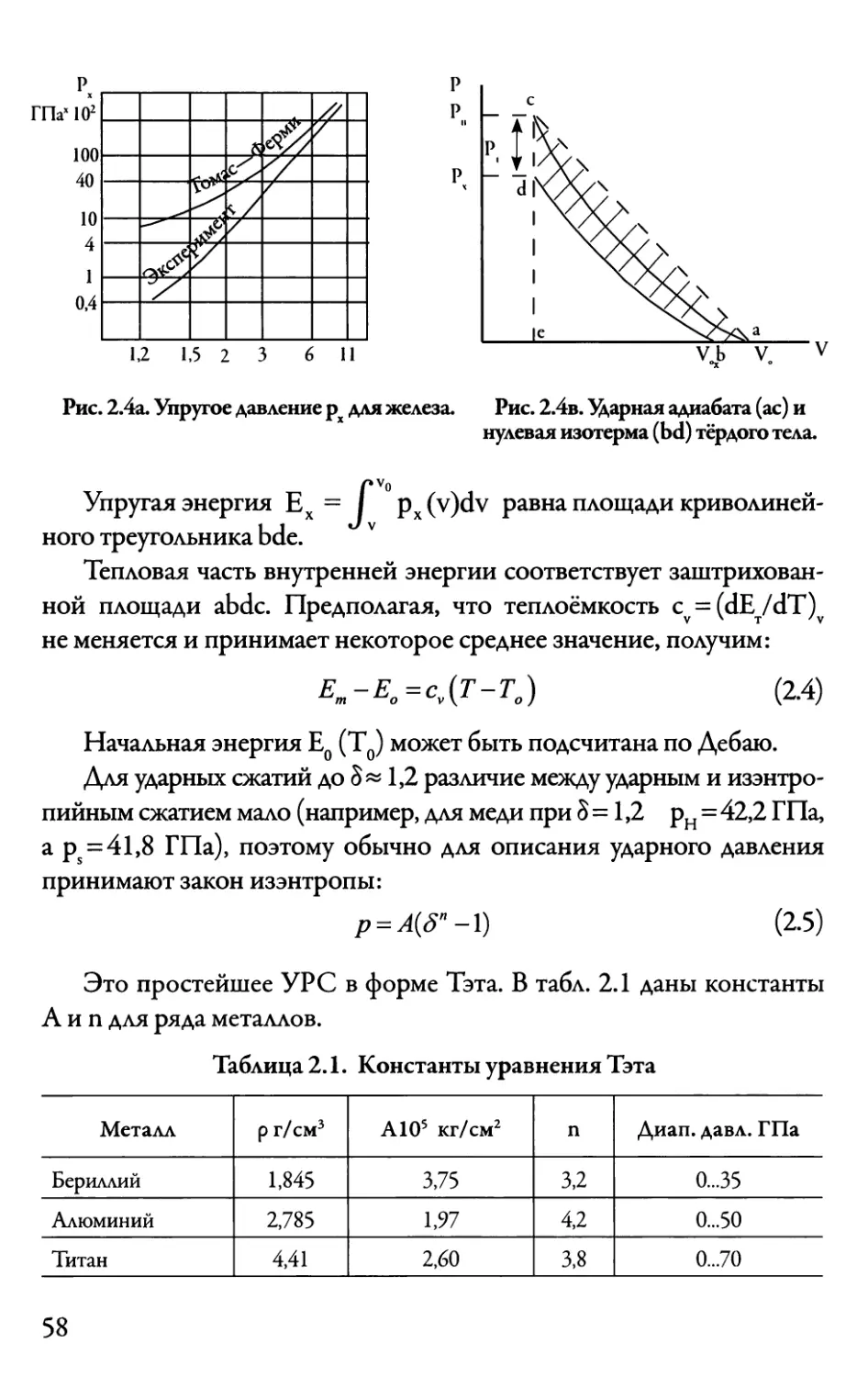
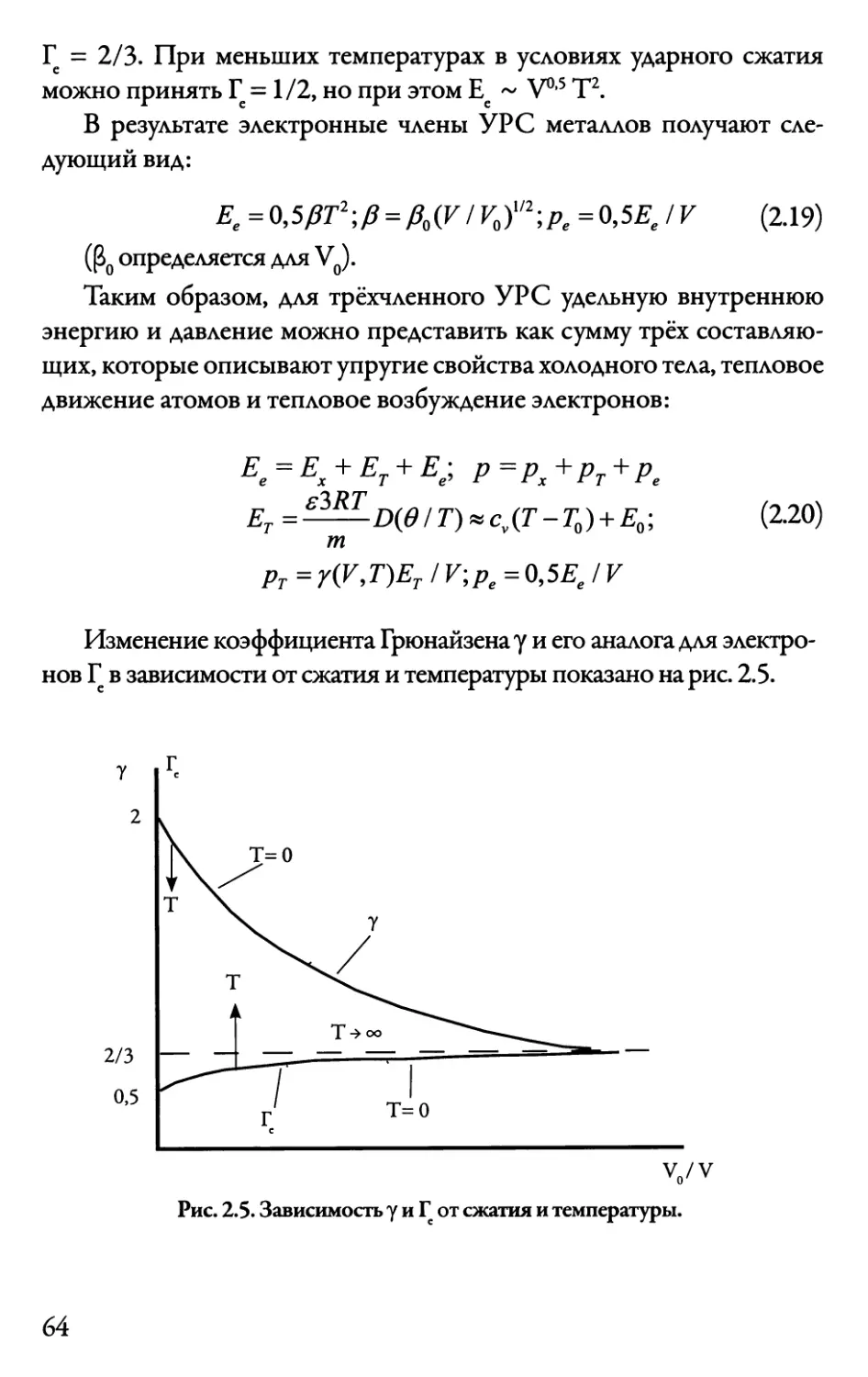
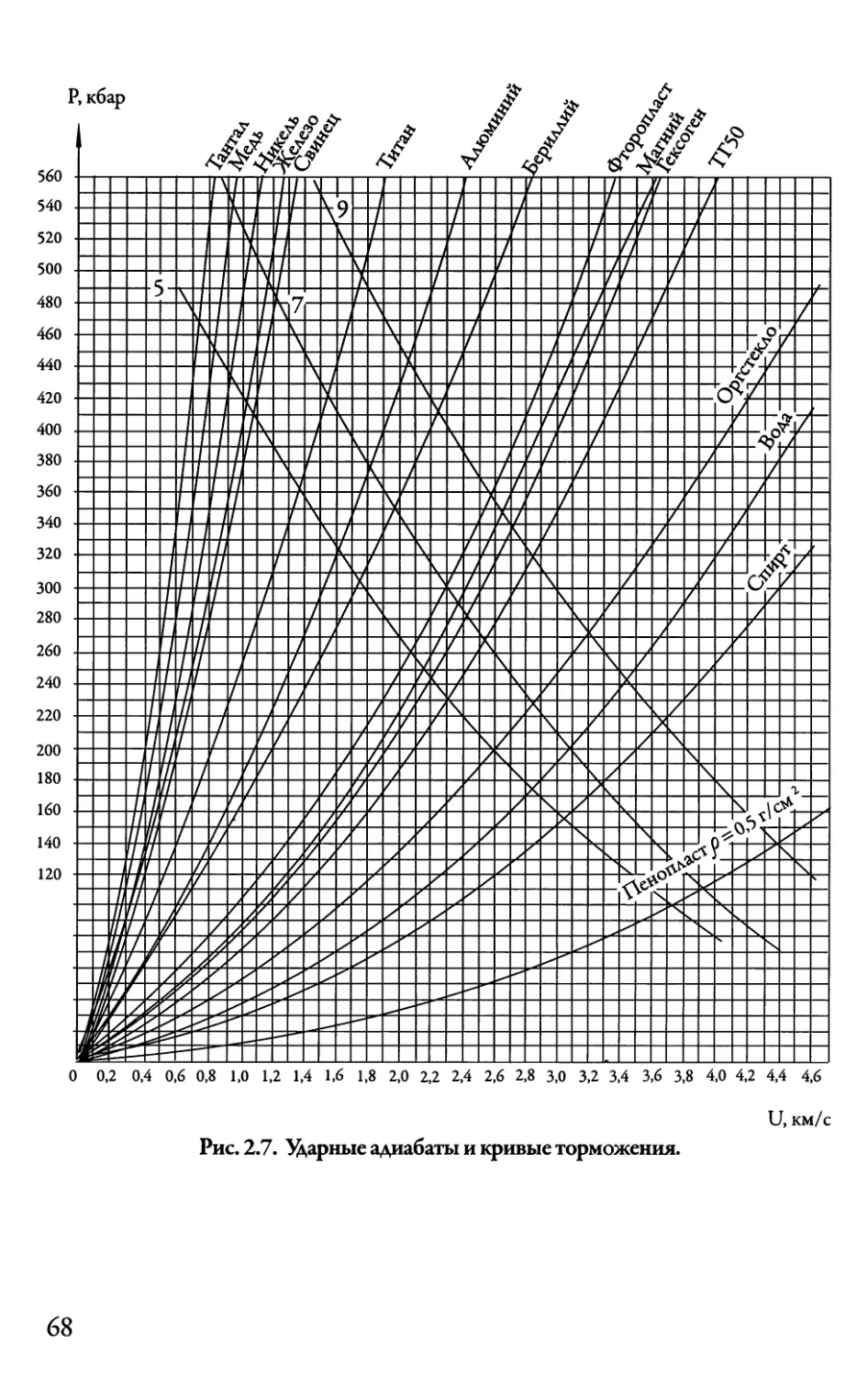
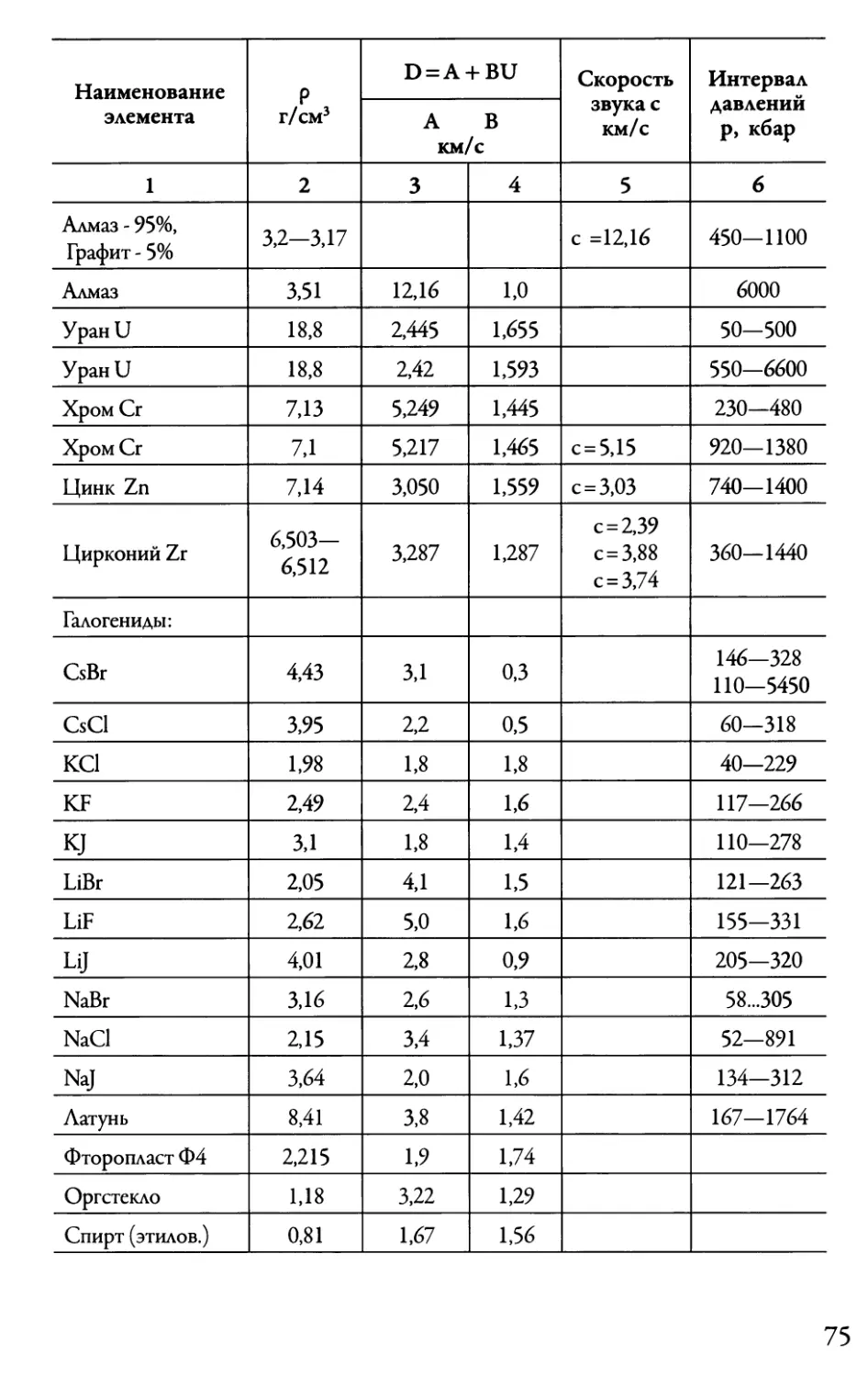
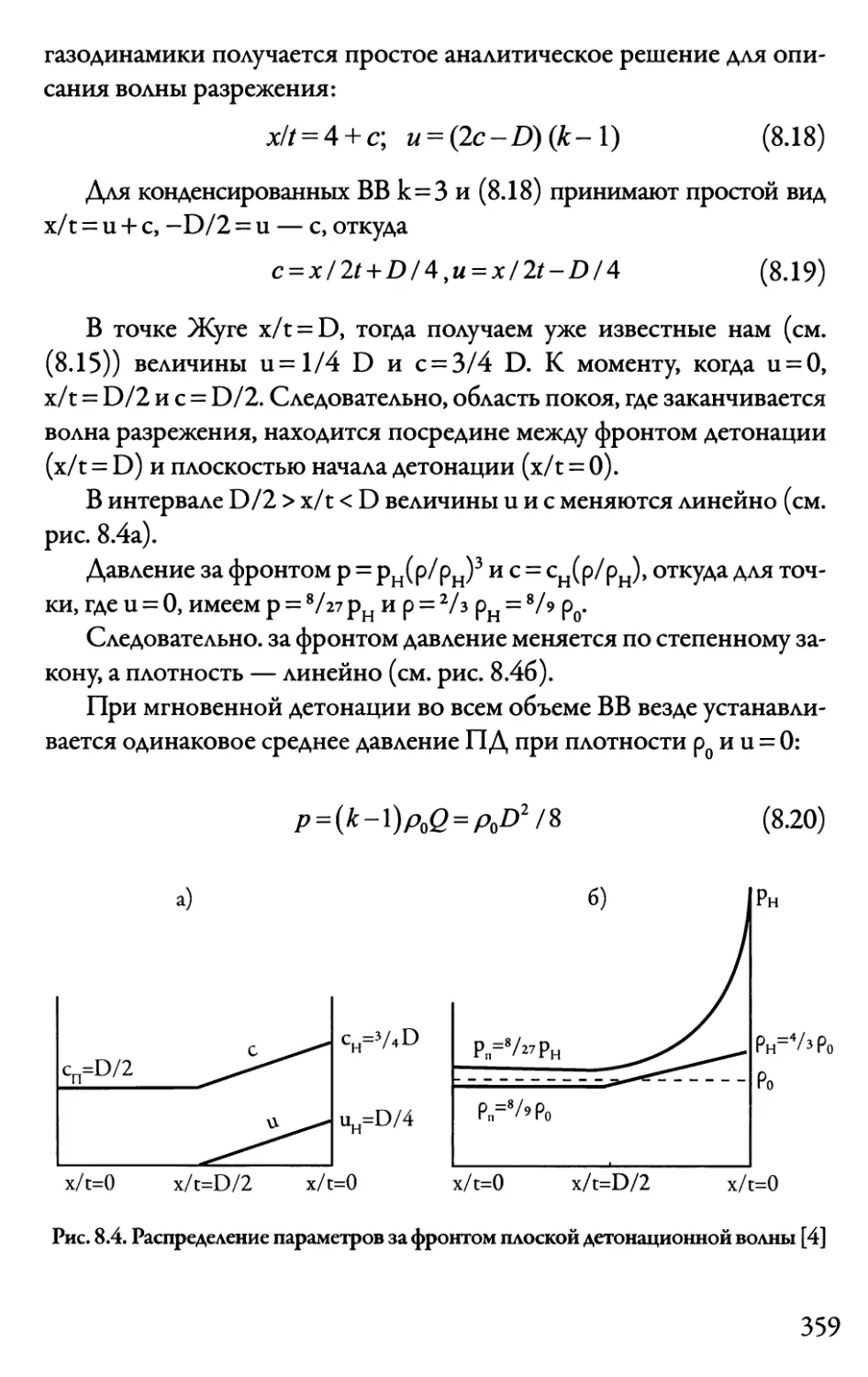
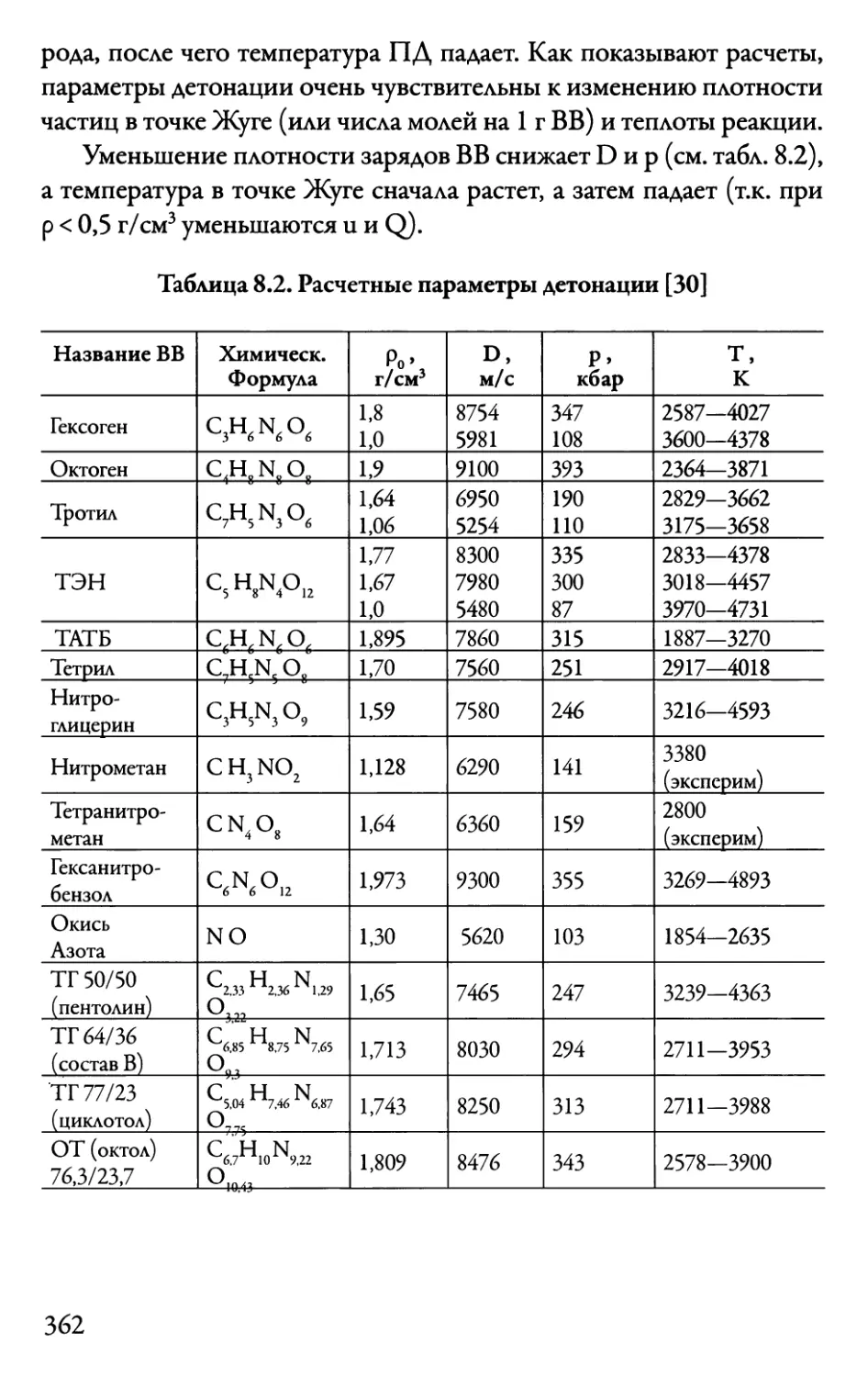
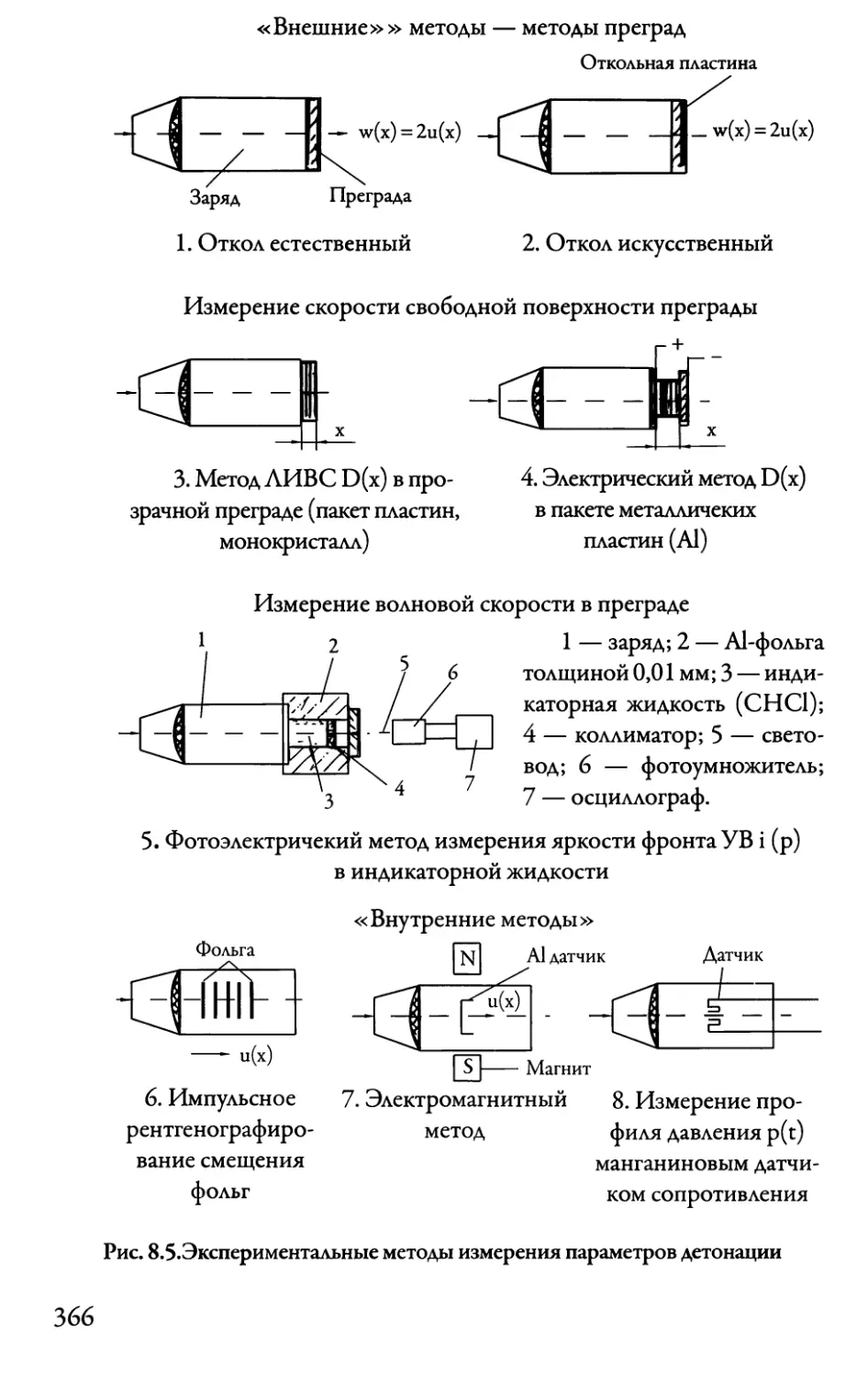
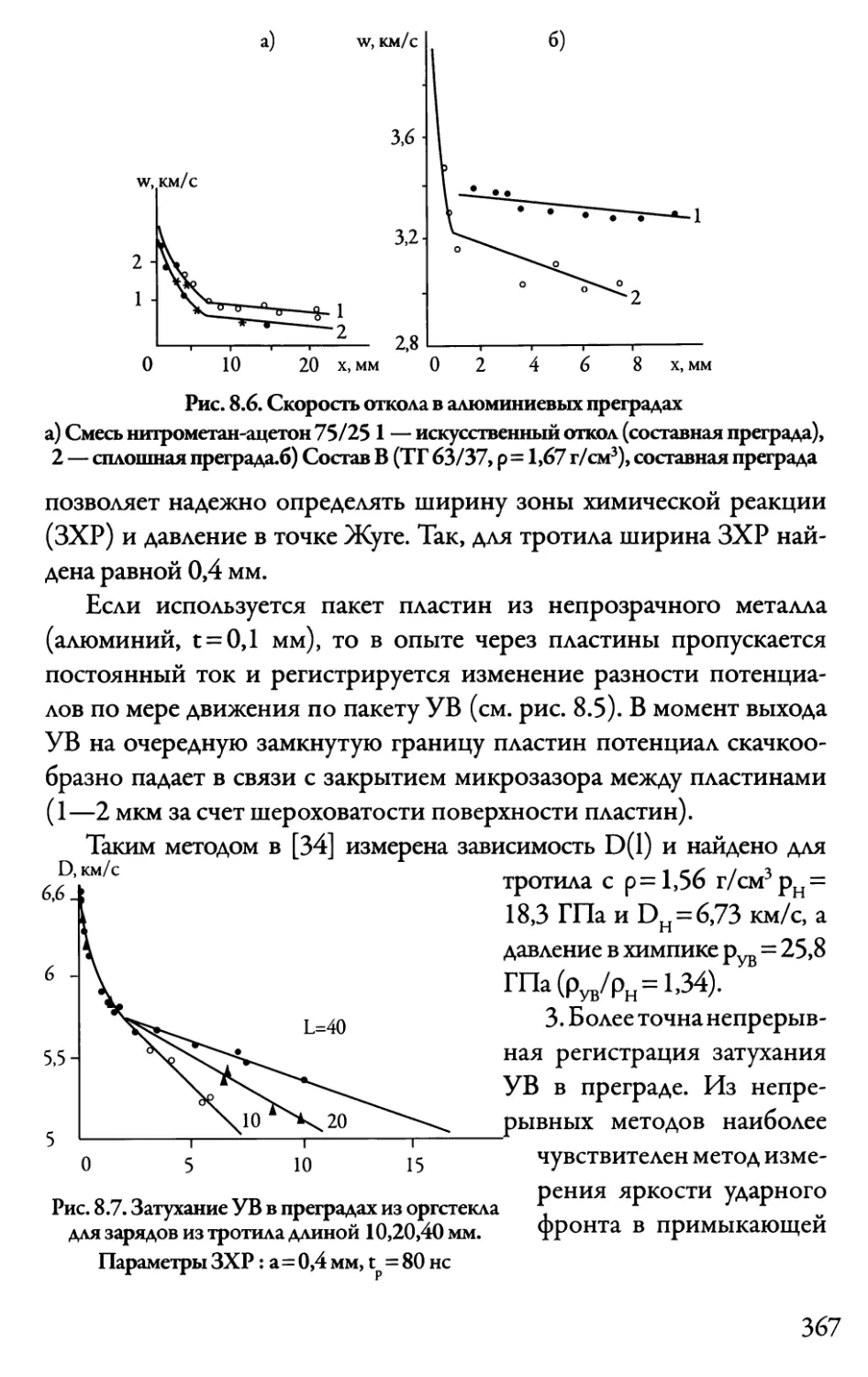
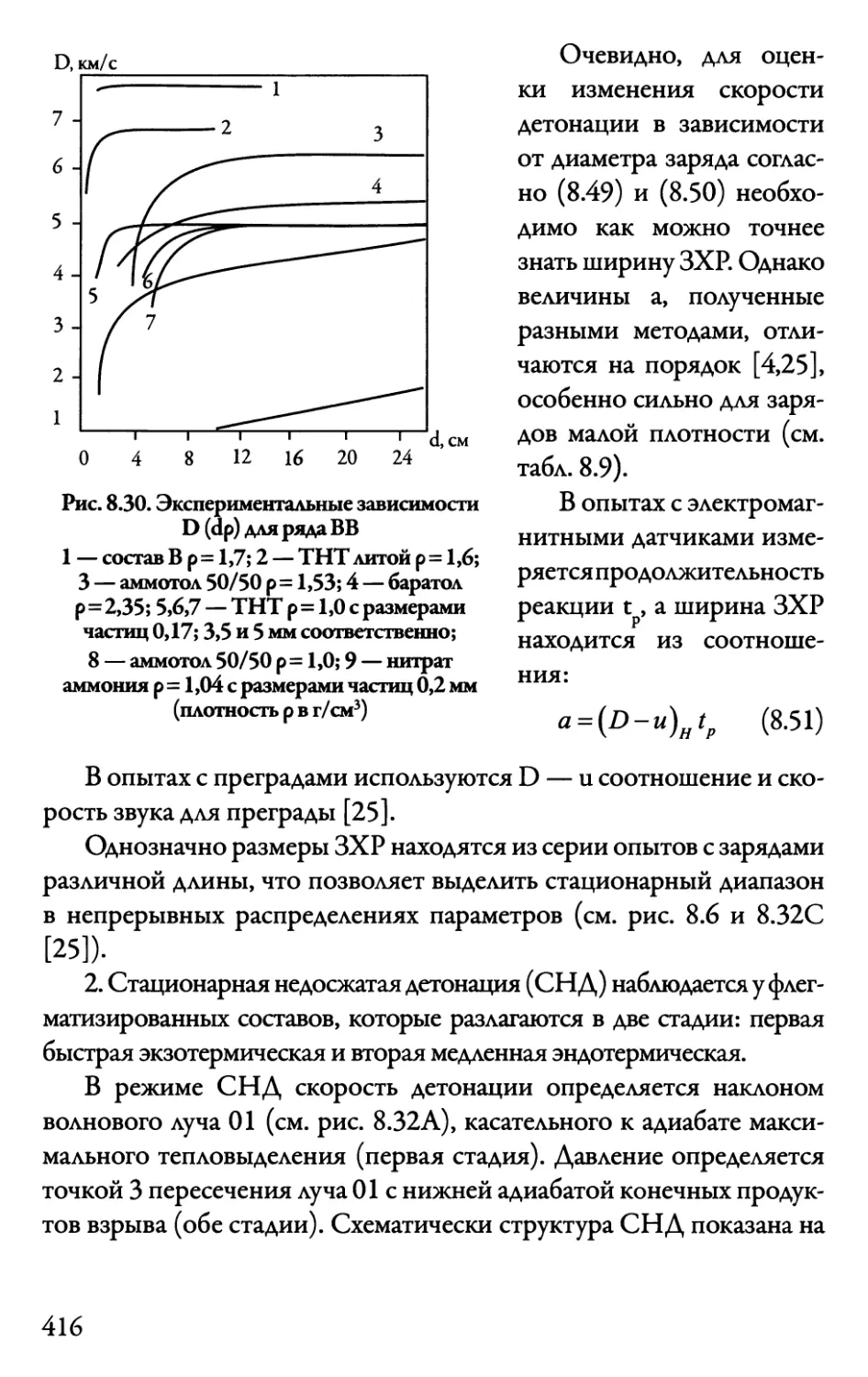
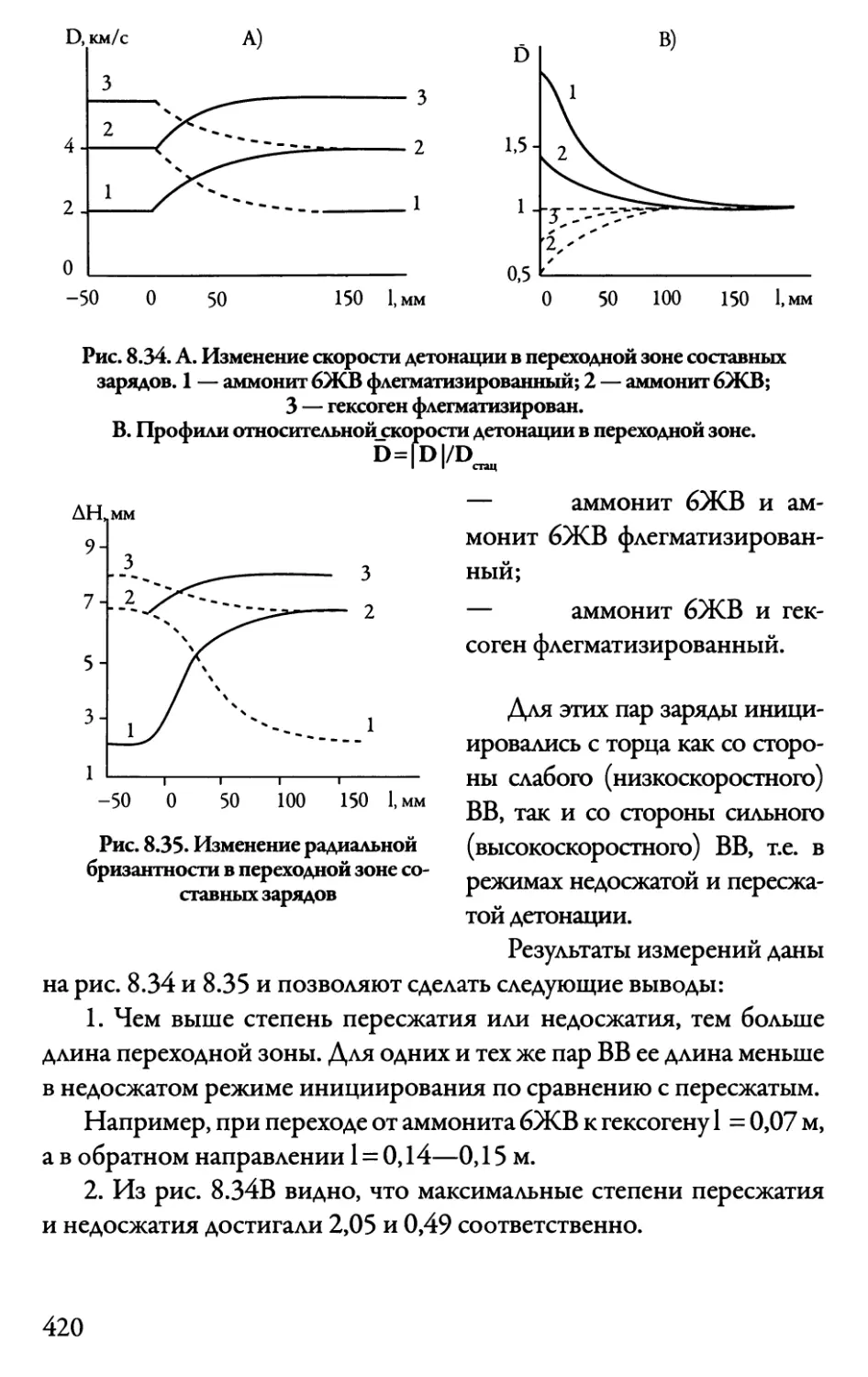
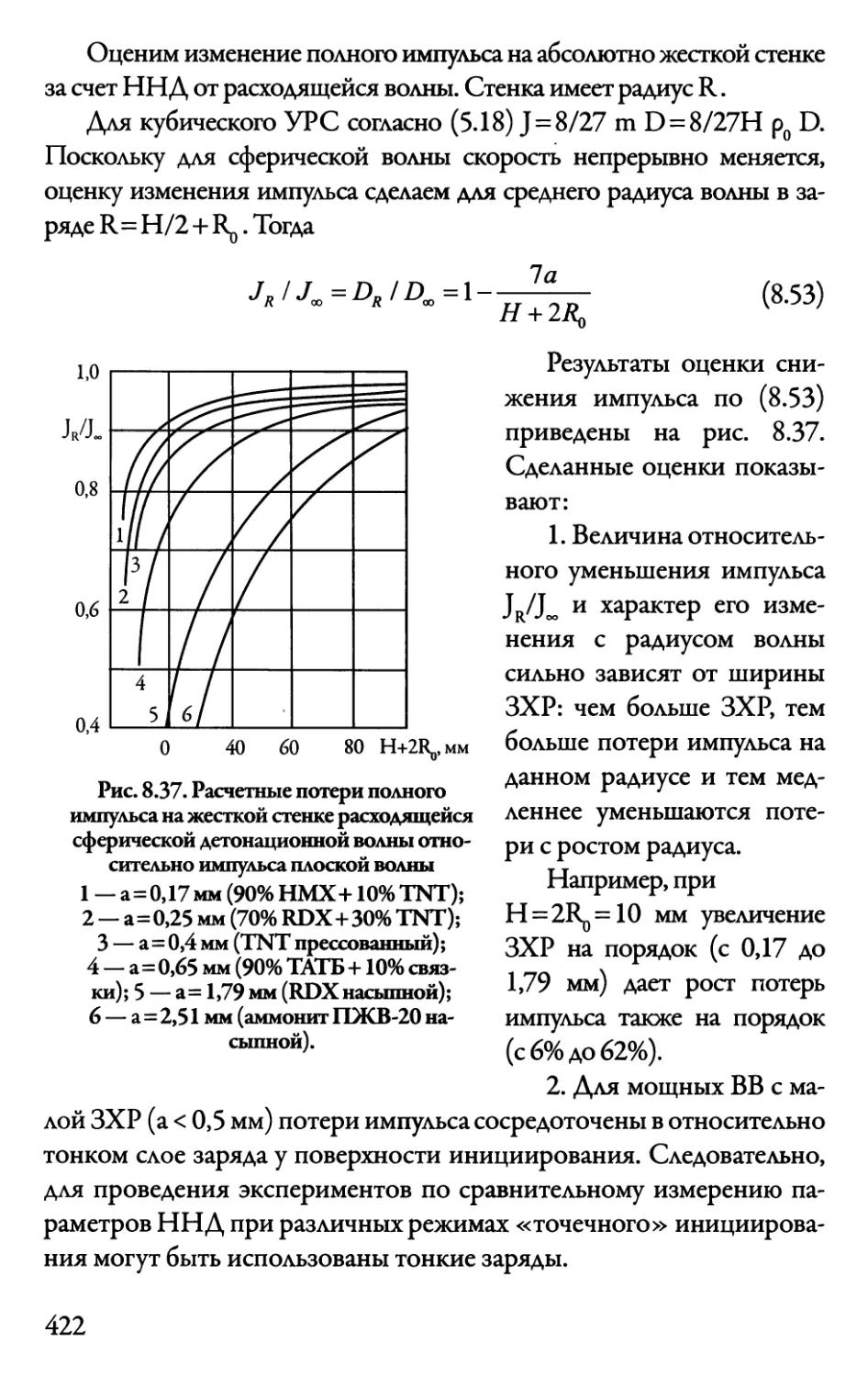
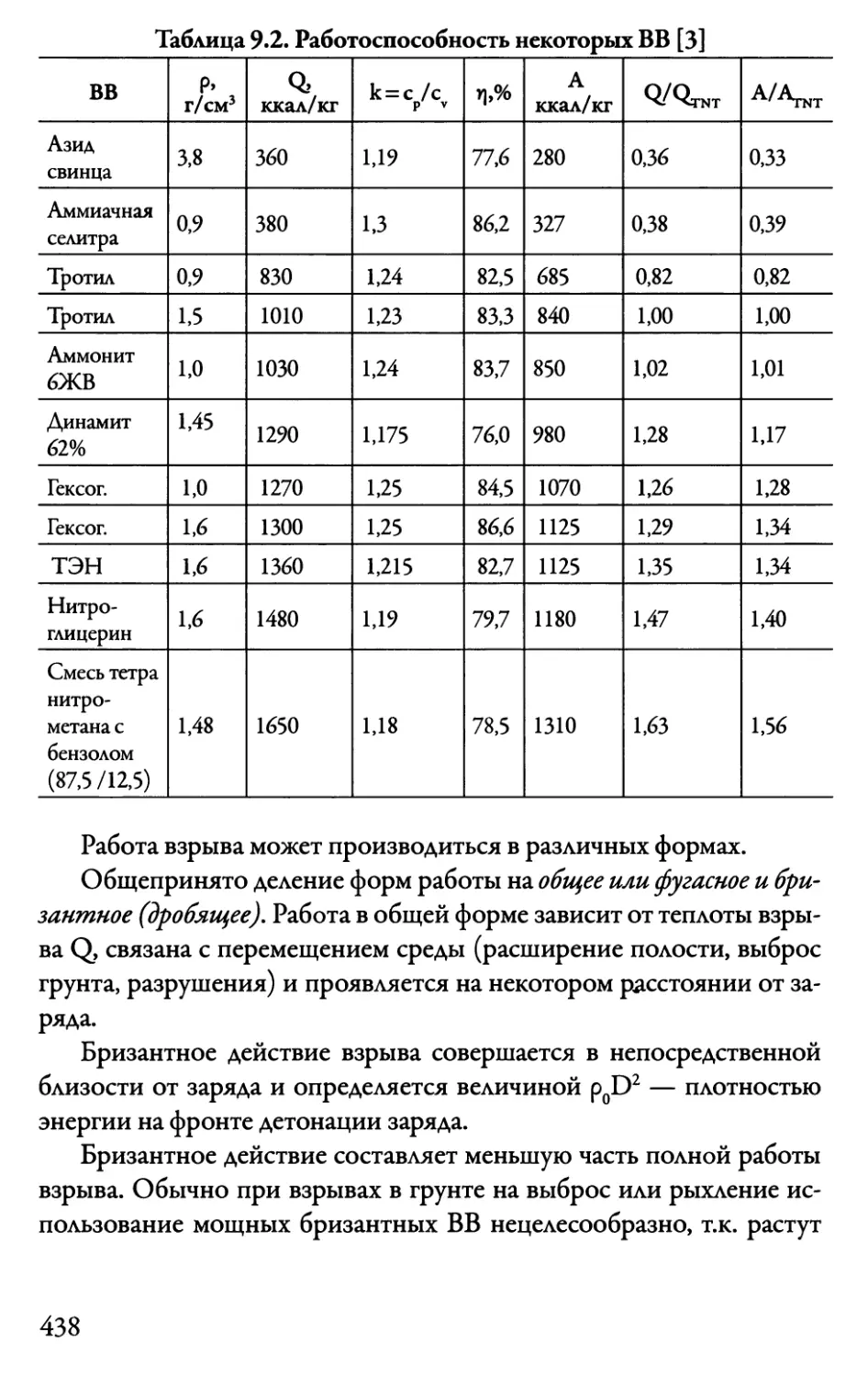
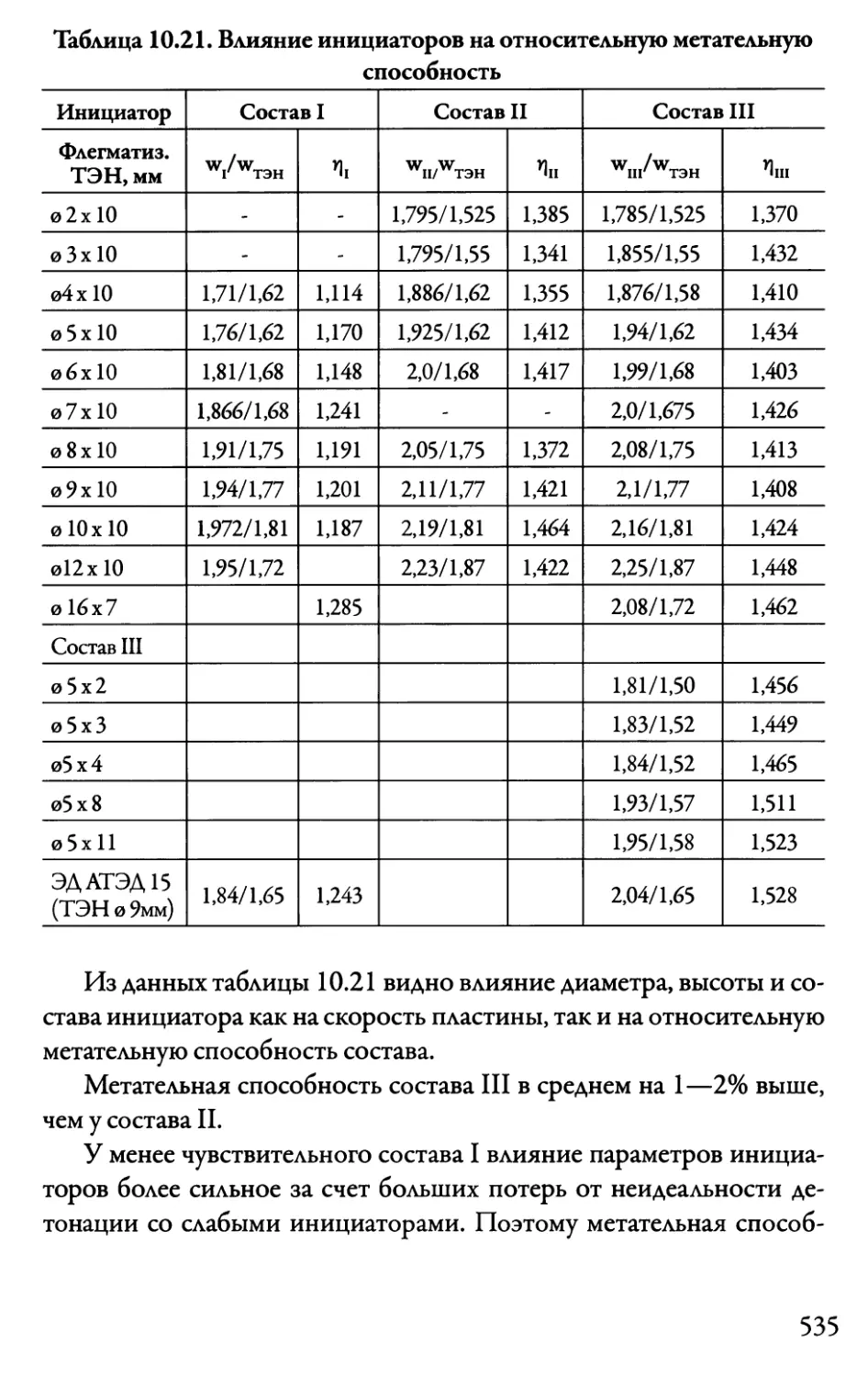
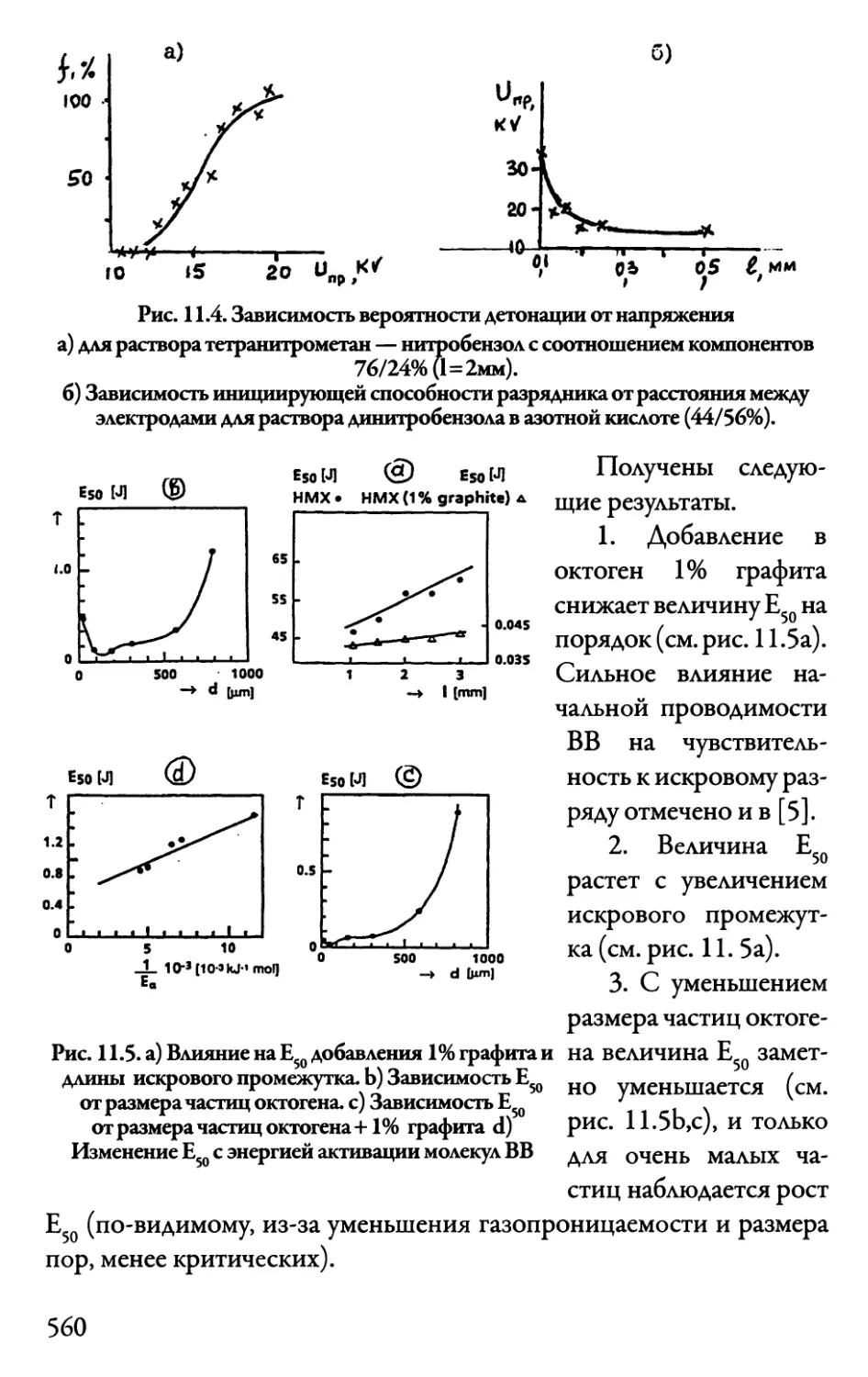
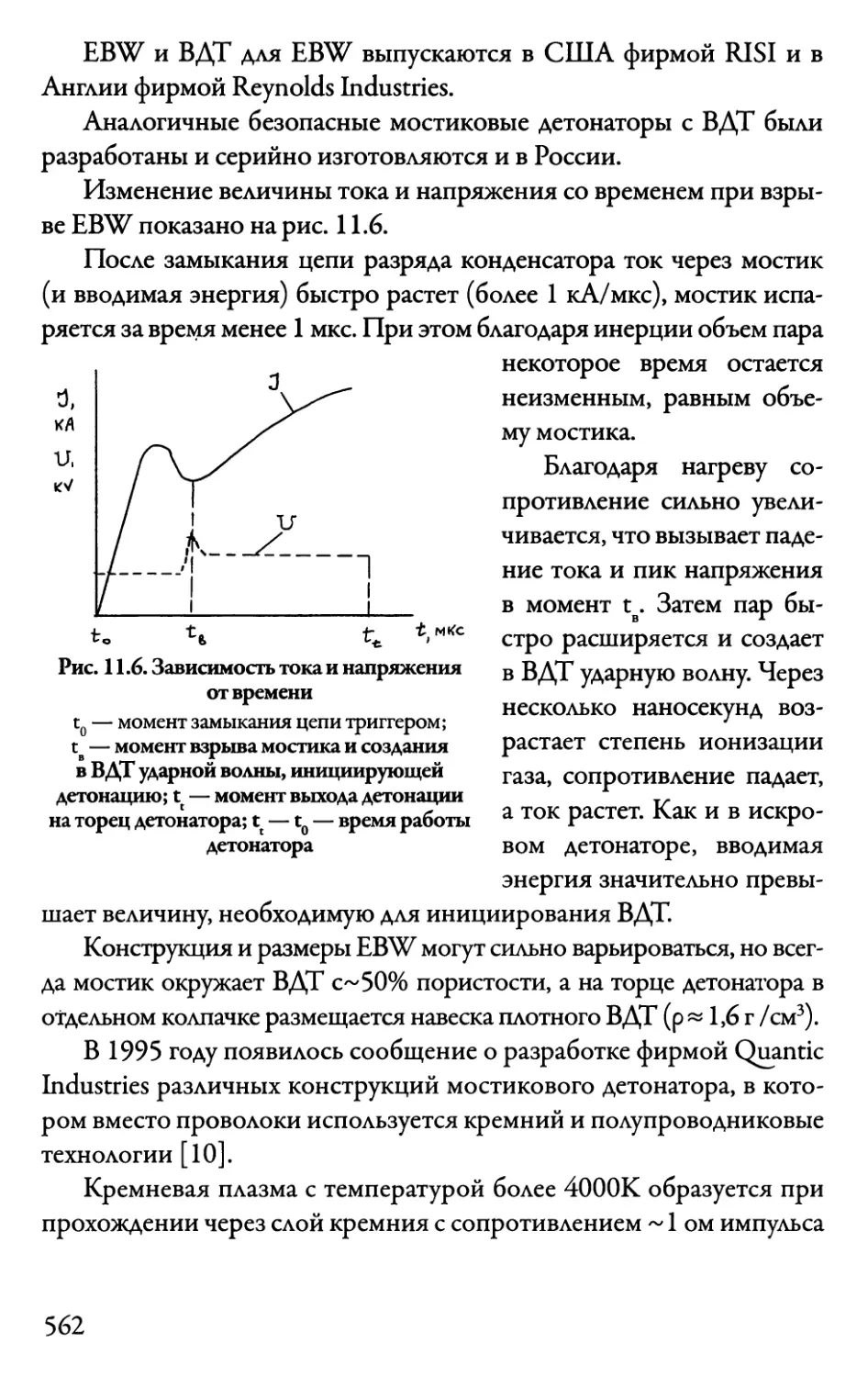
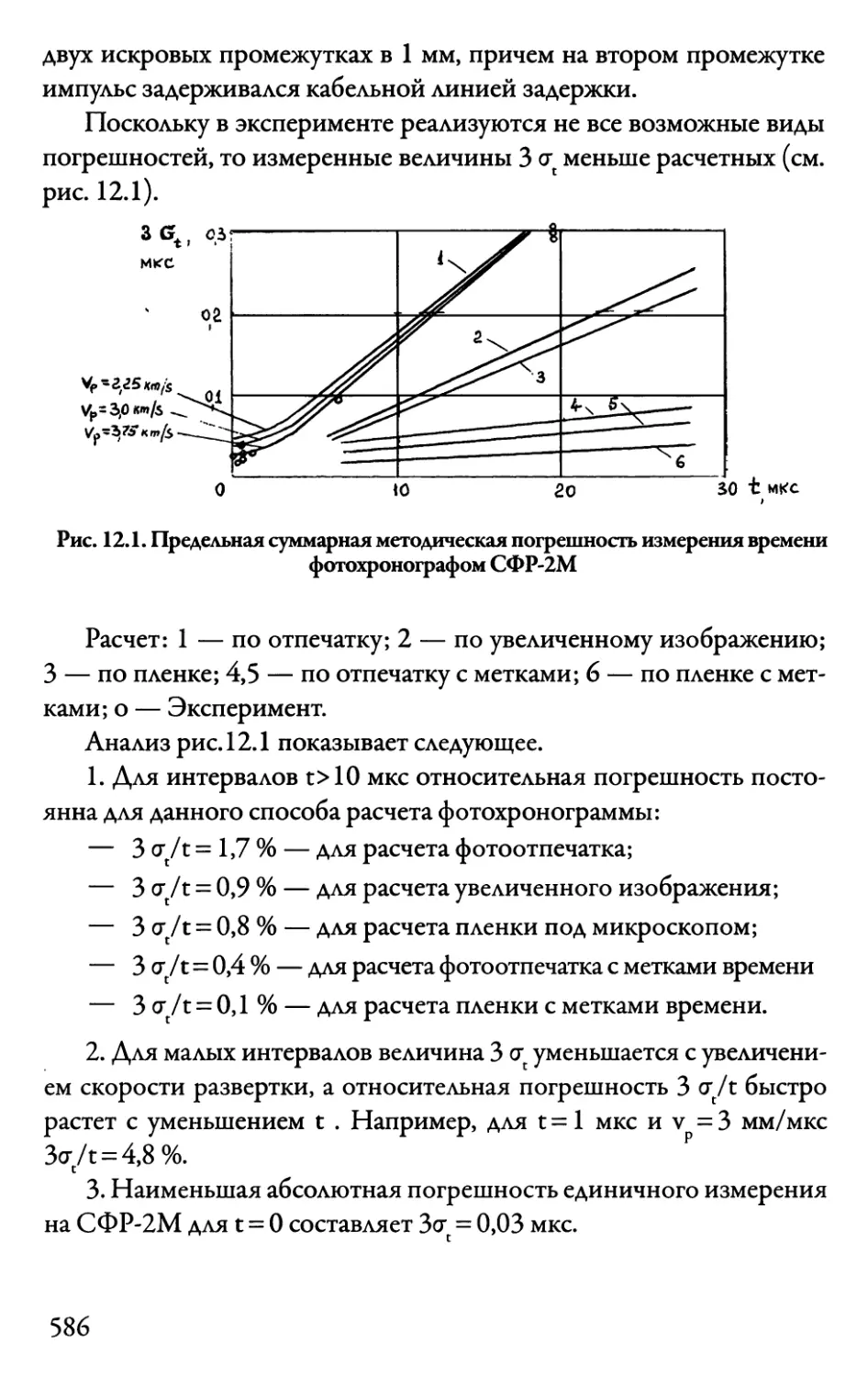
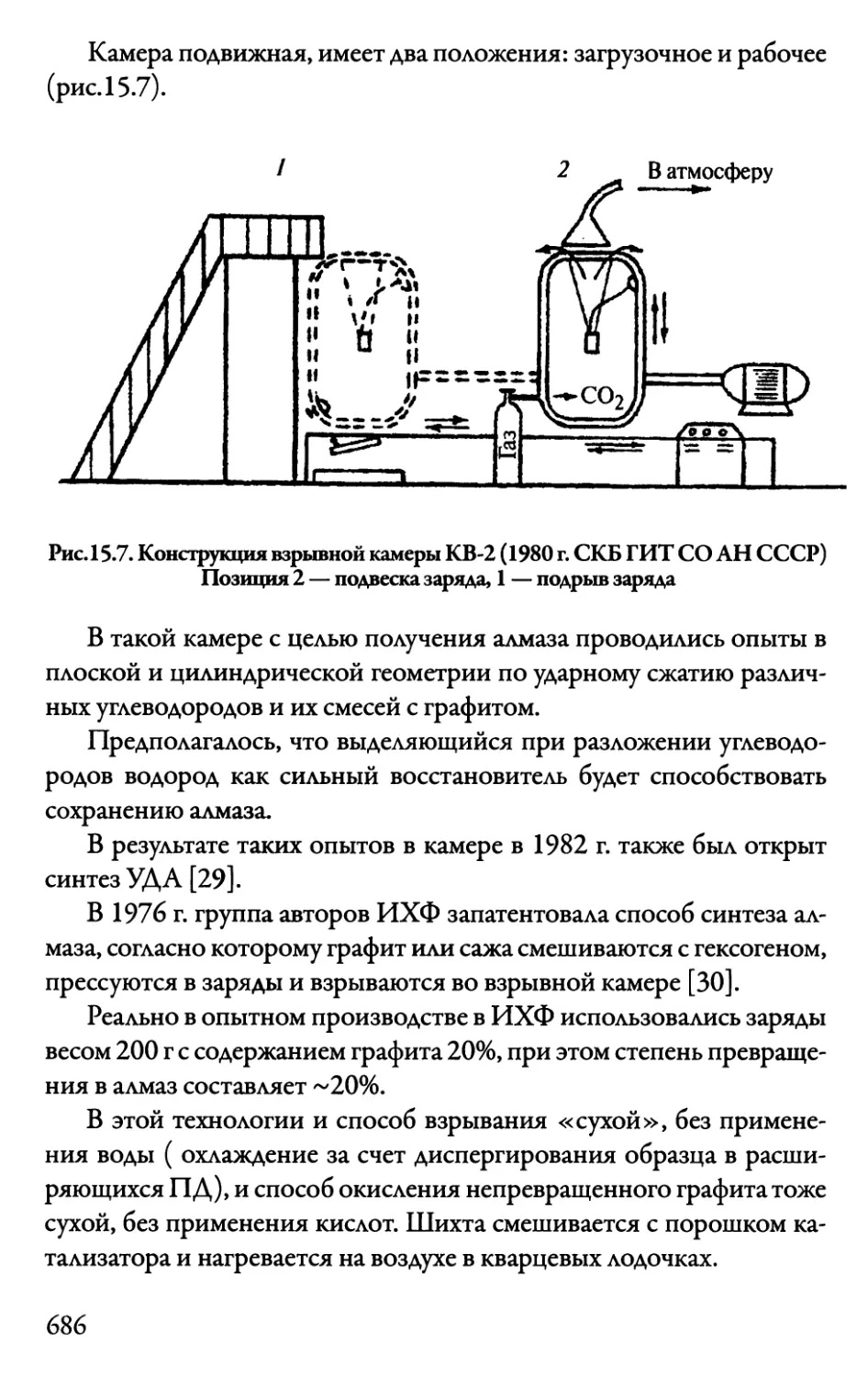
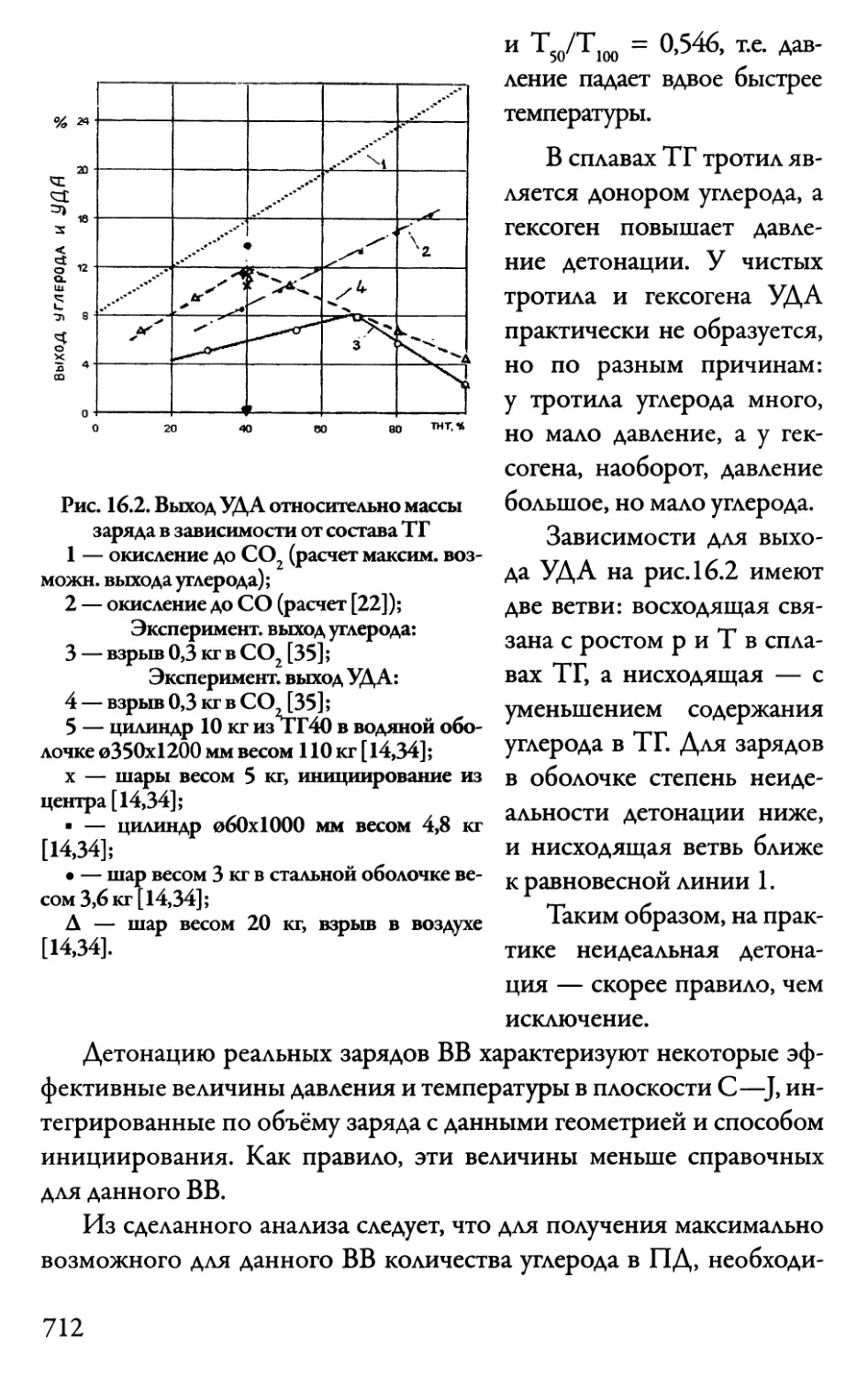
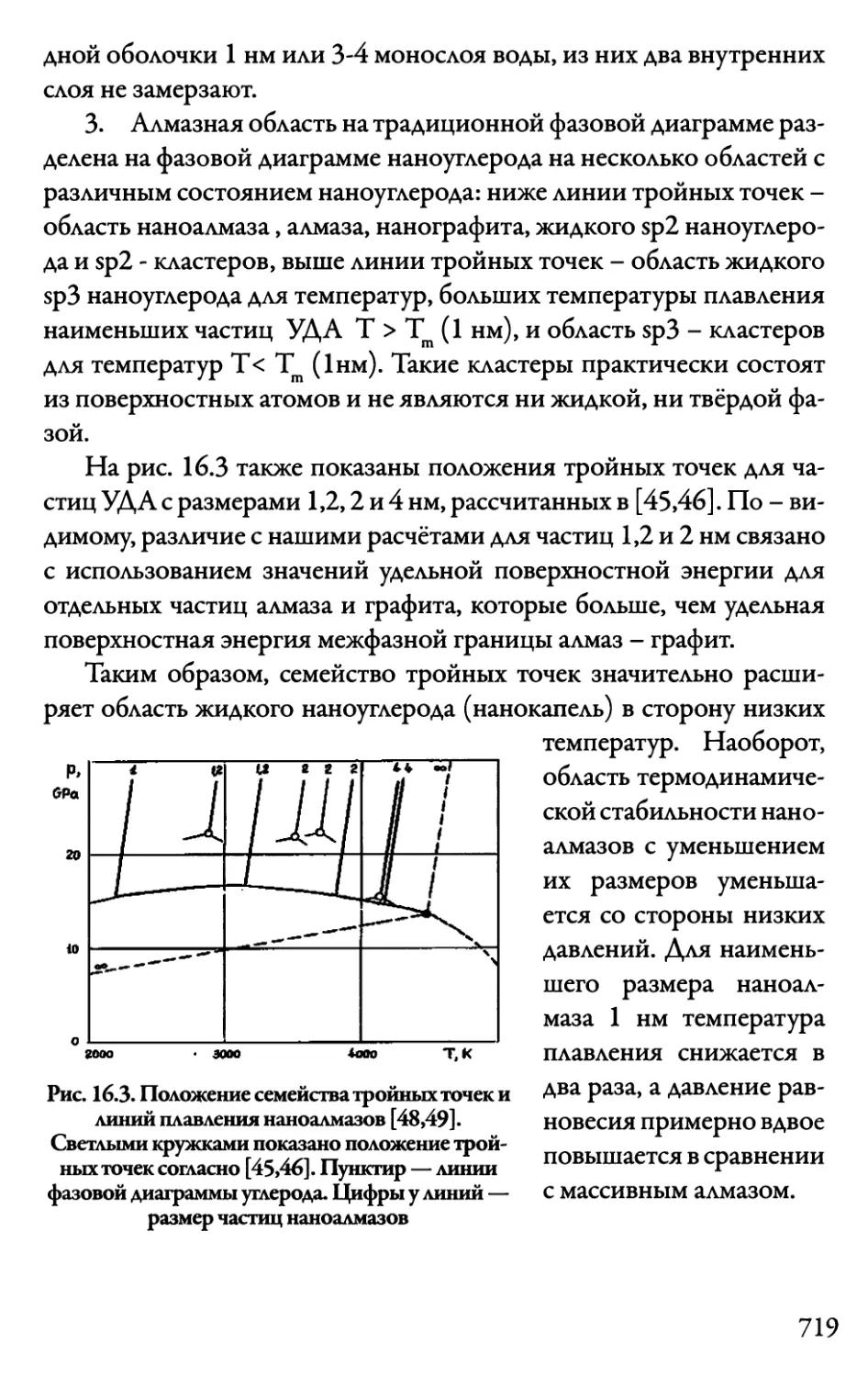
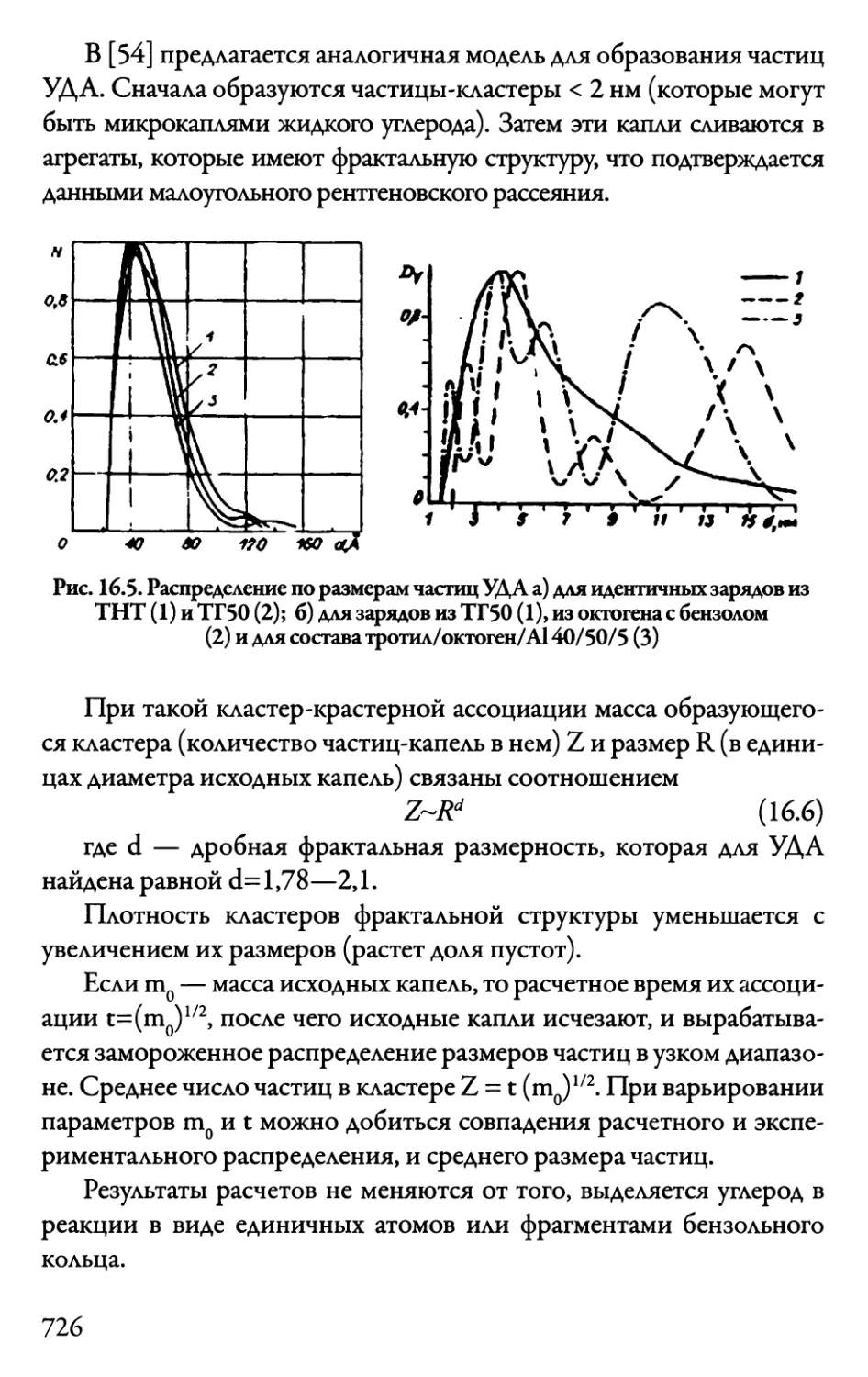
Автор: Даниленко В.В.
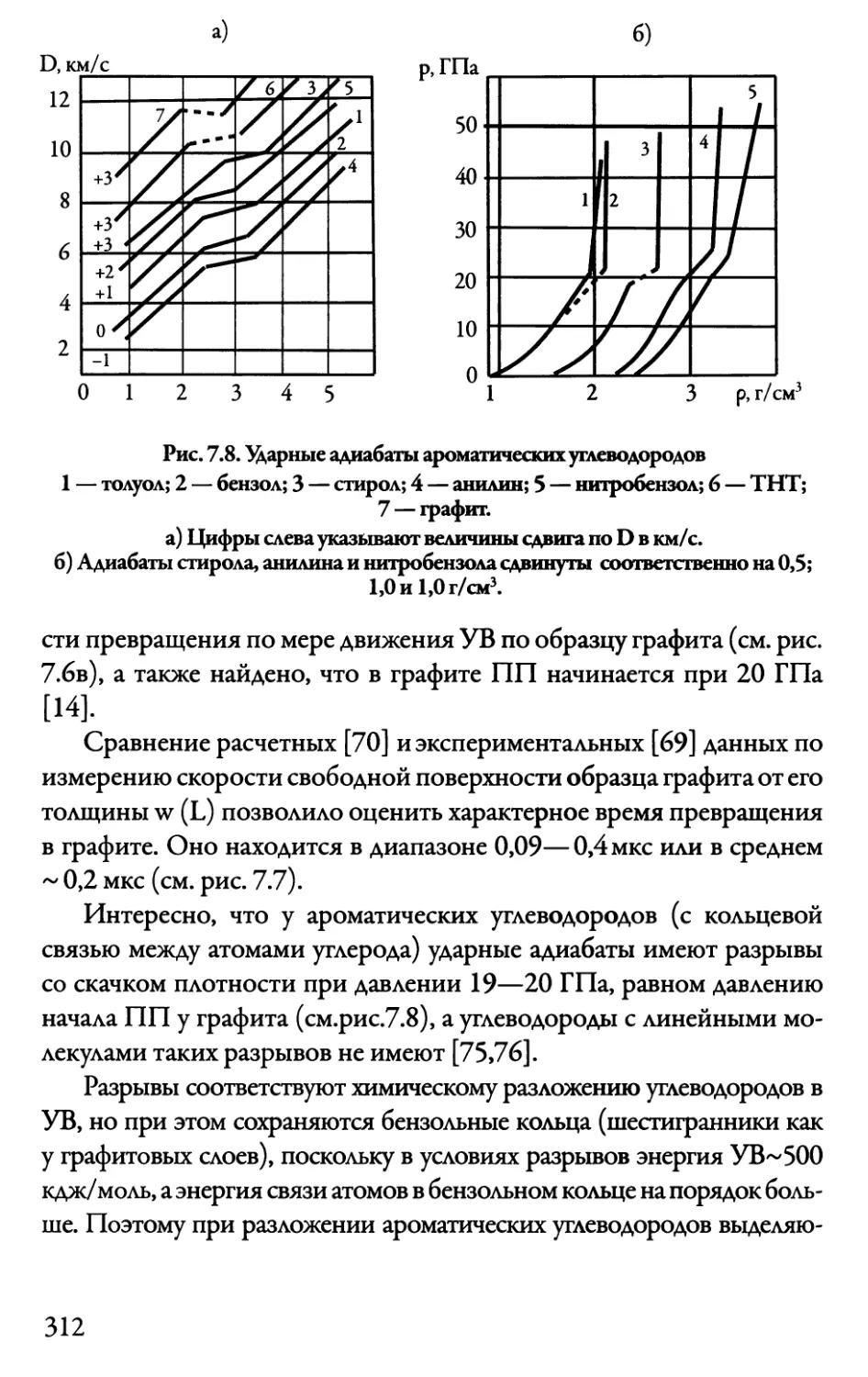
Теги: свойства и структура молекулярных систем химическая технология химические производства физика взрывчатые вещества энергоатомиздат издательство энергоатомиздат взрывная техника
ISBN: 978-5-283-00857-8
Год: 2010
В. В. ДАНИЛЕНКО
ВЗРЫВ
ФИЗИКА • ТЕХНИКА
ТЕХНОЛОГИЯ
Москва
Энергоатомиздат
2010
УДК 539.2,621.7.044.2
ББК 35.46
Д18
Даниленко В. В.
Д 18 Взрыв: физика, техника, технология. — М.: Энергоатомиздат,
2010. —784 с: ил.
ISBN 978-5-283-00857-8
В книге доктора техн. наук В. В. Даниленко в систематическом виде
рассматривается широкий круг вопросов, связанных со взрывом и
использованием его энергии: элементы газовой динамики и теории ударных волн,
уравнения состояния, теория детонации, кумуляция, фазовые
превращения при ударном сжатии, высокоскоростной удар, методы измерений бы-
стропротекающих процессов, свойства ВВ, взрывы в различных средах,
средства инициирования взрыва, техника проведения взрывных работ,
технологии динамического синтеза и спекания алмаза, в частности,
детонационный синтез ультрадисперсных алмазов (или детонационных нано-
алмазов),
Для научных работников, инженеров, технологов,
специализирующихся в области прикладной физики взрыва и взрывных технологий. Может
быть полезна аспирантам и студентам вузов соответствующих
специальностей.
УДК 539.2,621.7.044.2
ББК 35.46
V. V. Danilenko. Explosion: physics, engineering, technology.
In the book in a systematic aspect the broad class of problems, bound with explosion
and using of its energy is considered: elements of gas-dynamics and theory of
shockwaves, equation of state, theory of a detonation, cumulation, phase changes
at a shock compression, high-velocity shock, measurement methods of high-speed
phenomenons, properties of explosive, explosions in different environments,
facilities of initiation of detonation, engineering of conducting of blastings, know-
how of dynamic synthesizing and sintering of diamond, in particular, detonation
synthesizing of ultra dispersed diamonds (or detonation nanodiamonds).
The book is intended for the students, post-graduate students, physicists,
engineers, technologists specialize in the area of applied physics of explosion and
explosive technologies.
ISBN 978-5-283-00857-8
© B.B. Даниленко, 2010
СОДЕРЖАНИЕ
Предисловие 11
Глава 1. Элементы газовой динамики 15
1.1. Уравнения газовой динамики 15
1.2. Характеристики уравнений газовой динамики.
Простые волны. Автомодельность 17
1.3. Элементарная теория ударных волн 23
1.4. Примеры взаимодействия волн. Распады разрывов 33
1.5. Скорость звука 41
Литература к главе 1 49
Глава 2. Уравнение состояния 51
2.1. Краткий обзор 51
2.2. Квазигармоническая модель твердого тела 57
2.3. Учет плавления и испарения 65
2.4. Табличные и аппроксимационные
уравнения состояния 65
2.5. Экспериментальные ударные адиабаты различных
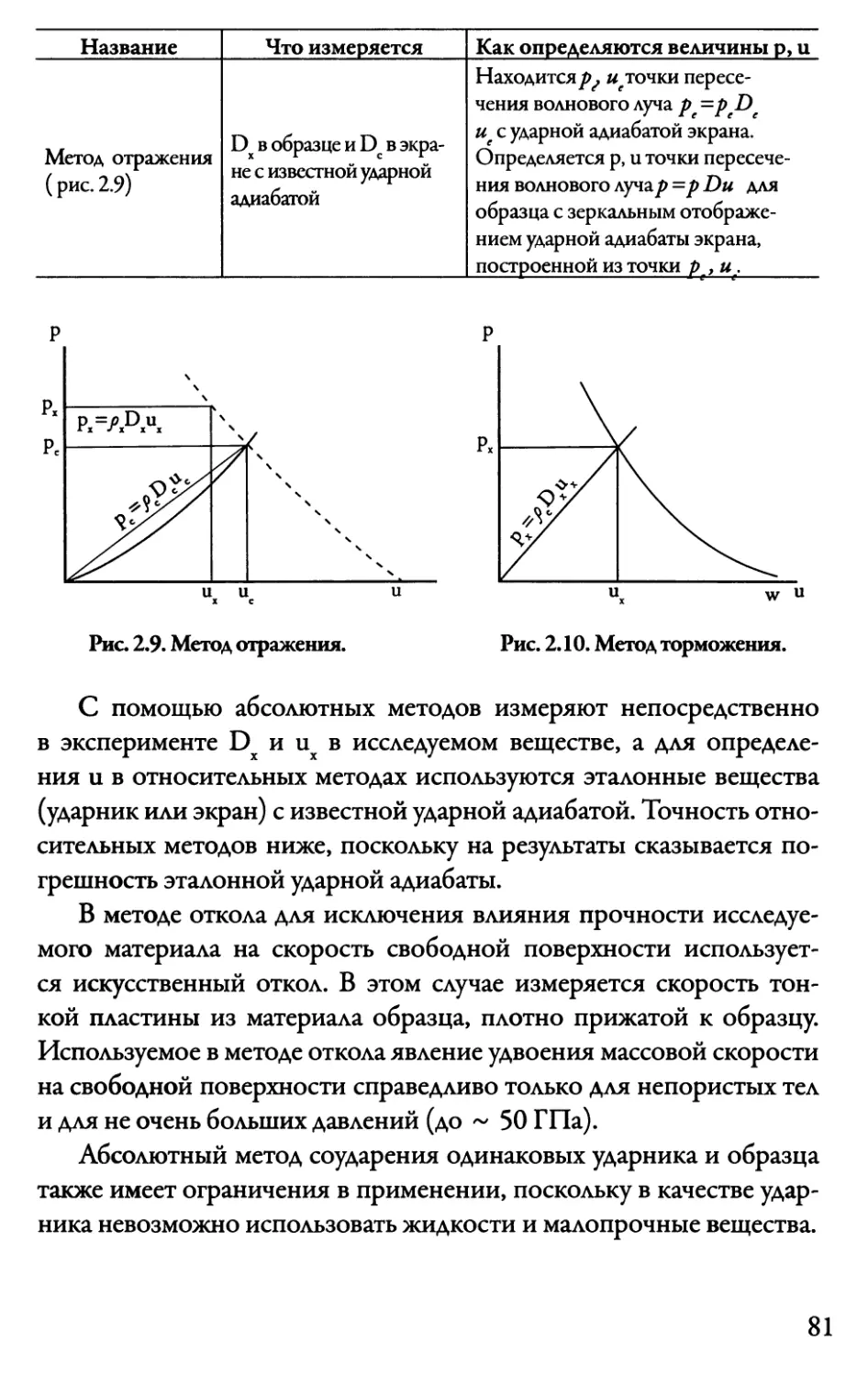
веществ и методы их нахождения 67
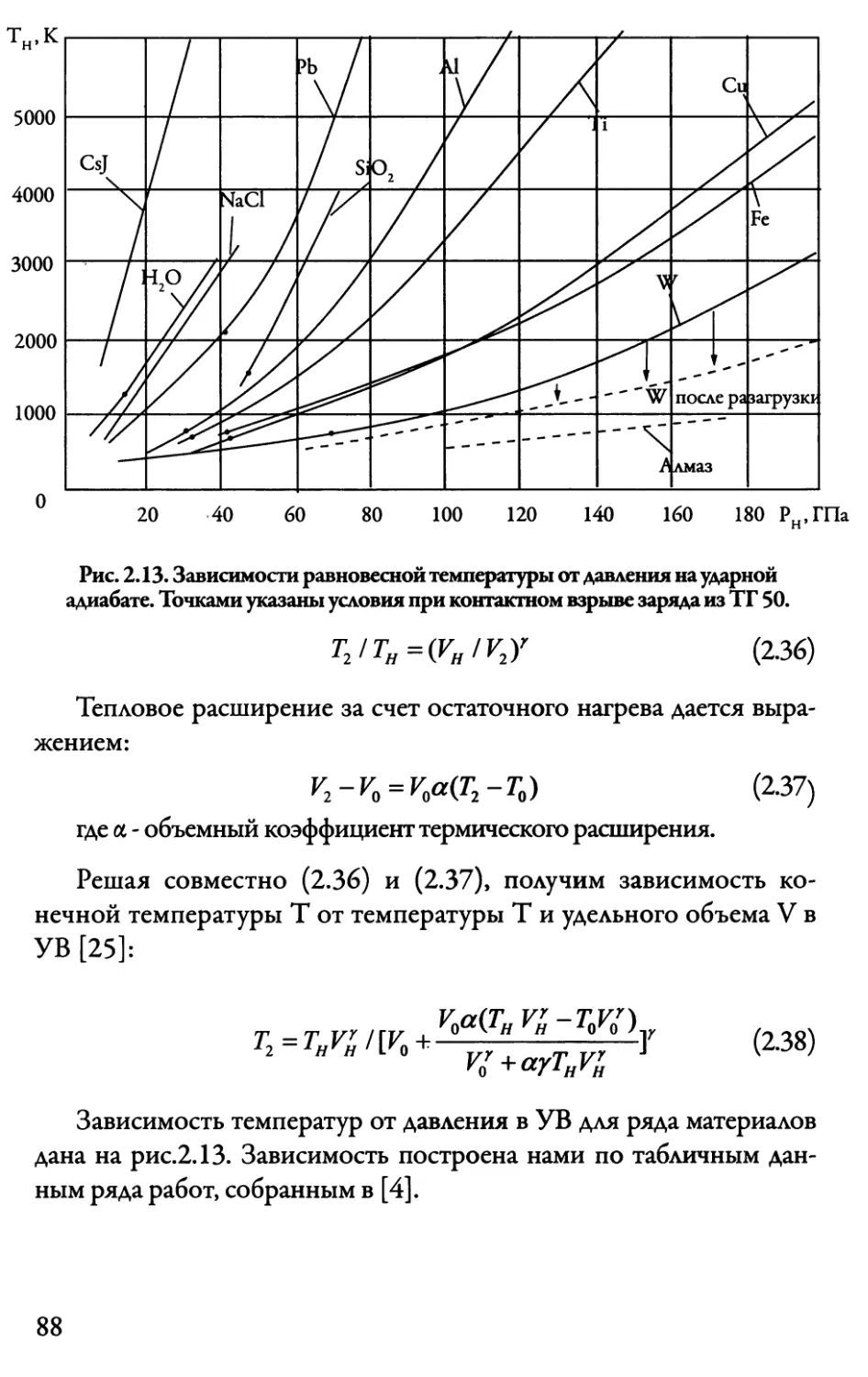
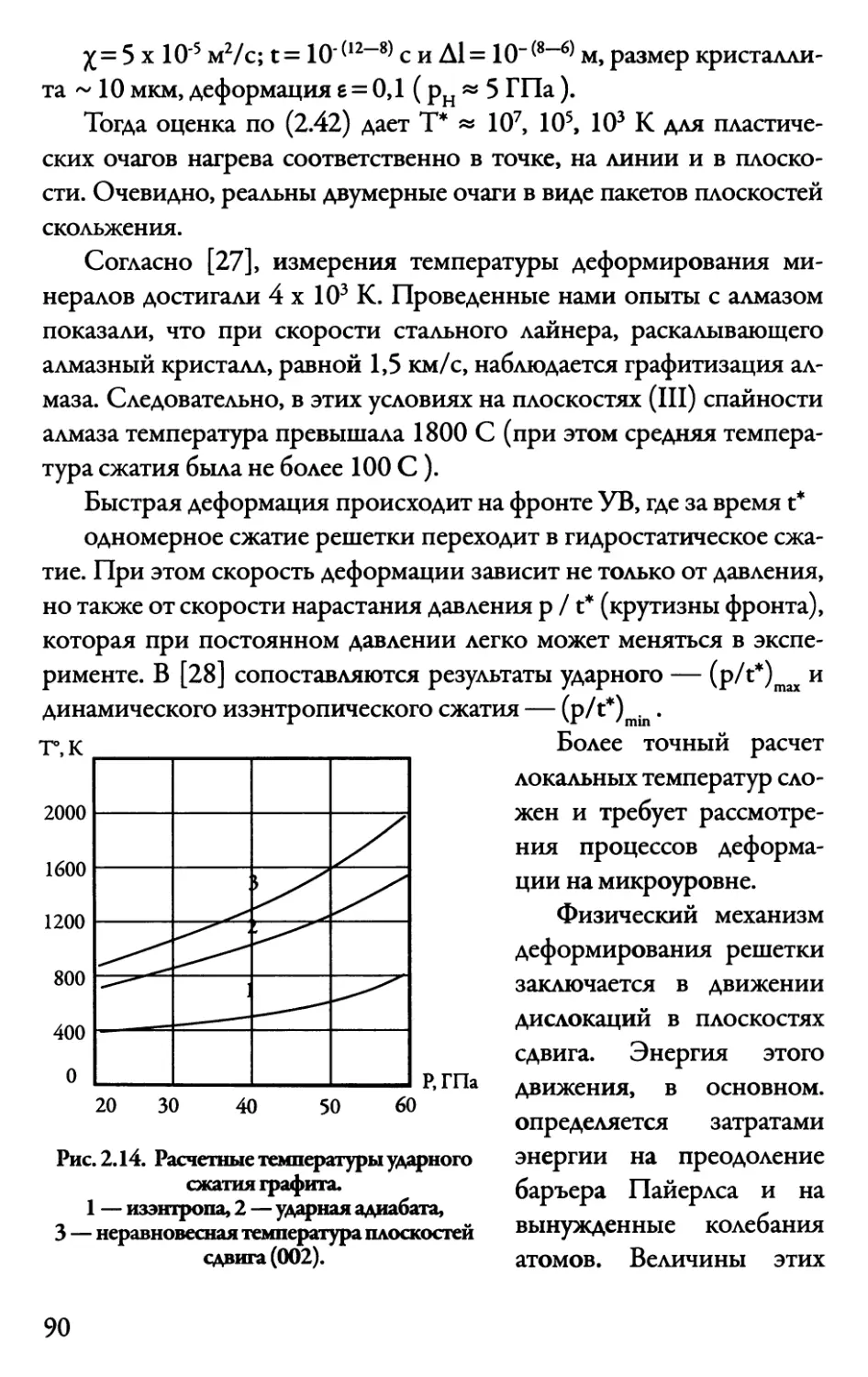
2.6. О температуре ударного сжатия 83
2.7. Уравнение состояния BKW 91
Литература к главе 2 95
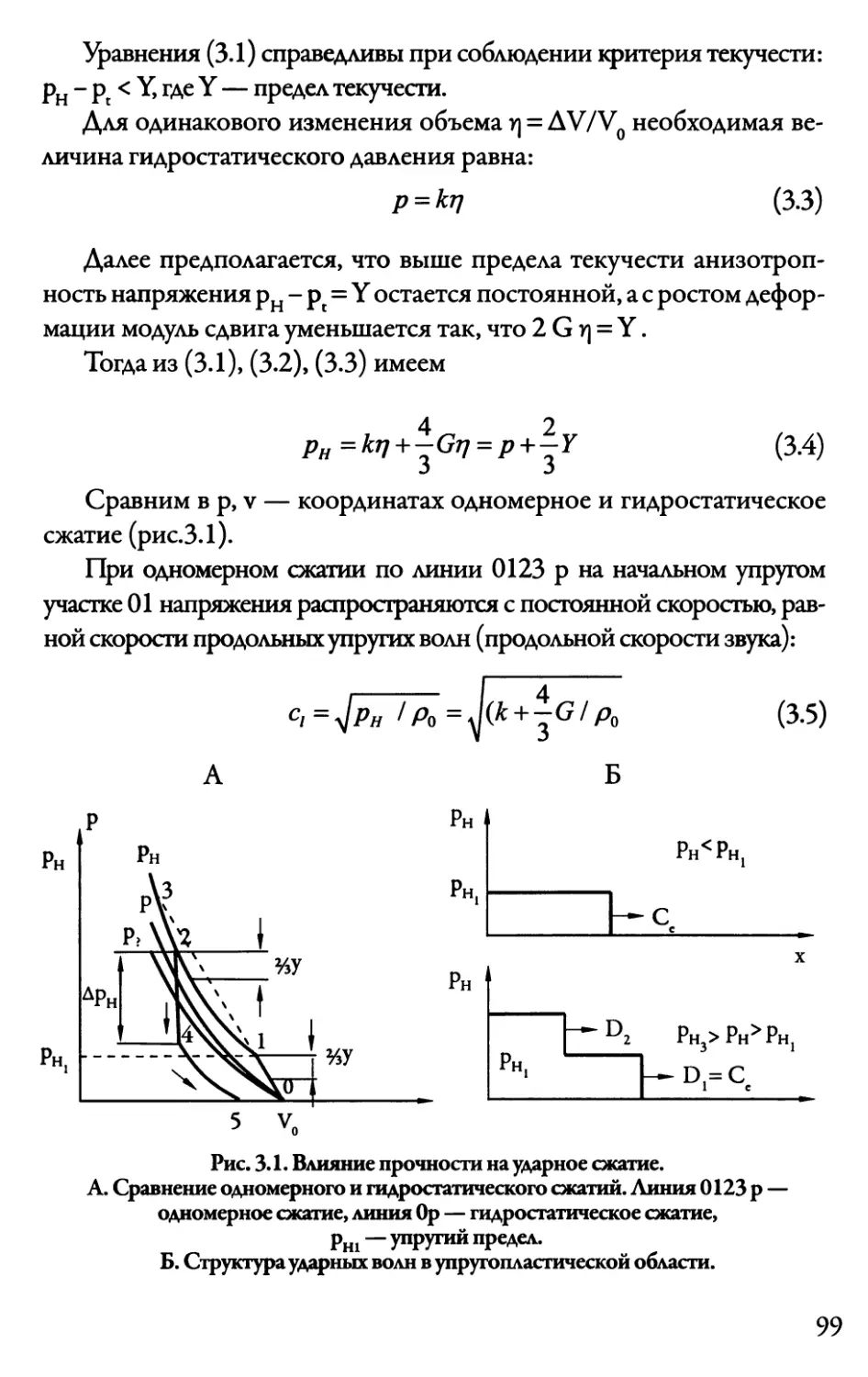
Глава 3. Динамическая прочность 98
3.1. Влияние прочности на ударное сжатие и разгрузку 98
3.2. Динамическое деформирование материалов 102
3.3. Разрушение материалов при импульсном
нагружении. Откольная прочность 108
3.3.1. Взаимодействие волн при отколе 108
3
3.3.2. Типы отколов 110
3.3.3. Методы измерения откольной прочности 111
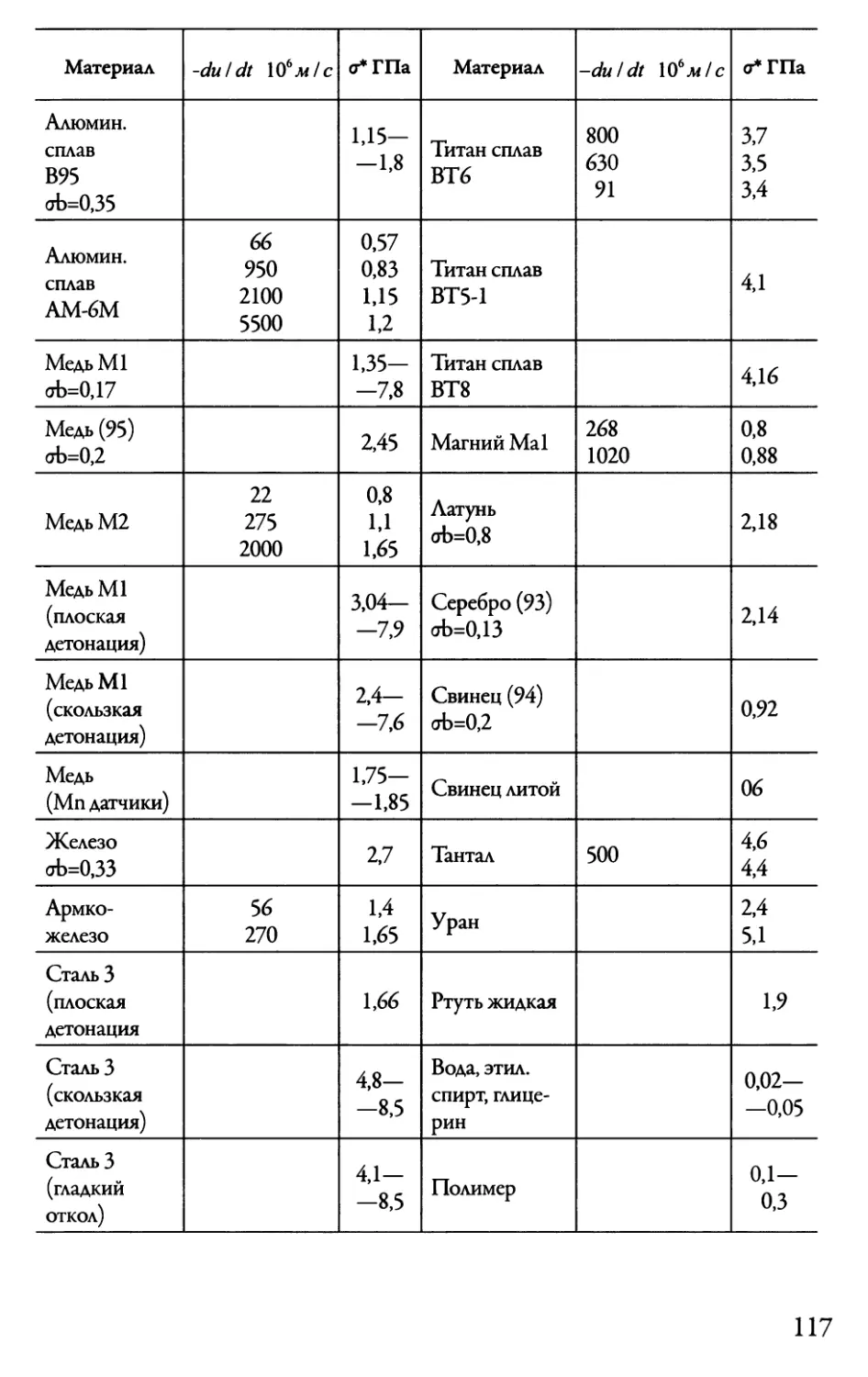
3.3.4. Экспериментальные результаты 115
3.3.5. Механизм и кинетика откольного разрушения 124
3.3.6. О локализации деформации и разрушения
при отколе 128
Литература к главе 3 132
Глава 4. Ударное сжатие пористого вещества 136
4.1. Вид ударных адиабат пористых тел 136
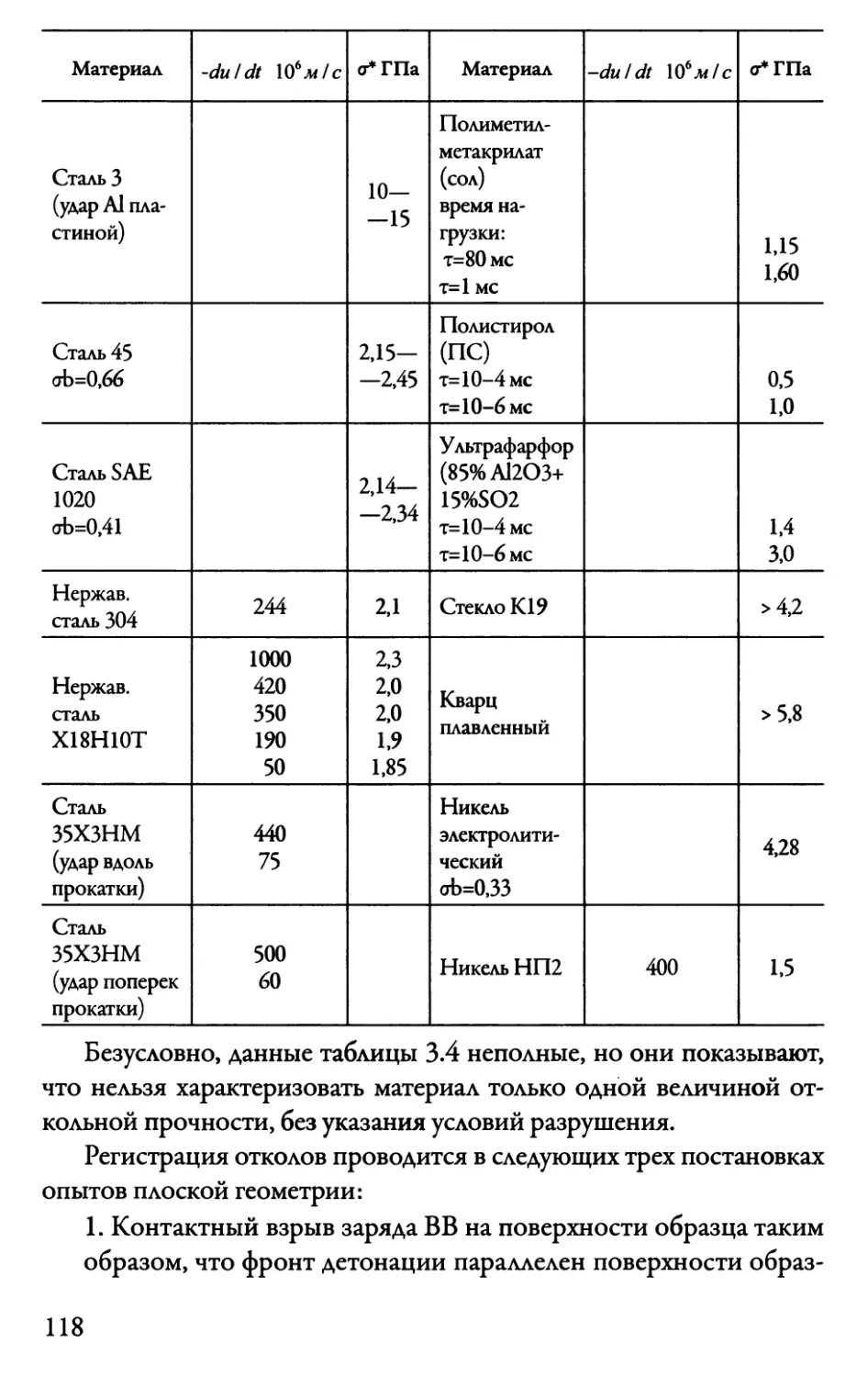
4.2. Ударное сжатие пористых тел
в области малых давлений 140
4.3. Модели пористого тела 144
4.4. Волны расширения в пористых телах 147
4.5. Ударная сжимаемость кубического
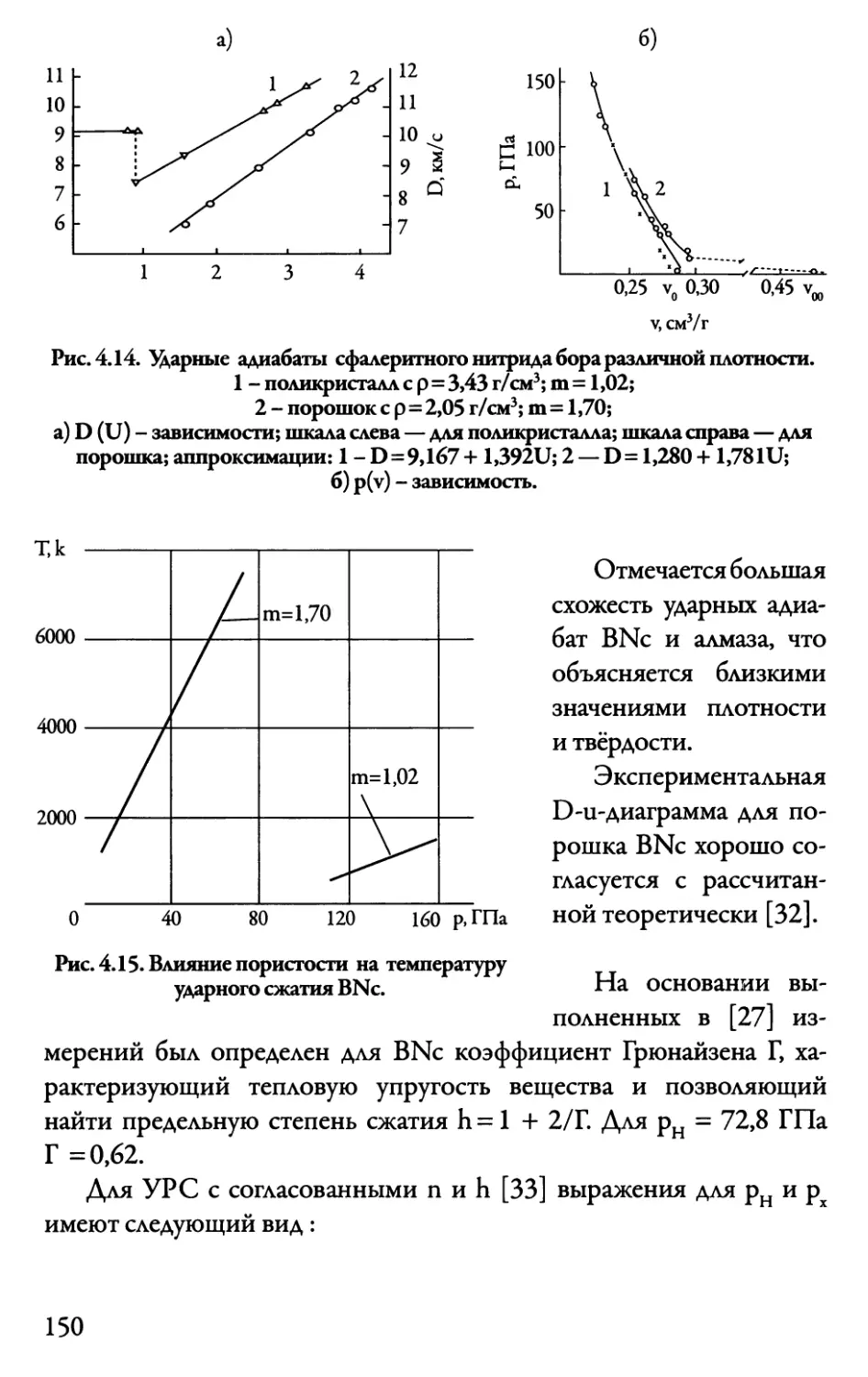
нитрида бора 148
4.6. Ударное компактирование алмазных порошков 151
4.7. Ударная сжимаемость алмазных порошков 153
4.7.1. Эксперименты 153
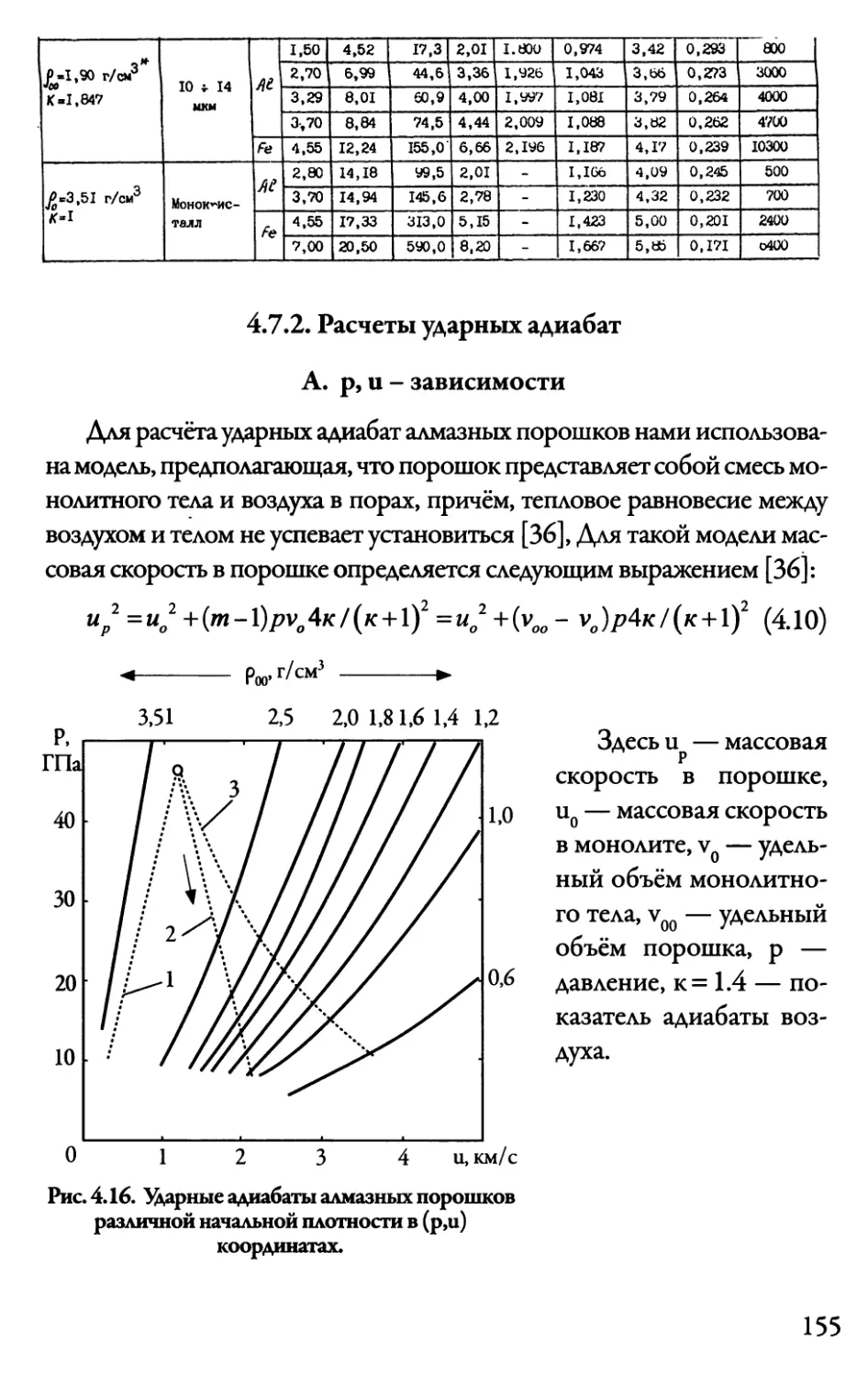
4.7.2. Расчеты ударных адиабат 155
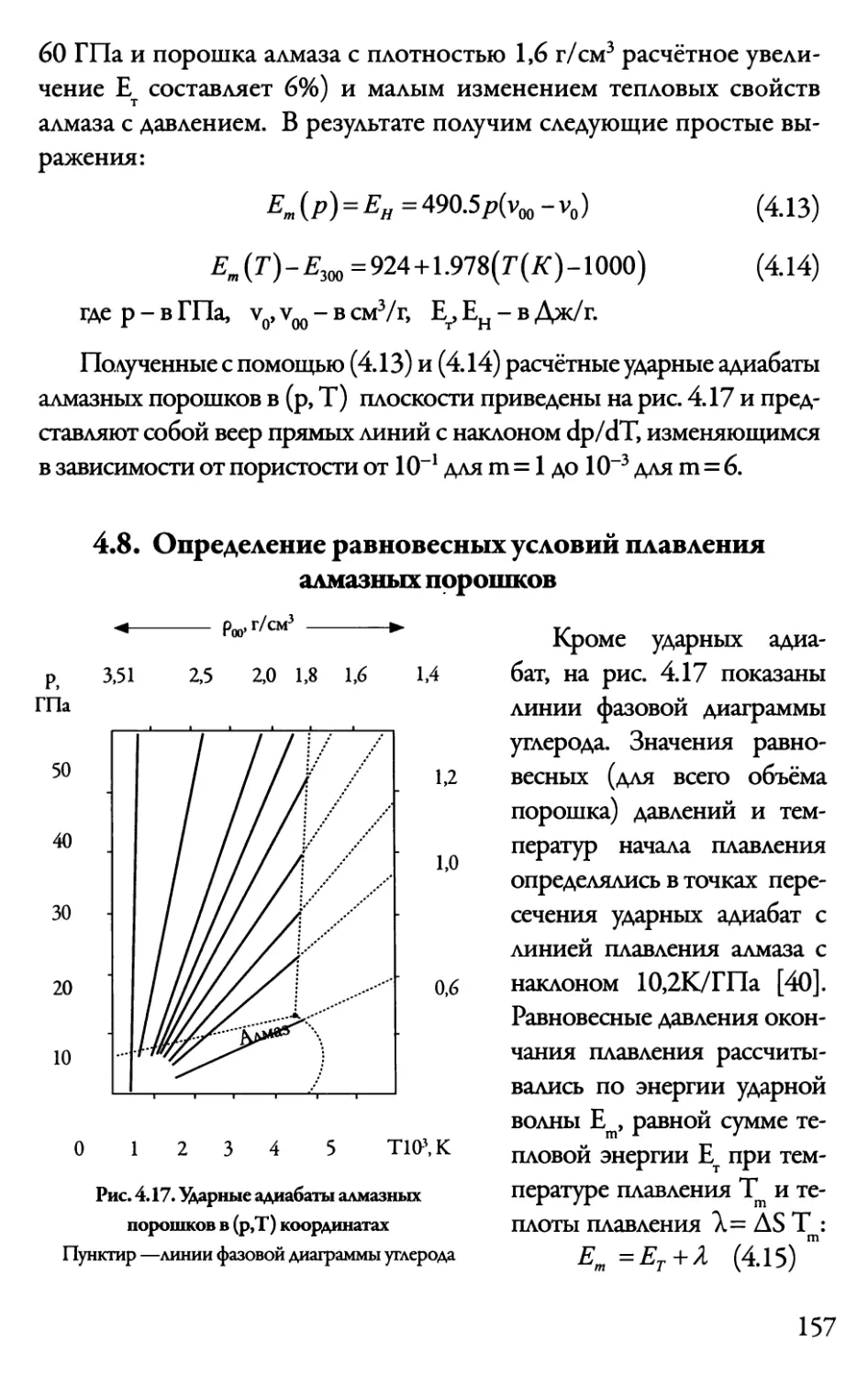
4.8. Определение равновесных условий плавления
алмазных порошков 157
4.9. Тепловая неравновесность
ударного сжатия порошков 159
Литература к главе 4 161
Глава 5. Кумуляция 165
5.1. Разновидности кумуляции 165
5.2. Прямое отражение УВ от преграды 168
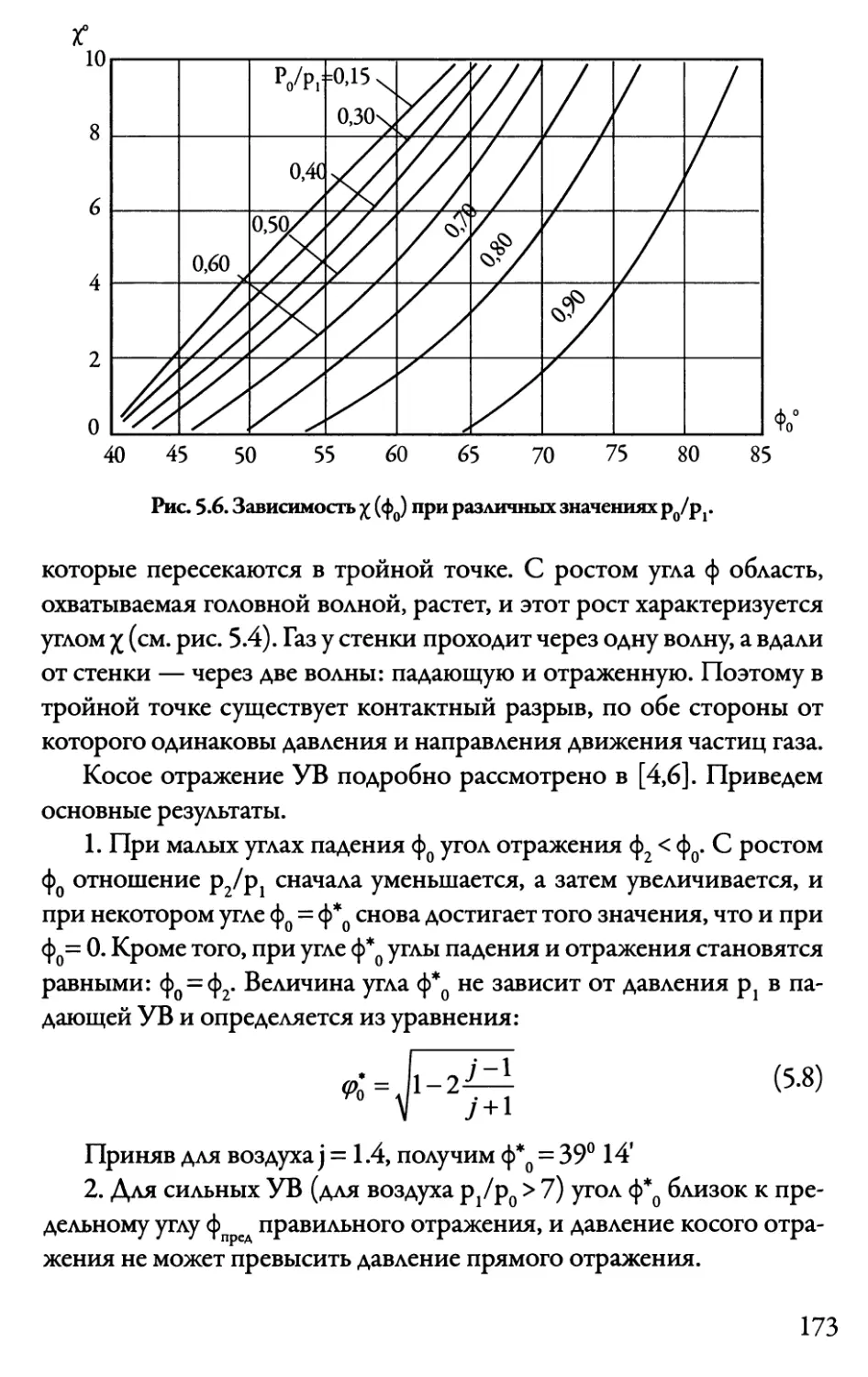
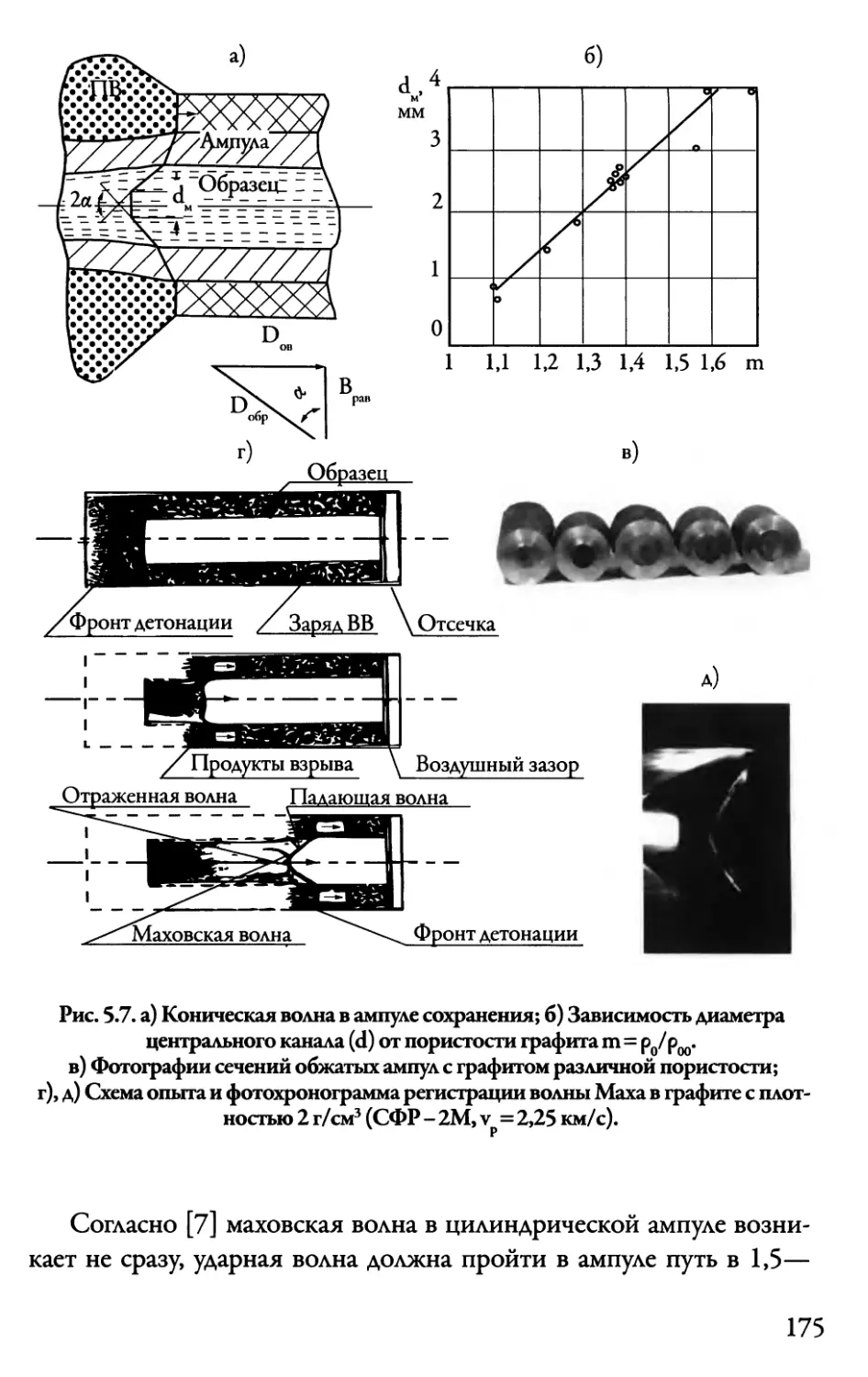
5.3. Косое столкновение волн. Маховские волны 171
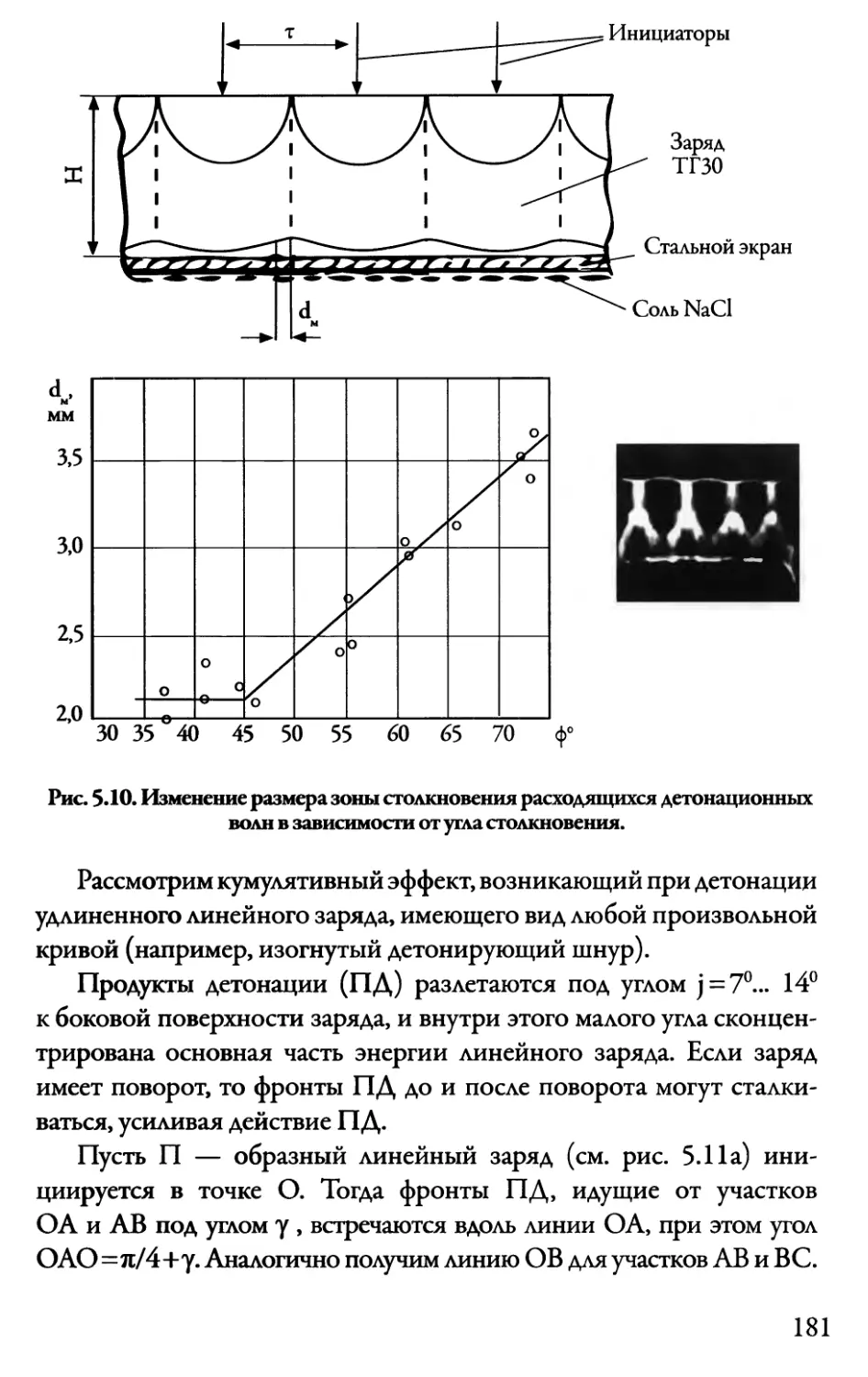
5.4. Столкновение детонационных волн 178
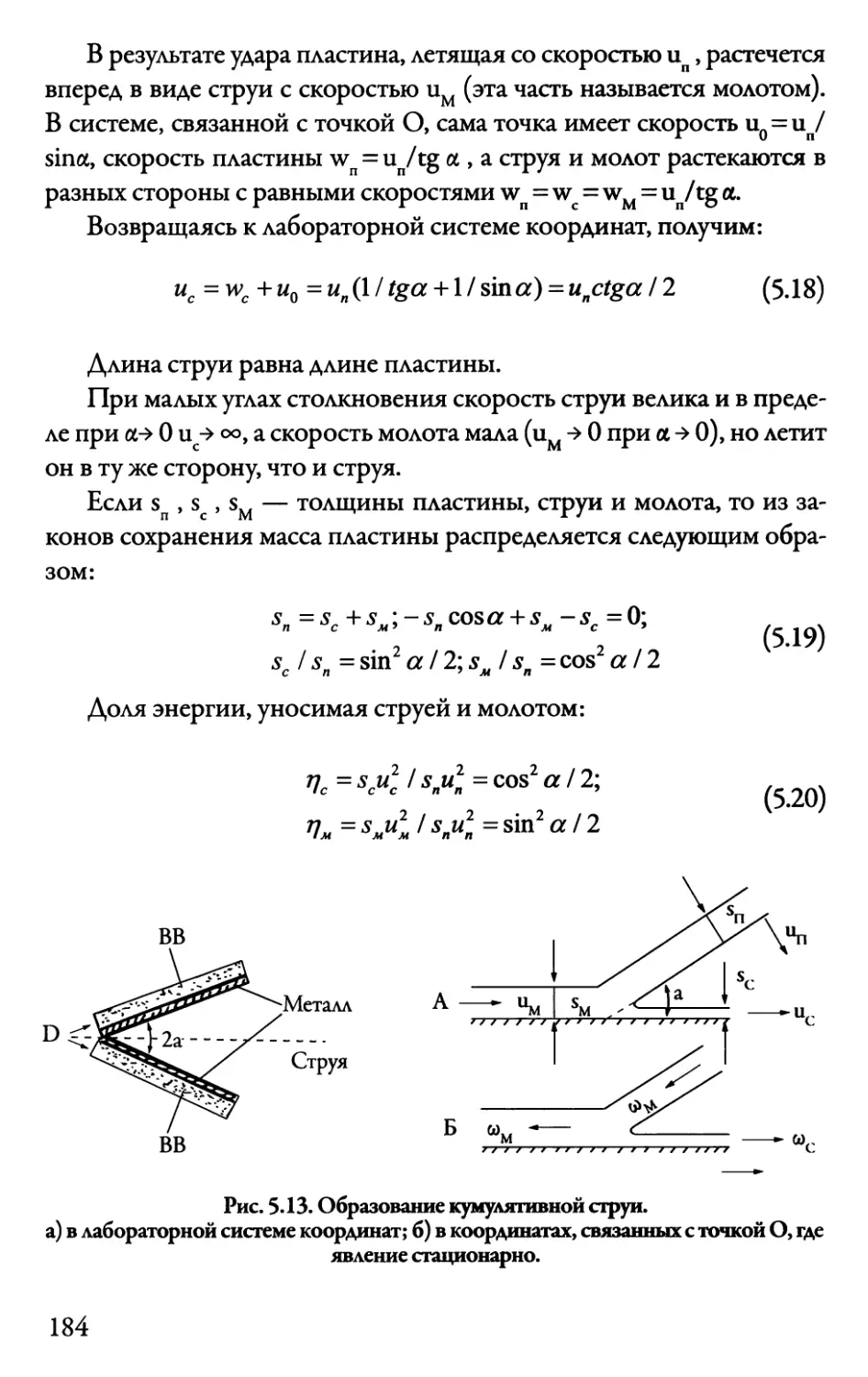
5.5. Кумулятивные струи 183
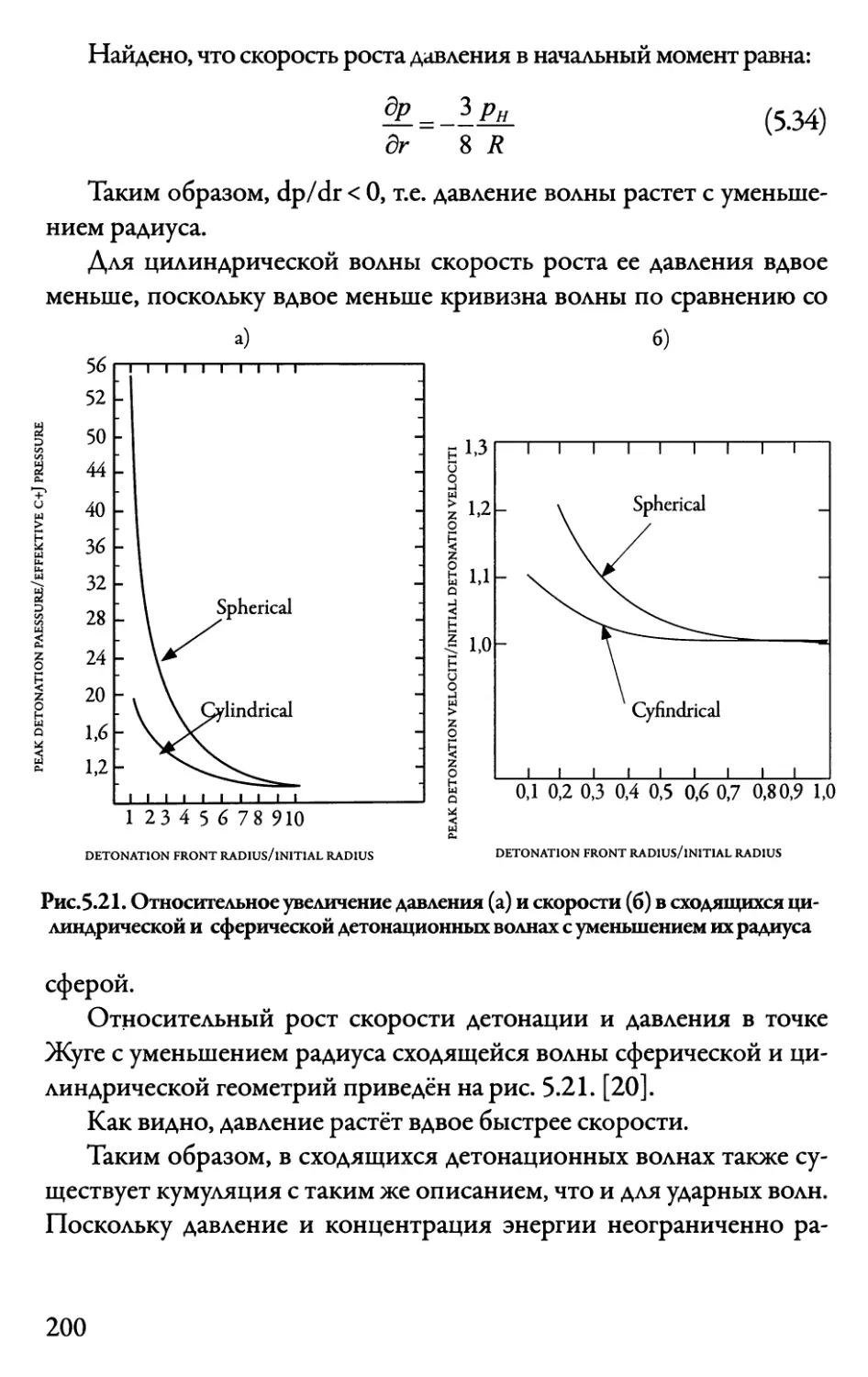
5.6. Сходящиеся сферические ударные волны 192
5.6.1. Фокусировка упругого предвестника 196
5.6.2. Фокусировка УВ с фазовым переходом 197
5.6.3. Фокусировка УВ в теплопроводном газе 198
5.7. Сходящаяся сферическая детонационная волна. 199
4
5.8. Схлопывание полости.
Пузырек в сжимаемой жидкости 201
5.9. Неустойчивость схлопывания.пузырьков 202
5.10. Кумуляция в слоеных системах 205
5.11. Примеры прекращения неограниченной
кумуляции 208
5.12. Неустойчивость контактных границ 211
5.13. Безударное сжатие шара 216
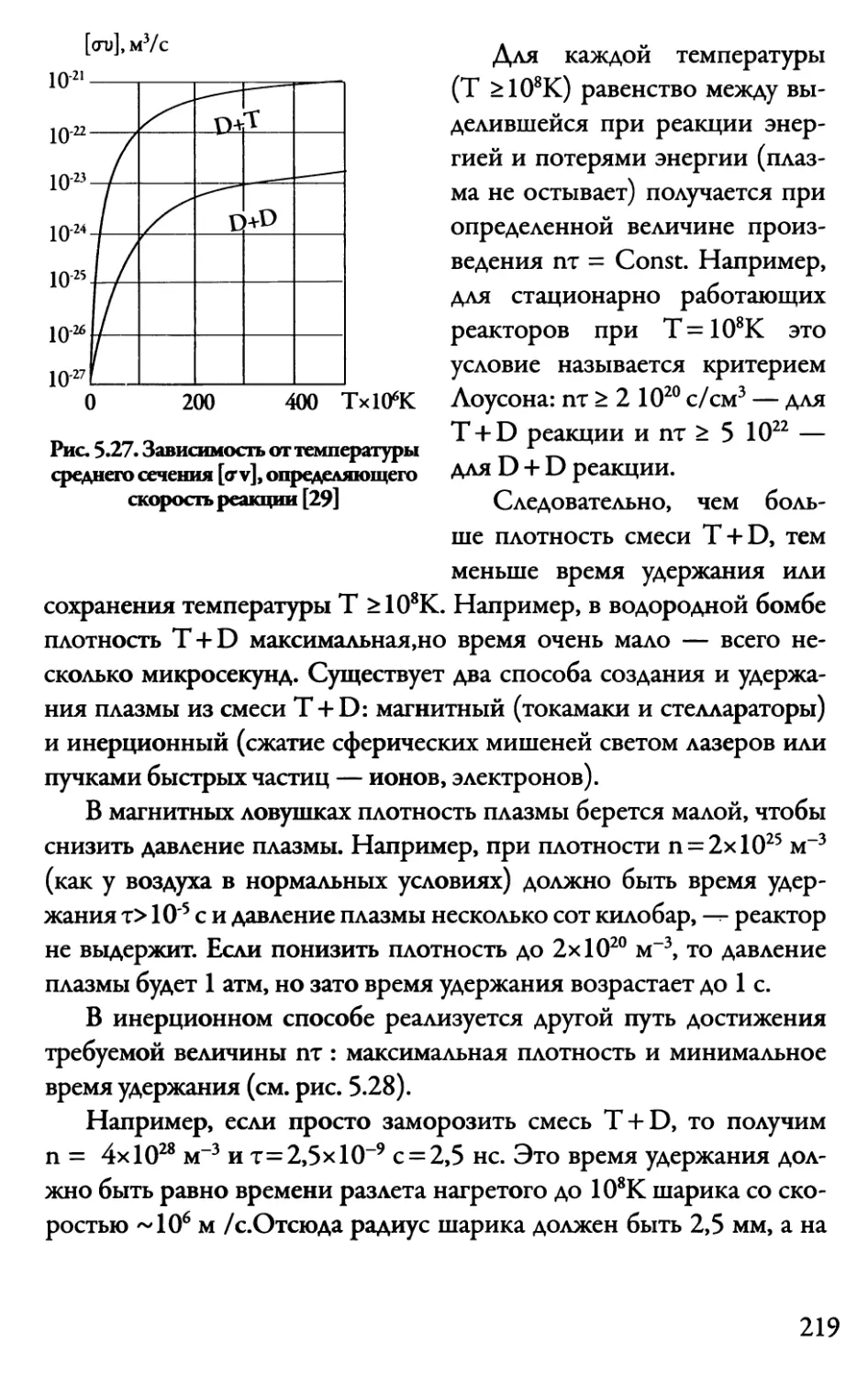
5.14. Сжатие мишеней термоядерного синтеза 218
5.15. Ускорение частиц с помощью
газокумулятивных зарядов 223
Литература к главе 5 226
Глава 6. Высокоскоростной удар 229
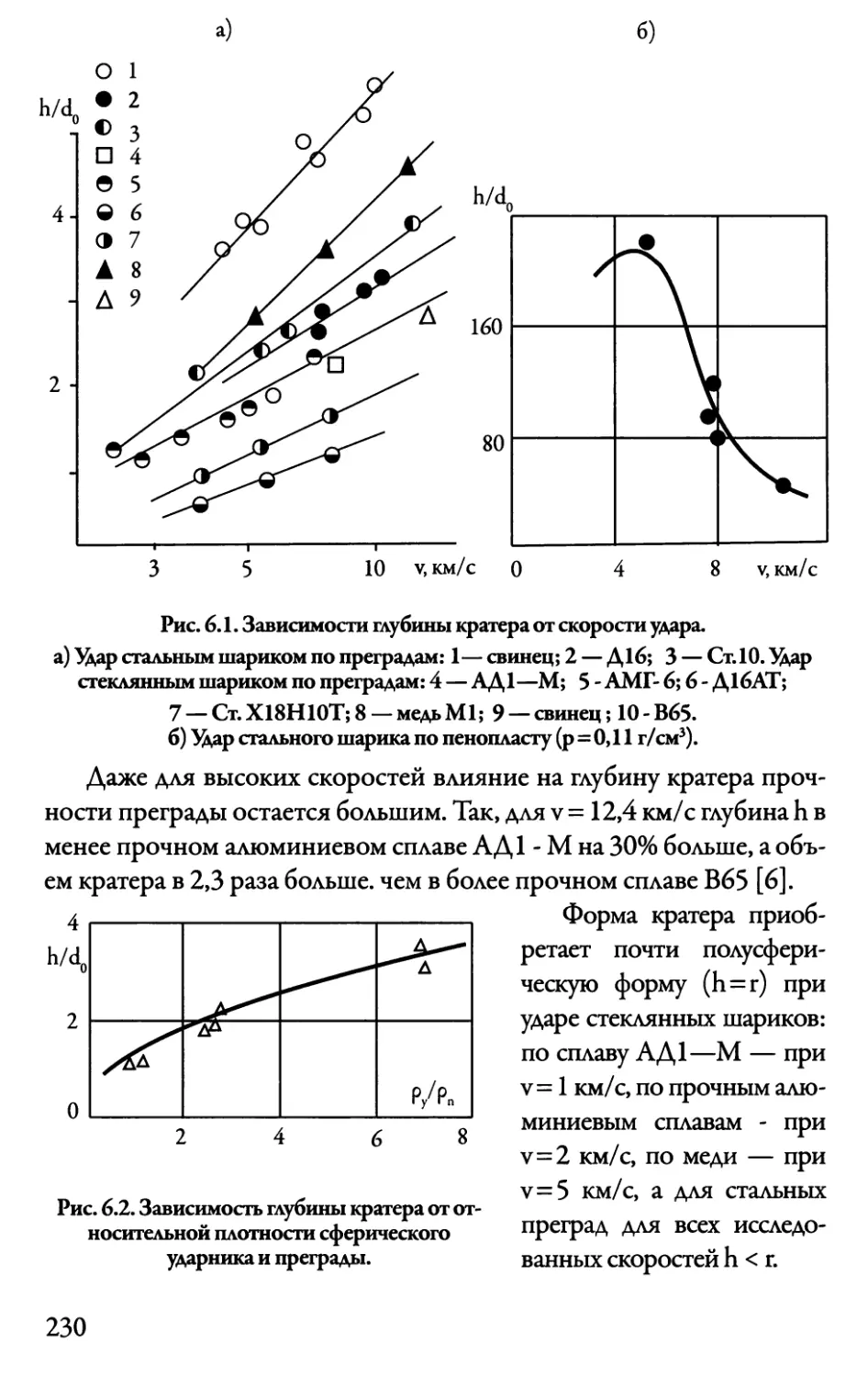
6.1. Соударение частицы с преградой 229
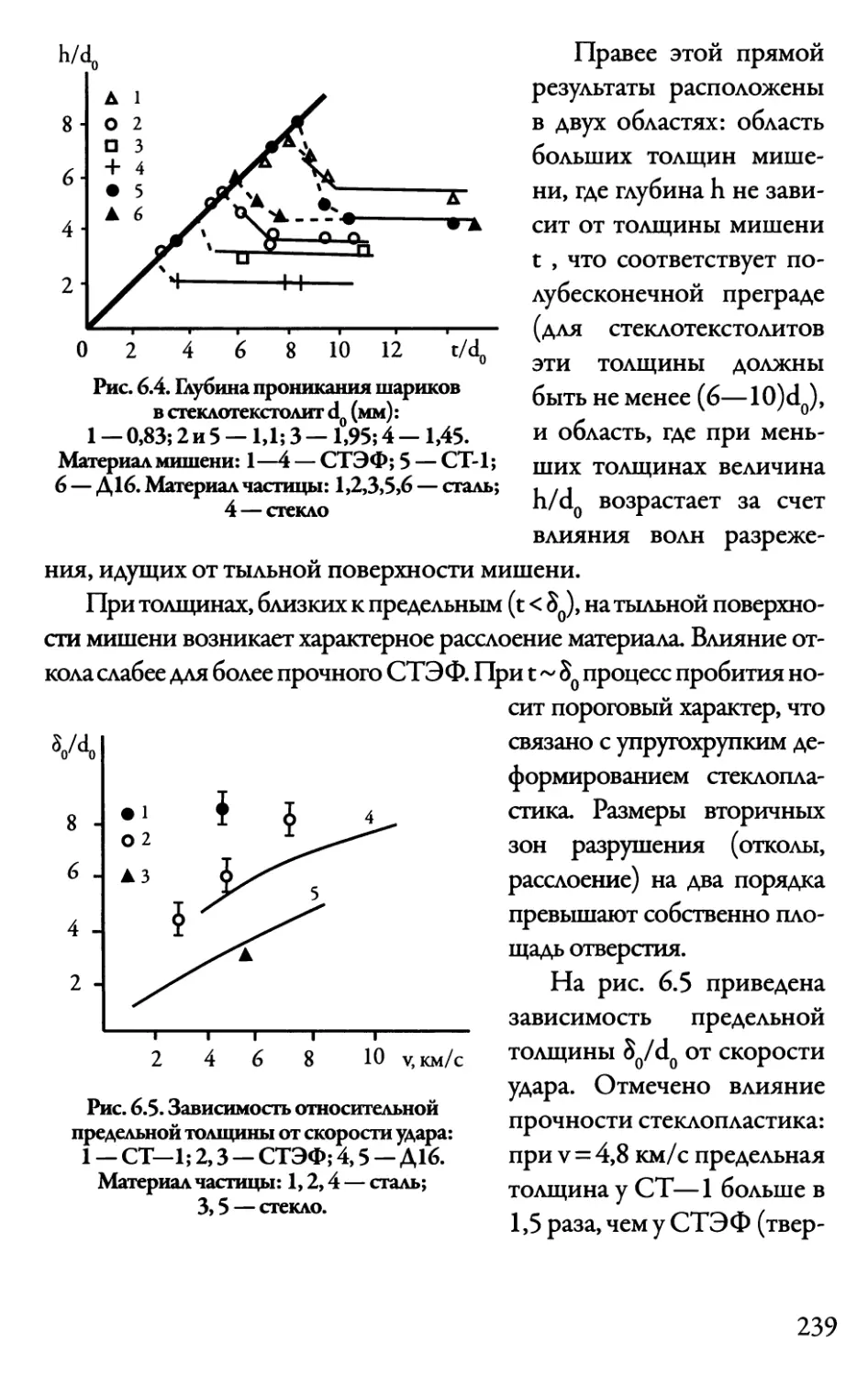
6.2. Сквозное пробивание стеклотекстолита 238
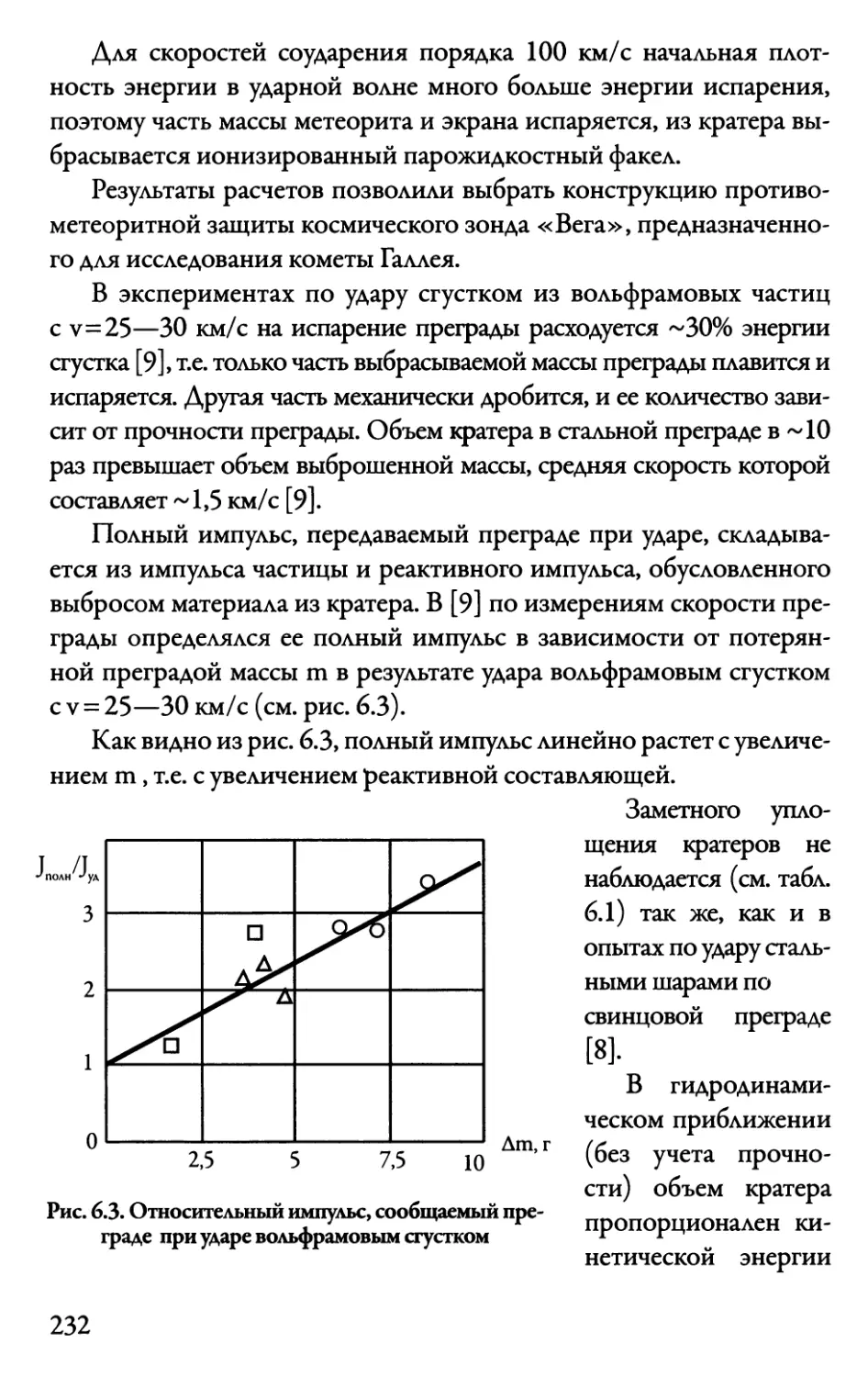
6.3. Соударение длинных стержней
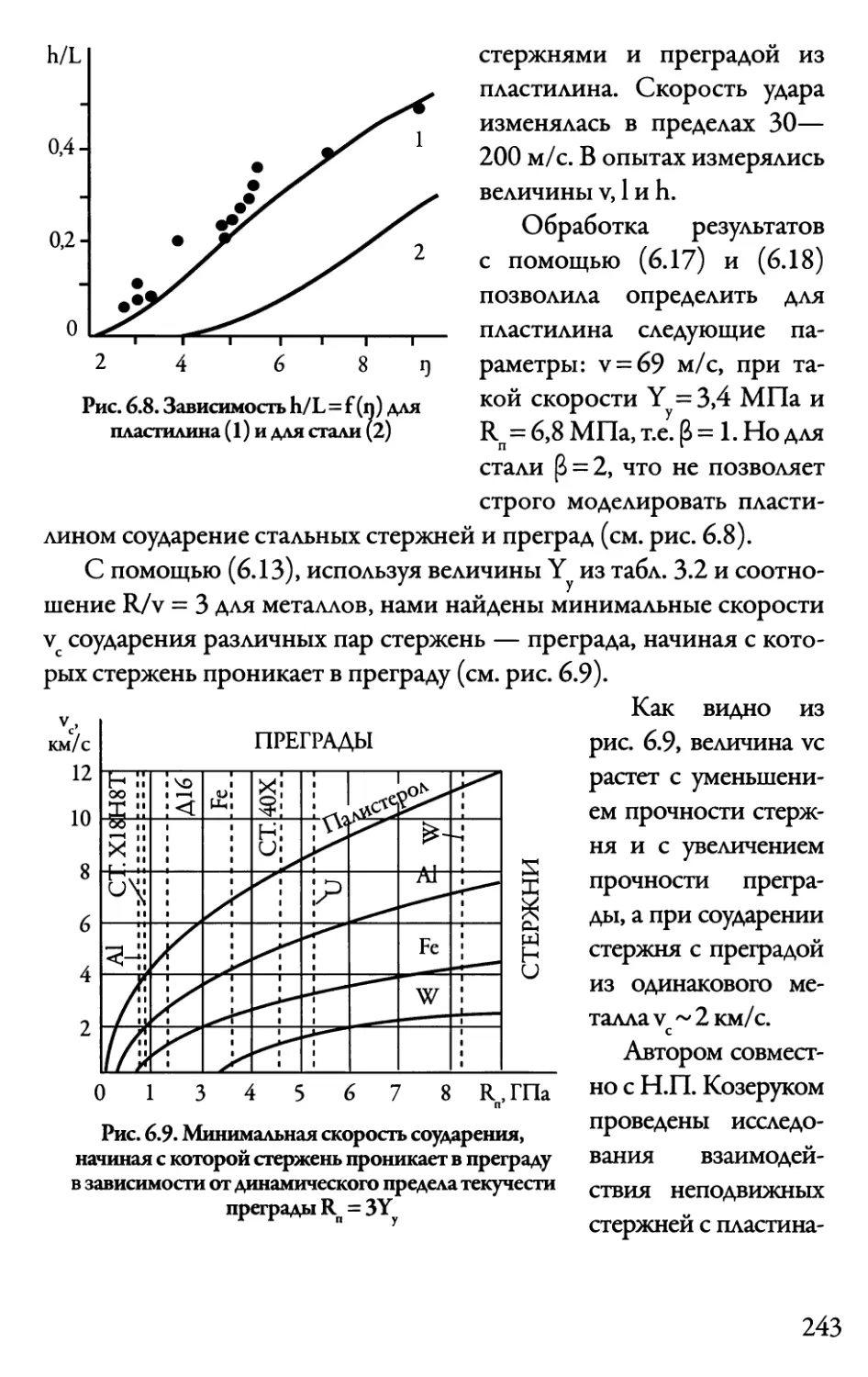
с полубесконечной преградой 240
6.4. Взаимодействие с преградой потока частиц 247
6.4.1. Детонационное напыление 248
6.4.2. Сверхглубокое проникание порошковой струи ... 254
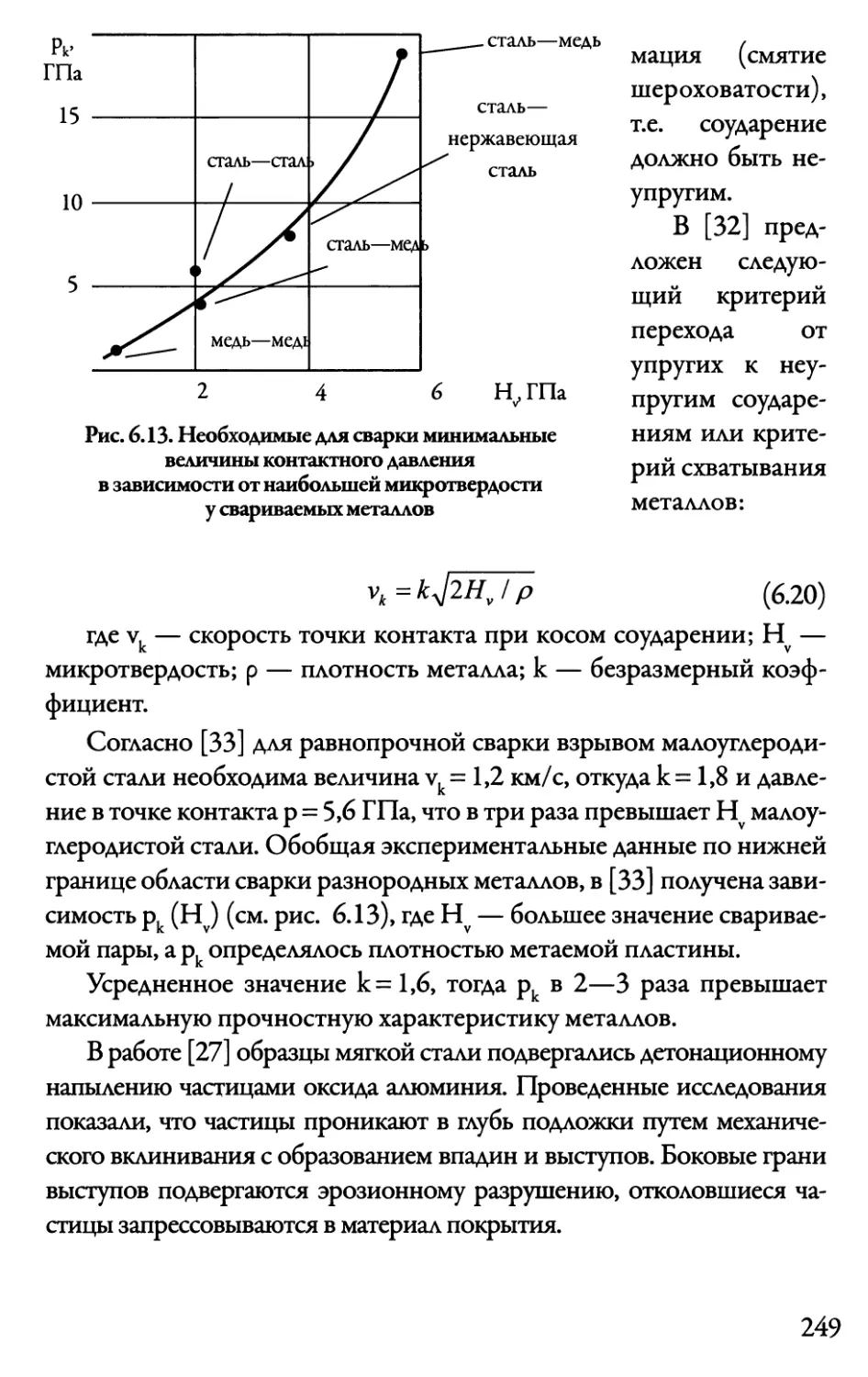
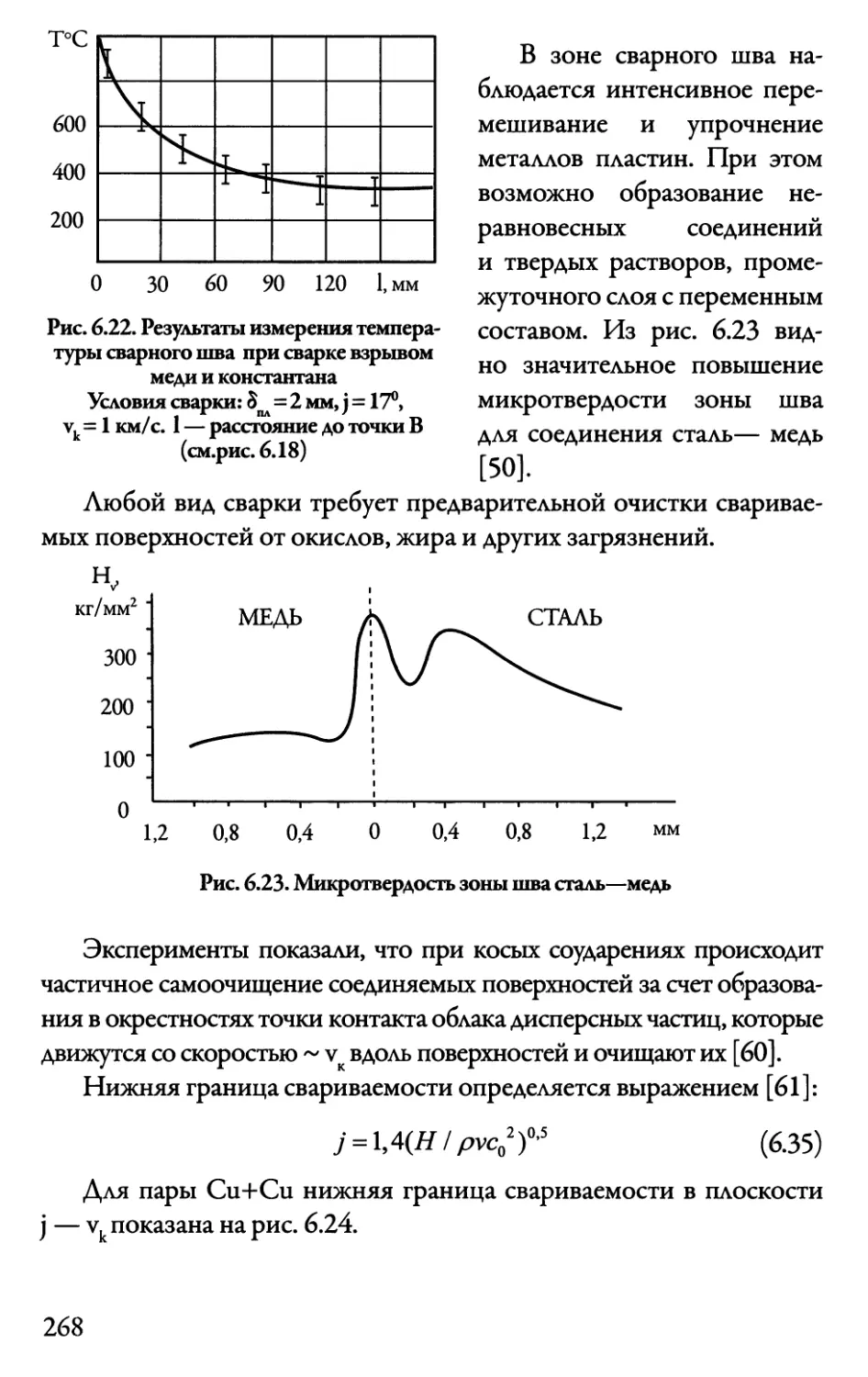
6.5. Соединение пластин при их косом
столкновении (сварка взрывом) 261
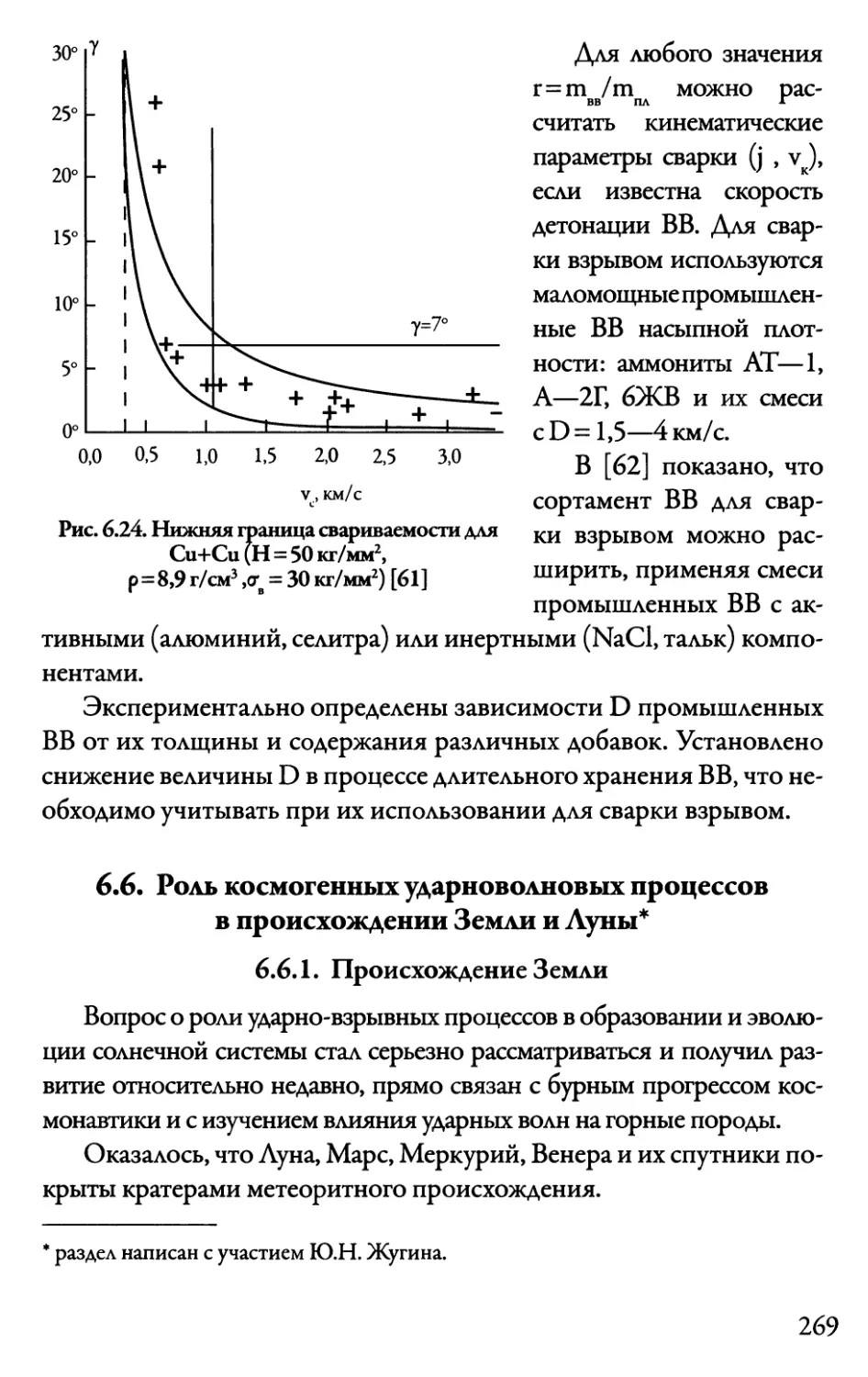
6.6. Роль космогенныхударноволновых процессов
в происхождении Земли и Луны 269
6.6.1. Происхождение Земли 269
6.6.2. Происхождение Луны 273
Литература к главе 6 276
Глава 7. Фазовые превращения в ударных волнах 281
7.1. Полиморфизм. Термодинамика и кинетика 281
7.2. Особенности полиморфных превращений
в ударных волнах 293
7.3. Примеры полиморфизма при ударном сжатии 302
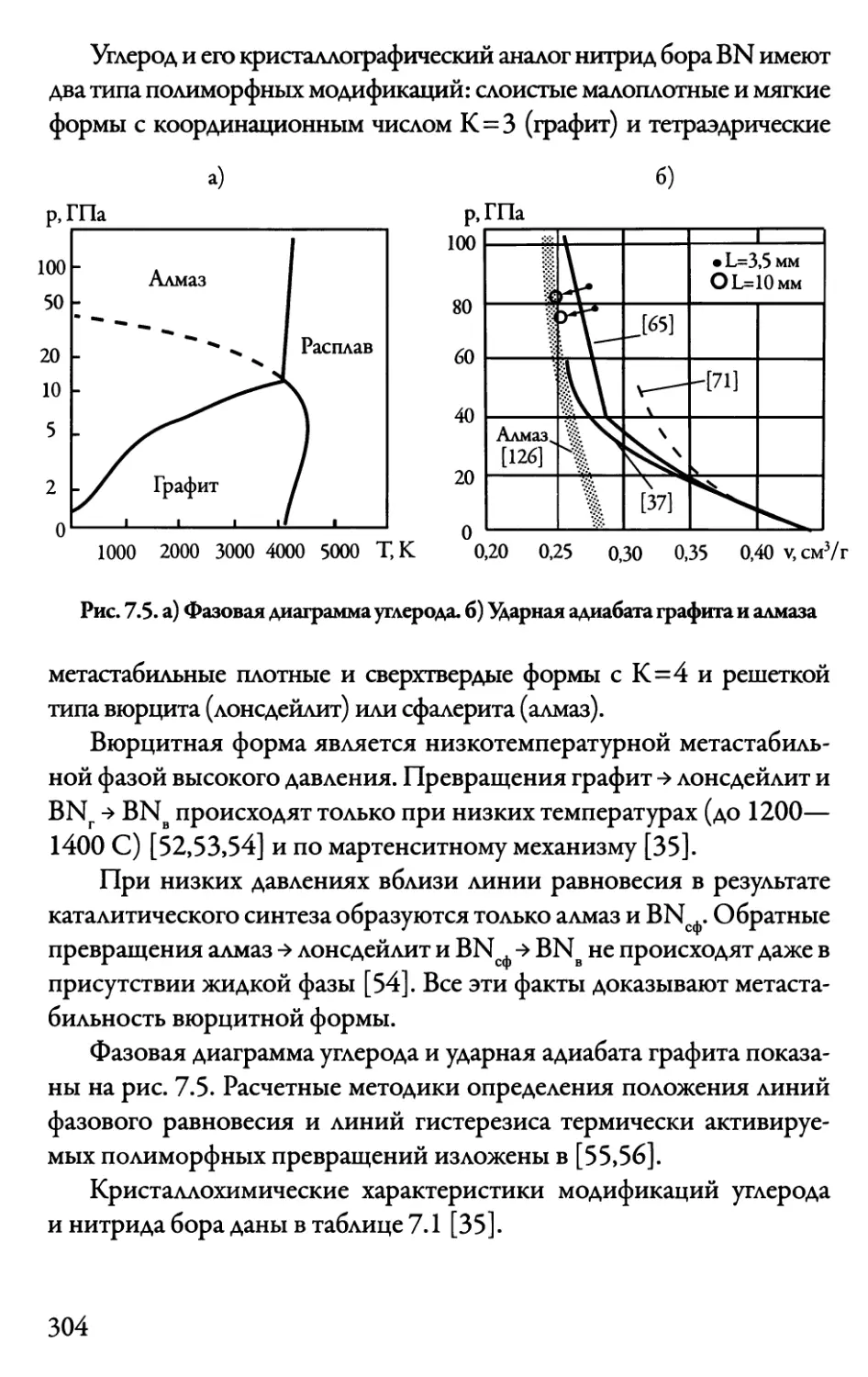
7.3.1.Железо 302
7.3.2. Олово 303
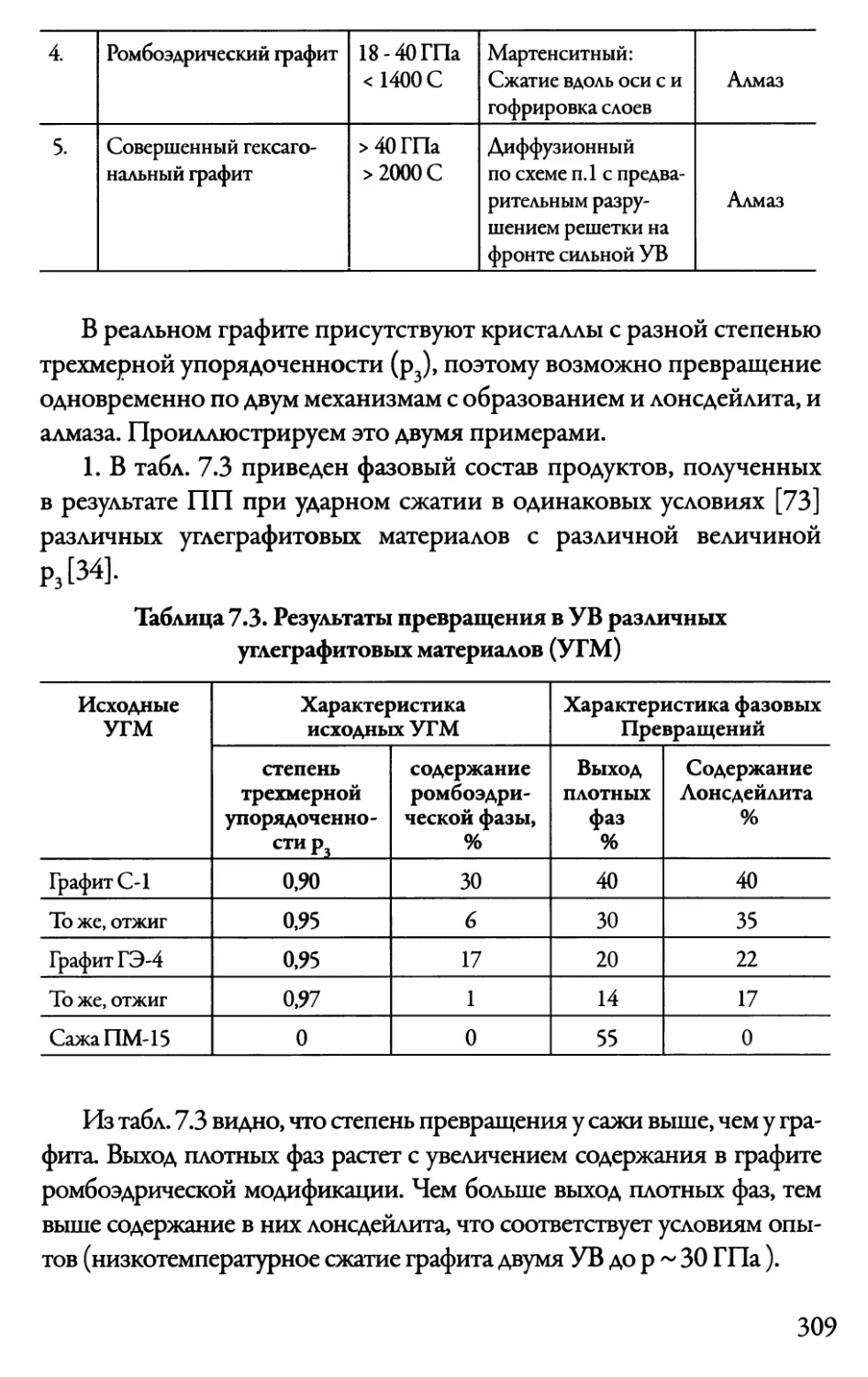
7.3.3. Углерод 303
5
7.3.4. Нитрид бора 313
7.3.5. Кремний 317
7.3.6. Двуокись кремния 318
7.3.7. Горные породы 322
7.4. Плавление при ударноволновом сжатии 323
7.4.1. Основные представления о плавлении
под давлением ° 323
7.4.2. Плавление в ударной волне 329
Литература к главе 7 333
Глава 8. Детонация 341
8.1. Гидродинамическая теория детонации
(модель ЗНД) 341
8.2. Модифицированные модели ЗНД 347
8.3. Вычисление параметров детонации 355
8.4. Измерение параметров детонации 364
8.4.1. «Внешние» методы измерений 364
8.4.2. «Внутренние» методы измерений 368
8.4.3. Исследование структуры зоны химической
реакции при детонации твёрдых ВВ 373
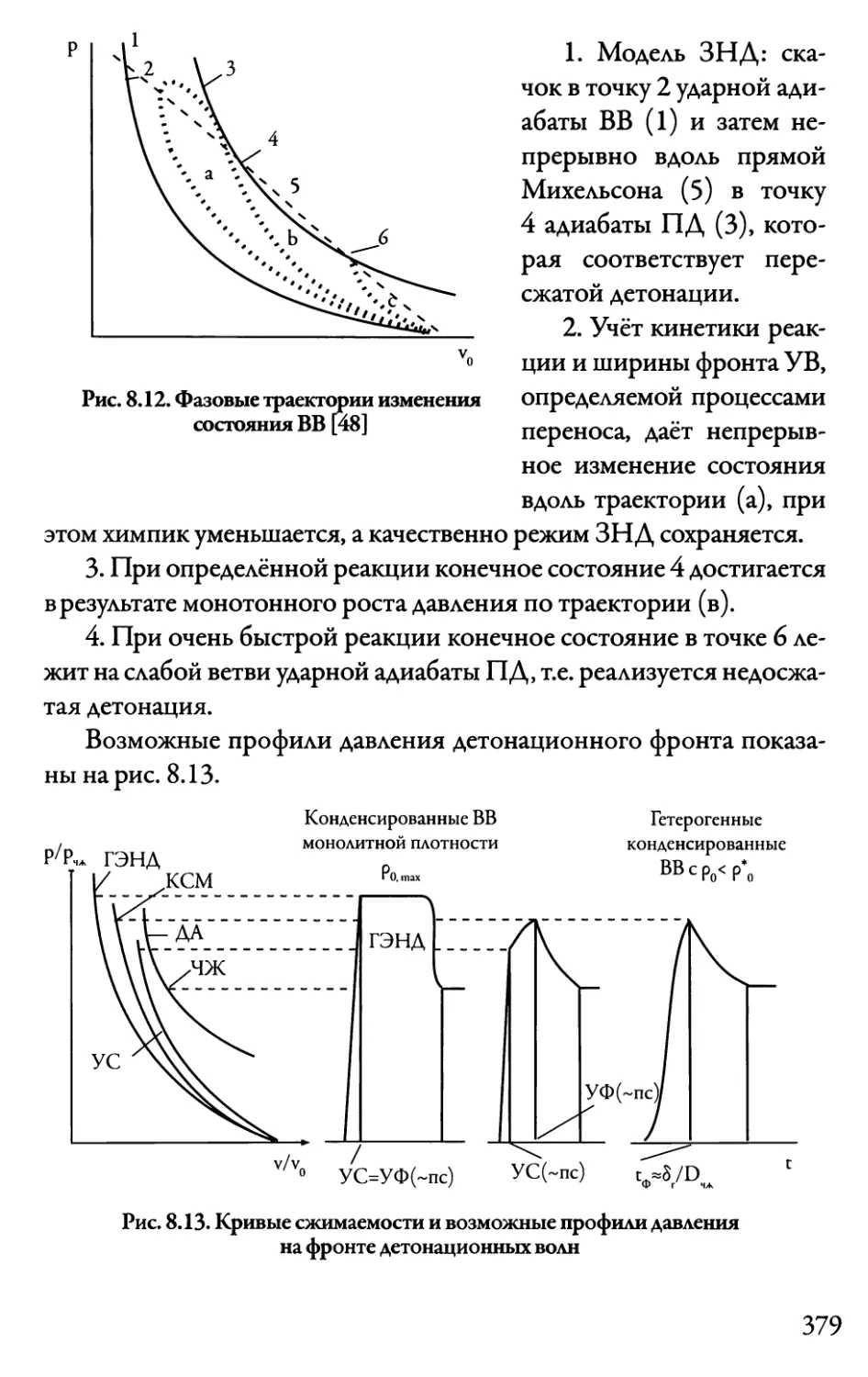
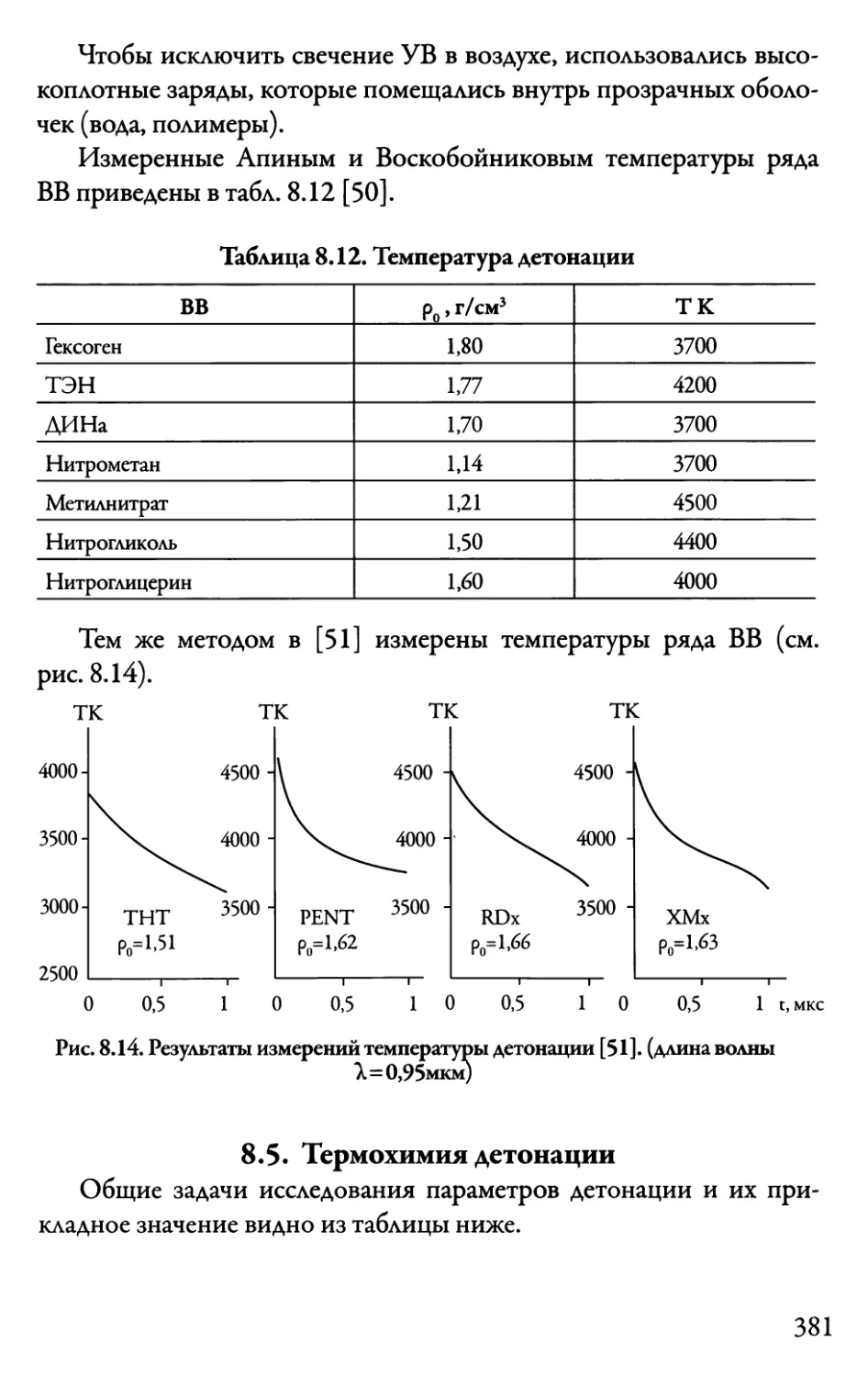
8.4.4. Измерение температуры ПД 380
8.5. Термохимия детонации 381
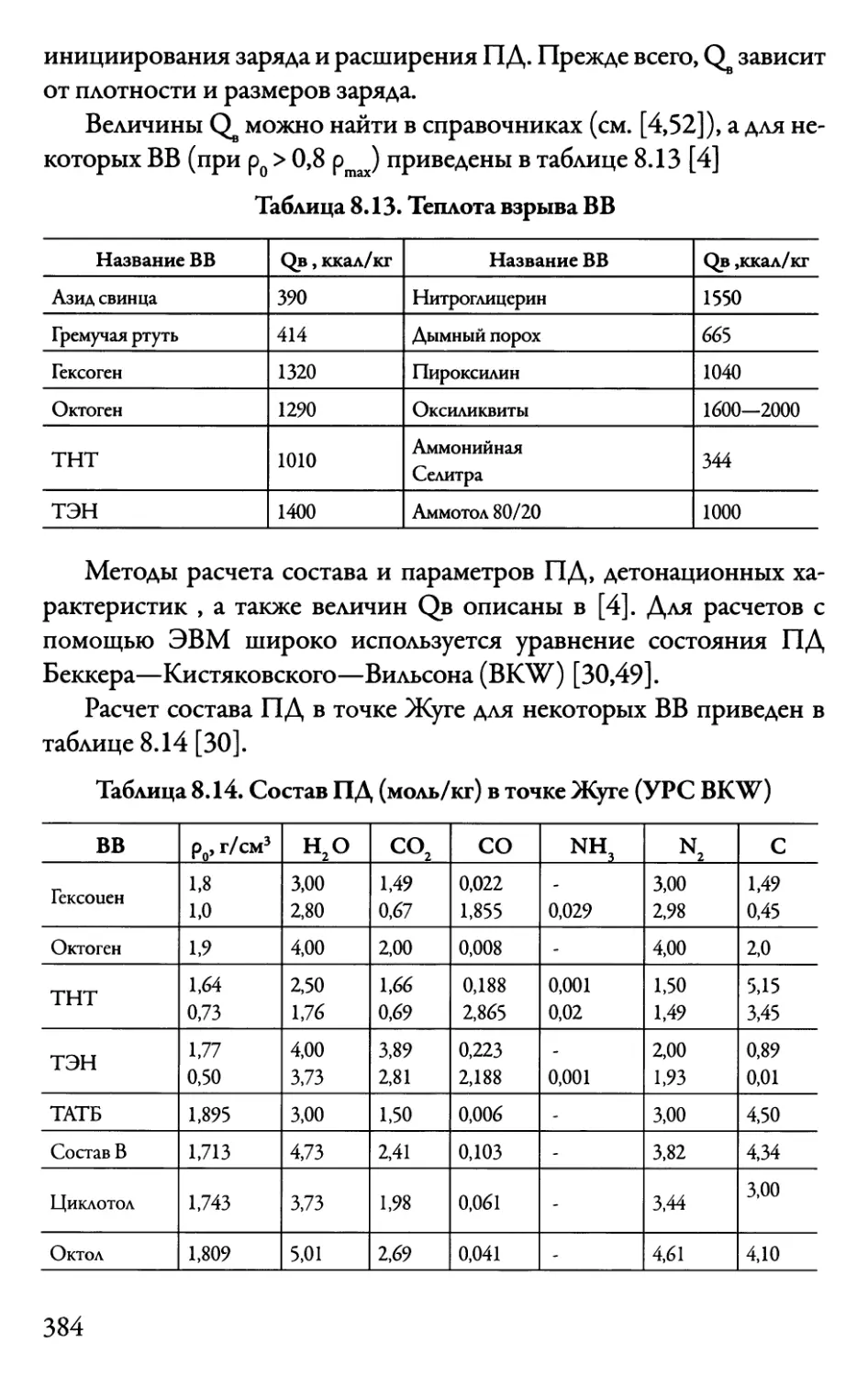
8.6. Возбуждение детонации 385
8.6.1. Очаговый механизм возбуждения детонации
в пористых ВВ 387
8.6.2. Возбуждение детонации гомогенных ВВ
(адиабатный взрыв) 399
8.6.3. Возбуждение детонации ударом пластины
или стержня 401
8.6.4. Инициирование лазерным импульсом 410
8.7. Неидеальная детонация 413
8.8. Обобщенное описание детонации 425
Литература к главе 8 428
Глава 9. Взрыв в различных средах 434
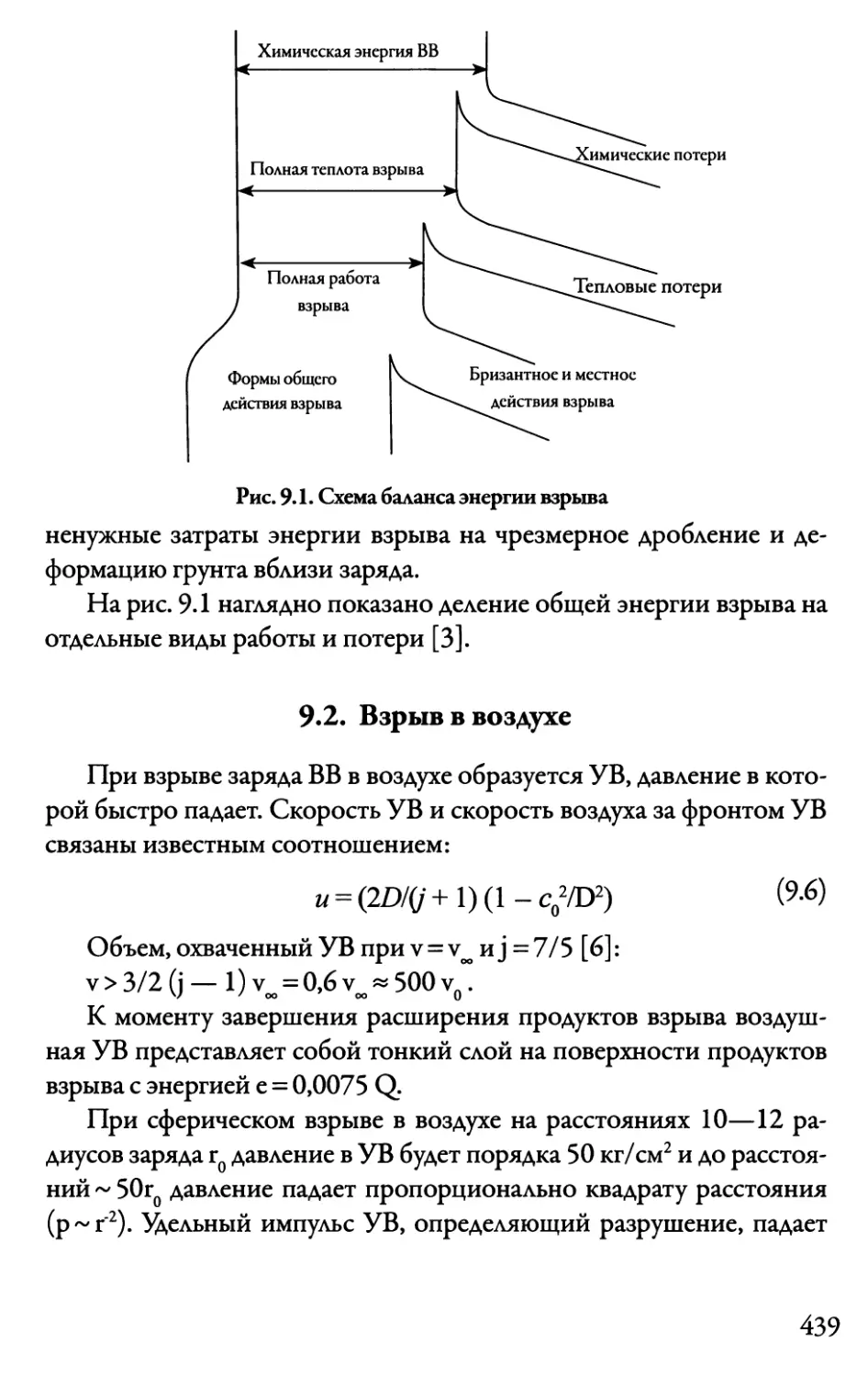
9.1. Понятие взрыва. Работа взрыва 434
9.2. Взрыв в воздухе 439
6
9.3. Взрыв в воде 443
9.4. Взрыв в грунте 447
9.4.1. Камуфлетный взрыв 449
9.4.2. Взрывы на выброс 452
9.5. Взрывные работы. Управление взрывом 458
9.6. Мирные атомные взрывы 463
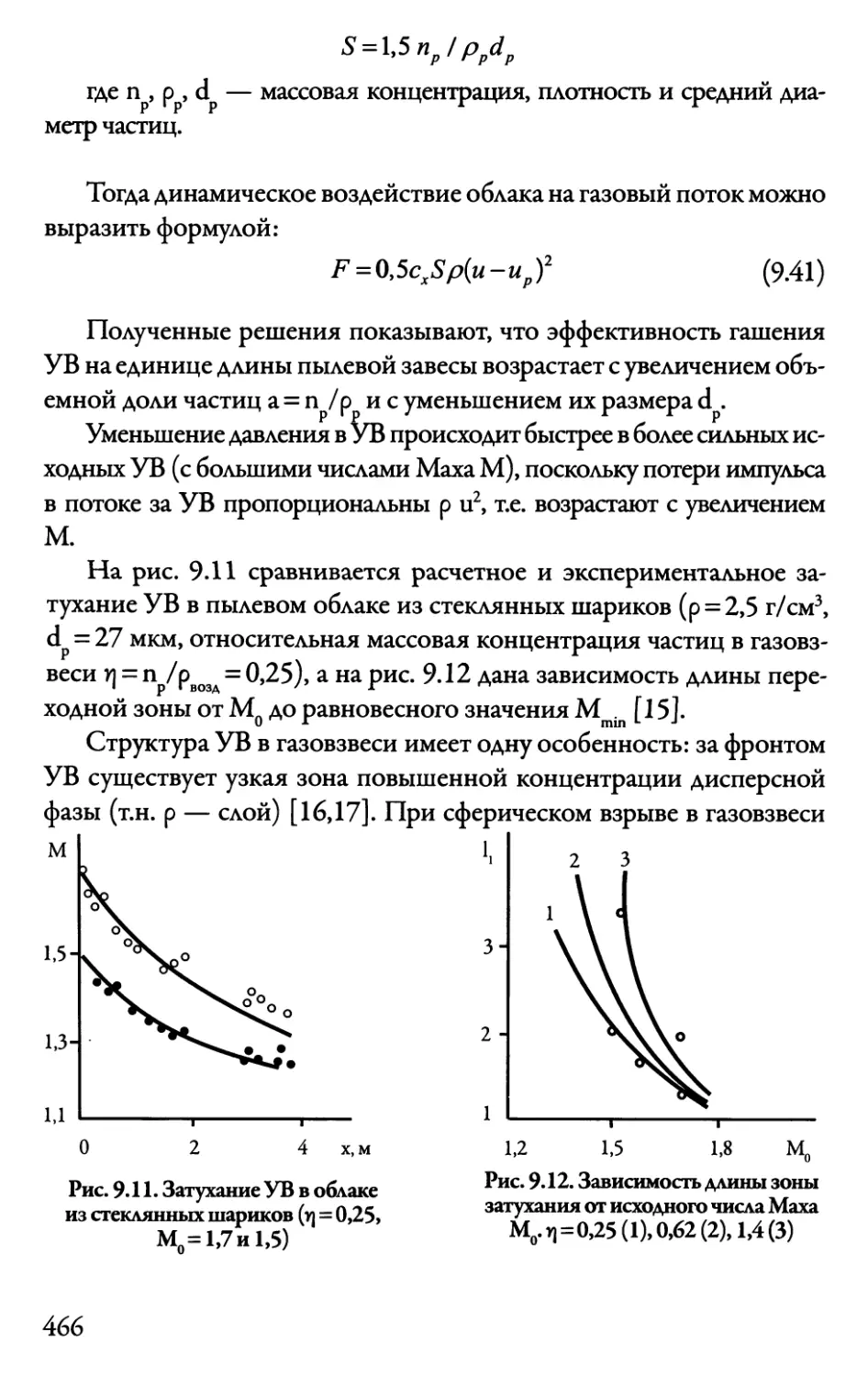
9.7. Взрыв в газовзвесях и в пене 465
9.8. Термический взрыв 471
Литература к главе 9 473
Глава 10. Взрывчатые вещества 475
10.1. История создания ВВ 475
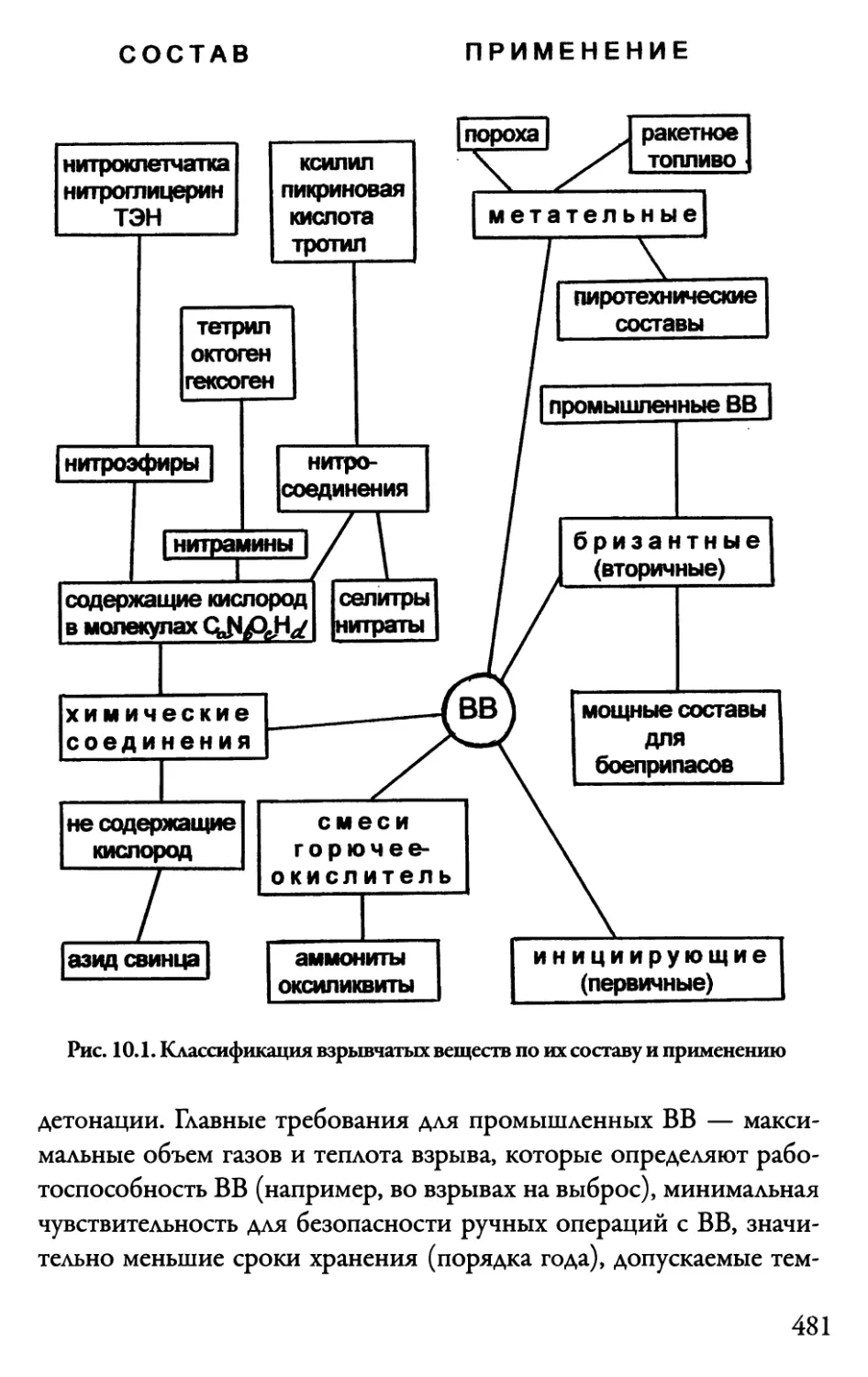
10.2. Общая характеристика и классификация ВВ 478
10.3. Промышленные взрывчатые вещества 482
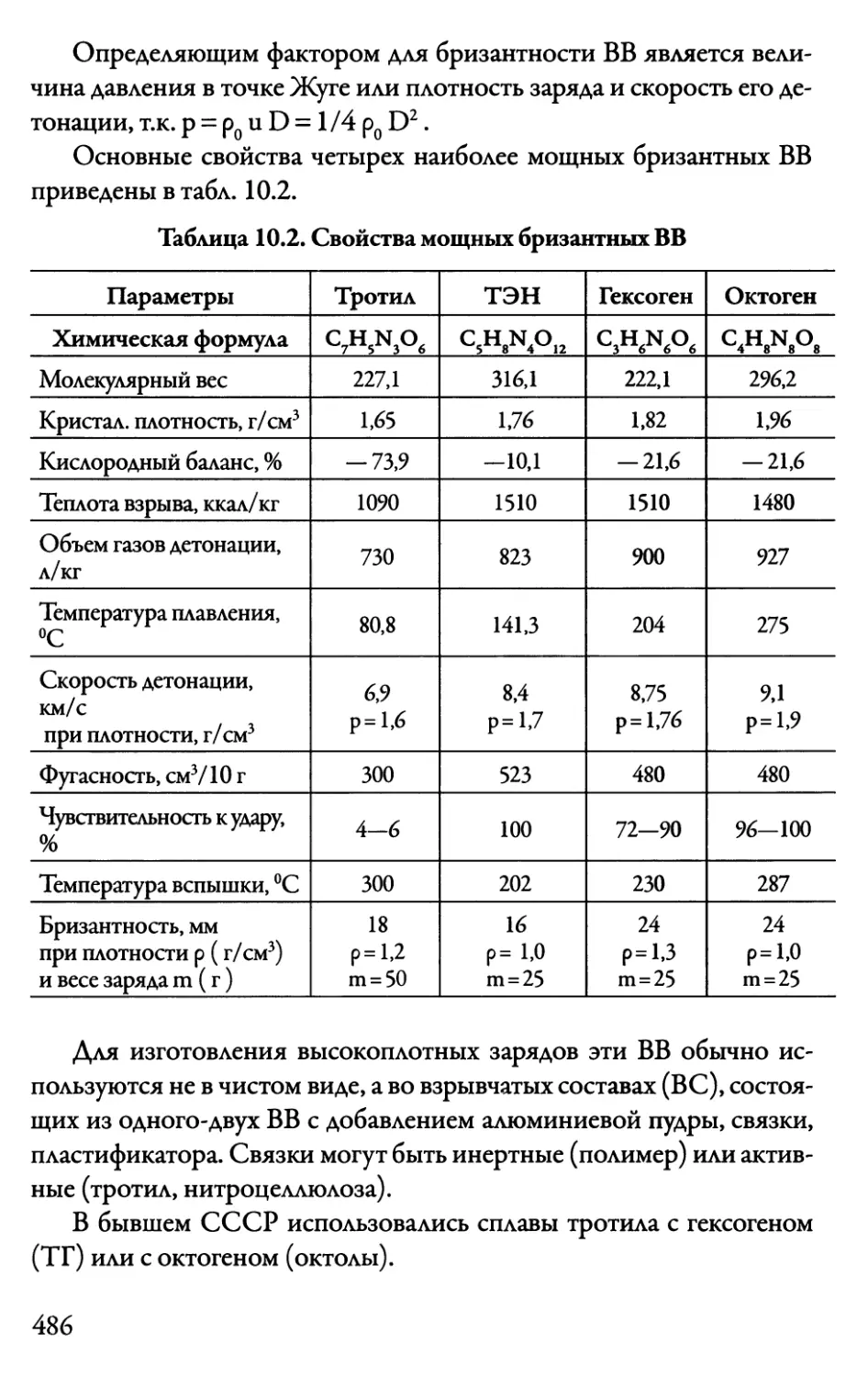
10.4. Мощные бризантные ВВ и составы 485
10.5. Технологии изготовления зарядов 490
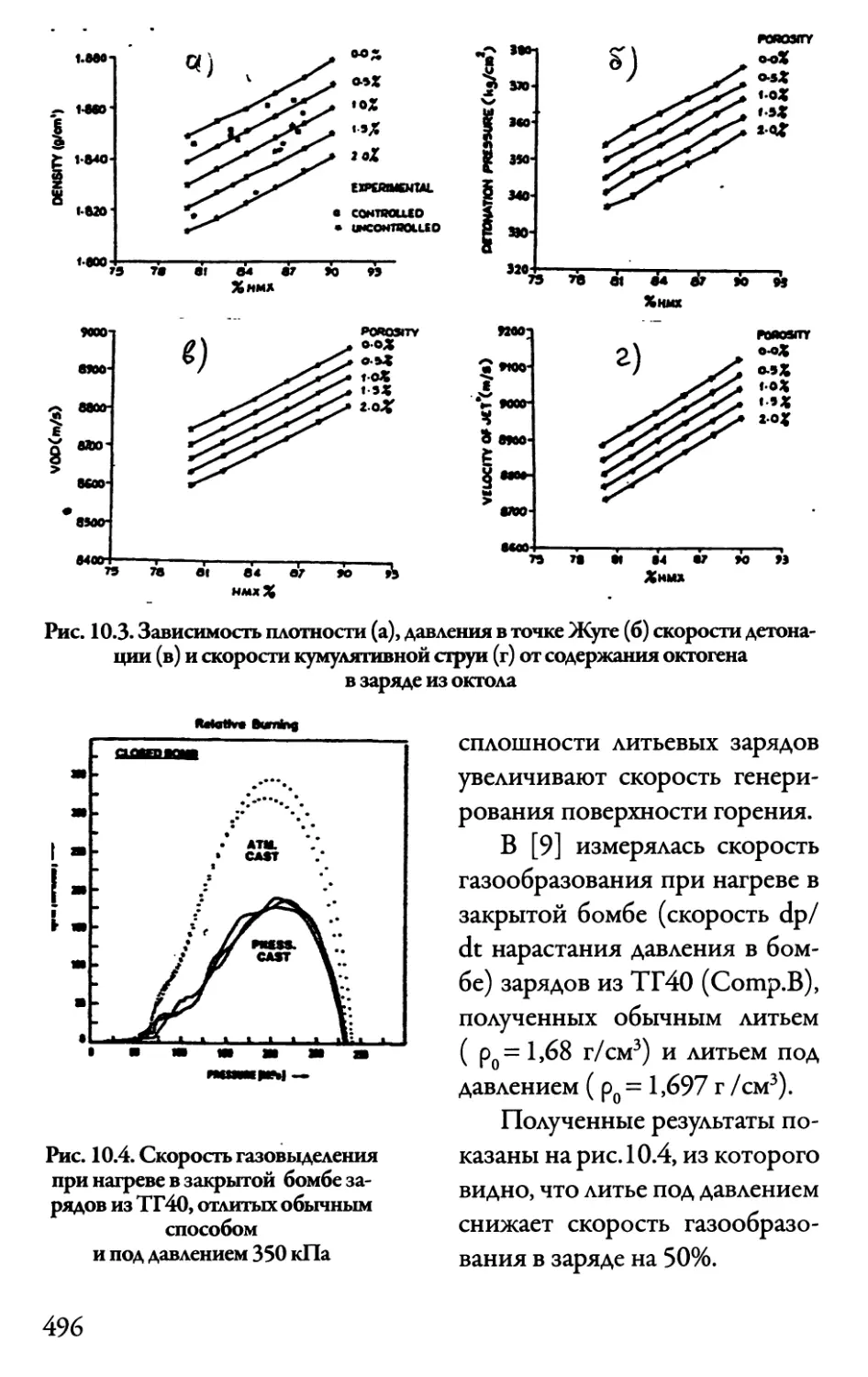
10.5.1..Влияние технологии литья на свойства заряда ... 494
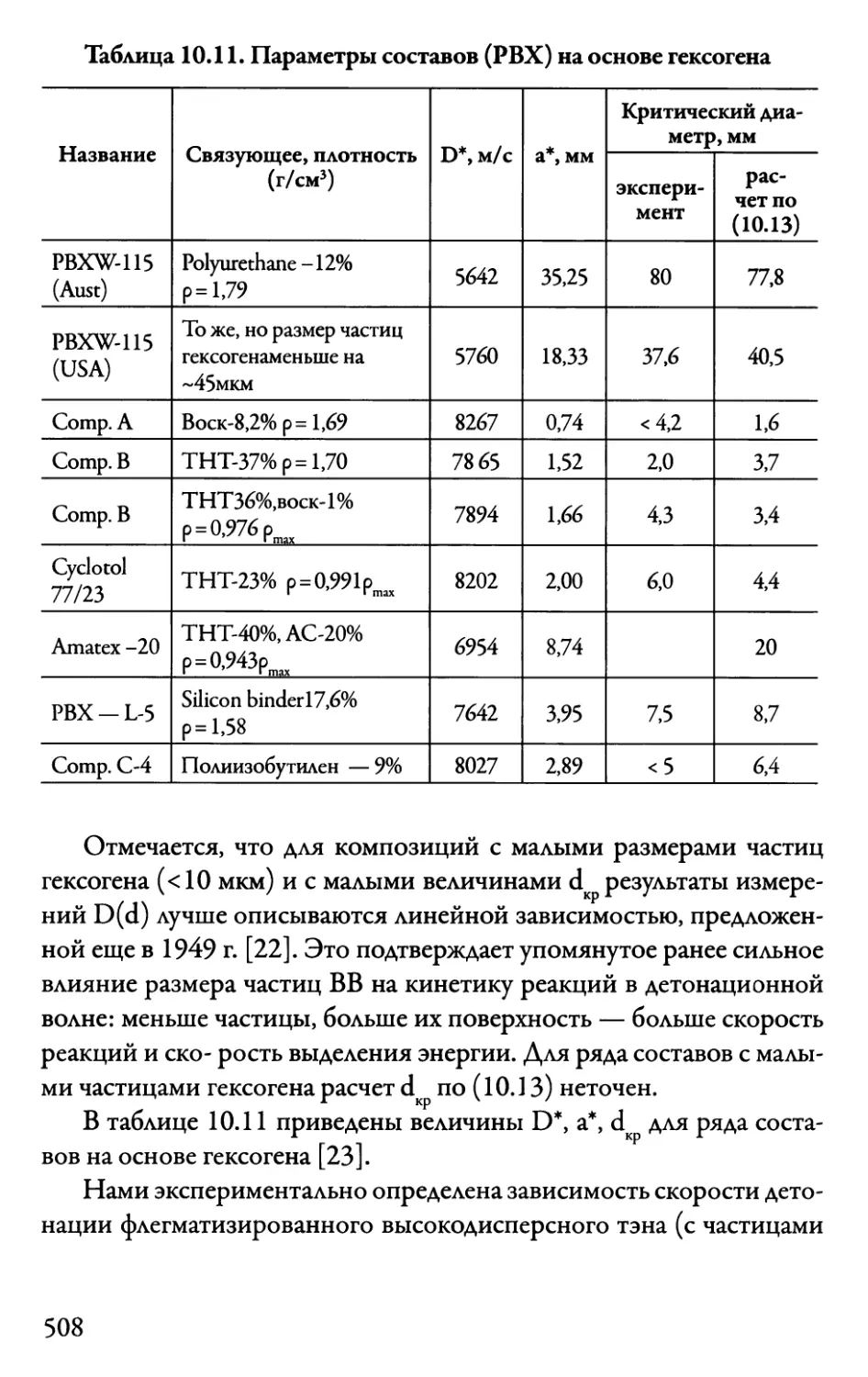
10.6. Детонационная способность ВВ 497
10.6.1. Критический диаметр заряда 497
10.6.2. Зависимость скорости детонации
от диаметра заряда 505
10.6.3. Детонация с «внутренней» разгрузкой 509
10.6.4. Зависимость скорости детонации
от плотности заряда 510
10.7. Чувствительность ВВ 511
10.7.1. Общая характеристика чувствительности 511
10.7.2. Чувствительность к удару 515
10.7.3. Чувствительность к прострелу пулей 517
10.7.4. Чувствительность к термическому дмпульсу 517
10.7.5. Минимальный инициирующий импульс 518
10.7.6. Чувствительность к инициированию
ударной волной 519
10.8. Формы работы взрыва.
Бризантность и фугасность ВВ 520
10.9. Метание продуктами взрыва 524
10.9.1. Метание пластин 525
7
10.9.2. Метание сферической оболочки 527
10.9.3. Метание при инициировании заряда от пластин. .528
10.9.4. Метание цилиндрической оболочки 529
10.9.5. Метание скользящей детонацией 531
10.9.6. Влияние на метание неидеальности
детонации заряда 531
10.10. Основы техники безопасности при работе
с взрывчатыми материалами 533
10.10.1. Организация работ с ВМ 536
10.10.2. Требования к персоналу 537
10.10.3. Гигиена труда и промсанитария 538
10.10.4. Общие правила обращения с ВМ 538
10.10.5. Транспортировка ВМ 539
10.10.6. Учет и хранение ВМ 540
10.10.7. Общие правила ведения взрывных работ 541
Литература к главе 10 543
Глава 11. Средства взрывания и инициирующие
устройства 546
11.1. Способы взрывания 546
11.2. ОШ и ДШ 550
11.3. Капсюли-детонаторы 552
11.3.1. Высоковольтные (быстрые) детонаторы 557
11.3.2. Искровые ЭД 558
11.3.3. Детонаторы с взрывающимся мостиком 561
11.3.4. Детонаторы с взрывающейся фольгой 563
11.3.5. Лазерные детонаторы 564
11.4. Взрывные линзы 565
11.5. Многоточечные системы 570
11.5.1. Конструкция систем 570
11.5.2. Начальная асимметрия и разнодинамичность
детонационного фронта 572
Литература к главе 11 575
Глава 12. Методы регистрации быстропротекающих
процессов 577
12.1. Классификация методов регистрации 577
8
12.2. О точности измерений временных интервалов 581
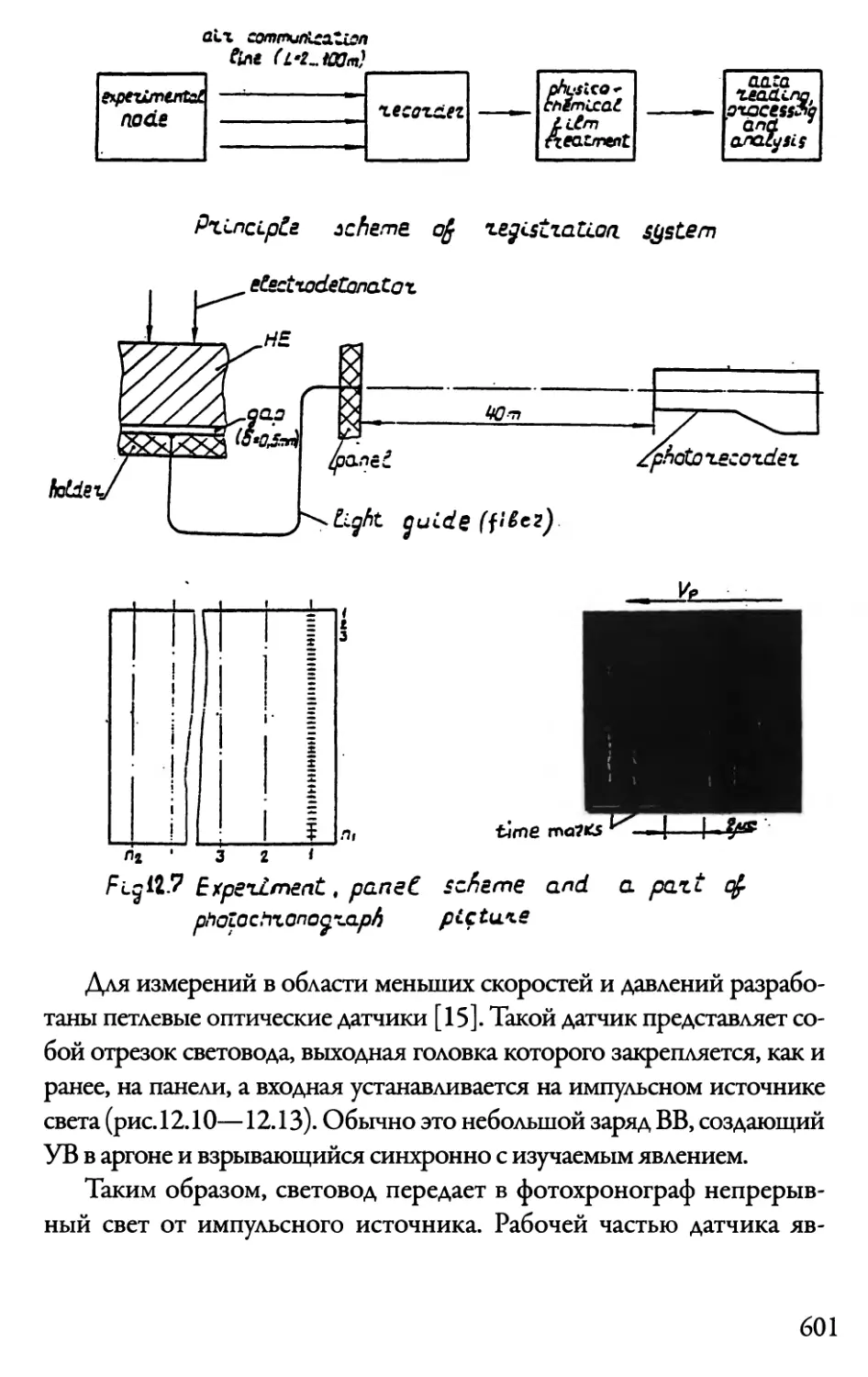
12.3. Измерения с помощью фотохронографа 589
12.3.1. Краткое описание фотохронографа 589
12.3.2. Режимы регистрации явления 591
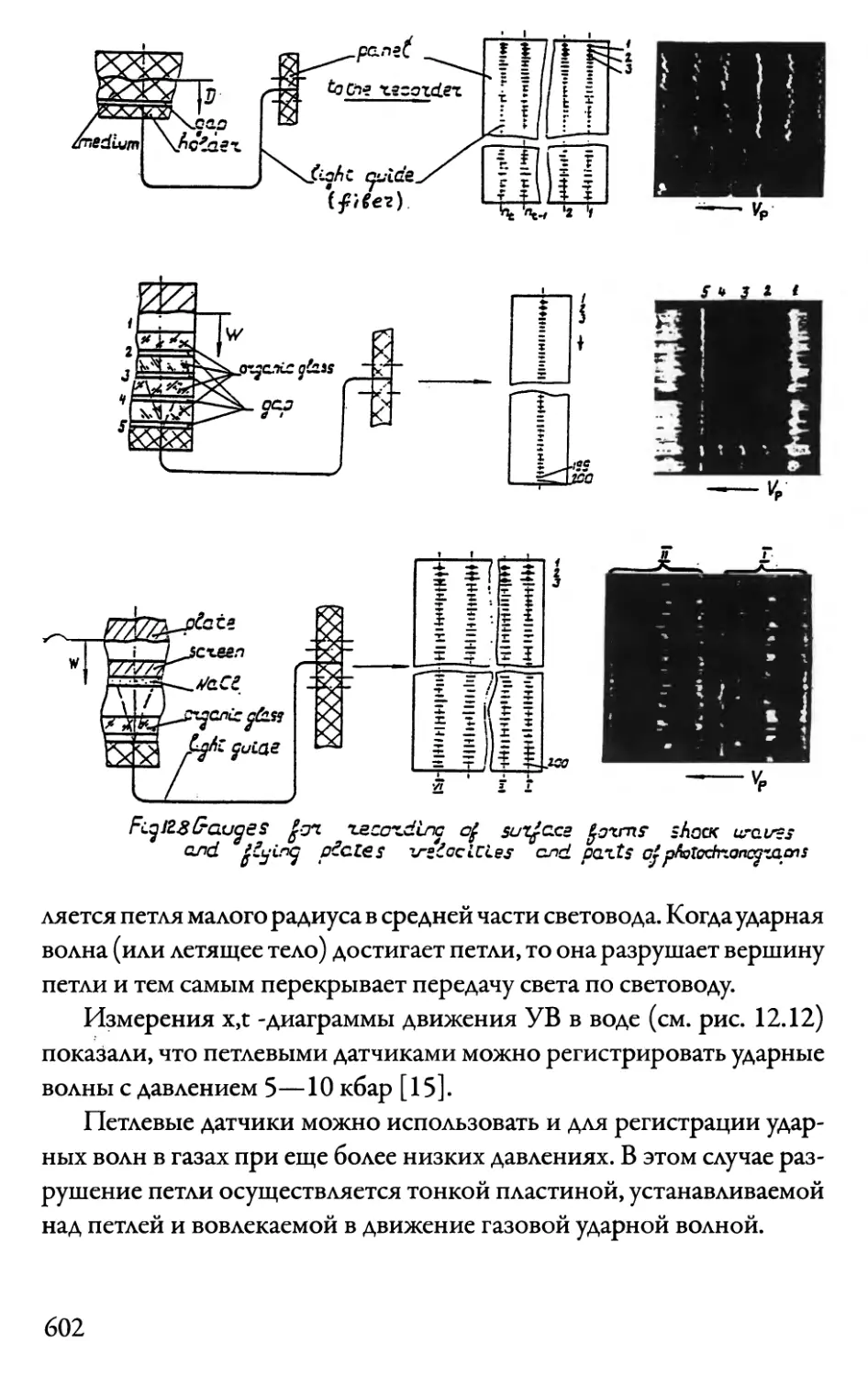
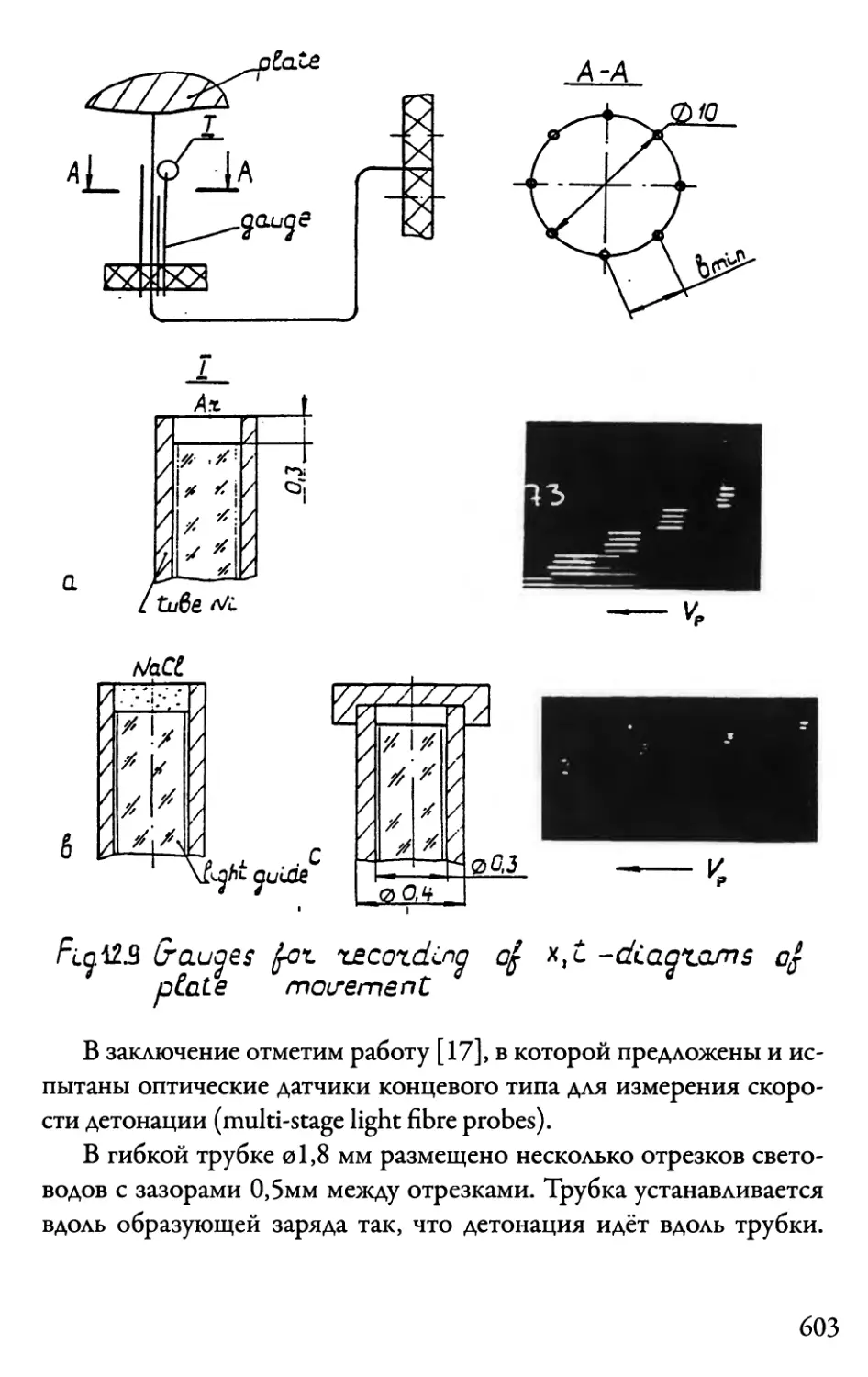
12.4. Многоканальные измерительные системы
с применением оптических световодов 595
12.5. Метод оптического рычага 605
12.6. Электроконтактная многоканальная методика
регистрации х, t - диаграмм 606
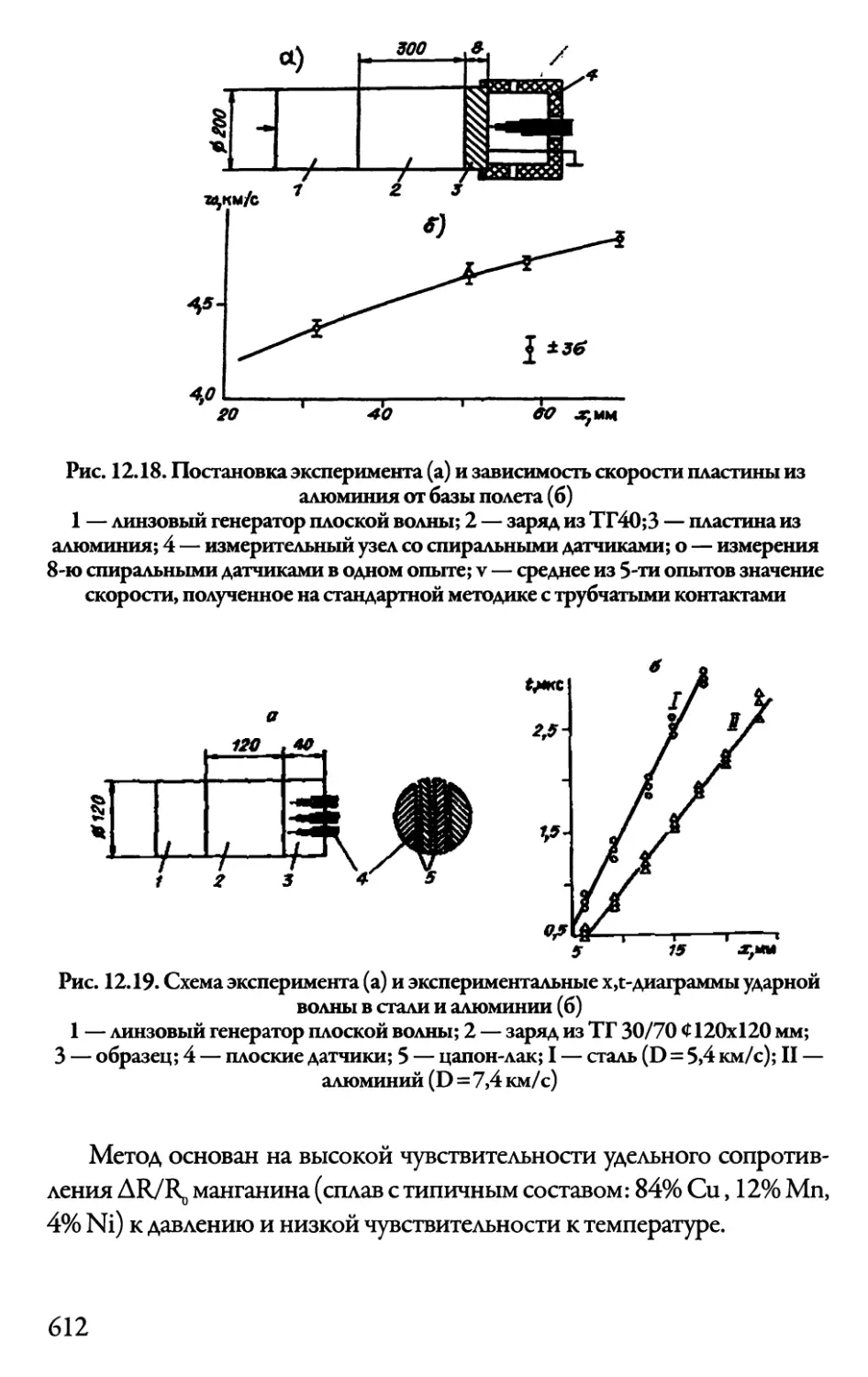
12.7. Измерение давления манганиновыми датчиками ...611
Литература к главе 12 614
Глава 13. Взрывные камеры 617
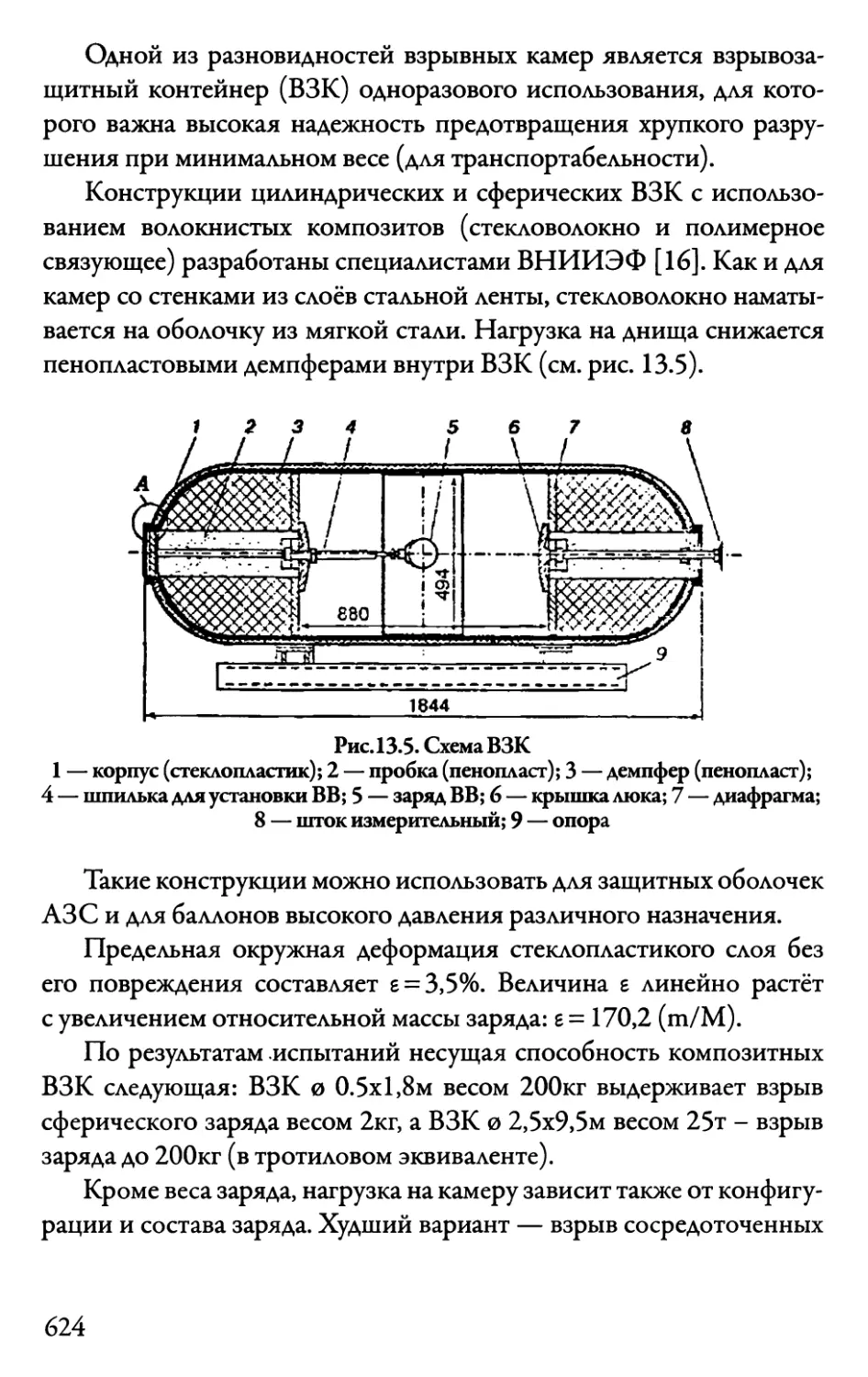
13.1. Общее описание камер 617
13.2. Способы снижения взрывных нагрузок
на стенки камеры 628
13.3. Расчеты импульсных нагрузок на стенки камеры... 630
13.4. Циркуляция ударных волн и
температурные поля в камере 635
13.5. Определение несущей способности
железобетонных взрывных камер 637
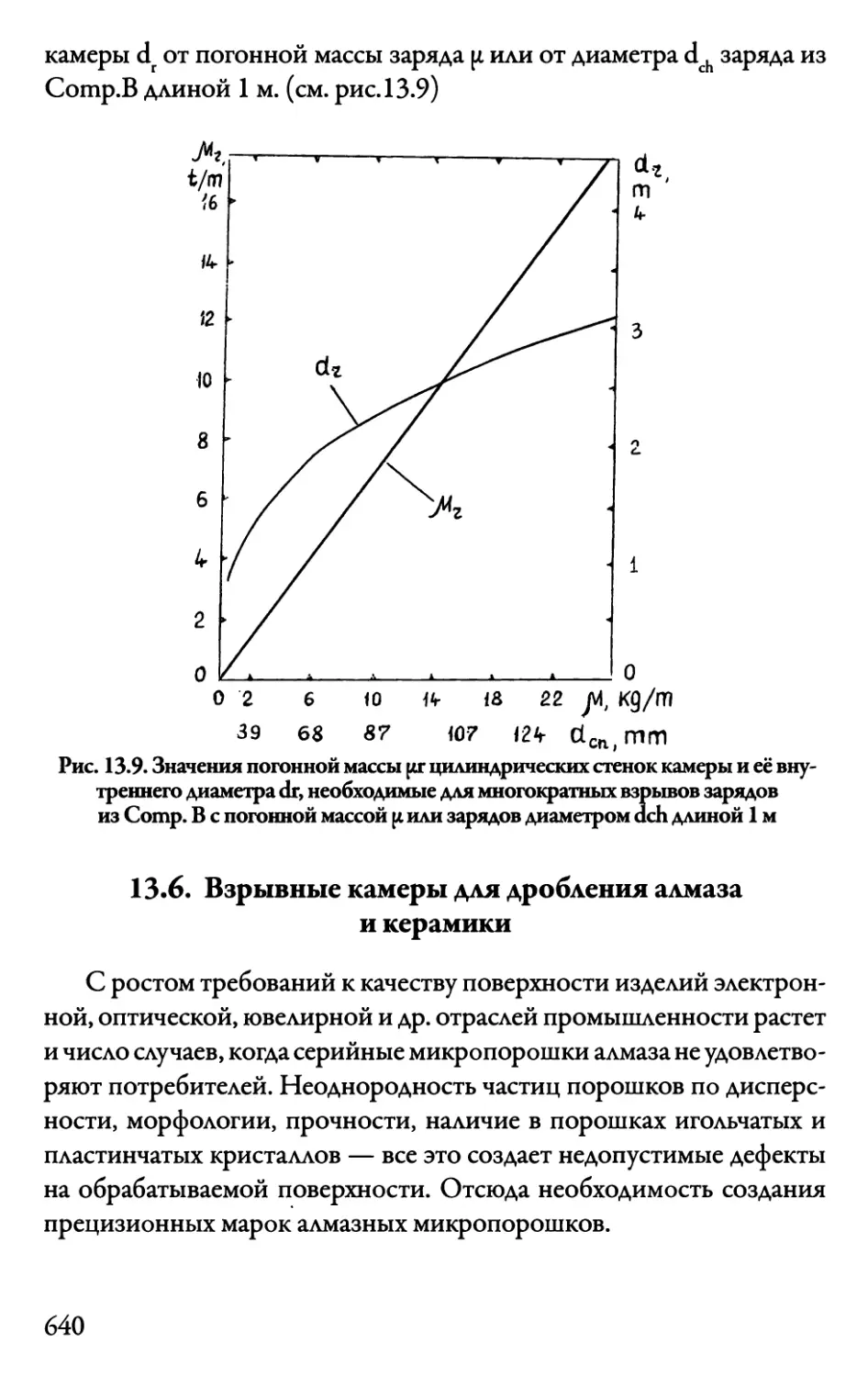
13.6. Взрывные камеры аая дробления алмаза
и керамики 640
Литература к главе 13 643
Глава 14. Алмаз 646
14.1. Алмаз: свойства, синтез, применение 646
14.2. Графитизация алмаза 652
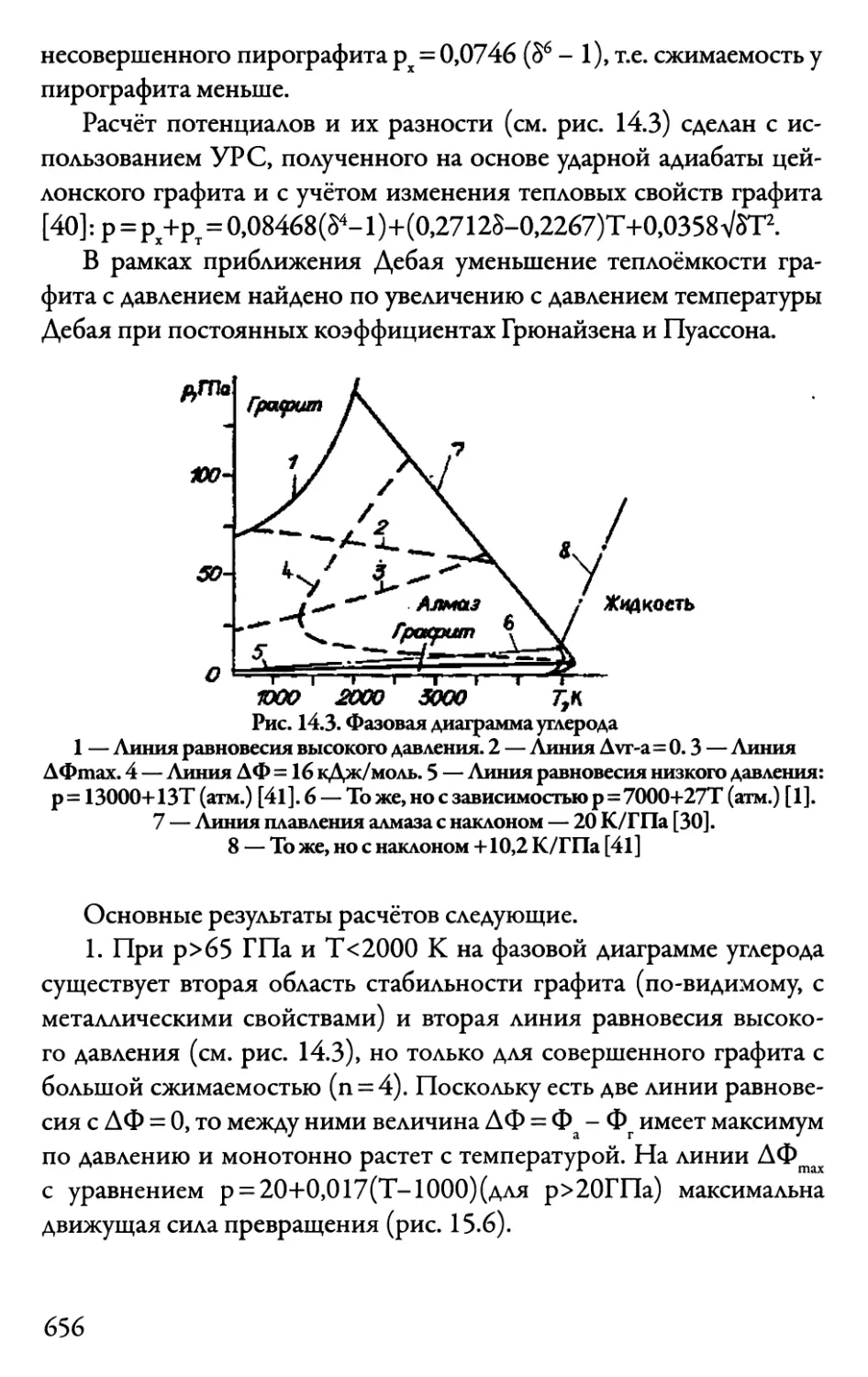
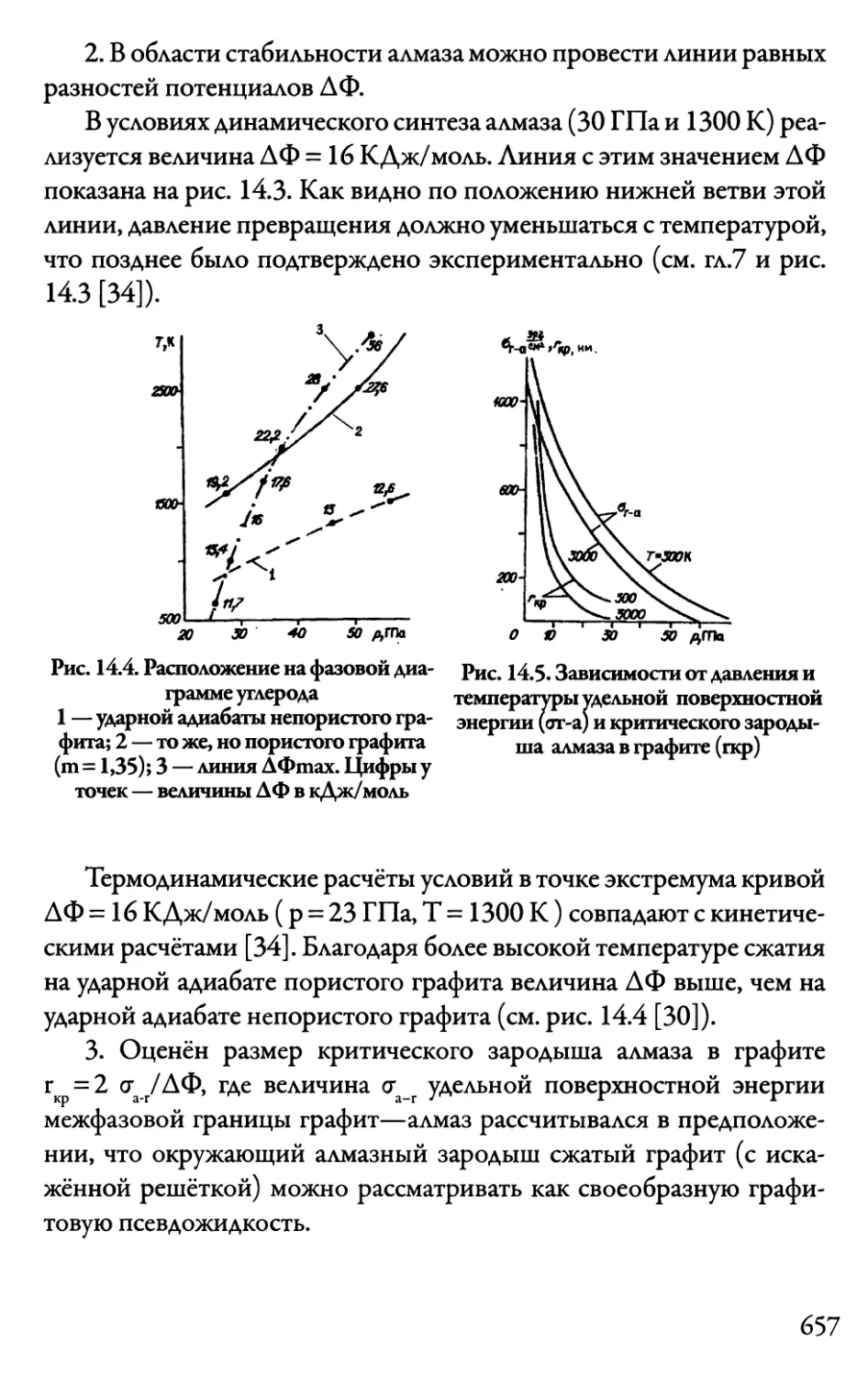
14.3. Превращение графит—алмаз 655
14.3.1. Термодинамика 655
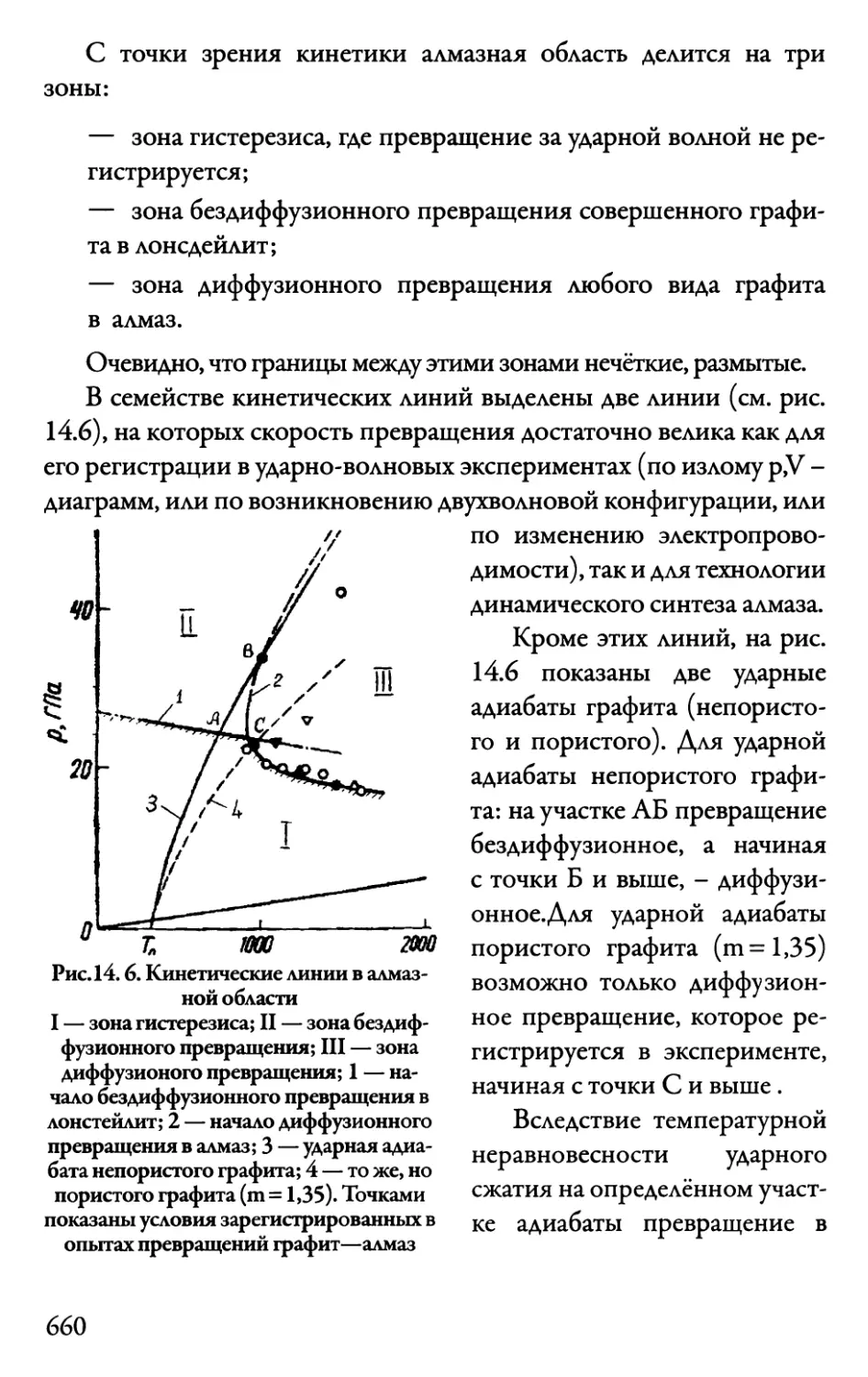
14.3.2. Кинетика 659
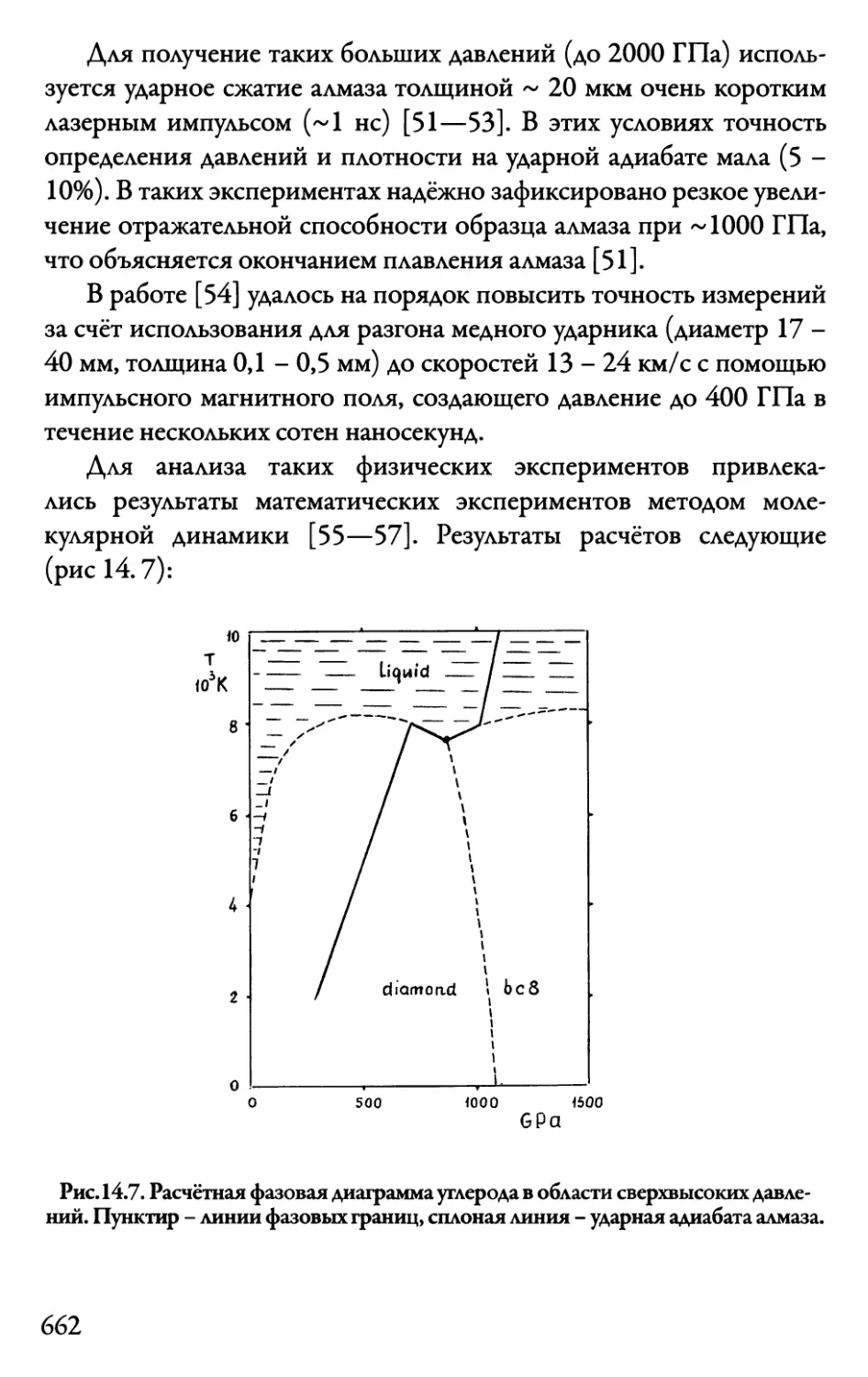
14.4. Плавление алмаза 661
Литература к главе 14 663
Глава 15. Угарно-волновой синтез алмаза 668
15.1. История открытия и разработки синтеза 668
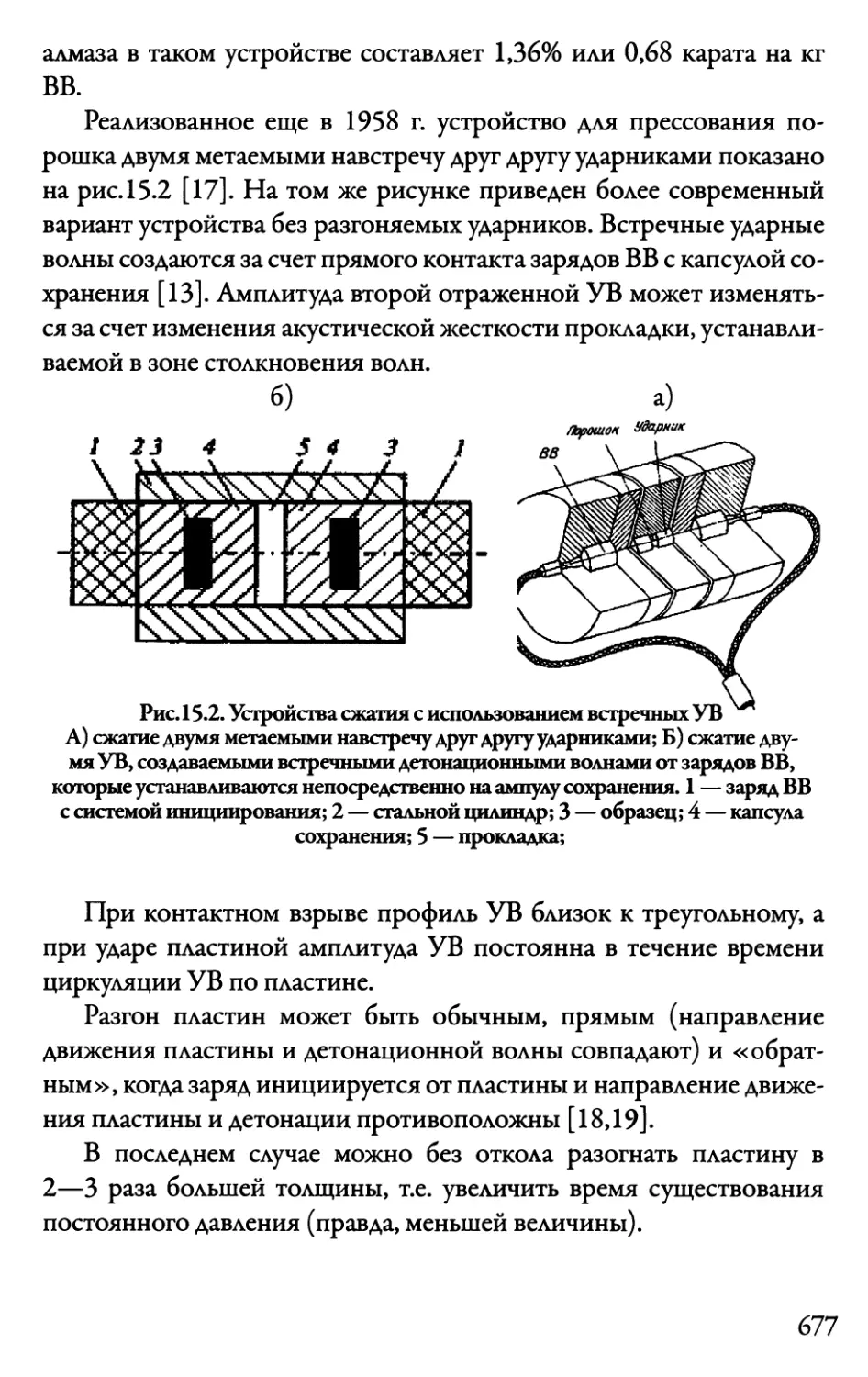
15.2. Особенности ударно-волнового синтеза алмаза 671
15.3. Метод плоского нагружения 676
9
15.4. Осесимметричные устройства 678
15.5. Сферические устройства 681
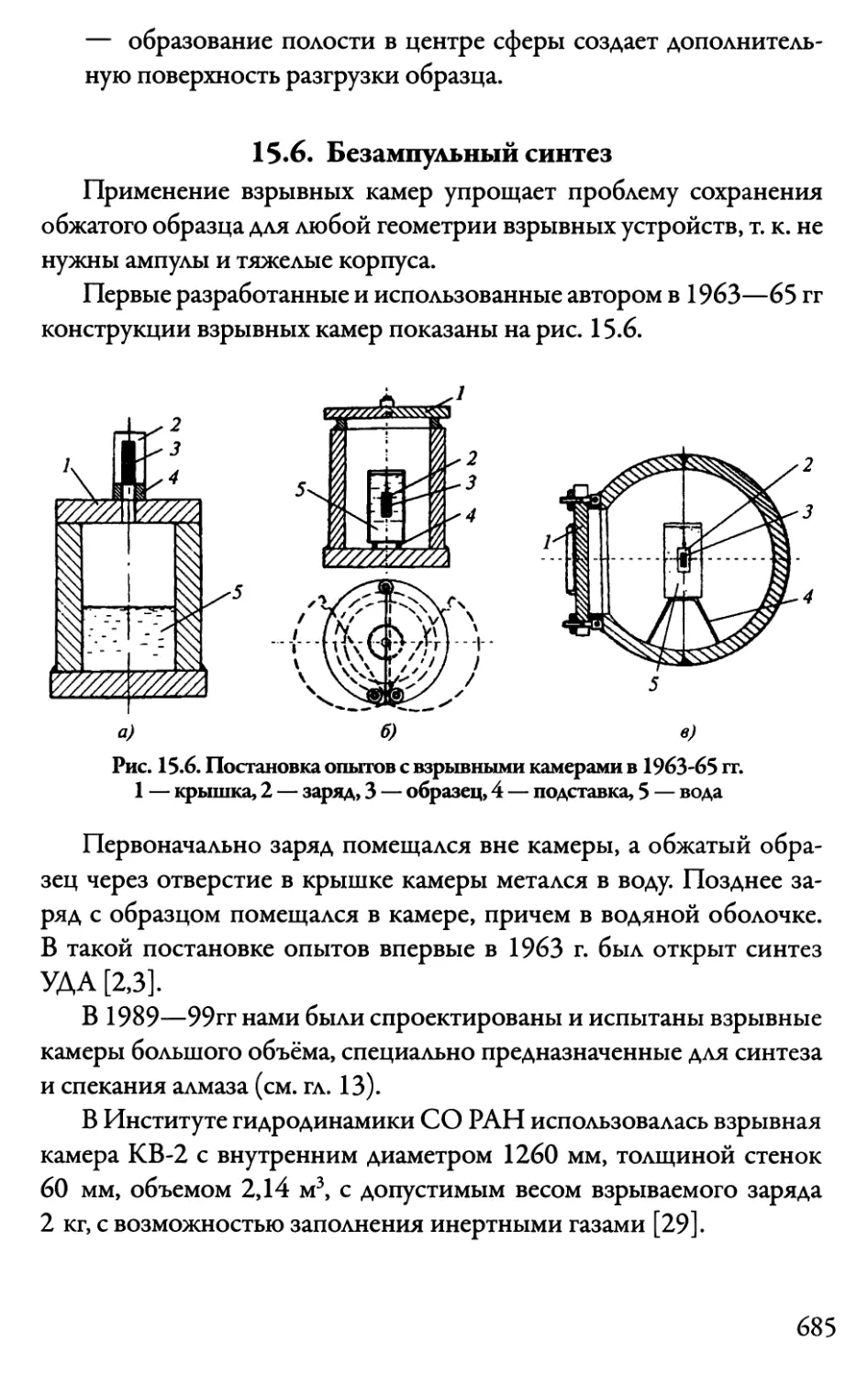
15.6. Безампульный синтез 685
15.7. Динамико-статическое сжатие 687
15.8. Свойства взрывных алмазов 689
Литература к главе 15 692
Глава 16. Детонационные наноалмазы 695
16.1. %ътрадисперсная среда.
Наноматериаловедение и нанотехнологии 695
16.2. История открытия синтеза
детонационных наноалмазов 705
16.3. Конденсация углерода в ПД. Влияние состава
ВВ и условий взрыва 708
16.4. Особенности синтеза УДА 713
16.4.1. Анализ представлений о синтезе УДА 713
16.4.2. Фазовая диаграмма наноуглерода 717
16.4.3. Образование УДА на изэнтропе ПД 720
16.5. Аморфизация наноуглерода 723
16.6. О коагуляции углеродных кластеров
в детонационной волне 724
16.7. Технология синтеза УДА 730
16.8. Свойства УДА 740
16.9. Модификация УДА 749
16.10. Применения УДА 753
16.11. Графитизация УДА 756
16.11.1. Кинетика графитизации 756
16.11.2. Термодинамическая оценка температуры
начала графитизации 760
16.11.3. Графитизация и окисление наноалмазов 762
16.12. О плавлении детонационных наноалмазов
в ударной волне 764
16.13. Эксперименты по спеканию наноалмазов 767
16.14. Образование УДА и параметры детонации 771
Литература к главе 16 772
ПРЕДИСЛОВИЕ
Взрыв интересует человечество с момента открытия пороха и его
использования в военном деле (~ 12 век). Причина тут в огромной
удельной энергии и мощности, реализуемой при взрыве. Благодаря
малому времени выделения энергии расчетная величина мощности
взрыва 1 кг взрывчатого вещества (ВВ) равна ~ 108 л. с.
В 20-м веке получены выдающиеся результаты в деле изучения
и использования взрыва. Созданы новые мощные взрывчатые составы
(ВС) и технологии изготовления из них зарядов, новые методы
использования различных взрывных явлений: ударных волн (УВ), детонации,
скоростного удара, кумуляции, динамической прочности, фазовых
превращений и т.п. Достигнуто более глубокое понимание физических
процессов, проходящих в этих явлениях.
Бурное развитие компьютерной техники (с увеличением скорости
счета до 1010 операций в секунду) позволило проводить достаточно
точное численное моделирование сложных взрывных процессов.
Венцом всех достижений можно считать осуществление в 40—50-х
годах 20 века атомного и термоядерного взрывов. Причем атомный
взрыв (за счет энергии цепной реакции деления атомов урана или
плутония) был использован для создания условий более мощного
термоядерного взрыва (за счет энергии реакции синтеза атомов гелия из
атомов тяжелых изотопов водорода).
В 1962 году в России проведен взрыв термоядерного заряда с
рекордной мощностью 50 мегатонн тротилового эквивалента (надеемся,
что этот рекорд никогда в будущем не будет превзойден).
Рекордно большие взрывы зарядов обычного химического ВВ
также впервые осуществлены в России. Например, в 1964 году двумя взры-
11
вами зарядов общей массой 28000 тонн в скалах проложено 36 км Аму-
Бухарского канала и выброшено 6 млн м3 скальных пород.
Таким образом, взрыв используется в трех направлениях: военном,
гражданском и в научных исследованиях. В этой книге в основном
изложены результаты научных исследований взрывных явлений.
Физика высоких давлений как наука о поведении вещества в
условиях сильных сжатий берет свое начало с уникальных экспериментов
П. Бриджмена в 1920—40-х годах.
Совершенствование техники эксперимента позволили ему
поднять давление статического сжатия до 100 кбар, а в 1980—90-х годах
с помощью алмазных наковален микроскопические навески вещества
удалось сжать до 5 Мбар (правда, только при низких температурах),
что достаточно для перевода многих изоляторов в металлическое
состояние.
Другой метод получения высоких динамических давлений с
помощью сжатия вещества ударными волнами начал интенсивно развиваться
с конца 1940-х годов в крупных лабораториях США и России в связи
с разработками новых ядерных боеприпасов.
Уже в конце 1950-х гг в России в лабораторных условиях с
помощью специального заряда ВВ уран был сжат давлением ~13 Мбар.
Использование подземных ядерных взрывов подняло эту величину
до 50 Мбар.
В результате в физике возникло новое направление — физика
взрыва.
При ударном сжатии конденсированных сред возникают
экстремально высокие концентрации энергии, превосходящие энергии связи
твердых тел, перестройка и возбуждение молекулярной и электронной
структур, фазовые превращения, высокоскоростная деформация и
разрушение материала.
Изучение ударноволнового сжатия имеет большое практическое
значение для разработки таких новых технологий, как: термоядерный
синтез, сварка, штамповка, упрочнение взрывом, синтез сверхтвердых
материалов, противометеоритная защита космических аппаратов,
создание новых боеприпасов. Развитие методов сохранения ударносжатых
12
образцов привело к созданию «взрывного» материаловедения,
динамических и детонационных технологий синтеза алмаза.
Наряду с решением прикладных проблем ударноволновые
исследования имеют и чисто научное значение, т. к. позволяют получать в
лабораторных условиях экстремально высокие давления, температры,
сжатия, скорости нагружения, недостижимые другими способами.
Получаемые результаты используются для описания
термодинамических состояний при высоких давлениях и температурах (составление
уравнений состояния), массопереноса и перемешивания на границах
сред, кинетики полиморфных превращений, для изучения
геофизических процессов в центре планет, понимания роли ударных процессов
в эволюции создания планет и формировании их поверхности.
Трудность экспериментирования с ударными волнами состоит
в краткости существования динамического давления (обычно не
более нескольких микросекунд), что требует использования специальной
скоростной оптики и электроники. Сейчас временное разрешение
измерительной аппаратуры составляет пикосекунды. Это позволяет
изучать тонкую структуру фронтов ударных и детонационных волн.
Начиная с 1960-х гг, наблюдалось резкое возрастание объема
исследований в таких слабо связанных друг с другом направлениях, как:
уравнения состояний, измерительные методики, детонационные
процессы, явления кумуляции, разработка новых мощных взрывчатых
составов и способов их инициирования, скоростной удар, фазовые
превращения и синтез сверхтвердых материалов, динамическая прочность
и откольные разрушения. Полученная за это время новая интересная
информация содержится в огромной массе книг, журнальных статей
и в трудах различных научных конференций.
Нами предпринята попытка кратко изложить в этой книге
результаты исследований в перечисленных направлениях. Более подробные
сведения по конкретным вопросам можно найти, используя указанную
библиографию (более 800 наименований). Большинство цитируемых
работ — работы русских ученых.
Кроме того, в книге приведены оригинальные результаты,
полученные автором, научные интересы которого в разное время
фокусировались в области методов измерений, систем инициирования, фазовых
превращений, взрывных технологий синтеза и спекания алмаза.
13
Динамические методы синтеза и спекания алмаза — одно из
наиболее интересных применений энергии взрыва. Поэтому этой тематике
посвящены последние две главы книги. /^,ля развития ряда нанотехно-
логий особый интерес представляют детонационные наноалмазы.
Книга может быть полезна как научный обзор, как справочное
и учебное пособие для студентов, аспирантов, инженеров, научных
работников.
Автор стремился сделать книгу интересной как можно более
широкому кругу специалистов — от газодинамика и взрывника до
материаловеда и технолога.
Автор благодарит свою супругу В. Н. Даниленко за большую
работу по подготовке книги к изданию.
Глава первая
ЭЛЕМЕНТЫ ГАЗОВОЙ ДИНАМИКИ
Теория ударных волн была создана еще в второй половине 19-го
столетия трудами Римана, Ренкина, Гюгонио.
Современный математический аппарат газовой динамики, физика
волновых и ударных процессов подробно изложены в книгах Ландау
и Лифшица [1], Зельдовича и Райзера [2], Куранта и Фридрихса [3],
Станюковича [4], Годунова [5], Баума, Станюковича и Шехтера [6],
Зельдовича и Компанейца [7], Зельдовича [8].
Нами приводятся только краткие сведения по простым и
ударным волнам.
1.1. Уравнения газовой динамики
Рассматривается адиабатическое движение идеальной жидкости,
т. е. без учета процессов диссипации энергии и теплообмена между
отдельными элементами жидкости и между жидкостью и средой.
Если в некоторый начальный момент энтропия всех частиц
жидкости (газа или другой среды) была одинакова и равна So, то в
адиабатическом движении жидкости энтропия остается постоянной
S = S0 =Const или dSIdt = 0
Такое движение называется изэнтропическим.
Уравнение изэнтропы: р = А рп.
Скорость звука на изэнтропе: с2 = (Эр/Эр)5.
Пример: волны разгрузки в ударносжатом веществе.
В случае, когда в любой заданной точке среды ее параметры
меняются со временем, движение среды называется неустановившимся.
15
Когда же параметры среды со временем не меняются, движение
называется установившимся. Установившееся движение
описывается уравнением Бернулли, которое аля одномерного изэнтропиче-
ского движения принимает вид:
U2/2 + i = i0=Const
io — удельное теплосодержание среды в покое.
В явлениях взрыва, детонации, ударного сжатия наблюдаются
в основном неустановившиеся течения. Во многих случаях
движения среды изменением ее плотности (т.е. сжимаемостью) можно
пренебречь, и о таком движении говорят как о движении
несжимаемой жидкости. Допущение о несжимаемости значительно упрощает
описание многих явлений.
Если движение среды происходит только в зависимости от одной
координаты х (или от радиуса г fi^ сферы), то такое движение
называется одномерным. Волна, распространяющаяся только в одном
направлении, называется простой или бегущей. Примером простой
волны является волна разрежения в однородно сжатой среде.
Для описания и анализа ударноволновых экспериментов часто
достаточно рассмотреть одномерное движение вещества, т. к.
большинство опытов имеет простую плоскую геометрию.
Уравнения газовой динамики выводятся из законов сохранения
массы, количества движения и энергии [1,2]. Для получения
замкнутой системы уравнений, определяющих при заданных граничных
и начальных условиях четыре параметра среды (плотность р или
удельный объем v= 1/р, скорость U, давление р и температуру Т),
к этим трем законам сохранения надо добавить четвертое
уравнение — уравнение состояния вида:
р = р(р,Т), p = p(p,S)wiuE = Е(р,р) (1.1)
где Е — удельная внутренняя энергия.
При этом предполагается, что бесконечно малый объем среды
все же содержит достаточно много молекул, и размеры этого
малого объема много больше длины свободного пробега молекул в этой
среде.
16
Уравнения газовой динамики можно записать в координатах
Эйлера или Лагранжа. По методу Эйлера параметры среды
определяются а^я каждой фиксированной точки в пространстве в любой
момент времени, т.е. как функция координат х, у, z и времени t.
По методу Лагранжа изменение параметров среды со временем
определяется а^я каждой частицы среды в т. н. субстанциональных
координатах, связанных с веществом. Этот метод удобен аая описания
одномерных движений.
В координатах Эйлера уравнения газовой динамики могут быть
записаны в векторной или в координатной форме (более удобной
для решения).
В случае изэнтропических одномерных движений, а также изэн-
тропических движений с осевой (цилиндрической) и центральной
(сферической) симметрией все параметры среды зависят от одной
пространственной координаты г и уравнения газовой динамики
принимают вид:
du/dt + udu/dr + l/p6p/dr = 0,
dp / dt + udp / дг + рди/ дг + Npu/ г = О
где: N = О аая плоских течений; N = 1 аая движений с
цилиндрической симметрией; N = 2 аая движений со сферической симметрией.
1.2. Характеристики уравнений газовой динамики
Простые волны. Автомодельность.
В общем случае в движущейся среде скорость распространения
слабых возмущений в каждой точке складывается из местной
скорости движения среды и местной скорости звука:
dx/dt = U + ac
dy/dt = V + ac (13)
dz/dt = W + ac
Решение этой системы дает некоторую гиперповерхность f (х, у,
z, t) = 0, определяющую фронт возмущения и называемую
характеристической поверхностью или характеристикой. Характеристики
17
описывают распространение в веществе слабых возмущений.
Возмущения могут распространяться в виде волн сжатия, в которых
давление в среде возрастает или волн разрежения, в которых
давление падает.
Для одномерных неустановившихся движений f (х, t) = 0, и
характеристики будут линиями в плоскости х, t, наклон которых dx/dt
в каждой точке равен местной скорости звука относительно
неподвижной системы координат.
Для возмущений, распространяющихся в положительном
(вправо) или отрицательном (влево) направлениях, будем иметь два
семейства характеристик — С+ и С , ^ая которых
(dx/dt)+=U+c; (dx/dt)_ = U-c (1.4)
Для простых изэнтропических волн на этих характеристиках
постоянны величины:
J+ =U + [2/(n-l)]c = Const , .
J_ = U-[2/(n-l)]c = Const
которые называются инвариантами Римана.
Таким образом, вдоль каждой характеристики
соответствующего семейства С+ или С_ остается постоянной скорость, а,
следовательно, и все остальные параметры среды. Каждое состояние в среде
будет перемещаться с постоянной, присущей этому состоянию,
скоростью U+c или U-c. Отсюда следует, что С+ и С характеристики
на плоскости х, t представляют собой прямые линии. С достаточной
степенью точности это справедливо и аая слабых ударных волн (с
малым изменением энтропии), что сильно упрощает решение многих
задач.
Для наглядного представления о характеристиках рассмотрим
следующие два случая [2].
А. Поршень выдвигается из закрытой трубы с газом.
При этом в газе возникает простая волна разрежения, для
которой характеристики С+ представляют собой расходящиеся прямые,
образованные на кривой х (t), описывающей движение поршня (см.
рис. 1.1).
18
с
III /
вЫ
Движение^
поршня
D,
л
it
/
II
//7/
/ / / /
/ Область покоя
/ 1
О х
Рис. 1.1. Семейство С+ характеристик для
простой волны разрежения, возникающей
при выдвижении поршня из трубы с газом.
Линия
поршня
Справа от
характеристики х = cQ t расположена
область I неподвижного
газа, в которой все
характеристики —
параллельные прямые с
наклоном dx/dt = c0. В момент
t = 0 поршень начинает
ускоряться на участке
ОВ от нулевой скорости
по закону w (t) до
некоторой постоянной скорости
U в точке В. Закон
движения поршня х (t) при этом
превращается в прямую
x(t) = -Ut.
Начальное
возмущение от поршня — простая
волна, бегущая вправо
со скоростью звука вдоль
С+ характеристики ОА:
x = c0t.
Рис. 1.2. Семейство С+ характеристик
для центральной волны разрежения.
На границе с поршнем
скорость газа совпадает
с отрицательной
скоростью поршня w (t). Поэтому скорость звука, а также давление и
плотность газа будут меньше начальных.
Поскольку поршень только ускоряется, характеристики С+
только расходятся, т.к. их наклон (d x/dt)+ = u + c = cQ + u(n + l)/2 все
время уменьшается.
Это область II между характеристиками ОА и ВД. Левее линии
ОД в области III поршень движется с постоянной скоростью,
скорость газа на линии поршня одинакова, и все газодинамические
величины постоянны: и = -U; с = с0 - и (п - 1)/2. В области III все
характеристики С+ одинаковы с величиной J+ = и+(2/п — 1) с
19
На рис. 1.1 сечение FF аля данного момента времени t
представляет собой область, охваченную волной разрежения. Очевидно,
со временем эта область будет расширяться. Предположим теперь,
что начальное ускорение поршня очень велико, и поршень
практически мгновенно получает постоянную скорость w = — U. Тогда
участок ОВ, где скорость поршня переменна, исчезает, в пределе точки
О и В (откуда выходят С+ характеристики ОА и ВД) совпадают. Обе
характеристики выходят из одной точки х = 0, t = 0. И вообще все
характеристики, заполняющие область II переменного течения, также
выходят из одной точки О в виде веера.
Таким образом, когда поршень сразу начинает двигаться с
постоянной скоростью, картина на плоскости х, t приобретает вид,
показанный на рис. 1.2.
Из центральной точки О выходят все характерные линии: линия
«головы» волны ОА, линия «хвоста» волны ОД и линия поршня.
Такая волна называется центрированной простой волной.
Для нее уравнение характеристик имеет вид:
x=[u+c(u)]t, где \u\ = [2/(n+l)](cQ-x/t) (1.6)
Как видно, скорость среды в центральной волне разрежения
линейно зависит от х. " Голова" волны, где и = 0, движется вдоль
линии x = ct, а "хвост" волны, где u =— U, движется вдоль линии
x=(Cl-u)t=[(c0-(n+l)/2u)]t
Таким образом, простая волна всегда примыкает к области покоя
или стационарного течения, а скорость ее фронта — это скорость
перемещения границы между двумя этими областями.
Из уравнений газодинамики и интегралов Римана в лагранжевых
координатах следуют выражения а^я расчета изменений внутренней
энергии и удельного объема вещества в простых волнах:
р
du
р
du)
*-*+M.fJ* "-и-М£
Ро v ' Pq
dp
(1.7)
,dP)
Несколько слов об автомодельности движения.
Решение для скорости среды в центрированной волне имеет вид:
20
М=4т(со-7] (h8)
П + 1{ t)
Как видно, газодинамические величины, описывающие
движение, зависят от координаты х и времени t не порознь, а только в
комбинации x/t.
Что касается областей постоянного течения I и III на рис. 1.1 и 1.2,
то они ограничены прямыми x/t = c (область I), x/t = w, x/t = w + c
(область III). Распределения (профили) всех величин по оси х не
меняют своей формы со временем, оставаясь подобными самим себе
и изменяясь только за счет изменения масштабов величин (в данном
случае масштаба длины с t или w t). Такие движения называются
автомодельными.
Для центрированной волны разрежения масштабы
газодинамических величин остаются неизменными: с течением времени
профили u (х, t) и с (х, t самоподобно растягиваются только по оси абсцисс,
но не меняются по оси ординат.
Физическую причину автомодельности можно объяснить, исходя
из размерности. Уравнения газовой динамики и термодинамики не
содержат никаких характерных длин и времен (длина свободного пробега
молекулы в газе характеризует лишь микропроцессы вязкости и
теплопроводности, но не макродвижение). В описание газодинамических
движений входит только один размерный параметр вещества —
скорость звука. Таким образом, если начальные и граничные условия не
содержат характерных длин и времен, движение может зависеть только
от комбинации x/t, имеющей размерность скорости.
В задаче о центрированной волне разрежения в начальные и
граничные условия входят только скорости с и w, плотность р, давление
р, но не длина и время.
Автомодельные движения имеют большое значение для
газодинамики, т. к. на них основываются динамические методы изучения
уравнений состояния. Уменьшается на единицу число независимых
переменных (вместо х и t — x/t), и одномерные течения
описываются уравнениями не в частных производных, а обыкновенными
дифференциальными уравнениями, что математически очень упрощает
решение задач.
21
Рис. 1.4. Деформация
Рис. 1.3. Семейство С характеристик для волны сжатия
простой волны сжатия, возникающей при
вдвижении поршня в трубу с газом.
Кроме того, автомодельное движение всегда изэнтропично.
В сложных задачах газодинамики, где точное решение
неизвестно, часто удается найти предельное решение, заранее предположив,
что оно автомодельно.
Б. Теперь рассмотрим случай, когда поршень ускоренно
вдвигается в трубу с газом (см. рис. 1.3).
При каждом элементарном ускорении от поршня пойдут волны
сжатия, причем каждая последующая волна будет распространяться
по газу, уплотненному предыдущей волной. Поэтому амплитуда и
скорость волны будут непрерывно увеличиваться, значит, будет расти и
наклон С+ характеристик к оси ординат. Получается, что «хвост» волны
движется быстрее, чем «голова» волны: [(n+1)/2] w+cQ > cQ
Сходящийся пучок характеристик на рис. 1.3 в конце концов
приводит к пересечению характеристик, что физически
бессмысленно, т. к. в одной точке не может быть два различных состояния газа.
Следовательно, в этом случае непрерывного решения не
существует. Эта трудность вызвала появление разрывных решений уравнений
газовой динамики, что привело к созданию теории ударных волн.
На рис. 1.3 точка С пересечения характеристик может
рассматриваться как место возникновения разрыва — ударной волны.
Таким образом, центрированная волна сжатия невозможна,
поскольку она неизбежно переходит в ударную волну.
Физически это очевидно: в более сжатом газе больше скорость
звука и массовая скорость, направленная в сторону распростра-
22
нения звука. Волна сжатия не может распространяться, не
деформируясь: гребни волны, где (u + c)max будут двигаться быстрее
других точек, будут выдвигаться вперед, становиться все круче
(см. рис. 1.4).
Наконец, фронт станет вертикальным — это момент
возникновения ударной волны.
Образование скачков, поверхностей разрывов величин р, р, Т
означает изменение энтропии. Для ударных волн уже нельзя
пренебрегать теплопроводностью среды, поскольку даже при малом
коэффициенте теплопроводности \ неограниченное возрастание
градиента температуры dT/dx приводит к неограниченному росту
потока энергии^. dT/dx.
Таким образом, возникновение разрывов приводит к
повышению энтропии, т. е. к диссипации энергии, а это обуславливает
сильное затухание волны.
1.3. Элементарная теория ударных волн
Уддрноволновые процессы играют ключевую роль в
механическом воздействии взрыва на различные материалы, а также в
механизме создания и распространения детонационных волн.
Фронт ударной волны — это поверхность, на которой
претерпевают разрыв ряд параметров, характеризующих состояние и
движение среды.
Скорость фронта направлена по нормали к поверхности. Разрыв
можно рассматривать как предельный случай очень больших
градиентов газодинамических величин, когда толщина переходного слоя,
где происходит изменение этих величин, стремится к нулю.
Для идеальной среды, не имеющей вязкости и
теплопроводности (т. е. без учета молекулярной структуры среды) нет ограничений
в возможности существования сколь угодно тонких переходных
слоев, в пределе сводящихся к разрыву.
При учете вязкости и теплопроводности газа появляется
масштаб длины — длина свободного пробега молекул 1, и как
следствие — конечная ширина разрыва, определяемая этим масштабом
(см. рис. 1.5).
23
р2 1
I p
Волна
разряжения (разгрузки)
Фронт
ударной волны
Невозмущенное вещество
а б
Рис. 1.5. Фронт ударной волны в идеальной (а) и реальной (б) ударной волне.
На основании молекулярно-кинетических выражений аая
коэффициентов вязкости и теплопроводности Зельдович оценил ширину
фронта ударной волны d ~ 1 р/ Ар ~ 1 cQ/u, где с0 — объёмная скорость звука.
Эти оценки показывают, что ширина фронта того же порядка,
что и длина свободного пробега молекул в газе.
Еще одна причина конечной ширины фронта заключается в том,
что изменение состояния газа в ударной волне происходит
быстрее, чем увеличение теплоемкости до ее равновесного значения.
Относительно медленный рост теплоемкости связан с медленным
возбуждением колебательного движения молекул, а также с
медленными процессами диссоциации частиц и возбуждением электронов.
Поэтому температура на фронте меняется от более
высокого неравновесного значения (соответствующего неравновесно
низкой теплоемкости только поступательной и вращательной степеней
свободы, возбуждающихся практически мгновенно) до более низкой
равновесной величины.
При этом давление на фронте плавно увеличивается на
ширине порядка D t, где t — время возбуждения или время достижения
равновесной теплоемкости, D — скорость ударной волны.
Таким образом, тонкая структура фронта реальной ударной
волны состоит из двух частей: сначала изменение параметров быстрое,
а затем относительно медленное (см. рис. 1.5).
Дифференциальные уравнения газовой динамики содержат
четыре закона сохранения, но в разрыве выполняются только три из них,
кроме закона сохранения энтропии. На разрыве энтропия всегда
возрастает. Причем величина возрастания энтропии при ударном
24
сжатии определяется только тремя законами сохранения и не
зависит от механизмов диссипации энергии, которые определяют только
ширину разрыва или толщину фронта ударной волны.
Законы сохранения, положенные в основу уравнений газодинамики
не требуют обязательного сохранения непрерывности параметров
среды и не содержат никаких предположений о свойствах вещества.
Соотношения между параметрами среды по обе стороны
ударной волны наиболее просто выводятся на основе законов
сохранения а^я плоской ударной волны в цилиндре единичного сечения.
Закон сохранения массы: р0 (D - uQ) = р{ (D - и).
Закон сохранения импульса и количества движения за
единичное время: р2 - р0 = р0 (D - u0) (u, - uQ).
( 2 2\
Закон сохранения энергии: -^—-— ° ° = (Е.ЕЛ +
(D-u0)p0
и{ и0
2 2
Здесь индекс 1 относится к параметрам за фронтом ударной
волны, а О — перед фронтом; u{i uQ — массовая скорость, E{i EQ —
внутренняя энергия.
Из законов сохранения получаются выражения для массовой
и волновой скоростей:
^-Uo^fo-PoXVo-v,); D-u0 = v0>/(p1-Po)/(Vo-v1)
Практически всегда р = 0, и = 0, и тогда законы сохранения
имеют вид:
p=p0Dul
E-E0 = 05pbv
Последнее уравнение называется уравнением Гюгонио.
Для среды, подчиняющейся политропическому закону
pvn = Const, считая nQ = n1 = n = Const (для не слишком сильных
ударных волн):
Е0 = М/(п-1); E, = (p1y1)/(n-l) (МО)
25
После преобразований (1.10) получим выражения,
связывающие р и v перед и после ударной волны:
Р\ =(л + 1)р|-(||-1)Ро Ру =У0^(/2 + 1)р1-(/2-1)Ро ,И1,
Ро (if + l)p0-(i-l)Pi Pq v, (/i + l)p0-(/i-l)Pl
Эти уравнения называются ударной адиабатой или адиабатой
Гюгонио.
Обычно ударную адиабату графически изображают и
анализируют в р — v,p — uhD — и координатах.
Таким образом, задаваясь значением какого-либо одного из
параметров, можно определить все остальные параметры.
Для сильных ударных волн в газах (р{ > > р0) соотношения между
параметрами имеют особенно простой вид:
Ul = 2/(n + l)D
Pl = 2/(n+l)p0D2
Pl/p0=(n+l)/(n-l) (1.12)
T/T0 = p/p0[(n-l)/(n+l)]
Из (1.12) видно, что плотность на фронте ударной волны
стремится к конечному пределу h=(n+l)/(n — 1), зависящему только
от величины п, т. е. в конечном итоге от температуры на фронте.
Энтропия ударносжатой среды возрастает (dS > 0) с ростом
ударного давления (S -> оо при р -> ©о). Температура ударного сжатия
растет пропорционально давлению.
Сравним в плоскости р, v относительное положение изотермы,
изэнтропы и ударной адиабаты (см. рис. 1.6).
Изотерма и изэнтропа дают последовательность состояний,
которые могут быть пройдены непрерывно, а ударная адиабата дает все
состояния, в которое может переходить вещество из данного
начального состояния в результате ударного сжатия, фарная адиабата —
это набор точек, определяемых начальным состоянием вещества
и распространением по нему одной стационарной ударной волны.
Скорость ударной волны по невозмущенному веществу
(D = vQ (p/Av)05 графически на р, v — диаграмме ударной волны (см.
26
рис. 1.6) определяется наклоном прямой АВ, проведенной из
начального в конечное состояние. Чем выше давление, тем больше
наклон прямой и тем больше скорость ударной волны.
Поскольку в пределе а^я слабой ударной волны S -> 0, a D -> с0
(с0 — скорость звука в невозмущенном веществе), то в начальной
точке А ударная адиабата касается адиабаты Пуассона, проходящей
через эту точку. Вообще же наклон прямой АВ всегда больше
касательной в точке А, т. е. всегда D > cQ.
фарная адиабата всегда проходит выше обычной адиабаты (из-
энтропы), поскольку рост энтропии при ударном сжатии означает
и рост давления при равном конечном объёме.
Рассмотрим энергию, необходимую аая сжатия вещества из
начального состояния до заданного конечного (от объема v0 до объема v2).
Для трех сравниваемых процессов можно записать:
дР
изотерма-AE = I%TdST -\\pdVT = \\T^-dVT-\\pdV,
изэнтропа — АЕ = J^ pdVs
ударная адиабата — ДЕ = О,5p(V0 -Vx)
дТ
(1-13)
Графически на рис. 1.6 увеличение внутренней энергии при
ударном сжатии равно площади треугольника ABC. За фронтом ударной
волны вещество приобретает удельную (на 1 г) кинетическую
энергию, равную и2/2 =1/2 (р2 -p0)(v0 -v2) (1-14)
Эта энергия численно равна площади треугольника ABC.
Площадь прямоугольника
ABCG — это полная
энергия вещества (сумма
внутренней и кинетической),
которая аая сильной
ударной волны (р2 >> р0)
поровну делится между
внутренней и кинетической
с a v энергиями (сравн. (1.13)
р л г , и (1.14)).
Рис. 1.6. р, v — диаграммы. 1 — ударная
адиабата, 2 — изэнтропа, 3 — изотерма
1 в
Ек
v!
\:
3
1
G
Vo
27
Для изэнтропы энергия определяется площадью АДС под изэн-
тропой АД. Для изотермы энергия меньше площади АЕС под
изотермой на величину отрицательного первого члена в (1.13).
Таким образом при заданном сжатии энергия и температура
вещества увеличиваются при переходе от изотермы к изэнтропе и
далее к ударной адиабате.
Для подавляющего большинства исследованных веществ
экспериментально D — и зависимости могут быть аппроксимированы
прямой линией
D = A + Bu (1.15)
где А и В — эмпирические коэффициенты, определяемые аая
каждого вещества в результате обработки экспериментов. Причем, их
величины выше определённого давления могут изменяться в связи с
кристаллической или электронной перестройкой.
Значения А и В ^^я многих веществ приведены в табл. 2.3 гл.2.
Для грубых оценок:
— A~c(npnu = OD = c);
— из уравнения изэнтропы (^ая слабых УВ) р = А(5П - 1)
следует, что величина В зависит от показателя п (или от сжимаемости):
В = И(п+1).
Например, для твердого алмаза В = 1, а а^я мягкого полиэтилена
В = 2,35. Методы определения р, и — диаграмм см. раздел 2.5.
Способ представления ударной адиабаты в D — и координатах
обычно используется для решения задач о распаде разрыва [2, 9].
При решении таких задач рассматривается комбинация ударных
волн и центрированных волн разрежения, распространяющихся
от места разрыва параметров и разделенных областью с
постоянными параметрами Здесь возможны две типичные ситуации:
а) ударные волны распространяются б обе стороны от разрыва
(случаи соударения пластин и отражения ударной волны от
границы с более жестким веществом) и
б) в одну сторону движется ударная волна, а в другую — простая
волна разрежения (отражение волны от границы с менее
жесткой средой).
28
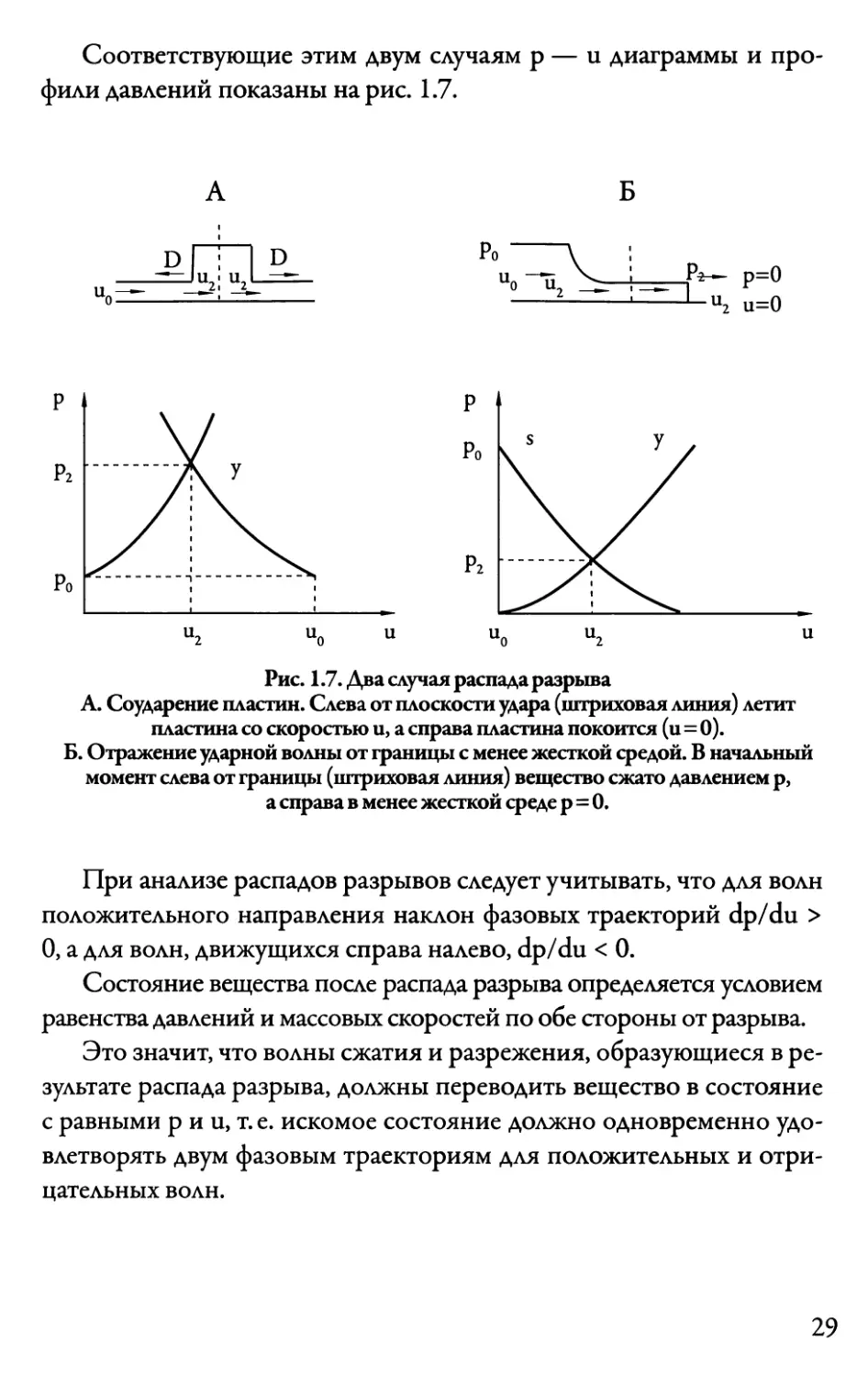
Соответствующие этим двум случаям р — и диаграммы и
профили давлений показаны на рис. 1.7.
D
D
Ро
р=0
и=0
Рис. 1.7. Два случая распада разрыва
А. Соударение пластин. Слева от плоскости удара (штриховая линия) летит
пластина со скоростью и, а справа пластина покоится (и=0).
Б. Отражение ударной волны от границы с менее жесткой средой. В начальный
момент слева от границы (штриховая линия) вещество сжато давлением р,
а справа в менее жесткой среде р=0.
При анализе распадов разрывов следует учитывать, что а^я волн
положительного направления наклон фазовых траекторий dp/du >
0, а для волн, движущихся справа налево, dp/du < 0.
Состояние вещества после распада разрыва определяется условием
равенства давлений и массовых скоростей по обе стороны от разрыва.
Это значит, что волны сжатия и разрежения, образующиеся в
результате распада разрыва, должны переводить вещество в состояние
с равными р и и, т. е. искомое состояние должно одновременно
удовлетворять двум фазовым траекториям а^я положительных и
отрицательных волн.
29
Таким образом, величины р и и непрерывны на поверхности
раздела и на границах, поэтому аля анализа распадов чаще всего
используют х, t и р, и — диаграммы.
Укажем следующие основные особенности, характерные а^я
ударных волн:
1. Скорость ударной волны всегда больше скорости звука в
невозмущенной среде, но меньше скорости звука в ударносжатой
среде. Поэтому любые возмущения за фронтом ударной волны
(например, волны разрежения) всегда догоняют фронт.
2. На фронте ударной волны параметры среды меняются скачком.
3. фарные волны сопровождаются перемещением среды в
направлении движения ударной волны.
4. Скорость ударной волны зависит от давления на ее фронте
(увеличивается с давлением).
5. Энтропия среды, сжатой ударной волной, возрастает. Поэтому
в сравнении с другими процессами сжатия температура ударного
сжатия наибольшая.
6. фарная волна не имеет периодического характера, а
распространяется в виде одиночного скачка уплотнения.
7. Время существования давления ударного сжатия конечно
(обычно не более нескольких микросекунд), давление всегда
снимается волнами разгрузки.
8. При конечном увеличении давления однократного ударного
сжатия максимально достигаемая величина сжатия
(уменьшение объема) всегда конечна и аая каждого вещества своя, что
объясняется ростом температуры с давлением в УВ. При
определённом давлении тепловое расширение начинает превышать
сжатие.
9. Энергия ударной волны расходуется поровну на создание
кинетической энергии движения ударносжатой среды и на
увеличение ее внутренней энергии.
10. В твердом веществе ударная волна с амплитудой больше
предела текучести вещества создает на фронте одноосное сжатие
с быстрой сдвиговой деформацией, а за фронтом вещество сжато
гидростатически.
30
До сих пор речь шла о сжатии одной ударной волной. Посмотрим,
какменяется состояние веществапри последовательном сжатии
несколькими ударными волнами.
Пусть конечное давление постоянно. Разбивая адиабатическое
сжатие на любое число этапов, мы всегда будем получать одну и ту же
плотность, если задан только один параметр — конечное давление.
В отличие от адиабаты Пуассона адиабата Гюгонио зависит от двух
параметров (v и р). Поэтому сжатием несколькими ударными
волнами нельзя получить такое же конечное состояние, как при
сжатии одной ударной волной. Например, одноатомный газ одной
сильной ударной волной можно сжать максимум в четыре раза (/^
n = 5/3h = (n+ 1)/(п — 1)= 4), а если пропустить по газу одну за
другой две сильные волны с тем же конечным давлением, то газ
сожмется уже в 16 раз (или в общем случае в [(п + 1)/(п — 1)] раз).
р — v — диаграмма на рис. 1.8 иллюстрирует различные способы
сжатия вещества. Если сжимать вещество многими слабыми волнами
(каждую такую волну можно считать простой волной сжатия с S=const),
то получим такой же объем, как и при адиабатическом сжатии.
Отметим, что вещество в основном нагревается в первой
ударной волне. Прирост температуры во второй и последующих
волнах незначителен (поскольку уменьшается сжимаемость вещества,
сжатого первой волной).
Рассмотрим различия в ударном сжатии газов и твердых тел.
1. Газы
1. Давление в газе носит тепловой характер и всегда
пропорционально температуре: р = n к Т.
2. Газы легко сжимаются. Предельное сжатие достигается при
давлении за фронтом порядка 0,1 кбар. Если принять за меру
интенсивности ударной волны степень её приближения к давлению
предельного сжатия, аая газа волна с давлением 0,1 кбар является
сильной волной.
3. Её скорость значительно больше скорости звука в исходном
газе (D >> с0), а массовая скорость газа за фронтом сильной волны
близка к скорости самой волны (u -> D).
31
4. Благодаря большой
сжимаемости, газ
легко нагревается сильной
ударной волной до
температур в десятки тысяч
градусов. Например, для
воздуха при 3 кбар Т=
30000°Кир/р0=9,5[6].
Рис. 1.8. Однократное, многократное ударное, адиабатическое сжатия до
одинакового давления р Н, Н, Н — ударные адиабаты, для которых начальными
являются точки А, В, С. П — адиабата Пуассона.
2. Твёрдые тела
Природа возникновения давления при ударном сжатии твердых
тел двояка. Это упругая (или «холодная») составляющая давления,
обусловленная преодолением межатомных сил отталкивания,
которые быстро возрастают при сближении атомов и никак не связаны
с температурой.
Нагревание в ударной волне приводит к появлению тепловой
составляющей давления, обусловленного тепловым движением атомов
и электронов. В пределе с ростом амплитуды ударной волны
тепловое давление возрастает настолько, что твёрдое вещество ведёт себя
как газ, а упругим давлением можно пренебречь. Однако а^я
давлений в миллионы кбар упругая и тепловая составляющие
сравнимы между собой. А при давлениях в сотни кбар тепловое давление
(и температура сжатия) мало и преобладает упругое давление.
Например, железо при давлении в ударной волне, равном 200 кбар,
сжимается на 10%, а тепловое давление составляет только 3—4% от
всего давления. Соответственно пренебрежимо мала температура сжатия.
Правда, температура ударного сжатия различных твёрдых тел
сильно различается в зависимости от их сжимаемости. Например,
ударная волна с давлением в 1 Мбар нагревает монокристалл
алмаза всего на 500 К, а свинец — на 7000 К. Для свинца при
давлении 4 Мбар сжатие близко к предельному (р/р0=2,2), а температура
\ \ \н> 1
1 \ Н}Х\
\ с \
п \
1 н,
в
*^_
А V
32
достигает 26000 К; при этом тепловое давление составляет 32%
от полного давления, а половина тепловой энергии принадлежит
электронам [2]. Таким образом, а^я многих твёрдых тел давления
в ~ 100 кбар являются слабыми. Для таких волн справедливо
приближение «адиабатичности» ударного сжатия, когда ударная волна
практически совпадает с изэнтропой.
Это упрощает решение многих задач а^я реальных давлений,
создаваемых с помощью взрыва. Скорость слабых ударных волн
мало отличается от скорости звука, а массовая скорость за фронтом
составляет всего несколько процентов от волновой скорости (так,
Аая железа при р = 200 кбар и = 0,06 D).
1.4. Примеры взаимодействия волн.
Распады разрывов
Ранее было показано, что любое автомодельное движение в
газах или в конденсированных средах может быть создано из трех
элементов: областей постоянного течения, волн разрежения и ударных
волн. С одним ограничением: в одну сторону не может двигаться
более одной волны. Например, если по веществу идет ударная волна,
то следующая за ней волна разрежения, а тем более ударная волна,
обязательно догонит ее через некоторое время. Но в силу
автомодельное™ обе волны выходят из одной точки х = 0 и в одно время
t = 0, т. е. вторая волна уже в начальный момент догнала первую
волну, и они обе движутся как одна волна.
Итак, если в веществе возник произвольный разрыв
(скачкообразное изменение р, v, u, Т), то движение среды может быть
построено только в виде какой-нибудь комбинации из двух типов
волн — ударной и разрежения, распространяющихся в
противоположные стороны от начального разрыва и разделенных областями
постоянного течения. При этом очевидно, что в силу непрерывности
давления и скорости по обе стороны разрыва совпадают. Возможны
три типичных случая распада разрыва: в обе стороны идут ударные
волны, волны разрежения и в одну сторону — ударная волна, а в
другую — волна разрежения.
33
а;
1
t3---
tl
aN
>^ Образец
ft
'#-
s
X
&■
1 °*
^
W
У
Я"
8
Он
vo
О
б)
в)
max
IV
III/ II I I
vft Vi V
r)
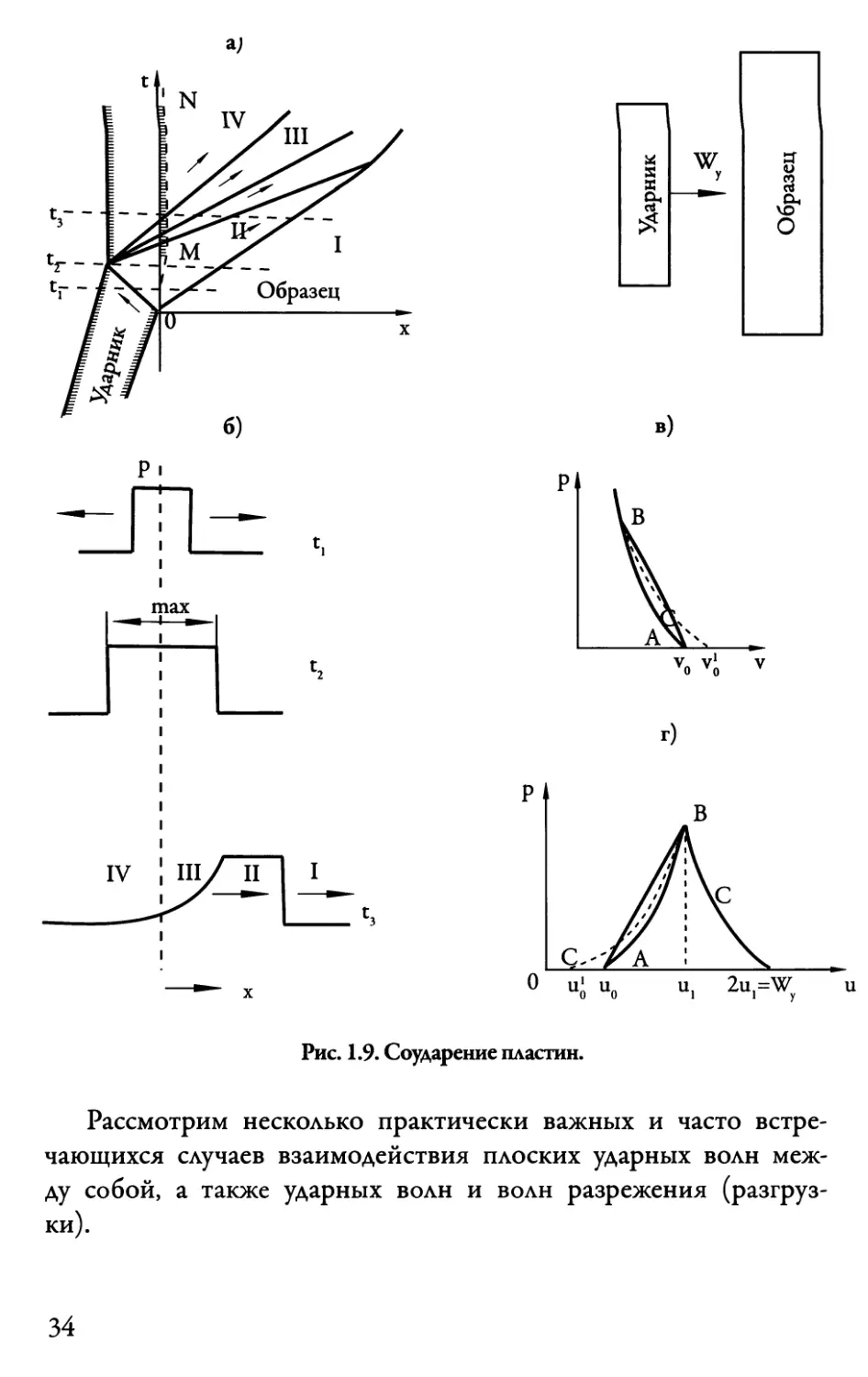
Рис. 1.9. Соударение пластин.
Рассмотрим несколько практически важных и часто
встречающихся случаев взаимодействия плоских ударных волн
между собой, а также ударных волн и волн разрежения
(разгрузки).
34
Такое рассмотрение проведем в х, t, р, и- и р, v —
координатах в гидродинамическом приближении (т.е. без учета
прочности). Это поможет получить более глубокое и наглядное
представление об общепринятых способах графического описания
ударных волн и их взаимодействиях между собой и с волнами
разрежения.
1. %ар летящей пластины по мишени (см. рис. 1.9)
Для простоты считаем, что материал пластины и мишени один
и тот же. При ударе по мишени и по пластине пойдут ударные волны.
Центрированная волна разгрузки возникает в виде расходящегося
веера характеристик в момент выхода на тыльную поверхность
пластины ударной волны торможения (рис. 1.9 а). Первая волна
догоняет фронт ударной волны в мишени в точке К, и с этого момента
ударная волна начинает затухать, траектория волны искривляется,
т. к. скорость и давление уменьшаются.
Линия OMN — траектория границы пластина — мишень (или
траектория поршня).
Область I — начальное состояние мишени (р0, vQ, uQ)
Область II — состояние за фронтом ударной волны (р2, у2, и{)
Область III — область волны разрежения, где давление и скорость
вещества плавно уменьшаются.
В области IV давление вновь равно р0, но объем и скорость
мишени отличаются от vQ и uQ.
Профиль давления в мишени показан на рис. 1.9 б. На р, v —
диаграмме (см. рис. 1.9 в)) сжатие материала идет от состояния
А в состояние В на адиабате Гюгонио. В волне разрежения вещество
расширяется вдоль изэнтропы ВС (пунктирная линия) до
объема v0 и начального давления pQ. Этот же процесс в р, и —
координатах показан на рис. 1.9 г с теми же обозначениями.
Прямая Михельсона АВ имеет наклон dp/du = р0 (D - uQ).
Напомним, что графики на рис. 1.9 отражают связь между ударно-
сжатым и исходным состояниями, которая описывается
уравнениями:
Простая волна
разрежения описывается
уравнением характеристик: и -
"о = 1-
1 =
10,где
= / dp/pc.
JPl
Рис. 1.10. Общий вид р, и — диаграммы.
Эти основные
соотношения не содержат членов,
зависящих от времени (т.е.
движение автомодельно).
фарное нагружение
пластины и мишени в р,
и — координатах иллюстрирует рис. 1.9 г. Летящая пластина
имеет скорость w и полностью разгружена— р = 0 (точка С). У
мишени в исходном состоянии р = 0 и и = 0 (точка А). При ударе
пластина тормозится до скорости Uj и нагружается давлением р2 по адиабате
СВ, а мишень нагружается по той же адиабате АВ до тех же величин
Pj, ur Адиабата СВ а^я волны, движущейся по пластине в
отрицательном направлении (УВ-), является зеркальным отражением
адиабаты АВ аая волны в мишени, движущейся в положительном
направлении (УВ+).
Общий вид р, и — диаграммы взаимодействия волн показан
на рис. 1.10.
Выше начальной точки О — ударные адиабаты OQ и ОН,
а ниже — изэнтропы разгрузки. В начальной точке О ударные
адиабаты и изэнтропы имеют касание второго порядка (равные первые
Ро=°
Р. .Ь^Рг
u. "и=0' и,
И
УВ
Р2>и:
До столкновения После столкновения
Рис. 1.11. Столкновение двух ударных волн.
36
и вторые производные). Для не очень сильных ударных волн,
пренебрегая изменением энтропии, заменяют изэнтропу ударной
адиабатой и также используют прием зеркального отображения аая волн,
идущих в отрицательном направлении.
2. Столкновение двух ударных волн
На рис. 1.11 две ударные волны (УВ), разделенные однородным
состоянием р = О, и = 0, движутся навстречу друг другу. На р, и —
диаграмме состояние за ударными волнами показаны точками (р2,
Uj) и (р2, и2). После столкновения образуются две удаляющиеся друг
от друга волны, разделенные новым состоянием (р3, и3). Эти волны
распространяются в среде в состояниях (р2, и{) и (р2, и2).
Рис. 1.12. Столкновение двух волн разрежения.
Состояние (р3, и3), разделяющее расходящиеся после
столкновения волны, однородно по давлению и массовой скорости
вследствие непрерывности этих величин при распаде разрывов.
Находится это состояние в точке пересечения двух адиабат Гюгонио,
выходящих из точек (р2, и2) и (р2, и2) и соответствующих двум
ударным волнам: УВ+ и УВ _.
3. Столкновение двух волн разрежения (см. рис. 1.12)
Рассуждения такие же, как и в предыдущем случае. Две волны
разрежения (pj, Uj) и (р2 и2) разгружают с двух сторон исходное состояние.
Конечное состояние (р3, и3) однородно и лежит в точке пересечения из-
энтроп ВР+ и ВР, проходящих через точки (р{, и{) и (р2, и2).
37
\™М*>
P,'u, ^>
yBv^
\/.Po'uo=°
p2,u2=0
u 0 v0 v
Рис. 1.13. Отражение ударной волны от жесткой стенки.
Отметим, что р3 < 0, т. е. столкновение волн разрежения создает
в материале растягивающее напряжение, и если оно больше предела
прочности, то на линии столкновения будет разрыв материала — так
называемый, откол (см. гл. 3). Практически откол возникает в
пластине при взрыве на ее поверхности относительно тонкого заряда
ВМ от столкновения волн разгрузки, идущих от двух поверхностей
пластины.
4. Отражение ударной волны от жесткой стенки (см. рис. 1.13)
Исходная УВ переводит вещество из состояния (р0 = 0, uQ =0)
в состояние (р2, и2). Конечное состояние (р2, и2 = 0) возникает
за отраженной волной, связано с состоянием (р2, и2), лежит на
ударной адиабате сжатия вещества второй обратной ударной волной
УВ_ и одновременно — на оси абсцисс, т. к. на стенке и = 0. Этим
условиям отвечает точка А на р, и — диаграмме. В реальном случае
абсолютно жесткая стенка эквивалентна плоскости столкновения
двух одинаковых движущихся навстречу друг другу ударных волн.
Рис. 1.14. Отражение ударной волны от свободной поверхности.
38
5. Отражение ударной волны от свободной поверхности
(см. рис. 1.14)
В этом случае конечное состояние лежит на изэнтропе
расширения в точке р = 0. Заменяя изэнтропу ударной адиабатой, находим
точку В (р = 0, u2 = 2Uj) как пересечение с осью абсцисс зеркального
отображения адиабаты относительно вертикальной линии,
проходящей через точку А (р2, их).
Закон удвоения массовой скорости на свободной поверхности
нарушается только аля пористых тел и ^ая очень сильных УВ, где
и2 > 2иг Этот случай типичен ^ая разгона пластин продуктами
взрыва. В процессе разгона по пластине циркулируют волны разрежения
(от свободной поверхности) и ударные волны (от границ с
продуктами взрыва).
В результате пластина увеличивает скорость не плавно, а
скачками. Амплитуда первого скачка u2 = 2и2 максимальна, а затем
амплитуда скачков быстро затухает (см. рис. 1.15).
W 1
км/с
X, мм
Рис. 1.15. Разгон пластины продуктами взрыва.
6. Прохождение ударной волны через границу двух сред
Пусть у среды II ударная адиабата расположена выше, чем у
среды I. фарная волна идет из среды I в среду II (см. рис. 1.16 а)
Конечное однородное состояние (р2, и2) одинаково а^я обеих
сред и создается обратной УВ в среде I, идущей из состояния (р2, и2),
и прямой УВ в среде II, идущей из состояния (р0 = 0, uQ = 0).
Если ударная адиабата Нп среды II лежит ниже ударной адиабаты
Нг среды I, то обратная волна в среде I является волной разрежения
(рис. 1.166)
39
а) б) а)
Рис. 1.16. Распад разрыва на границе двух сред.
Аналитическое выражение аая амплитуды р2 волны, отраженной
в среду I и прошедшей в среду II, можно легко получить из условий
на ударном скачке, написанных аая падающей, отраженной (и
прошедшей) волн:
D-uQ = V^(px- р0) / (v0-vx)
Щ~Щ= V(A-Po)K-vi) (1.16)
/?, (рп,д /^д^ + Сро/Д /Рп//Д)
где р01, рои — начальная плотность среды I и среды II; р — плотность
за падающей волной; D{ — скорость падающей волны.
D2r~ скорость отраженной волны относительно среды, сжатой
падающей волной: D21 =ui— D21; D21— скорость отраженной
волны в лабораторной системе координат; D2 — скорость
прошедшей волны в среде II.
Произведения pD в (1.16) называются волновым
сопротивлением по аналогии с акустическим сопротивлением рс (для предельно
малой амплитуды волны).
В случае, когда среда II абсолютно жесткая стенка, pD->ooh(1.16)
получает следующий вид:
^ = (p0Dl+PlDil)/p0D (1.17)
А
В акустическом приближении, когда р; -»р0, р2/р; -> 2.
40
Величина волнового сопротивления равна наклону хорды,
соединяющей начальное и конечное состояния в р, и — координатах
(T.K.p = p0Du).
1.5. Скорость звука
Волновая и массовая скорость УВ позволяют найти давление
и плотность ударного сжатия.
Не менее важна скорость звука в ударно-сжатом материале,
которая определяет скорость слабых УВ и волн разгрузки за
фронтом УВ. Знание величины скорости звука нужно а^я правильной
постановки экспериментов с УВ (определение неразгруженной
области), а также а^я геофизичеких исследований и а^я
построения уравнений состояния. Например, изэнтропические модули
упругости в ударно-сжатом веществе определяются из
соотношений объемной сь и продольной с{ скоростей звука. Объёмная или
изэнтропическая скорость звука cb = V2>/5p/5v характеризует
наклон изэнтроп или изэнтропическую сжимаемость вещества.
Существует три способа измерения скоростей звука в ударно-
волновом эксперименте.
1. Метод боковой разгрузки
Разработан Альтшулером и Кормером с сотрудниками [10].
При ударном сжатии цилиндрического образца ступенчатой
формы боковая разгрузка из точки О (рис. 1.17) ослабляет перифе-
Рис. 1.17. Боковая разгрузка цилиндрического образца.
41
рийную часть плоской волны. Поэтому фронт волны искривляется,
начиная с точки В. Рассматривая треугольники OBF и ABF, можно
связать скорости звука со скоростью D и тангенсом угла разгрузки:
c = D[tg>a + (£j±ffJ (1.18)
Если ударная адиабата известна, то задача сводится к измерению
Dna.
Фиксируя фотометодом «отсечки» фронт волны на торце
образца, определяют по пленке точку В и, зная геометрию образца, —
угол разгрузки а.
Величина а четко фиксируется по форме УВ fi^ жидкостей,
имеющих только одну скорость звука. Для металлов фронт разгружается
плавно, сначала слабо за счет разгрузки ударной волны со скоростью
с{ (упругий предвестник), затем сильно за счет пластической волны
с меньшей скоростью сь.
Существование двух скоростей звука затрудняет точное
определение границы «пластической» разгрузки у материалов, имеющих
прочность. Поэтому был разработан другой способ.
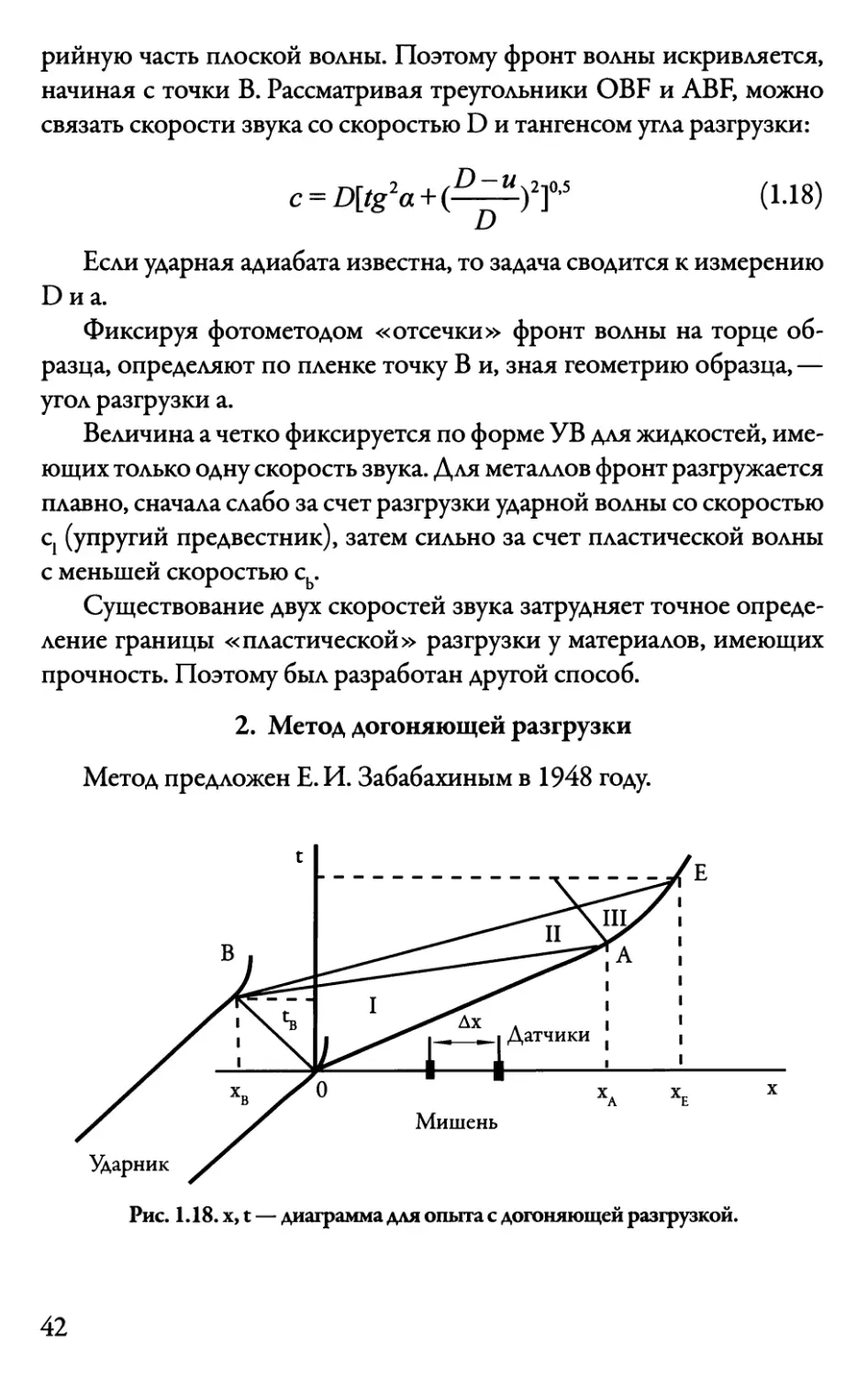
2. Метод догоняющей разгрузки
Метод предложен Е. И. Забабахиным в 1948 году.
Рис. 1.18. х, t — диаграмма для опыта с догоняющей разгрузкой.
42
Образец нагружается ударом пластины, х, t — диаграмма
процесса показана на рис. 1.18.
Центрированная волна разгрузки от точки В догоняет фронт УВ
в точкеА и далее УВ затухает, ее скорость уменьшается. Расстояние
догонах равно:
хА = [(1+Щ1-ЩА (1.19)
где: А — толщина ударника, М = (D - и)/с — число Маха.
Отсюда находится скорость звука, если D — и и х— известны.
Здесь также велика погрешность в определении х— из-за
опережающей упругой волны разгрузки. Поэтому используются три варианта
этого метода. В первом варианте находится наклон а —
характеристики W а^я точки Е, находящейся в заведомо разгруженной
области: WE = uE + cE, где W£ = (x£-xB)/(t£- tB), а и находится
непосредственно или по измерению D.
Расчетная формула а^я с£ = W£ - u£:
DJE-A
где cjj = D1/(D1 - Uj) hDj — параметры в неразгруженной
области.
По второму варианту в двух сечениях образца с расстоянием Ах
регистрируются профили давления р (t) манганиновыми датчиками.
Зная Ах и определив по осциллограммам промежутки времен между
моментами прихода к датчикам УВ и волны разрежения, легко
найти их скорости.
Наконец, в третьем варианте метода догоняющей разгрузки
скорость фронта волны разрежения измеряется оптической
методикой, основанной на регистрации изменения яркости свечения
УВ в прозрачной индикаторной жидкости (например, в СНС13.
см. раздел 8.4) [11].
43
3. Метод стимулированного бриллюэновского рассеяния
Метод основан на рассеянии световых волн на звуковых
колебаниях (фононах). Как известно, в любой кристаллической решетке
всегда существует термически возбуждаемые колебания. Поскольку
эти колебания распространяются со скоростью звука, наблюдается
допплеровское смещение частоты света в зависимости от
направления движения звуковых волн. Стимулированное бриллюэновское
рассеяние наблюдается в случае, когда интенсивность света
настолько велика, что биения, возникающие при сложении падающей и
рассеянной световых волн, усиливают акустические колебания
решетки, на которых свет рассеивается за счет электрострикции.
Допплеровское смещение частоты пропорционально скорости
звука с в теле:
Av = vo2/ic/asin0/2 (1.21)
где v — частота падающего света; п — показатель преломления тела;
а — скорость света; 0 — угол дисперсии.
Измерения скорости звука проводятся с помощью рубинового
лазера (плотность потока 104 Мвт/см2) и интерферометра Фабри —
Перо [12] в прозрачных телах с временным разрешением 0,1 мкс
и с точностью 0,5%.
4. Расчет скорости звука
Трудоемкость измерения скорости звука за фронтом УВ
стимулировала поиски методов ее расчета. Рассмотрим некоторые из них.
Объемная скорость звука сь может быть рассчитана, исходя
из экспериментального факта, что в р, и — координатах для
непористых веществ при не слишком больших давлениях изэнтропа и
ударная адиабата D = а + bu мало отличаются (не более 3%).
В приближении их совпадения получим:
" A5=A*=A>(« + 2^) (1.22)
аи аи
cb = (a + 2bu)(v/v0)
44
Рассчитанные по (1.22) значения сь хорошо согласуются с
результатами измерений. Это свидетельствует о широкой применимости
и обоснованности квазиакустического приближения, согласно
которому скорость УВ есть средняя величина лагранжевых скоростей
звука за и перед фронтом УВ: D = (cQ + cb)/2.
Зная cb, можно в предположении постоянства коэффициента
Пуассона [л рассчитать соответствующие величины продольной
скорости звука с}:
c,(p)/ch(p) = j3(l-M)/(l + M) (1.23)
Сопоставляя расчетные и экспериментальные значения с} (р),
можно видеть, что хорошее согласие наблюдается до определенного
давления, выше которого продольная скорость Cj уменьшается до совпадения
с объемной скоростью звука с^, что объясняется плавлением данного
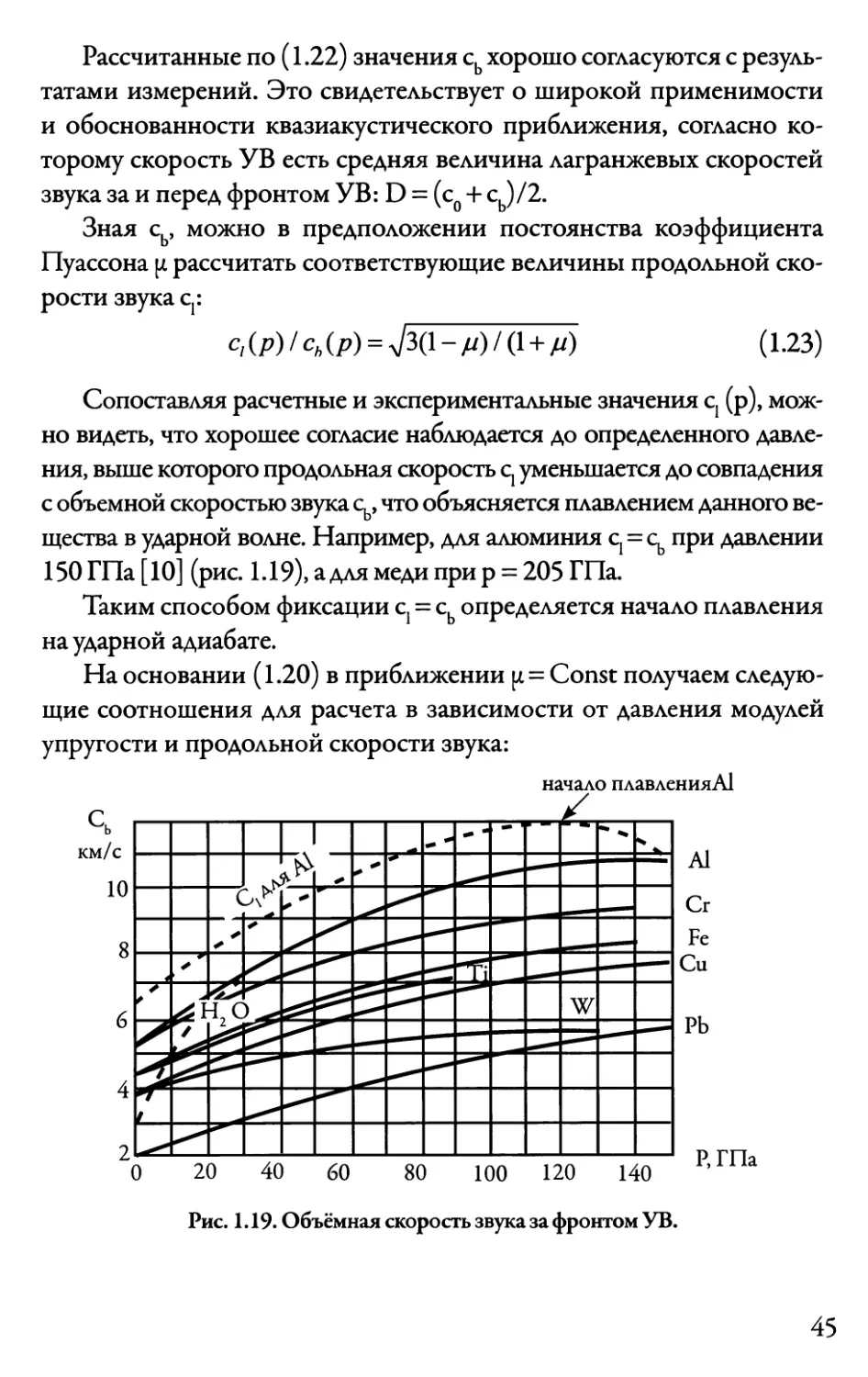
вещества в ударной волне. Например, АА^ алюминия с} = с^ при давлении
150 ГПа [10] (рис. 1.19), а для меди при р = 205 ГПа.
Таким способом фиксации Cj = cb определяется начало плавления
на ударной адиабате.
На основании (1.20) в приближении [л = Const получаем
следующие соотношения для расчета в зависимости от давления модулей
упругости и продольной скорости звука:
начало плавленияА!
0 20 40 60 80 100 120 140
Рис. 1.19. Объёмная скорость звука за фронтом УВ.
45
k = &- (к0+4Ьр)
P
G = *[G0 + 6bp£^]
P (1 + /0 (1.24)
Отметим, что для веществ с полиморфизмом под давлением
(железо, кварц, углерод, висмут и др.) коэффициент Пуассона не
постоянен и формулы (1.24) неприменимы.
Изменение с давлением объемной скорости звука аая ряда
металлов и аая воды показаны на рис. 1.19. Быстрый рост сь аая воды
объясняется сильным увеличением с давлением плотности и модуля
упругости воды. Например, удвоение плотности в УВ происходит
в воде уже при 30 ГПа, а у меди — при 900 ГПа.
Выражение а^я скорости звука можно получить из
уравнения состояния а^я данного вещества, однако если взять
наиболее точное трехчленное УРС, то выражение а^я сь получается
довольно громоздким. Кроме того, расхождение с
экспериментом растет с сжатием и, например, а^я свинца составит 20% при
400 ГПа.
Для веществ, не имеющих экспериментальных данных,
можно оценить скорость звука с помощью следующей эмпирической
формулы [13]:
ДА АА ^ '
Если известна ударная адиабата в виде D = А+Ви, то, используя
известные выражения р = р0 Du и <7=p/p0 = D/(D— и), получим
уравнение ударной адиабаты в виде [13]:
Рн =p0c20(r(cT-l)[(h-l)/(h-a)]2 (126)
где h — предельное сжатие.
Предполагаем, что коэффициент Грюнайзена изменяется при
сжатии как Г = Г0/<т (что найдено для РЬ и А1).
46
с. с.
км/с *) км/с б)
100 200 300 Р,ГПА 100 200 300
Рис. 1.20. Зависимость от давления продольной (пунктир) и объёмной скоростей
звука в железе (а) и меди (б).
Используя уравнение Е = 1/2р (VQ-V), дифференцируем (1.26) пост
и подставляем в дифференциальное уравнение аая изэнтропы. В итоге
получим следующее выражение аая расчета скорости звука [13]:
_ _*-!_ |2*(а-1) _,.Мр£^ (1.27)
0 h-(j\ h-a °a(h-a)
Эта формула дает хорошее согласие с экспериментом (в пределах
5%) до с ~ 1,7, а выше заметен вклад электронов, и предположение
Г = Г0/<7 неверно.
В [13] получено следующее выражение аля сь у пористого тела
с пористостью m = V /V:
fo_ (<J-l)(mcr + l) + (h-m<j) (1.28)
crv A - ma
Для непористого вещества (m = 1):
Рис. 1.21. Зависимость угла боковой разгрузки от сжатия.
Измеренная продольная скорость звука в железе хорошо
согласуется с расчётом по (1.27) до 125 ГПа. При более высоких давлениях
величина с} падает и при 150 ГПа становится равной объёмной
скорости звука. Уменьшение с} объясняется плавлением вещества в
ударной волне (см. рис. 1.19.) и уменьшением коэффициента Пуассона
до величины [л = 0.5, присущей жидкости [14].
Результаты оптических измерений (по яркости свечения
индикаторной жидкости) скоростей звука в Fe и Си показаны на рис. 1.20.
Для железа резкое изменение с} при 200 ГПа связано се — j
превращением а плавление (с} = сь) достигается при 240 ГПа.
Аналогичные измерения а^я тантала показали, что он начинает
плавиться в У В при 295 ГПа.
Давления, при которых с} = сь согласуются с расчётной оценкой
точки плавления в УВ [15].
Для корректной постановки экспериментов с ударными
волнами необходимо правильно выбирать размеры образцов, чтобы
область измерений не была охвачена боковой разгрузкой.
Для этого нужно знать угол а боковой разгрузки, который
зависит от скорости звука согласно (1.18) или в явном виде:
"-Щ^ (ио)
Наименьшее расхождение с экспериментом дает следующая
формула [13]:
3-а
\2
I 2а J
+б£±-1
(1.31)
На рис. 1.21 даны зависимость а (с), рассчитанная по (1.31),
и результаты измерения а [10]:
В работе [16] найдено, что продольная скорость звука у твердой
керамики с давлением растет линейно:
с, =с1о+Ли (1.32)
где и — массовая скорость за фронтом УВ, определяемая по
измеренной волновой скорости D и по уравнению состояния керами-
khD = A + Bu.
Исходные данные аля расчета величин Cj у трёх различных видов
керамики приведены в таблице 1.1.
Таблица 1.1. Некоторые параметры керамики [16]
Параметр
р0, г/смЗ
с,о,км/с
1
А км/с
В
SiC
3,166
11,7
1,25
8,29
0,62
ZrOz+ 12,5%Y02
5,602
7,11
3,0
3,68
2,12
в4с
2,516
14,07
1,8
8,11
1,61
Литература к главе 1
1. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика, т. 6
Гидродинамика. М.: Наука, 1986.
2. Зельдович Я. Б., Райзер Ю. П. Физика ударных волн и
высокотемпературных гидродинамических явлений. М.: Наука,
1966.
3. Курант Р., Фридрих К. Сверхзвуковое течение и ударные вол-
ны.М.: Из-во иностр. лит., 1950.
4. Станюкович К. П. Неустановившиеся движения сплошной
среды. М.: Гостехтеориздат, 1955.
5. Годунов С. К. Элементы механики сплошной среды.М.: Наука,
1978.
6. БаумФ.А., Станюкович К. П., Шехтер Б. И. Физика взрыва.
М.: Из-во физ-мат. лит., 1975.
7. Зельдович Я. Б., Компанеец А. С. Теория детонации. М.: Гос-
техтеоретиздат. 1955.
8. Зельдович Я. Б. Теория ударных волн и введение в
газодинамику. М.: Из-во АН СССР, 1946.
9. Альтшулер Л. В. Применение ударных волн в физике высоких
давлений.//Успехи физических наук, 1965, 85, N2, с. 197.
10. Альтшулер Л.В., Кормер СБ. и др. ЖЭТФ, I960, Т. 38,№ 4,
С. 1061.
11. Me Queen R.G., Fritz J.N. Rev. Scient. Jnstrum., 1982,53, N2,
p.245.
12. Kceler R. N., Bloom G. H., Mitchell A. C. Physical Review Letters,
1966, N16
13. Рыбаков А. П. Твердые тела в условиях давлений и
температур ударного сжатия (учебно-метод. пособие), ЦНИИ-
атоминформ, М, 1978, 87 с.
14. Линд В. Д. Корпускулярная природа динамического
прессования. Тр. конф. Metallurgical Application of Shock- Wave and
High-Strain-Rate Phenomena, Santa Fe, 1985, c, 65.
15. Кормер С. Б., Синицын М. В., Кириллов Г. А., Урлин В. Д. ЖЭТФ,
1965, т. 48, в.4, с. 1033.
16. Скрыпняк В, А, Скрыпняк Е. Г., Жукова Т. В. ФГВ, 2001, 37, 5,
с. 121 — 127.
50
Глава вторая
УРАВНЕНИЯ СОСТОЯНИЯ
2.1. Краткий обзор
Поведение вещества при его динамическом нагружении
описывается двумя разными моделями, отражающими физические свойства
вещества и его напряжённо-деформированное состояние.
Физическое состояние вещества как сплошной среды
характеризуется пятью функциями: р, Т, р, Е, S. Связь между ними даётся основным
уравнением термодинамики dS = dE/T + pdv/T и уравнением
состояния (УРС), которое может быть задано в различной форме: р=р (v, Т),
p=p(v,S),T=T(p,v),E=E(p,v),E=E(v,T)S = S(p,v),S=S(v,T).
Если принять в качестве независимых переменных удельный
объём v = 1 /р и температуру Т, то УРС в форме Е = Е (v, р) называют
калорическим, а в форме р = р (v, Т) — термическим.
Уравнение состояния является фундаментальной
характеристикой вещества, которая позволяет использовать общий
математический аппарат термодинамики и газодинамики аля решения
прикладных задач физики высоких плотностей энергии, таких, как:
реализация идеи управляемого термоядерного синтеза, расчёты
взрывных ядерных устройств, противометеоритная защита
космических аппаратов, фазовых превращений и др.
Уравнения состояния, замыкающие при расчётах систему
уравнений движения среды, определяют точность и надёжность
получаемых результатов.
В период I960—90-е гг. разработаны полуэмпирические модели
уравнений состояния АА^ широкого диапазона давлений и температур.
51
В этих моделях общий вид уравнения состояния устанавливается
на основе теоретических соображений, а данные экспериментальных
измерений (в частности, ударных адиабат и изэнтроп) используются
Аля определения численных значений коэффициентов в уравнениях
состояния.
Такие лабораторные измерения стали возможны только
благодаря использованию сильных ударных волн как способа воздействия
на вещество.
В этом направлении фундаментальные исследования проведены
в связи с разработкой и испытанием атомных боеприпасов в США
и в России, в основном, в Лос-Аламосской и Ливерморской
лабораториях США, в ядерных центрах России в г. Саров (ВНИИЭФ)
и в г. Снежинск (ВНИИТФ).
Начиная с 1940-х годов благодаря совершенствованию
лабораторных методик измерения и измерительных устройств непрерывно
расширялся диапазон давлений, в котором изучалась ударная
сжимаемость веществ, т. е. определялась связь между давлением,
плотностью и энергией [1].
Например, в России уже в 1947 году ударная сжимаемость
железа и урана была изучена до давлений 40 и 50 ГПа, в 1948 году— до
350 ГПа, а к 1955 году диапазон давлений был увеличен до 1,3 ТПа с
помощью сферических кумулятивных зарядов, обеспечивающих плавный
(«безнагревный») квазиизэнтропический разгон ударника [1].
Дальнейший рост давлений до 10 ТПа (в железе) был достигнут
за счёт использования сильных ударных волн, возникающих при
подземных ядерных взрывах.
Общие схемы фазовой диаграммы вещества показаны на
рис. 2.1 а, б.
Теоретические модели уравнений состояния рассматривают
микросвойства веществ на уровне ядер и электронов. Как известно,
холодное разрежённое вещество имеет только связанные с ядрами
электроны. При ионизации высокими давлением и температурой
часть электронов становятся свободными, т. е. в системе растет число
частиц, что увеличивает давление и энергию, и должно быть учтено
вУРС.
52
нтовыи
кристалл
V 10"5 10"3 КГ1 1 Ю2
Рис. 2.1. Схемы фазовой диаграммы веществ [2]
104 vo/v
а) I — плавление, II — равновесие жидкость — пар
Стрелками указаны направления уменьшения межчастичного взаимодействия.
б) Диаграмма для алюминия. Епот, Е — потенциальная и кинетическая энергии
частиц.
У нейтрального газа межчастичное взаимодействие мало и может
быть учтено в рамках вириального уравнения состояния, но с ростом
плотности газа такое описание ухудшается и заставляет использовать
чисто эмпирические формулы, а при сверхкритических условиях —
модели жидкости.
С ростом температуры газ ионизируется и превращается в
плазму, термодинамические свойства которой описываются
уравнениями ионизационного равновесия. По мере сжатия плазмы в ней
усиливается кулоновское взаимодействие, что приводит к снижению
потенциалов ионизации. При низких температурах в плотной
плазме важную роль играют квантовые эффекты, которые описываются
методом Монте-Карло.
Неидеальная ячеистая плазма — такая плазма, где ионы
нейтрализованы (экранированы друг от друга) окружающими электронами.
В такой плазме среднее расстояние между ионами R примерно равно
дебаевскому радиусу. Плотная плазма описывается с помощью
модели ограниченного атома, учитывающей размер иона и влияние на его
спектр плазменного окружения.
53
Рис.2.2. Изменение с давлением атомных объёмов элементов. (Z — атомный
номер.)
В области чрезвычайно высоких давлений и плотностей
электронные оболочки атомов оказываются раздавленными, и
осуществляется однородное распределение электронной плотности, описываемое
моделью Томаса-Ферми. Дальнейший рост плотности или температуры
позволяет использовать формулы а^я идеального электронного газа.
54
Р,ГПа
105 |—
102 ■ ■ ■ ■
10 15 20 25 30 35 40 45 55 60
p, г/см3
Рис.2.3. Сопоставление расчёта и эксперимента для Fe, Си, Cd, Pb.
На рис. 2.2 показано изменение с давлением атомных объёмов
элементов. Выше 1 ТПа периодичность V (Z), отражающая
индивидуальную структуру оболочек атомов в нормальных условиях,
практически исчезает. Соответственно при очень высоких давлениях
нивелируются и ударные адиабаты.
При понижении давления и температуры поведение
конденсированного вещества определяется конкретной оболочечной
структурой атома, а также симметрией кристаллической решётки. В этой
области теоретические квантомеханические модели очень сложны и
приближённы, поэтому используются эмпирические УРС,
получаемые экспериментально.
Сопоставление расчета по Томасу — Ферми и эксперимента аля
Fe, Си, Cd и РЬ показано на рис. 2.3. Как видно, лучше всего стыкуется
с расчётом ударная адиабата свинца. Поэтому свинец используется как
эталон в косвенных сравнительных измерениях при очень высоких
давлениях, получаемых при проведении подземных ядерных взрывов.
УРС кристаллических веществ усложняется при учёте
прочности и полиморфизма. При достаточно высоких давлениях во всех
твёрдых телах реализуются структуры с плотной упаковкой атомов.
Наиболее трудна и малоизученна область жидкого состояния, где
сильное взаимодействие и неупорядоченность затрудняют теоретиче-
55
ское описание. Здесь реалистические модели основаны на
использовании упрощённых потенциалов твёрдых и мягких сфер, позволяющие
применить численные методы молекулярной динамики и Монте-
Карло, причём параметры парного межчастичного потенциала
находятся путём сравнения расчётных данных с результатами
экспериментов.
Отметим, что плазма схожа с жидкостью, только в плазме
в электронной жидкости «плавают» ионы с различными зарядами.
Поэтому описать плазму труднее, чем жидкость.
Таким образом, теоретическое описание неидеальных сред
приводит к использованию сложных квантовомеханических или
статистических моделей, применимых в ограниченной области
параметров и связанных с очень громоздкими численными расчётами.
В настоящее время теоретическое описание неупорядоченности
и сильного межчастичного взаимодействия в сжатой и разогретой
жидкости и в плотной плазме малоэффективно, поэтому эдесь
основную роль играют полуэмпирические У PC, построенные на основе
экспериментальной информации. В то же время ^ая точного описания
реальных физических систем очень важны трёхмерные программы
численных расчётов с использованием точных УРС и мощных ЭВМ.
Например, в настоящее время реализация всех этих трёх факторов
настолько повышает точность и надёжность расчётов ядерных зарядов,
что отпадает необходимость их испытаний в натурных условиях.
Термодинамические свойства сред имеют общенаучное значение
и ^ая облегчения их использования любым специалистом в своих
расчётах в лабораториях Лос-Аламоса и Ливермора создан банк
данных или библиотека УРС «Сезам». В РФЯЦ — ВНИИТФ
(г. Снежинск) такой банк данных называется «Арсмус, а в
институте математического моделирования (Москва) — «Тнернус».
Причём, УРС могут быть даны в любой форме: таблицы,
полиномы, степенные зависимости с коэффициентами, найденными
экспериментально.
Отметим, что все вещества можно разделить на термодинамически
равновесные, а^я которых все параметры определяются в зависимости
только от плотности и температуры, и реологические вещества, у кото-
56
рых нет равновесия, и нужны дополнительные реологические
зависимости (например, от степени фазового превращения).
Здесь рассматриваются только термодинамически равновесные
среды.
Далее подробнее анализируются УРС твёрдого тела [1—5].
2.2 Квазигармоническая модель твёрдого тела
Традиционно полуэмпирическое УРС твёрдого тела имеет две
составляющие: холодную и тепловую.
р=рЛу)+рЛг-т) (2.1)
Из общего термодинамического соотношения TdS = dE + pdV
при Т = О следует:
Px=-dEx/dV (2.2)
Смысл (2.2) простой: приращение энергии равно работе
сжатия, р и Е называются «холодными», т. к. равны полным давлению
и удельной внутренней энергии при абсолютном нуле температуры,
определяются только силами упругого взаимодействия между
атомами, зависят только от плотности и не зависят от температуры.
Зависимости р (V) получают из результатов опытов по ударному
сжатию.
При очень больших р и р атомы теряют свою индивидуальную
структуру (см. рис. 2.2), и ^ая описания состояния вещества
применима статистическая модель Томаса — Ферми, которая даёт
следующий предельный закон а^я холодного сжатия:
А-Г*3 (2.3)
При достижимых в опытах сжатиях S = р/р = 1,5— 2 модель
Томаса — Ферми значительно завышает давление (см. рис. 2.4 а).
На рис. 2.4 в показана ударная адиабата твёрдого тела (ас) и
изотерма при Т = 0° К (bd). При Т = 0° К изотерма строго совпадает с из-
энтропой, а в обычных условиях адиабатическая сжимаемость
пренебрежимо мало отличается от изотермической.
57
р
ГПах 102
100|
40
10
4
1
0,4
<*£'
V
tf
J}
t/
ts
£
^ /
/
4t
у
/
/A 1
P h h
1,2 1,5 2 3
6 11
Рис. 2.4a. Упругое давление px для железа. Рис. 2.4в. фарная адиабата (ас) и
нулевая изотерма (bd) тёрдого тела.
pvo
Упругая энергия Ех = I px(v)dv равна площади
криволинейного треугольника bde.
Тепловая часть внутренней энергии соответствует
заштрихованной площади abdc. Предполагая, что теплоёмкость с = (dE /dT)
не меняется и принимает некоторое среднее значение, получим:
Em-E0=cv{T-T0) (2.4)
Начальная энергия Е0 (Т0) может быть подсчитана по Дебаю.
Для ударных сжатий до S« 1,2 различие между ударным и изэнтро-
пийным сжатием мало (например, аая меди при S = 1,2 рн=42,2 ГПа,
а р =41,8 ГПа), поэтому обычно для описания ударного давления
принимают закон изэнтропы:
p = A(S'-l) (2.5)
Это простейшее УРС в форме Тэта. В табл. 2.1 даны константы
А и п для ряда металлов.
Таблица 2.1. Константы уравнения Тэта
Металл
Бериллий
Алюминий
Титан
р г/см3
1,845
2,785
4,41
А105 кг/см2
3,75
1,97
2,60
п
3,2
4,2
3,8
Диап. давл. ГПа
0...35
0...50
0...70
58
Металл
Железо
Кадмий
Молибден
Свинец
Тантал
Золото
Платина
р г/см3
7,84
8,64
10,2
11,34
16,46
19,24
21,37
А105 кг/см2
2,15
0,77
7,29
0,86
4,58
3,16
5,39
п
5,5
6,3
3,8
5,3
4,0
5,7
5,3
Диап. давл. ГПа
25—100
0...70
0...70
0...50
0...50
0...70
0...50
фарные адиабаты можно описать трёхчленным уравнением:
Р=А(д-1)+В(д-1)2 + С(д-1)3
Значения коэффициентов А, В, С а^я ряда металлов приведены
в таблице 2.2.
Таблица 2.2. Значения коэффициентов А, В и С (в ГПа) для
некоторых металлов
Металл
Берилий
Кадмий
Хром
Кобальт
Медь
Золото
Свинец
Магний
Молибден
Никель
Серебро
Торий
Олово
А
118,2
47,9
207,0
195,4
140,7
142,7
41,7
37,0
268,6
196,3
108,8
57,2
43,2
В
138,2
108,7
223,6
388,9
287,1
526,7
115,9
54,0
424,3
375,0
268,7
64,6
87,8
С
0
282,9
702,9
173,8
233,5
0
101,0
18,6
73,3
0
252,0
85,5
193,5
Металл
Титан
Цинк
Алюминий
Латунь
Индий
Ниобий
Палладий
Платина
Радий
Тантал
Галлий
Цирконий
А
99,0
66,2
76,5
103,7
49,6
165,8
174,4
276,0
284,2
179,0
31,7
93,4
В
116,8
157,7
165,9
217,7
116,3
278,6
380,1
726,0
645,2
302,3
93,8
72,0
С
124,6
124,2
42,8
327,5
0
0
1523,0
0
0
0
148,5
0
59
Частным случаем УРС Тэта является кубическое уравнение
состояния. Если р ~ р3, то АА^ скорости звука с2 ~ dp/dp ~ р2, т.е. с ~ р, что
резко упрощает уравнения газодинамики и решение задач.
Кубическое УРС достаточно точно аая продуктов взрыва
конденсированных ВВ. Так, аля детонации u/D = 1/(п + 1)и при п = 3 u/D = 1/4,
что подтверждается экспериментально.
Для холодных твердых тел давление определяется упругостью
атомов
Р = [(р0с02)/3](ё3-1) (2.6)
где р0, с0 — плотность и скорость звука в несжатом веществе.
Если предположить, что тепловое давление также
пропорционально р3, то с учетом нагрева кубическое УРС будет иметь вид:
p=^L(ssi_l) (2.7)
где S — энтропийный множитель.
Если кубическое УРС записать в традиционной форме
р = рх + pv где рт = р (п — 1) Ev то получим полное кубическое
уравнение состояния:
p = -^-(S3-l) + 2pQS(E-Ex)
Ex=^-(S2-3S + 2) (2.8)
од
Е = Е+Ет=-?— + ^(--1)
х т 2p0S 2 S
Для описания экспериментальных точек ударных адиабат часто
используют УРС с согласованными п и h (иначе УРС с предельной
плотностью) [6].
Рассмотрим тепловое давление, которое можно представить как
сумму двух составляющих, определяемых тепловым движением
атомов в кристаллической решётке и для больших температур —
тепловым возбуждением электронов: рт = р + ре
60
Для вычисления первой составляющей р (V, Т) используется
квазигармоническое приближение Дебая, согласно которому
кристалл рассматривается как совокупность 3 N гармонических
осцилляторов.
Реальный вид спектра колебаний атомов в решётке и его
зависимость от объёма очень сложны. Модель Дебая задаёт фононный
спектр в акустическом приближении, причём твёрдое тело
предполагается однородным и изотропным. В дебаевском приближении
тепловые составляющие энергии и давления имеют вид:
Ep=3RTD(0/T)
y(V) (2-9)
где D (9/Т) — дебаевская 0 функция, обеспечивающая а^я
теплоёмкости низкотемпературную су ~ Т3 и высокотемпературную
су « 3 R асимптотики. 0 — температура Дебая, при которой
возбуждены все степени свободы и теплоёмкость максимальна.
Для относительно невысоких температур ударного сжатия (до
рн= 100 ГПа) пренебрегают термическим возбуждением
электронов и успешно применяют квазигармоническую модель —
уравнение состояния Ми—Грюнайзена:
p(V,T) = рх(у) + ГЮ.[Е-Ех(У)-\ (2.10)
где рх (V) = - d Ex/d V, а у (V) — коэффициент Грюнайзена, равный
отношению теплового давления к плотности тепловой энергии
решётки, у (V) = р /Е /V. Коэффициент Грюнайзена в обобщённой форме
зависит от объёма и рх следующим образом:
V(V)~ (2-И)
Значение параметра t=0 соответствует приближению Слэтера —
Ландау, t = 1 — модели Дугдейла — Макдональда, a t = 2 приводит к
теории свободного объёма Ващенко — Зубарева.
61
Если из опыта найдена линейная связь D = А + В и, то давление
на ударной адиабате:
„ _ с20(У0-У)
Р» {V-B{V0-V)f (2-12)
Параметр t можно связать с экспериментальными
величинами — наклоном ударной адиабаты В и коэффициентом Грюнайзена
при нормальных условиях уо = у (VQ):
; = 3(2Я-у0)-2 (2.13)
Для любого вида зависимости у (V) должна выполняться
асимптотика у = 2/3 при Т -> оо, уо = а с02/су при нормальных условиях
и правильно описывать ударное сжатие пористых веществ.
Аппроксимирующая зависимость у (V), удовлетворяющая этим
условиям, предлагается в [2] в следующем виде:
г(У) = \НгА)^тЗ (2.14)
тп
где S=VQ/V— относительное сжатие. Для различных металлов
а =0,5—0,9.
m
Точная зависимость у (V) может быть найдена только с учётом
реального спектра частот колебаний атомов в кристалле. Из
уравнений (2.10) и (2.11) не удаётся однозначно найти у (V), поскольку
производные от рх в (2.11) определяются по экспериментальной
адиабате очень неточно. При этом различные у (V) одинаково
хорошо описывают эксперимент.
Отметим, что /^ая больших температур эксперименты указывают
на необходимость учёта изменения у не только с объёмом, но и с
температурой. По данным [7] величина у с температурой уменьшается.
С ростом температуры колебания решётки становятся ангармо-
ничными. В рамках УРС Ми — Грюнайзена учёт ангармоничности
может быть сделан различными способами (см. [2]).
Например, вещество рассматривается как равновесная смесь
гармонических осцилляторов и идеального газа, причём
обеспечивается идеальногазовая асимптотика (переход от с = 2/3 R при Т -> 0
KCv = 3RnpnT->oo).
62
Рассмотрим электронную составляющую ре.
Как известно, в металлах валентные электроны образуют
электронный газ, подчиняющийся квантовой статистике Ферми- Дирака.
В соответствии с принципом Паули при Т = О К электроны
занимают наиболее низкие энергетические состояния и обладают энергией,
не превышающей
Е ~ п ^з-v273 (2Л5)
О е
где пе — число свободных электронов. Эта энергия включается
в упругую или «холодную» энергию и не является тепловой. С
ростом температуры в пределах Т < Т* (Т* — температура Ферми)
число возбуждённых электронов растёт, и каждый получает
дополнительную энергию порядка кТ.
Тепловая энергия электронов в 1 г металла равна:
Ее=О,50Т2 (2.16)
где коэффициент (2 зависит от плотности:
P = №'VQ)m (2.17)
Цельная теплоёмкость электронов при V=Const
пропорциональна температуре:
с„=РГ (2.18)
В нормальных условиях с на два порядка меньше теплоёмкости
решётки су = 3 NK, но уже при Т = 50000 К теплоёмкость
электронов становится выше теплоёмкости решётки.
При Т > Т* Е ~ V273 Т2 и су = 2/3 Nek — ^ая идеального
электронного газа.
В условиях ударного сжатия (до температур (3—5)104 К)
теплоёмкость электронов пропорциональна температуре по (2.18),
причём с ростом плотности эта пропорциональность сохраняется до всё
более высоких температур.
По аналогии с решёткой, определяя коэффициент Грюнайзена
из р = Г Е /V, получим, что ^ая свободного электронного газа
63
Г = 2/3. При меньших температурах в условиях ударного сжатия
можно принять Г = 1/2, но при этом Ее ~ V0,5 Т2.
В результате электронные члены У PC металлов получают
следующий вид:
Ee=0,5fiT2;fi = fi0(V/V0)l,2;pe=0,5Ee/V (2.19)
((J0 определяется аля Vq).
Таким образом, аля трёхчленного УРС удельную внутреннюю
энергию и давление можно представить как сумму трёх
составляющих, которые описывают упругие свойства холодного тела, тепловое
движение атомов и тепловое возбуждение электронов:
Ее=Ех + ЕТ + Ее'> Р=Рх+Рт+Ре
Ет= £>(в/Т)*су(Т-Т0) + Е0;
(2.20)
m
pT=y(V,T)ET/V;pe=0,5Ee/V
Изменение коэффициента Грюнайзенау и его аналога для
электронов Г в зависимости от сжатия и температуры показано на рис. 2.5.
V./V
Рис. 2.5. Зависимость у и Г от сжатия и температуры.
64
2.3. Учёт плавления и испарения
С ростом давления и температуры ударного сжатия неизбежно
плавление вещества (в ударной волне или на изэнтропе разгрузки), которое
слабо влияет на кинематические характеристики (D, и), но заметно ска-
° зывается на ход экспериментальных температурных зависимостей.
Наиболее точный учёт плавления осуществлён добавлением к Ет
функции, свободные параметры которой обеспечивают точное
описание экспериментальных скачков энтропии и плотности при плавлении.
Далее, при расширении очень сильно сжатых и нагретых веществ,
кроме плавления, возникает испарение, описать которое можно,
например, с помощью классического УРС Вандер—Ваальса:
(p-a/V2)(V-b) (2.21)
где параметры а и b подбираются по экспериментальным данным.
Проведение сквозных гидродинамических расчётов в широком
интервале изменения физических условий потребовало создания
широко диапазонных более сложных полуэмпирических УРС,
описывающих свойства вещества на фазовой диаграмме с
согласованным учётом эффектов плавления, испарения, ионизации и т. п. Такие
УРС были получены аая ряда металлов, воды и NaCl [2].
2.4. Табличные и аппроксимационные уравнения
состояния
Основное использование УРС — численные расчёты физических
процессов. По мере повышения точности УРС и расширения
диапазона его применимости усложняется форма УРС, возникает
необходимость вычисления положения фазовых границ плавления и испарения,
что значительно увеличивает время счёта при численном
моделировании. Сокращает затраты машинного времени задание УРС в табличной
форме, причём в качестве исходной информации используются как
теоретические модели, так и полуэмпирическое описание экспериментов.
Таблицы составлялись следующим образом. Проводилась
процедура двумерной гладкой сшивки отдельных участков фазовой
диаграммы и затем в узлах заданной табличной сетки определялись
значения термодинамических величин.
65
Табличный способ позволяет легко заменять часть расчётных
данных на новые, более точные. Недостаток табличной формы
У PC — возможные термодинамическая несогласованность
участков, немонотонность и разрывы производных, что может мешать
проведению расчётов.
Аппроксимационные УРС имеют более сложную структуру,
но более точны и обеспечивают согласованность расчётных данных.
^ддрноволновые эксперименты определяют УРС в неполном
калорическом виде Е (р, V) и требуют дополнения в виде зависимости
T(p,V).
Эта зависимость находится из решения следующего
линейного неоднородного дифференциального уравнения в частных
производных, которое получается, исходя из первого начала
термодинамики и экспериментальной зависимости Е (р, V):
_ . т^ лзт ,дЕ. дт / ч
^^ак^ф-^'ак (2-22)
Калорическое УРС Е (р, V) строилось на основе аппроксимации
экспериментальных точек в виде полинома:
Eq(p^=Tk,<_Xe^kvl (223)
k+l<q
где коэффициент еы находится методом наименьших квадратов.
Точность расчётной температуры определялась в зависимости
от погрешности экспериментальных точек и их расположения на р,
V плоскости с использованием метода Монте-Карло.
Статистический анализ показал, что для описания всех
имеющихся точек достаточно выбрать значение q = 3.
Таким способом получена УРС, например, аая никеля, вольфрама
и Li F, причём с описанием полиморфного перехода у LiF и с
характерной ступенькой на ударных адиабатах, вызванной плавлением. Точность
интерполяционного УРС АА^ вольфрама иллюстрирует рис. 2.6.
Подробно об УРС со ссылками на литературу можно прочитать
в [1,2].
66
1 2 3 4
Рис. 2.6. Описание ударных адиабат вольфрама аппроксимационным УРС:
m=Vw/ V0 — пористость, о — эксперимент [7].
2.5. Экспериментальные ударные адиабаты различных
веществ и методы их нахождения
Как было показано, УРС конденсированного вещества основано
на ударной адиабате этого вещества, которая определяется
экспериментально в определенном диапазоне давления в виде линейной
зависимости D=А + Ви, из которой легко рассчитать давление и плотность:
р = p0Du = р0(Аи + Ви2)
D (А + Ви) i/D п (2.24)
D-u А
Подставляя в (2.24) с известными р0, А, В значения и от 0 до
требуемого значения, например, через 0,1 км/с, можно построить р-и
диаграмму данного вещества.
В таблице 2.3 приведены ударные адиабаты многих веществ
согласно данным американских лабораторий в Ливерморе [8] и в Лос-
Аламосе [9]. На рис. 2.7 изображены некоторые р-и диаграммы,
построенные по (2.24) и данным табл. 2.3. Там же приведены т. н.
кривые торможения (изэнтропы продуктов детонации) а^я трех
взрывчатых составов различной мощности:
— кривая 5 — для зарядов из состава, состоящего из 50% ТНТ
и 50% гексогена (RDX);
— кривая 7 — для зарядов из состава 30% ТНТ и 70%
гексогена;
67
Р, кбар
о ^
О 0.2 0,4 0,6 0,8 1.0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3.0 3,2 3,4 3,6 3,8 4,0 4,2 4,4 4,6
U, км/с
Рис. 2.7. Ударные адиабаты и кривые торможения.
68
р, Ю''мбар
Рис. 2.8а. Ударные адиабаты металлов и кривые торможения ВВ.
— кривая 9 — аля зарядов из смеси 90% октогена (НМХ)
иЮ%ТНТ.
Пересечение кривой торможения с р-и диаграммой дает
величину давления и массовой скорости вещества при контактном
взрыве заряда из данного состава на поверхности данного
вещества (лобовое столкновение детонационного фронта с веществом).
Например, согласно рис. 2.7 плоская детонационная волна в
заряде из ТГ50 создает: в железе — 410 кбар, в алюминии —325 кбар,
в воде — 177 кбар.
69
PRESSURE (kbars)
0 0,5 10 15 20 25 30
PARTICLE VELOCITY (cm/ц sck)
Рис. 2.86. Ударные адиабаты некоторых веществ. Изэнтропы систем ВВ + А1.
Прямая Релея и кривая торможения для Сотр. В (расчёт по УРС BKW) [10].
70
На рис. 2.8 а приведены р, и — диаграммы ряда металлов и
кривые торможения некоторых маломощных ВВ [31].
фарные адиабаты ряда веществ и кривая торможения аля
Сотр.В показаны на рис. 2.8 б [10].
Пересечение прямой Релея (линия, на которой постоянна
скорость стационарной детонации) с кривой торможения даёт условия
в точке Жуге. Выше точки Жуге кривая торможения является
ударной адиабатой ПД, а ниже — изэнтропой разгрузки.
На рис. 2.8 б. пунктирные линии — это кривые торможения
экспериментальных систем, состоящих из заряда различных ВВ
в контакте с алюминиевой пластиной. Цифры означают давление
в кбар, создаваемое зарядом в алюминии. Например, 350 означает,
что Сотр.В создаёт в алюминии давление в 350 кбар, а тротил —
только 240 кбар. Пересечение пунктирных линий с ударными
адиабатами даёт величины р и и, создаваемые в веществе
экспериментальными системами ВВ + А1.
Подчеркнём, что кривые торможения и ударные адиабаты сняты
в условиях плоской стационарной детонации. Учёт многомерности
детонационной волны требует применения численных методов
моделирования, также, как и глубокая разгрузка ПД в малоплотные среды (газы).
Сохранение линейного D-u соотношения ^^я всех веществ
можно объяснить сходным характером потенциалов отталкивания всех
видов атомов, молекул, ионов (а при ударном сжатии преобладает
энергия отталкивания). Каждое данное D-u соотношение
пригодно только аая одной данной фазы, т. к. наклон прямой при фазовом
переходе меняется.
Если линейность сохраняется вплоть до низких давлений, когда и —>
0, то скорость D и величина коэффициента А должны быть равны
пластической или гидродинамической скорости звука с = Jdp I dp -
Коэффициент В или наклон линейной D-u зависимости
определяется следующим выражением [11].
в ■ iv\#pidv\ (225)
4 V(dp/dV)s
71
Таблица 2.3. Экспериментальные D—и соотношения веществ [1,8,9]
Наи> [енование
элемента
1
АзотЫ
Т=77,4 К
Т=77К
Алюминий А1
Алюминий А1
Алюминий А1
Пористый А1
Пористый А1
Пористый А1
Пористый А1
Пористый А1
Алюминий А1
Алюминий А1
Аргон Аг
Бериллий Be
Ванадий V
Висмут Bi
Висмут Bi
Вольфрам W
Германий Ge
Железо Fe
Р
г/см3
2
0,808
0,808
2,7
2,71
2,78
1,816
1,348
1,919-
1,93
1,575-
1,590
1,344-
1,350
2,7-
2,586
2,794
1,400-
1,409
1,851
6,10
9,767-
9781
9,8
19,17
5,239-
5,327
7,82—
7,86
D=A+BU
А В
км/с
3
1,588
1,219
5.38
5,38
5,355
-0,128
-0,057
2,08
1,12
0,426
5,39
5,24
0,84
8,056
5,108
1,58
2,00
4,005
1,52
4,955
4
1,360
1,622
1,337
1,35
1,345
2,76
2,03
1,71
1,78
1,83
1,32
1,77
2,07
1,145
1,210
1,61
1,34
1,268
1,83
0,454
Скорость
звука с
км/с
5
с =0,849
с =0,857
с = 6,2
с = 63
с = 0,848
с = 8,137
с=7,934
с = 5,18
с=186
с = 4,05
с = 3,77
с = 3,82
с = 3,24
Интервал
давлении
р, кбар
6
20—400
10—170
640—920
690—1970
15—1020
65-170
40—130
184—530
210—430
170-370
280—660
25-50
1—40
150—910
200—1250
70-855
350-3450
390—2070
350—900
40—130
72
Наименование
элемента
1
Железо Fe
Железо (армко)
Кадмий Cd
Магний Mg
Медь Си
Молибден Мо
Никель Ni
Олово Sn
Олово Sn
Платина Pt
Свинец Pb
Серебро Ag
Скандий* Sc
Тантал Та
Тантал Та
Р
г/см3
2
7,82—
7,86
7,85
8,64
1.78
8,9
10,20
8.86
7,28
7,28
21.43
11,34
10,49
2.996-
3,035
16.46
16,66
D=A+BU
А В
км/с
3
2.049
3,8
3,809
4,65
3.944
5,143
4,796
2,49
2,64
3,646
2,006
3,271
4,45
3,139
3.453
4
3,79
1,58
1,226
1,20
1,514
1,255
1,254
1,59
1,476
1,535
1,538
1,575
0,87
1,531
1,197
Скорость
звука с
км/с
5
с = 4,64
с = 4,65
с = 2,93
с = 5,60
с = 4,46
с = 2,26
с = 4,7
с = 3,92
с=5,19
с = 2,96
с = 5,63
с = 4,47
с =2,674
с = 2,76
с = 2,76
с =1,79
с = 4,08
с = 3,51
с=3,41
с = 0,6
с = 2,16
с=1,59
с = 3,6
с = 3,09
с =3,25
с =5,69
с =4,28
с = 3,35
с = 2,07
с = 4,15
с = 3,39
с = 3,41
Интервал
давлении
р, кбар
6
135—320
400—4870
300—9400
60-740
210—500
230—4950
230—510
150—1000
780-1370
320—2710
80—1400
210—515
80—750
270—540
280—2300
73
Наименование
элемента
1
Титан Ti
Титан Ti
Пирографит
Пирографит
Графит пористый
Графит пористый
Графит пористый
Графит порист.
Графит порист
Графит порист
Пирографит
Пирографит
Пирографит
Графит технич
Графит Цейлон
прессованный
Графит
технический
Графит пористый
Графит пористый
Графит пористый
Графит пористый
Р
г/см3
2
4,51
4,51
2,2
2,2
2,11—
2,14
1,91-
1,97
1,93-
1,96
1,96
1,88
1,88
2,2
2,2
2,2
1,628
2.185—
2,170
1.812—
-1,673
1.76-
—1,81
1,81—
1,76
1,52-
1,56
1,56.-
1,52
D=A+BU
А В
км/с
3
4,695
4,779
4,67
4,14
4,13
3,36
2,13
3,81
1,78
4,01
3,91
5,01
4,2
1,162
3,9
3,32
1,45
3,41
0,51
2,72
4
1,146
1,089
1,514
1,21
1,06
1,13
2,01
0,99
2,02
0,89
2,14
1,05
1,66
1,822
1,177
0,99
1,93
0,985
2,10
1,05
Скорость
звука с
км/с
5
с = 4,84
с = 4,84
с = 3,45
с = 3,9
с =1,65
с = 2,54
с = 1,68
с=11,2
Интервал
давлении
р, кбар
6
150—3100
760—1060
110—430
650—800
280—720
410—700
80—250
250—650
70—210
210—630
30...130
130—270
270—460
40—210
310—570
160—610
70—200
200—600
50-160
160-530
74
Наименование
элемента
1
Алмаз - 95%,
Графит - 5%
Алмаз
Уран U
Уран U
Хром Сг
Хром Сг
Цинк Zn
Цирконий Zr
Галогениды:
CsBr
CsCl
КС1
KF
KJ
LiBr
LiF
Lij
NaBr
NaCl
NaJ
Латунь
Фторопласт Ф4
Оргстекло
Спирт (этилов.)
Р
г/см3
2
3,2-3,17
3,51
18,8
18,8
7,13
7,1
7,14
6,503-
6,512
4,43
3,95
1,98
2,49
3,1
2,05
2,62
4,01
3,16
2,15
3,64
8,41
2,215
1,18
0,81
D=A+BU
А В
км/с
3
12,16
2,445
2,42
5,249
5,217
3,050
3,287
3,1
2,2
1,8
2,4
1,8
4,1
5,0
2,8
2,6
3,4
2,0
3,8
1,9
3,22
1,67
4
1,0
1,655
1,593
1,445
1,465
1,559
1,287
0,3
0,5
1,8
1,6
1,4
1,5
1,6
0,9
1,3
1,37
1,6
1,42
1,74
1,29
1,56
Скорость
звука с
км/с
5
с =12,16
с = 5,15
с = 3,03
с = 2,39
с = 3,88
с = 3,74
Интервал
давлении
р, кбар
6
450—1100
6000
50—500
550—6600
230—480
920—1380
740—1400
360—1440
146—328
110—5450
60—318
40—229
117—266
110—278
121—263
155-331
205—320
58...305
52—891
134—312
167—1764
75
Наименование
элемента
1
Пенопласт
Пенопласт
Пенопласт
Пенопласт
Пенопласт
Воздух
Полиэтилен
Полиэтилен
Вода Н О
Р
г/см3
2
0,51
0,50
0,365
0,33
0,32
0,00129
0,82
0,917
1,0
D=A+BU
А В
км/с
3
0,71
0.70
0,31
0,22
0,2
0,269
2,95
1,57
1,91
4
1,32
1,31
1,299
1,291
1,29
1,046
1,39
2,37
1,56
Скорость
звука с
км/с
5
Интервал
давлении
р, кбар
6
[176]
Жидкие органическ. вещества:
Спирты,
ненасытен.
Углеводороды,
КИСЛОТЫ,
Ангидриды, кето-
ны (ацетон)
0,816
(средн.)
2,05
1,464
100—600
Жидкие алканы:
Гексан С Н
Гептан С Н
Декан С Н
Гексадекан С Н
Тротил [178]
Тротил
Состав В-3
(Г-60%,ТНТ-40%)
Гексоген
ТЭН
Октоген / тротил
75/25
0,661
0,691
0,741
0,778
1,614
1,80
1,73
1,81
1,738
1,808
1,970
2,127
2,39
2,372
2,71
2,87
2,17
2,02
1,446
1,450
1,458
1,464
2,05
2,16
1,86
1,61
1,91
2,36
2,572
0-363
0-387
0—406
0—425
16—126
3,68—24,2
21-70
76
Наименование
элемента
1
Кварц SiOz
Оргстекло [177]
Р
г/см3
2
D=A+BU
А В
км/с
3
2,32
2,58
4
1,04
1,525
Скорость
звука с
км/с
5
3,69
Интервал
давлении
р, кбар
6
Интервал
и, км/сек
1,726—3,88
0,5-2,63
Горные породы
Магматические:
Граниты
Туфы
Сиениты
Габбро
Порфиры
Осадочные:
Сланцы
Известняки
Доломиты
Глины глубин
Песчаники
2,60
2,74
2,74
2,89
2,62
2,77
2,72
2,84
2,21
2,65
2,435
3,75
2,69
3,814
2,76
3,35
2,098
2,77
3,75
4,99
3,32
2,02
4,53
1,525
1,28
1,55
1,327
1,50
1,46
1,617
1,54
1,44
1,24
1,02
1,65
1,24
2,16-5,10
8,9-5,10
2,5—4,8
6,0—4,8
2,15—6,25
1,8—4,0
2,2—6,25
2,2—6,1
4,2—0,8
8.6-1,1
4,7-2,8
6,2—2,3
8,8-6,2
Кривые торможения ПВ
Наименование ВВ
ТГЗО
(гексоген — 70%, тротил — 30%)
Кривая 7 на рис. 2.7.
р,кбар
563
490
374
304
181
111
81
1,04
и,км/с
1,014
1,785
2,313
3,287
3,80
4,34
8,68
77
Наименование ВВ
Октол
(октоген — 90%, тротил — 10%)
Кривая 9 на рис. 2.7.
р,кбар
671
570
456
382
348
282
221
130
102
99
1,229
и,км/с
0,91
1,41
2,07
2,65
2,59
3,24
3,69
4,204
4,52
4,73
9,415
Однако определение производных по экспериментальным изэн-
тропам очень неточное. Различные теории твердого состояния дают
различные расчетные величины наклона В, которые могут отличаться
от экспериментальных значений до 25%. Так, согласно теории Слэтера
В=у/2 + 1 /3, по теории Дугдайла-Магдональда В=у/2 +1 /2, а согласно
модели Томаса-Ферми для металлов наклон В меняется от 1,1 для самых
легких до 1,5 для самых тяжелых, и кроме того, В не может оставаться
строго постоянной с ростом давления.
Для большинства веществ В = 3/2 при умеренных давлениях,
а при р -> оо преобладает тепловая энергия, любое вещество
превращается в идеальный газ, для которого В = 4/3.
Вот почему в таблице 2.2 аля величин А и В указан интервал
давления.
Отметим, что при сохранении линейности D — и соотношения
Аая р -> оо величина предельного сжатия твердых тел в одной ударной
волне (V/VQ)max = (В — 1)/В, что следует из выражения ^ая давления
на ударной адиабате в р, V координатах:
-А\У/У0-\)
р v0(B-i-BV/v0f (226)
Для В = 3/2 максимальное сжатие Smax = (V/V0)max =1/3 (аая
идеального газа (V/V ) = 1 /4).
78
Как показано в [12], при одинаковых степенях сжатия
величины В для различных веществ группируются возле трех значений: 1,0,
1,2 и 1,5, причем аля каждого значения В любые две ударные
адиабаты в координатах р, S будут пропорциональны или подобны, т. е.
р (S) = k р (S), где к — постоянный коэффициент подобия.
Таким образом, величина В является критерием подобия
ударных адиабат. С тем же коэффициентом подобны и нулевые изотермы
[13]. На основе такого подобия в [14] предложен метод расчета
температур ударного сжатия.
Для более точного описания ударных адиабат в
широком диапазоне давлений используется трёхчленное уравнение
D = aQ + а{ u +а2 и2, параметры которого аая 6-ти металлов даны
в табл. 2.4
Таблица 2.4. Параметры ударных адиабат в виде
D=aQ + aJu +л2и2
Metal
Fe
Си
Cd
Mo
Pb
Al
a0, kms1
3,664
5,869
6,982
3,899
5,905
2,456
4,251
5,08
6,711
1,972
3,18
5,331
6,371
ui
1,79
1,239
1,190
1,534
1,212
1,734
1,182
1,294
1,149
1,571
1,169
1,417
1,164
a2, km'1
-0,0342
0,00017
0,00011
-0,0129
3,76 xlO5
-0,0424
7xl05
-0,00288
34,1 x 10-5
-0,0335
5,52 x 105
-0,015
io-5
Range of
applicability
1,4<U<8
8<U<22
U>22
U < 12,5
U > 12,5
U<6,5
U>6,5
U < 22,5
U > 22,5
U<6
U>6
U<8,2
U>8,2
Остановимся кратко на экспериментальных методах
нахождения ударных адиабат. [32]
79
Как было показано, задача определения калорического
уравнения состояния Е = Е (р, V) в области, перекрытой ударными
адиабатами, сводится к измерению волновых и массовых
скоростей в стационарных ударных волнах или в простых волнах
разгрузки.
В свою очередь измерение D или и требует измерения
расстояний и промежутков времени, что может быть сделано с высокой
точностью с помощью дискретных измерительных методик и
аппаратуры.
Одна точка ударной адиабаты определяется измерением
двух независимых параметров ударного сжатия — D и и. А вели-
чины р, V, Е затем вычисляются по известным D и и на основании
законов сохранения. Скорость ударной волны измеряется
непосредственно любой дискретной методикой (оптической или
электроконтактной), а для определения массовой скорости
используется анализ распада разрыва на границе ударник — образец или
экран — образец.
Существует два абсолютных и два относительных
метода определения точек ударной адиабаты данного вещества (см.
табл. 2.5).
Таблица 2.5. Методы определения ударной
адиабаты вещества
Название
Что измеряется
Как определяются величины р, и
Абсолютные методы
Метод откола
Соударение
ударника и образца
из одинакового
материала
D в образце и скорость
свободной поверхности
образца w — 2 их
D в образце и скорость
ударника w = 2u
Dxu их = w/2 — в эксперименте
Dxu ux=w/2— в эксперименте
p = pnD и
*x *0 x x
Относительные методы
Метод
торможения (рис. 2.10)
D в образце и скорость
ударника w с известной
ударной адиабатой
Определяются координаты/^ их
точки пересечения волнового луча
р =pQDxux для образца и зеркальной
ударной адиабаты ударника,
построенной из точки р = 0, u = w.
80
Название
Что измеряется
Как определяются величины р, и
Метод отражения
(рис. 2.9)
Dx в образце hDb
экране с известной ударной
адиабатой
Находится/^ «точки
пересечения волнового луча р =pDe
ие с ударной адиабатой экрана.
Определяется р, и точки
пересечения волнового луча/> =р Du для
образца с зеркальным
отображением ударной адиабаты экрана,
построенной из точки р , и£
Г)
Г,
п
1с
\
\
р =pD u
Гх Jx х х
*\у/
У/
\
\
У
7
\
\
\
\
ч
ч
ч
ч
ч
Рис 2.9. Метод отражения.
w и
Рис. 2.10. Метод торможения.
С помощью абсолютных методов измеряют непосредственно
в эксперименте D и их в исследуемом веществе, а аля
определения и в относительных методах используются эталонные вещества
(ударник или экран) с известной ударной адиабатой. Точность
относительных методов ниже, поскольку на результаты сказывается
погрешность эталонной ударной адиабаты.
В методе откола а^я исключения влияния прочности
исследуемого материала на скорость свободной поверхности
используется искусственный откол. В этом случае измеряется скорость
тонкой пластины из материала образца, плотно прижатой к образцу.
Используемое в методе откола явление удвоения массовой скорости
на свободной поверхности справедливо только для непористых тел
и а^я не очень больших давлений (до ~ 50 ГПа).
Абсолютный метод соударения одинаковых ударника и образца
также имеет ограничения в применении, поскольку в качестве
ударника невозможно использовать жидкости и малопрочные вещества.
81
В методе отражения (см. рис. 2.9) при распаде разрыва на
границе экран — образец в экран пойдет либо отраженная ударная волна,
либо изэнтропическая волна разрежения. Такое отражение волн ^ая
умеренных давлений с хорошей точностью описывается в р — и
координатах зеркальным отражением ударной адиабаты экрана
(относительно любой известной точки ре, ие на адиабате). Преимущество
метода отражения в том, что измеряются только волновые скорости,
а это проще измерений массовой скорости.
Тем не менее, метод торможения (см.рис. 2.10) также широко
используется, поскольку обычно в этом методе применяется установка
(т.н. «пушка»), разгоняющая ударник до скорости w, измеренной
заранее с большой точностью.
При проведении экспериментов с экстремально высокими
давлениями (десятки Мбар), выходящими за диапазон давлений, при
которых найдена эталонная ударная адиабата, в качестве эталонной
используется интерполяционная зависимость, связывающая
экспериментальный участок адиабаты (р < 10 Мбар) с расчетными
величинами, определяемыми квантово — статистической моделью
Томаса—Ферми (р > 100 Мбар). Поскольку расчеты по Томасу-
Ферми более надежны аля металлов с большими атомными номерами,
в качестве эталона используют тяжелые металлы, например свинец [15].
Во всех методах предъявляются высокие требования к ударнику
после его разгона:
— к геометрии поверхности (плоская, сферическая);
— к температуре (ударник не должен заметно нагреваться);
— к целостности (ударник не должен разрушаться, расслаиваться)
Измерения должны проводиться в условиях однородного
ударного сжатия, т. е. в таком объеме образца, где нет влияния боковых
и задних волн разгрузки.
В заключении назовем имена ученых, внесших наиболее
значимый вклад в экспериментальные исследования ударных адиабат
твердых веществ: Л.В. Альтшулер, СБ. Кормер, К.К. Крупников,
Р. Ф. Трунин, М. Н. Павловский, М. А. Подурец, С. А. Новиков,
В. Н. Зубарев, В. Д. Урлин, Г. В. Симаков и др. — в России.
82
M.Walsh, R.H.Christian, D.Mallory, B.I.Alder, D.Bankroft,
R.G.MeQueen, M.H.Rise, Van Thiel, S.RMarsh, D.S.Hughes,
I. Wackerle и др. — в США.
2.6. О температуре ударного сжатия
Специфика экспериментов по определению ударных адиабат
состоит в том, что измеряются только скорости, что позволяет найти
связь энергии, давления и объема, т. е. получить У PC в неполном
калорическом виде Е = Е (р, v).
Для расчета процессов, связанных с теплопереносом, с
кинетикой фазовых превращений нужно знание температуры. К
сожалению, измерение температуры одновременно с измерением скоростей
обычно невозможно. Поэтому приходится температуру
рассчитывать. Ниже рассматриваются некоторые методы таких расчетов.
Основы расчетных методов изложены в работах [2,15—22].
Предварительно сделаем несколько общих замечаний о
специфике ударноволнового нагрева вещества.
1. При прохождении УВ температура вещества повышается
практически скачком, как и давление, и величина температуры
растет с давлением.
2. Причем этот рост температуры за фронтом УВ более сильный,
чем при адиабатическом сжатии за счет необратимых потерь
энергии при быстрой пластической деформации ударносжатого
вещества. Температуру и энергию за фронтом УВ можно
представить состоящей из двух частей: обратимой (изэнтропиче-
ской) и необратимой. Поэтому после разгрузки остаточная
температура вещества будет меньше на величину обратимой части
и будет определяться необратимыми потерями энергии ударного
сжатия.
3. Эмиссионные спектры ударносжатых веществ [18,19]
показали, что цветовая температура может на порядок превышать
расчетную температуру на ударной адиабате, которая определяется
в предположении однородного нагрева всего сжатого объема.
Микроструктура образцов, сохраненных после сжатия, также
свидетельствует о локализации зон пластической деформации.
83
Следовательно, необратимые потери энергии ударного сжатия
распределяются в веществе неоднородно, нагревают какие-то
выделенные зоны (например, границы зерен, полосы скольжения,
примеси, поры).
Со временем за счет теплопроводности более высокая локальная
температура выравнивается до величины, одинаковой аая всего
объема. Таким образом, можно говорить о существовании двух температур
ударного сжатия — неравновесной (локальной) и равновесной.
Неравновесная температура определяется диссипацией энергии
не во всем объеме v однородно, а в некоторых выделенных областях
объемом v < < v. Геометрия этих областей нагрева может быть
различной: точка, линия или плоскость.
Расчет равновесной температуры на ударной адиабате.
При ударном сжатии единичного объема вещества увеличение
внутренней энергии составляет:
ЕТ=ЕН-ЕХ (2.27)
^ ET=cv(TH-T0) (2.28)
Откуда легко найти Тн, если известна удельная теплоемкость су.
Согласно теории Дебая fi^ кристаллической решетки
cv=jn4kN(T/ef (2.29)
где: к — постоянная Больцмана, N — число степеней свободы, 0 —
дебаевская температура, выше которой в кристаллической решетке
возбуждены все степени свободы, и величина теплоемкости су по
правилу Дюлонга и Пти постоянна и равна су = 3 R на моль или су=3 R/m
на грамм, где m — атомный или молекулярный вес.
Отсюда
1/?
cv=—D(e/T); ET=cv(TH-T0) (2.30)
m
где D (Т/6) — функция Дебая. При Т > 0 D (Т/0) = 1.
84
С другой стороны, по определению 9 = (hcomax/k), где h —
постоянная Планка, а сотах — частота, ниже которой энергия
кристаллического осциллятора Е = hco быстро падает до нуля с уменьшением
температуры от 9 до нуля.
Поскольку частота и упругая скорость звука с связаны, можно
вывести другое выражение аля 9:
Ля V к
(2.31)
где N/V — число атомов в единице объема.
Поскольку с~£ (^— сжимаемость), то ^ая изменения дебаев-
ской температуры с объёмом получим [23,24]:
в 100 = Cr0 / Z)V2(V I V0)mf(M) (2.32)
Если принять коэффициент Пуассона [л = Const, то. f ([л) = 1. Как
видно, увеличение 9 с давлением больше у того вещества, у которого
больше уменьшение сжимаемости и объема. Для простейшего У PC
в форме Тэта 9/9Q = (S)(3n-1)/6 [20], что аая предельных сжатий
(идеальный газ с = 5/3) дает асимптоту 9 ~ S2/3.
Сделанные нами расчеты для графита [20]) показали, что 9
сильно растет с давлением, а, следовательно, теплоемкость су пада-
зооо
2000
Р,ГПа
Рис. 2.11. Зависимость от давления температуры Дебая (сплошные линии)
и удельной теплоемкости (штриховые) графита.
85
lg[(T+1000)10-3]
О 1 2
Рис. 2.12. Изменение теплоемкости решетки с температурой.
ет (Рис. 2.11), что заметно повышает расчетную температуру
ударного сжатия. Например, &ля Т=1300 К и р=30 ГПа: 9/90=1,9,
cv/cv =0,68, Ег/Ет0=0>6> S/S0=0,5.
В [2] приведены другие зависимости 9(v). Решеточная
составляющая тепловой части термодинамического потенциала твердого
тела в [2] задается выражением:
F{VJ) = 3RT]n[0(S) IТ] (2.33)
содержащим только одну эмпирическую зависимость 9( S), В
пределе аля больших сжатий 9 (S) ~ S2/3.
Таким образом, мы получили, что при Т < 9 теплоемкость
уменьшается с ростом сжатия решетки.
Поскольку основной нагрев обусловлен быстрой пластической
деформацией ударносжатого вещества, то а^я расчетов температуры
надо брать среднюю величину теплоемкости в интервале Тн—Т0 а^я
решетки, сжатой до объема V на ударной адиабате.
Обычно берут максимальное значение су = 3R / т, поскольку аля
большинства веществ 9 < < Тн, т.е. в расчетах температур не
учитывают уменьшение теплоемкости.
86
Такой учет впервые был сделан в работе [21] при анализе
результатов ударного сжатия пористых металлов, когда тепловая энерги
настолько велика, что металл может плавиться и даже превратиться в
высокоплотный газ.
Как известно, теплоемкость жидкости с ростом температуры
уменьшается от величины 3R до значения 3R /2, характерному а^я
газов. Поскольку увеличение плотности эквивалентно уменьшению
температуры, то с ростом плотности будут увеличиваться
температуры, при которых заметно снижение теплоемкости.
Для расчета теплоемкости предложено следующее выражение:
cv(T,V)=^R[l + (l + zy2] (2.34)
где z=l R Т / с - величина, уменьшающаяся с объемом и
пропорциональная отношению тепловой и упругой частям давления, причем,
1 — эмпирический параметр, определяемый из ударных экспериментов
с пористыми образцами, cx2 = 3Rx/3p — упругая скорость звука, через
которую учитывается влияние объема.
Изменение су с температурой согласно (2.34) аая А1, Си, Ni, Pb
при S = 1 и S = 2 дано на рис. 2.12.
Для высоких температур (Т >>9) с учетом изменения
теплоемкости по (2.34) тепловые составляющие энергии и давления имеют
вид [2]:
1 2 + 7
TV 1 2 1 + Z
(2.35)
Ъу + zRT
Pt(v>t) = — —
1 + z 2
В [25] получено явное аналитическое выражение аая расчета
температуры в зависимости от коэффициентов А и В ударной адиабаты,
величины сжатия, коэффициента Грюнайзена и теплоёмкости.
После изэнтропической разгрузки ударно-сжатого материала его
остаточная температура Т2 связана с температурой Тн на ударной
адиабате уравнением изэнтропы:
87
Рис. 2.13. Зависимости равновесной температуры от давления на ударной
адиабате. Точками указаны условия при контактном взрыве заряда из ТГ 50.
T2/TH=(VH/V2y
(2.36)
Тепловое расширение за счет остаточного нагрева дается
выражением:
V2-V0=V0a(T2-T0) (2.37)
где а - объемный коэффициент термического расширения.
Решая совместно (2.36) и (2.37), получим зависимость
конечной температуры Т от температуры Т и удельного объема V в
УВ [25]:
VMTHVrH-T0V")
тг =THvrHi[к + ° Ун н——у
2 н н l0 V'+ayTHV>
(2.38)
Зависимость температур от давления в УВ для ряда материалов
дана на рис.2.13. Зависимость построена нами по табличным
данным ряда работ, собранным в [4].
88
Как видно, нагрев в УВ у разных материалов разный и
растет с ростом сжимаемости. Например, при давлении 50 ГПа
свинец нагревается ударной волной на 24300 , а вольфрам — только
на 1800.
Оценка неравновесных температур ударного сжатия.
Согласно [26], величина необратимых потерь энергии на
пластическую деформацию г вещества в ударной волне составляет:
АЕрЛр0А2Ве2 (2.39)
Предполагая, что эта энергия нагревает в УВ не весь объем v
кристалла, а только некоторую часть v*, найдем первоначальную
максимальную температуру Т* этого объема:
су V 3cv V
Величина Т* — это локальное превышение температуры над
температурой однородного изэнтропийного нагрева, достигаемое за время
нарастания давления на фронте УВ. Затем со временем за фронтом эта
температура выравнивается за счет теплопроводности, и в результате
мы получаем равновесные температуры, величины которых были
рассчитаны выше, исходя из тепловой энергии ударного сжатия.
В [26] сделаны оценки Т* при следующих предположениях.
В каждом кристаллите размером 1 есть только один очаг
тепловыделения и тогда
V/V=(l/Alf-r (2.41)
где г = 0, 1, 2 - размерность очага (точка, линия, плоскость),
А1 = (7Г £ t)0,5 - длина прогрева за время t, £ - коэффициент
теплопроводности.
Тогда (2.40) получает вид:
Л2Яръ /3_г
Г = £ , 1 (2.42)
Типичные величины для металлов:
89
Х= 5 х 10"5 м2/с; t = 10"(12_8) с и Al = 10"(8"6) м, размер
кристаллита ~ 10 мкм, деформация г — 0,1 (рн « 5 ГПа).
Тогда оценка по (2.42) дает Т* « 107, 105, 103 К для
пластических очагов нагрева соответственно в точке, на линии и в
плоскости. Очевидно, реальны двумерные очаги в виде пакетов плоскостей
скольжения.
Согласно [27], измерения температуры деформирования
минералов достигали 4 х 103 К. Проведенные нами опыты с алмазом
показали, что при скорости стального лайнера, раскалывающего
алмазный кристалл, равной 1,5 км/с, наблюдается графитизация
алмаза. Следовательно, в этих условиях на плоскостях (III) спайности
алмаза температура превышала 1800 С (при этом средняя
температура сжатия была не более 100 С).
Быстрая деформация происходит на фронте УВ, где за время t*
одномерное сжатие решетки переходит в гидростатическое
сжатие. При этом скорость деформации зависит не только от давления,
но также от скорости нарастания давления р /1* (крутизны фронта),
которая при постоянном давлении легко может меняться в
эксперименте. В [28] сопоставляются результаты ударного — (p/t*)max и
динамического изэнтропического сжатия — (р/^)т1п •
Более точный расчет
локальных температур
сложен и требует
рассмотрения процессов
деформации на микроуровне.
Физический механизм
деформирования решетки
заключается в движении
дислокаций в плоскостях
сдвига. Энергия этого
движения, в основном,
определяется затратами
энергии на преодоление
барьера Пайерлса и на
вынужденные колебания
атомов. Величины этих
Т°,К
2000
1600
1200
800
400
0
[ -
]
\ ^/
уЛ
20 30
40
50
60
Р,ГПа
Рис. 2.14. Расчетные температуры ударного
сжатия графита.
1 — изэнтропа, 2 — ударная адиабата,
3 — неравновесная температура плоскостей
сдвига (002).
90
энергий зависят от модуля сдвига вещества и от скорости движения
дислокаций. Обе эти величины растут с давлением в УВ, поэтому и
температура растет.
При малом давлении дислокации начинают двигаться только в
одном семействе плоскостей решетки, имеющем наименьшее
критическое напряжение сдвига (упорядоченный сдвиг). Затем с ростом
давления сдвиг охватывает и другие плоскости и идет
одновременно на нескольких пересекающихся плоскостях (неупорядоченный
сдвиг). При этом движение дислокаций останавливается, растут
точечные дефекты.
Таким образом, с ростом давления в УВ увеличивается степень
аморфизации кристаллической решетки, растут плотность зон
локального разогрева и скорость выравнивания локальных температур.
В заключение отметим решающую роль локального разогрева при
инициировании гетерогенных ВВ слабыми УВ. Вследствие физической
неоднородности заряда ВВ (поры, включения) часть энергии ударного
сжатия локализуется в « горячих точках», что приводит к возбуждению
в них экзотермической реакции разложения ВВ. Наконец, очень
короткое время (~ 10"10 с) на фронте УВ существует высокая неравновесная
температура, обусловленная возбуждением только одной
поступательной степени свободы молекул ВВ.
Нами сделана оценка локального нагрева базовых плоскостей
(002) графита за счет диссипации энергии движущихся в этих
плоскостях краевых полудислокаций с вектором Бюргерса, равным 1/3.
Такие дислокации при одномерном сжатии переводят обычный
гексагональный графит с чередованием слоев типа АВАВ в
ромбоэдрический графит с алмазным чередованием слоев типа АВСАВС.
На рис.2.14 даны расчетные равновесные температуры на из-
энтропе, на ударной адиабате и температуры плоскостей (002)
идеального непористого графита в интервале давлений превращения
графит—алмаз.
2.7. Уравнение состояния BKW
УРС Беккера-Кистяковского-Вильсона (BKW) широко
используется а^я расчета параметров стационарной детонации, состава
91
продуктов детонации (ПД), изэнтропы расширения ПД любых
взрывчатых составов [10,29,30]. Это УРС построено на основе
межатомного потенциала отталкивания вида U = А / г" и вириального
уравнения состояния.
УРС BKW имеет следующий вид:
pV/RT = l + xefix; х = к^-^ = кК/У(Т + в)а (2.43)
где х., Ц - относительное количество молей и коволюмы отдельных
видов продуктов детонации; х. = а /п (п - количество молей ПД);
К=X х. Ц - ковалюм П Д; к, (2 - константы УРС.
Подбор величин к и (2 дает соответственно совпадение расчетной
и экспериментальной скоростей детонации и наклона зависимости
скорости детонации от плотности.
Коволюм каждого продукта детонации определяет его
потенциал отталкивания. Коволюм находится по экспериментальным
результатам ударного сжатия каждого ПД, из которых наиболее важны
Аая ВВ типа CHNO вода, азот, двуокись углерода, окись углерода
и углерод.
Одной совокупностью параметров УРС BKW не удается хорошо
описать свойства гексогена и тротила вследствие большой разницы
в содержании углерода в ПД.
Поэтому в расчетах используются два семейства параметров:
RDX — параметры — для ВВ с малым содержанием в ПД твердого
углерода и TNT - параметры — для ВВ с большим содержанием
твердого углерода в ПД. BKW параметры даны в табл.2.6 [10].
Таблица 2.6. Параметры УРС BKW
Параметры
RDX
TNT
Р
0,16
0,09585
К
10,91
14,15
а
0,50
0,50
6
400
400
Коволюмы
со2
250
250
СО
600
600
N*
390
390
НР
80
380
92
Кован и Фиккет [30] добавили к Т величину 9 с целью ограничить
давление при Т -> 0 и всегда аая любого объема иметь (dp/ dT)v > 0.
Кроме того, нужно знание термодинамических свойств каждого
из ПД. Методы расчета термодинамических функций компонентов
ПД и коволюмов изложены в [10].
В общем случае ПД представляет собой смесь газообразных
и твердых компонентов, для которой справедливо соотношение:
g = nG+nG (2М)
о g g s s
где g — любые свойства в расчете на единицу массы; G — то же в
расчете на моль; n , ns — количество молей газообразных и твердых
компонентов ПД.
Для газов используется УРС идеального газа, а а^я твердых
компонентов (например, графита) обычно используется трехчленное
УРС в форме, предложенной Кованом [30]:
р = рг (S) + a(S)T+b(S)T2 (2.45)
где S=р/р0 — относительное сжатие, Т в ev
Пределы применимости УРС: Т < 2; S < 2,5.
Первые расчеты ВВ типа CHNO с использованием УРС BKW
сделаны в 1954 году Кованом и Фикетом [30]. Затем во многих
научных центрах мира были созданы практически идентичные
компьютерные программы, отличающиеся различными названиями,
например, Arpege (Комиссия по атомной энергии), RUBY (Ливермор),
TIGER (Stanford Research Institute).Программа а^я персонального
компьютера дана в [ 10].
О точности расчетов по УРС BKW можно судить по данным
табл. 2.7, где сравниваются расчетные и экспериментальные
величины скорости детонации и давления в точке Жуге.
Обычная точность расчета D — несколько процентов, а рн ~
10...20%. Худшая точность расчета давления в точке Жуге (с
помощью любых типов УРС) объясняется нестационарностью,
турбулентностью и трехмерностью процессов в зоне химреакции, а также
неравновесностью состава ПД. Расчетные температуры детонации
всегда значительно занижены.
93
Результаты расчетов по У PC BKW углубляют наше понимание
особенностей детонационных процессов и энергетики.
Например, становится понятной слабая связь между давлением
и теплотой взрыва. Давление в точке Жуге в основном определяется
не тепловой, а упругой составляющей, сильно зависящей от
плотности частиц в точке Жуге (или от числа молей на грамм).
В свою очередь плотность частиц повышается с ростом
содержания водорода в молекуле ВВ (или с увеличением воды в
ПД). Благодаря этому, например, величина рн у нитрогуаниди-
на и Сотр. В одинакова, хотя теплота взрыва нитрогуанидина
вдвое меньше.
С другой стороны, окисление таких добавок в ВВ, как А1, В,
увеличивают только тепловую составляющую давления, дают твердые
ПД, поэтому у таких ВВ р меньше, чем у ВВ с большим
содержанием водорода.
Таблица 2.7. Точность расчетов по УРС BKW
ВВ
Гексоген, р = 1,80
Тротил, р = 1,64
Октоген, р = 1,90
ТЭН,р=1,77
ТАТВ,р = 1,895
Октол.р =1,809
(76,3/23,7HMX/TNT)
Cyclotol,p= 1,743
(77/23 RDX/TNT)
Сотр. В, р = 1713
(64/36 RDX/TNT)
D, м/с
эксперим.
8754
6950
9100
8300
7860
8476
8250
8030
расчет
8754
6950
9159
8421
7860
8555
8311
8084
Рн > кбар
эксперим.
347
190
393
335
315
343
313
294
расчет
347
206
395
318
297
333
305
284
94
Литература к главе 2
1. Свойства конденсированных веществ при высоких
давлениях и температурах. Информ. издание, (сб статей) / Под ред.
Р. Ф. Трунина. Министерство атомной энергетики и
промышленности, ВНИИЭФ, 1992,398 с.
2. Теплофизика и динамика интенсивных импульсных
воздействий. / А. В. Бушман, Г. И. Канель, А, Л, Ни, В. Е. Фортов.
Ин-т химфизики АН СССР, Черноголовка, 1988,200 с.
3. Станюкович К. П. Неустановившиеся движения сплошной
среды. М.: Гостехтеориздат, 1955.
4. БаумФ.А., Станюкович К. П., Шехтер Б. И. Физика взрыва.
М.: Из-во физ-мат. лит., 1975.
5. Забабахин Е. И., Забабахин И. Е. Явления неограниченной
кумуляции. М.: Наука, 1988,172 с.
6. Дуболадов И. П., Ракитин В. И., Сутулов Ю.Н., Телегин Г. С.
ПМ-ТФ, 1969,№4,с. 148—151.
7. Крупников К. К., Бражник М. И., Крупникова В. П.//Журнал
эксперимент, и технич. физики, 1962, с 42.
8. Compendium of shock wave data. Lawrence radiation laboratory.
UCRL — 50108, Vol.1, Sect.A-1, A-2,1966.
9. Marsh Stanley P. «LASL Shock Hugoniot Data». University of
California Press, 1980 and «Selected Hugoniots». Los Alamos
Scientific Laboratory Report LA — 4167 — MS, 1969.
10. Mader S. L. Numerical Modeling of Explosives and Propellants.
Second Edition, CRC Press, 1998, p. 439.
11. Афанасьв A. H., Богомолов В. M., Воскобойников И. М
Обобщённая ударная адиабата конденсированных веществ.
Журнал прикладной механики и технической физики, 1969,
№4.
12. Анисичкин В. Ф. ^удрно-волновые данные и уравнения
состояния конденсированных сред. Физическая механика
неоднородных сред, Новосибирск, ИТПМ, 1984, с. 142.
13. Анисичкин В. Ф.//Физика горения и взрыва. 1979, № 1, С. 15.
14. Долгушин Д. С, Анисичкин В. Ф.//Физика горения и взрыва,
1992, №4, с. 80.
95
15. Трунин Р.Ф., Подурец М.А, Симаков Г. В. и др.//Журнал экс-
пер. и технич. физики, 1972, Т. 62.
16. Зельдович Я. Б., Райзер Ю. П. Физика ударных волн и
высокотемпературных гидродинамических явлений. М.: Наука,
1966.
17. Алдер Б. Физические эксперименты с сильными ударными
волнами. Сб. «Твердые тела под высоким давлением.» М.:
«Мир», 1966, с. 430—471.
18. Кормер С. Б., СиницынМ.В., Кириллов Г. А.//Журнал экс-
пер. и технич. физики, 1965,21, с. 689.
19. Kondo К., Ahrens Т. Phys. Chem. Miner., 1983,9, Р.173.
20. Даниленко В. В. / Физика горения и взрыва, 1988, № 5,
с. 137.
21. Кормер С. Б., Фунтиков А. И., Урлин В. Д., Колесникова А. Н. /
Журнал экспер. и.технич. физики, 1962, Т. 42, с. 686.
22. Высокоскоростные ударные явления./Мак-Куин Р., Марш С,
Тейлор Дж. и др.М.: «Мир», 1973.
23. РябининЮ.Н., Родионов К. П., Алексеев А. С. ЖТФ, 1964,
34,11.
24. Рябинин Ю. Н., Родионов К. П., Алексеев А. С. ФММ, 1960,
10,1.
25. Голубев В. К., Трунин И. Р. ФГВ, 1990, № 3, с. 105.
26. Машаров Н. В., Бацанов С. С. ФГВ, 1989, № 2, с. 138.
27. Скороход В.В., Солонин СМ. // Физико-металлургические
основы спекания порошков. М.: Металлургия, 1984.
28. АдадуровГ.А. О роли пластических деформаций в
динамических экспериментах и сопоставлении результатов
динамических и статических исследований //«Химическая
физика процессов горения и взрыва». Детонация и ударные
волны. Материалы VIII Всес. симпозиума по горению и
взрыву, Черноголовка, 1986, с. 3.
29. Becker R. Zeitschrift fur Technische Physic, 1922, 3, p. 249.
30. Cowan R. D. and Fickett W.J. of Chem. Phys., 1956,24, p. 932.
31. Дерибас А. А. Физика упрочнения и сварка взрывом,« Наука»,
Новосибирск, 1972.
96
32. Методы исследования свойств материалов при
интенсивных динамических нагрузках. Монография под общей ред.
М.В.Жерноклетова. РФЯЦ —ВНИИЭФ, Саров, 2003.
402 с.
Глава третья
ДИНАМИЧЕСКАЯ ПРОЧНОСТЬ
3.1. Влияние прочности на ударное сжатие и разгрузку
Рассмотрим особенности ударного сжатия твердого тела,
связанные с прочностью тела. Если давление велико, то влиянием
прочности можно пренебречь и рассматривать изменение плотности
как результат всестороннего сжатия вещества (т.е. изменение только
объема без изменения формы тела).
Однако в общем случае ударное сжатие создает в твердом теле
анизотропную систему напряжений. Соотношения Гюгонио
остаются справедливыми, лишь гидростатическое давление заменяется на
компоненту напряжения, нормальную к фронту волны.
При одноосном сжатии согласно простейшей теории упругости
нормальная (рн) и поперечная (pt) компоненты напряжения
определяются следующим образом:
Рн=к + -СЪ Рг=(к--°)Ъ Рт=7^-Рн (ЗЛ)
3 3 1- /и
где: [л - коэффициент Пуассона; У) = 1 - V/ VQ = AV/ VQ — нормальная
деформация.
Поскольку все смещения нормальны к фронту, то поперечная
деформация отсутствует, k, G, Е — модули объемного сжатия и Юнга
соответственно.
Модули связаны между собой следующими соотношениями:
3(1-2,0) 2(1 + //) 3 (1 +/0(1-2//) V >
98
равнения (3.1) справедливы при соблюдении критерия текучести:
рн - pt < Y, где Y — предел текучести.
Для одинакового изменения объема у] = AV/V0 необходимая
величина гидростатического давления равна:
Р = кч (3.3)
Далее предполагается, что выше предела текучести
анизотропность напряжения рн - pt = Y остается постоянной, а с ростом
деформации модуль сдвига уменьшается так, что 2 G У] = Y.
Тогда из (3.1), (3.2), (3.3) имеем
4 2
PH=krl + -Gr] = P + -y
(3.4)
Сравним в р, v — координатах одномерное и гидростатическое
сжатие (рис.3.1).
При одномерном сжатии по линии 0123 р на начальном упругом
участке 01 напряжения распространяются с постоянной скоростью,
равной скорости продольных упругих волн (продольной скорости звука):
Ci=4Ph /po=^(k + -G/p0 (3.5)
Рн
Рн,
Ph<PHi
Рн
Рн,
X
— D2
Phj>Ph>Ph1
-D,= C
Рис. 3.1. Влияние прочности на ударное сжатие.
А. Сравнение одномерного и гидростатического сжатий. Линия 0123 р —
одномерное сжатие, линия Ор — гидростатическое сжатие,
Phi ~~ УПРУ1™ предел.
Б. Структура ударных волн в упругопластической области.
99
Эта скорость определяется наклоном прямой 013 и может быть
получена из выражения аля скорости ударной волны в точке 1
подстановкой и = 0, р = 0, рН1 = (к + 4/3 G) У]г
Начиная с точки 1, материал деформируется пластически по линии
123 р, которая описывается уравнением (3.4). Линия 123 р
параллельна кривой гидростатического сжатия 0 р. Поскольку величина к растет
с давлением, то линия 123 р выпукла вниз так же, как и для жидкости.
При ударном сжатии линия 123 р является адиабатой Гюгонио.
Из рис. 3.1 видно, что на участке 123 скорость ударной волны
D < Ср следовательно, в диапазоне давлений от рН1 до р3 по веществу
пойдут две волны: упругий предвестник с давлением рш и скоростью
Cj, а затем — пластическая волна с давлением рн - рш и скоростью
D=Vj л/ (рн - pH1)/(vj - v) относительно материала за упругой
волной. Предельно малая скорость пластической волны, когда рн -> рш,
определяется как сь = л/k/p, что соответствует пластической скорости
звука.
В точку 3 приходит прямая Михельсона с наклоном упругого
участка 01, т.е. в этой точке скорости пластической и упругой волн
становятся одинаковыми. Выше точки 3 напряжения создаются
одной ударной волной со скоростью D = v0yl(pH -p0)/(vo ~~v)-
Таким образом, с ростом нормального давления в ударной волне,
член 2/3 Y в (3.4) относительно уменьшается и в конце концов
становится пренебрежимо малым. Это позволяет считать напряжения
в твердом теле с прочностью изотропными и описывать
нестационарные течения так же, как и в жидкости.
По определению динамический предел текучести
Y = PH-pT = l-^PHl (3.6)
1-//
В статических условиях сжатия величина Y сильно растет с
давлением, но при ударном сжатии этот рост меньше, т. к. он частично
компенсируется увеличением температуры сжатия (см.табл. 3.1).
Поэтому с ростом давления Y проходит максимум и затем
падает до нуля (при плавлении). Так, а^я свинца при р>400 кбар
Y = 0 [1]. Для меди Y = 28 кбар при давлении 800 кбар [2],
арпл > 1,9Мбар.
100
Таблица 3.1. Динамический предел текучести металлов
Металл
Алюминий
« «
"_"
"_"
«_«
Алюминий
р„,кбар
100
ПО
175
300
345
680
Y, кбар
8,2
8,6
12,5
17
22
29
Металл
Медь
","
"_"
Свинец
Железо
Железо
рн, кбар
340
800
1200
460
1110
1850
Y, кбар
18
28
16
0
11
27
Таблица 3.2. Динамические пределы упругости рш и текучести Y [9,10]
Материал
Алюминий 2024
Алюминиеый сплав Д16
отжиг
закалка
Алюминиеый сплав АМ-6М
Магний
Сталь 1018
Сталь 3
Сталь 40
Сталь 30ХГСА
Сталь 35ХЗНМ
Нержавеющая сталь 304
Нержавеющая сталь Х18Н10Т
Титан ВТ6
Титан
Бериллий
Никель
Молибден
Вольфрам
Вольфрам
Уран- молибден (98/2 %)
Карбид вольфрама WC
Карбид бора В С
Окись бериллия ВеО
Корунд А10
Сапфир (А10 + Сг)
Карбид кремния SiC
г/см3
2,78
2,71
2,61
1,73
7,86
7,85
7,89
7,9
4,45
1,85
8,9
10,2
19,2
18,6
15,01
2,50
2,84
3,97
3,98
3,09
км/с
5,25
5,3
4,45
4,63
4,6
4,51
4,57
5,11
7,93
4,63
5,19
4,02
4,05
2,46
4,98
9,62
8,14
7,94
7,71
км/с
6,36
6,4
5,92
5,88
5,77
5,74
6,15
13,8
5,22
3,33
6,75
3,78
1,54
10,83
11,4
РН1»
ГПа
0,6
0,47
0,76
0,38
1,1
1,4
1,4
1,91
1,98
2,3
0,2
0,45
2,0
1,85
0,33
1,0
1,6
4,0
3,2
2,1
4,6
15
8,2
11,2
12..21
8
Y,
ГПа
0,29
0,26
0,42
0,18
0,7
0,82
0,87
1,2
1,25
1,3
0,12
0,26
0,92
0,88
0,32
0,57
0,92
2,4
1,83
1,4
3,1
11,5
6,2
7,8
6,5
Экспериментальные значения пределов упругости рш и
динамических пределов текучести Y приведены в таблице 3.2 [3,4].
Кроме металлов, переход от упругого состояния в пластическое
за ударной волной зафиксирован у таких хрупких материалов, как
стекло, кварц, кремний (рш =40—70 кбар).
Наличие прочности влияет на процесс расширения (разгрузки)
ударно-сжатых материалов, находящихся в состоянии
пластического течения. При снижении давления (за счет догона ударной волны
задней или боковой волнами разгрузки) и изменении направления
деформации материалы вновь приобретают способность к упругой
деформации.
В упругой стадии расширения полный перепад напряжений
равен 2Y, отсюда амплитуда упругой волны разгрузки
Измеряя величину Арн, из (3.7) определяется предел текучести
или критическое напряжение сдвига Y (р,Т).
Таким образом, из начальной точки 2 на рис.3.1 вещество
упруго расширяется со скоростью с{ в точку 4 на величину Дрн . Далее
из точки 4 в точку 5 идет пластическая разгрузка с меньшей
скоростью сь.
Поскольку Cj > cb, волна разгрузки расщепляется на две волны:
упругую, уменьшающую давление на величину Дрн> и
пластическую.
Из рис.3.2 видно, что наличие прочности у материала приводит
к сдвигу влево кривой разгрузки в р,и и p,v — координатах.
Приращение скорости Ди и величина Дрн = р0 с( Ди оказываются
меньшими, чем при разгрузки материала без прочности.
3.2. Динамическое деформирование материалов
В плоских.волнах сжатия и разрежения происходит одномерная
деформация тел:
Е =Е = 0; (Г =сг *0.
у z у я
102
Рн
Рн,
РН !
Рн,
Г
дрн m
1 \\
* !W4
~~~'"Yv
р! \л
V
Рис. 3.2. Расширение упругопластического тела при выходе на свободную
поверхность ударной волны с давлением >рш. Г — ударная адиабата; S — изэнтропа
разгрузки без прочности; Р— разгрузка с прочностью.
В упругой области продольная сжимаемость кх меньше объемной
кили
, , 1 dV 1 1 dV 1
к <к или = < = — (<хо\
V dax k+4G/3 V dp к &8)
Из закона Гука следует, что 3 р = <7 + 2 р, где р — напряжение
сжатия в перпендикулярных направлениях.
В пластической области продольная и объемная сжимаемости
равны.
Переход от упругого к пластическому деформированию
происходит при напряжении
к ?.
(3.9)
х иих X\2G 3/
Условие пластичности: <7х- pt = ± рН1 (р, Т), где рш — предел
прочности.
После завершения цикла одномерного сжатия-разгрузки в
материале должна наблюдаться остаточная деформация, равная
бх=2/3(р/к)[3].
Экспериментальная регистрация волновых профилей a (t)
позволяет найти зависимости «продольной» (упругой) с{ и
«объемной» (пластической) сь скоростей звука (следовательно, модулей
упругости), а также предела текучести Y от давления ударного
сжатия.
Пластическое деформирование металлических материалов
сопровождается возрастанием сдвиговых напряжений т, что означает
деформационное упрочнение. С учетом упрочнения зависимость
напряжения течения т от величины пластической деформации у имеет вид:
* = **+ЯУ1 (ЗЛО)
где q, п — константы.
В реальных металлах наблюдается эффект Баушингера, который
можно определить как временное разупрочнение при смене
направления деформирования. Эффект Баушингера приводит к
асимметрии кривой деформирования в цикле сжатие-разгрузка и к
соответствующему искажению волнового профиля.
Наблюдаемая зависимость напряжения течения от скорости
деформирования в расчетных моделях описывается как проявление
вязкости материала. Простейшей моделью среды с вязкостью
является модель Максвелла, в которой упругий и вязкий элементы
включены последовательно, и общая деформация у есть сумма упругой у
и пластической упл составляющих [5,6]:
. dy . . г г
где У) — коэффициент вязкости.
В случае фиксированной скорости деформирования у*
напряжение возрастает до некоторой предельного значения, определяемого
значениями у* и У):
r = 7;r*[l-exp(-G*/77)] (3.12)
В данной модели отношение y)/G есть время релаксации.
Модель упруговязкого тела улучшается введением параллельно
вязкому элементу элемента трения и нелинейной вязкости [6].
Согласно [7] аая металлов справедлива следующая
логарифмическая зависимость напряжения течения т от скорости
деформирования у*(для 10 "3 < у* < 103 с"1):
T = TC+J3ln/ (3.13)
104
где т — напряжение при квазистатическом деформировании. Тогда
вязкость определяется как
// = /?ехр[-(г-гс)//?] (3.14)
Значения ттах на фронте УВ определяются отклонением прямой
Михельсона от кривой всестороннего сжатия р (V, Т) [8], растут
с амплитудой УВ и даже могут превзойти теоретический предел
сдвиговой прочности, равный 0.1 G.
Анализ результатов измерений, сделанных с помощью лазерных
интерферометров [9], показал, что а^я очень больших скоростей
деформации е*= 10 7 ... 109 с'1 связь между амплитудой У В <7тах и е*
описывается зависимостью:
*'=Л<т1 (3.15)
Максимальные сдвиговые напряжения в УВ примерно
пропорциональны квадрату ее амплитуды. Отсюда скорость пластической
деформации
/р1=А(т-ат/2)2 (3.16)
где величины А равны: А1— МО8, Си— 3-Ю8, Ве = 5107, Fe —
ЗЛО7 (ТШ/с)'1 [9].
Особенность импульсного деформирования упруговязкого тела
заключается в том, что всегда за участками с большими градиентами
параметров следуют релаксационные зоны с асимптотическим
приближением к конечным состояниям [5].
Другой особенностью быстрого деформирования при ударном на-
гружении является адиабатический сдвиг, при котором тепловыделение
катастрофически снижает сопротивление деформированию твердого
тела. Если снижение напряжения течения из-за разогрева превышает
деформационное упрочнение, то процесс теряет устойчивость.
Деформация локализуется в узких зонах, где материал
разогревается вплоть до плавления. Полосы адиабатического сдвига четко
выявляются при металлографическом анализе. Локализация деформации
характерна для высокотвердых материалов с низкой теплопроводностью
(керамика, минералы). О полной потере сдвиговой прочности у таких
материалов за фронтом УВ
свидетельствуют измерения
скорости звука, которая оказалась
близка к объемной
(пластической), а также вид ударной
адиабаты (рис. 3.3 [10]).
При давлениях выше рн
состояние ударного сжатия
приближается к гидростатическому,
т.е. без прочности.
Прямым доказательством су-
0,26 0,30 0,34 у,см3/г s
ществования адиабатических
Рис. 3.3. фарная адиабата керамики ВеО. сдвигов являются резуль-
Штриховая линия —кривая всестороннего Тагы исследования образ-
сжатия по данным ультразвуковых измерений.
3 r 3 г цов монокристаллического
кварца, сохраненных после
ударного сжатия. Материал стал блочным, причем блоки разделены
прослойками кварцевого стекла (результат плавления кварца).
Кроме того, в [11] наблюдалось свечение кристаллического
кварца, локализованное в плоскостях сдвига.
Таким образом, гетерогенный характер динамического
деформирования высокотвердых материалов не вызывает сомнений.
Рассмотрим кратко микроскопическую модель деформирования.
Как известно, в основе физического механизма деформации лежит
представление о зарождении, движении и размножении дислокаций.
В отличие от низких скоростей деформирования ударноволновое
нагружение активирует дополнительные плоскости скольжения и
процесс двойникования. Уменьшаются размеры ячеек дислокационных
сеток, резко увеличивается плотность дислокаций и точечных дефектов,
что и определяет более высокую степень упрочнения металлов.
Обычно кинетику пластической деформации описывают
выражениями, предложенными Орованом:
dyP, = bdNJS; dypl = bdSdN (3.17)
где bd — вектор Бюргерса (элементарное смещение,
вызываемое единичной дислокацией и равное межатомному расстоянию,
106
bd « 10 8—10 7 cm); N — плотность дислокаций, S - смещение
подвижных дислокаций
В простейшем случае скорость со движения дислокаций на
участке без препятствий определяется законом вязкого торможения:
co = xbdIBd (3.18)
где Bd — коэффициент торможения (Bd « 10"4 Па с).
Максимально возможная скорость дислокаций не может быть
больше поперечной скорости звука ct. Реально ситуация осложняется
взаимодействием движущихся дислокаций друг с другом, с точечными
дефектами, с границами зерен. Для описания средней скорости
дислокаций Гилманом предложено эмпирическое соотношение [12]:
со = сх exp(-d I г) (3.19)
где d=Const.
В процессе деформации плотность дислокаций возрастает [12]:
N = N0+Mrpl (3.20)
где М — коэффициент размножения.
Но за счет блокирования на препятствиях доля подвижных
дислокаций убывает:
N = (N0+Mypl)exp(-<prpl) (3.21)
Таким образом, кинетика пластической деформации
описывается уравнениями (3.17), (3.19), (3.21) с использованием четырех
эмпирических констант d, N, М, ф.
При высоких сдвиговых напряжениях в УВ, больших скоростях
движения дислокаций, большой плотности различных препятствий
Аля их движения деформация определяется процессами зарождения
и размножения дислокаций.
Применение дислокационных моделей в расчетах быстрой
деформации в УВ осложнено реальной картиной и трудностями в
определении констант материала.
Ширина пластической волны сжатия определяется
вязкостью в условиях быстрой пластической деформации на фронте УВ.
Результаты измерения структуры волны сжатия в алюминиевом
u
м/с
400
200
0,2 0,4
0,6
0,8 t, мкс
Рис. 3.4. Волновые профили ударного сжатия
в алюминиевом сплаве 6061-Т6 [13].
сплаве 6061-Т6 (см. рис.3.4
[13]) показали, что с ростом
амплитуды УВ наблюдается
резкое сокращение
ширины ее фронта, что означает
уменьшение вязкости с
ростом сдвиговых
напряжений в УВ,
Например, для
давления в УВ, равного 9 ГПа
коэффициент
вязкости уменьшается с 103-104 Пас до У] < 30 Пас аая алюминия и до <
20 Пас х\я меди. При этом средняя скорость деформирования
6* = 7 106 с"1. При таких больших скоростях происходит переход от
термофлуктуационного механизма преодоления дислокациями
различного рода препятствий к непрерывному надбаръерному атермиче-
скому движению дислокаций, которые тормозятся в основном
вязкостью газа фононов [12].
3.3. Разрушение материалов при импульсном нагружении.
Откольная прочность
3.3.1. Взаимодействие волн при отколе
Измерение разрушающих напряжений в материалах при различных
импульсных напряжениях основывается на регистрации откольного
разрушения или динамических разрывов в материале.
Первым описал явление откола Гопкинс в 1914 году, а первые
измерения откольной прочности металллов сделаны Рейнхартом
в 1951 году. В многочисленных последующих работах развиты
различные методы исследования откола и изучены отколы в самых
разных материалах, в том числе в жидкостях.
Установлено, что откольная прочность значительно превышает
величины, получаемые в статических условиях ( величину предела
прочности). В отличие от разрыва образца на разрывной машине,
разрушение при импульсном нагружении происходит не в одном наиболее
слабом месте, а одновременно из многих очагов путем слияния многих
108
u
рЦк.-
Рис. 3.5. Схема волн и эпюры напряжений и скоростей при соударении двух тел.
микротрещин. Развитие откольного разрушения требует времени,
сравнимого с длительностью ударного импульса, но на 6—8 порядков
меньше, чем при статических испытаниях на разрыв.
Для понимания, как при ударном сжатии образца в нем возникают
растягивающие напряжения, рассмотрим одномерное упругое
соударение двух тел в плоскости х, t (см. рис. 3.5) [3].
После удара направо и налево пойдут ударные волны on и оа,
которые к моментам tx и t2 достигнут свободных поверхностей тел и
отразятся от них в виде волн разгрузки.
Направо пойдет волна пс, оставляя за собой область покоя, а
налево — волна ас, за которой напряжения будут равны нулю, а
скорость удвоится и будет равна скорости соударения и.
В момент t идущие навстречу друг другу волны разгрузки
встретятся в точке с. В этот момент во всем материале напряжения равны
нулю, но слева от точки с материал будет в покое, а справа — имеет
скорость и. Поэтому при t > tc от точки с будет распространяться
волна растяжения.
Если возникшая величина растягивающего напряжения будет
больше предела прочности материала, то правая часть образца
отколется и полетит вправо.
Чем выше напряжение растяжения, тем меньшее время требуется
Аая наступления разрушения. Разрушение материала приводит к
возникновению новой свободной поверхности, на которой напряжения
равны нулю. Вправо от этой поверхности по растянутому материалу
пойдет волна сжатия («откольный импульс»). К моменту выхода
откольного импульса на правую свободную поверхность падающая волна
разрежения уменьшает ее скорость от начальной wQ до величины wm.
Во фронте откольного импульса скорость поверхности вновь
возрастает и в процессе многократных отражений в откольной части
величина w(t) испытывает затухающие колебания, стремясь к
конечному значению wk = (wQ + wm)/2.
В результате первого откола образуется новая свободная
поверхность, и если амплитуда ударной волны достаточно велика, то
взаимодействие волн разрежения повторится, и может произойти второй
откол и т.д.
Таким образом, растягивающие напряжения выше предела
прочности возникают в материале в результате взаимодействия волн
разгрузки, идущих от свободных поверхностей сжатого образца.
Аналогичная волновая картина будет наблюдаться при взрыве
заряда ВВ на поверхности преграды.
3.3.2. Типы отколов
Известны следующие три типа откола.
1. При очень больших ударных давлениях и градиентах давления
(использование тонких пластин и больших скоростей соударения)
условия а^я разрушения реализуются не в одной плоскости, а в
целой зоне, и вся эта зона разрушается
Такая картина разрушения наблюдается также в случае, когда
после сильного ударного сжатия в волне разгрузки материал плавится,
и его прочность резко снижается.
2. Обычно откол возникает, когда растягивающие напряжения
превышают предел прочности материала на одной поверхности, а
материал не испытывает фазовых превращений. Поверхность откола всегда
шероховатая, причем шероховатость уменьшается с уменьшением
времени разрушения или с повышением растягивающего напряжения (т. к.
при этом инициируются больше и более мелких очагов разрушения).
3. Отколы с гладкой поверхностью обнаружены в железе и стали
при давлениях выше фазового перехода (> 132 кбар).
Схема ударной адиабаты и профиля давления в железе показаны
на рис. 3.6 [14].
В зависимости от давления по железу может идти одна (р > р4), две
(р3 < р < р4) или три (р3 > р > рс) волны: первая — упругая с
давлением pd = 11,6 кбар (Dj = 6 км/с), вторая — с давлением рп = 132 кбар
фазового перехода (D2 = 5,l км/с) и третья волна с давлением р2
ПО
2
-Г g£-
О v о 0,5 1 1,5 0 х
Рис. 3.6. p,v — диаграмма и профиль давления в железе и стали.
(D3 < D2). При давлении р < рп тоже будет распространяться две
волны: упругая и ударная.
На адиабате есть выпуклый участок, где возможно
распространение ударной волны разрежения с максимальной амплитудой рс — р§
и с крутым фронтом с5. Спереди и сзади ударной волны разрежения
распространяются простые волны разрежения oS и с2.
Гладкий откол в стальных и железных образцах объясняется
взаимодействием двух ударных волн разрежения. При их встрече высокие
разрывающие напряжения возникают в очень узкой зоне (~ 0,01 мм), что и даёт
гладкую поверхность откола, как при чистовой токарной обработке.
При встрече простых волн разрежения зона разрыва более
широкая, поэтому и поверхность откола шероховатая.
Условия получения гладкого откола просты: контактный взрыв
заряда толщиной ~ 100 мм из ТНТ или ТГ 50/50 на поверхность
стальной плиты толщиной 30—100 мм.
Откол возникает также и в результате взаимодействия с волнами
разгрузки, идущими от боковых или цилиндрических свободных
поверхностей. В этом случае откольная часть имеет форму не пластины,
а конического сердечника.
3.3.3. Методы измерения откольной прочности
1. Естественный откол
Используя мягкое торможение, сохраняют откольную пластину
и измеряют ее толщину. Далее, зная условия опыта, рассчитывают
111
все волновые процессы в образце и определяют максимальное
растягивающее напряжение в плоскости откола.
Этот метод не учитывает кинетику зарождения микротрещин, в
гидродинамических расчетах не учитываются эффекты вязкости и
сдвиговой прочности, поэтому значения откольной прочности
систематически завышаются.
Более точные результаты получаются при микроструктурном
исследовании развития микротрещин в сохраненных образцах без
отделившегося откола (см. 3.4) и при измерении манганиновым
датчиком профиля давления в плоскости откола.
Профиль падающей УВ может быть построен также по скорости
свободной поверхности w (t).
2. Измерение скорости свободной поверхности
Если любым дискретным методом измеряется только начальная
wQ и конечная wk скорости откола, то:
0"*=А>соК-*Ь) (3.22)
где cQ — объемная скорость звука.
Здесь предполагается треугольный импульс нагрузки, и в этом
случае конечная скорость откола близка к среднему значению:
w « (wn + w )/2.
к ч О m '
Наиболее точные и достоверные результаты получаются при
использовании методик непрерывной регистрации скорости свободной
поверхности w (t), например, с помощью емкостного датчика [15], или
лазерного интерферометра [16,17]. В этом случае величина а*
определяется по разности Aw=wQ - wm между максимумом и первым
минимумом скорости [18]:
a=0,5p0c0(Aw +Sw) (3.23)
где: поправка S w= (h/cQ - \v/c{ )[(со1-со2)/(со1+со2)], h— толщина
откола, с — продольная скорость звука, Wj и со2 — градиенты
массовых скоростей в падающей волне разрежения и во фронте отколь-
ного импульса (считаются постоянными, т. к. профили волн близки
к треугольным).
112
6 7 8
Эта поправка Sw тем
больше, чем круче фронты
волн, поэтому без учета S w
значение скорости wm
завышается, а а* — занижается.
Если измерено время At,
через которое достигается
первый минимум скорости wm, то
толщина откола определяется
просто: h=0,5AtcQ. При
сохранении откола его толщина
может быть надежно
определена путем точного взвешивания
откола и оставшегося образца.
На рис. 3.7 в качестве
иллюстрации приведены экспериментальные профили скорости w
свободной поверхности стальных образцов. Для Ст.З w (х) измерялась автором
с Н. И. Куракиным электроконтактными (спиральными) датчиками [ 19]
(в одном опыте 10 датчиков с базами измерения 0,3 мм и 1 мм), а аая Ст.
35ХЗНМ w (t) измерялась непрерывно емкостным датчиком [3].
3. Регистрация профиля давления манганиновыми
датчиками [20]
С помощью линзового заряда в образце создается плоская УВ со
спадающим давлением за фронтом. Манганиновый датчик давления
t, МКС
Рис. 3.7. Профили скоростей стальных
образцов.
а)Ст.З;б)Ст.35ХЗНМ.
113
2
\ /^IVfB
\//CwA
|^^ВВ| образец
X)
преграда
Датчик
Рис. 3.8. х, t — диаграмма и профиль давления на границе образец—преграда.
1—область разрушения; 2 — магистральная трещина; OD — профиль падающей
УВ; DK — откольный импульс; пунктир — профиль УВ без откола.
располагается на границе образец—преграда из более «мягкого»
материала. В результате распада разрыва на границе в образец
отражается волна разрежения.
На рис. 3.8 показана волновая картина в образце в х, t—
координатах и форма импульса, регистрируемая датчиком.
По зарегистрированным датчиком значениям ртах и pmin и
известным ударным адиабатам в р, и — координатах образца и
преграды определялось максимальное растягивающее напряжение сг*
(рис. 3.9).
Принимается, что изэнтропы и ударные адиабаты в р, и —
координатах совпадают, а сдвиговая прочность равна нулю.
4. Импульсная рентгенография
Импульсная рентгенография
позволяет получать рентгеновские
снимки образцов с отколами и
измерять плотность разрушенных
частей образцов. Например, с
помощью установки Mevex (1 Mev,
размер фокусного пятна 2 мм,
выдержка 50 не) исследовались от-
Рис. 3.9. Схема определения о*. кольные разрушения в свинце
1 — ударная адиабата преграды, \2^^
2 — ударная адиабата образца *■ ■■'
114
33.4. Экспериментальные результаты
Все известные методы регистрации откола дают лишь косвенную
информацию о напряжениях разрушения сг*, поэтому важен выбор
метода, обеспечивающего получение наиболее полной и надежной
информации, а также наиболее точной теории расчета а* .
Полученные разными методами и разными авторами
результаты довольно сильно отличаются друг от друга (см. табл. 3.4).
На величину откольной прочности данного материала
влияют градиент давления (или скорости) в ударной волне Ар /Ах и
исходное состояние материала (отжиг, закалка, прокатка,
литье). Ограничивая время нагрузки, можно получить картину
от пол-ного разрушения (откола) до появления только первых
признаков разрушения (микротрещин). Все это и
обуславливает большой разброс результатов измерения откольной
прочности.
Значения сг* аая металлов растут с увеличением градиента
давления Ар/Ах в растягивающем импульсе [20]:
<J*=crh + а^Ар/Ах (3.24)
Для треугольного импульса Ар/Ах = o*/h.
В [22] отмечается, что подобный критерий аля откольной
прочности успешно используется в численных программах аля расчета
процесса взрывного нагружения.
Данные таблицы 3.3 [23] показывают, как растет откольная
прочность с градиентом давления ^ая медных образцов (рг — давление в
УВ, hj, h — толщины зарядов ВВ и образца).
Результаты по определению толщины откола могут быть
представлены в виде [23]:
hjh^l + myfhjhi (3.25)
где коэффициенты 1 и m составляют: А1 — 0,012 и 0,33; Ni — 0,016
и 0,42; Си — 0,012 и 0,30; РЬ — 0,004 и 0,18.
Как видно из табл. 3.3, с ростом градиентов в УВ толщина откола
уменьшается.
115
Таблица 3.3. Откольная прочность меди [23]
Толщина, мм
h
е
100
51
38,1
25
12,7
19
12,7
6,37
h
t
25
25
25
25
25
12
12
6
h
S
2,4
2,2
1,95
1,7
1,65
1,3
1,2
0,85
Давление, ГПа
Рг
36,1
32,1
30
26,7
21,2
30,3
27,1
27,2
о*
ГПа
3,04
3,04
4,20
4,61
5,13
5,55
5,98
7,98
Ар/Ах
ГПа/мм
1,27
1,85
2,15
2,71
3,11
4,27
4,98
9,39
Результаты работ [17,24] показали, что при уменьшении
длительности исходного импульса сжатия в 100 раз величина откольной
прочности увеличивается менее чем в 2 раза. Амплитуда УВ и начальная
температура не оказывают заметного влияния на откольную прочность
металлов, что упрощает модельное описание откола.
Однако в [23] влияние амплитуды УВ выявлено и
предложена более точная, чем (3.24), двухпараметрическая зависимость
o* = f (Ар/Ах, рг).
Экспериментальные величины откольной прочности сг* fi^ ряда
материалов приведены в таблице 3.4 [14,3,23,17,20,25,26].
Таблица 3.4. Результаты измерения откольной прочности
Материал
Алюминий
(95)
оЪ=0,51
Алюмин.
сплав
2024
оЪ=0,19—0,48
-duldt \06м/с
315
ст* ГПа
1,35
1,15
Материал
Титан чистый
т=10-6с
Титан чистый
т=10-8с
-duldt \06м/с
ст* ГПа
~3
~6
116
Материал
Алюмин.
сплав
В95
оЪ=0,35
Алюмин.
сплав
АМ-6М
Медь Ml
ofa=0,17
Медь (95)
ofa=0,2
Медь М2
Медь Ml
(плоская
детонация)
Медь Ml
(скользкая
детонация)
Медь
(Мп датчики)
Железо
оЪ=0,33
Армко-
железо
Сталь 3
(плоская
детонация
Сталь 3
(скользкая
детонация)
Сталь 3
(гладкий
откол)
-duldt \Оьм/с
66
950
2100
5500
22
275
2000
56
270
сг*ГПа
1Д5-
—1,8
0,57
0,83
1,15
1,2
1,35-
-7,8
2,45
0,8
1,1
1,65
3,04—
-7,9
2,4-
-1,6
1,75-
-1,85
2,7
1,4
1,65
1,66
4,8-
-8,5
4,1-
-8,5
Материал
Титан сплав
ВТ6
Титан сплав
ВТ5-1
Титан сплав
ВТ8
Магний Mai
Латунь
оЪ=0,8
Серебро (93)
оЪ=0,13
Свинец (94)
оЪ=0,2
Свинец литой
Тантал
Уран
Ртуть жидкая
Вода, этил,
спирт,
глицерин
Полимер
-duldt 106л*/с
800
630
91
268
1020
500
сг*ГПа
3,7
3,5
3,4
4,1
4,16
0,8
0,88
2,18
2,14
0,92
06
4,6
4,4
2,4
5,1
1,9
0,02—
—0,05
0,1—
0,3
117
Материал
Сталь 3
(удар А1
пластиной)
Сталь 45
оЪ=0,66
Сталь SAE
1020
оЪ=0,41
Нержав,
сталь 304
Нержав.
сталь
Х18Н10Т
Сталь
35ХЗНМ
(удар вдоль
прокатки)
Сталь
35ХЗНМ
(удар поперек
прокатки)
-duldt \06м/с
244
1000
420
350
190
50
440
75
500
60
сг*ГПа
10—
-15
2,15—
-2,45
2,14—
-2,34
2,1
2,3
2,0
2,0
1,9
1,85
Материал
Полиметил-
метакрилат
(сол)
время
нагрузки:
т=80мс
т=1мс
Полистирол
(ПС)
т=10-4мс
т=10-6мс
Ультрафарфор
(85%А1203+
15%S02
т=10-4мс
т=10-6мс
Стекло К19
Кварц
плавленный
Никель
электролитический
оЪ=0,33
Никель НП2
-duldt \06м/с
400
сг*ГПа
1,15
1,60
0,5
1,0
1,4
3,0
>4,2
>5,8
4,28
1,5
Безусловно, данные таблицы 3.4 неполные, но они показывают,
что нельзя характеризовать материал только одной величиной от-
кольной прочности, без указания условий разрушения.
Регистрация отколов проводится в следующих трех постановках
опытов плоской геометрии:
1. Контактный взрыв заряда ВВ на поверхности образца таким
образом, что фронт детонации параллелен поверхности образ-
118
ца. Для создания плоской УВ в образце используются
специальные линзовые заряды. Время существования откольных
напряжений ~ 10"4 с.
2. Контактный взрыв заряда ВВ на поверхности образца. Фронт
детонации перпендикулярен поверхности образца (скользящая
детонация), в образце создается косая УВ. Время существования
откольных напряжений ~ 10"5 —10~6 с.
3. Соударение пластин. Большая скорость пластины—ударника
и малая ее толщина позволяют уменьшить время
существования откольных напряжений до ~ 10~7—10~8 с и получить тем
самым максимальные величины сг* Например, в [24]
времена ~ 10"8 с были получены при воздействии на образец
мощного ионного пучка (на установке «Калиф») или при
ударе пластины из алюминия толщиной 0,05 мм со скоростью
4,1 км/с.
При любой постановке опыта аля получения откола должны
выполняться следующие два условия.
1. рг > сг*. При невыполнении этого условия в образце не
возникают напряжения, достаточные аля его разрушения.
2. Ар/Ах >сг*/2 hs, т.е. скорость падения давления за
фронтом падающей волны должна быть достаточно большой, чтобы
при воздействии падающей УВ и отраженной волны
разрежения в образце возникли критические растягивающие
напряжения.
Реализация этих условий в экспериментах с накладными
зарядами ВВ (первые две постановки) определяется
отношением толщин образца и заряда ht/HBB. При большом ht/HBB
(толстый образец, тонкий заряд) нарушаются оба условия. При
малом ht/HBB не выполняется второе условие — при толстом
заряде давление за фронтом детонации падает слишком
медленно.
Таким образом, получение откольного разрушения возможно
при изменении ht/HBB только в определенном диапазоне,
ограниченном и сверху, и снизу.
119
В [27] этот диапазон определен экспериментально а^я
алюминиевого сплава AMg - 6 при изменении ht/HBB от 1 до 30 (скользящая
детонация):
h/Hnn < 1,5 — откола нет.
t DD
h /Hn= 1,5— 2,5 — один отколЬ /h =0,3 — 0,15; w, =0,8 км/с.
С DD St US
h /HnTJ = 2,5—11 — два откола.
t DD
h/b-L=ll—13 — одинотколЬ/h =0,2 — 0,1; w, =0,55 км/с.
t DD St IIS
h /HDT1 > 23 — откола нет.
t DD
В [26] верхний и нижний пределы отношений ht/HBB
(скользящая детонация) определены ^ая стали 3 и меди (см. табл. 3.5),
причем показано влияние технологии производства материала: у
образцов из прутка откольная прочность выше, чем у образцов из листа.
В [28] найдено, что у стали 35ХЗНМ вдоль направления прокатки сг*
больше, чем поперек.
Таблица 3.5. Откольная прочность стали 3 и меди [26]
Материал
Сталь 3 пруток
Сталь 3 листа
Медь Ml пруток
Медь Ml лист
рсГПа
8,1—13,2
4,1—14
(b/Hj^
67
10
15,06
14,5
(VHBB) min
0,83
0,78
0,66
0,62
а . -<г ,
nun max
ГПа
4,8-8,5
4,1—8,1
2,4-7,6
2,1-6,4
Из табл. 3.5 видно, что с увеличением толщины заряда ВВ
величины рг и сг* увеличиваются в ~ 1,5 раза для стали и в ~3,5 раза
Аая меди (у меди сильнее затухание УВ). При этом наблюдается
смещение плоскости откола вглубь образца до величины h = h /2, что
приводит к увеличению энергии разрушения в ~ 9 раз ^ая стали и в
~ 30 раз ^Ая меди.
Это можно объяснить ростом упрочнения материалов с
давлением ударного сжатия (микротвердость сохраненных образцов
увеличивается в 1,2—1,5 раза).
В связи с ростом сг* при уменьшении времени действия
растягивающих напряжений возникает вопрос: нельзя ли получить величи-
120
ны а*, близкие к теоретическому пределу прочности при растяжении
<7 = ОДЕ (Е — модуль Юнга). Величина о* соответствует
одновременному разрыву без пластической деформации всех межатомных
связей в сечении образца.
Экспериментально при t ~ 10"8 с в меди, никеле, титане были
получены гладкие отколы, причем отсутствовали разрушения в виде
микропустот [29,30]. В этих опытах достигнуты величины а* = 8"10 ГПа,
близкие к с.
Согласно [24] снижение времени нагрузки на два порядка (с 10"6
до 10"8 с) увеличивает откольную прочность чистого титана вдвое,
до сг* = 6 ГПа. Уменьшить время t можно, используя встречные
ударные волны разрежения в стали. Приведенный в [25] теоретико-
расчетный анализ результатов работ [31,32] показал, что при
гладких отколах сталь способна выдерживать а* = 10— 15 ГПа, близкие к
<7 . При этом время разрушения < 0,01 мкс. Но даже при столь малых
временах разрушение сопровождается пластической
микродеформацией, поэтому теоретический предел прочности не достигается.
Неожиданно высока откольная прочность у стекла, которое
выдерживает кратковременное растягивающее напряжение 5 ГПа [33].
По-видимому, причина высокой прочности стекла — в его
внутренней однородности, бездефектности. При импульсном нагруже-
нии стекла давлением, меньшим динамического предела упругости
(8,8 ГПа), по образцу со стороны нагружаемой УВ поверхности
распространяется со скоростью 1—1,5 км/с волна хрупкого
разрушения, вызванная разгрузкой УВ.
Дробление инициируется сеткой трещин сдвига (слой
раздробленного стекла) на поверхности образца. При р > 8,8 ГПа
пластичность стекла препятствует его хрупкому разрушению.
Для низкопрочных и легкоплавких металлов (свинец, олово)
характерно беспорядочное разрушение образцов, начинающееся
со свободной поверхности и проходящее как с плавлением, так и
без плавления.
У всех металлов наблюдается микроразрушение свободной
поверхности при выходе на нее УВ в виде микроструй, вылетающих
из впадин микрорельефа поверхности. Это явление в значительной
121
степени устраняется нанесением на поверхность масляной пленки
(простым смазыванием).
В работе [34] в диапазоне t= 104 — 10"6 с исследованы
закономерности разрушения трех хрупких материалов: полиметилмета-
крилата (ПММА) марки СОЛ, полистирола (ПС) и ультрафарфора
(85%Al203+15%Si02).
Поскольку откольная прочность зависит от времени
существования растягивающих напряжений, по результатам экспериментов
[34] были построены зависимости логарифмов долговечности lgr от
величины разрушающих напряжений (рис. 3.10).
Как показал фрактографический анализ, при т > 10"4 с разделение
образца на части происходит за счет роста одной, реже двух трещин,
которые зарождаются на поверхности, как и при квазистатическом
нагружении.
При т < 10~4—10"5 с и увеличенных напряжениях наблюдается
переход от разрушения одноочагового с поверхности к
характерному многоочаговому разрушению. Долговечность определяется
закономерностями процесса одновременно растущих и
взаимодействующих микротрещин.
Из рис. 3.10 видно, что взаимодействие при больших а*
одновременно растущих микротрещин при их большой концентрации суще-
4
3 I-.X
-зТ
~4Г
-6
lgr
в)
-I L.
сЛ кг/мм2 10 15 20 25 30 35 о*, кг/мм2
Рис. 3.10. Временные зависимости прочности полистирола (а), полиметиметакри-
лата (б), ультрафарфора (в)
• — разрушение с поверхности, А — многоочаговое разрушение объема материала
122
ственно изменяет зависимость lgr(cr*) по сравнению с долговечностью
при малых сг*,определяемой ростом изолированной микротрещины.
Полученные результаты исследований кинетики разрушения
ПММА представлены данными таблицы 3.6.
Таблица 3.6. Кинетические параметры разрушения ПММА [34]
р,ГПа
1Д5
1,30
1,35
1,40
1,55
1,60
т ,мкс
р
80
25
15
10
2
1
Т, мм
4,4
0,8
0,3
0,25
0,035
0,018
тЗ, м/с
56
30
20
25
20
15
,—*.
3
т —время разрушения,
I — среднее расстояние между микроочагами разрушения,
v — средняя скорость развития откола.
Обычно падающая на образец плоская волна сжатия ослабляется
на периферии боковыми волнами разгрузки,
идущими радиально от свободной
цилиндрической поверхности образца. Поэтому
напряжения и запас энергии уменьшаются
радиально от центра образца.
Если вблизи оси образца реализуется
магистральная трещина с отделением откола, то
на периферии образуются только
зародышевые микротрещины, и далее на больших
расстояниях от оси импульс нагрузки ослабевает
настолько, что вообще не вызывает
разрушения.
В зависимости от кинетической энергии
1-Ъс. 3.11. Процесс отколовшейся центральной части движение
образования откола г
в преграде. может прекратиться (частичное разрушение с
образованием куполообразного выступа), либо продолжиться до
полного отрыва от образца (см. рис. 3.11 [35])
Работа образования откола складывается из энергии на
образование новой поверхности, энергии деформации откольной
пластины, работы отрыва пластины от преграды по окружности и
кинетической энергии откольной пластины.
Поскольку после образования магистральной трещины
кинетическая энергия откола пропорциональна его площади, а работа
отрыва пропорциональна длине его окружности, то аля каждой
данной постановки опыта существует критический диаметр откольной
пластины, меньше которого кинетическая энергия будет меньше
работы отрыва, и отделения откола не произойдет.
Действительно, при двукратном увеличении диаметра откола его
кинетическая энергия увеличивается в 4 раза, а работа отрыва
откола по краям только в 2 раза.
В работе [35] аая образца из титана ВТ5—1 h = 4 мм,
нагружаемого ударом Al t = 2 мм со скоростью 660 м/с, найдено: h = 1,91 мм,
сг* = 4,1 ГПа, удельная работа разрушения Е = 2,5 10"5 дж/м2,
удельная кинетическая энергия откола Е = 0,5ph w2 = 5,7 105 дж/ м2 и
критический диаметр отрыва равен 17,5 мм. Полностью оторваться от
преграды может откол диаметром больше критического.
3.3.5. Механизм и кинетика откольного разрушения
Механизм зарождения и развития разрушения подробно
анализируется в [36—39, 3]. Если ^ая оценки теоретической
прочности с использовать ударную адиабату D = А + В и, то получим
a«PoAV4B.
Для металлов теоретическая прочность составляет десятки
ГПа, что на 1.. 2 порядка выше измеряемого в опытах предела
прочности.
Решение проблемы было дано в 1920 году Гриффитсом, который
разработал энергетический критерий разрушения: работа
приложенных напряжений расходуется на увеличение поверхностной энергии
и энергию упругой деформации при росте длины трещины:
124
aD=\-^- (3.26)
где: г - радиус трещины, и - удельная поверхностная энергия.
Оценки <70 показывают, что реальная прочность объясняется
наличием в материале гриффитсовых трещин микронных размеров.
Все реальные материалы дефектны. Дефекты возникают в процессе
изготовления или обработки материала. Микротрещины
образуются в районе скопления дислокаций, около пор и включений,
О роли дефектности свидетельствует высокая прочность
бездефектных «усов» микронного диаметра, в 10 раз большая прочности
монокристаллов обычных размеров. С другой стороны, увеличение
пористости материала на 1 % снижает величину сг* на 1 ГПа.
В данном объеме тела случайно распределены дефекты
различной степени опасности (а^я разрушения). Вероятность наличия в
теле дефекта, понижающего его прочность, растет с увеличением
приложенных напряжений, времени их действия и объема тела.
Статистический и энергетический характеры прочности
проявляются в т.н. масштабном факторе, когда прочность падает с ростом
объема (размера) образца, детали, конструкции. Действительно,
при одинаковых напряжениях запас упругой энергии выше в
крупных деталях.
Согласно энергетическому критерию величина разрушающих
напряжениий обратно пропорциональна корню квадратному из
размеров образца [40].
Влиянием масштабного фактора можно объяснить
происходящие время от времени внезапные разрывы магистральных
трубопроводов высокого давления.
В условиях откола статистический характер прочности проявляется
в увеличении инициируемых очагов разрушения с ростом напряжения.
При малых временах существования напряжений отдельные крупные
дефекты не оказывают существенного влияния на прочность.
Однако важны зародышевые малые дефекты, включения,
границы зерен. Поэтому откольная прочность зависит от исходного
состояния материала (поставка, отжиг, закалка, прокатка, литье и т.п.).
С другой стороны, слабое влияние температуры и амплитуды давле-
ния УВ указывают на малый вклад отдельных дислокаций и
тепловых флуктуации в развитие откольного разрушения.
Изменение зависимости долговечности от напряжения
(см. рис. 3.10) связано с изменением механизма пластической
деформации: при низких напряжениях — большое влияние тепловых
флуктуации и разрушение за счет развития одиночной трещины, а
при высоких напряжениях — быстрое надбаръерное движение
дислокаций и разрушение за счет многих одновременно растущих и
взаимодействующих трещин.
В условиях откола характерная вязкость процесса роста трещин
составляет 10—100 Пас. Такую же величину коэффициента
вязкости дают измерения ширины фронта УВ.
Для расчетного описания откольного разрушения используется
континуально-кинетический подход, при котором развитие
разрушения рассматривается как непрерывный процесс накопления
повреждений под влиянием растягивающих напряжений. В качестве
меры разрушения в моделях повреждаемых сред выбираются
размеры или объем трещин, остаточная прочность материала или
некоторые формальные параметры.
Процесс образования микроповреждений (МП) задается
одним интегральным или двумя (зарождение и развитие МП)
кинетическими уравнениями а^я скалярного параметра
повреждаемости.
Определяющие соотношения носят полуэмпирический характер
с несколькими константами, которые находятся путем сравнения
экспериментальных данных с результатами моделирования
экспериментов на ЭВМ.
Широко известна кинетическая концепция разрушения твердых
тел, предложенная С. Н. Журковым [41,42].
Разрушение трактуется как накопление разрывов межатомных
связей. Потенциальные баръеры преодолеваются за счет тепловых
флуктуации, а напряжения придают процессу диссоциации связей
необратимую направленность.
Теория соответствует экспериментам с образцами
разнообразных материалов при долговечностях 10~2—107 с.
126
По этой концепции долговечность т зависит от растягивающих
напряжений с согласно следующему кинетическому уравнению [34]:
T = T0exp[{uQ-ja)/RT] (3.27)
где т0 — период тепловых колебаний атомов, uQ и j — энергия
активации и активационный объем.
Наиболее распространена модель NaG (nucleation and
growth — зарождение и рост) [43], которая дает выражение а^я
скорости разрушения с двумя слагаемыми (зарождение и рост
трещин) и с 6-ю константами. Константы находятся с помощью
металлографического анализа статистики разрушений в
сохраненных образцах.
Модель роста сферических пор [44] предполагает
существование в материале исходных пор одинакового размера, которые
начинают расти при создании пороговых напряжений. Дается
выражение а^я кинетики разрушения с тремя константами
материала.
В работах [45,46] предложено эмпирическое выражение а^я
динамики разрушения в широком диапазоне времен. Выражение
содержит пять констант и учитывает наличие в материале спектра
очагов разрушения, инициируемых при различных уровнях
напряжений.
Варьированием параметров можно описывать как относительно
хрупкое, так и вязкое, затянутое разрушение.
Обычно предполагается, что по мере разрушения предел
текучести, модуль сдвига и коэффициент вязкости уменьшаются. В
расчетах момент разрушения не фиксируется, но в зоне разрушения
асимптотически стремится к нулю сопротивление материала
растяжению.
Другое описание разрушения дано в [47,48]. Вводится условный
параметр повреждаемости, который меняется от нуля (монолитный
материал) до единицы (полное разрушение). С ростом параметра
повреждаемости снижается сопротивление растяжению. В
полученных соотношениях определяется связь между растягивающей
127
нагрузкой и скоростью разрушения с учетом формы
микроповреждений.
Названные кинетические модели успешно применяются в
двумерных расчетах аля описания динамических разрушений при
действии на преграды взрыва или высокоскоростного удара.
В моделях используются динамические характеристики
прочности, получаемые в опытах по одномерному отколу.
33.6. О локализации деформации и разрушения
при отколе
Экспериментально измеряется только две характеристики от-
кольного разрушения — длительность импульса нагружения и
нормальное напряжение сг* в зоне откола, причем, как видно из табл.3.4,
величина сг* имеет большой разброс.
Кроме того, в формировании откольной поверхности участвуют
сдвиговые процессы, не учитываемые величиной сг*.
На откольной поверхности имеются участки не только
нормального разрыва, параллельные фронту УВ, но и продольного
локального сдвига.
На микрошлифах откольной поверхности наблюдается
значительный разброс продольных и поперечных ступенек по
размерам, а также реализуются ступеньки под углом 45° к фронту волны
[49,50].
В [50] выполнены детальные металлографические анализы от-
кольных поверхностей на различных стадиях откола при различных
скоростях соударения и с целью исследования механизмов
зарождения, развития и локализации разрушения.
Как показали исследования, процессы локализации при отколе
можно разделить условно на следующие две категории:
1). Локализация в форме нормальных разрывов (параллельно УВ);
2). Локализация в форме микросдвигов и трещин,
перпендикулярных фронту УВ или под углом 45° к фронту.
Все нормальные разрывы развиваются из исходных микропор,
дающих начало распространению микротрещин при напряжениях
128
выше некоторых критических. С увеличением скорости и за УВ
микроразрывы объединяются в микротрещины, также параллельные
свободной поверхности (или УВ) и расположенные на разных
расстояниях от нее, образуя зону откола.
Локализация сдвиговой деформации является следствием
неоднородности динамического деформирования, которое обусловлено
распределением частиц по скоростям в УВ. Наличие продольных
микросдвигов свидетельствует о том, что движение среды за фронтом
УВ и при взаимодействии встречных волн разгрузки происходит в
виде микропотоков, имеющих разброс по скоростям. В результате на
границе соседних микропотоков происходят микросдвиги, которые
хорошо видны на поперечных шлифах образцов после их ударного
нагружения.
Результаты статистической обработки геометрических размеров
продольных и поперечных микроразрушений в образцах,
нагружаемых с различной скоростью соударения и, выявили существование
четырех масштабных групп микротрещин: h и Н - а^я продольных
сдвигов и d и D — fiiA^ нормальных разрывов (см. табл.3.7 [50]).
Таблица 3.7. Средние размеры микротрещин в стали 30Х2Н2МФА
it, м/с
300
340
400
Размеры микроразрушений, мкм
I масштабируемый
уровень
d
11
25
11
h
10
12
9
II масштабируемый
уровень
D
190
180
Н
165
Ди, м/с
117
155
20
При малых скоростях и образуются только микроразрушения
первого масштабного уровня (d и h). По мере роста и реализуются
все более крупномасштабные разрушения (D и Н), и при достаточно
больших значениях и микроразрывы размера D соединяются с
микросдвиговыми трещинами размера Н, что и формирует откольную
поверхность.
Размеры d нормальных разрывов определяются расстоянием
между продольными микросдвигами размера h, а размеры D зависят
129
от расстояния, которое успевает пройти поперечная трещина за
время действия растягивающих напряжений в зоне откола.
Поскольку во всех описываемых опытах длительность импульса
нагрузки была ~ 0,35 мкс, a D= 180 мкм, то отсюда скорость
поперечной трещины равна ~ 500 м/с, что совпадает с прямыми
измерениями, приведенными в [51].
Процесс формирования откольной зоны зависит от ширины
распределения частиц по скорости.
Если разброс скорости частиц соизмерим с их средней
скоростью ( А и * и ), то откольная щель имеет ступенчатый характер.
Если а^я данного материала характерно узкое распределение
скоростей (А и < 0,1 и), то откольная щель имеет сдвиговый характер.
Полученные в [50] кривые распределения микроразрушений по
их ориентации по отношению к фронту УВ показали следующее.
При малых скоростях нагружения (и < 300 м/с) материал
разрушается главным образом за счет микроразрывов, параллельных фронту
УВ (размеры d =10—30 мкм).
При больших скоростях (и > 400 м/с) разрушение осуществляется в
основном в виде локальных сдвигов, либо перпендикулярных к фронту
УВ, либо ориентированных под углом 45° (по плоскостям максимального
касательного напряжения), что свидетельствует об уменьшении ширины
распределения частиц по скорости и о более однородном характере
деформирования материала при больших скоростях нагружения.
Испытания показывают, что минимальное значение откольной
прочности сг* соответствует максимуму ширины распределения
скорости частиц и, а максимальное значение сг* достигается при Аи . .
Уменьшение сг* с ростом Аи можно объяснить увеличением
вероятности зарождения очень большого числа микротрещин на
боковых поверхностях микропотоков.
В хрупких материалах (керамика) продольных микросдвигов нет,
а диссипация энергии происходит за счет густой сети микротрещин
и за счет фрагментации материала.
Таким образом, на основании проведенных в [50] исследований
процесс локализации деформирования и разрушения материала при
отколе описывается следующим образом.
130
1. При малых и, создающих близкие к пороговым напряжения
продольного сдвига, возникают продольные микросдвиги
(сдвиговая релаксация напряжений) и нормальные микроразрывы как
результат взаимодействия волн разгрузки. Реализуется низший
масштабный уровень локализации (с размерами d и h).
2. При увеличении и возникает второй масштабный уровень
откольного процесса — образование нормальных макроразрывов
и продольных макросдвигов. Размеры макроразрывов определяются
длительностью существования растягивающих напряжений в зоне
откола и скоростью поперечных трещин. Продольные макросдвиги
также возникают при взаимодействии волн разгрузки и соединяют
нормальные макроразрывы.
3. При очень больших и откольных разрушений первого
масштабного уровня может не быть вообще. Продольные микросдвиги
не возникают из-за очень узкого распределения микропотоков
материала по скорости, а нормальные микроразрывы сразу реализуются
в виде макроразрывов.
В общем случае с уменьшением длительности нагрузки в
интервале от 10"6 с до 10"7 с и с ростом откольной прочности
уменьшаются дефекты разрушения металлов от 10—100 нм до 1—10 нм [52].
Изучение временной зависимости энергии откольного
разрушения металлов подтверждает существование при отколе масштабного
эффекта. Оказывается,удельная энергия разрушения X (на единицу
откольной поверхности) не постоянна, а зависит от времени нагру-
жения t или от толщины образца о [53].
С учётом влияния масштабного фактора в [53] получено
соотношение
a2/(l-m)S = const (3.28)
где а - напряжение в плоскости откола, am- масштабный
коэффициент, который определён экспериментально и составляет: медь — 0,57;
Ст.З — 0,61; свинец — 0,55; Ст. 12Х18Н10Т — 0,67; титан — 0,71.
Чем прочнее металл, тем сильнее влияние масштаба (больше
величина т).
Для описания результатов опытов по отколу с геометрически
подобными сборками с толщиной образцов, варьируемой в пределах
S = 1,5... 15 мм был принят следующий вид зависимости:
Л=^4Г=М"Г (3.29)
Таким образом, с уменьшением времени нагружения
(толщины образца) напряжение растет, а удельная энергия откольного
разрушения, наоборот, падает. Например, уменьшение толщины
образца из Ст. 3 с Змм до 0,05мм в 22 раза снизило величину
энергии разрушения (за счёт уменьшения затрат на пластическую
деформацию). Поэтому быстрый (гладкий) откол в условиях
встречных ударных волн разрежения используется в технологиях
разрушения металлических конструкций и позволяет сократить
затраты ВВ.
Литература к главе 3
1. Новиков С. А., Синицына Л. М.//Ж. прикладной механики
и техн.физики,1970, N6.
2. Альтшулер Л. В., Бражник М. И., Телегин Г. С. ПМТФ, 1971,
N6.
3. Теплофизика и динамика интенсивных импульсных
воздействий. /А. В. Бушман, Г. И. Канель, А, Л, Ни, В. Е. Фортов.
Ин-т химфизики АН СССР, Черноголовка, 1988.
4. Высокоскоростные ударные явления. Под ред.Кинелоу P.M.:
Мир,1973.
5. Годунов С. К. Элементы механики сплошной среды. М.: Наука,
1978.
6. Степанов Г. В. Поведение конструкционных материалов в
упруго-пластических волнах нагрузки. Киев: Наукова думка,
1978.
7. Campbell J. D. Material Science and Engineering, 1973,12, N1, p.3.
8. Cowan G. R. Trans. Metal. Soc. AIME, 1965,233, N6, p.l 12.
9. Swegle J. W., Grady D. E.J. Appl. Phys., 1985,28, N2, p. 692.
132
10. Gust W. H., Royce E. B.J. Appl. Phys., 1971,42, N1, p.276.
11. Brannon P.J., Konrad C, Morris R. W., Jones E. D., Asay J. R. J.
Appl. Phys., 1983,54, N11, p. 6374.
12. Gilman J.J.J. Appl. Mechanics Rev., 1968,21, N8, p.767.
13. Johnson J.N., Barker L.M.J. Appl. Phys., 1969,40, N11, p.4321.
14. Баум Ф. А., Станюкович К. П., Шехтер Б. И. Физика
взрыва. М.: Из-во физ-мат. лит., 1975.
15. Иванов А. Г., Новиков С. А.//Приборы и техника
эксперимента. 1963, № 1, С. 135—138.
16. Barker L.M.,HoUehbachR.E.//J. Appl. Phys., 1972, V. 43, № 11,
P.4669—4675.
17. Разоренов СВ., Канель Г.И.//Детонация и ударные
волны. Материалы VIII Всес. симп. по горению и взрыву.
Черноголовка, 1986, С. 46—49.
18. Степанов Г. В. Проблемы прочности, 1976, N8, с. 66...69.
19. Куракин Н. И., Даниленко В. В., Козерук Н. П.//Физика
горения и взрыва. 1989, № 5, С. 89—92.
20. Батьков Ю. В., ГлушакА.Б., Новиков С. A.//IV Всес.
совещание по детонации, Телави. 1988. Доклады, Т. 1, С. 154—157.
21. Lambourn В. D., BealingR., Mears A.Jntern. Confer. "Shock
waves in condensed matter", St. Peterburg, Russia, 1994, Abstracts,
p.8.
22. Мейдер Ч. Численное моделирование детонации. M.: Мир,
1985.
23. Голубев В. К., Трунин И. Р. ФГВД990, № 3, С. 105.
24. Razorenov S. V., Utkin А. V., Kanel G. J., Yarunichev A. S. "Shock
waves in condensed matter", Jntern.conf., St. Peterburg, 1994,
abstracts, p.7.
25. Ахмадеев H.X., Болотова P.X.//Детонация и ударные волны.
Материалы VIII Всес. симпозиума по горению и взрыву.
Черноголовка, 1986, С. 23—26.
26. Иванов А. Г., Огородников В. А. и др. IV Всес.совещание по
детонации. Телави. 1988, доклады т. 1, с. 175—179.
27. MuzyriaA.K.Jnter.Conf. "Shock waves in condensed matter",
St.Peterburg, Russia, 1994, Abstracts, p. 11.
28. ГлузманВ.Д., КанельГ.И. и др. Проблемы прочности, 1985,
N8, с. 52.
29. Новиков С. А., Погорелов А. П., Синицын В. А. Ж. прикл.
мех. и техн. физики, N3, с. 136... 139.
30. Breed В. R., Mader С. L., Vehable P. J. J. Appl. Phys., 1967, 38, 8,
3271.
31. Erkman J. O.J. Appl. Phys., 1961,32, N5, p.939—944.
32. Молодец A. M. Динамика сплошной среды. Новосибирск,
1980, вып. 48, с. 111...115.
33. Канель Г. И., Разоренов С. В. и др. IV Всес. совещание по
детонации, Телави, 1988, доклады, т. 2, с. 104... 110.
34. Беллендир Э. Н., Пугачев Г. С, Синани А. Б. IV Всес.
совещание по детонации, Телави, 1988, доклады, т. 1, с. 279...285.
35. Разоренов С.В., КанельГ.И. IV Всес. совещание по
детонации, 1988 доклады, т. 2, с. 77...83.
36. Либовиц Г. Разрушение (сборник). М.: Мир, 1973.
37 Мороз Л. С. Механика и физика деформаций и разрушения
материалов. Л.: Машиностроение, 1984.
38. Кукуджанов В. Н. Успехи механики. 1985, т. 2, N4, с. 21—65.
39. Ахмадеев Н.Х. Динамическое разрушение твердых тел в
волнах напряжений. Уфа, 1988.
40. Иванов А. Г. ФГВ, 1985, N2, с. 97.
41. Журков С. Н. Вести АН СССР, 1968, N3, с. 46.
42. Регель В. Р., Слуцкер А. И., Томашевский Э. Е. Кинетическая
природа прочности твердых тел. М.: Наука, 1974.
43. Barbee Т. W., Seaman Jr.L., Crewson R.J.J. Materials, 1972, N3,
p.393.
44. Johnson J.N.J. Appl. Phys., 1981,52, N4, p.2812.
45. Сурак С. Г., Канель Г. И. и др. ФГВ, 1983, N2, с. 121.
46. КанельГ.И., Разоренов СВ., Фортов В. Е. Ж. прикл. механ.
и техн. физики, 1984, N5, с. 60.
47. Ахмадеев Н.Х., Нигматулин Р.И. ДАН СССР, 1082,266, N5,
с. 158.
48. АхмадеевН.Х.Ж. прикл. механ. и техн. физики, 1983, N4,
с. 158.
134
49. Мещеряков Ю. И. ЖТФ, 1988,58,3, с. 628.
50. АтрошенкоС.А., БейлинаО.Я., ГладышевС.А. и др. ФГВ,
1990.N3.C.65...71.
51. Златин Н.А.,Пугачев Г.С.,ВоловецЛ.Д.идр.ЖТФ,1981,51,7,
с. 1506.
52. Огородников В. А. ФГВ, 2002 № 4, с. 119.
53. Огородников В. А., Иванов А. Г. ФГВ, 2001, № 1, с. 133—136
135
Глава четвертая
УДАРНОЕ СЖАТИЕ ПОРИСТОГО ВЕЩЕСТВА
4.1. Вид ударных адиабат пористых тел
Одна ударная адиабата дает информацию о свойствах вещества
при высоких давлениях и температурах только вдоль одной линии
на р, u; р, v или р, Т — диаграммах. Регистрация серии ударных
адиабат а^я образцов вещества с различной начальной плотностью (с
пористостью) позволяет расширить область, доступную а^я
исследований в направлении более высоких температур. Поведение пористых
материалов в УВ представляет большой интерес в связи с задачами
исследований уравнений состояния, динамического прессования,
спекания, синтеза.
Впервые предложил исследовать ударное сжатие одного и того же
вещества с различной начальной плотностью Я. Б. Зельдович [1].
Изучению ударного сжатия пористых металлов посвящены
ставшие уже классическими работы СБ. Кормера, Л.В. Альтшулера,
К.К. Крупникова [2,3,4,5].
Способом варьирования плотности является приготовление
образцов из порошка с различной пористостью m = р0/р(Ю = v^/v^ где
р0 — плотность сплошного вещества, р^ — средняя плотность
пористого образца.
При сжатии пористого образца сначала затрачивается работа
на «закрытие» пор и уплотнение образца от р^ до р0. Эта работа
связана с преодолением сил трения между частицами и их
деформацией. Для этого требуется сравнительно малые давления,
определяемые прочностью (до ~1 ГПа).
136
Эти давления в десятки раз меньше давлений на ударной
адиабате, поэтому можно считать, что давление уплотнения равно нулю,
и на участке v — vQ адиабата пористого вещества представляет
собой отрезок оси абсцисс (модель Зельдовича).
Общий вид ударной адиабаты пористого вещества в р, v
-координатах показан на рис. 4.1.При сжатии внутренняя энергия
возрастает на величину Е-0,5р (v^— v)9 равную площади
треугольника vQQ ^.Потенциальная (упругая) энергия равна площади vQ vc
и не зависит от v^. Следовательно, с ростом vw или пористости
возрастает доля тепловой энергии и теплового давления. Поэтому вру v —
координатах ударная адиабата идет круче, а значит, ^\я сжатия вещества
до одного и того же объема необходимо приложить большее давление,
что и видно из рис. 4.1.
Например, ^ая
железа с пористостью т= 1,4
при сжатии в vQ/v=l,22,
v00/v = 1,74 и прирост
давления рА/рв= 2,63 [5].
При достаточно
большой пористости роль
тепла может оказаться
настолько большой, что
тепловое расширение
превысит уменьшение объема
при сжатии, т.е.
увеличение давления УВ приведет
к уменьшению плотности
(адиабата N6 на рис. 4.3).
Существование такой
аномальной адиабаты было доказано Зельдовичем на примере
уравнения состояния Ми— Грюнайзена [1].
Если в уравнение ударной адиабаты Е — Е0 = 1/2 р (vQ — v)
подставить Е = Ех+Е^ выразив тепловую часть Етчерез тепловое давление
Р— Рх = Рт = ГоЕЛ Е = Ет + v (р— р0)/Г0, (Г0— коэффициент
Грюнайзена), то получим уравнение ударной адиабаты в форме:
1
А
Рспл
л
1
'пор
\ \
\ \
\ \
ч \ \
<м - \
/\
tf& \
Рис.4.1. Ударное сжатие пористого вещества.
Рн =
(h-\)px-2EJV
h-VJV '
(4.1)
где Ь=(2/Г0)—1 — предельное сжатие в ударной волне (при
р -> оо vQ /v -> h).
Напомним, что h = (j + l)/(j — 1) аля газов, а Г0=j — 1 (j —
показатель адиабаты газа).
Уравнение (4.1) получено для небольших давлений в
предположении Г = Г0 = Const, энергия и давление электронов малы, а Е0
также можно пренебречь, причем вещество может быть как сплошным
(с vQ), так и пористым (с v^). В последнем случае уравнение ударной
адиабаты ^ая пористого вещества получает вид:
Уравнение (4.2) описывает семейство ударных адиабат с
различными vQ0 или с различной пористостью m = vQ0 /vQ. Начальная точка
рн = 0, v = vQ удовлетворяет уравнению (4.2) при любом начальном
объеме v00, так что семейство адиабат выходит из одной начальной
точки (см. рис. 4.2 [6]).
Рис. 4.2. Семейство ударных адиабат вещества с различной пористостью
m=voo/vot6l-
138
Рис. 4.3. Виды адиабат веществ с
различной пористостью [7]:
I тип — сплошные линии, II тип —
пунктир.
Предельный объем
v = v„ /h. При небольшой
пр 00 лГ
пористости m < h
адиабаты имеют нормальный вид,
а при m > h ход кривых
аномален: при увеличении
давления объем увеличивается.
При больших
давлениях картина усложняется за
счет возрастания роли
электронных членов. Используя
уравнение состояния с
электронными членами, можно
показать возможность
существования адиабат с чередованием участков с положительными и
отрицательными значениями производных (Эр/Э а )н, где а = vQ /v.
Изменение знака (Эр/Эо) объясняется тем, что при малых
давлениях и температурах ударная адиабата определяется
поведением решетки, а при больших — поведением электронов. Знак
(Эр/Эо) и вид адиабаты определяются соотношением величин тс
и коэффициентов Грюнайзена аля решетки (Гр) и /^ля
электронов (Гэл). Адиабаты пористых веществ могут быть двух типов (см.
рис. 4.3).
1тип Г<2/(т<7-1).
При<7> 1 (Эр/Эс) >0 (N 1,2,3).
При <7< 1 (Эр/Эо) знакопеременна (N4).
II тип Г>2/(т<7-1).
При с> 1 (Эр/Э с) знакопеременна (N 5).
npH<r<l(3p/3<r)<0(N6).
Предельная плотность достигается при Г = 2/(т с- 1) (N7).
Адиабата вида N 7 получена экспериментально для никеля с m = 3
[7], N4 — для вольфрама [3], N2 — для железа [5].
Обработка экспериментальных данных по ударному сжатию
пористых металлов, имеющих экстремально высокие температуры при
небольших сжатиях <7, позволяют выявить температурные
зависимости теплоемкости (от 3R до 3/2 R) и коэффициентов Грюнайзена Гр
и Гэл (см. гл. 3).
4.2. фарное сжатие пористых тел в области малых
давлений
При малых давлениях, сравнимых с прочностью, ударные волны
в пористом теле имеют сложную структуру. Здесь простая модель
однородного пористого тела Зельдовича неприменима. Вид адиабат
пористого тела при низких давлениях показан на рис. 4.4.
Р
Рис. 4.4. Начальный участок адиабат пористого тела.
Как и аая монолитного тела с прочностью, на первой стадии,
пористое тело реагирует на нагрузку упруго, т.е. существуют упругий
предвестник и упругий предел Гюгонио, выше которого адиабата
меняет свой наклон и переходит в пластическую область.
В пористом упругопластичном теле амплитуда упругого
предвестника рН1 и его скорость D меньше, чем аля сплошного тела, что
иллюстрирует таблица 4.1 [9,10].
Таким образом, пористость снижает сопротивляемость тела
ударному нагружению, т.е. величина рш уменьшается с ростом т.
Из рис. 4.4 видно, что при некотором давлении полного
уплотнения р ударные адиабаты пористого тела близки, или совпадают с
ударной адиабатой сплошного тела. Полученные в [11,12]
экспериментальные величины рк приведены в таблице 4.2.
140
Таблица 4.1. Зависимость параметров упругой волны
от пористости
Металл
Be
Be
Be
Be
Fe
Fe
Пористость, m
1,0
1,16
1,32
1,49
1,47
1,76
рН1,кбар
3,3
2,2
1,3
2,2
1,3
D, км/с
13,8
9,0
Из табл. 4.2 видно, что рк зависит от пористости. Для алюминия
с m = 2—3 состояние полного уплотнения не достигается, как и а^я
ультрадисперсного алмаза [31]. Обычно рк > рн1.
Таблица 4.2. Давление полного уплотнения в зависимости
от пористости
Металл
Медь
Медь
Медь
Молибден
Молибден
Вольфрам
Вольфрам
Вольфрам
р, г/смЗ
7,41
6,05
5,10
5,10
3,40
12,64
9,70
6,40
rti
1,2
1,47
2,00
2,00
3,00
1,52
2,00
3,00
Рк, ГПа
2,0
2,0
4,0
4,0
2,0
5,0
6,5
3,0
Начальные участки ударных адиабат пористого и монолитного
вольфрама показаны на рис. 4.5 [11], а для горячепрессованных
образцов бериллия различной плотности — на рис. 4.6 [12].
На рис.4.7—4.9 приведены экспериментальные результаты а^я
пористых стекла, мрамора и окиси магния [13], а на рис. 4.10 — а^я
кварца [14].
Рн,
ГПа
0 0,05 0,06 0,07 у,см3/г
Рис. 4.5. Начальные участки
адиабат вольфрама [11].
0,05 0,10 0,15 0,20 (v-v0)/v
Рис. 4.6.Уплотнение бериллия при
одноосном сжатии [12].
Здесь также наблюдается картина, отличающаяся от
предсказываемой моделью Зельдовича. Нет свидетельств того, что у адиабат
с разными m возможны общие состояния р = 0, р = р0. Каждая
начальная плотность p^ является начальной точкой своей адиабаты.
Кроме того, на рис. 4.7, 4.8 ясно видна еще одна особенность
адиабат — существует область давления, где тела с большей
пористостью обладают большей сжимаемостью, в отличие от обычной
картины уменьшения сжимаемости с ростом m . Эти своеобразные
Рн
кбар
500
300
100 L
0,25 0,30 0,35 0,40 у,см3/г
Рис. 4.7. Ударные адиабаты стекла:
1 — т=1;2 — т=2,1
0,2 0,3 0,4 у,см3/г
Рис. 4.8. Ударные адиабаты
мрамора: 1 — т=1;2 — т = 1,18
142
Рн,
кбар
400
200
100
Рн.
коар
600
400
200
0
6
1
>"7
————^^^У^1'
i Г --JT / 1/
5
1 ' уГ
Л
4 3
L
2 1
II
i » i i
0,1 0,2 0,3 0,4 у,см3/г 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 у,см3/г
Рис. 4.9. Ударные адиабаты окиси
магния:
1— т=1,05;2 — т=1,95;
3 — т=2,52;4 — т = 2,64;
5 — т=7,41.
Рис. 4.10. Ударные адиабаты кварца:
1 —т=1;2 — т=1,2;
3 — т=1,52;4 — т=1,71;
5 —т=1,9б;6 —т=2,30
особенности сжатия пористых тел наблюдаются при давлениях
фазовых превращений и объясняются кинетикой перестройки
кристаллической решетки и существованием неравновесных состояний
за фронтом УВ.
Таким образом, при больших давлениях различие ударных
адиабат пористого и монолитного материала связано с аномально
высоким тепловым давлением у пористого тела. Экспериментально
показано, что при сильном ударном сжатии высокопористых материалов
реализуются газофазные и плазменные состояния [15].
Приведем результаты экспериментов по динамической
сжимаемости хрупкого полидисперсного порошка аминопласта (р0 = 1,453 г/ см3)
с р(Ю=0,95 г/см3 при давлениях менее 1 ГПа, когда существенным
становится влияние на сжатие порошка поверхностно-прочностных
эффектов [16].
В опытах волновая и массовая скорости измерялись
электромагнитным методом с помощью 3-х П — образных датчиков из
алюминия.
По измеренным значениям D и и рассчитывались давление
сжатия р = р00 Du и степень сжатия р00/р = 1 - u/D. Полученные
кривые динамической сжимаемости порошка аминопласта
показаны на рис. 4.11 а,б.
б)
рГПа
0,3
0,2
0,1
0
- 1
1 •
1 *
1 *
• '—-»^
0 0,1 0,2 0,3 и,км/с 0,6 0,8 1,0 pjp
Рис. 4.11. Кривые динамической сжимаемости порошка аминопласта [16].
На (D,u)—диаграмме четко выделяются четыре различных
режима динамического уплотнения порошка:
— область I квазиупругой деформации с характерным двухвол-
новым профилем u(t). С уменьшением и волновая скорость D
возрастает, стремясь к продольной скорости звука в порошке.
— области II—IV неупругой необратимой деформации (и > 100 м/с).
В области II деформация определяется переупаковкой частиц
в условиях сухого трения. В области III деформация
сопровождается хрупким разрушением (дроблением) частиц порошка, чем можно
объяснить наличие участка с D = Const.
В области III достигается предельное уплотнение порошка на
фронте УВ. Параметры состояния в области III зависят от скорости
нагружения порошка (скорости роста давления в волне), что
объясняется существованием при сжатии предельной скорости
скольжения частиц порошка относительно друг друга.
При более высоких давлениях в области IV определяющим
становится сжимаемость частиц аминопласта и (D,u)-диаграмма
принимает общепринятый линейный вид.
4.3. Модели пористого тела
В [17] пористое тело рассматривается как агломерат зерен
сплошного вещества, разделенных промежутками. Поэтому движение УВ яв-
144
ляется дискретным: в зернах УВ идет со скоростью D, а свободные
поверхности зерен движутся со скоростью w. Такой процесс идет от зерна
к зерну с некоторой средней скоростью D*, фиксируемой в опыте:
\иу„ил+х.ил
D
w
(43)
Каждое зерно испытывает сжатие и разрежение в точках М и N (см.
рис 4.12). Гидродинамическое состояние вещества описывается изэн-
тропой сплошного тела S. Колеблясь вначале (в падающей волне) между
точками N и М, состояние вещества стремится к равновесному,
поскольку ударные волны и волны разрежения, идущие назад в зерне, догоняют
каждая последующая предыдущую. Отраженная УВ стремится к слабой
волне сжатия, идущей со скоростью звука .Однако равновесное состояние
L достигается не фазу за фронтом падающей волны. Место точек L на
рис 4.12а — кривая С, которая на рис. 4.126 совпадает с ударной
адиабатой сплошного тела и не зависит от пористости.
Если учитывать воздух в промежутках между зернами, то сжатие
можно характеризовать средними значениями v*,u*, D*, р*, которые
устанавливаются в результате циркуляции волн между воздухом
и зернами. Зерна сжимаются и разогреваются до v и Т,
соответствующих сплошному веществу при давлении р*, а при многократном
сжатии воздуха предполагается сильными только две первые волны
с предельным сжатием в каждой волне.
Считается, что у воздуха теплового излучения нет (Т < 10 6 К) и для
длительности волны 1мкс между зернами и воздухом выравнивается
только давление, а термическое равновесие не успевает установиться.
а) б)
N u N
Рис 4.12. Диаграмма сжатия пористого тела.
Считается, что если число Фурье F = a t/R2<<l, то выравнивания
температуры не происходит (а — теплопроводность, t — время, R —
размер). Например, для меди с зернами ~ 10 мкм F = 0,1.
Цельный объем пористого тела будет равен сумме удельных
объемов воздуха и сплошного тела, умноженных на их весовые доли:
r=F + F0(m-l)(^)2 (4.4)
Для сжатия:
l/o-* =1/ст + (т-1)(^)2 (4.5)
/ + 1
Для массовой скорости:
u=[u2+(m-l)pVo7^ (4.6)
где а=v0/v, у — показатель адиабаты воздуха, величины без индекса
относятся к сплошному телу.
Выражения (4.5) и (4.6) позволяют рассчитать адиабату пористого
тела по известной адиабате сплошного тела. Согласие с экспериментом
хорошее до давлений порядка 100 ГПа (см. рис. 4.13) [18,19].
Отметим работу [20], согласно которой вакуумирование
пористых образцов сульфата аммония не влияет на D, и — зависимость
в интервале D < 6 км/с, и < 3 км/с. Следовательно, влияние
воздушных пузырьков между зернами пренебрежимо мало.
Модель равномерно распределенных сферических пор
используется в [21,22] а^я описания поведения пористых тел в ударных
волнах. При этом учитывается инерционность и вязкость материала в
окрестности поры. Хорошая точность расчета ширины
пластической волны сжатия в алюминии достигается при использовании
величины коэффициента вязкости у] = 1—10 Пас.
Широко используется также т.н. р - а модель Германа (Herrmann)
[23], согласно которой поведение пористого материала описывается с
помощью одного параметра состояния а, который определяется как
относительный объем сплошной матрицы и зависит только от давления.
Связь между давлением и удельным объемом дается в виде р = р (v, а)
146
р кбар
1000
3,5 и,км/с 0,8 1,0
1,2
1,4 1,6
Рис. 4.13. Сравнение расчетных и экспериментальных результатов по сжатию
пористых тел [18,19].
или более точно р = а р (v, а) [24] или р = (ас/с0) р fya) [25], где с и с0 —
скорости звука в пористом и сплошном материалах.
На модели пористого тела, имитируемого набором стальных
шариков, показано, что деформация пористого тела локализована вблизи
поверхности частиц [26], температура которой может превысить
температуру плавления. Адиабатический разогрев приповерхностных слоев
частиц облегчает их деформацию и снижает общее сопротивление
ударному уплотнению в сравнении со статическим прессованием.
4.4. Волны расширения в пористых телах
Процесс разгрузки ударносжатых пористых тел изучен слабо.
Анализ имеющихся результатов [18] показывает, что разгрузка
определяется изэнтропическим расширением зерен сплошного тела, а
объем воздуха в порах практически не меняется и остается равным
значению в исходном сжатом состоянии перед разгрузкой.
По-видимому, два конкурирующих процесса — изэнтропиче-
ское расширение и сжатие воздуха при его охлаждении за счет
теплопроводности окружающими менее нагретыми зернами -
компенсируют друг друга. Плотность тела после сжатия и разгрузки выше,
чем первоначальная (см. рис. 4.6).Следовательно, в p,v — плоскости
возрастают наклон кривой разгрузки и скорость звука.
Особенность разгрузки пористых тел состоит в том, что волна
разгрузки быстрее догоняет фронт УВ по сравнению со сплошным
телом, т.е. выполняется соотношение:
(-^-)пор>(-^-)спл (4.7)
Поэтому в пористых телах ударные волны затухают быстрее,
а угол а боковой разгрузки больше, чем в сплошном веществе.
Выражение для расчёта угла а (т, а) получено в [19]
В таблице 4.3 сравниваются экспериментальные и расчетные
значения угла а для пористых вольфрама и меди [19].
Таблица 4.3. Сравнение экспериментальных и расчетных по (4.8)
значений угла боковой разгрузки
Металл
Вольфрам
Вольфрам
Вольфрам
Медь
Медь
Медь
m
1,8
1,8
1,8
3,01
3,01
1,0
а
1,212
1,065
1,017
1,03
1,03
1,2
Угол боковой разгрузки, а0
эксперимент расчет
38,5
44,5
67,0
64,0
60,0
41,0
35,4
50,0
69,0
59,0
59,0
28,0
Из таблицы 4.3 на примере меди видно, что пористость заметно
увеличивает боковой угол разгрузки.
4.5. фарная сжимаемость кубического нитрида бора
Сравним ударные адиабаты сплошного и пористого вещества
на примере сверхтвердой модификации нитрида бора с кубической
(сфалеритной) решеткой (BNc).
В [27] экспериментально исследована до давления 147,7 ГПа
ударная сжимаемость поликристаллов BNc (р0=3.43 г/см3, р(Ю=3,34 г/см3,
m = 1,018, модуль Е = 911 ГПа, твердость по Виккерсу 60 ГПа,
получены ударноволновым спеканием порошка зернистостью 28-40 мкм
[28]) и порошка BNc (р(Ю = 2,05 г/см3, т=1,7, с той же
зернистостью).
Точки ударной адиабаты определялись методом «отражения»
(см.раздел 2,5), использовались экраны и ударники из алюминия и
148
стали, электроконтактами измерялась в образце волновая скорость
D и скорость свободной поверхности w.
В поликристалле до давления 100 ГПа перед пластической
волной распространяется упругий предвестник со скоростью 12,2 км/с
и давлением р{ = р u2D .
Давления во второй пластической волне р2 измерялись
манганиновым датчиком [29].
Зная р2, р2, Uj = 0,5 Wj, u2 = 0,5 w2, вычислялись остальные
параметры сжатия [27].
Полученные D - и зависимости а^я поликристалла и а^я
порошка BNc с р00 = 2,05 г/см3 приведены на рис. 4.14.
Величина энергии «холодного» сжатия Ех вычислялась
методом последовательных приближений с использованием дебаевской
удельной теплоемкости с (температура Дебая а^я BNc равна 1720 К
[30]). При расчете температуры до давлений 95 ГПа принималось,
что ударная адиабата совпадает с кривой «холодного» сжатия
(рн = рх), а энергия сжатия от р00 до р0 считалась тепловой. Тогда
температура на ударной адиабате рассчитывалась по формуле:
0,5р (V -V)-E
ТК = 280 + ^—У *- (4.8)
с
v
Полученные результаты приведены на рис. 4.14, 4.15. Видно,
что пористость резко увеличивает температуру ударного сжатия.
Для полного закрытия микропор в BNc требуются большие
давления: ~ 8 ГПа аая образцов с р00 = 3,43 г/см3 и ~ 23 ГПа аая
образцов с р00 = 2,05 г/смЗ. Это давление а^я алмазного порошка с
р00 = 2,02 г/см3 равно 20 ГПа [31,8].
Полученные D(u) и p(v) зависимости не имеют изломов (нет
перестройки решетки).
фарная сжимаемость BNc выше 50 ГПа хорошо согласуется со
статической сжимаемостью BNc, полученной в [32]. При низких
давлениях ударная адиабата отличается от кривой гидростатического сжатия
вследствие влияния большой прочности BNc при одностороннем
сжатии в ударной волне.
б)
0,25 v0 0,30 0,45 v00
v, см3/г
Рис. 4.14. фарные адиабаты сфалеритного нитрида бора различной плотности.
1 - поликристалл с р=3,43 г/см3; m = 1,02;
2 - порошок с р=2,05 г/см3; m=1,70;
a) D (U) - зависимости; шкала слева — для поликристалла; шкала справа — для
порошка; аппроксимации: 1 - D = 9,l67 + 1,392U; 2 — D= 1,280 + 1,781U;
6) p(v) - зависимость.
T,k
6000
4000
2000
0
у
/
/
m=l,70
m=l,02
\
^
40
120
160 р.ГПа
Отмечается большая
схожесть ударных
адиабат BNc и алмаза, что
объясняется близкими
значениями плотности
и твёрдости.
Экспериментальная
D-u-диаграмма а^я
порошка BNc хорошо
согласуется с
рассчитанной теоретически [32].
Рис. 4.15. Влияние пористости на температуру
ударного сжатия BNc.
На основании
выполненных в [27]
измерений был определен аая BNc коэффициент Грюнайзена Г,
характеризующий тепловую упругость вещества и позволяющий
найти предельную степень сжатия h = 1 + 2/Г. Для рн = 72,8 ГПа
Г =0,62.
Для УРС с согласованными п и h [33] выражения ^ая рн и рх
имеют следующий вид:
150
Р0С0 Г/7 Л + lv П 2П /7 141
Ри= ,, ° А(Ь -)<тн + -<т-(й + 1)];
п(п-т<7) п-\ п-\ иу\
л = ЯЙ.(<т-_1)
Расчет рн по (4.9) хорошо согласуется с
экспериментальными точками ударной адиабаты поликристаллов (т= 1,02) при
следующих параметрах У PC для BNc: р0=3,492 г/см3, с0=9,826 км/с,
п = 4,074; h = 4,3.
4.6. фарное компактирование алмазных порошков
Цель ударного компактирования алмазных порошков —
получение абразивных поликристаллов спеканием частиц. Для порошков
из хрупких и прочных материалов наиболее вероятен механизм жид-
кофазного спекания за счёт частичного плавления частиц в
окрестностях схлопывающихся пор. Косвенным свидетельством плавления
является резкое (на 2—3 порядка) измельчение структуры
поликристалла BNc в местах пор. Такое же резкое измельчение структуры
наблюдается при плавлении центральной части образцов различных
материалов, сжатых сферически сходящейся ударной волной в
ампулах сохранения [34]. Причина измельчения — в большой скорости
охлаждения расплава («закалки») окружающим более холодным
объёмом нерасплавленного материала.
Трудность жидкофазного спекания алмаза состоит в сочетании
его рекордно высокой температуры плавления (4470 К в тройной
точке) и рекордно низкой сжимаемости (низкой тепловой энергии
ударного сжатия), а также большого различия температур спекания
и графитизации (~2500 К и ~1500 К соответственно). Поэтому
сохранить алмаз можно только при его охлаждении под давлением до
температур менее 1500 К.
Для обеспечения необходимого времени охлаждения требуется
максимально замедлять скорость разгрузки после ударного сжатия за
счёт использования заряда взрывчатых веществ (ВВ) большой массы
и массивных оболочек вокруг заряда или вокруг алмаза.
Как известно, при ударном сжатии порошков вблизи пор между
частицами температура существенно выше средней за счёт
кумулятивных явлений. Поэтому по сравнению с монокристаллом
плавление порошков начинается в порах при значительно меньших
давлениях. Это облегчает получение условий а^я жидкофазного
ударно-волнового спекания порошков алмаза.
Малый нагрев монокристаллических частиц алмаза при ударно-
волновом спекании порошков играет и положительную роль: алмаз,
сильно нагретый в порах вплоть до расплавления, быстро
охлаждается за счёт теплообмена с холодным внутренним объёмом частиц
(охлаждение т.н. «внутренним» холодильником [31]). Этому
способствует и рекордно высокая теплопроводность алмаза (2000 W/
(т-К)). Если ударной волной расплавить весь объём порошка
алмаза, то а^я охлаждения (и кристаллизации под давлением)
потребуется т.н. «внешний» холодильник, например, в виде металлической
матрицы, не образующей карбиды (медь, серебро, свинец) и ещё
меньшая скорость разгрузки [31].
Например, расчетное время внешнего охлаждения от 2300К до
1300К гранулы размером 0,6 мм из алмазного микропорошка
расплавленным в УВ свинцом составляет 80 мкс[31]. Эти расчеты
показывают, что применение обычно используемых в экспериментах
зарядов и сборок с длительностью давления порядка 1 мкс
малопригодно для жидкофазного спекания алмазных порошков.
Обзор имеющихся экспериментальных результатов по ударно-
волновому компактированию алмазных порошков сделан нами в [31].
Необычный механизм жидко-фазного спекания в плотной
газовой среде ( в плотных продуктах детонации) обнаружен нами в 1987
г. при проведении экспериментов по синтезу УДА взрывом зарядов
из ТГ40 массой 5 - 10 кг в воде. В результате детонации образуются
нанокапли sp3 углерода с размерами 3-8 нм. В процессе
относительно медленной разгрузки в интервале 25-8 ГПа (более 60 мкс) эти
нанокапли сталкиваются, сливаются и кристаллизуются с
образованием абразивных поликристаллов с размерами более 10 мкм [31]. В
1991 г. в результате взрыва в водной оболочке заряда из ТГ40 массой
140 кг обнаружены поликристаллы с размерами до 85 мкм [44].
152
4.7. фарная сжимаемость алмазных порошков
Для оценки условий плавления в ударной волне необходимо
знание ударных адиабат алмазных порошков. Экспериментальное
определение ударной сжимаемости алмазных порошков сделано
лишь а^я нескольких образцов с определёнными значениями
пористости и дисперсности [31,35]. Поэтому нужна информация,
позволяющая оценить условия ударного сжатия алмазных порошков
с любыми значениями пористости и дисперсности. Нами сделаны
расчёты ударных адиабат и условий плавления алмазных порошков
Аая давлений однократного ударного сжатия порошков в пределах
~ 60 ГПа [8]. При таких давлениях алмаз можно считать слабо
сжимаемым и пренебрегать энергией его упругого сжатия, что упрощает
расчёты адиабат.
4.7.1. Эксперименты
Методом отражения (см. разд. 2.5 и 4.5) М.Н. Павловским
экспериментально исследована ударная сжимаемость алмаза различной
пористости. Исследуемые образцы получались холодным
прессованием следующих алмазных порошков:
- ультрадисперсный детонационный алмаз (УДА) или наноал-
маз с частицами 2—10 нм, р00 = 0,607 г/см3;
- АСМ-В 1/0 с частицами 0,1—1 мкм, р00 = 1,79 г/см3;
- АСМ 14/10 с частицами 10—14 мкм, р00 = 1,90 г/см3;
- АСМ 40/60 с частицами 40—60 мкм, р00 = 2,02 г/см3;
- АСН 40/60 с частицами 40—60 мкм, р00 = 2,23 г/см3
(частицы покрыты никелем).
Полученные результаты сравнивались с ударной сжимаемостью
монокристаллического алмаза (ро = 3,51 г/см3), исследованного
ранее тем же методом и тем же автором (М.Н. Павловским) [35].
В опытах электроконтактным методом измерялась скорость D
ударной волны в образцах, а величины массовых скоростей в
экранах (и ) были известны. Температура ударного сжатия оценивалась
так же, как а^я BNc [27] (см. разд. 4.5). В расчётах теплоёмкости
температура Дебая аля алмаза принималась равной 2000 К.
Результаты опытов представлены в табл. 4.4. Для монокристалла
алмаза D = 12,16+1,00 и. На этой прямой не лежит одна последняя
точка адиабаты (р = 590 ГПа, Т = 6400К), что может быть связано с
плавлением алмаза (см. раздел 14.4).
Из-за большой начальной пористости температура ударного
сжатия УДА значительно выше, чем у обычных алмазных
микропорошков. Например, при 20 ГПа у УДА Т = 7000 К, а у АСМ1/0
Т = 2000 К. Поэтому УДА с р00 = 0,607 г/см3 не сжимается до
беспористого состояния, получение которого важно /щя спекания
алмаза.
ВсеточкиударнойадиабатыУДАлежатнапрямойВ=0,5б+1,19и,
даже точка с Т = 7200К, где должно быть плавление.
Вследствие большого содержания в порошке АСН 60/40 никеля
(более плотного, чем алмаз), ударная адиабата этого порошка лежит
левее ударной адиабаты монокристалла алмаза в p,V - координатах.
Полученные результаты могут быть использованы /^ выбора
оптимальных условий ударноволнового спекания алмазных
порошков при их однократном сжатии. При сжатии двумя и более
ударными волнами (например, в цилиндрической ампуле) температура
будет ниже, а сжатие выше, чем измеренные в этих опытах.
Таблица 4.4.
Экспериментальные точки ударных адиабат алмаза различной пористости.
Начальная
плотность
образцов
I
9 = 0,607 JL
Г- см3
К= 5,7625
Р = 1,789 •£-„
5- см3
* =1,962
v*-™%
Фракция.
Размер
зёрен.
2
УДА
204-100 А
АСМ-В 1/0
0,14-1 МКМ
АСН 60/40
40*60 мкм
Материал
экрана.
3
км/о
4
1,45
2,07
2,70
3,29
1,45
2,07
2,70
3,29
1,45
2,07
2,70
3,29
Ъ
км/с
5
3,60
4,65
5,85
6,96
4,56
5,65
6,79
7,89
3,99
5,04
6,27
7,35
Р
ГПа
6
5,57
9,77
15,94
22,73
16,15
27,49
41,91
57,49
17,26
29,55
46,28
64,08
7Л
км/с
7
2,55
3,46
4,49
5,38
1,98
2,72
3,45
4,12
1,94
2,63
3,31
3,91
8
3,429
3,908
4,301
4,405
1,767
1,928
2,033
2,093
1,946
2,091
2,118
2,137
G
9
0,593
0,675
0,744
0,762
0,900
0,983
1,036
1,067
<?
г/см3
10
2,08
2,37
2,61
2,67
3,16
3,45
3,64
3,74
4,34
4,66
4,72
4,76
см3/?
II
0,480
0,422
0,383
0,374
0,316
0,290
0,275
0,267
0,230
0,214
0,212
0,210
т°к
I?
1900
3200 |
5100 |
7200
1300 1
2100
3100 1
4100 1
154
Р-1,90 г/см3
\Jeo
«С-1,847
/>=3,51 р/см3
\к*1
1
ЫКМ
Монокристалл
Fe
М
fe
1,50 |
2,70'
3,29
3,70
4,55
1 2,80
3,70
4.55
7,00
4,52
6,99
8,01
8,84
12,24
14,18
14,94
17,33
| 20,50
17,3
44,6
60,9
74,5
| 155,0"
| У9,5
145,6
| 313,0
1 590,0
2,011
3,36'
4,00
4,44
6,66
2,01
[2,78
5,15
| 8,20
I.60O
1,926
1,997
2,009
2,196
-
j -
-
-
0,974
1,043
1,081
1,088
1,187
1,166
1,230
1,423
| 1,667
3,42
3,66
3,79
3,82
4,17
4,09
4,32
5,00
5,tib
0,293
0,273
0,264
0,262
0,239
0,245
0,232
0,201
0,171
800 |
3000 ]
4000
4700
10300
500
700
2400
с400
4.7.2. Расчеты ударных адиабат
А. р, и - зависимости
Для расчёта ударных адиабат алмазных порошков нами
использована модель, предполагающая, что порошок представляет собой смесь
монолитного тела и воздуха в порах, причём, тепловое равновесие между
воздухом и телом не успевает установиться [36], Для такой модели
массовая скорость в порошке определяется следующим выражением [36]:
ир2 =и02Цт-1)ру04к/(к + 1)2 =и02 +(v00- v0)p4k/(k + 1)2 (4.10)
+ Роо>г/см3 ►
3,51 2,5 2,0 1,81,6 1,4 1,2
Здесь и —массовая
р
скорость в порошке,
1,0 и0 — массовая скорость
в монолите, vQ —
удельный объём
монолитного тела, vQ0 — удельный
объём порошка, р —
°>6 давление, к= 1.4 —
показатель адиабаты
воздуха.
0 12 3 4 и, км/с
Рис. 4.16. Ударные адиабаты алмазных порошков
различной начальной плотности в (р,и)
координатах.
ГПа
40
30
20
10
\%/j III/А
1мШ/\
V 1W//V У\
Для монокристалла алмаза [35]:
Do=l2A6 + uo,p = poD0u0=3.5l(l2.\6uo+uo2) (4.11)
где DQ — скорость ударной волны.
Задавая ряд значений uQ, по (2), находим соответствующий им ряд
давлений. Затем задаёмся рядом значений v00 порошков и по (1)
находим соответствующие значения и . Полученные таким образом р, и —
зависимости приведены на рис. 4.16. Кроме того, на рис. 4.16 приведены
ударные адиабаты монокристалла алмаза и железа, изэнтропа разгрузки
железа после сжатия взрывчатым составом Сотр.В, а также кривая
торможения аля Сотр.В [37]. Эти зависимости позволяют оценить
давление в порошках алмаза различной плотности как в стальных плоских
ампулах сохранения (аая контактного взрыва заряда на ампуле), так и в
смеси с Сотр.В.
1 и 2 — ударная адиабата и изэнтропа разгрузки железа,
нагруженного УВ от детонации заряда из взрывчатого состава Сотр.В;
3 — кривая торможения Сотр. В.
Для низких плотностей порошков алмаза расчётные значения
массовой скорости выше экспериментальных на 5%, а а^я высоких
плотностей, наоборот, ниже на 5%.
Б. р, Т-зависимости
фарные адиабаты в (р,Т) координатах рассчитывались путём
сравнения зависимостей тепловой энергии Е (р) ударного сжатия
порошков алмаза от давления и внутренней энергии алмаза от тем-
пературыЕт(Т)-Е300 [38,39]:
Ет{р) = Ен-Ех=0.5р^-ч)-сй2{дг-Ъд+2)/68 (4.12)
где Ен - полная энергия ударной волны, Ех—упругая (« холодная »)
энергия сжатия (в (4.12) дана аая кубического уравнения состояния
[38]), с0 = 13 км/с - объёмная скорость звукав алмазе, S=vQ/v — сжатие
алмаза, Е3(Ю - энтальпия алмаза при 300К, Т(К) > 1000К —
температура алмаза.
Для принятых в расчётах давлениях до 60 ГПа пренебрегаем
малыми значениями S и Ех (например, при таком допущении аля
156
60 ГПа и порошка алмаза с плотностью 1,6 г/см3 расчётное
увеличение Ет составляет 6%) и малым изменением тепловых свойств
алмаза с давлением. В результате получим следующие простые
выражения:
Ет{р) = Ен = 490.5/Kv00-v0) (4.13)
Ет(Т)-Еш =924 + 1.978(Т(К)-1000) (4.14)
гдер-вГПа, vQ, v^ - в см3/г, Е^Е^вДж/г.
Полученные с помощью (4.13) и (4.14) расчётные ударные адиабаты
алмазных порошков в (р, Т) плоскости приведены на рис. 4.17 и
представляют собой веер прямых линий с наклоном dp/dT, изменяющимся
в зависимости от пористости от Ю-1 аа^ m = 1 до 10~3 аа^ m=6.
4.8. Определение равновесных условий плавления
алмазных пороппсов
+ Роо>г/см3 ►
р,
ГПа
50
40
30
20
10
3,51
0
1
2,5 2,0 1,8 1,6
1,4
1,2
1,0
0,6
ТНР.К
Рис. 4.17. Ударные адиабаты алмазных
порошков в (р,Т) координатах
Пунктир —линии фазовой диаграммы углерода
Кроме ударных
адиабат, на рис. 4.17 показаны
линии фазовой диаграммы
углерода. Значения
равновесных (аля всего объёма
порошка) давлений и
температур начала плавления
определялись в точках
пересечения ударных адиабат с
линией плавления алмаза с
наклоном 10,2К/ГПа [40].
Равновесные давления
окончания плавления
рассчитывались по энергии ударной
волны Е , равной сумме
тепловой энергии Ет при
температуре плавления Т и
теплоты плавления \= AS Т :
m
Ет=ЕТ+Я (4.15)
157
Для всех давлений до
60 ГПа скачок энтропии
при плавлении
принимался в расчётах постоянным
и равным его значению в
тройной точке (AS = 1,6
Дж/(гК) при р= 13,5 ГПа
[41]).
Полученные таким
образом зависимости
равновесных давлений начала и
окончания плавления от
начальной плотности
алмазных порошков
приведены на рис. 4.18 и в табл. 4.5.
Как видно, значения этих
давлений растут с
увеличением плотности порошков, стремясь к очень большим давлениям в
800—1000 ГПа для монокристалла алмаза [42].
Таблица 4.5. Результаты расчётов параметров плавления
алмазных порошков.
р, г/см3
Ьс m
stPm-GPa
EJ/g
E+XJ/g
,. p , GPa
hn i m
T,K
cq
p ,GPa
st i pore
0.6
4700
12.5
8352
12201
18.26
3840
10.0
1.0
4500
23.0
7840
15040
42.88
3218
14.5
1.2
4600
30.5
8090
15450
57.48
3025
18.0
1.4
4750
40.0
8387
15987
75.97
2854
21.0
1.6
4800
52.0
6419
16100
96.53
2611
26.5
1.8
5000
67.0
8912
16912
127.23
2439
27.5
2.0
5200
88.0
9303
17623
167.11
2236
31.5
Рт,ГПа
0,6 0,8 1,0 1,2 1,4 1,6 1,8 Poo, г/см3
Рис.4.18. Зависимости давления плавления
алмазных порошков от их начальной плотности.
1 —окончание равновесного плавления;
2 — начало равновесного плавления;
3 — начало плавления алмаза вблизи пор.
Заштрихована зона давления со смесью алмаза и
жидкости.
158
Между линиями начала и окончания плавления лежит область
смеси алмаза и его расплава. Массовую долю расплава L можно
оценить с помощью следующего простого выражения [31]:
L = p{vw-v0)/2[cp {Тя-Т0)+Л] (4.16)
где Т0 — начальная температура алмаза, с - удельная теплоёмкость.
Из (4.16) следует очевидный вывод: массовая доля расплава растёт с
увеличением давления, пористости и начальной температуры.
4.9. Тепловая неравновесность ударного сжатия порошков
Тепловая неравновесность, обусловленная концентрацией
тепловой энергии вблизи пор, существует при условии, что время
уплотнения и плавления t много меньше времени th релаксации
тепла до однородной температуры по всему объёму порошка. Если
рассматривать сжатие отдельной частицы, то при каком-то размере
dK время нагревания центра частицы th = d2/4H сравнивается с
временем прохождения ударной волны по частице, равном t = d / D.
В этом случае у частицы поверхность и центр температурно
неразличимы. Для частицы алмаза ( Н = Ю-4 м2/с, D = 15 км /с) это
происходит при dK = 26 пм (t = ^ = 0.07пс), следовательно, нагрев
ударной волной частиц наноалмазов с d = 2 - 8 пм всегда будет
равновесным. При этом внутренний объём наночастиц уже не может
играть роль «внутреннего» холодильника.
Неравновесность ударного сжатия порошков можно
характеризовать отношением температур пор в порошке к равновесной
температуре -Т /Т . Для порошков алмаза таких
экспериментальных данных нет. В работе [43] проведены измерения яркост-
ной температуры и сделаны расчёты равновесной температуры
ударного сжатия порошков магния с плотностью 1 г/см3 (т = 1.73).
Показано, что неравновесность сжатия падает с уменьшением
размера частиц, от Т оге/Те =40 - 50. аая частиц размером 0,5 мм
до Т огс / Те =2 — 4 fiiA^ частиц размером 1 — 5 мкм. С ростом
давления в интервале 6,5-18 ГПа неравновесность
увеличивается.
Нами оценена неравновесность ударного сжатия до
беспористого состояния (оптимального а^я спекания) трёх алмазных порошков,
Аая которых имеются экспериментальные ударные адиабаты [31,35].
В расчётах мы пренебрегали малым сжатием и нагревом
монокристальных частиц порошков алмаза и считали, что вся энергия сжатия
до беспористого состояния Ет =0,5 pm(v00 -v ) является тепловой и
сосредоточена в объёме пор. Тогда температуру пор можно оценить
из простого соотношения [31]:
Тpore lTeq=Vроге ' ^ = (1" Роо / Л)) (4.17)
Результаты расчётов приведены в табл. 4.6, из которой видно, что
при ударном сжатии до беспористого состояния микропорошков
алмаза с р00 < 2 г/смЗ часть алмаза, закрывающая поры, должна плавиться.
При этом равновесная (и остаточная после разгрузки) температура
превышает температуру начала быстрой графитизации. С ростом
пористости неравновесность ударного сжатия уменьшается.
Для алмазного порошка с частицами 40 — 60 мкм и
р00 = 2,02 г / см3 (т = 1,73, как у порошка магния) при р = 20 ГПа
расчётное значение неравновесности Т /Т =2,3 согласуется с
измерениями на магнии (Т /Т = 3,7 аая частиц 1-5 мкм при
р=18ГПа [43]).
Рассчитаем давления ударного сжатия порошков алмаза
любой пористости, при которых начинается плавление только части
алмазных частиц, закрывающей поры. При этом локальная
температура вблизи пор равна температуре начала плавления: stT ок = stTm.
Подставляя в (4.17) значения stTm из табл. 4.6, найдём
значения равновесной температуры Те =stTm р0/(р0 - р00), затем с
помощью (4.14) рассчитываем значения тепловой энергии Ет(Те ) =
ET(stp ). По Ет(Те ) с помощью (4.13) определяем значения
давлений stp , при которых начинается плавление вблизи пор
(см. табл. 4.6 и рис. 4.18). Эти давления в 1,5—2,5 раза меньше
равновесных давлений начала плавления всего объёма алмазного
порошка, причём, это различие растёт с увеличением плотности
порошка.
160
Таблица 4.6. Результаты расчёта неравновесности ударного
сжатия алмазных порошков до беспористого состояния
Роо>8/ст3
m
p,GPa
Teq,K
Троге, К
Tpore/Teq
2.02
1.73
20.0
1660
3900
2.35
1.90
1.85
27.6
2200
4880
2.22
1.79
1.96
32.1
2420
4920
2.03
Сравнивая значения давлений из рис. 4.16 и 4.18, можно сделать
неутешительный вывод: с помощью сжатия алмазных порошков
любой плотности плоской УВ в стальной ампуле сохранения (при
контактном взрыве на ампуле заряда из Сотр.В или при ударе по
ампуле стальным ударником со скоростью 1 км/с) невозможно
достигнуть даже начала равновесного плавления алмаза. Необходимое
увеличение давления можно получить, только используя различные
кумулятивные схемы ударного сжатия алмазных порошков.
Своеобразной кумуляцией световой энергии можно считать
получение гигантского наносекундного импульса лазерного излучения,
плавящего алмаз [42].
В опытах с использованием энергии взрыва возможно
получение двух видов кумуляции: микрокумуляции при схлопывании пор
в сжимаемом порошке и макрокумуляции при использовании
сходящихся или сталкивающихся ударных или детонационных волн
[34,38]. При сжатии порошков возможно сочетание обоих видов
кумуляции. Для любых кумулятивных процессов рост давления
ограничивается неустойчивостью границ сжимаемой системы,
длительностью импульса сжатия и вязкостью [38]. Последнее ограничение
особенно актуально при схлопывании поры в алмазе.
Литература к главе 4
1. Зельдович Я.Б. ЖЭТФ, 1957, N6.
2. Альтшулер Л.В. Применение ударных волн в физике высоких
давлений. // Успехи физических наук, 1965, 85, N2, с.197.
161
3. Крупников К.К., Бражник М.И., Крутикова В.П. // Журнал
эксперимент, и технич. физики, 1962.42.
4. Кормер СБ., Фунтиков А.И., Урлин В.Д., Колесникова А.Н.
ЖЭТФ, 1962. N3
5. Marsh Stanley P. "LASL Shock Hugoniot Data". University of
California Press, 1980 and "Selected Hugoniots". Los Alamos
Scientific Laboratory. Report LA - 4167 - MS, 1969
6. Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и
высокотемпературных гидродинамических явлений. М.: Наука, 1966.
7. Кормер СБ., Фунтиков А.И., Урлин В.Д., Колесникова А.Н.
ЖЭТФ,1962,№.
8. Даниленко В.В. ФГВ, 2009, т.45, N6, с. 1-9.
9. Lysne Р.С., Halpin W.J.J. Appl. Phys., 1968, N12.
10. Eden, Smith D.M. V Symp. (Jnt.) on Detonation, California, 1969.
11. Boade R.R.J. Appl. Phys., 1969,40, N9, p. 3781.
12. Beasley D., Turner G.J., Edwards K.L. Journ. of Mater. Sci., 1975,
10, p. 436.
13. Трофимов B.C., Ададуров Г.А., Першин СВ., Дремин А.Н.
ФГВ, 1968,N2
14. Трунин РФ., Симаков Г.В., Подурец A.M. "Известия АН
СССР, Физика земли", 1971, N2.
15. Хвостов Ю.Б. ДАН СССР, 1987, т.294, N2, с. 302...306.
16. Аттетков А.В., Бойко М.М. и др. V Всес. совещание по
детонации. Красноярск, 1991, Сб. докладов, т.1, с. 31...35.
17. Thouvenin J. Journal de Physique, 1966, N3...4.
18. Алексеев Ю.Л., Ратников В.П., Рыбаков А.П. ЖЭТФ,
1971,N2.
19. Рыбаков А.П. Твердые тела в условиях давлений и
температур ударного сжатия (учебно-метод. пособие), ЦНИИ-
атоминформ,М, 1978.
20. Johnson J.O., Wackerle J.J. Transactions of Symposium on High
Dynamics Pressures, Paris, Sept. 1967.
21. Buteher B.M., Carroll M.M., Holt A.C. J. Appl. Phys., 1974, 45,
N9,p.3864.
22. Carrol M.M., Holt A.C.J. Appl. Phys., 1972,43, N4,p.l626.
162
23. Herrman W. J. Appl. Phys., 1969,40,p.2490.
24. Carrol M.M., Holt A.C.J. Appl. Phys., 1972,43, N2, p. 759.
25. Sadyrin AJ. "Shock waves in condensed matter", Jntern. conf.,
St.Peterburg, 1994, abstracts, p.9.
26. Беляков Г.В. Доклады АН СССР, 1974,218,N6,c. 1280.
27. Конгун В.И., Павловский М.Н. и др. ЖТФ, 63, № 1, 1993,
с.54 —60.
28. Ковтун В.И., Трефилов В.И. Порошковая металлургия, 1989,
№11,с.85—90.
29. Павловский М.Н., Комиссаров В.В. ЖЭТФ, 1990, т. 13, вып.
5(11),с.1748-1751.
30. Курдюмов А.В., Пилянкевич А.Н. Фазовые превращения в
углероде и нитриде бора. Киев: Наукова думка, 1979,с. 186.
31. Даниленко В.В. Синтез и спекание алмаза взрывом. М. Энерго-
атомиздат, 2003,272 с.
32. Knitde Е., Wetzcovitch R.M., Jeanloz R., Cohen М.Н. Nature,
1989, v 337, p. 349-352.
33. Дуболадов И.П., Ракитин В.И., Сутулов Ю.Н., Телегин Г.С.
ПМТФ, 1969,№4,с.148-151.
34. Козлов Е.А., Лебедев М.А., Литвинов Б.В. ФГВ, 1993, Т.29,
№2, с. 118—122.
35. Павловский М.Н. ФТТД971, Т.13, вып.З, с. 893.
36. Афанасенков А.Н., Богомолов Б.М., Воскобойников И.М.
Обобщенная ударная адиабата конденсированных веществ //
Журн. прикл. механики и техн. физики, 1969, № 4, С. 137.
37. Mader С. L. Numerical Modeling of Explosives and Propellants.
Second Edition. CRC Press, Boca Raton, N.Y. 1998,439 p.
38. Забабахин Е.И. Явления неограниченной кумуляции. М.
«Наука», 1988,172 с.
39. Даниленко В.В. Сверхтв. Мателиалы, 2006, № 6, с. 3— 11.
40. Togaya М. Thermophysical properties of carbon at high
pressure // Advanced Materials'96: Proc. of the 3rd NIRIM Intern.
Symp. on Advanced Materials (ISAM'96), Tsukuba, Japan, March
4-8,1996, P. 251—256.
41. Даниленко В.В. ФГВ, 2005, T.41, №4, с. 110—116.
163
42. D.K. Bradley, J.H. Egert, D.G. Hicks, P.M. Celliers, S.J. Moon,
R.C. Cauble, and G.W. Collins. Phys. Review Letters, 2004, V. 93,
No 19, P. 195506-1—195506-4,
43. Беляков Г.В., Родионов B.H., Самосадный В. ФГВ, 1977, № 4, с.
614—619.
44. Выскубенко Б.А., Даниленко В.В., Лин Э.Э. и др. ФГВ, 1992,
N2, с. 108.
164
Глава пятая
КУМУЛЯЦИЯ
5.1. Разновидности кумуляции
В взрывном деле кумулятивный эффект — это резкое повышение
местного действия взрыва. А в общем случае кумуляция (от
латинского слова cumulatio — увеличивать, суммировать, накоплять) —
это концентрация в малом объеме какой-либо физической
величины (энергии, давления, температуры).
Причем, часто при описании различных кумулятивных
процессов обнаруживается, что кумуляция неограниченная, т.е. хотя бы в
одной точке и на один момент энергия возрастает неограниченно,
или, иначе говоря, происходит фокусировка.
В технике явление кумуляции используется ^ая создания
условий протекания ядерных реакций в атомных зарядах и в лазерных
термоядерных мишенях (сферическая сходящаяся ударная волна), в
кумулятивных зарядах аля пробивания брони и ^ая резки
различных конструкций (направленная осевая кумуляция).
В основе эффекта кавитации (разрушающей быстроходные
гребные винты кораблей) лежит кумуляция при схлопывании пузырьков
в жидкости. С другой стороны, созданная в специальных аппаратах
кавитация хорошо «работает» для дробления, смешивания,
приготовления эмульсий.
До сих пор остается открытым вопрос о том, что же
ограничивает кумуляцию в реальных условиях схождения волн (размеры атомов
или молекул — слишком маленький предел). Полный учет в
расчетах сжимаемости, диссипации энергии из-за вязкости и теплопро-
165
водности не устраняет неограниченную кумуляцию в сходящихся
волнах [1].
Единственной реальной физической причиной остается
неустойчивость, развитие которой не только вызывает быстрый рост
малых начальных возмущений, но и полностью останавливает
кумуляцию.
По-видимому, неограниченная кумуляция возможна лишь в
идеальных условиях или с нулевой вероятностью [1], т.е. существует
лишь теоретически, но указывет на возможность достижения
экстремально высоких плотностей энергии.
В физике взрыва давно известна и хорошо изучена ограниченная
кумуляция, возникающая при соударении пластин, струй, ударных и
детонационных волн, при взаимодействии их с преградами, в
конической УВ с образованием диска Маха.
С помощью кумуляции можо значительно усилить действие
взрыва в заданном направлении, получив давление, больше, чем в
детонационной волне.
Кумулятивный эффект может быть создан как в газах,так и в
конденсированных средах. Кумуляция может быть как нестационарной, так и
стационарной (коническая волна поля) [1], связанная и не связанная с
сходимостью ударных волн.
Например, в случае создания УВ в центральных областях
звезды расходящаяся волна движется к поверхности звезды по газу с
уменьшающейся плотностью. Поэтому энергия сообщается
неограниченно уменьшающейся массе вещества, значит, плотность энергии
неограниченно возрастает [2] (точно так, как и в сходящейся волне,
где сжимаемая масса тоже уменьшается).
Кумуляция интересна тем, что, создавая в веществе экстремально
высокие давления, плотности, температуры, она тем самым создает
условия а^я новых физических явлений, «включает» новые
физические факторы, например, лучистую теплопроводность в схождящей-
ся У В (термоядерный синтез).
Открыто и изучено много разновидностей кумулятивных
процессов (см. рис. 5.1).
Так, кумуляция может быть:
166
Сходящиеся
сферические и
цилиндрические
УВ
Сходящиеся
детонационные
волны
Схлопывание
полости (пузырек
в жидкости)
Слоеные системы
с периодической
автомодельностью
Безударное сжатие
шара
Статическая
кумуляция в
разрезном шаре
Рис. 5.1. Разновидности кумуляции
— ограниченная и неограниченная теоретически (хотя бы одна
величина в расчетах неограниченно растет);
— сильная (две и более величины -> оо);
— слабая (только одна величина -> оо , например,
кумуляция пылевидной материи в космосе, когда р = О, Т = 0 и только
р->°о);
— в газах, в конденсированных веществах, в электромагнитном
поле, в периодических системах - слойках;
Столкновение
тел, ударных
детонационных
волн
Кумулятивные
струи
УВ в узкой
клиновидной или
конической полости
с газом
Сходящиеся
конические волны
(волны Маха)
Схождение
многогранной УВ
с образованием
сталкивающихся
волн Маха
Кумуляция
электромагнитного
поля
Слабая кумуляция
пылевидной
материи в космосе
Т=0,р=0,р->оо
Слабая кумуляция
при входе УВ на
границу атмосферы
Т>оо,р=0,р-*х>
— в плоских, сходящихся и расходящихся УВ;
— при схождении полостей (пузырек в жидкости);
— стационарная и настационарная;
— динамическая и статическая (сжатие разрезного шара [ 1 ]).
Для осуществления кумуляции важно, чтобы среда была
непрерывной и вела себя закономерно. Количественно процесс кумуляции
Аая сходящихся движений можно оценить показателем кумуляции
к, который определяет скорость роста параметров с уменьшением
радиуса: и~ 1/гк_1 ир^и2^г2^1).
Вблизи фокусировки движение автомодельное и описывается
безразмерной переменной г — v/K t" [2], где показатель
автомодельное™ а = 1/к.
Описанием кумулятивных процессов занимались многие
выдающиеся ученые: Ландау, Станюкович, Гудерлей, Зельдович,
Тейлор, Лаврентьев, Покровский, Баум. Особенно отметим работы
Е.И. Забабахина, много лет систематически исследовавший явления
неограниченной кумуляции [1]. Он впервые описал кумуляцию в
слоеной системе без участия сходящихся волн и стационарную
кумуляцию конической волны поля; исследовал влияние на кумуляцию
различных видов диссипации энергии и неустойчивость
контактных границ [1,3].
5.2. Прямое отражение УВ от преграды
Рассмотрение взаимодействия УВ с преградой имеет
практическое значение. При столкновении УВ с различного рода
препятствиями массовый поток за фронтом УВ тормозится на препятствии,
поэтому давление и пульс, сообщаемые препятствию, увеличиваются
по сравнению с параметрами свободно движущейся УВ.
В любых средах столкновение двух одинаковых УВ
эквивалентно отражению одной УВ от абсолютно жесткой стенки. При
отражении от стенки создается новая, отраженная УВ, идущая от стенки.
Применяя к границе между падающей и отраженной волнами
законы сохранения и уравнение Гюгонио, можно вычислить
параметры отраженной волны.
168
Фронт отраженной УВ x=D2t
Фронт падающей УВ x-Dt
Стенка
Рис. 5.2. Прямое отражение УВ от жесткой стенки.
Рассмотрим прямое отражение от жесткой стенки стационарной
плоской УВ в идеальном газе, х, t-диаграмма отражения показана на
рис. 5.2.
Параметры газа: перед фронтом — р0, р0, uQ = 0; за фронтом
падающей У В рр р{9 D л^; за фронтом отраженной волны — р2, р2,
Очевидно, между стенкой и фронтом отраженной УВ
существует область покоя, т.е. и2 - их = 0.
Соотношения между параметрами падающей и отраженной
ударными волнами следующие [4]:
Pi=Pi+-
VPi(Pi-Po)
(У -1) А + (У + 1)Ро
(j — показатель адиабаты)
Для сильной волны (pj > > р0)
(5.1)
(5-2)
А/л=(зу-1)/а-1)
что для j=с /су= 1,4 (воздух) дает р2 = 8 рг
Для слабой У В (р2« р0) р{ = 2 р0, как и аая отражения звуковой
волны.
Скорость отраженной УВ:
р2-р0, кг/см2
50
40
30
20 I
Ю I
0
123456789 10 РгР0.кг/см2
Рис. 5.3. Зависимость между давлением в отраженной и падающей УВ в воздухе
Скачок плотности:
Рг1 Р\=Т~.
JP\
U-l)Pi+Po
(5-4)
Для сильной УВ в воздухе имеем: p2/pj = 3,5 и р2/ р0 = 21, т.е.
плотность воздуха в результате отражения от стенки резко возрастает.
Давление отражения может быть представлено приблизительно
как сумма двух компонентов: удвоенного давления падающей волны
(а^я слабых волн) и «ветрового» давления, определяемого
скоростным напором (/^ сильных волн) [5]:
p2=2Pl+(j + l)Plw2/2 (5.5)
На рис. 5.3 дана расчетная зависимость а^я воздуха между
давлениями в падающей и отраженной ударных волнах [5].
При отражении УВ возрастает не только давление, но и импульс.
Например, при взрыве в воздухе заряда из ТНТ весом М (кг) на
расстоянии R (м) импульс отражения от жесткой стенки можно оценить
по формуле [5]:
J = АМ11Ъ /R(кг сек /м2) (5.6)
где А= 50—60.
Для зарядов из других ВВ в качестве М надо брать тротиловый
эквивалент.
Если размер препятствия ограничен, в частности меньше длины
волны, то возникает явление обтекания препятствия ударной вол-
170
ной. В начальный момент на всей отражающей поверхности
давление будет равно р2. Затем от краев преграды к ее середине пойдут
волны разрежения со скоростью звука с в сжатом воздухе. Через
время t = 1/с (1 - половина ширины преграды) давление упадет с р2
до р* (р* - давление обтекания), и установится режим обтекания.
Ориентировочно р* = 0,5р2, откуда с учетом (5.5) и j + 1 = 2 можно
оценить величину максимального давления обтекания:
p* = Pl+Plw2/2 (5.7)
Такое давление будет на передней площадке преграды, а на
заднюю площадку будет действовать давление порядка рг
При этом результирующее давление приблизительно равно
скоростному напору р2 wV2. Благодаря явлению обтекания а^я
разрушения, например, забора из столбов нужна УВ гораздо меньшей
интенсивности по сравнению с УВ, способной сломать один столб.
До сих пор мы рассматривали отражение от стенки УВ в газе
(воздухе). Легко найти давление в отраженной УВ (при
столкновении УВ) ^ая конденсированной среды, используя простое
кубическое уравнение состояния (см. Гл. 2). В [1] показано, что скачки
плотности на падающей и отраженной волнах одинаковы аая любой
амплитуды падающей волны и ^ая любого состояния перед ней.
5.3. Косое столкновение волн. Маховские волны
Рассмотрим отражение УВ от стенки под углом — т. н. косое
отражение.
Для наглядности пусть взрыв происходит в воздухе в точке А над
поверхностью земли (см. рис. 5.4).
В разных точках волна падает на плоскость под разными углами
ф. При ф = О отражение нормальное или лобовое, при ф = 90° волна,
не отражаясь, скользит вдоль плоскости. При малых углах ф < фп
идущая от центра взрыва А падающая ударная волна П отражается
от плоскости и дает отраженную волну О. Для слабой УВ в
акустическом приближении отраженная волна О идет как бы из мнимой
точки В, которая является отражением точки А.
А
\ Регулярное отражение
Л п о J1 Ч/
Нерегулярное отражение
Волна
Маха
А
т
в
D
Рис. 5.4. Схема отражения УВ, падающей на пласкость
В зависимости от угла падения ф различают два режима
отражения: регулярный и нерегулярный (или маховский). При регулярном
отражении линия пересечения падающей и отраженной волн лежит
на поверхности преграды (точки С, D на рис. 5.4). При
нерегулярном отражении линия пересечения падающей и отраженной волн
находится над преградой (точки Е, F).
Нерегулярное отражение возникает, начиная с некоторого угла
фп , который зависит от амплитуды УВ. При ф > ф характер
отражения меняется. Часть фронта отраженной волны, двигаясь с
скоростью, большей скорости падающей волны, догоняет падающую
волну и, сливаясь, образует новую волну, которую называют головной
или маховской. Образуется конфигурация из трех волн (П, О и Г),
ф
пред
Не существует правильного отражения
о р„/р,
Рис. 5.5. Зависимость предельного угла регулярного отражения от давления в
падающей УВ.
172
40 45 50 55 60 65 70 75 80 85
Рис 5.6. Зависимость ^ (ф0) при различных значениях р0/рг
которые пересекаются в тройной точке. С ростом угла ф область,
охватываемая головной волной, растет, и этот рост характеризуется
углом % (см. рис. 5.4). Газ у стенки проходит через одну волну, а вдали
от стенки — через две волны: падающую и отраженную. Поэтому в
тройной точке существует контактный разрыв, по обе стороны от
которого одинаковы давления и направления движения частиц газа.
Косое отражение УВ подробно рассмотрено в [4,6]. Приведем
основные результаты.
1. При малых углах падения ф0 угол отражения ф2 < ф0. С ростом
ф0 отношение р2/р2 сначала уменьшается, а затем увеличивается, и
при некотором угле ф0 = ф*0 снова достигает того значения, что и при
ф0= 0. Кроме того, при угле ф*0 углы падения и отражения становятся
равными: ф0 = ф2. Величина угла ф*0 не зависит от давления р2 в
падающей УВ и определяется из уравнения:
Приняв аая воздуха j = 1.4, получим ф*0 = 39° 14'
2. Для сильных УВ (аля воздуха р/р0 > 7) угол ф*0 близок к
предельному углу фп е правильного отражения, и давление косого
отражения не может превысить давление прямого отражения.
3. Зависимость предельного угла регулярного отражения фп е от
скачка давления в падающей УВ p0/pj показана на рис. 5.5 [4].
4. При переходе к маховскому отражению отношение р2/р2 сначала
скачкообразно падает, а затем плавно уменьшается с увеличением ф0 или
с ростом области головной волны до р2/рх = 1 при ф0 = 90°.
5. Угол £ расширения области головной волны (см. рис. 5.4)
приближенно определяется в предположении, что головная волна
прямая и перпендикулярна к отражающей поверхности.
Расчетная зависимость £ (ф0) дана на рис. 5.6 [4].
Нерегулярное отражение УВ в твердых телах изучено слабее, чем
в газах, что объясняется сложностью создания, измерения и
расчетов этого режима при возникающих экстремально высоких
давлениях и температурах. Этот принцип кумуляции энергии интересен аая
изучения уравнений состояния, а^я сжатия и разогрева
термоядерной плазмы в конических мишенях, а^я сжатия веществ в
цилиндрических ампулах сохранения.
Рассмотрим довольно сложную неоднородную картину движения
конической УВ в цилиндрической ампуле сохранения (см. рис. 5.7).
Скользящая детонационная волна создает в стальной стенке
ампулы коническую ударную волну (см. рис. 5. 7а), которая
преломляется на границе сталь—образец, и в образец идет коническая волна
с другим давлением и с другим углом при вершине конуса. Этот угол
конуса 2а определяется величинами скорости детонации заряда ВВ
вокруг ампулы и скорости УВ в образце.
Скорость конической УВ имеет радиальную составляющую,
направленную к оси образца, т.е. волна сходящаяся, и давление в ней растет
с приближением к оси. При этом отраженная от оси УВ может создать
в образце канал. Кроме того, при сжатии смеси порошков наблюдается
разделение (сепарация) смеси: тяжелая компонента собирается у оси
ампулы. Например, при сжатии в ампуле окиси свинца происходит её
разложение, а весь выделяющийся свинец оказывается в осевой зоне.
В случае образования маховской волны образец вблизи оси
сжимается одной УВ со скоростью, равной скорости детонации, а весь
периферийный объем образца сжимается двумя волнами —
падающей и отраженной от тройной точки.
174
Рис. 5.7. а) Коническая волна в ампуле сохранения; б) Зависимость диаметра
центрального канала (d) от пористости графита m=Рд/р^.
в) Фотографии сечений обжатых ампул с графитом различной пористости;
г), д) Схема опыта и фотохронограмма регистрации волны Маха в графите с
плотностью 2 г/см3 (СФР - 2М, v = 2,25 км/с).
Согласно [7] маховская волна в цилиндрической ампуле
возникает не сразу, ударная волна должна пройти в ампуле путь в 1,5—
3 диаметра ампулы. По сечению маховская волна занимает 20—50%
внутреннего диаметра ампулы.
Чтобы исключить образование маховской волны и обеспечить
более однородное двукратное сжатие образца, часто на оси ампулы
устанавливается стальной стержень.
Автором проведена серия опытов с цилиндрическими ампулами
без центрального стержня. Размеры: заряд из ТГ40 обО х 120 мм,
ампула из Ст. 3 оЗО х 100 мм, образец о16,5 х 75 мм.
Исследовалось сжатие порошка графита различной
пористости т. Результаты измерения диаметра центрального канала d (m)
приведены на рис. 5.7б). Для всего исследованного диапазона
пористости т=1,10—1,76 величины d линейно растут с
пористостью. Давление однократного сжатия графита с т=1,1 вблизи
оси > 40 ГПа. Графит в маховской волне превращается в алмаз, а
после разгрузки алмаз полностью графитизируется, превращаясь в
сажу.
Граница сажа—графит очень четкая, поэтому величину d легко
измерять. В таких же опытах с пористым вольфрамом (т = 1,8) в зоне
вблизи оси канал не образуется, но четко фиксируется по
микроструктуре плавление вольфрама (остаточная температура > 3700 К).
Эти примеры показывают, что столкновение сходящейся
конической УВ создает в веществе достаточно большие давления и
температуры.
В таблице 5.1 [8] приведены результаты измерения параметров
сжатия пяти веществ при косом столкновении УВ под углом 2а = 40°
(регулярное отражение, угол отражения 2(2 = 50°).
В таблице 5.2 [9] даны результаты экспериментов по
нерегулярному отражению УВ в металлах. На двух гранях призмы с углом
при вершине 2а = 90° синхронно создавались плоские УВ, которые
в плоскости симметрии призмы сталкивались с образование волн
Маха.
Результаты численных расчетов [10] маховской волны в меди
Аая плоских и конических УВ показали, насколько эффективнее
конические УВ.
176
Таблица 5.1. Сжатие при регулярном отражении УВ (2а = 40°)
Материал
Парафин
р0=0,9г/см3
Вода
р0=1 г/см3
Плексиглас
р()=1,18г/см3
Магний
р0=1,74г/см3
Алюминий
р0=2,71г/см3
Падающая волна
Р,, ГПа
15,4
14,9
18,4
26,2
36,0
Dj, км/с
6,66
5,77
6,38
7,16
7,71
Р/Ро
1,628
1,815
1,623
1,415
1,288
Отраженная волна
р2, ГПа
54,6
58,6
, 65,3
73,5
95,2
D2, км/с
10,04
8,96
9,62
9,10
9,72
Р2/Ро
2,215
2,59
2,21
1,84
1,57
Таблица 5.2. Сжатие при регулярным отражении УВ (2а = 90°)
Материал
Алюминий
Медь
Железо
Pj, ГПа
97
179
171
Плоскость симметрии
Р,ГПа
425
721
642
D ,км/с
17,36
13,07
13,38
Тройная тоскаа
Р^ГПа
425
628
608
D^km/c
17,36
12,39
13,10
Так, для а = 45° в меди Dc= 13,1 км/с, aDT= 14,54 км/с.
Для конуса с а=30° DT=20 км/с, что соответствует давлению в
меди 2000 ГПа (за счет сходимости конический УВ и более сильной
волны Маха).
Отметим, что при схождении конической волны к оси ее
скорость будет возрастать, а это значит, что угол при вершине конуса
будет притупляться и появится маховская волна или струя с
конечной скоростью и давлением. Поэтому в веществе с конической
УВ невозможна неограниченная осевая кумуляция (строго это
доказывается в [6]).
Единственным примером стационарной неограниченной
кумуляции является кумуляция в вершине конической УВ магнитного
поля. Скорость УВ равна скорое ги света, а вершина конуса
движется вдоль оси со сверхсветовой скоростью [1].
Согласно расчетам, амплитуда волны неограниченно растет как
1/г0,5 и сохраняется на отраженной от оси волне. Однако такая
стационарная кумуляция возможна только при идеальной симметрии
и нулевой ширине фронта волны, что практически невозможно
реализовать.
5.4. Столкновение детонационных волн
Для кубического
уравнения состояния просто
решается и задача отражения
детонационной волны при взрыве
заряда ВВ на абсолютно
жесткой стенке (или задача о
столкновении двух плоских волн
детонации).
Заряд толщиной Ь иници-
Рис. 5.8. Взрыв заряда ВВ на жесткой стенке. ируетСЯ на Свободной
поверхности (см. рис. 5.8).
На х, t-диаграмме от точки А пойдет детонация с скоростью D,
давлением р и веер [2 — характеристик: (2 = и - с = (х—b)/t.
В момент t = b /D детонация дойдет до стенки и на ней
возникнет давление р ~ р3 ~ с3, т.е. р/рн = (c/cj3.
Для кубического У PC параметры детонационной волны :
c=3/4D;u=l/4D;p=puD=l/4pD2(cM.Dv.8).
На стенке х=0, и=0, с=b/t. Тогда р/рн = (Ь/сн t)3.
Учитывая, что сн = 3/4 D , получим аля давления на стенке:
Р = -РА—? (5-9)
и 21 н DHt
В момент t=b/D выхода детонации на стенку начальное давление на
стенке будет р = (64/27) рн = 2,37 рн.
178
р
2,37Рн
2Рн
Рн
8/27Рн
4
(D/b)t
Изменение с
временем давления на стенку,
согласно (5.9), показано
нарис.5.9[4].
Очень быстро, за
время t=2 b/D давление
падает дор=(8/27) рн
(например, для D=8 км/с и
Ь=20см г=50мксек).
В продукты взры-
1 2 3
ва пойдет отражённая
РисЗ^Падениедавлениянастенкесвременемприспраже-уз^ началыше Параме-
нии детонационной волны. u г
1 — жесткая стенка; 2 — медь; 3 — алюминий; тры КОТОрОИ ^,АЯ куби-
4—вода. ческого УРС
следующие [4]: р2 = 2,37 рн ;
D2=-0,75D;c2=D;p2/pH=4/3 = l,33.
Для реальной сжимаемой преграды с известными u , D
зависимость давления от времени имеет вид [4]:
/ 64 6 з
Pi Рн =-=(—)
(1-й))3
2TDt' {l-a>0[l-(b/Dt)<>-l]}W-l) (5'10)
где: со= u/D - находится с помощью р, и - диаграммы вещества
преграды, а величина (2 определяется приближенным соотношением [6]:
PHaJ = l + 0,02(p0c0)0-24 (5.11)
Начальное давление на сжимаемой преграде в момент t = b/D
составляет:
-*,.(.-.>■
(5.12)
На рис. 5.9 показаны зависимость р (t) а^ преград из меди,
алюминия и воды. Как видно, рост сжимаемости преграды заметно
снижает давление на преграде и замедляет спад давления.
Полный импульс давления на жесткой стенке:
J =—pbDH
27 и
(5.13)
Посмотрим, что изменится, есш инициировать заряд ВВ не со
свободной поверхности, а от стенки. При этом до прихода разрежения на
стенку от свободной поверхности через время t=b/D+2 b/D = 3 b/D
давление на стенку все это время будет постоянно и равно:
8 2
Pi=—Ph=—PoD2h (5.14)
Суммарный импульс на стенке оказывается точно таким же, как
при инициировании заряда ВВ снаружи со свободной поверхности.
Косые столкновения детонационных волн характерны аля
многоточечных систем инициирования зарядов ВВ (см. гл. 11). В этих
системах синхронно во многих точках на поверхности заряда
создаются расходящиеся детонационные волны, после столкновения
которых в заряде формируется один детонационный фронт.
Давление на этом фронте колеблется от нормального (р ) под точками
инициирования до более высокого давления (р2) в зонах
столкновения волн между точками. В свою очередь, величина давления р2
и размеры зон, где оно создается, зависит от угла столкновения ф.
На поверхности инициирования ф = 0 (р2= 2,37 рн), а в заряде на
глубине Н от поверхности инициирования ф = агс tg (Н/г) (г —
кратчайшее расстояние между точками инициирования). При ф > ф*
регулярный режим столкновения сменяется на нерегулярный, где
размер зоны с волной Маха растет с ростом ф, а давление в этой зоне
падает, стремясь к рн.
Автором измерен размер dM зоны повышенного давления
при столкновении расходящихся детонационных волн в заряде из
ТГЗО/70 в зависимости от угла столкновения ф (см. рис. 5.10).
В опытах тонкий слой соли NaCl (0,2 мм) на стальном экране
(1 мм) служил отлетающим индикатором с более ярким свечением
в зонах столкновения. Измерения проводились с помощью камеры
СФР - 2М в режиме фоторегистратора.
Как видно из рис. 5.10, до углов ф = 40°—45° (регулярное
отражение) размер dM зоны повышенного) давления в стальном экране
меняется слабо, а при углах ф > 45° величина dM возрастает
пропорционально углу столкновения.
180
Инициаторы
Заряд
ТГЗО
Стальной экран
Соль NaCl
м
3,5
3,0
2,5
2,0
О
—в—
о
О
о
1
г О
у
О
о/
о
oJ
°
ДА*'
30 35 40 45 50 55 60 65 70 ф°
Рис. 5.10. Изменение размера зоны столкновения расходящихся детонационных
волн в зависимости от угла столкновения.
Рассмотрим кумулятивный эффект, возникающий при детонации
удлиненного линейного заряда, имеющего вид любой произвольной
кривой (например, изогнутый детонирующий шнур).
Продукты детонации (ПД) разлетаются под углом j = 7°... 14°
к боковой поверхности заряда, и внутри этого малого угла
сконцентрирована основная часть энергии линейного заряда. Если заряд
имеет поворот, то фронты ПД до и после поворота могут
сталкиваться, усиливая действие ПД.
Пусть П — образный линейный заряд (см. рис. 5.11а)
инициируется в точке О. Тогда фронты ПД, идущие от участков
ОА и АВ под углом у , встречаются вдоль линии ОА, при этом угол
ОАО=я/4+у. Аналогично получим линию ОВ мя участков АВ и ВС.
А фронты идущие от параллельных участков ОА и ВС, встречаются на
линии ОЕ.
б)
в1
А
0
\
\
\
\
\
\
^ «— "
1 F
]
\
\
Г
В
1 ---"
С1
^ -*■
Рис. 5.11. а) Детонация П - образного заряда.
б) Удлиненный заряд в виде логарифмической спирали.
При инициировании заряда в точке О все фронты П Д
сталкивается в одном точке О'.
Точка О' имеет координаты: х=АВ cos (45 — j); у=ОА—АВ/2 cos2j.
В общем случае, при детонации линейного заряда в какой-либо среде
sinj = u/D, где D — скорость детонации, и — скорость УВ в среде.
Если П-образный заряд поместить на металлическую
пластину, то наибольшая деформация металла будет на линиях АО', О'В и
О'Е.
Таким образом, на этих линиях столкновение фронтов ПД
создает кумулятивный эффект. Очевидно, наибольшая кумуляция ПД
будет создана, если выбрать такую форму удлиненного заряда, при
которой все фронты сталкиваются в одной точке.
Такая «кумулирующая» кривая, дающая сходящуюся круговую
волну , известна — это логарифмическая спираль (см. рис. 5.116) с
уравнением:
и I с0 = tgaj 2(1+ tga) I (l-tga) (5.15)
Для логарифмической спирали угол между касательной в любой
точке А и радиусом вектором есть величина постоянная, равная 90—j.
Спираль инициируется в точке О. Если с помощью
логарифмической спирали образовать поверхность вращения вокруг оси OF, то
182
получим кумулирующую поверхность, дающую сходящуюся в точке
F сферическую волну.
5.5. Кумулятивные струи
До сих пор мы рассматривали столкновения различных
ударных и детонационных волн. Теперь рассмотрим косое столкновение
сжимаемых пластин. Здесь также в зависимости от угла
столкновения возможны два режима: регулярный с образованием отраженной
УВ и нерегулярный с образованием струи.
Предполагая, что аая несильных сжатий любых непористых
веществ давление пропорционально плотности (р = с02(р-р0)) в [1]
найдены условия возникновения этих двух режимов (см. рис. 5.12):
и I с = tga^2(\ + tga) I {\-tga) (5 16)
На рис. 5.12 область R соответствует регулярному отражению
без струи, а область S — с струей. В начале кривой u/cQ мало и аая
малых сжатий аая любых веществ:
u/c0=tgayf2 (5Л7)
При больших сжатиях граница уже зависит от У PC и аля разных
веществ может быть разной (пунктир на рис. 5.12).
Далее будем рассматривать только нерегулярное столкновение с
образованием струи.
Как и а^я УВ, столкновение двух пластин эквивалентно удару
одной пластины о жесткую скользкую стенку (см. рис. 5.13).
3
и/с0
2
1
О 0,5 1 ща
Рис. 5.12. Зависимость предельного угла столкновения пластин от их скорости
Область столкновения /
без струи
+' Область столкновения
со струей
В результате удара пластина, летящая со скоростью ип, растечется
вперед в виде струи с скоростью им (эта часть называется молотом).
В системе, связанной с точкой О, сама точка имеет скорость uQ = un/
sina, скорость пластины wn = Wtg a , а струя и молот растекаются в
разных стороны с равными скоростями wn = wc=wM = un/tg a.
Возвращаясь к лабораторной системе координат, получим:
uc=wc+uo= ип (1 / *8а +1 / sina) = unctga 12
(5.18)
Длина струи равна длине пластины.
При малых углах столкновения скорость струи велика и в
пределе при а-> 0 ис-> оо, а скорость молота мала (им -> 0 при a -> 0), но летит
он в ту же сторону, что и струя.
Если sn , sc, sM — толщины пластины, струи и молота, то из
законов сохранения масса пластины распределяется следующим
образом:
sn=sc+sM;-sncosa + sM-sc=0'9
sc/sn =sin2a/2;sM/sn =cos2a/2
Доля энергии, уносимая струей и молотом:
(5.19)
Л, = smI I su] = cos2 a 12;
1С с с п п '
T}M=sMu2M/syn=sm2a/2
(5.20)
А— "м
Б со
/////////// /// ///////
Рис. 5.13. Образование кумулятивной струи.
а) в лабораторной системе координат; б) в координатах, связанных с точкой О, где
явление стационарно.
184
Таким образом, чем меньше угол столкновения а, тем тоньше
струя, тем большую энергию она имеет. При а -> О струя уносит всю
энергию пластины, и происходит неограниченная кумуляция.
Однако при малых а кумуляцию ограничивает влияние
сжимаемости пластины, благодаря чему струя вообще не образуется (регулярный
режим). Отметим, что, если заменить пластины схлопыванием конуса
или цилиндра, то струя образуется всегда, даже в сжимаемом
материале.
Если параллельные пластины разгоняются детонацией со скоростью
D, то при их столкновении образуется струя со скоростью 2D. Если же
взять вместо пластин сужающуюся коническую трубу, то скорость
точки О может быть больше D, а скорость струи — больше 2D.
Явление образования высокоскоростной кумулятивной струи
используется в т. н. кумулятивных зарядах, в которых имеется
выемка (обычно коническая), облицованная металлом. Кумулятивные
заряды широко использовались ещё во время второй мировой
войны как бронебойное средство. Кумулятивные снаряды пробивали
броню не сами, а металлической струей, выбрасываемой ими вперед
при взрыве.
Гидродинамическую теорию кумулятивных зарядов с облицовкой
разработали впервые в 1943 году М. А. Лаврентьев и Г.И. Покровский.
Качественнно она такая же, как и /^ пластин. Небольшие
сжатия облицовки (при w= 1 км /с Др/р = 0,2) и большие напряжения
в металле (больше его прочности) позволяют принять в расчетах
облицовку несжимаемой жидкостью.
Схема заряда с конической облицованной выемкой и стадии
формирования струи показаны на рис. 5.14 [5].
Под действием давления детонационной волны облицовка
двигается к оси заряда и смыкается. После смыкания материал
облицовки делится на две части. Слева от точки смыкания из наружных
слоев облицовки образуется пест, в который переходит большая часть
массы облицовки, но который не играет никакой роли в бронепро-
бивании. Справа от точки смыкания из внутренних слоев
облицовки образуется струя, имеющая малую массу, но большую скорость,
благодаря которой и пробивается броня.
185
Облицовка
Фронт детонации
\
Пест
Рис. 5.14. Формирование струи в кумулятивном заряде
1 — исходный заряд с конической выемкой; 2 — схлопывание выемки; 3,4,5 —
стадии образования песта и струи (импульсная рентгенография)
Отметим, что угол 2$ между движущимися стенками облицовки
будет больше первоначального угола конуса 2а. Из теории следует,
что длины струи и песта одинаковы и равны длине образующей
конуса. Общая масса m облицовки делится между струей и пестом
следующим образом:
тс =y(l-cos/?); тп =y(l + cos/?)
(5.21)
На практике применяют конусные выемки с углом а = 30°—40°,
облицованные сталью, медью или алюминием толщиной 0,5—3 мм.
Исследование движения струи показало, что головная ее часть
имеет скорость большую, чем ее тыльная часть. Поэтому струя
растягивается, ее длина растет, и затем струя распадается на отдельные
части, а ее бронепробивная способность падает. Следовательно,
существует оптимальное расстояние (фокус) между зарядом и броней,
при котором пробивное действие струи максимально.
Например, цилиндрический заряд об5 х 180 мм с конической
выемкой, облицованной сталью t = 2 мм, пробивает насквозь броню
толщиной 200 мм.
Как мы показали, скорость струи umax = 2 D при а -> 0 , т.е. а^я
D = 8 км/с и = 16 км/с. Однако такая струя будет неустойчивой. При
а = 30° скорость струи приблизительно равна скорости детонации, а
скорость схождения стальных стенок конуса (t = 1... 2 мм) составляет
1... 2,5 км/с. В струю переходит 6...20 % массы облицовки. В качестве
ВВ обычно используется сплав ТГ 50 с D = 7,6 км/с.
186
Пест движется сравнительно медленно, со скоростью 0,5.. 1 км/с.
Результаты измерения скорости головной части струи приведены в
таблице 5.3 [4]. Заряд из ТГ 50, оЗО х 70 мм, облицовка выемки из
стали или алюминия t = 1 мм.
Как видно из таблицы 5.3, скорость струи возрастает с
уменьшением угла конуса в полном соответствии с (5.17), а также с
уменьшением атомного веса металла облицовки и сильно зависит от формы
выемки (гипербола — наилучшая, т.к. больше длина образующей и,
значит, больше длина струи).
Таблица 5.3. Скорость кумулятивной струи
Параметры выемки
форма
Полусфера
Конус
Конус
Конус
Гипербола
диаметр
основания,
мм
28
27,2
27,2
27,2
27,2
угол конуса
2а
60
35
27
Скорость головной части струи
сталь
3,00
6,50
7,30
7,40
9,50
алюминий
6,05
7,65
8,50
9,0
При соблюдении геометрического подобия кумулятивных
зарядов и при одинаковых материалах скорость струи не зависит от
диаметра заряда и выемки (меняется только длина струи).
Условия формирования струи предполагают быструю
пластическую деформацию металла облицовки. Однако, кроме пластических
свойств металла, отмечается влияние на формирование струи типа
кристаллической решетки : лучше — у металлов с кубической
решеткой (Al, Fe, Си), хуже — у металлов с гексагональной решеткой
(Cd,Co,Mg).
Для обжатия облицовки с образованием струи необходимы
некоторые минимальные величины давления р и скорости обжатия
облицовки.. Эти условия не выполняются при а-> 7г/2, при использовании
маломощных ВВ и малой массы активной части заряда относительно
массы облицовки (М/т). Соотношение аая определения оптимальной
толщины облицовки и отношения ее массы к активной массе заряда
даны в [4]. Ориентировочно рп = 7 ГПа; М/т = 0,21 аая ТГ 50.
Активная масса заряда — та часть массы, которая при взрыве
двигается в сторону облицовки и увеличивает ее кинетическую энергию.
Активная часть цилиндрического заряда достигает своего предельного
значения при высоте заряда, равной Нп =2 r+h, где 2 г — диаметр
выемки, ah — ее высота. Обычно в кумулятивных боеприпасах
используют заряды высотой, меньше предельной, поскольку с уменьшением
Н активная масса и скорость струи уменьшаются медленнее, чем масса
всего заряда.
Минимальная скорость стальной струи, при которой броне-
пробивание прекращается, составляет 2 км/с аля обычной стали и
2,2 км/с а^я закаленной стали. При такой скорости давление струи
уравновешивается инерционными силами и силами прочностного
сопротивления брони. Для струи из алюминия минимальная
скорость выше: 2,9—3,3 км/с.
Максимальная измеренная скорость струи из бериллия (р= 1,5 г / см3)
равна 90 км/с и получена с помощью заряда, схема которого дана на рис.
5.15 [5].
Детонация огибает массивный экран, в результате чего волна
падает на облицовку под переменным углом.
npHa=0HJ^0uc^2D,npHJ^90°uc^oo.EcAHJ^0,TOuc= 2D/cosj.
Полученная в вакууме струя из бериллия обладает очень малой массой
и плотностью, поэтому быстро тормозится даже в разреженном воздухе
с давлением 0,1 мм ртутного столба.
Процесс пробивания струей брони описывается просто (см.
рис. 5.16).
В системе координат, связанной с точкой О, струя и броня текут
навстречу друг другу. При одинаковой их плотности скорость точки О
u0=u/2.
Глубина пробивания равна длине струи L и не зависит от ее
скорости (а^я преграды без прочности)), но чем больше скорость,
тем кратер больше. Если плотности струи и брони разные, то
они натекают на точку О с разными скоростями wc и w6 , причем
pcwc2 = p6w62.
188
^ч:—
Ли
/
/
г
J.
г г
f
Рис. 5.15. Схема кумулятивного заряда
1 — заряд ВВ; 2 — стальной экран;
3— цилиндрическая облицовка
из бериллия (а=0)
Броня
Струя
Рис. 5.16. Внедрение струи
в броню.
Время пробивания t=L/w., а глубина кратера L6 = t w6 = Lc (рс/рб)0,5
и тоже не зависит от скорости струи и определяется лишь ее длиной и
плотностью.
Реально глубина пробивания зависит еще от прочности
(твердости) брони и от того, насколько струя компактна (не распылена) и не
искривлена.
Зависимость глубины пробивания от прочности (твердости)
иллюстрирует таблица 5.4.
Таблица 5.4. Влияние твердости брони на глубину ее пробивания
струей
Заряд из ТГ 50 о42 х 84 мм, гиперболическая выемка с
облицовкой из алюминия толщиной 2 мм.
Материал преграды
Сталь
Сталь
Алюминиевый сплав
Алюминиевый сплав
Твердость по Брюнелю
100
350
50
200
Глубины пробивания, мм
111
80
327
256
Отметим, что при расчетах пробивания нельзя брать длину
струи, равной образующей конической облицовки Lk. Поскольку
струя растягивается, то всегда L > Lk. Расстояние от заряда до брони,
на котором струя максимально растягивается до L , еще оставаясь
компактной, соответствует максимальной глубине пробивания и на-
зывается фокусным расстоянием R кумулятивного заряда. Таким
образом, Lmax= Lk+ R. Для стальных конусов Lmax = 3 Lk.
Поскольку длина струи должна возрастать с увеличением
высоты и диаметра выемки, на практике применяют конические выемки
с диаметром, почти равным диаметру заряда и с высотой, равной
1 —1,5 диаметра выемки (а = 30°—40°). Увеличение высоты выемки
снижает устойчивость струи, как и уменьшение толщины конуса.
Причины возникновения неустойчивости кумулятивной
струи
1. Большие градиенты скорости, приводящие к разрыву и
диспергированию струи.
2. Падение плотности струи в процессе ее движения и
радиальное расширение струи из-за сопротивления воздуха.
3. Искривление струи,обусловленное погрешностями
изготовления заряда, несимметричности точки его инициирования,
взрывного импульса и оси выемки.
4. Вращение кумулятивного заряда. Под влиянием
центробежных сил происходит радиальное расширение струи по мере ее
движения. Например, стандартный снаряд калибра 76 мм пробивает
броню толщиной 205 мм без вращения и только 82 мм с вращением
(20000 об /мин).
В реальных условиях в разной мере сказываются все эти факторы.
Неустойчивость струи снижает ее пробивную способность,
поскольку при этом энергия струи дополнительно расходуется либо на
расширение одной пробоины, либо на создание вместо одной
пробоины нескольких кратеров.
Современные кумулятивные боеприпасы способны пробивать
броню толщиной 600 мм и более,поэтому актуальна проблема
антикумулятивной защиты бронемашин.
Широко применяется активная динамическая защита, в которой
источником энергии является слой пластического ВВ, расположенный
между двумя металлическими пластинами. Такая защита исследована
в 1957-61 гг в Институте гидродинамики (Новосибирск) [11].
190
Механизм работы защиты следующий (рис. 5.17). Струя
пересекает антикумулятивный слой и инициирует в нем ВВ. Пластины
слоя начинают двигаться под некоторым углом к струе, сообщают
ей импульс, под действием которого струя разрушается. Её энергия
тратится на расширение отверстия в слое, а не на пробивание брони.
Для ослабления струи решающим является величина угла между струей
и пластиной (см. рис 5.17),а при толщине ВВ более 7 мм глубина
проникания струи перестает уменьшаться.
Кроме бронебойных кумулятивных снарядов, разработаны
специальные кумулятивные заряды - перфораторы для пробивания глубоких
отверстий в стенах старых нефтяных скважин с целью повышения
добычи нефти. В некоторых конструкциях перфораторов используются
тяжелые облицовки из урана-238 (р = 18,6 г /см3).
Наконец, необходимо упомянуть об удлиненных кумулятивных
зарядах (УКЗ), которые применяются для резки металлов
кумулятивной струей. В частности, УКЗ эффективны для резки на
металлолом старых кораблей, подводных лодок, самолетов и т.п.
По конструкции УКЗ представляет собой обычную
металлическую трубку, диаметром 20... 100 мм (Си, Pb, Fe, А1), наполняемую
Рис. 5.17. а) Размещение кумулятивного заряда 1, антикумулятивного слоя из
пластин 2,4 и брони 5
б) Зависимость глубины проникания струи от угла а. (1 =1 =70 мм, толщина ВВ —
4 мм, пластины из алюминия толщиной 2,5 мм). 2,4 — расчет, 1,3 — эксперимент,
3,4 — нижние пластины заменены на сталь толщиной 50 мм
порошком гексогена и затем
профилируемую на
специальных станках (см. рис. 5.18).
В результате в трубке по
всей ее длине формируется
кумулятивная выемка. Чем
больше диаметр трубки, тем
толще разрезаемая сталь. УКЗ
инициируется с одного торца.
Схлопывание выемки с
образованием струи происходит за счет давления скользящей детонации.
В артиллерийской академии (Москва) разработаны гибкие УКЗ
с оболочкой из полимеров. Эти УКЗ дешевле и удобнее, но могут
разрезать меньшие толщины стали, чем УКЗ из медной трубки.
а)
Рис. 5.18. Конструкция УКЗ (сечение):
а) исходная трубка с гексогеном; б) та же
трубка после профилирования.
5.6. Сходящиеся сферические ударные волны
Сходящаяся сферическая УВ была первым примером
кумуляции, рассчитанной количественно для вполне реальной физической
постановки как ^ая газов, так и /^ля конденсированных веществ.
При описании сферической УВ был открыт новый класс
автомодельных движений, а^я определения которых недостаточно
соотношений размерностей.
При решении автомодельных задач используется безразмерная
переменная е = г/А ta , где a — параметр автомодельное™, который
входит в систему дифференциальных уравнений в качестве
параметра, и а^я задач с плоскими и расходящимися волнами определяется
до решения задачи из соображений размерности [2].
Задача о сходящихся волнах относится к второму типу
автомодельных задач, в которых величина а находится не из исходных
условий, а требует интегрирования уравнений, т.е. находится из решения
полной неавтомодельной задачи. Предельное автомодельное
решение справедливо только вблизи момента фокусировки, когда радиус
фронта УВ мал, причем вид решения не зависит от начальных
условий [2].
192
В отличие от плоских детонационных и ударных волн, на
фронте сильной сходящейся УВ энтропия не постоянна, а всегда
возрастает с уменьшением радиуса волны. Кроме того, сходящиеся
УВ конечной ширины обязательно должны содержать и зону
сжатия, и зону расширения, что следует из закона сохранения
массы [12].
Задача о движении вблизи фокусировки была впервые решена
немецким ученым Гудерлеем в 1942 году [13], независимо от него
Ландау и Станюковичем в 1944 году [14].
В общей форме описание сферической УВ есть в книгах [2,12].
Приведем результаты расчетов, сделанные в [1] ^^я кубического
урсо=з).
Изменение радиуса УВ с временем взято степенным:
t~Rk;(k = l/a) (5.22)
где степень предстоит найти, а время отсчитывается от момента
фокусировки (t = 0, R=0). До нее t<0. Обозначая r/R = r и вводя
вместо р, и и с новые безразмерные функции
р = p0Sr\ и = ^о(гУ, с2 = (y)2<f(r•) (5.23)
получим АЛ^ этих функций три дифференциальных уравнения ji^
автомодельного движения, из которых получается одно уравнение,
связывающее У) и 6:
до = Л2рл£) ,524)
где А2, А - детерминанты системы уравнений.
Это уравнение можно интегрировать, задаваясь величиной к.
При верно угаданном к обратятся в нуль все детерминанты.
Вычисленная методом попыток величина к оказалась равной
1,571. Тогда
u~l/Rk~l ~l/R057l;p~u2 ~l/R1142 (5.25)
т.е. при R -> 0 р -> <х> - происходит неограниченная кумуляция.
Кроме того, на фронте УВ Т * <*> В момент фокусировки (г'-> <х>)
величины и и с всюду конечны, кроме центра, а плотность постоянна
(не зависит от координат) и сжатие Sf = р/ро = 2,73.
После фокусировки от центра идет отраженная волна, в которой
сжатие максимально (SJ. В центре после фокусировки плотность
равна нулю (давление конечно, а энтропия бесконечна).
На рис. 5.19 показано распределение сжатия аая трех моментов: до
фокусировки, в момент ее и после нее.
В таблице 5.5 приведены главные параметры сходящихся
автомодельных УВ а^я веществ с j = 5/3,2 и 3.
Таблица 5.5. Расчетные параметры сходящейся волны
j
5/3
2
3
к
1,452
1,499
1,571
к
пр
1,451
1,500
1,588
*■
9,33
5,60
2,73
5
m
24,3
10,2
3,35
Ю.С. Вахрамеев [15] рассмотрел общий случай, когда
предельное сжатие h на фронте сильной УВ и показатель адиабаты j не
связаны обычным соотношением h = (j + l)/(j-l). Вычисленные к а^я
сферической волны приведены в таблице 5.5.
Гудерлей [16] проводил расчеты аля траектории сходящейся волны
в виде г=A (tf — t)a, где г — радиус волны, А=Const, t — время
достижения волной центра (у нас t=0), a — показатель автомодельности.
Для цилиндрической УВ в воздухе с j = l,4 согласно расчетам
Гудерлея a=0,835, а согласно расчётам Ю.С. Вахромеева [ 15] a=0,856.
Кроме того, аая сильной сферической волны Гудерлеем [16]
и Станюковичем [17] найдено аая j=7/5 значение a=0,717
(k= l/a = 1,395), а для j = 3 Станюкович нашел a=0,638 или k= 1,567,
(что близко к рассчитанному Забабахиным к= 1,571 [1]), а также
установил, что в пределе j -> 1, a -> 1.
С использованием показателя автомодельности законы
изменения параметров сходящейся У В с радиусом ее фронта следующие:
R~t\D~ ta~l ~ Ra~Va; р - t1{a~X) ~ д2(e-|)/e; Е ~ R5~2,a (5.26)
194
Рис. 5.19. Распределение сжатия по радиусу
для сильной сходящейся волны [1]
диусу в момент фокусировки (t = 0) следующие [2]:
Поскольку с временем
размеры автомодельной
области уменьшаются, то
полная энергия этой
области также уменьшается,
хотя вблизи фронта УВ
энергия
концентрируется, и в рамках
автомодельного решения во всем
пространстве энергия
бесконечна.
Предельные законы
распределения
газодинамических величин по ра-
Л-а
■г 1~а;р-
(5.27)
р= Const.
Для j = 7/5 S1 = pn е/р0 = 21,6, а на фронте отраженной УВ
Sm = poT /р0= 137,5, т.е. плотность в отраженной волне в 23 больше
плотности в падающей волне [2], (где р/р0 = 6).
Таким образом, в моменте фокусировки сходящейся волны
давление и температура (энергия) бесконечны, а плотность конечна.
Если сферическая волна слабая (слабый толчок сферического
поршня, | и | < < с), то на фронте А р ~ А V, а сам объем V
уменьшается как г2, т.к. ширина зоны возмущения постоянна.
Поэтому полная энергия Е ~ V А р; А V ~ Ар2 г2, откуда а^я
слабой сферической волны в любом веществе [1]:
Ар~г~\ и~г~х (5.28)
Этот простой закон не годен ^ая пористых тел (где
несправедливо А р ~ А V) и ^ая очень короткого начального импульса, когда
затухание УВ сравнимо с ее усилением от уменьшения радиуса.
Отметим, что сходящаяся волна не обязательно должна быть
сферической или цилиндрической. Например, если заменить сферу
многогранником (допустим, кубом), то в его вершинах и гранях
будут возникать волны Маха (тришоки), которые, сталкиваясь,
образуют новый многогранник, он порождает новые тришоки и так далее с
возрастанием давления по степенному закону.
В этом случае кумуляция (и автомодельность) носит не
непрерывный, а периодический характер.
Таким образом, сильные сходящиеся УВ создают сильную,
теоретически неограниченную кумуляцию.
До сих пор мы рассматривали схождение одной УВ, но часто
волна расщепляется на две волны, например, в твердом теле из-за
его прочности или фазового перехода (появление упругого и
фазового предвестника), а в газе - из-за его теплопроводности. Как
такое расщепление влияет на характер кумуляции проанализировал
Е.И. Забабахин в [1].
5.6.1. Фокусировка упругого предвестника
фарная адиабата вещества с прочностью имеет излом при
давлении, равном динамическому пределу упругости р* (см. гл. 3).
Впереди пластической волны с постоянной скоростью сие
постоянной амплитудой р* движется упругая волна или упругий
предвестник. Для коэффициента Пуассона [л=1/3 в упругой области
одноосного сжатия (на предвестнике) справедливы следующие
соотношения:
^Ц- = с2; р* = 4Г; Y = \Ej (5.29)
ар 2 р 8 ч
где Е — модуль Юнга; Y* — прочность на сдвиг (динамический
предел текучести); Y — касательное напряжение; j — текущий угол
сдвига.
При давлении р > р* в области пластической деформации:
Y = Y* = const при j > j*; dp/dp = Е/р = cn2 (5.30)
где j* — предельный угол сдвига (при р=р*).
196
При схождении к центру упругого предвестника в прочном шаре
на его фронте происходит либо разгрузка, либо пластическая
деформация. Области упругого и пластического течений чередуются. Для
каждой области найдены законы автомодельного движения.
В [1] показано, что при схождении упругого предвестника
неограниченной кумуляции нет, но она возникает после
фокусировки:
p/p0=0,467\nR/r (5.31)
Кумуляция не сильная, лишь логарифмическая. Диссипация
энергии и нагрев шара малы.
5.6.2. Фокусировка У В с фазовый переходом
Как и в предыдущем случае, ударная адиабата имеет излом в
точке начала фазового перехода, и волна распадается на две. Вперед
уходит УВ с постоянной скоростью и давлением (это постоянство D и р
сохраняется даже если У В сходящаяся). Ее можно назвать фазовым
предвестником.
В [1] найдено решение вблизи центра а^я случая , когда вторая
волна с увеличивающейся амплитудой не успевает догнать первую
волну до ее фокусировки.
Найдено автомодельное решение аа^ кубического УРС, из
которого следует,что до фокусировки (t = 0) вещество ускоряется, а после нее
замедляется. На отраженной от центра волне (r/t=с) скорость
обращается в нуль, что означает, что эта волна вырождается в слабый разрыв.
Сделан вывод, что а^я фазового предвестника нет
неограниченной кумуляции ни при его схождении к центру, ни после отражения
от центра.
Влияние на сферическую кумуляцию фазового перехода в
стали показано в [18] при исследовании сохранённых шаров после их
ударного сжатия сферическими зарядами. Шары из сталей с а - Fe
(с фазовым а -> е переходом и фазовым предвестником) имели в
центре полость объёмом вдвое меньшим, чем у таких же шаров из стали
12С18Н10Т с j - Fe (без фазового перехода, поэтому с более сильной
кумуляцией УВ).
197
5.6.3. Фокусировка УВ з теплопроводном газе
Поскольку вблизи фокусировки сходящейся УВ температурные
градиенты растут неограниченно, то теплопроводность становится
одяим из ведущих механизмов диссипации энергии, и неясно,
приведет ли это к ограничению кумуляции.
Этот вопрос исследован в [1] аая случая УВ в идеальном газе
(j = 5/3), когда перенос тепла осуществляется излучением. За счет
теплопроводности перед УВ появляется зона прогрева, в которой
газ не только нагревается, но и начинает двигаться и уплотняться.
Поэтому фронт этой зоны можно назвать тепловым
предвестником.
Ширина зоны
<? = 0,007^- (5.32)
где: L = Const, <7 — постоянная Стефана- Больцмана.
Внутри зоны сжатие увеличивается от 1 до (j +1)/2, и далее
скачком до (j +1) (j — 1). Как видно, ширина зоны S растет со скоростью
волны D ~ А/г1*-1, т.е. в сходящейся волне S увеличивается, поэтому
ее фронт (тепловой предвестник) фокусируется до основной волны
(точка В на рис. 5.20).
Распределения температуры и плотности в УВ и схема ее
фокусировки в газе с теплопроводностью показаны на рис. 5.20.
На сходящейся волне температура Т~ A2/R г2^"1^ а
максимальная температура в момент фокусировки будет равна:
^ = const[(p01 /а)2**"" Д3*-2Л2]"<5*-4> (533)
где 1 = L р0/р — свободный пробег излучения.
Значение А характеризует начальную интенсивность сходящейся
УВ, величины Const определяются из численных расчетов. За первой
волной АВ идет вторая волна СЕ (см. рис. 5.20), при фокусировке
которой р -> оо, Т -> Const, т.е. процесс изотермичен в отличие от обычной
кумуляции УВ без теплопроводности, когда Т -> оо и р -> Const.
Таким образом, сходящийся тепловой предвестник (волна АВ)
не создает неограниченной кумуляции.
198
у+1 ,
y-l
2
P/Po
s
X
T/Tt
I m
S X
m ►
АСт
Рис. 5.20. Фокусировка УВ в газе с теплопроводностью
Во всех трех рассмотренных случаях ращепления сходящейся УВ
с образованием различной природы предвестников фокусировка
предвестников не создает неограниченной кумуляции.
5.7. Сходящаяся сферическая детонационная волна
Нормальная детонационная волна стационарна, т.е. имеет
определенную амплитуду, минимальную скорость, соответствующую
условию Жуге (и + с = D, т.е. на фронте звук движется со скоростью
фронта, см. гл. 8). Это справедливо а^я плоских и расходящихся
волн, но не выполняется а^я сходящихся: по мере схождения
давление на фронте растет, нарушается условие Жуге, и звук может
догонять фронт. В отличие от нормальной такую волну называют
пересжатой (подробно см. в [19]).
В частности, нестационарный (затухающий) режим пересжатой
детонации возникает в зоне инициирования заряда, если давление
инициирования больше давления в точке Жуге (например, если
инициатор изготовлен из более мощного ВВ, чем заряд).
Для сходящейся детонационной волны пересжатие не затухает,
возникает самопроизвольно (вне связи с инициирующим
давлением), и объясняется геометрией волны (кривизна и сокращение
поверхности фронта с временем).
В [1] факт самопроизвольного пересжатия доказывается \ля
сферы, используя кубическое У PC и ограничиваясь только началом
процесса. В начальный момент детонация нормальная,
инициирована на радиусе R и движется внуть сферы, а продукты детонации
свободно разлетаются.
199
Найдено, что скорость роста давления в начальный момент равна:
(534)
др
дг
IEil
8 R
Таким образом, dp/dr < 0, т.е. давление волны растет с
уменьшением радиуса.
Для цилиндрической волны скорость роста ее давления вдвое
меньше, поскольку вдвое меньше кривизна волны по сравнению со
б)
pU
1,2
ё 1д
1,0
Cyfindrical
J I I I L
J L
12345678 910
DETONATION FRONT RADIUS/lNITlAL RADIUS
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,80,9 1,0
DETONATION FRONT RADIUS/lNITlAL RADIUS
Рис.5.21. Относительное увеличение давления (а) и скорости (б) в сходящихся
цилиндрической и сферической детонационных волнах с уменьшением их радиуса
сферой.
Относительный рост скорости детонации и давления в точке
Жуге с уменьшением радиуса сходящейся волны сферической и
цилиндрической геометрий приведён на рис. 5.21. [20].
Как видно, давление растёт вдвое быстрее скорости.
Таким образом, в сходящихся детонационных волнах также
существует кумуляция с таким же описанием, что и а^я ударных волн.
Поскольку давление и концентрация энергии неограниченно ра-
200
стут, то калорийность ВВ вблизи фокусировки не играет никакой
роли.
Анализ, сделанный в [1], показал, что, если сходящуюся
детонационную волна поместить в сильное магнитное поле, то это не
усиливает и не изменяет кумуляцию волны.
5.8. Схлопывание полости. Пузырек в сжимаемой жидкости
Рэлей решил задачу о пузырьке в идеальной несжимаемой
жидкости. Возникает вопрос, а как изменится кумуляция при схлопывании
пузырька, если учесть сжимаемость жидкости? Задача аналогична задаче
о схождении к центру толстой сжимаемой оболочки.
Этот вопрос исследовали Зельдович, Забабахин, Гельфанд, Хантер,
Брушлинский и Каждан.
В [1] решение задачи о схлопывании пузырька излагается аля
кубического УРС, что упрощает выкладки, т.к. с ~ р.
Решение уравнений движения в переменных Римана (а = и + с и
(2 = и - с) показало, что а^я неизвестной степени кумуляции к в
интервале 1,411 < к < 1,5 существует не одно, а множество решений.
Решение с к = 1,411 выделено как наименьшее, т.е. дающее
наименьшую степень кумуляции.
Множество предельных решений означает, что существует
множество движений стенок пузырька к центру с искусственно
подобранными начальными условиями, которые соответствуют самим решениям.
Найденное решение показало, что сжимаемость не устраняет
неограниченной кумуляции, которая не есть следствие идеализации
при постановке задачи, а реальное свойство явления схлопывания
полости.
Поскольку вблизи фокусировки всюду, кроме свободной
границы полости, р -> оо, то начальная плотность р0 не играет никакой
роли. Это значит, что найденное решение описывает схлопывание
полости как в газе с р = А р3, так и в жидкости с р = А (р3 — р03).
Учет сжимаемости изменил кумуляцию по сравнению с тем, что
было в несжимаемой жидкости. Массовая скорость и плотность
неограниченно растут по закону
201
u-p-r™ (5.35)
Температура также расходится, если у газа была начальная
температура (адиабатическое сжатие). Если же Т = 0 (давление
только упругое), то температура остается нулевой до фокусировки.
Степень кумуляции к а^я разных веществ (разных j) приведена
ниже:
j
к
1
1
5/3
1,064
2
1,176
3
1,411
7
1,801
оо
2,5
5.9. Неустойчивость схлопывания пузырьков
Рассмотрим вопрос неустойчивости движения стенок пузырька,
ограничивающей кумуляцию при схлопывании пузырька.
Процесс схлопывания газонаполненных полостей в объеме
жидкости изучался в [21,22] применительно к инициированию
жидких взрывчатых веществ (ЖВВ) схлопыванием газовых
включений.
Не удавалось объяснить взрыв ЖВВ простым теплообменом
адиабатически нагретого газа (до 1300К) со стенками схлопываю-
щегося пузырька или вязким разогревом сходящейся поверхности
пузырька. В [22] было показано,что причиной взрыва могут быть
микрокапли ЖВВ (порядка микрон), образующиеся в полости при
ее схлопывании.
В свою очередь образование микрокапель объясняется
нестабильностью поверхности схлопывающейся полости. Принципиальная
неустойчивость движения поверхности пузырьков приводит к
появлению внутри пузырька микроструй жидкости [23,24]. В [25]
показано, что такие струи при кавитации воды на стальной
поверхности (например, гребного винта судна) создают короткие импульсы
давления с амплитудой ~1 ГПа , превышающей предел прочности
стали, и являются причиной ее эрозии.
На основе теоретического анализа формы сферического
пузырька в [26,27] сделан вывод о нестабильности формы
захлопывающейся полости. Таким образом неустойчивость движущейся
поверхности полости ограничивает кумуляцию (т.е. максимально
202
достижимые в центре полости величины температуры , давления и
плотности) и приводит к образованию высокоскоростной
кумулятивной струи.
Эта струя внедряется в противоположную стенку пузырька
еще до остановки движения стенок, при этом струя
диспергируется на капли, а полость разбивается на множество более мелких
частей.
Сделанный в [21] анализ показал, что взрыв нитроглицерина с
пузырьками возможен только, если внутри пузырьков количество
образующихся капель будет оптимально. Если капель мало, то даже
при большой степени сжатия пузырька (S = 65) адиабатического
разогрева газа в пузырьке недостаточно а^я взрыва, так же, как и
теплоты сгорания капель.
Слишком большое количество капель охлаждает полость
настолько, что температура стенок опускается ниже критической
величины, требуемой аая взрыва. Оптимальная масса капель примерно
равна массе газа в полости.
Увеличение вязкости нитроглицерина за счет его желатинизации
(введением коллоксилина) незначительно изменяет время и
скорость движения границы полости, но значительно уменьшает
скорости кумулятивной струи и процесса дробления струи на капли, что и
снижает чувствительность.
Таким образом, инициирование нитроглицерина с пузырьком
воздуха происходит только в результате принципиальной
неустойчивости движения границ пузырька. С этим явлением связана и
неустойчивость движения струй внутри пузырька (в смысле изменений
вектора скорости и формы струй).
Теоретически невозможно предсказать условия начала развития
неустойчивости, т.к. они определяются конкретной совокупностью
малых начальных возмущений. В [21] указываются лишь некоторые
критерии устойчивости сходящегося движения.
1). Ускорение границы Э u/Э г < 0;
2). При г -> 0 Э u/Э г растет быстрее, чем ~ г2.
Смена знака ускорения свидетельствует о начале
неустойчивости, так же, как рост первоначально малых возмущений.
203
В [21] экспериментально показано, что из-за неустойчивости
формы круглая в сечении полость при схождении превращается в
эллиптическую. Почему? Если разложить близкий к кругу контур в
ряд по гармоническим функциям, то первым наиболее влиятельным
членом в этом ряду будет функция, определяющая эллипс (гармони-
KaNl).
Скорость границы вдоль большой полуоси эллипса больше, чем
вдоль малой, поэтому постепенно вдоль большой полуоси
образуется кумулятивная струя.
46,5
25
77,5
40
90
а)
б)
в)
Проблема
неустойчивости схлопывания
пузырьков важна не
только аля изучения
инициирования ЖВВ
или эрозии гребных
валов, но также аая
сжатия мишеней
термоядерного синтеза
(см. раздел 5.13).
Способы
снижения неустойчивости
контактных границ
рассматриваются в
разделе 5.12.
Рис.5.22. Кинокадры схлопывания воздушных полостей в жидкости.
а) Сферический воздушный пузырек 610 мм в водном растворе глицерина.
б) То же в нитроглицерине.
в) Эллиптическая полость с полуосями 2,65 и 5 мм в нитроглицерине.
Цифры на кинокадрах означают время в мкс после начала движения границ полости
Развитие неустойчивости схлопывания воздушных полостей
в жидкости иллюстрируется кинокадрами рис. 5.22, полученными
в работе [21].
204
5.10. Кумуляция в слоеных системах
До сих пор неограниченная кумуляция была связана с
центростремительным движением к центру или к оси. Оказывается, это
геометрическое условие не является обязательным а^я возникновения кумуляции.
Например, при движении УВ по газу с убывающей плотностью (выход
на границу атмосферы) также реализуется автомодельность, причем и и
Т на волне растут неограниченно, но р -> 0, т.е. энергия единицы массы
велика, но ее объемная плотность стремится к нулю[28].
Е.И. Забабахину удалось построить слоеную систему из
чередующихся легких и тяжелых слоев, в которой УВ неограниченно
усиливается [1]. Качественно принцип усиления в слойке такой же, как и
при соударении последовательности несжимаемых пластин с убы-
вающейся толщиной. Поскольку энергия постоянна, а масса падает,
то скорость пластин растет.
В слоёной системе (см. рис. 5.23) относительные толщины всех
легких слоев одинаковы ед = b./x. = Const. Для тяжелых слоев тоже
6 = Const.
т
При подобном изменении размеров исходной системы в (1 —б)
(1—6) раз новая система совпадает с исходной, и распределение
плотности р (х) в ней будет исходное.
Слоеная система может быть построена не только из пар слоев,
но и из любых повторяющихся профилей плотности.
Если скорость поршня, вызвавшего движение в слойке,
достаточно долго постоянна, то на волне в слойке установится
периодическое изменение давления. При переходе волны из слоя в слой
давление меняется скачками. Кроме того, при отражении от границ слоев
возникают вторичные УВ, которые догоняют первый фронт и также
скачком увеличивают на нем давление (см. рис. 5.23).
Для соответствующих значений х (например, на правых
поверхностях тяжелых слоев) давление на фронте подчиняется закону
р = а/хп. Для других х (например, ^ая середин легких слоев) закон
будет тот же, но с другой величиной а. Зависимость р (х) удобно
строить в логарифмических координатах (рис. 5.23), т.к. в них шаг между
парами уменьшающихся по толщине слоев будет постоянный.
205
Рис. 5.23. Автомодельная система из легких и тяжелых слоев.
Описание движения УВ в слойке сложнее, чем в рассмотренных
ранее случаях схождения УВ в однородной среде, поскольку аая решения
задачи надо знать все профили р (х, t) и р (х, t) аая целого периода
слойки на площади плоскости х, t. Поэтому необходимо решать уравнения
в частных производных численным методом. Цель численных
расчетов — найти показатель кумуляции п в законе р ~ 1/х" или Е ~ 1/хп.
Признаком автомодельное™ в расчетах является появление
повторяющихся профилей в зависимости In р от In х.
Если в системе нет потерь энергии при передаче ее от слоя к
слою, то Е ~1/х, т.е. верхним пределом аая степени кумуляции УВ
в плоской слойке является п = 1.
Из общих соображений можно ожидать, что степень кумуляции
будет расти с увеличением различия в плотностях слоев. Был сделан
численный расчет плоской газовой (j = 5/3) слойки с отношением
плотностей, равным 25 и с относительными толщинами г = 0,1, ед = 0,2.
Получено, что УВ усиливается по мере ее движения от толстых
пар слоев к тонким, при этом п = 0,23.
Показатель п определен по наклону ломаной на
зависимости lnp(lnx). Он невелик, но превосходит погрешности расчета.
Экспериментально факт кумуляции в плоской слойке был
подтвержден К.К. Крупниковым в РФЯЦ—ВНИИТФ.
Для получения кумуляции в слойке из конденсированных
веществ необходима достаточно сильная исходная УВ, входящая
в слойку, такая, чтобы вещества слойки вели себя как идеальные
206
газы, а скорости УВ в слоях были заметно больше скоростей звука
в них.
Если исходная волна слабая, то отраженные вторичные волны
будут иметь ту же скорость звука, что и фронт первой волны, значит,
не смогут ее догнать и усилить. Поэтому первая волна в этом случае
будет затухать.
Таким образом, аая конденсированной слойки существует
критическая интенсивность начальной волны.
С целью получения сильной начальной волны целесообразно
использовать генератор сферической сходящейся ударной или
детонационной волны, а слойку сделать сферической.
В сферической слойке степень кумуляции будет значительно
выше, чем в плоской, поскольку УВ будет усиливаться за счет суммы
двух факторов: сферичности (сходимости) и слоистости системы.
По-видимому, в сферической слойке можно получить
наибольшую степень кумуляции. Например, при j = 5/3:
Аая сферической волны к = 1,452 и р ~ R-2^'1) ~ R-0»904 у
Аля плоской слойки р ~ х~°23,
аая сферической слойки р ~ R-°'904-0»23 ~ R-U34 ^
что соответствует степени кумуляции к = 1,567.
Увеличение степени кумуляции означает при прочих равных
условиях увеличение сжатого объема, в котором будут требуемые высокие
значения р, р, u, Т (или увеличение параметров в заданном объеме).
В слойке движение периодическое, и автомодельность
периодическая. Такая периодичность может быть и при двумерном
схождении исходной УВ в виде квадратной призмы. В ее углах образуются
волны Маха, которые превращают квадрат в восьмиугольник, затем
снова в квадрат и т.д.
Возможно и трехмерное периодическое движение волн,
например, идущих от граней куба внутрь с периодической автомодельно-
стью и кумуляцией.
Таким образом, аая получения неограниченной кумуляции не
обязательна фокусировка с цилиндрической или сферической
симметрией.
Итак, аая эффективной работы слойки необходимо соблюдение
следующих условий:
1. Максимально возможное различие в плотностях слоев.
2. Убывающие по постоянному закону толщины слоев.
3. Достаточно большое количество пар (хотя обычно достаточно
4-х пар). Конечное количество слоев ограничивает и кумуляцию.
4. Максимально возможная амплитуда начальной УВ.
5.11. Примеры прекращения неограниченной
кумуляции
Рассмотрим примеры кумуляции, а^я которых найдены и
количественно обоснованы ясные физические причины прекращения
теоретически неограниченной кумуляции [1].
1. Сжимаемость. Согласно (5.24) при очень малом угле а
столкновения несжимаемых пластин энергия струи равна энергии
пластины, и вся она кумулируется в бесконечно тонкой струе, т.е.
происходит неограниченная кумуляция. Однако сжимаемость пластин
ограничивает кумуляцию, и при малых а струя не образуется
(регулярный режим, см. рис. 5.11).
2. Вязкость. Одним из первых теоретически описанных
примеров неограниченной кумуляции (Рэлей, 1917г.) является
фокусировка пустого сферического пузырька радиусом а в несжимаемой
жидкости с давлением р0. Решение этой задачи автомодельно (т.е.
безразмерные величины u/u2 зависят только от г/г2, где индексом 1
отмечены величины на поверхности пузырька):
щ*1^£У=А/гГ (536)
Как видно, при г -> 0 скорость иг неограниченно растет, т.е. мы
имеем неограниченную кумуляцию.
Перед фокусировкой и давление неограниченно растет.
Например, при уменьшении радиуса пузырька в воде в 100 раз
давление в нем р = 16 ГПа, при этом сжатие vQ/v > 2, т.е. будет существенна
сжимаемость жидкости (см. раздел 5.8.).
208
Кроме сжимаемости, на процесс фокусировки может влиять вязкость
жидкости, которая приводит к диссипации энергии со скоростью [ 1 ]
— = -16ю]ги: (5.37)
dt
где У] - коэффициент вязкости, г и и - на поверхности пузырька.
Кинетическая энергия жидкости 1^ = 2 п г3 ри2 и т.к. d/at = u (d/ar),
то
dEk/dt=ud(r3u2)/dr (5.38)
Приравнивая (5.37) и (5.38), получим квадратное уравнение из
решения которого видно, что поверхность пузырька может достичь
центра, но может и остановиться (и = 0 на радиусе г2).
Радиус остановки г2 определяется выражением:
лЯ^ = 1+^ (539)
где и=У]/р — кинематическая вязкость, uQ, rQ — начальные условия
(причем uQ<0).
Поверхность пузырька останавливается (нет фокусировки) при
l+u0r0/8u>0.
Величина uQ rQ/v = R е — число Рейнольдса.
Тогда критическая величина Re = 8. При Re < 8 пузырек не схло-
пывается, его стенки не достигают центра, останавливаются. При
Re > 8 происходит неограниченная кумуляция в центре, где скорость
бесконечно велика.
Таким образом, при Re > ReK вязкость не устраняет кумуляции и
даже не меняет ее степени (и = А г3/2 как а^я жидкости без вязкости,
так и с вязкостью).
Результаты численного интегрирования:
1). Re = 8,4.
2). Для данных р и р существует критический начальный радиус
пузырька величиной
a=%,AvJ^Fp (5.40)
При а<ак пузырек сходится медленно, т.е. вязкость
устраняет кумуляцию. При а>ак скорость вблизи центра растет
неограниченно по тому же закону и = А г"3/2, но с меньшей
величиной А.
Величина ак очень мала, т.е. вязкость устраняет кумуляцию
только в очень маленьких пузырьках. Например, аля воды он равен
0,8 мкм, fiiA^ глицерина — 0,5 мм. Роль вязкости уменьшается из-за
нагрева жидкости у быстро движущейся к центру поверхности
пузырька.
3. Вращение. Рассмотрим инерционное (без давления на
поверхности) движение к оси жидкой несжимаемой цилиндрической
оболочки. Для такого радиального движения иг = Const и кинетическая
энергия единицы длины цилиндра
Ер = л:ри2г21п(Д / г) = Const (5.41)
где и — скорость внутренней границы, R и г — наружный и
внутренний радиусы.
Отсюда видно, что при схождении оболочки к оси (г -> 0) и -> оо,
т.е. происходит неограниченная кумуляция. Посмотрим, как
влияет на этот процесс схождения одновременное вращение оболочки.
В этом случае будет две сохраняющиеся постоянными энергии:
радиальная Е и вращательная Е = к р v2 г2 In (R/r), где v — вращатель-
р
ная скорость внутренней границы, растущей как 1/ г.
Кроме того, сохраняется момент количества вращательного
движения Q, который для момента остановки радиального движения
равен Q= mvr, где m — масса единицы длины цилиндра.
Из этих условий получаем выражение аая максимальной
скорости вращения:
2]
© = — ехр(—-§-) /542)
mr KpQ \J-^J
При Q Ф 0 v конечна и при Q->0 v -> оо.
Следовательно, сколь угодно слабое начальное вращение
оболочки (Q=mvr -> 0 и v -> 0) при ее схождении (г -> 0), бесконечно
усиливается и разрушает кумуляцию.
210
Из сравнения формул &ля Е и Ев видно, что величина v точно
совпадает с той скоростью, которую имела бы невращающаяся
оболочка с той же энергией, на том же радиусе, но направлена скорость
не по радиусу, а по окружности (v = и).
Это единственный пример, доказывающий неустойчивость
кумуляции, когда введение дополнительной степени свободы
(вращения), бесконечно слабо возбужденной, отнимает всю энергию
основного (радиального) движения и полностью разрушает кумуляцию.
Отметим реальное и существенно отрицательное влияние
вращения кумулятивных снарядов на бронепробивание (см. раздел 5.5. и [4]).
4. Геометрические ограничения.
Слабая кумуляция в расходящейся УВ, движущейся по газу с
уменьшающейся плотностью, будет ограничена, если конечная
плотность мала, но не нулевая,
Кумуляция в слоеной системе ограничивается конечной
толщиной последнего слоя.
Кумуляция в сходящейся сферической УВ в газе будет
ограничена, если вблизи центра поместить малую твердую частицу,
Кумуляция УВ, входящей в узкую коническую или клиновидную
полость с газом, ограничивается любым притуплением конуса или
угла полости.
Наконец, любая кумуляция нарушается неустойчивостью
границ к малым возмущениям. В результате их развития в процессе
движения форма сходящейся УВ или полости отклоняется от
идеальной (сферы или цилиндра), что и ограничивает кумуляцию. Причем
Ю.С. Вахрамеев показал, что чем сильнее кумуляция, тем сильнее и
неустойчивость [15].
5.12. Неустойчивость контактных границ
Ниже кратко излагаются результаты исследований неустойчивости
границ, полученные сотрудниками РФЯЦ—ВНИИТФ (г.Снежинск),
Е.И. Забабахиным, А.Р. Птицьшым, Н.Н. Анучиной, А.В. П олионовым,
В.Н. Огибиной, Л.И. Шибаршовым, ЮА. Кучеренко, Н.В. Птициной,
В.И. Читайкиным, В.Е. Неуважаевым, В А. Лыковым [3].
211
Для сходящихся движений очевидной причиной ограничения
кумуляции является искажение, неустойчивость геометрической
формы поверхности, отклонение ее от идеальной сферы или
цилиндра. Развитие возмущений на контактной границе двух сред с
различной плотностью приводит к перемешиванию, хаотизации
движения и к ухудшению кумуляции, а аля неустойчивых процессов
и к полному ее разрушению.
Очевидный путь улучшения кумулятивных процессов —
тривиальное прецизионирование исходной системы (например, лазерной
мишени), поскольку чем меньше начальное возмущение, тем ближе
мы к идеальной или расчетной картине процесса.
Стабилизирующее влияние на развитие возмущений оказывает
вязкость, диффузия и поверхностное натяжение вещества.
Однако принципиально неустранима неустойчивость границ
двух жидкостей, когда ускорение направлено от легкой жидкости к
тяжелой (ртуть на воде). В этом случае малые вомущения на границе
растут, переходя в турбулентное перемешивание. Эта неустойчивость
называется конвективной, гравитационной или рэлей-тейлоровской
и часто встречается в кумулятивных процессах (метание,
сходящиеся волны в многослойных системах, сжатие газа тонкой оболочкой в
лазерных мишенях).
Гравитационная неустойчивость возникает, когда газ ускоряет
более плотную оболочку (или пластину). На стадии разгона
оболочки к центру давлением газа снаружи неустойчива внешняя граница
газ - оболочка, а при торможении сходящейся оболочки на газе
неустойчива внутренняя граница.
В общем случае контактная граница неустойчива, если в
процессе нестационарного движения двухслойной системы легкое
вещество ускоряет тяжелое или когда границу разноплотных веществ
проходит ударная волна.
Развитие малых возмущений на такой контактной границе
описывается формулой Тейлора:
r = Fkg(£zR (5.43)
(S+1)
212
где к=2 я/1 — волновое число, 1 — длина волны возмущения, F —
его начальная амплитуда^—ускорение границы, S=рт/рл — отношение
плотностей жидкостей на границе, г — ускорение роста амплитуды Е
Возмущения на границе неограниченно растут с временем,
и если в спектре начального возмущения представлены все длины
волн (широкий спектр гармоник), то граница раздела быстро
разрушается. Образуется зона турбулентного перемешивания, ширина
которой быстро растет с временем. Основная часть энергии
возникающего турбулентного течения содержится не в вихрях, а в
хаотических беспорядочных струях тяжелой жидкости, проникающей
в легкую. Идет непрерывный процесс разрушения струй и
возникновения новых, более крупных.
Энергия, затрачиваемая на эти процессы, берется из энергии
тяжелой жидкости, что меняет динамику течения в целом и снижает
характеристики процесса.
Экспериментально показано [3], что изменение величин
вязкости и поверхностного натяжения жидкостей не меняет
автомодельный характер турбулентного перемешивания, интенсивность
которого определяется только отношением плотностей жидкостей, или
при заданном S — величиной смещения границы 1 = 1/2 g t2. Кроме
того, найден период индукции, в течение которого не наблюдалось
разрушение границы.
Возможно, причина этого скрытого периода обусловлена
естественным размытием резкой границы из-за взаимной
молекулярной диффузии жидкостей. В 1883 году Рэлей показал, что размытие
границы между жидкостями (не скачок, а плавное изменение
плотности) уменьшает скорость роста возмущений. На основе
тейлоровской зависимости а^я случая изменения плотности в переходном
слое шириной b по экспоненте найдена величина уменьшения
ускорения роста амплитуды возмущений [1,3]:
Гт/Го = (^АШ//3 = 0,5^^^-]пЗ (544)
т ° (S-l) b2(S-l) { '
где г — ускорение при скачке плотности, rm — ускорение на
размытой границе.
У t
i
3
2
1
(
Рис. 5.24. Ограничение тейлоровской неустойчивости размытием скачка
плотности на границе
Результаты расчета rm/rQ даны на рис. 5.24.
Как видно, при размытии границы на толщину, равную длине
волны возмущения (Ь/1= 1), ускорение роста возмущения
уменьшается втрое (rm/rQ = 0,3). Значит, путь границы g t2/2 до момента
появления турбулентности увеличится также втрое.
Числовое моделирование процесса турбулентного
перемешивания на границе из-за тейлоровской неустойчивости подтвердило
этот вывод. Если к определенному моменту времени на границе без
переходного слоя реализуется зона перемешивания шириной L, то
оптимальная ширина переходного слоя h = L/3.
При данной фиксированной ширине ослабление роста зоны
перемешивания тем сильнее, чем слабее начальное возмущение.
Кроме того, невозмущенная гравитационно-неустойчивая система с
распределенной плотностью в переходной зоне на границе остается
устойчивой, если длина волны возмущения не превышает
некоторой критической величины. Для систем с резкой границей такого
ограничения нет, и достаточно малых фоновых возмущений &1\я
возникновения турбулентного перемешивания.
Экспериментально найдена зависимость пути L*, пройденного
границей с переходной зоной ширины h от величины возмущений z
(см. рис. 5.25).
Например, согласно данным рис. 5.24, а^я переходной зоны
шириной h = 5 мм, S = 4 и z = 1 мм путь, проходимый границей без
турбулентности, будет равен L* = 15 х 5 = 75 мм.
214
L7h
25
20
*i
H
15
10
0"
Uj~
"02"
"ОТ"
UJ~
"ДГ
us~
Z/h
Рис. 5.25. Зависимость задержки в развитии возмущений на границе
с переходным слоем от размера возмущения
• — 8=4,°—8=2. Ускорение границы g= 1000 g^
А. Р. Птицын показал, что замена плавного распределения
плотности в переходном слое многоступенчатым также ограничивает
тейлоровскую неустойчивость [3].
Изучение неустойчивости процесса сжатия газа сходящейся
сферической оболочкой имеет прямое отношение к процессам,
происходящим при сжатии и горении мишеней инерциального термоядерного
синтеза (например, лазерного). Развитие возмущений на оболочке
приводит к ограничению кумуляции и к потерям сжатия газа, величина
которых оценена Л И. Шибаршовым следующим образом [3].
Пусть идеальный газ с j = 5/3 сжимается сосредоточенной
сферической оболочкой, движущейся по закону
*('W*L+w2'2
(5-45)
где R . — минимальный радиус, w — максимальная скорость,
t=0 — момент максимального сжатия.
Объем сжимаемого газа представим в виде
4
(5.46)
где 6 — поправка, связанная с отклонением оболочки от
сферичности в процессе ее движения и определяемая гармоническим составом
возмущений (номерами п сферических гармоник):
*(0 = Е>„(0 (5.47)
Влияние данной гармоники падает с увеличением ее номера п.
Напомним, что 1-я гармоника возмущений формы — это смещение
точки фокусировки от геометрического центра (за счет
разновременности движения полюсов); 2-я гармоника — это
разновременность движения полюсов и экватора сферы; 4-я гармоника — это
превращение сферы в куб и т.д. Кроме того, существуют
гармонические возмущения, связанные с перетеканием массы.
Величину относительной потери максимального сжатия можно
оценить с помощью следующего выражения:
v«/vc =1 + ^(0 (5.48)
Если на разгоняемой газом пластине или толстой несжимаемой
оболочке заданы синусоидальные возмущения у = a sin к х, то их
развитие идет по закону
a~expjkgt (5.49)
(g - ускорение оболочки)
Этот же закон справедлив и а^я развития возмущений на
границе толстой несжимаемой оболочки с ускоряющим ее газом.
В.А. Лыков исследовал условия подавления гравитационной
неустойчивости оболочек мишеней термоядерного синтеза потоком
импульса частиц, возникающих в результате объемных реакций при
горении газа мишени, либо частиц от внешнего источника (поток
тяжелых ионов) [3].
Показано, что возможна полная стабилизация части спектра
коротковолновых возмущений границы в результате взаимодействия
гравитационной апериодической моды с колебательной модой,
которая обусловлена анизотропией тензора напряжений кинетических
частиц (объемные силы).
5.13. Безударное сжатие шара
Для осуществления инерционного термоядерного синтеза
необходимо получение больших плотностей, чего нельзя добиться
сжатием ударной волной — мешает нагрев.
216
а)
б)
в)
Р/Ро
103
102
ю
7=5/3 II
//
/ 7=3
Р/Ро
103
ю2
10
т-
/-
5/3
х
/
/
7=3
-1 -ю-1
-102 -103
t/T
-1 -ю-1 -102
-ю-3
t/T
Рис. 5.26. Безударное сжатие шара,
а) — Схема движения поршня, б) — Давление на поршне, в) — Средняя
плотность шара
Оказывается, шар можно сжать до высоких плотностей без его
нагрева ударной волной.
Общее решение задачи о безударном сжатии шара дано
Станюковичем [12], а в [1] излагается наиболее простое решение аая
кубического УРС. Условием безударного сжатия является задание
такого закона движения сферического поршня, когда все (2 - характеристики
приходят в центр одновременно, т.е. формируется центрированная
волна сжатия. Схема движения поршня показана на рис. 5.26.
Время сжатия поршня с начальным радиусом R равно Т = R/c ,
текущее время t отсчитывается от фокусировки (t < 0). При t = 0 шар
коллапсирует в точку. Уравнения движения записывается в
переменных Римана (а = и + си(2 = и-с), их решение ищется в
автомодельной форме с помощью численного интегрирования.
Вблизи фокусировки асимптотика дает: d r/d t=r/4 t, r~t —1/4 ,
.-9/4,
.-9
p-cMr/t)3
Бесконечно большая энергия сжатия Е~г"6 по порядку
величины совпадает с внутренней энергией сжатого шара £~р2~г"6.
Следовательно, потери на кинетическую энергию невелики в
отличие от сжатия шара ударной волной, где они связаны с нагревом и
стремятся к 100 %.
В общем случае а^я любых] и любой геометрии волны:
r~t\p~tM
(5.50)
где У) = 2/[ [х(у-1) + 2] , [л= 1, 2V 3 — для плоской, цилиндрической
и сферической волн.
Зависимости давления на сферическом поршне и среднего
сжатия S = (г0/г)3 от t/T даны на рис. 5.26 б), в).
Полученные результаты относятся и к конденсированным
веществам
Если волна сжатия не будет центрированной ((J —
характеристики не сходятся к центру), то движение остается автомодельным, но
в момент фокусировки шар не превращается в точку (неполный
коллапс), скорость всех частиц одинакова и направлена в центр. После
фокусировки из центра идет ударная волна, за которой газ
покоится.
Таким образом, если на поверхности однородного шара создать
давление, растущее по специальному закону, то можно реализовать
любое безударное сжатие шара вплоть до полного коллапса (р -> ©о),
т.е. неограниченная кумуляция может быть получена и без
сходящихся УВ. Только используя такой режим безударного (и безна-
гревного) сферического сжатия, можно получить рекордно высокие
плотности вещества, что является решающим условием
осуществления термоядерного синтеза - как неуправляемого, так и
управляемого.
5.14. Сжатие мишеней термоядерного синтеза
%се около полувека физики всего мира работают над решением
невероятно сложной проблемы управляемого термоядерного синтеза
(УТС). Суть проблемы — научится осуществлять и использовать
громадную энергию реакции ядерного синтеза — превращение водорода в
гелий. Сложность этой проблемы в том, что для наиболее быстрой
реакции T+D -> Не + п+17,5 Мэв необходимо создать и некоторое время
сохранять температуру 50—100 млн градусов. При такой температуре
близка к максимальной усредненная по рапределению Максвелла
величина эффективного сечения [сг v] реакции Т+D (см. рис 5.27), поэтому
максимальна и скорость реакции п [с v], где п — число частиц в
единице объема или плотность водорода.
218
р*р
200
400 TxltfK
Рис 5.27. Зависимость от температуры
среднего сечения [cry], определяющего
скорость реакции [29]
L(ruJ,M/c д^ каждой температуры
(Т >108К) равенство между
выделившейся при реакции
энергией и потерями энергии
(плазма не остывает) получается при
определенной величине
произведения пт = Const. Например,
Аля стационарно работающих
реакторов при Т=108К это
условие называется критерием
Лоусона: пт > 2 1020 с/см3 — аля
T + D реакции и пт > 5 1022 —
для D + D реакции.
Следовательно, чем
больше плотность смеси T + D, тем
меньше время удержания или
сохранения температуры Т >108К. Например, в водородной бомбе
плотность T + D максимальная,но время очень мало — всего
несколько микросекунд. Существует два способа создания и
удержания плазмы из смеси T + D: магнитный (токамаки и стеллараторы)
и инерционный (сжатие сферических мишеней светом лазеров или
пучками быстрых частиц — ионов, электронов).
В магнитных ловушках плотность плазмы берется малой, чтобы
снизить давление плазмы. Например, при плотности п = 2х1025 м-3
(как у воздуха в нормальных условиях) должно быть время
удержания т> 10"5 с и давление плазмы несколько сот килобар, —г- реактор
не выдержит. Если понизить плотность до 2x1020 м~3, то давление
плазмы будет 1 атм, но зато время удержания возрастает до 1 с.
В инерционном способе реализуется другой путь достижения
требуемой величины пт : максимальная плотность и минимальное
время удержания (см. рис. 5.28).
Например, если просто заморозить смесь T + D, то получим
n = 4Х1028 м"3 и т=2,5х10"9 с = 2,5 не. Это время удержания
должно быть равно времени разлета нагретого до 108К шарика со
скоростью ~106 м /сОтсюда радиус шарика должен быть 2,5 мм, а на
1
ю-2
ю-4
ю-6
Область выполнения
критерия Лоусона
дляП+Т
ю-8
ю-1
Инерционное
удержание
ю-18
ю-2
ю-2:
ю-2
ю-2
ю-2!
ю-3
Рис. 5.28. Два способа реализации критерия Лоусона [29]
его нагрев до 108К нужно ~ 107 дж энергии, что практически
нереально.
А вот если сжать смесь Т + D в 10 раз до плотности 1 кг/см3, то на
нагрев нужно всего 200 кдж, и диаметр шарика можно уменьшить до
0,2—0,4 мм, а время удержания — до 0,1 не.
Это уже реальные размеры. Опыты с такими шариками в начале
1980-х годов дали выход нейтронов 1010 и п т= 1018 с/м3.
Для отработки лазерного термоядерного синтеза нужны очень
мощные, сложные и точные лазерные системы, фокусирующие
световой синхронный импульс многих лазеров на очень маленький
шарик—мишень.
Для исследования лазерного синтеза в Ливерморской лаболато-
рии (США) построена уникальная лазерная система Shiva (24
лазера, 2,5 кдж, длительность импульса 100 пс), на которой получено
Зх 1010 нейтронов за импульс.
О необходимости сверхточности говорит тот факт, что на
второй в мире по мощности лазерной установке «Искра-5» (12
лазеров, РФЯЦ—ВНИИЭФ, г. Саров) работают только ночью, когда
нет движения транспорта на дорогах и можно добиться требуемой
настройки оптической системы лазеров.
В начале 1990-х годов на этой установке плазму удалось нагреть
до 108К, а вот с плотностью дела обстоят похуже - пока получается
лишь 1 г/см3 вместо требуемых 100 г/см3.
Для увеличения плотности, кроме высочайшего уровня преци-
зионирования установки и мишени, необходимо повысить степень
220
Мощность
к лазера безударности сжатия
мишени одновременно двумя
способами.
1. Тщательно
профилировать световое давление
на мишень, которое должно
Время, не плавно нарастать по заранее
Рис. 5.29. Форма лазерного импульса для рассчитанной кривой и обе-
безударного сжатия мишени [29] спечивать безударное сжатие
мишени (см. рис. 5.29).
На последнюю 0,1 не должно приходится половина мощности
импульса. При этом первая половина энергии тратится в основном
на сжатие мишени, а вторая — на нагрев до зажигания
термоядерной реакции.
После зажигания температура поддерживается за счет энергии
реакции, т.к. образующиеся нейтроны и ядра гелия не вылетают из
мишени, а отдают свою энергию другим частицам.
2. Правильно выбрать конструкцию мишени.
Чем сложнее мишень, тем проще лазер. Просто стеклянный
шарик с смесью D + Т не может обеспечить высокое сжатие. По мере
проведения исследований мишень все более усложнялась, ее стенки
сделались многослойными, причем каждый слой имеет свою
определенную функцию.
Схема трех конструкций мишени показаны на рис. 5.30 [140].
Внешняя толстая и легкая оболочка (бериллий, LiH,
фторопласт) испаряется, за счет чего создается реактивная сила, которая
будет сжимать внутреннюю тяжелую оболочку из тантала.
Тяжелая оболочка сохраняется неиспаренной, защищает D + Т
от воздействия быстрых электронов и рентгеновских лучей, а
главное — служит «холодным поршнем», обеспечивающим безударное
сжатие смеси D+T. Кроме того, бериллиевая оболочка отражает
образующиеся быстрые нейтроны (с энергией 14,1 Мэв) назад в D-T
смесь, что увеличивает скорость реакции. А танталовая оболочка
увеличивает отбор энергии плазмы легкой оболочки, идущей на
сжатие топлива.
стекло
полимер
бериллий
тантал
пористая пластмасса
золото
LiH
тантал
памороженный слой D+T
полость
золото
Рис. 5.30. Схемы многослойных мишеней для лазерного термоядерного синтеза
В более сложной конструкции на рис. 5.30 в) слой пористого
пенопласта защищает D + Т от быстрых нейтронов, а внутренняя
оболочка из золота — от рентгеновских лучей. Топливо D + Т
разделено на две части: намороженный слой дает максимальное сжатие,
а центральная часть внутри золотой оболочки — максимальную
температуру для зажигания реакции.
Точность изготовления мишени по современной
технологии очень высокая: отличие от идеальной сферы не превышает
0,3 мкм.
Технология изготовления таких точных стеклянных шариков
несложная. Компоненты стекла растворяют в воде. Капли
раствора падают внутри вертикальной печи и при Т=1000 К из раствора
образуется стекло, а вода, испаряясь, выдувает из стекла полые
шарики диаметром от 20 до 800 мкм с толщиной стенки в несколько
микрометров. Затем путем отсева отбирают шарики нужного
диаметра.
Основная трудность получения симметричного сферического
сжатия мишени заключается в подавлении развития
неустойчивости, которая может быть следующих двух видов:
1. Интенсивность лазерного света на поверхности мишени
достигает 1020 Вт/см2. При этом давление света состаляет 300 ГПа
Внешняя оболочка мишени испаряется, образуя плазму. На
расстоянии ~ Змкм от мишени давление плазмы резко падает и примерно
222
D+T
D+T
I
*■*•*.:».» •
1 2
ш
т
4 3 2 1
D+T П &Щ>>
° 5 4 3 2 1
а)1-
2-
6)1-
2-
3-
4-
2-
3-
4-
5-
сравнивается с давлением света. Вот в этой области и развивается
турбулентность плазмы, рождаются сильные поля и быстрые
электроны, которые могут нагреть топливо до его сжатия.
Турбулентность связана также с неоднородностью давления на
поверхности мишени в связи с небольшим количеством
используемых лазеров (12—24 штук).
2. Очень большие ускорения границ между веществами с
большим различием в плотности обусловливают быстрое развитие
гравитационных возмущений на границах (см. раздел 5.12).
Уменьшить эти неустойчивости и повысить тем самым
симметрию и степень сжатия можно следующими путями:
1). Увеличить толщину внешнего легкого слоя. Это позволит
увеличить длительность импульса, следовательно, уменьшить
интенсивность света, что, в свою очередь, снизит турбулентность плазмы.
Возможно применение вместо бериллия (или вместе с ним в нано-
композите) наноалмаза, который наилучший отражатель
нейтронов и при испарении создает более плотную и более энергичную
плазму.
2). Увеличить равномерность освещения поверхности мишени
за счет увеличения количества лазеров.
3). Ввести в конструкцию мишени слои с плавным или
ступенчатым изменением плотности, что уменьшит скорость развития
гравитационной неустойчивости.
4). Использовать взамен лазеров и света ускорители и пучки
тяжелых ионов.
Пробег таких ионов в веществе маленький, поэтому с ними
можно получить большую степень сжатия мишени, значит, уменьшить
энергию а^я поджигания реакции.
5.15. Ускорение частиц с помощью газокумулятивных
зарядов
Высокоскоростное метание тел имеет как научный, так и
практический интерес. Соударение тел с высокими скоростями позволяет
получать экстремально высокие величины р, р, Т и моделировать удар
метеоритов по конструкциям космической техники. Кумулятивные
заряды являются одним из простых, но эффективных ускоряющих
устройств, с помощью которых можно ускорять микрочастицы до
высоких скоростей, сравнимых с космическими скоростями
метеоритного удара (максимум функции распределения скоростей
метеоритов оценивается величиной 20... 40 км/с).
Распределение метеоритов по их массе можно описать
зависимостью N (т) = А/т. Верхняя граница массы оценивается т= 1 г [30].
Для обеспечения надежного измерения формы, размера и
агрегатного состояния ускоряемых частиц нижнее значение массы частиц
т« 10"4г, что соответствует размерам не менее десятых долей
миллиметра.
Для разгона в газовом потоке наиболее выгодна шаровая форма
частиц. Важнейшим параметром любого струйного метания
является отношение удельных масс разгоняющего потока газа и метаемой
частицы [30]:
(<*Р)шара
Скорость метания возрастает с увеличением (2.
Чтобы скорость тела была сравнима со скоростью струи,
необходимо выполнить условие ($ > 1.
Чтобы при ускорении тело не разрушалось, должно выполняться
второе условие:
ри2 < аа (5.52)
где и — скорость струи, о* - предел прочности материала, а=Const,
определяется свойствами материала.
Простейший газокумулятивный заряд ^ая метания твердых
частиц представляет собой длинный трубчатый заряд ВВ (до 200 d),
инициируемый с торца вспомогательной шашкой (см. рис. 5.31 а).
В полости заряда диаметром d формируется кумулятивная струя,
скорость которой достигает максимума на расстоянии от торца
х = 20 d для воздуха при нормальном давлении и на х = 50 d для воз-
224
Рис. 531. Газокумулятивные заряды [30,31].
1 — капсюль-детонатор, 2 — трубчатый заряд, 3 — ускоряемая твердая частица,
4 — инертный диск, 5 — кумулятивный заряд — генератор металлической струи,
6 — слойка из 3... 4-х пар слоев тяжелый—легкий металл, 7 — метаемое тело,
8 — линзовый заряд, 9 — металлическая пластина, 10 — стальная обойма
с сферическим полированным углублением
духа при давлении 1 Торр. Для этих двух случаев и заряда из ТГ 50
скорость струи составляет и =13,5 км/с и и =18 км/с.
a a J max max
Простым трубчатым зарядом удается разгонять частицы до
8 км/с. Более высокие скорости достигаются с помощью составного
заряда из двух цилиндров разного диаметра. Максимальные
скорости до 14 км/с получены при разгоне в вакууме нихромовых шариков
диаметром 80... 100 мкм, а шарики ol мм разгонялись до скоростей в
диапазоне 3...12 км/с.
Для имитации удара каменных метеоритов стеклянные шарики
диаметром от 1,56 до 5,2 мм разгонялись до umax = 7,8 км/с.
В связи с малым отношением масс частицы и заряда ^кя метания
частиц массой 1—2 г требуется трубчатый заряд массой 10—100 кг.
На рис. 5.31 в изображена схема легкогазовой пушки, в которой
в качестве поршня используется металлическая кумулятивная струя.
Ускорение тела в такой пушке можно рассматривать как задачу о
движении в трубе двух поршней, разделенных в начальный момент
слоем газа с давлением р и объемом V.
При условии, что масса метаемого тела М много меньше массы
струи, в [30] оценена максимальная скорость тела:
v =v + iv* + 2j?ovo
max c V C AfO"-l)
где vc — скорость струи, j — показатель адиабаты газа.
Видно, что при vc > > 2p0VQ/M (j -1) можно получить vmax« 2 vc.
В этом устройстве можно использовать кумулятивную плоскую
слойку из нескольких слоев пар тяжелый — легкий металл. Это
увеличит скорость УВ в газе от струи.
Используя подобные кумулятивные устройства, получили
компактные частицы вольфрама (сгустки) плотностью 1 г/см3,
движущиеся со скоростью до 27 км/с [3,32]. Получение компактных
частиц (вместо пара) связано с тем, что расширение ударносжа-
того вещества происходит с большим отклонением от адиабаты
идеального газа с j = Const. Например, аля гидрида лития и
вольфрама в [32] найдено, что в области давлений р >> 10 бар
адиабаты расширения имеют аномальные участки с у < 1 (d2 p/d V2 < 0),
где у (р) = — (v/p) (d p/d v) — эффективный показатель адиабаты.
Уникальны кумулятивные генераторы сильных УВ в газах
(генераторы Войтенко [31], см. рис. 5.31 г), в которых газ сжимается в
условиях остроугольной геометрии при движении пластины внутрь
сферической чаши с газом. С их помощью легко получить скорость
УВ в воздухе 40—45 км/с при нормальном давлении, а при замене
воздуха на аргон генератор дает мощную вспышку жесткого
ультрафиолетового света. Однако при попытке ускорять шарики
выяснилось, что условие (5.65) не выполняется, и шары разрушаются уже
при и= 18 км/с.
Литература к главе 5
1. Забабахин Е.И., Забабахин И.Е. Явления неограниченной
кумуляции. М.: Наука, 1988,102 с.
2. Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и
высокотемпературных гидродинамических явлений. М.: Наука, 1966.
3. Вопросы атомной науки и техники (ВАНТ), серия: теоретич.
и прикл. физика, М, 1988,вып.1.
(5.53)
226
4. Баум Ф.А., Станюкович К.П., Шехтер Б.И. Физика взрыва. М.:
Из-во физ-мат. лит., 1975.
5. Андреев К.К., Беляев А.Ф. Теория взрывчатых веществ. М.:
1960.
6. Курант Р., Фридрих К. Сверхзвуковое течение и ударные
волны. М.: Из-во иностр. лит., 1950.
7. Ададуров Г.А., Дрёмин А.Н. и др. ФГВ, 1967,3,2, с.281 -285.
8. Альтшулер Л.В., Петрунин А.П. ЖЭТФ, 1961,31,вып.6.
9. Альтшулер Л.В., Кормер СБ., Баканова А.А. и др. ЖЭТФ,
1961,41, вып.5,с.1382
10. А.В. Бушман ,Г.И. Канель ,А,Л, Ни, В.Е.Фортов. Теплофизика
и динамика интенсивных импульсных воздействий. Ин-т хим-
физики АН СССР, Черноголовка, 1988.
11. Бэрри Р.С., Смирнов Б.М. ЖЭТФ, 2000,117,3, с.562 -570.
12. Станюкович К.П. Неустановившиеся движения сплошной
среды. М.: Гостехтеориздат, 1955.
13. Guderley G. Luftfahrschung, 1942,Bd,19,p.302.
14. Ландау Л.Д., Станюкович К.П. ДАН СССР, 1945, т.46, N9,
с.399.
15. Вахрамеев Ю.С. ПММ, 1966, т.30,вып.4,с.774.
16. Guderley G. Luftfahrschung, 1942, Bd,19, р.302.
17. Станюкович К.П. Неустановившиеся движения сплошной
среды. М.: Гостехтеориздат, 1955.
18. Kozlov Е.А., Shock compression of condensed matter. 1991,
Elsevier Science Publishers B.V., 1992.
19. ЗельдовичЯ.Б.,Компанеец A.C. Теория детонации.М.: Гостех-
теоретиздат.1955.
20. Mader S. L. Numerical Modeling of Explosives and Propellants.
Second Edition, CRC Press, 1998,439 p.
21. Дубовик A.B., Боболев B.K. Чувствительность жидких
взрывчатых систем к удару. М.: "Наука", 1978.
22. Iohansson С.Н. Ргос. Roy. Soc. Lond, 1958, А246, р.160.
23. Корнфельд М.И. Упругость и прочность жидкостей. М.-Л.:
Гостехтеоретиздат, 1951.
24. Кнэпп Р., Дейли Дж., Хэммит Ф. Кавитация. М.: "Мир",
1974.
25. Kornfeld M., Suvorov L. J. Appl. Phys., 1944,15, p.495.
26. BirkhoffG. Quart Appl. Math., 1956,13, N4, p.451.
27. Plesset M.S.J. Appl. Phys., 1954,25, N1, p.96.
28. Гандельман Г.М., Франк-Каменецкий Д.А. ДАН СССР,
1956,t.107,N6,c.811.
29. Воронов Г.С. Штурм термоядерной крепости. М.: Наука,
1985.
30.. Мержиевский Л.А., Титов В.М., Фадеенко Ю.И., Швецов ГА.
ФГВ, 1987.N5, с.77.
31. Войтенко А.Е. ЖТФ, 1966,30,5,1,178.
32. Русаков М.М., Ногин В.Н. ФГВ, 1989, N1, с.140.
228
Глава шестая
ВЫСОКОСКОРОСТНОЙ УДАР
Изучение явления высокоскоростного соударения актуально в
связи с задачами метеоритной защиты космических аппаратов,
вопросами космогонии (удар по горным породам), проблемами
эрозионного износа лопаток турбин и сопел двигателей, разработки
технологий детонационных напылений (защитных покрытий), сварки
взрывом и т.п.
Развитие этого научного направления прямо связано с успехами
в создании методов ускорения твердых тел (см. разд.5.15). Однако
трудности в получении скоростей тел более 10—12 км/с
стимулировали работы по численному моделированию явлений
высокоскоростного взаимодействия [1—4].
Представление о современном состоянии этого направления
можно получить по обзорам [5,6] и монографиям [2,7, 8].
6.1. Соударение частицы с преградой
Детальное описание явления дано в [2, 5]. Обычно при
скоростях соударения v > 2 км/с в преграде образуется кратер, объем и
размеры которого больше, чем у ударяющей частицы, а глубина растет со
скоростью удара. Форма кратера зависит от скорости и определяется
отношением плотностей и прочностных параметров материалов
частицы и преграды. Экспериментальные зависимости глубины
кратера h относительно диаметра частицы d от скорости удара показаны
на рис.6.1а [6, 8].
а)
б)
О 1
h/cL
160
80
5
v, км/с 0
8 v, км/с
Рис. 6.1. Зависимости глубины кратера от скорости удара.
а) У^ар стальным шариком по преградам: 1— свинец; 2 — Д16; 3 — Ст.10. %др
стеклянным шариком по преградам: 4 — АД 1—М; 5 - АМГ- 6; 6- Д16АТ;
7 — Ст. Х18Н10Т; 8 — медь Ml; 9 — свинец; 10 - В65.
б) %др стального шарика по пенопласту (р=0,11 г/см3).
Даже аля высоких скоростей влияние на глубину кратера
прочности преграды остается большим. Так, а^я у = 12,4 км/с глубина h в
менее прочном алюминиевом сплаве АД 1 - М на 30% больше, а
объем кратера в 2,3 раза больше, чем в более прочном сплаве В65 [6].
Форма кратера
приобретает почти
полусферическую форму (h=r) при
ударе стеклянных шариков:
по сплаву АД1—М — при
v= 1 км/с, по прочным
алюминиевым сплавам - при
v=2 км/с, по меди — при
v=5 км/с, а аля стальных
преград аля всех
исследованных скоростей h < г.
4
h/4
/&
Д^
Р/Рп
Рис. 6.2. Зависимость глубины кратера от
относительной плотности сферического
ударника и преграды.
230
В то же время при ударе стальной частицы по алюминиевому
сплаву Д16 со скоростью 7,3 км/с h/r > 2.
Для пористых преград с ростом скорости частицы наблюдаются
следующие три режима внедрения.
1. При малых v (точнее, при малых кинетических энергиях)
напряжения в частице невелики, меньше ее прочности, и частица
сохраняет компактную форму.
2. С ростом v напряжения превышают прочность частицы,
которая разрушается на ряд осколков, что приводит к уменьшению
глубины проникания.
3. При больших скоростях удара трещины в частице не успевают
раскрыться, и частица ведет себя как вязкая жидкость, а каверна в
преграде приобретает вид широкой выемки.
Названные режимы наблюдаются при проникании стального
шарика (d = 3,35 мм) в пенопласт с плотностью р = 0,11г/см3 (см.
рис. 6.16). При v=5,l км/с h/d = 230 и соответствует наибольшей
скорости, при которой шарик еще не разрушается [6,8].
Зависимость глубины кратера от относительной плотности
ударника (р /р ) показана на рис.6.2 [9]. Парник сферической формы,
скорость 6 км/с.
Измерения размеров кратеров в преградах при ударе
вольфрамовых сгустков позволили оценить размеры кратера при ударе с
космической скоростью 80 км/с по защитному экрану из алюминиевого сплава
АМГ—6 метеоритов массой 10"7 г и 10"11 г (см. табл. 6.1) [9].
Таблица 6.1. Размеры кратеров в защитном алюминиевом экране
космического аппарата при соударении с микрометеоритами (р = 1 г/см3)
со скоростью 80 км/с
Источник
информации
Экстраполяция
экспер. результатов
[91
Двумерные числен-
ныерасчеты [10]
Масса метеорита
10 7 г
Диаметр
Глубина
мкм
420
500
450
300
1011 г
Диаметр
Глубина
мкм
18
23
20
14
231
Для скоростей соударения порядка 100 км/с начальная
плотность энергии в ударной волне много больше энергии испарения,
поэтому часть массы метеорита и экрана испаряется, из кратера
выбрасывается ионизированный парожидкостный факел.
Результаты расчетов позволили выбрать конструкцию противо-
метеоритной защиты космического зонда «Вега»,
предназначенного а^я исследования кометы Галлея.
В экспериментах по удару сгустком из вольфрамовых частиц
с v=25—30 км/с на испарение преграды расходуется ~30% энергии
сгустка [9], т.е. только часть выбрасываемой массы преграды плавится и
испаряется. Другая часть механически дробится, и ее количество
зависит от прочности преграды. Объем кратера в стальной преграде в ~10
раз превышает объем выброшенной массы, средняя скорость которой
составляет ~1,5 км/с [9].
Полный импульс, передаваемый преграде при ударе,
складывается из импульса частицы и реактивного импульса, обусловленного
выбросом материала из кратера. В [9] по измерениям скорости
преграды определялся ее полный импульс в зависимости от
потерянной преградой массы m в результате удара вольфрамовым сгустком
с v = 25—30 км/с (см. рис. 6.3).
Как видно из рис. 6.3, полный импульс линейно растет с
увеличением m, т.е. с увеличением реактивной составляющей.
Заметного
уплощения кратеров не
наблюдается (см. табл.
6.1) так же, как и в
опытах по удару
стальными шарами по
свинцовой преграде
[8].
В
гидродинамическом приближении
2,5 5 7,5 ю АтГ (^ез Учета
прочности) объем кратера
Рис. 6.3. Относительный импульс, сообщаемый пре- пропорционален „,_
граде при ударе вольфрамовым сгустком г г^
нетической энергии
•^ полн •'ул
\^Уи
□
У^Д
232
частицы. Тогда в предположении, что кратер имеет полусферическую
форму, получаем:
h/dQ~vm (6.1)
Действительно, экспериментальные результаты описываются
зависимостью
h/d = kva (6-2)
Величина а колеблется в пределах 0,3 < а < 0,85.
Отклонение величины а от 2/3 объясняется отличием реальной
формы кратера от полусферы вследствие влияния прочности. Учесть
прочность можно, предполагая, что кинетическая энергия частицы
полностью переходит в работу пластического деформирования
преграды, которая определяется напряжением течения а*, зависящем от
скорости деформирования: сг* = Ае|3 (е ~ v/d0 ~ 106 —107 с"1).
Тогда получим следующее соотношение [6]:
hr2 \р/ hr2 1
з " н,^>4 (6-3)
d0 8 (Т+ d0 8
-или—г- = -ру
Для разных материалов величина $ колеблется в пределах
(3 = 0,13—0,45. Величины Аи^ уменьшаются с уменьшением
прочности преграды. Например, аая стали Х18Н10Т А =5,06 и (3=0,42,
а для мягкого алюминия АД 1—М А = 0,63 и (3 =0,2 [6].
Если считать, что h = г (полусфера), то из (6.3) следует :
h \\PyV2 h 2-f (64)
— = — з——или v 3 УР'*)
d 2\ a, d
Такое приближение справедливо для v < 10 км/с, когда нет
существенного испарения преграды, влияние которого уменьшает
показатель а в (6.2).
Из (6.3) следует, что размер частиц слабо влияет на
относительные размеры кратера, что подтверждается экспериментами, в
которых d изменялось на два порядка.
Кратерообразование в хрупких преградах (горные породы,
стекло) имеет свои особенности [6,11,12]. При ударе стальным
шариком по стеклу с v = 5—12 км/с вокруг кратера образуется зона
радиально-кольцевых трещин, имеющая форму конуса с диаметром
D>>d и углом раствора 140°—150°. Этот угол оценивается как
арксинус отношения скоростей поперечных и продольных
звуковых волн [2].
Максимальные хрупкие разрушения наблюдались при ударе под
углом 45°—60°.
Для горных пород не выполняется условие, что масса
раздробленного и выброшенного материала пропорциональна
кинетической энергии ударника.
Исследовано угловое распределение осколков горной породы,
выбрасываемых при ударе с v = 3—10 км/с [6]. Определены три
угловые зоны разлета осколков: зона кумулятивного выплеска быстрых
осколков на стадии формирования кратера (а = 25°—28°), зона
бокового выброса медленных осколков (0,8 массы всех осколков) на
последней стадии образования кратера за счет разрушения
(скалывания) преграды у поверхности (а = 80°) и зона выброса осколков по
нормали при упругом восстановлении формы преграды после
сжатия (2а = 10°).
Не более 5% осколков имеют скорость, превышающую 1 км/с.
Масштаб размеров осколков - десятки микрон.
Изучено влияние на глубину кратера слоя пыли, покрывающего
базальт [3]. Кратер не образуется, если произведение толщины пыли
на ее плотность равно произведению глубины кратера в преграде без
слоя пыли на плотность преграды.
До сих пор рассматривался удар по полубесконечной преграде.
Теперь посмотрим, как изменяется картина соударения с
уменьшением толщины преграды. Для данных условий удара (материалы
ударника и преграды, скорость удара, форма ударника) можно
выделить три характерные толщины преграды.
1. Толщина, при которой при формировании кратера начинает
сказываться влияние тыльной свободной поверхности преграды.
Перемычка между дном кратера и свободной поверхностью
выпучивается или образуется откол под кратером (если растягивающие
234
напряжения превышают прочность материала преграды). Волна
сжатия от удара успевает отразиться от поверхности преграды в виде
волны разрежения, которая возвращается к кратеру еще до
остановки пластического течения преграды, следовательно, изменяет
глубину кратера.
2. Предельная толщина SQ, при которой наступает сквозное
разрушение преграды (хотя бы в виде сквозных трещин). Величина SQ,
в основном, зависит от отношения плотностей ударника и
преграды (от этого зависит амплитуда УВ в преграде) и от динамической
прочности преграды.
При ударе стали по алюминию величина SQ определяется
радиальными разрывами преграды, а при ударе стали по стали или стекла
по алюминию начало разрушения преграды связано с откольными
эффектами.
Исходя из определяющей роли кинетической энергии
ударяющей частицы, удалось описать экспериментальные данные разных
авторов единой линейной зависимостью [6,13]:
.2
^«1,15(з^--0,7] (6.5)
(v в км/с).
(6.5) не описывает удар сталью по свинцу и магнию.
Когда роль откола в преграде мала, аля оценки SQ можно
использовать соотношение:
S0*kh (6.6)
где к = 1,4.—1,5 аля алюминиевых сплавов [4].
3. Толщина S < SQ, при которой в преграде возникает сквозное
отверстие. Парник вместе с выбитой частью преграды проникает за
преграду, при этом деформируется, а выше определенной скорости
удара разрушается. Различают диаметры входного и сквозного
отверстий. Диаметр сквозного отверстия dx с изменением толщины S
от нуля до SQ изменяется от dQ до нуля, проходя через максимум при
какой-то промежуточной толщине.
В [14] предлагается линейная связь dt/d с параметром
v(s/don
Механизм пробоя металлических преград зависит от формы
ударника [15]. Если торец цилиндрического ударника плоский, то
пробой происходит по схеме выбивания пробки по механизму
сдвига с образованием отверстия в преграде лепесткового типа. При этом
в преграде наблюдаются области адиабатической локализованной
деформации. Цилиндрический ударник с острым коническим тор-
цем вызывает радиальное течение металла преграды и образование
пластичного отверстия.
Оценим скорость w облака осколков, проникающих за
пробитую преграду, предполагая, что кинетическая энергия неупругого
соударения (Е0) расходуется на пробивание (Е2), а остаток
передается осколкам (Е2), т.е. Е0 = Ег + Е2.
Отсюда получаем скорость осколков:
где аая сферического ударника z = S рп / (0,875 dQ р ) и аля
цилиндрического ударника длиной Н z = S р /Нр ;v — минимальная скорость
пробивания преграды, определяется из (6.5), где SQ отождествляется с
толщиной преграды.
Оценка скоростей и размеров осколков за преградой важна а^я
решения задачи о пробивании экранированной мишени. Если перед
мишенью установить тонкий экран, то на мишень будет
воздействовать не одна частица, а осколки частицы и экрана, распределенные
по площади мишени, во много раз большей сечения частицы. Это
вместе с потерей импульса на пробивание экрана и определяет
защитное действие экрана.
Площадь, занимаемая облаком осколков на мишени, зависит от
расстояния S между экраном и мишенью. При малых S поражение
мишени определяется воздействием компактного, еще не
разошедшегося облака осколков. При больших S показателем защитных
свойств экрана служит глубина h наибольшей из образующихся на
мишени каверн.
236
Эксперименты показали, что с ростом S величина h сначала
убывает, а начиная с S/d > 15—20 становится постоянной.
При больших S поражение мишени определяется толщиной
экрана S и скоростью удара v. При малых v и тонких экранах значительная
часть металлического ударника остается неразрушенной. С ростом v
и (или) S происходит полное разрушение ударника, причем сначала
размеры каверн от отдельных осколков близки. Такая структура
называется структурой равномерного разрушения.
При дальнейшем повышении v > 10—12 км/с четко выделяются
большими размерами краевые каверны, что означает переход к
кольцевой структуре поражения. В этом случае наблюдается сильное
диспергирование тела на мельчайшие осколки, частичное их плавление
и испарение.
Для стеклянных частиц во всем диапазоне v и S/d поражение
мишени характеризуется равномерным полем каверн.
Таким образом, оптимальная толщина экрана такая, при
которой происходит полное дробление ударника. При этом прочность
тонкого экрана слабо влияет на его защитные свойства.
До сих пор рассматривался удар по нормали к преграде. Однако
в действительности соударение, например, метеорита с оболочкой
космического аппарата должно происходить под различными углами
j к поверхности конструкции. Влияние угла соударения j изучалось
в [5,16]. Оказалось, что объем кратера V(j) пропорционален sinj, т.е.
V(j) = V0sin v, а его форма перестает быть симметричной
относительно нормали к поверхности. Наиболее глубокая часть кратера
формируется со стороны, откуда двигался ударник.
Отношение предельных толщин S(j)/SQ = (sin j)2/3.
Поэтому а^я удара под произвольным утлом (6.5) получает
вид:
^«U5(3p^-0,7)(sinyr (6-8)
d0 V Рп
При высоких скоростях удара из (6.8) следует:
^lA5h(VSinJ)2 (6.9)
При пробое преграды отверстие имеет форму эллипса,
вытянутого в направлении удара, причем большая ось эллипса d2 < d{ sin j.
При j = 30° площадь отверстия в 1,5 раза больше площади
отверстия при нормальном ударе.
При пробое преграды осколки из материала преграды
приобретают запреградную скорость w}, направление которой близко к
нормали к поверхности преграды. В то же время осколки от
разрушающегося ударника двигаются в направлении удара со скоростью w2
При ударе стальных шаров по алюминиевой преграде всегда
w2>Wj [17].
Для определения максимальной запреградной скорости
осколков можно использовать (6.7), где вместо z ввести z{ = z/sinj.
6.2. Сквозное пробивание стеклотекстолита
В изделиях аэрокосмической техники используются
композитные материалы, поэтому представляет интерес исследование
высокоскоростного взаимодействия частиц с конструкциями из
слоистых органо- и углепластиков.
В работе [18] исследовано пробивание пластин толщиной t из сте-
клотекстолитов при ударе стальных и стеклянных шариков диаметром
d= 1—2 мм, которые ускорялись трубчатым зарядом ВВ до скорости
v=3—7,3 км/с. В опытах использовались стеклотекстолит
полотняного переплетения марок СТ—1 (связующее — фенолформальдегидная
смола, р = 1,71 г/см3, твердость по Бринелю — 36 кг/мм2) и СТЭФ
(связующее — эпоксидная смола, р = 1,85 г/см3, твердость — 63 кг/мм2).
Полученные экспериментальные данные приведены на рис. 6.4
в виде зависимостей относительной глубины проникания шарика
h/d0 от относительной толщины мишени t/d0. Если мишень
пробита или возникли разгерметизирующие сквозные трещины, то
h = t= SQ, и все точки, соответствующие пробитию, лежат на прямой
h/d0=t/d0.
238
Рис. 6.4. Глубина проникания шариков
в стеклотекстолит dQ (мм):
1 - 0,83; 2и 5-1,1; 3-1,95; 4-1,45.
Материал мишени: 1—4 — СТЭФ; 5 — СТ-1;
6 — Д16. Материал частицы: 1,2,3,5,6 — сталь;
4 — стекло
Правее этой прямой
результаты расположены
в двух областях: область
больших толщин
мишени, где глубина h не
зависит от толщины мишени
t , что соответствует
полубесконечной преграде
(аля стеклотекстолитов
эти толщины должны
быть не менее (6—10)dQ),
и область, где при
меньших толщинах величина
h/dn
*0 возрастает за счет
влияния волн
разрежения, идущих от тыльной поверхности мишени.
При толщинах, близких к предельным (t < SQ), на тыльной
поверхности мишени возникает характерное расслоение материала. Влияние
откола слабее для более прочного СТЭФ. При t ~ SQ процесс пробития
носит пороговый характер, что
*«ч
6 J
4 -I
2
-г~
4
8 Ю v,km/c
Рис. 6.5. Зависимость относительной
предельной толщины от скорости удара:
1 — СТ—1; 2,3 — СТЭФ; 4,5 — Д16.
Материал частицы: 1,2,4 — сталь;
3,5 — стекло.
связано с упругохрупким
деформированием
стеклопластика. Размеры вторичных
зон разрушения (отколы,
расслоение) на два порядка
превышают собственно
площадь отверстия.
На рис. 6.5 приведена
зависимость предельной
толщины S0/d0 от скорости
удара. Отмечено влияние
прочности стеклопластика:
при v = 4,8 км/с предельная
толщина у СТ—1 больше в
1,5 раза, чем у СТЭФ (твер-
1/2
2 -I
1 -|
0
дость CT—1 ниже на
70%).
Для стеклянного
шарика по сравнению
со стальным величина 5„
0,4
08
Г"
1,2
уменьшается в ~2 раза.
, z Предельные толщины у
стеклопластиков выше,
Рис. 6.6 Зависимость относительной предельной чем у дюралюминия
Д16.
Наиболее точно
экспериментальные резуль-
толщины от параметра z
Заштрихованная область — результаты
для металлических преград
таты обобщаются зависимостью (см. рис. 6.6):
(S0/d0)°-5=-l + 2,5z
(6.10)
где z = (р vVp ) — параметр, определяемый отношением
кинетической энергии частицы к начальному давлению в преграде р ,
вычисляемому по ударным адиабатам материалов ударника и
мишени.
6.3. Соударение длинных стержней с полубесконечной
преградой
Механизм соударения стержня аналогичен пробиванию брони
кумулятивной струей (см. разд. 5.4).
Проникание стержня в преграду включает в себя два процесса:
образование кратера в преграде и разрушение стержня внутри
кратера. Для описания этих процессов в [19] использовано
модифицированное уравнение Бернулли:
/7 = 0,5pfv-M)2+7=0,5py + /?n
(6.11)
у\ / у
где р — давление на контактной поверхности между стержнем
и преградой; и — скорость проникания; v — скорость твердой части
стержня; р, рп — плотности стержня и преграды; Y, Rn —
динамическая прочность стержня и преграды.
240
Отсюда скорость проникания (скорость движения границы
стержень- преграда):
и=- j(y-^v2 + A)
l-ju
(6.12)
M = y[pJP~y A = 2^^(l-M2)
Py
Критическая (минимальная) скорость стержня v, при которой
отсутствует проникание и и = 0:
v<=i2^^ (6-13)
Предполагая, что уменьшение длины стержня при проникании
не влияет на его скорость, из (6.11) получаем оценку глубины
проникания в гидродинамическом приближении:
h = L4py'Pn (6.14)
где L — начальная длина стержня.
Замедление жесткой части стержня описывается уравнением,
найденным, исходя из предположения, что давление, действующее
на стержень, не может быть больше динамической прочности стерж-
няУ:
с
где 1 и v — текущие длина и скорость стержня.
Скорость укорочения стержня:
dl , ,
^ = -"- (6.16)
Из (6.16) следует, что р^я высоких скоростей соударения, при
которых и и v постоянны, длина стержня линейно убывает со временем, что
подтверждают двумерные численные расчеты (см.рис. 6.7) [20].
Рассмотрим случай, когда материалы стержня и преграды одинако-
вы и р = рп=р. В [ 19] показано, что аая одинаковых материалов Rn > Y,
причем АА^ металлов R /Y = 3. Согласно [21], конечная длина жесткой
части стержня ls и глубина проникания h связаны с параметрами
проникания следующим образом:
L -(Vc)R"~
L V Г
-exp[-p(v02+vc2)/47]
(6.17)
- = -(2v2x-£)x/> exp[v2(x2 -1)]Л
L £ x
(6.18)
rAev*2=pv074Y ^ = v/v0>(2 = R /Y - 1
Из (6.17) и (6.18) видно, что величины ls и h полностью
определяются двумя безразмерными комплексами:
7 =
™;/?=*-1
(6.19)
Поэтому при моделировании проникающего действия стержней
(при изменении материалов и скоростей удара) необходимо
одновременное выполнение условий rj = const и (3 = const, т.е. одновременно
учет
гидродинамических и прочностных
условий проникания.
Такое
моделирование упрощает
эксперимент, т.к.
позволяет снизить скорость
удара при
одновременном уменьшении
прочности стержня
и преграды. В [21]
проведены
модельные эксперименты со
80 t, мке
Рис. 6.7. Внедрение стержня из сплава вольфрама
в стальную преграду
Расчет для L=7,62 см, d=0,636 см, v=3 км/с [20]
242
h/L
0,4-
0,2-
-
0
•
i
•
—r-
• >^
1 1 I-
^/^ 1
•^ 2
—i 1
Рис. 6.8. Зависимость h/L=f (n) для
пластилина (1) и для стали (2)
стержнями и преградой из
пластилина. Скорость удара
изменялась в пределах 30—
200 м/с. В опытах измерялись
величины v, 1 и h.
Обработка результатов
с помощью (6.17) и (6.18)
позволила определить а^я
пластилина следующие
параметры: v = 69 м/с, при
такой скорости Y = 3,4 МПа и
Rn= 6,8 МПа, т.еУ. (2 = 1. Но для
стали (3 = 2, что не позволяет
строго моделировать
пластилином соударение стальных стержней и преград (см. рис. 6.8).
С помощью (6.13), используя величины Y из табл. 3.2 и
соотношение R/v = 3 А^я металлов, нами найдены минимальные скорости
v соударения различных пар стержень — преграда, начиная с
которых стержень проникает в преграду (см. рис. 6.9).
Как видно из
рис. 6.9, величина vc
растет с
уменьшением прочности
стержня и с увеличением
прочности
преграды, а при соударении
стержня с преградой
из одинакового
металла v ~2 км/с.
с
Автором
совместно с Н.П. Козеруком
проведены
исследования
взаимодействия неподвижных
стержней с пластина-
V,
км/с
12
10
оо •■
5 »
Г ', ■■
■I
и
га-::
1 ч
/11
/ "
ш
1 1-Н
:<
/Г
Uhi
ПРЕГРАДЫ
X; 1
Si
иц
:^v
|Я
1*^
й^*
А 1
А1
Fe
W
S
DC
1
IS
0 1
8 Я,ГПа
Рис. 6.9. Минимальная скорость соударения,
начиная с которой стержень проникает в преграду
в зависимости от динамического предела текучести
преграды Rn = 3Y
ми, разгоняемыми до vc> 1,5 км/с продуктами взрыва. Необходимость
исследований возникла в связи с обоснованием корректной постановки
опытов по измерению скорости пластин (точнее, регистрации х, t -
диаграмм движения пластин) электроконтактными датчиками (см.гл.12),
а также с помощью мононитей из полистирола (световодов). В опытах
датчики должны замыкаться невозмущенной поверхностью пластины,
вне зоны влияния датчиков верхних уровней.
Измерения проводились с помощью фотохронографа СФР— 2М
в режимах лупы времени и съемки через щель с использованием
взрывной подсветки (см.рис. 6.10—6.12). Подсветка обеспечивалась за счет
свечения ударной волны в аргоне, создаваемой взрывом заряда ВВ.
Датчики моделировались стержнями диаметром 1,5—5 мм.
Результаты опытов показали, что в зависимости от скорости
пластины и материалов пластины и стержня возможны следующие три
режима взаимодействия.
1. Давление на торце стержня не превышает его динамического
предела текучести, т.е. стержень абсолютно жесткий и не расходуется
(v = и), а пластина мягкая (Y >>R ). Поэтому стержень проникает в
пластину с минимальной деформацией пластины вокруг стержня.
Пример: проникание стержня из твердой стали У8 (HRC = 55)
в пластины из мягкого алюминия или свинца при v < 2 км/с.
2. Пластина абсолютно жесткая, а стержень мягкий (Rn>>Y).
Проникание отсутствует или очень медленное. Материал
деформируемого стержня накапливается на поверхности пластины.
Пример: стальная пластина и стержень из мягкого алюминия
или из полистирола при v < 2 км/с.
3. И пластина, и стержень пластически деформируются
(контактное давление превышает и Y, и R ). Образуется кратер, в котором
формируется поток из материала пластины и стержня,
направленный в сторону, противоположную прониканию, т.е. из кратера
выходит струя в виде конуса.
В начале взаимодействия и вблизи поверхности пластины конус
сплошной, но со временем и по мере удаления от пластины он
распадается на отдельные частицы, размер которых на порядок меньше
диаметра стержня. Со временем по мере углубления кратера угол
244
а)
У/////}//У'~'/Л
v = 1,4 км/с
АЛЛ
v =2,2 км/с
I ТУТ
<1=5мм
т=3мкс
с1=1,5мм
т=2,5мкс
d= 1,5 мм
т= 5 мкс
d=l,5MM
т= 9 мкс
Рис. 6.10. Исследование взаимодействия стержней и пластин
а) — постановка опытов:
1— линзовый заряд ВВ; 2 — зазор; 3 — пластина t=3—10 мм;
4 — стержень d = 1,5—5 мм; 5 — матовый экран; 6 — взрывная подсветка.
Фотохронограммы взаимодействия стальной пластины t = 3 мм
б) — с различными стержнями d= 1,5 мм при скоростях 1,4 и 2,2 км/с;
в) — с медным стержнем при разном времени взаимодействия (v=2 км/с)
пластина — Д16
стержень — Д16
Отражатель
*J
ЩельСФР
WF
пластина — сталь 3
стержень — полистирол
пластина — сталь 3
стержень — медь
Рис. 6.11. Измерение размера возмущенной области на пластин вокруг стержня
диаметром 3 мм
245
конуса растет, по-видимому, из-за увеличения диаметра кратера
на поверхности пластины. Например, при проникании латунного
стержня в стальную пластину (d. = 5 мм, vc = 1,9 км/с) угол конуса
увеличивается за 20 мкс взаимодействия с~ 13° до ~25° . При этом
диаметр кратера вырастает с ~ 4 d до ~ 10d .
Время, мкс
12
16
20
Riaei-
ииа,
Скорость,
С 1.3,
2 км/с
С1 ерл-
снь,
Диаметр,
Латунь,
5 мм
Рис. 6.12. Фотохронограммы взаимодействия пластин со стержнями. Постановка
опытов — на рис. 6.10. Съёмка на СФР-2М в режиме лупы времени.
Кроме того, вокруг кратера на пластине образуется кольцевой
валик. Измеренная в опытах высота валика составляет ~ 2d. аая пары
сталь—медь и ~ 3d. а^я пары алюминий—алюминий (см. рис. 6.8).
Измерения длины сохраненных после опытов стержней
показали, что расход стержня при проникании в стальную пластину
толщиной 3 мм уменьшается с увеличением твердости стержней.
246
Например, у твердой стали У8 (HRC = 55) расход вдвое меньше, чем
у мягкого железа.
У пластичных стержней (Fe, Си, А1) взаимодействующий с
пластиной торец имеет грибовидное утолщение — полусферическую
шляпку со следами радиального пластического течения. У стержня
из твердой стали У8 такой шляпки нет, и на торце имеются следы
хрупкого разрушения (сколы).
Таким образом, на основании проведенных измерений диаметра
возмущенной области на пластине были выбраны допустимые
минимальные расстояния между соседними датчиками двух уровней
(равные с запасом lOd.) [22].
Кроме того, показано, что возникающие струи не могут сдвинуть
или преждевременно замкнуть нижележащий датчик.
6.4. Взаимодействие с преградой потока частиц
В газовых турбинах и в ракетных двигателях поверхности
лопаток и сопел подвергаются разрушающему действию быстрого
потока твердых частиц. Пример созидательного действия потока
микрочастиц — плазменное и детонационное покрытия,
защищающие поверхность от эрозионного износа. Для образования
защитного покрытия при газотермическом напылении необходимо
обеспечить такие условия соударения потока микрочастиц с
поверхностью, при которых возникает прочная связь частиц с
поверхностью.
Согласно одним авторам, необходимым условием образования
прочной связи является диффузия, зависящая от температуры и
условий деформаций при соударениях [23,24]. Другие авторы
обнаруживают аномально высокий массоперенос при импульсном нагру-
жении металлов: величина коэффициента диффузии на 6—7
порядков превосходит его значение в жидкости [25].
При детонационном напылении в переходной зоне также
обнаружено взаимное проникновение материалов частиц и подложки
на большие глубины [26,27]. При напылении возможно проникание
железа в алюминий, хотя железо в алюминии не растворяется.
247
При разгоне частиц размером до 100 мкм кумулятивным зарядом
обнаружено сверхглубокое проникание частиц (до 10d) [28,29,30],
что противоречит законам сохранения импульса и энергии.
Авторы [24,27,31] считают, что кратковременность действия
высоких давлений и температур при детонационном напылении и
сварке взрывом не позволяют развиться диффузионным процессам.
Рассмотрим кратко два процесса: детонационное напыление
и сверхглубокое проникание.
6.4.1. Детонационное напыление
При газодетонационном способе напыления покрытие
формируется серией выстрелов, причем после одного выстрела обычно слой не
сплошной, а состоит из отдельных частиц с расстоянием между ними
(2—3) dQ. Если за один выстрел формировать сплошное покрытие, то
при остывании оно не выдерживает термических напряжений.
Частицы ускоряются до скоростей 0,5—1 км/с при помощи
специальной ствольной установки (например, типа АДУ ОБЬ), в
которой создается детонация обычно метанкислородной смеси. Порция
порошка впрыскивается в детонирующий газ. Покрываемая
поверхность располагается перпендикулярно оси ствола на некотором
расстоянии.
При одном выстреле частицы подлетают к подложке
неодновременно, поэтому первые частицы взаимодействуют с холодной
поверхностью, а последние - с подогретой предыдущими частицами.
Время между выстрелами (доли секунды) много больше времени
остывания, поэтому перед каждым выстрелом массивную подложку
можно считать холодной. Обычно за один выстрел формируется
защитное покрытие толщиной 1—10 мкм.
Защищаемую поверхность предварительно делают шероховатой
в результате пескоструйной обработки. Шероховатость увеличивает
сцепление частиц с поверхностью.
Процессы соединения при контакте поверхностей под давлением
имеют общий характер аая нанесения покрытий, сварки взрывом и
взрывного компактирования (спекания порошков). Во всех случаях
Аля прочного соединения необходима пластическая микродефор-
248
нержавеющая
сталь
Рис. 6.13. Необходимые для сварки минимальные
величины контактного давления
в зависимости от наибольшей микротвердости
у свариваемых металлов
медь /
мация (смятие
шероховатости),
т.е. соударение
должно быть
неупругим.
В [32]
предложен
следующий критерий
перехода от
упругих к
неупругим
соударениям или
критерий схватывания
металлов:
vk=kj2Hv/p
(6.20)
где vk — скорость точки контакта при косом соударении; Ну —
микротвердость; р — плотность металла; к — безразмерный
коэффициент.
Согласно [33] аая равнопрочной сварки взрывом
малоуглеродистой стали необходима величина vk = 1,2 км/с, откуда к = 1,8 и
давление в точке контакта р = 5,6 ГПа, что в три раза превышает Ну
малоуглеродистой стали. Обобщая экспериментальные данные по нижней
границе области сварки разнородных металлов, в [33] получена
зависимость рк (Ну) (см. рис. 6.13), где Ну — большее значение
свариваемой пары, а рк определялось плотностью метаемой пластины.
Усредненное значение к= 1,6, тогда рк в 2—3 раза превышает
максимальную прочностную характеристику металлов.
В работе [27] образцы мягкой стали подвергались детонационному
напылению частицами оксида алюминия. Проведенные исследования
показали, что частицы проникают в глубь подложки путем
механического вклинивания с образованием впадин и выступов. Боковые грани
выступов подвергаются эрозионному разрушению, отколовшиеся
частицы запрессовываются в материал покрытия.
Ширина зоны механического перемешивания не превышает
60 мкм. Микровыступы подложки пластически деформируются,
следствием чего является измельчение структуры и увеличение
микротвердости до двух раз. Наряду с упрочнением в микровыступах
имеется система трещин.
Отмечается, что после пескоструйной обработки различные
участки шероховатой поверхности находятся в разных
газодинамических условиях по отношению к потоку: выступы нормальны к
потоку, а на боковые грани поток частиц действует под углом.
Угол максимальной эрозии зависит от свойств материала:
мягкий материал стоек при нормальном падении потока и больше
разрушается при малых углах соударения. Наоборот, твердый и
хрупкий материал больше разрушается при нормальном падении
потока.
В [34] исследуются канальные нарушения сплошности преграды
при соударении с ударниками ограниченных размеров. Канальная
повреждаемость при импульсном нагружении поверхности —
явление общее и наблюдалось при эрозионном изнашивании
потоком абразивных частиц [35], при импульсном лазерном облучении
поверхности [36], при ударе струи воды [37], при ударе пластины,
имеющей брускообразные или кольцевые выступы [34].
В [38] образование канального фокусируемого откола под
зоной контакта названо эффектом «ужаления», который возникает
только при высокоскоростном внедрении индентора в преграду.
Причина возникновения продольной трещины под ограниченной
зоной приложения нагрузки заключается в фокусировке волн
разгрузки, идущих от боковых граней частицы и создающих области
растягивающих напряжений как в преграде, так и в частице.
Если растягивающие напряжения превышают откольную
прочность, то возникает канальный откол. Критерием откола может быть
условие превышения радиальной составляющей скорости
растяжения некоторой критической величины, которая определяется от-
кольной прочностью.
Продольная повреждаемость преграды под частицей не
возникает, если угол наклона боковой грани частицы превышает угол ко-
250
нуса сжимаемости (угол, при котором скорость фронта УВ в частице
равна скорости звука).
Таким образом, выше некоторой критической скорости
соударения частиц с преградой в последней возникают два
противоположных процесса: упрочнение поверхностного слоя за счет
пластической деформации и его разупрочнение за счет появления канальных
микротрещин.
В [23] оценивается влияние температуры и скорости частиц,
а также условий деформации частиц на прочность сцепления
покрытия с подложкой при газодетонационном напылении.
Весь процесс соударения и образования покрытия можно
разделить на два этапа: динамический (деформация частицы при ударе)
и статический (остывание частицы после завершения движения).
Для получения прочной связи частицы с подложкой в зоне
контакта необходима взаимная диффузия на глубину нескольких (т = 3—10)
межатомных расстояний dA. Чтобы диффузия успела произойти,
необходимо, чтобы характерное время диффузии было меньше
характерного времени остывания контактной поверхности:
<^>2<*1>4l (6.21)
D a v
где D — коэффициент диффузии; а — коэффициент
температуропроводности; h — окончательная толщина деформированной после
удара частицы с начальным диаметром dQ « 3h.
В свою очередь, для статического этапа время остывания должно
быть больше характерного времени деформации d0/v, где v —
скорость удара частицы. Это условие выполняется для v > 3 м/с, т.е. для
всех видов напыления.
Отсюда следует, что для получения прочной связи частицы
с подложкой коэффициент диффузии в зоне контакта должен
быть достаточно большой, больше некоторого критического
значения Dk = a(mdA/h)2. Для типичных значений параметров
металлов:
D>D. « 4(10"14 — КГ13) м21с (6.22)
Если на контактной поверхности происходит плавление одного
из материалов, то условие (6.22) всегда выполняется, т.к. аая расплава
D«(109— 108)м2/с.
Вблизи температуры плавления D«2(10"13—10'12)м2/с, а при
уменьшении температуры на каждые 15% величина D падает
примерно на порядок. Поэтому диффузионная связь в твердом
состоянии возможна в очень узком интервале температур, вблизи
температуры плавления. Можно считать, что минимальная критическая
температура равна Т* « 0,9Тт.
Для шероховатой поверхности прочность сцепления покрытия
с подложкой будет максимальной (<7тах), если условие Т > Т*
выполняется во всех точках поверхности. Если же Т* достигается только на
выступах шероховатости с относительной пллощадью S, то получим
покрытие с пониженной прочностью сцепления с=S <7тах.
К начальной температуре частиц надо добавить температуру,
обусловленную переходом кинетической энергии частицы в тепловую при
ударе: ДТ^=vV2c . При увеличении скорости частицы с 0,3 до 1 км/с
величина АТ^ возрастает на порядок и играет решающую роль.
Для динамического механизма образования покрытий должно
выполняться условие: время диффузии меньше времени
деформации частицы при ударе:
(ШС1а)2 к^ (623)
D v
т.е. D должно быть больше некоторого критического значения
Db=(m dA)2d0 / v«4 (Ю-12—10"11) м2/с. Это условие с запасом
выполняется аля жидкости.
Если при ударе частица плавится и растекается по твердой
подложке, то скорость жидкости в образующемся динамическом
ламинарном пограничном слое распределена по закону [38]:
u = u„<P(0,5yJvt) (6.24)
где у — расстояние от подложки; v - кинематическая вязкость.
Необходимая аля образования прочной связи с подложкой
интенсивность диссипации энергии в пограничном слое достигается
252
при скорости растекания, примерно на порядок превышающую
начальную скорость частицы и близкую к скорости звука в металлах
(и «с «4 км/с).
Следовательно, соединение материалов по рассматриваемому
динамическому механизму возможно только в местах образования
кумулятивных струй при малых углах соударения а < и/с « 0,1.
Возможен и твердофазный динамический механизм
образования покрытий, основанный на том, что в условиях интенсивной
пластической деформации коэффициент диффузии может возрасти на
шесть порядков [39]. Отсюда условие связи частицы с подложкой:
D0>4(10-17— 10-16)м2/с.
С учетом зависимости DQ (Т) аля металлов аая соединения
необходима температура Tk>2/3Tm, а частица в исходном
состоянии перед деформацией должна быть хотя бы частично
расплавлена.
Давление в окрестностях точки контакта, где образуется
кумулятивная струя, р « 0,5pvctga должно быть выше предела текучести
ст.. Тогда условие существования деформации принимает вид:
а < а. = arctg^pv1 /2ат (6.25)
А соответствующая (6.25) относительная площадь контактной
поверхности S = 1 — cosa = а I а . Относительная прочность связи
a max а
может быть оценена по формуле:
Например, ^ая р = 104 кг/м3 и <7. = 0,5 ГПа при скорости частиц
0,1, 0,3 и 0,5 км/с получим v/vmux = 0,05, 0,3 и 0,5 соответственно.
Дальнейший рост прочности связи возможен лишь за счет
статического механизма при Т0 ~ 1,5Тт.
В общем виде зависимость прочности сцепления частиц от
их температуры при ударе v/vmzyi = f (TQ + AT^J при постоянной
скорости частиц имеет двухступенчатый характер, что отражает два
механизма образования покрытия: низкотемпературный
(динамический механизм) и высокотемпературный (статический механизм).
did
max
0,75.
0,50
0,25
0
2000 3000 Т/Г^К
Рис. 6.14. Зависимость относительной
прочности покрытия от температуры
частиц [23].
Пунктир — динамический механизм;
штрихпунктир — статический
механизм; точки — эксперимент
При ТЛ + ДТ.. <Т ПО-
* 0 kin m
крытие вообще не образуется,
при T0 + ATkin = Tm прочность
скачком возрастает до
значения, определяемого скоростью
частиц. С ростом
температуры прочность плавно растет
до 0,5(Ттах, а при температуре
частиц, достаточной fi^
полного прогрева всей
шероховатой поверхности, прочность
скачком достигает <7тах (см. рис.
6.14). Из рис. 6.14 видно, что
только совместный учет двух
механизмов образования
покрытия дает хорошее согласие с экспериментом.
6.4.2. Сверхглубокое проникание порошковой струи
Итак, соударение потока микрочастиц с преградой при
скоростях частиц 0,3—1 км/с образует на поверхности преграды
покрытие. Проникание частиц в преграду невелико: зона перемешивания
порядка 60 мкм. Одиночная частица при ударе может создать в
металлической преграде кратер глубиной максимум до ~ 5d0, причем
масштабный фактор не влияет на кратерообразование.
Однако авторы работ [28,29,30,40] экспериментально
обнаружили аномально глубокое проникание микрочастиц в обычные
металлические преграды — до 103dQ. Поток микрочастиц
создается с помощью обычного заряда ВВ с кумулятивной выемкой, в
которую помещается порошок, а выемка закрывается крышкой (см.
рис. 6.15).
Скорость частиц — до 1—1,5 км/с , т.е. практически такая же,
как и при детонационном напылении. Однако эффект наблюдается
только ^ая малых частиц, с размером не более 100 мкм.
После обработки потоком частиц в образце наблюдаются глубокие
каналы, на дне и стенках которых имеются остатки частиц. Каналы мо-
254
Рис. 6.15. Постановка опытов
по сверхглубокому прониканию
1 — заряд ВВ с кумулятивной
выемкой;
2 — облицовка выемки;
3 — порошок;
4 — крышка;
5 — преграда
гут быть закрыты и искривлены (по-видимому, вследствие ударновол-
новой деформации поверхностных слоев образца). Эти каналы
трактуются как траектории проникающих частиц (см. рис. 6.18).
Выдвинуты самые разные объяснения этого феномена, связанные в
основном с появлением у преграды аномальных прочностных свойств
под влиянием ударной волны от потока частиц.
В частности, в [41,42,43] сверхглубокое проникание
объясняется скачкообразным падением прочности в окрестности движущейся
частицы — переходом вещества в сверхпластичное состояние с
аномально низким сопротивлением движению частиц.
Каналы рассматриваются как трещины, инициируемые
частицами или осколками облицовки кумулятивной выемки (канальный
фокусируемый откол [34]).
В [44] высказывается мнение о возможности захвата частиц
фронтом УВ. Ранее в [45] была показана возможность захвата
заостренных (веретенообразных) удлиненных тел фронтом УВ в газе.
Это явление напоминает движение спортсмена на серфинге,
подхваченного гребнем морской волны.
Для частиц с размерами, близкими к ширине Н фронта УВ,
перепад давления во фронте будет создавать силу и ускорение частицы
в направлении движения фронта. Характерный градиент давления
dp/dx ~ р/Н, а связанная с ним сила, действующая на частицу, равна
F =47гг3р/ЗН . Торможение частицы потоком вещества можно
оценить по формуле Стокса: Ft=6 тс (D— u) vr.
Здесь волна сжатия близка к акустической, скорость фронта
близка к скорости звука и совпадает со скоростью частицы. Очевидно,
если сила вязкого трения Ft > F , то частица отстает от фронта, ее
скорость будет равна массовой скорости вещества за фронтом УВ,
т.е. проникания частицы в вещество не будет.
Условие Ft=F соответствует стационарному движению частицы на
фронте и позволяет оценить размер частиц, увлекаемых фронтом УВ,
равный r~4 [vH (D — u)/p]0,5. Для типичных значений D«cQ«3 км/с,
и = 0,5—1 км/с получим, что в условной жидкости с вязкостью
v~ 10 см2/с характерный размер вовлекаемых частиц составляет сотые
доли микрона, а аая сред с v ~ 100 см2/с — десятки микрон.
Таким образом, имеется принципиальная возможность
увлечения микрочастицы размазанным фронтом УВ в конденсированном
веществе, однако, только в случае, если частица уже имеет скорость
этой волны. Авторы [44] предполагают, что благодаря
неоднородности порошковой среды и локальным кумулятивным процессам
отдельные частицы могут приобрести такую скорость.
Однако результаты численного моделирования явления
проникания в напряженную среду микрочастиц, движущихся в потоке
порошкообразного вещества, показали, что глубина проникания не
превышает 15 dQ, т.е. никакого аномального эффекта нет [46].
В 1987 году в Минске на секции научного совета ГКНТ СССР
автор предложил свое объяснение сверхглубокого проникания,
согласно которому разгадка этого явления лежала не в каких-то
экзотических свойствах преград, а в свойствах кумулятивного генератора
потока частиц.
Оказывается, эффект наблюдался только в случае, если порошок
закрыт крышкой 4 (см.рис. 6.15). Почему? Дело в том, что под
давлением порошка крышка деформируется и затем разрывается на
отдельные куски. В момент разрушения между кусками крышки
образуются щели и отверстия, в которые инжектируются под давлением
струи порошка (см.рис.6.15). Таким образом, перед однородным
порошковым телом формируется некое подобие порошкового душа со
струями, состоящими из частиц, движущихся строго друг за другом.
Выстраиванию летящих в воздухе частиц в виде цепочек
способствует явление затягивания каждой последующей частицы в
турбулентный след с пониженным давлением за частицей. По-видимому,
по этой причине при напылении часто наблюдается маловероятное
попадание двух частиц строго в одну точку поверхности преграды.
256
Такие порошковые струи аналогичны стержням, но с
переменным сечением и с дискретной прочностью (между частицами связи
нет). Сечение струи повторяет форму зазора между частями
разрываемой крышки 4 и в принципе может быть любым. А аая быстро-
летящего стержня глубина его проникания в преграду определяется
только длиной стержня (см. рис. 6.14) при условии, что скорость
стержня больше некоторой критической величины v (см. рис. 6.9).
В экспериментах по сверхглубокому прониканию обычно
реализуются условия, когда контактное давление превышает
динамические пределы текучести материалов и преграды (обычно стали) и
порошка (обычно диборида титана). Следовательно, в процессе
проникания частица разрушается (хрупко или пластически), и материал
частицы «размазывается» по стенкам кратера (или частично уходит
из кратера в виде струи), освобождая дно кратера /а^я удара
следующей частицы.
По сравнению со сплошным прочным стержнем частица из того
же материала разрушается быстрее из-за тыльного откола и
переменного сечения.
Скорость расходования стержня при проникании
определяется соотношением твердости стержня и преграды Н* = Н /Н . Для
сплошного стержня чем больше Н*, тем при заданной длине
стержня глубже его проникание и меньше расход стержня (меньше
концентрация материала стержня в канале).
Но аая порошковой струи из дискретных частиц картина
проникания с уменьшением твердости преграды может быть другой. Кроме
длины струи, плотности и прочности частиц порошковая струя
характеризуется еще одним параметром — расстоянием между частицами,
которое определяет частоту ударов частиц по дну кратера.
Время полного разрушения частицы равно t* = d0/(u - v), где
скорость проникания и определяется прочностью преграды и частицы
согласно (6.12). С уменьшением прочности преграды величина t*
увеличивается, т.е. процесс разрушения частицы в мягкой преграде
замедляется. Время между ударами частиц At = 1/v, где 1 —
расстояние между частицами в струе. Если At > t* , то каждая частица струи
ударяет по «чистому» дну кратера, что соответствует
максимальному внедрению частицы. В этом случае глубину внедрения струи мож-
257
но оценить как произведение глубины внедрения одной частицы на
количество п частиц в струе: (h/d0) = n (h/d0)4acr.
Если At < t*, то часть материала частицы остается на дне кратера
и тормозит внедрение следующей частицы, которая ударяет не по
преграде, а по остаткам предыдущей частицы.
Поэтому глубина проникания порошковой струи с постоянными
значениями 1, t и v в зависимости от величины Н* должна меняться не
монотонно (см.рис.6.16). С уменьшением Н* внедрение начинается при
достижении условия v = v., затем глубина (h/d0) растет при At > t*,
достигая максимума при At=t*, после чего при At < t*, глубина проникания
Поэтому глубина
проникания твердых
частиц в мягкую
преграду (например, в
алюминий) должна быть
меньше, чем в твердую
преграду (например,
в сталь), т.к. частицы
в кратере в алюминии
не успевают
разрушиться, т.е At < t*.
Для данных
условий проникания
порошковой струи концентрация материала частиц струи не должна
меняться по длине канала в преграде.
В [30] приведены следующие результаты экспериментов по
прониканию частиц порошков диборида титана (40—63 мкм) и
кобальта (< 40 мкм) в образец из армко — железа с различной
температурой (77 К —1160 К), т.е. с различной прочностью (см. рис. 6.17 а).
1. Средняя концентрация материала частиц по глубине каналов
практически постоянна, что характерно а^я струй, а не а^я
отдельной частицы.
2. Изменение концентрации с изменением размеров частиц dQ.
пропорционально изменению объема частиц (dQ1/d02)3. Следовательно,
h/d
At<t,
At=tt
Н.1
Н1
Рис. 6.16. Зависимость глубины проникания
каждой частицы в струе из дискретных частиц
с постоянным расстоянием между частицами
от соотношения Н* динамических прочностей
частицы и преграды
258
О 5 10 15 20 30 35 40 45 50 55 h'MM
Рис. 6.17 б. Структура перлита в зоне
Рис. 6.17 а. Результаты измерения сред- канала в ст.45 от сверхглубокого
ней концентрации бора и кобальта при проникания порошка
проникании порошка Ti В с частицами 30 - 100 мкм.
(d=40—63 мкм) и Со (<1<40мкм) в
образец из армко-железа с различной
температурой
количество струй от кумулятивного заряда не меняется с изменением
размера частиц (не меняется характер разрушения крышки заряда, а
меняются зазоры между частями крышки, при которых начинается ин-
жекция частиц).
3. С ростом температуры образца концентрация диборида бора
растет, а кобальта падает, что можно объяснить замедлением
проникания твердого диборида титана (At < t*), и ростом проникания
кобальта (At >t*),
Поскольку струи образуются за счет инжекции частиц под
давлением в зазоры (равные dQ) между частями разрушающейся крышки
заряда, процесс увеличения зазоров идет одновременно с процессом
падения давления в порошке за счет задней и боковой разгрузок.
Поэтому каждой величине зазора соответствует свое давление
инжекции и своя скорость частиц.
Для данной конструкции заряда существует максимальная
величина зазоров и соответствующая ей величина d0, при которой
давление инжекции снижается настолько, что скорость частиц в струе
становится меньше критической (v < v), и проникание прекращается.
Упрочнение стали (легирование) за счет сверглубокого проникания
твердых частиц имеет практическое значение (например, упрочнение
резцов аля горных комбайнов). Упрочнение растет с увеличением
концентрации введенных частиц, которого можно достичь, по мнению
автора, за счет оптимизации конструкции кумулятивного заряда.
В частности:
1. Увеличить количество струй на единицу поверхности за счет
сетки рисок на крышке, по которой крышка будет
разрушаться закономерно, а не случайно. В этом случае сечение струй
будет прямоугольник длиной, равной шагу сетки, и
шириной dQ.
2. Увеличить концентрацию можно, если получить струи с
частицами ~ 100 мкм, скоростью частиц v > vc и интервалами
между частицами At < t*. По- видимому, а^я этого надо увеличить
время существования высокого давления в порошке,
например, за счет увеличения размеров заряда, мощности ВВ, толщин
крышки и облицовки, применения тяжелой оболочки вокруг
заряда.
Экспериментальное изучение движения порошковой струи
удобно проводить на одной плоской струе, получаемой при разрушении
крышки по одной линии (вдоль одного предварительно сделанного
в крышке паза).
Таким образом, по мнению автора, причиной сверхглубокого
проникания является создание порошковых струй кумулятивным
зарядом. Подобно длинным стержням, глубина проникания таких
порошковых струй зависит от их длины, плотности, твердости, а
также и от расстояния между частицами.
Согласно [47], развитие пластической деформации в преградах
при проникании в них плоских струй происходит подобно течению
турбулентной жидкости с турбулизацией на различных масштабных
уровнях. Внутренняя поверхность каверн от струй оплавлена и
имеет вид макрогребней, которые , в свою очередь, состоят из
микрогребней оплавленного металла, внутри которых имеются очень
мелкие (2—3 мкм) поры и трещины.
Возможно, аналогичную структуру имеют и стенки каналов от
порошковых струй, только меньшего масштаба (см. рис. 6.176).
260
6.5. Соединение пластин при их косом столкновении
(сварка взрывом)
В разделе 5.4 был рассмотрен нерегулярный режим косого
столкновения пластин с образованием кумулятивной струи. Еще в 1944—46
годах при изучении различных режимов образования кумулятивных
струй М.А. Лаврентьевым с сотрудниками было обнаружено явление
сваривания металлов при метании пластин и конусов [8].
Систематические исследования сварки взрывом начались в 1960-х
годах в СССР и США и привели к созданию промышленной
технологии. В СССР основные результаты получены А.А.Дерибасом,
С.К. Годуновым и В.А. Симоновым.
Очевидно, не всякий регулярный режим косого столкновения
пластин приводит к их свариванию. Поэтому прежде всего
необходимо определить критерии сварки, параметры, влияющие на этот
процесс, границы их изменения (область сварки), понять и описать
физические процессы, происходящие при сварке взрывом.
Схема взрывной сварки металлических пластин показана на
рис. 6.18.
Свариваемые пластины устанавливаются на некотором
расстоянии друг от друга с углом а между ними. Нижняя неподвижная
пластина лежит на жесткой опоре, а верхняя пластина метается
продуктами взрыва при инициировании заряда ВВ у угла в точке А.
Режимы соударения пластин определяются тремя
кинематическими параметрами: скоростью пластины v , скоростью точки
контакта vk и углом соударения j.
Скорость метания пластины скользящей детонацией
определяется скоростью детонации D и отношением масс ВВ и пластины
r=(pS)BB/(pS)nA. В одномерном приближении, считая детонацию
мгновенной, получим [48]:
v = Dr[31 (к2 - 1)(г2 + 5г + 4)]0'5 (6.27)
где к~ 3 — показатель адиабаты продуктов взрыва.
При разгоне пластина поворачивается на угол (2 , поэтому угол
соударения
j = a + fi = a + 2arcsiny / 2D (6.28)
261
Важным параметром сварки является скорость vk точки В
контакта пластин:
vk = D(sin(j - a) I sin j (6.29)
Если пластины установлены параллельно (а = 0), то vk = D.
Для осуществления регулярных режимов столкновения угол а
должен быть мал, меньше того критического значения, при котором
образуется струя. В окрестностях точки контакта пластин возникают
высокие давления, много больше прочности металлов, поэтому для
описания явлений при соударении обычно используется
гидродинамическая модель [8,49,50]. При этом в точке контакта течение может
быть дозвуковым или сверхзвуковым в зависимости от скорости v и
угла j. Сварка взрывом осуществляется в дозвуковом режиме.
В [50] показано, что в окрестностях точки контакта форма
свободной поверхности пластин представляет собой параболу с
радиусом кривизны в точке контакта, равным /^ля бесконечно толстой
неподвижной пластины:
Я = (4/;г)(1-у,2/с02)0-5£>п772 (6.30)
где с0 — скорость звука в материале пластины.
Размер зоны высокого давления пропорционален радиусу
кривизны.
Критерием образования прочного соединения при соударении
является возникновение на контактирующих поверхностях
пластических деформаций, которые зависят от прочностных свойств
свариваемых металлов (см.(6.20) и рис.6.13). В течение нескольких
микросекунд в окрестностях точки контакта металл находится в
пластическом состоянии, когда он способен течь как вязкая
жидкость, поскольку напряжения в несколько раз превосходят
прочность [33].
Таким образом, сварка взрывом занимает промежуточное
положение между сварками в твердом и жидком состояниях.
При сварке взрывом при совместной пластической деформации
двух металлов процесс их соединения представляет собой
совокупность трех последовательных стадий [51]: активация контактных
поверхностей, образование физического контакта и объемное взаи-
262
модействие металлов. Сварка взрывом разнородных металлов и
образование биметаллов имеет еще один существенный фактор —
неравномерность деформации и связанные с ней фихико-химические
превращения на контактных поверхностях [52]. В переходной зоне
соединения обнаруживаются твердые растворы, легкоплавкие
эвтектики, различные интерметаллидные соединения.
Например, при сварке взрывом алюминия со сталью в
переходной зоне шириной 27—42 мкм образуются два твердых раствора
(Fe2Al и FeAl3) и семь интерметаллидных соединений с
содержанием алюминия от 25 до 78% [52].
Процесс сварки взрывом определяется технологическими,
кинематическими и физическими параметрами, причем последние
наименее изучены. На образующиеся связи влияют несоответствие
параметров решеток соединяемых металлов, различия их
кристаллических структур и электронных свойств, диффузионные эффекты.
Авторы [53] рассмотрели условия соединения сваркой взрывом
многих пар металлов и пришли к выводу, что соединение
обеспечивается взаимодействием объемных атомов, а не тех, что находились
на исходных поверхностях. «Раскрытие» объемных атомов и
образование связей происходит в процессе больших пластических
деформаций поверхностей, сопровождаемых срывом поверхностных
слоев, т.е. самоочищением.
Толщина R приконтактной зоны, где степень пластической
деформации g> 100%, растет с увеличением значений vk, j и
уменьшается с уменьшением шероховатости. Для разных металлов
величина R составляет 0,8—1,5% от толщины метаемой пластины [54].
Величина g растет по мере приближения к шву, причем этот рост
неравномерен: в зависимости от (vk, j) наблюдаются один или два
скачка [54]. Деформационное состояние зоны контакта может быть
выявлено методом рекристаллизации [54].
Типичной формой пластической деформации свариваемых
пластин на контактной поверхности является волнообразование (см.
рис. 6.18). Многочисленными исследованиями было установлено
следующее выражение а^я длины волны!:
Я = 26£ sin2y72 (6.31)
Рис. 6.18. Схема сварки взрывом
1 — заряд ВВ; 2 — метаемая пластина; 3 — неподвижная пластина; 4 — жесткое
основание
При этом амплитуда волны а = 0,21.
Из (6.31) следует, что на степень пластической деформации,
обеспечивающей прочность соединения пластин, влияет только угол].
Волны на поверхности контакта образуются не в момент
соударения, а позже. Поэтому волнистость начинается на некотором
расстоянии 1 от точки контакта.
Волнообразование является автоколебательным процессом,
начальным возмущением которого служит волна разрежения,
приходящая от свободной поверхности метаемой пластины [50].
Размер зоны 1 от точки контакта, до которой еще не доходит
разрежение и в которой не образуются волны, в акустическом
приближении равен [50]:
l = 2S„,vk/(c02-vk2r (632)
Автоколебательный процесс волнообразования поддерживается
тепловой энергией, выделяющейся в узкой зоне соударения и
составляющей ~3% от кинетической энергии метаемой пластины [55]. По-
видимому, основной источник этой энергии — трение между
соединяющимися поверхностями пластин. Зона тепловыделения на порядок
меньше амплитуды волн [50].•
В плоскости j—vk область сварки схематически показана на
рис. 6.19 [56].
Вблизи нижней границы области сварки осуществляется сварка,
во-первых, наиболее качественная, с минимальным объемом расплавов
пластин и, во-вторых, наиболее экономичная, с минимальным
потреблением ВВ. При этом прочность шва обычно превышает прочность
слабейшего из соединяемых металлов.
264
г
20
Ю Н
F Е
9 1 •
гч4
о,
q
о
♦ • •
оо
о о
©о
•©о
+ о
о
о
о
4 v, км/с
Рис. 6.19. Схема области сварки
взрывом.
1 — нижняя граница сварки;
2 — граница сверхзвуковой
области; 3 — верхняя граница сварки
Рис. 6.20. Результаты исследования
косого соударения пластин t=5 мм из
малоуглеродистой стали
(Н = 1500—1700 МПа) [33]
• — равнопрочная сварка;
© — частичная сварка; О - нет сварки.
В плоскости j — vk нижняя граница области сварки представляет
собой гиперболу v . = const, где v —МИНИМаЛЬНОе ЗНаЧеНИе
СКОРОГО J mm mm а
сти метаемой пластины [57]. При скорости vmin давление соударения
в 2—3 раза превосходят максимальную прочностную
характеристику свариваемых металлов и обеспечивает пластическую деформацию
в окрестности точки контакта.
В [57] предложен критерий (6.20) схватывания металлов в
условиях сварки взрьюом. представляемый на плоскости j — vkB виде прямой
vk = const, разделяющей упругие и неупругие соударения.
Экспериментальные данные о положении прямой vk = const
Аая сварки взрывом малоуглеродистой стали представлены на
рис. 6.20.
Прямая Е — переход к стабильной равнопрочной сварке при
vk> 1,6 км/с. В области между прямыми Е и F при vk= 1 1,4 км/с
прочность сварки нестабильна и существенно зависит от свойств
поверхностей. Для стали vk = 1,2 км/с.
Толщина околошовного слоя R, где степень пластической
деформации g> 100%, выражается формулой [33]:
R = 2,6Ssin2j/2
(6.33)
т.е. линейные размеры, характеризующие степень пластической
деформации, изменяются так же, как и длина волн на контакте
поверхностей.
Из (6.31) и (6.33) следует, что степень пластической
деформации, обеспечивающая равнопрочность соединения пластин, зависит
только от угла j. Таким образом, в фиксированном интервале
скорости vk нижняя граница сварки представляется отрезком j=j . [58].
В [58] качество соединения в каждом опыте оценивалось
средней сг = сг /сг и максимальной сг = сг /от , где сг = 200 МПа аая меди
I ср в 2 max в " в " "
и <7в = 350 МПа а^я стали. Полученные зависимости сг1 (j и <j2 (j)
приведены на рис. 6.21.
При j = 2° ^ = 0^ = 0, поверхности пластин остаются гладкими.
Увеличение j на 1°—2° дает
быстрый рост ст, а сг2>1,
т.е. условие равнопрочно-
сти выполняется локально,
в зоне шва наблюдаются
микрорасплавы и
локальные волновые дорожки. Это
углы нестабильных
переходных режимов. Условие а > 1
(равнопрочность по всей
поверхности шва) выпол-
2 10 20 т° няется при j=7° и 5° соот-
„_ ,~л ~ ветственно для меди и стали
Кис. 6.21. Экспериментальные зависимости .
отугла соударения средней (1) (нижняя граница области
и максимальной (2) прочности соединения сварки).
пластин из меди и стали т> . ^о ^лп
В интервале j = 7—20°
аая меди величина 0^ =
const, а аая стали максимум а1 и сг2 достигается в интервале j = 7°— 15°
с последующим резким спадом при j = 20°. Экспериментально
найдено, что аая сварки стали с алюминием угол j » 20° является
критическим и определяет верхнюю границу области сварки взрывом.
Реализация условия равнопрочности (а1 > 1) совпадает с
устойчивым волнообразованием в зоне шва с минимальным размером R
0*, 0*
l,b -
.
1,0-
0,7-
2
Г г
J/r-2^
wT?
t
/
3 2 ^
\/ Cu
Л
\\ Си
\ Ст.
\ Ст.
266
(см. 6.31). В этой зоне степень пластической деформации достаточна
Аая образования равнопрочного соединения по всей площади
сварки.
Таким образом, критерий схватывания vk = const (6.20) и
критерий j=jmin нижней границы сварки являются необходимыми и
достаточными условиями а^я нижних кинематических параметров
косого соударения пластин при сварке взрывом.
Рассмотрим тепловую динамику сварного шва (толщину зоны
расплава и время затвердевания). Для получения прочного шва
необходимо, чтобы затвердевание успело пройти за время tQ существования
высоких давлений, до прихода волны разрежения в точку контакта:
'o=2<^/(C2-v2)0,5
(6.34)
В [59] решалась несимметричная, нестационарная задача
теплопроводности Стефана, связанная с локальным мгновенным
выделением тепла в плоскости соударения, расплавлением и
затвердеванием зоны шва. Результаты расчетов а^я медных и стальных пластин
t = 5 мм и плотности энергии их соударения Q= 3 кал/см2
приведены в таблице 6.2.
Расчеты показали, что расплав начинает затвердевать изнутри, от
контактной поверхности. Таким образом, внутри расплава
возникает твердый «островок», и далее затвердевание идет с двух сторон —
изнутри и снаружи.
Таблица 6.2. Динамика фазовых переходов в сварном шве [59]
Материал
пластин
Медь—медь
Ст.25-Ст.25
мкм
3,625
1,94
6
max
МКМ
6,23
3,87
t
max
МКС
0,26
1,34
t
s
МКС
1,53
6,0
6ПИ 6
О max
— начальная и максимальная полуширина
расплавленной зоны; tmax — время, за которое достигается emax; t — время
затвердевания расплава.
Представление о распределении температуры контактной
поверхности при сварке взрывом дают измерения температуры при сварке
меди с константаном, проведенные с использованием
термоэлектрического эффекта [60] (см.рис. 6.22).
т°с
600
400
200
к
N
Чч.
ф^1
^^^1—±
—±
о
30 60 90 120 1,мм
Рис. 6.22. Результаты измерения
температуры сварного шва при сварке взрывом
меди и константана
Условия сварки: 8=2 мм, j = 17°,
vk = 1 км/с. 1 — расстояние до точки В
(см.рис. 6.18)
В зоне сварного шва
наблюдается интенсивное
перемешивание и упрочнение
металлов пластин. При этом
возможно образование
неравновесных соединений
и твердых растворов,
промежуточного слоя с переменным
составом. Из рис. 6.23
видно значительное повышение
микротвердости зоны шва
Аая соединения сталь— медь
[50].
Любой вид сварки требует предварительной очистки
свариваемых поверхностей от окислов, жира и других загрязнений.
СТАЛЬ
1,2 0,8 0,4 0 0,4 0,8 1,2 мм
Рис. 6.23. Микротвердость зоны шва сталь—медь
Эксперименты показали, что при косых соударениях происходит
частичное самоочищение соединяемых поверхностей за счет
образования в окрестностях точки контакта облака дисперсных частиц, которые
движутся со скоростью ~ v вдоль поверхностей и очищают их [60].
Нижняя граница свариваемости определяется выражением [61]:
j = l,4(H/pvcQ2)0-5 (6.35)
Для пары Cu+Cu нижняя граница свариваемости в плоскости
j — vk показана на рис. 6.24.
268
30°
25°
20°
15°
10°
S°
n°
7 ,
I +
\+
\+
V
\-f
1 1
4- +
-lE:
7=7°
Z±z
-
0,0 0,5 1,0 1,5
2,0 2,5
v., км/с
3,0
Рис. 6.24. Нижняя граница свариваемости для
Cu+Cu(H = 50 кг/мм2,
р=8,9 г/см3 ,<тв = 30 кг/мм2) [61]
Для любого значения
r=m /m можно рас-
ВВ ПЛ А
считать кинематические
параметры сварки (j , v),
если известна скорость
детонации ВВ. Для
сварки взрывом используются
маломощные
промышленные ВВ насыпной
плотности: аммониты AT—1,
А—2Г, 6ЖВ и их смеси
с D= 1,5—4км/с.
В [62] показано, что
сортамент ВВ а^я
сварки взрывом можно
расширить, применяя смеси
промышленных ВВ с
активными (алюминий, селитра) или инертными (NaCl, тальк)
компонентами.
Экспериментально определены зависимости D промышленных
ВВ от их толщины и содержания различных добавок. Установлено
снижение величины D в процессе длительного хранения ВВ, что
необходимо учитывать при их использовании а^я сварки взрывом.
6.6. Роль космогенных ударноволновых процессов
в происхождении Земли и Луны*
6.6.1. Происхождение Земли
Вопрос о роли ударно-взрывных процессов в образовании и
эволюции солнечной системы стал серьезно рассматриваться и получил
развитие относительно недавно, прямо связан с бурным прогрессом
космонавтики и с изучением влияния ударных волн на горные породы.
Оказалось, что Луна, Марс, Меркурий, Венера и их спутники
покрыты кратерами метеоритного происхождения.
* раздел написан с участием Ю.Н. Жугина.
На Земле до 1960-х годов был известен лишь один крупный
Аризонский метеоритный кратер, а к 1987 году число доказанных
метеоритных структур на Земле приблизилось к 230. Зондирование
земной поверхности из космоса и последующие геологические
исследования позволили выявить многочисленные кольцевые
структуры, кратеры диаметром от сотен метров до 2—3 - х тысяч
километров [63].Только на территории бывшего СССР их насчитывается
около 4-х тысяч [64].
Одна часть геологов считает, что все кольцевые структуры на Земле
имеют ударно-взрывное происхождение по аналогии с Луной, Марсом.
Другая часть относит к метеоритным лишь те структуры, в породах
которых обнаружен ударный метаморфизм (плотные фазы,
специфические деформационные структуры в кварце и полевом шпате).
Многие ученые как в России, так и за рубежом поддерживают
гипотезу ударно-взрывной тектоники.
Более того, американский ученый Э. Шумейкер утверждает [65],
что соударение плотных тел в космосе является фундаментальным
процессом, без которого не могли возникнуть планеты и их спутники.
Наконец, экспериментально установлено, что при динамическом
сжатии идет процесс полимеризации, и аммонийные соли акриловой,
метакриловой. кротоновой, фумаровой и малеиновой кислот
превращаются в аминокислоты [66]. А это первый шаг перехода от неживой
материи к живой, и условия аа^ него мог создать метеоритный удар.
В 1940-х годах О.Ю. Шмидтом была предложена
космогоническая гипотеза, согласно которой наша планетная система и, в
частности, Земля возникла в результате сгущения окружавшего Солнце
холодного допланетного газопылевого облака. Как считал Шмидт,
разогрев первично холодной Земли произошел за счет тепла
радиоактивного распада составляющих ее веществ.
Однако развитие этой гипотезы учениками Шмидта привело к
выводу о незначительности роли радиоактивности в разогреве Земли.
Так, B.C. Сафронов предположил, что основным источником
тепла Земли была энергия высокоскоростных ударов космических
тел, падающих на планетозималь, ставшей зародышем Земли. Среди
этих тел были и крупные, размером в несколько сотен километров.
270
Чем крупнее сталкивающийся с Землей астероид, тем больше
глубина, на которой высвобождается энергия удара, и, следовательнодем
большая доля энергии аккумулируется Землей. Теплопроводность
усиливалась за счет интенсивного перемешивания вещества при
ударе. Скорости ударов оцениваются величинами более 10 км/с.
Расчетные температуры разогрева Земли при таких ударах
превышают 1500 С и достигаются на глубине ~ 500 км.
Таким образом, вещество при ударе плавится. Когда доля
расплава составит около половины вещества, должна произойти
гравитационная дифференциация - тяжелые составляющие вещества Земли
опускаются к центру, формируя ядро Земли, а легкие вещества
поднимаются вверх, образуя мантию.
Ученые считают, что соударения планетозималей и образование
ядра Земли произошли 4,2—4,6 млрд. лет назад [65,67].
Сафронов предполагал, что континенты образовались над
сильно разогретыми областями ударов крупных астероидов.
Рост массы Земли за счет присоединения части массы
ударяющих астероидов увеличивал гравитационное поле Земли,
соответственно возрастали масса и количество бомбардирующих молодую
Землю астероидов. Возможно, распределение ударов было ассиме-
трично (с одной стороны Земли), в виде подковы. Получившаяся к
концу архея (2,7—2,8 млрд. лет назад) серповидная суша (Пангея)
является вероятным воспроизведением этого распределения
ударов.
По-видимому, последующий распад Пангеи на континенты и их
дрейф обусловлен фрагментарностью Пангеи, возникшей в
результате космической бомбардировки Земли на раннем этапе ее истории.
Исследования последних десятилетий (см.ссылки в [68])
показали, что о Землю ударялись многие планетозимали массой 0,001...0,01
массы Земли. Крупнейшая после Земли планетозималь, которая
могла образоваться в зоне Земли и затем столкнуться с Землей, могла
иметь массу 0,03—0,1 массы Земли.
Грандиозность такого удара соответствует, например, столкновению
Земли (диаметр 13000 км) с Луной (диаметр ~ 3500 км, масса 0,01) или
с Марсом (диаметр ~ 7000 км, масса 0,1).
271
При таких ударах Земля оказывается проплавленной насквозь, и
запасенное в результате ударов тепло в дальнейшем определяет
уникальную геологическую и биологическую истории нашей планеты.
О периодическом ударном подогреве Земли говорят оценки
[69], согласно которым время остывания Земли (1012 лет) более, чем
в 200 раз превосходит время ее существования.
Если бы на начальном этапе истории Земли не было теплового
потока из недр Земли, она бы полностью оледенела, и на ней никогда
бы не возникла жизнь [70].
Столкновение Земли с крупным астероидом возможно и в наше
время, и это вызывает тревогу. Ведь при падении на Землю астероида
диаметром 1 км выделится энергия, эквивалентная взрыву 25000
водородных бомб. В 1976 и в 1989 годах такие безымянные астероиды
проходили на расстоянии от Земли немногим более 1 млн.км.
Вероятность падения крупных астероидов на Землю
оценивается по-разному [71]. Например, считают, что каждый миллион лет
падает три астероида размером более 1 км. Вероятные интервалы
падения астероидов диаметром 10 км — 40—100 млн.лет.
Возможно, в будущем человечеству придется создать систему
защиты от астероидов, обеспечивающую их разрушение до подлета к Земле.
В результате столкновений с астероидами на Земле возникли
гигантские взрывные кратеры, в земной коре сформировались
структурные неоднородности, зоны растяжения, прогибы
геосинклиналей и другие региональные структуры.
Многие геологи, сторонники гипотезы ударно-волновой
тектоники, считают, что Тихий океан — это гигантская метеоритная структура
[71,72]. Геолог Б.С. Зейлик к гигантским астроблемам (древнегреч. —
звездные раны) относит также Антарктиду с окружающим ее океаном,
северный полярный бассейн с Гренландией, Мексиканский залив,
Черное море, восточное Средиземноморье и др.
Интересно, что в гальках пляжей черноморского курорта Сочи
часто встречаются характерные деформационные структуры в
кварце, свидетельствующие о метеоритном ударе в этом районе.
Большой интерес геологов к метеоритной гипотезе связан с тем,
что у них имеется множество примеров четкой связи распределения
272
нефтяных, газовых и рудных месторождений с кольцевой
тектоникой, в том числе и гигантской. Кроме того, есть доказательства, что
ударные волны, возникшие в зонах крупных кольцевых структур,
должны ускорять на много порядков созревание нефти и углефика-
цию растительных осадков.
Например, Прикаспийский нефтегазовый район окружен по
периферии « бортовым уступом », к которому примыкает цепь газовых
и нефтяных месторождений, а в центре имеется крупное нефтяное
месторождение.Аналогичное концентрическое распределение
нефтегазоносное™ наблюдается и в бассейне Мексиканского залива.
Одно из рудных месторождений Казахстана имеет в плане форму
круга, ограниченного кольцевым разломом, причем породы в кольце
несут признаки ударного метаморфизма.
При ударе крупных метеоритов о Землю фокусировка
поверхностных волн приводит к образованию трубок взрыва — сквозных
проколов в области антипода удара (на другом конце радиуса Земли)
[73,74]. Неоднородность коры Земли обуславливает образование в
этой области сразу нескольких трубок взрыва (поля диатрем).В
геологических процессах трубки взрыва могут служить каналами
выноса глубинного вещества на поверхность. Например, кимберлитовые
трубки выносят вещество мантии, и если в них образуются пробки,
то это создаёт условия fi^ роста алмаза.
При ударе о молодую ещё горячую планету (Венера, возраст
всего 400 млн лет) фокусировка сейсмических волн приводит к
формированию уединённых вулканов (У Венеры 1600 таких вулканов).
Если сила удара метеорита достаточно болыыая,то УВ проходит
через всю Землю и на противоположном конце диаметра Земли возможен
откол коры с образованием впадины и выбросом породы в атмосферу.
Таким образом, поиск и изучение метеоритных структур
является не только научной проблемой, но и практически важной задачей
современной геологии.
6.6.2. Происхождение Луны
Одной из первых была гипотеза Георга Дарвина (сына
знаменитого биолога Чарльза Дарвина), который в 1878 году предположил, что
273
молодая расплавленная Земля должна была вращаться все быстрее
и быстрее, и в результате резонансного взаимодействия с
солнечными приливами гигантская масса лавы оторвалась от Земли в районе
Тихого океана и образовала Луну.
Однако физики не подтверждают эту гипотезу, т.к. аля такого
отрыва части массы Земли ее вращение должно быть в 4 раза быстрее,
чем это было на самом деле. Кроме того, возраст дна Тихого океана
слишком мал — всего 200 млн. лет.
Другая теория утверждает, что Земля и Луна возникли
одновременно из гигантского облака пыли и камней. Эта теория
опровергается отсутствием железа на Луне.
Третья гипотеза допускает, что Луна сформировалась в
другом месте солнечной системы, затем при движении по
нерегулярной траектории сблизилась с Землей и была ею притянута.
Американский физик Камерон утверждает, что это маловероятно.
Если такая большая планетная масса, как Луна, войдет в контакт с
гравитационным полем Земли, то она либо столкнется с Землей,
либо будет выброшена во внешнее пространство, но не станет
спутником Земли.
Близость средней плотности Луны (3,34 г/см3) к плотности
верхней мантии Земли (3,30—3,40 г/см3) указывает на возможность того,
что Луна каким-то образом была вырвана из мантии Земли.
По расчетам Хартмана и Дэвиса [75] удар о Землю планетозимали
с массой ~ 0,5 массы Луны со скоростью 13 км/с обладает достаточной
энергией, чтобы отторгнуть от мантии массу в две лунные массы,
сообщив ей скорость, близкую ко второй космической. Половина этой
энергии идет на нагрев, а половина на кинетическую энергию выброса.
Большая часть выброшенного вещества попадает на
геоцентрическую орбиту, образуя диск или кольцо осколков, из которых и
формируется Луна.
Годом позже, в 1976 году группа американских астрофизиков
во главе с Камероном выдвинула новую гипотезу, согласно которой
Луна сформировалась от слияния осколков, возникших при
столкновении Земли с другой планетой, близкой по массе к Марсу, со
скоростью более 11 км/с [70,75].
274
Была создана компьютерная модель этого явления и наглядно
показаны все стадии удара. Он не был центральным, исходя из того,
что Земля после столкновения приобрела существующую сейчас
скорость вращения. По обеим планетам пробегает ударная волна,
нагревая вещество выше температуры плавления. Оба тела
сливаются, при этом во все стороны летят осколки. Наиболее быстрая часть
осколков покидает систему, наиболее медленная часть возвращается
на Землю, но примерно сотая часть полной массы остается на земных
орбитах. Через некоторое время «рой» осколков на высоте ~ 22000
км мягко сливается, образуя Луну.
По этой модели Луна образуется из внешних силикатных
оболочек планет, а их железные ядра сливаются. Запасенное при ударе
тепло не дает Земле остыть (в отличие от близкой по массе Венеры) и
создает условия ^ая возникновения и развития жизни на Земле.
Первоначально Луна была в 20 раз больше, чем сейчас. Это был
гигантский красно-коричневый шар на небе. Постепенно в течение
сотен миллионов лет гигантские приливные силы солнца отдалили
Луну от Земли на теперешнее расстояние в 380000 км. Измерения
радаром показывают, что Луна продолжает удаляться от Земли со
скоростью 4 см в год.
Астрономы и астрофизики Токийского технологического
института создали 27 различных компьютерных моделей в попытках
описать процесс возникновения Луны при ударе. Оказалось, что во
внешних областях вращающегося вокруг Земли диска осколки легко
соединяются друг с другом. Наоборот, во внутренних областях
диска благодаря влиянию притяжения Земли осколки отталкиваются
друг от друга.
В каждой модели только 15—40% осколков диска идет на
создание Луны, причем формирование Луны происходит очень быстро —
менее, чем за год.
Астроном Робин Кануп из американского университета в
Колорадо утверждает, что не все так просто, как представлялось 10
лет назад [76]. Согласно его расчетам, ударившая по Земле планета
должна быть втрое тяжелее Марса, чтобы масса осколков была
достаточна для создания Луны.
275
Возможно, подтверждение правильности этих компьютерных
моделей мы сможем найти в анализах лунного грунта, привезенного
астронавтами. Следы происхождения Луны могут отыскаться и при
тщательном изучении мантии Земли.
Литература к главе 6
1. Теплофизика и динамика интенсивных импульсных
воздействий. А.В. Бушман ,Г.И. Канель, А, Л, Ни, В.Е.Фортов. Ин-т
химфизики АН СССР, Черноголовка, 1988.
2. Высокоскоростные ударные явления, М.: Мир, 1973.
3. Уилкинс М.Л. В кн. Вычислительные методы в
гидродинамике, М.: Мир, 1967.
4. Гулидов А. И., Фомин В.М., Яненко Н. Н. В кн. Проблемы
математики и механики, Новосибирск, 1983.
5. Эйгербергер Р., Кайнике Дж. В кн. Физика быстропротекающих
процессов, т.2, М.: Мир, 1971.
6. Мержиевский Л.А., Титов В.М. ФГВ, 1987, N5, с.92.,.108.
7. Динамика удара, М.: Мир, 1985.
8. Лаврентьев М.А., Шабат Б.В. Проблемы гидродинамики и их
математические модели, М.: Наука, 1973.
9. Русаков М.М., Лебедев М.А. Вопросы атомной науки и техники,
сер. Теор. и прикл. физика, 1988, N1, с.81—84.
10. Агурейкин В.А., Анисимов СИ., Бушман А.В. и др.
Теплофизика высоких температур, 1984, т.22, N5, с.964.
11. Механика образования воронок при ударе и взрыве, М.:
Мир,1977.
12. Титов В.М. ПМТФ, 1976,4.
13. Аникиева А.П., Мержиевский Л.А., Титов В.М. ПМТФ,
1977,3.
14. Никифоровский В.С, Шемякин Е.И. Динамическое
разрушение твердых тел. Новосибирск,Наука,1979.
15. Woodward R.L. Jntern. Jorn. of Jmpact Eng., 1984,2,N2,p.l21—
129.
16. Степанов Г.В. Прикладная механика, 1969,5,8.
17. Мержиевский Л.А., Урушкин В.П. ФГВ,1980,16,5.
276
18. Горшков Н.Н., Пластинин А.В., Сильверстов В.В. ФГВ, 1992,
N4,c.ll5...120.
19. Тейт А. Теория торможения длинных стержней после удара по
мишени, М.: Мир,19б8.
20. Холт А. ФГВ,1990,Ы2,с.131...137.
21. Бухарев Ю.Н., Морозов В.А. и др. ФГВ,1992Жс.108...113.
22. Куракин Н.И., Даниленко В.В., Козерук Н.П. // ФГВ. 1989,
№5,С.89-92.
23. Гавриленко Т.П., Николаев Ю.А и др. ФГВ, 1990, N2,
С.110...123.
24. Бартенев С.С, Федько Ю.П., Григоров А.И. Детонационные
покрытия в машиностроении, Л.: Машиностроение, 1982.
25. Лариков Л.И., Фальченко В.М. и др. ДАН СССР, 1975, 221, 5,
1073.
26. Шмирева Т.П. ФГВ, 1983,19,N5,c.l43...l46.
27. Киселев Ю.Н., Миронов Э. А., Попов В. А. и др. О механизме
взаимодействия потока микрочастиц с преградой, «Химическая
физика процессов горения и взрыва», Детонация и ударные
волны, Материалы VIII Всес. симпозиума по горению и
взрыву, Черноголовка, 1986, с.7б.
28. Козорезов К.И., Максименко В.Н., Ушеренко СМ. Избранные
вопросы современной механики, М.: Из-во МГУ, 1981,с. 114.
29. Роман О.В., Андилевко С.К., Горобцов В.Г., Ушеренко СМ.
Порошковая металлургия, 1987, N3, с. 100—102.
30. Романов ГС, Ушеренко СМ., Юрии СЕ. Влияние исходной
температуры железа на процесс сверхглубокого проникания, IV Всес.
совещание по детонации, Телави,1988, Сб. докладов, т.П, с. 152.
31. Кудинов В.М., Коротеев АЛ. Сварка взрывом в металлургии,
М.: Металлургия, 1978.
32. Дерибас А.А. II Междунар.семинар «Использование энергии
взрыва для производства металлических материалов с новыми
свойствами», Сб. докладов, 1973, Пардубице.
33. Симонов В.А. ФГВ, 1991,27, N1, С.127...130.
34. Ададуров Г.А., Беликова А.Ф., Буравова СН. ФГВ, 1922, 28,
N4,c.95.
35. Brown R., Kosco S., Jun J.E. Wear, 1983,8, р.181...193.
36. Беликова А.Ф., Буравова C.H. и др. Поверхность, 1989, N10,
с. 134—139.
37. Боуден Ф.П., Тейбор Д. Трение и смазка твердых тел, М.:
Машиностроение, 1968, с. 544.
38. Лойцянский Л.Г. Механика жидкости и газа, М.: Наука, 1978.
39. Ларионов Л.Н., Исаичев В.И. Диффузия в металлах и сплавах,
Киев.: Наукова думка, 1987.
40. Горобцов В.Г., Козорезов К.И., Ушеренко СМ. Порошковая
металлургия, 1982, N6.
41. Григорян С.С. ДАН СССР, 1987,292, N6, с. 1319... 1323.
42. Черный Г.Г. ДАН СССР, 1987,292, N6, с.1324—1328.
43. Альтшулер Л.В., Авдилевко С.К., Ушеренко СМ. и др. Письма
вЖЭТФ, 1989,15, вып.5,с.55...57.
44. Симоненко В.А., Скоркин Н.А., Башуров В.В. ФГВД991, 27,
N3,c.46—51.
45. Забабахин Е.И., Забабахин И.Е. ПМТФ, 1980, N2.
46. Симоненко В.А., Скоркин Н.А., Башуров В.В. ВАНТ, сер.
Теоретич. и прикл. физика, 1988, вып.1, с.85—91.
47. Барахтин Б.К., Савенков Г.Г. IV Всес. совещание по
детонацииДелави, 1988, Сб.докладов, т.П, С.194...197.
48. Noskin N.E., Allan J. и др. IV Simp, on Detonation, 1965.
49. Годунов CK. Элементы механики сплошной среды. М.: Наука,
1978.
50. Дерибас А.А. Физика упрочнения и сварка взрывом, «Наука»,
Новосибирск, 1972.
51. Каракозов Э.С Сварка металлов давлением, М.:Машино-
строение,1986,280 с.
52. Гульбин В.Н., Архангельская О.В. и др. V Всес. совещание по
детонации, 1991, Сб.докладов, т.1, с.117—120.
53. Oberg A., Martensson N., Schweitz J.A. Metallurgical Trans.,
1985, N16A.
54. Бондарь М.П., Нестеренко В.Ф. ФГВ, 1991, N3, С.103...117.
55. Годунов С.К., Дерибас А.А. и др. ФГВ, 1971, N1.
56. Дерибас А.А. ФГВ, 1987, N5, с.148—158.
278
57. Прюммер Р. Обработка порошкообразных материалов
взрывом (пер.с нем.) М.: « Мир», 1990.
58. Симонов В.А. ФГВ, 1990, N4, с.132—136.
59. Качан М.С., Курочкина Е.П. ФГВ, 1992, N2, с.98—103.
60. Пай В.В., Ишуткин С.Н. IV Всес. совещание по детонации,
Телави,1988, Сб.докладов, т.П, с.98—103.
61. Deribas A. Explosive welding: weldability Range. Shock-assisted
synthesis and modification of materials. Ed. by A. Deribas, Yu.
Scheek. M., TORUS PRESS, 2006, p.28—34.
62. Кожевников B.E., БезшапошниковЮ.П.и др. ФГВ, 1990, N3,
с.115—118.
63. Брюханов В.Н., Буш Б.А., Глуховский М.З. и др. Кольцевые
структуры континентов Земли,М.:Недра,1987.
64. Хрянина Л.П. Метеоритные кратеры на Земле, М.гНедра,
1987.
65. Масайтис В.Л., Данилюк А.Н.и др. Геология астроблем, Л.:
НедраД980.
66. Ададуров ГА. О роли пластических деформаций в
динамических экспериментах и сопоставлении результатов
динамических и статических исследований. // «Химическая
физика процессов горения и взрыва». Детонация и ударные
волны. Материалы VIII Всес. симпозиума по горению и
взрыву, Черноголовка, 1986,С. 3.
67. Гудвин А.М., Масайтис В.Л., Данилюк А.Н.и др. Геология
астроблем, Л.:НедраД980. Гигантская метеоритная
бомбардировка и развитие континентальной земной коры, В кн. Ранняя
история Земли, М, 1980, с.87—107.
68. Риигауд А.Е. Происхождение Земли и Луны, Пер.с англ. М.:
НедраД982
69. Жарков В.Н., Трубицин В.П. Физика планетных недр, М.:
Наука, 1980.
70. Бялко А.В. Наша планета Земля, М.: Наука, 1989.
71. Хрянина Л.П.Метеоритные кратеры на Земле,М.:Недра, 1987.
72. Зейлик Б.С. О происхождении дуговых и кольцевых
структур на Земле и других планетах (ударно-взрывная тектони-
279
ка), М.:Обзор ВИЭМС, Сер. Общ. и регион, геол.
картирование, 1978.
73. Симоненко В.А., Шишкин Р.И. К ударному образованию кимбер-
литовых трубок. Конференция «Космическая защита Земли»
Евпатория, 11-15 сентября 2000, тезисы докладов, с.45.
74. Симоненко В.А., Шишкиш Н.И. Трубки взрыва и вулканы
в антиподе удара. Забабахинские научные чтения,Снежинск,
8—12 сентября 2003, тезисы, с.22.
75. Риигауд А.Е. Происхождение Земли и Луны, Пер. с англ.
М.:Недра,1982.
76. Кануп Р. Астрономический журнал, сентябрь 1998.
280
Глава седьмая
ФАЗОВЫЕ ПРЕВРАЩЕНИЯ В УДАРНЫХ ВОЛНАХ
7.1. Полиморфизм. Термодинамика и кинетика
У многих кристаллических веществ (элементы, сплавы,
химические соединения) наблюдается полиморфизм, т.е. возможность
существования различных кристаллических модификаций в
зависимости от величин давления и температур.
Переходы из одной модификации в другую являются фазовыми
переходами первого рода (как и плавление), поскольку
сопровождаются изменением объема, тепловых свойств, выделением или
поглощением скрытой теплоты.
Наиболее известно, хорошо изучено и имеет огромное
практическое значение полиморфное превращение железа, которое при
910 С и нормальном давлении превращается из а-фазы в у-фазу
с уменьшением объема на 2,5%. На полиморфизме железа основана
термообработка стали.
Полиморфные превращения часто наблюдаются при сжатии
вещества. Полиморфизм под давлением в статических условиях изучал
П. Бриджмен [1]. Обнаруженные им полиморфные переходы
позднее были найдены и в условиях ударного сжатия. Яркий пример
полиморфизма под давлением — превращение мягкого графита в
твердый алмаз.
Фазовые превращения при высоких давлениях исследованы
почти в 2000 веществ [2]. В большинстве из них при сжатии
наблюдается полиморфизм.
281
Движущей силой полиморфного превращения является
разность термодинамических потенциалов фаз: АФ = Ф2- Ф , где
0 = E-TS + pv = \cvdT - Т\%1Т + pv (7.1)
Для протекания превращения необходимо, чтобы АФ < 0, т.к.
переход происходит в фазу с меньшей энергией:
A<D = AE-TAS + pAv<0 (7.2)
Линия термодинамического равновесия фаз в р,Т координатах
соответствует условию АФ = 0.
Условия ДФ<0 недостаточно аая протекания превращения,
поскольку при возникновении новой фазы в исходной кристаллической
матрице затрачивается энергия на создание межфазной поверхности
(Епов) и на деформацию исходной матрицы и нового кристалла (Е .).
Необходимое и достаточное условие превращения —
понижение полной энергии системы:
АФ + Е^+Е^кО (7.3)
Тогда линия кинетического равновесия в р,Т координаиах
соответствует условию АФ = Е + Е ..
' ' пов деф
Разница между термодинамическим и кинетическим
равновесием определяет гистерезис превращения^ В зоне гистерезиса
превращение не идет и фазы метастабилъны.
Таким образом, всегда фазовое превращение протекает в
термодинамически неравновесных условиях, поэтому экспериментально
найти точное положение линии равновесия АФ = 0 нельзя.
Приближение к равновесным условиям достигается за счет
применения катализаторов — растворителей, снижающих активацион-
ный барьер образования плотных фаз аая таких превращений, как
графит -> алмаз и BNf->BN .
Типичный вид фазовой диаграммы показан на рис. 7.1.
Со стороны высоких температур фазовая диаграмма твердых
модификаций ограничена областью жидкого состояния. Линии плавления
фаз пересекаются с линией фазового равновесия АФ=0 в тройной
точке А, откуда выходят и линии гистерезиса АФ+Епов + Е . = 0.
282
о к м т
Рис. 7.1. Типичный вид фазовой диаграммы вещества с полиморфным переходом
ON и OQ- ударные адиабаты
С понижением температуры линии гистерезиса расходятся
и зона метастабильности быстро растет. Линии гистерезиса не
пересекают ось давления, поскольку превращение требует термической
активации и не идет при Т = О К.
Экспериментальное положение линии гистерезиса зависит от
чувствительности методов измерения и от времени выдержки в
данных условиях. Поэтому гистерезис в статических и в динамических
условиях может не совпадать, a fi^ диффузионных превращений
зона метастабильности в ударноволновых экспериментах должна
быть больше из-за краткости существования давления.
Увеличение давления действует на вещество подобно снижению
температуры: уменьшается подвижность атомов, растет прочность.
Для уменьшения зоны гистерезиса при комнатной температуре
Бриджмен применял сжатие образца с большой деформацией
сдвига (с помощью вращающейся наковальни [1]). Сдвиг под давлением
позволял снимать метастабильность и получать превращения в зоне
283
гистерезиса, когда превращение не шло при той же величине
давления, но гидростатического (без напряжений сдвига).
О решающей роли сдвиговых напряжений /^ля мартенситного
превращения говорят следующие результаты опытов. Сталь в виде
порошка, свободного от напряжений, при охлаждении не имела
мартенситного превращения, который наблюдался у массивных
образцов той же стали. Только сдвиг под давлением (р > 3,5 кбар)
позволяет получить ромбоэдрическую модификацию графита.
Следовательно, энергия сдвиговой деформации R=T6 может
играть роль движущей силы превращения аналогично АФ. Это дает
основание нанести на фазовой диаграмме линии гистерезиса в
условиях сдвиговых напряжений, на которых выполняется условие
Е + Е =ДФ + К(см.рис.7.1).
пов деф \ г /
Линии гистерезиса Е + Е . =АФ определяют зону метаста-
а пов деф a J
бильности при гидростатическом сжатии, а линии гистерезиса
Епов + Е = АФ + R — в условиях одноосного (и ударного) сжатия
или искусственно созданной сдвиговой деформации под давлением.
В области между этими двумя линиями превращение идет только в
течение времени существования сдвиговых напряжений. На фронте
УВ эти напряжения релаксируют очень быстро — за < 10"7с
независимо от того, происходит или не происходит превращение в данном
веществе.
Линии Епов + Е = АФ + R пересекают ось давления, поскольку
сдвиг заменяет термическую активацию.
Для низкотемпературного мартенситного превращения
касательное напряжение активирует ту систему сдвига, которая
переводит старую решетку в новую. А аая высокотемпературного
диффузионного механизма сдвиг разрушает исходную решетку и ускоряет
диффузионные процессы.
Область мартенситного превращения со стороны высоких
температур ограничивается линией рекристаллизации (Т к ~(0,4—0,6)
Тпл), правее которой высокая скорость диффузионных процессов
разрушает упорядоченный сдвиг, необходимый /i^L мартенситного
механизма.
С другой стороны, в низкотемпературной области скорость
мартенситного сдвигового механизма много больше скорости диффузи-
284
онного превращения, поэтому возможно образование новой
плотной метастабильной фазы с решеткой, отличающейся от решетки
стабильной фазы (правило Освальда). Это наблюдается у углерода
(лонсдейлит взамен алмаза) и у нитрида бора (вюрцитный BN
взамен сфалеритного).
Если нанести на фазовую диаграмму ударные адиабаты и изэн-
тропы разгрузки непористого и пористого вещества, имеющего
полиморфные переходы, то линии диаграммы разделят адиабаты и из-
энтропы на ряд характерных участков (см.рис. 7.1).
а). Непористый образец.
ОВ — сжатие стабильной исходной фазы;
ВС — сжатие метастабильной исходной фазы;
CD — мартенситное (сдвиговое) превращение только на фронте
УВ в течение времени действия сдвиговых напряжений
(одностороннее сжатие);
DE — превращение как на фронте (одноосное сжатие), так и за
фронтом УВ (гидростатическое сжатие);
ЕР — высокотемпературное диффузионное превращение;
PN — плавление исходной фазы.
Разгрузка из точки Е.
EF — продолжение образования новой фазы;
FG — разгрузка новой фазы без обратного перехода;
GK — обратное превращение в исходную фазу за счет влияния
сдвиговых напряжений.
Поскольку на схеме рис. 7.1 точка К находится в зоне метаста-
бильности, то после разгрузки возможно сохранение части новой
фазы. Это невозможно, если точка К расположена правее линии
гистерезиса.
б). Пористый образец.
Ударная адиабата OQ не проходит через низкотемпературную
область превращения, а сразу из зоны гистерезиса попадает в
высокотемпературную область (правее линии рекристаллизации).
Сдвиговая деформация на фронте УВ неупорядочена и разрушает
решетку.
Поэтому мартенситная фаза не образуется. Превращение идет
по диффузионному механизму в стабильную плотную фазу.
При разгрузке обратный переход происходит на участке RM
и завершается после разгрузки, т.к. точка М лежит правее линии
гистерезиса, в зоне стабильности исходной фазы.
Рассмотрена идеальная схема, а в действительности в связи с
термической неоднородностью ударного сжатия (особенно пористых
образцов) ударная адиабата представляет собой не линию, а
полосу. Поэтому в одном опыте различные части объема образца могут
попадать в различные характерные области фазовой диаграммы. В
результате в опыте может получаться смесь различных плотных фаз,
например, лонсдейлит и алмаз, вюрцитная и сфалеритная
модификации нитрида бора, стишовит и коэсит (при сжатии Si02).
Рассмотрим кинетику полиморфного перехода.
Превращение может протекать по двум механизмам:
бездиффузионному и диффузионному.
Бездиффузионное превращение реализуется в случае, когда
скорость роста кристалла новой фазы определяется процессами на
границе раздела фаз: движением дислокаций, адсорбцией, химическим
разложением. В этом случае линейные размеры частиц новой фазы
пропорциональны времени ее роста.
Диффузионный рост зародышей новой фазы требует
переноса к поверхности зародыша атомов на значительные расстояния.
Скорость роста пропорциональна скорости диффузии,
следовательно, размер зародыша растет пропорционально корню
квадратному из времени роста.
Бездиффузионный механизм в кристалле может осуществляться
кооперативным (одновременным и согласованным) перемещением
атомов на доли межатомного расстояния (направленный сдвиг в
исходной решетке за счет движения дислокаций). Такой механизм
называют мартенситным, поскольку так получается мартенсит при
закалке стали.
Скорость v бездиффузионного роста кристалла в жидкости
определяется концентрацией атомов п у поверхности растущего кристалла и
частотой у перехода атомов через межфазную границу: v =п у.
Кинетика диффузионного механизма определяется решением
соответствующего уравнения диффузии.
286
5
О
a)
xV^
v°x
X J^~
^-^^ДФ
Зарожд. ак Рост
Бездифф.
превр.
Нет
превращения
Рис. 7.2. Изменение полной энергии F=AO+E + Е . с ростом степени
Г ^ пов деф *
превращения а при различной неравновесности АФ.
а) Зона гистерезиса (АФ < АФ ); б) Двухэтапное превращение: зарождение
и рост (АФг < АФ < АФм)
в) Бездиффузионное превращение без этапа зарождения (АФ> Ф )
Два возможных механизма превращения можно кратко описать
так: старый порядок — новый порядок и старый порядок —
беспорядок — новый порядок.
Та или иная кинетика превращения определяется степенью
термодинамической неравновесности АФ и исходной
структурой вещества (дефектностью решетки). На рис. 7.2 показано, как
с ростом неравновесности меняется зависимость полной энергии
F = АФ + Епов + Едеф от степени превращения а [3].
При малой неравновесности превращение не идет, т. к. с самого
начала рост новой фазы увеличивает полную энергию (зона
гистерезиса, где АФ < АФг).
В некотором интервале неравновесности, где АФг<АФ<АФм
превращение идет в два этапа. На этапе зарождения величина F
увеличивается до максимума при а , соответствующей
критическому зародышу новой фазы. При а > а полная энергия уменьшается,
и зародыши растут.
При дальнейшем увеличении неравновесности, начиная с
некоторой АФм этап зарождения исчезает,т.к. d (Епов + Е .)/da = — dДФ/da
и полная энергия уменьшается с самого начала превращения, при
а^О.
Превращение без этапа зарождения может протекать по двум
механизмам — высокотемпературному диффузионному или
низкотемпературному бездиффузионному.
1). При АФ>АФм скорость зарождения (плотность зародышей
в единице объема) настолько велика, что зародыши сливаются, не
достигая критических размеров. При этом слияние зародышей с
образованием малоугольных границ между блоками поликристалла или даже
с образованием монокристалла — процесс рекристаллизационный, т.е.
относительно медленный и требующий высокой температуры.
2). Рост новой фазы начинается на определенного вида линейных
дефектах в исходном кристалле (дислокациях) и представляет собой
движение дислокаций без участия рекристаллизации и диффузии, т. е.
этот процесс низкотемпературный, мартенситный. Определенного
вида сдвиги в исходной решетке дают решетку новой фазы.
При заданной постоянной величине АФ > АФм превращение идет
до величины атах, при которой за счет увеличения Епов+Е . полная
энергия начинает расти, и превращение останавливается (см. рис. 7.2 в).
Для получения степени превращения а > атах необходимо
компенсировать рост Епов + Е . увеличением неравновесности ДФ. Например, при
изотермической выдержке углеродистой стали образуется мало
мартенсита, и аля увеличения его количества требуется непрерывное
охлаждение стали, т. е. непрерывное увеличение АФ.
Рассмотрим понятие критического зародыша при гомогенной
кристаллизации.
Если Ag — разность потенциалов фаз в расчете на один атом,
то объемный выигрыш энергии при образовании зародыша из i
атомов будет равен i Ag.
Связанный с образованием межфазной поверхности проигрыш
энергии пропорционален поверхности (i2/3) и удельной
поверхностной энергии межфазной границы с:
Тогда Епов = (2 i2/3 а; где (2 — геометрический коэффициент,
учитывающий форму частиц. Для сферического зародыша (3—п/6.
Таким образом, полное изменение энергии при образовании
зародыша новой фазы i Ag-h (^ i2/3 <j=AG становится отрицательным,
начиная с некоторого числа атомов в зародыше i , которое
находится из условия d AG/d i = 0:
288
i =(^)3 (7.4)
Радиус сферического критического зародыша:
гкр=2а/АФ (7.5)
Энергетический барьер, который необходимо преодолеть для
образования критического зародыша из iK атомов, равен:
iG,=MV (76)
кр 27Ag V }
Из условия термодинамического равновесия зародыша с
окружающими его атомами можно найти число N критических
зародышей (способных к росту):
N^N^xpi-AGjKT) (7.7)
где NQ — число атомов.
Плотность стабильных центров роста новой фазы,
возникающих в единицу времени в единице объема (скорость зарождения v),
определяется частотой со, с которой происходит присоединение
атомов к критическим зародышам:
v=coN (7.8)
3 кр
Отметим, что термодинамический подход при описании
фазовых превращений не является всесторонним и исчерпывающим.
Не всегда термодинамические расчеты соответствуют результатам
эксперимента. Основные причины этого в следующем:
1. Выводы термодинамической теории справедливы только при
малых отклонениях от состояния равновесия.
2. В рамках этой теории трудно учесть флуктуации, играющие
решающую роль в образовании зародышей.
3. В сильно неравновесных условиях предпочтительнее идут те
процессы, скорость которых максимальна, а не те, которые обеспечивают
максимальный выигрыш свободной энергии, т.е. кинетика оказывается
более сильнодействующим фактором, чем термодинамика.
Например, при пиролизе метана в присутствии водорода на
подложку осаждается метастабильный алмаз, а не термодинамически
стабильный графит. Согласно правилу Освальда органические
молекулы при диссоциации могут переходить в ближайшее устойчивое
состояние, а не в состояние с наименьшей энергией.
Например, при распаде молекул оксалата никеля может
образовываться металл (Е=75 ккал/моль), а не окисел (Е=56 ккал/моль) [4].
4. Отметим, что поверхностное натяжение является
макрохарактеристикой вещества и неприменимо к зародышам и частицам размером
менее ~ 1 мкм [5]. Это связано с существованием на границе раздела фаз
переходного слоя — ширины межфазной границы толщиной S=o/Ap,
где Ар — разность плотностей фаз. Обычно S«10—100 нм. Поэтому
Аля малых зародышей разделение энергии на объемную и
поверхностную невозможно.
Величина о\ межфазной границы всегда меньше, чем значение об
у новой фазы на границе с вакуумом. Например, на некогерентной
границе кристалл - расплав [6]:
аф = 2/ЗавАУ/У (7.9)
где AV/V — относительное изменение удельного объема при
кристаллизации.
На когерентной границе растущего мартенситного кристалла
поверхностная энергия минимальна (~0,1 <7в).
Для фазовых превращений под давлением характерно
уменьшение скачка удельного объема AV с увеличением давления. Согласно
(7.9) <7 ~AV, следовательно, величина а должна уменьшаться
с давлением так же, как и радиус критического зародыша (соглас-
но (7.5) [7].
Таким образом, мы видим, что действительно при большой
степени неравновесности г -> 0 и этап зарождения исчезает. Роль
зародышей играют определенного вида дислокации в исходной
кристаллической решетке, а рост новой фазы идет за счет движения этих
дислокаций и направленного сдвига исходной решетки.
Кинетика сдвиговой деформации описывается уравнением:
1 dr
L™=-bNmV (7.10)
290
где b — вектор Бюргерса, Nm — плотность подвижных
дислокаций, v — их средняя скорость, которая зависит от сдвигового
напряжения т следующим образом:
v = с, exp(-const 1т) (7.11)
где ct — сдвиговая скорость звука.
В общем виде скорость увеличения объемного содержания а
новой фазы в образце определяется напряжением сдвига т и
плотностью дислокаций N:
da/dt-rN (7.12)
где величины т и N зависят от скорости деформации или от dp/dt
на фронте УВ.
Если превращение идет под давлением в веществе, сжатом
на Ь = v0/v, то b = b0 S"1/3 и Nm = N0S2/3, где bQ, NQ относятся к
исходному несжатому единичному объему.
С учетом размножения дислокаций при их движении аля
плотности дислокаций N можно записать:
' N = Nw-cAds (7.13)
где N^ — начальная плотность дислокаций, а величина а > 0
характеризует скорость размножения дислокаций.
Если при умеренном давлении ударного сжатия (до ~ 10 ГПа)
создаются достаточно большие неравновесности АФ, то вероятен
мартенситный механизм.
Отметим некоторые характерные особенности мартенситных
превращений (МП), обнаруженные металловедами при изучении
МП у металлов и сплавов [8]:
— минимальное перемещение атомов (доли межатомных
расстояний); превращение идет за счет упорядоченных сдвигов
определенных плоскостей кристаллической решетки; в свою
очередь сдвиги осуществляются движением определенного вида
дислокаций;
— строгая взаимная ориентировка и сопряженность фаз;
— когерентность межфазовых границ с минимальной
поверхностной энергией; срыв когерентности останавливает МП;
— большой гистерезис превращения (Фм);
— МП протекает в определенном диапазоне температур: при
высоких температурах МП подавляется конкурирующими ре-
кристаллизационными процессами или диффузионным
превращением, а при очень низких температурах АФ мало, а Е
велико, и МП «замораживается»;
— ограниченность степени превращения в условиях
постоянства неравновесности (при ДФ=Сош1:); увеличить количество
мартенситной фазы можно только за счет такого изменения
условий МП, при котором АФ возрастает;
— активирующая роль сдвиговых напряжений и малых
пластических деформаций, уменьшающих гистерезис;
— затруднение МП при больших деформациях,
увеличивающих дефектность кристалла;
— невозможность МП в очень дефектных или несовершенных
кристаллах, в аморфных материалах;
— Аая кристаллов, полученных в результате МП, характерна
высокая дефектность и пластинчатая форма с поверхностным
рельефом (равновесная форма мартенситного кристалла —
двояковыпуклая линза);
— размер мартенситных кристаллов всегда меньше размера
кристалла исходной фазы, поскольку МП происходит внутри
кристалла или внутри монокристаллического блока
поликристалла. В результате МП исходная кристаллическая структура
измельчается (отсюда упрочнение материала после МП).
На основе этих особенностей МП можно предложить
следующие рекомендации ^ая получения максимальной степени МП
в условиях ударного сжатия:
— использование достаточно совершенных кристаллов с
минимальной плотностью дислокаций;
— использование устройств, обеспечивающих многократное
ударное сжатие с целью увеличения термодинамического
стимула МП (А Ф) в каждой последующей УВ;
292
— ограничение амплитуды ударных волн и начальной
пористости сжимаемого образца, связанные с необходимостью
сохранения только одного семейства плоскостей сдвига &ая МП
и с ограничением скорости сдвига (локальной температуры).
При больших амплитудах УВ и пористости сдвиги возникают
в нескольких пересекающихся плоскостях, решетка разрушается,
температура поднимается выше температуры рекристаллизации,
и МП заменяется диффузионным превращением с другой более
медленной кинетикой (вместо кооперативного сдвига переход
« атом за атомом »);
— с целью сохранения решетки при высоких ударных
давлениях осуществлять ударное сжатие исходных кристаллов в смеси
с другим менее прочным веществом (жидкостью, например).
7.2. Особенности полиморфных превращений
в ударных волнах
Особенности распространения ударных волн в веществах,
претерпевающих превращения с уменьшением объема, рассмотрены
многими авторами, например, в работах [9-21].
Рис.7.3. Ударное сжатие вещества с полиморфным переходом
a) p,v - диаграмма; б) Профиль давления при сжатии и разгрузке (рА < р < рт);
в) Изменение скорости звука
293
Перестройка кристаллической решетки при ударном сжатии
прежде всего отражается на виде ударной адиабаты, поскольку
исходная фаза и новая более плотная фаза имеют различную
сжимаемость (рис. 7.3).
На рис. 7.3а ОА — ударная адиабата исходной фазы. В точке А
начинается перестройка кристаллической решетки с образованием
новой более плотной фазы. АВ — смесевой участок адиабаты, на
котором идет перестройка исходной решетки и увеличивается
количество новой фазы. За счет перехода объем уменьшается быстрее и
требует меньшего давления в сравнении с обычным сжатием, поэтому
смесевой участок более пологий, но не горизонтальный, т.к. теплота
превращения q ^ 0.
В точке В превращение заканчивается. ВМт4 — адиабата
новой фазы. В любой промежуточной точке между А и В состав
термодинамически неравновесной смеси двух модификаций может
быть найден по «правилу рычага» отношением, в котором данная
точка делит расстояние между адиабатами первой и второй фаз.
Если провести прямую ОАт, то выше точки m образец
сжимается одной волной, особенность которой состоит в увеличенной
длительности фронта («завале» фронта) на время, требуемое для
фазового превращения (обычно это доли микросекунды). Вначале
ударное сжатие исходной фазы приводит к промежуточному
состоянию М на экстраполированной ударной адиабате исходной
фазы (без фазового перехода). Например, в КС1 и КВг ,
испытывающих превращение при 20 кбар [14], метастабильная исходная
фаза при 100 кбар существует в течение времени порядка Ю-11—
10'12 с [17].
Затем на фронте УВ начинается переход, переводящий вещество
из точки М в точку М1 на адиабате плотной фазы. Для
промежуточных давлений в интервале рА < р < рт происходит расщепление
ударной волны на две независимые волны, поскольку наклон прямой An
меньше, чем у прямой ОА, следовательно, скорость волны с
давлением рА больше, чем у волны с давлением рп.
В первой волне вещество сжимается до давления рА,
соответствующего началу фазового перехода. Скорость первой волны:
294
Рл-Ро
A=v0l£-£L (7.14)
V -V
'О Y А
За первой волной следует вторая, в которой вещество сжимается
от давления рА до давления рп со скоростью
°2ЫкГ^ (7Л5)
Скорость D2° второй волны относительно наподвижной
исходной фазы будет больше D2 на величину массовой скорости UA
в первой волне:
D2°=D2+UA (7.16)
Всегда D2 > D2 и со временем по мере движения по образцу вторая
волна все больше отстает от первой волны. Поскольку фазовое
превращение происходит во второй волне за конечное время, то фронт второй
волны сильно размыт в отличие от первой волны (см. рис. 7.3 б).
Признаком фазового превращения является излом или разрыв
линейных D-u соотношений, т.к. сжимаемость фаз различна, и
каждая фаза имеет свой наклон D-u зависимости [12].
В р, v — координатах точка В обычно плохо фиксируется, и сме-
севой участок плавно переходит в амплитуду плотной фазы.
Разгрузка вещества с фазовым переходом может проходить по
двум вариантам.
1. При полном сохранении фазы высокого давления в метаста-
бильном состоянии (превращение необратимо) происходит
разгрузка по изэнтропе плотной фазы (кривая mnl на рис. 7.3а). При
неполном сохранении плотной фазы конечное состояние
располагается правее точки L. Пример — нитрид бора BN.
2. Если при снижении давления происходит обратная
перекристаллизация в исходную фазу (превращение обратимо), то изэнтропа
расширения имеет излом, и появляются ударные волны разрежения
[9]. Сначала разгрузка идет по изэнтропе плотной фазы до точки п
(см. рис. 7.36). Затем давление скачкообразно снижается в ударной
волне разрежения от точки п до точки 2\ и далее разгрузка идет по
изэнтропе исходной фазы в точку К. Примеры: железо, олово,
висмут, КС1,
Возникновение ударных волн разрежения связано с аномальным
ходом ударной адиабаты в окрестности точки А, где вторая
производная cPp/dV2 отрицательна, хорда, соединяющая какие-либо две
точки адиабаты, целиком лежит ниже адиабаты, а изменение
скорости звука также носит аномальный характер [9]: при снижении
давления в точке А происходит скачкообразный её рост (см. рис. 7.3в).
Как и аая прямого превращения, обратная перекристаллизация
в исходную фазу также имеет гистерезис, т.е. превращение
начинается при давлениях, отличающихся от равновесного давления рд. На
рис. 7.3а дана идеальная схема без гистерезиса, а реально обратное
превращение начинается не в точке п , а ниже, при давлениях р<рА-
Если аля прямого перехода время превращения (ширина
фронта УВ) уменьшается с ростом давления сжатия, то ширина фронта
ударной волны разрежения, характеризующая время обратного
превращения, постоянна (обычно меньше 0,2 мкс).
Расщепление У В на две волны в интервале рА<р<рм не
происходит, если вещество испытывает быстрое мартенситное превращение
на фронте УВ в течение короткого времени существования
касательных напряжений. В этом случае участок адиабаты, соответствующий
смеси двух фаз, будет представлять собой отрезок волнового луча
ОАт с наклоном, равным минимальной скорости ударной волны
Аля начала превращения в точке А.
Поскольку мартенситное превращение всегда неполное, то
непосредственно за фронтом превращение продолжается, но уже в
условиях гидростатического давления и по другому, более медленному
механизму. В этом случае фронт УВ имеет два различных участка:
малой длительности до давления мартенситного превращения рм,
а выше — значительно более длительный «затянутый» участок.
Такая структура фронта найдена у кварца в интервале давлений
превращения его в стишовит (23—29 ГПа) [22]. Аналогичный двух-
стадийный процесс наблюдается при превращении графита в алмаз,
судя по скорости увеличения электросопротивления ударносжатого
графита [16].
296
Поскольку аая превращения нужно какое-то конечное время
(обычно в интервале 0,1—1 мкс), то существует зависимость
измеряемых параметров УВ и изэнтропы разгрузки от толщины
образца — т.н. масштабный эффект. При уменьшении толщины образца
уменьшается степень превращения, и регистрируются
неравновесные состояния с увеличенным содержанием метастабильной
исходной фазы.
Превращения протекают с уменьшением удельного объема,
поэтому в веществе, превращающемся в более плотную фазу,
наблюдается более сильное затухание УВ — т.н. «внутренняя или фазовая
разгрузка». Давление уменьшается от точки М на адиабате
метастабильной исходной фазы по изэнтропе до точки М' на адиабате новой
фазы (см. рис. 7.3 а). Аномально сильное затухание УВ в образце
является признаком фазового превращения.
Как следствие «внутренней разгрузки» начальная скорость
превращения da/dt падает по мере распространения волны по образцу
согласно выражению, полученному в [23]:
л pJ3D-A)— -B[l-D2(D + Buy2](^-)L , ч
/fta\ =^oV } dt l v } }KdtJL (7.17)
dth B(V2-Vx)plD2
где a — массовая доля новой фазы; (da/dt) — начальная скорость
превращения в сечении образца на расстоянии L от входа в образец
УВ (т.е. L — текущая толщина образца); А и В — коэффициенты D,
и — соотношения исходной фазы; V{ и V2 — удельные объемы фаз;
р0 — начальная плотность исходной фазы; dD/dt — изменение
скорости УВ по образцу ; (dp/ dt) — изменение давления в сечении L .
Например, согласно [13] начальная скорость превращения
графита в алмаз в сечении L = 2 мм в ~ 5 раз меньше, чем а^я L = 0
(u= 1,78 км/с).
Несмотря на различие в масштабе времени (~ в 10 раз) и в
методах измерений регистрируемые давления фазовых
превращений в статических и динамических условиях вполне сопоставимы
[120]. Это указывает, с одной стороны, на гидростатичность
давления за фронтом УВ, но с другой стороны,говорит о резком уско-
рении не мартенситных превращений в условиях ударного сжатия.
Причинами повышения скорости перестройки кристаллической
решетки за фронтом УВ могут быть следующие факторы.
1. Эффекты, возникающие при очень быстром одноосном
сжатии на фронте УВ. Во-первых, на фронте не успевают возбудиться
все степени свободы атомов в кристалле, поэтому теплоемкость
мала, а, соответственно, неравновесная температура на фронте
высока, во много раз больше равновесной температуры за фронтом.
Во-вторых, быстрые неупорядочные сдвиги на фронте УВ создают
точечные дефекты - междуузельные атомы и вакансии. Эстафетный
механизм перемещения комплексов междуузельных атомов имеет
малую энергию активации (порядка 0,1 эу [123]) и скорость,
близкую к скорости звука. На решающее влияние фронта УВ на фазовое
превращение указывают следующие результаты.
В статических условиях а^я превращения красного фосфора
в черный необходимо давление 8 ГПа без сдвига [24] и 4,5 ГПа со
сдвигом [25], а при ударном сжатии это превращение происходит
при 2,5—3,5 ГПа [26].
Если за счет использования слоеных ударников увеличить
длительность фронта УВ (до 10 мкс и более [27]), то будут резко
снижены градиенты давления и касательные напряжения на фронте. В
результаты получим сжатие, близкое к изэнтропическому. В отличие
от ударного сжатия, в этих условиях не происходит полимеризация
мономера (например, акриламида) и превращение гексагонального
BN в вюрцитный [28].
2. В результате температурной неравновесности и
неоднородности ударного сжатия (особенно пористых образцов) отдельные
микрообъемы нагреваются ударной волной значительно сильнее
среднего (вплоть до плавления) и поэтому имеют более высокие
скорости зарождения и роста.
Например, очень медленный полиморфный переход в NaCl,
обнаруженный в статических условиях при 1,8 ГПа [29],
становится быстрым и фиксируется только при расплавлении NaCl ударной
волной с давлением ~ 170 ГПа [20].
3. С момента образования объемных зародышей новой фазы
среда становится гетерогенной и представляет собой движущую-
298
ся смесь двух фаз различной плотности. Скорость более плотных
частиц новой фазы должна быть меньше скорости исходной фазы,
поэтому может возникать обтекание частиц новой фазы исходной
фазой как вязкой жидкостью. При этом скорость роста должна
возрасти, т.к. к межфазной границе поставляются все новые атомы. Это
явление аналогично скоростной неравновесности (сепарации),
возникающей в ударносжатом порошке, состоящем из смеси легкой и
тяжелой компонент [30,31].
Как меняется характер превращения с ростом давления в УВ?
1. Согласно линейной термодинамики неравновесных состояний
скорость превращения растет с увеличением давления относительно
равновесного давления.
2. Сжимаемость у исходной фазы больше, чем у плотной фазы,
поэтому с давлением скачок удельного объема Av при превращении
уменьшается, следовательно, согласно (7.9) уменьшается удельная
поверхностная энергия <7ф межфазной границы [7].
3. С ростом АФ и уменьшении <7ф уменьшается размер критического
зародыша гкр=<7ф/ДФ, а ширина межфазной границы Ьф=<7ф/Др,
наоборот, растет.
В результате с давлением количество кристаллов новой фазы в
единице объема растет, а объем каждого кристалла падает. В пределе
при гк ->8ф невозможно получить объемные кристаллы, и
превращение получает характер критического перехода.
Экспериментально наблюдается сильное измельчение
кристаллической структуры после полиморфного перехода в УВ
(независимо от того, переход обратимый или необратимый).
Например, такое измельчение зерна в железе после его ударного
сжатия давлением выше 13 ГПа и превращения а-у является
причиной упрочнения железа. Кварц после сжатия УВ с р = 50 ГПа и
перехода в стишовит и обратно становится аморфным — у него исчезают
максимумы на рентгеновских дифрактограммах [32].
Полученные в результате мартенситного превращения
микропорошки лонсдейлита и вюрцитного BN имеют размеры монокристаллов
несколько сотых микрометра [33,34,35], причем кристаллы плоской
формы. Интересно, что алмаз, полученный из сажи не мартенситным
механизмом, имеет размер изометричных кристаллов на порядок боль-
299
ше [34], что можно объяснить меньшей скоростью зарождения в саже,
чем в графите (в саже нет дислокаций), а также большей температурой
сжатия. Причем, размер частиц алмаза превосходят частицы сажи, что
свидетельствует об их спекании под давлением [34].
По-видимому, процесс формирования кристаллов новой фазы при
ударном сжатии может проходить в три последовательные стадии [8,
124,125].
1. Быстрое (< 10"7с) образование на фронте УВ мартенситных или
не мартенситных зародышей (в зависимости от вещества и условий
сжатия).
2. Более медленный (106—10"5 с) не мартенситный рост
кристаллов за фронтом УВ до их смыкания.
3. Еще более медленный (> 10"5 с) рекристаллизационный процесс
спекания образовавшихся монокристаллов в прочные
поликристаллы за счет взаимной подстройки решеток соседних монокристаллов
и формирования малоугольных границ или даже с образованием
более крупных монокристаллов. Эта стадия характерна а^я порошков
и в обычных опытах (t~10~6 с) не успевает завершиться, хотя ее
протекание ускоряется малыми размерами, дефектностью и
напряженным состоянием кристаллов плотной фазы.
Таким образом, существует два уровня масштабного эффекта
ударноволновых превращений: аая второй и аая третьей стадий.
Повышение давления однократного сжатия неизбежно
приводит к плавлению вещества за фронтом УВ. При плавлении
разрушается дальний порядок (решетка), но вблизи линии плавления
(при небольших перегревах жидкой фазы) сохраняется ближний
порядок (координационное число), и он может изменяться с
изменением объема, что проявляется в аномальном ходе ударных
адиабат.
Такие аномалии в области жидкой фазы обнаружены у NaCl, КС1,
КВг [20], которые трактуются как фазовый переход с изменением
координационного числа. При этом высокая подвижность атомов в
жидкой фазе уменьшает время перехода.
Например, при небольшом давлении 2—4 ГПа вода
превращается в лед VII, т.е. замерзает за время 0,1 мкс [36].
300
Перестройка кристаллической решетки под давлением
происходит к более плотным упаковкам атомов с большим числом
соседей в последовательности: неплотная гексагональная (слоистая типа
графита) — объемно-центрированная кубическая (о.ц.к.) — гра-
нецентрированная кубическая (г.ц.к.) или гексагональная плотная
упаковка (г.п.у.).Переходы в обратной последовательности
давлением тормозятся.
Однако существуют переходы со скачком объема, но без
изменения типа решетки. Это т.н. электронные переходы, обусловленные
перестройкой под давлением электронных оболочек атомов —
«вдавливанием» внешних электронов на внутренние незаполненные
d-уровни. При этом резко уменьшается удельное
электросопротивление. Например, такой переход без изменения г.ц.к. решетки имеет
церий при 0,7 ГПа со скачком объема 14%.
Электронные перестройки обнаружены у всех щелочных,
щелочноземельных, редкоземельных и переходных металлов. После
завершения s-d переходов дальнейшее сжатие металлов с ростом давления
описывается гладкими зависимостями (без переходов).
Ионные кристаллы, минералы, горные породы, имеющие
различные исходные структуры, под влиянием давления совершают
переходы первого рода к плотнейшим ионным упаковкам, которые
сохраняются при дальнейшем увеличении давления.
Конечной стадией структурных перестроек у любых веществ
(полупроводников, изоляторов) является металлическое состояние,
наступающее при перекрытий зон (давление уменьшает до нуля
ширину зоны запрещенных энергий). Одновременно с металлизацией
возможна и перестройка решетки.
Например, проводимость всех диэлектриков при давлении
ударного сжатия 50 ГПа возрастает более, чем в 1010 раз, а концентрация
свободных электронов составляет 1018 см'3 [37 — 41].
У кремния, начиная с давления в УВ ~ 15 ГПа образуется
металлическая фаза с большим количеством электронов в зоне
проводимости, что обнаружено по резкому возрастанию коэффициента
отражения лазерного света [42]. Сера также была превращена в металл [43].
В заключение перечислим измерительные методики, которые
используются а^я регистрации фазовых превращений в УВ.
301
1. Измерение кинематических параметров (скоростей) обычным
методом отражения.
2. Измерение амплитуды и профиля УВ манганиновым датчиком.
3. Измерение структуры и давления УВ методом индикаторной
жидкости (с известной зависимостью яркости излучения от давления).
4. Измерение массовой скорости в образце электромагнитным
методом.
5. Измерение скорости свободной поверхности образца
различной толщины электроконтактами, индуктивным датчиком или
лазерным интерферометром.
6. Измерение отражения и преломления света.
7. Измерение электрической проводимости за фронтом УВ.
8. Регистрация рентгеновских дифрактограмм образцов под
давлением УВ.
9. Исследование сохраненных после ударного сжатия образцов
(рентгеноструктурный анализ, электроннооптические
исследования, металлография, дифференциально-термический анализ,
плотность, магнитные свойства, электропроводность и др.).
7.3. Примеры полиморфизма при ударном сжатии
7.3.1. Железо
15 р,ГПа
t, МКС
Рис. 7.4. а) Фазовая диаграмма железа, б) Профиль напряжения в армко-железе (1)
и стали 35ХЗНМ (2). Нагружение ударом А1 пластины со скоростью 2,06 км/с.
302
Обратимое полиморфное превращение (ПП) в УВ
зафиксировано впервые в [44] при р=13 ГПа, а затем подтверждено в
статических условиях по скачку электросопротивления при 13,3 ГПа
[45]. Позднее рентгеноструктурные исследования в статических
условиях показали [46], что это переход а -> е фаз (о.ц.к. % г.п.у.) с
уменьшением объема на 6%. Фазовая диаграмма железа показана на
рис. 7.4а.
Экспериментальным подтверждением перехода с ударными
волнами разрежения является явление гладкого откола [см. разд. 3.3.2].
Вид ударной адиабаты железа показан на рис. 3.6. Превращение идет
с образованием двух УВ. Зарегистрированные манганиновыми
датчиками профили напряжений бх (t) в армко-железе и в прочной
легированной стали 35ХЗНМ показаны на рис. 7.4 [47].
Такая регистрация дает величины напряжений, соответствующих
началу прямого и обратного переходов ос % е, равные соответственно
12,6 и 12,3 ГПа [48], т.е. гистерезис превращения в УВ меньше, чем
в статике (12,6 и 13,3 ГПа).
Ударное нагружение) — Fe (например, стали 12С18Н10Т) не
даёт ПП вплоть до плавления [49].
Полиморфизм железа и стали сказывается на их упрочнении
(измельчение структуры), а также влияет на картину напряжений и
разрушений преград при ударном и взрывном воздействии [50].
7.3.2. Олово
В статических условиях при 25° С в олове наблюдается ПП при
9,4 ГПа. Измеренное манганиновыми датчиками ударное давление
начала ПП составляет 8,9 ГПа (D = 3,37 км/с), а амплитуда ударной
волны разрежения равна ~7,8 ГПа [51]. Наблюдается расщепление
УВ на две волны.
7.3.3. Углерод
Полиморфизм углерода рассмотрим подробнее, поскольку он
является основой промышленного синтеза алмаза и хорошо
изучен.
303
Углерод и его кристаллографический аналог нитрид бора BN имеют
два типа полиморфных модификаций: слоистые малоплотные и мягкие
формы с координационным числом К=3 (графит) и тетраэдрические
а)
б)
р,ГПа
100
50
20
10
5
Г Алмаз
1 ^
Г х
L / Графит
Г i i i i
1 Расплав
р.ГПа
100
80
60
40
20
Алмаз^
[126]
,[65]
\
[37]
1
• L=3,5mm
OL=10mm
'[71]
ч.
о1 ■ ■ ■—u ■ о
1000 2000 3000 4000 5000 Т, К 0,20 0,25 0,30 0,35 0,40 v, см3/г
Рис. 7.5. а) Фазовая диаграмма углерода, б) Ударная адиабата графита и алмаза
метастабильные плотные и сверхтвердые формы с К=4 и решеткой
типа вюрцита (лонсдейлит) или сфалерита (алмаз).
Вюрцитная форма является низкотемпературной метастабиль-
ной фазой высокого давления. Превращения графит -> лонсдейлит и
BN. -> BNb происходят только при низких температурах (до 1200—
1400 С) [52,53,54] и по мартенситному механизму [35].
При низких давлениях вблизи линии равновесия в результате
каталитического синтеза образуются только алмаз и BN,. Обратные
превращения алмаз -> лонсдейлит и BN -> BNb не происходят даже в
присутствии жидкой фазы [54]. Все эти факты доказывают метаста-
бильность вюрцитной формы.
Фазовая диаграмма углерода и ударная адиабата графита
показаны на рис. 7.5. Расчетные методики определения положения линий
фазового равновесия и линий гистерезиса термически
активируемых полиморфных превращений изложены в [55,56].
Кристаллохимические характеристики модификаций углерода
и нитрида бора даны в таблице 7.1 [35].
304
Таблица 7.1. Кристаллохимические характеристики полиморфных
модифиций углерода и нитрида бора
Полиморфная
модификация
Графит
гексагональн.
Графит
ромбоэдрич.
BNr
BNp
Алмаз
Лонсдейлит
BNb
ВЫсф
К
3
3
3
3
4
4
4
4
Пространст
группа
p63/mmc
R3m
p63/mmc
R3m
Fd3m
p63/mmc
p63/mmc
Fd3m
Чередован,
слоев
ABAB....
ABCABC...
A AAA...
ABCABC...
aa bb cc...
aa bb aa...
aa bb aa...
aa bb cc...
Параметры решетки A
а с
2,4611
2,46
2,5040
2,504
3,567
2,516
2,550
3,615
6,7076
10,05
6,6612
10,01
-
4,18
4,230
-
P
г/см3
2,267
2,26
2,279
2,275
3,512
3,478
3,460
3,492
Если говорить о перестройке атомных связей, то &ая ПП
необходимо превратить sp2 — гибридные электронные орбитали атомов
углерода в графите в sp3 — гибриды в алмазе, изменить
межатомные расстояния 1,42А в слоях и 3,55 А между слоями графита на 1,54
А в алмазе, изменить углы химических связей между атомами в
решетке с 120° в слоях графита на тетраэдрическую систему с
центральным углом 109,5° в алмазе.
Геометрически /^ля перестройки решетки графита в алмаз
необходимо сжать графит вдоль оси с, упорядоченными сдвигами слоев
изменить их чередование АВАВ... на ABCABC... и гофрировать слои
графита (путем смещения атомов из плоскости слоя).
Предложенная в [57] схема превращения графита в лонсдейлит
предусматривает образование промежуточной структуры с
чередованием слоев АДАД... (слой Д смещен на 1/4 большой диагонали
гексагона графита), сжатие ее по оси с и продольный изгиб слоев
(001) графита, переходящих в плоскости (100) лонсдейлита.
Структурные механизмы ПП в углероде и BN рассмотрены в [35].
Модель диффузионного ПП графит—алмаз с помощью движения
комплексов вакансий и междуузельных атомов предложена в [58].
Превращения графит -> лонсдейлит и графит— алмаз
зафиксированы как в статических, так и в динамических условиях. В опытах
305
Р. Венторфа [59] прямое (без катализаторов) ПП графита в алмаз
наблюдалось прир= 11,5—17,5 ГПаи Т= 1500—2500 К, причем а^я
Т=1500 К нужна была выдержка около часа при р = 15 ГПа, и
синтезировалась смесь лонсдейлита и алмаза, а аая Т = 2500 К было
достаточно нескольких минут, и синтезировался только алмаз.
Условия ПП в опытах Ф. Банди [60]: р= 12 ГПа,Т=3000—4100 К.
Первая работа, в которой по виду ударной адиабаты обнаружено
ПП графита, была опубликована в 1961 г. [61]. Перечень работ,
выполненных до 1976 г. по исследованию ударного сжатия различных
видов графита, приведен в [62].
ПП графита в УВ практически полностью обратимо, т.к.
содержание плотных фаз в ударносжатых и сохраненных образцах чистого
графита не превышает 1—2%. Обратный переход ускоряется сдвиговыми
деформациями в волне разгрузки, высокими остаточными
температурами, дисперсностью и дефектностью получаемых плотных фаз.
В [63,64] кинетика ПП изучалась с помощью манганиновых
датчиков, которые более информативны, чем волновые измерения. Дело
в том. что на ударной адиабате графита (см. рис. 7.56 [65]) нет
закрытых участков, в области смеси фаз адиабата идет круче волновой
прямой Михельсона (ОАт на рис.7.3а), поэтому две волны не могут
возникнуть [66,67,68],что затрудняет фиксацию начала ПП.
Двухволновую конфигурацию удается наблюдать
манганиновыми датчиками методом ступенчатого сжатия [64]. Сначала вещество
сжимается прямой УВ до давления ниже точки А, а затем — второй
УВ, отраженной от тяжелого экрана (например, медного). Эта
отраженная волна уже как обычно расщепляется на две волны,
Таким методом найдена следующая зависимость давления начала
перехода от начальной температуры графита [64]:
ГС -196 +20 +300
рГПа 23,3+1 19,6 ±0,5 17,5 ±1
Уменьшение давления начала ПП (рА) с ростом температуры
получено в результате термодинамических расчетов [7], т.к. с
температурой растет движущая сила превращения АФ. Меньшая величина
306
рА у пористого графита также может быть объяснена повышенной
температурой его ударного сжатия.
О начале превращения в веществе судят также по
аномальному затуханию скоростей УВ и свободной поверхности образцов
[13,14,69,70].
Полученные разными авторами на различных марках графита
величины давления начала превращения сильно отличаются.
Так, искусственный пиролитический графит имеет излом
ударной адиабаты при 42 ГПа [66], при 34 ГПа [67], а в [71] до 50 ГПа не
обнаружено изменения наклона адиабаты. Для марок природного
графита (цейлонский, тайгинский, завальевский) диапазон
критических давлений составляет 18—25 ГПа [13,64 - 67,72,61].
Можно назвать следующие причины такого большого разброса
экспериментальных данных.
I. Прежде всего, это различие в кристаллическом строении
различных видов графита. Отсюда различие в сжимаемости ( [7],см.
табл. 2.2), температуре сжатия и кинетике ПП.
Природный графит имеет совершенную кристаллическую решетку
с законом упаковки плоских слабо связанных слоев типа АВАВ Сдвиг
слоев под небольшим давлением (движением частичных дислокаций в
плоскости (001) с вектором Бюргерса b = 1 /3) приводит к образованию
дефектов упаковки с «алмазным» чередованием слоев ABC ABC... т.е. к
образованию ромбоэдрического графита.
Гексагональный и ромбоэдрический графиты отличаются лишь
укладкой слоев и являются простейшими политипами —
двухслойным и трехслойным.
В природных графитах содержится до 30% ромбоэдрической
модификации, которая может быть превращена в алмаз бездиффузион-
но, простым сжатием (без сдвигов) вдоль оси с с гофрировкой слоев.
На основании структурных исследований продуктов
статического и ударного сжатия совершенного графита в [35] показано, что
перестройка графита в алмаз осуществляется по мартенситному
механизму в две стадии через образование лонсдейлита как
промежуточной структуры.
Для несовершенного графита с дефектами упаковки слоев типа
АА—ВВ и для сажи такой мартенситный механизм невозможен,
307
и происходит высокотемпературное (> 2000 К) диффузионное
превращение за счет перемещений междуузельных атомов и вакансий
[58]. Требуемый нагрев при ударном сжатии обеспечивается более
высокими давлениями в УВ или повышенной пористостью графита.
Таким образом, в углеграфитовых материалах могут
происходить:
— мартенситные превращения в лонсдейлит и алмаз при
ударном сжатии совершенного непористого графита умеренными
давлениями, не разрушающими решетку (< 40 ГПа, < 1400 С);
— диффузионное превращение любого вида графита и сажи
при сильном ударном сжатии (> 40 ГПа, > 2000 С). Начальная
пористость, увеличивая температуру, снижает требуемое
давление (сажа — пористая структура).
Все названные случаи сведены в табл. 7.2.
Таблица 7.2. Условия и механизмы полиморфного превращения в УВ
различных видов графита
NN
1.
2.
3.
Исходная форма
углерода
Несовершенный графит
с дефектной упаковкой
слоев и сажа
Совершенный
гексагональный графит
Совершенный
гексагональный графит
Условия
ударного
сжатия
> 40 ГПа
>2000 С
18-40 ГПа
<1400 С
18-40 ГПа
<1400 С
Механизм
Превращения
Диффузионный
за счет движения
Комплексов
междуузельных атомов и
вакансий
Мартенситный:
образование
чередования АДАД,
сжатие вдоль оси с
и продольный изгиб
слоев (001)
Мартенситный:
а) сжатие по оси с,
сдвиги слоев в
положение АВСАВС и
гофрировка слоев;
б) из лонсдейлита
Плотная
Фаза
Алмаз
Лонсдейлит
Алмаз
308
4.
5.
Ромбоэдрический графит
Совершенный
гексагональный графит
18-40ГПа
< 1400 С
>40ГПа
> 2000 С
Мартенситный:
Сжатие вдоль оси с и
гофрировка слоев
Диффузионный
по схеме п.1 с
предварительным
разрушением решетки на
фронте сильной УВ
Алмаз
Алмаз
В реальном графите присутствуют кристаллы с разной степенью
трехмерной упорядоченности (р3), поэтому возможно превращение
одновременно по двум механизмам с образованием и лонсдейлита, и
алмаза. Проиллюстрируем это двумя примерами.
1. В табл. 7.3 приведен фазовый состав продуктов, полученных
в результате ПП при ударном сжатии в одинаковых условиях [73]
различных углеграфитовых материалов с различной величиной
Р,[34].
Таблица 7.3. Результаты превращения в УВ различных
углеграфитовых материалов (УГМ)
Исходные
УГМ
Графит С-1
То же, отжиг
Графит ГЭ-4
То же, отжиг
СажаПМ-15
Характеристика
исходных УГМ
степень
трехмерной
упорядоченности р3
0,90
0,95
0,95
0,97
0
содержание
ромбоэдрической фазы,
%
30
6
и
1
0
Характеристика фазовых
Превращений
Выход
плотных
фаз
%
40
30
20
14
55
Содержание
Лонсдейлита
%
40
35
22
17
0
Из табл. 7.3 видно, что степень превращения у сажи выше, чем у
графита. Выход плотных фаз растет с увеличением содержания в графите
ромбоэдрической модификации. Чем больше выход плотных фаз, тем
выше содержание в них лонсдейлита, что соответствует условиям
опытов (низкотемпературное сжатие графита двумя УВ до р ~ 30 ГПа).
309
2. За счет легкосжимаемых добавок в [74,75] изменялась
температура сжатия графита и сажи при одинаковом давлении 30 ГПа.
Результаты опытов приведены в табл.7.4, из которой видно, что с
ростом температуры у сажи степень превращения в алмаз растет
при полном отсутствии лонсдейлита, а у высококристаллического
графита содержание лонсдейлита в получаемой плотной фазе
падает.
Уменьшение выхода плотных фаз из графита при 4200К
объясняется графитизацией высокодисперсного лонсдейлита (размер
частиц ~ 0,01мкм) под действием высоких остаточных температур.
Таблица 7.4. Влияние температуры на фазовые превращения графита
и сажи при ударном сжатии
Исходные
УГМ
Графит С-1
СажаП-803
Температура К
ударного сжатия
1600
3600
4200
1600
3600
4200
Выход плотных
фаз, %
30
40
40
30
55
75
Содержание
лонсдейлита, %
40
30
IS
0
0
0
II. Вторая причина разброса экспериментальных результатов -
масштабный эффект, т.е. зависимость степени превращения от
толщины образца, а разные авторы использовали в опытах различные
толщины образцов.
Быстрое мартенситное превращение на фронте УВ дает не
полное превращение, которое продолжается за фронтом УВ, но уже по
более медленному диффузионному механизму [16]. Эта вторая часть
превращения и зависит от толщины образца.
С ростом давления в УВ решетка разрушается, температура
растет, что подавляет мартенситное превращение и, наоборот, ускоряет
диффузионное.Такая смена кинетики должна сказываться на ходе
ударной адиабаты.
Еще в первой работе по превращению графита в УВ [61] была
отмечена зависимость скорости свободной поверхности w от толщины
образца L. Зависимость w (L) у графита и BN измерена в работах [69,14].
310
,ГПа
4 L, мм
,км/с
0 2
—f—i—
4
(Эо/Эс)Ц
8-
4-
о
L, мм i
МКС 1
\
\
°\
\
\
ч
о ч
ч
«ч о
1 1 1
3 1 2 L, мм
Рис. 7.6. Зависимости от толщины L образца природного графита
а) максимального давления на границе графит—бромоформ; б) мгновенных
скоростей УВ; в) начальной скорости превращения (расчет по (7.17)).
Массовая скорость в экране из алюминия и = 1,78 км/с.
Затухание скорости УВ D (х) в образце толщиной 10 мм при
р ~ 80 ГПа измерено в [70], что свидетельствует о продолжении ПП
за фронтом УВ даже при таком
высоком давлении.
Таким образом, все полученные
в опытах ударные адиабаты
графита не характеризуют равновесное
состояние, и экспериментальные
точки в р, v — координатах лежат
правее ударной адиабаты алмаза
(см. рис. 7.56). При увеличении
толщины образцов (базы
измерения) экспериментальные точки
приближаются к адиабате алмаза, а
при малых толщинах — к метаста-
бильному участку адиабаты
графита (см. рис. 7.5б).
На рис. 7.6 приведены
экспериментальные данные по
затуханию УВ в природном графите
(р= 2,03—2,08 г/см3) в зоне ПП
W,
6 -
5 -
4
км/с
о ^
У
/ 1
1
1
—г"-"
л1°
•Л
1
2
-т
4 L* 8
L, мм
Рис 7.7. Зависимость скорости
свободной поверхности образца
графита от его толщины
о — эксперимент [69]; 1 — расчет для
быстрого ПП с t^=0,09 мкс; 2 —
расчет для медленного ПП с t^=0,4 мкс;
3—расчет для «замороженного» ПП
ct->oo Излом кривых при L*
соответствует приходу разгрузки со стороны
ударника
(измерения яркости свечения индикаторной жидкости на границе
с графитом). По этим данным рассчитано по (7.17) падение скоро-
311
а) б)
D, км/с р, ГПа
Рис. 7.8. Ударные адиабаты ароматических углеводородов
1 — толуол; 2 — бензол; 3 — стирол; 4 — анилин; 5 — нитробензол; 6 — ТНТ;
7 — графит.
а) Цифры слева указывают величины сдвига по D в км/с.
б) Адиабаты стирола, анилина и нитробензола сдвинуты соответственно на 0,5;
1,0 и 1,0 г/см3.
сти превращения по мере движения УВ по образцу графита (см. рис.
7.6в), а также найдено, что в графите ПП начинается при 20 ГПа
[14].
Сравнение расчетных [70] и экспериментальных [69] данных по
измерению скорости свободной поверхности образца графита от его
толщины w (L) позволило оценить характерное время превращения
в графите. Оно находится в диапазоне 0,09—0,4 мкс или в среднем
~ 0,2 мкс (см. рис. 7.7).
Интересно, что у ароматических углеводородов (с кольцевой
связью между атомами углерода) ударные адиабаты имеют разрывы
со скачком плотности при давлении 19—20 ГПа, равном давлению
начала ПП у графита (см.рис.7.8), а углеводороды с линейными
молекулами таких разрывов не имеют [75,76].
Разрывы соответствуют химическому разложению углеводородов в
УВ, но при этом сохраняются бензольные кольца (шестигранники как
у графитовых слоев), поскольку в условиях разрьшов энергия УВ~500
кдж/моль, а энергия связи атомов в бензольном кольце на порядок
больше. Поэтому при разложении ароматических углеводородов выделяю-
312
щийся углерод конденсируется в виде ультрадисперсного алмаза, но не
по одному атому, а блоками-шестигранниками.
Такая же картина наблюдается и при детонационном
разложении ТНТ с начальной плотностью ро > 1,6 г/см3 [76].
7.3.4. Нитрид бора
Фазовая диаграмма [77] и ударная адиабата нитрида бора [14]
б)
юк;
1зань
р,.ГПа
15
10
5
0
**»
>i на рис. 7.9.
а)
р, Мбар
U 3
I
BN /BNL \о-
**-.1 з/ I 2
^4/ / 1
>>2 ♦' /BN /
/ / 7
. / / . / Q
1000 2000 3000 0
4
1
\
\
\
3V
5
Ч.
1
0
0,20 0,25 0,35
0,45
Рис. 7.9. Фазовая диаграмма (а) и ударная адиабата (б) нитрида бора
а) Линия гистерезиса: 1,2 — для BNb, 3,4 — для BNc<|>.
б) 0 — исходное состояние пористых образцов; 013 — линия постоянной
скорости УВ D=4,65 км/с; 34 — адиабата плотных фаз; 15 — участок адиабаты
метастабилбного BN г; — состояния для образцов толщиной L=4 мм; — то же
для L = 10 мм
Кристаллографическая аналогия и близость термодинамических
свойств углерода и нитрида бора обусловливают подобие фазовых
диаграмм, но а^я BN все величины давления и температуры
меньше. Аналогично углероду существуют два вида плотных фаз:
низкотемпературная метастабильная вюрцитная (BNJ и
высокотемпературная сфалеритная (BN ). Превращение BN,—>BNb проходит
по мартенситному механизму (в совершенном BNr), а превращение
BNp—►BN. диффузионное.
Для прямого превращения BNp->BN в статических условиях
требуется 6—7 ГПа [54], а при ударном сжатии — 12 ГПа [ 12]. В интервале
8 L, мм
Рис. 7.10. Зависимость скорости
свободной поверхности нитрида бора
от толщины L образца (р ~ 45 ГПа)
12— 19 ГПа скорость УВ
постоянна (~ 4,65 км/с),что
свидетельствует о двухволновой
конфигурации УВ при этих давлениях.
В интервале 19—90 ГПа
экспериментальные точки лежат
правее ударной адиабаты BN,, что
свидетельствует о
незавершенности превращения в условиях
опытов (аля толщины образца
4 мм и базы измерения или пути
УВ, равной 2 мм). Возможно, в
этом интервале давлений идет
неполное превращение в BNb по мартенситному механизму.
При давлениях р > 100 ГПа скорость ПП возрастает, и
экспериментальные точки ложатся на адиабату BNc(j) (см. рис. 7.96).
Следовательно, при высоких давлениях времена ПП столь малы,
что на глубине 2 мм образца превращение успевает завершиться.
Как и &ая графита, увеличение толщины образца до 10 мм
приближает точки к адиабате BN. (см. рис. 7.9б).
Вследствие фазовой разгрузки, обусловленной ПП с
уменьшением объема, скорость свободной
BN->.% поверхности W падает с
толщиной L образца (см. рис. 7.10).
В отличие от графита
нитрид бора имеет высокую
степень необратимости
превращения (при р= 12—20 ГПа
сохраняется до 70—80%
плотных фаз [74,78,79], из них не
более 10% BN ф [78]), о чем также
свидетельствует отсутствие при
разгрузке ударной волны
разрежения [14]. Возможно,
причина большей необратимости —
-196 0
Рис. 7.11. Выход BNb в зависимости
от начальной температуры
х — ударное сжатие, о — квазиизэнтро-
пическое сжатие
314
в большей, чем у алмаза, термостойкости BNb и BN и в меньшей
остаточной температуре.
Полученные в [78] экспериментальные результаты влияния на
выход плотных фаз BN начальной плотности сохраняемых образцов,
начальной температуры и давления ударного сжатия представлены в
табл. 7.5.
Условия опытов: многократное сжатие ударными волнами за ~1
мкс до максимальных давлений, указанных в табл.7.5, в плоских
ампулах сохранения; толщина образцов 1—1,5 мм; время выдержки
под давлением 5—7 мкс; разгрузка за ~ 2 мкс.
Из данных табл. 7.5 видно, что с ростом пористости и начальной
температуры выход плотных фаз падает (по-видимому, из-за
влияния высоких остаточных температур). Основной получаемой фазой
является вюрцитная. С увеличением давления и температуры
ударного сжатия увеличивается содержание сфалеритной фазы.
В [79] сравнивалось ПП нитрида бора при ударном и квазиизэн-
тропическом сжатии образцов с L = 2 мм в ампулах сохранения до
давления 20 ГПа. Квазиизэнтропическое сжатие с сильно затянутом
по времени фронтом УВ и поэтому с уменьшенной температурой на
фронте достигалось за счет применения составных ударников
(оргстекло, алюминий, медь). Вюрцитная форма в этом случае не
образовывалась (см. рис. 7.11) в интервале начальных температур 77—
293 К. Однако предварительный нагрев образцов всего до 150 С
обеспечивал ПП BNr -> BNb и в условиях ДИС. Увеличение нагрева
выше ~ 350° С снижал выход BNb (см. рис. 7.11).
Таблица 7.5. Результаты фазового анализа сохраненных после ударного
сжатия образцов нитрида бора [78]
Начальная
плотность,
г/.см3
1,98
1,98
1,98
1,98
Начальная
температ.,
К
300
300
300
300
Давление
р, кбар
500
350
200
Температ.
ударного
сжатия, К
1400
1300
1200
650
Количество
алмазной
модифик.%
.10
_8_
_8_
8
Количест.
вюрцит-
ной
модиф. %
64
63
73
68
Начальная
плотность,
г/.см3
0,8
0,8
0,8
0,8
1,98
1,98
1,98
1,98
0,8 + 1,98
1,98
Начальная
температ.,
К
300
300
300
300
800
800
800
800
300
120
Давление
р, кбар
500
350
200
120
500
350
200
120
< 100
350
Температ.
ударного
сжатия, К
1900
1500
1350
850
2100
1800
1400
1300
-
-
Количество
алмазной
модифик.%
16
14
11
7
11
13
10
10
0
10
Количест.
вюрцит-
ной
модиф. %
52
56
53
63
36
37
30
50
0
65
хк
1300
900
500
Эти опыты доказали, что
мартенситное превращение
BNr -> BNb может происходить
и без сильных
микросдвиговых деформаций на фронте
УВ и является термически
активируемым процессом.
В [74,80] исследовано
влияние на ПП в нитриде бора
степени его трехмерной
упорядоченности р3. Во всех
опытах ударное сжатие
проводилось в одинаковых условиях до
давления 30 ГПа и
температуре сжатия ~ 3600 К. Менялся
только исходный BNp.
Полученные результаты даны в табл. 7.6, из которой видно, что
уменьшение упорядоченности структуры исходного BNb приводит
к замене мартенситного превращения BN -> BNb на диффузионное
превращение BNp->BN . Благодаря высокой температуре сжатия и
Рис. 7.12. Диаграмма зависимости
фазовых превращений BNr от совершенства
его структуры (величина р3)
начало ПП—50% ПП.
316
резкому охлаждению после разгрузки из турбостратного BN, (р3= О,
размер зерна 0,01 мкм) впервые удалось получить очень высокую
степень превращения в BN (50%).
Таблица 7.6. Влияние совершенства кристаллов исходного BNr на его
фазовое превращение в УВ.
Степень трехмерной
упорядоченности BNr, р
0,95
0,60
0,40
0,13
0,15
0
вкв+вксф
%мас.
70
60
10
9
10
50
BN„
%мас.
70
55
5
2
следы
0
BNA
сф
%мас.
0
5
5
7
10
50
Эти результаты согласуются с данными по ПП BNr с различной
величиной р3 в статических условиях [35,81].
На рис. 7.12 показана диаграмма фазовых превращений BNr в
зависимости от температуры и величины р при статическом давлении
11Гпа[81].
Диффузионное превращение турбостратного BNr (р3=0, зерно
0,01 мкм) в BN, начинается при 500° С и заканчивается при 1200° С.
Столь низкие температуры обусловлены исключительно высокой
дисперсностью исходной структуры.
Высококристаллический BNr (р3 = 1, зерно 5 мкм) испытывает мар-
тенситное превращение в BNb уже при комнатной температуре, и
скорость ПП с температурой растет. В BNp с промежуточной структурой
(р3=0,6, зерно 0,25 мкм) образуются обе модификации — BNb и BN ,
причем температура превращения максимальна, т.к. дефекты в
кристаллах BNp препятствуют развитию мартенситного ПП, а большой размер
зерна не обеспечивает столь большую скорость ПП, как в BNp с
ультрадисперсным зерном.
7.3.5. Кремний
Полиморфизм кремния в области высоких давлений весьма
многообразен. Исходная алмазоподобная фаза Si I переходит в фазу
Si II (типа P-Sn) при 8—12 ГПа. При снятии статического давления
Si II переходит в Si III с объёмноцентрированной кубической
решёткой, которая при нагреве до 200—600° С преобразуется в фазу Si IV
с гексагональной структурой.
При 16 ГПа наблюдается переход Si II-Si V с простой
гексагональной решёткой, которая при 40 ГПа преобразуется в структуру
с гексагональной упаковкой.
При сжатии ударной волной переход Si I-Si II даёт классическую
двухволновую картину [82]. Переход обратимый, т.к. в сохранённых
образцах нет новых фаз.
В упругопластической волне при 3,5—6 ГПа резко
увеличивается электропроводность (в 30—50 раз).
Металлизация кремния в ударной волне изучена в [42] по
измерению коэффициента отражения лазерного излучения от ударносжатого
монокристалла кремния р-типа. Коэффициент отражения резко
возрастает при появлении в зоне проводимости свободных электронов.
При 15—18 ГПа зафиксирован резкий скачок коэффициента
отражения с ~ 30% до ~ 80%, характерных fi^ металлов.
Таким образом, начиная с 15 ГПа, в кремнии образуется
металлическая фаза (возможно, Si II или Si V), которая после разгрузки
переходит в метастабильную фазу также с высокой
электропроводностью (возможно, Si III или Si IV).
7.3.6. Двуокись кремния
Изучение полиморфизма двуокиси кремния Si02 (кварца,
кварцита, глинозема) имеет особый интерес ^ая геофизики,
поскольку это соединение является главной составляющей мантии
Земли [83].
У кварца (p=2,65 г/см3) в условиях статического давления
найдено две высокоплотные модификации, устойчивые при нормальных
условиях: коэсит (р = 3,01 г/см3) и стишовит (р = 4,3 г/см3) [84,85].
Затем переход кварц-стишовит был обнаружен и в условиях
ударного сжатия [86,87].
Эти открытия объясняют ход р-р диаграммы Земли [88] с
резким возрастанием плотности вещества мантии в области слоев В
318
р>к(
юоо
500
0 3 4 5 р,г/см3
Рис. 7.13. Ударные адиабаты Si02 с различной начальной плотностью
1 — кварц; 2 — коэсит; *— начало перехода коэсит-стишовит
и С. Величина гистерезиса перехода кварц-стишовит в УВ
значительно больше, чем в статике — 12—14 ГПа вместо 5 ГПа. Еще
больше различие у перехода коэсит-стишовит — 30 ГПа вместо 6 ГПа.
Характерные времена переходов в УВ на 10 порядков меньше, чем
в статике.
фарная сжимаемость кварца и кварцита исследована в
абсолютных измерениях до 650 ГПа и относительно алюминия — до
2000 ГПа [89]. В диапазоне от 40 ГПа до ~ 2000 ГПа получена
плавная монотонная р-р зависимость без каких-либо скачков плотности,
т.е. без перестройки кристаллической структуры стишовита. При
~2000 ГПа наблюдается резкий излом адиабаты, связанный, по-
видимому, с плавлением.
В [90] исследовалось ударное сжатие Si02 с изменением
исходной плотности в диапазоне р00= 0,2—1,75 г/.см3 (см. рис. 7.13).
Весь набор адиабат с различными р00 можно разделить на три
группы:
1). Стишовитная группас р00 > 1,55 г/см3. Наблюдается типичная
картина ПП первого рода со скачком плотности и смесевым
участком адиабаты.
2). Коэситная группа с р00 < 1 г/см3. Скачок плотности
отсутствует , переход к коэситной ветви адиабаты характеризуется лишь
резким изменением наклона адиабаты dp/dp.
3). Промежуточная группа с 1 <р00< 1,55 г/см3, где , по-видимому,
происходят одновременно переходы кварц-коэсит и кварц-стишовит.
Превращение кварц - коэсит может быть только диффузионным,
поскольку их решетки очень сильно отличаются (16 ячеек кварца
надо перевести в 3 ячейки коэсита). Поэтому в УВ этот переход
может идти только при высокой температуре, что и имеет место при
сжатии сильнопористых образцов кварца.
Также затруднено превращение коэсит - стишовит (из одной
ячейки коэсита надо получить 8 ячеек стишовита), поэтому столь
велик гистерезис по давлению начала превращения (см. рис. 7.13).
Мартенситное превращение кварц-стишовит имеет следующие
особенности [91—94].
1. Постоянство скорости УВ в области фазового перехода
(D =5,72 км/с) без образования нестационарной двухволновой
конфигурации, т.е. смесевой участок ударной адиабаты совпадает в p,v-
плоскости с прямой Михельсона, проходящей через точку первого
излома адиабаты (точку А на рис. 7.3а). Смесевой участок на
адиабате простирается до 38 ГПа.
0,1 0,2 0,3 0,4 т,мкс
Рис. 7.14. Профиль УВ в кварце в зоне превращения в стишовит
320
2. Превращение протекает очень быстро только на фронте УВ
в течение времени существования на фронте сдвиговых напряжений
(< 10"7 с). Поэтому масштабный эффект &ля мартенситного
превращения в стишовит отсутствует.
3. Превращение носит пороговый характер и начинается в момент
потерь кварцем сдвиговой прочности, равной ^ = 14,5 ГПа [95].
4. Как всякое мартенситное превращение переход кварц ->
стишовит незавершенный, до 20% кварца остается непревращенным
[91]. Остаточный кварц переходит в стишовит при повторной
нагрузке второй УВ или при резкой разгрузке. Поэтому после
мартенситного перехода «стишовитные» ветви ударных адиабат отвечают
неравновесным состояниям (с остаточным кварцем).
5. До р ~40 ГПа адиабаты кварца и кварцита отличаются [95],
что можно объяснить разным их кристаллическим строением и
поэтому разной степенью мартенситного превращения в стишовит.
Исследования с помощью манганиновых датчиков профиля УВ
в кварце до давлений 29 ГПа с образцами толщиной L = 0,5—10 мм
показали следующее (см. рис. 7.14) [22].
1. До 23 ГПа а^я любой толщины образца фронт УВ имеет
обычный прямоугольный профиль (быстрое мартенситное превращение
в стишовит только на фронте УВ).
2. В интервале 23—29 ГПа проявляется двухстадийный характер
превращения: быстрая стадия до 23 ГПа и более медленная стадия
выше 23 ГПа. Вторая стадия длится около 0,35 мкс, что на 2—3
порядка больше длительности первой стадии.
Вторая стадия проявляется только после прохождения УВ
толщины образца 5—6 мм, т.е. масштабный фактор существует только
Аая второй стадии, которую можно считать диффузионным
превращением кварца в стишовит за фронтом УВ.
С ростом давления в УВ скорость диффузионного превращения
должна увеличиваться и, соответственно, длительность фронта УВ
(«завал» фронта на рис. 7.14) должна уменьшаться. Ускорению
диффузионного превращения должно способствовать плавление кварца
в зонах быстрого адиабатического сдвига [96].
При обеспечении в опытах достаточного времени
существования давления > 30 ГПа (достаточных толщин образца и ударника)
321
можно надеяться на достижение за счет диффузионной стадии
превращения равновесного состояния с практически полным
переходом кварца в стишовит.
Таким образом, кинетика ПП кварца в стишовит соответствует
общей картине полиморфных переходов, изложенной в разд. 7.1 и
7.2.
7.3.7. Горные породы
Интерес к исследованиям ударной сжимаемости различных
горных пород связан с решением геофизических вопросов (строение
мантии Земли), с построением уравнений состояния, знание
которых необходимо, например, а^я измерений мощности ядерных
зарядов при подземных испытаниях.
Сейчас накопилась информация по ударной сжимаемости более
чем 100 горных пород до давлений 100—400 ГПа, например, см.
работы [92,97—106]. Поэтому естественны попытки обобщения этих
данных, получения зависимостей, пригодных аая описания кривых
ударного сжатия различных типов пород. Наиболее удачное прибли-
Дкм/с а) 2 Л / 4 Дкм/с б)
■ и, км/с
и, км/с
Рис. 7.15. Адиабаты магматических (а) и осадочных (б) пород
а) 1 - габбро (D + 2 км/с); 2 - сиениты (D +1 км/с); 3 - туфы; 4 - граниты; 5 -
порфиры (D -1 км/с); 6 - совокупность данных по магматическим породам (D - 3 км/с)
б) 7 - магнетит; 8 - доломиты; 9 - известняки; 10 - алевриты; 11 - глины; 12 -
сланцы (D - 3 км/с); 13 - песчаники (D - 4км/с)
322
жение к эксперименту до 150 ГПа — полученные в [108] уравнения
множественной регрессии.
Приведенные эксперименты показали, что у всех горных пород и
минералов при ударном сжатии происходят изменения, связанные с
фазовыми переходами в более плотные и менее сжимаемые
модификации. Как обычно, это отражается в скачках плотности и в
изменении наклона ударных адиабат. Наблюдаются два типа D,u
-соотношений: два прямых отрезка, соединенных примерно горизонтальным
участком в зоне фазового перехода или две пересекающиеся прямые
с разным наклоном (см. рис. 7.15).
На рис. 7.15 приведены ударные адиабаты в D,u — координатах
Аля двух основных классов горных пород: магматических (граниты,
туфы, габбро, сиениты, порфиры) и осадочных (песчаники, глины,
сланцы, доломиты). Для всех пород область фазовых переходов
находится в интервале р=10—40 ГПа, где обычно проявляется
масштабный эффект. По-видимому, при существенно более высоких
давлениях скорость ПП велика, превращения заканчиваются полностью,
и ударные адиабаты могут рассматриваться как равновесные.
Т°С
7.4. Плавление при ударноволновом сжатии
7.4.1. Основные представления о плавлении под давлением
В системе фазовых
переходов плавление
(переход твердое тело -
жидкость) является
универсальным физическим
явлением, наблюдаемым
практически у всех
веществ. Плавление
происходит при строго
определенной температуре и
сопровождается
скачкообразным изменением
объема (Av) и энтропии
(всегда AS>0), т.е. является
200
150
100
50
Жидкость
■/ l 1
( Тв. 1
1 1_!_
II
Тв.
IV
/ ш
0 10 20 30 40 50 р.кбар
Рис. 7.16. Фазовая диаграмма цезия
фазовым переходом первого рода с метастабильными состояниями
по обе стороны линий плавления.
При плавлении в кристалле разрушается дальний порядок и
изменяется координационное число. Поскольку нет дальнего порядка,
то жидкость изотропна, в то время как кристаллы всегда
анизотропны. Структура жидкости характеризуется радиальной функцией
распределения, которая вычисляется из данных по рассеянию
рентгеновских лучей и нейтронов.
Вдоль линии плавления справедливо уравнение Клаузиуса-
Клапейрона: dT AV AVT
ф=^~Г (7-18)
где Т, р — температура и давление плавления, L — скрытая
теплота плавления.
Изменение объема Av может быть как положительным, так и
отрицательным и определяет согласно (7.18) знак наклона линии
плавления. Однако еще Бриджмен установил, что вещества с
отрицательным наклоном линии плавления (Av<0) испытывают фазовый
переход под давлением в более плотные фазы, после которого
наклон их линий плавления становится положительным (аргон, вода,
кремний, германий, галлий и др.).
Кроме того, широкий круг веществ имеет максимум на кривой
плавления (цезий, теллур, рубидий, барий, сурьма, сера, селен и др.).
Все эти вещества также имеют фазовый переход, так что после
максимума обязательно следует тройная точка кристалл I —
кристалл II — жидкость, и затем наклон линии плавления снова
становится положительным (см.рис. 7.16). Возникновение максимума (где
Av=0) есть следствие аномального уменьшения скачка объема вдоль
линии плавления.
По-видимому, температурные максимумы отражают
своеобразные процессы в жидкости, связанные с перегруппировкой ее частиц,
причем в этом случае превращение в жидкости опережает
превращение в твердой фазе [107].
Важные выводы следуют из анализа фазовой диаграммы цезия
(см. рис. 7.16). Как видно, линия плавления Cs-II имеет
отрицательный наклон, и, следовательно, объем Cs-II при плавлении уменьша-
324
ется. Но Cs-II уже имеет наиболее плотную упаковку (г.ц.к.), и
жидкость не может быть плотнее при тех же атомных размерах.
Следовательно, в жидком цезии происходит электронный переход
аналогично такому переходу в твердом теле. При плавлении Cs -II
плотность жидкого цезия увеличивается при сохранении
координационного числа за счет уменьшения размеров атома при переходе электрона из
состояния 6s в состояние 5d.
Изменения термодинамических и структурных свойств при
плавлении достаточно индивидуальны, поэтому нет какого-то
закона, описывающего плавление всех веществ. Однако существует
корреляция между структурами кристалла и жидкости и величинами Av
[107] (см. табл. 7.7).
При плавлении плотноупакованных структур
координационное число К уменьшается, а межатомные расстояния существенно
не меняются. При этом объемный скачок Av=4—15% определяется
значением К в жидкости. При плавлении веществ с рыхлыми
структурами проявляется тенденция к увеличению Кик уменьшению Av
вплоть до смены знака.
Температура плавления веществ с плотноупакованными или
близкими к ним структурам растет с увеличением давления
(dT/dp>0). Наибольшими начальными значениями dT/dp (при
р=0) обладают вещества с большим молярным объемом и
слабыми межатомными силами. Наклон линий плавления с давлением
уменьшается (d2T/dp2<0), что указывает согласно (7.18) на более
быстрое уменьшение скачка объёма по сравнению с уменьшением
скачка энтропии вдоль линии плавления. Имеющийся
экспериментальный материал показывает, что Av и AS с ростом давления не
стремятся к нулю, а наиболее вероятно при р->оо Av/vtb = Const 1 и
AS = Const2.
На линии плавления сжимаемость жидкой фазы всегда больше,
чем твердого тела.
Рассмотрим три различных способа описания плавления.
1. В 1927 году Симон попытался связать параметры линии
плавления со свойствами сосуществующих фаз [108].
Преобразовав (7.18) к виду
325
d\ap АН
(7.19)
d\aT AVp
Таблица 7.7. Характеристика плавления металлов при р = 1 атм [107]
Металл
Литий
Натрий
Калий
Алюминий
Медь
Серебро
Золото
Свинец
Цинк
Кадмий
Индий
Олово
Сурьма
Висмут
Германий
Галлий
Кристаллическ.
структура
о.ц.к.
о.ц.к.
о.ц.к.
г.ц.к.
г.ц.к.
г.ц.к.
г.ц.к.
г.ц.к.
г.п.у.
г.п.у.
тетрагональн.
гранецентрир.
тетрагональн.
объемноцентр.
ромбоэдрическ
ромбоэдрическ
кубическая
алмазная
ромбическая
Av/v,
%
1,65
2,5
2,55
6,0
4,15
3,8
5,1
3,5
4,2
4,0
2,0
2,8
-0,95
-3,35
-5,0
-3,2
AS,
кал/моль
гр
1,59
1,68
1,65
2,74
2,30
2,19
2,21
1,90
2,55
2,44
1,82
3,41
5,25
4,78
6,28
4,41
Наклон
линии
плавления
dT/dp
град/кГсм2
0,0032
0,0084
0,0166
0,0054
0,0032
0,0044
0,0058
0,0081
0,0036
0,0052
0,0042
0,0031
-0,00078
- 0,0035
-0,0026
- 0,0020
Координацией
число К
ТВ. жидк.
8
8
8
12
12
12
12
12
6+6
6+6
4+8
4+2+
+ 4
3+3
3+3
4
1+2+
+2+2
9,5
9
9
10,6
11,5
11,0
11,0
11,7
10,8
10,3
8,5
8,2
6,1
7,6
8,0
11,0
где Н — теплота плавления, а АН/(р Av) — безразмерная величина,
Симон обнаружил, что в координатах In (р+а) — 1пТ все линии
плавления становятся прямыми с очень близкими наклонами, что облегчает
экстраполяцию их в область высоких давлений.Отсюда следует
уравнение линии плавления Симона:
1п(/7 + а) = clnT + Ъ или
326
pia = (T/T0)c -1или
р + а = ЬТс или (7.20)
d\n(p + a) АН _
— = = Const
dlnT AV(p + a)
где А ,а, b, с — константы, причем величина с аля большинства
неметаллов порядка двух, а - это внутреннее давление, которое требуется
преодолеть, чтобы расплавить вещество при Т=0 К.
Например, аая NaCl Т = 1073 К, А = 1,6 ГПа, с = 2,7.
Из (7.20) следует линейная зависимость AH/Av от давления и,
таким образом, знание величин Т, р, Av и АН в одной точке на
линии плавления позволяет определить постоянные а и с и получить
уравнение линии плавления исследуемого вещества.
Параметр с в (7.20) связан с показателем п , характеризующим
потенциал взаимодействия между атомами Ф (г) ~ 1/г11.
Если обозначить р* = р/а и Т* = Т/Т0, то уравнение Симона
получит вид:
р* = (Т*)с-1 (7.21)
откуда следует, что линии плавления всех веществ с
одинаковой постоянной с будут изображаться одной кривой в координатах
р*—Т*.
Поэтому уравнение Симона может быть названо законом
соответственных состояний [107]
Уравнение Симона выдержало проверку временем, оно хорошо
описывает положение всех экспериментальных линий плавления,
в том числе и в области очень высоких ударно-волновых давлений
[109].
2. В 1910 году Линдеман предположил, что плавление наступает,
когда при нагреве амплитуда колебаний атомов в решетке достигает
определенной доли межатомного расстояния.
Из соотношения, связывающего энергию гармонического
осциллятора по Дебаю с амплитудой колебаний Линдеман получил
следующее уравнение [ПО]:
тв2У2/3 /Тт=С2 (7.22)
где m — масса атома; 0 — температура Дебая; v — объем; Тт —
температура плавления; С — постоянная Линдемана,
пропорциональная амплитуде колебаний и почти одинаковая а^я многих
веществ.
В точке плавления среднеквадратичное смещение атомов
составляет около 1/8 межатомного расстояния.
Позднее Гилварри преобразовал (7.22) в рамках теории
упругости [111]:
RT = nkmVm (7.23)
где R — газовая постоянная, km — модуль объемной упругости в
точке плавления, Vm — объем в точке плавления, П = (S m/C )2, Sm=f (G),
G — коэффициент Пуассона.
Эксперименты со свинцом показали, что выше 100 ГПа кривая
Линдемана завышает температуру плавления по сравнению с
экспериментом [112]
3. Если предположить, что при высоких температурах и
давлениях свойства веществ определяются только отталкивающей частью
потенциала взаимодействия, то твердые сферы могут быть хорошей
моделью атомов реальной системы. Твердые сферы могут
находиться либо в «кристаллическом» состоянии (в узлах решетки), либо
в неупорядоченном жидкоподобном состоянии, когда
пространственная корреляция сфер существует лишь на малых расстояниях
порядка нескольких диаметров сферы.
«Машинные» эксперименты с такой молекулярно-кинетиче-
ской моделью позволяют фиксировать переход между этими
двумя состояниями как фазовый переход I рода. Для таких
компьютерных расчетов очень важен выбор межчастичного
потенциала.
Например, потенциал парного взаимодействия Ленард—Джонса
[113] хорошо описывает изменение объема, но АА^ описания
деформации с изменением формы необходимо к нему добавить трехчастичный
потенциал Киттинга [114].
Условие плавления твердых сфер:
328
PV0/NkT= Const (7.24)
т.е. плавление наступает при определенном отношении общего
размера к суммарному размеру частиц.
7.4.2. Плавление в ударной волне
Повышение давления ударного сжатия неизбежно приводит
к плавлению вещества, т.е. ударные адиабаты (особенно пористых
веществ) проходят в области жидкой фазы. Поэтому представляет
интерес вопрос о влиянии плавления на положение ударной
адиабаты, а также проблема экспериментального определения линии
плавления в условиях динамического сжатия. Обычно факт плавления на
фронте УВ не учитывается, поскольку плавление слабо сказывается
на кинематических параметрах УВ и на положение ударной
адиабаты в p,V — координатах.
Значительно более чувствительной к плавлению является
температура сжатия, однако ее прямое измерение а^я непрозрачных
веществ затруднительно, но возможно а^я прозрачных кристаллов
путем регистрации свечения фронта УВ через слой еще несжатого
вещества. Такие измерения при давлениях до 80 ГПа сделаны аая
прозрачных монокристаллов NaCl и КС1 [115].
Яркостные температуры фронта УВ определялись сравнением
световых потоков, излучаемых фронтом и эталонным источником
света при двух длинах волн (4780 А и 6250 А).
Поведение ударной адиабаты при ее пересечении с линией
плавления аналогично плавлению в обычных условиях: при нагревании
температура не повышается, пока не расплавится все вещество. Но
увеличение тепловой энергии в УВ связано с ростом давления,
поэтому процесс плавления проходит не при Т = Const, а вдоль линии
плавления.
Полученные в [ 115] экспериментальные ударные адиабаты
монокристаллов NaCl и КС1 в р, Т-координатах показаны на рис. 7.17.
фарная адиабата твердой фазы доходит до линии плавления,
затем претерпевает излом, идет вдоль линии, пока не расплавится весь
сжимаемый объем, и снова с изломом выходит в область жидкой
фазы.
329
х ю3к aj X103К
О 200 400 600 р.кбар 0 200 400 р.кбар
Рис. 7.17. Ударные адиабаты NaCl (а) и КС1 (б)
о — измеренная температура; 1 — адиабата твердой фазы; 2 — участок
плавления (область сосуществования фаз); 3 — адиабата жидкой фазы; 4 — адиабата
«перегретой» твердой фазы; 5 — расчет линии плавления по [109]; 6 — расчет
по уравнению Симона с параметрами, найденными в [ 115]
Границы области сосуществования фаз у NaCl и КС1 следующие:
Материал Начало плавления Завершение плавления
р,ГПа ТК р,ГПа ТК
NaCl 54 3500 70 3700
КС1 33 3800 48 4100
Учет плавления приводит к уменьшению температуры жидкой
фазы по сравнению с расчетом без такого учета (пунктир на рис.
7.15) на величину
Т4-Т3=^— = = — (7.25)
4 3 3Rn ЪЯп cv К J
Для большинства веществ скачок энтропии при плавлении
S ~ 0,5 су. Если принять, что AS не меняется с давлением, то для NaCl
(Т3 = 4450 К) получим Т4 - Т3 = 2200 К, т.е. температура
оказывается очень чувствительной к плавлению.
На основании полученных экспериментальных результатов
в [115] сделаны следующие выводы.
1. Наклоны линий плавления, вычисленные по (7.18), хорошо
согласуются с полученными экспериментально.
330
2. Скачок энтропии AS вдоль линии плавления остается почти
постоянным, а скачок объема Av сильно уменьшается: ^ая NaCl —
с 20—25% прир = 0до2%прир = 70ГПа; для КС1 — с 20% при
р=1,9ГПадо4% прир = 48ГПа. Поэтому согласно (7.18) наклон
линии плавления с давлением уменьшается.
3. Из факта уменьшения с давлением скачка объема следует
также, что в условиях сильного сжатия на линии плавления твердая
и жидкая фазы различаются меньше, чем при атмосферном
давлении.
4. Вплоть до 70 ГПа у NaCl и КС1 нет критической точки на
линиях плавления, что подтверждает вывод Бриджмена [1].
5. Температура и теплота плавления (при AS = Const) вырастают
примерно в 4 раза при сжатии в 1,7 раза по сравнению с величинами
при р = 0. Следовательно, при сжатии растет высота
потенциального барьера, который нужно преодолеть атому ^ая разрушения
кристаллической решетки.
6. При плавлении не возникает двухволновой конфигурации
(как при ПП в кристалле) и в В,и-соотношении нет характерной
ступеньки и часто даже нет заметного излома. Адиабаты твердой и
жидкой фаз в D, u-координатах всегда отличаются своими
наклонами. У жидкой фазы наклон всегда меньше, т.к. меньше средний
коэффициент Грюнайзена Г = (р - рх)/р(Е - EJ. Причем с давлением
наклон плавно уменьшается, что связано с увеличением роли
электронной составляющей в УРС [114].
В [114] на основе УРС твердой и жидкой фаз предложен метод
расчета ударных адиабат твердой и жидкой фаз, изэнтроп разгрузки
и линии плавления как границы между фазами (из условия фазового
равновесия АФ = Фте — Ф = 0). Этот расчетный метод был успешно
применен ^ая описания экспериментов [115] с NaCl и КС1, и затем
с его помощью были рассчитаны ударные адиабаты и линии
плавления а^я А1, Си, РЬ и Ni (см. рис. 7.18).
Для всех рассмотренных веществ температура на кривой
плавления при равном давлении выше, чем на изэнтропе. Следовательно,
энтропия твердой фазы вдоль линии плавления возрастает. Отсюда
ясно, что если ударно-сжатое вещество не перешло в жидкую фазу,
331
а)
Т,К
6000
4000
2000
-
-
/* ж
/> 1
»
»
» /
» /
t /
1 1
» /
* / ^
1 1
X
6000
5000
4000
3000
Ni
Си
1000
РЬ
к
-
J*1 ж <S
7* i S ^r
1
/ /
» /
i i
' -^^^^ У
/ -т/'"
i i__
*
# ^^0 +'
1
2 p, Мбар
4 р,Мбар
Рис. 7.18. Ударные адиабаты, изэнтропы разгрузки и линии плавления алюминия
(а), никеля, меди и свинца (б)
оно может частично расплавиться при разгрузке из сжатого
состояния. И наоборот, разгрузка из жидкого состояния не может
перевести вещество в твердое состояние.
Не исследован вопрос о времени t необходимом а^я плавления.
На рис. 7.17 и 7.18 приведены расчетные ударные адиабаты и линии
плавления аая двух предельных случаев: когда t мало по сравнению с
временем существования давления в опыте и когда t велико
(«перегретая» твёрдая фаза).
Кроме прямых измерений температуры, экспериментально факт
плавления в У В может быть установлен по изменению:
1) скорости звука, которая уменьшается при переходе от
твердой фазы к двухфазной области и к жидкой фазе [114,116] или
упругая скорость звука с{ а^я твердой фазы плавно уменьшается с
началом плавления до пластической скорости звука сь (см.рис.1.19
гл.1);
2) показателя преломления света и его производной, которые аля
ионных кристаллов увеличиваются при плавлении в УВ в 1,5—1,7 раза,
что объясняется различием в зависимостях показателя преломления от
плотности аля твердой и жидкой фаз [ 117,118];
332
3) вязкости, которая резко уменьшается при плавлении [119].
Область плавления в УВ для любого вещества может быть
рассчитана, если известно точное уравнение состояния этого
вещества.
Например, согласно расчетам на основе У PC &ля алюминия
[120] двухфазная область твердое - жидкое на ударной адиабате
соответствует давлениям 113—184 ГПа, что хорошо согласуется с
давлением начала плавления алюминия р > 100 ГПа, установленным по
измерениям вязкости [119] и скорости звука [121].
В заключение отметим аномальное поведение ударных адиабат
ионных кристаллов NaCl, КС1, КВг в области жидкой фазы [122],
где обнаружены скачки плотности Ар/р = 4—9%, характерные
Аая фазового перехода. Возможная причина этого явления - в
изменении координационного числа в жидкой фазе. Например, &ая
твердого NaCl К = 6, и вблизи линии равновесия число ближайших
соседей не меняется в принципе или очень велико время такого
изменения.
До давлений 130—170 ГПа реализуется неравновесное жидкое
состояние с К = 6, а с повышением давления и температуры ударного
сжатия, т.е. с удалением от линии плавления в область жидкой фазы
координационное число увеличивается, частицы в жидкости
приобретают более плотную упаковку со скачком плотности ( для жидкой
NaCl величина скачка Ар/р = 9%).
Литература к главе 7
1. Бриджмен П.Твердые тела под высоким давлением. М.: Мир,
1966.
2. Тонков Е.Ю. Фазовые диаграммы соединений при высоком
давлении. М.: Наука, 1983,с.280
3. Delinger V. Phys. Chemistry Met. Solutions and Jntermetalic
Compounds, Vol.2, London, 1959
4. Морохов И.Д., Трусов Л.И., Чижик СП. %ътрадисперсные
металлические среды. М.: Атомиздат,1977,с.2б4
5. Щербаков Л.М. ДАН СССР, 1966,т.168,с 388...391
333
6. ЗадумкинСН. ДАН СССР, 19б0,т.130,с.4.
7. Даниленко В.В. // Физика горения и взрыва, 1988, №5,
С.137.
8. Даниленко В.В. Динамический синтез алмаза. Доклад на
семинаре по новым материалам. United nations. Economic
commission for Europe Eng. Aut/sem. 10/R, 31, 22 July 1992
9. Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и
высокотемпературных гидродинамических явлений. М.: Наука,
1966.
10. Теплофизика и динамика интенсивных импульсных
воздействий. / А.В. Бушман ,Г.И. Канель Л,Л, Ни, В.Е.Фортов. Ин-т
химфизикиАН СССР, Черноголовка, 1988.
11. Альтшулер А.В. Применение ударных волн в физике
высоких давлений // Успехи физических наук, 1965, 85, N2,
с.197.
12. Свойства конденсированных веществ при высоких
давлениях и температурах. Информ. издание.// Под ред. Р.Ф. Трунина.
Министерство атомной энергетики и промышленности,
ВНИИЭФ,1992,398с.
13. ГогуляМ.Ф. ФГВ,1989,Ш,с.95—104.
14. Альтшулер, Л.В.,Павловский М.Н., Дракин В.П. ЖЭТФ,
1967,52,2,400.
15. Hayes D.B. J. Appl.Phys., 1974,54,3,1208.
16. Жугин Ю.Н., Крупников К.К., Овечкин Н.А. Ж. Химическая
физика, 1987, N10, с.1447.
17. Кормер СБ., Юшко К.Б., Кришкевич Г.В. Письмв в ЖЭТФ,
,19б6,3,с.64.
19. DuffR., Minshall F. Phys.Rev., 1957,108,1207.
20. Кормер СБ., Синицын М.В. и др. ЖЭТФ, 1964,47,1202.
21. Подурец М.А., Симаков Г.В., Трунин Р.Ф. Изв. АН СССР,
Физика земли, 1976,3,3.
22. Жугин Ю.Н., Крупников К.К. Проблемы нелинейной
акустики. Сб. трудов симпозиума по нелинейной акустике. II часть,
Новосибирск, 1987, с.196—200,
23. Канель Г.И. ПМТФД977, 5,117.
334
24. Bridgman P. Proc. Am. Acad. Arts. Sci. 1948,76,55.
25. Bridgman P. Proc. Am. Acad. Arts. Sci. 1937,71,124.
26. Гарбер P. И., Поляков Л. M. Физика металлов и металловедение.
Т.П. вып. 5, с. 730—740.
27. Ададуров Г.А., Гольданский В.И. Успехи химии. 1981, 50,
с.1810—1827.
28. Ададуров Г.А. О роли пластических деформаций в
динамических экспериментах и сопоставлении результатов
динамических и статических исследований // «Химическая физика
процессов горения и взрыва». Детонация и ударные волны.
Материалы VIII Всес. симпозиума по горению и взрыву,
Черноголовка, 1986.С. 3.
29. Евдокимова В.В., Верещагин Л.Ф. ФТТ, 1962,4,1965.
30. Костюков Н.А. ПМТФ,1988,Ю,с.54...59.
31. Костюков Н.А., Яковлев И.В. ФГИ, 1992, N2, с. 109... 111.
32. Герман В.Н., Подурец М.А., Трунин Р.Ф. ЖЭТФД973, т.64,
Nl,c.205.
33. Курдюмов А.В., Пилянкевич А.Н. Фазовые превращения
в углероде и нитриде бора. Киев: Наукова думка, 1979,
с.186.
34. Балан Т.Р., Боримчук Н.И., Бочко А.В.,Курдюмов А.В.
и др. «Химическая физика процессов горения и взрыва».
Детонация и ударные волны. Материалы VIII Всес.
симпозиума по горению и взрыву. Черноголовка, 1986, с.80.
35. Влияние высоких давлений на вещество. Под ред. А.Н. Пиля-
нкевича, т.1, Киев: Наукова думка, 1987, с.6—20.
36. Кормер СБ., Юшко К.Б., Кришкевич Г.В. ЖЭТФ.1968,
54(3).
37. Alder В, Cristian R. Phys. Rev., 1956,104, р.550.
38. Бриш А.А., Тарасов М.С., Цукерман Б.А. ЖЭТФД960, 38,
с.22.
39. Альтшулер Л.В., Кулешова Л.В., Павловский М.Н. ЖЭФТ,
1960,39,с.1б.
40. Alder В. В сб. « Solids unter Pressure », N.Y., 1963.
41. Кормер СБ., Синицын М.В. и др. ЖЭТФ, 1965,49, с.135.
42. Запорожец Ю.Б., Минцев В.Б., Фортов В.Е. «Химическая
физика процессов горения и взрыва». Детонация и ударные
волны. Материалы VIII Всес. симпозиума по горению и
взрыву. Черноголовка,1986,с.82.
43. David H.G., Hamanu S.D. J. Chem. Phys. 1958,28,1006.
44. Bancroft D, Peterson EX., Minshall S.J. Appl. Phys. 1956,27, N3,
p.291.
45. Balchan A., Drickamer H.G.J. Rev. Scient. Jnstrum. 1961,32, N3,
p.308.
46. Clendenen R.L., Drickamer H.G. J. Phys.Chem.Solids. 1964,25,
N8,p.865.
47. Глузман В.Д., Канель Г.И. и др. Проблемы прочности.1985,
N8, с.52.
48. Ананьин А.В., Дремин А.Н., Канель Г.И. ФГВ, 1981, N3,
с.93.
49. J.M.Brown, R.G. Mc Queen. J. Geophys.Rev., 19$6, 91, В7,
7485.
50. Сучак С.Г., Канель Г.И., Фортов В.Е., Стельмах.В.Г. ФГВ, 1983,
N2,c.l21.
51. Павловский М.Н., Комиссаров В.В. ЖЭТФ,1990,т.98,
вып.5(11),с.1748.
52. Bundy F.P., Kasper J.S. J. Chem. Phys.,1967, 46, N9,
p.3437...3446.
53. Bundy F.P., Wentorf R.H. J. bit,1963,38, N5, p.l 144...1149.
54. Corrigan F.R., Bundy F.J. Chem.Phys.1975, 63, N11,
p.3812...3820.
55. Мейер К. Физико-химическая кристаллография, М.:
Металлургия., 1972.
56. Эстрин Э.И. В сб. Проблемы металловедения и физики
металлов, 1975, N5, с. 28...39.
57. Курдюмов А.В. ДАН СССР, 1975,221, N2, с. 322...324
58. Хоменко А.А., Ганкевич Л.Т. и др. Синтетич. алмазы, 1975,
вып.З, с. 3.
59. Wentorf R.H. Adv. Chem. Phys., VoLIX, 1965.
60. Bundy F.P. Science, 1964,146, N3552.
336
61. Alder B.J., Christian R.H. Phys. Rev. Lett.,1961,7,10,367.
62. Duvall G.E., Graham R.A. Rev. Mod. Phys. 1977,49,3,523.
63. Ананьин A.B., Дремин A.H., Канель Г.И. и др. ПМТФ, 1978,
3,с.П2.
64. Разоренов СВ., Канель Г.И., Овчинников А. А. В сб. Детонация.
Черноголовка, 1981, вып.2, с.70.
65. Павловский М.Н., Дракин В.П Письма в ЖЭТФД966, т.4,
в.5,с.169.
66. Мс Queen R.G., Marsh S.P. Behaviour of dense media unter high
dynamic pressures. Paris, N.Y., 1968, p. 207.
67. Gust W.H. J. Phys. Rev. ВД980,22,10,4744.
68. Doran D.G. J. Appl. Phys., 1963,34,844.
69. Алексеев Ю.Л., Волков K.B. ПМТФ, 1979,2,105.
70. Кравченко М.Н., Нигматулин РИ. Детонация и ударные
волны. Материалы VIII Всес. симпозиум по горению и взрыву.
Черноголовка, 1986, с. 104... 107.
71. Coleburn N.L. J. Chem. Phys., 1964,40,1,71.
72. Ананьин A.B., Дремин А.Н., Канель Г.И. и др. В сб. Детонация.
Критические явления. Физико-химические превращения в
ударных волнах.Черноголовка,1978.
73. Балан Т.Р., Боримчук Н.И., Бочко А.В. и др. Сверхтвердые
материалы, 1983, N3, с.19—23.
74. Боримчук Н.И., Курдюмов А.В., Ярош В.В. V Всес.
совещание по детонации (Красноярск), 1991, Сб. докладов, т.1,
с.43—47.
75. Трунин РФ., Жерноклетов М.В. и др. 4-е Всес. совещание по
детонации (Телави),1988, Сб. докладов, т.1, С.166...171.
76. Анисичкин В.Ф. V Всес. совещание по детонации (Красноярск),
1991, Сб. докладов, т.1, с. 20...26.
77. Пятернев СВ. V Всес. совещание по детонации, Красно-
ярск,1991, сб. докладов, т. 2, с. 214...218.
78. Дулин И.Н., Альтшулер Л.В., Ващенко В.Я., Зубарев В.Н.
ФТТ, 1969, т.11,вып.5,с.1252.
79. Ададуров Г.А., Бавина Т.В., Бреусов О.Н. ФГВД981, N17,
с.159—162.
80. Курдюмов А.В., Бритун В.Ф., Боримчук Н.И., Ярош В.В.
Мартенситные и диффузионные превращения в углероде
и нитриде бора при ударном сжатии. Киев, из-во Куприянова,
2005,191 с.
81. Курдюмов А.В., Гладкая И.С., Голубев А.С. и др. Изв. АН
СССР, сер. Неорганические материалы, 1982, N11, с.1835—
1838.
82. Павловский М.Н. Физика твердого тела, 1967, 9, № 11,
с.3192.
83. Стишов СМ. Геохимия, 1962, N8.
84. Coes L.J. Science, 1953,118,131.
85. Стишов СМ., Попов СВ. Геохимия, 1961,10,837.
86. Wackerly J. J. Appl. Phys., 1962,33, N3, p.922.
87. Альтшулер Л.В., Трунин Р.Ф., Симаков Г.В. Изв. АН СССР,
Физика Земли,19б5,Ш0.
88. Буллен К.Е. Сб. «Физика и химия Земли», М.: Изд. иностр.
лит.,1962.
89. Трунин РФ., Симаков Г.В., Подурец М.А. и др. Изв. АН
СССР, Физика Земли, 1971, N1, с. 13.
90. Симаков Г.В., Трунин Р.Ф. Изв. АН СССР, Физика Земли,
1991, N11, с. 72.
91. Подурец М.А., Симаков Г.В., Трунин Р.Ф. Изв. АН СССР,
Физика земли, 1976,3,3.
92. Трунин Р.Ф., Симаков Г.В., Подурец М.А. и др. Изв. АН
СССР, Физика Земли, 1971, N1, с. 13.
93. Симаков Г.В., Трунин Р.Ф. Изв. АН СССР, Физика Земли,
1991,N11,72.
94. Подурец М.А., Трунин Р.Ф. ФГВ, 1987, N1.
95. Wackerly J. J. Appl. Phys., 1962,33, N3, p.922.
96.. Ананьин A.B., Бреусов O.H., Дремин А.Н. и др. ФГВ, 1974,
N4, с. 578.
97. Трунин Р.Ф., Гонынакова В.И., Симаков Г.В., Галдин Н.Е.
Известия АН СССР, сер. Физика Земли, 1965, N9, с.1.
98. Дремин А.Н., Ададуров Г.А. ДАН СССР, 1959, т. 128,
с.261.
338
99. Калашников Н.Г., Павловский М.Н., Симаков Г.В., Трунин
Р.Ф. Известия АН СССР,сер.Физика Земли, 1973, N2,
с.23.
100. Симаков Г.В., Павловский М.Н., Калашников Н.Г., Трунин
Р.Ф.Известия АН СССР.сер.Физика Земли, 1974, N8, с.11.
101. Симаков Г.В., Трунин Р.Ф. Изв. АН СССР ,сер. Физика
Земли,1985, N2.
102. Трунин Р.Ф., Симаков Г.В. и др. Изв. АН СССР, сер.Физика
Земли,1988,Ш.
103. Huges D.S., McQueen R.G. Trans. Amer. Geophys. Union,1958,
v.39,N5.
104. Butkowich T.R. J. Geophys.Rev., 1965, v.70, N4.
105. Справочник физических констант горных пород, М., Мир,
1969.
106. Телегин Г.С., Антошев В.Г., Бугаева В.А. и др. Изв. АН СССР,
сер. Физика Земли, 1980, N5, с.22.
107. СтишовСМ. УФН,1968,т.96,вып.З,с.46-496.
108. Simon ЕЕ., Glatzer G.Z. Anorg. u. allgom. Chem.,1929, 178,
309.
109. Кормер СБ., Синицын М.В., Кириллов Г.А., Урлин В.Д.
ЖЭТФ, 1965, т.48, в.4, с.1033.
110. Lindeman ЕА. Phys. Z., 1910,11,609.
111. GilvarryJJ. Phys.Rev.,1956,102,308.
112. Godwal B.K., Meade Ch. et. Al. Science, 1990, V.248, p.462-
465
113. Магаметов M.M. Ж. физ. химии, 1 989,t.63,N 11 ,с.2943.
114. Урлин В.Д. ЖЭТФ, 1965, т.49,вып.2(8), с.485.
115. Кормер СБ., Синицын М.В., Кириллов ЕА., Урлин В.Д.
ЖЭТФ, 1965, т.48, в.4, с.1033.
116. McQueen R.G., Fritz J.N., Morris CE.Shock waves in Condensed
Matter. Elsevier Science Publ. B.V., 1984, p.95-98.
117. Кормер СБ., СиницынМ.В.и др. ЖЭТФ,19б5,т.49, вып. 1(7),
с.135.
118. Кормер СБ. II Всес. симпозиум по горению и взрыву,
Черноголовка, 1969, сб. авторефератов докладов, с.250.
339
119. Сахаров А.Д., Зайдель P.M., Минеев В.Н., Олейник А.Г. ДАН
СССР, 1964,159,1019.
120. Альтшулер Л.В. Детонация. Критические явления. Физико-
химические превращения в ударных волнах. Черноголовка,
1978, с. 119-1212.
121. McQueen R.G., Fritz J.N., Morris СЕ. Shockwaves in Condensed
Matter. Elsevier Science Publ. BY., 1984, p.95...98.
122. Кормер СБ., Синицын M.B. и др. ЖЭТФД964,47,1202.
123. Дамаск А., Дине Дж. Точечные дефекты в металлах. М., Мир,
1966.
124. Даниленко В.В. VBcec. Совещ. по детонации. Красноярск, 1991,
Сб. Докл., т. 1,с.146.
125. Даниленко В.В. Синтез и спекание алмаза взрывом. М.
Энергоатомиздат, 2003.
126. Павловский М.Н. ФТТ, 1971, т.13, вып.З, с. 893.
340
Глава восьмая
ДЕТОНАЦИЯ
8.1. Гидродинамическая теория детонации (модель ЗНД)
Все взрывные процессы могут проходить в двух принципиально
различных формах — горение и собственно взрыв. Горение зависит
от внешних условий, определяется теплопроводностью и может
протекать с переменной скоростью. Взрыв от внешних условий почти
не зависит, в передаче взрыва определяющую роль играет не
теплопроводность, а ударная волна, при этом наблюдается очень большое
местное повышение давления.
Скорость горения всегда меньше скорости звука в исходном ВВ,
а скорость взрыва — всегда больше. Горение может скачкообразно
переходить во взрыв, а взрыв может протекать в форме детонации.
Детонация имеет максимально возможную постоянную скорость
Аая данного ВВ и а^я данных условий инициирования ВВ.
Явление детонации в газах было открыто в 1881 году независимо
Бертло и Вьелем, а также Малляром и Ле-Шателье в ходе
исследований горения газов в трубах. В 1883 году появилась теория взрывной
волны» Бертло, согласно которой первым этапом инициирования
взрывчатой смеси капсюлем является быстрое сжатие прилегающего
слоя смеси, который разогревается при этом до очень высокой
температуры, что и определяет большую скорость реакции разложения
смеси.
Таким образом, реакция распространяется от слоя к слою за счет
трех различных явлений: механических (сжатие), термических
(разогрев) и химических (реакция).
341
Результатом развития этих представлений явилась современная
гидродинамическая теория детонации, Основоположниками
теории являются Михельсон (1889 г.), Чепмен (1899 г.), Жуге (1905 г.),
Крюссар(1907г.).
Дальнейшее развитие гидродинамическая теория детонации
получила в работах Ландау, Зельдовича, Гриба, Деринга, Станюковича,
Неймана, Щелкина, Трошина, Дремина и др.
В соответствии с гидродинамической теорией [1—6] детонация
ВВ обусловлена идущей по ВВ ударной волной, которая возбуждает
экзотермическую реакцию.
Энергия реакции идет на поддержание постоянства параметров
детонации. Существует максимальная стационарная скорость
детонации, которая не зависит от условий инициирования и
определяется только энергией химической реакции разложения ВВ (теплотой
взрыва Q) и УРС продуктов взрыва.
По сравнению с ударной волной детонационная волна обладает
более сложной структурой и включает в себя ударную волну, зону
химической реакции постоянной ширины (химпик) и нестационарную
область расширяющихся продуктов взрыва (рис. 8.1). Конкретная
структура зоны реакции определяется кинетикой превращения ме-
тастабильного ВВ в конечные продукты взрыва. Для
гидродинамической теории детонации не имеет значения ширина зоны реакции.
Ро
Н
0 т
Рис. 8.1. Структура стационарной детонационной волны
А А — ударная адиабата ВВ; S — ударная адиабата ПД; Н — точка Жуге;
О А и ОВ — прямые Рэлея — Михельсона; О А — ударное сжатие ВВ; АН — зона
химической реакции.
342
Поверхность, которая разделяет зону реакции и продуктов
взрыва, называется поверхностью Чепмена—Жуге, а параметры ПД на
этой поверхности называются параметрами детонации,
параметрами Чепмена—Жуге или параметрами в точке Жуге.
При переходе от ударных волн к детонационным уравнения
сохранения остаются в силе и в р, v-координатах дают уравнение
прямой Рэлея—Михельсона
V -V 2
Ph=Po+-^T-d (8.1)
проходящей через начальную точку (p0v0). Как видно, квадрат
скорости детонации определяется тангенсом угла наклона этой
прямой к оси ординат.
Уравнение Гюгонио принимает вид:
Ен -Е0=0,5(рн -Po)(yo-VH) + Q (8.2)
Поскольку за счет выделения энергии Q продукты детонации
имеют повышенную энергию, то равновесная ударная адиабата ПД
лежит выше ударной адиабаты ВВ (см. рис. 8.1).
Чепмен и Жуге предложили аая газов, а затем Зельдович в 1940г.
в общем случае доказал, что процессу детонации отвечает лишь одно
состояние ПД, характеризуемое точкой Н-точкой касания прямой
Михельсона ударной адиабаты П Д. В этой точке скорость детонации и
энтропия минимальны, а химическая реакция завершается. Кроме того,
используя условие касания (pH-p0)/(vQ-vH) = (9p/9v)H = (9p/9v)s и
законы сохранения, было доказано, что D-u = с, т.е. скорость детонации
относительно движущихся ПД точно равна местной скорости звука в
ПД (условие Жуге). К такому же результату позднее пришел в 1942 г.
Деринг в Германии, а в 1943 г. фон Нейман в США.
Итак, согласно модели ЗНД детонационная волна,
распространяющаяся по ВВ со скоростью идеальной или нормальной
детонации, движется относительно ПД с местной скоростью звука.
Поверхность Чепмена — Жуге неподвижна относительно
фронта УВ, поэтому скорость газа на ней относительно УВ равна местной
«замороженной» скорости звука.
Движение вещества в области разлета ПД является
сверхзвуковым относительно детонационной волны, поэтому возмущения из
области расширения ПД не проникают в зону химической реакции.
А внутри зоны течение дозвуковое (с > D-u), что обеспечивает
поступление выделяющейся при реакции энергии на фронт УВ.
Таким образом, переход от ударной адиабаты АА' исходного
ВВ к ударной адиабате S продуктов детонации совершается по
прямой Михельсона от точки А к точке Н (см. рис. 8.1), т.е. обязательно
сверху.
Три закона сохранения, уравнение состояния и правило
отбора D (условие касания или D-u = c) дают пять уравнений аая
нахождения пяти неизвестных величин детонации — рн, vH, uH, DH, Тн
(заданы начальные условия и теплота взрыва Q).
Вследствие дополнительного разогрева при ударном сжатии ВВ
температура детонации больше, чем температура мгновенной
химической реакции при постоянном объеме: Тн > Q/cy.
Режим, соответствующий прямой АН называется нормальным
режимом детонации, а минимальная скорость детонации (в условии
касания в точке Н) называется нормальной скоростью детонации.
Если мощным инициатором реализовать в ВВ ударное давление,
соответствующее точке В (см. рис. 8.1), то возникает пересжатый
режим детонации (точка С) со скоростью, большей, чем нормальная
скорость детонации.
При пересжатом режиме скорость потока П Д относительно
фронта детонации — дозвуковая, т.е. D-u < с или и+с > D, возмущения
догоняют фронт, и режим детонации поэтому нестационарен, неустойчив.
Через какое-то расстояние от места инициирования детонация
становится нормальной. Однако при инициировании наружных
поверхностей цилиндрического или сферического зарядов весь объем заряда
будет охвачен пересжатой детонацией (эффект кумуляции).
Если до момента окончания химической реакции скорость
тепловыделения становится отрицательной Э Q/ Э t < 0 (например, за
счет диссоциации ПД тепло не выделяется, а поглощается), то
состояние частиц ПД может перемещаться от точки С до точки D.
Тогда скорость детонации определяется меньшим наклоном прямой
Михельсона не к равновесной конечной адиабате S , а к промежу-
344
точной адиабате, соответствующей тому составу ПД, при котором
произошла смена знака Э Q/ Э t. В этом случае будет идти
стационарная недосжатая детонация.
Экспериментальное доказательство существования химпика
подтверждает правильность гидродинамической теории детонации
и, кроме того, позволяет наиболее надежно оценить время реакции
во фронте детонационной волны, т.е. время перехода от
реагирующего ВВ к продуктам полного превращения или время перехода от
точки А к точке Н Жуге (см. рис. 8.1).
Это время t определяется кинетикой химической реакции и во
много раз больше времени нарастания давления на фронте ударной
волны (соответственно 0,3—0,4 мкс и 1 не аа^ прессованного тротила).
Сжатие исходного ВВ ударной волной происходит настолько
быстро, что химический состав ВВ не успевает измениться. Химическая
реакция происходит в уже сжатом веществе. Выделение энергии Q
при этом увеличивает температуру и объем ПД, но давление
несколько снижается (см. рис. 8.1).
Большая ширина детонационного фронта обусловливает резкое
уменьшение градиентов в зоне химпика, что позволяет пренебречь в
этой зоне влиянием вязкости и теплопроводности. Роль теплового
потока в передаче детонации мала.
Для современных мощных взрывчатых составов время реакции
составляет доли микросекунды (см. табл. 8.9). Отметим, что аля
пересжатой детонации время реакции настолько мало, что
превращение ВВ в ПД происходит непосредственно на фронте УВ, без
химпика [7— 10].
Ряд экспериментальных фактов несовместим с одномерной
теорией ЗНД [8].
Во-первых, многомерная пульсирующая детонация в газах и
в жидкостях.
Во-вторых, по теории ЗНД величина критического диаметра dK
должна быть пропорциональна времени химреакции t. Но
структура гетерогенных зарядов (дисперсность частиц, твёрдое или жидкое)
при одинаковой плотности слабо влияет на время детонационного
превращения t, но очень сильно — на dK. Например, у жидкого
тротила d = 60 мм, а у твёрдого прессованного d = 5—10 мм.
Третье противоречие с теорией ЗНД относится к гомогенным
жидким ВВ, у которых скорость детонации почти не зависит от
диаметра заряда, но при этом у них большая величина d . Например, у
нитрометана dK = 18 мм, но скорость D = 6,3 км/с меняется с
диаметром заряда на доли процента. У гетерогенных ВВ в соответствии
с теорией ЗНД, чем больше d , тем сильнее зависимость скорости
детонации от диаметра заряда.
Эти факты объясняются явлением срыва химической реакции
во фронте ударной волны под влиянием волн разрежения. Явление
срыва связано с изменением кинетики реакции в боковой разгрузке,
с переходом от быстрой реакции к медленной.
У гомогенных ВВ стационарная детонация характеризуется
быстрой реакцией с малым временем индукции. Боковая разгрузка
ослабляет детонационный фронт настолько, что время индукции
увеличивается и становится больше времени нахождения ВВ в удар-
носжатом состоянии. И тогда проявляется срыв детонации.
Таким образом, критический диаметр определяется не
закономерностями быстрой реакции на оси заряда, а медленной реакцией
(или реакцией в горячих точках для гетерогенных ВВ) в зоне
действия боковой волны разгрузки.
У гомогенных ВВ нормальная детонация всегда возникает из
пересжатого режима. Если при переходе из пересжатого режима в
нормальный срыва детонации нет, то детонация будет устойчивой, а
при срыве — пульсирующей.
Для пульсирующей детонации характерно существование
отдельных очагов расходящейся пересжатой детонации со
сферическими волнами большой кривизны. Параметры этих волн быстро
снижаются, и происходит срыв реакции. Но волны из очагов
сталкиваются с образованием маховских волн большей амплитуды, в
которых срыв преодолевается. Измерения показали, что в маховской
волне давление близко к давлению в точке Жуге, а не в химпике по
модели ЗНД,
Для каждого гетерогенного ВВ существуют характерные
величины давления ударной волны р* и плотности р0*, ниже которых
реакция идёт в основном по механизму горячих точек и зависит от
346
структуры заряда, а при больших р и р — реакция преимущественно
гомогенная и не зависит от структуры заряда, а только от структуры
молекул ВВ.
Аля р0 = р0* давление в точке Жуге р* = 0,5рн(р0 = pm J
ПРиРо<Ро*:
— максимальное выделение энергии — на фронте УВ, что даёт
химпик острый и прогнутый вниз;
— ширина фронта УВ (несколько частиц) намного больше, чем
у ударного скачка при р0 = ртах;
— величина химпика зависит от доли ВВ, прореагировавшего
на фронте УВ: чем больше эта доля, тем меньше химпик.
В теории ЗНД возбуждение всех степеней свободы молекул ВВ
подразумевается мгновенным. Но на ширине ударного скачка
порядка пикосекунд успевают возбудиться только поступательные
степени свободы. При этом энергия идёт прежде всего на наиболее
быстро возбуждаемые, т.е. на наиболее прочные связи, которые
разрушаются (связи бензольного кольца).
Возникает сверхнеравновесная поступательная температура (см.
рис. 8.2), что уменьшает сжимаемость ВВ в ударном скачке и создаёт
высокую концентрацию активных радикалов.
8.2. Модифицированные модели ЗНД
1. Модель с турбулентностью
Из одномерных уравнений газодинамики и кинетики реакции
/^ля гомогенных ВВ следует теория детонационной волны с
гладким фронтом и ламинарным течением. Однако экспериментально
установлено, что только в некоторых жидких ВВ фронт гладкий, в
остальных случаях фронт негладкий, и поток внутри химпика носит
турбулентный пульсирующий характер.
Основная причина этого в том, что ударная волна, входящая в
детонационный комплекс, всегда взаимодействует с зоной тепловы-
деления, т.е. существует положительная обратная связь УВ с химпи-
ком, поскольку существует влияние температуры на фронте УВ на
скорость тепловыделения, с одной стороны, и влияние
тепловыделения на параметры УВ, с другой стороны.
Если Q/t сильно зависит от Т, то обратной связи достаточно а^я
возникновения пульсаций волны или ^^я т.н. тепловой
неустойчивости детонационной волны [11].
Таким образом, предположение модели ЗНД о ламинарном
течении среды в плоской одномерной детонационной волне в общем
случае неверно. Из-за указанной тепловой неустойчивости, а также из-за
исходной неоднородности ВВ это течение турбулентное. Поэтому
теорию детонации надо строить путем пространственно —
временного усреднения параметров детонации [12]. Согласно такой общей
теории: 1) в основных соотношениях pH = pQDu и Ен-Е0 = 1/2(рн-р0)
(vQ-vH) под рн и Ен надо понимать не средние, а эффективные
величины; 2) из-за турбулентности ударное сжатие ВВ в разных местах
детонационной волны происходит неодновременно; 3) в исходном ВВ
D2 > с2 , а где-то в детонационной волне (D—и)2 < с 2; 4) правило
отбора Чепмена—Жуге обосновывается в точном соответствии со схемой
Зельдовича [1—4]; 5) при завершении реакции в зоне химпика
турбулентность затухает.
Таким образом, имеется полное сходство основных идей и
представлений ламинарного течения по модели ЗНД и фактически более
точной и более общей теории усредненного турбулентного течения
в детонационной волне.
2. Многопроцессорная модель
Рассматривая детально с учетом кинетики физический механизм
детонации в рамках модели ЗНД, надо отметить существование
экспериментальных данных, которые указывают на то, что в области
низких и высоких давлений в УВ детонационные процессы
протекают по-разному.
Поэтому нельзя описывать одним механизмом поведение ВВ
в широком интервале давлений от десятков до сотен кбар. Так, при
низких давлениях справедлив очаговый механизм «горячих то-
348
чек», обусловленный гетерогенностью, неоднородностью исходной
структуры ВВ. Обычно это поры в твердом ВВ или воздушные
пузырьки в жидком ВВ. При их схлопывании в ВВ возникает высокая
температура , и в этих «горячих точках» начинается быстрая
реакция разложения ВВ. Менее нагретая масса ВВ сгорает затем в волнах
реакции, распространяющихся из очагов.
Необходимость введения понятия «горячие точки» связана с тем,
что при ударно-волновом инициировании с давлением р < р*
равновесная температура в УВ оказывается слишком низкой, чтобы вызвать
наблюдаемую быструю реакцию. Размеры создаваемых УВ «горячих
точек» пропорциональны размерам имеющихся в ВВ неоднородностей.
Чтобы началась реакция в объеме ВВ, размер очага должен быть больше
некоторого предельного аая данного давления и температуры в УВ. С
ростом давления в УВ возрастает количество предельных очагов и
соответственно растет объемная скорость реакции.
С другой стороны, увеличение количества и удельной
поверхности неоднородностей в исходном ВВ снижает требуемое давление
инициирования и ускоряет реакцию, т.к. при этом растет объемная
концентрация «горячих точек».
Для расчетов очаговой макрокинетики разложения ВВ обычно
используется выражение [6]:
^*kNS(a)u(p,T) (8.3)
где da/dt — скорость разложения ВВ; N — концентрация
активных очагов; S — средняя площадь поверхности очага; и (р,Т) —
скорость горения.
Очаговый механизм разложения гетерогенных ВВ влияет не
только на режим инициирования, но и на установившийся режим
детонации, о чем свидетельствует зависимость длительности химпи-
ка и критического диаметра от физической структуры заряда.
При высоких давлениях (больше некоторого р*) очаговый
механизм вытесняется другим, обусловленным гомогенным нагревом
внутри зерен ВВ. Так, при р > р* время реакции или ширина зоны химпика
в прессованном ТНТ не меняется при заполнении пор жидкостью.
Физический механизм гомогенного разложения ВВ предложен
в работах [13,14]. Согласно многопроцессорной модели детонации
гомогенный распад проходит в две стадии.
На первой стадии происходит распад некоторой части молекул
ВВ с образованием активных радикалов и ионов на фронте УВ за
время ~1010с. Вторая стадия — это догорание ВВ за фронтом УВ
за время ~106с.
Рассмотрим эти стадии подробнее.
/ стадия. Расчеты методом неравновесной молекулярной
динамики [15] показали, что одномерное сжатие в УВ многоатомных
молекул возбуждает сначала только поступательную степень свободы
за время порядка 10"12с, а затем более медленно, за время 109—10'10 с
возбуждаются колебательные степени свободы.
Возбуждение только одной степени свободы означает малую
теплоемкость молекулы, следовательно, высокую неравновесную
температуру (см. рис. 8.2).
Амплитуду неравновесной температуры можно оценить
выражением:
T£=T0+(N-Wp-TQ) (8.4)
где N — число атомов в молекуле.
Равновесная Т
за фронтом
Зона сжатия t = 10 12с
Зона T,v релаксации t = 10 9—10 10с
Рис. 8.2. Неравновесная температура на фронте УВ
350
Для типичных ВВ типа тротил, гексоген, октоген при давлении УВ
р= 100 кбар, Т= 1000—1500 К, а Татт=20000—30000 К (2—Зет).
При таких высоких температурах будут протекать процессы очень
быстрого электронного возбуждения (Е=2—5ev) с образованием
активных радикалов, что экспериментально найдено в [16,17].
II стадия протекает за фронтом УВ, когда наступает
термодинамическое равновесие. Главным процессом здесь является взаимодействие
молекул с радикалами и образование вторичных радикалов: М + R2 = R^.
Процесс идет до полного разложения ВВ и образования равновесных
продуктов детонации (N2, Н20, С, СО, С02, NO, N02).
Для реакций с участием активных радикалов характерны низкая
энергия активации (5—15 ккал/моль) и, как следствие этого,
высокая скорость и слабая зависимость от температуры.
Именно поэтому изменение в эксперименте давления в УВ от
50 до 200 кбар слабо уменьшает ширину химпика в ТНТ (от 1,5 до
0,2 мкс), хотя аая классической реакции разложения (без активных
радикалов) изменение температуры от 500К до 1000К должно
увеличить скорость реакции на 5—10 порядков.
Суть многопроцессорной модели детонации в том, что очаговый
и гомогенный механизм детонационного распада действует
параллельно, но с изменением давления их вклад в общую кинетику
распада меняется непрерывным образом.
На основе этой физической модели в [14,18] разработана
расчетная модель детонации, которая позволяет определять параметры
детонации любых взрывчатых составов.
3. Одностадийная реакция по Аррениусу
Классической модели ЗНД соответствует структура
детонационной волны у тех ВВ, основная часть энергии взрыва которых
выделяется за УВ, реакция протекает одностадийно и за время, много
меньше времени детонации заряда ВВ.
Так, АА^ прессованного ТНТ большой плотности (> 1,57 г/см3)
и состава РВХ-9502 на УВ реализуются сжатия непрореагировавшего
ВВ, а давление в химпике превышает давление в точке Жуге в 1,42— 1,47
раза.
351
Для описания детонации ВВ с затянутыми реакциями
разложения, завершающимися в расширяющихся ПД, используется
модифицированная модель ЗНД, в которой распределение за УВ
массовой скорости соответствует кинетике разложения по Аррениусу
(рис. 8.3) [18,19]:
— = -va ехр(-Еа IRT) или
dt
^- = -оар^хр(-Г/Т)
dt
(8.5)
(8.6)
где а — концентрация неразложившегося ВВ; t — время;
Е — энергия активации; Т — температура; р — давление
ударного разрыва в данном лагранжевом элементе; j, n, Т* —
константы.
и, км/с
1 L—х, мм
Рис. 8.3. Распределение массовой скорости за фронтом УВ
Расчет кинетики разложения по Аррениусу [18].
Длина заряда L, мм: 1 — 39,56; 2 — 19,75; 3 — 9,36; 4 — 4,89; 5 — 1,83.
Точками обозначены сечения, для которых выполняется условие Жуге D=и+с
Формула (8.5) хорошо описывает распределение скоростей для
состава В и ТГ 50/50 [18], а (8.6) — аая составов на основе ТАТБ
[19].
352
4. Двухстадийные режимы детонации
В [20] предложена двухстадийная модель детонации,
согласно которой реакция идет в две стадии. Основная часть
энергии Q освобождается на первой, «быстрой» стадии (96—98%),
а ее остаток — во второй, «медленной» стадии. С такой двух-
стадийной кинетикой хорошо согласуются экспериментальные
профили массовых скоростей за фронтом детонации у состава
LX-14.
Другой вид двухстадийной кинетики реализуется в режиме
стационарной недосжатой детонации (СНД) [21], обнаруженном у
флегматизированных составов [22].
На первой стадии идет быстрая экзотермическая реакция с
выделением энергии Qj, а на второй, медленной стадии, идет реакция
эндотермическая с поглощением энергии Q2 < < Q2, что связано с
деструкцией молекул флегматизатора.
При этом относительное снижение давления детонации
или для j = 2/3 и п = 3: Ар/р« 0,58(0^0,)
Как показали экспериментальные исследования структуры
детонационного фронта, двухстадийные режимы энерговыделения
широко распространены.
5. Детонация без химпика
Это предельный случай, когда весь объем ВВ реагирует в ударном
скачке [23]. Такой режим наблюдается у высокоплотных
актированных зарядов из гексогена и октогена и характерен очень высоким
давлением в УВ и очень узкой зоной реакции.
В отличие от модели ЗНД внутри зоны давление возрастает,
сначала очень быстро, а затем идет «медленное» завершение
реакции.
Для наглядности все рассмотренные модели детонации сведены
в таблицу 8.1.
Обзор работ по исследованию макрокинетики разложения ВВ в
детонационной волне дан в [4,6,24,25].
Таким образом, современное численное моделирование
детонации основано на физической модели ЗН Д (или различных ее
модификациях) и на результатах точных, с высоким разрешением
экспериментов.
В настоящее время численные методы используются не только
Аая воспроизведения и оценки достоверности экспериментов, но
также дают подробную информацию там, где прямой эксперимент
невозможен.
Таблица 8.1. Различные модели детонации
Модель детонации
Гидродинамическая
теория — модель
знд
Модифицированная
модель ЗНД с
турбулентностью
Многопроцессорная
модель
Двухстадийная
модель нормальной
детонации
Особенности кинетики
Одностадийная реакция
с выделением всей энергии
за фронтом УВ.
На УВ сжимается нереаги-
рующее ВВ. Фронт УВ
гладкий, течения ламинарные.
То же, но в зоне реакции
течениетрбулентное
с эфективными значениями
энергии и давления.
Параллельно существуют
внутри зоны (очаговая)
и гомогенная (объемная)
две кинетики разложения
с вкладом каждый в
зависимости от давления.
Реакция начинается
на фронте в условиях
перегрева с образованием
активных радикалов.
Разложение ВВ в две
стадии. На первой «быстрой»
стадии реагирует %—98%
ВВ, остаток на второй
«медленной» стадии.
Наблюдается
уВВ
ТНТср>1,57
г/см3 Состав
РВХ-9502
У всех 12
гетерогенных
составов
Любые ВВ
LX-14
Литература
1,2,4,5,6
14,15
20
354
Модель детонации
Детонация без
химпика
Одностадийная
реакция с кинетикой
по Аррениусу
Двухстадийная
модель
стационарной недосжатой
детонации
Особенности кинетики
Полное разложение ВВ на
фронте УВ. Зона реакции
очень мала, внутри зоны
давление растет.
Относительно медленная
реакция разложения,
завершающаяся в
расширяющихся ПД
На первой стадии —
экзотермическая реакция,
на второй —
эндотермическая реакция деструкции
молекул флегматизатора.
Наблюдается
уВВ
Мощные
высокоплотные
агатированные
ВВ (гексоген,
октоген)
Сплавы тротил-
гексоген.
Составы на
основе ТАТБ
Флегматизи-
рованные
составы
Литература
23,24
18,19
21,22
8.3. Вычисление параметров детонации
Для количественной характеристики процессов детонации ВВ
необходимо знать пять следующих параметров в точке Жуге: рн,
рн, DH, uH, Тн. Их определяют , решая следующие пять уравнений:
Ен -Е0=0,5(рн -pQ)(yQ-VH) + Q;
D2^v2Ph_Z£o_
Vo-Vh
£а^Л=(-*),=Лря/Гя;
v0-vH v ev's FH h
Рн=/(Рн>Тн)
(8.8)
"2=(Ph-A)Xvo-vh)
Величины po, p0, Q считаются известными.
Для детонации в идеальной газовой смеси (например, 2Н2 + 02)
пятое уравнение состояния идеального газа имеет вид:
Рн = Рн*?» = РнТ„сЛк ~ 1) (8.9)
355
а уравнение изэнтропы — рх^=Const, поэтому Е = pv/(k — 1), где
к=с /с. Предполагая к = Const после преобразований, пренебрегая
р0 < < рн и Е0 < < Ен, получим для детонации газовых смесей:
pH=2(k-l)pQQv;
D2=2(k2-l)Qv; u2H=2Qy^;
^=(* + 1). (8.10)
Ра к
2k Q
T =
1н
(h + l)cv
где Q = Q/ 427 г м2/сек2, Q— теплота взрыва в ккал/кг.
Сравним давления и объемы в УВ (точка А на рис. 8.1) и в точке
Жуге при одинаковой скорости D:
2p0D2
Руд-Ро
Рн~Ро =
уд - (k+l)(l-c2/D2)
PqD2 V0-Vyd_
(к + \)<\-41&) V0 (k + \){\-c2JD2)
Vq-Vh _ 1 (8.11)
V0 (k + \)(\-c2/D2)
Как видно, рув « 2рн и VyB = 2vH - v„.
Таким образом, при выделении тепла происходит расширение ПД,
и давление в точке Жуге вдвое меньше, чем на фронте УВ в газах.
Приведем расчетные параметры гремучей смеси (2Н2 + 02):
v0/vH = 1,88; рн/р0 = 18,0; D=2819 м/сек; Тн = 3583 К.
Уравнения для параметров детонации в газах были
выведены в предположении, что плотность ПД невелика и они
подчиняются законам идеальных газов. При этом давление в точке Жуге
(р « 4—6 кбар) является тепловым (р~Т).
При детонации конденсированных ВВ плотность ПД в точке Жуге
очень велика (до 2,7 г/см3), больше плотности исходного ВВ, а
давления достигают ~400 кбар. В этих условиях объем газа, приходящий-
356
ся на одну молекулу, сравним с собственным объемом молекулы, а
УРС а^я идеальных газов неприменим.
Ландау и Станюкович впервые рассмотрели такое сверхплотное
состояние газов по аналогии с кристаллической решеткой твердого
тела и показали, что ^ая очень плотных ПД можно пренебречь
тепловыми составляющими и считать энергию и давление упругими
[1]. Допустив, что при рн > 1 г/см3 давление зависит только от
плотности, но не от температуры, можно по экспериментальной
зависимости D(p) установить уравнение состояния р(р).
Измерения в интервале р0= 1—1,7 г/см3 показали, что скорость
детонации пропорциональна плотности: D = Ар0.
Предположим также из общих соображений, что плотность в
точке Жуге пропорциональна исходной плотности : рн = h pQ.
Из уравнений сохранения:
D2 = V°2lTirU Ph=D2£sL(Ph-Po) (8.12)
Vo~Vh Рн
Подставляя в (8.12) D = Ар0 и ро = hp0, получим [5]:
р = Вр3; В = А2^-
(8.13)
Таким образом, из факта, что D ~ р0, мы получили простейшее
кубическое уравнение состояния ПД.
Подставляя (8.13) в (8.12), получим:
D2_ РнРн _В Р4
Ро(Рн -Ро) Ро(Рн -Ро) ^'14^
Согласно правилу отбора (условие касания) или правилу Жуге
нормальная детонация идет с наименьшей возможной скоростью.
Поэтому из (8.14) найдем Dmin при данных В и ро:
¥—r*-^l*A<»-аГ-xuI-tAf*'У =0 (8..5)
dp Ро(Ри-Ро) Ро(Рн-Ро)
Откуда следует:
р = 4/3р0; p = l/4p0D2; и = [(рн -р0)//>„]; D = l/4D (8.16)
Скорость звука в точке Жуге с = D - u = 3/4D.
Эти соотношения достаточно точны, поскольку более точные
расчеты с учетом теплового давления дают а^я уравнения изэнтро-
пы р = Врп в точке Жуге значение п = 2,7—3,2, причем величина
давления мало чувствительна к небольшому изменению п. Поэтому
очень часто выбирают п = 3, что резко упрощает уравнения
газодинамики и позволяет просто решать задачи, связанные с одномерным
разлетом ПД [27].
Таким образом, в результате детонации за время порядка 10"7 с
атомы метастабильных молекул исходного ВВ перестраиваются с
выделением энергии в устойчивые молекулы ПД, которые сразу после
реакции (в точке Жуге) упакованы более плотно, чем до детонации.
Можно доказать, что формула (8.10) D2 = 2(k2- 1) Q, найденная
Аая газов, справедлива и аля конденсированных ВВ при условии, что
вся химическая энергия Q переходит в упругую энергию ПД (для р0
больше некоторого предельного значения). Этой формулой удобно
пользоваться при решении различных прикладных задач.
Методы расчета параметров детонации ВВ с р0 > 1г/см3
приведены в [4,5]. Учитывается, что, как и в твердом теле, энергия и давление
П Д имеют две составляющие: упругую (потенциальную) и тепловую
(кинетическую).
В общем виде а^я конденсированных ВВ с ударной адиабатой
D = cQ + S и и показателем изэнтропы п соотношение давлений на УВ
и в точке Жуге будет:
= р0Р2 рн = л + 1
FH S(l-c0/DyPyd S(l-c0/D) V ' ;
Найдем распределение параметров детонации за фронтом
детонационной волны [4].
Поскольку в точке Жуге энтропия со временем не меняется, то
за фронтом происходит изэнтропийное автомодельное расширение
ПД. Для одномерного течения по изэнтропе р = А рп из уравнений
358
газодинамики получается простое аналитическое решение а^я
описания волны разрежения:
x/t = 4 + c; u = (2c-D)(k-l) (8.18)
Для конденсированных ВВ к=3 и (8.18) принимают простой вид
x/t = и + с, -D/2 = и — с, откуда
c = x/2t + D/4)u = x/2t-D/4 (8.19)
В точке Жуге x/t = D, тогда получаем уже известные нам (см.
(8.15)) величины и =1/4 D и с = 3/4 D. К моменту, когда и = 0,
x/t = D/2 и с = D/2. Следовательно, область покоя, где заканчивается
волна разрежения, находится посредине между фронтом детонации
(x/t = D) и плоскостью начала детонации (x/t = 0).
В интервале D/2 > x/t < D величины и и с меняются линейно (см.
рис. 8.4а).
Давление за фронтом р = рн(р/рн)3 и с = сн(р/рн), откуда а^я
точки, где и = 0, имеем р = 8Л? рн и р = 2/з рн = 8А pQ.
Следовательно, за фронтом давление меняется по степенному
закону, а плотность — линейно (см. рис. 8.46).
При мгновенной детонации во всем объеме ВВ везде
устанавливается одинаковое среднее давление П Д при плотности р0 и и = 0:
p = (k-l)p0Q = p0D2/8
(8.20)
cn=D/2
а)
cH=3/4D
uH=D/4
Р„=8/27РН
б) 1
Р„=8Аро
Рн
Рн=4/зр0
Ро
x/t=0 x/t=D/2 x/t=0 x/t=0 x/t=D/2 x/t=0
Рис. 8.4. Распределение параметров за фронтом плоской детонационной волны [4]
Детонационное давление в идеальном газе (см. 8.10):
Рн=2(к-!)роа
Таким образом, давление на фронте детонации в два раза больше,
чем при мгновенном взрыве, что объясняется кинетической
энергией движущихся за фронтом ПД.
В случае цилиндрической и сферической расходящихся
детонационных волн численные методы расчета показали, что параметры
в точке Жуге не меняются в зависимости от геометрии фронта, но
с увеличением порядка симметрии (плоская, цилиндрическая,
сферическая) увеличивается скорость падения параметров за фронтом,
а также уменьшаются размеры и параметры области покоя.
В [28,29] получены аналогичные распределения параметров
детонации, но при помощи других методов расчета.
До сих пор мы использовали простейшее кубическое уравнение
состояния (без учета тепловых составляющих), которое позволяет
сделать только оценки. Ряд задач, связанных с разлетом ПД в
различные среды (воздух, вода, грунт), с отражением ПД от преград, с
метанием пластин и оболочек, требует знания точного
калорического УРС а^я ПД Е = Е(р,р). Для расчета же пяти параметров
детонационной волны нужно знание термического УРС р = р(р,Т).
Как и аая твердого тела, обычно используютУ Р С Ми-Грюнайзена
с упругой и тепловой составляющими давления. Однако а^я П Д
задача усложняется тем, что по мере расширения ПД и уменьшения
их плотности роль упругой составляющей падает, а тепловой —
возрастает, меняются состав и параметры ПД, показатель изэнтропы.
Кроме того, а^я каждого ВВ надо строить свое УРС, поскольку
П Д состоят из разного набора молекул. Точный теоретический
расчет УРС невозможен, поэтому используют полуэмпирические УРС
с привлечением экспериментальных результатов.
Кроме того, обычно используются предположения об
аддитивности вклада компонентов ПД в объем и энергию ПД и о
химическом равновесии (аая расчета концентрации компонентов).
Обзор способов получения УРС а^я ВВ дан в [4,30].
Наиболее часто используется и наиболее надежно уравнение
состояния Беккера—Кистяковского—Вильсона (BKW), которое при-
360
менимо для конденсированных ВВ любого состава с формулой СаНь
Nc Od в широком диапазоне плотностей в предположении
стационарности и химического равновесия процессов детонации:
р = pnRT[\ + ехр(/?х)] (8.21)
где x = pk(T + Q)"a , n = 1/М , М — средний молекулярный вес
газообразных ПД, Q, k, a , $ — коэффициенты, получаемые
сравнением с экспериментом. Например, а^я гексогена (р0= 1,8 г/см3)
к= 10,9; (3 = 0,16; Q = 400; а = 0,5.
Расчетные значения р, D, Т в точке Жуге, полученные с помощью
УРС BKW а^я ряда индивидуальных ВВ и взрывчатых составов,
приведены в таблице 8.2 [30].
УРС BKW помогает понять, почему нет прямой связи между
теплотой взрыва и давлением в точке Жуге. Оказывается, при
детонации ВВ с большой теплотой взрыва возникают ПД, состоящие из
молекул с большим молекулярным весом, следовательно, с низкой
плотностью частиц в ПД. При этом возрастает тепловая
составляющая энергии, но давление в точке Жуге меняется слабо.
Для повышения давления необходимо прежде всего увеличить
плотность частиц в ПД или число молей газа на грамм ВВ (а затем
теплоту взрыва). Этого можно достичь, увеличивая содержание
водорода в молекуле ВВ типа CHNO. Например, нитрогуанадин (С2 28
Н44 N4 02 2) имеет теплоту взрыва вдвое меньше, чем Сотр.В (С685
Н8 75 Ng 06 08 59), но такое же давление в точке Жуге.
Из всех параметров детонации наименее достоверен расчет
температуры. В опыте измеряется яркостная температура ПД,
движущихся на детектор. Эти результаты относятся к температуре
абсолютно черного тела с эквивалентной фотояркостью, но это не так,
если в П Д много кислорода.
Вероятно, расчет по BKW занижает температуру, поэтому в
таблице 8.2 дается также температура, рассчитанная по другому УРС
Леннарда—Джонсона—Девоншира (LJD) [30].
Значения по LJD завышены, и обе расчетные температуры дают
диапазон, внутри которого реальная температура ПД.
Тепловая энергия и температура ПД растут с увеличением
содержания С02 в ПД до тех пор, пока не появится избыток кисло-
рода, после чего температура ПД падает. Как показывают расчеты,
параметры детонации очень чувствительны к изменению плотности
частиц в точке Жуге (или числа молей на 1 г ВВ) и теплоты реакции.
Уменьшение плотности зарядов ВВ снижает D и р (см. табл. 8.2),
а температура в точке Жуге сначала растет, а затем падает (т.к. при
р < 0,5 г/см3 уменьшаются и и Q).
Таблица 8.2. Расчетные параметры детонации [30]
Название ВВ
Гексоген
Октоген
Тротил
ТЭН
ТАТБ
Тетрил
Нитроглицерин
Нитрометан
Тетранитро-
метан
Гексанитро-
бензол
Окись
Азота
ТГ 50/50
(пентолин)
ТГ 64/36
(состав В)
ТГ 77/23
(циклотол)
ОТ (октол)
76,3/23,7
Химическ.
Формула
с,нйм6о6
СЛЧ°«
C7H5N,06
C5H8N4012
СсНЛ°с
CRN, О,
C3H5N309
CH3N02
CN4Os
сло12
NO
2.33 2.36 1.29
^6,85 8,75 7,65
°-3
^5,04 "7,46 6.87
Ц.7"1<Л.22
Pn>
г/см3
1,8
1,0
1,9
1,64
1,06
1,77
1,67
1,0
1,895
1,70
1,59
1,128
1,64
1,973
1,30
1,65
1,713
1,743
1,809
D,
м/с
8754
5981
9100
6950
5254
8300
7980
5480
7860
7560
7580
6290
6360
9300
5620
7465
8030
8250
8476
P»
кбар
347
108
393
190
110
335
300
87
315
251
246
141
159
355
103
247
294
313
343
T,
К
2587—4027
3600-4378
2364—3871
2829—3662
3175-3658
2833—4378
3018—4457
3970-4731
1887—3270
2917—4018
3216-4593
3380
(эксперим)
2800
(эксперим)
3269—4893
1854-2635
3239-4363
2711-3953
2711-3988
2578—3900
362
Для расчета метательной способности ВВ и взаимодействия с
преградами важно знание изэнтропы расширения ПД. Из
основного уравнения термодинамики TdS = dE + pdv получим:
р = ~(^=Р(^)з'Л—)5 =JT 8.22
dV dp dp р
В таблице 8.3 даны результаты численного расчета
изэнтропы гексогена (р= 1,66 г/см3), полученные с использованием (8.22)
и УРС гексогена [4].
В таблице 8.3 представлены: рт — тепловая часть давления;
р — полное изэнтропийное давление; A = -Jpdp/p2 — работа из-
энтропийного расширения ПД; с = (dp/dp)s0,5 — скорость звука;
n = dlnp/dlnp — показатель изэнтропы.
Таблица 8.3. Расчетная изэнтропа ПД гексогена
р.
г/см3.
2,2
2,0
1,8
1,6
1,4
1,2
1,0
0,8
0,6
0,4
0,2
0,05
тк
4260
3910
3580
3270
2980
2720
2480
2240
2000
1720
1360
860
кбар
187,2
150,3
117,3
88,3
63,47
43,05
27,25
15,96
8,518
3,917
1,232
0,160
А,
кдж/г
0,00
1,17
2,24
3,22
4,10
4,87
5,23
6,07
6,52
6,90
7,27
7,73
Р>
кбар
290,2
223,1
166,3
119,1
81,04
51,53
30,06
15,78
7,308
2,887
0,851
0,130
с,
Км/с
6,02
5,56
5,09
4,61
4,10
4,87
5,23
6,07
6,52
6,90
7,27
7,73
п
2,75
2,77
2,81
2,85
2,91
2,95
2,94
2,81
2,52
2,06
1,52
1,26
Как видно, показатель изэнтропы п не постоянен.
В таблице 8.4 для двух сплавов ТГ приведены расчетные
величины давления и плотности на изэнтропе ПД.
363
Таблица 8.4. Плотность и давление на изэнтропе ПД [4]
вв
тг
50/50
ТГ
25/75
Р»
г/см3
р»
кбар
Р»
кбар
2,35
292
308
2,25
252
265
2,1
204
216
1,9
143
154
1,5
58,5
67,2
1,1
24,8
27,5
0,7
7,6
8,6
0,3
2,5
3,0
0,1
0,9
1,3
Совместное решение У PC и закона сохранения энергии
Е-Е0 = 1/2 (р + p0)(vQ-v) дает расчетное уравнение ударной
адиабаты ПД, которая лежит выше ударной адиабаты ВВ (см. рис. 8.1).
Расчетные УРС, изэнтропы и ударные адиабаты ПД
проверяются сравнением с экспериментальными параметрами детонации.
Кроме того, интегральная проверка УРС делается сравнением
расчетного закона движения сферических или цилиндрических
оболочек и плоских пластин с опытными зависимостями R(t) или L(t).
8.4. Измерение параметров детонации
Регистрация явлений в детонационной волне является
технически сложной задачей, т.к. требует высокой точности измерений на
малых базах.
Как правило, в опытах используются плоские детонационные
волны, создаваемые линзовыми системами. Методы измерений
можно разделить на «внешние» (датчики вне заряда) и «внутренние»
(датчики внутри заряда).
8.4.1. «Внешние» методы измерений
1. Наиболее старый и простой метод откола был предложен
Горансоном в 1945 году (Лос-Аламосская лаборатория, США) и
независимо развит Альтшулером и Крупниковым в 1947—48 гг.
[31].
Давления в П Д определяются по измерениям массовой скорости
u = w/2 преграды различной толщины с известной ударной
адиабатой (рис. 8.5). Вид получаемой кривой затухания скорости и давле-
364
ния в преграде отражает последовательное воздействие на преграду
зоны реакции и волны разгрузки. В разделяющей эти зоны
плоскости Чепмена—Жуге параметры ип, рп в преграде и ин, рн в точке Жуге
связаны соотношением:
2 1 2я
,л п -1ин -и„—-
'■-'•«+-2Г-ШБ?Г:
Ун - , ! » ин - Г
которое при известных р0, DH определяет параметры
стационарной детонации.
Скорость w занижается на Aw < pD <7 из-за влияния откольной
прочности с материала преграды. Эта погрешность устраняется при
использовании преграды с искусственным отколом толщиной в
десятые доли мм.
С целью исключения влияния на скорость преграды второй волны,
отраженной от П Д, база измерения S скорости w свободной
поверхности преграды толщиной d должна быть ограничена:
S<2dwlD
п
На рис. 8.6 приведены скорости откола в алюминиевых
преградах ^ая смеси нитрометан-ацетон и /^ля состава В (ТГ 37/63,
ро= 1,67 г/см3). Точки излома на кривых w(l) соответствует точке
Жуге.
2. Более точно и с лучшим временным разрешением (3—5 не)
измеряется затухание ударной волны в преграде в виде пакета тонких
пластин (0,1—0,5 мм) с микронными зазорами.
Если пластины из прозрачного материала (оргстекло), то
используется лазерный измеритель волновых скоростей (ЛИВС) (см.
рис. 8.5). В методе ЛИВС [32,33] лазерный луч отражается от
поверхностей пластин, фарная волна, последовательно закрывая
зазоры уменьшает суммарную интенсивность отраженного света,
который через систему зеркал и линз направляется на фотоумножитель.
Этим методом исследованы профили волн у тротила (см. рис. 8.7),
флегматизированных составов (СН Д) и у актированных ВВ. Метод
«Внешние»» методы — методы преград
Откольная пластина
■и
Заряд
-— w(x) = 2u(x)
Преграда
<з
Л _ w(x) = 2u(x)
1. Откол естественный 2. Откол искусственный
Измерение скорости свободной поверхности преграды
I
3. Метод ЛИВС D(x) в
прозрачной преграде (пакет пластин,
монокристалл)
4. Электрический метод D(x)
в пакете металличеких
пластин (А1)
Измерение волновой скорости в преграде
1 — заряд; 2 — А1-фольга
толщиной 0,01 мм; 3 —
индикаторная жидкость (СНС1);
4 — коллиматор; 5 —
световод; 6 — фотоумножитель;
7 — осциллограф.
5. Фотоэлектричекий метод измерения яркости фронта УВ i (р)
в индикаторной жидкости
«Внутренние методы»
Датчик
t
— u(x)
6. Импульсное
рентгенографиро-
вание смещения
фольг
Фольга Щ А1 датчик Да
|~S~| Магнит
7. Электромагнитный 8. Измерение про-
метод филя давления p(t)
манганиновым
датчиком сопротивления
Рис. 8.5.Экспериментальные методы измерения параметров детонации
w, км/с
3,6
,,км/с
3,2
2,8
20 х, мм 0 2 4 6 8 х, мм
Рис. 8.6. Скорость откола в алюминиевых преградах
а) Смесь нитрометан-ацетон 75/25 1 — искусственный откол (составная преграда),
2 — сплошная преграда.6) Состав В (ТГ 63/37, р = 1,67 г/см3), составная преграда
позволяет надежно определять ширину зоны химической реакции
(ЗХР) и давление в точке Жуге. Так, а^я тротила ширина ЗХР
найдена равной 0,4 мм.
Если используется пакет пластин из непрозрачного металла
(алюминий, t = 0,l мм), то в опыте через пластины пропускается
постоянный ток и регистрируется изменение разности
потенциалов по мере движения по пакету УВ (см. рис. 8.5). В момент выхода
УВ на очередную замкнутую границу пластин потенциал
скачкообразно падает в связи с закрытием микрозазора между пластинами
(1—2 мкм за счет шероховатости поверхности пластин).
Таким методом в [34] измерена зависимость D(l) и найдено аа^
тротила с р=1,5б г/см3рн =
18,3 ГПа и DH = 6,73 км/с, а
давление в химпике р^ = 25,8
ГПа(рув/рн = 1)34).
l=4q 3. Более точна
непрерывная регистрация затухания
УВ в преграде. Из
непрерывных методов наиболее
чувствителен метод изме-
п ^ тгт» рения яркости ударного
Рис. 8.7. Затухание УВ в преградах из оргстекла „
для зарядов из тротила длиной 10,20,40 мм. фронта в примыкающей
Параметры ЗХР: а=0,4 мм, t = 80 не
D, км/с
6,6
5,5 4
к заряду индикаторной жидкости (СС14, СНС13) с известной
зависимостью яркости от давления в У В (см. рис. 8.5) [35].
Способ позволил четко определить ЗХР в высокоплотных
тротиле, ТГ 50/50, гексогене и в составах на основе гексогена и октоге-
на [36].
4. Предельно высокой разрешающей способностью (0,3 не)
обладают лазерные интерферометры, измеряющие по отражению
лазерного луча скорости тонких (15—25 мкм) фольг на границе
заряда с прозрачными «окнами» из воды. В работе [37] на
интерферометре ORVIS изучены тротил и состав RBX-9502 на основе
ТАТБ.
и,км/с Составы на основе ТАТБ
имеют общие особенности:
отсутствие четких границ ЗХР и рост
скорости с длиной заряда, что
характерно аая неустановившейся
детонации.
В [38] в качестве «окна»
использовался монокристалл LiF,
а толщина отражающего слоя
из алюминия не превышала 0,2
мкм. Результаты таких опытов
с составом LX-14
подтверждают двухстадийную модель с
быстрой и медленной стадиями
(см. рис. 8.8).
2,3
1.9 Ч
1,5
1,1
1,3
—i—
1,5
t, МКС
Рис. 8.8. Скорость ПД на границе
с LiF для состава LX-14
Во всех этих методах профиль
массовой скорости в преграде
отождествляется с профилем
детонационной волны
8.4.2. «Внутренние» методы измерений
1. Импульсное рентгенографирование смещения фольг внутри
заряда в процессе его детонации [39]. Впервые метод был
разработан в 1948 году Цукерманом и применен для исследования ТГ 50/50
[40] (рис. 8.5).
2. Измерение давления манганиновыми датчиками
сопротивления [41,42] (рис. 8.5). Метод дает непосредственно профиль
изменения давления в детонационной волне.
368
3. Электромагнитный метод измерения массовой скорости. Идея
метода разработана Завойским [43] и заключается в следующем (см.
рис. 8.5). В заряд ВВ помещают П — образный датчик из тонкой
(0,07—0,1 мм) алюминиевой фольги. Рабочей частью датчика
является его перекладина. Заряд помещают в однородное магнитное
поле. При детонации заряда датчик вовлекается в движение, при
этом в нем возникает Э.Д.С. индукции Е (в), которая связана со
скоростью и (см/сек) датчика, его длиной 1 (см) и напряженностью
Н (э) магнитного поля соотношением: Е (t) = - Hlu 10"8.
С помощью осциллографа записывается E(t).
Предполагается, что датчик безынерционный, т.е. его скорость
равна массовой скорости продуктов детонации.
В действительности прохождение детонационной волны
через датчик вызывает нестационарные переходные процессы,
связанные с рассогласованием динамических импедансов pD датчика и
ПД. Точность измерений 2% при разрешении 10 нсек.
Модельные расчеты стационарной детонации позволяют
оценить, насколько искажаются реальные профили u(t) и D(t) в
зависимости от материала и толщины датчика.
Результаты таких расчетов для ТГ50/50 приведены на рис. 8.9 [44].
и, км/с
D,km/c
8 -
7 -
6 -
/
i
- *м 1
1
,
----->=*---
/
1
i i i i
2,4
2,2
2,0
1,8
5^=150 мкм
Идеальный датчик
=50 мкм
-0,5 0 0,5 1,0
0
50
i I
100 150
t, не
Рис. 8.9. Расчетные профили и (х) и D (х) при прохождении через датчик
стационарной детонации в ТГ 50/50
Сравнение «внешних» и «внутренних» методов сделано в
[25] по результатам измерений разными авторами давления в точке
Жуге а^я сплавов ТГ. Все результаты приводились к одному
составу а = 40/60 и к одной плотностиj)Qr = 1.73 г/см3 по формулам [45]:
Арн/рн = 2,30 Ар0/р0; Арн = 0,157 ГПа на 1% гексогена (см.
табл. 8.5).
Таблица 8.5. Сравнение результатов измерений различными методами
Методы
Р»
г/см3
а
%
Эксперимент
р,ГПа
Привед.
р,ГПа
п
Средние
рип
«В нешние» метод ы»
Откол
Откол
Откол
Откол
ЛИВС
1,715
1,67
1,713
1,73
1,692
35/65
37/63
36/64
40/60
46/60
29,2
27,2
29,2
29,2
28,1
29,0
29,0
29,2
29,2
29,6
2,74
2,74
2,72
2,72
2,67
Для «внешн.»
методов
р = 29,2
п = 2,72
«В нутренние» методы»
Электромагниты.
Рентген
Рентген
Магнитн.
Магнитн.
Магнитн.
Датчик
1,71
1,73
1,73
1,73
1,73
1,67
36/64
40/60
40/60
40/60
40/60
40/60
26,6
26,8
27,5
27,4
26,4
25,4
26,5
26,8
27,5
27,4
26,4
27,5
3,09
3,05
2,95
3,02
3,11
2,95
Для «внутр»
методов
р = 27,0
п = 3,02
Как видно из табл. 8.5, «внешние» методы дают систематически
более высокие давления, чем «внутренние» методы.
Это можно объяснить, основываясь на двухстадийной
детонации. Опыты с преградами фиксируют повышенные давления
затянутых реакций, а «внутренние» методы — профили волн
разрежения, характеризующие параметры стационарной
детонации.
Такая же картина наблюдается и у сплава ТГ 50/50: «внешние»
методы дают р = 25,5 + 0,5 ГПа ,а «внутренние» — р = 24 + 0,3 ГПа [25].
370
Сравнение параметров в точке Жуге, измеренных &ая тротила
(р0= 1,59 г/см3) разными авторами методами откола и
электромагнитным приведены в таблице 8.6 [4].
Таблица 8.6. Параметры Жуге для тротила
Метод
Откол
(естеств.)
Откол
(искусств.)
Электромагнитный
D,km/c
6,94
6,91
6,91
и,км/с
1,76
1,61
1,60
р,ГПа
19,4
17,8
17,6
ЗХР, а, мм
0,17
0,97
0,7
ЗХР, t, нс
39
200
100
В настоящее время величины рн определены ^\ая многих ВВ с
погрешностью не более 0,5 ГПа, а а^я показателя изэнтропы
возможные отклонения An « 0,1.
Для наиболее распространенных индивидуальных и смесевых
ВВ параметры Жуге даны в табл. 8.7.
Таблица 8.7. Параметры Жуге
ВВ
Тротил
Гексоген
Гексоген
Флегмати-
Зирован.
ТЭН
ТЭН
флегмати-
зирован.
РВХ — 9404
ТГ 50/50
ТГ 36/64
(сплав В)
р, г/см3
1,53
1,63
1,66
1,78
1,66
1,66
1,76
1,66
1,84
1,68
1,73
D,km/c
6,83
6,94
8,21
8,67
8,12
7,95
8,26
8,12
8,80
7,65
7,92
и,км/с
1,66
1,70
2,11
2,24
1,94
2,05
2,12
1,78
2,29
1,92
1,97
р,ГПа
17,7
19,2
28,8
34,5
27,0
27,0
30,8
24,0
36,0
24,6
27,0
п
3,10
3,10
2,88
2,88
2,90
2,90
2,95
2,98
3,02
371
На рис. 8.9а приведены экспериментальные зависимости
давления в точке Жуге от плотности зарядов из тротила, гексогена и ТЭНа
[25].
Тротилгь=3,1 Гексоген гь=2,9 ТЭНгь=2,9
РнДПа
гъ=3,2
1,55 1,59 р0,г/см3 1,6 1,7 р0,г/см3 1,6 1,7 р^г/см3
Рис. 8.9а. рн, р0 — диаграммы для тротила, гексогена и ТЭНа
При построении границ полосы разброса ТЭНа использовались
соотношения [45]:
при р0 < 1,65 г/см3: D = 4,78 + 3,7 (р0« 0,8);
при р0> 1,65 г/см3: D = 7,92 + 3,05 (р0« 1,65).
Экспериментальные величины давлений стационарной
детонации аля ряда наиболее распространенных ВВ обобщены на
рис. 8.10.
Рн.ГПа
35
30
25
20
Х2.93
15 \-z fz А А Ро-г/см3
ТГ 50/50
тнт
7
Х2.93
РВХ-9404^
Гексоген
ТЭН ^Ч
В \12
"^3.03
^2.95
Октоген
^22
1,6
1,7
1,9
Рис. 8.10. Номограмма детонационных давлений для семи распространенных ВВ
372
Как видно, величины
п = 3, что обеспечивает
правомерность
использования кубического УРС.
Там же указаны
усредненные показатели изэнтро-
пы п , характеризующие
расширение ПД.
Используя 51
измерение давления в точке Жуге
для различных составов
в интервале 17—39 ГПа
для плотностей зарядов
1,6—1,9 г/см3, нами получена следующая линейная зависимость (см.
рис. 8.11):
Рн,ГПа
36
32
28
24
20
16
I .. Гг
«г—-З^А
I 1 **/Л I I I
1,5
1,6
1,7
1,8 Ро,г/см3
Рис. 8.11. Зависимость p^pj
для составов CHNCJ
рн= 19 + 69 (р-1,6)
(8.25)
Выше этой линии расположены результаты измерений по методу
откола.
Зависимость (8.25) полезна fi^ проведения инженерных оценок
давления.
8.4.3. Исследование структуры зоны химической реакции при
детонации твёрдых ВВ
Структура и размеры ЗХР различных твёрдых ВВ подробно
исследованы в работе [10].
Для проведения измерений применялся усовершенствованный
фотоэлектрический метод (см. рис. 8.5) с временным разрешением
5 не.
В опытах в качестве индикаторной жидкости использовался
хлороформ СНС13 с ударной адиабатой D = 1,174+ l,724u-0,0497u2
(км/с) и зависимостью интенсивности I свечения фронта УВ от
давления р/р2 = (I./L)0'2.
Профиль давления на фронте УВ в хлороформе отражает
профиль давления в детонационной волне.
Полученные в [10] основные результаты измерений следующие.
1. Для всех исследованных ВВ, кроме актированных,
зарегистрирован химпик с временем нарастания, равным временному
разрешению методики (5 не).
2. Между зоной реакции и волной Тейлора отсутствует чётко
выраженная граница, но есть различия в законах затухания УВ в
хлороформе. Для расчёта времени реакции и ширины ЗХР было
принято, что реакция заканчивается в плоскости Жуге (хотя
выделение энергии за счёт коагуляции углерода может продолжаться
[46,47]).
В каждой области зависимости производных du/dt от времени
в полулогарифмических координатах — прямые линии, точка
пересечения которых соответствует плоскости Жуге.
Линейность du/dt указывает на экспоненциальную зависимость
u(t) в ЗХР (при t < t) в виде ехр(—t/t), где t, — характерное время
реакции, в течение которого количество а непрореагировавшего ВВ
уменьшается в е раз.
По измеренным величинам D, ин и t рассчитывалась ширина
3XP:xH=0D-u)dt
3. Массовая скорость на детонационном фронте на 30—50%
превышает скорость в плоскости Жуге и с точностью ~ 10% может быть
рассчитана по экстраполированной ударной адиабате ВВ (за
исключением актированных ВВ), Но этот факт не означает отсутствие
реакции на фронте, поскольку определить величину а по измерениям
массовой скорости невозможно.
4. Зависимость da/dt от а а^я а < 0,5 в логарифмических
координатах линейна с наклоном 1...1Д. Поэтому можно считать, что
последние 50% энергии в ЗХР выделяются благодаря реакции первого
порядка, для которой скорость реакции пропорциональна непро-
реагировавшему ВВ.
5. У актированных ВВ (прессованных с растворителем до
относительной плотности 0,99 и полупрозрачных) время реакции
меньше времени разрешения методики (меньше 5 не), т.е. зона реакции
374
очень узкая. Те же ВВ, но прессованные без растворителя до близкой
плотности 0,98 с мельчайшими порами имеют время реакции 0,05—
0,11 мкс. Следовательно, именно гетерогенность ВВ определяет
время реакции. Гетерогенность означает, что весь объём ВВ можно
разделить на две части:
— горячие точки (микропоры, трещины, границы зёрен), где
при Т> 1000 К происходит быстрый тепловой взрыв за время
~1 не;
— холодные точки (монокристальные частицы), в которых
первоначально Т<1000 К (слабый адиабатический нагрев), а
дальнейшее их нагревание идёт за счёт сравнительно медленной
теплопередачи от горячих точек.
Увеличение давления ударной волны, сжимающей ВВ, приводит
к росту средней температуры и, соответственно, к увеличению доли
гетерогенного ВВ с быстрой реакцией теплового взрыва, т.е. к
уменьшению до нуля влияния гетерогенности.
Таким образои два параметра определяют время реакции и
ширину ЗХР: степень и характер гетерогенности (распределение пор,
тип связки) и давления УВ, рост которого устраняет влияние
гетерогенности.
6. Давление в УВ коррелирует с давлением Жуге, поэтому ЗХР
зависит от давления Жуге. Для ТНТ, ТЭНа, гексогена, октогена,
тетрила, дины и составов на их основе эта зависимость
аппроксимируется выражением: t = 0,7exp(-pH/l4) (рн — в ГПа, t —
в мкс)
Увеличение давления Жуге на каждые 10 ГПа (независимо от
способа) уменьшает ширину ЗХР вдвое.
7. Химпик исчезает, когда с ростом давления ударная адиабата
ВВ сливается с адиабатой ПД. При этом реакция протекает
полностью на фронте УВ. Для малочувствительного ТАТБ химпик
исчезает в пересжатой детонации с давлением 40 ГПа.
Вместо химпика наблюдается монотонный рост давления.
Отметим, что в работе [48] измерениями с помощью
интерферометра VISAR показано, что для каждого ВВ существует критиче-
375
екая плотность, выше которой химпик исчезает (для гексогена —
р0* = 1,73 г/см3, для октогена — р0* = 1,84 г/см3.
Таблица 8.9. Ширина ЗХР для ряда ВВ [4,25,33,36]
ВВ Метод измерения
Тротил прессованный Электромагнитный метод
Тротил литой Электромагнитный метод
Тротил Метод откола
Тротил прессованный Метод преград
Гексоген Электромагнитный метод
ТГ 36 Электромагнитный метод
ТГ 50 Электромагнита, метод
ТЭН флегматизированный Электромагнитный
метод
ТГ 36+1% воска Метод откола
Порох баллист. Метод откола
Фотоэлектрический метод:
90% октогена +10% ТНТ
70% гексогена+30% ТНТ
90% ТАТБ +10% полим. Связки
Аммонит ПЖВ-20 d= 120 мм
Электромагнитный метод
г/см3
0,8
1,0
1,35
1,36
1,45
1,59
1,60
1,60
1,62
1,0
1,45
1,59
1,59
1,0
1,0
1,59
1,72
0,9
1,68
1,68
0,95
1,66
1,67
1,58
>1,8
>1,7
>1,9
0,9
1,7
а,
мм
2,53
1,75
2,14
1,35
1,0
1,0
1,35
1,64
1,41
0,32
0,19
0,17
0,4
1,79
1,26
<1
<0,7
2,16
<0,5
1,33
1,53
<0,5
0,13
0,12
0,17
0,25
0,65
2,51
1,62
МКС
0,85
0,50
0,47
0,32
0,20
0,20
0,22
0,33
0,30
0,100
0,048
0,039
0,08
0,34
0,30
<0,2
<0,1
0,6
<0,1
0,26
0,33
<0,1
0,024
0,033
0,025
0,042
0,120
0,75
0,37
376
8. Ширина ЗХР растёт по мере распространения детонации, т.е.
с увеличением диаметра и длины заряда. В совокупности с
влиянием плотности, типа и степени дисперсности, микротурбулентности
погрешностей разных методик, способов и критериев определения
разными авторами зоны реакции, получается достаточно большой
разброс экспериментальных данных по определению времени
реакции и ширины ЗХР.
Измеренные различными методами величины ЗХР и времени
реакции t а^я ряда ВВ приведены в таблицах 8.10 и 8.11.
Таблица 8.10. Результаты измерений и расчётов параметров зоны
химреакции [49]
Метод
Измер.
Бромо-
Форм
ферометр
Откол
Расчёт
Размер ЗХР,
мм
Сотр
В
0,4
0,2
0,14
РВХ
9502
0,8-
1,6
0,3
РВХ
9404
0,2
<0,1
0,1
0,7
Давление химпика
ГПа
Сотр
В
39,5
42,0
37,4
43,7
РВХ
9502
37,6
37,7
РВХ
9404
48,5
55,0
56,0
Давление в точке
Жуге,ГПа
Сотр
В
28,5
28,5
РВХ
9502
29,0
29,0
РВХ
9404
36,5
36,5
Более обоснованно не связывать ЗХР с количеством
выделившейся энергии или с кажущимся изменением зависимости u(l), а
определять зону реакции как зону от фронта УВ до звуковой
поверхности, где D = и + с (в одномерном случае это плоскость Жуге).
9. Полученные в [10] результаты измерений времени реакции и
ширины ЗХР приведены в таблице 8.11.
В общем случае, когда сопоставимы времена химических и
механических процессов (определяемых вязкостью, диффузией,
теплопроводностью), возможны следующие варианты изменения
состояния детонирующего ВВ при различной начальной скорости
химической реакции (см. рис. 8.12) [48]:
377
Таблица 8.11. Параметры зон реакции детонирующих ВВ
ВВ
ТНТ
(прессованный с подплавле-
нием)
ТНТ (литой)
ТНТ
(прессованный)
ТАТБ*
ТАТБ
ТАТБ/инерт
ТАТБ/инерт
Гексоген/ТНТ
50/50
Гексоген/ТНТ
70/30
Октоген/ТНТ
90/10
Октоген/инерт
Октоген/инерт
Гексоген
(актированный)
Гексоген
Гексоген
ТЭН
(актированный)
ТЭН
ТЭН
Октоген
Октоген
Гексоген/
инетрт94/6
Р(/ Ркрист.»
%
97,9
94,3
91,9
95,4
94,8
99,1
99,1
97,6
99,5
99,1
99,2
69,1
98,6
92,4
92,4
98,3
97,8
91,5
97,1
94,7
99,4
Размеры
ВВ,мм
0 60x100
060x100
060x100
040x10
0120x80
060x120
060x150
060x100
060x150
060x150
060x150
040x50
040x80
040x80
040x40
040x80
040x40
040x40
040x80
040x80
040x80
Т, НС
91 ±14
80 ±12
62±13
103 ±15
109 ±16
99 ±21
94 ±14
33 ±7
19±4
11 ±2
11 ±2
71 ±11
15+3
12±3
32±7
27 ±6
10±2
15±2
12±2
t3, МКС
0,33 ±0,05
0,29 ±0,04
0,19 ±0,04
0,31 ±0,04
0,24 ±0,03
0,26 ±0,05
0,21 ±0,03
0,13 ±0,03
0,08 ±0,02
0,07 ±0,01
0,06 ±0,01
0,19 ±003,
< 0,005
0,07 ±0,01
0,05 ±0,01
< 0,005
0,08 ±0,02
0,11 ±0,02
0,04 ±0,01
0,06 ±0,01
0,05 ±0,01
х3,мм
0,54 ±022,
0,36 ±0,19
0,87 ±0,17
056, ±0,22
0,18 ±0,17
0,24 ±0,25
0,03 ±0,14
0,64 ±0,13
0,44 ±0,09
0,37 ±0,07
0,36 ±0,05
0,80 ±0,11
<0,03
0,36 ±0,07
0,28±0,0б
<0,03
0,42 ±0,08
0,52 ±0,10
0,25 ±0,04
0,33 ±0,05
0,28 ±0,04
378
1. Модель ЗНД:
скачок в точку 2 ударной
адиабаты ВВ (1) и затем
непрерывно вдоль прямой
Михельсона (5) в точку
4 адиабаты ПД (3),
которая соответствует
пересжатой детонации.
2. Учёт кинетики
реакции и ширины фронта УВ,
определяемой процессами
переноса, даёт
непрерывное изменение состояния
вдоль траектории (а), при
этом химпик уменьшается, а качественно режим ЗНД сохраняется.
3. При определённой реакции конечное состояние 4 достигается
в результате монотонного роста давления по траектории (в).
4. При очень быстрой реакции конечное состояние в точке 6
лежит на слабой ветви ударной адиабаты ПД, т.е. реализуется недосжа-
тая детонация.
Возможные профили давления детонационного фронта
показаны на рис. 8.13.
Рис. 8.12. Фазовые траектории изменения
состояния ВВ [48]
гэнд
Конденсированные ВВ
монолитной плотности
Ро.п
Гетерогенные
конденсированные
ВВсРо<р*0
УС=УФ(~пс)
Рис. 8.13. Кривые сжимаемости и возможные профили давления
на фронте детонационных волн
8.4.4. Измерение температуры ПД
Температура ПД измеряется по излучению в предположении, что
оно является тепловым и равновесным, т.е. ПД считается абсолютно
черным телом. Метод измерения основан на определении отношения
яркостей при двух длинах волн (метод «красно-синего» сравнения).
По формуле Планка относительная спектральная яркость
абсолютно черного тела Ь(Х,Т) аля длины волны! равна:
Ыял=-—^
ехр(С2/ЯГ)-1
где Cj = 3,7 10"5 эрг см2/сек; С2 = 1,433 см х град.
Для температур Т < 6000 К ехр С2 ДТ > > 1, поэтому а^я данной
температуры Т и двух длин волн^ Д отношение яркостей
выражается соотношением:
К\,т) С1,Л , с2
In КУ '=5111-2- + -
6(4,г) л, ГЛ-Л
откуда (8.26)
Q 4~4
т_ \К
"toMZ)_5hi
Свечение ПД регистрируется фотоумножителем, ток
которого записывается осциллографом. Перед фотоумножителем система
объектив — щель вырезала свечение узкого участка ПД на оси
заряда.
При помощи двух светофильтров выделяли определенные части
спектра свечения ПД и определяли относительные яркости в
соответствующих интервалах длин волн.
Затем по этим экспериментальным данным рассчитывали по
(8.26) температуру ПД.
380
Чтобы исключить свечение УВ в воздухе, использовались
высокоплотные заряды, которые помещались внутрь прозрачных
оболочек (вода, полимеры).
Измеренные Апиным и Воскобойниковым температуры ряда
ВВ приведены в табл. 8.12 [50].
Таблица 8.12. Температура детонации
ВВ
Гексоген
ТЭН
ДИНа
Нитрометан
Метилнитрат
Нитрогликоль
Нитроглицерин
р0, г/см3
1,80
1,77
1,70
1Д4
1,21
1,50
1,60
ТК
3700
4200
3700
3700
4500
4400
4000
Тем же методом в [51] измерены температуры ряда ВВ (см.
рис. 8.14).
тк тк тк тк
4500 -\
4000
ХМх
3500
Р0=1,63
1 о
0,5
1 t, МКС
Рис. 8.14. Результаты измерений температуры детонации [51]. (длина волны
1=0,95мкм)
8.5. Термохимия детонации
Общие задачи исследования параметров детонации и их
прикладное значение видно из таблицы ниже.
381
Основные проблемы исследований характеристик
детонации
Предмет исследований
Определение теплоты взрыва,
Объема и состава ПД.
Определение давлений в химпике,
в точке Жуге и при расширении ПД
Прогнозирование свойств новых
ВВ.
Прикладное значение
Способность ВВ совершать работу
(фугасное действие взрыва).
Допустимость применения с точки зрения
безвредности ПД для человека.
Расчет местного действия взрыва:
Деформация, метание, кумуляция.
Увеличение бризантности, фугасности,
метательной способности,
безопасности,снижение токсичности ПД.
По своей сути детонация является быстрой экзотермической
реакцией. Поэтому необходимо знание уравнения реакции,
связывающего химическую формулу исходного ВВ с составом конечных П Д и
позволяющее рассчитать теплоту взрыва и объем ПД.
Расчеты затруднены тем, что, во-первых, константы равновесия
реакций для очень высоких давлений детонации точно неизвестны
и, во-вторых, обычно при детонации в П Д не успевает установиться
химическое равновесие, т.е. реакции не идут до конца, в ПД
содержится в больших или меньших количествах промежуточные
соединения. Это характерно аля зарядов ВВ малых размеров. Состав П Д
меняется также с изменением начальной плотности ВВ.
Экспериментальное определение состава холодных ПД не дает
информации о составе ПД в точке Жуге, поскольку в процессе
расширения состав П Д меняется.
Таким образом, и расчет, и эксперимент дают лишь
приближенные результаты.
Как правило, исходная формула ВВ имеет вид Са Hb Ос Nd .
Соответственно, в составе П Д могут содержаться С02, Н20, N2,02,
СН4, СО, NH3, N20, NO, HCN, С.
Обычно ВВ представляет собой нитросоединение, которое
содержит в каждой молекуле и «горючее» (углерод, водород), и
кислород, причем кислород связан с азотом.
Экзотермические реакции окисления углерода до СО и С02 и
водорода до Н20 и представляют собой источник энергии взрыва.
382
Если ВВ содержит кислорода как раз столько, сколько нужно аля
полного окисления входящего в его состав «горючего», то
кислородный баланс его равен нулю. При недостатке кислорода
(отрицательный кислородный баланс) в ПД появляется свободный углерод
(пример — ТНТ), который может быть в форме сажи или
ультрадисперсного алмаза в зависимости от давления в точке Жуге.
Состав П Д прежде всего зависит от положения равновесия двух
следующих реакций:
а)2СО,С02+С
б)Н2+СОгН2<Э+С
Равновесие реакции б) во всех случаях предельно сдвинуто
вправо, а для реакции а) равновесие сдвинуто вправо только а^я высоких
исходных плотностей ВВ р0 > 1,5 г/см3 (аля высоких давлений).
Следовательно, водород молекул ВВ всегда окисляется до Н20,
а углерод может окисляться до С02 полностью (аая высокоплотных
зарядов с р0->ртах)> либо распределяться между С02 и СО (а^я
малоплотных зарядов).
Важнейшей характеристикой ВВ является теплота взрыва,
которая представляет собой суммарный тепловой эффект первичных
химических реакций в точке Жуге и вторичных равновесных реакций в
расширяющихся ПД. Рассчитать тепловые эффекты каждой из этих
реакций затруднительно, однако суммарную теплоту определить
несложно, если воспользоваться законом Гесса, согласно которому
тепловой эффект химической реакции, протекающей при v = Const
или р = Const, не зависит от пути ее протекания, а определяется
начальным и конечным состояниями системы.
Для расчета теплоты взрыва (^ надо знать теплоту
образования (Q^ ) ВВ и ПД. Теплота образования реализуется при
создании одного моля данного соединения из простых веществ при
стандартных условиях (находится из термохимических таблиц, см. [4,50]).
Из закона Гесса следует:
Ив ~ Уобр. ПД ~ Уобр.ВВ (8.28)
Теплота взрыва не строго постоянная величина, поскольку
зависит от состава ПД, который меняется в зависимости от условий
инициирования заряда и расширения П Д. Прежде всего, (^ зависит
от плотности и размеров заряда.
Величины (^ можно найти в справочниках (см. [4,52]), а а^я
некоторых ВВ (при р0 > 0,8 ртах) приведены в таблице 8.13 [4]
Таблица 8.13. Теплота взрыва ВВ
Название ВВ
Азид свинца
Гремучая ртуть
Гексоген
Октоген
ТНТ
ТЭН
Qb , ккал/кг
390
414
1320
1290
1010
1400
Название ВВ
Нитроглицерин
Дымный порох
Пироксилин
Оксиликвиты
Аммонийная
Селитра
Аммотол 80/20
Qb ,ккал/кг
1550
665
1040
1600—2000
344
1000
Методы расчета состава и параметров ПД, детонационных
характеристик , а также величин Qb описаны в [4]. Для расчетов с
помощью ЭВМ широко используется уравнение состояния ПД
Беккера—Кистяковского—Вильсона (BKW) [30,49].
Расчет состава ПД в точке Жуге а^я некоторых ВВ приведен в
таблице 8.14 [30].
Таблица 8.14. Состав ПД (моль/кг) в точке Жуге (УРС BKW)
ВВ
Гексоиен
Октоген
ТНТ
ТЭН
ТАТБ
Состав В
Циклотол
Октол
р0, г/см3
1,8
1,0
1,9
1,64
0,73
1,77
0,50
1,895
1,713
1,743
1,809
н2о
3,00
2,80
4,00
2,50
1,76
4,00
3,73
3,00
4,73
3,73
5,01
со2
1,49
0,67
2,00
1,66
0,69
3,89
2,81
1,50
2,41
1,98
2,69
СО
0,022
1,855
0,008
0,188
2,865
0,223
2,188
0,006
0,103
0,061
0,041
NH,
0,029
-
0,001
0,02
0,001
-
-
-
-
N2
3,00
2,98
4,00
1,50
1,49
2,00
1,93
3,00
3,82
3,44
4,61
С
1,49
0,45
2,0
5,15
3,45
0,89
0,01
4,50
4,34
3,00
4,10
384
8.6. Возбуждение детонации
К началу 1970-х годов сформировались представления о
процессах перехода горения в детонацию благодаря работам Андреева,
Беляева, Боболева, Петровского, Боудена, Мачека, Тейлора, Гриф-
фитса, Прайса [53].
Для возбуждения детонации в заряде ВВ необходим начальный
импульс, величина которого определяется как видом самого
импульса (тепловой, ударный, механический, лучевой), так и
характеристиками самого ВВ (размеры заряда, пористость, величина частиц,
гетерогенность, наличие оболочки).
Инициирующий импульс должен иметь достаточную
энергию, чтобы вызвать химическую реакцию разложения молекул ВВ.
Причем эта энергия должна быть сконцентрирована в некотором
объеме (в очаге реакции), в котором образуется достаточно много
активных молекул.
Процессы инициирования детонации связаны с механизмами
протекания химических реакций в детонационной волне. Ю.Б. Хари-
тон выделяет три типа таких реакций: ударный, баллистический и
смесевой [4,54].
фарный механизм характерен ^ая гомогенных непористых ВВ,
химическая реакция идет за счет сжатия и разогрева всего объема ВВ
за фронтом ударной волны (адиабатный взрыв).
При баллистическом механизме превращение происходит не во
всем объеме, а в поверхностных слоях отдельных сгорающих частиц
(теория горячих точек), что характерно длч пористых зарядов ВВ. С
уменьшением размера частиц уменьшается время их горения и,
следовательно, уменьшается ширина зоны реакции.
Смесевой механизм наблюдается ^ая твердых взрывчатых смесей
типа горючее — окислитель, в которых реакция протекает лишь на
границе раздела компонентов.
Для любых типов ВВ их инициирование осуществляется той
частью начального импульса, которая повышает температуру
ВВ, поскольку скорость химической реакции пропорциональна
exp(-E/RT). При высокой температуре большая скорость
экзотермической реакции означает и большую скорость выделения энергии.
385
При этом потери энергии незначительны, и вся энергия реакции
(Е + Q) оказывается сосредоточенной в ее продуктах.
Высокая концентрация энергии в какой-то части объема ВВ
обеспечивает передачу выделившейся энергии соседним слоям ВВ, в
которых также возбуждается быстрая реакция. Такое самоускорение
реакции может происходить по трем основным механизмам [50]:
тепловое самоускорение (разогрев за счет выделяющегося при
реакции тепла), автокаталитическое самоускорение (за счет
каталитического действия промежуточных продуктов реакции) и цепное
самоускорение (в результате превышения разветвления над обрывом
цепей в цепных реакциях).
Распад ВВ представляет собой сложную многоступенчатую
совокупность последовательно и параллельно идущих реакций [50]. Ход
реакций и состав продуктов реакций может меняться как в
процессе разложения при постоянной температуре, так и при изменении
температуры и давления. Соответственно изменяются и величины
энергии активации реакций.
Например, а^я реакций при больших давлениях и
температурах в уже сформировавщейся детонационной волне энергия
активации в полтора раза меньше, чем а^я реакций медленного
разложения ВВ при температурах до 600 К (например, 25 и 40 ккал/моль)
[55].
Способность ВВ к самораспространяющейся реакции (или
легкость возбуждения детонации) определяется не абсолютной
величиной энергии активации Е, а соотношением между энергией распада
молекулы (возбуждающей распад сосоедних молекул) и энергией
активации, характеризующей устойчивость молекул.
Другой важной характеристикой самоускоряющихся реакций
ВВ и важным условием их перехода в детонацию являются
максимальная скорость реакции и время ее достижения.
Эти характеристики зависят от химического строения ВВ. Так,
нитросоединения и нитрамины разлагаются с относительно
малым ускорением, а аля нитроэфиров, наоборот, ускорение велико, и
очень быстро максимальная скорость достигает значения, в тысячи
раз большего начальной скорости разложения [50].
386
Таким образом, в зависимости от структуры ВВ (гетерогенной
или гомогенной) процесс возбуждения детонации может протекать
по двум различным механизмам: очаговому (нагрев в горячих
точках) и адиабатному (нагрев всего объема ВВ).
8.6.1. Очаговый механизм возбуждения детонации
в пористых ВВ
Поскольку возбуждение детонации начинается с реакции
разложения (горения) ВВ, то имеет смысл напомнить кратко некоторые
элементы кинетики химических реакций.
Согласно Аррениусу, реакция происходит при столкновении
только активных молекул, таких, которые обладают при столкновении
некоторой избыточной энергией, называемой энергией активации Е.
Число активных молекул в единице объема равно их общему
числу, умноженному на exp(-E/RT). Объемная скорость реакции
(число молекул, реагирующих за 1 секунду в 1см3) равна удвоенному
числу столкновений, при которых суммарная энергия сталкивающихся
молекул превышает энергию активации.
Скорость реакции в зависимости от температуры определяется
выражением:
K = Bcxp(-E/RT) (8.29)
где множитель В не зависит от температуры, а величина К есть
константа, характеризующая зависимость скорости реакции от
температуры. Чем больше энергия активации Е, тем сильнее растет
скорость с повышением температуры при условии Е > > RT.
Скорость реакции со временем падает, т.к. падает концентрация
реагирующих веществ в процессе реакции. Причем, это падение
зависит от числа молекул, участвующих в реакции. Практически во
всех реальных химических процессах участвуют только одна или две
молекулы, т.е. это реакции первого или второго порядка.
С нагревом разложение ВВ начинается с первичной
мономолекулярной реакции, которая протекает по закону реакции
первого порядка. Заметная скорость распада ВВ наблюдается уже при
100—200°С и характеризуется большим температурным коэффи-
387
циентом скорости: при повышении температуры на 10° скорость
распада многих ВВ увеличивается в 4 раза.
Для реакций первого (п = 1) и второго (п = 2) порядка скорость
реакции зависит от времени t следующим образом:
п = 1: dx/dt = aKtxp(-Kt)
(8.30)
п = 2: dx/dt = K(a-x)
где а и х — концентрации реагирующих веществ и продуктов
реакции соответственно.
Множитель В в (8.29) представляет собой вероятность распада
активной молекулы, равной обратной величине времени t ее жизни.
Для бимолекулярных реакций (п = 2) множитель В численно равен
удвоенному количеству соударений между молекулами за 1 сек в
единице объема. При концентрации реагентов а = 1 моль/л В ~10п.
К мономолекулярному распаду (п = 1) способны только
сложные молекулы с большим количеством связей. Для концентрации
энергии на одной разрываемой связи должно произойти за время
t перераспределение энергии между связями. Очевидно, величина t
не может быть меньше периода внутримолекулярных колебаний, т.е.
t= 1012—1014.ТогдаВ= l/t= 1012—1014.
Величины В и Е а^я первичной реакции разложения некоторых
ВВ при нормальном давлении даны в табл. 8.15 [50].
Из табл. 8.15 видно, что величина Е не постоянна и зависит от
температуры, давления и агрегатного состояния.
Разложение ВВ при его нагреве является экзотермической
реакцией горения, которая происходит как в конденсированной фазе,
так и в образующихся при нагреве ВВ газах (вследствие
летучести ВВ).
Теория горения газов (паров) была создана в 1938 году
Я.Б. Зельдовичем и Д.А. Франк-Каменецким. Тогда же А.Ф. Беляев
показал, что эта теория применима и к горению летучих
конденсированных ВВ, ^ая которых скорость испарения значительна уже при
умеренных температурах начала разложения. Поэтому превращение
в пар летучих ВВ является первым этапом их горения.
388
Таблица 8.15. Кинетические характеристики первичной реакции
разложения некоторых ВВ
вв
Нитроглицерин (пары)
Нитроглицерин
Нитроглицерин
Нитроглицерин
Нитроглицерин (р = 13,4ГПа)
ТЭН
ТЭН
ТЭН в растворе
Гексоген
Октоген
а-азид свинца
в - азид свинца
Гремучая ртуть
Т,С
150—160
125-150
90—125
75-105
641
145-171
160—225
171—238
213—299
245-275
237—252
100—115
Е,
Ккал/моль
36
45
43,7
40,3
39,3
39
47
39,5
47,5
52,7
55
40
30
lgB
15,5
19,2
18,6
17,1
15,6
19,8
16,1
18,5
19,7
Скорость тепловыделения реакции нелинейно зависит от
концентрации реагентов и от температуры. Выражая скорости
реакции и тепловыделения как функции температуры горения,
получим нелинейное уравнение второго порядка. Решая это уравнение,
Я.Б. Зельдович получил /^ля массовой скорости горения и следующее
выражение [50]:
uM=^(^-r+l(Tr-Torn\wTr (8.31)
где: Q— теплотворная способность ВВ; п — теплопроводность
паров ВВ; Т0 — начальная температура ВВ; Тг=TQ + Q/cv; w^ — скорость
реакции при температуре горения.
Это выражение позволяет получить явные зависимости
скорости горения от давления и температуры:
389
uu=B§\ (8>32)
Поскольку скорость газовой реакции n-го порядка меняется с
давлением по закону w = kpn, то
uM=Bjkf (8.33)
Таким образом, теоретически скорость мономолекулярной
реакции горения (п = 1) пропорциональна корню квадратному из
давления, а скорость бимолекулярной реакции горения (п = 2)
пропорциональна величине давления.
Экспериментально аая многих вторичных ВВ найдена линейная
зависимость скорости горения от давления вида и = А + Вр.
Скорость горения летучих ВВ в газовой фазе теоретически
растет с температурой следующим образом:
u=jTexp(-E/2RT)
(8.34)
Линейная скорость горения изменяется обратно
пропорционально изменению плотности ВВ.
Горение твердых ВВ происходит устойчиво (послойное горение
(ПГ)) только при малых давлениях (см. рис. 8.15).
Начиная с некоторого предельного давления, горение резко
ускоряется и становится пульсирующим (конвективное горение (КГ)).
Изменение режима горения
при больших давлениях
связано с прониканием
газообразных продуктов горения в ВВ
перед фронтом горения.
При большой скорости
и глубине проникания газы
прогревают и поджигают
слой ВВ заметной толщины.
Давление при таком горении
растет и усиливает
проникание газов и скорость горе-
и, г/см2с
0,254
конвективное горение
послойное горение
1 1
1 2 :
р, кг/см2
Рис. 8.15. Зависимость скорости горения
пористого пироксилина от давления [65]
390
ния. Ускорение горения зависит от соотношения между
газопритоком и газоотводом.
Схема развития горения в открытой трубке дана на рис. 8.16.
При давлении р2 зависящего от газопроницаемости ВВ,
скорость газоприхода начинает возрастать вследствие проникания
газов вглубь ВВ. Это начало конвективного горения (линии 2). Чем
выше давление, тем быстрее растет скорость горения.
к /
2
i
' ■
В
Ро Р. Р2
Вторичные ВВ р2 > рО
Р. Р2 Ро Р
Инициирующие ВВ р2 < рО
Рис. 8.16. Влияние давления на устойчивость горения различных ВВ [50]
ОВ — линия газоотвода; линия 1 — газоприход для устойчивого ПГ;
линия 2 — газоприход для КГ
При давлении р2 газоотвод и газоприход сравниваются, причем
производные (dm/d ) > (dm/d ), поэтому равновесие неустойчивое:
малейшее повышение давления вызывает рост превышения
газоприхода над газоотводом и прогрессивное возрастание скорости
горения.
Если р2 < р0(р0 = 1атм), то такие ВВ относятся к инициирующим.
У них скорость горения так велика, что небольшое повышение
давление при горении свободной поверхности ВВ вызывает
проникание газов и быстрое КГ, переходящее в детонацию.
Если р2 > р0, то такие ВВ относят к вторичным. Для них скорость
горения при атмосферном давлении недостаточна, чтобы вызвать
проникание газов и переход от ПГ к КГ.
Таким образом, возбуждение ускоряющегося КГ происходит
при достижении пороговых условий, которые определяются
давлением, диаметром пор и граничными условиями (условиями газоот-
вода). Например, в замкнутой прочной оболочке КГ существенно
ускоряется из-за быстрого роста давления в зоне горения.
Прогрессивный рост давления и скорости реакции в
нестационарном КГ приводит к возникновению стационарного
детонационного режима горения, при котором постоянное максимальное
давление достигается в ударной волне.
Таким образом, возбуждение детонации в пористых ВВ
проходит ряд стадий (см.табл. 8.16) [56].
Таблица 8.16. Развитие взрыва в пористых ВВ
Стадия
Послойное
горение
Конвективное
горение
Низкоскоростная
детонация в поры
Нормальная
детонация
Механизм возбуждения
Образование очага горения
в результате начального
импульса
Воспламенение поверхности
пор теплом нагретых газов
Формирование волны
сжатия критической
интенсивности, способной
инициировать реакцию в горячих
точках
Ударно-волновой разогрев
Механизм передачи
энергии
Молекулярная
теплопроводность, излучение
Конвективная теплопередача,
сопровождающая фильтрацию
газов в поры
Гидродинамический при
немонотонном неполном
тепловыделении
Гидродинамический при
полном тепловыделении
Для экспериментальных исследований КГ применялись
сложные комплексные методики: оптические с лазерными
интерферометрами, ионизационные (электроконтактные), рентгеноимпульсные,
пирометрические, метод квазитонких слоев.
Некоторые результаты этих исследований приводятся ниже.
1. До скоростей пламени ~150 м/с и аля не очень высоких
давлений определяющим является традиционный механизм
конвекционного разогрева за счет переноса энергии опережающим
фильтрационным потоком горячих газов. При больших скоростях и зерне
порядка 1 мм реализуется иной механизм нагрева поверхности
частиц, связанный с высокоскоростным трением газов о стенки пор.
392
2. Выделяются две стадии горения: ускоряющегося КГ и
стабилизированного КГ. На последней стадии, несмотря на рост
давления, скорость горения стабилизируется на уровне 400—500 м/с.
3. Давление горения у торца заряда растет по экспоненте.
4. В процессе КГ происходит уплотнение ВВ перед фронтом
пламени, что приводит к уменьшению газопроницаемости,
стабилизации скорости КГ и снижению темпа роста давления.
5. КГ вызывает в ВВ волну сжатия. Незадолго до возникновения
детонации пористость ВВ перед фронтом пламени близка к нулю.
Именно сжатие пористого ВВ с кумуляцией энергии в порах
является основным источником образования горячих точек.
6. Для сильно измельченных ВВ переход в детонацию
происходит с образованием позади фронта КГ мощной вторичной
волны. Детонация возникает в момент догона этой волной переднего
фронта КГ. Причина этого явления в том, что на начальной стадии
КГ затруднено горение малых пор, поэтому воспламеняется лишь
малая часть поверхности в наиболее крупных порах. А вторичная
волна возникает, когда давление КГ достигает уровня, достаточного
для воспламенения всех пор малого диаметра.
7. В [57] исследовано разложение ВВ в ударной волне. Получены
зависимости от времени величин давления, степени разложения п
(отношение массы продуктов горения к исходной массе ВВ), скорости
разложения dn/dt, температуры и плотности ВВ (см. рис. 8.17).
Как видно из рис. 8.17, максимум давления в реагирующем слое ВВ
возникает одновременно с достижением максимальной скорости
разложения и плотности ВВ. Этот момент соответствует моменту
соприкасания сферических фронтов горения, идущих из горячих точек.
8. Мерой чувствительности данного ВВ к переходу горения в
детонацию служит длина преддетонационного участка 1п .
Зависимость 1п от пористости и размера зерна (пор) носит
сложный характер с минимумом [53]. При сильном измельчении ВВ 1
возрастает, например, ^ая тетрила в ~3 раза при уменьшении
зерна от 470 до 20 мкм. Это согласуется с замедленным развитием КГ
в мелкозернистых ВВ.
9. Процесс возбуждения детонации инициирующей ударной
волной (ИУВ) с амплитудой до ~7 ГПа можно разделить на две стадии
393
Рис. 8.17. Результаты измерения параметров ударноволнового
разложения ТЭНа
[58]: инициирование химической реакции в отдельных горячих точках
(ГТ) и развитие процесса горения на весь объем ударносжатого ВВ.
Чувствительность первой стадии характеризуется минимальной
амплитудой ИУВ pmin, при которой еще возможно инициирование
локальной химической реакции. Чувствительность второй стадии
характеризуется критической энергией инициирования детонации
Ек , длиной преддетонационного участка 1п и критическим
давлением возбуждения детонации р*. Чем меньше все эти величины, тем
выше чувствительность ВВ.
Микроструктура ВВ характеризуется размером эквивалентных
сферических частиц rQ, размером пор а и удельной поверхностью S.
Эти параметры связаны между собой:
S=6(\-m)/r=6m/a (8.35)
где пористость т= 1—Р0/ртах-
Уменьшение rQ (увеличение S) увеличивает pmin, но снижает Ек ,
1 пр и р*, т.е. две стадии развития ГТ подчиняются различным
механизмам и закономерностям [59].
От амплитуды ИУВ скорость первой стадии зависит сильно, а
скорость второй — намного слабее.
При постоянной пористости с уменьшением размера пор или
размера частиц ВВ чувствительность ВВ увеличивается только а^я
достаточно сильных и коротких ИУВ, а ^ая слабых и длинных ИУВ,
наоборот, самыми чувствительными становятся крупнозернистые ВВ.
394
10. Разработаны различные физические модели образования
и горения ГТ: гидродинамического взаимодействия ИУВ с порами,
вязкопластического уплотнения пористых ВВ, фрикционного
разогрева поверхностей скольжения (краткий обзор см.[4,59]).
Наиболее полно объясняет эксперимент вязкопластическая
модель. По сравнению с гидродинамической, в этой модели
изменяется геометрическая форма ГТ и профиль температуры вокруг ГТ,
но сохраняется полная энергия, выделяющаяся вокруг ГТ. Передача
энергии от ГТ к «холодному» ВВ происходит не ударной волной, а
за счет теплопроводности.
Динамика роста ГТ определяется комплексом процессов
деформирования поры, теплопроводностью, диффузией и химической
реакцией в объеме и на поверхности поры. Модель дает величину
критической поры:
a^Hw/pJ (836)
где [л — эффективная вязкость; ^ — коэффициент
температуропроводности.
Самоподдерживающаяся реакция развивается в пористом ВВ
только с размерами пор больше критических.
Например, а^я рув = 3 ГПа, [л= 10 Па с и £=3,5 10'4 м/с согласно
(8.36) ак = 2 мкм.
Формула (8.36) объясняет изменение ударноволновой
чувствительности ВВ одной пористости, но с различной дисперсностью.
11. Пока нет строгой физической теории разложения пористых
ВВ при их ударноволновом инициировании. Поэтому а^я описания
нестационарных процессов в дополнение к УРС и уравнениям
движения используются эмпирические соотношения кинетики
горения, например, такие:
и=Ареехр0Т (8.37)
где £, (2, А — константы, определяемые из экспериментов; и —
скорость горения.
12. В [60] с помощью манганиновых датчиков исследовалась
кинетика разложения флегматизированного гексогена в плоской ИУВ
с амплитудой менее 8 ГПа (см. рис. 8.18).
р.ГПа
15
10
\г
V
р,ГПа
15
10
5
Л
f
1
р.ГПа
15
10
5
Л
/
/
t.MKC
t.MKC
Рис. 8.18. Изменение давления в процессе разложения флегматизированного
гексогена на границе алюминиевый экран—заряд
1,2,3 — для р = 1,41,1,60 и 1,67 г/см3 соответственно
Как видно из рис. 8.18, разложение ВВ ведет к росту давления на
контактной границе экран — заряд. Образуются характерные
максимумы давления, положение которых дает оценку времени реакции
в пограничном слое заряда.
В этих условиях средняя расчетная температура ударного сжатия
давлением 5,5 ГПа в заряде с р = 1,67 г/см3 составляет всего 110° С,
ниже температуры вспышки при времени задержки 300с. А в
эксперименте время реакции — 0,5 мкс — на много порядков меньше, что
доказывает очаговый характер разложения твердых ВВ в ИУВ.
13. У азида свинца, в отличие от других ВВ, при любых внешних
условиях и способах инициирования этапа горения не
наблюдается — взрывное превращение всегда происходит сразу в форме
детонации.
Однако воздействием очень коротких импульсов
ультрафиолетового (УФ) лазерного излучения в [61] удалось получить предварительное
разложение и понять причины неустойчивости КГ у азида свинца.
396
Инициирующая способность УФ излучения несравнимо выше,
чем у длинноволновой части спектра, поскольку выше поглощение
света и концентрация поглощенной энергии.
Для лазерного моноимпульса (30нс) видимого света порог
инициирования менее 0,01 дж/см2. Однако при коротком УФ
моноимпульсе (6 не) инициирование не удалось осуществить даже при
плотностях энергии 10 дж/см2. Поверхность образца темнела,
потемнение усиливалось с каждым новым импульсом вплоть до взрыва
через 5—6 импульсов. При плотности 0,6 дж/см2 аая возбуждения
взрыва необходимо было 100—150 лазерных импульсов.
Как известно, процесс разложения ВВ останавливается
потерями горячих продуктов реакции из зоны инициирования. Короткий
лазерный импульс прогревает очень тонкий поверхностный слой
заряда (0,2 мкм), для которого время разброса вещества (1 не) меньше
длительности импульса (6 не). Поэтому реакция затухает, несмотря
на очень высокую плотность энергии.
При увеличении длительности светового импульса растут
толщина нагретого слоя (> 1 мкм) и время разброса. Как следствие,
уменьшаются потери газов и развивается детонация.
То же самое происходит:
— если закрыть поверхность азида свинца стеклом;
— при предварительном облучении («тренировке») образца,
когда потемнение при частичном разложении азида свинца
связано с выделением металла, который уменьшает разброс газов, но
увеличивает глубину прогрева (за счет роста теплопроводности);
— при длительном старении образца азида свинца, в
результате которого на поверхности образуется защитная пленка
карбоната свинца, из-за которой порог инициирования снижается до
0,01 дж/см2.
— Крайняя неустойчивость горения азида свинца
объясняется в [61] отсутствием при его разложении относительно долго
живущих (> 10 не) промежуточных возбужденных продуктов
реакции.
397
14. Walker и Wasley [62] предложили в качестве критерия
инициирования детонации величину (р — р )2t (р — динамическая
прочность ВВ, t — время), которая определяется составом и
дисперсностью ВВ, пористостью заряда.
Критическая (минимальная) амплитуда р* инициирования
ударной волной сильно зависит от пористости ВВ. На рис. 8.19 по-
б)
р*, кбар
40
30
20
10
[и
МП
I
р , коар
80
,1/дарси
40
_*- л
J
1 1
1
1
1
' I
л
0,8
1,0
1,2 1,4 1,6 р0,г/см3 1,0
1,4
0
р0,г/см3
Рис. 8.19. Экспериментальные зависимости р (р) для тротила (а) и гексогена (б)
— обратная газопроницаемость
казаны экспериментальные зависимости р*(р0) А^я тротила и
гексогена [4].
Как видно из рис. 8.19, требуемое аая инициирования
минимальное давление ИУВ быстро растет при р0/ртах > 0,9, что
объясняется резким уменьшением газопроницаемости, числом и размером
пор (см. (8,36)).
Очевидно, с приближением к кристаллической плотности
величина р* будет стремиться к давлению ИУВ, характерному аая
гомогенных непористых ВВ (без ГТ). Для таких ВВ очаговый механизм
невозможен, и детонация возникает только в результате адиабатного
теплового взрыва при однородном нагреве за счет ударного сжатия
всего объема ВВ.
398
Критические температуры разогрева ВВ в горячих точках могут
достигать 700—1800 К.
8.6.2. Возбуждение детонации гомогенных ВВ
(адиабатный взрыв)
Для аррениусовской кинетики разложения важна средняя
температура ударного сжатия гомогенного ВВ, которая рассчитывается
при совместном решении системы уравнений, следующих из закона
сохранения энергии и уравнения состояния:
3«Kv),
J\ 2 Jv Mv
(8.38)
р,ГПа
18
14
10
/
'/
/
А
А
/
^
1
/
у
-о
/
^
S
/J
/
/
/
'
3
/
V
У
'4
S
5
<*
где р, u, Т— параметры
за фронтом ИУВ (р и и
известны); р (Т ) — изотерма
ВВ при температуре Т; v —
удельный объем; М —
молекулярная масса ВВ; j(v) —
коэффициент Грюнайзена.
Полученные В.М.
Богомоловым расчетные
зависимости температуры ударного
сжатия от давления ^кя ряда
ВВ приведены на рис. 8.20
[4].
Правильность расчетов
проверялась сравнением с
экспериментом: по измеренной
величине времени задержки
взрыва t вычислялась температура по известной формуле а^я
задержки адиабатного взрыва [4]:
t3 = (cvpRT2)/ (QzE)qxp(-E IRT) (839)
Зная температуру, легко найти давление р^ ударного сжатия. В
таблицах 8.17 и 8.18 приведены использованные в расчетах харак-
400 600 800 1000 ТК
Рис. 8.20. Расчетные зависимости
температуры от давления ударного сжатия для
некоторых гомогенных ВВ. 1 — гексоген; 2 —
ТЭН; 3 — нитроглицерин; 4 — жидкий ТНТ
(Т=85° С); 5 — нитрометан
теристики некоторых ВВ, а также опытные и расчетные параметры
инициирования этих ВВ.
Из табл. 8.19 видно, что критическое давление инициирования
ударом по очаговому механизму на порядок меньше давления
инициирования гомогенных ВВ за счет разогрева при адиабатном
ударном сжатии.
Таблица 8.17. Характеристики гомогенных ВВ
ВВ
Нитрометан
Тетранитрометан
Нитроглицерин
Тротил (Т = 85° С)
Тротил (Т = 20° С)
тэн
Гексоген
Тетрил
г/см3
1,14
1,64
1,59
1,45
1,64
1,77
1,80
1,73
км/с
1,34
1,04
1,74
1,55
2,16
2,42
2,62
2,17
Р.
103
град
1,32
1,06
0,86
0,70
0,32
0,50
0,51
0,32
Константа
реак
К = Вехр
LgB
13,7
17,53
14,0
11,4
11,4
16,1
15,5
16,0
скорости
ции
(-E/RT)
Е, ккал/
моль
49,2
40,9
35,0
34,4
34,1
39,5
41,5
40,0
Таблица 8.18. Парамет
ВВ
Нитрометан жидк.
ТЭН кристаллич.
Гексоген кристал.
Тетрил кристал.
Тротил кристал.
Тротил жидкий
Тетранитрометан
Нитроглицерин
р*.
кбар
опыт
93
112
170
125
86
ПО
рыИУВ
кбар
расчет
115
122
162
150
180
125
82
120
для гомогенных ВВ
МКС
опыт
1,0
0,3
1,0
1,0
0,7
0,7
1,0
0,3
т0>
к
293
298
293
293
293
358
293
293
Т
к
1200
700
770
810
1000
1000
700
760
Ркр>
Кбар
ДляГТ
4,8
7,0
8,4
11,0
400
Таблица 8.19. Сравнение гомогенного и гетерогенного
инициирования [49]
ВВ
Октоген
ТЭН
Нитро-
Метан
Физическое состояние
(плотность р0, г/см3)
Монокристалл, 1,905
Пресспорошок, 1,891
Монокристалл, 1,774
Пресспорошок, 1,000
Чистая жидкость, 1,128
Жидкость с песком, 1,128
Жидк.с пузырьками 1,128
Параметры
Инициирования
358 кбар,
t = 0,3 мкс
100 кбар
100 кбар
2 кбар,
85 кбар,
t = 2 мкс
23 кбар,
t=2MKc
85 кбар,
t = 0,1 мкс
Тип
Инициирования
Гомогенный
Гетерогенный
Гомогенный
Гетерогенный
Гомогенный
Гетерогенный
Гетерогенный
8.6.3. Возбуждение детонации ударом пластины или стержня
Первое условие возбуждения детонации ИУВ р > р* еще
недостаточно. Критические параметры ИУВ зависят также от размера
зоны сжатия на поверхности заряда ВВ, от длительности действия
ИУВ, крутизны нарастания давления на фронте ИУВ и спада
давления за фронтом ИУВ.
Рассмотрим второе условие — размер очага сжатия ИУВ.
Согласно принципу Ю.Б. Харитона [63] детонация в заряде
возможна только в случае, если время химической реакции меньше
времени движения боковой волны разгрузки. Отсюда критический
диаметр заряда:
d =2ct (8-40)
кр р
где с — скорость звука в П Д.
Однако из-за кривизны фронта детонации и задержки детонации
величина t растет с уменьшением диаметра заряда и не совпадает с
t для нормальной детонации. Поэтому правильны более общие
соотношения [64]:
401
d =kt d >2a
кр p кр
где к — коэффициент; а — ширина зоны реакции.
(8.41)
Рис. 8.21. Критические условия возбуждения
детонации ИУВ на участке поверхности
заряда диаметром dH
Н — сжатый объем заряда, не охваченный
боковой разгрузкой
Для критического
размера очага ударного
сжатия dH на
поверхности заряда второе условие
возбуждения детонации
формулируется
аналогично: время возбуждения
детонации^ должно быть
меньше времени прихода
боковой разгрузки t6 (см.
рис. 8.21) [4]:
*вр<*бр'>^
>d„,
(8.42)
Детонация должна возникнуть до момента, когда боковая
разгрузка уменьшит диаметр поверхности, сжатой ИУВ, до
критического значения.
Очевидно, критические параметры ИУВ снижаются с ростом
диаметра начальной зоны сжатия dH до тех пор, пока dH не достигнет
предельного диаметра а^я данного ВВ.
Угол боковой разгрузки а не постоянен — он максимален /^ая
инертного ВВ и уменьшается с развитием химической реакции. При
dH = dK угол а уменьшается в 2,5 раза.
Из экспериментов следует связь между глубиной развития
детонации и конечным диаметром очага сжатия:
Lp=2,5dm (8.43)
Принимая tg а = 1, получим область граничных значений для d :
2d <d <3d
кр u np
(8.44)
При<1 >3d критические параметры ИУВ не зависят от величины
dH (рис. 8.22), а при dH < d для возбуждения детонации необходимо
402
_ 2d 3d d
кр кр пр и
Рис. 8.22. Зависимость критических
параметров ИУВ от диаметра очага
инициирования на поверхности
заряда ВВ
создать пересжатую детонацию.
При d =d критические
параметры ИУВ соответствуют химпику
детонационной волны.
При инициировании
детонации ударом пластины
(осколком) диаметром dH в интервале
0,5 < dH/dK < 10
экспериментальные параметры ИУВ для ряда
ВВ могут быть описаны одной
зависимостью [4]:
"Ув U?=\,65exV(-0,5dJdnp)
ит-ит
кр пр
(8.45)
где u * — массовая скорость в химпике детонации при d3a =d ;
u * — массовая скорость за фронтом критической ИУВ при d > 3 d ;
пр -t i-t а а зар кр
Uyg* — массовая скорость за фронтом ИУВ при ударе пластиной
диаметром dH.
Значения постоянных в (8.45) для трех ВВ приведены в табл.
8.20 [4].
Таблица 8.20. Характеристики трех ВВ
ВВ
Тротил прессованный
Сплав ТТ40
Гексоген флегматизир.
г/см3
1,58
1,67
1,62
D ,
ММ
3,0
2,0
1.5
и *,
КР
м/с
2900
2800
2800
и *,
м/с
470
450
370
По данным табл. 8.19 и по (8.45) можно найти критическую
скорость пластины (осколка) данного диаметра. Например, аля сплава
ТГ40 при dH= 10 мм UyB* = 0,75 км/с и критическая скорость равна
0,88 и 1,04 км/с аля стального и алюминиевого осколка. При этом
критическое давление в ТГ40 будет равно 5 ГПа.
Толщина осколка не влияет на его критическую скорость, если
толщина более 0,5 d .
Рассмотрим механизм возбуждения детонации заряда ВВ
высокоскоростными стержнями или удлиненными элементами (УЭ) [65].
а)
6)
Начальная стадия
Без экрана
С экраном
Установ. проник.
/ Р-
2
Рис. 8.23. а) Схема взаимодействия УЭ с экранированным зарядом.
б) Профили давления на границе У Э — ВВ
Диаметр УЭ d0 сравним с dK, а удлинение H/d0 =10.
Процесс взаимодействия УЭ с ВВ разделяется на начальную
ударно-волновую стадию и стадию установившегося проникания
[66]. На начальной стадии давление значительно больше давления
установившегося проникания (см. рис. 8.23).
Для скоростей УЭ 3—8 км/с и для диаметров dQ = 0,5—5 мм
возбуждение детонации имеет ударно — волновую природу с
определяющим влиянием кривизны возникающих ударных волн.
На начальной стадии взаимодействия инициирующая
способность УЭ определяется следующей величиной [67]:
w = pv2d0 (8.46)
где р, v, dQ — соответственно плотность, скорость и диаметр УЭ.
Условие возбуждения детонации: w>w .
Величина w пропорциональна энергии ВВ, поглощенной на
начальной стадии, т.е. условие w > w эквивалентно энергетическому
критерию ударно-волнового возбуждения детонации.
404
Детонация возникает на начальной стадии при р = 50—150 ГПа
и d0 > (0,1—0,2) d . Если d > > d0, то возникающая пересжатая
детонация быстро затухает.
На второй стадии установившегося проникания формируется
баллистическая УВ, и если область высокого давления в этой волне
больше dK, то возникает детонация, причем этот процесс
характеризуется большим временем и глубиной.
На второй стадии инициирующая способность УЭ значительно
ниже, чем на первой стадии (т.к. меньше давления) и определяется
величинами J2 или J2:
4=1*4; J7=v2dayfe (8.47)
где и — скорость проникания.
Условия возбуждения детонации: Jt > JlK или J2 > J2k .
Экранировка зарядов ВВ изменяет характер нагружения ВВ.
Экран как бы «берет на себя» начальную ударно-волновую стадию
и тем самым снижает инициирующую способность УЭ.
Для тонких экранов с H/dQ < 3—4 и УЭ с v = 5—8 км/с
детонация возникает у ВВ с dK < 5 dQ [65].
При толстых экранах с H/dQ > 10—15 детонация не возникает.
Экранированное ВВ подвергается предварительному ударному
сжатию при проникании УЭ, что снижает чувствительность ВВ по
двум основным причинам: гомогенизация ВВ (закрытие пор,
повышение плотности) и снижение температуры за фронтом второй УВ.
Далее приведены экспериментальные результаты работы [68],
которые конкретизируют рис. 8.22. В этой работе изучалось
влияние диаметра ударника на критические параметры инициирования и
на характер развития детонации.
Использовались ударники из алюминия и стали диаметром
d0 = 4—50 мм, заряды из тротила (р0 = 1,56 г/см3, D = 2,74+ 1,37 и),
флегматизированных гексогена (р0 = 1,66 г/см3, D = 2,48 + 2,04 и) и
октогена (р0=1,78 г/см3, D = 2,28 И-2,24 и) с пористостью 4—6 %.
Критические скорости удара w* определялись экспериментально,
а критические давления р* рассчитывались по известным D — и
соотношениям.
pMTla
15
10
5
+
-5,
*
\Л
S^^*»^
Ч.
Al
Fe
о
•
*
w*, км/с
t
\
о
4 ^^"*"
i
Al
(
■--
)
-
0 10 20 30 40 50 d.MM
0 10 20 30 40 50 d,MM
Рис. 8.24. Порог инициирования: • — тротил, *— гексоген флегм., о — октоген
Из рис. 8.24 видно, что &ля d < 20 мм зависимость р (d)
одинакова как для алюминиевых, так и для стальных ударников. Значения р
и w при dQ > 40 мм соответствуют условиям инициирования плоской
УВ, а при dQ < 40 мм краевые эффекты приводят к росту критических
параметров.
Переход ИУВ в детонацию рассмотрен в [69]. Вначале ИУВ
распространяется по ВВ как по инертному веществу. Разложение ВВ,
D, км/с
а)
25 х, мм
р,ГПа
б)
-
\
-у»
1Г\|
- 20_ /
о
^'Ч
i ' i
7 t, мкс
Рис. 8.25. а) — Изменение скорости ИУВ. б) — Профили давления (цифры -
путь, пройденный ИУВ по заряду в мм)
406
сжатого с поверхности заряда, приводит к образованию волны
сжатия, которая, усиливаясь, догоняет ИУВ, после чего процесс быстро
переходит в детонацию.
Изменение скорости и давления в процессе эволюции ИУВ в
детонацию показано на рис. 8.25.
Волна сжатия за фронтом ИУВ не наблюдается, следовательно,
разложение ВВ идет в узком, примыкающем к фронту слое. Развитие
процесса в этом слое не зависит от материала ударника, а ширина
слоя определяется толщиной ударника. Давление и скорость плавно
нарастают, асимптотически приближаясь к значениям &ая
нормальной детонации.
Для инициирования ударом пластины характерны относительно
высокие начальные давления, аля которых определяющей становится
вторая стадия процесса — переход в детонацию. Эта стадия
ограничивается во времени воздействием волн разрежения, идущих с тыльной и
боковой поверхностей ударника.
Волна разрежения со свободной
поверхности ударника (пласт-ны)
не влияет на процесс перехода ИУВ
в детонацию, если длительность
ударного импульса с амплитудой р в
больше, чем t = Н/рУвт , где Н, т —
константы [70].
В [71] исследовались переходные
процессы при инициировании
зарядов из грубодисперсных ВВ
(тротила и граммонита 79/21 насыпной
плотности с частицами >2,5 мм)
другими зарядами (боевиками из
аммонита 6ЖВ, но меньшего
диаметра d3). Заряды инициировались
через пластину ПММА толщиной
10 мм треугольным импульсом
длительностью 7 мкс.
D,
з 41
2-\
1 А
км/с
0
i/a,
Рис. 8.26. Скорость детонации
в переходной зоне в зарядах
диаметром 80 мм из граммонита и
тротила (штрих) при их
инициировании боевиками из тротила с
р0= 1,55—1,62 г/см3 и давлением
р =11ГПа
* ИН
1 —d =80мм;2 —d =40мм;
ни ни
3 — d =23 мм.
Найдено, что переходная область не превышает 2d3, но
параметры за фронтом ИУВ достигают детонационных не постепенно
плавно понижаясь, а проходя через некоторое минимальное
значение на глубине 1 = d3, (рис. 8.26).
Чем меньше диаметр боевика, тем резче падение параметров
фронта. Снижение может быть ниже критического уровня а^я
нормальной детонации данного ВВ (Dmin = 1—2 км/с, см. рис. 8.26), что
объясняется несоответствием кривизны фронта ИУВ параметрам
данного ВВ, характерным а^я данной формы фронта.
Эти результаты опровергают справедливость в общем случае
критерия «незатухания» при инициировании ВВ [64].
Результаты измерения кривизны ИУВ для заряда из тротила
диаметром 80 мм и боевика из тротила о23х21 мм приведены в табл. 8.21.
Таблица 8.21. Результаты измерения кривизны фронта ИУВ
в тротиле
v±
0
0
0,3
0,5
1,0
1,5
R,mm
TQ ,мкс
*л
« — «
« — «
« — «
« — «
10
0,1
1
7,7
5,4
3,8
1,5
20
2,3
1
1,6
1,3
0,7
0,3
30
4,98
1
1,58
1,2
0,7
0,3
40
7,83
1
1,15
0,8
0,3
В табл. 8.20: l/d3 — расстояние от инициатора вдоль оси заряда
(R = 0); tj — время задержки появления фронта на расстоянии R от
оси заряда относительно его появления на оси аая заданного
расстояния l/d3; tQ — то же время а^я входящей ИУВ при l/d3 = 0.
Отношение tj/t определяет кривизну фронта.
Из табл. 8.20 видно, что в переходной области развития ИУВ в
детонацию сначала кривизна волны увеличивается (tj/t0 > 1) и лишь
затем уменьшается, причем уменьшение происходит раньше, чем
параметры достигнут минимума.
Общей особенностью развития детонации в
малочувствительных ВВ является сильная пространственная анизотропия, обуслов-
408
ленная возникновением в заряде вокруг инициатора т.н. темной
зоны — кольцевого слоя недетонирующего ВВ (толщиной ~dK), а
также более медленным развитием детонации в направлении,
перпендикулярном движению ИУВ (из-за значительно меньшего
давления в перпендикулярном направлении).
ь х 3
а)
б)
г)
Рис. 8.27. Развитие детонации (РД) в заряде из ТАТБ (1) при его инициировании
боевиками сеч. 10 х 15 мм из флегмат. октогена
1— инициатор; 2 — заряд; 3 — детонационная волна; 4 — ударная волна;
5 — сжатое и непрореагировавшее ВВ; 6 — прореагировавшее ВВ; а) — исходное
состояние сборки; б), в), г) — фазы РД через 2; 3,2 и 6 мкс после выхода детонации
из боевика на поверхность заряда с р0 = 1,9 г/см3; д), е) — фазы РД через 2 мкс для
зарядов с р0 = 1,84 и 1,78 г/см3 соответственно.
В [71] с помощью импульсной рентгеносъемки удалось
зафиксировать картину развития детонации в малочувствительной
композиции ТАТБ и фторопласта (р0= 1,9 г/см3), инициируемой боевиками
из флегматизированного октогена. Полученные в опытах
конфигурации фазы взрывчатого превращения показаны на рис. 8.27.
Из рис. 8.27 видно, что с быстрым ростом чувствительности при
уменьшении плотности заряда уменьшается объем непрореагировавше-
го ВВ, и заметно растет скорость в боковом направлении. Уменьшение
размера инициатора увеличивает объем 5 вплоть до отказа при сечении
инициатора 10x4 мм. Наоборот, полное заглубление в заряд
инициатора сечением 10x15 мм приводит к исчезновению объема 5.
Таким образом, при инициировании твердых ВВ сначала
возникает нестационарная и неидеальная детонация.
8.6.4. Инициирование лазерным импульсом
Изучение лазерного инициирования представляет как научный,
так и практический интерес в плане создания безопасных
быстродействующих детонаторов с использованием вторичных ВВ.
Световое инициирование начал изучать ещё Боуден (1958г.),
а в России пионером таких работ стал Зайцев (Москва) [72], а в
1970-90 гг большой объём исследований проведен Таржановым и
Зинченко (ВНИИТФ, г. Снежинск).Ниже кратко излагаются
результаты их работ [73,75].
Закономерности инициирования ТЭНа изучались с использо-
ваием лазера на ниодимовом стекле (к= 1,06 мкм) в режиме
модуляции добротности резонатора. Генерируемые импульсы имели
длительность на полувысоте t = 30 не и энергию до 4.5 дж.
В опытах использовался ТЭН с варьируемыми дисперсностью S
и плотностью р^. Навески ТЭНа закрывались со стороны импульса
прозрачным экраном (подложкой) из стекла толщиной А и с
акустической жесткостью р с .
Гп п
Вблизи границы отказов инициирование носит вероятностный
характер, поэтому пороговая энергия инициирования Е05
определяется как энергия, соответствующая 50% — ой вероятности подрыва
в сериях из 10—20 опытов с использованием метода максимального
правдоподобия.
Эффективный диаметр d облучаемой зоны определялся в
специальных экспериментах. По известным величинам Е05 и d
рассчитывалась пороговая плотность энергии инициирования
W = E05/(7rd2/4), которая является многопараметрической
функцией W = f (t,l, d, S, p^, pncn, dK). Инициирование осуществлялось как
прямым облучением ТЭНа, так и с помощью взрываемых лазерным
импульсом металлических плёнок на поверхности ТЭНа.
Основные результаты экспериментов следующие:
1. Пороговая энергия инициирования Е растёт с
увеличением длительности лазерного импульса.
2. С уменьшением толщины подложки до А = 0,1 мм величина
Е05 остаётся постоянной, а при дальнейшем уменьшении
растёт. Без подложки (А = 0) ТЭН не инициируется даже при
Е05 в 40 раз больше, чем Е05 а^я А = 0,1мм, т.к. быстрый раз-
410
лёт ТЭНа со свободной поверхности не позволяет развиться
химреакции.
3. Предложен двухстадийный механизм инициирования ТЭНа
лазером с поджиганием. Вводимая через подложку
световая энергия активирует химреакцию разложения ТЭНа.
Энергия химреакции выделяется в тонком слое вблизи
подложки. Образовавшийся пик химической энергии есть и пик
давления, который формирует в ТЭНе реакционную
ударную волну. Последняя переходит в детонационную волну
согласно [76].
4. Перед «запуском» химреакции лазерным импульсом в
ТЭНе наблюдается резкое уменьшение светопропускания,
обусловленное оптическим пробоем ТЭНа как
диэлектрика или фотоионизацией поверхностных слоев ТЭНа (30—
80мкм).При пробое роль воздуха в порах ТЭНа ничтожна.
На первой допробойной стадии поглощается около 1% всей
поглощаемой в импульсе энергии.
5. Зависимости WQ (рто) имеют минимумы, которые не зависят
от величины дисперсности S .
Связь оптимальной плотности opt р с S при d -> °° имеет вид: opt
p7Po=l4,4/(14,4+S^)
Оптимальная плотность ТЭНа лежит в интервале 0,8—1 г/см3.
6. С уменьшением диаметра облучаемой зоны d величины
Е05 уменьшаются, a WQ5 — растут (см. рис. 8.28). Для d = 0,3 мм
Е0'5 = 10 мДж, a W05 = 20...30 мДж/см2 (р00 = 0,9 г/см3).
7. Плотность энергии в очаге инициирования fi^ больших d ,
S = 3700 см2/г и р^ = 0,9 г/см3 оценена равной 1160 Дж/г, а расчётная
температура в очаге равна ~ 1120 К.
8. При замене поверхностного слоя ТЭНа на гексоген и тротил
с частицами ~50 мкм величина EQ 5 возрастает соответственно в 1,19
и 1,33 раза.
В [75] исследовано инициирование ТЭНа с помощью
взрываемой лазерным импульсом (t = 40 не) металлической плёнки. Плёнки
из Mn, Al, Си, Mg и РЬ наносились на стеклянную подложку
вакуумным напылением. Толщина плёнок А варьировалась в пределах (40—
411
12000) 10 "8 см. Использовался ТЭН с S = 8000 см2/г и р^ = 0,9г/см3.
Лазерный импульс фокусировался на плёнки линзой.
Измерения показали, что зависимости Е05(А) — это кривые
с минимумом при некоторых, оптимальных /^ каждого металла
1000
500
400
300
200
100
| 50
Р 40
30
20
10
\
\
\
1
\
-т—
\
\
**\
"^
^
«•
- >
**,
у
сг
\
\
\
\
\
\
\
\
\
>£
^99\
ч
ч
«£
ч22
i—Г
v I
\]
К
I ч
jftr?
*>
#
А
пУ
\К N
Ts^N4
fM
/г
* if
ч _ W0.5
v:—
^
7
jk
-J
о *
xA
1000
500
400
300 o-
X
200 A
100
50
40
30
20
w ?
10
0,1
0,2 0,3 0,4 0,5
d, мм
1,0
Рис. 8.28. Зависимости EQ 5 (d) (сплошные линии) и WQ 5 (d) (штриховые) для
opt p^ и различных S (указаны цифрами)
толщинах плёнки. При увеличении А > А величина Е линейно воз
opt
растает, что связано с необходимостью прогревания металла. При
А < Ао t значительная часть излучения пропускается плёнкой, не
поглощается в ней, что также повышает Е0 .
Е0 практически не зависит от вида металла плёнки, т.к. основная
энергия поглощается плёнкой на разлётной стадии, когда металли-
412
ческие свойства уже утеряны, и взрывающаяся плёнка превращается
в плазму. При разлёте в поры ТЭНа плёнка продолжает поглощать
энергию, и температура плазмы достигает 20000 К.
Таким образом, к концу лазерного импульса продукты взрыва
плёнки являются горячим поршнем, формирующим в ТЭНе
ударные волны с амплитудой 0,8 ГПа, соответствующей инициированию
ТЭНа в ударноволновых условиях с задержкой 0,1—0,2 мкс.
Очевидна полная аналогия между световым и электрическим
взрывами металлических плёнок. В обоих случаях это
взаимодействие свободных электронов металла с высокочастотным
электромагнитным полем.
8.7. Неидеальная детонация
Скорость идеальной детонации по данным [77] равна:
D\ =8,37 Ю37'0' + 2)0 (8.48)
где Q— теплота взрыва в кал/г, j — коэффициент Грюнайзена.
Многочисленные эксперименты показывают, что по разным
причинам в реальных условиях детонации химические реакции не идут по
пути образования продуктов, обеспечивающих максимальную
расчетную величину Q— реализуется неидеальная детонация (НД).
Неидеальный режим детонации характеризуется меньшими
параметрами (энерговыделение, скорость, давление) по сравнению с
максимально возможными /^ля данного ВВ.
На практике такой режим скорее правило, чем исключение.
При неидеальной детонации уменьшение энерговыделения
обусловлено внешним воздействием на поток (разгрузка, расходимость
потока, взаимодействие со стенкой трубы), эндотермической
реакцией (разложение пластификатора ВВ), недогоранием смесей за счет
диффузионных ограничений на границе горючее — окислитель.
Изменяется и структура детонационной волны: увеличивается
ширина зоны реакции, и поток в плоскости Чепмена—Жуге не
находится в состоянии равновесия (механического, физического,
химического).
413
Для газовой детонации в трубе обнаружены детонационные
пределы НД в зависимости от отношения теплопотерь к
тепловыделению [5,78].
Возможна стационарная и нестационарная НД. Основные
условия и причины возникновения НД приведены в табл. 8.22.
Таблица 8.22. Различные виды неидеальной детонации
ВидНД
Стационарная
Нестационарная
Условия возникновения
Заряд малого диаметра
Пластифицированный заряд.
Детонация распылов и смесей
горючее -окислитель
Газовая детонация в трубе
Слабое и очень сильное
инициирование заряда
(разгон детонации и пересжатая
детонация)
Детонация в жесткой
оболочке
«Точечное» инициирование
поверхности заряда
Физические причины НД
Боковая разгрузка и кривизна
фронта
Потери энергии на разложение
пластификатора.
Недогорание капель распыла и
горючего в смесях
Теплообмен и трение на стенке
трубы
Процесс перехода горения в
детонацию
Разгрузка сильной ИУВ в ВВ
Предварительное уплотнение
ВВ идущей по оболочке ударной
волной
Расходимость потока и
краевые эффекты на
стыке боковой поверхности
инициатора и заряда
Рассмотрим стационарную неидеальную детонацию (СНД).
1. Наиболее изучена СНД в зарядах малого диаметра. Влияние
диаметра заряда на скорость детонации обусловлено тем, что реакции
протекают не мгновенно, а в течение некоторого времени t в зоне ЗХР
шириной а=ct=3/4Dt. Если в эту зону входит боковая волна
разрежения, то давление и температура в зоне снижаются, реакции
замедляются, снижается энергия, поступающая в УВ, и скорость детонации падает.
Кроме того, фронт детонации искривляется.
Связь скорости детонации с диаметром заряда d и шириной
зоны реакции а была найдена Джонсом [79]:
414
'£
е)2=1-з,2(4)2
(8.49)
Рис. 8.29. Вид зависимости скорости
детонации от диаметра заряда
и Эйрингом [80]:
(8.50)
Недостаток теорий
Джонсона и Эйринга —
допущение а=const при d<d .
В интервале d <d<a
а кр пр
скорость детонации растет
с диаметром, стремясь
асимптотически к максимальной
величине D при d > d (см.
И А Пр х
рис. 8.29).
Выше предельного
диметра потери от боковой
разгрузки не влияют на скорость детонации. Размер интервала между
d и d меняется в зависимости от времени реакции, которое в свою
очередь зависит от состава ВВ, плотности заряда, размера частиц
ВВ, наличия тяжелой оболочки (см. разд. 10.6). Чем
чувствительнее ВВ (меньше dK), тем меньше разница dn — dK . Например, для
чувствительного, высокодисперсного, флегматизированного ТЭНа
с d =0,3 мм d < 5 dK (см. рис. 10.6), а а^я низкочувствительного
игданита с d = 150 мм d > 100 d .
" кр пр кр
Экспериментальные зависимости D(d) аая некоторых ВВ
приведены на рис. 8.30 [4,50,81].
Из рис. 8.30 и 8.31 видно, что с уменьшением размеров
кристаллов уменьшаются величины d и d и разница между ними, что
обусловлено сокращением ширины зоны реакции. В то же время
размер кристаллов никак не влияет на скорость детонации при d > dn ,
а только определяет насколько быстро достигается максимальное
значение скорости. Эта закономерность общая как а^я
цилиндрических зарядов диаметром d < d , так и ^ая зарядов в виде тонких
слоев толщиной h < hn (см. рис. 8.31 В).
D, км/с
d, см
Рис. 8.30. Экспериментальные зависимости
D (dp) для ряда ВВ
1 — состав В р = 1,7; 2 — ТНТ литой р = 1,6;
3 — аммотол 50/50 р= 1,53; 4 — баратол
р=2,35; 5,6,7 — ТНТ р = 1,0 с размерами
частиц 0,17; 3,5 и 5 мм соответственно;
8 — аммотол 50/50 р= 1,0; 9 — нитрат
аммония р = 1,04 с размерами частиц 0,2 мм
(плотность р в г/см3)
Очевидно, аая
оценки изменения скорости
детонации в зависимости
от диаметра заряда
согласно (8.49) и (8.50)
необходимо как можно точнее
знать ширину ЗХР. Однако
величины а, полученные
разными методами,
отличаются на порядок [4,25],
особенно сильно ^ая
зарядов малой плотности (см.
табл. 8.9).
В опытах с
электромагнитными датчиками
измеряется продолжительность
реакции t, а ширина ЗХР
находится из
соотношения:
a = (D-u)Htp (8.51)
В опытах с преградами используются D — и соотношение и
скорость звука а^я преграды [25].
Однозначно размеры ЗХР находятся из серии опытов с зарядами
различной длины, что позволяет выделить стационарный диапазон
в непрерывных распределениях параметров (см. рис. 8.6 и 8.32С
[25]).
2. Стационарная недосжатая детонация (СНД) наблюдается у флег-
матизированных составов, которые разлагаются в две стадии: первая
быстрая экзотермическая и вторая медленная эндотермическая.
В режиме СНД скорость детонации определяется наклоном
волнового луча 01 (см. рис. 8.32А), касательного к адиабате
максимального тепловыделения (первая стадия). Давление определяется
точкой 3 пересечения луча 01 с нижней адиабатой конечных
продуктов взрыва (обе стадии). Схематически структура СНД показана на
416
D, км/с
A)
Мелкие кристаллы
D, км/с
В)
П 1 1 1
2 4 6 8 Ь,мм
Рис. 8.31. Влияние размера кристаллов ВВ на зависимость D (d)
А — для ТНТ с р=0,85 г/см3 [50]; В — для слоя гексогена толщиной h с р = 1 г/см3
и с частицами: 45 мкм (1), 55 мкм (2) и 125 мкм (3) [82]
рис. 8.32В и состоит из ударного скачка (точка 2), круто
спускающегося участка 2-1 экзотермической реакции, более пологого участка
1—3 завершения первой стадии и автомодельно расширяющейся
области постоянного течения 3 — 3 (вторая стадия).
Снижение давления в СНД оценивается согласно (8.7).
Результаты измерения методом ЛИВС зависимости D(l) для
флегматизированного ТЭНа показаны на рис. 8.32 С.
3. СНД обусловленная неполным энерговыделением,
наблюдается также в смесевых взрывчатых составах типа горючее —
окислитель. Основным препятствием в достижении полного (расчетного)
энерговыделения является диффузионные затруднения на границе.
А)
В)
з у
О v
Рис 8.32. А) — р — v диаграмма СНД В) — структура НС Д. Цифрами
обозначены состояния на рис. 8.28 А. С) — режим СНД в ТЭНе с 6 % (2,3,4) и 10% (1)
флегматизатора. Длина заряда (мм):
1 — 50; 2 — 40; 3 — 20; 4 — 10. Метод ЛИВС
Обзор некоторых экспериментов со смесевыми составами дан в
[81].
Например, измеренная теплота взрыва при детонации
аммонитов на 8—13% ниже расчетной, что, возможно, связано с
эндотермическими реакциями образования окислов азота.
Максимум на зависимости Q(a) а^я аммонитов отвечает
содержанию селитры а = 21% (нулевой кислородный баланс, КБ = 0).
Однако максимальная скорость детонации достигается при а = 30—
35% (КБ = - 8—13%), и с дальнейшим ростом а величина (^падает, а
скорость детонации практически не меняется.
В экспериментах с помощью изотопной метки найдено, что при
детонации аммонита с 20% аммонийной селитры (АС) реагирует
только 12% АС.
Экспериментальные значения скоростей детонации игданитов
(ANFO) не соответствуют имеющемуся в них запасу химической
энергии. Согласно величине Q= 900 ккал/кг а^я игданитов можно
ожидать D = 6 км/с, а измерено только 2,3—3,5 км/с {аая d3 = 0,3 м),
что даже меньше, чем аая чистой селитры (D = 3,7 км/с).
Экспериментальные зависимости D(d) аая игданитов (см.
рис. 8.33) показывают, что а^я стехиометрической смеси селитры с
жидким топливом максимальная скорость детонации должна быть
близка к 4,75 км/с.
Ц,
км/с
0
—i г
ОД
—1 1 1 г
0,2 0,3
-I—л,—,—
0,4 5,5 Ам
Рис. 8.33 Экспериментальные зависимости D(d) для игданитов [81]
1,2,3 — игданит на основе гранулированной АС; 4 — игданит на основе измельченной АС
418
Таким образом, и &ля игданитов существенное влияние на D (d3)
оказывает размер зерна селитры. А учитывая влияние ряда других
факторов (масштаб, структура частиц, технология перемешивания,
содержание компонентов, окружающая среда), можно считать, что расчетное
прогнозирование величины скорости детонации ненадежно, поэтому
необходим в каждом случае экспериментальный контроль.
4. Скорость детонационной волны в распылах зависит от
размеров капель [78,83] и оказывается ниже расчетной (до 25%) в
предположении полного испарения капель. Здесь также имеется связь
между шириной ЗХР и параметрами детонации.
НСД в конкретных газокапельных смесях проанализирована в
[84,85,86]. Показано, что значительное недогорание смеси (более
50%) связано с кинетикой химических реакций. Обосновано
существование различных структур НСД.
Рассмотрим нестационарную неидеальную детонацию (ННД),
возникновение которой обычно связано с условиями
инициирования заряда. Если инициирующий и основной заряды различаются
по мощности, то последнему навязывается несвойственный ему
режим пересжатой или недосжатой детонации. На определенной
длине основной заряд детонирует с какой-то переменной скоростью,
постепенно переходя на стационарный режим. Характер перехода и
длина переходной зоны а^я различных пар ВВ и способов
инициирования исследованы недостаточно.
В [87] изучался процесс передачи детонации от низкоплотных
зарядов на основе гексогена (р = 0,15—0,6 г/см3) к контактирующим с ними
аналогичным зарядам большей плотности (р = 0,6—1,7 г/см3).
Полученные зависимости длины переходной зоны 1 от
плотности основного заряда имеют четкий минимум при р = 1,2—1,3 г/см3,
причем 1 растет с уменьшением р.
В [88] установлено, что как при сильном, так и при слабом
инициировании скорость детонации стремится сверху или снизу к
одинаковому стационарному значению.
В [89] проведены электроконтактные измерения скорости
детонации и радиальной бризантности (по обжатию брусков из Д16) по
длине переходной зоны fi^ контактирующих пар цилиндрических
зарядов из следующих ВВ:
419
-50 0 50
150 1,мм
50 100 150 1,мм
Рис. 8.34. А. Изменение скорости детонации в переходной зоне составных
зарядов. 1 — аммонит 6ЖВ флегматизированный; 2 — аммонит 6ЖВ;
3 — гексоген флегматизирован.
искоро
D=[D
|Л>«
АН,
В. Профили относительнойскорости детонации в переходной зоне.
— аммонит 6ЖВ и
аммонит 6ЖВ
флегматизированный;
— аммонит 6ЖВ и
гексоген флегматизированный.
Рис. 8.35. Изменение радиальной
бризантности в переходной зоне
составных зарядов
Для этих пар заряды
инициировались с торца как со
стороны слабого (низкоскоростного)
ВВ, так и со стороны сильного
(высокоскоростного) ВВ, т.е. в
режимах недосжатой и
пересжатой детонации.
Результаты измерений даны
на рис. 8.34 и 8.35 и позволяют сделать следующие выводы:
1. Чем выше степень пересжатия или недосжатия, тем больше
длина переходной зоны. Для одних и тех же пар ВВ ее длина меньше
в недосжатом режиме инициирования по сравнению с пересжатым.
Например, при переходе от аммонита 6ЖВ к гексогену 1 = 0,07 м,
а в обратном направлении 1 = 0,14—0,15 м.
2. Из рис. 8.34В видно, что максимальные степени пересжатия
и недосжатия достигали 2,05 и 0,49 соответственно.
420
Ph, кбар
400U
300 L
200 U
100
Рис. 8.36. Зависимость рн(1) при
инициировании плоской баратоловой
линзой зарядов из состава 9404, Сотр.В,
ТНТ и нитрометана
3. Сравнение рис. 8.34 и
8.35 показывает, что
кривые изменения D и ДН
качественно подобны. Связь
скорости детонации с
величиной бризантности
нелинейная, что
очевидно, поскольку АН ~p~D.
Относительные изменения
АН больше, чем D.
Результаты работ [87—
89] согласуются с
измерениями давления в точке Жуге
при инициировании
баратоловой линзы плоской
детонации в зарядах из состава
9404 (94% октогена, р = 1,84 г/см3, D = 8,8 км/с), Сотр.В, тротила и
нитрометана (см. рис. 8.36) [49].
Так, а^я наиболее мощного состава 9404 на расстоянии от
линзы 1= 12,7 мм рн = 303 кбар, а а^я 1= 101,6 мм рн = 375 кбар, т.е.
давление вблизи линзы на 20% ниже. При этом величина скорости
детонации изменяется незначительно — в пределах 100м/с [49].
Наоборот, а^я наиболее слабого нитрометана наблюдается
пересжатая детонации.
Режим ННД снижает давление в точке Жуге, что должно
уменьшать метательную способность заряда с зоной ННД. Кроме
мощности инициирующего заряда, второй причиной ННД является
«точечный» способ инициирования основного заряда. При этом в
заряде возникает сферически расходящаяся детонационная волна,
скорость которой растет с радиусом волны R [90,91,92]:
DR=Da(l-3,5a/R) (8.52)
где а — ширина ЗХР; R=Н + R^; Н — толщина заряда; R^ — радиус
РТУВ на поверхности заряда; D^ — скорость идеальной детонации аля
IUoo.
JRIJ„=DRID„=\-
1,0
VI
Оценим изменение полного импульса на абсолютно жесткой стенке
за счет НН Д от расходящейся волны. Стенка имеет радиус R.
Для кубического УРС согласно (5.18) J = 8/27 m D = 8/27H р0 D.
Поскольку аля сферической волны скорость непрерывно меняется,
оценку изменения импульса сделаем для среднего радиуса волны в
заряде R=Н/2+Rq . Тогда
Результаты оценки
снижения импульса по (8.53)
приведены на рис. 8.37.
Сделанные оценки показы-
0,8 1 /// I / I—/\ / I 1
1 '" '' 'х ■ х ' ' вают:
1. Величина
относительного уменьшения импульса
]к/]оо и характер его
изменения с радиусом волны
сильно зависят от ширины
ЗХР: чем больше ЗХР, тем
больше потери импульса на
данном радиусе и тем
медленнее уменьшаются
потери с ростом радиуса.
Например, при
H = 2R0=10 мм увеличение
ЗХР на порядок (с 0,17 до
1,79 мм) дает рост потерь
импульса также на порядок
(с 6% до 62%).
2. Для мощных ВВ с
малой ЗХР (а < 0,5 мм) потери импульса сосредоточены в относительно
тонком слое заряда у поверхности инициирования. Следовательно,
Аля проведения экспериментов по сравнительному измерению
параметров ННД при различных режимах «точечного»
инициирования могут быть использованы тонкие заряды.
0,6
0,4
4
ц,
7
\\
4
5]
^/
У
/
//
и
V
/
о
40 60 80 Н+г^мм
Рис. 8.37. Расчетные потери полного
импульса на жесткой стенке расходящейся
сферической детонационной волны
относительно импульса плоской волны
1— а=0,17мм(90%НМХ+10%ТЭТ);
2 — а=0,25 мм (70% RDX+30% TNT);
3 — а=0,4 мм (TNT прессованный);
4 — а=0,65 мм (90% ТАТБ +10%
связки); 5 — а= 1,79 мм (RDX насыпной);
6 — а=2,51 мм (аммонит ПЖВ-20
насыпной).
422
Например, а^я определения влияния НН Д на метательную
способность различных взрывчатых составов автор использовал заряды
толщиной Н = 10 мм [93].
Кроме расходимости потока в сферической волне и
относительной мощности ВВ инициатора, на режим ННД при «точечном»
инициировании влияют также конечный размер инициатора, малая
поверхность инициируемой зоны относительно всей поверхности
заряда.
По краям зон возникают боковые разгрузки, вследствие чего
некоторый объем поверхностного слоя заряда вокруг инициатора
полноценно не детонирует (см. рис. 8.27), что снижает метательную способность
заряда. По этой же причине в криволинейных прутках ВВ в местах
поворотов наблюдается непрореагировавший объем ВВ [94]. Эта т.н.
«темная зона» (без свечения ПВ на фотохронограммах) имеет ширину,
равную критическому диаметру ВВ.
Как правило, о режиме Н Д судят по измерениям волновой
скорости, которая малочувствительна к изменению режима или
степени Н Д. Величина снижения давления в точке Жуге при режимах Н Д
вдвое больше изменения скорости (т.к. p~D2 и Ар = 2AD) и прямо
влияет на энергию метаемой пластины.
В [93] нами проведены измерения влияния режима ННД на
метательную способность прессованных зарядов из различных сплавов
ТГ и ТНТ. Все заряды имели примерно одинаковую минимальную
пористость.
Степень неидеальности детонации зарядов определялась
параметрами инициатора: использовались цилиндрические инициаторы
из флегматизированного ТЭНа высотой 10 мм и диаметром,
изменяющимся от 2 до 15 мм, а также удар алюминиевой пластины со
скоростью 1 км/с.
Сложность этой задачи в том, что на энергию пластины влияют
сразу четыре взаимосвязанных фактора: кривизна детонационной
волны, ННД заряда, масса и размеры инициатора.
Для выделения влияния только ННД определялось изменение
энергии метаемой пластины в опытах с зарядами из исследуемых ВВ
по отношению к точно таким же зарядам из чувствительного флегмати-
423
зированного мелкодисперсного ТЭНа и с теми же инициаторами, т.е.
всегда анализировались пары опытов с одинаковыми инициаторами.
Заряд из высокочувствительного ТЭНа взят за эталонный,
поскольку он детонирует в идеальном режиме (без потерь от ННД) даже с
самым маленьким инициатором о2 мм. Поэтому измеренное
относительное изменение энергии пластины К=E/Ej^ будет обусловлено только
ННД заряда исследуемого ВВ, поскольку все другие три фактора в
сравниваемых опытах остаются постоянными.
Максимальная относительная энергия пластины К будет
измерена при отсутствии ННД, а потерь от ННД не будет, если инициатор
изготовлен из одинакового с зарядом ВВ и имеет диаметр <1ин > dn .
Если ВВ инициатора менее мощное, чем ВВ заряда, а <1ин > ап , то
возникают постоянные потери, названные предельными, которые
обусловлены только уменьшением давления инициирования:
A*v=l-V*»« (8-54)
В интервале d < d < d возникают дополнительные потери
энергии пластины, и суммарные потери составят:
Д£ин=1-*„„/*_ (8.55)
Полученные результаты показаны на рис. 8.38. Пластины из стали
или латуни разгонялись зарядами 0 60 х10 мм. Малая толщина заряда
усиливала влияние ННД на энергию метаемой пластины (см. рис. 8.37)
С помощью камеры СФР-2М измерялось время t движения пластины
на базе 10 мм в точке под проекцией оси инициатора. Относительная
энергия пластины определялась как:
k = E/E3m=(t,Jt)2 (8.56)
Погрешность измерений ±1%.
Как видно из рис. 8.38А, значения потерь ДК линейно
уменьшаются с ростом диаметра инициатора от d до d , а при d > d
становятся постоянными и равными АК .
А Пр
Для ТНТ АКп =0, т.к. ТЭН мощнее тротила, а а^я ТГ10
АКп = 5% поскольку давление в точке Жуге у флегматизированного
ТЭНа меньше, чем у ТГ10.
424
АК ,96
б)
АК ,%
Гг—'
0,25 0,5 0,75 Рии/рн
Рис. 8.38. Потери энергии метаемой пластины в зависимости:
А — от диаметра инициатора из флегматизированного ТЭНа; В — от давления
инициирования относительно рн.
1 — ТНТ; 2 — ТГ50; 3 — ТГЗО; 4 — ТГ10; 5 — удар алюминиевой пластины со
скоростью 1 км/с
Зависимость АК (d /d ) усиливается с уменьшением
восприимчивости к детонации (с ростом ЗХР). Например, при dHH = dK fi^
тротила потери составляют 25%, а для ТГ10 — 8% (см. рис. 8.38А).
В предположении, что предельные потери от НН Д
определяются различием между давлением инициирования р и давлением в
точке Жуге рн /^ая данного состава получена линейная зависимость
АК (ри„/Рн)» показанная на рис. 8.38В.
При инициировании заряда из ТГ10 ударом алюминиевой
пластины (рин = 4 ГПа) измерена величина задержки инициирования,
равная 0,8 мкс (глубина задержки 6 мм). При этом потери энергии
пластины от ННД составили 12%.
Таким образом, потери от ННД могут быть достаточно велики.
Полученные результаты позволяет правильно выбрать
инициатор в исследованиях, где важно учесть или исключить неидеальную
детонацию заряда.
8.8. Обобщённое описание детонации
До сих пор мы рассматривали обычную химическую
детонацию — сверхзвуковое распространение экзотермической
химической реакции в газовых или конденсированных средах. По своей
структуре детонация — это ударная волна, движение которой под-
держивается энерговыделением за её фронтом за счёт химической
реакции.
Для детонации возможны три режима: нормальный (D = u + c),
пересжатый (D<u + c) и недосжатый (см. рис. 8.1). Оказывается
энергетика детонации может быть различной природы, не только
химической, но и физической, связанной, например, с фазовыми
превращениями [95].
Для протекания детонации даже необязательно наличие у среды
освобождаемой энергии. Так, обнаружена световая детонация
воздуха, идущая за счёт введения в воздух внешней энергии лазерного
излучения [96,97].
Таким образом, возможна не только внутренняя, но и внешняя
энергетическая «подпитка» детонации, причём с изменением
режима детонации. Например, а^я реализации пересжатой детонации
нужен подпор П Д сзади поршнем, скорость которого больше массовой
скорости ПД в режиме нормальной детонации. Предварительное
ударное сжатие тротила увеличивает его скорость детонации на 25%
[98].
Анализируя режимы детонации с внешним энерговводом, В. И. Тар-
жанов предложил новое понятие — перегретая детонация [73,99],
представляющую собой нормальную стационарную детонацию ВВ при
дополнительном внешнем энерговводе в зону химреакции.
Осуществить перегрев химической детонации можно
следующими двумя способами:
1. После инициирования прозрачного ВВ (нитрометан)
лазерным взрывом металлической плёнки подача световой
энергии продолжается (навстречу волне, через нитрометан).
При этом поглощение энергии осуществляется в узкой зоне
(~30 мкм) на фронте волны детонации, перегревая её.
2. Заряд ВВ помещается между электродами малоиндуктивной
цепи сильноточного источника и создаётся мощное
магнитное поле, энергия которого также перегревает детонацию.
При этом энерговыделение в зоне реакции равно сумме
химической и магнитной энергий. Сделанные в [27] расчёты
показали, что при увеличении напряжённости магнитного
426
поля скорость детонации растёт, а давление, температура и
плотность снижаются. В пределе, при бесконечно большой
энергии магнитного поля сжатие ВВ отсутствует, D -> <*>, т.е.
детонация становится мгновенным безволновым
химическим превращением.
Таким образом получаются гибридные режимы светохимиче-
ской или магнитохимической детонации.
В [73] сделано общее рассмотрение плоской химической
детонации в идеальном газе с химическим энерговыделением
(калорийностью) при дополнительном энерговводе с постоянной плотностью
мощности. Используется У PC идеального газа Е = ру/(к — 1) (Е —
внутренняя энергия, к — показатель политропы) и обычные
уравнения сохранения потоков массы, импульса и энергии.
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
Рис. 8.39. Расчётные адиабаты Гюгонио и кривая состояния Жуге (13) для
идеального газа (к= 1,14)
а) 4 — адиабата инертного газа; б) 1,2,3 — адиабаты химической детонации с
различным энергосодержанием газа в) 5,6,7 — адиабаты перегретой детонации газа с
энерговводом ;г) 8,9,10,11 — адиабаты охлаждаемой детонации газа с
энергоотводом д) 12 — адиабата инертного газа с энерговводом
427
Получено уравнение, которое описывает весь спектр
стационарных процессов с ударным фронтом в реакционноспособной или
инертной среде с внешним энерговводом (отводом) или без него.
На рис. 8.39 показаны результаты расчётов адиабат Гюгонио
продуктов детонации с внешним воздействием и кривой состояний
Жуге (идеальный газ, к = 1,14).
Выше адиабаты 4 инертного газа расположено семейство адиабат
1,2,3 химической детонации с различной калорийностью. Выше
адиабаты 1 лежит семейство адиабат 5,6,7 перегретой детонации с
различным внешним энерговводом. Пересечения этих семейств с
кривой 13 дают состояния в точке Жуге аля нормальной детонации.
Таким образом, каждый из известных трёх классов детонации
(нормальная, пересжатая, недосжатая) может быть расширен
перегретой или охлаждаемой детонацией за счёт внешнего энерговвода
(отвода).
Литература к главе 8
1. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика, т.6
Гидродинамика. М.: Наука, 1986.
2. Станюкович К.П. Неустановившиеся движения сплошной
среды. М.: Гостехтеориздат, 1955.
3. Годунов С.К. Элементы механики сплошной среды. М.: Наука,
1978.
4. Баум Ф.А., Станюкович К.П., Шехтер Б.И. Физика взрыва. М.:
Из-во физ-мат. лит., 1975.
5. Зельдович Я.Б., Компанеец А.С. Теория детонации. М.:
Гостехтеоретиздат. 1955.
6. Теплофизика и динамика интенсивных импульсных
воздействий. А.В. Бушман ,Г.И. Канель ,А,Л, Ни, В.Е.Фортов. Ин-т
химфизики АН СССР, Черноголовка, 1988.
7. Авенян В.А., Ашаев В.К., Доронин Г.С. «Химическая
физика процессов горения и взрыва». Детонация и ударные
волны. Материалы VIII Всес. симпозиума по горению и взрыву,
Черноголовка, 1986, С.50.
8. Дрёмин А.Н. ФГВ, 2000, №6, с.31 -44.
428
9. Уткин А.В., Колесников С.А., Першин СВ. ФГВ, 2002, №5, с.
111 — 118.
10. Лобойко Б.Г., Любятинский С.Н. ФГВ, 2000,№6, с.45-64.
11. Кузнецов Н.М. «Химическая физика процессов горения и
взрыва». Детонация и ударные волны. Материалы VIII Всес.
симпозиума по горению и взрыву, Черноголовка, 1986, С.65.
12. Трофимов B.C. Там же, С.59.
13. Клименко В.Ю., Давыдова О.Н., Жолудева ТА., Дремин
А.Н. IV Всес. совещания по детонации, СССР, Телави, 1988.
Доклады, Т.2,С.261.
14. Klimenko VYu. Abstracts of Jnter. Conf. «Shock waves in
condensed matter», St. Peterburg, Russia, 1994, P.36.
15. Dremin A.N., Klimenko VYu., Davidova O.N., Zoludeva ТА.//
IX Symposium (Jnt.) on Detonation, USA, Pordand, 1989,
P.724.
16. Dufort S., Delpuech A. VIII Symposium (Jnt.) on Detonation,
USA, Albuquerque, NM, 1985, P. 847.
17 Delpuech A. IX Symposium (Jnt.) on Detonation, Pordand, 1989,
P. 172.
18. Бахрах СМ., Евстигнеев A.A., Зубарев В.Н. и др. ФГВ, 1981,
№6, С. 117.
19. Seitz W.L., Stacy H.J., WackerlyJ. 8th Symp. (Jnt.) on Detonation,
Albukerc, 1986.
20. Davis W.C., Ramsay J.B. 7th Symp.(Jnt.) on Detonation —
Annapolis,Maryland, 1981.
21. Детонационные волны в конденсированных средах. Дремин
А.Н., Савров С.Д., Трофимов B.C., Шведов К. К. М:, Наука,
1970.
22. Альтшулер Л.В., Балалаев В.В. и др. ПМТФ, 1982, №1, С. 128.
23. Дремин А.Н. Труды ин-та механики МГУ. — М.: Из-во МГУ,
1973, №21.
24. Ашаев ВТ., Доронин Г.С., Левин А.Д. ФГВ, 1988, №1, С. 24.
25. Альтшулер Л.В., Доронин Г.С., Жученко B.C. ФГВ, 1989, №2,
С.84.
26. Бордзиловский С.А., Караханов СМ., Лобанов В.Ф. ФГВ,
1987,№5,С132.
27. Забабахин Е.И., Забабахин И.Е. Явления неограниченной
кумуляции. М.: Наука, 1988.
28. Taybor J. Detonation in condensed explosives. Oxford, 1952.
29. Володин Г.Т. ФГВ, 1991, №1, C.123.
30. Мейдер Ч. Численное моделирование детонации.М.:
Мир,1985.
31. Альтшулер Л.В., Крупников К.К. и др. ЖЭТФ, 1958,34,4,874.
32. Ашаев В.К., Доронин Г.С., Жученко B.C. ФГВ, 1985, №1,
с.127.
33. Ашаев В.К., Доронин Г.С., Левин А.Д. ФГВ, 1988, №24, с.1.
34. Гатилов АЛ., Ибрагимов РА, Кудашов A3. ФГВ, 1989, №2, с.
82.
35. Альтшулер Л.В.,Кормер СБ. и др.ЖЭТФ, 1960, Т.38, №4,
с.1061.
36. Любятинский С.Н., Воробей В.А. V Всес. совещание по
детонации. Красноярск, 1991. Сб. докладов, Т.2, с. 39.
37. Sheffield S.A., Bloomquist D.D., Tarver СМ. J. Chem. Phys.,
1984,V.80,№8,P.3831.
38. Steinberg D., Chau H. 8th Symp. (Jnt.) on Detonation. —
Albucirc, 1986.
39. Дорохин B.B., Зубарев B.H. и др. ФГВ, 1985, №4, с.100.
40. АльтшулерЛ.В.,КормерСБ. и др. ЖЭТФ,1960,Т.38, №4,
с.1061.
41. Burrows К., Chilvers D.K., Cyton R. at al 6th Symp. (Jnt.) on
Detonation California, 1976.
42. Канель Г.И. ФГВ, 1978, №1, c.14.
43. Альтшулер Л.В. Применение ударных волн в физике высоких
давлений. Успехи физических наук, 1965,85, N2, с.197.
44. Лобанов В.Ф., Караханов СМ., Бордзиловский СА. ФГВ,
1982, №3, с. 90.
45. Hornig Н.С, Lee EX., Finger М. et.al. 5th Symp. (Jnt.) on
Detonation. Pasadena, California, 1970.
46. Tarver S.M., Fried L.E., Ruggiero A.J., Calef D.F. Proc. of the
10 -th Intern. Deton. Symp., Boston, Massachusetts, 1993, p.
3 — 10.
47. Даниленко B.B. Сверхтв. материалы, 2006, № 5, с. 9 — 24.
430
48. Уткин А.В., Колесников С.А., Першин СВ. ФГВ, 2002, 5,111.
49. Mader S. L. Numerical Modeling of Explosives and Propellants.
SecondEdition, CRC Press, 1998, p. 439.
50. Андреев K.K., Беляев А.Ф. Теория взрывчатых веществ. М.:
1960.
51. Kato J., Nori N., Sakai Н. 8th Symp. (Jnt.) on Detonation. New
Mexico,1985.
52. Авакян Г.А., Хмельницкий Л.И. Справочник по взрывчатым
веществам. ВИА им. Дзержинского, 1962.
53. Беляев А.Ф., Бобылев В.К. и др. Переход горения
конденсированных систем во взрыв, М.:Наука,1973.
54. Харитон Ю.Б. В сб. «Вопросы теории взрывчатых
веществ»,вып. 1, Из-во АН СССР, 1947.
55. Воскобойников И.М., Буланов И.В. IV Всес. совещание по
детонацииДелави, 1988, доклады,т.1, с.134—140.
56. Сулимов А.А., Ермолаев Б.С. «Химическая физика процессов
горения и взрыва». Детонация и ударные волны. Материалы
VIII Всес.симпоз. по горению и взрыву. Черноголовка, 1986,
с.134.
57. Андреев С.Г., Зюзин В.В., Имховик Н.А., Соловьев B.C. IV
Всес. совещание по детонации, Телави, 1988, доклады, т.1,
с.118.
58. Хоув П., Фрей Р., Тейлор Б., Бойль В. Детонация и взрывчатые
вещества (сборник статей), М.: Мир, 1981, с.236—254.
59. Хасаинов Б.А., Борисов А.А., Ермолаев Б.С. «Химическая
физика процессов горения и взрыва». Детонация и ударные
волны. Материалы VIII Всес. симп. по горению и взрыву,
Черноголовка, 1986, с.89.
60. Уткин А.В., Канель Г.И., Фортов В.Е. IV Всес. совещание по
детонации, Телави, 1988, доклады,т.1,с.104.
61. Александров Е.И. IV Всес. совещание по детонации, Телави,
1988, доклады, т.2, с. 132.
62. Walker Е Е., Wasley R.J. Combustion and Flame, 1970,15,233.
63. Харитон Ю.Б. Сборник по теории взрывчатых. веществ,
Оборонгиз,1941.
431
64. Дремин А.Н., Савров С.Д., Трофимов B.C., Шведов К.К.
Детонационные волны в конденсированных средах, М.:
Наука,1970.
65. Кобылкин И.Ф., Носенко Н.И., Соловьев B.C. IV Всес.
совещание по детонации, Телави, 1988, доклады, т.1, с.97.
66. Златин Н.А., Красильщиков А.П., Мишин Г.И., Попов Н.Н.
Баллистические установки и их применение в
экспериментальных исследованиях, М.: Наука, 1974, с.344.
67. Mader C.L., Pimbley G.H.J. Energetic. Materials, 1983, N1, p.3.
68. Жученко B.C. IV Всес. совещание по детонации, Телави,1988,
доклады, т.2, c.247.
69. Уокерли Дж., Раби Р. и др. Сб.» Детонация и взрывчатые
вещества», М.: Мир, 1981, с.269.
70. Лобавнов В.Ф. ФГВД986, N5, с.104.
71. Василенко В.Г., Ковтун А.Д., Макаров Ю.М., Фомичева Л.В.
и др. V Всес. совещание по детонации, Красноярск, 1991, сб.
докладов, т.2, с.351.
72. Бриш А.А., Галеев И.А., Зайцев Б.Н. и др. ФГВ, 1966,3,132.
73. Быстрое инициирование ВВ. Особые режимы детонации.
Сб. научных статей под ред. В.И.Таржанова. Изд-во РФЯЦ-
ВНИИТФ, Снежинск, 1998,166 стр.
74. Таржанов В.И., Зинченко А.Д., и др. ФГВ, 1996,4,113.
75. Таржанов В.И., Зинченко А.Д. и др. ФГВ, 1996,2,111.
76. Stirpe D.Johnson J., Wackerly J. J. Appl. Phys., 1970, V41, N9.
77. Salzman P.K., Irwin O.R., Anderzen W.H.J. AJAA, 1965,3,12.
78. Воронин Д.В. ФГВ, 1989, N2, c.l 16.
79. Jones H. Proc. Roy. Soc, 1947, A189,415
80. Eyring H. et al. Chem. Rev., 1949,45,69.
81. Колдунов C.A., Чухарев А.Э. IV Всес. совещание по
детонации, Телави, 1988, доклады, т.1, с.199.
82. Пырьев В.А., Соловьев B.C. ФГВ, 1992, N6,c.l 12.
83. Гельфанд Б.Е. Детонация, Черноголовка, 1977.
84. Николаев Ю.А., Фомин П.А. ФГВ, 1984,20,4,97.
85. Воронин Д.В. ФГВ, 1984,20,4,105.
86. Воронин Д.В., Митрофанов В.В. ФГВ, 1985,21,5,77.
432
87. Соловьев B.C., Власова Л.Н., Андреев С.Г. и др.
ФГВ,1981,17,5,135.
88. Мартынюк В.Ф., Сулимов А.А., Дубовицкий В.Ф.
ФГВД981,17,4,136.
89. Гржибовский В.В., Поплавский В.А. ФГВ, 1989,25,1,131.
90. Воробьев А.А. Материалы VI Всес. симпозиума по горению и
взрыву.Черноголовка, 1980.
91. Губкин К.Е. ФГВ, 1978,14,3.
92. Wood WW, Kirkwood J.G.J. Chem. Phys., 1954,22,11.
93. Даниленко B.B., Пачурин Ю.М. ФГВ, 1987,1,46.
94. Новиков С.А., Шутов В.И. ФГВ, 1980,16,3.
95. Radic R. L., Fowles G. R., Fickett W. Phys. Fluids, 1979, V22,
p.422.
96. Ramsdew S. A., Savic P. Nature, 1964, V 203, p.1217
97. Райзер Ю.П. Лазерная искра и распространение разрядов. М.:
Наука, 1974.
98. Таржанов В.И. ФГВ, 1977, 5,760-766.
99. Таржанов В.И. ФГВ, 1985,5,81-85.
433
Глава девятая
ВЗРЫВ В РАЗЛИЧНЫХ СРЕДАХ
9.1. Понятие взрыва. Работа взрыва
Определение взрыва было дано еще М.ВАомоносовым: «Взрыв —
это очень быстрое выделение большого количества энергии и больших
объемов газов». Правда, неясно, что значит «большое количество»
энергии и газов. Кроме того, при взрьюе атомного заряда газы вообще
не выделяются. Природа явления взрьюа сложна и многообразна,
поэтому можно сформулировать понятие взрьюа лишь в широком смысле
как «быстрое выделение энергии в ограниченном пространстве,
приводящее к разрушению, уплотнению и перемещению окружающей
среды» [1].
При взрыве содержащаяся в веществе потенциальная энергия
различного вида (химическая, атомная, термоядерная, тепловая)
быстро превращается в механическую работу, совершаемую сжатыми и
нагретыми газами или парами, образующимися при взрыве.
Работоспособность ВВ определяется величиной потенциальной
энергии в единице объема ВВ, которая освобождается при взрыве. Для
различных химических ВВ она составляет от 600 до 1600 ккал/кг. Эта
энергия невелика по сравнению, например, с имеющейся у бензина
(11000 ккал/кг), но работоспособность ВВ определяется скоростью
выделения энергии.
Например, при взрыве 1кг динамита в течение 2-10"5с
развивается мощность 3-108 л.с. С другой стороны, энергия ядерной реакции
синтеза гелия из водорода на единицу массы в 108 раз превышает
энергию взрыва ТНТ.
434
Другим фактором, определяющим силу взрыва, является
величина объема газов или пара, образующихся при взрыве 1 кг ВВ. Эта
величина а^я обычных химических ВВ колеблется в пределах 600—
1100 л при нормальном атмосферном давлении, причем эти газы
нагреты до 3000—4000 К, что и определяет их способность совершать
работу при расширении.
Быстрое химическое превращение конденсированных ВВ в
газообразные продукты взрыва протекает за счет реакции окисления
углерода и водорода кислородом, входящим в составе ВВ, т.е. без
притока кислорода извне.
Быстрота выделения и огромное давление сжатых газов при их
расширении создают в окружающей среде ударные волны, а
граница ВВ — среда начинает двигаться с большой скоростью,
уплотняя и разрушая среду. Начальные параметры взрыва заряда ТНТ
(р = 1,6 г/см3) в различных средах даны в таблице 9.1 [2].
Таблица 9.1. Начальные параметры взрыва в некоторых средах (заряд
ТНТ, р= 1,6 г/см3)
Среда
вакуум
воздух
вода
известняк
мрамор
гранит
сталь
Давление на
границе ВВ—среда,
кбар
0
0,57
136
185
237
251
300
Скорость границы
ВВ—среда, км/с
13
6.45
2,18
1.31
1.22
1.29
0,73
Начальная
скорость УВ в среде,
км/с
0
7,1
6,1
6У67
7,06
7,28
4,3
Из опыта известно, что уже на небольших расстояниях от заряда
(больших его размера) действия в среде не зависит от формы заряда
и аля любого компактного заряда будет эквивалентно взрыву
сферического заряда той же массы.
Максимальная скорость разлета газообразных продуктов взрыва
сферического заряда в вакуум (беспрепятственное расширение)
оценивается следующей зависимостью:
"max=(3*-iW2e(*2-i) (9.1)
где: к — средний показатель адиабаты расширения газов; Q —
теплота взрывчатого превращения.
Для типичных ВВ Q« 1 кал/г и к =5/4. Тогда согласно (9.1)
и = 11 км/с. При реальной детонации мощных ВВ и = 13—15 км/с.
При взрыве в средах с конечной плотностью продукты взрыва,
взаимодействуя со средой, вовлекают среду в движение.В
зависимости от соотношения акустической жесткости среды и продуктов
взрыва возможны два режима взаимодействия со средой:
1) аая очень плотных сред от границы в продукты взрыва пойдет
ударная волна, т.е. давление будет сначала возрастать за счет
торможения газов на границе со средой;
2) fiiA^ менее плотных сред граница раздела будет двигаться
быстрее газов за фронтом детонации, и с самого начала процесса
расширения газов давление в них будет падать. Во всех случаях в среду
пойдет волна сжатия.
Первоначально резкая граница со средой в процессе расширения
продуктов взрыва становится все более размытой за счет
турбулентности газов, их «диффузии» в среду и перемешивания со средой.
В результате расширения в неограниченной среде продукты взрыва
займут некоторый предельный объем, определяемый равновесием
между остаточным давлением газов и давлением (атмосферным)
окружающей среды (без учета прочности среды).
Для типичных ВВ (р=1,6 г/см3) продукты взрыва расширяются
примерно в 800—1600 раз, следовательно, аая сферического заряда
радиус предельного объема будет в 10—12 раз больше радиуса заряда.
Зная предельный объем v^, можно оценить энергию продуктов
взрыва после их расширения:
Е„=р v„(k-l) (9.2)
Начальная энергия взрыва заряда Е0 = р0 v0 Q=M Q (М -масса
заряда). Следовательно, в среду (в У В) переходит энергия:
ЕУВ =ЕН -Е„ =M[Q- рУ- ] (93)
(k-i)pnV„
436
При к = 7/5 Еув/Е0 = 0,97,априк = 5/4 Еув/Е0 = 0,91.
Таким образом, подавляющая часть энергии переходит в среду.
Оценим в общем виде работу А расширения продуктов взрыва
от начальных параметров p{i v{i Т{ до конечных р2, v2, Т2 [3].
Из уравнений адиабаты pvк = Const и уравнения состояния
идеального газа имеем:
ZL = (2i.)*-'=(ii)t*"1 (9.4)
Следовательно,
А = Q[\-(Щ'ь ] 7 = 4 = 1"(—)" = 1"(-)*"' (9-5)
>i Q Рх v2
2
Как видно, отношение A/Q тем больше, чем больше величина
к = с /с , которая зависит от молекулярного состава продуктов
взрыва. Например, в продуктах взрыва гексогена 2/3 молекул
двухатомных (СО, N2, Н2) и 1/3 — трехатомных (С02, Н20), что
соответствует к = 1,25. Увеличение доли многоатомных молекул увеличивает с^
снижает величину к и отношение A/Q. Особенно сильно снижаются
к и A/Q при наличии в продуктах взрыва конденсированной фазы
(Al203,NaCl,Si02).
При расширении в продуктах взрыва остается тепло q = Q — А,
которое зависит от степени расширения, т.е. от остаточного
давления, или от среды. При полном расширении газов до р = 1 атм.
получим полную работу взрыва. Отнесенная к единице веса полная
работа взрыва называется работоспособностью (см.табл.9.2).
Из таблицы 9.2 следует, что для многих ВВ расчетные
величины У) = 83—85%, однако в реальном процессе расширения величина
к меньше, чем для идеального газа, и существуют потери на
остаточное тепло (q). Поэтому полный к.п.д.ВВ меньше и составляет
у, = 65—75%.
Однако расчетные относительные значения
работоспособности A/ATNT меняются несущественно, и их можно использовать для
сравнения действия взрыва различных ВВ в виде т.н. тротилового
эквивалента.
Таблица 9.2. Работоспособность некоторых ВВ [3]
ВВ
Азид
свинца
Аммиачная
селитра
Тротил
Тротил
Аммонит
6ЖВ
Динамит
62%
Гексог.
Гексог.
ТЭН
Нитроглицерин
Смесь тетра
нитро-
метана с
бензолом
(87,5/12,5)
г/см3
3,8
0,9
0,9
1,5
1,0
1,45
1,0
1,6
1,6
1,6
1,48
Qi
ккал/кг
360
380
830
1010
1030
1290
1270
1300
1360
1480
1650
k = S/cv
1Д9
1,3
1,24
1,23
1,24
1,175
1,25
1,25
1,215
1,19
1,18
Г],%
77,6
86,2
82,5
83,3
83,7
76,0
84,5
86,6
82,7
79,7
78,5
А
ккал/кг
280
327
685
840
850
980
1070
1125
1125
1180
1310
Q/Qtnt
0,36
0,38
0,82
1,00
1,02
1,28
1,26
1,29
1,35
1,47
1,63
АЛАгнт
0,33
0,39
0,82
1,00
1,01
1Д7
1,28
1,34
1,34
1,40
1,56
Работа взрыва может производиться в различных формах.
Общепринято деление форм работы на общее или фугасное и
бризантное (дробящее). Работа в общей форме зависит от теплоты
взрыва Q, связана с перемещением среды (расширение полости, выброс
грунта, разрушения) и проявляется на некотором расстоянии от
заряда.
Бризантное действие взрыва совершается в непосредственной
близости от заряда и определяется величиной pQD2 — плотностью
энергии на фронте детонации заряда.
Бризантное действие составляет меньшую часть полной работы
взрыва. Обычно при взрывах в грунте на выброс или рыхление
использование мощных бризантных ВВ нецелесообразно, т.к. растут
438
имические потери
Тепловые потери
Рис. 9.1. Схема баланса энергии взрыва
ненужные затраты энергии взрыва на чрезмерное дробление и
деформацию грунта вблизи заряда.
На рис. 9.1 наглядно показано деление общей энергии взрыва на
отдельные виды работы и потери [3].
9.2. Взрыв в воздухе
При взрыве заряда ВВ в воздухе образуется УВ, давление в
которой быстро падает. Скорость УВ и скорость воздуха за фронтом УВ
связаны известным соотношением:
u = (2D/(j+l)(l-c02/D2) (9.6)
Объем, охваченный УВ при v = v^ и j = 7/5 [6]:
v>3/2(j-1)voo = 0>6vto«500v0"
К моменту завершения расширения продуктов взрыва
воздушная УВ представляет собой тонкий слой на поверхности продуктов
взрыва с энергией е = 0,0075 Q.
При сферическом взрыве в воздухе на расстояниях 10—12
радиусов заряда rQ давление в УВ будет порядка 50 кг/см2 и до
расстояний ~ 50rQ давление падает пропорционально квадрату расстояния
(р~г2). Цельный импульс УВ, определяющий разрушение, падает
приблизительно пропорционально г"1, поскольку
продолжительность действия УВ пропорционально rQ . Расстояние предельного
действия взрыва по давлению пропорционально М1/3 Q (М —
масса заряда), а при импульсном разрушении — пропорционально
M2/3Q.
Обычно параметры ударной волны даются в функции
приведенного расстояния:
R* = R/Mem (9.7)
где Ме = М Q/QTNT — масса тротилового эквивалента заряда.
Цельный импульс УВ fi^ R* > 0,5 оценивается просто:
J = AMem/R* (9.8)
Если сферический взрыв происходит на поверхности земли,
и УВ двигается вдоль поверхности, то давление в УВ будет выше в
сравнении с взрывом в свободном воздухе без взаимодействия с
земной поверхностью.
Для этих двух случаев падение избыточного давления Ар с
расстоянием R* показано на рис. 9.2.
Если УВ не сферическая, а плоская, то Ар ~ 1/R.
Для оценки разрушающего
Ар, кг/см2
10
8
6
4
2
0
\
2'
_J
lv
^
:==
^
10 12 R*
Рис. 9.2. Избыточное давление Ар
на фронте сферической УВ в воздухе
в зависимости от приведенного
расстояния R*
1 — взрыв на поверхности земли,
2 — взрыв в воздухе далеко от земли
действия воздушной УВ нужно
знать изменение давления со
временем.
Типичная запись профиля Ар
(t) показана на рис. 9.3.
Как видно, профиль р (х)
состоит из двух частей: фазы
сжатия с Ар > 0, импульсом сжатия J+
в течение времени t+ и фазы
разрежения с р < р0, импульсом J и
временем t .
В случае мощного взрыва,
когда длительность фазы сжатия t
превосходит период Т
собственно
ных колебаний элементов
сооружения (t > > Т, где Т
обычно не более
нескольких десятых секунды),
разрушающее действие взрыва
определяется величиной
избыточного давления
(статическое действие УВ за
Рис. 9.3. Изменение избыточного давления воемя t < t )
в УВ со временем * +
Если же t+ < < Т, то
сооружение приобретает
некоторое количество движения
под действием не давления (которое быстро снизится до нуля), а
импульса. Разрушение наступит, если импульса достаточно аая создания
предельной деформации сооружения. Разрушение произойдет за время
t>t (импульсное действие УВ).
Практически важно определить расстояния, безопасные по
действию воздушной УВ. Эта задача решается методами теории
подобия (см. (9.7)). Вид расчетной формулы зависит от того, чем
определяется разрушение: давлением или импульсом.
На расстоянии R*, Ар+ избыточное давление Ар_ уже
недостаточно аая разрушения данного вида сооружения. Тогда
R=R„,/M
1/3
ИЛИ
R^^M
1/3
(9.9)
Аналогично, если разрушение определяется импульсом, то
R6e3=k2M2/i (9.10)
Коэффициенты Ц и Ц зависят от свойств разрушаемого объек
-та. Поскольку часто t+ « Т и трудно решить, что определяет
разрушение, то в «Единых правилах безопасности при ведении
взрывных работ» дается формула с промежуточным показателем
степени:
441
R6e3=kMl/2 (9.11)
(R — в м, M — в кг). Величины k даются в таблице 9.3.
Таблица 9.3. Значения к в (9.11)
Возможные разрушения
Разрушение остекления, повреж дение рам,
дверей, легких перегородок, штукатурки
Разрушение рам, дверей, перегородок, бараков,
сараев
Разрушение обычных зданий, опрокидывание
ж.д. составов, по-вреждение линий
электропередач
Открытый Заряд, углу-
г оленныи на
заряд
г свою высоту
5—8 2-4
2—4 1,1—1,9
1,5—2,0 0,5—1,0
Из табл.9.3 видно, что при взрыве открытого заряда безопасное
расстояние аая населенного пункта будет равно
R6e3>lOMm (9.12)
В случае сверхмощных взрывов (атомных, крупных складов
ВВ), когда t >> Т оценить безопасное расстояние можно
выражением:
R6e3>30Mm (9.13)
До сих пор речь шла о взрыве сосредоточенных зарядов ВВ.
В воздухе возможен и другой вид взрыва — т.н. объемный взрыв,
который возникает при распылении в воздухе твердого или жидкого
горючего или при смешивании воздуха с горючим газом.
Очень часто объемные взрывы возникают в угольных шахтах,
где при разрушении угольных пластов выделяется метан и угольная
пыль. Метано-воздушная смесь взрывается при содержании метана
в воздухе от 5—6% до 14—16%. Наибольшая разрушительная силау
смеси с 9,5% метана по объему. Температура воспламенения метано-
воздушной смеси ~ 650—750 С с задержкой 10с. С ростом
температуры задержка воспламенения уменьшается до 1 с при 1000 С и до
нуля при 2200 К.
442
Еще опаснее смесь становится, если в воздухе есть угольная пыль.
Взрывная волна поднимает угольную пыль со стенок выработок
шахты, сжимает и нагревает пыле-воздушную смесь, что усиливает взрыв
метана и приводит к распространению взрыва в шахте на большие
расстояния.
Для предотвращения взрывов метана в шахтах:
1) используются специальные, т.н. предохранительные ВВ, в
которых температура взрыва снижена (меньше 1500 С) за счет добавок
1—3% солей NaCl или КС1. Кроме того, эти соли тормозят реакции
окисления метана кислородом воздуха;
2) одновременно с камуфлетными взрывами в призабойном
пространстве применяют водораспылительные завесы —
полиэтиленовые мешки с водой, в которые помещен заряд ВВ. Взрыв
этого заряда одновременно с основным взрывом разбрызгивает
воду по выработке, предотвращая взрыв метана и смачивая
угольную пыль.
Уменьшают опасность воспламенения метана все факторы,
способствующие завершению реакций детонации заряда до выхода
газов из шпура (величина заряда, влияние забойки, величина
свободного пространства и др.), поскольку воспламеняют метан активные
промежуточные продукты взрыва
93. Взрыв в воде
В результате взрыва в однородной водной среде возникает
пузырь из нагретых и сжатых газов. Расширяясь, газы создают в воде
УВ. Малая по сравнению с воздухом сжимаемость воды
обуславливает большие начальные давления в УВ (150—200 кбар а^я
типичных ВВ) и небольшой рост энтропии (температуры). Из-за меньших
тепловых потерь доля энергии УВ, идущая на перемещение (на
механическую работу) будет больше, чем у воздушной УВ (при равной
общей энергии УВ в воде и в воздухе) [23].
На начальной стадии движения УВ в воде давление резко падает:
р ~ г "3 и уже на расстоянии ~ 10 rQ Ар « 0,01 р0. При этом предельные
расстояния, на которых еще проявляется действие взрыва, пример-
но такие же, как и аля взрыва в воздухе. Сильное разрушительное
действие взрыва в воде проявляется в объеме пузыря.
Расширение пузыря приведет к тому, что в некоторый момент
времени давление в нем сравняется с гидростатическим давлением
в окружающей воде, но процесс расширения будет продолжаться по
инерции. Поэтому в момент остановки стенок пузыря давление в
нем будет меньше, чем в окружающей воде. Пузырь начнет
сжиматься и опять пройдет положение равновесия. В результате пузырь
будет некоторое время пульсировать около среднего диаметра (может
быть до 10 циклов пульсации).
Пульсирующий пузырь двигается вверх — всплывает в воде. При
этом пузырь отталкивается от свободной поверхности и
притягивается к жесткой стенке.
Кроме основной УВ, в воду излучаются также волны давления
при колебаниях пузыря. При первой пульсации в УВ
излучается ~ 60% всей энергии взрыва, а при второй — еще ~ 25% энергии.
При взрыве вблизи поверхности воды на ней образуется купол, а
затем происходит выброс воды с появлением водяного столба.
Вода имеет сравнительно большую скорость звука с0« 1,5 км/с,
поэтому при движении УВ ее скорость быстро падает до скорости
звука, и волна становится акустической, хотя давления на ней еще
большие (500—1000 кг/см2). Поэтому аая описания полей
подводного взрыва часто пользуются акустическим приближением
(D = c = Const).
Давление и импульс в воде значительно больше, чем в воздухе.
Так, давление отражения в воде можно оценить по формуле [4]:
Apomp=550/R* (9.14)
Для R* = 5 Арот в воде в 150 раз больше, чем в воздухе.
Величина импульса в воде может быть определена по
приближенной формуле:
У«930М2/3/Д (кг сек/м2) (9.15)
Сравнивая с импульсом УВ в воздухе (I = (50 — 60) M2/3/R)
видно, что при равных М и R импульс в воде в 15—20 раз больше.
444
Для расчетов параметров движения пузыря и УВ в воде, кроме
обычных уравнений сохранения и неразрывности, используют
различного вида У PC воды, из которых наиболее простым и
распространенным является УРС в форме ТЭТа [4]:
Руд-р0=В[(р/р0У-1] (9.16)
Аая р > 30 кбар В = 4,25 кбар и п = 6,29;
^ая р < 30 кбар В = 3,045 кбар и п = 7,15.
В интервале 0 < р < 450 кбар ударная адиабата воды имеет вид:
D = h 483 + 25,3061g (l+w/5,19) (9.17)
где D и u — в км/с.
Адиабата разгрузки воды может быть представлена в виде [4]:
р-р0=А(р/р0Г-В (9-18)
где константы А, В, п зависят от давления:
0 <р< 30 кбар А = В = 3045кг/.см2,п —7,15;
30 <р < 150 кбар А= 1220+0,0606р, В = 3045 кг/см2;
150 <р< 250 кбар А = 2680+0,0509 р, В = 6100 —0,0204 р
фарная абиабата и изэнтропа разгрузки в p,v координатах
представлена на рис. 9.4.
Экспериментально получена следующая зависимость
избыточного давления а^я сферической УВ в воде [4]:
Ар = А(г0/г)а (9.19)
где г0 — радиус заряда.
Для заряда из тротила (р = 1,6 г/ см3):
А = 37 кбар, а = 1,5 при 6 < г/г0 < 12;
А= 14,7 кбар, а = 1,13 при 12 < г/г0 < 240.
Найдены зависимости давления и импульса УВ от веса
заряда М:
Для заряда из тротила (р = 1,52 г/см3):
Аруд = 533(М1/3 / г),ЛЗ Jyd = 0,059М1/3(М1/3 / г)0'89 (9.20)
в интервале 1,57 < (М/г) < 0,078.
(9.21)
Для заряда из ТЭНа (р = 1,6 г/см3):
Аруд = 645(М,/3 / rf2\Jyd = 0,0772М,/3(М1/3 /г)0'92
в интервале 3,3 < (М1/3/г) < 0,067.
В результате численного решения задачи о взрыве в воде заряда
из ТЭНа получена следующая зависимость давления на
поверхности газового пузыря:
р=А{гй/гпГ (922)
где величины А и п равны: при rQ < гп < 1,2 rQ: А = 147,5 кбар, п = 3,8;
при 1,2 rQ < гп < 3 г0: А=44,3 кбар, п= 1,61;
при гп > 3 rQ: А= 13,4 кбар, п= 1,25.
Расчеты позволили получить распределение энергии в
зависимости от радиуса УВ. Полная энергия волны Е представляет собой
р, кбар
Изэнтропа
Ударная адиабата
1,0
0,75-
0,50-
0,25-
0
Е \ ^ 1
пв у
у^л
/Р~
III 1
£Z
Е
п
1 1 '
r/rft
1 2 3 5 10 20
50 100
1,2 v, см3/г
Рис. 9.4. Ударная адиабата
и изэнтропа разгрузки воды
Рис. 9.5. Распределение энергии взрыва
вводе
сумму кинетической Ек и внутренней Евн. Последняя делится на
потенциальную энергию сжатия воды Е и энергию необратимых
потерь Еп.
Распределение энергии взрыва в воде показано на рис. 9.5 [4].
Энергия волны Е быстро растет и уже при г/г0 = 5 Е = 0,75 Ею
Наоборот, энергия газов в пузыре быстро уменьшается от 1 до 0,14
при r/rQ = 10 и до 0,06 при г/г0 = 100. Энергия потерь Епот все вре-
446
мя растет и при r/rQ =100 составляет 0,46. Потенциальная энергия
сжатия воды сначала увеличивается от 0 до 0,12 при r/rQ = 6, затем
уменьшается до 0,1 при r/rQ = 100. Кинетическая энергия растет до
0,37 при г/г0 = 15 и затем остается постоянной.
В соответствии с законом сохранения полная энергия УВ равна
работе, совершаемой газами при расширении пузыря.
9.4. Взрыв в грунте
Поскольку подземный взрыв широко используется в горной
промышленности и в строительстве, то его изучение имеет большое
практическое значение. Однако эта задача крайне трудна и
неопределенна, поскольку свойства грунтов и горных пород крайне
разнообразны. Это многокомпонентные среды (твердые частицы — вода-
воздух) самого разнообразного состава, прочности, пористости,
слоистости. Поэтому каждый участок грунта требует
индивидуального изучения.
Отметим некоторые общие особенности ударного сжатия
грунтов и горных пород при подземном взрыве.
1. Грунт (песок, глина) называется сыпучей средой, поскольку в
нем силы сцепления между частицами много меньше сил сухого
трения между частицами при деформации грунта
Для такой среды справедливо условие предельного состояния
Кулона [4]:
тт=К + тр (9.23)
где т — касательное напряжение; р — среднее напряжение; m = tgQ
— коэффициент внутреннего трения (Q— угол внутреннего трения);
К — коэффициент сцепления.
Если внутреннее трение мало (т«0), то среда называется
пластической и аая нее т = К.
"^ m
Для различных грунтов варьируется доля твердой фазы (а2), воды
(а2) и воздуха (а3). Плотность грунта как трехкомпонентной среды будет
равна р0=aj р2+а2 р2+а3 р3, где р2 = 1 г/см3, а р3 = 1,29 X10'3 г/см3.
Коэффициент пористости грунта Кп = (а2+а )/а2.
Конкретно аля песка Кп = 0,2—0,35, аая глины Кп = 0,5—0,7, аая
мела Кп = 0,4 —0,5, аая гранита Кп = 0,001—0,05.
Как для любой пористой среды, сжатие грунта создает
необратимые объемные деформации, поэтому кривые нагрузки и разгрузки
не совпадают, причем после разгрузки плотность грунта оказывается
больше первоначальной, в отличие от воды и воздуха, где за счет
нагрева (необратимых потерь энергии в УВ) плотность после
разгрузки всегда меньше начальной.
В грунтах, как и в металлах, напряжения различны в различных
направлениях, а прочностные характеристики зависят от скорости
деформации.
2. В горных породах (гранит, мрамор, песчаник, известняк,
доломит, сланец и др.) твердые частицы соединены между собой
цементирующим материалом и между частицами существуют большие
силы сцепления.
Различают следующие типы разрушения горной породы:
а) Разрушение сдвига, когда касательные напряжения достигают в
данной точке значения сдвиговой прочности ст: т = <71 — (T2 = (Ts'
При этом в хрупких породах происходит скол, а в пластичных
грунтах возникает пластическая деформация.
б) Образование трещин, если одно из нормальных напряжений
достигает прочности горной породы на разрыв: а1 = <7В.
в) Раздавливание горной породы, если сжимающее главное
напряжение достигает предела прочности на сжатие: а>1 = о\
Естественная система трещин в массивах породы снижает
примерно вдвое прочность в сравнении с малыми образцами аая
лабораторных испытаний.
Прочность горных пород зависит от среднего давления
р = -1/3 (Cj+cr +сг3) и от времени приложения нагрузки (как аая
металлов).
При решении динамических задач, связанных с поведением
грунтов и пород при подземных взрывах, используют различные
допущения и простые модели. Так, аая описания упругих сейсмических
волн грунт рассматривают как упругую среду с применением теории
448
упругости. Для водонасыщенных пластичных грунтов используется
модель вязкой сжимаемой или несжимаемой жидкости [4].
Эти задачи автомодельны, и распределения скоростей,
деформаций, напряжений, энергии, температуры, плотности подобны для
взрывов различной полной энергии (различной массы зарядов).
9.4.1. Камуфлетный взрыв
Любой подземный взрыв в бесконечной горной породе
(камуфлетный взрыв) может быть рассчитан достаточно просто, если весь
процесс разбить на следующие четыре этапа [4].
1. На первом, гидродинамическом этапе в области, прилегающей
к заряду, давление велико, больше прочности частиц породы, что
позволяет считать породу жидкостью.
2. На втором этапе по породе распространяется УВ с давлением,
превышающим предел прочности породы на раздавливание, поэтому
порода дробится в УВ. Раздробленная порода движется между
полостью с продуктами взрыва и УВ, считается твердой средой, в которой
существуют касательные и нормальные напряжения.
3. На третьем этапе происходит динамическое безволновое
расширение взрывной полости до максимального радиуса, начиная с
момента, когда скорость фронта разрушения
становится меньше скорости УВ.
4. Четвертый этап начинается,
когда амплитуда радиальных
напряжений станет меньше прочности
породы на раздавливание (с), и по
породе начнет распространяться
упругая волна, излучение которой
идет от внешней границы зоны
дробления.
Схема разрушения горной
породы при подземном взрыве показана
на рис. 9.6 [4].
Приведем некоторые
выражения, полученные в результате
расчетов этапов.
Рис. 9.6. Схема разрушения
горной породы при подземном
взрыве
I — полость с продуктами взрыва
II — зона дробления; III — зона
радиальных трещин; IV — зона
упругих деформаций
449
Принимая, что вещество в полости расширяется как идеальный
газ с показателем изэнтропы к, находим давление в полости:
p=pH(aJRr(l-pJPir (9.24)
где а0 — радиус заряда, рх — плотность за УВ, R — радиус за УВ.
Расширение газов в полости начищается с давления рн = (к — 1)
PoQ
Равновесное давление газов в камуфлетной полости
определяется уравнением:
p = pH{a0/af (9.25)
Измерения показали, что давление в УВ в грунте очень сильно
зависит от пористости грунта (количества воздуха). Так, в водона-
сыщенном песке (а3 = 0) по сравнению с сухим песком (а3 = 0,04)
давление в 50—70 раз выше.
Максимальный радиус полости ат можно оценить
аппроксимирующей формулой:
4/3 я ajp0cy2 IE. = 38 (р0 су2/250ас)т (9.26)
где Ев — энергия взрыва.
Радиус зоны дробления (сферы сжатия) определяется
выражением:
b = rjam (9.27)
где У) = [Е (n+l)<j]1/(n+1), Е — модуль Юнга породы, п — показатель
изэнтропы продуктов взрыва (п«2—3), обычно радиус зоны
дробления в 4—9 раз больше радиуса полости.
Внешний радиус зоны растрескивания получим на основе
уравнений равновесия ^ая упругой среды:
be = b(afbrj» (9.28)
где <тв — предельное упругое растягивающее напряжение.
450
Для треугольного профиля упругой волны на радиусе b
максимальная массовая скорость породы равна:
u*lj(ae/E)cy (9.29>
Поскольку теоретические методы расчета параметров взрыва
неточны, большое значение имеют экспериментальные
исследования, а также обработки уже имеющихся результатов промышленных
взрывов. На основе опытных данных получена эмпирическая
формула ^ая радиуса камуфлетной полости:
К=уМввю{м) (9.30)
где Мвв — в кг. Величины коэффициента "ty ^\я различных грунтов
следующие: водонасыщенный песок и глина — 0,6—0,7; суглинок —
0,45; лесс — 0,35; скальные породы — 0,1—0,13.
Радиус сферы сжатия можно оценить по формуле:
6 = 0,062 (аМвв)ш (9.31)
где коэффициент а учитывает свойства пород и равен: аая скальных
пород — 10; для глин — 250; для грунтов средней плотности — 150.
Коэффициент а называется коэффициентом простреливаемое™ и
равен отношению объема раздавливания или уплотнения к объему
зарядной камеры.
На основании обработки 46 крупных камуфлетных взрывов
(в том числе и атомных), проведенных в США в различных породах
(туф, известняк, аллювий, гранит, соль), американскими учеными
предложена следующая эмпирическая формула а^я расчета радиуса
полостей R(m):
R = 2l(EBB°>306 Е°-516)/(р0°>ш /z0'576/*0'161) (9.32)
где Е и [л — модули Юнга и сдвига (Мбар), h — глубина заложения
заряда (м) с энергией взрыва Евв (кг тротилового эквивалента), р0 —
плотность породы (г/см3).
Эта формула согласуется с теоретическими формулами,
полученными в [5,6] в результате анализа движения грунта при подземном
взрыве.
Прочностные характеристики горных пород (статистические
испытания образцов), необходимые а^я расчетов параметров
подземных взрывов, приведены в таблице 9.4 [4].
Измеренные величины продольной скорости звука с} зависят от
направления относительно пласта: параллельно напластования с{
больше, чем перпендикулярно напластованию. Для разных пород
величина с{ изменяется очень сильно: 2,2—5,5 км/с а^я сланцев,
6,2—6,7 км/с а^я известняка и магнетовых роговиков. Велики и
пределы изменения скорости развития трещин в различных
породах при подземном взрыве: от 0,1 до 1 км/с.
Таблица 9.4. Модуль Юнга Е, коэффициент Пуассона [л и предельные
напряжения горных пород
Материал
Песчаник
Доломит
Известняк
Гранит
Мрамор
Сланец
Каменная соль
Е,кг/см2
(3-4) 10
9,810
(3,5-7) 10
6,210
(3,8.7,1)10
7,610
3,210
¥•
0,1—0,25
0,28
0,26-0,33
0,22
0,33
0,24—0,3
0,25—0,32
Сдвиг as
кг/см2
30-150
1200
30—110
100
-
70
-
Разрыв <т
кг/см2
20—60
340
30-50
80
150—240
50
10
Сжатие а
кг/см2
1700
1900
700—1600
1550
720-1200
1800
400—600
9.4.2. Взрывы на выброс
Если приближать заряд к поверхности земли или увеличивать
его вес, то зона разрушения будет терять сферическую симметрию.
В результате отражения УВ от свободной поверхности увеличится
область, в которой возникнут растягивающие напряжения больше
предельных, следовательно, в этой области грунт будет разрушаться,
интенсивно дробиться вследствие множественного откола.
В итоге увеличится объем и форма зоны разрушения: на
сферическую зону разрушения накладывается воронка рыхления (см.рис. 9.6).
Если продолжать приближать заряд к поверхности, то часть
грунта начнет двигаться и будет выброшена. В результате в грунте
452
Рис. 9.7. а) Схема воронки рыхления; б) Схема воронки выброса
образуется углубление — воронка выброса. Различают следующие
элементы воронки выброса (см.рис. 9.7): w — глубина заложения
заряда или линия наименьшего сопротивления (ЛНС); г — радиус
воронки; 2а — угол раствора воронки; n = r/w = tg а — показатель
действия взрыва [1].
Форма воронки зависит от грунта: самые мелкие воронки
получаются в глине и песчаниках, средние — в слабых наносных породах,
самые глубокие — в базальте.
Первые попытки инженерных расчетов взрывов на выброс
принадлежат французам де Биллю и С. Вобану. Первый предположил,
что масса заряда пропорциональна глубине его заложения w, а
второй — объему грунта, выбрасываемого взрывом. В дальнейшем
Б. Белидор заметил, что с ростом массы заряда при w = Const растут
глубина и раствор воронки. Поэтому он ввел понятия «заряд
нормального горна» (или нормального выброса) при п = 1, «заряд
усиленного горна» при п > 1 и «заряд уменьшенного горна» при п < 1.
При п < 0,7 образуется уже не воронка выброса, а воронка
рыхления. Русские инженеры М.М. Фролов и М.М. Боресков установили, что
масса заряда пропорциональна w3 (т.е. объему воронки) и зависит от
свойств грунта и некоторой функции показателя действия взрыва:
f(n) = A + Bn3 (9.33)
Боресков уточнил значения коэффициентов А и В и предложил
производить расчеты массы зарядов «на выброс» по формуле:
M=Kw3(0A + 0,6n3) (9.34)
Для w>25 миМ>105кг М.А.Садовским и Г.И.Покровским
предложена поправка к (9.35) аая расчетов зарядов усиленного
выброса (п > 1):
M = £w3(w/25)°,5(0,4 + 0,6w3), (кг) (9.35)
где коэффициент к (кг/м3) определяет расход данного ВВ,
необходимого аая выброса 1.м3 данного грунта или породы.
Приведем некоторые значения к для тротила или аммонита [4]:
глина, суглинок — 1—1,3; песок сухой — 1,5—1,7; песок
влажный — 1,2—1,3; доломит, известняк, песчаник — 1,3—2,1; гранит,
базальт — 1,5—2,3.
В скальных породах аая п < 2 видимая глубина воронки
определяется формулой [4]:
He=0,35w(2n-l) (9.36)
Для п < 1 в случае, когда в пределах конуса г = w порода сильно
раздроблена, вес заряда аая образования воронки рыхления
определяется выражением [4]:
М=0,33^3 (9.37)
Инженерные расчеты действия взрыва основаны на законе
подобия, согласно которому при сохранении характеристик заряда и
грунта действие взрыва (радиусы зон разрушения, параметры
воронки) одинаково на одинаковых относительных радиусах,
выраженных в радиусах заряда.
Из анализа большого количества накопленных за 70 лет
экспериментальных результатов по взрывам на выброс с изменением массы
зарядов от 0,8 г до 100 кт следует, что закон подобия М ~ w3 неточен
аая такого большого диапазона М.
Ю. С. Вахромеев показал [6,13], что аля задач о движении грунта при
подземном взрыве существует два типа автомодельных решений. В
обоих — кинетическая энергия грунта Е^ убывает с радиусом R по закону:
Ek=Bk/Rn (9.38)
454
По первому типу показатель автомодельное™ n = Т (j — 1), где
j — показатель адиабаты продуктов взрыва, а Т = 2 а^я сферы и Т = 1
Аля цилиндра. Величина п определяется из условия, что энергия газа
в полости пропорциональна Ек.
По второму типу (j велико и энергией газа пренебрегают)
показатель п находится в результате полного решения задачи
(подобно задачам о кумуляции). При этом п зависит от свойств
грунта [6].
Для автомодельности двумерного движения грунта при взрыве
на выброс необходимо постоянство отношения
E0/wa=Const (9.39)
где а= (Зп+4)/(п+3) — аая сферы и а= (Зп+3)/(п+2) — аая
цилиндра, EQ — начальная энергия взрыва.
В [6] сделан вьюод о том, что в реальном прочном грунте нет
строгого подобия явлений выброса с зарядами существенно разной мощности.
При малых лабораторных взрьюах (М < 1 г) размеры откольной зоны
определяются прочностью, т.к. коэффициент сцепления частиц грунта
к много больше атмосферного давления р. Кроме того, заметно влияют
сила тяжести и процессы массо- и теплообмена между продуктами
взрыва и грунтом. Однако аля натурных взрьюов существует приближенное
подобие выброса с показателем 3,5 < а < 4 [6].
Вопрос о подобии взрывов важен аля прогнозирования
результатов мощных взрывов (в т.ч. атомных) и аля обоснования
постановки с этой целью лабораторных опытов с малыми зарядами. При
больших взрывах влияние прочности грунта на образование
воронки мало, поэтому возможно приближенное моделирование крупных
взрывов малыми взрывами в непрочных средах.
На основе теории размерностей в [7] найден критерий подобия
в виде следующего безразмерного комплекса:
п0=ЕоаГ/^ш(р08Г(раГ (9.40)
где а3 — свободная пористость грунта (содержание воздуха в
единице массы грунта), g — ускорение сил тяжести, р0 — плотность грунта.
Тогда закон подобия имеет вид: 71 = Const.
На рис. 9.8 даны зависимости объема (vQ), глубины (Н0) и
радиуса (RQ) воронки выброса от 7iQ, полученные в [7] с использованием
результатов химических (М = 0,15 г—454 т) и атомных (М=1,2—
100 кт) взрывов в слабосвязанных грунтах (сухие и влажные пески,
лесс, аллювий).
Линейные зависимости рис. 9.8 подтверждают существование
подобия с найденным критерием.
В [6] на основе обработки 35 результатов взрывов обычных ВВ
(М = 80 кг—981 т) и 12 результатов атомных взрывов (М = 100 т—140
кг) получены линейные зависимости в координатах lg vQ—lg EQ/p0 а^я
разных грунтов (см. рис. 9.9).
Для прямых vQ1/3 = с (Е0/р0)1/3,6 найдены следующие значения с:
с = 1,59 — глины, глинистые сланцы;
с= 1,43 — песчаники, аргиллиты и алевриты с песчаником;
с = 1,27 — пески, аллювиальные почвы, алевриты;
с = 1,15 — базальт, сухой риолит.
Показатель 1/а= 1/3,6 соответствует п = 2 в а = (Зп+4)/(п+3)
(см.(9.39)).
Очевидно, что размеры воронки зависят от глубины заложения
данного заряда. Существует оптимальная глубина, при которой
объем воронки будет максимальным.
Рис. 9.8. Зависимость размеров Рис. 9.9.Связь между максимальным
воронки от критерия подобия 7Г0 [7] объемом воронки и энергией взрыва
(энергия атомных взрывов уменьшена
в 1,35 раза)
456
1,4
0,6
0,2
V'^-0,2 0,2 0,4 0,6 1,0 1,8 2,2 2,6 c Po
Рис. 9.10. Зависимость объема выброса от глубины заложения по 35 результатам
взрывов [6]
Для выяснения зависимости v (w) на рис. 9.10 в других
координатах отложены те же 35 результатов, которые использовались для
рис. 9.9.
Как видно, правее максимума, при приближении к камуфлету
разброс точек больше, т.к. сильнее влияние прочности. Когда
величины М малы, а грунт прочный, то точки располагаются хаотично
даже ^ая ряда взрывов одинаковых зарядов в одном и том же
грунте.
Выброшенная из воронки порода размещается после взрыва на
бортах и называется навалом. Максимальная высота Н гребня
породы вокруг воронки зависит от величин глубины заложения w и от
показателя взрыва п [2] следующим образом:
п 1,0 1,5 2,0 2,5 3,0
H* = H/w 0,15 0,22 0,30 0,37 0,45
Для заряда рыхления по (9.41) в таблице 9.5 приведены радиусы
разброса взорванной породы [2].
Таблица 9.5. Радиус разброса породы для заряда рыхления (м)
n\ W
1,0
1,5
2,0
1,5
200
300
350
2
200
400
500
4
300
500
700
6
300
600
800
8
400
600
800
10
500
700
900
12
500
800
1000
15
600
800
1000
20
700
800
1200
25
800
1000
1500
Отметим особенности взрывов в сильнопористых и в мерзлых
грунтах. В сильнопористых грунтах передаваемая грунту энергия
А*
кггт
<
-*J .
^N
•
•
ч
\
\
\
ч
•
t
^
' "*" ■*
: АгХб
взрыва уменьшается из-за истечения газов в поровое пространство
грунта. Соответственно конечные размеры полости уменьшаются
на 15—20% [8].
При промерзании грунта возрастает прочность льдоцементных
связей в грунте, поэтому уменьшается диссипация энергии и
затухание УВ, а давления в грунте возрастают [9].
9.5. Взрывные работы. Управление взрывом
Взрыв как мощный источник импульсных нагрузок широко
применяется в горной промышленности, в строительстве
(гидротехнические сооружения, плотины, дороги, котлованы), в нефтяной и
газовой промышленности (торпедирование скважин, прокладка
трубопроводов, строительство хранилищ), в ирригации и мелиорации
земель (строительство каналов, водоемов, дренажно-осушительные
работы).
С помощью взрыва добываются в год сотни и сотни миллионов
тонн руды, угля, камня. Только на открытых разработках ежегодно
дробятся и перемещаются десятки млрд.м3 породы. Наиболее
эффективны т.н. массовые взрывы, когда взрываются заряды в сотни и
тысячи тонн (см. табл. 9.6).
Кроме разовых работ по строительству плотин и каналов по
вскрытию рудных и угольных месторождений, массовые взрывы
постоянно применяются аая дробления руды на многих железорудных
карьерах мира. Например, в карьерах Криворожского
месторождения взрывы проводятся одновременно в 400—700 скважинах с
общей массой зарядов до 800 тонн.
Главным преимуществом взрывных технологий и методов
является возможность в кратчайшие сроки выполнять огромные объемы
земельных работ при минимальном использовании землеройной
техники и рабочей силы.
Однако а^я полной реализации этой возможности необходимо
выполнение следующих условий.
1. Комплексная механизация всех подготовительных работ
(изготовление взрывчатых смесей, их траспортировка, бурение, заряжание).
Для этих целей созданы и используются специальные машины [1,2].
458
Таблица 9.6. Параметры некоторых массовых взрывов [1]
Место и время взрыва
Вскрытие Коркинского угольного
месторождения (1936 г.)
Вскрытие Алтын-Топканского
месторождения свинца (1952 г.)
Там же в 1953 г.
Вскрытие Байинчанского
месторождения меди (1956 г.)
Железорудный каръер Петер
Митчел(США,1958г.)
Фарходская ГЭС на р.Сыр-Дарья
(1946 г.)
Отвод реки Колонии от
Покровского рудника (Урал,
1958 г.)
Строительство Аму-Бухарского
канала в пустыне Кызылкум
(1964 г.)
Селезащитная плотина в урочище
Медео около г.Алма-Ата
I серия — 21 октября 1966 г.
II серия — 14 февраля 1967г.
Байпазинский гидроузел на
р. Вахт (1968 г.)
Вес взорванного
заряда, т
1808
1180
1814
Три серии взрыв
1431
4003
9200
285
570
3100
28000
1-5294
II-3941
1904
Результат
Траншея 1 = 1км
h= 11—22м
Выброшено
0,552 млн. м3
0,6 млн. м3
Выброшено
9млн.м3
Выброшено
1,16млн.м3
80 тыс.м3
0,75 млн.м3
Новое русло реки длин.
115 км, глубин. 25 м,
шириной 100 м
6 млн. м3
В скалах проложен канал
длиной 36 км
Разрыхлено всего
5,48 млн.м3,
из них уложено в плотину
2,52 млн.м3, высота
плотины 91 м
В плотину
шириной 520 м уложено
0,778 млн м3
2. Замена дорогостоящих ВВ заводского изготовления (тротил,
аммонит) дешевыми взрывчатыми смесями на основе аммонийной
селитры (АС), сыпучими (гранулированными) или водонаполненными
(ВВВ), заливаемыми машинами прямо в скважины или траншеи. Очень
дешев и удобен аая механизированного заряжания игданит —
малочувствительная смесь АС с дизельным топливом или с маслом.
459
3. Применение методов управления взрывом, увеличивающих
его эффективность (объем разрушений и выброса). Механизм
разрушения пород зависит не только от свойств породы, но и от
параметров взрывного импульса.
При подземном взрыве на выброс возникает сложное поле
напряжений, в котором возможны три системы разрушений:
— образование радиальных трещин, распространяющихся от
заряда;
— разрушения у свободной поверхности, вызванные
отраженными волнами и распространяющихся в сторону заряда:
— разрушение концентрическими трещинами вокруг заряда,
обуслов ленными обратным движением среды в сторону заряда.
Изменение формы взрывчатого импульса меняет и соотношение
между объемами разрушений этих трех систем. Короткий импульс с
высоким давлением (от мощных бризантных ВВ) создает
интенсивное дробление породы вблизи заряда и только небольшое
количество радиальных трещин.
В случае длинного импульса с малым давлением (слабые ВВ на
основе АС) порода покроется и радиальными трещинами и
трещинами, вызванными отраженными волнами, т.е. интенсивность
разрушения и объем выброса будет больше.
Таким образом, удлинение импульса без увеличения массы
заряда будет снижать расход ВВ на 1м3 выброшенной или раздробленной
породы.
Во взрывных работах широко применяются следующие способы
удлинения импульса.
1. Увеличение зоны химреакции ВВ, достигаемое, в основном, за
счет гранулирования ВВ (гранулотол) и водонаполнения (ВВВ).
Гранулирование значительно облегчает механизированное
заряжание скважин. Воздушные промежутки между гранулами снижают
скорость и давление детонации.
При водонаполнении воздух между гранулами заменяется на
воду. Давление детонации вырастает, но энергия остается такой же,
как у сухих гранул, поскольку часть тепла расходуется на испарение
460
воды. Потери энергии на испарение имеет положительное значение,
т.к. за счет пара увеличивается импульс. Водосодержащие ВВ могут
быть различных типов: акватолы (смесь гранул АС, ТНТ и воды),
горячельющиеся ВВВ (взвесь гранулотола в горячем (70—80°С)
высококонцентрированном растворе АС с желатинирующими
добавками), ифзаниты (многокомпонентные жидкие смеси АС, ТНТ,
часто с добавлением алюминиевого порошка а^я увеличения
теплоты взрыва). Более медленное сгорание алюминия увеличивает время
тепловыделения и существования в газах высокого давления, т.е.
импульс растягивается во времени.
2. Форму импульса изменяет создание в скважине или в
камере между частями заряда воздушных полостей. Газы, заполняя при
взрыве воздушный объем зарядной камеры, снижают давление в
момент соударения с породой без существенных потерь энергии.
Многочисленные эксперименты показали, что при объеме воздуха,
равном 40—50% камеры полость камуфлетного взрыва
увеличивается на 25—30%, а объем воронок выброса возрастает в 1,5—2,5 раза.
Используются также водяные промежутки между зарядами в
скважинах.
3. Форма заряда также влияет на эффективность взрыва.
Например, согласно [10] ^ая скваженных зарядов выброса объем
воронки зависит от удлинения h/d цилиндрического заряда. Объем
максимален при h/d « 7. Форма заряда также сильно влияет на
размеры уплотненной зоны мягкого грунта вокруг заряда.
Если на одинаковой глубине взорвать сосредоточенный заряд
и удлиненный с равной удельной массой, то взрыв
цилиндрического заряда дает уплотненную зону в 1,5—2 раза большую, чем взрыв
сферического заряда.
Этот факт очень важен при строительстве взрывом
оросительных каналов и водоемов, поскольку максимально снижается
фильтрация воды из дна и стенок каналов — в 10—20 раз меньше, чем
для каналов, выкопанных землеройной техникой [1].
Кроме того, при взрывании сплошного горизонтального заряда
достигается как равномерное уплотнение стенок по всей длине, так и
равномерный выброс грунта (без механической доработки канала).
461
Наконец, расход ВВ при взрывании сосредоточенных зарядов
больше, чем при использовании удлиненных. Например, взрыв в суглинке
сферического заряда массой 5 кг на глубине 12 м образует воронку
объемом 5 м3, а взрыв цилиндрического заряда с удельной массой 5 кг/м на
глубине всего 0,8 м дает выемку с объемом 7,5 м3 на 1 м длины [1].
4. Применение короткозамедленного взрывания отдельных
зарядов и их частей. Взрыв многих зарядов в скважинах производят не
одновременно, а с замедлениями в тысячные и сотые доли секунды.
Этот способ применяется /^ая улучшения дробления породы, /^ая
направленного выброса, fiiA^ снижения сейсмического воздействия.
От взрыва первых зарядов в породе образуются трещины, т.е.
увеличиваются свободные поверхности, от которых идут
дополнительные волны растяжения при последующих (задержанных)
взрывов, что и способствует лучшему дроблению.
Кроме массовых взрывов в горной промышленности и в
строительстве, назовем еще несколько видов взрывных работ с
использованием взрывов малых зарядов:
— торпедирование скважин (в твердых породах) /^ая
увеличения дебита воды, нефти, газа и с целью ликвидации аварий при
бурении;
— дробление валунов и негабаритного камня;
— взрывные работы при добыче штучного (отделочного) камня;
— корчевка пней и валка деревьев;
— дноуглубительные работы;
— взрывание льда на реках перед ледоходом;
— образование колодцев, шурфов, малых водоемов;
— обрушение зданий и сооружений;
— дробление фундаментов;
— резка на металлолом старой техники (корабли, подводные
лодки, самолеты);
— тушение пожаров в лесах и на газонефтепромыслах.
Методы проведения взрывных работ и расчеты зарядов, схем
взрывания см. в [2].
462
9.6. Мирные атомные взрывы
В 20-м веке человечество овладело самой мощной энергией
взрыва — атомным и термоядерным взрывом. Прежде всего — а^я военных
целей.
В процессе гонки вооружений в эпоху «холодной войны»
разработаны, испытаны и освоены в серийном производстве надежные и
совершенные малогабаритные ядерные заряды с типичной мощностью
10—20 кт — аая атомных зарядов и 100—200 кт — аая термоядерных
зарядов.
Практически сразу после разработки ядерных боеприпасов был
поднят вопрос об их мирном применении, поскольку растет
потребность в проведении массовых взрывов, а стоимость энергии
ядерных взрывов очень низкая, во много раз меньше стоимости взрывов
обычных химических ВВ.
Принципиальный недостаток ядерных взрывов, сильно
ограничивающий их применение, — образование в результате взрыва очень
вредных радиоактивных изотопов.
Тем не менее в 1950—70-х годах был предложен ряд интересных
программ с применением ядерных взрывов. Часть их них даже
начала осуществляться, но затем работы были прекращены, в основном,
из-за экологических требований.
Наиболее перспективно применение ядерной энергии в
следующих направлениях:
— строительство гидротехнических сооружений — плотин,
каналов, водоемов, закрытых гаваней;
— сооружение подземных резервуаров, хранилищ, емкостей
Аля хранения жидких и газообразных продуктов, в том числе аая
захоронения вредных стоков и отходов промышленности;
— стимулирование добычи нефти и газа на месторождениях с
низким дебитом;
— вскрытие месторождений аая разработки открытым способом;
— газификация месторождений угля и сланцев;
— использование тепла земли.
Эффективность атомных взрывов на выброс иллюстрирует
таблица 9.7 [11,12].
463
Таблица 9.7. Параметры некоторых атомных взрывов на выброс
Название
Седан
Джанг-Y
Типпотесс
Деннибой
Кабриолет
Скунер
Т-1
1003
1004
Грунт, р
г/см3
Аллювий 1,6
« — «
« — «
Базальт 2,75
сухой ел.
риолит 2,2
Влажный
туф, 2,0
Песчаниюи,
аллергиты,
174
Алевролит, 2,0
Песчаниюи,
алевриты, 2,55
кт
100
1,2
1,2
0,42
2,2
31
0,2
1,1
140
Глубина
заложен.
м
193
5,2
20,4
33,5
52
108
31,4
48
200
Параметры воронки
радиус, м
185
40
44,5
33
55,2
130
37
62
207
глубина, м
98
16,2
27,5
19
35,6
63,4
21
20
83
объем, м3
5,1 Ю6
2,85104
7,7310*
2,710*
Л38105
175 108
4,1104
1,11105
6,4106
Как видно из табл. 9.7, опытные взрывы показали, что за один
взрыв может быть выброшено 5—6 млн м3 грунта с образованием
воронки глубиной и радиусом 200 м.
В России в I960—70-х годах были проведены следующие
эксперименты по мирным подземным атомным взрывам.
1. Серией взрывов вдоль параллели от Чукотки до Кольского
полуострова проведено геофизическое зондирование горных пород (с
целью поиска полезных ископаемых).
2. Под Астраханью в мощном соляном пласте созданы
хранилища аая жидких продуктов производства серы.
3. Взорваны первые заряды на трассе канала а^я переброски вод
северных рек на юг, в бассейн реки Волги.
4. Проведены успешные эксперименты по увеличению дебита
старых нефтяных скважин.
5. Взрывом заряда в наклонной скважине погашен крупнейший
газовый факел. Пожар возник на разведочной скважине, и
несколько месяцев не удавалось его погасить никакими другими способами.
464
В США в 1950-х годах был создан проект строительства с
помощью ядерных взрывов новой трассы Панамского канала (294 взрыва
до 10 кт, выемка длиной 73,5 км и сечением 100 х 300 м, общий
объем взрываемого грунта 4 км3).
В 1967 году в США предложена программа «Сандерберд»
подземной газификации бурого угля месторождения в штате Вайоминг с
запасами свыше 20 млрд.т. Предварительно взрыв мощностью 50 кт
дробит уголь и создает большую зону трещиноватости. Затем уголь
поджигают, а процесс горения регулируют подачей воздуха через
специальную скважину. Продукты газификации угля отсасываются
через другую скважину.
9.7. Взрыв в газовзвесях и в пене
Взрывы в стесненных условиях, когда рядом объекты, которые
надо защитить от воздействия взрыва, часто требуют применения
ослабляющих УВ экранов из водовоздушной пены или из
газовзвесей (пылевое или капельное облако).
Расчеты ослабления УВ в таких гетерогенных средах с учетом
межфазного взаимодействия сложные. Такие задачи решаются
численными методами на основе приближенных теоретических моделей.
1) Газовзвесь.
Свойства течения газа с предварительно подмешанными
твердыми частицами или каплями исследованы в [14].
В [15] найдены приближенные решения /^ газовзвеси,
позволяющие оценить длину переходной зоны, на которой скорость УВ
падает от исходного значения до равновесного.
Расчеты велись в предположении, что за фронтом УВ скорость
акустических возмущений равна скорости фронта УВ, следовательно,
возмущения за фронтом не влияют на движение УВ. Теплоотдачей от газа
к частицам пренебрегают, т.к. при высоких числах Рейнольдса очень
велики вихревые потери импульса газа при отрыве потока газа на
частицах, много больше потерь из-за трения на поверхности частиц. Для
Re=pud /\l -><*> коэффициент сопротивления частиц с =0,42 = Const.
Суммарная площадь миделева сечения всех частиц в единице
объема пылевого облака
S = l5np/ppdp
где n , p , d — массовая концентрация, плотность и средний диа-
р i р р
метр частиц,
Тогда динамическое воздействие облака на газовый поток можно
выразить формулой:
F = 0,5cxSp(u-u)2
(9.41)
Полученные решения показывают, что эффективность гашения
УВ на единице длины пылевой завесы возрастает с увеличением
объемной доли частиц а = п /р и с уменьшением их размера d .
Уменьшение давления в УВ происходит быстрее в более сильных
исходных УВ (с большими числами Маха М), поскольку потери импульса
в потоке за УВ пропорциональны р и2, т.е. возрастают с увеличением
М.
На рис. 9.11 сравнивается расчетное и экспериментальное
затухание УВ в пылевом облаке из стеклянных шариков (р = 2,5 г/см3,
d = 27 мкм, относительная массовая концентрация частиц в
газовзвеси У] = п /рвоз = 0,25), а на рис. 9.12 дана зависимость длины
переходной зоны от М0 до равновесного значения Mmin [15].
Структура УВ в газовзвеси имеет одну особенность: за фронтом
УВ существует узкая зона повышенной концентрации дисперсной
фазы (т.н. р — слой) [16,17]. При сферическом взрыве в газовзвеси
М I 1,
1,2
М„
Рис. 9.11. Затухание УВ в облаке
из стеклянных шариков (vj = 0,25,
М=1,7и1,5)
1,5 1,8
Рис. 9.12. Зависимость длины зоны
затухания от исходного числа Маха
М0.У!=0,25(1), 0,62(2), 1,4(3)
466
частицы около центра взрыва имеют скорость выше, чем удаленные.
Поэтому быстрые частицы догоняют более медленные.
Таким образом, получая различный начальный импульс,
частицы образуют зону повышенной концентрации. Поршневой эффект
этой зоны создает «полочку» на профиле давления. Кроме того,
температура частиц в р — слое в 4—5 раз меньше, чем у газа.
2) Пена.
Пена наиболее эффективно поглощает энергию взрыва и
позволяет снизить на порядок и более давление в воздушной УВ. При
взрыве в пене время формирования УВ конечно и релаксационный
характер волны надо учитывать при определении параметров УВ в
пене. На первой стадии формирования УВ в пене происходит
разрушение пенных ячеек.
Принято считать, что каналячейки образуюттри
соприкасающиеся дуги окружностей с одинаковым радиусом г (в сечении ячейка
имеет вид треугольника с вогнутыми сторонами). Например, а^я
пены, получаемой барботированием водного раствора алкилсульфа-
та натрия (поверхностное натяжение с=0,03 Н /м) средняя
плотность пены р « 4 кг/м3, объемная доля жидкости в пене $2 = 2,6 10"3, а
длина канала ячейки а колеблется от 0,3 до 3 мм [18].
В полиэдрических пенах радиус г связан с объемным
содержанием жидкости $2 и длиной ребра ячейки а соотношением:
1//?2=4,8(я/г)2+1 (9.42)
В работе [18] экспериментально изучалась кинетика
разрушения ячеистой структуры пены в ударных волнах. С приходом УВ
по воздуху в ячейках движется скачок давления. Движение воздуха
сохраняется, наблюдается смещение узлов и каналов ячейки за счет
эффекта парусности на расстояние, примерно равное длине канала.
Затем в момент прекращения движения канала происходит
разрушение пленок, поставляющих воздушному потоку жидкую фазу в виде
капель.
Разрыв каналов сопровождается формированием мелких
«факелов» и капельных струй в местах разрушения. Перемешивание
капель с потоком приводит к образованию равномерного тумана.
Согласно [19] радиус капель не превышает R=г/10 « 40 мкм.
С ростом интенсивности начальной УВ (с ростом MQ) динамика
разрушения ячеек существенно ускоряется и при MQ > 1,3
образование тумана начинается сразу за фронтом УВ. Для MQ = 1,22
измеренное время разрушения ячеек составляет 100 мкс, а время релаксации
давления много больше — 500 мкс.
Это свидетельствует о том, что разрушение пены — только
первая начальная часть процесса взаимодействия УВ с пеной, а
основной более длительный энергообмен капель с потоком происходит на
второй стадии — после разрушения ячеистой структуры и
образования тумана.
Поведение капли в потоке определяется балансом внешних и
внутренних сил (внешние деформируют каплю, а внутренние
поддерживают ее сферическую форму). Внешние силы определяются
динамическим давлением (ри2)во , а внутренние — давлением
поверхностного натяжения a /d, (о* — поверхностное натяжение
жидкости, образующей каплю диаметром d). Этот баланс сил
характеризуется числом Вебера:
We = (pJ)eo3dd/o (9,43)
С ростом We достигается некоторое критическое значение We,
при котором капля начинает деформироваться и разрушаться
потоком воздуха.
Кроме We, разрушение капли зависит также от числа Лапласа:
Lp = (pa//i)xd №
где р И [Л — плотность и вязкость жидкости.
Механизм разрушения капли, разгоняемой воздушным потоком,
определяется также неустойчивостью Рэлея-Тейлора, время
развития которой по данным [20] для жидкой пленки толщиной 10 мкм
составляет ~10 мкс при массовой скорости воздуха за УВ несколько
метров в секунду.
Согласно [14], когда величина We • Re а5> 0,5, то при обтекании
капли воздушным потоком происходит т.н. «обдирка»
поверхностного слоя капли. Для данной пены We Re"0,5 = 0,5—3,5, т.е. этот
критерий разрушения капли выполняется.
468
Кроме затрат энергии УВ на дробление капель, затухание УВ
определяется также тепловой релаксацией (затратами энергии УВ
на нагрев и испарение капель).
В работе [20] на базе механики двухфазной среды создана
модель прохождения УВ через пену и решена задача о взрыве заряда
ВВ в пене. При этом предполагается, что скорости и давления фаз
одинаковы, а тепловая релаксация происходит за счет контактного
теплообмена горячий газ — холодная жидкость без учета
испарения.
Задача о взрыве в пене заряда ВВ содержит три независимых
параметра: массовую концентрацию жидкости (22, радиус заряда гвв и
диаметр микрокапель жидкости d.
Причем в систему уравнений гвв и d входят только в виде
комбинации А = rBB/d2. Для точности расчетов затухания УВ в пене
принципиально важно точное знание величины диаметра капель.
На вопрос об устойчивости границы П Д — пена дает ответ
расчет изменения со временем плотности ПД и пены (см. рис. 9.13).
Как известно, граница неустойчива, когда ускорение
направлено от более плотной среды к менее плотной. В случае взрыва ВВ в
пене ускорение всегда направлено от П Д к пене, поэтому
устойчивость границы зависит только от соотношения плотностей ПД и
пены.
В начальный момент плотность ПД всегда больше плотности
пены, но со временем быстро убывает. А плотность релаксирующей
пены падает медленно или даже возрастает. Поэтому, начиная с
некоторого момента t* или с радиуса УВ R*, соотношение плотностей
меняет знак, и граница становится устойчивой.
Например, аля заряда массой 2 кг t* = 0,283 и R* = 0,196. Здесь
безразмерное время t* = t (рпены/рвоз )°,5/гвв>а приведенный радиус УВ
R* = г /Мвв1/3 (г — радиус фронта УВ).
Результаты расчетов затухания УВ в пене даны на рис. 9.14.
Сравнение с экспериментом показывает, что при R* > 0,25 м/кг1/3
расчет завышает давление и скорость УВ. Причина в том, что расчет
не учитывает испарения капель. При малых t* и R* давление и
температура больше критических аля воды (р* = 225 атм, Т* = 647 К),
поэтому капли не могут испаряться, и расчет в этой области
согласуется с опытом.
При больших R* энергии УВ уже нехватает &ая испарения
капель, и здесь также расчет и опыт совпадают.
Таким образом, в окружающей заряд ВВ пене можно выделить
три диапазона приведенных расстояний R* :
1) 0,053 < R* < 0,15 — закритическая область, испарения нет;
2) 0,15 < R* < 0,35 — нагрев водяных капель и их частичное
испарение;
3) R* > 0,35 — только нагрев капель без их испарения.
Таким образом, максимальное различие расчета и опыта по
давлению в 60% (при R* = 0,45) может быть отнесено за счет
испарения капель диаметром 35,5 мкм при их массовой концентрации
$2 = 0,9278 или при плотности пены 15 кг/м3.
С увеличением размера капель растут затраты энергии УВ на
дробление капель, а на их нагрев и испарение, наоборот, падают, т.к.
интенсивность теплообмена ~ d"2.
т* 0,5 1,0 т 0,05 0,1 0,2 0,4 0,6 0,8 К,м/кт]
Рис. 9.13. Зависимость от времени Рис 9.14. Изменение избыточного,
плотности П Д и пены давления УВ в пене от приведенного
М (кг): 1- 2 103; 2 — 2; 3 — 2 103 радиуса фронта УВ
470
9.8. Термический взрыв
Термический взрыв возможен при контактном взаимодействии
расплавленного металла с жидким охладителем (водой). Изучение
этого явления актуально в связи с проблемой взрывобезопасности в
металлургии и ядерной энергетике.
Возможны два режима такого взаимодействия: спокойного
кипения охладителя и интенсивного быстрого парообразования с
возникновением УВ большой амплитуды и импульса.
Для объяснения таких взрывных процессов взаимодействия
расплава с охладителем в [21] предложена модель термической
детонации, основанная на модели ЗНД по аналогии с химической
детонацией. Согласно этой модели жидкий металл взаимодействует с
водой по следующему механизму:
1) В результате перемешивания капель расплава с водой
начинается пленочное кипение на поверхности капель.
2) Если от любой внешней причины возникает ударная волна,
то паровая пленка на фронт УВ схлопывается, резко возрастают
плотность и давление (выше давления насыщения).
3) В результате взаимодействия капель с потоком воды
происходит гидродинамическое дробление капель с образованием
мелких (10—15 мкм) капель.
4) Резкое увеличение контактной поверхности мелких капель
приводит к интенсивному парообразованию, а смесь снова
переходит в трехфазное состояние. Поток тепла от капель расплава
— это источник энергии, который поддерживает такую
термическую детонацию, а роль газообразных П Д играет пар.
Сложность моделирования термической детонации состоит в
учете движения и взаимодействия четырех фаз: исходные крупные
капли расплава, мелкие капли, вода и пар.
Поскольку процесс тепло- и массообмена между фазами
достаточно медленный, то зона тепловыделения (аналогичная зоне хим-
реакции при обычной детонации) протяженная. Следовательно,
Аая термической детонации определяющую роль играют вопросы
потерь энергии в стенки трубы на трение и теплоотвод.
Поскольку плотность расплавленного металла больше
плотности воды, то капли воды разгоняются потоком до скорости потока.
В процессе разгона капли деформируются и разрушаются, причем
параллельно идет сдирание поверхностного слоя капель. Момент
начала дробления запаздывает относительно начала взаимодействия
потока с каплей. Гидродинамическое дробление оканчивается при
выравнивании скоростей капель и потока.
Эксперименты по дроблению капель жидкого азота показали,
что скорость дробления не зависит от наличия паровой фазы. Кроме
гидродинамического дробления возможно дробление за счет
проникания паровых струй внутрь капель.
Состояние аналогичное точке Жуге в химической детонации,
здесь также существует, зависит от начальных условий и
возникает в момент выравнивания скоростей капель и потока, когда в воде
достигаются параметры насыщения и начинается интенсивное
парообразование, а скорость звука в суспензии за счет пара резко
падает.
В [22] проведены расчеты для системы олово-вода при
массовой доле металла в пароводяной смеси, равной 4, температурах фаз
1070 К и 360 К. На рис. 9.15а представлены расчетные распределе-
а) б) в)
и, м/с
р.МПа
3
-
70 -
60 -
50
3
^
/^
1 1 1 1
1 ж
1 '
Дм/с
0
0,4
0,8 х,М
МПа
Цм/с
,МПа
Рис. 9.15. Расчетные параметры термической детонации в системе расплавленное
олово — вода
а) Распределение скорости капель олова (1), скорости суспензии (2) и давления
(3) в зоне реакции детонационной волны.
б) Влияние начального паросодержания на скорость (1) и давление (2)
термической детонации.
в) Зависимость скорости (1) и давления (2) детонации от времени задержки
начала дробления капель.
472
ния давления и скорости фаз в зоне реакции тепловой
детонационной волны в идеальном режиме (т.е. без потерь).
Профиль давления аналогичен профилю давления при
неидеальной детонации, а в точка Жуге производная d p/d х имеет
неопределенность типа 0/0. Потери на трение при движении в шероховатой
трубе снижают скорость детонации вплоть до срыва стационарного
режима при определенных значениях диаметра и шероховатости
трубы (а^я расчетного случая предельный диаметр трубы равен 76
мм при ее шероховатости, равной 1мм).
Другими параметрами, определяющими скорость D и давление р
термической детонации, являются начальное паросодержание перед
фронтом УВ (j) и задержка начала процесса дробления капель (t2).
Расчетные зависимости р (j), D (jj), р (t), D (t2) показаны на рис.
9.15 б), в).
Литература к главе 9
1. Вовк А.А. Укрощение взрыва. Киев, Наукова думка, 1979.
2. Справочник по буровзрывным работам на карьерах. Киев,
Наукова думка, 1973.
3. Андреев К.К., Беляев А.Ф. Теория взрывчатых веществ. М.:
1960.
4. Баум Ф.А., Станюкович К.П., Шехтер Б.И. Физика взрыва. М.:
Из- во физ-мат. лит., 1975.
5. Башуров В.В., Вахрамеев Ю.С., Демьяновский СВ. ПМТФ,
1979, N3,c.l53—160.
6. Вахрамеев Ю.С., Михальков Н.Г. ВАНТ, серия: теоретич.
и прикл. физика, М, 1988, вып.1, с.63—72.
7. Бондарь П.П., Плаксий В.А., Губенко СП. ФГВ, 1990, N3,
с.101 —105.
8. Кудряшов Н.А., Мурзенко В.В. ФГВ, 1989, N3, с.89—96.
9. Ляхов Г.М., Лучко И.А., Плаксий В.А., Ремез Н.С ФГВ, 1989,
N3,130.
10. Адушкин В.В., Камалян Р.З. ФГВ, 1992, N4, с.127—129.
11. Нифонтов Б.И., Протопопов Д.Д., Ситников И.Е., Куликов А.В.
Подземные ядерные взрывы. М.: Атомиздат, 1965.
12. Vortman L.J. Nucl. Appl. Techn., 1969,Vol.7,N3,p.269—304.
13. Вахрамеев Ю.С. Некоторые вопросы физики взрыва и
кумуляции (сб. статей), г. Снежинск, РФЯЦ-ВНИИТФ, 1997,172 с.
14. Ивандеев А.И., Кутушев А.Г., Нигматулин Р.И. Газовая
динамика многофазных сред. Ударные и детонационные волны
в газовзвесях. Итоги науки и техники. Сер. МЖГ, 1981,16,
с. 209.
15. Фролов СМ., Гельфанд Б.Е. ФГВ, 1991,Nl,c.l30—136.
16. Меньшов И.С. ДАН СССР, 1982,267,4,808.
17. Шамшев К.Н., Лапидзе А.М. и др. ФГВ, 1989,N3,c.l 15—117.
18. Британ А.Б., Зиновик И.Н., Левин В.А. ФГВ, 1992, N5,
с. 108—116
19. Борисов А.А., Гельфанд Б.Е. и др. ИФЖ, 1981,40, N1, с.64.
20. Ждан С.А. ФГВ, 1990, N2, с.103—110.
21. Board S.J., Hall R.W., Hall R.S. Nature, 1975, N 254, p.319.
22. Гельфанд Б.Е., Бартенев A.M., Фролов СМ. ФГВ, 1991,N5,
с.122—130.
23. Физика взрыва в 2-х томах под ред. Л.П. Орленко. М.:
Физматлит, 2002.
474
Глава десятая
ВЗРЫВЧАТЫЕ ВЕЩЕСТВА
ЮЛ. История создания ВВ
Первым в истории техники взрывчатым веществом был черный
или дымный порох — мелко измельченная смесь селитры и
древесного угля. Время и авторы открытия черного пороха неизвестны, но
впервые он был применен в Китае и Индии, откуда его заимствовали
арабы и народы Западной Европы.
Возможно, первое известное применение черного пороха как ВВ
относится к 1226 году, когда китайцы использовали его при обороне
Пекина от войск Чингисхана.
К русским огнестрельное оружие могло попасть как из Западной
Европы, так и более коротким путем с Востока. В летописях первое
упоминание об артиллерии, стреляющей дымным порохом,
относится к 1382 году (оборона Москвы от орд хана Тохтамыша).
Начиная с XVI века, порох используется и аая военно-
инженерных целей (осада Казани в 1552 году), а также и аая
проведения промышленных работ (очистка от скал русла реки Неман
в 1548—1572 гг.). Для горных работ порох впервые использовал в
Силезии К.Вейндель в 1627 году.
Впервые в мировой науке основы физики взрыва излагаются в
работе М.В.Ломоносова «Диссертация о рождении и природе
селитры» (1749 г.). В другой своей работе «О пользе химии» (1751 г.)
Ломоносов впервые открыл взрывчатые свойства органических
веществ, обработанных азотной кислотой. Такие нитросоединения
стали основой современных ВВ.
475
В 1778 году К. Гаусман в результате обработки азотной кислотой
фенола получил тринитрофенол или пикриновую кислоту, которая
долгое время использовалась как краситель. Только в 1872—86 гг.
Г. Шпренгель и Э. Тюрпен открыли и исследовали взрывные
свойства пикриновой кислоты. С 1895 года пикриновую кислоту
используют а^я снаряжения боеприпасов под названиями: мелинит — в
России и Франции, меллит — в Англии, пикринит — в Испании,
шимоз — в Японии.
Недостаток пикриновой кислоты в том, что она при хранении
дает с металлами боеприпасов очень чувствительные соединения —
пикраты. Поэтому пикриновая кислота была заменена на более
безопасный тринитротолуол (тротил), который был открыт в 1863 году
немецким химиком К.Вильбрандом.
Переворот в гражданской и военной взрывной технике
произошел после открытия А.А. Фадеевым пироксилина (1845 г.) и
итальянцем А. Собреро нитроглицерина (1846 г.).
Только в конце XIX века великий русский химик Д .И. Менделеев
на основе пироксилина создал бездымный порох (пироколлодий) и
безопасную технологию его производства. В 1892 году он был
успешно испытан адмиралом СО. Макаровым и принят на вооружение
военно-морского флота России.
Яркую страницу в историю разработки ВВ вписал знаменитый
А. Нобель, который в начале своей карьеры работал в России. Заслуга
Нобеля в организации промышленного производства созданных в
его лаборатории ВВ, что определило их широкое применение.
Нитроглицерин очень чувствителен, опасен в обращении и не
может быть использован в чистом виде. Нобель на основе
нитроглицерина создал гремучий студень и желатин — динамиты,
использовав открытое Менделеевым явление желатинизации
нитроглицерина коллоидным хлопком.
В 1860—63 гг. русский инженер В.Ф.Петрушевский предложил
новое ВВ — динамит, представляющий собой смесь из 75%
нитроглицерина и 25% углекислой магнезии. В России было построено
несколько динамитных заводов, выпускавших три сорта динамитов
с содержанием нитроглицерина 75%, 50% и 35% аая горных пород
различной крепости.
476
Используя работы Петрушевского, Нобель заменяет в динамите
магнезию а^я пропитки нитроглицерина на инфузорную землю
(кизельгур) и в 1867 году получает патент на гурдинамит. Его
производство к 1874 году составило 3120 тонн в год на 14-ти заводах.
В 1867 году шведские инженеры И.Ольсен и И.Норбин взяли
патент на более безопасные ВВ — аммониты, созданные на основе
аммиачной селитры. Нобель купил их патент, но использовал его
только через 12 лет. Добавив в аммонит нитроглицерин, Нобель
получил аммонжелатин-динамит.
В СССР с 1924 года использовались на открытых горных
работах низкопроцентные нитроглицериновые ВВ — аммониты с
содержанием нитроглицерина 5—15%.
Кроме разработки и производства новых ВВ, огромное значение
имело решение проблемы их инициирования. В 1812 году русский
ученый П.Л. Шиллинг открыл способ электровзрывания, который
сейчас с помощью электродетонаторов стал основным а^я взрывных
работ. Русские химики Н.Н. Зинин и В.Ф. Петрушевский
предложили аая надежного инициирования динамитов применять
промежуточный детонатор из небольшого заряда черного пороха. Такой
усовершенствованный и надежный детонатор с эффектом кумуляции
был использован Д.И.Андриевским.
Изучив изобретение Андриевского, Нобель разработал свой
вариант капсюля — детонатора (КД), в котором вместо пороха
использовалась гремучая ртуть. И в этом случае Нобель быстро
налаживает производство таких КД, что в свою очередь способствовало
развитию производства и применения динамитов. В горной
промышленности Европы в конце XIX века использовалось несколько
сот различных видов динамитов.
В 1877 году голландским химиком Ромбургом был получен
тетрил путем последовательной обработки серной и азотной
кислотами диметиланилина. Тетрил сильнее тротила и находит применение
при изготовлении КД как вторичное инициирующее ВВ.
Расширение масштабов взрывных работ потребовало
обеспечить одновременный взрыв многих зарядов, а^я чего в 1879 году
К. Мессеном был предложен детонирующий шнур (ДШ). Сначала
\
477
Аля начинки ДШ использовался пироксилин, затем в 1890 году
французы предложили ДШ из мелинита в оловянной оболочке, в
1904 году — из тротила в свинцовой оболочке, а в 1909 году — из
тетрила.
Шведские инженеры в 1919 году разработали ДШ из ТЭНа.
В СССР изготовлялись ДШ в нитяной оболочке из флегмати-
зированной смеси азида свинца и ТНРСа (1927 г.), из азида свинца
(1928 г.), из флегматизированной гремучей ртути (1931 г.), из смеси
гремучей ртути, тетрила и желатина (1934 г.). Сейчас в России
изготовляют ДШ из ТЭНа, имеющие трехслойную нитяную оболочку с
водоотталкивающим покрытием. Для специальных работ (высокие
температуры, взрыв в газовых средах) используются ДШ из гексоге-
на и октогена.
Для проведения взрывания огневым способом применяют
огнепроводный шнур (ОШ) из дымного пороха, который передает
пучок искр КД.
В конце XX века ~90% потребления ВВ в горной промышленности
составляют т.н. простейшие ВВ типа игданитов — механических смесей
аммиачной селитры (окислитель) с различными горючими добавками
(дизельное топливо, масла, мазут, древесная мука, мох и др.).
10.2. Общая характеристика и классификация ВВ
К взрывчатым веществам относятся химические соединения,
способные под действием внешнего импульса к быстрому
химическому превращению, протекающему с выделением большого
количества тепла и газов. Любая химическая реакция происходит в форме
взрыва, если удовлетворяет следующим четырем условиям [1]:
экзотермичность, образование газов, большая скорость, способность к
самораспространению.
Тепловой эффект взрыва определяется суммой двух
составляющих: эндотермичностью ВВ (если при синтезе ВВ тепло
затрачивалось, то при его распаде оно выделяется) и экзотермичностью
соединений (Н2С С02), образующихся из атомов ВВ при взрыве.
Экзотермичность превращения ВВ обусловлена тем, что прочность
478
связей между атомами в продуктах взрыва гораздо выше, чем в самом
ВВ, структура которого строится на слабых связях типа N—О, С—
N,0—0,N = N,C = C.
Основная масса современных химических ВВ содержит N02-
группу, которая может быть связана с углеродом непосредственно
(нитросоединения), через азот (нитрамины) или через кислород
(нитроэфиры). При взрыве таких соединений тепло выделяется в
результате окисления углерода (до СО и С02) и водорода (до Н20)
кислородом N02-rpynn.
Если скорость и тепловой эффект реакции разложения ВВ
достаточно велики, то эта реакция протекает в форме стационарной
тепловой волны, передаваемой по ВВ ударной волной (детонация). Выше
скорость реакции — меньше теплопотери и выше температура реакции.
Другим фактором, определяющим распространение реакции,
является реакционная способность молекулы ВВ, ее неустойчивость,
характеризуемая энергией активации, т.е. минимальной энергией,
которую должна получить молекула, чтобы прореагировать.
Малая устойчивость молекулы ВВ нежелательна, т.к. приводит
к высокой чувствительности и низкой химической стойкости ВВ.
Поэтому современные ВВ являются достаточно устойчивыми
соединениями, но с большой экзотермичностью реакции разложения.
Например, тротил труднее поджечь, чем бумагу, а пикриновая
кислота применялась как краситель в течение ста лет, прежде чем
узнали, что это сильное ВВ.
Образование при взрыве сильно сжатых и нагретых газов —
решающий фактор действия взрыва. Поскольку плотность газов
примерно в тысячу раз меньше плотности конденсированного ВВ и газы
нагреты до ~3000 К, то мгновенное превращение ВВ в газы при
неизменном объеме по уравнению Клапейрона дает давление ~5 кбар.
Это давление значительно увеличивается при детонации ВВ за счет
кинетической энергии газов, движущихся за фронтом детонации.
Наконец, понятие «взрывчатое вещество» не является
абсолютным, без указания условий, при которых ВВ взрывается:
размеры и плотность заряда, инициирующий импульс, наличие оболочки
и т.п.
479
Например, заряд любого ВВ не взрывается, если его диаметр
меньше критического, заряд из литого тротила не взрывается от
обычного капсюля-детонатора и требует применения
дополнительного заряда, усиливающего инициирующий импульс.
С другой стороны, удобрительная смесь из нитрата и сульфата
аммония не является ВВ в обычных условиях, однако тысячи тонн
плотной слежавшейся смеси взорвались в 1921 году на складе завода
в Оппау (Германия).
В принципе, взрывчатым веществом может быть любая смесь
горючего с окислителем. Как говорил академик Ю.Б.Харитон,
взорваться могут и дрова, нужны только соответствующие условия.
По агрегатному состоянию ВВ могут быть газообразными,
жидкими или твердыми. Мы будем рассматривать только твердые ВВ.
Все многообразие известных ВВ может быть классифицировано по
двум признакам: по составу ВВ и по его применению (см. рис. 10.1).
По применению ВВ делятся на метательные, бризантные и
инициирующие.
Основным видом превращения метательных ВВ является
горение, хотя они также способны детонировать при высокой плотности
заряжания.
Инициирующие ВВ очень чувствительны, детонируют от
небольшого импульса и используются в детонаторах, капсюлях,
взрывателях.
Мощные бризантные ВВ применяют ^ая изготовления
боеприпасов (снарядов, бомб, мин, ракетных боеголовок). Основные
требования к ВВ для боеприпасов: высокие плотность зарядов и скорость
детонации, минимально возможная чувствительность ко всем видам
внешнего воздействия, высокая химическая стойкость в
эксплуатационном интервале температур от — 40 С до+60 С, срок хранения
15 лет и более.
Особо высокие требования предъявляются к полым
кумулятивным зарядам (максимально возможные величины плотности,
скорости детонации и прочности), ^ая которых используются составы на
основе октогена как наиболее мощного ВВ.
Наоборот, ^ая промышленных ВВ не требуется высокая бри-
зантность, создаваемая большими значениями плотности и скорости
480
СОСТАВ
ПРИМЕНЕНИЕ
нитроклетчатка
нитроглицерин
ТЭН
ксилил
пикриновая
кислота
тротил
тетрил
октоген
гексоген
нитроэфиры
пороха I
ракетное
топливо \
метательные
нитро-
соединения
| нитрамины
содержащие кислород
в молекулах QflAH<*
химические
соединения
не содержащие
кислород
z
азид свинца
х
пиротехнические
составы
| промышленные ВВ |
бризантные 1
J (вторичные) 1
1 мощные составы 1
ДЛЯ
1 боеприпасов |
смеси
горючее-
окислитель
аммониты
оксиликвиты
инициирующие
(первичные)
Рис. 10.1. Классификация взрывчатых веществ по их составу и применению
детонации. Главные требования &ая промышленных ВВ —
максимальные объем газов и теплота взрыва, которые определяют
работоспособность ВВ (например, во взрывах на выброс), минимальная
чувствительность а^я безопасности ручных операций с ВВ,
значительно меньшие сроки хранения (порядка года), допускаемые тем-
пературы от — 25 С до+60 С в течение нескольких часов (взрывы в
глубоких шахтах), водостойкость в течение ~2-х часов.
Наконец, аля проведения постоянных массовых взрывов в горной
промышленности и строительстве очень важна низкая стоимость как
ВВ, так и буро-взрывных работ (за счет их максимально возможной
механизации). Поэтому широко используются дешевые маломощные
ВВ из смеси горючее — окислитель, изготовляемые на месте взрыва.
103. Промышленные взрывчатые вещества
Рассмотрим классификацию промышленных ВВ по условиям
применения и по составу [2]. Согласно существовавшей в СССР
единой классификации, все промышленные ВВ по условиям
применения делятся на шесть классов (см. табл. 10.1)
Таблица 10.1. Классификация промышленных ВВ по условиям
применения
Класс
I
II
III
IV
V
VI
Наименование ВВ по
условиям безопас-ности применения.
Непредохранительные
Непредохранительные
Предохранительные
Предохранительные
Повышенной
предохранительности
Высокопредохранительные
Условия применения
На открытых работах
Для подземных работ, кроме шахт,
опасных по газу и пыли
В шахтах, опасных по газу и пыли,
только в породных забоях
В угольных и смешанных забоях,
в шахтах, опасных по газу и пыли
Для шахт, опасных по газу и пыли
Для шахт, опасных по газу и пыли
В I класс входят любые ВВ, безопасные в обращении и
детонирующие от стандартных средств инициирования (КД, ДШ,
дополнительные детонаторы).
У ВВ II класса при их взрыве количество ядовитых газов не
должно превышать этот показатель у эталонного аммонита 6ЖВ.
482
ВВ III—VI классов должны соответствовать установленным а^я
них нормам по предохранительное™. ВВ III и IV классов испы-
тываются взрыванием в мортире заряда 600 г (класс III — только
по метану, класс IV — по газу и угольной пыли). ВВ V и VI
классов испытывают взрыванием открытых зарядов (V класс — 200 г,
VI класс — 1 кг) в атмосфере газа и угольной пыли.
Приведем названия некоторых применявшихся в СССР
предохранительных ВВ: аммониты ПЖВ-20, Т-19,1ЖВ, ЗЖВ, АП-4ЖВ,
АП-5ЖВ, победит ВП-4, углениты Э-6, N5, N7.
По составу промышленные ВВ разделяются на следующие шесть
групп.
1. Аммиачноселитренные (аммониты, динамоны, аммоналы, гра-
нулиты, зерногранулиты, игданиты).
Основой этих ВВ является аммиачная селитра (специальная
водоустойчивая марка ЖВ), которая смешивается с другими ВВ
(тротил, гексоген) или с горючими материалами (дизельное топливо,
масла, мазут, древесная мука, алюминий).
Селитра содержит около 20% избыточного кислорода и играет
роль окислителя. Смешивание селитры с горючим повышает
теплоту взрыва примерно в три раза.
Для уменьшения слеживаемости селитра гранулируется в виде
шариков оЗ—5 мм. Тогда смеси на ее основе называют зернограну-
литами.
Аммониты — это смесь измельченной селитры с тротилом.
Более мощные смеси, содержащие гексоген, называются
скальным аммонитом.
Аммониты, содержащие соли — пламягасители, называются
предохранительными.
Кроме того, аммониты обычно содержат различные добавки:
разрыхлители (древесная мука), гидрофобные (парафин, стеариты),
красители и др.
Аммониты с добавкой алюминия называются аммоналами.
Динамоны — это смесь порошков селитры и невзрывчатых
горючих веществ.
Смесь гранулированной селитры и минеральных масел
называется в странах бывшего СССР игданитами и гранулитами.
483
Обычно игданит — это смесь 94,5—95,5% гранулированной
аммиачной селитры и 4,5—5,5% солярового масла.
Игданиты готовят на месте взрывания одним из трех способов:
предварительной заливкой солярового масла в мешки с селитрой,
смешением селитры с маслом в процессе засыпки в скважины или
в специальных смесителях. Слабая чувствительность игданитов
требует применения а^я их инициирования дополнительных
детонаторов (обычно зарядов из аммонита 6ЖВ).
Благодаря высокой безопасности, механизации работ и низкой
стоимости игданиты широко применяются на открытых горных
выработках. Так, годовое потребление игданитов в США в 1970—80 гг.
превысило 0,5 млн. тонн.
Порошкообразные аммониты выпускаются промышленностью
россыпью в бумажных мешках по 40 кг или в патронах с
водостойким покрытием. Скальный аммонит изготовляется также в виде
прессованных шашек с плотностью 1,4—1,5 г/см3.
2. Нитроглицериновые ВВ делятся на высокопроцентные жела-
тинизированные или пластичные ВВ (динамиты) и
низкопроцентные (не более 15% жидких нитроэфиров) порошкообразные ВВ
(победиты, детониты). Выпускаются только в виде патронов из
парафинированной бумаги с весом заряда 200 г и 550 г.
Динамиты опасны в обращении (особенно в полузамерзшем
состоянии), при хранении теряют способность к детонации. Поэтому
после ~1970 года динамиты в бывшем СССР не применяются.
Детониты содержат 6—15% нитроглицерина с добавкой нитро-
дигликоля (а^я снижения температуры замерзания с +10 С до —
19,5 С) остальное — селитра, коллоидный хлопок, алюминий,
тротил и древесная мука.
Углениты и победиты имеют такой же состав, но с добавлением
соли — пламягасителя.
3. Нитросоединения — тротил, гексоген, ТЭН и их сплавы.
Используются в основном как составные части аммонитов и аая
изготовления шашек — детонаторов.
Для зарядки обводненных скважин в крепких породах часто
используется гранулированный тротил (гранулотол) и
гранулированный сплав тротила с алюминием (алюмотол).
484
Взрыв тротила в воде сдвигает равновесие в реакции
генераторного газа в сторону образования С02 и С с выделением
дополнительного тепла, что повышает эффективность взрыва.
Гексоген и ТЭН применяют аля изготовления ДШ, в
детонаторах (как вторичное инициирующее ВВ) и в сплаве с тротилом ^ая
производства литых шашек — детонаторов.
4. Оксиликвиты представляют собой горючие пористые
поглотители (уголь, сажа, торф, мох, древесные опилки), пропитанные
жидким кислородом. Приготовляют непосредственно на месте
заряжания. В виду опасности в обращении и быстрого изменения свойств
из-за испарения кислорода оксиликвиты примерно после I960 года
в бывшем СССР не применяют.
5. Дымный порох аля взрывных работ имеет следующий
состав: 75% калиевой селитры, 10% серы и 15% древесного угля.
Дымный порох гигроскопичен, допускаемая влажность не выше 1%.
Используется при изготовлении огнепроводного шнура и при
добыче ценного камня, мрамора, т.к. не имеет бризантности и в породе не
образуются трещины.
6. Водонаполненные ВВ (ВВВ) содержат в качестве
пластификатора водные гели (5—20%) и могут иметь консистенцию от легко
льющейся массы до тестообразной.
Состав ВВВ: аммиачная селитра, тротил, загуститель, часто
добавляют алюминий, нитраты кальция и натрия.
ВВВ, применяемые на открытых выработках, называются аквато-
лы, а ВВВ ^ая шахт — акваниты.
Для инициирования ВВВ требуются промежуточные
детонаторы (тротиловые шашки, патроны из аммонита).
10.4. Мощные бризантные ВВ и составы
Бризантность ВВ определяет разрушительное действие заряда
ВВ на среду, расположенную в непосредственной близости от
заряда. Максимально бризантность проявляется при контакте заряда с
преградой и определяет такие характеристики ВВ, как осколочное
действие, бронепробивание. метательная способность.
485
Определяющим фактором fi^ бризантности ВВ является
величина давления в точке Жуге или плотность заряда и скорость его
детонации, т.к. р = р0 u D = 1 /4 р0 D2.
Основные свойства четырех наиболее мощных бризантных ВВ
приведены в табл. 10.2.
Таблица 10.2. Свойства мощных бризантных ВВ
Параметры
Химическая формула
Молекулярный вес
Кристал. плотность, г/см3
Кислородный баланс, %
Теплота взрыва, ккал/кг
Объем газов детонации,
л/кг
Температура плавления,
°С
Скорость детонации,
км/с
при плотности, г/см3
Фугасность, см3/10 г
Чувствительность к удару,
%
Температура вспышки, °С
Бризантность, мм
при плотности р (г/см3)
и весе заряда m (г)
Тротил
C7H5N3°6
227,1
1,65
-73,9
1090
730
80,8
6,9
р=1,6
300
4-6
300
18
р=1,2
т = 50
ТЭН
C5H8N4012
316,1
1,76
—10,1
1510
823
141,3
8,4
Р=1.7
523
100
202
16
р= 1,0
т = 25
Гексоген
C3H6N6()6
222,1
1,82
— 21,6
1510
900
204
8,75
р=1,76
480
72—90
230
24
P=U
т = 25
Октоген
CHNO
4 8 8 8
296,2
1,96
— 21,6
1480
927
275
9,1
р=1,9
480
96—100
287
24
р=1,0
т = 25
Для изготовления высокоплотных зарядов эти ВВ обычно
используются не в чистом виде, а во взрывчатых составах (ВС),
состоящих из одного-двух ВВ с добавлением алюминиевой пудры, связки,
пластификатора. Связки могут быть инертные (полимер) или
активные (тротил, нитроцеллюлоза).
В бывшем СССР использовались сплавы тротила с гексогеном
(ТГ) или с октогеном (октолы).
486
В США выпускают ВС трех групп:
А — флегматизированный воском гексоген (RDX), который при
р = 1,71 г/см3 имеет D = 8,1 км/с;
В — составы, получаемые литьем из смеси гексогена с тротилом.
Например, &ая смеси с содержанием тротила 40% ир=1,б5г/ см3
D = 7,8 км/с (соответствует ТГ40);
С — композиции из гексогена и различных связок как
взрывчатых, так и инертных (см. табл. 10.3).
Таблица 10.3. ВС группы С [3]
Индекс
композиции
С
С-2
С —3
С-4
Содержание
гексогена
88,3
80,0
78,0
90.0
Содержание
связки
11,7
20,0
22,0
10,0
Тип
связки
инертный
взрывчатый
взрывчатый
полиизобутилен
Состав наиболее мощных ВС, выпускаемых в США, приведен в
табл. 10.4,10.5,10.6 [3,4].
Таблица 10.4. Состав и свойства ВС на основе октогена
Обозначение
LX-04—1
(RBHV-85/15)
LX —07 —2
(RX-04-BA)
LX-09 —0
(RX — 09 — СВ)
LX-10 —0
(RX —05 —DE)
LX-11—0
(RX-04-P1)
LX—14 —0
Octol 70/30
Состав
октоген, %
85
90
93
95
80
95
70
связка
Viton А
Viton А
DNPA
Viton А
Viton А
Estane
TNT
%
15
10
7
5
20
5
30
Свойства
р, г/см3
1,86
1,87
1,84
1,86
1,87
1,83
1,80
D, км/с
8,46
8,64
8,81
8,82
8,32
8,84
8,38
487
Обозначение
Octol 72/28
Octol 75/25
Состав
октоген, %
72
75
связка
TNT
TNT
%
28
25
Свойства
р, г/см3
1,821
1,81
D, км/с
8,48
8,64
Таблица 10.5. Состав и свойства мощных ВС [4]
Индекс ВВ
РВХ-9404-03
LX-07-0
X —0204
РВХ-9010
Cyclotol
RX —04 —AV
CompB
Состав ВВ
НМХ, NCCEF (94/3/3)
НМХ, Viton (90/10)
НМХ, Teflon (83/17)
RDX,KelF (90/10)
RDX, TNT (77/23)
НМХ, (CH) (92/8)
RDX, TNT (64/36)
p, г/см3
1,841
1,865
1,911
1,787
1,754
1,719
1,717
D,
км/с
8,80
8,64
8,42
8,39
8,25
8,63
7,99
Таблица 10.6. Мощные ВС на полимерной связке [3]
Обозначение
РВХ — 9010
РВХ —9011
РВХ-9404-03
РВХ —9205
РВХ-9501
PBXN—1
PBXN —2
PBXN —3
PBXN —4
PBXN —5
PBXN-6
PBXN -101
PBXN — 102
Состав
90%RDX,10%KelF
90%HMX,10%estane
94% HMX, 3% NC, 3% chlorocthylphosphate (CEF)
92% RDX, 6% polystyrene, 2% ethylhexylphthalate
95% HMX, 2,5% dinitropropyle acrylate- formalate,
2,5% estane
68% RDX, 20% Al, 12% nylon
95% HMX, 5% nylon
86% HMX, 14% nylon
94%TATB,6%nylon
95% HNX, 5% Viton A
95% RDX, 5% Viton A
82% HMX, 18% Laminae
59% HMX, 23% Al, 18% Laminae
488
Примечания:
1. Заряды из последних двух составов в табл. 10.6
изготавливаются литьем, остальные — прессованием.
2. Используемые полимерные связки: KelF — полиамидная
смола, Viton А — фторопласт, NC — нитроцеллюлоза, CEF —
пластификатор NC, estane — полиэфир.
В отдельную группу ВС надо выделить пластичные составы
(ПС), обычно имеющие вид паст различной консистенции или
гибких листов и пластин. Зарядам из ПС легко придать любую нужную
форму. В военной технике ПС применяются ^ая активной защиты
танков.
В США на основе октогена выпускаются пастообразные составы
LX — 02, LX — 03 и LX — 04 с плотностью 1,44; 1,42 и 1,53 г/см3
соответственно.
Содержание ВВ в ПС колеблется в пределах 85—90%. При
меньшем содержании возможны отказы в детонации, а при большем —
низкие механические свойства (хрупкость). В качестве связующих и
пластификаторов используются такие материалы, как полибутадиен,
полиизобутилен, полиуретан, акриловая кислота, воск, каучук.
Отметим ещё один состав, который предназначен /^ замены
Сотр. В или ТГ 40/60 аая изготовления зарядов методом литья. В
этом составе тротил заменён на более безопасный и дешёвый 2,4 ди-
нитроамизол (DNAN). Это вещество используется как краситель
и производится в США, Китае и Ю. Корее, перевозится не как
взрывчатое, а как пожароопасное вещество. Его основные свойства:
плотность — 1,34 г/см3, температура плавления — 94° С,
температура вспышки- 347°С, кислородный баланс — 96,9% (у ТНТ — 74%).
В Австралии создан состав ARX- 4027 (40% DNAN+60% RDX),
его основные свойства [5]: плотность — 1,61 г/см3, скорость
детонации — 7,4 (7,36) км/с, рн=22,5 (21,6) ГПа. В скобках даны
свойства в случае применения флегматизированного гексогена. Ещё
в 1944 г во II мировой войне Германия для снаряжения
боеголовок ракет Фау -1 использовала состав 50% DNAN, 35% NH4N03,
15% RDX [6].
Благодаря дешевизне состав ARX-4027 может найти
применение fiiA^ синтеза детонационных наноалмазов (см. гл. 16).
10.5. Технологии изготовления зарядов
В ряде случаев к зарядам предъявляются следующие
повышенные требования:
— максимальная плотность или минимальная пористость;
— минимальная разноплотность;
— однородность по составу;
— высокие механические характеристики (прочность);
— точность геометрических размеров заряда.
Выполнение этих требований необходимо, в частности, ^ая
кумулятивных зарядов.
Решающую роль в достижении высоких характеристик заряда
играет технология его изготовления. Высокоплотные заряды могут
изготовляться методом прессования и методом литья.
Прессованием получают заряды из очень мощных составов с
высоким содержанием гексогена или октогена (например, LX-10-0).
Прессование проводят по безлюдной технологии в специальных броне-
камерах с помощью стальных пресс-форм и прессов с дистанционным
управлением, поскольку этот процесс является опасным, с
относительно высоким процентом аварийных взрывов.
Значительно более безопасны технологии литья зарядов. Обычно
отливают заряды из составов, содержащих тротил. Эта простая
технология применяется ^ая изготовления боеприпасов (бомб,
снарядов, мин, боеголовок).
Низкая температура плавления тротила (80° С) позволяет
использовать ^ая его плавления очень простые котлы с паровым
обогревом, исключающим возможность опасного перегрева. Оптимальная
температура литья (90—110° С) определяется требованием
получения низкой вязкости расплавленного тротила и ограничения
величин усадки и газообразования.
Плохо отливаются заряды из чистого тротила, т.к. у тротила
большая усадка, и при его затвердевании образуются удлиненные
490
иглообразные рыхлые кристаллы, не позволяющие получать заряды
малой пористости.
Кристаллическая структура отливок из тротила может быть
улучшена за счет добавок в тротил гексанитростильбена.
При литье составов гексоген, октоген, ТЭН не плавятся
(вводятся в расплав тротила в виде порошка), поскольку их температуры
плавления опасно близки к температурам вспышки.
Часто используется плавление тротила под водой, затем к нему
добавляется гексоген, а вода отсасывается; состав сушится в вакууме.
Этот способ удобен, т.к. сокращает время плавки и не требует сушки
исходного гексогена, который аая безопасности транспортировки
увлажняется.
Существуют следующие методы литья зарядов:
1). Обычное классическое литье.
2). Кусковой метод.
3). Послойное литье.
4). Литье под давлением.
5). Центробежное литье.
6). Седиментационное литье (литье с выдержкой или с
отстоем).
7). Вибрационное литье.
1). При обычном литье в расплавленный тротил вводят при
перемешивании гексоген, и затем полученную смесь заливают в корпус
боеприпаса или в литьевую форму.
Параметры зарядов из ТГ40, получаемые классическим литьем [4]:
— D = 7,8+0,075 км/с;
— концентрация гексогена колеблется в пределах 58—67%;
— плотность колеблется в пределах 1,67— 1,7 г/см3;
— пористость 3—5%.
Пористость уменьшается, если применять вакуумирование
литейной формы.
Содержание гексогена более 73% сильно увеличивает вязкость
смеси, поэтому такие составы обычно не отливаются, а прессуются.
Большая усадка тротила не позволяет получать обычным литьем
относительно большие заряды с малой пористостью и с
равномерным составом (более плотный гексоген оседает в нижнюю часть
заряда).
2). Эти недостатки устраняются, если проводить отливку в два
приема. Сначала отливается много маленьких высокоплотных
зарядов, например, в виде гладких шаров. Вместо шаров можно отливать
тонкие пластины (толщиной 5—10 мм), а затем разламывать их на
куски (отсюда название — кусковой метод).
На второй стадии шары или куски засыпаются в форму, а
остающиеся промежутки заливаются жидкой смесью того же состава.
Куски не должны быть слишком малы, т.к. вязкий состав плохо
заполняет промежутки малых размеров.
Форму перед заливкой нагревают, что значительно уменьшает
концентрацию внутренних дефектов отливки.
Как обычно, при литье формируется рыхлая прибыль, которая
после затвердевания отливки отрезается или откалывается.
3). При послойной отливке смесь заливается в форму
малыми порциями и только после затвердевания предыдущей порции.
Отливка идет медленно, но зато заметно повышается плотность
и однородность.
4). Как всегда, литье под давлением ускоряет процесс и улучшает
структуру заряда. Обычно сочетается с вакуумированием формы.
5). При центробежном литье форма вращается на центрифуге.
Центробежные ускорения увеличивают скорость оседания
гексогена и его концентрацию в заряде. Время выдержки сокращается с
нескольких часов до 15 минут. Этот метод хорош а^я получения полых
осесимметричных кумулятивных зарядов.
6). При седиментационном литье состав выдерживается в
обогреваемой форме при высокой температуре до тех пор, пока
частицы гексогена не осядут. Таким образом можно увеличить
концентрацию гексогена от 65% до 75% и получить плотность 1,73—1,76
г/см3. Обедненная гексогеном часть отливки остается в удаляемой
прибыли.
Оптимальный режим литья: 110° С и выдержка 6 часов.
492
Наибольшие значения плотности и концентрации гексогена
достигаются в случае использования гексогена с частицами двух
размеров: мелких (10—60 мкм) и крупных (200—800 мкм) в
соотношении 1 часть мелких и 3 части крупных.
7). Вибрационное литье является наиболее совершенной
технологией литья. При оптимальном соотношении размеров частиц
гексогена за 20—60 минут можно изготовить заряд со следующими
параметрами [6]:
— скорость детонации 8400+10 м/с;
— концетрация гексогена 83—90%;
— пористость 1—2%;
— плотность 1,77—1,78 г/см3.
Рассмотрим более сложную технологию изготовления листов из
пластических составов [7].
Листы обладают достаточно высокой гибкостью, эластичностью,
прочностью, не трескаются и не ломаются при изгибах.
Состав ПС: 85—90% по весу мощного ВВ (октоген, гексоген,
ТЭН, тетрил), остальное — связующее. В качестве связующего
используется полиизобутилен (ПИБ, торговая марка Oppanol) с
молекулярным весом в интервале 5000—15000. ПИБ с большим
молекулярным весом имеет слишком большую вязкость, что затрудняет
его смешивание с ВВ. Поэтому в ПИБ добавляют 7— 15%
пластификатора (политетрафторэтилен) или растворяют ПИБ в хлороформе.
Величина молекулярного веса ПИБ определяет эластичность,
твердость и липкость получаемых листов ПС.
Для получения высокой детонационной способности ПС
частицы ВВ в нем должны быть маленькие (меньше 50 мкм). Лучшая
упаковка частиц достигается при бимодальном распределении частиц
по размерам. Например, один пик распределения при 20—25 мкм и
второй пик при 8—10 мкм.
Безопасное дробление частиц достигается после
смешивания ВВ со связующим в результате многократной прокатки ПС
на дифференциальных валках с зазором между валками порядка
0,05 мм.
Критический диаметр ПС уменьшается за счет использования
ВВ после его рекристаллизации, что дает частицы меньше 10 мкм.
Например, листы из ПС на основе мелкодисперсного ТЭНа (после его
рекристаллизации) надежно детонируют при толщине листов 0,5 мм.
Кроме дробления, такое многократное вальцевание ПС дает
хорошее перемешивание ВВ со связующим.
Изготовленный ПС сушится и окончательно прокатывается на
валках а^я получения листов требуемой толщины.
10.5.1. Влияние технологии литья на свойства заряда
В работе [8] исследовалось влияние технологии литья на
свойства кумулятивного заряда из октола. Сравнивались заряды,
полученные обычным литьем и литьем под давлением (300—400 кПа,
выдержка 30 мин) с вакуумированием октола (5 мм ртутного столба
в течение 30 мин) и с программированным режимом охлаждения
(95—80° С — 4 часа, 80—75° С — 16 часов, всего 24 часа) и без ва-
куумирования и программирования.
Для уменьшения остаточных напряжений в заряде при его
охлаждении градиент температуры между центральной частью и
периферией не должен превышать 10° С.
После изготовления двумя методами литья кумулятивные
заряды разрезались перпендикулярно оси на девять сегментов, аая
которых по трем образцам определялась плотность и содержание октоге-
на(НМХ)(рис.10.2)
По этим данным пористость каждого образца рассчитывалась
следующим образом:
% НМХ х плотность заряда % TNT х плотность заряда
% Пористости =100 - — [ — + — ' —
Теоретич. плотность НМХ Тсоретич. плотность TNT
Колебание плотности октола в заряде определяется двумя
факторами: колебанием содержания НМХ и TNT и пористостью.
При обычном литье плотность заряда растет в направлении к
нижней части заряда благодаря седиментации более тяжелого окто-
гена в жидком тротиле. При литье под давлением, наоборот,
плотность уменьшается от верхней к нижней части заряда.
494
Это объясняется следующими причинами. В верхней части
заряда часть жидкого TNT выдавливается через сетку проницаемого
плунжера, создающего осевое давление сверху вниз. Наконец,
сечение нижней части заряда очень мало, что затрудняет заполнение
формы.
Поскольку в нижней части заряда содержание октогена
одинаково а^я двух методов, то различие в плотности (0,03 г/см3, см.
рис. 10.2) определяется только пористостью.
Кроме влияния большой усадки тротила при затвердевании,
пористость возникает из-за воздуха, захватываемого частицами октогена при
перемешивании, при сливе октола в форму, при охлаждении заряда.
Пористость в виде полостей и пузырьков воздуха
регистрируется рентгеновским методом при обычном литье без давления и не
регистрируется при литье под давлением.
Изменения величин плотности, скорости детонации, давления
I в точке Жуге и скорости
кумулятивной струи (расчеты по УРС
BKW) показаны на рис. 10.3.
При % НМХ = Const
пористость, равная 2% снижает
плотность на 0,04 г/см3 (см. рис. 10.2 и
10.3), что уменьшает скорости
детонации и кумулятивной струи на
0,15 км/с, давление в точке Жуге
на 18 кбар, а энергию взрыва на
8%. Кроме того, колебание
плотности заряда уменьшает длину
струи.
Технология литья влияет
также на термическую
чувствительность зарядов из ТГ. Поскольку
горение является поверхностным
процессом, то пористость,
микротрещины и другие нарушения
А-
/ €
/ ? /
8 /
1. \
'9>
ф/4-5
Рис. 10.2. Результаты анализов
зарядов отлитых под давлением с вакууми-
рованием жидкого октола в миксере и
программным охлаждением отливки
и без вакуумирования и
программирования охлаждения
(см. Таблицу)
1-в20Н
О CONTROUCO
• UKCOMTSOtLEO
в4 «7
%ММЛ
8С00Ч
» |
esoo-f
6400-
в4 Q7
НМХ%
Хнмх
14
I- ш
Рис. 10.3. Зависимость плотности (а), давления в точке Жуге (б) скорости
детонации (в) и скорости кумулятивной струи (г) от содержания октогена
в заряде из октола
сплошности литьевых зарядов
увеличивают скорость
генерирования поверхности горения.
В [9] измерялась скорость
газообразования при нагреве в
закрытой бомбе (скорость dp/
dt нарастания давления в
бомбе) зарядов из ТГ40 (Сотр.В),
полученных обычным литьем
( р0= 1,68 г/см3) и литьем под
давлением ( р0= 1,697 г /см3).
Полученные результаты
показаны на рис. 10.4, из которого
видно, что литье под давлением
снижает скорость
газообразования в заряде на 50%.
Рис. 10.4. Скорость газовыделения
при нагреве в закрытой бомбе
зарядов из ТГ40, отлитых обычным
способом
и под давлением 350 кПа
496
Литье без вакуума и с обычным
охлажден.
% ОКТОГ.
87,18
86,56
86,02
86,39
86,38
84,67
83,07
80,43
78,81
плотность
1,853
1,843
1,846
1,844
1,837
1,827
1,830
1,818
1,810
пористость, %
1,02
1,30
1,38
1,35
1,75
1,87
1,79
1,88
2,07
Литье с вакуумом и програм.
охлажден.
% ОКТОГ.
87,85
87,25
87,52
85,47
83,38
82,98
83,00
80,49
78,94
плотность
1,873
1,863
1,851
1,86
1,848
1,851
1,849
1,846
1,843
пористость, %
0,05
0,54
0,60
10,87
0,60
0,60
0,64
0,37
0,30
10.6. Детонационная способность ВВ
10.6.1. Критический диаметр заряда
Критический диаметр является интегральной характеристикой
детонационной способности ВВ данного состава.
Для мощных однородных ВВ с увеличением плотности растут
давление и скорость химреакции, и соответственно уменьшаются
величины d и d .
кр пр
Для смесевых ВВ (аммонитов, игданитов) с увеличением
плотности вначале d и dn уменьшаются, а затем растут, что объясняется
ухудшением диффузии газов и уменьшением поверхности горения
при большой плотности.
Результаты измерений критического диаметра различных ВВ
имеют большой разброс, поскольку на d сильно влияют физическое
состояние ВВ (размер и дефектность частиц, плотность) и условия
взрывания (оболочка, инициирующий импульс).
Ориентировочные данные по величине d аая некоторых ВВ
приведены в табл. 10.7 [1,2,4].
497
Таблица 10.7. Критический диаметр некоторых ВВ (для порошковых
ВВ р = 0,9—1 г/ см3, размер частиц 0,05—0,2 мм)
ВВ
Азид свинца
ТЭН
Гексоген
Сплав ТГ (75/25)
Тетрил
Пикриновая кислота
Тротил
Аммонит N6 (21% ТНТ)
Аммонит N2 (12% ТНТ)
Аммонит N10 (8% ТНТ)
d , мм
0,01—0,02
1—3,2
1—4,4
5,5
7
6-9
8—20
10—12
15
20
ВВ
Аммонит N9 (5% ТНТ)
Аммиачная селитра
Тротил жидкий при 81 С
Тротил жидкий при 240 С
Тетранитрометан (ТНМ)
Нитроглицерин
ТНМ/бензол (87,5/12,5)
ТНМ/нитробензол(74/26)
Пластичный состав на
основе гексогена
Пластичный состав на
основе высокодисперсн.
ТЭНа
d ,мм
25
100
62
6
16
2
<0,1
<0,05
1,5—
-2,5
0,3-
-0,5
Предложенная Харитоном зависимость критического диаметра
от времени химреакции (dK =2cQ t [10]) не позволяет объяснить
различие в dK у литого и прессованного тротила, где t практически
одинаково [11], ad различаются на порядок [12].
Дело в том, что кроме величины t критический диаметр
определяется во многом структурой заряда, в частности, наличием
совокупности неоднородностей разного уровня:
— на кристаллическом уровне — дислокации, дефекты
упаковки, блочность кристаллов;
— на уровне микроструктуры отдельных частиц ВВ —
микропоры и микротрещины с размерами < 10"3 мм;
— на уровне микроструктуры заряда — границы отдельных
зерен и их величина, межкристаллические поры.
Неоднородности последнего уровня характерны для ряда
промышленных составов, состоящих из однородных ВВ с
порошковыми (инертными или активными) добавками или насыщенные
498
пузырьками (аэрированные) или полыми стеклянными
микросферами.
Для таких составов существует три типа экспериментальных
зависимостей d от содержания добавок: монотонно возрастающая, с
минимумом и монотонно убывающая.
Количественный анализ этих зависимостей выполнен в [13] на
основе развитой в [14] теории критического диаметра детонации.
Теория исходит из того факта, что d зависит от начальной скорости
разложения ВВ. Критический диаметр определяется следующим
образом:
d =4uc2cos(Pcm (10.i)
* rQPvw
где и — массовая скорость во фронте детонации; с — скорость звука в
ударно-сжатом ВВ за фронтом детонации; фс — угол наклона
детонационного фронта к поверхности заряда, обеспечивающий стационарность
детонации; Г — коэффициент Грюнайзена; <Э — тепловыделение при
разложении ВВ при постоянных объеме и давлении; w — начальная
скорость разложения ВВ в зоне химреакции.
Выражение (10.1) можно переписать в виде:
где А (р) — коэффициент пропорциональности, зависящий от
давления в точке Жуге и от сжимаемости ВВ.
Начальная скорость разложения может быть представлена
в виде:
w = wH(p,S)N (10.3)
где w (р, S) — характерный для данного типа ВВ коэффициент
пропорциональности, зависящий от давления во фронте и дисперсности
добавки, определяемой удельной поверхностью S (wH растет с S); N —
плотность неоднородностей.
N можно представить в виде суммы:
N = nB+nd (10.4)
где nQ — плотность очагов химреакции, присущая данному типу
и состоянию основного ВВ; nd — плотность введенных в ВВ неодно-
родностей, каждая из которых является эффективным очагом
химреакции.
Исходя из сравнения величин nQ и nd однородные ВВ можно
разделить на две группы:
— ВВ с медленной кинетикой, которые разлагаются в форме
теплового взрыва. Для них nQ мало и nd > > nQ;
— ВВ, у которых начальная скорость разложения
достаточно велика, так что введение добавки заметно не увеличивает w.
Поэтому nQ > > nd, w = wH и не зависит от добавок. Эти ВВ
детонируют с гладким фронтом в отличие от ВВ первой группы.
У составов на основе ВВ второй группы добавки влияют на d за
счет изменения Q. Ясно, что введение в ВВ второй группы
реагирующей добавки (например, гексогена в тротил) не изменит
значительно d , если теплоты разложения различаются не сильно.
Посмотрим теперь, как на d влияет пористость заряда m (m —
отношение объема пор к общему объему).
Поскольку с ростом пористости давление падает, необходимо
учесть зависимость w от давления. Предполагаем, что w ~р.
Так как р ~ рп, рс = (1 - т) р0, то аля начальной скорости
разложения пористого заряда имеем:
w = w0^[(l-m)pj (Ю.5)
где Vg — средний объем поры; п — показатель политропы продуктов
взрыва.
Подставляя (10.5) в (10.2), получим следующее соотношение для
d в зависимости от пористости заряда:
К =^-Пт) (10.6)
Так же, как у реальных аэрированных составов, функция d (m)
имеет U — образный вид.
ч>х
500
Для порошкообразных индивидуальных ВВ и их смесей величина
d уменьшается с ростом плотности (рис.10.5 [1]) в соответствии с ро-
кр-
стом О v и с уменьшением размера частиц (w растет согласно (10.3)).
а)
ММ
to Н
S i
о?
10 \tS Р,г/о»3
to -
4К?
мм
5 г
б)
^ Ч
h= « 1
»5
£*'
см"
Рис. 10.5. Зависимость критического диаметра от плотности
а) Для тротила: 1 — частицы 0,01—.0,05 мм; 2 — частицы 0,07—0,2 мм.
б) Для аммотола 50/50. — отказ, Н— детонация
Аммотол 50/50 при больших плотностях ведет себя как тротил, а
при малых — как пористая смесь (см. рис. 10.56)).
Влияние размера частиц на dK иллюстрируют данные табл. 10.8
[1]. Из рис.10.5а следует, что ^ая тротила d ~а (а — размер
частиц).
У крупных совершенных монокристаллов ВВ величина d
значительно больше, чем у ВВ в виде спрессованного порошка (т.к. мала
начальная скорость разложения). Например, у литого
крупнокристаллического тротила критический диаметр в 15 раз больше, чем у
порошка [ 1 ], а монокристаллы имеют следующие величины d [4]:
ТЭН — 5мм; гексоген — 7мм; октоген — 18мм; тротил —
110мм.
Величину d уменьшает наличие оболочки вокруг заряда,
которая в первом приближении эквивалентна увеличению диаметра
заряда. Прежде всего влияет удельный вес материала оболочки
(свинцовая эффективнее железной), затем ее прочность.
Если же взять материал оболочки, у которого скорость ударной
волны будет выше скорости детонации заряда, помещенного в такую
оболочку, то происходит инициирование химреакции ударной
волной в оболочке, идущей впереди детонационной волны.
Характеристики некоторых материалов с высокой скоростью УВ
приведены в табл. 10.9 [15].
Таблица!0.8. Влияние размера частиц ВВ на критический диаметр
ВВ
Тротил
Пикриновая кислота
ТЭН
Гексоген
г/см3
0,85
0,8
0,7
0,95
1,0
1,0
Размер частиц
мм
0,01—0,05
0,07—0,2
0,01—0,05
0,05—0,07
0,1-0,75
<0,01
0,025—0,1
0,15—0,25
0,025—0,15
Критический диаметр,
мм
4,5-5,4
10,5—11,2
2,08—2,28
3,6-3,7
8,9-9,25
0,1—0,3
0,7—0,86
2,1—2,2
1,0—1,15
Таблица 10.9. Характеристики некоторых материалов
Матер.
Be
Si
BN
в4с
AiA
Si С
A1B
Плотн.,
г/см3
1,82
2,34
2,30
2,52
3,96
3,22
2,54
Коэф-т
Пуассона
0,115
0,214
0,180
0,180
0,230
0,170
0,077
Скор.
продол.
волн,
км/с
12,9
9,1
19,6
14,3
10,9
11,6
11,8
Скор.
объем.
волн
км/с
8,4
6,5
13,5
9,9
7,9
8,5
7,4
Скор.
волн в
стержн.,
км/с
12,7
8,6
18,8
13,7
10,1
11,2
11,7
Гюгоние
вский
Упругий
Предел,
ГПа
0,38
7,1
-
15,4
11,2
8,0
8,7
Динам,
жесткость
Рос'
г км/с см3
15,3
15,3
31,1
25,0
31,3
27,4
18,8
В [16] найдено, что скорость детонации ВВ на основе ТАТБ
возрастает на границе со стенкой из бериллия.
В работе [15] использовалась оболочка о48 х о7б мм из
самосвязанного карбида кремния (с0= 11,1—11,2 км/с).
502
Измерения показали, что скорость детонации увеличилась
только благодаря влиянию оболочки из SiC:
— Аля литого тротила ( р0 = 1,6 г/см3) — с 6,4 км/с до 7,2 км/с ;
— Аля гексогена ( р0 = 1,1 г/см3) — с 6,4 км/с до 7,5 км/с;
— для ТГ 36/64 ( р0 = 1,69 г/см3) — с 8,0 км/с до 8,9 км/с.
При этом максимально измеренное давление в тротиле
увеличилось с 17 до 24 ГПа.
Эти эксперименты показывают, что прочные и жесткие
оболочки создают новые режимы детонации с повышенными давлением и
скоростью, соответственно, с меньшими величинами d .
Понятие критического диаметра относится только к
цилиндрическому заряду. Возникает вопрос, а каковы критические размеры
зарядов другой формы, например, в виде пластин, листов?
Чтобы установить соответствие между критическими размерами
цилиндрического и плоского зарядов в [17] введено понятие
удельного объема заряда М, представляющего собой отношение объема
заряда к его поверхности. Это понятие обосновывается теорией
Харитона. Очевидно, аая цилиндра:
M = ^L = d/4 (10.7)
Andh
где d, h — диаметр и длина заряда.
Для плоского заряда:
M = abh/2(a + b)h = ab/2(a + b) (10.8)
где а, Ь — толщина и ширима заряда соответственно.
Выражая ширину заряда через его толщину (b = п а), получим:
М = па/2(п + 1);(1экв=2па/(n + l) = ma; т = 2п/(п = 1) (10.9)
С увеличением п от 1 до оо m меняется от 1 до 2, т.е. толщина
листа бесконечной ширины эквивалентна половине диаметра
цилиндрического заряда, или
в„=0,5«/_ (10.10)
Экспериментально установлено [17}, что скорости детонации
плоских и цилиндрических зарядов одинаковы, если а = 0,5 d.
Таким образом, понятие удельного объема позволяет оценить
критический размер заряда с любой формой поперечного сечения
Очевидно, если слой ВВ лежит на жесткой подложке,
ограничивающей разгрузку, то удельный объем увеличивается вдвое, а
критическая толщина слоя уменьшается вдвое.
Для трёх типичных условий определения критических размеров
ВВ (диаметра или слоя) — в воздухе, на подложке и в оболочке —
экспериментально определены следующие соотношения [18]:
^крвозд ' ™кр обол = 3 ~°> "к/> возд I акрподл = 3 "^ акр подл ' акр обол — *>*
В [ 19] для ряда мощных ВВ определена критическая толщина де-
тонационноспособного слоя при высокой относительной плотности
(0,9—0,93), причем слой расположен на подложке из алюминия.
В табл. 10.10 даны
критические толщины слоев, а
также наименьшие диаметры
ударника, способного
возбудить детонацию этих слоев.
Кроме того, в [19] получена
зависимость величины
критической толщины слоя гек-
согена от размера его частиц
(см. рис. 10.6).
Как видно из рис. 10.6,
уменьшение размера частиц
на порядок уменьшает критическую толщину гексогена втрое.,
Экспериментальное определение малых критических
диаметров — достаточно сложная задача. Взамен можно определять
критическую толщину. Прекращение детонации с уменьшением
толщины слоя ВВ легко устанавливается методом «свидетеля». Например,
слой ВВ в виде диска помещается внутрь стального или
алюминиевого неразрушаемого кольца и инициируется в центре. Если диск
сдетонировал (а> ак), то на внутренней поверхности кольца
останется чёткий след.
ми
02
ш
0 гоо Ы мкм
Рис. 10.6. Зависимость критической
толщины слоя гексогена от размера
его частиц
504
Таблица 10.10. Детонационная способность и чувствительность к удару
для слоев различных ВВ
вв
Тротил
Пикриновая кислота
Тетрил
Октоген
Гексоген
ТЭН
Азид свинца
Критическая толщина
слоя, мм
1,34
0,91
0,55
0,81
0,45
0,22
-0,02
Миним. диаметр ударника,
мм
-170
-83
-45
19
18
8
-0,1
Для определения ак можно также использовать тот факт, что при
повороте детонации на 90° в слое образуется т. н. «тёмная зона»
(без детонации, поэтому не светится), толщина которой равна а
кр
Поэтому, если инициировать детонатором слой ВВ с а < а , то сдето-
нирует только слой под детонатором, но повернуть в слое детонация
не сможет. В результате в таком слое под детонатором образуется
отверстие, а остальная часть слоя сохранится (или будет частично
разрушена).
10.6. 2. Зависимость скорости детонации от диаметра заряда
Стационарное распространение детонации возможно лишь а^я
зарядов, диаметр которых больше критического. При d = d
скорость стационарной детонации минимальна ( D ), априс1 = а —
максимальна (DJ.
Отношение dK /d выражает степень отклонения процесса
детонации от идеального:
dK /d= 1 — критический режим детонации;
dKp/d = 0 (d -> оо ) — идеальный режим детонации.
Согласно [20] зависимость скорости детонации от диаметра заряда
лучше всего описывается следующим образом: 1/D = f (d /d) или
D =
ВД
Dk+(Du-Dk)(dKp/d)
(10.11)
505
Обработка многих экспериментов показала, что между 1/D
и d /d существует линейная зависимость, а точка излома в области
критических параметров соответствует истинным значениям dK и
Dk (см. рис. 10.7 [20].).
Для данной плотности заряда величины Dk и Dh являются
независимыми характеристиками ВВ данного состава, а величина dK
зависит еще и от дисперсности
компонентов. Например,
Аая литого и
прессованного тротила с одинаковой
р0 = 1,62 г/см3
критические диаметры
отличаются почти в 5 раз (15 мм и
3,2 мм), но в координатах
1/D — dK /d все
экспериментальные точки лежат
на одной прямой, соответ-
Ф,ъА
;
06
о2
01 о€ iO )Ь d<f/cf
\ ) ) i '
Рис. 10.7. Зависимость 1/ D=f (d /d) для
смеси гексогена с NaCl (85/15), р0 = 1,2 г /см3.
Излом при d=d
ствующей Dk = 6,63 км/с и
D =7,05 км/с
Кроме того, а^я показателя политропы п продуктов детонации
зависимость 1/n = f (d /d) также является линейной (рис. 10.8).
Имея эти две линейные зависимости и зная d , можно а^я
^ кр
любого диаметра заряда определить величины D и п ;
используя их, рассчитать другие параметры детонации : u = D/(n+l);
p = p0uD.
J- X-
0 ) п.
</n '
р7~
—о —
^_i 1
о ■ о ■ '"* ^° ***
ог
ОЬ-
I
об
08
>
<t<
/d
Рис. 10.8. Линейные зависимости 1 /D = f (d /d) и 1 / n = f (d /d) для литого троти
ласр0=1,62г/см3
506
Кроме более точного определения параметров детонации,
линейная зависимость l/D = f(dK/d) может быть использована а^я
контроля качества изготовления данного ВВ. Для этого необходимо
измерить величину скорости детонации в заряде определенного
диаметра и по заранее известной зависимости 1/D = f (dK /d)
определить величину d.
В [21] критически проанализированы результаты
измерения скорости детонации D(d) а^я ряда композиций на основе гек-
согена (плотность зарядов > 95% теоретической) и найдено, что
наилучшим образом эксперименты описываются следующим
уравнением:
D2 (d) = £>*2 [1 - (a*/d)2] (10.12)
где D* и а* — константы, величина которых легко может быть получена
из линейной зависимости D (1/d).
Кроме того, оказалось, что величины критического диаметра dK
и а* а^я анализируемых композиций лежат на прямой
^ = 2,208а* (10.13)
проходящей через точку dK = 0, а* = 0.
Таким образом, если а^я данного состава известна зависимость
(10.12), то из нее легко находится величина критического диаметра
и отпадает необходимость проведения большого числа
экспериментов а^я определения dK.
Из (10.12) и (10.13Тполучаем:
[D (d)/D*f = 1 - (dJ2,20Sd)2 (Ю-14)
(10.14) позволяет определить минимально возможную скорость
детонации при dK:
DMmi=°>892D* (10-15)
Таблица 10.11. Параметры составов (РВХ) на основе гексогена
Название
PBXW-115
(Aust)
PBXW-115
(USA)
Сотр. А
Сотр. В
Сотр. В
Cyclotol
77/23
Amatex -20
РВХ — L-5
Сотр. С-4
Связующее, плотность
(г/см3)
Polyurethane -12%
р=1,79
То же, но размер частиц
гексогенаменьше на
~45мкм
Воск-8,2%р=1,69
ТНТ-37%р=1,70
ТНТЗб%,воск-1%
р = 0,976 р
Г Гтах
ТНТ-23% р = 0,991ртах
ТНТ-40%,АС-20%
р = 0,943р
1 I max
Silicon binder 17,6%
р=1,58
Полиизобутилен —9%
D*,m/c
5642
5760
8267
78 65
7894
8202
6954
7642
8027
а*, мм
35,25
18,33
0,74
1,52
1,66
2,00
8,74
3,95
2,89
Критический
диаметр, мм
эксперимент
80
37,6
<4,2
2,0
4,3
6,0
7,5
<5
расчет по
(10.13)
77,8
40,5
1,6
3,7
3,4
4,4
20
8,7
6,4
Отмечается, что для композиций с малыми размерами частиц
гексогена (<10 мкм) и с малыми величинами dK результаты
измерений D(d) лучше описываются линейной зависимостью,
предложенной еще в 1949 г. [22]. Это подтверждает упомянутое ранее сильное
влияние размера частиц ВВ на кинетику реакций в детонационной
волне: меньше частицы, больше их поверхность — больше скорость
реакций и ско- рость выделения энергии. Для ряда составов с
малыми частицами гексогена расчет dK по (10.13) неточен.
В таблице 10.11 приведены величины D*, a*, d для ряда
составов на основе гексогена [23].
Нами экспериментально определена зависимость скорости
детонации флегматизированного высокодисперсного тэна (с частицами
508
менее 10 мкм) от площади сечения прутков D(S). Эта зависимость
позволяет оценить критический и предельный диаметры этого
состава (см. рис. 10.9).
7,75
?,?
7,65
I I
I ш • I I e_J
^*т*" I *# г
XX* I
ЕЖ
0Ъ5
0,5
0,6
1
1,15
1*
1(5в
2
1,60
2,5
SfMMX
<Ь<р,мм
Рис. 10.9. Зависимость скорости детонации прутков флегматизированного ТЭНа
от площади сечения прутков, d = 1,128 S0,5
Для однородных ВВ с ростом плотности величины d , d и
разница между ними значительно уменьшаются, но вблизи
кристаллической плотности dK резко растёт (экспоненциально).
Обобщенная зависимость D(d) следующая [18]:
D{d)/Doo=\-2A/{d-0^11dKp)
Для различных составов найдены следующие величины
коэффициента А:
Состав ТНТ ТНТ Сост.В ТГ23/77 Октол 23/77 РВХ9404 РВХ9501
А 6,Г 11,2 1,94 2.44 1,34 0,553 0,48
10.6.3. Детонация с «внутренней» разгрузкой
Как было показано выше, все взрывчатые составы (ВС) имеют
скорость детонации, увеличивающуюся с диаметром заряда d от
^min ПРИ ^кР А° ^тах ПРИ ^пР' Эти зависимости D(d) определяются
условиями «внешней» разгрузки заряда с его боковой
поверхности [18].
509
Нам представляется возможным создание ВС с зависимостью
D(d), определяемой «внутренней» разгрузкой. Модель структуры
такого ВС следующая. На шарики инертного вещества с радиусом
г нанесён слой ВВ толщиной t и затем шарики спрессованы в заряд.
При d>>r и r>>t скорость детонации такого состава зависит не
от «внешней» разгрузки, а от следующих трёх «внутренних»
параметров: жесткости шариков (подложка а^я ВВ),толщины слоя ВВ и
отношения t/r.
Кроме того, измеряемая скорость детонации заряда будет
меньше физической скорости детонации слоев ВВ из-за разницы длины
заряда и пути детонации вокруг шариков. Например, если слой ВВ
имеет критическую толщину и детонирует с D . ,то измеряемая
скорость заряда D3 = Dmin/(7r/2) и не будет зависеть от диаметра (или от
толщины слоя ВС) т.е. d = d .
7 кр пр
Реально такой состав может быть изготовлен из смеси крупных
инертных частиц и примерно на два порядка меньших частиц ВВ.
Создание таких ВС с минимальной и постоянной скоростью
детонации в слоях малой толщины представляет интерес для сварки
взрывом тонких конструкций [38].
10.6.4. Зависимость скорости детонации от плотности
заряда
Для плотностей зарядов более 1г/см3 скорость детонации
линейно возрастает с плотностью [4]:
D = D0+M(p-p0)9
где DQ — скорость детонации при плотности р0, М —
коэффициент, постоянный а^я данного ВВ.
Величины р0, DQ, М приведены в таблице 10.12.
Для смесевых ВВ с увеличением плотности скорость детонации
сначала растёт, достигает максимума, а затем быстро падает.
Нам представляется возможным создание ВС с зависимостью
D(d), определяемой только «внутренней» разгрузкой, т.е. внутри
самого ВС.
510
Таблица 10.12. Коэффициенты зависимости D (р)
Название ВВ
Азид свинца
ТЭН
Гексоген
Тротил
Состав А (гексоген+воск)
Состав В
Аммотол 50/50
Октоген
р0, г/см3
4,0
1,0
1,0
1,0
1,6
1,6
1,0
1,0
D0, км/с
5,100
5,550
6,080
5,010
8,180
7,540
5,100
9,05
М, (км/с)/(г/см3)
4,560
3,950
3,590
3,225
4,000
3,080
4,150
3,34
10.7. Чувствительность ВВ
10.7.1. Общая характеристика чувствительности
ВВ различаются по чувствительности к внешним воздействиям
[1,2,3,4].
Чувствительность характеризуется минимальной величиной
начального импульса, который необходим а^я возбуждения взрыва.
Чувствительность зависит от вида внешнего воздействия: нагрев,
удар, трение, детонационный импульс от первичных ВВ, передача
детонации на расстоянии, электрический разряд.
Чувствительность прямо связана с механизмом инициирования
взрыва. Принципиально отличаются критические параметры
инициирования гомогенных ВВ (жидких без пузырьков, монокристаллов,
твёрдых актированных) и гетерогенных ВВ (литых, прессованных).
Рассмотрим чувствительность более широкого класса
структурно неоднородных гетерогенных ВВ, инициируемых по механизму
горячих точек. При инициировании структурные неоднородности
являются источником генерации локального тепла. Различные
механизмы такой генерации показаны на рис. 10.10 [24].
Эффективность этих механизмов не равнозначна и в порядке
возрастания образует следующий ряд: деформационный
макроразогрев — ударно-волновой разогрев — фрикционное
тепловыделение — вязкопластический локальный разогрев.
511
Источники
локальной генерации тепла
Диссипативные
*
Различными
авторами предложено доста-
^аэогрев в вершине
развивающейся
трещины
Эффекты развития
микрокумуляции
Разогрев
от сгоревших
частиц
Эффекты торможения
язкопластический микроструй
разогрев Зоны
сдвига
Кумулирующие Трансляционные ТОЧНО МНОГО Критериев
* I ударно-волнового
инициирования : минимальные
критические величины
давления, массовой
скорости, энергии, импульса
и скорости их изменения
(см.[24]).
Например, известный
критерий p2t = const
может быть уточнён, если
учесть, что возникновение
детонации определяется
как химической реакцией
на фронте ударной волны,
так и возможностью её
развития после спада
давления.
Чувствительность ВВ
зависит не только от
величины импульса, но также
от его профиля. Любое
размытие фронта импульса
снижает температуру
удара и, как следствие, ведёт к
снижению чувствительности.
Изменение чувствительности в зависимости от начальной
температуры может быть немонотонной и отражает влияние изменения
с температурой физико-механических и структурных свойств ВВ.
Зависимости критического давления инициирования от начальной
температуры показаны на рис. 10.11 [24].
Чувствительность — одно из важнейших свойств ВВ,
определяющее условие их практического применения. Поэтому это понятие
требует точного количественного определения.
Множественное
струе -
гсколкообраэование
Эффекты
отражений
от жестких
включений
Рис. 10.10. Источники локальной генерации
тепла
512
В промышленности и
Аая боеприпасов
используются ВВ с низкой
чувствительностью, чтобы избежать
случайных взрывов при
производстве,
транспортировке, при пожарах и
других авариях. Взрыв таких
малочувствительных
взрывчатых составов
обеспечивается практически только
при помощи специальных
устройств АА^ возбуждения
взрывов или
дополнительными зарядами.
Для получения нужной чувствительности часто используются
специальные добавки: сенсибилизаторы, повышающие
чувствительность или флегматизаторЫу понижающие чувствительность.
Примеры: сенсибилизаторы — добавки твердых порошков (песка),
пузырьки воздуха в жидких ВВ; флегматизаторы — добавки мягких
веществ (воск, парафин), воды (при транспортировке гексогена), тротила
в сплавах ТГ.
Иногда само смешение компонентов играет флегматизирующую
или сенсибилизирующую роль. Например, оба компонента
нитроглицеринового пороха (нитроглицерин и нитроклетчатка) сами по
себе легко детонируют, а вязкий порох детонирует плохо, только
при больших диаметрах заряда. Наоборот, жидкие тетранитрометан
и нитробензол малочувствительны (нитробензол вообще не ВВ), но
при их смешивании получается очень чувствительное ВВ с
критическим диаметром в сотые миллиметра.
В общем случае чувствительность зависит от химической
структуры ВВ (строения и состава молекулы) и от его физико-механических
характеристик (плотности, размера кристаллов, агрегатного
состояния, полиморфной формы). А такие характеристики ВВ, как энергия
активации и теплота взрыва, сами по себе прямо не определяют
чувствительность.
/ГНТ монокристалл
^Гексоген монокристалл
Тэн монокристалл
ТНТ жидкий
ТГ2СУ1В0
160 Г0.°С
Рис. 10.11. Влияние начальной температуры
на критическое давление инициирования
513
Чувствительность обуславливается скоростью разложения ВВ
при нагреве и скоростью тепловыделения. В этом отношении нитро-
эфиры спиртов и углеводов более чувствительны к теплу и удару, чем
нитросоединения бензольного ряда. С другой стороны, введение
четвертой нитрогруппы в бензольное кольцо резко повышает
чувствительность к нагреву, поэтому тетранитросоединения не
применяются, хотя они по мощности превосходят тринитросоединения.
Устойчивость молекулы ВВ изменяет взаимное влияние атомов и
групп в молекуле, но это трудно поддается анализу.
Введение в бензольное кольцо аминогруппы СН3 значительно
снижает чувствительность. Увеличение числа групп СН3 и ОН в ни-
тросоединениях дает рост чувствительности, а увеличение NH2 —
групп, наоборот, снижает чувствительность.
Общий вывод: чем больше в молекуле непрочных связей, тем
выше чувствительность к удару.
Рассмотрим кратко влияние на чувствительность физико-
механических характеристик ВВ.
1. Размер кристаллов.
С увеличением степени измельчения вторичных ВВ их
чувствительность к взрывному импульсу (определяемому минимальным
весом заряда азида свинца) сильно возрастает. Например, при сильном
измельчении тротила необходимый ^ая его инициирования вес
азида свинца уменьшается с 0,10 г до 0,04 г.
2. Агрегатное состояние.
Известно, что если нитроглицерин и динамит замерзали
медленно, при высокой температуре (+10° С), то образовывались крупные
кристаллы с высокой чувствительностью. При низкой температуре
(—11° С) получались мелкие кристаллы с чувствительностью,
меньшей чем у жидкого нитроглицерина.
Нужно учитывать также, что замерзший динамит становится
твердым и уже не смягчает удара так, как пластичный незамерзший
динамит.
Переход от кристаллического состояния к аморфному
(переохлажденный расплав) снижает реакционную способность и
чувствительность ВВ [25].
514
Расплавленный тротил имеет большую чувствительность, чем
твердый. Однако в общем случае при переходе от твердого к
жидкому состоянию чувствительность может как увеличиваться, так и
уменьшаться. Это зависит от того, приводит или нет изменение
текучести к возникновению местного нагрева при ударе.
3. Полиморфные формы.
Многие ВВ могут существовать в различных кристаллических
модификациях, чувствительность которых различна. Так,
ромбоэдрическая модификация нитроглицерина более чувствительна, чем
его кристаллы триклинной системы. Неустойчивая $ — форма азида
свинца более чувствительна устойчивой а — формы. Октоген имеет
четыре кристаллические модификации, сильно различающиеся по
чувствительности.
4. Плотность.
С увеличением плотности зарядов их чувствительность понижается.
Далее рассмотрим чувствительность ВВ к различным видам
начального импульса и методы ее определения.
10.7.2. Чувствительность к удару
Для сравнения ВВ по чувствительности к удару созданы
специальные установки — копры.
Груз падает с определенной высоты на образец ВВ, помещенный
на наковальне в специальном штемпельном приборчике. Ролики
приборчика, между которыми помещено ВВ, могут иметь или не иметь
фасок. Фаски создают кольцевой зазор, в который может течь ВВ,
нагреваясь, поэтому чувствительность измеряется более высокая, чем у
роликов без фаски и без быстрой пластической деформации ВВ.
Поскольку чувствительности разных ВВ сильно различаются,
при испытаниях на копре варьируют как вес груза, так и высоту его
падения. Увеличивая высоту падения груза, мы постепенно
переходим от 100% отказов к 100% взрывов.
Характерной для данного промышленного ВВ высотой считают
максимальную высоту, при которой после 6 испытаний нет ни
одного взрыва (метод горного бюро США).
515
Для мощных ВВ и составов проводят 25 опытов при высоте 25
см и грузе 10 кг. Устанавливают процент взрывов, который и служит
характеристикой чувствительности к удару. Этот метод неточен в
области около 0 и 100%.
Кроме того, чувствительность выражают как минимальную
энергию удара в кгм, при которой в 6-ти опытах наблюдается хотя бы
один взрыв [3].
Для инициирующих ВВ чувствительность определяют на малом
рычажном копре Велера. Навеска весом 0,02 г запрессовывается в
гильзу капсюля. На каждой высоте делают по 5 опытов.
Мерой чувствительности считают верхний (Н) и нижний (h)
пределы. Нижний предел — это максимальная высота, на которой
происходят 5 отказов. Верхний предел — это минимальная высота,
при которой наблюдаются 5 взрывов.
Нижний предел характеризует восприимчивость к детонации и
безотказность работы, а верхний предел показывает степень
опасности в обращении. Желательно, чтобы разность между этими
пределами была как можно больше.
Например, а^я азида свинца Н = 230 мм и h = 70 мм, а а^я
гремучей ртути Н = 85 мм и h = 55 мм.
Некоторые результаты испытаний приведены в табл. 10.12а и
10.13 [ 1 ] и дают возможность сравнить различные ВВ по их
чувствительности к удару.
Таблица 10.12а. Чувствительность ВВ к удару (минимальная высота
L падения груза 2 кг, при которой происходит хотя бы один взрыв
из 10-ти опытов)
ВВ
Тротил
Пикриновая кислота
Тетрил
Гексоген
L, см
100
82
26
18
ВВ
Октоген
ТЭН
Азид свинца
Гремучая ртуть
L, см
32
17
11
5
516
Таблица 10.13. Чувствительность ВВ к удару (груз 10 кг, высота 25 см,
навеска ВВ 0,05 г, серия 25 опытов)
ВВ
Тротил
Аммотолы
Пикриновая кислота
Тетрил
ТГ 50/50
Частота
взрывов, %
4-8
20—30
24—32
50—60
40
ВВ
ТГ 30/70
Гексоген
Бездымный порох
Октоген
ТЭН
Частота
взрывов, %
64
70—80
70—80
96—100
100
10.7.3. Чувствительность к прострелу пулей
Такие испытания проводят &ля ВВ, применяемых в
боеприпасах.
В одном из вариантов испытаний исследуемое ВВ помещают
в закрытую чугунную трубу и простреливают ее из винтовки с
расстояния 9 м.
Число взрывов из 10-ти опытов: тротил — 0,5; тетрил — 7;
гексоген, ТЭН, нитроглицерин — 10.
10.7.4. Чувствительность к термическому импульсу
Определяется температурой вспышки.
Существуют два варианта испытаний.
При первом варианте в баню из масла или легкоплавкого
металла при 100°С вводят пробирку с 0,1 г ВВ и нагревают со скоростью
20° в минуту, отмечая температуру вспышки (со слабым звуком или
взрывом).
При втором варианте навеску ВВ вводят в пробирку, уже
нагретую в бане до фиксированной температуры. Измеряют задержку
взрыва t. Для многих ВВ зависимость в координатах lg t — 1/Т
линейная, что соответствует автокаталитическому и цепному
механизмам теплового взрыва.
Температура вспышки /^ая ряда ВВ даны в табл. 10.14 [1].
517
Таблица 10.14. Температура вспышки (ТС) различных ВВ
вв
Тротил
Гексоген
Октоген
ТЭН
Тетрил
Аммониты
Азид свинца
Т,С
285—300
215—230
287
205-215
190—200
280—320
325—340
ВВ
Гремучая ртуть
Нитроглицерин
Коллоксилин
Пироксилин
Бездымный порох
Черный порох
Аммиачная селитра
Т,С
170—180
200—210
204—205
195—200
180—200
290—315
280—350
Большинство промышленных ВВ при поджигании на открытом
воздухе горят без взрыва, но в закрытых емкостях и при больших
массах горение может перейти во взрыв. Осторожно надо относиться к
уничтожению сжиганием аммонитов и дымного пороха: они могут
взрываться.
10.7.5. Минимальный инициирующий импульс
Для каждого вторичного ВВ имеется свое значение
критического давления ИУВ (рк), которое зависит от химической структуры
ВВ, пористости, размера частиц, диаметра заряда.
Ориентировочные величины рк составляют [2]:
— Аая порошковых промышленных ВВ и тротила ( р0= 1,1—
1,35 г/см3) рк = 6— Юкбар;
— для высокоплотных прессованных зарядов из гексогена или
ТЭНа (р0 ~1,8 г/см3) ркр= 120—170 кбар;
— для литого тротила ( р0 = 1,6 г/см3 )рк =35—115 кбар;
— Аая жидкого нитроглицерина рк =120 кбар.
— Величина р зависит также от времени его действия,
поэтому часто говорят не о критическом давлении, а о критическом
импульсе.
— Если ИУВ создается взрывом ВВ, то очевидно, что в этом
случае инициирующий импульс пропорционален как давлению
детонации, так и массе ВВ, а а^я одного и того же
инициирующего ВВ — только его массе.
518
Поэтому чувствительность различных ВВ к инициирующему
импульсу выражается в минимальной навеске гремучей ртути или
азида свинца в граммах, требуемой аая возбуждения взрыва (см.
табл. 10.15 [1,2]).
Таблица 10.15. Минимальный инициирующий импульс
для некоторых ВВ
ВВ
Тротил
Аммониты
Гексоген
ТЭН
Тетрил
Пикриновая кислота
Навеска гремучей ртути, г
0,25—0,36
0,25—0,29
0,14—0,19
0,15—0,17
0,15—0,29
0,30
Навеска азида свинца, г
0,09
-
0,05
0,01—0,02
0,025
0,025
10.7.6. Чувствительность к инициированию ударной волной
Широко применяется методика, в которой регистрируется
передача детонации от заряда — донора через различные инертные слои
к заряду — акцептору из исследуемого ВВ.
За характеристику чувствительности к ударно-волновому
импульсу в этих испытаниях принимается такая толщина инертного
слоя, которая соответствует 50% вероятности инициирования
заряда — акцептора. При этом в конкретных условиях
испытаний (размеры, материалы) в заряде — акцепторе создается ударная
волна с наименьшими для инициирования давлением и
импульсом.
Такие испытания проводятся для контроля технологии
производства ВВ, обеспечивающей стабильность чувствительности ВВ.
В [26] проведена серия экспериментов по передаче детонации
через различные металлические и неметаллические слои толщиной
от 0,1 до 10 мм, что соответствует изменению р от 0,8 до 20 ГПа.
Измерялись профили давления р( t).
Показано, что критическая толщина слоев линейно растет с
диаметром заряда — донора. Инициирование через малые воздушные
519
зазоры происходит легче благодаря термическому воздействию
продуктов взрыва.
Найден общий интегральный критерий передачи детонации
через любые инертные слои:
г
K = jpdt = Const (10.16)
о
где t — время, за которое давление падает до известной аля данного ВВ
критической величины. К=const аая данного ВВ, независимо от
условий испытаний.
В табл. 10.16 приведены величины критерия К а^я ряда мощных
ВВ [26].
Таблица 10.16. Величины критерия К для мощных ВВ
ВВ
тэн
ТЭН/воск(95/5)
Пластичное ВВ на основе ТЭНа
Гексоген/воск (99/1)
Тетрил
Тротил
Октоген/воск (96,5/3,5)
Гексоген/воск (95/5)
Октоген/тротил (84/16)
Гексоген/А1/воск (75/20/5)
ТГ 36/64
Гексоген/тротил/А1/воск (40 /38/18/4)
р0,г/см3
1,57
1,64
1,50
1,64
1,57
1,58
1,75
1,66
1,80
1,70
1,70
1,70
К, ГПа мкс
1,9
4,6
5,6
6,8
7,3
10,2
11,8
13,7
19,4
20,7
56,3
80,0
10.8. Формы работы взрыва.
Бризантность и фугасность ВВ
Бризантность ВВ определяет воздействие взрыва на среду
вблизи заряда (дробление), а фугасность — это общая работа взрыва.
520
Если фугасность пропорциональна полному импульсу взрыва
(рис. 10.12), то бризантность определяется головной частью
импульса (заштрихованной на рис.
10.12), следовательно,
пропорциональна максимальному
давлению детонации заряда
P = P„DV4.
Без учета химических и
термодинамических потерь
полная работа взрыва
определяется следующими
соотношениями:
Рис. 10.12. Полный импульс взрыва
заряда ВВ
(Р2>
Tl V2 А
(10.17)
где Q— теплота взрыва; п = с /с — показатель политропы
расширения продуктов взрыва; Т2 ,v , р2 — начальные параметры
продуктов взрыва; Т2, v2, р2 — конечные параметры после совершения
работы.
Обычно Д.епл/Амех < 0,4—0,6, а на полезную работу расходуется
всего 10—15% энергии взрыва. Лишь при взрыве в воздухе в
энергию УВ передается около 85% энергии взрыва.
Фугасные формы работы взрыва совершаются в течение
миллисекунд, а бризантные — в течение микросекунд.
Оценку общей работоспособности данного ВВ проводят с
помощью т.н. пробы Трауцля. Образец ВВ весом 10 г взрывают в
свинцовом цилиндре (бомбе) о200 х 200 мм с несквозным каналом
начальным объемом 61 см3.
После взрыва бомба расширяется, и разность объемов в см3 (за
вычетом 30 см3 от капсюля -детонатора) является показателем
работоспособности ВВ. Работа расходуется на пластическую деформацию свинца
и составляет от 0,5 до 0,67 исходной теплоты взрыва.
На расширение бомбы влияет плотность ВВ: с ростом плотности
образцов одного и того же ВВ расширение уменьшается. Поэтому
испытания проводят при постоянной плотности 1 г/см3.
Другим способом определения работоспособности является
испытание на баллистическом маятнике.
Суть метода в том, что взрыв заряда ВВ совершает работу по
отклонению свободно подвешенного груза, и работоспособность ВВ
можно оценивать по измеренным абсолютным значениям
импульсов взрыва:
J = Mxg(27r/T) (10.18)
где М — масса маятника; Т — полупериод колебания; х —
измеряемое линейное отклонение в результате взрыва; g — ускорение силы
тяжести.
Зная величину импульса, можно оценить и значение энергии:
E = Mgh = J2/M (10.19)
где h — высота подъема маятника.
По результатам баллистических испытаний можно определять
относительную работоспособность ВВ, например, по весу
испытуемого ВВ, дающего такое же отклонение маятника, как заданный вес
тротилового заряда, взятого за эталон.
После проведения лабораторных измерений итоговым полевым
испытанием может быть метол воронок, который прямо определяет
фугасное действие ВВ по величине воронки, образованной взрывом
в грунте. Этот метод неточен из-за влияния колебаний свойств
грунта и неточного определения объема воронки по ее размерам.
Бризантность ВВ определяют по величине обжатия свинцового
цилиндрика о40 х 60 мм взрывом на его торце заряда о40 мм весом
50 г и плотностью 1 г/см3 (проба Гесса). В результате взрыва верхняя
часть свинца расплющивается, приобретает грибовидную форму с
уменьшением высоты цилиндрика. По измеренной в четырех
опытах величине усадки цилиндрика оценивают бризантность ВВ в мм.
Недостатки пробы Гесса: обжатие нелинейно связано с работой
деформации свинца, аая малочувствительных ВВ (dn > 40 мм) влияет их
детонационная способность, применение пробы Гесса невозможно для
очень мощных бризантных ВВ (свинец сильно разрушается).
С увеличением плотности заряда при постоянном его весе
величина усадки линейно возрастает.
522
Величины фугасности и бризантности некоторых ВВ приведены
втабл.10.16а[1,2].
Таблица 10.16а. Фугасность и бризантность некоторых ВВ
ВВ
Тротил
Гексоген и октоген
Коллоксилин
Тетрил
ТЭН
ТГ 50/50
Аммонит Ы6ЖВ
Аммонит скальный N1
Фугасность, см
285-300
450—495
310
340—390
500
380
360—380
450—480
Бризантность, мм
16—17
24 (вес 25 г)
12
20—22
-
14 (вес 25 г)
14—18
22—28
Другая аналогичная проба Каста основана на обжатии взрывом
медного крешера. Известны и современные модификации проб
Гесса и Каста [27].
Дополнительно а^я оценки бризантности ВВ проводят
испытания снаряженных ими боеприпасов (снарядов, мин), целью которых
является определение характера и интенсивности дробления
оболочки боеприпасов, а также скорости осколков.
После взрыва боеприпаса в броневой яме собирают все осколки,
распределяют их по весу, производят подсчет числа осколков, затем
делят эти числа на общий вес всех осколков и получают числа а2, а2, а3...
Величина этих чисел и их сумма полностью описывают характер и
интенсивность дробления оболочки боеприпаса.
Скорость осколков определяется по методу круговых мишеней.
Вокруг подрываемого боеприпаса по концентрическим
окружностям располагают деревянные или стальные щиты. После
подрыва определяют число осколков, пробивших и не пробивших щиты.
Начальная скорость осколков полностью определяется
импульсом, действующим на боковую поверхность оболочки. Величину
этого импульса можно рассчитать в зависимости от размеров заряда
и скорости его детонации [1].
523
10.9. Метание продуктами взрыва
Можно предположить, что бризантное действие ВВ
определяется не давлением, а импульсом, отраженным от поверхности
разрушаемого тела. Тогда зависимость бризантности от скорости детонации
будет менее сильная, линейная, а не квадратичная, т.к. р = pQD2/4,
а импульс на жесткой стенке J = 8/27 (ma D), где ma — активная часть
массы заряда, продукты взрыва которой движутся в сторону
поверхности тела [4]. Если цилиндрический заряд взрывается без
оболочки, то часть заряда будет охвачена боковой разгрузкой и не создаст
импульса а^я метаемого тела.
Согласно [4], аля открытого заряда диаметром d максимальная
длина конической активной части заряда составляет 1 = 2,25d.
Дальнейшее увеличение длины заряда не увеличивает импульс.
Заключение заряда в тяжелую оболочку ограничивает боковую
разгрузку, та растет, соответственно значительно возрастает и
удельный импульс (см. табл. 10.17).
Таблица 10.17. Влияние стальной оболочки толщиной 5 на удельный
импульс (J/J5=0)
Заряд 1/d = 2,5; р0 = 1,3 г/см3
Тротил
Гексоген флегматизированный
S/d = 0,257
3,12
2,24
a/d=0,119
2,19
1,56
В общей постановке задача о метании тел продуктами взрыва
является сложной трехмерной и нестационарной задачей. Однако
упрощенные одномерные модели удается легко рассчитывать.
Создаваемый при взрыве на поверхности тела (пластины,
оболочки) импульс позволяет метать тело. При этом мерой
совершенной кратковременной работы является приобретаемая телом
кинетическая энергия или его скорость при известной массе.
Таким образом, точное измерение скорости метаемого тела
является методикой определения бризантности мощных взрывчатых
составов или их метательной способности.
Для измерения скорости используют самые различные методы:
электроконтактный, оптический, рентгеноимпульсный, электромаг-
524
нитный. Обычно измеряют либо x,t — диаграмму разгона, либо
конечную скорость в конце разгона.
В общем случае метательная способность сложных взрывчатых
составов (особенно содержащих такие добавки, как алюминий)
зависит от масштаба опыта и от степени расширения продуктов взрыва.
Поэтому наиболее правильно определять метательную способность
в конкретных условиях применения ВВ.
Обычно определяют относительную метательную способность
данного ВВ, относительно какого-то ВВ, взятого за эталон.
Существуют следующие схемы метания (см. рис. 10.13).
1. Метание пластин или оболочек при инициировании заряда в
направлении к метаемой пластине так, что движение
детонационной волны совпадает с движением пластины.
2. Метание при инициировании заряда от пластины так, что
направления детонации и движения пластины противоположны.
3. Метание пластины скользящей детонационной волной.
4. Метание скользящей детонационной волной
цилиндрической оболочки (заряд внутри оболочки, детонация идет вдоль оси
цилиндра).
Рассмотрим кратко эти схемы.
НИН.
ZZZZZZZZ2
' /х/
N ьъ
£225*
EZ
г
N
N
К]
N
\
( il i
3
и
и
р)вв
W
\\
К1
И
И ! И
И |/|
\Л
\л
\л
И
И
И
Рис. 10.13. Схемы метания продуктами взрыва
10.9.1. Метание пластин
Эту задачу решили в 1951 году независимо Е.И. Забабахин [28]
и К.П. Станюкович [4].
Для разгона несжимаемой пластины (если пластина тонкая, то ее
сжимаемостью можно пренебречь) открытым зарядом с d -> <х> (без
учета боковой разгрузки) и кубического уравнения состояния
продуктов взрыва получено следующее выражение аая максимальной
скорости пластины wm [28]:
27 п 16 ,
= (1 +—к-
\вк 27
\ + —k)D
(10.20)
rAek=mBB/MnA=pBBhBB/(pnAhJ.
В зависимости от длины разгона х скорость пластины равна:
u*=T-[-rHl+ir)2z]
I^BB I^BB "'ВВ
(10.21)
где z = (16/27) k.
Часто необходимо выбрать такую массу (толщину) метаемой
пластины, чтобы ее энергия была максимальна, т.е. решить задачу о
к.п.д. метания.
Полная тепловая энергия заряда Е = mBB Q= mBBD2/16, а
кинетическая энергия пластины Е = Мпл wm2/2. Отсюда:
72
Еш kyDJ Ъ2къ
/1 167 1 32/Л2
(1 +—к-А\ + —к)2
27 V 27
(10.22)
Зависимость у) (к) показана на рис. 10.14 [28].
Функция (10.22) имеет максимум при к = 2,53, при этом:
г) = (16/27) «0,35 и wm/D = l/3.
Для несжимаемой
пластины набор скорости
происходит плавно, а ^ая
сжимаемой пластины ее
поверхности набирают
скорость скачками (рис.
10.15 [4]),
соответствующим циркуляции ударных
волн и волн разрежения
по пластине.
nji |
1
i
/
/
1
Рис. 10.14. Зависимость к.п.д. заряда от
относительной массы метаемой пластины
526
Ц fcfrf/c
U^W^j
u ~
—'L^r—
L I
5 Xcm
3 i икс
Рис. 10.15. Скачкообразное изменение скорости
а) раздела ВВ — стальная пластина (hBB=50,8 мм, h = 5,08 мм, ТГ 36/64);
б) свободной поверхности стальной пластины (hfiB=48,3 мм, h=2,8 мм, ТГ 36/64).
разгон несжимаемой пластины
Как известно, при взаимодействии волн разрежения в пластине
возникают растягивающие напряжения, которые при относительно
толстой пластине и тонком ВВ могут превзойти предел прочности,
и тогда произойдет откол.
Согласно расчету, растягивающие напряжения а при
циркуляции волн затухают медленно. Например, а^я условий рис. 10.156)
в первой волне <7=94 кбар, а в восьмой волне с=78 кбар.
Отметим, что если в толще пластины образовалась откольная
трещина, то она сначала расширяется, а затем обе части пластины
схлопываются.
При первом отражении УВ от свободной поверхности пластины
ее энергия составляет 40% полной кинетической энергии,
получаемой в конце разгона, а после третьего отражения — 80%. При этом
после третьего отражения пластина проходит расстояние, равное
двум толщинам заряда.
10.9.2. Метание сферической оболочки
На рис. 10.16 показаны результаты проведенных автором
измерений скорости внутренней поверхности стальных сферических
оболочек трех различных толщин, разгоняемых сферическим
зарядом, в котором создается сферически сходящаяся детонационная
волна.
Измерения проводились электроконтактной методикой с
использованием спиральных датчиков [29] и оптической методикой с
помощью полистирольных оптических нитей [30,31].
«м/с
X
Л*Ъ«*
^W~
' f-СЛМр. ДАТСКИ
: ф-отгич. нити
t^T^JYh^
-/
£»(Омм
60
70
20 30 40 SO ьо yo г 14И
Рис. 10.16. Измерения динамики разгона внутренней поверхности стальных
оболочек различной толщины
Заряд из ТГ 30/70 толщиной 45 мм
Как видно из рис. 10.15, с увеличением толщины пластины или
оболочки сильнее проявляется скачкообразный характер
разгона. Оболочки толщиной 8 и 10 мм испытывают откол (скорость с
уменьшением радиуса не растет), который затем смыкается.
По характеру движения траекторию метаемых пластин и
оболочек можно разделить на два участка: разгонный и инерционный.
На инерционном участке скорость пластины постоянна, а скорость
сферически сходящейся оболочки растет по закону и=А г"а [28].
При этом на скорость оболочки сильнее влияют потери
энергии, связанные с ее пластической деформацией (или с вязким
течением).
10.93. Метание при инициировании заряда от пластины
В этом случае детонация идет от пластины, давление на пластину
уменьшается вдвое, разгон становится более мягким, «безнагрев-
ным». Давление на пластину удерживается до прихода волны
разрежения от открытого торца заряда.
Если торец закрыть массивной крышкой, то на пластину придет
ударная волна, и скорость пластины возрастет.
При реализации такого способа метания обычно заряд
заключают в тяжелую оболочку, чтобы задержать боковую и заднюю
разгрузку. Заряд инициируется от пластины относительно тонким
многоточечным устройством [32,33].
528
Независимо от состава ВВ и толщины пластины, предельная
длина открытого заряда (выше которой скорость пластины не
растет) составляет 1 = 0,65 d [33].
' max L J
По сравнению с обычным разгоном относительно тонких
пластин этот способ проигрывает по скорости пластины [34], но зато
позволяет без откола разгонять толстые пластины (например,
толщиной более 30 мм).
10.9.4. Метание цилиндрической оболочки
Для определения относительной метательной способности
мощных индивидуальных ВВ и взрывчатых составов широко
используется т.н. «цилиндр — тест», суть которого в измерении скорости
разгона медной трубки взрывом заряда внутри трубки [35]. Измерения
обычно проводят с помощью фоторегистратора в направлении
перпендикулярном оси трубки и на расстоянии, равном 7 диаметрам
трубки от места инициирования заряда на торце трубки.
Медная трубка не разрушается вплоть до радиуса R/RQ = 2,24.
Максимальная скорость трубки достигается при расширении
продуктов взрыва в 7 раз. 75% кинетической энергии трубка
приобретает на расстоянии R ~1,33 R0 и 90% — на расстоянии R ~2 RQ.
Величины у] = ( WDD/W ) относительной метательной способ-
I ч ВВ этал '
ности зависят от расстояния или от степени расширения продуктов
взрыва: на малых расстояниях различия между ВВ больше, чем на
больших (см. табл. 10.18 и 10.19 [1,36,37]).
Таблица 10.18. Результаты «цилиндр — теста» для ряда ВВ
ВВ
Октоген
Тротил
ТЭН
ТАТБ
ТГ 36/64
ТЭН/ТНТ 50/50
Р0> г/см3
1,891
1,63
1,765
1,854
1,717
1,700
W, км/с
R =6мм
1,69
1,23
1,60
1,32
1,44
1,39
W2, км/с
R=20mm
1,87
1,41
1,79
1,47
1,64
1,59
i,=(W1
/W*)2
1,00
0,530
0,896
0,610
0,726
0,676
1 =
(w2/w*)2
1,00
0,569
0,916
0,618
0,769
0,723
w* — скорости для октогена как эталона.
Таблица 10.19. Относительная метательная способность некоторых
мощных взрывчатых составов (эталон — Сотр. В)
Индекс
TNT
Сотр. В
Cyclotol
РВХ — 9010
LX —04—1
X —0204
Octol
РВХ-9404-03
НМХ
Состав
Тротил
ТГ 36/64
ТГ 23/77
RDX — Kdf (90/10)
НМХ —Viton (85/15)
НМХ-Teflon (83/17)
НМХ —TNT (72/22)
HMX-NC-CEF (94/3/3)
Октоген
р0, г/см3
1,63
1,717
1,754
1,787
1,865
1,911
1,821
1,841
1,891
Г|ДЛЯ
R=5mm
0,72
1,00
1,10
1,09
1,14
1,16
1,21
1,28
1,41
г) Для
R=19mm
0,76
1,00
1,09
1,10
1,10
1,11
1,15
1,22
1,30
В отличие от метания пластины, на разгон оболочки
затрачивается гораздо больше энергии взрыва — 60—75%, т.е. к.п.д. заряда,
заключенного в оболочку, выше к.п.д. открытого заряда, что очевидно.
В табл. 10.18 приведены экспериментальные значения скоростей
разлета медной оболочки на базе R=6 мм и К=20 мм [36,37], а
также значения относительной метательной способности ВВ
относительно октогена, взятого за эталон.
Таблица 10.20.Относительная метательная способность ряда ВВ при
7-кратном расширении ПВ (эталон — тротил) [35]
ВВ
Тротил
Нитрометан
ХТХ-8003
ТАТБ
ТГ40/60
ТЭН
Октоген/ТНТ 78/22
Октоген
Гексоген
БТФ
р0> г/см3
1,60
1,14
1,554
1,854
1,728
1,765
1,813
1,894
1,80
1,859
1
1,0
1,120
1,265
1,349
1,492
1,629
1,606
1,715
1,641
1,682
530
В табл. 10.19 [4] приведены экспериментальные величины
относительной метательной способности у) некоторых мощных
взрывчатых составов (за эталон взят ТГ 36/64), найденные по скоростям
оболочки при R= 5 мм и R= 19 мм.
В таблице 10.20 [35] даны значения у] а^я ряда ВВ при 7-кратном
расширении ПВ (за эталон взят ТНТ).
10.9.5. Метание скользящей детонацией
Такое метание слоями ВВ широко применяется при сварке взрывом,
при обработке металла взрывом, в металлических взрывных линзах, в
измерениях динамической прочности и в других экспериментах.
Скорость метаемой пластины связана со скоростью детонации
D и углом разворота пластины 9 при ее разгоне следующим
соотношением:
w = 2Dsm0/2 (10.23)
или аля малых углов w=D 9.
Вместо экспериментальных D и 9 часто используют их
численные оценки, из которых распространены следующие две:
1). Формула Гарни [38,39] для максимальной скорости
пластины, полученная в приближении мгновенного взрыва:
*,=>/26 ,2к^ (Ю.24)
где к=твв/Мпл=рвв Ьвв/(Рпл h^ ); Q — теплота взрыва единицы
массы ВВ, которая оценивается выражением: Q = D2/[ 2 (п — 1)].
2). Уравнение аля угла разворота пластины, полученное на
основе сравнения двумерных расчетов с экспериментом [40]
£ + 2,71 + 0,184/;/* (10'25)
где п — интегральный показатель политропы ПВ (п=1,75—2,5);
y*=y/hBB , ay — расстояние, пройденное пластиной перпендикулярно
ее поверхности.
Часто &ая оценки wmax малым членом 0,184/у* в (10.25)
пренебрегают.
Для расчета угла поворота сжимаемой пластины надо учитывать
начальный угол поворота 90, обусловленный сжимаемостью, и
максимальный угол поворота 9^ , на который поворачивается пластина
при метании данным зарядом [41]:
0o=2arcsin(w/£>) (10.26)
где и определяется по р,и — диаграмме материала пластины.
0да = 2arcsin(w/ 2D) (10.27)
Экспериментально измеренное в [41 ] изменение угла поворота в
процессе разгона пластины хорошо описывается формулой:
0(Л = 0о+(0оо-0о)[1-ехр(-2/)
(10.28)
В.И. Шутовым, А.В. Губачевым и В.А. Вакиным в 1971 году
найдено следующее эмпирическое выражение &ая максимальной
скорости пластины, разгоняемой тонким слоем ВВ:
Рвв"вв
Эта зависимость показана на рис. 10.17.
(10.29)
i»«*.
км/с
2
0.5
.P«/.fi
пп
& ifi fee" h
ее
Рис. 10.17. Зависимость скорости пластины от ее массы относительно массы ВВ
532
На скорость пластины влияет наличие корпуса, закрывающего
слой ВВ. Это влияние сказывается только при относительной массе
пластины к < 3,2, причем влияние корпуса линейно уменьшается с
уменьшением массы корпуса в области т* = Мко п/тпл < 0,9.
Для слоя флегматизированного ТЭНа максимальный отбор
энергии Епл/ Евв « 0,38 наблюдается при к = 2 без корпуса и E^/Egg «
0,48 при к= 1 с корпусом. Эти данные полезны ^ая отработки
плоских металлических линз.
10.9.6. Влияние на метание неидеальности детонации заряда
I. Метание скользящей детонацией.
Рассмотрим влияние на скорость пластины неидеальности
детонации зарядов ВВ с толщиной меньше предельной [42].
Здесь действуют следующие два фактора:
1). Известно, что показатель политропы п растет с уменьшением
D в области dK < d < dn [43]. Поэтому согласно (10.25) угол 9
растет, и согласно (10.23) растет скорость пластины. Для согласования
расчета с экспериментом величина п должна уменьшиться с 2,5 до
1,75. Физическое объяснение этому — рост зоны химреакции, что
увеличивает время и импульс давления ПВ на пластину.
2). Рост неидеальности детонации при уменьшении толщины
заряда приводит к увеличению кривизны детонационного фронта.
При этом уменьшается угол падения детонации к пластине,
появляется нормальная составляющая в косой ударной волне в пластине.
Поэтому скорость пластины растет, несмотря на падение
параметров детонации.
Экспериментально зафиксированное аномальное влияние на
скорость пластины неидеальности детонации слоя насыпного гексо-
гена толщиной 1,6 мм иллюстрируется рис. 10.18 [42].
II. Метание пластины расходящейся детонационной волной.
При инициировании заряда одиночным инициатором степень
неидеальности детонации зависит от размеров, массы и мощности
состава инициатора.
Нами проведена серия опытов по определению метательной
способности трех мощных взрывчатых составов на основе гексогена
533
и октогена относительно
флегматизированного ТЭНа, который
взят за эталон, поскольку он
детонирует идеально со всеми
использованными в опытах
инициаторами.
Часть полученных результа-
/ тов приведена в [44 J и в разде-
Рис. 10.18. Экспериментальная и ле 8 7
расчетная зависимости скорости ила- " '
станы от ее относительной массы & опытах использовались:
1—медь; 2 —дюраль; 3 —расчет по — заряды 0 60 хЮ мм из четырех
(10.19) и по (10.21) для D = 5,65 км/с г *«" г^
и п=2 8 Г381 составов: флегматизированныи
ТЭН (эталон), состав I (70% гексо-
гена, 30% связки на основе
тротила), состав II (90% октогена, 10% связки на основе тротила) и состав
III (92% октогена, 8% полимерной связки);
— цилиндрические инициаторы о(2—16) мм, высотой 2—15 мм
из флегматизированного ТЭНа, состава III, а также
использовался электродетонатор АТЭД15, в котором инициатором был ТЭН
(р0 =1,6 г/см3) диаметром 9 мм
Плотность всех зарядов составляла 0,99—0,995 максимальной.
В опытах с помощью фотохронографа СФР-2М измерялась
средняя скорость w стальной пластины толщиной 1 мм на базе полета
10 мм.
Относительная метательная способность определялась как
у] = (w./wT3H)2 в двух опытах с одинаковым инициатором, но с
зарядами из исследуемого состава и из эталонного флегматизированного
ТЭНа.
Таким образом, влияние на скорость пластины массы
инициатора и начальной кривизны ИУВ, входящей в заряд, в обоих
сравниваемых опытах были одинаковы. Опыты отличались мощностью
составов и степенью неидеальности их детонации.
Полученные результаты приведены в табл. 10.21.
534
Таблица 10.21. Влияние инициаторов на относительную метательную
способность
Инициатор
Флегматиз.
ТЭН, мм
о2х10
оЗхЮ
04x10
05x10
06x10
07x10
08x10
09x10
0 10x10
012x10
0 16x7
Состав III
05x2
05x3
о5х4
о5х8
05x11
ЭДАТЭД15
(ТЭН о9мм)
Состав I
W/WT3H
-
-
1,71/1,62
1,76/1,62
1,81/1,68
1,866/1,68
1,91/1,75
1,94/1,77
1,972/1,81
1,95/1,72
1,84/1,65
1i
-
-
1,114
1,170
1,148
1,241
1,191
1,201
1,187
1,285
1,243
Состав II
WII/WT3H
1,795/1,525
1,795/1,55
1,886/1,62
1,925/1,62
2,0/1,68
-
2,05/1,75
2,11/1,77
2,19/1,81
2,23/1,87
1„
1,385
1,341
1,355
1,412
1,417
-
1,372
1,421
1,464
1,422
Состав III
WIl/WT3H
1,785/1,525
1,855/1,55
1,876/1,58
1,94/1,62
1,99/1,68
2,0/1,675
2,08/1,75
2,1/1,77
2,16/1,81
2,25/1,87
2,08/1,72
1,81/1,50
1,83/1,52
1,84/1,52
1,93/1,57
1,95/1,58
2,04/1,65
1ш
1,370
1,432
1,410
1,434
1,403
1,426
1,413
1,408
1,424
1,448
1,462
1,456
1,449
1,465
1,511
1,523
1,528
Из данных таблицы 10.21 видно влияние диаметра, высоты и
состава инициатора как на скорость пластины, так и на относительную
метательную способность состава.
Метательная способность состава III в среднем на 1—2% выше,
чем у состава II.
У менее чувствительного состава I влияние параметров
инициаторов более сильное за счет больших потерь от неидеальности
детонации со слабыми инициаторами. Поэтому метательная способ-
535
ность состава I относительно состава III колеблется от У] = 0,82—0,83
при инициировании слабыми инициаторами до п = 0,86—0,88 при
инициировании сильными инициаторами.
10.10. Основы техники безопасности при работе с
взрывчатыми материалами
10.10.1. Организация работ с ВМ
1. Организация работ с ВМ основывается на Кодексе о
труде, «Единых правилах безопасности при взрывных работах»,
ведомственных положениях и руководствах по ТБ. Кроме того,
вопросы ТБ отражаются в должностных инструкциях,
определяющих права, обязанности и ответственность работников данного
предприятия.
2. На предприятии с учетом его особенностей должен быть
составлен перечень видов опасных и особо опасных работ. К
категории особо опасных работ относятся такие работы, при выполнении
которых возможны аварийные ситуации с тяжелыми последствиями
не только а^я исполнителя, но и а^я окружающих лиц, не занятых
на этих работах. Таким образом, все работы с ВМ являются особо
опасными.
3. На каждый вид работ с ВМ составляется инструкция по
ТБ, отражающая специфику работ и действия в аварийных
ситуациях.
Выполняются работы с ВМ только по специальным нарядам или
заданиям особого образца в составе группы не менее двух человек.
При совместной работе двух и более групп назначается один
старший руководитель групп.
4. Все помещения, здания, оборудование, связанные с работой
с ВМ, должны быть в установленном порядке приняты в
эксплуатацию и иметь весь требуемый комплект документации: чертежи,
планы размещения оборудования, технические описания и
паспорта, инструкции по эксплуатации, акты испытания оборудования, акт
о приемке в эксплуатацию, приказ по предприятию о назначении
эксплуатационного персонала.
536
Здания, в которых проводятся работы с ВМ (или хранятся ВМ),
должны иметь средства пожаротушения, грозозащиту, контур
заземления вокруг здания, заземляющие шины в каждом помещении.
Между зданиями с ВМ должны соблюдаться безопасные
расстояния по разлету осколков (породы), по сейсмике и по воздушной
волне согласно «Инструкции по определению безопасных расстояний
при взрывныых работах и хранения ВМ» (см.»Единые правила»).
С целью сокращения безопасных расстояний здания могут
окружаться земляными валами.
10.10.2. Требования к персоналу
Все лица, обеспечивающие руководство и выполнение работ с
ВМ, должны быть назначены приказом по предприятию, пройти
обучение в объеме утвержденных программ и предварительную
проверку знаний по ТБ, должны проходить периодический инструктаж
по ТБ под роспись в журнале инструктажа.
К руководству взрывными работами допускаются лица с
высшим образованием или окончившие специальные учебные
заведения, дающие на это право. Руководители взрывных работ должны
проходить аттестацию не реже одного раза в три года.
Взрывные работы выполняются взрывниками, имеющими
«Единую книжку взрывника». Взрывники аттестуются
квалификационными комиссиями предприятия не реже одного раза в два
года.
В помощь взрывнику назначается помощник взрывника,
который может работать со средствами инициирования (СИ) только
совместно с взрывником или под его руководством и наблюдением.
К монтажным и вспомогательным работам с ВМ без права
работы с СИ допускаются лица, прошедшие обучение и инструктаж.
Весь персонал, работающий с ВМ, должен быть не моложе 18 лет
(взрывники — старше 19 лет) и должен проходить периодическое
медицинское освидетельствование.
Персонал должен уметь пользоваться первичными средствами
пожаротушения и оказывать первую помощь пострадавшим при
несчастном случае.
537
10.10.3. Гигиена труда и промсанитария
Все ВМ и продукты их взрыва — вредные. Поэтому а^я цеха,
участка, лаборатории, где ведутся работы с ВМ, возможно введение
санитарного паспорта (по решению руководства предприятия и
санэпидемстанции). В соответствии требованиям паспорта проводят
периодические замеры вредности, контроль вентиляции и другого
оборудования.
Работы с ВМ проводятся персоналом только в спецодежде и в
спецобуви, а в отдельных случаях с применением защитных средств
(например, респираторов). После окончания работ спецодежда
снимается и хранится в специальных помещениях.
Запрещается курить и принимать пищу на рабочих местах.
Администрация должна обеспечивать своевременное
прохождение персоналом обязательных предварительных и периодических
медицинских осмотров персонала.
В производственных помещениях должны быть медицинские
аптечки, укомплектованные необходимыми медикаментами.
10.10.4. Общие правила обращения с ВМ
При выполнении любых операций с ВМ должна
соблюдаться максимальная осторожность. Запрещается подвергать ударам,
толчкам, бросать, волочить, перекатывать изделия с ВМ и тару
сВМ.
Запрещается при всех работах с ВМ курить и проводить работы
ближе ста метров от открытого огня, иметь при себе огнестрельное
оружие, спички и другие курительные принадлежности (кроме
случая огневого взрывания).
Запрещается проводить доработку зарядов ВВ при монтаже
экспериментальных узлов и сборок (кроме пластичных составов).
Применяемый инструмент должен быть изготовлен из
омедненной стали или из цветного металла, не дающего искр
(измерительный инструмент может быть стальным).
Заряды ВВ и другие изделия из ВМ должны переноситься только
в специальной таре (ящик, сумка) или перевозиться на специальной
ручной тележке.
538
10.10.5. Транспортировка ВМ
Транспортировка ВМ железнодорожным и водным транспортом
производится согласно «Правилам перевозки по железным
дорогам и водным путям сообщения боеприпасов, взрывчатых и
сильнодействующих ядовитых веществ» (см. также Transport of Dangerous
Goods, United Nations, New York, 1970), «Инструкции по
транспортированию ВМ» (см.приложение 5 к «Единым правилам—»),
а также согласно ведомственным инструкциям.
Разрешается перевозка до 5 кг ВМ в пассажирском поезде,
обязательно в отдельном купе группой не менее двух человек
(ответственный за перевозку и вооруженная охрана).
Запрещается перевозка ВМ вместе с другими грузами в одном
транспортном средстве (за исключением взрывных машинок и
легкого инструмента).
Погрузка и выгрузка должны выполняться на специальных
огороженных и охраняемых площадках.
Запрещается перевозка ВМ в общественном транспорте (метро,
троллейбус, трамвай, автобус, такси), в самосвалах, а также на
личных автомашинах.
Для перевозки ВМ автотранспортом используются только
специально оборудованные а^я этих целей автомобили, отвечающие
«Правилам перевозки взрывчатых материалов автомобильным
транспортом».
Перевозка осуществляется только по установленному маршруту,
при строгом соблюдении Правил дорожного движения со
скоростью, обеспечивающей полную безопасность движения.
В перевозке автотранспортом участвуют: ответственный за
перевозку, водитель и вооруженная охрана (размещается в кузове). При
перевозке автоколонной ответственный находится в передней машине,
а в кузове последней машины — один из вооруженных охранников.
В процессе транспортировки персоналу запрещается: курить,
отлучаться от машины с ВМ, останавливаться без надобности,
отвлекаться посторонними делами, перетаривать груз.
При доставке ВМ со склада к месту работы разрешается
совместная перевозка ВВ и СИ с размещением СИ в передней части авто-
539
мобиля в специальных плотно закрывающихся ящиках с мягкими
прокладками внутри.
Доставка ВВ и СИ (раздельно) к месту взрывания может
производиться вручную в специальной таре. При совместной переноске ВВ и
СИ взрывник может переносить не более 12 кг, а ВВ без Си — 24 кг.
10.10.6. Учет и хранение ВМ
Учет и хранение ВМ производится согласно «Инструкции о
порядке хранения, транспортирования, использования и учета
взрывчатых материалов», «Инструкции по устройству и эксплуатации
складов ВМ» (см.приложения к «Единым правилам»).
Контроль за соблюдением этой инструкции осуществляют
органы госгортехнадзора и органы внутренних дел.
ВМ хранятся в таре на специальных охраняемых складах —
базисных или расходных, стационарных или временных. По своему
устройству склады могут быть поверхностные, углубленные или
подземные.
Организация хранения должна исключать утрату или порчу ВМ.
В научных и учебных организациях ВМ могут храниться в
специальных сейфах. Каждый склад ВМ должен иметь паспорт, в котором
указывается сколько и какого вида ВМ можно хранить на данном
складе.
Предприятие в лице завскладом ведет учет прихода и расхода
ВМ на складе в Книге учета прихода и расхода ВМ (форма N1) и в
Книге учета выдачи и возврата ВМ (форма N2).
Наряд — накладная (форма N3) выдается бухгалтерией
предприятия и служит а^я отпуска ВМ с одного склада на другой.
Наряд — путевка (форма N4) служит аая отпуска ВМ
взрывникам и подписывается руководителем взрывных работ.
На складе должны быть заверенные образцы подписей лиц,
имеющих право подписывать наряд — накладные и наряд — путевки.
Наряд — путевка является основанием ^^я записи выданных
ВМ в Книгу выдачи и возврата, а заполненная и подписанная после
окончания взрывных работ — для списания ВМ по Книге учета
прихода и расхода.
540
ВМ не выдаются взрывникам, не отчитавшимся в
израсходовании ранее полученных ВМ.
10.10.7. Общие правила ведения взрывных работ
Общие правила ведения взрывных работ определяются
«Едиными правилами».
Промышленные взрывные работы (на открытых и подземных
горных выработках, на строительстве, сейсморазведке и т.п.)
проводятся по проектам или паспортам, в которых указываются все
сведения по взрыванию: способы инициирования, расчеты
взрывных цепей, масса и вид взрываемых ВМ, определение опасной зоны,
меры ТБ, места укрытия персонала, оцепление и ограждение места
взрыва, предупредительные сигналы, связь и т.п.
При производстве взрывных работ обязательно подача
взрывником звуковых сигналов (сиреной), значение которых следующее:
1) Первый сигнал — «Предупредительный» (один
продолжительный). Подается перед заряжанием.
После окончания работ по заряжанию и удалению связанных с
этим лиц взрывники приступают к монтажу взрывной сети.
2) Второй сигнал — «Боевой» (два продолжительных).
После этого сигнала производится взрыв.
3) Третий сигнал — «Отбой» (три коротких). Означает
окончание взрывных работ.
Опытные, научно-исследовательские и контрольные работы с
ВМ проводятся только на специально оборудованных, огороженных
и охраняемых площадках, которые строятся по специальным
проектам с учетом требований ТБ и безопасных расстояний.
На площадках имеются прочные сооружения (казематы) ^\ая
размещения оборудования, аппаратуры и укрытия людей во время
взрыва.
Прибывающая на площадку группа сотрудников а^я ведения
взрывных работ регистрируется у диспетчера площадки и получает
разрешение на проведение работ у начальника площадки с отметкой
в письменном задании. Группу возглавляет руководитель взрывных
работ, имеющий «Книжку взрывника».
Все виды взрывных работ, проводимых на площадке, должны
иметь инструкции по ТБ, а общий порядок работы на площадке
определяется отдельной инструкцией.
На площадке имеется расходный склад, на котором взрывник
получает необходимые ВВ и СИ.
Подготовка изделий из ВМ и их монтаж без СИ проводится на
рабочем поле перед казематом или в специальных сооружениях.
Не допускается одновременная работа с ВВ и с СИ.
Звуковые сигналы подаются диспетчером площадки по
требованию взрывника (передаваемому по телефонной связи).
Перед установкой СИ взрывник запрашивает первый звуковой
сигнал, укрывает в каземате персонал, обесточивает всю аппаратуру,
закорачивает подрывную линию и вместе с помощником выходит на
поле для установки СИ.
После установки СИ запрашивается второй звуковой
сигнал. Время от второго сигнала до взрыва не должно превышать
10 минут. При задержке свыше 10 минут берется дополнительный
сигнал.
После взрыва разрешается выходить из каземата не ранее, чем
через 5 минут.
Особо опасными являются действия по ликвидации отказа,
которые специально подробно оговариваются инструкцией по ТБ.
Отходы и остатки ВМ уничтожаются (сжиганием или
взрыванием) в тот же день согласно специальной инструкции.
Неизрасходованные ВМ сдаются в тот же день на склад площадки.
Производство взрывных работ на площадке запрещается в
следующих случаях:
— при отсутствии санитарной машины,
— при возникновении пожара,
— при несчастном случае,
— во время грозы и сильного снегопада,
— при очень низких температурах (ниже 30 С),
— при неисправных звуковой и световой сигнализациях, а
также при нарушении телефонной связи.
542
Литература к главе 10
1. Андреев К.К., Беляев А.Ф. Теория взрывчатых веществ. М.:
1960.
2. Справочник по буровзрывным работам на карьерах. Киев,
Наукова думка, 1973.
3. Meyer R. Explosives. Volgar Chemie, 1981.
4. Баум Ф.А., Станюкович К.П., Шехтер Б.И. Физика взрыва. М.:
Из-во физ-мат. лит., 1975.
5. Davies P.J., Provatas A. Australian Government, Department of
Defence. Defence Science and Technology Organisation. Report
DSTO-TR-1904 (2007).
6. FedorofFB.T. Dictionary of Explosives, Ammunition and Weapons
(German Section), Picatinny Arsenal Technical Report 2510
(1958).
7. Jones W.T., Willy J. Explosive Composition. Патент
Великобритании N1,082,641 от 6 сент. 1967.
8. Gharia I.S., Kumar A.S., Raghavendra L.N. and Vadali S.R.
Propellants, Explosives, Pyrotechnics, 1996, 21, p.36—39.
9. Spero Nicolaides, Rodolf W. Velicky and H.William Voigt.
Propellants,Explosives, Pyrotechnics, 1991,16, p.299—304.
10. Харитон Ю.Б. Сборник по теории взрывчатых веществ,
Оборонгиз,1941.
11. Шведов К.К., Колдунов С.А. Горение и взрыв (сборник),
М.:Наука,1972, с.439—443.
12. Юхансон К., Персон П. Детонация взрывчатых веществ,
М.:Мир,1973,с.352.
13. Кобылкин И.Ф., Соловьев B.C. «Химическая физика
процессов горения и взрыва», Детонация и ударные волны,
Материалы VIII Всес. симпозиума по горению и взрыву,
Черноголовка, 1986,с.72.
14. Кобылкин И.Ф.,Соловьев В.С.,Бойко М.М. ФГВД983, №4,
с.120.
15. Балаганский И.А., Кобылкин И.Ф., Разоренов СВ.,
Соловьев B.C., Уткин А.В. V Всес. совещание по детонации,
Красноярск, 1991, сб. докладов, т.2, с.345—350.
16. Edex G., Belcher R.A. The Ninth Symp.Qnt.) on Detonation,
1989, vl,p.322—330.
17. Элиэбарашвили Т.Ш. IV Всес. совещание по детонации,
Телави, 1988, сб. докладов,т.1,с.148—153.
18. Физика взрыва в 2х томах под ред.Л. П. Орленко. М.,
Физматлит, 2002
19. Афанасьев Г.Т., Бедов В.И., Сергиенко О.И. ФГВД981, №17,
С.158..159.
20. Кукиб Б.Н., Лавров В.В., Шведов К.К. IV Всес. совещание по
детонации, Телави, 1988, сб.докладов, т.П, с.40—46.
21. Whelan D.I., Bocksteiner G. J. of Energetic Materials,1995, V.13,
p.15.34
22. Eyring H., Powell R.E., Duffey G.H., Darlin R.B. Chem.Rev.,
1949,45, p. 65-181.
23. Spero Nicolaides, Rodolf W. Velicky and H.William Voigt
Propellants,Explosives, Pyrotechnics, 1991,16,p.299—304.
24. Соловьёв B.C. ФГВ, 2000, №6, с 65 — 76.
25. Василенко В.Г., Ковтун А.Д., Макаров Ю.М., Фомичева Л.В.
и др. V Всес. совещание по детонации, Красноярск, 1991, сб.
докладов, т.2, с.351.
26. Zuchenko VS., Shikunov N.V «»Shock waves in condensed
matter.», St-Peterburg, Russia, 1994, abstracts, p. 18.
27. Струков Г.В., Еременко Л.Т., Дубнов Л.В. и др. «Химическая
физика процессов горения и взрыва», Детонация (сборник),
Черноголовка, 1980, с.24—27.
28. Забабахин Е.И., Забабахин И.Е. Явления неограниченной
кумуляции. М.: Наука, 1988.
29. Куракин Н.И., Даниленко В.В., Козерук Н.П. ФГВ, 1989, №5,
с. 89.
30. Kozeruk N.P., Danilenko V.V., Telichko J.V. Optical Fiber Ganges
for Gas-Dynamic Investigations, 20-th Congress on High-Speed
Photography and Photonics, Victoria, 1992,SPIE Vol.1801,
p.138—146.
31. Kozeruk N.P., Danilenko V.V. et.al. Multichannel Optical Fiber
System to Measure Time Intervals at Investigations of Explosive
544
Phenomena, 20-th Congress on High-Speed Photography and
Photonics, Victoria,1992,SPIEVol.l801, p.981—988.
32.. Патент США N3430563, кл. 102-22, публикация 1969.
33. Лебедев М.А. ФГВ, 1989, №2, с.140—142.
34. Иванов А.Г., Кариенко ГЛ. ФГВ, 1980.N2, с.84.
35. Методы исследования свойств материалов при
интенсивных динамических нагрузках. Монография под общей ред.
М.В. Жерноклетова. РФЯЦ-ВНИИЭФ,Саров,2003,402 с.
36. Short J.M., Helm F.H., Figner М. et al. Comb. Flame, 1981,
43,1,99.
37. Kamlet M.J., Short J.M., Figner M. et al. Comb. Flame, 1983, 51,
3,325.
38. Дерибас A.A. Физика упрочнения и сварка взрывом,» Наука»,
Новосибирск, 1972.
39. DeCarli P.S., Megers М.А. Shock waves and High-Strain-Rate
Phenomena in Metals, Plenum Press., N-Y.,1981, p.34l— 373.
40. Кузьмин Г.Е. Динамика сплошной среды, Новосибирск,
1977,вып.29,с.137—142.
41. Киселев В.В. ФГВ, 1995.N1, с.138—142.
42. Пырьев В.А., Соловьев B.C. ФГВ, 1992, N6, с. 112.
43. Дремин А.Н., Савров С.Д., Трофимов B.C., Шведов К.К.
Детонационные волны в конденсированных средах, М.:
Наука, 1970.
44. Даниленко В.В., Пачурин Ю.М. ФГВ, 1987, N1, с.46.
545
Глава одиннадцатая
СРЕДСТВА ВЗРЫВАНИЯ И ИНИЦИИРУЮЩИЕ
УСТРОЙСТВА
11.1. Способы взрывания
Способы взрывания можно классифицировать по трем признакам:
— по применяемым средствам взрывания;
— по последовательности взрывания зарядов;
— по характеру инициирования поверхности заряда.
I. Классификация способов взрывания зарядов по применяемым
средствам взрывания приведены в табл.11.1 [1].
Таблица 11.1. Классификация способов взрывания зарядов
Название
Огневой
Электроогневой
Электрический
Инициирование
детонирующим шнуром
Особенности способа
Взрыв от капсюля-детонатора
(КД), который инициируется
искрой от огнепроводного
шнура (ОШ)
Как в огневом способе, но
ОШ поджигается патроном
с порохом от электрического
тока
Взрыв от электродетонатора
(ЭД)
Взрыв заряда от ДШ, который
инициируется КД или ЭД
Средства взрывания
КД, ОШ и средства
зажигания ОШ
КД, ОШ, зажигательный
патрон с электрозапалом
Электродетонаторы.кабели,
провода, взрывные
электромашинки-источники
тока, контрольно-
измерительные приборы
ДШ, КД или ЭД и средства
их инициирования
546
1. Огневой способ хорош своей простотой и низкой стоимостью (не
нужны источники тока, сети), но имеет недостатки: более опасен ^ая
взрывника при зажигании рядом с местом взрыва, низкая
производительность, невозможность контроля качества подготовки к взрыву,
невозможность взрывания одновременно большого количества зарядов.
Огневое взрывание применяется только /^ая вспомогательных
работ и в условиях, не опасных по газу и пыли. Для детонации
зарядов при огневом взрывании служит зажигательная трубка,
состоящая из КД и ОШ длиной не менее 1 м. Конец ОШ вводится в КД
и закрепляется в нем путем обжимания дульца КД специальными
щипцами, если капсюль металлический или с помощью изоленты,
если гильза К Д бумажная.
Если используются заряды из малочувствительных составов, то
для их взрывания применяют патроны-боевики: в патрон с ВВ
вводится КД зажигательной трубки и закрепляется.
Зажигательная трубка зажигается только с помощью
тлеющего фитиля, отрезком ОШ или зажигательным патроном. Спичкой
можно поджигать только одиночную трубку ^ая взрывания одного
заряда. Зажигательные патроны марки ЗП-5 позволяют
одновременно поджигать от 7 до 37 отрезков ОШ.
Для обеспечения безопасности взрывания огневым способом
применяют контрольную трубку, которая имеет ОШ на 60 см
короче, чем ОШ в зажигательных трубках, поджигается первой и ее
взрыв предупреждает взрывника о необходимости укрыться в
безопасном месте.
2. Электроогневое взрывание отличается от огневого только
применением электрозажигательных патронов типа ЭЗП-Б, которые
выпускаются пяти калибров диаметром от 18 до 41 мм, так что в них
можно поместить от 7 до 37 концов ОШ. Патроны ЭЗП-Б
поджигаются электрозапалом.
3. Электрический способ взрывания обеспечивает безопасность
взрывника, т.к. при подключении ЭД к цепи он находится в
укрытии, но имеет следующие недостатки:
— сложность выполнения электровзрывной сети;
— опасность при ликвидации отказов;
547
— опасность появления блуждающих токов в сети;
— высокая стоимость взрывания.
В этом способе источниками тока аля подрыва ЭД могут быть:
электроосветительные линии, взрывные машинки, батареи из
аккумуляторов или элементов.
Другое применяемое оборудование: линейный мостик а^я
измерения сопротивления ЭД и сети, щит с рубильником, вольтметр,
пульт ^ая испытания взрывных машинок.
При электрическом взрывании должны быть соблюдены
следующие условия:
— токи, проходящие через различные ЭД в сети, — близкие по
величине и не меньше гарантийного аая данного ЭД;
— импульс тока, поступающий в сети, — не меньше импульса,
необходимого аля воспламенения наименее чувствительного
детонатора;
— ЭД проверены и подобраны по сопротивлению;
— Электрозврывная сеть точно рассчитана, правильно
смонтирована и проверена.
Электровзрывная сеть — наиболее сложная и ответственная
часть схемы элктрического взрывания — состоит из ЭД, проводов
и источника тока.
Провода сети: питательные, магистральные, соединительные,
концевые, участковые. Согласно «Единым правилам» сечение
магистральных проводов должно быть не менее 0,75 мм2.
Для монтажа ЭД в цепь может применяться любая схема
соединения: последовательная, параллельная или смешанная.
Самая простая, легко рассчитываемая и контролируемая схема
последовательного соединения ЭД.
Недостатки схемы: невозможность использования большого
количества ЭД и массовый отказ при неисправности хотя бы одного ЭД.
При параллельной схеме различают параллельно- ступенчатое и
параллельно-пучковое присоединение ЭД к магистральным проводам.
Недостатки схемы: сложность схем и сложность их расчета,
большой расход проводов, требуется большой ток.
548
Смешанное соединение бывает параллельно-последовательное
и последовательно-параллельным (ЭД в группах соединены
параллельно, а группы — последовательно, и наоборот).
Важным этапом подготовки электрического взрывания является
проверка ЭД. Сопротивление мостика накаливания ЭД
проверяется на расходном складе или в специальном помещении с помощью
специального прибора — ЛМ-48, у которого строго ограничен ток
проверки ЭД.
ЭД с сопротивлением выше нормы подлежит отбору и
уничтожению.
Перед монтажом сети все провода проверяются на
проводимость и целостность изоляции.
Монтаж сети производят в направлении от зарядов к источнику
тока. Магистральные провода должны быть все время замкнуты
накоротко, и размыкаются они только после окончания монтажа при
присоединении к источнику тока.
После монтажа сети проверяется ее сопротивление. Расхождение
между расчетной и измеренной величинами сопротивления не
должно превышать 10%.
При соединении проводов сети применяют различного типа
сростки, которые затем изолируют изолентой.
II. По последовательности взрывания отдельных зарядов
возможны три способа взрывания:
— мгновенный, без регулируемых интервалов времени между
взрывом отдельных зарядов; используется ДШ или ЭД;
— короткозамедленный, с интервалами 10—15 мс;
используются ЭД короткозамедленного взрывания и пиротехнические
замедлители КЗДШ;
— замедленный — соседние заряды или группа зарядов
взрываются с интервалами 0,5—1 с с помощью ЭД замедленного
действия.
Многорядный короткозамедленный способ является самым
распространенным способом взрывания в промышленности и
строительстве как в подземных условиях, так и в карьерах.
III. Характер инициирования заряда.
549
Детонацию заряда можно инициировать в одной точке (КД,
ДШ, патроном-боевиком), по всей поверхности (взрывными
линзами) или одновременно во многих точках (специальными
многоточечными устройствами).
11.2. ОШиДШ
1. Огнепроводный шнур (ОШ) предназначен для передачи с
определенной скоростью (1 см/с) пучка искр капсюлю-детонатору.
ОШ состоит из слабо спрессованной сердцевины из зерен
дымного пороха (78% калиевой селитры, 12% серы и 10% древесного
угля), заключенной в три слоя хлопчатобумажной оплетки,
пропитанной водоизолирующей мастикой.
В зависимости от марки ОШ имеет наружную оболочку из
асфальта или полихлорвинила (марки ОЩ-А, ОШ-ДА, ОШ-П).
Выпускается ОШ диаметром 5—6 мм бухтами по 10 м.
Испытывают ОШ на скорость горения — фиксируют время
горения отрезков длиной 60 см, которое должно быть в пределах 60—69 с.
2. Детонирующий шнур (ДШ) предназначен а^я передачи
детонации от капсюля-детонатора к заряду ВВ. Имеет строение,
аналогичное ОШ, но в отличие от ОШ ДШ окрашен в красный цвет
и имеет сердцевину из высокобризантного ВВ (гексоген, ТЭН), со
скоростью детонации 7 км/с, выпускается бухтами по 50 м.
В России аая промышленных нужд выпускаются несколько марок
ДШ: ДШ-А, ДШ-Б, ДШ-В с погонным весом ВВ 12—13 г/м и
температурой применения от -35 С до +50С; термостойкие ДЩТ-165,
ДШТ-180 с сердцевиной из гексогена (14 г/м) и ДШТ-200 (до
200 С) с сердцевиной из октогена (14 г/м) с оплеткой из
стеклонитей и фторопласта. Для шахт, опасных по пыли и газу, выпускаются
предохранительные ДШП-1 и ДШП-2 с сердцевиной из ТЭНа с
пламягасителями (12 г/м).
В Европе выпускается специальный усиленный ДШ с навеской
40 и 100 г/м для инициирования малочувствительных игданитов
(ANFO). С другой стороны, в США производится ДШ только а^я
передачи детонационного импульса без инициирующей
способности. Такой ДШ содержит только 1 г/м ТЭНа в свинцовой оболочке
550
и известен под названием « mild detonating fuses». Другой ДШ,
содержащий 2 г/м ТЭНа, называется «Primadet» [2].
Аналогичные ДШ из пластифицированного высокодисперсного
ТЭНа в хлопчатобумажной или алюминиевой оболочке
разработаны и в России.
Такие ДШ имеют минимальный боковой разлет и могут быть
использованы в системах аварийной автоматики (сброс фонаря
самолета, разъединение частей ракеты и т.п.). Для усиления слабого
детонационного импульса на конце ДШ применяется усилитель —
концевик, снаряженный ТЭНом.
Для осуществления короткозамедленного взрывания зарядов
скважин с помощью ДШ применяют пиротехнические замедлители
КЗДШ, которые вставляются в магистральную линию ДШ между
соседними скважинами. Детонация левой вставки ДШ вызывает сначала
горение замедлителя, а затем взрыв КД и детонацию правой вставки
ДШ. В КЗДШ возможно замедление взрыва на 10,20,35 и 50 мс.
При необходимости взрыва с помощью ДШ нескольких
зарядов к магистральному ДШ плотно прикрепляют (узлом, примоткой
шпагатом) боковые ответвления ДШ. КД также прикрепляется к
ДШ с помощью шпагата.
Для надежности инициирования заряд обычно обвязывается
ДШ. При испытаниях ДШ должен подрывать стандартную шашку
из тротила весом 200 г.
Давно известен простой и надежный метод Дотриша для
измерения с помощью ДШ скорости детонации ВВ.
С 1972г. а^я передачи детонационного импульса получила
распространение ударно — волновая трубка (УТВ), которая
представляет собой полимерную трубку, на внутреннюю поверхность
которой нанесён тонкий слой ВВ в смеси с алюминиевой пудрой.
Содержание ВВ в УТВ минимально — 17 — 40 мг/м, скорость
детонации — 1.5—2 км/с. УТВ может инициироваться с помощью ЭД,
ДШ, капсюлем — воспламенителем, искровым разрядом.
С 1994г. в России начато производство инициирующих систем
«Эдилин», в состав которой, кроме УТВ, входят детонатор с
замедлением и устройства соединения и разводки УТВ. Соединители
УТВ бывают активные (с детонатором) и пассивные — а^я
соединения УТВ с ДШ.
11.3. Капсюли — детонаторы
КД любой конструкции, типа, марки представляет собой гильзу
(корпус), в которой, как правило, запрессованы две навески ВВ:
— заряд чувствительного к тепловому импульсу
инициирующего ВВ (гремучая ртуть, азид свинца);
— высокоплотный заряд вторичного ВВ (тетрил, гексоген,
ТЭН), который инициируется взрывом ИВВ и обеспечивает
высокую инициирующую способность КД.
В КД тепловой импульс создает пучок искр от горящего ОШ, а в
электродетонаторе (ЭД) — от нагретого током мостика, от мостика,
взорванного токовым импульсом или от электрической искры,
лазерным импульсом.
Классификация и основные параметры электродетонаторов
приведены в табл.11.2, а схемы конструкций ЭД показаны на рис. 11.1.
Из табл. 11.2 видно, что существуют ЭД « медленные»(время
действия миллисек. и сек.) и « быстрые» (время действия микро-
сек.), низковольтные и высоковольтные.
Все ЭД можно также разделить на два класса:
— относительно опасные в обращении ЭД с применением
чувствительных ИВВ (ЭД с низкой энергией подрыва);
— безопасные ЭД без применения ИВВ (ЭД с высокой
энергией подрыва).
ЭД с ИВВ требуют защиты от электростатических зарядов и
блуждающих токов. В ФРГ применяют более безопасные мостиковые ЭД,
т.н. « U» — детонаторы, аля инициирования которых требуется
увеличенный токовый импульс мощностью 16 mw и « HU» — деттонаторы
с требуемой мощностью импульса 2500 mw — [2].
Относительно опасные ЭД с низкой энергией подрыва (LEI)
должны выдерживать без подрыва два испытания: на чувствитель-
552
ность к электростатическим зарядам и на допустимый ток через
эд.
Таблица 11.2. Основные типы ЭД
NN
п.п.
I.
II.
III.
IV
V
Принцип
действия
Поджигание ВВ
Мостиком
накаливания
а) ЭД мгновен. дей
ствия (ЭД-8)
б)ЭД короткозамед
ленного действия
(ЭД-КЗ,ЭД-3-Н)
в) ЭД замедленного
действия (ЭД-ЗД)
Инициирование
детонации ВВ
взрывом мостика
Инициирование
детонации ВВ
электрической искрой
Инициирование
ударом пленки,
ускоряемой
взрывающейся фольгой
(Slapper detonator)
Инициирование
лазерным
импульсом
Состав ВВ
Навески:
1).Тетрила, гексо гена
илиТЭНа
2).Гремучей, ртути или
азида свинца
3). Мостиковый
электровоспламе
нитель
Для ЭД типов б) и в)
между
воспламенителем и гремучей ртутью
имеется замедлитель
из горючей смеси
Высокоплотный ВДТ
или гексоген,
пористые азид свинца или
ВДТ
То же, что для п.П.
Высокоплотные
мощные ВВ
Азид свинца, гексоген,
ТЭН
Время
действия
а) 2—Юме
6)15—1000 мс
в) 0,5—Юс
2—3 мке
2—3 мке (с
азидом свинца)
5—10 мке (с
ВДТ)
<2мкс
<2мкс
Ток
срабатывания при
групп,
подрыве, амп
Константано-
вый мостик 2
(2,5)
Нихромовый
мостик 1 (3,5)
-1000
-1000
-1000
Примечания: 1. ВДТ — высокодисперсный ТЭН (после
перекристаллизации, с частицами < 10 мкм); 2. В скобках указана
величина тока при использовании сети переменного тока.
553
а) б) в) г)
Д)
Рис. 11.1. Конструктивные схемы различныз типов ЭД
а) ЭД мгновенного действия (ЭД-8):1 — тетрил, ТЭН; 2 — гремучая ртуть;
3 — мостиковый электровоспламенитель.
б) ЭД короткозамедленного (ЭД-КЗ, ЭД-З-Н) и замедленного действия
(ЭД-ЗД):4 — замедлитель передачи теплового импульса из горючей смеси.
в) ЭД с взрывающимся мостиком с ИВВ: 1 — высокоплотный ВДТ;
2 — пористый ВДТ; 3 — азид свинца, г) ЭД с взрывающимся мостиком без ИВВ.
д) ЭД с инициированием ИВВ электрической искрой: 1 и 2 — ВДТ;
3 — азид свинца; 4 — боковые электроды.
е) ЭД с инициированием ВДТ электрической искрой (возможная конструкция):
1 — пористый ВДТ; 2 — плотный ВДТ.
ж) ЭД с взрывающейся фольгой (см. рис. 11.8): 1 — электроды; 2 — фольга;
3 — пленка; 4 — зазор; 5 — мощное ВВ.
з) Лазерный детонатор: 1 — световод; 2 — азид свинца; 3 — ТЭН или гексоген.
Для первого теста может использоваться модельная
электрическая схема (см. рис. 11.2), в которой электростатический заряд
распределяется между руками (0,1 мН, 10 pF, ПО ом) и остальной
частью тела (0,5 мН, 400 pF, 250 ом) [3].
Для второго теста ЭД должен выдерживать в течение 5 минут
1 а /1W и как минимум ток 0,25 а [3].
554
26 kv:
l400pF
10 pF
I
LEI
Рис. 11.2. Электрическая схема испытания ЭД
на чувствительность к электрическим зарядам
Безопасные ЭД без ИВВ
могут быть с традиционным
мостиком накаливания и
навеской воспламенительно-
го состава в толстостенном
стальном колпачке [ 1 ].
Наиболее безопасны
ЭД, в которых ВДТ
инициируется взрывом
мостика (фольги) при подаче на
него сильного импульса тока (такие ЭД не взрываются даже при их
подключении в сеть 220 в).
Искровые ЭД и ЭД с взрывающимся мостиком имеют очень
короткое время срабатывания (микросекунды), которое может быть
стабилизировано за счет высокой точности изготовления ЭД
(малые допуска на размеры и навески) и большой крутизны фронта
импульса тока.
Такие ЭД используются в экспериментах, где требуется высокая
степень синхронизации инициирования зарядов (в пределах
микросекунды) или поверхности одного заряда (например,
инициирование одновременно двух торцев цилиндрического заряда а^я
получения высоких давлений в зоне столкновения двух, идущих навстречу
ударных или детонационных волн).
Приведем некоторые технические характеристики наиболее
распространенных промышленных ЭД-8-Ж с мостиком накаливания
(индекс « Ж»означаетжесткое крепление мостика) [1]:
— диаметр и длина — 0 7,2x60 мм;
— время срабатывания — 2—10 мс;
— навеска ВВ — 1,02г тетрила и 0,5г гремучей ртути;
— электровоспламенитель — мостик накаливания из нихромо-
вой проволоки 0 30 + 2 мкм длиной от 2 до 5 мм, воспламени-
тельная головка твердая, двухслойная в виде капли из различных
легковоспламеняющихся составов: пикрат и пикроминат
свинца, бертолетовая соль и др.;
— выводные провода — стальная или медная одножильная
проволока диаметром 0,5 мм и длиной 2; 2,5; 3; 3,5 или 4 м с
полихлорвиниловой изоляцией;
— сопротивление ЭД-8:
— с константановым мостиком — 0,65—2 ома,
— с нихромовым мостиком — 2—4,2 ома.
Характеристики по току.
Максимальный безопасный ток — верхний предел постоянного
тока, который независимо от времени действия не вызывает нагрева
мостика до температуры вспышки головки. Эта величина
характеризует устойчивость ЭД к блуждающим токам и определяет
допустимый ток в контрольно-измерительных приборах.
Хотя ЭД не взрываются от тока 0,18 а в течение 5 мин, в
измерительных приборах принята безопасная величина тока 0,05 а (чтобы
исключить возможное разложение воспламенительного состава).
Максимальный длительный воспламеняющий ток — нижний
предел тока, вызывающего вспышку головки.
Этот ток гарантирует надежное срабатывание одиночных ЭД
и групп ЭД, соединенных параллельно.
Минимальный длительный ток (без ограничения времени) а^я
ЭД с константановым мостиком — 0,6—0,725 а, а а^я ЭД с
нихромовым мостиком — 0,3 а.
Минимальный стомиллисекундный ток — это ток, при котором
воспламенение ЭД происходит в течение 100 тс. Этот ток
обеспечивает надежное воспламенение одиночных ЭД и равен для константа-
новых мостиков 0,75—0,9 а, а а^я нихромовых мостиков — 0,75 а.
Импульс воспламенения ЭД K=Jt (амперсекунд) позволяет по
заданной величине тока определить время воспламенения. Обратная
импульсу величина S = 1/К называется чувствительностью ЭД.
Для ЭД с константановым мостиком К= 17—40 ас, с
нихромовым мостиком — К = 0,6—30 а с.
Верхнего предела по току для ЭД не существует.
Для группового взрывания последовательно соединенных ЭД
важное значение имеет величина времени срабатывания Q—
времени горения состава до передачи горения ИВВ.
556
Должно выполняться условие: Qmin>(tmax_t min)> т-е- все ЭД
в цепи взорвутся, если минимальное время передачи Q^ будет не
менее разности между временем воспламенения наименее
чувствительного и наиболее чувствительного ЭД.
Для группового взрывания ЭД с константановыми мостиками
подбирают по сопротивлению так, чтобы разница не превышала 0,3 ома.
Проводят следующие виды испытаний ЭД:
1. Испытания на групповой подрыв (200 штук ЭД из партии
в 10 тыс. шт.).
2. Испытания на полноту детонации данных используемых
зарядов ВВ от ЭД.
3. Испытание инициирующей способности ЭД по пробою
свинцовой пластинки толщиной 5 мм.
Гарантийный срок хранения ЭД — 1,5 года. После этого срока
ЭД должны быть повторно испытаны на соответствие требованиям
ТУ или ГОСТа.
11.3.1. Высоковольтные (быстрые) детонаторы
Для подрыва таких детонаторов необходим специальный
высоковольтный генератор. Принципиальная электрическая схема
инициирования детонатора показана на рис. 11.3.
Основной частью генератора является малоиндуктивный
высоковольтный конденсатор 1 (0,1—1 mF, 5—50 кв, 5—10 пН),
который заряжается высоковольтным источником постоянного тока 2
и разряжается на детонатор 3 при включении высоковольтного
разрядника (триггера) 4.
Получаемый таким образом импульс тока (0,5—1,5 кА)
передается к детонатору через коаксиальный кабель. Для нормальной
(синхронной) работы высоковольтных детонаторов очень важно
получение импульса с крутым передним фронтом, длительностью
0,1—1 мкс, что требует максимального снижения индуктивности
всей электрической схемы.
Триггеры могут быть различной конструкции. Например, в виде
разрядной трубки с электродами, зазор между которыми заполнен
сжатым воздухом, водородом, аргоном, SF6 или вакуумирован.
557
импульс
Рис. 11.3. Схема высоковольтного генератора для подрыва ЭД
Зазор пробивается при подаче на триггер низковольтного импульса
(200—300 в).
Триггер обеспечивает длительность переднего фронта импульса
тока 10—100 не и разброс времени срабатывания 20—40 не.
Возможны и другие варианты схемы. Например, в
фотохронографе СФР-2М высоковольтный импульс вырабатывается
импульсным трансформатором, первичная обмотка которого замыкается
обычным тиратроном на 400 в.
11.3.2. Искровые ЭД (рис. 11Лд)
Искровые ЭД наиболее простые по конструкции, но и наиболее
опасные, поэтому сейчас редко применяются даже в военных целях.
Два электрода, между которыми имеется искровой промежуток
(< 1мм) погружаются в пористый азид свинца (р « 3 г/см3). При
подаче на электроды высоковольтного импульса (обычно с энергией
10—100 мдж на один детонатор) между электродами возникает
искра, от энергии которой детонирует азид свинца. От азида свинца
детонация передается пористому ВДТ (р ~ 1,3 г/см3), а от него —
плотной навеске ВДТ (р« 1,6 г/см3). Для увеличения безопасности
параллельно электродам может быть установлено сопротивление.
Процесс искрового инициирования конденсированных ВВ
исследован в работах [4,5,6,7] и др.
В [5,6] исследовано электроискровое инициирование (и =10—
150кв) чувствительных жидких ВВ: растворы нитросоединений в
высококонцентрированной азотной кислоте, растворы
нитробензола (горючее) в тетранитрометане (окислитель) Прозрачность этих
558
растворов позволило использовать оптический метод измерений
с помощью электронно-оптического хронографа ФЭР-1.
Для искрового разряда характерны малые размеры, быстрое
выделение энергии и высокая ее плотность. При искровом пробое
детонация возбуждается за счет создания ударной волны и
сильного разогрева ВВ. Пробой происходит не мгновенно. Различают три
стадии пробоя: скрытую (до появления свечения на электродах),
формирование и движение от электродов т.н. «лидеров», стадию
развития канала искры [8].
При зажигании разряда на одном из электродов в сторону другого
электрода начинает распространяться «лидер», за которым создается
плазменный шнур с высокой проводимостью и температурой.
Скорость отбора энергии максимальна в районе встречи двух
«лидеров» примерно в середине искрового промежутка. Поэтому в
этом месте и возникает чаще всего детонация. Скорость замыкания
электродов проводящим каналом превышает 200 км/с.
Поскольку детонация возникает в одной области, а
электрическая энергия затрачивается на нагрев, ионизацию и испарение ВВ
вдоль всего искрового промежутка, то отсюда следует, что
затраченная электрическая энергия значительно превышает энергию,
необходимую а^я возбуждения детонации.
Вероятность возникновения детонации f при прочих
неизменных условиях зависит только от напряжения Un между электродами
разрядника, причем эта зависимость подчиняется нормальному
закону (см. рис. 11.4а). Значение U50, соответствующее 50% взрывам,
является мерой чувствительности данного ВВ к искровому разряду.
При больших U детонация возникает сразу после пробоя (без
задержки) на оси искрового промежутка. Инициирующая
способность разрядников с электродами типа острие — острие слабо
зависит от расстояния 1 между электродами, заметно уменьшается только
при малых 1 (см. рис. 11.46). Рост U начинается при 1 ~ dK.
В [7] изучалась чувствительность октогена к искровому
разряду, т.е. определялась для различных условий минимальная
электрическая энергия искрового разряда Е50, в 50% случаев вызывающая
вспышку порошка октогена (навеска 6 mg).
559
б)
зо4
20
-40-
К
01
Ob
9
"■• г—
05 £; мм
Рис. 11.4. Зависимость вероятности детонации от напряжения
а) для раствора тетранитрометан — нитробензол с соотношением компонентов
76/24% (1=2мм).
б) Зависимость инициирующей способности разрядника от расстояния между
электродами для раствора динитробензола в азотной кислоте (44/56%).
т
1.0
0
EsoUl
-
i ■ i
©
г\...\
EsoUl
нмх.
@ EsoM
НМХ (1% graphite) л
1000
Получены
следующие результаты.
1. Добавление в
октоген 1% графита
снижает величину Е50 на
порядок (см. рис. 11.5а).
Сильное влияние
начальной проводимости
ВВ на
чувствительность к искровому
разряду отмечено и в [5].
2. Величина Е50
растет с увеличением
искрового
промежутка^, рис. 11. 5а).
3. С уменьшением
размера частиц октоге-
Рис. 11.5. а) Влияние на Е50 добавления 1% графита и на величина Е замет-
длины искрового промежуткаЪ) Зависимость Е50 HQ уменьшается (см.
от размера частиц октогена. с) Зависимость Е50 '
от размера частиц октогена+1% графита d) рис. 11.5Ь,с), и только
Изменение Е с энергией активации молекул ВВ для очень малых
частиц наблюдается рост
Е50 (по-видимому, из-за уменьшения газопроницаемости и размера
т
1.2
0.8
0.4
0
Е50(Л
.
"■
■ 1 i i I
<а>
•у^^
\ „1 г i .1 i i J
5 Ю
_L 10-3(103kJ'moq
Еа
Г
0.5
п
EsoM
-
-
©
_,_!.., . . 1
1000
d bim]
пор, менее критических).
560
4. Чувствительность к искре зависит от энергии активации Еа
молекулы ВВ следующим образом (см. рис. 11.5d): Е50 = 94,29/Еа + 0,51
(Е50 — в дж, а Еа — в килодж)
В [4] с помощью искрового разряда (с = 1 mF, U = 4—8,5 кв)
инициировалась нормальная детонация ВДТ с частицами d=10 мкм
и плотностью 1 г/см3. ВДТ был помещен в массивную
стальную оболочку (внутренний диаметр 3—6 мм и толщина стенок
А = 8—15 мм).
В этих условиях скоростное неустойчивое конвективное горение
(СКГ) переходит в нормальную детонацию на длине~25 мм. Это
объясняется тем, что увеличение поверхности горения и удержание
образующихся газов оболочкой увеличивает давление в ВДТ до
критического давления р*, при котором достигается ударноволновое
возбуждение детонации.
Согласно [9],
Р*~Ъ{рр)т1(сР1Ъг) (И-1)
где: D — скорость СКГ, t=2 A/D — время удержания давления р*
в оболочке.
11.3.3. Детонаторы с взрывающимся мостиком
Если в искровом детонаторе с ВДТ соединить электроды
микропроводом (Ni, Au, 0 20—30 мкм), то высоковольтный импульс с
крутым передним фронтом (длительностью 0,1—1 мкс) взорвет провод.
При взрыве образуется плазма, давление и температура которой
достаточны ^ая инициирования детонации ВДТ.
В результате получим «быстрый» детонатор с взрывающимся
мостиком (EBW). Как и ^ая искрового детонатора, здесь также
необходима большая скорость ввода энергии, т.е. минимальная
индуктивность цепи.
EBW был изобретен в Лос-Аламосе Луисом Альваресом и с
1968 года выпускается в США ^ая баллистических ракет (Polaris,
Poseidon и др.)
Для получения EBW с минимальным током срабатывания
необходимо использование в детонаторе ВДТ с оптимальными
плотностью и удельной поверхностью.
EBW и ВДТ &ая EBW выпускаются в США фирмой RISI и в
Англии фирмой Reynolds Industries.
Аналогичные безопасные мостиковые детонаторы с ВДТ были
разработаны и серийно изготовляются и в России.
Изменение величины тока и напряжения со временем при
взрыве EBW показано на рис. 11.6.
После замыкания цепи разряда конденсатора ток через мостик
(и вводимая энергия) быстро растет (более 1 кА/мкс), мостик
испаряется за время менее 1 мкс. При этом благодаря инерции объем пара
некоторое время остается
неизменным, равным
объему мостика.
Благодаря нагреву
сопротивление сильно
увеличивается, что вызывает
падение тока и пик напряжения
в момент tB. Затем пар
быстро расширяется и создает
в ВДТ ударную волну. Через
несколько наносекунд
возрастает степень ионизации
газа, сопротивление падает,
а ток растет. Как и в
искровом детонаторе, вводимая
энергия значительно
превышает величину, необходимую для инициирования ВДТ
Конструкция и размеры EBW могут сильно варьироваться, но
всегда мостик окружает ВДТ с~50% пористости, а на торце детонатора в
отдельном колпачке размещается навеска плотного ВДТ (р ~ 1,6 г /см3).
В 1995 году появилось сообщение о разработке фирмой Quantic
Industries различных конструкций мостикового детонатора, в
котором вместо проволоки используется кремний и полупроводниковые
технологии [10].
Кремневая плазма с температурой более 4000К образуется при
прохождении через слой кремния с сопротивлением ~ 1 ом импульса
КА
U
t м«с
to Ч t;
Рис. 11.6. Зависимость тока и напряжения
от времени
tQ — момент замыкания цепи триггером;
tB — момент взрыва мостика и создания
в ВДТ ударной волны, инициирующей
детонацию; t — момент выхода детонации
на торец детонатора; tt — tQ — время работы
детонатора
562
тока с максимальной амплитудой всего 10—20 ампер (аая EBW
требуется^ 1000 ампер).
11.3.4. Детонаторы с взрывающейся фольгой
Конструкция детонатора с взрывающейся фольгой (EFI)
отличается от EBW, была разработана в Lawrence Livermore Laboratory,
USA [11] и названа «slapper detonator».
Основные части детонатора показаны на рис. 11.7.
WWE КТО EXPLOSIVE RESULTING
*f DETONATION
Рис. 11.7. Схема детонатора с взрывающейся фольгой
На изоляционном диске с отверстием в центре расположена
прочная полимерная пленка (Карton, Mylar). На пленке лежит
тонкая металлическая фольга (может получаться напылением металла
на пленку). Фольга закрыта изоляционной крышкой. Под диском с
отверстием расположен заряд из вторичного ВВ с большой
плотностью (близкой к кристаллической).
При подаче высоковольтного импульса фольга взрывается,
образующаяся плазма разгоняет пленку в отверстии диска до скорости,
достаточной для инициирования заряда УВ при ударе пленки по
заряду.
Для нормальной работы EFI еще более ужесточаются
требования к скорости ввода энергии, т.е. к взрывной схеме.
По сравнению с EBW фольговый детонатор имеет ряд
преимуществ: металлический мостик полностью отделен от инициируемого
заряда ВВ, который имеет большую плотность и малую
чувствительность, может быть с полимерной связкой, т.е. EFI более безопасен;
имеет большую инициирующую способность; аая работы EFI
требуется меньшая энергия; большая стабильность и большие сроки
хранения; большая допустимая температура применения; простота
конструкции.
Благодаря этим качествам постепенно EFI вытесняет EBW в
арсеналах США.
11.3.5. Лазерные детонаторы
Лазерное инициирование ВВ — относительно новый способ и
представляет интерес как в научном, так и в технологическом плане.
Используется твердотельный лазер (обычно на неодимовом стекле с
\= 1,06 мкм) с диодной накачкой и с модулированием добротности
резонатора. Создаваемый лазером короткий (40 не) гигантский
импульс фокусируется на поверхности порошка ВВ через прозрачную
стеклянную или полимерную крышку толщиной 1 — 2 мм. Крышка
предохраняет ВВ от быстрой разгрузки и является обязательным
условием инициирования. В работах РФЯЦ—ВНИИТФ
исследовано взаимодействие света с ВВ и найдена пороговая энергия
инициирования [12]. Основные результаты следующие.
1. Пороговая энергия инициирования (50% вероятность
подрыва) ТЭНа растёт с увеличением длительности лазерного импульса
и практически не зависит от формы импульса и эффективного
диаметра d области облучения. Оптимальные параметры: плотность
ТЭНа — 0,8—1 г/см3, d = 0,2—0,5 мм, удельная поверхность
(дисперсность) — (1—2) 104 см2/г, пороговая энергия 20—40 мДж.
2. Толщина прозрачной крышки не влияет на пороговую
энергию в пределах от 1,7 мм до 0,1 мм, при меньших толщинах она
растёт. Без крышки не было инициирования при увеличении энергии
в 40 раз. Следовательно, инициируется тонкий слой ТЭНа, приле-
564
гающий к подложке. Применение оргстекла вместо стекла повышает
порог на 15—20%.
3. При замене ТЭНа на гексоген и тротил с частицами 0,05 мм
пороговая энергия возрастает на 19% и 33% соответственно.
4. Параметром, определяющим лазерное инициирование,
является не мощность, а плотность энергии в объёме инициирования.
Возможно использование следующих трёх видов лазерных
детонаторов.
1. В лазерных детонаторах (рис. 11.1з) короткий световой
импульс инициирует обычно азид свинца или ТЭНа, поверхность
которого закрыта прозрачной крышкой. Лазерный импульс передается
детонатору с помощью волоконного оптического кабеля, что
позволяет организовать систему с синхронным инициированием многих
детонаторов.
2. В лазерном детонаторе используется порошок гексогена с
удельной поверхностью не менее 104см2/г. Такой детонатор
устанавливается на заряд, взрываемый во взрывной камере аля синтеза
наноалмазов. Лазер находится вне камеры, и импульс передаётся по
воздуху через прозрачное окно в крышке камеры. Такое
инициирование обеспечивает не только безопасность работ, но «чистый»
синтез наноалмазов, без примесей металлов.
3. В лазерных детонаторах используется светочувствительный
перхлорат меди с полиазотистой гетероцикличной лигандой
торговой марки Purpald с химической формулой
Cu(C2 H3N6 S)2. Пороговая энергия 0,5 Дж/см2 (у гремучей
ртути 1 Дж /см2, у стифната свинца 0,4 Дж/см2) [13].
Лазерная система инициирования безопасна и помехоустойчива.
11.4. Взрывные линзы
Капсюли — детонаторы инициируют заряд практически в одной
точке и таким образом создают в заряде сферически
расходящуюся волну. Однако, а^я точных измерений давлений и скоростей во
взрывных экспериментах необходимо создание волн и других
геометрий: плоской, сферической или цилиндрической сходящейся.
565
Наиболее часто в опытах используются плоские
детонационные и ударные волны, которые формируются с помощью взрывных
линз.
Взрывные линзы — это устройства, где расходящаяся от КД
детонационная волна преобразуется в плоскую ударную волну,
которую используют а^я инициирования в примыкающем
заряде ВВ плоской детонационной волны, с помощью которой можно
разгонять пластины — ударники или получать плоскую УВ в
образце.
Взрывные линзы или генераторы плоской УВ представляют со-
а) б) б)
Рис. 11.8. Типы плоских взрывных линз
а) 1 — заряд ВВ; 2 — линза из боратола; б) 3 — линза из пенопласта или свинца;
в) металлическая линза, 4 — конический лайнер из AI, Fe, Си
бой цилиндрический заряд со скоростью детонации D. Заряд сверху
по оси инициируется КД, а снизу имеет профилированную выемку,
в которую устанавливается собственно линза (см. рис. 11.8).
Эта линза обычно может быть изготовлена либо из ВВ с малой
скоростью детонации (боратол), либо из инертного материала с
малой скоростью D ударной волны (пенопласт, свинец). Наконец,
выемка может быть облицована слоем металла (Al, Fe, Си), скорость
движения которого внутри полой выемки будет меньше скорости
детонации заряда.
Таким образом, условие работы первых двух линз: D2 < D , причем
в первом приближении собственно линзы имеют коническую форму.
Исходя из равенства времени выхода УВ из линзы по оси и на краю,
угол при вершине конуса линзы должен определяться условием:
cos/? = Z)2/A (П-2)
566
Однако, на практике, поскольку в линзу входит косая УВ с
переменным углом падения, линза не конус, а имеет более сложное
сечение.
Кроме одновременности выхода УВ на плоский торец линзы,
необходимо выполнить еще одно условие: амплитуда У В должна быть
достаточной ^^я инициирования основного заряда ВВ.
Это условие трудновыполнимо а^я центральной зоны инертных
линз, если отношение Ьвв/Ьд мало (линзы низкие), а основной заряд
ВВ малочувствителен.
В этом случае затухание УВ в линзе велико, и центральная зона
основного заряда либо не инициируется, либо инициируется с
большой глубиной задержки. Поэтому экспериментальную
отработку взрывных линз проводят обязательно вместе с основным
зарядом, но малой толщины (например, толщиной 10 мм), чтобы
точнее выявить влияние возможной задержки в инициировании на
разновременность плоской детонационной волны. Обычно у линз
h /h >5.
ВВ л
Приведем величины глубины задержки детонации Ьз в ТГ 30/70
от давления, создаваемым ударом алюминиевой пластины
толщиной 1 мм и 0,5 мм.
р.
кбар
h ,мм
3
t
55
7
= 1 мм
А1
70
4
85
3
105
2
Ь
120
1,5
75
8
d = 0,5 мм
95
2,5
115
1,7
140
0
Для давлений более 90 кбар глубина задержки практически
одинакова у всех мощных малопористых взрывчатых составов.
В линзе третьего типа (см. рис. 11.8в) металлический
лайнер метается зарядом ВВ, который обычно представляет собой
относительно тонкий слой ВВ в виде порошка или листа из
пластического состава. Условие работы этой линзы W < D , где W —
скорость лайнера, разгоняемого скользящей детонационной
волной.
Лайнер представляет собой конус с углом при основании:
0 = 2arcsin (11.3)
Очевидно, этот угол должен быть равен углу, на который
поворачивается пластина при ее разгоне скользящей детонацией (см. разд.
10.8.2).
Значение скорости лайнера W рассчитывается по формуле Гарни
(см. (10.20), (10.25)).
Трудность отработки металлической линзы тоже связана с
центральной зоной вблизи оси конуса, но тут сложности в том, что
конус должен в результате метания ПВ превратится в пластину,
одновременно подлетев к плоской поверхности заряда.
При этом поверхность металла уменьшается, появляется
«лишний» металл, который образует складки, волны вблизи центра, где
«лишнего»металла больше всего.
Чем выше конус (быстроходнее лайнер), тем труднее
отработать линзу. Обычно симметрия улучшается, если в вершине конуса
сделать отверстие которое будет заполняться «лишним»
металлом.
Например, ^ая металлической линзы с параметрами:
диаметр 80 мм, высота конуса 18 мм 9 = 21°40\ конус из алюминия
t = 0,3 мм, метание слоем флегматизированного ТЭНа (р = 1,5 г/см3,
D = 7,5 км/с) толщиной 2 мм, диаметр отверстия в вершине конуса
должен быть 5 мм, чтобы устранить асимметрию в центре линзы.
Достигаемая разновременность инициирования определяется
точностью изготовления линзы и растет пропорционально
диаметру линзы и базе полета лайнера (высоте конуса) или времени
работы линзы.
Металлические линзы дают худшую симметрию плоской УВ, чем
ударноволновые линзы, но имеют меньшую массу и высоту при
высокой инициирующей способности.
Если линзовая система используется /^ая определения
метательной способности ВВ, то надо иметь в виду, что сам этот эталон не
постоянен, т.к. любая реальная линзовая система имеет свой баланс
двух противоположных факторов, влияющих на метательную
способность заряда — увеличение энергии за счет массы системы (т.н.
568
w ,
км/с
28
;
26
I
2,2
20
епира/ibH. тг30 медь полимер
пластин.
ев
/
у/
У
>
\
г
-♦-"'
■"•^
,*.♦•**"
-*—«J
.••—•■
_«—
^-•-^~
•—•-
-—
»•——<•
t,
мм
10
го
so
40
50
Рис. 11.9. Скорость пластины при инициировании
заряда 0120x40 мм из ТГ 30/70 ударом медной фольги
«подпор») и потерь энергии за счет неидеальной детонации
заряда.
На рис. 11.9 приведены постановка и результаты опытов
(проведены автором совместно с Н.П.Козеруком), которые показали, что
при одновременном инициировании всей поверхности заряда его
метательная способность заметно меняется при изменении
скорости инициирующего удара медной фольгой. При « быстром»ударе
исчезают потери от НД и растет « подпор».
Инициированиее ударом медной фольги (0,3 мм)
Толщина заряда
на фольге, мм
7,5 (зависимость 1)
2,5 (зависимость 2)
а0
20
11
Wr , км/с
Си
2,9
1,6
l-(w2/w,)2
0,12
11.5. Многоточечные системы
11.5.1. Конструкция систем
Для зарядов большого диаметра линзовая система становится
очень массивной и её трудно отработать. В таких случаях детонация
заряда может быть инициирована одновременно во многих точках
поверхности заряда с помощью специального устройства,
запатентованного в США в 1969 году [14].
Устройство состоит из слоя инертного материала (как правило,
полимерного), в котором расположены пазы детонационной
разводки (параллельно поверхности заряда) и отверстия
(перпендикулярно поверхности заряда). Пазы и отверстия заполнены ВВ, как
правило, пластичным взрывчатым составом.
Прутки ВВ в пазах инициируются в одной общей точке капсюлем-
детонатором, и от этой точки до любого отверстия длины прутков
детонационной разводки одинаковы, что обеспечивает
одновременность инициирования прутков в отверстиях и, соответственно,
заряда в точках под отверстиями.
Схема устройства показана на рис. 11.10.
Недостатки таких устройств:
— большое количество прутков разводки с поворотами, что
обусловливает высокую трудоемкость изготовления
устройства;
Рис. 11.10. Устройство многоточечного инициирования
1 — корпус; 2 — прутки детонационной разводки в пазах корпуса; 3 — точка
начала инициирования разводки капсюлем-детонатором; 4 — инициирующие
прутки в отверстиях корпуса; 5 — заряд; 6 — детонационный фронт
570
— в инициируемом заряде создается характерная негладкость
детонационного фронта, связанная с конечными расстояниями
между инициаторами устройства.
В заряде устройство создает систему расходящихся от
инициаторов волн, после столкновения которых образуется единый
детонационный фронт (ДФ, см. рис. 11.10).
На этом фронте точки столкновения волн отстают относительно
точек под инициаторами и, кроме того, в этих точках возникают ма-
ховские волны с повышенным давлением. Диаметр этих зон растет с
увеличением угла столкновения волн (см. рис. 5.10).
Таким образом, создаваемый многоточечным устройством
детонационный фронт характеризуется разновременностью At и разно-
динамичностью др. По мере движения по заряду ДФ сглаживается,
величины At и Ар уменьшаются.
Очевидно, гладкость ДФ увеличивается при уменьшении
расстояния между инициаторами устройства. Минимально возможное
расстояние определяется сечением прутков разводки и диаметром
инициаторов, обеспечивающих надежное инициирование заряда
данного состава.
Минимально допустимое сечение прутков разводки должно
быть близко к значению предельного диаметра ^ая применяемого в
прутках взрывчатого состава.
Таким образом, /^ая каждого данного состава прутков и их
сечения, для каждого состава заряда существуют свои
минимально допустимые толщины инертных слоев вокруг прутка,
надежно обеспечивающие нормальную работу многоточечного
устройства.
Эти толщины и диаметр инициатора определяют минимально
возможное расстояние между инициаторами (шаг а сетки
инициаторов), а также толщину устройства. Толщина устройства — это
высота инициатора, уменьшение которой снижает надежность
инициирования заряда вплоть до отказа.
В принципе заряд можно инициировать тремя способами: по
всей его поверхности, по линии или в точке.
Очевидно, эффективность этих трех способов инициирования
различна. Например, если оценивать эффективность способов по со-
571
отношению поверхности разгрузки продуктов взрыва и их объема,
образовавшегося за одно и то же время, то получим ряд 1—1,27—
1,5, т.е. точечное инициирование в 1,5 раза хуже инициирования по
всей поверхности.
Автором проведены эксперименты (см. рис. 8.33) по измерению
энергии пластины, метаемой зарядом толщиной 10мм при
инициировании заряда тремя названными способами.
Полученные результаты показали, что по сравнению с
инициированием в точке энергия пластины в 2 и в 1,5 раза больше при
инициировании по всей поверхности и по прямой линии
соответственно.
Таким образом, цилиндрический пруток является инициатором
самым простым по конструкции, но и худшим по эффективности —
по симметрии создаваемого фронта и по метательной способности
заряда.
11.5.2. Начальная асимметрия и разнодинамичность
детонационного фронта
Основной характеристикой многоточечного устройства (УМ)
является создаваемая им величина начальной асимметриии
детонационного фронта (в момент смыкания волн, идущих от
инициаторов).
Несмотря на многообразие используемых инициаторов,
начальную асимметрию ДФ можно легко рассчитать, если взять за основу
асимметрию от точечных инициаторов, которая определяется
только шагом сетки точек.
Сетка точек может быть квадратной, треугольной или
смешанной (искаженной). Оказывается, величина начальной асимметрии
от вида сетки мало зависит, поэтому за начальную асимметрию
точек можно взять радиус круга R, равновеликого площади
поверхности заряда S, приходящейся на одну точку инициирования.
Для всех реальных инициаторов величина асимметрии будет
меньше R.
т
Нами проведены измерения начальной разнодинамичности ДФ
в зависимости от тангенса угла столкновения волн tg ф = AR/H, где
572
дМГ / W
1f$R 7w = 0,35 40,74 tgv\
и ~ *
о и ~ Флегм- тэн
• 4 -ТГ 10/90
• - Прутки фЪМОмул
к д- £ольц% дегиц'-ры
Рис. 11.11. Начальная разнодинамичность детонационного фронта
многоточечных устройств
Н — толщина заряда, A R — расстояние от инициатора до точки
столкновения волн. В опытах использовались квадратные сетки с
шагом а = 6—20 мм инициаторов 0 3x10 мм, которые можно
считать точечными. Например, /^ая квадратной сетки точек
инициирования со стороной а : AR=a/2 — fi^ столкновения двух волн;
AR=a/V 2 — ^ая столкновения четырех волн.
В опытах с зарядами Н = 10 мм измерялась скорость w тонкого
слоя соли NaCl (рис. 11.11) в точках под и между инициаторами.
Соль служила « отлетающим индикатором», и поэтому ее скорость
отражала только начальную разнодинамичность ДФ.
Полученные результаты приведены на рис. 11.11 в виде
зависимости Aw/w = f( AR/H), где Aw — разница в скоростях NaCl, aw —
скорость под инициаторами.
Из рис. 11.11 следует:
1. В интервале AR/H = 0,2— 1,3 зависимость Aw/w = f (R/H)
линейная: Aw/w = 0,35 + 0,74 aR/H.
2. Все экспериментальные точки независимо от числа
сталкивающихся волн и типа инициатора ложатся на одну прямую для заряда
данного состава.
3. По сравнению с зарядом из флегматизированного ТЭНа ^ая
заряда из менее чувствительного состава ТГ10 измерена меньшая
разнодинамичность, что объясняется преломлением
детонационных волн на границе инициатор-заряд. В результате асимметрия ДФ
уменьшается, и фактические величины AR оказываются меньше
расчетных.
Рис. 11.12. Разновременность движения стальной пластины в точках под
и между инициаторами
Разнодинамичность ДФ должна сказываться на асимметрии
пластины, разгоняемой зарядом с многоточечным инициированием.
Нами проведены измерения разновременности движения
стальной пластины t= 1 мм после ее разгона на базе 10 мм
зарядом Н= 10 мм. Измерялась разность At = tH — tM времени
подлета точек пластины под и между инициаторами в зависимости от
tgc|> = AR/H.
Полученные результаты приведены на рис. 11.12.
Как видно из рис. 11.12, разновременность пластины линейно
уменьшается с уменьшением AR/H или при Н = const — с
уменьшением расстояния между инициаторами. До tg ф = 0,16
разновременность определяется опережением пластины в точках под
столкновениями волн. С уменьшением угла столкновения давление в этих
точках падает, и поэтому опережение уменьшается.
Нетривиальным результатом является смена знака
разновременности при tgcj><0,16 — пластина под зонами столкновения волн
начинает отставать. В зонах столкновения давление выше, но и
скорость разгрузки выше. По-видимому, при tgcj> < 0,16 давление
уменьшается настолько, что импульс, получаемый пластиной от ПВ
становится меньше, чем в зонах под инициаторами.
Таким образом, у пластины после разгона At = 0 становится
дважды: при AR/H = 0,16 — за счет равенства импульсов в точках
под и между инициаторами и при AR=0 — при отсутствии
столкновения волн и гладком фронте.
574
На систематическую разнодинамичность и разновременность
ДФ, обусловленную конечным шагом сетки инициаторов,
накладывается влияние разновременности работы инициаторов.
Разновременность работы инициаторов изменяет фактический
шаг сетки: у опережающих инициаторов он больше, чем у
отстающих. Если инициатор отстает от соседа на величину a/2D,
то он «отключается», на его месте возникает столкновение
волн от соседних инициаторов с вдвое большей разнодинамич-
ностью.
Отсюда следует, что с уменьшением шага сетки инициаторов
должны возрастать требования к разновременности их работы.
Литература к главе 11
1. Справочник по буровзрывным работам на карьерах. Киев,
Наукова думка, 1973.
2. Meyer R. Explosives. Volgar Chemie, 1981.
3. H & SM Supplement 24.9 — Low Energy Initiator (LEI)
Operation ht 17/09/21.
4. Андреев B.B. ФГВ, 1993,N2,c.87—90.
5. Зотов E.B., Красовский Г.Б., Козырев A.C. ФГВ,1982,Ы4,
c.107.
6. Зотов Е.В., Козырев A.C. и др. ФГВ, 1082, N4, с. 110.
7. Roux М., Auzanneau and Brassy С. Propellants, Explosives,
Pyrotechnics, 1993,18, p. 317—324.
8. Трофимов Н.Б. В сб. «Пробой диэлектриков и
полупроводников »М.-Л.: « Энергия», 1964.
9. Беляев А.Ф., Боболев В.К., Короткое А.Н. и др. Переход
горения конденсированных систем во взрыв, М.: Наука,
1973.
10. Willis К. and Whang D. « Semiconductor bridge Technologies ».
Report at the 31st AIAA/ASME/SAE/ASEE Joint Propulsion
Conf. July 10—12,1995.
11. Stroud, John R. « A new kind of detonator — the slapper».
UCRL 7739 Lawrence Livermore Laboratory.
12. Быстрое инициирование ВВ. Особые режимы детонации.
Сб науч. статей под ред. В.И. Таржанова. Изд-во РФЯЦ-
ВНИИТФ, Снежинск, 1998,168 с.
13. Илюшин М.А., Целинский И.В., Бачурина И.В., Козлов А.С.,
Королёв Д.В. Влияние строения лиганда на лазерное
инициирование перхлоратных комплексов переходных металлов
с замещёнными 1,2,4-триазолами. В сб. Физика и техника
высокоэнергетической обработки материалов. Днепропетровск,
АРТ-ПРЕСС,2007,с.З-9.
14. Патент США №3430563, Кл. 102—22, публикация 1969 г.
Глава двенадцатая
МЕТОДЫ РЕГИСТРАЦИИ БЫСТРОПРОТЕКАЮЩИХ
ПРОЦЕССОВ
12.1. Классификация методов регистрации
Трудно переоценить роль измерительных методов в развитии
физики взрыва и ударных волн.
О большом значении, которое придают ученые развитию
методов регистрации быстропротекающих процессов, говорит тот факт,
что регулярно проводятся международные научные конференции
по высокоскоростной фотографии.
Мощное ускорение получило развитие измерительных методик
после II Мировой войны в связи с разработкой атомного оружия.
Затем в 1970-е годы потребовалось повысить временное разрешение
измерений а^я исследований микромишений термоядерного
синтеза и аля более детального изучения детонационных процессов.
По временному разрешению в интервале 10"3—10"13 с все
известные приборы аля регистрации быстропротекающих процессов
можно разделить на три группы [1].
— 103— 106 с — приборы аля изучения динамического
поведения сложных систем и объектов;
— 105—109 с — приборы а^я изучения ударного сжатия
материалов, детонации, разгона тел, явлений кумуляции,
скоростного удара и проникания, баллистики и др.;
— 10"10— 10'13 с — приборы а^я изучения сжатия мишеней
термоядерного синтеза.
Разнообразие исследовательских задач и направлений второй
группы обусловило и создание большого разнообразия методов измерений.
Перечень основных методов приведен в таблице 12.1.
Таблица 12.1. Методы регистрации быстропротекающих процессов
Метод
Оптический
Электрический
Электронно-
оптический
Импульсная
рентгеносъемка
Разновидности метода
Измерения с помощью фотохронографа с зеркальной
разверткой:
— съемка покадровая; съемка в режиме
хронографа с помощью щели и растра;
— многоканальные измерения с помощью
световодов;
— съемка светящихся объектов и с импульсной
подсветкой в проходящем и отраженном свете;
— измерения скорости поверхности с помощью
лазерного интерферометра (метод ЛИВС).
Измерения:
— давления манганиновыми датчиками;
— волновых и массовых скоростей
ионизационными датчиками (электроконтактами);
— массовой скорости емкостными датчиками;
— массовой скорости магнито-электрическим
методом;
— температуры термопарным методом.
— Измерение профилей давления и временных
интервалов с помощью индикаторной жидкости;
— измерение яркостной температуры
детонации и ударного сжатия.
— Измерение формы и плотности ударнос-
жатых тел: одно- и многокадровая съемка
с использованием импульсного источника
рентгена или в лучах собственной радиации
(а^я термоядерных мишеней).
Мы выделили в табл. 12.1 четыре группы методов, с помощью
которых получена основная масса научных результатов в физике взрыва и
ударных волн. Методы исследования детонационных процессов пере-
578
числены на рис. 8.5 (Гл.8). Измерительные методики подробно описаны
в прекрасной монографии, изданной РФЯЦ-ВНИИЭФ (г. Саров) [2]
Для измерения временных интервалов необходима развертка
изображения или сигнала во времени с точно известной скоростью.
Такая развертка осуществляется в фотохронографах с помощью
вращающегося зеркала или электростатическим отклонением потока
электронов в камерах с электронно-оптическим преобразователем
[3,4]. Электрические сигналы разворачиваются во времени
осциллографами с линейной или спиральной разверткой, позволяющими
оценивать также амплитуду и форму импульсов.
Временные интервалы могут быть измерены также с помощью
электронных цифровых счетчиков (типа СУПИ-30). Такие
счетчики считают количество импульсов п (генерируемых генератором
счетчика с частотой f), прошедших за время между срабатыванием
двух электроконтактов, отпирающих и запирающих схему счета.
Измеряемый интервал времени t = n/f. Разрешающая способность
счетчиков определяется частотой f и может быть доведена до 1 пс.
Данные измерений получаются сразу в числовом выражении и
могут быть переданы на принтер или в ЭВМ.
Оптические методы позволяют без взаимодействия с изучаемой
системой получать неискаженную датчиками информацию.
В фотохронографах для регистрации изображения используется
чувствительная фотопленка, преимущество которой — наглядность
получаемой информации.
Если пленка размещена на окружности радиусом R вокруг
зеркала, вращающегося с угловой скоростью w, то линейная скорость
отраженного от зеркала луча (скорость развертки на пленке) будет
v = 2wR. Например, для старого и надежного фотохронографа СФР-
2М w=1250 об/с, v = 3,75 мм/мкс, временное разрешение 10 не
[5]. А для современных фотохронографов с зеркальной
разверткой в вакууме характерны следующие параметры: w= 18000 об/с,
у = 26 мм/мкс и временное разрешение 2,5 не.
В электронных камерах на основе ЭОП достигаются v ~ 10 мм/ мке
и временное разрешение ~10 пс. С 80-х годов 20 века широкое
распространение получили лазерные интерферометрические системы [2].
579
В 90-х годах использовалось более ста видов таких систем, прежде
всего в исследованиях детонации. Различные лазерные интерферометры
(VTSAR, ORVTS, ЛИФП, метод ЛИВС) уникальны своей высокой
точностью измерений и временным разрешением (< 5нс).
Кроме временного разрешения, важнейшей характеристикой
любой оптической системы является пространственное или линейное
разрешение. Например, аая СФР-2М оно составляет 16 линий/мм и
ограничивается в основном воздушными возмущениями вокруг
вращающегося зеркала.
В электронно-оптическом методе возникающее в исследуемом
объекте свечение преобразуется в электрический сигнал с
помощью ФЭУ, а затем этот сигнал регистрируется осциллографом (см.
рис. 8.5)
При импульсной рентгеносъемке, наоборот, теневое
изображение объекта в рентгеновских лучах преобразуется в видимый свет
при помощи флуоресцирующего усиливающего экрана (Baryum
Fluoride), а^я которого характерна задержка в появлении свечения,
равная примерно 6 мкс. Для получении одного снимка сразу за
экраном помещается фотопленка.
Для регистрации нескольких кадров («рентгеновское кино»)
изображение на экране регистрируется высокоскоростной
электронной камерой («Jmacon 790»). Разрешение получаемых рентгеновских
снимков низкое — не более 8 линий/мм, хотя разрешение самой
камеры 10—20 линий/мм [6]. Получена частота снимков до 4 107 в секунду.
Просвечивающая способность рентгеновских лучей зависит от
используемого в источнике напряжения — от 10 kv для
исследования движения малых частиц низкой плотности до 30 Mv для
исследования формы и степени сжатия массивных тел высокой плотности.
Например, линейный ускоритель Лос-Аламосской лаборатории в
США создает 30 Mv рентгеновский импульс, способный
просвечивать слой стали толщиной не менее 150 мм [6].
В [7] с помощью щелевой рентгеновской камеры исследовалось
сжатие и нагрев мишеней лазерного термоядерного синтеза в лучах
собственной рентгеновской эмиссии (мишени диаметром 0,13—
0,18 мм, лазерный импульс 100 пс с энергией до 20 дж).
580
Методы регистрации быстропротекающих процессов могут быть
дискретные и непрерывные, одноканальные и многоканальные.
В исследованиях ударной сжимаемости веществ давно и широко
используются дискретные методы измерения волновых и массовых
скоростей с помощью электроконтактных датчиков и
осциллографов, а также с помощью метода вспыхивающих зазоров и
фотохронографа в режиме щелевой развертки.
Непрерывно регистрируются: профили давлений —
манганиновым датчиком и индикаторной жидкостью, массовая скорость —
емкостным датчиком, магнитоэлектрическим и лазерным допплеров-
ским методами.
В одном измерительном канале можно регистрировать один
временной интервал или несколько последовательных интервалов, т.е.
подробную (квазинепрерывную) x,t — диаграмму. Многоканальные
измерения необходимы, если фронт ударной волны или
движущейся поверхности не одномерны, а искривлены, перекошены или
движение разнодинамично.
Подробная регистрация x,t — диаграмм во многих точках
поверхности наиболее информативна, точна и надежна, т.к. позволяет
в одном опыте измерить и динамику, и симметрию исследуемой
поверхности.
Поэтому мы уделили много внимания разработке
многоканальных методик, как оптических, так и электрических.
12.2. О точности измерений временных интервалов
Обычно блок-схема измерения временных интервалов состоит
из традиционных частей:
Явление
Датчики
Регистратор
Фотопленка
У каждой части имеется своя величина и свои причины дисперсии •
временных интервалов. Например, если измеряется скорость
пластины, метаемой детонацией заряда ВВ, то колебание ее скорости (или
581
времени пролета пластиной известной базы измерения) определяется
колебаниями состава, плотности, и веса заряда, а также веса пластины,
асимметрии и разнодинамичности движения ее поверхности.
Определяя фактические параметры заряда, пластины, датчика,
скорости развертки в регистраторе, мы можем часть случайных
колебаний величин перевести в разряд систематических и в виде
расчетных поправок ввести в результат данного опыта.
Случайные и систематические составляющие колебаний
результатов измерений можно разделить на величины, определяемые
изучаемым явлением и методикой измерения. Очевидно,
дисперсия явления должна быть много больше суммарной методической
погрешности. Но это соотношение должно выбираться в разумных
пределах, например, порядка 10:1.
По аналогии, нет смысла измерять среднюю ширину грубого
кухонного стола только в одном месте микрометром. Результат будет
точен, но будет относиться не ко всему столу, это будет «местная»
ширина в одной точке. Проще провести измерения линейкой, но
в нескольких местах с последующим усреднением.
Точно так же обычно используемые в газодинамических опытах
объекты недостаточно прецезионны, чтобы измерения в одной
точке считать представительными (результат может содержать
неизвестную систематическую погрешность).
Надежные результаты можно получить только измерениями
одновременно во многих точках, а высокая точность будет
достигнута усреднением этих измерений. Тем более такие измерения имеют
смысл, если вас интересует асимметрия и разнодинамичность
движущейся поверхности.
Таким образом, уточнение результата достигается усреднением
многих измерений.
Суммарная предельная погрешность 3 <7 среднего из п
измерений может быть записана в виде [8]:
3<7 = V(3<7,./V^)2+Z<S;2 (12.1)
где S — систематическая погрешность.
582
Как уже было сказано, часть систематических погрешностей
может быть учтена в виде поправок в результаты опытов.
с — дисперсия нормального закона распределения
ошибок,равная:
o-2=yft"'g) (12.2)
t — единичное измерение, t = 1/n £t. — среднее арифметическое
из п измерений.
Рассмотрим структуру методической погрешности измерения
временных интервалов с помощью фотохронографа СФР-2М.
В [9] нами определены отдельные виды методических
погрешностей, которые были разделены на две подгруппы: погрешность
собственно фотохронографа и погрешность расчета фотохронограмм
по пленке или по увеличенному отпечатку на фотобумаге.
Измеряемое время t определяется следующим образом:
t = Hvp (12.3)
при расчете по пленке, где 1 — расстояние между почернениями на
пленке, a v — скорость развертки СФР-2М;
р
* = L/*v =1/—v, (12.4)
Р Р
т
при расчете по отпечатку с увеличением k=М/т, где М и т — шаги
перфорации на отпечатке и пленке.
Таким образом, погрешность измерения времени определяется
погрешностью измерения величин v , 1, L, М, т. Для каждой из них
определены несколько случайных независимых погрешностей (см.
табл. 12.2)
Кроме того, в расчетах учитывались две систематические
погрешности: разрешающая способность глаза человека — 0,2 мм [8]
и временное разрешение СФР-2М—0,01 мкс при v =3,75 мм/мкс
[5].
Как известно, с увеличением экспозиции края изображения
светящегося объекта размываются. Следовательно, на пленке (отпечат-
ке) размер почернений (линий, пятен) может меняться. Нами
найдено, что в зависимости от экспозиции Н изображение щели СФР-2М
изменяет свою ширину h линейно:
h/h0=aH/H0 (12.5)
где hQ — ширина щели при минимальной экспозиции HQ.
Для пленки а = 0,13, а аля отпечатка а = 0,19 (Н/Н0< 10).
Таблица 12.2. Виды случайных погрешностей измерений с помощью
СФР-2М
Параметр
Скорость
развертки, V
р
Расстояние на
пленке, 1
Источник погрешности
Погрешность СФР-2М
Замена улитки Паскаля
Неточность тахометра
Расчет по пленке
Усадка пленки после ее обработки
Перенос щели с предварительного
снимка
Неточность отсчета под микроскопом
БМИ-1
Качество изображения (влияние
различной экспозиции):
Расчет по краям почернений
Расчет по центрам почернений
Величина
относительной
погрешности 3 ajx. у %
0,5
0,1
0,4
(0,1/1) 100
(0,05/1) 100
(0.06/1) 100
(0,03/1) 100
Расстояние на
отпечатке, L
Коэффициент
увеличения, к
Расчет по отпечатку
Перенос щели с предварительного
снимка
Неточность измерения линейкой
Качество изображения:
Расчет по краям почернений
Расчет по центрам почернений
Неточность шага перфорации пленки
Неточность измерения линейкой (для
расстояния 200 мм)
Искажение оптики фото увеличителя
Неравномерность вытяжки фотобумаги
в результате проявления и сушки
(1/L) 100
(0,5/L) 100
(0,11/L) 100
(0,03/L) 100
0,3
0,25
1,1
0,9
584
Влияние качества изображения (экспозиции) определено аая
расчета фотохронограмм как по краям, так и по центрам
почернений (см. табл. 12.2).
Из табл. 12.2 видно, что при расчете по центрам погрешность
вдвое меньше, чем при расчете по краям почернений.
Исходя из (12.3) и (12.4), можно записать выражения а^я
относительной погрешности:
— для пленки
3t7/ _о lrUl\2 , rvP\2
f-W-fYH-f-Y (,20
для отпечатка
За,
, = w>2+Ф2+(—)2+(—)2 (127)
Если подставить в (12.6) и (12.7) все составляющие погрешностей из
табл. 12.2, то легко заметить, что все формулы аля 3(7 сводятся к виду:
3at=y]B2t2+C2/vp (12.8)
где В, С — коэффициенты.
2
Р
Из (12.8) следует:
а) а^я больших интервалов времени t, когда В212> >C2/v
3<j,~f (12.9)
и практически не зависит от скорости развертки СФР-2М.
б) а^я малых интервалов, когда C2/v 2>>В2 t2 абсолютная
погрешность практически не зависит от времени и определяется
скоростью развертки:
3<7,~l/vp (12.10)
Например, при расчете по центрам почернений малых
интервалов времени 3 а* =0,116/v .
Результаты расчета величины 3 о* показаны на рис. 12.1.
Кроме расчетов, нами проведены 2000 измерений временных
интервалов (в пределах 20 мкс) между искрами от импульса 20 kv на
двух искровых промежутках в 1 мм, причем на втором промежутке
импульс задерживался кабельной линией задержки.
Поскольку в эксперименте реализуются не все возможные виды
погрешностей, то измеренные величины 3 <7 меньше расчетных (см.
О «О 20 30 t мкс
Рис. 12.1. Предельная суммарная методическая погрешность измерения времени
фотохронографом СФР-2М
Расчет: 1 — по отпечатку; 2 — по увеличенному изображению;
3 — по пленке; 4,5 — по отпечатку с метками; 6 — по пленке с
метками; о — Эксперимент.
Анализ рис. 12.1 показывает следующее.
1. Для интервалов t> 10 мкс относительная погрешность
постоянна а^я данного способа расчета фотохронограммы:
— 3 cj/t = 1,7 % — А^я расчета фотоотпечатка;
— 3 <7/t = 0,9 % — А^я расчета увеличенного изображения;
— 3 с /t = 0,8 % — а^я расчета пленки под микроскопом;
— 3 (J/t = 0,4 % — аля расчета фотоотпечатка с метками времени
— 3 <7 /t = 0,1 % — а^я расчета пленки с метками времени.
2. Для малых интервалов величина 3 о* уменьшается с
увеличением скорости развертки, а относительная погрешность 3 с /t быстро
растет с уменьшением t . Например, для t = 1 мкс и v = 3 мм/мкс
Зет/t = 4,8%.
3. Наименьшая абсолютная погрешность единичного измерения
на СФР-2М для t = 0 составляет Зет = 0,03 мкс.
586
4. Использование световых меток времени от датчика ДВ-2
с кварцевым генератором [10] заметно снижает погрешность
измерения больших интервалов времени и бесполезно а^я измерения
малых интервалов. Метки времени наносятся на пленку одновременно
с регистрацией интервалов времени в опыте.
5. По сравнению с отпечатком расчет пленки под микроскопом
снижает погрешность примерно вдвое.
По-видимому, ошибка расчёта изображения, полученного на
мониторе компьютера с помощью сканирования плёнки, близка к
ошибке расчёта оптически увеличенного изображения.
Увеличение скорости развертки заметно снижает погрешность
Аая малых интервалов времени только до v ~5 мм/мкс, а
дальнейший рост v малоэффективен и, кроме того, требует повышения
чувствительности пленки.
Погрешность собственно СФР-2М относительно невелика
(0,7%), поэтому а^я снижения суммарной погрешности важно
применение более современных способов расчета фотохронограмм.
Временное разрешение регистратора составляет только малую
часть суммарной методической погрешности.
Отметим различие в поведении составляющих дисперсии
результатов при увеличении числа измерений в одном опыте (на
одной пленке). Усреднение п измерений на движущейся
поверхности уменьшает в Vn раз составляющую погрешности
результата, связанную с явлением, но при этом методическая погрешность
уменьшается слабо, поскольку в Vn раз уменьшаются только две ее
составляющие: расчет линейкой и качество изображения. Поэтому
методически вся совокупность измерений на одной пленке
представляет собой практически единичное измерение (с
погрешностью согласно рис. 12.1).
Из (12.1) следует, что при п -> <х> на m -> <х> пленках методическая
погрешность среднего 3(7 = VS S.2 = 0,02 мкс.
Погрешность измерения интервала времени, обусловленная
точностью базы измерения датчика (ЗстДх) зависит от измеряемой
скорости (w):
3<j=3(tJw (12.11)
3 G/t, %
KM
^ 1 l44^^
t, мкс
Рис. 12.2. Расчетная зависимость относительной ошибки электроконтактных
измерений от измеряемого интервала времени
Регистратор — осциллограф ИВ-ЗОМ со спиральной разверткой 5мкс/круг.
1 — без учета ошибки датчика. 2 — с учетом ошибки спирального датчика при
скорости замыкающей поверхности, равной 2 км/с
Например, у изготовленных по шаблону спиральных
электроконтактных датчиков колебание измерительных баз не более 3 а^ = 0,015мм
[11].Тогда аля измеряемой скорости поверхности w «2 км/с
3(7=0,015/2= 7,5 не.
Однако это только часть погрешности, вносимой датчиком.
Для электроконтактного датчика колебание измеряемого
времени также вызывается качеством поверхностей у движущегося тела
(пластины) и у проволочного контакта, влиянием на процесс
замыкания контакта воздуха или другого газа, точностью установки
многоконтактного датчика целиком (точность не баз Ах, а координаты х).
Расчетная зависимость относительной методической ошибки
измерений от измеряемого интервала времени ^ля спиральных датчиков
и осциллографов ИВ-ЗОМ со спиральной разверткой (5 мкс/круг)
показана на рис. 12.2.
Осциллографы с круговой (спиральной) разверткой (без меток
времени) имеют свою структуру методической ошибки со своими
составляющими: крутизна фронта импульса, ширина линий
осциллограммы, радиус кругов развертки и др.
Из рис. 12.2 видно, что влияние погрешностей, связанных с
датчиком и его работой, на общую относительную погрешность очень
велико а^я малых интервалов времени и ослабевает с ростом
измеряемого интервала.
588
Точность измерения времени и, соответственно, скорости
повышается при многоканальной подробной регистрации x,t -диаграмм.
Например, пусть мы хотим измерить скорость пластины после
ее разгона зарядом ВВ. На инерционном участке скорость пластины
w = const и х = a+wt. Если имеется m каналов измерения, то
обычными датчиками вы можете измерить m интервалов и после
усреднения получить скорость с точностью, определяемой m измерениями.
Если же на каждом из m каналов регистрировать x,t —
диаграмму в п точках, то методом наименьших квадратов точность w в
аппроксимирующем x,t — диаграмму уравнении (в данном случае
x = a+wt) будет определяться уже по nxm измерениям. Точность
выше а^я точки х, находящейся в середине регистрируемого
участка x,t-диаграммы. Выше и надежность результата, опирающегося на
положение всей x,t -диаграммы.
12.3. Измерения с помощью фотохронографа
12.3.1. Краткое описание фотохронографа
Рассмотрим оптическую регистрацию быстропротекающих
процессов фотохронографом с зеркальной разверткой типа СФР-2М
или ВФУ-1 (эти хронографы имеют одинаковую конструкцию
камеры и отличаются пультом управления).
Основные части фотохронографа: оптическая система,
развертывающая зеркальная система, устройство измерения скорости
вращения зеркала и узел синхронизации [5,12,13].
Оптическая система (см. рис. 12.3) состоит из двух линз с
общей фокальной плоскостью, в которой помещается щель или растр.
•—Н1+
г
Рис. 12.3. Оптическая схема фотохронографа
1,4 — объективы; 2 — узел щели и растра; 3 — затвор; 5 — вращающееся зеркало;
6 — фотопленка
Применение светосильных и длиннофокусных объективов
позволяет проводить измерения на достаточном удалении от взрываемого
заряда с достаточной освещенностью изображения.
Второй объектив через вращающееся зеркало строит
изображение щели или растра на пленке. Перед вторым объективом
установлен электромагнитный затвор, который ограничивает время
освещения пленки через вращающееся зеркало и тем самым уменьшает
фоновое потемнение пленки.
Развертывающий механизм состоит из скоростного
электродвигателя, вращающегося зеркала и датчика. В катушке датчика
генерируются импульсы, число которых в единицу времени равно числу
оборотов зеркала, что и используется /^ измерения скорости
развертки.
Датчик может быть повернут вокруг оси зеркала, за счет чего
импульс от датчика может быть получен при любом заданном
положении вращающегося зеркала . Это и позволяет синхронизировать
(согласовать) положение зеркала и подачу инициирующего импульса
на электродетонатор. При вращении зеркала изображение процесса
перемещается по пленке, размещенной на фокальной поверхности
второго объектива. Таким образом пленка экспонируется, и
регистрируется развитие явления во времени.
Ось вращения зеркала не совпадает с отражающей плоскостью
зеркала (зеркало толстое, чтобы при вращении исключить его
прогиб). В этом случае геометрическим местом изображения точки при
развертке таким зеркалом является улитка Паскаля.
Точное изготовление поверхности по этой кривой
затруднительно, поэтому улитка Паскаля аппроксимируется окружностью, центр
которой не совпадает с осью вращения зеркала. В этом случае при
равномерном вращении зеркала скорость развертки на пленке
неравномерна и подчиняется закону:
vp =2mr[l + (a/r)cos<p] (12.12)
где w — угловая скорость вращения зеркала; г — радиус развертки
(у камеры СФР-2М г=239 мм); а — расстояние между осью и
отражающей поверхностью зеркала (у СФР-2М а= 5 мм); ф- угол поворота
зеркала относительно оптической оси СФР.
590
Таким образом, неравномерность растет с углом ф, но не
превышает 0,5%.
Ошибка измерения числа оборотов зеркала стробоскопическим
методом составляет 0,1%.
Максимальная скорость вращения зеркала равна 75000 об/мин,
что дает максимальную линейную скорость развертки на пленке
v = 3,75 мм/мкс.
Для регистрации процесса используется обычная 35 мм
перфорированная фотопленка длиной 1,6 м в стандартных фотокассетах
с чувствительностью 800—1200 единиц (цветная или черно-белая
типа РФ или КН-2). Размер одного кадра — 25 х 375 мм.
Недостатки зеркального фотохронографа:
— небольшая светосила, связанная с малым размером зеркала
и ограничивающая регистрацию самосветящихся явлений;
— необходимость жесткой синхронизации явления и
положения вращающегося зеркала, когда момент съемки задается не
процессом, а хронографом. При изучении быстропротекающих
процессов, связанных со взрывом, такая синхронизация
требует применения специальных импульсных электродетонаторов
с малым микросекундным временем работы (с взрывающимся
мостиком). Обычные дешевые промышленные ЭД с мостиком
накаливания здесь неприменимы.
12.3.2. Режимы регистрации явления
\.Кадрированная съемка (режим лупы времени) производится с
помощью трех сменных объективных вставок, которые
устанавливаются между зеркалом и пленкой:
— светосильная вставка дает 49 кадров диаметром 10 мм;
— двухрядная вставка дает 60 кадров диаметром 10 мм;
— четырехрядная вставка дает 240 кадров диаметром 5 мм.
Частота съемки — от 25 103 до 2,5 106 кадров /с.
Обычно кадрированная съемка требует применения
импульсной подсветки — лампой вспышки или свечением УВ в аргоне,
создаваемым взрывом специального заряда ВВ рядом с исследуемым
объектом.
Съемка может быть в проходящем или в отраженном свете.
Примеры получаемых снимков в проходящем свете приведены
нарис.6.12 (гл.6).
2.Съемка в режиме хронографа.
Возможно три вида съемки:
— съемка «на окно» обычно используется /^ля получения
предварительных снимков при неподвижном зеркале;
— съемка «на растр» применяется для измерения
разновременности выхода УВ по всей контрольной поверхности. Растр
представляет собой стеклянный диск с непрозрачным зеркальным
покрытием, в котором имеется ряд параллельных щелей шириной
0,1мм.
Растры отличаются шагом между щелями. Растры
устанавливаются вместо щели в фокальной плоскости между объективами
хронографа.
Съемка «на растр» требует использования короткой вспышки
света в зазоре между контрольной поверхностью (например,
заряда ВВ или пластины) и т.н. «отсечкой» из прозрачного блока
оргстекла.
При ударном давлении > 10 кбар оргстекло теряет свою
прозрачность — отсюда и термин «отсечка» света. Контрольная
поверхность и вспыхивающий зазор устанавливаются перпендикулярно
оптической оси хронографа. Вспышка в зазоре не только
короткая, но и более яркая по сравнению со светом от детонирующего
на открытом воздухе заряда.
— съемка «на щель» — наиболее распространенный вид
регистрации. Вертикальная щель с регулируемой шириной
(обычно используется щель 0,05—0,25 мм) вырезает из
наблюдаемого объекта узкую полосу, которая и разворачивается по
пленке. Обычно щель располагается по центру (по оси)
объекта.
В зависимости от взаимного расположения щели и вектора
скорости у наблюдаемого явления возможны следующие три режима
съемки «на щель» (см. рис. 12.4).
592
Xq Xj И
X > _ A
I 3 ш
Рис. 12.4. Возможные режимы съемки «на щель»
I — измерение скорости; II — измерение разновременности;
III — измерение профиля
I — измерение скорости (вектор скорости параллелен щели и
перпендикулярен оптической оси).
II — измерение разновременности (вектор скорости
перпендикулярен щели и параллелен оптической оси).
Этот режим аналогичен съемке «на растр», но наблюдается
разновременность только в одном сечении объекта, где установлена щель.
III — измерение профиля явления (вектор скорости
перпендикулярен щели и оптической оси).
В одном опыте можно с помощью одной щели совместить
измерения скорости детонации заряда и разновременности выхода
волны на торец заряда, если установить зеркало под 45° к торцу заряда.
Детонационный профиль в том же опыте можно наблюдать, если
часть щели с помощью призмы повернуть на 90° [14].
Кроме величины разновременности, съемка «на щель» во II
режиме позволяет измерить скорость УВ и ее затухание в прозрачном
пакете слоев из оргстекла (метод вспыхивающих зазоров).
На рис. 12.5. показана постановка такого опыта и одна из
хронограмм, полученных нами в процессе отработки плоской стальной
линзы о 80 х 8 мм.
При съемке «на щель» экспозиция пленки равна ширине щели,
деленной на скорость развертки. Для увеличения точности
измерений стремятся уменьшать ширину щели и увеличивать скорость
развертки. При этом экспозиция снижается и для регистрации
требуется применять более чувствительную пленку и повышать яркость
свечения непрерывной продувкой вспыхивающих зазоров аргоном.
593
«)
21 12
Отсечка ( оргстекло )
( оргстекло )
ш - e- Jfe6*£!3*«6
At «Q/fMKC
О It & 12 X ми
Рис. 12.5. Постановка опыта и полученные результаты по отработке плоской
стальной линзы о 80 х 8 мм (генератора плоской ударной волны — ГУВ)
а) Симметрия УВ; б) Затухание УВ в оргстекле; на графике даны скорость и
давление в оргстекле в зависимости от расстояния от линзы. 1 — линза;
2 — стальной корпус; 3 — пленка 0,2 мм; 4 — зазор; 5 — пластины оргстекла
t=2 мм; 6 — щель СФР; 7 — хронограмма
При измерении по I схеме съемка мгновенной скорости УВ или
детонации искомая скорость D находится по формуле:
D = (yple)tgy/ (12.13)
где v — скорость развертки; у—угол наклона касательной на
пленке к кривой путь-время; в<1 — коэффициент увеличения
фотохронографа.
Ошибка в измерении угла у определяет в основном погрешность
скорости, которая будет минимальна при условии Db/v = 1. Это
условие выполняется аая D = 6—8 мм/мкс, в = 0,25—0,5, v = 2—3
мм/мкс, т.е. при измерении с помощью СФР-2М.
12.4. Многоканальные измерительные системы
с применением оптических световодов
Недостаток описанных выше трех режимов съемки «на щель» —
регистрация явления только в одном сечении в месте расположения
щели.
Точность и информативность измерений в одном опыте резко
повышаются за счет применения многоканальных систем,
позволяющих проводить измерения во многих точках контрольной
поверхности любого вида: фронта ударной или детонационной
волны, при искривленной поверхности летящего тела (пластины,
оболочки).
Рассмотрим разработанные нами совместно с Н.П. Козеруком
многоканальные измерительные системы с применением
оптических световодов в виде мононитей из полистирола [15,16].
1. Измерение разновременности и формы ударной или
детонационной волны.
Схема устройства показана на рис. 12.6.
Основной частью устройства являются отрезки мононитей
световодов, которые одновременно служат датчиками световых
вспышек, возникающих при выходе в зазор ударной или детонационной
волны. Наиболее дешевы и удобны аля монтажа световоды 0 0,3—
1,5 мм из хорошо очищенного (двойной перегонкой) полистирола.
По световоду свет распространяется за счет эффекта полного
внутреннего отражения, поэтому светопропускание световода
сильно зависит не только от качества очистки, но и от качества
поверхности световодов. Для увеличения светопропускания световоды могут
покрываться пленкой полиметилметакрилата. Величина
светопропускания таких световодов достигает 70%/м. Светопропускание
падает с уменьшением диаметра световодов и радиуса их изгиба.
На свету и в изогнутом состоянии световоды из полистирола
относительно быстро стареют, покрываются сеткой микротрещин, что
снижает светопропускание и делает световоды хрупкими. Поэтому
не рекомендуется долго хранить изготовление измерительные
устройства с изогнутыми световодами
Концы отрезков световодов имеют входные и выходные головки,
которые легко получаются оплавлением полистирола..
Индикатрисса светопропускания световода на входе и выходе
света достаточно острая: внутри телесного угла в 20%
пропускается ~80% света. Поэтому ^^я максимальной передачи света входные
части световодов должны быть перпендикулярны контрольной
поверхности, (на которой возникает вспышка света), а выходные части
6
Рис. 12.6. Схема многоканального измерительного устройства со световодами
1 — объект испытания; 2 — зазор 0,2—0,5 мм; 3 — держатель входных головок
световодов; 0,3—1,5 мм и длиной 0,1—0,5 м; 4 — световоды; 5 — держатель-
планка выходных головок световодов; 6 — зеркальный фотохронограф
со специальным растром
световодов должны быть переллельны оптической оси
фотохронографа (см. рис. 12.6).
Входные и выходные части световодов закрепляются в отверстиях
держателей. Входные головки распределяются по контрольной поверх-
596
ности любым способом: равномерно, вдоль образующей
цилиндрического заряда или под проекциями каких-то характерных точек.
А выходные головки световодов размещаются на панели в одну
линию или в несколько рядов. Далее выходящий из световодов свет
передается по воздуху в зеркальный фотохронограф. Таким образом
пространственное размещение входных головок преобразуется в
линейное размещение выходных головок.
Обычно входные головки делают плоскими, заподлицо с
поверхностью держателя, а выходные головки — полукруглые. Диаметр
головок составляет примерно два диаметра световода.
С целью уменьшения фоновой экспозиции пленки регистрация
в фотохронографе осуществляется через щель или с помощью
специального растра, имеющего столько щелей, сколько рядов
световодов на панели. Кроме того, делается экранировка фонового свечения
продуктов взрыва.
Как уже упоминалось, при необходимости усиления вспышек
света, зазор заполняется аргоном или мелким порошком соли NaCl.
Чем больше измерений в одном опыте (больше световодов),
тем выше точность и надежность получаемых результатов. Поэтому
естественно стремление увеличить число световодов в одном
измерительном устройстве.
Максимально возможное количество используемых в устройстве
световодов зависит от диаметра световодов и размера контрольной
поверхности, а также от условий регистрации световых вспышек
фотохронографом.
Количество п световодов в одном ряду определяется
минимальным диаметром пятна d почернения на пленке от вспышки,
передаваемой одним световодом:
np = ht/(d+VN) (12.14)
где hf — высота рабочей части пленки (h = 24 мм); N — линейное
разрешение хронографа (аая СФР-2М N = 20л/мм).
Реально различимо пятно диаметром d = 0,05 мм.
Тогда в одном ряду можно разместить максимум п = 240 световодов.
Расстояние А1 между рядами световодов на пленке
(соответственно и на панели AL = А1/в ) должно быть больше, чем максимальный
597
разброс пятен от вспышек одного ряда световодов, обусловленный
ожидаемой максимальной разновременностью на контрольной
поверхности Al> At v .
a max р
При этом пятна почернений от соседних рядов не будут
перепутываться (иначе невозможен расчет фотохронограммы).
Для многих постановок опытов максимально допустимое
количество рядов световодов N также имеет ограничение, связанное
с возникновением регистрируемого световодами длительного
вторичного свечения воздуха при достаточно быстром движении
тыльной поверхности держателя входных головок световодов.
Между вспышками света в зазоре на входных головках и этим
вторичным свечением существует пауза в свечении длительностью
t = H/D, где Н — толщина держателя, a D — скорость УВ в нем.
Чтобы вторичное свечение от нового ряда световодов не
накладывалось на рабочие почернения последнего ряда, необходимо
выполнить условие:
Hp>MNIvp (12Л5)
Практически в опытах с СФР-2М автор использовал максимум
шесть рядов световодов о 0,8—1,2 мм по 200 шт. в ряду, всего 1200
световодов в одном измерительном устройстве.
2. Измерение разновременности подлета движущегося тела
(например, пластины, разогнанной продуктами взрыва) к контрольной
поверхности.
Конструкция устройства аналогична представленному на рис. 12.6.
Отличие лишь в том, что вводится непрозрачный экран,
устанавливаемый с зазором над входными головками световодов.
3. Измерение в одном опыте времени движения тела и
разновременности его подлета к контрольной поверхности.
В этом случае на поверхность тела (пластины) наносится тонкий
слой соли NaCl (0,2 мм), который дает яркое свечение в момент
выхода УВ на поверхность пластины. Тем самым фиксируется начало
движения пластины.
Экран над головками световодов делается прозрачным, чтобы
зарегистрировать начало свечения соли. Толщина экрана из
оргстекла должна быть достаточно большой (3—5 мм), чтобы зазор под
598
экраном захлопывался не от соли, летящей впереди пластины, а от
пластины.
Чтобы получить время движения пластины (и ее среднюю
скорость), надо из измеренного времени вычесть время движения УВ
по экрану (t = h /D ) и время закрытия зазора шириной S экраном
(t, = 8/2U,).'
4. Измерение разновременности и скорости УВ при ее
движении в слоеном приемнике (метод вспыхивающих зазоров).
Приемник изготовляется из ряда прозрачных слоев (обычно из
оргстекла), разделенных зазорами по аналогии со схемой на рис. 12.5.
Последний зазор — над держателем входных головок световодов.
Каждый световод фиксирует ряд последовательных вспышек при
закрытии зазоров ударной волной над входной головкой световода.
Таким образом, каждый световод регистрирует x,t -диаграмму
движения УВ в точке над осью световода, что исключает ошибку,
связанную с асимметрией волны. В опыте измеряется изменение
асимметрии, разнодинамичности УВ и ее затухание при движении
по приемнику. Кроме того, такая постановка опыта позволяет
определить, был ли откол у пластины.
5. Регистрация x,t -диаграммы движения свободной поверхности
тел ( пластин или оболочек.)
На пути движения пластины на различных известных
расстояниях от начального положения пластины устанавливаются
световоды, которые могут быть открытого или закрытого типа (без экранов
или с экранами на входных головках).
У открытых головок момент подлета поверхности пластины к
головке фиксируется по прекращению свечения, а у экранированных
световодов — по вспышке света, возникающей в момент закрытия
зазора между экраном и головкой.
При необходимости увеличить яркость свечения пространство
под пластиной заполняется аргоном, а в зазор между экраном и
головкой световода помещается пористая соль NaCl.
При регистрации x,t -диаграмм максимальное количество
световодов в одном устройстве имеет два ограничения.
1). Световоды должны размещаться только под
неразгруженной зоной круглой пластины — внутри конуса, угол при верши-
599
не которого можно брать «с запасом», равным 100°. Поэтому
количество световодов уменьшается с увеличением базы полета
пластины.
2). Расстояние между световодами разных уровней должно быть
достаточно большим, чтобы обеспечить взаимодействие нижележащего
световода с пластиной вне зоны возмущения поверхности пластины,
создаваемой соседним световодом предыдущего уровня [11,16]. (см.
раздел 6.3)
Диаметр возмущенной зоны пропорционален диаметру
световода dc, скорости пластины (см. гл. 6 и рис. 6.12) и времени
взаимодействия (базе измерения). При достаточно больших скоростях в
пластине образуется кратер, из которого вылетает струя. При малых
скоростях кратер не образуется, а материал световода накапливается
на поверхности пластины.
Практически аля всех встречающихся постановок опытов по
регистрации x,t -диаграмм можно установить расстояние между
соседними световодами разных уровней, равное 5 d .
Для обеспечения жесткости и прямолинейности световоду малого
диаметра каждый световод помещается в тонкостенную металлическую
трубку. Световоды могут группироваться в трубчатые многоканальные
оптические датчики аналогично электроконтактному спиральному
датчику (см. разд. 12.5 [И]). Фотохронограф СФР-2М надежно фиксирует
вспышки света от световодов диаметром более 0,3 мм.
Все рассмотренные схемы измерений показаны на рис. 12.7, 12.8,
12.9.
В перечисленных устройствах световоды используются как
оптические датчики концевого типа: достаточная а^я регистрации
вспышка света возникает на конце световода (на его входной головке).
При регистрации вспышек с помощью СФР-2М нижний предел
использования таких датчиков — световодов:
— по скорости удара по головке
— в воздухе ~2 км/с
— в аргоне ~1,5 км/с
— по давлению — 50—80 кбар.
600
alx comrnurilcaZisn
node
zecozzez]
phusico<*
ChimicaC
LLtm
fzeazment
\oiace$$$*
* ana 7
analysis
hide
PxincipCe scheme ofi zegistzatLoa system
„ eCectxodeConatoz
Lr„;
40n
/panei
Light guide (fl&ez)
5
x
I
^pnotoxscozdez
Vent
ttme malts
n% ' з 2 *
fig 12.7 Experiment. pans С scheme and a pazt eg-
pholQchzQnogzaph ptc tuis
Для измерений в области меньших скоростей и давлений
разработаны петлевые оптические датчики [15]. Такой датчик представляет
собой отрезок световода, выходная головка которого закрепляется, как и
ранее, на панели, а входная устанавливается на импульсном источнике
света (рис. 12.10—12.13). Обычно это небольшой заряд ВВ, создающий
УВ в аргоне и взрывающийся синхронно с изучаемым явлением.
Таким образом, световод передает в фотохронограф
непрерывный свет от импульсного источника. Рабочей частью датчика яв-
ляется петля малого радиуса в средней части световода. Когда ударная
волна (или летящее тело) достигает петли, то она разрушает вершину
петли и тем самым перекрывает передачу света по световоду.
Измерения x,t -диаграммы движения УВ в воде (см. рис. 12.12)
показали, что петлевыми датчиками можно регистрировать ударные
волны с давлением 5—10 кбар [15].
Петлевые датчики можно использовать и ^ля регистрации
ударных волн в газах при еще более низких давлениях. В этом случае
разрушение петли осуществляется тонкой пластиной, устанавливаемой
над петлей и вовлекаемой в движение газовой ударной волной.
602
£ОЖ*'
late
А-А
hJaCt
И
б У
*
к
JaIM
\(sjht auLde
FiyilS Groups fat recording o£ x,£ -diagrams c£
piate mocremenC
В заключение отметим работу [17], в которой предложены и
испытаны оптические датчики концевого типа а^я измерения
скорости детонации (multi-stage light fibre probes).
В гибкой трубке о 1,8 мм размещено несколько отрезков
световодов с зазорами 0,5мм между отрезками. Трубка устанавливается
вдоль образующей заряда так, что детонация идёт вдоль трубки.
deb.
lighting
~9 • v~ *— detonation uratre ~i
eC3cZzod*Canci.az cLixurcttathe Sux/ace/ si
HE
ааи$г x
tot^etfcatc'ft ?
\-shcci плите educe.
RjgSlJQScnama and phcCocAzanogzam
usiin Саар $au$s
Zlantatg i shock urave
the catttzaC
surface
OSi
i^Z^v,
to be tscazdet
Fin.lZft. Uooo qauces and phazcchianontarns
aScalned a 6u them.
Qpanet
s ; A , wazex *£
£ \Д£ pbte £
etactzodetonatozs
J 1С
N
I
3 J
<^
\
/
p
'D
J
<
«^+_
Q 5
so
40
10
2fl
с
in
a
0
FisOLlzTest schems fox
determine
Ltmm
Fin\H$/etocit$ and piessuxe
dependence on the.
acscance la uratez
nation <ф gauge fjrazxing capacity.
604
Вспышки света, возникающие при закрытии зазоров передаются в
фотохронограф. Использование нескольких датчиков позволяет
измерить и скорость, и форму детонационной волны.
12,5. Метод оптического рычага
В исследованиях динамической прочности, фазовых переходов,
развития детонации и др. часто используется оптический метод
непрерывной регистрации волновой и массовой скорости - т.н. метод
оптического рычага [18,19,20].
Суть метода состоит в регистрации смещения отполированной
зеркальной поверхности клиновидного образца в момент выхода на
поверхность упругих и пластических волн, а также волн разгрузки.
Постановка опыта и типичная фотохронограмма показаны на
рис. 12.14.
Рис. 12.14. Схема измерения волновых и массовых скоростей методом
оптического рычага и типичная фотохронограмма. Нагружение скользящей детонацией
1 - ПВ; 2 - заряд ВВ; 3 - образец; 4 - светоотражающая поверхность; 5 -
линейчатый растр; а - точка выхода упругого предвестника; в - точка выхода
пластической волны
С помощью фотохронографа регистрируется свет, отражаемый от
поверхности образца. Свет создаётся аргоновым источником. На пути
света стоит линейный растр, создающий на плёнке ряд светящихся
полос, на которых фиксируются смещения, возникающие за счёт поворота
отражающей поверхности в момент выхода на неё волн.
Величина излома прямо связана с величиной смещения
поверхности, т.е. с массовой скоростью.
605
Применение клиновидного образца позволяет изучать в одном
опыте различные волновые явления в зависимости от толщины
образца.
Волновые скорости определяются по скоростям, с которыми
волновые фронты пересекают отражающую поверхность клина.
Формулы для расчёта волновых и массовых скоростей
получаются из рассмотрения геометрических соотношений
экспериментальной сборки [18,19].
Погрешности измерения: волновых скоростей — 1%, скорости
свободной поверхности образца — 3—4%, расчёта давления по
измеренным скоростям — 5%.
Для изучения детонации ударно-сжатого тротила в [19]
использовалась измерительная сборка, отражающая поверхность
которой погружена в жидкость с ударной адиабатой, близкой к
адиабате тротила. Использовался раствор бромоформа в этиловом
спирте (р = 2,35 г/см3) со следующими ударной адиабатой и
зависимостью коэффициента преломления п от массовой скорости:
D = 1190+1,86и(м/с), п = 1,54+0,35 103и
Применение жидкости позволяет увеличить время ударного
сжатия образца и повысить точность вычисления массовой скорости в
образце по методу отражения. Максимальные давления ограничены
потерей прозрачности жидкости (не более 30 ГПа).
12.6. Электроконтактная многоканальная методика
регистрации х, t - диаграмм
Задолго до разработки оптических методик с применением сво-
товодов широко использовалась электроконтактная методика а^я
измерения скоростей ударных и детонационных волн, скоростей
свободной поверхности метаемых тел [2,21]. С ее помощью
регистрируются моменты замыкания проволочных или фольговых
контактов (ионизационных датчиков) какой-либо движущейся
поверхностью, ударной или детонационной волнами.
При замыкании контактов короткие импульсы создаются за счет
разрядки (или зарядки) небольших конденсаторов и
регистрируются либо осциллографами с линейной или спиральной разверткой
606
(старый метод) или современными цифровыми счетчиками
временных интервалов.
Для измерения скорости свободной поверхности обычно
используются массивные трубчатые датчики с экранами,
защищающими контакты в трубках от преждевременного замыкания воздушной
ударной волной.
Поскольку контакты разных уровней размещаются в разных точках,
на точность измерения временных интервалов влияет изменение
формы замыкающей поверхности (например, отклонение от плоскости).
Точность измерений снижают колебания амплитуды и формы
электрических импульсов, получаемых при замыкании контактов.
Нами совместно с Н.И. Куракиным разработана модификация
электроконтактной методики регистрации подробных x,t —
диаграмм с использованием новой конструкции миниатюрного
многоконтактного датчика, повышающего точность и информативность
измерений [11].
Датчик представляет собой (см. рис. 12.15) цилиндр из тонкой
конденсаторной бумаги, по образующей которого наклеены медные
проволочки (контакты) из обмоточного провода ПЭВ. Каждая
проволочка обрезается вместе с бумагой на определенную высоту (в
зависимости от базы измерения), так что торцы проволочек лежат на
спирали (отсюда название датчика — спиральный). Датчик с
десятью контактами имеет диаметр 2,3 мм.
* в
Рис. 12.15. Многоконтактный датчик
а) спиральный; б) плоский; в) разрез по АА: 1 — база измерения; 2 —
конденсаторная бумага толщиной 0,01 мм; 3 — провод ПЭВ-2 диаметром 0,06 мм;
4 —клейБФ-2
Предварительно на специально сконструированном
намоточном станке готовятся плоские заготовки, которые затем
покрываются клеем БФ-2, сворачиваются в цилиндр и в таком виде полиме-
ризуются при температуре 130 С. Проволочки у плоских заготовок
обрезаются шаблоном, который позволяет изготовлять датчики с
колебанием измерительных баз в пределах 0,015 мм. Общая
толщина бумаги и клея в датчике не превышает 0,04 мм, однако трубчатая
форма придает датчику достаточную жесткость.
Большое внимание было уделено выбору расстояний между
проволочками датчика, исключающих взаимное влияние контактов друг на
друга. При взаимодействии датчика с движущимся телом в последнем
образуется кратер, из которого вылетает струя, содержащая материал
движущегося тела и контакта [22,23]. Она может создать мостик
проводимости аля соседних контактов и нарушить их работу. По краям
кратера образуется валик, поэтому соседний контакт надо удалять
настолько, чтобы он попадал на невозмущенный участок поверхности.
Проведенные исследования по взаимодействию движущихся
тел со стержнями показали (см. гл. 6, рис. 6.11, 6.12), что в
зависимости от материалов тела и стержня диаметр возмущенной области
достигает величины dB = 10dQ (dQ — диаметр стержня, скорость тела
~5 км/с.) Поэтому а^я спирального датчика с контактами из
провода диаметром 0,06 мм взято расстояние между контактами 0,6 мм,
что в 2 раза больше размера возмущенной зоны (гв = 5dQ = 0,3 мм).
Опыты показали, что вылетающая из кратера струя не может
замкнуть или сместить соседний контакт, так как она не непрерывна, а
состоит из отдельных частиц, которые не образуют электрические цепи,
и по размерам частицы на порядок меньше диаметра контакта. Таким
образом, группировка контактов в одном спиральном датчике малого
диаметра снижает погрешность измерений, связанную с асимметрией
поверхности (каждый датчик регистрирует x,t — диаграмму движения
практически одной точки поверхности), упрощает монтаж
измерительного узла и увеличивает плотность размещения контактов.
Так как торцы контактов не изолированы (а^я простоты
экспериментальной сборки и для более надежного замыкания с
движущимся телом), работа датчика зависит от ионизации газовой среды,
608
в которой проводятся измерения. Так, /а^я воздуха скорость тела не
должна превышать 2,5 км/с. При большей скорости воздух за
фронтом УВ, идущей перед движущимся телом, ионизирован настолько,
что нарушает нормальную работу контактов (они замыкаются не
поверхностью тела, а воздушной УВ),
Для измерений при больших скоростях применена газовая защита
спирального датчика, заключающаяся в замене воздуха перед
движущимся телом другим газом, с меньшей степенью ионизации за фронтом
УВ [24,25]. Можно использовать гелий (с высоким потенциалом
ионизации) или многоатомные газы (углекислый газ, метан, пропан и др.),
которые имеют большую теплоемкость и меньше нагреваются в УВ, чем
воздух [26,12]. Для воздуха, углекислого газа, гелия и пропана нами
сделаны оценки температуры и степени ионизации j газа за фронтом УВ в
зависимости от скорости движения в газе изучаемого тела.
Полученные зависимости приведены на рис. 12.16.
Рис. 12.16. Расчет зависимостей температуры за фронтом УВ в газах от скорости
пластины (а) и степени ионизации газов от температуры (б)
1 — воздух; 2 - С02; 3 — гелий; 4 — пропан
При проведении измерений в воздухе без защиты контактов
Аая максимально допустимой скорости тела 2,5 км/с за фронтом
воздушной УВ Т = 3000К, j = 0,01. Приняв, что и в других газах
допустимы измерения открытыми контактами, если j<0,01, получим
приведенные в таблице 12.3 значения Т и предельных скоростей w,
которые можно замерить спиральным датчиком. Практически в
экспериментах пространство вокруг датчиков делается замкнутым (но
не герметичным) и непрерывно продувается пропан-бутаном.
609
Таблица 12.3. Допустимые скорости измерений в различных газах
Газ
Воздух
Углекислый газ
Гелий
Пропан
Т,К
3000
12500
20000
10000
w,„,km/c
2,5
5,5
11,0
11,0
Для измерений с помощью спиральных датчиков разработан
многоканальный измерительный комплекс (см. рис. 12.17), имеющий
следующие параметры: число измерений в опыте (число контактов) 200
(20 датчиков по 10 контактов или 10 датчиков по 20 контактов);
напряжение на контактах 50 В; временное разрешение 50 не.
Измерительный
\usejr со спираль-
1 мыма
датчиками
\бло/гфсрми-
Хрования
UMftt/JTbCOS
а
Усилатель-
дмрмироеа-
тель
Измеритель
бремени
(]Rl150h
Д1Д*М
|iC!300
Т^пит
150к f]R10150K
г*4А1°
ф
Д10Д14
уСЮЗОО Д2256
MR11150
f Т го*
Г -L 150
II
-^ш-ру]
2:0140,1
Л16В2П
Рис. 12.17. Блок-схема (а) и электрическая схема (б) одного канала измерительного
комплекса
Блок формирования импульсов (БФИ) обеспечивает получение
коротких выходных импульсов практически постоянной амплитуды
независимо от количества сработавших контактов в датчике. Малая
длительность импульсов (50 не) достигается применением
конденсаторов малой емкости (150—300 пФ), а постоянство амплитуды —
610
введением диодов Д1—Д10, которые выделяют положительную
полуволну колебаний, возникающих из-за паразитных емкостей
и индуктивностеи в схеме при замыкании контакта, и устраняют
влияние ранее сработавших контактов на амплитуду формируемых
импульсов. Для улучшения формы импульсов БФИ размещается за
бронезащитой как можно ближе к датчикам.
При малом напряжении питания датчиков и значительном
затухании коротких импульсов при передаче по кабелю чувствительность
используемых в комплексе осциллографов ИВ-ЗОМ мала аая регистрации
импульсов от БФИ. Поэтому в канал измерения введен усилитель —
формирователь, который генерирует импульс с амплитудой 150 В и
длительностью переднего фронта 10 не. В качестве такого
формирователя использована спусковая схема на лампе 6В2П с вторичной эмиссией
[27]. Через диод Д11 подается нулевой импульс, относительно которого
измеряется время срабатывания контактов датчика.
Ошибка измерения временных интервалов (см. рис. 12.2)
зависит от используемого измерителя времени и точности изготовления
баз датчика. При использовании датчиков, изготавливаемых по
шаблону, и осциллографов ИВ-ЗОМ случайная погрешность измерения
временных интервалов не более 20 не
Для выявления систематической ошибки в одинаковых условиях
опыта проведено сравнение измерений с помощью спиральных
датчиков с измерениями по общепринятой электроконтактной
методике (с экранированными трубчатыми датчиками [21]). Результаты
такого сравнения, приведенные на рис. 12.18, свидетельствуют об
отсутствии заметной систематической погрешности в измерениях с
помощью разработанной методики.
Примеры измерений на разработанном комплексе показаны
также на рис. 12.19, рис. 11.3, рис. 3.7а, рис. 10.9.
12.7. Измерение давления манганиновыми датчиками
Широко применяется непрерывная регистрация профилей
давления с помощью манганиновых датчиков в исследованиях
полиморфизма, упругопластических свойств, детонации и т.п.
611
АО
СО jpfUH
Рис. 12.18. Постановка эксперимента (а) и зависимость скорости пластины из
алюминия от базы полета (б)
1 — линзовый генератор плоской волны; 2 — заряд из ТТ40;3 — пластина из
алюминия; 4 — измерительный узел со спиральными датчиками; о — измерения
8-ю спиральными датчиками в одном опыте; v — среднее из 5-ти опытов значение
скорости, полученное на стандартной методике с трубчатыми контактами
Рис. 12.19. Схема эксперимента (а) и экспериментальные x,t-диаграммы ударной
волны в стали и алюминии (б)
1 — линзовый генератор плоской волны; 2 — заряд из ТГ 30/70 С 120x120 мм;
3 — образец; 4 — плоские датчики; 5 — цапон-лак; I — сталь (D = 5,4 км/с); II —
алюминий (D=7,4 км/с)
Метод основан на высокой чувствительности удельного
сопротивления AR/Rq манганина (сплав с типичным составом: 84% Си, 12% Мп,
4% Ni) к давлению и низкой чувствительности к температуре.
612
р/Щ
Q5 Щ uRjRo
Рис. 12.20. Зависимость относительного
изменения электросопротивления манганина
от давления
Для измерения
статических давлений
манганин использовал впервые
Бриджмен. Затем в [28,29]
было показано, что
зависимость AR/Rq (р) у
манганина одинаковая как в
статических, так и в динамических
условиях. В [30] найдено,
что до ударных давлений не
ниже 7... 10 ГПа эта
зависимость обратима (нет
гистерезиса в изменении AR/
RJ и не зависит от профиля
давления в УВ. При полной
разгрузке в связи с наклёпом у манганина появляется необратимая
составляющая AR/Rq , но не более 2,5% от R^ .
Зависимость AR/Rq от давления у манганина показана на
рис. 12.20 [31]. Результаты измерений калибровочной зависимости
AR/RQ (р) манганина приведены в [31].
Согласно [29] величина давления по результатам измерения AR/Rq
у манганинового датчика рассчитывается по формуле:
р = 34,5АЛ//г0+7,5(АЛ//г0)2 (12.16)
В [30] предлагается несколько иная расчётная формула:
P = 34AR/Ro + 7(AR/R0f (12.17)
Применимость этой формулы проверена до ПОГПа в работе
[32].
По конструкции плоский манганиновый датчик аналогичен тен-
зорезистору, делается из проволоки или фольги толщиной 10...30
мкм, занимает площадь 0,1 — 1см2. Датчик закладывается внутрь
исследуемого образца (между пластинами) и при необходимости
отделяется от материала образца тонкими изолирующими прокладками
(тефлон, слюда).
Максимальное давление, измеряемое манганиновым датчиком,
ограничивается давлением, до которого прокладки сохраняют свои
изолирующие свойства (не более 100 ГПа). Максимальное время
измерения ограничивается разгрузкой образца, при которой
обрываются электровводы в сборку.
Для проведения измерений через датчик пропускается
стабилизированный импульс тока длительностью примерно 100 мкс и
осциллографом регистрируется падение напряжения на датчике,
которое растёт с давлением. Измерение величины AR/Ro проводят с
помощью моста сопротивлений.
Применение изолирующих прокладок вносит в показания
датчика небольшую инерционность, искажающую профиль давления
[31], но обычно это заметно только при измерениях малых
давлений.
На измеряемую величину AR/I^ , кроме давления, влияет
изменение длины манганина в условиях одноосной нагрузки. Для учёта
этого фактора в одной измерительной сборке используется ещё один
датчик из константана (с малым пьезоэффектом), или второй
манганиновый датчик, устанавливаемый перпендикулярно фронту УВ.
Максимальная погрешность измерения давления составляет 10%.
Литература к главе 12
1. Hallock F. Ргос. of the 13th Inter. Congress on High Speed
Photography and Photonics, Tokyo, 1978, p.8—18.
2. Методы исследования свойств материалов при интенсивных
динамических нагрузках. Монография под общей ред. М.В.
Жерноклетова. Изд-во РФЯЦ-ВНИИЭФ, г. Саров, 2003,402 с.
3. Thomas Е. Holland, Thomas J. Healey and Charles H. Bagley
«Ultrahigh — speed photographic instruments». ISA
Transactions — January, 1966.
4. Z. Ziolcowski, H. Derentowicz J. of Tech.Phys.,1975, 16,2, p.
185—195.
5. Дубовик A.C. Фотографическая регистрация быстропроте-
кающих процессов. М.: Наука, 1975.
614
6. Hallock F. Proc. of the 13th Inter. Congress on High Speed
Photography and Photonics, Tokyo, 1978, p.8—18.
7. Key M.N., Lamb M.I., Lewis C.L.S., Moore A., Evans R.G. Appl.
Phys. Lett. 34(9), 1979/
8. Зайдель A.H. Ошибки измерения физических величин, Л.:
Наука,1974.
9. Даниленко В.В., Козерук Н.П. Журнал научн. и прикл.
фотографии и кинематографии, 1989, т.34, N5, с.336—340.
10. Болотов Ф.Ф., Ловягин Б.М., Ильин Н.В. Журнал научн. и
прикладной фотографии и кинематографии, 1977, т.22, N6,
с.415.
11. Куракин Н.И., Даниленко В.В., Козерук Н.П. // Физика
горения и взрыва. 1989, №5,С. 89 — 92.
12. Баум Ф.А., Станюкович К.П., Шехтер Б.И. Физика взрыва. М.:
Из-во физ-мат. лит., 1975.
13. Шнирман Г.Л., Дубовик А.С., Кевлишвили П.В.
Высокоскоростная фоторегистрирующая установка СФР, Из-во
техн.-эконом. информации АН СССР, 1957.
14. Held М.В., Nikowitsch P.P. Intern. Congress jn High Speed
Photography and Photonics. San Diego, 1982, SPIE Vol.348, p.
939—947.
15. Kozeruk N.P., Danilenko V.V., Telichko J.V. Optical Fiber
Ganges for Gas-Dynamic Investigations, 20-th Congress on
High-Speed Photography and Photonics, Victoria, 1992,SPIE
Vol.l801,p.l38—146.
16. Kozeruk N.P., Danilenko V.V. et.al. Multichannel Optical Fiber
System to Measure Time Intervals at Investigations of Explosive
Phenomena, 20-th Congress on High-Speed Photography and
Photonics, Victoria, 1992,SPIEVol. 1801 ,p.981—988.
17. Held M. and Nikowitsch P. High Speed Photography, 1984, v.491,
p. 619.
18. Fowles G. R. J.Appl.Phys., 1961,38,1475.
19. Таржанов В. И. ФГВ, 1976, №6, с. 924 - 930.
20. Козлов Е. А., Музыря А. К. и др. ФГВ, 1984,20,4,123.
21. Альтшулер Л.В. Применение ударных волн в физике высоких
давлений. Успехи физических наук, 1965, 85, N2, с.197.
615
22. Драчев Н.М., Морозкин В.И., Потапов И.В. ИФЖ, 1972,
22,3.
23. Сагомонян АЛ. Проникание. М.: Из-во МГУ, 1975.
24. Duff, Honston. J. Chem.Phys., 1955,23,7.
25. Goranson, Bancroft et. al. J. Appl. Phys., 1955,26,1472.
26. Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и
высокотемпературных гидродинамических явлений. М.: Наука,
1966.
27. Глебович Г.В., Моругин Л.А. Формирование импульсов нано-
секундной длительности. М.: Сов. радио, 1958.
28. Leel M.J.J. Appl. Phys., 1973,44, N9, p.4017.
29. Ананьин A.B., Дремин A.H., Канель Г.И. ФГВ, 1973, N3,
с.437-443.
30. Канель Г.И., Вахитова ГГ., Дремин А.Н. ФГВ, 1978, N2, с.130.
31. Теплофизика и динамика интенсивных импульсных
воздействий. А.В. Бушман, Г.И. Канель, А,Л, Ни, В.Е.Фортов. Ин-т
химфизикиАН СССР, Черноголовка, 1988.
32. Постнов В,И. Сб. «Нестационарные проблемы
гидродинамики». Институт гидродинамики СО АН СССР, вып.48,1980,
с.116.
616
Глава тринадцатая
ВЗРЫВНЫЕ КАМЕРЫ
13.1. Общее описание камер
Во всех случаях взрывная камера — это локализатор взрыва,
т.е. стенки камеры ограничивают некоторый объем, из которого не
должны разлетаться продукты взрыва и осколки [1].
Назначение взрывных камер (ВК) может быть следующим.
1. Камеры а^я проведения исследований, ^^я измерения
параметров новых ВС и новых взрывных устройств, а^я испытаний брони
и других материалов.
2. Камеры для сварки взрывом, а^я упрочнения взрывом.
3. Камеры для синтеза порошков (алмаза, керамики) и ^^я их
безампульного спекания.
4. Камеры для взрывного дробления хрупких порошков (алмаз,
керамика).
5. Камеры для безопасной перевозки ВС и взрывных устройств.
6. Передвижные камеры ^^я уничтожения взрывоопасных
предметов, найденных в аэропортах, вокзалах, автостанциях.
По своей конструкции ВК могут быть:
— сферические или цилиндрические, с горизонтальной или
вертикальной осью, с плоскими или эллиптическими днищами;
— герметичные или негерметичные;
— стальные, железобетонные, из полимерных композитов;
— с люком или из двух разделяющихся частей для доступа
внутрь ВК;
— заполненные ПД (от предыдущего взрыва), инертным газом
(С02, N2), воздухом или вакуумируемые;
— полностью сварные или составные из частей, соединяемых
болтами;
— однократного или многократного применения;
— с защитой от осколков и без такой защиты
Прежде всего, камеры отличаются своим внутренним объемом,
от которого зависит максимальный вес взрываемого в камере заряда.
В качестве первой грубой оценки можно считать, что на каждый кг
заряда необходимо 1 —4 м3 объема камеры.
В 1980 году в России были построены две сферические камеры
диаметром 12 м, толщиной стенок 100 мм и объемом 905 м3,
рассчитанные на взрыв зарядов до 1 т (см. фото. 13.1). Для камер
использовалась специальная очень прочная и пластичная сталь АК-36
(<7 = 110 кг/мм2, б = 22%). В одной из таких камер с участием автора
проведен уникальный эксперимент по синтезу ультрадисперсного
алмаза взрывом в водяной оболочке заряда из ТГ40 весом 140 кг
И.
Для взрывов сосредоточенных зарядов сферические камеры
наилучшие, т.к. обладают равнопрочностью.
Обычно а^я исследовательских и технологических целей
строятся цилиндрические камеры гораздо меньшего объема и длиной
в пределах 2—7 диаметров. Такие камеры проще изготавливать, но
они не равнопрочные — их слабым местом является центральное
сечение (в котором взрывается заряд) и днища.
В [3] показано, что при нагружении взрывом цилиндрические
оболочки так же прочны, как и сферические, но их разрушение
менее катастрофично и носит локальный характер (обычно
разрушается только центральное сечение камеры).
Согласно измерениям, сделанным в [4], при одинаковых
радиусе камер и массе заряда, максимальное давление на стенке
сферической и цилиндрической камер одинаково, но длительность импульса
на~30% меньше в цилиндрической камере (благодаря боковой
разгрузке центрального сечения), причем кольцевые деформации
стенок камеры в~7 раз больше осевых.
618
Фото. 13.1. Сферическая взрывная камера 012м. в транспортном положении
и после установки в бетонный колодец
619
Отметим, что при статической нагрузке напряжение в
цилиндрической камере вдвое больше, чем в сферической тех же размеров.
С 1963 года автор проектировал, строил и эксплуатировал
различные конструкции камер, в одной из которых впервые автором
был получен наноалмаз из продуктов взрыва [1,5—8].
Например, в 1992 году &ля фирмы «Алит» построена и
успешно эксплуатируется стальная цилиндрическая камера 02,5x17,5 м (см.
фото. 13.2), состоящая из трех частей, соединяемых болтами:
центральная неподвижная часть с трехслойными стенками общей толщиной
300 мм и две подвижные боковые части с толщиной стенок 70 мм [9].
Для лучшего охлаждения алмаза и снижения нагрузки на
стенки камеры перед взрывом по всей длине камеры создавался водяной
душ. Камера рассчитана на взрыв в воздухе зарядов до 30 кг.
При синтезе и спекании алмаза увеличение массы заряда
позволяет получать более крупные и более совершенные моно- и поли-
Рис. 13.4. Схема воздушно-водяной системы камеры для синтеза алмаза
1— камера; 2— воздушный ресивер; 3 — расходный водяной бак; 4 —
вентилятор; 5 — компрессор (Юатм.); 6 — электроклапан; 7 — вентиль; 8 — трубы;
9 — водяной насос; 10 — бак осаждения суспензии; 11 — горизонтальная оса-
дительная центрифуга с автоматической выгрузкой; 12 — главный водяной бак;
13 — фильтр-сетка для отделения крупных частиц; 14 — ёмкость для осколков;
15 — датчик уровня воды; 16 — электроклапан
620
^l^^^^y
Фото 13.2 Взрывная камера для синтеза алмаза (100м3) фирмы «АЛИТ»
Фото 13.3. Взрывная камера ВНИИТФ с «отлетающей» при взрыве массой на
торцах камеры (V=22м3)
621
кристаллы, а также повысить производительность камеры. Отсюда
и стремление к увеличению объема и прочности камеры.
В 1999—2000 годах автором спроектирована цилиндрическая
камера о 4,6 х 19 м объемом 315 м3, рассчитанная на многократный
взрыв сосредоточенных зарядов до 70 кг. Схема воздушно-водяной
системы камеры показана на рис. 13.4.
Снаружи центральная часть камеры на длине 9 м усилена
железобетоном квадратного сечения 7,6 х 7,6 м весом 700 т. В камере перед
взрывом может создаваться водяной душ и вакуум. Днища камеры и
их крепление к цилиндру усилены ребрами и пластинами,
установленными в камере перед днищами. При обтекании пластин ударной
волной между пластинами и днищем создается турбулентность,
снижающая и растягивающая импульс на днище.
В 2008 г. автором спроектирована вертикальная цилиндрическая
камера оЗ,2х7,5 м (V = 60 m3) с плоскими днищами и трёхслойными
стенками (сталь—бетон—сталь) толщиной 0,6 м [10]. Камера
предназначена а^я синтеза и спекания наноалмазов взрывом зарядов
массой до 20 кг.
При проектировании таких больших взрывных камер
необходимо учитывать масштабный эффект энергетической природы,
снижающий фактическую прочность камеры.
Влиянием масштаба может быть объяснено хрупкое разрушение
в упругой области крупных объектов, изготовленных из пластичной
стали [12]. С точки зрения статистики, чем больше толщина стенки
камеры t, тем больше вероятность появления в стенке дефекта,
снижающего напряжение разрушения а . При этом ^^я геометрически
подобных камер (t/R= Const) со стенками толщиной t{ и t2
выполняется соотношение:
'Л2=('Л)-1/т <ш>
где т~8 — характеристика дефектности стали.
Согласно энергетической концепции, работа хрупкого
разрушения объекта (работа движения трещин) осуществляется за счет
упругой энергии деформации, при этом выполняется то же
соотношение (13.1), но при m = 2, т.е. влияние масштаба более сильное, что
подтверждается работами [11,12].
622
Влияние масштабного эффекта можно значительно снизить, если
цилиндрическую оболочку изготавливать из многих слоев,
например, из тонкой стальной ленты или из стеклопластика [13]. У
многослойной оболочки во много раз возрастает сопротивление
движению трещины.
Наибольшей удельной прочностью обладают полимерные
композиции: очень прочные полимерные нити (кевлар, лавсан) наматываются в
определенном порядке на тонкую стальную технологическую оболочку
и пропитываются полимерной смолой. Такие оболочки
нечувствительны к исходным дефектам и к динамичности нагружения, обладают
высоким сопротивлением к распространению трещин.
Сотрудниками ВНИИТФ (г. Снежинкск-70) спроектирована,
изготовлена на заводе Уралхиммаш и успешно испытана цилиндрическая
камера 01,5x12,5 м, стенки которой толщиной 70 мм изготавливались
намоткой с натягом стальной ленты на цилиндр из нержавеющей
стали толщиной 10 мм. Камера рассчитана на заряд весом до 40 кг. В
камере применена оригинальная защита плоских днищ (см. фото 13.3).
Снаружи к днищам плотно прижаты стальные болванки, которые
могут передвигаться вдоль оси камеры на рельсовых тележках. При взрыве
импульс передается от днищ к болванкам, в результате днища остаются
практически неподвижными, а болванки начинают двигаться на
тележках и затем тормозятся (эффект бильярдных шаров).
Эта камера была использована автором ^^я синтеза алмаза
взрывом заряда весом до 20 кг в водяной оболочке и без оболочки.
В качестве характеристики удельной взрывной нагрузки на
камеру можно принять отношение массы заряда m к массе М
цилиндрической оболочки камеры длиной, равной двум диаметрам камеры
[14]. Это отношение т/М пропорционально кольцевой
деформации наиболее нагруженного центрального сечения камеры [14], а
распределение максимальных величин т/М по длине камеры
пропорционально проекции удельного импульса на нормаль к
поверхности оболочки [15].
Если для обычной стальной оболочки предельная разрушающая
нагрузка составляет (m/M)max = (1—3) 103, то /^ая оболочек из
полимерных композиций (m/M)max = (10—20) 103 [13].
623
Одной из разновидностей взрывных камер является взрывоза-
щитный контейнер (ВЗК) одноразового использования, ^^я
которого важна высокая надежность предотвращения хрупкого
разрушения при минимальном весе (аая транспортабельности).
Конструкции цилиндрических и сферических ВЗК с
использованием волокнистых композитов (стекловолокно и полимерное
связующее) разработаны специалистами ВНИИЭФ [16]. Как и а^я
камер со стенками из слоев стальной ленты, стекловолокно
наматывается на оболочку из мягкой стали. Нагрузка на днища снижается
пенопластовыми демпферами внутри ВЗК (см. рис. 13.5).
12 3 4 5 6 7 8
Рис.13.5. Схема ВЗК
1 — корпус (стеклопластик); 2 — пробка (пенопласт); 3 — демпфер (пенопласт);
4 — шпилька для установки ВВ; 5 — заряд ВВ; 6 — крышка люка; 7 — диафрагма;
8 — шток измерительный; 9 — опора
Такие конструкции можно использовать &ая защитных оболочек
АЗС и для баллонов высокого давления различного назначения.
Предельная окружная деформация стеклопластикого слоя без
его повреждения составляет 6 = 3,5%. Величина е линейно растёт
с увеличением относительной массы заряда: г — 170,2 (т/М).
По результатам испытаний несущая способность композитных
ВЗК следующая: ВЗК о 0.5x1,8м весом 200кг выдерживает взрыв
сферического заряда весом 2кг, а ВЗК о 2,5x9,5м весом 25т - взрыв
заряда до 200кг (в тротиловом эквиваленте).
Кроме веса заряда, нагрузка на камеру зависит также от
конфигурации и состава заряда. Худший вариант — взрыв сосредоточенных
624
зарядов — сферических или цилиндрических с L/d = 1—2. При
одинаковой массе заряда нагрузка на цилиндрическую камеру
уменьшается с увеличением длины заряда (распределенное осесимметричное
нагружение), а также, если заряд плоский (диск) с L/d<l. Для
плоского заряда нагрузка определяется только частью заряда,
разлетающейся в радиальном направлении, а размер зоны деформации
камеры не зависит от толщины заряда [17], если L /(Rk t)0,5< 1, где Rk,
t — радиус и толщина стенки камеры, L- толщина диска.
Кроме того, в реальных системах возможны отклонения от
симметричной схемы нагружения камеры, связанные с нарушением
симметрии положения заряда или с асимметричным разлетом
продуктов детонации.
Согласно [18], смещение заряда от центра сферической камеры
на величину с = e/R^ изменяет величину импульса и деформации 8
камеры (т.к. e~i/co, где со — частота свободных колебаний оболочки)
следующим образом:
iJi={Rk + eflR^ = {\+cf (13.2)
При взрыве заряда в камере стенки камеры смещаются от положения
равновесия и затем начинают колебаться с собственной частотой со0.
Во многих работах экспериментально показано, что длительность
динамической нагрузки на стенках камеры меньше четверти периода
ее собственных колебаний (t<TQ/4), т.е. характер нагружения камер
импульсный [20]. Поэтому максимальное смещение оболочки
относительно положения равновесия определяется соотношением [21]:
д =J/pt®n (13.3)
max г ~ s s 0 ч '
где Jr— импульс, отраженный от стенок, ps, tg — плотность и
толщина стенок.
Интересно, что деформация сферической и короткой
цилиндрической (L/d =1) камер в первом полупериоде камер не является
максимальной. Уже после затухания УВ нагрузки наблюдается
раскачка колебаний с увеличением амплитуды до трех раз. Такая раскачка
объясняется возбуждением и взаимодействием равноправных форм
собственных колебаний оболочки с близкими частотами [4,18].
Для бесконечной круговой цилиндрической оболочки частота
свободных радиальных колебаний равна:
/0 = со0/2я (13.4)
Во всех зонах цилиндрической камеры, кроме окрестностей
защемленных торцев, регистрируемый при взрывах процесс
колебаний носит гармонический характер [4].
Для цилиндра с днищами, при взрыве возникают, кроме
радиальных, изгибные колебания, при которых максимальные
напряжения наблюдаются вблизи днищ и в центре днища [22].
При изгибных колебаниях пластические деформации реализуются
лишь в поверхностных слоях стенок камеры, которые при
многократном нагружении будут изменять свою структуру, разрыхляться, терять
прочность. Соответственно реальная толщина несущего слоя оболочки
будет уменьшаться. Поэтому разрушение от высоких циклических
изгибных напряжений должно иметь усталостный характер [22].
При расчете цилиндрических камер на многократный взрыв
максимально допустимый вес заряда надо выбирать с учетом
зависимости числа циклов п знакопеременных напряжений от
относительного напряжения сгк/<7 (<7 — предел текучести стали, из которой
сделана камера) в упругой области (см. рис. 13.6). Например, ^ая сталей,
применяемых в судостроении п -> оо при -><7k/<7s = 0,2.
Отметим, что по результатам испытаний камер из сталей 25 и
35 динамический предел упругости этих сталей на 40% больше, чем
с =40 кг/мм2 аая статических условий [23].
Различие между
статической и динамической
прочностью взрывных камер связано
с колебательным характером
деформации камер при взрыве.
Например, чем больше масса
отдельных узлов и деталей, жестко
прикрепляемых к гладкой обо-
_ % *, _ лочке, тем больше дополнитель-
Рис. 13.6. Зависимость количества циклов
знакопеременной нагрузки от упругих ные изгибные колебания в зоне
напряжений
626
таких «присоединенных масс». В результате «усиленная»
массивными деталями камера разрушается быстрее и при меньших весах
взрываемых зарядов.
Чтобы не искажать колебаний, взрывные камеры всегда
свободно устанавливаются на опорах или подвешиваются на шарнирах.
Срок эксплуатации камер многоразового использования
(например, fiiA^ синтеза наноалмазов) определяется усталостным
разрушением, которое ускоряется большими величинами знакопеременных
деформаций стенок камеры при взрыве. Поэтому конструкция
таких камер должна обеспечивать минимальные деформации.
К камерам, предназначенным ^ая динамического синтеза и
спекания алмаза, предъявляются дополнительные требования,
связанные с необходимостью сохранения алмаза.
Во-первых, синтезируемый алмаз имеет низкую температуру
начала окисления (400 С), поэтому газовая атмосфера в камере
должна быть бескислородной, иначе весь алмаз сгорит. Действительно,
взрыв в воздухе не позволяет сохранить ультрадисперсный алмаз.
Наиболее просто проводить взрывы в атмосфере ПД от
предыдущих взрывов, поскольку в ПД практически отсутствует
свободный кислород.
Во-вторых, температура синтеза алмаза (3500—4000 К)
значительно выше температуры начала графитизации алмаза (~1300 К).
Поэтому алмаз нужно очень быстро охладить от 4000 К до 1300 К.
Охлаждение возможно только с поверхности частиц алмаза за счет
теплообмена с более холодными ПД.
В свою очередь, быстро охладить ПД можно только за счет
совершения газообразными ПД работы по ударному сжатию и
ускорению окружающей заряд среды — газовой, жидкой или твердой.
В различных технологиях в качестве такой среды используются П Д,
углекислый газ, слой воды или льда вокруг заряда, смесь ПД с
распыленной водой.
Очевидно, масса среды, ускоряемая и сжимаемая
расширяющимися П Д, должна быть достаточно большой. Следовательно, должен
быть достаточно большой объем камеры.
Другим важным требованием к камерам является обеспечение
максимально возможной «чистоты» синтеза: в получаемой алмазной
627
шихте должно быть минимальное содержание неуглеродных примесей.
«Чистота» синтеза обеспечивается применением дистанционного
лазерного инициирования взамен электродетонаторов, облицовкой
стенок камеры нержавеющей сталью и отказом от использования металла
Аая подвески заряда и оболочек из воды или льда.
13.2. Способы снижения взрывных нагрузок
на стенки камеры
Применение специальных способов ослабления воздушной УД,
действующей на стенки камеры при взрыве в камере заряда ВВ,
позволяет улучшить надежность работы камеры при многократном
взрывании зарядов или увеличить предельно допустимую массу
заряда.
Очевидный способ - устранение воздуха путем вакуумирования
камеры. Но технически это не всегда возможно, кроме того, остаётся
давление ПД, которое падает пропорционально кубу расстояния до
сосредоточенного заряда.
Принцип работы других применяемых устройств состоит в
окружении заряда пористой средой (пена,пенопласт, песок, водно-капельные
завесы — любые газосодержащие многофазные среды, см.[24]).
Исследования степени ослабления воздушной УВ показали, что
решающая роль принадлежит сжимаемости и инерционности
пористой среды. Сжимаемость характеризуется скоростью звука в среде
е.. Для водно-воздушной пены с.<св (св - скорость звука в воздухе),
а а^я взвеси пузырьков воздуха в воде с <с <с (с — скорость звука
в воде).Инерционность среды определяется массой пористой
оболочки вокруг заряда.
Степень ослабления воздушной УВ при взрыве заряда из
тротила в пене относительно взрыва в воздухе видна из рис. 13.7.
В подземных выработках давно и широко применяется защита
от воздушных ударных волн с помощью воздушно-водяной завесы
[25,26].
При взаимодействии ударной волны с водно-воздушной смесью
быстрое затухание волны вызвано затратами энергии на [25]:
628
— отражение УВ от отдельных капель и струй как от жесткой
пространственной решетки — 20%;
— рассеивание энергии УВ на элементах решетки — каплях и
струях — 30%;
— распыление капель и струй — 40%;
— испарение поверхностных слоев воды — 1%;
— перемещение паро-водо-воздушного поршня и преодоление
сил трения о стенки выработки — 9%.
За счет этих факторов распыленная вода может снижать
давление и импульс воздушной УВ в 1,4—4 раза [25].
Таким образом, водяной душ, создаваемый в камере перед
взрывом, не только усиливает охлаждение П Д и алмаза, но также
значительно уменьшает нагрузки на камеру.
Нами синтез УДА проводился с использованием водяной
оболочки вокруг заряда [27,28,2], и было неясно, как оболочка изменяет
давление на стенки камеры. Согласно прочностным расчётам камеры
«АЛИТ» вода вокруг заряда увеличивает деформацию стенок камеры.
С другой стороны, опыты, проведенные в 1986г. в камере ВНИИТФ
(г. Снежинск) с отлетающей массой на днищах, показали, что при взрыве
в водяной оболочке расстояние отлёта массы от днища в два раза
меньше, чем при взрыве такого же заряда (20кг) в воздухе. Следовательно,
оболочка вдвое снижает давление на днища.
В работе [30] экспериментально показано, что ослабление
амплитуды воздушной УВ при взрыве заряда из тротила в
водяной оболочке с массой, равной примерно четырём массам
заряда, практически такое же, как при использовании пены (см.
рис. 13.7)
Например, а^я приведенного расстояния R* = R/m1/3 (R —
расстояние до заряда массой т) , реализованного в наших опытах в
камере, измеренное в [30] на открытом воздухе ослабление
составило рв/рж = 90/30 = 3, т. е. больше, чем в камере (жесткая труба), что
вполне естественно.
По-видимому, в этих опытах одинаковое с пеной ослабление УВ
связано с компенсацией меньшей сжимаемости воды большей её мас-
629
сой (по сравнению с пеной) и
с увеличением массы
оболочки ослабление должно расти.
Как показала
фоторегистрация разлета водяной
оболочки, начиная с R=2r
(г - радиус сферического
заряда) оболочка теряет
устойчивость, разрушается на
отдельные части, между
которыми прорываются ПД.
Начинается интенсивное
турбулентное перемешивание
воды с ПД, сопровождаемое
дроблением воды на капли. В
итоге получается такое же
распределение потерь энергии,
как аля воздушно-капельной
завесы.
Отметим, что измерялись только величины амплитуд давления, а
вопрос об уменьшении импульса остаётся открытым.
Очевидно, одновременное применение вакуумирования,
водяного душа и водяной оболочки даст максимальное снижение
нагрузки на камеру.
Трудной является проблема защиты стенок камеры от осколков.
При взрыве даже легкие пластмассовые детали сборок оставляют на
стенках заметные следы. Основной способ защиты — экранировка.
Кроме водяных струй, могут быть использованы деревянные
щиты, асбоцементные трубы. Если известно направление движения
основной массы осколков, то в определенном месте на стенку
камеры можно установить толстый стальной экран.
13.3. Расчеты импульсных нагрузок на стенки камеры
Обычно численные расчеты взрывной камеры проводятся в два
этапа.
Ар,
/00
600
500
400
300
200
100
0
кПа
\2
\ 7
^V
V ▲
Л^ч^
С,кг:
А 0,1
О 1.0
12 3 4 Я'.м/кг1*
Рис. 13.7. Зависимость амплитуды
воздушной УВ от приведенного расстояния до
заряда из тротила
1 — для открытого заряда; 2 — для заряда в
водно-воздушной пене; заштрихованная
область — заряды в оболочках из жидкости
630
На первом этапе определяются газодинамические нагрузки на
стенки камеры (внутреннее давление), а на втором этапе проводят
упругопластические расчеты напряженно-деформированного
состояния конструкции камеры от действия нагрузок, полученных на
первом этапе.
При расчете нагрузок численно интегрируются двумерные
уравнения газовой динамики с использованием лагранжево-эйлеровых
разностных сеток, т.е. движущихся с произвольными скоростями
[31].
Уравнение состояния ПД может быть взято из [32] в виде
р = p(j,E), либо может быть рассчитано по УРС типа идеального газа
с переменным показателем адиабаты. Например, а^я заряда из ТГ40
j = l,33+l,67p/p0 ,где р0 = 1,67 г/смЗ.
Обычно в расчетах задается мгновенное инициирование
зарядов по всему объему, поскольку нагрузки на камеру слабо зависят от
способа инициирования заряда.
Газ, заполняющий камеру, в расчетах принимается идеальным с
постоянным показателем адиабаты.
В случае использования вокруг заряда водяной оболочки аая
описания разлета воды может быть использовано УРС воды с
параметрами: с= 1,5 км/с; п=7,15; Г=0,105.
Для численных расчетов может быть использован комплекс
программ СИГМА [33] или ВОЛНА — 81 [34].
Если заряд и камера сферические, то требуется решить более
простую одномерную задачу. Результаты ее решения, полученные в
[21], приведены ниже в табл. 13.1.
Таблица 13.1. Расчетные величины давления и импульса на стенке
сферической камеры
R./r
к о
10
12
15
20
р, атм.
43,79
30,30
19,81
10,93
Р , атм.
г
314,11
208,28
127,40
57,60
Р/Р
7,17
6,87
6,43
5,27
1
10,944
9,493
9,804
7,448
Обозначения в табл. 13.1: R^ го — радиусы камеры и заряда из ТГ50;
р — давление в воздушной УВ, падающей на стенку камеры; рг —
давление в УВ, отраженной от стенки; Jr — безразмерный импульс
положительной фазы сжатия.
Расчетные величины рг согласуются с результатами измерений
давления в [4] (р = 210 атм а^я Rj/r =11).
Величины рг и Jr в зависимости от приведенного расстояния до
заряда Z = R/M173 можно определить по графикам [1.20].
Отметим, что отношение давлений в отраженной и падающей
волне зависит от давления УВ и изменяется от р /р = 2 аля слабой
звуковой волны до рг/р = 13,92 ^ая сильной УВ [20].
Зная давление и импульс на стенке камеры в предположении
треугольного профиля давления, можно оценить время импульса.
В отличие от сферической камеры, взрыв сосредоточенного заряда в
цилиндрической камере создает неодномерную картину нагружения.
При взрыве УВ падает на стенку цилиндрической камеры под
разными углами ф (ф — угол между нормалью к стенке и
направлением движения УВ). Для центрального сечения камеры и центра днищ
ф = 0.
Согласно [20], рассчитать удельный импульс падающей на стенку
УВ можно с помощью следующих формул:
JTIJN = coscp + (Rk I r0) sin ф (13.5)
где JT, JN — импульсы ^ая скользящей (ф = 90°) и нормальной
(ф = 0)УВ.
IN =54 mm/Rk (13.6)
(m — в кг, R — в м).
При отражении от стенки импульс на стенку удваивается.
Расчет импульса на стенке цилиндрической камеры показывает,
что на расстоянии от центрального сечения, равном радиусу камеры,
импульс на стенке камеры уменьшается в 2,2 раза (см.рис. 13.8).
Давление на стенку (величина рг) зависит от трех взаимосвязанных
параметров: радиуса камеры, расстояния до центрального сечения
камеры и от угла отражения УВ от стенки.
632
Для центрального сечения зависимость рг от радиуса такая же,
как аля сферической камеры, а аля других сечений увеличиваются и
расстояние до заряда и угол падения УВ на стенку.
До углов ф~40° а^я сильной волны и до ф~70° а*я слабой волны
можно считать, что рг не зависит от угла [20].
Расчетные давления на стенку цилиндрической камеры
(Rk= 1,25м, m= 1 кг) приведены на рис. 13.8 [35].
Как видно из рис. 13.8, давление (как и импульс) быстро падает с
расстоянием от центрального сечения камеры: при S = 21^ давление
уменьшается в 6 раз и далее практически не меняется.
Если а^я камеры с Rj/r^ 12 (соответствует взрыву 1 кг ВВ в
камере объемом 1 м3), заполненной воздухом (средняя молекулярная
масса м = 29) рг = 208 атм, [36] то при заполнении той же камеры
С02 (м = 44) рг = 130 атм [21]. Меньшее давление в С02 можно
объяснить большим затуханием УВ за счет больших затрат энергии на
возбуждение всех степеней свободы молекулы С02 и на ее
ионизацию (поэтому у С02 теплоемкость больше, чем у воздуха).
8
с
р
МЛа 6
х
3-
о
с.
1
0
Ч
>
ж
А
1
\
~~^А
\
1 \
1 \'2 ^
\ А*
/1 \
Г 1 N
1 1 Ч
V
Н,
\Ч
■
i«J**V,
г\>
h
Ь
t
09
OS
oC
I
;
f
05
/
t>Z
t
oi
0.5
1.5
2.0
2.5
S,m
wx
N
Рис. 13.8. Изменение давления (расчет согласно [35]) и импульса на стенке
цилиндрической камеры в зависимости от расстояния до центрального сечения (вес
заряда 1 кг, диаметр камеры 2,5 м)
Таким образом, приведенные здесь данные позволяют оценить
нагрузки на стенки камер без проведения двумерных численных
расчетов.
Ниже приводятся основные результаты прочностных
расчётов камеры 02,5x17,5 м фирмы «АЛИТ». Расчёты сделаны с
использованием пакета прикладных программ (ППП) ДИСК,
разработанного во ВНИИЭФ (г. Саров). Нагрузкой на камеру
является внутреннее давление от взрыва зарядов из ТГ40.
Временная зависимость давления определена из газодинамических
расчётов.
ППП ДИСК предназначен а^я решения двумерных задач
нестационарного деформирования конструкций, состоящих из
деформируемых оболочек и недеформируемых твёрдых тел.
В ППП ДИСК в качестве физических соотношений приняты
уравнения теории течения с линейным кинематическим и
изотропным упрочнением. Вариационное уравнение движения
формируется в смешанной форме (усилия - перемещения), исходя из принципа
возможных перемещений.
Численное решение основано на конечно-разностной
аппроксимации вариационного уравнения движения по пространственной
переменной и явной схеме интегрирования по времени.
О корректности использования ППП ДИСК
свидетельствует согласие с экспериментальными данными результатов расчётов
большого числа тестовых задач.
В результате расчётов взрывной камеры получены эпюры
максимальных деформаций стенок и днища, временные зависимости
давления в центральном сечении и на днище.
В таблице 13.2 приведены параметры шести расчётных
вариантов и максимальные величины деформаций камеры ^ая каждого
варианта. В любой точке камеры допустимы только упругие
деформации (< 0,2%).
Основные результаты расчётов следующие:
1. Как и ожидалось, максимальные деформации и давления
наблюдаются в центральном сечении на длине, близкой к длине
заряда. Затем давление на стенках падает и не превышает 10 атм.
634
2. Заряды весом 40 кг в оболочке из воды создают в
центральном сечении пластическую деформацию, поэтому многократный
подрыв таких зарядов недопустим.
3. единение заряда весом 40 кг снижает вдвое нагрузки на
днище.
4. Максимальная нагрузка на днище составляет 800 т и может
быть удержана болтами, без применения отлетающей массы.
5. Без учёта турбулентного перемешивания воды с ПД
применение водяной оболочки увеличивает нагрузку на камеру.
Однако проведенные нами на камере ВНИИТФ эксперименты
показали, что применение водяной оболочки толщиной, равной
радиусу заряда, снижает давление на днище камеры в два раза по
сравнению с взрывом такого же заряда, но без оболочки.
Таблица 13.2. Результаты прочностных расчётов вариантов
нагружения взрывной камеры фирмы «АЛИТ»
№№
вар.
1
2
3
4
5
6
Масса, кг
ВВ
40
40
30
20
20
20
н2о
400
400
300
200
80
0
Диаметр, м
ВВ
0.127
0.249
0,12
0,10
0.10
0,10
н2о
1,90
0,50
1,60
1,50
0,44
0
Длина, м
ВВ
0.70
0,48
0,46
0,40
0,40
0,40
н2о
1,04
2,34
1,95
1,85
0.60
0
Макс, деформ., %
продол
0,60
0,53
0,30
0,175
0,09
0,07
Кольцев.
0,47
0,28
0,20
0.15
0,042
0,035
13.4. Циркуляция ударных волн и температурные
поля в камере
До сих пор мы оценивали параметры ударноволнового
нагружения стенок камеры при отражении первой наиболее сильной УВ.
Но циркуляция ударных волн в камере определяет температуры П Д
[36], что очень важно аа^ сохранения синтезируемого в камере алмаза.
В сферически расширяющихся ПД давление падает очень быстро.
Поскольку плотность П Д падает как г-3, то давление уменьшается как
г3', где а^я плотных ПД j = 3 до г=2 rQ, а далее j~5/4 [37].
635
Начиная с r~10 rQ, УВ в воздухе отрывается от ПД. Давление в
ПД оказывается меньше, чем в окружающем ударносжатом воздухе.
Поэтому от границы раздела ПД — воздух в ПД к центру камеры
идет т.н. внутренняя ударная волна. Скорость этой УВ относительно
воздуха меньше скорости воздуха за фронтом УВ, поэтому
внутренняя УВ сносится потоком.
В момент подхода УВ к стенке камеры слабая внутренняя волна
успевает сжать основную массу ПД.
Таким образом, можно различать в камере два вида ПД:
разреженное ядро и более плотную «оболочку», которую сжала
внутренняя УВ [36].
Согласно расчётам [36] аая камеры с малым относительным
радиусом 1^/^=12 отраженная сходящаяся к центру сферы УВ догоняет
внутреннюю УВ, сливается с ней и сжимает малоплотное ядро П Д.
В результате плотная оболочка ПД сжимается двумя УВ, а
разреженное внутреннее ядро — одной УВ. Поэтому температура ядра
очень высока. Согласно расчетам, во внешнем слое ПД Т<2000 К, а
для ядра достигаются значения (6—8) 103 К.
Далее волна отражается от центра, доходит до стенки и циркуляция
волн повторяется с уменьшающимися амплитудами. После затухания
УВ в камере реализуется существенно неоднородное температурное
поле: очень горячее ядро ПД (25% массы ПД), затем сравнительно
холодный слой ПД и опять сильно нагретый газ. Перемешивание этих
слоев будет ускорять выравнивание температур.
Из этих расчетов следует вывод: а^я снижения температуры ПД
внутренняя УВ должна сжать всю массу ПД (чтобы не было
разреженного ядра в ПД). Этого можно достичь двумя способами:
— увеличить размеры камеры (R^ /rQ> 12), что задержит приход
УВ, отраженной от стенки);
— увеличить плотность газа в камере, что увеличит скорость
внутренней УВ.
Рассмотрим особенности взрыва в вакуумированной камере [36].
Поскольку нет среды, поглощающей энергию ПД, расширение
ПД и циркуляция УВ в ПД происходит при постоянной полной
636
энергии П Д. Но в начальный момент примерно половина всей
энергии ПД является упругой. После разлета ПД эта часть энергии
перейдет в тепловую. Следовательно, средняя температура в П Д будет
выше, чем в случае взрыва в газе. Поэтому наноалмазы не
сохраняются при взрыве заряда из ТГ50 в вакууме.
При разлете ПД в вакууме скорость ПД имеет линейный
профиль с максимальным значением 7—8 км/с на границе ПД. Поэтому
максимальные температуры в ПД достигаются на периферии при
ударе П Д о стенку камеры.
Таким образом, вакуум в камере с одной стороны полезен, т.к.
снижает нагрузку на стенки и устраняет кислород (предохраняет
синтезируемый алмаз от окисления), но с другой стороны, вреден,
т.к. увеличивает температуру ПД (наноалмаз графитизируется) и
увеличивает скорость разгрузки ПД (наноалмаз аморфизируется).
С целью максимального снижения температуры ПД, последние
должны совершать работу по разгону не газа, а воды в виде капель,
создаваемых душем в камере или в виде оболочки вокруг заряда
(которая в процессе ускорения также быстро распадается на капли).
13.5. Определение несущей способности
железобетонных взрывных камер
Под несущей способностью взрывных камер (ВК) понимается
предельная масса заряда данной конфигурации и состава, подрыв
которого не приводит к появлению пластических (остаточных)
деформаций в стенке ВК.
Несущая способность данной ВК может быть определена либо
расчетами, либо измерениями деформаций стенки ВК,
проводимыми в процессе взрывных испытаний ВК с помощью тензорезисторов,
наклеенных на наружную поверхность ВК в центральном сечении и
на днищах.
Для проведения численных расчетов ВК могут быть использованы
различные пакеты прикладных программ, например, ADINA (США),
LUSAS (Англия), DISK (Россия). Подобные программы описаны в
[38,39]. Однако с помощью таких программ оболочку из бетона невоз-
637
можно рассчитать, поскольку бетон практически не имеет прочности на
растяжение. Об этом свидетельствуют результаты взрывных испытаний
трехслойных камер сталь — бетон — сталь [40].
При нагружении бетон разделяется радиальными трещинами на
отдельные блоки, толщина которых остается постоянной, а окружная
деформация осуществляется за счет удаления блоков друг от друга.
Тем не менее, применение бетона удваивает несущую
способность испытанных в [40] камер.
Очевидно, несущая способность стальных ВК повышается за
счет увеличения массы стали, т.е. увеличения толщины стенок ВК,
радиуса ВК, либо одновременно того и другого. Однако в связи с
трудностями изготовления и транспортировки ВК обычно
существуют определенные пределы максимально возможных веса и
размеров сварных стальных ВК. (Например, вес 200—300 т и диаметр
4,5—5 м). Увеличить эти пределы можно, используя железобетон.
Слой железобетона вокруг ВК изготавливается после установки
стальной ВК в стационарное рабочее положение.
По-видимому, такие конструкции ВК являются наиболее
простым вариантом /^ля цилиндрических камер большого диаметра и
объема с несущей способностью более 20кг, предназначенных,
например, ^ая синтеза и спекания алмаза.
Несущая способность цилиндрических железобетонных камер
исследована в [41]. В расчётах принято, что на растяжение работает
только кольцевая арматура, а бетон только упруго сжимается.
При взрыве в цилиндрических ВК удлиненных
цилиндрических зарядов с различной погонной массой [л (кг/м) нагружение
камеры одномерное, что упрощает расчеты несущей способности.
Детонация считается мгновенной, при этом расчетный импульс
несколько завышается, поскольку не учитывается разлет П Д с торцев
заряда и нерадиальность движения ПД.
Рассчитанный импульс отличается не более 15% от измеренного
импульса и от величины импульса, полученного интегрированием
расчетной зависимости p(t) /^ая первого удара по стенке [41].
Основной отбор энергии железобетонной стенкой ВК
происходит за время прохода ударной волной по стенке ВК. Далее стенка
638
движется по инерции (сумма кинетической и потенциальной
энергий постоянна), а давление компенсируется напряжениями в стенке.
Вклад тонкой стальной внутренней оболочки в несущую
способность ВК невелик.
В [41] рассчитана несущая способность железобетонных ВК,
используя энергетический подход и одномерную модель ВК.
Получена следующая формула аля оценки максимально
допустимой погонной массы заряда [л^*, взрыв которого не вызовет
пластической деформации стальной внутренней обечайки:
Мвв* = 27/64 a (fi^ Щ {RkIRflEpcQT 03.7)
где <7 - предел текучести внутренней стальной обечайки,^ —
погонная масса железобетона, [л. - погонная масса i -го слоя арматуры, Е,
рс — модуль упругости и плотность стали, Q- калорийность ВВ.
Как видно из (13.7), |^в*~(Ккб)°'5 •
Расчетные величины [х^* на 10—20% меньше экспериментальных
[41]. Кроме величин в (13.7), на [х^* в не меньшей степени влияет
качество изготовления железобетонной ВК, прежде всего качество сварки,
плотность и сплошность бетона. Кроме того, бетон должен быть покрыт
внешней стальной оболочкой, поскольку разрушение бетона
начинается с внешней поверхности (отколы, разрыхление).
Основные результаты работы [40] по испытаниям трёхслойной
взрывной камеры (сталь - бетон - сталь):
1. Радиальные смещения внутренней и наружной стальных
труб одинаковы, т.е. бетон работает как абсолютно жесткое
несжимаемое тело, но в нём возникают трещины.
2. Разрушение камер начинается с появления трещин во
внутренней трубе при деформациях г = 0,3% и [хвв = 2,2 кг/м. При
усъв = 2,0 кг/м и меньше деформация стенок ВК отсутствует.
3. Применение слоя бетона между трубами удвоил несущую
способность камеры - с 1 кг/м (аа^ двух труб без бетона) до 2 кг/м.
Анализ результатов исследований цилиндрических
железобетонных камер позволил нам получить зависимости необходимых
величин погонной массы камеры ([л, т/м) и внутреннего диаметра
камеры d от погонной массы заряда [л или от диаметра dch заряда из
Сотр.В длиной 1 м. (см. рис. 13.9)
0 2 6 w \ь i& 22 ja, кд/т
39 68 87 Ю7 iZk Ctctl|mni
Рис. 13.9. Значения погонной массы \хх цилиндрических стенок камеры и её
внутреннего диаметра dr, необходимые для многократных взрывов зарядов
из Сотр. В с погонной массой [л или зарядов диаметром dch длиной 1 м
13.6. Взрывные камеры для дробления алмаза
и керамики
С ростом требований к качеству поверхности изделий
электронной, оптической, ювелирной и др. отраслей промышленности растет
и число случаев, когда серийные микропорошки алмаза не
удовлетворяют потребителей. Неоднородность частиц порошков по
дисперсности, морфологии, прочности, наличие в порошках игольчатых и
пластинчатых кристаллов — все это создает недопустимые дефекты
на обрабатываемой поверхности. Отсюда необходимость создания
прецизионных марок алмазных микропорошков.
640
Кроме того, традиционные мельницы (шаровые,
электромагнитные, планетарные), используемые аля дробления алмазного сырья
при производстве микропорошков, имеют ряд существенных
недостатков: малая производительность, малый выход мелких фракций,
большой расход электроэнергии, большое загрязнение алмаза
материалом мелющих тел, быстрый износ мельниц.
Для производства прецизионных микропорошков алмаза в
ИПМ АН Украины (г.Киев) Г.И. Саввакиным был предложен метод
взрывного дробления алмаза. Этот метод позволяет управлять
процессом дробления и лишен недостатков традиционных мельниц.
Кроме алмаза, целесообразно проводить взрывное дробление
различных керамических порошков перед их спеканием. Как ^ая
инструментальной, так и аля конструкционной керамик взрывное
дробление активирует процесс спекания. В частности,
значительно — до 400 градусов — снижается температура спекания, что
позволяет получить керамику более мелкокристаллическую, значит,
более прочную.
Дробление алмаза с помощью взрыва в ИПМ было опробовано
в трех конструктивных вариантах:
1. Алмазное сырье смешивалось с порошком ВВ, и эта смесь в
полиэтиленовом пакете взрывалась в обычной взрывной камере.
Алмаз загрязнялся продуктами взрыва и полиэтиленом,
результаты плохо воспроизводились, большие потери алмаза.
2. Алмаз помещался в плоский контейнер, закрывался
крышкой, на которой подрывался заряд ВВ. В' этом способе
увеличен расход ВВ, энергия которого используется неэффективно.
Крышка быстро разрушалась, при этом алмаз терялся.
3. Для дробления алмаза использовалась цилиндрическая
ампула сохранения с центральным стержнем. Недостатки такого
метода: увеличение стоимости дробления из-за необходимости
изготавливать ампулы, большой расход ВВ, большие потери
алмаза при его извлечении из ампулы, неоднородность давления
в ампуле.
Автором предложена, спроектирована и после изготовления
опробована и запущена в эксплуатацию специальная взрывная каме-
641
pa, предназначенная только а^я дробления порошков алмаза и
керамики [1,29].
Несущая способность камеры — плоский заряд порошка гексо-
гена весом 100 г. Производительность одной такой камеры — 1 кг
алмазного или керамического сырья в час. Расход порошка гексоге-
на — 100г на 1 кг алмаза. Это в 20—30 раз меньше расхода ВВ при
дроблении в ампулах сохранения.
Основная особенность ВК состоит в том, что алмазный порошок
слоем толщиной 5 мм помещается в двух одинаковых контейнерах
из прочной броневой стали, закрытых стальными пластинами
толщиной 0,8—1,5 мм. Между этими пластинами насыпается гексоген
слоем толщиной 1—3 мм. В этом устройстве слой гексогена
«работает» в обе стороны, разгоняя скользящей детонацией (от
электродетонатора) сразу две пластины и сжимая две навески порошка.
Кроме гексогена, расходуются только стальные пластины.
Требуемая степень измельчения достигается изменением
толщины стальных листов между ВВ и алмазом, а также толщины
гексогена. Чем толще стальной лист и тоньше слой гексогена, тем меньше
скорость сжатия порошка и степень его дробления.
При малых скоростях сжатия разрушаются только непрочные
сростки, трещиноватые и дефектные частицы порошка. С ростом
скорости дробятся практически все кристаллы.
Эксплуатация ВК показала [ 1 ], что взрывное дробление
алмазного сырья резко увеличивает содержание наиболее дефицитных
мелких фракций. Например, после однократного дробления примерно
половина частиц имеет размеры менее 6 мкм, а после повторного
дробления таких частиц в порошке алмаза уже около 90%.
Результаты дробления показали, что по данной технологии
можно получать качественные как шлифпорошки, так и микропорошки
алмаза, причем с хорошим выходом всех фракций.
2. Кроме производства алмазных микропорошков, представляет
интерес исследование воздействия взрывного дробления различных
керамических порошков на температуру и кинетику их спекания, а
также на прочность получаемых спеканием керамических изделий.
Нами проведено взрывное дробление порошка А1203. И в этом
случае достигается сильное измельчение: средний размер частиц
642
уменьшился с 41,3 до 1,9 мкм, после дробления 97,8% частиц имеют
размеры менее 6 мкм [1].
Литература к главе 13
1. Даниленко В.В. Синтез и спекание алмаза взрывом. М. Энерго-
маш, 2003,272с.
2. Выскубенко В.А., Даниленко В.В., Толочко А.П., Лин Э.Э.
MAp.OrB,1992,N2,c.l08.
3. Цыпкин В.И., Иванов А.Г., Минеев В.Н. и др. Атомная
энергия, 1976,41,5, 303.
4. Белов А.И., Корнило В.А., Клаповский В.Е. и др. ИФЖ, 1990,
N3,111.
5. Даниленко В.В. Динамический синтез алмаза. Доклад на
семинаре по новым материалам. United nations. Economic
commission for Europe Eng. Aut/sem. 10/R, 31,22 July 1992.
6. Волков K.B., Даниленко B.B., Елин В.И. ФГВ, 1990,3,123.
7. Даниленко В.В, Из истории открытия синтеза алмазов. ФТТ,
2004, т.46, вып.4, с581 - 584.
8. Vyacheslav V. Danilenko. On the Discovery of Detonatoin nano-
diamond.In book: UltraNanocrystalline Diamond. Synthesis,
Properties,and Applications. Ed. by Olga A. Shenderova and
Dieter M. Gruen.William Andrew Publishing, Norwich, N.Y,
USA. 2006,600 p.
9. Даниленко B.B., Трефилов В.И., Даниленко В.Н. Взрывная
камера для синтеза сверхтвердых материалов. Патент СССР SU
181329 A3 с приор, от 12.05.91.
10. Даниленко В.В., Даниленко Е.В. Взрывная камера для
синтеза детонационных наноалмазов. Патент РФ № 2327515 от 27
июня 2008г
11. Иванов А.Г., Рыжанский В.А. и др. ФГВ, 1981, 1,102.
12. Иванов А.Г., Новиков С.А., Синицын В.А. ФГВ, 1972, 8, 1.
13. Сырунин М.А., Федоренко А.Г., Шитов А.Т. ФГВ, 1989, 4,
108.
14. Цыпкин В.И. и др. МКМ, 1981,2,249.
15. Иванов А.Г., Цыпкин В.И. МКМ, 1987,3,472.
16. Сырунин М. А., Федоренко А, Г., Иванов А. Г. ФГВ ,2002,38,
З.с.127-136.
17. Могилев В.А., Иванов А.Г. и др. ФГВ, 1981,17,2.
18. Белов А.И., Клаповский В.Е. и др. ФГВ, 1984,3,71.
19. Демчук А.Ф. В сб. Второй Международный симпозиум.
Обработка металлов взрывом. Т2, Прага, 1974.
20. Baker W.E. et.ol. Explosion Hazards and Evaluation Elsevier Scien.
Publ.Co. Amsterdam — Oxford — N.Y., 1983 (русский перевод
в 2x книгах, M:. «Мир», 1986).
21. Ждан СЯ. ФГВ, 1981,2,142.
22. Корнев В.М., Адищев В.В., Митрофанов А.Н., Греков В.А.
ФГВ, 1979,6,155.
23. Иванов А.Г., Новиков С.А., Синицын В.А. ПМТФ, 1968, V9,
N6,c.94.
24. Гельфанд Б. Е. Сальников М. В. и др. ФГВ, 2001, 37, 5, с.128
-133.
25. Бузухов А.А., Сварский Б.М., Щекотихин Б.А. Защита от
воздушных ударных волн в подземных выроботках с помощью
воздушно-водяной завесы. Новосибирск, Изд-во ИГД СО
АН СССР, 1971, с.18.
26. Бузуков А.А. ФГВ, 2000, № 3.
27. Волков К.В., Даниленко В.В., Елин В.И. ФГВ, 1990,3,123.
28. Волков К.В., Даниленко В.В. и др. «Взрыв, удар, защита»,
Информ.бюлл. ИГ СО АН СССР, вып. 17, 1987, Новоси
бирск.
29. Даниленко В.В., Трефилов В.И., Мильман Ю.В. и др. а.с. СССР
N1496114 от 22.03.89.
30. Гельфанд Б. Е. Сальников М. В. и др. ФГВ, 2001, 37, 5,
с. 128-133.
31. Годунов ГС. (редактор). Численные решения многомерных
задач газовой динамики. М:.»Наука», 1976.
32. Куропатенко В.Ф. В кн. Численные методы механики
сплошной среды, т.8, вып. 6, Новосибирск, 1977.
33. Баталов М.В., Бахрах СМ. и др. Комплекс СИГМА а^я
расчета задач двумерной газодинамики. Труды Всесоюзного се-
644
минара по численным методам механики вязкой жидкости.
Канев, 1968, Новосибирск, «Наука», 1969.
34. Куропатенко В.Ф., Коваленко Г.В. и др. Ж. Проблемы атомной
науки и техники. Сер. Математ. моделирование физич.
процессов, 1989,1,9.
35. Mukoid V.P. Intern. Appl. Mech. 1999, Vol.35, N3,288.
36. Ершов А.П., Куперштох А.Л. ФГВ, 1986,3,118.
37. Баум Ф.А., Станюкович К.П., Шехтер Б.И. Физика взрыва. М.:
Из-во физ-мат. лит., 1975.
38. Уилкинс М.Л. В сб. Вьиислительные методы в гидродинамике.
М:.»Мир», 1967.
39. Быченков В.А., Гаджиев В.В., Куропатенко В.Ф. В сб.
Численные методы механики сплошной среды, т. 3, N2, 1972,
Новосибирск.
40. Иванов А.Г., Могилев В.А. и др. ФГВ, 1982, N4, с.88.
41. Горбунов Е.Ф., Иванов А.Г., Могилев В.А. и др. ФГВ, 1991, N5,
с.107.
Глава четырнадцатая
АЛМАЗ
Для успешного развития взрывных методов синтеза и спекания
алмаза полезна информация о свойствах алмаза, особенно о его гра-
фитизации, о термодинамике и кинетике превращения графит—
алмаз, об уже существующих промышленных технологиях синтеза и
спекания алмаза с использованием высоких статических давлений.
14.1. Алмаз : свойства, синтез, применение
Среди всех используемых человеком материалов, алмаз -
чемпион по своим свойствам. И прежде всего по твердости и
прочности. Не зря по-гречески алмаз («адамас») означает «нерушимый»,
«непреодолимый». Алмаз вдвое твёрже других лучших абразивных
материалов ( карбида и нитрида бора).
Являясь лучшим диэлектриком, тем не менее, по
теплопроводности алмаз также чемпион и в 2—3 раза превосходит медь и серебро.
В природе миллионы лет алмаз сохраняется неизменным, благодаря
своей высокой химической стойкости — его не берет даже «царская
водка», растворяющая золото и платину.
Подробнее о свойствах алмаза можно узнать в [1 - 14].
По-видимому, в 21 веке важным станет то, что алмаз ещё и
лучший материал а^я электроники [10]. Алмаз становится
полупроводником при легировании его бором, литием, фосфором методом
ионной имплантации. Развитие нанотехнологий приведет к
созданию алмазных микрочипов с максимальной мощностью при ми-
646
нимальных размерах. Сегодня уже производятся и используются
дискретные теплоотводы из алмаза аля мощных малогабаритных
полупроводниковых приборов. Созданы алмазные транзисторы и
диоды, детекторы радиации, датчики температуры аля агрессивных
сред. Показана возможность создания алмазных светодиодов,
фоторезисторов, лазеров. Применение алмазов резко ускорит развитие
оптоэлектроники.
Сочетание экстремально высоких электрической и оптической
прочности, теплопроводности с высокой дрейфовой скоростью
носителей делает алмаз идеальным материалом а^я пикосекундной
оптоэлектроники (оптоэлектронных коммутаторов, генераторов
мощных импульсов, фотоприемников). Для генерации плазмы в
алмазе можно использовать мощное оптическое излучение и сильные
электрические поля, не опасаясь разрушения алмаза под
воздействием импульса тока или джоулева тепла.
«Слабостями» алмаза является низкая температура его
окисления на воздухе (начиная с ~700 С) и легкая раскалываемость по
плоскостям (111).
В конце 50 -х годов 20 века человечество совершило важный
технологический прорыв — научилось делать алмазы. Промышленный
синтез алмазов проводится в области его термодинамической
устойчивости и основан на технике высоких статических давлений.
Вследствие большого различия в кристаллических решетках прямой
переход графит — алмаз требует создания большой
неравновесности: в статике необходимо давление более 10 ГПа, а в динамике
(ударноволновое сжатие графита) — более 20 ГПа.
Синтез при более низких статических давлениях 4—6 ГПа
вблизи линии равновесия оказался возможным при предварительном
разрушении решетки графита путем его растворения в металлах —
катализаторах (обычно используются сплавы Ni — Mn, Fe — Ni,
Fe — Со). Несмотря на растворение, вид графита влияет на процесс
синтеза [2].
При охлаждении под давлением из пересыщенного раствора
углерод выделяется и кристаллизуется в форме алмаза. Размер
алмазных кристаллов растет пропорционально корню квадратному от
времени синтеза [3], а доля прочных монокристаллов с правильной
647
огранкой растет с уменьшением массовой скорости превращения [2].
Общим недостатком синтетических алмазов является содержание в
них примеси металлов — катализаторов, что снижает прочность и
термостойкость алмазов.
Первыми синтез алмаза осуществили шведские исследователи
(1955), затем американские (1956). Независимо от этих работ в I960
году алмаз был получен в России. Основы технологии синтеза алмаза
даны в [2,6,9].
Успех исследований был определен созданием эффективных
аппаратов высокого давления (АВД): типа «belt» в США, типа
наковальня с углублением в России.
Например, в АВД «belt» объёмом 1000см3 создаются 6 ГПа и
1800 К за несколько минут с точным компьютерным управлением
параметрами.
Во второй половине 20 века в мире создана и быстро
развивается мощная индустрия синтетических алмазов и алмазных
инструментов. Например, в США в период 1980—1995 гг. производство
алмазов выросло в 6 раз, с 20 до 115 тонн в год (мировая добыча
природных алмазов в 1999 году составила 23,3 т). Структура
применения алмазов в США ( на 1998 год ): машиностроение — 33%,
буровые работы — 18%, обработка керамики — 17%, производство
абразивов — 16%, строительные работы — 13%, прочее — 3%. Во
всех этих применениях идёт замена монокристаллов на
поликристаллы, получаемые спеканием под давлением алмазных порошков.
Лучшие марки алмазных поликристаллов без связки по твердости не
уступают природному алмазу.
Синтезирующие алмаз предприятия выпускают свою
продукцию в виде различных алмазных порошков [2, 5]. После химической
очистки получаемое алмазное сырье в виде сростков, друз, осколков
кристаллов дробится и классифицируется по размерам частиц.
В зависимости от размеров частиц (зернистости)
промышленность изготавливает следующие три вида порошков:
— шлифпорошки с размером зерен от 3000 до 60 мкм;
— микропорошки с размером зерен от 60 до 1 мкм;
— субмикропорошки с размером зерен от 1 до 0,1 мкм и мельче.
648
Микропорошки предназначены аая доводочных и
полировальных работ. Используются в основном в незакрепленном виде в
составе паст и суспензий.
Основные характеристики микропорошков — абразивная
способность и шероховатость обработанной ими поверхности,
зернистость, содержание примесей. Лучшими являются микропорошки
«Mypolex», имеющие поликристаллические сфероидальные
частицы и получаемые из ударносжатого графита.
Повышение качества шлифпорошков связано с развитием и
широким применением методов их сортировки по магнитным,
электрическим, адсорбционным и геометрическим характеристикам
зерен [2,4,5].
Особый интерес представляют поликристаллические шлифпо-
рошки АРСЗ, АРС4, получаемые спеканием и используемые в
инструментах, работающих в особо тяжелых условиях (бурение,
обработка камня и бетона, правка шлифкругов). Велика потребность в
таких порошках с частицами 0,8 - 3 мм.
Одним из перспективных способов увеличения ударной
прочности поликристаллов является повышение дисперсности спекаемых
алмазов,т.е. повышение концентрации частиц и числа контактов
между ними в единице объема [2]. Поэтому перспективно
использование а^я спекания очень дисперсных порошков алмаза,
получаемых с помощью взрыва. Но при этом возникают технологические
трудности: малая и нестабильная начальная плотность, большое
количество примесей на поверхности частиц.
Обычно в промышленном производстве синтезируются
монокристаллы размером не более 1 мм. Однако в 1970—80 годах все
три крупнейших производителя алмаза — Дженерал Электрик, Де
Бирс и Сумитомо — объявили об освоении производства крупных
совершенных (gem-quality) безазотных монокристаллов алмаза
желтого цвета весом до двух карат, имеющих максимальные прочность и
теплопроводность и минимум примесей (аая теплоотводящих
подложек в электронике).
Например, японская компания Сумитомо продает кристаллы
массой 0,1—0,4 карат за $60—140, а в 1985 году эта фирма создала
649
технологию синтеза безазотных кристаллов массой 12 карат (размер
6 мм). Аналогичные результаты получены и компаниями Де Бирс
и Дженерал Електрик. Прогресс в технологии теплоотводов был
ускорен внедрением лазерной резки и трехслойной металлизации
алмаза (Ti/Pt/Au).
Появление на рынке большого объёма относительно дешёвых
синтетических алмазов привело к подлинной революции во многих
производствах. На изготовление каждого автомобиля расходуется
0,3 г алмаза. Без алмазных буровых коронок невозможно бурение
в твёрдых породах. Бытовые пластмассовые изделия удешевляются
потому, что отливочные формы а^я них полирует алмаз, и формы
работают дольше. Сейчас без применения алмазов функционирование
современной индустрии немыслимо.
Следует упомянуть ещё один интенсивно совершенствуемый
способ синтеза алмазных плёнок без применения высоких
давлений, в области стабильности графита. Оказывается, при пиролизе
метана в присутствии водорода существуют условия, при которых
свободный углерод конденсируется на подложку в виде алмазной
плёнки. Это явление объясняется не термодинамикой, а
кинетикой: скорость роста у алмазного кристалла оказывается выше, чем
у графита.
На рис. 14.1 показана фазовая диаграмма углерода, на которой
нанесены области синтеза алмаза различными способами. При
низких температурах под давлением образуется не алмаз, а лонсдей-
лит — другая плотная и сверхтвёрдая модификация углерода с
плотной гексагональной решеткой.
В любых методах синтеза алмаза нет полного превращения
углерода в алмаз, всегда в результате синтеза получается смесь алмаза с
неалмазными формами углерода (шихта синтеза). Поэтому важной
составляющей синтеза алмаза является технология извлечения
алмаза из шихты синтеза и очистки алмаза от различных примесей.
Обзоры методов очистки алмаза даны в [15 — 22].
Обычно технология химического выделения и очистки
синтетического алмаза состоит из трёх этапов: растворение металлической
составляющей, растворение неалмазных форм углерода (НФУ) и
650
тонкая очистка от примесей. Эта
технология трудоёмка (до 40%
стоимости алмаза) и
экологически вредная — много ядовитых
стоков, солей, газовых
выбросов). 70—90% общей
химической обработки приходится на
долю окисления НФУ.
Любые способы окисления
основаны на более высокой
реакционной способности НФУ
по сравнению с алмазом, причем
различие возрастает с
увеличением дисперсности , дефектности,
аморфности НФУ. Поэтому аая
динамических методов синтеза
алмаза (в частности, а^я синтеза
УДА) возможно использование более простых и более дешевых
технологий с применением более мягких окислительных сред с
меньшими объёмами вредных стоков. Кроме того, важно, что
применяемый окислитель НФУ влияет на состав адсорбированных алмазом
примесей.
Обычно в промышленности используется жидкофазное
окисление НФУ. Требуемая а^я окисления температура ~230 С
обеспечивается кипячением шихты в смеси концентрированной серной
кислоты с различными окислителями: хромовым ангидридом, калиевой
селитрой, азотной кислотой.
Специально а^я очистки детонационных наноалмазов
разработана дешевая и экологически чистая технология с применением
только азотной кислоты. Для повышения ее температуры кипения
с 80 С до 230 С применяется титановый автоклав непрерывного
действия [19]. Для отделения алмаза от жидких окислителей и воды
вместо декантации и центрифугирования в [22] разработан метод
отделения алмазов и наноалмазов с помощью титановых фильтров с
порами 0,5—7мкм.
ГПо
0 iGCQ 20GC 30С0 4-ССО ТК
Рис. 14.1. Условия различных видов
синтеза алмаза на фазовой диаграмме
углерода
1 — прямой переход графит—алмаз
в условиях ударного сжатия; 2 — то
же, но в статике; 3 — переход графит—
лонсдейлит; 4 — каталитический
синтез алмаза; 5 — синтез алмазных
плёнок пиролизом метана
651
14.2. Графитизация алмаза
Одной из фундаментальных и практически важных характеристик
алмаза является кинетика его графитизации при нагреве. С одной
стороны, это частный вопрос общей проблемы обратимости
полиморфных превращений. С другой стороны, графитизация определяет
термостойкость алмазных инструментов и является ключевой проблемой
технологии динамического синтеза и спекания алмаза.
Графитизацией алмаза мы здесь называем процесс превращения
алмаза в неалмазные формы углерода - кристаллические,
аморфные, кластерные с перестройкой углеродных связей от sp3 к sp2
типу. Поэтому, наряду с обычным рентгеноструктурным анализом,
используется метод определения степени графитизации алмаза по
потере веса графитизированного алмаза после его кислотной
обработки, при которой окисляются до С02 и графит, и все другие
неалмазные формы углерода.
Обзор работ, посвященных графитизации алмаза при его
нагреве, сделан в [12,23,24].
Установлено два типа графитизации: поверхностная - при
относительно низких температурах (до 1400—1700 С) и объёмная -
при более высоких температурах. Совершенные алмазы графитизи-
руются только с поверхности, а у дефектных алмазов наблюдаются
оба типа графитизации. Обнаружены два механизма
графитизации [25]:
— до 1800 С — диффузионный с энергией активации 340 кдж/
моль (соответствует энергии разрыва одной связи углерод -
углерод);
— выше 1800 С — мартенситный с энергией активации
42 кдж/моль.
На температуру начала графитизации влияет дисперсность
алмаза — а^я частиц 100 мкм она снижается до 1000 С [15]. Для очень
мелких и дефектных алмазов динамического синтеза (из графита)
мартенситная графитизация зафиксирована при гораздо более
низких температура (~600 С) вследствие имеющихся в алмазе
когерентных зародышей из остаточного графита.
652
На кинетику графитизации сильно влияют дефекты, примеси в
алмазе и окружающая среда. В частности, графитизация ускоряется
в присутствии кислорода и никеля [12, 15]. Отсюда большой
разброс в результатах эксперимента.
При мартенситной графитизации внутри алмазного кристалла
образуются графитовые пластины со следующей
кристаллографической ориентацией: ось с графита перпендикулярна плоскости (111)
алмаза, или параллельны плоскости (002)г и (111 )а. Следовательно,
скорость роста графитовых плоскостей (002) в плоскостях (111)
алмаза много больше скорости роста по оси с.
Графитизация происходит с очень большим скачком объёма
(почти 50%), поэтому образующийся внутри алмаза графит сильно
сжат (расстояние между слоями уменьшено с 0,335 нм до 0,310—
0,315 нм), а в алмазе возникает сильное напряженное состояние,
которое может приводить к раскалыванию алмаза по плоскостям (111)
даже при малой степени графитизации. Данные по графитизации
алмаза позволили оценить прочность алмаза на растяжение, равное
2,5ГПа[2б].
Графитизация алмаза обнаружена автором (рентгеноструктурным
анализом) при ударноволновом сжатии алмазного порошка
зернистостью 200 мкм стальным лайнером со скоростью более 1,5 км/с [13].
В этом случае графитизация ускоряется сочетанием быстрой сдвиговой
деформации и высокой локальной температуры.
Очевидно, давление должно повышать температуру начала
графитизации, что впервые показал Бриджмен [27]. Более детально
графитизация под давлением исследована в [28], где а^я описания
экспериментальных данных используются уравнения, описывающие
двухстадийное (образование и рост зародышей) полиморфное
превращение в металлах [29].
Кинетика графитизации определяется временем л, за которое
происходит превращение на 50 %. Таким образом, при л=0 графитизация
происходит мгновенно, а при л=оо алмаз не графитизируется.
В [28] получено уравнение, связывающее степень превращения и
время. С его помощью рассчитаны следующие величины л,
реализованные в условиях экспериментов (см. табл. 14.1).
653
Таблица 14.1. Величины л для графитизации алмаза
р,ГПа
3,2
3,2
3,2
3,9
тк
2270
2410
2580
2410
л, сек.
600
100
18
280
Расчёт по результатам экспериментов даёт &ая графитизации в
условиях р = 3.2 и 3.9 ГПа и Т = 2270—2560 К величины суммарной
энергии активации Н = 270 ккал/моль и суммарного активационно-
го объёма V* = 59 смЗ/моль.
На фазовой р,Т-диаграмме углерода зона гистерезиса
превращения алмаз—графит заполнена веером кинетических линий с
различными л, исходящими из тройной точки (см. рис. 14.2).
По данным табл. 14.1 в линейном приближении нами найдено
следующее положение линии с л = 0 с тремя точками: р= 13 ГПа,
Е = 4000 К; р = 3,2 ГПа, Т = 2620 К; р = 0, Т = 2170 К (см. рис.14.2):
Тр = 2170+140р [13].
Линии л=const являются многопараметрическими функциями, их
положение зависит не только от р и Т, но также от совершенства алмаз-
WOO 2000 2€20 ЗОСО 400О "Г К
Рис. 14.2. Кинетические линии графитизации на фазовой диаграмме углерода
654
ного кристалла, его размеров и формы, от наличия кислорода, никеля,
сдвиговых и растягивающих напряжений, зародышей графита.
14.3. Превращение графит—алмаз
14.3.1. Термодинамика
Вид фазовой диаграммы углерода давно интересует
исследователей в связи с проблемами синтеза алмаза.
Для построения фазовой диаграммы в широком диапазоне
давлений и температур, интересном а^я динамического синтеза и
спекания алмаза, экспериментальных данных пока недостаточно. Нужны
полуэмпирические УРСы графита и алмаза, чтобы рассчитывать
величины их термодинамических потенциалов. Разность потенциалов
ДФ = Фа - Фг определяет движущую силу превращения и
критический радиус зародыша алмаза в графите.
Эти параметры необходимы а^я описания кинетики
превращения в разных точках области термодинамической стабильности
алмаза.
Разными авторами проблема превращения графит - алмаз
рассматривалась с разных точек зрения, в различных аспектах: квантово-
механические (sp2 - sp3 переход) и физико-химические условия
(зарождение, пересыщение), термодинамика с учётом поверхностной
энергии и энергии деформации, кристаллография превращения,
диффузионные и бездиффузионные механизмы превращения,
гистерезис превращения (например, см. [30—36]).
Большой вклад в экспериментальное изучение превращения
графит - алмаз в статических условиях сделан Bundy F.P. [37, 38, 39].
В частности, он показал, что в тройной точке диаграммы гистерезис
превращения графит - алмаз отсутствует [39].
В 1967 году нами проведён расчёт термодинамических
потенциалов цейлонского графита и алмаза в интервале 300—3000 К а^я
давлений до 100 ГПа [30]. Для каждого типа графита (со своей
упаковкой и размерами слоев) должно быть своё У PC, прежде всего
отличающееся показателем п в выражении р =A(Sn - 1). Например,
для совершенного цейлонского графита р =0,08468 (S4 - 1), а для
655
несовершенного пирографита рх = 0,0746 (S6 - 1), т.е. сжимаемость у
пирографита меньше.
Расчёт потенциалов и их разности (см. рис. 14.3) сделан с
использованием У PC, полученного на основе ударной адиабаты
цейлонского графита и с учётом изменения тепловых свойств графита
[40]:p = px+pT = 0,08468(S4-l)+(0,2712S-0,2267)T+0,0358VST2.
В рамках приближения Дебая уменьшение теплоёмкости
графита с давлением найдено по увеличению с давлением температуры
Дебая при постоянных коэффициентах Грюнайзена и Пуассона.
Рис. 14.3. Фазовая диаграмма углерода
1 — Линия равновесия высокого давления. 2 — Линия Avr-a=0.3 — Линия
ЛФтах. 4 — Линия АФ = 16 кДж/моль. 5 — Линия равновесия низкого давления:
р= 13000+13Т (атм.) [41]. 6 — То же, но с зависимостьюр=7000+27Т (атм.) [1].
7 — Линия плавления алмаза с наклоном — 20 К/ГПа [30].
8 — То же, но с наклоном +10,2 К/ГПа [41]
Основные результаты расчётов следующие.
1. При p>65 ГПа и Т<2000 К на фазовой диаграмме углерода
существует вторая область стабильности графита (по-видимому, с
металлическими свойствами) и вторая линия равновесия
высокого давления (см. рис. 14.3), но только а^я совершенного графита с
большой сжимаемостью (п = 4). Поскольку есть две линии
равновесия с АФ = 0, то между ними величина АФ = Ф - Ф имеет максимум
по давлению и монотонно растет с температурой. На линии АФт
с уравнением р = 20+0,017(Т-1000) (для р>20ГПа) максимальна
движущая сила превращения (рис. 15.6).
656
2. В области стабильности алмаза можно провести линии равных
разностей потенциалов АФ.
В условиях динамического синтеза алмаза (30 ГПа и 1300 К)
реализуется величина АФ = 16 КДж/моль. Линия с этим значением АФ
показана на рис. 14.3. Как видно по положению нижней ветви этой
линии, давление превращения должно уменьшаться с температурой,
что позднее было подтверждено экспериментально (см. гл.7 и рис.
14.3 [34]).
7,К
2500-
txxh
2&//^г
7
1 f*r
№00
20
30
40 50 дГПа
200Л
50 дГПа
Рис. 14.5. Зависимости от давления и
температуры удельной поверхностной
Рис. 14.4. Расположение на фазовой
диаграмме углерода
1 — ударной адиабаты непористого гра- энергии (от-aj и критического зароды-
фита; 2 — то же, но пористого графита ша алмаза в графите (гкр)
(т = 1,35); 3 — линия АФтах. Цифры у
точек — величины АФ в кДж/моль
Термодинамические расчёты условий в точке экстремума кривой
АФ = 16 КДж/моль (р = 23 ГПа, Т = 1300 К) совпадают с
кинетическими расчётами [34]. Благодаря более высокой температуре сжатия
на ударной адиабате пористого графита величина АФ выше, чем на
ударной адиабате непористого графита (см. рис. 14.4 [30]).
3. Оценён размер критического зародыша алмаза в графите
г =2 а /АФ, где величина а_ удельной поверхностной энергии
межфазовой границы графит—алмаз рассчитывался в
предположении, что окружающий алмазный зародыш сжатый графит (с
искажённой решёткой) можно рассматривать как своеобразную
графитовую псевдожидкость.
Поэтому /^ля оценки а _ было использовано выражение а^я
границы кристалл—расплав [42,43]:
а -2/3a (V-V)IV
a-r a v г а' г
где а = (5,4—5) 10"4 Дж/см2 [51 ] соответственно для Т = 300—3000
Кис давлением не меняется; Ava_ г - разность удельных объёмов алмаза
и графита; v — удельный объём графита.
Поскольку разность в удельных объёмах графита и алмаза с
давлением уменьшается, то <7а и размер гк также быстро падает (см.
рис. 14. 5) и при р>20 ГПа гк < 10 нм.
С другой стороны, с давлением должна увеличиваться толщина
поверхностного слоя (толщина межфазовой границы) S _ = а _ /Ар
(Ар —разность плотностей). При г = Sr или на линии Av = 0 (см.
рис. 14.3) превращение получает характер критического перехода,
при котором невозможно получить устойчивые объёмные
кристаллы алмаза.
Таким образом, расчёты гк а^я алмаза количественно подтвердил
общую закономерность, согласно которой с увеличением
неравновесности условий превращения новая фаза получается всё более
дисперсной.
В [36], рассчитаны термодинамические потенциалы твёрдого и
жидкого углерода. На фазовой диаграмме найдены положения
линий равновесия и плавления,а также ударных адиабат графита,
которые согласуются с экспериментальными данными. Расчёты
проведены в приближении Эйнштейна с использованием выражения
для коэффициента Грюнайзена T(v,T) [32] (см. гл. 2) и подгоночных
параметров, получаемых из экспериментальных изотерм и ударных
адиабат.
Гистерезис првращения графита в алмаз можно рассчитать, если
кроме термодинамических потенциалов учесть энергию межфазной
поверхности и энергию упругого деформирования. Сделанные в
[44] расчеты показывают, что вклад энергии внутренних
напряжений, возникающих в графите и алмазе, определяет наблюдаемую
величину гистерезиса.
658
14.3.2. Кинетика
Другим семейством линий, покрывающим алмазную область,
является семейство кинетических линий, вдоль которых постоянна
скорость превращения. В соответствии с двумя различными
механизмами и кинетикой превращения существуют два вида таких
линий: а^я бездиффузионного (или мартенситного) и ^^я
диффузионного превращений.
Теория полиморфного превращения под давлением по этим
двум механизмам разработана Эстриным в [45], а в [34]
использована а^я оценок кинетики превращения графит - алмаз. Напомним,
что по бездиффузионному механизму может превращаться только
совершенный кристаллический графит (см. гл.7).
Согласно [46,47], при ударном сжатии превращение развивается
в две стадии: сначала быстрая мартенситная, затем более медленная
диффузионная. Но если первая быстрая стадия невозможна в силу
высоких температур, несовершенства или разрушения в УВ
кристаллической решётки (высокие значения давлений или пористости),
то медленная стадия может не успеть проявиться за короткие
времена ударного сжатия (по-видимому, такая ситуация у несовершенного
пирографита и при сжатии тонких образцов графита).
Прямой бездиффузионной перестройкой решётки графита можно
получить только лонсдейлит при относительно низких температурах
(примерно в интервале 1200— 1600 К [31 ]). При нагревании лонсдейлит
переходит в алмаз. Превращение графит—алмаз протекает только по
диффузионному механизму при высоких температурах сжатия (> 1300 К).
Бездиффузионное превращение возможно также аая
ромбоэдрического графита,который всегда содержится в совершенных природных
графитах как дефект упаковки слоев (ABC—ABC вместо АВ—АВ).
Область бездиффузионного превращения ограничена как со
стороны низких температур (мала величина АФ), так и со стороны
высоких температур (превращение подавляется конкурирующими
диффузионными процессами).
Отметим совпадение и формы, и расположения расчётной линии
с АФ = 16 КДж/моль [30] и расчётной кинетической линии
диффузионного превращения [34].
659
С точки зрения кинетики алмазная область делится на три
зоны:
— зона гистерезиса, где превращение за ударной волной не
регистрируется;
— зона бездиффузионного превращения совершенного
графита в лонсдейлит;
— зона диффузионного превращения любого вида графита
в алмаз.
Очевидно, что границы между этими зонами нечёткие, размытые.
В семействе кинетических линий выделены две линии (см. рис.
14.6), на которых скорость превращения достаточно велика как а^я
его регистрации в ударно-волновых экспериментах (по излому p,V -
диаграмм, или по возникновению двухволновой конфигурации, или
по изменению
электропроводимости), так и а^я технологии
динамического синтеза алмаза.
Кроме этих линий, на рис.
14.6 показаны две ударные
адиабаты графита
(непористого и пористого). Для ударной
адиабаты непористого
графита: на участке АБ превращение
бездиффузионное, а начиная
с точки Б и выше, - диффузи-
онное.Для ударной адиабаты
пористого графита (т=1,35)
возможно только
диффузионное превращение, которое
регистрируется в эксперименте,
начиная с точки С и выше .
Вследствие температурной
неравновесности ударного
сжатия на определённом
участке адиабаты превращение в
Тл № 2Ш
Рис.14.6. Кинетические линии в
алмазной области
I — зона гистерезиса; II — зона
бездиффузионного превращения; III — зона
диффузионого превращения; 1 —
начало бездиффузионного превращения в
лонстейлит; 2 — начало диффузионного
превращения в алмаз; 3 — ударная
адиабата непористого графита; 4 — то же, но
пористого графита (т = 1,35). Точками
показаны условия зарегистрированных в
опытах превращений графит—алмаз
660
разных точках объёма графита может идти одновременно по двум
механизмам.
В алмазе, синтезированном ударным сжатием графита, всегда
присутствует лонсдейлит, что свидетельствует о реализации
бездиффузионного механизма.
14.4. Плавление алмаза
Изучение углерода в условиях очень высоких давлений и
температур представляет интерес а^я астрофизиков. Например, планеты
Нептун и Уран на 10 - 15 % состоят из углерода, который под
давлением ледяного покрытия планет может конденсироваться в форме
алмаза.
Изучение плавление алмаза нужно а^я его применения в
капсулах инерционного термоядерного синтеза (см. раздел 5.14).
Экспериментальная регистрация плавления ударно-сжатого
непористого алмаза является предельно сложной задачей. Это связано
с тем, что необходимые сверхвысокие давления (500 - 1500 ГПа)
можно создать на очень короткое время (наносекунды), что резко
снижает точность и надёжность измерений.
В первых работах по исследованию плавления алмаза [37,39]
считалось, что наклон линии плавления отрицательный (см. рис. 14.1),
как и у элементов IV группы с алмазной решёткой (кремний,
германий). Алмазная решетка не самая плотная, и отрицательный наклон
означает, что жидкий углерод плотнее.
Однако позднее, начиная с работ [38, 47, 48] и затем в работах
[41,49, 50] доказывается, что наклон линии плавления
положительный. В [41] даны экспериментальные координаты тройной точки
алмаз - жидкость - графит (13,5 ГПа, 4470 К) и наклон линии
плавления, равный 10,2 К/ ГПа (см. рис. 14.1).
С учётом этих данных и расчётов равновесных температур на
ударных адиабатах алмаза в работе [32] установлены точки
начала плавления: 74 ГПа, 5200 К — для пористого алмаза (порошок
АСМЮ/14, m = 1,847) и 688 ГПа, 8300 К — для монокристалла
алмаза.
661
Для получение таких больших давлений (до 2000 ГПа)
используется ударное сжатие алмаза толщиной ~ 20 мкм очень коротким
лазерным импульсом (~1 не) [51—53]. В этих условиях точность
определения давлений и плотности на ударной адиабате мала (5 -
10%). В таких экспериментах надёжно зафиксировано резкое
увеличение отражательной способности образца алмаза при ~1000 ГПа,
что объясняется окончанием плавления алмаза [51].
В работе [54] удалось на порядок повысить точность измерений
за счёт использования &ая разгона медного ударника (диаметр 17 -
40 мм, толщина 0,1 - 0,5 мм) до скоростей 13-24 км/с с помощью
импульсного магнитного поля, создающего давление до 400 ГПа в
течение нескольких сотен наносекунд.
Для анализа таких физических экспериментов
привлекались результаты математических экспериментов методом
молекулярной динамики [55—57]. Результаты расчётов следующие
(рис 14. 7):
ю
т
<о3К
в
б
г
о
О 500 Ш00 №0
GPa
Рис. 14.7. Расчётная фазовая диаграмма углерода в области сверхвысоких
давлений. Пунктир - линии фазовых границ, сплоная линия - ударная адиабата алмаза.
/
/
—/
—'
\-ч
п
п
7 j
i I
( /
Liquid
/ \
/ \
I \
1 \
diamond
_ / 1
/ "~
\ Ьс8
1
662
— найдены положения ударной адиабаты алмаза и линий
фазовой диаграммы углерода а^я давлений до 2000 ГПа;
— при давлениях более 1000 ГПа существует область более
плотной, чем алмаз твёрдой фазы углерода - т.н. Ьс8;
— линия плавления алмаза меняет свой наклон при ~500 ГПа и
8000К, при больших давлениях наклон становится отрицательным;
— координаты тройной точки алмаз - Ьс8 - жидкость: 875 ГПа,
7500К при плотности алмаза 6>6 г/см3;
— в окрестности тройной точки наклон линии плавления фазы
Ьс8 положительный;
— ударная адиабата алмаза пересекает линию плавления при
699 ГПа, а смесевой участок адиабаты проходит через тройную точку.
Полученные экспериментальные точки ударной адиабаты
алмаза соответствуют этим расчётам. Смесевой участок состоит из двух
сегментов с разным наклоном линии плавления: до тройной точки
(700 - 875 ГПа, плотность 6,08 - 6,53) и после тройной точки (875 -
1064 ГПа и плотность 6,67 - 7,01). Эти параметры определялись по
измеренным массовой скорости медного ударника и волновой
скорости в прозрачном образце алмаза.
Литература к главе 14
1. Физические свойства алмаза: Справочник / Под ред. Н.В.
Новикова Киев: Наукова думка, 1987.
2. Синтез алмазов. Новиков Н.В., Федосеев Д .В., Шульженко А. А.,
Богатырева Г.П./Киев: Наукова думка, 1987.
3. Санжарлинский Н.Г., Самойлович М.И.// Докл. АН СССР,
1981,259, №5,1106.
4. Алешин В.Г., Смехнов А.А., Богатырева Г.П., Крук В.Б. Химия
поверхности алмаза/Киев:Наукова думка, 1990, 200с.
5. Никитин Ю.И., Уман СМ., Коберниченко Л.В.,
Мартынова A.M. Порошки и пасты из синтетических алмазов/Киев:
Наукова думка, 1992.
6. Amanda S. Barnard. The diamond formula. Butterworth—
Heinemann, Oxford, 2000.
663
7. Шумилова Т.Г. Алмаз, графит, карбин, фуллерен и другие
модификации углерода. УрО РАН, Екатеринбург, 2002.
8. New Diamond : Abstracts of Conference reports. First Int.Conf.
on the New Diamond Science and Technology. Tokyo, Oct. 1988,
p.80.
9. Properties of Diamond. EdJ.Field. Lnd, N-Y.: Academ.
Press., 1979.
10. Алмаз в электронной технике: Сб. статей под ред. В. Б. Кваскова.
М.: Энергоатомиздат,1990
11. Оситинская Т.Д., Подоба А.П. Поверхностные и тепло-
физические свойства алмазов. Киев: ИСМ АН Украины,
1985.
12. Сверхтвердые материалы. Получение и применение. Том
1. Синтез алмаза и подобных материалов. Монография под
ред. А.А, Шульженко. Киев, ИСМ им. В.Н. Бакуля, 2003,
320 с.
13. Даниленко В.В. Синтез и спекание алмаза взрывом. Москва,
энергоатомиздат, 2003,272 с.
14. Поликристаллические материалы на основе алмаза./
Шульженко А.А., Гаргин В.Г., Шишкин В.А. и др. Киев: Наукова
думка, 1989.
15. Гатилова Е.Г, Колесниченко Г.А., Малоголовец В.Г., Кос-
тюк Б.Д.// В кн. «Физическая химия конденсированных
фаз, сверхтвердых материалов и их границ раздела». Киев:
Наукова думка, 1975, с. 110-113.
16. Кугель ТУ, Иванова М.Л. // Алмазы и сверхтвердые
материалы, 1982, вып.8, С. 12 — 13.
17. Исаев Р.Н. // Сверхтвердые материалы, 1989, № 2, С.ЗО - 34.
18. Коноков Г.Х., Аникеев А.И., Аникин В.Н. // Исследование
и разработка теор. проблем в обл. порошк. металлургии и
защитных покрытий. Мат-лы Всес. конф., Минск, 1983 ч.1,
С.78 — 81.
19. Патент России 210 9683 №01 А 31/06. Метод выделения
синтетических алмазов. Долматов В.Ю., Сушев В,Г., Марчу-
ков В.А., Публ.5.03.96.
664
20. Губаревич Т.М., Сатаев P.P., Долматов В.Ю. // V Всесоюзное
совещание по детонации, Красноярск, 1991. Сб.трудов, Т.1,
С.135- 139.
21. Международная заявка PCT/SU 90/00169. Способ вы
деления алмазов из алмазосодержащей шихты./ Шебалин А.И.,
Молокеев В. А., Сакович Г.В., др. Заявл. 19.07.88.
22. Губаревич Т.М., Гаманович Д.Н.,др. // Новые материалы и
технологии. Тезисы докладов на конференции ассоциации
«НОМАТЕХ», Минск, 1994, СИЗ.
23. Хоменко А.А., Ганкевич Л.Г. и др. // Синтетические алмазы,
1974,№1,С9.
24. Сверхтвердые материалы. Киев, «Наукова думка», 1980,
С.157—159.
25. Андреев В.Д., Созин Ю.И., Оситинский Т.Д. // Воздействие
высоких давлений на материалы. Сб. научных трудов ИПМ
АН Украины, Киев, 1993, С. 77 — 87.
26 Андреев В.Д., Созин Ю.И., Симкин Э.С.// Сверхтвердые
материалы, 1990, № 2, С.13 — 15.
27. Bridgman P.W. //J. Chem. Phys. 1947,15, P. 92 — 98.
28. Horton R.M., Horton M.D. // High Temperature—High
Pressure, 1972, P. 39-48.
29. Christian J.W. The theory of Transformation in Metals and Alloys.
Pergamon Press, N.Y., 1965, P. 18.
30. Даниленко B.B. // Физика горения и взрыва. 1988, №5, С. 137
31. Курдюмов А.В., Пилянкевич А.Н./Фазовые превращения в
углероде и нитриде бора. Киев: Наукова думка, 1979.
32 Молодец А. М. // Физика горения и взрыва. 1998, №4,
С.94—101.
33. Слободской В.Я., Соболев В.В., Баранов П.А. // Физика
горения и взрыва. 1990, №3, С. 119 —122.
34. Пятернев СВ., Першин СВ., Дремин А.Н. // Физика горения
и взрыва. 1986, №6, С125 -130.
35. Альтшулер Л.В. // Детонация. Критические явления. Физико-
химические превращения в ударных волнах. Черноголовка,
1978, С119—122.
36. Молодец А.М., Молодец М.А., Набатов С.С. // Физика
горения и взрыва. 2000, №2, С. 88 - 93.
37. Bundy F.P. // Koninkl. Nederl. Academie van Wetenschappen.
Proceedings, Ser. B, 1969, V. 72, № 5, P.302 - 316.
38. Bundy F. P. // Proc. Xl-th AIRAPT Inter. Conf., Kiev,: Naukova
Dumka, 1988, V.l, P. 326 — 336
39. Bundy F.P. //J. Chem. Phys. 1963, V.38, №3, P. 618.
40. Cowan R.D., Fickett W. //J. Chem. Phys., 1956, V. 24, P.5.
41. Togaya M. // Proc. of the 3 rd NIRIM Jntern. Symp. On Advanced
Materials (ISAM196). Tsukuba, Japan, 1996, P.251—256
42. Задумкин C.H. ДАН СССР, 1960, т.130, С. 4.
43. Задумкин C.H. Физика твердого тела, 1960, № 11, с. 5.
44. Лущук А.А., Новиков Н.В., Левитас В.И. Сверхтв. матер.,
2002, № I.e. 49-57.
45. Эстрин Э.И. // В сб. Проблемы металловедения и физики
металлов, 1975, №5 С. 28 - 39.
46. Жугин Ю.Н., Крупников К.К. // Сб. трудов симпозиума по
нелинейной акустике. Новосибирск, 1987, 2-я часть, С. 196 -
200.
47. ShanerJ.W., BrownJ.M. et.al. //J. De Physique (Paris), 1984, V.45,
№11, P. 235 —237.
48. Weathers M.S., Bassett W.A. // Phys. Chem. Minerals, 1987, V. 15,
№2,P.105—112.
49. Averin A.B., Dremov, Samarin S.J., Sapozhnikov A.T. // Shock
Compression of Cond. Mat., 1995. Schmidt and Tao (Eds), 1996,
Pt.l,P.65 —68.
50. D.K. Bradley, J.H. Egert, D.G. Hicks, P.M. Celliers, S.J. Moon,
R.C. Cauble, and G.W. Collins. Shock Compressing Diamond to
a Conducting Fluid // Phys. Review Letters, 2004, V. 93, No 19,
P. 195506-1 - 195506-4.
51. H. Nagao et al., Phys. Plasmas, 2006,13,052705.
52. S. Brygoo et al, Nat. Mater., 2007,6,274.
53. M. D. Knudson, M. P. Desjarlais, D. H. Dolan. Shock-wave
Exploration of the High-Pressure Phases of Carbon. Science, 2008,
Vol.322, p. 1822-1825.
54. A. A. Correa, S. A. Bonev, G. Galli. Proc. Natl. Acad. Sci. USA,
2006,103,1204.
55. N. A. Romero, W. D. Mattson, Prys. Rev. 2007, В 76,214113.
56. G. E. Duvall, R. A. Graham, Rev. Mod. Phys., 1977,49,523.
57. В.Д. Андреев. ФТТ, 1999, т. 41, вып.4, с. 695 - 701.
667
Глава пятнадцатая
УДАРНО-ВОЛНОВОЙ СИНТЕЗ АЛМАЗА
15.1. История открытия и разработки синтеза
Первые единичные и неудачные попытки синтезировать алмаз с
помощью энергии взрыва были предприняты в СССР еще в 1946 г.
Васильевым и в 1956 г. Рябининым [1].
После разработки в СССР в 1960 г. каталитического синтеза
алмаза в статических условиях в том же году научный
руководитель ВНИИТФ (г.Снежинск) академик Е.И.Забабахин показал, что
ударная адиабата графита должна входить в область существования
алмаза на фазовой диаграмме углерода, следовательно, возможен
ударноволновой синтез алмаза. На этом основании по инициативе
Забабахина и под его руководством во ВНИИТФ были начаты
систематические исследования в двух направлениях: снятие ударной
адиабаты графита и разработка технологий синтеза алмаза
взрывом с сохранением сжатых образцов. Работы по второму
направлению были начаты группой газодинамиков в составе К.В. Волкова,
В.В. Даниленко и В.И. Елина. Выделением и очисткой алмаза
занималась группа химиков во главе с СЕ. Саниной.
Первой наиболее трудной задачей были создание сферических
и цилиндрических устройств сохранения образцов графита
достаточно большого объема (> 100 см3), ударносжатого до давления
>30 ГПа. Эта проблема была успешно решена к началу 1962 г. В том
же году анализ первых образцов сохраненного сжатого графита по-
668
казал, что алмаз образуется как в сферических, так и в
цилиндрических взрывных устройствах.
В 1963 г. удалось увеличить выход с 1,5—2,5% до 19—20%
сжатием в сферических устройствах смеси порошков графита и
различных металлов (Ag, Си, РЬ (20:80 об.%) с оптимальной пористостью
Р«/Роо=1>35[2].
Было показано, что алмаз образуется из всех известных марок
природного и искусственного графита. Значительно лучший по
качеству алмаз получается не из графита, а из сажи.
В 1963 г. в цилиндрических ампулах был впервые в помощью
взрыва получен вюрцитный натрид бора с выходом до 67%.
В том же 1963 г. при переходе от цилиндрических ампул
сохранения к безампульному синтезу во взрывных камерах был впервые
открыт детонационный синтез ультрадисперсного алмаза (УДА) или
детонационного наноалмаза. (см. гл. 16)
Результаты всех названных работ были изложены в закрытых
отчетах ВНИИТФ. В 1986 г. основная часть этих отчетов была
разослана во все научные центры СССР, занимающихся синтезом алмаза
и затем опубликованы [2,3].
В 1965 г. продолжение работ во ВНИИТФ по динамическому
синтезу алмаза было признано нецелесообразным в связи с бурным
и успешным развитием в те годы производства алмазов в
статических условиях. Исследования возобновились во ВНИИТФ только в
1986 г. и только по синтезу УДА.
Правда, в 1970 годах были сделаны две попытки
использовать аая синтеза алмаза энергию подземного ядерного взрыва.
С этой целью в горные породы в ближней зоне ядерного взрыва
закладывались стальные трубы с графитом. К сожалению, через три
года после проведения опытов найти и достать трубы из грунта не
удалось.
Основные даты, имена и события истории динамического
синтеза алмаза сведены в таблицу 15.1, из которой видна ведущая роль
российских ученых.
669
Таблица 15.1. История динамического синтеза алмаза
Авторы
Васильев
Рябинин
Забабахин
(ВНИИТФ)
B.A.Alder, R.H.Cristan
Павловсюий
(ВНИИТФ),
Крупников
(ВНИИТФ),
Дремин,Першин
(ИХФ)
PJ.DeCarli,
A.CJamisson
Волков, Даниленко,
Елин (ВНИИТФ)
_«_
_«_
Ададуров (ИХФ)
Фирма Дюпон
(США)
Саввакин (ИПМ)
Титов, Ставер,
Лямкин, Петров (ИГ
СО АН СССР)
Бреусов, Дробышев,
Ададуров, Дремин
(ИХФ)
Сакович с
сотрудниками (НПО
«Алтай»)
Год
1946
1956
1960
1961
1963
1968
1961
1962
1963
1963
1965
1976
1982
1982
1983
1984
Содержание работы
Неудачные попытки динамического синтеза.
Обоснование возможности синтеза алмаза
ударным сжатием графита, начало
экспериментальных работ во ВНИИТФ.
Получение ударной адиабаты графита и вывод
о его превращении в алмаз.
Синтез алмаза с сохранением ударно-сжатого
графита в плоской ампуле.
То же, но в сферических и цилиндрических
ампулах. Выход алмаза -2%.
Синтез алмаза сжатием смесей Г+Ме,
сажа+Ме. Выход алмаза -20%.
Синтез УДА из углерода ПВ. Выход 8-12% от
веса заряда из ТГ40.
Синтез алмаза из графита.
Пром. производство алмаза сжатием в
цилиндрических ампулах. Смеси Г+Cu зарядами
весом 5т.
Синтез УДА.
Синтез УДА.
Опытное производство ДАЛАН'а взрывом в
камере смеси графита с гексогеном.
Опытно-промышленное производство УДА
670
В США алмаз был получен в 1961 г. ударным сжатием графита в
плоском устройстве сохранения [4].
С тех пор техника и технология получения взрывных алмазов
значительно усовершенствована.
Во всех развитых странах получена масса патентов (см.обзор [5].
Тем не менее на сегодня можно отметить только следующие три
разработки, доведенные до реального производства:
— организация в США в 1976 г. фирмой «Дюпон»
промышленного производства алмазного микропорошка («Mypolex») с
поликристаллическими частицами до 60 мкм (сжатие в
цилиндрических ампулах смеси графита с медью зарядом весом 5 т;
объем производства — до 3 т алмаза в год). Порошки Mypolex
— лучшие аая полировочных работ;
— ампульный синтез вюрцитного нитрида бора (BNb ),
доведенный в 1974 г. до опытного производства в СКТБ Института
проблем материаловедения (ИПМ) АН Украины (г.Киев);
— опытное производство поликристаллических
микропорошков алмаза с частицами до 5мкм путем взрыва в камере
прессованных зарядов весом 200 г. из смеси гексогена с графитом (ДАГ)
или с сажей (ДАС); организовано в 1982 г. в Институте химфи-
зики РАН (пос.Черноголовка Московской обл.).
Позднее, независимо от работ ВНИИТФ, исследования
динамического синтеза алмаза и BN проводились в ИХФ РАН
(О.Н.Бреусов, Г.А.Ададуров, В.Н.Дробышев, С.В.Першин,
А.Н.Дремин и др.), в Институте сверхтвердых материалов АН
Украины (В.Д.Андреев, В.А.Лукаш, В.Р.Малик и др.), в Институте
гидродинамики РАН (А.М.Ставер, А.И.Лямкин, А.А.Дерибас,
В.А.Петров, В.М.Титов и др.), в ИПМ АН Украины (В.В.Ярош,
Н.И.Боримчук, Г.И.Саввакин, В.И.Трефилов), в Днепропетровском
горном институте (В.В.Соболев, Р.П.Дидык).
15.2. Особенности ударно-волнового синтеза алмаза
Взрывной метод синтеза алмаза имеет следующие преимущества
перед статическим синтезом:
— высокая производительность, поскольку отсутствуют
принципиальные ограничения на величины сжимаемых объемов и
массы взрываемых зарядов, с ростом которых увеличивается
время существования высоких давления и , как следствие этого,
повышается качество и размер синтезируемых частиц алмаза; за
один взрыв можно получать до 104 карат алмаза;
— не нужны расходуемые детали из дефицитных твердых сплавов,
легированных сталей, не нужны металлы-катализаторы (Ni, Mg);
— в результате синтеза в сильно неравновесных условиях
получаются уникальные поликристаллические порошки алмаза с
нанокристаллическои структурой; каждая частица алмаза имеет
множество мельчайших режущих кромок, что обеспечивает
наивысшее качество полировки;
— величины давления, скорости нагружения, температуры
сжатия и остаточные температуры могут регулироваться
способом сжатия (однократное, многократное ударное или квазиизэн-
тропическое), мощностью ВВ, начальной пористостью, сжатием
смесей с различной сжимаемостью и теплопроводностью,
применением предварительного нагрева или охлаждения;
— прямой переход углеграфитовых материалов в алмаз
позволяет получать чистый алмаз без примесей металлов-катализаторов,
снижающих прочность и термостойкость алмаза.
Наряду с этим перечнем достоинств, взрывной метод имеет и
следующие недостатки:
— взрывные работы, изготовление и транспортировка зарядов
являются особо опасными, проводятся вручную; синтез в
ампулах сохранения требует проведения взрывов на специальных
полигонах, достаточно удаленных от населенных пунктов и
охраняемых;
— А,ая синтеза алмаза обычно требуются заряды из дорогих
и мощных ВВ (гексоген, сплав ТГ40), которые используются,
в основном, а^я изготовления боеприпасов, поэтому такие
заряды обычно изготавливаются только на оборонных
предприятиях;
672
— относительно высокая стоимость энергии взрыва мощных
ВВ, примерно в 20 -30 раз дороже электроэнергии, поэтому
экономически выгодно крупномасштабное производство алмаза
(что и сделано фирмой «Дюпон»);
Эти недостатки частично устраняются за счет проведения
безампульного синтеза в взрывных камерах и механизации
изготовления зарядов.
— рост энтропии при ударном сжатии обусловливает
остаточные температуры у обжатого материала, которые растут с
увеличением температуры сжатия и часто приводят к отжигу
получаемых метастабильных фаз (алмаза). Охлаждение образцов
после разгрузки возможно только за счет теплопроводности, а
это требует времени, намного большего времени существования
давления в УВ;
— быстрая разгрузка создает в образце быстрые сдвиговые
деформации, снимающие метастабильность фаз (аналогично
остаточным температурам);
— превращение графит-алмаз в УВ носит многостадийный
характер [6,7] и требует определенного времени аая роста
алмазных кристаллов; если быстро снять давление, то степень
необратимости превращения резко уменьшится.
Поэтому взрывные устройства а^я синтеза алмаза должны иметь
достаточно большие размеры (см. устройства фирмы «Дюпон»),
чтобы обеспечить и максимально возможное время существования
высокого давления (>20 ГПа), и минимальную скорость разгрузки,
и максимальную степень охлаждения полученного алмаза за счет
теплообмена с окружающим алмаз наполнителем.
Противоречие между требованием высокой температуры сжатия
графита и низкой остаточной температурой алмаза может быть
разрешено сжатием смеси графита или любого углеграфитового
материала (УГМ) с наполнителем. Для синтеза алмаза могут
использоваться два типа наполнителя.
1. Наполнитель с акустической жесткостью (рос) большей, чем
у УГМ. Общее с УГМ давление смеси повышается, а температура
сжатия наполнителя всегда будет ниже, чем у УГМ, и наполнитель
станет охлаждать УГМ с алмазом тем лучше, чем больше его
теплопроводность и разность температур AT с УГМ. Примеры такого
наполнителя — порошки серебра и меди. Но лучшим охладителем
является порошок алмаза, у которого максимальны и
теплопроводность, и AT.
2. Наполнитель с величиной pQc, меньшей, чем у УГМ (например,
KI, КС1). Общее давление смеси понизится, а температура сжатия
наполнителя будет выше, чем у УГМ. При достаточном времени
существования давления и малых размерах частиц УГМ происходит
теплообмен, в результате которого УГМ нагревается под давлением,
а наполнитель охлаждается. При изэнтропической разгрузке
наполнитель с большой сжимаемостью охладится до более низких
температур, чем УГМ и будет охлаждать УГМ после разгрузки. Этот метод
управления температурой успешно опробован в [8,9]. Выход алмаза
из сажи удалось поднять до 75% (см. табл. 2.4).
Авторами [10] предложен и опробован комплексный метод
синтеза алмаза, в котором на первом этапе с помощью ударного сжатия
серого чугуна в графите чугуна создаются затравочные
микрокристаллы алмаза (< 10 мкм), а на второй стадии в процессе
многократной термообработки чугуна при нормальном давлении происходит
рост метастабильного алмаза (до 400 мкм после пяти циклов нагрев-
охлаждение), по мнению авторов, за счет распада пересыщенного
твердого раствора углерода в железе.
По нашему мнению, росту алмаза в этих условиях
способствуют два обстоятельства: графит в чугуне остается сжатым, что
сближает межатомные расстояния и снижает скачок объема при
превращении, кроме того, межфазная граница графит-алмаз остается
когерентной, что на порядок снижает межфазную поверхностную
энергию.
Общий недостаток всех методов синтеза с охлаждением — в
необходимости диспергирования УГМ, в результате синтезировались
только дисперсные порошки алмаза. Кроме того, наполнитель надо
было удалять, как правило, дорогостоящими и вредными
химическими методами.
674
О решающей роли специальных методов сохранения
синтезированного взрывом алмаза свидетельствует следующий факт.
В 1963 г. во ВНИИТФ К.К. Крупниковым была исследована
ударная сжимаемость цейлонского графита и по виду ударной
адиабаты подтвержден вывод работы [11] о полном превращении
графита в алмаз при 40 ГПа. Затем, не меняя постановки опыта,
сжатый при 40 ГПа образец графита улавливался в воду и
подвергался химической очистке смесью H2S04+KN03. К большому
удивлению всех исполнителей, не было обнаружено даже следов
алмаза.
Рассмотрим классификацию схем и устройств сжатия.
Существуют две принципиальные схемы ударноволнового на-
гружения УГМ.
Контактная схема, при которой УГМ находится в контакте с
зарядом либо непосредственно, либо через слой металла. В этом
случае давление обычно не превышает 30 — 40 ГПа.
Безконтактная схема, при которой на УГМ воздействует
металлический ударник (лайнер), разгоняемый зарядом ВВ. Давление
в УГМ зависит от скорости ударника и может достигать 100 ГПа и
более.
В обеих этих схемах энергия сжатия может создаваться либо
скользящей, либо лобовой детонационной волной. За счет
столкновения УВ, воздаваемых в УГМ этими видами детонационных
волн, образец может сжиматься второй ударной волной до более
высоких давлений. Противоположно направленные импульсы
ударных волн уравновешиваются, что облегчает сохранение
образцов [13].
По своей геометрии устройства ударноволнового нагружения
естественно делятся на плоские, осесимметричные
(цилиндрические) и сферические (с центральной симметрией). В двух последних
используется явление кумуляции за счет создания в УГМ
сходящихся ударных волн.
Рассмотрим некоторые известные устройства всех трех
геометрий [2,5,7,9,12,13,14].
Рис. 15.1. Схема плоского
нагружения
1 — свинцовый контейнер;
2 — стальной стакан; 3 — углегра-
фитовый образец; 4 — метаемая
пластина-ударник; 5 — заряд ВВ
153. Метод плоского нагружения
Плоское нагружение образцов широко используется для
исследования ударных адиабат. Параметры плоских УВ легко
измерять и рассчитывать. Здесь мы рассматриваем только
устройства, которые могут иметь массовое технологическое
применение.
Наиболее распространенная
схема плоского нагружения с со-
храненим образцов описана в
патенте США [15] (см.рис. 15.1).
На сжимаемый образец
метается с помощью заряда ВВ плоская
пластина толщиной 0,5—5 мм со
скоростью до 6,5 км/с. В
образце создается УВ с амплитудой до
200 ГПа. Массивный свинцовый
контейнер обеспечивает
сохранение ~90% объема образца. В этом
устройстве использовалось сжатие смеси графита с металлами-
охладителями (на ~5 лет позже работ ВНИИТФ). Результаты
применения такого устройства: при сжатии чугуна степень превращения
графита в чугуне — 52% или 1,25% от массы чугуна, Выход алмаза —
42,5 карата на кг заряда ВВ.
Подобная схема запатентована и аая синтеза вюрцитного
нитрида бора. При сжатии смеси 85% Cu+15% BNr выход BNb составлял
70—90% от массы исходного BNr.
В 1973—80 гг запатентовано множество вариантов конструкции
плоской схемы (см. [5,13]).
Из них интересны схемы со столкновением
противоположно направленных УВ. По японскому патенту [16] образец
помещается в гнезда стальной плиты, которая служит устройством
сохранения.
С двух сторон платы под углом 10° устанавливаются пластины-
ударники, разгоняемые скользящей детонацией зарядов ВВ,
инициируемых по линии с помощью генератора линейной волны. Выход
676
алмаза в таком устройстве составляет 1,36% или 0,68 карата на кг
ВВ.
Реализованное еще в 1958 г. устройство аая прессования
порошка двумя метаемыми навстречу друг другу ударниками показано
на рис. 15.2 [17]. На том же рисунке приведен более современный
вариант устройства без разгоняемых ударников. Встречные ударные
волны создаются за счет прямого контакта зарядов ВВ с капсулой
сохранения [13]. Амплитуда второй отраженной УВ может
изменяться за счет изменения акустической жесткости прокладки,
устанавливаемой в зоне столкновения волн.
б) а)
/Ьрошок Ударник
Рис. 15.2. Устройства сжатия с использованием встречных УВ
А) сжатие двумя метаемыми навстречу друг другу ударниками; Б) сжатие
двумя УВ, создаваемыми встречными детонационными волнами от зарядов ВВ,
которые устанавливаются непосредственно на ампулу сохранения. 1 — заряд ВВ
с системой инициирования; 2 — стальной цилиндр; 3 — образец; 4 — капсула
сохранения; 5 — прокладка;
При контактном взрыве профиль УВ близок к треугольному, а
при ударе пластиной амплитуда УВ постоянна в течение времени
циркуляции УВ по пластине.
Разгон пластин может быть обычным, прямым (направление
движения пластины и детонационной волны совпадают) и
«обратным», когда заряд инициируется от пластины и направление
движения пластины и детонации противоположны [18,19].
В последнем случае можно без откола разогнать пластину в
2—3 раза большей толщины, т.е. увеличить время существования
постоянного давления (правда, меньшей величины).
15.4. Осесимметричные устройства
Именно с помощью таких устройств впервые были сохранены
ударносжатые образцы [ 1 ].
В этих устройствах цилиндрическая стальная капсула с УГМ
может нагружаться двумя способами (см.рис. 15.3):
а) б)
Рис.153. Цилиндрические устройства
А,Б — контактный и бесконтактный варианты. 1 — капсюль-детонатор;
2 — заряд ВВ; 3 — верхняя крышка; 4 — цилиндр; 5 — образец УГМ;
6 — нижняя крышка; 7 — метаемый цилиндр; 8 — центральный стержень
— контактным, когда капсула помещается внутри заряда ВВ,
а сходящиеся к оси капсулы УВ создаются скользящей
детонацией, распространяющейся по заряду вдоль оси капсулы;
— безконтактным, когда капсула нагружается метаемой коакси-
ально цилиндрической оболочкой.
Во всех случаях в образце создается трехударная
конфигурация: сходящаяся к оси коническая волна, зона однократного
сжатия (волна Маха) у оси и расходящаяся волна, отраженная от этой
зоны.
678
Чтобы исключить волну Маха и повысить однородность сжатия
образца, в центре вдоль оси капсулы располагают стальной стержень.
Контактный способ и капсула со стержнем используется а^я
синтеза вюрцитного нитрида бора [9]. В этом способе образец
сжимается до давлений обьино не более 12—15 ГПа, что достаточно
Аля синтеза BNb.
Более высокие давления (до 40 ГПа) требуемые а^я синтеза
алмаза, позволяет получить бесконтактный способ, который
использует фирма Дюпон а^я промышленного производства алмазного
поликристаллического порошка.
Такой способ синтеза алмаза подробно описан в заявке Франции
2013326 и в патенте США 3667911.
Согласно указанным патентам для синтеза алмаза используется
смесь из металла-охладителя и 3—12% графита с плотностью,
равной 20—80% теоретической. Степень превращения графита
достигает 75,9% или 6,25% от массы смеси. Обычно используются смесе-
вые взрывчатые составы со скоростью детонации 4—5 км/с.
Синтез алмаза при ударном нагружении смеси графита с
металлом-охладителем описан также в [2,20].
В таблице 15.2 приведены расчетные параметры соударения
метаемой стальной оболочки со стенкой стальной капсулы а^я
различных отношений массы оболочки к массе ВВ [14].
Таблица 15.2. Параметры соударения оболочки и капсулы
Отношение массы оболочки к
массе ВВ
Скорость движения оболочки,
м/с
Давление соударения, ГПа
0,2
1948,5
42,5
0,4
1923,5
41,0
0,6
1731,5
36,0
0,8
1546,5
31,0
1,0
953,3
19,6
Переходя из стенки капсулы в графит, ударная волна
разгружается, поэтому давление в образце графита в капсуле будет меньше
указанного в табл. 15.2.
В1959—65 гг. автор проводил исследования по синтезу алмаза и BNb
в цилиндрических устройствах контактного типа с зарядами из ТГ40
плотностью 1,68 г/см3 и D=7,8 км/с в капсулах радиусом, равным
половине радиуса заряда [2,7].
В такой постановке капсула диаметром более 20 мм не
сохраняется. Установлено, что аая сохранения капсул любого размера
необходимо использовать тяжелую оболочку (корпус) вокруг
заряда. Например, из чугуна с толщиной, равной толщине заряда
(рис. 15.4).
2 3 4
Рис. 15.4. Цилиндрическое устройство с тяжёлым корпусом
1 — ЭД, 2 — оболочка, 3 — заряд ВВ, 4 — капсула, 5 — образец
Таблица 153. Постановка опытов и их результаты
Масштаб
-
1
1.67
2
4
Размеры
заряда,
мм
о60х120
о60х240
0100x480
0120x480
0240x960
Размеры
ампулы.
мм
030x100
030x200
050x380
060x400
0120x800
Размеры
графита,
мм
016.5x75
016,5x150
027x260
038x300
080x660
Вес
графита. Г
25,5
51
238
548
5320
Выход
алма-
за,%
0,5
1,4
1,7
1,4
1,3
Выход
алмаза, г
1,3
7,1
40,5
77
690
680
С применением тяжелой оболочки проведена серия опытов по
синтезу алмаза из графита с изменением масштаба опытов в 4 раза.
Постановка опытов и их результаты приведены в таблице 15.3 [2,7].
Было сконструировано и испытано устройство с предварительным
электронагревом графита до 2000° С (6V, 1200А) и с улавливанием
обжатого графита в воду [7]. К сожалению, алмаз получен не был.
Результаты опытов позволили сделать следующие выводы.
— алмаз получен из всех опробованных видов УГМ;
— в зависимости от начальной пористости графита степень
превращения имеет максимум 1 - 2% при пористости т=1,35
(р00 =1,63 г/см3);
— изменение масштаба опыта в 4 раза не влияет на степень
превращения;
— повторное обжатие цилиндрической капсулы практически
удваивает степень превращения (с 1,3% до 2,3%);
— обжатие УГМ в смеси с металлами (15:75) повышает выход
алмаза до 19%;
— степень превращения в капсуле растет с расстоянием от
точки инициирования, поэтому увеличение вдвое длины заряда и
ампулы (от 100 до 200 мм) повысило степень превращения от
0,5% до 1,4%;
— на оси и на поверхности образцов графита выход алмаза не
зарегистрирован: на поверхности исходный графит не изменяется,
а на оси в зоне волны Маха превращается в сажу, по-видимому,
как результат полной графитизации алмаза (в этом причина
снижения выхода).
В самом большом заряде выход алмаза составил 60 кар. на кг заряда.
15.5. Сферические устройства
Плоские и цилиндрические устройства сохранения имеют один
принципиальный недостаток — эффекты боковой или торцевой
разгрузки, искажающие одномерность сжатия. Сферическая
система лишена этого недостатка.
Внутри сферического заряда помещена сферическая капсула с
образцом (рис. 15.5).
Рис. 15.5. А. Сферическое устройство: 1 — тяжелый корпус; 2 — система
инициирования; 3 — заряд; 4 — капсула; 5 — образец; Б — фото сохраненного
образца с полостью
Наружная поверхность заряда синхронно инициируется
специальной инициирующей системой или многими
электродетонаторами. В результате в заряде создается сферически сходящаяся
детонационная волна, а в капсуле и в образце - сходящаяся УВ. Для капсулы
о 184 мм и толщины заряда 18 мм на поверхности капсулы создается
УВ с амплитудой 60 ГПа и с треугольным профилем длительностью
5 мкс [21]. На радиусе 3 мм в стальном шаре расчетное давление
достигает 1000 ГПа с длительностью 0,5—2 мкс. Согласно расчетным
оценкам в образце кварца о 48 мм на фронте сходящейся УВ
реализуются на радиусе 1-2 мм давления 300—100 ГПа и плотность
энергии 30—10 кдж/г [22,23].
Увеличение размеров сферической системы позволяет получать
те же состояния на более высоких радиусах и увеличить
длительность импульса давления.
Вблизи фокусировки в центральной части сферического образца
вещество плавится, а отраженная от центра волна образует в
образце полость (см.рис. 15.5 б), а при выходе на свободную поверхность
сферической капсулы создает в материале капсулы растягивающие
напряжения. Если эти напряжения превысят откольную прочность,
682
то капсула разрушается на мелкие фрагменты, что и наблюдалось в
первых опытах со сферической системой, проведенных в 1960—61г
в ВНИИТФ Волковым, Даниленко и Елиным [2].
Уже в 1961 г. было найдено простое решение проблемы
сохранения сферических капсул, которое заключалось в применении
тяжелого металлического корпуса (свинец, чугун), внутри которого
взрывался сферический заряд. Масса корпуса должна быть такой,
чтобы к моменту выхода на поверхность капсулы отраженной от
центра ударной волны давление в П Д оставалось достаточно
большим, чтобы нейтрализовать растягивающие напряжения в капсуле и
предотвратить откол.
По аналогии с плоским нагружением, возникновение откола в
сферической капсуле определяется отношением радиуса капсулы г к
толщине заряда h. При r/h=8—10 откола нет благодаря затуханию
ударных волн в капсуле. Наиболее сложно сохранить капсулу при
r/h=4—6, т.к. амплитуда отраженной УВ достаточна а^я откола, а
ПД тонкого заряда разгружаются быстро, еще до прихода УВ (даже
с корпусом). Хорошо сохраняется капсула с корпусом при r/h= 1 —2,
причем импульс сжатия образца в такой системе максимален.
Кроме корпуса, большое влияние на сохранность сферической
капсулы оказывают материал и конструкция капсулы.
Лучшим материалом ^^я капсулы является нержавеющая сталь
(напр. 1X18НЮТ), пластичность которой устраняет опасность
хрупкого разрушения капсулы, а отсутствие фазового превращения
уменьшает затухание сходящейся УВ.
Нами с одинаковым успехом применялись следующие
конструкции капсулы:
— с резьбовой пробкой;
— из двух свинчивающихся полусфер;
— из двух свариваемых полусфер.
Серия опытов по синтезу алмаза, проведенных в 1962—65 гг.,
позволили сделать выводы, которые изложены выше а^я
цилиндрических устройств. Кроме того, показано большое влияние
теплопроводности металла на выход алмаза при сжатии смеси графит+Ме:
выход возрастал в ряду Pb—Zn—Си—Ag.
683
Опытработы со сферической системой, полученный авторами [2],
через четверть века был использован во ВНИИТФ Е. А. Козловым с
сотрудниками [13,21,24], но не а^я синтеза алмаза, а а^я
исследования образцов различных сплавов с полиморфизмом, горных пород,
минералов и т.п., ударносжатых в диапазоне давлений, недоступных
Аая других устройств.
Сферическое устройство а^я синтеза алмаза запатентовано в
США [25]. Заряд синхронно инициируется во многих точках
электродетонаторами мгновенного действия.
В 1999 г. в США опубликована работа [26], в которой также
используется тяжелый корпус а^я сохранения капсулы, а заряд
инициируется 14-ю капсюлями.
Целью этой работы был синтез алмаза из фуллерена С60 и
синтез нитрида углерода C3N4, твердость которого должна быть такая
же или даже выше, чем у алмаза. К сожалению, положительных
результатов не получено. Причины неудачи, по нашему мнению две:
малый размер устройства (диаметры образца и капсулы всего 6,3 и
25,4 мм) и несовершенная система инициирования (система 14-ти
расходящихся волн от детонаторов не трансформируется в заряде в
одну сходящуюся сферическую волну).
Сложность создания в образце сходящейся УВ состоит в
синхронности инициирования всей поверхности сферического заряда.
Для решения этой проблемы японскими исследователями
предложено использовать металлическую фольгу, покрывающую заряд
и взрываемую электрическим импульсом [27,28]. Синхронность
инициирования можно получить, если покрыть поверхность заряда
слоем светочувствительного ВВ и инициировать его лазерным
импульсом (см. гл.11).
Недостатки сферических устройств аая синтеза алмаза:
— сложность инициирующей системы аая создания
достаточно гладкой сферической сходящейся детонации;
— большая неоднородность условий нагружения по радиусу
образца: если на поверхности образца давление а^я синтеза
алмаза оптимально (30—40 ГПа), то вблизи центра на малых
радиусах давление чрезмерно высоко и алмаз графитизируется;
684
— образование полости в центре сферы создает
дополнительную поверхность разгрузки образца.
15.6. Безампульный синтез
Применение взрывных камер упрощает проблему сохранения
обжатого образца а^я любой геометрии взрывных устройств, т. к. не
нужны ампулы и тяжелые корпуса.
Первые разработанные и использованные автором в 1963—65 гг
конструкции взрывных камер показаны на рис. 15.6.
а) б) в)
Рис. 15.6. Постановка опытов с взрывными камерами в 1963-65 гг.
1 — крышка, 2 — заряд, 3 — образец, 4 — подставка, 5 — вода
Первоначально заряд помещался вне камеры, а обжатый
образец через отверстие в крышке камеры метался в воду. Позднее
заряд с образцом помещался в камере, причем в водяной оболочке.
В такой постановке опытов впервые в 1963 г. был открыт синтез
УДА [2,3].
В 1989—99гг нами были спроектированы и испытаны взрывные
камеры большого объёма, специально предназначенные для синтеза
и спекания алмаза (см. гл. 13).
В Институте гидродинамики СО РАН использовалась взрывная
камера КВ-2 с внутренним диаметром 1260 мм, толщиной стенок
60 мм, объемом 2,14 м3, с допустимым весом взрываемого заряда
2 кг, с возможностью заполнения инертными газами [29].
685
Камера подвижная, имеет два положения: загрузочное и рабочее
(рис.15.7).
/ 2 В атмосферу
Рис.15.7. Конструкция взрывной камеры КВ-2 (1980 г. СКБ ГИТ СО АН СССР)
Позиция 2 — подвеска заряда, 1 — подрыв заряда
В такой камере с целью получения алмаза проводились опыты в
плоской и цилиндрической геометрии по ударному сжатию
различных углеводородов и их смесей с графитом.
Предполагалось, что выделяющийся при разложении
углеводородов водород как сильный восстановитель будет способствовать
сохранению алмаза.
В результате таких опытов в камере в 1982 г. также был открыт
синтез УДА [29].
В 1976 г. группа авторов ИХФ запатентовала способ синтеза
алмаза, согласно которому графит или сажа смешиваются с гексогеном,
прессуются в заряды и взрываются во взрывной камере [30].
Реально в опытном производстве в ИХФ использовались заряды
весом 200 г с содержанием графита 20%, при этом степень
превращения в алмаз составляет ~20%.
В этой технологии и способ взрывания «сухой», без
применения воды ( охлаждение за счет диспергирования образца в
расширяющихся ПД), и способ окисления непревращенного графита тоже
сухой, без применения кислот. Шихта смешивается с порошком
катализатора и нагревается на воздухе в кварцевых лодочках.
686
Название получаемого таким способом алмаза Д АГ (из графита)
и ДАС (из сажи) или ДАЛАН — а^я обоих видов алмаза.
Он имеет поликристаллические частицы, аналогичные частицам
алмазного порошка Mypolex.
Судя по изломам D(p) — зависимостей детонации смесей гексо-
гена с 25% коллоидного графита, превращение графит — алмаз
начинается при 12 ГПа, а оканчивается при 16 ГПа [31]. Более низкие
величины давления превращения в детонационной волне по
сравнению с ударной волной (18 и 40 ГПа) объясняются более высокой
температурой, до которой успевают прогреться мелкие частицы
графита. Согласно термодинамическим расчётам [32], требуемая
Аая превращения величина разности термодинамических
потенциалов с ростом температуры достигается при меньших давлениях (см.
гл. 14).
15.7. Динамико-статическое сжатие
Как известно, подавить графитизацию алмаза можно или
понизив его температуру, или повысив давление.
При проведении экспериментов по синтезу алмаза и BNb
в цилиндрических капсулах было замечено, что выход
снижается, когда капсула разрывается, частично разрушается с выбросом
части образца. Если образец содержал какую-либо органику
или воду, то иногда капсулы «взрывались» в процессе ее
разрезки на токарном станке, что свидетельствовало о
значительном остаточном давлении газов в капсуле (см. расчёты капсулы
в [7]).
Наши исследования стали -3, из которой была сделана
капсула, показали, что в результате взрывного нагружения сталь-3
сильно упрочнилась: исчезла площадка текучести на диаграмме
растяжения (т.е. сг=сгв), а предел прочности повысился втрое, с 30 до
99 кг/мм2.
Следовательно, всегда стальная капсула удерживает внутри себя
какое-то остаточное давление, но на это не обращали внимание,
считая давление небольшим.
Рис. 15.8. Схема динамико-статического сжатия
а -динамическое нагружение; б — разгрузка;
с — статическое давление; d — спад температуры;
е — область отжига плотной фазы в отсутствии
давления
Идея
превратить капсулу после
ее ударного сжатия
в автоклав, тем
самым совместив
динамическое и
статическое сжатие была
всесторонне развита
С. С. Бацановым с
сотрудниками
после 1980 г. [33,34].
Схема
динамико-статического сжатия
показана на рис. 15.8.
Были
опробованы следующие
способы создания достаточного давления в капсуле:
— добавка к образцу вещества, выделяющего газ под действием
остаточной температуры, например воды, гексогена;
— использование в качестве источника давления твердых тел,
испытывающие при нагреве фазовые превращения или
плавление с увеличением объема на 10-20%.
Согласно [33] капсулы из специальных сталей о50х70мм со
сферическими торцами, выдерживают давление до 15 кбар.
В результате динамико-статического сжатия (ДСС) с
использованием прочной капсулы и заряда из ТГ40 был получен
монолитный образец BNb с плотностью 3,35 г/см3. В аксиальной
области образец имел особо твердое пятно с твердостью по Виккерсу
5000—7000, а на периферии образца твердость падала до 1000—
1500 единиц.
В условиях ДСС компактирование алмазного порошка дало
монолитный образец с плотностью 3,32 г/см3 и твердостью до 5000
единиц по Виккерсу.
688
15.8. Свойства взрывных алмазов
Свойства взрывных алмазов зависят от условий синтеза и от вида
УГМ.
Подробно исследованы свойства алмазов, полученных из
графита или сажи:
— в капсулах сохранения или при ударном сжатии чугуна;
— при детонации смеси с гексогеном во взрывных камерах.
Основные свойства алмазного порошка, синтезированного
в 1962—65 гг. из смеси графита или сажи с медью или серебром в
сферических устройствах, были определены во ВНИИТФ и
приведены в табл. 15.4 [2].
Таблица 15.4. Свойства алмаза из смеси УГМ+Ме
Наименование
Внешний вид
Размеры частиц
Размер ОКР (монокрист.
блоков)
Тип частиц
Форма частиц
Плотность
Тип алмаза
Плотность дислокаций
Искажения кристалл,
решетки
Температура начала
окисления на воздухе
Измеренные параметры
Порошок черного цвета
От 0,01 до40 мкм; одна треть частиц — более 10
мкм; 0,7—2 мкм — по величине удельной
поверхности
5—12 нм — для алмаза из графита;
15—20 нм — для алмаза из сажи
Поликристаллы
Преимущественно пластинчатая — для алмаза из
графита; округлая — для алмаза из сажи
3,3—3,4 г/см3
I — поглощение у ИК-спектра при 8—10 мкм
2.10,2см-2
Да/а=4.10-3
550° С
Таким образом, взрьюной алмаз представляет собой
полидисперсный порошок с поликристаллическими частицами. Каждая частица
состоит из очень малых монокристальных блоков, а плотность дислока-
689
ций очень высокая (как у сильно наклепанного металла), на 3—4
порядка выше, чем у поликристаллов статического синтеза и типа карбонадо.
Эти свойства определяют ценность алмаза как лучшего образи-
ва а^я полировки. Каждая частица имеет тысячи режущих
микрокромок, при полировке частица разрушается, но такие же кромки
все время остаются, воспроизводятся, что обеспечивает уникальное
сочетание высоких значений и абразивной способности, и чистоты
поверхности.
У частиц обычного синтетического алмазного микропорошка
режущие кромки сопоставимы с размером самих частиц, а с
разрушением частиц в процессе полировки размер кромок уменьшается.
Качество порошка определяется изометричностью частиц (или
коэффициентом формы, равным d /d . ). Алмаз, полученный из
графита имеет много частиц в виде пластин, линз, игл (d /d . >2),
т.е. не лучшего качества, т.к. пластинки легко разрушаются, но могут
давать глубокие царапины.
Поэтому лучшим по качеству является алмаз, полученный из
сажи, с округлыми изометричными частицами.
В 1964 г. алмаз, полученный сжатием смеси графита с медью в
сферических устройствах ВНИИТФ был фракционирован
(классифицирован) стандартным методом седиментации на ряд фракций от
1/0 до 60/40 мкм без предварительного дробления.
Для каждой фракции измерена абразивная способность (а.с.)
и сравнена с а.с. промышленных порошков. Оказалось, что а^я всех
фракций, кроме 1/0 и 2/1, величина а.с. ниже у взрывного алмаза.
Для указанных самых мелких фракций а.с. у взрывного алмаза чуть
выше а.с. промышленного порошка.
Наоборот, шероховатость поверхности после полировки у
взрывного алмаза на 1—2 класса выше.
У неклассифицированного порошка алмаза а.с. падает с
увеличением начальной пористости графита, по-видимому, из-за
уменьшения размера частиц.
В 1983—89 гг исследованы свойства алмаза, полученного с
помощью цилиндрических устройств и взрывом смеси УГМ + гексоген
[35,36].
690
Найдено, что в алмазе, полученном из графита, содержится 10
-20% лонсдейлита. Лонсдейлита нет у алмаза, полученного из сажи.
Сравнение некоторых свойств алмаза из графита (ДАГ) и из сажи
(ДАС), синтезированных безампульным способом в ИХФ,
приведено в таблице 15.5.
Таблица 15.5. Сравнение свойств алмазов типа ДАГ и ДАС
Параметр
Массовое содержание летучих при нагреве в вакууме до
1000 С, %
Удельная поверхность, м2/г
Содержание лонсдейлита
Размеры ОКР, нм
Размер частиц под электронным микроскопом, нм
ДАГ
2-4
20—25
10—20
7-8
10—50
ДАС
2-4
35
0
18—20
20—80
У алмазов ДАГ морфология и субструктура частиц
неоднородна, что отражает различные механизмы превращения графита при
детонационном сжатии.
Мелкие частицы графита успевают прогреться в детонационной
волне и дают округлые зерна (подобно частицам ДАС) по
диффузионному механизму. Более крупные зерна, содержащие лонсдейлит,
сохраняют признаки слоистого строения графита и, по-видимому, возникали
при более низких температурах по мартенситному механизму.
Влияние на выход УДА степени прогрева частиц графита в
зависимости от размера частиц видно из табл. 15.6 [37].
Таблица 15.6. Влияние размера частиц графита на выход УДА при
детонационном синтезе смесей графита с гексогеном (заряд ©40x100
мм,р0=1,6 г/см3, концентрация графита в смеси 25%).
№
1
2
3
4
5
Размер частиц, мкм
250— 800
70—140
0—40
0-9
Сажа, < 0,7
Выход УД А,%
4,4
6,3
22
22
35
691
В этих условиях давление начала превращения резко
уменьшается и составляет 6 ГПа, что объясняется высокой температурой
синтеза.
Литература к главе 15
1. Рябинин Ю.Н. Журнал технической физики, 1956, Т. XXXVI,
вып. 12.
2. Волков К.В., Даниленко В.В., Елин В.И. и др. "Взрыв, удар,
защита". Информ.бюлл. ИГ СО АН СССР, вып. 17, 1987,
Новосибирск.
3. Волков К.В., Даниленко В.В., Елин В.И. ФГВ, 1990, №3,
С. 123.
4. De Carli P. J., Jamisson A. С Science, 1961, V.133, P. 3467.
5. Лукаш B.A., Марков А.И. Сверхтв.материалы,1983, №6,
С. 13—19.
6. Даниленко В. В. V Всес. совещ. по детонации. Красноярск, 1991.
Сб. докладов, Т.1, С.146.
7. Даниленко В.В. Синтез и спекание алмаза взрывом М.
Энергоатомиздат, 2003,272 с.
8. Боримчук Н.И., Курдюмов А.В., Ярош В.В. V Всес. совещание
по детонации (Красноярск), 1991, Сб. докладов, Т.1, С.43 -
47.
9. Курдюмов А.В., Бритун В.Ф., Боримчук Н.И., Ярош В.В.
Мартенситные и диффкзионные превращения в углероде и
нитриде бора при ударном сжатии. Киев, Из-во Куприянова,2005,
191с.
10.. Слободской В.А., Соболев В.В., Губенко СИ. Материалы VIII
Всес. симп. по горению и взрыву. Черноголовка, 1986, С. 3.
11. Alder B.J., Christian R.H. Phys. Rev. Lett.,1961, V.7, №10, P. 367.
12. Прюммер P. Обработка порошкообразных материалов
взрывом (пер.с нем.) М.: Мир, 1990.
13. Козлов Е.А., Лебедев М.А., Литвинов Б.В.,ФГВ., 1993, №2,
С.118.
14. Лукаш В.А., Петушков В.Г., Дидык Р.П., Марценкевич Г.И.
Синтетические алмазы. 1976, №5, С. 21—26.
692
15. Патент 3401019 (США). G.R. Cowan и др. Опубл. 10.09.68.
16. Акцептованная заявка 51-14994 (Япония)./С. Танака и др.
Опубл. 13.05.76.
17. La Rocca E.W., Pearson J. Rev. Sci. Instrum., 1958, V.29, P. 848.
18. Патент США N3430563, кл. 102-22, публикация 1969.
19 Лебедев М.А. ФГВД989, №2, С.140 -142.
20. Дерибас А.А., Ставер A.M. ФГВ, 1977,№3, С.38.
21. Kozlov Е.А. Shock compression of condensed matter. 1991,
Elsevier Science Publishers B.V., 1992.
22.. Kovalenko G.V., Kozlov E.A., et al. Bull. Am. Phys. Soc, 1991, V.
36, №6, P. 1831.
23. Патент 3499732 (США). Methods for making diamonds. D.R.
Garrett. Опубл. 10.03.70.
24. Литвинов Б.В., Козлов E.A., Жугин Ю.Н. и др. V Всес. Совещ.
по детонации, Красноярск, 1991, сб. докл., Т. 1, С. 197.
25. Патент 3499732 (США). Methods for making diamonds./D.R.
Garrett. Опубл. 10.03.70.
26. С. Grant Willson./Shock Compression Synthesis of Hard
Materials Amarillo National Resource Center for Plutonium.
ANRCP -199-13. Report of Department of Chemistry The
University of Texas. 1999.
27. Акцептованная заявка 47—5089 (Япония). Способ
синтеза сверхтвёрдых материалов. Кумамото Дайгакутё. —
Опубл.14.02.1972.
28. Акцептованная заявка 48 — 32517 (Япония). Устройство а^я
создания высокого давления с помощью взрывчатого
вещества. Фудзимура Мэйко. — Опубл. 16.10 1973.
29. Ставер А.М., Лямкин А.И. %ътрадисперсные материалы.
Получение и свойства. Межвуз. сб. тр., Красноярск, 1990,
С. 3—28.
30. А.с. № 565474 / Ададуров Г.А., Бавина Т.Б. и др. от
23.07.1976.
31. Цаплин Д.Н., Першин СВ. V Всес. совещ. по детонации.
Красноярск, сб. докл., Т.2, С. 322—325.
32. Даниленко В.В. ФГВ, 1988, №5, С.137.
33. Бацанов С.С. ФГВ, 1994, №1, С.125.
34. Бацанов С.С, Вазюшин В.А. Дидюков ГГ. и др. V Всес. совещ.
по детонации. Красноярск, 1991, сб. докл., Т.1, С. 48—53.
35. Балан Т.Р., Боримчук Н.И., Бочко А.В. и др. Сверхтвердые
материалы, 1983, №3, С.19 — 23.
36. Курдюмов А.В., Бреусов О.Н. и др. ФГВД989, №3, С. 126.37.
Дробышев В.Н., Ананьин А.В., Дрёмин А.Н., Першин СВ.,
Рогачёва А.И. Исследование процесса синтеза алмаза в
детонационной волне. Физика импульсной обработки материалов.
Сб. статей под ред. В.В. Соболева. Днепропетровск, АРТ-
ПРЕСС,2003,с.45—70.
694
Глава шестнадцатая
ДЕТОНАЦИОННЫЕ НАНОАЛМАЗЫ
16.1. Ультрадисперсная среда.
Наноматериаловедение и нанотехнологии
С помощью «взрывных» технологий получены
ультрадисперсные порошки алмаза, сажи, окиси алюминия, окиси циркония и др.
Особое место занимают детонационные наноалмазы (УДА)
благодаря своим уникальным свойствам, широкому спектру применений и
возможностью производства УДА десятками тонн в год.
Поэтому в этой книге появился раздел об ультрадисперсных
средах как об особом конденсированном состоянии вещества с новым
комплексом свойств.
В ультрадисперсных частицах (УДЧ) существует особый тип
дальнего порядка, при котором межатомное расстояние
закономерно изменяется от центра частиц к ее поверхности, причем среднее
межатомное расстояние существенно (до 10%) меньше, чем в масив-
ном материале.
Уи>традисперсные среды отличаются и от поликристаллов.
Например, благодаря влиянию сил поверхностного натяжения
локальная плотность в ультрадисперсной среде не постоянна, а
колеблется относительно среднего значения, примерно равного
плотности массивного материала. УДЧ всегда термодинамически
неравновесны, имеют неравновесное распределение размеров и
формы, являются результатом своеобразной закалки искусственно
созданного неравновесного состояния.
695
Обсуждение особенностей известных технологий получения
ультрадисперсных порошков полезно а^я понимания процесса синтеза
ультрадисперсного алмаза (УДА) (или детонационных наноалмазов)
при конденсации углерода за фронтом детонации. С точки зрения
позиций материаловедения перевод материала в ультрадисперсное
состояние столь же эффективен, как, например, термообработка и
легирование. Поэтому в конце 20 века стали бурно развиваться
исследования наноматериалов и нанотехнологий. В том числе
углеродных кластеров (фуллеренов, трубок, ультрадисперсного алмаза и
продукта его графитизации - луковичного графита).
Подробнее о свойствах, методах получения и исследованиях
ультрадисперсных порошков можно узнать из [1—15].
За последние 15 лет материаловедение переживает настоящую
революцию, основанную на изучении и применении различных
систем с наноструктурой. С начала 21 века активно создаётся и
развивается новое научное и технологическое направление - нано-
структурное материаловедение, изучающее структуры с размерами
в интервале 1 —100 нм, АА^ которых влияние на свойства
поверхностей раздела очень велико.
Создаваемые и исследуемые наноструктуры подразделяются на
одномерные (плёнки), двумерные (многослойные плёнки,
углеродные нанотрубки) и трёхмерные (наночастицы как в виде порошков,
так и консолидируемые).
Для получения консолидируемых наноматериалов требуется
решить ряд сложных проблем: синтезировать наночастицы
требуемого качества с помощью воспроизводимой и масштабируемой
технологии, создать методы консолидации, позволяющие получать
наноструктуры с высокой плотностью и однородностью.
Особо перспективно развитие нанотехнологий, связанных с
созданием нанокомпозитов. Это наиболее обширный класс
наноматериалов, в которых стабильно соединяются на наноуровне самые
разнообразные составляющие: полимеры, керамика, металлы, на-
ноуглерод, белки и др., а также нанокристаллические и аморфные.
Частным случаем объёмных наноматериалов является класс
пористых материалов. В нанопорах происходят самые разнообразные
696
процессы: химический синтез, сорбция молекул, белков и
биологически активных групп, полимеризация, катализ.
В технологиях консолидации наиболее сложны следующие
проблемы: стабильность и воспроизводимость наноструктур, очистка
поверхности или её направленная модификация, диспергирование
наночастиц, которые всегда создают прочные и многоуровневые
агрегаты с размерами уже в микродиапазоне. Проблема
стабильности наноструктур в термических, радиационных и деформационных
полях обусловлена наличием в наноструктурах неравновесных фаз
и поверхностей с избыточной свободной энергией Гиббса. В
результате с уменьшением наночастиц возрастает динамическая
неустойчивость наносистем, приводящая к явлению «неповторяемости»
структур и свойств в реально используемых технологиях.
В промышленности давно используются технологии получения
наночастиц, в которых применяются физические процессы
испарения и конденсации. Эти процессы могут проходить в неподвижном
или движущемся инертном газе или в вакууме. В полной мере это
относится и к технологиям получения разновидностей наноуглерода:
наноалмазов, алмазных плёнок, фуллеренов и нанотрубок.
Общепринято представление, что наночастицы и
наноструктуры начинаются с размеров менее 100 нм [15] или с появления
новых свойств и явлений. Общая причина появления новых свойств
состоит в том, что существенная часть атомов наночастиц находится
на их поверхности. Например, у частицы размером 10 нм четверть
всех атомов поверхностные. У частицы наноалмаза размером 2 нм
число объемных и поверхностных атомов примерно одинаково
(по ~600 атомов) Поэтому вклад поверхностной энергии в
свободную энергию наночастицы оказывается значительным.
Состояние атомов в объёме частицы и на поверхности можно
рассматривать как своеобразный фазовый переход от трёхмерного
к двухмерному состоянию. Тогда наночастица представляет собой
двухфазную систему, состоящую из трёхмерного ядра и двухмерной
оболочки. Таким образом, ^ая каждого свойства данного вещества
существует зависимость свойства от размера частиц, которая
определяется соотношением количества объёмных и поверхностных ато-
697
мов [10]. С этой точки зрения размерный ряд частиц ограничен с
одной стороны массивным монокристаллом, у которого отсутствует
влияние поверхности, и с другой стороны - кластером, у которого
все атомы - поверхностные. В этих пределах находятся все макро-,
микро- и наноструктуры. Границы между ними размыты, и аля их
количественного определения нами предлагается использовать
описание вероятностного процесса в переходной зоне отказ — работа аля
многих приложений в технике, механике, физике. Такая переходная
зона обычно характеризуется 50 %-ым уровнем отказов или работы.
По этой аналогии и учитывая определяющую роль
поверхности, нами предлагается следующий критерий положения размытой
границы между микро- и наночастицами: а^я каждого вещества и
условий его существования нанообласть начинается с размера
частиц, при котором внутренняя энергия Ed и поверхностная энергия
Es частицы равны (или поверхностная энергия составляет 50 % всей
энергии частицы).
Из условия равенства энергий получим следующее выражение
Аая определения граничного размера dna сферических частиц:
3, = (Vv„)£0; E0 = lcvdT; (vd/v0)=pndJ/6
Е =aS, = oTid 2
s а па
Из условия Ed = Я, dna = 6а 103 / (рЕ0), (им) (16.1)
где: с — удельная поверхностная энергия, Дж/м2, Е0 —
удельная внутренняя энергия, Дж/г, су — удельная теплоёмкость, Дж/гК,
р —плотность, г/см3, v/vQ— отношение объёма частицы к удельному
объёму.
Расчёты с помощью (16.1) дают для нормальных условий
следующие значения: dna = 4,37 и 107 нм соответственно а^я серебра,
алмаза и графита.
Как видно, а^я разных веществ расчётные значения dna
существенно различаются. Кроме того, с ростом температуры
внутренняя энергия значительно увеличивается, а поверхностная энергия
изменяется незначительно. Поэтому значения d с температурой
уменьшаются. Например, для алмаза при 1000 К d уменьшается в
ЕШ00/Е300 = 4,58 раз и составляет 8 нм.
698
Возможен и другой критерий определения наночастиц: размер
наночастицы должен быть соизмерим с характерными длинами
процессов массопереноса, поглощения и эмиссии, другими волновыми
процессами.
С уменьшением числа атомов в частице уменьшаются энергия
Ферми и энергия связи, а потенциал ионизации растет.
Деформация электронной структуры и особенно ее квантование
у малой частицы сказывается на ее электронных, оптических и
парамагнитных свойствах.
Малую частицу можно называть кластером, если ее размер
настолько мал, что исчезает различие между поверхностью и объемом.
Учитывая, что переходная область в 2—3 атомных слоя имеет
толщину 1—1,5 нм, можно оценить размер кластера d < 3 нм. При таких
и меньших размерах невозможно представлять термодинамические
функции в виде суммы объемной и поверхностной частей.
Снижение поверхностной энергии в малых частицах
достигается за счет сферической формы или огранения только плотно-
упакованными гранями, следовательно, гранями с минимальной
поверхностной энергией (для алмаза это грани октаэдра и
плоскости (111)).
Некомпенсированные связи наружных атомов создают
всестороннее сжатие частицы - т.н. лапласово давление р = 2 а/К (<т —
поверхностное натяжение, R — радиус частицы).
Так, металлическая частица радиусом 10 нм испытывает
давление 10—100 МПа, что уменьшает параметры решетки и
стабилизирует фазы высокого давления.
Кроме того, меняется фононный спектр (обрезается его
длинноволновая часть), усиливаются поверхностные релеевские волны.
В результате изменяются низкотемпературная теплоемкость,
теплопроводность, температура Дебая, критические температуры
перехода в сверхпроводящее состояние.
Вводимая в малую частицу мощность прежде всего приводит к
разогреву электронов. Увеличивается число электронов с энергией,
превышающей работу выхода, т.е. меняются эмиссионные свойства
частицы.
699
Изменение оптических свойств малой частицы связано с тем, что
равновесное испускание и поглощение света запрещено, если длина
световой волны в W2 раз превышает размер частицы.
При переходе от компактного к ультрадисперсному состоянию
меняются термодинамические свойства вещества, смещаются линии
равновесия химических реакций и фазовых превращений, в
частности, уменьшается температура плавления.
Высокая энтальпия малых частиц облегчает их спекание
(увеличивает скорость спекания, снижает температуру спекания).
Например, спекание ультадисперсных частиц никеля (внутри
агрегатов частиц) протекает уже при комнатной температуре [9].
Температура рекристаллизации ультрадисперсного алмаза
детонационного синтеза снижается до Т/Т = 0,4 по сравнению с
Т /Т = 0,8—0,9 у обычного алмаза каталитического синтеза [16].
С другой стороны, ультрадисперсные порошки (УД П) имеют
малую насыпную плотность и плохо прессуются. Большая поверхность
частиц увеличивает содержание адсорбированных примесей. Все это
усложняет технологию получения качественных изделий из
ультрадисперсных порошков. Одним из наиболее характерных свойств
ультрадисперсных порошков является их коагуляция, которая
обусловлена электростатическим взаимодействием между
ультрадисперсными частицами различных размеров [ 1 ]. Трудности
прессования УДП связаны с существованием в УДП конгломератов, которые
в процессе прессования выступают как объекты уплотнения. При
этом образуются прочные каркасы, препятствующие равномерному
уплотнению, а процесс уплотнения носит стадийный характер,
вызванный периодическим образованием и разрушением каркасов.
Прочность агрегатов возрастает с уменьшением их размера
вплоть до отдельных частиц, прочность которых значительно выше
прочности массивного тела. Поэтому кривая уплотнения УДП
является ломаной линией, каждое звено которой соответствует своей
стадии уплотнения с разрушением конгломератов определённого
размера и прочности [18,19].
Локально неоднородное пористое тело грубо можно описать
кластерной моделью, согласно которой пористое тело разбито на
700
микрообъёмы с плотнейшей упаковкой частиц — кластеры с
максимальным числом контактов между частицами (8—12), а сами эти
кластеры расположены хаотично, с минимальным числом
межчастичных контактов (4). Таким образом, имеются два типа границ:
I — внутри кластеров (аналог межзёренных границ) и II — границы
между кластерами (границы пор). В наночастицах отсутствуют
дислокации, поскольку размер дислокационных петель больше размера
частиц. Это означает резкое снижение пластичности наночастиц,
поэтому пластическая деформация может идти при спекании только
с зернограничным скольжением кластеров.
Твердофазное спекание УДП протекает по двум механизмам
массопереноса: взаимное проскальзывание кластеров (коагуляция)
и жидкоподобная коалесценция. Эксперименты показывают, что
процесс спекания и усадки проходит в два этапа. Первый этап
быстрый, с наиболее активной рекристаллизацией одновременно по
двум названным механизмам или только по одному из них в
зависимости от температуры.
Второй этап медленный и носит характер собирательной
рекристаллизации.
Таким образом, изменение различных свойств начинается с
размера частиц в диапазоне от 3 до 100 нм. Промышленных методов
производства таких частиц пока очень мало. Механическое
измельчение не дает ультрадисперсного состояния. В порошковой
металлургии используются порошки с частицами микронных размеров,
поэтому невозможно получить какие-то необычные свойства у
изделий из таких порошков.
Для получения УДЧ могут быть использованы различные типы
фазовых превращений (пар—жидкость—твердое тело, жидкость—
твердое тело, твердое — твердое тело) и различные процессы
(конденсация пара, кристаллизация раствора, реакции разложения
химических соединений).
По-видимому, условия образования УДЧ в парогазовой среде
наиболее близки к условиям образования наноалмазов за фронтом
детонации. Рассмотрение может проводиться с позиций
термодинамики, кинетики или статистики [17].
701
Общим условием формирования ультрадисперсных частиц является
сочетание высокой скорости образования центров кристаллизации
(зародышей) с малой скоростью их роста.
Рост зародыша может проходить по бездиффузионному и
диффузионному механизмам. В первом случае атомы встраиваются в
решетку зародыша в результате процессов сорбции или химических
реакций, зависящих от колебательных спектров и электронного
состояния на поверхности зародыша. Размер частицы
пропорционален времени ее роста и определяется частотой встраивания
свободных атомов в решетку зародыша.
Во втором случае скорость роста зародыша определяется
скоростью диффузии атомов к зародышу и требует перемещения атомов
на значительное расстояние. Размер растущей частицы
пропорционален корню квадратному из времени роста.
Для конденсации металлического пара в виде дисперсной фазы
необходимы три условия [7]: высокое пересыщение пара,
присутствие в конденсирующемся паре нейтрального газа и создание
определенного режима течения парогазовой среды.
Нейтральный газ служит:
— дисперсионной средой, препятствующей росту частиц, и
содержащей ионы, активные примеси, облегчающие зарождение
частиц;
— хладоагентом, переносящим теплоту, выделяемую при
образовании частиц;
— переносчиком самих частиц, удаляя их из зоны конденсации;
— разбавителем пара, замедляющим его доставку к частицам.
Движущей силой процесса является разность температур
начального и конечного состояния пара. Свойства частиц зависят от
условий тепло- и массообмена в зоне конденсации.
При малых пересыщениях пара конденсация может протекать
только гетерогенно на охлаждаемой поверхности, а при больших
пересыщениях — гомогенно в объеме.
Гетерогенное образование ультрадисперсного порошка —
быстрый процесс, с высокой скоростью тепло- и массообмена, с
образованием переходных структур.
702
Гомогенное образование порошка в объеме парогазовой смеси
инициируется высоким пересыщением пара и происходит при
следующих условиях:
— адиабатическое расширение газовой среды, что снижает
внутреннюю энергию смеси;
— смешивание пара с холодным нейтральным газом, что
вызывает переохлаждение пара;
— введение в объем инертной или химически активной готовой
дисперсной фазы, облегчающей объемную конденсацию.
Когда температура газовой среды выше 0,7 температуры
плавления конденсируемого вещества, частицы имеют сферическую форму,
образуясь по механизму пар—жидкость—твердое.
При более низкой температуре частицы имеют огранённые
формы (призмы, пирамиды, пластины) и образуются по схеме пар—
кристалл.
В первом случае частицы имеют поликристаллическую
структуру, а во втором случае могут образовываться монокристаллические
частицы.
По-видимому, эти общие закономерности полностью относятся
и к процессу образования за фронтом детонации сферических
частиц наноалмазов и относительно больших монокристальных
пластин лонсдейлита [14].
В [3,8] разработана математическая модель объемной
конденсации частиц аэрозольного размера. Модель основана на
представлениях о гетерогенной структуре пересыщенного пара, зародышеобра-
зовании кластерным путем с участием нейтрального газа в качестве
переносчика энергии и росте частиц коагуляцией кластеров. Модель
хорошо описывает процесс конденсации неметаллических веществ
при смешении струи холодного газа с эжектируемым паром.
Для разбавленных газовых смесей под большим давлением
(например, продукты детонации) процесс конденсации лимитирован
диффузионной доставкой пара к частицам, и размер частиц d ~ t. При t -> <х>
положение максимума кривой распределения частиц по размерам ас-
симптотически стремится к постоянной величине, т.е. при увеличении
длительности роста частиц их средний размер будет постоянен.
703
Например, расчетный средний размер частиц, образующихся
при пиролизе солей органических кислот при t -> <х> , постоянен и
равен ~50 нм [1]. Это объясняется саморегулированием процесса
конденсации: в результате образования частиц скорость их роста
снижается вследствие истощения парогазовой среды.
Скорость конденсации может значительно возрасти, если к
растущей частице присоединяются не одиночные атомы, а группы
атомов.
Например, в состав молекулы тротила входит бензольное
кольцо. Энергия связи между атомами углерода в кольце выше, чем между
углеродом и кислородом или азотом. Поэтому в результате
детонационного разложения тротила фрагменты бензольных колец могут
сохраняться и участвовать в образовании ультрадисперсных частиц
сажи или (и) алмаза (в зависимости от условий взрыва).
Конденсация пара сопровождается интенсивным выделением на
границах растущей частицы скрытой теплоты кристаллизации, что
приводит к перегреву прилегающих к частице слоев газа.
Рост частиц происходит в условиях межфазной турбулентности,
возникновение которой связано с неодинаковой плотностью сред, с
градиентами концентраций и температур, с эффектом торможения
потока на частицах с развитой поверхностью, с изменением
поверхностного натяжения. Турбулентные потоки способствуют отводу
тепла кристаллизации от растущей частицы. Однако всегда
температуры газа и частиц не равны.
Разность температуры растет с ростом скорости конденсации и
по мере увеличения разрежения среды.
Таким образом, условия тепло - и массопереноса обеспечивают
отвод тепла конденсации пара, а инертный газ является хладоаген-
том.
На практике а^я получения из парогазовой фазы
ультрадисперсных порошков металлов и различных тугоплавких соединений
(нитридов, боридов, карбидов) используются как химическая, так и
физическая газовые фазы [5]. В первом случае частицы формируются
в результате реакций между газовыми компонентами и гомогенной
конденсации образовавшегося пересыщенного пара.
704
Во втором случае происходят только процессы
испарения—конденсации. Минимальный размер получаемых сферических наноча-
стиц зависит от температуры плавления [123] : А1 - 70 нм , Си - 25
нм, Мо - 5 нм, графит - 2 нм (для графита расчётное значение).
Алюминиевые частицы коагулируют и частично спекаются.
Способы нагрева и испарения: электронно-лучевой, лазерный,
плазменный, с помощью электрической дуги высокого напряжения.
Например, испарение металла в плазменной струе азота дает
активные порошки нитридов. Исходные пар и газы подаются в
реактор, где в присутствии углеводородов идет образование карбидов, а
в присутствии треххлористого бора — боридов.
Технологические сложности консолидации УДП делают
перспективными технологии получения наноструктур в известных
материалах с микроструктурой (например, за счёт их обработки
ударными волнами, многократной циклической термообработкой с
фазовыми превращениями и пластической деформацией).
16.2. История открытия синтеза
детонационных наноалмазов
История открытия синтеза детонационных наноалмазов (УДА)
уникальна. На протяжении 25 лет его открывали четырежды
разными авторами в разных научных институтах [14,20,21].
Впервые детонационный синтез УДА открыт в 1963 году в
процессе проведения с I960 года исследований динамического
синтеза алмаза в РФЯЦ—ВНИИТФ (г.Снежинск Челябинской обл.)
группой в составе К.В. Волкова, В.В. Даниленко, В.И. Елина (см.
табл. 15.1). С целью упрощения синтеза автором была предложена и
реализована в 1962 году замена ампульного синтеза алмаза на безам-
пульный с проведением взрывов во взрывной камере (см.гл.15). При
этом графит помещался непосредственно в цилиндрический заряд
из ТГ40, а а^я подавления графитизации и снижения скорости
разгрузки образующегося алмаза заряд окружался водяной оболочкой.
Первый же опыт в такой постановке дал резкое увеличение
выхода алмаза. Затем в июле 1963 года был проведен контрольный опыт с
705
зарядом без графита, который подтвердил предположение о синтезе
алмаза из углерода П Д.
В 1963—1964 гг. было проведено около 100 опытов по
исследованию влияния условий взрыва, состава и конфигурации зарядов,
свойств получаемого УДА [22,23].
В то время работы по методам синтеза алмаза в СССР
относились к совершенно секретным, поэтому полученные результаты были
изложены только в закрытых отчетах ВНИИТФ.
Аналогичным образом (но без водяной оболочки) в 1982
году синтез УДА был открыт A.M. Ставером, А.И.Лямкиным и
Е.А. Петровым в Институте гидродинамики РАН (г.Новосибирск)
[24,25] и Г.И. Саввакиным в Институте проблем материаловедения
АН Украины (г.Киев) [26].
В США первые сообщения о синтезе УДА появились только
в 1987 и 1988 годах [27,28]. Это четвёртое открытие синтеза УДА
было результатом исследований продуктов детонации (газов, сажи)
от различных ВВ. Эксперименты проводились в атмосфере аргона
в взрывной камере в Fraunhofer Institute for Chemical Technology
(Германия) руководителем отдела этого института Fred Volk и Roy
Greiner из Los Alamos National Laboratory (США). Целью опытов
не было получение алмаза. Более детальное исследование образцов
сажи от детонации Сотр. В и др. смесей на основе гексогена было
проведено R. Greiner с соавторами в США. В результате также
неожиданно в саже были обнаружены наноалмазы.
Четыре обстоятельства так надолго задержали развитие этого
интересного направления науки и технологии:
— общая неподготовленность промышленности к развитию на-
номатериалов и нанотехнологий в 60-х годах 20-го века (сохраняется
до сих пор).
— режим секретности, существовавший в СССР на любые
работы по синтезу алмаза;
— в условиях бурного развития в эти же годы исследования и
производства алмазов каталитического синтеза параллельное
развитие альтернативных методов в Правительстве СССР было признано
нецелесообразным;
706
— открытие синтеза УДА было сделано в РФЯЦ-ВНИИТФ,
профиль работ которого был далёк от алмазной тематики. Только
инициатива, заинтересованность и реальная поддержка научного
руководителя ВНИИТФ академика Е. И. Забабахина дало возможность
небольшому коллективу в течение 6 лет плодотворно заниматься
динамическим синтезом алмаза, в том числе УДА.
В 1983—1995 годах большой объем работ по изучению
закономерностей синтеза УДА проведен в Институте
гидродинамики А.И. Лямкиным, A.M. Ставером, В.Ф. Анисичкиным,
И.Ю. Мальковым, Е.А. Петровым, А.П. Ершовым, В.М. Титовым.
В 1984 г. специалисты ИХФ РАН сообщили впервые о
термодинамических расчетах детонации с учетом фазового состояния
углерода [29], а в 1989 г. — с учетом влияния дисперсности углерода на
его термодинамические свойства. Из доклада 1991 г. этих же авторов
[30] следует, что ими впервые был теоретически предсказан синтез
УДА и сформулированы оптимальные условия синтеза и требования
к ВВ. Правда, этот синтез задолго до того уже четырежды был
открыт и детально исследован.
Начиная примерно с 1991 г, детальное исследование свойств и
применений УДА проводилось в ФТИ РАН и СТКБ «ТЕХНОЛОГ»
(г.С.Петербург).
В 1984 г. в НПО «АЛТАЙ» (г. Бийск, Россия) было впервые
создано опытно-промышленное производство УДА и исследован
ряд нетрадиционных а^я алмаза применений УДА. (гальванические
покрытия, смазки, полимерные композиты).
В1990 гг в бывшем СССР были созданы опытные производства
УДА в ВНИИТФ (г. Снежинск), в НПО «СИНТА» (г. Минск),
в Политехническом Институте в г. Красноярске, в «Алмазном
Центре» (г. С. Петербург), на комбинате «Электроприбор»
(г. Лесной Свердловской обл.).
В 1991 г в Украине автором спроектирована и затем изготовлена
уникальная взрывная камера объёмом 100 м3 [14,31] и на её основе
совместно с В.И. Падалко в г. Житомире создана фирма «АЛИТ»
Аая производства УДА. Работы по химической очистке УДА,
изготовлению из него порошков и их применению проводятся в И СМ
НАН Украины.
707
В 21 веке резко возросло количество публикаций по исследованию
УДА, что свидетельствует о расширении круга учёных и научных
центров во всём мире, занимающихся этой тематикой (к сожалению, не по
синтезу, а по свойствам, их модификации и применению УДА).
Полученная в 20 веке информация по синтезу УДА может быть
разделена на две части:
1. Результаты исследований по физике образования УДА в
детонационной волне.
2. Экспериментальные данные по количеству получаемого УДА
(выходу) относительно веса заряда, по содержанию УДА в
детонационном углероде (или алмазной шихте - АШ), по влиянию условий
взрыва на синтез УДА. На основании этих данных создаётся
оптимальная технология производства УДА.
16.3. Конденсация углерода в ПД. Влияние состава ВВ
и условий взрыва
Напомним, что детонационная волна — это единый комплекс из
ударной волны, зоны химической реакции (ЗХР) и изэнтропы
расширения продуктов детонации (ПД). Сверхзвуковое течение в ЗХР и
дозвуковое на изэнтропе разделяет плоскость Чепмена - Жуте (С —J),
давление и температура на которой характеризуют индивидуальное
взрьючатое вещество (ВВ) или взрывчатый состав.
Мощные ВВ состава CNHO в детонационной волне разлагаются
с образованием газообразных П Д состава N2, Н20, СО, С02, причём
кислород молекул ВВ окисляет весь водород до воды, а углерод — до
СО и С02. Если кислорода в молекулах ВВ не хватает (кислородный
баланс ВВ отрицательный), то выделяется свободный углерод.
Как известно, образование конденсированного углерода в ПД
взрывчатых составов с отрицательным кислородным балансом
определяется протеканием следующих двух реакций:
2СО^С02+С (16.2.)
СО+Н2^Н20+С (16.3)
Максимальное выделение углерода в ПД происходит, когда
кислород молекул ВВ окисляет весь водород до воды, а остаток кислоро-
708
да расходуется на окисление углерода до С02. При этом состав П Д
в точке Жуге соответствует максимально возможным величинам
теплоты взрыва, давления и температуры (идеальная детонация). Но
реально окисление углерода идёт с образованием и СО, и С02.
Кроме величины кислородного баланса, количество свободного
углерода /^ данного ВВ определяется пористостью заряда ВВ и
степенью неидеальности детонации заряда. Поскольку реакция (16.2)
сдвигается влево с повышением температуры и вправо с
повышением давления, то пористость , повышающая температуру, и
неидеальность детонации, снижающая давление, сдвигают равновесие влево,
что уменьшает количество углерода. Соотношение СО/С02 в ПД
характеризует уменьшение реально выделяющегося углерода
относительно максимально возможного [32,33].
В таблице 16.1 приведены /^ая ряда взрывчатых составов
параметры в точке Жуге а^я идеальной детонации и количество свободного
углерода в ПД, рассчитанное из условия, что кислород в молекулах
ВВ окисляет углерод до СО или до С02 [22].
Таблица 16.1. Параметры идеальной детонации
и количество свободного углерода
ВВ
Тротил
Гексоген
ТГ50
ТГ40
Тетрил
ТЭН
г/см3
1,64
1,82
1,67
1,68
1,7
1,62
Условия в точке Жуге
р,ГПа
20,6
(19)
34,7
(34,7)
25
(24—25,5)
26
25,1
(28,3)
31,8
(33,5)
т,к
2937—3662
(3600)
2587-^*200
(4500 и 3700)
2711—3953
2711—3953
2917-4018
(4300)
3018-^457
(4600 и 4200)
Свободный углерод в
ПД, % к массе заряда
Окисление до
СО
18
0
9
7
2
0
со2
28
8
18
15
18
4
709
В скобках указаны экспериментальные значения.
Меньшие значения температуры в табл. 16.1 получены расчётом
по У PC BKW, который занижает температуру в т. Жуге.
Степень неидеальности детонации зависит от способа
инициирования заряда, его размеров и конфигурации (см.раздел 8.7).
При переходе от слабого к сильному инициатору реакция (16.2)
смещается вправо, в сторону увеличения свободного углерода (см.
табл. 16.2 [33]).
Таблица 16.2 Влияние инициирующего импульса на состав ПД тротила
(р= 1,52 г/см3)
Условия взрыва
Слабый импульс
Сильный импульс
Состав ПД в гмоль/кг
С
6,6
15
со,
1,78
5,30
СО
18,63
8,79
Н,°
4,25
7,05
Н,
5,34
1,69
При «точечном» инициировании заряда (например,
электродетонатором) в ВВ возникает расходящаяся детонационная волна с
давлением pR, зависящем от радиуса R волны следующим образом
[32,34]: pR = рто - 7 D^ a/R, где р^ и D^ — параметры идеальной
детонации с R = оо, а — ширина ЗХР (см. табл. 16.5). Поэтому с
увеличением расстояния от точки инициирования степень неидеальности
детонации уменьшается.
Примыкающие к свободной поверхности заряда объемы
(толщиной примерно равной критическому диаметру) также
детонируют неидеально, т.е. с меньшими величинами р, Т и выхода углерода.
В этих объемах реакции разложения ВВ не идут до конца,
«замораживаются» быстрой разгрузкой. Поэтому выход углерода должен
зависеть от формы заряда (от соотношения объема заряда и его
свободных поверхностей) и от места инициирования заряда. Этот вывод
подтвержден экспериментально (см. рис. 16.1 [22]).
В одинаковых условиях взрыва содержание УДА в шихте
заметно выше в удлиненном цилиндре (1/d > 3), чем в диске и шаре.
Для случаев быстрого расширения ПД (например, взрыв заряда
весом 0,1—0,6 кг без оболочки) наблюдаемый в экспериментах выход
710
mo/mc
% _
i
80
60 . /
40 i / >
20 Ш
°(T~
10
cylinder
disc
^ball
20 30
•
,
cover,
mm
Рис. 16.1. Содержание УДА в
конденсированном углероде (шихте) в
зависимости от толщины оболочки
и от геометрии заряда из ТГ40 весом
100 г [22]
углерода составляет примерно 67,5%
для тротила и примерно 54% аля
ТГ40 от максимально возможного.
Измеренный в [35] выход углерода
(взрью заряда весом 300 г в
атмосфере С02) из различных сплавов ТГ
показал, что тротил дает углерода около
17% своей массы в сплаве, а гексо-
ген — 2,5%, т.е. окисление в тротиле
идет только до СО (см. табл. 16.1).
Взрыв заряда в оболочке
снижает скорость разгрузки ПД,
приближая состав П Д к равновесному
при окислении углерода до С02.
Кроме того, водяная оболочка
увеличивает время существования
давления в области стабильности
алмаза. Например, аля ТГ50 давление в ПД на границе с водой
равно 18ГПа при нулевом угле падения детонационной волны и 7,5 ГПа
при угле 90° (скользящая детонация) [22].
Рис. 16.2 показывает, насколько отличаются реальные условия
детонации зарядов из сплавов ТГ от идеальной детонации, в
которой реакция разложения ВВ протекает до конца по равновесной
схеме Н20—С02 с максимальной теплотой взрыва и с максимальным
выходом углерода.
Экспериментальное количество углерода при взрывах малых
зарядов массой 300 г в атмосфере С02 заметно меньше расчётного
(см. рис. 16.2), что связано с неидеальностью детонации. Так, а^я
тротила углерод окисляется до СО (т.е. величины р, Т ниже
паспортных данных), а аая сплавов ТГ с увеличением гексогена в ТГ
растет степень окисления до С02. Очевидно, неидеальность
реальной детонации не только уменьшает количество углерода в ПД, но
снижает давление и температуру в точке Жуге. Например,
согласно расчётам [36] при завершенности реакции в ЗХР на 50% имеем
Р5о/Р10о = °337
711
% *»
а:
3)
-""
f*
..••"' «
**■'
X
>
I
./^м
.1
<u
3 ^
/■"1
"*"
< 1
Л
и VTioo = °>546> TX-
Деление падает вдвое быстрее
температуры.
В сплавах ТГ тротил
является донором углерода, а
гексоген повышает
давление детонации. У чистых
тротила и гексогена УДА
практически не образуется,
но по разным причинам:
у тротила углерода много,
но мало давление, а у
гексогена, наоборот, давление
большое, но мало углерода.
Зависимости ^ая
выхода УДА на рис. 16.2 имеют
две ветви: восходящая
связана с ростом р и Т в
сплавах ТГ, а нисходящая — с
Рис. 16.2. Выход УДД относительно массы
заряда в зависимости от состава ТГ
1 — окисление до С02 (расчет максим, воз-
можн. выхода углерода);
2 — окисление до СО (расчет [22]);
Эксперимент, выход углерода:
3 — взрыв 0,3 кг в С02 [35];
Эксперимент, выход УДД:
4 — взрыв 0,3 юг в СО Л 35]; ^ уменьшением содержания
5 — цилиндр 10 кг из ТГ40 в водяной обо- __,._ А
лочке 0350x1200 мм весом 110кг[14,34]; углерода в ТГ. Для зарядов
х — шары весом 5 кг, инициирование из в оболочке степень неиде-
центра [14,34]; альности детонации ниже,
■ — цилиндр 060x1000 мм весом 4,8 кг s
[14,34]; и нисходящая ветвь ближе
• — шар весом 3 кг в стальной оболочке ве- к равновесной линии 1.
сом 3,6 кг [14,34]; г ^ ^
А - шар весом 20 кг, взрыв в воздухе Таким образом, на прак-
[14,34]. тике неидеальная
детонация — скорее правило, чем
исключение.
Детонацию реальных зарядов ВВ характеризуют некоторые
эффективные величины давления и температуры в плоскости С—J,
интегрированные по объёму заряда с данными геометрией и способом
инициирования. Как правило, эти величины меньше справочных
для данного ВВ.
Из сделанного анализа следует, что /^ая получения максимально
возможного для данного ВВ количества углерода в ПД, необходи-
712
мо создавать во взрываемых непористых зарядах режим детонации,
максимально приближенный к идеальному. Этого можно
достигнуть при следующих условиях:
- максимально возможная плотность заряда;
- взрыв заряда в оболочке;
- «сильное» инициирование заряда;
- оптимальная форма в виде удлинённого цилиндра или шара,
инициируемого из центра.
16.4. Особенности синтеза УДА
16.4.1. Анализ представлений о синтезе УДА
Тривиальное сопоставление фазовой диаграммы углерода и
параметров в точке Жуге для детонации мощных ВВ показывает, что
свободный углерод ПД должен конденсироваться в форме алмаза
[22]. Очевидно также, что для получения свободного углерода в
ПД необходимо использовать ВВ с отрицательным кислородным
балан- сом. Такие взрывчатые составы одновременно являются
источником и энергии, и углерода. По сравнению с синтезом алмаза
из графита, преимущество конденсации атомарного углерода в
алмаз состоит в том, что не требуется расходовать энергию и время на
разрушение или перестройку исходной кристаллической решетки
графита.
Поскольку процесс образования алмазов идет с очень большой
скоростью и в сильно неравновесных условиях, для предсказания и
описания детонационного синтеза алмаза необходимы знания
кинетики образования и роста алмазов в ПД, условий сохранения
алмаза, подавления его графитизации.
Экспериментально установлено, что диапазон давления (15-
20 ГПа), в котором начинается образование алмаза из УГМ, слабо
зависит от природы УГМ (графит, сажа, углеводороды). Полное
превращение графита в алмаз достигается при 40 ГПа [37,38]. Что
касается температуры ударного сжатия, то с увеличением
температуры уменьшается давление начала превращения (до 12 ГПа) и сильно
возрастает степень превращения (т.к. растет величина АФ - движу-
713
щей силы превращения, см. гл.7). Например, а^я сажи увеличение
температуры сжатия с 1600К до 4200К приводит к росту выхода
алмаза с 30% до 75% (см. табл. 7.4.).
Эти данные позволяют сделать предварительный вывод, что
достижимые при детонации современных мощных ВВ давления (20-
40 ГПа) и температуры (3000-4000 К) достаточны аля синтеза
алмаза за фронтом детонационной волны из свободного углерода молекул
ВВ. Несмотря на убедительность теоретических предпосылок,
только эксперимент 1963 года впервые показал, что образование алмаза
в детонационной волне действительно происходит.
Оставалось неясным, где происходит образование алмазов (в ЗХР
или на изэнтропе), какова кинетика этого процесса, почему в
получаемом после взрыва углероде, кроме алмазов, всегда присутствуют
неалмазные формы, в частности, сажа, почему содержание алмаза в углероде
из сплава ТГ40 составляет 70—80 %, а из тротила только 10-15%, хотя
отличие параметров С—J небольшое.
В [14, 35, 39—43] подробно изложены полученные в России в
1960 - 90 годах результаты исследований синтеза УДА. Эти
результаты сводятся к следующему.
1. При детонации мощных взрывчатых составов с
отрицательным кислородным балансом выделяющийся при распаде молекул
ВВ углерод конденсируется в виде наноалмазов в зоне химической
реакции (ЗХР) детонационной волны за время 0,3—0,5 мкс.
2. Высокая дисперсность углеродных частиц повышает давление
перехода алмаз — графит [30], и выше этого давления в ЗХР
образуется наноалмаз, а ниже — нанографит. В [44] утверждается, что
благодаря малым размерам частиц УДА термодинамически более
стабилен, чем графит.
3. Для сохранения УДА нужно подавить графитизацию быстрым
охлаждением УДА («заморозкой») и исключить окисление НА,
проводя взрывы в инертной атмосфере.
Из этих представлений следуют три вывода.
1. Поскольку УДА образуется в ЗХР ( в зоне сверхзвукового
течения), то этот процесс не зависит от массы взрываемого заряда и
среды вокруг заряда.
714
2. Если увеличивать массу заряда, то скорость охлаждения УДА
будет падать, следовательно, степень графитизации будет расти, а
выход УДА - уменьшаться.
3. Для лучшего сохранения УДА целесообразно использовать ВВ
с меньшей температурой детонации [30].
Существует следующий ряд экспериментальных фактов,
противоречащих сложившимся в 20-м веке представлениям о синтезе УДА
и указывающих на то, что эти взгляды требуют пересмотра.
1. Если УДА образуются в сверхзвуковой зоне химреакции, то ни
масса заряда, ни среда, окружающая заряд, не могут влиять на
синтез УДА. Однако, проведенные нами в 1986 - 1991 годах опыты с
зарядами массой 5 - 140 кг в оболочках из воды впервые показали,
что масса заряда и оболочки влияют на свойства и количество УДА.
[34,48,50,51,53]. Увеличение на порядок массы заряда уменьшило
удельную поверхность УДА вдвое (с 400 до 200 м2/г), причём выход
УДА не уменьшается, а даже увеличивается. Таким образом, нами
обнаружено влияние на размеры частиц УДА масштабного фактора
(т.е. времени существования условий превращения, определяемого
массами заряда и оболочки) [50,51,53]. Такого влияния не может
быть, если УДА образуются в сверхзвуковой ЗХР.
Данные по влиянию масштабного фактора на синтез алмаза в
ударных и детонационных волнах приведены в таблице 16.3.
Таблица 16.3. Влияние масштабного фактора
Параметр
Масса заряда,
kg
Средний
размер частиц
Синтез алмаза из
графита
0.1
5цт
10
20pum
5000
60 цт
^Поликристаллы с
размером зёрен 10—20 nm
Синтез алмаза из углерода ВВ
0.2—2
3—4nm
10—20
5—бпти
поликрист.
до 20fim
140
8 nm и
поликристаллы
до 85 fim
Это влияние слабое: &ля увеличения размера частиц в два раза
требуется увеличить время существования высоких давлений и темпе-
ратур синтеза примерно на два порядка. Но увеличивается количество
абразивных поликристаллов (до 85 мкм).
Влияние масштабного фактора чётко проявляется на
зависимости удельной поверхности УДА от массы взрываемого заряда: 0,1
кг - 643 м7г [125], 0,6 кг - 350 м2/г [109], 10 кг - 200 м2/г [14,124].
Отметим, что процессы синтеза УДА ударным сжатием графита
и конденсацией углерода в детонационной волне совершенно
разные.
2. Время химреакции ^^я сплавов ТГ ( табл. 16.4) [52] заметно
меньше найденного по изменению электропроводности ПД
времени образования УДА (0,3 - 0,5 мкс). Например, нами получены УДА
при взрыве состава ТНТ/ОКТ 10/90, у которого время реакции
составляет всего 0,07 мкс [52]. Кроме того, в зоне химреакции
температура растёт, и углерод не может охлаждаться, что необходимо аля
кристаллизации УДА.
Таблица 16.4. Результаты измерения параметров ЗХР для ВВ,
используемых в синтезе наноалмазов [52]
ВВ
ТНТ литой
ТГ 50/50
ТГ 36/64
ТГ 30/70
ТНТ/Октоген 10/90
Время химреакции, мкс
0,22—0,29
0,09—0,13
0,10
0,08
0,07
Ширина ЗХР, мм
1,23—1,47
0,12—0,68
0,13—0,60
0,44
0,37
3. В [30] утверждается, что fi^ синтеза УДА лучшим является
ВВ с высоким давлением и низкой температурой детонации. Такое
ВВ имеется. Это ТАТБ (р = 25 - 31ГПа, Т = 2100 - 3100К). Однако,
при взрыве ТАТБ УДА получается в несколько раз меньше, чем при
взрыве ТГ40/60, у которого при примерно равном давлении
температура детонации выше на 800 - 1800К.
4. Продукты детонации охлаждают УДА только за счёт
теплообмена, эффективность которого зависит от плотности ПД. Но в
области графита (где требуется «заморозка» УДА) плотность ПД
мала - 0,05 г/см3 [32] , поэтому они не могут охлаждать УДА. По
716
этой причине УДА не синтезируются при взрыве в вакууме, когда
ПД имеют максимальные скорости расширения и охлаждения.
5. УДА сохраняются при взрыве в воздухе зарядов из ТГ40/60,
заключённых в оболочку из металла (Al, Fe, Pb) [22], который не
может служить охладителем УДА. Тем не менее, в этих условиях
температура УДА понижается ниже температуры окисления УДА в
воздухе (400°С). Таким образом, требование создания в взрывной камере
инертной атмосферы относится только к взрыву открытых зарядов
(без оболочек).
Учитывая эти результаты, нами предложен и обоснован
расчетами иной механизм конденсации углерода в детонационной волне с
образованием наноалмазов и сажи [34,48—51]. По нашему мнению
синтез УДА проходит согласно общим закономерностям гомогенной
конденсации ультрадисперсных фаз в сильно пересыщенном паре по
схеме пар—жидкость—кристалл с образованием сферических
частиц. Необходимым условием кристаллизации является охлаждение
инертным газом. В связи с быстрым истощением парогазовой среды
средний размер наночастиц практически не растёт с увеличением
времени существования условий роста. Свидетельством
кристаллизации УДА из жидкой фазы является распределение частиц УДА по
размерам, характерное а^я жидкокапельной коалесценции [35].
16.4.2. Фазовая диаграмма наноуглерода
В описании механизма образования УДА важную роль играет
вид фазовой диаграммы наноуглерода.
Известно, что влияние поверхностной энергии наночастиц
изменяет вид фазовых диаграмм дисперсных систем в сравнении с
таковыми а^я массивных монокристаллов [1-4]. Появляется ещё одна
переменная - размер частиц, и диаграмма становится трёхмерной.
Изменяются границы жидкой фазы и равновесные давления
полиморфных превращений. Поэтому использование известной фазовой
диаграммы массивного углерода а^я анализа условий образования
наноалмазов некорректно.
Фазовая диаграмма наноуглерода ещё не изучена. В [48,49] нами
рассчитаны положения линий плавления и равновесия на фазовая
717
диаграмме наноуглерода в зависимости от размера частиц УДА.
В расчётах учитывалось только влияние поверхностной энергии
межфазной границы алмаз - турбостратный (аморфный) графит,
что соответствует структуре частицы УДА (алмазное ядро
диаметром d, покрытое аморфным sp2 - углеродом). Получены следующие
расчётные формулы:
Аая температуры плавления частиц УДА
та/т.=о^[1+(1-1/<Щ;
Аая равновесных давлений (ГПа)
Pd = Poo + Ps = (^ + 2,9-10-3T) + 240(0,3-10-5T) (v-vd)vd/vad,
где ps - повышение равновесного давления за счёт
поверхностной энергии, vd, va - удельные объёмы алмаза и аморфного графита.
Наклон линий плавления принят таким же , как а^я
массивного алмаза и равным 10.2 К / ГПа. Минимальный диаметр
алмазного ядра в частице УДА принят равным d = 1 нм (~ 200 атомов).
Предполагается, что при меньших размерах объёмные свойства
алмаза исчезают, и частица превращается в sp3 - кластер.
Полученная фазовая диаграмма наноуглерода показана на
рис. 16.3. Её особенности:
1. Вместо одной тройной точки появляется семейство
тройных точек в зависимости от размера частиц наноуглерода, лежащее
в интервалах
р = 13,5 - 16,5 ГПа и Т = 2230 - 4470 К.
2. Температура плавления быстро падает у частиц размером
менее 2 нм и медленно у частиц более 3 нм, а у частиц размером
более 10 нм она практически такая же, как у массивного алмаза. По
сравнению с монокристаллом температура плавления предельно
малых частиц УДА (1 нм) в два раза меньше, а равновесное
давление примерно вдвое выше. Аналогичная зависимость измерена а^я
наночастиц золота: а^я d = 4 нм Т = 500С, а а^я d=16 нм Тд =
1000С [123]. Вокруг частиц УДА найдена нанофаза воды также с
пониженной до - 8С температурой плавления [127]. Толщина во-
718
дной оболочки 1 нм или 3-4 монослоя воды, из них два внутренних
слоя не замерзают.
3. Алмазная область на традиционной фазовой диаграмме
разделена на фазовой диаграмме наноуглерода на несколько областей с
различным состоянием наноуглерода: ниже линии тройных точек -
область наноалмаза, алмаза, нанографита, жидкого sp2
наноуглерода и sp2 - кластеров, выше линии тройных точек - область жидкого
sp3 наноуглерода а^я температур, больших температуры плавления
наименьших частиц УДА Т > Тт (1 нм), и область sp3 - кластеров
Аая температур Т< Тт (1нм). Такие кластеры практически состоят
из поверхностных атомов и не являются ни жидкой, ни твёрдой
фазой.
На рис. 16.3 также показаны положения тройных точек а^я
частиц УДА с размерами 1,2,2 и 4 нм, рассчитанных в [45,46]. По -
видимому, различие с нашими расчётами аая частиц 1,2 и 2 нм связано
с использованием значений удельной поверхностной энергии а^я
отдельных частиц алмаза и графита, которые больше, чем удельная
поверхностная энергия межфазной границы алмаз - графит.
Таким образом, семейство тройных точек значительно
расширяет область жидкого наноуглерода (нанокапель) в сторону низких
температур. Наоборот,
область
термодинамической стабильности нано-
алмазов с уменьшением
их размеров
уменьшается со стороны низких
давлений. Для
наименьшего размера
наноалмаза 1 нм температура
плавления снижается в
два раза, а давление
равновесия примерно вдвое
повышается в сравнении
с массивным алмазом.
20
1 * «г
/J
г—
[«&-—■"■—"""""
и л г г
\Щ
_LiX
1 44 тЛ
Jl
■ \
гооо • аооо 4ооо т,К
Рис. 16.3. Положение семейства тройных точек и
линий плавления наноалмазов [48,49].
Светлыми кружками показано положение
тройных точек согласно [45,46]. Пунктир — линии
фазовой диаграммы углерода. Цифры у линий —
16.4.3. Образование УДА на изэнтропе ПД
Сопоставим полученную фазовую диаграмму наноуглерода с
величинами давлений и температур в плоскости С—J аля непористых
сплавов ТГ (рис. 16.4) [34,48,50,51].
I — линии плавления;
II — линия тройных
точек; III — линии
термодинамического равновесия;
IV - линия мгновенной
графитизации алмаза; V
— изэнтропа
расширения ПД аля ТНТ; VI -
пунктирные линии
максимальных температур
начала аморфизации на-
нокапель углерода с
размером 1, 2, 4 нм при их
охлаждении.
Цифры у линий
плавления, равновесия и
аморфизации означают
размеры частиц УДА в нм.
Для оценок давления
и температуры
идеальной детонации в плоскости С—J у непористых сплавов ТГ в ряду
тротил—гексоген на основании наиболее надёжных литературных
данных нами были получены следующие соотношения [50].
p=19 + 69(p-l,6) (ГПа); Т = 3500 + 38(р-19) (К),
где: р - плотность непористого смесевого состава ТГ; р -
давление С-J для смесей ТГ.
Отметим, что у реальных зарядов из гетерогенных ВВ по ряду
физических причин С J -параметры - это не точка в р.Т -
плоскости, а площадка, размеры которой растут с увеличением степени
неидеальности и пористости заряда. Например, C-J - параметры в
Рис. 16.4. Фазовая диаграмма наноуглерода и
параметры детонации ВВ. А, В, С, D —
параметры Жуге идеальной детонации
непористых зарядов из гексогена, ТГ 36,
ТГ 50 и тротила соответственно; Е, F — то же
для пористых зарядов из ТГ 50 с плотностью
1,43 г/см3 и 1,25 г/см3 соответственно.
720
расходящейся детонационной волне при «точечном»
инициировании непористого тротила попадают в область жидкого наноуглеро-
да только при радиусе волны более 26 мм [34].
Из рис. 16.4 видно, что для сплавов ТГ состояния в плоскости C-J
Аая идеальной детонации находятся в области жидкого наноуглеро-
да. Следовательно, в ЗХР образуются нанокапли углерода, которые
затем кристаллизуются (или аморфизируются) на изэнтропе
расширения ПД О кристаллизации УДА из жидкой фазы свидетельствует
также сферическая форма частиц УДА и их распределение по
размерам, характерное ^^я жидкокапельной коалесценции.
Анализ зарегистрированных в [38] профилей
электропроводности ПД R (t) показывает, что образование УДА в детонационной
волне имеет две стадии: первую быструю в ЗХР и вторую медленную
на изэнтропе.
Таким образом, УДА образуются по известной а^я других
материалов схеме: пар - жидкость - кристалл [ 1 ].
На рис. 16.4 показана изэнтропа ПД, которая всегда отражает
уменьшение давления и температуры в расширяющихся П Д, а масса
и форма заряда, масса и плотность среды влияют только на скорость
движения вдоль изэнтропы.
На изэнтропе расширения П Д можно выделить следующие три
участка (рис. 16.4).
1. Участок между C-J - параметрами и линией тройных точек
(давление более 16,5 ГПа). Здесь происходит коагуляция углерода
и образование нанокапель, размер которых определяется временем
расширения ПД на этом участке (масштабный фактор) и
параметрами ПД (концентрация углерода, плотность, температура).
2. Участок между линией тройных точек и линиями равновесия
Аая частиц различного размера. На этом участке изэнтропы в
интервалах давления от 16,5 до 9 ГПа и температуры от 3400 до 2900 К
происходит кристаллизация УДА из полученных на первом участке
нанокапель размером более 2 нм. Для кристаллизации нанокапель
на этом участке важны минимальные скорости расширения ПД и
охлаждения нанокапель продуктами детонации (рост скорости
охлаждения увеличивает вероятность аморфизации нанокапель),
721
например, за счет увеличения массы заряда и заключения заряда в
массивную оболочку (масштабный фактор).
3. Участок полного расширения П Д от равновесных давлений до
нуля. На этом участке образуется сажа и нанографит (как результат
недостаточного охлаждения нанокапель и графитизации УДА). Не
исключено продолжение кристаллизации УДА, поскольку
равновесные и кинетические линии фазовых превращений не совпадают.
Из рис. 16.4 видно, что с увеличением содержания гексогена в
сплавах ТГ растут плотность и температура ПД, а также удаление
C-J - параметров от линии тройных точек, что способствует
коагуляции и увеличению количества нанокапель с размерами более 2 нм
(кристаллизация которых на изэнтропе дает УДА). Однако, при этом
снижается количество конденсирующегося в ЗХР углерода, т.е.
снижается общая масса получаемых нанокапель. Поэтому а^я данных
условий взрыва должен быть один оптимальный состав ТГ, дающий
максимальный выход УДА. Для взрывов зарядов в оболочке
(«мокрое охлаждение») такой состав экспериментально найден - это
ТГ 40/60, а а^я взрывов в инертном газе («сухое» охлаждение) -
ТГ 60/40 или ТГ 70/30 (рис. 16.2).
Таким образом, образование наноалмазов в детонационной
волне состоит из последовательной цепочки следующих процессов
(указана ориентировочная длительность процессов t).
a) В ЗХР - распад молекул ВВ с образованием активных
макромолекул (плоские «ароматические» кластеры из бензольных
колец) -1 = 1 не и затем из них первичных трёхмерных кластеров
(d< 2нм)-г=10нс;
b) В ЗХР и в области жидкого наноуглерода - коагуляция
кластеров с образованием нанокапель (d > 2 нм) - t = 102 - 103 не;
c) На изэнтропе ПД - ниже линии тройных точек
кристаллизация нанокапель в алмазной области с образованием
наноалмазов в условиях достаточного времени их охлаждения П Д или амор-
физация нанокапель и кластеров с образованием сажи - t > 103 не.
Оставшиеся в П Д макромолекулы участвуют в образовании у частиц
УДА пористых оболочек из аморфного углерода.
В таблице 16.5 перечислены фазовые переходы, проходящие в
углероде на изэнтропе П Д при детонации сплавов ТГ (условия пере-
722
ходов основаны на расчетной равновесной фазовой диаграмме на-
ноуглерода [48,49]).
Таблица 16.5. Фазовые переходы в углероде на изэнтропе ПД
Давление,
ГПа
>16,5
16,5—9
<9
Область на фазовой
диаграмме
Жидкого наноуглерода
Наноалмаза для с1>2нм
Нанографита для d <2нм
Нанографита
Фазовый переход
Образование кластеров —
sp3 гибридизации
Жидкий наноуглерод — на-
ноалмаз
Кластеры sp3 -> кластеры sp2
sp3-> эр2для любых размеров
кластеров
Остается открытым вопрос о возможности «кинетической»
кристаллизации sp3 — нанокапель в области стабильности sp2 —
наноуглерода (т.е. вдоль всей изэнтропы).
Таким образом, на синтез УДА решающее влияние оказывают
следующие три параметра: расположения на фазовой диаграмме
наноуглерода С—J — параметров ВВ относительно линии тройных
точек, минимальный размер нанокапель (2 нм), способный
кристаллизоваться, и время существования в ПД условий синтеза УДА.
16.5. Аморфизация наноуглерода
Если нанокапли кристаллизуются на изэнтропе ПД, то
возникает необходимость рассмотрения возможности их аморфизации как
процесса, конкурирующего с кристаллизацией наночастиц УДА.
Температура Td замены кристаллизации на аморфизацию зависит
от размера частиц d, от удельной поверхностной энергии ст. а
межфазовой границы кристалл - аморфная фаза, от удельного объема
аморфной фазы v и от теплоты плавления 1 следующим образом [1]:
Т/Т =1+2о- vAd (16.5)
а оо с-а a v '
где Тм — постоянная ^^я данного вещества температура, при
которой аморфным может быть массивное тело (с d=<x>).
Как видно, температура аморфизации растет с уменьшением
размера частиц, что увеличивает вероятность аморфизации наноуглеро-
да на изэнтропе. В результате проведенных нами расчётов [34,50,51]
найдены положения линий аморфизации нанокапель углерода на
фазовой диаграмме (см. рис. 16.4).
Из рис. 16.4 видно, что на изэнтропе кристаллизация
нанокапель с размером 1 нм вообще невозможна, нанокапли с размером до
2 нм аморфизируются в алмазной области, а более 2 нм — в области
графита. С ростом давления температура аморфизации
уменьшается. Очевидно, что слишком быстрое охлаждение под давлением
нанокапель более 2 нм также является причиной их аморфизации.
По-видимому, основная масса свободной сажи в ПД является
продуктом аморфизации наноуглерода.
16.6. О коагуляции углеродных кластеров
в детонационной волне
Исследования синтеза УДА, основанные на результатах анализа
твердых П Д во взрывной камере, не дают информации об условиях
и кинетике образования УДА. Поэтому нужны теоретические
модели процессов синтеза.
Для образования УДА прежде всего важны процессы выделения
свободного углерода и его коагуляция.
Кинетика разложения молекулы ВВ в зоне реакции и
конденсации углерода в ПД мало изучены. В зоне химреакции углерод
образуется одновременно с формированием среды N2, СО, С02, Н20,
причем плотность среды высокая, примерно 2,3 г/см3 и ее трудно
считать газообразной. Тем не менее, по-нашему мнению, синтез
УДА должен проходить по общим закономерностям гомогенной
конденсации ультрадисперсной фазы в сильно пересыщенном паре
(см.раздел 16.1).
Такая аналогия подтверждается следующим.
1) Если Та >0,7 Тд, то конденсация пара идет по схеме пар—
жидкость—кристалл, а частицы-поликристаллы и имеют
сферическую форму, что справедливо и для частиц УДА
724
2) Скорость роста частиц быстро снижается вследствие
истощения парогазовой среды. Поэтому с увеличением длительности
существования условий роста частиц их средний размер остается
практически постоянным. Средний размер сферических частиц УДА также
мало меняется с увеличением массы взрываемых зарядов на три
порядка.
3) Конденсация пара в смеси с холодным нейтральным газом
проходит по диффузионному механизму и требует интенсивного
турбулентного перемешивания, которое всегда возникает за
фронтом детонации твердых и смесевых ВВ.
Предположение о росте частиц УДА в режиме диффузионного
броуновского движения сталкивающихся атомов углерода не
оправдывается, т.к. требует на 3—4 порядка больше времени роста, чем время
химреакции. Частота столкновения частиц возрастает при взаимном
движении объемов среды (при турбулентности ПД) и при различной
инерции частиц разной массы. Расчет коагуляции в изотропном
турбулентном сдвиговом течении уменьшает на три порядка время
возникновения частиц УДА [43]. Поскольку турбулентность ускоряет
коагуляцию, то аа^ синтеза УДА представляет интерес анализ способов
повышения турбулентности в детонационной волне (например, выбор
размера зерна ВВ, способа инициирования заряда и др.).
Время коагуляции еще более уменьшается, если предположить,
что рост частиц идет не путем диффузии отдельных атомов, а за счет
коагуляции групп атомов углерода.
Например, энергии ударной волны в химпике а^я тротила
недостаточно fiiA^ разрыва всех связей в его молекуле. Прежде всего
разрываются связи С—Н а бензольное кольцо разрушается частично
так, что связанные друг с другом три атома углерода выделяются при
химреакции одновременно и затем коагулируют, создавая в ЗХР
первичные кластеры углерода. Экспериментальные распределения
частиц УДА по размерам (см. рис. 16.5) всегда имеют крутой
передний фронт и длинный спад в сторону частиц больших размеров, что
характерно аая жидкокапельной коалесценции [35].
Объемную конденсацию пара неметаллов хорошо описывает
двухстадийная модель [3,8], по которой сначала образуются
кластеры, а затем рост частиц идет за счет слияния кластеров.
725
В [54] предлагается аналогичная модель а^я образования частиц
УДА. Сначала образуются частицы-кластеры < 2 нм (которые могут
быть микрокаплями жидкого углерода). Затем эти капли сливаются в
агрегаты, которые имеют фрактальную структуру, что подтверждается
данными малоугольного рентгеновского рассеяния.
Рис. 16.5. Распределение по размерам частиц УДД а) для идентичных зарядов из
ТНТ (1) и ТГ50 (2); б) для зарядов из ТГ50 (1), из октогена с бензолом
(2) и для состава тротил/октоген/А140/50/5 (3)
При такой кластер-крастерной ассоциации масса
образующегося кластера (количество частиц-капель в нем) Z и размер R (в
единицах диаметра исходных капель) связаны соотношением
Z~Rd (16.6)
где d — дробная фрактальная размерность, которая аая УДА
найдена равной d=l,78—2,1.
Плотность кластеров фрактальной структуры уменьшается с
увеличением их размеров (растет доля пустот).
Если mQ — масса исходных капель, то расчетное время их
ассоциации t=(m0)1/2, после чего исходные капли исчезают, и
вырабатывается замороженное распределение размеров частиц в узком
диапазоне. Среднее число частиц в кластере Z = t (m0)1/2. При варьировании
параметров т0 и t можно добиться совпадения расчетного и
экспериментального распределения, и среднего размера частиц.
Результаты расчетов не меняются от того, выделяется углерод в
реакции в виде единичных атомов или фрагментами бензольного
кольца.
726
Расчет и эксперимент хорошо согласуются аая вполне реальных
величин т0 = 103 атомов (2 нм) и t = 0,1 мкс, т.е. образование кластеров
идет в зоне химреакции еще до разлета ПД. При этом размер кластера
R~Z1/2 состоит примерно из десяти исходных кластеров. При
увеличении температуры детонации величина mQ возрастает и размеры
получаемых за то же время кластеров несколько увеличиваются.
Еще больших размеров частиц можно ожидать, если их
образование и рост проходит в области жидкого углерода. Наши расчеты
фазовой диаграммы наноуглерода показывают, что а^я наночастиц
углерода область жидкого состояния расширяется за счет алмазной
области (см. рис. 16.3)
Интересные результаты получены при моделировании
коагуляции углеродных кластеров в П Д методом молекулярной динамики.
В [55] изучалась кинетика термического разложения гексогена
различной плотности при различной температуре. Найдено, что
быстрее всех образуются молекулы N , затем Н2С а скорость
образования СО и С02 зависит от плотности. При низкой плотности
СО образуется так же быстро, как Н20, С02 не образуется, а
углеродные кластеры малы и имеют в среднем всего по 24 атома. При
высокой плотности (2,11 г/см3) СО не образуется, скорость
образования С02 меньше, чем Н20, а размер углеродных кластеров
значительно увеличивается, причем резкий рост кластеров наблюдается
при увеличении температуры, начиная с 2000—2500 К. Этот вывод
согласуется с экспериментальной зависимостью размера частиц на-
ноалмаза от температуры детонации [56]. Следовательно, большие
размеры нанокапель получаются в П Д с максимальными
температурой и плотностью.
Кроме понижения температуры плавления, общая особенность
плавления любых кластеров состоит в том, что они плавятся не на
линии Т = const, а в зоне плавления, где сосуществуют и жидкая, и
твёрдая фазы [57]. Плавление начинается с поверхности кластера, и
в зоне плавления каждой температуре соответствует своя доля
расплава кластера.
Поверхностные атомы кластера имеют в 1,5 - 2 раза меньше
соседей, чем внутренние атомы. Поэтому их энергия связи меньше,
727
энергетические барьеры ниже, разрыв связей и миграция атомов
по поверхности возможна при температурах, меньше температуры
плавления массивного кристалла алмаза.
Это значит, что при нагревании должно происходить послойное
плавление кластера. Поскольку с уменьшением размера кластера
растёт доля поверхностных атомов, то а^я каждой температуры
существует критический размер кластера, при котором он
расплавляется полностью [58]. Даже частичное поверхностное расплавление
кластеров должно облегчать их слияние подобно жидким каплям
или подобно жидкофазному спеканию с образованием
поликристаллов.
Коагуляция кластеров — экзотермический процесс,
вызывающий повышение их температуры. За счёт уменьшения
поверхностной энергии оценки [59] дают прирост температуры ДТ=4000 N~1/3
(N — число атомов в кластере). Кроме того, крупные частицы
растут за счет потока на их поверхность малых частиц. При
растекании малой частицы (100 атомов) по поверхности бесконечно
большой частицы средняя температура повышается на 1000 К.
Согласно [57] повышение температуры в результате полной
коагуляции одиночных атомов углерода, выделившихся в ЗХР, составляет
-3200 К.
Коагуляция малых кластеров (менее 2 нм) — процесс очень
быстрый (порядка не), поэтому энергию их коагуляции можно считать
частью энергии основной химреакции в ЗХР.
Нами в [50] сделана оценка роста температуры кластеров с
увеличением их размера более 2 нм при следующих допущениях.
1). Температура кластеров размером 2 нм и меньше равна
известной температуре детонации данного ВВ (например, а^я ТГ 40/60
это3900К).
2). Кластеры сферические и уменьшение их поверхности с
увеличением размерас dj до d2 составляет AS=6 v/d2 - 6 v /d= 6v (d2 - d1)/(d1d2).
При этом выделяется энергия, равная AE=AS<7, а температура
кластеров повышается на AT =AE/cv, где а^я нанокапель при Т>3500
К удельный объём v = 0,31 см3/г [43,44], удельная поверхностная
728
энергия нанокапель а = 1,7 Дж/м2 [45] и удельная теплоёмкость
с =2Дж/гК.
v ' '
Тогда ДТ = 1,58 103 ( d2 - d1)/(d1 d ) и температура кластеров
Т=ТГТ + ДТ\
с C-J с
Результаты оценки увеличения температуры кластеров с ростом их
размеров для состава ТГ 40/60 приведены в табл. 16.6.
Таблица 16.6. Оценка температуры кластеров для ТГ 40/60
d, нм
ТС
ТС
0—2
0
3900
2—4
395
4295
4—6
132
4427
6—8
66
4493
8—10
40
4533
Как видно, температура кластеров всегда выше температуры
газообразных ПД — а^я частиц 6—8 нм на 600 К. Увеличение
температуры кластеров с ростом их размеров способствует плавлению
и образованию нанокапель. Хотя а^я сплавов ТГ температура в
С—J - плоскости соответствует плавлению частиц УДА размером
~2 нм (см. рис. 16.4), расчётная температура реально получаемых
частиц размером 4—6 нм лежит в области их жидкого состояния,
следовательно, такие кластеры представляют собой нанокапли.
Отметим, что с ростом размеров кластеров скорость их коагуляции
быстро уменьшается, так что а^я получения частиц размером 8 нм
необходимо взрывать большие заряды (более 20 кг) в массивной
оболочке (более 200 кг) [53].
Назовём ещё два явления в ПД, которые ускоряют коагуляцию.
1. Сепарация в ПД. Для кристаллизации нанокапель на изэн-
тропе необходимо их охлаждение более холодными молекулами
расширяющихся газообразных ПД. Очевидно, что кроме разности
температур, ^ая охлаждения требуется интенсивное обтекание
нанокапель молекулами газов ПД. Такое обтекание обеспечивается в ПД
микротурбулентностью и сепарацией [60]. Микротурбулентность
возникает в ЗХР и обусловлена неоднородностью ВВ
(гетерогенность, пористость, анизотропия), а сепарация также начинается в
ЗХР, но развивается на изэнтропе.
729
Явление сепарации — это разделение в потоке первоначально
однородной смеси частиц разной массы. Для П Д — это ряд из азота,
воды, двуокиси углерода и углеродных кластеров. П Д начинают
двигаться за фронтом детонации с массовой скоростью u = D/4~2 км/с
вдоль оси заряда, и в процессе движения значительно более тяжелые
кластеры начинают постепенно отставать, тем самым увеличивая
в задней части потока концентрацию кластеров и вероятность их
столкновений и слияний. Отставание растёт с массой кластеров и
со временем движения, а затухает с уменьшением скорости потока.
Поэтому аля достижения максимальной степени сепарации важно
уменьшение разгрузки (как боковой, так и задней), что
достигается формой заряда (удлинённый цилиндр) и влиянием масштабного
фактора.
Кроме того, усиление сепарации связано с тем, что в середине
длины заряда скорость газообразных П Д меняет знак из-за влияния
задней разгрузки. Но более инерционные кластеры меняют скорость
с запаздыванием, которое растёт с массой кластера. Возникающее
при этом увеличение скорости обтекания кластеров, во-первых,
улучшает их охлаждение, а во-вторых, увеличивает вероятность
столкновений кластеров разной массы и скорость их коагуляции.
2. Торможение ПД. При взрыве заряда в оболочке ПД
тормозятся на границе с оболочкой. При этом тяжёлые кластеры по инер-
ии двигаются быстрее газового потока, что также увеличивает
концентрацию кластеров вблизи границы.
Реализация обоих названных процессов растёт с увеличением
длины заряда, о чём свидетельствует проведённый автором
эксперимент: выход УДА, равный 12% от веса заряда, был получен при
взрыве в водяной оболочке заряда длиной 1м [14,34,50].
16.7. Технология синтеза УДА
В синтезе детонационных наноалмазов использование
углеводородного сырья идёт по следующей цепочке: изготовление тротила и
гексогена - изготовление из их смеси зарядов - детонация зарядов во
взрывной камере (или в реакторе) с последующей конденсацией и
730
сохранением выделяющегося при этом свободного углерода,
содержащего УДА. За последние 20 лет получена обширная информация
о свойствах УДА, найден широкий спектр самых различных их
применений. Реализация этих применений в промышленности может
многократно увеличить объём потребления УДА как сырья а^я
создания новых более качественных материалов и изделий.
Однако существующие в настоящее время небольшие опытные
производства УДА (в России, Украине, Белоруссии, Китае, Чехии)
не в состоянии надежно обеспечить прогнозируемые
потребности промышленности. Их нерентабельность и монополизм
приводит к повышению цены на УДА в несколько раз. Производство
УДА ведётся с применением различных технологий, как правило, не
оптимальных. Различия в технологиях влияет на свойства УДА,
следовательно, и на результаты исследований их применений. Можно
утверждать, что в настоящее время не существует единого
материала под названием «детонационные наноалмазы». Всё это тормозит
применение УДА в промышленных масштабах ( потребление
десятки тонн в год).
Отметим один важный положительный фактор, который
помогает создать производство УДА. Это острая необходимость
экологически чистой утилизации огромных арсеналов различных
боеприпасов, ВВ из которых является сырьём аля синтеза УДА.
По нашему мнению, необходим переход от несогласованных,
неоптимальных и небольших национальных производств к
крупномасштабному промышленному производству стандартизованных
детонационных наноалмазов, с гарантированным качеством и
поставками, дешёвых и в любом требуемом количестве.
Условия промышленного производства УДА должны быть
хорошо оптимизированы, причём на основе современных знаний
особенностей образования и сохранения УДА в детонационной волне.
Рассмотрим следующие три вопроса:
- конструкции взрывных камер;
- способы охлаждения УДА в камере;
- критерии оптимальности технологии синтеза УДА.
1. Взрывные камеры (ВК). Для синтеза УДА применяются
специализированные ВК, обеспечивающие удобство установки зарядов
731
в ВК, извлечения шихты и безопасность эксплуатации ВК,
определяемую, в основном, прочностью ВК (см. гл.13) [14].
Обычно объём ВК относительно массы взрываемого заряда
составляет 1—5 м3/кг. В настоящее время а^я синтеза УДА
применяют ВК объёмом 2—20 м3 (кроме ВК фирмы «АЛИТ»), в
которых взрывают заряды массой 0,5—2 кг. Легко подсчитать, что а^я
производства 10 т. УДА в год, надо одновременно эксплуатировать
примерно десять таких ВК, что проблематично. По-видимому,
проще построить одну большую ВК для взрыва зарядов массой 10—
20 кг.
По геометрии ВК могут быть сферические и цилиндрические, с
одно- и многослойными стенками (см. гл. 13). Их расчёт на
прочность делают, определяя предельные значения на стенках ВК
динамических давлений и импульса. При многократных взрывах
разрушение ВК носит усталостный характер и начинается с появления
микротрещин на внутренней поверхности стенок. Поэтому
наилучшей сталью а^я ВК является максимально пластичная нержавеющая
сталь.
Цилиндрические камеры проще в изготовлении и не
разрушаются катастрофически (перед полным разрушением появляются
сквозные трещины в стенках).
Внешний вид горизонтальной цилиндрической ВК фирмы
«АЛИТ» показан на фото [14,31].
2. Способы охлаждения УДА в ВК. Необходимое аая синтеза
и сохранения УДА охлаждение возможно только за счёт
теплообмена с более холодными ПД, эффективность которого зависит как от
разности температур, так и от плотности ПД. При разлёте в вакуум
плотность ПД очень быстро падает, поэтому УДА не охлаждаются
и полностью графитизируются. Для снижения температуры
газообразные П Д должны производить работу по сжатию и разгону
окружающей заряд среды. Среда может быть инертная газовая или в виде
оболочки из воды или льда. Охлаждение газовой атмосферой
определяется теплоёмкостью газа в ВК и его удельным весом (наилучший
С02), а охлаждение водой (льдом) зависит от массы воды, намного
более эффективное и поэтому не требует инертной атмосферы в ВК.
732
Фото камеры «АЛИТх
Кроме охлаждения, оболочка увеличивает время коагуляции и
кристаллизации нанокапель, что уменьшает в наноуглероде долю
малых (<2 нм) аморфизирующихся кластеров.
733
Увеличить теплоёмкость и плотность газовой среды можно за
счёт повышения давления газа в ВК. Сильное влияние на синтез
УДА давления азота в ВК видно из табл. 16. 7 (ВК 0,17 м3, заряд из
ТГ50массой100г)[125].
Таблица 16.7. Влияние ни синтезУДД давления азота в ВК
Давление, атм
S,M2/r
Sp3/Sp2,%
D,hm
р, г /см3
1
643
10
4
2,79
2,5
468
30
4,5
2,85
7
450
75
5
2,89
10
415
75
5
3,09
3. Критерии оптимальной технологии синтеза УДА.
Очевидно, что в производстве УДА должна использоваться
оптимальная технология синтеза.
Оптимальность синтеза УДА можно рассматривать как в
отношении количества, так и качества УДА.
Показателем оптимальности синтеза в количественном
отношении является получение максимального выходаУД А. Оптимальность
качества УДА определяется их конкретным применением и тоже
зависит от условий синтеза, в частности, от влияния масштабного
фактора.
А. Количественные критерии. При оптимальном синтезе УДА
должны быть максимальны:
а) количество углерода, получаемого в результате взрыва заряда
данного состава;
б) содержание УДА в получаемом углероде или алмазной шихте
(АШ).
При одновременном выполнении этих условий будет
максимален и выход УДА относительно массы взрываемого заряда.
На основании сделанного выше анализа условия оптимального
синтеза в количественном отношении (максимальный выход УДА
относительно массы заряда) приведены в табл. 16.8. [34,50].
734
Таблица 16.8. Условия оптимального синтеза детонационных
наноалмазов
Условия синтеза
Конденсация максимального для
данного ВВ количества свободного
углерода.
Конденсация углерода в области
жидкого наноуглерода.
Максимально возможные времена
существования в ПД условий жидкого
наноуглерода и его кристаллизации
при давлениях в ПД более ~10 ГПа.
Проведение взрывов в условиях,
обеспечивающих отсутствие процессов
аморфизации, окисления и графити-
зации
Способы реализации условий
синтеза
Детонация зарядов ВВ с минимальными
пористостью и степенью неидеальности.
Использование сплавов ТГ с давлением
в плоскости С—J более ~22 ГПа
Детонация зарядов с массой более ~5
кг и в водяной оболочке с массой более
~ 10-ти масс заряда.
Взрыв зарядов в массивной водяной
оболочке
Как видно из табл., &ая получения максимального выхода
наноалмазов необходимо:
- максимально реализовать два позитивных процесса -
коагуляцию кластеров в области жидкого наноуглерода до размеров более
2 нм и затем их кристаллизацию в области алмаза;
- максимально подавить три негативных процесса - аморфиза-
цию нанокапель, графитизацию и окисление полученных
наноалмазов.
При «сухом» синтезе (взрыв в собственных продуктах
детонации или в С02) содержание УДА в АШ составляет примерно
15 —30% при выходе УДА 4—6%, а при «мокром» (взрыв в
оболочке из воды или льда) — 60—70% при выходе УДА 8—10%.
Б. Качественные критерии. Качество получаемой алмазной
шихты (АШ) характеризуется двумя основными параметрами:
соотношением sp3/sp2 и степенью связности частиц УДА. За счёт
изменения условий синтеза получаемые параметры качества могут
варьироваться в следующих пределах:
sp3/sp2 - от 15% до 75%; степень связности частиц - от
агрегатов 50 - 200 нм до поликристаллов 10-100 мкм. Получить АШ без
примеси неалмазного углерода или с одиночными частицами пока
не удаётся. Из-за разнородности условий синтеза в объёме
детонирующего заряда всегда по степени связности УДА полидисперстен.
Третьим параметром качества АШ, связанным с условиями
синтеза, является степень загрязнения АШ неуглеродными и несгораемыми
примесями (металлы). Здесь также пока не удаётся получать чисто
углеродную АШ, но может помочь лазерное инициирование зарядов.
Сложнее определить оптимальность качества УДА.
Во-первых, ^ая разных применений УДА требуется различное
его качество. Поэтому производство УДА должно быть гибким,
способным быстро переходить с одной технологии на другую в
соответствии с требуемым качеством УДА. К сожалению, для многих
возможных применений ещё не определено оптимальное качество
УДА, обеспечивающее максимальное увеличение эксплуатационных
характеристик изделий. Но всегда качество материала будет
улучшаться с уменьшением агрегатов УДА, вводимых в материал.
Во-вторых, качество УДА зависит от условий синтеза, в
частности, от влияния масштабного фактора.
Например, при взрыве заряда массой 10 кг в ледяной оболочке
на границе ПД—лёд давление 9 ГПа сохраняется ~60мкс. За это
время в процессе охлаждения нанокапель с 3500—4000 К до 1600К
кристаллизуются частицы кубического алмаза, а при температурах
ниже 1600 К образуются и монокристаллы лонстейлита размером
до 10 мкм, и трёхфазные сростки алмаз-лонсдейлит-нанографит
[14,61]. Очевидно, УДА такого качества нельзя использовать /^ля
суперфинишной обработки или аая смазок. По-видимому, такое
сырьё необходимо фракционировать.
Как видно из табл. 16.3, масштабный фактор слабо влияет на
средние размеры частиц УДА. Но влияние масштабного фактора
заметно сказывается на два идущих параллельно процесса в ПД:
формирование и укрупнение нанокапель за счёт коагуляции
кластеров и взаимодействие нанокапель с образованием агломератов
нанокапель, а после их кристаллизации - агломератов частиц УДА с
прочными ковалентными связями и с размерами 20—200 нм. Этот
второй процесс образования прочных агломератов во многом
определяет качество УДА.
736
Кроме увеличения времени за счёт массы заряда и массивной
оболочки вокруг заряда, на эти процессы влияют также температура,
давление и концентрация углерода в ПД. С их увеличением идёт
последовательный переход от фрактальной структуры с 1—3 связями у
частиц к пористым поликристаллам с 4—8 связями и в пределе — к
ликвидации пористости с образованием поликристаллов с
частицами, связанными по всей их поверхности (рис. 16.6). Такое прочное
связывание частиц УДА с появлением абразивных свойств можно
рассматривать как разной степени спекание в плотной газовой
среде продуктов детонации (впервые обнаружено нами в 1987 г [14]).
Поскольку в детонационной волне условия неоднородны (в центре
заряда и на его поверхности), то при одном взрыве может возникать
вся гамма названных структур.
Синтез поликристалличных УДА соответствует общим законам
конденсации пара [1] и обсуждается в [62—64]. При взрыве заряда
массой 140 кг в водяной оболочке обнаружены поликристаллы
размером 85 мкм [53].
Синтез поликристалличных УДА соответствует общим законам
конденсации пара [1] и обсуждается в [62—64]. При взрыве заряда
массой 140 кг в водяной оболочке обнаружены поликристаллы
размером 85 мкм [53].
Время синтеза, с
Тип агрегатов
Тип связи частиц
КЦ—10*
Фракталы
Одноточечная
Синтез
Ю-'—105
Пористые
поликристаллы
Многоточечная
(6— 8 связей)
Ю-*—-Ю-4
Непористые
поликристаллы
Связь по всей
поверхности
Эскизы агрегатов
Я?
Рис. 16.6. Влияние условий детонации на качество ЗДА, определяемое степенью
связности частиц
О связывании частиц с уменьшением их поверхности (за счёт
общих участков связи) свидетельствует тот факт, что удельная
поверхность, рассчитанная по размерам частиц, всегда больше измеренного
значения удельной поверхности [65].
Таким образом, по степени связности частиц качество УДА
можно характеризовать линейкой качества, на концах которой два
предельных случая: одиночные, не связанные частицы и УДА,
образующие непористые поликристаллы. В реальных условиях
синтеза качество получаемых УДА всегда лежит где-то посредине этой
линейки.
Возможности движения вдоль линейки качества за счёт
вариации условий синтеза ограничены.
Для снижения связности частиц этот процесс надо ограничить
во времени, например, используя заряды малой массы без оболочки
(«сухой» синтез). Но при этом в два раза и более падает выход УДА
и растёт содержание в шихте сажи. В первую очередь на связность
влияет температура ПД, но её можно варьировать только вместе с
давлением и плотностью ПД. Снижение давления вместе с
температурой приближает параметры синтеза к линии тройных точек, что
уменьшает время коагуляции в области жидкого sp3 наноуглерода и
также снижает выход УДА. Поскольку процессы коагуляции и
связывания идут параллельно, то по-видимому, синтез только одиночных
частиц невозможен.
Для повышения связности и получения абразивных
поликристаллов надо использовать заряды большой массы и оболочки с
массой ~10 масс заряда. Такие заряды сложно и изготовлять, и
применять. Кроме того, требуется дорогостоящая взрывная камера
(реактор) большого объёма
В таблице 16.9 а^я порошков УДА, полученных у различных
производителей, приведены: измеренные средние величины
размера частиц dex, рассчитанные по ним величины удельной поверхности
Sd, измеренные удельные поверхности Sex и рассчитанные по Sex
величины эквивалентных диаметров частиц d = 6/(р S ).
Из табл. 16.9 видно, что у различных порошков УДА, размер
частиц и удельная поверхность сильно отличаются, причём, всегда
738
удельная поверхность Sd, рассчитанная по диаметру частицы,
значительно больше экспериментального значения Sex. Соответственно,
всегда de > dex. Наибольшее отличие - &ая синтеза взрывом в
ледяной оболочке (синтез в Снежинске и в «АЛИТЕ»). Возможная
причина этого - в связности синтезируемых частиц, у которых
поверхность уменьшена за счёт их частичного объединения с
образованием прочных ковалентных связей. Исходя из этого и используя
экспериментальные значения dex и Sex, измеренные аая ряда УДА
разных производителей, нами рассчитаны размеры а общих
связующих участков на поверхности частиц и размеры пор вп между
частицами (табл. 16.9). В расчётах принято, что упаковка частиц плотная
и число ближайших соседей у каждой связанной частицы равно 8.
Тогда значения а и размер пор в между частицами находятся из
условия:
S /S=l-2(a/d )2; в =<2{d -а)
exp a v с exp' 7 п v е с7
Такие пористые агломераты оптимальны для применений УДА,
где нужна абсорбция в нанопорах различных веществ.
С увеличением масштабного фактора будет расти и содержание в
УДА непористых абразивных поликристаллов и монокристаллов.
Таблица16.9. Параметры связанных частиц ДНА
различных производителей [65]
Producer
Snezhinsk,
ozone cleaning
Snezhinsk,
ordinary cleaning
Krasnoyarsk
Petersburg
«ALIT»,
d ,
nms
3.1
4.7
4.4
4.5
6
Su,m2/g
616
407
434
425
318
s ,
2X?
m2/g
350
284
337
274
187
d >
e4
nms
5.0
6.2
5.2
6.4
9.4
Scxp/Sd
0.57
0.70
0.78
0.64
0.59
nms.
1,44
1,82
1,46
1,91
2,72
в .
ii
nms
3,88
6,13
5,87
5,76
7,56
16.8. Свойства УДА
Для всех ультрадисперсных порошков характерны большая
удельная поверхность и ее влияние на свойства частиц порошков,
склонность к агрегированию, специфическая округлая форма
частиц.
Ярким примером ультрадисперсной среды со всеми ее
особенностями является ультрадисперсный алмаз детонационного синтеза.
При среднем размере частицы УДА всего 4 нм она состоит из ~ 12000
атомов углерода, из которых примерно 3000 являются
поверхностными. Отсюда большое влияние поверхности УДА на его свойства.
Несмотря на малые размеры частиц, УДА сохраняет основные
свойства алмаза: кристаллическую решетку и химическую инертность,
позволяющую выделять УДА из шихты с помощью традиционной
обработки кислотами.
В получаемой в результате взрыва заряда исходной шихте
углерод находится во всех трех состояниях: sp3 (алмаз), sp2 (графит) и
sp (карбин).
На свойства УДА влияют условия его синтеза (вес, форма и
состав заряда, способ охлаждения ПД) и очистки (кислотами,
кислородом воздуха, озоном).
Впервые свойства УДА были исследованы в 1963-64 гг. во
ВНИИТФ (г.Снежинск) непосредственно после открытия
синтеза УДА при конденсации углерода ПД [22,23]. Полученные
тогда данные о свойствах УДА в 1980-2003 гг. были подтверждены,
расширены и углублены в лабораториях института
гидродинамики (г. Новосибирск), Красноярского технического университета
(г. Красноярск), НПО «Алтай» (г. Бийск), ВНИИТФ, института
проблем материаловедения (г. Киев), Института сверхтвердых материалов
(г. Киев), НПО «СИНТА» (г. Минск), АОЗТ «Алмазный центр»
(г. Санкт-Петербург).
Детальное изучение свойств УДА важно для разработки
технологий применения УДА. О результатах исследования свойств
УДА можно прочитать, например, в работах [14,20,22,23,39,40,
66-80].
740
Морфология частиц УДА
Порошок УДА состоит из сфероподобных частиц с удельной
поверхностью от 200 м3/г (синтез из ТГ40, вес зарядов 3—10 кг, взрыв
в воде, удельная поверхность исходной шихты 184 м3/г) до 400 м3/г
(синтез из ТГ60, вес зарядов 0,6кг, газовое охлаждение). При
нагреве до 1000 С удельная поверхность не меняется.
Каждая частица УДА состоит из сверхтвердого и инертного
алмазного ядра, покрытого пористыми оболочками из аморфного
углерода и из различных функциональных групп, способных
активно участвовать в различных химических реакциях [78]
Детально строение частицы изучить не удается, но по
электронно-микроскопическим снимкам размер частиц равен 2—6
нм аая УДА с S = 400 м3/г и 3—13 нм — аая УДА с S = 200 м3 /г.
Микроэлектронограммы от них представляют собой сплошные
размытые кольца. В [35] установлено логарифмически нормальное
распределение частиц УДА с максимумом ~ 4 нм, что совпадает с
величиной ОКР.
В сухом виде УДА — полидисперсный светлосерый порошок
с насыпной плотностью 0,4 г/см3, состоящий из агломератов
размером 1—200 мкм. В водной суспензии после диспергирования
ультра- звуком частицы УДА имеют размер примерно 0,05 мкм.
Вероятно, такие агрегаты имеют максимальную степень
связанности.
Таким образом, УДА является кластерным материалом с
определенной иерархией уровней агрегации.
В зависимости от способа синтеза и очистки плотность частиц
УДА колеблется в пределах 3—3,4 г/см3.
Фазовый состав и кристалическая структура УДА
В зависимости от условий синтеза УДА состоит либо только из
кубического алмаза, либо с примесью (до 5%) монокристаллов лон-
сдейлита с размерами до 10 мкм. Под электронным микроскопом
обнаруживаются однофазные (алмаз, лонсдейлит, графит) и
трехфазные частицы (алмаз-лонсдейлит-графит.[ 14,61]. Свободные части-
741
цы графита в ввиде скоплений усов наблюдаются только в образцах
УДА после 22-х летнего хранения .
Рентгеновская дифрактограмма УДА имеет 5 отражений:
Индекс плоскости
Интенсивность для
УДА
Интенсивность аая
эталонного алмаза
(ш)
85
44
(220)
14
22
(из)
0,5
18
(400)
0,3
4
(331)
0,2
12
Ширина дифракционных линий на порядок больше, чем у
алмаза, синтензированного в статических условиях.
Высокая интенсивность (111), по-видимому, связана со
сферической формой частиц. Практически на дифрактограммах
фиксируются три линии.
Очень высокие значения микронапряжений второго рода и
искажений решетки у УДА не меняются при нагреве до 1200 С [66].
По нашим данным при 900 С и выдержке 1 час структура УДА
несколько улучшается.
Поверхностные примеси
Для УДА характерно большое количество трудноудаляемых
летучих (СО, С02, N2, 02, Н20, остатки HN03, H2S04) и
твердофазных (оксиды, карбиды, соли) примесей. Количественный состав
примесей сильно зависит от тщательности и способа очистки УДА и
обычно колеблется в широких пределах:
С — 79—98% (из них графита< 1%): Н — 0,1—1,5%; N — 1,3—
2,5%; О — 4,5—17%; несгораемый остаток — 0,1—8%.
Несгораемый остаток УДА содержит окислы и карбиды с
содержанием С — 29 ат.% и кремния 51 ат.%.
Кроме того, УДА содержит примеси кремния и металлов (в %):
Si — 0,1—1,0; Са — 0,05; Fe — 0,2—1,0; Ti — 0,01—0,3; Cr —0,02—
0,1; Pb — до 0,6.
742
Химики Института сверхтвердых материалов (г.Киев) показали,
что УДА может быть очищен до зольности 0,1 %, но стоимость
глубокой очистки резко возрастает.
По данным ИК-спектроскопии на поверхности УДА
присутствуют карбонильные, карбоксильные, метильные и нитридные
группы. Информацию о составе поверхностных соединений
дает анализ десорбированных при нагреве газов (см. табл. 16.10
[67]).
Таблица 16.10. Состав адсорбированных газов (%)
т, К
573
773
сн4
3
43
со2
62
15
N2
4
4
NH3
-
7
СО
15
11
HCN
16
20
Общее
газовыделение, см3 /г
4,6
15,05
Таблица 16.11. Содержание неалмазных форм углерода
№№ пп
1
2
3
4
5
6
7
8
Наимен.
Образца
Шихта
Шихта
УДА
УДА
УДА
УДА
УДА
УДА
Условия синтеза
и очистки
Охлаждение: ледяная
оболочка и водяной душ
Охлаждение только
водяным душем
Очистка смесью H2SO4+H2
СЮ4
Образец № 3, очистка
водородом, 850 С, 2 часа
Образец № 4, очистка
водородом, 940 С, 2,5 часа
Образец № 4, очистка
водородом, 1050 С, 2 часа
Образец № 3, глубокая хим.
очистка до зольности 0,15%
Образец № 7, очистка
водородом, 1050 С, 2 часа
Содерж.неалмазн.
форм, %
10,0
22,0
0,84
1,4
1,3
5,7
0,37
2,0
743
Энергия активации десорбции С02, сСН4 и N2 при
нагревании УДА изменяется в пределах 23...48,5 дж/моль, что ,может
свидетельствовать о химических связях этих газов с поверхностью
УДА. Поверхность УДА заряжена, величина зарядки составляет
+3,3 эв. В спектре ЭПР сигнал от УДА представляет собой синглет
с ж-фактором 2,003, что соответствует спектру ЭПР от разорванных
связей на поверхности алмаза.
В табл. 16.11 приведены результаты определения содержания
неалмазных форм углерода ^ая различных условий синтеза и очистки
УДА производства фирмы «Алит» (г.Киев) [14].
Согласно [74], в УДА содержание sp2 углерода колеблется в
пределах 3—10% (в виде монослоя на поверхности частиц).
Окисление УДА воздухом
Дифференциально-термический анализ (ДТА) 4-х различных
порошков УДА показал следующие результаты [14].
1. УДА НПО «Алтай» и исходная шихта теряют массу
(окисляются до СО и С02) уже начиная со 100 С.
2. Для порошков УДА фирмы «Алит», очищенных смесью
H2S04 + Н2СЮ4 (зольность 8%) и дополнительно очищенных до
зольности 0,1% в интервале 350—400° С наблюдается небольшое
увеличение массы, что объясняется реакцией 2С+02 = 2СО.
Образующаяся окись углерода не удаляется, а формирует на
поверхности частиц адсорбированный слой.
З.Для всех исследованных порошков быстрое окисление
начинается с температур 400—430° С.
4. При 500° С наибольшая потеря массы наблюдается у УДА с
зольностью 0,1% ,возможно, за счет уменьшения частиц при
дополнительной очистке. По-видимому, по той же причине УДА,
очищенный в токе водорода при 850 С, окисляется с большей скоростью в
более узком диапазоне температур (460—610 С).
Связь между температурой начала окисления на воздухе и
удельной поверхностью для алмазных порошков различного синтеза
показана в табл. 16.12 [ 14].
744
Таблица 16.12. Начало окисления алмазных порошков
детонационного синтеза с различной удельной поверхностью
№№
пп
1
2
3
4
5
6
Параметры образца порошка алмаза
Наименование
Шихта УДА, алмаза 8%; углерода в
сумме 84%
Шихта УДА, алмаза 30%; углерода в
сумме 89%
УДА, алмаза 100% углерода в сумме
88%
УДА, алмаза 100% углерода в сумме
94%
ДАГ, синтез при детонации смеси
гексоген+графит
ДАС, синтез при детонации смеси
гексоген+сажа
SM2/r
440
430
252
200
27
18
Температура
начала окисления, С
300
315
430
475
570
590
Диэлектрические и магнитные свойства
Такого рода исследования полезны не только аая новых областей
применения УДА, но также для оценки качества УДА.
В промышленности синтетических алмазов давно используется
величина магнитной восприимчивости х как показатель качества
алмазного порошка. Идеальный алмаз (без дефектов и примесей)
диамагнитен и имеет величину х = -6,2 108 м3/кг. Парамагнитные и
ферромагнитные включения (Ni, Mn, Fe) и поверхностные примеси,
с одной стороны, изменяют величину х , а с другой стороны,
существенно влияют на абразивную способность, прочность,
термостойкость алмаза. Поэтому величина х является косвенным показателем
качества технологий производства и очистки алмаза
К наличию примесей чувствительны и величины
диэлектрической проницаемости Е.
Для идеального алмаза Е = 5,68. Для хорошо очищенного и
высушенного УДА измерены следующие величины, близкие к
идеальному: Е = 6,2—9,2, х = -(3,6—6,2) К)"8 м/кг.[14]
Проводимость УДА после сушки при 300° С имеет
минимальную величину ~ 1012 ом м.
745
При нагреве в атмосфере СО при 900° С происходит резкое
падение сопротивления до 2,3 104 ом м [66], что подтверждает
обнаруженный нами факт начала графитизации УДА при 900° С.
Адсорбционная способность (АС)
АС зависит от состояния поверхности частиц, которое
определяется условиями синтеза и химобработки (диапазон изменения
АС — до 50 раз).
Максимальную АС имеют порошки, полученные сухими
методами синтеза (газовое охлаждение продуктов взрыва) и очистки
(окисление озоном, тлеющим разрядом в воздухе, кислородом).
АС газов выше, чем АС ионов металлов. Например, а^я паров
хлороформа — 12—19 моль/кг, а аая ионов Fe, Ni, Сг — 0,1—
10 моль/кг.
АС зависит от рН раствора, который определяет степень
диссоциации поверхностных групп УДА.
В [80] обнаружено, что в процессе окисления шихты величина
удельной адсорбции изменяется не монотонно, а достигает
максимума при содержании окисляемого углерода в шихте 18—20%. По
сравнению с шихтой в максимуме удельная адсорбция увеличивается
на порядок. Экстремальный характер зависимости отражает переход
в процессе окисления от неалмазных форм к алмазу. Последние 18—
20% окисляемого углерода являются периферийной частью частиц
УДА. По-видимому, АС определяется активными центрами с
переходной sp3—8р2-гибридизацией.
На величину селективной АС влияет гидрофильно —
гидрофобный баланс поверхности УДА [81]. Гидрофильность
поверхности увеличивается в результате электрохимической обработки
УДА — электролизом в соляной кислоте. При этом на поверхности
увеличивается количество атомарного кислорода, который ускоряет
каталитические процессы. В частности, впервые обнаружено
каталитическое окисление СО до С02 на поверхности УДА (до 80% при
380—400 С).
В [82] показано, что промотированный УДА в силу своего
высокого адсорбционного потенциала активно участвует в реакции
746
электровосстановления кислорода и может быть перспективным
катализатором кислородного электрода топливного элемента.
На гидрофильной поверхности белки адсорбируются лучше и
заполняют свыше 60% поверхности [81]. Наоборот, ионы хрома,
железа, никеля лучше адсорбирует гидрофобная поверхность
(заполнение до 80%). При нагреве УДА до 150 С происходит десорбция
физически адсорбированной воды (втрое больше а^я гидрофильной
поверхности), а выше 150 С (до 400 С) преобладает десорбция хемо-
сорбированной воды.
Высокая агрегация УДА сдерживает его применение, в том
числе и как сорбента. Получаемые спеканием УДА новые пористые
порошки [83,84] лишены этого недостатка и могут быть использованы
Аая очистки жидких сред (воды, плазмы крови), аая извлечения
редких металлов из разбавленных растворов. Благодаря высокой
прочности, инертности и термической стойкости эти порошки легко
регенерируются, их можно использовать многократно, что удешевляет
их применение.
Седиментационная устойчивость
В производстве и применении УДА роль седиментационной
устойчивости (СУ) противоположна. С одной стороны, малая СУ в воде и
кислотах полезны, т.к. упрощают технологии синтеза и очистки.
С другой стороны, а^я применения УДА в полировочных
составах, АЛЯ введения УДА в масла, полимеры, резину, в
гальванические составы необходима высокая СУ, и эту проблему нельзя считать
полностью решенной.
Для получения суспензий обычно пользуются ультразвуковым
диспергированием сухого порошка УДА. В результате получают
суспензии с агломератами частиц УДА размером 0,2—0,5 мкм. По
нашим данным, в воде такая суспензия устойчива только при малых
концентрациях УДА — не более 0,2%. Согласно [85], после 20 мин.
обработки ультразвуком 90% частиц водной суспензии УДА имеют
размеры в интервале 18—32 нм, но через 2 часа после обработки
начинается агрегирование частиц и выпадение их в осадок.
Для повышения СУ ультрадисперсных порошков используется
два способа: модификация поверхности частиц порошка (см. разд.
16.9) и выбор дисперсионной среды.
Для полярных жидкостей (вода) УДА должен быть
гидрофильным за счет насыщения кислородом поверхности частиц,
например, обработкой в кислородной плазме, а в воде добавляют
поверхностно-активные вещества (ПАВ) а^я предотвращения
агломерации и образования устойчивых в воде комплексов. В качестве
ПАВ можно использовать, например, полиоксиэтилированный ал-
каламид (синтамид-5).
Для неполярных органических жидкостей частицы УДА
должны быть гидрофобны (например, в результате восстановления в токе
водорода).
В работе [86] показано, что УДА, очищенный кислотами,
обладает низкой СУ во всех дисперсионных средах как полярных, так
и неполярных. Суспенсии УДА, очищенного сухим окислителем,
устойчивы до 40 часов в воде и более 120 часов в органических
средах. Влияние ПАВ меньше, чем способ очистки УДА.
В [85] предложена и опробована методика твердофазного
химического модифицирования поверхности УДА прививкой триметил-
силильных групп. В результате силилирования происходит
очистка от адсорбированной воды и гидрофобизация поверхности, при
этом средний размер частиц суспензии УДА в толуоле снизился до
14,5—18 нм, что позволяет получать устойчивые суспензии.
Абразивная способность
Использование а^я синтеза зарядов до ~0,5 кг без оболочки дает
частицы УДА со средним размером 4 нм. При увеличении веса
зарядов до ~10 кг и использовании водяной или ледяной оболочки
синтезируются сферические частицы кубического алмаза с размерами
5—12 нм и, кроме того, хорошо ограненные частицы лонсдейлита с
размерами до 10 мкм.
В первом случае абразивная способность у УДА полностью
отсутствует и даже проявляются антифрикционные свойства.
748
Во втором случае нами зафиксирована количественно абразив- ная
способность УДА [14]. Величине съема монокристалла кремния (0,0015
мкм) испытанный УДА соответствует промышленному ал- мазному
субмикропорошку АСМС5-01 по ГОСТ 9206-80, но при этом
измерена повышенная шероховатость (0,08 мкм). Кроме того, по размерам
царапин и сколов на полированной пластине корунда и твёрдого
сплава нами показано, что такой УДА содержит крупные (до ~ 20 мкм) и
прочные частицы (по-видимому, лонсдейлита) [14] Эти данные имеют
прямое отношение к возможности применения УДА водного синтеза в
качестве полировальных составов и антифрикционных присадок в
смазочные материалы. В этом случае, требуется фракционирование УДА.
16.9. Модификация УДА
Уникальность свойств УДА определяется сочетанием в
структуре частицы инертного и твёрдого сферического алмазного ядра и
очень активной неалмазной оболочки вокруг ядра. В этом сочетании
перспективы различных примененией УДА. С другой стороны,
применение УДА тормозят следующие его недостатки:
— неуглеродные и несгораемые примеси, вносимые в процессе
синтеза и требующие дорогостоящей кислотной очистки;
— большая склонность к агрегированию (в связи с большой
поверхностной энергией);
— большая прочность агрегатов менее 200 нм, создаваемых в
процессе синтеза;
— полидисперсность прочных агрегатов в диапазоне 20 -
200 нм;
— большое разнообразие состава оболочки в отношении как
форм неалмазного углерода, так и функциональных групп и ге-
тероатомов;
— как следствие всех перечисленных недостатков малая
стабильность суспензий УДА (стойкие суспензии нужны
практически ^ая всех применений УДА).
С начала 21 века многие учёные пытаются хотя бы частично
устранить эти недостатки путём модификации свойств поверхности
749
УДА. Общая проблематика модификации - научится управлять
количеством и качеством групп на поверхности частиц с целью
создания материалов с требуемыми свойствами.
Для модификации широко используются дешевые газофазные
обработки. Поскольку в агрегатах часть поверхности остаётся
закрытой аая обработки, то наилучшие условия а^я модификации
будут созданы при использовании исходного УДА без агрегатов, или
при предварительном разрушении агрегатов. К сожалению,
реализация этих условий весьма проблематична.
Природа прочных связей частиц в агрегатах УДА пока не
установлена. Предложено две модели:
1). Агрегация УДА такая же, как у сажи. Алмазные ядра не ка-
саюся друг друга, а «плавают» в sp2 углероде, т.е. агрегация без
ковалентных связей между частицами [63,131].
2). Агрегация как результат частичного спекания ядер в процессе
синтеза с возникновением прочных ковалентных связей (см.раздел
16.7) [65].
Очевидный способ разрушения агрегатов состоит в частичной
графитизации УДА с последующим окислением графита, или просто
в окислении воздухом (тоже с потерей части алмаза). Размер
агрегатов уменьшается, но пока не удаётся модифицированием получить
единичные частицы УДА. Их можно получить размолом агрегатов
циркониевыми микрошариками (30 мкм) [63,131] , но этот метод
дорогой (надо дополнительно очищать частицы от циркония и
графита) и малопроизводительный.
Различные способы модификации преследуют следующие цели:
— увеличить соотношение sp3/sp2 в УДА;
— унифицировать состав поверхностных групп (что можно
рассматривать и как дополнительную очистку поверхности);
— уменьшить размеры агрегатов;
— получить стойкие суспензии в различных средах;
— закрепить на поверхности группы или молекулы,
необходимые для данного применения.
Исследованные виды модификации и полученные результаты
приведены в табл.16.13.
750
По-видимому, наиболее значимы три вида модификации УДА:
— аминирование а^я создания прочных ковалентных связей с
полимерной матрицей;
— хлорирование а^я прививки белков, биопрепаратов,
лекарств;
— очистка водородом ^ая получения спеканием металлических
и керамических композитов.
Кроме того, обработка водородом с частичной графитизацией
позволяет получить исходный «нулевой» уровень ^ля любых
модификаций, когда всё разнообразие групп устранено.
При обработках водородом, кислородом или хлором
содержание азота не меняется, значит азот входит в состав алмазных ядер
частиц.
В [119] показано, что модифицирование позволяет получать
стойкие суспензии даже с крупными агрегатами (100 - 200 нм).
На изменение свойств УДА сильно влияет время обработки, что
видно из табл. 16.14, составленной нами по результатам [114].
Обзор работ по модификации УДА сделан в [105].
Таблица 16.13. Способы модификации УДА
№
1
2
3
4
Ссылки
[106-
109]
[ПО]
[111]
[111,20]
Способ обработки
УМ
Окисление воздухом
в интервале 380 -
600 С
Окисление смесью
озона с воздух, при
120-400 С
Обработка хлором
при 850 С
Обработка смесью
Аг/СС14при450С
Результаты обработки
Увел-е: sp3/sp2, кислородных
групп, гидрофильности,
устойчивости суспензий
Тоже
Условия аая прививки белков,
удаление окислов Al, Сг, Fe, Si,
но Си остаётся
Увелич. sp3/sp2, С1 +6,8%, О
-7%, гидрофильность
уменьшилась в 20 раз.
751
№
5
6
7
8
9
10
11
12
Ссылки
[HI]
[112,
113,116]
[114]
[111]
[115]
[114]
[117]
[118]
Способ обработки
УДА
Обработка Н2 при
850 С
Обработка Н2 при
800 С
Обработка Н2 при
900 С
Обработка NH3 при
600-850 С
Фторирование
Окисление воздухом
при400С 1-5час.
Графитизация в N2
при 1000 С 1 час,
затем окислен, возд.
При 450 С
Н2,800 С, 2 часа
425 С воздух, 5 часов
C^^OOCl час
NH3,850C,l4ac
Результаты обработки
валяется 95% всех групп, Н
+1%
Монофукционализация, уве-
лич. Адсорбции, уменьш. О с
9% до 1 %, сохран. гр. С-Н О-Н
Содерж. С увел, с 78% до 89%,
содерж. О уменьш. с 19 до 7%,
увел, стойкость к окислению, уд.
поверхн. увел, с 283 до 427 м2/г,
появились связи С-Н и изолир.
ОН - группы
Очистка по реакции
C+NH3=HCN+H2, С-С связи
исчезли, гидрофильн. уменьш.
в4раза
+ 9% фтора, ковал, связь со
стеклом через NH2
Содерж. С увел, на 4%, уд. пов.
Увел, с 283 до 415 м2/г, уменьш.
устойчивость к окислению
В суспензии 50% частиц
< 50 нм, но остались агрегаты
1000 - 2000 нм (водный синтез
УМ)
С=0 убраны, С-Н увелич., но
остались О-Н С-Н убраны,
увел. С-О и в103 электропро-
водн. Активн. хлорир. поверхн.
АЛЯ аминирования
С=0 уходят, созд. С-Н и C-N
АЛЯ полимеров
752
№
13
14
15
Ссылки
[119]
[120]
[121]
Способ обработки
УДА
Обработка
octadecylamine
(ODA)
Графитизация при
1800-1900Ксоб-
разов. OLC
Аминирование и
силицирование
Результаты обработки
Композит ND-ODA с ковал,
связями, флюоресц. голубым
светом, образует стойкие
суспензии, хотя агрегаты 100 —
200 нм.
Увелич. теплопроводности мя
микроэлектроники.
Снижает размер агрегатов от
170 нм до 20 нм.
Таблица 16.14. Влияние времени обработки на результаты
модификации
Изменение удельной
поверхности, м2/г
Расчёт для
с1=5нм
450
Исходный
образец
283
Водородное
3 час.-414
5 час.-427
7 час.-393
Воздух -
400С
1 час-415
Зчас.-371
Потери массы после окисления
на воздухе (723К, 15 мин.), %
Исходный
образец
6,91
Водород-
900С
3 час-1,04
5 час.-0,48
7 час-0,22
Воздух -
400С
1 час-6,42
5 час. -
15,01
16.10. Применения УДА
После создания в 1984г. промышленного производства УД А,
специалисты НПО «Алтай» первыми провели исследования и
определили широкий спектр нетрадиционных ^ая алмаза применений
УДА. Начиная с конца 90-х гг эти исследования были продолжены
и расширены в научных центрах Москвы, Киева, Санкт-Петербурга,
Минска, Красноярска, Новосибирска, затем и во многих научных
центрах США, Японии, Китая, Европы [14,39,74 - 87]. Подробные
обзоры применений сделаны В.Ю. Долматовым в [39,74,79], а также нами в
[14].
753
Показана высокая эффективность применения УДА в
следующих областях:
— Моторные масла (ускор. обкатка двиг., экономия топлива);
— Технологические смазки (холодная и горячая штамповка,
вытяжка, волочение);
— Композиционные электрохимические износостойкие
покрытия (хромовые аля инструмента и оснастки, золотые и
серебряные а^я контактов в электронике и др.);
— Полимерные композиты с повышенной прочностью и
износостойкостью (в том числе резины);
— Полировочные составы а^я суперфинишной обработки и
хонингования;
— Получаемые частичным спеканием в статических условиях
пористые микропорошки, которые используются как мягкий
абразив (аая текстурирования поверхности магнитных
носителей), как сорбент с нанопорами, как катализатор.
— Абразивные поликристаллические микропорошки (типа
Mypolex).
Смесь алмазных микропорошков с УДА может быть
использована а^я производства спеканием износостойких волок а^я получения
стальной проволоки (например, а^я корда автопокрышек).
— Электронная полевая эмиссия в вакууме, в которой
центрами эмиссии являются частицы УДА. Строение частиц идеально
подходит а^я такой эмиссии: теплоотводящее диэлектрическое
ядро и нагреваемая током оболочка. Успех в этих исследованиях
позволит создать устройства а^я передачи и приёма
изображений с увеличенной в миллионы раз разрешающей способностью.
Здесь главные проблемы - диспергирование частиц и их
коммутация.
— Создание новых биоактивных препаратов и лекарств на
основе водных и спиртовых суспензий УДА с модифицированной
поверхностью: антиоксиданты, противовирусные и противоми-
кробные препараты (например, УДА как носитель антибиотиков
в добавках в корм животных), средства, нормализующие работу
754
желудка и кишечника, онкологические препараты,
флюоресцирующие маркеры и др.
Медицинские и биологические применения очень
перспективны, хотя серьёзные исследования в этом направлении ещё впереди.
Предварительно показано, что в отношении человека УДА
безвреден и биологически совместим.
Значительно улучшается качество CVD алмазных плёнок, если
перед осаждением на подложку нанести частицы УДА, служащие
зародышами.
Всегда при добавлении в материалы УДА играет роль мощного
структурообразователя, обеспечивая дисперсионное упрочнение,
повышение твердости и износостойкости.
К началу 21 века УДА получило промышленное применение
только в гальванике (где потребление УДА небольшое - 200 - 500 кг
в год). В производстве масел и смазок, а также fi^ полирования УДА
прошли опытно - промышленное применение и апробацию.
По-видимому, в 21 веке промышленость будет использовать
УДА двух видов: УДА, не очищенные от sp2 углерода (АШ), и
модифицированные УДА.
Получению максимального соотношения цена/качество /^ая
изделий и материалов с УДА способствуют следующие причины:
— простая технология синтеза УДА позволяет легко создать
промышленное производство с низкой себестоимостью УДА,
которая определяется, в основном, стоимостью ВВ;
— во многих известных применений УДА допустимо
использовать неочищенную исходную шихту, которая в 2 - 4 раза дешевле
очищенного УДА;
— положительный эффект достигается при введении в материал
малых добавок УДА, как правило, в пределах 0,5—3%.
Тормозит промышленное применение УДА , в основном,
трудность диспергирования агрегатов и высокая цена очищенного и
модифицированного сырья. Рынок наноалмазного сырья пока не
сформирован. Существующие мелкие производители изготовляют
не более тонны АШ в год, что нельзя назвать промышленным
производством. Прогнозируемое потребление АШ ^ая полимеров, ре-
755
зин, полирования, масел и смазок составляет десятки тонн в год. Для
большинства применений ещё не найдено оптимальное качество
УДА, обеспечивающее максимальное увеличение эксплуатационных
свойств изделий с УДА.
В качестве примера требований, прдъявляемых
промышленностью к качеству УДА, приведём требования к УДА аля полирования,
сформулированные в [122]:
— УДА должны быть хорошо отфракционированы, например,
фракции 0-20 нм, 20 - 50 нм и т.д.;
— УДА должны сохраняться в водных суспензиях;
— должна быть хорошая воспроизводимость от партии к
партии физико-химических свойств УДА;
— УДА не должны содержать химических примесей, что важно
для микроэлектроники;
— по цене УДА должны быть сопоставимы или быть ниже цены
промышленных микропошков алмаза;
— с перечисленными требованиями УДА должны выпускаться
в объёме несколько тонн в год.
16.11. Графитизация УД А
16.11.1. Кинетика графитизации
Температура начала графитизации и её кинетика определяет
термостойкость УДА, которая важна как аля анализа возможных потерь
УДА в результате различных окислительных и восстановительных
термообработок, так и ^ая ряда применений УДА. Целенаправленно
изменяя степень графитизации, можно получать различные sp3/sp2
нанокомпозиции.
Основные результаты исследований графитизации алмаза и УДА
следующие [14,88—92].
1. Температура начала графитизации снижается с уменьшением
размера частиц алмаза и наименьшая аля УДА. Но как она зависит
от размера частиц УДА (или удельной поверхности) не
исследовано.
756
2. Графитизация всегда начинается с поверхности алмаза,
подчиняется закону Аррениуса, но имеет разную кинетику:
а) в области низких температур (1300—1900 К) энергия
активации мала (45 kkal/mol), и поверхность алмаза трансформируется
в графит без разрыва С—С связей у алмаза; линейная скорость
графитизации мала и при 1800 К равна 1 nm/h;
б) в области высоких температур (больше температуры Дебая
/^ля алмаза, равной 1910 К) энергия активация велика (252 kkal/
mol), графитизация идёт с разрывом С-С связей у алмаза; резко
увеличивается линейная скорость графитизации: при 2000 К она равна
1000nms/h[90].
3. На температуру и скорость графитизации огромное
каталитическое влияние оказывает даже ничтожное содержание
кислорода или водорода в атмосфере вокруг УДА и на поверхности частиц.
Кроме того, при этом меняется и структура образующегося
графита.
Кинетика изотермической графитизации может быть описана
на основании модели уменьшающейся сферы [90], согласно которой
граница алмаз — графит движется от поверхности сферических
частиц по радиусу к их центру одновременно у всех частиц и с
постоянной линейной скоростью Ц.п(Т), зависящей только от температуры.
В рамках этой модели объём образовавшегося графита
относительно исходного объёма алмаза v /v^ можно рассчитать с помощью
следующего выражения:
vJvdia = k,SDtSlvdia (16.7)
где, t — время графитизации при данной температуре, S —
удельная поверхность исходного УДА.
Для одиночных сферических частиц УДА S=6/pQd, где
р0 =3.07 g/cm3 [90], d — диаметр частицы. Поскольку в УДА
имеется распределение частиц по их диаметру и практически все частицы
в той или иной степени связаны, то можно оперировать в расчётах
только некоторым эквивалентным диаметром частиц: de = 6/(р0 S ),
где Sex — измеренная удельная поверхность аая данного порошка
УДА, полученного в данных условиях синтеза и очистки.
Цельный объём порошка УДА vd = 1/ р00, где р00 = 0,4 g/cm3 —
насыпная плотность сухого порошка УДА [14]. Подставляя эти
значения в (16.7), получим выражение а^я расчёта степени объёмной
графитизации в зависимости от температуры, времени и размера
частиц УДА [65]:
VvA = ek!№pJ(p0 d) = 0,78 kHn{T)tlde (16.8)
Из (16.8) видно, что судить о величине температуры начала
графитизации Т г можно, только задаваясь временем графитизации и
минимальным содержанием sp2 углерода в УДА, которое
обнаруживается данной методикой. Чем меньше время выдержки при каждой
температуре и меньше чувствительность используемой методики,
тем выше получаемая величина Т
Примем, что минимальное содержание sp2 углерода в УДА,
надёжно определяемое современными методами, составляет 0,2%.
Тогда согласно (2) время аля получения v r/vdia = 0,002 можно
рассчитать следующим образом:
(=0,0026 dJklin(T) (16.9)
Используя данные [93], а^я расчёта величины Ц.п (Т) нами
получена следующая линейная зависимость:
log Ц.п(Т) = -0,985(104 /Т-5,55) (16.10)
Скорость графитизации определена в опытах в интервале
температур 1420—1800 К, т.е. без влияния кислорода, но а^я какой-то
неизвестной степени связности частиц УДА. Кроме того, при
измерениях в [93] предполагается , что величина Ц.п (Т) постоянна и не
зависит от размера частиц.
Выражения (16.8), (16.9) и (16.10) определяют зависимость t (Т, dj.
Эта зависимость в интервале Т = 1200— 1800 К показана на рис. 16.7.
Как видно, время получения 0,2%-й графитизации УДА резко
увеличивается с уменьшением температуры, что определяется уменьшением
в 1000 раз линейной скорости графитизации в этом интервале
температур.
На рис. 16.7 также показана зависимость степени графитизации
УДА от температуры при условии часто используемой изотермической
758
выдержки в 1 час. При такой выдержке заметить графитизацию (без
влияния кислорода) при Т< 1500 К очень трудно. За 1 час выдержки
при 1400 К на поверхности УДА формируется только 1—2
графитовых слоя, а за час при 1800 К графитизируется ~85% УДА [90].
Большую зависимость
результатов измерений степени
графитизации УДА от
незначительных изменений условий
опытов можно объяснить
наличием кислорода на поверхности
частиц УДА, который
полностью удаляется в глубоком
вакууме только при температурах
начала графитизации. При низких
температурах (1000—1300 К)
кислород ещё остаётся,
поэтому его влияние на скорость
графитизации больше, чем после
высокотемпературного отжига
в вакууме. Например,
сравнение зависимости на рис. 16.7 с
результатами опытов автора по
графитизации УДА в
герметичной ампуле при 1173 К (на 10%
после выдержки 5 час.) [14]
показывает, что наличие
кислорода на поверхности УДА ускоряет графитизацию в 20 раз. Разными
авторами появление в УДА sp2 углерода фиксировалось после нагрева
до 943 К, до 1003 К, до 1173 К [90]. Образцы УДА нагревались нами
в токе водорода до 1050 С с выдержкой 2 часа. В результате в 4—6 раз
увеличилось содержание в УДА неалмазных форм углерода [14]
Впервые обнаруженная нами 5%-я графитизация УДА после
22-х лет его хранения в нормальных условиях [14] показывает, что в
сравнении с расчётом по (16.8) при 300К кислород ускоряет
графитизацию на три порядка.
Рис 16.7. Кинетика графитизации.
Сплошные линии — зависимость от
температуры времени изотермической
выдержки, необходимой для получения
0,2 %-й графитизации УДА
Штриховые линии — зависимость от
температуры степени графитизации
при изо- термической выдержке 1 час.
!, 2,3 — расчёт для диаметров частиц
УДА, равных 3,5 и 10 nms
соответственно
Как видно из (16.8), уменьшение размера частиц УДА в процессе
графитизации приводит к ускорению графитизации.
Таким образом, проделанный анализ показывает, что процесс
графитизации УДА многофункционален и не поддаётся простому
описанию, в основном, благодаря неопределённому влиянию
кислорода и связности частиц. Кроме того, фиксация начала
графитизации усложняется тем, что при низких температурах образуется
аморфный sp2 углерод, тесно связанный с алмазным ядром.
Интересен результат графитизации УДА при температурах
1400—1800 С, значительно выше температур начала графитизации
[92]. Из УДА получена новая луковичная структура графита,
состоящая из 7-8 вложенных друг в друга замкнутых концентрических
оболочек. Оболочки представляют собой графитоподобные сетки в
форме полиэдров со взаимной ориентацией. Расстояние между
оболочками равно 0,35 нм. Как и а^я кластера С^ образование
оболочек объясняется стремлением системы к минимуму поверхностной
энергии за счет замыкания углеродных связей. Для создания таких
оболочек требуется определенная тепловая энергия, поскольку
синтез фуллеренов идет в узком диапазоне температур (2100 С). По-
видимому, для более низких температур энергии недостаточно и на
поверхности алмазного ядра образуются только отдельные
незамкнутые фрагменты графитовых слоев.
16.11.2. Термодинамическая оценка температуры
начала графитизации
Рассмотрим графитизацию УДА с позиций термодинамики, без
учёта её кинетики. Как показано выше, графитизация - термически
активируемый процесс, и начало графитизации на границе
гистерезиса фазового превращения алмаз - графит определяется
температурой алмаза или его энтальпией EQ (Т). Значения EQ (Т) аля
массивного алмаза рассчитывались в приближении Дебая с температурой
Дебая, равной 2000 К. Для совершенного массивного
монокристалла алмаза поверхностная графитизация начинается при Т = 1800 К,
или при расчётной величине EQ(Tr) = 32,3 kj/mol.
Энтальпия алмазных наночастиц Е больше, чем у
монокристалла алмаза, на величину поверхностной энергии Es:
760
EyJT,S) = E0(T) + E:
(16.11)
Оценим температуру Т г начала графитизации УДА, исходя из
предположения, что она определяется только величиной энтальпии
УДА, которая в начале графитизации такая же, как у монокристалла,
т.е. Еу (Т, S) = 32,3 kj/mol. Тогда температура начала
графитизации определится из следующего выражения:
£0(7;) = 32,3-£s (16.12)
Согласно [46], поверхностная энергия Es в объёме одного моля
зависит от числа атомов п в сферической частице УДА следующим
образом :
Е3=Е{(пУ» (16.13)
где Ej = 293 Kj/mol - удельная поверхностная энергия алмаза в
расчёте на один атом.
Определив значения Es, по (16.13), из (16.12) находим
соответствующие значения EQ (Т г) и по ним - значения температуры начала
графитизации Тг в функции размера частиц УДА. Результаты
расчётов приведены в табл. 16.15
Таблица1б.15. Результаты расчёта температуры начала графитизации
частиц УДА
d, nms
S,m2/g
n (atoms)
Es, kj/mol
ВДг),
kj/mol
Tgr,K
2,01
950
969
29,6
2,7
250
3,01
635
2925
20,46
11,8
870
4,02
475
6545
15,7
16,6
1110
4,78
400
10660
13,3
19,0
1220
7,04
271
32509
9,2
23,1
1410
9,3
205
73150
7,0
25,3
1510
10,56
181
105995
6,2
26,1
1540
Полученная зависимость T (d) показана на рис. 16.8.
Как видно из табл. 16.15, с уменьшением размера частиц УДА
или с увеличением удельной поверхности УДА расчётная температура
начала графитизации частиц уменьшается с 1800 К аая монокристалла
до 870 К аля УДА с частицами диаметром 3 nms.
После разгрузки
температуры ПД, равные
1000—860 К,
практически совпадают с
расчётными температурами начала
поверхностной
графитизации частиц УДА с
размерами 3 nms. А частицы
с размерами 2 nms и
меньше в этих условиях могут
графитизироваться
полностью. По-видимому, sp2
оболочки у частиц УДА
образуются сразу после
разгрузки как результат
частичной графитизации.
Кроме того, из
полученных данных следует,
что сам факт разрушения
агломератов с меньшей удельной поверхностью до получения
одиночных частиц размером 2—4 нм может приводить к началу
графитизации.
16.11.3. Графитизация и окисление наноалмазов
Из рис. 16.8 видно, что температуры начала окисления на
воздухе алмазных микропорошков (см. табл.16.12 [14].) сравнимы с
расчётными значениями температуры начала графитизации частиц
УДА с размером частиц 2—4 nms. При окислении УДА на воздухе
каталитическое влияние кислорода может на порядки ускорить гра-
фитизацию, что позволяет по-новому анализировать и объяснять
результаты опытов по окислению УДА [93] с учётом их
графитизации.
Кроме того, известно, что графит, осаждённый на поверхность
алмаза, начинает окисляться при меньших температурах, чем
алмаз, и при Т< 850 К окисляется быстрее алмаза [94]. Согласно [95]
it a rtm$
Рис. 16.8. Зависимости от диаметра частиц
УДА и их удельной поверхности:
температуры начала окисления — 1 [14]
и температуры начала графитизации:
2 — для одиночных частиц и 3 — для
связанных частиц. 4 — диапазон результатов
измерений температуры начала
графитизации (отнесён к среднему размеру частиц
4 nms). Пунктиром показан расчёт
температуры начала графитизации, сделанный
в [71] с учётом sp2 оболочки у частиц УДД
762
температура начала окисления алмазного порошка АСМ 3/2 равна
756 К, а графита — 723—733 К.
По-видимому, при окислении УДА на воздухе при температурах
~ 800 К [93] окисляется не алмаз, а аморфная sp2 оболочка частиц
УДА, которая по мере её газификации непрерывно
воспроизводится за счёт поверхностной графитизации, ускоряемой кислородом
воздуха. При этом кинетика окисления определяется кинетикой
графитизации. Кроме влияния кислорода, скорость графитизации
растёт благодаря уменьшению размера алмазного ядра (см.(1б.8)).
При определённой степени окисления (по потере массы УДА),
когда алмазное ядро данной частицы становится меньше ~ 4 nms,
скорость графитизации возрастает настолько, что приводит к
быстрой графитизации всего ядра частицы. Переход от частичной к
полной графитизации частицы никак не меняет ни режим
окисления, ни массу УДА, и в экспериментах по окислению это не
фиксируется. В результате получается смесь частиц УДА с алмазными
ядрами >4 nms и сажи с большей удельной поверхностью. Поэтому
при больших степенях окисления удельная поверхность образцов
увеличивается и становится больше значений, рассчитанных по
диаметру частицы [93].
Таким образом, минимальный устойчивый размер частиц на-
ноалмазов определяется условиями, в которых они находятся или
находились (температура, давление, наличие кислорода). Поэтому в
различных проводимых с УДА исследованиях надо учитывать всю
предыдущую историю образцов УДА, в которой, возможно,
уничтожались «маленькие» наноалмазы. Например, такие процессы,
как «сухой» синтез УДА с высокими остаточными температурами
в взрывной камере малого объёма (до 1400К) [96]), очистка УДА
окислителями или водородом, разрушение пористых
поликристаллов УДА с увеличением удельной поверхности.
Результаты наших расчётов позволяют а^я каждого вида
окислительной или восстановительной термообработки УДА оценить
минимальный размер частиц УДА, меньше которого все частицы будут
графитизированы (см. табл. 16.16 [65]).
763
Таблица 16.16. Минимальные размеры частиц УДА после различных
термообработок
Kinds of heat
treatment
Temperature,°C
Min d,nms
Ozone
cleaning
130-150
2.5
Acid
cleaning
220-260
3
Oxidation
on air
430-530
3
Oxidation
by water
650
3.5
Treatment
by
hydrogen
750-850
4
16.12. О плавлении детонационных наноалмазов
в ударной волне
Эксперименты по плавлению наноалмазов ударным сжатием
представляют интерес аля получения поликристаллов с
наноструктурой или даже монокристаллов [14,99].
В разделе 16.3 было показано, что влияние на плавление
поверхностной энергии частиц наноалмаза приводит к заметному
снижению их температуры плавления (см.рис.16.3) [48,49]. Для
наименьшего возможного размера наноалмаза, равного 1 nm, температура
плавления вдвое ниже, чем у массивного алмаза.
Но с увеличением размеров частиц температура плавления
быстро растёт и а^я типичного размера в 4 nm она всего на 7% меньше,
чем у монокристалла.
В процессе плавления ударной волной частицы наноалмазов
сливаются, и при этом выделяется поверхностная энергия. В этом
случае энергия УВ (Ен) расходуется на нагрев наноалмазных частиц
до температуры плавления (Ет) и на плавление (X), но при этом
требуемая энергия меньше на величину выделяющейся при слиянии
частиц поверхностной энергии (Е):
EH(d) = 490,5pJy00-v0) = Em(d) + X(d)-Es(d) (16.14)
Рассмотрим зависимости составляющих (16.14) от размера
частиц наноалмазов в диапазоне d = 2—8 nm.
1. Тепловая энергия Em(d) определяется по (4.14) температурой
плавления по (16.4), считая Т^ = 4470 К (как в тройной точке):
E(d) = 924 + 1,978 {2235 [1 + (1-1/</)°'5]-1000} (16.15)
764
2. Теплоту плавления \ = AS(d) Tm(d) рассчитываем с учётом
структуры частицы наноалмазов: сферическое алмазное ядро
покрыто аморфной оболочкой толщиной 0,4 nm [20]. Энтропию
аморфной оболочки принимаем такой же, как у расплава. Скачок
энтропии при плавлении считаем постоянным и равным
значению в тройной точке, причём он будет относиться только к ядру
частицы диаметром (d - 0,8) nm. Получаем следующее
выражение:
X{d) = [1,6 (d-0.8)3 Щ 2250 [1 + (l-l/d)°>5] (16.16)
3. Поверхностная энергия сферической частицы определяется
выражением Es = 6<j/pd, где аая алмаза а = 5,3 10"4J/cm2 [95], А^я
ядра частицы наноалмазов р = 3,51 g/cm3. Расчётная формула
получает следующий вид:
Es = 9060/J (Я в Jig, d в nm) (16.17)
4. Рассчитав с помощью (16.15), (16.16) и (16.17) все три
составляющие правой части (16.14), получим значения энергии ударной
волны EH(d).
Результаты расчётов энергетических параметров плавления
наноалмазов приведены в табл. 16.17.
Таблица 16.17. Энергетические параметры плавления наноалмазов
d, nm
Tm(d), К
AS, J/g
К kJ/g
Es, kJ/g
Em, kJ/g
EH, kJ/g
1,4
3430
0.126
0.43
6.47
5.73
-0.31
2
3815
0.346
1.32
4.53
6.49
3.28
3
4059
0.630
2.56
3.02
6.98
6.52
4
4170
0.819
3.42
2.27
7.19
8.34
5
4234
0.950
4.02
1.81
7.32
9.53
6
4275
1.040
4.45
1.51
7.40
10.34
8
4326
1.160
5.02
1.13
7.50
11.39
765
Рис. 16.9. Зависимости давления окончания плавления от начальной плотности
и от размера частиц наноалмазов. Пунктир - та же зависимость,
но для микропорошков алмаза. Цифры у линий - размер частиц в nm.
Задавая ^ая каждого размера частиц, различные значения v00, с
помощью (16.14) получим соответствующие значения давлений р
плавления наноалмазов в ударной волне:
рт = [EJd)+W - Es (d)]/490,5 (v^-v^ (16.18)
Рассчитанные таким образом зависимости pm (d, р00) приведены
на рис. 16.9.
Отметим некоторые особенности плавления наноалмазов.
1. С уменьшением размера частиц детонационных наноалмазов
уменьшаются величины теплоты плавления и энергии нагрева до
температуры плавления, но растёт поверхностная энергия,
выделяемая при слиянии расплавленных частиц (см. табл. 16.17). В
результате расчётное значение давления плавления наноалмазов вдвое
меньше, чем у обычных алмазных порошков и, кроме того,
снижается в ~ 4 раза при уменьшении частиц от 8 до 2 nm (см. рис. 16.9).
Следовательно, более перспективны попытки расплавить наноалма-
зы с наименьшими частицами.
766
2. Расчётная энергия УВ, требуемая ^ая плавления наноалмазов
при d = 1,4 nm, практически обращается в ноль (см. табл. 16.17). Это
означает, что а^я наноалмазов с такими малыми частицами возможно
возникновение частично самоподдерживающейся волны плавления
по аналогии с детонационной волной. Как и в детонации,
сжимающая наноалмазы ударная волна определённой начальной амплитуды
инициирует плавление. Но затем ^^я поддержания этого режима
нужна слабая УВ или просто изэнтропическое сжатие с массовой
скоростью, достаточной аля обеспечения слияния расплавленных
частиц и компенсирующей уменьшение удельного объёма порошка.
Отметим, что такой режим плавления возможен только
теоретически, в рамках наших расчётов, поскольку частицы детонационных
наноалмазов менее 1,8 nm не образуются [35]. Однако, этот режим
может существовать ^ая наноалмазов с толщиной аморфной
оболочки, большей 0,4 nm.
3. Благодаря малой теплоте плавления, давления начала и
окончания плавления близки, т.е. у наноалмазов смесевой участок на
ударной адиабате меньше, чем у обычных порошков алмаза.
16.13. Эксперименты по спеканию наноалмазов
Кинетика спекания алмазных порошков или кинетика
уменьшения пористости 9 под давлением описывается следующим
соотношением [100]:
In0/00 = -3pt/4fi, (16.19)
где 90 - начальная пористость, р - давление, t - время спекания,
у) - эффективная вязкость при данной температуре спекания.
Как видно, кинетика спекания зависит от начальной пористости.
Требуемое аая хорошего спекания значение pt можно получить,
увеличив давление и уменьшив время, что и происходит при ударном
сжатии.
Существует оптимальная температура спекания, при которой
получаемый поликристалл алмаза имеет максимальные твёрдость
и износостойкость. Для статического давления 10 ГПа оптимальна
температура 2300 - 2500 К. При меньших давлениях и температурах
свойства поликристаллов снижаются за счёт влияния пористости, а
при больших температурах - за счёт возрастающей графитизации.
Задача спекания наноалмазов как в статических условиях, так и в
условиях ударно-волнового сжатия усложняется следующим.
1. На поверхности частиц присутствуют аморфный углерод,
примеси в виде воды.и различных радикалов, в частности, содержащих
кислород, который сильно ускоряет графитизацию.
2. Необходимая аая спекания пластическая деформация частиц
затрудняется высокой прочностью алмазных ядер у наночастиц.
Повидимому, поэтому а^я спекания давления в 8 - 9 ГПа
недостаточно [101].
3. Порошки наноалмазов очень плохо компактируются. Так,
прямое прессование при статическом давлении 8 ГПа увеличивает
их плотность только до 1.8 г/см3 [101]. Мешает противодавление
адсорбированных газов [129].
Сложность спекания УДА отражает общую проблему компак-
тирования любых нанопорошков. Например, а^я частиц 5 нм и
толщине межзёренных границ 1 нм в объёме границ будет 49% всех
атомов [123]. Из них большая часть относится к разного рода
примесям, ослабляющим прочность границ.
Далее дан краткий обзор результатов экспериментов с наноалма-
зами.
1. Спеканием УДА в статических условиях не удаётся получить
прочные беспористые поликристаллы [14,101,124,129,130]. При
4,5-7 ГПа и 1400С получают пористые спёки [124]. После
дробления и классификации по размерам порошки из пористых частиц
могут использоваться как мягкий абразив, как сорбенты и
биофильтры.
В [130] исследована спекаемость УДА, модифицированных
добавлением В, Ti, Si (твердость спёков 25 - 30 ГПа), A1N (твердость
13-20 ГПа).
Основные закономерности процесса спекания под давлением
< 10 ГПа следующие [14].
— Скорость уплотнения максимальна в первые 10 с, а далее
плотность медленно растёт до 2,9 г/см3 при 1500С; при 2000С,
768
наоборот, плотность быстро падает. Оптимальное время
спекания - 36 с.
— Начиная с 1000С и выше по границам агрегатов (в нанопо-
рах) развивается графитизация.
— Эволюция структурного состояния УДА в процессе
спекания типична для спекания любых УДП с многоуровненвой
структурой (зерно - агрегат 1 - агрегат 11). Вначале идёт
спекание внутри плотных агрегатов 1. При 8 ГПа и 1500С в УДА
спекается только 20% агрегатов 1, а при 2000С появляются
монокристальные зёрна (10-30 нм).
2. Названные выше трудности спекания наноалмазов не
существуют в условиях синтеза УДА, где частицы наноалмазов
рождаются в виде «чистеньких и голеньких» нанокапель при температурах
выше ЗОООК. Для их спекания нужно только обеспечить достаточно
большую величину pt.
В 1986—1988 гг нами проведены эксперименты по синтезу
наноалмазов детонацией зарядов из ТГ40 массой 5—20 кг в массивных
оболочках из воды. Впервые обнаружены поликристаллы
наноалмазов с абразивными свойствами, а также монокристаллы лонсдейлита
размером до 10 мкм [14]. В 1991 г. аая синтеза наноалмазов был
использован заряд из ТГ40 массой 140 кг в водяной оболочке и также
были получены поликристаллы размером до 85 мкм [53]. Таким
образом, показано, что кроме синтеза наноалмазов, в плотной газовой
фазе (в продуктах детонации) протекают процессы и спекания на-
ночастиц, и кристаллизации монокристаллов.
Эти процессы наиболее вероятны вблизи границы с оболочкой,
где газовые продукты детонации тормозятся сильнее, чем во много
раз более массивные углеродные кластеры и нанокапли. В
результате в этой зоне увеличивается концентрация наночастиц и частота их
столкновений с образованием ковалентных связей. Если нанокапли
полностью сливаются и успевают кристаллизоваться при
охлаждении водой при температурах меньше 1600К, то образуются
монокристаллы лонсдейлита. Безусловно, все эти процессы требуют
достаточно большого времени существования в продуктах детонации
давления более ~10 ГПа (десятки мкс). По-видимому, используя за-
769
ряды и оболочки большой массы, оптимальные геометрию и состав
зарядов, кумулятивные эффекты, можно повысить в синтезируемых
наноалмазах содержание ценных абразивных поликристаллических
микрочастиц.
3. Опыты по динамическому компактированию порошков на-
ноалмазов с плотность 0.5—1.0 г/см3 давлением 11 ГПа показали,
что сжатие таких порошков не имеет ударного характера,
давление нарастает длительное время (20 мкс), и зона сжатия
охватывает многие тысячи частиц [102,103], Многоступенчатое сжатие
порошка наноалмазов объясняется существованием в нём
конгломератов различной плотности и прочности, выступающих как
объекты уплотнения, а также лёгкими примесями на поверхности
частиц. Получены частицы с размерами 1—200 мкм и плотностью
3.1—3,2 г/см3 [103].
4. Ещё в 1965 г. нами проведена серия опытов по сжатию смеси
порошков наноалмазов и свинца (как охладителя) в
цилиндрических капсулах зарядами из ТГ50 [14]. Во всех опытах зафиксирована
графитизация УДА, которая прежде всего наблюдается в зоне
однократного сжатия (в волне Маха), где давления более 20 ГПа и
температура конгломератов наноалмазов с плотностью 0.6 г /см3 более
7000К [14]. В такой же постановке нами проведены опыты с
графитом разной пористости.
Во всех опытах только в зоне волны Маха графит полностью
превращался в аморфный углерод, по-видимому, после плавления, или
после превращения в алмаз и затем его графитизации.
5. Из неудачных опытов 1965 г. нами были сделаны выводы о
необходимости увеличивать исходную плотность гранул наноалмазов,
удалять поверхностные примеси на частицах наноалмазов,
увеличивать и давление, и время сжатия, и объём однородного сжатия (без
волн Маха).
В 1994 г. нами были разработаны технологии очистки
наноалмазов водородом и приготовления из наноалмазоа гранул
плотностью 1,8—2,7 g/cm3. Смесь таких гранул со свинцом была сжата во
взрывной камере давлением до 100 ГПа, возникающим при
лобовом столкновении двух плоских УВ, которые создавались синхрон-
770
ной встречной детонацией двух зарядов из ТГ40 массой по 5 кг,
заключённых в ледяную оболочку [14,99,104]. В результате получены
поликристаллы и неожиданно-единичные монокристаллы алмаза в
виде прозрачных октаэдров с размером 0,6 мм. По-видимому, это
результат полного расплавления гранулы и кристаллизации под
давлением при относительно медленном охлаждении расплавленным
свинцом.
16.14. Образование УДА и параметры детонации
Обычно зависимость D (р) для ВВ считается линейной.
Еще в 1961 г. у ТНТ нарушение линейной зависимости D(p),
при р = 1,55 г/см3 были измерены в [97], но эти результаты не были
правильно объяснены и не были приняты во внимание. Только в
1987 г. СВ. Першин (ИХФ), уже зная об образовании в ПД УДА,
повторил измерения D (р) и четко зафиксировал изломы на D(p) —
зависимости аая ряда ВВ [38,98].
Начиная с р = 1,55 г/см3 с ростом плотности D (р) - зависимость
все больше отклоняется от первоначальной линии, что объяснялось
ростом доли алмаза в ПД с повышением давления детонации. На
— зависимости зарегистрированы 1-й и 2-й изломы,
которые объяснялись началом и окончанием образования алмаза в ЗХР.
Давления в точке Жуге, при которых наблюдаются изломы в D(p) -
зависимости, приведены в табл. 16.18 [38].
Таблица 16.18. Давления в точке Жуге в изломах
D (р) — зависимостей
ВВ
ТНТ
ТГ75
ТГ50
Пикриновая кислота
Тетрил
р—v адиабата непористого графита
Давление, ГПа
1-й излом
16,6
18,6
18,0
19,0
20—21
20
2-й излом
-
19,5
20,5
-
-
40
Dp)
771
Согласно излагаемым в этой главе представлениям, эти изломы
обусловлены пересечением С—J давления линии тройных точек и с
переходом в область жидкого sp3 наноуглерода на фазовой
диаграмме. Участок между изломами - это смесь нанографита и жидкого на-
ноалмаза (в ЗХР температура растёт, и кристаллизация
невозможна).
Параметры C-J аая ТНТ с плотностью 1,55 г/см3 находятся
вблизи линии тройных точек (р=1б,5 ГПа). Поэтому излом D(p) -
зависимости, наблюдаемый при этой плотности (р = 16,6 ГПа) [38],
обусловлен началом замены сажевых наночастиц в зоне химреакции
на sp3 кластеры или нанокапли sp3 углерода, но полной замены не
достигается. Для сплавов ТГ параметры С - J находятся глубоко в
области жидкого наноуглерода, поэтому наблюдается и второй
излом (р=20,5 ГПа), означающий окончание такой замены или
конденсацию углерода в ЗХР полностью в виде sp3 кластеров.
Хорошее описание изломов с помощью УРС алмаза и графита
[36], можно объяснить близостью УРС алмаза и жидкого наноалма-
за, на что указывает невозможность регистрации плавления наноал-
маза по виду ударной адиабаты [14]. Поэтому расчёты параметров
детонации ВВ не должны измениться при замене УДА на жидкий
sp3 наноуглерод.
Таким образом, излом D(p) зависимости аналогичен излому
ударной адиабаты при пересечении линии плавления.
Изучение кинетики формирования УДА с помощью
малоугольного Re излучения от синхротрона 25 keV при экспозиции 1нс
показало, что УДА не образуются на фронте и за фронтом
детонации в течение 0,3 - 0,5 мкс [132, 133]. В [134] предложена физико-
химическая модель синтеза УДА, согласно которой УДА образуются
на изэнтропе П Д.
Литература к главе 16
1. Морохов И.Д., Трусов Л.И., Чижик СП. У^ьтрадисперсные
металлические среды. М.: Атомиздат,1977,с.2б4.
2. Петров Ю.И. Физика малых частиц. М.: Наука, 1982,360с.
772
Петров Ю.И. Кластеры и малые частицы. М.: Наука, 1986,
368с.
Непийко С.А. Физические свойства малых металлических
частиц. Киев: Наукова думка, 1985,248с.
КосолаповаТ.Я., Прилуцкий Э.В. Свойства и применение
дисперсных порошков. Сб. научных трудов. Киев: Наукова думка,
1986, с. 13—20.
Nepijko S.A., Pinpel Е, Wolteradorf Т. Phys.status solidi (а), 1980,
V.6l,N2,p.469.
Фришберг И.В. Свойства и применение дисперсных
порош- ков. Сб. научн. трудов, Киев: «Наукова думка», 1986,
с.З—13.
Сутугин А.Г. Образование аэрозолей при объемной
конденсации быстрого типа. Автореферат дисс. докт. хим. наук,
М.,197б,с.19.
Кипнис А.Я., Михайлова Н.Ф., Померанцева Л.А. Получение,
свойства и применение тонких металлических порошков. Сб.
докладов Всес. конф. Киев: «Наукова думка», 1971.
Борзяк П.Г., Непийко С.А. Свойства и применение
дисперсных порошков. Сб. научн. трудов, Киев: «Наукова думка»,
1986, с.63.
520. Kroto H.W. et al. Nature, 1985, V 318, p. 162.
Елецкий A.B., Смирнов Б.М. УФН, 1991, т.161, № 7, с.173-
192.
Шпак А. П., Куницкий Ю.А., Лысов В.И. Кластеры и нано-
структурные материалы. Киев, Академпериодика,2002, 539 с.
Даниленко В.В. Синтез и спекание алмаза взрывом. М.
Энергоатомиздат, 2003,272 с.
Gleiter Н. Acta Materialia, 2000, V.48, N1, P. 1 - 29.
Пилянкевич А.Н., Олейник Г.С., Бритун В.Ф. Влияние
высоких давлений на свойства материалов. Сб. научн. трудов ИПМ
АН Украины, Киев, 1999, с.4—22.
Костюков Н.А. ПМТФ,1988,№,с.54—59.
Скороход В.В. Свойства и применение дисперсных порошков.
Сб. научных трудов, Киев, «Наукова думка», 1986, с. 91—98.
773
19. Акимов Г.Я., Бельгейзимер Я.Е. и др. Физика и техника
высоких давлений, 1999, Т.9, № 2, С. 44.
20. Synthesis, Properties and Applications of Ultrananocrystalline
Diamond. Ed. by Dieter M. Gruen, Olga A. Shenderova and
Alexander Ya. Vul. NATO Science Series. — Dordrecht, The
Netherlands: Springer, 2005. - P. 401.
21. Даниленко B.B. ФТТ, 2004, T.46, вып .4, с. 581 - 584.
22. Волков K.B., Даниленко В.В., Елин В.И. ФГВ, 1990,3,123.
23. Волков К.В., Даниленко В.В. и др. «Взрыв, удар,
защита», Информ.бюлл. ИГ СО АН СССР, вып. 17, 1987,
Новосибирск.
24. Ставер A.M., Лямкин А.И. %ътрадисперсные материалы.
Получение и свойства. Межвуз. сб. тр., Красноярск, 1990,
с.З—28.
25. Лямкин А.И., Петров Е.А., Ершов А.П., Сакович Г.В.,
Ставер А.М., Титов В.М. ДАН СССР, 1988, т.302, № 3, с.611-
613.
26. Петрунин В.Ф., Погонин В.А., Саввакин Г.И., Трефилов
В.И.,Порошковая металлургия, 1984, № 2, с.20-24.
27. Van Triel М.Дее F.N. UCRL -Preprint 95839, Livermore, USA,
1986 and J. Appl. Phys., 1987, v. 62, N5, p. 1761.
28. Greiner N.Roy, Philips P. S., Johnson J. D. Nature, 1988, 333 p.
6172.
29. Губин C.A., Одинцов B.B., Пепекин В.И. Хим.физика,
1984, 5,
30. Акимова Л.Н., Губин С.А., Одинцов В.Д., Пепекин В.И. V
Всес. совещ. по детон.. Красноярск, 1991, сб. докл. т.1. с. 14.
31. Даниленко В.В., Трефилов В.И., Даниленко В.Н. Взрывная
камера fiiA^ синтеза сверхтвердых материалов. Патент СССР SU
181329 A3 с приор, от 12.05.91.
32. Баум Ф.А., Станюкович К.П., Шехтер Б.И. Физика взрыва. М.:
Из-во физ-мат. лит., 1975.
33. Андреев К.К., Беляев А.Ф. Теория взрывчатых веществ. М.:
1960
34. Даниленко В.В.. ФГВ, 2005.41. № 5. С. 104 - 116.
35. Титов В.М., Анисичкин В.Ф., Мальков И.Ю. ФГВ, 1989, № 3,
с. 117.
36. Mader S. L. Numerical Modeling of Explosives and Propellants.
Second Edition, CRC Press, 1998, p. 439.
37. Ананьин A.B., Дремин A.H., Канель Г.И. и др. В сб. Детонация.
Критические явления. Физико-химические превращения в
ударных волнах.Черноголовка,1978.
38. Першин СВ., Цаплин Д.Н. V Всес. совещ. по детонации.
Красноярск, 1991. Сб. докл., т.2, с.237-244.
39. В.Ю. Долматов. >^ьтрадисперсные алмазы детонационного
синтеза. Получение, свойства, применение. - СПб. Изд-во
СПбГПУ, 2003.
40. А.Л.Верещагин. Детонационные наноалмазы. Барнаул:
Издательство Алтайского госуд. технич. университета ISBN
5-9257-0012-0,2001,176 с.
41. Ставер А.М., Лямкин А.И. Уилрадисперсные материалы.
Получение и свойства. Межвуз. сб. тр., Красноярск, 1990,
с.З—28.
42. Лямкин А.И., Петров Е.А., Ершов А.П., Сакович Г.В.,
Ставер А.М., Титов В.М. ДАН СССР, 1988, т.302, № 3,
с.611-613.
43. МалковИ.Ю.ФГВ,1994,№5,С155.
44. Gamarnik M.Y. Phys. Rev. В. -1996. - 54, - P. 2150 - 2156.
45. J.A.Viecelli and EH. Ree. J. of Appl. Phys. - 2000. - 88, N 2. —
P. 683—690.
46. J.A. Viecelli, S. Bastea, J.N. Glosli and EH. Ree. J. of Chem. Phys.
2001. -115, N 6. - P. 2730 - 2736.
47. Huang Fenglei, Tong Yi, Yun Shourong. Физика твердого тела.
2004.46. вып. 4. С. 601 - 604.
48. V.V. Danilenko. Proceedings of the NATO Advanced
Research Workshop on Synthesis, Properties and Applications
of Ultrananocrystalline Diamond Edited by D.M. Gruen,
O.A. Shenderova and A.Y. Vul, St. Petersburg, Russia. 7 - 10 June
2004. - Netherlands: Springe, 2005. P. 181 -198.
49. Даниленко B.B.. ФГВ, 2005.41. № 4,. С. 110 - 116.
775
50. Даниленко В.В. Сверхтв. материалы,2006 № 5, с.9 - 24.
51. Даниленко В.В. Физика и техника высокоэнергетической
обработки материалов (Сб. научн. статей). Днепропетровск,
АРТ-ПРЕСС.2007, с.92 - 107.
52. Б.Г. Лобойко, С.Н. Любятинский. ФГВ, 2000,36, № 6, С. 45—
64.
53. Б.А. Выскубенко, В.В. Даниленко. Э.Э. Лин, В.А. Мазанов,
Т.В. Серова, В.И. Сухаренко. А.П. Толочко. ФГВ, 1992, 28,
№ 2, С. 108 -109.
54. Ершов А.П., Куперштох А.Л. ФГВ, 1991, № 2, с.111-117.
55. A. Strachan and Е. М. Kober. J. of Chem. Phys., 2005,122, P. 1.
56. Мальков И.Ю., Филатов Л.И., Титов В.М. и др. ФГВ, 1993,
№4. С. 131.
57. Бэрри Р.С., Смирнов Б.М. ЖЭТФ, 2000,117,3, с.562—570.
58. Куперштох А.Л., Ершов А.П., Медведев Д.А. ФГВ, 1998, №4,
с.102—109.
59. А.П. Ершов, А.Л. Куперштох. Письма в ЖТФ. - 1993. - 19. -
№ 2. с. 76—80.
60. EH. Ree. J. Chem. Phys. - 1986. - 84 (10). - P. 5845 - 5856.
61. Даниленко B.B., Мельникова В.А., Минаков В.Н. Механика
и физика разрушения хрупких материалов. Сб.трудов ИПМ
АН Украины. Киев, 1992, с. 186-189.
62. Bursil L.A., Peng J.L., Praver S. Plasmonresponse and structure of
nanocrystalline diamond powder. // Phil. Mag. A. - 1997. - 74. -
769-781.
63. Kruger A., Kataoka E, Osawa M., Fujino Т., Susuki Y., at al.
Unusually tight aggregation in detonation nanodiamond:
identification and disintegration. // Carbon. - 2005. - A. -
P. 1722 -1730.
64. E. Osawa. 3-th International Symposium «Detonation Nanodia-
monds: Technology, Properties and Applications. Programme &
Abstracts. - St. Petersburg, Russia: 2008. - P. 5.
65. Даниленко B.B.CTM, 2009, №4.
66. Верещагин А.Л., Комаров В.Ф. и др. V Всес. совещание по
детонации. Красноярск, 1991, Сб. докладов, т.1, с.99—103.
776
67. Верещагин А.Л., Ульянова Г.М., др., СТМ, 1990, № 5,
с. 20 -22.
68. Губаревич Т.М., Костюкова Н.М., др. СТМ, 1991, № 5,
с.30-34.
69. Губаревич Т.М., Кулагина Л.С., Ларионова И.С. V Всесоюзное
совещание по детонации. Красноярск, 1991, Сб. докладов, т.1,
с.130-134.
70. Игнатенко А.В., Солохина А.Б., Ирданеева М.В. V Всесоюзное
совещание по детонации. Красноярск, 1991, Сб.докладов, т.1,
с.166.
71. Даниленко В.В. СТМ, 2006, № 6, с.З - 11.
72. Ставер A.M., Лямкин А.И. %ътрадисперсные материалы.
Получение и свойства. Межвуз. сб. тр., Красноярск, 1990,
с.3-28.
73. Петрунин В.Ф., Погонин В.А., Саввакин Г.И., Трефилов В.И.,
Порошковая металлургия, 1984, № 2, с.20-24.
74. Долматов В.Ю. УХН, 2001, т.70 (7), с.607- 626.
75. Труды научного семинара по нанометрическим алмазам. Киев,
апрель 2002. Сверхтвёрдые материалы 2002, №6.
76. Детонационные наноалмазы: получение, свойства и
применения. Труды первого междунар. Симп. Санкт-Петербург,7-
9июля, 2003, ФТТ, 2004, том. 46, вып.4.
77. Proceedings of the NATO Advanced Research Workshop on
Synthesis, Properties and Applications of Ultrananocrystalline
Diamond Edited by D.M.Gruen, O.A.Shenderova and A.Y. Vul,
St. Petersburg, Russia. 7 - 10 June 2004. - Netherlands: Springe,
2005.
78. Алексенский A.E., Байдакова M.B., Буль А.Я., Сиклицкий В.И.
ФТТ,1999,т.41,с.740.
79. Долматов В.Ю. Успехи химии, 2007, т. 76 (4), с. 375 - 397.
80. Губаревич Т.М., Костюкова Н.М. и др. V Всес. совещание по
детонации. Красноярск. 1991 г. Сб.докл., т.1, с. 112-115.
81. Богатырёва Г.П., Маринич М,А. и др., Труды научного
семинара по нанометрическим алмазам. Киев, апрель 2002.
Сверхтвёрдые материалы 2002, №6. с. 10 -15.
82. Жутаева Г.В., Маринич М.А. и др. Там же, с. 55-59.
83. Новиков Н.В., Богатырёва Г.П., Волошин М.Н. и др. СТМ,
2002,№б,с.4-9.
84. Пат.38541А Украина, МПК7 COIB 31/06. Алмазный
порошок и способ его получения. Кирилин К.В., Падалко В.В.
Опубл. 15.05.01,Бюлл.№4.
85. Возняковский А.П., Фуджимура Т. и др. СТМ, 2002, № 6,
с. 22 - 27.
86. Захаров А.А., Семенова О.В. и др. %ътрадисперсные
материалы. Получение и свойства. Межвуз.сборник. Красноярск,
1990,с.181-185.
87. Сакович Г.В., Комаров В.Ф., Петров Е.А. и др. V Всес. совещ.
по детонации. Красноярск, 1991 г. Сб. докл., т.2, с.272-277.
88. Zhao D.S. et al. Diamond and Related Materials, 2002 V.ll,
p.234
89. V.I. Kuznetsov and Yu.V. Butenko Proceedings of the NATO
Advanced Research Workshop on Synthesis, Properties and
Applications of Ultrananocrystalline Diamond Edited by
D.M.Gruen, O. A.Shenderova and A.Y. Vul, St. Petersburg, Russia.
7 - 10 June, 2004. Dordrecht, The Netherlands: Springer, 2005.
P. 199.
90. V.I. Kuznetsov and Yu.V. Butenko Ultrananocrystalline Diamond,
Synthesis, Properties, and Applications. Ed. by Olga L. Shenderova
and Dieter M Gruen. W.Andrew Pulishing, Norwich, New York,
U.S.A.,2006,P.405
91. Yu. VButenko et al. J.Appl.Phys., 2000, v.88, N7, p. 4380.
92. Мальков И.Ю., Титов B.M., Кузнецов В.Д., Чувилин А.Л. ФГВ,
1994, № 1, с. 130-132, а также Chemical Physics Letters, 1994,
222,р.343-348.
93. Гордеев С.К., Корчагина СБ.. Сверхтв. материалы. 2004, № 6,
с. 34.
94. Федосеев Д.В., К.С. Успенская К.С.. Журнал физ. Химии,
1974,XLVlll,№6,c.l528.
95. Физические свойства алмаза: справочник под ред. Н.В.
Новикова., Наукова думка, Киев, 1987,188 с.
778
96. Мазанов В.А. ФТТ, 2004,т. 46, вып. 4. с. 614.
97. Urizar М. J., James Е., Smith L. С. Physics of Fluids, 1961,4,262.
98. Першин СВ. IV Всесоюзное совещание по детонации. 1988.
Телави, Сб. докл., т.1, с.1-5.
99. Даниленко В.В. З^арноволновое спекание наноалмазов //
ФТТ, 2004, Т.46, вып.4, С. 693—697.
100. Новиков Н.В., Федосеев Д.В., Шульженко А.А. и др. Синтез
алмазов. Киев, Наукова думка, 1987.
101. Даниленко В.В., Петруша И.А., Олейник Г.С., Даниленко Н.В.
Эволюция структуры компакта при спекании нанодисперс-
ных алмазов в условиях высоких давлений. // Сверхтв.
материалы, 1999, № 4, С.53 - 61.
102. Скоков В.И., Лин Э.Э., Медведкин В.А., Новиков С.А. О
характере ударной нагрузки при динамическом компактиро-
вании ультрадисперсных алмазов // ФГВ, 1998, Т. 34, № 3,
С.105—106.
103. Лин Э.Э. Импульсное нагружение объектов при сильном
расширении продуктов взрыва твёрдых взрывчатых веществ
(обзор) // ФГВ, 2005, Т. 41, № 3, С. 3—28.
104. Козлов Е.А., Лебедев М.А., Литвинов Б.В. Взрывные
устройства для динамического компактирования и синтеза
материалов // ФГВ, 1993, Т.29, № 2, С. 118—122.
105. Anke Krueger. J. Mater. Chemistry, 2008,18,1485 - 1492.
106. Gordeev S.K., Kruglikova S. Superhard Mater. 2004,6,34.
107. X.Y.Xu, Z.M.Yu, YW. Zhu, B.C. Wang. J.Solid State Chem.,
2005,178(3), 688.
108. O. Shenderova, I. Petrov, J. Walch, et al. Diam. Rel. Mater., 2006,
15(11-12),1799.
109. S. Osswald, G. Yushin, V. Mochalin, et al. JACS, 2006,128
(35),11635.
110. I. Petrov, O. Shenderova, et al. Diam. Rel. Mater. 2007,16,2098 -
2103.
111. D.V. Spitsyn, J.L. Davidson, et al. Diam. Relat. Mater. 2006, 15
296 - 299.
112. T.Jiang and K.Xu. Carbon, 1995, V.33,N 12, p.1663- 1671.
779
113. V.V. Korobkov, LI. Kulakova, B.N. Tarasevich, G.V. Lisichkin.
Diam. Rel. Mater., 2007,16, p. 2129 - 2132.
114. И.И. Кулакова. Ж. Рос. Хим. общ. им Д.ИМенделеева, 2004, т.
XLVIII,N5,c.97-106.
115. Yu Liu, V.N. Khobashesku, N.J. Halas. JACS, 2005,127, 3712 -
3713.
116. O.A. Besedina, A.N. Eremenko, et al. Russ. J. of Appl.Chem.,
2006, V. 79, N 12, p. 1940 - 1942.
117. Kong Xu, Qunji Xue. ФТТ, 2004, т.46, в.4, с. 633 - 634.
118. Vadim Mochalin, Sebastian Osswald, et al. Mat. Res. Soc. Symp.
Proc, 2008, Vol.1039.
119. V N. Mochalin, Yu. Gogotsi. J. Am. Chem. Soc. 2009, 131 (13),
4594-4595.
120. O. Shenderovam T.Tyber, et al. Diam. Rel. Mater. 2007,16,1213 -
1217.
121. H.B. Сироткин, А.П. Возняковский, A.H. Ершова. ФТТ, 2004,
т. 46, в.4.
122. А.С. Артёмов. ФТТ, 2004, т. 46, вып. 4, с. 670 - 678.
123. S.C. Tjong, Haydn Chen. Mater. Science and Engineering, 2004,
R15,p.l-88.
124. G.N. Yushin, S. Osswald, V.I. Padalko, G.P. Bogatyreva, Y. Gogotsi.
Diam. Rel. Mater., 2005,14, p. 1721 - 1729.
125. I.Yu. Mal'kov, V.L. Kuznetsov, et al. Carbon, 1994, V. 12, N5,
p. 873 - 882.
126. Jian Chen, S.Z.Dong, et al. Appl. Phys. Lett., 1999, Vol.74, N24, p.
3651-3653.
127. M. V. Korobov, N.V. Avramenko, et al. j. Phys. Chem. C, 2007,
111,7330-7334.
128. Быстрое инициирование ВВ. Особые режимы детонации.
Сб науч. статей под ред. В.И. Тарханова. Изд-во РФЯЦ-
ВНИИТФ, Снежинск, 1998,168 с. ,,
129. А.А. Бочечка. Сверхтв. Матер., 2002, № 6, с.37 - 42.
130. PA. Vityaz, V.T. Senyut. Phys. Solid State, 2004, Vol.46, N4,
p. 764-766.
131. Eiji Osawa. Diam. Rel. Mater., 2007,16, p. 2018 - 2022.
780
132. Титов В.М.,Толочко Б.П. и др. Joint Intern. Conf. Nanocarbon &
Nanodiamond 2006. Progr. and Book of Abstracts. Sept. 11-15,
2006, St. Petersburg, Russia.
133. Титов В.М.,Толочко Б.П. и др. Diamond and Related Mater. 2007,
V.l6,issuel2,p.2009-2013.
134. Толочко Б.П., Титов B.M. и др. Diamond and Related Mater. 2007,
V.16,issuel2,p.20l4-2017.
781
Научное издание
Даниленко Вячеслав Васильевич
Взрыв: физика, техника, технология
Авторская редакция
Комльютерная верстка Е. А. Морозова
Художник переплета В. В. Дёмкин
Подписано в печать 10.11.2009. Формат 60x90/16.
Бумага офсетная № 1. Усл. печ. л. 49,11. Уч. изд. л. 49,34.
Тираж 400 экз.
ОАО издательство «Энергоатомиздат»,
107031, Москва, ул. Рождественка, д.5/7
Отпечатано в типографии ООО «Галлея-Принт»
УДК 539.2,621.7.044.2
Даниленко В. В. Взрыв: физика, техника, технология. — М.:
Энергоатомиздат, 2009. — 784 с.: ил.
В систематическом виде рассматривается широкий круг вопросов,
связанных со взрывом и использованием его энергии: элементы газовой
динамики и теории ударных волн, уравнения состояния, теория детонации,
кумуляция, фазовые превращения при ударном сжатии,
высокоскоростной удар, методы измерений быстропротекающих процессов, свойства
ВВ, взрывы в различных средах, средства инициирования взрыва, техника
проведения взрывных работ, технологии динамического синтеза и
спекания алмаза, в частности, детонационный синтез ультрадисперсных
алмазов (или детонационных наноалмазов).
Для научных работников, инженеров, технологов,
специализирующихся в области прикладной физики взрыва и взрывных технологий. Может
быть полезна аспирантам и студентам вузов соответствующих
специальностей.
V. V. Danilenko. Explosion: physics, engineering, technology.
In the book in a systematic aspect the broad class of problems, bound with
explosion and using of its energy is considered: elements of gas-dynamics and
theory of shockwaves, equation of state, theory of a detonation, cumulation,
phase changes at a shock compression, high-velocity shock, measurement
methods of high-speed phenomenons, properties of explosive, explosions in
different environments, facilities of initiation of detonation, engineering of
conducting of blastings, know-how of dynamic synthesizing and sintering of
diamond, in particular, detonation synthesizing of ultra dispersed diamonds
(or detonation nanodiamonds).
The book is intended for the students, post-graduate students, physicists,
engineers, technologists specialize in the area of applied physics of explosion
and explosive technologies.
Даниленко Вячеслав Васильевич
wdan@list.ru