ФИЗИКА ВЗРЫВА
издание третье, дополненное и переработанное
Том II
Под редакцией
Л. П. ОРЛЕНКО
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 2004

УДК 532.5, 539.5
Ф84
ББК 24.54
Авторы:
С.Г. Андреев, А.В. Бабкин, Ф.А. Баум, Н.А. Имховик, И.Ф. Кобылкин,
В.И. Колпаков, СВ. Ладов, В.А. Одинцов, Л.П. Орленко, В.Н. Охитин,
В.В. Селиванов, B.C. Соловьев, К.П. Станюкович, В.П. Челышев, Б.И. Шехтер
Физика взрыва / Под ред. Л. П. Орленко. — Изд. 3-е, испр. — В 2 т. Т. 2. — М.:
ФИЗМАТЛИТ, 2004. - 656 с. - ISBN 5-9221-0220-6.
В книге в систематизированном виде излагается комплекс вопросов, касающихся законо-
закономерностей взрывных процессов и действия взрыва в различных средах (газах, жидкостях и
твердых телах). Рассматриваются общие свойства взрывчатых веществ, механизм и условия
их превращения в продукты детонации в зависимости от различных физико-механических
факторов, основные закономерности детонации, параметры взрыва газовых смесей, метание
тел продуктами детонации и формирование осколочных полей, кумуляция, электромагнит-
электромагнитные поля, возникающие при взрыве, условия использования энергии взрывчатых веществ
в промышленности, проблемы моделирования взрывных процессов, а также результаты
численного решения многих задач, связанных с взрывными процессами.
Второй том посвящен формированию осколочных полей, кумуляции, действию взрыва в
твердой среде, электромагнитным полям, сопровождающим взрыв, моделированию взрыв-
взрывных процессов и использованию энергии взрыва в разных областях промышленности.
Книга адресована широкому кругу специалистов, занимающихся физикой взрыва, ас-
аспирантам и студентам старших курсов.
© С.Г. Андреев, А.В. Бабкин, Ф.А. Баум, Н.А. Им-
Имховик, И.Ф. Кобылкин, В.И. Колпаков, СВ. Ла-
Ладов, В.А. Одинцов, Л.П. Орленко, В.Н. Охитин,
В.В. Селиванов, B.C. Соловьев, К.П. Станюкович,
ISBN 5-9221-0220-6 (Том 2)	В.П. Челышев, Б.И. Шехтер, 2002, 2004
ISBN 5-9221-0218-4	© ФИЗМАТЛИТ, 2002, 2004

Оглавление
15.Метание тел продуктами детонации	1
15.1.	Определение импульса взрыва при отражении детонационной волны
от стенки		1
1.	Параметры состояния продуктов взрыва за фронтом ДВ		1
2.	Импульс при отражении ДВ от стенки 		10
15.2.	Определение скорости и законов движения оболочки заряда		23
1.	Максимальная скорость при одномерном метании оболочек		23
2.	Законы движения одномерных оболочек 		26
15.3.	Одномерное метание пластин продуктами детонации 		31
15.4.	Высокоскоростное метание компактных металлических частиц. ...	37
15.5.	Метание осесимметричных оболочек продуктами детонации		42
15.6.	Пространственные (трехмерные) задачи метания		58
16.Осколочное действие взрывных систем	62
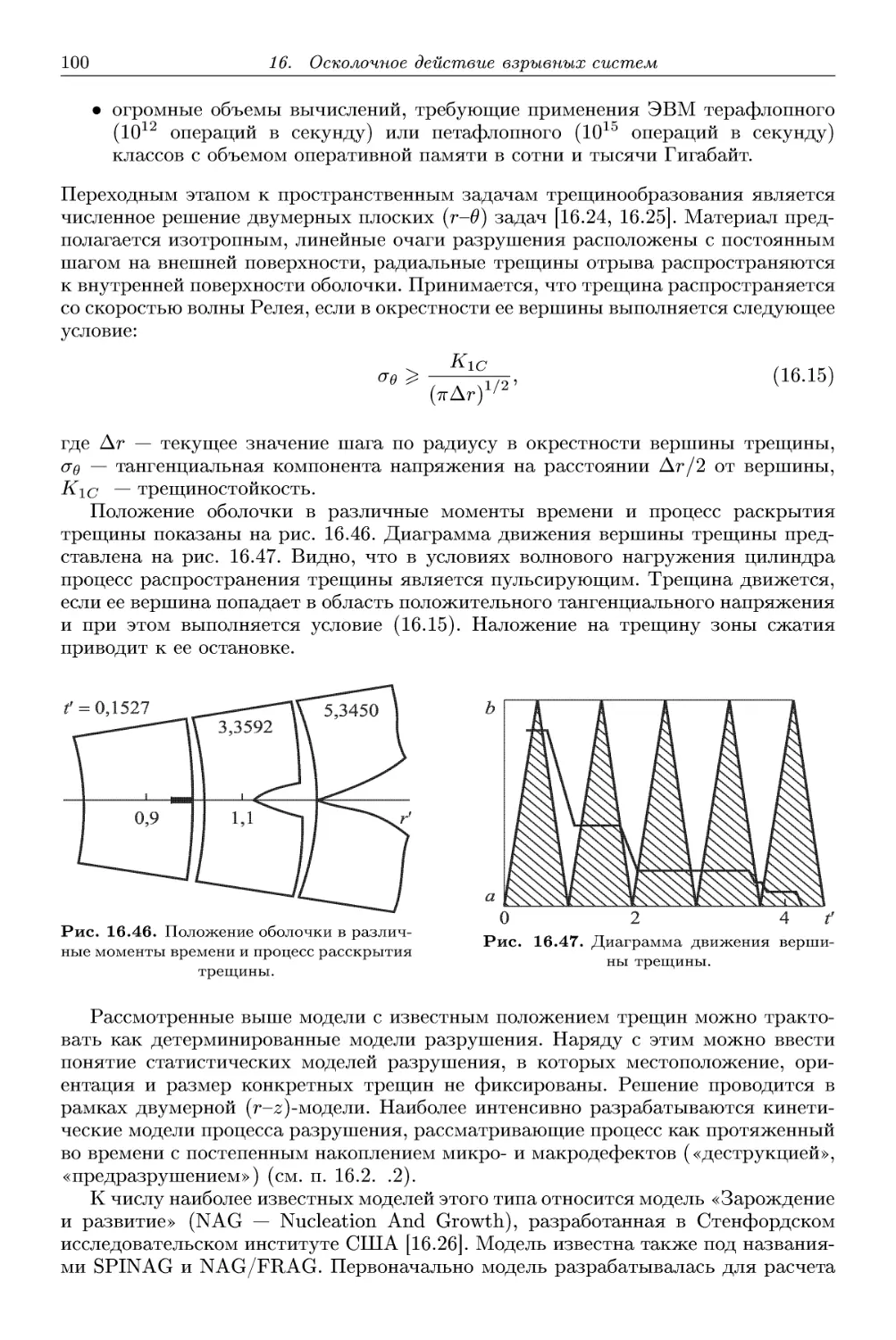
16.1.	Экспериментальные наблюдения процесса расширения и разруше-
разрушения металлической оболочки и получающихся осколочных спектров	62
1.	Оптическая и рентгеноимпульсная съемка оболочек		62
2.	Камерные и щитовые испытания		70
3.	Основные особенности осколков естественного дробления		75
4.	Металлографическое исследование осколков		79
16.2.	Модели процессов расширения и разрушения оболочек		89
1.	Одномерное расширение жесткопластической несжимаемой оболочки. 89
2.	Одномерное расширение сжимаемой упруго-пластической оболочки.	91
3.	Модели разрушения оболочек		98
16.3.	Основные соотношения при дроблении оболочек		107
1.	Масштабный эффект при разрушении и осколкообразовании. Ана-
Анализ размерностей		107
2.	Радиус разрушения оболочки		113
3.	Соотношения для характеристик дробления оболочки 		116
4.	Соотношения для общего числа осколков		122
5.	Прогноз характеристик спектра		124
16.4.	Статистическое распределение осколков		127
1.	Пространственно-массовые распределения осколков		127
2.	Общие соотношения осколочной статистики		130
3.	Основные статистические модели спектров		133
16.5.	Стандартные осколочные цилиндры		143
1.	Основные типы и параметры стандартных осколочных цилиндров .	143
2.	Численное моделирование процессов в стандартных осколочных ци-
цилиндрах		150
3.	Экспериментальные данные испытаний стандартных осколочных
цилиндров		154
4.	Исследование масштабного эффекта		166
16.6.	Действие осколков		170
1.	Модели и параметры формы осколков естественного дробления ...	170
2.	Баллистика осколков		182
3.	Классификация механизмов взаимодействия осколков с преградами.	184

IV
4.	Предельно пробиваемые толщины преград и предельные скорости
пробития		186
5.	Критерии для оценки действия осколков		188
17.Кумуляция	193
17.1.	Общие сведения		193
1.	Понятие кумуляции. Кумулятивные заряды		193
2.	Краткие исторические сведения		195
3.	Механизм формирования кумулятивной струи. Возможные режимы
кумуляции		196
4.	Проникание кумулятивной струи в преграду		201
17.2.	Теория кумуляции		205
1.	Теория струй несжимаемой жидкости		205
2.	Теория образования кумулятивной струи		206
3.	Критические условия струеобразования		208
4.	Теория проникания кумулятивной струи в преграду		213
5.	Определение диаметра каверны в преграде		220
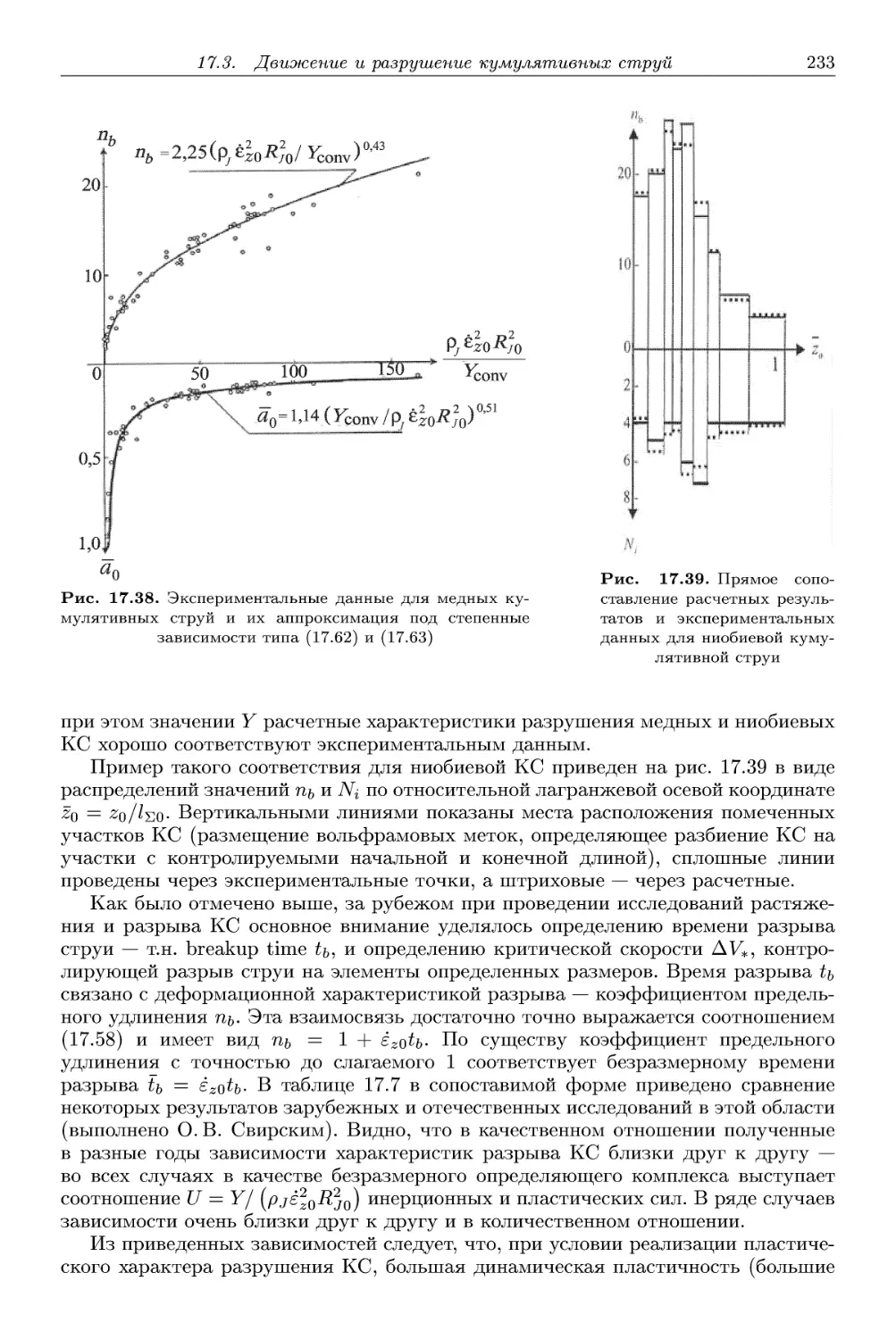
17.3.	Движение и разрушение кумулятивных струй из различных мате-
материалов 		224
17.4.	Структурное состояние материала кумулятивной струи и песта . . .	234
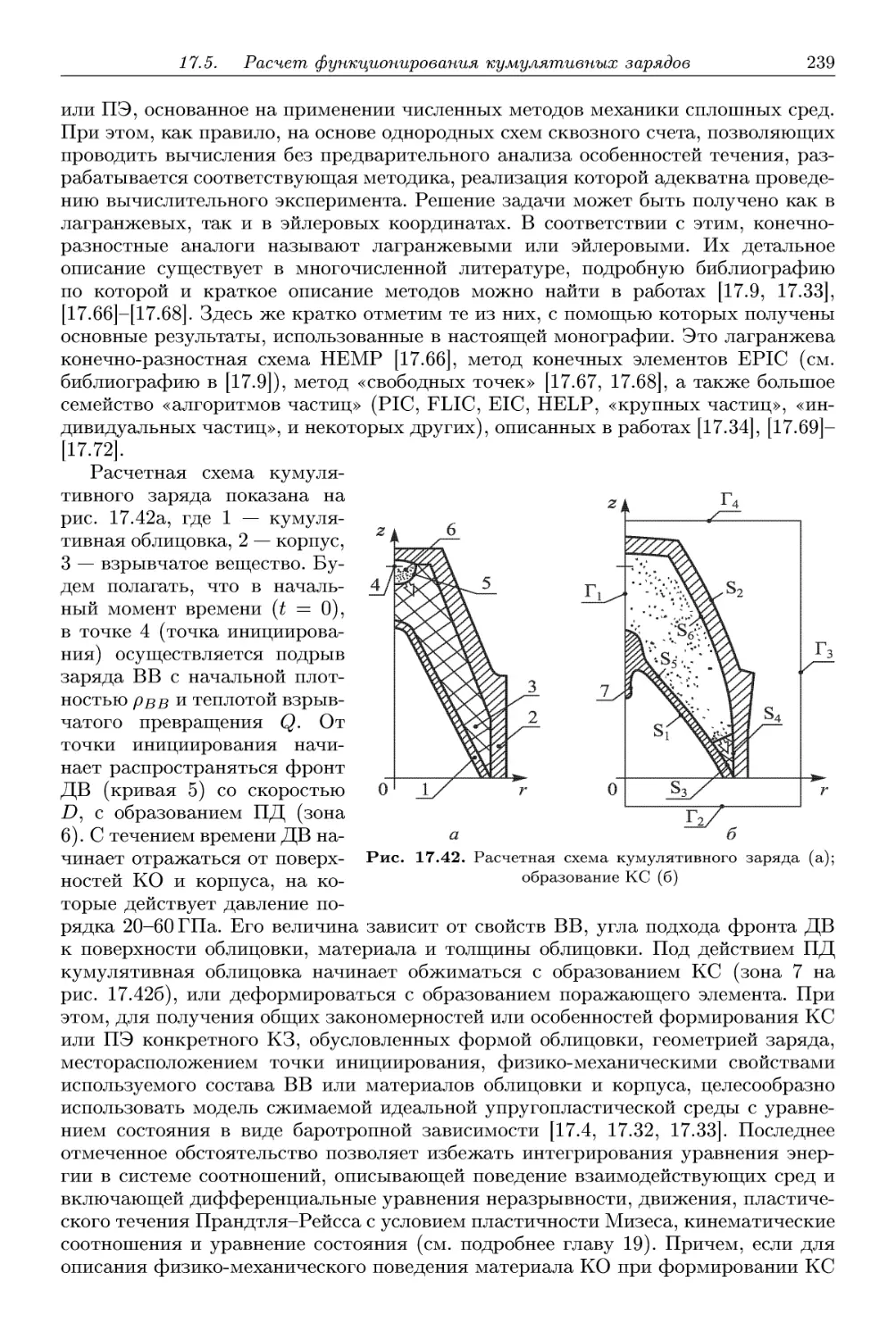
17.5.	Расчет функционирования кумулятивных зарядов		238
1.	Численные методики расчета параметров кумулятивной струи. . . .	238
2.	Инженерные методики расчета параметров функционирования ку-
кумулятивных зарядов с высокими коническими облицовками		247
3.	Расчет полусферических и сегментных оболочек		258
4.	Методика расчета формирования кумулятивного «ножа» удлинен-
удлиненных зарядов с клиновидной выемкой		273
5.	Методика оценки температуры кумулятивной струи		279
17.6.	Влияние конструктивных параметров заряда 		286
1.	Облицовка кумулятивной выемки		286
2.	Заряд взрывчатого вещества и корпус		292
3.	Узел управления детонационным фронтом		296
4.	Технология изготовления кумулятивного заряда		299
5.	Неидеальность детонационных процессов в кумулятивном заряде. .	303
17.7.	Влияние условий применения на действие кумулятивных зарядов . .	308
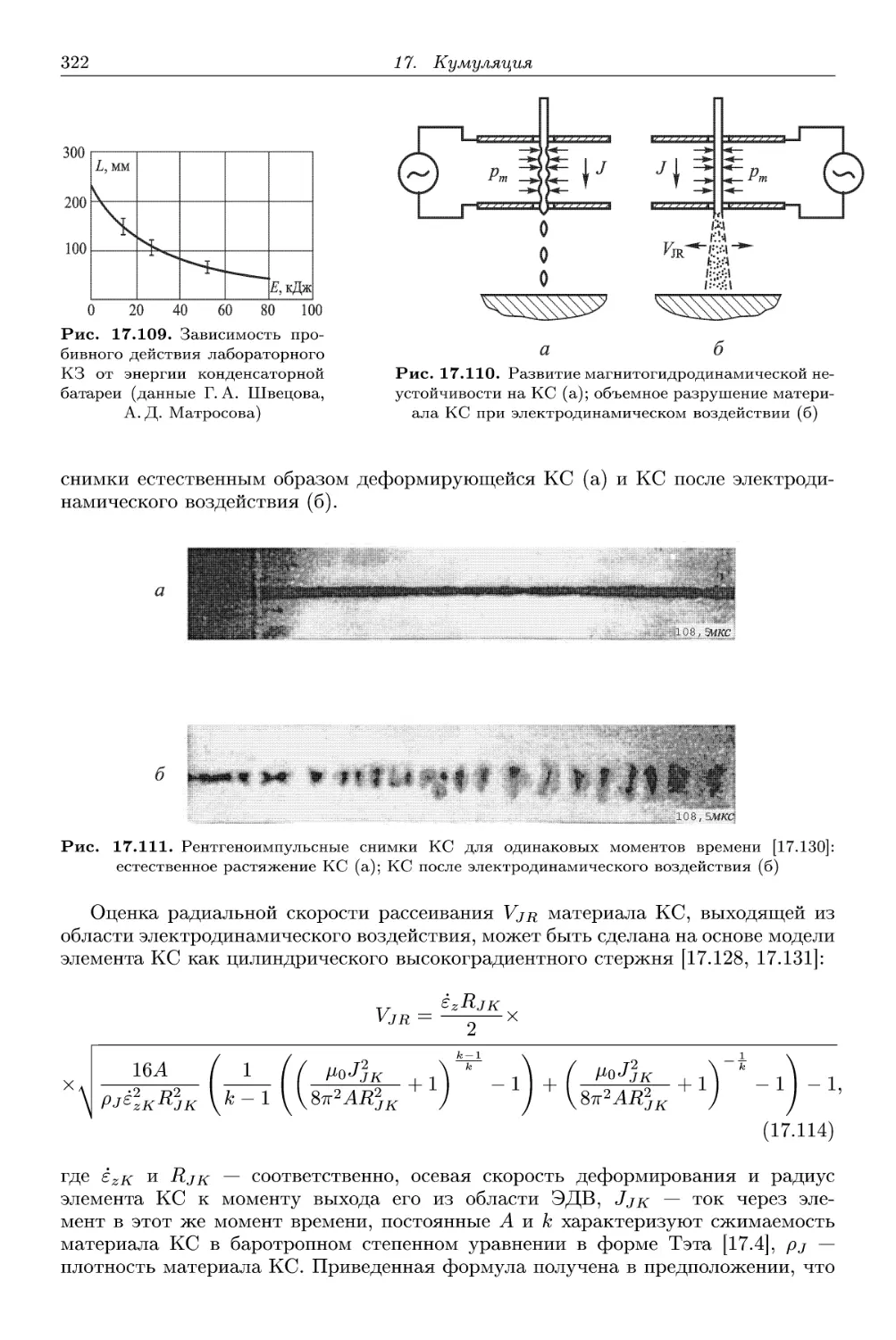
1.	Фокусное расстояние кумулятивного заряда		309
2.	Влияние вращения на кумулятивный эффект		311
3.	Влияние электромагнитных воздействий на кумулятивный эффект.	318
4.	Влияние предварительного нагрева облицовки заряда на кумуля-
кумулятивный эффект		331
5.	Влияние гидростатического давления и температуры на кумулятив-
кумулятивный эффект		338
6.	Взаимодействие кумулятивной струи с динамической защитой. . . .	345
18.Электромагнитные явления при взрыве конденсированных взрыв-
взрывчатых веществ	351
18.1.	Феноменология электромагнитных явлений при взрыве		351
18.2.	Физические и математические модели электромагнитных процессов
при взрыве		364
18.3.	Метод оценки теплового излучения взрыва КВВ		378
18.4.	Экспериментальные исследования процессов электромагнитной и ра-
радиационной газодинамики при взрыве КВВ		382

	V
19.Взрыв в твердых телах	389
19.1.	Уравнения адиабатического движения упругопластических сред . .	389
19.2.	Уравнения состояния и ударные адиабаты жидких и твердых тел. .	400
1.	Уравнения состояния конденсированных веществ		400
2.	Экспериментальные методы определения динамической сжимаемо-
сжимаемости веществ		409
3.	Свойства веществ при ударном сжатии		414
19.3.	Высокоскоростное деформирование и разрушение сжимаемых упру-
упругопластических сред 		426
1.	Плоская ударная волна в упругопластическом полупространстве . .	427
2.	Предел упругости на ударной адиабате Гюгонио. Фазовый переход.
Упругие и пластические волны		435
3.	Механика и морфология высокоскоростного деформирования. . .	443
4.	Динамический предел текучести		453
5.	Ударные волны в пористых средах		458
6.	Критерии разрушения при ударноволновом нагружении		463
7.	Динамическое разрушение материалов в режиме импульсного объ-
объемного разогрева		477
8.	Откольное разрушение материалов		480
9.	Динамическое разрушение преград при взрыве зарядов ВВ		491
10.Динамическое разрушение алюминийсодержащих преград		496
19.4.	Диссипативные процессы в ударных волнах в различных средах . .	506
19.5.	Электромагнитные явления при ударном сжатии твердых сред . . .	521
20.Моделирование взрывных процессов	525
20.1.	Теория моделирования взрывных процессов		525
20.2.	Моделирование процессов взрыва в разных средах		527
20.3.	Моделирование процессов кумуляции и разрушения оболочек про-
продуктами взрыва		530
1.	Моделирование кумулятивных процессов		530
2.	Моделирование сложных систем		531
3.	Моделирование разрушения оболочек при взрыве		533
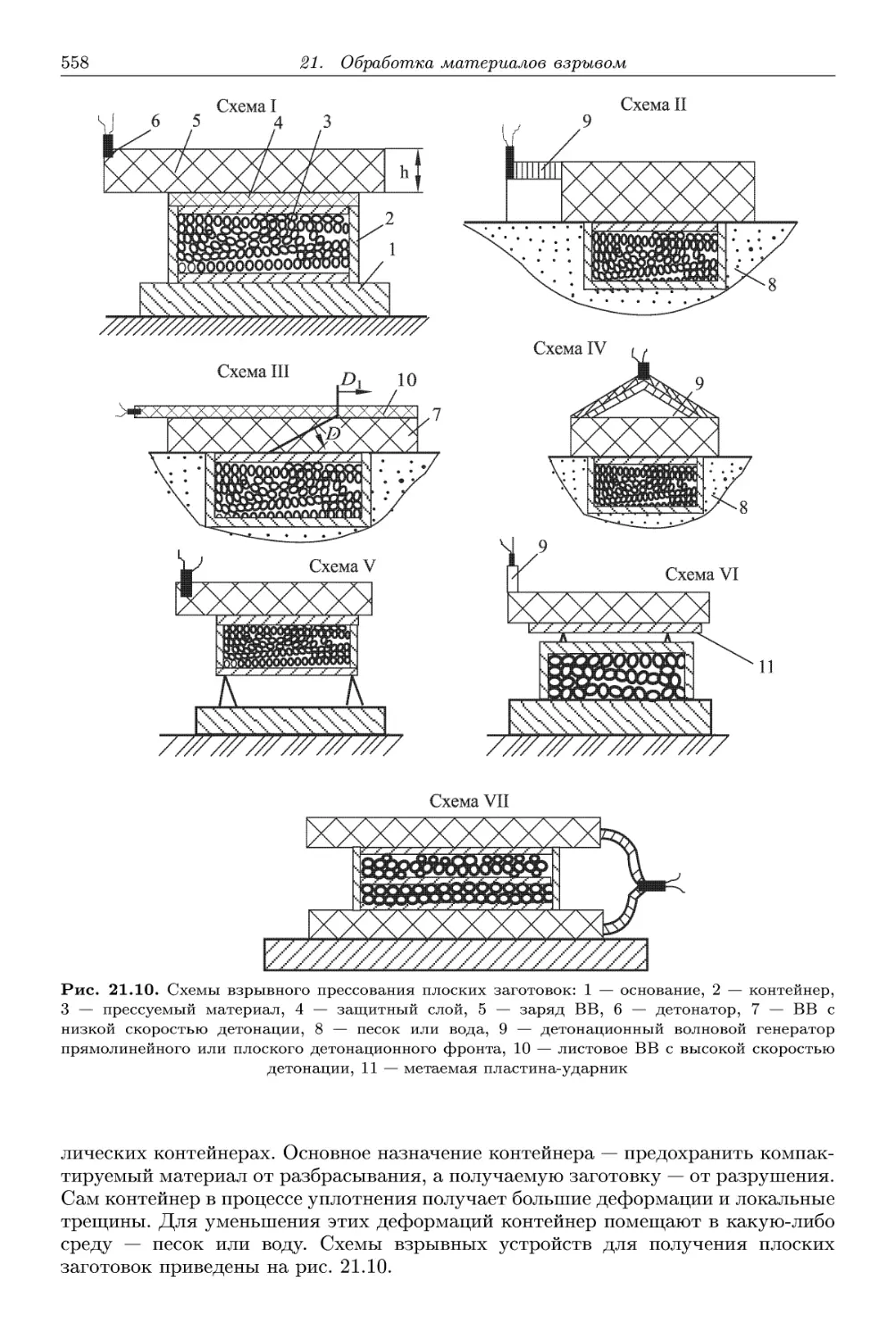
21. Обработка материалов взрывом	536
21.1.	Упрочнение металлов взрывом		536
21.2.	Сварка взрывом		541
1.	Основные схемы и параметры процесса сварки взрывом		542
2.	Основные закономерности сварки взрывом		548
3.	Формирование соединения при сварке взрывом		549
4.	Особенности взрывной сварки крупногабаритных листов [21.13]. . .	552
21.3.	Взрывное прессование пористых материалов		555
1.	Модели уплотнения пористых материалов		555
2.	Взрывное прессование плоских заготовок		557
3.	Взрывное компактирование осесимметричных заготовок		562
21.4.	Штамповка металлов взрывом		565
1.	Основные понятия штамповки взрывом		565
2.	Действие подводного взрыва на заготовку 		566
3.	Расчет энергии, передаваемой заготовке		568
4.	Расчет работы формообразования деталей		569
5.	Расчет массы заряда ВВ		572
6.	Особенности гидровзрывной штамповки		574
21.5.	Ударно-волновой и детонационный синтез сверхтвердых материалов	576

VI
1.	Ударно-волновой синтез сверхтвердых материалов	577
2.	Детонационный синтез сверхтвердых материалов	579
Приложения	583
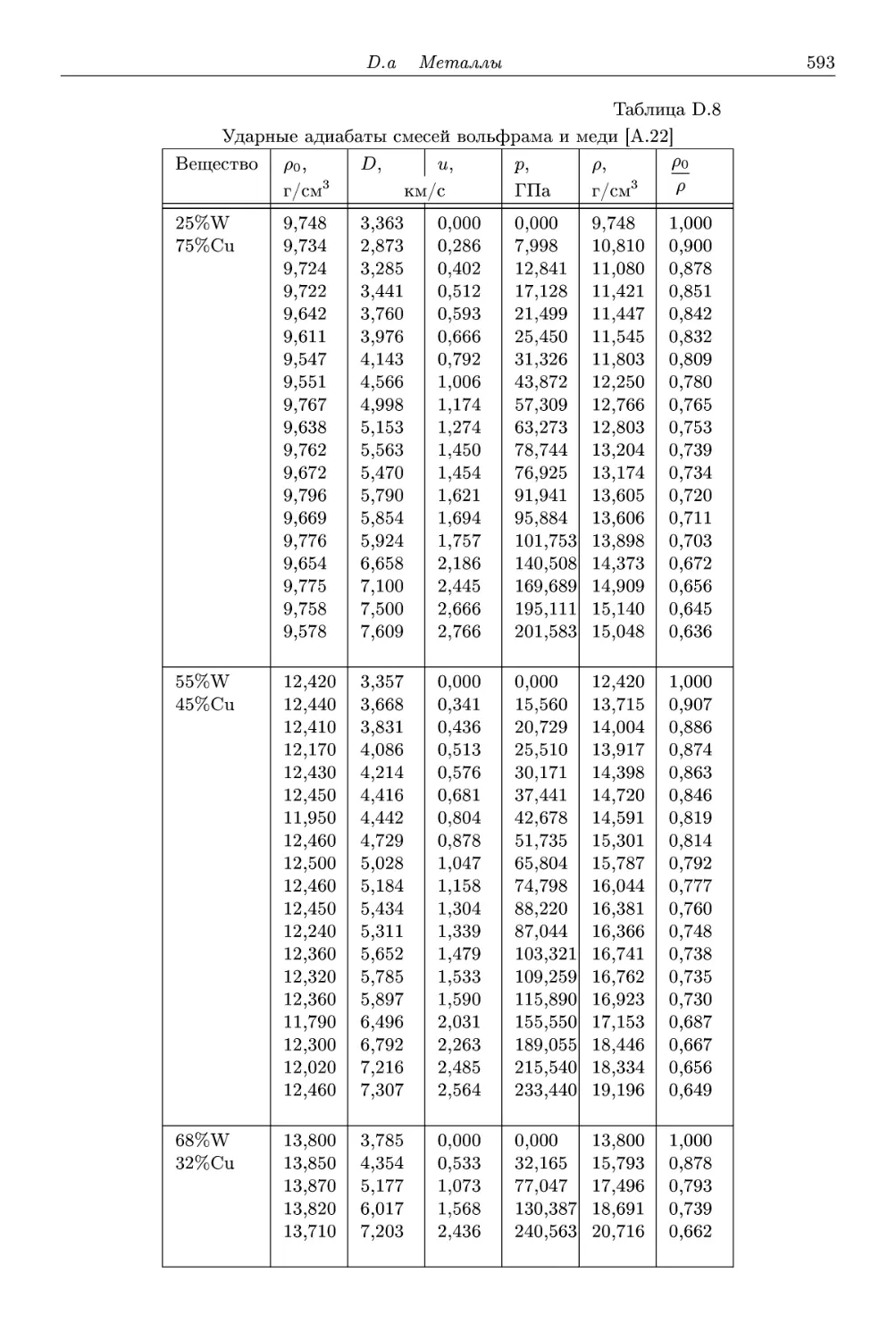
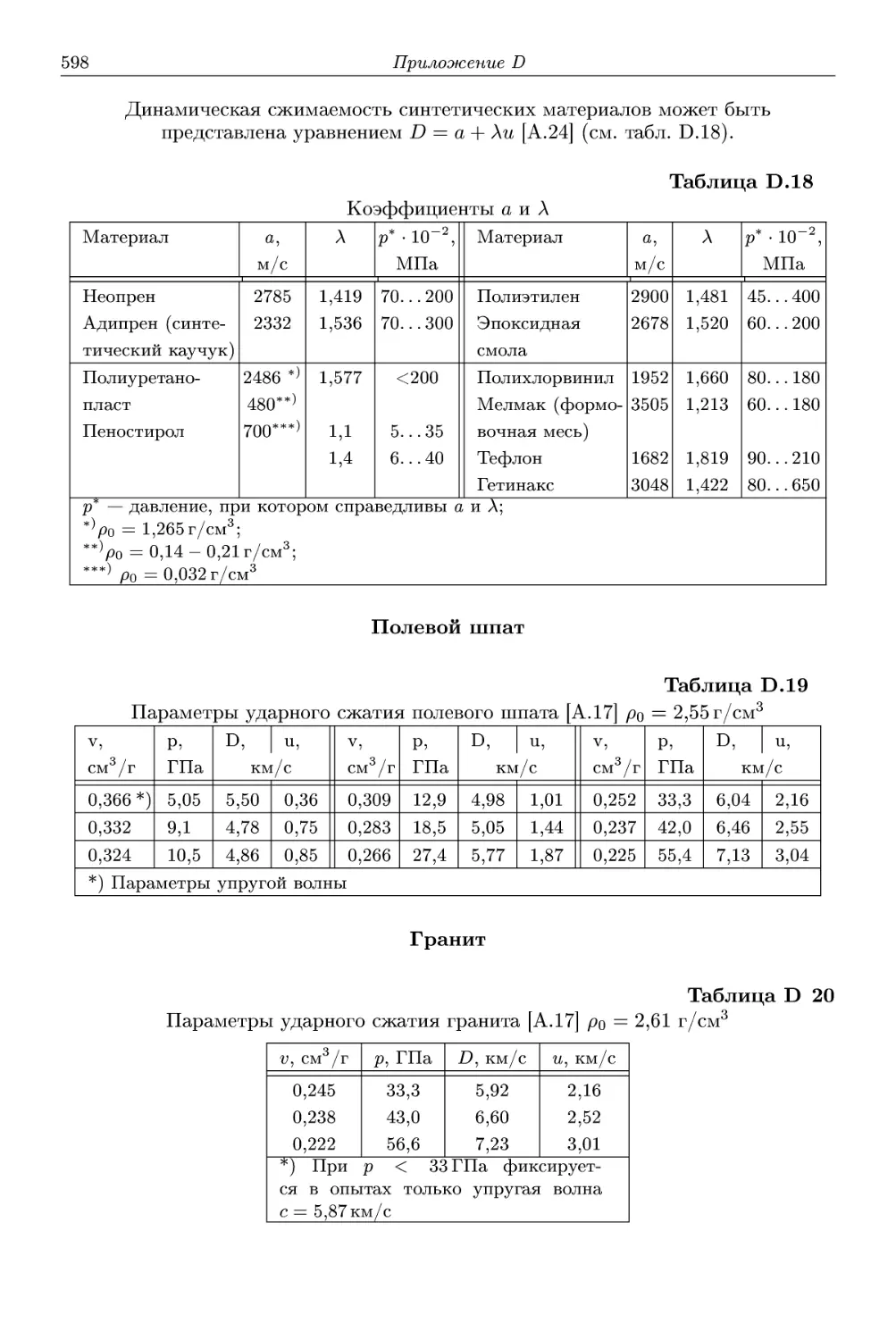
D Динамическая сжимаемость веществ	583
D.a	Металлы		583
D.b	Пористые материалы		594
D.c	Столкновение ударных волн		595
D.d	Щелочные металлы и щелочно-галоидные соединения		596
D.e	Неметаллы		597
D.f	Жидкости 		600
D.g	Ударные адиабаты 		603
Список литературы 	609

Глава 15
Метание тел продуктами детонации
15.1. Определение импульса взрыва при отражении детонационной
волны от стенки
1. Распределение параметров состояния продуктов взрыва за фрон-
фронтом детонационной волны. Детонационной волне в продуктах детонации
всегда сопутствует волна разрежения. Она появляется сразу по окончании реак-
реакции. Объясняется это тем, что непосредственно за зоной превращения продукты
реакции перемещаются со скоростью и в направлении распространения детонации
и находятся вследствие этого под повышенным давлением.
Поскольку на фронте детонационной волны в точке Чепмена-Жуге для любого
момента времени энтропия остается постоянной, то за фронтом волны имеет место
изоэнтропийное движение газа.
Движение продуктов детонации за фронтом детонационной волны наиболее
просто решается для одномерного, плоского случая, если уравнение изоэнтропы
имеет вид р = Арк(к = const). В этом случае может быть получено простое
аналитическое решение. Для цилиндрического же и сферического случаев для
изоэнтропы р = Арк(к = const) нельзя получить аналитическое решение для
задачи о движении ПД. В этом случае задача решается численными методами.
Численные методы необходимо также использовать для определения движения
продуктов взрыва за фронтом детонационной волны в плоском, цилиндрическом
и сферическом случаях, если изоэнтропа имеет произвольный вид р = р(р)
или к = к(р). Рассмотрим аналитическое и численные решения, определяющие
движение ПД за фронтом одномерных детонационных волн.
В случае плоской детонационной волны для изоэнтропы р = Арк(к = const) все
параметры за фронтом волны зависят только от координаты х и времени t.
Напишем основные уравнения газодинамики в следующем виде (см п. 3.1):
ди ди 2 дс Л	,1Л
*+"& + FrTcS = 0-	A5Л)
к — 1 dt к — 1 дх дх
Эти соотношения, как известно, приводят к уравнениям C.7):
д_
№

15. Метание тел продуктами детонации
В том случае, когда
2с
и = - ± —	— + const,	A5.4)
[к - 1)
уравнение A5.3) удовлетворяется тождественно, и исходная система уравнений
может быть приведена к виду
? + (.±«>|-0.	,1,5,
что сразу дает возможность написать решение
х = (u±c)t + F(u).	A5.6)
Напомним, что это решение описывает распространение волны только одного
направления, что, в частности, характерно для детонационной волны.
Если волна распространяется слева направо в сторону возрастающих ж, то
решение надо брать со знаком плюс, а для волны, бегущей в обратном направ-
направлении, — со знаком минус. Применим эти решения для определения параметров
за фронтом детонации:
2С
x = (u±c)t + F(u), u = ±j-j	г + const.	A5.7)
(k — 1)
Пусть детонация началась у закрытого конца трубы (х = 0) в момент времени
t = 0 и распространяется слева направо. Следовательно, в уравнениях A5.7)
выбирается знак плюс.
Поскольку движение в момент времени t = 0 определено при х = 0, то F(u) = 0,
следовательно,
x = (u + c)t.	A5.8)
На фронте сильной детонационной волны, как известно, иц = D/(k -\- 1) и
сн = kD/(к + 1). Отсюда постоянная в уравнении A5.4)
const = -V^Ty	A5-9)
Таким образом, волна разрежения должна описываться следующими уравне-
уравнениями:
Поскольку конец трубы в точке х = 0 закрыт, то эти уравнения являются
действительными только до значений ж, при которых скорость и не равна нулю и
газ не приходят в состояние покоя. Начиная с этой точки, все параметры состояния
газа, вплоть до точки х = 0, остаются постоянными.
Для продуктов детонации конденсированных В В (сильная детонационная вол-
волна) показатель изоэнтропы к = 3. В этом случае уравнения A5.10) принимают
наиболее простой вид:
х	D
-=и + с, -—=и-с,	A5.11)

15.1. Импульс взрыва при отражении ДВ от стенки
откуда
D
D
A5.12)
Во фронте детонационной волны, т.е. когда x/t = Z),
моменту времени, когда и = О,
x/t = D/2 и сп = D/2.
= D/4 и сн = 3D/4. К
A5.13)
Из A5.12) следует, что в интервале D/2 ^ x/t ^ D скорость потока и скорость
звука изменяются по линейному закону. В интервале 0 ^ x/t ^ D/2 и = 0 и
с = Z)/2. Распределение иисза фронтом детонационной волны для какого-либо
заданного момента времени показано на рис. 15.1.
D
1-П	--- --Л
Ги	Г2 Ги
Рис. 15.1. Распределение и и с
за фронтом плоской детонационной
волны (А: = 3)
Рис. 15.2. Распределение р и р за, фронтом плос-
плоской детонационной волны (к = 3)
Точка, в которой заканчивается волна разрежения и начинается область покоя,
находится как раз посередине между фронтом детонационной волны и местом, где
произведено инициирование взрыва.
При показателе изоэнтропы к = 3, р = Рн{р/рнK
и с = снр/рн, откуда для точки, в
которой и = 0, имеем
Ри = -Рн = -
Таблица 15.1
Давление и плотность продуктов
детонации в зоне покоя для различных
значений к
A5.14)
Таким образом, за фронтом дето-
детонационной волны плотность меняет-
меняется по прямой, а давление — по сте-
степенному закону. Характер распреде-
распределения pup показан на рис. 15.2.
Поскольку все параметры состояния зависят только от ж/?, то с течением
времени волна будет растягиваться, не изменяясь по форме, т.е. будет реализо-
реализоваться автомодельное самоподобное движение газа. Приведенное выше решение
принадлежит Грибу [15.1]. В табл. 15.1 приведены результаты вычислений для
отношений ри/рн и Ри/Рн ПРИ различных значенияях показателя изоэнтропы к.
к
3,0
1,66
1,40
Рп
Рн
0,30
0,33
0,34
рп
Рн
0,67
0,51
0,46
к
1,20
1,0
Рп
Рн
0,35
0,369=1/е
?п_
Рн
0,42
0,369

15. Метание тел продуктами детонации
Из таблицы видно, что отношение ри/рн сравнительно мало меняется даже
при существенном изменении к.
Если бы детонация протекала в замкнутом объеме, то вскоре после ее окон-
окончания в продуктах взрыва везде установилось бы одинаковое давление рс при
плотности, равной ро- Это давление легко может быть определено из уравнения
состояния Е = pvj(k — 1) или pcvo/(k — 1) = Qv, откуда
pc = {k-l)p0Qv.	A5.15)
Для давления во фронте детонационной волны в совершенном газе (гл. 5):
Рн = *(л ~~ ±)PoQv, Рс = ~тг-	A5.15)
и, км/сек
Давление во фронте детонационной волны в этом случае в два раза больше, чем
среднее давление продуктов взрыва. Повышенное давление во фронте компенсиру-
компенсируется пониженным давлением в остальных частях газа, находящихся позади волны
разрежения: рп = 0, 6рс.
Если бы химическая реакция протекала во
всем объеме ВВ мгновенно, то максимальное
давление продуктов взрыва равнялось бы рс.
Следовательно, при мгновенной детонации мест-
местный эффект взрыва в непосредственной близости
от заряда оказался бы заметно меньшим, чем в
условиях нормальной детонации. Суммарное же
действие продуктов взрыва, определяемое потен-
потенциальной энергией ВВ, при этом не изменилось
бы.
Экспериментальное исследование движения
ПД за фронтом плоской детонационной вол-
волны, проведенное электромагнитным методом для
зарядов ТГ50/50 разной длины, показало, что
если в экспериментальных кривых (массовая
скорость—время) выделить стационарную зону
ОДмксек, то последующее движение можно счи-
считать автомодельным [15.2]. В этом случае, счи-
считая, что изоэнтропа ПД имеет произвольный вид
р = р(р), автомодельное движение ПД можно
2,5
1,5
1
0,5
0,5 0,6	0,8	1,0
Рис. 15.3. Изменение массовой ско-
скорости и за фронтом детонационной
волны для ТГ50/50 в зависимости
от: 1 — опыт (по Зубареву), 2 —
к = 2,7, 3 -к = 3
/
3
ц
описать уравнениями (п. 3.2)
A5.17)
или, поскольку для изоэнтропийного течения du/d In p = с и dp = pcdu, то
интегрируя эти уравнения от точки Чепмена-Жуге, получим
(и(г}) Л	и(г})
~с\' P(f])=PH+ / cpdu.	A5.18)
Экспериментальное значение и = u(rj) для ТГ50/50 (ро = 1,68г/см ) представлено
на рис. 15.3 (кривая 1). С помощью первого уравнения A5.17) в параметрическом
виде определяется с = с(и). Численное интегрирование уравнений позволяет
определить р(г]) и р(т]).

15.1. Импульс взрыва при отражении ДВ от стенки
Показатель изоэнтропы при этом
определяется с помощью следующе-
следующего уравнения:
Таблица 15.2
Экспериментальные изоэнтропийные
параметны ПД ТГ50/50
к =
d Inp
сПпр
pdp
pdp
Р
V
1
0,968
0,933
0,880
0,815
0,747
0,679
0,611
0,543
0,475
и
ъ
0,271
0,24
0,21
0,18
0,15
0,12
0,09
0,06
0,03
0
с
ъ
0,729
0,728
0,723
0,700
0,665
0,627
0,589
0,551
0,513
0,475
/ 3
г/см
2,30
2,21
2,12
2,03
1,95
1,86
1,77
1,68
1,58
1,49
Р,
ГПа
26,5
23,6
20,9
18,3
15,9
13,8
11,8
10,1
8,6
7,2
h
2,70
2,9
3,10
3,18
3,17
3,10
3,04
2,96
2,83
2,73
Результаты этих расчетов, приве-
приведенных на основе эксперименталь-
экспериментальной кривой и = u(rj), представлены
в табл. 15.2.
Зависимость р = р(р), представ-
представленная в табл. 15.2, является изо-
энтропой ПД для ТТ50/50, полу-
полученной на основе экспериментальной
зависимости и = u(rj) (рис. 15.3). На
этом рисунке представлены зависи-
зависимости и = и(г]) для ТГ50/50 также
и в том случае, когда изоэнтропа ПД
определяется уравнениями р = Ар3
ир = ВР2>7.
Для автомодельной волны имеем d(x/t) = du + dc, или d(x/t) = du(l-\--\-dc/du).
Так как du = cdlnp, то d(x/t) = du(l + dInc/dInp), или
du
drj
D
1 + d In c/d Inp 1 + jfe(l + (p/k2)dk/dp)'
A5.19)
Последнее выражение получается, если формулу к = с2р/р прологарифмировать,
а затем продифференцировать по In p.
Если к = const, то из A5.19) следует, что
du
drj
2D
*)
= const.
A5.20)
Из уравнения A5.19) следует, что большему наклону кривой и = u(rj) (см. рис. 15.3)
по сравнению с к = к(рн) = const должна соответствовать отрицательная
производная dk/dp. Это означает, что с уменьшением р величина к возрастает.
Рассмотрим распределение параметров состояния продуктов взрыва за фрон-
фронтом плоской, цилиндрической и сферической детонационных волн для произволь-
произвольного уравнения изоэнтропы.
В случае одномерных волн все параметры за фронтом волны зависят только
от координаты г и времени t.
Поскольку во фронте детонационной волны для любого момента времени
энтропия остается постоянной, а за фронтом волны начинается изоэнтропийное
расширение газа, то с помощью соотношения с2 = (dp/dp)s первые два уравнения
газодинамики B.19) приводятся к виду
ди
ди
дг
р дг
ot дг or r
До тех пор, пока мы ограничиваемся процессом распространения детонации в
однородной среде внутри заряда взрывчатого вещества, ни уравнения, ни гранич-
граничные условия не дают нам величины с размерностью длины и времени. Поэтому из

6	15. Метание тел продуктами детонации
теории автомодельных движений следует, что искомое решение — переменное во
времени, пространственного поля плотности, давления и других величин, может
содержать независимые переменные rut только в определенной комбинации
размерности скорости r/t.
Введя замену переменных Р = r/t и используя элементарные соотношения
д _1 d д _ г d _ p d
дг t dp' dt t2 dp t dp'
уравнения A5.21) приводятся к системе двух дифференциальных уравнений в
полных производных:
du	Nc2u
A5.22)
dp p(u — Р) du
~dp =	с~2 Jp'
Квадрат скорости звука с определяется как функция плотности из уравнения
состояния продуктов взрыва с помощью соотношения с2 = (dp/dp)s- В случаях
плоской волны (N = 0), кроме тривиального решения и = const, p = const, кото-
которое, как указывалось, не удовлетворяет реальной детонации, из A5.22) получаем
с2 -(и-РJ = 0.	A5.23)
С помощью A5.23) система A5.22) для описания плоской детонационной волны,
распространяющейся в направлении оси /3, переходит в уравнения
с = р-щ	A5.24)
dp/du = р/с = р(Р - и).	A5.25)
Переменная /3 меняется от /3 = 0 в центре заряда до /3 = ин + сн = Р во
фронте детонационной волны. В центре заряда из соображений симметрии должно
выполняться условие
и = 0.	A5.26)
Во фронте волны при Р = D должны выполняться условия (см. п. 5.4)
Рн_ = fc + 1 u = D c = kD	= ррР2 к=р /ф\
fJQ	гь	гь ~\~ -L	ги ~\~ ±	гь ~\~ A.	JJ у LLfJ J а
Соотношения A5.26) и A5.27) служат граничными условиями для интегриро-
интегрирования системы 15.22. При к = const, т.е. для изоэнтропы расширения продуктов
взрыва типа
р = Арк	A5.28)
для плоской детонационной волны из уравнений A5.24) и A5.25) нетрудно найти
аналитическое решение A5.10). Заменяя в A5.24) скорость звука выражением
)/2,	A5.29)

15.1. Импульс взрыва при отражении ДВ от стенки
получим
VAkp(k-3V2dp = du,	A5.30)
интегрируя которое, найдем
и - VAk	р^-1)/2 = и- с	= const.	A5.31)
Константа в A5.31) находится из граничных условий A5.27):
и - ckh =ин ~ CHkh = -*зт •	A5-32)
Исключая отсюда с с помощью A5.24), получим
^-v или и = *тт*-*тг A5-33)
Для скорости звука из A5.24), получаем решение
'=гтт*+1?г	A5'34)
С помощью A5.28) и A5.29) нетрудно получить распределение давления и
плотности в детонационной волне. Как видно из A5.33) и A5.34), распределение
скорости звука и массовой скорости частиц в плоской детонационной волне линей-
линейно, причем при /3 = D/r скорость частиц обращается в нуль. При этом с = D/2.
Для того чтобы выполнялось второе граничное условие A5.26), необходимо, чтобы
в области 0 $J [3 $J D/2 неизвестные иже имели постоянные значения
и = const = 0, с = const = D/2,	A5.35)
которые также удовлетворяют уравнению A5.25).
В случае цилиндрической или сферической детонационной волны, а также для
более сложного уравнения состояния продуктов взрыва системы A5.22) не имеют
аналитического решения.
Из уравнений A5.22) следует, что для любого уравнения состояния во фронте
волны при /3 = и-\- с = D решение имеет особенность, du/d[3 и dp/d[3 обращаются
в бесконечность. Значит, за фронтом цилиндрической и сферической детонацион-
детонационных волн параметры падают быстрее, чем в плоском случае. При и = 0, du/df3 = 0,
за исключением двух подлежащих исследованию случаев, C = 0 и C = с. Анализ
решения показывает, что в интервале 0 ^ C ^ с везде и = 0, с = const. На границе
области покоя, т.е. в точке /3 = с, du/d/З = 0, d2u/df32 = ос.
На рис. 15.4—15.7 представлены распределения скорости, плотности и давления
в плоской, цилиндрической и сферической волнах, приведенные к значениям в
детонационной волне, в зависимости от безразмерной пространственной коорди-
координаты для состава ТГ36/64 (р0 = 1,717 г/см , рн = 29,5 ГПа, ин — 2153 м/сек, рн =
2,35157г/см ) с помощью численного интегрирования системы1) [15.3]. В решении
1^Для удобства сравнения разных вариантов расчеты проводились для детонационных волн с
одними и теми лее параметрами рн-> PHt иН-

15. Метание тел продуктами детонации
0,25	0,5 0,75	1,0 х
Рис. 15.4. Распределение р = р/рн, Р = р/рн-,
п = и/D от х = x/Dt за фронтом плоской де-
детонационной волны для состава ТГ36/64: 1 — для
изоэнтропы A5.36), 2 — для изоэнтропы A5.37), 3 —
для изоэнтропы A5.38).
0,25 0,5 0,75 1,0 х
Рис. 15.5. Распределение р = р/рн-,
р = р/рн, п = u/D от х = x/Dt
за фронтом цилиндрической детона-
детонационной волны для состава ТГ36/64.
Обозначения — как на рис. 15.4
использовалось три уже описанные (см. п. 5.5) изоэнтропы разгрузки продуктов
взрыва:
Г Po^i ] n f P0-R21 ^ f p\
p = A exp <	> + В exp <	> + С —
I P J	I P J	VPo/
;	A5.36)
A5.37)
где p = p/pH, p = pjpH, W = 0,94435, G = 0,055667, n = 3,2752, 7 = 0,34, и
простейшая изоэнтропа с постоянным к = 3:
= Ар3
A5.38)
Параметры во фронте детонационной волны имеют одну и ту же величину
для всех трех случаев симметрии, однако с увеличением порядка симметрии
увеличиваются скорости их падения за фронтом волны, а также уменьшаются
размеры и параметры области покоя. Как следует из рис. 15.4—15.7, все три
изоэнтропы разгрузки дают близкие результаты, поэтому для расчета параметров
ПД без разлета с достаточной для практики точностью можно использовать
простейшую изоэнтропу A5.38).
Для оценки возможности использования различных уравнений состояния для
решения более сложных задач детонации рассмотрим задачу о разлете плоского
детонирующего заряда в пустоту с торца, в котором произошла детонация. Для
решения этой задачи можно воспользоваться уравнением A5.25), из которого
следует, что в волне выполняется соотношение
интегрируя которое, будем иметь
Г / 1 /ф\
и — \ ^ \ — ар = const.
У Vp2 Vdp/5
A5.39)
A5.40)

15.1. Импульс взрыва при отражении ДВ от стенки
0,25-
0,25 0,5 0,75 1,0 х
Рис. 15.6. Распределение р, р, и от х за
фронтом сферической детонационной вол-
волны для состава ТГ36/64. Обозначения — как
на рис. 15.4
Рис. 15.7. Разлет ПД в пустоту за фронтом
плоской детонационной волны для ТГ36/64.
Обозначения — как на рис. 15.4
Для изоэнтропы разгрузки в форме A5.28), как уже было показано, интеграл
в A5.40) можно вычислить и получить решение задачи в виде формул A5.33)
и A5.34). На границе разлетающегося газа должно выполняться условие с = 0, в
этом случае для координаты /3 из A5.34) получаем
D
а для скорости разлета газа в пустоту из A5.33)
D
Umax ~ ~ к_ 1-
A5.41)
A5.42)
Для случаев, когда изоэнтропы разгрузки продуктов взрыва используются в
виде A5.36) и A5.37), интеграл в A5.40) необходимо вычислять численно.
На рис. 15.7 представлено распределение давления, плотности и скорости
частиц в разлетающемся газе, приведенные к значениям на детонационной волне,
в зависимости от безразмерной координаты для трех изоэнтроп разгрузки продук-
продуктов детонации A5.36)-A5.38).
Как видно, в области высоких давлений все три уравнения дают близкие
результаты, однако при малых давлениях простейшая изоэнтропа A5.38) дает
большие ошибки, особенно в значении максимальной скорости разлета газа в
пустоту. Изоэнтропа, полученная из упрощенного уравнения состояния, дает ре-
результаты, совпадающие с решением для изоэнтропы A5.36).
Для изучения влияния вида уравнения состояния ПД на закон движения
оболочки заряда был численно рассчитан осесимметричный разлет ПД массой
т (длина цилиндрического заряда Iq, радиус г о) и найден закон движения цилин-
цилиндрической оболочки массой М (без учета прочности и сжимаемости оболочки) под
действием плоской скользящей детонационной волны, которая в момент времени
t = lo/D отражалась от жесткой стенки [15.3]. Для момента времени t > lo/D рас-
рассчитывалось движение ПД и оболочки заряда в зоне отраженной ударной волны
(см. систему уравнений B.15)). Схема процесса разлета ПД и движения оболочки

10
15. Метание тел продуктами детонации
Фронт разлета ПДр = 0, р = 0
Оболочка
0,5
Рис. 15.8. Схема метания цилиндрической
оболочки при детонации заряда В В
0,25
V/D
1
- - ¦""	"~
го/г
о
1	1,5	2,0
Рис. 15.9. Зависимость скорости оболочки
у жесткой стенки V/D от расстояния г/го
заряда для t < lo/D изображена на рис. 15.8 Во фронте детонационной волны па-
параметры равны рн, рн, ин. Eh, во фронте истекающих в пустоту ПД: р = 0, р = 0.
На оси симметрии v = 0, для t ^ lo/D на жесткой стенке W = 0. Граничное условие
на оболочке заряда имеет вид dMdV/dt = pds cos 5, dMdW/dt = pds sin 5, где 5 —
угол между вертикалью и нормалью к поверхности оболочки, V, W — радиальная
и осевая компоненты скорость элемента оболочки, имеющего массу dM и площадь
ds.
Указанная задача решалась для пентолита, как с помощью уравнения E.88),
так и с использованием уравнения состояния для ПД E.110).
На рис. 15.9 представлен график набора скорости оболочки для случая т/М = 2,
Iq/vq = 2 вблизи жесткой стенки для обоих уравнений; сплошная линия соответ-
соответствует уравнению E.110), штрих-пунктирная — уравнению E.88). Разница в ко-
конечных результатах ~ 6 %. Приведенный анализ показывает, что для приближен-
приближенных расчетов газодинамических задач действия вырыва можно воспользоваться
простым уравнением состояния и его изоэнтропой E.88), коэффициенты в которых
определяются для любого ВВ по известным параметрам в точке Чепмена—Жуге.
2. Импульс при отражении детонационной волны от стенки. Рас-
Рассмотрим теоретический расчет импульса при отражении детонационной волны от
стенки [15.4].
Пусть плоская детонационная волна начинается у левого открытого конца
заряда ВВ (в начале координат). Длина заряда /; у правого конца при х = /
помещена недеформируемая стенка (рис. 15.10).
Уравнения газовой динамики для одномерного изоэнтропийного течения имеют
вид C.7):
д_
dt
и±
fc-1
ох
Запишем A5.43) для случая к = 3:
at
Решение A5.44) согласно п. 3.5 будет
х = (и + c)t + Fx{u + с),
= (и- c)t + F2(u - с),
A5.43)
A5.44)
A5.45)

15.1. Импульс взрыва при отражении ДВ от стенки
11
где Fi и F2 — произвольные функции. Для отраженной волны решение определено
при t = l/D, x = I. При этом и = 0, с = D; из этого следует, что F\ = l — (D/D)l = 0,
следовательно,
х = (и +
A5.46)
Функция i^2 определяется из условия,
что на стенке при х = I будет и = 0 при
любом значении t. Тогда / = @ — c)t +
F2@ —с). Учитывая, что при t = Z/Z? имеем
с = D. получаем / = -Dl/D + F2@-c), т.е.
F2 = 2/. Следовательно,
21.
A5.47)
Из A5.46) и A5.47) определим иис:
(х-I)
I
с = -.
A5.48)
О
Рис. 15.10. К теоретическому расчету им-
импульса при отражении детонационной вол-
волны от недеформируемой стенки
Последняя зависимость позволяет легко установить закон изменения давления,
действующего на стенку, во времени.
Определим закон движения фронта отраженной ударной волны, распростра-
распространяющейся по продуктам детонации со скоростью (см. п. 4.4)
A5.49)
где и\ и с\ — массовая скорость и скорость звука перед фронтом ударной волны.
Эти параметры определяются формулами A5.11). Параметры и и с определяются
уравнениями A5.48). Поскольку во фронте ударной волны, если она изучается в
акустическом приближении, и + с = и\ + ci, то, подставив это равенство в A5.49),
получим:
dx
D I
A5.50)
Интегрируя это уравнение при условии, что х = / при t = l/D, получим закон
движения фронта отраженной ударной волны:
Dt VIDt
2/.
A5.51)
Из уравнения изоэнтропы р = Ар3 следует, что р/рн = (р/рнK', поскольку при
к = 3 имеем с ~ р, то
Рн
A5.52)
Подставляя A5.52) в значение с из A5.48) и учитывая, что сн = 3.D/4, получим
64
P=27PH \DtJ
v
A5.53)

12
15. Метание тел продуктами детонации
Уравнение A5.53) дает закон изменения давления у стенки. Графически эта
зависимость представлена на рис. 15.11 Полный импульс при отражении дето-
детонационной волны от стенки
1/D
l/D
где S — площадь поперечного сечения заряда ВВ. Поскольку рн = PoD2/4, то
окончательно будем иметь
I = -SlpoD = —mD,
Z /	Z /
A5.55)
где Slpo — масса заряда.
Как видно из рис. 15.11, давление у стенки падает чрезвычайно резко. Из этого
следует, что импульс, обусловливающий местное действие взрыва (изображен на
графике заштрихованной площадью), передается преграде в основном за весьма
короткий промежуток времени т ~ 2//Z), равный времени пробега волны разре-
разрежения по заряду. В случае D = 8000 м/сек и / = 20 см, г = 5 • 10~5 с. За это время
давление падает до значения рт = (8/27)рн, которое все же еще достаточно велико
и обычно превосходит предел упругих деформаций соответствующих материалов.
При подобных расчетах сле-
следует учитывать истинное мак-
максимальное давление, которое
возникает на границе разде-
раздела сред при отражении и су-
существенно зависит от соотно-
соотношения между плотностью и
сжимаемостью продуктов де-
детонации и самой среды. Ме-
Методы теоретического вычисле-
вычисления этих давлений подробно
рассмотрены в гл. 11.
Рассмотрим влияние дви-
движения границы раздела ПД и
0	1	2	3	4 HDt
Рис. 15.11. Падение давления, действующего на стенку,
при отражении детонационной волны
плотной сжимаемой среды на
закон изменения давления и
импульса на границе плотной
среды.
Закон движения границы ПД и плотной среды можно рассматривать прибли-
приближенно, считая, что движения отраженной волны в ПД и ударной волны в плотной
среде являются изоэнтропийными. В этом случае движение ПД в отраженной
волне определится общими решениями для к = 3 (см. п. 3.5):
х = (и + c)t + Fi(u + с), х = (и- c)t + F2{u - с),
а волна в плотной среде - особым решением1).
2
и =
п
— (с - с0), x =
¦c)t
«К
A5.56)
A5.57)
^Если ударная волна слабая и ее движение можно рассматривать с помощью акустической
теории (см. п. 4.4).

15.1. Импульс взрыва при отражении ДВ от стенки	13
где со — скорость звука в невозмущенной плотной среде. Изоэнтропийную связь
между давлением и плотностью возьмем для ПД в виде
р = Ар3 = Вс3.	A5.58)
Для плотной среды
«— \ п	\	/ / _ \ 2п/(п — 1)	\
поскольку с2 = dp /dp ~ рп~1. Численные коэффициенты Ann для разных
плотных сред приведены в гл. 19.. Движение границы раздела ПД и плотной среды
можно определить без полного решения задачи о движении волн в ПД и плотной
среде. Для этого достаточно определить функцию F\(u + с) в уравнении A5.56).
Эта отраженная волна сопрягается с падающей простой волной A5.11):
x = (u + c)t, u-c=-D/2.	A5.60)
Поскольку на границе падающей и отраженной волн величина и + с является
непрерывной, то F\(u-\-c) = 0. Тогда решение A5.56) в области отраженной волны
примет вид
х = (и + c)t, x = (u-c)t + F2{u - с).	A5.61)
На границе раздела ПД и плотной среды, вследствие закона равенства действия
и противодействия и условия неразрывности среды, давление и скорость равны
соответственно
dx
р = р, — = и = п.	A5.62)
Используя уравнения A5.58), A5.59) и первое уравнение A5.62), получим
-ч2п/(п-1)	\
)
Поскольку, согласно уравнениям A5.57) и A5.61), на границе раздела ПД и
плотной среды
х dx _ _ п — 1 dx
с = 1~^ ~с = ~с« + —те	A5-64)
то, подставляя эти уравнения в A5.63), получим дифференциальный закон дви-
движения границы раздела ПД и плотной среды:
Это уравнение необходимо интегрировать численно. Начальными условиями явля-
являются t = l/D, x = /. Отсюда в момент отражения детонационной волны от плотной
преграды
|= D = uo + c0.	A5.66)

14	15. Метание тел продуктами детонации
Это соотношение позволяет определить начальную скорость границы раздела ПД
и плотной среды щ из уравнения A5.65):
_//	Г}_1 \2n/(n-l)	\
B(D-uoK = Al М +—_uoj	-I •	A5.67)
Начальное давление на границе ПД и плотной среды определяется формулой
A5.68)
где рн = poD2 /4, сн = 3D/А. Поскольку закон движения границы раздела ПД и
плотной среды определяется интегрированием уравнения A5.65)
rf, — гг(+ \	0, — 0,{+ \	(ЛТ\ CZQ\
то, следовательно, на границе раздела в ПД можно определить t* = ip(u — с) и
х* = ф(и — с); это позволяет определить F2(u — с) в уравнении A5.61)
F2(u -c)=x*-{u- c)U.	A5.70)
Это определяет закон движения ПД в отраженной волне с помощью уравне-
уравнений A5.61) и A5.70).
Для определения f(u) в уравнениях A5.57) опять используем известный закон
движения границы раздела A5.69), что позволяет найти t\ = t\(u) и х\ = х\{и)\
отсюда
/ = х\ — (и + c]t\.	A5.71)
Это определяет закон движения плотной среды.
Найдем закон движения фронта ударной волны в плотной среде в акустическом
приближении (см. п. 4.4):
^уд = ~г~ = —(п + с + по + со),	A5.72)
dt 2
где поч Со — известные массовая скорость и скорость звука перед фронтом волны,
X — координата фронта ударной волны в плотной среде.
Используя уравнения A5.57) и A5.71), получим
--п + с.	A5.73)
Для фронта волны
dx к^-,л _ _ ,	A574)
Интегрируя это уравнение при начальных условиях при t = l/D, x = I, получим
закон движения фронта ударной волны X = X(t).

15.1. Импульс взрыва при отражении ДВ от стенки
15
В рамках рассматриваемого (акустиче-
(акустического) приближения (без учета прочности)
полученный закон движения границы раз-
раздела и закон движения ПД и плотной
среды справедливы как для ударных волн
разрежения, так и для ударных волн в ПД.
Поэтому уравнения A5.56)-A5.74) могут
быть использованы для таких сред, как
вода, грунт, металлы.
Согласно расчетам [15.5], закон одно-
одномерного движения границы раздела слоя
ПД и сжимаемой плотной преграды, полу-
полученный численным интегрированием урав-
уравнения A5.65), можно аппроксимировать
следующей степенной зависимостью:
3,0
2,5
2,0
1,5
1,0
0,5
О 1 2 3 _4_ 5_ 6 7
PqCq-W~~7, кг/м2-сек
Рис. 15.12. Зависимость величины C о
свойств преграды
Гтт /~\
JtlLovJ'
Be
Cd
*—^->
Cu
—	—
Та
Mo
An
-~-—m
A5.75)
где luq = uq/D, uj = u/D, щ — начальная скорость границы раздела, /3 — некоторая
константа, определяемая свойствами заряда и преграды, D — скорость детонации.
Величина /3 определяется приближенным соотношением
/3 = 1 + 0,02(р0соH'24,	A5.76)
где Cq = (dp/dp)o — скорость звука в материала преграды при р = ро, ро —
начальная плотность материала преграды, [pqCq] — в кг/сек • м2. Величина C
для ряда материалов представлена на рис. 15.12 Зависимость позволяет получить
аналитическое уравнение для определения давления на границе ПД-плотное тело
с учетом сжимаемости последнего.
Поскольку uj = (l/D)dx/dt, то A5.75) из следует
dx
dt
Интегрируя это уравнение, можно получить
1/A-/5)
откуда
A -
A5.77)
A5.78)
A5.79)
В области отраженной волны в ПД, согласно A5.61), справедливо уравнение
x/t = и-\-с. Подставим в это уравнение x/t и и = ujD из уравнений A5.78) и A5.79),
в результате получим
с
A5.80)

16
15. Метание тел продуктами детонации
Уравнение A5.80) определяет закон изменения скорости звука в продуктах де-
детонации, контактирующих с поверхностью преграды. Учитывая, что р/рн = {с/сн)
и сн = 3.D/4, молено записать теперь формулу, определяющую зависимость
давления на контактной поверхности рх от времени:
Рх_
Рн
64
27
/
v 3/3/@-1) •
A5.81)
Если считать преграду абсолютно несжимаемой (luq = 0), то уравнение A5.81)
полностью совпадает с уравнением A5.53). Для сжимаемой преграды (cjq > 0) в
момент выхода фронта детонационной волны на поверхность преграды (?0 = 1/D)
имеем:
64
Ро=27
A5.82)
Величину ujq удобно определять графоаналитическим решением уравнения A5.82)
с помощью (р-и)-диаграммы вещества преграды. Расчеты по этой формуле дают
результаты, близкие к полученным в гл. 11.
Величина импульса на преграде для любого момента времени t > l/D опреде-
определяется интегралом
t= I —(—}
J PH27 \Dt)
l/D
(l-ujoKdt
A5.83)
P
2,37pH
Рн
1
0,5
0,4
0,3
0,2
0,1
ч
II
?
1
>
— -
—	—
и—	—
4
——	—
——	¦¦
1	2	3	4	12468 10
а	б
Рис. 15.13. Зависимость давления (а) и импульса (б) взрыва от времени с учетом сжимаемости
разных преград: 1 — жесткая преграда, 2 — медь, 3 — алюминий, 4 — вода
Расчеты показывают, что для любых реальных преград /3 > 1. В силу этого спад
давления продуктов детонации на контактной поверхности должен происходить
медленнее, чем это следует из уравнения A5.53). На рис. 15.13а представлены
кривые p(i), рассчитанные по формуле A5.81) для нескольких комбинаций «ВВ-
преграда» с учетом значений ujq и /3, найденных из соотношений A5.65) и A5.75) по
методу наименьших квадратов. Сопоставляя эти кривые, можно заключить, что
удельный импульс взрыва должен в меньшей степени зависеть от сжимаемости
преграды, чем начальное давление ро.

15.1. Импульс взрыва при отражении ДВ от стенки
17
На рис. 15.136 представлены расчетные значения импульсов взрыва на сжима-
сжимаемые преграды из Си, А1 и воды по формуле A5.83). Из этого рисунка видно,
что для металлов величина импульса слабо зависит от их сжимаемости. Для
воды же величина импульса существенно зависит от ее сжимаемости. Опытные
данные подтверждают, что импульс взрыва слабо зависит от механических свойств
твердой преграды (грунт, бетон, сталь), максимальное же давление на преграде
существенно зависит от свойств преграды (см. гл. 11).
Из выражения A5.55) следует, что удельный импульс, обусловливающий (в
первом приближении) местное, бризантное действие взрыва, зависит не только от
скорости детонации и плотности ВВ, но и от веса и геометрических параметров
заряда.
Из A5.55) следует, что при прочих равных условиях, импульс должен линейно
расти с увеличением скорости детонации. Отсюда следует, что импульс заряда
данного ВВ может быть заметно увеличен за счет увеличения плотности заряда;
поскольку D = ApQ, то, следовательно, должна выполняться следующая зависи-
зависимость:
/ = Кр%	A5.84)
Уравнение A5.55) предполагает линейную зависимость между импульсом и
длиной заряда, что в действительности не наблюдается. Объясняется это тем,
что на практике не представляется возможным реализовать строго одномерное
движение продуктов детонации и полностью исключить боковой их разлет даже
при заключении заряда в достаточно прочную оболочку.
Однако зависимость A5.55) может быть использована не только для одномер-
одномерного, но и для трехмерного случая. Для этого необходимо вместо полной массы
заряда подставить массу активной его части, которая может быть в каждом
частном случае рассчитана приближенно.
Теория активной части заряда разраба-
разрабатывалась Власовым, Покровским и полу-
получила дальнейшее развитие в работе Баума
и Станюковича. Под активной частью за-
заряда понимают ту часть заряда, продукты
детонации которой разлетаются в задан-
заданном направлении. С увеличением длины
заряда при заданном его диаметре актив-
активная масса активной части заряда может
быть рассчитана следующим образом.
Пусть инициирование цилиндрического
заряда производится в произвольном сече-
сечении, разделяющем заряд на две части (а и б), как это показано на рис. 15.14. Из
теории одновременного разлета продуктов детонации известно, что в этом слу-
случае для разлетающихся в противоположных направлениях продуктов детонации
справедливы следующие соотношения [15.4]:
< а >
< Ъ >
Рис. 15.14. Разлет продуктов детонации
цилиндрического заряда с торцов
9
т2 =
A5.85)
где ttzi и т>2 — массы, разлетающиеся в левую и правую стороны соответственно.
Если инициирование заряда осуществляется у левого конца, то в сторону
распространения детонации (вправо) разлетается 4/9 общей массы заряда. Однако
вследствие одновременного разлета продуктов детонации с боковой поверхности
активная масса заряда уменьшается

18
15. Метание тел продуктами детонации
Если с — скорость волны разрежения, распространяющейся от боковой поверх-
поверхности к оси заряда, а его радиус — г о, то предельная длина активной части заряда
определяется из условия
ГО _ \а_ * _
с D
A5.86)
а активная масса будет занимать объем конуса с радиусом основания г о и высотой
/о, т.е.
A5.87)
где mnp — предельная активная масса заряда.
Приняв с достаточным для практики приближением с ^ D/2 и относя актив-
активную массу к единице поверхности основания заряда, получим
тир _ 2
тгг? 3
A5.88)
Из A5.85) и A5.86) видно, что предельное значение активной массы при заданном
диаметре заряда достигается при длине заряда / = 9/2го- Отсюда следует, что
увеличение удельного импульса при увеличении длины заряда должно проис-
происходить лишь до известного предела. При увеличении длины заряда выше его
оптимального значения /пр = 9/2го (при этом 1а = 4/9/пр) увеличение импульса не
должно наблюдаться (рис. 15.15).
« '''У'?г(\'$!??^а'*:9 пр™™™**
Рис. 15.15. Активная части открытого за-
заряда При / > /Пр-
Рис. 15.16. Активная части открытого за-
заряда при / < /пр.
Если длина заряда / < 9/2го, то активная масса заряда определяется объемом
усеченного конуса, высота которого равна 4/9/ (рис. 15.16).
Масса активной части заряда выражается в этом случае следующей зависимо-
зависимостью:
8 '2 И ^ '	A5.89)
Применяя те же рассуждения, можно показать, что активная часть заряда, а
следовательно, и удельный импульс, должны также возрастать и при увеличении

15.1. Импульс взрыва при отражении ДВ от стенки
19
диаметра заряда, асимптотически приближаясь к определенному пределу (см.
табл. 15.3).
В табл. 15.3 сопоставлены значения импульсов, установленных эксперименталь-
экспериментально и рассчитанных по формуле A5.55) для тротиловых зарядов на основании
данных об активной части заряда A5.89). Как видно из таблицы, рассчитанные
значения находятся в удовлетворительном согласии с опытными.
Выведенные выше зависи-
зависимости позволяют определить	Таблица 15.3
импульс при детонации от- Расчетные и опытные значения удельных
крытого заряда ВВ на по- импульсов
верхности жесткой или сжи-
сжимаемой стенки. Если же за-
заряд ВВ находится в оболоч-
оболочке из инертного вещества (на-
(например, стальной), то вели-
величина импульса, действующего
на стенку, будет существенно
больше, чем для открытого
заряда.
Определим импульс, пе-
передаваемый длинным цилин-
цилиндрическим зарядом, заклю-
заключенным в оболочку, на поверх-
поверхность плиты1 >. В этом случае
разлет продуктов детонации
будет задерживаться инерт-
инертной оболочкой, причем, чем
толще эта оболочка, тем медленнее будет разлет продуктов детонации и, следо-
следовательно, тем больший импульс будет действовать на поверхность плиты.
Удельный импульс, действующий на площадь контакта заряда и плиты, легко
определить, если считать, что имеет место мгновенная детонация. В этом случае
давление в ПД внутри длинной цилиндрической оболочки определяется законом
ее движения.
Закон движения цилиндрической оболочки возьмем в виде A5.143):
A5.90)
где г — текущий радиус, г о — начальный радиус заряда, т — масса ВВ, заключен-
заключенная в оболочке, М — масса оболочки, D — скорость детонации, t — время. Так как
масса газа в начальный момент времени равна тггд/рсь а в любой другой момент
времени эта же масса газа равна тгг2/р, где / — высота заряда ВВ, р — текущая
плотность ПД, то отсюда получим г^ро = г2р. Давление р ~ р3, поэтому
MM
80
80
80
80
70
70
70
43
61
67
d
MM
20,0
23,5
31,4
40,0
20,0
23,5
31,4
40,0
40,0
40,0
P
г/см3
1,40
1,40
1,40
1,40
1,50
1,50
1,50
1,30
1,30
1,30
D
м/сек
6320
6320
6320
6320
6640
6640
6640
6025
6025
6025
i • 10hc/m2
опыт
0,162
0,217
0,305
0,378
0,205
0,266
0,325
0,296
0,316
0,318
расчет
0,178
0,208
0,280
0,360
0,200
0,234
0,314
0,272
0,305
0,310
Р_
Рс
A5.91)
При расширении цилиндрической оболочки от начального радиуса го до теку-
х) Задача решена Л. П. Орленко

20	15. Метание тел продуктами детонации
щего радиуса г среднее текущее давление ПД р будет равно
Здесь принято, что в начальный момент среднее давление в цилиндре равно
давлению мгновенной детонации рс = pqD2/S. Подставим в уравнение A5.92)
значение г/vq из A5.90), в результате получим
Эта зависимость определяет закон изменения давления на площади соприкосно-
соприкосновения заряда и плиты с учетом расширения оболочки в зависимости от времени.
Удельный импульс г2 на поверхности плиты равен
где d = 2гд. Из этой формулы следует, что при отсутствии оболочки (М = 0)
импульс %2 = 0. Очевидно, что формула, определяющая импульс на плиту с учетом
оболочки, должна при М —)> 0 превращаться в формулу, определяющую импульс
открытого заряда на плиту %\.
Удельный импульс открытого заряда %\ с помощью уравнений A5.55) и A5.88),
A5.89) определяется формулами:
8	/4 8 / 16 /2
16	9
Ч = —Dporo	для / ^ —.	A5.96)
81	2г0
Этот импульс %\ действует весьма малые промежутки времени (см. рис. 15.13).
Полный удельный импульс, который передает заряд в оболочке на плиту, равен
сумме импульсов i\ A5.96) и %2 A5.94):
^	A5.97)
При М —>> 0 г* = ii. Зависимость A5.97) справедлива для длинных зарядов в
оболочке при / > 2,25с/, где d = 2го-
При детонации коротких зарядов (/ ж d) уравнение A5.97) дает завышенные
значения удельного импульса, так как при выводе этой зависимости было принято,
что имеет место разлет продуктов детонации с осевой симметрией. Определим
удельный импульс на поверхности плиты при детонации заряда в оболочке в
том случае, когда разлет продуктов детонации имеет точечную симметрию. Тогда
среднее текущее давление продуктов детонации будет меняться как р ~ 1/г9. Так
как в этом случае rjjpo = r3p, то аналогично A5.91) получим

15.1. Импульс взрыва при отражении ДВ от стенки	21
а зависимость скорости движения оболочки от расстояния г для данного случая
равна (см.A5.132)
Л™	I / Л \ /	™6 \
A5.99)
где А = (ро/24)?оГо/М, So — начальная поверхность оболочки заряда.
Удельный импульс представим состоящим из двух составляющих i[ и г^, так лее,
как и при разлете продуктов детонации с осевой симметрией, причем i[ = %i будет
определяться формулой A5.95), ai'2- следующим приближенным соотношением:
м
UDro4m- A5Л°0)
Эта зависимость справедлива для зарядов, у которых I ~ d. Если требуется
определить удельный импульс на поверхности плиты для зарядов в оболочке,
имеющих d < I < 2,5б/, то следует вычислить интерполяционное значение удельно-
удельного импульса между значениями, вычисленными по формуле A5.94) (для / = 2,5с/)
и A5.100) (для / = с/).
Интерполяционное значение удельного импульса для зарядов в оболочке, имею-
имеющих высоту d < I < 2,5б/, можно определить по формуле
A5.101)
Полученные выше соотношения для импульса при взрыве подтверждаются ре-
результатами экспериментальных исследований (см. табл. 15.4).
Если заряд заключен в оболочку, то в детонирующем заряде в большей или
меньшей степени ограничено распространение боковых волн разрежения, что
приводит к соответствующему увеличению удельного импульса на его торце. С
увеличением прочности и толщины оболочки импульс заметно возрастает. Неко-
Некоторые данные, иллюстрирующие влияние этих факторов на удельный импульс,
приведены в табл. 15.4.
Необходимо отметить, что наличие оболочки приводит к значительному повы-
повышению воздействия ПД на преграду.
В табл. 15.4 приведены расчетные (по формулам A5.97), A5.100) и A5.101) и
экспериментальные значения удельных импульсов взрыва. В формуле A5.101) ве-
величина i[ = i\ при / > 2,25б/ (см. формулу A5.96). Толщина оболочки обозначена 5.
Согласно данным табл. 15.4 значения расчетных удельных импульсов с точностью
до 15 % совпадают с опытными значениями удельных импульсов для отношений
М/тп > 1. Из таблицы видно, что расчетные удельные импульсы превышают
экспериментальные импульсы, кроме первого случая (/ = 30 мм).
Если заряд ВВ, который детонирует в контакте с жесткой преградой, находится
в воде, то импульс взрыва на преграду приближенно можно рассчитать по анало-
аналогии с расчетом импульса для зарядов в оболочке. Пусть на жесткой преграде в воде
детонирует сосредоточенный заряд (I & d). Как в формуле A5.97), будем считать,

22
15. Метание тел продуктами детонации
Таблица 15.4
Удельные импульсы для зарядов в оболочках, г • 10~5нс/м
вв
Тротил
Тротил
Тротил
Гексоген
флегмати-
зированный
мм
30
50
60
60
Оболочка стальная
мм
23,5
23,5
23,5
23,5
6 = 0
Ро
г/см3
1,3
1,3
1,3
1,3
D,
м/сек
6025
6025
6025
6875
— без оболочки
6 =
опыт
0,523
0,635
0,678
0,830
6 мм,
расчет
0,484
0,655
0,729
0,834
6 =
опыт
0,388
0,430
0,475
0,578
Змм,
расчет
0,381
0,497
0,551
0,630
6 = 0
опыт
-
-
0,217
0,370
что полный удельный импульс г определяется двумя составляющими: г = i\ -\- %2-
Величина %\ для 1/г$ = 2, согласно A5.95) определится формулой
Н = 0,0815?>/ро = O,163i>opo-
A5.102)
Величина г2 может быть определена по аналогии с формулой A5.100), если
известен закон движения границы ПД-вода г = r(i) или и = и(г). Тогда справед-
справедливы соотношения A5.98):
A5.103)
=Рв(т) = Vte) '
Р~усх ~ ' - 8 \r(t)J ' " df
Величина импульса, определяемая влиянием воды, будет равна
dr
r9u(r)
A5.104)
Закон движения границы раздела воды и ПД описывается уравнением (см.
гл 13).
0,4
г = г0 ( 1 + 77—
A5.105)
Давление в ПД практически равно одной атмосфере (вблизи поверхности воды)
при г/г0 « 10 и t = Т = 315го/гусо.
Подставим A5.105) в уравнение A5.104):
-3,6
21г]с0
_	сЛ
\ r
A5.106)
Следовательно, импульс сосредоточенного заряда на преграде (на небольшой
глубине) в воде равен
г = г\ + г2
0,163 +
A5.107)

15.2. Определение скорости и законов движения оболочки заряда	23
15.2. Определение скорости и законов движения оболочки заряда,
метаемой продуктами детонации
1. Определение максимальной скорости при одномерном метании
оболочек. Метание оболочки заряда, ее разрушение и разлет осколков проис-
происходит за счет энергии, выделяющейся при детонации ВВ. Если ВВ заключено в
оболочку, масса которой превосходит массу ВВ, то при расчете скорости оболочки
можно, в первом приближении, пользоваться гипотезой мгновенной детонации,
поскольку отражение волн произойдет несколько раз, прежде чем оболочка раз-
разрушится и осколки начнут разлетаться.
Максимальную скорость растяжения оболочки одинаковой толщины для за-
закрытого со всех концов заряда (например, шара или длинного цилиндра) можно
определить из уравнения
Ми2
Ес + Ек + Еи + ЕФ + —— = mQ,	A5.108)
z
где и — максимальная скорость оболочки, М — масса оболочки, т — масса ВВ,
Q — теплота взрывчатого разложения, Ес — энергия, которая передается среде
(воздуху, воде, грунту), окружающей оболочку, Ек — кинетическая энергия ПД,
Ец — внутренняя потенциальная энергия ПД, Еф — энергия формоизменения
(затрачивается на пластическую деформацию оболочки и ее разрушение).
Найдем энергии Ес, Ек, Ей и Еф. Верхнее, максимальное значение энергии Ес,
передаваемой в ударную волну, распространяющейся в окружающей метаемую
оболочку среде, может быть определено, если известна максимальная скорость
оболочки, которая может быть определена из опыта либо расчетным путем без
учета энергии Ес. В этом случае массовая скорость за фронтом ударной волны
в среде равна максимальной скорости оболочки и, следовательно, давление на
оболочку снаружи будет равно р = pcuD(u), где рс — начальная плотность
среды, D — скорость ударной волны в среде, которая может быть определена по
известной скорости и (см. гл. 19). Давление на оболочку со стороны среды будем
считать постоянным. Тогда передаваемая в среду энергия равна работе, которую
совершает оболочка против сил противодавления со стороны среды:
где R — внешний радиус оболочки, соответствующий полному разгону оболочки,
Rq — начальный внешний радиус оболочки. Для сферы V = 4/3tt.Rq, TV = 3,
для цилиндра V = ttRqH, N = 2 (Н — высота цилиндра), для плоского случая
V = soRo, so = const, TV = 1.
Если снаружи оболочки находится воздух, то принимая его за идеальный газ,
для сильных ударных волн получим
, 1 // п\*	\
A5.110)
Здесь величина R = Rup соответствует моменту получения оболочкой максималь-
максимальной скорости. Значение Rup определяется по опытным данным либо расчетным
путем. Так, например, для цилиндрической медной оболочки, когда детонация
расположенного внутри оболочки заряда ВВ распространяется вдоль его оси,

24	15. Метание тел продуктами детонации
величина Rup = 2,24i?0, где Rq — начальный наружный радиус оболочки (см.
п. 10.3).
Для воды, грунта, если D = а + Хи (см. приложение D ), то
= Vpcu(a + \u) — -1 .	A5.111)
Приближенно кинетическая энергия ПД Е^ легко вычисляется при одномер-
одномерном метании сферической, цилиндрической и плоской оболочек, если известны
зависимости скорости и плотности ПД от координаты.
В качестве примера найдем Ек при метании ПД сферической оболочки. Пусть
скорость ПД от центра до оболочки определяется уравнением п = (p(t)rn, где
(p(t) — произвольная функция времени, п — числовой показатель, плотность ПД
р = f{t) не зависит от координаты, тогда полная кинетическая энергия ПД в
каждый фиксированный момент времени будет равна
u2dm Г ip2r2n^r2pdr 27rR3pip2R2n	Ъти2	/1
=	=	A
Г u2dm Г
= J — = )
где и — скорость оболочки, т = 4/ЗтгД3р — масса ПД, г = R — координата
оболочки.
При метании сферической, цилиндрической и плоской оболочек величину ки-
кинетической энергии можно записать в следующем виде:
Ек = ^,	A5.113)
где для сферического разлета ф = 2Bп + 3)/3, для цилиндрического ф = 2п + 2
и для плоского ф = 2Bп + 1). Из A5.113) следует, что можно рассматривать
кинетическую энергию ПД Е^ как кинетическую энергию определенной массы ПД
777,1, движущейся с постоянной скоростью и, т.е. Ек = miu2/2. Эта часть массы ПД
для сферического, цилиндрического и плоского случая, например, соответственно
равна (для п = 1):
777,1 = 3m/5, mi = т/2, mi = т/3.	A5.114)
Определим величину внутренней энергии ПД по формуле Ей = теп, где еп —
внутренняя (потенциальная) энергия единицы массы ПД:
= fpdv,	A5.115)
v — удельный объем, который занимают ПД к моменту полного разгона оболочки.
Уравнение изоэнтропы при расширении ПД от объема v до ос можно предста-
представить в различном виде (см. п. 5.7). Если приближенно принять р = Арк, причем
к = const, то удельная энергия, рассчитанная на единицу массы ПД, определяется
уравнением
/-к Pv P
Av dv = 	= —	-.

15.2. Определение скорости и законов движения оболочки заряда	25
Отсюда внутренняя энергия продуктов ПД
Соответствующие моменту получения оболочкой максимальной скорости дав-
давление р и плотность р могут быть приближенно определены, например, для
цилиндрической оболочки следующим образом:
{) ,	A5-117)
где рс = pqD2/S — среднее давление при мгновенной детонации. Опыт показал,
что полный разгон медной оболочки заканчивается при ро/ р = v/vq = 7 (см. гл. 10)
и г/го = л/7- Поэтому
w if?-	A5Л18)
Следовательно, в этом случае
б	^	A
Точность вычислений по этой формуле существенно зависит от величин к\ и
&2- Величина к\ обычно меняется от 2,5-3 при р = ро ДО примерно 1,5-1,7 при
р = ро/7, а &2 = &i при р = ро/7 и /^2 = 1.2 при р —>> 0.
Точное значение величины еп молено получить по формуле A5.115), если
известна изоэнтропа ПД р = p(v). Результатом такого вычисления ед является
зависимость E.114), полученная для состава ТГ36/64 (р0 ~ 1,717г/см ).
Энергия разрушения (формоизменения) оболочки Еф определяется уравнением
м с	м
ЕФ =	 / endsi =	Ар,	A5.120)
Рм J	рм
о
где Mjрм = Ум — объем метаемой оболочки,М — ее масса, рм — плотность
оболочки, Ар — энергия разрушения единицы объема материала, G{, s\ — интенсив-
интенсивность напряжений и интенсивность деформаций, ер — интенсивность деформаций,
соответствующая разрушению материала; численные значения Ар для некоторых
материалов приведены в гл. 19. Следовательно, полное уравнение энергии A5.108)
при метании в воздухе можно записать в виде
^ + ^ + -J^ + gg + V^k + ^ W^ ~ ^ = mQ. A5.121)
Рм	Ф р{к - 1) 2	2
При плоском метании Еф = 0, тогда скорость метаемой оболочки, если прене-
пренебречь Ес, будет равна
2/3	A5.122)
где j3 = m/M.

26	15. Метание тел продуктами детонации
Далее для удобства будем пользоваться формулой D = у/2(/с2 — 1)Q. Следует
заметить, что эта формула, справедливая для идеальных газовых систем, является
теоретически необоснованной для конденсированных ВВ (см. гл. 5). Для многих
ВВ большой плотности (ро = 1,6... 1,8г/см ) эта формула дает завышенные зна-
значения скорости детонации на 10-15 % при к = 3. В этом случае D = Ал/Q. В ряде
случаев более точное значение скорости детонации получается при к = 2,7, при
этом D = 3,5\/Q- При уменьшении плотности данного ВВ D всегда уменьшается,
a Q для ряда ВВ не зависит от начальной плотности ВВ. Использование формулы
D = \Ji(k2 — 1)Q в этом случае теряет свой смысл.
Формула A5.122) не учитывает истечения продуктов детонации вдоль оси
заряда для цилиндрических оболочек конечной толщины и истечения ПД при
разрыве оболочки; не учитывает она и взаимодействия детонационной волны
с оболочкой. Затем следует заметить, что эта формула предполагает толщину
оболочки вдоль образующей постоянной, в противном случае скорости различных
частей оболочки будут разными. Зависимость A5.122) выведена для плоского и
шарового заряда или для цилиндрического заряда бесконечной протяженности.
Для различных других случаев эта формула определяет завышенные значения
некоторой средней скорости (например, для случая короткого цилиндра без днищ).
В уравнении энергии A5.121) во многих случаях можно пренебречь энергией
разрушения Еф и величиной энергии ударных воздушных волн. В этом случае
скорость разлета оболочки равна
Если принять, что численно для больших ро выполняется Q — Ей ~ D2 /16, то
A5.124)
Если считать, что вся энергия mQ расходуется на метание оболочки, то
Ми2/2 = mQ.
Эта формула при условии D = 4\/Q может быть записана в виде
A5.125)
и дает верхний теоретический предел скорости метания оболочки ПД.
Учитывая, что для плоской оболочки ф = 6, для цилиндрической ф = 4 и
сферической ф = 10/3 из A5.124) соответственно получим
A5.126)
2. Определение законов движения одномерных оболочек, метаемых
продуктами взрыва. Рассмотрим закон движения сферической оболочки в
предположении мгновенной детонации заряда, что допустимо для М/т > 1.
Будем считать, что энергия ПД расходуется на метание оболочки массой М и

15.2. Определение скорости и законов движения оболочки заряда	27
метание самих ПД. Если считать, что скорость продуктов детонации линейно
меняется от центра до оболочки, то со скоростью оболочки в каждый данный
момент движется масса ПД mi A5.114). С учетом этой массы закон движения
оболочки запишется в следующем виде:
(М + \т) ^ = (М + \т)и^ = sp,	A5.127)
о dt	о div
где s = 4тгг2 — поверхность расширяющейся сферической оболочки; начальное
значение s = sq = 4тггд, отсюда
s = so(-J.	A5.128)
Поскольку для конденсированных ВВ р/рс = (р/роK> а из закона сохранения
массы г3р = rjjро> т0 V — Рс{го/Г)9, или
Подстановка A5.128) и A5.129) в A5.127) дает
D2r7 f _7л	cikiq^
dr- A5Л30)
М 3\ ? 2 soPoD2r7o
0	r0
После интегрирования, с учетом, что /5 = т/М и m = <soPoro/3, получим
2 Y E + 3/3J
Если /3 мало, то формула приобретает вид
Если (го/rN <С 1, то из формул A5.131), A5.132) получим соответственно форму-
формулы A5.124) и A5.125).
Чтобы найти закон движения сферической оболочки, надо в уравнении A5.131)
положить и = dr/dt, в результате чего получим
*= D
2г0 /2E + 3/3) Y° X3
/ то
Если считать, что оболочка состоит из готовых осколков, то в уравнении A5.127)
надо положить s = sq:
тE + 3C) du PoD2

28	15. Метание тел продуктами детонации
что после интегрирования дает
15/3
2 V 8E + 3/3)
Отношение предельных значений скоростей готовых осколков и целой оболочки
согласно формулам A5.131) и A5.135) равно \/3/4 ж 0,87. Следует заметить, что
это отношение завышено, поскольку формула A5.135) не учитывает истечения ПД
через зазоры между готовыми осколками.
Определим теперь скорость цилиндрической оболочки, рассматривая оболочку
все время как целое или считая, что она заранее состояла из готовых осколков1). В
первом случае, рассматривая тяжелую оболочку (М/т > 1) и применяя уравнение
сохранения импульса, можно написать с учетом массы продуктов ПД A5.114).
777 \ fill	/	777 \ fill
™)™ = (М+-)и— = 8р	A5.136)
2 / dt V	2 / dr
где s — текущая площадь боковой поверхности цилиндрической оболочки. Оче-
Очевидно, что s = so(r/ro), где sq — начальная боковая поверхность цилиндра, г о —
начальный радиус цилиндра.
На начальной стадии расширение ПД подчиняется закону
;	A5.137)
подставив это выражение в A5.136), получим
/	т\ dn В2	/ г \5 D2 И
f Л/Г I	1	I \	0	(л г 1QQ\
I М + — I — = —soPo I — I = ~ГШ^"'	A5.138)
V	2 / аг 8	\го/	4 г°
или
бЫ2 _ 2/3 Р2г4
dr ~ 2 + f3 2 г5'
Интегрирование дает выражение для скорости оболочки
A5.139)
При г —>- сю получим A5.126), Так как ?j = dr/dt, то, обозначая Л = r/го и
г = Dt/ro, придем к уравнению движения цилиндрической оболочки
т (при г = 0, Л = 1).
A5.140)
v л** — ± ^vz"^p
1
Левая часть A5.140) может быть представлена в виде эллиптического интеграла
и аппроксимируется выражением
л
A5.141)
^Задача решалась Баумом и Станюковичем.

15.2. Определение скорости и законов движения оболочки заряда	29
На основании A5.140) и A5.141) получим
v +4B + /?)) '	A5Л42)
Если /3 -С 2, то
А = (l + ^т2) .	A5.143)
Это уравнение представляет закон движения цилиндрической оболочки. Если
s = sq, интегрирование A5.136) дает
A5Л44)
при г —>• 0, uu/D = у7'yS/5B + /3). Полученное таким образом отношение скоростей
завыпгено, поскольку мы не учли истечения ПД через зазоры в случае метания
готовых элементов (осколков).
Рассмотрим приближенно влияние пластического сопротивления цилиндра на
величину его скорости. Если считать материал цилиндра идеально пластичным
и пренебрегать упругими деформациями, то давление внутри тонкого цилиндра,
которое уравновешивает пластическое сопротивление цилиндра, определится по
формуле
Ps = ^,	A5.145)
где h — толщина оболочки, crs — динамический предел текучести. Из усло-
условия несжимаемости материала получим Br + h)h = Bro + ho)ho = Л, отсюда
h = yV2 + A — г. Если h <С 2г, то h = A/Br) и ps = Ars/Br2). В этом случае
уравнение A5.136) можно написать в виде
^)^=S(p-ps),	A5.146)
или, если ps = (yV2 + ^4 — г) crs/r,
+)и	ггп^
2 / б/г 4 г5 г0
Если ps = Лсг5/2г2, то
т \ du D2 Tq sq A<js
dr 4 r5 ro 2r
Интегрирование этого уравнения дает
'-^wmV-d) -i^rK A5Л47)

30
15. Метание тел продуктами детонации
U/D
0,4
0,3
0,2
0,1
/
//
W
Г
***
—. ¦—
р.	* ^
-.	-
Полученные выше соотношения для основной части оболочки или готовых
осколочных элементов сохраняются и при детонации В В в длинном цилиндре,
открытом с торцов. Для длинного заряда, длина которого в несколько раз пре-
превышает его диаметр, элементы оболочки, находящиеся на некотором удалении от
торцов заряда, успеют переместиться на значительное расстояние, прежде чем
осевые волны разрежения успеют проникнуть вглубь заряда.
Величина г в формуле A5.139), A5.147) соответствует либо некоторому пре-
предельному внутреннему радиусу гр, при котором оболочка получает максимальную
скорость, если оболочка расширяется до гр без разрыва, либо тому радиусу
Гр, при котором происходит разрушение оболочки. Так, например, для медных
оболочек гр > 2,6го (см. гл. 10). Менее пластичные материалы разрываются
раньше, чем оболочка наберет максимально возможную скорость (если движение
осуществляется без разрыва оболочки). Так, например, по опытным данным
Санасаряна гр = 1,84го для оболочек из стали 45, причем величина гр практически
не зависела от относительной толщины оболочки /го/^о = 0,208—3,33. Аналогичные
результаты гр = A,6...2,1)го были получены при разрушении труб из мягкой
стали другими исследователями.
Из формул A5.139), A5.147) следует, что
при г = 1,45го оболочка набирает около
88% максимальной скорости; при г = 1,88го
оболочка приобретает 95 % максимально воз-
возможной скорости щ, а при г = 2,64rg
и = О,99^о- Эти значения близки к имею-
имеющимся экспериментальным данным для сколь-
скользящей детонационной волны. Так, по данным,
изложенным в п. 10.3 при R/Ro = 1,33 (при
этом г/го = 1,45) и = @,8.. .0,86)гло, при
R/Ro = l,65(r/r0 = l,88)iz = 0,89...0,92?io, при
R/Ro = 2,24(r/r0 = 2,64)u = 0,95...0,97iz0, где
R — наружный радиус оболочки.
На рис. 15.17 представлены зависимости ско-
скорости цилиндрической оболочки и в долях скоро-
скорости детонации D при осевой детонации (детона-
(детонация начинается на оси заряда) и при мгновенной
детонации, полученные путем численного инте-
интегрирования дифференциальной системы одно-
одномерных уравнений для осевой симметрии [15.6],
описывающих адиабатическое движение продук-
продуктов детонации (см. гл. 2). Прочность и сжи-
сжимаемость оболочки не учитывалась. Показатель
изоэнтропы ПД считался постоянным и равным
трем. Обозначим C = т/М, где т — масса
заряда ВВ, М — масса оболочки заряда. Для
легких оболочек (f3 > 1,25) скорость оболочки
при осевой детонации больше, чем при мгновен-
мгновенной. Для более тяжелых оболочек (/3 = 0,25—1,25)
максимальная скорость оболочки (при r/rg = 1,5) при мгновенной детонации
больше, чем при осевой. Для тяжелых оболочек /3 < 0,25 стирается различие в
величинах максимальных скоростей при мгновенной и осевой детонациях.
В начальный период при осевой детонации набор скорости всегда идет более
быстрым темпом, чем при мгновенной детонации. Затем закон изменения скорости
оболочки с расстоянием существенно зависит от величины /5, что связано с законом
11
}0,5
10,25
1,0 1,1 1,2 1,3 1,4 г/г0
Рис. 15.17. Зависимость скорости
цилиндрической оболочки от
расстояния для осевой детонации
(сплошные линии) и при мгновенной
детонации (штриховые линии) для
разных р = т/М.

15.3. Одномерное метание пластин продуктами детонации	31
движения оболочки в начальный период и законом движения ударной волны,
отраженной от оси заряда (при осевой детонации). Если оболочка легкая, то при
отражении детонационной волны она настолько быстро разгоняется в начальный
период, что ударная волна, отраженная от оси заряда, ее не догоняет. Для
тяжелых оболочек отраженная от оси заряда ударная волна догоняет оболочку
и увеличивает скорость оболочки. В то же время ударная волна, отраженная
от оболочки и двигающаяся к центру, уносит с собой заметную часть энергии,
давление около оболочки быстро падает (быстрее, чем при мгновенной детонации)
и разгон оболочки уменьшается более быстро, чем при мгновенной детонации. В
результате при /3 = 0,25-1,25 максимальная скорость оболочки (при r/rg = 1,5)
оказывается больше при мгновенной детонации, чем при осевой (рис. 15.17).
15.3. Одномерное метание пластин продуктами детонации
Рассмотрим движение тела, метаемого продуктами детонации конденсирован-
конденсированного ВВ, для строго одномерной задачи (движение газа и тела в трубе) [15.4].
Пусть в точке х = 0 началась детонация: налево продукты детонации истекают
в пространство, которое можно принять пустым (наличие воздуха практически
не изменит результата вычислений). Направо идет детонационная волна, которая
для бризантных взрывчатых веществ характеризуется законом изоэнтропы
р = Арк.	A5.148)
Одномерное движение продуктов детонации описывается уравнениями A5.10)
и=Ц^-,	A5.149)
х = (и + с%	A5.150)
где р — давление, р — плотность продуктов детонации, и — скорость потока, с —
местная скорость звука, D — скорость детонационной волны.
Пусть длина заряда есть / и с правой его стороны находится тело, масса
которого М. Очевидно, что масса ВВ равна т = s/po, где s — сечение заряда,
ро — его начальная плотность.
В момент времени t\ = l/D детонационная волна дойдет до тела и, отражаясь
от него, сообщит ему движение. Поскольку, как известно, даже при ударе дето-
детонационной волны об абсолютно твердую стенку, энтропия во фронте отраженной
ударной волны увеличивается весьма незначительно, то с точностью до нескольких
процентов задачу об отражении волны от твердого тела можно рассматривать в
акустическом приближении (см. п. 4.4).
Для этого случая (при к = 3) имеем C.7):
что, как известно, дает
х = (и + c)t + F^u + с), х = (и- c)t + F2(u - с).	A5.152)
Здесь и -\- с ж и — с определяют параметры отраженной волны.

32	15. Метание тел продуктами детонации
Краевыми условиями данной задачи будут условие сопряжения отраженной
волны с волной, описываемой уравнениями A5.149) и A5.150), и условие на
поверхности твердого тела:
=* «=!¦
Первое условие показывает, что F\(u + с) = 0 и, следовательно,
х = (u + c)t.	A5.154)
Учитывая, что р = pi(c/ciK, где р\ = F4/27)ря = A6/27)ро^2 и ci = D,
уравнение A5.153) можно привести к следующему виду:
= rjc3/W,	A5.155)
dt 27MD
где rj = A6/27)т/М и spo = т/1. Дифференцируя A5.154) по t, получим
—du/dt = c/t + dc/dt. Сравнивая это выражение с A5.155), будем иметь
dc с с3
— -\	h 77-— = 0.	A5.156)
dt t 'ID	y	j
Для решения уравнения A5.156) применим подстановку с = z/\/i. Тогда уравнение
примет вид
= 0.	A5.157)
Разделяя в этом уравнении переменные, получим dz/(z/2 + rjz3/ID) = —dt/t, или
dz2/(z2(l + 2r]z2/ID)) = —dint. После интегрирования это уравнение примет вид
Inz2-ln( l + -^z2 1 = -In*-In С,	A5.158)
или Ct = 1/z2 + 2rj/lD, где G — постоянная интегрирования. Так как с = z/y/i, то
В момент отражения детонационной волны от жесткого тела при t = l/D, с = D,
поэтому С = A + 2rj)/l2. С учетом этого значения G уравнение A5.159) можно
записать в виде с = W/t, где # = A + 27/A - l/Dt))'1/2. Из A5.154) находим
^ ^	A5.160)
dt	t
Общее решение этого линейного неоднородного уравнения:

15.3. Одномерное метание пластин продуктами детонации
33
где С\ — постоянная интегрирования, которая определяется из того условия, что
при t = l/D, x = I. Интегрируя, находим
Подставив найденное значение х в A5.160), получим
что дает зависимость скорости тела и от времени t.
Определим теперь величину и — с. Очевидно, что
и _ с =
- 21ВIt,
откуда следует, что F2(u — с) = 201. На основании A5.152) получим
х = (u-
Поскольку
Отсюда следует, что
Р(г) + 1) - V(u - с)
x-2l(V
A5Л62)
A5Л63)
A5.164)
A5.165)
A5.167)
Уравнения A5.154) и A5.165) полностью решают поставленную задачу. Рас-
Рассмотрим два предельных случая. Пусть М = 0 и rj —)> оо; тогда задача сведется
к изучению движения продуктов детонации при их разлете в пустоту. Уравне-
Уравнение A5.168) при этом дает
Пусть теперь М —>• ос и rj = 0, при этом задача аналогична рассмотрению
отраженной волны от абсолютно твердой стенки:
L
A5.170)
Это выражение вытекает также из уже ранее полученных нами зависимо-
зависимостей 15.47.
В заключение выведем предельные формулы, описывающие законы движения
метаемого тела при М/тп < 1 и М/тп > 1. При М/тп < 1 и соответственно

34
15. Метание тел продуктами детонации
больших значениях ту, используя уравнения A5.162) и A5.163), получим с помощью
разложения этих выражений в ряд по степеням 1/y/rj:
Dt
Dtp
2fl\
A5.171)
-1/(Dt))
При больших M/m, разлагая выражение по степеням rj, получим
I
и
ъ
I2
{Щ2
A5.172)
при t —>> ос, x/l = 1 — т? + (rj/2)Dt/l, и/D = ту/2. Очевидно, что при М = 0 импульс
метаемого тела / = 0, при М —>> ос, / = Afi/, = A6/27)mu/rj, при /; —)> оо, г^ = Drj/2,
следовательно, / = (8/27)mZ), что, как ранее было установлено, соответствует
полному количеству движения продуктов детонации при их разлете.
Мы видим, что при больших М/т в зависимости ж от ту отсутствует свобод-
свободный член; для того чтобы определить зависимость / от ту, необходимо сделать
разложение ж по ту до членов, содержащих т?2.
Проведя вычисления для и ж I при t —>- ос, получим
^	о
-г)).	A5.173)
Таблица 15.5
Сопоставление опытных и расчетных скоростей пластин, метаемых взрывом
заряда ВВ
171, Г
22,8
22,8
22,8
22,8
11,8
ро,г/см3
1,30
1,40
1,50
1,60
1,40
D, м/сек
6880
7315
7690
8000
7315
М, г
6,60
6,80
6,82
6,79
6,91
2,04
1,98
1,87
1,98
1,18
г^оп, м/сек
2440
2540
2700
2830
2030
^расч, м/сек
2670
2790
2450
3060
2170
^расч
91,6
90,5
91,5
90,3
93,5
В заключение укажем, что если продукты детонации разлетаются во все сторо-
стороны (детонация открытого заряда), то выведенные зависимости остаются справед-
справедливыми, если под величиной массы заряда m понимать массу его активной части
Результаты экспериментальных исследований хорошо подтверждают развитую
теорию, что видно из табл. 15.5, в которой сопоставлены опытные и расчетные (вы-
(вычисленные по зависимости A5.163)) скорости пластин в случае заряда из флегма-
тизированного гексогена. Заряд помещался в толстостенной стальной трубе. Выше
была рассмотрена задача метания жесткой пластины без учета волновых явлений
в пластине. Одномерное метание пластины может быть рассчитано численно, с
учетом волновых явлений как в продуктах детонации, так и в метаемой пластине.

15.3. Одномерное метание пластин продуктами детонации
35
На рис. 15.18 представлен про-
процесс движения волн в ПД и пласти-
пластине в координатах расстояние—время,
(x-t), где ADEM — траектория дви-
движения границы раздела ПД и пла-
пластины, CNK — траектория дви-
движения свободной поверхности пла-
пластины. В этом случае на границы
раздела пластины толщиной /го и
В В падает детонационная волна О А,
при этом в ПД отражается ударная
волна А В, а по пластине движет-
движется ударная волна АС. При выходе
этой ударной волны на свободную
поверхность (точка С), от свободной
поверхности внутрь пластины будет
отражаться центрированная волна
разрежения CDE, которая отража-
отражается от границы ПД-пластина (DE).
Происходит ускорение этой грани-
границы, что служит источником образо-
образования волны сжатия (DNKE), и т.д.
За время t^ — tc внешняя поверхность пластины тормозится,
уменьшается до момента прихода волны сжатия DNKE.
Поскольку и в ПД, и в пластине распространяются ударные волны (АВ и АС),
то течение в этих зонах является неизоэнтропийным и для его математического
описания необходимо использовать все три семейства характеристик C.41)—C.43),
учитывая, что на границе ПД и пластины в любой момент времени давление и
скорости должны быть равны. Для численного решения этой задачи необходимо
для продуктов детонации и материала пластины иметь уравнение состояния
р = p(p,S) или р = р(Е,р). На рис. 15.19 представлены результаты численно-
Рис. 15.18. Разгон сжимаемой стальной пластины
продуктами детонации в плоскости (x-t).
и ее скорость
и, км/сек
3
и, км/сек
0	12	3
Рис. 15.19. Закон изменения скорости гра-
границы раздела ВВ-стальная пластина при
изменении расстояния полета х: 1 — несжи-
несжимаемая, 2 — сжимаемая пластина.
0	12	3
t, мксек
Рис. 15.20. Закон изменения скорости сво-
свободной границы стальной пластины со вре-
временем полета: 1 — опыт, 2 — численный рас-
расчет для сжимаемой пластины, 3 — расчет
для жесткой пластины по A5.163).
го решения задачи о плоском метании пластины методом характеристик [15.7].

36
15. Метание тел продуктами детонации
г t, мксек
Пластина из нержавеющей стали толщиной 5,08 мм металась слоем ВВ (состав
ТГ36/64, р0 = 1,714г/см3, D = 7990м/сек) толщиной 50,8мм. Для продуктов
детонации использовалось упрощенное уравнение состояния ПД р = (к — 1)рЕ,
где к — постоянный показатель изоэнтропы.
Из рис. 15.19 видно, что набор скорости границы раздела ВВ-пластина осу-
осуществляется четко выраженными скачками, соответствующими отражению волны
разрежения от этой границы (см. рис. 15.18)
Если пластину считать несжимаемой (см. A5.163)), то набор скорости будет
осуществляться плавно (линия 1 на рис. 15.19), наибольшее расхождение между
скоростями жесткой и сжимаемой пластинами при этом получается в начале
движения.
На рис. 15.20 представлены численный расчет и опытная зависимость скорости
свободной поверхности от времени полета для пластины из нержавеющей стали
толщиной 2,8 мм (толщина слоя ВВ 48,3 мм из ТГ36/64). В пределах первого
отражения волны это совпадение удовлетворительное. Штриховая кривая 3 на
рис. 15.20 рассчитана для жесткой пластины по формуле A5.163).
Отметим медленное затухание расчетных
максимальных напряжений при отражениях
волн разрежения и сжатия в пластине. Так, в
первой волне разрежения (после отражения
ударной волны от свободной поверхности)
максимальные растягивающие напряжения
составляли 9,4 ГПа, в первой волне сжатия
напряжение сжатия было равно 18,3 ГПа, в
восьмой волне разрежения напряжения рас-
растяжения достигали 7,8 ГПа, в волне сжатия
8,7 ГПа. Также отметим условный характер
этого расчета, поскольку задача решалась в
газодинамическом приближении.
При первом отражении волны пластина
приобретает 40 % полной кинетической энер-
энергии, которую пластина получает при мета-
метании, а после третьего отражения — 80 %
полной энергии. Пластина после третьего от-
отражения проходит расстояние, равное при-
примерно двум толщинам пластины. Опыты с
разгоном цилиндра при распространении де-
детонационной волны вдоль оси цилиндра по-
3 -
1 -
С
О
1
0,5
1,0
X, СМ
Рис. 15.21. Образование откола в сталь-	казывают, что для состава ТГ36/64 на рас-
ной пластине (численный расчет): ОС —	стоянии двух толщин медная оболочка акку-
ударная волна в пластине,О?>? - гра-	мулирует 72 % полной кинетической энергии
ница ПД и пластины, 1А — волна, обра-	/„ 10 3)
зующаяся при разрыве пластины, 2В —	-,-г
волны, образующиеся при схлоиывании ПРИ отражении ударной волны от сво-
пластины	бодной поверхности возникает зона растяги-
растягивающих напряжений. Если растягивающие
напряжения превосходят предел прочности на разрыв, в пластине образуется
откольная трещина. Очевидно, что при расчетах толщины откола необходимо
знать величину разрывающего напряжения или, если известна толщина откола (из
опыта), то можно определить, какое напряжение соответствует этой толщине. Для
пластины из нержавеющей стали толщиной 5,08 мм эта величина разрывающего
напряжения оказалась равной около 6,5 ГПа. Интересно отметить, что образую-
образующаяся в пластине откольная трещина (точка 1, рис. 15.21) сначала расширяется,

15.3. Метание металлических частиц
37
а затем обе половинки разорванной пластины вновь схлопываются. При этом от
места удара распространяются две ударные волны (от точки 2, рис. 15.21).
15.4. Высокоскоростное метание компактных металлических частиц.
В настоящее время в околоземном пространстве находится большое количество
мусора искусственного происхождения. Он возник в результате самоликвидации
космических объектов, их разрушения вследствие аварий и т.п. Этот космический
мусор как правило представляет собой частицы из алюминиевых сплавов (остатки
разорванных оболочек ракет и спутников), массой от долей грамма до десятков
и сотен грамм. Большие элементы мусора могут быть обнаружены заранее ра-
радиолокационными методами, что позволяет управляемому космическому объекту
уйти от столкновения с ними. От мелких частиц, массой от долей грамма до
нескольких грамм, летящих с относительными скоростями 3... 16 км/с, а также
от метеорных частиц, имеющих скорости 30 ... 70 км/с, необходима защита косми-
космических объектов. Для исследования и конструирования такой защиты необходимо
уметь разгонять на земле мелкие компактные частицы до высоких скоростей.
Для этой цели используются, во-первых, легкогазовые пушки [15.8]. Они поз-
позволяют разгонять массу до десятка грамм до скоростей Vo = 7,5 км/с. Проведение
массовых экспериментов такого рода затруднено ввиду их высокой стоимости. Во-
вторых, для разгона металлических частиц могут быть использованы взрывные
устройства различной конструкции.
На рис. 15.22 показана схема метательного устройства, основанная на исполь-
использовании кумулятивного заряда [15.8]. Это метательное устройство состоит из
8
0dT
а	о	\^*^ в
Рис. 15.22. Схема высокоскоростного метания с использованием кумулятивного заря-
заряда. Метательное устройство (а); высокоскоростной элемент (б); кратер (в).
детонационного устройства 1, взрывчатого вещества 2, кумулятивного конуса 3,
вкладыша 4 и отсекающего механизма, состоящего из металлической пластины 5,
взрывчатого вещества 6, детонирующего шнура 7. Из части кумулятивной воронки
образуется кумулятивная струя, летящая со скоростью Vo, от которой отсекается
элемент с помощью метания пластины 5 сбоку на струю, или же вместо устрой-
устройства 5, 6, для отсекания струи используется детонация бокового заряда ВВ [15.8].
С помощью устройства такого типа, как на рис. 15.22а, были получены высо-
высокоскоростные элементы (рис. 15.226), а также кратеры глубиной hk и диаметром
dk (рис. 15.22в).
В таблице 15.6 представлены основные экспериментальные данные о метаемых
элементах и результатах их удара в алюминиевые преграды [15.9].
Угол а в таблице 15.6 определяется с помощью рентгеноскопии, он равен углу
между осью элемента и нормалью к преграде.
На рис. 15.23 изображена схема взрывного метания, использующая газовую
кумуляцию [15.10]. Устройство работает следующим образом. Детонатор A) воз-

38
15. Метание тел продуктами детонации
Таблица 15.6
CD ^
s §
Al
Mo
Ni
Экспериментальные данные о
0) &
A16061-T6
A16061-T6
Чистый Al
A16061-T6
A16061-T6
та,
03 0)
0,31
0,74
1,15
2,5
4,0
1,11
1,94
?
4
о ^
11
11,17
11,28
11,68
11,81
10,85
10,75
hk,
(cm)
2,69
2,93
4,88
4,3
3,7
3,2
4,0
метании
(см)
2,72
4,45
6,15
5,5
5,3
5,1
6,8
[ частип
/о,
(см)
1,14
1,39
1,72
3,04
3,34
2,01
2,06
dj,
(см)
0,38
0,52
0,53
0,32
0,42
0,31
0,37
a°
0
18
7
0
32
90
56
Рис. 15.23. Схема метательного устройства, использующего газовую кумуляцию.
буждает детонацию взрывчатого вещества B), в результате образуется газо-
газовая кумулятивная струя. Одновременно, или с задержкой, детонирует заряд
взрывчатого вещества C). С помощью детонатора D), детонирующего шнура
E) и детонирующего устройства F) продукты детонации заряда C) разгоняют
метаемый элемент G) в трубе (8). После детонации заряда C) на разгон элемента
воздействует газовая кумулятивная струя. С помощью такого ускорителя был
разогнан стальной элемент, диаметром 24 мм и массой 20 г до скорости 4,9 км/с.
Масса заряда B) была равна 1,65кг (ТГ 40/60). Труба имела длину 150мм,
внутренний диаметр 24 мм, внешний — 60 мм.

15.4- Высокоскоростное метание компактных металлических частиц.
39
Рис. 15.24. Схема газокумулятивного ме-
метательного устройства.
ЛГУ
ПСУ
Рис. 15.25. Метательное устройство ком-
комбинированного типа.
На рисунке 15.24 показан газокумулятивный заряд для разгона сферических
металлических элементов [15.11] Метательное устройство состоит из стальной
трубы A), заряда взрывчатого вещества B), полости D) и метаемого элемента C).
При детонации заряда с торца возникает газовая кумулятивная струя, которая
разгоняет элемент C). Численные расчеты процесса газовой кумуляции для раз-
разных параметров метательного устройства показали, что газовая струя состоит из
двух частей: основной (головной), увеличивающейся со временем, где плотность,
скорость и давление практически остаются постоянными, и хвостовой струи, дли-
длиной l,6di, расположенной непосредственно перед фронтом детонационной волны,
в которой происходит сильный рост плотности и давления продуктов детона-
детонации [15.12]. Параметры основной части газовой струи для типичных взрывчатых
веществ определяются соотношениями:
плотность
массовая скорость
давление
р= @,25d- 0,02) г/см3;
и = 1,8?>(км/с);
р= @,7d-0,4)-100MIIa,
где d = с/2/^ъ D — скорость детонации.
Газокумулятивное устройство позволяет метать частицы массой 0,01 г до ско-
скоростей 12 км/с. Для метания массы в один грамм до скоростей 8 км/с, требуется
заряд взрывчатого вещества в 100 кг.
На рис. 15.25 показана схема разгона сферического металлического элемента
комбинированного типа [15.12]. Сначала элемент разгоняется с помощью легкога-
легкогазовой пушки (ЛГУ), затем он попадает в газокумулятивное устройство (ГКУ), где
дополнительно разгоняется газовой струей. Детонация ГКУ осуществляется ше-
шестью детонаторами, расположенными в торцевой части заряда ВВ. Их взведение
осуществляется с помощью контактного датчика, расположенного перед ГКУ. С
помощью ЛГУ шарик из стали ШХ15 диаметром 7,8 мм, массой 2,1 г, разгонялся
до 4,5 км/с и 6,5 км /с , затем его скорость увеличивалась, соответственно, до
5,5 км/с и 8,5 км/с.
Параметры ГКУ были равны: d\ = 40 мм,
с^2 = 80 мм, длина / = 0,5 м для перво-
первого опыта и Z = 1 м для второго опыта.
Соответственно, массы В В были равны
3,4 кг и 6,9 кг. Расчеты показывают, что,
при увеличении заряда В В до 32 кг, можно
получить скорость метания элемента 7-
11 км/с при его массе 20—1 г.
На рис. 15.26 изображена схема двух-
каскадного взрывного метательного устрой-
устройства [15.12]. Метательное устройство со-
состоит из двух каскадов. Первый каскад
состоит из заряда ВВ A) и металлического ударника B), который после разгона
ударяет по заряду ВВ C) второго каскада, продукты детонации которого метают
/VI
1
3//4
Рис.
15.26. Схема двухкаскадного взрыв-
взрывного метательного устройства.

40
15. Метание тел продуктами детонации
металлическую оболочку в виде сферического сегмента D). В первом каскаде удар-
ударник разгоняется до 4,5 км/с. Его удар по заряду ВВ второго каскада возбуждает
в нем пересжатую детонационную волну, которая отражалась от металлического
сферического сегмента. Под действием продуктов детонации оболочка разгонялась
и одновременно формировался компактный элемент Движение элемента должно
проводится в вакуумной камере E) для предотвращения его неустойчивости за
счет торможения в воздухе. При метании железного элемента, массой 0,8-3 г были
получены скорости 6,8—8 км/с . Плотность элемента была меньше начальной и
составляла 2-4,8г/см3.
БУ
КЗ
Ударник-
отсекатель
Метательный
элемент
V0=Vy+Vk
Рис. 15.27. Схема двухступенчатой метательной установки.
На рис. 15.27 представлена схема двухступенчатого разгона элемента, состоя-
состоящая из баллистической установки (БУ) и кумулятивного заряда (КЗ), который
выстреливается из БУ [15.12]. Сначала кумулятивный заряд A) с металлической
облицовкой B) в поддоне C) разгоняется с помощью легкогазовой или пороховой
баллистической установки, затем, с помощью взрывательного устройства, дето-
детонирует взрывчатое вещество кумулятивного заряда, в результате чего образуется
компактный элемент, летящий со скоростью Vo-
С помощью кумулятивного заряда из ТГ 50/50 с закругленной облицовкой,
формируется компактный элемент с массой 3,5—4,0 г, скоростью 4,5—4,7 км/с. При
использовании ВВ на основе октогена, скорость элемента увеличивается до 5,8 км/с,
плотность формируемых железных элементов 4,1-6,1 г/см3.
2 3 4 5
Рис. 15.28. Метательное устройство, ис-
использующее цилиндрическую кумуляцию.
ш
Рис. 15.29. Трехкаскадная схема высоко-
высокоскоростного метания металлических элемен-
элементов.

15.4- Высокоскоростное метание компактных металлических частиц.
41
Экспериментально двухступенчатое метательное устройство было опробовано с
помощью пороховой баллистической установки калибром 100 мм и КЗ с ТГ 50/50,
диаметром 70 мм и массой 0,93 кг. КЗ формировал элемент массой 8 г, летящий
со скоростью 4,6 ± 0,21 км/с . Инициирование ВВ осуществлялось при ударе по
каналам с ВВ D), расположенным в поддоне, при пролете КЗ через отверстие в
отсекателе. КЗ в оболочке, вместе с поддоном массой 3,2 кг, метался со скоростью
1 км/с. Была получена суммарная скорость элемента 5,8 км/с, массой 8 г. Согласно
расчетам, метательное устройство (рис. 15.27) позволяет метать массу 3,5—20 г со
скоростью 9—6 км/с. На рис. 15.28. представлена схема метательного устройства,
использующая цилиндрическую кумуляцию [15.13]. Устройство работает следую-
следующим образом. Детонатор 1 возбуждает детонацию во взрывчатом веществе 2,
находящемся в стальном корпусе 3. Внутри заряда находится инертная линза
4 и цилиндрическая трубка 5, из которой образуется кумулятивная струя. В
трубку вставлен металлический вкладыш 6 с отверстием для пролета кумулятив-
кумулятивной струи. Вкладыш 6 смыкается к оси и отсекает часть кумулятивной струи.
Устройство опирается на плиту 7. По данным ЦНИИМАШа, при массе заряда
ВВ около 1,4 кг средняя скорость составляла около 11 км/с, а масса алюминиевого
элемента — около грамма [15.13]. Скорость измерялась с помощью рам-мишеней,
а масса элемента — рассчитывалась по объему каверны в алюминиевой плите.
На рис. 15.29 представлена трехкаскадная схема высокоскоростного метания
металлических элементов [15.14]. Метательное устройство состоит из заряда ВВ и
трех каскадов A,11,III). Каждый каскад включает в себя ВВ A,4,7), отсекающую
пластину B, 5, 8) и метаемый элемент C, 6, 9). При детонации основного заряда
ВВ A) метается элемент C), он ударяет по ВВ D), в котором возникает пересжатая
детонация. При этом продуктами детонации метается элемент F). Он детонирует
ВВ третьего каскада и элемент (9) приобретает скорость Vo-
С помощью однокаскадного ме-
метательного устройства были достиг-
достигнуты: для медного элемента, массой
1,55 г — скорость 5,6 км/с, для алю-
алюминиевого элемента, массой 0,2 г —
скорость 7,2 км/с. При использова-
использовании двухкаскадной схемы метания,
были получены: для стали, массой
9 г — скорость 9,5 км/с; для трех-
каскадной схемы (алюминий, масса
1,75 г) — скорость 13,8 км/с.
На рис. 15.30 показана схе-
схема взрывного метания, использую-
использующая кумулятивный эффект [15.15].
Устройство состоит из заряда ВВ A), плиты B) и полости C) в плите. При
детонации заряда В В A) плоская детонационная волна отражается от плиты,
в которой возникает плоская ударная волна. Эта ударная волна схлопывает
полость в плите, в результате из материала плиты образуется метаемый элемент
(рис. 15.306). В конечном итоге формируется струя D), утолщенный элемент E) и
головная струя F). Для одного из вариантов метательного устройства (материал —
алюминий), скорость элемента E) составила 8,8 км/с, а головной струи — 21,5 км/с.
Экспериментально было исследовано влияние размеров полости (d, h, r) на
параметры метаемого элемента. В таблице 15.7 показаны величины скоростей
головных струй, полученные экспериментально для алюминиевых и медных плит,
для диаметра заряда ВВ 150 мм.
Рис. 15.30. Схема взрывного метания, использую-
использующая кумулятивный эффект

42
15. Метание тел продуктами детонации
Рис. 15.31. Асимметричное кумулятивное метательное устройство.
Таблица 15.7	На рис. 15.31 показана схема вы-
Скорости головных струй.	сокоскоростного метания элементов
кумулятивной струи, состоящая из
детонатора A), заряда ВВ B) и ку-
кумулятивной облицовки C). Детона-
Детонатор сдвинут относительно оси заря-
заряда, в результате струя D) изгиба-
изгибается. Это позволяет отсечь от нее
элемент с помощью плиты, имеющей
щель [15.8]. Скорость головных ча-
частей металлических струй достигает
8... 12 км/с.
На рис. 15.32 представлена схе-
схема кумулятивного заряда, предна-
предназначенная для метания мелких ме-
металлических частиц. Метательное устройство состоит из детонатора A), заряда ВВ
B) и смеси ВВ с металлическим порошком C), которой облицована кумулятивная
выемка. Экспериментально были получены скорости алюминиевых и вольфрамо-
вольфрамовых частиц E—25 мкм) до 12—15 км/с.
плита
А1
Си
d, мм
20
20
20
30
20
20
30
30
h, мм
20
20
30
30
20
20
30
30
г, мм
1
5
10
15
1
5
3
15
vo, км/с
21,5
20
9,7
9,3
19
14,5
15,5
5,3
Рис. 15.32. Схема высоко-
высокоскоростного метания метал-
металлических порошков.
15.5. Метание осесимметричных оболочек продуктами детонации
На рис. 15.33 представлены результаты численного
решения осесимметричной двумерной задачи о разлете
железной цилиндрической оболочки (предел текуче-
текучести <jsd = Юкбар, метаемой зарядом ВВ (РВХ-9404-
03, см табл. 10.14 из гл. 10), который инициируется
одновременно с двух концов по всей торцевой по-
поверхности заряда [15.17]. Осесимметричный разлет ПД
описывается в этом случае системой газодинамических
уравнений B.15). На рис. 15.33 представлено решение
в двух вариантах: а) железная оболочка без учета
прочностного сопротивления материала, б) с учетом
прочности и сжимаемости железной оболочки.
В этом случае движение материала оболочки описывается системой урав-
уравнений A3.35), учитывающих сжимаемость и прочностные свойства материала
оболочки. На границе раздела ПД и оболочки давление равно нормальному
напряжению, и нормальные составляющие скорости ПД и оболочки равны друг
другу. Дифференциальные уравнения были численно решены методом конечных
разностей с использованием искусственной вязкости.
Результаты решения представлены в виде картинок процесса в плоскости
симметрии в разные моменты времени. Вся среда (ПД и оболочка) разделена на
ячейки, интенсивность затемнения которых соответствует степени сжатия ячеек

15.5. Метание осесимметричных оболочек
43
(элементов среды).
На рис. 15.33 в момент вре-
времени t = 2,11050 (время от-
относительное) видно, как при
столкновении детонационных
волн в центре заряда обра-
образуется темная зона, соответ-
соответствующая образованию отра-
отраженных ударных волн. Срав-
Сравнение результатов расчетов
движения железного цилин-
цилиндра с учетом и без учета его
прочности показывает, что ес-
если учитывается прочность ци-
цилиндра, то его толщина ме-
меняется незначительно, и он
в большей степени сохраняет
первоначальную форму, чем
в гидродинамической модели
без прочности.
Резкий перегиб оболочки
(см. рис. 15.33а) в районе
инициирования заряда В В яв-
является результатом не физи-
физики процесса, а некорректности
принятой схемы расчета ПД в ближайших к торцу узлах на внутренней поверх-
поверхности оболочки (для сравнения см. рис. 15.34 и 15.35).
Двумерные нестационарные задачи о движении оболочки при двустороннем и
осевом инициировании заряда ВВ решались в работах [15.18, 15.19] А. В. Кашир-
Каширским, Ю. В. Коровиным, В. А. Одинцовым и Л. А. Чудовым.
Материал оболочки учитывался только как инерционная масса без прочности
и сжимаемости. Продукты детонации истекают в вакуум. В качестве ВВ взят
пентолит (сплав тротила с тэном 50/50) с начальной плотностью ро = 1,65 г/см ,
теплотой взрывчатого превращения Q = 0,0536 Мбар-см3/г и скоростью детона-
детонации D = 0,7655 см/мксек. Уравнение состояния продуктов детонации принято в
форме A5.116). При заданном уравнении состояния ПД и способе инициирования
заряда, определяющими параметрами задачи будут Л = L/ro и C = 7?г/М, где L —
длина заряда, г о — начальный радиус заряда.
Система уравнений газовой динамики для продуктов детонации в эйлеровых
переменных имеет вид (см. гл. 2):
t = 2,1490
6	'-¦''1™ 6
а	б
Рис. 15.33. Разлет железного цилиндра при двусторон-
двустороннем инициировании заряда (показана 1/4 часть оболочки):
оболочка без прочности (а); оболочка «с прочностью»
(б). 1 — середина заряда, 2 — железная оболочка, 3 —
место инициирования заряда, 4 — заряд, 5 — столкновение
двух детонационных волн, 6 — фронт отраженной ударной
волны.
dv
ot
wdp
dv
dv
—
oz
dv dw
I dp
pdr
pv
A5.174)
dw	dw	dw 1 dp
dt	dr	dz pdz
dE dE dE	p (dv dw\ pv
ot or	oz	p \ or oz) pr
Здесь р, г;, w, E, p — плотность, радиальная и осевая компоненты скорости,

44
15. Метание тел продуктами детонации
внутренняя энергия и давление продуктов детонации соответственно. Система
замыкается уравнением состояния ПД.
Уравнение движения оболочки таково: dM dU/dt = pdsn. Здесь U — вектор
скорости элементарной массы оболочки dM, п — единичный вектор, нормальный к
оболочке, ds — поверхность, соответствующая массе dM. Записывая это уравнение
в проекциях на оси координат, получим
dV
dM — = pds cos J,
dt
dW
dM	= pds sin J,
dt
A5.175)
где V и W — радиальная и осевая компоненты скорости элемента оболочки, 5 —
угол между вертикалью и нормалью к поверхности оболочки.
Граничное условие на оболочке
Un =
A5.176)
где Un и ип — проекции векторов скоростей оболочки и продуктов детонации,
соответственно, на нормаль к оболочке.
Граничные условия во фронте истекающих продуктов детонации имеют вид:
р = 0, р = 0.
A5.177)
В силу осевой симметрии задачи радиальная составляющая скорости продуктов
детонации на оси
= 0.
A5.178)
Граничные условия во фронте детонационной волны имеют вид:
A5.179)
где рн, Рн-> ин — давление, плотность и массовая скорость продуктов детонации
в точке Чепмена-Жуге.
Поскольку рассмотренные задачи симметричны относительно плоскости z = 0,
то решение проводилось только для правой части заряда. Граничное условие на
плоскости симметрии
= 0.
A5.180)
1
/
\
j 0,018^
у \ j -С?
\
Л
\
,005
\
w
\
\<
г=3,796
\
\
\
0	1	2	3 4 5 z
Рис. 15.34. Распределение давлений в ПД
при двустороннем инициировании заряда: 1 —
оболочка заряда, 2 — фронт разлета ПД в
пустоту, р — давление в ПД
1
0,11
0,15
Ц.19Л
0,3
1= 3,796
0	12 3 4 5 2
Рис. 15.35. Распределение скоростей в ПД
при двустороннем инициировании заряда: 1 —
оболочка заряда, 2 — фронт разлета ПД в
пустоту, w — скорость ПД

15.5. Метание осесимметричных оболочек
45
Конечно-разностная аппроксимация уравнений газовой динамики выполнена
при помощи явной двухшаговой схемы второго порядка [15.20].
Результаты решения задачи о двустороннем инициировании представлены на
рис. 15.34 и 15.35. В этом случае плоские детонационные волны возбуждаются
одновременно на обоих торцах заряда. На рис. 15.34 показаны изобары р = const в
момент времени t = 3,796. Здесь f = r/ro, z = z/ro, р = p/(poD2), t = Ш/ro-
На рис. 15.35 показаны линии равных скоростей w = const в тот лее момент
времени (w = w/D). Ввиду симметрии изображена только правая часть заряда.
Стрелки на рис. 15.35 представляют векторы скоростей ПД в масштабе. При
г
\\
7=2
,735
o.oi4
0,02
р- 0.004 ~"""
-J.
S
>\
/
No.c
1 1
0,0004 1
5
.2
\
Г
и
	1
/3
= 0,1
I I
г
,07/
7=2
4
Ч4
,735
0,16/^
).»
/
J,22
</
V:
Д
0Д2
— >
/2
\
0	1	2	3	г
Рис. 15.36. Распределение давлений в ПД
при осевом инициировании заряда: 1 — обо-
оболочка заряда, 2 — фронт разлета ПД в пусто-
пустоту, 3 — фронт отраженной ударной волны в
ПД, 4 — фронт волны разрежения.
0	1	2	3 1
Рис. 15.37. Распределение скоростей в ПД
при осевом инициировании заряда: 1 — обо-
оболочка заряда, 2 — фронт разлета ПД в пу-
пустоту, 3 — жесткая стенка, 4 — линия, где
скорость звука равна скорости потока ПД.
осевом инициировании детонация возбуждается одновременно по всей оси заряда.
Распределения давлений и скоростей в момент времени t = 2,735 представлены
соответственно на рис. 15.36 и 15.37.
Задача о метании цилиндрической оболочки конечной длины зарядом ВВ при
точечном инициировании заряда решалась численно Л. А. Чудовым, А. В. Кашир-
Каширским и Ю.В. Коровиным [15.21].
На правом, открытом торце в цен-
центральной точке возбуждается сфериче-
сферическая детонационная волна. Продукты де-
детонации истекают в вакуум. После выхо-
выхода детонационной волны на левый откры-
открытый торец, начинается распространение
ПД влево от заряда, вправо от торца
по продуктам детонации идет волна раз-
разрежения. При решении этой задачи ис-
использовались формулы A5.174)—A5.180).
Положения оболочки и газового облака в
различные моменты времени представле-
представлены на рис. 15.38. Интенсивное истечение
продуктов детонации приводит к быст-
быстрому падению давления ПД в торцевой
зоне, поэтому часть оболочки, близкая к торцу, получает относительно мень-
меньшие ускорения и значительно отстает от центральной части. Облако продуктов
детонации на правом торце слабо распространяется влево от торца, т.е. имеет
место небольшое «затекание» ПД на оболочку. Изобары при i = 6,12 — во
время развитого процесса движения оболочки, — представлены на рис. 15.39.
Картина изобар отражает взаимодействие торцевых и боковых волн разрежения.
/
Т-.
= 6,i:
1^
щ
2,9
^-
\
\
\
\
\
\
\
3
2
1
О
-3-2-101234562
Рис. 15.38. Положение оболочки заряда A)
и облака ПД B) в разные моменты времени
их движения t (ВВ — взрывчатое вещество,
ДВ —- детонационная волна.

46
15. Метание тел продуктами детонации
-3-2-101234562
Рис. 15.39. Положение оболочки заряда и
изобар в момент времени t = 6,12
-3 -2 -1 0
Рис. 15.40. Положение оболочки заряда и
линии тока ПД. 1 — дозвуковая область те-
течения, 11 — сверхзвуковая область течения
На рис. 15.40 представлены линии тока продуктов детонации в тот же момент
времени. Штриховой линией показана звуковая линия (ЗЛ), где скорость звука
равна массовой скорости течения ПД. Дозвуковая зона по мере развития процеса
уменьшается.
Обзор работ по метанию несжимаемых тон-
тонких жидких оболочек (НТЖ-оболочек) приведен в
[15.22].
Решение г—z двумерных (осесимметричных) за-
задач, как правило, имеет главной целью построение
законов распределения масс и скоростей по меридио-
меридиональному углу разлета (рис. 15.41).При этом обычно
принимаются следующие допущения [15.23]:
-	размеры оболочки пренебрежимо малы по срав-
сравнению с размерами поля, т.е. все траектории
Рис. 15.41. Сферические ко-	частиЧ исходят из одной точки;
ординаты (ip—О)	/
—	скорость по данному направлению разлета (го-
(годограф скорости vo((p)) определяется един-
единственным образом.
Здесь if Е [0, тг] — меридиональный угол, который обычно отсчитывается от
луча,направленного из центра оболочки к точке инициирования.
Функция распределения масс U((p) задается как
> ад
где М(Т < (р) — масса оболочки, разлетающаяся в конусе с углом при вершине
2<?, Mq — полная масса оболочки.
Плотность распределения массы определяется соотношением
и((р) =
При этом, очевидно
dM{T < if)
d(p
= / u(ip) dip.
о

15.5. Метание осесимметричных оболочек	47
Масса оболочки, движущаяся между коническими поверхностями, образующие
которых наклонены к оси под углами <pi, <??2? определяется как
Pl-(p2 = Mq
Ч>2
= Мо J u{v) dtp.
Массовая медиана, т.е.угол ц>ме, по разные стороны от которого движутся равные
массы Мо/2, определяется из выражения U((Pme) = 0,5.
Средневзвешенный угол определяется как
= / ipu((p) dip.
Мода распределения ф находится из условия
du(<p)
= 0
Если оболочка симметрична относительно экваториальной плоскости, и иници-
инициирование производится в центре ее, то (рмЕ = Ф = Ф = тг/2. Кинетическая
энергия оболочки в телесном угле,ограниченном коническими поверхностями с
углами <??i, if2-> равна
Этот телесный угол равен Q = 2tt(cos ip\ — cos ^2)-
Начальная кинетическая энергия оболочки,содержащаяся в единице телесного
угла (стерадиане)
И	4тг cos (fi — cos if2
Требуемые в настоящее время уровни S составляют 5-20МДж/ср [15.24], Полная
кинетическая энергия оболочки [if G [0, тг])
= ~y /
При этом для первоначально неподвижной оболочки с зарядом ВВ, имеющим
массу m должны выполняться условия
И^о + ЕПд = mQv, /0 + /Пд = 0,
здесь Ецд — полная (внутренняя и кинетическая) энергия ПД, Qy — удельная теп-
теплота взрыва ВВ, /пд — импульс продуктов детонации. При отсутствии у оболочки
доньев, распределение и((р), как правило, является унимодальным. Предложен ряд
аналитических выражений для описания таких полей, например, в виде:

48
15. Метание тел продуктами детонации
A5.181)
Медиана такого распределения определяется как
2А + 1
График этой функции, при А = 0,005, v = 8, представлен на рис. 15.42 (<?>ме
= 0,515тг = 92,7°). Поле смещено по направлению распространения детонации
на угол 2,7°. Этот угол склонения потока по физическому смыслу близок к углу
Тэйлора.
Кинетическая энергия в телесном угле ((р± —
и(ф)	^21 6i — ^2M ПРИ заданном годографе скоростей
определяется соотношением
-f/7
0	90	180
Рис. 15.42. График функции рас-
расЧисленное решение R-Z двумерной задачи о
разлете осесимметричной прочной толстостенной
оболочки получено В. А. Одинцовым, Ю.М. Си-
Сипределения массы по меридиональ- Доренко И В. С. ТуберОЗОВЫМ [15.25], Процесс яв-
явному углу разлета.	ляется двумерным, и может рассматриваться в
континуальной постановке только до момента раз-
разрушения оболочки, после чего процесс превращается в трёхмерный, и должен
рассматриваться в координатах (г, #, z). По данным оптической съемки процесса
взрыва стальных цилиндрических оболочек известно, что оболочки из средне-
углеродистых сталей, в частности, из штатных снарядных сталей С-60 и 45X1,
сохраняют сплошность до относительного радиуса bf = 1,4,... 1,5 (bf = fe//feo>
где bo, bf — начальный внешний радиус оболочки и радиус в момент разрушения,
соответственно) [15.18, 15.26, 15.27]. Отсюда следует, что численное моделирование
в рамках континуальной модели до этого момента времени является физически
адекватным.
Подробное описание двумерной программы «Гефест» приведено в [15.25]. Ис-
Используется система уравнений в эйлеровых цилиндрических координатах. Рас-
Распространение детонации, инициируемой в вершине снаряда, рассматривается вне
общей системы уравнений и задаёт границу области, охваченную течением. Рас-
Расширение продуктов детонации (ПД) описывается изэнтропой в форме Джонса-
Уилкинса-Ли (JWL) в виде:
р = А • ехр {-R^} + В • exp {-R2V} + С • V~^+1\
здесь р — давление, V = V/Vq = Ро/р — относительный объём продуктов
детонации, Vo, Ро — соответственно удельный объём и плотность исходного ВВ,
У, р — те же величины для текущего состояния ПД, А, 5, G, R\, R2, и —
параметры изэнтропы данного ВВ. Поведение металла описывается уравнениями
пластического течения Прандтля — Рейсса, заменяемыми в численной реализации
соотношениями Гука и процедурой Уилкинса.

15.5. Метание осесимметричных оболочек
49
Система уравнений решалась модифицированным методом крупных частиц,
в котором использована комбинация геометрического и физического расщеп-
расщеплений с локализацией контактных разрывов по алгоритму концентраций. Для
этой цели система уравнений была дополнена соотношением сохранения концен-
концентраций [15.28]. Рассмотрим пример расчёта процесса взрыва 152 мм осколочно-
0 мкс
28 мкс
76 мкс
124 мкс
ш
Рис. 15.43. Картина процесса взрыва 152 мм
ОФ снаряда
18
12
6
28 мкс (
к
А
Л
16 мкс 1
р'.
О 200 400 600 Z,mm
Рис. 15.44. Распределение давления и мас-
массовой скорости по оси симметрии ОФС в
различные моменты времени
фугасного снаряда. Общая масса снаряда составляет 43,4 кг. Корпус снаряда
массой 36,455 кг выполнен горячей штамповкой из стали С-60, снаряжение ТНТ
массой 5,86 кг (коэффициент наполнения а = 0,135) выполнено методом шнекова-
ния. Полная длина снаряда с взрывателем — 706 мм D,64 клб.) Расчёт проводился
на сетке 120 х 720 = 86400 ячеек (размер ячейки 1,25 х 1,25 мм). Характеристики
металла: 7о = 7850кг/м3, G = 81ГПа, as = 0,4ГПа, уравнение состояния
в форме Тэта: р = А (G/70)™ — 1) ? А = 21,5 ГПа, п = 5,5. Характеристики
ВВ: ро = 1630кг/м3, D = 6930м/с, Уравнение состояния ПД в форме JWL
(А = 371,2ГПа, В = 3,231 ГПа, С = 1,045ГПа, В,г = 4,15, R2 = 0,95, ш = 0,3).
Счёт проводился с фиксированным шагом по
времени At = 1 мкс. Процесс рассчитывался до
момента времени 170мкс A70 временных слоев),
что примерно соответствует удвоенному времени
пробега детонационного фронта по длине заряда
ВВ Lo = 570мм (tD = Lo/D = 82мкс). Время
счёта задачи составило 28 ч.
Общая картина процесса взрыва снаряда
представлена на рис. 15.43. Распределение дав-
давления по оси снаряда в различные моменты
времени (t\ = 28 мкс, t2 = 76 мкс) представлено
на рис. 15.44а. При схождении отраженной ко-
косой ударной волны к оси симметрии, возникает
второй пик давления р'. Схождение волн проеле-
живается и на распределении массовой скорости
вдоль оси симметрии (рис. 15.446). Это распределение значительно отличается от
7 6
Рис. 15.45. Конфигурация косых
ударных волн в ПД. 1 — сфериче-
сферический ДФ; 2,6 — кольца Маха; 3,5,7 —
отраженные ударные волны; 4 —
диск Маха

50
15. Метание тел продуктами детонации
линейного, определяемого для одномерного течения за детонационным фронтом
(ДФ) при открытом левом торце и к = 3 соотношением:
z D
Конический фронт сходящейся ударной волны в ПД, возможное нерегуляр-
нерегулярное отражение его от оси симметрии с образованием диска Маха (рис. 15.45) и
последующие волновые процессы в ПД в рамках данного метода с достаточной
определенностью не выявляются. Картины изобар и линий равных модулей ско-
скоростей в ПД представлены на рис. 15.46. Из графиков распределения по радиусу
21 16 8 4 3 2 1,5
1100 900 750 250 500 1100 900
и = 750 м/с
Рис. 15.46. Картины изобар и линий равных модулей скоростей в ПД
давления и радиальной скорости в сечении Z = 340 мм (от границы расчетной
области) в различные моменты времени, представленных на рис. 15.47 видно, что
выравнивание давления по сечению (переход к равновесной схеме расширения ПД)
происходит только на поздней стадии процесса. Аналогичным образом обстоит
дело и с формированием линейного закона распределения скоростей по радиусу в
соответствии с моделью Покровского-Джерни.
Волновые процессы в стенке оболочки детально воспроизведены на рис. 15.48.
Уверенно просматриваются четыре пульсации волн. Давление в металле в момент
падения ДФ рх и угол поворота потока вх (начальные параметры) определяются
как параметры в точке пересечения ударных поляр сжатия ПД в отраженной
ударной волне и сжатия стали. Эти значения составили рх = 22,3 ГПа, вх = 4,3°.
Угол а между первым ударным фронтом и образующей составляет 45°, что
соответствует скорости ударного фронта в стали S = D sin a = 4900 м/с [15.30].
Отметим, что картина пульсаций, воспроизводимая гидрокодом, кардинальным
образом зависит от принятой модели поведения материала в области растягиваю-
растягивающих напряжений. Экспериментальные данные о поведении кривой р = /G) B этой
области отсутствуют, и обычно предполагается, что в область растягивающих (в
данном случае отрицательных) напряжений может быть экстраполирован закон
Тэта (рис. 15.49). Уилкинс [15.17] предложил в этой области ограничивать рас-
растягивающие напряжения величиной A/3)ат>, что вытекает из модели разрушения
при одноосном растяжении:
iA 1
(Л = сгТ, сг2 = сг3 = 0, а = —р = - > di = -стт-
6 i=i	6
Очевидно, что это ограничение не соответствует реальному поведению мате-
материала, когда разрушение наступает при напряжениях, намного превышающих
эту величину. По данным [15.31], для различных сталей напряжение разрушения
при отколе может достигать D-6) ГПа , т.е. в 20-30 раз превышать величину
-ат = 0,20,... 0,30. Отсюда следует, что ограничение Уилкинса должно приводить

15.5. Метание осесимметричных оболочек
51
р, ГПа
52 мкс
uR, м/с
55 мкс
15
10
5
0
10
5
О
10
5
О
5
О
5
О
2
О
20
40
Ь ГПа 55 мкс
	¦—	««.
	.
р, ГПа 60 мкс
———
р, ГПа 65 мкс
>, ГПа
\
70]
\
У1ЖС
р, ГПа 86 мкс
60
R, мм
200
400
200
600
400
200
600
400
200
О
800
600
400
200
\
0
uR, м/с 60 мкс
у
0
%, м/с 65 мкс
л
/
0
%, м/с 70 мкс
^^
/
Щ, м/с 90 мкс
у
о
20 40
60
R, мм
Рис. 15.47. Распределение давления р и радиальной скорости иг по радиусу в сечении Z в
различные моменты времени
к полному искажению волновой картины в стенке оболочки. Соответствующий
численный эксперимент полностью подтвердил этот вывод. Ограничение приводит
к тому, что гидрокодом воспроизводится только одна пульсация, а в дальнейшем
материал переходит в безволновое состояние сжатия. Следует также отметить, что
при двумерном моделировании, вследствие небольшого числа ячеек по толщине
стенки (обычно не более 20) и значительного «размазывания» фронтов по сетке,
получение достаточно точных амплитудных величин затруднительно. В этом
случае существенную помощь оказывает одномерное моделирование процесса на
частой лагранжевой сетке C00-500 ячеек по толщине стенки). В данном случае
моделирование проводилось с использованием алгоритма [17.78] для обоих извест-
известных одномерных схем нагружения (мгновенная детонация и осевая детонация)
при к = 3. Рассчитывалась конфигурация, соответствующая среднему сечению
снаряда (do = 152 мм, da = 104 мм, 5о = 24 мм, коэффициент наполнения сечения
<^ = 0,154 при ро = 1630кг/м3 (ТНТ)). Асимптотическая скорость оболочки
г>о, независящая от схемы нагружения, определялась по формуле Покровского -
Джерни: vq = —w	, и составила 1002,6 м/с. Законы движения внутренней,

52
15. Метание тел продуктами детонации
0,90
•
•
0,95
•
1,00
•
•
•
р,
-10
¦5
j
/
<
--5
--10
ГПа 7
У
/
1,05 1
:ут/3«0,3
ДО
Р/ро
ГПа
Рис. 15.48. Волновая конфигурация в стенке оболочки
Рис. 15.49. Объемная сжимаемость стали. — закон Тэта; - - - экстраполяция закона Тэта в
область растягивающих напряжений; - . - ограничение Уилкинса; *- напряжение, полученное в
одномерном расчете по программе HEMP
внешней поверхностей и центра масс сечения для обоих моделей представлены
на рис. 15.50, моменты окончания пульсаций и значения скоростей центра масс,
набранные к концу соответствующей пульсации — в таблице 15.8. В таблице пред-
представлены также средние значения этих величин, которые могут быть использованы
в качестве приближённых оценок.
и, м/с
v, м/с
600
300
20 40 60 80 t,MKc
О
ё
г
л
V
V
ш
ш
VVvs
20 40 60 80 t,MKC
а	б
Рис. 15.50. Законы движения внутренней A), внешней B) поверхностей оболочки и центра масс
сечения C) ОФ снаряда при мгновенной (а) и осевой (б) детонации
После отражения ДФ от дна корпуса, в донной части камеры формируется зона
высокого давления. Сильное радиальное выдавливание металла действует только
в относительной близости ко дну, в результате чего донная камера приобретает
форму опрокинутого колокола. В результате сложного взаимодействия косых волн
и прямой ударной волны, в дне формируется ударный фронт S\Vzi, близкий
по форме к сферическому (рис. 15.51). После выхода сферического ударного
фронта на внешнюю поверхность дна, возникает сферический же фронт волны
разрежения К\Уд. Взаимодействие этого фронта с косыми волнами разрежения
RWi приводит к возникновению конической зоны растяжения R—R, по которой
происходит в дальнейшем отделение (угловой откол) дна. Численное моделиро-
моделирование придонных процессов играет важную роль в процессе проектирования ОФ
снарядов и позволяет определять пути целенаправленного воздействия на процесс

15.5. Метание осесимметричных оболочек
53
Таблица 15.8
Набор скоростей оболочкой по пульсациям.
Мгновенная
детонация
Осевая
детонация
Усредненные
значения
t, МКС
г>о,м/с
t, МКС
г;о, м/с
t, МКС
wo, м/с
№ пульсации
I
8
375
15(9)
470
8,5
423
II
17(9)
670
24(9)
600
9
635
III
26(9)
850
33(9)
690
9
770
IV
34(8)
940
41(8)
810
8
875
V
41G)
980
48G)
860
7
920
VI
48F)
1010
54F)
890
6
950
Рис. 15.51. Волновые процессы в дне снаряда
дробления придонной части корпуса.
Процесс взрывного разгона оболочки отслеживался с помощью «вморожен-
«вмороженных» в неё маркеров, (рис. 15.52). Картина набора меридионального угла разлёта:
if = arctg (vr/vz) между осью снаряда и вектором скорости, отсчитываемого от
луча, направленного из центра снаряда к взрывателю, имеет ярко выраженный
пик, что указывает на определяющую роль первой пульсации. Практически этот
процесс заканчивается за время первой пульсации, включающей в себя 2 косых
волны: косую ударную волну SW\ и косую волну разрежения RW\. Отсюда, в
частности, следует, что нет оснований ожидать существенного увеличения общего
угла разлёта для ВВ с затянутым энерговыделением, например, алюминесодержа-
щих, типа A-IX-20.
Распределение компонент скорости вдоль оболочки в конце разгона представ-
представлены на рис. 15.53. Для оценки эффективности основной интерес представляет
распределение осевой компоненты скорости vz. Из рис. 15.53 видно, что в оболочке
по её длине возникают 2 зоны с пиковыми значениями осевых компонент скорости
vz в торцевых зонах, приближающихся по порядку величин к радиальным ско-
скоростям, что и приводит к достаточно большому углу разлета оболочки, а в свою
очередь, и осколков.
Из графика меридионального угла разлёта (р видно, что по длине снаряда
выделяются три характерных зоны:
— средняя часть с плавным (небольшим) изменением угла <??, в которой заметно

54
15. Метание тел продуктами детонации
и», м/с
-300
vR, м/с
30
60
90
t, МКС
Рис. 15.52. Набор радиальной vr, осевой vz,
полной v скоростей и меридионального угла
разлета ср маркерами (М5, М12 и т.д. — номе-
номера маркеров)
900-
600-
300-
n
^^^ 	^
V
\
vz, м/с
600-
300-
0-
100-
/
/
v, м/с
900
800
700
600
A J
у
1 /
1 /
\1
ф
150°-
120°
90°-
Г
j
0	200	400 s, мм
Рис. 15.53. Распределения радиальной vr,
осевой vz, полной v скоростей и меридиональ-
меридионального угла разлета ср вдоль оболочки ОФС в
конце разгона
формирование устойчивого угла Тейлора (из расчетов 6,4°), причём эта
зона доминирует, что приводит к тому, что разлетающаяся масса корпуса
сосредоточена в сравнительно небольшом угле (рис. 15.54).
- головная и донная части с большим градиентом угла (р по маркеру.
Распределение масс по меридиональному углу разлета удовлетворительно опи-
описывается соотношением A5.181). Достоверность расчёта (адекватность численной

15.5. Метание осесимметричных оболочек
55
М, кг
15
10
5
0
¦
...1
1
1.
Щ, м/с
900-
600»
300™
III
30
5 10 15 20 25 30 0 5 10 15 20 25
Номер угловой зоны	Номер угловой зоны
Рис. 15.54. Распределения массы М и скорости разлета vo корпуса ОФС по 6-градусным
угловым зонам
схемы) проверяется по выполнению в конце разгона балансов осевой компоненты
импульса и энергии:
к
MjVOj cos (fj + /Пд = О
= mQ
v
где /пд — импульс продуктов детонации, И^пд — кинетическая энергия ПД,
Ецд — внутренняя энергия ПД, С — масса заряда ВВ, Qv — удельная теплота
взрыва.
Невязка балансов не превышала 5%, что является вполне приемлемым для
задач данного класса.
В [15.32] численно воспроизводился процесс разлета тонкостенных снарядов
при двух схемах инициирования — головной и центральной. Последняя применя-
применяется для увеличения меридионального угла разлета. Картина процессов представ-
представлена на рис. 15.55, 15.56. В случае центрального инициирования после отражения
расходящейся сферической ДВ от внутренней поверхности корпуса в продуктах
детонации возникает сходящаяся к оси симметрии ударная волна, фронт которой
представляет часть поверхности тора. Распределение скоростей и меридиональ-
меридионального угла разлета вдоль оболочки для обоих схем в моменты, соответственно,
108 и 88 мкс, представлено на рис. 15.57, 15.58. Пик скорости в средней части
оболочки является следствием нормального падения фронта ДВ на внутреннюю
поверхность корпуса снаряда. По разные стороны от этого сечения углы Тейлора
имеют разные знаки, что, собственно и является причиной увеличения угла разле-
разлета. Меридиональные углы разлета Д<?>80%, А(р90% при центральном инициировании
существенно возросли и составили соответственно 42° и 114° (табл. 15.9). В таблице
также приводятся расчетные и экспериментальные данные для штатного 152 мм
снаряда. Углы разлета для обоих снарядов с головным инициированием близки
друг другу.
Другой обширный класс осесимметричных двумерных задач связан с осевым
метанием круглых пластин с торца заряда ВВ (в общем случае снабженного
оболочкой).
Основными техническими применениями являются метание тонкой вогнутой
пластины для формирования в последующем «ударного ядра» (EFP — Explosively
Formed Projectile) и метание однослойного набора готовых поражающих элементов

56
15. Метание тел продуктами детонации
О мкс
¦¦¦ \
8 мкс
28 мкс
76 мкс
104 мкс ^.—•
\
18 мкс
28 мкс
38 мкс
58 мкс
/ш
Рис. 15.55. Картина взрыва 152 мм тонко- Рис. 15.56. Картина взрыва 152 мм тонкостенного
стенного снаряда с головным инициирова-	снаряда с центральным инициированием
нием
Таблица 15.9
Меридиональные углы разлета.
Снаряд
Тонкостенный (Г)
Тонкостенный (Ц)
Штатный (расч.)
Штатный (эксп.)
Углы разлета
80°
А(р, град
30
42
30
29,6
Границы угла
72 ... 102
66 ...114
78 ... 108
-
90°
А(р, град
66
114
48
47,2
Границы угла
54 ... 120
24 ... 138
66 ...114
73,3 ... 120,5
Г — головное инициирование, Ц — центральное инициирование.
(ГПЭ) для создания направленного осколочного потока [15.33]. Численное решение
этой задачи приведено в [15.34].
Метательный блок с наружным диаметром 110 мм выполнен в тонкостенном
стальном корпусе толщиной Змм. На переднем торце блока уложена круглая
осколочная пластина (слой ГПЭ или пластина заданного дробления) толщиной
10 мм и массой 667 г. Снаряжение выполнено составом A-IX-2. Моделирование
производилось для конфигураций блока с высотой заряда ВВ 1=20, 40 и 60 мм.

15.5. Метание осесимметричных оболочек
57
/'„ м/с
1400
1000
600
200
900
600
300
о
-300
-600
г
к
г> м/с
У
*
\
	, J
V 9 м/с
1400
1200
1000
800
с
150
120
90
60
\ i
\J
I
1600
1200
800
400
1000
500
О
-500
-1000
i
1600
1300
1000
J
V
Гг, м/с
/
/
(
Г, м/с
\
А
У
Ф,град
Ф,град
150-
120-
90-
60-
(
\
О
200
400
600 s, мм
Рис. 15.57. Распределение скоростей и ме-
меридионального угла разлета вдоль оболочки
тонкостенного ОФС (Г) в момент t = 108 мкс
о
200
400
600
Рис. 15.58. Распределение скоростей и ме-
меридионального угла разлета вдоль оболочки
тонкостенного ОФС (Ц) в момент t = 88 мкс
Характеристики зарядов и расчетные значения скоростей пластины представлены
в таблице 15.5. (С — масса заряда ВВ, Q — общая масса блока, а = C/Q —
коэффициент наполнения, vez, ve — соответственно условно-конечные скорости на
оси пластины и среднее значение для пластины, te — условный момент окончания
разгона. Картина процесса взрыва метательного блока (/ = 20 мм) представлена
на рис. 15.59.

58
15. Метание тел продуктами детонации
Таблица 15.10
Характеристики зарядов и конечные значения скоростей
/,мм
20
40
60
С, г
289
578
866
1417
1864
2310
а
0,204
0,310
0,375
?е, мкс
20,8
21,6
23,6
Vez
725
950
1200
Ve
705
889
1182
15.6. Пространственные (трехмерные) задачи метания
?
I
0 мкс
1,6 мкс
5,6 мкс
11,6 мкс
В настоящее время в связи с быстрым развитием взрывных устройств с направ-
направленным потоками ГПЭ [15.35, 15.36] интенсивно разрабатываются программы для
решения трехмерных задач метания (ЗЮ-гидрокоды) [15.37]—[15.39].
Трехмерное моделирование
требует применения ЭВМ ги-
гафлопного A09 операций/с)
и терафлопного A012 опе-
операций/с) диапазонов с объ-
объемом оперативной памяти в
сотни гигабайт. В зависимо-
зависимости от рассчитываемой кон-
конфигурации используются раз-
различные системы координат.
Для цилиндрических зарядов
со смещенными от оси точ-
точками инициирования и заря-
зарядов, форма которых близка к
цилиндрической, целесообраз-
целесообразно использование цилиндри-
цилиндрической системы координат г—
0-z (рис. 15.60).
Для зарядов плоской или
близкой к ней формы целесо-
целесообразно использовать декар-
тову систему координат x-y-z
3.5 мкс
18,8 мкс
(рис. 15.61).	Рис. 15.59. Картина процесса взрыва метательного блока
Распределение ГПЭ и их
скоростей в направленных потоках с учетом малости размеров метательного
блока по сравнению с размерами поля строится обычно в сферической системе
координат (p-0-r (<р — меридиональный угол, в — экваториальный угол, <p Е [0, 2тг],
0е[О,2тг]).
При заданной функции распределения U((p, плотность распределения массы
определяется как
и(<р,в) =
Масса металла, заключенная в телесном угле <р\ — <f2, Oi —62, определяется

15.6. Пространственные задачи метания
59
о
о
о
о
а	б	в	г
Рис. 15.60. Конфигурации зарядов с трехмерным разлетом в координатах r — 6 — z: одноточечное
инициирование на образующей заряда (а); многоточечное инициирование на образующей заряда
(б); односторонняя выемка (желоб) на заряде (в); блок менисков на заряде (г)
Рис. 15.61. Пространственные конфигурации взрывных метательных устройств: боевая часть
зенитной управляемой ракеты, нацеливаемая поворотом ракеты по крену (патент №5003885
США) (а), метательный блок активной защиты танка (патент №2127861 РФ) (б), мина осколочная
направленная МОН-50 (в), управляемая ракета типа «Осколочное крыло» (патент №2032138 РФ)
(г); 1 — заряд ВВ, 2 — слой ГПЭ, 3 — пластина заданного дробления
соотношением
i-(p2ie1-e2=M0 // u(<p,
d<pde.

60	15. Метание тел продуктами детонации
Плотность массы поля на сфере радиуса г (кг/м2) определится как Пм = dM/dS,
где
dM = Мои (<р, 0) dipdO
dS = r2simpd(pd6,
откуда
Mou((p,0)
Пм =
r2simp
В случае равномерного распределения масс по сфере разлета
и(<Р> °) = 4^ sin <р'
Согласно теореме умножения плотностей, пространственно-угловая плотность мас-
массы может быть представлена в виде
и(<р, в) = иг(в) и2{р\6), и{р, в) = Ul(<p) и2(в\<р).
Первая форма и входящая в нее величина безусловной плотности распределения
и\F) по экваториальному углу является предпочтительной при оценке интенсив-
интенсивности перераспределения масс по углу в для радиально-направленных боевых
частей. В этом случае интенсивность перераспределения («уровень нацеливания»)
может быть охарактеризован величиной
здесь ui (в) = 1/2тг — плотность равномерного распределения по углу в.
Кинетическая энергия в телесном угле ipx-ipi, Q\-Qi при заданном годографе
скоростей vo((p,6) определяется соотношением
WVl-V2ei-e2 = —
В [15.37] приводятся расчетные и экспериментальные результаты исследования
процесса разлета осколочной БЧ при боковом инициировании.
В [15.8] приводятся расчетные и экспериментальные результаты исследования
процесса разлета осколочной БЧ при боковом инициировании. Боевая часть имеет
отношение длины к диаметру 1,5, снаряжение PBXN-107. На торцах расположе-
расположены алюминиевые крышки толщиной 12 мм. Несущая оболочка толщиной 3,3 мм
выполнена из алюминиевого сплава. Использовались стальные ГПЭ в форме
параллелепипеда трех типов:
-	тип 1 - 7,35x7,35x6,35 мм, двуслойная укладка
-	тип 2 12x12x0,7 мм, однослойная укладка
-	тип 3 10x10x10 мм, однослойная укладка
Инициирование БЧ проводилось по образующим, расположенным симметрично
относительно плоскости нацеливания с экваториальным углом 20 между радиуса-
радиусами, направленными к образующим, 45° (рис. 15.62).

15.6. Пространственные задачи метания
61
Линии инициирования
Рис. 15.62. Расчетная кон-
конфигурация БЧ с инициирова-
инициированием по двум образующим
09 м/с
направление
нацеливания"
^^— тип 1
—	- тип 2
-	- - тип 3
3000
2500
2000
1500
1000
500
0 60 120 180 240 300 360
Рис. 15.63. Расчетная диаграмма распределения
скоростей по экваториальному углу; 1 — ГПЭ тип
1, 2 — ГПЭ тип 2, 3 — ГПЭ тип 3
\
центр инициирования
в, град :
Расчетные диаграммы распределения скоростей по экваториальному углу пред-
представлены на рис. 15.63.
Нанесена также линия, соответствующая осевому инициированию. На рис. 15.64
представлено распределение по экваториальному углу кинетической энергии поля
(для ГПЭ типа 2).
Расчет проводился с помо-
помощью трехмерного гидрокода LS-	ц/ жлж
DYNA3D. Согласование расчет-
расчетных и экспериментальных данных
было удовлетворительным.
Эти результаты показывают,
что способ нацеливания поля с по-
помощью скользящего инициирова-
инициирования не обеспечивает интенсивной
концентрации потока в направле-
направлении цели (увеличение кинетиче-
кинетической энергии по отношению к изо-
изотропному разлету не превышает
25
20
15
10
5
направ^шиеТнаце4иванщ
/¦
; центр инициирования;
¦\
9, град
О 60 120 180 240 300 360
Рис. 15.64. Расчетная диаграмма распределения ки-
50%).
нетической энергии поля по экваториальному углу

Глава 16
Осколочное действие взрывных систем
16.1. Экспериментальные наблюдения процесса расширения и
разрушения металлической оболочки и получающихся
осколочных спектров
1. Оптическая и рентгеноим-
пульсная съемка оболочек. Опти-
Оптическая (высокочастотная или щелевая)
съемка оболочек обычно применяется
для регистрации начальных стадий рас-
расширения оболочки до момента прорыва
ПД или натекания их на оболочку со
стороны открытых торцев.
С помощью этого метода опреде-
определяются радиусы трещинообразования
и прорыва ПД, скорость распростра-
распространения продольных трещин по оболоч-
оболочке и т.п. Для защиты фоторегистрато-
фоторегистратора применяется съемка через зеркало
(рис. 16.1).
Рентгеноимпульсная съемка (РИС)
может проводиться на всех стадиях
процесса. Защита от осколков рент-
рентгеновских трубок и кассет с пленкой
осуществляется с помощью толстых
A0. ..15 мм) дюралюминиевых листов,
что ухудшает качество регистрации.
Недостатком РИС является и малое
число кадров (обычно 2.. .4).
По данным высокочастотной съемки
можно определить следующие количе-
количественные характеристики процесса:
-	относительные радиусы трещино-
трещинообразования и разрушения Ъс и^;
-	угол наклона оболочки #т;
-	число окружных делений по;
Пульт
СФР
|СФР
—1
Рис. 16.1. Схема оптической съемки процессов
расширения и разрушения оболочек (высокоча-
(высокочастотная фотография) 1 — защитный стальной
экран; 2 — заряд задней подсветки; 3 — труба
задней подсветки; 4 — боковые защитные экра-
экраны; 5 — исследуемая оболочка; 6 — стеклянные
трубы передней подсветки; 7 — заряд передней
подсветки; 8 — защитное стекло амбразуры; 9 —
экран; 10 — зеркало
—	скорость движения вершин магистральных трещин vc\
—	радиальные скорости цилиндра (методом двух засечек);
—	скорость движения дна;

16.1. Наблюдения процесса и осколочных спектров	63
- время разрушения tf (время от момента инициирования до момента полного
разрушения всех частей оболочки).
Определение необходимой частоты съемки производится по формуле:
fo = O,7v/3cNL,
где v — скорость развития явления (в данном случае максимальная радиальная
скорость оболочки); /Зс — масштаб съемки; Nl — разрешающая способность оптики
(линий/мм).
Например, для типичных условий съемки v = 106 мм/с, /Зс = 1/20, Nl = 20
лин/мм, откуда /о = 106 кадр/с. При съемке оболочек стандартной камерой СФР-
2М обычно используется максимальная частота, достигаемая при двухрядной
вставке (/о = 625 • 103 кадр/с, период смены кадров То = 1,6 мкс). Здесь и
в дальнейшем используются обозначения: ао,^о — соответственно внутренний и
внешний радиусы цилиндрической оболочки, 5 о = bo — clq — толщина стенки, Lq —
длина заряда ВВ, do = 2bo — наружный диаметр, da = 2ао — внутренний диаметр,
Sd = 5o/do — относительная толщина стенки, Aq = Lq/ da — относительная длина
заряда, L — полная длина оболочки (с доньями). Для стальных оболочек прини-
принимают, что процесс разрушения заканчивается за время tf ~ 2tr>(tr> = Lq/D —
время пробега детонационной волны по заряду ВВ). При длине заряда малого
стандартного цилиндра Lq = 100 мм и скорости детонации D=8000 м/с = 8
мм/мкс, получаем ^=12 мкс, что при частоте съемки 625 тыс. кадр/с дает за
весь процесс разрушения 15 рабочих кадров (п = itj^jT = 24/1,6 = 15). Такое
число кадров обеспечивает достаточно подробный анализ процесса разрушения.
Схема оптического эксперимента подробно описана в [16.1]—[16.3]. Съемка, как
правило, проводится через зеркало с использованием всесторонней взрывной под-
подсветки. Задняя подсветка осуществляется с помощью заряда ВВ (шашка A-IX-
I массой 15. ..20 г), помещенного в стальную трубу диаметром 250. ..300 мм и
длиной 800.. .1500 мм. Воздушная ударная волна в трубе излучает яркий световой
импульс продолжительностью t « Lm/2 (Lm — длина трубы в мм, t, мкс). Торец
трубы, обращенный к прибору, затягивается калькой, на которую черной тушью
наносятся № опыта и реперные отметки.
Передняя подсветка также осуществляется двумя взрывными источниками све-
света (ВИС), представляющими стеклянные трубки диаметром 30.. .40мм и длиной
150.. .200мм с помещенными внутри зарядами ВВ массой 5.. .Юг.
Повышение качества съемки может быть достигнуто применением зеркал с
внешним отражающим слоем и использованием цилиндров с белой матовой по-
поверхностью. Однако кардинальное улучшение качества регистрации, требующее
фотографического разрешения порядка 80.. .100 лин/мм, обеспечивающего фик-
фиксацию положения вершин трещин, не может быть достигнуто с помощью обычных
зеркальных разверток. Наиболее перспективным здесь является использование
высокоскоростных затворов типа ячеек Керра или Поккельса, дающих небольшое
число оптически высококачественных кадров. Наличие таких камер, в частности,
позволило бы решить проблему съемки осколков на полете с целью определения
их истинных размеров и формы, не искаженных вторичным разрушением в
улавливателе с тормозящей средой. Съемка осколков производится после выхода
их из облака ПД.
Характерные высокочастотные фотографии представлены на рис. 16.2-16.7. На
рис. 16.2 показан процесс расширения тонкостенной Ed = 1/12) медной оболочки,
снаряженной шашками A-IX-L В процессе расширения оболочка приобретает
форму усеченного конуса с углом наклона образующей к оси 0Т = 2 arcsin (vq/2D).
Прорыв ПД через оболочку начинается при относительном значении внешне-
внешнего радиуса bf = bf /bo порядка 3, т.е. динамическая деформация оболочек до

64
16. Осколочное действие взрывных систем
,#
Рис. 16.2. Высокочастотная фотография процесса расширения медной оболочки (медь М1/А-
IX-1, Sj = 0,083).
Умке
Рис. 16.3. Высокочастотная фотографии процесса расширения стальной оболочки, сталь С-
60/ТГ50, do = 27 мм, da = 20 мм, ё0 = 3,5 мм, Sd = 0,13, Lo = 123 мм, Ло = 6,15, камера СФР-2М,
625 тыс. кадр/с
разрушения значительно превосходит предельные деформации, полученные из
статических разрывных испытаний (для меди 5 = 30... 35%). Это явление —
динамическая сверхпластичность — объясняется специфическими условиями де-
деформации оболочек под действием контактной взрывной нагрузки, а именно
равномерным распределением деформаций по окружности без локализации их.

16.1. Наблюдения процесса и осколочных спектров
65
Явление имеет ту же природу, что и сверхпластичность кумулятивной струи,
также реализуемая за счет принудительного распределения деформаций по всей
длине струи.
9,6 мкс
19,2 мкс
28,8 мкс
Рис. 16.4. Высокочастотная фотографии процесса расширения стальной оболочки, сталь
45XI/THT, do = 27 мм, da = 20 мм, Lo = 110 мм, Ло = 5,5, /о = 625 тыс. кадр/с
Рис. 16.5. Высокочастотная фотографии процесса расширения стальной оболочки, Арм-
ко/ТНТ, d0 = 30 мм, da = 20 мм, ё0 = 5 мм, Sd = 0,167, Lo = 110 мм, Ло = 5,5, /о = 625
тыс. кадр/с
Достигаемая предельная деформация для тонкостенных оболочек сильно за-
зависит от разностенности оболочки, однородности ВВ, качества сборки заряда и
т.п. В отдельных удачных случаях достигались значения bf ж 5. Наблюдались
кольцевые «прострелы» оболочки газокумулятивными струями, образующимися
вследствие недостаточно плотной сборки шашек A-IX-I в оболочке.
На рис. 16.3—16.7 представлены оптические регистрации стальных оболочек.
Видно, что донья с относительно небольшой толщиной Hq ~ а$ обеспечивают
закрытый в осевом направлении характер расширения вплоть до полного раз-
разрушения оболочки.
Несмотря на резкий перепад импульсов в зонах оболочки — прилегающей к
верхней крышке и в соседней, контактирующей с зарядом ВВ, в течение довольно
длительного времени происходит их совместное движение с сохранением плав-
плавного контура образующей, что обеспечивается пластическим течением металла
на границе этих зон. Момент образования зазора с прорывом кольцевого облака

66
16. Осколочное действие взрывных систем
Рис. 16.6. Высокочастотная фотографии процесса расширения стального цилиндра, сталь SAE
1015/С-З, d0 = 127 мм, da = 114,3 мм, 50 = 6,35 мм, Sd = 0,05, Lo = 254 мм, Ло = 2,22, /0 = 500
тыс. кадр/с, Центр морского оружия (NWC) США, камера "Cordin"
Рис. 16.7. Высокочастотная фотография процесса расширения 30-мм ОФ снаряда. 1 — 0 мкс;
2 — 6,4 мкс; 3 — 12,8 мкс; 4 — 19,2 мкс; 5 — 25,6 мкс; 6 — 32 мкс;
ПД, наиболее четко выявляемый оптической съемкой, соответствует безразмер-
безразмерному времени т = D • t/Lo = t/to ~ 1- Аналогичное явление значительного
пластического изгиба стенки имеет место в донной части оболочки, несмотря на
то, что здесь на контактную часть оболочки действует значительно большая по
амплитуде (вследствие отражения детонационной волны от дна) и длительная

16.1. Наблюдения процесса и осколочных спектров
67
нагрузка. Кольцевой прорыв ПД в донном сечении происходит примерно при
г « 2. Осевой сдвиг доньев за время разрушения цилиндра незначителен.
Искривление оболочки охватывает только
торцевые зоны. В остальной части реализуется
«стационарная» зона, в которой оболочка при-
приближенно сохраняет форму конуса. Относитель-
Относительная длина «стационарной» зоны колеблется в
пределах 0,7.. .0,9.
Щелевая съемка в плоскости, перпендикуляр-
перпендикулярной оси симметрии оболочки, используется для
определения закона разгона оболочки в данном
сечении.
Для дальнейшего описания процесса введем
следующие характерные радиусы расширения
(рис. 16.8): Ъс — радиус трещинообразования (по-
(появления трещин на внешней поверхности); bf —
радиус разрушения (появления сквозных тре-
трещин, фиксируемых по прорыву ПД на внешнюю
поверхность).
Отметим, что если прорыв ПД фиксируется
относительно четко, то появление трещин до-
достоверно выявляется оптической съемкой лишь
тогда, когда трещины уже достигают значитель-
значительного раскрытия. Дальнейшее развитие метода
определения радиуса трещинообразования связа-
связано с разработкой оптических высокоскоростных камер, дающих фотографическое
разрешение порядка 100 линий/мм (существующие камеры типа СФР-2М дают
разрешение 20.. .30 линий/мм).
Относительные значения радиусов трещинообразования и разрушения Ъс = bc/bo
и bf = bf/bo представлены в табл. 16.1.
Для пластических материалов характерным является развитие длинных пря-
прямолинейных трещин, распространяющихся по направлению детонационного фрон-
фронта («бегущих» трещин). В отдельных случаях бегущие трещины проходят через
всю длину оболочки. Измерение скоростей вершин бегущих трещин vc вдоль обо-
оболочки с помощью оптической съемки дает значения vc в диапазоне 2000.. .4000 м/с.
Верхнее значение существенно превышает теоретический верхний предел скорости
распространения трещин под действием постоянных растягивающих напряжений,
равный скорости cr поверхностной волны Релея (для стали сц = 2980 м/с).
Число п$ магистральных трещин по окружности при относительной толщине
стенки оболочки Sd = 1/8—1/6 в зависимости от характеристик стали и ВВ
меняется в диапазоне 20.. .50.
Радиус разрушения оболочки может быть также определен по измеренному
экспериментально утончению оболочки 5 = S/5о E — толщина осколка) с помощью
соотношения:
Рис. 16.8. Радиусы трещинобразо-
вания и разрушения оболочки
В [16.4] приведены результаты оптической съемки процесса взрыва крупнога-
крупногабаритных цилиндров. Использовались открытые на торцах цилиндры с внешним
диаметром 127мм E дюймов), внутренним диаметром 114,3мм D,5 дюйма) и
длиной 254мм A0 дюймов), изготовленные из обычной низкоуглеродистой ста-
стали SAE 1015, имеющей предел текучести 480 МПа и твердость Rb = 75... 85.

68
16. Осколочное действие взрывных систем
Таблица 16.2
Скорости оболочек в конце фаз
Таблица 16.1
Значения относительных радиусов
трещинообразования и разрушения
Материал оболочки
Сталь 45Х термообр.
Сталь 35
Армко
Медь Ml
bc
1,25
1,4
2,1
-
h
1,5
2,0
2,8
4,0
Фаза
1
2
3
4
t, С
27
-79
27
-79
27
-79
27
-79
v, м/с
1250
1281
1647
1677
1967...2074
1982...2074
1891
1878
t — температура образца,
v — скорость в конце фазы.
Фазы процесса взрыва по [16.4]
Таблица 16.3
фазы
1
2
3
4
Вид фазы
Упругопластическое рас-
расширение
Пластическое расширение
с раскрытыми трещинами
Процесс дробления внут-
внутри облака продуктов дето-
детонации
Полет осколков за преде-
пределами облака ПД
Признак конца фазы (КФ)
Образование трещин на по-
поверхности
Прорыв ПД через оболочку
Вылет осколков из облака ПД
Прибытие осколков к мише-
мишени, находящейся на расстоя-
расстоянии 6м
Время
КФ, мкс
9
24.. .27
650
3200
Отн. радиус
вКФ
1,2
1,6
21
Толщина стенки 6,35мм @,25 дюйма), относительная длина заряда 2,22. Сна-
Снаряжение производилось составом С-3. Испытания проводились при нормальной
температуре оболочки 27 С и низкой температуре -79 С. Съемка производилась
высокоскоростной лупой времени «Кордин» с частотой съемки 333 тыс. кадр./сек.
Передняя двухсторонняя подсветка процесса осуществлялась с помощью двух
трубчатых аргоновых бомб.
Автор работы выделяет четыре фазы процесса взрыва (табл. 16.3).
В 4-м и 5-м столбцах таблицы приводятся данные испытаний при нормальной
температуре. Данные для низкой температуры практически не отличаются. Дан-
Данные относятся к сечению Lq/2.
Скорости оболочек в конце каждой фазы представлены в табл. 16.2.
Волосовидные трещины на поверхности цилиндра, появляющиеся в конце 1-й
фазы, ориентированы вдоль образующих оболочки. В ходе 2-й фазы эти трещины
расширяются как в осевом, так и в тангенциальном направлениях, приобретая
вид относительно узких эллипсов с острыми концами. Одновременно происходит
появление новых трещин. В фазе 3 возможности наблюдения процесса быстро
уменьшаются из-за экранировки оболочки истекающими через нее продуктами

16.1. Наблюдения процесса и осколочных спектров
69
детонации. Тем не менее некоторые качественные особенности процесса описы-
описываются. При продолжающемся расширении оболочки продолжается рост трещин
в длину и ширину, но значительно более быстрыми темпами, чем в фазе 2.
Образуется система перемычек между параллельно расположенными трещинами.
Картина осложняется бифуркацией трещин. Излом по перемычкам приводит к
выделению из оболочки длинных осколков. В торцевых зонах краевые эффекты
приводят к образованию более мелких осколков.
Процесс разрушения может продолжаться уже после выделения осколка из
оболочки. В этом случае решающую роль играет градиент осевой компоненты
скорости, приводящей к делению осколка по длине.
10,4 мкс 15,7мкс	26мкс
Рис. 16.9. Рентгеноимпульсная съемка
процесса расширения медной трубки.
da = 20 мм; do = 24 мм; Lq = 140 мм, 1 —
0 мкс; 2 — 10,4 мкс; 3 — 15,7мкс; 4 — 26 мкс;
5 — 31,8 мкс
18мкс	22мкс	32мкс
Рис. 16.10. Рентгеноимпульсная съемка про-
процесса расширения стандартного осколочного
цилиндра № 7
Предложенная 4-х фазная модель разрушения в части, касающейся фаз 3, 4
представляется спорной. Если концы фаз 1,2 соответствуют достижению сечения-
сечениями оболочки радиусов Ъс и bf , то фаза 3 сформирована достаточно произвольно,
т.к. выход осколков из облака продуктов происходит намного позднее полного
разрушения оболочки и, строго говоря, не имеет отношения к модели разрушения.
Аналогично обстоит дело и с фазой 4. Другим недостатком модели является то,
что она не рассматривает разрушение в контактной зоне и взаимодействие этого
разрушения с трещинами, распространяющимися с внешней поверхности.
Рентгеноимпульсные регистрации процесса расширения оболочек представле-
представлены на рис. 16.9 - 16.11.
В работах [16.5, 16.6] рассматривается применение рентгеноимпульсной съемки
для изучения поля разлета осколков. В качестве рентгеновского источника исполь-
используется рентгеноимпульсная установка типа ЭРИДАН со следующими параметра-
параметрами: энергия 0,8 МэВ, длительность импульса 0,2.. .0,4 мкс, «игла» анод 2.. .10 мм,
просвечивающая способность на 1 м-45 мм Fe. Регистрация производится на рент-
рентгеновские кассеты различного формата. Размер кассет от 30x40 см до 2,3x2,6 м.
Показано, что при определении масс осколков по рентгеновским изображениям
имеет место систематическое занижение массы, зависящее от формы и материала
осколков, а также от условий съемки.
В [16.7] рентгеноимпульсная съемка использовалась для определения угло-
углового распределения ПЭ осколочной БЧ при различных схемах инициирования
(центральное, единичное боковое, двойное боковое). Боевая часть выполнена в
форме бочки с высотой 197 мм, максимальным диаметром 157 мм и массой заряда
ВВ 3,5 кг (РХ-80). БЧ помещалась внутри двух концентрически расположенных
цилиндров, имеющих продольную щель (рис. 16.12). Готовые ПЭ (куб со стороной

70
16. Осколочное действие взрывных систем
А -..А
39,7 m
А
49,2
А
Рис. 16.11. Рентгеноимпульсная съемка процесса расширения снарядов: а — макет осколочно-
фугасного снаряда, б — 30 мм ОФ снаряд под углом к его оси. Выделяется пояс А низкоско-
низкоскоростных осколков от придонной толстостенной части снаряда)
3,85 мм), пролетающие через щель, регистрировались двумя рентгеноимпульс-
ными установками. Векторы скорости осколков определялись ЭВМ с помощью
специальной программы.
2. Камерные и щитовые испытания. Распределение осколков по массе
определяется в результате подрыва цилиндров в специальных камерах, снабжен-
снабженных уловителями осколков. Тормозящей средой уловителей служат песок, вода,
опилки, пена и т.п.
В научной литературе большое внимание уделяется оценке достоверности дан-
данных, получаемых при камерных испытаниях. Существенное влияние на характер
спектра может оказывать как тип тормозящей среды, так и диаметр воздушной
полости D, в которой осуществляется подрыв. По данным [16.8] испытаний в песча-
песчаном уловителе осколочных гранат калибра 30 мм, снаряженных смесью гексоген-
алюминий, диаметр воздупеной полости должен превышать диаметр снаряда не
менее чем в четыре раза.
В работе [16.9] описаны сравнительные испытания осколочных гранат калибра
150 мм, снаряженных тротилом, в песочной и водяной камерах при различных
диаметрах воздушной полости. В обоих случаях увеличение диаметра полости
способствует уменьшению осколков. Сделан вывод, что для получения неиска-
неискаженного распределения осколков, соответствующего подрыву в неограниченной
воздушной среде («истинного» спектра осколков), отношение D/cIq при водяном
уловителе должно составлять не менее 5, а при песочном — не менее 10.

16.1. Наблюдения процесса и осколочных спектров
71
6
Рис. 16.12. Схема рентгеноимпульсной съемки поля готовых ПЭ боевой части: 1 — боевая часть,
2 — стальные цилиндры, 3 — щель, 4 — кассеты, 5 — экран, 6 — рентгеноимпульсные трубки
Рис. 16.13. Конгломерат слабосвязанных сабель, полученный при воздушном разлете
Таблица 16.4
Распределение Ni осколков по
массовым группам
Наиболее распространенное объяснение явле-
явления роста числа осколков с увеличением отно-
относительного диаметра полости D/do состоит в
том, что на начальной стадии свободного полета
осколков в них продолжаются процессы пласти-
пластического течения, разрыхления и разрушения. Пе-
Перехват осколка плотной средой приводит, с одной
стороны, к быстрому отбору энергии осколка, с
другой — подавлению процессов разрыхления,
происходящих под действием растягивающих на-
напряжений.
Предполагается также, что реальная картина
разрушения цилиндра при камерных испытаниях
осложняется доломом (вторичным дроблением)
осколков при ударе о тормозящую среду. Кри-
Критерии реализации дол ома рассмотрены в [16.3].
В результате спектр, полученный при камерных
испытаниях, может рассматриваться лишь как
некоторое приближение к «истинному».
«Истинный» спектр фрагментов, не искажен-
искаженный процессом улавливания, в принципе может
быть получен одним из следующих методов:
1) воздушным торможением осколков с после-
последующим сбором их с местности (с бето-
бетонированной или асфальтированной секторной площадки, имеющей длину
500.. .800 м) при помощи электромагнитного подборщика. Оценочное сравне-
сравнение десяти наиболее длинных осколков 122 мм осколочно-фугасных снарядов,
полученных при подрыве в опилочной бронекамере и собранных с местности
после щитовых испытаний в секторе, противоположном щиту, показали, что
отношение максимальных длин осколков, полученных при свободном разлете
и в камере составляет 1,87, а средних длин — 1,53 (рис. 16.13);
массовая
группа
0,5-1
1-2
2-3
3-4
4-6
6-8
8-10
10-15
15-20
20-30
30-50
50-75
75-100
>100
Снаряд
53ОФ540
704
632
560
213
288
196
152
268
176
199
192
87
32
21
ЗОФ25
1159
1045
314
371
491
329
235
401
221
224
149
40
9
1

72
16. Осколочное действие взрывных систем
2) рентгеноимпульсной съемкой расширяющегося поля осколков с последую-
последующим пересчетом параметров плоских изображений осколков на массы. Ана-
Аналогичный метод может быть реализован высокочастотной оптической съем-
съемкой после выхода фрагментов из облака ПД.
Таблица 16.5
Фракционный состав
осколочных масс
Снаряд
53-ОФ-540
З-ОФ-25
Мм
0,17
0,19
0,28
0,42
Мк
0,55
0,39
канал Б
После испытания в камере осколки с помощью
электромагнита извлекаются из опилок и сорти-
сортируются по массовым группам. Нижняя граница
сбора осколков ms принимается обычно для ОФ
снарядов средних калибров 0,5 г, для стандарт-
стандартного осколочного цилиндра № 12 — 0,25 г, для
малокалиберных снарядов — 0,1г. В практике
осколочных испытаний США обычно принима-
принимается ms = 1 гран, т.е. 0,0648 г. Границы массовых
групп для ОФС средних калибров составляют:
0,5-1; 1-2; 2-3; 3-4; 4-6; 6-8; 8-10; 10-15; 15-20; 20-30; 30-50; 50-75; 75-100; > 100 г,
для стандартных осколочных цилиндров № 12 — 0,25-0,5; 0,5-1; 1-2; 2-3; 3-4; 4-5;
5-6; 6-7; 7-8; 8-9; 9-10; 10-12; 12-15; 15-20; 20-30; 30-50; > 50 г. Распределение
осколков по массовым группам для двух типов 152 мм ОФ снарядов представлено
в табл. 16.4:
Наряду с числом осколков в данной массовой группе определяется их суммар-
суммарная масса в группе. Определяется также суммарная масса осколков, имеющих
т < ms («пыли»). Опыт считается корректно выполненным, если отношение
суммарной собранной массы всех осколков (включая массу несчетной группы
т < ms) к массе корпуса составляет не менее 0,95.
В табл. 16.5 приводится фрак-
фракционных состав осколочной мас-
массы этих снарядов (/хм — от-
относительное содержание мелкой
фракции 0 < т $J 4 г, /ic —
относительное содержание сред-
средней фракции D < т ^ 20г),
/iK — относительное содержание
крупной фракции (т > 20г).
Отметим, что для обоих снаря-
снарядов содержание средней фрак-
фракции не удовлетворяет современ-
современным требованиям (/ic ^ 0,45).
Характеристики формы оскол-
осколков в различных массовых груп-
группах определяются либо прибли-
приближенно, например, измерением
длины и ширины осколка, либо
точно с помощью компараторов.
В СКВ НИИ «Геодезия» разра-
разработана автоматическая система
«Спектр», позволяющая опреде-
определять массу осколка, минималь-
минимальную, среднюю (из 15 измерений) и максимальную площадь проекции осколка
(рис. 16.14).
Развитие процесса разрушения цилиндра может быть исследовано методом его
остановки на различных стадиях расширения с помощью массивного цилиндра-
канал А
Г*
4
i
7
1
8
9
Рис. 16.14. Прибор «Спектр» НИИ «Геодезия» для
измерения характеристик формы осколков; 1 — весы; 2 —
устройство сброса и ориентирования ПЭ; 3 — контейнер;
4 — блок обработки сигналов; 5 — излучатели; 6 — фото-
фотоприемники; 7 — ЭВМ; 8 — ЦПУ; 9 — пульт управления

16.1. Наблюдения процесса и осколочных спектров
73
остановщика. Впервые метод остановки был предложен профессором В. А. Кузне-
Кузнецовым в 50-х годах XX века. Воздушный зазор между испытываемым цилиндром
и остановщиком определяет деформацию цилиндра в момент остановки.
Основная трудность при работе с данным методом заключается в отделении
эффектов, вызываемых расширением цилиндра, от эффектов, связанных с удар-
ударной остановкой.
Уменьшение амплитуды напряжений в момент удара может быть достигнуто за
счет использования демпфера 2 (рис. 16.15а). Облегченная разборка остановщика
после подрыва может быть достигнута при использовании выплавляемого сплава
Вуда (рис. 16.156). При необходимости одновременной остановки оболочки полость
остановщика должна быть выполнена конической с углом наклона образующей,
равным углу Тейлора (рт = arcsin (vq/2D) (рис. 16.15в).
В работе [16.10] при металлографическом анализе остановленных оболочек в
поперечном сечении обнаружены срединные радиальные трещины, не выходящие
ни на одну из поверхностей оболочки. На рис. 16.16 показана внешняя поверхность
остановленной оболочки с нанесенным электронным лучом швом. Видно, что
продольные трещины на поверхности возникают преимущественно на швах.
Рис. 16.15. Цилиндр-остановщик в сборе:
варианты с цилиндрической камерой (а, б);
вариант с конической камерой (в); 1 — кор-
корпус остановщика; 2 — демпфер; 3 — подры-
подрываемый образец; 4 — сплав Вуда
Рис. 16.16. Остановленная оболочка с на-
нанесенными электронно-лучевой обработкой
швами. Видны очаги разрушения по швам
Щитовые испытания
Щитовые испытания предназначены для определения распределения осколков
и их скоростей по меридиональному углу разлета. Щитовая (мишенная) обста-
обстановка выполняется в виде полуцилиндрической вертикальной стенки, обшитой
металлическим (дюралевым или стальным) листом. Снаряд устанавливается в
центре полуцилиндра в горизонтальном положении (рис. 16.17а). На внутренней
стенке полуцилиндра нанесены контуры проекции части сферы, ограниченной

74
16. Осколочное действие взрывных систем
двумя меридиональными сечениями с углом АО между ними, а также линии
границ угловых секторов с шагом А(р. Развертка щитовой обстановки показано
на рис. 16.176. Испытуемый боеприпас или стандартный осколочный цилиндр
устанавливается на высоте средней линии АВ. В результате опыта определяется
а	б
Рис. 16.17. Щитовые испытания. 1 — снаряд; 2 — щит; 3 — противорикошетный щит; 4 —
скоростные кинокамеры
число счетных осколков пу, попавших в каждый угловой сектор «линзы» АВ и
общее число счетных осколков, попавших в площадь «линзы». Отбор счетных
осколков, например, с массой, большей 0,5 г (ns = ^0,5) на щите проводится
по площади отверстий, т.е. учитываются только те отверстия, площадь которых
больше So,5- Площадь So,5 рассчитывается по соотношению:
То
A6.1)
При 7о = 7,85 • 10 Зг/мм3, Ф = 2, получаем So,5 = 32 мм2. Число осколков в j-й
угловой зоне Nq^j и общее число осколков N^5 определяются по соотношениям:
360°
Следует отметить, что числа осколков данной оболочки, определенные по резуль-
результатам камерных испытаний (АГ^5) и щитовых испытаний (АГ^5) могут отличаться
друг от друга, причем, как правило, iVJ5 > -^о^б- -^ отдельных случаях отношение
Nq5/N^5 может достигать 1,5.. .1,8.
Указанное явление обычно объясняют, с одной стороны, вторичным дроблени-
дроблением осколков в тормозящей среде («додрабливанием»), с другой — методическими
ошибками в измерении площади пробоин и процедуре пересчета по формуле A6.1).

16.1. Наблюдения процесса и осколочных спектров
75
В"
R
Как правило, испытания по определению уг-
углового распределения осколков совмещаются с
измерением углового распределения скоростей
(годографа скоростей). Для этого с помощью
скоростных кинокамер фиксируется время At
между двумя моментами: освещением щита при
подрыве и моментом удара осколков о щит. Сред-
Средняя скорость в данном направлении определяет-
определяется как vj = R/Atj, где R — расстояние от места
расположения боеприпаса до щита. Момент при-
прибытия осколков к щиту при высоких скоростях
(г; > 1000 м/с) и щитах, выполненных из дюра-
дюралюминиевых листов, фиксируется по вспышкам
при ударе. Свечение может быть усилено за счет Рис 16 18 Основные (А) и сопут-
покрытия листов составом, содержащим магние-	ствующие (В) осколки
вый порошок. При низких скоростях и стальных
листах момент удара фиксируется по появлению пробоин в щите, подсвеченных
пиротехническим источником света, расположенным сзади щитов.
В заключение отметим, что оба указанных метода (камера и щит) как по-
порознь, так и в комбинации друг с другом, не позволяют достоверно определить
пространственно-массовое распределение осколков, определяемое двумерным мас-
массивом N^ (N^ — число осколков г-й массовой группы, движущихся в j-й угловой
зоне). Выход заключается в замене обоих испытаний одним испытанием по методу
углового улавливания осколков. На устройство соответствующего стенда получен
патент № 2131583 РФ [16.11]. Основная трудность разработки заключается в
создании разборных улавливающих блоков многократного использования.
3. Основные особенности осколков естественного дробления. При
исследовании осколков выявляются следующие характерные особенности:
1. В общем случае в спектре осколков вы-
выделяются две разнородные морфологические
совокупности осколков — крупные (основ-
(основные, квазирегулярные) осколки типа А, обра-
образованные магистральными трещинами и со-
содержащие обе исходные поверхности цилин-
цилиндра) и сопутствующие мелкие осколки типа
В, содержащие одну исходную поверхность
(рис. 16.18) [16.12, 16.13].
Спектр осколков типа В включает в себя
два подкласса: В'— осколки контактной зоны,
примыкающей к заряду ВВ, образованные
поверхностями сдвига, В" — осколки зоны,
расположенной у внешней поверхности ци-
цилиндра, образованные в основном (для сред-
Таблица 16.6
Зависимость относительной
массы основных осколков от
толщины стенки цилиндра
do ,мм
Sd
ст. 20
ст. 60
5о , мм
7,5
45
1/6
0,52
0,47
10
50
1/5
0,69
0,56
15
60
1/4
0,91
0,78
неуглеродистых и высокоуглеродистых сталей) хрупкими отрывами радиального
направления.
Относительная масса основных осколков /ха при фиксированном типе ВВ
увеличивается с увеличением относительной толщины стенки и снижением содер-
содержания углерода в стали.
В табл. 16.6 приводятся данные подрывов открытых цилиндров с фиксиро-
фиксированными диаметром заряда 30 мм и длиной заряда 120 мм (Aq = 4), снаряженных
ТНТ, при различных толщинах стенок.

76
16. Осколочное действие взрывных систем
Число осколков типа А определяется как Na = тт^п^, где n#, п^ — средние числа
осколков, на которые делится цилиндр по окружности и длине соответственно.
Средняя масса осколка типа А та = Mofia/Na (Mq — масса оболочки).
2. Осколки типа А и значительная часть осколков типа В имеют более или
менее значительное удлинение по образующей оболочки. Это удлинение обычно
характеризуют показателем Л* = /// (/ — длина, / — средняя ширина осколка)
или более объективным показателем
А =
где т, V — соответственно масса и объем осколка.
Введена следующая классификация осколков по величине удлинения Л:
4 ^ А	— компактные осколки;
8 ^ А > 4	— нормальные осколки;
15 ^ Л > 8	— длинные осколки;
Л > 15	— сверхдлинные осколки.
A6.2)
I =	156 мм 167 мм	137 мм	145 мм	159 мм	137 мм	142 мм	130 мм
т=	41,5 г 35,2 г	24,5 г	39,2 г	35,2 г	25,7 г	27,0 г	23,2 г
X =	26,8 32,2	28,0	24,7	30,0	28,1	29,0	27,3
т' =	2,66г/см 2,11	1,79	2,70	2,21	1,88	1,90	1,79
Рис. 16.19. Осколки стандартного цилиндра № 12 (сталь 60 и сталь 45 с длиной, равной длине
оболочки («полосы»)
Наличие в спектре длинных и в особенности сверхдлинных осколков («сабель»)
указывает на неудовлетворительное дробление. В наиболее неблагоприятных слу-
случаях (вязкий металл, низкобризантное ВВ, волокнистая структура включений и
т.д.) могут образовываться осколки с длиной, равной длине оболочки («полосы»).
Характерные полосы и близкие к ним по длине осколки цилиндров №12 (ст. 60
и ст. 45) показаны на рис. 16.19 (табл. 16.7).

16.1. Наблюдения процесса и осколочных спектров
77
Таблица 16.7
Характеристики сверхдлинных
осколков («полос»)
В качестве примера приведем данные по выборке 20 наиболее длинных осколков
цилиндра №12 (ст.20/ТНТ). Корпус цилиндра изготовлен холодным обратным вы-
выдавливанием и имеет высокие пластические свойства (^=50%, ан=860 КДж/м2).
Погонная масса осколка т' рассчитывалась по формуле т = т/1. Числа осколков
составляли 7V0,25=521, 7V0,5=396, 7V1=291.
Средняя масса осколка т — 31,5 г
Средняя длина осколка / — 93 мм
Средняя погонная масса га' — 3,31 г/см
Среднее удлинение Л — 14,4.
Выборочное среднеквадратическое откло-
отклонение 8Ш' погонной массы составляло 0,69
г/см, коэффициент вариации V = 5т'/га' = 0,21,"
что указывает на достаточную стабиль-
стабильность величины т'. Уравнения регрессии
/ = 1,62га + 3,94, га = 15,7га'- 20,6, где /=[см],
772= [г/см] имеют коэффициенты корреляции
соответственно 0,76 и 0,92, что свидетель-
свидетельствует о наличии значимой положительной
корреляции между этими величинами. Приве-
Приведем также данные для осколка максимальной
массы
Максимальная масса осколка ттах —
59,2 г
Его длина Z — 133 мм
Погонная масса т'— 4,45 г/см
Удлинение Л — 17,7.
3. Поверхность разрушения основных осколков имеет, как правило, две зоны:
поверхность хрупкого отрывного разрушения (зона R), прилегающую к внешней
поверхности осколка, и поверхность сдвигового разрушения по площадкам сколь-
скольжения (зона S), прилегающую к внутренней поверхности осколка. Обозначим глу-
глубину зоны отрывного разрушения у, тогда тип разрушения может быть охаракте-
охарактеризован отношением у = у/5. Для осколков хрупких сталей характерны значения
у = 0,5—0,8 (рис. 16.20а), для осколков низкоуглеродистых и легированных сталей
характерно разрушение по схеме сквозного сдвига (у = 0) (рис. 16.206).
1.
2.
3.
4.
1.
2.
3.
4.
1, мм
Сталь 60/ТНТ
156
167
137
145
сталь 45/ТНТ
159
137
142
130
т, г
41,5
35,2
24,5
39,2
35,2
25,7
27
23,2
Л
26,8
32,2
28
24,7
30
28,1
29
27,3
Рис. 16.20. Схема разрушения хрупких сталей (а) и пластичных сталей (б)
В цитированной выше работе Дж. Пирсона [16.4] показано, что 127 мм ци-
цилиндры из низкоуглеродистой стали SAE 1015, при нормальной температуре
разрушающиеся по схеме сквозного сдвига (у = 0), при пониженных температурах
начинают разрушаться по комбинированной схеме «отрыв—сдвиг». При темпера-

78
16. Осколочное действие взрывных систем
турах испытания 51 С и —79 С относительные глубины у зоны хрупкого отрывного
разрушения составляли соответственно 0,25 и 0,35.
Выделяются две основные схемы разрушения сквозным сдвигом. В первом
случае в основном образуются сдвиговые осколки трапециевидного или треуголь-
треугольного сечения, причем широкое основание трапеции может располагаться как на
внутренней, так и на внешней поверхности стенки. Второй, менее распространен-
распространенный тип сквозного сдвигового разрушения характеризуется образованием пластин
скольжения, сдвигающихся относительно друг друга по плоскостям скольжения
одного семейства (по «черепичному» механизму) (рис. 16.21). В отдельных случаях
получаются пластины скольжения («лопасти») с отношением ширины к толщине
4—5. Сквозной сдвиг по отношению к комбинированному разрушению ухудшает
форму осколка.
В толстостенных оболочках Sd > 1/5
разрушение, как правило, происходит по
схеме «сдвиг-отрыв-сдвиг».
Сложность контура поперечного сече-
сечения осколков может быть охарактеризован
параметром сечения Q = Р/у/~В, Р — пери-
периметр, В — площадь сечения. Для осколка
квадратного сечения Q = 4. Большие зна-
значения ?7^5 приводят к ухудшению аэро-
аэродинамической формы осколка (увеличе-
(увеличению его среднего миделя <S>). Параметр
Q увеличивается с уменьшением величины
у по приближенной зависимости:
п = 6 - 2у, (К
1.
При сквозном сдвиге в отдельных слу- ^ -, ~ «-, ^
1	„	„	т^ Рис. 16.21. Схема разрушения по «чере-
чаях значения п достигают п = 7. На	пичному» механизму
внутренней поверхности осколков имеются
множественные ступеньки скольжения Т.
Значительная часть мелких осколков образуется вследствие выкрашивания ме-
металла по этим ступенькам.
Таким образом, роль сдвига в осколкообразовании неоднозначна. Множествен-
Множественный сдвиг в контактной зоне (зоне «перемола») является полезным фактором, так
как он способствует увеличению массы мелкой (сопутствующей) части спектра.
Напротив, сквозной сдвиг (у = 0) по всей толщине оболочки является негативным
фактором, ухудшающим как массовое распределение, так и форму осколков.
Характерные конфигурации на кон-
контактной поверхности представлены на
рис. 16.22 (открытый цилиндр, До = 4,
da = 25 мм, сталь 20-окфол, Sd = 1/4,5).
Показаны оба типа осколков А и В в поло-
положении, непосредственно предшествующим
отделению.
Видны отчетливо сформированная сту-
ступенька скольжения и развивающаяся тре-
трещина, разделяющая осколки по осевому
направлению. На рис. 16.23 показан ча-
частично отделившийся осколок с малой шириной (так называемая «лопасть»).
Таблица 16.8
Размеры ступенек скольжения, мм
вв
тнт
A-IX-2
Окфол
Сталь
Ст. 20
4,0
3,8
3,2
Ст. 45
3,7
3,3
2,8
Ст. 60
3,5
3,1
2,6

16.1. Наблюдения процесса и осколочных спектров
79
5 мм
Рис. 16.22. Осколки на контактной поверх-
поверхности в положении, непосредственно пред-
предшествующем отделению
Рис. 16.23. Частично отделившийся оско-
осколок с малой шириной («лопасть»)
В табл. 16.8 представлены средние значения величин Д5, мм для различных
комбинаций сталь-ВВ (стандартный осколочный цилиндр №12).
С увеличением содержания углерода в стали и мощности ВВ наблюдается
закономерное уменьшение величины AS.
В дальнейшем для оценки минимальной массы осколка, включаемой в спектр,
с приданием ей ясного физического смысла использовалась модель осколка типа
В в виде призмы треугольного сечения с гипотенузой Д?, в качестве последней
принимался нижний доверительный предел случайной величины AS = 3,3 ±0,5 мм
с доверительным пределом 0,8, полученный при усреднении данных табл. 16.8.
4. Металлографическое исследование осколков Вопросы металлогра-
металлографических исследований осколков рассматривались в работах [16.1]—[16.3], [16.14,
16.15].
Исследование поверхностей разрушения
Поверхности разрушения осколков исследуют с помощью электронных мик-
микроскопов — просвечивающего электронного микроскопа (ПЭМ) или растрового
(сканирующего) электронного микроскопа (РЭМ). При использовании ПЭМ про-
просвечиваются тонкие слепки с поверхности разрушения (реплики). По сравнению
с ПЭМ растровый электронный микроскоп имеет то преимущество, что позволя-
позволяет непосредственно изучать топографию деформированного рельефа в широком
интервале увеличений при глубине фокуса на 2-3 порядка больше, чем в опти-
оптическом микроскопе. При этом трудоемкость исследований на РЭМ существенно
меньше, чем на ПЭМ. Фотографирование поверхностей разрушения с помощью
сканирующего электронного микроскопа показывает, что на поверхности отрыва R
разрушение происходит по комбинированному механизму с образованием фасеток
скола (рис. 16.24) и участками вязкого волокнистого разрушения ямочного типа
(рис. 16.25), причем доля последних увеличивается с увеличением пластичности
металла. Ямки (лунки) представляют следы полостей, возникающих и разви-
развивающихся в металле под воздействием растягивающих напряжений. Большая
часть полостей развивается вокруг неметаллических включений в стали (карбидов,
нитридов и т. д.).
Фрактографические исследования поверхностей скольжения в контактной зоне,
проведенные на сканирующем электронном микроскопе JSM—U3 ИМЕТ показали,

80
16. Осколочное действие взрывных систем
У
v y\v\
\
!
Рис. 16.24. Фрактография поверхности отрыва с образованием фасеток скола, Х2000
Рис. 16.25. Фрактография поверхности отрыва на участке вязкого волокнистого разрушения
ямочного типа, х500
что для этой стали на всей плоскости скольжения реализуется вязкий ямочный
сдвиг. Вершины параболических ямок на сдвиговой поверхности данной части
направлены в сторону ее сдвига относительно первоначально примыкающей к ней
другой части металла. Опасения относительно того, что при взаимном скольжении
поверхностная тонкая структура будет стерта или сильно искажена, в целом не
подтвердились.
В ряде случаев на поверхности скольжения в зоне, прилегающей к внутренней
поверхности, наблюдалось появление системы ступенек с шагом hs = 0,02 ... 0,05 мм.
Аналогичные исследования, проведенные на осколках из сталей 40Х, 45, 60, 65Г,
показали, что в этом случае на поверхностях скольжения в зоне глубиной до

16.1. Наблюдения процесса и осколочных спектров
81
1,5. ..2 мм имеет гладкая поверхность, на которой рельеф не выявляется даже
при увеличении 3000. Молено предполагать, что эти поверхности являются по-
поверхностями разрушения по плоскостями адиабатического скольжения (ПАС).
В зоне, более удаленной от внутренней поверхности, ПАС сменяется обычной
вязкоямочной структурой.
Исследование шлифов
В основном исследовались шлифы поперечных разрезов осколков.
1)	Контур сечения осколка. В подавляющем большинстве случаев поперечное
сечение осколка не является выпуклой фигурой. Параметр формы сечения
Q в целом уменьшается с увеличением содержания углерода в стали и
составляет для низкоуглеродистых сталей 5,5—7, для среднеуглеродистых —
5-6, для высокоуглеродистых — 4,5-5,5.
2)	Пластическая деформация оболочек прослеживается по деформации зерен.
Деформация зерна, характеризуемая отношением больших осей зерна, умень-
уменьшается по направлению от внутренней к внешней поверхности осколка и
составляет для внутренней зоны 1,6.. .2,3, для средней зоны 1,4.. .1,7, для
наружной зоны 1,1.. .1,3.
3)	Характер разрушения на уровне микроструктуры существенно зависит от
содержания углерода в стали. Для низкоуглеродистых сталей имеет место
преимущественно внутризеренное (интеркристаллитное) разрушение с за-
заметным двойникованием. В среднеуглеродистых ферритно-перлитных ста-
сталях разрушение происходит преимущественно в перлитной фазе, а также на
включениях. Для высокоуглеродистых заэвтектоидных сталей (С>0,83%),
имеющих цементитную сетку, разрушение происходит по сетке.
4)	В средней по толщине зоне осколков оболочек, изготовленных из среднеуг-
среднеуглеродистых и высокоуглеродистых сталей, часто отмечается так называемая
деструкция, т.е. возникновение внутренних трещин и пор (полостей разрыва
W). Появление этой разрывно-волновой зоны (РВЗ) обычно связывают с
действием волн разрежения.
Полости разрыва в основ-
основном имеют вытянутую конфи-	Таблица 16.9
гурацию, ориентированную Распределение трещин разрыва по углу
преимущественно в радиаль- ориентации
ном направлении. Распределе-
Распределение трещин по углу ориента-
ориентации Xi T-e- острому углу, об-
образованному осью трещин с
радиусом, представляет убы-
убывающую функцию экспонен-
экспоненциального типа. Средняя дли-
длина трещины 1С с увеличением
угла х убывает. Экспериментальное распределение трещин разрыва по углу х
представлено в табл. 16.9 для открытой оболочки из стали 60 (da = 25 мм, Aq =
4, 5d = 1/6).
Экспериментальные исследования откольно-разрывной зоны на оболочках раз-
различных типов при нагружении обычной скользящей детонацией показали, что
этот эффект сильнее проявляется для оболочек открытого типа и, во-вторых,
характеризуется довольно низкой воспроизводимостью. Отмечались случаи на-
наличия и отсутствия откольно-разрывной зоны в однотипных условиях экспе-
эксперимента. Более того, в экспериментах с кольцами имели место случаи, когда
X, град
Рг
1С, мкм
0-15
0,55
460
15-30
0,25
420
30-45
0,10
360
45-60
0,06
230
60-75
0,03
180
75-90
0,01
105
Pi — отношение числа микротрещин данной ори-
ориентации к полному их числу

82
16. Осколочное действие взрывных систем
Таблица 16.10
Характеристики разрывно-волновой зоны
Показатель
Число радиальных трещин пс
Максимальная длина трещины Lmacc, мм
Коэффициент выхода осколков r\f = пе/пс
рас _
пв — ncrjf
Тип ВВ
ТНТ
51±5
2,4
0,24
12,2
A-IX-2
48±6
2Д
0,29
13,9
Окфол
64±4
2,2
0,26
16,6
разрывная зона возникала только на части окружности кольца. Следует отметить,
что указанное явление отмечалось как при шашечном снаряжении, так и при
наполнении заливкой, что устраняет предположение об определяющем влиянии на
нестабильность эффекта величины зазора между ВВ и внутренней поверхностью
оболочки. Можно предполагать, что существенное влияние на развитие процесса
порообразования оказывает неоднородность свойств и структуры материала.
Основные количественные результаты
были получены при исследовании осколков
стандартных цилиндров открытого типа
№4 - 0, изготовленных из стали 20 и стали
С-60 (обе стали в нормализованном состоя-
состоянии). Выяснилось, что степень развития
разрывных эффектов в стенке оболочки
зависит от положения сечения по длине
оболочки.
Изменение максимальной длины тре-
трещины внутреннего разрыва в различных
сечениях по длине оболочки показано на
рис. 16.26. В дальнейшем для обозначения ближней и дальней к точке иниции-
инициирования зон оболочки будем использовать термины соответственно «передняя» и
«задняя» зоны.
В торцевых зонах величина 1шах больше, чем в средних сечениях, что, по-
видимому, объясняется более интенсивной разгрузкой ПД в этих зонах. Небольшое
увеличение значения /тож в передней зоне может быть объяснено усилением
откольных эффектов при малых значениях угла падения old детонационного
фронта.
В развитом виде разрывно-волновая зона включает в себя крупные радиальные
внутренние трещины (каверны) с относительно периодическим расположением
скопления микро- и макропор. Рассмотрим последовательно эти образования.
Характеристики набора каверн для стали С-60 при различных ВВ (тротил, А-
IX-2, окфол) представлены в табл. 16.10. В последней строке таблицы представлено
расчетное значение числа щ.
Величина пс определялась с помощью соотношения
Перед.	Средн. Задн.сеч.
2=20-30 мм 2=40-60 2=70-80 мм
Рис. 16.26. Изменение максимальной дли-
длины трещины внутреннего разрыва
Пг —
2тгг0
где г0 — средний радиус оболочки (r0 = a0 + So/2 = а0 A — Sd) / A - 2^)); х —
среднее расстояние между радиальными трещинами (шаг трещин). В таблице
указаны величины доверительных интервалов для величины пс при доверительной

16.1. Наблюдения процесса и осколочных спектров
83
вероятности 0,8. Коэффициент выхода осколков по данным эксперимента опреде-
определялся с помощью соотношения:
пс — число радиальных трещин в данном осколке.
Рис. 16.27. Периодические разрывы (каверны) в осколках. Цилиндр №4-О, ст 60. а — ТНТ; б —
A-IX-2; в — окфол.
Характерные виды расположения периодических радиальных трещин в оскол-
осколках из стали С-60 представлены на рис. 16.27. При приближении трещины к
внутренней поверхности, направление ее развития отклоняется от радиального,
что указывает на переход к сдвиговому разрушению.
Увеличенные изображения некоторых радиальных трещин (х80) показаны на
рис. 16.28, 16.29. Видно, что конфигурация и структура каверн имеют более
сложный характер, чем представляется при небольшом увеличении, и отличаются
Рис. 16.28. Слияние радиальных трещин
Рис. 16.29. Полоса деструкции.
большим разнообразием. Наиболее типичной конфигурацией является радиальная
цепочка пор с различной степенью их слияния. Весьма условно можно выделить

84
16. Осколочное действие взрывных систем
два основных типа каверн — свободные полости и полости деструкции. К первому
типу относятся образования (рис. 16.28), ко второму — рис. 16.29.
Характерную конфигурацию представляет образование «D» (рис. 16.28). Здесь
зафиксировано положение, непосредственно предшествующее слиянию двух до-
достаточно крупных радиальных трещин. На основании данной и аналогичной
фотографий можно предположить, что радиальная каверна может формироваться
не только за счет линейного развития в одном направлении, но и за счет слияния
нескольких трещин, возникающих с небольшим временным сдвигом.
Полосы деструкции представляют собой удлиненные в радиальном направ-
направлении зоны множественных разрывов (рис. 16.29). Ширина полос колеблется
в пределах от 100 до 450 мкм. Предельной формой полосы является открытая
полость, содержащая отдельные конгломераты зерен. Размеры этих включений
достигают в отдельных случаях 100.. .150 мкм.
У значительной части радиальных каверн имеются отходящие трещины. Ча-
Частость появления каверн с различным числом отходящих трещин по отношению
к общему числу каверн (цилиндр №12, сталь С - 60, A-IX-2) представлена в
табл. 16.11.
Таблица 16.11
Частота появления каверн с различным числом отходящих трещин
Число отходящих трещин
Частота
0
0,76
1
0,12
2
0,07
3
0,03
4
0,01
5 и более
0,01
Величина острого угла, образованного отходящей трещиной с радиальной осью
каверны, колеблется в пределах 40.. .70.
Следует отметить, что в шлифах встречается также большое количество ком-
компактных полостей с отходящими трещинами небольшой длины. Не исключено,
что полости данного типа (компактные полости — узлы трещин) представляют
не первичное, а вторичное явление, т.е. сами образуются в месте пересечения
трещин. Это явление представляется, однако, маловероятным вследствие очень
низкой плотности независимых линейных трещин.
Более вероятным является образование разрывных полостей в месте пересече-
пересечения полос адиабатического сдвига. В этом случае процесс, по-видимому, является
двухстадийным. На первой стадии в месте пересечения полос адиабатического
сдвига возникает разрывная полость, а затем на второй стадии происходит полное
или частичное раскрытие отходящей трещины вдоль полосы.
Развитие линейных трещин от полостей разрывного происхождения феномено-
феноменологически представляет весьма интересный процесс. При этом очагами отходящих
трещин могут служить микроразрывы, возникающие на поверхностях разрывной
полости при ее раскрытии. Однако небольшая доля полостей — узлов трещин
указывает на то, что роль этого явления в общем процессе разрушения для
исследованных сталей, по-видимому, невелика.
В отдельных радиальных полостях оболочек из стали 45X1 и С-60 отмечалось
образование полости разрывом по полосе адиабатического сдвига. Характерным
признаком этого явления является наличие по краю полости узкой белой кромки
бесструктурного мартенсита. Для стали 20 это явление не обнаружено. Не исклю-
исключено, что сравнительно редкая фиксация этого явления связана с выкрашиванием
хрупкой мартенситной пленки при механической обработке поверхности шлифа.
В отдельных случаях обнаружены (цилиндр № 7, ст. 45X1/A-IX-2) внутренние
радиальные полости, образованные разрывом ПАС и послужившие очагом фор-
формирования радиальной трещины разрыва на внешней поверхности. На вторичный

16.1. Наблюдения процесса и осколочных спектров
85
характер наружной трещины в данном случае указывает наличие в осколках
большого числа внутренних полостей такого же типа, не приводящих к развитию
наружных радиальных трещин. Распределение микропор по размеру L удовлетво-
удовлетворительно описывается показательным законом:
П5(>Ь)=Поехр(--М,
где Us (> L) — поверхностная плотность микропор, имеющих линейный размер
больше L; Ls — характеристический размер микропоры.
Математическое ожидание раз-
размера поры < L >= Ье- Значения па-	Таблица 16.12
раметров распределения представ- Параметры распределения пор по
лены в табл. 16.12. размерам
При снижении пластических ха-
характеристик сталей разрывно-волно-
разрывно-волновые явления усиливаются. На рис.
16.30 показаны характерные ви-
виды внутренних разрывов в крем-
кремнистой 60 С 2 и высокоуглероди-
высокоуглеродистой перлитно-цементитной стали
110 Г2С (da = 40мм, 5d = 1/6). Эти разрывы в осколках стандартного цилин-
цилиндра №12 имели место при всех трех типах снаряжения (ТНТ, A-IX-2, окфол).
Разрывно-волновые эффекты усиливаются также при увеличении толщины обо-
оболочки и при Sd ^ 0,2 отчетливо проявляются практически для всех сталей.
Сталь
Сталь 20
С-60
По,
1/см2
150
550
Ls,
мкм
580
410
In По
5,0
6,3
Lc In По
2900
2580
Рис. 16.30. Внутренние разрывы: а — в кремнистой стали 60С2; б — в высокоуглеродистой стали
110Г2С, х5
Откольно-разрывные эффекты могут быть резко усилены при использовании
более интенсивных нагрузок острого профиля и более хрупких материалов, напри-
например, чугунов. Пусть в общем случае спад нагрузки описывается экспоненциальным

86
16. Осколочное действие взрывных систем
законом:
= рт ехр
Разлагая правую часть в ряд и ограничиваясь первыми двумя членами разложе-
разложения, в первом приближении заменим экспоненциальную волну волной треуголь-
треугольного профиля:
Р = Р
Для этой волны условие реализации откола в оболочке толщиной 5q с напря-
напряжением разрушения af и скоростью звука cq имеет вид:
1.
A6.3)
сосг/т
Таким образом, для цилиндра фиксированной толщины определяющую роль иг-
1
10
?
I
а
——-m
,\
б
\
\
II
в
\
\
III
г
\
\
IV
\
\
кбар
' МКС
2 4 6 8 10 12 14
Рис. 16.31. Области реализации различ-
различных видов откольно-разрывных явлений:
а — скользящая детонация; б — полый за-
заряд; в — осевая детонация; г — кольцевой
ударник; I — откольных явлений нет; II —
вутренние разрывы; III — откол с части по-
поверхности; IV — откол по всей поверхности.
*,
Рис. 16.32. Сечение контактной зоны
рает параметр рш/т. Как уже указывалось выше, откол существенно облегчается
при увеличении хрупкости металла, которую условно охарактеризуем величиной
ф~1. На рис. 16.31 по данным [16.3] представлены области реализации различных
видов откольно-разрывных явлений на плоскости аргументов pm/r и 1/ф. Для
данного типа ВВ величина рш/т может значительно изменяться в зависимости от
схемы заряда. Наименьшее значение параметра дает скользящая детонация (а).
При нагружении цилиндра полыми зарядами кольцевого сечения (б) или зарядом
с осевой детонацией (в) могут быть получены как сплошные кольцевые отколы,
так и неразвитые.
Сплошные кольцевые отколы возникают также при нагружении оболочки уда-
ударом по ее внутренней поверхности кольцевым ударником, разгоняемом взрывом
(г). В 1978 году сотрудниками Армейского центра по механике и материалам был
получен патент № 4089267 США на этот способ дробления осколочных оболочек.
Однако исследования этой схемы в СССР проводились значительно ранее. В 1976

16.1. Наблюдения процесса и осколочных спектров	87
году была опубликована статья (Известия АН СССР, МТТ, 1976, №6), в которой
было исследовано развитие гладких фазовых кольцевых отколов под действием
ударных оболочек.
Порообразование в осколках приводит к снижению их средней плотности.
Средняя плотность осколка определяется соотношением:
7 = 7оA " К),
а относительная плотность 7 = 7/70 — соотношением:
7 = 1 - К,
где Vv — относительный объем пор.
Экспериментальные измерения плотности осколков ЕД средних фракций ци-
цилиндров №12 (сталь 60 нормализованная) при снаряжении ТНТ, A-IX-2 и окфолом,
проведенные методом параллельного взвешивания осколков в воздухе и воде,
дали средние значения плотности соответственно 7,5 ± 0,2; 7,4 ± 0,3; 7,2 ± 0,2
(относительные плотности при 70 = 7,85 г/см3 соответственно 0,95; 0,94 и 0,92,
относительные объемы пор и трещин соответственно 0,05; 0,06 и 0,08). В то
же время следует отметить, что для осколков ЕД мелких и крупных фракций
снижение плотности незначительно и не выходит за пределы точности измерений.
Сечение контактной зоны, перерезанной множественными ступеньками сколь-
скольжения, показано на рис. 16.32 (fs — ширина ступеньки скольжения, hs — высота
осколка после излома, М — магистральная плоскость сдвига). Наиболее вероятно,
что излом по поверхностям "И"происходит под действием изгиба после некоторого
расширения оболочки.
Трещины сдвига распространяются с внутренней поверхности как в виде си-
систем трещин одного семейства, так и двух семейств. Типичным является случай
остановки трещины при пересечении ею трещины другого семейства (осколок А).
Очень характерным является остановка
трещины сдвига на малом расстоянии от
внешней поверхности, причем в отдель-
отдельных случаях это расстояние не превышает
долей миллиметра. В средней по толщи-
толщине зоне сдвиговых осколков наблюдаются
многочисленные разрывные полости.
m	„	Рис. 16.33. Характерные сечения сдвиго-
1олщина локализованной зоны сдви-	оп
^	^	вого осколка из ст. 20
га уменьшается с увеличением углерода
в стали и для низко-, средне- и высо-
высокоуглеродистых сталей составляет соответственно 100.. .150 мкм, 60. ..80мкм,
20. ..50мкм.
На рис. 16.33 показано треугольное сечение осколка сквозного сдвига с ярко
выраженным уплощением (а± р^ а2 ~ 30°), приводящим к резкому ухудшению
формы. Значение показателя формы сечения в данном случае достигает величины
?} = 7,4 (Р = 59,6 мм; В = 64,4 мм ). Отметим, что это значение Г? соответствует
обычно используемому в анализаторах изображений (например, типа «Видео-
«Видеоплан») параметру Fp = АттВ/Р2 = 0,23 (Fp = 4тг/^2, п = ^Tr/FpI/2, для круга
Fp = 1).
На рис. 16.34 показано довольно часто встречающееся явление — полость
разрыва в конце сдвиговой трещины. Вопрос о последовательности образования
полости и трещин сдвига пока не вполне ясен.

16. Осколочное действие взрывных систем
:#¦>:
Х50
Рис. 16.34. Полость разрыва с конце сдви-
сдвиговой трещины.
Х50
Рис. 16.35. Полосы локализованного сдви-
сдвига в осколках.
Рис. 16.36. Полосы адиабатического сдвига
Характерные сдвиговые эффекты в осколках ст.45Х1 показаны на рис. 16.35,
16.36. Легирование этой стали хромом подавляет развитие трещин хрупкого отры-
отрыва и способствует разрушению по схеме сквозного сдвига, ухудшающему форму
осколков. На рис. 16.35 показана полоса локализованного сдвига, на рис. 16.36 —

16.2. Модели процессов расширения и разрушения оболочек	89
полосы адиабатического сдвига (ПАС). Развитие ПАС при разрушении оболочек
и литература по этом вопросу рассмотрены в [16.3].
Характерной особенностью осколков сдвигового происхождения является нали-
наличие в них острого режущего ребра. Изменение остроты режущей кромки осколков
из стали 80Г2С, проведенные Волыновой и Одинцовым на сканирующем электрон-
электронном микроскопе в ЦНИИЧермет, показали, что радиус при вершине режущего
ребра может составлять до 5.. ЛОмкм, что соответствует остроте заточки хирур-
хирургического инструмента. Действие такого осколка по тканевым бронежилетам при
подходе режущим ребром вперед существенно отличается от действия притуплён-
притуплённых тел типа пуль, имитаторов осколков в виде шариков или цилиндров и т.п.
16.2. Модели процессов расширения и разрушения оболочек
1. Одномерное расширение жесткопластической несжимаемой обо-
оболочки. Рассмотрим процесс расширения жесткопластической оболочки под
действием продуктов мгновенной детонации с начальным давлением: р0 = Ро •
D2/2 • (fc + 1) (рис. 16.37) [16.16, 16.17]. Процесс расширения ПД будем считать
равновесным, т.е. примем, что происходит мгновенное выравнивание давления по
всему объему, занятому ПД.
Система уравнений в эйлеровых координатах для материала оболочки в общем
случае имеет вид:
^7 d(^fv) 7^	/	\
——I	1	=0 (уравнение неразрывности)
ot от т
fdv dv\ даг ав - ar
7 т;—Ь ^тг~ = —	(уравнение движения)
\ot от) от	т
7 = / (сгг, <jq, crz) (уравнение объемной сжимаемости) A6.4)
F (сгг, сг#, az) = 0 (условие пластичности)
1 /	ч /
<jz = - [аг + ае) (условие стесненности
осевой деформации (ez = 0))
Система 5 уравнений содержит 5 зависимых переменных г>, 7? ^п ^в^ °~г-
Граничными условиями являются следующие:
аг = — р на внутренней поверхности оболочки (г = а)
аг = 0 на внешней поверхности оболочки (г = Ь)
Примем материал оболочки несжимаемым G = 7о = const). В этом случае все
производные плотности обращаются в нуль и уравнение неразрывности приобре-
приобретает вид:
от г
Интегрирование этого уравнения приводит к соотношению:
v=C®	A6.5)
т
Функция C{t) определяется из условий на внутренней поверхности. При г = а,
v = а, откуда С (t) = aa и, следовательно:
v = a-	A6.6)

90
16. Осколочное действие взрывных систем
а = da/dt — скорость движения внутренней поверхности оболочки.
Подставляя A6.6) и производные
Т
dv da + a2
~dt ~ r '
в уравнение Эйлера:
dv dv
\dt or J or
dv
dr
dar
аа
Т2
— ar
а также используя условие пластичности:
ав - аг = ХУ	A6-7)
получим:
Рис. 16.37. Напряженное состояние тол- дGг
стостенной оболочки под действие ПД.
дGг	Y
ОГ	Г
da + а2 а2 а2
, A6.8)
d = d2a/dt2 — ускорение внутренней поверхности.
В выражении A6.7) х = 1 ПРИ условии пластичности Сен-Венана—Треска
и х = 2/л/З при условии пластичности Мизеса—Генки (деформация плоская,
аг = A/2) (стг + ств).
Интегрируя A6.8) по г от а до текущего значения и учитывая граничное
условие аг = — р при г = а, имеем:
(Уг = -Р + XYln - + 7о [аа + а ) In - + 70 1 о 2
Используя внепЕние граничные условия сгг = 0 при г = 6, выраж:ение для давления
мгновенной детонации ро = PoD2/8, учитывая условие несж:имаемости:
Ь2 — а2 = Ь2) — а2,
и закон равновесного расширения ПД в виде:
получим нелинейное уравнение:
где
1 = Ро — )
а /
а =
A6.9)
A6.10)
2aln(b/a)
In (Ь/a) a'
7о V а1п(Ь/а)
Начальными условиями являются:
a@) = a0, d@) = 0.

16.2. Модели процессов расширения и разрушения оболочек
91
Интегрирование уравнения A6.10) при
различных толщинах оболочки и условиях
пластичности подтвердило, что распреде-
распределение напряжений по толщине оболочки в
любой момент времени можно считать ли-
линейными (с точностью до 5-7%), откуда:
tD/h
а г = --
р(Ъ — г)
p(b-r)
Для глубины растянутой зоны, отсчиты-
отсчитываемой от внешней поверхности оболочки,
можно записать:
у = 5—
V
или, учитывая A6.9):
У =
5Y (а/а0)
2к
На рис. 16.38 представлены законы дви-
движения поверхностей оболочки, а также по-
поверхностей aq = 0 и аг = — aq для значения
0,8	1,0	1,2	1,4
Рис. 16.38. (R-t)-диаграмма процесса рас-
расширения несжимаемой жесткопластической
оболочки под действием первоначально по-
покоящихся ПД
Таким образом, в оболочке, находящейся под действием взрывной нагрузки,
возникают две зоны. В зоне, прилегающей к внешней поверхности, реализуется
смешанное напряженное состояние (аг < 0, а$ > 0), во внутренней зоне —
состояние всестороннего неравномерного сжатия. По мере расширения цилиндра
граница зон (<jq = 0) перемещается к внутренней поверхности.
По Тейлору разрушение сплошной оболочки происходит в тот момент, когда
внешняя зона распространяется на всю толщину оболочки. Радиус разрушения а/
определяется выражением:
= ао \Т7
)
A6.П)
В указанном выводе неявно предполагается, что разрушение оболочки происходит
в растянутой зоне путем хрупкого отрыва.
2. Одномерное расширение сжимаемой упруго-пластической оболоч-
оболочки. Численное исследование напряженно-деформированного состояния оболочки
в начальной (волновой) стадии ее расширения проводилось в одномерной поста-
постановке [16.18]. Для воспроизведения нагрузок от скользящей детонационной волны
использовалась следующая модель.
В момент t = 0 продукты детонации (ПД) имеют постоянную по радиусу
плотность ро> равную плотности взрывчатого вещества, и радиальную скорость,
распределенную по параболическому закону и = щ (R/uq) (uq — начальный
внутренний радиус оболочки, R — радиальная координата). Величины скорости
г^о и начального давления ПД р^ (или скорости звука в ПД со) определяются
единственным образом из баланса энергии на единицу длины заряда:
СЕ0+ j ^u2 dC = CQV,
с

92
16. Осколочное действие взрывных систем
и условия равенства давления отражения ПД от оболочки фронтальному дав-
давлению детонации pc-J> где С —масса заряда взрывчатого вещества на единицу
длины, Eq — начальная внутренняя энергия ПД, Qv —- удельная теплота взрыва.
Для продуктов детонации, описываемых политропой Ландау-Станюковича р =
Арк имеем (D — скорость детонации)
Qv =
D2
2(к2 - 1)'
PC-J =
РоР2
к + 1
— 0,1736, с0 —
— 0,587,
В безразмерном виде при к — 3 получим: и'о —
Ро = Po/poD2 = 0,155, D = Ay/Q~v.
Движение оболочки происходит в условиях плоской деформации (ez = 0),
напряжения сгг, сг#, <jz являются главными.
Уравнения механики сплошной среды для продуктов детонации и материала
оболочки записаны в линейных лагранжевых переменных. Уравнение состояния
металла (стали), единая процедура расчета в упругой и пластической области
с приведением девиаторов напряжения на круг текучести, начальные и гра-
граничные условия и безразмерные переменные приняты такими же, как в [16.19].
Ограничений на величину растягивающего напряжения в волнах разрежения не
накладывалось.
Начальные условия для ПД имеют вид р = ро, и = щ (R/clq) , где а$ —
начальный внутренний радиус оболочки.
Определяющими безразмерными параметрами задачи являются: G' = G/p$D2,
Y' = Y/p0D2, ш0 = 7О/Ро, Sd = 60/2Ъ0.
Здесь G — модуль сдвига, Y — динамический предел текучести, 7о — начальная
плотность металла, 5q = (bo — clq) — начальная толщина стенки.
Конечно-разностная аппроксимация уравнений выполнена при помощи явной
одношаговой схемы второго порядка точности. Регуляризация решения прово-
проводилась посредством линейного сглаживания. Диссипативный член в формуле
сглаживания соответствует псевдовязкому давлению, введенному в [16.20].
Значения относительного радиуса полости \о = ао/Ьо =1—2J^, коэффициента
нагрузки /3 и коэффициента наполнения сечения ? (/3 = С/MX = С/(С + М),
где С, М — масса взрывчатого вещества и оболочки на единицу длины), а
также расчетное значение конечной скорости оболочки vq = A/2) • D((/{2 —
С)I/2, представлены в табл. 16.13 (скорость в м/с) На рис. 16.39 представлено
распределение давлений в продуктах детонации р' и радиальных напряжений в
оболочке о'г в различные моменты времени для 5d = 1/6. Линейный масштаб в
ПД и металле различен.
Рассчитаны варианты, соответствую-
соответствующие значениям ?0=1/8 и 1/6, при этом
G = 81ГПа, Y = 1ГПа, 7о = 7,85 •
103кг/м3, ро = 1,7- 103кг/м3, D=8000m/c.
В ПД возникает отраженная ударная
волна с характерным плато давления. При
схождении отраженной ударной волны к
оси симметрии формируется расходящаяся
ударная волна, амплитуда которой быстро
убывает. В дальнейшем в ПД устанавливается процесс, близкий к равновесному
расширению.
Амплитудное давление на контактной поверхности ПД—металл равно 18,3 ГПа,
что близко к расчетному давлению распада разрыва при скользящей детонации.
Таблица 16.13
Характеристики цилиндров
1/8
1/6
Хо
0,75
0,667
0
0
Р
,278
,173
0
0
С
,218
,148
1390
1030

16.2. Модели процессов расширения и разрушения оболочек
93
Наблюдается расщепление ударной волны в оболочке на упругий предвестник,
первую пластическую волну с амплитудным давлением фазового перехода 13 ГПа
и вторую пластическую волну, также наблюдается поэтапная разгрузка.
Амплитуда первой удар-
ударной волны в оболочке затухает
сначала медленно, а затем, по
мере приближения к внешней
поверхности, быстро.
Амплитуда волны разре-
разрежения нарастает по мере дви-
движения вглубь оболочки, до-
достигая максимума сгг = 4,8 ГПа
на относительной глубине у° =
0,72, а затем быстро убывает.
(R-t1)-диаграмма процесса
для обеих толщин представ-
представлена на рис. 16.40. Здесь по
оси абсцисс отложена безраз-
безразмерна^ лагранжева коорди-
координата R = (R — а0)/(bo -
ао),&о ^ R ^ ^о- Сплош-
1,546
Рис. 16.39. Распределение давлений в ПД и радиальных
напряженияй в оболочке в различные моменты времени
t' = Dt/ao
ная линия ад = 0 разде-
разделяет зоны с растягивающи-
растягивающими и сжимающими (заштри-
(заштрихованная область) тангенциальными напряжениями. На первых трех пульсаци-
пульсациях у внутренней поверхности сохраняется состояние тангенциального сжатия.
В дальнейшем зоны сжатия возникают пульсирующим образом только внутри
оболочки, причем толщина этой зоны со временем уменьшается. С некоторого
момента времени в оболочке существуют только растягивающие тангенциальные
напряжения (для случая Sd = 1/8, t' « 7, девятая пульсация, рис. 16.40).
В дальнейшем, несмотря на существование внутри цилиндра значительного
давления ПД, практически весь материал цилиндра переходит в разгруженное
состояние (по всей толщине среднее напряжение а > 0) (для случая Sd = 1/8 это
происходит в момент времени t' й 8). Значения величин в моменты окончания 1—
5-й пульсаций для обеих толщин представлены в таблице 16.14 (первые 4 столбца
относятся к случаю 8а = 1/8, остальные — Sd = 1/6, № — номер пульсации),
Ь = b/bo — относительный внешний радиус. Средняя скорость определялась по
формуле (ее величина дана в м/с)
(v) = — v dM
М J
м
Размерные значения времени (в мкс) приводятся для оболочки с внутренним
радиусом ао=2Омм.
Для обеих толщин оболочек относительные радиусы b в моменты окончаний
соответствующих пульсации отличаются менее чем на 3%. История изменения
напряжений ад и деформаций \sr\ (кривая 1) и sq (кривая 2) в средней точке
оболочки (на срединной поверхности) (R = 0,5) представлена на рис. 16.41
E^=1/6). Римскими цифрами помечены моменты окончания соответствующих
пульсаций. Амплитудные значения растягивающих тангенциальных напряжений
убывают сравнительно медленно, что свидетельствует о возможности разрушения
как в первой, так и в последующих волнах разрежения.

94
16. Осколочное действие взрывных систем
10
6 -
4 -
2 -
2 -
0	0,5	10	0,5	1
Рис. 16.40. (R-t') диаграмма расширения упругопластической сжимаемой оболочки
В то время как деформация растяжения по координате 0 возрастает с течением
времени монотонно, радиальная деформация сжатия возрастает (по модулю)
пульсирующим образом. Моменты пересечения кривых (se=\sr\) соответствуют
нулевой объемной деформации. При дальнейшем расширении, с затуханием вол-
волновых процессов и уменьшением объемного сжатия оболочки, соотношение между
деформациями приближается к соотношению ?Q=-sr , справедливому для несжи-
несжимаемого материала при плоской деформации (табл. 16.14).

16.2. Модели процессов расширения и разрушения оболочек
95
Таблица 16.14
Характеристики разгона к моменту окончания соответствующей пульсации
№
1
2
3
4
5
t'
1,0059
2,0244
2,8646
3,7526
4,5612
t
2,5148
5,0610
7,1615
9,3815
11,4030
b
1,0323
1,0993
1,1689
1,2516
1,3320
(v)
659,9
917,2
1045,5
1124,8
1170,0
t'
1,5173
2,8550
4,2605
5,6640
6,7906
t
3,7933
7,1375
10,6513
14,1600
16,9765
b
1,0377
1,1016
1,1859
1,2818
1,3649
(v)
577,4
774,3
873,1
956,9
988,4
0,05 -
О
-0,05 -
0,3"
0,2-
0,1-
CJQ
,
1
I
1
Pv
II
I
A
/ 3 \
III
I
Л
/4
I si
IV
I
V
I
A
VI
I
У 8
о
12345678
Рис. 16.41. История изменения тангенциального напряжения и деформаций на срединной
поверхности цилиндра
Значения величин в средней точке R = 0,5 в момент окончания первой
пульсации представлены ниже, значения напряжений и удельной энергии фор-
формоизменения As даны в ГПа, а скорости деформации — в 1/с (первая строка
соответствует 8а = 1/8, а вторая — 8а = 1/6) (табл. 16.15)
Таблица 16.15
Значение величин в средней точки в момент окончания первой пульсации
о-в
4,56
4,72
СГГ
3,50
3,67
3,89
4,04
а
3,98
4,14
?в
0,039
0,050
Sr
-0,013
-0,020
0,026
0,030
ее
27456
22220
ir
-28600
-30372
As
0,27
0,35
В этот момент все три напряжения (<jr, <7q, crz) являются растягивающими,
т.е. имеет место состояние всестороннего неравномерного растяжения; достигнута
значительная тангенциальная деформация растяжения D.. .5%), а радиальная
деформация сжатия к этому моменту достигает локального минимума. Средняя

96
16. Осколочное действие взрывных систем
объемная деформация в этот момент также положительна.
Распределение напряжений, деформаций и удельной энергии формоизменения:
As = Videi
о
по толщине оболочки в момент окончания первой и второй пульсации представлено
на рис. 16.42 Ed = 1/6). Таким образом в момент окончания первой пульсации в
¦-0,2
а)	6)
Рис. 16.42. Распределение напряжений, деформаций и удельной энергии формоизменения по
толщине оболочки в момент окончания первой и второй пульсаций
средней зоне оболочки возникает состояние, близкое к всестороннему растяжению.
В соответствии с утверждением Ю. Н. Работнова трехосное напряженное со-
состояние, близкое к состоянию всестороннего растяжения, приводит к хрупкому
разрыву даже в том случае, когда материал является пластичным в обычных
условиях испытания.
Специфической особенностью здесь является тот факт, что радиальное рас-
растягивающее напряжение действует в условиях отрицательной радиальной дефор-
деформации. В этом случае условия откольного разрушения становятся иными, чем в
одномерном плоском случае.
Наличие значительных тангенциальных напряжений, превосходящих на 30%
радиальные, по-видимому, и приводит к первоочередному развитию радиальных
трещин.
При дальнейших численных исследованиях процесс расширения оболочки с
самого начала рассматривался как пластически-деструкционный. Использовалась
динамическая статистическая модель, в которой местоположение, ориентация и
размер конкретных трещин не фиксирован, а степень деструкции характеризуется
некоторой обобщенной величиной D = / (?, г) (где t — время, г — лагранжева ко-
координата), причем эта характеристика может быть как скалярной, так и векторной
или тензорной величиной.
Для описания пластически-деструкционного процесса нами использовалась
величина о;, предложенная Ю. Н. Работновым [16.21] для описания процессов

16.2. Модели процессов расширения и разрушения оболочек	97
ползучести и названная им поврежденностью. Величина поврежденности для
сплошного материала равна нулю, является монотонно неубывающей по времени
и не превышает 1. Введено также понятие «сплошности» материала ф = 1 — си.
Трудность использования функций со, ф для полного описания процесса разру-
разрушения оболочек заключается в том, что характер поврежденности (деструкции) в
разных по толщине зонах стенки оболочки различен. В средней по толщине зоне
стенки имеет место образование множественных микро- и макроразрывов. У внеш-
внешней поверхности оболочки разрушение идет главным образом за счет радиального
разрыва, у внутренней поверхности — за счет сдвига по плоскостям скольжения.
Описание всех этих физически разнородных видов разрушения единой функцией
поврежденности о;, помимо чисто теоретических трудностей, порождает большие
затруднения при параметризации экспериментально наблюдаемой деструкции в
различных по толщине зонах оболочки. Поэтому при помощи кинетических урав-
уравнений поврежденности и родственных им критериев разрушения имеет смысл
описывать только начальную стадию разрушения оболочек — стадию образования
и роста зародышей магистральных трещин или, при определенных условиях (когда
возможен откол), процесс накопления поврежденности, приводящий к отколу.
При расчетах [16.22] использовалось кинетическое уравнение поврежденности
в виде:
dt y '
При этом для определения константы ад и функции A(<Ji) были использо-
использованы экспериментальные данные о зависимости разрушающего напряжения ар
от времени его действия tp, приведенные в [16.23] для стали 3. В этом случае
ао=О,89ГПа, а функция A(ai) представляется в виде:
AyCTi) = (-/о — \P"i — ^о) ^о) •>	A6.13)
где /0 = 1,14 • 10ГПа2с, t0 = 0,176 • ИГ6 с, А'1^) = 0 при а{ = ат,
ат = 8,95 ГПа. Вводилось условие, что при достижении любым из компонентов
тензора напряжений сгш, соответствующий компонент uji обращается в единицу,
что соответствует мгновенному разрушению.
Снижение предела текучести при нарастании поврежденности учитывалась
зависимостью:
{--)¦
A6.14)
Yq — динамический предел текучести для сплошного материала (си = 0, ф = 1);
иос — характеристическое значение поврежденности;
uj — некоторая усредненная (скалярная) поврежденность, определяемая по
з
соотношению uj = A/3) J^ c<;^ либо из кинетического уравнения поврежденности
с подстановкой в него среднего напряжения.
Очевидно, что расчеты деструкционного процесса с помощью уравнений ме-
механики сплошной среды справедливы только до тех пор, пока среда находится в
рамках континуальной модели, т.е. пока рассеянные микроповреждения не слились
в развитые трещины. Это условие может быть представлено в виде си

16. Осколочное действие взрывных систем
— значение поврежденности, соответствующее появлению развитых трещин
(макротрещин).
Система уравнений механики сплошной среды, дополненная соотношениями
A6.12—16.14), записанными для лагранжевой частицы, интегрировалась при тех
же значениях характеристик металла и ВВ, как и в случае сплошной упруго-
пластической среды. Результаты расчетов представлены на рис. 16.43. Результаты
со
со
0,25
0,20
0,15
ОДО
0,05
t'= 1,51
-
-
-
-
со
0,25-
0,20-
0,15-
0,10-
0,05-
1
Г= 5,22
Г\
\(Ж\
R
0	0,5	1,0 0	0,5	1,0 0	0,5	1,0
Рис. 16.43. Распределение компонентов поврежденности по толщине стенки в различные
моменты времени [5^ = 1/6).
расчетов показывают, что поврежденность в средней части оболочки нарастает до
критических величин в течение одной—двух пульсаций. Общая кинематика обо-
оболочки при этом практически не меняется по сравнению со сплошным материалом.
В течение всего процесса тангенциальная компонента поврежденности ujq суще-
существенно превышает поврежденность ujr в радиальном направлении. Отношение
повреждений ujr/uJo колеблется в диапазоне 0,45.. .0,55 и сравнительно слабо зави-
зависит от величины параметра иос. Таким образом в средней зоне оболочки в первую
очередь следует ожидать развития радиальных трещин. Это подтверждает вывод,
сделанный выше на основе сравнения радиальных и тангенциальных деформаций.
На рис. 16.44 приведена расчетная кривая нарастания поврежденности ujq в
зависимости от времени в средней по толщине зоне стенки. Кривая нарастания
поврежденности является монотонно неубывающей, ступенчатой, так как по своей
природе поврежденность может возрастать только в периоды действия растяги-
растягивающих напряжений. Ступенчатая форма кривой возрастания поврежденности
является следствием волновой природы процесса расширения и разрушения обо-
оболочки. На рис. 16.45 приведена (R—tf)-диаграмма пульсаций волн и нарастания
поврежденности (зона сив > 0,05 заштрихована). Пунктирная линия соответ-
соответствует границе зон сжатия и растяжения. Видно, что с течением времени зона
поврежденности расширяется, расширение зоны происходит в периоды действия
растягивающих напряжений.
Однако зона поврежденности не проникает до внутренней поверхности, в
окрестности которой в течение длительного времени действуют сжимающие на-
напряжения. Описанные выше критерии разрушения непригодны для моделирова-
моделирования зарождения и роста очагов разрушения сдвигом при сжатии.
3. Модели разрушения оболочек. Процесс деформации и разрушения
оболочки под действием ПД уже после первой волновой пульсации и возникно-

16.2. Модели процессов расширения и разрушения оболочек
99
О,2 -
од -
О	2	4	t
Рис. 16.44. Нарастание тангенциальной
поврежденности в зависимости от времени
в средней по толщине стенки области
4 -
2 -
О	О,5	1
Рис. 16.45. (R-t')-диаграмма пульсацций
волн и нарастания поврежденностей в стен-
стенке оболочки
вения в волне разрежения первичных очагов разрушения является трехмерным.
Для его описания необходимо включение в систему уравнений механики сплошной
среды уравнений, описывающих трещинообразование и осколкообразование, яв-
являющиеся последовательными стадиями процесса. При этом возможны следующие
модификации трехмерных моделей:
•	оболочка имеет исходные однородные свойства (выполнена из изотропного
материала), внутри нее в координатах (r—6—z) заданы расположение очагов
разрушения (например, включений цементита, неблагоприятно ориентиро-
ориентированных перлитных колоний и т.п.) и для каждого очага — некоторый пара-
параметр его интенсивности;
•	материал оболочки анизотропен, т.е. для каждой лагранжевой ячейки зада-
задается конкретные значения прочностных и деформационных характеристик
материала, а также характеристик механики разрушения. В этой модели
возникновение очагов разрушения происходит в самом процессе численного
моделирования в неизвестные заранее моменты времени и в неизвестных
заранее местах.
Трехмерное моделирование при тщательном отборе наиболее важных и пред-
представительных ситуаций позволит получить ясную физическую картину образо-
образования полей напряжений и деформаций, взаимодействия полей трещин друг с
другом, преимущественного развития отрывных или сдвиговых разрушений, мест
образования зон хрупкого скола или вязкого волокнистого разрушения, типовых
механизмов слияния трещин и начальной стадии осколкообразования. В принципе
могут быть учтены такие тонкие эффекты как ветвление трещин, схлопывание
раскрытых трещин под действием пульсирующих волн сжатия, изменение направ-
направления распространения трещин и т.п.
К трудностям реализации трехмерных детерминированных моделей относятся
следующие:
•	трудность получения экспериментальной информации по пространственному
расположению дефектов и анизотропии свойств;
•	отсутствие на сегодняшний день достоверных критериев разрушения при
больших пластических деформациях;

100
16. Осколочное действие взрывных систем
• огромные объемы вычислений, требующие применения ЭВМ терафлопного
A012 операций в секунду) или петафлопного A015 операций в секунду)
классов с объемом оперативной памяти в сотни и тысячи Гигабайт.
Переходным этапом к пространственным задачам трещинообразования является
численное решение двумерных плоских (r-в) задач [16.24, 16.25]. Материал пред-
предполагается изотропным, линейные очаги разрушения расположены с постоянным
шагом на внешней поверхности, радиальные трещины отрыва распространяются
к внутренней поверхности оболочки. Принимается, что трещина распространяется
со скоростью волны Ре лея, если в окрестности ее вершины выполняется следующее
условие:
A6.15)
(.ДгI/2'
где Аг — текущее значение шага по радиусу в окрестности вершины трещины,
а $ — тангенциальная компонента напряжения на расстоянии Аг/2 от вершины,
К ic — трещиностойкость.
Положение оболочки в различные моменты времени и процесс раскрытия
трещины показаны на рис. 16.46. Диаграмма движения вершины трещины пред-
представлена на рис. 16.47. Видно, что в условиях волнового нагружения цилиндра
процесс распространения трещины является пульсирующим. Трещина движется,
если ее вершина попадает в область положительного тангенциального напряжения
и при этом выполняется условие A6.15). Наложение на трещину зоны сжатия
приводит к ее остановке.
f = 0,1527
Рис. 16.46. Положение оболочки в различ-
различные моменты времени и процесс расскрытия
трещины.
О	2	4 f
Рис. 16.47. Диаграмма движения верши-
вершины трещины.
Рассмотренные выше модели с известным положением трещин можно тракто-
трактовать как детерминированные модели разрушения. Наряду с этим можно ввести
понятие статистических моделей разрушения, в которых местоположение, ори-
ориентация и размер конкретных трещин не фиксированы. Решение проводится в
рамках двумерной (г—г)-модели. Наиболее интенсивно разрабатываются кинети-
кинетические модели процесса разрушения, рассматривающие процесс как протяженный
во времени с постепенным накоплением микро- и макродефектов («деструкцией»,
«предразрушением») (см. п. 16.2. .2).
К числу наиболее известных моделей этого типа относится модель «Зарождение
и развитие» (NAG — Nucleation And Growth), разработанная в Стенфордском
исследовательском институте США [16.26]. Модель известна также под названия-
названиями SPINAG и NAG/FRAG. Первоначально модель разрабатывалась для расчета

16.2. Модели процессов расширения и разрушения оболочек	101
откола и проверялась экспериментально при плоском ударе пластин. В дальней-
дальнейшем она применялась для расчета кратерообразования в горных породах и дру-
других динамических процессах. Для расчета спектров осколочных оболочек NAG-
модель впервые была использована сотрудниками Центра надводного оружия
флота (NSWC) в 1976г. [16.27], причем сама NAG-модель применялась только
для радиального разрушения, а сдвиговое разрушение описывалось специальной
моделью SNAG.
NAG-модель включает в себя две модификации, описывающие независимо
хрупкое и вязкое разрушение. Хрупкое разрушение представляется как процесс
образования и роста множественных дискообразных трещин и характерно для ста-
сталей, в том числе и низкоуглеродистых, включая Армко-железо. Вязкое разрушение
представляется как процесс образования и роста множественных сферических пор
и характерно для алюминия и меди.
NAG-модель для хрупкого разрушения последовательно рассматривает четыре
стадии процесса — зарождение трещин, рост трещин, слияние их и образование
осколков, причем для каждой стадии определяется зависимость скорости процесса
от мгновенного значения растягивающего напряжения, вычисляемого в каждой
частице материала в данный момент времени с помощью двумерных упруго-
пластических программ.
Зарождение трещин начинается в данной точке при условии, что напряжение
в ней, независимо от его ориентации, превышает некоторый пороговый уровень
сгпо- При выполнении этого условия скорость зарождения трещин определяется
соотношением:
	 = Щ ехр < 	— > ,	A6.16)
at	[ G\ J
где TVq, o"i, crno — эмпирические константы, а текущее распределение данной «ге-
«генерации» трещин по размерам имеет вид
Г ~}•	A6.17)
Рост характеристического размера распределения Rc в данной частице в функции
от времени описывается линейным дифференциальным уравнением:
^ - Т, (а - а ) R	A6 18)
dt	U 9°> с'	( '
где 7\ — эмпирический параметр; адо — пороговый уровень напряжения, при
котором начинается рост трещин.
Величина адо может быть определена с помощью соотношения:
где К\с — трещиностойкость материала.
Общий спектр трещин в каждый момент времени определяется как результат
суммирования трещин различных генераций на разных стадиях их роста:

102	16. Осколочное действие взрывных систем
(здесь и ранее величина N есть число трещин в единице объема).
Процесс слияния трещин описывается с помощью понятия области трещины,
представляющей некоторый объем, построенный вокруг дискообразной трещины
и определяемый соотношением:
V) = TCR3.
Безразмерный коэффициент Тс имеет величину порядка единиц для очень пла-
пластичных материалов и порядка 20 для очень хрупких материалов. Относительный
объем областей трещин в любой момент находится суммированием для трещин
всех размеров и ориентации:
В пределах данной расчетной ячейки слияние трещин считается законченным,
когда сумма объемов областей трещин становится равной объему ячейки (Vs = 1).
Распределение осколков по размерам в ячейке рассчитывается непосредственно
по распределению трещин по размерам при условии выполнения критерия полного
слияния трещин. Вводятся два эмпирических безразмерных коэффициента:
т.е. предполагается, что размер осколка Rf (его средний радиус) пропорциона-
пропорционален радиусу трещины G ~1), а число осколков пропорционально числу трещин
(для компактных восьмигранных осколков, например, /3f = 1/4). Распределение
осколков по размерам имеет ту лее форму, что и распределение трещин:
т.е. оно определяется параметрами распределения трещин и коэффициентами
Для вязкого материала соотношения NAG-модели записываются в виде, ана-
аналогичном A6.16) и A6.17), однако величиной R в данном случае является радиус
сферической поры, а не радиус дискообразной трещины, как в случае хрупкого
разрушения. Константа Т\ в уравнении роста поры будет равна 1/47/, где rj —
динамическая вязкость материала. При вязком разрушении важную роль играет
величина относительного объема пор в материале, которая при экспоненциальном
распределении размеров пор:
определится выражением:
В процессе порообразования происходит изменение модуля сдвига и предела
текучести, описываемое соотношениями:
G = С A - К7*1), F = 15±^-, У = Го A-4-^7)	A6-19)

16.2. Модели процессов расширения и разрушения оболочек
103
где Go, Yq — модуль сдвига и предел текучести для сплошного материала; 7 ~~
средняя плотность материала; v — коэффициент Пуассона. Условие разрушения
представляется в виде Vv ^ V?r.
Как уже указывалось выше, в работе [16.27] NAG-модель использовалась для
описания процесса радиального разрушения оболочек. Сдвиговые процессы моде-
моделировались с помощью геометрической аналогии краевых дислокаций, вследствие
чего кинетика распределения описывалась уравнением Орована:
iV,b =
3/2
1/2
\AtEcrJ \kvsb
, н =
kEcAt
1/2
3/2 / k \ V2
7ocy7
где Nsb — плотность подвижных сдвиговых полос; Н — ширина полосы; В — коэф-
коэффициент, характеризующий распространение полосы; 7о — плотность материала;
Су — теплоемкость при постоянном объеме; к — теплопроводность; Ер = Су At —
пластическая работа; Есг — величина внутренней энергии; 7 = ^sbBVsb — сдвиго-
сдвиговая скорость деформаций (соотношение Орована).
Значения констант, определяемых главным образом из экспериментов с плоско-
плосковолновым нагружением пластин, представлены в табл. 16.16 для двух материалов,
резко отличающихся по свойствам (высокоосколочная заэвтектоидная кремнисто-
марганцевая сталь HF-1 и Армко-железо)
Таблица 16.16
Характеристики стали HF-1 и Армко-железо.
Материал
Сталь
Армко
V
2724
417
(У до
-
2-Ю8
Ro
3,3-Ю-3
5-1(Г5
О~п0
1010
3-Ю9
3
4,
,1 •
56-
109
109
4
4,
No
,6-108
6 • 1012
в
2500
190
2
W
,5 6,75
200
Размерности для этих величин: rj — [дин-с/см2], адО: апО: а — [дин/см2], Ro —
[см], Б, W — [мкм], No — [1/см3с].
Начальный радиус трещины Rq в стали HF-1 почти на два порядка превышает
соответствующую величину для Армко-железа, т.е. скорость роста трещины в
первом случае будет значительно выше. Этот результат физически очевиден. В
то же время константа скорости зарождения Nq в стали HF-1 на четыре порядка
меньше, чем в Армко-железе. Прибегая к некоторой условности, можно сказать,
что из двух сторон процесса «зарождение-развитие» в стали HF-1, и вообще
в хрупких сталях, доминирует развитие трещин, а в Армко-железе и других
пластичных материалах доминирует их зарождение.
Полученные с помощью модели NAG/SNAG расчетные осколочные спектры
удовлетворительно совпали с экспериментальными данными для обоих материа-
материалов.
Следует отметить, что применимость рассмотренной модели к расчету спек-
спектров осколочных оболочек в широком диапазоне условий вызывает определенные
сомнения. Главное возражение состоит в том, что NAG/SNAG-модель описывает
разрушение и образование осколков компактной формы в толще металла, тогда
как при разрушении оболочек важную роль играют свободные поверхности, а
осколок имеет заведомо некомпактную удлиненную форму, причем продольное и

104	16. Осколочное действие взрывных систем
окружное деление оболочки по существу представляет два разнородных процесса.
Если модель с нарастанием и слиянием дискообразных трещин еще в какой-то
степени может быть применена к окружному делению, то для продольного, в
котором важную роль играет взаимодействие независимых и бегущих трещин,
она в принципе неприемлема.
Существенным недостатком модели также является большое число эмпири-
эмпирических параметров (восемь), определение которых требует применения сложных
экспериментальных методов.
Из отечественных работ, посвященных моделям разрушения осколочных обо-
оболочек, наиболее известны исследования В. А. Кузнецова. В. А. Кузнецов впервые
указал, что при исследовании процесса разрушения оболочки главное внимание
целесообразно уделить исследованию начального периода ее динамической дефор-
деформации. Этот начальный период в соответствии с терминологией, используемой
при изучении колебательных процессов, В. А. Кузнецов называл «переходным
периодом» или «периодом возбуждения оболочки». Он также предположил, что
рассмотрение колебательного процесса имеет физический смысл только для на-
наружной зоны упругой и упруго-пластической деформации материала оболочки,
а наиболее существенный интерес представляет развитие волновых явлений в
некотором тонком цилиндрическом слое металла толщиной А?о, имеющем радиус
срединной поверхности гт, где происходит возникновение основной массы трещин
разрушения. В. А. Кузнецов считал, что при схематическом описании процесса
деформации оболочки в период ее возбуждения, материал оболочки, находящийся
во внутренней зоне деформации, можно считать не участвующим в колебатель-
колебательном процессе, поскольку он находится в состоянии интенсивного пластического
течения. Таким образом, изучение начального периода деформации оболочки
при взрыве сводилось к исследованию упругих колебаний цилиндрического слоя
толщиной А^о при действии на этот слой импульсной нагрузки, меняющейся вдоль
оболочки по определенному закону. При исследовании этот слой рассматривался
как тонкая оболочка, поверхности которой свободны от внешней нагрузки.
Вынужденные колебания оболочки с открытыми торцами описываются систе-
системой линейных уравнений. При этом образуется п волн по окружности радиуса гт
и m полуволн по длине прямолинейной образующей этой поверхности, при этом
числа пит определяются выражениями
гТ
п = ш
сь V З-i/ '	тгСеУ З-i/ "
Для достаточно тонкой и длинной оболочки расчет общего числа первичных
очагов разрушения, которое при определенных условиях будет равно общему
количеству регулярных осколков, может быть произведен по формуле:
V,
8 /л	фЛа^^сь^Ь)	\\-\-v\ <jq I <jq
Значение параметров г = 0, 1 ,2... и j = 0, 1, 2... соответствует числу
максимумов, которые реализуются в момент потери устойчивости оболочкой в
период возбуждения последней.
Высказанное В. А. Кузнецовым предположение о том, что волновые процессы
на начальной стадии предопределяют дальнейшее разрушение оболочки, имело
важное значение для развития теории дробления. Идеи В. А. Кузнецова, оформ-
оформленные в виде так называемой «стартовой теории трещин» в дальнейшем разви-
развивались в работах Т. Г. Стаценко, С. А. Кренева, В. Б. Попова, В. А. Сидорова.

16.2. Модели процессов расширения и разрушения оболочек
105
Из отечественных работ последних лет, посвященных моделям взрывного раз-
разрушения оболочек, отметим работы Колобановой А.Е., Селиванова В. В. [16.28,
16.29]. Изложение этих результатов приведено в главе 19.
В. А. Одинцовым в [16.30] предприня-
предпринята попытка построения в рамках двумер-
двумерной (r-z) задачи статистической модели
разрушения как процесса распростране-
распространения конечного числа продольных трещин.
В основу этой пространственно-временной
модели положено представление о процес-
процессе разрушения цилиндра как о взаимо-
взаимодействии трех систем трещин: первичных
магистральных, вторичных («компенсаци-
(«компенсационных») и распределенной (диффузной)
поврежденности ш. После расширения ле-
левой торцевой зоны цилиндра до определен-
определенного радиуса в ней возникает «решетча-
«решетчатый» фронт магистральных трещин, дви-
движущийся на некотором переменном рас-
расстоянии Zff от детонационного фронта со
скоростью г>с, меньшей скорости детона-
детонации (рис. 16.48). При этом
Рис. 16.48. (z—t) диаграмма процесса раз-
разрушения оболочки: 1 — траектория детона-
детонационного фронта; 2 - траектория «решетча-
«решетчатого» фронта магистральных трещин.
Zff = ZD — Zc,
где Z?>, zc — соответственно координа-
координаты ДФ и фронта магистральных трещин
(МТ). Фронт магистральных трещин от-
отчетливо виден на высокочастотной фото-
фотографии рис. 16.3.
После прохода ДФ через сечение z цилиндра в момент времени t = z/D
начинается расширение сечения, сопровождающееся нарастанием пластической
тангенциальной деформации е и поврежденности uj. Нарастание поврежденности
в виде порообразования (деструкции) приводит к частичной разгрузке материала
вокруг пор. Подходящие в данное сечение магистральные трещины частично
захватываются разгруженными зонами и останавливаются. При этом скорость
выбывания МТ определяется как накопленной поврежденностью о;, так и изви-
извилистостью контура Y подходящих магистральных трещин. С увеличением изви-
извилистости скорость выбывания первичных трещин возрастает. После выбывания
МТ первичного семейства происходит компенсационный процесс формирования
вторичных трещин, генетически и морфологически отличающихся от первичных.
Система уравнений, описывающих конкурентное взаимодействие пришедших в
данное сечение п магистральных трещин первичного семейства, п вновь возник-
возникших «компенсационных» трещин и диффузной поврежденности ш имеет вид:
D —
Со
dn ts
— = К
dt
<- -
(п0 - п
dn
1 - ехр <	——-Y > ) ; — =
\	у ш*(пв) ) ) at
где c'R — скорость волны Релея с учетом поврежденности; п$ = п + п — общее
число окружных трещин; uq — начальное число первичных МТ; еш — критическая

106	16. Осколочное действие взрывных систем
тангенциальная деформация
Параметры, входящие в систему, молено определить по соотношениям:
* / ч	Г
, (ne)=exp|
Начальные условия имеют вид: zc(ts) = 0; ш (ts) = о;7; n (ts) = пс;
n(ie)=0; У(*в) = 1.
Полученные в результате интегрирования системы законы изменения n(z),
n(z), о; (z), У (z) и их производных позволяют прогнозировать изменение
спектра по длине цилиндра, т.е. определять параметры \±а (z) , itia(z) тпв (z).
Наряду с указанными величинами можно вычислить средние показатели для
всего цилиндра:
Lo	Lq	Lq
= I. [ щ (Z) dz. {ш) = J_ f ш {z)dz, (у) = -1 f Y (z)dz,
^0 J	b0 J	\ /	Lq J
а в зависимости от них — параметры то, т^, а, /3, ? гипервейбулловского
бимодального спектра.
В зависимости от скорости выбывания первичных трещин может быть реали-
реализован один из трех режимов (рис. 16.49):
1)	деление цилиндра целиком на «полосы», т.е. осколки с длиной, равной длине
цилиндра Lq, n(z) = const = uq. Важным показателем процесса является
условие dn/dt = 0, что обеспечивает реализацию строго прямолинейных
трещин.
2)	частичное образование «полос», п > п (Lq) > 0. Основной показатель
процесса — относительная сохранность vl = п (Lq) /uq первичных трещин
в момент выхода «решетчатого» фронта трещин на задний торец цилиндра.
3)	отсутствие «полос» в спектре. В этом случае трещины первичного семейства
полностью выбывают в некотором сечении z* = z.
Величина z*, определяющая максимальную длину
лю|\^^	1	1	первичного осколка, также является важной харак-
характеристикой процесса дробления. Для выявления ее
щ(?0) истинного значения, очевидно, должно выполняться
условие Lq ^ z*, откуда при 5а = 1/8... 1/6, da = 40 мм
и 50 < Fq < 150 получим следующее условие для
удлинения камеры цилиндра:
Рис. 16.49. Режимы разру-
разрушения цилиндра
= 3,7... 3,9.
Результаты численного интегрирования системы уравнения представлены на
рис. 16.50 Ed = 1/6, Ао = 4, а0 = 20 мм, г0 = 25 мм, сталь 20/ТНТ, р0 = 1550кг/м3,
D = 6700м/с, G = 81ГПа, Es = 1400кДж/м2, Fo=29, nc = 25, 7о=785Окг/м3,

16.3. Основные соотношения при дроблении оболочек
107
0,30
0,20
0,10
о
у
/
/
/
/
А
/
щ> щ, щ
1,20 20
1,10
1,00 о
<
N
/
>
/
/
/
\
О 40 80 120 2, мм о 40 80 120 «, мм
а)	б)
Рис. 16.50. Изменение характеристик по длине цилиндра: характеристики разрушения (а);
число трещин (б).
/3=0,158, ^о=9О6 м/с, CR = 2970 м/с, ?0=5mkc, ts = 4мкс, еш = 0,3, В0 = Змкс"\
knl = 20 мкс, кП2 = 5 мкс, кг = Imkc, v = 1, ujs = 0,1).
Средние значения величин по длине цилиндра по длине составили:
= 27,
= 0,027, (У) = 1,16.
Для данной комбинации цилиндр №12 — ст.20/ТНТ прогнозируется режим 2
(частичное образование «полос», vl « 0,1). Этот прогноз подтверждается нали-
наличием в экспериментальных спектрах одиночных «полос» с длиной 120. ..140 мм.
Экспериментальное измерение числа окружных делений методами выкладки и
высокоскоростной оптической съемки составило по = 28.
16.3. Основные соотношения при дроблении оболочек
1. Масштабный эффект при разрушении и осколкообразовании. Ана-
Анализ размерностей. Масштабному эффекту (МЭ) при разрушении тел, т.е.
влиянию размеров тела на прочность и предельную пластичность как в случае
статического, так и динамического нагружения, посвящено большое число работ
(см., например, обзор [16.31]). В теории осколочных оболочек наибольший интерес
представляет влияние характеристического размера оболочки на характеристики
спектра. Хотя теория МЭ такого типа в принципе может быть построена на основе
тех же физических идей, этот эффект практически не изучен и не учитывается в
подавляющем большинстве расчетных зависимостей для спектров.
Существует два основных взгляда на природу масштабного эффекта. Согласно
первому из них МЭ имеет физическую природу, а его формальное описание может
быть проведено на уровне изотропной среды и не требует введения характеристик
распределения дефектов в материале. Имеется несколько физических концепций
МЭ, главными из которых являются энергетическая и деформационно-скоростная.
Согласно второму взгляду, масштабный эффект имеет статистическую природу
и связан с понятием «опасный дефект материала». Чем больше объем объекта
(в данном случае оболочки), тем больше вероятность появления более опасного
дефекта, приводящего к локальному разрушению объекта.

108	16. Осколочное действие взрывных систем
Энергетическая концепция масштабного эффекта при разрушении впервые
была введена в работах Н. Н. Давиденкова. Масштабный эффект вытекает непо-
непосредственно из баланса запаса упругой энергии в теле и энергии, затрачиваемой на
разрушение. Запасенная упругая энергия Ее и затрачиваемая энергия разрушения
Df определяются соотношениями:
Ee~^f, Df~L2Es
L — характерный размер тела; а — действующее напряжение; Es — удельная
энергия разрушения [Дж/м2], Е — модуль Юнга.
Из условия Ee=Df получаем:
т-3 2 тр — 1 г 2 тр
откуда разрушающее напряжение:
af ~ (ESEI/2 -^	A6.20)
Аналогичным образом баланс энергии может быть использован и для оценки числа
осколков N. Если принять обычное положение линейной механики разрушения,
что разрушение происходит за счет запаса упругой энергии в теле и учитывая, что
в момент разрушения оболочка находится в состоянии общей текучести, получим:
dlYE'1 ~ SfvEa	A6.21)
SfY, — суммарная площадь поверхности разрушения, do — диаметр цилиндра.
Предполагая, что оболочка разрушается на Ne одинаковых осколков, имеем:
где А = 1,1/2 и 1/3 соответственно в случае линейного разрушения кольца,
плоского разрушения оболочки и объемного разрушения.
Из A6.21) получаем Ne ~ dj , откуда в случае кольца Ne ~ d0, (N = щ),
в случае плоского разрушения Ne ~ d^ в случае пространственного разрушения
Ne - dl (N = nenLn6).
Введем зависимость динамического предела текучести от скорости танген-
тангенциальной деформации, например, в виде Y = Bsq. Так как ее ~ ^o/^(h т0
Y = В (vo/do)n и, следовательно, Ed%~n ~ d%N*.
1 /9
Принимая п = 1/2, получаем в случае кольца Ne ~ d0' (Ne = n^), в случае
плоского разрушения Ne ~ c/q, в случае пространственного разрушения Ne ~ <i0
(Ne =
Недостаток изложенной концепции заключается в том, что реальный запас
упругой энергии Ее мал по сравнению с энергией Df образования поверхности
разрушения. Для цилиндрической оболочки объем определяется соотношением:
Уц = тг (Ь% - al) L,
а суммарная поверхность разрушения при разделении на N продольных осколков
выражением:
S/e = (Ьо - «о) L?XN,

16.3. Дробление оболочек	109
где ?х ^ 1 — коэффициент, зависящий от ориентации плоскости разрушения. При
радиальном разрушении ?х = 1, при сдвиговом разрушении приближенно молено
принять ?х = 1,4.
Из баланса энергии Ее = V4A = Df = E$Sfz, получаем
_ Afirdp A -
где Af — удельная упругая энергия в момент разрушения. В качестве оценки
примем Af = Y2 /2E.
При динамическом пределе текучести У=1ГПа (= 100кг/мм2), Е = 200ГПа,
Af = 0,25 • 105 Па. При радиальном хрупкоотрывном разрушении можно принять
?х = 1, Es = Сю = Ю5КДж/м2. Принимая также d0 = 53,3 • 10~3 м, 5d = 1/8
(стандартный цилиндр № 11), получим Ne = 0,036, т.е. разделение оболочки только
за счет запасенной в ней упругой энергии невозможно.
Из изложенного следует, что при построении баланса необходимо включать в
располагаемый запас энергии также некоторую часть rjwW кинетической энергии
оболочки W = Mvq/2. В этом случае, пренебрегая запасом упругой энергии,
получим
Если предполож:ить, что величина rjw H^ зависит от геометрических харак-
характеристик оболочки, то приходим к уже известному виду: Ne ~ do. Принимая
rjw = 0,005 для рассмотренных выше условий (при vq = 1000 м/с, 7о = 7850 кг/м3),
получим Ne = 30.
Деформационно-скоростная концепция МЭ исходит из положения, что кри-
критическое значение деформации возрастает с увеличением скорости деформации.
А. Г. Иванов [16.32] получил для вязкопластичных тел, описываемых реологиче-
реологическим соотношением Шведова-Бингана
а = сг0 + rje,
(его — статическое значение предела текучести, rj — динамическая вязкость)
следующую зависимость ef = / (е):
\^e2ef {sf + 2) + е B/х^ - а) + In {ef + 1) = 0, /i = ^-, а =
Z	его
При ?/ < 1 выражение упрощается
ёа
т.е. деформация разрушения достигает максимума a/4/i при ё = /i, а затем
уменьшается. В случае мягких сталей (rj = 2,5 • 103 кг- с/м2 = 2,5 • 104 Па-с,
его = 25кГ/мм2 = 25 • 107 Па) функция имеет максимум при ё = 104 1/с. Этот
теоретический вывод подтвержден результатами экспериментов по взрывному
разрушению труб.

110	16. Осколочное действие взрывных систем
Реологическая зависимость ?f = / (ё) может быть описана либо линейной
функцией
где еЩ — предельная статическая тангенциальная деформация; КТ — некоторый
коэффициент (зависящий от пластичности материала), либо степенной
л -2/3
ев/ = А2ев'
Принимая выражение для средней скорости тангенциальных деформаций в виде
ев = Wro> получим:
В общем случае ев/ = А^, (п < 1) имеем:
ne=2J^lr^ f = A3(^\ .	A6.24)
В данном выралсении масштабный эффект учитывается за счет снижения
показателя при vq. Так как по экспериментальным данным этот показатель A — п)
близок к единице, то отсюда п <С 1.
Оценка МЭ может быть получена также непосредственно из анализа размерно-
размерностей. Рассмотрим разрушение цилиндрической оболочки с размерами ао, So, Lo.
В процессе взрыва образуется осколочный спектр с некоторой характеристической
массой тпс. Эта масса является некоторой функцией геометрических характери-
характеристик ао, #о, Lo, свойств ВВ po,D и металла 7(b G, Е$'.
mc = f (а0, So, Lo, p0, D, 7o, G, Д5).	A6.25)
Это уравнение связывает п = 9 размерных параметров. Согласно тг-теореме, оно
может быть заменено уравнением, связывающим п — к безразмерных величин (к —
число независимых размерностей, в данном случае к = 3, т.е. п — к = 6). Пять из
них могут быть указаны сразу: относительная масса характеристического осколка
т^с/то^о? относительная толщина стенки 5о/2 (ао + #о), относительная длина каме-
камеры Lo/2ao, отношение плотностей ро/7о и общепринятый в динамических задачах
2
Для определения последнего параметра, включающего величину Д^> проведем
формальный анализ размерностей. Запишем в общем виде:
es,	A6.26)
где dim р0 = ML~3; dim D = LT~X\ dim a0 = L\ dim as = ML~1T~2; dim
Es = MT~2
Для безразмерной величины:
dimFo = M°Lor°,

16.3. Дробление оболочек	111
откуда получаем:
dimFo = (МЬ~3)а (Lf (LT-1I (ML^T'2N (MT~2)? =
^a+/3+??-3a+/3+7-<^-7-2?-2e Qg 27)
что приводит к системе уравнений:
а + /3 + ? = 0, -За +C + ^-5 = 0, 7 + 25 + 2е = 0.	A6.28)
Из 1-го и 3-го уравнений сразу находим 7 = 2а. Это указывает на появление в
параметре Fq комбинации (ро-^2) • Принимая а = 1 G = 2), получим
е = -/3, 5 = 13-1.	A6.29)
Из физических соображений очевидно, что е ^ О, откуда /3^0. Система A6.29)
позволяет получить произвольное множество безразмерных комбинаций вида:
Fo = PoD244E%.
Например, при /5 = 0, ? = О, S = — 1 получаем параметр Fq в виде F' = poD2/as-
При /3 = 1, ? = —1, 5 = 0 параметр Fq приобретает вид F" = poD2cio/Es. При
/5 > 1 получаем параметр Fq в виде, соответствующем энергетической концепции
Давиденкова-Иванова (см. выше), согласно которой показатели при величинах Es
и G имеют разные знаки. Например, при C = 3/2, е = —3/2, S = 1/2, получаем
Из изложенного очевидно, что для замыкания системы уравнений необходимо
привлечение некоторых дополнительных соображений. Возвращаясь с этой целью
к уравнению A6.25) заметим, что величину тс можно трактовать и как массу
квазирегулярного осколка, получаемого делением оболочки на п$ продольных
полос. Используем для по градиентное соотношение:
A6.30)
vcr
где vcr — некоторая величина, являющаяся параметром металла и имеющая
размерность скорости. Выражения для vcr будем искать в виде:
Проводя построения, аналогичные вышеприведенным, а также учитывая экспери-
экспериментальное соотношение uq ~ A/ао) (см. ниже), получим v = —1/2, fi = —1/2,
Л = 1/4, х = 1/4, т.е.
л
A6.31)
7о «о'~

112	16. Осколочное действие взрывных систем
Начальная скорость оболочки vq определяется известным соотношением:
которое в диапазоне C = 0,15... 0,30 может быть с хорошей точностью (до 2%)
аппроксимировано выражением:
Учитывая, что /3 = С/М1 = (ро/то) (Хо/ О- ~ Хо)) (гДе Хо = 1 - 25d = ао/Ьо),
получим:
_ D
0 3
Подставляя A6.31), A6.32) в A6.30), получаем:
,Г>2пУ2
A6.33)
Таким образом, при заданных пропорциях оболочки, число окружных делений
единственным образом определяется безразмерной комбинацией pqD2uq /Es G1'2.
Ее показатели полностью удовлетворяют системе уравнений A6.28). Отождеств-
Отождествляя эту комбинацию с величиной F, получаем а = 1, C = 1/2, 7 = 2,5 = —1/2,
е = —1/2 и, следовательно,
F0 = ^^.	A6.34)
Для 64 =1/8 и 1/6 значения \о составляют соответственно 0,75 и 0,667, отсюда
получаем
*	2'37
п
при о
1	1^87 ^-	A6.35)
при 5d = - щ =	^~
6 ""' Со v u
Коэффициент Со в диапазоне 5d = 0,1... 0,2 равен 0,41. При Sj = 1/6 (стандартный
осколочный цилиндр №12) получаем по = 4,6\/?о. Из A6.33) следует:
TlQ ^ Uq , Z/ = U,ZO,
т.е. МЭ при окружном делении на основные осколки является слабым. Полученное
значение v близко к величине v = 1/3, полученной в теоретической работе
А. Е. Колобановой [16.33] в предположении, что разрушение цилиндра начина-
начинается при относительно малых деформациях, а заканчивается при относительно
больших деформациях.

16.3. Дробление оболочек	113
2. Радиус разрушения оболочки. По Тейлору (см. п. 16.2. .1) разрушение
сплошной оболочки происходит в тот момент, когда внешняя зона распространя-
распространяется на всю толщину оболочки. Радиус разрушения af определяется выражени-
выражением A6.11):
/Ро\1/2*
af = ао [у)
Относительный внешний радиус bf = bf/bo в этот момент определится как:
1 . -I	ао	а/
g + I, Xo = Vq, af = -.
В указанном выводе неявно предполагается, что разрушение оболочки происходит
в растянутой зоне путем хрупкого отрыва.
Для сферической оболочки:
af — ^u у у j
В работе Хоггата и Рехта (см. [16.1]) предложена более сложная модель разруше-
разрушения. Предполагается, что одновременно с процессами хрупкого отрыва может идти
разрушение путем сдвига по площадкам скольжения во внутренней сжатой зоне,
и к моменту прихода границы зон материал уже разрушен по этим площадкам.
Однако фактическое разрушение оболочки (разделение на осколки) произойдет
позднее, когда нормальные напряжения в площадке скольжения станут равными
нулю. Это соответствует напряженному состоянию чистого сдвига.
ав = ~(тг, az = 0, а = - (аг + (те + (tz) = 0.
о
В расчетах учитывалось наличие в оболочке упругой зоны. В этом случае относи-
относительный радиус разрушения получается примерно на 3,5% меньше, чем по соот-
соотношению Тейлора. Для случая жесткой л астической оболочки радиус разрушения
определится выражением:
1/2к
а = ао -г—
/	^ Y
При фиксированных значениях величины po/Y и к = 3 отношение а%/df = 1,12.
В работе Аль-Хассани и Джонсона (см. [16.1]) излагается теория разрушения
на осколки упрочняющейся, чувствительной к влиянию скоростей деформаций
оболочки. Условие пластичности принято в виде:
где 5, n, m — константы материала.
Условие полного разрушения выведено на основе следующего допущения: рас-
распространение радиальной трещины сквозь стенку оболочки может происходить
тогда, когда окружное напряжение в зоне, расположенной впереди кончика трещи-
трещины, превышает некоторую долю от предела прочности на растяжение материала
сПр- Это приводит к следующему условию распространения разрушения:
ав ^ каир 0 ^ к < 1.

114	16. Осколочное действие взрывных систем
Выражение для радиуса разрушения приобретает вид:
l/2fc
I	РО	\
CLf = UQ
В случае к = 0 имеет место формула Тейлора.
В результате преобразований получают соотношение для радиуса разрушения
в виде:
1/2к
а0
С уменьшением радиуса оболочки и, следовательно, с увеличением скорости де-
деформации, относительный радиус разрушения возрастает. Аналогичным образом
влияет увеличение скорости метания оболочки.
Недостатком всех вышеуказанных соотношений является то, что в них не
учитываются пластические свойства материалов, характеризуемые предельным
относительным удлинением 5$, 5ю, сужением ф, вязкостью разрушения Kjq-, удар-
ударной вязкостью KCU, KCV, КСТ и т.д.
Простое соотношение для относительного радиуса разрушения может быть
получено с использованием критерия предельного относительного сужения [16.2].
Относительное сужение меридионального сечения оболочки в момент разрушения:
= Fp - Ff = (ftp - а0) - (bf - af)
Fo	b0 - a0
Учитывая условие несжимаемости Щ — aj = 6q — а§, исключая из уравнения af и
учитывая, что (bo — ao)/2bo = 5d получаем:
h = i + ^^ (i - 5d B - ф))
В случае тонкой оболочки (Sd —> 0): bf = 1/ A — ф).
Величина относительного суж:ения оболочки при динамическом разрушении в
общем случае не равна значению ф, полученному при статическом разрыве, вслед-
вследствие различного характера напряженно-деформированного состояния образцов в
момент разрыва. Однако даже допущение о примерном равенстве этих величин
дает неплохое совпадение с экспериментом. Например, расчетные значения bf для
стали 45Х, стали 35, Армко и меди Ml (ф соответственно 0,30; 0,45; 0,60; 0,70)
составляют 1,43; 1,82; 2,50 и 3,30, что близко к экспериментальным значениям этих
радиусов, приведенных в табл. 16.1.
В работе А. Г. Иванова (см. [16.1]) приведена следующая оценка влияния
масштабного фактора на радиус разрушения. Оболочка длиной Lo, радиусом Ro
и толщиной 5о имеет запас упругой энергии:
Ei rsj ?1R05qL0,
где Е\ — запас упругой энергии в единице объема оболочки.

16.3. Дробление оболочек	115
Для разрушения оболочки необходима энергия:
где Е\ — энергия разрушения на единицу поверхности материала.
Из равенства Ei=E2 с учетом RoSo = RS вытекает:
Rf s2 I
Rq Si Rq
т.е. радиус разрушения обратно пропорционален начальному радиусу оболочки.
Эта зависимость качественно подтверждена результатами эксперимента.
В работе В. В. Селиванова приведена простая оценка радиуса разрушения
оболочки при следующих допущениях:
1)	распространение фронта разрушения начинается от внешней поверхности
оболочки, а его положение определяется границей раздела между сжимаю-
сжимающими и растягивающими тангенциальными напряжениями (сг#=О) по зависи-
зависимости Тэйлора у = SY/р, где у — толщина растянутой зоны, отсчитываемая
от внешней поверхности оболочки, 5 — текущая толщина оболочки; Y —
динамический предел текучести материала оболочки; р = ро(ао/аJк —
текущее давление на внутренней поверхности оболочки; pq = pqD2 /B(к-\-1))
— давление мгновенной детонации; р$ — плотность ВВ; D — скорость
детонации; к — показатель изэнтропы;
2)	разгрузке подвергается только растянутая зона, расходующая запасенную
энергию на разрушение (считается, что развитие разрушения есть распро-
распространение трещин отрыва), а величина энергии, запасенной в объеме растя-
растянутой зоны, равна величине Еу = AeyryL^^ где А = const; ey ~ Y2/Е —
удельная объемная энергия в растянутой зоне; Е — модуль Юнга; R = BЪ —
у)/2 — средний радиус зоны растяжения; Lq — длина заряда ВВ;
3)	вся запасенная в объеме энергия затрачивается на образование поверхностей
отрывного разрушения, т е. Еу = Es, где Е$ = BssSLq — энергия обра-
образования новых поверхностей; ss — энергия, затрачиваемая на образование
единичной площади свободной поверхности (ее можно считать равной какой-
либо из характеристик разрушения материала, например, KCU, Gic, Jjc и
т.д.); В = const.
При выполнении этих условий можно путем элементарных алгебраических преоб-
преобразований прийти к зависимости:
Обработка результатов экспериментов позволила привести полученную аналити-
аналитически пропорциональность к конечному соотношению:
b-L « 0,0019
b
« 0,0019 (YV
bo	\ а0 J
KCU [кДж/м2], ао[мм]; ро[кг/м3]; D [м/с]. Средняя погрешность полученной за-
зависимости составляет 11%, а максимальное отклонение от экспериментальных
значений не превышает 20% при максимальной погрешности измерений ~ 15%.

116	16. Осколочное действие взрывных систем
3. Соотношения для характеристик дробления оболочки. Число
окружных делений.
Указанные соотношения могут быть разделены на три основные группы, опре-
определяющие в зависимости от сочетания «металл-ВВ-геометрия» (М-В-Г) следую-
следующие характеристики:
1)	число основных окружных делений оболочки или кольца щ,
2)	общее число осколков с массой, превышающей некоторую величину ms,
3)	параметры статистического распределения осколков по массе.
Соотношения для числа щ.
В ранних отечественных работах конца 40-х — начала 50-х годов выражение
для числа по принималось в виде
щ = —,	A6.36)
ас
где ас — центральный угол осколка, являющийся функцией М—В—Г.
Наиболее простая формула для величины ас была предложена К. П. Станюко-
Станюковичем. Он предположил, что ширина осколка по внутренней поверхности оболочки
равна толщине оболочки. Отсюда:
#о	2тга0	, Л
ас = —, по = —z—	A6.37)
Число продольных осколков, таким образом, не зависит от свойств металла и ВВ.
Эту формулу можно представить в виде:
пв = тг (j - 2\	A6.38)
При значениях 5^ = 1/12, 1/10, 1/8, 1/6 число щ, округленное до целых значений,
составляет соответственно 31, 25, 19 и 13.
Г. И. Покровский для определения числа ас ввел формулу
ас = —.	A6.39)
Величина критической скорости определяется соотношением [16.34]
Vcr = C()—	A6.40)
Г. И. Покровский вкладывал другой смысл в понятие критической скорости, чем
обычно, а именно он принимал, что это наименьшая разность скоростей на концах
стержня, достаточная для его разрыва. При этом естественно получались более
низкие значения vcr. Например, для стали среднего качества с ав = 0,5 ГПа при
Е = 200 ГПа и со=6ОООм/с получим vcr = 15 м/с.
В 1949 году В. А. Кузнецовым было предложено при расчете числа продольных
осколков цилиндрической оболочки величину угла ас определять по формуле:

16.3. Дробление оболочек	117
A6.41)
где cl\ — внутренний радиус оболочки в момент начала потери сплошности,
определяемый по формуле:
а1=а0
где Ъ\ — наружный радиус оболочки в момент начала потери сплошности оболоч-
оболочкой; ф — относительное сужение в момент разрыва; /с* — показатель политропы
ПД в момент начала потери сплошности оболочкой;
К = 4,lV/^e-°'702cj + 1,15,
где /сд — коэффициент, учитывающий динамический характер деформации мате-
материала оболочки, принятый равным 1,6.
Формула для определения показателя политропы к* получена опытным путем
на основании обработки экспериментальных данных по дроблению цилиндриче-
цилиндрических оболочек при взрыве.
Наиболее широкое распространение для оценки щ получил градиентный метод,
основанный на представлении о существовании некоторой критической векторной
разности скоростей на концах осколка. Например, в соответствии с [16.35] имеем
vcr
f = r0 —,	A6.42)
Vcr	Щ
где го — средний радиус оболочки; vcr — критическая разница скоростей на концах
фрагмента
Vcr =
О
Величина vcr в данном случае отождествляется с критической скоростью растя-
растягивающего удара, при которой разрушение происходит на нагружаемом конце
стержня (у подвижного захвата). Для сталей значения vcr по данным [16.35]
составляет 30.. .150 м/с.
Изложенное представление имеет ряд существенных недостатков:
1)	используются величины начального радиуса оболочки и конечной скорости,
т.е. схема мгновенного ускорения оболочки;
2)	перенос в данную схему понятия критической скорости г>сг, заимствован-
заимствованного из терминологии ударных разрывных испытаний стержней, является

118	16. Осколочное действие взрывных систем
искусственным. Нагружение стержня при разрывных испытаниях осуществ-
осуществляется волновым механизмом, деформации в пластической волне распреде-
распределяются неравномерно и разрушение осуществляется разрывом. В кольцах
и оболочках нагружение осуществляется высокоскоростным «безволновым»
механизмом с равномерной деформацией, а разрушение является сложным
процессом — комбинацией разрыва во внешней зоне со сдвигом во внутрен-
внутренней зоне оболочки. Формальное использование понятия vcr в данной схеме
обсуждалось в [16.36].
Для линейно упрочняющегося тела (da/ds = const) имеем:
?f
и, следовательно:
щ = ^ f = cro?-l.	A6.43)
C?f	Vq
О. Е. Власовым [16.37] получена другая формула, позволяющая определить
число фрагментов щ, на которое разрушится кольцо:
по пв
где Vf = ^2Af /70; Af — критическое значение удельной энергии деформации на
единицу объема.
Формулу A6.44) можно представить в явном виде относительно числа осколков
или ширины осколка. С этой целью проведем разложение в ряд, ограничиваясь
двумя членами
sin (тг/пр) ^ _ (тг/пр)
7Г/Щ	6
х 2\ V2
где Т = (vf/vji) — относительная потерянная энергия на деформацию осколка.
Подставляя вышеприведенные аппроксимации в A6.44), получаем:
7Г
по =
Принимая Af = f didsi = Yef, получаем
о
щ = ->=Д==	A6.45)
A6.46)

16.3. Дробление оболочек	119
В работе Мотта [16.38], которая в зарубежной литературе считается основопола-
основополагающей, выводится следующее выражение для средней ширины осколка:
2rj.	A6.47)
где К\ — экспериментальная константа; Pf — предел текучести; Sf — предельное
сужение в момент разрыва кольца; P<i — величина, имеющая размерность напря-
напряжения и соответствующая модулю упрочнения.
Формулы A6.42) и A6.47) по своему виду близки друг к другу, хотя они
получены из принципиально различных представлений об определяющих фак-
факторах разрушения. По Мотту этим фактором является полная деформация 6/,
т.е. разрушение наступает после исчерпания пластичности. Авторы [16.39] с более
общих позиций, используя постулат Друккера, показали, что любой критерий раз-
разрушения при импульсивной нагрузке необходимо основывать на скорости дефор-
деформаций, а не на общей деформации, как это предлагалось Моттом. Это утверждение
подвергнуто сомнению в работе [16.40].
В работе В. М. Кузнецова [16.41], посвященной разрушению идеально-пластиче-
идеально-пластических несжимаемых металлических колец вкладными зарядами ВВ, вводится пред-
представление о фронте разрушения, несущем некоторую предельную деформацию е*
и распространяющемся с внутренней поверхности. Для оценки времени разруше-
разрушения тонкого кольца предлагается формула:
,, * 2*°ShD	A6.48)
Ширина осколка определяется из соотношения:
f- S tf,	A6.49)
где с — скорость разгрузки, которая принимается равной «стержневой» скорости
звука со
из A6.48) и A6.49) следует:
/ <* m^ri.	A6.50)
Нетрудно видеть, что все рассмотренные выше формулы для средней ширины
осколка A6.42, 16.46, 16.47, 16.50) имеют одну и ту же структуру
где L — некоторый характерный линейный размер кольца; (в соотношениях A6.42,
16.46, 16.47) L = го, в соотношении A6.50) L = So), cc — некоторая характерная
величина скорости или характеристическая величина, имеющая размерность ско-
скорости.

120	16. Осколочное действие взрывных систем
Отметим еще, что соотношение / = г о (vcr/vo) представим в другой форме,
введя понятие о градиенте тангенциальных скоростей Gq (м/с • 1/м) = vo/ro = ее-
В этом случае:
f _Усг _ Усг
1 " Go " ев '
Г. В. Степанов [16.42, 16.43], используя соотношение, описывающее вероятность
разрушения р в зависимости от величины деформации е в виде:
dp
—
as
получил следующую формулу для числа
(e\
пе = 0,624-	 L°g	^ 1,96^-,	A6.51)
2cc(l + LA/B)	coc
где Lq — длина окруж:ности кольца; ё — скорость деформации; Со — скорость
звука; В — расстояние между очагами разрушения по окружности;
Общим недостатком формул A6.37, 16.39, 16.41, 16.42, 16.44, 16.47, 16.50)
является неучет масштабного эффекта, т.е. для геометрически подобных оболочек
с одинаковым металлом и ВВ предсказывается п$ = const.
В последние годы теоретически разработан ряд зависимостей для определе-
определения по с учетом МЭ. В работе А. Г. Иванова с сотрудниками [16.44] (смотри
также [16.45]-[16.47]) для определения числа п$ используется подход, близкий
к [16.41]. Рассматривается расширяющееся с постоянной радиальной скоростью
vq кольца. Принимается, что разрушение происходит за счет упругой энергии при
sp <С 1, материал кольца вязкопластический а = ао + rjs (а, ао — соответственно
динамический и статический пределы текучести. Согласно [16.32] деформация при
разрушении:
ёа
Предполагается, что развитие трещин по толщине стенки заканчивается на пути
от го до г, т.е. ?р = (г — го) /го = vot/ro и что дробление кольца завершится к
моменту времени t, откуда, с учетом ё = vo/r = vo /((I + ер) г о) получается:
п = (	 ) (г0	f
или, при:
г)	4ЕХ
—, а =
СГ0
Зависимость указывает на наличие МЭ и имеет минимум при г =
При го = const зависимость имеет вид квадратичной параболы.

16.3. Дробление оболочек
121
Еще более сильный МЭ предсказывается формулой, полученной А. Г. Ивано-
Ивановым и В. Н. Минеевым [16.31]
пв =
ЕЕ,
A6.53)
В работе [16.48] с помощью оптической съемки определялось число п$ при раз-
разрушении открытых цилиндрических оболочек со следующими характеристиками
Lo=127 мм, da = 50,8 мм, Ло = 2,5, относительная толщина стенки в основном
варианте Sd = 1/Ю, изготовленных из пяти различных сталей и снаряженных
ТНТ, баратолом, составами В и 9404, октолом. Показано, что достаточно точно
выполняется зависимость
= пво +
Таблица 16.17
Значения констант
Сталь
52100 С
52100 СВА
PR-2
HF-1
ВЕАРСАТ
Мв,
с/км
49,6
52,4
46,8
79,9
49,2
Пво
4,42
9,86
2,74
7,8
7,39
Коэффициент
корреляции
0,978
0,944
0,960
0,985
0,967
Vcr,
м/с
127
120
134
78,6
128
где v0 =[км/с]
Значения констант приве-
приведены в табл. 16.17.
Пренебрегая в первом при-
приближении свободным членом
пв0 получим значения крити-
критической скорости vcr = 2тг/Mq.
Эти значения приведены в
последнем столбце таблицы.
Аналогичные измерения п#0
проводились в работе [16.40].
Эти опыты проводились на
коротких открытых цилин-
цилиндрах (б/а=38,1 мм, с/о=42,672 мм,
So =2,286 мм, L0=25,4mm, 5j
=0,0536,
Aq=0,667, Лц=0,595) для четырех сталей. Результаты нашей обработки этих
опытов представлены в табл. 16.18. Приводятся также экспериментальные зави-
зависимости Nq = f(vo). Соответствующее перестроение показывает, что зависимость
Nq = f(n$) удовлетворительно аппроксимируется формулой Nq = Сщ .
В случае сферической оболочки постоянной толщины число квазирегулярных
осколков может быть определено соотношением:
Nq = П3П6,
где ns — число площадок деления на поверхности оболочки.
В случае сферы для
Таблица 16.18 произвольного числа ns тео-
Параметр Мо и критическая скорость для	ретически нельзя получить
различных материалов	одинаковые по конфигура-
ции осколки. Как известно,
максимальное число гра-
граней для правильного вы-
выпуклого многогранника со-
составляет 20 (икосаэдр).
Сталь
Мо, с/км
Vcr, м/с
0,07%С
(А)
36,1
174
0,98%С
1,4% Сг (В)
153,0
41,1
А л. сплав
2024 (С)
55,1
114
А л. сплав
7075 (D)
73,3
85,7

122	16. Осколочное действие взрывных систем
Выражение для числа
ns можно получить, ис-
используя концепцию критической скорости. В этом случае ширина осколка, изме-
измеряемая вдоль дуги большого круга
vcr 2тгЬ0
f = %— =	•
^о по
Величина площадки SB на внешней поверхности и число площадок ns определя-
определяется соотношениями:
2	, (vo\2 п2в
j
При центральном инициировании сферического заряда ВВ, или близком к
нему, реализуется нормальное падение расходящейся детонационной волны на
оболочку, что приводит к появлению растягивающих напряжений большой ам-
амплитуды и, как следствие, к развитию частичного или полного откола (щ = 2).
Наличие откола = на 50% поверхности оболочки было показано для сферических
оболочек из стали 50Л, изготовленных литьем в металлическую форму с после-
последующим отпуском при t = 650 С в течение 1,5 часов и охлаждением на воздухе.
4. Соотношения для общего числа осколков. Эти соотношения в основ-
основном являются эмпирическими. Широко известна формула Юстрова для опреде-
определения общего числа осколков массой более 1 г.
Л^/Зо^Ц^,	A6.54)
где /3q — коэффициент, зависящий от свойств ВВ (для ТНТ C$ = 46); С —
масса заряда ВВ, г; do — калибр оболочки, см; ае — предел упругости метал-
металла, кгс/мм2; ав — временное сопротивление металла разрыву, кгс/мм2; 5± —
относительное удлинение при разрыве, % ; % — коэффициент, зависящий от
конструкции оболочки и равны для оболочек с коэффициентами наполнения 7, 10
и 15% соответственно 1,8, 1,5 и 1,4.
Близкий к формуле Юстрова вид имеет формула Юловского (АНИИ)
Nlfi=0o^^=	A6.55)
^ 0"
где В = /(V7) — коэффициент, характеризующий свойства металла; ф — относи-
относительное сужение металла оболочки;
И. В. Долининым предложена формула для числа осколков iV"o.5, разработанная
применительно к артиллерийским снарядам калибра 76—152 мм с тротиловым
снаряжением
Щ,5 = dJ.ei9+D.-™)/iooo>	A6.56)
где do — калибр, мм.
В. А. Кузнецов и Р. С. Саркисян [16.49] предложили использовать для опреде-
определения полного числа осколков статистическое соотношение:

16.3. Дробление оболочек
123
где Мо — масса оболочки; (т) — математическое ожидание массы осколка.
Последняя величина определяется в предположении о том, что распределение
осколков по массе есть C — распределение с известными параметрами, с помощью
соотношения:
(т) = 0,0609ттаж
A6.58)
Максимальная масса осколка тшах определяется с помощью введенной модели
разрушения (см. п. 16.1. .2) соотношением:
ттах =
а/2166V
¦а/4 )
Т(ан)
A6.59)
2A-^2)
3-i/
а —
Ро D2
7о сеср
^°	rji /ОП -0,3 1П\
= -	, Т=129ая' -101 ,
Ln сР	V	/
где х ~ коэффициент, зависящий от конструкции оболочки (для оболочки с
закрытыми торцами х — 0,2); v — коэффициент Пуассона; се, ср — соответственно
скорость распространения упругих и пластических деформаций в металле оболоч-
оболочки; ан — ударная вязкость металла оболочки (кгс м/см ).
В. А. Одинцовым предложена формула для числа осколков с массой более
0,5г [16.3].
jVo,5 = K^-dlD2,	A6.60)
где К — коэффициент, зависящий от геометрии оболочки (для ОФС к = 70 ... 100);
а, ф — коэффициент наполнения и относительное сужение материала оболочки
(оба в долях единицы или в процентах); do - внешний диаметр оболочки (калибр),
дм; D — скорость детонации заряда ВВ, км/с.
Все указанные форму-
Таблица 16.19
Числа эффективных осколков по различным
формулам.
лы за исключением соотно-
соотношения A6.56) могут быть
представлены в виде:
кг(Д)
iN0,5
N(o)
iN0,5
N@) / дт(Д)
iN0,5/ iN0,5
Калибр do, мм.
85
1383
1420
1,03
100
1968
2000
1,02
122
2977
2980
1,00
125
3145
3120
0,99
130
3440
3380
0,98
152
4747
4620
0,97
Ns = %,
где А — коэффициент, за-
зависящий от пропорций сна-
снаряда, свойств металла и
ВВ; п = 2 во всех со-
соотношениях, кроме форму-
формулы A6.57).
На величину показателя п оказывает влияние как физический масштабный
эффект, так и «кажущийся» масштабный эффект, проистекающий из-за незави-
независимости границ сбора ms от величины калибра.
Эмпирическая формула И. В. Долинина A6.56) дает зависимость, близкую к
степенной при п = 2. Сопоставление результатов для различных калибров ОФ
снарядов по формулам A6.56) и A6.60) представлено в табл. 16.19. Расчеты
по формуле A6.60) проводились для тех же условий, для которых справедлива
формула A6.56) т.е. для ОФ снарядов калибра 76-152 мм из штатных средне-
углеродистых сталей с тротиловым снаряжением. Приняты значения а = 0,15,
ф = 0,35, D = 6,7 км/с, К = 100. Во всем диапазоне калибров расхождение
результатов не превышает 3%.

124	16. Осколочное действие взрывных систем
5. Прогноз характеристик спектра. Законы распределения осколков по
массе применяется как в числовой F(ra), /(га), так и в массовой ?/(га), и{т)
формах:
ТУ (М < га)	dF(m) _ 1 <i7V (M < га)
где N{M < га) — число осколков, имеющих массу, меньшую m; No — полное число
осколков;
ТТ f ч М^(М < га)	, ч <Я7 (га) 1 dME (M < га)
I 1 ( ТУ) 1 — 	 7/ ( ТУ) 1 — 	 —
Мо	dm	Мо	dm
М^(М < га) — суммарная масса осколков, масса каждого из которых меньше га;
Мо — полная масса оболочки.
Числовая форма ориентирована на расчет действия, массовая форма — пре-
преимущественно на выявление ресурсов массы металла.
Наиболее широко применяемым в зарубежной литературе числовым распреде-
распределением является закон Мотта:
{/ \1/21	М
-( — ) > , (ш) = /хГ C) = 2/х, 7V0 = -A
Распределение Мотта является однопараметрическим законом, т.е. зависит только
от параметра /i, представляющего характеристическую масс распределения. Для
представления спектров, подчиняющихся закону Мотта, используются как прави-
правило специальные координаты: ln7V(M > га) и га. Так как:
{/ \V2>|
_ /га\ I
то, логарифмируя, получаем:
ln7V(M>ra) =ln7V0- -^ra1/2
В указанных координатах функция распределения Мотта представляет прямую
линию, имеющую угловой коэффициент (—1//11/2) и отсекающую на оси ординат
отрезок ln(TVo)- Для оболочек с одинаковой массой Mq спектры с более мелким
дроблением изображаются крутыми линиями, а спектры крупных осколков —
пологими. По величинам отклонений экспериментальных точек от прямой можно
судить о степени соответствия реального распределения осколков закону Мотта.
В большинстве зарубежных источников указывается, что модель Мотта обес-
обеспечивает вполне удовлетворительное согласие с экспериментом. Предложен ряд
зависимостей (например, в [16.50]) для определения характеристической массы
/i как функции размеров оболочки и характеристик ВВ и металла, задаваемых
параметром В:
= в
(Мотт)
(Мотт)
^о (da + ^о)

16.3. Дробление оболочек
125
Для геометрически подобных оболочек при соответствующих преобразованиях
соответственно получим:
el,66
г2,33
0
Таким образом, обе зависимости Мотта предсказывают наличие масштабного
эффекта (МЭ) при дроблении, согласно формуле Джерни-Сармусакиса МЭ отсут-
отсутствует.
В некоторых исследованиях делаются попытки построения зависимости ха-
характеристической массы /1 и параметра No от характеристик линейной механики
разрушения. В работе [16.50] при обработке экспериментальных данных получены
следующие зависимости величин /х, Щ от отношения \ — Kib/Kic (^ic> К\в —
соответственно трещиностойкость и сопротивление ветвлению):
для стали HF-1 /х = 0,1622х4'61 [мг], No = 1,15 • 106х'36
для стали FS-01 fi = 0,0158%4'49 [мг] No = 3,35 • 107х'75
В более поздней работе тех же авторов [16.51] было показано, что более точной
является зависимость указанных параметров от отношения х = Кн/К\с:
для стали HF-1 /х = 1,10х3'53 [мг] Щ = 2,82 • 106х'30
для стали FS-01 /х = 0,14х3'37 [мг] No = 3,16 • 106х'54
Обращает на себя вни-
внимание чрезвычайно сильный	Таблица 16.20
характер указанных зависи- Экспериментальные характеристики
мостей. Выборочные значе- высокоосколочных сталей
ния экспериментальных ха-
характеристик представлены в
табл. 16.20. В работе [16.52]
отмечалось расхождение рас-
расчетных результатов, получен-
полученных по формуле Мотта, с
экспериментальными данны-
данными. Исследовалось распреде-
распределение осколков стандартных
цилиндров NOL из стали AISI
1045, снаряженных различными ВВ. Собирались осколки массой более 1 грана
(~ 0,0648г). Средняя масса осколков изменялась в пределах от 0.73г (снаряжение
флегматизированным гексогеном RDX/Wax 95/5) до 2,53 г (снаряжение аммото-
лом 80/20).
Практически для всех исследованных типов В В экспериментальное распреде-
распределение в координатах ln7V(M > m), m1/2 представляет выпуклую кривую, а не
прямую линию, отвечающую соотношению Мотта:
Сталь
FS-01 (А)
FS-01 (С)
HF-1 (А)
HF-1 (В)
СО,2
ГПа
2,57
1,78
1,23
0,95
к1с
21,7
31,4
32,5
37,5
Кн
Ша(м)
91,6
156,6
79,0
124,1
Кв
1/2
118,9
216,1
104,8
141,6
No
18910
10280
16360
5740
/i,
мг
19,0
34,1
23,3
70,7
=ln7V0-
На основании этих данных в работе сделан вывод, что для открытых цилиндров
формула Мотта удовлетворительно описывает опытное распределение только в
средней части спектра. Для крупной части спектра показатель 1/2 должен быть
заменен некоторым значением 0,5 < А < 1, а спектр мелкой части аппрокси-
аппроксимируется с помощью степенного закона. Таким образом, распределение в целом

126	16. Осколочное действие взрывных систем
описывается соотношениями:
N = 7V/777/,	77li < ГП ^ 777,2,
{/ \1/21
- ( 	 ) > ,
{
- (
777,2 < ГП < 777,3
Граница между областями I и II определяется соотношением:
2	5/4
777, = 1 + - (Ш - 1) ,
а между областями II и III -соотношением:
т = 0,236т1'77
Зависимость показателя Л от средней массы га задается некоторой функцией.
Экспоненциальное распределение в массовой форме использовалось в работах
Пэймена. Закон распределения записывается в виде:
U (М > т) = ехр {—С777,}
или в виде:
здесь:
1 * Мо 1
с= —, с* = 	 = —
777,с	777,с 777,с
где гас — характеристическая масса распределения;
гас = itic/Mq — относительная характеристическая масса распределения.
В указанных источниках параметры с, с* называются параметрами Пэймена.
При обработке экспериментальных данных испытаний открытых цилиндриче-
цилиндрических оболочек AISI 9260 и HF-1 с постоянным коэффициентом нагрузки /3 = 0,3
и переменной толщиной стенки Eq = 2,3—10,4 мм, Sd = 0,117 ~ 1/8,5, Ло = 2,62)
получены следующие соотношения:
— In с = А + В In 5о, In /i = P + Q In 5q •
Приводятся экспериментальные значения коэффициентов i, Б, Р, Q и произведе-
произведения fie = /i/mc для вышеуказанных сталей при различных термообработках.
Более общая форма массового закона распределения осколков породы при
взрывном дроблении в виде
U(m) = 1-ехр |- ( —
предложена в [16.53, 16.54]. Распределение по существу представляет закон Вей-
булла, примененный для описания распределения «масса по массе». В зарубежной
литературе такую форму описания обычно называют законом Розина—Раммлера.

16-4- Статистическое распределение осколков	127
М. Хельд предложил своеобразную форму представления распределения оскол-
осколков по массе в виде двухпараметрического закона [16.55]:
М{П)	г	Л.
1
где п — порядковый номер осколка в спектре (осколки расположены в порядке
убывания их масс); М(п) — суммарная масса всех осколков с номером, меньшим
или равным щ Мо — масса оболочки; Л, В — константы.
Масса осколка т(п), имеющего номер п, определится как:
т (п) =
СИП
1 ехр {-Впх} .
Параметры распределения В, А для каждого конкретного осколочного боеприпа-
са находятся в результате статистической обработки эксперимента. Физический
смысл этих параметров не вполне ясен. Соотношения, определяющие их зависи-
зависимость от свойств металла и ВВ, в [16.55] отсутствуют.
Основным методическим преимуществом представления осколочных спектров
в форме Хельда по сравнению с распределением Мотта является исключение
параметра Nq (число осколков с массой, большей нуля), представляющего аб-
абстрактную величину, не поддающуюся экспериментальному определению. Недо-
Недостатком метода является отход от общепринятого аппарата статистических функ-
функций распределения с аргументом в виде случайной массы осколка, что исключает
возможность определения моментов распределения (математического ожидания
массы осколка, дисперсии и т.д.) и возможность перехода к распределениям более
высокого порядка.
16.4. Статистическое распределение осколков
1. Пространственно-массовые распределения осколков. Как уже ука-
указывалось выше (п. 15.5. ), основной целью эксперимента или расчета процесса
взрыва осесимметричных оболочек является получение распределений осколков
по массе и по меридиональному углу разлета (р Е [О,тг], а также получение
распределения скоростей разлета по углу (р (годографа скоростей).
Пространственно-массовое распределение осколков экспериментально опреде-
определяется с помощью стенда углового улавливания (Патент № 2131583 РФ). Ре-
Результаты эксперимента позволяют построить двумерную матрицу A^j, где Nij —
число осколков г-ой массовой группы в j-той угловой зоне. Ширина угловой зоны
А(р обычно принимается в пределах 2... 5°. Пример экспериментальной матрицы
Nij, полученной при подрыве опытного образца (открытый цилиндр с конической
внешней поверхностью, Lo = 100 мм, da = 25 мм, наружные диаметры на торцах
32 и 40 мм, ст. C-60/A-IX-20) представлен в табл. 16.21 (представлены данные
только для 4-х угловых зон, расположенных около экваториальной плоскости).
Отбор осколков производился, начиная с массы 0,25 г. В таблице представлены
также общее количество осколков JV- ' в угловых зонах, общие количества
осколков N> ' в массовых группах и суммарные массы осколков М\ в
этих группах. Приведены средние данные по двум подрывам без промежуточной
разборки улавливателя при угле экваториального сектора 60°, что приводит к
числам осколков 7V^-, кратным трем.

128
16. Осколочное действие взрывных систем
Таблица 16.21
Пространственно-массовое распределение осколков (N^25)
угловые
зоны
87-90°
90-93°
93-96°
96-99°
N@,25)
М<°'25\г
массовые группы, Am, г
0,25-0,5
24
15
15
12
66
24,75
0,5-1
21
18
12
12
63
47,25
1-2
6
12
18
15
51
76,5
2-3
-
9
12
9
30
75,1
3-4
-
3
9
6
18
62,9
4-5
-
-
6
3
9
40,4
5-6
-
-
6
-
6
33,1
6-7
-
-
3
-
3
19,5
^@,25)
51
57
81
57
246
Как видно из таблицы, распределения по массе в угловых зонах для оболочки
с переменной по длине толщиной стенки существенно отличаются друг от друга.
К сожалению, метод прямого определения двумерной матрицы Nsij с помощью
углового улавливания осколков так и не был внедрен в практику отечествен-
отечественных полигонных испытаний. Фактически согласно ГОСТ он заменяется двумя
отдельными испытаниями — подрывом снаряда в мишенной обстановке с целью
определения величины Nsj и подрывом в бронекамере с улавливающей средой
с целью получения величины Ns{. Определение величины Nsij при этом обычно
производится с помощью соотношения:
Nsij=Nsj-^,	A6.61)
Ns
основанного на весьма грубом допущении о подобии распределения по массе
во всех угловых зонах. Отметим, что общее число осколков 7VS, определенные
щитовыми испытаниями (Ns = TiNsj) и камерными испытаниями (Ns = ^Nsi),
часто значительно отличаются друг от друга GVJ > Щщ , Щ /Щ = 1,2 ... 2).
Причины этого явления до настоящего времени не выяснены. Одно из возмож-
возможных объяснений связано с явлением вторичного разрушения осколков («доломом»)
при ударе об улавливающую среду. Более вероятно, что расхождение является
следствием систематической погрешности при пересчете площадей пробоин в щите
на массы осколков.
Восстановление массы осколка т по площади пробоины S производится с
помощью соотношения:
771 = 70
-)
3/2
где 7о — плотность металла, Ф — средний параметр формы осколков. Учитывая,
что измерение S производится весьма приближенно (как правило, по двум раз-
размерам пробоины), а величина Ф даже в пределах одной массовой группы имеет
значительный статистический разброс, ошибка при восстановлении массы может
достигать 30-40%. Аналитическое выражение плотности двумерного распределе-
распределения /(<??, га) {if Е [О,тг], т Е [0,оо)) строится как аппроксимация дискретной
плотности:
1
N ¦ ¦
Sl3

16-4- Статистическое распределение осколков	129
Очевидно:
d2F(^m)
f(<p,m) =
dip dm '
где F((p,m) — совместная функция распределения двух случайных величин (М, J-)
N(J- < ю М < га)
F((p, га) = Р[Т < <р, М < га) = —	Щ	-,
где N(J- < (р, М < 7тг) — число осколков, разлетающихся в конусе с углом 2(р при
вершине и имеющих массу, меньшую га, Nq — полное число осколков с массой,
большей нуля (теоретическая константа).
Число осколков в интервале масс rai-ra2, движущихся в угловой зоне (pi~(f2
определяется как
A^J^, = Nq / / f ((p,m) dm dip.
j j
о о
Согласно теореме умножения плотностей двумерная плотность /(<?>, га) может
быть представлена в одной из следующих форм:
f(ip,m) = f1(ip)f2{m\ip), /(га) = /з(т)/4(<Р | га),
где /i (<?>), /з(?77,), /2G77,1^M /4(^5 ш) — соответственно безусловные и условные
плотности распределения.
В частном случае, когда случайные величины ip ж т являются независимыми,
теорема умножения плотностей принимает вид:
f(<p,m) = f1{ip)f2{m).
Использование этого соотношения эквивалентно использованию соотношения
A6.61). Как мы видели ранее (табл. 16.21), величины ip и т являются зависимыми.
Проверка полученных пространственно-массовых плотностей распределения
/(<?>, 777,) и годографа скоростей ^о(^) производится по выполнению балансов осевой
компоненты импульса и энергии. При этом должны выполняться условия:
^2	cos <pj + /Пд = О,
i=i
Mivli
где С — масса заряда ВВ, Qy — удельная теплота взрыва, /пд — осевая компо-
компонента импульса продуктов детонации, Еид и И^пд — соответственно внутренняя
и кинетическая энергия продуктов детонации.
При известной пространственно-массовой плотности распределения f((p,m)
распределение /(га) по массе определяется как:
TV
= / f(<p,
f(m) = / f(<p,m) dip.

130	16. Осколочное действие взрывных систем
Это распределение, по существу, представляет вторичный продукт, который не
может быть без дополнительных допущений использован в расчетах эффектив-
эффективности, но, учитывая, что экспериментальные распределения /(га) (осколочные
спектры) дают важную информацию о физике осколкообразования и морфологии
осколков, позволяют проводить качественное сравнения и прогноз дробимости при
различных комбинациях металл-ВВ-геометрия, распределение /(га) по-прежнему
сохраняет определенную роль в теории осколочных полей поражения.
2. Общие соотношения осколочной статистики. Масса осколка является
случайной положительной величиной, в общем случае заданной на интервале
т G [mmin,mmax]. Используются законы распределения со следующими областя-
областями задания [16.56]:
1)	полуось т G [0, оо) (распределения Вейбулла, Нукияма-Танасава, гипервей-
булловское и др.);
2)	луч т G [га*,оо) (распределение Парето);
3)	отрезок т G [0,гатаж] (бета-распределение).
Функция распределения случайной величины вводится в виде
, , 7V(M<ra)
F(m) = —-	-,
где N(M < т) — число осколков, имеющих массу, меньшую га, Nq — полное число
осколков.
Функция распределения имеет следующие общие свойства:
1) функция распределения — неубывающая функция своего аргумента, т.е. при
77i2 > rai, F(rri2) ;
2)	на левой границе области распределения тш{п функция распределения рав-
равна нулю;
3)	на правой границе области определения ттах (в частном случае на плюс
бесконечности) функция распределения равна единице.
Медианой распределения га называется такое значение га = гаме, для которого:
F(mMe) = 1/2.
Число осколков в данном интервале rai-m^:
iVmi_m2 = No (F (то2) -
Плотность распределения определяется соотношением
dF(m) _ 1 dN(M < то)
f(m) =
dm Nq	dm
В отличие от функции распределения, которая является безразмерной, плотность
распределения имеет размерность 1/г.
Ее основные свойства:
1) плотность распределения есть неотрицательная функция, т.е. /(га,) ^ 0;

16-4- Статистическое распределение осколков	131
2) интеграл от плотности распределения в пределах от левой до правой границы
области распределения равен единице
ГПтах
I /(ra)dra = l,
mmin
т.е. площадь под кривой /(га) равна единице.
Модой величины га называется то ее значение га, при котором плотность веро-
вероятности /(га) максимальна. Если кривая плотности распределения имеет одну
моду, распределение называется унимодальным, при наличии нескольких мод —
полимодальным (в частности, при наличии двух — бимодальным). В частных
случаях мода может совпадать с границей области определения.
Число осколков в интервале масс m\-m<i
mi
Nmi_m2 = No (F(m2) - F(mi)) =N0J f(m) dm.
mi
Число осколков с массой, большей ms
ГПтах
Ns=N0(l-F(ms)) = N0 j f(m)dm.
ms
Математическое ожидание массы осколка:
Штах
(т) = / mf(m) dm.
Полное число осколков Nq определяется как:
(га)
где Мо — масса оболочки.
Используя выражение /(га) = A/JVq) (dN [M < га) /dm) и соотношение dN [М <
т) = dM (M < т) /т, получаем:
/ \ / 1 ldM(M<m) ,	1 /',,.,,. ч Мо
(га) = / га—	Ц	J-dm=— I dM (M < га) = -—.
J Norn	dm	No J	v	J No
Подбор аналитической модели распределения к данному экспериментальному
спектру, полученному при подрыве в камере с улавливающей средой, обычно
проводится по условию минимума критерия Пирсона х2. Эмпирическое значение
X2 вычисляется по формуле:

132	16. Осколочное действие взрывных систем
где к — число массовых групп, Ni — число осколков в данной массовой группе,
определенное по результатам подрыва, Ni — расчетное число осколков в данной
массовой группе. Пусть, например, используется двухпараметрическая модель
распределения с параметрами гао и Л. Так как величина Ni является функцией
параметров гао, Л, то и величина %2 также является функцией этих параметров.
Параметры, соответствующие минимуму х2, принимаются в качестве параметров
статистической модели. Проверка согласия экспериментального распределения и
теоретической модели может быть проведена по критерию Романовского:
Наряду с распределениями в форме «число по массе» F(ra), /(га) широко ис-
используется также распределения в форме «масса по массе» Е/(га), и{т). Функция
распределения U(rn) и плотность распределения и(т) вводятся соотношениями:
ТТ( . M(<m) ( Л dU(m) I dM(<m)
v J	Mo ' v ' dm Mo dm '
где Mq — масса корпуса, М(< га) — суммарная масса осколков, масса каждого из
которых меньше га.
Учитывая, что
1 dN(<m)	I dM(<m)	dM (< т)
I \ 11L ] —	•	LJL \ 11L ] —	• LLJ. V I <\v lib) —	•
Nq dm	Mq dm	m
связь меж:ду числовой и массовой плотностями распределения определяется соот-
соотношением:
, ч ra7V0
которое можно также представить в виде
и{т) = Й/м'
Из этого выражения следует, что для распределений, заданных на полуоси
777, ^ 0, график ?х(га) всегда проходит через начало координат. Очевидно также,
что при 7тг = (га) значения и{т) и /(га) совпадают. Масса осколков, заключенная
в интервале rai-ra2, определяется формулами
= Мо (U(m2) - U{m1)) = Мо / и(т) dm.
Распределение «масса по массе», представленное в виде гистограммы и(т) =
(Mi/Mq)A /Ami), ПРИ анализе баланса осколочной массы значительно более ин-
информативно, чем числовое /(га). Оно дает ясное представление о размерах потерь
осколочной массы на бесполезные осколки. Кроме того, массовая гистограмма
значительно четче, чем числовая выявляет бимодальный характер спектра.
Более компактное представление о составе спектра может быть получено с
помощью введения осколочных фракций — мелкой @ < га ^ mf\), средней
(га/1 < 7тг ^ га/г) и крупной (га > 771/2), соответственно с массами Мм, Мс и

16-4- Статистическое распределение осколков	133
Мк (Мм + Мс + Мк = Мо) и относительными массами /хм = Mm/Mq, /ic = Mc/Mq,
/iK = Mk/Mq, (/iM + Me + Мк = 1)- Выбор границ основных фракций m/i, m/2
определяется главным образом размерами оболочки. При известной плотности
распределения и(т) относительные массы фракций определяются как
ra/i	га/2
1лш = и(т) dm, /ic = / и{т) dm.
О	ra/i
Наглядное представление о фракционном составе осколочной массы может
быть получено с помощью треугольной фракционной диаграммы, по осям которой
отложены содержания мелкой и средней фракций (рис. 16.64,см. стр. 157). Ука-
Указанный способ позволяет нанести на один график данные большого числа экспери-
экспериментов. Состав каждой осколочной массы изображается при этом одной точкой. В
данном случае показано расположение внутри фракционного треугольника линий,
отвечающих составам, описываемым числовым распределением Вейбулла при
Л = const, то = var (rrifi = 1г, m/2 = 4г). При движении вдоль параметрически
заданной линии /ic = /(/iM) от /iM = 0 до /iM = 1 интенсивность дробления
возрастает, при этом характеристическая масса то уменьшается от ос до 0. На
восходящем участке кривой происходит одновременное возрастает масс мелкой и
средней фракции за счет уменьшения крупной фракции. Гипотенуза треугольной
диаграммы /iM + fic = 1 отвечает нулевому содержанию крупной фракции. На
нисходящем участке кривой крупная фракция в основном исчерпана и дальнейшее
возрастание массы мелкой фракции происходит за счет уменьшения средней
фракции.
3. Основные статистические модели спектров
Распределение Вейбулла
Наибольшее распространение для описания распределения осколков по массе
получило распределение Вейбулла. Применение закона Вейбулла для описания
осколочных спектров при произвольном значении Л впервые введено в [16.3].
В [16.57, 16.58] показано, что закон Вейбулла может быть строго выведен на основе
предположений о пуассоновском распределении окружных трещин и о наличии
функциональной зависимости между площадью В поперечного сечения осколка и
его длиной L.
При пуассоновском распределении трещин имеет место экспоненциальное рас-
распределение площадей В
*(Ь) = 1ехр(-А\.
bo { bo J
В общем случае примем L = ABV', откуда масса осколка
М = joLB = A^oBu+1.
Если В — непрерывная случайная величина с плотностью t(b), а случайная
величина М связана с ней функциональной зависимостью М = (р(В), то плотность
распределения случайной величины т:
где ф — функция, обратная (р. Эта функция и ее производная имеют вид:
1	1
т \ V+1	1 / т
^l , ф'(т) = —Ц(^
ч

134	16. Осколочное действие взрывных систем
откуда
т) =
обозначая:
1
= Л, 7о^4^о = т®->
у + 1
получим плотность распределения по массе в виде:
{I.	A6.62)
Функция распределения определяется как
Л
F(m) = / /(m) dm = 1 - exp \ - ( — ) I .	A6.63)
J	I Vmo/ I
0	^	'
Распределение A6.62, 16.63) является двухпараметрическим распределением Вей-
булла, заданным на полуоси т G [0, оо). Величина uiq представляет характеристи-
характеристическую массу распределения, величина Л — показатель качества дробления (при
увеличении Л спектр становится более однородным). В зарубежной литературе
закон Вейбулла при Л = 0,5 называют законом Мотта. При Л > 1 распределение
является унимодальным и имеет моду тоA — l/AI^, при Л = 1 превращается
в экспоненциальное распределение, при Л < 1 имеет асимптотой ось ординат.
Возможность использования закона Вейбулла для описания принципиально раз-
различных типов дробления является его очевидным преимуществом.
Медиана распределения определяется как:
Ме = шоAп2I/Л.
Математическое ожидание массы осколка:
оо
(т) = / mf{m) dm = ш0Г ( 1 + — I ,
где Г (ж) — гамма-функция.
Число осколков в интервале масс m\-m<i'.
—4-Ш
Число осколков с массой, большей ms
iVs=7Voexp<!-( —
Теоретическая константа АГ0
Мп	Мп

16-4- Статистическое распределение осколков
135
где Мо — масса корпуса.
Значение т^, при котором имеет значение максимум 7VS, и число
деляется соотношениями:
опре-
опреДифференциальный закон распределения «масса по массе» имеет вид
и(т) =
т0ГA
m \
m
и при любом значении Л проходит через начало координат.
Относительная масса осколков фракции m\—m<2 определяется как:
7712
/
тп1-тп2 = / u(m)dm.
A6.64)
В случае произвольного значения Л это выражение не может быть получено в
квадратурах. При Л = z, где z — целое положительное число, выражение A6.64)
можно получить в виде конечных формул. Например, при Л = 0,5 (распределение
Мотта) получаем
mi	[rn^ \	Г
— + 2W— + 2 exp -
m0 у m0 J {
/
- P + 2,p + 2 exp
\m	у ш
Показатель z/, следовательно, и показатель Л, зависят от свойств металла и В В, в
первую очередь от содержания углерода в стали. Для каждого класса сталей (низ-
(низкоуглеродистые С<0,3%, среднеуглеродистые 0,3<С<0,7%, высокоуглеродистые
С>0,7%) диапазон изменения величины v довольно широк (имеет место перекры-
перекрытие диапазонов), тем не менее по средним значениям тенденция прослеживается
достаточно четко: с возрастанием содержания углерода показатель v уменьшается.
Таким образом, для низкоуглеродистых пластичных сталей наблюдается сильная
корреляционная зависимость средней длины осколка от площади его поперечного
сечения {у > 1), что способствует образованию большого числа удлиненных
осколков, то есть ухудшению качества осколочного спектра.
Для высокоуглеродистых, крем-
кремнистых и марганцевокремнистых	Таблица 16.22
сталей зависимость L = f(B) явля- Средние значения показателей v и Л для
ется относительно слабой {у < 1). различных классов сталей
Образование удлиненных осколков
(«сабель») затруднено вследствие
большой хрупкости сталей, что при-
приводит к повышению качества спек-
спектра. Среднеуглеродистые стали с
линейной зависимостью L = АВ
[у = 1) занимают промежуточное
положение.
сталь | Диапазон v
Низкоуглеродистая
Среднеуглеродистая
Высокоуглеродистая
1,0... 2,0
0,5... 1,5
0,4. ..1,0
V
1,5
1,0
0,7
Л
0,4
0,5
0,6

136
16. Осколочное действие взрывных систем
Значение показателей v и Л для различных классов сталей представлены в
табл. 16.22.
Распределение Вейбулла может применяться для описания как общих спек-
спектров, так и спектров в угловых зонах. В табл. 16.23 приводятся результаты стати-
статистической обработки эксперимента с угловым улавливанием осколков конического
цилиндра (табл. 16.21).
Таблица 16.23
Параметры распределения Вейбулла в угловых зонах и общего распределения
осколков
Спектры по угловым
зонам
зоны
87-90°
90-93°
93-96°
96-99°
Общий спектр
Л
0,2
0,4
0,5
0,7
0,7
т0, г
0,01
0,75
1,65
2,44
0,87
<т>, г
0,67
2,49
3,3
3,09
1,1
No
626
167
126
134
378
х2
10,36
2,24
0,54
2,78
6,42
R
6,62
0,12
1,01
0,70
0,45
Как видно из таблицы, закон Вейбулла с высокой точностью описывает все
угловые спектры (кроме спектра первой угловой зоны) и общий спектр. При этом
значения параметров распределения Л и uiq во всех угловых зонах различны,
что подтверждает высказанное выше положение о невозможности использования
в расчетах формулы пропорционального пересчета A6.61). Увеличение по ме-
меридиональному углу разлета характеристической массы uiq очевидным образом
объясняется увеличением толщины стенки по направлению ко дну оболочки.
Стабильное увеличение по углу разлета показателя качества дробления Л, т.е.
увеличение однородности спектра, физически менее очевидно и, с одной стороны,
может быть объяснено менее стабильными условиями взрывного нагружения
верхней части оболочки вследствие быстрой осевой разгрузки ПД и резкого
изменения угла падения детонационного фронта, а с другой — интенсивным
разрушающим действием волны разрежения, распространяющейся от нижнего
торца оболочки.
Гипервейбулловское распределение
Закон Вейбулла неприемлем при описании осколочных спектров с двумя вы-
выраженными модами плотности и{т), отвечающими морфологическим совокупно-
совокупностям осколков А и В.
Для описания бимодальных распределений и(т) (и-бимодальных спектров) в
работах [16.59, 16.60] предложено использовать суперпозицию законов Вейбулла
(гипервейбулловское распределение) в виде:
F(m) = 1 - ? • ехр \ -
т
тп.
A6.65)
где то, т^, а, C — соответственно характеристические массы и показатели каче-
качества дробления основного и сопутствующего спектров, ? — коэффициент, устанав-
устанавливающий соотношение этих частей спектра.
Математическое ожидание массы фрагмента:
(га) = ?та ¦ Г { 1 + - ) + A - 0 тьТ

16-4- Статистическое распределение осколков
137
Дифференциальный закон распределения масса по массе имеет вид:
и{т) =
ехр
-
—
\тъ)
ехр
A6.66)
Это распределение имеет обе моды больше нуля.
Гипервейбулловское и-бимодальное распределение в общем случае содержит
пять параметров и позволяет описывать осколочные спектры, в том числе и спек-
спектры заданного дробления, в широком диапазоне сочетаний металл-ВВ-геометрия.
Прогнозирование параметров ma, т^, а, /3, ? по известной геометрии снаряда и
свойствам металла и В В в настоящее время не может быть проведено с достаточ-
достаточной достоверностью. Можно лишь привести наиболее общие соображения:
1)	показатель качества дробления а основного спектра должен быть больше,
чем соответствующая величина C для сопутствующего спектра, т.к. по свой
физической природе основной спектр является более однородным (квазире-
(квазирегулярным) ;
2)	относительное число осколков основного спектра ? должно быть существенно
меньше 0,5;
3)	отношение характеристических масс ть/та должно находится в диапазоне:
A/50... 1/10), что вытекает из особенностей формирования основных оскол-
осколков продольными магистральными трещинами и сопутствующих осколков
трещинами сдвига в контактной («перемольной») зоне.
а)
м(ж)х100
24
16
м(ш)х100
Ift
б)
\
Для практических расче-
расчетов желательно уменьшить
число параметров распределе-
распределения. В работе [16.60] показано,
что в ряде случаев осколоч-
осколочные спектры удается описать
с помощью гиперэкспоненци-
гиперэкспоненциального распределения, пред-
представляющего частный случай
гипервейбулловского распре-
распределения при а = /3 = 1
(рис. 16.51).
Более детальный анализ
спектров стандартных оско-
осколочных цилиндров и различ-
различных типов ОФ снарядов пока-
показал, что в аспекте использо-
использования двухкомпонентной мо-
модели для прогнозирования спектров при проектировании методически более
целесообразно фиксировать оба показателя качества дробления и относительное
число ?, а в качестве подбираемых параметров принять характеристические массы
та и тъ.
В качестве примера проводится подбор статистической модели для ОФС калиб-
калибра 152 мм [16.61]. Корпуса снарядов были изготовлены горячей штамповкой из сна-
снарядной стали С-60 и снаряжены ТНТ методом шнекования E3-ОФ-540) и A-IX-20
О 1 3 5 7 9 12 20 50 О 1 3 5 7 9 12 20 50
Рис. 16.51. и-бимодальные гиперэкспоненциальные оско-
осколочные спектры цилиндра №12: сталь 20/ТНТ (а); сталь
60/флегматизированный октоген (б)

138
16. Осколочное действие взрывных систем
Таблица 16.24
Основные характеристики 152 мм
испытуемых ОФС
методом порционного прессования (З-ОФ-25 «Гриф»). Основные характеристики
снарядов представлены в табл. 16.24 [16.62]. Снаряды подрывались в бронекамере
с опилочным улавливателем. В табл. 16.25 представлены распределения осколков
по массовым группам.
Для снаряда 53-ОФ-540 приводится
средние значения группы опытов из 7 под-
подрывов, для снаряда З-ОФ-25 — средние
значения из 12 подрывов. Гистограммы в
форме «масса по массе» представлены на
рис. 16.52а,б.
Фракционный состав осколочных масс
представлен в табл. 16.26 (/хм — отно-
относительное содержание мелкой фракции
(О < т ^ 4 г), /хс — относительное содер-
содержание средней фракции D < т ^ 20 г),
/хк — относительное содержание крупной
фракции (т > 20 г)). Отметим, что для
обоих 152 мм снарядов содержание средней
фракции не удовлетворяет современным
Тип
53-ОФ-540
З-ОФ-25
Q
43,4
43,63
ВВ
ТНТ
A-IX-20
С
5,86
6,57
а
0,135
0,151
Q — масса снаряда со взрывателем,
кг; С — масса ВВ, кг; а — коэффи-
коэффициент наполнения.
требованиям (/ic ^ 0,45).
Таблица 16.25
Распределение осколков по массовым группам
Снаряд
53ОФ540
ЗОФ25
0,5-1
704
1159
1-2
632
1045
2-3
314
560
3-4
213
371
Число
4-6
288
491
6-8
196
329
осколков в
8-10
152
235
10-15
268
401
массовых группах
15-20
176
221
20-30
199
224
30-50
192
149
50-75
87
40
75-100
32
9
> 100
21
1
и(т)Л/г
0,025
0,020
0,015
0,010
0,005
30
т,г 50
и(т\1/т
0,045
0,040
0,035
0,030
0,025
0,020
0,015
0,010
0,005
02 6" 10 15 20
30
б)
т, г 50
02 6 10 15 20
а)
Рис. 16.52. Гистограммы распределения осколков снарядов в форме «масса по массе»: 53-ОФ-
540 (а); З-ОФ-25 (б)
Полученные средние значения общих чисел осколков 7Vo,5 c массой более 0,5 г
достаточно точно описывается формулой (см. 16.60):
.OL

16-4- Статистическое распределение осколков
139
Снаряд
53-ОФ-540
З-ОФ-25
0,
0,
м
17
19
/ic
0,28
0,42
1
0
0
,55
,39
где К = 70; а, ф — коэффициент наполнения Таблица 16.26. Фракционный со-
и относительное сужения материала оболочки	став осколочных масс
в момент разрыва (оба в долях единицы или
в процентах); do — калибр, дм; D — скорость
детонации заряда ВВ, км/с (для ТНТ и A-IX-
20 принято соответственно 6,7 и 8,1км/с). Зна-
Значение ф принято равным 0,3 для обоих типов
снарядов. Расчетные значения 7Vo,5 составляют
соответственно 3267 и 5341, т.е. расхождение с
экспериментом не превышает 6%.
Анализ гистограмм в форме «масса по массе» (рис. 16.52 а, б) позволяющий
наиболее отчетливо выявить характер спектра, показал, что оба распределения
существенно отклоняются от унимодального распределения Вейбулла.
Проверка на согласие вейбулловской и гиперэкспоненциальной моделей дала
отрицательный результат.
Таблица 16.27
Результаты подбора параметров распределения при фиксированных значениях
а,/8, С
Снаряд
53-ОФ-540
З-ОФ-25
та, г
14,0
8,0
тъ, г
0,24
0,19
12,71
14,57
R
1,53
2,02
дтрасч.
3490
5264
дгэксп.
3453
5234
дтрасч.
iV0,5
ДГЭКСП.
iV0,5
1,011
1,006
(га) г
4,56
2,74
7V(a)
1895
2979
iV0,5
1594
2285
Результаты подбора параметров гипервейбулловского распределения представ-
представлены в табл. 16.27, 16.28. В табл. 16.27 представлены результаты подбора пара-
параметров та и тъ при фиксированных значениях а = 0,8, C = 0,4, ? = 0,25. В
обоих случаях подобранные аппроксимации удовлетворяют критерию Романов-
Романовского R ^ 3. Поведение параметров распределения правильно отражает усиление
дробления при переходе от снаряжения ТНТ к A-IX-20. В табл. 16.28 представлены
результаты аппроксимации при свободной вариации всех пяти параметров.
Таблица 16.28
Результаты подбора параметров распределения при вариации всех параметров
Снаряд
53ОФ540
З-ОФ-25
а
0,7
0,9
Р
0,4
0,3
та, г
11,4
9,8
гаь, г
0,15
0,11
0,25
0,1
х2
1,83
1,43
R
1,38
1,49
дтрасч.
3464
5238
дтрасч.
/уэксп.
iV0,5
1,003
1,001
(т) , г
3,98
1,94
N(a)
2080
1748
iV0,5
1383
3489
Для снаряда З-ОФ-25 на рис. 16.53 построены линии уровня %2 = const на
плоскости та — тъ . Для этого же снаряда на рис. 16.54 изображены графики
подобранных плотностей распределения и(т) в форме «масса по массе» отдельно
для обоих частей спектра и их композиция.
Статистическая обработка экспериментальных спектров цилиндров показала,
что большую часть их удается описать с помощью гиперэкспоненциального рас-

140
16. Осколочное действие взрывных систем
10
6,0 6,4 6,8 7,2 7,6 8,0 8,4 8,8 9,2 9,6 9,8 '
Рис. 16.53. Линии уровня %2 = const на
плоскости характеристических масс та—тъ
(З-ОФ-25)
0,051
0,046
0,041
0,036
0,031
0,026
0,020
0,015
0,010
0,005
0
5 10 15 20 25 30 35 40 45 т, г
Рис. 16.54. Графики подобранных плотно-
плотностей распределения и(т) для обеих частей
спектра и их композиция (З-ОФ-25)
пределения, представляющего частный случай гипервейбулловского распределе-
распределения при а = C = 1.
(га) = ?гао + A - &тъ,
Дифференциальный закон распределения «масса по массе» в этом случае
представляет композицию гамма-распределений
и (га) = {т) [ ?	ехр

ma
га	\ ( т
- О — ехр <^ - —
Числа осколков типа А и Б и их относительные массы определяются соотно-
соотношением:
°' а (га) '
а относительные массы фракций — соотношениями:
(га)
тпъ
Н
ехр
1 + ^ ехр -
тъ ) [ \mi,

16-4- Статистическое распределение осколков	141
Распределение Нукиямы-Танасава [16.63]
Распределение является трехпараметрическим, что позволяет описывать весь-
весьма разнообразные распределения. Использование этого распределения для описа-
описания осколочных спектров предложено в [16.64]. Плотность распределения имеет
вид:
п
га0Г
п
этот закон включает в себя как частные случаи экспоненциальное распределение
(при uj = 0, п = 1), распределение Вейбулла (при ш = п — 1) и гамма распределение
(при п = 1).
Математическое ожидание массы:
мода распределения:
га = га0 —
Распределение Паретпо
Значительный интерес в методическом плане представляют статистические мо-
модели, позволяющие получить все четыре распределения (/(га), F(ra), iz(ra), U{m))
в виде конечных формул. Наиболее простую форму имеет двухпараметрическое
распределение Парето, используемое для описания распределения случайных ве-
величин, заданных на интервале m G [га*, ос).
Числовое распределение описывается зависимостями
F(m) = l-(^.Y, /(m) = -?-(-)
V т /	га* V га /
Медиана распределения: гаме = 2G?г*/р).
Математическое ожидание: (га) = 	га*.
Число осколков в интервале тх—т^'-
Ш*
Число осколков с массой, большей ms (ms > га*)
Массовое распределение описывается соотношением:
U (т) = 1 - (		, и(т) =
V т /	га* V т )
Масса осколков в интервале масс m\-m<i
г1_Ш2 = Мо 	 .	.	.
VVmi/	\Ш2/

142	16. Осколочное действие взрывных систем
Выше были рассмотрены распределения с правой границей области т —>• оо.
Формальным недостатком таких распределений является невыполнение очевидно-
очевидного условия т < ттах, где ттах — максимальная масса осколка в данном спектре,
в пределе равная массе оболочки Mq. Известным распределением, заданным на
интервале т Е [0, ттаж], является бета распределение.
Бета-распределение
Плотность вероятности бета-распределения имеет вид:
/(ш)= 1 Г(а + /3) ( m \ (Л m
тшах Т(а)Г(/3) \mmaxj \ тшс
При а > 1, /3 > 1 бета-распределение унимодально с модой в точке ттах(а —
1)/(а-\- /3 — 2). Если а = [3 = 1, то бета распределение является равномерным.
Математическое ожидание массы осколка:
Применение бета-распределение для описания осколочных спектров было пред-
предложено Р. С. Саркисяном и В. А. Кузнецовым [16.49]. Согласно их данным мак-
максимальная масса осколка, получающегося при дроблении закрытого цилиндра,
определяется соотношением:
где
2A-i/2)	_POj^l b-^_P_.
3 - v	70 cecp '	Ьо ce '
z/ — коэффициент Пуассона металла оболочки; ср, се — соответственно скорость
распространения упругих и пластических волн в материале оболочки; х ~~ коэффи-
коэффициент, зависящий от конструкции оболочки (для оболочек с закрытыми торцами
X = 0,2).
Описание распределений, заданных на интервале т G [0, тшах] с достаточным
приближением может быть осуществлено с помощью трехпараметрической моди-
модификации закона Вейбулла:
777/
F (т) = 1 - ехр I - '
{гпшах - т)
где /1 <С 1 — параметр распределения.
Медиана распределения:
тМе =
1 +
Исходя из представления об образовании «полос», максимальная масса осколка
в спектре определяется выражением: ттах =

16.5. Стандартные осколочные цилиндры
143
а)
В
D
Е	F	G	н
Рис. 16.55. Схемы осколочных цилиндров: открытый тип (а); закрытый тип (б)
16.5. Стандартные осколочные цилиндры
1. Основные типы и параметры стандартных осколочных цилиндров
Схемы и пропорции осколочных цилиндров.
Стандартные осколочные цилиндры предназначены для исследования дробимо-
сти материала оболочек боеприпасов (главным образом сталей) и для определения
метательно-дробящих свойств ВВ [16.64].
Модификация используемых цилиндров сводится к основным типам представ-
представленным на рис. 16.55. Цилиндры открытого типа (см. рис. 16.55 а) получили
более широкое распространение, что обусловлено, с одной стороны, простотой их
изготовления, а, с другой — физически более однородным спектром.
Основным недостатком открытых цилиндров считается наличие открытых
торцев, приводящее к значительной осевой разгрузке продуктов детонации, а
следовательно, и к неравномерному дроблению цилиндра по его длине. Кроме
того предполагается, что свободное торцевое истечение сильно сказывается на
действии ВВ с затянутым энерговыделением, к которым относится большинство
современных смесевых ВВ, содержащих алюминиевую пудру. В этом случае тор-
торцевая разгрузка может приводить к неполному разложению ВВ в торцевых зонах
заряда, а следовательно, к значительному искажению моделируемого процесса. В
работе [16.65] с помощью интерферометрического метода Фабри-Перо показано,
что составы с 5.. .10% содержания алюминия полностью реагируют в течении
12 мкс, тогда как составы с 20% содержанием алюминия реагируют не полно-
полностью. Применение подгрузочных зарядов, расположенных на торцах, увеличивает

144
16. Осколочное действие взрывных систем
6,35,
п
111
050,8^
^063,
6,35
в»»
5
3
\
6,4
о
1 1
; Я
6,35
1
!>
b)	c)	d)
Рис. 16.56. Унифицированные осколочные цилиндры США
расход ВВ на опыт, ограничивает возможность их проведения на лабораторных
установках, вредно с экологической точки зрения, но, как показывают расчеты, не
устраняет полностью торцевых эффектов.
Схема F (см. рис. 16.556) морфологически наиболее близка к схеме реальных
конструкций. При изготовлении цилиндра прессовыми операциями она позволяет
наиболее полно воспроизводить особенности структуры и анизотропии металла.
Недостаток схемы G, а отчасти и схемы F заключается в том, что в зонах Q и
R дробление цилиндра происходит не под действием контактной нагрузки ПД, а
под действием ослабленного импульса, передаваемого через донья цилиндра, т. е.
физика дробления этих зон меняется.
Этот недостаток устранен в схеме Н, где осколки доньев (в случае их дробле-
дробления) полностью отделяются от осколков спектра цилиндра.
Характерные типы унифицированных цилиндров открытого типа, используе-
используемых в зарубежных исследованиях показаны на рис. 16.56, их основные характери-
характеристики приведены в табл. 16.29.
Основными безразмерными параметрами (см. параграф 16.3. 1), определяю-
определяющими геометрию цилиндра, являются относительная толщина стенки 5d = So/do
и удлинение камеры Aq = L0/da. Диапазон изменения 5а в конструкциях обычно
составляет 0,05.. .0,20 A/20.. .1/5 ).
При Sd > 1/4 реализуется пространственно-определенное разрушение, при
котором визуально можно определить поясную принадлежность каждого осколка
основного спектра.
Рациональный ряд значений 8d, состоящий из девяти членов вида 5а = 1/3, 1/4
..., 1/п (п — целое число) может быть получен суммированием трех параметри-
параметрических рядов (по три члена в каждом) со знаменателем прогрессии Щ = 2 и
основаниями Sd = 1/20, 1/16, 1/12. Этот ряд представлен в табл. 16.30, где также
даны значения: хо = ^о/^о = 1 - 2Sd, <Vao = A - Хо)/хо = <W@, 5 - 5d), коэф-
коэффициенты нагрузки /3 = ро@,5 — JdJ/Go^d(l ~ ^d))? коэффициенты наполнения

16.5. Стандартные осколочные цилиндры
145
Таблица 16.29
Основные унифицированные цилиндры США
Организация
МО США
РА
AMMRC
NOL
NSWC
d'o
1,0
2,5
2,5
4,75
d0,
мм
25,4
63,5
63,5
120,7
d'a
0,75
2,0
2,0
3,0
da,
MM
19,05
50,8
50,8
76,2
S'o
0,125
0,25
0,25
0,875
So,
MM
3,175
6,35
6,35
22,25
L'o
2,0
5,0
9,0
8,0
MM
50,8
127,0
228,6
103,2
So
1/8
1/10
1/10
1/5,43
Ao
2,67
2,5
4,5
2,67
Mo,
г
88,4
1137
2045
10966
Источник
[16.66]
[16.48]
[16.67]
[16.68]
РА — Пикатиннский арсенал; AMMRC — Американский исследователь-
исследовательский центр по механике и материалам; NOL — Морская артиллерийская
лаборатория; NSWC — Морской центр надводного оружия.
сечения ? = /3/A + /3), значения начальных скоростей vq = {D/2)^{Ct/{2 — ?))
(принято ро = 1700 кг/м3, 7о = 7850 кг/м3, DQ = 8200 м/с). Удлинение цилиндра
Таблица 16.30
Изменения характеристик цилиндров в зависимости от относительной толщины
стенки
sd
Хо
5о/ао
Р
С
г>о, м/с
1/20
0,900
0,111
0,923
0,480
2304
1/16
0,875
0,143
0,707
0,414
2095
1/12
0,833
0,200
0,492
0,330
1823
1/10
0,800
0,250
0,385
0,278
1647
1/8
0,750
0,333
0,278
0,218
1434
1/6
0,667
0,500
0,173
0,148
1159
1/5
0,600
0,667
0,122
0,109
984
1/4
0,500
1,000
0,072
0,067
763
1/3
0,333
2,000
0,027
0,026
471
можно охарактеризовать двумя показателями:
удлинением заряда Ao = Lo/da = Lq/2uq.
удлинением цилиндра Лц = L/do = L/2bo.
Эти две величины связаны соотношением:
Ац = Хо(Ао + ft) = A - 2*d)(A0 + ft),
где h = h^/da — суммарная относительная толщина доньев (для открытой схемы
ft = 0).
Молено ввести также показатель удлинения меридионального сечения стенки
цилиндра А^ = Lq/^o, который имеет существенное значение при построении
расчетных сеток для численного решения двумерных осесимметричных задач о
взрывном расширении цилиндра.
После введения безразмерных параметров Sd и Ао, А^, Ац построим общую мор-
морфологическую матрицу для цилиндров. Для открытых цилиндров она приведена
в табл. 16.31.
Каждая ячейка таблицы 16.31 содержит некоторый набор значений Sd (на-
(например, Sd = 1/12, 1/8, 1/6). Изменение Sd может быть достигнуто вариацией

146
16. Осколочное действие взрывных систем
одного из радиусов ао, &о ПРИ фиксированном значении другого радиуса либо при
фиксированной толщине 8$.
Комбинация указанных
вариантов построения по-	Таблица 16.31
перечных сечении и удли-	Морфологическая матрица для открытых
нений дают девять воз-	цилиндров
можных схем формирова-
формирования цилиндра открытого
типа. Ячейки I, V, IX, рас-
расположенные по диагонали
(см. табл. 16.31), соответ-
соответствуют не только подоб-
подобным конфигурациям, но
и одинаковым размерам
заряда, внешнего контура
цилиндра и его меридио-
меридионального сечения.
Вариант 5 о = const
(ячейки VII, VIII, IX) явля-
является наиболее трудным для
экспериментальной практики, так как имеет место наиболее сильное изменение
объема заряда при изменении 8^- Например, для схемы VII соответствующая
зависимость имеет вид:
Подобие
Подобные заряды
Lq = 2aoAo
Подобные внешние
контуры Lo = 2&оАц
Подобные
меридиональные
сечения цилиндра
Lq = 5q\s
а0 = const
bo = var
I
II
III
bo= const
a0 = var
IV
V
VI
So = const
a0 = var
VII
VIII
IX
г-= 7
= '-X,dl = ^
В принятом диапазоне 5 a = 1/12...1/6 объем заряда при 8 о = const увеличива-
увеличивается в 6,25 раз. Большой диапазон масс зарядов усложняет унификацию экспери-
эксперимента (однотипная защита, стандартные безопасные расстояния для аппаратуры,
улавливатели осколков и т.п.).
Схемы с фиксированным наружном диаметром с/0 = 260 (IV, V, VI) имеют ряд
технико-методических преимуществ, в том числе:
1)	появляется возможность построения кодировочных сеток с фиксированной
длиной ячейки по окружности;
2)	упрощается техника баллистических испытаний цилиндров;
3)	упрощается проведение экспериментов, поскольку в качестве элемента из-
измерительной базы используется внешняя поверхность цилиндра (например,
контактный и емкостный методы измерения скорости метания);
4)	упрощаются испытания в улавливающей камере, при которых исходной вели-
величиной для расчета размеров ловителя, в том числе диаметра его воздушной
полости, служит внешний диаметр цилиндра.
Основные преимущества схем с фиксированным внутренним диаметром da (ячей-
(ячейки I.. .III):
1) отсутствие масштабного эффекта вследствие неполноты детонации в наруж-
наружном слое заряда ВВ;

16.5. Стандартные осколочные цилиндры
147
15, мм
2)	отсутствие МЭ по ширине ступеньки скольжения на внутренней поверхности
цилиндра;
3)	возможность унификации операций снаряжения и прессового оборудования
для этих целей;
4)	возможность унификации технологической оснастки при изготовлении ци-
цилиндров, в частности оправок, для раскатки и поперечно-винтовой прокатки.
Аналогичное рассмотрение вариантов по удлинениям совместно с вышеприведен-
вышеприведенным приводит к выводу, что наиболее перспективной для унификации является
схема I (da = const, Lo = const).
Оптимальное удлинение камеры Aq = L0/da
определяется из условия реализации макси-
максимальной длины первичного осколка с целью
выявления склонности металла корпуса к саб-
леобразованию, то есть к образованию длин-
длинных осколков, в том числе и осколков с дли-
длиной, равной длине цилиндра («полос»).
Для определения границ Aq проводились
подрывы цилиндров с внутренним диаметром
da = 25мм, толщиной стенки 5 о = 6,25 мм
Ed = So/do = 1/6), толщиной дна и крышки
12,5 мм (/гк = /гд = 0,5), изготовленных из
сталей 20 и 60. Варьировалась длина камеры
Lo, а, следовательно, и удлинение камеры
Ао = Lo/da. В каждом подрыве определялось
среднее значение /5 для выборки 5 наиболее
длинных осколков спектра. Результаты экспе-
эксперимента представлены на графике (рис. 16.57)
(О — сталь 20, А — сталь 60). Для обеих сталей кривые /5 = /(^о) имеют
максимум при Lo = 100 мм, то есть при Aq = 4. Наличие максимума объ-
объясняется тем, что с увеличением длины цилиндра склонность к разрушению
образовавшихся «полос», то есть осколков с длиной, равной длине цилиндра,
непрерывно возрастает. Это объясняется как статистическим накоплением в
осколке опасных дефектов, так и возрастанием вероятности излома длинного
осколка при внедрении его в тормозящую среду ловителя. Допустимые границы
отклонения Aq = 4 ± 0,2 устанавливаются из анализа взаимодействия систем
продольных трещин [16.30, 16.64]. Это отношение защищено патентом №2025646
РФ [16.69]. В [16.64] обоснована также величина h/da = 0,5 относительных толщин
доньев. Для указанных цилиндров введено обозначение RSFC (Russian Standard
Fragmenting Cylinder) [16.95].
Размеры цилиндров
В соответствии с ГОСТ 6636—69 параметрический ряд цилиндров должен быть
организован по принципу геометрической прогрессии, при этом устанавливается
четыре основных ряда нормальных линейных размеров (Ra5, RalO, Ra20, Ra40),
для которых знаменатели геометрической прогрессии Щ соответственно состав-
составляют: 101/5 = 1,5849 « 1,6; 101/10 = 1,2589 « 1,26; 101/20 = 1,1220 « 1,2;
10V40 = 1,0593 « 1,06.
Обычно используется ряд RalO, включающий следующие 11 значений внутрен-
внутреннего диаметра da: 20; 25; 32; 40; 50; 63; 80; 100; 125; 160; 200мм. Отношение масс
цилиндров /ii в соседних градациях точного (неокругленного) параметрического
0 12 3 4 5
Рис. 16.57. Зависимость средней дли-
длины осколка выборки пяти наиболее
длинных осколков от длины цилиндра

148	16. Осколочное действие взрывных систем
ряда со знаменателем Щ:
что при U = 1,2589 дает значение /ii = 1,995 ~ 2. Значение /ii « 2 обеспечивает
важное преимущество ряда RalO — возможность пропорционального изменения в
определенном диапазоне границ массовых групп при сохранении фиксированных
границ этих групп, принятых в практике.
В качестве основного выбран цилиндр с внутренним диаметром da = 40 мм.
Этот выбор обусловлен следующими соображениями:
1)	согласно результатам одномерного моделирования при da = 40 мм, 5d = 1/6
в средней по толщине зоне стенки цилиндра реализуется удельный им-
импульс растяжения ц = 5 ГПа-мкс, достаточный для образования разрывно-
волновой зоны, что позволяет проверить на цилиндре действие разрывно-
волновых эффектов;
2)	для ряда материалов сохраняется возможность определения характеристик
механики разрушения материала цилиндра, в частности трещиностойкости
К 1С- При использовании метода изгиба цилиндрических образцов с кольце-
кольцевой трещиной на диаметр образца dr накладывается ограничение:
4^0,2,
где К\с в Н/мм3/2; ао,2 в Н/мм2; dr в мм.
Для перспективных материалов отношение -?G.c/<7o,2 может снижаться до
0,8.. .1,5, что позволяет использовать образцы, вырезанные непосредственно
из стенки цилиндра, толщиной 6,67 и 10 мм соответственно при Sj = 1/8 и
1/6. В последнем случае из стенки может быть вырезан стандартный образец
A0 х 10 х 55мм) для определения ударной вязкости ан (KCU, KCV, КСТ);
3)	ограничение снизу da ^ 40 мм вытекает из условия полноты детонации
заряда ВВ, особенно для смесевых ВВ с большим содержанием алюминиевой
пудры, перхлората калия и т.п. Известно, что при стандартном определение
бризантности В В по обжатию свинцового цилиндра (ГОСТ 5984—51) диаметр
заряда составляет 40 мм;
4)	ограничение сверху da ^ 40 мм определяется условиями подрыва основного
цилиндра в лабораторных вакуум-камерах, максимальная масса заряда ВВ
для которых обычно не превышает 400. ..500 г. Аналогичное ограничение
вытекает из условий высокоскоростной оптической съемки процесса разру-
разрушения цилиндров.
Длина камеры основного цилиндра и соответственно открытого цилиндра
составляет Lg = 160 мм, общая длина закрытого цилиндра L = 200 мм. Внеш-
Внешний диаметр б/д, нумерация основных цилиндров и их массы в зависимости от
относительной толщины представлены в табл. 16.32 (рис. 16.58).
Характеристики типовых ВВ, массы зарядов С и обозначения ВВ, приме-
применяемые на графиках и треугольных фракционных диаграммах, приведены в
табл. 16.33.
Важным методическим вопросом камерных испытаний является выбор нижней
границы 7715 масс отбираемых осколков. Теоретически масса т$ должна опреде-
определяться по условию включения в спектр морфологической совокупности осколков,

16.5. Стандартные осколочные цилиндры
149
дающей наиболее мелкую фракцию. Такая совокупность образуется мелкими сдви-
сдвиговыми осколками в контактной («перемольной») зоне. Принята модель сдвигового
осколка, образованного поверхностями скольжения, развивающимися под углом
45° к внутренней поверхности.
Масса осколка:
т = О,257оАдА|,
где Ад — удлинение осколка,
Ад = //As-
Ширина ступеньки сколь-
скольжения A s связана с линейной
плотностью П полос адиаба-
адиабатического сдвига (ПАС) соот-
соотношением [16.64]:
к
д
где к — относительное число
ПАС, переходящих в ступень-
ступеньки скольжения.
Многочисленные измерения
ширины ступенек скольже-
скольжения и удлинений контактных
сдвиговых осколков стандарт-	а	&
НЫХ ЦИЛИНДРОВ №12 при раз- Рис. 16.58. Стандартный осколочный цилиндр RSFC:
ЛИЧНЫХ комбинациях металл—	закрытый тип (а); открытый тип (б)
В В и их статистическая обра-
обработка показали, что нижние
доверительные пределы при доверительной вероятности 0,8 составляют для As
2,9 мм, для А^ 5,2 мм, откуда т$ = 0,249 ~ 0,25 г. Это значение и принято в
качестве массы осколков ms для основных цилиндров (da = 40 мм).
В исследованиях, проводимых в
Таблица 16.32
Нумерация и массы основных осколочных
цилиндров
США, значение ms обычно прини-
мается ms = 1 гран @,0648г).
Экспериментальные обработки спек-
спектров осколков цилиндров №12 по-
показали, что нижний доверительный
предел для осколков типа А и
верхний доверительный предел для
осколков типа В составляет соответ-
соответственно 1 и 4г. Интервал [16.1, 16.4]
содержит смесь осколков обоих ти-
типов и может рассматриваться как
средняя фракция с относительным
содержанием /ic. Мелкая фракция
т G [0,1 г] с относительным содер-
содержанием /хм включает в себя преиму-
преимущественно осколки типа В, а круп-
крупная фракция т G [4, оо) с относительным содержанием /iK — преимущественно
осколки типа А.
sd
1/12
1/10
1/8
1/6
do, мм
48
50
53,33
60
Закрытый
цилиндр
9
10
11
12
Мо, г
1065
1305
1730
2660
Открытый
цилиндр
9-0
10-О
11-0
12-0
Мо, г
695
890
1225
1975

150
16. Осколочное действие взрывных систем
Таблица 16.33
Характеристики типовых ВВ и массы зарядов
вв
тнт
A-IX-2
Октоген флег-
матизированный
ро, кг/м3
1550
1700
1750
D, м/с
6200
7900
8600
p0D2, Гпа
59,6
106,1
129,4
Pc-j, ГПа
14,9
26,5
32,4
С, г
305
336
346
Символ
о
э
•
Оценка качества дробления проводится с использованием классификационной
диаграммы, построенной для цилиндра №12 с пересчетом спектра последнего на
спектр натурных осколочно-фугасных снарядов калибра 100-152 мм с коэффици-
коэффициентом наполнения 0,15. ..0,20 в предположении, что распределение осколков по
массе подчиняется распределению Вейбулла.
Для каждой комбинации показателей цилиндра А^о,255 Мс прогнозируются па-
параметры осколочного поля снаряда и, соответственно, ущерб, наносимый одним
снарядом конгломерату целей, включающей мягкие цели, небронированную тех-
технику и легкобронированные цели.
г=1
где П^ — плотность целей данного класса на местности A/м2); Supi — приведенная
площадь поражения для целей данного класса (м2), Щ — стоимость одной цели
данного класса (у. е. с).
Построенные на плоскости (-/Vo,25~aO линии равных ущербов и заключенные
между ними зоны с достаточным приближением могут быть аппроксимированы
прямоугольными областями. Построенная на основе указанного подхода клас-
классификационная диаграмма iVo,25~Mc [16.70] представлена на рис. 16.59 (класс I
(высококачественное дробление) соответствует условиям 7Vo,25 ^ 2000, /ic ^ 0,45,
класс II (качественное дробление) — условию iVo,25 ^ 1500, fic ^ 0,4, класс III
(удовлетворительное дробление) — условию А^о,25 ^ 1500, /ic ^ 0,3), класс IV
(неудовлетворительное дробление): iVo,25 < 1000, /ic < 0,3.
Эти нормативы прошли международную апробацию [16.71]. Максимальный
прогнозируемый уровень числа 7Vo,25 для цилиндра №12 по данным [16.64] со-
составляет 3000. Пересчет результатов испытаний стандартного цилиндра №12, т.
е. числа iVo,25 на прогнозируемое число осколков 7Vo,5 Для некоторой конкретной
оболочки диаметром do с примерно той же относительной толщиной стенки и при
том же сочетании металл-ВВ, может быть проведен с помощью соотношения
где d0 в дм.
2. Численное моделирование процессов в стандартных осколочных
цилиндрах. Как уже указывалось выше (п. 16.1. 3), при формировании про-
продуктивного осколочного спектра наиболее негативную роль играет процесс разру-
разрушения оболочки продольными трещинами, движущимися по образующим цилин-
цилиндра и приводящим к образованию тяжелых длинных осколков (так называемых
«сабель»).

16.5. Стандартные осколочные цилиндры
151
500	1000	1500	2000	2500
Рис. 16.59. Классификационная диаграмма качества дробления стандартного цилиндра №12
Выявление склонности металла к «саблеобразованию» требует создания вдоль
цилиндра максимально протяженной зоны с однородным кинематически-напряженным
состоянием, в первую очередь с минимальным градиентом осевых скоростей.
 Г*-
О кшс	Ю икс	?5 мне	S0* "«	S°b
Рис. 16.60. Картина процессов расширения для закрытого цилиндра №12 без отделения дна
Рис. 16.61. Волновые процессы в стенке цилиндра

152
16. Осколочное действие взрывных систем
Таблица 16.34
Характеристики разгона по
пульсациям
ь
v, м/с
№ пульсации
1
1,033
650
2
1,1
760
3
1,166
820
4
1,25
850
С целью более детального изучения
влияния типа цилиндра (закрытый-откры-
(закрытый-открытый) и для второго типа — способа торце-
торцевой подгрузки на процесс высокоскорост-
высокоскоростной деформации и напряженное состоя-
состояние проводилось моделирование процесса
с помощью двумерной программы [17.34].
Характеристики металла и ВВ (A-IX-20)
приняты такими же, как и в п. 16.4.1.
Рассчитывались конфигурации цилин-
цилиндров, расположенные в порядке возраста-
возрастания «закрытости» схемы (схема I — откры-
открытый цилиндр со свободными торцами, схема II — открытый цилиндр с односторон-
односторонней торцевой подгрузкой, схема III — открытый цилиндр с двухсторонней торцевой
подгрузкой, схема IV — закрытый цилиндр). Во всех случаях диаметр заряда
равен 40 мм, длина осколкообразующей части цилиндра 160 мм (удлинение заряда
4), высота подгрузочных шашек 40 мм.
Картина процесса взрыва для закрытого цилиндра №12 (схема IV) без отде-
отделения дна представлена на рис. 16.60. При схождении отраженной косой ударной
волны к оси симметрии в ПД возникает второй пик давления. Схождение ударных
волн проележивается и на распределении массовой скорости вдоль оси симметрии.
Волновые процессы в стенке цилиндра (рис. 16.6^воспроизводятся детально,
уверенно просматриваются четыре пульсации волн. Время одной пульсации со-
составляет около 8 мке, протяженность зоны пульсации около 25 мм. Относитель-
Относительный внешний радиус цилиндра Ъ = b/bo, и средняя скорость стенки v к концу
соответствующей пульсации представлены в табл. 16.34.
Фронты косых ударных волн в стенке цилиндра 2D- гидрокодом воспроизво-
воспроизводятся со значительным размытием, что с одной стороны объясняется относительно
небольшим числом эйлеровых ячеек по толщине стенки B0), а с другой стороны
(для второй и последующих пульсаций) — тем, что волна сжатия SW2, возни-
возникающая при отражении от внутренней поверхности волны разрежения RW\, не
успевает трансформироваться в ударную волну. Последний вывод подтверждается
одномерным моделированием процесса на частой лагранжевой сетке C50 ячеек
по толщине сетки). В данном случае моделирование производилось по программе
HEMP для обоих известных одномерных схем нагружения (мгновенная детонация
и осевая детонация) при к = 3.
\ /
RWB
Рис. 16.62. Волновые конфигурации в дне цилиндра и схема разрушения дна; 1 — откольная
тарелка, 2 -диск лицевого откола, 3 — поверхность сдвига, 4 — кольцевой прорыв продуктов
детонации, 5 — осколки придонного кольца
После отражения ДФ от дна цилиндра, в результате сложного взаимодействия

16.5. Стандартные осколочные цилиндры
153
косых волн и прямой ударной волны, в дне формируется ударный фронт
близкий по форме к сферическому (рис. 16.62). После выхода сферического
ударного фронта на внешнюю поверхность дна возникает сферический же фронт
волны разрежения RWb- Одновременно происходит сдвиг по поверхности 3. В
результате имеет место сложная картина разрушения дна. Высокоскоростная
Г1?5,м/с
F1M?m/c
1 6 11 16 21 26 31 36
Кг1>8,м/с
1 6 11 16 21 26 31 36
11 16 21 26 31 36
Номер маркера
Рис. 16.63. Изменение кинематических характеристик в зависимости от степени «закрытости»
схемы
оптическая съемка моделей цилиндров показала, что для всех низкоуглеродистых
сталей и подавляющего большинства среднеуглеродистых сталей, в том числе
закаленных, при падении детонационного фронта на дно цилиндра происходит его
значительный пластический прогиб, а отделение дна, фиксируемое по кольцевому
прорыву продуктов детонации, происходит при времени t > 2^, где tu = Lq/D —
время пробега детонационной волны по заряду ВВ длиной Lo, (D — скорость
детонации). На фоторегистрациях (см. п. 16.1. 1) видно, что дно еще не отделено
в момент разрушения оболочки, определяемый по прорыву продуктов детонации
по всей боковой поверхности цилиндра.
Процесс взрывного разгона оболочки отслеживался с помощью «вморожен-
«вмороженных» в стенки цилиндра маркеров. Распределение условно-конечных радиальных
и осевых скоростей вдоль цилиндра показано на рис. 16.63. Значения скоростей
взяты в момент расширения данного сечения цилиндра до фиксированных зна-
значений относительных внешних радиусов Ъ = 1,5 и 6 = 1,8, условно считаемых
радиусами конца разгона для хрупких и пластических сталей соответственно.
Скорости при относительном радиусе 1,8 незначительно (на 2.. .2,5%) превышают
скорости при радиусе 1,5, взаимное расположение графиков скоростей вдоль

154
16. Осколочное действие взрывных систем
цилиндра не изменяются. Принципиальное отличие закрытой схемы состоит в
изменении хода графиков скоростей в придонной зоне (для открытых схем I—III
полные скорости к торцу понижаются, а осевые скорости быстро возрастают, для
закрытой схемы IV полные скорости повышаются, осевые скорости уменьшаются
по направлению ко дну).
С увеличением степени «закрытости» схемы осевая компонента в придонной
зоне уменьшается, но тем не менее остается значительной даже для схемы III
(двухсторонняя нагрузка). Негативное влияние большого градиента осевых скоро-
скоростей в придонной зоне на сохранность формируемых «сабель» подтверждается
экспериментально — достаточно сравненить длины осколков придонной части
закрытого цилиндра №12 (схема IV) и торцевой части цилиндра (схема II).
Результаты сравнения представлены в
табл. 16.35 (сталь 45/ТНТ).
Сравнение общих показателей кинема-
кинематической однородности схем I-IV пред-
представлено в табл. 16.36.
Здесь vmax, Vjnin — максимальная и ми-
минимальная условно-конечные скорости зон
цилиндра, (v) — средняя условно-конечная
скорость оболочки, Avz — перепад осевых
скоростей. Из таблицы и графиков следует,
что все открытые схемы создают более
жесткие условия, способствующие деле-
делению осколков по длине и в этом смысле
являются менее приемлемыми в качестве
стандартных испытательных образцов.
Таблица 16.35
Сравнение характеристик осколков
схемы II и IV
Характеристика
Максимальная длина
ОСКОЛКа, \maxi ММ
Средняя длина в вы-
выборке 5 шт наиболее
длинных осколков, мм
Макеты
II
62
51
83
67
Таблица 16.36
Общие показатели кинематической однородности
Характеристики
Ь= 1,5
Ъ= 1,8
Vmax 1 М/С
Vmin , м/с
Vmax 1 ^тгп
(v), м/с
Avz, M/c
Vmax, М/С
Vmin , М/С
Vmax / Vrnin
(v), м/с
Avz, м/с
Расчетная конфигурация
т
844
391
2,159
725
268
889
287
3,098
759
275
тт
853
533
1,60
761
228
895
556
1,61
798
216
ттт
848
526
1,612
764
208
899
554
1,623
803
192
IV
Вез отделения
дна
941
612
1,537
774
101
963
656
1,468
817
92
U отделением
дна
932
612
1,523
773
104
957
658
1,454
815
95
3. Экспериментальные данные испытаний стандартных осколочных
цилиндров. Испытания дробимости различных углеродистых и легированных
сталей в широком диапазоне изменения содержания углерода (С=0,1.. .1,1%) про-

16.5. Стандартные осколочные цилиндры
155
водились в стандартном осколочном цилиндре JV512 RSFC при стандартном наборе
ВВ, рекомендованном [16.64] (ТНТ, A-IX-2 и окфол). Испытания проводились
подрывом в осколочной камере при диаметре полости уловителя 360 мм F<io)-
Для каждой комбинации проводилось три подрыва. Определялись следующие
характеристики осколочных масс: числа осколков с массой т > 0,25, 0,5 и 1г
(^V"o.25j -No.5? -Ni,o)? Мм, Me, Мк — относительные содержания мелкой (т $J 1г),
средней A < т $J 4 г) и крупной (т > 4 г) фракций осколков. Определялись
также следующие морфологические характеристики осколков: максимальное от-
относительное удлинение Л = у 7о^3/ш (То — плотность металла), а также для
выборки 20 наиболее длинных осколков — средняя длина /20 • Для ряда комбинаций
измерялись также характеристики формы Ф, атт фракции 1-2 г. Результаты
испытаний представлены в табл. 16.37, треугольная фракционная диаграмма и
классификационная плоскость на рис. 16.64, 16.59.
Таблица 16.37
Результаты испытаний стандартных осколочных цилиндров №12
Сталь
Ст. 10
Ст.20
Ст.35
Ст.45
Ст.С-60
Ст.60С2
Ст.60С2
мнлз
Ст.40Х
Ст.45Х1
Ст.60Г2С
Ст.80Г2С @,7)
Ст.80Г2С @,9)
110Г2С
закалка с
ВВ
ТНТ
A-IX-2
ТНТ
A-IX-2
Окфол
ТНТ
A-IX-2
Окфол
ТНТ
A-IX-2
ТНТ
A-IX-2
Окфол
ТНТ
A-IX-2
Окфол
ТНТ
A-IX-2
Окфол
ТНТ
A-IX-2
ТНТ
A-IX-2
A-IX-2
A-IX-2
A-IX-2
ТНТ
A-IX-2
N0,25
515
608
547
670
1271
707
832
1304
796
934
885
1131
1456
1039
1358
1661
1017
1293
1569
626
712
683
740
1590
1912
2133
1932
2103
N0,5
382
468
423
490
874
552
670
950
604
718
684
867
1072
814
1020
1166
788
985
1136
493
514
502
669
1223
1345
1346
1295
1324
N1,0
316
348
332
362
564
383
472
588
408
520
511
617
695
588
680
710
562
670
716
360
488
378
503
873
763
645
727
627
Мм
0,05
0,10
0,06
0,12
0,27
0,12
0,16
0,22
0,18
0,20
0,15
0,18
0,24
0,16
0,25
0,35
0,16
0,23
0,28
0,09
0,11
0,11
0,12
0,30
0,33
0,49
0,40
0,53
0,09
0,11
0,10
0,12
0,28
0,16
0,21
0,33
0,20
0,26
0,26
0,35
0,42
0,32
0,42
0,45
0,30
0,41
0,45
0,21
0,23
0,20
0,23
0,46
0,50
0,45
0,51
0,42
Мк
0,86
0,79
0,84
0,76
0,45
0,72
0,63
0,45
0,62
0,52
0,59
0,47
0,34
0,52
0,34
0,20
0,54
0,36
0,27
0,70
0,66
0,69
0,65
0,24
0,17
0,06
0,09
0,05
120,ММ
65,2
52,3
59,7
49,8
43,4
53,5
47,0
38,3
49,4
42,3
46,2
44,0
38,8
43,4
40,5
38,2
42,7
42,4
41,1
51,1
43,7
60,5
46,3
38,1
37,8
36,2
46,2
40,3
Лтах
20,1
19,7
18,2
17,4
12,8
17,1
166
14,9
16,7
16,3
16,5
16,0
14,3
13,1
12,6
7,8
13,9
12,3
7,7
18,3
16,3
22,3
19,5
10,3
9,1
7,8
10,3
8,6
Ф
2,21
2,18
2,16
2,07
2,01
1,98
1,98
2,04
1,96
1,98
1,91
1,84
1,84
1,83
2,02
2,17
2,09
1,83
1,80
1,78
1,83
0~тт
7,72
6,79
7,62
6,48
6,62
5,48
6,81
7,05
6,26
5,29
5,02
4,67
5,38
4,92
6,20
6,75
7,63
4,64
4,57
4,52
5,12

156
16. Осколочное действие взрывных систем
Сталь
отпуском
110Г2С
нормализ.
с отпуском
100ХГС
закалка
с отпуском
ВВ
Окфол
ТНТ
A-IX-2
Окфол
ТНТ
A-IX-2
Окфол
N0,25
2411
2057
2345
2602
1469
1972
2187
N0,5
1337
1382
1320
1304
1068
1270
1239
Ni,0
799
727
548
452
709
664
623
0,67
0,47
0,65
0,72
0,38
0,50
Me
0,32
0,48
0,34
0,26
0,43
0,40
/iK
0,05
0,05
0,05
0,02
0,29
0,10
bo,мм
38,5
42,1
36,8
35,2
46,0
42,3
34,1
Атаж
7,9
10,1
8,2
7,4
10,3
7,8
7,7
Ф
1,82
1,80
1,92
1,87
0~mm
5,23
4,64
5,60
5,22
Оценка статистической достоверности результатов проводилась по величине
коэффициента вариации V числа осколков iVo,25 {V = sn/Nq^5i sn — выбороч-
выборочное среднеквадратическое отклонение числа осколков, Щ^5 ~~ средневыборочное
значение числа осколков). Согласно [16.56] результаты серии опытов считаются
достаточно стабильными, если коэффициент вариации не превышает 0,2. Во всех
случаях это условие выполнялось. В табл. 16.38 приведены примеры статисти-
статистических оценок для трех сталей: результаты по отдельным подрывам в группе,
средневыборочные значения 7Vo,25 с доверительными пределами при доверитель-
доверительной вероятности 0,8 и значения коэффициента вариации. Для опытных снарядных
сталей 60С2 и 110Г2С выполняется условие V < 0,1.
Таблица 16.38
Статистические оценки результатов испытаний
Сталь
С-60
60С2
110Г2С
ТНТ
N0,25
815
1061
778
951
1055
1044
1790
2043
1963
N0,25
885±168
1017±62
1932±141
V
0,174
0,056
0,067
A-IX-2
А^0,25
1374
992
1028
1322
1238
1318
2088
2304
1916
АГ0,25
1131±230
1293±52
2103±212
V
0,186
0,037
0,092
Окфол
А^0,25
1268
1697
1403
1713
1515
1479
2520
2358
2356
АГ0,25
1456±239
1569±137
2411±103
V
0,151
0,08
0,039
Группа углеродистых сталей
Механические характеристики исследованных сталей представлены в табл. 16.39.
Зависимости основных характеристик дробимости от содержания углерода (при-
(принятого номинальным значением по марке стали) представлено на графиках рис.
16.65—16.67. Зависимость числа осколков от безразмерного параметра дробления
Fo представлены на рис. 16.68.
Как видно из графиков, увеличение содержания углерода в данном диапа-
диапазоне 0,1<С<0,6% приводит к улучшению как числовых и балансно-массовых
характеристик спектра, так и характеристик формы осколков. Наиболее низко-
низкокачественное дробление имеют низкоуглеродистые (С<0,3%) стали 10 и 20 при
снаряжении ТНТ. Для этих пар имеет место четко выраженный и-бимодальный

16.5. Стандартные осколочные цилиндры
157
0,8
0,6
0,4
0,2
о
0,2
0,4
0,6
0,8
1,0
Рис. 16.64. Треугольная фракционная диаграмма. 1 — сталь 10; 2 — сталь 20; 3 — сталь 35;
4 — сталь 45; 5 — сталь С-60; 6 — сталь 60С2; 7 — сталь 60С2 МНЛЗ; 8 — сталь 40Х; 9 —
сталь 45X1; 10 — сталь 60Г2С; 11 — сталь 80Г2С @,7С); 12 — сталь 80Г2С @,9С); 13 — сталь
110Г2С (закалка с отпуском); 14 — сталь 100ХГС; заливка знака определяет вид ВВ: знак не
залит — ТНТ; залит наполовину — A-IX-2; залит полностью — окфол. Ак — серия опытов с
нормализ. сталью С-60, № 1 - ТНТ; 2 - ТНТ/А1 80/20; 3 - ТГ 40/60; 4 - A-IX-1; 5 - A-IX-2;
6 — гексоген/А1/перхлорат калия 65/20/15; 7 — окфол; 8 — октоген/А1 90/10; 9 — октоген/А1
70/30; 10 — октоген/А1/перхлорат калия 80/10/10
спектр длинных осколков сдвигового происхождения с доминирующим содер-
содержанием крупной фракции (/iK соответственно 0,86 и 0,84). Неудовлетворитель-
Неудовлетворительное дробление при данных комбинациях металл-ВВ подтверждается наличием в
спектре сверхдлинных осколков с относительной длиной Л > 15. Относительные
максимальные длины осколков / = /тОж/-^0 составляют соответственно 0,92 и
0,88, т.е. процесс приближается к режиму образования «полос» — осколков с
длиной, равной длине камеры цилиндра. Характерное для низкоуглеродистых
сталей разрушение сдвигом почти по всей толщине цилиндра приводит к большому
значению относительного периметра ?} = 5,6. В отдельных осколках значение ?}
достигало 6,0-6,5. Для сравнения укажем, что для сечения ромбической формы
с острым углом 45° величина Г2 составляет 4,76. О ярко выраженном неравно-
неравномерном характере дробления свидетельствует также большая величина (г = 0,70)

158
16. Осколочное действие взрывных систем
Таблица 16.39
Механические свойства углеродистых сталей
Сталь
10
20
35
45
С-60 норм.
С-60 улуч.
сгО;2, МПа
390
500
520
560
670
920
сгв, МПа
510
630
550
680
790
1020
E, %
33
19
4
22
23
18
Ф,%
62
52
27
47
39
47
ан,КДж/м2
1300
1270
420
670
400
400
НВ
174
178
254
187
217
285
N0,25
No,5
Рис. 16.65. Зависимость числа осколков от содержания углерода: масса больше 0,25г (а); масса
больше 0,5 г (б)
коэффициента корреляции г = cov (Bl) /\/DbDi между величинами Bui как
зависимыми компонентами случайного вектора (В, Z), (cov(i?, /) — ковариация
(корреляционный момент) случайных величин В, /; Db-> Di — дисперсии этих
величин). Уравнение регрессии имеет вид / = 12,75 + 3,94 G, см; В, см2).
Поскольку для зависимых величин В, I математическое ожидание объема осколка
определяется соотношением
< V >=< В >< I >+соу(Б,/),
где < В >, < I > — соответственно математические ожидания площади попереч-
0,4
0,3
032
ОД
О
С, %
0,2 0,4 0,6
0,9
0,8
0,7
0,6
0,5
0,4
0,3
о
с, %
0,2 0,4 0,6
Рис. 16.66. Зависимость относительного содержания фракции от содержания углерода: средней
(а); крупной (б)

16.5. Стандартные осколочные цилиндры
159
а)
ОД 0,2 0,3 0,4 0,5 0,6	0,1 0,2 0,3 0,4 0,5 0,6
Рис. 16.67. Зависимости характеристик формы осколка от содержания углерода: средней длины
осколка в выборке наиболее длинных осколков (а); параметра формы осколка (б)
1500
1000
500
^0,25, ^1,0
7
' ТА
¦^1,0
О	50	100	150
Рис. 16.68. Зависимость числа осколков от безразмерного параметра дробления
ного сечения и длины осколка, то наличие положительной ковариации неблаго-
неблагоприятно влияет на осколочный спектр, увеличивая средний объем осколка.
Среди среднеуглеродистых сталей @,3<С<0,7%) наибольший интерес пред-
представляют характеристики дробления стали С-60, являющейся основной отече-
отечественной штатной снарядной сталью [16.62]. Сталь С-60 по химическому составу
соответствует конструкционной стали ст. 60, но имеет расширенные пределы по
фосфору и сере.
Как следует из данных табл. 16.37, осколочные характеристики стали С-60 по
современным нормативам являются неудовлетворительными. Это объясняется как
низкокачественным крупным спектром, так и плохой формой осколков. Из класси-
классификационной диаграммы А^о,25~/^с (рис. 16.59) следует, что комбинация С-60/ТНТ
попадает в область неудовлетворительного дробления (класс IV), а основная
комбинация C-60/A-IX-2 находится вблизи нижних границ удовлетворительного
дробления (класс III). Даже при снаряжении окфолом сталь С-60 не попадает в
область качественного дробления (класс II), очень велики относительные массы

160	16. Осколочное действие взрывных систем
/iK крупной фракции (для ТНТ и A-IX-2, соответственно 0,59 и 0,47). Низкокаче-
Низкокачественная форма осколков выявляется как по данным выборки крупных (основных)
осколков (аномально высокое значение Лтож = 16 для A-IX-2, соответствующее
классу сверхдлинных осколков, /20 = 44мм, В20 = 21мм2, Г? = 5,1), так и по
характеристикам формы осколков мелкой фракции 1—2 г (Ф = 1,96, сгтгп = 6,26).
Кремнистые стали
Испытывались стандартные цилиндры из стали 60С2, полученной отливкой в
изложницу и методом непрерывного литья заготовок (МНЛЗ). Сталь относится
к классу рессорно-пружинных сталей и содержит 2% кремния, увеличивающего
хрупкость стали. Использование кремнистой стали 60С2 в осколочных боепри-
боеприпасах защищено патентами №№2079099, 2095740 РФ. В США для производства
осколочно-фугасных снарядов используется кремнистая сталь того же состава,
имеющая индекс AISI-9260.
Кремнистая сталь при невысокой стоимости легирующего элемента обеспе-
обеспечивает стабильное, хотя и не очень высокое преимущество перед сталью С-60,
как по массово-численным характеристикам спектра, так и по характеристикам
формы. Обеспечивается прирост числа осколков 7V"o.25 Для ТНТ, A-IX-2 и окфола
соответственно на 17, 20 и 14%, а относительного содержания средней фракции —
соответственно на 23, 20 и 12%.
Хромистые стали
Хромистые стали 40Х и 45X1 испытывались при двух типах ВВ — ТНТ
и A-IX-2. Сталь 45X1, как и сталь С-60 является штатной снарядной сталью.
Присутствие хрома в стали приводит к подавлению радиальных трещин отрыва
и преимущественному развитию сдвигового разрушения, что в свою очередь
повышает относительный периметр сечения до величины Г? = 6-6,5. Именно в
этих сталях отмечается разрушение с образованием пластин. Отмечается весьма
высокое содержание крупной фракции (для стали 45X1 при снаряжении ТНТ и
A-IX-2 соответственно 0,69 и 0,65), сравнимое с соответствующими величинами
для низкоуглеродистых сталей, и значительное уменьшение числа осколков iVo,25
(на 30-35%) по сравнению со сталью С-60.
Кремнемарганцовистые стали
Испытывались стали с легирующей группой Г2С при изменении содержания
углерода в пределах 0,6—1,1%. Эта группа сталей в настоящее время вызывает при-
пристальный интерес. Еще в 1970 году фирмой «Бетлехем стил корпорейшен» США
была запатентована высокоуглеродистая заэвтектоидная кремнемарганцовистая
сталь HF-1 с цементитно-перлитной структурой (патент №3547032 США), по
составу примерно соответствующая отечественной индексации 110Г2С. Эта сталь
применялась в производстве ОФС калибров 155 мм (ХМ708) и 203 мм (ХМ711,
ХМ762), а также боевых частей активно-реактивных снарядов калибров 155 мм
(М549) и 203 мм (ХМ560). Существенным недостатком стали HF-1 (High Fragmen-
Fragmentation) является ее низкая пластичность, из-за чего в ряде случаев не обеспечива-
обеспечивается необходимые ствольная и ударная прочность. Кроме того, эта сталь требует
сложной дорогостоящей изотермической обработки. Еще более существенным не-
недостатком этой стали, в особенности при высокобризантном снаряжении, является
снижение относительной массы средней фракции.
Т. Ф. Волыновой и В. А. Одинцовым в результате многолетних исследований
было установлено, что одним из наиболее перспективных материалов для из-
изготовления корпусов ОФ снарядов является эвтектоидная сталь 80Г2С [16.72]-
[16.74]. Теоретическим основанием этой разработки явилось предложенная автора-
авторами концепция взрывного разрушения сталей, близких по составу к эвтектоидным.
При эвтектоидном составе @,83%С) сталь имеет чисто перлитную структуру в
виде тонких пластинок цементита, равномерно распределенных в основной массе

16.5. Стандартные осколочные цилиндры	161
феррита (рис. 16.69).
Рис. 16.69. Взаимодействие косой волны разрежения с колониями перлита различной ори-
ориентации: 1 — корпус; 2 — заряд ВВ; 3 — детонационный фронт; 4 — продукты детонации;
5 — фронт косой ударной волны; 6 — фронт волны разрежения; 7—9 — колонии перлита с
цементитными пластинами, ориентированными соответственно параллельно, перпендикулярно
и под произвольным углом к фронту волны разрежения; 10 — трещина хрупкого отрыва
Угол ориентации пластинок х является случайной величиной, распределенной
по некоторому закону с плотностью /(х). Следовательно, взаимодействие с ме-
металлом косых ударных волн и волн разрежения, возникающих в стенках оско-
осколочного корпуса при скольжении вдоль него детонационной волны, также будет
иметь локально-случайный характер, что приведет к появлению распределенных
очагов разрушения, роль которых в до- и заэвтектоидных сталях выполняют со-
соответственно перлитные и цементитные включения. Данный процесс реализуется
в области, близкой к эвтектоидному составу, при содержании С 0,7.. .0,9%. В
дальнейшем этот состав обозначается как сталь 80Г2С.
Марганец в количестве 1,5-2,5% по массе при содержании в стали 0,7.. .0,9%С
обеспечивает необходимую прочность (его,2 > 500 МПа) за счет упрочения кар-
карбидной составляющей в перлитной матрице. Изменение указанного интервала в
сторону уменьшения содержания Мп сопровождается разупрочнением стали и
ухудшением дробления вследствие образования в структуре феррито-перлитной
смеси и появления ферритной составляющей на границах зерен. При содержании
Мп более 2,5% в структуре стали образуется мартенсит, что приводит к повы-
повышению прочности, твердости и снижению технологичности при температурно-
деформационном переделе.
Кремний в количестве 0,8.. .1,2% упрочняет ферритную составляющую пер-
перлитной матрицы и снижает ее пластичность. При содержании Si менее 0,8%
уменьшается прочность стали. При содержании более 1,2% кремний стабилизирует
феррит, повышает твердость стали, температуру нагрева и время выдержки при
горячей пластической деформации, снижает технологичность.
В соответствии с термокинетической диаграммой [16.75] выбираются такие
режимы горячей деформации и термической обработки, чтобы обеспечить обра-
образование перлита с оптимальным размером цементитных пластинок.
Опытная сталь выплавлялась в открытой индукционной печи (две плавки).
Состав плавок представлен в табл. 16.40. Механические свойства металла пред-
представлены в табл. 16.41.

162
16. Осколочное действие взрывных систем
Таблица 16.40
Состав опытных плавок стали
80Г2С, %
Таблица 16.41
Механические свойства стали
80Г2С (опытные плавки)
Номер
плавки
1
2
С
0,75
0,87
Si
0,85
0,86
Мп
1,57
1,58
S
0,005
0,004
Р
0,005
0,005
Номер
плавки
1
2
°,2,
МПа
536
640
сгв,
МПа
1080
1160
6,%
15
12
30
21
2200
2000
1800
1600
А
110Г2С
80Г2С
(плавка 2)
80Г2С
плавка 1)
60Г2С
0,45
0,40
0,35
1400"	<	>	>	> 0,30
0,6	0,8	1,0 С, %	0,6	0,8	1,0 С9%
Рис. 16.70. Зависимости числа осколков и массовой доли средней фракции от содержания
углерода
У испытанных составов ста-
стали предел текучести не ме-
менее 500 МПа, что удовлетворя-
удовлетворяет требованиям по ствольной
и ударной прочности корпусов
артиллерийских ОФС. Значе-
Значение относительного сужения
ф в момент разрыва были
не ниже 15%, что обеспечива-
обеспечивало достаточную устойчивость
против хрупкого разрушения
в момент выстрела и удара о
преграду.
Компьютерное моделиро-
моделирование процесса высокоскорост-
высокоскоростной деформации стандартно-
стандартного осколочного цилиндра №12
RSFC под действием продук-
продуктов детонации подтвердило,
что в данном диапазоне из-
изменения предела текучести распределение масс и скоростей по углам разлета
практически не зависит от этой величины.
0,50 -
0,45
0,425
0,40
0,35™
0,30
-
/* у.
/# v
/60Г2С^
I
80Г2С (плавка 1)
•а.
ц — q 50™0 590~6(iV
vJ
• 80Г2С
^(плавка 2) I
п
110Г2С
0
i
1500 1750 1850 2000 2180
2500
^0,25
Рис. 16.71. Условия реализации нормального дробления
материалов для корпусов осколочных боеприпасов с уче-
учетом статистического рассеивания

16.5. Стандартные осколочные цилиндры	163
Оценки допустимых пределов по содержанию С в предлагаемой стали проведе-
проведены на основании анализа результатов испытаний цилиндров №12, изготовленных
из трех сталей с одной и той же легирующей группой Г2С B% Мп, 1% Si).
Экспериментальные зависимости TVo.25 = /(С) и Me = /(С) представлены на
рис. 16.70. С увеличением содержания С число осколков монотонно возрастает, а
относительное содержание средней фракции имеет максимум при С~ 0,75%. Сдвиг
местоположения максимума в меньшую сторону от номинального эвтектоидного
состава @,83% С), по-видимому, объясняется снижением фактического содержа-
содержания С в эвтектоиде за счет влияния легирующих элементов Мп и Si. Зависимость
/ic = /(^Vo.25)? таким образом, является соотношением, заданным параметрически,
которое может быть аппроксимировано зависимостью:
/ic = 0,50 ... 0,59 • 10GV0 25 - 1850J.
Рассматривая область нормального дробления как совокупность доверительных
интервалов 7Vo.25 = 1750=Ь250 для восходящей ветви кривой и /ic = 0,425=Ь0,025 для
нисходящей ветви соответствующие условия реализации нормального дробления
с учетом статистического рассеивания примем в виде:
^0.25 > 1750; /ic ^ 0,425.
Кривая /ic = /(iVo.25) пересекает указанные вертикаль и горизонталь в точках
JVo.25 = 1750 и 2180 (рис. 16.71), откуда с использованием кривой 7Vo.25 = /(С)?
(рис. 16.70) и округлением до десятых долей процентов получаем:
С™„ = 0,7%, Стах = 0,9%.
Изменение морфологических характеристик дробления и характеристик формы
осколков в зависимости от содержания С для сталей с легирующей группой Г2С
представлены на рис. 16.72.
Испытания метательно-дробящих свойств В В проводились с помощью подры-
подрывов стандартных цилиндров №12 RSFC, изготовленных из нормализованной стали
С-60. Испытывались составы на основе ТНТ, гексогена и октогена, включающие
в качестве окислителя перхлорат калия, а в качестве горючего — алюминиевую
пудру [16.71, 16.76, 16.77]. Характеристики испытуемых составов представлены в
табл. 16.42,
Для каждого состава проводилось два подрыва. Дополнительно к вышеуказан-
вышеуказанным параметрам формы основных осколков определялась максимальная длина
осколка в спектре 1шах и средняя площадь поперечного сечения В20 по выбор-
выборке 20 шт. наиболее длинных осколков. Результаты экспериментов приведены в
табл. 16.43. В первом столбце приведено отношение чисел осколков 7Vo,25 ПРИ
снаряжении цилиндра данным составом и ТНТ. Для величин iVo?25j Мс> Vn^ Imax
и i?2o строились корреляционные зависимости их от скорости детонации D (м/с).
Они имеют следующий вид (г — коэффициент корреляции)
jV0>25 = -1183,4 + 0,342L> r = 0, 95
fic = -0, 538 + 1, 23 • 10~4D r = 0, 99
Viv = 0,4 - 4, 3 • Ю~5?>	г = 0, 82
Imax = 296, 5-0,029D	г = 0, 92
Б20 = 66, 5 - 5,62 • 10-3?> г = 0, 94.

164
16. Осколочное действие взрывных систем
/20, мм
38
37
36
35
\
h
Л
Л/20
/
^тпах
10
9 1,75
1,65
i
V
л
\
ЧучФ
Г
сттт
4,60
4,55
4,50
0,4 0,6 0,8 1,0 С,%	0,4 0,6 0,8 1,0 С, %
Рис. 16.72. Изменения средней длины выборки крупных осколков I20, максимального удлине-
удлинения \maxi параметра формы Ф и перепада миделей crmm осколка в зависимости от содержания
углерода для сталей с легирующей группой Г2С
Таблица 16.42
Исходные характеристики взрывчатых составов
и/и
1
2
3
4
5
6
7
8
9
10
Состав
ТНТ
ТНТ/алюминий80/20
ТНТ/гексоген 40/60
Гексоген флегматизированный
Гексоген/алюминий 80/20
Гексоген/алюминий/перхлорат калия
65/20/15
Октоген флегматизированный
Октоген/алюминий 90/10
Октоген/алюминий 70/30
Октоген/алюминий/перхлорат калия
80/10/10
Ро,
г/см3
1,59
1,80
1,67
1,65
1,81
1,79
1,73
1,80
1,91
1,85
А
м/с
6800
6600
7700
8300
8200
7400
8450
8400
7900
8100
ккал/кг
1040
1530
1160
1190
1565
1720
1215
1450
1750
1750
а
0,364
0,296
0,502
0,531
0,43
0,494
0,559
0,481
0,370
0,432
Qv — удельная теплота взрыва, а — кислородный коэффициент.
Строились также корреляционные зависимости указанных величин от параметра
PoD2, но оказалось, что они являются более слабыми.
Число iVo?25 линейно возрастает с увеличением скорости детонации D, коэф-
коэффициент вариации Удг линейно убывает. Последнее указывает на то, что с увели-
увеличением интенсивности нагрузки процесс дробления становится более стабильным.
Число осколков 7Vo,5 и TVio также монотонно возрастают с увеличением скорости
детонации D. Отношение ^0,5/^0,25 и ^1,0/^0,25 изменяются в небольших преде-
пределах и в среднем составляют соответственно 0,71 и 0,45. Все полученные осколочные

16.5. Стандартные осколочные цилиндры
165
Таблица 16.43
Результаты экспериментов
п/п
1
2
3
4
5
6
7
8
9
10
V
1,00
0,74
1,26
1,22
1,24
1,08
1,44
1,34
1,24
1,17
Vn
0,02
0,12
0,01
0,06
0,06
0,09
0,04
0,01
0,10
0,04
/iM
0,25
0,15
0,29
0,30
0,24
0,21
0,33
0,30
0,29
0,26
Me
0,32
0,25
0,44
0,48
0,47
0,38
0,49
0,51
0,44
0,46
/iK
0,43
0,60
0,27
0,22
0,28
0,41
0,18
0,19
0,27
0,28
1>тах ?
MM
84,5
112,8
74,6
48,1
61,3
109,0
57,0
59,0
56,0
71,7
15,5
18,0
16,1
14,0
11,7
20,4
14,0
14,9
10,0
17,0
bo,
MM
49,6
55,0
44,2
41,6
41,0
41,2
44,2
38,9
43,1
43,8
?>20,
мм2
25,0
32,2
21,7
18,0
21,1
24,7
18,1
19,5
24,3
23,4
спектры имеют унимодальный характер. Фракционный состав осколочной массы
также изменяется с изменением скорости детонации. Наиболее тесным образом
от скорости детонации зависит относительное содержание средней фракции /ic.
Эта связь близка к функциональной (г = 0,99). Полученные экспериментальные
точки /jLm—{ic внесены в общую треугольную фракционную диаграмму (рис. 16.64).
Расположение экспериментальных точек для смесевых В В у вершины кривой
1лс = /(/iM) указывает на то, что составы осколочных масс близки к оптимальным.
Максимальное значение /ic составило 0,51 (октоген/алюминий 90/10).
Образование осколков при нагружении смесевыми ВВ происходило по схеме,
характерной для среднеуглеродистых сталей: хрупкий отрыв радиального направ-
направления во внешней зоне стенки — разрушение сдвигом по плоскостям скольжения
во внутренней (контактной) зоне стенки. Максимальные длины осколков для всех
составов изменялись в диапазоне 48.. .112 мм, а удлинения — в диапазоне 10.. .20.
Наличие в спектре сверхдлинных осколков с удлинением Л > 15 [16.3] указывает на
сравнительно низкокачественный характер дробления стали С-60. Максимальная
длина осколка /тож стабильно убывает с ростом скорости детонации (г = 0,92).
Средняя площадь поперечного сечения осколка В20 для выборки 20 наиболее
длинных осколков колеблется в довольно узких пределах и составляет в среднем
21,5 мм2. Убывание площади В20 с ростом скорости детонации D описывается
линейной зависимостью, близкой к функциональной (г = 0,94).
Таким образом, для исследованных смесевых ВВ большинство характеристик
дробления, в первую очередь число осколков 7Vo,25 и содержание средней фракции
/ic, связано достаточно тесными линейными корреляционными зависимостями со
скоростью детонации. Одно из возможных объяснений этого факта состоит в
том, что основная характеристика, определяющая процесс дробления цилиндра —
число по окружных делений на крупные осколки типа А, теоретически линейно
зависит от скорости детонации. Этот вывод можно получить, используя извест-
известные соотношения: формулу Покровского-Мотта для числа окружных делений
по = 2ttvq/v* (vq — радиальная скорость стенки цилиндра в конце разгона, v* —
модуль критической векторной разности скоростей на концах осколка) и формулу
Станюковича-Джерни для начальной скорости осколков vq = Dy/]3/ B\/2) (/3 —

166
16. Осколочное действие взрывных систем
отношение массы ВВ к массе цилиндра), что приводит к выражению:
пв =
в, =
y/2'
С другой стороны, наличие непосредственной связи скорости детонации с
характеристиками дробления цилиндров может быть объяснено влиянием этой
скорости как кинематического параметра, определяющего процесс накапливания
разрушения в зоне, расположенной между фронтом детонации и фронтом маги-
магистральных трещин, движущимся в общем случае со скоростью vc < D.
4. Исследование масштабного эффекта при осколкообразовании с
помощью стандартных осколочных цилиндров. Экспериментальное ис-
исследование МЭ проводилось с применением стандартных осколочных цилиндров,
имеющих внутренний диаметр da = 40 мм (№ 12) и 50 мм (№16); удлинение
камеры До = LQ/da = 4, где Lo — длина заряда ВВ; относительную толщину
стенки Sd = So/do = 1/6. Цилиндры изготовлены механической обработкой из
нормализованной снарядной стали С-60 [16.78].
Параметры стандартных цилиндров приведены ниже:
Цилиндр
Внутренний диаметр, мм
Наружный диаметр, мм
Толщина стенки, мм
Масса, г
Длина заряда ВВ, мм
Объем камеры под заряд ВВ, см
№12
40
60
10
2660
160
200
№16
50
75
12,5
5195
200
390
Отношение линейных размеров L = 50/40 = 1,25, отношение объемов камер и
масс цилиндров L3 = 1,253 = 1,95.
Цилиндры снаряжали четырьмя различными составами ВВ, характеристики
которых представлены в табл. 16.44. В таблице Qv — удельная теплота взрыва,
а — кислородный коэффициент.
Таблица 16.44
Характеристики взрывчатых составов
Состав
Е (гексоген/ алюминий 80/20)
F (октоген флегматизированный)
G (октоген/ алюминий 80/20)
Н (октоген/ алюминий/перхлорат
калия 70/20/10)
ро, г/см3
1,81
1,73
1,89
1,91
Д м/с
8200
8450
8300
7900
Q, ккал/кг
1565
1215
1600
1700
а
0,412
0,559
0,431
0,483
Цилиндры подрывали в бронекамере с улавливающей средой (опилками) при
диаметре внутренней полости улавливателя 6do. Границы массовых групп при
сортировке осколков цилиндра №16 относятся к соответствующим границам для
цилиндра №12 как 2:1 (табл. 16.45).
Результаты экспериментов по числам осколков в сходственных массовых груп-
группах и отношения чисел осколков ТУ,
(№16)
для каждого состава приведены

16.5. Стандартные осколочные цилиндры
167
Границы сходственных групп для цилиндров (г)
Таблица 16.45
Цилиндр
№12
№16
Номер массовой группы
I
0,25-0,5
0.5-1
II
0,5-1
1-2
III
1-2
2-4
IV
2-3
4-6
V
3-4
6-8
VI
4-5
8-10
VII
5-6
10-12
VIII
6-10
12-20
Ш61Ш2)
15'
10
5
0
I III V VII
I III V VII
I III V VII
мГИ
I III V VII
(№16)
15
10
5
• 0
Среднее
I III V VII
Рис. 16.73. Изменение чисел осколков в сходственных массовых группах при увеличении
размеров цилиндра
в табл. 16.49 и на рис. 16.73 (пунктирная линия N^ 1^1 = 1 соответствует
равенству чисел осколков в сходственных массовых группах, что наблюдается
при полном подобии процесса дробления (при отсутствии МЭ)). Во всех случаях
при увеличении размера цилиндра (при переходе от цилиндра №12 к цилиндру
№16) стабильно увеличивается число осколков в группах с малыми массами
осколков и уменьшается в группах крупных осколков, т.е. происходит несомненное
проявление МЭ.
Сравнение спектров цилиндров № 12 и 16 по балансно-массовым и морфо-
морфологическим характеристикам представлено в табл. 16.47, в которой /iM, /iC5 Мк —
соответственно содержание мелкой, средней A < т $J 4г)иB < т $J 8 г)
соответственно для цилиндров № 12 и 16) и крупной фракции; 1шах — максималь-
максимальная длина осколка в спектре; /5, ho — средние значения длин в выборке 5 и 20
наиболее длинных осколков спектра; В20 — средняя площадь сечения осколка для
выборки 20 наиболее длинных осколков спектра. Изменение фракционного состава
осколочных масс при увеличении размеров цилиндра полностью соответствует
отмеченному выше явлению перемещения осколочной массы в группы с малыми
массами осколков. При этом различие в содержании сходственных средних фрак-
фракций мало (отношение 1,02), т.е. увеличение содержания мелкой фракции проис-
происходит практически целиком за счет уменьшения содержания крупной фракции.
Единственное исключение представляет направление изменения фракционного
состава при снаряжении относительно низкобризантным составом Н с максималь-

168
16. Осколочное действие взрывных систем
Таблица 16.46
Числа осколков в сходственных массовых группах и их отношения
Цилиндр
№12
№16
N{KЫ6) AyCN*12)
Состав
Е
F
G
Н
Е
F
G
Н
Е
F
G
Н
среднее
Номер массовой группы
I
450
624
448
422
468
752
544
503
1,04
1,21
1,16
1,19
1,15
П
362
452
421
407
433
604
532
501
1,22
1,34
1,26
1,23
1,26
III
351
408
350
329
361
458
343
416
1,03
1,12
0,98
1,26
1,10
IV
183
177
175
170
165
154
159
184
0,90
0,87
0,91
1,08
0,94
V
89
76
100
89
69
50
69
81
0,78
0,66
0,69
0,91
0,76
VI
51
34
54
48
42
20
37
37
0,82
0,59
0,68
0,77
0,72
VII
29
25
28
22
23
9
15
15
0,79
0,36
0,54
0,68
0,59
VIII
34
21
20
34
27
6
16
12
0,79
0,29
0,59
0,39
0,59
Таблица 16.47
Балансно-массовые и морфологические характеристики спектров
Цилиндр
№12
№16
х(№16)
Jf(№12)
Состав
Е
F
G
Н
Е
F
G
Н
Е
F
G
Н
среднее
Мм
0,24
0,33
0,29
0,29
0,28
0,45
0,38
0,32
1,16
1,36
1,31
1,10
1,23
0,47
0,49
0,49
0,47
0,48
0,47
0,47
0,53
1,02
0,96
0,96
1,13
1,02
/iK
0,29
0,18
0,22
0,24
0,24
0,08
0,15
0,15
0,83
0,44
0,68
0,62
0,64
^тах
до
6,13
5,70
5,64
10,5
6,94
6,30
7,46
6,08
1,13
1,11
1,32
0,58
1.03
/5
So
5,10
4,91
4,95
5,74
5,00
4.98
6,07
5,18
0,98
1,01
1,23
0,90
1,03
ho
So
4,10
4,42
4,17
4,50
4,65
4,02
4,64
4,26
1,13
0,91
1,11
0,95
1,03
В20 мм
21,1
18,1
20,6
18,6
36,8
19,9
25,5
26,9
-
-Е>20
*1
0,211
0,181
0,206
0,186
0,235
0,127
0,163
0,172
1,11
0,70
0,79
0,92
0,88
ным суммарным содержанием добавок окислителя и горючего C0%). В данном
случае проявление МЭ заключается в преимущественном возрастании не мелкой,
а средней фракции (fic = 0,53). Отметим, что наибольшее значение fic полученное
в сериях предыдущих опытов с цилиндром № 12, составляло 0,51 [16.71].

16.5. Стандартные осколочные цилиндры
169
Морфологический анализ осколков типа А проводился на выборках 5 и 20 наи-
наиболее длинных осколков спектра, а также по измерениям осколка максимальной
длины. Для выявления МЭ все длины и площади представлялись в безразмерном
виде. Для длин осколков обычно используется отношение / = I/Lq, где 1 — длина
осколка. Величина / четко выявляет склонность металла к саблеобразованию, а
в предельном случае — к образованию «полос» G = Lq,1 = 1). В данном случае,
для увеличения компактности записи, относительная длина осколка представлена
в виде
Очевидно, для цилиндров № 12, 16 величины /#, / связаны соотношением:
Is = 16/".
Для безразмерных величин /шаж/?(ь /5/^0 и Ьо/^о отношение ж(№16)/ж(№12) не
имеет закономерного характера и со значительным разбросом колеблется около
1 (средние значения отношений для всех трех величин составили 1,03, однако
оценка по критерию Фишера не подтвердила принадлежности наборов величин
Ж(№16) и ж(№12) к различным совокупностям). Таким образом, проявление МЭ при
формировании длин осколков типа А не наблюдается.
Из табл. 16.47 видно изменение относительных средних площадей сечений
крупных осколков при увеличении размеров цилиндров для различных соста-
составов. За исключением состава Е (гексоген/алюминий 80/20), точки для цилин-
цилиндра №16 располагаются ниже точек для цилиндра №12, что указывает на на-
наличие МЭ при формировании площади сечения осколка. Среднее отношение
[«О-2Р16)/[?2(Л-2Р12) Д^ всех
четырех составов составляет 0,88, а	Таблица 16.48
для трех составов при исключении Общие сходственные числа осколков и их
аномальной точки состава Е — 0,88,	отношения
т. е. МЭ является значительным.
Изменение общих сходственных
чисел осколков YVq 25 ? -*>о 5 -> и их
q 25
о 5
отношения
= TV
o 5
/дГ
?25
ПРИ
Состав
Е
F
G
Н
N(№12)
1560
1820
1600
1530
N(№16)
1590
2055
1715
1750
дг(№16)
iV0,5
дг(№12)
1,019
1,129
1,072
1,143
N(№16)
1980
2790
2270
2400
различных составах представлено в
табл. 16.48. В табл. 16.48 приведена
также в качестве справочных дан-
ЛГ(№16)
ных значение A/q 25 '.
Все значения Щ 25 ' удовлетво-
удовлетворяют критерию нормального дроб-
дробления для цилиндра №12 GVo,25 > 1500, /ic > 4) [16.70]. Масштабный эффект по
общему сходственному числу осколков значителен (среднее значение отношения
составляет 1,09) и по критерию Фишера определяется как достоверный. При этом
обнаруживается более высокое значение показателя v в зависимости ? = L^,
чем в зависимости для числа окружных делений п$ — а% {у = 0,2... 0,3, см.
выше), а именно v ж 0,4 A,250'4 = 1,09). Аномальное положение точки Щ 5 ^
для низкобризантного состава Н, как и отмеченное выше аномальное увеличение
содержания средней фракции /хс для этого состава, объясняется, по-видимому,
спецификой МЭ при нагружении низкобризантными ВВ с большим содержанием
окислителя и горючего.

170	16. Осколочное действие взрывных систем
16.6. Действие осколков
1. Модели и параметры формы осколков естественного дробления
(ОЕД). Основной характеристикой формы осколков является безразмерный
параметр формы:
Ф= <*>
где E), V — соответственно средний мидель (математическое ожидание площади
проекции осколка на плоскость, нормальную к направлению полета) и объем
осколка. Параметр формы в указанном виде впервые был введен в [16.3]. Для вы-
выпуклого тела средний мидель, согласно лемме Коши, определяется соотношением:
(S) = Ss/4, где Sy, — суммарная площадь поверхности осколка.
Наряду с параметром формы используются и другие характеристики формы,
производные от среднего миделя (?), в том числе:
т
q = -у—г — поперечная нагрузка осколка;
{Ь)
Q	9 /Ч
?0 = ——- = 7о /Ф — относительная поперечная нагрузка;
/
(S) 1
Kw = _,_ =	параметр Е. С. Вентцель.
7тг2/з ?0
Основным недостатком величин (S), Ф как показателей формы является то, что
они практически не выявляют реальные особенности конфигурации ОЕД. Вели-
Величина (S) лишь косвенно характеризует форму осколка, не отражает наличие таких
важнейших эффектов, как саблеобразование и сквозной сдвиг, и в конечном счете
не указывает причин низкого качества осколочных спектров и пути его улучшения.
Поэтому существует настоятельная потребность во введении, дополнительно к
характеристикам формы (S), Ф, предназначенным в основном для расчета эффек-
эффективности осколочных боеприпасов, также и морфологических характеристик ОЕД,
важнейшими из которых является удлинение осколка и характеристика формы
его поперечного сечения. Для ОЕД в виде прямой призмы длиной / с сечением
выпуклой формы, имеющим площадь В, периметр Р и наибольший отрезок,
размещающийся в площади сечения Z)s, введем характеристики удлинения
х 1 х 1
Эти характеристики связаны соотношениями:
\ Хв л D>
Форма поперечного сечения задается относительным периметром:
Вторым крупным недостатком среднего миделя как показателя формы, особенно
отчетливо проявляющимся при оценке проникания ОЕД в малопрочные цели и
поперечного действия в них, является неучет реальной величины возможного

16.6. Действие осколков
171
диапазона изменения миделя ОЕД. Отсюда вытекает необходимость введения в
систему нормативных данных величин минимальной и максимальной площадей
проекций Smin, Smax и соответствующих безразмерных величин:
с
итах
С . '
дтгп
(У а, =
С
итах
W
(S)
Площади Smin, (?), Smax Для ОЕД определялись экспериментально с помощью
многолучевого анализатора изображений. Как показали тарировочные экспери-
эксперименты с телами правильной геометрической формы, величины Smax и (S) опре-
определяются с достаточной точностью, а при определении Smin необходимо вводить
постоянную поправку, что приводит к расчетной формуле:
о(к) _
°тгп —
(п)
где S^ln — величина проекции, полученная на приборе; S^in — скорректированная
величина проекции, кэ = 0,45 ... 0,55 (в зависимости от типа прибора).
Определение характеристик формы осколков мелких фракций проводилось
в два этапа. На первом этапе проводились сравнительные измерения осколков
натурных осколочно-фугасных снарядов (ОФС) калибра 122, 125 и 152 мм и
осколков стандартных осколочных цилиндров №12 с тем лее сочетанием металл-
ВВ. Результаты сравнительных измерений для массовой группы 1-2 г представ-
представлены в табл. 16.49 (ф(ц\ <Jmm — характеристики формы для осколков цилиндра,
.(<=)
— характеристики формы для осколков снарядов).
Таблица 16.49
Результаты сравнительных измерений
осколков снарядов и стандартных цилиндров
Таблица 16.50
Относительные площади
проекций осколков цилиндров
№12 (фракция 1-2 г)
Калибр,
мм
122
125
152
152
Снаряд
корпуса
53-ОФ-462
З-ОФ-19
53-ОФ-540
З-ОФ-25
Металл
ст. С-60
ст. 45X1
ст. С-60
ст. С-60
ВВ
ТНТ
ТНТ
ТНТ
A-IX-20
ф(ч)
ф(с)
0,85
1,07
0,89
1,09
п-(ц)
и mm
0~mm
0,92
0,94
1,12
0,98
Сталь
20
45X1
С-60
60С2
80Г2С
110Г2С
0~mm
6,48
7,63
6,26
4,67
4,52
4,64
1,34
1,28
1,36
1,50
1,62
1,44
(?г
0,207
0,168
0,217
0,321
0,358
0,310
Расхождение показателей не превышает 15%, что может считаться вполне
удовлетворительным, учитывая ограниченный характер выборок (п = 20 шт.).
После установления идентичности осколков ОФС и цилиндров RSFC проводи-
проводились измерения характеристик формы Ф, сгшш осколков стандартных цилиндров
№12, изготовленных из применяемых и перспективных снарядных сталей при трех
типах ВВ (выборки по 50 шт. осколков фракции 1—2г). Результаты измерений
представлены в табл. 16.37 и на графике рис. 16.74. В табл. 16.50 для ряда сталей
представлены относительные величины максимальной и минимальной проекций
(снаряжение A-IX-2).
С увеличением содержания углерода в стали происходит устойчивое улучшение
формы осколка, проявляющееся в одновременном уменьшении параметра формы
Ф и отношения проекций crmm.

172
16. Осколочное действие взрывных систем
Е. С. Вентцель предложена модель осколка в виде параллелепипеда а х b x с
(а > b > с). Эта модель является одной из наиболее простых (форма задается
двумя безразмерными параметрами, что обусловило ее широкое применение.
Средний мидель (S) (ма-
crmm,	,	.	.	,	, тематическое ожидание про-
проекции) согласно лемме Коши
определяется как
Метод определения E), при-
применяемый на практике, осно-
основан на измерении массы т
и двух размеров наибольшего
основания осколка — длины
а и ширины Ь. Для оскол-
осколка принимается модель парал-
параллелепипеда, и, следовательно,
толщина с может быть опреде-
определена как с =
откуда:
та
#А
п
LJ
л
\*
О'
1,7 1,8	1,9	2,0 2,1	2,2 Ф
Рис. 16.74. Результаты измерения параметра формы и
перепада миделей для осколков цилиндров из различных
сталей
ab
Значения Smin, Smax найдем, проектируя параллелепипед на произвольно ори-
ориентированную плоскость, положение которой определяется единичным вектором
нормали к этой плоскости, в свою очередь задаваемым углами (р и в в сферической
системе координат. Выражение для площади проекции имеет вид
S((p, в) = be sin (p + ab cos (p cos в + ас cos (p sin 0.
Поскольку направления единичного вектора равновероятны, дифференциаль-
дифференциальный закон распределения случайных углов (р и в имеет вид
[о, |], ее [о,
Площадь минимальной проекции равна площади наименьшей грани, т.е.
площадь максимальной проекции:
Smax =
Значения углов (р и 0, при которых реализуется максимальная площадь, находятся
из условий:
откуда:
(°)s=max =
дв
D>)S=max =
be
cos ^ + ac sin ^

16.6. Действие осколков
173
В дальнейшем примем обозначения: /, /, h — соответственно длина, ширина и
толщина осколка (/ > / > К). Для безразмерных переменных Ai = ///г, Л2 = l/h
получаем:
ф = ^-
А1А2 + А2
ч2/3
J
э и гага
.1/2
2Ai
A1A2 + A2
_
2 ¦ (Aj +
А|)
1/2
Расчетные значения безразмерных па-
параметров для ряда параллелепипедов
представлены в табл. 16.51.
Для отбора пробоин на щитах, отвечаю-
отвечающих осколкам с массой, не менее задан-
заданной, с помощью анализаторов изображе-
изображений, представляют интерес соотношения
для периметров проекций осколков. Про-
Проводя аналогичные построения, для ОЕД в
форме параллелепипеда получим:
+ A1A2 + A2
Таблица 16.51
Безразмерные характеристики
формы для параллелепипедов
7Г
2
Ртах =
1xAixA2
lxlxl
1x1x2
1x1x8
1x2x2
1x4x4
Ф
1,50
1,58
2,13
1,59
1,89
0~тт
1,73
3,00
11,36
2,25
4,24
СГг
0,667
0,400
0,118
0,500
0,333
СГа
1,15
1,20
1,34
1,12
1,42
или в безразмерных переменных:
_ Ртах _ 3 A + Ах + А2)
^mm — "^	— ^	1 _|_ \	'
±min	^	1 -h Ai
Pmin 4 A + Л)	Pm,
Aj
,1/2
(P) тг 1 + Ai + A2'
(P)	7Г
1 +
A2
Линии уровня Ф = const на плоскости (Ai — А2) показаны на рис. 16.75.
График Ф = const убедительно подтверждает положение о недостаточности
параметра формы для характеристики реальной конфигурации осколка. Осколки,
соответствующие точкам А и В, имеют совершенно различную форму (А —
длинный брусок квадратного сечения 1x1x6,4, В — пластина 1 х 4,7 х 4,7),
тем не менее оба этих осколка имеют одинаковый параметр формы Ф = 2 и,
следовательно, имеют при равных массах одно и то же значение средней проекции.
Точка начала координат A,1) на рис. 16.75 соответствует конфигурации куба,
ось ординат — брускам квадратного сечения, биссектриса Ai-A2 — квадратным
в плане пластинам. Условные границы между различными морфологическими
типами осколков выделены на рис. 16.75 штрих-пунктирными линиями (I —
область компактных осколков, II — область «брусков», III — переходная область,
IV — область «пластин»).
При параметрическом задании функции ашш = /(Ф) в общем случае, для
квадратных пластин (Ai = A2 = А) и призм квадратного сечения (Ai = 1, А2 = А)
могут быть получены аналитические зависимости:

174
16. Осколочное действие взрывных систем
10
9
8
7
6'
5
4
3
2
1 23456789 10
Рис. 16.75. Линии уровня параметра фор-
формы и морфологические зоны для модели
осколка в виде прямого параллелепипеда
в случае квадратных пластин 1 х Л х Л
имеем:
Ф =
2 + Л
2AV3
5 u mm
откуда:
Ф =
- 2
xl/6'
в случае призмы квадратного сечения 1 х
1 х Л:
ф =
откуда:
1 + 2Л
2Л2/з '
&тт
Ф =
Семейства кривых <Jmm = /(Ф) для
параллелепипедов с различными пропор-
пропорциями представлены на рис. 16.76 (А —
1 х 1 х А, В - 1 х 2 х А2, С - 1 х 3 х А2,
D — 1 х 4 х Л2).
Здесь лее пунктиром нанесен отрезок,
снятый с графика рис. 16.74 и отвечающий
расположению экспериментальных точек.
Видно, что удовлетворительное описание
параметров ОЕД с помощью модели Вент-
цель может быть получено только для
сильно уплощенных пластин, форма кото-
которых не отвечает реальной конфигурации
осколков. Другим существенным недостат-
недостатком параллелепипеда как модели ОЕД яв-
является отсутствие у него режущих ребер.
В [16.79] описан целый ряд имитато-
имитаторов ОЕД, применяемых за рубежом при
исследовании действия осколков. Наиболее
известным из них является имитатор FSP
(Fragment Simulating Projectile), разрабо-
разработанный Уотертаунеким арсеналом США. Имитаторы FSP имеют форму цилиндра
h : d = 1,3 с двумя скосами на переднем торце. Для герметизации пороховых
газов имитаторы снабжены фланцем. Твердость имитаторов составляет 28 ... 32 по
шкале «С» Роквелла. Размеры, порядок изготовления и применения имитаторов
FSP регламентированы военным стандартом MIL-P-46593 США и позднее вве-
введенным стандартом НАТО STANAG 2920. Из изложенного выше очевидно, что
характеристики формы имитатора FSP не соответствуют даже приблизительно
и
5
0
7/
//
/у
/
D
/
ф
1,5	2,0	2,5
Рис. 16.76. Зависимость перепада миделей
от параметра формы для параллелепипедов
с различными пропорциями

16.6. Действие осколков
175
характеристикам реальных ОЕД. Действительно, параметр формы для цилиндра
с высотой h и диаметром d определяется выражением:
ф= -
W3 ' h d~
При h = 1,3, получаем Ф = 1,4, в то время как реальный диапазон этой величины
для ОЕД составляет Ф = 1,8... 2,2 (см. табл. 16.50). При этом имеет место тот же
недостаток, что и в модели Вентцель, т.е. отсутствие режущих ребер. Стандартом
STANAG 2920 предусмотрен параметрический ряд имитаторов с массой от 0,0875
до 53,8 г, однако на практике наибольшее распространение получил имитатор с
массой 1,1 г A7гран).
Такая цепочка совершенно очевидного
занижения нормативов привела к тому,	v Mjc
что осколочная опасность стала рассмат-
рассматриваться по отношению к пулевой как вто-
второстепенная, с избытком нейтрализуемая
СИЗ 1-го класса защиты. В этом смысле
введение стандарта STANAG 2920 сыгра-
сыграло негативную роль. Следствием являлась
потеря интереса к исследованиям действия
осколков по СИЗ как в России, так и за
рубежом. Между тем, эти исследования,
интенсивно проводившиеся в 70-80х годах,
уже тогда выявили серьезные противоре-
противоречия в подходах к оценке реального оско-
осколочного действия. Эти результаты были
2*
V1
==5
1000
500
0
0,01 ОД 1 10 100 т, г
Рис. 16.77. Зависимость скорости проби-
пробития г?50 °т массы осколка для различных
типов преград: 1 — сталь; 2 — Дайнема SK
66 fabric, M/ = Юкг/м2; 3 — Дайнема SK
66, М/ = 5кг/м2; 4 — Дайнема "Fraglight",
М/ = Зкг/м2;
подтверждены исследованиями последних лет. В качестве примера рассмотрим
экспериментальные данные фирмы DSM (Нидерланды) по стойкости тканевых
бронематериалов DYNEEMA к действию осколков 155 мм осколочно-фугасного
снаряда (рис. 16.77). Экспериментальная зависимость г>5о = / (тп) (т — масса
осколка) для стального листа с удельной массой М' = 20 кг/м2 (кривая а) неплохо
аппроксимируется формулой:
124/гФ
где г>5о — скорость пробития, м/с; h — толщина листа, мм (/г — 2,54 мм); Ф —
безразмерный параметр формы осколка.
Для шара, цилиндра 1:1 и куба параметр Ф соответственно равен 1,21, 1,38
и 1,50, для осколка естественного дробления в среднем Ф = 2,0. Расчетная
кривая по этой формуле нанесена на графике рис. 16.77 пунктиром. Зависимость
непосредственно вытекает из формулы для скорости г>юо 100% пробития сталь-
стальной преграды, предложенной автором и соответствующей критерию удельного
импульса: г = mv/ (S)
155/гФ
гкр =
с учетом соотношения г>5о = О,8г>юо-
Зависимость г>5о = f(jn) Для материалов DYNEEMA (кривые 6, с, d) также
описываются формулами вида г>5о = С/та, но со значительно меньшей величиной
показателя а. Наиболее низкое значение а ~ 0,1, не соответствующее ни одному из

176
16. Осколочное действие взрывных систем
Таблица 16.52
Соотношение между массой и скоростью ударника при различных критериях
пробития
Критерий
Импульс
Кинетическая энергия
Удельный импульс
Удельная энергия
Зависимость для матери-
материала DYNEEMA Fraglight,
М/ = Зкг/м2 рис. 16.77
^проб — предельная скорость ]
Условие пробития
mv ^ С\
mv2 ^ G2
m1/3v ^С3
m1/3v2 ^ Са
m1/10v ^ Съ
пробития.
г>проб
v rsj 1/т
v rsj 1/у/т
v ~ 1 / \/гп
v ~ 11 \fm
v ~ 1 / 1tym
известных критериев пробития (табл. 16.52), имеет место для нетканого материала
DYNEEMA Fraglight (кривая d).
Сравнение пробивной способности осколка естественного дробления (ЕД) и
имитатора FSP ввиду отсутствия экспериментальных данных по пробитию имита-
имитатором FSP той лее преграды (М' = Зкг/м2) молено провести на основе сопостав-
сопоставления величин энергопоглощения: Э = W/M'. Согласно [16.80, 16.81] значение
г>5о при действии имитатором FSP т = 1,8г по преграде DYNEEMA Fraglight
(Mf = 1,2кг/м2) составляет 450 м/с.
Расчетные значения кинетической энергии W и энергопоглощения Э представ-
представлены в табл. 16.52. Из нее следует, что энергопоглощение при действии осколка ЕД
оказывается в 2,2 раза ниже, чем для имитатора FSP. При удлиненных осколках
Таблица 16.53
Сравнение величин энергопоглощения при пробивании нетканного материала
Дайнема "Fragligth"имитатором FSP и осколком ЕД
ПЭ
Имитатор
Осколок ЕД
m, r
1,1
1,0
М'
, кг/м
1,2
3,0
г>5о , м
450
500
/с
W, Дж
111
125
э,
Дж/(кг/м2)
92,5
41,6
наиболее неблагоприятным для цели является такой случай встречи осколка с пре-
преградой, при котором его большая ось оказывается близкой к нормали к преграде.
Статистическая оценка этой опасности может быть проведена с использованием
модели осколка в виде отрезка длины /, произвольно вращающегося вокруг центра
масс с равномерным распределением f((f),O) = cos(/>/4tt по углам ориентации ф,6.
В этом случае случайная длина а проекции отрезка на фиксированную плоскость
изменяется в пределах @... /). Вводя относительную величину проекции у = а//,
получаем плотность распределения этой величины в виде
У

16.6. Действие осколков	177
Функция распределения имеет вид
у
G(y) = Jg(y)dy =
= 1 - Л/1 -2/2-
о
Математическое ожидание относительной длины проекции
1
у д(у) dy = — ж 0,785.
о
Медиана распределения
Уме = sin f arccos - 1 « 0,866.
V	2/
Последнее означает, что 50% отрезков падают на площадку с проекцией более
0,866, т.е. практически «плашмя». В то же время достаточно велик и процент
отрезков, падающих на площадку с малым углом к нормали. Так, 10% отрезков
падают на площадку с относительной проекцией менее 0,435, а 5% — с проекцией
менее 0,312, и 1% с проекцией менее 0,14.
Статистический диапазон опасных по пробитию углов падения значительно
расширяется, если отрезок вращается только в плоскости, нормальной к площадке.
В этом случае плотность и функция распределения проекций определяются как
2	2
д(у) = 	Л	G(y) = 1	arccos у.
Математическое ожидание и медиана относительной длины проекции определя-
определяются следующим образом
<!/> = -» 0,637, уме = cos j » 0,707.
7Г	4
В данном случае 25% отрезков падает на площадку, когда их ось составляет менее
23° от нормали, а 10% падают с углом менее 9°, т.е. в условиях, когда осколок
будет пробивать преграду как стреловидный поражающий элемент. По критерию
удельного импульса, при равных массах, скорости пробития должны относиться
для удлиненной призмы, падающей продольной осью перпендикулярно к цели, и
шара как:
уи _ Su _ Фп
уш Бш Фш
Для призмы Фп = 1/Xj , для шара Фш = (тг/4) F/тг) ' = 1,209, отсюда:
vn _ 0,827
~7Г ~ Л 2/3 '
При А# = 8 (верхняя граница диапазона нормальных осколков) для пробития
призмой теоретически нужна скорость в 5 раз меньшая, чем для пробития шаром.

178	16. Осколочное действие взрывных систем
Сравнение экспериментальной кривой для стальной преграды М' = 20 кг/м2 с
расчетной проводилось при Ф = const. Это допущение, в первом приближении при-
приемлемое при ударе в стальную преграду вследствие высокой амплитуды давления,
сильной пластической деформации ударника и быстрого поперечного волнообмена
в броневой плите, при ударе в низкоплотный материал с локализованным низко-
низкоамплитудным энергообменом уже не может считаться приемлемым. Записывая в
общем случае, при h = const, в соответствии с критерием удельной энергии:
и принимая Ф = К2тк, получаем:
"U m(l/6-fe/2) '
По оценкам к = 1/12, откуда г>5о ~ 1/m1/8, что близко к экспериментальной
кривой для преграды DYNEEMA «Fraglight».
Снижение энергопоглощения при пробитии реальным осколком ЕД по срав-
сравнению с пробитием имитатором FSP, наряду с большим перепадом миделя ашш,
объясняется появлением такого фактора, как режущее действие острых сдвиговых
ребер осколка. Вследствие перерезания нитей, уже в начальной стадии внедрения
в ряде случаев не наблюдается образования схемы «крест» [16.82].
Морфологические модели осколков. Патент № 2025644
Из изложенного выше в п. 16.1. следует, что в общем случае в осколочном
спектре выделяются две разнородные морфологические совокупности осколков —
крупные (основные, квазирегуляторные) осколки типа Л, образованные маги-
магистральными трещинами и содержащие обе исходные поверхности цилиндра, и
сопутствующие мелкие осколки типа В, содержащие одну исходную поверхность.
Методологические вопросы построения моделей осколков типа А и В и со-
соответствующих имитаторов рассматривались в [16.83, 16.84]. Сформулированы
следующие основные требования к имитаторам ОЕД:
1)	характеристики формы имитаторов должны соответствовать характеристи-
характеристикам формы ОЕД, т.е. точка Ф — ашш для имитатора должна лежать внутри
соответствующей зоны для ОЕД, определенной экспериментально;
2)	имитатор должен иметь режущие ребра;
3)	набор геометрических характеристик имитатора (пропорций и углов) должен
отражать форму поперечного сечения и удлинение ОЕД;
4)	имитатор должен иметь две модификации, первая из которых воспроизводит
ОЕД мелких фракций типа В, а вторая — квазирегулярные осколки типа А
(осколки крупных фракций).
К числу дополнительных требований относятся следующие:
1)	с целью соблюдения преемственности желательно, чтобы имитатор включал
в себя модель Е. С. Вентцель как частный случай;
2)	имитатор должен быть прост и технологичен в изготовлении.

16.6. Действие осколков
179
Таблица 16.54
Зависимость характеристик формы от угла C
Сталь
Низкоуглеродистая
Среднеуглеродистая
Высокоуглеродистая
/3, град
45
60
75
п
4,76
4,30
4,07
*^ЭКСП
4,5...5,0
4,2...4,5
4,0...4,2
А
2,20
1,86
1,61
Учитывая последнее тре-
требование, наиболее перспектив-
перспективной конфигурацией следует
считать прямую или косую
призму, изготавляемую рез-
резкой прутка заданного сечения.
Форма сечения прутка фикси-
фиксирована (равносторонний тре-
треугольник, квадрат), либо за-
задана одним параметром (ромб,
равнобедренный треугольник,
прямоугольник), или двумя параметрами (параллелограмм, трапеция).
Проведенный анализ показал, что оп-
оптимальной формой сечения является ромб,
задаваемый острым углом /3, причем вели-
величина угла определяется типом стали (см.
табл. 16.54).
Модель ОЕД мелких фракций (тип В).
D
Рис.
16.78. Имитатор осколка
фракции
мелкой
Эта модель получена сечением призмы
с ромбическим основанием под углом ? к
ребру при угле 180° — /3 и представляет со-
собой плоскосимметричный параллелепипед
(рис. 16.78). Форма определяется тремя
параметрами: двумя углами /3, ? и отно-
относительной длиной ребра \р = l/D (D —
большая диагональ ромба).
Площадь и периметр ромба определя-
определяется соотношениями
;- = a2sin/3,
Р =
2D
cos (/3/2)'
Безразмерные характеристики сечения имеют вид:
д =
tg(/?/2) •
Угол а между боковой гранью и основанием определяется соотношением:
а = arccos
/	0
cos ? • cos —
V
Объем параллелепипеда V и математическое ожидание площади проекции (S)
определяются как:
/ - 1/п2 ^ - Xd°3 &
Параметр формы определится соотношением:
Ф =
4sm?cos(/3/2)((AD/2)tg(/3/2))
2/3 '
A6.67)

180
16. Осколочное действие взрывных систем
0
С'тт
р=50° ж
^ \Р=90° \
^=90°
р=зо° ~
р=40°^Г
п
\ р=70°
ф
1,5
2,0
2,5
Выражение для произвольной площади проекции имеет вид:
S = Sr sin (p + Sp cos(n, ni) + 5p cos(n, П2),
где n — вектор нормали к плоскости проекции; ni, n^ — соответственно векторы
нормалей к боковым граням призмы; Sr = Bq/ sin? — площадь основания; Sp = I-
л/Bq/sin/3 — площадь боковой грани.
Выражение для площадей проекций
10 i	1	1 Smim Smax получается из условий:
о ^о
dip ' дв
Расчетные значения величин Ф, сгшш
представлены в табл. 16.55 в виде функций
от исходных параметров /3, ?, Xd-
На рис. 16.79 представлено семейство
кривых amm = /(Ф) при относительной
длине ребра Л^ = 1. Каж:дая кривая по-
построена при фиксированном значении C и
изменении угла ? в диапазоне от 30 до 90°.
Промежуточные черные точки на кривых
соответствуют значениям ?, равным 40 и
60°. Видно, что в одном и том же диапазо-
диапазоне углов 30.. .90 градусов величина угла /3
оказывает более существенное влияние на
положение точки в плоскости Ф — crmm, чем
величина угла ?.Нижняя ветвь семейства
отвечает диапазону компактных осколков
ЕД, осколков заданного дробления и готовых ПЭ (для куба Ф = 1,5, (Jmm — 1,75).
Верхняя ветвь семейства соответствует осколкам очень плохой формы, получаю-
получающимся при дроблении оболочек из низкоуглеродистых сталей. Модули производ-
<ЭФ	Ватт	п
ных -— и —7^7Г~ существенно увеличиваются с уменьшением угла р.
ор	ор
В результате совместного анализа расчетных и экспериментальных зависимо-
зависимостей <Jmm — /(Ф) Для модели типового имитатора ОЕД мелких фракций выбрана
следующая комбинация определяющих параметров: /3 = 50°, ? = 40°, Л^ = 1, что
соответствует: Ф = 1,94, <7тт = 5,57. Эта комбинация входит в число комбинаций,
защищенных патентом №2025644 «Имитатор осколка естественного дробления
боеприпасов» РФ [16.85]. Для данного имитатора было предложено обозначение
RFSP (Russian Fragment Simulating Projectiles).
Указанная точка показана на графиках знаком Q. Разработан параметриче-
параметрический ряд масс имитатора, организованный по принципу геометрической прогрес-
прогрессии 777,^+1 = Uoirii со знаменателем Щ = 2 (т = 0,25; 0,5; 1,0; 2,0; 4,0г).
Модель квазирегулярных осколков (тип А)
В соответствии с вышеизложенным, модель имеет форму прямой призмы
ромбического сечения с удлинением Л^ = 4... 8. Расчетная зависимость для
параметра Ф при ? = 90° приобретает вид:
Рис. 16.79. Зависимости отношений про-
проекции от параметра формы для имитатора
ОМФ (Аг>=1)
Ф =
sin (/3/2) + 2XD
4cos(/3/2)((AD/2)tg(/3/2)J/3'
A6.68)

16.6. Действие осколков
181
Расчетные значения
функции от исходных
Таблица 16.55
характеристик формы в
параметров
Ad
0,5
1
1
2
е
30
40
60
90
30
40
60
90
30
40
60
90
30
40
60
90
Ф
0~тт
Ф
0~тт
Ф
0~тт
Ф
0~тт
Ф
0~тт
Ф
0~тт
Ф
0~тт
Ф
0~тт
Ф
0~тт
Ф
0~тт
Ф
0~тт
Ф
0~тт
Ф
0~тт
Ф
0~тт
Ф
0~тт
Ф
0~тт
/3°
30
2,38
5,56
2,20
5,02
2,04
4,42
1,98
3,86
2,40
7,15
2,27
6,62
2,14
6,01
2,09
5,44
2,49
9,25
2,38
8,71
2,27
8,10
2,23
7,53
2,81
16,7
2,74
16,2
2,68
15,5
2,65
15,0
40
2,22
4,59
2,02
4,06
1,83
3,47
1,77
2,92
2,19
5,76
2,03
5,23
1,89
4,63
1,84
4,07
2,22
7,30
2,10
6,76
1,98
6,15
1,94
5,59
2,45
12,8
2,37
12,2
2,29
11,6
2,27
11,0
50
2,13
4,00
1,92
3,48
1,72
2,90
1,65
2,37
2,07
4,91
1,90
4,38
1,75
3,79
1,69
3,23
2,07
6,10
1,94
5,57
1,81
4,97
1,76
4,40
2,22
10,4
2,14
9,82
2,06
9,21
2,03
8,64
60
2,10
4,16
1,87
3,09
1,66
2,52
1,57
2,00
2,00
4,33
1,83
3,81
1,66
3,22
1,60
2,68
1,98
5,29
1,84
4,76
1,70
4,16
1,65
3,61
2,08
8,72
1,99
8,18
1,91
7,57
1,87
7,00
70
2,09
4,64
1,85
3,06
1,62
2,24
1,54
1,74
1,98
3,91
1,78
3,39
1,61
2,81
1,54
2,28
1,93
4,70
1,78
4,17
1,64
3,58
1,58
3,03
1,99
7,51
1,89
6,98
1,81
6,37
1,77
5,80
90
2,15
5,82
1,87
3,74
1,62
2,16
1,52
1,41
2,00
4,63
1,78
3,05
1,58
2,25
1,50
1,75
1,92
3,86
1,74
3,35
1,58
2,77
1,52
2,24
1,91
5,82
1,80
5,29
1,70
4,69
1,66
4,12
В частном случае, при C = 90°, приходим к бруску квадратного сечения, для
которого получаем
ф =
2\/2А
D
24/зл2,/3

182	16. Осколочное действие взрывных систем
или, учитывая, что Хр = А#/\/2,
Ф = —
Значения Smin, Smax находятся по формулам, приведенным выше, с учетом
/3 = 90°.
В случае прямой призмы функции аргументов четко разделены: величина угла
/3 отражает форму поперечного сечения, величина Хр — удлинение осколка.
Экспериментальные измерения параметров Ф, сгшш для квазирегулярных оскол-
осколков цилиндров №12, изготовленных из низко-, средне- и высокоуглеродистых
сталей, проводились с помощью прибора «Спектр» института «Геодезия» и раст-
растрового анализатора «Квантимет». В качестве величины типового удлинения была
принята середина интервала нормальных осколков [16.3] т.е. Л^ = Л = 6. Для
реальных выборок из 10 осколков величина половины доверительного интервала
Д (А^) = 6± А) при доверительной вероятности 0,8 колебалась в пределах 1,2.. .1,7.
Наблюдается вполне удовлетворительное согласие по величинам угла /3, принятым
для указанных сталей в табл. 16.54.
Рекомендуемый диапазон удлинения Хц = 4... 8 при А = 1 совпадает с диа-
диапазоном удлинения нормальных осколков по классификации [16.8]. Углы для раз-
различных классов сталей приняты в соответствии с данными табл. 16.54. Размеры D
(8, 10, 12, 16, 20 и 25 мм) являются членами ряда нормальных линейных размеров
RalO. Регламентируемый диапазон масс при этом является весьма значительным,
например, при /3 = 60°, Л = 8, 7о = 7,85 г/см3 он составляет т = 9,3... 283 г. Это
позволяет использовать имитатор для оценки противоосколочной стойкости как
средств индивиндуальной защиты (СИЗ), так и легкобронированной техники.
2. Баллистика осколков. Движение осколка в воздухе рассмотрим при
следующих допущениях:
1)	плотность воздуха рв вдоль траектории постоянна;
2)	влияние силы тяжести пренебрежимо мало;
3)	площадь миделя осколка на полете можно считать равной среднему значению
4)	коэффициент лобового сопротивления сх не зависит от скорости осколка.
Уравнение движения осколка в этом случае приобретает вид
где v — текущая скорость осколка (ПЭ).
Это уравнение можно представить в виде:
^L	p{S)C	A6.70)
Av\ A.
dt	2га
Величина А называется баллистическим коэффициентом и имеет размерность
1/м. Интегрируя уравнение A6.70) при начальных условиях v@) = г>о, ж@) = 0,
получим следующие законы движения осколка:
v = ——-—-, х = — In A + Avot).
1 + Avot	A

16.6. Действие осколков	183
Наибольший интерес для практики представляет закон падения скорости ПЭ в
функции от пройденного расстояния х. Используя замену dv/dt = (dv/dx) (dx/dt) =
vdv/dx, представим уравнение A6.69) в виде:
^ = -Av.	A6.71)
ах
Начальным условием является ^@) = vq. Интегрируя A6.71) получаем:
In— = -Ах.	A6.72)
Откуда
v = vq exp{—Ах}.	A6.73)
Это выражение известно как закон экспоненциального затухания скорости осколка
на полете.
Из A6.71) следует, что величина Av есть потеря скорости на пути 1 метр.
При значениях баллистического коэффициента для реальных осколков А =@,01—
0,03) 1/м и v = 1000 м/с получаем А^/Аж = A0 ... 20) (м/с)-A/м).
Непосредственно из A6.72) получаем выражение для убойного интервала,
т.е. расстояния от места взрыва, на котором осколок еще сохраняет скорость,
необходимую для поражения цели (убойную скорость г>уб).
/y6 = Iln—,	A6.74)
где vq — начальная скорость осколка (ПЭ).
Выражение для баллистического коэффициента можно представить в виде:
А =
mi/3'
где 7о — плотность материала осколка, В — баллистический параметр (при
размерностях А [1/м], т [г] для осколков ЕД можно в среднем принять В ~ 0,03).
Значение коэффициента лобового сопротивления сх для осколков естественного
дробления обычно принимают 1,21.
Принятое выше допущение о усреднении миделя на полете приемлемо далеко
не всегда. Реальная площадь миделя (проекции площади осколка на площадку,
нормальную траектории) в полете является переменной величиной (случайной
функцией времени), колеблющейся в пределах Зш{п-Зшах. Усреднение миделя
неприемлемо при оценке безопасных по осколочному действию расстояний, на-
например, при расчете безопасности хранилищ, безопасности самолетов—носителей
авиабомб при метании их с малых высот и т.п.
Допущения о постоянстве коэффициента лобового сопротивления сх также
приемлемо лишь для приближенных оценок. При точных расчетах необходимо
учитывать зависимость коэффициента сх осколка от его скорости v (или от числа
Маха М = v/co, cq — скорость звука в воздухе). В дозвуковой области (М < 1) ко-
коэффициент сх примерно постоянен и равен 0,5. В области М ~ 1, вследствие смены
режимов обтекания и возникновения присоединенной (баллистической) ударной

184	16. Осколочное действие взрывных систем
волны, сопротивление воздуха резко возрастает. Согласно [16.86], зависимость
Сх = f{v) может быть аппроксимирована следующими соотношениями:
0,5	при v $J 150 м/с
A,49 + 0,51 • sin(860° - 350lgv)) при 550 ^ v > 150 м/с
с, = <	/ 50
0,865 ( 1 + — 1	при v > 550 м/с
3. Классификация механизмов взаимодействия осколков с преграда-
преградами. Рассмотрим удар в нормаль осколка (ПЭ) по преграде со скоростью vq.
Масса и форма ПЭ, физические и ме-
р	.	ханические свойства ПЭ и преграды зада-
?1	/	ны. Наиболее важными характеристиками
I	/	действия являются следующие:
/ _	__ /	1) глубина Lqq внедрения в полубеско-
' ^ *" ¦' '	нечную преграду;
2) толщина /гпр предельно пробиваемой
конечной преграды (плиты, листа).
Эти величины связаны соотношением:
/гпр = г/Loo, (у > 1)	A6.75)
где у — коэффициент, учитывающий вспо-
вспомогательное действие тыльных эффектов
при пробитии (коэффициент конечности
преграды).
0	1000	2000	% м/с	В зависимости от скорости удара и со-
Рис. 16.80. Классификация механизмов отношения свойств ПЭ (ударника) и пре-
внедрения на плоскость (vo-P)	грады, ударник при внедрении может со-
сохранять свою форму, либо претерпевать
различные деформации. При этом будут иметь место различные механизмы
внедрения и пробивания. Области реализации этих механизмов могут быть
представлены на плоскости Р — vq (рис. 16.80), Р = Gу/7п) ехр{(сгу — <7и) /сгу}
— параметр соударяемой пары; 7у> 7п — соответственно плотности ударника и
преграды; сгу, аи — пределы текучести ударника и преграды.
На рис. 16.80 зоны А, П и К соответствуют «аэродинамическому», переходному
и кратерному механизмам внедрения.
Аэродинамическая схема внедрения реализуется, например, при внедрении
стальных осколков или ГПЭ при скоростях до 1500 м/с в такие низкоплотные
среды как жидкости, пластмассы, дерево, твердое топливо, тканевые преграды
из арамидных или полиэтиленовых волокон и т.п., а также в модельные среды
(пластилин, петролатум, глицерин и т. п.). Кадры высокоскоростной фотореги-
фоторегистрации процесса внедрения шара в воду показаны на рис. 16.81. Для преград из
алюминиевых сплавов аэродинамическая схема может сохраняться при внедрении
стальных ударников при скорости до 800 м/с.
Наиболее важный в прикладном плане класс образуют переходные схемы
внедрения с более или менее значительной деформацией ударника. Вид кратера
при переходном механизме внедрения показан на рис. 16.82. Высокочастотная
фотография процесса пробивания стальной преграды с выбиванием пробки пред-
представлена на рис. 16.83. При заданных физико-механических характеристиках
ударника и преграды степень деформации ударника определяется как скоростью,
так и толщиной преграды. При выполнении условия v > г>псп, т.е. при наличии

16.6. Действие осколков
185
Рис. 16.81. Высокочастотная фоторегистрация внедрения стальной сферы в воду
Рис. 16.82. Сечения кратеров в стальной преграде при внедрении по переходному механизму
запреградной скорости ударника, важную роль, в особенности при пробивании
разнесенных преград, играет критическая величина скорости г>сг, при которой
происходит разрушение ударника на первой преграде. При разрушении ударника
резко снижается пробивное действие по дальнейшим преградам. При кратерной
схеме, реализуемой при высоких скоростях удара, в преграде образуется кратер,
близкий по форме к полусфере, а ударник растекается по стенкам кратера. При
этом в преграде распространяется сильная ударная волна, вызывающая откол
на тыльной поверхности. Остающаяся толщина преграды пробивается по типу
выбивания пробки. Коэффициент конечности при этом может достигать значений
у= 1,2... 1,5.

186
16. Осколочное действие взрывных систем
Рис. 16.83. Высокочастотная фотография процесса пробивания стальной плиты
4. Предельно пробиваемые толщины преград и предельные скорости
пробития.
«Аэродинамический» механизм.
Уравнение движения жесткого недеформируемого ударника в среде с инерци-
инерционным и прочностным сопротивлением имеет вид:
dv
A6.76)
где m — масса ударника, S — мидель, Hq — удельное прочностное сопротивление
среды.
Представим уравнение A6.76) в виде:
dv	* 2 л
— = -Av2 - С,
dt
где А = -^
2т	т
Произведя замену dv/dt = vdv/dx и интегрируя в пределах от 0 до L^ и от
до 0 получим выражение для глубины внедрения в пространство
A6.77)
A6.78)
Предельно пробиваемая толщина преграды определится как /гпр = yL
р — у^оо
С

16.6. Действие осколков	187
Предельная скорость пробития vucu (предел сквозного пробития) преграды данной
толщины h определится соотношением
В данном случае вероятность пробития преграды р описывается ступенчатым
законом:
Р = 0 При V < ^псп,
Р = 1 При V ^ ^псп-
В реальных условиях, даже для тел с постоянной величиной миделя S (шар,
стабилизированное тело), вследствие статистического разброса физико-механичес-
физико-механических характеристик преграды, вероятность пробития представляет возрастающую
функцию скорости, причем р = 0 при v = 0, р —>• 1 при v —>• оо. Зависимость
р = f(v) может быть описана, например, функциями:
р = 1-
где г>*, п, Р, ? — параметры, зависящие от свойств ударника и преграды.
В некоторых случаях используется кусочно-линейная аппроксимация
р = 0 при v ^ Vmin,
р = 	_mm	при vmin < v ^ 1)таж,
р=1 при v > ушах.
При пробивании преград осколками, имеющими случайную величину миделя
S Е [Smim Smax] в момент удара о преграду баллистический диапазон суще-
существенно расширяется. При оценке противоосколочной стойкости преград, в том
числе средств индивидуальной защиты (СИЗ) в качестве характеристики обычно
используют значение скорости г>5о, при которой вероятность пробития преграды
составляет 0,5.
Кратерная схема.
Предполагая, что кинетическая энергия ударника Wo затрачивается на рас-
расширение полусферической полости в преграде с постоянным противодавлением
р0 = zaTU от радиуса, равного нулю, до некоторого конечного радиуса Д, получим:
R
/2
r2dr= -
о
R
/
откуда:
Loo = R = \ 3 ° ¦	A6.80)
Относительная предельно пробиваемая толщина определяется как
1/3
m1/3 m1/3

188	16. Осколочное действие взрывных систем
Для стальной и дюралевой преград среднего качества получаем соответственно
^пр _ к or 2/3	_^__iii 2/3	ПВЯП
где берется /гпр — в мм, т — в г, vq — в км/с.
Переходная схема
Для пар «сталь—сталь», «сталь—дюраль» в диапазоне скоростей до 2000 м/с
для оценки пробиваемой толщины используется критерий удельного импульса
г = tuvq/ (s) ^ гкр, причем принимается, что критическое значение удельного
импульса линейно зависит от толщины преграды:
Отсюда
hnp
A6.82)
ml/3
Для пары «сталь-сталь»
л,™ = 155/^Ф-	A6.83)
/гпр
155Ф	т1'3
Для пары «сталь-дюраль»:
Лпр	^	66/г^Ф
"ТТз = ^Ж' "пел = -^-,	16.84
га1/*3 66Ф	га1/*3
где /г — в мм; т — в r; v — в м/с.
При компактной форме ударника в виде цилиндра 1:1 (Ф = 1,38) для пар
«сталь-сталь» и «сталь-дюраль» получаем соответственно
mi/3 --"""' mi/3 -•"¦"»'
где hup — в мм; т — в г; vq — в км/с.
Более точные оценки пробиваемых толщин могут быть получены при чис-
численном моделировании процессов пробития (двумерных при нормальном ударе
осесимметричных тел и трехмерных при ударе под углом) (см., например, [16.87,
16.103].
5. Критерии для оценки действия осколков. При оценке действия оскол-
осколков, наряду с расчетом пробиваемых толщин (стальных или дюралевых эквивален-
эквивалентов объектов), широко используется также критериальный подход. Согласно этой
концепции, поражение объекта достигается при выполнении условия К ^ -Ккр? где
К = /(га, г;, (s)...) — некоторая физическая величина или комбинация параметров
ударника, Ккр — эмпирический параметр цели. В качестве величины К наиболее
широко используется кинетическая энергия осколка Wo, удельная кинетическая
энергия Еуд = Wo/ (s) и удельный импульс г = /q/ (s).
Критериальные оценки наиболее целесообразно использовать в тех случаях,
когда поражение объекта нельзя свести к простому пробитию преграды, например,
в случаях физически сложных комбинаций пробития с последующим зажжением,
инициированием и т.п. Важным преимуществом критериального подхода является

16.6. Действие осколков
189
Таблица 16.56
Критерии поражения целей
Критерий
Полная кинетическая
энергия
Удельная энергия
Удельный импульс
Предельное условие
mv2 w
2 кр
2
2 < 5 > Еуя
mv
Критическая скорость
/2Wkp~
^кр - \
V т
1 2Екр
кр у t^om1/3
2кр
Связь
ттгг»2 const
тг>6 const
ттгг»3 const
возможность построения вероятностно-статистических моделей поражения объек-
объектов, задаваемых как правило, функциями р = f(K).
Выше приводится сводная табл. 16.56 вышеперечисленных критериев, соответ-
соответствующие зависимости для критической скорости и связь массы и скорости при
фиксированном значении К (т/ (s) = q = ^т1/3).
Характерные значения параметров WKp, ^уд.кр и ^кР для трех основных клас-
классов объектов приведены в табл. 16.57. Важным и относительно слабоизученным
Таблица 16.57
Критические величины для трех классов целей
Объект
Незащищенные "мягкие"цели
Небронированная техника
Легкобронированная техника
WKP, Дж
100
300-1000
2000-5000
-Ьуд.кр
кгс • м
СМ2
10
30-100
200-500
Дж
мм2
1
3-10
20-50
i кр.кПа-с
5
30-100
100-300
разделом теории осколочного действия является противоосколочная стойкость
средств индивидуальной защиты (СИЗ). Современные методы испытания защит-
защитных свойств СИЗ ориентированы в основном на их противопульную стойкость. Все
принятые в настоящее время классификация СИЗ по уровням защиты, в том числе
и ГОСТ Р50744-95 «Бронеодежда» построены по видам стрелкового оружия.
Для оценки противоосколочной стойкости СИЗ в отечественной практике ис-
используется шарик диаметром 6,3 мм (масса 1 г). В зарубежной практике испытания
СИЗ проводятся по стандарту НАТО STANAG 2920, согласно которому противо-
противоосколочная стойкость СИЗ определяется стрельбой по ним имитатором осколка
FSP (Fragment Simulating Projectiles), разработанным Уотертаунским арсеналом
США. Стандартом STANAG 2920 предусмотрен параметрический ряд имитаторов
с массой от 0,0875 до 53,8 г, однако на практике наибольшее распространение
получил имитатор массой 1,1 г A7 гран).

190
16. Осколочное действие взрывных систем
Таблица 16.58
Основные марки текстильных бронематериалов
Материал волокна
Арамид
Высокомолекулярный
полиэтилен
Марка
Кевлар
СВМ
Армос
Тварон
Дайнима
Фирма, страна
Дюпон, США
Россия
Россия
Акзонобель, ФРГ
DSM, Нидерланды
В настоящее время наибольшее распространение получили тканевые СИЗ. Наи-
Наиболее известные марки текстильных бронематериалов представлены в табл. 16.58.
Основной особенностью полиэтиленового волокна является чрезвычайно высо-
высокая скорость распространения упругих волн в нем (9000.. .10000 м/с), т.е. примерно
на 40% более высокая, чем в арамидном волокне G500 м/с), вследствие чего
энергия осколка быстро рассеивается по площади. Наряду с тканевыми СИЗ
широко используются бронепанели из керамики на основе оксида алюминия,
карбидов бора, кремния, титана и т.п.
Вопросам механики пробития тканевых и керамических бронематериалов по-
посвящена обширная литература [16.88]-[16.94]. Данные об осколочной стойкости
леи лета и каски, изготовленных из слоистого кевлара и составляющих комплект
СИЗ PASGT сухопутных войск США (Personnel Armour System Graund Troops)
представлены в табл. 16.59 (стандартный имитатор FSP массой 1,1г.).
Таблица 16.59
Характеристики комплекта СИЗ PASGT
Элемент СИЗ
!Жилет
Каска
Масса, кг
4,1
1,45
Удельная масса, кг/м2
6,5
10,8
^50,м/с
485
605
W™, Дж
129
201
В [16.91]—[16.93] показано, что процессы пробития тканевых СИБ шариком или
имитатором FSP и реальными осколками естественного дробления существенно
отличаются друг от друга. Это объясняется как большим перепадом миделей атт
осколка ЕД, так и появлением такого фактора как режущее действие острых
сдвиговых ребер осколка, в особенности при подходе режущим ребром вперед.
Вследствие перерезания нитей уже в начальной стадии внедрения в ряде случаев
не наблюдается их вытягивание из утка и основы ткани по схеме «крест».
Наиболее рациональной мерой мог бы стать переход к испытаниям проти-
воосколочных СИЗ имитатором RFSP (Russian Fragment Simulating Projectiles,
патент № 2025644 РФ) в виде косой призмы ромбического сечения. Испытания
указанными имитаторами ОЕД являются более трудоемкими по сравнению с
испытание шаром или цилиндром, так как они требуют определения ориентации
имитатора в момент подхода к преграде и значительного увеличения объема
эксперимента, но дают более объективные и полные данные о реальной проти-

16.6. Действие осколков
191
воосколочной стойкости СИЗ.
На рис. 16.84 приводятся результаты стрельб
по 30-слойному пакету арамидной ткани СВМ
осколками ЕД (масса 0,95.. .1,05 г) 152 мм оско-
осколочно-фугасного снаряда 30Ф25 и имитаторами
RFSP массой 1 г. Штрих-пунктирными линия-
линиями нанесены значения скорости г>5о = 550 м/с
и границы конечнобаллистического диапазона
г>нп = 520 м/с и г>1Оо%п = 580 м/с, полученные при
отстреле такого же пакета шариком диаметром
6,3мм (масса 1г) в [16.94].
Для осколка ЕД и имитатора RFSP были
получены результаты пробития при скоростях
458 и 443 м/с, т.е. предельная скорость пробития
ЕД
RFSP
> Jo- *-— w-o w—
э еД#- - ¦¦ -о-*- о-*-»
400 450 500 550 600 v, м/с
Рис. 16.84. Результаты стрельб по
30-ти слойному пакету арамидной
ткани СВМ осколками ЕД и имита-
имитаторами RFSP; (о — непробитие, • —
пробитие )
имитатором снизилась на 15% по сравнению со скоростью пробития шариком.
Пробивание разнесенных преград.
Реальная аэродинамическая цель обычно представляет набор разнесенных пре-
преград («пакет»). При ударе со скоростью vq ^ г>кр после пробития первой преграды
происходит разрушение ПЭ (рис. 16.85).
11 мксек	46 мксек
Рис. 16.85. Рентгеноимпульсная регистрация процесса разрушения ПЭ на тонкой преграде
Хотя общий импульс и энергия потока за первой преградой («экраном») умень-
уменьшаются незначительно, происходит их перераспределение на большую площадь,
что резко снижает пробивное действие потока по дальнейшим преградам. Влияние
разнесенности преград молено характеризовать показателем Cz
cz =
пр

192	16. Осколочное действие взрывных систем
где /гпр — предельная толщина одиночной преграды, пробиваемой при заданных
параметрах удара: I ^ ^пР ) — суммарная максимальная толщина некоторой
г=1	/ Пр
комбинации преград из того лее материала, пробиваемая при тех же параметрах.
В данном случае величина Cz представляет относительное снижение массы
преграды, достигнутое за счет разнесенности. В общем случае, когда преграды
изготовлены из различных материалов с плотностями 71,72 ? • • • ? In ? относительное
снижение массы определится как
г=1	/ Пр
Г
Экспериментально показано, что при удачном подборе толщин и материала
преград при vq > 2000 м/с значение Cz может быть снижено до 0,4.
В заключение главы отметим, что дальнейшее развитие боеприпасов осколоч-
осколочного действия происходит как в направлении совершенствования обычных кон-
конструкций с круговыми полями, в том числе естественного дробления [16.95, 16.96],
заданного дробления и готовых ПЭ [16.97], так и в направлении развития новых
схем ОБП, в том числе кассетных [16.98] и с направленными полями ГПЭ [16.99]-
[16.102].

Глава 17
Кумуляция
17.1. Общие сведения
1. Понятие кумуляции. Кумулятивные заряды. Термин «кумуляция»
происходит от латинского cumulato — «скопление» или cumulo — «накапли-
«накапливаю» и дословно означает увеличение или усиление какого-либо эффекта за
счет сложения или накопления нескольких однородных с ним эффектов. Эффект
концентрации энергии в определенном направлении или в определенном месте и
является кумуляцией. Если при обычном взрыве энергия «разбрасывается» во
все стороны, то при кумулятивном она «собирается» в некотором направлении.
Кумулятивный эффект есть существенное повышение местного действия взрыва
в одном направлении [17.1]—[17.6]. Этот эффект получается при использовании
зарядов, имеющих на одном из концов полость — кумулятивную выемку. Если
такой заряд инициировать с противоположного конца, то эффект действия в
направлении оси выемки оказывается значительно большим, чем при действии
обычных зарядов. Если же к тому же поверхность кумулятивной выемки покрыть
сравнительно тонкой металлической облицовкой, то пробивное действие такого
заряда во много раз увеличится.
Сравнительный эффект действия обыч-
обычных и кумулятивных зарядов (КЗ) проил-
проиллюстрирован на рис. 17.1. Такие простые
опыты были впервые описаны в фундамен-
фундаментальных работах [17.7, 17.8] и впоследствии
вошли во многие издания, посвященные
вопросам кумуляции. При детонации за-
заряда взрывчатого вещества (ВВ) без ку-
кумулятивной выемки наблюдается неглубо-
неглубокая вмятина в материале преграды (а),
при незначительном удалении заряда от
преграды эффект воздействия на преграду
резко снижается (б). Наличие кумулятив-
кумулятивной выемки в заряде приводит к концентрации плотности энергии, что прояв-
проявляется в увеличении глубины вмятины в материале преграды (в). С удалением
рассматриваемого КЗ от преграды эффект взрывного воздействия также резко
снижается (г). Применение металлической облицовки в КЗ приводит к резкому
увеличению пробивного действия, при этом глубина проникания кумулятивной
струи (КС) существенно зависит и от расстояния КЗ от преграды (д, е). Различия
в степени воздействия КЗ без облицовки кумулятивной выемки и с металлической
облицовкой связаны с физическими особенностями реализуемых режимов про-
@
Рис. 17.1. Схематическое изображение ре-
результатов взрывного воздействия обычных
и КЗ на преграду из мягкой стали [17.8]

194
17. Кумуляция
странственной концентрации плотности энергии. В первом случае эффект кумуля-
кумуляции проявляется в формировании газокумулятивной струи, представляющей собой
высокоскоростной направленный поток продуктов взрыва (ПВ) повышенной плот-
плотности энергии (скорость такой струи может превышать даже вторую космическую
скорость — 11,2 км/с). Однако такая газокумулятивная струя имеет относительно
низкую эффективность действия по преграде, особенно на некотором удалении
от нее, что обусловлено быстрым расширением газообразных ПВ вследствие
неравномерного распределения по длине струи и наличия поперечных пульсаций в
струе. Это приводит к радиальному рассеиванию и быстрому снижению плотности
продуктов взрыва.
В присутствии металлической облицовки на поверхности выемки, как уже было
отмечено, наблюдается очень резкое усиление кумулятивного эффекта. Несмотря
на это обстоятельство, в данном случае сохраняются те физические особенности,
которые характерны для взрыва КЗ без облицовки выемки. Однако картина
рассматриваемого явления при этом существенно меняется.
В результате экспериментальных и теоретических исследований было установ-
установлено, что усиление кумулятивного эффекта при наличии облицовки связано с
весьма сильным и своеобразным перераспределением энергии между ПВ и матери-
материалом металлической облицовки, а также переходом части металла в кумулятивную
струю. Основная часть энергии активной части КЗ «перекачивается» в металл
облицовки так, что оказывается сконцентрированной в его тонком слое, который
собственно и образует кумулятивную струю. Вследствие этого достигается значи-
значительно большая плотность энергии в струе, чем при подрыве заряда без облицовки
выемки. Максимальное отношение диаметра выемки к диаметру струи для заряда
без облицовки равно 4-5. Для заряда с металлической облицовкой выемки это
отношение значительно больше, так как диаметр КС значительно меньше, чем
для зарядов без облицовки.
Структурная характеристика КЗ обусловлена особенностями их конструктив-
конструктивного оформления и функциональным назначением. Различают сосредоточенные
(осесимметричные) и удлиненные (плоские) кумулятивные заряды (рис. 17.2).
Представленные схемы КЗ включают следующие структурные элементы: 1 —
заряд ВВ с кумулятивной выемкой, 2 — облицовка кумулятивной выемки, 3 —
корпус КЗ, 4 — средство инициирования.
Наибольшее значение для
а	б	практики имеет направленная
осевая кумуляция. Этот вид
кумуляции может быть реали-
реализован при подрыве осесиммет-
ричных зарядов (рис. 17.2а),
имеющих выемку той или
иной формы (конус, полу-
полусфера, парабола, гипербола и
т.п.). Такие КЗ с оптимально-
оптимального расстояния Fm = A,5-6) do
способны пробивать насквозь
стальные преграды, или создавать в них каверны глубиной L = E—6) do и более,
со средним диаметром отверстия Do = @,1-0,3)do, где do — внутренний диаметр
кумулятивной облицовки (рис. 17.1е).
Удлиненные КЗ с плоской симметрией (рис. 17.26) имеют кумулятивную вы-
выемку, поперечное сечение которой может иметь форму угла (клиновидные обли-
облицовки), параболы, полуокружности (полуцилиндрические облицовки) и т.п. При
взрыве они формируют пелену или кумулятивный «нож:», который и разрезает
Рис. 17.2. Сосредоточенный (а) и удлиненный (б) куму-
кумулятивные заряды

17.1. Общие сведения	195
преграду. Основными элементами удлиненного КЗ являются корпус 3, заряд
взрывчатого вещества 1 и металлическая облицовка 2 кумулятивной выемки,
причем последняя, как правило, формируется из заготовки совместно с корпусом.
Чаще всего инициирование осуществляется с одного из открытых торцов заряда
при расположении детонатора посередине слоя ВВ в любом удобном месте среза
заряда, однако наиболее стабильные и лучшие результаты получаются при под-
подводе инициирующего импульса непосредственно к ребру облицовки (установка
детонатора в вершине облицовки строго по оси заряда). При таком способе
инициирования с торца, ноле при своем формировании и действии как бы бежит
вдоль заряда. При функционировании удлиненных КЗ глубина реза стальных
преград с оптимального расстояния Fm = @,5-1)^ составляет L = @,8-1)^, где
dk — внешний диаметр корпуса-трубки с полуцилиндрической медной облицовкой.
Область использования кумулятивного эффекта определяется конструктив-
конструктивными особенностями и функциональным назначением кумулятивных зарядов.
Сосредоточенные осесимметричные КЗ используются в военной технике для про-
пробития сильнозащищенных и бронированных целей; в кумулятивных перфора-
перфораторах — для пробивания обсадных труб нефтяных, газовых, нагнетательных и
водозаборных скважин; для образования шпуров под заряды В В в массивах
материалов, негабаритах горных пород и металлических скрапах; для «прошивки»
отверстий в плитах из различных материалов и т.п. [17.1, 17.5, 17.10, 17.11].
Удлиненные КЗ применяются для взрывной резки и разделки материалов и
конструкций, разделения ступеней ракет, перерубания свай, кабелей, тросов и т.п.
[17.5, 17.11, 17.12, 17.13]. В основе явления, известного как сварка взрывом, лежит
частный случай плоской кумуляции, реализуемой при метании двух пластин под
определенным углом друг к другу (см. гл. 21).
2. Краткие исторические сведения. Открытие кумулятивного эффекта
связывают с разработкой взрывных петард, вошедших во всеобщее употребление
в горнодобывающей промышленности во второй половине XVIII века. Горным
инженерам уже тогда было известно, что некоторую часть энергии взрыва можно
сконцентрировать, если придать заряду соответствующую форму. В 1792 г. (по
другим данным — в 1799 г.) немецкий минный инженер и естествоиспытатель
Франц фон Баадер (Baader) впервые сфокусировал энергию фугасного заряда,
создав в нем полость [17.9]. Дальнейшее развитие кумулятивный эффект получил
во второй половине XIX века. В 1864 г. русский военный инженер М. М. Борес-
ков выявил повышенный эффект действия у инженерных мин с кумулятивной
выемкой и использовал его для разрушения твердых пород при строительстве
фортификационных сооружений, а уже в 1865 г. в России, для усиления направлен-
направленного действия при взрыве, был применен первый капсюль-детонатор с конической
кумулятивной выемкой. Примерно в это же время подобный капсюль-детонатор
был предложен известным изобретателем Альфредом Нобелем (Nobel).
Первые научные работы по исследованию кумулятивного эффекта полых необ-
лицованных зарядов ВВ были опубликованы в Германии М. Ферстером (Foerster) в
1883 г. и Е. Нейманом (Neumaun) в 1914 г., а в Великобритании и США — К. Монро
(Munroe) в 1888г. [17.9]. В период с 1910г. по 1914г. в Великобритании и Германии
были получены первые патенты на применение металлических облицовок кумуля-
кумулятивных выемок и использование кумулятивного эффекта в бронебойных снарядах,
однако перевести работы в полностью практическое русло для военных целей
не удалось до начала второй мировой войны. В России первые систематические
исследования явления кумуляции были проведены в 1923-1926 г. г. профессором
М. Я. Сухаревским, который показал целесообразность использования КЗ в ка-
качестве эффективных подрывных средств и установил зависимость пробивного

196	17. Кумуляция
действия КЗ без облицовки от формы кумулятивной выемки и ряда других
факторов.
Качественным скачком, обусловившим широкое применение кумулятивного
эффекта, явилось использование металлической облицовки кумулятивной выемки.
При взрыве заряда с кумулятивной выемкой без облицовки образуется газовая
струя, а с металлической облицовкой — металлическая кумулятивная струя. Хотя
скорость у газовой струи выше, чем у металлической, но, вследствие большого
диаметра и малой плотности, ее воздействие на преграды во много раз слабее.
Облицовку обычно делали из меди, цинка, алюминия, железа или стали. Кумуля-
Кумулятивный эффект увеличивался при установке облицованного КЗ на определенном
расстоянии от преграды.
Результаты экспериментальных и теоретических исследований явления ку-
кумуляции позволили к началу второй мировой войны создать первые образцы
боевой техники. В 1939—1943 гг. в Германии были разработаны 75-мм бронебойные
кумулятивные снаряды, 30-мм и 40-мм кумулятивные гранаты, а в России — 76-
мм и 122-мм бронебойные кумулятивные снаряды, тяжелая ручная кумулятивная
противотанковая граната РПГ-6. В первой открытой публикации по основам
теории действия КЗ с металлической облицовкой выемки [17.7] приведена схема
головной части американского снаряда «базука» и описан принцип его действия.
На рис. 17.3 показано поперечное сечение головной части ракеты «базука» [17.5].
Когда баллистический колпачок 1 встречает поверхность поражаемой прегра-
преграды, удар вызывает инерционное смещение ударника во взрывателе 3 и происходит
детонация заряда 2. Взрыв сминает стальной конус облицовки 4, образуется струя
высокой скорости и плотности, которая пробивает преграду и может поразить раз-
различные объекты и агрегаты, находящиеся за ней. Указанные разработки надолго
определили основное направление практического использования кумулятивного
эффекта — в военных целях.
Параллельно с практической реализа-
реализацией кумулятивного эффекта, примерно
с 1941 по 1949 г г, была создана теория
этого явления, которая в дальнейшем по-
получила исключительное развитие во всех
странах. Приоритет в развитии гидродина-
гидродинамической теории кумуляции принадлежит
Рис. 17.3. Схема головной части американ-	иканским и российским ученым. В
скои армейской ракеты «базука»	лттт д	„	^	»r-	m»
США над этой проблемой работали 1эи-
лор (Taylor), Биркхофф (Birkhoff), Мак-
Дугал (MacDougall), Пач (Pugh), Эйчельбергер (Eichelberger) и др., в России —
Лаврентьев, Покровский, Баум, Станюкович и др. В настоящее время крупные
исследования в области кумуляции проводятся в США, Германии, Великобрита-
Великобритании, Франции и России.
3. Механизм формирования кумулятивной струи. Возможные режи-
режимы кумуляции. Совместные теоретические и экспериментальные методы иссле-
исследований позволяют получить представление о процессе образования кумулятивной
струи. Всесторонними экспериментальными исследованиями, применяя методы
мгновенной рентгенографии, искровой фотографии и т.п., удалось установить
природу КС и механизм ее формирования. Особенно плодотворным при иссле-
исследовании явления кумуляции в присутствии металлической облицовки оказался
метод мгновенной рентгенографии.
Наиболее подробно процесс изучен на осесимметричных зарядах с кониче-
конической и полусферической облицовками выемок. В итоге этих исследований было

17.1. Общие сведения
197
а
установлено, что металлическая облицовка под воздействием ПВ обжимается,
в результате чего ее элементы последовательно захлопываются с образованием
тонкой металлической струи, обладающей большой скоростью.
Общая картина процесса деформирова-
деформирования металлической облицовки и образо-
образования КС показана на двух сериях рент-
рентгеновских снимков для конической (а)
и полусферической (б) форм облицовок
(рис. 17.4). Они фиксируют начальный мо-
момент процесса обжатия облицовки и дви-
движения струи во времени. При этом дав-
давление продуктов детонации на облицовку
имеет порядок 20—60 ГПа, в зависимости от
материала облицовки, угла подхода фрон-
фронта детонационной волны (ДВ) к поверх-
поверхности облицовки и характеристик ВВ, а
скорость метаемой тонкой металлической
облицовки имеет порядок 1-3 км/с. В ре- Рис 17 4 Рентгенограммы начальной ста-
Зультате СТОЛЬ СИЛЬНОГО И быстрого об- дии формирования КС зарядами с кониче-
I
I
ской (а) и полусферической (б) облицовками
[17.14]
жатия облицовки, при последовательном
деформировании и захлопывании отдель-
отдельных ее элементов, образуется компактная
монолитная масса — пест и формируется тонкая металлическая струя, скорость
которой может в несколько раз превышать скорость обжатия металлической об-
облицовки. Образованию остающегося песта можно в значительной мере воспрепят-
воспрепятствовать, формируя слой облицовки, образующий пест, из материала, который под
воздействием ПВ может сгорать или испаряться (специальные биметаллические
облицовки) [17.6].
Рис. 17.5. Формирование КС при обжатии металлической облицовки осесимметричного куму-
кумулятивного заряда
Картина формирования КС при обжатии металлической конической облицовки
осесимметричного КЗ схематично показана на рис. 17.5. Фронт ДВ 2 в заряде
ВВ 3 начинает распространяться от детонатора 1 со скоростью детонации D.
Образующиеся продукты детонации (ПД) взаимодействуют с облицовкой 4 ку-
кумулятивной выемки. При последовательном схлопывании облицовки образуется
пест 5 и кумулятивная струя 6.
Результаты обработки рентгенограмм показывают, что, в случае использова-
использования конических медных облицовок, в струю переходит в среднем 10-20% массы
облицовки, скорость головных участков струи составляет 9-10 км/с, а хвостовых
2-2,5 км/с. Скорость струи от полусферической облицовки приблизительно в два
раза меньше, но масса ее в три-четыре раза больше, так что общая энергия струи
от полусферической облицовки сравнима с энергией струи от конуса такой же
массы.

198
17. Кумуляция
:¦-¦*-
Рис. 17.6. Микрофотография шли-
шлифов песта (латунь)
При обжатии облицовки толщина ее увели-
увеличивается, а энергия концентрируется преимуще-
преимущественно в ее внутреннем слое. Механизм обра-
образования КС связан с течением материала внут-
внутренних слоев облицовки, что является следстви-
следствием высокоскоростного соударения ее элементов
в момент захлопывания, при этом струя как
бы «выжимается» из металлической облицовки
в процессе осевого схлопывания ее внутренних
слоев. Подтверждением того, что КС связана с
течением металла, кроме приведенных резуль-
результатов, могут служить следующие данные [17.4].
Если на внутреннюю поверхность стального ко-
конуса гальваническим путем нанести слой меди
толщиной 0,05 мм, то обнаружить в песте какие-
либо следы меди не удается. Если же слой меди
нанести на наружную поверхность конуса, то в
песте обнаруживаются полосы окисленной меди.
При обследовании песта вдоль его оси удается
обнаружить узкий канал, наличие которого яв-
является показателем того, что внутренние слои
металла имеют резко повышенные скорости по
сравнению с наружными. О характере деформа-
деформации металла облицовки в процессе ее обжатия
можно также судить по результатам металлогра-
металлографических исследований пестов в сечениях, раз-
различно удаленных от оси (см. подробнее в п. 17.4).
На всех фотографиях микроструктур (рис. 17.6)легко обнаруживается ориентация
и вытягивание структурных составляющих в осевом направлении. Ориентация и
вытягивание увеличиваются по мере приближения соответствующих слоев к оси.
Как следует из рентгенограмм, в течение некоторого времени пест и струя
составляют единое целое, однако их движение совершается с различными скоро-
скоростями. Пест движется сравнительно медленно (со скоростью 0,5—1км/с). Струя,
наоборот, обладает весьма большой скоростью поступательного движения. Однако
скорость эта различна в различных частях вдоль струи: головная часть струи
имеет наибольшую скорость, а скорость хвостовой части близка к скорости песта.
В зависимости от формы и природы металла облицовки, свойств ВВ заряда и
других факторов, скорость головной части струи может изменяться в широких
пределах. Например, для алюминиевой облицовки гиперболической формы ско-
скорость головной части достигает 11км/с [17.4]. Некоторые данные по скорости
головной части КС для состава ВВ — сплав тротила с гексогеном (D = 7600 м/с),
приведены в табл. 17.1.
В реальных условиях, как уже отмечалось, различные участки формируемой
КС движутся с различными скоростями, при этом скорость вдоль струи суще-
существенно возрастает от хвостовых к головным ее элементам. Различие в скоростях
движения элементов КС может достигать 5—6 км/с и более, значения начальных
градиентов скорости — 104-105с~1, что приводит к удлинению (растяжению)
струи при ее движении в свободном пространстве и затем к ее распаду на конечное
число отдельных фрагментов, в дальнейшем не изменяющих своей длины.
Картина растяжения и последующего разрыва КС многостадийна, она по-
подробно рассматривается в п. 17.3. На рис. 17.7 схематично показаны основные
стадии образования (а), растяжения (б) и фрагментации (в) в свободном полете

17.1. Общие сведения
199
Таблица 17.1
Зависимость скорости головной части КС от основных параметров
Размеры
заряда
d,
мм
30
30
30
30
30
42
н,
мм
70
70
70
70
70
85
Характер облицовки
Материал
сталь
дюралюминий
сталь
дюралюминий
сталь
дюралюминий
сталь
дюралюминий
сталь
дюралюминий
сталь
дюралюминий
S,
мм
1
1
1
1
1
4
1
Параметры выемки
Форма выемки
Полусфера
Конус
Конус
Конус
Гипербола
Гипербола
do,
мм
28
27,2
27,2
27,2
27,2
37,2
2а, °
-
60
35
27
-
-
Скорость
головной
части
струи,
м/сек
3000
6050
6500
7650
7300
8500
7400
9000
9500
7150
10700
d — диаметр заряда, Н — высота заряда, S — толщина облицовки,
do — диаметр основания, 2а — угол раствора конуса.
кумулятивной струи. При этом элементы фрагментированной КС в процессе
движения под воздействием внешних возмущений и с учетом технологических
факторов могут отклоняться от оси в пределах некоторого телесного угла разлета,
изменяющегося в зависимости от точности изготовления КЗ в пределах 0,5—1,5°.
На основании изложенного можно заключить, что наиболее эффективное дей-
действие КС может быть обеспечено лишь при определенном сочетании физико-
механических свойств металла. При этом необходимо иметь в виду, что свойства
металла в условиях быстрых деформаций могут значительно отличаться от его
свойств, определяемых при обычных скоростях деформаций. Например, чугун,
хрупкий в обычных условиях, при взрыве КЗ ведет себя как металл с относительно
высокой пластичностью.
Условия формирования КС определяются микроструктурой металла облицов-
облицовки и способностью его структурных составляющих к пластической деформации.
Однако пластичность металла в условиях обжатия под действием взрыва не опре-
определяется однозначно его стандартными характеристиками. Отмечена зависимость
между способностью металла к быстрому обжатию и типом кристаллической ре-
решетки. Тяжелые пластичные металлы, в частности гранецентрированные металлы
с кубической решеткой группы меди, и некоторые сплавы образуют сплошные
струи, плотность которых не более, чем на 10% ниже плотности материала об-
облицовки, и которые при большом удлинении (примерно в 10 раз по сравнению с
исходной длиной образующей облицовки) не разрываются и сохраняют высокую
плотность. Другие металлы, такие, например, как железо и цинк, на начальных
стадиях образуют сплошные струи, которые, в отличие от описанных выше, при
растяжении разрываются гораздо раньше. Хрупкие металлы, такие, в частности,
как вольфрам, титан, а также металлы с высокой пористостью, получаемые

200
17. Кумуляция
спеканием, вообще не образуют сплошных струй, они формируют дискретные
струи, состоящие из отдельных твердых частиц. В этом случае растяжение струи
приводит не к уменьшению ее диаметра, как в сплошных струях, а к снижению
средней плотности струи. Поражающая способность таких струй, по сравнению со
сплошными, значительно ниже.
Путем улавливания КС и песта в неко-
некоторых неплотных средах и последующего
металлографического анализа установле-
установлено, что в процессе формирования струи
не происходит плавления металла. Однако
температура КС, в зависимости от мате-
материала облицовки, может достигать 900-
1000°С [17.4].
Нормальный процесс струеобразования
приводит к формированию классической
сплошной монолитной высокоградиентной
КС, обладающей наибольшей пробивной
способностью. Однако, могут существо-
существовать условия, при которых струя либо во-
вообще не образуется, либо образуется в виде
диспергированного потока частиц, или в
виде компактного поражающего элемен-
элемента (ударного ядра). Критические условия
струеобразования подробно рассматрива-
рассматриваются в п. 17.2. В общем случае переход от
^	соударения с образованием сплошной КС
а	б	в	к соударению с образованием диспергиро-
Рис. 17.7. Основные стадии формирования ванной КС имеет место тогда, когда точка
и движения КС: образование струи при соударения (точка контакта) движется со
обжатии облицовки (а); растяжение струи сверхзвуковой СКОрОСТЬЮ. При Очень ма-
вследствие наличия градиента скорости (б); леньких углах схлопывания Струя вообще
I
фрагментация (разрыв) струи на отдельные
элементы в свободном полете (в) [17.15]
может не образовываться. При увеличе-
увеличении угла схлопывания вероятность струе-
струеобразования повышается, однако условием
образования сплошной монолитной КС будет являться обеспечение дозвуковой
величины скорости точки контакта [17.6, 17.16]. В ряде работ верхний предел
скорости головной части сплошной КС определяется близким к удвоенной ско-
скорости звука материала облицовки (к примеру, для меди он не должен превышать
~ 10км/с). Так, по данным работы [17.17], скорость головной части сплошной КС,
ограниченная сверху условиями обеспечения дозвуковой величины скорости точки
струеобразования, не должна превышать Vj $J 2,41cq, где cq — скорость звука в
материале облицовки.
Вместе с тем, для экспериментальной физики представляет интерес получение
газовых и металлических струй, движущихся со скоростями порядка многих де-
десятков километров в секунду. Такие распыленные струи могут быть реализованы
в условиях цилиндрической кумуляции при достаточно высокой скорости схло-
схлопывания элементов облицовки и достаточно малых значениях углов схлопывания
[17.4]. В работах [17.18]—[17.20] описаны КС, скорость которых существенно пре-
превышает величину, допускаемую гидродинамической теорией с учетом критериев
струеобразования (см. п. 17.2). Так, в [17.18] при использовании цилиндрических
трубок из бериллия, окруженных толстым слоем ВВ, получены КС со скоростью
до 90 км/с.

17.1. Общие сведения
201
Рис. 17.8. Различные режимы кумуляции: клас-
классическая кумуляция (а); «обратная кумуляция»
(б); промежуточный режим (в)
При существенном увеличении уг-
углов схлопывания (переходе на поло-
пологие конические или полусферические
облицовки), наряду с классическим
режимом кумулятивного струеобра-
зования, возможен так называемый
режим «обратной кумуляции», свя-
связанный с механизмом выворачивания
кумулятивной облицовки [17.21].
На рисунке 17.8 схематично пока-
показаны различные режимы кумуляции,
связанные с изменением угла кониче-
конической облицовки и профиля полусфе-
полусферической облицовки. В зарядах с вы-
высокими конусами реализуется режим
классической кумуляции (а), приводящий к формированию высокоскоростной
и высокоградиентной КС (выход металла в струю до 30%, скорости головных
элементов порядка 9—10 км/с, хвостовых элементов порядка 2—2,5 км/с, пробитие
стальной преграды до (8-10)с?о)- В зарядах с пологими конусами с углом раствора
порядка 150-160° и сегментными облицовками высотой до @,1-0,2)с/0 реализует-
реализуется режим обратной кумуляции (б), приводящий к формированию компактного
поражающего элемента с практически 100%-ым выходом материала облицовки
в ударное ядро, скоростью порядка 2,2—2,8 км/с и пробитием стальной преграды
толщиной @,5—0,8) do. Указанный режим образования компактного тела связан
с влиянием прочности материала кумулятивной облицовки (КО) на процесс
обжатия и определяется верхним пределом струеобразования [17.16]. На рис. 17.8в
показан промежуточный режим, характерный для конических облицовок с углами
раствора 100—120° и полусферических облицовок, и приводящий к образованию
массивной малоградиентной струи (выход металла облицовки в струю порядка
50—60%, скорости головных элементов порядка 4,5—5 км/с, хвостовых элементов —
порядка 1,5-2км/с, пробитие стальной преграды до D-5)do)- Приведенные выше
количественные характеристики зависят также от толщины КО, заряда ВВ и
относятся к медным КС и ударным ядрам.
4. Проникание кумулятивной струи в преграду. При взаимодействии
КС с преградой, на границе между материалом струи и преграды возникает
очень высокое давление, на один—два порядка превосходящее предел прочности
материала преграды. В результате возникающего давления КС разворачивается
и «срабатывается», ее материал растекается в направлении, обратном скорости
ее движения. Материал преграды также «уходит» из зоны высокого давления,
причем часть материала выносится вместе со струей к свободной поверхности, а
другая часть, за счет пластического деформирования, перемещается в радиальном
направлении. Таким образом, образуется кратер, диаметр которого существенно
превышает диаметр кумулятивной струи.
В целом глубина проникания струи в преграду зависит от:
-	размеров и формы КЗ;
-	формы, геометрии и материала КО;
-	качества, энергосодержания, плотности и скорости детонации ВВ;
-	расстояния заряда от преграды;
-	наличия «линзы»;
-	точности изготовления различных деталей КЗ и точности их сборки.
Подробно данный вопрос рассматривается в пп. 17.6. и 17.7. На глубину

202
17. Кумуляция
L/d
— F
1
i
2
3 F/d
О	1
Рис. 17.9. Экспериментальная за-
зависимость относительной глубины
проникания от относительного рас-
расстояния КЗ до стальной плиты
пробития существенно влияют также плотность и прочность преграды. Для не
слишком малых зарядов с достаточной точностью справедлив закон подобия:
размеры кратера увеличиваются в той лее степени, что и размеры заряда. Таким
образом, можно указывать поражающую способность зарядов данного типа, отно-
относя глубину внедрения струи к диаметру заряда (d) или к внутреннему диаметру
кумулятивной облицовки (do).
Большое значение для образования кратера
(пробоины) в преграде имеет так называемое
«фокусное расстояние», ассоциируемое с таким
минимальным расстоянием заряда от преграды,
при котором КС обладает максимальной про-
пробивной способностью. На рис. 17.9 показана за-
зависимость поражающей способности одного из
стандартных зарядов от расстояния F между
зарядом и стальной преградой [17.6]. Видно, что
достигаемая при этом глубина пробития L, по
мере увеличения расстояния между зарядом и
преградой, вначале возрастает, а затем убывает.
При увеличении расстояния F увеличивается и
разброс значений глубины внедрения КС (см.
зашрихованную зону на рис. 17.9). В этом случае глубина пробития достигает
максимального значения при подрыве КЗ на оптимальном («фокусном») расстоя-
расстоянии Fm от преграды, которое изменяется в зависимости от конструкции заряда,
материала облицовки, точности изготовления, и обычно составляет от двух до
шести диаметров заряда [17.5, 17.6, 17.9].
В табл. 17.2 приведены зна-
значения относительной глубины
проникания КС в преграды из
разных материалов примени-
применительно к взрыву стандартного
заряда [17.6]. Глубина кавер-
каверны в мягкой стали L$ приня-
принята за единицу. Следует отме-
отметить, что относительная глу-
глубина L/Ls зависит от кон-
конструкции КЗ и материала об-
облицовки.
В табл. 17.3 приведены дан-
данные о влиянии прочности соот-
соответствующих металлов на глу-
глубину проникания кумулятив-
кумулятивной струи [17.4]. Опыты про-
проводились с зарядами из сплава
ТГ 50/50 диаметром 42 мм и
высотой 84 мм, кумулятивная
выемка была гиперболической
формы с облицовкой из алю-
алюминиевого сплава толщиной 2 мм. Влияние прочности на глубину проникания
данной КС в преграду с одинаковой начальной плотностью, но разной прочностью,
объясняется более быстрым «срабатыванием» струи в прочной преграде.
При проникании струи в преграду максимальное давление возникает в лежащей
на оси струи точке соударения струи и преграды. Давление в зоне контакта струи
Таблица 17.2
Зависимость относительной глубины проникания
КС от плотности материала преграды
Материал преграды
Мягкая сталь
(эталон)
Броневая сталь
средней твердости
Свинец
Бетон
Плексиглас
Полиэтилен
Парафин
Резина
рт ¦ 1(ГЛ,
кг/м3
7,8
7,8
11,3
2,3
1,2
0,92
0,9
1,1
L/Ls
1,0
0,8
1,3
3,5
2,8
5,0
7,2
6,4
рт — плотность материала преграды,
L/Ls — относительная глубина проникания.

17.1. Общие сведения
203
Таблица 17.3
Зависимость проникающего действия
струи от твердости преграды
Материал преграды
Сталь
Сталь
Алюминиевый сплав
Алюминиевый сплав
Нв
100
350
50
200
L, мм
111
80
327
256
Л в — твердость по Бринеллю,
L — глубина пробития.
и преграды по перпендикулярному к оси струи направлению быстро уменьшается
до нуля на цилиндрической поверхности пробитого струей отверстия в преграде.
Материал преграды перетекает из зоны высокого давления в зону низкого
давления. Чем прочнее преграда, тем хуже происходит пластическое течение
материала преграды, тем меньше глубина пробития.
Очевидно, что этот эффект зависит
не только от прочности, но и от пла-
пластических свойств материала преграды в
условиях высокого среднего давления и
высоких скоростей деформации. Если ма-
материал преграды будет в этих условиях
оставаться хрупким, то пластическое тече-
течение материала из зоны высокого давления
будет затруднено, и в этом случае глубина
проникания струи в преграду будет соот-
соответственно меньше.
Экспериментальные и теоретические
исследования показывают, что не вся дли-
длина струи обладает способностью проби-
пробивать преграду. Та часть струи, которая
участвует в пробитии преграды, называется эффективной длиной струи. Мини-
Минимальную скорость, которую имеют элементы эффективной части струи, называют
критической — Vj . Некоторые средние значения критической скорости по данным
ряда авторов приведены в табл. 17.4, однако в зависимости от характеристик
используемых КЗ, метода определения критической скорости и существующих
расхождений в том, что принимать за критическую скорость в опыте, эти данные в
ряде случаев имеют значительный разброс. Наличие критической скорости объяс-
объясняется тем, что струя при скорости Vj < Vj уже не создает в месте контакта струя-
преграда необходимого поля давления, чтобы «раздвинуть» материал преграды,
а сама струя «срабатывается» в глубине преграды.
Объем кратера можно считать зависящим от энергии струи и прочности ма-
материала преграды. При этом оказывается, что расход энергии на образование
определенного объема с увеличением скорости струи возрастает. Существенным
образом влияет на форму кратера также и геометрия преграды. Это становится
понятным из того, что расширение кратера в значительной степени происходит
благодаря вытеснению материала преграды в радиальном направлении. Поэтому
диаметр кратера тем больше, чем меньше энергии требуется для пластическо-
пластического течения материала преграды. Вследствие этого, в блоках с ограниченным
поперечным сечением диаметр отверстия оказывается большим, чем в плитах,
поперечный размер которых велик по сравнению с их толщиной. В наборах
пластин с воздушными промежутками и прокладками из легкодеформируемых
материалов, диаметр кратера также получается большим, чем в однородных
толстых пластинах.
С другой стороны, разброс величин глубины проникания уменьшается с ростом
радиуса кратера. Это связано с тем, что в кратерах большого диаметра элементы
струи, имеющие некоторое отклонение от оси симметрии, попадают на дно кра-
кратера, образованного предыдущими элементами, а в кратере меньшего диаметра
соударяются с его стенками, вследствие чего глубина кратера не увеличивается,
а лишь нарушается его симметрия. Кроме того, участие песта и близких к нему
по скорости хвостовых элементов струи в пробитии преграды зависит от того,
позволяет ли диаметр кратера двигаться им без разрушения. Уже по этим причи-
причинам глубина внедрения струи должна зависеть от твердости материала преграды

204
17. Кумуляция
Таблица 17.4
Зависимость критической скорости струи от твердости преграды и материала
кумулятивной облицовки
Материал преграды
Сталь закаленная, HRC 50
Сталь, НВ = 125
Сталь, НВ = 125
Дюралюминий, НВ 115
Сталь прочная
Бетон
Песок
Мрамор
Известняк
Песчанник
Бетон
Лед
Грунт мерзлый
Материал КС
Сталь
Сталь
Дюралюминий
Дюралюминий
Медь
Медь
Медь
Медь
Медь
Медь
Сталь
Медь
Сталь
Vj, м/с
2200
2050
3300
2900
3000
1500
1000
1600
1500
1300
1900
1800
1000
Ссылка
[17.4]
[17.22]
[17.23]
[17.24]
.1
и ее геометрии; по результатам, полученным на материале с одними свойствами,
нельзя с уверенностью судить о возможной глубине пробития преграды с иными
прочностными характеристиками.
Если преграда имеет конечную толщину, то после ее пробития КС в запреград-
ное пространство проникают, помимо оставшейся части самой струи, вторичные
осколки, образующиеся в результате взаимодействия струи с тыльной частью
преграды, ПД и баллистические ударные волны (УВ). Каждый из указанных
факторов по-разному влияет на степень поражения объектов в запреградном
пространстве, однако главным образом она определяется энергией оставшейся
после пробития преграды части кумулятивной струи.
На рис. 17.10 представле-
представлена рентгенограмма (а) и схе-
схема процесса действия (б) КС
в запреградном пространстве.
В результате взрыва кумуля-
кумулятивного заряда 1, иницииру-
инициируемого детонатором 2, образу-
образуются КС 6, ПД 3 и падаю-
падающая на преграду воздушная
У В 4. После пробития такой
преграды 8, в запреградное
пространство проникают эле-
элементы КС 7 и поток осколков
а	б	от преграды 10, впереди ко-
Рис. 17.10. Рентгенограмма (а) и схема пробнтня (б) КС ™РЫХ распространяется УВ
стальной преграды конечной толщины	(воздушная взрывная 9 И бал-
листические 11,12 от потока
осколков и элементов КС). С
наружной поверхности преграды распространяется отраженная воздушная У В 5.
12,
7&

17.2. Теория кумуляции
205
Указанное явление необходимо учитывать при оценке эффективности действия
КЗ по преградам конечной толщины, особенно в случае защиты ими объектов с
замкнутым воздушным пространством.
Рассмотренные выше особенности действия КС по преградам относятся, в
основном, к металлическим преградам. При переходе на такие нетрадиционные
материалы преград, как скальные породы, бетон, лед, мерзлый грунт, вода, стек-
стеклопластик, керамика, пористые материалы и т.п., к которым в последнее время
проявляется определенный интерес в связи с возможностью расширения области
использования КЗ, появляются принципиально новые факторы, которые необхо-
необходимо учитывать при оценке пробивной способности кумулятивных зарядов. Как
правило, такие материалы имеют небольшую плотность по отношению к стали,
некоторые из них характеризуются инерционным движением среды и хрупким
характером разрушения; помимо срабатывающихся элементов КС, существенный
вклад в глубину их пробития может вносить пест, проникающий как жесткое тело.
17.2. Теория кумуляции
1. Теория струй несжимаемой жидкости. Процесс формирования куму-
кумулятивных струй при косом соударении пластин, метаемых продуктами детонации,
или при взрывном обжатии осесимметричных металлических облицовок, впервые
объяснила гидродинамическая теория кумуляции, основанная на модели идеаль-
идеальной несжимаемой жидкости [17.7, 17.8, 17.25]. В основе гидродинамической теории
образования кумулятивной струи лежит теория струй идеальной несжимаемой
жидкости.
Рис. 17.11. Схема соударения двух струй
несжимаемой жидкости
Рис. 17.12. Схема соударения одной струи с
идеально гладкой поверхностью
Рассмотрим картину симметричного соударения двух струй идеальной несжи-
несжимаемой жидкости под углом 2а (рис. 17.11). Так как процесс соударения струй
симметричен, то можно рассматривать только верхнюю часть течения струй
(рис. 17.12). При этом будем считать, что поверхность симметрии абсолютно
гладкая, то есть при движении жидкости по этой поверхности трение отсутствует.
Обозначим: щ, М — скорость и масса сходящейся струи (масса жидкости,
протекающая через поперечное сечение струи в единицу времени), uj, Mj —
скорость и масса струи, движущейся вправо вдоль оси Ож, us, Ms — скорость
и масса струи, движущейся влево, в отрицательном направлении оси Ох. В
этой задаче считаются заданными величины щ,М и а, необходимо определить
параметры образующихся струй: uj, us, Mj и Ms. К данному процессу применим

206	17. Кумуляция
законы сохранения массы, импульса и энергии. По закону сохранения массы:
М = Mj + Ms.	A7.1)
Согласно закону сохранения количества движения, изменение количества движе-
движения равно импульсу действующих сил. Поскольку вдоль оси Ох на жидкость не
действуют никакие силы в данной задаче, то изменение количества движения
равно нулю:
(Mjuj cos 0° + Msus cos тг) - щМ cos(tt + а) = 0	A7-2)
или
Mjuj - Msus = -щМ cos a.	A7-3)
Проекцию уравнения сохранения количества движения на ось Or в данной
задаче можно не находить, так как искомые струи текут в перпендикулярном
направлении к оси Or.
Поскольку процесс соударения струй является стационарным, то закон сохра-
сохранения энергии можно записать в виде:
Mju2j Msu2s = Mul
2	2	2 '	{ ' }
Из уравнений A7.1), A7.4) получим, что абсолютные значения скоростей струй
равны:
щ = uj = us.	A7-5)
С учетом этого уравнения, а также уравнений A7.1) и A7.3), получим:
Mj-Ms = -Mcosa.
Отсюда определим Mj и
M(l-cosa)	. 2 а	(Л^ ^
=	2	L = Msm2 -,	A7.7)
M(l + cosa)	о а	,^п,
Ms = v 2	 = Mcos2 -.	A7.8)
2. Теория образования кумулятивной струи. Рассмотрим переход от
теории струй несжимаемой жидкости к теории образования кумулятивной струи.
Пусть облицовка кумулятивной выемки получает скорость Vo •> перпендикулярную
к образующей облицовки (рис. 17.13). Разложим этот вектор по двум направле-
направлениям: вдоль образующей облицовки и вдоль оси Ох. В результате получим (см.
рис. 17.13):
^	^	A7.9)
tg a	sin a
Теперь рассмотрим процесс движения струй относительно каждой из этих состав-
составляющих вектора Vq —скорости обжатия кумулятивной облицовки. При этом схема

17.2. Теория кумуляции
207
//////////////////////////т/УУУУУУУУ
О	vK
Рис. 17.13. Схема процес-
процесса образования кумулятив-
кумулятивной струи в несжимаемой
жидкости
а	б
Рис. 17.14. Схема разложения процесса формирования куму-
кумулятивной струи
течения, представленная на рис. 17.13, распадается на две части (рис. 17.14).
На рис. 17.14а мы имеем схему течения струй, такую же, как на рис. 17.12. В
этом случае, согласно уравнению A7.5), образуются две струи, скорости которых
равны и, с учетом A7.9), определяются выражением и$ = uj = щ = Vo/tga.
На рис. 17.146 показана скорость Vk = Vb/sina, представляющая собой скорость
движения точки схлопывания кумулятивной облицовки (точки 0).
Соединяя оба эти течения, получим:
Vf,
+
- cos a
= Vk - us =
sin a tga
_Vo	Vb_
sin a tga
sin a
1 - cos a
sin a
= Vr
o a
2 cos2-
a a~
2 sm — cos —
a
Vr
> a a
2 sin — cos —
2 2
°a, A7.10)
2
= yotgj. A7.11)
Формула A7.10) определяет скорость кумулятивной струи Vj, а формула A7.11) —
скорость песта Vs\ соответственно, по формуле A7.7) определяется масса кумуля-
кумулятивной струи М/, а по формуле A7.8) — масса песта Ms-
Определим кинетическую энергию кумулятивной струи и песта:
MjFJ
a
a
~2
MV* 2 a
—-C°S 2'
^•sin2^
2	2'
A7.12)
A7.13)
где MVq/2 = Eq — кинетическая энергия обжатия кумулятивной облицовки,
имеющей массу М и скорость обжатия кумулятивной облицовки Vo-
Согласно гидродинамической теории, кумулятивная струя образуется при лю-
любом угле а и любой скорости Vo. Так, при а —> 0, по формулам A7.7), A7.8),
A7.10)-A7.13) получим Mj -+ 0, Ms -* М, Vj -+ ос, Vs -+ 0, Ej -+ Ео, Es -+ 0.
Однако практика не подтверж:дает эти предельные величины. Если скорость
щ = Vo/tga сверхзвуковая л а < а&, где а^ — некоторый критический угол
схлопывания, то кумулятивные струи не образуются [17.26].
С другой стороны, если а > ап, где ап — предельный угол схлопывания, то
кумулятивная струя также не образуется из-за того, что радиальная проекция
скорости метания облицовки становится недостаточной для того, чтобы обеспечить

208
17. Кумуляция
схлопывание (деформацию) материала, обладающего прочностью, не учитывае-
учитываемой в гидродинамической модели [17.16]. Деформирование облицовок с малыми
значениями радиальной скорости, реализуемое при углах схлопывания облицовки,
близких к ап, приводит к формированию компактных поражающих элементов —
ударных ядер (см. п. 17.5. ).
3. Критические условия струеобразования. Согласно гидродинамиче-
гидродинамической теории кумуляции, основанной на модели несжимаемой жидкости, кумуля-
кумулятивная струя образуется при любых углах схлопывания кумулятивной облицовки.
Эксперименты же показывают, что при малых углах схлопывания кумулятивная
струя не образуется [17.26]. Для объяснения этого эффекта необходимо учитывать
сжимаемость материала кумулятивной облицовки в процессе ее схлопывания. В
основе этой модели лежит теория косых ударных волн. Рассмотрим процесс сим-
симметричного схлопывания двух плоских струй сжимаемой жидкости под углом 2а
со скоростью щ в системе координат, связанной с точкой соударения 0 (рис. 17.15.)
На рис. 17.156 вектор скорости потока до и после фронта косой ударной волны
а	б
Рис. 17.15. Схема процесса соударения двух струй сжи-
сжимаемой жидкости
Рис. 17.16. Схема формирова-
формирования кумулятивной струи в сжи-
сжимаемой жидкости
Uo и u разложены на две составляющие: нормальные иоп, ип и параллельные
фронту щт, ит. Сжимаемый сверхзвуковой поток со скоростью щ поворачивается
на угол а и при этом тормозится. Такое торможение сверхзвукового потока
осуществляется с помощью фронта ОМ косой ударной волны. В этом случае поток
перед фронтом ударной волны ударно не сжат. Резкое повышение давления имеет
место за фронтом косой ударной волны ОМ и кумулятивная струя в направлении
Ох не образуется. Согласно теории косых ударных волн, между углом поворота
сверхзвукового потока а и углом наклона фронта косой ударной волны /3 для
данной скорости щ существует зависимость а = а (C). При увеличении угла
а присоединенный фронт ударной волны ОМ может существовать только до
некоторого угла а < а& (рис. 17.15). При углах а ^ а& фронт косой ударной
волны ОМ отходит в сторону набегающего сверхзвукового потока (рис. 17.16).
При этом интенсивность фронта ударной волны ММ' возрастает. Жидкость за
фронтом ударной волны ММ' ударно сжата, но, вследствие того, что поверхность
AM О свободна от давления, то жидкость на участке ОМ начинает истекать
вправо, и образуется кумулятивная струя. Угол а = а к определяется из условия
невозможности существования присоединенного фронта косой ударной волны с
помощью ударной поляры, которая определяет все возможные значения скорости
потока за фронтом и и углы а и /3 для данной скорости uo-
Рассмотрим определение критического угла а^. На фронте косой ударной
волны при pj = 0, согласно законам сохранения массы и импульса, существуют

17.2. Теория кумуляции
209
соотношения (см. гл. 4):
= ипр,
(иОт = ит),
A7.14)
A7.15)
A7.16)
где р и р — давление и плотности на фронте косой ударной волны.
Вместо уравнения энергии и уравнения состояния возьмем ударную адиабату:
где е =
PJ-1
A7.17)
Скорости uqu и ип из уравнений A7.14), A7.15) молено выразить следующим
образом:
Щп =
Из рис. 17.156 видно, что
иОт = ит =
V
, u=
A7.18)
A7.19)
Поскольку tgf3 = ——, a tg(yS — а) =
- tga
tg^tga
, то
tga=
A7.20)
При заданных щ и pj для каждого конкретного значения е можно, по форму-
формулам A7.17)—A7.19) и A7.20), определить и$п, ип, ит, и, а, что позволяет по вели-
величине и и а найти точку ударной поляры в координатах иу, их, где их совпадает по
направлению с г/о (рис. 17.17 и рис. 17.18). Ударная поляра на рис. 17.18 строится
по точкам для каждого ?, которая меняется от е = 0 (звуковая волна, точка К)
до еп (прямая ударная волна, точка А). Угол наклона касательной ОВ к ударной
поляре определяет критический угол а&. При а ^ aj~ интенсивность фронта косой
му, км/с
О	2	4	6	8 мх,км/с
Рис. 17.18. Графическое определение кри-
критического угла при соударении двух пластин
из алюминия
\
ч
В
м-	^»
\
0	мх	м0	и
Рис. 17.17. Разлолсение векторов скоростей
ударной волны возрастает, и он отходит вверх по течению (рис. 17.16). В результате
создаются условия для образования кумулятивной струи.

210
17. Кумуляция
Для расчета а*, надо определить а через е. В этом случае давление р, плотность
р и скорость и за фронтом прямой ударной волны М'М (рис. 17.16) молено опреде-
определить по формулам A7.17), A7.18), если в них положить щп = щ, ип = и. При этом
скорость щ = Vo/tga, где Vo — скорость схлопывания пластин или кумулятивной
осесимметричной облицовки. Затем, зная ударную адиабату материала облицовки
кумулятивной выемки D = D(u), можно по эмпирической формуле определить
с =
-1)
в ударно-сжатом металле. Если
изоэнтропическую скорость звука
р < 500 ГПа, то, согласно [17.27]
с = Dl 0,49 +
Выразим в формуле A7.20) щп, ип, ит через е с помощью A7.18), A7.19):
е
Р
tg a =
? + 1
Р
2а,;
60
40
20
Г
А
о
о
о
о
^-———
— В
A7.21)
Поскольку е непрерывно увеличивается
вдоль ударной поляры, а величина а при
перемещении вектора и из положения ОК
до ОВ сначала возрастает, а затем умень-
da
шается до нуля, то —— = 0 при а = а&, по-
ае
da dig2 a
этому —— « —	 = 0. Дифференцируя
зависимость A7.21), получим при а = а&:
dp
~de
р(р -
A7.22)
0	12	3	4 V0,km/c
Рис. 17.19. Расчетные кривые и экспери-
экспериментальные точки при соударении двух пла- Это выражение, совместно с A7.17) и про-
стин из мягкой стали	изводной dp/de, определяет критические
значения р^ и е^ для заданных pj и щ. Подставляя р^ и Sk в A7.21), получаем
а^. Если данный расчет провести для разных значений скорости щ и учесть, что
Vo = uotga (рис. 17.13), то можно построить кривую в координатах Bа, Vo).
На рис. 17.19 представлены расчетные кривые для симметричного соударения
двух пластин из мягкой стали и нанесены экспериментальные точки [17.16, 17.26].
В экспериментах, представленных на рис. 17.19, в нижней части струи обра-
образовывались в виде потока отдельных частиц. Линия А В определяет границу
зоны а = afc(Vo). Точки, лежащие ниже нее, соответствуют тому случаю, когда
кумулятивная струя не образуется, а точки сверху кривой А В образуют область
существования кумулятивной струи. Такое положение имеет место, если щ больше
скорости звука cq в материале кумулятивной облицовки.
В рамках данной модели, когда прочность материала не учитывается, эта
скорость звука с? — \ тг \ должна определяться в исходной, невозмущенной
\opJso
ж;идкости. Реальная оболочка имеет прочность, и под со надо понимать скорость
« - - 1К + D/3)G	^	й
объемной упругой волны Cq = W	, где il — модуль объемного сжатия,
V	PJ

17.2. Теория кумуляции	211
a G — модуль сдвига, pj — плотность облицовки. В зависимости от амплитуды
ударной волны величина cq может быть больше, меньше или равна скорости
ударной волны. Для стали, например, D > cq только при р > 60 ГПа. Величина
/lT + D/3)G	к .. .
со = \ 	для железа, алюминия и меди, соответственно, равна 5,94 км/с,
V pj
6,39 км/с, 4,76 км/с.
Если щ < со, то кумулятивная струя должна образовываться как для модели
несжимаемой, так и сжимаемой жидкости, при любых углах 2а.
Аналогичный по существу критерий отсутствия струеобразования можно по-
получить на основе следующего условия. В системе координат, где покоится пест,
скорость точки соударения должна быть сверхзвуковой, т.е. по формулам A7.9) и
A7.11) получаем [17.6, 17.16]:
*E*) *	A7.я)
vK* ,() >*
since \ since tgaj tga
где с — местная скорость звука в точке соударения 0 (рис. 17.16). В этом случае
пест покоится, а точка соударения 0 перемещается со скоростью Vo/tga ^ с, т.е.
ни одно возмущение не может обогнать точку контакта 0, в результате струя не
образуется. Для образования струи должно выполняться условие:
a^arctg—.	A7.24)
с
Это соотношение справедливо как для плоских, так и для осесимметричных
кумулятивных облицовок. Максимальная скорость струи по A7.10) равна
Vjrn =	\- т	•
sinafe tgak
Из A7.24) имеем с = Vo/tga^. Так как
smak =	=	,	A7.26)
/l + t2	/2 + V2
tg2 ak
то из A7.25) получим максимальную скорость струи, соответствующую критиче-
критическому углу ак:
'	A7.27)
Численное решение задачи о двумерном (плоском и осесимметричном) схлопы-
вании кумулятивной облицовки без прочности, в сочетании с экспериментальными
исследованиями, позволили построить более детальные критерии струеобразова-
струеобразования [17.16]:
1) если щ дозвуковая, то образуются сплошные, неразорванные кумулятивные
струи.
Для соударения плоских пластин условие образования монолитной струи
определяется формулой:
а*к > arctg (Щ ,	A7.28)
\со/

212	17. Кумуляция
где со — начальная скорость звука в материале пластин. Кривая АС на
рис. 17.19, построенная на основе этой формулы, делит плоскость Bа, Vq) на
две части. В зоне ВАС образуются диспергированные струи, выше кривой
АС— монолитные струи;
2)	если щ сверхзвуковая и а > а&, то струя представляет собой поток частиц,
расширяющихся в радиальном направлении;
3)	если щ сверхзвуковая и а < а&, то струи не образуется.
Вся теория, изложенная выше, не учитывает прочности материала схлопываю-
щихся поверхностей.
Для приближенной оценки влияния прочности на струеобразование можно
предположить, что давление при соударении определяется по уравнению Бер-
нулли для несжимаемой жидкости через нормальную составляющую скорости
схлопывания пластин [17.16]:
p = e!^a>trt	A7-29)
где а — некоторая величина, характеризующая прочность пластин. При р ^ а
струя не образуется, потому что силы прочности сдерживают движение материала
из зоны схлопывания.
Из уравнения A7.29) определяется критическая скорость соударения Voki ПРИ
которой струеобразования не существует:
A7.30)
cos a
Отсюда находится линия AD в плоскости Bа, Vb), где прочность ликвидирует
струеобразование (рис. 17.19). Для этого случая
at* =arccosA/	.	A7.31)
V рУок
Ha рис. 17.19 линия AD построена для а = 0,45 ГПа.
При схлопывании пластин скорость кумулятивной струи с учетом прочно-
прочности должна быть меньше, чем скорость жидкой струи, определяемая форму-
формулой A7.10):
Vj =	A + cos a).
sin а
Эта формула, с поправкой на прочность, имеет вид:
A7.32)
S111CK \	у	/JVq I
тт	2	2<J / п
При cos a — 	2 ^ 0, получаем скорость точки соударения, соответствующую
скорости точки контакта из формулы A7.9): Vk = Vb/sina.
Рассмотренная выше теория струеобразования неоднократно проверялась экс-
экспериментально путем метания двух пластин навстречу друг другу [17.26, 17.28].

17.2. Теория кумуляции
213
В этих опытах можно сохранять постоянными скорость схлопывания Vo, угол
схлопывания а, наблюдать появление струй (неразорванных и диспергированных).
Что же касается осесимметричных кумулятивных облицовок, то аналогичная
проверка очень сложна, поскольку скорость Vo переменна по длине облицовки,
угол а также меняется весьма существенно, а струю можно увидеть (с помощью
съемки в рентгеновской области спектра) только после ее выхода за пределы
конуса. Поэтому для кумулятивного конуса с малым углом 2а, верхняя часть
конуса будет схлопываться с большой скоростью и относительно малым углом,
что обеспечивает отсутствие струеобразования, а нижняя часть конуса будет
схлопываться с относительно малой скоростью и большим углом, что обеспечит
образование струи из этой части конуса. Поэтому определение критического угла
ak должно осуществляться для верхней части конуса кумулятивного заряда.
4. Теория проникания кумулятивной струи в преграду. В процессе
проникания кумулятивной струи в преграды (сталь, алюминий, бетон и т.п.) вели-
величина давления, возникающего на границе между материалами струи и преграды,
на один-два порядка превосходит прочностные характеристики преграды. Это
относится к тем частям кумулятивной струи, которые имеют скорость Vj > 4 км/с.
В этом случае прочностью струи и преграды можно пренебречь.
Рассмотрим приближенную теорию проникания элемента кумулятивной струи
в гомогенную преграду. Обозначим длину элемента — /, его начальную скорость —
Vj, плотность — pj, скорость проникания в преграду — их, начальную плотность
преграды — рт-
На рис. 17.20 изображены две схемы: до проникания кумулятивной струи в
преграду (а) и в процессе проникания (б). Под действием большого давления на
границе кумулятивная струя-преграда, кумулятивная струя «срабатывается», и ее
материал растекается в направлении, обратном скорости ее движения. Материал
преграды также «уходит» из зоны высокого давления, причем часть этого ма-
материала выносится вместе со струей к свободной поверхности преграды, а другая
часть, за счет пластических деформаций некоторой части преграды, перемещается
из зоны образующейся пробоины.
Pj
Pj
У////////
Рис. 17.20. Схема проникания элемента ку-
кумулятивной струи в преграду
Рис. 17.21. Схема проникания элемента ку-
кумулятивной струи в системе координат, свя-
связанной с границей проникания струи в пре-
преграду
На рис. 17.20 представлен процесс проникания кумулятивной струи в преграду
в системе координат, в которой преграда является неподвижной. Перейдем к си-

214	17. Кумуляция
стеме координат, где неподвижной является граница проникания струи в преграду
(точка X).
В этом случае скорость элемента кумулятивной струи будет равна Vj — их, а
скорость преграды — их (рис. 17.21).
Время «срабатывания» (около точки X) элемента кумулятивной струи и обра-
образования пробоины глубиной L равно
tL = — = т^	•	A7.33)
их Vj - их
Отсюда получим формулу для определения глубины пробития:
На основе этой зависимости могут быть построены приближенные формулы для
различных моделей как несжимаемой, так и сжимаемой жидкости, а также, в
первом приближении, можно учесть влияние прочности на процесс проникания.
1. Рассмотрим случай, когда материалы кумулятивной струи и преграды яв-
являются идеальными несжимаемыми жидкостями. Поскольку процесс проникания,
изображенный на рис. 17.21, является стационарным, то для него справедливо
уравнение Бернулли:
Pj{Vj-uxJ	рти\
	2	VVJ = —2	Ьрт =рх,	A7.35)
где pj, pj — начальные давление и плотность струи, рт, рт — начальные давление
и плотность преграды. рх — давление в точке X на границе струя—преграда, где
скорости струи и преграды равны нулю. Так как рх ^> pj и рх ^> рт, при pj = рт
из уравнения A7.35) получим:
pj{Vj-uxJ=pTu2x.	A7.36)
Отсюда
A7.37)
Давление и скорость проникания идеальной несжимаемой струи в идеальную
несжимаемую преграду равны
Рх=рт + р-^; их = ^.	A7.38)
На основе формул A7.34) и A7.38) получим формулу для определения глубины
пробития [17.7, 17.8, 17.25]:
A7.39)
По этой формуле глубина пробития зависит только от длины струи, плотности
струи и преграды, и не зависит от скорости струи Vj, сжимаемости материалов
струи и преграды и их прочности. Эта формула дает удовлетворительное совпа-
совпадение с опытными данными, определяющими глубину пробития для относительно
больших скоростей струи Vj > 4 км/с, когда можно пренебречь прочностью
преграды и струи, а сжимаемости материалов струи и преграды близки между
собой.

17.2. Теория кумуляции
215
2. Рассмотрим приближенный учет сжимаемости
материалов струи и преграды для случая стационарно-
стационарного сверхзвукового проникания элемента кумулятивной
струи (рис. 17.22). При этом в струе и преграде обра-
образуются фронты ударных волн CD и АВ.
В этом случае, рассматривая струю как симметрич-
симметричное тело, из условия непрерывности давления в точке
торможения (точка X), с помощью уравнения Бернулли
можно получить [17.29]:
Pj(Vj-uxJ
Xj
= Ptux
А
A7.40)
где Xj = 1 - pj/pjx, Ат = 1 - рт/ртх, pjx, Ртх —
плотности, соответственно, в струе и преграде в точке
контакта струи и преграды.
Из уравнения A7.40) получаем:
Рис. 17.22. Схема процес-
процесса сверхзвукового проника-
проникания элемента струи в прегра-
ДУ
Vj-ux
Используя уравнение A7.34) получим
L =
A7.41)
Ат)"
A7.42)
Если сжимаемости струи и преграды одинаковы, т.е. Xj = Ат, то получим формулу
L = l\/Pj /рт > которая совпадает с формулой A7.39).
Для определения величин pjx и ртх нужно решать систему уравнений на
фронте прямой ударной волны в системе координат, связанной с этим фронтом
(рис. 17.22). В этом случае поток сжимаемой жидкости (преграда) с параметрами
uxi Рт втекает во фронт ударной волны А В л тормозится в точке X.
Уравнения Бернулли для сжимаемого материала преграды и струи имеют вид:
К
для преграды : — + / — = / —
dp
Тх
для струи :
(Vj - uxf
Jx
где интегралы, стоящие слева, определяются на основе уравнений изоэнтропы для
материалов преграды и струи, соответственно. При этом для преграды р = рт, а
для струи р = pj. Интегралы в правой части уравнений определяются на основе
ударных адиабат, соответственно, материалов преграды и струи. Поскольку на
границе струи и преграды ртх = Pjx = Рх ? т0 из ДВУХ уравнений можно определить
рх и их, т.е. давление и скорость стационарного проникания сжимаемой струи в
сжимаемую преграду.
Для определения давления рх и скорости их при нестационарном проникании
сжимаемой струи в сжимаемую преграду, а также глубины пробития L, можно вос-
воспользоваться формулами для определения начальных параметров ударных волн
при соударении двух тел: струи и преграды [17.4]. Из закона сохранения импульса

216	17. Кумуляция
на фронте ударной волны, пренебрегая начальными давлениями в преграде и струе
(рт = Pj ~ 0), получим:
для преграды: рх = pTuxDT,
для струи:	рх = pj(Vj - ux)Dj.
Если известны ударные адиабаты материалов преграды и струи Dt = Dt(ux) и
Dj = Dj(Vj — ux), то из двух уравнений определяются рх и ?хж на границе в момент
соударения струи с преградой. Такой подход имеет смысл, если струя состоит из
отдельных разорванных кусочков. Из уравнений A7.43) получим:
pTD^^ = ZL^L±L	^1.	A7.44)
Из закона сохранения массы для фронтов ударной волны имеем в преграде:
PtDt = Ptx{Dt - их), в струе: pjDj = pjx(Dj - их), откуда Хт = 1 -
Рт их pj Vj - их
	 = —— и Aj = 1	= ——	. Используя эти соотношения, получим
РТх	DT	pjx	Dj
PjD27 XT
из уравнения A7.44): 	^- = —. С другой стороны, на основе уравнений A7.34)
PtDt Xj
и A7.44) можно получить зависимость:
т 1 \PJ PJDJ i IfJ "I-	(-\7 ЛХ>\
у рт PtDt xi -
3. Рассмотрим простейший учет прочности с помощью уравнения Бернулли
для несжимаемой жидкости [17.16], [17.29]—[17.31]. В этом уравнении A7.35) pj
и рт представляют собой начальные давления в материалах струи и преграды,
если их считать несжимаемыми жидкостями. Для учета прочности принимаем,
что эти величины включают прочностное сопротивление, соответственно, струи
и преграды. Прием этот носит искусственный характер, поскольку уравнение
Бернулли есть интеграл уравнений Эйлера для идеальной среды, где прочность
отсутствует. Но такая интерпретация величин pj и рт как характеристик проч-
прочности, определяемых из опыта, — удобный прием для создания инженерных
методов расчета проникания стержней в преграду с использованием опытных
данных. Поскольку металлические кумулятивные струи нагреты до 600—1000°С,
а их материал — обычно медь или мягкая сталь, то их прочность много меньше
прочности стальной преграды. Поэтому можно принять pj ж 0, а рт = Y, где
Y — некоторая характеристика, учитывающая упругопластическое сопротивление
преграды, разорванность струи, сжимаемость, нестационарность процесса прони-
проникания и т.п.
В работе [17.31] эта характеристика названа «диссипативным» давлением,
описывающим соответствующие потери энергии, а в [17.16] она ассоциирована с
динамической твердостью Нр материала преграды, также учитывающей диссипа-
диссипацию энергии. Уравнение Бернулли A7.35), с учетом изложенных выше замечаний,
запишем в виде:
Pj{VjUJ P^ + (PT-Pj),	A7.46)
где в дальнейшем будем считать, что pj ж 0, а рт = Y.

17.2. Теория кумуляции
217
Отсюда определим скорость проникания струи в преграду их:
еслл fi=J—/1,то — =
A7.47)
Глубину пробития на основе формул A7.34), A7.47) молено определить из следую-
следующих уравнений:
если /1 = 1,то L = I
если \i ф 1,то L =
A7.48)
Эти уравнения не учитывают процесс деформирования струи и преграды и поэто-
поэтому носят условный характер.
Экспериментальные данные показывают,
что, при относительно высокой скорости куму-
кумулятивной струи Vj > 4 км/с, процесс прони-
проникания следует гидродинамической теории про-
пробития без учета прочности струи и прегра-
преграды. На рис. 17.23 показаны эксперименталь-
экспериментальные данные зависимости ux/Vj от Vj для
кумулятивного заряда со стальной облицов-
облицовкой толщиной 0,9 мм и углом раствора конуса
2а = 44°, снаряженного ВВ — пентолит 50/50
со скоростью детонации D = 7510 м/с. Там же
приведена расчетная зависимость (кривая 1)
по формуле A7.47), удовлетворительно апрок-
симирующая экспериментальные данные при
Y = 3,5 ГПа [17.16]. При этом значение динами-
динамической твердости для мягкой стали составляет
= 1,5 ГПа, что в 2 раза меньше подгоноч-
подгоноч1 7
оРо
/
2
0^
]рь-П-"	*т!
|JpU
Vj, КМ/С
0,4
0,2
О	2	4	6	8
Рис. 17.23. Расчетная зависимость
ux/Vj от Vj; о, ? —экспериментальные
точки, проникание стальной струи в
стальную преграду
ной величины Y =3,5 ГПа. Прямая B) соответствует расчету по формулеA7.37).
О влиянии прочности преграды на глубину внедрения в нее кумулятивной
струи можно судить по экспериментальным данным, согласно которым при увели-
увеличении твердости стальной плиты в 4—6 раз глубина пробития уменьшается на 25—
30%, причем закон уменьшения глубины пробития близок к линейному. Основное
снижение пробивного действия происходит за счет уменьшения вклада хвостовых
элементов кумулятивной струи, имеющих скорости менее 4 км/с.
Формулы A7.42) и A7.45) по разному оценивают влияние сжимаемости мате-
материалов струи и преграды на глубину проникания L. При проникании медных (же-
(железных или стальных) кумулятивных струй в стальные преграды, сжимаемость

218
17. Кумуляция
взаимодействующих сред играет несущественную роль, поскольку \j « Лт- Если
лее медная или железная струя проникает в сильносжимаемые преграды (вода,
резина, грунт и т.п.), то сжимаемость материала преграды, согласно формулам
A7.42) и A7.45), играет заметную роль в определении глубины проникания первой
во вторую.
Количественная оценка такого влияния получена в работах [17.32, 17.33] по-
посредством численного решения осесимметричной задачи высокоскоростного про-
проникания железного цилиндрического элемента в воду. При этом для обеих сред
принималась модель идеальной сжимаемой жидкости. Численное интегрирование
исходной системы уравнений с учетом начальных и граничных условий осу-
осуществлялось по алгоритму, описанному в [17.34, 17.72], с выделением контактных
границ по методу концентраций. Конкретные расчеты проводились для железного
цилиндрического элемента длиной / = 6dj в диапазоне скоростей Vj = 3 — 7 км/с.
На рис 17.24 представлены
типичные стадии деформиро-
деформирования элемента КС и распре-
распределение давления в воде по
мере развития процесса. Вре-
Время г указано в безразмерном
виде в зависимости от диа-
диаметра элемента dj. При под-
подстановке реальных значений
диаметров КС в миллиметрах,
получаются значения текуще-
текущего времени процесса в мик-
микросекундах. С течением вре-
времени площадь контакта меж-
между деформируемым элемен-
элементом и каверной, образованной
в жидкой преграде, постепен-
постепенно увеличивается; из его ма-
материала формируется пелена,
растекающаяся по профилю
каверны. Результатом этого течения является, с одной стороны, постепенное
уменьшение начальной длины и массы центральной части стержня, а с другой
стороны, увеличение массы пелены, контактирующей с каверной жидкости. Будем
называть подобный процесс процессом «срабатывания» стержня. Например, в
текущий момент времени, соответствующий т = 0,94<ij (рис. 17.246), примерно
50% его начальной длины сработалось о жидкость, а в момент времени т = 2,04<ij
(рис. 17.24в) величина сработавшейся части стержня увеличилась до 75%. В
дальнейшем пелена из материала стержня утончается по всей поверхности,
контактирующей с каверной жидкости, а сама каверна продолжает расширяться
и углубляться.
На рис. 17.25—17.27 представлены количественные результаты, характеризую-
характеризующие изменение различных параметров процесса проникания элемента КС в жидкость.
Скорость точки контакта элемента струи с жидкостью их вдоль оси в зави-
зависимости от глубины проникания L/1 непрерывно падает (рис. 17.25). Первый
крутой спад скорости связан с начальным этапом внедрения. В дальнейшем темп
изменения скорости увеличивается после того, как сработалась длина элемента,
примерно равная 0,75/, что связано с изменением характера движения. Пунктиром
на рис. 17.25 для каждого частного случая показана скорость проникания, рас-
рассчитанная по теории несжимаемой жидкости A7.37). Величины их, полученные
с/.
г	U
—
а
1,
Рис. 17.24. Стадии деформирования железного цилин-
цилиндрического элемента струи при проникании в воду

17.2. Теория кумуляции
219
и..-, км/ с
d,., ГИа
¦¦¦¦¦¦	„1
1
1
50
25:
о
	—
^^
	¦—
L.-1
3
j, км/с
Рис. 17.25. Зависимости скорости проникания элемента железной струи в воду их от относи-
относительной глубины проникания L/1: 1 — Vj = 7 км/с, 2 — Vj = 5 км/с, 3 — Vj = 3 км/с.
Рис. 17.26. Изменение давления рх на границе железного элемента с водой (точка х) при
проникании: 1 — для сжимаемых сред, 2 — для несжимаемых сред
путем численного расчета и по теории несжимаемой жидкости, заметно расхо-
расходятся между собой в начале и в конце процесса проникания, где, например, для
Vj = 5 км/с, это расхождение достигает 2-х раз. Еще большая разница имеет
место для давлений на границе двух сред, причем это отличие возрастает с
ростом скорости удара (рис. 17.26, где 1 — давление на границе сжимаемого
стержня с водой; 2 — давление на границе стержня с водой, описываемое моделью
несжимаемой жидкости). На рис. 17.27 представлена зависимость диаметра пятна
контакта dg цилиндрического элемента с водой от длины его сработавшейся части.
В момент времени, соответствующий /; ~ 0,7<ij, диаметр пятна контакта достигает
значения dg ~ 2,2c/j и далее, до конца срабатывания стержня, практически не
увеличивается.
2
1
0
0,5
1 /'/*
Рис. 17.27. Зависимость диаметра головки железного элемента струи от длины его сработав-
сработавшейся части
Рис. 17.28. Зависимости сработавшейся части длины железного элемента от глубины его
проникания в воду
Представленное численное решение проникания стержня в жидкость позволяет
оценить существующие приближенные теоретические подходы к решению этой
задачи. На рис. 17.28 показаны зависимости сработавшейся длины элемента /;
от глубины его проникания в жидкость, соответствующие численному расчету
для разных начальных значений скоростей ударника Vj = 3 — 7 км/с (линии
1 и 2). Линия 3 представляет собой зависимость A7.39), следующую из теории
несжимаемой жидкости (гидродинамическая теория проникания), согласно ко-
которой глубина проникания элемента КС в среду не зависит от скорости струи.
На участке 0А до /' = 0,75 / (линия 1) существует линейная связь между /' и
L. Для скоростей стержня 3 — 5 км/с глубина проникания в жидкость с учетом
сжимаемости примерно на 15% больше глубины проникания, рассчитанной по
теории несжимаемой жидкости, а для Vj = 7 км/с, это расхождение составляет

220
17. Кумуляция
около 30%. На участке / ^ /' > 0,75 / линии 1 и 3 существенным образом
расходятся, а конечные значения L на этих кривых отличаются в 1,7 раза. Такая
большая разница объясняется различным характером увеличения L на участках
0А и АВ. На участке 0А идет срабатывание элемента КС (см. рис. 17.246), а на
участке АВ — растекание пелены из материала элемента по каверне в жидкости
(см. рис. 17.24в).
По формуле A7.45) построены прямые 5, 6, 7 на рис. 17.28, соответственно, для
скорости стержня 7 км/с, 5 км/с и 3 км/с, а по формуле A7.42) — прямая 4, которая
практически не зависит от скорости стержня при ее изменении от 3 км/с до 7 км/с
и достаточно близка к линии 3, рассчитанной по формуле A7.39). Из соотношений
A7.42) и A7.45) следуют диаметрально противоположные оценки влияния сжима-
сжимаемости материалов взаимодействующих тел на величину L. Зависимость A7.42)
фактически неверно оценивает влияние сжимаемости на глубину проникания КС в
жидкость, а зависимость A7.45) неоправданно завышает это влияние; например,
для /' = 0,75 / и Vj = 3 — 5 км/с — более чем в 1,4 раза, а для Vj = 7 км/с —
более чем в 1,7 раза. Таким образом, полученные результаты математического
моделирования процесса проникания элемента КС в воду позволяют, с достаточной
для практических целей точностью, описать особенности движения образующейся
в жидкости каверны, в зависимости от геометрических (c/j,/), кинематических (Vj)
и физико-механических (инерционных) характеристик взаимодействующих тел,
как до момента полного срабатывания внедряющегося элемента (гидродинамиче-
(гидродинамическая стадия проникания), так и после момента срабатывания (инерционная стадия
проникания).
5. Определение диаметра каверны в преграде. Эффективность дей-
действия КЗ определяется как глубиной проникания КС, так и диаметром пробитого
в преграде отверстия. При этом диаметр отверстия и время на его образова-
образование существенно влияют на глубину пробития: при конкретных параметрах КС
(скорость, диаметр, угол рассеивания) с уменьшением диаметра отверстия растет
непроизводительное расходование струи на стенках пробоины («намазывание»).
Результаты экспериментальных иссле-
исследований процесса проникания КС в раз-
различные преграды, проведенные с помощью
высокоскоростной оптической съемки и
мгновенной рентгенографии, показывают,
что, в зависимости от характеристик КС
и преграды, форма каверны может быть
конической, сужающейся к концу, цилин-
цилиндрической или волнообразной. При этом
существенное влияние на форму и раз-
размер кратера оказывает свободная поверх-
поверхность — в случае полубесконечной прегра-
преграды, и толщина — в случае относительно тонкой преграды, пробиваемой насквозь.
На рис. 17.29 представлены типовые профили пробоин при проникании КС в
тонкую преграду толщиной Нт — (а) и в полубесконечную преграду (б). Поэтапно
формирование каверны в общем случае выглядит следующим образом: образо-
образование цилиндрической полости некоторого начального радиуса, ее последующее
расширение до максимального радиуса и возможное инерционное расширение
(послетечение) после «израсходывания» элемента кумулятивной струи.
Из физических соображений следует, что объем каверны должен быть прямо
пропорционален энергии КС (диаметру и скорости струи) и обратно пропорци-
пропорционален характеристике прочности (сопротивляемости) материала преграды. Как
Рис. 17.29. Профили пробоин при прони-
проникании КС в преграду: конечной толщины
(а); полубесконечную (б)

17.2. Теория кумуляции	221
указывалось выше, конструктивное оформление и материал преграды также могут
оказывать влияние на формирование каверны. Для теоретического определения
диаметра каверны (пробоины) необходимо (при подходе струи к преграде под
прямым углом) численно интегрировать осесимметричные уравнения движения
прочной сжимаемой среды (см. главу 19.). При этом скорость, масса и диаметр
струи должны быть заданы. В некоторых случаях, при оценке среднего диаметра
пробоины Do, на основе ряда допущений могут быть использованы более про-
простые подходы, в которых можно получить аналитические или полу эмпирические
зависимости диаметра пробиваемого в преграде отверстия. Один из возможных
подходов изложен в предыдущем издании книги [17.4]. Он основан на рассмотре-
рассмотрении энергетического баланса системы, при котором основная часть кинетической
энергии КС затрачивается на необратимое пластическое деформирование матери-
материала преграды. При проникании элементов КС в преграду, ее кинетическая энергия
расходуется на срабатывание самого г-го элемента струи в процессе проникания,
на генерирование УВ, на разрушение материала преграды и его пластическое
деформирование. При этом принимается, что каверна глубиной Li и переменным
диаметром DOi (рис. 17.296) образуется за счет того, что часть материала преграды
разрушается и уносится в направлении поверхности преграды. Образованная
при этом каверна имеет переменный диаметр по глубине вследствие влияния
двух факторов: наличия свободной поверхности и неравномерного распределения
кинетической энергии вдоль кумулятивной струи. Наличие свободной поверхности
облегчает пластическое деформирование преграды, в результате диаметр у этой
поверхности имеет наибольшую величину (рис. 17.29). Неравномерность в распре-
распределении кинетической энергии вдоль КС приводит к тому, что величина каверны
по длине проникания меняется неравномерно. С учетом основного допущения
можно записать, что Ел = aEwi, где Ел — кинетическая энергия г-го элемента
КС; Ewi — энергия формоизменения деформируемой преграды при действии г-
го элемента КС; а — коэффициент, учитывающий, какая часть энергии элемента
струи расходуется на пластическое деформирование преграды, а также ряд дру-
других факторов. С учетом дополнительных приближений энергию формоизменения
можно записать в виде
ird2
EWi = anSiWi = <TD?i—Li,	A7.49)
где <jd — динамический предел текучести материала преграды; Si — усредненная
интенсивность деформации по деформированному объему W{, d — диаметр за-
заряда. Определяя среднюю интенсивность деформации по известной зависимости,
получаем промежуточную формулу для определения диаметра отверстия [17.4]:
V2
, A7.50)
где т = °Vc/, &d — 840 МПа (для стальной преграды).
Расчет показывает, что окончательно эту формулу можно представить в виде
следующей аппроксимирующей зависимости :
A7.51)
где определяющую роль в точности расчета среднего диаметра отверстия играет
экспериментальный коэффициент а, зависящий от конкретных параметров КЗ и
преграды.

222	17. Кумуляция
Полуэмпирическая зависимость диаметра каверны от диаметра КС и скорости
ее проникания в преграду, полученная обработкой конкретных экспериментальных
данных, приведена в работе [17.10]:
( ^)°'37,	A7.52)
где dj — диаметр КС, (см); рт — плотность материала преграды, (г/см3); их —
скорость проникания струи в преграду, (км/с); Нр — динамическая твердость ма-
материала преграды, (кг/мм2). Однако применение данной формулы ограничивается
диапазоном скоростей проникания и кругом рассмотренных при ее определении
материалов и типов преград.
За рубежом для определения диаметра каверны при проникании КС в преграду
широко используется подход, предложенный М. А. Куком (Cook) [17.31, 17.35].
При этом в рамках модифицированной гидродинамической теории, учитывающей
прочность материала преграды, конечный диаметр каверны определяется из вы-
выражения [17.35]:
где as — предел статической прочности материала преграды; рт, Pj — плотно-
плотности материала преграды и струи; dj, Vj — диаметр и скорость КС в момент
соударения с преградой; Л — безразмерный коэффициент, изменяющийся от 1
для сплошных струй невысокой скорости до 2 для высокоскоростной разорванной
струи.
После преобразования данная формула принимает вид :
.	A7.54)
y/pj)
Рассмотрим более подробно еще один энергетический подход, в котором счи-
считается, что кинетическая энергия элемента струи пропорциональна работе, ко-
которая необходима для образования каверны диаметром D^ и длиной 1^, а са-
сама каверна имеет цилиндрическую форму (рис. 17.296). Тогда можем записать :
Ел = 	г_^1± = AyyWi, где Мл, Vji — масса и скорость г-го элемента КС; Aw —
ttD2
удельная работа вытеснения единицы объема материала; W{ = 	—Li — объем
образуемой каверны. Преобразуя эту зависимость, получаем формулу для расчета
диаметра отверстия:
На удельную работу вытеснения единицы объема материала влияют не только
свойства материала преграды, но и конкретная конструкция КЗ, а также рас-
расстояние от рассчитываемого сечения каверны до свободной поверхности преграды
(вблизи поверхности значение Aw не является постоянным, что и определяет
резкое расширение отверстия и образование характерной полости). Как правило,
данную величину определяют экспериментальным путем, но возможны и расчет-
расчетные оценки [17.36].

17.2. Теория кумуляции
223
Таблица 17.5
Физико-механические характеристики металлов мишеней и сопоставление
расчетных и экспериментальных значений параметров процесса соударения
[17.36]
Материал мишени
Плотность металла мишени,
г/см3
Твердость по Бринеллю ме-
металла мишени Нв, ГПА
Динамическая твердость ме-
металла мишени Но, ГПА
Удельная работа
вытеснения
объема Aw, ГПа
Расчет
Эксперимент
Техн.
чистое
железо
7,85
0,9
2,0
2,9
2,8
Дюра-
люми-
люминий
2,8
1Д
1,4
2,5
2,2
Медь
8,9
0,45
0,72
1,17
1,2
Алю-
Алюминий
2,7
0,3
0,56
0,86
0,83
Свинец
11,34
-0,05
-0,08
-0,13
-0,1
В табл. 17.5 приведены некоторые данные по физико-механическим характери-
характеристикам материалов при соударении с высокоскоростными стальными ударниками
с конической головной частью в глубинных слоях металлической мишени, где
значение Aw можно считать постоянной. Анализ работы [17.36] и табл. 17.5,
в частности показывает, что величину удельной работы вытеснения объема в
глубинных слоях материала можно представить как Aw ~ Нр + Ив-, что предо-
предоставляет широкие возможности для определения Aw и для других материалов,
для которых известны стандартные величины Hp и В. в-
Экспериментально-теоретические
данные указывают, что под глу-	Таблица 17.6
бинными слоями материала мишени Значения коэффициента А для различных
следует считать такие, для которых материалов при проникании медной КС в
выполняется условие L > 2db для
J	° ^	преграду
цилиндрического ударника с кони-
конической головной частью, где db —
диаметр (калибр) ударника, и усло-
условие L > lOdj — для проникаю-
проникающей кумулятивной струи. В зоне
0 $J Li/dji ^ 10, значение Aw будет
изменяться, оно может быть оценено
следующей ступенчатой функцией :
Aw = К—	\-
d
где для случая пробития проч-
прочной стальной преграды медной КС
можно принять Aw о = 0,3 •
1010 Дж/м3, К = 0,3 • 109 Дж/м3. В
зоне Li/dji > 10 для тех же условий
значение Aw будет постоянным и может составлять Aw ~ 0,6 • 1010 Дж/м3.
Зависимость A7.55) после ряда преобразований можно использовать и в виде
Материал
Конструкционная
сталь
Алюминиевый
сплав
Титан
Медь
Свинец
Лед
Бетон
Тяжелый суглинок
Рт,
г/см3
7,80-7,82
2,7
4,5
8,9
11,3
0,95
2,2-2,6
1,75
А,
Дж-^мм3/2
0,55-0,6
0,6-0,8
0,44
0,9
2,2
2,7
0,8
4,0

224
17. Кумуляция
[17.24, 17.37]:
A7.56)
— диаметр и скорость
где А — коэффициент удельной работы вытеснения; dji,
г-го элемента кумулятивной струи.
В табл. 17.6 приведены значения коэффициента А для различных материалов
при проникании медной КС в полубесконечную преграду.
Расчет диаметра отверстия в преградах конечной толщины ведется, как прави-
правило, по полу эмпирическим зависимостям, в основу вывода которых положен закон
сохранения энергии.
17.3. Движение и разрушение кумулятивных струй из различных
материалов
t
Формирующиеся при кумулятивном взры-
взрыве металлические КС представляют собой вы-
высокоскоростные удлиненные осесимметричные
(или плоскосимметричные) тела. Образующее-
Образующееся в процессе взрывного формирования распре-
распределение осевой скорости движения различных
частей КС характеризуется наличием перепада
от головных к хвостовым элементам, при этом
головная часть имеет скорость порядка первой
космической, а хвостовые элементы, как прави-
правило, движутся со скоростью около 2 км/с.
Характер распределения осевой скорости дви-
движения по длине КС задает величину начального
градиента szq , локальное значение которого опре-
определяется отношением перепада осевой скорости
AVj к начальной длине /о элемента КС, кото-
которая, как принято считать, равна длине соответ-
соответствующего участка образующей металлической
кумулятивной облицовки. Значение начального
градиента осевой скорости szq меняется по длине
КС и определяет начальную скорость дефор-
деформирования элементов струи. Большинство осе-
симметричных КС характеризуется значениями
Рис. 17.30. Рентгенограммы рас-
растягивающейся высокоградиентной
медной КС лабораторного 50-мм
КЗ: t = 70 мкс, стадия равномерного
растяжения (a); t = 160мкс, стадия
развития шеек и разрыва струи (б)
Под действием градиента скорости, КС в свободном полете растягиваются в
осевом направлении с одновременным уменьшением поперечного размера. При
этом, для большинства струй, на начальной стадии их существования характерно
равномерное по всей длине растяжение без сосредоточенной деформации и с
сохранением близкой к цилиндрической или слабоконической формы (рис. 17.30а,
где приведена рентгенограмма КС лабораторного КЗ диаметром d = 50 мм на
момент 70 мкс от начала развития взрыва). Такую стадию в некоторых случаях
называют инерционной. Далее растяжение постепенно локализуется в областях
образующихся на струе множественных шеек (шеечная стадия растяжения). В
итоге КС распадается на отдельные безградиентные элементы, в дальнейшем не

17.3. Движение и разрушение кумулятивных струй
225
меняющие свою длину (рис. 17.306, где показана рентгенограмма той лее, что и на
рис. 17.30а, КС, но для более позднего момента времени).
ИерехЫ) к
шееч пой cmади и
\Ралрыв КС
I, i
Рис. 17.31. Пространственно-временная (z — t) диаграмма процесса растяжения и разрыва
кумулятивной струи
На рис. 17.31 приведена характерная пространственно-временная (z — t) диа-
диаграмма процесса растяжения и разрыва таких КС, где прямая 1 соответствует
распространению ДВ по заряду ВВ, кривая 2 характеризует последовательное
схлопывание различных элементов облицовки (время t и осевую координату z
образования соответствующих элементов струи), прямые 3 показывают изменение
координат элементов струи со временем. На диаграмме выделены три характерных
области: область равномерного деформирования КС 4, область шеечной стадии 5
и область разорванной струи 6.
Характер разрушения КС на отдельные элементы различен и зависит от
свойств материала КО и от геометрических и кинематических характеристик КС
(начальный радиус элементов Rjq, начальный градиент осевой скорости izo). Так,
медные высокоградиентные струи разрываются на отдельные элементы удиви-
удивительно закономерным образом, подобным показанному на рентгенограмме (рис.
17.306). Для такого типа разрушения (пластического разрушения) характерно
образование геометрически подобных отдельных элементов с развитыми шейками,

226	17. Кумуляция
радиус которых близок к нулю. Аналогичным образом происходит разрушение КС
из никеля, ниобия, чистого алюминия.
Рис. 17.32. Характер растяжения и объ-
объемное разрушение свинцовой кумулятивной	Рис. 17.33. «Квазихрупкое» разрушение
струи	стальной кумулятивной струи
Иной характер имеет разрушение струй из других материалов. Так, КС из
свинца, вольфрама разрушаются объемно, как это показано на примере свинцовой
струи на рентгенограммах рис. 17.32 для трех последовательных моментов време-
времени. Разрыв струй, образованных КЗ со стальными облицовками, в большинстве
случаев происходит без образования выраженной шейки, путем «квазихрупкого»
отрыва (рис. 17.33). Подобный вид разрушения характерен в некоторых случаях и
для медных струй (см. рис. 17.34, где приведена рентгенограмма медной массивной
низкоградиентной КС в момент ее разрыва).
Показанная на рис. 17.31 пространственно-временная z — t диаграмма процесса
растяжения и разрыва характерна для пластически разрушающихся кумулятив-
кумулятивных струй. Анализ этой диаграммы позволяет ввести в рассмотрение количе-
количественные характеристики этого процесса. В отечественной научной литературе
в основу этого положена концепция предельного удлинения [17.38], в соответствии
с которой основной количественной характеристикой растяжения и разрыва явля-
является коэффициент предельного удлинения, определяемый отношением суммарной
длины /$] отдельных элементов, образовавшихся после разрыва определенного
участка струи, к его начальной длине /о (длина соответствующего участка по
образующей КО): щ = /ц//о- Коэффициент предельного удлинения по существу
является показателем динамической пластичности или же деформационным кри-
критерием разрушения материала, деформируемого в условиях кумулятивной струи.
Еще одной характеристикой разрушения является количество отдельных эле-
элементов N{, образующихся при разрыве определенного участка струи, или же всей
струи в целом — N. В связи с явственным выделением на (z — t) диаграмме
области равномерного деформирования КС и области развития шеек на струе,
в качестве дополнительной количественной характеристики процесса растяжения
КС может быть рассмотрен т.н. коэффициент инерционного удлинения п\ = Ii/Iq,
определяемый длиной 1\ участка струи в момент начала развития на нем шеек,
и характеризующий завершение стадии равномерного деформирования данного
участка. Следует отметить, что в зарубежной литературе в качестве основной
характеристики разрыва КС рассматривается время разрыва струи на отдельные
элементы tb (breakup time) [17.9]. Коэффициент предельного удлинения щ и время
разрыва струи tb взаимосвязаны, и по существу являются разными формами
представления одной и той же информации.

17.3. Движение и разрушение кумулятивных струй
227
Рис. 17.34. Характер разрушения медной
массивной низкоградиентной кумулятивной
струи
Общее свойство для всех материалов
в условиях КС — их аномально высокая
по сравнению со статическими условиями
пластичность. Так, медные высокогради-
высокоградиентные КС после разрыва имеют общую
длину элементов, примерно в 10 раз превы-
превышающую начальную длину неразорванной
кумулятивной струи. Некоторые участки
КС испытывают еще большие удлинения
до разрыва. Например, для некоторых
участков ниобиевых КС значение коэф-
коэффициента предельного удлинения может
достигать щ = 26. Именно за счет аномально высокой пластичности материалов
в условиях растягивающейся КС, обеспечивается значительная длина струи к
моменту ее взаимодействия с преградой, и именно этим обстоятельством объяс-
объясняется высокая пробивная способность кумулятивных зарядов. Это определило
значительное внимание, уделяемое вопросу растяжения и разрушения КС иссле-
исследователями кумулятивного эффекта [17.9, 17.15, 17.32], [17.38]-[17.63].
При исследовании растяжения и разрыва КС, используются эксперименталь-
экспериментальные методы импульсной рентгенографии, оптической синхробаллистической съем-
съемки, а также расчетно-теоретические методы, основанные на физико-математиче-
физико-математическом моделировании процесса с позиций механики сплошных сред, с примене-
применением численных и аналитических методов определения параметров исследуе-
исследуемого процесса. Взаимно дополняя друг друга, экспериментальные и расчетно-
теоретические методы к настоящему времени позволили получить стройную си-
систему взглядов о закономерностях поведения КС в свободном полете.
В отечественной экспериментальной практике значительную роль сыграл пред-
предложенный в 1956 г В. М. Титовым метод «меченой струи» [17.38]. В изначальном
варианте метки из свинцовой фольги наносились на внутреннюю поверхность КО
в фиксированных ее местах. При схлопывании КО метки «переходили» на струю и
легко идентифицировались на рентгенограммах. В последующем для уменьшения
искажений, вносимых в струю, метки на внутреннюю поверхность КО наносились
вольфрамовым порошком с помощью шеллачно-канифольного лака.
О 5 ^,мм О 8 16 пь О 5 10 74
Рис. 17.35. Лабораторный 50-мм КЗ с медной КО и характеристики формируемой кумуля-
кумулятивной струи: схема кумулятивного заряда (а); условная начальная конфигурация струи (б);
коэффициенты предельного удлинения выделяемых метками участков струи (в); количество
отдельных элементов, образовавшихся после пластического разрушения выделяемых метками
участков струи (г)
На рис. 17.35а приведена схема лабораторного КЗ из флегматизированного
гексогена с баратоловой линзой и КО постоянной толщины с углом раствора 50°

228
17. Кумуляция
[17.57]. Цифрами 1-6 на рис. 17.35а показаны положения меток из вольфрамового
порошка, а цифра 7 соответствует основанию КО, из которого формируется
хвостовой элемент струи. С помощью импульсной рентгенографической съемки
определялись осевые скорости движения Vj и уравнения движения z = Vjt + Ъ
помеченных вольфрамовыми метками элементов КС, образующихся из соответ-
соответствующих элементов A-7) кумулятивной облицовки, при этом в каждом опыте
использовалось не более двух меток, расположенных достаточно далеко друг от
друга — для исключения их взаимного влияния. На рис. 17.356 в координатах
Rjo — zq приведена начальная конфигурация КС от данного заряда, где начальная
длина /о выделяемых метками элементов струи соответствует расстоянию по
образующей между этими метками (см. рис. 17.35а), Z^o — начальная длина КС,
равная длине образующей КО, Rjo — начальный радиус элементов КС, zq — осевая
лагранжева координата, отсчитываемая вдоль начальной длины кумулятивной
струи. На рис. 17.35в приведены значения коэффициента предельного удлинения
щ, на рис. 17.35г — количество отдельных безградиентных элементов А^, на кото-
которые разделились соответствующие участки КС после пластического разрушения.
Количество отдельных элементов N{ и их
суммарная длина fe определялись путем сопо-
сопоставления рентгенограмм полностью разорван-
разорванной непомеченной (неискаженной влиянием ме-
меток) КС с пространственно-временной (z — t)
диаграммой движения ее помеченных элементов,
что позволяло осуществлять привязку участков
разорванной струи к определенному элементу
начальной конфигурации струи и его начальной
длине /q.
По значениям /$], /о и Ni определялись зна-
значения коэффициента предельного удлинения
щ = Zs/Zo и начальной длины участка струи,
формирующего после разрыва отдельный эле-
элемент: ао = Iq/N{.
На рис. 17.36 обобщенно показаны получен-
полученные в начале 70-х годов В. М. Марининым ре-
результаты экспериментов по определению коэф-
коэффициента предельного удлинения для медных КС, и приведена соответствующая
линейная аппроксимирующая зависимость щ от произведения начального гради-
градиента осевой скорости szq (mkc) и начального радиуса Rjq (mm) элементов КС.
Подобным же образом аппроксимированы экспериментальные результаты и для
ряда других материалов [17.37]:
Щ
20
15
10
5
0
©Ар
(
оо
0,4
0,8
1,2 1,6
I, ММ/МКС
Рис. 17.36. Зависимость коэффи-
коэффициента предельного удлинения пь
медных КС от произведения началь-
начальных градиента осевой скорости ezo и
радиуса RJ0
Си:
Ni:
Nb:
Ст.20 :
щ = 1,8
nb = l,8
nb = 1,6 + SezoRJo.
A7.57)
Отметим, что в экспериментальных работах зарубежных исследователей идеи
«привязки» элементов разорванной струи к определенному участку кумулятивной
облицовки значительного развития не получили — в большинстве зарубежных ра-
работ с помощью рентгеноимпульсной или синхробаллистической съемки [17.9, 17.48]
непосредственно определялось время tb разрыва КС на отдельные элементы,
количество отдельных элементов, их форма, скорости движения. Аналогичные

17.3. Движение и разрушение кумулятивных струй	229
работы на современном этапе экспериментальных исследований проведены и оте-
отечественными учеными [17.45].
Недостатком эмпирических формул A7.57), полученных статистической об-
обработкой экспериментальных данных, является отсутствие в них в явном виде
характеристик физико-механических свойств материала — эта зависимость скрыта
во входящих в эти формулы числовых коэффициентах. Кроме того, малопонятен
сам характер зависимости коэффициента предельного удлинения от параметров
кумулятивной струи. Например, при стандартных испытаниях материалов на
растяжение, пластичность материалов как правило уменьшается с увеличением
скорости деформаций, тогда как КС ведет себя прямо противоположным обра-
образом. Экспериментальные методы изучения КС в свободном полете не позволяют
ответить на эти вопросы и объективно весьма ограниченны, по существу позволяя
фиксировать лишь геометрические и кинематические параметры данного сверхвы-
сверхвысокоскоростного объекта, не обеспечивая возможность получать более тонкую ин-
информацию о поведении КС, например, параметры напряженно-деформированного
состояния, другие параметры состояния материала.
Ключ к объяснению закономерностей поведения КС в свободном полете дают
расчетно-теоретические методы физико-математического моделирования [17.32,
17.39, 17.40, 17.44, 17.47], [17.53]-[17.57]. В большинстве моделей рассматривается
динамическое растяжение выделяемого из КС элемента (расчетного элемента)
при постоянном перепаде осевой скорости между ограничивающими его плоскими
сечениями и в системе отсчета, связанной с одним из этих сечений.
Простейшей моделью растягивающегося элемента КС является модель цилин-
цилиндрического несжимаемого жесткопластического стержня [17.47, 17.53]. Эта модель
позволяет оценить характер эволюции напряженно-деформированного состояния
в КС при ее инерционном деформировании и составить некоторые «опорные»
представления о механизме этого процесса. Основные физические результаты
здесь таковы.
Геометрически элемент КС характеризуется коэффициентом текущего удлине-
удлинения
п = {- = 1 + izOt,	A7.58)
где / и 10 — текущая и начальная длина растягивающегося элемента. Осевому дви-
движению материала струи Vjz = szqz/ (I + szot) обязательно сопутствует его ради-
радиальное (направленное к оси симметрии) движение Vjr = — O,5rezo/ (I + ?zot), и, со-
соответственно, кинетической энергии осевого движения Ezq = Ez = Мё^01$/6 соот-
соответствует кинетическая энергия радиального движения материала Ег = Его/п3 =
М?^оДо/16п3, где М — масса элемента, г — радиальная координата. В начальный
момент времени кинетическая энергия радиального движения материала мала по
сравнению с кинетической энергией осевого движения в масштабах всей струи.
Однако в системе отсчета и в масштабах участка струи с начальной длиной ао,
формирующего после разрыва отдельный элемент, энергия радиального движения
доминирует над энергией осевого движения, и ее необходимо учитывать, пытаясь
объяснить механизм деформирования и разрушения кумулятивной струи. Анализ
эволюции напряженного состояния, которое описывается тензором напряжений
az=Y + ar,	A7.59)
8 п1
(где Y — эффективный предел текучести материала КС, pj — его плотность,
аг, <Т0, gz — соответственно, радиальная, тангенциальная и осевая компоненты

230
17. Кумуляция
тензора напряжений), приводит к парадоксальному выводу: на ранних стади-
стадиях растяжение КС может происходить в условиях всестороннего сжатия. При
этом сжимающие осевые напряжения могут достигать значительной величины
и определяются начальной удельной кинетической энергией pjs^qR^q радиаль-
радиального движения материала элемента кумулятивной струи. Растяжение элемента
происходит при выполнении энергетического баланса Ero = Er + Ed + Ad, где
Ed = M(Y/pj) Inn — внутренняя энергия элемента, aij- работа, совершаемая
элементом над окружающими его элементами в составе струи. Анализ характера
изменения напряжений и энергетического баланса элемента позволяет указать
пределы нахождения коэффициента предельного удлинения
3 pji2z0R2J0
16 Y
A7.60)
при этом нижняя граница соответствует переходу среднего осевого напряжения
от сжимающего к растягивающему, а верхняя граница определяется из условия
ErQ = Ed полной диссипации и перехода во внутреннюю энергию начального
запаса кинетической энергии радиального движения материала.
> 6 1 8 9 10
Рис. 17.37. Радиальные колебания в растягивающейся кумулятивной струе, по модели цилин-
цилиндрического сжимаемого упругопластического стержня: изменение радиальной скорости боковой
поверхности стержня (а); изменение давления на оси стержня (б)
Представления о поведении КС в свободном полете существенно уточняются,
когда при физико-математическом моделировании учитываются сжимаемость и
упругопластические свойства, реально присущие материалу кумулятивной струи
[17.54]. В этом случае обнаруживается существование колебательного процесса
(см. рис. 17.37), когда параметры движения, например, радиальная скорость
боковой поверхности элемента Vr = Vr/(e;zoRjo), и параметры состояния, на-

17.3. Движение и разрушение кумулятивных струй	231
пример, давление на оси симметрии элемента ро = ?>o/(pj^o^jo)> колеблют-
колеблются относительно значений, характерных для несжимаемого жесткопластического
стержня, показанных на рис. 17.37 штриховыми линиями. Колебания происходят
с переменным периодом Т и затухают, при этом в течение одного цикла колебаний
распределение напряжений по радиусу элемента КС меняется плавно с сохране-
сохранением параболического характера.
Как показал анализ результатов численных расчетов, параметры колебатель-
колебательного процесса зависят от трех безразмерных комплексов
V	ТС
n = l + izOt, U = —^-j-, S = —^-j-,	A7.61)
первый из которых является текущим коэффициентом удлинения, второй харак-
характеризует соотношение пластических и инерционных сил, а третий характеризует
соотношение внутренних сил, связанных со свойством сжимаемости, и инерцион-
инерционных сил (здесь К — модуль объемного сжатия материала кумулятивной струи).
Безразмерный комплекс S определяет амплитуду колебаний (с уменьшением S
амплитуда увеличивается), а комплекс U — затухание колебаний по мере удли-
удлинения (с увеличением U происходит более интенсивное затухание радиальных
колебаний).
Наиболее полная информация по растяжению и разрыву КС получается при
рассмотрении элемента КС, как сжимаемого упругопластического стержня пере-
переменного сечения, путем численного решения соответствующей двумерной нестаци-
нестационарной (r — z — i) задачи. Первые попытки именно такого подхода к исследованию
деформирования КС были предприняты в работах [17.39, 17.40] и в дальнейшем
получили развитие в работах [17.32, 17.44], [17.53]-[17.57].
В работах [17.39, 17.40] было предложено исследовать процесс растяжения
и разрыва КС в связи с развитием поверхностных возмущений на струе. Ки-
Кинематический и динамический анализ [17.44] результатов авторов [17.39, 17.40]
показал, что при таком подходе воспроизводятся основные особенности, присущие
пластически разрушающимся кумулятивным струям. Так, расчет растяжения
элемента КС с начальным гармоническим поверхностным возмущением предска-
предсказывает развитие шейки по заранее заданному ослабленному сечению элемента.
Развитие шейки сопровождается перераспределением радиальной и осевой скоро-
скоростей по длине элемента, постепенным формированием безградиентных областей и
прогрессирующей локализацией деформирования в области шейки. Такой процесс
завершается пластическим разрушением элемента КС — чисто геометрическим
разделением на отдельные безградиентные части при достижении шейкой нулево-
нулевого радиуса. Расчеты показывают, что подобная неустойчивость процесса дефор-
деформирования КС связана с наличием у материала упругопластических свойств и
должна рассматриваться как пластическая неустойчивость.
Применяя более сложные поверхностные возмущения, можно расчетным путем
выявить существование жестких функциональных зависимостей характеристик
растяжения и разрыва от безразмерного комплекса U = Y/ (pj^^0JRj0), опре-
определяющего соотношение пластических и инерционных сил [17.55]—[17.57]. Эти
зависимости имеют вид:
/ -2 с>2 \ °>32
п\ = 2,78 ( 	z	j ,
\	/
/ -2 р2 \ °>39
пь = 5,38 ( Pj?z? J0j ,	A7.62)

232	17. Кумуляция
у	N 0,51
а0 = 0,65
При этом последнее соотношение в A7.62) фактически не отличается от выраже-
выражения
а0 = -^- = 0,65,/ .fp2 ,	A7.63)
откуда следует, что начальная длина отдельного элемента uq не зависит от началь-
начального радиуса струи и определяется некоторым характерным перепадом скорости
между ограничивающими его плоскими сечениями AVj = ДУ* = ?zoao = 0,65* —,
V PJ
зависящим от прочности и плотности материала КС. С учетом этого можно найти
число отдельных элементов, образующихся при пластическом разрушении части
КС, ограниченной плоскими сечениями с лагранжевыми осевыми координатами
zqi и ZQ2, движущимися с осевыми скоростями Vji и Vj2-
Z02	Z02
dz0 f iz0 7	Vj2 -
42 = "
ZQl
Если считать, что Vj2 — скорость головного элемента КС, a Vji — скорость ее
«хвоста», из A7.64) следует формула для определения общего числа N отдельных
элементов, образующихся при разрушении всей КС. Полученные численными
расчетами зависимости A7.63), A7.64) соответствуют так называемой концепции
критической массовой скорости [17.42, 17.46, 17.63].
Формулы A7.62) и A7.64) неплохо соответствуют экспериментальным дан-
данным для пластически разрушающихся медных и ниобиевых КС, полученным
В. М. Марининым. Результаты сопоставления для медных КС, сформированных
лабораторными КЗ диаметром d = 50 мм, различающимися составом снаряжения,
конструкцией линзового узла, толщиной и углом раствора КО, показаны на
рис. 17.38. В связи с неопределенностью значения предела текучести материа-
материалов в условиях деформирования КС, безразмерный определяющий комплекс U
определен при некотором условном значении эффективного предела текучести
Y = Yconv = 108 Па. Кружками показаны экспериментальные данные, сплош-
сплошными линиями — их обработка по методу наименьших квадратов под степенные
зависимости типа A7.62) и A7.63). Видно, что экспериментальные данные хорошо
аппроксимируются подобными степенными зависимостями (а не только эмпириче-
эмпирическими линейными зависимостями A7.57)), причем показатели степени (а именно
они несут в данном случае полезную информацию) для величины а$ практически
совпадают с расчетным значением, а для щ — весьма к нему близки.
Обработка экспериментальных данных непосредственно под расчетные зависи-
зависимости A7.62), A7.63) позволяет оценить значения эффективного предела текуче-
текучести материала Y в условиях КС, при которых имеется наилучшее соответствие
коэффициента предельного удлинения (Yn) и относительной начальной длины
отдельных элементов (Ya). По этим двум, по существу независимым оценкам,
значение эффективного предела текучести материала в условиях КС составля-
составляет: для медных КС Yn = 0,46 ГПа и Ya = 0,28 ГПа, а для ниобиевой КС —
Yn = 0,26 ГПа и Ya = 0,32 ГПа. В качестве окончательной оценки эффективного
предела текучести может быть принята величина Y = 0,5 (Yn + У^). Полученные

17.3. Движение и разрушение кумулятивных струй
233
t
-
У-

¦Л
<**УУ!УУ
1
h
Рис. 17.38. Экспериментальные данные для медных ку-
кумулятивных струй и их аппроксимация под степенные
зависимости типа A7.62) и A7.63)
Рис. 17.39. Прямое сопо-
сопоставление расчетных резуль-
результатов и экспериментальных
данных для ниобиевой куму-
кумулятивной струи
при этом значении Y расчетные характеристики разрушения медных и ниобиевых
КС хорошо соответствуют экспериментальным данным.
Пример такого соответствия для ниобиевой КС приведен на рис. 17.39 в виде
распределений значений щ и N{ по относительной лагранжевой осевой координате
zq = zq/I^q. Вертикальными линиями показаны места расположения помеченных
участков КС (размещение вольфрамовых меток, определяющее разбиение КС на
участки с контролируемыми начальной и конечной длиной), сплошные линии
проведены через экспериментальные точки, а штриховые — через расчетные.
Как было отмечено выше, за рубежом при проведении исследований растяже-
растяжения и разрыва КС основное внимание уделялось определению времени разрыва
струи — т.н. breakup time tb, и определению критической скорости AV*, контро-
контролирующей разрыв струи на элементы определенных размеров. Время разрыва tb
связано с деформационной характеристикой разрыва — коэффициентом предель-
предельного удлинения щ. Эта взаимосвязь достаточно точно выражается соотношением
A7.58) и имеет вид щ = 1 + szoh- По существу коэффициент предельного
удлинения с точностью до слагаемого 1 соответствует безразмерному времени
разрыва tb = izoh- В таблице 17.7 в сопоставимой форме приведено сравнение
некоторых результатов зарубежных и отечественных исследований в этой области
(выполнено О. В. Свирским). Видно, что в качественном отношении полученные
в разные годы зависимости характеристик разрыва КС близки друг к другу —
во всех случаях в качестве безразмерного определяющего комплекса выступает
соотношение U = Y/ (pj?^0.Rj0) инерционных и пластических сил. В ряде случаев
зависимости очень близки друг к другу и в количественном отношении.
Из приведенных зависимостей следует, что, при условии реализации пластиче-
пластического характера разрушения КС, большая динамическая пластичность (большие

234
17. Кумуляция
Таблица 17.7
Сравнение формул для коэффициента предельного удлинения и критической
скорости разрыва КС
Авторы
Hirsh E., 1979 [17.42]
Haugstad В.,1983 [17.46]
МГТУ, 1984 [17.57]
Chou P. С, Flis W.J., 1986
[17.58]
Chou P. С, 1992 [17.59]
Carleone J., 1993 [17.61]
Chantaret P. Y, 1998 [17.62]
Пъ
l + ly/pjelo&jjY
2y/pje%0R*J0/Y
5,38 (pji2z0R2J0/YH'39
2 + 3,75y/pje2z0R?J0/Y -
0,125 (pji2z0R%/Y)
5(pjeloR2JO/YI/S
5,44 (pjil0R2J0/YH'352
7,5 (Pjil0R%/YI/3
AV*
0,87^/Y/pj
0,65л/?/р~]
0,68^/Y/pj
значения коэффициента предельного удлинения) соответствует высокоплотным
и малопрочным материалам, а также более высокоградиентным и более мас-
массивным кумулятивным струям. Это объясняет характер эмпирических зависи-
зависимостей A7.57). Однако современная теория кумулятивного действия зарядов не
в состоянии заранее точно предсказать, в каких случаях действительно будет
реализовываться пластическое разрушение КС, а в каких растяжение струи (на
стадии равномерного растяжения или на стадии развития шеек) будет прерывать-
прерываться квазихрупким, или же объемным разрушением. Особенно сложно теоретически
предсказать квазихрупкое разрушение, являющееся следствием развивающегося
на фоне больших пластических деформаций (порядка 1000%) процесса зарожде-
зарождения микроповреждений, их слияния, образования макротрещин и последующего
разделения струи на отдельные элементы. Предпринимавшиеся попытки использо-
использования кинетических моделей разрушения (например, модели зарождения и роста
повреждений — NAG-модели), или же макроскопических критериев накопления
поврежденности, к успеху не привели. Некоторые качественные соображения
причин отклонения в характере разрушения КС от пластического (на уровне
тенденций) следуют из особенностей радиальных колебаний при равномерном
растяжении кумулятивной струи [17.54, 17.56]. Однако в целом вопрос прогно-
прогнозирования разрушения струи в настоящее время является проблемой. До решения
этой проблемы для определения поведения КС в свободном полете в общем
случае их геометрических, кинематических параметров и физико-механических
характеристик материала, экспериментальные методы остаются незаменимыми.
17.4. Структурное состояние материала кумулятивной струи и песта
Условия формирования КС во многом определяются микроструктурой мате-
материала облицовки, способностью его структурных составляющих к пластической
деформации. Отмечена также зависимость между степенью обжатия материала
облицовки под действием ПД и типом кристаллической решетки обжимаемого
материала [17.4]. Например, большая степень обжатия наблюдается у облицовок из

17.4- Структура материала струи и песта	235
металлов с кубической решеткой (Al, Fe, Си); существенно меньшая — у металлов
с гексагональной решеткой (Cd, Co, Mg). Гидродинамическая теория кумуляции
не может объяснить сути процессов пластической деформации, проходящей в
материале облицовки. Поэтому о ее характере обычно судят по результатам
металлографических исследований пестов [17.64, 17.65], улавливание которых, как
правило, производится в песок или опилки. Однако, при проникании песта в такие
улавливатели в нем происходят структурные изменения, вызванные нагревом
материала песта за счет трения с материалом преграды. С этой точки зрения
определенным преимуществом обладает водная преграда. При попадании в воду
пест не деформируется и сохраняет ту структуру, которая у него была в момент
подлета к преграде.
В настоящее время проведено детальное исследование структурных особен-
особенностей медных, железных и стальных пестов. Оно показало, что по форме и
размеру зерен поверхность шлифа можно разбить на характерные зоны, в пре-
пределах которых части поверхности шлифа имеет одинаковую микроструктуру.
Границы зон следует считать условными, т.к. переход одной зоны в другую
носит плавный характер. В зависимости от толщины, угла раствора и диаметра
основания облицовки меняется площадь той или иной зоны поверхности шлифа,
однако порядок их чередования всегда остается неизменным (рис. 17.40).
Для медных пестов микроструктура об-
области, контактирующей со взрывчатым ве-
веществом, в дальнейшем называемой внеш-
внешней зоной (см. рис. 17.40, зона 4), отлича-
отличается от исходной структуры наличием т.н.
ударных «двойников». Их возникновение
характерно для металла при приложении
к нему импульсных нагрузок. Зона 4 пе-
переходит в зону вытянутых зерен 3, на-
направленных в сторону выхода струи под
некоторым углом к оси песта, разделяю-	19	% А
щей его примерно на две равные половины.
Отмеченный факт фиксируется при рас-	Рис* 17.40. Распределение зон в пестах с
СМОТренИИ Микроструктуры Шлифов ПОД	°Динаковой микроструктурой [17.64]: 1 -
* ± о о ± х	внутренняя зона: 2 — зона течения с рав-
МИКРОСКОПОМ. При приближении К ОСИ пе-	ноосными зернами рекристаллизации; 3 -
Ста, на фоне СИЛЬНО деформированных ВЫ-	Зона течения с сильно деформированными
тянутых зерен ПОЯВЛЯЮТСЯ также мелкие	вытянутыми зернами; 4 — внешняя зона
равноосные зерна, названные зернами ре-
рекристаллизации (зона 2). Их количество увеличивается в месте отрыва струи от
песта, причем в этом месте и в центральной части песта наблюдаются зоны только
с равноосными (мелкими и крупными) зернами.
Анализ структуры медных пестов показывает, что почти всегда относитель-
относительный объем 1-ой зоны примерно одинаков (за относительный объем принимается
отношение объема характерной зоны к общему объему песта). С увеличением
угла раствора облицовки увеличивается относительный размер внешней зоны.
При постоянном угле раствора облицовки с увеличением ее толщины эта зона
увеличивается в размерах. Увеличение размеров зоны сопровождается изменением
конфигурации песта, который становится тупым, а не заостренным [17.64].
Форма пестов из технически чистого железа отличается от медных, а их
микроструктура в целом аналогична рассмотренной выше микроструктуре мед-
медных пестов, как по расположению зон, так и по относительным размерам и
форме зерен. В стальных пестах, наряду с общими закономерностями, обнаружены
и более сложные структурные превращения, чем у пестов из железа и меди.

236	17. Кумуляция
Например, было замечено, что, независимо от содержания углерода и термической
обработки стальных облицовок, практически во всех случаях структура внешней
зоны пестов соответствует исходной структуре облицовки. По мере приближе-
приближения к центру песта, его структура приобретает осевую направленность (зона
3). При переходе от 3-й зоны ко 2-й, ферритные и перлитные зерна пестов из
отожженных стальных облицовок вытягиваются сильнее. При этом зерна пер-
перлита меняют свою окраску при травлении и становятся белыми. Белые зерна
имеют микротвердость значительно большую, чем зерна перлита, из которых они
образовались. В переходной зоне встречаются также зерна смешанного типа, в
которых структурными особенностями белых зерен охвачена только часть зерен
перлита. Ферритные зерна, при переходе от 3-й ко 2-й зоне, вытягиваются. На этом
фоне, при приближении к 1-й зоне, наблюдаются отдельные равноосные зерна,
появление которых позволяет сделать предположение о начавшемся в этом месте
процессе рекристаллизации. Во 2-й зоне рекристаллизация полностью заканчи-
заканчивается, а в 1-й зоне ферритные зерна имеют большие размеры, что объясняется
собирательной рекристаллизацией. Таким образом, ферритные и перлитные зерна
претерпевают различные превращения: феррит пластически деформируется и
рекристаллизуется, а перлит деформируется и превращается в плохо травящиеся
белые зерна. Установлено также, что механизм образования последних связан
с локальным разогревом и последующим быстрым перераспределением тепла в
металле. В результате этого в теле песта образуются структуры закалки с высокой
твердостью. Повышение микротвердости феррита и перлита во внешней зоне песта
объясняется взаимодействием материала КО с распространяющейся в нем УВ, в
результате которого появляется большое количество «двойников» и реализуется
механизм множественного скольжения между ними. Причем феррит, в условиях
воздействия с УВ, как и в условиях обычного статического нагружения, упрочня-
упрочняется сильнее, чем перлит. Высокую микротвердость феррита в 1-й зоне можно
объяснить только повышенной плотностью дефектов структуры внутри зерна.
Увеличение содержания углерода в стали способствует повышению температуры
при обжатии облицовки и проявляется в итоговом разупрочняющем действии
центральных зон пестов на структурные составляющие.
Проведенные металлографические исследования [17.65] позволили разработать
модель процесса пластической деформации, происходящей при схлопывании ме-
металлической КО и последующем формировании струи и песта (рис. 17.41). После
срабатывания заряда ВВ, по КО распространяется УВ, формирующаяся при
выходе фронта ДВ на границу раздела ВВ-металл. При прохождении У В по
облицовке, в зернах ее кристаллической структуры образуется большое количество
дефектов, и вся деформация происходит внутри зерен. О сильной внутризеренной
деформации можно судить по структуре внешней зоны пестов. В зернах этой
зоны имеется большое количество «двойников», между которыми наблюдаются
следы множественного скольжения; увеличивается количество блоков; возрастает
плотность дислокаций, которые образуют ячеистую структуру. Все это приводит
к значительному упрочнению тела зерна, повышению его твердости и прочности
(например, для меди предел прочности увеличивается в 1,5—2 раза), уменьшению
пластичности. В то же самое время уровень значений температуры, возникающий
в материале облицовки вследствие прохождения УВ, способствует уменьшению
прочности границ зерен, которая становится существенно ниже прочности тела
самого зерна. Создавшихся условий оказывается достаточно для протекания пла-
пластической деформации по механизму межзеренного проскальзывания, когда зерна
материала КО под действие ПД начинают перемещаться относительно друг друга
по направлению к оси. Зоны вытянутых зерен в пестах (зона 3 на рис. 17.40)
образуются в результате деформации скольжения уже после разделения обли-

17.4- Структура материала струи и песта
237
Рис. 17.41. Схема процессов деформирования металлической КО, формирования струи и песта
[17.65]: А — зона взаимодействия УВ с КО; В — зона схлопывания облицовки; С — зона
формирования струи; D — зона деформирования песта; 1 — граница разлета ПД; 2 — фронт
ДВ; 3 — фронт УВ; 4 — фронт волны разрежения
цовки на струю и пест. При этом переход от равноосных деформированных
зерен (зона 4) к вытянутым зернам (зона 3), в результате выделения тепла при
пластической деформации, сопровождается падением прочности и увеличением
пластичности. Наконец, центральная зона песта (зона 2), имеющая равноосные
зерна, аналогична по своей структуре структурному состоянию струи. В этой
зоне находятся металлические зерна, которые должны были бы перейти в струю,
однако, из-за особенностей струйного течения, остались в теле песта.
В процессе формирования струи, за счет обжатия облицовки и интенсивно-
интенсивного трения различных слоев металла, возникают температуры, достаточные для
осуществления процесса рекристаллизации. В теле песта рекристаллизованная
структура испытывает дополнительные нагрузки, которые вызывают увеличение
плотности дефектов без изменения формы зерна. Этим объясняется повышенное
значение прочности и твердости материала центральной зоны по сравнению с ее
исходным значением. Процесс рекристаллизации, начавшийся в момент схлопыва-
схлопывания облицовки, протекает и в КС одновременно с ее пластической деформацией,
причем именно реализацией процесса динамической рекристаллизации можно
объяснить возможность многократного увеличения начальной длины струи при
ее последующем удлинении.
Таким образом, изложенная модель процесса пластической деформации ме-
металлической КО при взрывном обжатии показывает, что по толщине она испы-
испытывает неодинаковые тепловые и деформационные воздействия. В этом плане к
материалу КО можно предъявить различные требования. Например, материал
внутренних слоев облицовки, идущий в струю, кроме высокой плотности, должен
обладать низкой температурой рекристаллизации, способствующей большему вы-
выходу металла в струю и большему растяжению последней в полете. Наружные

238	17. Кумуляция
слои облицовки целесообразно выполнять из малопрочных, хрупких и легкоплав-
легкоплавких металлов. Наконец, средние слои облицовки целесообразно изготавливать
из высокопластичных металлов, способствующих большему выходу материала
внутреннего слоя облицовки в кумулятивную струю.
17.5. Расчет функционирования кумулятивных зарядов
Существует два метода расчетного определения параметров функционирова-
функционирования кумулятивного заряда. Первый из них заключается в численном интегриро-
интегрировании системы дифференциальных уравнении, описывающей поведение составных
элементов КЗ на разных стадиях кумулятивного действия: обжатия (схлопывания)
кумулятивной облицовки под действием продуктов детонации, образования КС
или формирования поражающего элемента (ПЭ), растяжения и разрыва КС,
проникания КС или ПЭ в преграду. Данный метод расчета требует обычно состав-
составления нескольких взаимосвязанных программ, знания свойств ВВ и материалов
КО, корпуса, «линзы» и других составных элементов заряда.
Второй метод, получивший название «инженерный расчет», основан на гидро-
гидродинамической теории кумуляции, а также ряде приближенных соотношений по
определению активной массы заряда, скорости метания облицовки, угла схло-
схлопывания отдельных элементов облицовки и экспериментальных данных. В силу
широкого использования экспериментальных данных для тарировки или определе-
определения отдельных параметров функционирования КЗ, данный класс методов иногда
называют расчетно-экспериментальным.
Необходимо отметить, что, по мере развития вычислительной техники, расши-
расширения представлений о поведении материалов при динамическом нагружении, су-
существенно выросли значение и практическая ценность исследований, проводимых
на основе численных методов механики сплошной среды. Тем не менее, такой рас-
расчет функционирования КЗ в рамках единой методики — от момента инициирова-
инициирования до окончания пробития преграды, в настоящее время сопряжен, прежде всего,
с неудовлетворительной точностью получаемых результатов, вызванных несовер-
несовершенством физико-математических моделей и самих численных методов, а также
со сложностями технического характера, связанными с обменом данных между
отдельными взаимосвязанными программами, чрезмерно высокими требованиями
к быстродействию, электронной и дисковой памяти ЭВМ. Наиболее эффективно
использование численных методов при исследованиях отдельных стадий куму-
кумулятивного действия, перечисленных выше. Поэтому увязка численных (конечно-
разностных) методов расчета с инженерными (расчетно-экспериментальными)
методиками в настоящее время обеспечивает наиболее полное моделирование
функционирования КЗ с приемлемой точностью.
1. Численные методики расчета параметров кумулятивной струи.
Изучение процессов обжатия (схлопывания) облицовки и образования КС или ПЭ,
как для осесимметричных, так и для удлиненных КЗ, целесообразно проводить
в двумерной постановке (в цилиндрической или декартовой системе координат
соответственно). Естественно, в первом случае не учитывается асимметрия в
изготовлении и инициировании заряда ВВ, во втором — протяженность и про-
пространственная кривизна реальных кумулятивных зарядов. Решение этих задач
экспериментальными методами затруднено из-за малой длительности процесса,
наличия импульсных нагрузок, а также потому, что структура течений в зоне
взаимодействия в процессе деформирования КО, а также в самой струе во время
растяжения и разрыва, скрыта от исследователя. В этом плане особое значение
имеет математическое моделирование явлений, сопровождающих образование КС

17.5. Расчет функционирования кумулятивных зарядов
239
или ПЭ, основанное на применении численных методов механики сплошных сред.
При этом, как правило, на основе однородных схем сквозного счета, позволяющих
проводить вычисления без предварительного анализа особенностей течения, раз-
разрабатывается соответствующая методика, реализация которой адекватна проведе-
проведению вычислительного эксперимента. Решение задачи может быть получено как в
лагранжевых, так и в эйлеровых координатах. В соответствии с этим, конечно-
разностные аналоги называют лагранжевыми или эйлеровыми. Их детальное
описание существует в многочисленной литературе, подробную библиографию
по которой и краткое описание методов можно найти в работах [17.9, 17.33],
[17.66]—[17.68]. Здесь же кратко отметим те из них, с помощью которых получены
основные результаты, использованные в настоящей монографии. Это лагранжева
конечно-разностная схема HEMP [17.66], метод конечных элементов EPIC (см.
библиографию в [17.9]), метод «свободных точек» [17.67, 17.68], а также большое
семейство «алгоритмов частиц» (PIC, FLIC, EIC, HELP, «крупных частиц», «ин-
«индивидуальных частиц», и некоторых других), описанных в работах [17.34], [17.69]—
[17.72].
Расчетная схема кумуля-
кумулятивного заряда показана на
рис. 17.42а, где 1 — кумуля-
кумулятивная облицовка, 2 — корпус,
3 — взрывчатое вещество. Бу-
Будем полагать, что в началь-
начальный момент времени (t = 0),
в точке 4 (точка инициирова-
инициирования) осуществляется подрыв
заряда ВВ с начальной плот-
плотностью рвв и теплотой взрыв-
взрывчатого превращения Q. От
точки инициирования начи-
начинает распространяться фронт
ДВ (кривая 5) со скоростью
D, с образованием ПД (зона
6). С течением времени ДВ на-
начинает отражаться от поверх-
поверхностей КО и корпуса, на ко-
которые действует давление по-
порядка 20-60 ГПа. Его величина зависит от свойств ВВ, угла подхода фронта ДВ
к поверхности облицовки, материала и толщины облицовки. Под действием ПД
кумулятивная облицовка начинает обжиматься с образованием КС (зона 7 на
рис. 17.426), или деформироваться с образованием поражающего элемента. При
этом, для получения общих закономерностей или особенностей формирования КС
или ПЭ конкретного КЗ, обусловленных формой облицовки, геометрией заряда,
месторасположением точки инициирования, физико-механическими свойствами
используемого состава ВВ или материалов облицовки и корпуса, целесообразно
использовать модель сжимаемой идеальной упругопластической среды с уравне-
уравнением состояния в виде баротропной зависимости [17.4, 17.32, 17.33]. Последнее
отмеченное обстоятельство позволяет избежать интегрирования уравнения энер-
энергии в системе соотношений, описывающей поведение взаимодействующих сред и
включающей дифференциальные уравнения неразрывности, движения, пластиче-
пластического течения Прандтля-Рейсса с условием пластичности Мизеса, кинематические
соотношения и уравнение состояния (см. подробнее главу 19). Причем, если для
описания физико-механического поведения материала КО при формировании КС
0
а	б
Рис. 17.42. Расчетная схема кумулятивного заряда (а);
образование КС (б)

240	17. Кумуляция
можно ограничиться газодинамической моделью, то для определения формы и ки-
кинематических характеристик ПЭ, особенно на поздних стадиях движения, важным
является учет проявления упругопластических свойств матери