Текст
Е.М.М0Р030В, гп.никишков
МЕТОД КОНЕЧНЫХ
ЭЛЕМЕНТОВ
В МЕХАНИКЕ
РАЗРУШЕНИЯ
I
МОСКВА «ПАУКА*
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО МАТЕМАТНЧЕСКОИ ЛИТЕРАТУРЫ
1980
М КП
УДК 531
Морозов Е. М., II п кп ш ко в Г. П. Метод конечных элементов в
механике разрушения.— М.: Наука. Главная редакция физико-математиче-
ском литературы, 1980.— 256 с.
В книге изложены современные представления о методе конечных
элементов и способах его реализации в задачах линейной и нелинейной
механики разрушения. Ее содержанием, охвачен широкий крут вопросов —
от методов расчета коэффициентов интенсивности напряжении в плоских
и осесимметричных телах мри механическом и термическом нагружении,
пластически деформированных областей и параметров локального разру-
шения в случае развитой пластической зоны и до ряда вычислительных
экспериментов, помогающих решению сложных вопросов механического
поведения упруго пластических тел с трещинами. В приложении к книге
даны алгоритмы решения основных задач, оформленные в виде программ
для ЭВМ па языке фортран.
Jкнига предназначена для научных п инженерно-технических работни-
ков, занимающихся вопросами механики разрушения и численными мето-
дами решения краевых задач механики деформируемого тела, а также для
аспирантов и студентов старших курсов по специальностям «физика проч-
ности», «механика твердого тела» п «прочность деталей машин».
М 2|,:|1>5~~ 074 163-80.170ЖШХЮ
053(02) SO
'С Издательство «Наука».
Главная редакция
физико-математической литературы. 1980
ОГЛАВЛЕНИЕ
Предисловие....................................................., 5
I । а в а I. Метод конечных элементов для решения задач теории
упругости...................................................... 7
§ 1. Введение...................................... 7
§ 2. Изопараметрпческие коночные элементы.......... 8
§ 3. Интерполяция перемещений...................... 9
§ 4. Матрицы жесткости.............................11
§ 5. Приведение реальных и фиктивных нагрузок к узлам 14
§ 6. Вырождение четырехугольных элементов в треугольные 15
§ 7. Сборка и решение системы уравнений равновесия . . 16
§ 8. Методические примеры с использованием квадратичных
элементов................................................17
§ 9. Расчет напряжении в роторе среднего давления турбппы
К-300-240 ЛМЗ...................................’ . . 20
I .1 ава II. Решение задач линейной механики разрушения с по-
мощыо МКЭ......................................................23
§ 10. Введение................................................23
§ 11. Моделирование сингулярного характера распределения
напряжений и деформаций в окрестности вершины тре-
щины ....................................................24
§ 12. Методы определения коэффициента интенсивности на-
пряжений 1 рода при термоспловом пагруженпп ... 26
§ 13. Методические примеры определения коэффициента ин-
тенсивности напряжении...................................37
§ 1 i. Коэффициент ивтонсивпо.стп напряжений для ДКБ-об-
разца при нагружении силой и моментом....................46
§ 15. Коэффициент пптенсивности напряжении у кольцевых
трещин в толстостенных трубах при растяжении . . 49
§ 16. Анализ хрупкой прочности корпуса реактора АЭС «Лови
мза» при. разрыве трубопроводов..........................51
г лава III.Несимметричные задачи линейной механики разрушения 58
§ 17. Введение ......... w . . . 58
§ 18. Критерии локального разрушения..........................58
§ 19. Методы расчета параметров разрушения с помощью МКЭ 61
§ 20. Задача о растягиваемой пластине с наклонной трещиной 64
§ 21. Моделирование распространения трещины л основании
нлотипы..................................................67
I jaualV. Определение целей упруго-пластических деформаций и
напряжений................................................... 70
§ 22. Введение................................................70
? 23. Основные уравнения шшзотермической теории течения
при изотропном упрочнении ...............................70
!!♦
ОГЛАВЛЕНИЕ
4
§ 24. Уравнения МКЭ в приращениях п условие равновесия
упруго пластического тела...................................73
§ 25. Метод начальных напряжении для решения физически
нелинейных задач и критерии сходимости .... 74
§ 26. Методика определения конечных приращений напряже-
ний в процессе упруго-пластпческого деформирования 76
§ 27. Ускорение сходимости итерационного процесса ... 78
§ 28. Методика подсчета приращений от равновесных значе-
ний величин................................................ 79
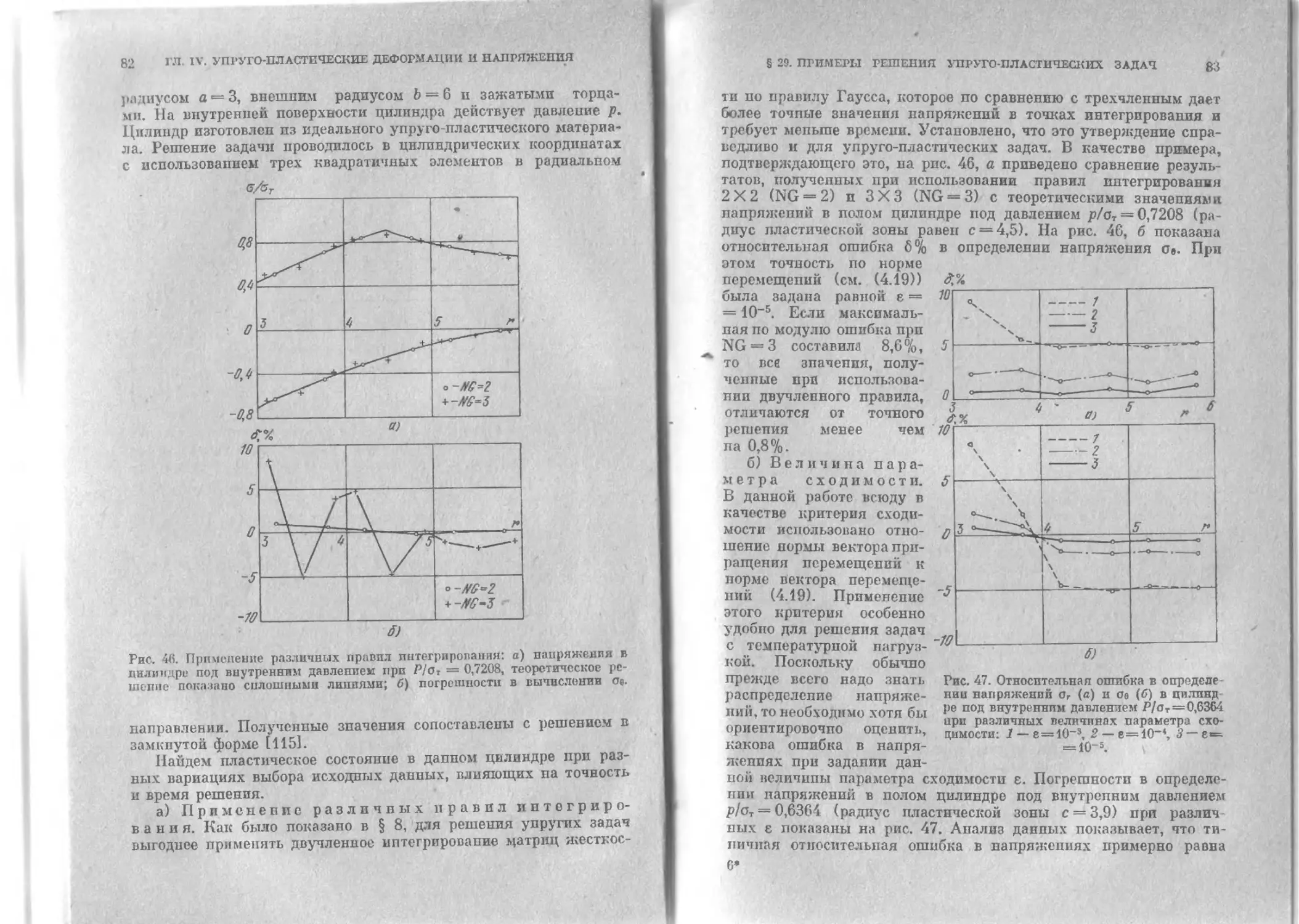
§ 29. Методические примеры решения * упруго пластических
задач.......................................................81
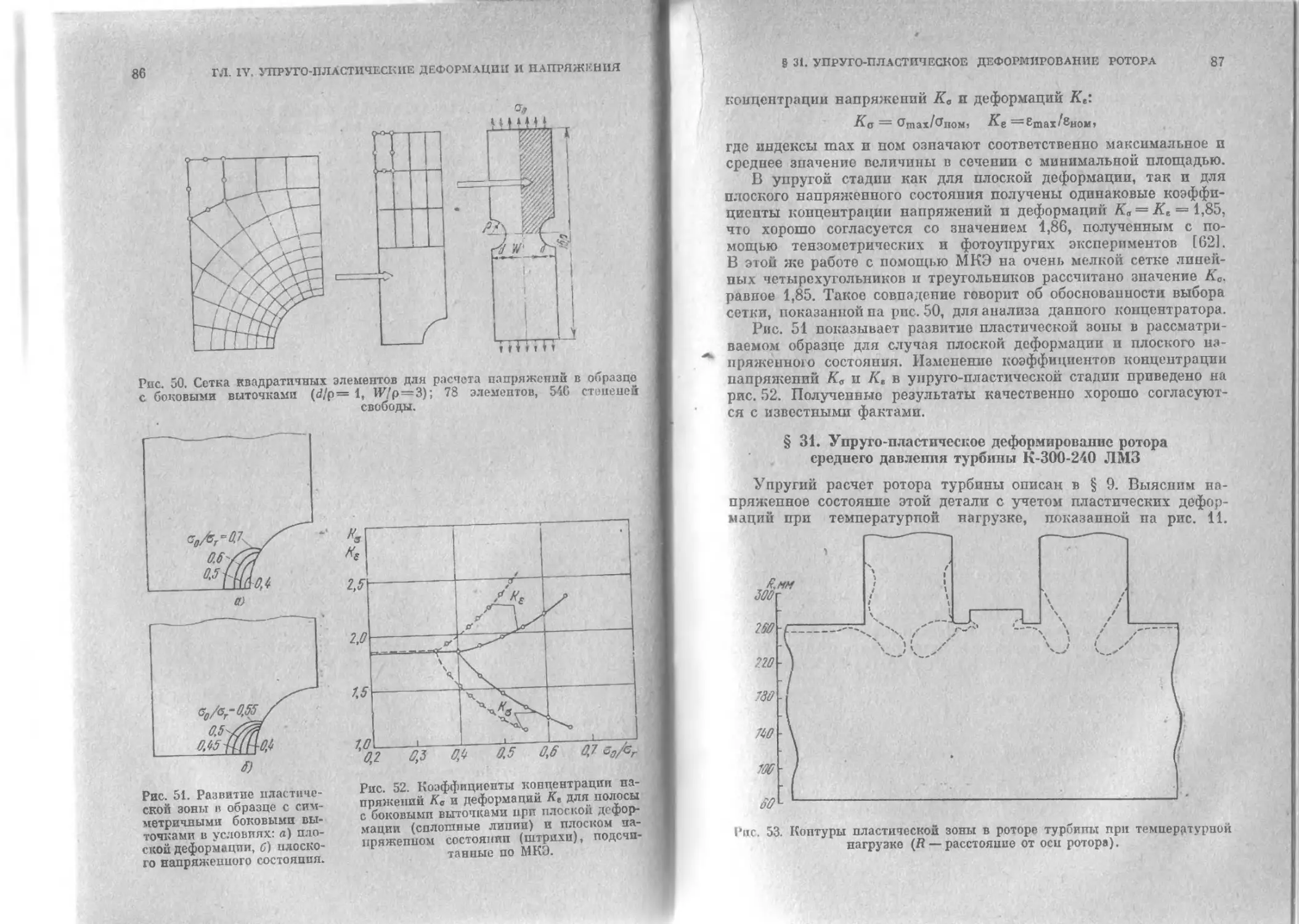
§ 30. Расчет коэффициентов концентрации дня образца с бо-
ковыми выточками............................................85
§ 31. Упруго пластпческоо ’(сформирование ротора среднего
давления турбины К-300-240 Л М3.............................87
Глава V. Решение упруго-пластических задач механике разруше-
ния с использованием теории течения..............................89
§ 32. Введение.............................................89
§ 33. Интеграл Черепанова — Райса в нелинейной механике
разрушения.............................................90
§ 34. Расчетное определенно величины интеграла Черепано-
ва-Райса ...................................................94
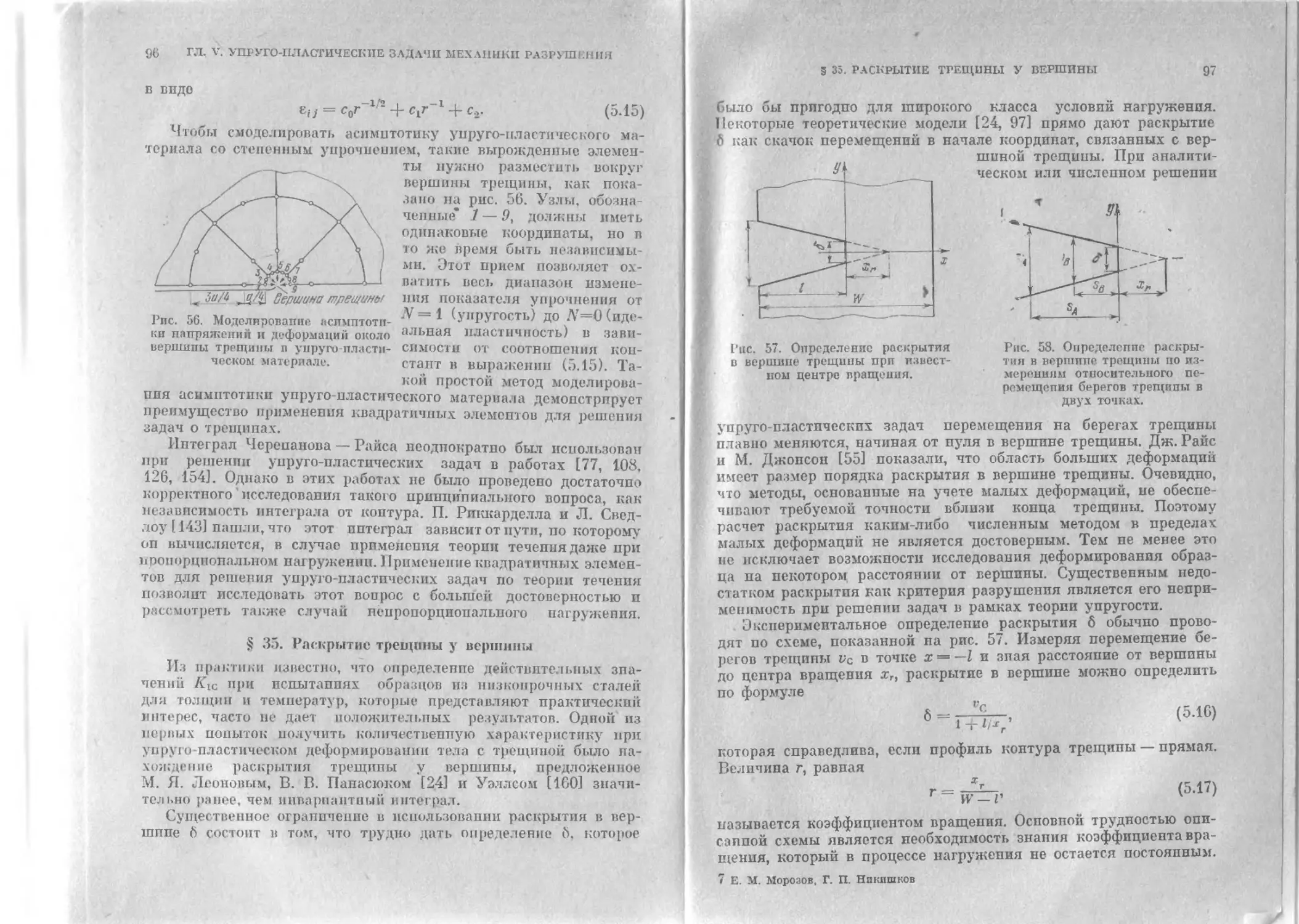
§ 35. Раскрытие трещины у вершины.....................96
§ 36. Локализованное пластическое течение у вершины тре-
щины при плоской деформации О4*
§ 37. Исследование независимости от контура интеграла Че-
репанова — Райса.......................................99
§ 38. Погрешности линейной механики при предсказании ло-
кального разрушения в упруго-пластических телах . . 102
§ 39. Энергетические затраты на развитие трещины при изо*
термическом процессе.....................................104
§ 40. Компактный образец................................1«‘7
§ 41. Анализ хрупкой прочности корпуса реактора АЭС «Ло-
вииза» с учетом эффектов пластичности . . . . . 112
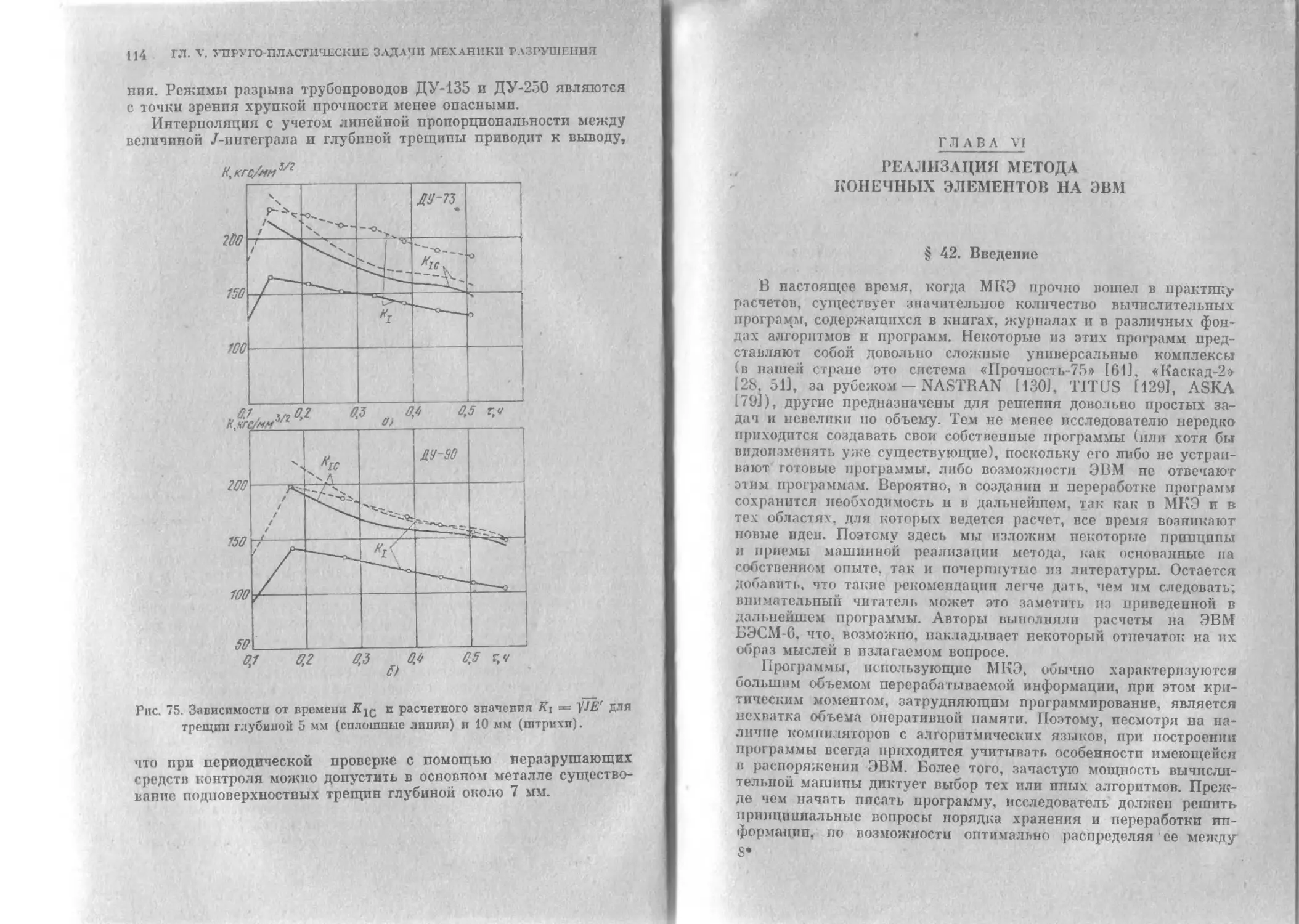
Г л а в а VI. Реализация метода конечных элементов на ЭВМ . . 115
§ 42. Введение............................................115
§ 43. Дискретизация и входная информация..................116
§ 44. Вычисление матриц жесткости элементов .... 125
§ 45. Сборка системы алгебраических уравнений равновесия 129
§ 46. Решение системы уравнений равновесия ..... 138
§ 47. Получение и обработка результатов ...... 144
Приложение. Описание программ................................. 149
Литература . . . » ..........................247
ПРЕДИСЛОВИЕ
Проведение расчетов на прочность, учитывающих всо многообразие
поведения реальных конструкций, становится все более актуальным. Внед-
рение методик расчета с позиций механики разрушения особенно важно
tin крупногабаритных тел из металлпчеепкх материалов сродной нрочно-
гти и для конструкций из высокопрочных материалов. Поэтому изучение
»лкопомерностен механики разрушения имеет большое значение для мно-
। их отраслей современной техники.
Если материал сохраняет свойство линейной упругости до разруше-
ния, за исключе1шем небольшой окрестности вер
mi
щы трещины, то учет
влияния трещины па прочность тела может быть сделан с позиций линей-
ной упругой механики разрушения, которая хорошо обоснована, особенно
ini трещин нормального отрыва. Однако определение упругих парамет-
ров разрушения — с южная математическая задача. Аналитические реше-
ния получены только для частных случаев. Для задач со сложной геомет-
рией и условиями нагружения обычно применяют численные методы.
Реальные металлические тела при разрушит и всегда испытывают не-
которую пластическую деформацию. Если прп этом реализуется концеп-
ции квазихрункого разрушения по Оровану — Првппу, то можно приме-
ojjil линейную механику. Очевидно, что во многих практических расчи-
пх упругое решение задач о трещинах пе дает их корректного описания,
«чеюда вытекает необходимость развития методов решения нелинейных
лндач механики разрушения с учетом перераспределения напряжений и
смещений вследствие пластической деформации.
Среди численных методов решения линейных п нелинейных задач о
1 рицинах наибольшее распространение получил метод конечных элементов
(МКЭ). Сравнение МКЭ с традиционными конечно-разностными методами
(МВТ) показывает его преимущества, состоящие в легкости расчета на-
пряженного состояния тел пз нескольких материалов с нерегулярными
। рапицамв, возможности сгущения сетки в местах ожпдаелюй концентра-
ции напряжении, простоте учета различных граничных условий. Гак как
МКЭ основан ла вариационных принципах, то потенциально он более то-
*!<• и. Важной особенностью МКЭ является то, что тело делится ла области
(конечные элементы), в каждой пз которых могут быть установлены своп
анконы, связывающие узловые силы и перемещения. Это дает возможность
« пнзывать в одной сетке различные элементы и значительно повышает эф-
фективность метода.
II последнее время многими исследователями ведется активная рабо-
|.т по численной реализации метода граничных интегральных уравнений
ПРЕДИСЛОВИЕ
Ci
(ГПУ) и на этом пути достигнуты немалые успехи. Основная привлеките, ib-
иля черта метода ГИУ состоит в снижении размерности рассматриваемой
задачи на единицу, следовательно, метод приводит к решению системы
линейных алгебраических уравнении меньшего порядка. Однако матрица
>гой системы обычно является полностью заполненной, в то время как
МКЭ приводит к разреженным или ленточным матрицам, которые весьма
удобны для решения. Па сегодняшний день теория и методы реализации
МКЭ развиты лучше, чем у метода ГПУ, это делает МКЭ пока более уни-
версальным методом. Немаловажное .значение для исследователя имеет
естественность механической трактовки МКЭ, что дает возможность по-
строения некоторых моделей на основе физического, а не математического
подхода. Все это позволяет утверждать, что МКЭ и ГИУ не исключают
друг друга, а требуют сочетания преимуществ обоих методов. Уже появи-
лись работы, в которых часть тела моделируется конечными элементами,
а решение в остальной области ищется С помощью ГИУ.
В настоящей монографии излагается применение метода конечных
элементов к задачам теории упругости и пластичности, линейным и нели-
нейным задачам механики разрушения. Изложение ограничено методом
перемещений и использованием пзопараметрпческпх конечных элементов.
Это — простой и логичный подход, позволяющий эффективно решать
многие задачи. Главное внимание уделено применению квадратичных эле-
ментов, которые за счет использования интерполирующих функций более
высоких степенен позволяют строить дискретную модель с мопыпим чис-
лом степеней свободы. Эти элементы особенно выгодно использовать в за-
дачах механики разрушения, поскольку опи легко позволяют точно мо-
делировать асимптотику в окрестности вершппы трещины.
Главы I и IV содержат основные соотношения МКЭ для решения уп-
ругих и упруго пластических задач п снабжены числовыми примерами.
В главах II и III рассматриваются методы определения коэффициентов
интенсивности напряжений для упругих тел. В главе V представлены ре-
зультаты некоторых вычислительных экспериментов для упруго-пластиче-
ских тел с трещинами. В книге рассматриваются лишь двумерные задачи.
Обобщение вычисли тельных методов механики разрушения на случай трех
измерений принципиальных трудностей не встречает. Глава VI посвящена
обсуждению различных аспектов реализации МКЭ на ЭВМ; в этой главе
нашли отражение некоторые работы авторов в этой области. В приложе-
нии приводится пример вычислительной программы для решения упруго-
пластических задач.
Выражаем глубокую признательность В. А. Постнову и Г. П. Черепа-
нову, взявшим пл себя нелегкий труд прочтения рукописи данной книги.
.1 вторы
ГЛАВА Т
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
ДЛЯ РЕШЕНИЯ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
$ 1. Введение
Метод конечных элементов (МКЭ) является эффективным об-
щим численным методом для решения широкого круга краевых
задач механики сплошной среды. Он основан на замене исследу-
емого объекта совокупностью конечного числа дискретных элемен-
тов, связанных между собой в узлах. В этом случае схема созда-
ния математической модели следующая: исследуемый объект —
идеализированная расчетная схема — система линейных алюбраи-
•нтких уравнении. Непосредственный переход к расчетной схеме
из соображений механики дает возможность естественно форму-
лировать граничные условия, произвольно располагать узлы сеткп
элементов, сгущая ее в местах ожидаемого большого градиента
искомых величин, применять метод для исследования областей,
состоящих пз фрагментов различной физической природы и т. д.
При обеспечении непрерывности перемещений и использова-
нии вариационных принципов для построеппя матрицы жестко-
сти, дающей связь между усилиями п перемещениями узлов эле-
мента, с математической точки зрения МКЭ тождествен методу
Ритца. Однако основное отличие МКЭ .состоит в кусочно-непре-
рывном определении полей, которое с достаточной простотой но-
П’.отяет рассматривать нерегулярные границы тела. Вторым су-
щественным достоинством такого кусочного определения является
ю, что уравнения равновесия образуют ленточную матрицу, для
которой эти уравнения легко решаются прямыми пли итерацион-
ными методами.
Важно отметить естественность механической трактовки МКЭ.
. lei кость физической интерпретации конечно-элементных моделей
позволяет без труда обнаруживать грубые ошибки в формулиров-
ке задачи. Кроме того, становятся ясными некоторые неожидан-
ные возможности метода, которые используются только на основе
физической пптуицип.
Котя некоторые идеи метода, прежде всего связанные со све-
lenncM континуальных систем к одномерным стержневым, извест-
ны давно [60], начало истории МКЭ следует отпести к середине
50-\ годов. Понятие конечных элементов было впервые введено
М. Горнером, Р. Клафом, X. Мартпном п Л. Тонном [153] в
8
ГЛ. I. РЕШЕНИЕ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
I9.ii) г. Не случайно, что это произошло вскоре после появления
ЭВМ, поскольку решение практических задач с помощью МКЭ
может быть осуществлено только при использовании быстродей-
ствующих машпн.
Дальнейшее развитие метода отражено в работах зарубежных
исследователей Дж. Аргпрпса, Е. Л. Вильсона, М. Р. Айронса,
Р. У. Клафа, Дж. Пржемппицкого, У. М. Дженкинса, О. К. Зен-
кевича и др. Значительный вклад в теорию МКЭ содержится в
отечественных работах А. В. Александрова, А. М. Масленникова,
Л. А. Розина, А. Г. Угодчикова, Н. Н. 1Папошпикова, В. А. Пост-
нова, II. Я. Хархурпма, Д. В. Вайпберга, А. С. Сахарова, В. Г. Кор-
неева и др.
Литература, посвященная теорпи и реализации МКЭ, весьма
обширна (в последило годы изданы книги [16, 42, 50, 56, 64]).
История метода и современное его состояние отражены в отлич-
ных обзорах О. К. Зенкевича 115] и Д. В. Вайпберга и др. [27].
Также следует отметить книги О. К. Зенкевича [16] и В. А. Пост-
нова и II. Я. Хархурима [50]. В первой исчерпывающе изложена
теория метода, вторая дает ясное представление о его реализации
па ЭВМ.
В дальнейшем всюду мы будем рассматривать подход, извест-
ный как метод перемещений. В этом случае метод эквивалентен
минимизации полной потенциальной энергии системы, выраженной
через поле перемещений. Такая трактовка обуславливает следу-
ющую последовательность проведения расчета по МКЭ:
1. Разбиение тела на конечные элементы и назначение узлов,
в которых определяются перемещения.
2. Определение зависимостей между усилиями и перемещени-
ями в узлах элемента, т. е. построение матриц жесткости.
3. Составление системы алгебраических уравнении равновесия
(сборка).
4. Решение системы уравнений.
5. Опре деление компонентов напряжений-деформированного
состояния тела.
Опишем некоторые теоретические п вычислительные особенно-
сти используемых алгоритмов и приведем числовые примеры.
§ 2, Изопараметрпческие конечные элементы
Выбор типов применяемых конечных элементов является важ-
ным шагом, сильно влияющим па эффективность расчета. Про-
стейшая форма идеализации двумерной задачи состоит в исполь-
зовании треугольников с узлами, расположенными в вершинах
[153J. Эти элементы использовались в числе первых. Впоследст-
вии было замечено, что при увеличении числа степеней свободы,
связанных с элементом, снижается общее число степеней свободы
§ 3. ИНТЕРПОЛЯЦИЯ ПЕРЕМЕЩЕНИИ
9
спст.емы. необходимой для достижения заданной точности. Однако
при использовании более сложных элементов возрастает время
вычисления матриц жесткости элементов и увеличивается шири-
на лепты матрицы системы уравнении равновесия, что также ве-
дет к росту времени счета. Ряд исследований указывает на эффек-
тивность применения в расчетах более сложных элементов. Па-
пример, в работе [91] посредством конформного отображения бы-
ло получено точное решение смешанной краевой задачи для об-
ласти нерегулярной формы. Это решение использовалось для
Рис. 1. Изопараметрпческие четырехугольные элементы: а) линейный,
6} квадратичный.
оценки точности треугольных элементов с тремя, шестью и де-
сятью узлами и изопараметрпческпх линейного и квадратичного
элементов. В результате сравнения точного и приближенного
решений было найдено, что из перечисленных наиболее эффек-
тивным с точки зрения точности и времени вычислении является
изолараметрпческпй квадратичный элемент. Преимущества ис-
пользования более сложных элементов показаны в работах [12, 23].
В данной работе в качестве базового используется пзопараметри-
ческий квадратичный элемент (рис. 1, б), для решения некоторых
задач применяется линейный четырехугольный элемент (рис. 1,а).
§ 3. Интерполяция перемещений
Введем в изопараметрическом четырехугольном элементе ло-
кальную координатную систему с, ц [1], которая удовлетворяет
условиям
— 1 Т) 1.
Па рис. 1 штриховой линией показаны линии, получающиеся.
1 огда одна из локальных координат фиксирована, а другая
пробегает все возможные значения. Эти координаты связываются
1U
ГЛ. I. ГНИЕНИЕ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
с глобальной (например, декартовой) системой с помощью за-
висимостей
(1.1)
где X/, уг~ глобальные координаты узлов, ЛГД|, ц)—так называ-
емые функции формы, которые выражаются через локальные ко-
ординаты. Число членов суммы равпя-
---------------------°--------------------->> ется числу узлЗв. В пзопараметриче-
ст ских элементах функции формы ирп-
fменяются также для интерполяции пс-
$--------------------. л ремещенпй по их узловым значениям
а> [98, 123]:
Рис. z. Иерархическая схе-
ма построения элементов с
числом узлов от 4 до 8.
и = У NiUi, v = У Nii'i. (1.2)
Здесь и, и — перемещения по осям х,
у в произвольной точке элемента,
и», Vf — перемещения узлов. Отметим,
что Ari также называют интерполиру-
ющими плп аппроксимирующими
функциями.
Для линейного четырехугольника
эти функции равны
1У{ = 4-(1 + ^1)С + ти). (1.3)
гдр щ — значения локальных коор-
динат в узле i. В квадратичном элементе эти функции имеют вид
2V; = 4 (1 + на (1 + 1рЬ) _ 4(i _ (1 + ipii) _
-4(1 + йд(1-П2) для I = 1,3, 5,7; (1.4)
А\ = 4"(1 — й)(1+ ‘Pli) для i = 2, 6;
1 (1-5)
= 4- (1 + ЙО (1 ~ ’I2) Для i = 4, 8.
А
Легко видеть, что любая угловая функция формы G=l, 3, 5, 7)
может быть выражена как линейная комбинация функций
(1.3) п (1.5), что открывает возможность конструирования эле-
ментов с числом узлов от четырех до восьми.
Наглядная схема так называемого иерархическою подхода
дана в работе [155]. Пусть угловой узел с квадратичного элемента
имеет единичное перемещение, а остальные — нулевые. Это пере-
мещение показано единичным вектором на рис. 2, д. Для просто-
ты предполагаем, что узлы имеют одну степень свободы в направ-
§ 4. МАТРИЦЫ ЖЕСТКОСТИ
11
лепии, перпендикулярном плоскости элемента. Если для интерпо-
ляции перемещенnii мы возьмем функцию формы линейного эле-
мента V, (1.3), то окажется, что перемещения промежуточных
узлов s ut будут равны не нулю, а 0,5. Вычитание из угловой ли-
нейной функции формы половин функций промежуточных узлов
квадратичного элемента восстанавливает верное распределение
перемещений. Это вычитание иллюстрируют рис. 2, б и 2, в. Если
же какого-либо промежуточного узла нет, то вычитания произво-
дит!. не надо. Таким образом, при построении элемента с числом
узлов от четырех до восьми угловые функции формы считаются
по формуле
лг« = Nt —L (Д'8 4- ,vt).
где в качестве функций формы N9 и Nt берутся выражения (1.5)
в случае присутствия промежуточных узлов пли нуль в случае
их отсутствия.
§ 4. Матрицы жесткости
Матрица жесткости [7d позволяет выразить вектор узловых
усилий {/?} через вектор узловых перемещении {д):
{/?} = [&]{</}. (1.6)
Здесь и всюду далее вектором названа матрица-столбец ком-
понентов некоторой величины, которая по своему физическому
смыслу может не совпадать с общепринятым определением век-
юра. Эти величины заключены в фигурные скобки, а квадратные
или прямоугольные матрицы — в квадратные скобки.
Пусть мы имеем соотношения, позволяющие по перемещениям
определить векторы деформации {с} п напряжения (о):
{с} = (В1{д}, (1.7)
(о) = [/)]<£}. (1.8)
Здесь [В] — матрица дифференцирования перемещений, [£>] —
матрица упругости. Заметим, что соотношение (1.8) записано для
случая отсутствия начальных деформаций (например, температур-
ных).
Но принципу возможных перемещений сумма работ всех
внешних {/?} и внутренних {о) сил на возможном перемещении
(6с4 равна нулю:
(6?)т [/?]— f (6ejr [a] dV 0.
V
Здесь V—объем элемента. Подставляя сюда выражения (1.7) —
(1.8) и сокращая обе части па {бд}т, получаем выражение для
12
ГЛ. I. РЕШЕНИЕ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
определения матрицы жесткости конечного элемента
[А-1 = f [В]Т[П] [В] dV.
(1-9)
Для того чтобы записать закон Гука для плоской задачи в
матричной форме, .представим матрицу упругости в виде
[D] -
Е
(l-FvXi-vj
1 О
1 О
1 •
о о —
(1.10)
где vj = v — для плоского напряженного состояния, vi «
== v/(l — v)—для плоской деформации. Такая запись матрицы
упругости подразумевает, что деформации объединены в вектор
в следующем порядке:
— I Ех 8^ 8х»;|«
Если при решении осесимметричной задачи вектор деформации
записан как
[в] — [ег 8т 8гг Eq[,
то матрицу упругости следует брать в впдо
1 — v v 0 v
v 1 — v 0 м
1/9] = 1 1 (l-bv)d-2v) 1 — 2v 0 0 —0 4м - (1.11)
—V v 0 1 — v_
Матрица [В] получается при помощи дифференцирования соот-
ношений (1.2) и состоит из блоков. Ш1сло которых равно числу
узлов элемента:
IB] -[В, В2 В3 ...].
Для различных координатных систем эти блоки имеют вид:
в декартовых координатах —
(1.12)
§ 4. МАТРИЦЫ ЖЕСТКОСТИ
13
в полярных координатах —
- dNi
dr
О
1 а-v.-
г (>0
(1.13)
1 dN. ду. Л’.
г д\) иг г
в цилиндрических координатах —
— О
дг
<)Ь\
dN- dN{
dz dr
Поскольку матрицы дифференцирования перемещений запи-
сываются через одни и те же функции формы и их производные,
нетрудно включить все три координатные системы в одну прог-
рамму. Производные функции формы по глобальным координа-
там легко получить. используя матрицу Якоби:
(1.15)
дх ’
aTj
(1.16)
Компоненты матрицы Якоби получаются посредством диффе-
ренцирования соотношений (1.1). Элемент объема dV в локаль-
ных координатах записывается через определитель [J] и для раз-
личных глобальных координатных систем будет равен:
в декартовых координатах —
dV = det [J] d^dx}\
в полярных координатах —
dV = г det [Л d£ dr);
ГЛ. I. РГП1ЕНИЕ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
в цилиндрических координатах —
dV == !лг det U] d£ dip
.интегрирование выражения (1.9) проводится численно по
квадратурным формулам Гаусса. При этом встас т вопрос о том,
сколько точек интегрирования необходимо использовать для обес-
печения сходимости решения к точному.
В работе [103] ^формулирована теорема, которая гласит: если
интерполирующие функции являются полным полиномом степени
р, то при решении краевых задач п задач о собственных значени-
ях в любой криволинейной (пзопараметри ческой) системе коорди-
нат полная скорость сходимости достигается в том случае, если
каждый член выражения энергии интегрируется по правилу, обес-
печивающему точное интегрирование йрлипома стспепи 2(p — w),
где т — высшии порядок производной в выражении энергии.
Экспериментальная проворна этой теоремы [ 1U4J показала, напри-
мер, что при решении задачи о колебаниях упругого диска с мс-
пользовапнем квадратичных элементов полная скорость сходимо-
сти прь ннтегрпрованпп по правилу Гаусса 2X2 достигается уже
прп двух элементах в радиальном направлении.
Использование интегрирования 2X2 для квадратичные эле-
ментов удобно также потому, что, как показано в [81], самые точ-
ные значения напряжений получаются при их вычислении в точ-
ках двучленного интегрирования ио методу Гаусса. Наилучшле
значения напряжений для линейного элемента соответствуют его
геометрическому центру.
§ 5. Приведение реальных и фиктивных нагрузок к узлам
Пусть рассматриваемый элемент нагружен объемными силами
повер> постными усилиями
а также претерпел начальную деформацию вследствие термичес-
кого воздействий
{ег)^[аТ <хГ 0].
Запишем перемещение произвольной точки элемента в виде
{/} = {u p} = [/v]{q}, (L17)
где
ГА\ 0 -V2 0
= 0 Л’ 0 N ’
-г * *=
§ 6. ВЫРОЖДЕНИЕ ЧЕТЫРЕХУГОЛЬНЫХ ЭЛЕМЕНТОВ
15
Тогта по принципу возможны v перемещений
{&7)т ((Яу) R I Rs} + Р»)) = У {ф l*M dV +
+ J Щ}т iPsl dS + f '6ejr ID] (er) dV.
s
V
Здесь {Z?v} n {Rs}—век'йры приведенных к узлам объемных и
поверх постных сил, {hl — фиктивная у зловая температурная на-
грузка (термический вектор). Используя формулы (1.17), (1.7),
получаем следующие выражения:
(1.18)
г
[«sl= f [АТ {Л< dS, (l.l’.'Y
s
[Л) = I [Bp [D] (er) dV. (1.20)
v
В случае термоспловой нагрузки напряжения должны подсчиты-
ваться с учетом температурных деформаций
|а) = [2>] ((e) - }ег)). 0.21)
Очевидно, что при интегрировании выражений (1.18) —(1.20) до-
статочно использовать формулы той же точности, что и при вы-
числении матрицы жесткости.
§ 6. Вырождение четырехугольных
элементов в треугольные
При построении сеток конечных элементов часто бывает вы-
годно среди четырехугольных элементов использовать несколько
। реугольпых. Для Вычисления матриц жесткости треугольных
элементов можно применить специальную подпрограмму. Однако
Рис. 3. Вырождение квадратичного элемента в треугольны!ь
16
ГЛ. I. РЕШЕНИЕ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
при программировании это неудобно. Другим приемом, достаточ-
но простым в реализации, может служить стягивапио одной пз
сторон четырехугольника в точку, т. о. вырождение четырех-
угольных элементов в треугольные. При этом для линейного
элемента не требуется делать никаких изменений, нужно лишь
присвоить двум узлам одинаковый помер.
При вырождении квадратичного элемента должны быть изме-
нены функции формы (1.4) —(1.5). Пусть в точку стягивается
сторона 5-6-7 элемента, показанного на рис. 3. Тогда должны
быть модифицированы (см. [136]) функции М, 2Уз, Л^з, которые
для вырожденного элемента помечены звездочкой:
Л\* = Л\ 4- ДЛ',
Л'* = - 2A2V,
N* = N3 + AxV,
X = N6 + Ne + N-,
(1-22)
где A2V = (1 — s2)(l — t]2)/8, Отметим, что по-прежнему, как и для
невырожденного элемента, У Лг{ = 1, что является необходимым
условием для отображения постояппой деформации.
§ 7. Сборка и решение системы уравнений равновесия
Имея матрицы жесткости [fcj отдельных элементов, можно
получить глобальную матрицу жесткости рассматриваемой обла-
сти [Я] следующим образом [3]:
= (1-23)
Здесь [а,] — матрица связи номеров степеней свободы при гло-
бальной (для всей области) и локальной (для данного элемента)
нумерациях.
Матрицы [а<] малозаполпенные, поэтому операция (1.23) вы-
полняется с помощью непосредственного суммирования.
В работе [124] эта методика названа методом кодовых чисел;
в работе [501 опа же называется суммированием с помощью мат-
рицы индексов. Эта методика состоит в том, что при реализации
(1.23) неявно выполняются операции только с ненулевыми элемен-
тами [а,-]. Суммирование вектора правых частей производится
аналогичным образом. После сборки решение задачи сводится к
определению неизвестных перемещений из системы уравнений
равновесия
[К1Ш = {П, (1.24)
где {б) — вектор перемещений, {F} — вектор нагрузки, в котором
§ 8. ПРИМЕРЫ РАСЧЕТА С КВАДРАТИЧНЫМИ ЭЛЕМЕНТАМИ
17
просуммированы внешние механические нагрузки, приведенные
к узлам, п фиктивные нагрузки от температуры. Решение систе-
мы уравнений (в общем случае высокого порядка) сильно упро-
щается тем, что матрица системы положительно определена, сим-
метрична и имеет ленточную структуру.
§ 8. Методические примеры
с использованием квадратичных элементов
Поскольку свойства простейших элементов достаточно хорошо
известны, здесь мы приведем несколько примеров, иллюстриру-
ющих точность квадратичных элементов, а также сравним резуль-
таты при использовании различных правил интегрирования. Все
расчеты этой главы проведены по разработанной вами программе
NISTEL.
Пример 1. Полый цилиндр под внутренним давлением.
С учетом циклической симметрии для нахождения напряжений в
полом цилиндре, подверженном действию равномерного давления
р па внутренней поверхности, применялись три квадратичных
элемента в полярных координатах (рис. 4). Отношение внутрен-
него и внешнего радиусов цилиндра равно а/Ь == 0,5. Вычислитель-
ная программа позволяет применение дву- пли трехчленного
правила интегрирования в гауссовых квадратурах для вычисле-
ния матриц жесткости. Сравнение перемещений, полученных при
использовании правил интегриро-
вания 2X2 и 3X3, показывает,
что они отличаются менее чем на
о,03%. В табл. 1 п 2 напряжения
но МКЭ в точках интегрирования
матриц жесткости сравниваются
с теоретическим решением [G61,
им же приведена относительная
♦ нипока S в процентах. Анализ
результатов указывает па выгод-
ное । ь применения двучленного
интегрирования, поскольку в этом
случае вдвое снижается время
выполнения операции численного
интегрирования и получаются бо-
лт точные значения напряжений.
Рис. 4. Рептрпио задачи о цилинд-
ре под втгутренппм давлением с
использованием трех квадратич-
ных элементов в полярных коор-
динатах.
высокой степенью точности.
Перемещения для различных пра-
вил интегрирования совпадают с
Пример 2. Вращающийся круглый диск. Идеализированная
гягмд решения осесимметричной задачи расчета напряжений в
шиком круглом диске радиуса b с круговым отверстием в центре
г м. Морозов, Г. П. Никишков
18
ГЛ. I. РЕШЕНИЕ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
представлена на рис. 5. Диск изготовлен из материала с плот-
ностью р и вращается с угловой скоростью в>. При расчете приня-
то, что alb — 0,5, р(«>2а2 = 1, коэффициент Пуассона v = 0,3. Ре-
зультаты счета но МКЭ и теоретическое решение показаны на
рис. 6. Несмотря на то, что использовались всего два квадратич-
ных элемента, максимальная ошибка в напряжении оР составила
Таблица I
Напряжения в полом цплппдрс под внутренним давлением
при интегрировании 2X2
г Ъ °г/р V1’
Теория МКЭ б, % Теория МКЭ б. %
0.5352 —0.8303 —0,8316 +0,2 1,497 1,498 +0.06
0.6315 —0,5027 —0,50! 7 -0.2 1.169 1,1(18 —о,| и?»
0.7019 —0,3433 —0.3436 +0,1 1,010 1,010 0,00
0,7981 —0,1900 —0,1897 —0.2 0.8566 0,8564 —0.02
0.8688 —0.1О85 —0,1(187 +0.2 0.7752 0.7753 +0,01
0.9648 —0,0248 —0,0247 —0.4 0.6914 0,6913 —0,01
4,1%, в напряжении ов — около 0,2%• В этом п остальных приме-
рах данной главы использовалось правило интегрирования 2X2.
Пример 3. Сферический сосуд под действием внутреннего
равномерного давления» Сферический сосуд с внутренним радпу-
Т а и л и ц а 2
Папря;кения в полом цилппдре под внутренним давлением
при интегрировании 3X3
г ь <тг/р °н/р
ТеОрИЯ МКЭ б, % Теория МКЭ %
0.5168 —0,9052 —0.8723 •—3.6 1,572 1.587 +1.0
0.5833 —0.64(53 —0,6816 +5,5 1.313 1.298 — 1,1
0.0479 —0.4608 —0,4356 —И.О 1.127 1.137 +0,9
0,6855 —0.3761 —11.3(545 —3.1 1,048 1.048 +0.5
0,7500 —0,2593 —0.2721 +4.9 0.9259 0,9203 —0.6
0.8146 —0,1691 —0.1597 —5,5 0.8357 0,8393 +0.4
0,8521 —0,1257 —0.1207 —4.0 0.7924 0.7946 +0.3
0,9167 —0.0634 —0.0691 +9.1 0.7300 0.7275 —0,3
0,9812 —0.0129 —0.0086 —33,0 0,6796 0,6812 +0,2
сом а и наружным b нагружен внутренним давлением р (рис. 7).
Отношение а!Ъ = 0,5, для расчета четверть сечения разбпта ла
сетку 2X2 квадратичных осесимметричных элементов. Сравпе-
§ 8. ПРИМЕРЫ РАСЧЕТА С НВАДРа/иЧНЫМП ЭЛЕМЕНТ АМН
19
ипо теоретических [G6] п рассчптаппых по МКЭ зпачсппй напря-
жений в сечениях 1 и 2 дапо па рис. 8. Относптолъпая ошибка оп-
ределения пан ряжения or 1 — 2%,
лишь в одной пз точек ин-
тегрирования она составила 0,0%.
Ошибка в определении ой заклю-
чена в пределах от 0,5 до 3,0%.
Рис. 5. Идеализация задачи о вращаю-
щемся круглом диске с центральным
круговым отверстием.
Рис. 0. Напряжения по вращаю-
щем с л диске: 1—МКЭ, 2— точ-
ное решение.
Пример 4. Тонкий круглый диск с концентрическим отвер-
стием под действием стационарного теплового потока. Проверка
правильности работы программы
в случае термического нагруже-
ния заключалась в вычислении
напряжений в топком диске ради-
Рпс. 7. Сферический сосуд под
дрГгствлем внутреннего давления.
Крестиками показаны точки ин-
тегрирования.
Рис. 8. Напряжения в сфериче-
ском сосуде: 1 — МКЭ, сеч. 7; 2—
МКЭ, сеч. 2\ о—точное решение.
уса b с концентрическим отверстием радиуса а и теплоизолиро-
ванными боковыми поверхностями, который подвержен действию
• лацпоиариого теплового потока. Если температура на внутренней
»»
*
20
ГЛ. I. РЕШЕНИЕ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
поверхности диска (г = а) равна Д7\ а на внешней поверхности
(г == 6) пулевая, то распределение температуры по радиусу дается
1’ис. 9. Напряжения в топком диске
г коттпоптрпческпм отверстием от
действия стационарного теплового
иотока: 1 — МКЭ, 2 — точное реше-
ние.
езтельпая ошибка для сгг равна
чину порядка 1%.
известным выражением
т (г) = -.-%. In —.
4 7 In (b/a) г
Принято, что а/Ъ = 0,5, коэф-
фициент Пуассона v = 0,3. Рас-
четная схема полностью анало-
гична показанной па рис. 4, за
исключением того, что вместо
трех использовались два квад-
ратичных элемента в радиаль-
ном направлении. На рис. 9 по-
казаны расчетные п теоретиче-
ские [261 значения напряжении,
которые масштабированы вели-
чиной СаАГ, где G — модуль
сдвига, а — коэффициент тем-
пературного расширения. Срав-
нение расчета по МКЭ с теоре-
тическими зависимостями по-
казало, что максимальная отно-
4%, ошибка для о* имеет велп-
§ 9. Расчет
напряжении в роторе среднего давления
турбины К-300-240 ЛМЗ
В качестве примера, иллюстрирующего возможности метода
л программы, рассмотрим решение осесимметричной задачи расче-
та напряжении в роторе среднего давления турбины К-300-240
ЛМЗ1) возникающих под действием температурного поля и цент-
робежных сил. Сетка конечных элементов показана па рис. 10.
Она содержит 153 квадратичных элемента п приводит к решению
системы из 10G0 уравнении с шириной симметричной части лепты
70. В качестве внешнего накопителя использовалась магнитная
лепта.
Возможности программы позволили практически точно опи-
сать поверхность концентратора (при дисковой канавки), а соотно-
шение размеров конечных элементов в этой зоне с характерными
!) Аверкина П. В., Федорова Л. В. Исследование теплового
и напряженного состояния ротора ЦСД и возможности повышения манев-
ренности турбин типа К-300-240.— В сб.: Исследование и разработка энер-
гетического оборудования.—Труды ЦКТИ, 1976, вып. 138, с. 9—14.
§ 9. РАСЧЕТ НАПРЯЖЕНИИ В РОТОРЕ
21
размерами концентратора пе превышало величины 0,2 0,07. Та-
кое соотношение обеспечивает достоверный результат даже при
простейших типах конечных элементов.
Рпс. 10. Разбиение ротора турбины на квадратичные элементы. Число эле-
ментов 153, число степеней свободы 10G0.
Рис. 11. Распределение температуры по радиусу и напряжения, возникаю-
щие в срединном сечении диска Л-Л: 7 — результаты, получоппыс* по про-
грамме NISTEL; 2 — решение по программе ВТИ.
Па рис. И показано сравнение температурных напряжений
в срединном ссчсппи диска турбины, полученных по программе
NISTEL, с известными нз работы [49]. Характер изменения тем-
пературных напряжений в зоне придпековой тепловой канавки,
ГЛ Т. РЕШЕНИЕ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
а также напряжений, вызванных воздействием центробежных сил
при скорости вращения ротора 3000 об/мин, представлен на
рис. 12.
Результаты расчета показали, что максимум температурных
напряжений возникает в зонах перехода от цилиндрической по-
верхности вала к поверхностям галтелей диска и диафрагменного
Рис. 12. Распределение папряжеппй в зоне при дисковой тепловой капавкп:
Д 2 — осевые аг и эквивалентные (по Мизесу) температурные напряжения;
и, 4 — окружные оТ0Сс и радиальные ОуСс напряжения от центробежных
сил; 5, 6 — aj}6c п о’хбс в сечении В-В.
уплотнения. Максимум напряжений, вызванных действием цент-
робежных сил, возникает под углом около 75° от точки сопряже-
ния придпековой галтели с валом. В зоне максимума температур-
ных напряжений эффект напряжений от центробежных сил прак-
тически пренебрежимо мал. В зоне концентрации ообс и о>бс эф-
фект температурных напряжении весьма существен. Высокая кон-
центрация осевой составляющей температурных напряжений и
радиального напряжения от центробежных сил показывает, что
зона придпековой тепловой канавки является весьма паи ряженной.
ГЛАВА IT
РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ
РАЗРУШЕНИИ С ПОМОЩЬЮ МКЭ
§ 10. Введение
Линейная механика разрушения изучает состояние тел с тре-
щинами в предположении, что материал сохраняет свойство ли-
нейной упругости вплоть до разрушения во всем объеме тела, за
исключением, может быть, небольшой окрестности вершины тре-
щины. Наблюдения показывают, что практически во всех конст-
рукциях существуют начальные трещины. Поэтому для практики
важным является вопрос, приведет ли к разрушению (или даль-
нейшему росту трещины) присутствие трещппоиодобпого дефекта
такого размера, что он надежно обнаруживается неразрушающи-
ми средствами контроля после изготовления пли в процессе экс-
плуатации изделия.
Первая задача о критическом состоянии тела с трощппой
была решена А. А. Гриффитсом [105] с позиций общего энергети-
ческого балапса. Затем Дж. И. Снеддон [151] нашел распределе-
ние напряжений у вершины трещины в упругом теле. Основыва-
ясь па его результатах, Дж. Г. Ирвин [122] предложил в качестве
критических величин использовать параметры системы урав-
нений пз решения Снеддона. Эти параметры были названы коэф-
фициентами интенсивности пап ряжений. Силовой критерий ло-
кального разрушения Ирвина состоит в сравнении рассчитанных
значений коэффициентов интенсивности напряжений с их крити-
ческими значениями, которые могут быть определены из экспе-
римента. Одновременно Ирвнп показал эквивалентность предло-
женного им силового критерия п энергетического подхода Гриф-
фитса.
Следующим крупным достижением механики разрушения
явилась концепция квазнхрупкого разрушения, впервые сформу-
лирования Дж. Р. Ирвином [121] и Е. О. Орованом [137].
Эта концепция состоит в том, что удельная поверхностная
энергия твердого тела заменяется работой пластической дефор-
мации в малой окрестности вершины трещины. Эту концепцию
можно сформулировать следующим образом — величина необра-
тимой работы, затраченной па образование единицы площади по-
верхности тела при развитии трещины, является постоянной ма-
териала, не зависящей от нагрузок, формы и размеров тела (см.,
24 ГЛ. И РЕШЕНИЕ ЗАДАЧ ЛППЕЙНОП МЕХ ШИКИ РАЗРУШЕНИЯ
например, [71]). Большое практическое значение концепции ква-
зихрупкого разрушения обусловлено тем, что она позволяет при-
менять все достижения механики хрупкого разрушения и для ре-
альных металлов в тех случаях, когда пластическая область име-
ет небольшие размеры и перемещается вместо с концом трещины.
Дальнейшее развитие механика разрушения получила в тру-
дах зарубежных исследователей И. Лариса, Дж. Cir, А. А. Уэл-
лса, Дж. Сроуад; У. Ф- Брауна, Ф. Макклпятока, Г. Лпбовица,
Дж. Райса, Ф. Эрдогана и советских ученых Л. И. Седова 581,
В. 13. Новожилова, Г. 1L Черепанова [711, М. Я. Леонова [24],
В. В. Панасюка ИЗ), В. 3. Партона [46, 47] и др. Очерк разви-
тия этой науки содержится в обзорах Д. Д. Ивлева [18] и
В. 3. [артона и Г. II. Черепанова [481.
В случае симметричной деформации берегов трещины (нор-
мальны! отрыв) расчет на хрупкую прочность сводится к опре-
делению единств ‘иного параметра и сравнению его с критической
величиной. Данная глава посвящена разработке и реализации ме-
тодов определения коэффициента интенсивности напряжении пер-
вого рода при произвольном термосиловом нагружении двумер-
ных тел с помощью МКЭ.
§ 11. Моделирование сингулярного характера распределения
напри келпи и деформации в окрестности вершины трещины
Из Теоретических решений известно, что напряжения it де-
формации в непосредственной близости от вершины острой тре-
щины пропорциональны К Jr, где К — коэффициент интенсив-
пости напряжений, г — расстояние дайной точки от врршппы.
Очевидно, что при определения коэффициентов интенсивности
напряжений с помощью МКЭ результат будет том точнее, чем
лучше будет смоделировало поле напряжений п деформации в ок-
рестности вершины трещины. Поскольку обычные конечные эле-
менты строят па основе представления поля перемещений с по-
мощью полинома с целыми степенями, то такое моделирование
сильно затрудняется.
Для преодоления этого затруднения многие авторы применя-
ли сильное ш ущелие сетки элементов у вершины трещины [78,90,
159]. Такой прием приводит к необходимости решения громозд-
ки* систем лилейных уравнений, чго значительно увеличивает
времд счета, а зачастую и количество х^сходных данных, если не
имен, в своем распоряжении подходящей программы автомати-
ческого построений сетки.
Избежать таких громоздких вычислении позволяет введение
в сетку одного или нескольких спецпальных элементов, модели-
рутощих сингулярность напряжений. Сиеппальпымп эти элемен-
§ 11. МОДЕ ЛИРОВАНИЕ СИНГУЛЯРНОСТИ
25
ты называются потому, что при вычислен и I матрицы жесткости
в ппх задаются отличные от обычных функции перемещений, ко-
торые содержат член, пропорциональный 1 S’. В этом направлении
многими исследователями пыл проделан значительный объем ра-
боты. Было предложено большое количество различных видов ко-
не тых элементов (например, Г§6, 1371). Типичными недостатка-
мп этих элементов является либо несовместность с обычными
а)
Рис. 13. Сдвиг узлов па четверть длины стороны для модплттроваппя сингу-
лярности 11аиряи;опий в вершине трещины: а) квадратичный четырехуголь-
ный элемент, б) квадратичный вырожденным элемент.
элементами, либо неспособность отображать перемещение тела
как целого. Неудобно также то, что для вычисления матриц
жесткости таких элементов необходимо иметь отдельную под-
жрогрлмму.
В работах [82, 112] было показано, что если промежуточный
узел изопарамстрпческого квадратичного элемента поместить,
сдвинув его на четверть длины стороны по направлению к вер-
шине трещины, то распределение перемещений вдоль этой сто-
роны дается выражением
1г + С3г, (2.1)
где г — координата, отсчитываемая от вершины трещины, Cj, 6’2,
Сз — независимые константы. Очевидно, что такая функция пере-
мещений правильно моделирует поле в окрестности вершины.
Для моделирования сингулярного характера распределения на-
пряжений у вершины трещины в области, занимаемой данным
элементом, необходимо сдвинуть про межуточные узлы па сторо-
нах, примыкающих к вершине (рис. 13). При этом в вершине
трещины определитель матрицы Якоби (1.16) становится равным
нулю. Однако, поскольку при интегрировании обращение этой
матрицы производится в точках внутри элемента, то это позво-
ляет не вносить никаких изменений в алгоритм. В работе [82]
также отмечено, что вырожденные в треугольник квадратичные
элементы со сдвинутыми узлами (рлс. 13, б) дают лучшие резуль-
таты, чем такие же четырехугольные элементы.
26
ГЛ II РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИИ
Сконструированные таким образом сингулярные элементы об-
ладают следующими положительными свойствами: они полностью
совместны с обычными квадратичными элементами, отражают
смещение тела как целого, для них остаются справедливыми тео-
ремы о сходимости решения к точному для обычных элементов,
для вычисления матриц жесткости сингулярных элементов не тре-
буется каких-либо специальных подпрограмм.
§ 12. Методы определения коэффициента интенсивности
напряжений 1 рода при термосиловом нагружении
Определен пр коэффициента пнтепсивпостп напряжений Ki
является сложной математической задачей. Применение анали-
тических методов ограничено частными случаями и зачастую весь-
ма трудоемко. Поэтому для практических задач этп методы обыч-
но не применяются. Достаточно простой метод расчета тре-
бующий знания распределения напряжений только в одном сече-
нии в теле без трещины, предложен в работах [31, 46]. Недостат-
ком метода является то, что, хотя во многих случаях он дает
приемлемые значения Аг, тем по мепсо в общем невозможно
предсказать ошибку вычисления.
На практике для задач со сложной геометрией и условиями
нагружения чаще всего применяется различные численные мето-
ды, среди которых определенные преимущества перед другими
имеет метод конечных элементов в силу некоторых своих особен-
ностей, а также хорошо развито!? теории метода. Применению МКЭ
для решения упругих симметричных задач о трещинах посвящено
значительное число публикаций (например, [78, 82, 80, 90, 109,
112, 138, 142, 157, 1591). Однако почти везде рассматриваются те-
ла под действием поверхностных нагрузок*. Большинство же эле-
ментов современных энергетических установок испытывает зна-
чительные температурные градиенты: Поэтому актуальным явля-
ется вопрос учета термических напряжений при расчете изделий
па хрупкую прочность. Рассмотрим различные методы вычисле-
ния коэффициента интенсивности напряжений [36], производя,
где нужно, обобщение на случай действия температуры.
12.1, Прямые методы вычисления К[. Если на тело действуют
только поверхностные нагрузки и заданные перемещения, то
распределение напряжений Оц п перемещений Ut в малой окрест-
ности вершины трещины подчиняется соотношениям
Ki
2G
(9
у у
(2-3)
§ 12. КОЭФФИЦИЕНТ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ I РОДА
27
Здесь г, 0 — полярные координаты с началом в вершине трещины,
расположенной вдоль отрицательной части оси гг. G — модуль
сдвига. Тригонометрические функции /,7 и Fi ;\:ih трещин нор-
мального отрыва равны
, О Л . О . 30 \
Jx = COS — 1 — sin — sin — ,
V «-• *a I
где x == 3—4v для плоской деформации и х = (3— v)/(l+v) для
обобщрппого плоского напряженного состояния.
Дж. Си [59] показал, что формулы (2.2) остаются справедли-
выми и в случае термосилового нагружения. Получим прибли-
женное выражение для перемещений в окрестности вершины с
учетом температуры. Для этого запишем закри Гука для точки
с температурой Т вблизи вершины трещины, используя выраже-
ния для напряжений (2.2) и предполагая, например, что соблю-
даются условия плоской деформации:
ди К,
« (1 + v) Т = —|(1 - v’-) /х - v(1 + v) /J,
(fx Л у 2лг
Известно, что в отсутствие температурной нагрузки (Т = 0) ре-
шение этой системы имеет вид (2.3). Простой подстановкой про-
веряется, что если считать температуру постоянной в окрестно-
сти вершины, то решениями системы (2.4) будут функции
и‘=Ф- +а <i+v)Тх"
(2-5)
где Т\~х, Х2=^у — декартовы координаты с началом в вершине
трещины. Для плоского напряженного состояния множитель
(1 + v) в формулах (2.5) следует опустить. Эти соотношения по-
казывают, что для вычисления по перемещепшо их при
28
ГЛ. II. РЕШЕНИЕ ЗАДАЧ ЛИНЕПНОИ МЕХАНИКИ РАЗРУШЕНИЯ
О = л/2 и но иу при 0 = л можно использовать формулы (2.3),
поскольку в этом случае поправочный член равен нулю.
Для нахождения коэффициента интенсивности напряжении с
использованием формул (2.1), (2.4) следует достаточно хорошо
моделировать сингулярность напряжении в вершине трещины,
что становится возможным при окружении вершины квадратич-
ными элементами со сдвинутыми промежуточными узлами. Оче-
видно, что значения А'г, полученные по перемещениям, должны
быть точнее, чем по напряжениям, так как применение числен-
ного дифференцирования (1.7) вносит дополнительную погреш-
ность.
Соотношение (2.5) не учитывает вид функции перемещений
элемента. Более совершенная методика расчета коэффициента
иптенспвностп напряжений по перемещениям узлов квадратич-
ного элемента со сдвинутыми узлами предложена в работе [156].
Пусть rzJO), щ(А/4) и u<(D— компоненты перемещения узла в
вершине трещины, промежуточного узла, сдвинутого па четверть
длины стороны, и углового узла соответственно. Здесь L — длина
стороны, расположенной вдоль луча с началом в вершипе трещи-
ны. Тогда константы в выражении для распределения перемеще-
ний (2.1) могут быть записаны в виде
Ci = Щ (0),
= T7z 14u‘(L/4) “ Ui ~ 3u‘ (°)]’ <2G>
Cs = 4 [2“i (L) + 2«i (0) - 4u, (L/4)].
Величина C\ отражает перемещение вершины трещины, С2 —
ту часть перемещения, которая соответствует асимптотике (2.3),
Сз — постоянную деформацию и вращение тела как целого. При-
равнивая второй член (2.1) выражению (2.3) п считая щ(0) рав-
ным пулю, получаем
= (2.7)
i \
К достоинствам формулы (2.7), кроме повышеппя точности,
следует отнести возможность се применения в случае термического
воздействия.
Другой подходе улучшению точности расчета Кт по перемеще-
ниям рассмотрен в работах [93, 91]. Для бесконечного тела с тре-
щи ной длиной 2Z при равномерном растяжении распределенной
нагрузкой р0 поверхность трещины может быть описана уравне-
нием эллипса
§ 12. КОЭФФИЦИЕНТ ИНТЕНСИВНОСТИ НАПРЯЖЕНИИ I РОДА
29
где х, у — координаты с началом в вершине трещины, а отрица-
тельная часть оси х расположена вдоль трещины. Применяя
асимптотическую формулу (2.3) с учетом того, что 0 = л, имеем
ии (X, 0) = (х + 1) ) Ч - (2.9)
Это выражение совпадает с обычной асимптотикой при г<с2/.
Однако для точек, расположенных на некотором удалении от вер-
шины, применение формулы (2.9) значительно улучшает точность
результатов. Очевидно, что это особенно важно для простейших
элементов. В работе [93] описано применение п других кониче-
ских сечений для аппроксимации профиля трещины. Для учета
температурного расширения формула (2.9) должна быть модифи-
цирована добавленном последнего члена выражения (2.5).
К прямым методам относятся также такие, в которых коэф-
фициенты интенсивности напряжений и, быть может, пекоторые
другие параметры, относящиеся к вершине трещины, включают-
ся в систему уравнений равновесия тела в качестве неизвестных.
Примером такого подхода может служить метод Хилтона [ИЗ].
В нем асимптотические формулы (2.3) используются в преде-
лах окружности небольшого радиуса, описанием вокруг верши-
ны трещины, а остальная часть тела дискретизируется обычны-
ми конечными элементами. Для узлов, лежащих на окружности,
задаются граничные условия в виде (2.3), а в число неизвестных
входят коэффициенты интенсивности напряжений и величины,
характеризующие перемещение и вращение вершины трещппы.
В расчетах коэффициента интенсивности напряжений, осо-
бенно с применением прямых методов, большое влияние па
точность результатов оказывает выбор сетки элементов. Значи-
тельное число различных сеток для вычисления Л\ опробовано
в работе [107].
В указанно]”! работе даются следующие рекомендации по по-
строению сетки:
1) Размер элементов в окрестности вершины должен быть
мал по сравнению с длиной трещпны. Для простых элементов
оптимальный характерный размер таких элементов должен быть
равен 1/200 длины трещины. (Наш опыт расчетов показал, что
для квадратичных элементов это отношение может составлять
1/25.)
2) В области с характерным размером порядка длины тре-
щппы размеры элементов должны плавно возрастать.
‘ 3) Отношение длины любого элемента к его ширине пе долж-
но превышать 50.
12.2. Энергетические методы определения Kj. В энергетиче-
ских методах используется связь между производной потенци-
альной энергии тела П по длине трещины I и коэффициентом
30
ГЛ. II. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
интенсивности напряжении А\:
дП М
Е'
(2.10)
где Е' равно модулю упругости Е для плоского напряженного
состояния и Е' = Е/(1 —V2) в условиях плоской деформации.
Получим выражение для потенциальной энергии тела при
термосиловом нагружении в матричной * форме. Будем при
этом пользоваться обозначениями гл. I и выписывать все соот-
ношения для отдельного элемента, имея в виду, что суммирова-
ние скаляров или сборка векторов и матриц, относящихся к эле-
ментам, дадут нам соответствующие величины для рассматри-
ваемого тела.
Запишем выражение для потенциальной энергии в виде [1121
и=4.| Мт И- (2.11)
V
Используя соотношения (1.7), (1.21), имеем
П = 4-[er)dV +
V V
+ 4.f Ы Ы dF-ltfEP).
V
С учетом (1.9), (1.20) и того, что вектор нагрузки {F} в (1.24)
равен
И) = l«s] + (7*1, (2.12)
а вектор перемещений можно вынести за знак интеграла, получаем
П = 4 Мт W (?) - [?)г (Л + (2-13)
где введено обозначение Ео = -Е I [ег}т [Z>] [ег) dV. Псполь-
V
зул уравнение равновесия (1.24), выражение для потенциальной
энергии можпо представить в другом виде:
п =----rl?lTIWo- (2.14)
А»
Имея два вида записи потенциальной энергии в матричной фор-
ме, можпо реализовать с помощью МКЭ вычисление KL двумя
методами.
а) Метод податливости. Для определения коэффици-
ента интенсивности напряжений продифференцируем выражение
§ (2. КОЭФФИЦИЕНТ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ I РОДА
31
(2.14) по длине трещины. Учитывая (2.10), получим
(2.15)
(2.16)
Соотношения (2.15), (2.16) позволяют определять коэффици-
ент интенсивности напряжении в самом общем случае — напри-
мер, когда нагрузки и распределение температуры зависят от дли-
ны трещины, а упругие свойства материала — от температуры.
Рис. 14. Изменение длины трещины по-
средством запрещения разного количества
степеней свободы на липни разреза при
расчете но методу податливости.
Для практических целей часто можпо считать, что прирост
длины трещины не влияет на силовые и термические нагрузки,
т. с. при неизменной сетке элементов
01
OF
dl
4гГИ)-
(2.17)
При реализации этого метода на ЭВМ проводим решение для
трещин длиной I и Z + AZ (рис. 14), применяя одну и ту же сетку.
Коэффициент определяем но приближенной формуле
(2.18)
Использование одпоп и той же сетки позволяет при дифферен-
цировании исключить систематическую ошибку и тем самым
повысить точность вычислений. Данный метод выгодно приме-
нять .в том случае, когда необходимо знать зависимость коэффи-
32
ГЛ. II. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
цпепта интенсивности напряжении в более или мепее широком
диапазоне длин трещин. Имея N решений в перемещениях для
последовательного ряда длин трещин с небольшим шагом, мо-
жем получить N — 1 значений Ki ио формуле (2.18). В этом
случае для улучшения точности можно использовать более слож-
ные правила дифференцирования, которые учитывают значения
функции в нескольких соседних точках.
Экономичная модификация метода податливости для оты-
скания зависимости Кх от длины трещины предложена в рабо-
те [11]. Пусть необходимо найти коэффициент интенсивности
для Z* = Zi, I?, ..., 1п длин трещин. Для этого следует решить
систему уравнении с п правыми частями для сетки с максималь-
ном длиной трещины Ц:
1*1 (^} = • • •> Ип} (* = I.. •*), (2.19)
где {Fj} — вектор заданных внешних поверхностных нагрузок,
{Гп) — векторы нагрузки, в каждом из которых отли-
чен от нуля лишь один компонент — единичное усилие, прило-
женное в fc-й вершило трещипы и перпендикулярное липли раз-
реза. Далее, для каждой из длин трещины lh (к = 2, ..., п) необ-
ходимо определить систему сил
h
Vj = 0 (/ = 2, к).
(2.21)
такую, чтобы
где Vj — перемещепия узлов на поверхности разреза с ажоорди-
натами, равным или большими координаты положения па оси .г
вершины трещины текущей длины 1к. Таким образом, будем
иметь систему (п — 1) линейных алгебраических уравнений.
Решая для каждой lh систему (2.21), найдем искомое поле
перемещений
h
= {71} + i Th} {7j1• (2.22)
j=i
Здесь Tw —усилия в узлах (2.21), необходимые для моделиро-
вания трещины длиной Z*.
Таким образом, решив систему уравнений с единственной
глобальной матрицей жесткости, по с п правыми частями, мы
получим поля перемещений (2.22); этп же поля перемещений
могут быть получены n-кратпым решением системы уравнений
с глобальными матрицами, соответствующими различным дли-
нам разреза. Такой прием значительно сокращает время счета
на ЭВМ. Затем для каждой пары найденных полей неремеще-
§ 12. КОЭФФИЦИЕНТ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ I РОДА
33
ний, относящихся к соседним длинам трещины, можно вычис-
лить коэффициент интенсивности по формуле (2.18).
При вычислениях ио методу податливости для того, чтобы
Д? было мало, естественно применять простые элементы. При
неизменной сетке исключается возможность использования син-
гулярных элементов.
б) Метод смещения узла в вершине трещины.
Дифференцирование соотношения (2.13) с учетом (1.24) даст
<22з>
Это выражение позволяет определить при произвольной тер-
мосиловой нагрузке п ее изменении в зависимости от длины
трещины. Оно нс содержит производной вектора перемещений,
поэтому коэффициент интенсивности напряжений определяется
по единственному решению задачи. Если можно считать, что на-
грузка и температура не являются функциями длины трещины,
то выражение (2.23) упрощается:
Е'
(2.24)
-4-мг
В этом выражении осталась производная термического вектора,
так как в процессе вычислений изменяется геометрия сетки
ментов. Для отыскания производных
сместим узел, находящийся в вершине
трещины, на малую величину AZ вдоль
липин трещпны, как показано на
рис. 15. При этом изменится геомет-
рия элементов, окружающих вершину,
и производные матриц и векторов мо-
гут быть подсчитаны по приближенной
эле-
Рпс. 15. Изменение геомет-
рии элементов при смеще-
нии узла в вершине тре-
формуле
ОД __ [ДЛ]_
. oi J “ ~дГ'~ д1
щины.
Такой прием применен в работе [109].
Другим подходом является сдвпг как целого ядра элементов вокруг
вершины [138]. Этот подход менее удобен при реализации на
ЭВМ, особенно в случае решения осесимметричных задач, когда
матрицы жесткости элементов зависят не только от разности ко-
ординат узлов, но и от расстояния от оси симметрии. В расчетах
по методу смещения узла возможно применение как обычных,
так и сингулярных элементов.
в) Использование интеграла Черепанова —
Райса. В работах Г. П. Черепанова [70] и Дж. Райса [54]
3 Е. М. Морозов, Г. П Ни к ишков
34
ГЛ. II. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
был предложен не зависящий от контура интеграл, который
можно применять для определения коэффициента интенсивности
напряжений:
— = j — СГу ds. (2.25)
Рис. 16. 7, 2— типичные контуры
для подсчета интеграла Черепа-
нова — Райса. Крестики — точки
интегрирования матриц жесткос-
ти. Кружками показал сдвш' то-
чек при вцтегрпроваттпи углом.
Здесь С — контур, который обходится против часовой стрелки
вокруг вершины трещины, лежащей вдоль отрицательной части
оси х; Э — плотность энергии деформаций; п, — компонента еди-
ничного вектора внешней нор-
мали к контуру. В наиболее об-
щей форме этот интеграл рас-
смотрен в работе Г. П. Черепа-
нова [71], где показано, что он
применим при произвольной
комбинации температурных и
поверхностных нагрузок, при
условии отсутствия потоков
тепла и внешних усилий на по-
верхности трещины.
Как известно, матрицы же-
сткости мзопара метрических
элементов интегрируются чис-
ленно по квадратурным форму-
лам Гаусса. Поскольку в интеграл Черепанова — Райса входят
члены того же порядка, что м при вычислении матриц жесткости,
то естественно выбирать контур проходящим через точки ин-
тегрирования матриц жесткости и пользоваться тем же прави-
лом интегрирования. Типичные контуры интегрирования пока-
заны па рис. 16. Если контур пересекает элемент и проходит,
например, в направлении т) = const, то интегрирование ведется
по другой локальной координате * и вклад от данного элемента
в интеграл составит
1
f [(4-[от}((е)-18т))-Ох-Й
-1
dv \
~~°хч~дг)
dy
<11
ди
dv
Входящие сюда величины производных dx/d^ и dy/d^ легко из-
влечь из матрицы Якоби (1.16), которая определяется для каж-
дой точки интегрирования при вычислении матрицы дифферен-
цирования перемещений (1.12)—(1.14).
Если контур в данном элементе содержит угловую точку, то
интегрирование проводится по лнпиям | == const, ц = const с
§ 12. КОЭФФИЦИЕНТ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ I РОДА
35
изменением пределов интегрирования, что достигается сдвигом
точек интегрирования (см. рис. 16),
Интеграл (2.25) в случае термосилового нагружения при
подсчете величины Э, так же как и в формуле (2.26), хотя и
имеет предел /<?/Е' при С 0, тем не менее не является не-
зависимым от контура [111J.
Как было отмечено И. Л. Биргером [8], для нагретого тола
понятие «потенциальная энергия» теряет смысл, поскольку пе
удовлетворяется естественное требование, чтобы результат не
зависел от порядка приложения внешних сил и нагрева.
До-ввдимому, использование интеграла Черепанова — Райса
в температурных задачах требует привлечения термодинамиче-
ской модели среды [17]. Для этого необходимо воспользоваться
представлением интеграла в виде [71]
J = J - оъ- ar + )"J ds- &.21)
С
Входящие сюда величины: CZq — удельпая внутренняя энергия
и qj — компоненты вектора теплового потока могут быть запи-
саны через конкретные выражения для плотности свободной
энергии и плотности энтропии; компоненты вектора теплового
потока можно определить по закону Фурье [22].
Вопросы расчета /-интеграла в присутствии произвольного
температурного поля рассмотрены в работах [40, 87, 88, 162].
В последней из них получен инвариантный вид J для условий
плоском деформации:
ди.
ds -|—
S
(2.28)
Второй член подсчитывается по площади S внутри контура С.
Нетрудно получить другое представление /*, пригодное для
плоской деформации и плоского напряженного состояния:
где J-интеграл вида (2.25). В случае подсчета Э интегрированном
по формулам (5.11) — (5.12), выражение (2.29) инвариантно от-
носительно контура и в упругопластическом случае.
Расчет инвариантного интеграла в осесимметричном случае
при использовании цилиндрических координат Z)=r, =
£з = () рассмотрен в работе 180]. Выделив из цилиндра клип с
3«
36
ГЛ. П. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОП МЕХАНИКИ РАЗРУШЕНИЯ
гранями, лежащими в плоскостях rz и наклоненными друг
к другу на небольшой угол d0, и взяв выражение интеграла для
трехмерного случая, авторы работы [80] провели интегрирова-
ние по всей поверхности тола и получили
J -Тг 4г)r ds~4j J (Э - Г° ~г) dS- (2.30)
С S
Здесь первый интеграл вычисляется по контуру, а второй по
площади, заключенной внутри этого контура. Компоненты уси-
лия, нормального к контуру, выражаются через напряжения и
компоненты единичного вектора внешней нормали:
J4 г — Г ~Н
Т z О'»^Л. г —}—
(2.31)
Формула (2.30) дает значение интеграла па единицу длины
фронта трещины глубиной I.
При вычислении интеграла по любой пз приведенных здесь
формул следует иметь в виду, что чем хуже моделируется рас-
пределение напряжений в окрестности вершппы трещины, тем
больше должна быть длина контура для достижения приемлемой
точности результатов. Возможно использование различных эле-
ментов, в том числе и сингулярных.
г) Вычисление Кт с помощью интеграла закры-
тия трещины. Согласно Дж. Р. Ирвину [120] интенсивность
освобождения упругой энергии G можпо рассчитать по работе
усилий cvdx на перемещениях v, необходимой для того, чтобы
превратить трещину длиной I в трещину длиной (Z — ДО:
2 Л1
G = = — lim .7^Л auv dx. (2.32)
о
При вычислениях с помощью МКЭ удобно аппроксимировать
формулу (2.32) выражением
G = lim , (2.33)
Д1-0 Ai
где — реакция в узле, расположенном в вершине трещины
длины I — ДZ; Vl-ы — перемещение того же узла прп длине трещины
I. Реакция Fi-ы может быть определена по формулам (2.19)—
(2.20), для чего необходимо решить систему уравнений равно-
весия с двумя правыми частями 1).
’) Имеется в виду решение двух систем уравнений, отличающихся пра-
выми частями. С вычислительной точки зрения решение системы с двумя
правыми частями требует гораздо меньше машинного времени сравнитель-
но с решением двух систем уравнений.
§ 13. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ИНТЕНСИВНОСТИ 37
Авторы работы [1471 предложили модификацию метода за-
крытия трещины, упрощающую п сокращающую вычисления.
Если вокруг вершины трещины расположить элементы одина-
кового размера и определить поле перемещении для трещины
длиной Z, то
Fi.
(2.34)
Здесь предполагается, что если Af < I, то изменением реакции,
возникающей в вершине трещины при начальном развитии ее,
можно пренебречь. Тогда формулу (2.33) можпо переписать в
виде
G =
AZ-» О
(2.35)
Из-за использования соотношения (2.32) величина Ы в мо-
дифицированном методе закрытия трещины должна быть мень-
ше, чем в методах, описанных в пункте а) данного параграфа.
§ 13. Методпческпе примеры определения коэффициента
интенсивности напряжений
В примерах, которые будут приведены в этом параграфе,
использованы как линейные, так* п квадратичные изопарамет-
рические элементы. Линейный элемент является базовым для
разработанной нами программы CRACK4, в которой для вы-
числения коэффициента интенсивности напряжений применяет-
ся только метод податливости. Эта программа ориентирована на
решение задач несложной геометрии и имеет подпрограмму ав-
томатического построеппя сетки элементов. Система уравнений
равновесия формируется один раз — для трещины максималь-
ной длины и записывается па магнитный барабан. В дальней-
шем из нее посредством запрещения соответствующего числа
перемещений узлов на поверхности разреза получают системы
уравнений равповеспя для трещин меньшей длины. Основное
ограничение по размеру задачи состоит в том, что система урав-
нений должна размещаться в оперативной памяти.
Квадратичный элемент использован в программе NISTEM,
которая предназначена для определения коэффициента интен-
сивности напряжений у трещины единичной длины. В про-
грамме реализованы все методы вычисления Кь описанные в
§ 12, за исключением метода податливости. Предусмотрено эко-
номичное решение для нескольких нагрузок. Для хранения мат-
рицы системы уравнений равновесия, которая обрабатывается
по блокам, используются магпптпые барабан и лепта.
38
ГЛ. II. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХ АНИКИ РАЗРУШЕНИЯ
13.1. Использование линейных четырехугольных элементов.
Рассмотрим два примера определения коэффициента интенсив-
ности напряжений, один из которых относится к плоской зада-
че, а второй — к осесимметричной.
а) Полоса с краевой трещиной. Бесконечная поло-
са с краевой трещиной моделировалась пластиной с шириной В
и высотой GB (рис. 17, а). Идеали-
зация симметричной части этой
пластины конечными элементами по-
казана на рис. 18. Сетка состоит из
195 линейных элементов п имеет
448 степеней свободы. С использо-
ванием алгоритмов, описанных в [2,
1651, для ее построения потребова-
лось задать координаты только
10 точек.
При вычислениях принято, что
В = 2, внешняя равномерно распре-
Рис. 17. а) Полоса с краевой трещи-
ной, б) цилиндр с кольцевой трещи-
ной, в) пластина с симметричными
трещинами па кромках.
Рис. 18. Сетка для расчета Кт в
полосе с краевой трещиной (195
линейных элементов, 418 степеней
свободы). Для автоматического
построения сетки задавались ко-
ординаты точек 1—10.
деленная нагрузка о=1. Сравнение значений К\, полученных
с помощью МКЭ по методу податливости, с известным решением
Гросса I 15] показано па рис. 19. Относительная ошибка соста-
вила lzi% для Z = 0,05 В, около 7% для I = 0,1 В и 0,15 В\ в
остальных точках ошибка колеблется от 4,0 до 4,5 %.
б) Круглый цилппдр с кольцевой трещиной
(рис. 17, б). Для вычисления Кт у кольцевой трещины в круг-
лом стержне диаметром D и высотой 32? использовалась сетка,
§ 13 ПРИМЕРЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ИНТЕНСИВНОСТИ 39
состоящая из 240 элементов с 544 степенями свободы. Па рис. 20
показаны результаты МКЭ, полученные при D = 2 и а=1,
и значения, полученные аналитическими методами [45, 46]. От-
носительная ошибка МКЭ по сравнению с результатами
X. Ф. Бюкнера [45] составляет около 8% при относительной
глубине трещины (Z) — d)/D = 0,1, в остальных точках ошибка
Рис. 19. Зависимости от длтпты
трещипгл для полосы с краевом тре-
щиной, полученные Гроссом [45]
(сплошная линия) и МКЭ (кружки).
Рис. 20. Зависимости от глубины
кольцевой трещины для круглого
стержня, полученные аналитически-
ми методами в работах [45] (сплош-
ная линия), [46] (штрихи) и МКЭ
(кружки).
находится в пределах от 2,4 до 3,4%. По сравнению с резуль-
татами работы [46] эта ошибка еще меньше.
13 .2. Использование квадратичных элементов. Исследование
точности методов с использованием квадратичных элементов в
примерах, показанных па рис. 17, проводилось [36] па сетке лз
38 квадратичных элементов с 271 степенями свободы (рис. 21).
Размеры элементов в об-тастп вершины трощппы образуют ариф-
метическую прогрессию. Четыре вырожденных элемента, окру-
жающие вершину трещины, имеют длину катета, равную
1/25 длины трещины, и легко превращаются в сингулярные
посредством сдвига промежуточных узлов па четверть длины
стороны.
Рассмотрим несколько примеров расчета коэффициента ин-
тенсивности напряжении, показывающих эффективность исполь-
зования квадратичных элементов.
а) Прямоугольная пластина с симметричными
краевыми трещинами. На рис. 17, в показана пластина
шириной 2В, общей высотой 6Z? с двумя трещинами длиной
1 = В/2, нагруженная растягивающим напряжением о. Для дан-
40
ГЛ. II. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
пои конфигурации
образца О. Бови [10] получено решение с
ожидаемой ошибкой в 1%
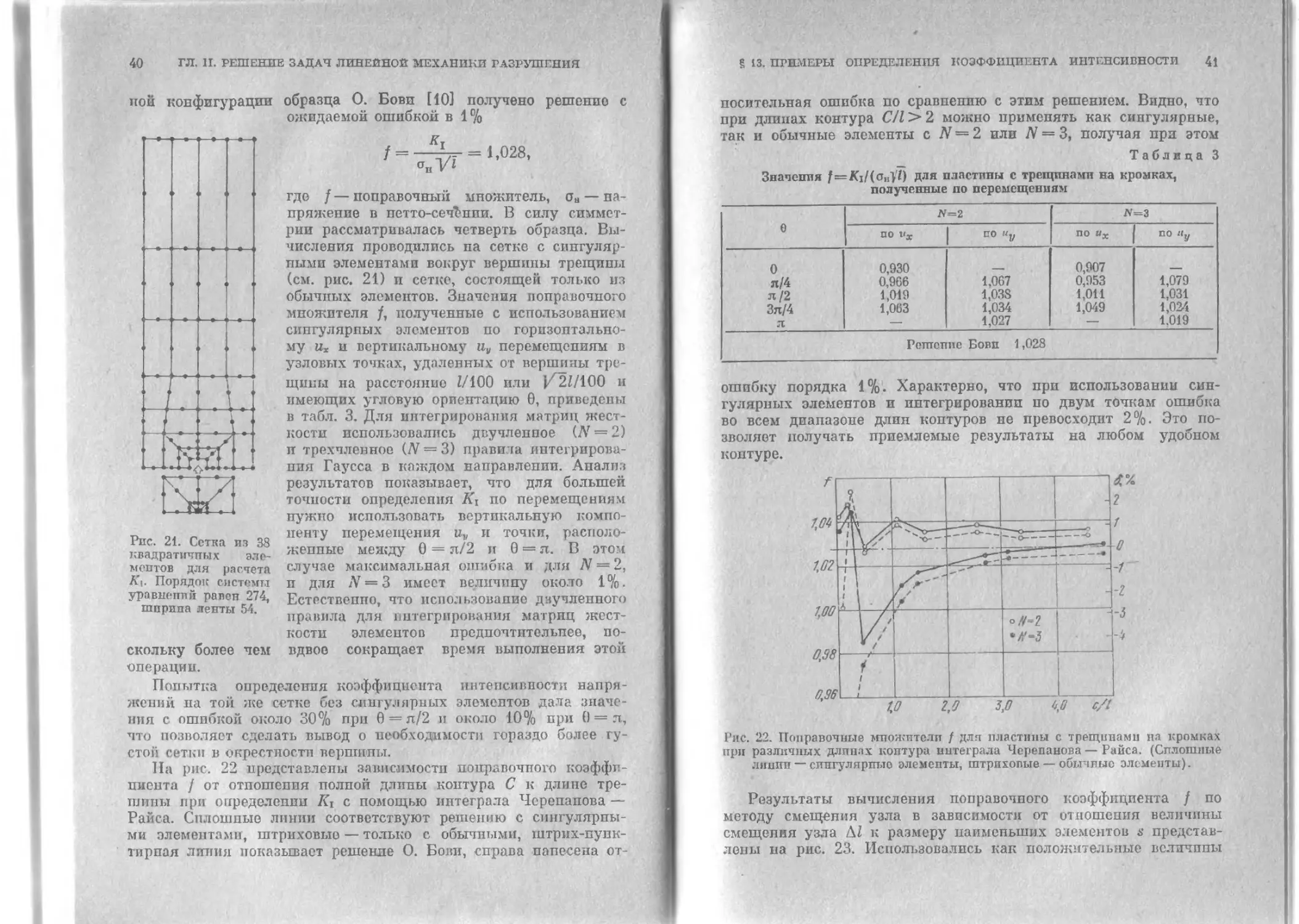
Рис. 21. Сетка из 38
квадратичных эле-
моптов для расчета
Ль Порядок* системы
уравнений равен 274,
ширина ленты 54.
—ГТ = 1.028,
стн¥г
где / — поправочный множитель, оа — на-
пряжение в петто-сечёппп. В силу симмет-
рии рассматривалась четверть образца. Вы-
числения проводились па сетке с сингуляр-
ными элементами вокруг вершины трещины
(см. рис. 21) и сетке, состоящей только пз
обычных элементов. Значения поправочного
множителя /, полученные с использованием
сингулярных элементов по горизонтально-
му их и вертикальному иу перемещениям в
узловых точках, удаленных от вершины тре-
щины на расстояние И100 пли i 2Z/100 и
имеющих угловую ориентацию 0, приведены
в табл. 3. Для интегрирования матриц жест-
кости использовались двучленное (А = 2)
и трехчленное (А = 3) правила интегрирова-
ния Гаусса в каждом направлении. Анализ
результатов показывает, что для большей
точности определения по перемещениям
нужно использовать вертикальную
центу перемещения и точки,
жеппые между 6 = л/2 и 0 = л,
случае максимальная ошибка и для А = 2,
и для А = 3 имеет величину около 1 %.
Естественно, что использование двучленного
правила для интегрирования матриц жест-
кости
вдвое
ком по-
ра сп оло-
13 этом
элементов предпочтительнее, по-
сокращает время выполнения этой
скольку более чем
операции.
Попытка определения
/копий па той же сетке без сингулярных элементов дала значе-
ния с ошибкой около 30% при 0=л/2 и около 10% при 0 = л,
что позволяет сделать вывод о необходимости гораздо более гу-
стой сетки в окрестности вершины.
Па рис. 22 представлены зависимости поправочного коэффи-
циента / от отношения полной длины контура С к длине тре-
щины при определении Ki с помощью интеграла Черепанова —
Райса. Сплошные линии соответствуют решению с сингулярны-
ми элементами, штриховые — только с обычными, штрих-пунк-
тирная линия показывает решение О. Бови, справа папесена от-
коэффициента интенсивности наиря-
g 13. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ИНТЕНСИВНОСТИ 41
посительная ошибка по сравнению с этим решением. Видно, что
при длинах контура C7Z>2 можно применять как сингулярные,
так и обычные элементы с Лг-2 или ZV = 3, получая при этом
Таблица 3
Значения f=Kj/(aHyO для пластины с трещинами на кромках,
полученные по перемещениям
е N—2 N=3
по vx ПО Uy по их | по «у
0 л/4 л/2 Зл/4 я 0,930 0,966 1,019 1,063 1.067 1,038 1,034 1,027 0,907 0,953 1.011 1,049 1,079 1,031 1,024 1.019
Гептспие Бови 1,028
ошибку порядка 1%. Характерно, что при использовании син-
гулярных элементов и интегрировании по двум точкам ошибка
во всем диапазоне длин контуров пе превосходит 2%. Это по-
зволяет получать приемлемые результаты на любом удобном
контуре.
Рис. 22. Поправочные множители / для пластины с трещинами па кромках
при различных длинах контура интеграла Черепанова — Райса. (Сплошные
линии — сингулярные элементы, штриховые — обычные элементы).
Результаты вычисления поправочного коэффициента / по
методу смещения узла в зависимости от отношения величины
смещения узла AZ к размеру наименьших элементов з представ-
лены па рис. 23. Использовались как положительные величины
42
ГЛ. II. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
Д/, дающие увеличение длины трещины, так и смещения узла
в сторону уменьшения длины трещины. В области больших сме-
щений узла имеем большую ошибку из-за нелинейности вследст-
вие искажения элементов, в области малых Д/ сказываются
ошибки округления. Для ЭВМ БЭСМ-6 с 6-бантовой структурой
Рис. 23. Зависимости поправочного мпожп-
теля / для пластины с трещинами па кром-
ках, подсчитанные по методу смещения уз-
ла, от отношения величины смещения узла
Д2 к размеру элемента $, окружающих вер-
шину трещины. (Сплошные* линии — син-
гулярные элементы, штриховые — обычные
элементы.)
слова следует использо-
вать ^0~5 1Д/А1 10~3.
Использование правила
интегрирования N = 2 да-
ет результаты выше, чем
решение с 2V = 3, пример-
но па 0,5 % • В данном слу-
чае расчет с применением
обычных элементов дал
значения /, более близкие
к решению Бови, чем
расчет с сингулярными
элементами. Однако ут-
верждать, что применение
обычных элементов пред-
почтительное, нельзя, по-
скольку ошибка имеет тот
же порядок, что и ошиб-
ка решения Бови. Все ре-
зультаты для lAZ/sl от
10~5 до 10~3 имеют ошиб-
ку не более 2%.
б) Полоса с краевой трещиной. Бесконечная полоса
моделировалась пластиной шириной В, общей высотой GB с од-
носторонним разрезом длиной I — В/2 при растяжении напря-
жением о (рис. 17, а). Для поправочного множителя F =
—Ki (о| л/)при данной длине трещины Гроссом и Бови L45J
аналитическими методами найдены зпачеппя 2,82 и 2,86.
В табл. 4 приведены значения множителя F, полученные раз-
личными методами с использованием МКЭ. Поправочные мно-
жители, подсчитанные по значению интеграла Черепанова —
Ганса, даны для длины контура C7Z = 5,2—5,6, при расчетах
методом смещения узла использовались lAZ/s| = 10~4. Макси-
мальное отклонение полученных результатов от решения Грос-
са около 2%, от решения Бови—около 3,5%• Наилучптие ре-
зультаты получены с сингулярными элементами п интегриро-
ванием по двум точкам.
в) Сплошной круглый стержень с кольцевой
трещиной. Для моделирования бесконечного стержня ис-
пользовался круглый цилиндр диаметром О, высотой 37) с тре-
щиной глубиной Z = CD — d)/2 =Z>/4, показанный на рис. 17, б.
§13 ПРИМЕРЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ИНТЕНСИВНОСТИ 43
При напряжениях в потто-сечении оп результат X. Ф. Бюкнера
[45] для поправочного множителя можно представить в виде
F = Aj/(an] nD) = 0,240. Значения F, полученные различными
методами с использованием сингулярных элементов, даны в
Таблица 4
Поправочные множители F=Ki/(or]W)
для полосы с краевой трстцппой
Метод Сингу.тарные элементы Обычные элементы
Л’=:2 А’=3 Л’==2 N=3
Перемещения, 0 = л/2 2.79 2,75 — —
Перемещения, 0=л 2,80 2,77 —
Плтеграл Черепано- ва — Райса 2,82 2,78 2,80 2,76
Смещение узла 2,85 2,82 2,81 2,76
Решение Гросса 2,82
Решение Бови 2,86
табл. 5. Применение различных правил интегрирования дает
весьма близкие результаты. Максимальная ошибка не превос-
ходит 2%.
Приведенные выше примеры позволяют сделать вывод, что
применение квадратичных пзопараметричсскпх элементов более
Таблица 5
Множители F=A'i/(anYnD) для цилиндра
с кольцевой трещиной
Метод N=2 N=3
Перемещения, 0=л/2 0,242 0,240
Перемещения, 0=л 0,239 0,238
Интеграл Черепанова — Райса 0,243 0,242
Смещение узла 0,245 0,244
Решение Бюкпера 0,240
Решение Кудрявцева и Партона 0,234
выгодно, чем использование лилейных элементов. При одном и
том же объеме вычислений квадратичные элементы дают более
точные результаты. Одпако в случаях, когда необходимо найти
зависимость коэффициента интенсивности напряжений в широ-
44
ГЛ. II. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
ком интервале длин трещин для образцов простой геометрии,
применение линейных элементов может быть более удобным.
г) Коэффициент интенсивности напряжений
у кольцевых трещин в полом цилиндре с лога-
рифмическим распределением температуры по
толщине [33]. На практике довольно часто встречается слу-
чаи, когда реальная геометрия
приводит к расчетной схеме ти-
па бесконечного полого цилппд-
ра со свободными торцами.
Приведем расчет коэффициента
интенсивности напряжений для
цилиндрической оболочки сред-
него радиуса 7?т, высотой 27?,
толщиной стенки t с внешней
кольцевой трещиной глубиной/
(рис. 24, а). Пусть па внутрен-
ней и внешней поверхностях
Рис. 25. Сепса для расчета Ki в
полом цилиндре с логарифмиче-
ским распределением температу-
ры (55 квадратичных элементов,
388 степеней свободы).
Рис. 24. Полый цплипдр, со-
держащий: а) внешнюю
трещину, б) внутреннюю
трещину.
цилиндра поддерживаются постоянные температуры, тогда для
точки с радиусом г температура Т дается выражением
где АГ — перепад температуры по толщине стенки.
Примем 7?т// = 5 и вылепим, какая высота цилиндра доста-
точна для приемлемого моделирования условия бесконечности
цилиндра. Расчеты были проведены на сетке из 55 квадратич-
§ 13. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ИНТЕНСИВНОСТИ 45
ных элементов, показанной на рис. 25. Вершина трещины ок-
ружена вырожденными сингулярными элементами. Для интег-
рирования всюду использовалось двухточечное правило Гаусса.
Для выяснения влияния высоты пплпндра па коэффициент
интенсивности напряжений значения Кт при глубине трещины
l/t = 0,5 были рассчитаны на сетке согласно рис. 25 п сетках,
Таблица 6
Безразмерные множители F для подлого цилиндра с внешней кольцевой
трещиной и логарифмическим распределением температуры
1Н Метод 0,1 0.2 0,3 0.4 1 0,5
Интеграл Черепано- ва — Райса Смещение узла Перемещение uv, 0=л Напряжение ау» 0 = = 12° 0,688 0,090 0,676 0,702 0,648 0,651 0,642 0,667 0,615 0,618 0,611 0,634 ' 0,581 0,584 0,578 0,600 0,541 0,544 0,539 0,558
получающихся из пес отбрасыванием верхних элементов. Если
значение Кг при hit = 14,5 принять за единицу, то коэффици-
енты интенсивности для h!ty равных 8,8 и 5,6, будут иметь со-
ответственно величины 1,009 и 1,070. На сетке высотой 14,5 h
был также выполнен расчет с одновременным действием темпе-
ратурном нагрузки и момента па верхнем торце, который под-
бирался из условия перпендикулярности торца и оси цилиндра.
Оказалось, что значеппе Кг в этом случае отличается от рассчи-
танного без момента всего лишь па 0,02%, что свидетельствует
о практически точном моделировании условия бесконечности при
h/t = 14,5.
При расчетах цилиндрических оболочек обычно принимается,
что краевые эффекты в районах торцов затухают на длине
2,51 Анализируя полученные результаты, можно предполо-
жить, что для приемлемого моделирования геометрии типа бес-
конечного цилиндра со свободными торцамп достаточно иметь
полувысоту не менее
= 2,5/1?^+6Z. (2.36)
Для рассматриваемого цилиндра эта величина равна Л/£ = 8,6.
В дальнейшем при вычислениях использовалась сетка с
h/t = 14,5. Для получения трещин разном длины блок из восьми
элементов, среди которых четыре вырожденных сингулярных,
перемещался вдоль нижнего ряда элементов сетки, заменяя со-
бой два квадратных элемента. Результаты расчета коэффици-
46
ГЛ II. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ РЛЗРУШЕН1 Я
ента интенсивности напряжений Кт с помощью интеграла Чере-
панова — Райса, метода смещения узла, а также по перемеще-
ниям и напряжениям приведены в табл. 6 и показаны па рис. 26
в виде безразмерных множителей
а&ТЕ ~[/л1
Принимая в качестве наиболее точных значения F, полученные
Рпс. 26. Зависимость множителя F =
= Кт/(аЕЕТул1) от относительной глуби-
ны трещины l/t, определенная с помощью:
1 — интеграла, 2— метода смещения узла
в вершине, 3 — перемещения иу при 0 = л,
4 — напряжения при 0 = 12°.
при помощи энергетиче-
ских вычислений, оцепим
точность прямых методов.
Наилучшие значения
У7-по перемещениям полу-
чаются для компоненты
иу в ближайших к верши-
не трещины узлах и углах
6 от л/2 до л. Величины
множителя F, подсчитан-
ные по перемещению ии
точки r/t = 0,03, 0 = л, от-
личаются от тех же велм-
чин, вычисленных ио энер-
гетическим методам, ме-
нее чем на 2%. Установ-
лено, что для определения
А\ по напряжениям необ-
ходимо использовать ком-
поненту Gy и ближайшие
к вершине точки интегрирования, лежащие в области малых уг-
лов 0. Безразмерные множители, полученные по напряжению
для точки r/t = 1,37 • 10~3 и 0 = 12°, завышены па 2—4% по
сравнению с энергетическими величинами.
Ожидаемая погрешность приведенных в табл. 6 результатов
по энергетическим методам составляет менее 2%, поскольку та-
кая ошибка была получена при проверке использованной сетки
элементов на решении задачи о растяжении сплошного цилинд-
ра с кольцевой трещиной.
§ 14, Коэффициент интенсивности напряжений
для ДКБ-образца при нагружении силой и моментом
Образцы типа двухконсольпой балки (рис. 27) весьма выгод-
ны для определения критических значений коэффициента ин-
тенсивности напряжений в момент старта п остановки трещи-
ны, условия которых можно многократно создавать па одном и
том же образце. Использование ДКБ-образцов затруднено от-
§ f4 КОЭФФИЦИЕНТ ИНТЕНСИВНОСТИ ДЛЯ ДКБ-ОБРАЗЦА
47
сутствием в литературе зависимостей коэффициента интенсив-
ности паиряжсппй А\ от длины трещины для образцов конеч-
ных размеров. Получим эти зависимости и оценим точность и
область применимости формул для А\, выведенных методами
сопротивления материалов [34].
Расчеты по методу податливости выполнялись па двух сет-
ках, первая пз которых состоит из 156 линейных элементов п
Рис. 27. а) Геометрия образца типа двухконсо.тьнои балки: b — La t, h —
« 1,25 /, а = 0,75 t, d = 1,5 /, to = 0,4 t; б) погружение образца моментом;
в) нагружение силой.
189 узлов, а вторая (рис. 28) пмеет 276 элементов и 329 узлов.
Построение сеток выполнялось автоматически. Время счета на
одну длину трещины для второй сетки составило около -о с
на ЭВМ БЭСМ-6.
Рис. 28. Сетка для расчета Ki в ДКБ-образцс (276 линейных элементов,
678 степеней свободы).
а) Нагружение моментом. Производя расчет для
симметрично]! части образца как для жестко заделанной балки,
которая имеет длину, равную длине трещины, и нагружена па
свободном конце моментом Л/, получаем, что коэффициент ин-
тенсивности напряжений но зависит от длины трещины п равен
кг == тчт1Л/’ 1 >h- <2-37>
hyh
48
ГЛ. II. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
Здесь принято, что образец плоский и имеет единичную толщи-
ну. Запишем решение (2.37) прп помощи безразмерного коэф-
фициента
Fm —
Кгк УЯ
2 Уза/ ’
Для теоретического решения (2.37) F* = 1 (штриховая линия
Л/ на рис. 29). Зависимости полученные методом конечных
элементов на сетках 1 и 2, показаны кривыми iM и 2М. Ока-
залось, что Ki постоянен с высокой степенью точности на уча-
стке 2h < I < с — 2Л, где I отсчитывается от силы, раскрываю-
щей трещину. На участке постоянства* па сетке 1 получено
FM — 0,959, сетка 2 дала результат FM~ 0,987. Учитывая, что
МКЭ оценивает точное решение снизу, следует считать, что за-
висимость (2.37) соблюдается весьма точно, начиная с момента,
когда вершина трещины отстоит от силы, закрывающей трещи-
ну, на 0,8Л. Нарушение постоянства Ki происходит на расстоя-
нии 2h от торца образца.
б) Нагружение силой. При нагружении ДКБ-образца
силой Р формула для Kh полученная аналогично формуле
(2.37), имеет вид
К* = 717ГР1' l^h‘
h у h
(2.38)
Вводя безразмерный коэффициент FP в виде
_ K{}/h
р~ гУзР ’
получаем, что теоретическое решение (2.38) дает зависимость
FP — l/ht которая на рис. 28 показана штриховой линией Р.
Кривые для FP, рассчитанные МКЭ па сетках 1 и 2, показаны
там же и обозначены 1Р и 2Р, Опп с высокой точностью ли-
нейны на участке l,8h<l<c — 2h и описываются соотноше-
ниями
= 0,960 (l/h + 0,610),
F2P = 0,987 (Z/A 4-0,630).
(2.39)
Сравнение этих решений с рассчитанными значениями попра-
вочного коэффициента для момента дает основание считать, что
тангенс угла наклона прямой для силы на участке линейности
весьма хорошо описывается формулой (2.38). Линейная экстра-
поляция соотношений (2.39) на теоретический угол наклона да-
ет следующую зависимость коэффициента интенсивности напря-
§ 15. КОЭФФИЦИЕНТ ИНТЕНСИВНОСТИ У КОЛЬЦЕВЫХ ТРЕЩИН
49
жепий в ДКБ-образце при нагружении его силой Р\
(2.40)
Для учета влияния боковых канавок необходимо полученные
значения Кг умножить па коэффициент, равный J Z/t0> где t
и to — брутто- и нетто-толщины образца соответственно.
§ 15. Коэффициент интенсивности напряжений
у кольцевых трещин в толстостенных трубах
мри растяжении
Рассмотрим толстостенный полый цплипцр со средним ра^
дпусом стенки Лт, толщиной стенки t с кольцевой трещиной
глубиной Z, нагруженной растягивающим напряжением о»
(рис. 24). Найдем коэффициенты интенсивности напряжений
для различных отношений RrJt. Для расчетов применялась сет-
ка линейных элементов, подобная изображенной на рпс. 18. Она
содержала 240 элементов с 544 степенями свободы. Значения
коэффициента интенсивности напряжений Kt были вычислены
с помощью метода податливости для разных длин трещин при
Rm/ty равных 2, 5, 10, 20, 50, и представлены в виде [35]
где оя — напряжение в нетто-ссчепии тела с трещиной. Зависи-
мости поправочных множителей F от относительной длины
трещины l/t для полых цилиндров разной кривизны Rmft с
внешней кольцевой трещиной представлены па рис. 30. Посколь-
ку погрешность вычислений для 7?m/Z = 0,5 и В.т/Ь — °° известна
и составляет величину 2,5—3,5% для всех’ длин трещин, кроме
1ft «0,1, то можно предполагать, что эта погрешность харак-
терна и для остальных кривых.
Коэффициент интенсивности напряжений для полого цилинд-
ра с внешней кольцевой трещиной при растяжении может быть
аппроксимирован формулой (при 2C7?m/t^50 и 0,15 ^l/t^
0,45)
Ki = 2B(Z/t)BoH I nt,
В = 0,2777 (7U/00 2300,
(2.41)
где напряжение в нетто-сеченип описывается соотношением
0 _____
Н ~ ('
(2.42)
4 Е. М. Морозов, Г. П. Никишков
50
ГЛ. II. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
Рис. 29. Безразмерные коэффициенты иитспсивпостп напряжений для на-
гружения ДКБ-образца силой FP и моментом FM. (Сплошные липли — рас*
чет МКЭ, штриховые — решение методами сопротивления материалов.)
Рис. 30. Зависимости множителей F для полых цилиндров различной кри-
визны Rm/t с внешней кольцевой трещиной.
§ 16. АНАЛИЗ ХРУПКОЙ ПРОЧНОСТИ КОРПУСА РЕАКТОРА
51
Максимальная погрешность аппроксимации составляет 6%, при-
чем она имеет место только в крайних точках при некоторых
значениях Rmft.
Вычисления, проведенные для полого цилиндра с внутрен-
ней кольцевой трещиной, показали, что в этом случае поправоч-
ные мложителп F меньше поправочных множителей для ци-
линдра с внешней трещиной приблизительно па 1,5% при
Rm/t = 2' в остальных случаях отличие составляет менее 1%
и стремится к нулю при Rm/t «>. Это позволяет рассчитывать
коэффициент интенсивности напряжений цилиндра с внутрен-
ней трещиной также по формуле (2.41) с учетом того, что на-
пряжение в нетто-сеченип теперь
Оц =
(2.43)
Таким образом, отношение для внешней трещины к та-
ковому для внутренней трещины ври одинаковых размерах ци-
линдра н равных растягивающих нагрузках приближенно равно
Ki 7Лм’1 W
(2.44)
Получеппыс формулы для коэффициентов интенсивности на-
пряжений в толстостенных трубах представляют интерес при
оценке хрупкой прочности соответствующих деталей конструкций.
§ 16. Анализ хрупкой прочности корпуса
реактора АЭС «Ловииза» при разрыве трубопроводов
Реактор АЭС «Ловииза» был спроектирован и изготовлен в
СССР ио заказу Финляндии1). Неразрушающне средства конт-
роля позволяют обнаружить дефшеты по меньше характерного
для данного метода дефектоскопии размера. Отсюда вытекает
возможность существования трещинолодобных дефектов в эле-
ментах конструкции реактора. Расчет па хрупкую прочность
должен дать гарантию, что трещины размером меньше обна-
руживаемых не должны приводить к катастрофическому разру-
шению при всех режимах эксплуатации. Наиболее опасные ус-
ловия нагружения корпуса реактора возникают в аварийных
ситуациях разрыва входных трубопроводов.
При разрыве входных трубопроводов различного сечения
срабатывает система аварийного охлаждения активной зоны и
*) Иванов А. Л. Строительство АЭС в Финляндии.— Атомная энер-
гия, 1978, т. 44, вып. 2, с. 193—194.
4*
ГЛ. IL РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
Рис. 31, Распределение температуры по толщине степки для различных мо-
§ 16. АНАЛИЗ ХРУПКОЙ ПРОЧНОСТИ КОРПУСА РЕАКТОРА
53
ментов времени т при разрывах трубопроводов ДУ-73, ДУ-90, ДУ-135, ДУ-250.
54
ГЛ. IT. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
в реактор поступает вода с температуре * 30 °C, которая течет
по части внутренней поверхности стенки, в то время как ос-
тальная поверхность остается горячей, В рассматриваемой об-
ласти корпус реактора представляет собой составной полый
цилиндр с внутренним радиусом 1823 мм и наружным радиусом
Рис. 32. Изменение по времени сум-
марного осевою напряжения ох при
разры ва х различных трубопроводов.
Ряс. 33. Температурные зависимости
модуля упругости Е и коэффициен-
та температурного расширь пин а для
основного металла (сплошная ли-
пли) и металла наплавки (штрихи).
1970 мм. Внутри находится наплавка, выполненная из стали
ОХ18Н10Т, основной металл (12Х2МФА) имеет толщину
140 мм.
Здесь мы по будем обсуждать выбор расчетной схемы, по-
скольку эго выходит за пределы настоящего исследования. Мо-
дель для анализа хрупкий прочности представляет собой полый
двухслойный цилиндр с кольцевой подповерхностной трещиной
в основном металле, одна из вершин которой находится ла гра-
нице сплавления. При разрыве трубопроводов ДУ-73, ДУ-90,
ДУ 135 и ДУ-250 по толщине корпуса возникает значительный
температурный перепад. Радиальное распределение температу-
ры для 23 расчетных моментов времени приведено на рис. 31,
а — г. На рис. 32 даны зависимости растягивающего напряже-
ния о,, которое представляет собой сумму Напряжений от пере-
пада температуры до периметру стенка корпуса* от остаточного
Давления и веса корпуса. При расчете учитывается зависимость
упругих свойств матерпалов (модуля упругости Е и коэффици-
ента температурного расширения а) от температуры; эта зави-
симость показана на рис. 33.
> !G. АНАЛИЗ ХРУПКОЙ ПРОЧНОСТИ КОРПУСА РЕАКТОРА
55
Для вычислений использовалась сетка, состоящая из 83
квадратичных элементов с о84 степенями свободы (рис. 34).
Вершина трещины окружена четырьмя сингулярными элемен-
тами с узлами, сдвинутыми па четверть длины стороны. Полу-
высота рассчитываемого цилиндра
Рис. 34. Сетка для расчета на хрупкую
прочность цилиндрической части корпуса
реактора «Лониила» (S3 квг тратичпых эле-
мента. число степеней свободы 584).
Йыорана в соответствии с
формулой (2.36) и соста-
вила 1550 мм. Время сче-
та одного варианта соста-
вило около 3 мин па ЭВМ
БЭСМ-6.
Носко тыку перазруша-
ющими средствами конт-
роля наделено обнаружи-
ваются трещиноиодобиые
дефекты с характерном
размером 5 мм, то очевид-
но, что удовлетворение
условии хрупкой прпчно-
СПМОСТ1» критического коэффп-
ниопта ичтепсплпостп папря
тнпш для осповппго металла.
сги для кодьцерой трещппы глубиной 5 мм будет представляю
собой консервативную (в запас прочности) опенку для корпуса
реактора. В соответствии с этим расчет производился для трещин
глубиной. 5 мм и 10 мм.
I» качестве критического значения коэффициента интенсив-
ности напряжений А\с использовалась кривая рис. 35, которая
приведена в зависимости от разности достигнутой температуры
и критической температуры хрупкости. Эта кривая пре(славян-
от собой огибающую, построенную по экс'перимоптальиым данным
56 ГЛ. II РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
• I0-2 мм. О
§ 16. АНАЛИЗ ХРУПКОЙ ПРОЧНОСТИ КОРПУСА РЕАКТОРА
57
различных организации. Критическая температура хрупко-
сти для вершины трещины глубиной 5 мм и 10 мм с учетом
сдвига от облучения и накопления циклических повреждений
составляет соответственно 102 °C и 101 °C.
Результаты расчетов приведены па рис. 36, а — г, где пока-
заны коэффициенты Кь полученные по интегралу Черепанова —
Райса, по перемещениям и напряжениям, а также зависимости
от времени критического коэффициента интенсивности ЛК> От-
метим, что не приведенные здесь значения Ai, вычисленные по
методу смещения узла в вершине, хорошо совпадают с величи-
нами, определенными по инвариантному интегралу. Весьма
близкие значения к приведенным здесь значениям коэффициента
интенсивности по перемещению в точке г = 0,1 мм, 0 = л получают-
ся и для других ближайших точек для 6 от л/2 до л, а также при
использовании компоненты их. Ближайшие к вершине две точки
интегрирования с малыми углами 0 при использовании напря-
жения для определения Кг дают результаты выше и ниже
значений по интегралу, а их усредненное значение хорошо сов-
ладает со значением, полученным методом перемещений. Хоро-
шее совпадение коэффициентов Аь полученных качественно раз*
ными методами, позволяет надеяться, что результаты достоверны.
Анализируя произведенный расчет, можно заключить, что
эксплуатация корпуса реактора безопасна с точки зрения хруп-
кого разрушения с учетом периодической проверки с помощью
неразрушающнх средств контроля. Допускается существование
подповерхностных трещин в основном металла глубиной до
10 мм. Для 10 мм трещины наиболее опасным является момент
времени 0,328 ч при разрыве трубопровода ДУ-73, когда отно-
шение Aic/A'i составляет 1,09. Расчеты (здесь не приведенные)
для трещины глубиной 15 мм показало, что в этом случае ус-
ловия хрупкой прочности не выполняются.
ГЛАВА Ш
НЕСИММЕТРИЧНЫЕ ЗАДАЧИ
ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
§ 17. Введение
До настоящего времени большая часть работ по механике*раз-
рушения была посвящена трещинам нормального отрыва (I ти-
па). В этом случае для формулировки критерия разрушения до-
статочен один параметр — коэффициент интенсивности напря-
жении I типа Ki.
Однако в практических задачах, которые могут быть сведены
к двумерным, чаще реализуется несимметричное поле напряже-
ний относительно трещины и асимптотика у вершины трещины
описывается двумя параметрами и А’п. Критерий локального
разрушения для таких задач должен ответить па два вопроса:
при каком значении нагрузки начнется развитие трещины и в
каком направлении начнет распространяться трещина. Различны-
ми исследователями (Ф. Эрдоганом, Дж. Си, Е. Иоффе, В. В. Па-
пасюком, Г. П. Черепановым) предложено несколько критериев
такого рода. Однако экспериментальных данных па сегодня не-
достаточно, чтобы решить, какой из них точнее описывает реаль-
ное поведение материалов. Поскольку аналитические решения
для несимметричного нагружения трещин получить исключитель-
но трудно, численные методы являются основным инструментом
исследования таких задач.
§ 18. Критерии локального разрушения
Рассмотрим несколько известных критериев локального раз-
рушения, которые не могут быть выражены одни через другой.
Эти критерии, помимо расчета критической нагрузки, позволяют
также определить угол начального направления роста трещин
вдоль радиуса, крове ценного из вершины трещины.
18.1. Критерий максимальных растягивающих напряжений.
Этот критерий был впервые предложен Е. Иоффе [164] для ре-
шения динамических задач и затем применен Ф. Эрдоганом и
Дж. Си [72], а также В. В. Панасюком п Л. Т. Бережницким
[43, 44] для статических двумерных задач.
Согласно этому критерию трещина начинает распространять-
ся в направлении 0q. перпендикулярном действию максимальных
§ 18. КРИТЕРИИ ЛОКАЛЬНОГО РАЗРУШЕНИЯ
59
растягивающих напряжений ое, когда величина Со па некотором
расстоянии от вершины достигнет критического значения. Для
острой трещины асимптотика По в окрестности вершины описы-
вается соотношением
/ <0)’
у 2л г
f (0) = [ АГ? (1 + cos0) — ЗКц sin 0] cos
(3.1)
Начальный угол распространения трещины Оо (рис. 37) опре-
деляется условием
<?/ (0)
<70
= 0
О=но
что приводит к уравнению для определения 0о’
Ki sin 0о + А'ц(3 соз 0 — 1) = 0.
Зиая коэффициенты интенсивности напряжений в момент стра-
гпвания трещины, можно определить 0О
. II. Мое-
Рыбка [30] предло-
18.2. Критерий максимума потока
энергии. Г. И. Черепанов 171], Л. В. Кр-
шов и Д. Д. Ивлев [141. В. II. Мос-
саковский и М. Г. Рыбка [30] предло-
жили следующий энергетический кри-
Рпс. 37. Система координат,
связанная с вершиной тре-
щины (0г,— начальный угол
распространения трсщппы).
терпи локального разрушения: трещина
начнет распространяться в направлении
максимума потока энергии в вершину
трещины, когда величина этого по-
тока достигнет критического значения.
Для несимметричных двумерных трещин вектор потока энер-
гии имеет следующие компоненты [71] (см. рис. 37):
(3.3)
Значения величин в этом выражении уже пояснялись в гл. II.
Для изотропною тела рост трещины будет происходить в направ-
лении вектора потока энергии J. Компоненты вектора потока
энергии связаны с коэффициентами интенсивности напряжений:
7 (1 + v) (1 + X) ГгЛ2 . rr2 \ г (1 "Г у) (1 + х) гл дг /о /к
jx =-----£g----(Л1 JU -------2L------АгАпДЗ. i)
где х = 3 — iv для плоской деформации и х = (3 — v)/( 1 + v)
для плоского напряженного состояния.
69
ГЛ. Ш. НЕСИММЕТРИЧНЫЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
Угол распространения трещины 0о равен
( 2КЖи \
e0 = arctg --. (3.5)
Локальное разрушение происходит при выполнении условия
18.3. Критерий минимума плотности энергии деформации.
Найдем энергию йРИ, накопленную в элементе обт>ема d.l, пока-
занного на рис. 38:
(3-7)
деформаций их асимптотпче-
Подставляя вместо напряжений и
Рпс. 38. Напряженное состоя-
ние* элемента объема в окрест-
ности вершины трещины.
скпе значения, получаем, что
окрестности вершины равна
плотность энергии деформации в
dW
dA
(3-8)
Коэффициенты квадратичной формы зависят от угла 6 и от
коэффициента Пу асе опа v:
«п = “Йг + cos ~ cos °)’
= l2cos0_(z~ 01 sin 0, (3.9)
«22= йт К* + О 0 - cos е) + (1 + cos в) (3 cos е -1)].
Дж*. Сп [149] предложил в качестве параметра разрушения
величину
dW
5 = (3.10)
которую назвал коэффициентом плотности энергии деформации.
Критерий локального разрушения состоит из двух предполо-
жений:
।
§ 19. МЕТОДЫ РАСЧЕТА ПАРАМЕТРОВ РАЗРУШЕНИЯ
61
1) трещина начинает расти в направлении минимума вели-
чины S:
dS
00
— л < 0о < л;
(311)
2) локальное разрушение происходит при достижении вели-
чиной 5 некоторого критического значения «$с.
Критическое значение коэффициента плотности энергии де-
формации SG можно выразить через вязкость разрушения:
(14-v)(x-l) L'2
с =------------Alc-
(3.12)
В общем случае нагружения параметр S можно подсчитать по
формуле
s =4"°ij(8ij —аГ8и)>
л*
(3.13)
где а — коэффициент температурного расширения, Т — темпера-
тура рассматриваемой точки, бу—символ Кронекера.
Проверка рассмотренных критериев разрушения с помощью
эксперимента обычно затруднена тем, что в образцах не удается
получить идеально острой трещины. Учет конечности радиуса
в вершине трещины сделан в работе [102].
§19. Методы расчета параметров разрушения с помощью МКЭ
В рассмотренных в предыдущем параграфе критериях локаль-
ного разрушения фигурируют различные параметры. Известно,
что асимптотика в случае несимметричных двумерных трещин
описывается коэффициентами интенсивности напряжении Кт и
Ктъ через которые выражаются введенные параметры локально-
го разрушения. Поэтому уделим здесь основное внимание опреде-
лению коэффициентов Aj и А'п. При этом будем использовать
методы, развитые в гл. II.
19.1. Прямые методы. В общем случае термомеханмческого
нагружения сингулярное поле напряжений вблизи вершины тре-
щины описывается теми же формулами, что и в случае силового
нагружения:
0у = [Kifij (0) + Яиф« (0)1.
у 2лг
(3-14)
где /у даются теми же выражениями, что и в (2.4), а (ру равны
• 9 (л । 0 30 i /о л
<р = — sm— 2 + cos — cos—тг“ ], (3.15)
Lt \ «и •— j
62
ГЛ. III. НЕСИММЕТРИЧНЫЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
. е о зо
Сру = SID — COS — COS—.
А /. . 0 . 30\
фх„ = cos— 1 — sin — sin— ,
(3.15)
Поле перемещений в окрестности вершины трещины при термо-
силовом воздействии можпо найти интегрированием поля дефор-
маций, получаемых пз (3.11) по закону Гука. Обозначим через
7’о температуру в вершине трещины, а через 71] температуру рас-
сматриваемой точки. Считая, что температура между этими точ-
ками изменяется по линейному закону, находим выражения для
перемещений щ в следующем виде:
== 3? I(°)! + (316)
Здесь G — модуль сдвига; Т7, — тригонометрические функции,
входящие в (2.5); Xi— одна пз декартовых координат; а'= а—
для плоского напряженного состояния, а' = а(1+т) — для пло-
ской деформации. Выражения для функций Ф, имеют вид
* Ф.т (6) = sin (х + 1 + 2 cos2
О/ (зл7>
Фу (6) = — cos — (х — 1 — 2 sin2 —].
Получив с помощью МКЭ значения напряжений и перемеще-
нии у вершины трещины, можно найти коэффициенты интенсив-
ности напряжений и Ап пз решения двух уравнений, состав-
ленных с использованием выражений (3.14), (3.16). Очевидно, что
для достижения приемлемых результатов выгодно использовать
сингулярные элементы (§ 11).
Расчет коэффициентов интенсивности напряжений Кт и Кп
можно выполнить также с помощью метода Хилтона С1131 и ему
подобных.
19.2, Энергетические методы. Зная компоненты вектора пото-
ка энергии Jx и Jth можпо определить коэффициенты интенсивно-
сти напряжений из решения системы уравнений (3.4). Для по-
лучения единственного решения необходимо знать знак разности
(А1 — А'ц), что требует привлечения прямых методов. Это весьма
неудобно при реализации вычислений, поэтому, вероятно, целе-
сообразнее в практических расчетах для определения критическо-
го состояния и начального угла распространения трещины опе-
рировать компонентами /х и Jy. В методических целях определе-
ние коэффициентов интенсивности напряжений вполне оправда-
ло. Рассмотрим три метода расчета параметров локального
разрушения.
§ 19. МЕТОДЫ РАСЧЕТА ПАРАМЕТРОВ РАЗРУШЕНИЯ
63
а) Метод виртуального роста трещины. Диффе-
ренцируя соотношение (2.13) пи длине трещины при произволь-
ном направлении ее развития, получим интенсивность освобож-
дения упругой энергии в направлении dl:
т ] । । т d К fi i ( i т е/”1 (j - Q.
J = = - —1?1Г[— Ш + М — >--тг- <ЗЛ8>
Задавая подрост трещины в направлении вдоль касательной в
вершине трещины к ее линии и в перпендикулярном направ-
лении получаем компоненты потока энергии Jx и Jv соответ-
ственно [1101.
Производные матрицы жесткости и вектора нагрузки вычи-
сляем как отношение разности этих величин в первоначальной и
измененной вследствие подроста трещины сетках к величине под-
роста. Суммирование производится только по элементам с изме-
нен ной геометр и ей.
б) Нен неродственное вычисление интеграла
Череп ан ива — Р а й с а. Компоненты вектора потока энергии
можно определить непосредственным интегрированием выраже-
ний (.3,3). При положительном (против часовой стрелки) обходе
контура компоненты вектора нормали к контуру равны
du dx
Пх — "Г"» ==-----Г"-
ds ’ у as
В явном виде компоненты потока энергии записываются так:
(3.19)
Эти выражения интегрируются при помощи формул типа (2.26).
Контур интегрирования, как и раныпе, выбирается проходящим
через точки интегрирования в гауссовых квадратурах. Отличие
состоит в том, что все пан ряжения, деформации п производные
в (3.19) должны относиться к системе координат, связанной с
трещиной. Такая система показала па рис. 37. В ней ось х сов-
падает с касательной к линии трещины в ее вершине. Разбиение
тела на элементы производится в системе, выбираемой из сообра-
жений удобства подготовки исходных данных, а в осесиммет-
ричном случае ориентировка осей координат фиксирована. Поэ-
тому при вычислении подынтегральных выражений нужно при-
вести перемещения, деформации и напряжения к системе коор-
динат, связанной с вершиной трещины.
G4 гл. ш. несимметричные задачи механики разрушения
в) Определение коэффициентов интенсивно-
сти с помощью интеграла закрытия трещины.
Обобщая формулу (2.32) на случай деформирования берегов
трещины по I и II типу, запишем согласно работам [120, 147]
выражения для интенсивностей освобождения упругой энергии
в ВИДО
№ 4 £
Gi = -вг = Нт — | a^v dx, (3.20)
о
К2
Си = = 1пи —j I ахуи dx, (3.21)
A/-# О -
где и, v — относительные перемещения точек берегов в направ-
лении вдоль линип трещины и в перпендикулярном направлении.
Окружая трещину одинаковыми элементами с размером Д£
и решая систему уравнений равновесия для дискретизации с тре-
щиной длиной Z, вычисляем величины и Gn по следующим
формулам:
Gi = lim A Fl (vt-м - (3-22)
Gn = lim Ti — uJLaJ. (3.23)
д/~* о
Здесь Ft и Ti — реакции в узле, находящемся в вершине трещи-
ны, в перпендикулярном и параллельном линии трещины направ-
лениях; знаки плюс и минус у компонент перемещений доказы-
вают, что они относятся к разным берегам трещины.
§ 20. Задача о растягиваемом пластине с наклонном трещиной
Проведем сравнение различных критериев разрушения и ме-
тодов расчета коэффициентов интенсивности напряжений па при-
мере решения задачи о прямоугольной пластине с наклонной тре-
щиной в поле растягивающих папряжений (рис. 39). Для беско-
нечной пластины такого вида известно теоретическое решение
________________________________ г
К\ == оу/л/sin2 В,
_ К (3.24)
Л~п = о j л/ sin р cos р,
где о напряжения на бесконечности, I — полудлина трещины,
р— угол наклона трещины к направлению о.
§ 20. ЗАДАЧА О ПЛАСТИНЕ С ПАНЛОННОЙ ТРЕЩИНОЙ
65
Квадратная пластина с отношенном длины трещины к стороне
квадрата 21/а = 0.032 моделировалась сеткой из 112 квадратич-
ных элементов с 700 степенями свободы,
которая показана на рис. 40. Размер наи-
меньшего элемента составлял 1/250 дли-
ны трещины. Сгущение сетки элементов
производилось у одной пз вершин. Изме-
нение наклона трещины достигалось де-
формпрованиехМ и вращением блока эле-
ментов, обозначенного на рпс. 40 бук-
вой Л. При расчете принято1)
(5
а=1, 2Z=10, v = 0,3.
Па рис. II приведены теоретические
* Рис. 30. Пластина с тре-
щиной длиной 2Z, пакло-
нениой под углом (3 к на-
правлению внешней на-
грузки о. Трещина начи-
нает распространяться
в направлении 0о-
и расчетные данные зависимости пачаль-
ного угла распространения трещины Оо
от ее ориентации по отношению к внеш-
ней нагрузке (3. Сравнение критериев мак-
симальных растягивающих напряжений,
минимума плотности энергии деформаций
и максимума потока энергии показывает,
что все три критерия дают близкие ре-
зультаты в интервале 50° С р 90°. Отметим, что па практике
распространение трещин происходит в большинстве случаев
именно в этом интервале.
Пз рассчитанных с помощью МКЭ значений 0о паилучшее
согласно с теорией в области больших углов р имеют величины,
Рпс. 40. Сотка для решения задачи о наклонной трещине (112 элементов,
700 степеней свободы). Для изменения ориентации трещины производилось
деформирование п вращение сетки блока Л.
полученные при помощи критерия максимального потока энер-
гии. При этом при определении компонент ппварпаптпого пнте-
*) Авторы благодарят В. II. Пшеничного за проведение расчетов по
III гл.
5 Е. М. Морозов, Г. П. Ншпипков
66 ГЛ. III. НЕСИММЕТРИЧНЫЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
града /* п Jv наблюдалась их зависимость от контура (особенно
/Д когда контур проходил в области влияния второго конца
трещины, где сингулярность моделировалась плохо. Расчеты по
/-интегралу и с помощью непосредственного отыскания макси-
мума потока энергии по методу смещения узла в вершине дали
Рис. 41. Зависимости направле-
ния распространения Оо от ори-
ентации ₽ по критериям макси-
мальных растягивающих напря-
жений (7), минимума плотности
энергии деформации (2) и макси-
мума потока энергии (5).
по критерию максимального
лы [71]
хорошее согласие в области боль-
ших р. В области малых р метод
смещения узла даст весьма слабо
выраженным максимум, поэтому
результаты, которые оказываются
выше, чем по /-интегралу, пе яв-
ляются достоверными.
Минимум плотности энергии
деформации S искался непосред-
ственно по значениям S в бли-
зка
<|и
шх к всршпне точках инте-
грирования. Хотя эти точки распо-
ложены достаточно редко (в сред-
нем с интервалом 22,5°), наличие
четко выраженного минимума по-
зволило получить неплохое согла-
сие с теорией.
Значительный разброс значе-
нии напряжений ое в окрестности
вершины трещины привел к не-
обходимости отыскивать углы Oq
растяжения с помощью форму-
0О = 2 arctg
где в качестве и А'п брались усредненные зпачеппя этих ве-
личин, определенных по напряжениям ох и оу в интервале 0 от
— л/2 до л/2.
В целом следует отметить, что существующие в настоящее
время опытные даппыс пока еще не дают возможности четко
разграничить области применения рассмотренных выше критери-
ев локального разрушения к тем пли иным классам материалов.
Сравнение коэффициентов интенсивности Кт и Кп для пла-
стины с наклонной трещиной, полученных по напряжениям о»,
ov, перемещениям н, и и энергетическими методами, с теоретиче-
скими зависимостями от угла р показано на рис. 42. По напря-
жениях! наиболее точные значения получены в ближайших к
вершине точках интегрирования, лежащих в пределах — л/2 <
С 0 < л/2. На рис. 42 приведены величины, усредненные по это-
§21. РАСПРОСТРАНЕНИЕ ТРЕЩИНЫ В ОСНОВАНИИ ПЛОТИНЫ
67
му интервалу. Коэффициенты А’т и Кц по перемещениям опре-
делены в узлах па линии трещины при 0 = ±л. При расчете
коэффициентов интенсивности напряжений энергетическими
Рис. 42. Зависимости Ад и Ац от угла наклона трещины р, полученные по
напряжениям (7), перемещениям (2) п энергетическими методами (5).
Сплошные линии — теоретическое решедпе.
методами использовались зависимости (3.4), которые, например,
для А\ > Ки дают
Расчеты» значения А\ имеют меньший разброс, чем АП. В об-
ласти больших В, т. е. для трещин, близких к трещинам нормаль-
ного отрыва, точность результатов по всем методам лучше, чем
в области малых р.
§ 21. Моделирование распространения трещины
в основании плотины
Критерии начального направления роста трещины, следую-
щие из критериев локального разрушения, позволяют рассчитать
траекторию трещины. Интересно взаимно сопоставить результаты
расчета траектории трещины как по разным методам, так гт с эк-
спериментом. Для примера возьмем задачу об отыскании траек-
тории развития трещины в основании плотины.
Гипсовая модель1) плотины (£’ = 2,3-104 кгс/см2, v = 0,22) бы-
ла жестко заделана па части границы и нагружалась с помощью
гидравлических домкратов, действие которых показано па рис. 43
') Эксперимент был проведен в лаборатории прочности МИСИ
М. Г. Зерцаловым и ТО. Я. Шипиловым.
5*
68 ГЛ. III. НЕСИММЕТРИЧНЫЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
распределенными усилиями р\ и рг- Постоянная вертикальная
нагрузка Р\ == 5,1 кгс/см2 препятствовала закритпческому росту
трещины, поэтому реализовался квазистатпчсский рост трещины
при увеличении нагрузки р%.
Область предполагаемой траектории распространения трещины
была обклеена тензодатчиками. Нагрузка в момент прохождения
Рис. 43. Схема эксперимента и траектория трещппы в модели основания
плотины.
Рис. 44. Одна из сеток для моделирования развития трещины в основании
плотины.
трещины фиксировалась по резкому увеличению сигнала тензо-
датчика. Для расчета использованы довольно редкие сетки, одна
пз которых показала па рис. \ ь Результаты расчета критических
параметров /с, Л: и начального угла распространения трещины
0о приведены в табл. 7. Для моментов прохождения конца тре-
щины через точки 1—4 получены приемлемые значения 0о. Ка-
чественно неправильный результат для точки 5 объясняется тем,
что, начиная с этой точки, происходят налегание берегов тре-
щппы друг па друга. Вместе с тем в данной постановке это об-
§ 21. РАСПРОСТРАНЕНИЕ ТРЕЩИНЫ В ОСНОВАНИИ ПЛОТИНЫ
69
стоятелъство не учитывалось, что приводит к взаимному проник-
новению берегов трещины в дискретной модели. Это было обна-
ружено с помощью анализа полей перемещений. Рассмотрение
такого поведения трещины возможно только с помощью реше-
ния контактной задачи итерационным путем, что ие входило в
задачи данного исследования.
Таблица 7
Параметры разрушения и начальный угол распространения
при росте трещины в модели основания плотины
.Чс точки •>* кгс/см" кгс/см3 “ КП' кге/гм 2 ZC’ кгс/см^ °0* град
VJcE'- кгс/см^
1 4.4 22,8 5,4 45 25 9 «и
о 4.6 25.3 4,4 50 26 2
3 5.0 29.5 5,6 62 33 2
4 5.3 36,2 6,3 73 38 —3
5 5.5 41.5 7,2 80 8
Анализ результатов показывает, что критические параметры
/с и /с» которые должны оставаться постоянными, монотонно
возрастают по мере продвижения трещины. Этот рост не может
быть объяснен неточностью вычислений. Вероятно, это обуслов-
лено тем, что вследствие пеучета сил трения экспериментально
определенные условия нагружения не соответствуют действи-
тельны м.
ГЛАВА IV
ОПРЕДЕЛЕНИЕ ПОЛЕЙ УПРУГО-ПЛАСТИЧЕСКИХ
ДЕФОРМАЦИИ И НАПРЯЖЕНИИ
§ 22. Введение
Вследствие повышения напряженности элементов современ-
ных конструкции и энергетических установок желательно в про-
цессе их проектирования использовать более совершенные мето-
ды расчета, учитывающие как реальные особенности деформиро-
вания, так п реальную геометрию тела. Этим требованиям при
определенных условиях отвечает применение теории пластично-
сти в сочетании с методом конечных элементов.
Охватить все термопластические свойства материала, прояв-
ляющиеся в многообразии условий работы, в рамках единой тео-
рии — задача пока неосуществимая. Поэтому для решения прак-
тических задач целесообразно использовать некоторые частные
варианты теории пластичности, достаточно правильно описываю-
щие важнейшие стороны данного явления. Наиболее частое при-
менение находят деформационная теория пластичности и теория
течения. Уравнения деформационной теории пластичности уста-
навливают связь между напряжениями и деформациями; урав-
нения теории течения — между бесконечно малыми приращения-
ми этих величин. Как известно, в случае простого нагружения
обе теории дают одинаковый результат. Однако па практике
даже при пропорцпопальпом возрастании нагрузки условия про-
стого нагружения могут не соблюдаться. Дифференциальная фор-
ма уравнений теории течения позволяет, по сравнению с дефор-
мационной теорией, более полно отразить историю нагружения,
что особенно важно в задачах термопластичпости. В данной ра-
боте решение задач проводится на основе теории течения, основу
которой при условии текучести Мизеса [29] составляют уравне-
ния Прандтля — Рейса [141].
§ 23. Основные уравнения неизотермической теории течения
при изотропном упрочнении
В уравнениях теории течения установлена зависимость между
бесконечно малыми приращениями деформаций и напряжений,
самими напряжениями п некоторыми параметрами пластического
* 23. УРАВНЕНИЯ НЕПЗОТЕРМИЧЕСКОЙ ТЕОРИИ ТЕЧЕНИЯ
71
состоятся. Далее предполагается, что упругие свойства и кривая
деформации материала не зависят от температуры.
Теория пластического непзотермического течения с изотроп-
ным упрочнением базируется на следующих трех основных по-
ложениях [9, 651:
1. Приращение полной деформации представляется в виде
суммы
{de) = {dee] 4- {dep} 4- {der|, (4.1)
где {dej, {deP} и {deT} — приращения соответственно упругой,
пластической и температурной частей вектора деформаций.
Приращение вектора упругой деформации выражается через
приращение вектора напряжений {do} и матрицу упругости
формулой
(de<f} = [D]-1{da). (4.2)
Компоненты вектора температурных деформаций равны
d&F = adT8i}, (4-3)
где а __ коэффициент температурного расширения, dT — прира-
щение температуры в данной точке. 6^ — символ Кропекера.
Предполагается также, что относительное изменение объема ма-
ло и является упругой деформацией, следовательно,
Ve’i = o.
2. Накопленная пластическая деформация {еР} при активном
нагружении для любых напряженных состояний определяется од-
ной и той же функцией текучести
/({а|, {ер}, х) = 0.^ (4.4)
Здесь под {о) подразумевается текущий вектор напряжений, х —
параметр упрочнения. Функция текучести характеризует пере-
ход материала из упругого состояния в пластическое. В частно-»
сти, при / < 0 материал деформируется по упругому закону, при
/ = 0 наступает состояние текучести. Принято, что состояние
/ > 0 не может быть реализовано.
3. В случае ассоциированного закона течения приращение
вектора пластической деформации {dep} пропорционально векто-
ру производных функции текучести по напряжениям:
где л — некоторый неотрицательный неопределенный скалярный
множитель. Соотношение (4.5) означает, что пластическое течение
развивается по нормали к поверхности текучести.
72 ГЛ. IV. УПРУГО-ПЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
Перейдем к формулировке соотношений между приращениями
напряжений и деформаций в упруго-пластической среде при тер-
мосиловом пагружепии. Используя формулы (4.2) — (4.5), можпо
переписать соотношение (4.1) в виде
(de) = [Z>]-1 [da] + X[fl} + {<*ет}- (4-6)
Умножим слева one часта этого равенства на величину {я}’’ [О].
В результате получим
{a)T [Р] {de} = (aj^ (da) + {«)г [D] X {а] [jD] {deT). (4.7)
Для того чтобы получить величину {a}T{do}, продифференцируем
условие текучести (4.4):
Отсюда
fajT do] — 4л,
Можно показать, что при изотропном упрочнении величина А
есть наклон кривой деформирования материала Н' для текущего
состояния, т. е. А = Н'.
Введем обозначения
= [D] {я),
Р= {OJT[d} = |a)r[O] {a). (4,8)
Тогда равенство (1.7) запишется в виде
{d}r {de} = АХ-Ь0Х+ ]d|T{deT|.
Отсюда сразу находим выражение для неопределенного множи-
теля X:
{<1}т ({*}- [*.т|)
.1 т- Р
(4.9)
Подставляя это .значение в уравнение (1.6) и решая его отно-
сительно {dal, имеем
[do] = ([Z3] - [Z)p])([de} - [deT}) - [Dep] ({de} - {der}), (4.10)
UVI = |d] [d}*7(4 + 0). (4.11)
Матрица [Z)ep] занимает место матрицы упругости, связывая
приращения напряжений и деформаций в упруго-пластической
области. Ода симметрична и имеет смысл независимо от того,
равен ли нулю наклон кривой деформирования. Впервые эта
матрица была введена в работе [163].
§ 21. УРАВНЕНИЯ МКЭ В ПРИРАЩЕНИЯХ
73
§ 24. Уравнения МКЭ в приращениях и условие равновесия
уIIруго-пластического тела
Будем (как и ранее в гл. II) все уравнения для тела выпи-
сывать как для отдельного элемента, имея в виду, что примене-
ние стандартных правил сборки позволяет перейти от величин,
относящихся к одному элементу, к соответствующим матрицам и
векторам для всего тела.
Для любых бесконечно малых приращений величин в упруго-
пластической области уравнение равновесия тела запишется в
виде
(М
(4Л2)
где [А‘ер] — упруго-пластическая матрица жесткости, {dq} — при-
ращение вектора перемещений, {dP} — приращение вектора си-
ловой нагрузки, {dbeil} — приращение фиктивной нагрузки от
температуры.
Выражения для матрицы жесткости и термического вектора
в упруго-пластической области полностью аналогичны упругим
величинам (1.9), (1.20) с заменой матрицы упругости [/9J на
матрицу [Z)Cp] из (4.10):
[М = ,f [Я]Т [Ргр] [Z?J dV,
\dh..p} = j [/?]rfZ)ep}((?fc-r)dr.
(4-13)
(4.14)
Подставляя выражения (4.13), (4.14) в уравнение равновесия
(4.12) и используя соотношения (1.7) и (4.10), получаем, что
равновесные приращения напряжений должны подчиняться ус-
ловию
[ [fl]rM<7| dV = [dP].
(4Д5)
Отметим, что для упругого состояния тела (еР = 0) все соотноше-
ния гл. I совершенно аналогичны формулам (4.12)—(4.15) и по-
лучаются из последних опусканием индекса РР. При этом прира-
щения рассматриваемых величии могут быть конечными. Поэтому
условие равновесия тела при любом уровне нагрузки получают
суммированием выражений тина (4.15):
J[Z?jr(0) dV = |Р].
V
(4.16)
Здесь I^P; = dPi] —достигнутый уровень силовой нагрузки.
74
ГЛ. IV. УПРУГ041ЛАСТНЧЕСКИЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
§ 25. Метод начальных напряжении для решения
физически нелинейных задач и критерии сходимости
Обычно для решения упруго-пластических задач используют
итерационные методы, в которых путем последовательных при-
ближений удовлетворяется условие (4.16). В методе коночных
элементов в основном используются следующие три итерацион-
ные процедуры.
В методе касательной жесткости (который также называют
методом Ньютона — Рафсона или методом переменных парамет-
ров упругости) на каждой итерации для всех элементов н пла-
стической зоне ищутся новые матрицы [Д»Р] (4.10)—т (4.11). По
этим матрицам строят касательные матрицы жесткости [fcPP]
(4.13) и вычисляют невязку уравнения (4.16). Существенным не-
достатком этого метода является необходимость формирования и
полного решения системы уравнений равновесия па каждой ите-
рации, что занимает слишком много времени.
Метод начальных деформаций выгодно отличается от преды-
дущего тем, что глобальная матрица жесткости тела остается в
процессе вычислений постоянной. На каждой итерации при до-
стигнутом уровне напряжений корректируются деформации,
а невязку уравнения равновесия (4.16) используют в качестве
новой правой части.
Метод начальных напряжении (метод упругпх решений) в
основном аналогичен предыдущему, за исключением того, что
вместо начальных деформаций используются начальные напря-
жения. необходимые для приведения упругого решения в соот-
ветствие с реальными папряжеппями нрп достигнутых деформа-
циях. Этот метод известен давно. Он впервые был применен для
решения задач теории пластичности с помощью МКЭ Зенкеви-
чем и др. [166]. Дальнейшее усовершенствование этого подхода
было сделано Наяком и Зенкевичем в работе [134].
Существенным достоинством метода начальных напряжений
является то, что он сходится для любой зависимости между на-
пряжениями и деформациями. Расходимость означает, что данное
тело исчерпало способность к деформированию. С другой сто-
роны, в отличие от метода начальных деформация, метод началь-
ных напряжений применим и для идеально пластичного материа-
ла. Это решающее преимущество метода начальных напряжений
делает iro наиболее выгодным из известных в настоящее время
итерационных схем. Метод начальных напряжений автоматиче-
ски учитывает разгрузку, поэтому оп весьма перспективен для
применения в задачах о трещинах и при циклической пагрузке.
Следует также упомянуть о так называемой модифицирован-
ной схеме Ньютона — Рафсона, которая состоит в том, что гло-
бальная касательная матрица жесткости строится па одной из
§ 25. МЕТОД НАЧАЛЬНЫХ НАПРЯЖЕНИИ
75
первых гтерацпй и затем остается постоянной, а вычисления ве-
дут по методу начальных напряжений. Как показывает опыт
[134], эта схема позволяет сократить время счета по сравнению
с методом начальных напряжений. Однако эффективная реализа-
ция модифицированной схемы Ньютона — Рафсона возможна при
наличии достаточного объема внешней памяти (магнитные ба-
рабаны и диски) для хранения необработанной системы линей-
ных уравнений. Поскольку у многих находящихся в настоящее
время в эксплуатации ЭВМ этого пет, то наиболее подходящим
для реализации решения физически нелинейных задач оказыва-
ется метод начальных напряжений.
Алгоритм метода начальных напряжений можно коротко за-
писать в виде
(A?i) = [Ле]-1 hh-1},
{?«} = + (Affib
|<Ji] = {CTi-i} + {A<Ti},
V
(4-17)
Здесь индекс i означает номер итерации. Тем самым решение
нелинейной задачи сводится к последовательности решения уп-
ругихчи адач с постоянной матрицей жесткости [7cJ, в качестве
нагрузки при этом используется невязка {i|'} условия равновесия
(4.16). Па первой итерации используются накопленные значения
перемещении {qoi и напряжений {ooh а правая часть равняется
сумме приращений силовой и фиктивной температурной нагру-
зок:
ШНАР} + {АМ-
(4ЛЗ)
Итерационный процесс продолжается до тех пор, пока не
будет выполнен выбранный критерий сходимости. Несколько кри-
териев сходимости описано в работах [6, 134]. Обычно в этих
критериях сравнивают с заданными значениями нормы векторов
приращения перемещений 1 A^JI пли повязок НфД а также макси-
мальные величины компонент этих векторов. В настоящей работе
итерационный процесс оканчивается при выполнении условия
|^Г
е,
(449)
где 8 — заданная точность вычислений. В работе [134] рекомен-
довано выбирать 8 в диапазоне от 10~4 до 10“5.
76 ГЛ. IV. УПРУГО-ПЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
§ 26. Методика определения конечных приращений напряжений
в процессе упруго-пластического деформирования
Рис. 45. Перемещение 1-2 точ-
ки интегрирования элемента
по кривой деформпроваипя в
пространстве деформации-на-
пряжении при конечных’ ша-
гах изменения нагрузки (от—
предел текучести).
Соотношения § 23 между приращениями перемещений и на-
пряжений справедливы только для бесконечно малых изменений
этих величии. Опишем методику [1311, позволяющую данной ма-
териальной точке достаточно точно следовать по кривой дефор-
мирования материалов при конечных шагах.
Рассмотрим точку иптегрирова-
ппя конечного элемента, после того
как элемент получил приращение
вектора перемещенпп {Лд} вслед-
ствие реальной или фиктивной на-
грузки (рпс. 45). Пусть до прираще-
ния точка находилась в положении
7, имела накопленные значения эк-
вивалентного напряжения с,—х п эк-
вивалентной деформации e,-i и на-
ходилась в упругом состоянии, а по-
сле приращения нагрузки перешла в
пластическую область. При этом по
существенно, по каким формулам
подсчитаны эквивалентные величины
и функция текучести. Заметим толь-
ко, что если в состав нагрузки входит
фиктивная часть вследствие темпера-
турного воздействия, то при подсче-
те е из деформаций следует вычесть
температурные составляющие (4.3).
Значение функции текучести в начале шага меньше пуля:
/{-1 = /({а<_1])<0.
Считая шаг упругим,
подсчитываем напряжения в конце шага
{о*} = {Oi.xl
{Дое},
{ЛсгД = |/Л ([5] {А<71 - (Аег]).
(4-20)
Естественно, что в этом случае /* = / (1оч I) > 0,что является не-
допустимым состоянием. Опре делим коэффициент г, указываю-
щий, какая часть приращения напряжений упругая. Правильно
подобранный коэффициент г должен удовлетворять условию
/({«Ч-ll -г г {Аае]) = 0.
Первое приближение для коэффициента и найдем с помощью
§ 26. МЕТОДИКА ОПРЕДЕЛЕНИЯ ПРИРАЩЕНИЙ НАПРЯЖЕНИЙ
77
линейной интерполяции:
Однако при несоблюдении условий простого нагружепия вследст-
вие нелинейности оказывается» что
= +г1{Дде])^О.
Улучшенная оценка /д дастся выражением
Напомним, что вектор {«} есть вектор производных функции те-
кучести по напряжениям и уже встречался в выражении (4.5).
Таким образом, часть приращения напряжений г{ДаЛ являет-
ся упругой, остальную же часть приращения точка должна сле-
довать по кривой деформирования материала. При этом для вы-
числения напряжений используются соотношения (4.10)—(4.11),
которые можно представить в виде
!а11 —- (tfi-ll + iA^ej
(4,23)
где X и {d} определяются соотношениями (4.8)—(4.9). Значение
напряжений в конце шага обозначено через {oj), поскольку это
первое приближение, полученное по формуле, справедливой толь-
ко для бесконечно малых изменений. Вследствие этого значение
функции текучести /| ==/({oi)) ¥=0. Коррекция напряжений осу-
ществляется по формуле, аналогичной (4.22):
{«} {<0
(424)
Очевидно, что точность вычисления напряжений но уравнениям
(4.23), (4.24) будет различной для различных приращении нагруз-
ки, или, конкретнее, опа будет зависеть от величины (1 —г) {Дое),
или, что то же самое, от /г . Чтобы сделать точность подсчета на-
пряжений независимой от приращения нагрузки, следует интер-
вал упруго-пластического деформирования разбить па некоторое
количество шагов
(4.25)
па каждом пз которых используется формула, аналогичная (4.23),
п коррекция (4.24). При вычислении т округление производится в
большую сторопу, а Д/ имеет величину порядка 10"1 от предела
текучести от.
73 ГЛ. iv. УПРУГО-ПЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
§ 27. Ускорение сходимости итерационного процесса
Как уже упоминалось, итерационный процесс метода началь-
ных напряжений является безусловно сходящимся для физически
нелинейных задач. Однако в некоторых случаях, когда зона плас-
тичности сильно развита, этот процесс протекает весьма медлен-
но. Желательно поэтому иметь некоторую. процедуру, которая
позволяет ускорить сходимость в таких случаях. Один пз мето-
дов ускорения сходимости был предложен Наяком и Зенкевичем
[1351 и назван ими методом «-ускорения при постоянной жест-
кости.
Идея данного метода ускорения сходимости состоит в том,
чтобы при топ же скорости сходимости, чго и в итерационной
схеме Ньютона — Рафсона, все вычисления выполнять с упругой
матрицей жесткости.
Пусть при реализации метода начальных на пряженец (4.17)
получено приращение вектора перемещений {AgJ. Улучшенную
оценку приращения перемещений па i-й итерации можно полу-
чить как
{Д/il =. а<_ [Agf], (4.26)
где | af_J— пока неизвестная диагональная матрица ускоряю-
щих коэффициентов. Эти коэффициенты будем искать из усло-
вия, что {Ад,} равны приращениям перемещений в схеме Ньюто-
на — Рафсона:
ер] 1 А?Л = ([A 'el [^р]) I “ Г» ( 1-2< :
Здесь [&ер] —касательная матрица жесткости, [7rJ — упругая мат-
рица жесткости. Умножая обе части этого равенства па [fce]"\
получаем
Гсц_1 {Atfi) - [АеГЦАр] М = (AJ-* {iTs-iI = {A<?fb (4-28)
Значение {Ад/} аппроксимируем величиной
[ДдЛ«{ДдГ1 ЛДд<). (4.29)
Тогда значения ускоряющих коэффициентов могут быть вычис-
лены из уравнения
(Г*; J-Г* J) (A?i} = |Д^Ь (4.30)
где / J—единичная матрица, а вектор {AuJ найден пз упру-
гого решения
|Aui} = [ЬЛ-1 [Ар] {Ад?} = [А-еГ1 {i$. (4.31)
В этом выражении вектор {яр?) получается при помощи интегри-
§ 28. ПОДСЧЕТ ПРИРАЩЕНИЙ ОТ РАВНОВЕСНЫХ ВЕЛИЧИН
79
ровапня дополнительных напряжений
{До|} = {Д0е(Д?*)} — |Дст(Д<7*)),
НД = ' 1#Г U<41 <4-32^
Здесь {До) — действительное приращение напряжений от перс
мещений {А//*}. На первой итерацпи в качестве '~a0_J использу-
ется единичная матрица.
Дальнейшее развитие метода a-ускорения сходимости итера-
ционного процесса при неизменной глобальной матрице жесткости
дано в работе [96]. Предложенный там подход требует при сбор-
ке вектора невязки проделывать вычисления только для элементов,
в которых присутствуют пластические деформации.
§ 28. Методика подсчета приращении от равновесных
значений величии
Рассмотренный итерационный метод начальных напряжений
(4.17) вместе с ускоряющей процедурой (4.26), (4.30)—(4.32)
весьма эффективен для решения задач теории пластичности в
скоростях деформаций. Однако оп не свободен от некоторых не-
достатков. Так расчеты показали, что при накоплении напряжений
на каждой итерации (4.17) может иметь место так называемая
«неверная» разгрузка. Ото происходит вследствие того, что поля
перемещений и напряжений в упругом и упруго-пластическом
состоянии пе являются подобными. Поэтому на первой итерации
(упругий шаг) в некоторых точках напряжения могут стать че-
ресчур большими и вынудить данную точку в последующих ите-
рациях разгружаться по упругому закону. Для устранения невер-
ной разгрузки можно пли значительно уменьшит ь шаги прира-
щения нагрузки, или иметь средства обнаружения «неверной»
разгрузки, с тем чтобы вместо разгрузки двигаться по кривой де-
формации в обратном направлении. Первое сильно увеличивает
время счета, второе неудобно с точки зрения программной реали-
зации. Следует отметить, что описанный эффект неверной раз-
грузки во многих задачах выражен весьма слабо.
Второй замеченный недостаток описаппой схемы состоит в
том, что применение «-ускорения также может вызвать неверную
разгрузку или в некоторых случаях даже привести к расходимос-
ти. Очевидно, что это происходит из-за приближенного характе-
ра соотношения (4.29).
Для решения задач принципиального характера (например,
задач об исследовании независимости от контура интеграла Че-
репанова — Райса) желательно иметь такую схему решения,
so
ГЛ. IV. УПРУГО-ПЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
в которой разгрузка всегда была бы истинной. Особенно это важно
для задач с непропорциональным изменением внешней нагрузки.
Поэтому второй вариант организации вычислений состоит в том,
что приращения напряжений вычисляются на каждой итерации
ст их равновесных значений. Обозначив равновесные значения пе-
ремсщенпй п напряжений через {#} и {о}, можно схему (4.17\
видоизменить так:
{Ад} = О
{Ад, ] = [М ’’ [4ч-1|
(Ад) = (Ад) + {Ад;|
{Ao} = {Аа}([ \g|)j
v
Достигнута ли сходимость?
Igi = Igl + (Ag)
{о) = {ст} -ь {До}
(4.33)
Здесь приращеппе напряжений (Ао) каждый раз подсчитыва-
ется от полного вектора приращения перемещений, накопленного
в процессе итераций вследствие приращения внешней пагрузкп.
Очевидно, что такой процесс устойчивее описанною выше, по-
скольку менее чувствителен к возмущениям в поле перемещений.
Это позволяет вместо вычисления диагональной матрицы! а_______h
что эквивалентно еще одной итерации, производить ускорение
сходимости посредством умножения всех компонент вектора {ДдЛ
на единую константу. Даже если при таком систематическом ум-
ножении процесс начнет расходиться, то отказ от ускорения про-
цесса сходимости снова приведет к его сходимости. Как было
выяснено в расчетах по методике (4.17), ускоряющие коэффици-
енты в зависимости от номера итерации растут приблизительно в
арифметической прогрессии, поэтому этот же закон был принят
для изменения единой константы:
= cZi-i + Да.
Обычно такой рост применяется на нескольких первых итерациях,
а затем эту константу стабилизируют.
Недостаток методики подсчета приращений от их равновесных
значений состоит в увеличении времени на вычисление (Да), так
как при этом точка несколько раз проходит одни и те же участки
кривой деформации.
§ 29. ПРИМЕРЫ РЕШЕНИЯ УПРУГО-ПЛАСТИЧЕСКИХ ЗАДАЧ
81
В заключение приведем выражения для функции текучести и
эквивалентных величин напряжении и деформаций. Используем
условие текучести Мизеса
/([о|» (8р1) = 1 За —Т' = 0, (4.34)
где мгновенный пре дел текучести Y задан в виде степенной функ-
ции
У = от + (4.35)
а эквивалентные величины ер и о определяются по формулам
Здесь stJ — девиаторные напряжения, равные
(4.37)
Приведсппая выше схема решения упруго-пластпческпх задач
фактически не зависит от конкретного вида условия текучести за-
кона упрочнения и т. п. Это позволяет без труда вводить в прог-
рамму ЭВМ различные поверхности текучести п законы течения.
§ 29. Методические примеры решения
упруго-пластических задач
Сравнение алгоритмов решения упругих и упруго-пластпческпх
задач методом конечных элементов показывает, что в последнем
случае вводится несколько параметров, которые можно варьиро-
вать. Па эффективность и точность решения задачи влияют вы-
бор правила интегрирования, точность, при которой прекращает-»
, ся итерационный процесс, применение ос-ускорения сходимости.
Кроме того, точность и скорость сходимости зависят от размера
пластической зоны и характера распределения перемещений. Пе-
ребор всех этих вариантов приводит к необходимости решения
значительного количества тестовых задач, что и было сделано при
проверке выбранной методики и составленной программы. Здесь
приведены лишь некоторые примеры, достаточно наглядно ил-
люстрирующие основные особенности метода начальных напря-
жений. Все расчеты этой главы выполнены по разработанным на-
ми программам NEPTUN и NEPTAL.
29.1. Полый цилиндр под действием внутреннего давления.
В качестве простейшего примера, который имеет аналитическое
pt шейпе, рассмотрим полый цилиндр (см. рис. 4) с внутренним
G Е. М. Морозов, Г. П. Пи ниш ков
82 ГЛ. IV. УПРУГО-ПЛАСГПЧЕСКИЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
радиусом а«=3, внешним радиусом Ь = 6 и зажатыми торца-
ми. На внутренней поверхности цилиндра действует давление р.
Цилиндр изготовлен пз идеального упруго-пластического материя-*
ла. Решение задачи проводилось в цилиндрических координатах
с использованием трех квадратичных элементов в радиальном
Рис. 46. Применение различных правил интегрирования: а) напряжения в
днлиндре под внутренним давлением при Р/от = 0J208, теоретическое ре-
шение показано сплошными линиями; б) погрешности в вычислении Оо.
направлении. Полученные значения сопоставлены с решением в
замкнутой форме [1151.
Найдем пластическое состояние в данном цилиндре прп раз-
ных вариациях выбора исходных данных, влияющих на точность
и время решения.
а) Применение различных правил интегриро-
вания. Как было показано в § 8, для решения упругих задач
выгоднее прпменять двучленное интегрирование матриц жесткое-
§ 29. ПРИМЕРЫ РЕШЕНИЯ УШ’УГО-ПЛАСТИЧЕСНИХ ЗАДАЧ
83
в определении напряжения о». При
Рис. 47. Относительная ошибка в опроделе
нии напряжений ог (а) и ао (б) в цилинд
ре под внутренним давлением Р/от=0,6364
прп различных величинах параметра схо-
димости: 1 — е=2 — е=10~\ 3 —
= 10-5. \
тп по правилу Гаусса, которое по сравнению с трехчленным дает
более точные значения напряжений в точках интегрирования и
требует меныпе времени. Установлено, что это утверждение спра-
ведливо и для упруго-пластических задач. В качестве примера,
подтверждающего это, па рис. 46, а приведено сравнение резуль-
татов, полученных при использовании правил интегрирования
2X2 (NG = 2) и 3X3 (NG = 3) с теоретическими значениями
напряжений в полом цилиндре под давлением р/от = 0,7208 (ра-
диус пластической зоны равен с = 4,5). На рпс. 46, б показана
относительная ошибка б %
этом точность по норме
перемещений (см. (4.19))
была задана равной е =
= 10“5. Если максималь-
ная по модулю ошибка прп
NG = 3 составила 8,6 %,
то все зпачеппя, полу-
ченные при использова-
нии двучленного правила,
отличаются от точного
решения менее чем
па 0,8%.
б) Величина пар а-
метра сходимости.
В данной работе всюду в
качестве критерия сходи-
мости использовано отно-
шение нормы вектора при-
ращения перемещений к
норме вектора перемеще-
ний (4.19). Применение
этого критерия особенно
удобно для решения задач
с температурной нагруз-
кой. Поскольку обычно
прежде всего надо знать
распределение напряже-
ний, то необходимо хотя бы
ориентировочно оценить,
какова ошибка в напря-
жениях при задании дай-
ной величины параметра сходимости е. Погрешности в определе-
нии напряжений в полом цилиндре под внутренним давлением
р/ат = 0,6364 (радиус пластической зоны с = 3,9) прп различ-
ных е показаны на рис. 47. Анализ данных показывает, что ти-
пичная относительная ошибка в напряжениях примерно равна
6*
84
ГЛ. IV. УПРУГО-ПЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
удвоенной величине ) е. Этот коэффициент при । 8 для оценки
точности напряжений, разумеется, не будет постоянным, посколь-
ку зависит от множества факторов. Нужно учитывать, что сюда
же накладывается погрешность вследствие дискретности копечпо-
элементной модели. Однако множество решенных задач указыва-
qг а
Рис. 48. Кривая деформации полого
цилиндра под внутренним давлени-
ем. Показана разгрузка с последую
щеп нагрузкой. / — точное решение;
2 —МКЭ, 5 шагов; 5 — МКЭ, 1 шаг.
ет на то, что ошибка в опреде-
лении напряжении имеет поря-
док квадратного корня из ве-
личины параметра сходимости
по норме приращения переме-
щений. Другой вывод состоит
в том. что для практических
задач достаточно задавать г в
пределах 10~4—10~5.
в) Величина шага при-
ращен и я и а г р у з к и. Урав-
нения теории течения строго
справедливы только для беско-
нечно малых изменений входя
щих в них величии. С точки
зреппя экономии времени сче-
та выгодно при решении задач
применять достаточно большие
приращения нагрузки.
На рис. 48 показана зависимость приложенного давления от
перемещения н.(Ь) внешней поверхности цилиндра, полученная при
точности но норме перемещений е = 10~5. Нагружение производи-
лось за пять шагов и за один шаг. При нагружении за пять ша-
гов после 3-го шага были выполнены разгрузка до нуля и после-
дующее нагружение до прежнего уровня давления. Видно, что в
данном случае полученное решение практически нс зависит ог
шага нагрузки и хорошо соответствует теоретической кривой. Хо-
тя такое поведение решения типично для многих упруго-пласти-
ческих задач при пропорциональном изменении нагрузки, сущест-
вуют задачи, где применение слишком большого шага нагруз-
ки приводит к некоторому отклонению от правильного резуль-
тата.
29.2, Толстостенная труба под действием температурной на-
грузки. Для проверки принятой методики решения задач термо-
пластичности определим температурные напряжения в полом
цилиндре (трубе) с отношением внутреннего радиуса к внешне-
му, равным а/b = 0,5. Материал, из которого изготовлена эта
толстостенная труба,— сталь с пределом текучести от — 22 кге/мм2
и пулевым показателем упрочнения, модуль упругости Е — 1,85 •
• 104 кге/мм2, коэффициент Пуассона v=l/3, коэффициент тем-
пературного расширения а = 1,72 • 10“51/°С. Установившаяся раз-
§ 30. РАСЧЕТ КОЭФФИЦИЕНТОВ 1ЮНЦЕНТГЛЦИИ
85
пость температур между холодпоп п горячей внутренней поверх-
ностями 250°. Для данной геометрии, материала и условий нагру-
жения Б. Ф. Шорром было получено решение [73], которое пока-
зано парне.49, б сплошными линиями. Там же приведены напря-
жения, подсчитанные с помощью МКЭ па сетке (рис. 49, а). При
этом путь нагружения был следующим: ДГ = 100° -> 150°
Рве. 49. я) Сетка конечных элементов, б) температурные напряжения в ци-
линдре с логарифмическим распределением температуры. 1 — решении
В. Ф. Шорра [73], 2 — МКЭ.
200° 250°. Наблюдается удовлетворительное согласие между
обоими решениями. Незначительные отклонения могут быть объ-
яснены тем, что вместо трубы бесконечной длины рассмотрена
труба с отношением высоты к внешнему радиусу —
§ 30. Расчет коэффициентов концентрации
для образца с боковыми выточками
Для демонстрации возможностей используемой методики при
решении задач о концентрации напряжений и деформаций рассмот-
рим растяжение образца с боковыми выточками в виде полуок-
ружности. На рис. 50 изображена сетка для расчета напряжеино-
дефирмированпого состояния в таком образце с отношением
расстояния между выточками к радиусу выточки W/p = 3. Для
получения деформаций и напряжений па поверхности выточки (а
одном из угловых узлов элемента) использовано локальное сглажп
ванне по методу наименьших квадратов 1114] в предположении,
что сглаживаемые величины распределены по билинейному зако-
ну. По значениям па контуре определялись коэффициенты
86
ГЛ. IV. ЗТЕРУГО-ПЛАСТИЧЕСКПЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
Рнс 50 Сетка квадратичных элементов для расчета напряжений в образце
с боковыми выточками (d/p = 1, И7р=3); 78 элементов, 516 степеней
свободы.
Рис. 51. Развитие пластиче-
ской зоны в образце с сим-
метричными боковыми вы-
точками в условиях: а) пло-
ской деформации, б) плоско-
го напряженного состояния.
Рис. 52. Коэффициенты концентрации на-
пряжений Ка и деформаций для полосы
с боковыми выточками при плоской д 'фор-
мации (сплошные линии) и плоском на-
пряженном состоянии (штрихи), подсчи-
танные по МКЭ.
§ 31. УПРУГО-ПЛАСТИЧЕСКОЕ ДЕФОРМИРОВАНИЕ РОТОРА
87
концентрации напряжений Ка и деформаций
Ко = Отах/^пом) — Етах/вново
где индексы max и пом означают соответственно максимальное п
среднее значение величины в сечении с минимальной площадью.
В упругой стадии как для плоской деформации, так и для
плоского напряженного состояния получены одинаковые коэффи-
циенты концентрации напряжений и деформации Ка = = 1,85,
что хорошо согласуется со значением 1,86, полученным с по-
мощью тензометрических и фотоупругих экспериментов [62].
В этой же работе с помощью МКЭ па очень мелкой сетке линей-
ных четырехугольников и треугольников рассчитано значение Ка,
равное 1,85. Такое совпадение говорит об обоснованности выбора
сотки, показанной па рис. 50, для анализа данного концентратора.
Рис. 51 показывает развитие пластической зоны в рассматри-
ваемом образце для случая плоской деформации п плоского на-
пряженного состояния. Изменение коэффициентов концентрации
напряжений Кс и Кл в упруго-пластической стадии приведено на
рис. 52. Полученные результаты качественно хорошо согласуют-
ся с известными Фактами.
§ 31. Упруго-пластическое деформирование ротора
среднего давления турбины К-300-240 Л М3
Упругий расчет ротора турбины описан в § 9. Выясним на-
пряженное состояние этой детали с учетом пластических дефор-
маций при температурной нагрузке, показанной на рис. И.
Рпс. 53. Контуры пластической зоны в роторе турбины при температурной
нагрузке (R — расстояние от оси ротора).
88 ГЛ. IV. УПРУГО-ПЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ II НАПРЯЖЕНИЯ
1 • расчете приняты следующие свойства материала: Е =
2,02 • 104 кгс/мм2, v = 0,3,’ а = 1,48 КУЧ/Х, ат = 20 кгс/мм2.
Диаграмма деформации с линейным упрочнением задана в виде
о от = 1 + 0,005 ер,
где о» Ер — эквивалентные напряжения и пластическая деформа-
ция. Использована сетка, приведенная па рис. 10. Коптуры рас-
считанной пластической зоны приведены па рис. 53. Результаты
Рис. 54. Зависимости коэффициентов
конц“птрацпп интенсивности дефор-
маций п напряжений рас-
считанные по формулам Нейбера
(J), Махутова (2) и с помощью МКЭ
(.?); сц — упругий коэффициент кон-
центрации.
расчетов упругого коэффициента концентрации «а* п коэффициен-
тов концентрации интенсивности деформаций Kti и напряжении
А’^в зоне прпдпековой галтели даны на рис. 51. Под коэффици-
ентом концентрации здесь понимается отношение максимальной
интенсивности величины (по Мизесу) па поверхности концентра-
тора к номинальному значению на этом же радиусе гладкого вала.
Сравнение полученных результатов с расчетом Kt. по формуле
Нейбера
о__Е
а2
(4.3S)
подтверждает известный факт, что зависимость Нейбера дает за-
вышенные значения Kg. с уменьшением упрочнения и ростом
концентрации. Сопоставление значении, полученных с помощью
МКЭ, с усовершенствованной II. А. Махутивым [25] зависимостью
(4.38) дает приемлемое их согласие.
Г . I В Л V
РЕШЕНИЕ УПРУГО-ПЛАСТПЧЕСКПХ ЗАД VI
М БХ ЛИПКИ РАЗРУШЕНИЯ
С ИСПОЛЬЗОВАНИЕМ ТЕОРИИ ТЕЧЕНИЯ
§ 32. Введение
Методы линейной упругой механики разрушения хорошо
обоснованы как теоретически, так и экспериментальпо и доста-
точно широко применяются при проектировании ответствеппых
конструкций. С другой стороны, очевидна ограниченность лпнеп-
Hoij механики разрушения. Реальные металлические тела при раз-
рушении всегда испытывают некоторую пластическую деформа-
цию. Если при этом реализуется концепция квазихрупкого разру-
шения (фактически это означает малость пластической области),
то может применяться лилейная механика. В настоящее время яс-
но. что во многих практически важных случаях упругое решение
задич о трещинах недостаточно для корректного их описания.
В противоположность механике упругого разрушения моголы
исследования в упруго-пластическо! г области развиты значительно
слабое. Поэтому применение численных методов и особенно доста-
точно универсального метода конечных элементов весьма привле-
кательно и может дать существенные результаты.
Применение упруго-плас• шчс< кого моделированья тел с тре-
щинами необходимо для анализа общих закономерностей проте*
капля пластического деформирования в окрестности вершины тре-
щины и выяснения пределов применимости и ошибок meiiiioir
механики разрушения. Указанное моделирование полезно также
для анализа деформирования применяемых па практике образцов
с целью определения вязкости разрушения, для оценки опасности
разрушения реальных конструкций сложной геометрии при про-
извольном нагружении. Представляет интерес сравнение различ-
ных крит> риев разрушения с помощью вычислительного экспе-
римента.
Одной из первых работ во механике упруго-пластического раз-
рушения стал расчет пластической зоны у вершины трещины при
аптпплоскон деформации, выполненный Дж. Хультом н Ф А. Мак-
luii шоком L1161 в 1956 г. Однако, вслецстйие математически х
трудностей^ аналогичная задача для случая трещин типа I до сих
нор не имеет точного аналитического решения. Поэтому для изу-
ченья локализованного пластического течения в окрестности вер-
шины трещины нормального отрыва применялись различные
90
ГЛ. V. УПРУГО-ПЛАСТИЧЕСКИЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
численные методы л, в частности, метод конечных элементов
(41, 150].
Учесть пластическую зону в виде топкой линии перед концом
трещины прп плоском напряженном состоянии позволяет модель
Леонова — Панасюка [24]. Экспериментальное и аналитическое
изучение пластических зон такого типа было проведено Д. С. Даг-
дейлом [97], С. Я. Яремой и др. [13, 57, 74].
Для идеально пластического тела в работе [32] предложен
интегральный вариационный принцип теории трещин. Предложен
также метод расчета па прочность прп наличии трещин, основан-
ный па понятии предела трещиностомкости [133]. В этом методе
расчет выполняют по упругим зависимостям. а пластические эф-
фекты учитывают с помощью специального эксперимента.
В нелинейной механике разрушения до сих пор не решен од-
нозначно вопрос о критерии локального разрушения. Был пред-
ложен ряд критериев разрушения, большинство из которых невоз-
можно проверить с точки зрения их применимости вследствие ма-
лой изученности окрестности вершины трещины прп упруго-
пластическом деформировании материала.
В настоящее время практически применяют (здесь мы нс рас-
сматриваем тонкие пластины) два критерия. Один из них основан
на использовании пе зависящего от контура интеграла Г. II. Че-
репанова [70] и Дж. Р. Райса [54]. Другой предложен А. А. Уэл-
лсом [160], М. Я. Леоновым п В. В. Панасюком [24] и исполь-
зует в качестве характеристики разрушения максимальное рас-
крытие трещины в ее кодце. Данная глава в основном будет
посвящена упруго-пластическим расчетам па основе этих двух
критериев.
§ 33. Интеграл Черепанова — Райса
в нелинейной механике разрушения
Записав закон сохранения энергии для тела с трещиной,
Г. П. Черепанов и Дж. Р. Райс получили, что величина интеграла
дх
п, ds
(5-1)
является параметром разрушения для трещин I типа и не зави-
сит от контура интегрирования. Здесь u,-, — компоненты пере-
мещений и напряжений; nj — компонента нормали к элементу
контура ds; Э = j — плотность энергии деформаций. Этот
интеграл уже рассматривался в гл. II, III в применении к реше-
нию упругих задач. Замечательным свойством J-интеграла являет-
ся то, что он в одинаковой степени пригоден для решения как
упругих, так и упруго-пластических задач.
§ 33. ИНТЕГРАЛ ЧЕРЕПАНОВА — РАПСА
91
Г. П. Черепанов рассмотрел интеграл в более общей форме,
чем Дж. Райс, включив температурные воздействия и объемные
силы, дал его физическую трактовку и указал область приме-
нимости.
По мнению Дж. Райса [53], интеграл (5.1) строго справедлив
только для упругих тел, поэтому для решения упруго-пластиче-
ских задач следует использовать деформационную теорию (не-
линейная упругость) вместо более адекватной физически теории
течения.
С точки зрения Г. П. Черепанова [71], физический смысл
величины интеграла J тесно связан с точностью постановки
задачи деформирования сплошного тела. В общем случае эта
величина равна удельной необратимой работе деформаций в
окрестности края трещины (неучитываемых в принятой поста-
новке задачи). В рамках заданной модели величину J можно
считать некоторой фиктивной поверхностной энергией, определя-
емой из опыта. Прп этом плотность энергии деформаций Э явля-
ется функцией деформации в данной точке тела только для
упругих сред. В случае сред с необратимыми деформациями
величина Э представляет собой некоторый функционал, завися-
щий от истории процесса нагружения всего тела и от его тепло-
вого режима.
Условия начала разрушения в металлах в большинстве слу-
чаев близки к условиям изотермического процесса. Рассмотрим
изотермический процесс, когда выделяемое вследствие необрати-
мых процессов деформации тепло мгновенно распределяется по
всему телу [71]. Будем считать, что достаточно учитывать лишь
механическую и тепловую энергию. Взамен интеграла (5.1) вос-
пользуемся более общим выражением для инвариантного интег-
рала
дх
(5-2)
Здесь Uo — удельная внутренняя энергия, qj — компоненты векто-
ра теплового потока. Примем следующее выражение для скорости
изменения Uq:
где с — удельная теплоемкость, — упругие деформации, Т—
температура, точкой обозначены производные по времени. Ло-
кальное уравнение энергии будет иметь вид
* Р I f i 7’
аУеУ + •
(5-4)
Ч 1 ГЛ. V. УПГУГО-П.ЧАСТПЧЕСКИЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
)!(щв<ц’ слагаемое в левой части итого уравнения представляет
теплового источника.
, что около 9/10 ра-
собой удельную мощность объемного
(Эксцеримеитальпые данные [7] показывают,
боты пллстическпх деформаций переходит в тепло.)
Выберем контур С прп интегрировании (5.2) таким образом,
чтобы ои проходил в упругой области. Согласно (5.3), (5.4) при
изотермическом процессе
f n/ls = - 1 f f = - £2
> dx J ; JJ ,J v SI
C Dp
( cTnxds = 0, Q = J j Gi^.dV.
C Dp
Здесь Dp пластическая область, Q — мощность тепловыделения
в пластической области. Таким образом, интеграл (5.2) 'можно
записать в виде
£<?
si ’
(5.6)
где /о — интеграл вида (5.1).
В выражении (5.6) J представляет собой удвоенную эф-
фективную поверхностную энергию, a Jo — удвоенную «истин-
ную» (в данной постановке задачи) поверхностную энергию.
Принимая в соответствии с концепцией квазихрупкого разруше-
ния, что вязкость разрушения А'с характеризует всю необрати-
мую работу при подросте трещины па единицу длины (при еди-
ничной толщине), получаем из (5.6)
9Q
dl ’
(5.7)
Здесь Jic — критическая величина инвариантного интеграла (по-
верхностная энергия 2у0 в соответствии с терминологией Г. П. Че-
репанова). Для определения величины dQ/dl можпо использо-
вать прямой эксперимент или решение нестационарной упруго-
пластической задачи по теории течения о начале движения
трещины.
Практическому применению развитой теории для определе-
ния критической величины 71С положили начало эксперименты
Дж. Л. Бигли и Дж. Д. Лапдеса [8Б, в которых использовалась
связь между величиной интеграла и производной потенциальной
энергии деформации образца
J = -fftt/dl.
(5.8)
Здесь п далее под J будем подразумевать выражение (5.1).
§ 33. ПЦТЕГРЛЛ ЧЕРЕПАНОВА — РАПСА
93
В соотношении (5.8) П — потенциальная энергия деформации,
которую подсчитывают как площадь вод кривой «сила — переме-
щение», / — длина трещины. Соотношение (5.8) получено при
использовании деформационной теории пластичности.
Дальнейшие экспериментальные исследования тех же авто-
ров [ 128] показали, что величина /1С ие зависит от геометрии
образца и, следовательно, может быть использована в качестве
параметра разрушения.
Дж. Райсом с соавторами [144] было получено соотношение,
позволяющее определить величину J ио диаграмме деформации
единственного образца:
М = 2,
(5.9)
где Р — приложенное усилие, v — перемещение точки приложе-
ния силы, vG — его конечное значение, b — размер по липин тре-
щины неразрушенного сечения. Эта формула справедлива для
Нзгибпых образцов с глубокой трещиной. По оценкам авторов
глубина трещпиы
I > 0,61У,
(5.10)
где W — ширина брутто-сечепия образца. Если значение vc будет
соответствовать моменту страгпванпя трещины, то при обеспе-
чении надлежащих размеров образца мы получим критическую
величину интеграла JIC.
Использование формулы (5.9) для обработки эксперименталь-
ных кривых значительно удобнее, чем использование выраже-
ния (5.8), поскольку позволяет избежать операции дифференци-
рования, которая обычно дает большую ошибку.
Отметим, что были предложены и более сложные зависи-
мости J от работы деформации (см., например, [125]). Методиче-
ски сложным вопросом остается определение момента страгива-
ют трещины (величины ис). Лапдес и Бигли [127] предложили
для этого проводить испытания серии образцов с приложением
различных величин нагрузки. Разгружая образцы и доламы-
вая их таким образом, чтобы пметь возможность определить
достигнутый прирост трещины, можно построить зависимость
величины подрастания трещины от нагрузки и экстраполяцией
получить момент страгивания трещины.
В связи с тем, что изложенный метод весьма перспективен
для определения величины JIC, желательно с помощью упруго-
пластического расчета по методу конечных элементов уточнить
коэффициент перец интегралом в формуле (5.9) для различных
длин трещпп.
94 ГЛ. V. УПГУГО-ПЛАСТПЧЕСКПЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
§ 34. Расчетное определение величины интеграла
Черепанова — Райса
Методика вычисления У-иптеграла в процессе решения задачи
с помощью МКЭ аналогична той, что была описана в гл. II.
Основное отличие состоит в том, что величина энергии деформа-
ции Э зависит от истории нагружения. Поэтому в процессе при-
ращения напряжений накапливается тот 4леп интеграла (5.1),
в котором присутствует Э;
I 9nxds =
с
(5.11)
= -у J ((ai} + {°ri+i})T({8i+i} — {в(}) nxds. (5.12)
с
Здесь приращение деформации {Де,} = {ef+1} — {ej получается
в результате деления интервала деформирования на некоторое
количество шагов в соответствии с формулой (4.25), а напряже-
ния {of+il вычисляются с использованием соотношении (4.23),
(4.24). Разумеется, если на данном шаге материал деформирован
упруго, то отпадает необходимость деления этого шага на части.
Интегрирование по контуру С в пределах каждого элемента,
как и раньше, ведется по квадратурным формулам Гаусса. Для
подсчета У по достижении критерия сходимости итерационного
процесса используются накопленное значение Уэ и достигнуты©
уровни перемещении и напряжении.
Некоторое затруднение при использовании методики, описан-
ной в гл. II, возникает в том случае, когда контур интегрирова-
ния должен пройти через данный элемент «углом» (рис. 55, а).
При решении чисто упругой задачи затруднение удавалось dSpii-
ти сдвигом точек интегрирования и вычислением подынтеграль-
ных членов в этих новых точках. В упруго-пластической области
этого пельзя сделать вследствие того, что напряжения являются
накапливаемыми величинами. Поэтому можно применить сле-
дующий прием. При подготовке сетки разобьем каждый элемент,
в (Котором контур интегрирования образует угол, па два треу-
гольных вырожденных, как показано па рис. 55, б. Такое раз-
биение добавляет всего лишь одпп узел и позволяет проинтег-
рировать необходимые величины не только по участку 1-2, но
и по пути 3-4, что затруднительно при сдвиге точек интегриро-
вал ня вследствие значительного ухудшения точности.
Для вычисления У-интеграла, как производной потенциальной
энергии по длине трещины (5.8), молено применить уже упоми-
навшийся в гл. II п III метод смещения узла в вершине трещи-
ны [139]. При этом пет практически никаких усложнений по
сравнению с расчетом аналогичном величины в упругом случае.
§ 34. РАСЧЕТ ИНТЕГРАЛА ЧЕРЕПАНОВА — РАЙСА
95
Однако трактовка интеграла Черепанова — Райса, как производ-
ной потенциальной энергии по длине трещины, есть только
частный случай, справедливый для нелинейной упругости (де-
формационная теория пластичности). Поэтому подсчет /-интег-
рала по производным матриц жесткости элементов имеет гораздо
Рис. 55. Замена одного квадратичного элемента двумя вырожденными для?
осуществления интегрирования углом при решении упруго-пластпческог.
задачи. Крестиками отмечены гауссовы точки интегрирования.
меньшие перспективы применения для исследования разрушения
упруго-пластических тел, хотя и может быть удобным численным
методом при определенных условиях деформирования и нагру-
жения.
Г. П. Черепанов [71],
Г. П. Черепанов [71], Дж. Хатчинсон [117] и Дж. Райс л
Г. Розенгрип [145] показали, что если зависимость между экви-
валентными напряжением и деформацией стремится к степен-
ной: ___
о = (5.13)
то асимптотическое поведение полой напряжений п деформаций
в малой окрестпостп вершины трещины имеет вид
N
1+"sy(0),
1
(5.14)
Здесь (0), Ef/O)— некоторые тригонометрические функ-
ции угла 0. Отсюда видно, что выражение для энергии дефор-
мации Э имеет при г->0 особенность вида 1/г. Эту особенность
можно смоделировать с помощью уже использованного в гл. II
и III сдвига промежуточных узлов пзопараметрического квадра-
тичного элемента [82]. Однако при этом напряжения и деформа-
ции имеют упругую асимптотику г"1'?.
Точное моделирование асимптотики (5.14) возможно при ис-
пользовании приема, предложенного Р. С. Барсоумом [8?>], ко-
торый показал, что вырожденный квадратичный элемент с уз-
лами на четверти стороны моделирует сингулярность деформаций
96 ГЛ. V. УПРУГО-ПЛАСТИЧЕСКИЕ ЗАДАЧИ МЕХ АНИКИ РАЗГУ ШИ ПЛ
В ВИДО
ег> = сог 12 + + с2- (5.15)
Чтобы смоделировать асимптотику упруго-пластического ма-
териала со степенным упрочнением, такие вырожденные элемен-
ты нужно разместить вокруг
. вершины трещины, как пока-
X ——-о > лево па рис. 56. Узлы, обозна-
z ченные 1 — должны иметь
Z.\ * одинаковые координаты, по в
/ <> / \ то же время быть независимы-
/ \ мп- Этот прием дозволяет ох-
J,______-А—1 ватить весь диапазон измеие-
S Вершина треш инш ппя показателя упрочнения от
Рпс. 56. Моделирование аслмптоти- (упругость) до Л-— 0 (пде-
кп напряжений и деформаций около альпая пластичность) в завы-
вершины трещины п упруги-пл а сти- симости от соотношения кои-
чоском материале. стапт в выражении (5.15). Та-
кой простой метод моделирова-
ния асимптотики упруго-пластического материала демонстрирует
преимущество применения квадратичных элементов для решения
задач о трощппах.
Интеграл Черепанова — Райса неоднократно был использован
при решении упруго-пластических задач в работах [77, 108,
126, 154]. Однако в этих работах нс было проведено достаточно
корректного исследования такого принципиального вопроса, как
независимость интеграла от контура. П. Рлккарделла и Л. Свед-
лоу [ 143] нашли, что этот интеграл зависит от пути, по которому
он вычисляется, в случае применения теории течения даже при
иропорцпопалыюм нагружении. Применение квадратичных элемен-
тов для решения упруго-пластических задач по теории течеппя
позволит исследовать этот вопрос с большей достоверностью и
рассмотреть также случай непропорционального нагружения.
§ 35. Раскрытие трещины у вершины
Из ирактиьи известно, что определение действительных зна-
чений Kia при испытаниях образцов из низкопрочных сталей
для толщин и температур, которые представляют практический
интерес, часто не дает положительных результатов. Одной из
первых попыток получить количественную характеристику5 при
упруго пластическом деформировании тела с трещиной было на-
хождение раскрытия трещины у вершины, предложенное
М. Я. Леоновым, В. В. Папасюком [24] и Уэллсом [1G0] значи-
тельно ранее, чем инвариантный интеграл.
Существенное ограничение в использовании раскрытия в вер-
шппе 6 состоит в том, что трудно дать определение 6. которое
s 35. РАСКРЫТИЕ ТРЕЩИНЫ У ВЕРШИНЫ
97
было бы пригодно для широкого класса условий нагружения.
Некоторые теоретические модели [24, 97] прямо дают раскрытие
б как скачок перемещении в начале координат, связанных с вер-
шиной трещины. Прп аналити-
ческом или чнслеппом решении
Рас. 57. Определение раскрытия
в вершине трещины прп извест-
ном центре вращения.
Гис. 58. Определение раскры-
тия в верптипе трещины но из-
мерениям относительного пе-
ремещения берегов трещппы в
двух точках.
упруго-пластических задач перемещения на берегах трещины
плавно меняются, начиная от пуля в вершине трещины. Дж. Райс
и М. Джонсон [55] показали, что область больших деформации
имеет размер порядка раскрытия в вершине трещины. Очевидно,
что методы, основанные на учете малых деформаций, не обеспе-
чивают требуемой точности вблизи конца трещины. Поэтому
расчет раскрытия каким-либо численным методом в пределах
малых деформаций не является достоверным. Тем пе менее это
не исключает возможности исследования деформирования образ-
ца па некотором расстоянии от вершины. Существенным недо-
статком раскрытия как критерия разрушения является его непри-
менимость при решении задач в рамках теории упругости.
Экспериментальное определение раскрытия б обычно прово-
дят по схеме, показанной на рпс. 57. Измеряя перемещение бе-
регов трещины Vc в точке х = —I и зная расстояние от вершины
до центра вращения хг, раскрытие в вершине можно определить
по формуле
(5.16)
которая справедлива, если профиль контура трещины — прямая.
Величина г, равная
г = (5.17)
называется коэффициентом вращения. Основной трудностью опи-
санной схемы является необходимость знания коэффициента вра-
щения, который в процессе нагружения не остается постоянным.
7 Е. М. Морозов, Г. П. Нпкишков
98 ГЛ. V. УПРУГО ПЛАСТИЧЕСКИЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
Схема, изображенная на рис. 58, свободна от этого недостат-
ка, поскольку перемещения иА и vB измеряются на разных рас-
стояниях от вершины и sB. Имея систему двух лппейпых
уравнений, можно определить обе неизвестные величины:
SAVB ~ SBVA SAVB ~' $BVA
--------- =----------------
(5.18)
Если профиль трещины не будет прямой линией, то измерения
па различных базах будут давать разные величины 6. Это поз-
Рис. 59. Сетка из 100 квадратичных эле-
ментов, 682 степени свободы. Размер
наименьшего элемента равен Z/50. Штри-
хи показывают типичные контуры инте-
грирования.
воляет использовать данную
схему для осуществления
численного эксперимента по
исследованию определения б.
§ 36. Локализованное
пластическое течение
у вершины трещины
при плоской деформации
Поскольку для трещин
нормального отрыва в упру-
го- пластической стадии до
настоящего времени но по-
лу чепо решений в замкнутом
виде, то для проверки разра-
ботанной методики прове-
дем сравнение с результатами
работы [1501, которые были
уточнены в 1551. II. Леви и
др. с помощью МКЭ при ис-
пользован ин линейных че-
тырехугол ы гиков получили
решение упруго-пластиче-
ской задачи в окрестности
вершины трещины, задавая
в качестве граничных усло-
вии упругую асимптотику
напряжений (2.2).
Нами для сравнения был
выполнен расчет упруго-пла-
стического состоя пня в рас-
тянутой напряжением о по-
лосе с краевой трещиной
при использовании сетки из 100 квадратичных элементов с 682
степенями свободы (рис. 59). Размер наименьшего элемента
составлял 0,02 длины трещины.
§ 37. НЕЗАВИСИМОСТЬ ОТ КОНТУРА ИНТЕГРИРОВАНИЯ
99
Очертания полученной пластической зоны, малой ио
сравнению с длиной трещины, приведены па рис. 60 в
нормализованных координатах. В работе [55] приводятся данные
о том, что при коэффициенте Пуассона v = 0,3 наибольшее рас-
стояние от конца трещины до упруго-пластической границы
Рдс. G0. Пластическая зона в условиях локализованного пластического тече-
ния у вершины трещины при плоской деформации.
rp nwx = 0,175(А7от)2 достигается при угле 6р = 70°, на продолже-
нии трещины расстояние до этой границы составляет гРо =
= 0,032(Л7от)2. Здесь А' — коэффициент интенсивности напряже-
ний. от— напряжение текучести.
В наших расчетах эти величины получены равными: гртах =
= 0,170 —0,175(А7от)2, 0₽ « 68°, rpQ = 0,030 - 0,034(А/ог)2, что на-
ходится в хорошем согласии с приведенным выше решением.
Решение с применением сингулярных элементов не дает сущест-
венного отличия от решения па сетке, состоящей только из обыч-
ных элементов.
§ 37. Исследование независимости от контура
интеграла Черепанова — Райса
Применение квадратичных изопара метрических элементов и
сильного сгущения сеткп у вершины трещины позволяет про-
нести исследование инвариантности интеграла Черепанова —
Райса (5.1) в широком диапазоне длин контуров.
В работах [154. 146] с использованием теории течения было
найдено, что этот интеграл не зависит от контура при пропорцио-
нальном нагружения даже в случае развитой пластической зоны.
7*
100 ГЛ. V. УПРУТО-ПЛАСТИЧЕСКИЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
Рпс. 61. Сетка из 92 квад-
ратичных элементов с
630 степенями свободы.
Относительная глубина
трещины 1/4 ширины.
Штрихами отмечены ти-
пичные контуры интег-
рирования.
Исследование инвариантности J-интеграла при решении уп-
руго-пластической задачи с учетом как физической, так и гео-
метрической нелинейности проделано в работе [131]. Найдено,
что интеграл зависит от контура только в весьма малой окрест-
ности вершины трещины с радиусом примерно в шесть раз
больше раскрытия в вершине. Именно
таков примерный размер зоны локализа-
ции больших деформаций. Вычислим зна-
чения /-интеграла на разных контурах
интегрирования для задач с непропорци-
ональным нагружением с целью установ-
ления степени зависимости /-интеграла
от контура.
Произведем расчет при непропорцио-
нальном нагружении в условиях плоской
деформации полосы с краевой трещиной
относительной глубппы Z/Z? = 0,25. Ис-
пользуем сетку пз 92 квадратичных эле-
ментов с 630 степенями свободы, приве-
денную па рис. 61. Путь нагружения —
растяжение сг/<гт = 0,2 -* 0,4 -> 0,5, затем
трехточечный изгпб 7И/(<М)=42 -> 24 -*•
36. Развитие пластической зоны и рас-
считанные па различных контурах вели-
чины интеграла показаны на рис. 62, с.
Точки в виде треугольников показывают
максимальный размер пластической зоны
при точности по норме перемещений
в = 10“5. Слева от треугольника па
рис. 62, б контур интегрирования пересе-
кает пластическую зону, справа — по пе-
ресекает. Максимальное отклонение /-ин-
теграла, определенного на контуре с ра-
диусом гаф// = 0,1, от стабилизированного
значения составляет около 4%.
Для моделирования полосы с краевой
трещиной Z/jB = 0,5 в условиях плоской
деформации применим сетку согласно
рис. 59. Осуществим нагружение «растя-
разгрузка о7от = 0,3 0,15 0, трехто-
чечный изгиб J//(oTZ) = 3040». Для окончания итерационного
процесса возьмем точность по норме перемещений е — 10” \ Кон-
туры упруго-пластической границы для некоторых нагрузок и
результаты расчета интеграла вдоль контуров различной длины
даны на рис. 63. Наибольшие отклонения величины интеграла
ог постоянной имеют место в процессе разгрузки. Вдоль контура
жоппе о/от = 0,2 -> 0,3
§ 37. НЕЗАВИСИМОСТЬ ОТ КОНТУРА ИНТЕГРИРОВАНИЯ
101
Рис. 02. Непропорциональное нагружение полосы с краевой трещиной 1/В —
== 0.2а растяжение + изгиб», а) Развитие пластической зоны; 6) значения
интеграла, определенные на контурах с различными эффективными радиу-
сами.
Гпс. 63. Непропорциональное нагружение полосы с краевой трещиной 1/В —
= 0,5 ^растяжение — разгрузка — изгиб», а) Контуры пластической зоны;
б) значения интеграла, рассчитанные по различным путям.
102 ГЛ V. УПРУГО-ПЛАСТИМЕСКПЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
гаф// = 0,08 значение /-интеграла после разгрузки даже становит-
ся отрицательным. Этот эффект можно объяснить тем. что при
разгрузке норма приращения перемещении в процессе итераций
падает довольно быстро и может уже не характеризовать точ-
ность решения в области вершины. В дальнейшем при активном
нагружении величине! интеграла опять стабилизируется с высо-
кой точностью. *
Проделанные па ЭВМ эксперименты (в том числе и пе при-
веденные здесь) показали, чти интеграл Черепанова — Райса в
пределах точности вычислений не зависит от контура пе только
при пропорциональном, по и при непропорциональном (по край-
ней мере, активном) нагружении. При этом безразлично, пере-
секают или не пересекают контуры интегрирования пластиче-
скую зону.
Следует отметить, что вычисление интеграла па различных
контурах может служить некоторой мерой качества решения
унруго-иластпческой задачи о трещине. Так, наличие неверной
разгрузки в процессе вычислеппй (см. § 28) приводит к большей
нестабплыюстп значении J.
§ 38. Погрешности линейной механики прп предсказании
локального разрушения в упруго-пластических телах
Оценим погрешность линейной механики разрушения при
простом растяжешш образцов пз идеального упруго-пластиче-
ского материала с краевой и центральной трещиной [39].
Будем рассматривать изотермический процесс как наиболее
типичный для металлов при умеренных скоростях нагружения.
При этом выделяющееся вследствие пластической деформации
тепло будет рассеиваться, пе изменяя напряженно-деформиро-
вапного состояния рассматриваемого тела. В соответствии с кон-
цепцией Г. II. Черепанова локальное разрушение произойдет
в момент достижения величиной J, подсчитанной но формуле
(5.1). критического значения 2vo = /ic. Здесь 270 — некоторая ис-
тинная в пределах точности постановки задачи поверхностная
энергия. В упругом случае она связана с Аю соотношением
Kic/E' = 2у0.
(5.19)
Подчеркнем еще раз, что концепция позволяет определить
моап‘1!т локального разрушения, т. е. страгпвания трещины.
Вопрос о ее дальнейшем развитии мы здесь не рассматриваем.
Очевидно, что при изотермическом процессе и простом нагруже-
нии страгпваппе трещины в упруго-пластическом теле и в нели-
нейно-упругом теле с той же диаграммой деформирования прои-
зойдет при одном п том же значении внешней нагрузки.
§ 38. ПОГРЕШНОСТИ ЛИНЕЙНОЙ МЕХАНИКИ РАЗРУШЕНИЯ
103
Для постановки вычислительных экспериментов применялись
сетки, изображенные на рис. 59, 61. Контуры пластических зон
для исследуемых образцов прп различных отношениях среднего
по нетто-сечснию напряжения са к напряжению текучести от
приведены па рис. 64. Сравнение значении J-иптеграла прп ре-
шении упруго-пластической и упругой (т. е. Je~Ki/E'} задач
Рпс. 64. Развитие пластической зоны при растяжении полосы с краевой
трещиной 1/В — 0.5 (a, б); 1/В = 0,25 (в, г); с центральной трощппой 1/В =
— 0.5 (б); Z/B=0,25 (е). Варианты б, г соответствуют условиям плоскою
напряженною состояния, остальные — плоской деформации.
сделано па рпс. 65. С учетом того, что значение J пропорциональ-
но квадрату коэффициента интенсивности напряжений, погреш-
ность линейного подхода в определении нагрузки страгивания
трещины имеет величину б = yrJe/J — 1.
104 ГЛ. V УПРУГО-ПЛАСТИЧЕСКИЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
Обычно считают, что лилейная механика разрушения может
применяться вплоть до напряжения в петто-сечении, равного 0,8
предела текучести ат. Анализ полученных результатов показы-
вает, что пределы применимости линейного подхода сильно за-
висят от степени стеснения деформации. Так, для образца с крае-
Рис. 65. Зависимости отношения величины J-
интеграла с учетом пластических деформаций
к его упругому значению 1е от напряжения в
петто-сечении для различных образцов.
(Сплошные линии — плоская деформация,
штриховые — плоское напряженное состоя-
ние.)
вой трещиной глубиной
в половину сечения
1/В^— 0,5 в условиях
плоек о й дефо рма ци и
ошибка в определении
нагрузки составляет при
Он/От = 0,8 около 38 %.
Однако для аналогично-
го образца с 1/В = 0,25
погрешность при этом
составит менее 10%.
Для образцов с цент-
рал ьным и тре щи нам и
при таких же напряже-
ниях 6 — менее 4%. Для
пластины с краевой тре-
щиной 1/В == 0,25 при
пл ос ком на пр яжен н ом
состоянии ошибка в
10% будет достигнута
уже при сн/ат около 0,5.
Таким образом, мож-
но рекомендовать при-
менять зависимости линейной механики разрушения вплоть до
нетто-иапряжеппя ои = 0,8ат для краевых трещин в массивных
телах глубиной менее 0,25 сечения пли для подповерхностных
трещин размером мепее половины сечения. Эта оценка пригодна
для нагружения, близкого к растяжению. Следует иметь в виду,
что линейная механика дает неконсервативную оценку нагрузок,
поэтому применять ее следует с осторожностью.
§ 39. Энергетические затраты на развитие трещины
при изотермическом процессе [38]
()цепим необратимые удельные энергозатраты при начале дви-
жения трещины (эффективную поверхностную энергию) 7эф при
помощи решения нестационарной упруго-пластической задачи в
скоростях деформаций. Расчет осуществим на сетке из 70 квад-
ратичных элементов с 486 степенями свободы, которая позволяет
рассматривать трещины с относительной длиной 1/В. близкой к
0,5 (рис. 66) [38].
§ 35. ЭНЕРГЕТИЧЕСКИЕ ЗАТРАТЫ НА РАЗВИТИЕ ТРЕЩИНЫ
105
Решение состоит в том, что на линии симметрии запрещается
такие число узловых перемещений, чтобы относительная длина
трещины была 1/В = 0,5. Затем решается обычная упруго-пласти-
ческая задача. По достижении нагрузкой по-
меченного значения двум узлам у ближай-
шего к вершине элемента предоставляется
свобода перемещения. Тем самым длина
трещины увеличивается па размер элемента
(в данном случае прирост AZ = 0,01Z). При
этом напряжения в «освобожденном» эле-
менте уже не уравновешиваются реакциями
опор, поэтому возникают усилия, раскры-
вающие трещину. Такая методика моделиро-
вания роста трепшны привлекательна тем,
что позволяет с небольшими изменениями
использовать обычный алгоритм решения
упруго-пластических задач. Едиитвевным
существенным изменением является то, что
посте изменения граничных условий в пере-
мещениях необходимо снова осуществить
полное решение системы линейных уравне-
нии. Гис. 67 показывает эволюцию пласти-
ческой зоны при подросте трещины от I =
= 0,527 до /1 = 0,505/7. Кружками отмечены
те точки интегрирования, в которых есть
1 । ласт ические деформации^ но произошла
раз! рузка.
Для подсчета эффективной поверхност-
ней энергии по формуле (5.6) при определе-
нии величины dQ/dl в соответствии с фор-
мулой (5.5) была применена лднеари гация:
Л! Д/ J J
г‘р
Результаты расчетов в виде величин типа
коэффициентов интенсивности напряжений
приведены на рис. 68. Истинная в данной
66. Сетка из 70
зле-
Рис.
квадратичных
центов с 486 степеня-
ми свободы. Относп-
юльная глубина тре-
щины 1/В = 0,5.
(5.20)
приведены на рис. 68. Истинная в данной постановке, поверх-
ностная энергия 7о позволяет вычислить коэффициент Aict обыч-
но определяемой при стандартных испытаниях па вязкость раз-
рушения при почти полностью упругих деформациях (5.19 8 Эф-
фективная поверхностная энергия 7зф является суммой.
, 1 oQ
и соответствует некоторому коэффициенту Кс, характеризующе-
му полные необратимые энергозатраты па единицу поверхности
JOG ГЛ V. УПРУГО-ПЛАСТИЧЕСКИЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
трещины. График на рис. 68 показывает для данной геометрии,
что вязкость разрушения К1С можно определить путем диффе-
ренцирования необратимой энергии по длине трещины только
Гис. 67. Изменение пластической зоны при подросте трещины I—0,57/ па
Д/=0,0П. Нотто-папряжение ои=0,5от.
для нетто-напряженпп <тп < 0,2от. Это соответствует тому, что
пластическая зона должна иметь наибольший лилейный размер
около 1/25 длины трещины и менее. Поэтому такой метод опре-
деления вязкости разрушения экспериментально реализовать
практически невозможно.
С*
Гис. С8. Зависимость коэффи-
циентов типа A’i, соответству-
ющих полным необратимым
энергозатратам на единицу
длины и «истинной» по-
верхности энергия То от нетто-
напряжения оп для образца с
краевой трещиной l=Q,5B.
Предложенная здесь методика решения нестационарной упру-
го-пластической задачи при дальнейшем ее усовершенствовании
может быть впоследствии применена для моделирования разви-
тия трещины.
§ 40. КОМПАКТНЫЙ ОБРАЗЕЦ
107
§ 40. Компактный образец
Одним из самых распространенных образцов для испытаний
па вязкость разрушения является компактный образец, изобра-
женный на рпс. 69. Поскольку методика испытаний этого образ-
ца хорошо отработана, оп применяется для определения крити-
ческого значения инвариантного интеграла Лс-
Inc. G9. Разбиение компактного образца на квадратичные элементы. Штри-
хами показаны контуры ннтегрировалия.
Для изучения особенностей деформирования компактного
образца при развитой пластической зоне применялась сетка,
показанная на рис. 69. Расчеты проведены для стали 12Х2МФА,
применяемой при изготовлении корпусов атомных реакторов.
Экспериментальная диаграмма деформации этой стали с доста-
точной точностью аппроксимируется зависимостью
о/dr = 1 0,645вр3 \
(5.21)
Напряжение текучести, при котором появились первые пласти-
ческие деформации, равно от = 63,7 кгс/мм2.
Развитие пластической зоны в образце с относительной глу-
биной трещины Z/Mz = 0,5 в условиях плоской деформации и
плоского напряженного состояния показано на рпс. 70. Числа на
упруго-пластпческпх границах показывают нагрузку па единицу
толщины t образца. Здесь и далее принято, что нетто-шпрпиа
образца TF = 100 мм. При стандартной методике испытания с
использованием закономерностей лтшейпоп механики разруше-
108 ГЛ. V. УПРУГО-ПЛАСТИЧЕСКИЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
иия действительными считают значения А’1С)
УСЛОВИЮ
удовлетворяющие
t и
Z£ic\2
va *)
Вычисления интеграла (5.1) показало, что это условие для
рассматриваемого случая соответствует нагрузке около 300 кгс/мм.
Рис. 70. Рост пластической зоны в компактном образце при относительной
глубине трещины 1/W = 0,5. Числа на упруго-пластических границах ука-
зывают нагрузку на единицу толщины образца в кгс/мм. а) Плоская дефор-
мация, б) плоское напряженное состояние.
При этом размер пластической зовы даже па поверхности об-
разца составляет около 1/10 длины трещины. Таким образом,
стандартная методика испытания на вязкость разрушения на-
кладывает весьма жесткие ограничения на величину зоны
пластичности. Реальное страгивапие трещины1) прп комнатной
температуре соответствует нагрузке около 600 кгс/мм. Интерес-
’) Момент страгиванпя трещины установлен в экспериментах, выпол-
ненных Л. В. Васютиным.
§ 40. КОМПАКТНЫЙ ОБРАЗЕЦ
1г»9
пой особенностью напряженного состояния образца является то,
что пластическая зона в место контакта шпильки с образцом
образуется пе па вертикальной оси, а приблизительно под 45—
50° к вей. Расчет был выполнен при распределении приложен’
кого усилия по синусоидаль-
ному закону на верхней по-
луокружности отверстия под
шпильку [37].
Для проверки истинности
соотношения (5.8) в случае
применения тсорип течения
был выполнен следующий
вычислительный экспери-
мент. В условиях плоской
деформации для трещин глу-
биной //И7 = 0,50 п 0,51 про-
считаны кривые «нагрузка —
перемещение точки прило-
жения силы» (рис. 71, а).
Затем по разности работ
прп постоянном перемеще-
нии подсчитаны значения
инвариантного интеграла.
Рис. 71, б показывает, что
расчеты по податливости и с
помощью интегрирования но
контуру (5.1) дают одинако-
вые результаты. Это под-
тверждает справедливость
формулы (5.8) прп пропор-
циональном нагружении.
Интересной с практиче-
ской точки зрения является
задача уточнения коэффици-
ента М в формуле (5.9), по-
зволяющей рассчитать вели-
чину 7-интеграла по кривой
податливости единственного
образца. В процессе вычис-
лений выяснилось, во-пер-
вых, что замена распреде-
Гис. 71. а) Кривые деформация ком-
пактного образца; б) сравнение значе-
ний 7, подсчитанных с помощью непо-
средственного интегрирования (7) и по
податливости (2).
ленной нагрузки сосредоточенным усилием, приложенным в точ-
ке Р (см. рпс. 69), при подсчете работы практически не изменяет
результата. Во-вторых, что расчет работы, когда вместо переме-
щения точки Р берется перемещение точки С, па поверхности
надреза под силой дает результат, несколько отличающийся от
ПО ГЛ V. УПРУГО-ПЛАСТШГЕСКЦЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
верного. Поскольку в экспериментах перемещение, измеряется па
поверхности трещины, то этот факт следует учитывать. Резуль-
таты для коэффициента М в (5.9) при измерении перемещения
в точках Р и С\ а также в точке Е на краю образца для различ-
Таблица 8
Зависимость коэффициента в формуле (5.9) от точки измерения переме-
щения и от относительной глубииьгтрещины
I IV А,р •WC 1 У!е
Плоская деформация
0.5 2.28-2,26 2,46—2.42 1,66—1.64
0.6 2,20 2,30 1,64—1,67
0.7 2.18 2.24 1,66—1.65
Плоское пан ряженное состояние
0,5 2,30-2,20 2.48-2.30 1.67—1.61
0.6 2,21—2,14 2.32—2,17 1,63-1,59
0.7 2.16—2,13 2.21-2,17 1,65—1.64
пых относительных длин трещины сведены в табл. 8. В том слу-
чае, когда коэффициент не постоянен в процессе нагружения,
дан диапазон его изменения. Большая зависимость М от иагруз-
Рпс. 72. Зависимость раскрытия в вершине трещины от базы, па которой
оно определяется: а) плоская деформация, б) плоское папряжеапос со-
стояние.
§ io. компактный образец
1Н
кп наблюдается для более коротких трещин и для плоского на-
пряженного состояния. В процессе испытания поведение реаль-
ного образца, соответствует промежуточному состоянию между
плоской деформацией и плоским напряженным состоянием. Бли-
зость коэффициентов Л1 при разном стеснении деформации позво-
ляет при обработке результатов уверенно использовать един-
стве пный коэффициент.
Перейдем теперь к изучению деформации берегов трещины.
Подчеркнем, что применяемая методика, ограниченная малостью
деформаций, не может претендовать па определение достоверных
Гис. 73. Сравнение величин / интеграла (7) и произведения раскрытия па
предел текучести 6ат (?) для компактного образца с относи тельной глуби
нон трещины Z/П = 0,5 для плоской деформации (<т) н плоского напряжен
ного состояния (б).
значений раскрытия в вершине трещины, по позволяет рассмот-
реть деформацию профиля трещины па некотором удалении от
ее вершины. Для определения раскрытия представим, что каж-
дый угловой узел элемента, находящийся на поверхности тре-
щины,— это датчик перемещения. Каждый элемент можно пред-
ставить в виде двухточечного датчика, позволяющего определить
раскрытие по формуле (5.18). Зависимость раскрытия в вершине
от места измерения перемещений показана на рис. 72. Точки
показывают положение середины базы, па которой определено
раскрытие (х— координата от вершины трещипы). Графики по-
казывают, что если этот гипотетический датчик расположен под
отверстием для шпильки, то получаемые зпачепия 6С будут
сильно заплаченными. В то же время видно, что определение
раскрытия по перемещениям па краю образна может дать при-
емлемые результаты.
Для случая, когда пластическая зова существенно мала по
сравнению с длиной трешпньт, Уэллсом [160] предложена
112 ГЛ. V. УПРУГО-ПЛАСТИЧЕСКИЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
следующая зависимость между критериями J п б:
J — (У«гб«
(5.22)
Сравнение величин, стоящих в левой и правой частях этого ра-
венства, производится па рис. 73. Расчет выполнен для компакт-
ного образца при 1/W = 0,5. В качестве б использованы макси-
мальные значения на кривых, показанных на рис. 72. Обнару-
жено, что в пределах использованной вычислительной модели
равенство (5.22) лучше удовлетворяется при малых нагрузках
и в условиях плоского напряженного состояния.
В целом следует отметить, что вычислительные эксперименты
могут оказать существенную помощь исследователю при трак-
товке результатов реальных экспериментов.
§ 41. Анализ хрупкой прочности корпуса
реактора АЭС «Мовипза» с учетом эффектов пластичности
Поскольку выяснилось, что линейная механика разрушения
дает оценку допустимых нагрузок не в запас прочности, проде-
лаем уточненный анализ хрупкой прочности корпуса реактора
при возникновении одного из аварийных режимов. Воспользуем-
ся при этом расчетной схемой и исходными данными, описан-
ными в §16. В соответствии с доступными экспериментальными
данными для материалов, пз которых изготовлен корпус, приня-
ты следующие упругие константы и диаграммы деформации.
Наплавка на внутренней поверхности цилиндрического корпуса
имеет характеристики:
Е = 2,05-104 кгс/мм2; v = 0,3; а = 1,66-10“51/°С;
<гт = 35 кгс/мм2; а/ат = 1 4- 2,93бр440.
Основной металл:
£ = 2,13-104 кгс/мм2; v — 0,3; а = 1,09-10“% С;
ат == 44 кгс/мм2; о/от = 1 4~ 0,612ср35*-
Используемая методика решения упруго-пластической задачи
в скоростях деформаций позволяет отразить произвольную исто-
рию нагружения. При расчетах взят следующий путь нагруже-
ния. Вначале задавались условия нагружения, имеющие место
в рабочем режиме, осевое растягивающее напряжение о, =
= 7,6 кгс/мм2 и постоянная по толщине температура Т == 275 °C
(температура недсформированпого состояния 20 °C). Затем зада-
вались такие приращения осевой нагрузки и температуры, чтобы
моделировать изменение этих величин в соответствии с рис. 31,
<52. В силу значительного изменения условий нагружения пере-
§41. АНАЛИЗ ПРОЧНОСТИ КОРПУСА РЕАКТОРА
113
ход от рабочего состояния к первому расчетному моменту вре-
мени осуществляли пропорциональным образом за пять шагов.
Оказалось, что в рабочем режиме металл наплавки нахо-
дится в пластическом состоянии, причем осевые и окружные
напряжения являются сжимающими. Контуры пластической
Ряс. 74. Контуры «активной» пластической зоны дан трех моментов времени
при разрыве трубопровода ДУ-73 в случае существования трещины глубиной
10 мм (а) и 5 мм (г5) в моменты времени т=0,140 ч (7); т = 0,210 ч (2}* т=
= 0,269 ч (•?).
зоны в последующие моменты времени в случае разрыва трубо-
провода ДУ-73 для трещин глубиной 10 мм и 5 мм показаны на
рис. 71. На рисунке г — координата, отсчитываемая по радиусу от
поверхности сплавления корпуса. 5 — координата по высоте цилинд-
ра от места расположения трещины, t — толщина основного ме-
талла стенки корпуса. В момент времени т = 0,140 ч наплавка
снова почти полностью деформирована пластически, однако осе-
вые и окружные напряжения в ней оказываются растягивающи-
ми. В этот момепт времени пластическая зона имеет наибольшие
размеры, в дальнейшем она уменьшается и практически исчезает.
Результаты расчета параметра типа коэффициента интенсив-
ности напряжений ио значению инвариантного интеграла Ki —
= т' JE’, а также критические величины этого коэффициента
А’1С для случаев разрывов трубопроводов ДУ-73 и ДУ-90 приве-
дены па рис. 75. Сравнение с результатами, полученными в § 16,
показывает, что в наиболее опасный момент времени (0,328 ч,
ДУ-73) упругий расчет занижает значение А\ на 22% по срав-
нению с упруго-пластическим моделированием истории нагруже-
S Е. М. Морозов, Г. П. Ни киш ков
114 ГЛ. V. УПРУГ0-ПЛАСТ11ЧЕСКПЕ ЗАДАЧИ МЕХАНИКИ РАЗРУШЕНИЯ
ппя. Режимы разрыва трубопроводов ДУ-135 и ДУ-250 являются
с точки зрения хрупкой прочности менее опасными.
Интерполяция с учетом линейной пропорциональности между
величиной J-пнтеграла п глубиной трещины приводит к выводу,
Гис. 75. Зависимости от времени Я1С и расчетного значения A'i == f/E' для
трещин глубиной 5 мм (сплошные лпплп) п 10 мм (штрихи).
что прп периодической проверке с помощью неразрушающих
средств контроля можно допустить в основном металле существо-
вание подповерхностных трещин глубиной около 7 мм.
ГЛАВА VI
РЕАЛИЗАЦИЯ МЕТОДА
КОНЕЧНЫХ ЭЛЕМЕНТОВ НА ЭВМ
§ 42. Введение
В настоящее время, когда МКЭ прочно вошел в практик у
расчетов, существует значительное количество вычислительных
программ, содержащихся в книгах, журналах и в различных фон-
дах алгоритмов п программ. Некоторые пз этих программ пред-
ставляют собой довольно сложные универсальные комплексы
(в нашей стране это система «Ирочыость-75» [61], «Каскад-2»
[28.51], за рубежом - NASTRAN [130], TITUS [129], ASKA
[79]), другие предназначены для решения довольно простых за-
дач и невелики но объему. Тем не мспее последователю нередко
приходится создавать своп собственные программы (или хотя бы
видоизменять уже существующие), поскольку его либо не устраи-
вают готовьте программы, либо возможности ЭВМ не отвечают
этим программам. Вероятно, в создании п переработке программ
сохранится необходимость и в дальнейшем, так как в МКЭ и в
тех областях, для которых ведется расчет, все время возникают
новые пдеп. Поэтому здесь мы изложим некоторые принципы
и приемы машинной реализации метода, как основанные на
собственном опыте, так и почерпнутые из литературы. Остается
добавить, что такие рекомендации легче дать, чем им следовать;
внимательный читатель может это заметить пз приведенной в
дальнейшем программы. Авторы выполняли расчеты на ЭВМ
БЭСМ-6, что, возможно, накладывает некоторый отпечаток на их
образ мыслей в излагаемом вопросе.
Программы, использующие МКЭ, обычно характеризуются
большим объемом перерабатываемой информации, при этом кри-
тическим моментом, затрудняющим программирование, является
нехватка объема оперативной памяти. Поэтому, несмотря па на-
личие компиляторов с алгоритмических языков, при построении
программы всегда приходится учитывать особенности имеющейся
в распоряжении ЭВМ. Более того, зачастую мощность вычисли-
тельной машины диктует выбор тех пли иных алгоритмов. Преж-
де чем начать писать программу, исследователь должен решить
принципиальные вопросы порядка хранения и переработки ин-
формации. по возможности оптимально распределяя'ее между
8е
116
ГЛ. VI. РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ II \ ЭВМ
оперативной памятью, внешними быстрыми и медленными нако-
пителями.
Рассмотрим теперь подробно этапы расчета но методу копеч-
пых элементов, приведенные в § 1, обращая внимание па особен-
ности пх реализации на ЭВМ.
§ 43. Дискретизация и входная информация
Под дискретизацией (идеализацией) понимается пред-
ставление рассчитываемой области набором конечных элементов,
связанных в узлах. Нельзя дать конкретных указании, как раз-
бить тело на элементы, за исключением того, что в местах ожи-
даемого большого градиента искомых величин размеры элементов
должны быть меньше. Невозможно заранее определить, какое
число элементов будет достаточно для достижения заданной точ-
ности. Обычно этот вопрос решается па основании опыта проде-
ланных расчетов. С другой стороны, характер дискретизации для
небольших программ часто определяется возможностями этих
программ.
Разбитая па элементы область полностью описывается двумя
информационными массивами — глобальными координатами уз-
лов у{ и матрицей индексов элементов. Использование гло-
бальной координатной системы (т. е. общей для рассматриваемо-
го тела) предпочтительнее, чем задание размеров элемента, по-
тому что при решении задач в полярных плп цилиндрических
координатах для вычисления матрицы жесткости требуется рас-
стояние от оси симметрии.
Матрица индексов [Г] (этот термин введен в [50]) оп-
ределяет очертания элементов, а также позволяет установить,
как элементы связаны друг с другом. Под набором индексов дан-
ного элемента будем понимать глобальные номера узлов элемен-
та, выписанные в порядке возрастапия пх локальных номеров.
Глобальные номера узлов определяются порядком следования их
глобальных координат в соответствующем информационном мас-
сиве. Для того чтобы определить порядок локальной нумерации
узлов для линейных четырехугольных элементов, достаточно до-
говориться о направлении обхода вокруг элемента, для квадра-
тичных элементов нужно еще условиться и о том, с какого узла
начинать — с углового или промежуточного. Начало отсчета для
локальных номеров определяет положение локальной координат-
ной системы (см. § 3), поскольку по локальному номеру выби-
рается вид функции формы для данного узла.
Дадим пример разбиения некоторой области па шесть квад-
ратичных элементов (рпс. 76, а, глобальная нумерация узлов)
и соответствующей матрицы индексов (рис. 76. б). Здесь принято,
§ 43. ДИСКГГТИЗАЦПЯ Л ВХОДНАЯ ИНФОРМАЦИЯ
117
что локальная нумерация начинается с углового узла и продол-’
жается в направлении обхода элемента против часовой стрелки
(см. рис. 76, б). Элемент 4У вырожденный в треугольник, имеет
три совпадающих индекса, которые указывают, какие три узла
совмещены в одной точке. Матрица индексов имеет размерность
а)
Рис. 76. с) Пример дискретизации, б) соответствующая матрица индексов.
эле- мента МнОенсь/ 8
f 2 3 4 5 5 7
1 3 7 11 12 13 8 5 4
2 7 5 3 10 77 7 3 2
3 11 74 17 16 19 15 13 12
h 77 10 9 9 9 15 17 74
5 23 24 25 21 Т7 15 9 20
6 25 25 27 22 19 18 17 21
5)
/? X V, где R — количество узлов одного элемента, a W— общее
количество элементов. Матрица индексов позволяет поручить ма-
шине сборку системы уравнении равновесия. При этом необхо-
димы в конце концов индексы, связанные со степенями свободы
узла, а не номера узлов. Однако их нетрудно вычислить, если
условиться нумеровать степени свободы в определенном порядке,
например, сначала вдоль оси <т, а затем вдоль //.
После того как полностью описана геометрия рассчитываемого
тела, необходимо задать граничные условия. Как известно, МКЭ
имеет то важное преимущество перед некоторыми другими мето-
дами, что учет граничимх условий как в перемещениях, так и в
напряжениях чрезвычайно прост. Для задания граничных усло-
вий можно использовать как глобальную нумерацию, так и ло-
кальную в сочетании с номерами элементов. Использование той
пли иной возможности зависит от характера граничных условий
и от методики сборки системы уравнений. Например, если необ-
ходимо задать граничные условия для перемещений, направлен-
ных по осям глобальной координатной системы, то легче пользо-
ваться глобальными номерами узлов. При этом для сокращения
объема задаваемой информации можно применить следующий
простой прием. Если перемещение задано по оси х, то указыва-
ется положительный номер узла; если по осп у, то отрицатель-
ный. Впоследствии легко расшифровать эту информацию и пе-
рейти к глобальным номерам степеней свободы.
118
ГЛ. VI. РЕАЛИЗАЦИЯ МЕТОД/V КОНЕЧНЫХ ЭЛЕМЕНТОВ НА ЭВМ
С другой стороны, при задании граничных условий, сущест-
венно связанных с элементами, легче, вероятно, указывать номе-
ра элементов, чтобы потом не организовывать перебор членов
матрицы индексов для отыскания элементов. Например, если
нужно запретить перемещение в направлении, не совпадающем
ни с одной из глобальных координатных осей, то удобнее всего
это выполнить в момент вычисления матрицы жесткости. Поэто-
му при задании входной информации можно указать соответ-
ствующий помор элемента. Информацию о поверхностных нагруз-
ках также можно связать с номерами элементов, используя ло-
кальную нумерацию для определения стороны элемента, к кото-
рой приложена распределенная нагрузка.
К типичным внешним воздействиям относится также темпе-
ратурное поле. Наиболее эффективным путем определения напря-
женно-деформированного состояния от действия температуры
было бы последовательное решение с помощью МКЭ сначала
задачи теплопроводности, а затем па той же сетке элементов за-
дачи расчета напряжений. Однако исторически в настоящее вре-
мя сложилось такое положение, что зачастую задачи теплопро-
водности п расчета па прочность решаются разными исполните-
лями п, следовательно, по различным методикам и па различных
дискретных моделях. Поэтому возникает проблема ввода инфор-
мации о температурном поле. Можно предположить по крайней
мере два пути решеппя этой задачи. Во-первых, с помощью ин-
терполяции значения температур можно привести к узлам и за-
тем вывестп их на перфокарты нлп на какой-либо внешний нако-
питель. Во-вторых, для описания температурного поля можпо
построить функцию от глобальных координат. Второй путь для
конечно-элементной программы, вероятно, предпочтительнее, по-
скольку позволяет хранить информацию в более компактной
форме п легко подсчитывать температуру для любой точки, на-
пример для точки интегрирования. Довольно часто встречаются
ситуации, когда иоле температур зависит только от одной из
глобальных координат. Целесообразно предусмотреть этот случай
в программе.
Во входной информации также должны присутствовать дан-
ные о свойствах материалов, из которых изготовлена рассчиты-
ваемая конструкция. Для каждого материала задаются его физи-
ко-механические характеристики — модуль упругости, коэффици-
ент Пуассона, коэффициент температурного расширения, предел
текучести, вид диаграммы деформирования, плотность и др. Ко-
личество и вид этих характеристик зависят от конкретной поста-
новки задачи. Например, метод конечных элементов достаточно
просто позволяет учесть зависимость характеристик материала от
температуры. Если область состоит пз нескольких материалов,
то необходимо каким-либо образом указать принадлежность эле-
§ 43. ДИСКРЕТИЗАЦИЯ II ВХОДНАЯ ИНФОРМАЦИЯ
119
мента к данному материалу. Для этого можно внести массив,
ра {мерность которого равна числу копейных элементов. Числа,
стоящие в этом массиве, указывают номер материала. Другой
способ — расположить наборы индексов элементов таким обра-
зом, чтобы сначала они описывали все элементы из первого мате-
риала, затем из второго и т. д., а в информационном массиве
о материалах поместить номера элементов, которыми кончается
группа элементов из определенного материала.
До сих пор мы описывали информацию в такой форме, ко-
торую авторы [61] назвали оперативной. Оперативной является
такая информация, которую можно без значительной переработки
использовать в программе на всех этапах решения. Входная ин-
формация, задаваемая пользователем, может практически совпа-
дать с оперативной. Преимуществом такого ввода информации
является универсальность, недостатком — большой объем. Если
пользователь все-таки по каким-либо причинам остановился па
задании информации в почти оперативной форме, то ему полезно
применить некоторые прпомы ее сокращения. Приемы эти весьма
просты и зависят во многом от фантазии составителя программы.
Очевидным способом сокращения информации является, напри-
мер, опускание, т. е. замена пулями пли пробелами, координат
промежуточных узлов квадратичных элементов, если сторона эле-
мента — прямая. При интерпретации входных данных координаты
промежуточных узлов легко найти с помошыо интерполяции по
координатам угловых узлов. Если какие-либо целые числа в мас-
сиве образуют возрастающий или убывающий ряд, то можно
определить только первое из них, а остальные заменить па про-
белы. Для того чтобы отличить убывающий ряд от возрастающего,
можпо перед первым членом убывающего ряда поставить знак
минус. Возможно применить прием генерации опущенных дан-
ных, если в них наблюдаются повторения пли если они отлича-
ются друг от друга на постоянное слагаемое. Алгоритмы интер-
претации таких сокращенных данных весьма просты, но дают
заметный эффект, поскольку часто позволяют сократить коли-
чество задаваемых величин примерно вдвое, следовательно, вдвое
сокращается вероятность появления ошибки.
Несмотря на то, что оперативная информация должна быть
представлена в таком виде, чтобы ее можно было непосредствен-
но использовать с минимальной обработкой, желательно, чтобы
опа занимала в оперативной памяти как можпо меньший объем.
Достичь этого можно двумя путями. Первый — запись во внеш-
нюю память и считывание в некоторый рабочий массив части
информации, необходимой в данный момент времени. Обычно
наборы индексов элементов используются последовательно, поэто-
му их нетрудно хранить таким образом. С другой стороны, гло-
бальные координаты узлов требуются в процессе счета в случай-
ГЛ \1 14 АЛИ ЗАЦПП МЕюДЛ KOlir.’IJII.lX .».’Н МЕНТОВ н Л ЗГ.М
ном порядке, что вызывает усложнение логики алгоритма обмена
с внешними запоминающими устройствами, поскольку желатель-
но, чтобы транспортировка информации осуществлялась более
пли менее большими порциями. Второй путь экономии оператив-
ной памяти — сжатое хранение информации, т. е. упаковка нес-
кольких чисел в одно машинное слово. Например, в одно слово
ЭВМ БЭСМ-6 можно упаковать четыре целых положительных
числа, пе превосходящие 4095. Эго позволяет в четыре раза со-
кратить объем памяти, необходимый для размещения матрицы
индексов. Разрядность БЭСМ-6 позволяет хранить 12 значащих
десятичных цифр реального числа. Обычно представление коор-
динат не требует такой точности, поэтому объем оперативной
памяти для записи координат узлов можно сократить вдвое, если
упаковать две координаты узла в одно машинное слово. В фор-
тране — наиболее распространенном языке для написания конеч-
но-элементных программ — операции над частями слова не опре-
делены. Поэтому для написания подпрограмм, упаковывающих
и распаковывающих информацию, необходимо использовать язык
ассемблера.
Форматный ввод, характерный для фортрана, не всегда удо-
бен для записи исходной информации. В системе «Прочность-75»
для представления входных данных разработаны специальные
проблемно-ориентированные языки, которые позволяют вводить
бесформатные данные в произвольном порядке и пользоваться
принципом умалчивания. Принцип умалчивания состоит в том,
что если какие-либо данные пе были упомянуты во входном по-
токе, го нм присваиваются стандартные заранее обусловленные
значения. Создание транслятора с проблемпо-ориентпрованиого
языка — трудная задача. Поэтому рядовой проблемный програм-
мист может воспользоваться бесформатным вводом (соответствую-
щая подпрограмма есть в библиотеке БЭСМ-6), когда числа запи-
сываются в любом формате и отделяются друг от друга запяты-
ми. Однако бесформатный ввод нс дает возможности сокращен-
ной записи повторяющихся чисел, а также по позволяет вводитI»
различные массивы и переменные в произвольном порядке, что
характерно для проблемно-ориентированных языков.
Опишем простой прием, который применим для того, чтобы
ввод информации осуществлять способом, до некоторой степени
аналогичным проблемно-ориентированному языку. Напишем две
подпрограммы, которые будут осуществлять ввод исходных дан-
ных. Первая подпрограмма служит для того, чтобы с помощью
оператора DATA присвоить стандартные значения всем перемен-
ным и массивам, к которым применим принцип умалчивания.
Вторая подпрограмма пе является закопченной, опа может содер-
жать, например, только описания массивов. На ЭВМ БЭСМ-6
тексты программ обычно хранятся на магнитной лепте и могут
g ‘3. ДИСКРЕТИЗАЦИЯ И ВХОДНАЯ ИНФОРМАЦИЯ
121
исправляться с помощью средств редактирования, имеющихся в
операционной системе. Перед запуском программы на счет но
вторую подпрограмму’’ вставляются перфокарты, содержащие опе-
раторы DATA с соответствующими именами переменных, масси-
вов и списками присваиваемых значении. В этой подпрограмме име-
на желательно подобрать такие, чтобы они ясно указывали на
смысл задаваемых величии. Можно пе записывать операторы
DATA во входной информации, для этого они уже должны содер-
жаться в подпрограмме. Тогда с помощью средств редактирования
идентификаторы и списки дописываются в оставшиеся позиции
перфокарт пли переносятся па новую строку, а излишние опера-
торы DATA удаляются. Занесение информации, описанной в опе-
раторе DATA, в оперативную память производится па этапе
загрузки подпрограмм, поэтому нужно позаботиться, чтобы ре-
дактируемая вторая подпрограмма загрузилась после первой. Это-
го всегда можно добиться путем описания подпрограмм в опера-
торе EXTERNAL, а также с помощью динамической или стати-
ческой загрузки.
Если входная информация задается в оперативной или почти
оперативной форме» то она имеет слишком большой объем. На-
пример, для расчета ротора турбины, описанного в § 9, для зада-
ния матрицы индексов и координат узлов требуется около 2300
чпеел. С помощью простых приемов удается сократить количество
ненулевых чисел примерно до тысячи. Поэтому попятно стрем-
ление многих исследователей разработать приемлемые алгоритмы
автоматического построения сетки элементов. Примером генера-
тора сеток треугольных элементов является работа [41. Достаточ-
но легко автоматически построить сетку для тела некоторой
конкретной типовой формы. Некоторые большие программные
комплексы включают в себя множество подпрограмм для построе-
ния сеток в типовых областях. Одни пз путей генерирования
сеток — использование графических носителей информации. В этом
случае наиболее эффективный метод подготовки информации со-
стоит в организации диалога человек — машина с возможностью
непрерывно получать и корректировать графическую информа-
цию. В настоящее время рядовой пользователь пока еще лишен
возможности такого общения с ЭВМ н зачастую может рассчи-
тывать лишь па пакетную обработку своей задачи. В условиях
таких ограничений наиболее подходящей нам кажется схема ге-
нерирования сеток, предложенная О. К. Зенкевичем п Д. В. Фил-
липсом [165].
Основой схемы является представление идеализируемой обла-
сти в виде набора фрагментов, каждый из которых геометрически
представляет собой изопараметрическпп квадратичный элемент.
Фрагмент с постоянными шагами по локальным координатам %,
1] разбивается на прямоугольники, переход эго формулам (1.1)
122
ГЛ. VI. РЕАЛИЗАЦИЯ .МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ НА ЭВМ
к глобальным координатам позволяет получить набор узловых
точек, распределенных в соответствии с желаниями пользователя.
Т рансформация фрагмента из локальной координатной системы
в глобальную показана на рис. 77. Сдвиг промежуточных узлов
на любых сторонах фрагмента позволяет получить сгущение сет-
ки в той области, куда сдвигаются узлы. Однако слишком боль-
шой сдвиг промежуточных узлов может привести к тому, что
Рпс. 77. Получение координат узловых точек с помощью перехода от ло-
кальных координат с, т] к глобальным х, у.
некоторые узлы окажутся за пределами фрагмента. Вопрос о до-
пустимых положениях промежуточного узла на стороне рассмот-
рен в работе 1152]. Там показано, что если шаг разбиения по
локальной координате, лежащей вдоль данной стороны, равен
Д£, то область допустимых положений промежуточного узла оп-
ределяется неравенствами
1 — ДВ В З-Д?
2 (2 - Дё) Ь " 2 (2 - Д|) ’
Д$-2/п, (6.1)
где В — расстояние от промежуточного узла до углового, L —
длппа стороны, п — число разбиений по данной локальной коор-
динате (рис. 78). При сдвиге промежуточного узла па давний
стороне длины элементов. примыкающих к данной стороне, обра-
зуют арифметическую прогрессию. При большом чпсле разбиений
(/z ©о) неравенство (6.1) принимает вид
4
(G.2)
Таким образом, изопараметрнческое преобразование координат
баз труда позволяет получить глобальные координаты узлов в
каждом фрагменте, которые соответствуют прямоугольной сетко
в локальной координатной системе.
§ 43. ДИСКРЕТИЗАЦИЯ И ВХОДНАЯ ИНФОРМАЦИЯ
123
Для указания о том, как фрагменты состыкованы друг с дру-
гом, служит двумерный массив, называемый ключевой дпаграм-
мой. Элементами ключевой диаграммы могут быть номера фраг-
ментов. Если фрагмента не существует, то в соответствующем
месте ключевой диаграммы проставляется пуль. Геометрия фраг-
мента определяется но матрице индексов, которую мы применяли
для обычных квадратичных элементов. Пример деления области
па фрагменты п ключевая диаграмма показапы па рпс. 79.
Рис. 78. Фрагмент для построения
сетки в глобальных координатах.
Параметр В характеризует поло-
жение промежуточного узла.
Рнс. 79. а) Деление области па фраг-
менты, б) соответствующая ключе-
вая диаграмма.
Узлы, получающиеся в результате разбиения, нумеруются
вдоль строк или столбцов ключевой диаграммы. Четыре узловые
точки, соответствующие пересечению двух линий § = const с дву-
мя линиями т| = const, можно использовать в качестве вершин
линейного четырехугольного элемента. Если необходимо получить
треугольные элементы, то каждый четырехугольник нужно раз-
делить мепьшей диагональю на два треугольника. Для получения
квадратичного элемента с восемью узлами можно объединить
четыре линейных четырехугольника и исключить лишнюю узло-
вую точку в центре элемента. При этим в общем случае следует
откорректировать положение промежуточных узлов, так как эти
узлы могут быть расположены не в цептро стороны.
Описанная методика позволяет строить сетки для довольно
сложных областей, образуя в нужных местах сгущения. Основ-
ные недостатки этой методики состоят в том, что в каждой вер-
шине, за исключением некоторых граничных точек, может схо-
диться не более четырех элементов в виде четырехугольника
а также в том, что количество разбиений должно быть постоянно
вдоль каждой строки и столбца ключевой диаграммы. Пути прео-
доления этих недостатков, вероятно, состоят в объединении раз-
121
ГЛ. VI РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ НА ЭВМ
личных фрагментов,, как сгенерированных автоматически, так и
заданных вручную.
Поскольку количество входной информации для конечно-эле-
ментных программ велико, большое значение также приобретает
автоматизация проверки этой информации. Такой контроль мо-
жет быть эффективно сделай с помощью программы, описанной
в работе [99]. Эта программа па стандартном алфавитно-цифро-
вом печатающем устройстве позволяет распечатать любую сетку,
состоящую из различных типов элементов, пронумеровать эле-
менты, напечатать положения узлов с номерами пли какой-либо
другой цифровой информацией.
В заключение даппого параграфа коснемся вопроса о влиянии
порядка нумерации узлов па структуру матрицы системы линей-
ных алгебраических уравнений равновесия. Поскольку каждый
конечный элемент связан с ограниченным числом других элемен-
тов, то матрица системы уравнений (глобальная матрица жестко-
сти) всегда бывает редкозаполпеппой. При случайном порядке
нумерации узлов (этот порядок определяется последовательностью
задания координат в соответствующем массиве) ненулевые эле-
менты распределены в глобальной матрице жесткости также
случайным образом. Обычно при решеппп системы уравнений
желательно, чтобы ненулевые коэффициенты были сгруппирова-
ны вблизи главно!! диагонали матрицы, т. е. образовывали лепту.
Тогда, кроме порядка, матрицу можно характеризовать шириной
(точнее, полушириной) ленты, которая равна расстоянию от наи-
более удаленного ненулевого элемента матрицы до главной диа-
гонали. Ширина ленты матрицы зависит от максимальной разно-
сти узлов при переборе всех элементов. Она может быть опреде-
лена но формуле
II = 2 (maxTO (max ТтЛ — min ТтЛ) Ч~ 1).
(G.3)
Здесь индекс т означает помер элемента, индекс i — номер узла
в местной системе нумерации, Тт( — элемент матрицы индек-
сов [Т]. Предполагается, что каждый узел пмеет две степени сво-
боды. Изменения ширины ленты матрицы можно добиться с по-
мощью изменения порядка нумерации узлов. Так, если сетка
элементов можег быть отображена на некоторую прямоугольную
область, состоящую из квадратных элементов, то для получен ня
ленты минимальной ширины нужно нумеровать узлы последова-
тельно вдоль прямых в том направлении, где число элементов
меньше. Во многих реальных случаях порядок нумерации узлов
неочевиден. В этом случае можпо пронумеровать узлы произволь-
но, а работу по перенумерации узлов поручить ЭВМ. Способы
минимизации ширины ленты описаны, например, в работах
[75, 76].
§ 44. ВЫЧИСЛЕНИЕ МАТРИЦ ЖЕСТКОСТИ ЭЛЕМЕНТОВ
§ 44. Вычисление матриц жесткости элементов
Вычисление, матриц жесткости изопара метрических элементов,
исключая простейшие, возможно только с применением числен-
кого интегрирования выражения (1.9). Известны различные ме-
тоды интегрирования, однако в случае интегрирования матриц
жесткости наиболее эффективно применение гауссовых квадра-
тур, поскольку они обеспечивают наивысшую точность при за-
данном числе точек интегрирования.
Вычисление матрицы жесткости плоского элемента сводится
к последовательному вычислению двойного интеграла от функции
локальных координат t, ц:
1 1
7 = J р(с,п)<ЗД- (6.4)
-1 -1
Дважды применяя формулу Гаусса для интегрирования функции
одной переменной, получаем
п п
7 = S X' (6.5)
1=1 j=xl
где Wi — веса, а тр — абсциссы точек интегрирования, п —
число точек интегрирования в каждом направлении.
В действительности при интегрировании матрицы жесткости
проводить двойного суммирования не требуется. Простейшая вы-
числительная процедура сводится к тому, что подынтегральная
функция последовательно подсчитывается в каждой точке интег-
рирования и умножается па вес, который, например, в формуле
(6.5) равен Точки интегрирования в локальных координатах
ио обязательно должны образовывать некоторую квадратную
сетку, как всегда получается, когда дважды (или трижды в объ-
емном случае) применяется одномерное правило Гаусса. Особен-
но эффективна такая процедура в трехмерном случае [119], где
она примерно вдвое позволяет сократить число точек интегриро-
вания но сравнению со стандартной п X пХ п-точечпой формулой.
Как уже упоминалось в § 4, для интегрирования матрицы
жесткости двумерного квадратичного элемента достаточно при-
менение четырехточечпого правила Гаусса. Для линейных че-
тырехугольных элементов сходимость обеспечивается при интегри-
ровании по одноточечному правилу, т. е. просто при вычислении
матрицы жесткости в геометрическом центре элемента.
Однако исследования показали [140], что применение такого
приема может па реальных сетках привести к значительным по-
грешностям. Поэтому линейные элементы обычно также прихо-
дится интегрировать по двучленному правилу в каждом направ-
лении, что сильно снижает эффективность их применения. Тем
не менее линейные четырехугольники могут быть полезны в том
126
ГЛ. VI. РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ НА ЭВМ
случае, когда опи применяются совместно с болсо точными квад-
ратичными элементами. Целесообразно тогда расположить линей-
ные элементы в местах слабого изменения искомой функции. Это
позволяет снизить число степенен свободы, а иногда и ширину
ленты матрицы уравнений равновесия, и в то жо время не ус-
ложняет сетку.
Время, затрачиваемое на подсчет матриц жесткости конечных
элементов, обычно составляет не слишком большую часть от об-
щего времени решения задачи, но оно увеличивается в случае
применения более сложных элементов. Кроме уменьшения вре-
мени вычисления матриц жесткости за счет применения наи-
меньшего возможного числа точек интегрирования, можно исполь-
зовать прием рационального выполнения операций при интегри-
ровании. Матричная форма представления матрицы жесткости
(1.9) является очень наглядной, но весьма неэффективна при
расчетах. Эффективная схема организации вычисления численно
интегрируемой матрицы жесткости предложена в работе [1061.
Эта схема основана па тензорных обозначениях величин. Пере-
писывая формулы для интерполяции перемещений (1.2) в тензор-
ных обозначениях, имеем
U* = (6-6)
Здесь верхний индекс означает степень свободы, г. е. направле-
ние соответствующей глобальной координатной оси, а нижний —
номер узла в системе локальной нумерации. Подразумевается
суммирование по повторяющимся индексам. Тогда для матрицы
жесткости в декартовых координатах нетрудно получить следую-
щее представление для члена матрицы жесткости:
кУп= (6.7)
dxh дх1 7
где EiJ™ — компоненты тензора модулей упругости. Матрица жест-
кости в такой записи — это четырехмерный массив. Обычный
двумерный массив (Й (1.9) получается пз (6.7) с помощью опус-
кания верхних индексов, относящихся к степеням свободы, и уве-
личения в два раза областей изменения нижних индексов. Эта
операция эквивалентна переходу от узловой нумерации к номе-
рам степеней свободы.
^Численное интегрирование (6.5) состоит в том, что некоторый
набор вычислений повторяется (с изменением части аргументов)
для каждой точки интегрирования. Число операций можно сни-
зить, не вычисляя повторно ужо подсчитанные величины, а так-
же вынося за знак интеграла такие члены, которые не зависят
от координат точки интегрирования. Еслп компоненты тензора
модулей упругости постоянны по объему данного элемента, то
§ 44 ВЫЧИСЛЕНИЕ 31АТГИЦ ЖЕСТКОСТИ ЭЛЕМЕНТОВ
127
удобнее сначала произвести вычисление массива
ПП -
бх* дх*
(6.8)
Для этого нужно воспользоваться формулой численного интегри-
рования (6.5). Затем результаты интегрирования следует умно-
жить на упругие константы и тем самым получить члены матри-
цы жесткости
?.Ъ ___ /гбА/трМ
Л7ИП — -Ь 7ПМ*
(6.9)
Как показали расчеты па ЭВМ [ 106], применение выражений
(6.8), (6.9) для подсчета матрицы жесткости линейного трехмер-
ного элемента по правилу Гаусса 2X2X2 снижает время счета
в четыре раза ио сравнению со стандартной матричной методи-
кой. Если упругие свойства переменны, то эффект сокращения
объема вычислений не столь велик. Однако выполнение опера-
ций по схеме (6.7) занимает около 65% времени обычной матрич-
ной методики. Прп получении матрицы жесткости в полярных
пли цилиндрических координатах под интегралом в выражении
(6.7) будут стоять другие члепы, по в принципе вычисления мо-
гут быть организованы по рассмотренной методике. Поскольку
матрица жесткости симметрична, то достаточно при интегриро-
вании получать только члены, лежащие выше пли ниже главной
диагонали вместе с членами на диагонали.
Как мы видим, один из общих принципов уменьшения време-
ни счета — не повторять уже проделанные вычисления. Наиболее
очевидно применение этого принципа в том случае, когда все
тело состоит пз одинаковых элементов. Здесь достаточно одип раз
сформировать матрицу жесткости элемента п все время пользо-
ваться сю при сборке. Если идеализированная конструкция со-
держит небольшое количество групп одинаковых элементов, то
можно воспользоваться тем же приемом. Но такие случаи не
типичны для расчетов, особенно для сеток, состоящих из сложных
элементов. Обычно встречается достаточно много различных эле-
ментов и сокращение вычислений не компенсируется усложне-
нием логики программы. Поэтому в общем случае следует иметь
в виду, что придется считать матрицы жесткости всех элементов.
Сформированные матрицы жесткости всех элементов можно от-
править во внешнюю память и хранить до того момента, как за-
кончится сборка системы уравнений равновесия. Однако такой
образ действий нельзя признать удовлетворительным, поскольку
набор матриц жесткости требует значительного объема памяти
для своего хранения, хотя и позволяет избежать повторного вы-
числения этих матриц. Необходимости повторного вычисления
ГЛ. VI. РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ НА ЭВМ
матриц жесткости не возникает, если вся система уравнения
равновесия размещается в оперативной памяти. Прп этом сборка
системы уравнений заключается в последовательном переборе
элементов с вычислением их матриц жесткости и отправлении
коэффициентов этих матриц по соответствующим адресам. Одного
прохода по всем элементам достаточно для полного формирова-
ния системы.
Иначе обстоит дело, если система уравнений равновесия
велика по объему п формируется поблочно, а блоки пос-
ле завершения сборки отправляются на хранение во внешние
запоминающие устройства. При этом часто оказывается, что
часть коэффициентов матрицы жесткости данного элемента долж-
на отправиться в формируемым блок, а оставшиеся — в другие
блоки, для которых еще нет места в оперативной памяти. Тогда
при формировании этих блоков придется повторно вычислять ту
же матрицу жесткости. Причем частота повторных вычислений
возрастает при использовании более сложных элементов с боль-
шим числом узлов, поскольку это вызывает увеличение ширины
лепты матрицы и уменьшение числа уравнений, одновременно
формируемых в одном блоке. Рационально при переборе индек-
сов элементов вычислять только те коэффициенты матрицы жест-
кости, которые потребуются для сборки данного блока уравне-
ний. Соотношения (6.7)—(6.9) легко позволяют это сделать, что
является еще одним их преимуществом.
Если в программе рассматривается и температурная нагрузка,
то интегрирование термического вектора (1.20) удобно включить
в ту же подпрограмму, в которой вычисляется матрица жестко-
сти. Для термического вектора нетрудно получить формулу, ана-
логичную соотношению (6.7):
hl,n = JEijM 6”аЬТ dV. (6.10)
Здесь а — коэффициент температурного расширения, ДТ — при-
ращение температуры в данной точке, индексы у символа Кро-
некера б’7 стоят сверху, так как нижние индексы связаны с ло-
кальными номерами узлов. Если упругие свойства материала по
объему данного элемента постоянны, то члены KiJkl9 как и ранее,
выносятся за знак интеграла, а умпоженпо на них производится
после окончания интегрирования.
Для большей универсальности программа может содержать
подпрограммы для вычисления матриц жесткости элементов раз-
личных типов. Вероятно, нецелесообразно пметь все такие под-
программы в составе программы во время счета каждой задачи.
Лучше перед решением конкретной задачи отредактировать про-
грамму, включив в нее возможность использования только тех
§ 45. СБОРКА СИСТЕМЫ УРАВНЕНИЙ РЛВПОВЕСПЯ
129
элементов, которые будут встречаться. Естественно, что подпро-
граммы формирования матриц жесткости должны удовлетворять
некоторым соглашениям о связях, чтобы быть взаимозаме-
няемыми.
§ 45. Сборка системы алгебраических уравнений равновесия
Сборкой называют процесс суммирования реакции в узлах
элементов по направлению глобальных координатных осей. По-
скольку реакции представляют собой коэффициенты матриц жест-
кости элементов, а в одном узле сходится обычно несколько эле-
ментов, то сборка фактически состоит в том, чтобы для каждого
узла по каждому пз направлений степеней свободы просуммиро-
вать соответствующие коэффициенты матриц жесткости несколь-
ких элементов и отправить эту сумму по нужному адресу в па-
мять, предназначенную для размещения системы уравнений рав-
новесия. Матрицу системы уравнении равновесия тола называют
также глобальной матрицей жесткости.
Формально проблема сборки решается с помощью формулы
(1.23), которая предполагает перемножение трех матриц для каж-
дого элемента. Однако, как мы уже видели, матричные формулы
прекрасно подходят для изложения теории метода конечных эле-
ментов. но далеко не всегда эффективны при программной реали-
зации метода. При вычислении глобальной матрицы жесткости ио
формуле (1.23) большую часть времени ЭВМ будет занята бес-
полезным перемножением и суммировал нем нулей. Поэтому
сборку почти всегда производят с помощью матрицы индексов
[50, 124].
Для того чтобы пояснить сущность метода, предположим вна-
чале, что мы имеем бесконечную оперативную память и можем
в ней поместить полностью глобальную матрицу жесткости в впде
двумерного массива GK(N, N), где N —- число стопепсй свободы
дискретной модели тела. В качестве информации после ввода п
переработки исходных данных имеем матрицу индексов по сте-
пеням свободы IT(M, NEL); М -—число степеней свободы элемен-
та, NEL — количество элементов дискретной модели. Пусть под-
программа STIF(N, ЕЮ в результате своей работы дает матрицу
жесткости N-ro элемента ЕК(М, М). Алгоритм сборки состоит в
том, что для каждого элемента попарно следует перебрать все
индексы данного К-го элемента (включая и тот случай, когда
индекс образует пару сам с собой). Пара локальных номеров сте-
пеней свободы I, J дает адрес (т. е. строку и столбец) числа, ко-
торое должно быть выбрано пз матрицы жесткости элемента,
а пара индексов 1Т(1, К), IT(J, К) определяет адрес в глобальной
матрице жесткости, по которому должен быть просуммирован вы-
бранный коэффициент матрицы жесткости элемента. 11а языке
9 Е М. Морозов, Г. П. Никишков
130 ГЛ. VI. РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ НА ЭВМ
фортран алгоритм сборки может быть реализован в виде такой
подпрограммы:
SUBROUTINE ASMBL (GK, EK, IT, N, М, NEL)
DIMENSION GK(N. N) ЕК(М, М), IT (AL NEL)
DO 100 I = 1, N
DO 100 J = 1, N
100 GK(I, J) = 0.0
DO 200 Ki== 1, NEL
CALL STIF(K, EK)
DO 200 I = 1, M
IG = IT(I, K)
DO 2(Ю J = 1, M
JG = IT (J, K)
200 GK(IG, JG) .= GK(IG, JG) + EK(I, J)
RETURN
END
одесь предполагается, что первый индекс дает номер строки,
а второй — номер столбца. В приведенной подпрограмме в цикле
обрабатываются наборы индексов элементов в порядке возраста-
ния номеров элементов. Следствием этого будет то, что глобальная
матрица жесткости будет заполняться случайным образом. Как
уже упоминалось, глобальная матрица жесткости является ред-
ь’озаполпепной. Очевидно, что вследствие ограниченное гп опера-
тивной памяти невыгодно (в подавляющем большинстве задач
просто невозможно) хранить глобальную матрицу жесткости
ри с. 80. Лепточвая структура
глобальной матрицы жестко-
СТИ.
в виде двумерного массива N XN
чисел. Способ хранения, а следова-
тельно, и алгоритм сборки глобаль-
ной матрицы жесткости зависят не
только от конкретного типа ЭВМ,
по п от подпрограммы, с помощью
которой будет в дальнейшем осу-
ществляться решение сформирован-
ной системы уравнений равновесия.
Хотя способы решения систем •ли-
нейных уравнений будут рассмот-
репы в следующем параграфе, мы
вынуждены частично использовать
те сведения,
дальнейшем.
которые изложим в
1}сли решение системы проводится прямым методом с уче-
том симметричного и ленточного характера глобальной матрицы
жесткости, по предполагается использование только оператив-
ной памяти, то элементы глобальной матрицы жесткости лучите
расположить в одномерном массиве GK(N1), размерность кото-
§ 45. СБОРКА СИСТЕМЫ УРАВНЕНИИ РАВНОВЕСИЯ
131
рого равна произведению ширины ленты матрицы LH на коли-
чество неизвестных N. Тогда подпрограмма, собирающая верх-
нюю симметричную часть ленты с построчном записью (рпс. 80),
может выглядеть так:
SUBROUTINE ASMBL1 (GK, EK, IT, N, Nl, М, LU, NEL)
DIMENSION GK(N1), ЕК(М, М), ГГ(М, NEL)
DO 100 I = 1, N’l
100 GK(I) = 0.0
DO 300 К = 1, NEL
CALL STIF(K, EK)
DO 300 I = 1, M
1G = IT (I, K)
DO 300 J = 1, 4
JG = IT (J, K)
IF(IG — JG) 200, 200. 300
200 L = LU • (IG — 1) + JG — IG + 1
GK(L) = GK(L) + EK(I, J)
300 CONTINUE
RETURN
END
Эта подпрограмма формирует массив GK, подразумевая, что
длина строки постоянна, т. е. верхняя ленточная часть матрицы
дополнена пулевым треугольником. Элементы, лежащие левее
главной диагонали, пропускаются, если помер строки IG больше
номера столбца JG. Оператор с меткой 200 записан в разверну-
том виде, чтобы было яспо, как находится адрес L в массиве
GK, по которому необходимо отослать данный коэффициент мат-
рицы жесткости элемента. Если алгоритм решения такой, что
требует в качестве входной информации симметричную часть
лепты без дополнения пулевым треугольником, то после опера-
тора с меткой 200 следует поместить выражение
IFGG.GE.N - LH + DL =*
= L—(I —N + LH—1) * (I-N + LII-2)/2.
В силу симметрии глобальной матрицы жесткости, сформирован-
ная но строкам верхняя часть ленты эквивалентна сформирован-
ной по столбцам нижней части лепты, которая показана па
рпс. 80 вертикальной штриховкой. Как при построчном, так и
при постолбцовой занпсн симметричной части ленты каждая
строка пли столбец начинается с коэффициента, стоящего на
главной диагонали.
Разместить всю симметричную часть ленты глобальной мат-
рицы жесткости в оперативном запоминающем устройстве при
решении реальных задач удается весьма редко. Однако, дума-
9*
132
ГЛ. Л I. РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ ПА ЭВМ
Рис. 81. Запись глобаль-
ной матрицы жесткости
с переменной шириной
ленты по столбцам.
ется, что программы с такой оргаплзаппей храпения информации
могут иметь право ла существование. Во-первых, у современных
ЭВМ наблюдается тенденция к значительному увеличению объе-
ма оперативной намяты. Во-вторых, существуют задачи, для ко-
торых не требуются дискретные модели с больным числом сте-
пеней свободы. Например, можно себе представить некоторую
диалоговую программу с отображением ипф ормации па дисплее,
с помощью которой конструктор в необходимых случаях может
выполнять лриклдочпыс расчеты в процессе проектирования.
При расположении коэффгщиентов
глобальной матрицы жесткости в маг-
нитном оперативном запоминающем уст-
ройстве (МОЗУ) выгодно избавиться от
части лишней нулевой информации, со-
держащейся в лепте. Дело в том, что
ширина ленты бывает почти постоянной
только в том случае, когда сетка элемен-
тов может быть отображена на прямо-
угольник в локальных координатах. Та-
кне сетки нетипичны для реальных рас-
четов , поэтому ширина лепты в общем
является переменной величиной. С^тце-
ствуют алгоритмы решения, учитываю-
щие этот факт. Например, в работе [100J
обрабатывающая матрицу системы урав-
нений в виде, представленном па рис. 81. Система хранятся по
столбцам, каждый столбец начинается с элемента главной диа-
гонали и оканчивается самым верхним ненулевым элементом
данного столбца. Факой способ хранения сэмметрщшой части
глобальной матрицы жесткости имеет особые преимущества в
случае нерегулярной сетки со Сгущениями в местах концентра-
ции напряжений. Для характеристики массива, в котором хра-
нится коэффициенты глобальной матрицы жесткости, уже недо-
статочно только скалярных параметров. Необходимо ввести мас-
сив целых величин, характеризующих расположение элементов,
стоящих па главной диагонали. Ниже приводится подпрограмма
для нахождения массива LV(N), I-й элемент которого указыва-
ет, какой помер имеет диагональный элемент I-го столбца. Ис-
пользуются обозначения, уже введенные в данном параграфе:
SUBROUTINE NOLV(IT, LV, N, M, NEL, Nl)
DIMENSION (T(M NEL), LV(N)
LU 100 I « 1, N
100 LV(I) = 0
DO 300 К — 1, NEL
DO 300 1 =i 1, M
IG = IT(l, K)
приведена программа,
§ 45. СБОРКА СИСТЕМЫ УРАВНЕНИЙ РАВНОВЕСИЯ
MX = О
DO 200 J = 1, М
200 МХ=МАХ0(МХ, IG - IT(J, К))
300 LV(IG) = MAX0(MX, LV(IG))
LV(1) = о
IG -= 1
DO 400 I = 2, N
MX.= LV(I) + 1
LV(I) == LV(I — 1) + IG
400 IG = MX
Nl = LV(N) + IG
R ET I RN
END
Переменная Nl, также получающаяся в результате счета»
равна количеству элементов в массиве коэффициентов глобаль-
ной матрицы жесткости GK(N1). Для формирования этого мас-
сива в виде, показанном на рис. 81, пригодна следующая подпро-
грамма:
SUBROUTINE ASMBL2(GK, EK, IT. LV, N, Nl, M, NEL)
DIMENSION GK(N1), FK(M, M), IT(M, NEL), LV(N)
DO 100 I = 1, Nl
100 GK(I) = 0.0
DO 300 К = 1. NEL
CALL STIF(K, EK)
DO 300 I = 1, M
IG = IT(T, K)
DO 300 J = 1. M
JG = IT (J, K)
IF(IG —JG) 200, 200, 300
200 L = LV(JG) 4- JG — IG
GK(L) = GK(L)+EK(I, J)
300 CONTINUE
RETURN
END
Гис. 82. Блочное ттредставлеппе ленточной
симметричной матрицы.
Если же симметричная
часть ленты глобальной
матрицы жесткости в оперативной памятп не помещается, то
следует формировать ее блоками и отправлять на хранение во
внешние запоминающие устройства. Естественно, что блоки
могут быть выделены из лепты по разному. Наиболее
простой и довольно распространенный способ — это деление сим-
метричной части ленты па блоки, каждый из которых состоит из
целого количества строк матрицы (рпс. 82). Для определенпя
блока, кроме величин, уже введенных ранее, необходимо ука-
134
f.'L VI. РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ ПЛ ЭВМ
зать номер первого NFIRST и номер последнего NLAST уравне-
нии в блоке. Чтобы избегать повторного вычисления матрицы
жесткости, предположим, что в пашем распоряжении имеется
подпрограмма-функция COEF(I, J, Ю| вычисляющая коэффици-
ент па пересечении 1-й строки и J-ro столбца патрицы жесткости
К-го 'лемепта. Следующая подпрограмма фбрмируе-т блок с по-
стоянно!' ширппоп лепты, записывая его в одномерный массив
GK(N1):
SI BROUTINE ASMRL3(GK. IT, NL M, NEL. NFIRST, NLAST, LII)
DIMENSION GK(N1). lT(Mt NEL)
DO WO I =:1, Nt
100 GK(I) = 0.0
DO 400 К = 1. NEL
DO tOO I = 1, M
1G = 1T(L K)
IF{IG.LiT.NFlRST.OR.IG.GT.NLAST) GOTO 400
DO 300 J&1, M
JG — IT(J, K)
IFfiG—JG) 200, 200, 300
200 L = (IG — NFIRST) <LH 4- JG — IG -[ 1
GK(L) .= GK(L) -f-COEF(I, J, K)
300 CONTINUE
400 CONTINUE
RETURN
END
В случае решения системы Уравнений итерационными мето-
дами для выполнения операции в принципе необходимо хране-
ние только ненулевых коэффициентов. Нужно отметить, что
и при решении систем уравнений прямыми методами не все ко-
эффипиенты внутри ленты становятся ненулевыми в процессе
решения. N чет этого обстоятельства возможен, по значительно
усложняет алгоритм. Применение итерационных методов летко
позволяет выполнять операции только с ненулевым! коэффици-
ентами, что является основным принципом сокращение потреб-
пости в памяти и времени счета 195]. Упакованные формы хра-
нения матриц подробно описаны Р. Тыоарсоно.м [671. Для эффек-
тивного применения упакованных форм хранения нужно, чтобы
количество ненулевых «элементов было не только значительно
меньше квадрата числа уравнеипп в системе, по также, чтобы
упакованная форма храпения давала преимущества в экономии
памяти по сравп 'шпо с ленточной формой хранения. Проиллюст-
рируем это примером.
Пусть мы имеем регулярную сетку липе^шых четырехуголь-
ных элементов с двумя степеням!: свободы в каждом узле, кото-
рая показана на рпс. 83. Предположим также, что для упроще-
§ 45. СБОРКА СИСТЕМЫ УРАВНЕНИЙ РАВНОВЕСИЯ
135
Рис. 83. Регулярная
сотки л инок пых четы-
pi «угольных элемен-
тов. В наименьшем
измерении располо-
жено L элементов.
дпя итерационного алгоритма решения мы в упакованной форме
хотим хранить все коэффициенты системы уравнении без учета
симметрии. Если мы формируем уравнение с помором, совпадаю-
щим с тлобальпым номером одной из степеней свободы узла, от-
меченного па рпс. 83 буквой А, то в уравнение войдет столько
коэффициентов, сколько узлов имеет подоб-
ласть из четырех элементов с центром в
узле А. Ла рисунке эти узлы отмечены
кружками. Поскольку таких узлов девять
и каждый имеет до две степени свободы,
то уравнение будет иметь 18 ненулевых
коэффициентов. Если узел лежит на границе
регулярной дискретной модели из лилей-
ных четырехугольников, то соответствующее
уравнение будет содержать 12 отличных от
нуля членов, а рели в угловой точке грани-
цы, то всего лишь восемь. При хранении
уравнении в симметричной ленточной форме
на каждое уравнение понадобится память,
равная ширине лепты, которая для данной
сетки равна
Я = 2(£, + 3), (6.11)
г ie L — число элементов в наименьшем измерении сетки.
Пусть для храйццня в упакованной форме мы будем на каж-
дый коэффициент тратить три ячейки памяти, указывая в пих
величину и номера строки и толбца, на пересечении которых он
расположен. Тогда без учета граничных узлов применение у на-
кованной формы хранения будет более выгодно при L> 24 и не-
выгодно для / менее 24. Конечно, при упаковке коэффициентов
можно сократить количество информации. Например, все воли-
чины коэффициентов можно расположить в одномерном массиве,
другой одномерный массив такого же размера использовать для
указания номеров столбцов, в которых тоят коэффициенты. Тре-
тий массив будет указателем места расположения первого коэф-
фициента данного уравнения в массиве пх величин. Тогда па
каждое уравнение с 18 лепулевышг коэффициентами понадобят-
ся 39 слов оперативной памяти. Приравнивая это число выраже-
нию (6.11), получаем, что упакованную форму храпения выгодно
применять при числе элементов L в наименьшее измерении,
равном 16 и более.
Рассмотрения аналогичных сеток, состоящих из квадратичных
элементов, показывает, что обычно в одном уравнении находятся
42 ненулевых коэффициента. Ширина ленты матрицы для квад-
ратичных элементов равна
Я = 2(3£ + 5).
(6.12)
13(1
ГЛ. VL РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ НА ЭВМ
'Тогда, (ч-ли на указание адреса каждого коэффициента тратить
два машинных слова, то упакованную форму храпения выгодно
применять при £, равном пли более 20. При адресации начала
уравнений с помощью матрицы указателя упакованная форма
храпения эффективнее ленточной симметричной при L = 13
и более.
Хотя у упакованной формы храпения есть еще резервы эко-
номии памяти (например, упаковка нескольких чисел — указате-
лей адресов в одну ячейку памяти), тем не менее очевидно, что
при решении двумерных задач на сотках с не очень большим
числом узлов упакованная форма хранения не имеет существен-
ных преимуществ по сравнению с ленточной симметричной.
Алгоритмы формирования упакованной глобальной матрицы
жесткости несколько сложнее ленточных. Очевидно, что можно
в упакованной форме формировать уравнение за уравпеппем,
перебирая каждый раз всю матрицу индексов, если заранее не-
известно. где искать индексы элементов, примыкающих к данно-
му узлу. Второй способ состоит в организации единственного
цикла по элементам (предполагаем, что вся упакованная матри-
ца помещается в МОЗУ) и отсылке соответствующих членов.
При этом, поскольку структура матрицы заранее по известна, не
удается избежать многократных сдвижек группы чисел в масси-
ве— указателе столбцов и массиве величин коэффициентов.
Процесс сборки кроме формирования глобальной матрицы
жесткости включает в себя наложение граничных условий в на-
пряжениях и перемещениях. Приложенные внешние распреде-
ленные усилия приводятся к узлам. Затем узловые силы (в том
числе и фиктивные) с помощью матрицы индексов собираются
в правой части. Пусть различные нагрузки (поверхностные, объ-
емные, фиктивные, температурные) приводятся к узлам п распо-
лагаются в векторе нагрузки К-го элемента ЕН(М) с помощью
подпрограммы VLOAD(K, ЕН). Тогда глобальный вектор нагруз-
ки GH(N) можпо вычислить по такой подпрограмме:
SUBROUTINE ASMBL4(GH, Eli, IT, N, M, NEL)
DIMENSION GII(N), EH(M), IT(M, NEL)
DO 100 I = d, N
100 GH(I) = 0.0
DO 200 К = 1, NEL
CALL VLOAD (K, EH)
DO 200 I =1, M
IG = IT (I, K)
200 GII(IG) = EH(I)
RETURN
END
§ 45. СБОРКА СИСТЕМЫ УРАВНЕНИЙ РАВНОВЕСИЯ
137
Как видим, процедура сборки глобального вектора нагрузки
пз векторов нагрузки отдельных элементов состоит в переборе
индексов элементов и отправлении коэффициента с данным ло-
кальным номером по адресу, определяемому глобальным номе-
ром. Такую сборку удобно производить в том случае, если исход-
ные данные о нагрузке связаны с номерами элементов пли под-
считываются вместе с матрицей жесткости (как, например,
термический вектор). Если же усилия уже отнесены к глобаль-
ным номерам узлов или степеней свободы, то весь процесс
сводится к отправлению таких членов по адресам. При задании
граничных условий в перемещениях наиболее часто встречается
случай жесткого закрепления. Исключение жестко закрепленной
степени свободы из матрицы индексов (замена нулем) и пере-
нумерация (вычисление единицы) всех следующих глобальных
номеров степенен свободы приводят к удалению пз глобальной
матрицы жесткости одной строки и одного столбца и, следова-
тельно, экономят память. Тем пе менее, по нашему мнению, та-
кой способ нерационален, поскольку создает некоторые неудоб-
ства при программировании. Другой способ моделирования жест-
кой заделки данной степени свободы — это обнуление столбца
и строки, а также коэффициента в правой части с номером за-
прещаемой степени свободы. Элемент главной диагопали, стоя-
щий ла пересечении обнуленных строкп и столбца, следует поло-
жить равным единице.
Несколько сложнее реализуется задание ненулевого переме-
щения. В этом случае кроме обнуления строкп и столбца и зада-
ния на главной диагонали единицы должен быть видоизменен
глобальный вектор нагрузки. Это видоизменение состоит в том
[16], что пз правой части вычитается столбец глобальной матри-
цы жесткости (впоследствии обнуляемый), умпожеппый па за-
данное перемещение, а коэффициент с номером задаваемого пе-
ремещения полагается равным нужной величине.
В работе [16] предложен другой чрезвычайно простой способ
задания перемещений. Он состоит в том, что диагональный эле-
мент глобальной матрицы жесткости заменяется на некоторое
большое число (в зависимости от возможностей ЭВМ), а в пра-
вую часть ставится член, равный произведению этого большого
числа на величину заданного перемещения. Недостатком данного
метода является то, что после решения соответствующее неиз-
вестное будет лишь приближенно равно заданному граничному
условию.
Наиболее сложно осуществляется задание перемещений по
направлению, не совпадающему с направлениями глобальных
осой координат х, у (рис. 84). Наложение таких граничных усло-
вий можно выполнить па уровне формирования матриц жестко-
сти элементов, которым принадлежат узлы с нулевыми переме-
138
ГЛ. VI. РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ НА ЭВМ
[ новую систему
Рис. 84. Сетка с запрещени-
ем перемещений по направ-
лению, не совпадающему
ни с одной пз осей глобаль-
ных координат.
щепиями по направлению, по совпадающему с направлениями
глобальных координатных осей. Такое задание нулевого переме-
щения эквивалентно установлению линейной связи между пере-
мещениями по направлениям глобальных координатных осей,
координат х , у', одна пз осей которой
параллельна запрещаемому перемеще-
нию. Если мы знаем матрицу преобра-
зования [5] узловых перемещений из
новой координатной системы в старую:
{д} = [£]{/}, (6.13)
то можем вычислить матрицу жестко-
сти iZr'l, относящуюся к новой коорди-
натной системе х\ у' [561:
1*4 = |S]T 1*1 (SJ. (6.14)
Для матрицы [А'] задаем пулевое пе-
ремещение для нужной степени свобо-
ды посредством обнуления строки и столбца и засылки единицы
на главную диагональ. Затем производим обратное преобразова-
ние в старую координатную систему. После сборки пз таких мат-
риц жесткости элементов глобальной матрицы жесткости в пой
автоматически будет учтено граппчпое условно в перемещениях
по нужному направлению.
§ 46. Решен не системы уравнений равновесия
Подпрограммы, осуществляющие решение системы линейных
алгебраических уравнений, обычно невелики по объему в срав-
нении с объемом всей конечно-элементной программы. Но имен-
но от подпрограммы решения системы во многом зависят воз-
можности всего комплекса. Отметим также то, что процесс реше-
ния уравнений равновесия занимает большую часть времени
счета задачи, а это накладывает определенные требования па
тщательное составление алгоритма. Поэтому зачастую создаппе
программы, реализующей метод конечных элементов, начинается
с выбора алгоритма и написания подпрограммы решения систе-
мы уравнений. Проблеме решения систем линейных алгебраиче-
ских уравнений посвящено множество работ; хорошим введением
к этому вопросу служит книга Дж. Форсайта и К. Молера [68].
Применение метода конечных элементов к реальным практи-
ческим задачам приводит к матрицам высокого порядка. Досто-
инство метода конечных элементов в том, что эти матрицы по-
ложительно определены, симметричны и обычно хорошо обуслов-
лены. Важной особенностью глобальных матриц является их
§ 46. РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ РАВНОВЕСИЯ
139
низкая плотность, что прп правильном порядке нумерации узлов
приводит к сосредоточению коэффициентов вблизи главной диаго-
нали (ленточной структуре).
Способы решения систем линейных уравнений делятся па
прямые п итерационные. И те, и другие имеют своп преимуще-
ства и недостатки. В настоящее время в МКЭ наибольшее рас-
пространение имеют прямые методы. Они привлекательны преж-
де всего тем, что решение происходит за конечное число опера-
ций, количество которых можно заранее определить. Известные
большие конечпо-элемептпые комплексы T1TUS и NASTRAN
ориентированы на использование прямых методов. Чаще всего
применяются различные варианты метода исключения Гаусса,
алгебраически тождественные, ио отличающиеся порядком вы-
полнения операций и способом храпения матриц.
Основной идеей исключения по Гауссу является то, что си-
стема линейных алгебраических уравнений
[Я1Ы = {Л (6.15)
может быть записана в виде
[£][£7]Ы = {П, (6.16)
где [L] и [LZ]— нижняя п верхняя треугольные матрицы соот-
ветственно. После такого разложения исходной матрицы пе со-
ставляет труда решить две системы с треугольными матрицами:
[Ь]{у} = {Л, [СЛЫ = {?/}. (6.17)
Разложение матрицы [К] па две треугольные вместе с реше-
нием первой пз систем (6.17) относительно {у} обычно называют
прямым ходом, а решение второй из систем (6.17) — обратной
подстановкой пли обратным ходом. Для ленточных матриц нену-
левые элементы [L] и [Z7] также находятся в пределах той же
лепты. При наличии симметрии все вычисления возможно орга-
низовать только с коэффициентами симметричной части ленты,
включая элементы главной диагонали. Если всю информацию
удается разместить в оперативной памяти, то нахождение неиз-
вестных не составляет труда. Чрезвычайно компактная програм-
ма для решения систем но методу Гаусса, состоящая всего лишь
из 30 операторов фортрана, приведена в работе [89]. Опа требу-
ет расположения симметричной части лепты в МОЗУ построчно
и дополнительного рабочего массива с размерностью, равной по-
рядку системы. Чтобы обеспечить постоянную длину строки,
лепту нужно дополнить нулевым треугольником, как показано
на рис. 80.
Мы в своих расчетах для глобальных матриц, симметричная
часть лепты которых размещается в оперативной памяти, при-
меняли фортранный аналог программы, приведенной в работе
140
ГЛ. VI. РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ НА ЭВМ
163]. Эта программа также использует метод Гаусса, но не тре-
бует достаточного рабочего массива и дополнения лепты нулевым
треугольником. Единственное усовершенствование состояло в том,
что во внешнем цикле выполнялась проверка величины коэффи-
циента матрицы, и если этот коэффициент равнялся пулю, то
внутренний цикл не выполнялся. Такой простой прием в неко-
торых случаях позволяет значительно снизить время решения
системы линейных уравнений.
Более эффективную работу ЭВМ в смысле потребности опера-
тивной памяти и времени счета обеспечивает уже упомянутая
в § 45 программа [1001, которая оперирует с системой, записан-
ной по столбцам переменной длины (см. рис. 81). В качестве
алгоритма решения использован модифицированный метод Хо-
ледкого (квадратных корпей). Интересной особенностью програм-
мы является то, что учет граничных условии в перемещениях
выполняется в процессе решения системы уравнений. Это устра-
няет необходимость предварительной модификации глобальной
матрицы жесткости после ее сборки.
Большинство практических задач приводит к дискретным
моделям, информацию о глобальных матрицах которых в опера-
тивном запоминающем устройстве разместить не удается. В этом
случае матрица разбивается на блоки, которые хранятся во
внешней памяти, а в основную память считываются по мере на-
добности.
Рассмотрим блочный метод Гаусса для решения систем ли-
нейных алгебраических уравнений [5], который нами применялся
во всех программах с использованием квадратичных элементов
(одна из программ приведена в приложении). На рис. 82 показа-
ны матрица системы уравнении порядка N и симметричная не-
нулевая ее часть с шириной ленты Я, разбитая па блоки и до-
полнения нулевым треугольником. Ленточная часть матрицы за-
писывается в виде одномерного массива построчно. Поскольку
объем быстрой внешней памяти (типа магнитных барабанов)
у находящихся в настоящее время в эксплуатации вычислитель-
ных машин обычно ограничен, выгодно сократить количество об-
ращений к внешним запоминающим устройствам. Для этого пря-
мой ход решения нужно проводить сразу после формирования
очередного блока уравнений.
Размер рабочего массива в оперативной памяти должен по-
зволять размещение N\=N2~bNz строк уравнений шириной II.
Решение начинается с формирования блока из Ni уравнений.
Этот блок сразу обрабатывается прямым ходом, после чего от-
зываются исключенными ЛГ2 неизвестных. Поэтому первые N%
строк переписываются во внешнюю память и происходит сдвиж-
ка оставшихся коэффициентов па освободившееся место. «Снизу»
нриформировывается Лг2 уравнений, снова производится прямой
§ 46. РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИИ РАВНОВЕСИЯ
141
ход и т. д. Последним обрабатывается прямым ходом массив из
Ar2 + /V4 уравнений GV^jVj»). Если не предполагается произво-
дить в дальнейшем решение с новой правой частью, то этот по-
следний массив можно пс переписывать во внешнюю память,
экономя тем самым общее время решения. Подстановка неиз-
вестных (обратным ход) начинается с последних двух блоков Лг2
и Aft, а затем продолжается для всех остальных блоков в обрат-
ном порядке.
При переппсп последних блоков N2 и Nt во внешнюю память
может быть осуществлено экономичное решение с новой правой
частью, которое потребует намного меньше времени, поскольку
ври прямом ходе требуется только обработка правой части.
Описанный алгоритм позволяет принципиально решать систе-
му уравнений любого порядка, по накладывает ограничение па
ширину лепты матрицы, так как в МОЗУ должны размещаться
одновременно блоки N3 и Лг2. Принципиально необходимо, чтобы
блок ЛГ2 состоял не менее чем из одного уравнения. Желательно
иметь в этом блоке хотя бы несколько уравнений для сокраще-
ния числа обменов с внешними запоминающими устройствами.
Программа, апалошчпая описанной, по требующая одновремен-
ного размещения в МОЗУ двух блоков с числом строк не менее
чем ширина лепты, оппсапа в работе [148]. Очевидно, что такое
построение уменьшает возможности программы, но не увеличива-
ет се эффективности. В той же работе дан текст другой про-
граммы, которая предусматривает нахождение в оператшшой
памяти всего лишь одного блока с числом строк пе менее шири-
ны лепты, а обмен с внешней памятью производится построчно.
Эта программа является предельным случаем примененной на-
ми, когда в блоке iV2 содержится одно уравнение.
Еще одна программа с обменом по блокам, состящпм из лю-
бого количества строк симметричной части лепты, дана в работе
1161]. Для работы программы необходимо нахождение в основ-
ной памяти пе менее двух блоков, в каждом из которых не ме-
нее одного уравнения. Использован один из вариантов метода
Гаусса, вычисления организованы таким образом, что обходится
большая часть операций с нулевыми коэффициентами. Недостат-
ком программы является необходимость большого числа внешних
накопителей—для эффективной работы их требуется четыре.
Все описанные выше алгоритмы при обработке пе меняют
организацию блоков, на всех этапах обменов блоки записывают-
ся но строкам или по столбцам. Изменение структуры блоков
позволяет построить лепточпый алгоритм метода Гаусса с боль-
шим коэффициентом использования доступного объема оператив-
ной памяти — так называемый метод «бегущего треугольника».
Для исключения неизвестного с номером I используются коэффи-
циенты матрицы жесткости в пределах треугольника, ограничен-
142
ГЛ. VI. РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ Н \ ЭВМ
Рис. Я5. Организация об-
мена в методе «бегуще-
го треугольника».
кого 7-й строкой и 7-м столбцом. Следовательно, минимальное
количество информации в МОЗУ для метода Гаусса составляет
1НН+1)/2, где И — ширина ленты матрицы. Обмен с внешней
памятью в методе «бегущего треугольника» может быть органи-
зован так, как показано на рис. 85. Сформировав треугольник по
из пего первое неизвестное и отсылаем
первую строку во вцешнюю память. По-
скольку элементы в строке расположены
в памяти машины не подряд, то для их
накопления необходим некоторый буфер-
ный массив. Оставшийся в памяти тре-
угольник меньшего размера сдвигается
па освободившееся место и к нему при-
форми ровывается новый столбец. После-
довательные пересылки строк во внеш-
нюю память и добавление столбцов
передвигают треугольник пз верхнего
угла глобальной матрицы жесткости в
нижний.
Непрерывная переорганизация па-
мяти требует несколько большего числа
операций, чем в алгоритмах с прямоугольными блоками. Ал-
гольная программа с рабочим массивом в виде треугольника,
основанная па методе квадратных корней, приведена в ра-
боте [69].
Еще более эффективно используется память в методе разре-
женных матриц. Вычисления в нем могут быть построены в со-
ответствии с алгоритмом любого прямою метода. Для экономии
памяти используется тот факт, что даже внутри ленты перемен-
ной ширины существуют пулевые элементы, не все из которых
в процессе решения становятся ненулевым и. В методе разрежен-
ных матриц коэффициенты системы хранятся в упакованной
форме вместо с матрицей-указателем. Место под образовываю-
щиеся в процессе прямого хода новые ненулевые коэффициенты
отводится во время пх появления. Существуют способы [67], по-
зволяющие обеспечить наименьшее заполнение матрицы в про-
цессе решения. Программы, реализующие этп методы, весьма
сложны. Для снижения времени счета нужно использовать язы-
ки низкого уровня.
К методам разреженных матриц близок фронтальный метод
Б. Айронса [118]. Исключение производится по элементам вно
зависимости от нумерации узлов. Эффективность метода обуслов-
лена тем, что в пем теспо переплетены процессы сборки и реше-
ния. Каждое неизвестное исключается немедленно, как накопи-
лась информация, достаточная для этого. И хотя в фронтальном
методе фактически нет понятия ширины ленты матрицы, он не
§ 46. РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ РАВНОВЕСИЯ
143
снимает ограничения, связанные с объемом доступной оператив-
ной памяти.
Это позволяют сделать клеточные методы, в которых матри-
ца разбита па клетки, представляющие собой прямоугольный
пли квадратный блок. Программа такого типа, требующая разме-
щения в МОЗУ трех квадратных блоков любого размера и не
имеющая ограничений на ширину ленты матрицы, приведена
в работе [89]. Программа требует наличия внешних устройств
прямого доступа (такими устройствами комплектуются ЭВМ се-
рии ЕС). Если же в распоряжении пользователя ограниченный
(по все же больший МОЗУ) объем быстрой внешней памяти
(МБ) и магнитные ленты, то на основе клеточных методов мо-
жет быть организован вариант метода «бегущего треугольника»
с размещением треугольника на МБ.
Весьма эффективный вариант клеточного метода Гаусса опи-
сан в работе [92]. В нем предусмотрена экономия вычислении
за счет того, что пе формируются и не хранятся в памяти те
блоки внутри ленты переменной ширины, которые остаются ну-
левыми в процессе всего решения.
Все прямые методы решения систем линейных уравнений по-
зволяют при незначительном увеличении времени счета получить
решение для нескольких правых частей. При этом векторы на-
грузки могут храниться п обрабатываться совместно либо вво-
диться последовательно. В последнем случае для каждого нового
вектора требуется решить системы (6.17) без повой переработки
глобальной матрицы жесткости.
Из-за ограниченного количества значащих цифр в машинном
представлении чисел с плавающей запятой вектор решения
всегда получается неточным, что связано с накоплением ошибок
округления. Это менее характерно для ЭВМ БЭСМ-6, оперирую-
щей с G-байтовымп словами, и может представлять некоторую
проблему для вычислительных машин серии ЕС, которые имеют
слова длиной 4 байта. Получение меньших ошибок может быть
достигнуто выполнением операций над числами с двойной точ-
ностью. Одпако это приводит к сокращению вдвое объема до-
ступной основной памяти и значительному увеличению времени
счета. Другой прием—итерационное уточнение полученного ре-
шения. Он состоит в том, что в исходную матрицу производится
подстановка неизвестных н подсчитывается невязка с правой
частью. Эта невязка используется в качестве правой части для
нового решения тем же методом. Повое решение суммируется
с уже имеющимся, процесс продолжается до заданной точности.
Неудобство итерационного уточнения состоит в необходимости
хранить исходную систему уравнений.
Основное внимание мы уделили прямым методам в связи с пх
преимуществами (на сегодняшний день) перед итерационными.
144
ГЛ. VI. РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ НА ЭВМ
Простейшим п некогда распространенным итерационным методом
является метод Гаусса — Зейделя (последовательной релаксации).
Вариант этого метода с ускорением посредством умножения на
некоторую константу называется методом верхней релаксации.
Находят применение и другие итерационные процедуры, из ко-
торых значительное внимание уделяется методу сопряженных
градиентов. Существуют методы, называемые частичным исклю-
чением и состоящие в комбинации прямых и итерационных ме-
тодов. Один из таких методов освещен в работе [158], где выска-
зывается мнение, что для очень больших систем уравнений быст-
рые итерационные методы могут быть экономичнее пе только но
памяти, по п по времени вычислений.
§ 47. Получение и обработка результатов
Основной целью МКЭ является получение поля перемещений,
заданного в узлах. По этому полю можно получить все осталь-
ные элементы решения. Перемещения — неизвестные в системе
уравнений равновесия и определяются с помощью ее решения.
Пользователю в качестве результатов могут потребоваться самые
различные величины. Получаемый при этом объем информации
составляет от нескольких чисел до нескольких тысяч. Напри-
мер, основной целью решения двумерной задачи для тела с тре-
щиной является определение небольшого количества параметров
разрушения. Однако достаточно часто нужно получать п обраба-
тывать поля деформаций п напряжений. Эта операция прп рас-
чете на хрупкую прочность реальных изделий обычно предшест-
вует рассмотрению тела с трещиной. Чтобы определить наиболее
опасное место расположения трещины, вначале следует решить
задачу без трещины и проанализировать поле напряжений. Ана-
лиз поля напряжений п других полей — весьма трудоемкая опе-
рация, если выполняется вручную.
Большие копечпо-эломоптные комплексы имеют специальные
программы, предназначенные для трактовки результатов. Значи-
тельное внимание этой проблеме уделено в системе «Прочпость-
75», где обработка выходной информации производится в инте-
рактивном (диалоговом) режиме с использованием графических
носителей информации (дисплея и графопостроителя). Диалого-
вая подсистема позволяет получить изображения векторов в уз-
лах, построение сеток и пзолинпй поля. Несомненно, что буду-
щее за таким подходом. Сегодня пользователь решает свои за-
дачи в режиме пакетной обработки и зачастую располагает лишь
построчно печатающим устройством и внешним накопителем.
Поэтому оп вынужден рассчитывать своп программы па более
простые приемы обработки результатов.
§ 47. ПОЛУЧЕНИЕ II ОБРАВОТКА РЕЗУЛЬТАТОВ
145
Самый распространенный способ вывода напряжений п пере-
мощений— это печать в виде таблиц. Здесь следует предусмот-
реть печать различных величин, которые могут понадобиться,
например: подсчитать максимальное и минимальное напряжения
в точке, угол наклона максимального напряжения к одпоп пз
глобальных осей, эквивалентное напряжение. Поскольку объем
информации велик, то обязательно нужно
иметь возможность пе выводить на пе-
чать часть результатов. Удобно ввести
массив, указывающий, для каких элемен-
тов пли узлов должны быть выведены ре-
зультаты.
Например, если нужно напечатать
величины для элементов Nl, N2 и с N3
по К 4, то в массив, указывающий
сегменты вывода, можно поместить их
номера Nl, N2, N3, — N4. Знак минус
здесь применен для того, чтобы подпро-
грамма вывода могла объединить номера
N3 и N4 в пару.
Для квадратичных илопараметрпче-
скпх элементов значения напряжений
Рпс. 8G. Экстраполяция
величин из точек шттр-
гркровапия I — IV в уг-
ловые узлы 1 — 4 квад-
ратичного нзопара метри-
ческого элемента.
следует вычислять в гауссовых точках ин-
тегрирования 2X2, так как в этих точках они имеют наимень-
шую погрешность [81]. Часто возникает потребность рассчитать
величины напряжений в узлах. Метод отыскания производных
перемещении в узлах предложен в работе [1011. Затем по ним
легко определить узловые значения напряжений. Другая чрезвы-
чайно простая методика пересчета любых величин из точек ин-
тегрирования 2X2 в угловые узлы квадратичного элемента дана
в [114]. Опа основана па предположении о том, что данная вели-
чина имеет билинейное распределение ио элементу. Обозначим
искомые узловые значения величины индексами 1—4, а значения
в точках интегрирования римскими цифрами I—IV. как показа-
но па рис. 86. Зададим распределение величины / но элементу
функцией
/(В, ц) = а\ + сь£ + «зц +
(6.18)
Для определения неизвестных коэффициентов имеем че-
тыре уравнения вида
/ (В.-, 1ъ) = Ь.
(6.19)
где л, = ± 1/У 3 —абсциссы интегрирования, к = 1, ...
..., TV. Решая уравнения (6.19). находим, что величины в уз-
лах могут быть вычислены с помощью следующего матричного
10 Е. М. Морозов, Г. П. Пикпшков
110
ГЛ. VI. РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ НА ЭВМ
соотношения:
(6.20)
В качестве величины / могут фигурировать компоненты напря-
жений, деформаций, а также их эквивалентные значения. Нами
была использована формула (6.20) для экстраполяции нэнряже-
ипй па границу тела в задачах о концентрации напряжении и
установлено, что выражение (6.20) дает хорошие результаты.
В каждом узле, за исключением угловых, сходится несколько
элементов. Если в данном узле подсчитать значения напряже-
ний пи точкам интегрирования нескольких элементов, то они бу-
дут несколько отличаться друг от друга. Для получения досто-
верного значения их следует усреднить.
Можно порекомендовать в больших таблицах печатать значе-
ния по F-формату. Такое представление величии позволяет зна-
чительно быстрее просматривать таблицы с целью определении!
характерных значений (максимума, минимума и т. д.). Неудобст-
во по сравнению с печатью по Е-формату состоит в том, что не-
обходимо предвидеть, сколько позиции следует отвести для пред-
ставления величины, чтобы пе было переполнения поля. Следую-
щим шагом более наглядного представления результатов будет
печать сетки (мы уже упоминали программу в работе [99]) или
только границы рассматриваемой области и печать величин в тех
точках, к которым они относятся. Использование оператора
ENCODE легко позволяет решить эту и подобные задачи.
Очень наглядно и полезно представление ноля найденной
функции с помощью изолиний. Прикладные программы для гра-
фопостроителей обычно обеспечивают эту возможность. Однако
построение картины изолиний можно выполнить и на алфавитно-
цифровом печатающем устройстве, разумеется, разрешающая спо-
собность при этом будет меньше. Простой способ такого построе-
ния изложен в работе [132]. Если мы для квадратичных эле-
ментов имеем значения изображаемой величины во всех узлах,
то ее интерполяция для любой внутренней точки может быть
выполнена но формулам (1.2), (1.4)—(1.5). Поскольку аргумен-
тами при этом служат локальные координаты ц, то процесс
нахождения пути изолинии удобнее выполнять в локальной коор-
динатной системе. Для этого элемент в локальных координатах
разбивается прямыми £ = const, ц = const на квадраты, которые
авторы работы [132] называют «доменами». Такое разбиение по-
казано па рис. 87. Предполагается, что изображаемая функция
§ 47. ПОЛУЧЕНИЕ II OBVABOTKA РЕЗУЯЬТ ЧТОБ
147
2. Точка 3 ищется на сторонах домепа, соседст-
Рве. 87. Построение
липин посредством
изо-
ли-
нейной мптернолятгин в
лонал ьны х коордппат а х
линейна вдоль любой стороны домена. Процесс построения начи-
нается с того, что па какой-либо стороне элемента находится
точка, в которой функция равна заданному параметру изолинии.
Згой точке изолинии присваивается номер 1. Затем, после провор
кп остальных сторон домепа. линейной интерполяцией находится
точка изолинии
кующего с первым. Так продолжается до
тех пор, пока пе достигается сторона эле-
мента. Каждая точка пересечения изоли-
нии со стороной домена отображается
в глобальную координатную систему и
с использованием масштабов отсылается
на соответствующее место в массиве, где
формируется искомый графический образ.
Величину домена нужно подбирать такой,
чтобы точки были расположены достаточ-
но близко, либо между соседними точка-
ми образовывать дополнительные с по-
мощью линейной интерполяции.
Если изображаемая графически функ-
ция (например, напряжения) находится
в угловых узлах с помощью билинейной
экстраполяции (6.20), то эта же билинейная функция может быть
применена для отыскания изолинии. Такой подход дает то пре-
имущество, что в этом случае можно записать искомый контур
в виде явной функции одной из локальных координат от другой.
Еще один очень просто программно реализуемый способ гра-
фического представления поля функции от двух координат со-
стоит в разбиении па домены таких размеров, чтобы область, за-
нимаемая одним доменом, примерно соответствовала площади,
покрываемой одним символом построчно печатающего устройст-
ва на бумажной лепте. Область изменения представляемой ве-
личины разбивается па некоторое число интервалов л каждому
интервалу ставится в соответствие один из символов печатающе-
го устройства. После этого процесс формирования графического
образа состоит в последовательном переборе всех доменов в ло-
кальной координатной системе, нахождении символа, соответст-
вующего интервалу, и отображения точки в глобальные коорди-
наты. Символы можно чередовать с пробелами, тогда выведенная
па печать картина будет состоять из ряда полос, чередующихся
с чистой бумагой.
Приведенные примеры построения алгоритмов показывают,
что даже с использованием стандартного печатающего устройст-
ва можно легко получить графическое представление большого
объема выходной информации. Если окажется, что разрешаю-
щая способность печатающего устройства недостаточна, то мож-
10*
148
ГЛ. VI РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ НА ЭВМ
по применить прием разрезания чертежа на две пли большее
число частей п раздельного печатания каждой части.
Методики получения результатов, характеризующих состоя-
ние трещин (параметров разрушеппя), были достаточно подроб-
но описаны в предыдущих главах, и мы не будем еще раз к ним
возвращаться.
В данной главе рассматривалось построение программке для
решения упругих задач. Решение упруго-пластических задач но
итерационной схеме метода начальных напряжений сводится
к решению последовательности упругих задач. При этом полая
правая часть вычисляется отдельным блоком подпрограмм. Поэ-
тому решение нелинейных задач не вносит принципиальных ус-
ложнений в вычислительный алгоритм и хорошая упругая про-
грамма может быть развита в упруго-пластическую.^При этом
графическое изображение пластической зоны может быть полу-
чено с использованием приемов, описанных выше.
ПРИЛОЖЕН И Е
ОПИСАНИЕ ПРОГРАММ
Приводимый ниже программный комплекс для ЭВМ БЭСМ-6 состоит
из трех отдельных программ, связанных между собой посредством пере-
дачи информации через магнитную ленту.
Программа подготовки дискретной модели AIDA служит для автома-
тического построения сетки четырехугольных элементов в области произ-
вольного вида.
Программа NEPTUN предназначена для решения упруго-пластических
задач по теории течения с изотропным упрочнением при действии на тело
механических нагрузок и температурного поля. Для симметричной дефор-
мации берегов трещины предусмотрена возможность вычисления значе-
ния интеграла Черепанова — Райса.
Третья программа — COMPAS — выполняет графическое представление
полей напряжений в виде картины изополос.
Комплекс рассчитан на стандартные устройства ЭВМ БЭСМ 6 мини-
мального комплекта: читающее устройство с перфокарт, накопитель па
магнит нои ленте и построчно печатающее устройство. Почти все подпро
граммы паписапы па языке ЦЕР1Г-ФОТ'ГРАН. Для написания подпро
грамм, которые не могут быть реализованы на языке высокого уровня,
был применен язык ассемблера МАДЛЕН.
I. Программа построения сетки четырехугольных элементов
для произвольной двумерной области1)
Сеточный генератор AIDA дает пользователю следующие возможности:
I) Построение сетки пз линейных и/плп квадратичных четырех у голь-
пых элементов для двумерных одно- и многосвязных произвольных обла-
стей. состоящих из различных материалов.
2) Возможность часть сетки строить автоматически, а часть — вруч-
ную. Возможность корректировки сетки, ужо построенной данной про-
граммой.
3) Обеспечение автоматической перенумерации узлов для достижения
приемлемой ширины лепты глобальной матрицы жесткости.
4) Возможность графического отображения построенной сетки на
построчно печатающем устройстве.
В основу программы положена идея фрагментации дискретизируемой
области. При этом разные фрагменты могу г строиться различными сред-
ствами. Укруппенпая блок-схема программы AIDA представлена па
рис. 88.
Основная стратегия генерирования сетки состоит в следующем:
1) Произвольная двумерная область делится на фрагменты, каждый
из которых состоит из одпого материала; фрагмент может быть много-
связным.
’) Авторы благодарят Т. А. Черныш за участие в разработке и отлад-
ке программ AIDA и СОМ Г AS.
150
ПРИЛОЖЕНИЕ
Mri HFff-
число
ГФССЧ'77/ЛОс
fffac AfSEf
лсигуия
$ ?аг ^етяа
/гл
66jG
ASmo -. и/7ш<гесм}
7/i7';^fiCC.7Ue
ф-'гмслтеа
AS/co -. u/navecw
//cc^pce.'ue
ф г ‘гмекюсг
Утеяие '
фрагкея'ча
c Afasm/m-
ми лея.'яы)
йи^/скил^е
л 7 7
l Z^7>/
А нт'/фрагмент
4__----------—
C7^/7.r/5^Z7
t^T-WO
^101
Сть/нО&на
Фраз сената
Модификация
пасоида гранич-
ных >"зло&
| 'Ыонье/ение
‘ а/иринм ленты
| з/шммм
| hmmw
< JZW/4'^ >
f S'TW HU
HUtW/rwyn
печать графи-
ческого ойдаза
сетки
Рис. 88. Блок схема программы AIDA.
ОПИСАНИЕ ПРОГРАММ
151
Фрагмент может быть:
— построен вручите и введен с перфокарт:
— построен автоматически с помощью ключевой диаграммы [~165];
— считан с магнитной ленты (т. г. использованы результаты работы
программы AIDA, полученные ранее);
— авшфрагмептом, действие пад которым состоит в удалении из сет-
ки некоторых элементов с предписанными номерами.
2) После построения фрагмента производится отыскание узлрв, лежа-
щих пл границе фрагмента.
3) Текущий фрагмент (сели он не первый) стьп^ется с уже суще-
ствующей сеткой посредством перебора граничных узлов данного фраг-
мента и уже существующей сетки. Объединение двух узлов в один про-
исходи г в том случае, если их координаты отличаются не более чем ла
некоторую заданную величину.
4) Если среди фрагментов встречается аптпфрагмент, то происходит
уничтожение элементов с заданными номерами и модификация массива
граничных узлов.
'•) По исчерпании числа фрагментов посредством ряда итераций
отыскивается такая нумерация узлов, которая уменьшает ширину ленты
глобальной матрицы [75].
(j) Координаты и индексы построенной сетки могут быть отпечатаны
в виде таблиц, записаны па магнитную лепту пли отперфорированы. Гра-
фический образ сетки может быть выведен на печатающее устройство
[99|. Уменьшение птпршты лепты глобальной матрицы жесткости произ-
водства по модифицированному пазш алгоритму, предложенному в работе
[75]. Этот алгоритм состоит в том, что путем итераций находится нумера-
ция узлов сотки, удовлетворяющая следующим трем критериям: 1) вели-
чины сумм максимального и минимального членов строки матрицы свя-
зности должны быть расположены в возрастающем порядке; 2) удельные
суммы строк матрицы связности должны образовывать возрастающий ряд;
3) суммы членов строк одинаковой длины располагаются в возрастающем
порядке. Здесь под матрицей связности подразумевается набор строк, со-
стоящих пз поморов узлов элементов, в которые входит узел с номером
данной строки.
Программа ATDA позволяет строить сетки до 500 элементов и 1000 уз-
лов. что вполне достаточно для двумерной задачи. Сетка может быть об-
разована либо из элементов одного типа (с числом узлов 4 пли 8). либо
состоять из различных иерархи ясских элементов с числом узлов от 4 до 8.
Для работы программы требуется подключение подпрограмм FETCH.
РАСК4. UNP4, WBL'F. PAGE, NOPAGE. нмгисапных на ассемблере
МАДЛЕН (часть IV приложения), и расширение объема доступной опе-
ративной памяти с помощью управляющей карты ♦CALL F1CMEMOR*.
II сходные данные
Схема ввода исходных данных с указанием форматов приведена па
рис. 89. Переменные и массивы имеют следующий смысл:
NFR — число фрагментов для построения сетки (включая п антнфраг-
менты).
NMAT(NFR)—номера материалов, пз которых состоят фрагменты.
Первый фрагмент должен быть из материала 1.
LIST0 — графический вывод производится с отключением режима
листоватая, если он был задай операционной системой.
>0 — режим листованпя по изменяется.
Ввод данных, относящихся к каждому отдельному фрагменту, зависит
от ключевого параметра NSET, поэтому опишем отдельно четыре пути,
па которые разветвляется ввод.
152
ПРИЛОЖЕНИЕ
1bl5
Рис. 89. Схема ввода исходных данных в программе AIDA.
ОПИСАНИЕ ПРОГРАММ
153
NSET < О
NSET= —2 — ввод фрагмента с перфокарт с интерпретацией индексов.
Интерпретация производится так. Если группа индексов в пределах эле-
мента образует возрастающий или убывающий ряд. то можно указать толь-
ко первый индекс этой группы, а остальные заменить пулями пли пробелами.
Для убывающего ряда перед первым индексом ряда нужно поставить
знак минус. Знак минус подавляется в процессе интерпретации.
=—1 — ввод фрагмента с перфокарт без интерпретации индексов.
МТОО— печать введенных координат узлов и индексов элементов.
NNOD1 — число элементов фрагмента.
XELI — число узлов фрагмента.
EPS — модуль допустимой погрешности в каждой из координат сты-
куемых узлов.
FMT— текстовая постоянная, обозначающая формат, но которому бу-
дут вводиться координаты узлов фрагмента.
XY(2, NNOD1)—координаты узлов фрагмента. Задаются пары Х(1),
Y(I). Если сторона элемента прямая, то координаты промежуточного уз-
ла можно пе задавать (т. е. заменить их пулями пли пробелами)—они
будут пропитерпо.тировапы липейпо по угловым узлам.
ХС(8, NEL1)—индексы элементов фрагмента. Для каждого элемента
в направлении против часовой стрелки выписываются глобальные (для
даппого фрагмента) номера узлов. Начало обхода с любой угловой точки.
Угловым узлам соответствуют нечетные локальные номера, промежуточ-
ным — четные. Для вырожденного элемепта три или два индекса стороны,
которая стягивается в точку, равны между собой. Если промежуточный
узел отсутствует, то его индекс задается равным нулю (при этом не долж-
на производиться интерпретация индексов).
NSET = О
NSET — 0 — автоматическое построение фрагмента.
NTR
NNOD1
NEL1
— ле используются.
EPS — модуль допустимой погрешности в каждой из координат пр.
стыковке узлов.
NZONE— число непустых зон в ключевой диаграмме (см. рис. 79).
NIIZ— размер ключевой диаграммы по горизонтали.
NVZ— размер ключевой диаграммы по вертикали.
XS — число опорных точек для описания зон.
IA — количество узлов элемента (=4 пли =8).
1ZONE (8, NZONE) — индексы зон. Задаются но тем же правилам, что
и индексы элементов. Если координата промежуточной опорной точки ин-
терполируется, то индекс задается равным пулю.
КЕ\ (NIIZ, NVZ) — ключевая диаграмма, показывающая связь зоп. Если
зона существует, то задастся 1. в случае кустом зоны полагается равной 0.
ID1V(NHZ+NVZ)—число разбиений по зонам. Вначале ключевая диа-
грамма проходится по строчкам, затем по столбцам.
XYS (NS) — координаты опорных точек* для определения геометрии зол.
Если сторона зоны прямая, то промежуточную опорную точку на этой
стороне можно нс помещать и но учитывать в нумерации.
NSET > 0, #= 100
NSET — десятичный номер магпитний ленты, с которой необходимо
считать коордппаты и упакованные индексы фрагмента. Например, если
заказана МЛ 41Б» то NSET=33jo-
154
ПРИЛОЖЕНИЕ
NTR— десятичный номер зоны, с которой начинается запись инфор-
мации о фрагменте.
NNOD1— количество узлов фрагмента.
NEL1 — количество элементов фрагмента.
EPS — модуль погрешности в каждой из координат при стыковке узлов.
NSET = 100
NSET=100 — аптпфрагмепт.
NTR— количество чисел в массиве NESK.
NNOD1
NEL1 — нс используются.
EPS
NESK(NIR)— массив, определяющий номера исключаемых элементов.
Абсолютные величины номеров должны быть расположены в возрастаю-
щем порядке. Отрицательный помер означает, что исключаются элементы,
начиная с номера, указываемого предыдущим членом, по помер, опреде-
ляемый модулем данного числа. Например, если в массиве содержатся
2, 10, —15, 20, то будут исключены элементы 2-й, с 10-го по 15-й включи-
тельно и 20-й.
1 Го исчерпании числа фрагментов вводятся следующие данные:
ITER>*0—максимальное количество итераций для уменьшения шири-
ны .ленты глобальной матрицы жесткости.
г^0 — уменьшение ширины ленты пе производится.
IPLOT>0 — производится печать таблицы соответствия померов у,>
лов до и по. ie уменьшения ширины лепты.
^0 — печати нет.
JPR>0—на печать выводятся координаты п индексы построенной
сетки.
— печати нет.
NSET>0 — номер МЛ, на которую нужно записать координаты и индек-
сы построенной сетки.
^0 — записи не производится.
NTR — номер зоны, с которой начинается запись результатов (прп
NSET^sO пе используется).
NPUNCH>0— производится перфорация координат и индексов пост-
роенной сетки по форматам FMT и (1(‘Т5).
^0 — перфорации не производится.
FMT — текстовая постоянная, определяющая формат для перфорации
координат (вводится при NPUNCH>0).
NFR>0 — количество фрагментов для графического представления
построенной сепш (эти фрагменты пе обязательно совпадают с темп, ко-
торые испол!>зпвались для построения сетки).
^0—печати не производится.
IW = 6 — ширила печати 65 позиций,
==7 — 72 позиций,
=8—107 позиций.
= 10 — 117 позиций,
'= 12 — 127 позиций.
Если I\V=8, 10, 12, то чертеж помещается в центре 132-спмвольпой
строки. При IW=6, 7 он центрируется относительно 72-символьпого поля
печати.
KODE(4) — коды печати (нулевой код печати пе производит никакого
действия).
= 1 — печать положелий узлов с номерами.
= 2 — печать только положений узлов.
ОПИСАНИЕ ПРОГРАММ
155
= 3 — печать элементов.
= 13 — печать элементов с поморами.
= 23 — то же, что и 13, по без печати сторон.
HEAD — заголовок пе более чем из 18 символов.
ЕЕ1— номер первого элемента печатаемого фрагмента.
NE2 — номер последнего элемента печатаемого фрагмента.
(Если ЕЕ 1^0, то полагается ЕЕ1 = 1, NE2=NEL).
1АХ>0— ось х перпендикулярна направлению протяжки бумаги.
^0 —ось х вдоль направления протяжки бумагп.
EXES — размерность массива NESK.
XMIN 1 т v
чг г — вырезка фрагмента дг.умя линиями, параллельные осп 1.
ХМ АХ J
YMIN '
УМАХ.
— вырезка фрагмента двумя прямыми, параллельные оси х.
Если XMIN^XMAX, то они игнорируются, то же для YMIX, УМАХ.
NESK (Е NES) — массив, определяющий номера исключаемых из печа-
ти элементов. Правила его заполнения такие же, как для антпфрагмента.
Выходная информация программы
В процессе счета программа для контроля распечатывает исходные
данные, по требованию печатает координаты и индексы сетки, ее графи-
ческим образ, производит перфорацию координат и индексов или записы-
вает эту информацию па магнитную лепту.
Прл записи па магпптпую ленту координаты узлов располагаются с
нас з ла заданной зоны. Запись индексов, упакованных по четыре числа
г одно слово, начинается с начала зоны, следующей за концом записи ко-
ординат. Запись в бесформатном виде по 1024 числа в зону осуществляет-
с: автокодпбй программой WBUF. Для упаковки 4 целых чисел в одну
ячеч ьу используется автокодная подпрограмма РАСК4. Запись координат
и индексов па магнитную лепту является основным путем передачи ин-
формации другим программам комплекса.
Программа AIDA помещена па стр. 156—186.
II. Программа решения двумерных упруго-пластп веских задач
Программа NEPTI’X предназначена для рептопия двумерных упруто-
пластпчсских задач по теории течения с изотропным упрочнением и име-
ет следующие основные возможности:
1) Рассмотрение произвольной двумерной области с использованием
квадратичных изопараметрическпх элементов.
2) Возможность проведения решения в полярных, декартовых или ци-
линдрических координатах и использования сетки, построенной програм-
мой AIDA.
3) Задание граничных условий в перемещениях и напряжениях, воз-
можность термического воздействия.
4) Программа позволяет подсчитывать зна -юния интеграла Черепало
на — Райса по различным контурам вокруг вершины трещины.
5) Возможность записи результатов решения на магнитную ленту
для последующего их графического представ.ц мия.
Приппипвалъиая блок-схема программы показана на рпс. 90.
Итерационная схема решения упруго-пластпческой задачи построена
в соответствии с методом начальных напряжений (134]. Приращения напря-
жений на каждой итерации вычисляются, начиная от равновесных*)
*) П-юдолжение см. на стр. 188.
156
ПРИЛОЖЕНИЕ
PROGRA? AIDA
С
с •• программа автоматической подготовки *•
с •» ИСХОДНЫХ ДАННЫХ ДЛЯ РЕШЕНИЯ ApV-MgPpbX ••
с Задач методом конечных элементов • »
С ♦♦ • • • ♦ • о ♦* * < • ♦ *♦ <:• • • < •
с
COMMON /ец/А ( 155551 /6 L 2/X Ч ? » 1 0 о 0 3 .BL3
NC(2»500*
INTEGER Н Е А 0 ( 3 ) » ^ОО Е А 3 V N < 5 0 > , J I N116
ОМАТ( *)fымдт (10 > ,FMT {3)
О I V J N s : О N N Р R ( а , 1 )
EQUIVALENCE ( А( 500 1 ) *НРЯ )
I V = С
5 READ 1 0 ' *'F R j < ММ АТ ( 1 1 > I = 1 । ЧГ Я ) » L I S 7
Ю FORMAT(1615)
! V = 1 V 4 1
Р R | Ч Т 6 • I V
6 FORMAТ ( ///5Х, 'ВАРИАНТ ' г 14)
PRINT 50»NFR
50 FORMAT <///5, , 'СБОРКА ИСХОДНЫХ ЛАнНЫХ МКЭ И
3 ' Г
1 14.' ФРАГМЕНТ ОВ л)
I Г R - О
120 REAL- 1 5 j NsE Т > NT R , NNOD 1 . NE L 1 . EPS » xSU’ ,7SUM #
XMUL.VMUl
15 FORMAT < 4 I 5.ЗЕ 1 0. 0)
IFR=IFR41
PRINT 5 5 » J F R »N5ET »NTp . NnOO I .NEL 1 4’S ,Х$им r
VSUM , XMUL , VMUL
55 FORMAT </5Xe ФРАГМЕНТ НОМЕР'МЗ/
1 IlX.'HSET = » f I 4 г 9X , *N7R - ' . 1 5 > 1 О X ' '%‘NO D 1
= '» I 5 >BX, 'NFL 1 ='.!</
1 llXt'EFs = ' »E1 о.4»4X , 'X SUM = ' , E11 , ж,3X, *
4 SUM = ',
1 E 1 1 . 4 . 3X > ' kMUL = ' » E 1 ] . 4,3X , 'VMUL -'.Ец.
I F ( n S EI 1 1 5 0 । ?. 0 0 » 2 5 0
c •» з В ОД с П / к
C КООРДИНАТ И ИНДЕКСОВ ФРАГМЕНТА
150 CALt C00RD1 (KELTrNN0Dl,NSET,nTR )
GOTO 4UC
C АВТОМАТИЧЕСКОЕ ПОСТРОЕНИЕ ФРАГМЕ4’
200 C^LL c OORd 2 < NE L 1 , NNOD I )
GOTO 4 CO
25o IF (N5ET .NE . loo ) GO TO 300
MIT = NMAT ([fR )
C УДАЛЕНИЕ ненужных элементов
CALL SCR AT i NE L ,NhOD , NTR t Nf SK,N А , nOmaT >
ОПИСАНИЕ ПРОГРАММ
157
GO ТО 450
с СЧИТЫВАНИЕ с МП
С *•»- КООРдИНдТ И ИНДЕКСОВ ФРдГМЕНТд
ЗОС 0*11 COORo3(NSET,NTR»NNOOi#UEL1)
С СТЫКОВКА ФРАГМЕНТОВ
400 1 Г (XMUL.EQ.0. ) XMUL = 1.0
) Г ( уMUL , ЕQ.О . ) VMU1=1.О
DO 42С l=l»NNODl
A i 2 • 1 -1 >=A(2*I“1)*XMUL*XSUM
420 A(2*I)=A(2*M •VMuL♦VSUM
ALL CONNECtNE L 9NEL. 1 ,NNOD,NNOO1> NA »IF* »
i NFR,EPS,NOMA1.NMAT)
450 1r(JFR-NFr) 120’500'500
500 P^lNT 57,kNCD,NEl
5? rCRMAT (/5X» ’СБОРКА ОКОНЧЕНА, В СЕТКЕ*
Г5»' УЗЛОВ И’*.15>' ЭЛЕМЕНТОВ*)
Й Е Ad 10,llER,JPLOT,jPR>MS T,nTR,NPUnCH
1r (HPUNCH , ЕС . ) GO ТО 55n
REАО 30» (FMT (1 ),I =1 г 3)
30 F С P м дТ(3 A б )
55f ITCjTER .Lf.q ) GOTO 65o
C •••• УМЕНЬШЕНИЕ ШИРИНЫ ЛЕНТЫ
С •••« ЧдТРИЦЫ ЖЕСТКОСТИ
САЦ AR AN ( NNOO > 1 TER , jPLOT , »tL 1
f C TO 7 0 0
6 5 0 DC 660 1 = 1 » NNСC
Ad ) =XV ( 1 , I )
.i=T*100C
65C A fJ] ) = XV(2 • 1 )
7f г J r (NSET ) 900 » SOO» 8C0
800 S*LL SWSB
L *2*NN00
C ЗАПИСЬ НА МЛ КООРДИНАТ И ИНДЕКСОВ
С ПОСТРОЕННОЙ СЕТКИ
C*1L bBUF (NSET »NTR .XV ,L )
I’T R 1=NTR ♦( L-l )/102 4* 1
L1=2*NEL
гall wbjF(nset»ntri.nc»li)
rajNT 6 Q .NSET > NTr » L fr '.TR 1 , L 1
to FORMAT(/5Х. '•••♦• МЛ’,13/
1 10^’ 'КООРДИНАТЫ УЗЛОВ ЗАПИСАНЫ, НАЧИНАЯ*
I
1 * с зону ' >14 , *, длина Записи*,16/
1 icx,'Индексы элементов заЯисдны, Начиная
• t
1 ' С 30НЫ'»14»', ДЛИНА ЗАПИСИ''!*)
CALL RESB
900 IF(JPR) ЮЗО» 1030 . 930
930 IF (ITER) 1000» 1000.95С
С ПЕЧАТЬ КООРДИНАТ И ИНДЕКСОВ
С ПОСТРОЕННОЙ СЕТКИ
158
ДРИЛОЛШПИЕ
95с FRIN'T $4
64 FORMAT(//JX» 'ПОСЛЕ УМЕНЬШЕНИЯ Р A3JPЕ*Е Т
И МАТРИЦЫ*)
1000 PRJNT 65
65 FORMAT ( ///бХ , гКСОрДиНдТ Ы УЗЛОВ С £ 7 К'Л '
1 4 С зх , 'У ЗЕ л ' > 1IX , 'X * I 11,х » 'У ' ) >
FR|NT 70 > (J » (XV( 1 .J ) .I’ 1 ।2) » J = 1r N*3D >
7q FORMAT(4< I 7»2F1?.4 ) )
PRINT 75
?5 FORMAT (//OX. *ЭЛ*.23Х»*ИНЦЕКСЫ*»35*»
1 'ЭЛ ' , 27x » 'ИНДЕКСЫ *)
CALL UNP4(NPR ,nC,b*NEL)
PRI«T 80r (1 HNPRCK , 1 ) »K=1 >6) >t = i ,4Et ?
Ip rOR/AT(2llO«715»l22>110*7I5)
1030 oo 1050 IJ=1.NFR
IF (NOMAT(1 J ) . EQ.C) GO T - 1060
I J J - 1 J
1050 CONTINUE
I J = ]J J
GO TO 1100
1 0 6 C 1 J = J J - 1
•Ю0 PRINT 65> ( I .NOMAT( 1 ) »1 = 1>1 J>
ftj FORM AT (// 1 4X. '1 *, 5* , 'HOMEP П0СЛГД4Е'Z ?ГЕМ
EHTa '/
• 20X>»V’3 I-го MATfPHAЛА ' / <2 I 15>>
R E д 0 2fl.NFR.IW.K0DE.HEAD
20 FORMAT(6!5»3A6>
1 F(NF R > 20 00* 20 00, 120 0
1200 PRINT 9 0 » Ы Г R »1W- К О 0 E
9o FORMAT(///5X• ПЕЧАТЬ',13.
i > фрагментов СЕТКИr/10X•«ШИРИНд печати*»
1 I з, * .КОДЫ ПсЧдт. ' » 41 5)
DO 1900 N=i,NFR
READ 2 5 > Nc1.HE 2 * IAX , NNE S,ХМIN , XM * 5 vMI 4.УМ
AX
25 F CRM A T f kI 5 >4E 1q.0 )
PRINT 95» N > NE1,NE 2 »> NNES > XNI\ ,XM4X,MJ N
.УМАХ
$5 FORMAT ( / i OX • 'ФРАГМЕНТ ' » 1 3 / 1 flX > r , TX . f
NE 2 ' •
1 7Х» ' I AX ' ,6X . 'NNES'.llX. 'XMJ N ' ’ 1 IX • 'X^AX'
1 ЦХ, 'УМ1Ы'.цХ# «УМАХ '/I 13 » 3I1C, - E 1 5 >/J
I F<NE1 .GT.о) GOTO 1300
NE 1 = 1
NE2=NEL
1300 IICNNES) 1500,1500.1400
1 400 READ 10» (NESK(J ) , 1=! , NNES)
PRINT 100. (NESK < I ) .1 = l.NNES)
100 FORMAT (10X . 'NESK 2 0 I5>
ОПИСАНИЙ программ
159
1500 NESK(NNES*1)=с
I Г(LI ST .L[l0) CALL NCPAGE
DO ]900 К = 1 » А
I Г ( К О ОЕ (К ) ) 1900>1900/1600
1 6 Г о KD=KODE < К ) - 5
IF(IAX) 16 0 0 . 1 8 0 (1,1700
С ПЕЧАТЬ СЕТКИ
1700 CALL MfSHFL(КО,NE1.NE2,IW.HEaD,NESK,
1 А » А ( 1 О О 1 ) . XМIN,ХМА X > УМJ N.УЦДX )
GOTO 1 У О О
1800 С At L MEShPL(KD»NEl»NE2»lw»HEA0»WESK.>
1 A ( 1 001 ) ,A,УМih,УMA X .XMjN . ХМA X )
1900 CONTINUE
call pace
2 0 00 IHNPUMCH J0.3)50 TO 210 0
C • ПЕРФОРАЦИЯ К0СРД4НДТ И ИНДЕКСОВ
С • ПОСТРОЕННОЙ СЕТКИ
wR 1 Т Е ( 5?/F МТ ) ( (ХУ<: J • J) ,I =1 ,2) » J = 1*NNoO >
К - 8 • W Е L
CALL UHP4(NPR ,NC( 1 » 1 ) ,К )
W«!Т Е ( 3 2. 1 0 ) <М р R < I ) И =1* К )
PRINT 7 7» ГИТ
77 FORMAT</;„X» 'ПРОИЗОШЛА ПЕРФОРАЦИЯ КООРДИНД
' ПО ФОРМдТу ' . 3 А 6
* 5 X , * И ИНДЕКСОВ ПО ФОРмдТУ (161-)*)
2100 GO ТО 3
STOP
END
SUBROUTINE COORO L<\El » NNOD । NSET •NT R)
C СЧИТЫВАНИЕ С П/К
C ♦ КООРДИНАТ И ИНДЕКСОВ ФРдГМЕНТД
COMMON BL1/A< 1 0000 »
DIMENSION ХУ I2 > 1 ) » HC <6.1) , NC1(2»1» . ХЕ I 6) »У
£ < 8 )
EQUIVALENCE (A»XM)HA(2001bNCl>i(A<60Cl)>
NC )
INTEGER ГМТ(3)
DATA ЫРЕ/8/
PRINT 50»NNOD»M:L
50 FORMAT( /5Х . 'ВВОД С П К КООРДИЧАТ',1
1 ' УЗЛОВ И ИНДЕКСОВ '» I 5, * ЭЛ-ТОв')
READ 5 » (Г МТ(I ) »I -1>3)
5 FORmAT(3A6)
RE Ар FMT। ( (XV(I id ) И =1 » 2) , J“ 1 » NJ С п )
RE АО 15 г ((NC ( 1 .J )»I=1> NPE ) » U- 1 . NEL)
NSET =NSET♦!
DO 1ПС0 1=1. NEL
DO 7 00 J - 1 »NPE
1F (NSET > 2 50•60 0 »600
C ИНТЕРПРЕТАЦИЯ ИНДЕКСОВ
1G0
ПРИЛОЖЕНИЕ
253 If )) 400*500*300
? p n к -:
GOTO 600
4 0 0 к --1
nC (j ,I ) = -NC(J » I )
GOTO 600
*00 NC(J,I)=NC(J-1»I>*K
6OC J J s N C < J'» I I
XE I J )=XV(1,J J )
70C yE(J)=XV(2»J^)
DO 1000 J = 2 * NP E > 2
I I = J*1
1 F CI I .GT . NPE > I ] = 1
JJ=NC ( J , I )
I F ( J J ) 600*1000*600
£ •* »• ИНТЕРПОЛЯЦИЯ КООРДИНАТ
?0<. :г ( (XE( J ) ,NE .0. ' .0” • <VE 1 J > -NE -° • ” C0T0 10
03
xy(*»JJ) = (XECJ"l)*XE(II > ) / 2.0
xV(2*JJ) = CVE^-l>*yEH 1 >>'2’R
1000 CONTINUE
K=NPE*NEL
CAuL PACK4(NC »NC1 >K )
IF(NTR> 1200*1200,1100
t ПЕЧАТЬ КООРДИНАТ И ИНДЕКСОВ фрагмента
) I О о PRINT 60
60 FORMAT(/6х» 'КООРДИНАТЫ УЗЛОВ ФРАГМЕНТА'/'
1 4(ЭХ, 'У ЗЕ Л '• 1IX » 'X ' , 1IX , 'У ' ) )
PRINT 70» (J। (ХУ( I ,J) »1 = 1 » 2 ) ’ J s1'NNOD )
7Q FORMAT (4( I 7 » 2F12.4 ) )
PRINT 80
FO F0RMAT(/3x, '3 Л *» 23х * *ИНДЕКСЫ'»35х»
1 *ЗЛ ' ,27Х » 'ИНДЕКСЫ * )
PR 1ЫТ 90 » (I » (НС(К , I) ।К=1>В) •1=1 *NEI }
90 FORMAT(2110*7I5»122 , I Ю,7I5)
15 FORMAT( 16] 5 )
1200 RETURN
Е NO
SUBROUTINE CO 0 P. О 2 < H E L » H NO D )
l АВТОМАТИЧЕСКОЕ построение фрагмента
COMMON /Bl 1 /А С 1 0 0 0 0 >
DIMENSION IZONE(B»20)*KEyt20»20),lDIV(40)*J
XVS(2»100)t
} Хут ( 2 » NC ( 2 » ! I.'I NL ( 10 » 20) »NLB( 10 » 2o ) *
J xz(8 I, VZ(в),ХУТ8(2,1 J » JIN(16 >•NABS( a *
EQUIVALENCE (Д,Хут),<А<2001)»МС>г<А<бООШ
IZONEli
(А<62О1),КЕУ)> (A( 6 601 )> I D I V > • (A ( 670 1 > > KV
S)
iA(6901)»Nl> (Д(7’01)/МиВ)/<А(7501)»ХУТВ
ОПИСАНИЕ ПРОГРА1
lilt*
161
INTEGER ₽RPRe,Si,S2»S>,SPAN,0i,o2»
1 DO1.DDZ,О I 0,DDD2»ИC201
RFAD 10>NZONE,NHZ,NVZ,NS,Iд
10 FORMAT(16I5)
PRINT 50»NZONE,NHZ,nVZ»NS,|A
50 FORMAT ( /5x» 'АВТОМАТИЧЕСКОЕ ПОСТРОЕНИЕ ФРАГ
МЕНТД '
1 /5Х , 'ИЗ ',J 4» ’ ЗОН С КЛЮЧЕВОЙ ЛИдГРдмнОй»,
14»' НА ' । 14
1 /5х, 'ПО *,]5j * опорным точкам, элементы с*
,13,* УЗЛАМИ / )
READ 10»((IZOHEtl , J ) , I = 1 , 6 ) , J = 1 , NZONE )
PRINT 55» (J, (IZ0NE <I , J) , I = 1,в),J = 1,NZONE)
55 FORMAT(/З5Х, 'ИНДЕКСЫ 30H '/(5X, '3 оНД*,I 3, '
->',615))
READ 10 > ( (KEV(I » J ) , J = i»NHZ)» J =1»nVZ)
PRINT 60
60 FORMAT (/14X, 'КЛЮЧЕВАЯ ДИдГрД*Мд»)
DO 15 1=1,NVZ
15 PRINT 65» (KEV ( I , J ) , j = l,NHZ)
65 FORMAT ( I 10 » 1Й5 )
NHVZ=NHZ*NVZ
READ 10><1DIV(1),I=i,NHVZ)
PRINT 70
7o FORMAT(/5X, 'ЧИСЛО РдЭбИЕМИЙ ПО ЗОНдМ»)
PRINT 65*(1DIV(I),I=1,NHZ)
JJ = NH7 >1
PRINT 65» ( 101V(I ) = JJ , NHVZ >
READ 20 J (XyS(I,J) >I=1» 21» J = 1,NS)
20 FORMAT(16F5.0)
PRINT 75
75 FORMAT(/5х. 'ГООРДиНдТЫ СПОРНЫХ Т0Ч£К')
PRINT eO*(J/(XVS(l,J),l=l,2)»J=l,NS)
60 FORMAT ( 4 ( 6X » 'N'/цХ, *X ' t 1IX t 'Vr>/(4Cl7,2Fl
2.4)))
PR = O
PR 6 = 0
S1=C
S2 = 0
S5 = 0
nOZ = 1
HHVZ=NHZ*NVZ
I г(I A.EQ.4) GO TO 5 0
DO 40 I=1,NHVZ
40 I 0 I V С I ) = 2»IDIV(I )
50 CONTINUE
1=0
55 1=1*1
1F (KEV ( 1 ,[ ) ,NE . 0t0R4NVZ.EQ,1) GO TO 59
JF(KEV(2»I).NE.O) S3=S3*|D!V(!>
ilEM Морозов. Г, П. Ни киш ков
162
• ПРИЛОЖЕНИЕ
IF <КЕУ<2»Т ) . EG . О .AND . I .GT .1.
1 AND.KEV(2,I -1 >.NE«С I S3 = S3*1
GO TO 55
59 DO 330 S?AN = i ,NVZ
NSP = 0
DO «о 1 =1 , NHZ
IF(KEV(SPAN,I).NE.O)NSP=NSP*1DIV(1 )
I F ( I , E Q . 1) GO TO 60
IF(KEV<SPAN,I ).EQ.O»AND.KLT.NHZ.AND.<EV(S
PlNd-D.Ne.O» NSP-NSP*!
60 continue
1F(KEV($PaN»NHZ-1> .Ее.0 . ANO.KEV(SPAN,NHZ) •
EQ.O) NSP=NSP-1
D1=)DIV(NhZ*SPAN)
001=01*1
C ПОДСЧЕТ НОМЕРОВ
С • ••• КРАЙНИХ ЛЕВЫХ УЗЛОВ ПРОПЕТд
NKSPAN, 1)=PR+S1*1
NL С SPAN,2)=NU(SPAN,1)♦NSP *S2* 1
iFCDl.EQ.l) NL(SPan,2)=NL(SP AN » 2 ) *S3
IF (01-2) 100,90 , 70
70 DO 60 1=3,01
00 NL(SPAN,I)=NL<SPaN,2)*<!-2)*(NSP*1)
90 NL(SPAN,01*X)=NL(SPAN,01)>NSP*S3*l
IF <1 A.EQ.A) GO TO 100
H =0
lF(NSP-(NSP/2)«2.GT.o) LL = 1
NS₽ 6=NSP/2*IL
NL0(SP AN » 1)=₽R 0*S!♦1
NL0(SPAN,2)=NLe(SPAN,l)*NSP*S2>l
D1D=D1-1
IF (010 .LT . 3 > GO TO 90
DO 95 1=3, DID,2
NL 8 (SPAN,I ) =NL 8 ( SP AN » 1 - 1 ) *NSP 8 ♦ 1
95 NL 0( SP AN , I ♦! ) =NL0( SP AN » *NSP* 1
90 NL.6(SPANiDl*l)=NL8(SPAN,Dl)*NSP6*S3*l
100 V = 2.0/01
DO 175 1=1,001
175 W<1>=0
DO 280 1 1 = 1 »NHZ
C • ••♦ ПОДСЧЕТ КООРДИНАТ УЗЛОВ В ЗОНЕ
D2=!O1V<1!)
[F (КЕV($РAN» 1 I ) .ЕQ • 0 ) GO ТО 230
DO 101 1=1,4
101 NABS ( I ) = 0
IF(SPAN.EQ.NVZ.0r.KEV(SPAN*1,I I ) . E Q,0 )
1 NABS(1) = 1
IF (I I .EQ.NHZ ,OR.KEV(SPAN,!!*1>.EQ.O)
1 NaBS(2)=1
1F(sPAN.EQ.1.0R.KEV(sPAN-1,!1).EQ.0>
1 NABS(3)=1
ОПИСАНИЕ ПРОГРАММ
163
I HI 1 .EQ .1 .OR . КЕУ (SPAN, II -1 ) .tQ . O>
1 KA6 S(*)- 1
DO 110 I=1, ?, 2
JZONE = iZOnE<i , N О Z )
* Z < I 1 = X V S ( 1 , J z 0 N k )
110 SfZ ( I ) "X У S < 2 » JZONf )
DO 17C 1= 2» 6»2
К = ]ZONE ( I ,KOZ )
J = ] * 1
i г (j.gt.a) j = j-a
1 Г С К ) 120,130 » 120
12o xz( I ) = ХУ S < 1 , К )
GO TO 140
130 XZ( I ) = (XZ( J -1 ) ♦ XZfJ ) ) / 2
140 1F(К ) 150, ]60, 150
150 У2 ( I )=XMSf 2^ )
GO TO 170
160 VZtI)=<yZ(i-l)*yztJ))/2
170 CONTINUE
H = 2.0/02
002 = 02 * 1
DO юс 1 = 1, OD1
ET = 1 .o-v« ( J -i )
DO iac J=lrDD2
x I = - 1 . D+H*(J - 1 )
INL =NL <SPAM , 1 ) *W« J ) ♦ J-1
ХУТ < 1 , INL )=RR (XZ , ET ,X I >
180 ХУТ (2>INL)=RR(yZ , ET ,X I )
IF( 1 A, E Q.4) CO To 210
I = 3
J=D1-1
IF(NABS < 3 ) . EQ . о >I = 1
I F ( NABS (D.EQ.OMsDpl
DO 182 К 1 = I , J , 2
00 162 XJ=2>D2>2
INL=NL(SPaN,K I )♦W f К 1 ) ♦ К J - i
X УI « 1 » 1 ML ) = «-Х У T « i , I N L - 1 > * X у T ( 1, I ^L ♦ 1 ) ) / 2
le2 yyT<2»INL)=(XVT(2*lNL-l>*XyT(2*lNL*l))/3
1F( I - 2 >165» 105> I83
103 DO 164 К J = г . 02*2
IN L = N L < S P A N , 1 )+W(j 1 ♦ К J - 1
CALL Ve ( ХУ T ( 1 r 1 NL - 1 ) » ХУТ ( 2 , 1 N(_ - 1 ) . ХУ T (1
, INL ) ,
1 ХУТ(2,1М1),ХУТ(1,1НЕ*1),ХУТ(2,1
NL + i > )
164 CONTINUE
1&5 IF(J-D 1)166. 166*180
106 DO 167 KJ=2»02»2
I ML = NL «SPAN,DC 1)*W(DO 1)*K J-l
CALL AMOVE(ХУТ(1,lNL*l>»XVT(2»lNL-l),xyT(l
!!♦
ПРИЛОЖЕНИЕ
164
» INI ) ,
1 XVТ ( 2 , 1 N L > , X V Т ( 1 , 1 Nt ♦ 1 I > X У Т ( 2 » I
NL♦ 1 ) >
167 CONTINUE
166 1=3
J=D2-1
IF(NABS I 4 ) . EO . 0 > 1 = 1
] F ( NABS ( 2 ) . E Gl. 0 > J = OD 2 «
DO 189 К I=2,01,2
DO 189 КJ=I,J,2
lNLl=NL(SPANiKl-l)*W(Kl-l>*KJ-l
INL2=NL<SPAN»KI)>w<Kl)*KJ~l
I NL 3-N L ( 5 P AN * К I ♦ 1 )+W ( К I ♦ 1 1 *K J - 1
XVT(li[NL2)=<XyT(i,lNLl)*X9T(l,lNl5))/2
189 XV T (2ИЫ1-2> = (ХУТ (2»INLl)*XyT < 2* InXIP > /2
IF(1-2)192,192*190
190 DO 191 K!=2*01 » 2
1 N L 1 =N L ( S P AN » К 1 - 1 ) *W ( К I * 1 )
jNL2=NL(SPAN>K1)*W(K|)
] N L 3 = N L ( S P AN » К I ♦ 1 ) *W ( К 1 ♦ 1 )
CALL RMOVE(ХУТ (1,INL 1 ) »ХУТ (2»INL1 ) , ХуT ( 1 ,1
NL 2 ) »
1 ХУТ (2 »1NL 2 ) » XyT (1»1NL3 ) »XyT I 2 r I
NL 3 ) )
191 CONTINUE
192 1F(J-D2)193*195»195
193 DO 194 KI=2*01*2
1NL1=NL(SPAN,K1-1)*W(K!-1)*D2
1NL2=NL(SPAN,KI)*W(KI)*02
INL3=NL(SPAN»KI*1)*W(K1*i)*D2
CALL RM0VE(XVT (1,INL1),XVT (2 »1NL 1 > »XV T (1*1 ।
NL2) ,
1 xyT(2,lNL2),XyT(l.|NL3).XVT(2rl
NL31 >
194 CONTINUE
195 CONTINUE
DO 199 1=1,001*2
DO 199 J=1,DO2
jNL8=NL8(SPAN,I)*W(I) *J ~1
jNL=NL(SPAN*1 ) *H ( I )1
DO 199 K=1,2
199 XУT^(К»JNL8УТ(К»JNL)
DDD2=02/2*l
DO 200 I=2iD1»2
DO 200 J=i»0002
Kl =0
1F IW(T ) -<W(I )/2)<2.GT.0)KL = l
KNL8=NL8<SPAN»I )♦<*(] )*KL)/2*J~1
KNL=NL(SPAN*I )*H(1 ) ♦2>J”2
D 0 2 0 0 К - 1 • 2
ОПИСАНИЕ ПРОГРАММ
200 XVTft(К*KNl6)=ХУТ(К»KNL5
210 nOZ=NOI*1
DO 220 1=1»OD1
2 20 W C1 ) =W(J )<02
GO TO 280 *
230 IF (I I .LE . i.OR .U .GE.NHZIgO TO 2©0
I I 1 = 1 I -1
DO 231 JJ = 1.1 1 1
1 IJj =11-Jj
IF(КЕУ(SPAN , I JJJ ) .NE.0 )G0 TO 232
231 CONTINUE
GO TO 280
232 IF(SPAN.LE . 1 .DR .KEV($PAN - i . I 1 HE0 • 0> GO TO
233
Vi ( 1 ) =W ( 1 ) ♦ о 2
GO TO 234
233 IR=O
IF (SPAN ,LE . 1 .OR . (ХЕУ(SpAN-1 ,1 I ) .ER.0.AND.
• КЕУ(SPAN-1 ,I I-1>.ta.0) ) IR = 1
1F (КЕУ<$PAN , I J-1) .EQ • 0 , AND . IR.EQ . 1 ) GO TQ
W <1 I=W <1>♦!
234 IF (KEV(SPAN , I I-1) , ERt0 ) GO TO ^36
DO 236 1=2*01
W< J >=W(I )♦!
236 CONTINUE
iFCSPAN.GE.NVZ.OR.KEytSPAN^lfllleEQ-O^ 6O
TO 237
W(DD1)=W(DO1)*D2
GO TO 280
237 1RcC
IF(SPAN.Eq.Nv2.Or,(KEV(SPAN*l*tl).EQ.O.ANO
• КЕУ(SPan*1*II-l>?EQ.0)> 1R=1
IF(KEV<SPAN,I 1 -1).ER.0.and.IRЛR.1) GO TO
280
W<DO 1 I=W(DO 11♦1
280 CONTINUE
1Г<JAtEQ«4)G0 TO 283
PR8=NL8tSPANiDl)*NSP8
28£ PR’NL<SPAh»DI)*N$p
IF(Dl .GT,i) GO TO 285
DO 284 !=1»NHZ
!NHZ=NHZ-l♦!
1F(KEV(SPAN»!NMZ).NE.0> CO TO 285
1F(SPAN.Er.i.OR.KEV(SPAN-i,1 NHZ>.EQ.0 > CO
f- To 284
PR=PR*1D1V(1NHZ*
264 CONTINUE
263 CONTINUE
166
ПРИЛОЖЕНИЕ
Sl = 0
S2 = 0
S3=0
I F(SPANЛa.NVZ) GO TO 330
290 IFCKEVISPANH ) ,NE,0,AnD*KESHSPAN<.1>I ),EQ,G
) S 1 = S X ♦ I o 1 V И )
1 F ( SP AN* 1 . EO.. NVZ T GO TO 300
]F(KEV(SPAN*1,1 ),EU.0.aND.kEV(SPaN*2»| ).NE
.o) S3=S3*IO1V< I )
1F(1, EQ.1) GO TO jOo
IF(KEV(SPAN*l»l )eEQ.0’AND*KE^^SP*N*2*1 > . E®-
. 0 .
• AND*KEV<SPA*I*2,|-1).nE.O) S3=$3*l
300 JF(KE V(SPA N ♦ 1 ,I ) ,nE . 0 ) GO TO 310
1=1*1
GO TO 290
31Q J=NHZ . rn л
320 lF(KEV(SPAN.J).N£.0.AND.KEy(SPAN»lFJ).EQ.O
) S 2 = S 2 * 1 0 1 V ( J )
]F(КEV(SPAN* 1 , J ) .NE . 0 ) Go T° 325
J=J-1
GO TO 320
325 1=1*1
J =J - 1
J 1 =0
ГЕ ( I Дт . J ) CO TO 329
DO 32® K=1,J
IF(КEV(SPAN ♦ 1 >К ) .NE . 0 1 GO TO 320
JI = 1
I F (KEV(SPAN>K) ) 326,32?>326
326 S2 = S2* 101v <K )
GO TO 320
32? )F(KEV<SPAN,K*l>.NEtQ,OR,KHV(sPAN*l»K<i).W
E.O) S2=S2*1
32B CONTINUE
329 CONTINUE
1F(JI .EQ . 1> S2 = S2-1
330 continue
IF(I AtEQ.41 GO TO 333
N NO0 = N L 6 ( N V Z » 0 1 ♦ 1 ) *N S f
L=2
GO TO 333
333 NNOD=NL<NVZ,01*1)*NSP
1 = 1
335 CONTINUE
Nt I = 0
NOEL=0
dO 400 SPAN = 1»NVZ.
c •••• ПОДСЧЕТ ИНДЕКСОВ ЭЛЕМЕНТА
ОПИСАНИЕ ПРОГРАММ
167
О 1 = ID1 V(NHZ*SPAN>
001=01*1
00 АОО I =L »01 »L
W<1-1)=о
Н<1>=0
W < I ♦ 1 > = О
00 390 ll=l»NHZ
О 2 = I о I V ( t I )
I Г<КEУ(SPДN , | I ) .EQ . О ) G0 TO 371
DO 370 J =L » 02 » L
1F ( 1 A.Ea.fi) GO TO 360
NOEL = NOEL♦!
J IN(3 ) =NL(SPAN.1*1)*J *W(I♦!>
JIN(1)=JIN(3)-1
JIN(3)=NL(SPAN.! )♦ J *W(I )
JIN(7)=J1N(5)-1
DO 35fi К I =2 » В » 2
35B J IN(К I ) = 0
GO TO 370
360 NOEL =NOEL * 1
KL = о
1F(W(I > - < W < 1 )/2>*2.GT.0)KL = L
j!N(2)=NLB(5PAN,l*l)*W() ♦ 1 ) ♦ J- 1
J IN( 11=JIN(2 >-l
JIN(3>=JIN(2>*1
J 1N(6)=NLeI$PAN, l-l)4W(I-i>4j‘k
J1N(7)=J1N(6)-1
J I N ( 5 ) = J 1 N ( 6 ) ♦ 1
j!N(4)=NLB(SPAN,i ) ♦(W( 1 ) *KI♦J’<2
jlN(fi)=JIN(4)-l
5?o call pас к 4(jin»nc< i ♦ no el ). a)
W< I -1>=W<I-1 ) *02
I )=W(I 1402
W < I * 1 ) =W < 1 ♦ 1 ) ♦ 0 2
GO TO 390
371 IF (H .LE.i.OR.H.NHZ )C0 TO 390
111 = 11 -1
DO 372 JJ = 1 » I t 1
1 I J J =1 I -J J
1F(кЕУ(SPAN»I I JJ ) .NE . 0 )G0 To 374
3?2 CONTINUE
GO TO 390
374 IF(1 .NE.L ) GO TQ 37 7
IF(SPAN . LE . 1 .OR.КЕУ < SPAN - ] I I 1 •EG•0 > GO TO
W < 1 ) =W ( 1 ) 4.02
GO TO 377
375 I*=0
lF(5PAN.LE.i.OR.(KEy(SPAN-i,Jl).EQ.O.ANOe
• KEV(SPAN-l>tI-l)e£Q.Q)> .IRal
168
ПРИЛОЖЕНИЕ
iFCKESHSFANHl-U.EQ.O.AND.IR.EStl* GO TO
W<1 ) =W( 1 )♦!
37? U (К6У(SPAN।I 1-1> .EQ .0 1 GO TO 580
IF <1 .EQ.L ) GO TO 378
U =[ -L
W <IL♦1 ) IL ♦ 1 ) ♦1
376 1F(JA.EQ'4) GO TO 380
3 79 wU )=W(1 )♦!
38o IF (I .NE.Dx ) GO TO 38?
IF(SPAN,Ge,NVZ.OR,KEV(SPaN*1»H ) . EQ • 0 ) GO
TO 385
W ( DO 1)= W<0015 *02
GO TO 398
385 !R = 0
IF C S₽AN.Eq.NVZ .OR , (KEV < SPAn* 1 • И > *E Я.0.AND
• KEV(SPAN ♦ 1 , I I-i ) ,EQ.0) ) 1R = 1
IF(KEV(SPAN,11 - 1 I .EQ.0.AND.1RДQ.1> GO To
390
W<OD1>=W(DD1)*1
GO TO 390
387 IF(KE V(SPAN И I - 1) .NE .0) W ( I ♦ 1 ) = И ( I ♦ 1 | ♦ 1
390 CONTINUE
*00 NEL=NOEL
IF(IA.NE.8)GD TO 415
00 410 1=1»NNOD
00 41S K = 1 » 2
410 XVT(K , I )= XVT 8 (KJ)
415 CONTINUE
RETURN
End
FUNCTION RR(R ,ET ,Xl )
C • ••• ФУНКЦИИ ФОРМЫ
REAL R (1>
Elxl.O-ET
xi=i.o-xi
E2=1.0*ET
X2”l«0*Xl
RR = -0.25* ( E 1* ( R I j.) *X 1 • ( * 2*E* ) *R < 3 » *X 2* < x 1
ET ) ) ♦
1 E2*(R<5)«X2*(Xi-ETl4R(7)*Xl«(X2-ET)))*
L 0 . 5* ( X1*X 2»(R(2)eE1*P < 6)*E2 > *
1 E1*E2*<R(A>*X2*R<8'*xD>
RETURN
ENO
SUBROUTINE RMOVE(XI, Vl»X2»y2fX3>V3)
c •••« сдвиг Промежуточного узпд на стороне
С •••• ЭЛЕМЕНТА к ЕЕ СЕРЕДИНЕ по окружности^
DATA ЕР$/1.0Е*8/
ОПИСАНИЕ ПРОГРАММ
169
0Е11 = Х1к<У2*хЗ*У1*Х2*уЗ~хЗ«У2-Х1<УЭ-Хг*У1
ХУц=Х1*>2*М1**2
XV22-X2«•2*У2*•2
ХУЗЗ=ХЗ*«2*У3-*2
0Е12 = ХУ11е^2*ху22«У5*ху53>У1-Х^11<^3-ху22*
У1-ХУзЗ»У2
0Е13 = ХУ11»Х2*ХУ22»хЗ*ХУЗЗ«Х1-ХУ11*ХЗ-ХУ22#
Х1-ХУЗЗ-Х2
0Е14=ХУ11*Х2»УЗ*ХУ22*ХЗ*У1*ХУЗЗ*Х1вУ2-
1 ХУ11«ХЗ*У2-ХУ22#х1*уЭ-ХУЗЗ*х2«У1
Хй=(Х1*ХЗ)/2
У4=(У1*УЗ)/2
Х31=ХЗ-Х1
У31=УЗ-У 1
Д = (У31»«2*Х31**2)»0ЕИ
1Г(А.1_Т .1/EPS)GO ТО 600
6 = (- 2)*(х4*х31«’2*у4*Х31*У31)*0ВИ'
1 У31-»2*ОЕк2-Х31*Уз1<0ЬЬЗ
С=(У4«*2>У31>>2*х4*^2*х31*>2*2еХ4<у4>х51*У
31)»0Е1 !♦
1 (У4«У31**2*х4#х31вУ31)е°Е,-3-У31<*2«0Еи4
If(6••2~•А*С.LT,q) GO ТО BOO
DEL5=SQRT(B»e2*4»A*C)
X 21=(-В *OEL 5)/(2* A )
X22s <"В-OEl5)/(2*A )
у21зУ4-Х31«<Х21-Х4)/У31 ;}
у22=У4-Х31«(X22-X4)/у 31
Rl = <X21-X2>»*2*<y21-y2M»2
Л2*<Х22-Х2)*«2ЧУ22-У2)*»2
IF (R1-R2) 100 »100.200
100 X2=X21
У2=y21
RETURN
200 X2=X22
V2=V22
RETURN
BOD X2=(X1*X3)/2
у2=(У1*УЗ)/2
return
END
SUBROUTINE C00RD3<NSET,NTR>NN0D.NEl)
C *••• СЧИТЫВАНИЕ С МЛ
C •••• КООРДИНАТ И ИНДЕКСОВ ФРАГМЕНТА
DIMENSION Xyi(2»l)/NCl(2jl>»JINC16)»NPRB*
COMMON /DL1>A(10000)
EQUIVALENCE C A•XУ 1)< (A( 200 1 ♦NC1>
A » tAOOOl) >NPR)
|P«1S1GN(1»NTR >
nTR=IR«NTR
ПРИЛОЖЕНИЕ
170
PRINT 50»NSET,NTR,NNOD,NEL
50 FORMAT( /5Х » 'СЧИТЫВАНИЕ С МЛ',|3«' (ЭОНА'Л
‘ д , ' ) КООРДИНАТ ',
15»' УЭдОВ И ИНДЕКСОВ',I5» ' ЭЛЕМЕНТОВ')
L = 2»NN00
C*LL SWSB
CALL RBUF (NSET • NTR »XУ 1 »L )
NT R =NTR♦C L “ 1 )/ 1 024*1
C*LL RBuF(NSET»NiR,NCl»2*NEL>"
CALL RESB
J F (IP « LT . о) GOTO 460
G •••• Печать координат и индексов фрагмента
PRINT 430t(J,(X41(l»J),l=L,2)»J=l»NNoO)
430 FORMAT </5Х, 'KOOPдИНАТЫ УЗЛОВ ФРАГМЕНТА'//
♦ 4 ( ЗХ , 'У ЗЕЛ ' , 1 IX • 'X ». ЦХ । 'У * ) /
♦ < 4( 1 7,2F12 . 4 >> >
PRINT 440
440 FОRМАТ (/ВX » 'ЭЛ ' » 25X » »ИНДЕкСЫ * » 35X » *ЭЛ • к
• 27Х , 'ИНДЕКСЫ ' )
GALL UNPa(NPRiNCi>B<NEL)
PRINT 450,(1 . (NPR < К,| ),K = i,B)»I=l»NEL)
450 FORMAT(2110'7I5,122*110/715)
460 RETURN
ENO
subroutine scrat(nEl,nnod,nnes,nesk»na»мдТ
,NOMAT )
C •••• УДАЛЕНИЕ НЕНУЖНЫХ ЭЛЕМЕНТОВ
COMMON /BL1/AC1) /BL2/XV(2»1)
1 /BL 3/NC( 2 » 1 1
DIMENSION N E S К ( 1 ) , 1 N ( 1 ) » NP T С В > * 1 N 1 ( 1 ) t
1 I ON( 1 ) ,NOMAT ( 1 )
EQUIVALENCE (A»IN)»(A(1DO1)»1M1)
1 (A(4001),lON),tA<2001),NPT)
data nsl/b/
READ 10» (NESK (!),!=! ,NNES )
10 FORMAT <1615»
PRINT 45»(NESK(|),I=1»NNES)
45 FORMAT</5Х , 'УДАЛЕНИЕ ЗЛ-Т0В
QO 100 1=1» NNOD
INI (1 )xl
100 IN(!)=1
M V = 0 <
1 SE = 1
DO 700 N = 1., N E L
JSE=NESK(jSE>
nse=iabs(jse>
CALL UNP4(NPT,nC<i,N)»NSL>
IF(N>EQ<NsE) GO TQ 500
1 F ( ( JSE .LT . 0 ) . ANO.<N . LT tNSE) J GO TO 600
DO 30 0 1 = 1,NSL
K=NPT{I)
ОПИСАНИЯ ПРОГРАММ
171
IF (К ) 3 0 0 , 3 00 . 200
200 IN(К ) =0
30Q CONTINUE
K=N-MV
00 400 1=1»2
4 00 НС С I > К >=NC ( I » N )
GO ТО 700
500 ISE=ISE*1
600 MV’MV*!
DO 640 l=l»NSL
К =NPT ( I )
1 F (K ) 6 40,640. 620
620 X N1(К)= 0
640 CONTINUE
?00 continue
NE L =NEL-Mv
710 IF(NOMAT(MAT ) .EQ,0) GO TQ 720
NOMAT(MAT jrNOMAT (MAT)-MV
MAT-MAT ♦ 1
GO TO 710
720 °C 760 I=1,NNOD
K=IN(I)*!N1(I)
IF(К) 740,740,760
740 NA=NA*1
c новые граничные Узлы
1 ON(NA ) = I
760 CONTINUE
MW= 0
DO 1100 N=1,NNOD
I F ( 1 N ( N eo0»600»lo00
600 IN(N)=-MW
К =N-MW
DO 900 1 = 1*2
c перенумерация узлов
9 00 ХУ ( I , К ) =Xtj ( I , N )
GO TO 1100
1000 MW=MW*1
1100 CONTINUE
NNOD =NNOD-MW
00 1400 N=1,NEL
CALL UNP4(NPT ,NC( 1 ,N) ,NSL)
00 1300 1 =1 .NSL
KzNpT ( ) )
IF(K) 130 0 »1300 , 1200
C ИЗМЕНЕНИЕ ИНДЕКСОВ ЭЛЕМЕНТОВ
12 00 NPT(I ) =K♦IN (К )
1300 CONTINUE
call PACK4(nPT,NC(1,N)»NSL)
1400 CONTINUE
oo 1700 1 = 1,na
172
ПРИЛОЖЕНИЕ
С •••* ПЕРГСЧЕ- ГРАНИЧНЫХ УЗЛОВ
К =1 ON ( I )
1 Г( IN С К ) >15 О 0 » 1 50 0 > 1 О О
1 500 1 ON ( I ) = К ♦ 1 N (К )
GO ТО 1700
1600 I ОN( I ) - О
1700 CONTINUE
J =0 •
рО 2000 I - 1 • NА
1F ( ] DN < N 1 1900 » 1 900 » ЮСО
1600
I ON ( I J ) ~ I DhM 1 )
GO TO 2000
1900 J|A 1
2000 continue
nA = n a-j
POINT 50/MV/MW
50 FORMAT (/5Х » rsfHK4T0)*FH0 * , J 5 । ' ЗЛ-Т06 И*>
1 I 5 j 9 УЗЛОВ 9 >
RETURN
ENO
SUBROUTINE CCNNEC ( NEl. tNELj ,nnOO,NSOOi»NA , I
Г9 »NF R »EPS»NOMMT , NN AT )
C ««•* СТЫКОВКА ФРАГМЕНТОВ
COMMON Btl/A( 6000> /BL2zX9(2’D /Bl3/NC<?
> 1 *
DIMENSION LCN(l),ХУ 1(2/1),NC1<2.1>.IDN<1>«
1 1ON1(1),JIN(16) » X V C ( 2 ) ,NCMaT(5)iNMaT<10)
,NNCC(2)
EQUIVALENCE <AiXyi),(A(20Ci>’NCl)*(Ac300t’
,LCN ) ,
1 (A(4001)i1D1. )MA(5001>/I0Ni)
data npe/b/
DO ЮС 1 = 1»NNOD1
100 L^N(1)=0
DO 200 I=IFR , NFR
200 NOMAT(1)=o
nPF i=NPE-l
DO 600 N - 1 , NEL 1
CALL UNP A(J IN » NCi( 1 »N > »NP£)
DO 300 1 = 1 ,NPE 1 »2
Nl =J1N ( I >
300 IF (Nl ,GT.o> LCN(n1 )=LCN(N! 1*1
DO 500 1=2.NPE,2
N1 -JlN ( I )
500 1F(NI.GT.C) LCN(NI )=LCN(N1 )-i
600 CONTINUE
NA1 = O
DO 700 I=1»NNOD1
IF (lCN(I ) ,GT . 3 .OR.ICN<I ) ,iT . - i ) GOTO 700
оппсанш: ПРОГРАММ
173
N A 1=NA1* 1
с ПОДСЧЕТ ГРАНИЧНЫХ узлов
J 0N1 (ы Д1)si
700 CONTINUE
IF (I FR.LI . 2 ) GOTO 2200
ncon =0
00 eco I - 1 > NhlCDl
BOO LCN(I)=0
DO 1000 N=1»NA
Nl =[DN(N)
850 4 = 1/2
850 XVC(J ) = ХУ(J ,NI )
DO 1 00 0 1 = 1 ,NA1
Nl 1=IDN1(I )
I F ( N I 1 1 Ю 00 . 1 000 » *00
900 0° *50 J = 1।2
C •••• ОТОЖДЕСТВЛЕНИЕ ГРАНИЧНЫХ УЗЛОВ
IF(AB5(XVC(J>->Vi(J»N11)).GT.EPS) GOTO ioo
0 •
950 CON1Inue
LCN < WI 1 > = ION(N)
I On 1(1)-0
NCON=NCON*1
1000 CONTINUE
DO 1200 N~1,NNG&1
J F ( LCH ( N) ) 1100* 1100* 1200
11CD NNVD=NNOD*1
ICN(N)=NNqd
1200 CONTINUE
DO 1300 n=i,nnooi
К =lCN(N)
DO 1300 1=1,2
C •••• перенумерДЦИЯ узлов
1300 ХУ I 1 ,K ) =XU1(I ,N >
DO 1700 N=i,NEL1
nel-nel *1
CALL UNPa (jJN , NC 1 ( 1 ,N ) rNPE )
00 ]600 I = 1 * npe
Nl=J|N( 1 )
IF(Nl) 1 4 о (J , 1 A 0 0,1 5 0 0
14CC J I N < M" 0
GOTO 1600
1 500 J IN( I )=LCn f Nl 1
1600 continue
C ИЗМЕНЕНИЕ ИНДЕКСОВ ЭЛЕМЕНТОВ
1700 CALL PACK4<JlN,NC(i,NEL),NpE)
NB = o
DO 1900 N = 1 ,NA
NI=I BN(N)
I Г ( hi I > 1900 * 1900 » 1^00 C
ПРИЛОЖЕНИЕ
LfiOO
]ON(NB ) =NI
1900 COhTIKUf
00 2100 h = b Ь Л 1
N 1 =1 ON 1 < N)
I F (Nl 1 2100,2 1 00 , 2 000
2C0Q NB = NB♦ 1
1 ON ( NP> ) si CH ( N I )
2100 CONTINUE •
NA: NB
PR J NT 50* NC0N
50 F0rMAT (/5X, *ИДEНТ ИМИЧиPОВАНЫ*, I 4f * ПдР
OB')
К = NMAT ( I FR )
I Г()FR-2 » 21 10» 21 I 0 « 2 12C
211Q HOMAT (К ) = NE L
GO TO 21® 0
2120 D0 2130 1 = 1» Nfr
IFlNOMAU] ) ) 2130 » 2140*2130
2130 CONTINUE
2140 1F(К .EQ.I FR .0R . К , EC . I 1 GO TC 2110
NEt2 = NOMAT(K )
00 216C J"1 .NEL 1
M = NEL-Nt L1+J
DO 2150 J L = 1 » 2
2150 NN0CtJ L >-NC ( J L,M )
N ‘NE I-NE I 1 -NEL 2
DO 215 5 JM= 1 .N
NJM-JM
DO 2155 JL-1 . 2
2155 NC(JL,NJM>1)=NC(JL»NJM)
N E L 3 = N F L 2 * J
DO 215® Л = 1*2
2156 NC(JL , NEIM = NNCC (JL )
2160 continue
11=1-1
DO 2170 JN = K * 1 1
2170 NOMAT (JN)=NOMAT<JN ) ♦NEL 1
2180 RETURN
C ПгРЕКДЧкд КООРДИНАТ УЗЛОВ И ИНДЕКСОВ
С ♦••• ПЕРВОГО ФРАГМЕНТА
22G0 DO 2300 I=1»ЫД1
2300 1 ОN ( 1 ) =J DN 1 (1 J
NA=NA1
DO 2400 i=l»NEli
CALL UN»4(J1N,NC1(1,]),NPE)
CALL PACK4(JJN,NC(l*l).NPE)
2400 CONTINUE
nEl=nel1
DO 2500 l=l»NNODi
ОППС ШИЕ ПРОГРАММ
175
00 2500 л=1»2
25С0 XV (j , 1 ) = Ху 1 ( J » I )
nnod =nnod i
К =NMAT(1 )
НОМДТ(К) = NEL
return
END
SUBROUTINE ARANCeN,ITER,JPLOT,NEL)
| «••• УМЕНЬШЕНИЕ ШИРИНЫ ЛЕНТЫ МАТРИЦЫ
COMMON BLl/NNOOfMCtio, [ (j 0 q ) , MS (4 0 ) , KV I (J ‘
000 > »
1 1 V ( 1 000 ) • KW( 1 0 0 0 J »NE< 1000 ) »MVG< 1 О Г 0>»
1 1VN(5) BL2/XV(2fl) /BL3/NC(2,1)
DIMENSION ЛИ(в),ХХС1>,УУ(1)
EQUIVALEKCE(n№D,XX)#(MC(iO0O)'VV)
data NSL/$/
NNOo=IN
tCON=0
call CONMaT(NEL)
DO x50 I=1»NNQD
150 К V I ( I ) = I
I T 1 = 0
g? - L H = 1 0 0 0
if Ml
call MI NT ES(J T 1 rI H)
print ic
10 FORMAT (//xoX , УМЕНЬШЕНИЕ ШИРИНЫ*»
1 * ЛЕНТЫ ГЛОБАЛЬНОЙ МАТРИЦЫ ЖЕСТКОСТИ'//
1 1оХ,'В ИСХОДНОЙ МАТРИЦЕ*)
PRINT 20 » LH
2l FORMAT( 1 ОХ> 'ШИРИНА ЛЕНТы»,15)
160 lHs-lh
DO ।70 1 =1 • 5
1 7 О LVN(I ) = 0
200 IT =]T * 1
1E (IT .EQ.ITER ) GOTO 600
CALL SPAN
call MINTES <IT 1,| H)
I F ( 1 T 1 .GT , C ) GOTO 250
call POND
IF(nA(I CON) .GT .0) GOTO 250
CALL MINT E S(IT1.1 И)
J F ( I T 1 ) 2oC»2qO>25O
250 DO 270 I=1,5
270 LVN(I)=0
300 IT =1T*1
IF (XT. EG.ITER) GOTO 6CC
call POND
call MI NT ES(IT 1 И H )
IF(1T1,GT.0) GOTO AOO
176
ПРИЛОЖЕНИЕ
call sum
I f (na(icom .gt . о) goto *oo
CAuL MIntes(1T1» lh)
I F <Iт11 300 » 300 > A 00
40C IULH.LT.LHS) goto 16t
boo PRINT 3 о IT
3o FORMAT ( 1QXt 'В РЕЗУЛЬТАТЕr,I 5, * иТЕРдЧИЙ»)
PRINT 20,LH
DO 7 00 1 = 1 , IN « s
N=MVG(I)
NE(N)=I
4 XX( 1 )=XV(1,N)
700 УУ<I )=XV<2»N^
DO 750 1 = 1 ,IN
XV( 1, I )=Xy ( I )
7 5 li ХУ ( 2 , 1 ) = УЦ ( I )
DO 900 1=1,NEL
CALL UNP A(J 1N, XlC( j,1 ) . NSL >
DO Й00 J=1»N5L
N=JIN(J)
iFlN.GT.O) J 1 N < U)= NEIN)
BOO CONTINUE
9 00 CALL PACK 4(J In,NC(1»1 ) »NSU)
IF(JPLOT)1200,1200«1000
1000 PRINT 40
4o FORMAT ( /ч5оХ , 'ТАБЛИЦА ПЕ PEHyME РдЦИи УЗЛОВ')
Nl=-19
N2=0
DO 1100 N=1t100
Nl=Nl420
N2 = N'2*20
IF(N2.GT.1N) H 2 =1N
PRINT 50* U » 1 =NLN2)
50 FORMAT(/5Xг 'СТд₽Ый НОМЕР',20J3)
PRINT 60> ( NE ( I ) » UNi»N2)
60 F0RMAT(5X,' НОВЫЙ НОМЕР',2015)
IF(N2.EQ.IN) GOT 0 1200
1100 continue
1200 RETURN
END *
SUBROUTINE CONMAT(NEL)
C ФОРМИРОВАНИЕ МАТРИЦЫ СВЯЗЕЙ
D1MEN5 J ON NC(В)
COMMON /BL1/NNOD,MC( 1C»1COO>,MS(4O),KV1<1C
00) »
1 JVC 1000),NE( 1000 * /В13/Кс<2>1)
DATA NSL/B/
00 10D I=1,NNOD
100 HE(I)-0
DO 400 N=iiNEL
ОПИСАНИЕ ПРОГРАММ
CAlL UNP 4( NC,КС (1 ,Ч ) ,NSL )
DO 40 0 I» NSL
К I=NC U )
I F(K I ,EQ.Q) GOTO 400
KN = NF (К I )
IF(KN.Eft-<J) GOTO 150
CALL UNP4(MS»MC<1,K[)»KN)
150 00 300 J=1iNSL
КJ = NC(J )
IF(KJ.Efil.O) GOTO 300
DO 200 L=1»KN
I F (KJ .EGL.MS (L ) ) GOTO 300
20Q continue
KN=KN♦ 1
M S I к N ) ~ KJ
300 CONTINUE
Nt (К I ) =KN
MS ( KN+1)= о
CALL PACKAIMS,Me(1>Ki),Kn+1)
400 CONTINUE
DO 500 1 =1 » N N О 0
IF t n£(1 ) ) 600 > 600 >500
500 CONTINUE
RETURN
600 PRINT 50 » 1
50 FORMAT(5X,гОШИБКА В ТОПОЛОГИИ - УЗЕЛ*,15)
STOP
ENO
SUBROUTINE SPAN
C *•♦* УПОРЯДОЧЕНИЕ По СУММЕ MAX И MIN ЧЛЕНОВ P
ЯДА
COMMON /BL 1 /NNOD,MC( 10’1900) ,MS(4Q) > KV 1 <10
00 ) »
1 I V( 1000 >»KSS( 1 000 )
DATA NR 4(j
DO 300 K=1,NNOD
CALL UNP4(MS»MC(i,K),NR)
MlT =MS ( 1 )
MAT =MII
I V ( К ) = К
DO mo !=2’NR
M = MS ( I )
IF(M .L E . 0 ) GOTO 200
MIT=MINO<M1T ,M)
MAT =MAX 0(MAT ,M )
100 continue
2C0 K$S(К ) =MIT♦MAT
300 CONTINUE
400 IND=O
El M. Морозов, Г- П, Никишков
178
DO 600 1^2-WbOD
KL=KSS < I “1 )
K2=KSS <I )
j F (K2-K1) 500 > 600 » 600
530 KSS(1-1)-K2
KS S(I ) =K 1
INDzIV <I )
I V ( I >-174 1-1!»
1V(1-1)=1ND
600 CONTINUE
I Г < t ND ) 7 oO • 7 GO »400
700 C^LL change
return
end
SUBROUTINE POND
C УПОРЯДОЧЕНИЕ ПО УДЕЛЬНОЙ СУММЕ РЯДА
COMMOn/BLi/NNOD . МС ( 10.1000) .MS (4 Q > ’К71(100
о) »
1 !v<I00b»»p₽ti000>
DATA NR/Aq/
do 300 K=1,NNOD
I V(К)-К
P = 0 . О
N₽ = О
CAlL UNP 4(NS .MC( 1» К ) > NR )
DO 100 I= 1 »NR
M=MS ( I )
IF Im ,LE.0) GOTO 200
NP =NP*1
100 P=P*FLOAT(M)
2C0 PP(K)=P/NP
300 CONTINUE
400 !ND=D
DO 600 1=2tNN0d
P1=PP(I-1)
P 2 = P P ( J )
1 r (P 2-P 1 » 5QO»6Oo,6oO
5C0 PP(l-l»=p2
PF( I ) =P 1
IND=IV(I>
1 V < 1 J = 1 -e < 1 - 1 >
1 н I -1 ) = I ND
600 cr NTINUE
I F I I> ?D0 » 7 ОС »4 0 0
700 b'Ml. CHANGE
F IITUnr
SUBROUTINE SUM
G *?•«♦* У P Л ? Оn GHW С ГП Гр/УПЯАМ ПО СУММЕ MpEHOft
РЯД.3
ОПИСАНИЕ ПРОГРАММ
179
СОммОК /BL1/NN0D,МС с х 0 * 1000>,М$(40 ) » К V I < 1 о
ООН
1 I V(1 000 ) ,SЕ( 1 с о С 1 • NE(1 000 )
DATA NR/4q/
Ml = ЮС0
Йа = о
DO 300 K=j,NNCD
s = o. о
IV(K)=K
DO 10 0 I=1» NR
M=MS( I )
IF(M) 200,200,1 00
IOC S=S*rLOAT(M)
20Q SE(K)=S
M ) = M ! N 0 ( M I » J - 1 >
MA-MAX D(Мд,J - 1)
3CQ NE(К) “I - 1
DO 90D N'-MJ ,MA
DO 400 IM = 1 »NNOO
1F(NE(I)“N> 400»500»40D
400 continue
GOTO 900
500 M-1M
I ND = O
DO 600 I=lM.KNQp
I F(NE < I )-N) 800'6 0 0 > BOO
600 N2=l
Sl-SE(Nl)
S2=SE(N2)
IF(S2-S1 1 7 00 *600»BOO
700 SE(N1)=S2
SE(N2 ) = Si
INQ=t V(Nl )
t V C Nl ) = 1v(N2)
IV(N2)=1ND
N1-N2
600 CONTINUE
I F <I HD > 900 ’ 906 • 500
900 CONTINUE
CALI change
RETURN
E NO
subroutine change
c перенумерация и Перестановка Рядов
COMMON Z8l1/NNOD,mC(10.1000)»M5<40>»KVI<10
00 > >
1 I V < 1 о 0 0 ) • N N ( 1 О О 0 1
DATA nr ,NS/40 »10/
Dc 100 l=l»NN0D
180
ПРИЛОЖЕНИЕ
100
200
300
400
500
600
700
600
1000
1100
1200
1300
NN(NUi
DO 300 K=1»NNOD
CALL UNP4(MS>MC(1,K),NR)
00 200 1=1,NR
M=MS(1 )
I F ( M . L E , 0 ) GOTO з C 0
MS (I ) =NN(M )
CALL PACKa(MS ,MC( 1 ,K ) , I )
1ND = O
DO 700 I=2»NN0D
К 1 =HN ( I - 1 )
K2=NN( 1 )
IF(K2-K1 ) 500*700*700
NN(1-1 ) =K2
nn(i > =ki
DO ООО J = 1 ,NS
MM=MC( J » I )
MC ( j , I ) =MC (J ,I -1 )
MC(j,1-1)=MM
IND = KV I ( I )
KV| (1 ) =KV J (I -1 )
KVI (I -1> = 1 ND
CONTINUE
IF <IN0 7 1 300 * 130 0 > ®00
1ND = O
DO 1200 N=2»NNOD
1=NNO0-N♦2
К 1=NN C1-1 )
K2=NN ( I )
IF (K2-K1 1 1000*1200*1200
nN(J -1 )=K2
nN(i ) =k 1
DO 1100 J = 1*NS
MM=MC(J , 1 )
MC(j , I ) =Mc < J * 1 -1 ’
MC <J ,I - 1):MM
J ND = KVId)
KVI (I ) =KVJ d - 1 )
KVI(I-I)SJND
continue
IF(IND) 1300*1300*400
return
END
SUBROUTINE MINTES(IT1»LH6)
COMMON ZBL1/NNOD,MC<10,1000)*MS(4C>»KVI(40
00),MVG(1000),LVN(5)
data NR/40/
LH = 0
DO 300 K=1*NNOD
MA = 0
ОПИСАНИЕ ПРОГРАММ
181
C*LL UNP4(MS»MC(1»K),NR)
oo 100 1=1, NR
M = MS ( I )
I F(M,L E.Q ) GOTO 20 0
MA= MAX0(MA»M)
100 CONTINUE
200 LH=MAX 0(LH»MA-K1
300 continue
lh=lh*i
I T 1 = 0
00 500 1 =1 , 4
K=5-I
500 LVN(К♦1> = LVN(К I
LVN(1)=LH
I Г(LVN < 1 > .Eft.LVN<2 ) .AnD.LVN<2 > .Ea.цVN < 3) I
IT1 = 1
IE(LVN(1>.EQ.LVN(3) ,AND.LVN<3),E^.LVN(5) )
IT 1 = 1
IFtLH.CE.LHGl GOTO 700
DO 600 t=lrNKOD
6 00 мVG(1 ) =KVI (t >
LHG=LH
700 RETURN
E ND
FUWCTION NA( 1 CON)
COMMON /BL1/NNOD,MC(ioq40»»KVL(1)
I S = 0
DO 100 1=1/NNOD
100 ISx[s*I*KVl ( I )
IF(IS-ICOnj30Qi200»300
2oo N A = 1
RETURN
300 ICON=IS
NA = o
RETURN
end
SUBROUT I WE MESHPL(KODE.NE1,NE2* I**HEAD»
I NESK,Х,у,ХМ1,ХМД,VMi,УМА)
ПЕЧАТЬ ПОСТРОЕННОЙ СЕТкИ
COMMON /BL1/A(5ooq) /ВL3/МI ND(2> i >
DIMENSION NESK(i),X(i),y(i),LB(l).
1 NPT (в) ,X ц{2 1 ,VE(2 )
INTEGER HEAD(3)rP<l),F6(5)»F7(5)lF6(5Jf
182
ПРИЛОЖЕНИЕ
1 Fa /30н<//' 56X3A6//(26Х13А6»АЗ))
1 FiO /30Н(/// 56ХЗМ6//С16Х16Д6,А5))
/ *
1 F12. 30Н(,// 5бХЗАб'/( 6Х20д6/А1)5
/ .
DATA В LANK * A ST »Сн1»СН2 /6Н
1 6Н0 >6НХ , 6W ♦ /
DATA NAW.NWF,NPCX,ИРСУ /6,5,10,6/
DATA N SL» IP /в,1 С О 0 0/
NC=NSL
IF(NSL .GT , 4 ) NC =N SL/2
NC2 = 2*NC- 1
NCODE = MOD(KODE,10)
IF(KODE JL T .0 > NCODE =-i
DO 100 I =1 И P
100 p <1 ) =BLANk
I SE = L
J = 0
DO 200 N-NE1.NL2
J5E=NE5X <ISE)
NSE = [ AB S(JSEI
1 F(N . EQ.NSE) GOT 0 180
IF( (JSE .LT .0) .AND. (N.LT .NSE) ) GOrO 200
CALL U N P 4(N P T , MIN D( 1 »N ) ,N SL. )
DC 160 1=1-NC2»2
K = NPT(I )
IF (K .LE . 0 ) GOTO 160
I F ( j ,GT . 0 ) GOTO 14 0
J=l’
XMIN=X(К)
<K 5
XMAX=XMlN
У*АХ=УМ1N
GOTO 160
14 0 XX-- 1 N-AMI N 1 < ХМ I N » X ( К ) )
XMAX=AMAX1(XMAX,y(К))
1N=AMI Nit У M1N jV(K) )
УM AX = А*ЛА X i ( У M A X , у ( X 5 )
160 continue
GO TO 200
1 8 n 1 S E “I S E ♦ 1
200 CONTINUE
iF(XWA-XMi) 220»220*210
210 X^IN=XMI
X^AX =xma
220 1Е(УМА-УМ[) 240»2AC»230
230 УМ]Ч=УМ!
умдх=умд
ОПИСАНИЕ ПРОГРАММ
183
240
250
280
5 0 0
xD=xmax-xmin
VO-уМДХ-Ум!N
1F((XD.LE.o.).AND.JVD.LE.3.)> XD=1.0
KRP=NPCX*1W
NWR = 1 + KRP/NAW
NCPjIp /nwr
nX=XD/FLOAT(KRP)
OV=VD/FLGAT(NCP-2)
ХУ&ДТ = FLOAT (NPCV>/FLOAT(NPCX)
DX-aMAX1(ox,X4IRAT*DV)
dy = dx/ху«дт
NXMAX=XD/DX*2
N У M I X Г У D / 0 v * 2
1N =XM1N-OX
УМ IN-УМ1N -0У
nC P = У D /Г) У 4 2.5
NR P -N AW*Nv»R
NLP=NCP»NrP+Na^-x
nPW = NWR »ncp
ISS = 1
00 600 N=NE1,NE2
jSE =NESK( ISE )
N 5 E = 1 A 6$ ( J S E )
IF (N .E^.NsE) GOTq 550
iFttJSE^LT.Ol.ANC.lN.Ll.NSE)) СОТО 600
CALL UNP4(NPT,MINDI1»N).NSL>
NS I 0 =NC
L = N С 0 D E • N S J D - 3
I F< ( L« IL*L- 1 ) ) .EG • 0 1 GOTO 6QC
Dc 500 N S = 1 > NC2 > 2
К 1=NPT (NS)
K2 = NPT (NS*2 >
IF((NS.EQ.NC2).OR.(K2.1E«0)) K2^MP Г(1)
M^jti
К "NS♦1
IF (NSL .GI ,A ) M=NP T (К )
I =K 1
J =K2
IF ( M . L £•0) GOTO 300
KOUNT =-2
KOUNT =KOUNT♦1
J =M
I F (KOLIN1 ) 300 » 260,500
1 =<2
!F(HtLE.0).0R.(j,LE.05.DA,l|,EQ,J)> COTo
400
X1=X(I)-XMlN
У1=У(I )-VMjN
X2=X(J)-XMIN
У2-У(J ) -VMIN
184
ПРИЛОЖЕНИЕ
00 J20 K=i,2
NX = XE(К )/DX*O . 5
1F( (NХМАX-NX)•NX,LЕ . О ' GOTO 320
NV=yE(К )/DV + 0.5
IF( (NVMAX-NV ) *NV.IE . Q ) GOTO 320
L =NLP *NX-NRP•nV
LFsl/NAW
CALL STORCH (P (LP ) , 1*L-NAV> - LP » AST )
320 CONTINUE •
If! (KOBE. LT . 0 ) . OR. (К ODE.GE.2C1)* G°TO 400
X D-X2-X1
УП~У2-У 1
I Г < (XC ,EQ, 0 ) . AND . ( VO . Ей . (j ) ) GOTO *0 p
IFIABS(VD).GT.o.7*ABS(^0)) GOTO 3З0
L i^i
L 2--NRP
C=VD/XO
Cl=o.5*tvX-C»Xi)/0V
C2=C«0X Dy
NXsAMJN1<X1»X2)/DX*1.0
N2-ДМАХ 1 (X 1 » X2 ) /DX
NX#1-NXMAX
ИУМ1=НУМАХ
GOTO 350
330 Llr-NRP
L2= 1
C -XD/УО
C1 = 0 . 5*(X1-С*У 1 >/DX
C2=C«0S» DX
N1 = AMINl (У 1 ,У2 ) /0У + 1 . C
N2 = AM AX 1 (У 1>У2) OV
NXM 1 ’NVMA X
NVMx=NXMAX
3 5 0 If < N 2.L T♦N1) GOTO 400
NL=NLP♦Hl«t1
DC 330 N * = N 1,N 2
1 Г( (NXM1-NX )*NX .LE.о I GOTO 36fl
NУ = С 1♦C2•ГLОAT (NX)
If( (NVM 1-NV)•МУ .LE .01 GOTO 38C
L=NL *L2*nV
LP=L/NAW
К =i + L-NAW«l.P
NL=NL*L1
1NEW=CH1
CALL FETCh(P(LM,K»IOLD>
IFUOLD, Eq. BLANK) GOTO 360
I F ( ( I OLD ,Ей. AST ) ,GR . ( 1 OLD . EQ.CH2H GOTO 38
0
IF(IOLD.Eq.CHi) InEW=CH2
360 C*l-L ST ORCH ( P ( L P ) , К , 1 NE d )
ОПИСАНИЕ ПРОГРАММ
185
3fiC CONTINUE
400 IF(И .GT . О ) GOTO 250
5C0 CONTINUE
GOTO 600
550 !St^ISE*l
600 continue
IF’ < (KODE . GT . - 2 ) , AND, (KODe .LT . 1 0 ) )GOTQ 620
I SE = 1
о о в с 0 I. = N E 1 t N E 2
JSE -NESK(ISE)
NSE=1ABS(j£E)
IF (N .EQ .NSE ) GOTO 760
1F((JSE.LT.0).AND.(K.LT.nSE)) GOTO BoO
CALL Uh?4(NPT,MlHD(l>N)»NSL)
kCunT”0
6Z0 КOUWT=K0UnT♦1
1r (KCDE .LT . о ) GOT 0 630
N L = i
N v 0 ft К = 4
L =NCODE*ЫCORN
IF( (L . EQ.j ) . OR . (u . EQ>4> ) CO TO 800
Xl = o .
У 1-C .
DO 630 I - 1»NC2 >2
X =NPT ( I )
X1= X1*X(К )
630 У1=У1*У(К )
X1=X1/FLOAT(NCORN)-XMIN
M1=V1/FLOAT(NCORN)-VMIN
LABsN
GOTc 660
650 nl=nsl
K=NPT (KOUNT )
IF(K.LL.C) GOTO 750
lab = k
X1=X(K)-XM!N
У 1=У(К)-УМ I N
66o icH=1
L = 1C
00 680 J=L.NAW
I F ( L .GT . 1 ABS(LA₽)) GO TO 700
ICH=JCH*1
680 L = L« 10
70П IF(LAB.LT.O) ICH=JCH*1
1CH=MINO(ICHjNAW)
NX=X1/OX
IF(CNXMAX-HX)*NXtLE.оGO TO 750
NX=NX-FL0aT(1CH/2)*0.5
N* =MAX 0(NX >1 )
N* =M1 NO <NX » XR P-ICH*2 )
186
ПРИЛОЖЕНИЕ
NV=V1/DV*o.5
If((ИУМАХ-NV)«NV.LE.O> GOTO 750
J Г (KODE.GT.0) GOTO 7JG
nv =nv*i
LrNLP*NX-NV»NRP
DO 720 J=1»ICH
L.P -L /N AW
CALL FETCH<P I LP)>1*L-NAW»L₽ * I OLD)
IF ( I OLD . NE , BLANK) GOTO 750 *
720 L-L+l
730 ENCODECNAW.15.Л LAB
15 FORMAT(16)
CALl STRMQV(j,NAW+1-1CH•1 CH,P• < NCP-NV > >nrp
♦ NX )
750 If (KOUNT-NL ) 62Cr 800 »«00
7B0 I SE = ISE* 1
BOO CONTINUE
B20 DO 900 1 =1 ,NWF
I F < I * , EQ . 6 3 FMT ( I ) =F 6 ( I )
] F < JW.EQ . 7 ) FMT( I > =F 7 < I 1
I F(IW.EQ.В) FMT(1)=fв(I)
IF(lW.EQ.lO) FMT< i )sF10( I )
IF(IW,EQ.12) FMT ( 1 ) =F 12(I )
900 CONTINUE
PR IN7 FMT,HEAD, (P(I), ] = 1.NPW)
I Г( IW.GE ,6) PRINT 20
20 FORMAT!/* XXXXX СТОРОНА ПРИНАДЛЕЖИТ ОДНОМ
У ЗП-ТУ'
1 /, **♦*♦ СТОРОНА ПРИНАДЛЕЖИТ НеСКОЛЬКЙМ
зл -т ДМ *
1 /• 9 ПОЛОЖЕНИЯ УЗЛОВ'///)
1000 RETURN-
end
SUBROUTINE STRM0v(!S*1»N,JT>J>
DIMENSION IS(1 ) . J T(1 )
NWS = C 1-D/6*1
NWT = (J-1>/6*1
1L-MCD(I।6)
J 1-MOD(J » 6)
I F С I i.EG.O) I 1 = 6
IF(J1.EQ.O> Jl=6
DO 40 K=1»N
CALL FETCH(IS(NHS)»I1»M)
call STORCH(J T (NWT ) ,J 1»M)
11=11*1
J1=J1«1 3o
1 F ( I 1-6 J 20.20.10
10 U = 1 *°
NWS =NWS♦1
20 If(Jl-6) 40,40»30
Jl=l
NWT =NWT♦ 1
CONT 1NUE
RETURN
ENQ
ОПИСАНИЕ ПРОГРАММ
187
tiffed данных
о се/пне
/ОАВЧОАЛЧ
/ТЕЯ-0
ЮАПЧМТЕЛ-О
tiffed варианта
нагрузки
Сдорна глодальнод
матрице/
/кестности и
вектор а нагрузки
L0MJ*1NHT#*O
СЕорна
вентери нагрузка
//елное решение
сисшемь/
уравнении
Сокращенное
решение системыг*х
уравнении I 1
/ТЕЯ=/ТЕЯ+1
Подсчет .
приращении
напря/нении и
спорна вектора
невязки
* - -
Hem
Hem
Пет
Да
Нсvор-
его ла
лласгииесние
достиг-
'нута ли сходи-
мость?
ефорна-
До
ано ли число
ераиии
Да
Печать
результата//
Рнс. 90. Блок-схема программы NEPTUX.
188
ПРИЛОЖЕНИЕ
значений, т. е. эти приращения напряжений соответствуют полным прира-
щениям перемещения с момента приложения шага внешней нагрузки.
Этот прием позволяет сделать итерационную схему более устойчивой и
применить ускорение сходимости посредством умножения вектора при-
ращения перемещений на единый коэффициент.
Поскольку в процессе решения глобальная матрица жесткости остает-
ся постоянной, то ее обработка прямым ходом производится один раз,
а на последующих итерациях делается только преобразование правой ча-
сти и обратная подстановка. Для размещения промежуточных результатов
в процессе решения системы уравнений равновесия используются внешни»*
накопители (магнитные барабаны и лента). Поскольку итерационный ха-
рактер решения нелинейной задачи предполагает многократное решение
системы линейных уравнений равновесия, то желательно как можно боль-
ший объем промежуточных данных разместить па магнитных барабанах.
Системные операторы обмена позволяют использовать из фортрана пе бо-
лее 32 трактов, т. е. не более одного магнитного барабана. Поэтому для
обмена с внешней памятью написана автокодпая подпрограмма VX BUF,
позволяющая через системный буфер записать до 128 трактов МБ. а так-
же осуществлять обмен с МЛ. Применение этой подпрограммы позволяет
снизить коммерческое время решения задач по сравнению с использова-
нием системного обмена. Кроме WBUF используются подпрограммы
РЛСК4 и UXP4, производящие упаковку и распаковку индексов элементов.
В данном варианте программа позволяет использовать сетки пе более
чем из 200 квадратичных элементов с 1100 степенями свободы. Посредством
изменения размерностей общих блоков в головной программе число этих па-
раметров может быть увеличено. Для работы программы требуется расши-
рение объема оперативной памяти с помощью карты »САЬГ F1CMEMOR*.
Исходные данные
Порядок ввода и форматы исходных даппых ясны из схем, показан-
ных ла рис. 91. Полепим значения переменных и массивов.
IZ<0 — печать данных без решения задачи.
=0*—решение без печати координат узлов, матрицы индексов и
температур узлов.
>0—решение с полной печатью исходных данных.
NSET>0 — десятичный номер магнитной лепты с координатами уз-
лов и индексами элементов, записанными программой AIDA.
<0 — ввод координат и индексов с перфокарт.
NTR — десятичный помер зоны, с которой начинается запись коорди-
нат узлов и индексов элементов используемой сетки.
DAL— разность арифметической прогрессии в формуле для вычисле-
ния ускоряющего коэффициента а=1-ЬДа (/— 2), где I— помер итерации.
Первые две итерации всегда выполняются без ускорения. Рекомендуется
Да=0.5 — 0.7.
KQ—абсолютная величина этого числа указывает количество итера-
ций. в течение которых растет а. Максимальное значение а будет 14-Да
(|KQ|-1).
Если KQ>0. то затем полагается а=1. Если KQ<0, то после прекра-
щения роста а ускорение производится с достигнутым значением а.
Последняя итерация всегда выполняется без а-ускореипя.
MIC — заданное минимальное число итераций.
МАС—заданное максимальное число итераций. Если за МАС итера-
ций пе будет достигнута заданная точность, то для данного шага нагрузки
итерационным процесс окончится и произойдет печать результатов. При
решении упругой задачи следует задавать МАС-1, в противном случае
программа будет проделывать некоторый дополнительный объем вычис-
лений, чтобы обнаружить отсутствие пластических деформаций.
ОПИСАНИЕ ПРОГРАММ
189
Мэляие/е *янмяе
S&rf умных
плдлдагрсгммо'У
ММЛАТ
99о9 Цшж „
лвдъзегп'глг/юи
УА&МГ
99л9 ймм
/ЮдлрЯЭР^НМ
/?ШТ
Ыс
<?ЭД /Л7.^/Д*5,г>лл<7 ]
\nle>/)
WOffW. r),H2)M^L£)
________^г---
_------------А__
’-----*Сдо з врал7 j
Рис. 91. Схема ввода исходных данных в программу NEPTUN.
NEL — количество элементов сетки. Допускается использование только
квадратичных элементов с 8 узлами.
NNOD — число узлов.сетки.
NEM1—число элементов из материала 1. Если область состоит из двух
материалов, то в матрице индексов сначала должна быть определена то-
пология всех элементов из материала 1, затем — всех из материала 2.
Наличие более двух материалов не допускается.
190
ПРИЛОЖЕНИЕ
ISTR=1— полярные координаты г, <р,
=2 — декартовы координаты .т, уч
=3 — цилиндрические координаты х, г, 0.
NZ — число запрещенных степенен свободы.
IPS>0 — плоское напряженное состояние.
^0 — плоская деформации, при ISTR = 3, нужно задать IPS^O.
NG — число точек интегрирования (в каждом направлении локальной
координат пой системы) матрицы жесткости элемента и других величин
(=2 или =3). В точках интегрирования вычисляются напряжения. Реко-
мендуется применять NG=2. *
Если впоследствии предполагается производил» графическое представ-
ление результатов с помощью программы COMPAS, то следует полагать
NG=2.
JTP — десятичный помер магнитной лепты для промежуточных дан-
ных. Задается, если недостаточно МБ. Промежуточные результаты, по уме-
стившиеся па барабанах, .записываются, начиная с нулевой зоны.
NT — число трактов магнитных барабанов для промежуточных дан-
ных (^128).
NKEL — число элементов, через которые проходят контуры для вы-
числепия значений интеграла Черепанова — Райса.
RSUM— сдвиг сетки как целого по оси х. Удобно применять при ре-
шении осесимметричных задач.
ZMUL — растяжение сетки элементов в ZML’L раз по оси у.
PREC — величина параметра сходимости е. Нормальное прекращение
итерационного процесса происходит при выполнении условия
{Д()}т.{Д<2}/({0т{«)<е, где {Д<2} и {(?} — приращенпе вектора переме-
щеипй на данной итерации и полный вектор перемещений. Во многих за-
дачах можно полагать PREC = 10~4— 10~5.
ЕМ (К)—модули упругости К материалов (7С=1 при NEMKNEL,
К—2 при NEM1=NEL).
ANU (К) — коэффициенты Пуассона.
ALT (К) — коэффициенты температурного расширения.
ST (К) —пределы текучести.
AM (К)—показатели упрочнения тп _в формуле, аппроксимирующей
кривую деформации материала о— где о и — эквивалент-
ные по Мизесу величины напряжений и пластических деформаций.
Р»К (К) — коэффициент упрочнения /• в последней формуле.
XYT (2, NNOD) — массив координат узлов. Разрешается заменять нуля-
ми (т. е. пробелами) координаты любого числа промежуточных узлов эле-
ментов. Если обе координаты промежуточного узла равны пулю, то про-
грамма интерполирует их линейно по угловым узлам.
NC(8, NEL)—матрица индексов. Для каждого элемента прп обходе
против часовой стрелки выписываются номера узлов в системе единой
нумерации. Начало обхода с любой угловой точки. Для вырожденного
треугольного элемента три индекса стороны, которая стягивается в точку,
равны между собой. Если группа индексов в пределах одного элемента
образует возрастающий пли убывающий ряд, то можно указать только
первый индекс этой группы, а остальные заменить пулями. Для убываю-
щего ряда перед первым индексом нужно поставить минус. Например:
(6 1 2 3 12 -9 8 7) = (6 1 0 0 12 9 0 0).
Последние два масспва составляют основной объем исходных данных,
поэтому их целесообразно считывать с магнитной лепты (NSET>0).
MZD (NZ) — массив глобальных номеров узлов с запрещенными пере-
мещениями (по оси х — номер положителен, по у — отрицателен).
KEL (NKEL) — номера элементов, через которые проходят контуры
интеграла Черепанова — Райса. Номера должны быть выписаны в возра-
стающего порядке. Трещина должна быть расположена вдоль линии у =
ОПИСАНИЕ ПРОГРАММ
191
=const. Программа удваивает полученное значение интеграла, считая, что
рассматривается только одна из симметричных относительно трещины ча-
стей тела.
KS(NKEL)—соответствующий KEL массив, показывающий, к какому
пз контуров принадлежит отрезок интегрирования, проходящий через
данный элемент.
KF (NKEL) — массив, указывающий положение отрезка интегрирова-
ния в данном элементе. Указывается глобальный номер первого (при об-
ходе против часовой стрелки) узла на стороне, вдоль которой проходит
отрезок контура.
SCP=O — вводится новый вариант приращения нагрузки.
=/=0 — новый вариант приращения нагрузки пе вводится, а мас-
штабируется умножением на SCP введенное до этого приращение нагруз-
ки (пли уже полученное с помощью масштабирования), т. е. {AFJ =
=SCP • {AFi-J.
SCT — играет роль SCP при SCP=O. Если SCP =#0, то значение SCT
несущественно.
ЛЕР — число сторон, нагруженных распределенной нагрузкой, нор-
мальной к поверхности.
NP — число сосредоточенных усилий в узлах.
NTR— размерность массива TR. Если NTR^O, вводится произвольное
двумерное температурное поле в узловых точках. При NTR=0 темпера-
турная нагрузка отсутствует.
РР1 — если все элементы массива распределенной нагрузки РР равны
между собой, то этот массив пе вводится. При РР1¥=0 все участки будут
загружены равномерно с интенсивностью РР1. Если направление нагрузки
к поверхности (давление) РР1>0. если от поверхности РР1<0.
LPEL(NEP) — массив номеров элементов, к которым приложена рас-
пределенная нагрузка, нормальная к поверхности. Номера должны обра-
зовывать неубывающий ряд. Подряд могут следовать не более 5 одинако-
вых номеров.
LS(NEP) —соответствующий LPEL массив, указывающий, к какой
стороне данного элемента приложена раенределенная пагру.зка. Указыва-
ется глобальный помер первого узла па стороне при обходе элемента про-
тив часовой стрелки.
РР(2, ХЕР)—массив величии распределенной нормальной к поверхно-
сти нагрузки в начале и в конце стороны при обходе элемента против ча-
совой стрелки.
NFOR (NR) — массив номеров узлов, к которым приложены сосредото-
ченные усилия. Если усилие по оси х, то номер положителен, по у — от-
рицателен.
FO (NP)—соответствующий NFOR массив величин сосредоточенных
усилий. Величина усилия положительна, если совпадает с направлением
осп глобальной координатной системы.
TD (NNOD) — массив узловых температур в порядке возрастания гло-
бальных номеров узлов. Если температура промежуточного узла равна ну-
лю, то опа интерполируется лппойпо по угловым. Температура недеформп-
роваиного состояния 0°.
TR(XTR, 2)—задание одномерного температурного поля Т(х), Сна-
чала вводятся все координаты данной таблицы, а затем все температуры.
Для всех узлов температуры интерполируются линейно по заданной таб-
лице.
T.DIS2>0 — печать таблицы перемещений узлов.
— пет печати перемещений.
NLE — число сегментов вывода напряжений и других величин, относя-
щихся к элементам.
NSET>0 — десятичный номер магнитной лепты, на которую будут
записаны напряжения пА, о^, 0Ху* эквивалентные пластические дефор-
192
ПРИЛОЖЕНИЕ
мации и перемещения для дальнейшего использования в программе гра-
фического представления результатов. Имеет смысл прп NG—2.
^0 — записи результатов па магнитную лопту пе производится.
NTR — десятичный номер зоны, с которой начнется запись результа-
тов для данного шага нагрузки.
JOUT(2,NLE)—неубывающий ряд померов элементов» пары которого
указывают сегменты вывода. Например, если в массиве JOUT стоят числа
I 10 20 20, то будет напечатана информация для элементов с 1-го по 10-м
включительно и для 20-го. На каждый элемент приходится NG*#2 строк
построчно печатающего устройства АЦПУ-128.
Выходная информация программы
Под заголовком ОБЩИЕ ДАННЫЕ распечатываются исходные данные,
введенные подпрограммой COMDAT с обозначениями раздела 3.1. Затем
программа дает некоторую информацию о решаемой задаче. Печатаемые
параметры имеют следующий смысл:
MN — число уравнении;
LH — полуширина глобальной матрицы жесткости;
N2 — число строк уравнений в массиве, который является основным
прп объеме с МБ/МЛ;
МЕМОВ — общий объем внешней памяти, требующейся для размеще-
ния промежуточных результатов;
NFIL — число блоков, на которые разбивается глобальная матрица
жесткости для обмена с внешней памятью.
Далее, иод заголовком «Нагрузка N», где N — помер варианта изменяе-
мых данных, печатаются скаляры и массивы, введенные подпрограммой
VAHDAT.
Вывод результатов производится подпрограммой RESULT. Если на
данном шаге пластического деформирования материала пе происходило,
то печатается текст «УПРУГИЙ ШАГ». В противном случае «УПРУГО-
ПЛАСТМЧЕСКИЙ ШАГ. N ИТЕРАЦИЙ, ИЗ 1ПГХ М С АЛЬФА-УСК. ТОЧ-
НОСТЬ А НЕВЯЗКА В», где N—полное число итераций; М при нормаль-
ном ходе процесса должно быть равно KQ; А — отношение нормы прира
щеппя перемещений на последней итерации к норме вектора перемеще-
ний A = {A(?t}T{A<2i}/({C*lT{C«}), где Qi — компонента вектора переме-
щений; В — корень и.; нормы вектора повязки уравнения равновесия
/; = ]/ Где ai— невязка для даппой степени свободы.
Затем в зависимости от желания пользователя печатаются значения
интеграла Черепанова—Райса для заданных контуров, напряжения и дру-
гие вели чипы, относящиеся к точкам интегрирования, и вектор пе реме ще-
ми й узлов.
При выводе величин по элементам каждой точке интегрирования со-
ответствует одна строка АЦПУ-128. Приняты обозначения:
EL — помер элемента;
FP—величина, показывающая, находится ли точка па кривой дна-
граммы пластической деформации материала, и равная FP —100(УЗо—
— У)/от, где о — интенсивность касательных напряженпй по Мизесу,
У— мгновенный предел текучести (деформирующее напряжение);
X, Y — координаты точки;
SX. SY, SXY, SZ — напряжения ох, (Ту, оХ1/, ог;
SMAX, SMIN — максимальное и минимальное напряжения в плоскости
у;
SEQ — интенсивность касательных напряжении;
EPQ — эквивалентная пластическая деформация.
ОПИСАНИЕ ПРОГРАММ
193
При расчете в разпых координатных системах для соотношения обо-
значений программы с общепринятыми следует пользоваться таблицей
Обозначение программы
Полярные координаты
Декартовы координаты
Цилиндрические координаты
Диагностика ошибок
Программа нс проверяет исходных данных, об этом должен заботиться
пользователь, проводя подробную распечатку данных без решения. Однако
в процессе решения программа контролирует монотонность убывания нор-
мы вектора повязки системы уравнений равновесия. Если на данной ите-
рации порма невязки увеличилась, то отключается ускорение. После того
как трижды будет обнаружен факт увеличения нормы невязки, задача
снимается со счета с диагностическим текстом РАСХОДИМОСТЬ, ITER —
=N, где N — число выполненных итераций па данном шаге. Такая диаг-
ностика обычно вызывается неправильными исходными данными.
Программа NEPTUN помещена па стр. 194—221.
III. Программа графического представления результатов счета
по методу конечных элементов
В результате решения задачи методом конечных элементов получает-
ся значительный объем выходной информации. Например, прп решении
упруго-пластпческой задачи с использованием дискретной модели пз
150 квадратичных элементов с 500 узлами объем только основной выход-
ной информации после каждого шага нагружения составит более 3400 чи-
сел. Нужно также учесть, что все величины, за исключением перемеще-
ний, получаются в точках интегрирования, что неудобно при анализе ин-
формации в табличной форме.
Для облегчения обработки выходной информации МКЭ в программе
COMPAS предусмотрены следующие возможности:
1) Приведение значений, заданных в точках интегрирования, к узлам.
2) Вывод па построчно печатающее устройство картины изополос,
границы которых являются изолиниями рассматриваемой величины.
3) Вывод на построчно печатающее устройство положений узлов сет-
ки и значений данной величины, приведенных к узлам.
4) Возможность увеличения представляющего интерес фрагмента рас-
сматриваемой области.
Принципиальная блок-схема программы показана па рпс. 92. Програм-
ма позволяет графически представить результаты любого количества ва-
риантов решения задачи с помощью МКЭ на одной л той же сетке, что яв-
ляется характерным для упруго-пластических задач с несколькими усло-
виями нагружения. Должны использоваться только квадратичные и изо-
параметрические элементы (в том числе н вырожденные в треугольник)
и двухточечное в каждом направлении правило интегрирования по методу
Гаусса ♦).
♦) Продолжение см. на стр. 221.
13 Е. М. Морозов, Г. П. Никишков
19i
при. юла JIIL2
Program neptun
с
С ♦ ♦ • • •• • • •• .........• • •• »• ♦*
с • • программа для решения двумерных задал •«
С •• TfРМОПЛАСТИЦНОСТИ по ТЕОРИИ ТЕЧЕНИЯ. ♦ ♦
С • • МЕТОД НАЧАЛЬНЫХ НАПРЯЖЕНИЙ. ПОДСЧЕТ ••
С • * ПРИРДЫЕНИЙ ОТ РАВНОВЕСНЫХ ЗНАЧЕНИЙ. **
С •• ИСКРИВЛЕННЫЕ КВАДРАТИЧНЫЕ ЭЛЕМЕНТЫ. ••
С •• ВЫЧИСЛЕНИЕ ИНТЕГРАЛА ЧЕРЕПднОВ А-РАЙС А ••
с • ♦ • • • • •« •........ • • • • >« •• ♦.....
с
COMMON / В L 1 / А ( 1 5 8 О О )
1 /BL1A/LH.JTP , NT »А1( 1 10 С >
1/BL2/XVT(2 » 550 )
1 /В L 2 А / М2 0 ( 1 С 0 > t N N , N Е L » НЕМ 1 » N Z » NC < 2 , 2 О 3 )
1 /ВL3/ЕМ(2 ) * ANU(2 ) > ALТ ( 2 ) » ST (2) » АМ(2 ) / ВК(2
)
1 /BL4/X(3),C(3),!STR,lPS»NG,PREC»LD
1 /BL5/LPEL(90)>LS(90)»PP(2>9D)»NFOR(20)»FO
(20)»NEP>NP
1 /BL6/NTr.KW>PS1»PS2»RP(1100)
1 / ВL 7/XУ(8 » 2 >>T1(8)г Т N ( 8 )
1 /BL8/В(4»16),ОЕТ»Я»2»Т»&T
1 /BL9/0D(4,4),01(4,4)»AP(4)
1 BL10/IZ,MN0D,LOAD,KQ,MIC,APR,NFDG,maC
1 /BLxi/XSrVSf3(10),CJ <10 ) >KELt100 >»KS(11 0)
1 /BL12/Ak<16»16),DAL,TS(550)
1 /ВLS/NW(5 ) ,NR(5) * LL(3 ) » 11 ,J J » NB < 3 )
OA TA ( (3( I ) » !=1 » 10 > =10 I 0.0) >
DaTa((KEl<1)»I=1*10 0 >=100(0))
DIMENSION XP(l),yP(l)»EPQ(l)»FP(l)
EQUIVALENCE (A(10401),XP),(A(11731),VP),
1 (A( 1310 i>/FP ) »{A I 14451) , EPQ )
C ВВОД ОБШИХ ДАННЫХ
call loadgoc*сомолт*>
Nl=15800/LH
N3=LH-1
N2 = N 1 -N3
NF I L=(NN-N3 ) /N2 + 1
lr(N2>NF|L*N3.E^.NK) NF I L = NF1L-l
IFCNFIL-2) 10,20»20
10 N2=<NN-N3)/2*1
N 1 = N 2 ♦ N 3
NF IL = 2
20 NN2=N2*Lh
NN3=N3»LH
N4=NN-N2«(NF1L-1)
NN4=N4«LH
MSG=I+NNOO
MOL=MSG*4*NEL*Ng♦•2
ОПИСАНИЙ ПРОГРАММ
195
MDC=MOL*N4
МТ I Т=MDC♦HN-1
мп1=MDC- 1
J=NK«LH*mT!г
PR I HI 510«NN.LH,N2>J»NfIL
510 FORMAT(//18X,2HNN > 18X » 2HLH »18X » 2HN2,15X ,
1 5НМEMOR, 16X * 4HNF1L/5 I 20 )
DO 30 !=1»NN
30 R₽<P -0 » 0
DO 4 0 I - 1»MT I T
40 A( I } -0 . 0
lOAD=0
1тур=о
50 LOAO-LCAO+l
c • ввод варианта НАГРУЗКИ
CALL LOAOGOt 'VARDAT ' >
IF( I I ) 50,60,60
60 ITER=O
IQT = 0
JFjN=-l
A L=1 . O-Ca L
DO 65
J=MD1 ♦ 1
A(J ) =0 . 0
65 A 1( I ) = C,0
70 KW=1
NF0G = 0
IF < 1ТУР) 90,90,60
c сборка вектора нагрузки
BO call FORSEQ(1,NNt0,1)
C ♦ ••• РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ РАВНОВЕСИЯ
90 CALL SOLUT(MTIT'NN.NFIl*
1 ITyp,Nl,N2iN3,N4,NN2*NN3>NN4)
1TVP=1
1T1=1TER*1
1F{ITER) 148,148,100
ICO APR=0.0
DO 10 1 1 = 1 iNN
J=M01*I
К =4DL♦I - 1
101 APR = APR♦(A(J ) ♦ A(К ) >••2
APq = RNM(A 1 ,NN)/AP R
C ♦••• ПОСТИГНУТА ЛИ СХОДИМОСТЬ
IF(APR.LT . PREC ) JF1N=1
IF(ABS(KQ)-ITER*1> 104,103*104
103 KW=0
IF(K U.LT .0) KW:- 1
104 I F ( JF I N.GT ,Q) KW=0
IF(KW) 145,14ft,130
130 AL=AL*OAL
13*
ПРИЛОЖЕНИЕ
< 4? 03 147 1 = 1 *NN
Д=М01♦(
14? А Л = А < J К А 1 ( D • Д I
I аг = I ат +1
сз то 150
|Ад ос 149 1=1,NN
.1=431*1
1 4 О А - ) г A U ) ♦ А 1 ( П w
150 1Ч1Т1-М4С) 160»155»16q
|55 *1N=1
t f(MAC - 11 16С » 1 57 »150
J 5? J f I N« - 1
I ER = 1
160 :-(1T1.LT.MIC) JF1N=O
C ♦ ПОДСЧЕТ ПРИРАЩЕНИЙ НдПРЯЖЕНИА
CALL DS 1 GP(A(M5G) » A(MDL) >A(MDC)*
1 l’ER»XP»VP,FPrEPa,JFIN)
ITT ’ER=ITEP*1
II ( ITER*JFlN,Efi..l) GOTO 150
Г F C JF IN ) 180,90 »1Й0
C ПЕЧАТЬ РЕЗУЛЬТАТОВ
153 CALL LOADGO(A(MSG),A<MoL)»FP»EPQ।XP»
i ypjjFiNrNEL,nm,iter,iст>Result*)
G 9'0 5 0
STO>
E 10
SUBROUTINE COMDAT
ВВОД OBUIHX ДАННЫХ
C34M0N /8Ц;А<И ? L 1 A / L H » J T P , nT , A 1 ( 1 )
1 ВL 2 , XV у ( 2 » 1 ) / В L 2 А/МZ D ( 1 0 0 } > NN » N E L *
I NEM1.NZ,NCP<2»1)
1 /Bl5/EM(2)» AnU(2).ALT(2 > » ST < 2).AM(2 ) >BK ( 2
)
1 BL 4/X(3 ) ,C(3), ]STR, IPS•N3,PREC (LD
1 BL 7/XV(0 » 2)» T1(В),TN(В )
1 ZBL10/!I,NN GO 4CaD » К QiMIC »aPR » NFDG » MaC
1 BLll/Xs,yS»3<10)»CJ(10)»XEllinDJ»KS(t001
I eL12/AK(16»16)»OAL»TS(500>
п:ме-1$юм nc < e > i), kf c i), л n t e)
EQUIVALENCE (A >NC )»(A < 2000 ) > KF ) . (A <22 0 □ > ' 1
1 H )
CaTa X/-Q.577350269190.0.577350269190»» '
П д T Д C / 1.0 » 1.0 » 0 . 0
REAO 330,IZtNSET>NTR
REAQ 325,0AL»Ki>MlC,MAC
’ 2 > FORMAT(FB.0 » 3 I 5)
READ 333,NEL»NNQ0/NEm1»ISIR»NZ»
1 tPS»NG'jTP»NT »nKEl
F:AD 340 RSUM»Z?iuL,PREC
KK = 1
ОПИСАНИЕ ПГ0Г1 А>Ш
lfl7
I F(NEM1.LT .N£L) КХ = 2
READ 340 , (ЕМ < I >,ANU( I > » ALТ(I ) ,ST ( 1 ) » AM И > •
1 ВК( ! ), 1 = 1 ,КК )
NN=2*HN0D
IF(NSET . GT . О ) SO TO 5 10
read 320» < (X,tu, j »,1=;,2>»J-1»nnoc
320 format(16F5.0 >
READ 330,((NC( I »J } , Irli 8 ) , J =1» NEL )
330 FCRMaT(1615)
GOTO 350
510 call sws&
call rbuf<nset»ntr»xmt,nn)
NTR1=NTR*(NN-1)/1O24*1
Call rbuf(nset,ntRi»ncp,2>nel)
call resq
PRINT 52o»NSEt>NtR
520 FORMAT(///10X»КООРДИНАТЫ И ИНДЕкСЫ*,
1 * СЧИТАНЫ С МЛ»,15,*» НАЧИНАЯ С ЭСнЫ*,13»
Call unp4 ( нс , ncp > b»nelj
53o READ 33q, (MZC( I) . I -1 »NZ)
340 FORMAT(6E1o.2)
IF(NKEL) 2 »2»1
i Read 310»ckel( i i,ksh> ,kfiij,i = 1,Nnll>
310 FORMAT(d ( I 5» 1 1 > I 4 > )
LH = 0
00 550 IsbNKEL
I I=KEL ( I )
00 533 Jj=1.8
IF(NC(J J,I 1 ) . EQ.KF{I ) ) GO TO 535
533 CONTINUE
535
LH=LN*JJ
ОС 54C J=l,8
K = j4.J J
I F(К . GT.в ) К-K-6
540 JIN(J) = NCIK' I 1 )
DO 550 J=lrB
550 NC(J » II )=J IN(J )
I F(NStT.lE . 0.OR.LH.EQ.0) GOTO 2
call packing,NCp,ft*NEL)
Call swSq
call wbuf(nset»ntri»ncp,2»nel >
call R£Sd
PRINT 360
560 FORMAT(/10Х> '•••• ИНДЕКСЫ НА МЛ'»
1 ’ ОТКОРРЕКТИРОВАНЫ В COOTB. С КГ'
2 LH = 0
ИНТЕРПОЛЯЦИЯ координат,
• ••• ИНТЕРПРЕТАЦИЯ ИНДЕКСОВ» ПОДСЧЕТ Ы
198
ПРИЛОЖЕНИЕ
С • ••• ЛЕНТЫ СИСТЕМЫ УРАВНЕНИЙ
DO 22 1 = 1 । NEL
М А Х = С
МI № 1 О ООО
DO 7 J- 1 » 6
I F ( NC С J • I > > 4> 5,3
3 к = 1
GOTO 6
4 К = -1
NC(J , 1 > = “^С(J » I >
GOTO 6
5 NC(J,I)= NC(J-1,I)♦*
6 J 1 = NC < J । 1 )
1 F ( J J , G Т , М А X ) М А X = J J
JFIJJ.LT.М 1 N ) М IN-J J
ху(j»1) = хут(11jj )
7 хм( J » 2 >=ХУТ(2 > J J>
IF(МДХ-МIН.GT,Iй) LH=MaX-M1N
DO 20 J=2»fl>2
I 1 = J*1
1F( I 1 . GT .6 ) I 1 = 1
J J = NC(J » I )
lF((Xy(J»l)fNE.O.01.0R,(Xy(J,2i#NE.C.0)>GO
TO 20
DO 10 K=1»2
10 X V TIK , J J1 = (X У(J -1 » X ) ♦X У( I I .К ) ) f2 . 0
2o CONTINUE
call fac^4(nc,ncp,8«nEli
p R1 NT 2 о C
200 FORMAT ( //55X, 1 ВН • • * 0 6 Щ‘Л E ДАННЫЕ*»»!
PRINT 2 о 5, IZ,ОДL,КQ»M1 с »MAc
205 F0 RMAT( / / 1 8X » 2H i Z > 1 7X,jH0AL » 1 6X » 2HКQ > 1 7X,
1 3HMIC, 17x,ЗНМАС/120 » F 20.4,3120)
PRINT 210,Nel,NNOD,NEM1,ISTR,nZ,
1 ips,ng>jtp,nt,nkel
210 F 0 RM A T ( / ' 7 X , J H N E L » 6 X , AH NN G D » 6 X , 4H N £ M 1 ,
I 6X,4HISTR,8X,2HNZ,7X.3H|PS,BX,
1 2H NG • 7 X » JH J T P , 6 X » 2 H N T , 6 X • 4H NK E L / 1 0 1 i 0 )
PRINT 212 (EM( I ) ,ANU( 1 ) »A LT( I ) •ST( I ) »
1 AM < I ) > ВК ( I ) » 1 = 1 » KK >
212 F0RMA T(/1bX,2 HEM , 17X.3HANU » 17X•3HAL T ,
1 ieXi2HST>I6X»2HAM, 18 X,2НВК/< 6E20 • 4 ) )
PRINT 215,RSUM,ZmUL i PREC
215 FORMAT(Z15X,5H RSUm»16X,4H’mUL,
1 16X , ‘•HPREC/3F20 . 5)
IF(IZ.EQ.O) CO TO 40
PRINT 2 1 7
217 FORMAT(///4(ЗХ,4Н^00Е»11Х,1НХ,11Х,1НУ))
PRINT 220, ( J ,(ХУТ И ,J) , I - 1» 2) ,J = 1> MNoD)
220 FORM A T(4( I 7 , 2F 1 2 . 4) )
ОПИСАНИЕ ПРОГРАММ
199
PRINT 23 0 » (J, tNC( I .J) , J = 1 »6) ,J = 1,NEL )
23 0 r0RMflT(///6X»4HELEM>25x,2HNC,2<?X^HELEMt
I 2e.<,2hNC//(2ll0»7i5»Ii5/I10»7I5))
<• 0 D ( 3 C I = 1 » N N О C
xvt(i,:) = хут(i,i)* в sum
50 ХУТ (2, I > = xVT(2, I )• ZMUL
67 ►PJNT 2 5 0 , (M10( I ) / ! = 1,N Z )
250 FORMAt(///53X»3HmZD//( ]01 10) )
IF (NKEL) 7 5,75» ?Q
7c PRJkT 26 0 * (XEL ( 1 ) »КS( I ) »KF ( I ) » I = 1 »NKEL )
260 FORMAT (/ /6xf 1 1HK El/К S/ К Г / ( 7( I 9 , 1 H / , I 2, 1H
. i 4 ) ) )
♦ ••• АБСЦИССЫ и ВЕСА Ин T E Г P ИР О Ь АН И £ ПО ГАУССУ
75 ! г(NG- 2 ) 85'65/60
*0 Х(3)=0.7745966692*1
X ( 2 ) = 0 . О
X( I>--X(з )
С( 1 ) = 5 . О / 9 Ю
С(2)=8.0/9,0
С( 3)=С( 1 )
6 5 L. н= 2•(L Н♦1)
LD=3
!F ( I STR.ЕО . 3 ) LD = 4
• ••• ПРЕОБРАЗОВАНИЕ НОМЕРОВ УЗЛОВ в НОМЕРА
• СТПЕНЕй СВОБОДЫ
00 1 0 5 I г 1 » NZ
II=2*IABSCMZOlI))
! F(MZD( I ) ) 105.100,100
ЮС 11 = 11-1
105 м I: D( I )- I 1
RETURN
END
SUBROUTINE VaRDaT
ввод Варианта нагрузки
COMMON BL1/A(1)/BL1A/LH»JTP»NT»A111 )
1 /Bl 2 xyт< 2 > 1) / BL 2 A/mZDI100)»NN,NEL »
1 NEM1» NZ ,NC( 2 , 1 )
1 Bl5/LPEL(90) ,L S(9 0 ) »PP(2»90) ,NFORt20)»FC
( 20) ,Ngp , NP
1 /B16/NTR,kW«SCP,SCT,RF(1)
1 BL7/XV(6»2)»Tl(a),TN(d)
1 /6L10lZ.NNCD.LCA0iKQ.NSS,APR,NFOG
1 BL12/Ak(16»16),0al»TC(1)
1 /Ы S / NV. ( 5 ) , NR ( 5 ) , LL ( 3 ) . I I , J J
DiMENSjOn TR(100»2),jIN(6)
EQUIVALENCE < A < ЮО 0 0), TP) , ( A ( 1 c 3 CO, » J : N )
32: F 0 R M A T( 1 6 F5, 0 >
33c F0RM AT(16 I 5)
read 340,scp,sct
PRINT 2QQ/L0AD
2-Х)
ПРИЛОЖЕНИЕ
С
2G0
210
3*0
₽R?NTTifИ'‘’с’1Н'’/5в*'’ИНАГРУЗКА.!3>
PRINT 2 1 о , SCP , SCT
FORMAT(/з 9 X »4 Н S С Р =
FORMAT(2E10.0)
1 Е 1 2,5 * 5Х , АН SC Т
1 г S С; р ,N Е.О.О) GOTO 100
ззод изменяемых дднных
^Е A D 3 30 , N Е р г N р , n Т R
Read здо,ррi
5бо
г г < Е Р)6СО>600*560
READ 330, (LPELll )»LS( I )
L₽ EL(NEP* 1 ) = C
I = 1, nep )
!F(PPl)5e0/5?0,5E0
570 READ 320, ( (p p < I,j 5
G О T 0 6 Г 0
- I» 2 > । J = 1 » N E =>),
580 DO 590 lzl,NEP
DO 590 J - 1 • 2
59 С PP(J , I )=pp j
600 IF(NP) 2,2,1
i Read 33o,(NfOR(i),i=x>N₽)
READ 320 , (FO( 1 ), j =1,NP j
2 PRJNT 28o,HEP,Np,Ntr,РР
280 FORMAT( 42 *•3HNEP>8X<2HNP,7x •3HNTR»6X
1 6H FP1 /35Х,3[10,F12.4)
1 F < NEP ) 53,53,52
52 PRjnT 233
FORMAT < 4( I7,i3,FlC.4,p10
DO 72 0 I = 1,HE P
. 4 M
I 1 -LPEL ( J )
710
720
5 3
5 5
240
60
591
502
505
51 0
4 4
2 TO
35
CALL UNP4(J IN,NC( 1, I [ ) ,6 j
DO 710 JJ=1,3
J IN ) .EQ.LS( 1 } ) GO TO 720
CONTINUE
L S ( I ) = j j
JF(NP) 60,60/55
I NT : 40, (NFOP( I ) , FQ{ j ) , 1 = ! ,Np ,
FOrM4T(///50X,6HPOrcES//(5( I 10»E
IF(NTR) 505,501,510
DO 502 1 -i,b NCD
T EM I ) = 0 , 0
GOTO 89
GOTO
READ
320
320 ,
T D ( 1 >
= 1 »NNOD)
1/NT A )
DO 540 4t1,N|J00
0ПИС\Н1Е? ПРОГРАММ
201
RsXSIT < 1 » J >
DO 520 1 = 1,NTP
IFCR-TR<I*l#l>> 530*533,520
520 CONTINUE
5-3 0 T0(J) = TR(I,2)*CP-TR(I,l))»
1 ( T R( I ♦ 1 • 2 ) -TR( I >2 ) >/(TR( I *1,1 )-TR( I • 1) 1
5*0 CONTINUE
GOTO
550 DO 620 l=l»NEL
CALL UNP A ( J I n , hiC ( 1 , I ) » в )
DC 6 10 J = 1 » 8
JJzJ 1N(J )
610 T N(J)= T 0(J J )
DC 620 J-2.8,2
I 1 = J*1
JJzJlNlJ)
IF( I 1 ,GT.8) I I x 1
!F(TN(J).NEtO.O> GOTO 620
TD(JJ1=(TN(J-i)*TN(!I))/2,0
620 CONTINUE
IF( I I) 625,89,625
625 PRINT 295
295 FOrmaT(///6(4X»4HNOOE»11X,1HT) )
PRINT 300 , <1 ,TO( 1) , I-1,NNOC)
30 0 FORMA T<6(I8»F12.A)I
c ПРЕОБРАЗОВАНИЕ номеров 93ЛОВ В НОМЕРА
С •••• СТПЕНЕЙ СВОБОДЫ
89 DC 95 !=i,NP
I 1 = 2*1ABSlNFORl I ) >
IF(NFOP( I ) ) 95,90*90
9Q 11=11-1
95 NFQR( I ) - I 1
IF(SCT > 97,995,97
97 SCP=SCT
C МАСШТАБИРОВАНИЕ нагрузки
100 CO 110 !=1»NP
110 F0( I ) = FO( I )*SCP
00 120 ItliNEP
DO 120 J= 1 , 2
120 P P(J, I ) - P Pt J M )•5 CP
00 130 I=liNN00
13 0 T о(1 ) = TC( 1 ) •SCP
C •••• ПЛАНИРОВАНИЕ ВНЕШНЕЙ ПДМЯ’И
995 irtNT) 1 0 о 0 • 1 С 00» 1 005
1 jp 0 0 1?г=о
goto 1015
10 05 1 I=NT /32
IF( I 1*32.LT .NT) I I =! 1 >1
DO 10 10 1xi' I I
NW ( I > = 7 ♦ |
202
ПРШГОЖЕИНЕ
101G NR ( I 1 = 32 WI
1F<NR( 1 I ) ,GT .NT) HR( 1 I )=Wt
с сброс системного буфера
Lois Call srtse
I F(J Тр ) 1030,1030,1020
102С Nw( I I *1 ) =JTP
NQ( I I 4 1 )=512
юзе re turn
end •
SUBROUTINE F0RSEfi(LF,LL»M10,lFF)
C ФОРМИРОВАНИЕ БЛОКА СИСТЕМЫ уравнений
о ♦ -»• • равновесия
common /bli/a<i)/blia/lh»jip,nt,aiii)
1 /912 ХУТ (2» 1 ) /BL 2A/mZD(100)> NN , NEL,
1 NEM1» NZ,NC(2 >1)
1 OL 3/EM(2)» ANU(2) , д lT (2) .ST < 2)» ДМ < 2 ) • БК IZ
)
1 /BLWX(J),C(3),iSTr,ips,ng,Frec»LD
1 BL5/LPeL(9C)»LS(90)»PP(2,90)>NFOR<2o),FG
(20 ) > NEP »NP
1 /BL6/NTR,KW,PSi,PS2,RP(1)
I /BL 7/xy t fi , 2> » T1(В ) ,T N(В )
1 /BLB 8(^,16),DET»R»Z,T,0T
1 /BL12/AK(16rl6),DAL.0TT(i)
1 / В L H/AHi 1 6 ) , PH(16 )
DIMENSION LEC(16 ) , J IN(B )
IF(IFF) 5,5,11
5 JJ=(LL-LF*1>*LH
DO 1 С I = 1 , J J
J = MJ D»LH4I
10 A(J)- 0 . 0
11 mt s £
Call dooi<mt и ps > о )
ip = i
Do 60 JJ=1,NEL
call unp^c jin,nc(i,jj j,в j
I F(J J - 1 -NEM. 1) 1 5 >15 , 15
13 MT=2
call oddi(mt•Ip^ > о)
C ПРЕОБРАЗОВАНИЕ индексов в номера
с »••• степеней свободы
15 DC 20 1=1,6
К = 2* I
LEC(к-1)=JIN(1)>2-1
2 О LE С(К)=LEC(К -1 ) 41
1 = 1
X F( IFF ) 25,25,40
25 DO 30 1=1,16
С ДАЕТ Ли ЭЛЕМЕНТ ВКЛАД В ДдННЫй БЛОК
I F ( LEC ( I ) ,GE ,LF . AND . LEC ( I ) ,LE ,LL ) GOTO
ОПИСАНИЕ ПРОГРАММ
203
30 CONTINUE
!F(NEP>34,34,31
31 DO 33 J = l»5
IF(LPEL(IP)-JJ)34,33,34
33 IPr1P*l
34 GOTO *0
C ВЫЧИСЛЕНИЕ МАТРИЦЫ ЖЕСТКОСТИ И
С •••♦ ТЕРМИЧЕСКОГО ВЕКТОРА
40 CALL DGNR(JJiIG,JIN)
DO 49 K = 1>8
J<J I N (K )
T1(K ) =OTT(J )
ХУ(K » 1)=XVT( 1 »J )
49 ХУ(К,2)=ХУТ(2»J)
CALL ST IF < IFF,MT, IG)
1F(NEP> 44,44,41
C • ••* НАГРУЗКА от давления
41 CO 43 J=1।5
IF(LPEL( I P )-J J) 44,42* 44
42 CALL PRESS(LS< I P ) »PP(1» I P> *pp I 2 ’ 1P} ’₽H* 1S*
R )
43 !P=IP*1
C СВОРКА УРАВНЕНИЙ
44 DO SC J=I,16
lF(LEC(J),LT,LFeOR.LEC(J).GT.LL) GOTO 50
M=LEC(J)
A1CM)^A1CM)*AH(J)*PH(J)
RP(M)=RP(M)*PHCJ)
IF( IFF) 55,55,50
55 DO 45 K = 1 , 16
1 F(LEC(К> . LT.LEC(J) ) GOTO 45
m=(Lec(J)-lf*m:d)»lh*lec(k>-lec(j)*i ?
A ( M ) = A ( M ) ♦ A К ( J » К )
45 CONTINUE
50 CONTINUE
6q CONTINUE
* сосредоточенные усилия
DO 70 1 = 1,NP
IF{NF 0R( I) .LT , LГ.0R•NFOЛ( 1 ) • ОT . LL ) GOTO 70
J=NFOR<1)
/ 1 ( J)=A1(J)*FO( I )
RP ( J ) = R P ( J ) ♦ F О I I )
70 CONTINUE
C •••• ГРАНИЧНЫЕ УСЛОВИЯ В ПЕРЕМЕЩЕНИЯХ
DO 90 1=1,NZ
IF( IFF.GT . 0 ) GqTo 85
[F(MZD( I) ,LT,LF.OR.hZO( 1) .GT ,lL> GOTO 90
M=(MZ0(I)-LF*мID)•LH*1
J=M*LH-1
DO 80 K=M,J
204
ПРИЛОЖЕНИЕ
t Z A ( К ) = 0 . 3
A CM ) = 1,0
8 5 M =M Z D ( 1 >
Al(MlcO,O
90 CONTINUE
I Ft* 1 FF> GT . О I GOTO 110
00 100 !=LF,LL
DO 95 J=1,NZ
!rU ,IE,MZD(j)-Ih-O₽. I ,GE >2D( J И GOTO 2 J
A(M) = 0.0
95 CONTINUE
100 continue
110 RETURN
ENO
SUBROUTINE 0001(WT»IPS,101)
c • вычисление матриц упругости
С • ••• И ПОДАТЛИВОСТИ
COMMON /8L9/D0(4,4) •D1(4,4 ), АР < 4)
'• /в,-3 Е г 3 k »ANU ( 2 > » ALT ( 2 ) , $1 (2 ) , Дц< 2 > гвк ( 2 !
DO Ю 1=1,4
00 10 J=1,4
Ю D0(I,j ) = 0,0
ANUi = ANU(MT >
1F(!₽$) 20*20,30
2C ANUisANU(MT)/(1.O-ANU(MT))
>0 00(1*1)51,0
DD<1» 2)=aNU1
D0( 1,4) = ДNи1
00(2,2>=1.о
DO < 2 >1)=aNU1
DC<2,4)=amU1
DD(3,3> = ( 1,0-ANUl )/2.0
00(4*1)=ANU1
D0(4r 2 )=ANU1
DO(4 * 4)=1.0
DO 40 1=1,4
DO 40 J=l,4
40 DD(ItJ)= d Г(I , J)•E(MT >7 ((1.0*ANU(MT) ) •
I (1.0-ANulM
1F(ID1) 70>T0,5Г
50 DO 60 1=1,4
DO 60 J=1,A
60 Dl(!'J) = о.0
AW=ANU(Mt)/E(MT)
Dl(1»1)=1.0/E(MT)
D1<1» 2)=-AN
Dl( 1»4) = -aN
Dl ( 2 » 1 ) =-AN
Die:.z ' = 1 .G/с(мт )
ОПИСАНИЕ ПРОГРАММ
205
D1(2»4)--AN
&1 ( 3» 3)=2 . О* (1 . О*ANU(МТ ) )/Е(МТ )
01(4.l)x-AN
01 ( 4,2 > = - A N
Oi(4>4)sIto/E(MT>
АР( £)=Al|(MT)
I P(2> = ALT(MT )
P < 3 J = 0 » 0
AP(4)=ALt (MT )
7© return
END
SUBROUTINE OGNR(NE»IG,J1N)
C ВЫРОЖДЕН ЛИ ЭЛЕМЕНТ
DIMENSION JIN(B)
I Gx C
CQ 10 1=1.7,2
10 , 20 » 10
Ю continue
пе turn
20 1G=I*5
IF(IG.GT.8 ) 1 G = lG-8
RETURN
END
SUBROUT INE ST1F(]FF»mT.IG)
C ♦ ••• ВЫЧИСЛЕНИЕ М|т₽ииы ЖЕСТКОСТИ и
с • ••« термического вектора
COMMON /BL3/Em(2)»ANU(2),ALT(2).$T(2),
1 дМ<2).Вк(2)
1 /&L4/X(3)fC<3),l5TR,lPS,NG.PREC,LD
1 /BL6/NTr»KW,PS1,PS2»RP(1)
1 /BL8/B(4»16),DET»R»2,T»0t
1 /ВL 9/DO ( 4,4 ) » 0 1 ( 4,4 ) , ЕР T ( 4 )
1 /BL12/Ak(16»16),0aL,TS(1)
1 /BLH/АН( 16 ) » PH(16 )
DIMENSION СС(16.4 )
10 2 1 = 1» 16
РН( I ) =0 . С
Z ДИ( J ) = 0 . О
I Г(NTR.EQ.ОtANO.IFF.GT.О) GOTO
IF(IFF) 9,9,13
9 DO 1С 1=1,16
00 10 J=l»16
13 АХ 1 1,J ) =0 . О
С ИНТЕГРИРОВАНИЕ ПС ГАУССЧ
13 DO 40 M=1.NG
DO 40 N=1»NG
CALL CCB(X(M),X(N),IG)
DO 13 1=1,16
DC 15 J=1,LD
CC( I , J ) =0.0
206
ПгаДОЖЕИИЕ
DO 15 К = 1 ,LD
13 CC(!,J)=CC(I,J}*8(K»I>*DD(K,J>
1 F ( J F F ) 17,17,25
17 DO 20 1 = 1 » 16
DO 20 Jslfld
DO 20 K=1,LO
C • ЭЛЕМЕНТ МАТРИЦЫ ЖЕСТКОСТИ.
20 ДК ( I ,J ) = AK ( I , J > *CC( I , К )»B(К,4)•
1 С(M)*C(N)© DET
IF(NTR) 25,4; ,25
25 EPT(1) = aLT(MT >•DT
E₽T(2)=EPT(1)
EPT<*)=0,0
E F T ( 4 ) = E P T < 11
DO 30 I = 1 »16
DO 30 J=1»LD
C • *-> ЭЛЕМЕНТ ТЕРМИЧЕСКОГО ВЕКТОРА
30 AW( I )=AH( I >4CC( I »J)«EPT(J)*
1 C(M)»C(N)»DET
40 CCNT I NUE
50 RETURN^
END
$U8 ROUTINE C0B<XbET»lG)
C ♦••• ВЫЧИСЛЕНИЕ МАТРИЦЫ ДиФФЕPEHUMPODАНмЯ
С ПЕРЕМЕЩЕНИЙ
COMMON BL4/X(3),C(3),ISTR,1PS»NG>PREC,ID
1 /BL7/XV(6>2),Tl<e)»TN(8)
1 bla/B(4,i6)»DET,R/Z,T,0T
1 /BL11/XS,VS,3(1(I),CJ(10>»KEL(100)>KS(100)
DIMENSION AN(a),XEN(2'8)>DNE(2)>DNV(2)»AJ(
2,23
x1 = i-x:
X2-i
E 1 = 1-ET
E2-1*ET
C • ••* ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ
AN(1)=-Xl*E!♦(X2+ET)
AN(3)= X2*E!♦(X1-E2)
AN(5)= Х2*Е2»(E T-X1)
AN(7)S-X1*E2*(E1*X!)
Ал(2)=X1«X2*E1
A N ( 4) = E I * E 2 • X 2
AN(и > =X1»X2*E2
A N ( 8 ) = E 1 ♦ E 2 • X 1
C ПРОИЗВОДНЫЕ ФУНКЦИЙ ПО ЛОКАЛЬНЫМ
С КООРДИНАТАМ
XEN( 1 ।1)=Е1»(2* XI*ЕГ)
ХЕ N(2,1)- X1 *(2» Е Т♦XI)
X Е N ( 1 » 3 ) = Е 1 • ( 2« X 1 - Е Т )
X L N ( 2 » 3 ) - х 2 • ( 2 • Е Т - X I )
описание Программ
207
ХЕШ 1 > 5 ) ?Е 2» С 2«Х I *ЕТ )
XEN(2 » 5 ) хХ2«(2*£Т*Х| >
XEN(1»7)=E2»(2»XI’ET)
X Е К(2» 7 > = XI. •(2•Е Т-X!)
X Е N( 1,2)з-Х1»Е1
X Е N(2।2)=- 0.5* X 1 •X 2
XKN(1,4)=0.5кЕ1<Е2
X Е N ( 2 » 4 ) з - Е У • X 2
XЕN ( 1» 6>=-XI • Е 2
X Е N <2 >6)з-XEN(2»2 )
X Е N ( 1 । 8 ) = - X Е N ( 1 > 4 )
XЕN(2»8)з-ЕТ*Х1
DO 10 I = 1 » 7 » 2
AM I ) = 0 . 25*AN ( I )
AN(!*l)=0.5*AN(t*l)
XEN( 1, J ) = 0.25*XENd, I )
IQ XEN(2»!>=C.25*XEN(2.I)
I F< I G ) 14,14,11
C •••• модификация ФУНКЦИЙ ДЛЯ
С ♦ ••• ВЫРОЖДЕННОГО ЭЛЕМЕНТА
11 я з 0.1 2 5 » X1 • х 2•Е1•Е 2
2 з - 0.2 3 » X 1 ♦ Е 1 • Е 2
Тх-0.23<Х1*Х2*ЕТ
AN(IG-1 > =AN С I G - 1 )* Я
AN( I G>=AN( IG)-2«R
J = I G ♦ 1
IF <J.GT . 8) J = J-8
A N ( J > = A N ( J ) ♦ R
XEN(1»IG-1)=XEN(1»IG’1)*Z
XEN(2rlG-l)=XEN(2»!C-l)*T
X E N(1, IG)= X E N(1, !G }-2»Z
XEN(2 > I G ) =XEN(2 H G )-2«Т
XEN( 1 , J ) s KEN(1»J)*2
X E N ( 2 > J > = X E N ( 2 > J > ♦ T
14 P = « . 0
Z-0. 0
т r o. a
DT = O . 0
DO 15 1 = 1» 8
C КООРДИНАТЫ И ТЕМГЕРАТУРд ТОЧьГ.
RcR + ANll ) * XV < Id)
ZzZ^AN t I ) «XV( I » 2)
ТзТ>ДН(I)*TN(I)
DT = OT*AN( I ) • T 1 С I )
15 CONTINUE
C •••• МАТРИЦ л-ЯК0 5UAH
17 DO 20 1=1»?
DO 20 J=1>2
AJ(I । J)=0.0
DO 20 K=l»8
208
приложен ire
20 = К >*XV(X,J)
XS«aJ( 1» 1 }
VS = AJ <1,2 >
c • ••• обрамение якобиана
f k = aj ( ь i)
A J ( 1 > 1 ) s A J ( 2 # 2 )
A J(2♦2)= fK
Aj < 1 , 2 ) = -AJ( 1 » 2)
A J (2 . 1)=*AJ(2»1)
00 25 1 = 1,2
00 25 J=1.2
25 AJ( I , J ) =<J( I » J )/OET
00 30 1 = 1»4
00 30 Jsl.16
50 В ( I » J ) * 0 • 0
DO 55 K = 1 »a
ONE( 1 )=XEN(1,K)
ONE(2)xXEN(2,K)
C •»»» ПРОИЗВОДНЫЕ ФУНКЦИЙ ПО ГЛОБАЛЬНЫМ
С • ••• КООРДИНАТАМ
00 35 1=1.2
ONVC | ) = 0.О
DC 35 Jsl,2
35 ONv( I ) = ONy( I )>дJ( 1 ,J).one(J )
I 1 = 2*K-1
1 2=2»K
C • ••• ISTR=1 - ПОЛЯРНЫЕ КООРДИНАТЫ
lf( 1STR-1) 40.40.45
40 В С 1. I 1) = ОЫУ(1)
В(2»I1)=A4(K)/R
В ( 2 , I 2)=ONV(2)/й
В < 3 , I 1)=ONV(2)/Й
В <3 » I 2) = ONV(1 ) -AN < К ) /й
GOTO 55
С !$ТЙ=2 - ДЕКАРТОВЫ КООРДИНАТЫ
4 5 В(1» I 1) = ONV <1)
В(2 * 12) = 0NV(2)
В< 3> 1 I) = ONV(2)
В(3» t2)zDNV(l)
С •••• 1$ТЙ«3 • ОСЕВАЯ СИММЕТРИЯ
If( ! STR-3 ) 55,50.55
50 В(4. 1 1 ) =ДN(К)/R
55 CONTINUE
I f ( I STR-2 ) 60,70 »60
60 OET=DET*R
70 RETURN
END
SUBROUTINE PRESS(JS,PltP2,AH.lSTR)
C •••• ПРИВЕДЕНИЕ К УЗЛдМ PАСПPEДSЛEMHOй
ОПИСАНИЕ ПРОГРАММ
209
С НАГРУЗКИ» НОРМАЛЬНОЙ К ПОВЕРХНОСТИ
COMMON /BL7/xy(8,2),Tl(8)»TN(8)
DIMENSION АНЦ6)
DIMENSION XP(3,2)»AN(3),XIN(3),X(3),C(3)
DATA ((X(I),1=1,3 ) = - 0 .7745966692*1»
1 0.77*596669241.0.0)»
1 (<C(I), 1 = 1,3)=2<0.555555555556),
1 0.666688666889)
C • ВЫБОРКА КООРДИНАТ УЗЛОВ СТОРОНЫ
DO 10 1=1.3
J=I-JS-1
I F ( J . GT.8) J=1
XP < I » 1 )=XV(J, 1 )
10 XP( 1 , 2)=XУ(J,2)
C • ИНТЕГРИРОВАНИЕ По ГАУССУ
DO 90 М=1,з
X!=X(M)
X1=1 . 0-X I
X2 =1. 0*X I
C •••• ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ И ИХ ПРОИЗВОЛ-
с ♦ ••• НЫЕ ПО ЛОКАЛЬНОЙ КООРДИНАТЕ
AN( 1)=-0. 5»ХЬХ1
AN(2)=Х1*Х2
AN(3)=0.5*Х2*Х1
X I N ( 1 ) = 0.5 • ( 2 . О ♦ X I - 1 , 0 ) ‘
X I N ( 2 ) = - 2 , 0 • X 1
X I N ( 3 ) = 0.5 ♦ ( 2 . О • X I ♦ 1 , 0 )
Р=Р1*0.5*(Р2-Р1)«(1.0*Х1)
R = 0 . О
У$ = 0 , О
Х5 = о. О
DO 20 1=1,3
R=R*AN< I ) .XP( j , 1)
C • ПРОИЗВОДНЫЕ ГЛОБАЛЬНЫХ КООРДИНдТ
С •••• По ЛОКдЛЬНой координате
yS=VS*XlN(I )*ХР( I ,2)
20 X$=XS*X1N(I ) •XР( Ы,
I Г < I STR-1 ) 50.40,50
*0 У5=У5*Я
50 I F( I STR-3 ) 70,60,70
60 PzP.R
с сборка усилий
70 Do 80 1=1.3
Jb(I♦JS-1 ) »2
IF(J.GT.16 ) J = 2
AH(J-l)=AH(J-l)-AN(I)»ys»C(M)»P ‘
60 Ah(J)=AH(J)+AN(J>>XS*C(M)*P
9o continue
Return
end
E. M. Морозов, Г, П. Никишков
210
ПРИЛОЖЕНИЕ
с
с ♦ • •
с • • •
5
10
20
25
30
35
40
45
50
55
60
45
70
75
60
SUBROUTINE SOLUTCMT1T.NN.NFIL,
1 I ТУР,Nl,N2»NJtN4,NN2»NN3,NN4)
• решение системы линейных уравнений
• itvp.le.o - полное решение со своркой
• ITVP.GT.0 - СОКРАЩЕННОЕ РЕШЕНИЕ
COMMON / BL 1 / А С 1 ) ✓ В L 1 А / LH . J ТР , N Т , А 1 С1 )
Mcsq
Call wrs < mtiт.о,мс)
LF = 1
ll = ni
mi Dz о
11*1
DO 50 I I =2.NF IL
IF(ITVP> 5.5,25
IF( I 1-3) 20. 10.20
MlDsN3
Call forseq<lf»ll.mid»-1)
LF=LL*1
LL=LL*N2
Call STRt(L1 INl,N2 . -1 )
call wr$(nn2.itvp.mc )
I F < I T ¥ P ) 35 »35.30
call stRtcli.ni .n2 > i >
GOTO 45
Do 40 I=1»NN3
J:1*NN2
A ( I ) = A ( J )
li=li*n2
CONT INUE
iFCtTVP) 55*55.60
call forseQclf.nn.n3.-i)
call strt cli.ni.na.-i )
call wrs<nn4.itvp.mc)
IFCITVP) 70.70.65
call st*t cli .ni , na, i>
call bsub<li»ni,hi-na )
Call rback cnna,i»mc>
Do BO LL=2.NFIL
Do 75 1=1»NN3
JJ=NN3-1>1
I 1 =NN2*Jj
A( II )*A<JJ )
Call rbackcnn2,-i,mc )
L 1 = L1-N2
CALL BSUBCL1.N1»n3)
CONT INUE
call RBACK(MT it.О/МС)
RETURN
END
subroutine strtcli.ni.n.ib)
описание программ
ПРЯМОЙ ХОД РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ
ПО МЕТОДУ ГАУССА
COMMON /BL1/A(1)/BL1A/LH,JTP,NT,A1(1)
1 Ок=€N1 * 1)•LH ♦ 1
I D= 1
IH1=LH-1
L2=L1*N-1
00 40 1=L1,L2
101=10
00 20 Ml=l,1H1
I 01=I 01 ♦ LH
1F( IDl-I OK ) 5,3 , 3 0
5 I F ( 16) 7,7,15
7 J J=ID*M1
IF(A(J J) .EQ . 0.0)GOTO 1 5
MM =
00 10 M=1,MM
11= O1*M-1
KK=Jv*M-l
A<II)=A(!1)-A(JJ)/A(ID)*A(KK)
10 CONTI NUE
15 I 1=I *M1
JJ=IO*M1
A1(II) = A1(II)-AIJJ)/A(ID)>A1H3
20 CONTINUE
30 IO=ID*LH
40 CONTINUE
RETURN
END
SUBROUTINE BSUB ( LI , Nl, Ц)
••• ОБРАТНЫЙ ХОД РЕШЕНИЯ
••• системы уравнений
COMMON /BLl/А ( 1 >/BLlA/LH, JTPaWTaAK П
I OK = ( N 1 - 1 ) ♦ L H ♦ 1
I 01=I OK-Il*LH
Ml = 1 1*1
N2 = L 1*N1
MM = LH - 1
00 40 I=M1,Nl
5=0.0
IR=IDl
00 10 M=1,MM
IR=!R*LH
IF < I R-I OK) 5,5,20
5 I I = ] D1*M
JJ = N2- I*M
S = 5 ♦ A ( I I >♦A 1(JJ)
10 CONTINUE
20 Il=N2“l
Alt II ) = (Al(H)-$>/4«XDXJ
212
ПРИЛОЖЕНИЕ
30 IDlsJOl-LH
*0 CONTINUE
return
end
SUBROUTINE WRS(L.IWR*MC)
C •••• ЗАПИСЬ/СЧИТЫВАНИЕ С мБ/мЛ В ПРЯМОМ
С • ••• НАПРАВЛЕНИИ
COMMON /BL1/A(1)/BL1A/LH,JTP,NT,A1(1)
1 /BLS/NW( 5) , NR( 5) » LL( 3 ) ,•! I > J J >NB( 3 )
call tone(mc > l )
MC-MC♦<L- 1 ) / 1 024♦1
20 MA = 1
K= 1
DO 130 lsU*JJ
IF(IWR) 100/100*110
C ЗАПИСЬ НА УСТРОЙСТВО NW В ЗОНУ NE/
c ♦ ••• начиная c адреса мозу а, длиной ll
c • ••• слов через системный вуфер
юс call wbuf(NW(I)»nB(K)*a(ma)/LL(KH
GOTO 120
c • ••• ЧТЕНИЕ
110 CALL RBUF(NW(I),NB(K>,A(NA),LL(K>)
120 MA=MA*LL(K)
K = 1
130 CONTINUE
return
end
SUBROUTINE R 6 А С К ( L » L R E V * MC )
c •••• чтение С М6/МЛ В ОБРАТНОМ НАПРАВЛЕНИИ
COMMON /eLl/A(l)/BLlA/LH,JTp*NT.Al(l)
1 / В L S / NW { 5 ) * NR ( 5 ) » L L C 3 ) » I I * J J * NB ( 3 )
MCsMC-< L-1 ) /1024-1
'20 IF < L9EV) 1 10 » 1 10 * 130
Ho call tone <mc *l )
K= 1
МД= I
00 1 20 I Si I >
call rbuf(nw(I),nB(k>»a(ma)»lu(K)>
Мд = МА *ll<к )
к = к ♦ i
120 CONTINUE
130 RETURN
END
SUBROUTINE TON£(MC,L)
C •••♦ НдСТРОйКА НА ВНЕШНЮЮ ПАМЯТЬ
COMMON /BLS/NW(5),NR(5)*LL(3),II»JJ»NB(
DO 1 1-1,3
1 Nb(I)=0
MC1=MC*<L-1>/1O24*1
5 DO 10 1 I si |3
ОПИСАНИЕ ПРОГРАММ
213
IF(MC-NR(11)) 20 ,1D , 1 О
10 CONTINUE
20 N=C
JF(II.GT.l) H = NR( I 1-1)
NE(1)= MC-N
DO 30 JJ = 1 » 3
IF < MC1-NR(JJ)> 40*40.30
30 CONTINUE
*0 IF(I I -J J) 60,50,50
5 0 LL < 1 ) = L
return
60 LL(1) = (NRC I 1)-MC)*102 4
I F( I I ♦!-J J ) 00*70*70
7 0 LL(2 ) = L-LL(1 )
Return
00 LLC2) = <Nr(I I♦1 )-NR(I I ) ) •1024
LL(3) = L-LL(1 )-LL(2 )
RETURN
END
SUBROUTINE OSIGP(SG,.DL,DC,
1 1 D S , X P , у P , F P . E P Q , J F I N )
C ПОДСЧЕТ НАПРЯЖЕНИЙ В УПРУГО*
С ♦♦♦• ПЛАСТИЧЕСКОЙ СТАДИИ
COMMON /BLl/A(l)/BLlA/LH,jTpiNT,Al(l)
1 В L 2 /XУ N ( 2 , 1 ) /ft L 2 д / МZ 0 ( 1 0 0 ) , NN * NЕ L »
1 NCMI , NZ • NC < 2 , 1 )
1 /ВL 3/ЕM< 2) 91NU(ZI•ALT(2) *ST(2),AM ( 2 ) iВК(2
)
1 /&L4/X(3),C(3),tSTR,IPS»NG,PREC,LD
1 /BL6/NTR»KW,PS1,PS2»RP(1)
1 ZBL7/Xy(B»2) ,T 1 (6 ) *TN(8)
1 /BL6/B(4,16),0ET»R»ZtT,DT
1 /BL9/DD<4,4),O1(4,4)*AP(4)
1 /BLlO/lZ.NNoO,LOAD,KQ,NSS,APR*NF1
1 /BL11/XS,VS,3(10)»CJ(10>»KEL(100)*KS(100)
1 /BL12/AK(16,16),0AL»TS(l)
DIMENSION SG(4,l)*TT(l)»0L(l),
1 DC(1),FP(1350)>EPR(1350)»*P(1550)»
1 У P ( 1 3 5 0 ) , DDE L ( 1 6 ) , DE L ( 1 6 ) » A I ( 4 ) , ОI ( 4 > ,
1 DS1(4),DSEC4),EPP(4),51G(4),SB(4),PSI(16>
1 »FEP(4),CEP(4),S1(4),JIN(8)
EQUIVALENCE (A( 10000),ODEL)*(A(10016),DEL)
>
1 (A( 1 0032 ) , Al), (4(10036), 01),
1 (A(10040),DSI),(A(10044),DSE)>
1 (A(10046), EPP), (A( 10052), SIG)*
1 (A(10056),SB).<A(1006q)»pS1)
1 »(A(10076),FEP),<A(ie080)»CEP)
1 *(A(LOO84),S1),(A(1OOB8),JIN)
LK = 3
?Л4
ПРИЛОЖЕН!] I
IHlpS.Eft.C) LK = 4
КМзJFIN*1DS
DO 3 I sj , 10
3 CJ( I )=0. 0
IC = 1
DO 5 I = 1 » NN
5 A 1 < I ) = OtO
NG2=NG**2
MTsi
OELFsO.!•ST(1)
CALL DOD1(MT,о »1)
c •••• цикл ПО ЭЛЕМЕНТАМ
DO 350 NE = 1,ne L
CALL UNp4 ( J IN,NC(1>NE),6)
к j = o
>io k;;«"su“"c”
ICs 1 C * 1
520 IF(NE-NEMl-i) 7/6i7
6 MT = 2
OELF=O.1»ST(2)
CALL ODDI(MT,0/1)
7 DO io 1 = 1, e
J = J IN( 1 )
M = 2* J
K = 2* I
c •••• ВЫБОРКА nApAMETP0B ЭЛЕМЕ>
TN( 1 ) =д(j)
T 1 ( I ) = T S ( J ) >
XV( I ,1)=XVN( 1,J)
XV(I.2>=XVN(2,J)
DOELI К -1)= OC(M- 1)
DOEL<K)=OC(M)
0EL(k-1>=DL(M-1)
10 DE L(K > = DL(M)
I A=NG2«(NE-1)
00 15 1=1.16
15 P SI( I ) = o.0
CALL OGNRINE,IG,J1N)
°0 330 Ijcl.NG
00 330 Jj=1,NG
KL = 0
IF(KJ.KM) 17,18,17
17 IFOJ.EG.I) KL = 1
18 К:I4»NC»(I I -i ) »jj
00 28 1=1,4
20 S8<I)=SG( I ,K >
CALL C0B(X( I I ),x<J J),JG)
00 40 1=1,4
CEP( I ) = 0.0
ОПИСАНИЕ ПРОГРАММ
215
Oi (1 ) = о.о
00 30 J=l,16
CEF(1)=CeF(I)*6(!,J)«DDEI(J)
Зо DI(I)=DI(I)*n(I,J)*DEL(J)
ген i > = сер(I )*di (I)
35 СеР( I )=CEP( I )-ДР( ! )»DT
*0 continue
I F С IPS) 60*^0,50
5o CeP(4)=-aNU(MT)*(CEP(1)*CEP(2))/(1.-ANU(MT
) )
6o oo ao
Dsl ( 1 ) = 0 . 0
DSE( I ) =0.0
DO 70 j=l ,4
0 S I ( I ) = 0 $ I < 1 ) ♦ D 1 ( I , J ) • SB ( J )
70 OSE(l)-0SE(!)*DD(I,J)*CEp(J)
EPP(1)=DI(!)-DS!(|)-AP(I)»T
00 51G(I)=SB(I)*0SE(I)
I F(I PS) 100*100,90
90 EPP(4 ) =-(EPP(1 ) ♦EPP(2 ) )
100 F1=FT(SIg»EPP.MY,EEQ)
c •••• Fl.GT.o - ТОЧКА в ПЛАСТИЧЕСКОМ
С СОСТ ОЯнИИ
I F С F 1 ) 105*105*110
105 IF(KL) 261*261*106
106 DO 107 1=1*4
107 3<KJ)=3(kJ)*(SIG(I ) ♦SВ(1 ) ) «С ЕР ( I )*VS *C(I I )
GO TO 261
110 1 F С 1 0 S > 115*115.120
115 JFIN=O
12q Fq=FT(SB,EPP•MT,EEQ)
1 F(F0 ) 140*130*130
13 0 Rm = 0.0
Goto 165
140 Rm=-F0/(Fl'FO )
Do 150 1=1,4
150 SIG(I)=$B(I)4RM*DSE(1)
F q = FT(SIg*EPP *MT,EEQ)
call cai< s1g.ips,mt,ai )
C12Q
Do 160 1=1,4
160 C1 = C1*A1 ( I )*DSE( I )
c •••• rm - упругая часть прирашения
rm=rm-fo/ci
165 Mm=1NT(Fi/DELF )♦!
DO 170 1=1*4
S J G( 1 )=Sb< I )*RM»DSE( I )
IF < КL ) 170*1 70 *166
166 Э(КJ) = з(кJ ) *(5 I G( ! ) ♦SB(1 ) >*RM•
216
ПРИЛОЖЕНИЕ
СЕР < I >SC(P(1 ) •(1.О-RM l/MM
170 DS I ( I)=О$Е( 1 )•<1.О - RM ) / ММ
00 230 1x1,ММ
Вн=Н1(ЕРр,МТ)
CALL С А 1(516 » IpS » МТ » д J j
ВЕТ = О . О
С1 = 0 . О
00 190 J=l,4
01( I > = 0, О
DO 100 J=1 , 4
1 В О Dl(I)eD](I)*DD(I,J>*Al(J)
BET=fiET<A I ( I )*DI ( 1 )
19 О C1=C 1 ♦ A I ( I)•DSI ( 1 )
OLA = C1/(BH*6ETj
IF(DLA,LT ♦ 0 . 0 ) DLA = 0 , 0
C •••• ПРИРАЩЕНИЯ НАПРЯЖЕНИЙ И
С ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
DO 2 0 0 1 = 1,4
51(I ) = SIG ( I )
51G(1) = 5IG(I)*CSI(!)-CLA*OHI)
200 ЕРР(1)=ЕРР(1)401д«А1(1)
I F I IP 5 > 220,220,210
210 Е РР t4) = -(ЕРР(1)♦ЕРР(2 ) )
220 F1=FT(SIG,EPP,MT,EEQ>
С1 = 0. О
с •••• коррекция напряжений
DO 230 1 = 1 ,LK
2 3 0 С1=С1*А I ( I )»«2
DO 2 4 0 1 = 1 , LK
240 S1G( 1 1 = S I Gt 1 ) -I I ( I)•Fl / С• 1
IFjKL) 250,250,243
2*5 DO 246 1=1,4
246 3(KJ)=3(KJ)*(SIG(I)*Sl(t>)«CEP(l)»VS»C(II)
250 CONTINUE
C • УСИЛИЯ В УЗЛАХ
261 DO 270 1=1,16
DO 270 J= 1 , 4
270 PSl(l)=PSl(I)«-B(J,I)»siG(J)«C(I!)*C(JJ)»DE
310 IF(KM) 320,330,320
320 Fl=FT(SlG»EPP,MT,EEa>
FP(К) = 100.0*F1/ST <MT 1
EPQ(K)=EEG
DO 325 1=1,4
32 5 SG( 1 ,K) = SIC( J )
XP(К ) =R
VP(K)=Z
C •••• ПОДСЧЕТ ВКЛАДА В ИНТЕГРАЛ Ч.-Р.
IF(КL ) 330,330,326
32 6 VXxO . О
ОПИСАНИЕ ПРОГРАММ
217’
1 ^SJG(l)»F£p(X)*SlG(3)«VX>»VS
CJ(KJ>=CJ(KJ)*2.0Tl»C(Ii)
330 CONTINUE
00 340 1=1,e
1 1=2*J 1N < I )
К =2* I
c •••• ВЕКТОР НЕВЯЗКИ
00 360 !=1»NN
Л 1 ( I ) =RP( I ) -A 1 ( 1 )
36o CONTINUE
IF(KM.EO.0) GOTO 365
C НАКОПЛЕНИЕ ПЕРЕМЕЩЕНИЙ
DO 362 I=1,NN
362 DL( 1 )- 0L ( 1 ) ♦0C < 1 )
c суммирование температур
00 363 1 - 1 ,NNOD
363 A( 1 )= A( I}*T s( I )
365 Do 36? 1=1,NZ
• I I= MZ0( I )
36 7 A 1 ( I I ) =0.0
PS2=RNM(Al»NN)
P^2=SftRT(PS2 >
ir(JOS.LE.O) GOTO 373
IF(PS2.GT,PS1) GOTO 375
373 RETURN
375 NFl=NFI>i
kw= o
I ГcNF I-3) 373*377,377
377 PRINT 36o » IDS
360 FORMAT(//52X,18HPДСХОДИМОСТЬ,1TER=, I 3)
STOP
End
function Rnm(a»n>
c • ••• норма вектора
dimension a<1)
c=o. о
Do 10 I = !,N
10 CsC*A(I)•12
RNMxC
RETURN
end
function fT(S,ep,mt,eeo)
c •••• функция текучести
218
ПРИЛОЖЕНИЕ
COMMON /bL3/Em(2HANU(2)»ALT(2>»
.1 $T(2) »Ам<2) »ВК(2)
DIMENSION 5(4)» ЕР I 4 )
DATA (53=1.7320508076)
SM=(S(1)♦$(2)*5(4 ) ) /3 . o
$EQ3SQRT(O.5«(<S(1,>-SM>.*2MS(2)-SM)*.2
1 ♦ ( s I 4 ) - gM ) • • 2 ) ♦ s I 3 ) • *2 )
EEQsSQRT((2.0*(EP<l)«*2*EP(f)«»2*
1 EP(4)«*2>*E?(3)»*2)/3.0)
FT=S3»SEq-BK(mT)*EEQ*«АМЛmT )-ST(mT>
return
END
FUNCTION Н1(ЕР»МТ)
c • ••• НАКЛОН КРИВОЙ ДЕФОРМИРОВАНИЯ
COMMON /&L3/EH(2) , ANU(2) » ALT (2 ) » ST (2)»
1 AM(2) » Bk < 2 >
DIMENSION EP(4)
DATA (S3 = l . 73205 060 76 )
I F(ДМ(MT)-1,0) 2 0 • 1 0 * 2 0
10 H1=BK(MT) * ‘ I
RETURN
20 EEQ=SQRT((2.0»(EP(l)*»2*EP(2>»»2*
1 EP(4)»»2)*EP<3)«»2)/3.O)
Н1 = ВК(МТ)»АМ(МТ)»ЕЕО**1АМ(МТ > - 1 . 0 )
return
end
SUBROUTINE CAI IS, IPS,MT,Al )
C •••• ВЕКТОР ПРОИЗВОДНЫХ ФУНКЦИИ текучести
С По НАПРЯЖЕНИЯМ
COMMON /6l3/EM(2),ANU(2),ALT(2)»
1 ST(2 ) > Ам< 2) > ВК(2 )
DIMENSION S<4),AI<4)
Data < S3 = 1 . 732050«076 )
SM=(SI 1)♦$(2 > *S(4) )/3.о
A I ( 1 ) = S(1)-Sm
A I ( 2 ) = S ( 2 ) • Sm
A!(3)-2.0*S(3)
A I (4) = S< * >-SM
3EQ=saRT(0.5*(AI<l)»«2*Al(2).w2*
1 A I (4 ) ••2 > *S(3)«*2)
F=C.5«S3/SEQ
DO 10 1=1*4
10 A I ( I ) =F»A I ( I )
I F C JPS) 3 0,30,20
20 AI(4)=-ANU(MT).(AH1)*AK2))/(1.O-ANU(MT))
30 RETURN
ENO
SUBROUTINE RESULT(SG,DL,FP,EPfi*
1 X , у , J F I N , NE L * NN , I T E R r I QT )
C »••• сегментация и печать результатов
ОПИСАНИЕ ПРОГРАММ
219
COMMON /В Ll/Д(1)/BL1A/LH > JTP,NT »А М1>
1 /OL4/XX(3),C(3)HSTR,lP$»NG,PREC»LD
1 /BL6/NTR»KW,PS1»P$2»RP<1)
1 /ВL10/I 2,NNO0,LOAD,KQ,NS5,APR » NFDG
1 /BLll/XS»yS»3(lO)rCJ(iO)»KEL(100),KS(100)
1 /ftLS/NW(5)>NR(5)»MB(3),1W»JW
DIMENSION SG(4,l)»DL(l),Fp(lHEpQ(l).
1 X(1) »V(1>,B( 1 ) » JOUT (2,20)
EQUIVALENCE (A( 69 01 )>B(1> )
С •••• ВОССТАНОВЛЕНИЕ СИСТЕМНОГО БУФЕРА
CALL RESB
REaO 310»LDISiNLE>NSET,NTR
310 F0RMAT(16I5)
IF(NLE.LE.C) goto 5
read 310i((JOUT(1»J)»1=1»2)»J=1*NLE)
N$E=NG»»2
NP=290/NSE
PRINT 510
510 FORMAT (//ЮХ, 10B( 1M=) )
PRINT 520
52 0 FORMAT(/59X>lОН РЕЗУЛЬТАТЫ)
5 I F (JFIN) 10»10»20
10 PRINT 530
530 FORMAT(59X,11НУПРУГИА ШАГ)
GOTO 30
20 PRINT 540 • I TER • 1 » APR , P-S2
54q FORMAT ( 13Х,24нУПРУГ0-ПЛАСТИЧЕСКИй ШАГ.
1 15,17Н ИТЕРАЦИЙ» ИЗ НИХ»[3,
1 13Н С АЛЬФА-УСК. »ЗХ,БМТОЧНОСТЬtЕ10»3» I ОН
НЕВЯЗКА,Е 10.3)
30 1F( NLE.LE . С ) GOTO 110
DO 31 Jl=l»ll
IF(С J(JL ) ) 31 » 32,31
31 CONTINUE
33 DO 34 ]e!»JL
3 4 C J( I)=C J( I ) *3( 1 )
PRINT 525,(1,CJ(l>»lsl»JL)
525 F0RMaT(//14X,6HКОНТУР,?Х,вНИНТЕГРАЛ'
1 ( )20»E15.4) )
35 PRINT 550
550 FORMAT(//2Xj2HEL,5x»2HFP»13X,1HX,13X,
1 lHV»9X,2HSX,9X»2HSV»8X,3HSXy,9X,2HSI,
I 7X•4HSMAX,7X•4HSMIN»BX»3HSEQ»8Xt3HEPQ)
Jl*l
40 |1=O
50 LFsJOUT(1 , JL)
220
ПРИЛОЖЕНИЕ
1 Г С J J-NP ) 7 С•7 0 •60
60 LL=LL-JJ*NP
J J = NP
JOUT( 1,JL ) =Ll ♦ 1
JPR= 1
GOTO 60
70JL=JL*l
IF(JJ.EQ.NP) J F R-1
IF(JL.GT.NLE) JPRs-1
80 DO 90 I* H
DO 90 J=1/NSE
K=((11*1-LF)*NSE*J-1)*12
L = ( I ~ 1 ) *NSp*J
В(K* 1) = I
В(K + £)=Fp(L)
В ( К * 3 ) = X { L )
В ( К ♦ 4 ) - V ( L )
6(K*5)=Sg<1»L>
В(К* 6 > = SgI 2,I >
B(K*7)=Sg(3'C>
B(K*e)=SG(4»L)
R1MSG< 1,1 )*SG<2'L > )/2.0
R2=S0RT((SG<1»L)-5g<2»l>>o*2/4.C*
1 S G ( 3 r L J • • 2 )
SMAX = R 1 * R 2
Sm1N=R1-r2
В ( K*9)=SmIX
B(K*10)~$UlN
B(K*11)=SGRT(C(2*R2)*«2*CSMAX-SG(4,L>)»»2
1 *(SMIN-$G(4,L ) )•»2 )/6 . 0>
P(К * 1 2)xEPQ(I)
«о continue
11 = j J
IF(JPR) i oo» 50 > ICO
100 KK=12*NSe»JJ
PRINT 600,(B(!>,l=l»KK)
600 F0RMAT(F4.0^r7.1,2F14.5»7F11.3iE11.4>
IF(JPR) U0r4C»4C
110 IF < L DIS > 130/150*120
12o PRINT 61c
610 F0RMAT(7/46X»22HnEPEMEuJEHHfl UX 1 , UV 1 . . . )
PRINT t2o>(DL(I)»l=l.HN)
620 FORMAT C1cE12.4)
130 IF(NSET) 170*170*140
140 NP=NEL*NSE
DO 150 I= I » NP
I I = I*NP
JJ=I 1*NP
LL=JJ*NP
LF=LL*NP
ОПИСАНИЕ ПРОГРАММ
221
В( * )= SG( 1 , 1 )
В( I I )=SG( 2 , I )
B(JJ)=SG(3,1)
В(LL > = SG t kг I )
150 В(Lr ) =EPQ ( I )
00 160 I si ,NN
JsLF* I
160 B(J)xDL( J )
Call SWSb
call wbuf(nset ,ntr ,e, j j
PRINT 1 a 0,NsE T,NT R , J
1во PORMAT(/5x, * *•♦*• Mfl'il}/
1 ЮХ.’ПоЛЯ 3 АЛИСАнЫ,НАЧИНАЯ ' ,
1 * с-зоны*,I*»длина записи*,16)
call RESB
170 RETURN
end
Относительно исходных данных па магнитной лепте предполагается
следующее соглашение о связях. Вся информация должна быть записана
во внешнюю память в бесформатном виде по 1024 числа в зону. Каждый
новый набор данных должен начинаться с начала зоны. Координаты уз-
лов должны располагаться в одном наборе даппых, со следующей свобод-
noir зоны должны располагаться индексы элементов, упакованные по 4
числа в одно мантийное слово. Набор данных, состоящий из результатов
решения, представляет собой массив, в котором последовательно записа-
ны в точках интегрирования оХэ Су, и*у. ог, ер и перемещения узлов, ском-
понованные попарно.
Программа организована в виде бесконечного цикла по вариантам по-
лем и прекращает печать указанных изополос и значений в узлах по ис-
черпании исходных данных.
Приведение значений, в заданных точках интегрирования, к узлам
производится с помощью билинейной экстраполяции [114]. Для печати
графических образов используется программа STP1PL, построенная па ос-
нове подпрограммы MESHPL [99]. Для работы программы COMPAS к ней
должны быть присоединены автокодные подпрограммы WBUF, UNP4,
FETCH. NOPAGE, требуется расширение доступного объема оперативной
памяти с помощью управляющем карты «CALL FICMEMOR.
Исходные данные
Схема ввода исходных данных с указанием форматов приведена па
рпс. 93. Некоторые исходные данные, касающиеся печати сетки, имеют
такие же значения, как и в программе подготовки сетки AIDA.
NSET — десятичный номер МЛ, па которой записаны координаты п
индексы сетки.
NTR — десятичный помер зоны, с которой начинается запись коор-
динат.
NNOD — количество узлов сетки.
N EL — количество элементов сетки.
LISTED—отключается, если был задан ОС, режим печати с лпсто-
ванием.
>0 — если было задано ОС, печать производится с лпстовапием.
NSET — десятичный помер МЛ, на которой расположен очередной ва-
риант результатов счета МКЭ.
222
ПРИЛОЖЕНИЕ
Рис. 92. Блок-схема программы COMPAS.
ОПИСАНИЕ ПРОГРАММ
223
16/5___________________
NSFT,MTP, MMOF, MOL.L/ST
10/5 |
NSFT,NTF,FOLB
J/5,ЗА 6
KOLIMZO WUXI
NFF, /W. HOPF, MF AB
IFF-О
IFF -IFF «7 *
W5,bF10.0 |
HNFS-0
MOI,MF2, /АХ, MMF3,
X.M7M,XM.AXУ ММ, УМАХ
| ~NNFS^O_
16/5
(FFSM/QI-^ IMFS)_
(FSTF/FO), /-W)_
8F7FP_ I
(PFIFF (I), /-1,8)
8/10 |
(FFl/MSd) , /-1,8)
8F1O. О |
(SOALF(Z), /-1,8)
Mem
FF-NFF?
Да
Рис. 93. Схема ввода исходных данных в программу COMPAS.
224
ПРИЛОЖЕНИЕ
NTR — десятичный номер зоны, с кот орой записан набор данных с ре-
зультатами.
KOLD^O — происходит ввод исходных данных, задающих фрагмен-
тацию и вид печати полей.
>0 — ввода данных о печати пе происходит, а используются те,
которые были заданы для предыдущего набора результатов. Естественно,
что эти данные должны быть введены хотя бы один раз.
NFR— число фрагментов печати сетки. Допускается не более 5 фраг-
ментов.
J\V== 6 — ширина печати 66 позиций, *
= 7 — 72 позиций,
= 8 —107 позиций,
= 10 — 117 позиций,
= 12 —127 позиций.
KODE — код печати, влияющий па печать сетки с пзопллосамп. До-
пускаются значения:
= 1, 2 — печать только узлов,
= 3 — печать узлов и сторон элементов.
При печати узловых значений всегда печатаются только положения
узлов с числами пад ними.
HEAD — заголовок не более чем из 18 символов для идептпфпкацпп
всех печатаемых картин.
NE1 — номер первою элемента, входящего в данный фрагмент.
NE2 —помер последнего элемента. При ХЕ1=0 полагается NE1 = 1,
NE2=NEL.
ТАХ>0 — ось х перпендикулярна направлению протяжки бумаги.
=^0—ось х вдоль направления протяжки бумаги. В этом случае
печатается зеркальное отраженно фрагмента.
NNES — количество членов в массиве NESK.
XM1N 'l
Г “ ограничение ноля печати по осях. При XMIN > ХМАХ
ХМАХ J
игнорируются.
YMIN 1
vixav (—-ограничение поля по оси у. При YMIN>YMAX пгпорп-
I Al А X J
руются.
NESK (NNES) — массив для указания померов элементов, исключае-
мых из печати. Абсолютные величины членов этого массива должны об-
разовывать возрастающий ряд. Если необходимо, папример, исключить
элементы с 25-го ио 36-й включительно, в массив NESK, следует поместить
пару чисел 25 — 36.
KSTR1P(8)—элементы этого массива указывают, какие величины
должны быть представлены в виде пзополос.
Допустимые значения: 1 — ох; 2 — ои; 3 — оУу; 4 — ог; 5 — эквивалент-
нал пластическая деформация ёр = у -у (2екр + 2ерр + 2егр + 4Ур);
8—о1Пах в плоскости ху; 9 — Qmin в плоскости ху\ 10 — эквивалентное на-
пряжение о = "j/" — + Sy 5^) Н- ajy, гдеч5х, Sv. St — диагональные
компоненты девиатора напряжения; 0, 6, 7 игнорируются.
PRICE — соответствующие цепы полосы, т. е. отрезок, приходящийся
па полосу с символами плюс полосу чистой бумаги. Следует учитывать,
что как в положительную, так и в отрицательную сторону только 10 пер-
вых полос печатаются разными символами, а затем все время использу-
ется последний символ.
ОПИСАНИЕ ПРОГРАММ
225
KNUМВ (8) —элементы этого массива указывают, какие величины
должны быть приведены к узлам и отпечатаны в виде чисел над положе-
ниями узлов. Допустимые значения: 1 — Oxj 2—cv; 3—<txv; 4—ах; 5 —
эквивалентная пластическая деформация еР; 6 — перемещения по осп х\
7 — перемещения по осп У; 8—огаах; 9 — <утш; 10 — эквивалентное на-
пряжение о: 0 игнорируется.
SCALE (8)—соответствующие масштабы. После приведения к узлам
значения умножаются на масштаб, затем округляются до ближайшего це-
лого. При выборе масштаба нужно учитывать, что для печати числа от-
водится не более 6 символов, включая и знак минус.
Выходная информация программы
Результаты работы программы — графические картины, выводимые па
построчно печатающее устройство.
Для каждого фрагмента после распечатки походных данных печата-
ется столько образов этого фрагмента, сколько ненулевых. элементов в мас-
сивах KSTRIP и KNUMB. Для картин изополос дается расшифровка сим-
волов, которыми они печатаются. Для картин, представляющих узловые
значения, указывается значение масштаба. Пад каждой картиной печата-
ется текст, сообщающий о том, какая величина здесь представляется.
Программа COMPAS помещена на стр. 226—238.
IV. Описание подпрограмм на автокоде МАДЛЕН
Все программы комплекса используют подпрограммы на автокоде
МАДЛЕН, написание которых было продиктовано тем, что пх функции
невозможно реализовать на фортране. Поскольку в ряде случаев возникает
необходимость состыковки каких-либо программ с комплексом с примене-
нием при этом автокодных подпрограмм, мы приводим описание параметров
п правила их использования. Подпрограммы приведены па стр. 239—242.
WBUF-водпрограмма
Назначение: заппсь/счптыванпе с МБ/МЛ.
Вызов:
CALL \VBUF(LUN. NTR, A. L) — запись па МБ/МЛ,
CALL RBUF(LUN, NTR, A, L) — считывание с МБ/МЛ,
CALL SWSB — сброс системного буфера,
CALL RESB — восстаповлеппо системного буфера.
Параметры:
LUN — помор устройства, участвующего в обмене. Можно использо-
вать МБ <• десятичными номерами 8, 9, 10. 11 п МЛ с номерами 24—55.
NTR — десятичный помор тракта/зоны, с которого начинается за-
пись/считываптте. Тракты МБ имеют номера 0 — 31, зоны МЛ нумеруют-
ся. начиная с 0.
А — начальный адрес оперативной памяти.
L — длина записи в словах.
Подпрограмма WBUF осуществляет бесформатный обмен (аналог фай-
лов прямого доступа) без каких-либо проверок. В каждый тракт/зопу за-
писывается 1024 слова. Запись можно начать только с начала тракта/зо-
лы. Поскольку обмен идет через системный буфер, то предусмотрен сброс
и восстановление системного буфера (на 0-й тракт МБ 148), которыми не-
обходимо пользоваться, если после обмена с помощью WBUF происходит
обращение к системному обмену (в том числе п к вводу перфокарт).*)
*) Цродо гженне см. па стр. 238.
15 Е. М. Морозов, Г. П. Никишков
226
ПРИЛОЖЕНИЕ
PROGRAM COMPAS
С
С «• • • •• •• • ♦ •• •« •• •• • • •• •» •• «• *•
С • ♦ ПРОГРАММА ОБРАБОТКИ РЕЗУЛЬТАТОВ СЧЕТА <•
С •• С ПОМОЩЬЮ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ ••
С •• ПРИ ИСПОЛЬЗОВАНИИ КВАДРАТИЧНЫХ ••
С •• ИЗОПАР АМЕТРИЧЕСКИX ЭЛЕМЕНТОВ
с <• •.............• •........... • • • •
с
COMMON ВЦ/ А( 1 0 0 0 0 5 BL3/ NC(2»300)
1 /BL4Z LB(ICOO) /В15 СХ(8)»СУ(8>
DIMENSION XN(1000)>VN(1000)’XV(2,1000)»
1 NE 1 (5) »NE 2(5) >IAX( 5 ) ,NNE S(5) ,ХМ IN(5) ,
1 XMAX(5),yM!N(5)»yMAX(5),NESK(30#5>r
1 KSTRIP(6,5),PRICF(8f5>•К NUMBСВ > »
1 SCALE(B»5)fIT(3»lC>»rDC5000)iNF(e)»
1 w( 1 000 5
INTEGER НЕАО(З)
EQUIVALENCE (LB»WH(A,Xy)>(NF(l)rNFl)>
1 (NFUbNF2)»< 4F<3)>NF3)»(NF(4),NFA)
DATA NG2/U/
data i t / i вннапряжЕние s-x
1 1 ЙИНА ПРЯЖЕНИЕ S- y »
1 1 8 н К-. А с А Т . КАПР. S - X У >
1 хьннапряженме S-Z »
1 18НЭКВ. ПЛАСТ. ДЕФ.
1 1 8НПЕРЕМЕЧЕНИЕ D-X ,
I 18НПЕРЕМЕ<«ЕНИЕ D-У ,
1 18НМАКС. НДЛР, S-MAX ,
1 18НМИН. НАПР. S-MIN ,
1 18ИЭКВ. НАПРЯЖ, S-EQ /
READ 10 > NSEТ,МТ R,NNOD,NEL » L1ST
Ю FORMAT(1615)
L=2*NN0C
С •••• СЧИТЫВАНИЕ С МЛ КООРДИНдТ И ИНДЕКСОВ
CALL SWSB
CALL RBUFINSEТ» NT R•XV» L>
CALL RBUr(NSET,NTR*(L-l>/lG24*l»NC(2«NEL>
С ДlL RE SB
PRINT 5o»nset,ntr,nnod,nel
5q FORMAT (///5Х , »•••• МГ'МАр*» НАЧАЛО ЗАПИСИ
t
1 ,f - 30HAr.|4»** СЧИТАНЫ КООРДИНАТЫ*,
1 15, • УЗЛОВ И ИНДЕКСЫ*,I 3» * ЭЛЕМЕНТОВ*)
DO 200 1=1,NMOD
XN< I )-ХУ( IjI)
200 УH( I ) = XУ(2 >I)
250 ЯЕдО 10,NSET,NTR,KOLO
C НА МЛ ИНФОРМАЦИЯ - SX»SУ>SXУ»SItEP,A 1
C •••• ПОЛЯ В ТОЧКАХ ИНТЕГРИРОВАНИЯ 2X2
ОПИСАНИЕ H3PQ1PAMM
227
N 1p = .NCL
NFlsl
DO 300 1 = 2,6
300 NF( J ) =NF < 1-1)♦Nl?
NF ( 7 }=NF(6 J *MNOD
L = NF(7)♦NNOD-1
C •••• СЧИТЫВАНИЕ С МЛ ОМЛМШдЬ.ЫХ ПОЛЕЙ
САЦ swse
call rbuf(Nset»nt«,fo,l)
call resb
PR 3 NT 55 ,NS£T,NTR, KOLD
55 format<//5X» *♦••• вариант Полей считана
1 ' С МЛ*, !<♦,', НАЧИНАЯ С ЗЭНЫ',14,
1 '» KOLD= '> 15)
С • ••• ИЗМЕНЕН^ ПОРЯДКА ЗАПИСИ ПЕРЕМЕЧЕНИй
Lx2<NN0D
KcNF (*>-!
DO 400 I= 1 ,t
JeK* I
AGO A(t )=FD(j >
DC 500 1=1,NNOD
J=NF(6)*I-1
K-NF(7)♦I -1
FD<J)SXV( 1,1)
5 00 FO< К > = XV(2 » I )
IF(KOLD.GT.O) Go to 5 5 о
PEAD 1 5»nFR, IW,К 0DEiHEAO
15 FOPMAT(3j 5,ЗА6 )
PRINT 60,NFR,1W,KODE
60 FORMAT (//Bx, '♦ ПЕЧдТЬ'ЛЗг
1 ' ФРАГМЕНТОВ ПОПЕА'/ХОК.
1 ' ШИРИНА ПЕЧАТИ *, !4,
1 * КОД ПЕЧАТИ *, IЦ )
*ODE=KOOf~3
550 I Г(KqDE . lT , 0) KqOE=-1
1 F(KCDE.GE , 0 > КООЕ =0
м= о
600 М=М+1
IF(KOLD) 700» ТОО, 110 0
700 Read ?о,ne1(м),мег(м>,1 ах<м>,nnesiм),
1 XMIN(M),ХМАХ(М),VM1N(И),УМАХ(М)
2 о Format I4I5,4Е1 О.О )
PR;NT 65,М * NE1(М) ,NE 21М) 'I АХ(М)» NNES(И)«
1 XMIN(M) ,XMAX(M) ,VM 1 N <M),VMAX(M)
63 FORMAT(//BX, '= ФРАГМЕНТ I3//10X , 'NE1 ' ,
1 7X, *KE2',7X,'IAX',6X,*NN₽S',11Xi 'XMlNrfff
1 ЦХ> 'ХмДХ*,11Х,'УМ1.Ч',11Х,*УМАХ'/
1 I 13,31 ltJ,4E15. 4)
KsNNES(M)
IF(К) 10CO'1COO,900
15*
230
ПРИЛОЖЕНИЕ
С • ••• ДЕФОРМАЦИЯ
10 Do 20 1=1,N1P
20 W( I ) =F ( J >.SC
return
c ♦ ••• Перемещения
3o Do 35 !=1>NNOD
35 W< 1 > = F( I )<SC
return
c • ••• максимальное напряжения
*o DO 50 1=1,N1P
W( ! ) = (o . 5 е(SX( I ) ♦ $ V( J ) ) ♦
1 SaRT((sX(l)-Sy(I))»*2*0.25*SXV(I)**2J)
1 sc
50 continue
return
c •••• МИНИМАЛЬНЫЕ НАПРЯЖЕНИЯ
60 Do 70 I = 1 » N IP
W( 1 ) = (0.5«(SX < 1 ) *SV( 1 ) ) •
1 SQRT(<sX(I)-SV(I))**2«0.25*SXV(!)**2))
1 SC
70 CONTINUE
return
C • ••• ЭКВИВАЛЕНТНЫЕ НАПРЯЖЕНИЯ
BO DO 90 1 = 1,NIP
W< I)=saRT<0.5>((SX(l ) - SV(I ) ) ♦*2*
1 (SV(I).S2(I))**2*(SZ(;)-SX(I))**2>>
1 3.O*SXV(1>**2)»SC
9o CONTINUE
RETURN
end
SUBROUTINE NOOVaL(W.NEL>NNOD,IU)
C ПРИВЕДЕНИЕ к УЗЛАМ зндчений,за данных
С • ••• В ТОЧКАХ ИНТЕГРИРОВАНИЯ
DIMENSION W(1),T(4,4),SN<1),NPT(8),LK(1)
COMMON /8L1/A(1) /BL3/NC(2/1> ZBL4/LB<1>
EQUIVALENCE (SN,A),(A(2000)»LK)
Од T a T/l. 8660254,-0.5,0.1339746,-0.5*
1 -0.5'0.1339746,-0.5/1.B66U234,
1 -0.5, 1.6660254,-0. 5,0.1339746,
1 0.1339746,-0.5»1.8660254,-0.5/
Data nsl/8/
Do 100 IslfNNOO
SN( I ) = 0. о
100 LK(I)=0
DO 300 K=1,NEL
call unpainpt,Ncii,k),nsl)
Do 300 1=1,4
4 N=NPT(2>1-1)
c = o. 0
DO 200 J =1,4
ОПИСАНИЕ ПРОГРАММ
1 I = 4*(К- 1 ) ♦ J
200 С=С♦Т(|,j)•W(I|)
SN(N)=SN(N)*C
300 IK(N)=LKсN)♦!
DO 600 K= 1 ,NEL
САЦ UNP4(NPT,NC( 1,К) ,NSL )
DO 600 1 = 1,4
N=NPT(2«I-1)
J = 2* I *1
If(J.GT.8)J=1
NN = NPT(J )
N1=NPT(2* I )
SN(Nl>=(SN(N)/LK(N)*SN(NN)/LK(NN))/i
60 0 LK(Nl ) = 1
I F C IU- 1 ) 7 30 t 730 »630
630 DO 700 1=1,NNOD
IFfLKC I ) >700,700,650
650 C = SN( ! >
LB( I ) = C/LK ( I ) ♦$ I GN(0.5,C)
700 CONTINUE
GO TO 900
730
DO 800 1=1,NN0D
I f ( LK ( I ) ) 8 0 0 , В 0 0 , 7 5 Q
750 W( I )-SN( I ) /LK( I )
800 CONTINUE
900 RETURN
E NO
FUNCTION KEX(NPT,X,y,XM1N,XMAKt M4tN> УМАХ,
1 NXl.NET,DX)
DIMENSION NPT(l),X(D,v(l)
COMMON /BL3/XE(8) • УЕ(8 )
c проверка принадлежности элемента
с • ••» к рассматриваемой области
00 100 1=1,8
K=NPT(I>
ХЕ ( I ) = Х(К)
10 0 УЕ( I ) =У(К )
XMIE=AMIN1(XE(1),XE(3),XE(5),XE(7))
ХМаЕ=АМАХ1(ХЕ(1),ХЕ(3),ХЕ(5),ХЕ(7))
УМ!Е=АМ!Ы1(УЕ(1),УЕ(3),УЕ(5),УЕ(7))
УМаЕ=АМдХ1(УЕ(1),Уе(3),УЕ(5),УЕ(7))
IF(XMAE-XMIN)500,500,200
200 IF(XMIE-XMAX)3OO,500,500
300 1Г(УМАЕ-УМ1Н)500,500>400
400 IF(УМ 1Е *VMAX) 600,50 0> 500.
500 К Е Х= 1
С ЭЛЕМЕНТ НЕ ВХОДИТ В ОБЛАСТЬ
RETURN
600 КЕХ=О
С ЭЛЕМЕНТ ВХОДИТ В ОБЛдСТЬ
232
ПРИЛОЖЕНИЕ
С ••••
с •••♦ МиСЛО РАЗБИЕНИЙ В ЛОКАЛЬНЫХ КООРДИНАТА*
SXMAX-0.0
SVmAX=0.о
ОС 700 1=1,5,4
J = I * 2
SXmax=AMAX1(SXMaX>aBS(XEt J)-ХЕ (I)))
700 $УМАХ = АМАХ1(5умдх,ДВ5<УЕи>-УЕ(11>)
SMaX = AMAX1(SXMAX,D.6>SV max*)
NX I = SMAX/ОХ + 2
SXMA*=0.0
SVMAX = 0 t0
DO 600 1=3,7,4
J= ! *2
1 F( I . EQ . 7) J =1
SXMAX=AMAX1(SXMAX>aBS(XE(J)-XE(!))>
800 SVMAX = AMA X1 (SVMAX,ABS(У Ej J)-УЕ < 1 ) )>
SMAX = AMAxl<SXMAXrO , 6•SV MAX )
NE T = SMAX/ОХ*2
RETURN
end
TUNC II ON RP(R , X I , ET )
REAL R ( 1 }
E1 = 1. 0-E I
X1=1.o-x i
E 2=1.0 *E T
X 2=1 .0 * X I
RR=-C.25-(El«(Ril)«Xl-(X2*ET )*R(3>«X2»(X1*
ET M *
1 E2*(R(5)*X2*(X1-ET)*R(7)»X1*(X2-ET)>)*
1 0 . 5* ( X i • X2 • ( R ( 2 ) *E 1 *R ( t ) *E 2 ) *
1 E 1 • E 2 •(R(4 ) »X2*R c 8 ) «XI ) )
RETUPN
END
SUBROUTINE ST R 1 PL ( К 0 D E » N E 1 . N E 2 » 1 W , HE ДО ,
1 NESK.X,VtXMI,XMA,УМ1,ЧМA)
c •••• печать изополос и значений в узлах
COMMON /bL1/A(50 00 > /ВL3/МI ND(2» 1 )
1 /BL4/Lb<1> /Bl 5/СХ(8 ) , СУ (6>
DIMENSION NESK(l)»X(l).y(l),
1 NPT(6),xE(2bVE(2).W(4.1),WA(l)
Integer неаосзьр(1).Г6(5),г7(5)»гв(5),
1 F10<5)»ri2(5) , ГМТ'5 > » BLANK,A ST .L 2
EQUIVALENCE (Х1,ХЕ),(Х2»ХЕ(2М.(У1,УЕ),СУ2
.VE(2 > )
EQUIVALENCE (A,P).(LB»W1»CW.WA)
dimension msim(20),sg(4)
ЭдТд MSlM/feHl ,6H2 ,oH3 »
1 6H 4 , 6h 5 , e>H 6 »
1 6H7 , 6H 6 ,6H9
I
ОПИСАНИЕ ПРОГРАММ
233
1 6WI ,*ИА ,6НВ •
1 6HC ,6Н0 »6НЕ »
1 6HF »6Н6 »6НН *
1 6HK »6HL /
DATA F6 /50H( /// 26ХЗА6//I 5Х10А6» А1) )
1 FT /зоне/// 26ХЗА6// 1 1Х11А6•<5))
/ 9
1 F8 /зоне/// 36ХЗД6//(26Х13А6»АЗ))
/ 9
1 F 10 /зоне/// 56ХЗД6//(16Х16Д6»А5) )
1 X 2 /30Н(/// / » 56ХЗД6//С 6Х20А6» А1 ) )
ОдТд BLANK । A ST,СН1 , СИ 2 /6Н »
1 бН$ ,6НХ »6Н* /
Data naw,nwf,npcx»npcv /б»5,ю»б/
ОдТд KSL,1Р/6»10000/
NC=NSL
I F< NSL . GT .4) NC = NSL/2
NC2=2*NC-1
NCODESMOD(KODE »10)
! F(К0DE.LT . 0 ) NCODE= *1
DO 100 I=1»IP r
100 P( I ) sOLAnK
IFCXMa.Gt.XMU AND.VMA.GT.VMI ) Go TO 205
I S E = 1
J=0
DO 200 N=NE1»NE2
J$E=NESK(1SE)
N S E = 1 A 8 S ( J S E )
IF(N.EQ.nSE) GOTO 180
1 F( ( JSE . LT . 0) . AND . (N.LT.NSE)> GOTO 200
• CALL UNp4(NPT»m!NDl1,N}»NSL)
DO 160 |=1»NC2»2
K = NPT(1)
I F l К ,LE .0) GOTO 160 '•
IF(J.GT,0) GOTO 140
J= 1
ХМ I N = X(К)
УМ IN = V (К )
xmax=xmin
УМДХ=УМ1И
GOTO 160
140 XMIN = AM!N1(XMIN,X(K> )
ХМДХ = АМАХ 1 (XMAX , X < К ) )
VMfNrAMlNl (VMlN»y(K) )
УMAX = AMAX 1(УМАХ»У<X) >
160 CONTINUE
GO TO 200
234
ПРИЛОЖЕНИЕ
i
130 1Se=ISE*1
zoo CONTINUE
20.’ ir(XMA.XMj) 220,220,210
2Ю XMIN=XMI
ХМдХзХМА
220 IFtVMA-VMI) 240,240,230
23€ yMiN=yMj
УМдХхуцд
240 XO=XMAX-XMIN
^ОжУмАХ-Уя j ы
TfC<XO.LE.0.).AND.(VD.LE 0 J} XOK1
X ЯР = NP С X • ! w XD-l.C
1*KNP/NAW
NC Pz J p/ftWR
DX = XD/FLОЛT(К ЯP )
Oy=VO/FLOAT(NCP-2)
ХУВАТ-'-ЧОАТ (NPCV)/float (NPCXJ '
о =AMAXiCDX>xyRAT«Dy) f
OV=OX/XyRAT
HXMAX=XD/DX*2
ЫУМА№УО/ОУ*2
XMN = XMlVOX
УМ IN = YMIW^Dy
NCp = V0/Dy42f 5
NRprNAh.NhR,
NLP = NCP*NRP4NA^-.A
NPW = NWR « NC P
I Sg = l
DO 600 № NE 1 2 Z
JSE=NESK(ISE)
NSE=IABS(J$E)
(N . EQ,NSE) GOTO 550
IF ( (JSE,LTtо ) #дцрe T NSE))
all WHUPT.IIIIIIMMMS!.)
GOTO 600
L = NC0r>E*NSID-3
2F^JL* 1 *L“1>>.Ed.0) GOTO 3oo
i Nx!:NNE₽TT:;;y’xM,N'xwAx’yMi^«M*^
If(M.GT,0) GO TO 60S
DO 500 NS = 1,NC2,2 **
KlxNPT(NS)
K2 = NPT ( N5.J , ’>
^((М5.Еа^С21.Ой.(К2.1.€.0И K2 = NPT(l‘j
К =NS*1
IF(N$l,GT.4) M=NpT(K)
I -KI
J^K2
r1M.L E » Q ) GOTO 30Q
ОПИСАНИЕ ПРОГРАММ
235
250
230
300
320
330
350
KOUNT=-2
<OUNT=KCuNT*l
J = M
I F(KOUNT) 30 0 > 28C ,50C
I xK 2
iFHI.LE.O.ORMJ.LE.M.OR.lI.Efc.J)) GOTO
400
Xj.= <( I )-xM!N
V1=V(I>-VMlh
X2=X(J)-XMIN
V2rV(J1-VM1N
DO 320 K=1,2
N X = X E ( К ) / О X ♦ 0 . 5
IF<(NXMlx-NX)«NX,LE.0> GOTO 320
MV=UE(K)/OV*C.5
I F ( ( NУMA X-NУ)•NV . LE . 0 ) GOTO 320
L-NLP*NX-NRP«NV
LP=L/NAW
call storc.h(P(Lp > > i*L’Naw#lp , ast )
CONTINUE
IF((KOOE.LT.O).CR.(KODE.GE.2J)) GOTO 40 0
XD=X2-X1
V D = У 2 - У 1 *-
I F( (XD.Eq.0) .AND. ( VO . Ей.0) ) GOTO 400
IFIABS < УС ).GT.0. ? • AB 5 < XO ) ) GOTO 330
Ll- 1
L?=-NRP
CxVO/XD
C1 = 0.5*(у L-C*X1)/DV
С2=С*0Х/0У
N1=AM]N1(X1>X2)/DX*1.O
N2 = AMAX1(X1,X2 ) /С Х
NXMl=NXMaX
NVM1=NVMaX
GOTO 350
L1 = -NP.P
L2= 1
C-XD/УЭ
Cl=0.5*(xi"C*Vl)/DX
С2=С«ОУ/О*
N1 = AMIN1(У 1>У 2 )/DУ ♦ 1 »0
N2-АМДХ1(V1,У 2 ) /DV
NXM 1 = ЫУМдХ
NVM1=NXMaX
I Г(N2 . LT,N 1 ) GOTO 400
N L = N UP ♦ N1•Ll
DC 380 Nx=Nl»N2
I Г( (NXM1-NX)»NX.LE.3) GOTO 360
NV = С 1 2♦FLOAT(NX>
1Г((НУм1-НУ)*ЫУ.иЕ.О) GOTO.380
236
ПРИЛОЖЕНИЕ
L=NL*L2*NV
LP=L/NAW
К:l*L~NAw*LP
NL=NL*L1
1NEW=CH1
call fetch(p(lpj,к,iold)
I Г(I OLD.£Q.BLAN<) GOTO 360
IF((IrLD.EQ.AST).OR.(IOLD.EQ,CH2)) GOTO 3»
0
I F( I OLD. Ed,CHI ) !NEW = CH2
36o call storch<pclp),k,enew)
3B0 CONTINUE
400 IF(M.GT.0 ) GOTO ?50
500 CONTINUE
fFiKODE.Efi.-Z) GO TO 6q0
DO 505 1=1,4
J = NPT(2* I -1 )
505 SG ( 1 )=*»( J)
DXI=2 # 0/NXI
DET = 2,0/NET
DO 520 I = 1 , NX I
XI=-i,0*DXI*(FL0aT(1)-q,5)
XI 1=1-XI
X I2 = 1*XI
DO 52 C J= 1 ,NET
ET=-1.O*DET*(FLOAT(J)-o,5)
ETi-i-ET
€T2=1*ET
S 1 = 0.2 5* ( X I 1*ET 1* SG ( 1 > *X I 2• F. T 1«SG ( 2) *
1 XI2*ET2*SG(3)*XI1*ET2«5G(4))
1 -0 . DC CO 1
M=$l
I F(SIt GT.С.0) м = м*1
1 F(MODIM, 2 )) 510 , 520 , 5 1 0
510 X1xRR(С X>X I ,ET)-XWIN
У1 = RR(СУ , X | ,E T)-VM I к
NX = Xl/DX*0.5
I F ( ( NXMAX-Nx ) *NX . Le . 0 ) GO T() 520
NV=V 1 /0У*0.5
IF( (НУМДХ-NV)* NV.LF ,0) GO To 520
L = NLP♦NX - NRP*NV
LP=L/NAW
X = 1*L-NAW« Lp
CAlL FETCH(P(LP ) г К, ICLD )
IF(TOLD.NE.BLANK)- GO To 520
M = M/2* 1
IF(M.GT.IO) M=10
. I F(Si , LT,0.0 > M = -M*12
IF(M.GT.2O) M=20
I NgW = MSIM(M)
ОПИСАНИЕ ПРОГРАММ
CALL SToaCH(P(LP)jK,!Nc^)
523 CONTINUE
GOTO 630
550 ISE=ISE*1
600 CONTINUE
I Г ( (f.,ODt . GT , - 2 ) . ftNO . ( KODE , LT , 10 > ) GOTO 8 2 о
I Sf = 1
00 fiGO N=NE1,NE2
J3E=NLSK( ISE )
N S f = J A В S ( J S E )
If(N.EQ.NSE) GOTO 780
IF<(JSE,L’I.G).AND.(N.LT.NSE>) GOTO 800
CALL UNP4CNPT/M1ND(1»N),NSL)
К 0 и N T = 0
<20 XOUHT=KOUNT*1
650 NLi:NSL
}< =NPT (KOUNT )
I F (K.LE.0 ) GOTO 75c
L А В = I. В ( К I
X1 = X(К)-ХМ IN
V1 = У(К)-УМ J N
6 6 0 IС н-1
L = 10
DO 630 J = 1 , NAW
IFCL.GT. UBSC LAB) ) GO TO 700
ICH=1CH+1
680 l“L«IC
"ОС IFCLAB.LT.0) !CH=1C**1
I С H = A1 N 0 ( I С H • N A W >
NX=X1 OX
)F( (NXMAx-NX)*NX.LE . 0 > GO TO 750
NXsHX-FLo AT < I CH/2 > *0 .5
NX=MAX0< »JX > 1 )
N X- MIN0(ЧX 7 К R P" I С H * 2)
NV=V1/0У + П .5
lFC(N'j>MAx-NV)oNy.LE.O) GOTO 750
I F(KOOL.GT .0) GOTO 730
NV = NV+ 1
L = N< p < N X N У • 4k P
DO 720 J=1,1CH
LP=L/NAW
call fetch(p<lp).i*l-naw*lf,iold)
IF( 1 OLD . NT .BLANK ) GOTO 750
720 L=L+1
730 ENCODE(NaW,15»J) LAB
15 FORMAT С I 6 )
call strmov cj,naw*i-)ch >1ch>p»(ncp-nv > *nrp
Ш )
75o IF(KOUNT-NL) 62Q,800«600
730 I Str I SE* i
238
ПРИЛОЖЕНИЕ
800 CONTINUE
820 00 000 I=1»NWF
I F ( IW. e QL „ 6 ) FMT (I ) = F6CI )
1F(1W.EQ.7) FMT(I ) sF7 ( I )
1FClW.Ea.8) FMT С I > = F в <I )
iFtlW.EO.lO) FMT(I)sFlO(l)
iFdW.EO.li) FMT С I ) = F 12U )
900 continue
PP 1NT FMT, HE AO, (PCI), 1=1,NPW)
IFC|W.GE.ft) PRINT 20
20 F0RMAT(/r XXXXX СТОРОНА ПРИНАДЛЕЖИТ ОДНОМ
V ЭЛ-TV*
1 /' ♦♦♦*♦ СТОРОНА ПРИНАДЛЕЖИТ НЕСКОЛЬКИМ
ЭЛ-ТАМ'
1 /' О ПОЛОЖЕНИЯ ¥ЗЛОВ'>
1000 RETURN
END
SUBROUTINE STRMOV <IS,1»N,JT,J)
DIMENSION I SC 1 ) iJT( 1 )
NWS=(I-l)/8*l
NhTr(J-1)/6*1
1l-MODC1,6)
Jl=M0DCJ,6)
1 F ( I 1 . Eft. 0 ) 11=6
IFCJI.EU.O) JL=6
DO 40 K=1,N
call fetch(IS(Nwsj,u,m)
call $torch(jtcnwt),ji,m)
io n = i
NHSxNWS*1
20 IFCJ1-6) 40,60,30
30 Jl=l
NWT=NWT*1
40 continue
return
end
РАСК4-подпрограмма
Назначение: упаковка массива из целых положительных чисел, не
превосходящих 4095, по 4 числа в одно слово.
Вызов: CALL РАСК4 (1UN, IP, К).
Параметры:
1UN — адрес начала неупаковочпых чисел,
IP — адрес начала упаковки,
К — количество упаковываемых чисел.
1ЖР4-цодирограмма
Назначение: распаковка упакованных по четыре в одно слово целых
положительных чисел, не превосходящих 4095.
ОПИСАНИЕ ПРОГРАММ
239
ASSEMBLER
fetch: .name ,
11 ,VTM,1
,UJ,FS
STORCH:,ENTRV,
11 fVTM,
F5 : ,ST1,8«T
.STI .9,1
» ST I . 1 c. s
12,BASE »•
9.XT*.
,AT! ,9
ll.VZM, ST
10/XTA,
9,APX.MAC-1
.AOX»=6H*0**A0*’40**A0**40*'40*
8.ATX,
13 »UJ »
S т : e , X T A ,
9.AUX.MAC-1
1O.XTS,
9»AAX,МДС-1
io.aex.
15.A0X,
10 »дтх»
13,UJ >
MAC: .OCT,7?6
, ISO »6H'O' *377**0 **0'*0r*0*
, ! SO , 6H *0 * '0 **37j**0'r0**0*
,lSOi6H*Q**orFOr,r377**o'*0*
»IS О » 6H *0**O**O **0**377*. Q*
.LOG,377
.END,
PAGE : ।NAME,
iPRJNT * 1
13 ,UJ ,
'ENO,
nopage: ,name>
,PR INT •
13 »UJ,
'END,
240
ПРИЛОЖЕНИИ
РАСК4;/NAME,
>ST I , в .К г ЧИСЛО
iSTl,9.P = АДРЕС ЧПАКОВКИ
• STblO.UN = АДРЕС НЕуПАК.
12 । BA$E , •
6>XTA,
> AT 1 , В
NEW: , XT A ,=D
9, ATX,
11iVTMr-j
H,VT|b2A
word: io »xta,
।AAX,=7777
14,ASN>
9i AOX,
9 »ATX ।
а.итм, -i
8>VZM,ALL
10/UTM,1
14 >UTM >12
11 >VLM»WO₽D
9,UTM, 1.
>UJ »NEW
ALL : 13»UJ,
/END,
Onpa:,name,
I$TI,e.K = число
•ST1.9.P 2 АДРЕС УПАКОВКИ
rSTblO.UN = АДРЕС НЕуПАК.
12/BAsE ,♦
3/ХТА,
/ATI *8
new:ii>VTMt-з
14,VTM >100
WDRD'.OiXTA,
14»ASN •
,AAX,=7777
,aOx,=:64
10 tATX>
0 »UTM,-j
e,vzw,all
1C >UTM>1
14>UTM>*12
11>VLMtWORD
9/UTM,1
>UJ >NEW
ALL:13 >UJ >
,END, .
ОПИСАНИЕ ПРОГРАММ
241
wbuf: ,nam£ »
ю । V*M »
,UJ»R«B
swsb:,entry,
10 »VTM»
,UJ ,RW
rEsB:» Entry »
iо, vtm ,i
rw:iz» base »♦
» XTA» 43B
» AAX » =76000
>ASN » 64-20
» AOX > =140000
11 т s f i о
»ASN >64-39
15,AOX »
>ATX*IRW70
>•70»IRW70
13 »UJ ,
IRW70: >BSS »2
rBuf:» entry,
i о»vtm,x
rwB : » st j ,ц
i S T I ,14
I ST [ » 9
• ST 1 > 8
12,BASE»•
11.ХТА»
8 > XT A >
» ASN > 64-12
9 » XT S »
, AAX »=777
15>A0X>
* XTS > AJB
» » = 76000
। ASN > 64-20
15» AOX ,
» I TS » 10
» ASN » 64’39
15,AOX,
10»ATX,|RW?o
14 »MTJ , 9
10»VZM, ЗАПИСЬ
MTEH:10,«70,IRW70
1 0 , XT A , IRW70
» ARX» =1
10iATX,IRW70
14,vTM,-1023
ПЕР: ,WTc » 43B
16 E. M. Морозов, Г. П. Никишков
242
ПРИЛОЖЕНИЕ
14,ХТД, Ю23
9 tUTC,
1*» ДТХ t£023
ll>UTMr-L
13/UTC t
11 . VZM,
14»VlMrOEP
9/UTH, 1024
,UJ ,4TEH
запись:i4»vtm »-1023
ЗАП1:9 »UTC ,
1 4 » x T A » 1023
>WTc >438
14,ДTX > 1023
11 » UIM > - 1
11»VZM,КОПЕР
1 4,VLM,ЗДП1
9।UTM,1024
1 0i♦7 0 > JRW70
10>XTA , IRW70
, ARX,-1
1 0 » AT x,IrW70
» UJ »ЗАПИСЬ
КОПЕР : 1 0 , «70, IRW70
13 ,UJ ,
1 END»
Вызов: CALL UNP4 (I UN, IP, K).
Параметры:
IUN — адрес начала заппсп распакованных чисел,
IP — адрес начала упаковки,
К — количество распаковываемых чисел.
FETCH-подпрограмма
Назначение: байтовые операции со словами.
Вызов:
CALL FETCH (IS, I, IT) —перемещение I-го байта слова IS па место
первого байта слова IT. Байты со второго по шестой слова ГГ заполняются
пробелами.
CALL STORCH (IS, L IT)—перемещение первого байта слова IT па
место I-го байта слова 1S. Остальные байты слова остаются без изменения.
N ОР AGE-подп рогра мма
Назначение: блокировка режима лпстования при печати, установлен-
ного операционной системой.
Вызов: CALL NOPAGE
PAGE-подпрограм ма
Назначение: восстановления режима лпстования.
Вызов: CALL PAGE.
Подпрограммы па автокоде МАДЛЕН приводятся па стр. 239—242.
СПИСАНИЕ ПРОГРАММ
V. Пример расчета с использованием комплекса программ
AIDA — NEPTUN — COMPAS
В качестве примера расчета, иллюстрирующего применение представ
ленного выше программного комплекса, рассмотрим определение напря-
жен я о-дефор миро ванного состояния проушины с симметричными трещи-
нами, исходящими пз отверстия, под действием сосредоточенного усилия
(ряс. 94, о). Подчеркнем, что данный пример является чисто иллюстра-
тивным и служит в основном для демонстрации некоторых возможностей
программ автоматизации переработки входной п выходной информации.
Рис. Л4. а) Схема нагружения проушины с трещинами, б) Пестрое
пне дискретной модели пз фрагментов.
Рис. 94, б показывает одну из возможностей построения дискретной
модели из квадратичных элементов для симметричной части рассчитывае-
мого тела с помощью программы A1DA. Сетка строится посредством сты-
ковки пяти фрагментов. Рядом с номерам и фрагментов, которые строятся
автоматически, приведет»! ключевые диаграммы вместе с числами разбие-
пип по строкам и столбцам этих диаграмм.
фрагмент 1 строится автоматически.
Фрагмент 2— антифрагмент, который уничтожает 4 элемента фраг-
мента 7.
Фрагмент 3 строится автоматически и стыкуется с фрагментом 7.
фрагмент 4 вводится с перфокарт, состоит из 4 вырожденных сингу-
лярных элементов со сдвинутыми на четверть длины стороны промежу-
точными* уЗ±амп я стыкуется с фрагментом 3.
16*
Рис, 95. Сетка конечных элементов, построенная и «пар асов айна я*
с помощью программы AIDA.
II*
111Ц1 «
tl»M 4)11111
**k ими
се»
I*
i > i: i
iiiii
|*ьпв и» till
:cc ев» (* i n:«
22 ?2 »
77222i>7?72
• CCC BB 1*
ей CC fff H
t'PD CC BB *•*
• d te bb и
till
1!
II
27?2227222??27
727272?2227722777?27
г?:???? з ? г ?21?2:о
3f33t • 3 ??-’7
•> c
L H
ci op a I*
f О C8 *
rt #< fl *
27122
2722
3» 3 > ♦ 772
222?
3 9333J31333
>>>33331 0>13
222 « 33333 >33
72
72
l Г »B2i| 2 33
Bl’> 320333
4133
*
I 11111*0
22
9
6 *
5535935
535599505
33
22
02
22
33
3
1J
eBOjOOOOO »B « 9
4*11729 «3 00*600130**
0A11I 23 « 5 *B.*«C.«»o
«Д ll 2 >3tO>s> >*•
« 9599
5555995
в
BB
BB
220
222
22
23
11
227
BB
?22X
131333
211
222
l:
32222
1911111
22222
•?J712
J222222
1.1
I
22221122
117112122
2113232232
3332321133
1222222:3
2121122222
111:272222
21212332032
О
333399
>33333 ,
333333
333333
333333
«31333
333333
>33333
>33333
>333333
333335
>333333
3333133
3335)333
>3933)5
33333339
♦
22< 222:12:2:2
33333333J3
3333111,32213221
.23212211323211111
<<2122?.22222222222
222э:<1а;«22:122222:21
33321113 33illll32 21f
СИ:}:; 2221222222277
133123312213131311221
;;2222121221:22212222
27222222221222222213
«2322221:2222323223 0
77<2 212 ?< 2 2 2 7? 2 2 72
32231277121122212
>333333333
3333333513Э
>313 >01333
33331’3333>
>>33359333
3533335333
ЗЗЗЗУ1953333
>35333333133
1Э3133333333
333333331591
3333533333353
ЗЗЗЭЗЗЗОЭЗЗЗЗ
Э53339333533»
Э3333333353333
3333333333)313
•4*4*4**
*«*•4*4
22722222222272272
7772722372722122
2227122:2222222
2722121:223271
27212273222222
*22:277222»I 2
3335333335J933
>3>3333333>3>33
>3>>>>>9513391?
>33335>1333333>>
33333>313>5>13>3
•3353>333>o3>>3333
Pnc. 96. Картина изополос папряжрппй o„, полу то пн а я по программе
NEPTUN п «иарисоваппая» с помощью программы COMPAS.
246
ПРИЛОЖЕНИЕ
Фрагмент 5 строится автоматически и стыкуется с фрагментом 1.
В результате сборки получена сетка, состоящая из 64 квадратичных
элементов. Ширина глобальной матрицы жесткости для первоначальной
нумерации 125 узлов затем была уменьшена до 45 узлов. Распечатка гра-
фического образа сетки на ’АЦПУ-128 представлена на рис. 95.
Упругое решение задачи о деформации симметричной части рассчиты-
ваемой детали получено по программе NEPTUN при задании заведомо
большого предела текучести.
Одпа из возможностей графического представления результатов в шг-
др изонолос с помощью программы COMPAS показана на рис. 96. Задана
печать поля напряжений оу с ценой полосы 2PjDt (t — толщина детали,
равная единице). Поскольку цена полосы относится, собственно, к пологе
символов и соседней полосе чистой бумаги, то па данном рис^тгке сим во
лы соответствуют следующим диапазонам напряжений: 1 — от 0 до Р Dt,
2— от 2P/Dt до 3P!Dt п т. д. Для визуализации пзополос непосредственно
вблизи вершины трещины можно произвести увеличение интсрпсующего
нас района с помощью выборки его по поморам элементов или ограниче-
нием фрагмента двумя парами прямых, параллельных координатным осям.
ЛИТЕРАТУРА
1. Айронс М. Р. Инженерные прмло/кепия численного интегрирования
в методах жесткостей.—Ракетп. техн, н косм., I960, № 11, с. 216—219.
2. Александров IO. А., II и к и ш к о в Г. II. Автоматизация подготов-
ки исходных данных ври реализации МКЭ на ЭВМ.— В со.: Проекти-
рование металлических конструкций. Сер. 7 (ЦИНИС).— Союзметалл-
стройниипроект Госстроя СССР, 1974. выл. 8 (55), с. 26—31.
3. А р г и р и с Дж. Современные достижения в методах расчета конструк-
ций с примененном матриц.— М.: ПЛ, 1968.— 240 с.
4. Бабич К). II., Цыбенко А. С. Методы и алгоритмы автоматиче-
ского формирования сетки конечных элементов.—Киев: ИПИ АН УССР,
1978.— 93 с.
5. Белявский Е. И., К л импорт 10. 3. Статический анализ уп-
ругих стержневых систем произвольного вида.— В сб.: Алгоритмы и ал-
горитмические языки.—М.: ВЦ АН СССР, 1969, выл. 4. с. 95—ИЗ.
6. Бер г о и, К л а ф. Критерии сходимости итеративных процессов.— Ра-
кетн. техн, и косм., 1972, т. 10, № 8. с. 173—174.
7. Берн ер Р., Кронмюллер Г. Пластическая деформация моно-
кристаллов.— М.: Мир, 1969.— 272 с.
8. Биргер Н. А. Варпаппоппые методы в строительной механике тур-
бомашин.— М.: Оборопгпл, 1959.— 28 с.
9. Биргер И. А. Теория пластического точения при неизо термическом
нагружении.— Изв. АН СССР. Сер. «Механика», 1961, А? 3, с. 78—83.
10. Бови О. Растяжение прямоугольной пластины с симметричными тре-
щппамп на кромках.—Труды амер, об-ва ипж.-мсх. Сор. Е, 1964, т. 31,
№ 2, с. 56—61.
11. Вайншток В. А. Сравнение двух численных методов расчета ко-
эффициентов интенсивности напряжений.— Проблемы прочности, 1977,
№ 9, с. 80-82.
12. Вульф о вич II. А., Зару бае в В. П., Кор леев В. Г. Решение
тестовых задач теории упругости методом конечных элементов высо-
ких порядков точности.— В сб.: Числ. методы решения задач теории
упругости и пластичности. Ч. 1.— Новосибирск: СО АП СССР, 197S,
с. 33—52.
13. Витвицк ий П. М.. Леонов М. Я. Полосы скольжения прп неод-
нородной деформации пластинки.— В сб.: Вопросы механики реально-
го твердого тела, выл. 1.— Киев: АП УССР, 1962, с. 13—28.
14. Ершов Л. В., Ивлев Д. Д. Об условиях квази хрупкого разруше-
ния.— ПММ, 1967, т. 31, As 3. с. 537—542.
15. Зенкевич О. К. Метод конечных элементов: от иптупцин к общно-
сти.— Сб. переводов «Механика».— М.: Мир, 1970, № 6. с. 90—103.
16. Зспкевич О. К. Метод конечных элементов в технике.—М.: Мар,
1975.— 541 с.
17. Ибрагимов В. А. Инвариантный интеграл в теории трещин для
упруго пластических сред.— ДАН СССР, 1976. т. 228, № 2, с. 335—337.
18. II в л св Д. Д. О теории трещин квази хруп кого разрушения.— Журнал
Прпкл. мех. и техн, физики, 1967, As 6, с. 88—128.
19. Ильюшин А. А. Пластичность.— М.: АН СССР, 1963.— 271 с.
248
ЛИТЕРАТУРА
20. Качанов Л. М. Основы теории пластичности.—М.: Паука, 1969.—
420 с.
21. Качанов Л. М. Основы механики разрушения.— М.: Паука, 1974.—
311 с.
22. К о в а л о и к о А. Д. Термоупрхтость.— Киев.: Биша школа, 1975.—
216 с.
23. Корнеев В. Г. Оценки обусловленности для схем метода конечных
элементов.— Труды 3-й Beer. конф, по числ. методам решения задач
теории упругости и пластичности. Ч. 2.— ПойЪснбирск: СО АН СССР,
1974, с. 13—27.
24, Л е о н о в М. Я., П а н а с го к В. В. Розвпток пайдрибнйппх трпцпп
в твердому тйи.—Прикл. механика, 1959, т. 5. № 5, с. 391—401.
25. М а х у т о в Н. А. Концентрация напряжений и деформаций в упруго-
пластической области деталей.—Машиноведение. 1971, № 6, с. 78—83.
26. Мела н 3., П а р к у с Г. Термоуиругио напряжения, вызываемые
стационарными температурными полями.— М.: Физматгнз, 195Х.—
167 с.
27. Метод конечного элемента в механике деформируемых тел/Вайи-
берг Д. В.. Городецкий А. С.. Кнрнчевскпй В. В., Сахаров А. С.— Прикл.
механика. 1972, т. 8, Л? 8, с. 3—28.
28. Метод суиерэлементов в расчетах ниже норных спору жеппн/Поо •<
пов В. А., Дмитриев С. А., Елтышев Б. К., Родионов А. А.—Л.: Судо-
строение, 1978.— 288 с.
29. Мизес Р. Механика твердых тел в пластически деформированном
состоянии.—В кн.: Теория пластичности.—М.: ИЛ, 1948, с. 48—56.
30. Мосс а ко в скип В. И., Рыбка М. Т. Попытка построения теории
прочности хрупких материалов, основанной па энергетических сообра-
жениях Гриффитса.— ПММ, 1965, т. 29, № 2. с. 291—296.
31. Морозов Е. М. Метод сечении в теории трещин.— Пзв. вузов. Сер.
«Строительство и архитектура», I960, № 12. с. 57—63.
32. Морозов Е. М., Фридман Я. Ь. Некоторые закономерности в
теории трещин.— В со.: Прочность и деформация материалов в
перавпомерпых физических нолях. Выц. 2.— М.: Атомиздат, 1966,
с. 216- 253.
33. Иикитпков Г. П. Определение термоулругнх коэффициентов интен-
сивности напряжений с помощью метода конечных элементов.— В сб.:
Физика и механика деформации п разрушения. Вын. 4.— М.: Атомиз-
дат, 1977, с. 51—58.
34. Пик и hi ко в Г. П.. Краев А. Г. Коэффициент интенсивности напря-
жений для ДКБ-образца при нагружении силой и моментом.— В сб.:
Физика и механика деформации и разрушения. Вьш. 4.— М.: Атомиз-
дат, 1977, с. 59—61.
35. Н и к и ш к о в Г. П., Морозов Е. М. Коэффициент интенсивности на-
пряжений у кольцевых трещин в толстостенных трубах прп растяже-
нии.— Проблемы прочности, 1976, № 6, с. 44—48.
36. Пик пшков Г. 11., Морозов Е. М. Расчет коэффпциепта интенсив-
ности напряжений с использованием пзопараметрических квадратич-
ных элементов.— Прикл. механика. 1977, т. 13. № 4. с. 72—77.
37. Пик ишков Г. П., Морозов Е. М. Моделирован не на ЭВМ испыта-
ний компактного образца в упруго-пластическшй области.— Заводская
лаборатория, 1978, т. 44, № 8, с. 1008—1011.
38. П и к ишков Г. 11., Морозов Е. М. Песташтопарная упруго-пласти-
ческая задача о начале движения трещины в условиях изотермическо-
го процесса.— ФХММ, 1978, Лг 2, с. 113—117.
39. Ники шков Г. П., Морозов Е. М. Погрешности линейного подхода
при определении нагрузки старта трещпны в упруго-пластических те-
лах—ФХММ, 1978, №*3, с. 95-98.
ЛИТЕРАТУРЛ
24!)
40. Николаевский В. П. Термодинамика роста трещин. Разрушение
упругих, почти-упругих и вязких тел.— Механика твердого тела, 1979,
AI® 4, с. 95—106.
41. О локальной пластической зоне вблизи конца щоли/Кудрявцев Б.
Партон В. 3., Песков 10. Л.. Черепанов Г. 11.— Механика твердого тела,
1970, № 1. с. 61—64; № 5, с. 132—138.
42. О д е н Дж. Конечные элементы в нелинейной механике сплошных
сред.— М.: Мир, 1976.— 464 с.
13. Па пасюк В. В. Предельно* равновесие хрупких тел с трещинами.—
Киев: Паукова думка, 1968.— 246 с.
44. Па пасюк В. В., Берсжницкий Л. Т. Определение предельных
усилий ирн растяжении пластины с дугообразной трещиной.— В кн.:
Вопросы механики реального твердого тела. Вын. 3.— Киев: Наумова
думка, 1964, с. 3—19.
45. 11 а р и с П., С и Дж. Анализ напряженного состояния около трещин.—
В кн.: Прикладные вопросы вязкости разрушения.— М.: Мир, 1968,
с. 64—142.
46. Партон В. 3.. Морозов Е. М. Механика упруго-пластического раз-
рушения.— М.: Наука, 1974.— 416 с.
47. Партон В. 3., Перлин 11. П. Интегральные уравнения в теории
упругости.— М.: Наука, 1977.—311 с.
18. Партон В. 3., Черепанов Г. П. Механика разрушения.— В кн.:
Механика в СССР за 59 лет. Т. 3.— М.: Наука. 1972. с. 305—467.
49. Плоткин Е. Р.. Израилев 10. Л., Л у б и ы-Ге р ц ы к Л. Л. Кон-
центрация температурных напряжений в роторах паровых турбин.—
В сб.: Доклады Весе, сими, пп малоцикл. усталости при довыш. темпе-
ратурах.— Челябинск: Челябинск, политехи, институт, 1974, вьш. 1,
с. 129—141.
50. Постирв В. А., Хархурим П. Я. Метод конечных элементов в
расчетах судовых конструкций.—Л.: Судостроение, 1974.— 344 с.
51. Проблемы автоматизации метода суперэлемептов. Программный комп-
лекс «К/\СКАД-2»/Постпов В. А., Дмитриев С. А.. Елтышев Б. К., Ро-
дионов А. А.— В сб.: Применение численных методов в строительной
механике корабля.— Л.: Судостроение, 1976. с.-6—14.
52. Работпов Ю. II. Ползучесть элементов конструкций.— М.: Паука,
1966.— 752 с.
53. Р а й с Дж. Р. Математические методы в механике разрушения.— В кн.:
Разрушение. Г. 2.—М.: Мир. 1975, с. 205—335.
54. Райс Дж. Р. Не зависящий от пути интеграл и приближенный анализ
концентрации деформаций у вырезов и трещин.— Труды амер, об-ва
ипж.-мех. Сер. Е. 1968, т. 35, № 4. с. 340—350.
55. Райс Дж. Р.. Джоисоп М. Влияние больших геометрических из-
менений у конца трещины па разрушение в условиях плоской дефор-
мации.— Механика (сб. пер.), 1973, № 6, с. 94—119.
56. Розин JT. А. Метод конечных элементов в применении к упругим си-
стемам.— М.: Стройиздат, 1977.— 129 с.
57. Русин ько К. II. Об условиях возникновения полос пластичности
при растяжении пластинки в прямолинейной трещиной.— В сб.: Вопро-
сы механики реального твердого тела. Вын. 2.—Киев: Паукова думка,
1964. с. 27—37.
58. Седов Л. И. Механика сплошных сред. Т. 2.— М.: Наука, 1976.—
573 с.
59. Си Дж. О сингулярном характера температурных папрлжепий у вер
шипы трещины,— Труды амер, об ва ипж.-мех. Сер. Е, 1962, т. 29, № 3,
с. 157—159.
60. Синицын А. П. Метод конечных элементов в динамике сооруже-
ний.— М.: Стройиздаг, 1978.—231 с.
250
ЛИТЕРАТУРА
61. Система математического обеспечения прочностных расчетов простран-
ственных копструкпин/Исахапов Г. В., Кислоокий В. Н., Сахаров А. С.,
Синявский А. Л.— Проблемы прочности, 1978. № 11, с. 59—61.
62. С л о т Т., М о у р б о й Д. Замечания о коэффициентах концентрации
напряжений для симметричных U-образпых выточек в плоских образ-
цах—Труды амер, об-ва инж.-мех. Сер. Е, 1965, № 3, с. 211—242.
63. С о сп с П. М. Алгоритмических! язык АЛГОЛ-60 и применение его в
строительной механике.— Киев: Будх'вельипк, 1965.— 170 с.
64. Стренг Г., Фикс Дж. Теория метода конечных элементов.— М.:
Мир, 1977.— 349 с.
65. Терхюнрочность деталей машин/Под ред. П. А. Биргера, Б. Ф. Шорра.—
М.: Машиностроение, 1975.—455 с.
66. Тимошенко С. П., Г у д ь е р Д ж. Теория упругости.— М.: Наука,
1978.— 575 с.
67. Тью ар сон Р. Разреженные матрипы.— М.: Мир. 1977.— 189 с.
68. Форсайт Д ж., М о л е р К. Численное решении систем алгебраиче-
ских уравнений.— М.: Мир, 1969.— 166 с.
69. Ф р а д к иц Б. В., Л а з а р е в с к и й Е. С. Решение плоской задачи тео-
рии упругости методом конечных элементов.— В сб.: Применение ЭВМ
для решения задач, связанных с исследованием, проектированием, стро-
ительством и эксплуатацией гидросооружений ГЭС. Материалы к сим-
позиуму стран—членов СЭВ и СФРЮ? Ч. 1.—Л.: ВНПИГ им. Ведене-
ева, 1973, с. 237—240.
70. Ч е р е п а п о в Г. П. О распространении трещин в сплошной среде.—
НММ, 1967, т. 31, № 3, с. 476-488.
71. Черепанов Г. П. Механика хрупкого разрушения.—М.: Иахка,
1974.— 640 с.
72. Эрдоган Ф., С и Дж. О распространении трещин в пластинках под
действием нагрузки в плоскости и поперечного сдвига.— Труды амер,
об-ва ипж.-мех. Сер. Д., 1963, т. 85, № 4, с. 122—126.
73. Ш о р р Б. Ф. К расчету неравномерно нагретых цилиндров в упруго-
пластической области.— Изв. АН СССР. ОТН. Сер. «Механика и маши-
ностроение», 1960, № 6, с. 57—62.
74. Ярема С. Я. Исследование полос пластичности при растяжении плас-
тин с концентратом.— В сб.: Вопросы механики реального твердого
тела. Вып. 2.— Киев: Паукова думка, 1964, с. 177—190.
75. A k h г a s G., D h a 11 G. An automatic node relabelling scheme for mini-
mizing a matrix or network bandwidth.— Int. J. Numer. Meth. Eng., 1976,
v. 10, p. 787—797.
76. А к у u z F. A., U t к u S. An automatic node — relabelling scheme for
bandwidth minimization of stiffness matrices.— AIAA Journal, 1968, v. 6,
Л» 4. p. 728—730*
77. Anderson D. M. Fracture toughness parameters and elastic-plastic ana-
lysis of nonnnoderato fracture conditions using finite element methods.—
Eng. Fract. Meeh.. 1973, v. 5. A? 2, p. 223—240.
78. Anderson G. P., R u g g 1 c s V. L., S t i b о г G. S. Use of finite element
computer programs in fracture mechanics.—Int. J. Fract. Meeh., 1971,
v. 7, N 1, p. 63-76.
79. Argyris J. IL ASKA: automatic system for kinematic analysis — a
universal system for structural analysis based on the matrix displace-
ment (finite element) method.— Aucl. Eng. Des., 1969, v. 10, A* 2,
p. 441—447.
80. A s t i z M. A., E 1 i c e s M., Galvez V. S. On energy release rates in
axisymmetrical problems.— In: Advances in Research on the Strength and
Fracture of Materials/Ed. D. M. R. Taplin.— V. ЗА. Analysis and Mechanics.
Fourth Int. Conf, on Fracture. June 1977. Univ, of Waterloo.—Canada:
Pergamon Press, 1978, p. 395—400.
ЛИТЕРАТУРА
81. Darlow J. Optimal stress locations in finite element models.—Int. J.
Numer. Meth. Eng., 1976. v. 10, N 2, p. 213—251.
82. Barsnum R. S. Application of quadratic isoparametric finite elements in
linear fracture mechanics.— Int. J. Fract., 1974, v. 10, N 4, p. 603—605.
S3. В ar so u in R. S. Application of triangular quarter-point elements as crack
tip elements of power law hardening material.— Int. J. Fract., 1970, v. 12,
N 3, p. 463—466.
84. Begley J. A.. Landes J. D. The /-Integral as a fracture criterion.—
Fracture Toughness. ASTM STP 514, 1972, p. 1—20.
85. Ben z ley S. E. Nonlinear calculations with a quadratic quarter-point
crack tip element.— Int. J. Fract., 1976, v. 12, № 3, p. 477—780.
SO. Blackburn W. S. Calculation of stress intensity factors at crack tips
using special finite elements.— The Mathematics of Finite Elements and
Applications.— London; New York: Academic Press, 1973, p. 327—336.
87. Blackburn W. S. Path independent integrals to predict onset of crack
instability in an elastic-plastic material.— Int. J. Fract. Meeh., 1972, v. 8,
p. 343—346.
88. Blackburn W. S., Jackson A. D., Helion T. K. An integral as-
sociated with the state of a crack tip in a Don-elastic material.— Int. J.
Fract., 1977, v. 13, N 2, p. 183-200.
89. Can tin G. An equation solver of very large capacity.—Int. J. Num er.
Meth. Eng.. 1971, v. 3, N 3, p. 379-388. ’
90. C h a n S. K., Tuba I. S., Wilson W. K. On the finite element method
in linear fracture mechanics.—Eng. Fract. Meeh., 1970, v. 2, N 1, p. 1—17.
91. Cheng R. T. On the accuracy of certain C° continuous finite element
representations.— Int. J. Numer. Meth. Eng., 1974. v. 8, N 3, p. 649—657.
92. Cheung Y. К., К h a t u a T. P. A finite element solution program for
large structures.— Int. J. Numer. Meth. Eng., 197*1, v. 10, N 2, p. Ю1—412.
93. Chow C. L.. Lau K. J. A conic-section simulation analysis of two-di-
mensional fracture problems using the finite clement method.— Int. J.
Fract.. 1976, v. 12, N 5, p. 669—684.
94. Chow C. L., Lau K. J. On crack surface displacement approaches of
finite element analysis in evaluating stress intensity factors.— Int. J.
Fract., 1976, v. 12, № 3, p. 488—490.
95. Chow T. S., Kowal ik J. S. Computing with sparse matrices.—Int. J.
Numer. Meth. Eng., 1973, v. 7, N 2, p. 211—223.
96. Coch c i J. F., l)h a I t G. S. A modification of the Alpha constant tech-
nique.— Int. J. Numer. Meth. Eng.. 1977. v. 11, № 6, p. 1053—1054.
97. b a g d a I c D. S. Yielding of steel she ets containing slits.— J. Meeh. Phys.
Solids, 1960, v. 8, N 2, p. 100-104.
98. E г g a t о u d i s I., 1 г о n s B., Z i e. n к i e w i c z O. Cowed, isoparametric
quadrilateral elements for finite element analysis.— Int. J. Solids and
Structures, 1968. v. 4, N I, p. 31—42.
99. Felippa C. A. An alphanumeric finite element mesh plotter.— Int. J.
Nurner. Meth. Eng.. 1972. v. 5. N 2, p. 217—236.
100. Felippa C. A. Solution of linear equal ions with skyline-tored symmet-
ric matrix.— Comput. and Struct., 1975, v. 5. N 1, p. 13—29.
101. Fischer K. On the calculations of higher derivatives in finite ele-
ments.— Computer Meth, in Appl. Meeh, and Eng., 1976, v. 7, № 2,
p. 323-330.
102. Francis P. IL, Ko . L. The effect of root radius on the direction of
crack extension under combined mode loading.—Int. J. Fract., 1976, v. 12,
N 2. p. 243-252.
103. Fried I. Accuracy and condition of curved (isoparametric) finite ele-
ments.— J. Sound Vibr., 1973, v. 31, N 3, p. 345—355.
10L Fried 1. Numerical integration in finite element method.— Comput. and
Struct., 1974, v. 4, № 5, p. 921—932.
252
ЛИТЕРАТУРА
105. Griffith A. A. The phenomenon of rupture and flow in solids.—Phil.
Trans. Roy. Soc. Ser. A, 1920, v. 221. p. 163—188.
1^ 6. Gupta A. K., Mo hr as B. A method of computing numerically integ-
rated stiffness matrices.—Int. J. Numer. Meth. Eng.. 1972. v. 5. N 1
p. 83—89.
107. Guу d i s h J. /..Fleming J. F. Optimisation of the finite element mesh
for the solution of fracture problems.—Eng. Fract. Meeh., 1978. v. 10.
N 1, p. 31—42.
108. Hayes D. J.. Turner С. E. An application of finite element techni-
ques to post-yield analysis of proposed standart three-point bond fracture
test pieces.— Tnl. J. Fract.. 1974, v. 10. N 1. p. 17—31.
109. lie 11 on T. K. On the method of virtual crack ex tent ions.— Tut. J. Nu-
mer. Meth. Eng., 1975, v. 9. № 1, p. 187—207.
110. H c 11 e n T. K., Blackburn W. S. The calculation of stress intensity
factors for combined tensile and shear loading.—Int. J. Fract., 1975, v. 11,
X 4. p. 605-617.
111. He lien Г. K., Price R. IL, Harrison R. 1*. Thermal analysis of
cracked bodies using finite element techniques.—Tn: 3 rd Intern. Conf.
Struct. Meeh. Reach. Technol. London 1975.— Amsterdam: Amsterdam e. a.,
1975, v. 5. part. L. p. L7, 4/1—L7. 4/13.
112. Hen shell R. I).. Shaw K. G. Crack tip finite elements are unnessa-
ry.— Int. J. Numer. Meth. Eng.. 1975, v. 9, N 3, p. 495—507.
113. Hilton P. D„ Sih G. S. Application of finite element method to the
calculations of stress intensity factors.—In: Methods of Analysis and So-
lution of Crack Problems/Ed. G. S. Sih.— Leyden: Noordhoff* 1973, v. 1,
p. 426—489.
114 Hinton E.. Scott F. C., Ricketts R E. Local least square stress
smoothing for parabolic isoparametric elements.— Int. J. Numer. Meth.
Eng., 1975, v. 9, № 1, p. 235—238.
115. Hodge P. G., AVh ite G. II. A quantitative comparison of flow and de-
formation theories of plasticity.—J. App. Meeh., 1950, v. 17, As 3. p. ISO—1S4.
116. Hu It J. A. IL. McClintock F. A. Elastic stress and strain distribu-
tions around sharp notches under repeated shear.—In: 9-th Intern. Congr.
for Appl. Meeh.— Brussels, Noord ho ff. 1956, v. 8, p. 51—58.
117. Hutchinson .1. W. Singular behavior at the end of a tensile crack in
a hardening material.—J. Meeh. Phys. Solids, 1968, v. 16, N 1, p. 13—22.
118. Irons В. M. \ frontal solution program for finite element analysis.—
Int. J. Numer. Meth. Eng., 1970, v. 2, N 1, p. 5—32.
119. Irons В. M. Quadrature rules for brick based finite elements.— Ini.
J. Numer. Meth. Eng., 1975, v. 3. N 2. p. 293—294.
120. 1 r w i n G. R. Fracture.— Handbuch der Physik.— Berlin: Springer A’vrlag,
1958. v. 6.— 551 p.
121. Irwin G. R. Fracture dynamics: Fracturing of Metals, ASM Cleveland,
1948. p. 147—166.
122. Irwin G. R. Analysis of stresses and strains near the end of a crack
traversing a plate.—.I. Appl. Meeh.. 1957. v. 24, N 3, p. 148—152.
123. Iso-parametric and associated element families for two- and three-dimen-
sional analysis/Zienkewicz О. C.. Irons В. M.. Ergatoudis J., Ahmad S.,
Scott F. C.— Tn: Fenile Element Method in Stress analysis, ch. 13.— Tron-
dheim: Tapir, 1969, p. 162—167.
121. J enkins W. AL Matrix and Digital Computer Methods in Structural Ana-
lysis.— London: McGraw-Hill. 1969.— 423 p.
12л. Kanazawa T., Machida S.. К a n e d a S. On the J integral fracture
criterion.— J. Fac. Eng., Univ, of Tokyo, v. 33. N 4, p. 503—517.
120. Kobayashi A. S., Chiu S. T., Beuewkes R. A. A numerical and
experimental investigation on the use of /-integral.— Eng. Fract. Meeh.,
1973, v. 5, № 2, p. 293-305.
литература
253
127. Landes J. D., Begley J. A. Test results from /-integral studies: an
attempt to establish a /IC testing procedure.— In: Fracture Analysis,
ASTM STP 560, 1974, p. 170—18G.
12S. Landes J. D., Begley J. A. The effect of specimen geometry on
/IC — In: Fracture Toughness, ASTM STP 514, 1972, p. 24—39.
129. Launay P. et al. The tridimensional termoelastic computer code
«TITUS».— In: Prepr. 1-st Int. Conf. Struct. Meeh. React. Technol. Berlin,
1971.— Amsterdam: Amsterdam e. a.. 1971, v. 5, part II, p. M5—4/1—M5—
4/21.
130. Mac Neal R. IL, McCormic C. VV. The NASTRAN computer prog-
ram for structural analysis.— Comput. and Struct., 1971, v. 7, IS 1,
p. 32-35.
131. Me Mee king R. M. Finite deformation analysis of crack-tip opening in
eastic-plastic materials and implications for fracture.— J. Meeh. Phys. So-
lids, 1977, v. 25. N 5, p. 357—387.
132. Meek J. L., Beer G. Contour plotting of data using isoparametric ele-
ment represcentation.— Int. J. Numer. Meth. Eng., 4976, v. 10, N i, p. 954—
957.
133. Morozov E. M. Limit analysis for structures with flaws.— Eng. Fract.
Meeh., 1974, v. 8, N 3, p. 297—306.
134. N а у a к G. C., Zienkievvicz О. C. Elasto-plaslic stress analysis. A ge-
neralisation for various constitutive relations including strain softening.—
Int. J. Numer. Meth. Eng., 1973, v. 5, N 1, p. 113—135.
135. N a v a к G. C., Z i e n к i e w i c z О. C. Note on the alpha-constant stiffness
method for the analysis of non-linear problems.— Int. J. Numer. Meth. Eng..
1972, v. 4, № 4, p. 579—582.
136. Newton R. E. Degeneration of brick-type isoparametric elements.—Int.
J. Numer. Meth. Eng., 1973, v. 7, N 4. p. 579—581.
137. Or о wa n E. O. Fundamentals of brittle behavior of metals.— Falique and
Fracture of Metals.— N. Y.: Wiley. 1950. p. 139—167.
138. Parks D. M. A stiffness derivative finite element technique for deter-
mination of elastic crack lip stress intensity factors.— Int. J. Fract., 1974,
v. 10, N 4, p. 487-502.
139. Parks D. M. The virtual crack extension method for nonlinear
material behavior.— Computer Meth. Appl. Meeh. Eng., 1977, v. 12, N 3,
p. 353—364.
110. Pawsey S. F. Discussion of papers by О. C. Zienkiewicz, R. L. Taylor
and J. M. Too and S. F. Pawsey and R. W. Clough.— Int. J. Numer. Meth.
Eng., 1972, v. 4. N 3, p. 445—450.
141. Prandtl L. Spannungsverteilung in plastischen Korpern.— Proc. 1-th
Int. Congr. Appl. Meeh.— Delft, 1924, p. 43—54.
142. Reynen J. On the use of finite element method in fracture analysis of
pressure vessel components.— Trans. ASME. Ser. J., 1976, v. 98, N 1,
p. 8—16.
1 i3. R i с с a r d e 11 a P. C., S w о d 1 о w L. L. A combined analytical experi-
mental fracture study.— In: Fracture Analysis. ASTM STP 560, 1974,
p. 134-454.
144. Rice J. R., Paris P. C., Mercle J. G. Some further results of / in-
tegral analysis and estimates.— Tn: Progress in Flaw Growth and Fracture
Toughness Testing. ASTM STP 536, 1973, p. 231—245.
145. Rice J. R., R о s e n g r c n G. F. Plane strain deformation near a crack
tip in a power law hardening material.— J. Meeh. Phys. Solids, 1968, v. 16,
№ 1, p. 1-12.
146. Roche R. L. Use of the calculation of integral Д — Advances in Rese-
arch on the Strength and Fracture of Materials/Ed. D. M. R. Taplin.—
V. ЗА. Analysis and Mechanics. 4-th Int. Conf, on Fracture. June 1977.
Univ, on Waterloo.—Canada: Pergamon Press, 1978, p. 245—255.
254
ЛИТЕРАТУРА
147. Rybicki Е. F., Kanninen M. F. A finite element calculation of
stress intensity factors by a modified crack closure integral.—Eng. Fracl.
Meeh., 1977, v. 9, N 4, p. 931—938.
148. S e g u 1 W. T. Computer programs for the solution of linear algebraic equ-
ations.—Int. J. Numer. Meth. Eng., 1973, v. 7, N 4, p. 479—490,
149. Sih G. C. Strain-energy-density factor applied to mixed mode crack prob-
lems.— Int. J. Fract., 1974, v. 10, N 3, p. 305—320.
150. Small scale yielding near a crack in plane strain: a finite element analv-
sis/Lcvy N.. Marcal P. V., Ostergren W. J., Rice J. IL— Int. J. Fract. Meeh.,
1971, v. 7, N 2, p. 143-156.
151. Sneddon J. N. The distribution of stress in the neighbourhood of a
crack in a elastic solid.—Proc. Rov. Soc. Ser. A, 1946, v. 187, N 1008,
5. 229—260.
152. St ein mu ell er G. Restrictions in the application of automatic mosh
generation schemes by «isoparametric» coordinates.—Int. J. Numer. Meth.
Eng., 1974, v. 8, N 2, p. 289-294.
153. Stiffness and deflection analysis of complex structurcs/Turner M J., Clo-
ugh R. W., Martin H. C., Topp L. J.— J. Aeronaut Sci., 1956, v. 23. N 9,
p. 805-824.
154. Sumpter J. D. G., Turner С. E. Use of the ] contour integral in elas-
tic-plastic-fracture studies by finite-element methods.—J. Meeh. Eng* Sci.,
1976, v. 18, № 3, p. 97-112.
155. lay lor R. L. On completeness of shape functions for finite element
analysis.— Int. J. Numer. Meth. Eng., 1972, v. 4, N 1, p. 17—22.
150. Tracey D. M. Discussion of «On the use of isoparametric finite elements
in linear fracture mechanics by IL S. Barsonm».—Int. J. Numer. Meth.
Eng., 1977, v. 11. N 2. p. 401—402.
157. Tracey D. M. Finite elements for determination of crack lip elastic
stress intensity factors.—Eng. Fract. Meeh., 1971, v. 3, N 3, p. 255—265.
158. Tuff A. D., Jennings A. An iterative method for large systems of
linear structural equations.— Int. J. Numer. Meth. Eng., 1973, v. 7, N 2,
p. 175—183.
159. VVat wood V. B. The finite element method for prediction of crack be-
havior.—Nucl. Eng. and Des., 1969, v. 11, № 2, p. 323—332.
160. Wells A. A. Application of fracture mechanics al and beyond general
yielding.— BriL Weld. J., 1963, v. 10, N 11, p. 563—570.
161. Wilson E. L.. В a t h e K. J., D о h e r t у W. P. Direct solution of large
systems of linear equations.—Coinput, and Struct., 1974, v. 4, N 2, p. 363—
372.
162. Wilson W. K, Y u. 1. W. The use of the /^integral in tvrmal stress
crack problems.— Int. J. Fract., 1979, v. 15. N 4. p. 371—387.
163. Yamada Y., Yoshimura N., Sakurai T. Plastic sircss-strain
matrix and its application for the solution of elastic-plastic problems by the
finite element method.— Int. J. Meeh, Sci., 1968. v. 10, N 4, p. 343—354.
164. Y of f e E. H. The moving Griffith crack.—Philos. Mag., 1931, v. 42, N 330,
p. 739—750.
165. Zienkiewicz О. C., Phillips D. V. An automatic mesh generation
scheme for plane and curved surfaces by «isoparametric» co-ordinates.—
Int. J. Numer. Meth. Eng.. 1971, v. 3, № 4, p. 519—528.
166. Z ien к i ewicz О. C., Valliappan S., King I. Elasto plastic solu-
tion of engineering problems. Initial-stress finite element approach — Int.
J. Numer. Meth. Eng., 1969, v. 1, Л? 1. p. 75—100.
Евгений Михайлович Морозов,
Геннадий Петрович Никигиков
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
В МЕХАНИКЕ РАЗРУШЕНИЯ
М., 1980 г., 256 Стр. с илл.
Редакторы И. А. Маркузон, if. М. Овчинникова
Техн, редактор Н. В. К отделе ва
Корректоры Г. В. Подеолъская. Л. С. Сомова
ПЕ М 11295
Сдано в набор 18.01.80. Подписаио к печати 27.05.80. Т-11201. Бумага 60х.90’/|в,
тип. М 2. Высокая печать. Обыкновенная гарнитура. Условн. псч. л. 161-форзац 9,25.
Уч.-изд. л. 15,251-форзац 0,46. Тираж 5000 эка. Заказ № 21. Цена книги 2 р 40 к.
Издательство «Паука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
4-я типография издательства «Наука», €30077, Новосибирск, 77, Станиславского. 25