Автор: Bolian L. Hong-Jian L.
Теги: mathematics physics graph theory mathematical physics higher mathematics springer network theory
ISBN: 0-7923-6469-4
Год: 2000
Текст
Network Theory and Applications
Volume 3
Matrices in Combinatorics
and Graph Theory
by
Bolian Liu
Department of Mathematics,
South China Normal University,
Guangzhou, P. R. China
and
Hong-Jian Lai
Department of Mathematics,
West Virginia University,
Morgantown, West Virginia, USA,
KLUWER ACADEMIC PUBLISHERS
DORDRECHT / BOSTON / LONDON
A C.I.P. Catalogue record for this book is available from the Library of Congress.
ISBN 0-7923-6469-4
Published by Kluwer Academic Publishers,
RO. Box 17,3300 AA Dordrecht, The Netherlands.
Sold and distributed in North, Central and South America
by Kluwer Academic Publishers,
101 Philip Drive, Norwell, MA 02061, U.S.A.
In all other countries, sold and distributed
by Kluwer Academic Publishers,
P.O. Box 322,3300 AH Dordrecht, The Netherlands»
Printed on acid-free paper
All Rights Reserved
© 2000 Kluwer Academic Publishers
No part of the material protected by this copyright notice may be reproduced or
utilized in any form or by any means, electronic or mechanical,
including photocopying, recording or by any information storage and
retrieval system, without written permission from the copyright owner.
Printed in the Netherlands.
Contents
Foreword ix
Preface xi
1 Matrices and Graphs 1
1.1 The Basics 1
1.2 The Spectrum of a Graph 5
1.3 Estimating the Eigenvalues of a Graph 12
1.4 Line Graphs and Total Graphs 17
1.5 Cospectral Graphs 20
1.6 Spectral Radius 24
1.7 Exercises 38
1.8 Hints for Exercises 41
2 Combinatorial Properties of Matrices 47
2.1 Irreducible and Folly Indecomposable Matrices 48
2.2 Standard Forms 50
2.3 Nearly Reducible Matrices 54
2.4 Nearly Decomposable Matrices 58
2.5 Permanent 61
2.6 The Class #(r,s) 71
2.7 Stochastic Matrices and Doubly Stochastic Matrices 77
2.8 Birkhoff Type Theorems 81
2.9 Exercise 90
2.10 Hints for Exercises 92
3 Powers of Nonnegative Matrices 97
3.1 The EYobenius Diophantine Problem 97
3.2 The Period and The Index of a Boolean Matrix 101
vj Contents
3.3 The Primitive Exponent 107
3.4 The Index of Convergence of Irreducible Nonprimitive Matrices 114
3.5 The Index of Convergence of Reducible Nonprimitive Matrices 120
3.6 Index of Density 125
3.7 Generalized Exponents of Primitive Matrices 129
3.8 Fully indecomposable exponents and Hall exponents 136
3.9 Primitive exponent and other parameters 146
3.10 Exercises 150
3.11 Hint for Exercises 153
4 Matrices in Combinatorial Problems 161
4.1 Matrix Solutions for Difference Equations 161
4.2 Matrices in Some Combinatorial Configurations 166
4.3 Decomposition of Graphs 171
4.4 Matrix-TVee Theorems 176
4.5 Shannon Capacity 180
4.6 Strongly Regular Graphs 190
4.7 Eulerian Problems 196
4:8 The Chromatic Number 204
4.9 Exercises 210
4.10 Hints for Exercises 212
5 Combinatorial Analysis in Matrices 217
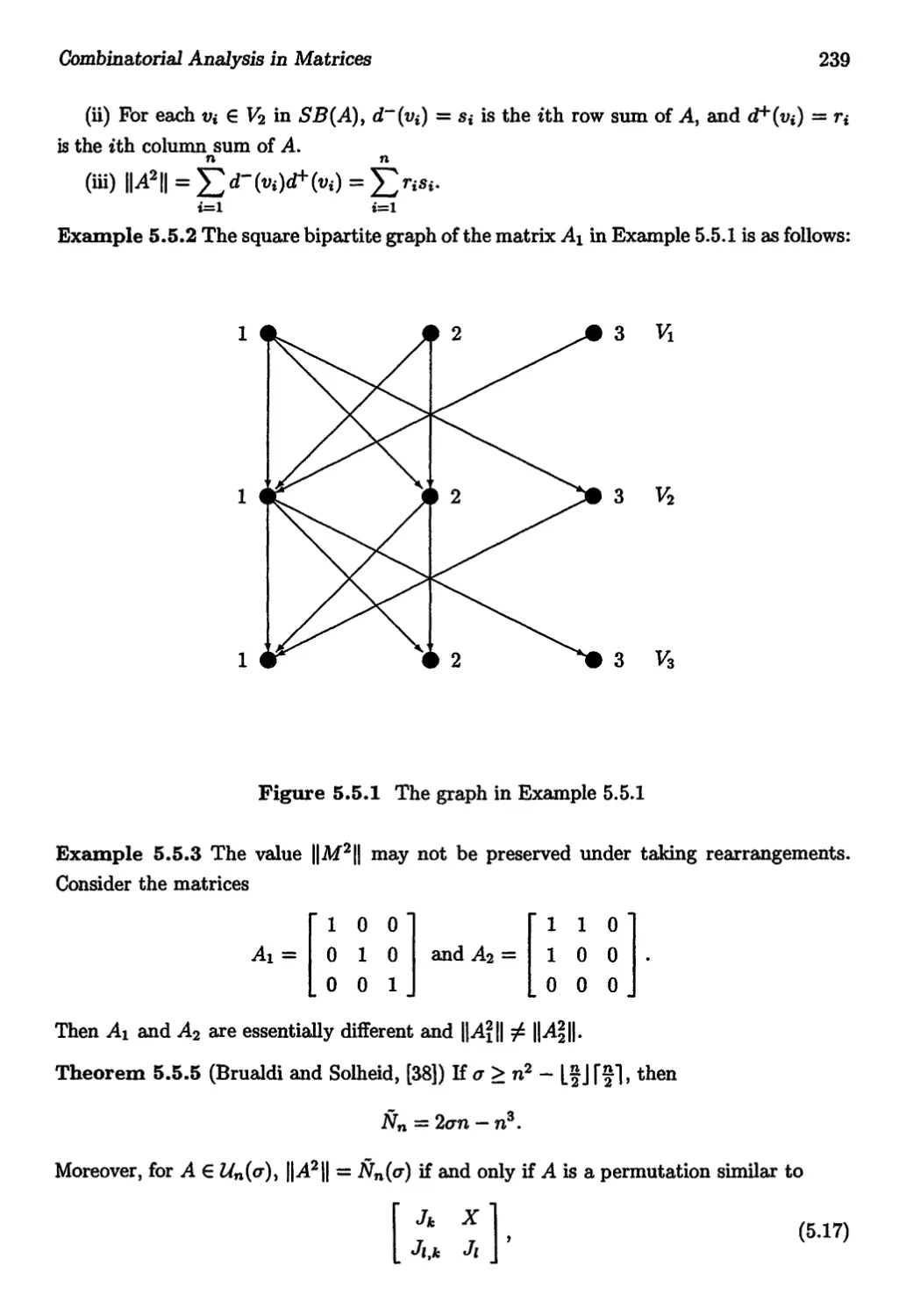
5.1 Combinatorial Representation of Matrices and Determinants 217
5.2 Combinatorial Proofs in Linear Algebra 221
5.3 Generalized Inverse of a Boolean Matrix 224
5.4 Maximum Determinant of a (0,1) Matrix 230
5.5 Rearrangement of (0,1) Matrices 236
5.6 Perfect Elimination Scheme 245
5.7 Completions of Partial Hermitian Matrices 249
5.8 Estimation of the Eigenvalues of a Matrix 253
5.9 M-matrices 261
5.10 Exercises 271
5.11 Hints for Exercises 272
6 Appendix 275
6.1 Linear Algebra and Matrices 275
6.2 The Term Rank and the Line Rank of a Matrix 277
6.3 Graph Theory 279
Contents vi
Index 28<
Bibliography 29 J
FOREWORD
Combinatorics and Matrix Theory have a symbiotic, or mutually beneficial, relationship.
This relationship is discussed in my paper The symbiotic relationship of combinatorics and
matrix theory1 where I attempted to justify this description. One could say that a more
detailed justification was given in my book with H. J. Ryser entitled Combinatorial Matrix
Theory1 where an attempt was made to give a broad picture of the use of combinatorial
ideas in matrix theory and the use of matrix theory in proving theorems which, at least
on the surface, are combinatorial in nature.
In the book by Liu and Lai, this picture is enlarged and expanded to include recent
developments and contributions of Chinese mathematicians, many of which have not been
readily available to those of us who are unfamiliar with Chinese journals. Necessarily, there
is some overlap with the book Combinatorial Matrix Theory. Some of the additional topics
include: spectra of graphs, eulerian graph problems, Shannon capacity, generalized inverses
of Boolean matrices, matrix rearrangements, and matrix completions. A topic to which
many Chinese mathematicians have made substantial contributions is the combinatorial
analysis of powers of nonnegative matrices, and a large chapter is devoted to this topic.
This book should be a valuable resource for mathematicians working in the area of
combinatorial matrix theory.
Richard A. Brualdi
University of Wisconsin - Madison
1Linear Alg. Applies., vols. 162-4,1992, 65-105
2 Cambridge University Press, 1991.
IX
PREFACE
On the last two decades or so work in combinatorics and graph theory with matrix and
linear algebra techniques, and applications of graph theory and combinatorics to linear
algebra have developed rapidly. In 1973, H. J. Ryser first brought in the concept
"combinatorial matrix theory". In 1992, Brualdi and Ryser published "Combinatorial Matrix
Theory", the first expository monograph on this subject. By now, numerous exciting
results and problems, interesting new techniques and applications have emerged and been
developing. Quite a few remarkable achievements in this area have been made by Chinese
researchers, adding their contributions to the enrichment and development of this new
theory.
The purpose of this book is to present connections among combinatorics, graph theory
and matrix theory, with an emphasis on an exposition of the contributions made by Chinese
scholars.
Prerequisites for an understanding of the text have been kept to a minimum. It is
essential however to be familiar with elementary set notation and to have had basic knowledge
in linear algebra, graph theory and combinatorics. For referential convenience, three
sections on the basics of these areas are included in the Appendix, supplementing the brief
introductions in the text.
The exercises which appear at the ends of chapters often supplement, extend or
motivate the materials of the text. For this reason, outlines of solutions are invariably included.
, who can
We wish to make special acknowledgment to Professor Herbert John Ryser
be rightfully considered the father of Combinatorial Matrix Theory, and to Professor
Richard Brualdi, who has made enormous contributions to the development of the theory.
There are many people to thank for their contributions to the organization and content
of this book and an earlier version of it. In particular, we would like to express our sincere
thanks to Professors Lizhi Hsu, Dingzhu Du, Ji Zhong, Qiao Li, Jongsheng Li, Jiayu Shao,
Mingyiao Hsu, Fuji Zhang, Kerning Zhang, Jingzhong Mao, and Maocheng Zhang, for
their wonderful comments and suggestions. We would also like to thank Bo Zhou and
Hoifung Poon for proof reading the manuscript.
Bolian Liu would like to give his special appreciation to his wife, Mo Hui, and his
favorite daughters, Christy and Jolene. Hong-Jian Lai would like to give his special thanks
to his wife, Ying Wu, and to his parents Jie-Ying Li and | Han-Si Lai |. Without our
families' forbearance and support we would never have been able to complete this project.
XI
Chapter 1
Matrices and Graphs
1.1 The Basics
Definition 1.1.1 For a digraph D with vertices V(D) = {vi,V2,--- ,vn}, let m(vi9Vj)
denote the number of arcs in D oriented from V{ to Vj. The adjacency matrix of D is an
n by n matrix A(D) = (a^), given by
dij =m(vitVj).
We can view a graph G as a digraph by replacing each edges of G by a pair of arcs
with opposite directions. Denote the resulting digraph by Dq. With this view point, we
define the adjacency matrix ofG by A(G) = A(Dg)> the adjacency matrix of the digraph
Dq- Note that A(G) is a symmetric matrix.
Note that the adjacency matrix of a simple digraph is a (0, l)-matrix, and so there
is a one-to-one correspondence between the set of simple digraphs D{V^E) with V —
{v\, • • • , vn} and Bn, the set of all (0,1) square matrices of order n: For each (0,1) square
matrix A = (aij)nxn, define an arc set E on the vertex set V by e = (vj,Vj) € E if
and only if ац — 1. Then we obtain a digraph 1?(Л), called the associated digraph of A.
Proposition 1.1.1 follows from the definitions immediately.
Proposition 1.1.1 For any square (0,1) matrix A, A(D(A)) = A,
Definition 1.1.2 A matrix A 6 Bn is a permutation matrix if each row and each column
have exactly one 1-entry. Two matrices A and В are permutation equivalent if there exist
permutation matrices P and Q such that A = PBQ; A and В are permutation similar if
for some permutation matrix P, A = PBP~l.
Let Л = (ay) and Б = (by) be two matrices in Mm>n. Write Л < Б if for each t and
j, a^ < 6^.
1
2
Matrices and Graphs
Proposition 1.1.2 can be easily verified.
Proposition 1.1.2 Let A be a square (0,1) matrix, and let D = D(A) be the associated
digraph of A. Each of the following holds.
(i) Each row sum (column sum, respectively) of A is a constant г if and only if d+ (v) = r
(d~(v) = r, respectively) Vv 6 V(D),
(ii) Let А, В € Вл. Then A < В if and only if D(A) is a spanning subgraph of D(B).
(iii) There is a permutation matrix P such that PAP"1 = В if and only if the vertices
of D(A) can be relabeled to obtain D(B).
(iv) A is symmetric with tr(A) = 0 if and only if D(A) = Z><j for some simple graph
G; or equivalently, if and only if A is the adjacency matrix of a simple graph G.
(v) There is a permutation matrix P such that
where Ai and A2 are square (0,1) matrices, if and only if D(A) is not connected,
(vi) There is a permutation matrix P such that
where В is a (0,1) matrix, then D(A) is a bipartite graph. (In this case, the matrix В
is called the reduced adjacency matrix of D(A)\ and D(A) is called the reduced associated
bipartite graph of B. )
(vii) The (i,j)-th entry of A1, the Z-th power of A, is positive if and only if there is a
directed (vi,Vj)-walk in D(A) of length l.
(viii) Ai is a principal square submatrix of A if and only if A\ = A(H) is the adjacency
matrix of a subgraph G induced by the vertices corresponding to the columns of A\.
Definition 1.1.3 Let G = (V,E) be a graph with vertex set V = {vi,v2,--- ,vn} and
edge set E = {ei,e2, ¦ • • , e^}, with loops and parallel edges allowed. The incidence matrix
of G is B(G) = (bij)nxg whose entries are defined by
{1 it Vf is incident with e**
0 otherwise
Let diag(ri,r2, • • • ,rn) denote the diagonal matrix with diagonal entries ri,r2, • • • ,rn.
For a digraph D = (V,!?) with vertex set V = {vi,v2,-** ,vn} and arc set E =
{ei,e2,-*- ,e9}, with loops and parallel edges allowed, the oriented incidence matrix of
Matrices and Graphs
3
the digraph D is B(D) = (Ьу)пхд whose entries are defined by
{1 it Vj is an out-arc of V{
—1 it vj is an in-arc of vi
0 otherwise
Given a digraph D with oriented incidence matrix Б, the matrix BBT is called the
Laplace matrix, (or admittance matrix) of D. As shown below, the Laplace matrix is
independent of the orientation of the digraph D. Therefore, we can also talk about the
Laplace matrix of a graph G, meaning the Laplace matrix of any orientation D of the
graph Ст.
Theorems 1.1.1 and 1.1.2 below follow from these definitions and so are left as exercises.
Theorem 1.1.1 Let G be a loopless graph with V(G) = {vi,V2>--* ,vn}, and let d{ be
the degree of vi in (?, for each % with 1 < i < n. Let D be an orientation of G, A be the
adjacency matrix of G and С = diag(di, d2i • • • , dn). Each of the following holds.
(i) If Б is the incidence matrix of G, then BBT = С + A.
(ii) If В is the oriented incidence matrix of D, then BBT = C — A.
Theorem 1.1.2 Let G be a graph with t components and with n vertices. Let D be an
orientation of G. Each of the following holds.
(i) The rank of the oriented incidence matrix В is n — t.
(ii) Let B\ be obtained from В by removing t rows from B, each of these t rows
corresponding to a vertex from each of the t components of G. Then the rank of B\ is
n — t.
Definition 1.1.4 An integral matrix A = (o^) is totally unimodular if the determinant
of every square submatrix is in {0,1, —1}.
Theorem 1.1.3 (Hoffman and Kruskal [127]) Let A be an m x n matrix such that the
rows of A can be partitioned into two sets Ri and R2 and such that each of the following
holds:
(i) each entry of A is in {0,1, —1};
(ii) each column of A has at most two non-zero entries;
(iii) if some column of A has two nonzero entries with the same sign, then one of the
rows corresponding to these two nonzero entries must be in Ri and the other in R2; and
(iv) if some column of A has two nonzero entries with different signs, then either both
rows corresponding to these two nonzero entries are in Ri or both are in R2.
Then A is totally unimodular.
Proof Note that if a matrix A satisfies Theorem 1.1.3 (i)-(iv), then so does any submatrix
of A. Therefore, we may assume that A is an n x n matrix to prove det(^4), the detenninant
4
Matrices and Graphs
of A, is in {0,1, —1}.
By induction on та, the theorem follows trivially from Theorem 1.1.3(i) when та = 1.
Assume that n > 2 and that Theorem 1.1.3 holds for square matrices with smaller size.
If each column of A has exactly two nonzero entries, then by (iii) and (iv), the sum of
the rows in R\ is equal to that of the rows in J?2> consequently det(A) = 0. If A has an
all zero entry column, then det(A) = 0. Therefore by (ii), we may assume that there is
a column which has exactly one nonzero entry. Expand det(A) along this column and by
induction, we conclude that det(A) € {0,1, —1}. []
Corollary 1.1.3A (Poincare [213]) The oriented incidence matrix of a graph if totally
unimodular.
Corollary 1.1.3B Let G be a loopless graph (multiple edges allowed) and let В be the
incidence matrix of G. Then G is bipartite if and only if В is totally unimodular.
Definition 1.1.5 For a graph G, the characteristic polynomial of G is the characteristic
polynomial of the matrix A(G), denoted by
Xg(A)= det(\I-A(G)).
The spectrum of G is the set of numbers which are eigenvalues of the matrix A(G), together
with their multiplicities. If the distinct eigenvalues of A{G) are Ai > Л2 > • • • > \Si and
their multiplicities are mi,r?i2, • • • , тя„ respectively, then we write
spec(<?)=( Al A2 "" As V
\ mi ГП2 • • • tns J
Since A(G) is symmetric, all the eigenvalues Ai's are real. When no confusion arises, we
write det<7 or det(<2) for det(A(G)).
Theorem 1.1.4 Let S(G,H) denote the number of subgraphs of G isomorphic to H. If
XG(A) = f>A"-\then
Co = 1, and
d = HO^dettfS^tf), 1 = 1,2,..-,*,
я
where the summation is taken over all non isomorphic subgraphs of G.
Sketch of Proof Since xg(A) = det(A/ - A) = An + • • •, C0 = 1, and for each г =
1,2,. • • , n, Ci = (-1)* ^2 detAi, where the summation is over all the ith order principal
Ai
submatrices of A. Note that Ai is the adjacency matrix of the subgraph H of G induced by
the vertices corresponding to the rows of Ai (Preposition 1.1.2(vii)), and that the number
of such subgraphs of G is 5(6?, Я). Q
Matrices and Graphs
5
Further discussion on the coefficients of XgW can be found in [226].
1.2 The Spectrum of a Graph
In this section, we present certain techniques using the matrix A(G) and spec(G) to study
the properties of a graph G. Theorem 1.2.1 displays some facts from linear algebra and
from Definition 1.1.5.
Theorem 1.2.1 Let G be a graph with n vertices, and A = A(G) be the adjacency matrix
of G. Each of the following holds:
(i) If 6?i, 6?2, * * * , Gk are components of G, then xgW = П*=а XG* (A).
(ii) The spectrum of G is the disjoint union of the spectrums of 6?i, where i = 1,2, • ¦ • , к.
(Hi) If f(x) is a polynomial, and if Л is an eigenvalue of Л, then /(A) is an eigenvalue
off (A).
Theorem 1.2.2 Let G he a connected graph with n vertices and with diameter d. If G
has s distinct eigenvalues, then n > s > d -f 1.
Proof Since n is the degree of х<?(А), n>s.
Let A = A(G) and suppose that $ < d. Then G has two vertices vi and Vj such that
the distance between Vi and Vj is 5. Let m^(A) be the minimum polynomial of A. Then
тпл(А) = 0. Since A is symmetric, the degree of гад (A) is exactly 5 and шд (A) = A* H .
By Proposition 1.1.2(vii), the (i,j)-entry of As is positive, and the (t,j")-entry of A1 is
zero, for each Z with 1 < / < s — 1. it follows that it is impossible to have тпа(А) = 0, a
contradiction. Q
For integer r,g > 1, an r-regular graph with girth g is called an (r,#)-graph, Sachs
[225] showed that for any r,g > 1, an (r,p)-graph exists. Let f(r,g) denote the smallest
order of an (r,^)-graph. An (r,y)-graph G with |V(<j?)| = f(r,g) is called a Moore graph.
Theorem 1.2.3 (Erdos and Sachs, [84])
r1 + 1 < /(r,5) < 4(r - l)(r2 - r +1).
Theorem 1.2.4 When g = 5, a Moore (r, 5)-graph exists only if r = 2,3,7, or 57.
Proof Let G be a Moore (r, 5)-graph. Then \V(G)\ = r2+l. Let V(G) = {vb v2, • • > , vra+1},
and let Л = (а#) denote the adjacency matrix of G, and denote A2 = (a\)).
Since ? = 5, <j has no 3-cycles, and so when o^ = 1, a\j = 0; and when a# = 0,
a^ = 1. It follows that
A2 + A = J+(r-l)J.
6
Matrices and Graphs
Add to the first row of A2 + A — A/ all the other rows to get
det(A2 + A - XI) = (r2 + r - A)(r - 1 - A)r2.
Therefore, spec(A2 + A) = [ . ).
V 1 r2 J
Let A», 1 < i < r2 +1, be the eigenvalues of A. Then by Theorem 1.2.1(iii), A2 + A* is
an eigenvalue of A2 + Л, and so we may assume that
\2 + Ai = r2 + r, and A2 + Ai = r - 1, for each г = 2,3, • • • ,r2 +1.
Hence we may assume Ai = r, and for some к with 2 < к < r2 + 1, A2 = A3 = • • ¦ =
ч -1 + л/аГ^З . . . -1-л/4Г^З e. +, r „
A*+i = and Afc+2 = ••• = Ar2+1 = r . Since the sum of all
eigenvalues of A is zero, solving
_ , fc(-i + >/5F33) , (r2^^)(,i^,/3^r3)
r + - + - =0,
t ftf (r2~2r) 2
we have 2A; = ч , ' + r2.
Since A; > 0 is an integer and since r > 2, either r = 2 or for some positive integer m,
4r — 3 = (2m + l)2 is the square of an odd integer. Thus if r > 2, then r = m2 + m + 1
and so
2* = 2m - 1 + 2! (2m + 3 - тт^-Л + (m2 + m + 1 )2.
4 \ 2m + 1/
As m2 and 2m + 1 are relatively prime, 2m + 1 must divide 15, and so m € {1,2,7}. It
follows that r € {2,3,7,57}, respectively. Q
Moore (r, 5)-graphs with r € {2,3,7} has been constructed. The existence of a Moore
(57,5)-graph is still unknown. (See [9].)
Theorem 1.2.5 (Brown [18]) There is no r-regular graph with girth 5 and order n = r2+2.
Sketch of Proof By contradiction, i^sume that there exists an (r, 5)-graph G with order
n = t2 + 2. For each v € V(G), let itf(v) denote the vertices adjacent to v in G.
Let vi € V{G) and let iV(vi) = {v2,-** ,vr+i}. Since the girth of G is 5, each
N(vi)C\N(vj) = {^i} for all 2 < г < j < fc + 1, and N(vi) is an independent set. It follows
that
r+l
I U&1 (tf(Vi) - M)\ = 53 |tffa) - {M| = r + r(r - 1) = r2. (1.1)
Since |F(<2)| = r2 + 2, it follows by (1.1) that for any v 6 V(<3), there is exactly one
v* € V(G) which cannot be reached form v by a path of length at most 2. Note that
(v*)* = v.
Matrices and Graphs
7
Let A = A(G) be the adjacency matrix of G. Since G has girth 5, it follows that
Л2 + Л — (r — 1) J = J — By where В is a permutation matrix in which each entry in the
main diagonal is zero. Therefore we can relabel the vertices of G so that В is the direct
n diagonal is zero.
¦-(lib
follows that both n and r are even. By Theorem 1.2.1(iii), if к is
an eigenvalue of Л, then k2 + fc - (r — 1) is an eigenvalue of Л2 + A — (r — 1)1. Direct
computation yields (Exercise 1.7(vi))
spec(A*+A-(r-l)D=(n-1 г -1 V
Since A is a real symmetric matrix, A has § real eigenvalues к satisfying к2 + к— (r — 1) =
1, or & = ^t^i where 5 = V4r +1; and A has § — 1 real eigenvalues к satisfying
k2 + fc — (r — 1) = 1, or к = z=^) where ? = -/4г — 7. Consider the following cases.
Case 1 Both s and t are rational numbers. Then s and ? must be the two odd integer 3
and 1, respectively. It follows that r = 2 and so G is a circle of length 6.
Case 2 Both s and ? are irrationals. If there is a prime a which is a common factor of
both s2 and t2 but a does not divide s or a does not divide t, then a divides s2 — ?2 = 8,
and so a = 2. But since s2 and ?2 are both odd numbers, none of them can have an even
factor, a contradiction.
Therefore, no such a exists. It follows that if ~x+* is an eigenvalue of J — B, then
""2"* is also an eigenvalue of J — B. In other words, the number of eigenvalues of J — В
in the form of z^? is even. Similarly, the number of eigenvalues of J — В in the form of
=^- is even. But this is impossible, since one of § and f - 1 must be odd.
Case 3 s is irrational and t is rational. Then t is an odd integer and so — 1 ± t is even.
Since s is irrational, the number of eigenvalues in the form :=^1 is even and the sum of all
such eigenvalues is ^f = ^f. However, since — 1 ± t is even, the sum of all eigenvalues
in the form of ^~ is an integer, and so the sum of eigenvalues in the form of rl*s is an
integer. It follows that r2 + 2 = n = 0 (mod 4), or r2 = 2 (mod 4), which is impossible.
Case 4 s is rational and t is irrational. Since t is irrational, the eigenvalues in the form
=2ф& must appear in pairs, and so the sum of all such eigenvalues is an integer. However,
the sum of these eigenvalues is ( — 1 (— — 1J. Let m denote the multiplicity of —-—.
Since G is simple, the trace of A is zero. By Proposition 1.1.2(vii) and by g = 5,
, m(—1 + s) /n \—1-5 f 1\ /n л /л лЧ
0=trA = r + -i-r^ + (--m)-1-+(--J(--l). (1.2)
s2-l
Since n = r2 + 2 and since r = —-—, substitute these into (1.2) to get
s5 + 2s4 - 2s3 - 20s2 + (33 - 64m)s + 50 = 0. (1.3)
8
Matrices and Graphs
Any positive rational solution of s in (1.3) must be a factor of 50, and so s € {1,2,5,10,25,50}.
Among these numbers only 5 = 1,5, and 25 will lead to these integral solutions
s = l ( s-Ь f s = 25
m = l < m = 12 < m = 6565
r = 0 [ r = 6 [ r = 156.
Since n = r2 + 2, we can exclude the solution when s = 1. We outline the proof that s
cannot be 5 or 25, as follows.
Since g = 5, the diagonal entries of A? must all be zero. By Theorem 1.2.1(iii), if Л
is an eigenvalue of A, then A3 is an eigenvalue of A3. It follows that tr(A3)=0. But no
matter whether s = 5 or s = 25, tr(A3) ф 0, and so s = 5 or s = 25 are also impossible.
?
Theorem 1.2.6 Let G be a graph with n vertices such that v G V(G). If G has eigenvalues
Ai > A2 > • * • An, and if G — v has eigenvalues pi > Ц2 > • * • А*п-ъ then
Ai > ii\ > A2 > \i2 > • • • Mn-i > An.
Proof Let A\ = A(G - v), and Л = A(G). Then there is a row vector u such that
Since Л is symmetric, A has a set of n orthonormal eigenvectors Xi,X2, • • • ,xn. Let e*
denote the n-dimensional vector whose i-th component is one and whose other components
are zeros.
Divide the eigenvalues Ai > • • • > An into two groups: Group 1 and Group 2. A A* is
in Group 1 if Ai has an eigenvector x* such that ef x* = 0; and a A» is in Group 2 if it is
not in Group 1. Note that if A» is in Group 2, then ef Xi Ф 0 (for all eigenvectors x$ of
Suppose Ai is in Group 1 and it has an eigenvector Xj such that efxi = 0. Let xj
denote the (n — l)-dimensional vector obtained from Xj by removing the first component
of Xi. Then as XiA = AiXj, AiAi = \{x!v It follows that \i = fa, for such Ai's.
Rename the eigenvalues in Group 2 so that they are Ai > A2 > • • • > \k- For notational
convenience, let x, 6 {xi,x2, • • • .xn} be the eigenvector corresponding to Ai, 1 < t < k.
Let y' be an eigenvector of Ai corresponding to an eigenvalue in Group 2; and let у
be the n-dimensional vector obtained from y' by adding a zero component as the first
component of y. Since the Xi's are orthonormal and by the definition of Group 1, both
У = Y,i=i bi*i ^ ei = X)iLi ^i, where d = ef Xi.
Matrices and Graphs
9
Since y' is an eigenvector of A\ corresponding to an eigenvalue \i (say), Aiy' — jxy'.
It follows that
к к к
Y^ *>ДгХг = A ]$Г Ь& = Ay = (uV)ei + /V = (uTy') Y, °&i + ^У;-
i=l i=l i-1
Therefore, for each j, the j-th component of both sides must be the same, and so
, . -(uTy')cj
Oj = s .
By the definition of y,
^4uVM=^^ = efy=0 (14)
Equation (1.4) has к vertical asymptotes at \i = A*, 1 < t < k. It follows that (1.4) has a
root /ц е (A,+i,Ai), whence
Ai > fix > A2 > Дг > * * * > Afc-i > ?*-i > Ajb.
This, together with the conclusion on the eigenvalues in Group 1, asserts the conclusion
of the theorem. []
Corollary 1.2.6A Let G be a graph with n > к > 0 vertices. Let V С V(G) be a vertex
subset of G with |V | = k. If C? has eigenvalues Ai > A2 > • • • An, then
\i>\i(G-V')>\i+k.
Corollary 1.2.6B Let G be a graph with n > 2 vertices. К G is not a complete graph,
then \2(G) > 0.
Proof Corollary 1.2.6A follows from Theorem 1.2.6 immediately. Assume that G has
two nonadjacent vertices и and v. Let V = V(<j?) — {u,v}. Then by Corollary 1.2.6A,
A2(G)>A2(G-V') = 0.n
Lemma 1.2.1 (J. H. Smith [71]) Let G be a connected graph with n > 2 vertices. The
following are equivalent.
(i) G has exactly one positive eigenvalue.
(ii) G is a complete fc-partite graph, where 2 < fc < n — 1.
Theorem 1.2.7 (Cao and Hong [43]) Let G be a simple graph with n vertices and without
isolated vertices. Each of the following holds.
(i) A2(G) = — 1 if and only if G is a complete graph with n > 2 vertices.
(ii) А2(<3) = 0 if and only if G Ф K2 and G is a complete fc-partite graph, where
10
Matrices and Graphs
2<k<n-l.
(iii) There exists no graph G such that -1 < M{G) < 0.
Proof Direct computation yields \2{Kn) = —1 (Exercise 1.7(i)). Thus Theorem 1.2.7(i)
follows from Corollary 1.2.6B.
Suppose that G Ф K2 and that G is a complete fc-partite graph with 2 < к < n — 1.
Then by Lemma 1.2.1 and Corollary L2.6B, \2(G) - 0.
Conversely, assume that \2(G) = 0 (then G ф K2) and that G is not a complete
fc-partite graph. Since G has no isolated vertices, G must contain one of these as induced
subgraphs: 2K2) Pa and K\ V (K\ U K2). However, each of these graphs has positive
second eigenvalue, and so by Corollary 1.2.6A, X2(G) > 0, contrary to the assumption
that \2(G) = 0. Hence G must be a complete fc-partite graph. This proves Theorem
1.2.7(ii).
Theorem 1.2.7(iii) follows from Theorem 1.2.7(i) and (ii), and from Corollary 1.2.6B.
?
The proofs for the following lemmas are left as exercises.
Lemma 1.2.2 (Wolk, [277]) If G has no isolated vertices and if Gc is connected, then G
has an induced subgraph isomorphic to 2K2 or P4.
Lemma 1.2.3 (Smith, [71]) Let #ь#2,#з and #4 be given in Figure 1.2.1. Then for
each i with 1 < i < 4, Х(Щ) > -.
о
-ft -ft -Ь й
H\ H2 H3 H4
Figure 1.2.1
Lemma 1.2.4 (Cao and Hong [43]) Let tf5 = Кп-з V (Kx U K2). Then each of the
following holds.
0) Xm = (A3 - A2 - 3(n - 3)A + n - 3)АЛ"4(А +1).
(ii) A2(tf5) < |.
Theorem 1.2.8 (Cao and Hong [43]) Let G he a graph with n vertices and without
isolated vertices. Each of the following holds,
(i) 0 < A2(C?) < I if and only if G S Я5.
Matrices and Graphs
11
(ii) If 1 > A2(G) > |, then G contains an induced subgraph H isomorphic to a member
in {2K2, P4} U {Щ : 12 < i < 4}, where the Hi's are defined in Lemma 1.2.2.
(iii) If ДМ = A2(#5), then A^ increases as n increases, and limn^oo A^ = |.
(iv) There exist no graphs Gk such that A2(Gfc) > i and lim A2(G*) = r.
0 fc-юо 3
Proof Part (i). By Lemma 1.2.4(ii), it suffices to prove the necessity.
Suppose 0 < A2(G) < |. If G has an induced subgraph H isomorphic to a member
in {2^2,^4} U {Hi : 12 < г < 4}, where the Hi's are defined in Lemma 1.2.3, then by
Corollary 1.2.6A, \2(G) > A2(#) > |, a contradiction. Hence we have the following:
Claim 1 G does not have an induced subgraph isomorphic to a member in {2J^2, P4} U
{H{: 12<i<5}.
By Claim 1 and Lemma 1.2.2, Gc is not connected. Hence Gc has connected
components Gb •• ,G* with A; > 2. But then G = GJ VGJ V ---V G%. We have the following
claims.
Claim 2 For each i with 1 < i < к, G? has an isolated vertex.
If not, then by Lemma 1.2.2, G\ has an induced subgraph isomorphic to 2K2 or P4,
contrary to Claim 1.
Claim 3 For some i, G\ = Kx U if2.
By A2(G) > 0 and by Theorem 1.2.7(ii), G is not a complete fc-partite graph, and
some GJ has at least one edge. By Claim 1, G* contains К\ U K2 as an induced subgraph.
If |V(CtJ)| > 3, then G\ must have an induced subgraph H isomorphic to one of 2K\ U
K2iKiUPs andK!UK3. Since к > 2, there exists a vertex it € У (G)- У (G?). It follows
that У (#) U {гх} induces a subgraph of G isomorphic to one of the H^s in Lemma 1.2.3,
contrary to Claim 1.
Claim 4 к = 2 and G2 ^ #п-3-
By Claims 2 and 3, we may assume that Gf = iifi U iT2. Assume further that either
к > 3 or fc = 2 and G2 has two nonadjacent vertices. Let it € y(G2 and v € V(Gs)
if fc > 3 and let u,v e V(G2) be two nonadjacent vertices in G2. Then y(Gi) U {u,v}
induces a subgraph of G isomorphic to #4 (defined in Lemma 1.2.3), contrary to Claim 1.
Thus it must be к = 2 and G2 = Kn-3.
From Claims 3 and 4, we conclude that G = #5.
Part (ii). It follows from the same arguments used in Part (i) and it is left as an
exercise.
Part (iii). By Corollary 1.2.6A, A<n) is increasing. Thus limn->oo A<n> = L exists. Let
/(A) = A3 - A2 - 3(n - 3)A + n - 3. Then by Lemma 1.2.4(i), /(A<n>) = 0, and so
3 + 3(n-3)1 ;
12
Matrices and Graphs
It follows that L = -.
«5
Part (iv). By contradiction, assume such a sequence exist. We may assume that for
all fc, 1 > \2(Gk) > x. By Theorem 1.2.8(H), all such Gu contains a member Я in
{2K2,P4} U {Н{: I2<i< 4}. By Corollary 1.2.6A, \2(Gk) > A2(#) > 0.334, therefore,
M(Gk) cannot have 1/3 as a limit. Q
Corollary 1.2.8A Let G be a graph with n vertices and without isolated vertices. If G
is not a complete fc-partite graph for some к with 2 < к < n — 1, then Лг(С?) > \2(Щ)у
where equality holds if and only if G ^ #5.
In 1982, Cvetkovic [69] posed a problem of characterizing graphs with the property
0 < A2(G) < 1. In 1993, P. Miroslav [200] characterized all graphs with the property
^2{G) < л/2 — 1. In 1995, D. Cvetkovic and S. Simic [72] obtained some important
properties of the graph satisfying X2(G) < ^-y1^ Cao, Hong and Miroslav explicitly
displayed all the graphs with the property X2(G) < ^^-. It remains difficult to solve the
Cvetkovic's problem completely.
1.3 Estimating the Eigenvalues of a Graph
We start with some basics from the classical Perron-Frobenius theory on nonnegative
square matrices. As the adjacency matrix of a connected graph is a special case of such
matrices, some of these results can be stated in terms of connected graphs as follows.
Theorem 1.3.1 (Perron-Frobenius, [211], [93]) Let G be a connected graph with |V(<?)| >
2. Each of the following holds.
(i) Ai(G) is positive, and is a simple root of XgW-
(ii) If xi is an eigenvector of Ai(6?), then Xi > 0.
(iii) For any e € E(G), AX(G - e) < Ai(<2).
Definition 1.3.1 Let G be a connected graph with \V(G)\ > 2. The value Ai (G) is called
the spectral radius of the graph G.
Theorem 1.3.2 (Varga [265]) Let G be a connected graph with A = A(G), let xi denote
an eigenvector of Xi(G). and let у be a positive vector. Then
|y|2 i<i<» yTej
where equality holds if and only if у = fcxi, for some constant k.
Proof Since Л is a real symmetric square matrix, we can find Xi, x2, • • • , xn such that the
Xj's are orthonormal and such that x» is an eigenvector of \i(G). By Theorem 1.3.1(H),
Matrices and Graphs
Vc
xi is positive. Note that x1}X2, • • • ,хл form a basis of the n dimensional vector spac*
over the reals.
Let у be a positive vector. Then у == Y%=i <W» Since the Xj's are orthonormal, it
follows by Axi = Xi%i that
(Ay)Ty _ T.U<?j>h ^ Ekcfo _ ,
where equality holds if and only if either C2 = C3 = • • ¦ = Cn = 0 or Ai = Л2 = • • • = An»
By Theorem 1.3. l(i), Ai > Л2 > An, and so
(Ayfy
if and only if у = CiXi. This proves the lower bound.
Again by у = 2|Li ЪЪ and by Axi = AjXi,
(Ay)Tei _ с?А< _
where equality holds if and only if t = 1, by Theorem 1.3.1(1). By Theorem 1.3.1(i),
xi = I^fLi &»е*> where h > 0 for each г with 1 < i < n. Since the x*'s are orthonormal
and by у = 22=i <№>
л _CiAx (Лу)гХ1 .Е^ЦЛу)** m bj^yfe,-
Al - ~ " ~F^T " ES-i *(yT*> - i<j<n ь,(у^) - Al»
where equality holds if and only if for each j, (Лу)те5- = Ai(yTe<7), and if and only if
у = CiXi. This proves the upper bound. Ц
Corollary 1.3.2A Let G be a connected graph with q = \E(G)\ and л = \V(G)\ > 2.
Exactly one of the following holds,
(i) ?2 < A2 < A(G).
(ii) — = Ai = A(G), G is regular and (1,1, • • • , 1)T is an eigenvector.
n
Corollary 1.3.2B(Hofbnan, Walfe and Hofineister [128], Zhou and Liu [289]) Let G be
a connected graph with q = |-Е(<7)| and n = |V(G)| > 2. Let d\y--- ,dn be the degree
sequence of G. Then
equalities hold if and only if there is a constant integer r such that d{dj = r2 for any
ij e E(G).
Proof Setting Xj = -y/SJ (1 < j < n) in Theorem 1.3.2, we obtain the inequalities in
Corollary 1.3.2B.
14
Matrices and Graphs
Suppose that there exists a constant integer r such that didj = r2 for any ij e E(G).
For г = 1, • - • , та, let d be the common degree of all the vertices j adjacent to г. Then
53 y/Tj=diVd = rVd,
j:ijeE(G)
so that r is an eigenvalue of A = Л(С?) with (л/ЗГ, • • • , V3Q* as a corresponding
eigenvector. Hence Ai = r.
Conversely, if the equality holds in Corollary 1.3.2B, we have
j:ijeE{G)
for all t.
If G is regular, we are done. Otherwise let 6 and A be respectively the minimal and
maximal degrees of G. Choose и and v such that the degrees of и and v are 6 and A.
Assume that there exists a vertex w with uw 6 E(G) and that the degree of w is less than
A. Then we have
Ai
On the other hand,
Ai
a contradiction.
Assuming existence of w where vw € E(G) and the degree of w is greater than 8 leads
to an analogous contradiction. We have proved that whenever ij e E(G), then the degrees
of i and j are 8 and A or vice versa, and that Ai = y/5K. Q
The study of the spectrum of a graph has been intensive. We present the following
results with most of the proofs omitted. More results can be found in Exercises 1.11
through 1.13, and in [71]. In [131], Hong studied bounds of A*(Tn) for general к (Theorem
1.3.7). Hong's results are recently refined by Shao [244] and Wu [278]. These refinements
will be presented in Theorem 1.3.8.
Theorem 1.3.3 (Hong, [130]) Let n > 3 be an integer, let G be a unicyclic graph (a
graph with exactly one cycle) with та vertices, and let S? denote the graph obtained from
-Ki,n-i by adding a new edge joining two vertices of degree one in iifi>n_i. Then each of
the following holds.
(i) 2 = Ai(Cn) < Ai(<3) < Ai(S?), where the lower bound holds if and only if G = Cn;
and where the upper bound holds if and only if G = S%.
(ii) 2 < Ai(6?) < Vn, where the upper bound holds if and only if G = Sf.
E Vf < E
j:ujeE(G) j:ujeE(G)
= v^A.
= .E i/KE ^=v*a.
jzvj€E(G)
j:vjeE(G)
Matrices and Graphs
15
Theorem 1.3.4 (Hofemeister, [121]) Let Tn denote a tree with n vertices. Then either
jn _ з
Аг(Тп) < W—-—, or n = 2s + 2 and Tn can be obtained from two disjoint Kit3's by
adding a new edge joining the two vertices of degree s.
Theorem 1.3.5 (Collatz and Sinogowitz, [62]) Let G be a connected graph with n =
\V(G)\. Then
2 cos
U+iJ"
Ai(G)<n-l,
where the lower bound holds if and only if G = Pn, a path of n vertices; and where the
upper bound holds if and only if G is a complete graph Kn.
Theorem 1.3.6 (Smith, [255]) Let G be a connected graph. Each of the following holds,
(i) If Ai(<2) = 2, then either G € {#1,4, Cn}, or G is one of the following graphs:
> <
T
:
Figure 1.3.1.
(ii) К Ai (G) < 2, then G is a subgraph of one of these graphs.
Theorem 1.3.7 (Hong, [131]) Let Tn denote a tree on n > 4 vertices. Then
0 < \k(Tn
•^e
for each к with 2
*s-
Moreover, if n = 1 mod fc, this upper bound of A* (Tn) is best possible.
Theorem 1.3.8 Let Tn denote a tree on n > 4 vertices and Fn a forest on n > 4 vertices.
Then each of the following holds^
(i) (Shao, [244]) A*(Tn) < J[^l - 1, for each к with 2 < [|]. Moreover, whenn ^ 1
16
Matrices and Graphs
(mod fc), this upper bound is best possible.
(ii) (Shao, [244]) When та = 1 (mod k)t strict inequality holds in the upper bound in
Theorem 1.3.8(i). However, there exists no e > 0 such that \k(Tn) < \ \т\ -1-е,
[тал
о" *
{[
(iii) (Shao, [244]) \k(Fn) < t/[r] - 1, for each к with !<[?]• This upper bound is
best possible.
(iv) (Wu, [278]) Let G denote a unicyclic graph with n > 4 vertices, then A*(C?) <
?]-! + !•*» each*wtth2<g].
We shall present a proof for Theorem 1.3.7. Two lemmas are needed for this purpose,
the proofs of these two lemmas are left as exercises (Exercises 1.14,1.15 and 1.16).
Lemma 1.3.1 Let T denote a tree on n > 3 vertices. For any к with 2 < к < — , there
exists a vertex subset V С V(T) with \V'\ = к — 1 such that each component of T — V
Гп-2]
4-1 vertices.
has at most
Lemma 1.3.2 Let G be a bipartite graph on та > 2 vertices. Then
\i(G) = — An+i_i, for each i with 1 < i < — .
Proof of Theorem 1.3.7 By Lemma 1.3.2, \k(T) > 0 for each i with 1 < i < [f ].
By Lemma 1.3.1, V(T) has a subset V with |V'| = к — 1 such that each component
of T - V has at most
+ 1 vertices. By Theorem 1.2.6,
\k{T)<\x{T
-m/
n-2
To prove the optimality of the inequality when n = 1 (mod к), write та = Ik + 1, for
some integer I > 2. Let Gi,(?2,''' ><2* be disjoint graphs each isomorphic to #1,1-1.
Obtain Tn by adding a new vertex v to the disjoint union of the Giys so that v is adjacent
to the vertex of degree I - 1 in Gi} for all i = 1,2, • • ¦ , fc. It follows by Theorem 1.2.6 and
by the fact that each component of Tn - v is a #1^-1 and that Tn has fc such components,
Ai(Tn -1>) = Ai(#!,,_!) = А*(ГП - v) = Ajkftfi,,-!) = л/ГП: = J
та-2
By Theorem 1.2.6, Ax(Tn -v)< \k(Tn) < Xk(Tn - v), and so \k(Tn) = y/[*f*\. This
completes the proof of Theorem 1.3.7. Q]
As we know, an edge subset M of ^(G) is called a matching of C?, if no two edges in
M are adjacent in G. A matching with maximum number of edges is called a maximum
Matrices and Graphs
17
matching and the size of it is called the edge independent number of G. The following
theorem provide a sharp bound of the fcth largest eigenvalue of a tree T with n vertices.
Theorem 1.3.9 (Chen [56]) Let T denote a tree on n vertices and edge independent
number q. For 2 < к < q, \k(T) > А*(5?1"^+2) with equality if and only if Г is isomorphic
to ^^2^+2» wnere Sn*^2k+2 1S a tree fc>rmed by making an edge from a one-degree vertex
of the path Ргк-ъ to the center of the star Kiyn-2k+i-
1.4 Line Graphs and Total Graphs
Definition 1.4 Л The line graph L(G) of a graph G is the graph whose vertices are the
edges of G, where two vertices in L(G) are adjacent if and only if the corresponding edges
are adjacent in G.
Definition 1.4.2 The total graph T(G) of a graph G is the graph whose vertex set is
E(G) U V(G), where two vertices in T(G) are adjacent if and only if the corresponding
elements are adjacent or incident in G.
Some elementary properties can be found in Exercise 1.20; and examples of line graphs
and total graphs can be found in Exercise 1.21. Results in these exercises are needed in
the proofs of the theorems in this section.
Theorem 1.4.1 Let G be a nontrivial graph. Each of the following holds,
(i) If A be an eigenvalue of L(G), then A > — 2.
(ii) If q > n, then A = -2 is an eigenvalue of L(G).
Proof Let A be an eigenvalue of L(G). By Exercise 1.20(H), A + 2 is an eigenvalue of
BTB. By Exercise 1.20(iv), BTB is a semi-definite positive matrix, and so A + 2 > 0.
When q > n, by Exercise 1.20(v), zero is an eigenvalue of BTB, and so by Exercise
1.20(H), A = -2 is an eigenvalue of L(G). ?
One of the main stream problems in this area is the relationships between XgW and
Xl(<?)(A), and between x<?(A) and Xr(<?)(A). The next two theorems by Sachs [227] and
by Cvetkovic, Doob and Sachs [71] settled these problems for the regular graph cases.
Theorem 1.4.2 (Sachs, [227]) Let G be a ^-regular graph on n vertices and q edges. Then
XL(G)(A) - (A + 2У~пха(\ + 2 - *).
Proof Let В — B(G) denote the incidence matrix of G. Define two n + gbyn + g
matrices as follows
18
Matrices and Graphs
By det(UV) = det(yr/), we have
A*det(AJn - BBT) = Andet(AJg - BTB).
Note that G is fc-regular, and so the matrix С in Exercise 1.28(i) is kln. These, together
with Exercise 1.28(i) and (ii), yield
XL(G)W = det(\Iq-A(L(G)))
= det((\ + 2)Ig-BTB)
= A*-ndet((A + 2)/n-?BT)
= \q-ndet((\ + 2-h)In-A(G))
= (A + 2)*~nXG(A + 2-fc).
This proves Theorem 1.4.2. ?]
Example 1.4.1 It follows from Theorem 1.4.2 that if
spec(G)=(* Al A> - 4
у 1 mi ТП2 • * • 771$ у
then
2k-1 к - 2 + Ai - • • fc - 2 + \s -2
specL(G) = %
1 77li Ш$ q — П
In particular,
Ttts\ /2n-4 n-4 -2 \
specL(tfn)=^ x n_n ^J.
Theorem 1.4.3 (Cretkovic, [71]) Let G be a ^-regular graph with n vertices and q edges,
,and let the eigenvalues of G be Ai > A2 > • ¦ ¦ > An. Then
n
XT(G)W == (A + 2)*~n Д(л2 - (2Ai + * - 2)Л + Л? + (* - 3)A* - *)•
Sketch of Proof Let A = A(G), В = B(G) denote the adjacency matrix and the
incidence matrix of G, respectively; and let L = A(L(G)) denote the adjacency matrix of
L(G). Then by the definitions and by the fact that G is fc-reguiar,
BBT = A + kl, BTB = L + 21, and A(T(G)) =
А В
BT L
Matrices and Graphs
19
It follows that
XT(G)(A)
(\ + k)I-BBT -B
-BT (\ + 2)I-BTB
(\ + k)I-BBT -Б
-(\ + k + l)BT + BTBBT (A+ 2)/
1
= (A + 2)*det
(»-
A+-^(A + kI)(A-(\ + l)I):
= (A + 2)«+n det(A2 - (2A - к + Z)A + (A2 - {к - 2)A - k)I)
П
= (A + 2)*+я Д(A? - (2A - к + 3)Ai + A2 - (fc - 2)A - к).
This proves the theorem.
In [235], the relationships between xg(A) a*id Xl(G)W> and between x<?(A) and
Xt{Q)W were listed as unsolved problems. These are solved by Lin and Zhang [165].
Definition 1.4.3 Let D be a digraph with n vertices and m arcs, such that D may have
loops and parallel arcs. The entries of the in-incidence matrix Bj = (b\j) of D are defined
as follows:
if vertex vi is the head of arc ej
otherwise
13 JO ol
The entries of the out-incidence matrix Bo = (by) of D are defined as follows:
bb
*-{!:
if vertex V{ is the tail of arc ej
otherwise
Immediately from the definitions, we have
A(D) = B0Bj, and A(L(D)) = Bf Б0,
and
A(T(D)) =
A{D) Bo
BJ A(L(D))
(1.5)
(1.6)
Theorem 1.4.4 (Lin and Zhang, [165]) Let D be a digraph with n vertices and m arcs,
and let AL = A{L(D)). Then
XHD)W = A"*-"Xd(A).
(1.7)
Proof Let
U =
A/„ -B„
0 Im
andW:
In B0
ВТ Mr,
20
Matrices and Graphs
Note that det(UW) = det(WU), and so
Am det(A/„ - B0Bj) = An det(AIm - B?Bi).
This, together with (1.5), implies that
Xl(d) (A) = det(A/ro - AL) = det(A/ro - BjB0)
= Am~n det(A/„ - B0Bj) = Am"n det(AJn - A(D)),
and so (1.7) follows. []
Theorem 1.4.5 Let D be a digraph with n vertices and m arcs, and let Al = A(L(D))
and Лг = Л(Г(1>)). Then
XT(D)W = Am"n det((A/n - A)2 - A).
(1.8)
A/n — BoBj —Bo
-Bf XIm-BfB0
-Bo
Proof By (1.6),
/w i Mn — A. —Bo
W(A) = | ^ A/m_^
\In-BoBf
-Bf-Bf(\In-B0Bj) AI,
A/n - BoBj + ^Во[-(1 + А)Б? + BjBoBj] 0
-(1 + А)Б? + BjB0Bf) A/,
= Am"n det(A2/n - ABoBf - (1 + A)B0Bf + B0BjB0Bj)
= Am-ndet(A2/n-AA-n(l + A)A + A2),
which implies (1.8). Q
Hoffman in [123] and [122] considered graphs each of whose eigenvalues is at least -2,
and introduced the generalized line graphs. Results on generalized line graphs and related
topics can be found in [123], [122] and [70].
1.5 Cospectral Graphs
Can the spectrum of a graph uniquely determine the graph? The answer is no in general
as there are non isomorphic graphs which have the same spectrum. Such graphs are call
cospectral graphs. Harary, King and Read [115] found that K\^ and K± U C± are the
smallest pair of cospectral graphs. Hoffman [125] constructed cospectral regular bipartite
Matrices and Graphs
21
graphs on 16 vertices. In fact, Hoffman (Theorem 1.5.1 below) found a construction for
cospectral graphs of arbitrary size. The proof here is given by Mowshowitz [206].
Lemma 1.5.1 (Cvetkovic, [65]) Let G be a graph on n vertices with complement Gc, and
let #<?(?) = I2?=o Nktk be the generating function of the number Nk of walks of length к
in G. Then
HG{t) = 1
XGc (—r)
Xoit)
(-1)
(1.9)
Sketch of Proof For an n by n matrix M = (m^), let M* denote the matrix (det(Jlf)M-1)T
(if M~l exists), and let \\M\\ = YZ=i E?=i mij- I* *s routine to verify that, for any real
number x, det(Af + xJn) = det(Af) + s||Af*||
Let A = A(G). By Proposition 1.1.2(vii), Nk = ||A*||. Note that when t < max^"1},
oo
]T) Aktk = (J - fA)-1 = (det(/ - tA))-1^ - tA)\
and so
But
ад-Ё^-Ё|А^=И
det(I - *A) *
(1.10)
(1.11)
||(/ - *A)*|| = i ( det(/ - «A + | J) - det(J - *A)) .
By A(GC) = J - / - A, (1.10) and (1.11), (1.9) obtains. Q
Lemma 1.5.2 Let G be an r-regular graph on n vertices and Gc its complement. Then
X^(A) = (-ir(^±i^)xG(-A-l).
Sketch of Proof Since each walk of length к can start from any of the n vertices and
each walk from a given vertex can have r different ways to continue, Nk = nrh. It follows
by Lemma 1.5.1 that (when \t\ < 1/r),
(-i):
*G' (JJr)
XG(})
Let Л = -(t + l)/t to conclude.
-1
=*«« = ХХ<* = гз^
*=o
„«.(.^(ijiii-jrt^.fl.
22
Matrices and Graphs
Theorem 1.5.1 For any integer k, there exist к cospectral graphs that are connected and
regular.
Proof Let Hi and #2 be two r-regular cospectral graphs. For each i with 0 < i < к — 1,
let Li be a graph with к — 1 components such that i of the к — 1 components of Li are
isomorphic to #i, and such that the other к — 1 — i components of Li are isomorphic to
#2; and let Gi = ??.
Clearly #i's are connected, regular and mutually nonisomorphic. By Theorem 1.2. l(i),
for each г with 1 < i < к - 1, лхДА) = xl0(A)- This, together with Lemma 1.5.2, implies
that XGi(A) = XGo (A), f°r eacn * witn 1 < t < fc — 1. ?
Schwenk [232] introduced cospectrally rooted graphs. A graph G with a distinguished
vertex v is called a rooted graph with root v. Two different rooted graphs G\ and G2
with roots vi and v2, respectively, are cospectrally rooted if both x#i(A) = Xg2(A) and
(A) — XG2-V2M n°ld- Graph pairs that are cospectrally rooted are characterized
by Herndon and Ellzey in [120]. We now turn to the construction techniques of cospectral
graphs.
Theorem 1.5.2 Let G\ and G2 be two graphs on n vertices with A{ = A(Gi)} i = 1,2.
The following are equivalent.
(i)Xc?1(A) = XG2(A).
(ii) tr(A{) = tr(^2), for j = 1,2,. •. , n.
(iii) There is a one-to-one correspondence between the collection of closed walks of
length j in Gi and that in G2, for each j = 1,2, • • • , n.
Sketch of Proof Let Ax = A(Gt) and A2 = A(G2). Note that tr(^) = ??=1 Ai^)*,
and so {Ai(-Ai), • ¦ • , A„(Ai)} and { tr(Ai), • • • , trA™} uniquely determine each other. The
same holds for A2. This establishes the equivalence between (i) and (ii).
By Proposition 1.1.2(vii) and by Exercise 1.5, (ii) and (iii) are equivalent. Q
Definition 1.5.1 (Generalized Composition, [234]) Let <j?i, G2 be two graphs with given
distinct subsets S\ С V(G\) and S2 Я V(G2)9 and let Б be a bipartite graph with
partite sets R = {wi,tt2, • • • ,ur} and S = {wi,w2i • • • ,«;«}. The generalized composition
?(<j?i,Si,(t2,S2) is formed by taking r copies of G\ and s copies of 6?2, every vertex in
the tth Gi is adjacent to every vertex in the jth G2 if and only if UiWj € E(B).
Theorem 1.5.3 (Schwenk, Heradon and Ellzey [234]) Let B(GUSUG2,S2) and B(G2iS2iGuStl
be defined in Definition 1.5.1. Then they have the same spectrum if one of the following
holds.
(i) r = s.
(ii) XGx(A) = Xg2(A).
Matrices and Graphs
23
Sketch of Proof By Theorem 1.5.2, it suffices to find a one-to-one correspondence ф
between the collection of closed walks of length j in G\ and that in 6?2, for each j =
l,2,— ,n.
Assume first that r = s. Let W he a closed walk in J?(Gri,5i,Cr2,&). If W is inside
an Щ, then since r = s, we can choose ^(W) to be the mirror image of W inside an Li
of B(G2,S2, Gi,Si). If W uses edges between the Я,-'в and the L/s, then again by r = s,
we can let <I>{W) to be the mirror image of W in B((?2,5г, Gi,Si).
Now assume that XGiM = Xg2(A). By Theorem 1.5.2, there is a one-to-one
correspondence between the closed walks in each Щ (Lj, respectively) in B(G\, 5i, ?2> ?2) zxid
the closed walks in each Hi (Lj, respectively) in B(G2,S2,Gi,Si). Closed walks using
edges between the fii's and the Lj's in B(GiiSi,G2iS2) can correspond to closed walks
between the same Hi's and the same ?/s in B(G2,S2,Gi,Si). Q
Definition 1.5.2 (Seidel, [236], Seidel Switching) Let G be graph and let it = {Ti,T2} is
a partition of V(G). Construct a graph G* as follows: V(G,r) = V(G) and two vertices
u,v € V(G*) are adjacent in <j?(Si) if and only if either u,v € Si and ш/ 6 #(<?), or
u, v € 52 and uv € E(G), or и € S\, v € S2 and uv ? E(G).
Under certain conditions, the Seifel Switching produces graphs with the same spectrum
(see [236]). An extension of the Seidel Switching is the Local Switching.
Definition 1.5.3 (Godsil and McKay, [101], Local Switching) Let G be graph and let
it = (Si,S2,- • • ,Sk,S) is a partition of V(G). Suppose that, whenever 1 < i,j < к and
v e S, we have
(A) any two vertices in Si have the same number of neighbors in Sj, and
(B) v has either 0, Щ- or щ neighbors in Si, where щ = |5»|.
The graph Gn formed by local switching in G with respect to it is obtained from G as
follows. For each v € S and 1 < i < к such that v has Щ- neighbors in Si, delete these ^
edges and join v instead to the other ^ vertices in 5».
Theorem 1.5.4 (Godsil and Mckay, [101]) Let G be a graph and let it be and a partition
of V(G) satisfying Definition 1.5.3(A) and (B). Then G and Gn are cospectral, with
cospectral complements.
Sketch of Proof Let sq = 0, Si = |5<|, where 1 < i < к; and let Sk+i = S and
s*+i = \S\. Then n = \V(G)\ = ??? Si. Label the vertices in V(G) (and in V^) also)
as V(G) = {vi, V2, • • • , vsi, vSl+i, • • • , vn} such that for each i with 1 <i <k + l,Vj 6 5*,
for J^Zq st +1 < j < St=o 5<* ket ^ = М@) ап^ Я = A(Gn) be the adjacency matrices
whose columns and rows are labeled with the labeling above.
We shall find a matrix Q such that QAQ"1 = A' to prove Theorem 1.5.4(i). The Proof
for Theorem 1.5.4(ii) is similar and is left as an exercise.
24
Matrices and Graphs
Recall that Jm denotes the m by m square matrix each of whose entries is a one. Define
2
Qm = «An """* *m-
m
Note that Qm = Jm. Define Q = diag(Q5l,Q52, • • • ,QS*>Iak+i) to be the n by n matrix
whose diagonal blocks are QSl, • • • , QSfc and ISh+l. It is routine to verify that QAQ~l = A1,
and so this proves Theorem 1.5.4(i). Q
Theorem 1.5.5 (Schwenk, Heradon, and EUzey [234]) If G\ is a regular graph and if
\V{GX)\ = 2|2\|, then B(GuTuG2)T2) and B(GuV(Gi) - TUG2,T2) have the same
spectrum.
Sketch of Proof Use the notation in Definition 1.5.3 with Si,S2 in Definition 1.5.3
replaced by Ti,T2 here in Theorem 1.5.6. Let к = |Ti| and s = \T2\. Then we can see that
Theorem 1.5.6 follows from Theorem 1.5.5(i) by taking n = {5i,52,--- tSk,S} in which
Si = V(#i), 1 < i < fc, and in which 5 = U?=1F(Z,i). []
Codsil and Mckay also proved that graphs with the same spectrum may be constructed
by taking graph products under certain conditions. We present their results below and
refer the readers to [101] for proofs.
Definition 1.5.4 Let A = (а^)тХп and В = (bij)pXq be two matrices. The Kronecker
product (also called the tensor product) of A and В is an mp x nq matrix A® B, obtained
from A by replacing each entry ац by a matrix a^B.
Theorem 1.5.6 (Godsil and Mckay, [101]) If XGi(A) = XG2M> an^L KX an<^ В are square
matrices with the same dimension, then
XH®I+X®Gi (A) = X#<8>/+X®G2(A).
Theorem 1.5.7 (Godsil and Mckay, [101]) If xg^A) = xg2(A), if *Gf (A) = x<?i(A), and
if C, Z), 25 and F are square matrices with the same dimension, then
XC&I+D® J+F®Gi+F®Gf (A) = XCO/+D® J+#®(?2+Fi8>G! (A)
It seems very difficult to determine if two given graphs have the same spectrum. Also,
very little is known about what classes of graphs which can be uniquely determined by
the spectrum. All these remain to be further investigated.
1.6 Spectral Radius
The spectral radius of a graph is defined in Definition 1.3.1. For a square matrix M, we
can similarly define the spectral radius of M, p(M), to be the maximum absolute value of
an eigenvalue of M.
Matrices and Graphs
25
When M = A{G) is the adjacency matrix of a graph G, p(G) = p(A(G))t by Theorem
1.3.1(i). Theorem 1.6.1 below summarizes some properties of non-negative matrices and
the associated digraph of a matrix in Bn.
Theorem 1.6.1 (Perron-Probenius, [96]) Let В € Bn be a matrix. Then each of the
following holds.
(i) Let u be an eigenvector of В corresponding to p(B). Then и > 0. Moreover, if
D(B), the associated digraph of ?, is strongly connected, then u is a positive vector.
(ii) Let ri, Г2, • • • , rn denote the row sums of B> then
min{ri,r2,— ,rn} <p{B) <max{ri,r2,-*' ,rn}.
(iii) Let z be a positive vector. If Въ > rz (or Въ < rz, respectively) then p(B) > r
(or p(B) < r, respectively). Moreover, p(H) = r holds if and only if both Въ — гъ and
D(G) is strongly connected.
Definition 1.6.1 Let n and e be integers. Let Ф(п,е) denote the collection of all n by n
(0,1) matrices with trace equal to zero and with exactly e entries above the main diagonal
being one. Let Ф*(п,е) denote the subcollection of Ф(п,е) such that A = (oy) € Ф*(п,е)
if and only if аы = 1 for all к < /, к < i and I < j whenever i < j and а# = 1. Define
/(n,e) = тах{р(Л) : A € Ф(п,е)} and
/*(n,e) = тах{/о(Л) : А €Ф*(п,е)}.
Lemmas 1.6.1 and 1.6.2 follow immediately from Definition 1.6.1, and from linear algebra,
respectively.
Lemma 1.6.1 Let A € Ф(п, e), and let P be a permutation matrix. Then PTAP € Ф(п, е)
andp(A)=p(PTAP).
Lemma 1.6.2 Let A and В be two square nonnegative matrices with the same dimension.
If, for some nonnegative vector x with |x| = 1, Bx = p(x) and хТЛх < хт?х, then
p(A)<p(B).
Lemma 1.6.3 Let A! = Js - Is, ег - (1,0, • • • , 0)r and let
Then p(A") > p(A').
Proof This follows from direct computation. []
Theorem 1.6.2 (Brualdi and Homnan, [30]) For each A € Ф(п, e), p(A) < /*(n, e), where
equality holds if and only if there exists a permutation matrix P such that PAP-1 €
Ф*(п,е).
26
Matrices and Graphs
Proof Choose A G Ф(п,е) such that p(A) = /(n,e). By Theorem 1.6.1(i), there exists a
non negative vector x such that p(A)x = Ax. and |x| = 1. By Lemma 1.6.1, we may assume
that x = (xi,r?2,• • • >?n)r such that x\ > X2 > • • -x^ > 0. Argue by contradiction, we
assume that A ? Ф*(п, е) and consider these two cases.
Case 1 There exist integers p and q with p < q, apq = 0 and ap>g+i = 1.
Let В be obtained from A by permuting apq and ap>g+i and ag+i,P and agp. Note that
Б — A has only four entries that are not equal to zero: the (p, q) and the (g,p) entries are
both equal to 1, and the (p, q+1) and the (</ + l,p) entries are both equal to -1. It follows
by xg > xq+i that
xTBx - xTAx = xr(? - A)x
= (••• ,xg -arg+i,— ,a;p,-xp,---)x
= 2Жр(Жд -Xg+l) >0.
Since Б is a real symmetric matrix and by |x| = 1, p(B) = xTBx. By Ax. = /?(Л)х
and by |x| = 1, we have p(B) — р(Л) > 2xp(xq - arg+i) > 0. As p(A) = /(n,e), and as
Б б Ф(п,е), it must be sp(#g — 2cg+i) = 0, and so p(B) = хгБх = р(Л).
If xp Ф 0, then xg = xg+i, and so xT?x - хтЛх = О. It follows that
(Ax)9 = (Bx)q = (Ax)q + (x)g,
and so xq = 0, contrary to the assumption that xq > 0.
Therefore, xq = 0, and so for some s < p — 1, xs >0 = xs+i = • • • = xn. Since
p(A) = /(n,e), A has an s by s principal submatrix A' = J — / at the upper left corner
and p(A) = p(A'). But then, by Lemma 1.6.3, /(n,e) > p(A") > p(A') = р(Л), contrary
to the assumption that p(A) =: /(n,e).
This completes the proof for Case 1.
Case 2 Case 1 does not hold. Then there exist p and q such that apq = 0 and fljH-i.g = 1.
Let В be obtained from A by permuting apg and aP+i,g and aqp and ag>p+i. As in Case
1, we have
xT?x - хтЛх = 2xq(xp - xp+i),
and so it follows that Bx = p(A)x and xq{xp — a:p+i) = 0.
We may assume that xp = xp+i. Then (Лх)р = p{A)xp = (Bx)p = (Ax)p 4- a?e, which
forces that #g = • • • = xn = 0. Therefore, a contradiction will be obtain as in Case 1, by
applying Lemma 1.6.3. ?~|
Lemma 1,6.4 For integers n > r > 0, let Fu be the r by r matrix whose (l,l)-entry is
r -1 and each of whose other entries is zero; let D = (dij)nxn be a nonnegative matrix such
Matrices and Graphs
27
that the left upper corner rxr principal square submatrix is Fu; and let a» = yJY^j^i ^tj >
where i = r + 1, • • ¦ ,n. Let i*i2 be the r by n — r matrix whose j-th column vector has
ar+<7* in the first component and zero in all other components, 1 <j <n — r. Define
F =
Fu F12
Then p(F) > p(D).
Proof Let x = (ari, • • • , xn)T be such that |x| = 1 and such that p(A)x = Ax. Let
У = (Vxi + A + • • • + x>,0,• • • ,0,a:r+i,— ,arn)T. Then |y| = 1, and
xTI?x = (r-l)a?J + 2 J2 ]Taw*tf*i
j=r+l \«=1 J
< (r-l)*? + 2 53 *,,
i=r+i
S^i
< (r-l)J>? + 2 53 x5
i=l j=r+l
= yTFy
Y*
]C*?<*i
and so Lemma 1.6.4 follows from the Rayleigh Principle (see Theorem 6.1.3 in the
Appendix). Q
Lemma 1.6.5 Let F be the matrix defined in Lemma 1.6.4. Each, of the following holds,
(i) p(F) is the larger root of the equation
s2-(r-l)s- JT, <**=0.
i-r+l
(ii) p(F)< к-1.
(iii) p(F) = fc - 1 is and only if r = к - 1.
Sketch of Proof By directly computing Xf(A), we obtain (i).
By the definition of the ai's, we have
^"-(0-
28
Matrices and Graphs
It follows by (i) and by r < к — 1 that
,_ r-l + V2fc2-r2-2fc + l r - 1 + i/(fc - l)2 + & - r2 , t
p(F) = ^ = 2 " * " L
By algebraic manipulation, we have p{F) = к — 1 if and only if r = к - 1, and so (iii)
follows. Q
¦-О-
Theorem 1.6.3 (Brualdi and Hoffman, [30]) Let к > 0 be an integer with e :
Then /(n, e) = fc — 1. Moreover, a matrix A€ Ф(п, е) satisfies р(Л) = к — 1 if and only if
Л is permutation similar to
(?:)¦
(1.12)
Proof Let Л = (oij) € Ф*(п, e). By Theorem 1.6.2, it suffices to show that p(A) < к -
and that p(A) = к — 1 if and only if A is similar to the matrix in the theorem.
Since A e Ф*(п,е), we may assume that
A =
/ J? *\
where r < fc — 1 and where all the entries in the first column of A\ are l's.
Since Jj? is symmetric, there is an orthonormal matrix U such that UTJ%U is a diag-
onalized matrix. Let V be the direct sum of U and In-n and let R be the r by r matrix
whose (1,1) entry is an r and whose other entries are zero. Then
—(о-:.)(Го')(?,1)
/ R-IT UAi \
\ (UAt)T 0 ) '
Obtain a new n by n matrix С from В by changing all the -l's in the main diagonal of
В to zeros. Note that for each nonnegative vector x = (arb • • • ,жп)т, xT?x = xrCx —
ESTi1 x\ ? ^Cx- ВУ Lemma 1.6.2, p(B) < p(C).
Obtain a new matrix D = (dy) from С by changing every entry in UA\ and in
(UAi)T into its absolute value. Then p(C) < p(D). Since D is nonnegative, p(D) has a
nonnegative eigenvector x = (xi, • • • ,arn)T such that |x| = 1. Let щ — JY^^i ^ijy where
t = r +1, • • • ,n. and let Fu be the г by r matrix whose (l,l)-entry is r — 1 and each of
whose other entries is zero; F\2 the rbyn-г matrix whose j-th column vector has ar+j
Matrices and Graphs
29
in the first component and zero in all other components, 1 < j < n — r. Define
L*S 0
By Lemma 1.6.4, p(F) > p(D) > p(A). By Lemma 1.6.5, /(n,e) = p(A) < p(F) < к - 1.
When p(A) = к — 1, by Lemma 1.6.5(iii) and by г < к — 1, we must have r = к — 1 and
so by e = fc(fc + l)/2, Л must be similar to the matrix in (1.12). Q
Theorem 1.6.4 (Stanley [256]) For any Л € Ф(п,е),
гл\ ^ -l + VlHFSe
p(A) < - >
к
and equality holds if and only if e = ( ) and A is permutation similar to
(?:)¦
Proof Let Л = (dij), ^t r»- be the zth row sum and let x = (a?i, • • • ,arn)T be a unit
eigenvector of A corresponding to p(A). Since Ax = p(A)x, we have p(A)x{ = ^ a^j.
Hence, by Cauchy-Schwarz inequality,
j з
Sum up over г to get
p(A)2 < 2e-?r«*J=2e-?<**? (1.13)
= 2e - 53 a*'i O*2 + ^?) < 2e - J3 2а^^ху
i<3 i<j
= 2e - 22 XiuijXj
= 2е-хгАж = 2е-р(А),
which implies the inequality of the theorem.
In order for the equality to hold in the theorem, all inequalities in the (1.13) must be
equalities. In particular, we have
aij(x2 +x)) -lOi^XiXj
for all г < j. Hence either Oy = 0 or ^ = Xj. Therefore, there exists a permutation
matrix P such that
Px = (VuVir~ )»ьй,!й,- 1У2,-' >yj,yj,~- уУз)
3Q
Matrices and Graphs
where 2/1,2/2, • * • >2/i эхе distinct. It follows that
/ M 0 \
PAPT =
V 0 A, J
where each Ai has an eigenvector (!,!,••• , 1)*. Hence each Ai has equal row sums, so
p(A) is the maximum row sum of A. So \Д + 8е is an integer, and e = ( ). Then
z
p(A) = fc — 1, and it follows that there is one nonzero block A\ = j?. This completes the
proof. []
Let Af = (rrtij) € Mn and let n and s» be the ith row sum and the ith column sum of
M, respectively, for each i = 1,2, • • • ,n. A digraph D is r-regular if for some Af 6 Mn,
D = D(M) such that n = Si=r for t = 1,2, ...n.
Theorem 1,6.5 (Gregory, Shen and Liu [100]) Let M = (т#) € Afn with trace 0 and let n
and Si be fth row sum and the ith column sum of M, respectively, for each i = 1,2, • • • , n.
Let r — mini<i<nri, 5 = maxi<*<nei, m = J2i<i<nr* ^^ ~k = тш1<*<п(г* - $»)• If
r > 0, then
" 0 M
Af* 0
Moreover, if
J < \Jm - r(n - 1) + (r - 1)5 + k.
has a positive eigenvector corresponding to its spectral radius,
0 M
_ M* °
the equality holds if and only if the adjacency digraph of M is either an r-regular digraph
or the undirected star Jff1>n_x.
" 0 M
Proof Let p denote p
non-zero vector
:]•
\[ Mt 0 J J" Let [ Ml 0 J [ у j
Then
My = px.
for some
(1.14)
Let x = (xf-Xi--*xn)T and у = (t/i • • • yi• • • 2/n)T- Since p > 0, by Exercise 1.21, we
may assume thatXi<i<nx! = J2i<i<nVi ~ *• by U-14) an^i Cauchy-Schwarz inequality,
Matrices and Graphs
31
for each г = 1,2,••• ,та,
* E <• E ti
= П(1- Е 2/D-
j:m{j:=0
Sum up the inequalities above over i to obtain
^ = EAL<E^- E ^«"Е* ? rf (1.15)
Now
> Er^.?+rE E tf
= ]?пУ?+г]?(п--1-*<)у?
i i
i г
> -fc^y?-(r-l)S^j,? + r(n-l)
t i
= -fc-(r-l)5 + r(n-l).
Therefore, by (L15), p < y/m - r(n - 1) + (r - 1)5 + k.
In order for equality to hold , all equalities in the above argument must be equalities.
In particular, for each i = 1,2, • • • , n,
(»ч-*)у« =-*y?,
and
(r-l)*<tf = (r-l)Sy?.
Suppose yi > 0. Then r* - Si = —fc, (r — l)s, = (r — 1)5, and n equals either rorn-1.
Since ?f rf = J^? 5i, we have r* = s» for all i. These implies that the adjacency digraph
of M is either an r-regular digraph or the undirected star Ki,n-i-
On the other hand, it is easy to verify that
p = y/m - r(n - 1) + (r - 1)5 + fc,
32
Matrices and Graphs
if the adjacency digraph of M is either an r-regular digraph or the undirected star K\%n~i.
и
Corollary 1.6.5A (Liu [172]) Suppose M is an n x n matrix with trace 0. Let r =
mini<i<nri, S = тах!<г<л5г, m = ?i<«<nr» and ~k = mini<i<n(rt- - s»). If r > 1,
then
/*(Af) < y/m - r(n - 1) + (r - 1)5 + k.
Moreover, if Af is irreducible then equality holds if and only if the D(Af), the associate
digraph of Af, is either an r-regular digraph or the undirected star Kitn-i.
Proof The inequality follows from Exercise 1.20 and Theorem 1.6.5 immediately. Now
suppose that equality holds and that Af is irreducible. Let x be an eigenvector of Af
corresponding to p(Af). Then x is a positive vector by Theorem 1.6.1. By Exercise 1.20
p(M)
/Го Af]\
~ p\[ м* о J;
and
0 Af
Af* 0
corre-
is a positive eigenvector of
sponding to p(Af). By Theorem 1.6.4, the adjacency digraph of M is either an r-regular
digraph or the undirected star ifi>n_i.
On the other hand, if D(Af) is either an r-regular digraph or the undirected star
-Ki,n-b then it is routine to verify that p(Af) = л/т - r(n — 1) + (r — 1)S + fc. Q]
Corollary 1.6.5B (Hong, [132]) Suppose Af is an n x n irreducible matrix with trace 0
and ri = si for i = 1,2, • • • ,n. Let m = 53i<*<« r»- Then
p(Af) < Vm-n+l
with equality if and only if Af is either the complete graph Kn or the star Jfitn-b
Corollary 1.6.5C (Cao, [42], Liu [172]) Let G be a simple connected graph with n vertices
and e edges. Then
p(G) < V2e-r(n-l) + (r-l)
with equality if and only G is either the star i^i,n-i or a regular graph.
Corollary 1.6.5D (Hong, [132]) Let G be a connected graph with n vertices and e edges.
Then
p{G) < V2e-n + l
with equality if and only if G is either the star Jfi,n-i or the complete graph Kn.
The next theorem consider the spectral radius of a bipartite graph. Thus we do not
assume that M is square or that tr(Af) = 0.
Theorem 1.6.6 (Gregory, Shen and Liu [100]) Suppose Af is an а х b matrix. Let
r = mini<i<an, R = maxi<,<0ri, s = mini<t<6Sj, S = maxi<i<bSi, m = ?i<i<ar**
Matrices and Graphs
33
Then
/Го м"|\ J
{[м- о JH
\ у/т -ar + 5r,
•s/m - 6s + i?s,
ar+fts I Sr+Rs
Moreover, if
has a positive eigenvector, then the spectral radius attains any
0 M
MT 0
of the above upper bounds if and only if r = R, s = S (and so ar = 6s).
Proof We only prove the first inequality. The second can be proved by replacing M* for
M, and the third follows from the first and the second easily. We shall adopt the notations
in the proof of Theorem 1.6.5. By (1.15),
p2 <m _?r< J- у)<т-г^ ]Г y)
i j:mij=0 i i:mi,-=0
= m — г У^(а — S) ^2 Vi =™> — a>r + Sr.
i i
Now suppose equality holds and yi > 0 for all i. Then r > 1. These imply r = Я and
s = S. On the other hand, if г = i?, s = 5 and ar = 6s, then it is easy to verify that
0 M
Ml 0
][;H
where x\ = л/б and од = v^ for all 1 < iI < o, 1 < j < b. By Theorem 1.6.1, p = y/rs =
y/m^~aFT~Sr^ []
Recently, Ellingham and Zha obtained a new result on p(G) for a simple planar graph
of order n.
Theorem 1.6.7 (Ellingham and Zha, [81]) let G be a simple planar graph with n vertices.
Then
p(G)<2 + V2n^-6.
An analogue study has also been conducted for nonsymmetric matrices in Bn.
Definition 1.6.2 Let M(n,d) be the collection of n by n (0,1) matrices each of which
has exactly d entries being one; and let M*(ni d) be the subset of M (n, d) such that A =
(aij) € Ф* if and only if Л 6 M(n, d) and for each i with 1 < i < n, ац > a^i > • * * > аы
and aii > ai2 > • • • > а»п. Denote
g(n,e) = тах{р(Л) : Л € Л1(п,е)} and #*(n,e) = max{p(A) : A € М*(п,е)}.
34
Matrices and Graphs
Example 1.6.2 The following matrices are members in Л4(3,7) achieving the maximum
spectral radius #(3,7) = 1 + V%- Only the first one is in M*(3,7).
The value of g(n, d) has yet to be completely determined. Most of the results on g(n, d)
and g*{n,d) are done by Brualdi and Hoffman.
Theorem 1.6.8 (Schwarz, [231]) g(n,d) = g*(nyd).
Theorem 1.6.9 (Brualdi and Hoffman [30]) Let A: > 0 be an integer. Then g(n, к2) = к.
Moreover, for A e M(n, fc2), p(A) = к if and only if there exists a permutation matrix P
such that
P~lAP =
Jk 0
0 0
Let к > 2 be an integer. Define
Zk =
Jk *
,^2 =
1110
10 0 0
10 0 0
0 0 0 0
l,Si =
' 0 1 0 1
10 0
_ 0 0 0 J
where there is a single 1-entry-somewhere in the asterisked region of Zk-
Theorem 1.6.10 (Brualdi and Hofbnan [30]) Let к > 0 be an integer. The p(n, k2+\) = к.
Moreover, for A € M (n, k2 + 1), p(A) = к if and only if there is a permutation matrix P
such that P'XAP = Zk.
Eriedland [92] and Rowlinson [221] also proved different upper bounds p(A), under
various conditions. Theorem 1.6.11 below extends Theorem 1.6.9 when s = 0; and Theorem
1.6.13 below was conjectured by Brualdi and Hofbnan in [30].
Theorem 1.6.11 (Friedland [92]) Let e
Л€Ф(п,е),
=0Ь
where s < к. Then for any
р(а)<*^±^НЕ1.
Theorem 1.6.12 (Friedland [92]) Let e
(0
+ к - 1, where к > 2. Then for any
Matrices and Graphs
35
ЛеФ(п,е),
P(A)<
k-2 + Vk?TW^l
where equality holds if and only if there exists a permutation matrix A such that P~lAP =
Hk+i + °> where
#Jfe-H =
**+i
JS-i
Theorem 1.6.13 (Rowlinson [221]) Let e
-(0
with к > s > 0. If A e Ф(п,е) such
that p(A) = $(n,e), then G(A) can be obtained from a if* by adding n — к additional
vertices Vi, • • • , vn-* such that vi is adjacent to exactly s vertices in Kk, and such that
V2, * * * , vn^jb are isolated vertices in G(A).
Theorem 1.6.14 (Friedland [92]) For d = к2 +1 where 1 < i < 2fc, and for each A €
М{п,е),
k + V&T^
P(A) < 5 .
Moreover, equality holds if and only if t = 2k and there is a permutation matrix P such
that
where d = к2 + 2Лг, and
Theorem 1.6.15 (PViedland [92]) For d = k2 + 2fc - 3 where jfe > 1, and for each A €
Л4(п,е),
P(A)<
* - 1 + VFT6F--7
Moreover, when к > 2, equality holds if and only if there is a permutation matrix P such
that
-'Н*г :)•
36
Matrices and Graphs
where for а к — 1 by 2 matrix L = J(k-i)x2,
Hk+i
To study the lower bound of р(Л), it is more convenient to classify the (0,1) matrices
by the number of entries equal to zero instead of by the number of entries equal to one.
Definition 1.6.4 Let n and r be integers. Let M(n,r) be the collection of n by n (0,1)
matrices each of which has exactly г entries being zero; and let M (п,г) be the subset
of M(n,r) such that A = (а#) € Ф*(п,г) if and only if A e ^Л(щг) and for each i with
1 < i < n, он > u2i > - • • > ani and ац > a# > * * * > a,n. Denote
§(n,e) = тах{р(Л) : A € М(щт)} and
p*(n,e) = тах{р(Л) : Л € .M (n,r)}.
Once again, a result of Schwarz in [231] indicates that д(щг) = p*(ra,r). Also, the
following are straight forward.
Therefore, it remains to study the value of <j(n, r) when r <
Theorem 1.6.16 (Schwarz, [231]) Let A € M(n,r) Then for some permutation matrix
Q, there exists a sequence of matrices Л о = QTAQi Ai, • • • , As = В such that
(i)BeJT,r)
(ii) Ai+i is obtained from Л» by switching a 0 and a 1 in Ai where the 0 immediately
precedes the 1 in some row or immediately follows the 1 in some column (г = 0,2, • • • , s—1),
(iii) p(A) > p(Ai) > p(B), (t = 1, • • • , s - 1).
The following Theorem 1.6.17 is due to Brualdi and Solheid. The proof here is given
by Li [160].
Theorem 1.6.17 (Brualdi and Solheid, [38]) Let r be an integer with 0 < r < [^-J, then
, ч n + \/n2 — 4r
9(n,r) = - .
Matrices and Graphs
37
Moreover, for A € M(n, r), p(A) = g(n,r) if and only if there is a permutation matrix P
such that P~XAP is equal to
f Jk C\
(1.16)
where fc, I are non negative integers such that к + / = n.
Proof Let Л = (aij) € Ф*(п,г). Let 74=71 — ?"=i a^, 1 < i < n. Since Л € ЛТ*(ra,r),
**i > ^2 > • * * > fn and 2?=i rn = **. Let x = (si,S2> • * • ,#n)T be a eigenvector of Л
corresponding to the eigenvalue p(A) such that |x| = 1. Then by p(A)x = -Ax, for each i
with 1 < i < n,
n—r* n
p(>l)xi = ]Г) хз = * - 53 *i-
It follows by р(Л) > О that
n
жп > жп-1 > • • • > я?ь ^ sj < пхп, (1 < г < n) (1Л7)
and
p(A)xn < 1. (1.18)
This implies that for each г,
n
p(A)a?i = 1 - 53 3j > 1 - пжп,
and so summing up for г yields
n
p(A) >n~Y^ nxn = n - rsn.
1=1
By p(A) > 0 and by р(4)жп < 1,
p(A)2 > p(A)(n - rxn) > np(A) - r.
Solving this inequality for p(-A) gives
/*0 > n + Vf^- (1-19)
Note that equality in (1.19) holds if and only if both (1.17) and (1.18) are equalities.
n
In other words, for each j with n - гг + 1 < j < n, both p(A)xj — V* s« = 1 and 77 = 0,
38
Matrices and Graphs
and so there exists a permutation matrix P such that P~lAP = В with к = n — гг and
I = ri.
It remains to show that if A G M(n> r) — Л4 (n, r) and if A is not permutation similar
to a matrix of the form in (1.16).
Consider a matrix A € Л?(п, r) and let Aq = QTAQi A\, • • • , As = В be matrices
satisfying Theorem 1.6.16. Since В € M (ra,r), if Б is not permutation similar to the
form in (1.16), then p(A) > p(B) > §(n, r). Thus we may assume that there is a number j
such that the matrix F = Aj+i has the form (1.16) and к = r, but the matrix 25 = A;- does
not have the form (1.16) for any k. Without loss of generality, we assume, by Theorem
1.6.16, that
where С is obtained from С by replacing a 0 at the (r, t) position of С by a 1, for some
t with 1 < t < n — r, and where D is obtained from Jn_r by replacing a 1 at the (1,?)
position by a 0.
Denote E = (e,j) and let x = (a?i, • • • ,xn)T with unit length be an eigenvector of E
corresponding to the eigenvalue p(E). By the choice of E, E does not take the form of
(1.16) for any k. In fact, for к = r+1, there is 0 in the first column of C". Let e$ = 1—ei>r+i,
then X)S=i ei > 0. Since the (r + 2) row of E does not have a 0, we can deduce, from the
r + 1 and the r + 2 rows of 2?х = p(E)x, that 0 < xr+i < xr+2 = хг+з = • • • = xn, and
/o(??)a:i = 1 - [(n - е»)жп + е»гсг+1].
Summing up for г yields
p(E) = n - (])Г(п - 6i)xn + 53e<a:r+l) > n ~ ГЖп'
and
\p(E)\2-np(E)+r>0.
It follows that
p(A) > p{E) > -(n + Vn2-4r) = д{щт),
which completes the proof. []]
1.7 Exercises
e =
Jn—r,r U
,F =
Jr С
Exercise 1.1 Prove Proposition 1.1.2.
Matrices and Graphs
39
Exercise 1.2 Prove Theorem 1.1.1 and Theorem 1.1.2.
Exercise 1.3 Let A = A(Kn) be the adjacency matrix of the complete graph of order n.
Show that
Ak=(in-l)'-(-l)*yn + (_1)kln.
Exercise 1.4 Prove Corollary 1.1.ЗА and Corollary 1.1.3B.
Exercise 1,5 The number trA* is the number of closed walks of length к in G.
Exercise 1.6 Let Jn denote the n x n matrix whose entries are all ones and let s,t be
two numbers. Show that the matrix sJn — tln has eigenvalues t (with multiplicity n — 1)
and ns +1.
Exercise 1.7 Let Kny Cn and Pn denote the complete graph, the cycle, the path with n
vertices, respectively, and let Kr>s denote the complete bipartite graph with r vertices on
one side and s vertices on the other. Let m = 2k be an even number, J be the m x m
matrix in which each entry is a 1, and В is the direct sum of к matrices each of which is
0 1
. Verify each of the following:
(i)spec(^)=(n-_1i "-1).
(ii) speeds) =( ° f ~f).
уr+s-2 1 1 J
(iii) spec(Cn) = j 2cos ( —J : j = 0,1,• ¦ • ,n - 1} .
(iv) spec(Pn) = J2cos (~jpy) • J = I**" >nj.
/ -г «ч I -l 1 m — 1 \
(v1)spec(7-B)=^_i k i j.
Exercise 1.8 Let G be a simple graph with n vertices and q edges, and let m(A) be the
number of 3-cycles of G. Show that
Xa(\) = An - q\n~2 - 2m(A)An-3 + . • ¦ .
Exercise 1.9 Prove Lemmas 1.2.2, 1.2.3, and 1.2.4.
Exercise 1.10 Prove Corollary 1.3.2A and Corollary 1.3.2B, using Theorem 1.3.2.
40
Matrices and Graphs
Exercise 1.11 Let G be a graph with n > 3 vertices and let Vi,V2 € V(G) such that v\
has degree 1 in G and such that v\V2 € E{G). Show that
XG{\) = AXG-Vl(A) - XG-{vUv2}W-
Exercise 1.12 Show that is G is a connected graph with n = |V(6?)| > 2 vertices and
with a degree sequence d\ < d2 < • • • < dn. Then each of the following holds.
(i) Al(G) < (max 2 J .
(ii) (H. S. Wilf, [275]) Let q = |E(G)|. Then Ai(G) < JMiZl).
V n
Exercise 1.13 Let Tn denote a tree with n > 2. Then
2cos (t^j) < MG) < Vn^I,
where the lower bound holds if and only if Tn = Pn, tbe path with n vertices; and where
the upper bound holds if and only Tn = Kit1l-i.
Exercise 1.14 Let T denote a tree on n > 3 vertices. For any к with 2 < к < n — 1,
there exists a vertex v e V(T) such that the components of T — v can be labeled as
Ouft, • • • , Gc so that either
CO |V(G,)| <
L K J
n-2
n~2l
—7— + 1, for all i with 1 < i < c; or
~p| +1, for all г with 1 < i < c-1, and |V(GC)| < n-2-
(ii) |K(G,)| <
Exercise 1.15 Prove Lemma 1.3.1.
Exercise 1.16 Let G be a graph on n > 2 vertices. Prove each of the following.
(i) (Lemma 1.3.2) If G is bipartite, then its spectrum is symmetric with respect to the
origin. In other words,
Ai(G) = -An+1_i(C?), for each i with 1 < г < |^J.
(ii) If G is connected, then G is bipartite if and only if — Ai(<3) is an eigenvalue of G.
(iii) If the spectrum of G is symmetric with respect to the origin, then G is bipartite.
Exercise 1.17 Let p(A) be the maximum absolute value of an eigenvalue of matrix A.
Show that for any matrix M € Bn,
p(M)<p\
/To м~\\
\[mt о \)
Exercise 1.18 If
0 M
MT 0
M
, then ||x|| = ||y|| whenever A # 0.
Matrices and Graphs
41
Exercise 1.19 Let G be a graph on n vertices and Gc be the complement of G. Then
p{G) + p(G°) < -\ + ^2(п-1Р + |,
Exercise 1.20 Let G be a loopless (n,g)-graph with a degree sequence <2i, tfe» - - - > ^n- Let
?((?) denote the incidence matrix of G (Definition 1.1.5), and let С = diag(di, ck, • • * ,^n)«
Show each of the following.
(i) A(L(G)) = BTB - C.
(ii) A(Z,(G)) = ВГВ - 2/д.
(ffi) If?>n, then Хв*в(А) = А*-п*ввт(А).
(iv) The matrix BTB is semi-definite positive (that is, a real symmetric matrix each
of whose eigenvalues is bigger than or equal to zero).
(v) If q > n, then zero is an eigenvalue of BTB.
Exercise 1.21 Let G be given below. Find L(G) and T(<3).
(i)G = K3.
(ii) G = K*.
(Hi) G is the graph obtained by deleting an edge from a K4.
(iv) What is the relationship between L{Ka) and T(Kz)7 Are they isomorphic?
(v) What is the relationship between L(Kn+i) and T(Kn)? Are they isomorphic? (See
И)-
Exercise 1.22 Let A € Ф(п,е) such that G(A) is a connected simple planar graph. Then
p(A) < VSn-ll.
Exercise 1.23 Let A € Ф(л, е) such that G(A) is a connected graph, and let Ai, • • • , An
be the eigenvalues of A. Then ?Г=2 A? > n — 1, where equality holds if and only if
C?(^)^ir1>n^orG(^)^irn.
Exercise 1.24 Let A be an n by n square matrix, and let В be an r by г submatrix of A
with r > 3. Then
p(A) < yJtr(AAT) - \2(BBT) - \B{BBT).
1.8 Hints for Exercises
Exercise 1.1 Apply the definitions.
Exercise 1.2 To prove Theorem l.l.l(i), note that when г ф j, the dot product of the ith
row and jth column of В is the number of edges joining v* and Vj in G; and when i = j,
42
Matrices and Graphs
this dot product is the degree of v*. The proof for (ii) is similar, taking the orientation
into account.
To prove Theorem 1.1.2, we can label the vertices of G so that the oriented incidence
matrix В of G is the direct sum of the oriented incidence matrix Bi of G», 1 < i < t,
where Gi, • • - ,G* are the components of G. Thus it suffices to prove Theorem 1.1.3 when
t = 1. Assume that t = 1.
Let a* denote the ith row of B. Since each column of В has exactly one 1-entry and
one (—l)-entry, Ya=\ a* = ®> an<^ so ^ne r&nk of В is at most n — 1. Assume then that
there exist scalars c,-, not all c* = 0, such that Yh=i <**» = 0> then use the fact that each
column of В has exactly one 1-entry and one (—l)-entry to argue that all c* must be the
same, and so Yh=i a» = 0. Therefore, the rank of В is exactly n — 1.
Exercise 1.3 Argue by induction on n. Note that A(Kn) = Jn — In.
Exercise 1.4 Apply Theorem 1.1.3 to the oriented incidence matrix of a graph with
1*2 = 0.
For Corollary 1.1.3B, note that G has a bipartition X and Y of V(G), which yields a
partition of the rows of the incidence matrix В into Ri and i*2, and so by Theorem 1.1.3,
В is unimodular.
Conversely, assume that G has an odd cycle or length r > 1, which corresponds to an
г by r submatrix B' of В with |det(2?')| = 2, and so В cannot be unimodular.
Exercise 1.5 - 1.7 Proceed induction on к in Exercise 1.5, and compute the corresponding
determinants in the other two exercises. Note that Exercise 1.7(v) and (vi) are equivalent.
Exercise 1.8 Apply Theorem 1.1.4. C0 = 1. Since det(A(Ki))=0, Сг = 0. Note that
det(A(K2)) = -1, and so G2 = det(A(K2))S(G,K2) = -q. Since det{A(K3)) = 2 and
S(G,KZ) = m(A), Cz = (-1)3 tet{A{Kz))S{G,Kz) = -2m(A).
Exercise 1.9 For Lemma 1.2.2, if G has two components, then G has an induced 2K2.
Hence we may assume that G has only one component. If G has an induced cycle of length
at least 5, then done. Since Gc is connected, |V(G)| > 6. If G has a vertex of degree one,
the we can easily find an induced 2K2 or a P4, as long as Gc is connected. Assume that
G has no vertices of degree one. Then argue by induction to G — v. Note that G — v has
no isolated vertices. If G — v is not connected, then v is a cut vertex of Gc, and so G — v
contains a spanning complete bipartite subgraph H with bipartition X UY. It is now
easy to find either an induced 2K2 or an induced P4. If G — v is connected, then apply
induction.
Lemma 1.2.3 can be done by straight forward computations.
For Lemma 1.2.4, it suffices to show that хя5(А) is equal to {by adding (-1)Column
Matrices and Graphs
43
1 to Column 2 and Column 3)
Л 0 0 -1
О Л -1 -1
О -1 Л -1
-1 -1 -1 Л
-1 -1 -1 О
(then expand along the Column 1)
-1
-1
-1
0
Л -Л -Л -1
О Л -1 -1
О -1 Л -1
-1 О О Л
-10 0 0
-1
-1
-1
о
= \»-2
Л -1
-1 Л
+E(-1)i+1(-1x-1)iAn"4
-Л -Л -1
Л -1 -1
-1 Л -1
Exercise 1.10 For Corollary 1.3.2A, let у = Ji,n. For Corollary 1.3.2B, let у = (л/ЗГ, \f<h, • • • ,
Exercise 1.11 Let G be a graph with n > 3 vertices and let vi,V2 € V(G) such that v\
has degree 1 in G and such that v\V2 € E(G). Show that
XG(\) = AxG-t*(A) -x<?4«b«a}M-
Exercise 1.12 Apply Corollary 1.3.2B to get Ai < max — У^ \AW,- By Cauchy-
l<i<n di ..j~«4
Schwarz inequality,
di
ij(zE(G)
= < / ^2 dj, which gives Part (i).
dj ]]ijeE(G)
Y,ijeE(G) \/didj
Apply Part (i) to show Part (ii). It suffices to show that for each i, ^ dj <
ijeE(G)
fyfo-1). This is true if ndi > 2q, since V dj <2q-di< Mizil.
ijeE(G)
For г with nd{ < 2q, then V cb < A(G)— < -SHZ_2.
Exercise 1.13 Apply the reduction formula in Exercise 1.11.
Exercise 1.14 Let T denote a tree on n > 3 vertices. Pick a vertex Vi € V(T). К vi is not
the desired vertex, then T — V\ has either a component with more than n — 2 — l(n — 2)/k\
vertices, or at least two components each of which has more than l(n - 2)/k\ +1 vertices.
Assume that 2\ is a component of T — v\ with more than [(n — 2)/fcJ +1 vertices. Let
V2 € V(Ti) be a vertex adjacent to v\ in T. Then in T - v2, the component containing vi
has at most n — 2 — [(n — 2)/fcJ vertices, and the other components of T - vi are subgraphs
of7\ -v2.
44
Matrices and Graphs
If again V2 is not the desired vertex, then Ti - v2 has a component T2 with more than
[(n — 2)/kj + 1 vertices. Let vs € Vffi) be a vertex adjacent to V2 in T. Then in Г — v$,
the component containing V2 has at most n — 2 — [(n — 2)/fcJ vertices, and the other
components of T — v$ are subgraphs of ТЬ — V3.
Repeat this process a finite number of times to get the desired v.
Exercise 1.15 Apply Exercise 1.14 when к = 2. Assume к > 3. By Exercise 1.14, we
assume that T has a vertex vi such that Exercise 1.14(H) holds. Let Ti = Gc in Exercise
1.14(H) and let щ = |V(Ti)|.
If ni < &, then V can be chosen to include vi, and as many vertices in V(Ti) as
possible. Thus assume that n\> к.
By Exercise 1.14, T has a vertex V2 such that T — V2 has a component T2 with ra2
vertices, and such that each other component of T — v2 has at most \{n\ — 2)/(к - 1)J +1
vertices, and
L^J+^L"-^:y*J-aJ+i?L^j.
Note that
^ л i wi - 2 .
П2 <ni-2-[fe_lJ.
Such a process may be repeated at most k — 1 times before we obtain a desirable subset
V.
Exercise 1.16 Let A = A(G) = (a#) and A» = А*((?). Note that Аг > 0.
(i) Assume that G is bipartite with a bipartition {S+,5~}. Let x = (ari,-*- ,xn)T be
such that A*x = Ax, Define, for each j = 1,2, • • • ,ra,
U- ifVieS+
and let w = (wi, • • • , wn)T. Then we can routinely verify that Aw = -A^w.
(H) Suppose —Ai is an eigenvalue. Assume Ax. = —Aix where x = (xi, ¦ • • , xn)T. Let
w = (|xi|,— ,|a?„|)T. Then
|xrAx| = I - AixTx| = AiXTx = AiwTw.
Thus
Aiwrw = — xTAx
< I - xrAx| = IX) S WW I
* j
* j
< AiwTw.
Matrices and Graphs
45
(Here we used the fact that Ai (G) = max{ . to }. See Theorem 6.1.3 in the Appendix) It
|uMol |u|2 J ™ '
follows that Aiw = Aw, By Theorem 1.3.1(H), and by the assumption that G is connected,
\xi\ > 0, for all г with 1 < i < n. It also follows that all inequalities above must be
equalities, and so all nonzero terms in
^Y^a^x, =-\i\x\2
* j
must have the same sign. Therefore, all summands must be negative, which implies that
if ay ф 0, then х{хй < 0. Let S+ = {vi: ж» > 0} and S~ = {vi: x{ < 0}. Then {S+,S-}
is a bipartition of V(G)t and so G is bipartite.
The other direction follows from (i).
(iii) Apply (ii) and argue componentwise.
Exercise 1.17 Suppose Mx = p(M)x for some non-zero vector x. Then xTMT =
p(M)xT and
¦([
0 M
MT 0
^ [xTxT]
I)'- ,
' 0
MT
TxT]
M 1
0 J
X
X
Г X |
1 X J
= х-м^м,=рт
Exercise 1.18 Since My = Ax and MTx = Ay, we have xTM — \yT and AxTx =
xTMy = AyTy.
Exercise 1.19 Note that G or Gc must be connected, and so we may assume that G is
connected. By Theorem 1.6.5 and its corollaries,
p(G) + p(Gc) < y/2e-n + l + [~ + J^ + n{n-l)-2el
мадб)+^)2
< (n-l)2 + i + 2J(2e-n + l))i + n(n-l)~
2e)
< 2(n-l)2 + :
Exercise 1.20 Apply definitions and Theorem 1.1.1.
Exercise 1.21 A formal proof for L(Kn+\) = T(Kn) can be found in [5], but we can get
the main idea by working on Ь{К±) = T{Kz).
Exercise 1.22 For a simple planar graph <3, \E{G)\ < Z\V{G)\ - 6.
Exercise 1.23 Note that ?JLX Af = 2e. Then it follows from Corollary 1.6.5D.
46 Matrices and Graphs
Exercise 1.24 Note that if P and Q are permutation matrices, then
{PAQ)(PAQ)T = PAATPT.
Hence we may assume that
A =
В С
D E
X
Y
Then ATA = XTX + YTY, and
AAT =
ххт XYr
yxt YYT
,ХХТ = ВВТ + ССТ.
Since YYT abd CCT are semidefinite positive,
\2{ATA) + \3(ATA) > \2(XTX) + \3(XTX) = \2(XXT) + \2(XXT)
= \2(BBT) + \3{BBT).
It follows by p(A)2 < \г{АтА) = tx(ATA) - ??=2 Ai(4T4) that
p(A)2 < tr(ATA) - \2(BBT) - Xz{BBT),
Chapter 2
Combinatorial Properties of
Matrices
Let F be a subset of a number field, and let Mm,n(F) denote the set of all m x n matrices
with entries in F, and let Mn(F) = Mntn(F). Note that Bn = Mn({0,l}). We write
M+ = Mn({r > 0| r is real}) and M* = Mn({r > 0| r is real}). When the set F is not
specified, we write МтгП and Mn for Мт,п(.Р) and Mn(F)) respectively.
Let A E Mm>n, and let к and r be integers with 1 < к < m and 1 < I < n. For
1 < ii < «2 < • • • < ik < m and 1 < Ji < J2 < • • • < jj < n, write a — (n,t2, • • • ,u) and
P = (ib J2> • * * ,ji). Let A[n, г2, • • • ,u|ii, j2, • • • ,#] = A[a|$ denote the submatrix of Л
whose (p, g)th entry is a*pjg. We also say that Л[ск|/3] is obtained from A by deleting the
rows not indexed in a and columns not indexed in /3.
Similarly, A[ti,t2, • • • ,?*|л,^2> • * * >ji) = A[a\/3) denotes the matrix obtained from A
by deleting the rows not indexed in a and columns indexed in /3; Л(а|/?] denotes the
matrix obtained from A by deleting the rows indexed in a and columns not indexed in fi;
and A(a\/3) the matrix obtained from A by deleting the rows indexed in a and columns
indexed in 0,
Nonnegative matrices can be classified as reducible matrices and irreducible matrices
by the relation ~p, or as partly decomposable matrices and fully indecomposable matrices
by the relation ~p.
47
48
Combinatorial Properties of Matrices
2.1 Irreducible and Fully Indecomposable Matrices
Definition 2.1.1 A matrix A € Mn is reducible if A ~p Ai, where
Ai =
Б О
and where В is an / by / matrix and D is an {n—l) by (n—/) matrix, for some 1 < I < n—1.
The matrix A is irreducible if it is not reducible. The next theorem follows from the
definitions.
Theorem 2.1.1 Let A = (a^-) € M+ for some n > 1, and let m denote the degree of the
minimal polynomial of A. The following are equivalent.
(i) A is irreducible.
(ii) There exist no indices 1 < n < %2 < • • • < ii < n with 1 < I < n such that
A[iV--t||ti,--- ,ij) = 0.
(iii) AT is irreducible.
(iv) (I + A^X).
(v) There is a polynomial f(x) over the complex numbers such that /(A) > 0.
(vi) 1 + A + • • • + A™-1 > 0.
(vii) (1 + А)т~1>0.
(viii) For each cell (?,i), there is an integer A; > 0 such that oj- , the (i,j)th entry of
A*, is positive.
(ix) D(A) is strongly connected.
Sketch of Proof By definitions, (i) <$=*> (ii) <=» (iii), (iv) =>• (v), (vi) ==> (vii) =»
(viii) => (i).
To see that (v) ==> (vi), let /(a:) be a polynomial such that /(A) > 0. Let тл(я)
denote the minimum polynomial of A. Then f(x) = ^(ж)тл(а;) + r(ar), where the degree
of r(x) is less than m, the degree of тл(х). Since гпа(А) = 0, r(A) = /(A) > 0, and this
proves (vi).
To see that (i) => (ix), suppose that D(A) has strongly connected components Di, D2, • •
for some к > 1. Then we may assume that D has not arcs from V(Di) to a vertex not
in V(Di). Let ti,t2, • • • }if) where 1 < i\ < ii • • • < ij < n, be integers representing the
vertices of V(Di). Then A[i\ • ¦ • *^|*i ¦ • • ij) = 0, contrary to (i).
It remains to show that (ix) => (vi), which follows from Proposition 1.1.1 (vii). Q
Definition 2.1.2 A matrix A € Mn is partly decomposable if A ~v Ai, where
А1 =
Б 0
С D
Combinatorial Properties of Matrices
49
and where В is an Z by Z matrix and D is an (n—Z) by (n—l) matrix, for some 1 < Z < n—1.
The matrix A is fully indecomposable if it is not partly decomposable.
Theorem 2.1.2 Let A = (a#) € M+ for some n > 1. The following are equivalent,
(i) A is fully indecomposable,
(ii) For any r with 1 < r < n, A does not have an r x (n — r) submatrix which equals
(iii) For any 0 ф X С V(D(A)), \N(X)\ > \X\, where N(X) = {v € T(-D(4)) : such
that D(A) has an arc (uv) from a vertex it € -X" to v}.
Proof By definition, (i) <=$> (ii). The graph interpretation of (ii) is (iii). []
Theorem 2.1.3 Let A = (а#) € Af+. Each of the following holds.
(i) If for any r with 1 < r < n, A does not have anrx(n-r) submatrix which
equals 0rx(n_r), then there exist no indices 1 < н < г2 < • • • < ц < n with 1 < I < n,
ji[*b---»i|ti,--- ,г*) = 0.
(ii) К Л is fully indecomposable, then A is irreducible.
(iii) Suppose that an > 0, for each i with 1 < i < n. Then A is fully indecomposable
if and only if A is irreducible.
(iv) A is irreducible if and only if A + / is fully indecomposable.
(v) (Brualdi, Parter and Schneider, [35]) A is fully indecomposable if and only if A ~p В
for some irreducible matrix В = (by) such that Ьц > 0, 1 < i < n.
Sketch of Proof (i) is straightforward, (ii) follows from Theorem 2.1.1(ii) and Theorem
2.1.2(ii).
Argue by induction on n to prove (iii). If A is not fully decomposable, then by Theorem
2.1.2(ii), and by the assumption that an > 0, A[i\ • • • %i\i\ • • • ц) = 0 for some »i, *2> • • • »*z>
and so A is not irreducible. The other direction follows from (ii).
(iv) follows from (iii) and (ii). []
Definition 2.1.3 A diagonal of a matrix A = (ay) € Bn is a collection T of n entries
fliii, G2t2, • • • , anin of A such that {n,гг, • • • , in} = {1,2, • • • , n}. A diagonal T of A is
a nonzero diagonal if no member of T is zero. An entry ay of Л is a 1-entry (0-entry,
respectively) if ay = 1 (ay = 0, respectively).
From this view point and by Theorems 2.1.2 and 2.1.3, the following can be concluded.
Theorem 2.1.4 (Brualdi, Parter and Schneider, [35]) Let A € Bn. Then A is fully
indecomposable if and only if every one entry of A lies in a nonzero diagonal, and every
zero entry of A lies in a diagonal with exactly one zero member.
Corollary 2.1.3 Let A € M+ with a nonzero diagonal. Then A is fully indecomposable
if and only if there is a permutation matrix P, such that PA is irreducible.
50
Combinatorial Properties of Matrices
Proof Since A has a nonzero diagonal, there is a permutation matrix P such that PA =
(a^) with the property а'н > 0, 1 < i < n. By Theorem 2.1.3(iii), PA is irreducible if and
only if PA is fully indecomposable. Q
2.2 Standard Forms
Certain canonical forms of a matrix A € M+ can be obtained in terms of irreducible
matrices and fully indecomposable matrices.
Theorem 2.2.1 Let A € M+. Bach of the following holds.
(i) A ~p В for some В € M+ with the following form (called the Frobenius normal
form of A):
(
B =
Аг
0
0
V 4b,i
0
A2
^9+1,9
4>9+2,9
0
^0+2,0+1
0
0
0
0
A9+2
\
Ak,g Ak,g+1
Ak )
(2.1)
where Aw- ,Ag,A9+i,• • • ,A* are irreducible matrices, and where for g < q < fc, some
matrix among Ag>1, • • • , Aq%q-\ is not a zero matrix.
(ii) If Ai € Mni, then the parameters A;,g and ni, • • • , n* are uniquely determined by
A.
Proof Let D — D(A). Note that the strong components of D can be labeled as
#ъА2>-** >Dk such that D has an arc from a vertex in V(A) to a vertex in V(Dj)
only if г < j. We may assume that Di, I>2, * * * > -^ are the source components, the strong
components with out degree zero.
For each i with 1 < i < к let a* = {j : Vj € V(A)}« Then А[^|а<] is irreducible by
Corollary 2.1.1.
By the labeling of the strong components of D, for each i with 1 <i <g, A[oci\ai) = 0;
for g < q < r < к} A[aq\ar) = 0. Since Dg+i, • * • ,Dk are not source components, some of
A[ag|ai], • • • , A[a9|ag-i] is not a zero matrix. This proves (i).
Since g represents the number of source components of D(A), к the number of strong
components of -D(A), and n^s are the number of vertices in the ith strong component of
D(A)t all these quantities are uniquely determined by D(A). This proves (ii). Q
Combinatorial Properties of Matrices
51
Example 2.2.1 Let X € M3, and let 03 6 Ms be the zero matrix. Let
Ai =
0 1 1
1 0 0
1 0 0
, Aa =
111
1 1 1
1 1 1
.A.
Г
X
.
03
Ai
Then Л is in a Frobenius normal form. If X — O3, then we can permute A\ and A2 to
get another Frobenius normal form. If X ф Оз, then the Frobenius normal form of A is
unique.
Example 2.2.2 If A ~p В and if Л is irreducible, then В is also irreducible, since ~p is
an equivalence relation. However, if A is irreducible and P, Q are permutation matrices,
then PA or AQ may not be irreducible. For example, the matrix obtained by permuting
the first two rows of the irreducible matrix A\ in Example 2.2.1 is reducible, by Theorem
2.1.1.
Example 2.2.2 indicates that certain reducible matrices may become irreducible by the
relation ~p. Therefore it is natural to ask what matrix A has the property that for some
permutation matrices P and Q, PAQ is irreducible? Note that PAQ = (PAPT)PQ,
and so we may only consider such matrix A that AQ is irreducibtei This is answered by
Brualdi in Theorem 2.2.2 below.
The proofs for the following two lemmas are left as exercises.
Lemma 2.2.1 Let A € M+ and let D = D(A) with V(D) = {vi, v2, • • • , vn}. Let P3it be
the matrix obtained from In € Mn by permuting the sth row with the tth row, and let
A' = APsj. Then D(A!) can be obtained from D(A) by changing all the in-arcs of vs in
D(A) into in-arcs of vt in D(A'); and by changing all the in-arcs of vt in D(A) into in-arcs
afv*in.D(A').
Lemma 2.2.2 Let D be a digraph with strong components Di, • • • , D* such that D does
not have a source (a vertex with in degree zero) nor a sink (a vertex with out degree zero),
and such that
(*) each arc of D goes from a vertex in a V(D{) to a vertex in Uj=rlV'(Dj), (1 < i < k).
Pick a vertex щ € V(A)> where 1 < i < fc, and denote щ — Uk- Obtain a new digraph
D' from D by the following Procedure Redirecting:
For each i = 1,2,-•• ,fc,
redirect all the in-arcs о/щ in D(A) to in-arcs о/щ-г.
Then D' is strongly connected.
Theorem 2.2.2 (Brualdi, [25]) Let A € M+. There exists a permutation matrices Q such
that AQ is irreducible if and only if A does not have a zero row or a zero column.
Proof If A has a zero row or a zero column, so does AQ, and so AQ is reducible.
52
Combinatorial Properties of Matrices
Conversely, assume that A has neither a zero row nor a zero column. By Theorem
2.2.1, we may assume that A has the following Probenius normal form
Ax 0
A2\ A2
Aki Ak2 Акз
0
0
Ак
If A; = 1, then A is irreducible. Hence we assume that к > 1. Therefore, D = D(A)
has к strong components Z>i, -• • ,-D* such that Ai = A(Di)> for each i with 1 < г < fc.
Moreover, each arc of D goes from a vertex in a V(D«) to a vertex in uj-х V(JDj)-
Pick a vertex «$ € V(-Dt), where 1 < i < kt and denote щ — it*. Obtain a new digraph
Z>' from D by Procedure Redirecting as in Lemma 2.2.2.
By Lemma 2.2.1, this procedure amounts to multiplying a permutation matrix Q to A
from the right, such that D' = D(AQ). By Corollary 2.1.1, it suffices to show that D' is
strongly connected. Therefore, the theorem follows from Lemma 2.2.2. Q
Example 2.2.3 By Theorem 2.1.4, if Л € M+ is fully indecomposable, then A must have
a nonzero diagonal. Also by Theorem 2.1.4, the identity matrix In 6 M+ has a nonzero
diagonal but In is not fully indecomposable.
The EVobenius form (2.1) can also be applied to obtain standard forms for matrices
A € M+ with pA = n under permutation equivalence relation, where рл stands for the
term rank of a matrix A (see Appendix, Section 6.2). The analogous result for non square
matrices can be similarly obtained, as stated in Theorem 2.2.4.
Theorem 2.2.3 Let A € M+ be such that pa = n. Then each of the following holds.
(i) A ~p В for some В б М+ with the following form (called the equivalence normal
form of A),
? =
Ax
0
0
Ag+l,l
Ли-2,1
0
A2
0
...
0
0
A9
Ag+l,g
Ag+2,9
0
Ag+l
Ag+2,g+l
0 •¦
0
0 •¦
0
Ag+2 ' •
¦ 0
• 0
• 0
• 0
• 0
Ak,]
Ak,t
Ak,g+l
Ak
(2.2)
where A\, • • • , Ag, Ag+i, • • • , Ak are fully indecomposable matrices, and where for g < q <
к, some matrix among Лдд, • • • , Aqiq-i is not a zero matrix.
Combinatorial Properties of Matrices
53
Л.
(ii) If Ai € Mn., then the parameters k,g and ni, • • • ,rifc are uniquely determined by
Proof Since pA = n, there is a permutation matrix Q such that Лф = (o^) with a# > 0,
1 < i < n. By Theorem 2.2.1, there is a permutation matrix P such that В = PT(^Q)P
is a Frobenius normal form in (2.1). Let В = (by). Since P is a permutation matrix, and
since а'н > 0, we have Ъц > 0, where 1 < i < n. By Theorem 2.2.1, each Ai is irreducible.
By Theorem 2.1.3(iii), each Ai is fully indecomposable. Q
In [163], a stronger conclusion on the uniqueness of (2.2) is proved. That is, if the
matrix A has an equivalence normal form В in (2.2), and is also permutation equivalent
to
A[ 0
0 AL
B' =
4+i,i
A'
dA+2,l
4.i
0
0
A1
A'
АД+2,Л
...
0
АЛ+1
^Л+2,Л+1
0
0
0
0
А'
Ah+2
¦ 0
• 0
• 0
¦ 0
• 0
4л
**,Л+1
А\
then к = I, д = h, and Л^,--- ,Лд can be obtained by permuting Ai,*-« ,Aff, and
^л+i»' * * >Ai can De obtained by permuting Ag+i, • • • , Л*.
Theorem 2.2.4 Let Л € M+>n such that A has no zero rows nor zero columns. Then A
is permutation equivalent to the following matrix
B =
where Al € Mrtl8n for some rj > s* with рдг = s*, where Ля € Mrhlsh> f°r some r& < s^
with рлн = rh> and where each Л*, 1 < i < fc, is a fully indecomposable square matrix.
Definition 2.2.1 Let A e Bn such that Л ф 0. Л has a total support if every 1 entry of
A lies in a nonzero diagonal.
AL 0 0 »
Л! 0 ..
A2 ..
*
• 0
• 0
• 0
A*
0 "
0
0
0
54
Combinatorial Properties of Matrices
Example 2.2.4 Let A = (а#) € Bn with the following form
X Z
0 Y
where X € M* and Y € Mi. If there is an entry a# = 1 in Z> then Л does not have a
nonzero diagonal that contains this entry. Assume such a diagonal T exists. Then a^ € T
and \T\ = n. Delete the ith row and jth column from A to get a matrix В € Мп_1. Then
T — {a#} must be a nonzero diagonal of B. However, the elements in T — {a^} must be in
either the first k—1 rows or the last /—1 columns, and so \T—{а^}| < (fc—1)+(J—1) = га—2,
contrary to |T| = n.
Example 2.2.4 indicates that if A has a total support, by Theorem 2.2.3, A is
permutation equivalent to a direct sum of fully indecomposable matrices. The converse holds
also, again using Theorem 2.2.3.
Corollary 2.2.3 Let A € Bn. Then A has a total support if and only if A ~p ?, where
Б is a direct sum of fully indecomposable matrices.
Theorem 2.2.5 Let A € Bn and А ф 0 and let G be the reduced associated bipartite
graph of A (see Proposition 1.1.2(vii)). Suppose ^that A has a total support. Then A is
fully indecomposable if and only if G is connected.
Proof If A is not fully indecomposable, then by Corollary 2.2.3, A ~p B, where В is the
direct sum of at least two matrices. Therefore, G is not connected.
Conversely, if G is not connected, then A is permutation equivalent to
A' =
X 0
0 Y
where X € MPtq with l<p + q<2n-l. Without loss of generality, assume p < q. Then
^A <p+{n — q)=.n—(q-p),b& the first p rows and the last n — q column of A1 contain
all positive entries of A1, Since A has total support, n = рл = Ад, and so p = q. It follows
that A1 has 0Р)П~д as a submatrix, and so A is not fully indecomposable.
2-3 Nearly Reducible Matrices
By Theorem 2.1.1, a matrix A € M+ is irreducible if and only if D(A) is strong. A
minimally strong digraph corresponds to a nearly reducible matrix.
Definition 2.3.1 A digraph D is a minimally strong digraph if D is strongly connected,
but for any arc e € E{D)i D — evs not strongly connected. For convenience, the graph K\
is regarded as a minimally strong digraph. A matrix A 6 M+ is nearly reducible if D(A)
is a minimally strong digraph.
Combinatorial Properties of Matrices
55
As an example, a directed cycle is a minimally strong digraph. Some of the properties
of minimally strong digraphs are listed in Proposition 2.3.1 and Proposition 2.3.2 below,
which follow from the definition immediately.
Proposition 2.3.1 Let D be a minimally strong digraph. Each of the following holds.
(i) D has no loops nor parallel arcs.
(ii) Any directed cycle of D with length at least 4 has no chord. In other words, if С =
V1V2 • • • vkvi is a directed cycle of ?>, then (vi, Vj) ? E(D) — E(C), for any V{, Vj € V(C).
(Ш) If |V(.D)| > 2, then D contains at least one vertex v such that d*"(v) = d~(v) = 1.
(Such a vertex is called a cyclic vertex of D.)
(iv) If D has a cut vertex v, then each v-component of D is minimally strong.
Definition 2.3,2 Let D be a digraph, and H a subgraph of D. The contraction D/H
is the digraph obtained from D by identifying all the vertices in V(H) into a new single
vertex, and by deleting all the arcs in E(H). If W С V(D) is a vertex subset, then write
D/W = D/DpPF].
Proposition 2.3.2 Let D be a minimally strong digraph and let W С V(D). If D[W] is
strong, then both D[W] and D/W are minimally strong.
Proposition 2.3.3 If D is a minimally strong digraph with n = |V(.D)| > 2, then D must
have at least two cyclic vertices.
Proof Since D is strong with n > 2, D must have a directed cycle, and so the proposition
holds when n = 2. By Proposition 2.3.1 (iii) and by induction, we may assume that D has
no cut vertices and that n > 3.
If every directed cycle of D has length two, then since D is minimally directed and by
n > 3, at least one of the two vertices in a directed cycle of length two is a cut vertex of
D. Therefore, D must have a directed cycle С of length m > 3. We may assume that
D ф (7, and so n - m > 1. Thus D/C has n — m + 1 > 2 vertices, and so by induction,
D/C has at least two cyclic vertices, Vi and V2 (say). If both v\> V2 € V(D) - V(C), then
they are both cyclic vertices of D. Thus we assume that v\ € V(D) — V(C) and V2 is the
contraction image of С in D/C, Then D has exactly two arcs between V(D) — V(C) and
V(C). Since |V(C)| = m > 3, С must contain a cyclic vertex of D. []
Definition 2.3.3 Let D = (У,??) be a digraph. A directed path P = vqV\ -*-vm is a
branch of D if each of the following holds.
(Bl) Neither vo nor vm is a cyclic vertex of Dy and
(B2) Each vertex in P° — {t/i, V2, • • • , vm_i} is a cyclic vertex of D (vertices in P° are
called the internal vertices of the branch P), and
(B3) ?>[V - P°] is strong.
56
Combinatorial Properties of Matrices
The number m is the length of the branch. Note that W = 0 or vq = vm is possible.
Proposition 2.3.4 Let D be a minimally strong digraph with n = |V(.D)| > 3. Then
either D is a directed cycle, or D has a branch with length at least 2.
Proof Assume that D is not a directed cycle. Let U = {ue V(D)\u is not cyclic}. Then
U Ф 0. Define a new digraph D' = (U>E') such that for any utu' € I/, (u,u') € 22' if and
only if D has a directed (u, tt')-path. Since D is strong, D' is also strong and has ho cyclic
vertices.
By Proposition 2.3.3, D' is not minimally strong and so there must be an arc e' € E'
such that D1 — e' is also strong. Since D is minimally strong, and since D' — e' is strong,
e' must correspond to a branch in ?>, which completes the proof. Q
Theorem 2.3.5 (Hartfiel, [118]) For integers n > m > 1, let Fx € M+_m>m such that
Fi = EiiSi for some s with 1 < s < m, F2 € Af^ n_m such that .F2 = ??t,n-m> for some t
with 1 < t < m, and let Aq € A^J"_m be the following matrix.
Л0 =
0
1
0
0
0 0 ••
0 0--
1 0 ••
0 1 ••
• 0
• 0
¦ 0
¦ 0
0
0
0
0
0 0 0
1 0
Then every nearly reducible matrix A € Bn is permutation similar to a matrix В € M+
with the form
B:
Ao Fi
F2 Аг
(2.3)
where A\ = (а^) е М+ is nearly reducible with a'u = 0.
Proof This is trivial if D is a directed cycle (m = 1 and A\ = A(Ki)). Hence assume n >
3 and by Proposition 2.3.4, D(A) has a branch vo^i • • • vm, and so there is a permutation
matrix P such that PAPT has the form of В in (2.3). []
Theorem 2.3.6 (Brualdi and Hedrick [29]) Let D be a minimally strong digraph with
n = |Fp)| > 2 vertices. Then
n < \E(D)\ < 2(n - 1).
Moreover, |#(D)| = n is and only if D is a directed cycle; and \E(D)\ = 2(n - 1) if
and only if D is obtained from tree T by replacing each edge of T by a pair of arcs with
opposite directions.
Combinatorial Properties of Matrices
57
Proof Since D is strong, d+(v) > 1 for each v € V(D). Thus \E(D)\ > \V(D)\ = n, with
equality holds if and only if every vertex of D is cyclic, and so D must be a directed cycle.
It remains to prove the upper bound.
The upper bound holds trivially for n = 1 and n = 2. Assume n > 3. By Proposition
2.3.4, D has a branch P — vqV\ • • • vt with t > 2 such that D' = D — P° is strong.
By induction, \E(D')\ < 2(\V(D')\ - 1). Since \E(D)\ = |#(I>')I + t and |V(D)| =
|V(D')|+t-l,
\E(D)\ = |Я(?>')| + * < 4\V(D')\ - 1) +1 = 2(n - 1) - (t - 2) < 2(n - 1).
Assume |?7(Z>)| = 2(n — 1). Then t = 2 and by induction, D' is obtained from a tree T'
with n — 1 vertices by replacing each edge of T' by a pair of oppositely oriented arcs. If
Щ Ф vt, then there is a directed (vo,v*)-path P'in D' with length at least one. Since P is
a (vo,v*)-path, all the arcs in P' may be deleted from ?>, and the resulting digraph is still
strong, contrary to the assumption that D is minimally strong. Hence vo = vt and so the
theorem follows by induction. Q]
Corollary 2.3.6 Let n > 2 and let к > 0 be integers. The there exists a minimally strong
digraph D with \V(D)\ = n and \E(D)\ = к if and only if n < к < 2(n - 1).
Proof The only if part following from Theorem 2.3.6.
Assume n < к < 2(n— 1). Construct a digraph Dk on the vertex set V = {vi, V2, • • • , vn}
with these arcs:
?7 = {(vivi+i),(vi+1Vi)\l <i<k-n}
U{(vk-n+jVk-n+j+l)\l < j < П - 1} U {(vnV*_n+l)}-
It is routine to check that D is a minimally strong digraph with n vertices and к arcs. Q
Definition 2.3.4 For a matrix A € Afn, the density of Л, denoted by ||A||, is the sum of
all entries of A. Note that when АбВП) ||Л|| is also the number of positive entries of A
Theorem 2.3.6 and Corollary 2.3.6 can be stated in terms of (0,1) matrices. The proof
is straight forward and is omitted.
Theorem 2.3.7 Let A € Bn be a nearly reducible matrix with n > 2. Then each of the
following holds.
(i)n<||A||<2(n-l).
(ii) || A || — n if and only if A = A(D) for a directed cycle D.
(iii) || A|| = 2(n - 1) if and only if A = A(G) for a tree G.
58
Combinatorial Properties of Matrices
2.4 Nearly Decomposable Matrices
In order to better understand the behavior of rally indecomposable matrices, we investigate
the properties of those matrices that are fully indecomposable matrices but the replacing
any positive entry by a zero entry in such a matrix will result in a partly decomposable
matrix. For notational convenience, we let Ец denote the matrix whose (i,j)-entry is one
and whose other entries are zero.
Definition 2.4.1 A matrix A = (a^) € Bn is nearly decomposable if Л is fully
indecomposable and for each apq > 0, A - apqEpq is partly decomposable.
Theorem 2.4.1 Let A € Bn be a nearly decomposable matrix. Each of the following
holds.
(i) There exist permutation matrices P and Q such that PAQ > I.
(ii) For each pair of permutation matrices P and Q such that PAQ > I, PAQ — J is
nearly reducible.
Proof By Theorem 2.1.3(v), there exist permutation matrices P and Q such that PAQ >
I. For the sake of simplicity, we may assume that A > I, By Theorem 2.1.3(iv), A — I
is irreducible. If for some В € Bn such that С is irreducible and С < A — I, then by
Theorem 2.1.3(iv), С + J < A is fully indecomposable. Since A is nearly decomposable, it
must be С = A — J, and so A — J is nearly reducible. Q]
Example 2.4.1 If Б is a nearly reducible matrix, by Theorem 2.1.3(iv), В +1 is fully
indecomposable. But В -h I may not be nearly decomposable. Let
B =
0 1 1
1 0 0
10 0
, and С =
Oil
1 1 0
1 0 1
Then В is nearly reducible and С is fully indecomposable. Note that С < В +1 and
С ф В + J. Hence В + J is not near decomposable.
Theorem 2.3.5 can be applied to obtain a recurrence standard form for nearly
decomposable matrices. The following notation for Ao will be used throughout this section. For
integers n > m > 1, let Aq € M*_m be the following matrix.
Ao =
10 0--
110--
0 1 1 ••
0 0 1--
¦ 0
¦ 0
• 0
• 0
0
0
0
0
0 0 0
1 1
Combinatorial Properties of Matrices
59
Lemma 2.4.1 follows from Theorem 2.2.5, and so its proof is left as an exercise.
Lemma 2.4.1 Let Б be a matrix of the form
B =
(2.4)
Ao F[
If Bi = (bij) e M+_m is a fully indecomposable matrix, if F[ has a 1-entry in the first
row, and if F2 has a 1-entry in the last column, then В is fully indecomposable.
Lemma 2.4.2 Let B\ = (bij) € M+ denote the submatrix in (2.4). If В in (2.7) is nearly
indecomposable, then each of the following holds.
(i) B\ is nearly indecomposable.
(ii) F[ = E\)S, for some s with 1 < s < m and F2 = Et%n-m> for some t with 1 < t < m.
(iii) If m > 2, then bts = 0.
Proof If some 1-entry of B\ can be replaced by a 0-entry to result in a fully
indecomposable matrix, then by Lemma 2.4.1, В is not nearly indecomposable, contrary to the
assumption of Lemma 2.4.2. Therefore, B\ must be nearly indecomposable. Similarly, by
the assumption that В is nearly indecomposable, Lemma 2.4.2(ii) must hold.
It remains to show Lemma 2.4.2(iii). Suppose m > 2. Since m > 2 and since B\ is
fully indecomposable, B\ ф 0. Given В in the form of (2.4), every nonzero diagonal of B\
can be extended to a nonzero diagonal of B.
If bts = 1, then let B( be the matrix obtained from В by replacing the 1-entry bts by a
0-entry. Since Bi is fully indecomposable, bts lies in a nonzero diagonal Lo?B\. Removing
bts from L, adding the only 1-entry in i*\ and F2, and utilizing the non main diagonal
1-entries of Ao, we have a nonzero diagonal of B1. Therefore, B' has total support. It is
easy to check that the reduced associated bipartite graph of B' is connected, and so by
Theorem 2.2.5, B' is fully indecomposable, contrary to the assumption that В is nearly
indecomposable. Thus bts = 0- П
Theorem 2.4.2 (Hartfiel, [118]) For integers n > m > 1, let Fi € Bn_m>m such that
Fi = EitSi for some s with 1 < s < m, F2 € Bm>n_m such that JF2 = ??t,n-m, for some
t with 1 < t < m. Then every nearly decomposable matrix A € Bn is permutation
equivalent to a matrix В € M+ with the form
? =
Ao Fx
F2 Ax
(2.5)
where either m = 1 and Ax = 0 or m > 3 and A\ = (o^) € Mm(0,1) is nearly
decomposable with a!ts = 0.
Proof By Theorem 2.1.3(v), A ~p A' with A' > I. By Theorem 2.4.1(ii), A! - J is nearly
irreducible. By Theorem 2.3.5, there is a permutation matrix P such that P(A,—I)P^1 =
60
Combinatorial Properties of Matrices
PA'p-i _ j nas the form in (2.5), Assume that m > 2, then by Lemma 2.4.2, Ai is nearly
indecomposable with at least one 0-entry. Since nearly indecomposable matrices in M}
has no 0-entries, m > 3. Q
Example 2.4.2 A matrix A € Bn with the form in Theorem 2.4.2 may not be nearly
decomposable. Consider
Аг =
110 0
10 11
0 110
0 10 1
andB-
110 0 0
0 110 0
0 10 11
10 110
0 0 10 1
Then A\ is nearly decomposable. However, В — Еъ$ is fully indecomposable and so B,
having the form in Theorem 2.4.2, is not nearly decomposable.
Theorem 2.4.3 (Mine, [194]) Let A € Bn be a nearly decomposable matrix. Then
П ifn = 1l<H|<(3n-2
In ifn>2 J -" "- \ 3(n-i;
ifn<2
ifn>3
(2.6)
Proof The upper bound is trivial if n < 2, and so we assume that n > 3. By Theorem
2.1.3(iv) and by Theorem 2.3.7, \\A — I\\ < 2(n - 1) with equality if and only if there is a
tree T on n vertices such that A — I = A(T). Note that if n = 2, then T has two pendant
vertices (vertices of degree one); and if n > 3, then T has at most n — 1 pendant vertices.
It follows that
и
-/n<i 2(n-1) ifn = 2
11 -\ 2(n-l)-l ifn>3,
which implies the upper bound in (2.6).
The lower bound in (2.6) is trivial if n = 1. When n > 2, note that each row of a fully
indecomposable matrix has at least two 1-entries, and so the lower bound in (2.6) follows.
?
Theorem 2.4.4 Let n > 3 and к > 0 be integers such that 2n < к < 3(n — 1). Then
there exists A 6 B„ such that A is nearly decomposable and ||A|| = k.
Sketch of Proof Write fc = 2(n - 1) + e for some s with 2 < s < n - 1. Let Ts
denote a tree on n vertices with exactly s vertices of degree one. (For example, Ts can be
obtained by subdividing edges in a KiiS.) Let T% denote the graph obtained from Ts by
attaching a loop at each vertex of degree one of Ts. Then A(T?) is nearly decomposable
andP(r*)||=*.n
Combinatorial Properties of Matrices
61
2.5 Permanent
Definition 2.5.1 Let n > m > 1 be integers and let A = (oy) € Mm>n. The permanent
of A is
Per(A) = ]Г aHl o2i2 • • • amitn,
(*1,*а,-,»т)€*&
where P? is the set of all m-permutations of the integers 1,2, • • • , n.
Both Proposition 2.5.1 and Proposition 2.5.2 follow directly from the related definitions.
Proposition 2.5.1 Let D be a directed graph with |V(D)| —n>l vertices and without
parallel arcs, and let G be a simple graph onn = 2m > 2 vertices.
(i) Let A = A(D). Each term in Per (A) is a one, which corresponds to a spanning
subgraph of D consisting with disjoint directed cycles. Thus Per (A) counts the number
of such subgraphs of D.
О В
(ii) Let A = A(G). If G is a bipartite graph with A =
then Рег(Б) counts the number of perfect matchings of D
BT 0
, for some В € Mw
Proposition 2.5.2 Let A = (ay) € Мт%п with n > m > 1. Each of the following holds.
(i) Let с be a scalar and let A* be obtained from A by multiplying the ith row of A by
с Then Per(A') = с Per(A).
(ii) Fix i with 1 < i < m. Suppose for each j with 1 < j < n, a# = a\^ + a?. Let A'
and A" be obtained from A by replacing the (i,i)th entry of A by o^ and a"j, respectively.
Then Per(A) = Per(A')+ Per(A").
(iii) If A ~p B, then Per(A) = Per(?).
(iv) If m = n, then Per(A) = Per(AT).
(v) If Di € Mm and D2 6 Mn are diagonal matrices, then Per(DiAD2) = Per(Di)
Per(A) Per(?>2).
The following examples indicate that permanent and determinant behave quite
differently.
Example 2.5.1 The permanent as a scalar function is not multiplicative. We can routinely
check that
Perl
1 1
0 1
1 1
1 0
) ф Per
J
1 1
0 1
Per
1 1
1 0
Example 2.5.2 We can also verify the following:
Per
an
0>21
Ol2
«22
= det
an
a>2i
—ai2
a22
62
Combinatorial Properties of Matrices
However, Polya in 1913 indicated that one cannot compute Per (A) by computing det(A'),
where A' is obtained from A by changing the signs of some entries of A. Consider A3 =
(aij) в Mz. Then
detAl3 = #11022^33 +fll2a23G3i + Q>13Q>2\0>Z2
—аца23°32 ~~ Q>l2a2lQ>ZZ — 0>1Z0>220>ZI'
Assume that the signs of some entries can be changed so that the last three terms in
det(As) can be positive. Then an odd number of sign changes is needed to make the last
three term positive. On the other hand, to keep the first three term remaining the same
sign, an even number of sign changes would be needed. A contradiction obtains.
For examples in Mn with n > 3, we can consider the direct sum of A3 and 1п_з and
repeat the argument above.
Theorem 2.5.1 (Laplace Expansion) Let A = (a#) € Mm%n with n > m > 1. Let
a = (ti,»2>"" ih) be a fixed k-tuple of indices with 1 < i\ < ••• < ** < m, and
P = (ji,J2, • • • ,jk) denote an general A;-tuple of indices with 1 < ji < • • • < jk < n. Then
Per(A) = J2 perA[a|^] PerA(a|^).
all possible 0
In particular, we have the formula of the expansion of Per(A) by the ith row:
n
Per(A) = ?>,-PerA(i|j).
Sketch of Proof Each term in PerA[a|/?] multiplying each term in PerA(a|/?) is one term
in Per (A). For a fixed /3, there are k\ terms in a fixed PerA[a|/3] and I I (rn — k)\
\ m — k J
terms in PerA(a|/3). There are I J different choices of p. Therefore, there are
(:)и(;::)<™-'"¦(:)'",
terms in the right hand side expression, which equals the number of all terms in Per(A).
?
To introduce Ryser's formula for computing Per (A), we need a weighted version of
the Principle of Inclusion and Exclusion (Theorem 2.5.2 below). Let 5 be a set with
\S\ = n > 1, let F be a field and let W : S »-> F be a function (called the weight function).
Let Pi, P2, * • • , Pn be N properties involving elements in S and denote P = {Pi, • • • , Pn}.
Combinatorial Properties of Matrices
For any subset {Pix, Pi2, • • • , Pir} С Р write
W(Pil}Pi2r.^Pir)^ J2 W&
63
(2.7)
and
all poestble {P^ ,Pt2,— ,P»r}CP
The following identities are needed in the proof of the next theorem.
\m )\k ) \m)\ t-fc ) *
(2.8)
(2.9)
Theorem 2.5.2 For an integer m with 1 < m < N, let
J5(rn) = ^{^(5) J 5 € 5 and s has exactly m properties out of P}.
Then
S(™) = ?(-l)>'
H^m + j).
Sketch of Proof Assume that an 5 € S satisfies exactly t properties out of P. Consider
the contribution of s to the right hand side of the equality. If t < m, then s makes
no contribution; if t = m, then the contribution of s is W(s); and if t > m, then the
contribution of $ is
?(-1)''
* + J )\m)
¦С)
TP(s)
W(s)
(0)^(5) = 0,
Then the theorem follows by (2.8) and (2.9). ?
Corollary 2.5.2 With the same notation in Theorem 2.5.2, we can write
?7(0) = W(0) - WQ) + W(2) - • • • + {-l)NW(N).
64
Combinatorial Properties of Matrices
Theorem 2.5.3 (Ryser, [197]) Let A € Mm,n with n > m > 1. For each r with 1 < r < n,
let Ar denote a matrix obtained from A by replacing some г columns of A by all zero
columns, S(Ar) the product of the m row sums of Ar, and ?S(j4r) the sum of the
S(Arys with the summation taken over all possible Л/s. Then
per(A)=x:(n"m+ME^n-m+,).
Proof Let 5 be the set of all m-combinations of the column labels 1,2, • • • , n. Then each
s € 5 has the form (ji,j2> * * * ,jm), where 1 < ? < j2 < • • • < jm < n. Define
W(s) = ТУ(ji, j2, • * • , jm) = fllix02j2 * • • Omim,
and Pi = ШьЛ,--- Jm) € S\i e {jija,— Jm}}, 1 < * < n. Then W(r) = ?5(А0
and so Theorem 2.5.3 follows from Theorem 2.5.2. ?]
Corollary 2.5.3 With the same notation in Theorem 2.5.3, we can write
Рег(Л) = S(A) - ? S(^) + 53 5(Л2) - • • • + (-1)-1 ? S^-x).
Both Theorem 2.5.1 and Theorem 2.5.3 are not easy to apply in actual computation.
Therefore, estimating the upper and lower bounds of Рег(Л) becomes important. The
proofs of the following lemmas are left as exercises.
Lemma 2.5.1 Let A = (o#) € Bm>n with n > m > 1. If for each », Y%=i a*i ^ ш> then
Рег(Л) > О.
Lemma 2.5.2 Let A = (а#) € Bm>n with n < m < 1. If for each fc with 1 < fc < m — 1,
every Ar x n submatrix of A has at least к+1 nonzero columns, then every (m — 1) x (n — 1)
submatrix A* of Л satisfies Рег(Л') > О.
Theorem 2.5.4 (Hall-Mann-Ryser, [116]) Let A € Bm>n with n < m > 1 such that each
row of A has at leat 11-entries. Then each of the following holds.
(i) If t > m, then Per(A) > tl/(t - m)!.
(ii) If t < m and if Рег(Л) > 0, then Рег(Л) > t\.
Sketch of Proof By Lemma 2.5.1, we may assume that Рег(Л) > 0 for eachjfr with
1 < t < n.
Argue by induction on m. The theorem holds trivially when m = 1. Assume rh > 1.
Case 1 For some 1 < h < m — 1 and В € Mh, A ~p A\ where
A \B °
A1=\C D
Combinatorial Properties of Matrices
65
Then each row of В must have all the t positive entries, and so t < h < m — 1.
Moreover, Per(>4) = Рег(Б) Per(?>) > 0. By induction, Per(?) > t\ and so Per(A) > tl.
Case 2 Case 1 does not occur.
Then for each к with 1 < к < m - 1, every kxn submatrix of A must have at least
к + 1 nonzero columns. By Lemma 2.5.2, for each submatrix A(i\j), obtained from A by
deleting the ith row and the jth. column, satisfies Per(A(i\j)) > 0. Note that each row of
A(i\j) has at least (t — 1) positive entries. By induction,
{(t -1)! ift-Km-1
It follows by ^2]Li aij ^ ttnat when t < m,
Рег(Л) = ^а^Рег(Л(1|Л)
i=i
and when i > m,
Per(A) = ?а«Рег(Л(1Ш)
» (t-1)! t\
fe^(*-m)!^(*-m)r
The theorem now follows by induction. ?]
Theorem 2.5.5 (Mine, [195]) Let A € Bn be fully indecomposable. Then
Рег(А)>||Л||-2п + 2. (2.10)
An improvement of Theorem 2.5.5 can be found in Exercise 2.14. Gibson [99] gave
another improvement.
Theorem 2.5.6 (Gibson, [99]) Let A e Bn be fully indecomposable such that each row
of A has at least t positive entries. Then
Раг(Л) > ||Л|| - 2n + 2 + ]T(i! -1).
An important upper bound of Рег(Л) was conjectured Mine in [196] and proved by
Bregman [16]. The proof needs two lemmas and is due to Schrijver [230]).
66 Combinatorial Properties of Matrices
Lemma 2.5.3 Let A € Bn with Per (A) > 0. Let S denote the set of permutations on n
elements such that а € S if and only if fliLi а1<т{%) — 1» Then each of the following holds.
(О Ц П ( ?<*Шк)Г'(Ат) = П П Рег(Л(»Кг))).
i=l o»fc=l a€5 *=1
n n
(ii) К rx, • • •, rn are the row sums of A, then JJ rfегЛ = JJ JJr*.
i=l <reS i=l
Sketch of Proof For fixed i and &, the number of Per(A(t|&)) factors on the left hand side
of (i) is Per(A(i|&)) when од = 1 and 0 otherwise; and the number of Рег(Д(г|&)) factors
on the right hand side of (i) is the number of permutations а € S such that a(i) = k,
which is Per(A(i|fc)) when од = 1 and 0 otherwise.
For (ii), the number of r* factors on either side equals Per (A). []
Lemma 2.5.4 Assume that 0° = 1. If tb t2, • - • , tn are non negative real numbers, then
Sketch of Proof By the convexity of the function x log x,
{ФИФ^-Ф^-
and so the lemma follows. []
Theorem 2.5.7 (Minc-Bregman,[16]) Let A € Bn be a matrix with row sums r\, r2, * • • , rn.
Then
n
Per(A)< JJ(r4!)n.
Proof Argue by induction on n. By Lemma 2.5.3,
(РегАГ"(л> - Щ?одР*А(»|А))
П-l aifcPer(A(«|*))
< П(ГГГ(Л) П (РегА(г|*))р"^1*»
By Lemma 2.5.4,
-- — — — Per(A(tKt)))
( Рег(А))пРег<л> < Д
(n*)n
Combinatorial Properties of Matrices
Apply induction to each (A(i\a(i))) to get
67
П РефОДаЮ)) < П ( П M*) ( П ((''i-1)0^1
П M*) ( П ((*v-1)0^1
= П
n
- П
i=i
(г,!)^((г,-1)!)^
where the last equality above is obtained by counting the number of (г$\)г* factors and
the number of (fo — l)!)^"1 factors: for fixed j and а € S, there are n—rj of i's satisfying
% Ф j and aja(i) = 0 and there are rj — 1 of i's satisfying г ф j and Q>j<r(i) = 1. It follows
that
П Per(A(i|a(i))) < J]
<r€S
lb n^o^fo-1)*
v-1
П Рег(Л)
= П(П("0'
<r€S \i=l
- GH
This proves the theorem. []
An upper bound of permanents of fully indecomposable matrices in M+ was obtained
by Foregger [90]. A few lemmas are needed for the proof.
Lemma 2.5.5 Let A = (a#) € Af+ with n > 2 be a fully indecomposable matrix with an
entry ars > 2. Then
Lemma 2.5.6 Let n > 3 be an integer. Then n! < 2n(n~2>.
Lemma 2.5.7 (Foregger, [90]) Let A € M+ be a fully indecomposable matrix. If each
row sum of A is at least 3, Then
рег(Л) < 2Ил"-2п.
Lemma 2.5.8 Let n > 2 and let A = (a^) € Af+ be a fully indecomposable matrix.
Then there exists a fully indecomposable В e Bn and an integer j > 0 such that В < Л,
INI - ||B|| = j and Рег(Л) < 2* Per(B) - {2? - 1).
68
Combinatorial Properties of Matrices
Sketch of Proof If A 6 Bn, then j = 0 and В — A. Therefore, we assume that A has
an entry ars > 2. Let A' = A — Ers. By Lemma 2.5.5 and since Per (А) = Per(A')+
Per(A(r|s)), it follows that
Per(A) < 2 Per(A') - 1.
Argue by induction on the number of entries bigger than one to complete the proof of the
lemma. []
Theorem 2,5.8 (Foregger, [90]) Let A € M+ be a fully indecomposable matrix. Then
per(A) < 2"л»-2я + 1.
Sketch of Proof Argue by induction on n and the theorem is trivial if n = 1. Assume
n > 2. By Lemma 2.5.7, we may assume that r\ € {1,2}. Since A is fully indecomposable
and by Theorem 2.1.2, r\ = 2 and we may assume that the first row of A is 1,1,0, • • • , 0.
Let A1 denote the matrix obtained from A by adding Column 1 to Column 2 of A, and then
deleting both Row 1 and Column 1. By Theorem 2.1.2, A' is also fully indecomposable
and||A'|| = ||A||-2.
Case li€B„. Then
Per(A) = Per(A(l|l)) + Рег(Л(1|2)) = Рег(Л;).
By induction, Рег(Л) = Per(A') < г^'И-2**-1) + 1 = 2^л^2п + 1.
Case 2 A has an entry at least 2. Then by Lemma 2.5.8, there exist a matrix В € Bn
and an integer j satisfying Lemma 2.5.8. Applying Case 1 to В to get
Per(A) = 2j Per(B) - (2j - 1)
< 2J'(2,|B,l~2n + 1) - (2j - 1) = 2|,лИ~2п + 1.
This completes the proof. Q
Foregger also characterized matrices which have equality in Theorem 2.5.8. Interested
reader are referred to [90]. Brualdi and Gibson noted that a matrix with total support
can be viewed as the direct sum of totally indecomposable matrices under the ~p relation,
Theorem 2.5.8 can be extended.
Theorem 2.5.9 (Brualdi and Gibson, [27]) Let A € M+ be a matrix with a total support
with t fully indecomposable blocks. Then
per(A) < 2»л»-2п+*.
Combinatorial Properties of Matrices
69
The upper bound of Рег(Л) for fully indecomposable matrices was further improved
by Donald et al [75].
Theorem 2.5.10 (Donald, Elwin, Hager, and Salomon, [75]) Let A = (a#) € M+ be а
fully indecomposable matrix with row sums n = EJLi. a*i» * ^ * ^ n» an(^ column sums
Рег(Л) < 1 + min
{П(^-1).П(^-1)}-
Brualdi et al considered upper bounds of Рег(Л) when A € Bn with restrictions on
||Л||. If a = || Л|| for some Л € Bn, then r = n2 — a is the number of zero entries of A
For r with 0 < r < n2, Let
W(n,r) = {^€Bn:|H|=n2~r}.
and
ц{щт) = max{ Per(A) : A € #(n,r)}.
Note that if r > n2 - n, then /*(n, r) = 0.
Theorem 2.5.11 (Brualdi, Goldwasser and Michael, [28]) Let A € U(nyr) with r < л2—п.
Let o- = n2 — r and г = [<r/nj. Then
Рег(Л) < (r!)sri^^((r + l)!)2^. (2.11)
Sketch of Proof By Theorem 2.5.7, we need to estimate П2=1 W)7* > under the conditions
that iVs are positive integers and that J2i=ir* = a<
To do that, we first we establish the following inequality. For integers m, t with m > 2
and t > 1,
((m + t-l)!)^A=r(m!)A > ((ro + t)!)*k((ro- 1)!)^. (2.12)
For any integer fc > 2, we have fc2 > (k — l)(fc +1) and so
k2k(k-i) > p _ i)(jfe + i)]*(*-i).
It follows that
fc(M*)(»-i) (fc+ 1)*(*-D (jfc-i)a
(fc - i)(*+D(*-2) > jb(*-i)(*-2)
and so
11 (jfe _ l)(*+l)(*-2) > 11 jfe(*-l)(*-2)
70
Combinatorial Properties of Matrices
Cancel the common factors from both the numerators and the denominators to get
s(*+2)(s-l) > (s + !).(«-l)((e _ Щ2 (2 13)
Multiplying ss2~s((s -1)!)2*2~2 to both sides of (2.13) and then raise both sides of (2.13)
to the power of l/(s(s — l)(s + 1)) yields
It follows that
m+t-l m+t-l
П (•')'> П ((*-l)!)A((s + 1)!)*, (2.14)
s=m e=m
and so (2.12) follows from (2.14).
By (2.12),
max < ТТ(г*!) r< : r.'s are positive integers and ]jP r» — а >
can be reached if there exists some integers a, b and r satisfying
[а + Ь =П (2.15)
\ ar + 6(r + l) = <r,
such that a of the rVs are equal to r = [o/nj, 6 of the r^s are equal to r +1.
Note that the unique solution of (2.15) is
{а =пг + п — а
b = a — rar.
Therefore, by Theorem 2.5.7
ц(п,т) = max{ PerA : Лб#(п,т)}
< max S TT(r**)^ : r*'s aie positive integers and У2Г{=а(
Ui « J
= (r!)*((r + l)!)*.
This completes the proof. Q
The bound in (2.11) is reachable, for certain integer values,
integers a and b such that
For example, choose
nr + n — а _ _ a — nr
a = qjhi ^ =
г г -Ы
Combinatorial Properties of Matrices
71
Let A be the direct sum of a Jr's and b Jr+i's. Then A € Ы{п,т) and Рег(Л) = (r!)a((r +
i)0*.
Brualdi, Goldwasser and Michael also proved the following in [28]. The extremal
matrices are characterized in [28].
Theorem 2.5.12 (Brualdi, Goldwasser and Michael, [28]) Let ra,r be integers such that
n > 3, n2 - 2n < r < n2 - n. Then
Ai(n,r) = 2^n2-r-n)/2J.
2.6 The Class W(r,s)
The study of the class U(r, s) was started by Ryser and Pulkerson, among others, in the
early 1950's. The central problems have been the existence of matrices in W(r,s), the
structure of W(r,s), and counting and estimating |?/(r,s)|.
Definition 2.6.1 Let r = (ri,Г2, • • • ,rm)T and s = (si, S2> • • • ,sn)T be two non negative
vectors. We say r is increasing if ri > тг > • • • > rm. Similar definition holds for s. Let
n
?/(r,s) denote the set of all matrices A = (а#) € Bm>n such that У^а# = r*,l < i <
m
m and yjaij = Sj, 1 < j <n.
When Л € ?/(r,s), r,s are called the row sum vector and column sum vector of A
The examples below present different views of the matrices in U(r, s).
Example 2.6.1 Given r = (ri,Г2, • • • ,rm)T and s = (sb «2, • • • >$п)т» the set W(r,s) # 0
if and only if there exists a bipartite graph with bipartition (X, Y) with X = {a?i, • • • , rrm}
and Y = {t/i, • • • , t/n} such that the degree of each ж» is n and the degree of each yj is $j.
Example 2.6.2 Suppose r = (ri,r2,'-* ,^m)T and s = (si,s2,*** ,sn)T satisfy both
г» > 0 and Sj > 0 for all г and j, and J2HLir* = ??=i si = *• ^et 21 be a set with ?
elements. Then W(r, s) ф 0 if and only if there exist two partitions of T
T = Fx U F2 U • • • U Fm = Gi U <32 U • • • U Gni
such that \Fi\ = rit \Gj\ = *,¦ and |.Р} П Gj\ € {0,1}, where 1 < i < m and 1 < j < n.
Definition 2.6.2 Given a non negative vector r = (ri,r2, • • • ,т*т)г» let
*« = (1,1,---,1,0э-.-,0)Т, (1<«<т)э
be an n dimensional vector with l's in the first r» components and O's elsewhere. A matrix
of the form
3=[*i,*2,...,tfm]r (2.16)
72
Combinatorial Properties of Matrices
is a maximal matrix with row sum vector r.
For two n-dimensional non negative vectors s = (si, s2, • • • , sn)T and s' = (s[, si2, • • • , $Q
The vector s is majorized by s', written
s -< s',
if each of the following holds after necessary subscripts renumbering:
(2.6.2A) sx > s2 > • • • > sn and si > s2 > ¦ • • > s'n,
(2.6.2B) For each г with 1 < г < n - 1, ?}=i s, < ?*=1 sj, and
(2.6.2С)е;=15, = е;=14
Proposition 2.6.1 summerizes two observations that follow from the definition.
Proposition 2.6.1 Let A be the matrix defined in (2.16). Then
(i) the column sum vector s = (s"i, S2, ¦ • * , sn)T of A is monotone, and
(Hi) W(r,S) = {A}.
Gale and Ryser independently proved the necessary and sufficient condition (Theorem
2.6.1 below) for ?/(r,s) to be non empty. Their constructive proofs can be found in [%}
and [223]. Gale and Ryser's proofs cannot be used to estimate \U(r, s)|.
The necessity of Theorem 2.6.1 is straightforward and is left as an exercise, The
sufficiency of Theorem 2.6.1 follows from Theorem 2.6.2, due to Wei [273], which also
gives a nontrivial lower bound for \U(r, s)|.
Theorem 2.6.1 (Gale [95] and Ryser [223]) Given non negative vectors г = (ri, r2, • • - 3rm)?
and s = (si, 52, • • • , sn)T with r^ < n for each г with 1 < г < т. Let s be defined as in
Definition 2.6.2. Then W(r, s) ф 0 if and only if s < s.
Definition 2.6.3 Suppose that s' = (si,--* ,s'n)T and s" = (si',--- ,s'r[)T are two при
negative monotone vectors with s" -< s'. Let v be the smallest subscript such that s"-s'u >
0 and /i be the largest subscript such that s^ — s'^ > 0. Define
W(s" s') =
K ' ' ' min{S;-s»>S»-S'J
and define a new vector s^1) = (s^ ,••• ,Sn )r according to the two different cases as*
follows:
(2.6.3A) When s^ - s? > s'l - s'u > 0,
(2.6.3B) When «'„' - s'v > s^ - s% > 0,
S = (5l> " " >S/i-lS/i>S/i+l> * " ' >Sl/-l)Sl/ + (SI/ _ Sv)>SV+l> ' ' ' >Sn) ¦
flombinatorial Properties of Matrices
73
We can routinely verify that s" -< s^ -< s' (Exercise 2.19). Moreover, there exist an
Integer к > 1 and non negative n-dimensional vectors s^s^, • • • ,s(fc) such that
s" = s^fc) -< s^"1) -< ( s^> -< s(°> = s',
which is called a whole chain from s' to s".
Theorem 2.6.2 (Wei, [273]) Given non negative vectors r = (n,^,--- ,rm)T and s =
fei^2,- • • ,5n)T with n <n for each i with 1 < i < m. Let s be defined as in Definition
16.2. If s is monotone and if s 4 s, then
k-i
|W(r,s)|>n^(s5s^)>l,
i=0
where s^,s^1), • • ,s^-1^ are the elements in the whole chain from s to s.
Froof Denote the whole chain from s to s by
s = s<*> -< s^"1) -< • • • -< s^ -< sW = s, (2.17)
where s is the vector defined in Proposition 2.6.1 (i).
Let s" be a one of the vectors in the whole chain (2.17), let s' be a vector satisfying
$f{ -< s' and let A' — (a^) 6 U{v> s'). Assume that s^ > s'v and let B' the m x 2 submatrix
Г a'l» *iv 1
B, = ^ ai„
L <M <„ J
ЩоЬе that B' has at least s'^ — s'u > 2 rows of the form (1,0). By Definition 2.6.3, to
construct the whole chain, we should exchange the elements in the s" — s'u rows of the
form (1,0), if (2.6.3A) holds, or exchange the elements in the s'^ — s'^ rows of the form
(1,0), if (2.6.3B) holds. In either case, elements in min{s^ - s'^s" - sJJ rows in B' that
^areof the form (1,0) should be exchanged. The number of different ways to perform these
exchanges is W(s">s')-
It follows by (2.17), by Proposition 2.6.1 (Hi) and by the argument above that we can
generate at least Пг^о* W'fosW) different matrices that are all in ?/(r,s). Q
Example 2.6.3 (Wei, [273]) Let
r = (7,5,5,4,4,3,2,2,1)T and s = (7,6,4,4,4,4,4)r.
74 Combinatorial Properties of Mstffie$
Then s = (9,8,6,5,3,1,1)T and s -< s. A whole chain from s to s can be found as fttlowsr
s<°> = s =(9,8,6,5,3,l,l)r, W(s,s(°>) =
s^ =(9,8,6,4,4,1,1)T) W(s)S^) =
s(2) =(9,8,4,4,4,3,1)T, ^s,s(2)) =
s<3> =(9,7,4,4,4,4,l)r, W(s,sW) =
s<4> = (9,6,4,4,4,4,2)T, W(s, s<°>) =
s(5> =s = (7,6,4,4,4,4,4)T.
Therefore,
|W(r,8)|<
12600.
In [268], Wan refined the concept of totals chains and improved the lower boujid in
Theorem 2.6.2. An application of Theorem 2.6.2 can be found in Exercise 2.20.
Example 2.6.4 (Ryser, [223]) Let
1 0
0 1
and A2 =
0 1
1 0
Suppose A € U(v, s) which contains a submatrix A\. Let A' be obtained from A by
changing this submatrix A\ into Л2, while keeping all other entries of A unchanged. Then
A' 6 U(t, s). The operation of replacing the submatrix A\ by A2 to get A' from A i$ called
an interchange, and we say that A' is obtained from A by performing an interchange oa
Ax.
Theorem 2.6.3 (Ryser, [223]) For A, A' 6 W(r,s), A' can be obtained from A by
performing a finite sequence of interchanges.
Proof Without loss of generality, we assume that both r = (n,--- ,rm)T an<Ls =
(si,-- ,5n)T are monotone. Argue by induction on n. Note that the theorem holds
trivially if n = 1, and so we assume that n > 2, and that the theorem holds for smaller
values of n.
Combinatorial Properties of Matrices
75
Denote A — (a^) and A' = (a^). Consider the m x 2 matrix
<n 1
L flmn Лтп J
The rows of M have 4 types: (1,1), (1,0), (0,1) and (0,0). Since A, A! € ?/(r,s), A and A'
have the same column sums and so rows of Type (1,0) and (0,1) must occur in pairs.
If M does not have a row of Type (1,0), then M can only have rows of Type (1,1) or
(0,0), which implies that the two columns of M are identical. The theorem obtains by
applying induction to the two submatrices consisting of the first n — 1 columns of A and
A.
Therefore we assume that M has some rows of Type (1,0) and (0,1). Let j = j(AiA')
oe the smallest row label such that Row j of M is either (1,0) or (0,1). Without loss of
generality, assume that (djniajn) = (0? 1)-
By the minimality of j, there exists an integer к with j + I < к <n} such that a*n = 1.
Since a'jn = 1 and since A and A' has the same row sums, A has at least a 1-entry in Row
j, Let ajix, • ¦ • , Oji, be the 1-entries of A in the jth row. Then 1 < I < rj.
Since г is monotone, rj > r*. As ajn = 0 and Ofcn = 1, we may assume that a*t = 0
for some t 6 {«1,12, •• • ,ij}- Thus M has a submatrix
1 <*>kt CLkn
=
10]
0 1 !
Let A\ be the matrix obtained from A by performing an interchange on B. Note that
](Ait A') > j(A, A') + l, which means we can perform at most m interchanges to transform
A to a matrix A" € ?/(r, s) such that the last column of A" is identical with the last column
oM', and so the theorem can be proved by induction. Q
Definition 2.6.4 If both r and s are monotone, then ZY(r,s) is normalized class. For a
matrix Л = (a^) in а normalized class ?Y(r,s), a 1-entry ajy is called an invariant 1 if
no sequence of interchanges applied to A makes a^- = 0. Thus by Theorem 2.6.3, for а
aormalized class U, either every matrix in U has an invariant 1, in which case we say that
U is with invariant 1; or none matrix in U has an invariant 1, in which case we say that U
ia-without invariant 1.
Theorem 2.6.4 (Ryser, [222]) The normalized class ^(r,s) if with invariant l's if and
only if every matrix A € ?/(r, s) can be interchanged into the form
M =
din
0>2n
Jef *
* 0
76
Combinatorial Properties of Matrices
Here the integers e and / may not be unique, but they are determined by r and s, and
are independent of the choice of Л € ?/(r,s).
Proof The sufficiency is trivial since every entry in J is an invariant 1. To prove the
necessity, assume that U = U(t, s) is with invariant l's and that every matrix of U has an
invariant 1 at the (e, /)th entry with e + / maximized.
Then each A s= (ay) € U can be viewed as
\WX]
[Y Z у
where W e Me,/(0,1). We must show that W = J and Z = 0.
If W Ф J, then by the monotonity of r and s, at most two interchanges applied to
A would change ae/ into a 0-entry, contrary to the assumption that oe/ = 1 is invariant.
Therefore, W = J and every entry in W is an invariant 1.
Note that since e + / is maximized, we may assume that a/,/+i = 0, for some t with
1 < I < e; for otherwise aej+i would be an invariant 1, contrary to the maximality of
e + /.
Now if Z has a 1-entry in Row t (say), then we may assume that <H,f+i = lj for
otherwise by the monotonity of r and s, an interchange can be applied to get a*,/+i — 1,
where e + 1 < t < m. If for some i with 1 < j < e, a^j = 0, then an interchange on
the entries aij, aij+i^j and atj+i would make aij = 0, contrary to the fact that every
entry in W is an invariant 1. Therefore, every <hj is also an invariant 1, 1 < j < e,
contrary to the maximality of e + /. It follows that Z = 0, as desired. Q
In [31], Theorem 2.6.4 was applied to study the lattice structure of the subspaces
linearly spanned by matrices in W(r,s):
?(r>s) = j Y^°iAi : Ai e w(r>s) and Ci € Z, 1 < г < П .
In [268], Wan studied the distribution and the counting problems of invariant l's in a class
Z/(r,e).
Using binary numbers, Wang [269] gave a formula of |W(r,s)|. For an integer к > О,
let I(k) denote the number of l's in the binary expression of the integer к — 1; let pi be
number of components of r that are equal to i, 1 < г < n; and for s = (si, • • ¦ , 5л)т, let
Qj = Sj-pni l<j<m.
Theorem 2.6.5 (Wang, [269])
№,.)1=епп(г;)'
Combinatorial Properties of Matrices 77
where п#* and m^* are functions oipi,qj and ?#*, given by the recurrence definition: for
1 < i < n - 1, l<i<n-landl<*< 2'-1,
tyjb if i + j — n < I(k) < г, (i and fc cannot be both equal to 1),
0 if I(k) > »,
mjk if /(A;) < i + j - n.
ni(7-i)h±L — ^i(j_i)*±i h° fc is odd and j > 1,
m«(i-i) I if fc is even ,
2.7 Stochastic Matrices and Doubly Stochastic
Matrices
Definition 2.7.1 Given a matrix A = (oy) G Af+(R), Л is a stochastic matrix if for each
г with 1 < i < та, ?"=1 aij = 1» anc* ^ is a doubly stochastic matrix if for each i with
1 < i < n, both SjLi %' = 1 and ?"=1 a^ = 1. Define
Qn = (P e Af+(R) | P is doubly stochastic}.
Theorem 2.7.1 Let A € M+(R). Each of the following holds.
(i) A is stochastic if and only if A J = J, where J = Jn.
(ii) Л is stochastic if and only if 1 is an eigenvalue of A and the vector e = JnXi is an
eigenvector corresponding to the eigenvalue 1 of A.
(iii) Л € fin if and only if A J = «7Л = J, where J =z Jn.
(iv) If Л is stochastic and if Л ~p 2?, then В is also stochastic.
(v) If Л € Пп and if Л ~p ?, then Б is also doubly stochastic.
(vi) Suppose Л be a direct sum of two matrices A\ and Л2. Then Л is stochastic if
and only if both A\ and Л2 are stochastic.
(vii) Suppose Л be a direct sum of two matrices Ax and Л2. Then Л € Пп if and only
if both Л1 and Л2 are doubly stochastic.
Proof (i)-(iii) follow directly from Definition 2.7.1; (iv) and (vi) follow from (i); (v) and
(vii) follow from (iii), respectively. Q]
Theorem 2.7.2 If Л € fin is doubly stochastic, then Рег(Л) > О.
Ttlijk = \
78
Combinatorial Properties of Matrices
Proof Suppose that A € ftn. If Рег(Л) = 0, then by Theorem 6.2.1 in the Appendix, A
is permutation similar to
X Y
B =
Opxg Z
where p + g = n +1. It follows that
n = \\B\\>\\X\\ + \\Z\\=p + q = n + l,
a contradiction. Q
The following Theorem 2.7.3 was conjectured by Van der Waerden [266], and was
independently proved in 1980 by Ealikman [85] and Egorysev[79]. A simpler proof of
Theorem 2.7.3 can be found in [199] and [163].
Theorem 2.7.3 (Van der Waerden-Falikman-Egorysev, [266], [85], [79]) If Л € Пп, then
Per(A)>^.
Example 2.7.1 Let A = - Jn. Then Рег(Л) = —.
n nn
Theorem 2.7.4 If A € €ln, then A ~p B, where В is a direct sum of doubly stochastic
irreducible matrices.
Proof Arguing by induction on n. It suffices to show that if A is a doubly stochastic
matrix, then A ~p B, where Б is a direct sum of doubly stochastic matrices.
Nothing needs a proof if A is irreducible. Assume that a doubly stochastic matrix A
is reducible. By Definition 2.1.1, A ~p В for some В € Mn of the form
B =
X Y
0 Z
where X € M* and Z € Mn-k for some integer к > 0. By Theorem 2.7. l(v), В is
doubly stochastic, and so both \\X\\ = к and \\Z\\ = n - к. It follows that n = ||B|| =
11*11 + 11*11 + l|2|| = k + \\Y\\ + (n - к), and so \\Y\\ = 0, which implies that Y = 0. By
Theorem 2.7.1 (vii), both X and Z are doubly stochastic. Q
Theorem 2.7.5 (Birkhoff, [8]) Let A € M+. Then Л € On if and only if there exist an
integer t > 0 and positive numbers ci, c2, • • • , c* with ci+c2H be* = 1, and permutation
matrices Pi,• • • , P* such that
t
Proof If Л = ?!=i CiP», then Л7 = YLi °ipiJ = ?i=i °iJ = J> Similarly, J A = J.
Therefore Л 6 fin by Theorem 2.7.1(iii).
Combinatorial Properties of Matrices
79
Assume now that A e ton. The necessity will be proved by induction on p(A), the
number of positive entries of A. By Theorem 2.7.2, p(A) > n.
If p(A) = n, then A is itself a permutation matrix, and so t = 1, c\ = 1 and Pi = A.
The theorem holds.
Assume p(A) > n. By Theorem 2.7.2, Per(A) > 0, and so there must be a
permutation 7Г on n elements such that the product а>1п(1)а>2тг(2\'' *Амг(п) > 0- bet c% =
nunfaiwCi)» u2tt(2) ,• • • ,аПтг(п)} 3^^ let Pi = (p^) denote the permutation matrix such
that pij = 1 if and only if (i,j) = (г,7г(г)), for 1 < i < n. Since A is doubly stochastic,
0 < ci < 1. If ci = 1, then ailt(i) = 1 for all 1 < г < n, and so by Theorem 2.7.1(iii),
A = Pi. Therefore, p(A) = n, contrary to the assumption that p(A) > n. Therefore
Ci < 1. Let
M = - (A - dPi),
1-Ci
Then Л1J = JAi = J and so Аг is also double stochastic with p{A{) = p(A) — 1. By
induction, there exist positive integers ?,c^, • - • ,cj with с^Л 1-cj = 1, and permutation
matrices P2, • • • ,P* such that
It follows that
Л = (1 - d)Ai + C^ = dPi + (1 - Ci)(c?fi + • • • + cJP*).
Since c\ + (1 - Ci)(c2 H h 4) = litne theorem follows by induction. Q
Definition 2.7.2 A matrix A € Bn is of doubly stochastic type if A can be obtained from
a doubly stochastic matrix В by changing every positive entry of В into a 1. Let Г2л
denote the set of all n x n doubly stochastic matrices.
A digraph D is k-cyclic if D is a disjoint union of к directed cycles. Let D be a
digraph on n vertices {vir" ,vn}> ш& ^et *ь*2>*** ,Jn be non negative integers. Then
Я(*ъ*2>--* yln) denote the digraph obtained from D by attaching U loops at vertex V{,
l<i<n.
Example 2.7.2 The matrix
[о i J *
is not of doubly stochastic type (Exercise 2.25).
Theorem 2.7.6 Let A € Bn. Then A is a matrix of doubly stochastic type if and only
if for some integers *,fci,--- ,fc* > 0, D(A) is a disjoint union of t spanning subgraphs
DiiD2)"- ,Dt of D(A), where Di is fc^-cyclic, 1 < i < L
80
Combinatorial Properties of Matrices
Sketch of Proof Note that P € Mn is a permutation matrix if and only if D(P) is a
fc-cyclic digraph on n vertices, for some integer A; depending only on P. Thus Theorem
2.7.6 follows from Theorem 2.7.5. ?
Definition 2.7.3 Let D be a digraph on n vertices {vi,--- ,vn}, and let luhr" Jn
be non negative integers. Then D(h, l2, • • • , /n) denote the digraph obtained from D by
attaching k loops at vertex v$, 1 < i < n.
A digraph D is Eulerian if for every vertex v € V(D), d*~(v) = d~(v).
Corollary 2.7.6 A digraph D is Eulerian if and only if for some integers /i, • • • ,/n > 0,
the adjacency matrix A(D(lit • • • , /n)) is of doubly stochastic type.
Sketch of Proof Note that D is Eulerian if and only if D is the disjoint union of directed
cycles C\, C?2>' * * , Ot of D. Since each d can be made a spanning subgraph by adding a
loop at each vertex not in Ci, and so the corollary follows from Theorem 2.7.6. Q]
Definition 2.7.4 Let r,s > 0 be real numbers and n > m > 0 be integers satisfying
rm = sn. Let ro denote an m-dimensional vector each of whose component is r, and let
s0 denote an n-dimensional vector each of whose component is s.
In general, for an integer к > 0, let s = k0 denote a vector each of whose component is
fc; and define Un(k) — W(k0,k0) П Bn. Thus every matrix A € Un(k) has row sum к and
column sum fc, for every row and column of A. In particular, Un(l) = On.
Theorem 2.7.7 Let A € Bm,n for some n > m > 0. Then A € W(ro,s0) if and only if
there exist integers t,ci, • • • ,c* > 0 and permutation matrices Pi, • • • ,P*, such that
A = ciPx + c2P2 + • • • + c*Pt.
Sketch of Proof If n = m, then r = s and so ?Л is doubly stochastic. Therefore,
Theorem 2.7.7 follows from Theorem 2.7.5.
Assume that m < n. Then consider
'A
Then A' € Un(5), and so Theorem 2.7.7 follows by applying Theorem 2.7.5 to A'. Q
Theorem 2.7.8 Let A € Bn. Then A € Un(k) if and only if there exist permutation
matrices Pi, • • • ,P* such that
A' =
Proof It follows from Theorem 2.7.5. Q
Combinatorial Properties of Matrices
81
Example 2.7.3 Let G be a fc-regular bipartite graph with bipartite sets X and Y. If
\X\ = \Y\ = n, then the reduced adjacency matrix of A is in Щк), and so by Theorem
2.7.8, E(G) can be partitioned into к perfect matchings.
Theorem 2.7.9 If Л € Ып{к), then
Рег(А)>^~0)П^.
Proof This follows from Theorem 2.7.3. ?
Another lower bound of Per (A) for A € Un(k) can be found in Exercise 2.26. When
к = 3, the lower bound in Theorem 2.7.9 has been improved to ([198])
Рег(Л)>б(|)" .
However, the problem of determining the exact lower bound of Per (A) for A € Un(k)
remains open.
2.8 Birkhoff Type Theorems
Definition 2.8.1 Recall that Vn denotes the set of all n by n permutation matrices, and
that fln denotes the set of all n by n doubly stochastic matrices.
For two matrices А, В € Mn, define
V(A,B) = {P€Vn : AP = PB)
V{A,B) = lY,^ : J2ci = laD&PieV(A9B)\.
Also define
Пп(Л,Б) = {РеПп : AP = PB}.
When A = B, write V(A), V(A) and Пп(А) for V(A, Л), V(A, A) and Г2П(Л, Л),
respectively. Note that when A = A(G) is the adjacency matrix of a graph G, V(A) is the set
of all automorphisms of G.
Example 2.8.1 Let G be the vertex disjoint union of a 3-cycle and a 4-cycle, let A = A(G)
and В — j J7. Then AB = В Л and so В € Q7(A). However, as there is no automorphism
of G that maps a vertex in the 3-cycle to a vertex in the 4-cycle, В ? V(A).
Definition 2.8.2 A graph G is compact if V(A((?)) = Sln(A(G)).
82
Combinatorial Properties of Matrices
Example 2.8.2 Note that G(In) is the graph with n vertices and n loop edges such that
a loop is attached at each vertex of G(In). Note that V(In) = Vn.
Thus Birkhoff Theorem (Theorem 2.7.5) may be restated as
which is equivalent to saying that G(In) is compact. Tinhofer [260] indicated that theorems
on compact graph families may be viewed as Birkhoff type theorems.
Definition 2.8.3 Let G be a graph with n vertices and without multiple edges. Let G*
be the graph obtained from G by attaching a loop at each vertex of G. Thus K? = G(Jn)
is the graph obtained from the complete graph Kn by attaching a loop at each vertex of
Kn.
The graph G can be viewed as a subgraph of K*. Moreover, if G is loopless, then G
can be viewed as a subgraph of Kn. The full completement of G is G*c = Kn — E(G). If
G is loopless, then the completement of G is Gc = Kn — E{G).
The proof of the following Theorem 2.8.1 is straightforward.
Theorem 2.8.1 Each of the following holds,
(i) If G is compact, then G*c is also compact,
(ii) If a loopless graph G is compact, then G* is also compact,
(iii) If a loopless graph G is compact, then Gc is also compact,
(iv) KnyKniKn are compact graphs.
Theorem 2.8.2 (Tinhofer, [260]) A tree is compact.
Theorem 2.8.3 (Tinhofer, [260]) For n > 3, the n-cycle Cn is compact.
Proof Let V(Cn) = Zn, the integers modulo n, and denote A = A(Cn) = (a#), where
J 1 if j = t ± 1 (mod n)
I 0 otherwise.
It suffices to show ПП(А) С *>(А).
Argue by contradiction, assume that there is an X = (xij) € Г2П(Л) \7>(Cn) such that
p(X), the number of positive entries of X, is minimized. To find a contradiction, we shall
show the existence of a real number e with 1 > e > 0, matrices Y e ftn and P € V(A)
such that X = (1 - e)Y + eP and such that p(Y) < p(X).
Since XA = ДХ,
Xi+ij + ar»-ij = Si^_i + a?,-,i+i, for all г, j with г, j € Zn.
It follows that for all г, j with 1 < i,j < n,
^i+lj-i — ^i,i-i-l = Xlj — Xn,j-1 BJld Xi+ij+i — Xij+i+i = Xij — Xnj+i.
Combinatorial Properties of Matrices
83
Note that the right hand sides are independent of t.
In each of the cases below, a matrix P = (pik) € V(A) is found with the property that
Xik > 0 whenever pa > 0. Let e = mm{xik\pik = 1}- If с = 1, the X = P € V(A), contrary
to that assumption that X is a counterexample. Hence 0 < e < 1. Let Y = ^n{X — cP).
Then p(Y) < p(X) and by XA = AX, PA = AP and by Theorem 2.7.1(iii), У € ftn(A),
and so a contradiction obtains.
Case 1 xij — arn>j_i > 0, for some fixed j.
Define P = (pik) as follows:
__ J 1 if fc s У + 1 — i (mod n)
| 0 otherwise.
As St+ij-i - Xij-i-i = xij - snj_i, Si* > 0 whenever p** > 0. Note that P is the
reflection about the axis through the positions ^±1 and n+p^1, and so P € ^(A).
Case 2 xij — ffn,i-i < 0, for some fixed j.
In this case, define P to be the reflection about the axis through the positions 2^ and
n+g~l. The proof is similar to that for Case 1.
Case 3 x\j — xnj+i > 0, for some fixed j.
Define P = (pit) as follows:
f i if;
" \ 0 otl
_ : fc = j +1 — 1 (mod n)
otherwise.
As Xi+ij+i — Xitj+i+i = a?i j - a:n,j+i > 0, ж«* > 0 whenever pik > 0. Note that P is a
clockwise rotation of Cn, and so P € ^(A).
Case 4 arij — xn,j+i < 0, for some fixed j.
In this case, define P to be an anticlockwise rotation, similar to that in Case 3.
Case 5 Xij = xnj+i = xn,j-i, for all j with 1 < j < n.
Then, а:1+1>)7- = tfij+i = a?i-ij = a^-i, for all i, j with 1 < i,j < n. It follows that
there exist matrices U, V and numbers a,/? > 0, such that X = C/ + V and such that
[ 0 otherwise, (^
/3 if i-j = l(mod2)
0 otherwise.
Note that if а > 0, then Z7 > the sum of some reflections; if 0 > 0, then У > the sum of
some reflections. Thus we can proceed as in Case 1-4 to express
Х = (1-€)К + бР,
for some P € V(A) and У € ПЛ(Л). If а = /? = 0, then X = 0.
84
Combinatorial Properties of Matrices
Therefore, in any case, if X ф 0, a desired P can be found and so this completes the
proof. []
Definition 2.8.4 Let A € Mn be a matrix. Define
Сопе(Л) = {В € Af+ : В А = AB}
*№ = I ? <*P : <*>oi.
It follows immediately from definitions that
V(A) С Сопе(Л).
Let <2 be a graph with A = Л(<2). If V(A) = Сопе(Л), then C? is a supercompact graph.
Theorem 2.8.4 Let At = \ ]T) cpP : cp > 0 > be a set of n x n matrices. Let G be
[Р€7>(Л) J
a graph on n vertices with A — A(G). Each of the following holds.
(i) If Y € Аи then G(Y) is a regular graph. (In other words, Y € Un(q) for some
number g.)
(ii) If Y € 'Р(Л) and if У # 0, then there exists a number q > 0 such that |У € Р(Л).
Moreover, q—lif and only if Y € Пп.
(iii) (Brualdi, [19]) If G is supercompact, then G is compact and regular.
Sketch of Proof (i) follows from Theorem 2.7.7. For (ii), note that Y = ?,РсрР.
Therefore let q = Y,p CP an<^ aPPty BirkhofF Theorem (Theorem 2.7.5) to conclude (ii).
For (iii), by definitions, V(A) С ?2П(Л). It suffices to show the other direction of
containment when G is supercompact. Let A = A(G) and assume that V(A) = Сопе(А).
By (i), G = (?(Л) is regular. By definitions and by (ii), Пп{А) С Сопе(Л) = V(A) С V(A).
D
Example 2.8.3 There exist compact graphs that are not supercompact. Let G be a tree
with n > 3 vertices. By Theorem 2.8.3, G is compact. Since n > 3, G is not regular, and
so G is not supercompact, by Theorem 2.8.4(i).
Example 2.8.4 A compact regular graph may not be supercompact. Let G be the disjoint
union of two -KVs. With appropriate labeling,
A = A(G) =
0 0 10
0 0 0 1
10 0 0
0 10 0
Combinatorial Properties of Matrices
85
Let
X =
10 0 0
0 0 0 0
0 0 10
0 0 0 0
We can easily check that XA = XA and so X € Сопе(Л). But by Theorem 2.8.4(i),
X & V{A)y and so G is not supercompact.
Theorem 2.8.5 (Brualdi, [19]) For n > 1, the n-cycle Cn is supercompact.
Theorem 2.8.6 (Brualdi, [19]) Let n, к > 0 be integers such that n = hi, let Я be a
supercompact graph on к vertices, and let G be the disjoint union of I copies of H. Then
G is compact.
Proof Let В = A(H) and A = A(G). Then A is the direct sum of / matrices each of
which equals B.
By contradiction, assume that G is not compact, and so there exists a matrix X €
Qn(A) — V(A) with p(X), the number of nonzero entries of X, is as small as possible.
Write
X =
X\\ X\2
|_ Хц Х12
X21
Xu J
where each X{j € M^. Since XA = AX, for all 1 < ij < l, ХцВ = BXij, and so
Xij € V(B)i by the assumption that Я is supercompact. By Theorem 2.8.4(i), there is
a number gy > 0 such that Xy € Z4(ftj)- Let Q = (</y) denote the / x 2 matrix. Since
X € Пп, Q € ft|. By Theorem 2.7.5, Q = ?Pe7>, cPP, where ? cp = 1. Therefore, there
exists a P = (pij) € Viy which corresponds to a permutation aon {1,2, • • • ,/}, such that
QsM*) > 0 for all 1 < s < Z.
Fix an s = 1,2, • • • ,/. Since XSta{s) € V(B), XSi<r{s) = T,PeVi(B) cPp> where cp ^ °-
Hence there exists a Ps € 7MB), which corresponds to an automorphism gs of Я, such
that for all 1 < и < fc, the (w,<7s(tt))-entry of X$i<7^ is positive.
Construct a new matrix R = (r^) € Afn as follows. Write
R =
Ru -R12
-R21 -R22
-Ri/
R21
Rn J
where Д
, =JPS iff
*'' \ 0 oth
= s and j = <t(s)
otherswise.
86
Combinatorial Properties of Matrices
Since PSB = BP3i RA = AR. Since Ps G Vk, R € Vn. Thus Л is an automorphism
of G and so R e V(A). Moreover, хц > 0 whenever r# = 1, for all 1 < i, j < n. Let
б = minfcij : r# = 1}. If с = 1, then since X, Д € Пп, X = R € V(A) С V{A), contrary
to the choice of X. Therefore, 0 < e < 1. Let Y = j~(X - сД). Then by Theorem
2.7.1(iii), and by X,R € ПП(Л), У € Пп(4) with р(У) < p(X). By the minimality of X,
Y e V(A)t and so X = (1 - б)У + €# € Р(Л), contrary to the choice of X. Q
Corollary 2.8.6 If G is the disjoint union of Ck (cycles of length fc), then G is compact.
When к = 1, Corollary 2.8.6 yields Birkhoff Theorem. Therefore, Corollary 2.8.6 is an
extension of Theorem 2.7.5. See Exercise 2.30 for other applications of Theorem 2.8.6.
Definition 2.8.5 Let k, m, n > 0 be integers with n = km, A graph G on n vertices is
a complete к-equipartite graph, (a C.fc - e graph for short), if V(G) = Ujg^ is a disjoint
union with \V{\ = к, for all 1 < i < m, such that two vertices in V(G) are joined by an
edge e € #(С?) if and only if these two vertices belong to different VVs.
Let G be a C.fc — e graph on n vertices. If к = 1, then G = JiT,»; if 2k = n, then
<7 = Ufa,a. Theorem 2.8.6 can be applied to show that C.k — e graphs are also compact
graphs (Exercise 2.30).
Theorem 2.8.7 (Brualdi, [19]) Let n = 2m > 2 and let M С Е(Кт>т) be a perfect
matching of 2fm>m. Then KmtTn — M is compact.
Proof We may assume that m > 3. Write V(Km>m — M) = Vi U V2, where
Vl = {vi,V2,--- ,Vm} and V2 = {Vm+l,Vm+2>--* ^2m}»
and Af = {ei | e,- joins v* to vm+i, where 1 < i < m}. Hence we may assume that
А = А(Кт,т-М) =
0 Jm ~~ -Im
Jm *т "
By contradiction, there exists an X € Un(A) — V(A) with p(X), the number of positive
entries of X, minimized. Write
X =
X\ X2
Xz X±
Then by AX = XA,
Xi(Jm — /m) = (Jm — 1гп)Ха
X±(Jm — Jm) = (Jm — Im)Xi
and so (Xi + X4) Jm = Jm(Xi + X4). It follows that there exists a number a > 0 such
that a is the common value of each row sum and each column sum of X\ + X*. Similarly,
Combinatorial Properties of Matrices
87
there exists a number b > 0 such that b is the common value of each row sum and each
column sum of X2 + X3.
Let ri, • • • ,rm denote the row sums of Xi and let si, • • • , sm denote the column sums
of Xi. Then the row sums and column sums of X4 are respectively a — n,-- ,a — rm and
Ь-Si,--- ,b-sm.
Let z^ denote the (г, j)-entry of X\. Since X\ — X4 = Xi Jm — JmX^ then (г, gentry
of X4 is гц + a — ti — Sj. By the definition of a, Jm(Xi + X4) = aJmi and so for fixed j,
m
i=l
= 2sj + ma - (ri + Г2 H 1- rm) - msj.
Thus by m > 2 that, for each j with 1 < j < m,
1
m-2
(m-l)a-]TVi
It follows that $1 = s2 = • • • = sm. Similarly, n — r2 = • • • = rm. Hence there exist
0i,a4 > 0 such that a = ai + a4, Xi € W(ai), X4 € W(a4), and
X4 = Xi + (a - 2oi) Jm.
Compare the row sums and column sums of the matrices both sides to see a — a\ = a± =
a\ + m(a — 2ai), and so
(m-l)(a-2ai) = 0.
Since m > 2, a = 2ai and so Xi = X±. Similarly, X2 = X3, and so
X =
Xi X2
X2 Xi
where Xi € W(ai), X2 € ?/(a2), and 01 + a2 = 1.
Suppose first that 01 ^ 0. Then ^-Xx € Пт and so by Theorem 2.7.5, there is a
Q = (^-) e pm such that ^ > 0 whenever qij = 1. Let r denote the permutation on
{1,2, • • • ,m} corresponding to Q, and let P € ft2m be the direct sum of Q and Q. Then
P corresponds to the automorphism of ifm>m — M which maps i/j to vT^) and vm+i to
um+r(i),andsoP€^(^)«
Let e = min{^ : qij = 1}. If e = 1, then X = P, contrary to the assumption that
X 0 P(3). Therefore, 0 < e < 1. Let У = j~(X - eP). Then by Theorem 2.7L(iii) and
by X, P € Г2П(Л), Y 6 ftn(A) with p(Y) < p(X) - 2. By the choice of X, У € V(A). But
then X = (1 - e)Y + eP € 7>(Л), contrary to the assumption that X ? Р(Л).
88
Combinatorial Properties of Matrices
The proof for the case when а<ъ Ф 0 is similar. This completes the proof. ?]
It is not difficult to see that Kmm — M (m > 3) is also supercompact.
Theorem 2.8.8 (Liu and Zhou, [187]) Let G be the 1-regular graph on n = 2m > 4
vertices. Then G is not supercompact.
Proof Let A — A{G) and consider these two cases.
Case 1 n = 0 (mod 4). Then A can be written as
A =
0 I2
h 0
0 0
Define
X =
0 0
Y 0 ••
0 У ••
• 0 "
• 0
, where Y =
" 1 0 1
0 0 J
Then X € Bn and AX* = ХЛ, and so X € Сопе(Л). However, as the row sums of X are
not a constant, X 0 ^(Л) by Theorem 2.8.4(i), and so G is not compact.
Case 2 n = 2 (mod 4). Let
Then A can be written as
A =
0 1
1 0
andy =
1 0
0 0
0
0
0
0
h
0 -
о ..
0 -
h •¦
0 ••
0
0
* Р(1Д) *
0
0
• 0
• h
• 0
• 0
• 0
h
0
0
0
0
Combinatorial Properties of Matrices
89
Define
Y
0
0
0
0
0 ••
Y ¦•
0 ••
о ..
0 ••
. 0 •«
. о ••
• h •¦
• 0 •
. о ••
• 0
• 0
• 0
• Y
• 0
0
0
0
0
Y
x =
Then X € Сопе(Л) \ V(A) as shown in Case 1, and so G is not compact. Q
Example 2.8.5 The complement of a supercompact graph may not be supercompact.
Let G = C4 denote the 4-cycle. Then G is compact. But Gc is a 1-regular graph on 4
vertices, which is not supercompact, by Theorem 2.8.8. Since Gc is not supercompact, it
follows by Definition 2.8.4 that G*c is not supercompact either.
Definition 2.8.6 Let k,m > 0 be integers. A graph G is called an (m>k)-cycle if V(G)
can be partitioned into Vi U V2 U ¦ • • U Vm with \V{\ = k, (1 < i < m) such that an edge
e € E(G) if and only if for some t, one end of e is in Vi and the other in K4-1» where
i = 1,2, • • • , m (mod m).
Example 2.8.6 An (m, l)-cycle is an m-cycle. When m = 2 or m = 4, an (m, fc)-cycle is
a complete bipartite graph Ifm* «ь. К Л(Ст) = J9, then an (m,fc)-cycle has adjacency
matrix В 0 Jm. For example, the adjacency matrix of the (4,2)-cycle is
0
J2
0
h
h 0 J2
0 J2 0
J2 0 J2
0 J2 0
Theorem 2.8.9 (Brualdi, [19]) Let m, к > 0 be integers. An (m, &)-cycle is supercompact
if either к = 1, or к > 2 and m = 4, or A; > 2 and m ^ 0 (mod 4).
Example 2.8.7 The (8,2)-cycle is not compact, and so it is not supercompact. To see
this, let A = A(Cs) 0 J2 be the adjacency matrix of the (8,2)-cycle, and let
if j — i = 0,1 (mod 4)
if j -i = 2,3 (mod 4)
Let X = (Xij) denote the matrix in M\q which is formed by putting each of the blocks
Xij, 1,< ij < 2 in the ijth position of a 2x2 matrix. ThenX € Qn(A)\V(A). (Exercise
2.31).
У = i
f
s.
'\ ol
0 0 J
" 0 0 1
1° \\
90
Combinatorial Properties of Matrices
Open Problems
(i) Find new compact graph families.
(ii) Find new techniques to construct compact graphs from supercompact graphs.
(iii) Construct new supercompact graphs. It is known that when к = 1, a C.k - e
graph is supercompact; and when к = 2, a C.k — e graph is compact. What can we say
for к > 3?
(iv) Is there another kind of graphs whose relationship with supercompact graphs is
similar to that between supercompact graphs and compact graphs?
2-9 Exercise
Exercise 2.1 (This is needed in the proof of Theorem 2.2.1) Let D be a directed graph.
Prove each of the following.
(i) If D has no directed cycles, then G has a vertex v with out degree zero.
(ii) D has no directed cycles if and only if the vertices of G can be so labeled v\, v2, • • •, vn
that (viVj) € E(D) only if i < j. (Such a labeling is called a topological ordering.)
(iii) If Di, D2i • • • , Dk are the strongly connected components of D, then there is some
D{ such that G has no arc from a vertex in V(D{) to a vertex V(D) — V(A)« (In this
case we say that Di is a source component, and write tf+(A) = 0» )
(iv) The strong components of D can be labeled as DX,D2, • - • ,?>* such that D has
an arc from a vertex in V(Di) to a vertex in V(Dj) only if г < j.
Exercise 2.2 Prove Lemma 2.2.1.
Exercise 2.3 Prove Lemma 2.2.2.
Exercise 2.4 Let A € Mn be a matrix with the form
A =
where each A{ is a square matrix, 1 < i < к. Show that A has a nonzero diagonal if and
only if each At has a nonzero diagonal.
Exercise 2.5 Let A = (а#) € М+. Then A is nearly reducible if and only if A is
irreducible and for each avq > 0, A — apqEpg is reducible.
Exercise 2.6 Prove Proposition 2.3.1.
Exercise 2.7 Let D be a digraph, let W С V(.D) be a vertex subset and let Я be a
subgraph of D. Prove each of the following.
Ai
*
*
*
0
A2
*
*
0
0
4*-l
*
0
0
0
Ak
Combinatorial Properties of Matrices
91
(i) If D is minimally strong and if D[W] is strong, then D[W] is minimally strong.
(ii) If D is strong, then D/H is also strong.
(iii) If both H and D/H are strong, then D is strong.
Exercise 2.8 A permutation (ai, a2, • • • , an) of 1,2, • • • , ra is an n-derangement if a* ^ i,
for each i with 1 < i < n. Show each of the following.
(i)Per(Jn) = n!.
(ii)Per(Jn-/n)=n!f;^.
Exercise 2.9 For n > 3, let A = (а#) € Afn be a matrix with a# = 0 for each i and j
with 1 < i < n -1 and г + 2 < j < n, (such a matrix is called a Hessenberg matrix). Show
that the signs of some entries of A can be changed so that Рег(Л) = det(A).
(Hint: change the sign of each ai,»+i, 1<г<п — 1.)
Exercise 2.10 A matrix A = (а#) € Mr,n with n>r>lisarxn normalized Latin
rectangle if ан = «, 1 < г < n, if each row of Л is a permutation of 1,2, • • • , n and if each
column of Л is an r-permutation of 1,2, • • • ,n. Let К(г,п) denote the number of r x n
normalized Latin rectangles. Show that K(2,n) = Per(Jn - Jn)-
Exercise 2.11 Prove Lemma 2.5.1.
Exercise 2.12 Prove Lemma 2.5.2.
Exercise 2.13 Prove Theorem 2.5.5.
Exercise 2.14 Let A € Af+ be rally indecomposable. Then Par (A) > \\A\\ - 2n + 2.
Exercise 2.15 Prove Lemma 2.5.5.
Exercise 2.16 Prove Lemma 2.5.6.
Exercise 2.17 Prove Lemma 2.5.7.
Exercise 2.18 Prove Theorem 2.5.9.
Exercise 2.19 Using the notation in Definition 2.6.3, Show that each of the following
holds.
(i) s" -< sW x s'.
(ii) there exist an integer k > 1 and k non negative n-dimensional vectors s^, s^2^, • • • , s^
such that
s" = s(fc)4sM^..4s(i)^s',
Exercise 2.20 Let r = s = (fc, ?, • • • , k)T be two nO-dimensional vectors. If fc|n, show
92
Combinatorial Properties of Matrices
that
|Z/(r,.)|
Exercise 2.21 Let A = (a^) € Mn, let x = (xux2r- >?n)T > 0 and let (Ax)* =
I2i=i °ti^i- Each of the following holds.
(Ax) - (Ax) -
(i) If A is nonnegative and irreducible, then min -—— = p(A) < max -——.
1<*<п Ж» l<t<n X{
(ii) If Л is nonnegative, then min -—— = p(A) < max -——.
Exercise 2.22 Show that if A is a stochastic matrix, then p(A) = 1.
Exercise 2.23 Let А, В € M+. Prove each о the following:
(i) If both A and В axe stochastic, show that AB is also stochastic.
(ii) If both A and В are doubly stochastic, show that AB is also doubly stochastic.
Exercise 2.24 If A € MJj" is doubly stochastic, then A ~ B, where В is a direct sum of
doubly stochastic fully indecomposable matrices.
Exercise 2.25 Show that the matrix A in Example 2.7.2 is not of doubly stochastic type.
Exercise 2.26 Show that if A € Un(k), then Per(A) > k\.
Exercise 2.27 Prove Theorem 2.8.1.
Exercise 2.28 Without turning to Theorem 2.8.2, prove the star K"i,n-i is compact.
Exercise 2.29 Prove Theorem 2.8.5 by imitate the proof of Theorem 2.8.3.
Exercise 2.30 Show that G is compact if
(i) G is a disjoint union of K^s.
(ii) G is a disjoint union of K^s.
(iii) G is a disjoint union of Tm% where Tm is a tree on m vertices,
(iv) G is a G.k — e graph.
Exercise 2.31 Show that X € U(A) \ V(A) in Example 2.8.7.
2-10 Hints for Exercises
Exercise 2.1 For (i), if no such v (a source) exists, then walking randomly through the
arcs, we can find a directed cycle.
For (ii), use (i) to find a source. Label the source with the largest available number,
then delete the source and go on by induction.
Combinatorial Properties of Matrices
93
For (iii), we can contract each strong component into a vertex to apply the result in
(0-
Exercise 2.2 Suppose that A = (oy) and Л' = (a^). Then aie = a'it and a« — a?e, for
each i with 1 < i < n. For each ais > 0, there are a{s arcs from v« to vs in D(A). Since
a(t = aiSi there are c^, ares from Vi to v* in D(A(). Thus all the arcs getting into v$ in
D(A) will be redirected to vt in -D(A;). Similarly, all the arcs getting into ty in D(A) will
be redirected to vs in -О(Л').
Exercise 2.3 We only show that case when к = 2. The general case can be proved
similarly.
Let и € V(D') = V(.D). We shall show that D' has a directed (tt2,tt)-path and a
(u,U2)-path. If it € V(A0> then since D2 is a strong component, P2 has a (tt2,w)-path
which is still in D*. Also, ?2 has a (u,u')-path for some vertex u' with (u'u2) € E(D2).
Note that in ZV, (и'щ) € E(D'). Since ui is not a source and by (*), there is a vertex
v € V(Z>i) such that (ущ) € E(D). It follows that D' has a (u,U2)-path that goes from
«, through u' and v with the last arc (v,«2)-
If и € V(Di), since щ is not a sink and by (*), there is a it" € V(Di) such that
(«"iti) € E(D), whence D' has a (u,U2)-path that contains a (it, u")-path in D\ with
the last arc (unU2). Also, since u2 is no a source, there is a vertex v e V(D2) such that
(v«2) € i?(.D). Hence P' has a (u2,u)-path that contains a (tt2,v)-path in Z>2> the arc
(w,«i), and a (tii,u)-path in D\.
Exercise 2.4 Induction on A;. By the definition of a diagonal, we can see that Ak must
have a nonzero diagonal. Argue by induction to the submatrix by deleting the rows and
columns containing entries in Ak.
Exercise 2.5 Apply Definition 2.3.1.
Exercise 2.6 Apply definitions only.
Exercise 2.7 (i) If D[W] has an arc a such that D[W] — a is strong, then D — a is also
strong, and so D is not minimal. Hence D[W] is minimally strong,
(ii) and (iii): definitions.
Exercise 2.8
(i) Show that Per( Jn) counts the number of permutations on n elements.
(ii) Show that Per(Jn — Jn) counts the number of n derangements.
Exercise 2.9 If Per (A) = 0, then A has a zero submatrix H € Ms,n-s+i(0), which has at
least n — m + 1 columns.
Exercise 2.11 If Л € Bmjn and if Рег(Л) = 0, then A has 0#X(n-«+i) as a submatrix, for
some s > 0 (Theorem 6.2.1 in the Appendix); and this submatrix has at least n — m + 1
94
Combinatorial Properties of Matrices
columns.
Exercise 2.12 In this case, each к x (n—1) submatrix of A has at least к nonzero columns,
and so by Theorem 6.2.1 in the Appendix, Раг(Л') > 0 for each (m—1) x (n-1) submatrix
A!.
Exercise 2.13 It suffices to prove Theorem 2.5.5 for nearly indecomposable matrices.
Argue by induction on n. When n = 1, (2.10) is trivial. By Theorem 2.4.2, we may
assume that
A =
Ao *i
F2 В
where В is nearly indecomposable. By induction,
Рег(Л) < Per(B) +1 > ||B|| - 2m + 2 + 1.
Exercise 2.14 Let A = (%)¦ If a# < 1, then this is Theorem 2.5.5. Assume that some
ar9 > 0. Let В = A — arsErs. By induction on \\A\\, we have
Рег(Л) = Per(?) + регЛ(ф) > ||B|| - 2n + 1
= ||Л||-2п + 2.
Exercise 2.15 Since n > 2 and since A is fully indecomposable, there exists at^s such
that art > 0. Hence
n
Рег(Л) = ?аг*Рег(Л(г|А;))
Jb=l
> ars Рег(Л(ф)) + art Рег(Л(г|*))
> 2 Per(^(r|s)) + 1
Exercise 2.16 Argue by induction on n > 3. Assume that (n - 1)! < 2(n-1><n-3>. Then
the theorem will follow if n < 22<n"2).
Consider the function f(x) = 2(x-2)-log2 x. Note that /(3) = 2-log2 3 > 2-log2 4 =
0, and f(x) > 0. Hence f(x) > 0 and so 3 < n < 22(n"2>.
Exercise 2.17 Let ri,r2, • * • >rn denote the row sums of A. If r» > 3 for each г, then by
Theorem 2.5.7 and by Lemma 2.5.6,
Рег(Л) < f[(ril)% < Jj2ri"2 = 2"лИ-2п.
Exercise 2.18 Argue by induction on t > 1 and apply Theorem 2.5.8.
Combinatorial Properties of Matrices
95
Exercise 2.19
(i). By Definition 2.6.2, the first \i — 1 components of s^ and s' are identical, and
Thus comparing the sum of the first к components and considering the cases
when к < A - 1 and к > A, we can conclude that s^ -< s'.
Note that sy > s? and sx > $'x. comparing the sum of the first к components and
considering the cases when к < \i — 1 and к > ц, we also conclude that s" X s^.
(ii). The number of identical components between s" and sM is more than that between
s" and s'. Apply (i) to s" and s*1* to find s<2> such that s" -< s<2> -< s^. Repeat this
process to get (ii).
Exercise 2.20 Apply Theorem 2.6.2.
Exercise 2.21 Let Y = diagfci,--- ,arn). Then Y~lAY — {a^Xj/xi), and A is
irreducible, Y~*AY is also irreducible, and p{Y"1AY) = p(A). It follows that
min &k = p(Y-lAY) = p(A) < majc ^.
l<t<n X{ l<*<n Xi
If Л is nonnegative, then let e > 0 be a real number and let A€ = A + eJn. Then by
the above,
mm — = p(A€) < max ~.
l<i<n Х^ 1<*<Л Xi
Thus (ii) follows by letting e -> 0.
Exercise 2.22 Since A is stochastic, 4j = A. Therefore apply Exercise 2.21 with x = j
to get
p(A) < max ^i = 1.
~ l<i<n 1
Show that if A is a stochastic matrix, then p(A) = 1.
Exercise 2.23 Apply Theorem 2.7.1(H) and (iii).
Exercise 2.24 Imitate the proof for Theorem 2.7.4.
Exercise 2.25 By contradiction, assume that there is a doubly stochastic matrix В =
№ibx2 such that only 621 = 0. Then apply Theorem 2.7.1(iii) to see that a\2 = 0.
Exercise 2.26 Apply Hall-Mann-Ryser Theorem.
Exercise 2.27 Let A = A(G). Then the adjacency matrices of G/c,C?* and Gc are
Jn — A>A + In and Jn— In — A, respectively. Apply these to prove (i)-(iii). For (iv), it
suffices to show Kn is compact, or H(Jn - In) = ?2n = V{Jn - In)-
Combinatorial Properties of Matrices
Exercise 2.28 Let G = -RTi,n-i and A - A(G). Then
A =
Oil-
10 0-.
10 0*.
. 1
• 0
. о
1 0 0
0
and so V(A) =
1 0
0 P
ePn,
where P € Bn_i is a permutation matrix. It suffices to show tln{A) С V(A). Let
Q e ?ln(A). Then since A = Q^AQ,
0 =
1 0
о Oi
for some Q\ € ftn-i. It follows that Qx = J^ CiQ'^ where Q\ are permutation matrices in
Bn_i. It follows that
Q = ]Г ъРг е V{A), where Pi =
1 0
0 Q\
Exercise 2.29 Let A = Л(СП) and 0 ф X = (a^) € Сопе(Л), X > 0 and XA = AX. In
the proof of Theorem 2.8.5, we know that there is a permutation a (corresponding to the
permutation matrix P = р%) € V{A)) such that xi<r(ij > 0 for all i. Let e = тт{х1а^), i =
1,2, • • • , n}. As P € 744), (X - eP) € Сопе(Л), and X - eP has one more 0-entry than
X.
Then argue by induction to show that X € V(A).
Exercise 2.30 (i)-(iii) follows directly from Theorem 2.8.6. For (iv), note that G*c is the
disjoint union of K?'s.
Chapter 3
Powers of Nonnegative
Matrices
Powers of nonnegative matrices are of great interests since many combinatorial properties
of nonnegative matrices have been discovered in the study of the powers of nonnegative
matrices and the indices associated with these powers.
A standard technique in this area is to study the associated (0,l)-matrix of a non-
negative matrix. Given a nonnegative matrix A, we associate A with a matrix A' € Bn
obtained by replacing any nonzero entry of A with a 1-entry of A'. Many of the
combinatorial properties of a nonnegative matrix can be obtained by investigating the associated
(0,l)-matrix and by treating this associated (0,l)-matrix as a Boolean matrix (to be
defined in Section 3.2).
Quite a few of the problems in the study of powers will lead to the Frobenius Diophan-
tine Problem. Thus we start with a brief introductory section on this problem.
3-1 The Frobenius Diophantine Problem
Certain Diophantine equations will be encountered in the study of powers of nonnegative
matrices. This section presents some results and methods on this topic. As usual, for
integers ai, аг, • • • , aSi let gcd(ai, • • • , as) denote that greatest common divisor of ai, • • • , as,
and let 1cm(ai, • • • , as) denotes that least common multiple of ai, • • • , as.
Theorem 3.1.1 Let ai,a2 > 0 be integers with gcd(ai,a2) = 1. Define ^(01,02) —
(01 — 1)(аг — 1). Each of the following holds.
(i) For any integer n > ^(01,^2), the equation a\Xx Л-а^х?, = п has a nonnegative
integral solution x\ > 0 and xi > 0.
97
98
Powers of Nonnegative Matrices
(ii) The equation a\X\ + a2x2 = ^(^1,^2) — 1 does not have any nonnegative integral
solution.
Proof Let n > (a\ — 1)(аг — 1)» Note from number theory that any solution x\ and x2
of aixi + a2x2 = n can be presented by
J x\ = x'x + 02*
I 12 = x2 — flit
where x'2, x2 are a pair of integers satisfying the equation, and where t can be any integer.
Since 01 > 1 and since x2 is an integer, we can choose t so that ait<x2< a\t + ai — 1.
Therefore x2 = x2 — ait > 0. Since n> a\a2 — ai —a2 and by this choice of t,
X\(X\ = (#! + a2t)d\ = n — (x2 — ait)a2
> a\a2 — ai — a2{a\ ~-1)^2 = ¦—fli
and so xi = xj + a2t > 0. This proves (i).
Argue by contradiction to prove (ii). Assume that there exist nonnegative integers
xi,x2 so that aixi + 02X2 = aia2 — a± — a2, which can be written as a\a2 = (xi +
l)a\ + (x2 + l)a2. It follows by gcd(ai, o2) = 1 that oi|(x2 +1) and o2|(xi +1). Therefore
X2 +1 > a\ and xi +1 > a2i and so a\a2 = (xi + \)a\ + (x2 + l)a2 > 2ага2, a contradiction
obtains. []
Theorem 3.1.2 Let s, n, a\, • • • , as be positive integers with s > 2 such that gcd(ax, • • • , as) =
1. There exists an integer N = iV(ai, • • • , as), such that the equation
Л1Х1 H 1- asxs = n,
has nonnegative integral solution xi > 0, X2 > 0, • • • , xs > 0 whenever n > N(ai, • • • , on).
Proof When s = 2, Theorem 3.1.2 follows from Theorem 3.1.1 with N(aua2) = (ax -
l)(a2 - 1) - 1.
Assume that s > 3 and argue by induction on s. Let d denote gcd(ai, • • • , aa_i). Then
gcd(d, as) = 1, and so there is an integer ds with 0 < bs < d — 1 such that a$b$ = n (mod
a*). Write a» = ajd, 1 < i < s — 1. Then the equation 01X1 H 1- a$xs = n becomes
a'1x1 + ..-+a,$_lxs-1 = ^^: (3.1)
By induction, there exists an integer iV(ai, o2, • * ¦ >a's-i) such that the equation (3.1) has
nonnegative integral solution xi = 61, • • • ,xs_i = 6s_i, whenever
n - QA . n-as(d-l) , , , .
_ > _ >iV(a1,a2)--- ,0^).
Powers of Nonnegative Matrices 99
Let N(ai, • • • , a3) = as(d-1) + dN(a[, • • • , а'5-1). Then a\X\ H a5x5 = n has
nonnegative integral solution x\ = bi, • • • xs = bs whenever n > JV(oi, • • • , a,), and so the theorem
is proved by induction. Q
Definition 3.1.1 Let s, ai, • • • , as be positive integers with s > 2 such that gcd(ai, • • • , as) -
1. By Theorem 3.1.2, there exists a smallest positive integer ф(а\, • • • ,as) such that any
integer n > ф(а>1,--- ,a5) can be expressed as n = aiari H asxs for some
nonnegative integers xi, • • • , ж5. This number #(ai, • • • , as) is called the Frobenius number. The
Frobenius problem is to determine the exact value of ф{аи • • • ) a*)-
Theorem 3.1.1 solves the EYobenius problem when 5 = 2. This problem remains open
when s > 3.
Theorem 3.1.3 (Ke, [143]) Let ai,a2,a3 > 0 be integers with gcd(ai, а2,а3) = 1. Then
3
ф(аг, a2, a3) < —-—^—г + a3 gcd(ab a2) - YV +1. (3.2)
gcd(aba2) ^
Moreover, equality holds when
a > QiQ2 01 Q2 /3 Зч
3 (gcd(aba2))2 gcd(aba2) gcd(aba2)*
Note that ах,а2,аз can be permuted in both (3.2) and (3.3).
Proof Let d = gcd(ai,a2) and write a\ = a'xd and a2 = a2d. Let tti,tt2, яо>Уо>я0 be
integers satisfying а^щ + a2ti2 = 1 and a\Xo + a2yo + 0320 = n respectively. We can easily
see (Exercise 3.1) that any integral solution of a\x + a2y + azz = n can be expressed as
{x = xo + a^i — ихазйг
2/ = 2/o - Mi - гх2азе2
2 = 2To + dt2i
where ?1, ?2 can be any integers. Choose t2 so that —dt2 < z0 < —dt2 + d — 1, and then
choose ?1 so that —a2t\ < x0 — uia3i2 < -a2*i + a2 "" *• Note that these choices of ?1
and «2 make x > 0 and 2 > 0. Let n > 8cd?^fa2s + аз gcd(ai,a2) — 2iLi ai + 1. By the
choices of ti, ?2 ad n,
a2y = ^2(2/0 — ei*i —11203*2)
= n — aia: —032 > n — ai(a2 — 1) — az(d — 1)
aitt2
= n azd + ai + аз > — аг.
a
Thus t/ > 0. This proves (3.2).
Now assume (3.3). We shall show that
3
aix + a2y + a3z = —-77-^—с + «з gcd(ai, a2) - Y) ab (3.4)
gcd(aba2) ~
100
Powers of Nonnegative Matrices
has no nonnegative integral solutions, and so equality must hold in (3.2). By contradiction,
assume that there exist nonnegative integers ж, у, z satisfying (3.4). Note that „„л}аг ч =
gCa(ai,a3)
da[a2 and that fl3gcd(ai,a2) = ^d, and so We have
з
da[a2 + Q>zd — ])P a* = axx + агу + a%z.
It follows that
d(a[a2 + a3) = da[(x + 1) + da'2(y + 1) 4- a3(z + 1).
Since gcd(d,a3) = 1, we must have d\(z + 1), and so z + 1 = dk for some integer к > 0.
Cancel d both sides to get
a[a2 = a[(x + 1) + 4(2/ + Ц + <*(* - !)•
If & > 1, then aja^ > a'x +a2+^3» contrary to (3.3). Thus к = 1. Then by gcd(oJ, a2) = 1,
a^l(y + 1) and а2|(ж + 1), which lead to a contradiction a[a2 > 2a[a2, Q
Some of the major results in this area are listed below. In each of these theorems, it
is assumed that s > 2 and that oi, • • • ,as are integers with a\ > 02 > • • • > as > 0 and
with gcd(ai, • • • ,as) = 1. Exercises 3.2 and 3.3 are parts of the proof for Theorem 3.1.7.
Theorem 3.1.4 (Schur, [158])
ф{аХу • • • ,a5) < (ai - l)(a5 - 1).
Theorem 3.1.5 (Brauer and Seflbinder, [15]) Let d{ = gcd(oi,o2, • • • ,a0, 1 < i < s - 1.
Then
«e1,...,e.)<^+x;^+e.*-a-?e<+i.
When 5 = 3, Theorem 3.1.5 gives inequality (3.2).
Theorem 3.1.6 (Roberts, [217]) Let a > 2 and d > 0 be integers with d /\a. Let
dj = a + jd, (0 < j < s), then
#(ao,ai,---,a,)< M^-^J + lj a +(d-l)(a-1).
Theorem 3.1.7 (Lewin, [158])
Powers of Nonnegative Matrices
101
Theorem 3.1.8 (Lewin, [156]) If5>3, then
w»i»*-- >а$) < L 2 -I*
Theorem 3.1.9 (Vitek, [267]) Let i be the largest integer such that ?*• is not an integer.
One of the following holds.
(i) If there is an a,j> such that there exist for all choices of nonnegative integers \i and
7, aj ф fias + 7а», then
#(ai,¦••,<».)< LyJ(ai-2).
(ii) If no such Oj exists, then
ф{а1Г • • ,a5) < (a* - l)(a* - 1).
Theorem 3.1.10 (Vitek, [267]) If s > 3, then
ф{а1Г-- ,as) < I J.
3.2 The Period and The Index of a Boolean Matrix
Definition 3.2.1 A matrix A € Bn can be viewed as a Boolean matrix. The Boolean
matrix multiplication and addition of (0,1) matrices can be done as they were real matrices
except that the addition of entries in Boolean matrices follows the Boolean way:
a + b = max{a, 6}, where a, b € {0,1}.
Unless otherwise stated, the addition and multiplication of all (0,1) matrices in this section
will be Boolean.
Theorem 3.2.1 Let A € Bn. There exist integers p > 0 and к > 0 such that each of the
following holds.
(i) If n > к and n — к = sp + r, where 0 < r < p — 1, then An = A*+r.
(ii) {1,Л,Л2,--- ,Afc,--- ,Л*+Р-1} with the Boolean matrix multiplication forms a
semigroup.
(iii) {Ak,-- ,Ak+p~1} with the Boolean matrix multiplication forms a cyclic group
with identity Ae afod generator Ae+1, for some e € {fc, fc + 1, • • • , к + p - 1}.
Proof It suffices to show (i) since (ii) and (iii) follow from (i) immediately.
Since |Bn| = 2n is a finite number, the infinite sequence J, Л, Л2, A3, • • • must have
repeated members. Let к be the smallest positive integers such that there exist a smallest
integer p > 0 satisfying Ak = A*+p.
102
Powers of Nonnegative Matrices
Then for any integer s > 0, A*+" = j4*+p+(«-i)p = 4*+p4(s-i)p = a*+(*-i)p
Л*, and so (i) obtains. Q
Definition 3.2.2 For a matrix A € Bn, the smallest positive integers p and A; satisfying
Theorem 3.2.1 are called the period of convergence of A and the index of convergence of
Л, denoted by p = р(Л) and fc = k(A), respectively. Very often p(A) and k(A) are just
called the period and the index of Л, respectively.
Definition 3.2.3 A irreducible matrix A € Mn is primitive if there exists an integer A; > 0
such that Ak > 0. An irreducible matrix A is imprimitive if A is not primitive.
Example 3.2.1 Let D be a directed n-cycle for some integer n > 2 and let A = Л(2Э).
Then since D is strong, Л is irreducible. However, A is not primitive.
Definition 3.2.4 Let D be a strong digraph. Let 1(D) = {/ > 0 : D has a directed cycle
of length /} = {li, l2i • • • , /*}. The mde# of imprimitivity of .D is d(D) = gcd(/i, Ь, * * * , '*)•
Theorem 3.2.2 Let Л € itf+ and let ?> = D(A). Then A is primitive if and only if both
of the following holds:
(i) D is strong, and
(ii) ЦР) = 1.
Proof Suppose that A is primitive. Then A is irreducible and so (i) holds. Moreover,
there is an integer к > 0 such that Ak > 0. Note that if Ak > 0, then AM > 0 also. It
follows by Proposition 1.1.2(vii) and by Exercise 3.4, that d(D) must be a divisor for both
к and fc + 1, and so d(D) — 1.
Conversely, assume that A satisfies both (i) and (ii). Then A is irreducible. Let
1(D) = {li,fe,--- ,U- ВУ (")> gcdflbfe,--- Л) = 1. By Theorem 3.1.2, ф{1и-~ Л)
exists.
Denote V(D) = {1,2,- •• ,n}. For each pair i,j € V(.D), by (i), D has a spanning
directed trail T(iJ) from i to j. Let d(«, j) = \E(T(i, j))\. Define
A; = max d(i,j) + ф(1г,•••,/*).
Then for each fixed pair ij e V(D)} к = d(i,j) + a, where a > ф(1\,--- ,ls)- By the
definition of ф(1\, • • • ,/5) and by Proposition 1.1.2(viii), D has a closed trail L of length
a. Since Г(г, j) is spanning, T(i,j) and L together form a directed (г, j)-trial of D. By
Proposition 1.1.2(vii), Afc > 0 and so A is primitive. Q
Definition 3.2.5 Let d > 2 be an integer. A digraph D is cyclically d-partite if V(D)
can be partitioned into d sets Vi, V2i • • • , V& such that ?> has an arc (щ v) € E(D) only if
u € Vp and v € V^ such that q— p=l or q— p=l — rf.
Lemma 3.2.1 Let D be a strong graph with V(D) = {vb V2, • • • , vn}. For each i with
Powers of Nonnegabive Matrices
103
1 < t < n, let d{ be the greatest common divisor of the lengths of all closed trails of D
containing vit and let d = d{D). The each of the following holds.
(i) d\ = db = • • • = dn = d.
(ii) For each pair of vertices Vi,Vj € V(D), if Pi and P2 are two {v^vj)-walks of D,
then \E{Pi)\ = |JE?(ft)| (mod d).
(iii) V(D) can be partitioned into Vi UP2 U • • • U Vd such that any (t/j, Vj)-trial T^* with
Vi € V* and Vj € V} has length |J5(T^-)| = j - * (mod d).
(iv) If d > 2, then D is cyclically d-partite.
Sketch of Proof (i). Fix vi,Vj € V(D). Assume that D has a (t/<, v^-trail T<j of length
s, a (vj,Vi)-trail Г^< of length t, and a (vj,Uj)-trail of length tj. Then both s + ? and
s +1 + tj are lengths of closed trails containing v,, and so di\(s +1) and d*|(s +1 + fy). It
follows that di|fy, and so di\dj. Since г, j are arbitrary, di = ^2 = • • • = dn = d', and d|d'.
Let I be a length of a directed cycle С of D. Then С contains a vertex vi (say), and
so d'|i. It follows that d'|d.
(ii). Let Q be a (v^,Vi)-trail. Then each Pi U Q is a closed trail containing v*. By (i),
|Я(Л)| + \E(Q)\ = |S(P2)| + \E(Q)\ (mod d).
(iii). Fix vi. For 1 < г < d, let VJ = {vi 6 V : any directed (v2, Vt)-path has length
i mod d}. If ^ 6 V% and v^ € V}, then D has a directed (vi,ty)-path of length /', and a
directed (v$, vj)-path of length l. Thus Z' = г mod d and Z + Z' = j mod d, and so I = j — i
mod d.
(iv) follows from (iii). Q
By direct matrix computation, we obtain Lemma 3.2.2 below.
Lemma 3.2.2 Let A € M+ be a matrix such that for some positive integers n\, n2, • • • , п<*
matrices A{ € Mnl>n.+I with each A{ having no zero row nor zero column,
Г ° Al 1
0 A2
A=\ . (3-5)
L Ad 0 J
Then each of the following holds.
(i) Ad = diag(?i,--« ,#d), where Bj = Yl^j"1 A% and where the subscripts are
counted modulo d.
(ii) If for some integer m > 0, Am = diag(Ji, J2, • • • , Jd), such that each Ji is a non-zero
square matrix, then d\m.
Theorem 3.2.3 Let A 6 M+ be an irreducible matrix with d = d(D(A)) > 1. Each of
the following holds.
104
Powers of Nonnegative Matrices
(i) There exist positive integers ni,7i2,-" ,n</ and matrices A\ e Mn.,ni+li and a
permutation matrix P such that PAP-1 has the form of (3.5).
(ii) Each Ai in (i) has no zero row nor zero column, 1 < % < d.
(Hi) nf=i Aiis primitive.
Proof (i). Let D = D(A). By Lemma 3.2.1(iii), V(D) has a partition Vx U V2 U • • • U Vd
satisfying Lemma 3.2.1(iii). Let щ = \Vi\, (1 < i < d). By Lemma 3.2.1(iii), any arc of D
is directed from a vertex in VJ to a vertex in 14ц, i = 1,2, • • • , d (mod d). With such a
labeling, D has an adjacency matrix of the form in (i).
(ii) follows from the assumption that D is irreducible.
(iii). Let 1(D) = {lul2,--- J*}- Then gcd(\>7>"* Л) = 1» a^ so ЬУ Theorem
3.1.2, *ь = ^,...,^) exists,
a a
Choose utv € Vi. Since D is strong, there exists a directed closed walk W(u, v) from
it to v. By Lemma 3.2.1(iii), d divides |??(W(tt,v))|. Let
u,vevi { d J
Then t > ко, and so for any u,v € Vi, td = |??(W(w, v))| + Ы for some integer к > ко. By
Theorem 3.1.2, and since V(W(ut v)) = V(D), for any pair of vertices u, v € V\, D has a
directed (tt,v)-walk of length id. It follows by Proposition 1.1.2(vii) that every entry of
the n\ x щ submatrix in the upper left cornier of (PAP~x)td is positive, and so by Lemma
3.2.2(i), B[ > 0. This proves (iii). []
The corollaries below follow from Theorem 3.2.3.
Corollary 3.2.3A Let A € M+ be irreducible with d = d(D(A)). Then d is the largest
positive integer such that D(A) is cyclically d-partite.
Corollary 3.2.3B Let A € M+ be an irreducible matrix with d = d(D(A)). Then each
of the following holds.
(i) К Л has the form (3.5) and satisfies Theorem 3.2.3(ii), then for each j with 1 < j < dt
Bj = Yli^j^1 Ai 1S primitive, where the subscripts are counted modulo d.
(ii) (Dulmage and Mendelsohn, [77]) There is a permutation matrix Q (called a
canonical transformer of A) such that
Q^AdQ= diag(BbB2,—,Д0,
where each Bi is primitive.
(iii) (Dulmage and Mendelsohn, [77]) Let Q be a canonical transformer of A. The
number d = d(D(A)) is the smallest power of Q_1 AQ which has the form of diag(?i, B2, • • •, Д/),
where each B{ is primitive.
Powers of Nonnegative Matrices
105
Corollary 3.2.3C Let A € M+ be a irreducible matrix with d{D(A)) > 1. Then p(A) =
d(D(A)).
Corollary 3.2.3D Let A E Bn. Each of the following holds,
(i) p(A) = 1 if and only if A is primitive,
(ii) If p = p(A) > 1, then A is similar to
[0 Ai I
L Ap 0 J
such that each A» is primitive. (The form (3.6) is called the imprimitive standard form of
the matrix A, and the integer p is the index of imprimitivity of A.)
Lemma 3.2.3 Let A € Bn be a matrix having the form (3.5) and satisfy Theorem 3.2.3(ii).
If Ili=i Ai1S irreducible, then A is also irreducible and d|p(A).
Sketch of Proof By Lemma 3.2.2(i),
Ad= dtoe(BuB2,~-,Bd),
where Bi = Ylt=i ^* *s irreducible. By Theorem 2.1.1(v), there is a polynomial f(x) such
that /(Bi) > 0.
Let g(x) = xf(x). Then for each i = 1,2, • • • , d,
g(Bi) = B«/(B«) = (^^х • • • Ad)/(B1)(A1 A2.. • А*-г).
Since A satisfies Theorem 3.2.3(H), each A* has no zero rows nor zero columns. It follows by
f{Bi) > 0 and by the operations of Boolean matrices that g(B{) > 0. Direct computation
leads to
(I + A + .-. + A^MA^X),
and so A is irreducible by Theorem 2.1.1(vi).
Let p = p(A). By Corollary 3.2.3C, p = d(D(A)). Let m > 0 be a length of a closed
trail of D(A). Then Am has a diagonal 1-entry. By Lemma 3.2.2(ii), d\m, and so d\p(A).
и
Theorem 3.2.4 Let BeBn such that В czp A for some A such that A has the form
in (3.5) with d > 1 and satisfies Theorem 3.2.3(ii) and Theorem 3.2.3(iii). Then В is
imprimitive and d = p(B).
Proof Since В ~p A, p(B) = p(A) and Б is primitive exactly when A is primitive. Thus
it suffices to show that A is imprimitive and p(A) = d.
106
Powers of Nonnegative Matrices
By Lemma 3.2.3 and since A satisfies Theorem 3.2.3(H) and Theorem 3.2.3(iii), A is
irreducible and d\p(A). Thus p(A) > 1 and so by Corollary 3.2.3D, A is imprimitive. It
remains to show that p(A)\d.
By Corollary 3.2.3D(ii) and Lemma 3.2.2, Ad = diag(?b?2,— ,?d), where the ??'s
are defined in Lemma 3.2.2(H). Since A satisfies Theorem 3.2.3(iu), B\ is primitive, and
so for some integer к > 0, both Bf > 0 and В*"1"1 > 0. It follows by Proposition 1.1.2(vii)
that D(A) has closed walks of length kd and (k + l)d, and so d(D(A))\d. By Corollary
3.2.3C, p{A) = d(D(A)), and so p(A)\dt as desired. []
Example 3.2.1 If A ~p ?, then D(A) and D(?) are isomorphic, and so by Corollary
3.2.3C and Corollary 3.2.3D that A is primitive if and only if В is primitive. However, if
A ~p B, then that A is primitive may not imply that В is primitive. Consider
A =
0 0 110
10 0 0 0
0 10 0 0
0 0 0 0 1
0 10 0 0
and B =
0 10 10
0 0 10 0
10 0 0 0
0 0 0 0 1
10 0 0 0
We can show (Exercise 3.11) that A is primitive, В is imprimitive and A ~p B.
Theorem 3.2.5 (Shao, [246]) Let A € Bn The there exists a Q € Vn such that AQ is
primitive if and only if each of the following holds:
(i) Each row and each column of A has at least one 1-entry;
(ii) A <? Vn\ and
(iii)
A*p
0 1
1 0
1 0
Theorem 3.2.6 (Moon and Moser, [204]) Almost all (0,l)-matrices are primitive. In other
words, if Pn denote the set of all primitive matrices in Bn, then
BmJg4-l.
n->oo |Bn|
Powers of Noimegative Matrices
107
3.3 The Primitive Exponent
Definition 3.3.1 A digraph D is primitive digraph if A(D) is primitive. Let D be a
primitive digraph with V = V(D). For u,v € V, let
7(tt, v) = min{& : D has an (it, v)-walk of length k} and
7(D) = max 7(u,v).
u,«?V(I>)
Let Л be a primitive matrix. The primitive exponent of A is 7(A) = 7(D(A)).
Propositions 3.3.1 and 3.3.2 below provide an equivalent definition and some elementary
properties of 7(A).
Proposition 3.3.1 Let Л be a primitive matrix and let D = D(A). Each of the following
holds.
(i) 7(A) = min{* : A* > 0}.
(ii) If 7(A) = fc, then for any utv 6 V(D), D has an (it, v)-walk of length at least k.
(iii) For u,v e V(D), let di>(u,v) be the shortest length of an (w, v)-walk in D, and let
1(D) = {luh,-"Л}- Then
7(w,v) <dr>(u,v)+ <?(/i,••• ,Z5).
Sketch of Proof Apply Proposition 1.1.2(vii) and Definition 3.3.1 to get (i). (ii) follows
from (i) and (iii) follows from (ii) and Definition 3.1.1. Q
Proposition 3.3.2 (Dulmage and Mendelsohn, [77]) Let D be a primitive digraph and
let A = A(D). Each of the following holds.
(i) For any integer m > 0, Am is primitive.
(ii) Given any и € V(D)i there exists a smallest integer hu > 0 such that for every
v € V"(D), D has an (w,v)-walk of length hu. (This number hu is called the reach of the
vertex it.)
(iii) Fix an и 6 V(D). For any integer h > hu, D has an (tt,v)-walk of length h for
every v 6 V(D).
(iv) If V(D) = {1,2, • • • , n}, then 7(D) = тах{Ль h2, • • • , Ы-
Sketch of Proof (i) and (ii) follow from Definitions 3.2.3 and 3.3.1, and (iv) follows from
(iii). (iii) can be proved by induction on h' = h — /iu. When Ы > 0, since D is strong,
there exists w e V(D) such that (w,v) € E(D). By induction D has an (u,w)-walk of
length /ц4 + Лг-1 = Л~1.
Theorem 3.3.1 (Dulmage and Mendelsohn, [77]) Let D be a primitive digraph with
\V(D)\ = n, and let s be the length of a directed cycle of D. Then
7(D) < n +s(n-2).
108
Powers of Nonnegative Matrices
Proof Let Cs be a directed cycle of D with length s. Note that D(AS) has a loop at each
vertex in V(CS).
Let uyv € V(D) = V(D(A*)) be two vertices. If и € V(CS\ then since D(4S) is
primitive (Proposition 3.3.2), and since D(A$) has a loop at u, D(AS) has an (u,v)-walk
of length n — 1. By Proposition 1.1.2(vii), the (u,v)-entry of As^n~^ is positive. Hence D
has a (u, v)-walk of length s(n — 1).
If w ft V(CS), then since P is strong, D has an (w,tu)-walk of length at most n — 5 for
some w e V(C8)t and so D has an («, v)-walk of length at most n—s+s(n—1) = n+s(n-2).
It follows by Proposition 3.3.2 that 7(D) <n + s(n- 2). []
Corollary 3.3.1A (Wielandt, [274]) Let D be a primitive digraph with n vertices, then
l(D) <(n- l)2 - 1.
Sketch of Proof By induction on n. When n > 2, D has a cycle of length s > 1, since D
is strong. Since D is primitive, s < n — 1, and so Corollary 3.3.1 A follows from Theorem
3.3.1. ?
Proposition 3.3.3 Fix i € {1,2} and let D be a primitive digraph with n > 3+г vertices.
Each of the following holds.
(i) If 7(D) = (n — 1)2 + 2-г, then D is isomorphic to A.
(ii) There is no primitive digraph on n vertices such that
n2-3n + 4<7(D)<(n-l)2.
Proof (i). Let s be the length of a shortest directed cycle of D. By Theorem 3.3.1,
(n - l)2 + 2 - г = 7(D) < n + s(n - 2). It follows that s = n -1. Build P from this n -1
directed cycle to see that D must be D\ or .D2.
(ii). By (i), s < n - 2, and so by Theorem 3.3.1, 7(D) < n2 - 3n + 4. ?
Example 3.3.1 Let Cn = v\v2 • • • , vnvi be a directed cycle with n > 4 vertices. Let Di
be the digraph obtained from Cn by adding an arc (vn-i,vi). Then by Proposition 3.3.2
and Theorem 3.1.2,
j(Dx) = max{hVi} = hVn=n + ф{щп - 1) = (n - l)2 + 1.
Thus the bound in Corollary 3.3.1 A is best possible.
Example 3.3.2 (Continuation of Example 3.3.1) Assume that n > 5. Let D2 be obtained
from Z>i by adding an arc (vn,V2). Note that 7CD2) = (n — l)2.
Proposition 3.3.3 indicates that Di is the only digraph, up to isomorphism, that have
y(D{) = (n — l)2 + 2 — i, (1 < i < 2). Moreover, there will some integers к such that
1 < к < (n — l)2 + 1 but no primitive digraph D satisfies 7(D) = k.
Powers of Nonnegative Matrices
109
Example 3.3.3 (Holladay and Varga, [129]) Let n > d > 0 be integers. If Л € M+ is
irreducible and has d positive diagonal entries, then A is primitive and ч(А) <2n — d—l
(Proposition 3.3.4(ii) below). Let A(n,d) € Mn be the following matrix
1 1
0
4(n,d) =
0
where Afad) has exactly d positive diagonal entries. Then у(А(щсЦ) = 2n — d — 1.
Proposition 3.3.4 Let D be a strong digraph with n = \V(D)\ and let d > 0 be an
integer. Then each of the following holds.
(i) If D has a loop, then D is primitive.
(ii) К D has loops at d distinct vertices, then 7(D) < 2n - d - 1.
(iii) The bound in (ii) is best possible.
Sketch of Proof (i) follows from Theorem 3.2.1.
(ii). By (i), D is primitive. For any u,v € V(D), D has an (u,w)-walk of length
n - d for some vertex w with a loop, and a (w, v)-walk of length at most n — 1. Thus
K<2n-d—l, and (ii) follows from Proposition 3.3.2(iv).
(iii). Compute y(A(n,d)) for the graph A(n,d) in Example 3.3.3 to see 7(Л(п,<2)) =
2n-d-l. Q
Definition 3.3.2 For integers 6 > a > 0 and n > 0, let
[a, 6]° = {fc : к is an integer and а < к < b}
En = {k : there exists a primitive matrix A € M^* such that *у(А) = fc}.
By Theorem 3.3.1 and by Proposition 3.3.3, En С [1, (n - l)2 + 1]°.
Theorem 3.3.2 (Liu, [168]) Let n-l>d>lbe integers let Pn(d) be the set of primitives
matrix in M+ with d > 0 positive diagonal entries. If к € {2,3, • • • , 2n — d — 1}, then
there exists a matrix A € Pn(^) such that <y(A) = fc.
Sketch of Proof For any integer к € {2,3, * • * , n} we construct a digraph D whose
adjacency matrix A satisfying the requirements.
Ifl<d<fc<n, the consider the adjacency matrix of the digraph D in Figure 3.3.1.
110
Powers of Nonnegative Matrices
т—s
d+1
fc-1
~N
<~4
-Л
fc + 1
fc + 2
n-1
Figure 3.3.1
Note that
7(«»JM <
= fc
if i = j = 1,
otherwise.
Thus 7(Л) = A; in this case.
Digraphs needed to prove the other cases can be constructed similarly, and their
constructions are left as an exercise. []
Theorem 3.3.3 (Shao, [245]) Let A € Bn be symmetric and irreducible,
(i) A is primitive if and only if D(A) has a directed cycle of odd length,
(ii) If A is primitive, then у (A) < 2n — 2, where equality holds if and only if
Л~РВ =
0
1
0
0
0
1
0
1
0
0
0 ••
1 • ¦
0 •
0 ¦•
0 ••
• 0
¦ 0
• 0
• 0
• 1
0
0
0
1
1
Powers of Nonnegative Matrices
111
Proof Let D = D(A). Since A is reduced and symmetric, D is strong and every arc of
D lies in a directed 2-cycle. Thus by Theorem 3.2.2, D is primitive if and only if D has a
directed odd cycle.
Assume that A is primitive. Then A2 is also primitive by Proposition 3.3.2. Since A is
symmetric, a loop is attached at each vertex of V(D(A2)) = V(D). Thus by Proposition
3.3.4(ii), 7(Л2) < n - 1, and so A2*"-1* > 0. Hence 7(A) < 2n - 2.
Assume further that 7(A) = 2ra — 2. Then in D(A2), there exist a pair of vertices щ v
such that the shortest length of a (w,v)-path in D(A2) is n — 1. It follows that D(A2)
must be an (it, v)-path with a loop at every vertex and with each arc in a 2-cycle. If D has
a vertex adjacent to three distinct vertices и\у',тг € V(D)t then u'v'w'u' is a directed
3-cycle in D(A2), contrary to the fact that D(A2) is an (w,v)-path with a loop attaching
at each vertex. It follows that D(A) is a path of n vertices and has at least one loop. By
7(A) = 2n — 2 again, D has exactly one loop which is attached at one end of the path. Q
Theorem 3.3.4 (Shao, [245]) For all n > 1, En С ??n+1. Moreover, if n > 4, then
En С En+i.
Proof Let t € En, and let A = (ay) € Bn be a primitive matrix with 7(A) = t. Construct
a matrix В = (by) € Bn+i as follows. The n x n upper left corner submatrix of В is
A, for 1 < i < n, &i>n+i = oi>n, for 1 < j < n, bn+i,j- = an>j, and &n+i,n+i = a,n,n- Let
F(D(A)) = {1,2,-•• ,n}. Then ?>(?) is the digraph obtained from D(A) by adding a
new vertex n + 1 such that (i,n + l) € E{D(B)) if and only if (г,п) € E(D(A)), such that
(n+l,i) 6 E(D(B)) if and only if (n, j) € E(D(A)), and such that (n+l,n+l) € ?(?>(?))
if and only if (щп) € E(D(A)). By Theorem 3.2.2, В is also primitive. By Definition
3.3.1 (or by Exercise 3.13(iv)), 7(B) = 7(A), and so t € En+i.
If n > 4, then by Example 3.3.1, n2 + 1 € En+i — Eny and so the containment must
be proper. Q
Ever since 1950, when Wielandt published his paper [274] giving a best possible upper
bound of 7(A), the study of 7(A) has been focusing on the problems described below. Let
A denote a class of primitive matrices.
(MI) The Maximum Index problem: estimate upper bounds of 7(A) for A € A.
(IS) The Set of Indices problem: determine the exponent set
En(A) = {m : m > 0 is an integer such that for some A 6 A, 7(A) = m}.
(EM) The Extremal Matrix problem: determine the matrices with maximum exponent
in a given class A. That is, the set
EM(A) = {A 6 A : 7(A) = max{7(A') : A! € A}}.
112
Powers of Nonnegative Matrices
(MS) The Set of Matrices problem: for a 70 € UnEn(A), determine the set of matrices
MS(A,7o) = {A e A : 7(A) = 7o}.
In fact, Problem EM is a special case of Problem MS.
We are to present a brief survey on these problems, which indicates the progresses made
in each of these problems by far. First, let us recall and name some classes of matrices.
Some Classes of Primitive Matrices
Notation Definition
Pn nxn primitive matrices in Bn
Pn(d) matrices in Pn with d positive diagonal entries
Tn matrices A € Pn such that D(A) is a tournament
Fn fully indecomposable matrices in Pn
DSn РпППп
CPn circulant matrices in Pn
NRn nearly reducible matrices in Pn
Sn symmetric matrices in Pn
SJJ matrices in Sn with zero trace
Problem MI
This area seems to be the one that has been studied most thoroughly.
Notation
Pn
Pn{d)
Tn
Fn
DSn
CPn
NRn
Sn
S°n
Authors and References
Wielandt, [274]
Dulmage and Mendelsohn, [77]
Holladay and Varga, [129]
Moon and Pullman, [205]
Schwarz, [232]
Lewin, [159]
Kim-Butler and Krabill [144]
Brualdi and Ross, [36]
Shao, [245]
Liu et al, [177]
Results
4(A) < (n - l)2 + 1
7(A) < n + s(n - 2)
7(A)<2n-d-l
7(4)<n + 2
7(Л) < n - 1
7(A) < i
f ,n3 лХ
if n = 5,6, or
n = 0 (mod4)
^ otherwise
7(A) < n - 1
7(A) < n2 - An + 6
7(A) < 2n - 2
7(A) < 2
n-4
Powers ofNonnegative Matrices
113
Problem IS
Let wn = (n - l)2 + 1. Wielandt (1950, [274]) showed that En С [l,wn]°; Dulmage
and Mendelsohn (1964, [77]) showed that En С [l,wn]°-
In 1981, Lewin and Vitek [157] found all gaps (numbers in [l,wn]° but not in En) in
[-^•J +1, wn\ and conjectured that 1, [-^J has no gaps.
Shao (1985, [247]) proved that this Levin-Vitek Conjecture is valid for sufficiently
large n and that 1, [—pj +1 has no gaps. However, when n = 11, 48 ? En and so the
conjecture has one counterexample.
Zhang continued and complete the work. He proved (1987, [282]) that the Levin-Vitek
Conjecture holds for all n except n = 11. Thus the set En for the class Pn is completely
determined.
Results concerning the exponent set in special classes of matrices are listed below.
Notation
Pn(n)
Pn{d)
Tn
F„
DSn
CP„
NRn
Sn
S°
Authors and References
Guo, [110]
Liu, [168]
Moon and Pullman, [205]
Pan, [209]
Shao and Hu, [249]
Shao, [245]
Liu et al, [177]
Results
[М-1Г
[2,2n-d-l]°
\<d<n
[3,n + 2]*
[l,n-l]'
Unsolved
Unsolved
Characterized
[l,2n-2]°\S
S = {m is an odd integer
and n < m < 2n — 3}
[2,2n-4]'\Si
Si = {m is an odd integer
and n — 2 <m<2n — 5}
Problem EM
In Proposition 3.3.3, it is indicated that
EM(Pn) = {PDiP * : P is a permutation matrix},
where D\ is defined in Example 3.3.1. However, for certain classes of primitive matrices,
the extremal matrices may not be unique under the ~p equivalence and are hard to
characterize, even when under the condition that the number of positive entries is minimized
([168]). Several such problems remain unsolved.
Results concerning Problem EM in special classes of matrices are summarized below.
114
Powers ofNonnegative Matrices
Notation Status Authors and References
Pn(d) Solved Liu and Shao, [182]
Tn Solved Moon and Pullman, [205]
Fn Partially Solved Pan, [209]
DSn Solved Zhou and Liu [290]
CPn Solved Huang, [135]
NRn Solved Brualdi and Ross, [36]
Sn Solved Shao, [245]
S° Solved Liu et al, [177]
Problem MS
This problem appears to be harder. Prom the view point of matrix equations, this is
to find all primitive matrices solution A to the equation Ak = J, for any к € En. The
study of this problem is just the beginning. See [209], [292] and [270], among others.
3.4 The Index of Convergence of Irreducible
Nonprimitiye Matrices
Throughout this section, the matrices and the matrix operations will also be Boolean.
Definition 3.4.1 Recall that p(A) denotes the period of a matrix A € Bn and k(A) the
index of convergence of A (Definition 3.2.2). For integers n > p > 1 with n > 1, define
IBn,p = {4€Bn : p(A)=p}.
Note that Шпд = Pn, the set of all n by n primitive matrices. Denote
k(n,p) = max{fc(A) : A € IBn>p}.
Theorem 3.4.1 (Heap and Lynn, [119]) Write n = pr + s for integers r and s such that
0 < s < p. Then
k(n,p) < p(r2 - 2r + 2) + 2s.
Equality holds when s = 0.
Note that Wielandt's theorem (Corollary 3.3.1 A) is the special case of Theorem 3.4.1
when p = 1. The next theorem, due to Schwarz (Theorem 3.4.2), implies Theorem 3.4.1.
The proof here is also given by Schwarz.
Theorem 3.4.2 (Schwarz, [233]) Write n = pr+s for integers r and s such that 0 < s < p
Powers of Nonnegative Matrices
115
and let
f r2-2r
+ 2 ifr>l
ifr = l.
Then k(n,p) < pu)n + s.
Some notations and lemmas are needed in the proof of Theorem 3.4.2.
Definition 3.4.2 Let A 6 Bn with p(A) = p. If Л is not primitive, then by Corollary
3.2.3D, A is permutation similar to
О Аг
0 A2
0 '-.
AP
Ap-i
0
(3.7)
where each Ai e Mn{jfl.+1, (г = 1,2,••• ,p (mod p)) is primitive. Denote the matrix
of the form (3.7) by (щ, Ax, n2, A2, • • • ,np, Api ni), or simply (AiiA2) • • • , Ap), when no
confusion should arise.
Fix an integer p > 1. For any integers m > 0 and ni,n2,-** >% > 0> and any
Z» 6 Мщ,щ+1, (t = 1,2, • • • ,p (mod p)), define (Zi, #2, • • • , Zp)m to be the block matrix
[Aij ] such that
4.;=J z* ifi"f
13 I 0 otherw
— t s m (mod p)
otherwise.
Thus (Ai, Л2,- • • , Ар) = (Ль Л2, • • • , Ap)i.
For any rriyj > 1, define
Aj+p = Ля А,(0) = Inji and А,-(т) = A,Ai+1... Ai+m«i.
The following three lemmas are obtained form the definitions and by straightforward
computations.
Lemma 3.4.1 If A = (Ai, A2, • • • , Ap), then
(i) Am = (Ai(m),A2(m),... ,Ap(m))m.
(ii) Ai(ph) = (А*(р))л, for each t = 1,2, • • • ,p (mod p), and for each integer h > 1.
(iii) For integers fc, j,/,g with fc, j,/ > 0, 5 > 0, j + 5 < p, and 1 < / < p, Л^(Аг) =
4fa)jl|+e(fc-4r).
Lemma 3.4.2 Let A,Be Bn. Bach of the following holds.
(i) If AB is primitive, then A has no zero rows and В has no zero columns.
116
Powers of Nonnegative Matrices
(ii) If A has no zero columns and В has no zero rows, and if AB is primitive, then В А
is also primitive. Moreover,
MBA)--r(AB)\<l.
(Hi) If A = (Ait A2, • • • , Ap) € Bn is an irreducible matrix with p(A) = p, then each
Ai(p) (1 < i < p), is primitive, and \y(Ai(p)) - 7(^j(p))l < If (1 < h3 < P)-
Lemma 3.4.3 Let A = (ni,Ai,n2,A2,--- ,np,Ap,ni) = (Ai,A2,-" ,AP) € Bn be an
irreducible matrix with p(A) = p. Then k(A) is the smallest integer A; > 0 such that
Ai(k) = J, for alH = 1,2, • • • ,p.
Lemma 3.4.4 Let A = (Ai, A2i • • • , Av) € Bn be an irreducible matrix with p(A) = p.
Let ? be an integer with 1 < t < p. If for 1 < ii < i2 < - - • < it < p, 7^ = ч(А^ (р)), then
fc(A) <ртах{7?1,7Ь,• • • ,<yit} + p-*.
Proof Let h = тах{7^, 7,2, - • , 7,,} and k = ph + p — t. Since /i > у{А{. (р)),
For any 1 < I < p, since
|{ti,---,**}| + |0,I + l,« + 2,...,I+p-t}|=p+l>pl
there exist j and q (1 < j < i, 0 < </ < p — t) such that some ij = l + q (mod p), and so
Aij = Aj+g. It follows that for each I = 1,2, • • • ,p,
Ai(k) = At(q)At+q(k-q)
= At (q)Ai+q (ph)Ai+q+ph (к-ph- q)
= At {q)Aii (ph)At+q+ph (k-ph- q)
= At(q) JAl+q+ph(p -t-q) = J.
Therefore k(A) < к follows by Lemma 3.4.3. Q
Lemma 3.4.5 Let A = (niiAitn2iA2l"- ,Ap,ni) € Bn be an irreducible matrix with
p(A) = p, and let m = min{ni,n2i • • • ,np}. Then
k(A)<p(m2-2m + 3)-l.
Proof It follows from Lemma 3.4.4 and Corollary 3.3.1 A. Q]
Proof of Theorem 3.4.2 Since fc(A) = fc(PAP-1) for any permutation matrix P, we
may assume that A = (ni, Ai, ra2, A2, • • • , rap, Ap, ni), where ni 4- n2 H 1- np = n. Let
m = min{ni, • • • ,np}. Since n = rp + s where 0 < s < p, m < r.
Powers of Nonnegative Matrices
117
Case 1 m < r — 1. Then r > m + 1 > 2, and so by Lemma 3.4.5,
k(A) < p(m2-2m + 3)-l<p(r2-4r + 6)-l
< p(r2 - It + 2) + s.
Case 2 m = r. Since 711+712 + hnp = n =pr + s = pm + s, there must be
1 < н < %2 < • • * < ip-s < P such that n^ = • • • = Щр_а = r. For each j = 1,2, • • • ,p — s,
Ai;(p) € Br is primitive, and 7^. = 70<Ц(р)) < r2 - 2r + 2 (by Corollary 3.3.1 A). It
follows by Lemma 3.4.4 with t = p — s that
А;(Л)<ртах{7^,-'-,7{р_Л+р-(р-в)<р(г2-2г + 2) + 5.
When r = 1, n = p + s. Thus among any s + 1 members in {ni, • • • ,np}, at least one
of them is 1. Accordingly, one of the matrices of A*, A{+i, • • • , Ai+s-i is a J, since these
matrices has no zero rows nor zero columns. It follows that Ai(s) = J, i = 1,2, • • • ,p, and
so fc(A) < s, by Lemma 3.4.3. []
Schwarz indicated in [233] that in Theorem 3.4.2, the upper bound can be reached
when n = 7 and p = 2. Can the upper bound be reached for general n and pi Shao
and Li [252] completely answered this question. Two of their results are presented below.
Further details can be found in [252].
Theorem 3.4.3 (Shao and Li, [252]) Let A € IBn>p with p = 2 and n = 2r + 1, r > 1.
Then fc(A) = k(ntp) if and only if there is a permutation matrix P such that PAP-1 €
{Mi, M"2, Af3}, where
Afi =
and where
[ 0 Я1 "
[yl ° .
, M2 =
0 #! "
y2 0
, Mz =
' 0 н21
У1 0 J
0
#1 =
tf2 =
and
J(r+l)xr
1 (r+l)xr
*1 =
,*2 =
1 1
J rx(r+l)
1 0
rx(r+l)
118
Powers ofNonnegative Matrices
Theorem 3.4.4 (Shao and Li, [252]) When r > 1, r = 1 and s > 0, or r = 1 and $ = 0,
the matrices A € IBn>p with k(A) = /b(ra,p) can be partitioned into 2s + 5 • 2S_1, 2*""1,
and 1 equivalence classes, respectively, under the relation ~p.
Theorem 3.4.2 can be viewed as a Wielandt type upper bound of the index of
convergence of irreducible nonprimitive matrices. In order to obtain a Dulmage-Mendelsohn
type upper bound, we need a few more notions.
Definition 3.4.3 Let A € IBn>p. For 1 < i,j < n, let кА(ъ^) be the smallest integer
к > 0 such that (Al+P)ij = (A')i^, for all / > k; and define тА(г, j) be the smallest
integer m > 0 such that (Am+ap)^ = 1 for all а > 0.
Example 3.4.1 Let A € IBn,p and let D = ?>(A) with V(I>) = {vi,v2,— ,vn}. By
Proposition 1.1.2(vii), Au(z,j) is the smallest integer к > 0 such that for each / > A;, D
has a directed (v», Vj)-walk of length / + p if and only if D has a directed (vi,Vj)-walk of
length /; and шл(г,Я is the smallest integer m > 0 such that for any а > 0, D has a
directed (v^, Vj)-walk of length m + op.
Definition 3.4.4 Let A € IBn>p and D = ?(Л) with V(-D) = {vi,-- ,vn}, /(Л) =
{^1,^2, — Js} denote the set of lengths of directed cycles in D(A), and let df(A)(*\i)
denote the shortest length of a directed (vi,Vj)-walk in D that intersects directed cycles
in D of lengths in 1(D).
Also, let p = gcd(fi, h, • • • , is) 1 and define
p p p
The following two results, due to Shao and Li [251], indicate that to estimate ЦА),
we can study d^D) and ф(1\> • • • ,/s), therefore the problem can be approached by graph
theory techniques and by number theory techniques.
Theorem 3.4.5 (Shao and Li [251]) Let A € IBn,p. For 1 < ij < n, each of the following
holds.
(i) k(A) -maxi<ij<n{kA(iJ)}, and
,j)-p+l ifmA(i,i) >p-l
,. л / rnA(hl
м = 10
(ii) кА{%„,
if шл(г,;) <p-l.
Proof It suffices to prove (ii). Let m = rriA(i,j) and к = kA(i,j). Let D = D(A) with
V(D) = {vi, —, vn}. Suppose that />m — p+lisan integer.
If / = m (mod p), then / = m + ap for some integer a > 0. By Definition 3.4.3,
(Al)itj = (^41+р)^^ = 1. Assume that / ф m (mod p). By Proposition 1.1.2(vii), D has a
directed (v», u/)-walk of length exactly m. It follows by Lemma 3.2.1(ii) that D does not
have directed (vt, v^)-walk of length exactly / and I + p, and so (Al)ij = (А^р) = 0.
Powers of Nonnegative Matrices
119
Thus for each I > m-p+1, (A% = (Al+P)ijy and so by Definition 3.4.3, к < m-p+1.
On the other hand, by Definition 3.4.3, (Лш-*%- =0^1 = (Ат)у, and so к > m-p+1.
П
Theorem 3.4.6 (Shao and Li [251]) Let A € 1ВЛ>Р and D = D(A). Let 1(D) =
{luhf-" Js}. For 1 <ij <n,
mA(i.j) < с4(л)(«,j) + Ф(кМ>• • • Л).
Proof Let W be a shortest directed (v*, t/j*)-walk which intersects directed cycles of each
length in 1(D). Then by the definition of the Probenius number, for an integer а > 0, D
has a directed (vi, Vj)-walk of length exactly d^(A)(*>i) + <t>(luh> • • * k} + ap, and so the
theorem follows by Definition 3.4.3. Q
By applying the techniques used in Theorems 3.4.5 and 3.4.6, Shao, Shao and Wu
obtained the Dulmage-Mendelsohn type upper bound.
Theorem 3.4.7 (Shao, [242], [243], Wu and Shao [279]) Let A € IBn,p, D = D(A) and
l = imn{liel(D)}. Then
Theorem 3.4.8 (Shao, [242]) Let A € IBn>p and D = D(A). Write n - pr + s, where
0 < s < p. If /(.D) contains three distinct cycle lengths different from p, then
r2 — 9r -1- 4
Definition 3.4.5 Let A € IBn>p. Define
m(A) = max rriA(i,j)
l<i,j<n
IMniP = {т(Л) : Л 6 IBn,p}
Jn,p = {k(A) : А в IBn,p}
Shao and Li [251] investigated the structure of Jn>p and found that Jn>p may have gaps.
The complete characterization of Jn,P is done by Shao and Li [251] and Wu and Shao [279].
Lemma 3.4.6 below can be obtained by quoting Lemmas 3.4.3 and 3.4.4 (with t = 1).
Lemma 3.4.6 (Shao and Li, [251]) Let A = (ЛЬЛ2,--- ,AP) € IBn,p. Then for г =
1,2,— ,p,
Pl(Ai(p)) -p +1 < ЦА) <py(Ai(p)) +p- 1.
120
Powers of Nonnegative Matrices
Theorem 3.4.9 (Shao and Li, [251]) Let п,р,&1,&2 be positive integers, such that n =
pr + s, where 0 < s < p. If for all к with ki < к < fe, к & Eri then for all m with
k\p <m< k2P, m ft In>p. In particular (when ki = Л?2 = к), if к ft Er, then kp & In>p.
Proof Suppose that there exists an m with k\p < m < fop and m € /n,p« Then there
exists an Л € IBn>p with m = k(A).
By Corollary 3.2.3D, we may assume that there exist matrices АьЛг,-" ,ЛР such
that A = (ni, Ai,ri2, A2, • • • ,rip, Api ni) satisfying Theorem 3.2.3.
Since n\ + ri2 Л + np = n = pr + s < p(r + 1), there must be some щ < г.
By Corollary 3.2.3B, Aj(p) is an щ х rij primitive matrix, and so by Theorem 3.3.4,
7i=7(^i(p))€Si,C^..
On the other hand, by Lemma 3.4.6,
P7i-p + l<m<pyi+p-ly
and so h < ji < k2, contrary to the assumption that any к with ki < к < k2 is not in
Br. П
Example 3.4.2 Dulmage and Mendelsohn [77] showed that if г > 4 is even, then for any
к with r2 - 4r + 7 < к < r2 - 2r, we have k?Er. By Theorem 3.4.9, for any p > 0, s > 0
and n = pr + s, we have pk & Jn>p, and so 1П)Р may have gaps.
Theorem 3.4.10 (Shao and Li, [251], Wu and Shao [279]) Let n = pr + s with 0 < s < p.
Then
/п,р = Л(п,р)и/2(га,р),
where
{r2 — 2r + 4 1
i,V-,pL 2 J+Sj and
Ып,р) = (J {r2g-i),...,r2^-2)+n}
л > *ч > rj > Ар
М + «*2 ? (г + 8>Р
gcd(ri,r2) =p
3-5 The Index of Convergence of Reducible Nonprim-
itive Matrices
In 1970, Schwarz presented the first upper bound of k(A) for reducible matrices in Bn.
Little had been done on this subject until Shao obtained a Dulmage-Mendelsohn type
upper bound in 1990.
Powers of Nonnegative Matrices
121
Theorem 3.5.1 (Schwarz, [233]) For each A € Bn, k(A) < (n - l)2 + 1. Moreover, if A
is reducible, then k(A) < (n — l)2.
Theorem 3.5.2 (Shao, [243]) Let A € Bn, D = D{A), and DUD2,-- ,A> the strong
components of D. Let no = maxi<i<c{|V(.Dj)|}, and let so be the maximum of shortest
lengths of directed cycles in each ?)«, 1 < i < c, if D has a directed cycle, or 0 if D is
acyclic. Then
^)<n + s0(^-2).
Theorem 3.5.2 implies Theorem 3.5.1 and Theorem 3.3.1 (Exercise 3.17). In Theorem
3.5.3 below, Shao [243] applied Theorem 3.5.2 to estimate the upperbound of k(A) for
reducible matrices A.
Lemma 3.5.1 Let X € Bn have the following form:
*=¦ B °
(3.8)
where В € Bn_i and а € {0,1}. Each of the following holds,
(i) If а = 0, then k(B) < k(X) < k(B) + 1.
(ii) К о = 1, then k(B) < k(X) < max{fc(?),n - 1}.
Proof The relationship between Xk+1 and Bk+1 can be seen in Exercise 3.19. Thus by
Definition 3.2.2, k(B) < k(X). When а = 0, Lemma 3.5.l(i) follows immediately from
direct matrix computation (Exercise 3.19(i)).
Assume that а — 1. Since В e Bn-~i, for any A; > n — 2, I + В + --Bk — I +
В Л h ?л~2, by Proposition 1.1.2(vii). By matrix computation (Exercise 3.19(ii)), if
m > max{fc(B),n - 1}, then Xm = Xm+*B\ and so k(X) < max{k(B),n- 1}. Q
Lemma 3.5.2 Let n > 3 be an integer and let A € Bn be a reducible matrix. If
k(A) > n2 — 5n + 9, then there exists a matrix X € Bn with the form in (3.8) such that
В e Bn_i is primitive, such that D(B) has a shortest directed cycle with length n — 1,
and such that either A ~p X or AT ~p X.
Proof Let D = D(A). К every strong component of D is a single vertex, then An =¦
дп+i __ q^ an^ so цд^ < n < тг2 — 5n + 9, a contradiction. Hence D must have a strong
component Dx with (Уфх)! > 1. By Theorem 3.5.2,
k(A)<n + s0(^+2), (3.9)
where so and no are defined in Theorem 3.5.2. Since A is reducible,
so < n0 < n - 1. (3.10)
122
Powers of Nonnegative Matrices
If so < n - 3, then by (3.9) and (3.10), k(A) < n + (n - 3)(n - 1 - 2) = n2 - 5n + 9, a
contradiction.
If $0 = n-2 and n0 = n-2, then by (3.9), fc(4) < n + (n -2)(n-4) <n2-5n + 9,
another contradiction.
If so = n — 1, then by (3.10), no = n — 1. Then I? has a strong component ?>i which
is a directed cycle of n — 1 vertices. Therefore we may assume that A or AT has the form
(3.8), and that the submatrix В in (3.8) must be a permutation matrix. It follows that
B° = In_! = B*-1, and so ?(?) = 0. By Lemma 3.5.1, &(Л) < max{fc(?) + l,n - 1} <
n — 1 < n2 — 5n + 9, a contradiction.
Therefore it must be the case that so = n—2 and no = n—1, and so we may assume that
A or AT has the form (3.8) and that the associate directed graph D(B) of the submatrix
В in (3.8) has shortest directed cycle length n — 2.
It remains to show that В is primitive. If not, then by Theorem 3.2.2, every directed
cycle of D(B) has length exactly n —2. Since D(B) is strong, В = #п-1, and so k(B) = 0,
which implies by Lemma 3.5.1 that k(A) < n2 — 5n + 9, a contradiction. Therefore, В
must be primitive. Q
Theorem 3.5.3 (Shao, [243]) Let A e Bn be a reducible matrix. Then
fc(4)<(n-2)2 + 2.
(3.11)
Moreover, when n > 4, equality holds in (3.11) if and only if A ~p Rn or AT ~p Rn,
where
Rn =
0
0
1
1
1
0
1
0
1
0
0
0 1 0
0 0 0
0 0 0
Proof Note that (3.11) holds trivially when n € {1,2}. Assume that n > 3. Since
n2 - 5n + 9 < (n - 2)2 + 2, we may assume that k(A) > n2 - 5n + 9. By Lemma 3.5.2,
we may assume that A or AT has the form (3.8). By Theorem 3.5.1 or Theorem 3.5.2,
k{B) < (n - l)2 + 1 and so (3.11) follows by Lemma 3.5.1.
Now assume that n > 4 and that A ~p Rn or AT ~p Rn. Then direct computation
Powers of Nonnegative Matrices
123
R(n~2)4l _
yields
0
0
0 1 — 10
and so k(Rn) = (n - 2)2 + 2. Thus ?(Л) = fc(#n) = (n - 2)2 + 2.
Conversely, assume that n > 4 and k(A) — (n — 2)2 + 2 > n2 — bn + 9. By Lemma
3.5.2, we may assume that A ~p X or AT c±p X, where X is of the form (3.8). Note that
k(B) < (n - l)2 + 1. If а = 1 in (3.8), then by Lemma 3.5.1,
k(A) = k(X) < max{fc(B), n - 1} < (n - 2)2 + 1,
contrary to the assumption that k(A) = (n - 2)2 + 2. Therefore we must have а = 0, and
so by
(n - 2)2 + 2 = k(A) = k(X) < k(B) + 1 < (n - 2)2 + 2,
k(B) = (n-2)2+l. By Proposition 3.3.1 and Proposition 3.3.3, D{B) must be the digraph
in Example 3.3.1 with n — 1 vertices, and so we may assume that В is the (n — 1) x (n — 1)
upper left corner submatrix of Rn, It remains to show that the vector in the last row of
Ain(3.8)isxT = (l,0,0,— ,0).
By direct computation,
?(n-2)2 = ° <7(n-2)xl
L ^lX(n-2) *7n-2
Sincek(X) = k(A) = (n-2)2+2,X(n"2)2+1 #X(n-2)2+2,andsoxB(n-2>2 ^хгБ(п~2>2+^
Therefore xT = (1,0,0, • • • ,0), and so A ~p Rn or AT ~p Rn. [J
Theorem 3.5.4 Let n > 1 be an integer. There is no reducible matrix A € Bn such that
n2 - 5n + 9 < k{A) < (n - 2)2. (3.12)
Proof By contradiction, assume that there exists a reducible matrix A € Bn satisfying
(3.12). Then n > 7. By Lemma 3.5.2, A c±p X or AT ^p X where X is the matrix
in (3.8) such that В is primitive and such that the shortest length of a directed cycle in
D(B) is n — 2. By Proposition 3.3.3 and Proposition 3.3.1, there are exactly two such
digraphs (as described in Proposition 3.3.3), and k(B) > (n — 2)2. By Lemma 3.5.1,
(n - 2)2 > k{A) = k(X) > k(B) > (n - 2)2, a contradiction. []
Theorem 3.5.5 Let n > 13 be an integer. If n is odd, then there is no matrix A € Bn
such that
n2 - 4n + 6 < k(A) < n2 - 3n + 2, or n2 - 3n + 4 < fc(A) < (n - l)2;
124
Powers of Nonnegative Matrices
if n is even, then there is no matrix A € Bn such that
n2 - 4n + 6 < k(A) < (n - l)2.
Sketch of Proof Assume such an A exists. By Proposition 3.3.1 and Proposition 3.3.3(ii),
A is not primitive. By Theorem 3.5.3, A is not reducible. Therefore, A must be irreducible
and imprimitive, and so p(A) = p > 2. Write n = pr + s with 0 < s < p. By Theorem
3.4.2,
k(A) < p(r2-2r + 2) + s
= p(r2 + 5)-2(pr + s)-3(p-s)
n2
< pr2 + bp - 2n - 3 < — 4- Ъп - 3
n2
< — + 3n - 3 < n2 - 4n + 6,
and so Theorem 3.5.5 obtains. []
For integers j, m, n > 0, let
??m + i = {а + j : аб&};
iJJn = {k : k(A) = kiov some reducible A € Bn};
?/n = {k : k(A) = к for some Л € Bn}
Jiang and Shao completely determined RIn and BIn. For Problem IS in other classes of
matrices, the study has just begun.
Theorem 3.5.6 (Jiang and Shao, [139])
n— 1 i
Rin = (J (J №»-<+')>
n-1 i
^« = (J \J(En-i+j).
t=0 jssO
Given a matrix A € Bn, if -D(A) has a directed cycle of length s and if one of the
length s directed cycle in D(A) has exactly t vertices, we say that A has s-cycle positive
elements on exactly t rows.
Theorem 3.5.7 (Zhou and Liu, [288]) Let n > t > 1 be integers. Let A 6 Bn be a matrix
such that with s-cycle positive elements on exactly t rows. К s = 1 or if s is a prime
number, then
Powers of Nonnegative Matrices 125
The upper bound is best possible except when t > n—Js(n — 1) 4- J—f and gcd(s, n) > 1.
Theorem 3.5.7 has been improved by Zhou [285]. An important case of Theorem 3.5.7
is when s = 1.
Theorem 3.5.8 (Liu and Shao, [183], Liu and Li, [179]) Let n > d > 1 be integers.
Suppose that A € Bn has d positive diagonal entries. Then
I 2n—3—y/4n~
{ (n-d-if + i ifi<d<L2n-3-/4n
\ 2n-d-l ifd>[-2n-3-V5EI1
4
Let Jn(d) = {k : A; = fc(A) for some A € Bn with d diagonal elements }. Liu et al
completely determined In(d) as follows.
Theorem 3.5.9 (Liu, Li and Zhou, [181])
Г {1,2, • • • , 2n - d - 1} U (l?od UU En-d-i+j)
Ш = 4
ifl<d< 2"-з-у3^з
2
{1,2,—,2n-d-l}
2n—3—л/4п—3
ifd> 2-
Theorem 3.5.10 (Liu, Shao and Wu, [184]) If A € Пп, then
¦*{&
, 4 .1] if n = 5,6 or n = 0 (mod 4)
otherwise.
Moreover, these bounds are best possible.
The extremal matrices of k(A) in Theorem 3.5.8 and Theorem 3.5.10 have been
characterized by Zhou and Liu ([288] and [287]).
3.6 Index of Density
Definition 3.6.1 For a matrix A € Bn, the maximum density of A is
^)=тах{|И"*||},
and the index of maximum density of A is
h(A) = min{m > 0 : ||Am|| = ц(А)}.
For matrices in IBn>p, define
Й(п,р) = тах{/1(Л) : A € IBn>p}.
126
Powers of Nonnegative Matrices
Example 3.6.1 Let A € Bn be a primitive matrix. Then ц(А) = n2 and h(A) = 7(A).
Thus the study of the index of density will be mainly on imprimitive matrices. For a
generic matrix A € Bn with p(A) > 1, /л(А) < n2 and h(A) < k(A)+p— 1 (Exercise 3.23).
Theorem 3.6.1 Let A = (ni,Ab712, A2,••• ,np,Ap,ni) € IBn,p and denote
0 1
0
I )
JTip ХПр J
0 ]
0
• I '
0 J
and Bi = Bj, 1 < г < p - 1. Then
fc(A) = min{rn > 0 : Am = BjJ = m (mod p),0 < j < p - 1}.
Proof Let
m0 = min{m > 0 : Am — Bj,j = m (mod p),0 < j < p — 1}.
Let A; = fc(A) and write к = rp + j, where 0 < j < p. Since each A*(p) is primitive,
y(Ai(p)) exists. Let e = шах1<1<р{7(Л^(р))}. Then Aep = Bo, and so
A* = Ak+ep = Л^г+e^,н",7.
However, as Ae*> = B0, A<r+e>p = B0 also, and so A* == Ak+e*> = A(r+e>p+' = By. Thus
mo < A;.
On the other hand, write тщ = lp + j with 0 < j < p. Then Am° = Bj, and so
Am0+p _ д^р _ в^ and so A; < m0. ?
Corollary 3.6.1 Let A = (ni,Ai,n2,A2>"- ,np,Ap,ni) € IBn>p and let 7* = 7(A*(p)).
Then for each i = 1,2, • • • ,p,
p(74-l)<A(A)<p(7l + l).
Proof Note that A0 = I, for each г, by the definition of 7i,
(Ai(p)p-1 < J => A***"1* < B0 =* *(A) > p(7i - 1).
?0 =
"ЩХШ
0 J,
0
П2ХП2
0
B,
О «Л11ХП2 0
0 0 jmx,
^ПрХП!
Powers of Nonnegative Matrices
127
To show k(A) < p(ji +1), for each j with 1 < j < p, it suffices to show that Aj{p{^i) -
1) = J. Write г = j+t (modp), where 0 < t < p. Then A* = Aj+t and so (Aj+tfo))7* = J.
It follows
^i(p(7i + 1) - 1) = A,(p7«+P-1)
= (Aj • • • л_/+1 • • • Aj+p-i) *Aj-¦• • Aj+p-2
= ^(t)(Ai+t(p))^ A^+t(p - 1 -1) = J.
U
Definition 3.6.2 Let aT = (ai, a2, • • • , ap) be a vector. The circular period of a, denoted
by r(a) or r(oi, a2, • • • ,ap), is the smallest positive integer m such that
(a>i>Q>2r-- ,o,p) = (am+i,— ,Op,oi,**- ,om).
With this definition, r(oi,аг, • • • ,ap)\p.
Heap and Lynn [119] started that investigation of h(A) and (n,p). Shao and Li [251]
gave an explicit expression of h(A) in terms of the circular period of a vector, and
completely determined h(n,p).
Theorem 3.6.2 (Heap and Lynn, [119], Shao and Li, [251]) Let A € IBn,p with the form
A = (ni, Ai, • • • , rip, Ap, rii), and let r = r(ni, П2, • • • ,np). Each of the following holds.
(ii) h(A) = min{m : m > fc(A), r\m} = rl ^J.
т
Sketch of Proof Let m > 0 be an integer with m = j (mod p), such that 0 > j < p.
Define щ = rij/ whenever j = / (mod p). By Theorem 3.6.1,
m > k(A) => A- = В, =» ||Am|| = f>ni+i,
and
v
m < fc(A) =» Am < S,- =» ||Am|| < YtWi+o-
p p -j p
As Yi n2 -Ynini+3 = о Юп* " ni+i)2 ^ °' for each inteSer m ^ °» WAmW ^ Si=i ni •
Moreover, ||Am|| = 52u=i ni ^ an<^ оп^У ^m — *С^) an<^n* = n*+j» *°r eac^ * = 1» 2, • • • ,p;
if and only if m > fc(A) and r^*. Thus (i) and (ii) follow from the definitions of fj,(A) and
h(A). а
128
Powers of Nonnegative Matrices
Theorem 3.6.3 (Shao and Li, [251]) For integers n > p > 1, write n = rp + s, where
0 < s < p. Let
k(m,p) = max{k(A) : A € IBn,p}-
Then
Hn,P) = pL^J
p(r2 - 2r + 2) if r > 1, s = 0
p(r2-2r + 3) if r > l,0<e<p
p ifr = l,0<s<p-
1 if г = 1, s = 0.
Moreover, if &(Л) = й(п,р), then h(A) = /i(n,p).
Sketch of Proof For each A € IBn,p, A ~p (щ, j4i, • • • , np, Лр, ni).
Let r = iow(ni, П2, • • • , rip).
By Theorem 3.6.2,
т p p
Assume that for some A ~p (щ, Au * * • > %> 4p, ni) € IBn>p, &(Л) = k(n,p). By Theorem
3.4.2 and Theorem 3.4.3, we may assume that (rii, 712, • • • , np) = (r+1, ¦ • • , r+1, r, • • • , r),
andsoM4)=K^%n
p ^
Definition 3.6.3 The index set for h(A) is
H(n,p) = (Л(Л) : A € IBn,p}.
Thus #(n, 1) = #n.
Theorem 3.6.4 (Shao and Li, [251]) For integers n > p > 1, write n = rp + s, where
0 < s < p. Each of the following holds.
(i) If к & Er and if ki < к < fe, then for each integer m with p&i < m < pk2,
m & H(n,p).
(ii) If r is odd and if r > 5, then \p(r2 - 3r + 5) + l,p(r2 - 2r)]° П H(n,p) = 0.
(iii) If г is even and if r > 4, then \p(r2 - 4r + 7) + l,p(r2 - 2r)]° П H{n,p) = 0.
Definition 3.6.4 For integers n > p > 1, let SIBn>p denote the set of all symmetric
imprimitive irreducible matrices.
Example 3.6.2 Let A € SIBn>2 and let D = D(A). Then D(A) is a bipartite graph and
the diameter of D is k(A) + 1.
Powers of Nonnegative Matrices
129
Theorem 3.6.5 Let A = (nb Abn2,42,ni) € SIBn>2. Then
¦ щ = r%2
f к(А)г?т
h(A)
• -*J^Jifni^n2.
Proof This follows from Theorem 3.6.2. Q
Example 3.6.3 Define
SKnt2 = {*(A) : A e SIBn.2} and S#n,2 = {h(A) : A € SIBn.2}.
For integers n > к 4- 2 > 3, let G(n, fc) to be the graph obtained from Kn~k,i by replacing
an edge of ifn-M by a path fc edges. Then we can show that k(A(G)) = к, and so
S*rn,2 = {l,2,---,n-2}.
The same technique can be used to show the following Theorem 3.6.6.
Theorem 3.6.6 (Shao and Li, [251]) Let n > 2 be an integer. Each of the following holds,
(i) If n is even, then SHn>2 = [l,n - 2]°.
(ii) If n is odd, then SHn,2 consists of all even integers in [2, n — 1]°.
For tournaments, Zhang et al completely determined the index set of maximum density.
Theorem 3.6.7 (Zhang, Wang and Hong, [284]) Let STn = {h(A) : A € Tn}. Then
STn = {
{1}
{1,9}
{1,4,6,7,9}
{1,2,...,8,9}\{2}
{l,2,..,n + 2}\{2}
{l,2,---,n + 2}
if n = l,2,3
if n = 4
if n = 5
if n = 6
if 11 = 7,8,--
if n > 16.
,15
3.7 Generalized Exponents of Primitive Matrices
The main purpose of this section is to study that generalized exponents ехр(щ к), /(n, к)
and F(nt fc), to be defined in Definitions 3.7.1 and 3.7.2, and to estimate their bounds.
Definition 3.7.1 For a primitive digraph D with V(D) = {v\, v2, • * • , vn}, and for v,, Vj 6
V(D), define expn{viy Vj) to be the smallest positive integer p such that for each integer
t > p, D has a directed (vi,ttf)-walk of length t. By Proposition 3.3.1, this integer exists.
For each i = 1,2, • • • , n, define
expo(v{) = max {expo(vi,vj)}.
130
Powers of Nonnegative Matrices
For convenience, we assume that the vertices of D are so labeled that
expt>(vi) < expnfa) < * • • < expD(vn).
With this convention, we define, for integers n > к > 1,
exp(n, k) = max {expo (v*)}.
D ia primitive and
|V(D)| - «
Let D be a primitive digraph with \V(D)\ = n and let X С V(D) with \X\ = A;. Define
expp(X) to be the smallest positive integer p such that for each и € V(D), there exists a
v € X such that .D has a directed (u, v)-walk of length at least p; and define the kth lower
multi-exponent of D and the kth upper multi-exponent of D as
f(Dyk) = ^min^{expp(X)} and F(D,fc) = xmn {expD(X)}t
respectively. We further define, for integers n > к > 1,
fin, к) = max {/(?>,&)} and
D ie primitive and
|V(0)| = »
F(n,k) = max {F(D,]fc)}.
17 U primitive and
|V(D)|=«
These parameters exp(n,k), f(n,k) and F(n,k) can be viewed as generalized exponents
of primitive matrices (Exercise 3.25).
Example 3.7.1 Denote exp(n) = ea:p(n,n). By Corollary 3.3.1A and Example 3.3.1,
exp(n) = (n - l)2 +1.
Definition 3.7.2 Let Dn denote the digraph obtained from reversing every arc in the
digraph Dx in Example 3.3.1, and write V(Dn) = {vi, V2, - • • , vn}. For convenience, for
j > n, define Vj = v* if and only if j = i (mod n). For each vi € V(A0 and integer t > 0,
let 12*(г) be the set of vertices in Dn that can be reached by a directed walk in D of length
t.
Lemma 3.7.1 Let vm € V(Dn), let ? > 0 be an integer. Write t = p(n — 1) + r, where
p, r > 0 are integers such that 0 < r < n — 1. Each of the following holds.
(i) If t > (n - 2)(n - 1) + 1, then Rt(l) = V(?n).
(ii) К t < (n - 2)(n - 1) + 1, then Rt{l) - {v-r, vi-r, • • • , v„_r, vp_r+i}.
(iii) К i > (n - 2)(n - 1) + m, then #*(m) = V{Dn).
Powers of Nonnegative Matrices
131
(iv) If 0 < t < m - 1, then Rt(m) = {vm-t}.
(v) If m - 1 < * < (n - 2)(n -1) + m, then Rt(m) = iu-m+i(l).
Proof (i) and (ii) follows directly from the structure of Dn. (iii), (iv) and (v) follows from
(i) and (ii), and the fact that in Dn, there is exactly one arc from v* to v*_i, 2 < к < п.
Theorem 3.7.1 Let n > к > 1 be integers. Each of the following holds,
(i) expDn (k) = n2 - 3n + fc + 2.
(ii) f{Dni k) = 1 + (2n - к - 2)L^J - H^J2.
Proof By Lemma 3.7.1,
expDn (k) = (n - 2)(n - 1) + к = n2 - 3n + к + 2.
Note that when fc = 1, (ii) follows by Example 3.3.1. Assume that к < п. Write n — 1 =
qk+sy where 0 < s < k. Then the right hand side of (ii) becomes (q-l)(n—l)+l+s(g+l).
We construct two subsets X and F in V(Dn) as follows.
Let X = {vij, Vj2, • • • , vik } such that ti = 1, and such that, for j > 2,
. _ Г ij-i +q + l i?2<j<s + l
*J "" \ ij-i +q if s + 2 < j < fc.
Let К = {vi.+q-i : 1 < j < s} and У = V(Dn) \ Y. We make these claims.
Claim 1 IfX* = {uuu2t • • • ,uk} С К(1)п), then
еаад,, (X*) > fo - l)(n - 1) + 1 + «fo + 1).
Note that from any vertex v € X*, v can reach at most n—s vertices by using directed
walks of length (n — l)(q — 1) + 1. If a vertex vi, where 1 < / < s(q + 1) - 1, cannot be
reached from X* by directed walks of length (n — l)(q — 1) + 1, then adding a directed
walk of length s(q + 1) — 1 cannot reach the vertex vn. Thus Claim 1 follows.
Claim 2 Every vertex in Y can be reached from a vertex in X by a directed walk of length
l + (n-l)fa-l)inD».
In fact, by Lemma 3.7.1,
#l+(n-l)(ff-l)(vii) = {vn-l,Vn,Vi,V2,'" yV^+q-z}
#1+(п-1)(д-1)(^г2) = {Vi2-l,Vi2,-" ,Vi2+g_2}
#l+(n-l)(g-l)(vu) = {Vifc-i,Vifc,--- ,Vife+g-2}.
Thus Claim 2 becomes clear since
/. ,ч /• Лч • . ( 2 if2< j<s + l
132
Powers ofNonnegative Matrices
Claim 3 Every vertex V{ € V(Dn) can be reached by a directed walk from a vertex in Y
of length s(q + 1); but not every vertex can be reached by a directed walk from a vertex
in У of length s(q + 1) - 1.
It suffices to indicate that vn cannot be reached by a directed walk from a vertex in
Y of length s(q + 1) — 1. In fact, since s(q + 1) — 1 = is + q - 1, if vn can be reached by
a directed walk in Dn of length s(q + 1) — 1, then the initial vertex of the walk must be
V5(g+1)-1 € У.
By Claims 2 and 3, f{Dn, k) < expDn (X) < (q- l)(n-1) +1 + s(q+1). This, together
with Claim 1, implies (ii). Q
Theorem 3.7.2 Let n > к > 1 be integers. Then
F(Dn,A:) = (n-l)(n-AO + l.
Proof Let X' = {vi,v2,-'- >tf]b_i,t;n}. By Lemma 3.7.1, Dn has no directed walk of
length (n - l)(n - A;) from a vertex in X' to vn. Thus F(Dni k)>(n- l)(n - k) 4-1.
On the other hand, by Lemma 3.7.1 again, for any vertex Vi € V(?>n), the end vertices
of directed walks from vi of length (тг—l)(n—fc)+l consists of n—k+1 consecutive vertices
in a section of the directed cycle V1V2 • --vnvi. Since any к distinct such sections must
cover all vertices of Dny for any X С V(Dn) with \X\ = к, ехрвп {X) < (n - l)(n- k) +1.
This proves the theorem. Q
Lemma 3.7.2 Let n > к > 1 be integers and let D be a primitive digraph with V(Dn) =
{vi, ^2, • • • , vn}. If D has a loop at V{, 1 < г < г, then
/ n - 1 if A; < r
[ n — 1 + fc - r ifA;>r.
Proof Assume that D has a loop at vi, V2, • • • ,vr. Then exp?>(v») <n — 1, l<»<r.
Thus if fc < r, then ехр&(к) < n — 1.
Assume fc > r and L = {vi, • • • ,vr}. Since D is strong, V(D) has a subset X with
|X| = A; — r such that any vertex in X can reach a vertex in L with a directed walk of
length at most fc — r, and any vertex in L can reach a vertex in X with a directed walk of
length at most к - r. Thus expD(v) < (n - 1) + (fc - r), Vv € X U L. Q
Lemma 3.7.3 Let n > к > 2 be integers and let D be a primitive digraph with |V(?)| = n.
Then
expo(k) < expp(k — 1) + 1.
Proof Assume that expo(vi) = еагрр(г), 1 < г < n. Since D is strong, D has a vertex v
such that (v»,v) € Я(-О). ?
Powers of Nonnegative Matrices
133
Theorem 3.7.3 (Brualdi and Liu, [33]) Let n > к > 1 be integers and let D be a primitive
digraph with |V(D)| = n. If s is the shortest length of a directed cycle of D, then
е*РВ(*)Л S(n_1) Xk<s
| s(n — l + k-s) if fc > s
Sketch of Proof Given D, construct a new digraph D^ such that V(D^) = V(D)t
where (ж, у) € E(D^) if and only if D has a directed (a:, */)-walk of length s. Then D' has
at least s vertices attached with loops, and so Theorem 3.7.3 follows from Lemma 3.7.2.
?
Theorem 3.7.4 (Brualdi and Liu, [33]) Let n > к > 1 be integers. Then
ехр(п, к) = n2 — 3n + к + 2.
Proof Let D be a primitive digraph with |V(D)| = n. By Lemma 3.7.3, ехро(к) <
ехрв(1) + (к — 1). Let s denote the shortest length of directed cycles in D. If s < n — 2,
then by Theorem 3.7.3, expoW <n2 —Zn + 2 and so the theorem obtains.
Since D is primitive, by Theorem 3.2.2, n < n — 1. Assume now s = n — 1. Since P is
strong, D must have a directed cycle of length n and so D has Dn (see Definition 3.7.2)
as a spanning subgraph. Theorem 3.7.4 follows from Theorem 3.7.l(i) and Theorem 3.7.3.
?
Shao et al [253] proved that the extremal matrix of ехр(щ к) is the adjacency matrix
of Dn. In [185] and [241], the exponent set for ехрв{к) was partially determined.
Lemma 3.7.4 Let n>fc>s>0be integers and let D be a primitive digraph with
|F(D)| =s n and with s the shortest length of a directed cycle of D. Then f(D,k) <n — k.
Proof Let Y С V(D) be the set of vertices of a directed cycle of D with \Y\ = s. Since
D is strong, V(D) has a subset X such that FcXC V(D) and such that every vertex
in X \ Y can be reached from a vertex in У by a directed walk with all vertices in X.
Thus any vertex in V(D) can be reached from a vertex in X by a directed walk of length
exactly n- k. [2
Lemma 3.7.5 Let n>s>k>lhe integers. If D has a shortest directed cycle of length
s, then
/(!>,*) <l + e(n-A-1).
Proof Let Cs = Х1Ж2 • • • ЯвЯх be a directed cycle in D. Since D is strong, we may assume
that there exists z e V(D) \ V(CS) such that (x1} z) € E(D).
134
Powers of Nonnegative Matrices
Let X = {xi,a:2,- •• >s*}, and let Y be the set of vertices in D that can be reached
from vertices in X by a directed path of length 1. Then {z, x2, * • • , Xk+i }СУ.
Construct a new digraph D<5> with V(D&) = V(D), where (и,у) € J5(.DW) if and
only if D has a directed (u, v)-walk of length s. Then D' has a loop at each of the vertices
X2y • • • ж*+1, and (0:2, г) € ??(D^S^). Thus, each vertex in D^ can be reached from a vertex
in У by a directed walk of length exactly n — к — 1, and so every vertex in D can be reached
from a vertex in X by a directed walk of length exactly 1 + s(n — к — 1). Ц
Lemma 3.7.6 can be proved in a way similar to the proof for Lemma 3.7.5, and so its
proof is left as an exercise.
Lemma 3.7.6 Let n>s>k>lhe integers such that k\s. Let D be a primitive digraph
with |V(D)| = n and with a directed cycle of length s. Then
/(p,t)^i+j(»-*-1).
Theorem 3.7.5 (Brualdi and Liu, [33]) Let n > к > 1 be integers. Then
/(n, k) < n2 - (k + 2)n + к + 2.
Sketch of Proof Any primitive digraph on n vertices must have a directed cycle of
length s < n - 1, by Theorem 3.2.2. Thus Theorem 3.7.5 follows from Lemmas 3.7.4 and
3.7.5. ?
Theorem 3.7.6 Let n > к > I be integers such that k\(n - 1). Let /*(n,A;) =
max{/(D, k) : D is a primitive digraph on n vertices with a directed cycle of length
s and k\s}. Then
**, ,ч п2-(к-2)п + 2к + 1
f (n>k) = .
Proof This follows by combining Lemma 3.7.6 and Theorem 3.7.1(H). Q
Lemma 3.7.7 Let D be a primitive digraph with |V(.D)| = n, and let s and t denote the
shortest length and longest length of directed cycles in D, respectively. Then
F(D, n - 1) < max{n - s, t}.
Proof Pick X С V(D) with \X\ = n - 1. If V(C) С X for some directed cycle С of
length p, where s < p < t, then any vertex in D can be reached by a directed walk from a
vertex in V(C) of length n — p. Hence we assume that no directed cycle of D is contained
in X. Let и denote the only vertex in V(D) \ X. Then every directed cycle of D contains
Powers of Nonnegative Matrices
135
Let C\ be a directed cycle of length t in D. Then и € V(Ci). Since D is strong, every
vertex lies in a directed cycle of length at most ?, and so every vertex in X can be reached
from a vertex in X by a directed walk of length exactly t.
Since D is primitive, and by Theorem 3.2.2, D has a directed cycle Ci of length q with
0 < q < t. Let t = mq + r with 0 <r <q. let v € V(Ci) be the (t — r)th vertex from u.
Then Ci has a directed (v, u)-path. By repeating C2 wi times, D has a directed (v, tt)-walk
of length t Hence expppO < max{n - s,t}. Q
Theorem 3.7.7 F(n,n- 1) = n.
Proof By Theorem 3.7.2, F(n,n - 1) > F(Dn,n - 1) = n. By Lemma 3.7.7, for any
primitive digraph D with \V(D)\ — n, F(D>n- 1) < max{n - s,t} < max{n- l,n} = n.
D
Lemma 3.7.8 Let n > ш > 1 be integers and let D be a primitive digraph with | V(D)| = n
such that D has loops at m vertices. Then for any integer к with n > к > 1,
* J ~ \ 2n - m -)
F(D,k)<{ л ,
- n fc < n — m.
Proof Let X С V(D) with |X| = fc. Assume first that D has a loop at a vertex v € X.
Then every vertex of D can be reached from v by a directed walk of length exactly n — 1,
and so .F(Z), fc) < n — 1. Note that when k>n-m1 X must have such a vertex v.
Assume then к <n — rn and no loops is attached to any vertex of X. Then X has a
vertex a: such that D has a directed (ж, w)-path of length at most n - m — к +1, for some
vertex w € V(D) at which a loop of .D is attached. Thus any vertex in D can be reached
from a vertex in X by a directed walk of length exactly 2n — m — к. ?]
Theorem 3.7.8 (Brualdi and Liu, [33]) Let n > к > 1 and s > 0 be integers. If a
primitive digraph D with |V(-D)| = n has a directed cycle of length s, then
F(D,k)<\s{n-l) л »*>» —
[ s(2n — s — к) if fc < n — s.
Sketch of Proof Apply Lemma 3.7.8 to I>(s). []
Theorem 3.7.9 (Liu and Li, [179]) Let n > к > 1 be integers, and let D be a primitive
digraph with |V(D)| = n and with shortest directed cycle length s. Then
F(Dt к) < (n - k)s + (n - s).
Proof It suffices to prove the theorem when n > к > 1. Let Cs be a directed cycle
of length s and let X С V(D) be a subset with |X| = к < п. Let v G У (-D) and let
136
Powers of Nonnegative Matrices
t > (n — k)s + (n — s). We want to find a vertex x € X such that D has a directed
(a:, v)-walk of length exactly t.
Fix v e V(D). Then there is a vertex x' € X such that D has a directed (a;',v)-walk
of length d < n — s. Since Cs is a directed cycle, then for any h > d, there exists a vertex
x" e V(CS) such that D has a directed (a:", v)-walk of length h.
Note that in D^s\ x" is a vertex at which a loop is attached. Since \X\ = A; and since
D^ has a loop atx", we can find x € X such that D^ has a directed (x, ar")-walk of
length n - &. Thus D has a directed (s, a;")-walk of length s(n - к), and so D has a
directed (я, v)-walk of length * > s(n - k) + (n- s), consisting of a directed (or, x'^-walk
and a directed (s',v)-walk. []
Theorem 3.7.10 (Liu and Li, [179]) Let n > к > 1 be integers. Then
F(n,fc) = (n-l)(n-fc) + l.
Proof Let D be a primitive digraph with | V(Z>)| = n and let s denote the shortest length
of a directed cycle of D. Since D is primitive, s > n — 1. Thus by Theorem 3.7.9,
F(D, к) = s(n - k) + n - s = s(n - k - 1) + n
= (n - l)(n -fc-l)+n = (n- l)(n - Jfe) + 1.
Theorem 3.7.10 proves a conjecture in [33]. By Theorem 3.7.2, the bound in Theorem
3.7.10 is best possible. The extremal matrices for F(D, к) have been completely determined
by Liu and Zhou [186]. The determination of /(n, к) for general values of n and к remains
unsolved.
Conjecture Let n>fc-f2>4be integers. Show that
/(n,fc) = l + (2n-fe-2)L^J-L!i^A-
3-8 Fully indecomposable exponents and Hall
exponents
Definition 3.8.1 For integer n > 0, let Fn denote the collection of fully indecomposable
matrices in Bn, and Pn the collection of primitive matrices in Bn. For a matrix A € Pn>
define f(A)y the fully indecomposable exponent of A, to be the smallest integer A; > 0 such
that Ак е Fn. For an integer n > 0, define
/П=тах{/(Л) : АбРл}.
Powers of Nonnegative Matrices
137
0
0
0
1
1
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
1
0
0
0
The Proposition 3.8.1 follows from the definitions.
Proposition 3.8.1 Let n > 0 be an integer. Then
Pn = {A : A e Bn and for some integer к > 0, Ak € Fn}.
Schwarz [232] posed the problem to determine /n, and he conjectured that /n < n.
However, Chao [53] presented a counterexample.
Example 3.8.1 Let
M5 =
Then we can compute Af|, for i — 2,3,4,5 to see that /(M5) > 6. In fact, Chao in [53]
showed that for every integer n > 5, there exists an A € Pn such that f(A) > n. However,
Chao and Zhang [54] showed that if trA > 0, then fn < n.
Example 3.8.2 For a matrix AePn and an integer к > 1, that Ak € Fn does not imply
Ak+1 e Fn. Let
A =
Then we can verify that A8, A9 € F7, A10, A11 ? F7, and A{ € F7 for all i > 12.
Definition 3.8.2 For a matrix A e Pn> define f*(A), the strict fully indecomposable
exponent of A, to be the smallest integer A; > 0 such that for every i > к, А1 € Fn. Define
/n = max{/*(A) : A e Pn}.
Thus in Example 3.8.2, f(A) = 8, f*(A) = 12.
Proposition 3.8.2 Let A € Pn- Then
0
0
0
0
1
1
1
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
ЯА)<Г(А)<у(А).
138
Powers of Nonnegative Matrices
Proof Let к = f(A). Then Ak € Fn, and so f(A) < f*(A). By Proposition 3.3.1, for
any and k' > 7(A), we have Ak' > 0, and so Ak' € Fn. Therefore, f*(A) < y(A). Q
Lemma 3.8.1 Let A € Bn and D = D(A) with V(D) = {vb v2, • • • , vn}. For a subset
Jf С V(D)y and for an integer t > 0, let il*(X) denote the set of vertices in D which can
be reached from a vertex in X by a directed walk of length t, and let Ro(X) = X. Then
for an integer A; > 0, the following are equivalent.
(0 Ak € Fn.
(ii) For every non empty subset X С V(D), \Rk{X)\ > \X\.
Proof This is a restatement of Theorem 2.1.2. Q
Lemma 3.8.2 Let D be a strong digraph with V(D) = {t/i,va,--- ,vn} and let W =
{vh > Vi2, • • • , v»,} С V(D) be vertices of D at which D has a loop. Then for each integer
*>0,
|Д*(И0|>т1п{в + *,п}.
Proof Suppose that Rt(W) ф V(D). Since D is strong, there exist и € Rt(W) and
v € V(D) \ Rt(W) such that (u,v) € #(?). Since v ? Rt(W)t we may assume that the
distance in D from Vix to w is ?, and the distance in D from V{s to it is at least t, for any
j with 1 < i < s. As the directed (vi19u) in ДДИО contains no vertices in W — {%},
№(W)| > (* - 1) + (* + 1) = * +1. ?
Theorem 3.8.1 (Brualdi and Liu, [31]) let n > s > 1 be integers. Suppose that A 6 Pn
has s positive diagonal entries. Then
/*(4)<п-* + 1.
Proof Let Z) = D(A) and let W denote the set of vertices of D at which a loop is
attached. Let X С V(D) be a subset with n > \X\ = к > 0. By Lemma 3.8.1, it suffices
to show that
\Rt(X)\ > \X\ + 1, for each t > n - s +1. (3.13)
Since n > fc, we may assume that |#tPOI < я. If X Л W ^ 0, then by Lemma 3.8.2 and
since ? > n — s + 1
\R4{X)\>\Rt{XViW)\>\X^W\^t>\XriW\^n-s + l>\X\ + l.
Thus we assume that X Л Ж = 0. Let я* € X and w* €W such that the distance d from
ж* to w* is minimized among all x € X and w € W. By the minimality of d,
^<п + 1-|Х|-|1У| = п--5 + 1-А;<*.
Powers of Nonnegative Matrices
139
Since w* € W, x* can reach every vertex in Rk(w*) by a directed walk in D of length
exactly t. By Lemma 3.8.2, \Rt{X)\ > |Д*({™*})| > \Rk(w*)\ > к +1, and so (3.13) holds
also. Q
Corollary 3.8.1A (Chao and Zhang, [54]) Suppose A € Pn with ti(A) > 0. Then
f(A)<f*(A)<n.
Corollary 3.8.IB Let A e Pn such that D(A) has a directed cycle of length r and such
that D(A) has s vertices lying in directed cycles of length r. Then f(A) < r(n — s + 1).
In particular, if D has a Hamilton directed cycle, then f(A) < n.
Corollary 3.8.1С Let A € Pn such that the diameter of D(A) is d. Then
f(A)<2d(n-d).
Corollary 3.8.1D Let A € Pn be a symmetric matrix with tr(4) = 0. Then f(A) < 2.
Proof Corollary 3.8.1A follows from Theorem 3.8.1. For Corollary 3.8.1B, argue by
Theorem 3.8.1 that (Аг)п~3~1 € Fn. If the diameter of D is d, then D has a directed
cycle of length r < 2d, and D has at least d + 1 vertices lying in directed cycles of length
r. Thus the other corollaries follow from Corollary 3.8.1В. Ц
Theorem 3.8.2 (Brualdi and Liu, [31]) For n > 1,
Proof Let Л € Pn and D = D(A). Since D is strong, D has a directed cycle of length
r > 0. Let s be the number of vertices in D lying in directed cycles of length r. By
Corollary 3.8.1B,
f(A) < r(n - s + 1) < r(n - r + 1).
When n is odd, since D is primitive, D must have a directed closed walk of length different
from (n + l)/2. Since r(n — r + 1) is a quadratic function in r, we have
fM)<|^ if n is even
Л '-{ abfcj-з if „is odd,
which completes the proof. []
Conjecture 3.8.1 (Brualdi and Liu, [31]) For n > 5, /n = 2n — 4. Example 3.8.1 can be
extended for large values of n and so we can conclude that /n > 2n — 4.
Liu [170] proved Conjecture 3.8.1 for primitive matrices with symmetric 1-entries.
140
Powers of Nonnegative Matrices
Example 3.8.3 Let n > 5 and к > 2 be integers with n > fc+3. Let D be the digraph with
V(D) = {vuv2i • • • ,vn} and with E(D) = {(vu vi+1) : l<i<n-k}U {(vn-*+i, Vi)}U
{(г7п_^1,^),(^,г71) : n-fc+2< j < n}. Let A = Л(?>) andlet Xk = {vk-k+i>-~ ,vn}-
Then we can see that for each i = 1,2, • • • , fc, |J?»(n-*)-i №01 = *» and so /*(Л) > fc(n-fc).
(See Exercise 3.25 for more discussion of this example.)
Lemma 3.8.3 Let D be a strong digraph with |V(D)| = n, and let Cr be a directed cycle
of D of length r > 0.
(i)IfXCV(Cr),then
Я«г+*(*) ? i*(i+1)r+i(X), (» > 0, 0 < j < r - 1).
(ii) If X = V(Cr), then ДДХ) С %+1)(Х), for each i > 0.
Proof (i). Let z € Rir+j(X) and x € X. Since ж € V(Cr), any direct (ar,2)-walk of
length ir + j can be extended to a direct (a:, z)-walk of length (i 4- l)r + j by taking an
additional tour of Cr.
(ii). Let z € #,(X) and a; e X = F(Cr). Let a:' e V(Cr) be the vertex such that
(a:', x) € E(Cr). Then P has a directed (ж', z)-walk of length г + 1. ?
Lemma 3.8.4 Let r > s > 0 be two coprime integers, and let Dbea digraph consists of
exactly two directed cycles Cr and C3i of length r and s, respectively, such that V(Cr)f)
V(CS) ф 0. If 0 ф X С V(Cr), then
\Ri(X)\ > min{n, \X\ + l}yi>lr<mdl> 1. (3.14)
Proof Let X^ denote the vertices in V(Cr) that can be reached from vertices in X by
a directed walk in Cr of length L Thus if i = j (mod r), X^ = XW.
Assume first that r < г < 2r. If X = F(Cr), then since г > r, |Jfc(X)| > min{n, |X| +
г}, and so (3.14) holds.
Thus we assume X ф V(Cr) and / = 1. If Ri(X) g V{Cr), then |#*(X)| > |X| +1.
Assume then Д*(Х) С V{Cr). If (3.14) does not hold when I = 1, then \ЩХ)\ = |X|,
and so Ri(X) = XW. Since Ri(X) С У(СГ), we have Ri-s(X) С Яг(Х), which impUes
that Х^"5> = X^. Therefore if У = Х<?-*> С V(Cr), then F« = У, contrary to the
assumption that r and s are coprime.
Now assume that / > 2 and argue by induction on I. Note that (3.14) holds if
|lty_i)r+^(X)| = n, and so assume that \R^^r+j(X)\ < n.
If Rir+j(X) = ity_1)r+,(X), then for each t > I - 1, -Rtr+i(X) = #(z_1)r+i(X).
Since .D is primitive, for t large enough, we have \Ry_i)r+j(X)\ = |iur+j(X)| = n,
a contradiction. Hence by Lemma 3.8.3, ity_i)r+j(X) = ifyr+j(X), for each j with
Powers of Nonnegative Matrices
141
0 < j < r - 1. It follows
\Rir+j(X)\ > \R{l_1)r+j(X)\ + l
> min{n,|X| + (Z~l)} + l
> min{n,|X| + 0
which completes the proof. Q
Theorem 3.8.3 (Brualdi and Liu, [31]) Let A € Pn- If D(A) has exactly 2 different
lengths of directed cycles,then
m<L(n±i>!j.
Proof Let D(A) has directed cycles CT and Cr, of lengths r and s, respectively, such
that r and s are coprime and such that V(Cr) Л V(C8) ф 0. Let D* denote the subgraph
of D induced by E(Cr) U E(C3).
Let Y С V(D) be a subset, where 1 < к = |У| < n-1. First assume that |УПУ(СГ)| >
р>1. By Lemma 3.8.4, |#?(У)| > fc +1, (г > (fc -p+ l)r), and so by r < n- (fc-p), it
follows that
(*-p + l)r<|i(n + l)2J.
Now assume that Y П V(Cr) = 0. Then r < n — к and D has a directed (y, ar)-walk from a
vertex у € У to a vertex ж € У (C7r) of length ?, where t<n-r-k + l. By lemma 3.8.4,
\Ri({x})\>k + l, i>kr.
Therefore \Ri{Y)\ > к + 1, for i > кг + n - r - fc + 1. It follows that
n2
fcr + n-r-fc-l-l< [—J +1.
Hence for all Y 0 ф Y С X,
|^(y)|>|y| + i,i>L^^J,
which completes the proof. []
Prom the discussions above on /* (see also Exercise 3.25), we can see that the order of
/* will fall between 0(n2/4) and 0(n2/2). It was conjectured that
?<L(« + 1)2/4J
and this conjecture has been proved by Liu and Li [178].
142
Powers ofNonnegative Matrices
Definition 3.8.3 A matrix A € Bn is called a Hall matrix if there exists a permutation
matrix Q such that Q <A. Let Hn denote the collection of all Hall matrices in Pn.
Hn = {A e Bn : Ak e Hn for some integer к}.
For an matrix A € Hn, h(A), the Hall exponent of A, is the smallest integer к > 0 such
that Ak € Hn. Define
hn = max{/i(A) : A € Hn П IBn},
where IBn is the collection of irreducible matrices in Bn.
Similarly, for an matrix A € Hn, h*(A), the strict Hall exponent of A, is the smallest
integer к > 0 such that A* € Hn, for all integer i > h. Define H*. = {A e B« :
Л*(А) exists as a finite number}, and
h*n = max{/i*(A) : A € Hn Л IBn},
Example 3.8.4 In general, Pn С Hn. When n > 1, if P is a permutation matrix with
tr(P) = 0, then P € Hn \ Pn.
Example 3.8.5 Let
A =
10 0 0 0
10 0 0 0
0 1110
0 0 0 0 1
0 0 0 0 1
0 0 0 0 1
1111110
Then we can verify that A G P7 \ H7. A2 € H7 but A3 ? H7, and A1 € H7, for all i > 4.
Proposition 3.8.3 follows from Hall's Theorem for the existence of a system of distinct
representatives (Theorem 1.1 in [222]); and the other proposition is obtained from the
definitions and Corollary 3.3.1 A.
Proposition 3.8.3 Let A € Bn and let D = D(A). Each of the following holds.
(i) A is Hall if and only if for any integers r > 0 and s > 0 with r + s>n,A does not
have an 0r Xs as a submatrix.
(ii) For some integer к > 0, A* € Hn if and only if for each nonempty subset X CV(D),
\Rk(x)\ > \x\.
Proposition 3.8.4 Each of the following holds:
(i)IfAeHn,then
h(A) < h*(A) < 7(A) < n2 - 2n + 2.
Powers of Nonnegative Matrices 143
(ii) Hi€Pft, then h(A) < f(A) and h*(A) < f*(A).
(in) For each n > 1, Fn С Hn.
Example 3.8.7 Let
Г 0 0 1 0 1
л 0 0 10
A =
0 0 0 1
[ 1 1 0 0 J
Then Ak e H4 if and only if 4|fc, and so A € Hn \ Щ.
Example 3.8.8 It is possible that h*(A) > f{A). Let
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
0
0
0
0
0
1
1
0
0
0
1
0
0
0
0
1
1
0
0
0
1
0
0
0
0
1
1
0
0
0
1
0
0
0
0
1
1
0
0
0
1
0
0
0
0
1
1
0
0
0
0
1
1
1
1
0
0
0
0
0
0
1
1
1
1
0
0
Then A 0 Ню, A2 € Fio, (and so A € Рю and A2 € Ню), A3 ? Ню but Ak € Fxo С HI0,
for any к > 4. Therefore,
hm(A) = f*(A) = 4 > 2 = f(A) = h(A).
Definition 3.8.4 Let A € Bn and let
I An 0 »• • 0 1
A\2 An ••• 0
|_ Api Ap2 • • • App J
le the Frobenius normal form (Theorem 2.2.1) of A. By Theorem 2.2.1, each Ац is
^reducible, and will be called an irreducible block of A, * = 1,2, • • • ,p. A block Ац is a
wivial block of A if Ац = Oixi.
By definition, we can see that if A has a trivial block, then A ? Hn, and so Lemma
18.5 obtains.
144
Powers of Nonnegative Matrices
0
0
0
Bh
Вг
0
0
0
0 •
в2 ..
о ..
о ..
0
0
* Bh-1
0
Lemma 3.8.5 Let A € Bn. Then A € Hn if and only if every irreducible block of A is a
Hall matrix.
Theorem 3.8.4 (Brualdi and Liu, [33]) Let A € Bn. Then A € Hn if and only if the
Probenius standard form of A does not have a trivial irreducible block.
Proof We may assume that A is in the standard form. If A has a trivial irreducible
block. Then for any k, Ak also has a trivial irreducible block, and so Ak ? Hn.
Assume then that A has no trivial irreducible block. Then each vertex vi e V(D(A))
lies in a directed cycle of length m», (1 < г < n). Let p = lcm(mi,m2, ¦ • • ,mn). Then
each diagonal entry of Ap is positive, and so Л € Hn. []
Definition 3.8.5 Recall that if A € Bn is irreducible, then A is permutation similar to
(3.15)
where B{ € М*<х**+1, (1 < * < h) and &л+1 = k\. These integers k^s are the imprimitive
parameters of A
Let P € Bh be a permutation matrix and let Y\, Y2i • • ¦ , Yh 6 B* be /i matrices. Then
P(Yi,y2> * * * ,Ул) denotes a matrix in В*ь obtained by replacing the only 1-entry of the
ith row of P by Yu and every 0-entry of P by a 0*Xfc, (I <i <h).
Theorem 3.8.5 (Brualdi and Liu, [33]) Let A € IBn. Then A € H* if and only if all the
imprimitive parameters are identical.
Proof We may assume that A has the form in (3.15). Define X\ = B\B2 • • • Bh, X2 =
B2B3 • • • BhBi, • • •, Xh = l?fci?i • • • Вл-i.
Suppose first that к = k\ = k2 = • • • = kh. Then the matrices Xi, X2i • • •, Хл are in
Р*, and so there exists an integer e > 0 such that Xf = Л, for any integer p > e and
1 < i < h.
Let q > eh be an integer and write q = /Л + r, where / > e and where 0 < г < Л.
Then A9 has the form P(Yi,Y2i--- ,Уд) for some permutation matrix P, where K* =
x{Ai~- Ai+r-i, (1 < t < h, and the subscripts are counted modulo h). Since / > e,
Xf = J; since A is irreducible, each Л* has no zero columns. It follows that Yi = J,
(1 < г < h)% and so A9 € Hn. Hence A € HJ.
Conversely, assume that A does not have identical imprimitive parameters. Without
lost of generality, we assume k\ < k2. Note that for each integer / > 0, A*h+1 takes
the same form as in (3.15) with X{B{ replacing Bit 1 < i < h. It follows that A^h has
Powers of Nonnegative Matrices
145
0(n-*i)x*2 ^ a submatrix. Since (n — кг) + fc2 > га, Л/Л 0 Hn, by Proposition 3.8.3. ?
The following results concerning the Hall exponent, analogous to those concerning
the rally indecomposable exponent, are obtained by Brualdi and Liu [33] with similar
techniques.
Theorem 3.8.6 (Brualdi and Liu, [33]) Let A € IBn. If tr(A) = s > 0, then h*(A) < n-s.
Theorem 3.8.7 (Brualdi and Liu, [33]) Let n > 3. Then
Theorem 3.8.9 (Brualdi and Liu, [33], Zhou and Liu, [286]) Let A € P„. Then h*(A) <
[n2/4].
Shen et a! [240] introduced the exponent of r-indecomposability as a generalization
of fully indecomposable exponents and Hall exponents. Several useful results have been
obtained in [240] and [176].
Definition 3.8.7 The exponents can be defined in a weak sense. For a matrix A € IBn,
the weak exponents are defined as follows.
(i) The weak primitive exponents of Л, denoted by ew(A), is the smallest integer p > 0
such that A + A2 + • • • + Ap e Pn-
(ii) The weak fully indecomposable exponent of Л, denoted by /Ю(А)> is the smallest
integer p > 0 such that A + A2 + • • • + AP € Fn.
(iii) The weak Hall exponent of Л, denoted by hw(A), is the smallest integer p > 0 such
that А + Л2 + '-- + ЛР€Нп.
Theorem 3.8.10 (Liu, [171]) For A € IBn,
e*(A)<2, Л*(Л)<ф+1, and/w(A)<r|l.
Moreover, each of these bounds is best possible.
Theorem 3.8.11 (Liu, [171]) For A € IBn, let WE(n),FE(n) and HE(n) denote the set
of integers that can be the value of ew(A), fw(A) and hw{A)i respectively. Then
WE{n) = {1,2}
FE(n) = {l,2,...,L|j + l}
HE{n) = {l,2,.-,r|l}.
146
Powers of Nonnegative Matrices
3.9 Primitive exponent and other parameters
The investigation of the relationship between 7(A) and the diameter of D(A), and between
7(A) and the eigenvalues of A has recently begun and is on the rise.
We use these notations in this section: For a matrix A € Bn and D = D(A), m = m(A)
denotes the degree of the minimal polynomial of A; d = d(D) denotes the diameter of D,
and d(vi,Vj) the distance from Vi to Vj in D.
Given a matrix A, let (А)# denote the (i,j)-entry of A. Therefore, if A = (%•), then
(A)ij = а#. Similarly, given an n-dimensiona! vector a, (a)j denotes the jth component
of a. Finally, for an integer к with 1 < к < n, let e* denote the n-dimensional vector
whose fcth component is a 1 and whose other components are 0.
Proposition 3.9.1 Let A € Pn, D = D(A), d = d(D) and m = ш(Л). Each of the
following holds.
(i) y(A) > d. Moreover, if each diagonal entry of A is positive, then y(A) = d.
(ii) If the length s of a shortest directed cycle of D is not bigger than d, then 7(Л) < dn.
(iii) (See [96])
J + A + '-' + A"1-1 >0
A + A2 + --Am >0
(iv)lfV(D) = {vi,va,--- ,vn}, then
0 if i ф j.
Proof (i) follows from the graphical meaning of 7(A). To prove (ii), consider the graph
D(SK Each vertex of a shortest directed cycle Cs is a loop vertex in D^s\ from which
any vertex can be reached by a directed walk of length at most n — 1. Thus in D, any
vertex и can reach a vertex in Cs by a directed walk of length at most d, and any vertex
in V(CS) to any other vertex v by a directed walk of length at most s(n — 1). It follows
that 7(A) <d + s{n-l) <d + d(n-l). [J
Problem 3.9.1 By examine the graph in Example 3.3.1, it may be natural to conjecture
that if A € Pn> Bud if d is the diameter of D(A), then
7(A) < <f + 1. (3.16)
Note that the degree m of the minimal polynomial of A and d are related by m > d +1.
A weaker conjecture will be
d(vi, Vj) < m — 1 + Sij, where $
И
7(A) < (m - l)2 + 1.
(3.17)
Powers of Nonnegative Matrices
147
Hartwig and Neumann proved (3.17) conditionally. Lemma 3.9.1 below follows from
Proposition 3.9.1 and Proposition 1.1.2(vii).
Lemma 3.9.1 (Hartwig and Neumann, [117]) Let A € Pn, D = D(A) and m = m(A).
Suppose V(D) = {vltv2, • • • ,vn}.
(i) If Vk is a loop vertex of D, then Am~1eii > 0.
(ii) If each vertex of D is a loop vertex, then A171"1 > 0.
Theorem 3.9.1 (Hartwig and Neumann, [117]) Let Л € Pn, D = D(A) and m = m(A).
Then 7(A) <(m-l)2 + l, if one of the following holds for each vertex v € V(D):
(i) v lies in a directed cycle of length at most m — 1,
(ii) v can be reached from a vertex lying in a directed cycle of length at most rn — 1
by a directed walk of length one, or
(Hi) v can reach a vertex lying in a directed cycle of length at most m — 1 by a directed
walk of length one.
Sketch of Proof Let V(D) = {vi,v2r" >vn} and assume that v* lies in a directed
cycle of length jk < m. Then v& is a loop vertex in D(A^h). Since A*h € Pn with
m(Al*) < m(A) = m, it follows by Lemma 3.9.1 that (A^)"1-^* > 0, and so
4(m-l)2ejfe = ^[(т-1)-Мт-1) [(^m-l^j > Q.
Thus (i) implies the conclusion by Lemma 3.9.1.
Assume then Vk can be reached from a vertex lying in a directed cycle of length at
most m — 1 by a directed walk of length one, then argue similarly to see that
A(m-i)4iek = A(m-V2(Aek) > 0,
and so (ii) implies the conclusion by Lemma 3.9.1 also.
That (iii) implies the conclusion can be proved similarly by considering AT instead of
A, and so the proof is left as an exercise. []]
Theorem 3.9.2 (Hartwig and Neumann, [117]) Let A € Pn with m = m(A). Then
7(A) < m(m — 1).
Proof Let D = D(A) with V(D) = {vi,v2,— ,vn}. By Proposition 3.9.1(iii), for each
Vk e V(D), there is an integer jk with 1 < jk < m such that vk is a loop vertex of D(Ajb).
By Lemma 3.9.1, (Ajk)m-lek > 0. It follows that
Am(m-l)e(k) = A(m-jk)(m-i) [(^ifcjm-l^J > q^
and so A"1^-1) > 0, by Lemma 3.9.1(H). ?
148
Powers of Nonnegative Matrices
Theorem 3.9.3 (Hartwig and Neumann, [117]) Let A € Pn be symmetric with m the
degree of minimal polynomial of A, Then у (A) < 2(m — 1).
Sketch of Proof As A is symmetric, every vertex of D(A2) is a loop vertex. Then apply
Lemma 3.9.1 to see (A2)™-^* > 0. []
Theorem 3.9.4 (Hartwig and Neumann, [117]) Let A € Pn such that D(A) has a directed
cycle of length к > 0, and let m and m^* be the degree of the minimal polynomial of A
and that of A*, respectively. Then y(A) < (m - 1) + fc(m^fe - 1).
Proof Let С к denote a directed cycle of length k. Then V(Ck) are loop vertices in D(Ak).
Any vertex in D(Ak) can be reached from a vertex in V(Ck) by a directed walk of length
at most тдк — 1, and so in D(A), any vertex can, reach another by a-directed walk (via
vertices in V(C*)) of length at most k(mAk — 1) + (m - 1). []
Theorem 3.9.5 (Hartwig and Neumann, [117]) Let A € Pn such that A has r distinct
eigenvalues. Then D(A) contains a directed cycle of length at most r.
Proof If p(A), the spectrum radius of A, is zero, then A2 = 0. Thus r — 1 and, by
Proposition 1.1.2(vii), -D(A) has no directed cycles. Assume that p(A) > 0 and that
*-w-(t ?::: t)-
Argue by contradiction, assume that every directed cycle of D(A) has length longer than
r. Then for each к with 1 < к < r, tr(A*) = 0, by Proposition 1.1.2(vii). Thus
Ai . Л2
Aj A2
Ar
A?
/1
«2
L ^1 A2 • • • Ar J L *r J
Note that (3.18) is equivalent to the homogeneous system
(3.18)
1
Ai
1
A2
" Xih '
\zh
. Kir .
=
" ° 1
0
о J
(3.19)
I ЛГ-1 ЛГ-1 V
L л1 л2 л
The determinant of the coefficient matrix in (3.19) is a Vandermonde determinant with
А» ф 'Aj, whenever i ф j. Thus the system in (3.19) can only have a zero solution
AiZi = A2Z2 = * • • Ar/r = 0, a contradiction. []
Corollary 3.9.5A ([117]) Let A € Pn with m = m(A). If A has at most m - 2 distinct
eigenvalues, then 7(A) < (m — l)2.
Powers of Noimegative Matrices
149
The conjectured (3.17) remains unsolved in [117]. In 1996, Shen proved the stronger
form of (3.16), therefore also proved (3.17).
For a simple graph G, Delorme and Sole [73] proved 7(G) can have a much smaller
upper bound.
Theorem 3.9.6 (Delorme and Sole, [73]) Let G be a connected simple graph with diameter
&. If every vertex of G lies in a closed walk of an odd length a€ most 2g + 1, then
7(G) < d + g. In particular, if G is not bipartite, then y(G) < 2d.
Example 3.9.1 The equality 7(G) = 2d may be reached. Consider these examples: G is
the cycle of length 2fc +1 (d = к and 7 = 2k); G = Kn with n > 2 (d = 1 and 7 = 2); and
G is the Petersen graph (d = 2 and 7 = 4).
The relationship between 7(A) and the eigenvalues of A is not clear yet. Chung
obtained some upper bounds of y(A) in terms of eigenvalues of A. For convenience, we
extend the definition of у {A) and define у (A) = 00 when A is imprimitive.
Theorem 3.9.7 (Chung, [58]) Let G be a ^-regular graph and with eigenvalues A* so
labeled that |Ai| < |A2| < • • • < |An|. Then
Proof Let ui, U2, • • • , un are orthonormal eigenvectors corresponding to Ai, A2, • • • , An,
respectively, such that
ii! = -7= Jnxi and \i = k.
yn
Thus if ( JT--7 J > n - 1, then
i
*¦ v~fcAr(u<)r(ui)s
- V-|A2|ro{?l(uiMui)i|}
> 0.
150
Powers of Nonnegative Matrices
Therefore, if m > L l0?g , V. J>then Am > 0. П
Llogfc-log|A2|J *-*
With similar techniques, Chung also obtained analogous bounds for non regular graphs
and digraphs.
Theorem 3.9.8 (Chung, [58]) Let G be a simple graph with eigenvalues A* so labeled
that |Ai| < |Аг| < ••• < |An|. Let ui be an eigenvector corresponding to Ai, let w =
mini{|(ui)i|} and let d(G) denote the diameter of G. Then
log|Ai|-log|A2|
Theorem 3.9.9 (Chung, [58]) Let A € Bn be such that each row sum of A is fc, and A
has n eigenvectors which form an orthonormal basis. Then
For further improvement along this line, readers are referred to Delorme and Sole [73].
For a matrix A € Bm>n, define its Boolean rank b(A) to be the smallest positive integer
к such that some F € Bm>* and G € В*>п, A = FG. With Lemma 3.4.2, Gregory et al
obtained the following.
Theorem 3.9.10 (Gregory, Kirkland and Pullman, [106]) Let A € Pn. Then 7(A) <
(6(A)-l)2+2.
The next theorem can be obtained by applying Lemma 3.7.3 and Exercise 3.23.
Theorem 3.9.11 (Liu and Zhou, [185], Neufeld and Shen, [207]) Let A € Pn and let r
denote the largest outdegree of vertices of a shortest cycle length with length s in D(A).
Then
l{A) < s(n - r) + n < (n - r +1)2 + r - 1.
Open Problem From Proposition 3.9.1(i), one would ask the question what the matrices
A with "y(A) = d are? In other words, the problem is to determine the set
{A e Pn : 7(A) = d, where d is the diameter of D(A)}.
3-10 Exercises
Exercise 3.1 Let ai,a2»u3 > 0 be integers with gcd(aiia2iaz) = 1. Let d = gcd(oi,a2)
and write a\ — a'xd and ai = a!2d. Let Wi,tt2, ^o»2/o»^o be integers satisfying a\u\ +
Powers of Nonnegative Matrices
151
a'2U2 = 1 and агхо + а2уо + аз*о = n respectively. Show that all integral solutions of
a\x + a,2y + аз2г = n can be presented as
{x = xo + a[ti - ttia3t2
У-Уо- ai*i - ге2аз*2
2 = zo + <U2,
where ti, ?2 can be any integers.
Exercise 3.2 Let s > 2 be an integer and suppose 74, Г2, • • • ,r* are real numbers such
that ri > r2 > • • • > rs > 1. Show that
Exercise 3.3 Assume that Theorem 3.1.7 holds for s = 3. Prove Theorem 3.1.7 by
induction on s.
Exercise 3.4 Let D be a strong digraph. Let d!(D) denote the g.c.d. of directed closed
trail lengths of D. Show that d'(D) = d(D).
Exercise 3.5 Let D be a cyclically к partite directed graph. Show each of the following,
(i) If D has a directed cycle of length m, then k\m.
(ii) К h\h, then D is also cyclically /i-partite.
Exercise 3.6 Show that if A G M+ is irreducible with d = d(D(A)) > 1, and if h\d, then,
there exists a permutation matrix P such that PAhP~x = diag(Ai, Л2, • ¦ • ,Л.л).
Exercise 3.7 Prove Corollary 3.2.3A.
Exercise 3.8 Prove Corollary. 3.2.3B. For (i), imitate the proof for Theorem 3.2.3(iii).
Exercise 3.9 Prove Corollary 3.2.3C.
Exercise 3.10 Prove Corollary 3.2.3D.
Exercise 3.11 Show that in Example 3.2.1, A is primitive, В is imprimitive and A ~p B.
Exercise 3.12 Let DltD2 be the graphs in Examples 3.3.1.and 3.3.2. Show that 7(A) =
(п-1)2 + 2-г.
Exercise 3.13 Complete the proof of Theorem 3.3.2.
Exercise 3.14 Prove Lemma 3.4.1.
Exercise 3.15 Prove Lemma 3.4.2.
Exercise 3.16 Prove Lemma 3.4.3.
Exercise 3.17 Prove Lemma 3.4.5.
152
Powers of Nonnegative Matrices
Exercise 3.18 Let A € Bp and let n0, s0 be defined as in Theorem 3.5.2. Apply Theorem
3.5.2 to prove each of the following.
(i) If A e IBn>p, then k(A) < n + s0 (- - 2 J.
(ii) Wielandt's Theorem (Corollary 3.3.1A).
(iii) Theorem 3.5.1.
Exercise 3.19 Let X be a matrix with the form in Lemma 3.5.1. Show each of the
following.
(i) If а = 0, then
X*+1 =
[ B*+1
[xTBk
0 1
0 J
(ii) К о = 1, then
Xk+1 =
[¦ Bk+l
[ xT(I + B + "- + B*)
0 1
1 J
Exercise 3.20 Suppose that A € B„ with p(A) > 1. Show that ц(А) < n2 and h(A) <
fc(A)+p-l.
Exercise 3.21 Let n > 0 denote an integer, and let D be a primitive digraph with
V(D) = {vi, • • • yvn} such that esppfai) < expvfa) < * • * < escp?>(vn)- Show that
(i) F(D, 1) = еа^Ы = liP) and /(?>, 1) = expD{Vl).
(ii) f(n,n) = 0, /(n, 1) = esp(n, 1), and ,Р(п, 1) = esp(n).
Exercise 3.22 Suppose that г is the largest outdegree of vertices of a shortest cycle with
length s in ?>. Show that ежрр(1) < s(ra — r) + 1.
Exercise 3.23 Let A € Bn be a primitive matrix and let D = D(A). For each positive
к < п> show each of the following.
(i) expn(k) is the smallest integer p > 0 such that Ap has & all one rows. (That is
Jkxn is a submatrix of A*\)
(ii) /(?,&) is the smallest integer p > 0 such that Лр has a fc x n submatrix which
does not have a zero column.
(iii) F(D,k) is the smallest integer p > 0 such that Ap does not have akxn submatrix
which had a zero column.
Exercise 3.24 Let n > к > 1. Then
(n-fc-l)(n~l)
f(Dn,k)
\ 2(n-fc)-l
if n - 1 = 0(mod к)
iff <fc<n-l
Powers of Nonnegative Matrices
153
Exercise 3.25 Show that /(n, n - 1) = 1 and /(n, 1) = n2 - 3n 4- 3.
Exercise 3.26 Prove Lemma 3.7.6.
Exercise 3.27 Let D be the digraph
(i) Show that /*(A) = k(n - к).
(ii) Show that for n > 5,
ФФ<К<п*-2п + 2.
Exercise 3.28 Let A € Pn with m = т(Л). If D(A) has a directed cycle of length at
most m — 2, then 7(A) < (m — l)2.
Exercise 3.29 Let A € Pn with m = тп(Л) > 4. If every eigenvalue of A is real, then
7(A) < 3(m - 1) < (m - l)2.
Exercise 3.30 Prove Corollary 3.9.5A.
Exercise 3.31 Let A € Pn with m = m(A). If A has a real eigenvalue with multiplicity
at least 3, or if A has a non real eigenvalue of multiplicity at least 2, then 7(A) < (m — l)2.
Exercise 3.32 Prove Theorem 3.9.10.
Exercise 3.33 Prove Theorem 3.9.11.
3.11 Hint for Exercises
Exercise 3.1 First, we can routinely verify that for integers ?ь*2>
{x = xo + a[ti - tiiu3t2
у = t/o - Q>ih - u2a3*2
satisfy the equation a\x + аг2/ + озя = п.
Conversely, let а:, у, z be an integral solution of the equation a\x+a2y+a>zz — n. Since
aiz + a%y + аз2 = n, and aixo + агУо + «з^о = n,
we derive that
d(ax{x - жо) + h(y - yo)) = -c(s - *o).
Since gcd(c, d) = 1, there exists an integer ?2 such that z = z0 + dt2. It follows that
ах(ж - ar0) + h(y - y0) = -ct2-
154
Powers of Nonnegative Matrices
Since a\ui + b\U2 = 1, we have a\(—ttic?2) + h(—U2ct2) = —c*2, and so
d\ (x - X0 + WiCt2) + &1 (У — 2/0 + U2C*2) = 0.
It follows that there exists an integer ti such that
x — a* + a'lh — wia3*2, and у = t/o — ai*i — «203*2-
Exercise 3.2 Argue by induction on s > 2.
Exercise 3.3 First prove a fact on real number sequence.
Let ui,U2 be real numbers such that щ > u2 > 1. Then
l + tt2 <tti.
u2
This can be applied to show that if щ > u2 > • • • > tt* > 1, then
Jb-l
For number ai,a2, • • • ,a* satisfying Theorem 3.1.7, let gcd(ai,cfe) = di, gcd(ax,02,03) =
<k> gcd(oi, • • • ,as-i) = aY-2, s — 1 > 2. Then
, ч Qia2 , 03^1 , , од-1^-з
«1 Ct2 G*-2
+a5as^2-53^ + 1
aio2 ,
< —j— + a3
01
Ш(&-к
This, together with the fact above on real number sequence, implies that
0(eir,# »^; < — ba3di.
If, among aba2,-»- ,a«, there are s — 1 numbers which are relatively prime, then by
induction, Theorem 3.1.7 holds. Therefore, d\ > 1.
If di = pa is a prime power, for some prime number p and integer о > 0, then ds-2 = ^
for some integer 6 with 0 < b < a. Hence we have gcd(ai, a2, • • • , as) — p5 for some integer
5 > 0, a contradiction. Therefore, d\ must have at least two prime factors. Thus d\ > 6,
a>2 < o>i — di, az < a2 — 2 < n — 8. As di\a,2, we have d\ < n/2y and so
floi, • • •, «,)< ^ + a3rf! < П(П 7 dl) + (n - dy - 2)^.
di ai
Powers of Nonnegative Matrices
155
As n(n~d*) is a decreasing function of dx, ad as dx > 6, we have both nin~dl) < (n - 2)2/4
and (n - di - 2)di < (n - 2)2/4.
Exercise 3.4 Note that d!\d since cycles are closed trails. By Euler, a closed trail is an
edge-disjoint union of cycles, and so d\d'.
Exercise 3.5 Apply Definition 3.2.5 and combine the partite sets.
Exercise 3.6 By Corollary 3.2.3A and argue similarly to the proof of Lemma 3.2.2(i).
Exercise 3.7 By the definition of d{D) (Definition 3.2.4).
Exercise 3.8 For (i), imitate the proof for Theorem 3.2.3(iii). (ii) is obtained by direct
computation.
Exercise 3.9 By Lemma 3.2.2(i), PAdP~x - diag(?b • • • , Bd), By Corollary 3.2.3B, Bi
is primitive. Therefore, В™{ > 0 for some smallest integer m* > 0. Let m = тах*{т*}.
Then Б{" > 0 and БТЛ+1 > 0, and so p(A) = d, by definition.
Exercise 3.10 (i) follows from definition immediately. Assume that p > 1. Then by
Corollary 3.2.3C, p = d = d(D(A)). Then argue by Theorem 3.2.3.
Exercise 3.11 It can be determined if Л is primitive by directly computing the sequence
А, Л2, • • •. An alternative way is to apply Theorem 3.2.2. The digraph D(A) has a 3-cycle
and a 4-cycle, and so d(D(A)) = 1, and A is primitive. Do the same for D(B) to see
d(D(B)) = 3. Move Column 1 of Л to the place between Column 3 and Column 4 of Л to
get Bt and so A ~p B.
Exercise 3.12 Direct computation gives 7(Di) = 7(vn,vn) and 7(^2) = 7(vi,vn),
Exercise 3.13 Complete the proof of Theorem 3.3.2. The following take care of the
unfinished cases.
If к € {2,3, • • • , n} and k<d<n — l<n, then write d = к + / for some integer / with
0</<n — к — 1. Consider the adjacency matrix of the digraph D in figure below.
156
Powers of Nonnegative Matrices
k + 1
fc + 2
k + l + 2
Figure: when к € {2,3, • • • , n} and k <d<n — I <n
Again, we have
У < к otherwise,
and so 7(A) = к in this case also.
Now assume that A; € {n + l,nH-2,-«- ,2n — d-1}. Note that we must haved<n-l
in this case. Write к = 2n — / for some integer I with d+l < I < n — 1. Consider the
adjacency matrix of the digraph D in the figure below
Powers of Nonnegative Matrices
157
T
1
л
l-d-l l-
P '
w
-d
"* ^
*w
l-l
.A .A
I
Figure: when к € {n + 1, n + 2, • • • , 2n - d — 1}.
Note that in this case, we must have d < n — 1. Thus
.. .ч Г =2n-/ = i
M)\<*i-I»i
if t = j and у = n,
otherwise,
and so y(A) = k, as desired.
Exercise 3.14 Definition 3.4.2.
Exercise 3.15 (i) follows from Definition 3.2.3.
(ii). Use (BA)k+1 = B(AB)*B and UJV = J.
(iii). Apply (ii).
Exercise 3.16 Let к be an integer such that А{(к) = J, Vt = 1,2,-¦• ,p. Then by
Lemma3.4.1, A* = (^(fc),--- ,4p(fc)b and Ak+*> = (Ai(*+p),— , 4p(fc+p))*+p. Thus
А{(к) = 4i(fc+p), Vi, and k+р = p (mod p), and so Л* = Ak+P. It follows that &(Л) < к.
Conversely, assume that for some j, Aj(k — 1) Ф J. Note that Ak~~x = (Ai(k —
1),.. • , Ap(k - 1))*_! and A**"1*? = (Ai(fc - 1 + p), • • • , Лр(* - 1 + p))*-i+p. Since
Aj(k - 1 + p) = J ф Aj(k - 1), Ak~x ф Ак~1+Р, and so k(A) > к - 1.
Exercise 3.17 Let m = щ for some ». Then A{(p) € Мт,т is primitive, and so by
Corollary 3.3.1A, j(Ai(p)) < m2 - 2m + 2. Apply Lemma 3.4.4 with tf = 1 and i\ = t to
get the answer.
Exercise 3.18 (i). When A is irreducible, n = no and p = d(D). (ii). Theorem 3.3.1
follows from (i) with p = 1. (iii). When A is reducible, apply a decomposition.
Exercise 3.19 Argue by induction on k.
158
Powers of Nonnegative Matrices
Exercise 3.20 By Definition (of primitive matrix), p,(A) = n2 if and only if A is primitive,
and if and only if p(A) = 1. The inequality of h(A) follows from the definitions of p(A)
and k(A).
Exercise 3.21 Let n > 0 denote an integer, and let D be a primitive digraph with
V(D) = {vi,- • • ,vn} such that expoiyi) < exprtfo) < • * • < ехрв(уп)- Show that
(i) F(D, 1) = expD(vn) = 7(D) and /(Д1) = espial).
(ii) f{n,n) = 0, /(n, 1) = exp(ny 1), and F(n, 1) = exp(n).
Exercise 3.22 Let w € V(CS) and d+(w) = r. Let Vi = {v \ (w,v) € E(D)}. Then
|Vi| = r. Denote V(CS) C\Vi = {wi}. Then D has a directed path of length s from it/i to
a vertex in Pi. In D5, there is at most one vertex, say x, which cannot be reached from
loop w\ by a walk of length n — r. Thus a path of length n — r + 1 from iz>i to x must
pass through some vertex z (say) of VL, and so there is a path of length n — r from z to
ж. It follows that there is a walk of length s(n — r) + 1 from w to x in -D(-A).
Exercise 3.23 Apply definitions.
Exercise 3.24 Apply Theorem 3.7.1.
Exercise 3.25 By Theorem 3.7.5, /(n, n -1) < 1 and /(n, 1) < n2 - 3n + 3. By Theorem
3.7.1(ii), f(Dn, 1) = л2 - 3n + 3.
Exercise 3.26 Let t = — and let Cs denote a directed cycle of length s. Pick X =
{ari,X2,--- ,ff*} Q V{Cs) such that Cs has a directed (a?j,a;i+i)-path of length i, where
a;^ = a:J whenever j = j' (mod к). Since D is primitive and since n > s, we may assume
that (a?i, z) € E(D) for some ^ € V(D) \ V(C7S). Let У be the set of vertices that can be
reached from vertices in X by a directed path of length 1. Then {a:^, • • • , Xih, z} С Y.
Construct D№ as in the proof of Lemma 3.7.5. Note that x^ • • *XihXix is a directed
cycle of D№ of length к and (xi,z) € E(D^). Thus any vertex in D^ can be reached
from a vertex in У by a directed walk of length exactly n — к — 1.
Exercise 3.27 First use Example 3.8.3 to show that /* < k(n — к). As a quadratic
function in к, k(n — к) has a maximum when к = n/2. The other inequality of (ii) comes
from Proposition 3.8.2 and Wielandt' Theorem (Corollary 3.3.1A).
Exercise 3.28 Apply Theorem 3.9.4 with mAk < m and к < m - 2.
Exercise 3.29 Since p(A) > 0 and tr(A) > 0, D(A) must have a directed cycle of length
2 < m - 2.
Exercise 3.30 Apply Theorem 3.9.5 and then Exercise 3.42.
Exercise 3.31 In either case, A has at most m - 2 distinct eigenvalues. Apply Corollary
3.9.5A.
Powers ofNonnegative Matrices 159
Exercise 3.32 Suppose that A = Хпх6УЬхп. By Lemma 3.4.2, y(A) < j(XY) + 1 <
(6-l)a + 2.
Exercise 3.33 Apply Lemma 3.7.3 and Exercise 3.22.
Chapter 4
Matrices in Combinatorial
Problems
4.1 Matrix Solutions for Difference Equations
Consider the difference equation (also called recurrence relation) with given boundary
conditions
m = ci, 0 < I < к — 1,
¦ + акип + Ьп
(4.1)
(4.2)
where the constants oi, • • • , a*, Co, • • • , c*_i and the sequence (bn) are given. A solution
to this equation is a sequence (un) satisfying (4.1) and (4.2). If bn = 0, for all n, then the
resulting equation is the corresponding homogeneous equation to (4.1).
Definition 4.1.1 The equation
Afc - ajA*"1 - a2A*~2 ак = О (4.3)
is called the characteristic equation of the difference equation in (4.1), and the matrix
Л =
0
0
0
Ofc
1
0
0
ufc-1
0 •
1
0 •
Ojb-2 •
¦ 0
• 0
• 0
0.2
0
0
1
Ox
(4.4)
is called the companian matrix of equation (4.3). Note that by Hamilton-Cayley Theorem,
Ak - aiAk
• a2Ak~2 akI = 0
161
162
Matrices in Combinatorial Problems
A usual way to solve (4.1) and (4.2) is to solve the characteristic equation of the
difference equation, to obtained the homogeneous solutiont which satisfies the difference
equation (4.1) when the constant bn on the right hand side of the equation is set to 0, and
the particular solutiony which satisfies the difference equation with bn on the right hand
side.
The homogeneous solution is usually obtained by solving the characteristic equation
(4.3). However, when к is large, (4.3) is difficult to solve. The purpose of this section is
to introduce an alternative way of solving (4.1), via matrix techniques.
Theorem 4.1.1 (Liu, [169]) Let A be the companian matrix in (4.4), and let
С = (со,сь--- ,с*-1)т
B, = (0,0,--.,0Л)г, j = 0,l,2,--.
and let
AmC + Am"lBo + Am~2B1 + • • • + Ак-хВт-к = (a(m), • ¦ )T. (4.5)
Then (a<m>) is a solution to (4.1).
Proof By (4.4),
к
AmC = ?а*Ат~*С7, and
к
Am4-iBj = ^^«^-^,7=1,2,....
Thus by (4.5),
(a<»+*\...)r
= An+kC + Ат+к~гВ0 + Ат+к~2В1 + • • • + Ak'1Bn
к к к
= Y, сцАп+к~'С + ]Г uiA"**-1"* A, + ••• + ]? *4*-'Д»-1 + Ah~xBn
i=l »-l i=l
= ai
+ ? агА^Вп-г + a3 Un+*-3C + ]Г 4n+*-3-i2?i-i )
i=2 V i=l /
+ Y, ыАм-1Вп-2 + • • • + а Л AnC + ? ^n~'*<-i
i=3 V i=l /
+a*A*-2?n-.fc+1+A*-1Bn.
Matrices in Combinatorial Problems
163
Note that
0 10
, fori = 0,l,2,--* ,Jfe-l.
AlBj = (0, — )T> 0 < г < Ar - 2, andanyj,
Ak'xBn = (6n,--)T-
It follows that
(a<n+*>,
•)T = o1(e(»«-1>). ..)T + a2(aC+*-2),...)T + (0,...)r
+аз(а("+*-3),"-)Т + (0,-")Т
+ •••
+^(а<п»,.-)Г + (0,-)Т + (6»,-)Г-
Therefore, a<n+fc) = J^, <ца(п+*-*> + 6„, for each n > 0, and so (4.1) is satisfied.
When 0 < n < A; — 1, by (4.5) again, we have
(аО\.--)Т = A°C = (co,-f
(о«,...)Г = Ж7=(С1)--)Т
(а(*-1),-..)Т = Л*-1С = (ск_1)-)Т
and so (4.2) is also satisfied. []
We shall find a combinatorial expression of the a^'s. Let Am = (e{™ )• Then by
(4.5), we have, for m > k> that
fe-l m-Jfe
(4.6)
i=o
t-0
Definition 4.1.2 For a matrix A = (a#) € Mn, define a weighted digraph D (called the
weighted associate digraph of A) as follows. Let V(D) = {1,2, ••• ,n}. For itj € V(D),
an arc (ij) € ??(-D) with weight w(i,j) = o# exists if and only if a# #0. If Г = vi -*
V2 -»• • • • -* v* is a directed walk of D, then the weight of T is w(T) = П?=1 w(vi> vi+i)-
Therefore if Am = (aW), then a\^ is the sum of the weights of all directed (г, j)-walks
of length m (the weighted version of Proposition 1.1.2(vii)).
Lemma 4.1.1 a\f = ag*1^.
164
Matrices in Combinatorial Problems
Proof Note that for 1 < m < к - 1,
a(m) = a(m+i-i) = f 1 ifm = j-l
13 jj \ 0 i{j<m<k-l.
Now assume m > к. Note that any directed (1, J)-walk of length m must be the form
1 -» 2 -» > j -» > fc -» > j,
which yields a one-to-one correspondence between all directed (г, j)-walks of length m and
the directed (j, j)-walks of length m - j + 1.
Since w(i,i + 1) = aM+x = 1, for all 1 < i < j - 1, we have a[f = a^14). Q
Lemma 4.1.2 Define /W = 0 for each t < 0, /C°> = 1 and
*г ? 0. (» = 1.2, ¦•• ,fc)
Then for j = 1,2,— ,fc,
eSt)=Ee*-w/(m"b+l"1) (4J)
Proof By Definition 4.1.2, D has these directed (k} fc)-walks:
Type Walk Length Weight
d k-bk 1 a\
C2 fc -* fc - 1 -* & 2 a2
Cz к-*к-2-+к-1-?к З а3
C* fc -» 1 -» 2 -» »fc А; a*
Therefore, any directed (fc, fc)-walk of length m must have s± of Type Ci, s2 of Type
C2,-- ,s* of TypeC*.
For any j with l<j<k — l,D has these directed (j,j)-walks:
Type Walk
Сi j -> ?k >k-+l-+2-+ >j
С2 j -> >k vk-*2-+Z-? У j
C'z j -> У к *> fc -» 3 -* 4 -* >j
C\ j-> >k >k-> j
Matrices in Combinatorial Problems
165
For each i with 1 < i < j, the first directed (j, fc)-walk of length к — j and the last
directed (k, j)-walk of length j - i +1 of C\ form a directed closed walk of length к - i +1.
Thus, for each j with 1 < j < к,
4?
30
= У У ( Sl+S2 + --+iSk-i+l-1) + - + Sk)al^--aV-
•i > 0, t ,4 k - i + 1
,t > 0, * = fc - i + 1
»t > 0,(1 =1,2, ••• ,fc)
Therefore the lemma follows by the definition of f(m\ ?]
Theorem 4.1.2 (Liu, [169]) The solution for (4.1) and (4.2) is
fc-l j m-fc+l
i=i t=i i=i
Proof This follows from Theorem 4.1.1, (4.6) and (4.7). []
Corollary 4.1.2A Another way to express um is
к j m-k+l
i=i i-i j-i
Corollary 4.1.2B (Tu, [261]) Let к and r be integers with 1 < r < к - 1. The difference
equation
{un+k = aun+r + bun + bn
Щ = Co,!*! = Ci, • • • ,ltjfe_i = Cjfc-i
has solutions
r-l Jb-l m-fc+l
«»=Ec*b/(m-*_i)+Ec^(m_i) + E ь*-!^—*-^.
i=o j-r i=i
where
0)
fc* + (fc-r)y = m \ " /
Proof Let a* = 6, a*_r = a and all other a* = 0. Then Corollary 4.1.2B follows from
Theorem 4.1.2. ?
166
Matrices in Combinatorial Problems
Corollary 4.1.2C Letting о = b = 1, bn = 0 r = 1, and cq = d = 1 in Corollary 4.1.2B,
we obtain the Fibonacci sequence
Example 4.1.1 Solve the difference equation
{
Fn+b = 2Fn+A + ZFn + (2n - 1)
FQ = l,Fi = 0,F2 = 1, Д = 2,F4 = 3.
In this case,
fc = 5,r = 4,a = 2,6 = 3,&n = 2n-l
Co = l,ci = 0,c2 = l,c3 = 2,c4 = 3.
and so
l(n-5)/5j
Fn = 3
i=0 \ * /
l(n-7)/5j / \
+3 ^ jn-^-7\3I2n_Sl_7
l(n^8)/5j / \
+6 ^ »-^-8 3.rw
+3 Е I , ) З^-51-4
n-4 l(«-4-i)/5j / _ . _ 4 _ . \
+I>'-3) E F2"
4.2 Matrices in Some Combinatorial Configurations
Incidence matrix is a very useful tool in the study of some combinatorial configurations. In
this section, we describe how incidence matrices can be applied to investigate the properties
of system of distinct representatives, of bipartite graph coverings, and of certain incomplete
block designs.
Definition 4.2.1 Let X = {x\, x2, • • • , xn} be a set and let Л = {Xi, X2, • • • , Xm] denote
a family of subsets of X. (Members in a family may not be distinct.)
Matrices in Combinatorial Problems
167
The incidence matrix of A is an matrix A = (ay) 6 Bm>n satisfying:
a.. f 1 if a?i€X<
aii \ о iixj&Xu
where 1 < г < m and 1 < j < n.
Example 4.2.1 The incidence of elements of X in members of A can also be represented by
a bipartite graph G with vertex partite sets X = {rri, a?2, • • • , xn} and Y = {t/i, 2/2, • • * , 2/m}
such that Eil/j € ??(C?) if and only if ж» € X,-, for each 1 < г < n and 1 < j < m. Let Л
be the incidence matrix of A, Note that a set of к mutually independent entries (entries
that are not lying in the same row or same column, see Section 6.2 in the Appendix) of
A corresponds to к edges in E(G) that are mutually disjoint (called a matching in graph
theory),
In a graph #, a vertex and an edge are said to cover each other if they are incident.
A set of vertices cover all the edges of H is called a vertex cover of H. Since a line in
the incidence matrix A of A corresponds to either an element in X or a member in A,
either of which is a vertex in G. Therefore, Theorem 6.2.2 in the Appendix says that in a
bipartite graph, the number of edges in a maximum matching is equal to the number of
vertices in a minimum vertex cover.
Definition 4.2.2 A family of elements (Xi : i € I) in S is a system of representatives (SR)
of A if Xi € Ai, for each г € I. An SR (xi : i € I) is a system of distinct representatives
(SDR) of A if for each i,j € I, if i Ф j, then xi Ф Xj.
Example 4.2.2 Let X = {1,2,3,4,5}, Хг = X2 = {1,2,4}, Xz = {2,3,5} and X4 =
{1,2,4,5}. Then both Dx = {1,2,3,4} and D2 = {4,2,5,1} are SDRs for the same family
X.
However, for the same ground set X, if we redefine X\ = {1,2}, X2 = {2,4},Хз =
{1,2,4} and X4 = {1,4}. Then this family {XuX2,XZ,XA} does not have an SDR.
Example 4.2.3 Let A be the incidence matrix of A. By Definitions 4.2.1 and 4.2.2, A
set of к mutually independent entries of A corresponds to a subset of к distinct elements
in X such that for some к members XiXiX^* • • ,Xih of A, we have Xj € X^, for each
1 < j < k (called a partial transversal of A). Thus a partial transversal of \A\ elements is
just an SDR of A,
Several major results concerning transversals are given below. Proposition 4.2.1 is
straightforward, while the proofs for Theorems 4.2.1, 4.2.2 and 4.2.3 can be found in [113].
Proposition 4.2.1 Let X = {a?i,a?2»"" »^n} be a set and let A = {Xi,X2,--- ,Хт}
denote a family of subsets of X. Let A € Bm>n denote the incidence matrix of A. Each of
the following holds.
168
Matrices in Combinatorial Problems
(i) The family A has an SDR if and only if pA, the term rank of A, is equal to m.
(ii) The number of SDRs of Л is equal to per (A).
Theorem 4.2.1 (P. Hall) A family A = {X{ \ г € /} has an SDR if and only if for each
subset J С J, | Ui€j Xj\ > \J\.
Given a family X = {Xi, X2, • • • , Xm}, N(X) = N(Xi, • • • , Xm) denotes the number
of SDRs of the family.
Theorem 4.2.2 (M. Hall) Suppose the family X = {Хг, X2, • • • , Xm} has an SDR. If for
each i, \Xi\ > k, then
xr/V4 f k\ iffc<m
ЩХ) >{ .,
Van Lint obtains a better lower bound in [162]. For integers m > 0 and ni,«•• ,nm,
let
-Fm(ni,n2, • • • ,nm) = IlgJ1 max{nt+i - i, 1}.
Theorem 4.2.3 (Van Lint, [162]) Suppose the family X = {XuX2r- >Xm} has an
SDR. If for each », \Xi\ > nu then
N(X)>Fm(nun2,--- ,пт).
Definition 4.2.3 Let 5 be a set. A partition of 5 is a collection of subsets {A\, A2, • • • , Am}
such that
(i)5 = U^4 and
(ii) А» П A, = 0, whenever г ^ j.
Suppose that S has two partitions {Ai,A2,-«- ,Am} and {Bi,B2,— ,Bm}. A
subset E С S is a system of common representatives (abbreviated as SCR) if for each
ij в {1,2,— ,m},
ЕП АъфЪ and EnnBj^ffi.
Theorem 4.2.4 Suppose that S has two partitions {A\, A2i • • • , Am} and {Bi, Б2, • • •, ?m}«
Then these two partitions have an SCR if and only if for any integer A; with 1 < /г < m,
and for any к subsets A^, il»a, • • • ,A$fc, the union U*_1Aii contains at most к distinct
members in {Bi, B2, • • • »Дп}-
Interested readers can find the proofs for Theorems 4.2.1-4.2.4 in [222] and [162],
Definition 4.2.4 For integers к, t, X > 0, a family {Хг, X2i • • • , Хь} of subsets (called the
blocks of a ground set X = {xi,x2i • • • ,xv} is a t-design, denoted by 5л(t, fc,v), if
Matrices in Combinatorial Problems
169
(i) \Xi\ = k, and
(ii) for each t element subset T of X, there are exactly Л blocks that contain T.
An 5x(2,fc,v) is also called a balanced incomplete block design (abbreviated BIBD, or a
(v,?,A)-BIBD) . A BIBD with b = v is a symmetric balanced incomplete block design
(abbreviated SBIBD, or a (v,fc,A)-SBIBD). An Si(2,k,v) is a Steiner system.
Example 4.2.4 The incidence matrix of an Si(2,3,7) (a Steiner triple system):
л =
1
0
0
0
1
0
1
1
1
0
0
0
1
0
0
1
1
0
0
0
1
1
0
1
1
0
0
0
0
1
0
1
1
0
0
0
0
1
0
1
1
0
0
0
0
1
0
1
1
Proposition 4.2.2 The five parameters of a BIBD are not independent. They are related
by these equalities:
(i) rv = bk.
(ii) \(v - 1) = r(k - 1).
Theorem 4.2.5 Let A = (a^) 6 Bb,v denote the incidence matrix of a BIBD S\(2, kt v).
И v > к, then
(i) ATA is nonsingular, and
(ATA)-1 = ((r - A)J„ + AJ.)"1 = ^j(lv- ^J.) •
(ii) (Fisher inequality) b > v.
Proof By the definition of an 5д(2, к, v), we have the following:
r(fc-l) = A(v-l)
AJV)b = kJb
ATA = (r-A)/v + AJv.
If v > kt then r > A, and so the matrix (r — \)IV + XJV has eigenvalues r + (v + 1)A
and A — r (with multiplicity v — 1). Since all v eigenvalues of ATA are nonzero, ATA is
nonsingular, and the rank of A is v. By direct computation,
((r-AK.+AJ.r-j^J.-Aj.).
170
Matrices in Combinatorial Problems
Note that A € B&>v and the rank of A is v. Fisher inequality b > v now follows. Q
Theorem 4.2.6 (Bruck-Ryser-Chowla, [222]) If a (v, fc, A)-SBIBD exists, and if v is odd,
then the equation
x2 = {k-\)y2 + {-\)^\z2
has a solution in x% y, and z, not all zero.
We omit the proof of Theorem 4.2.6, which can be found in [222]. In the following, we
shall apply linear algebra and matrix techniques to derive the Cannor inequalities.
From linear algebra, it is well known that the matrices P = A(ATA)^1AT and Q-h-
P, representing the projections to the column space of A and to is orthogonal complement,
respectively, are symmetric and semipositive definite. Therefore, by Theorem 4.2.5 and
by the definition of an S\(2, fc, v),
P = A(ATA)-1AT = A((r-\)Iv+\Jv)-1AT
- тк(**-*»*«)
and
By the definition of an incidence matrix, any mxm principal submatrix of Q can be
obtained as follows: Pick a subfamily A* = {Х'ЪХ'2, - • • ,X^} of A, Let \ii$ denote the
common elements in both X- and in Xj, (1 < i < m, 1 < j < m), and let U = (р#).
Then
is an m x m principal submatrix.
Since Q is semidefinite positive, det(Qm) > 0. Hence we have the following.
Theorem 4.2.7 (Cannor inequalities) With the notations above, if Qm is a principal
submatrix of Q = h — P, then det(Qm) > 0.
Note that there are 2b — 1 such inequalities. When m = 1, this yields Fisher inequality.
When m = 2, Cannor inequalities say that the number \i of common elements in two
Matrices in Combinatorial Problems
171
blocks must satisfy
(r-k)(r-\)>\\k-rfj,\.
Readers interested in design theory are referred to [76].
4.3 Decomposition of Graphs
Definition 4.3.1 Let G be a loopless graph. A bipartite decomposition of G is a
collection edge-disjoint complete bipartite subgraphs {(?i, G2, • • • > Gr} oiG such that E(G) =
Since a graph with a loop cannot have a bipartite decomposition, we assume all graphs
in this section are loopless.
Example 4.3.1 Let Я be a graph and let v € V(H). Denote Eh(v) the edges in H incident
with v. For a complete graph G = Kn with V(G) = {vi, v2i • • • , vn}> for 1 < i < n — 1, let
ft = (G-Ыг- ,Ч-1})[Ео-{91,...,9м}Ы]-
(Thus (•?* is the subgraph of G — {vi, • • • , Vi_i} induced by the edges incident with v in
G - {vi, • • • , Vj_i}.) Then {6гь<22, • • • , Gn-i} is a bipartite decomposition of Kn.
What is the smallest number r such that Kn has a bipartite decomposition of r
subgraphs? This was first answered by Graham and Pollak. Different proofs were later given
by Tverberg and by Peck.
Theorem 4.3.1 (Graham and Pollak, [105], Tverberg, [263], and Peck, [210]) If {Gu G2, • • • , GT}
is a bipartite decomposition of Kny then r > n — 1.
Theorem 4.3.2 (Graham and Pollak, [105]) Let G be a multigraph with n vertices with a
bipartite decomposition {Gi,G2> • • • ,Gr}. Let A = A(G) = (a#) be the adjacency matrix
of Gy and let n+,n_ denote the number of positive eigenvalues and the number of negative
eigenvalues of A, respectively. Then r > max{ra+,n_}.
Proof A complete bipartite subgraph G% of G with vertex partite sets X\ and Yi can be
obtained by selecting two disjoint nonempty subsets X\ and Yi from V(G). Therefore we
write (Xi.Yi) for Gu 1 < г < г.
Let 2i, • ¦ • ,zn be n unknowns, let z = (21,z2i • • • ,zn)T, and let
g(z) = zrAz — 2 ])P QijziZj-
l<i<j<n
For each (X^Yi),
#(z) =\YjZk~YjZl
•
172
Matrices in Combinatorial Problems
Since {(7i, Фа, • • • , G>} is a bipartite decomposition of G,
r
ф) = ггЛг = 2^#(г),
i=l
By the identity 4ab = (a + b)2 - (a - 6)2,
«(»> = 5 (ew) (??(¦)').
where Z|(z) and Z"(z) are linear combinations of 21,22, * * * ,?n-
Note that l[t 1'2, • • • , I J. will take zero values over a vector subspace W of dimension at
least n-r. Therefore, q(z) is semidefinite negative over W.
Let E+ denote the vector subspace spanned by the eigenvectors of A corresponding to
the positive eigenvectors. Then E+ has dimension n+ and q(z) is positive definite over
E+. It follows that (n — r) + n+ < n, and so r > n+. Similarly, r>n-. Ц
Note that Л(1(ГП) = Jn—In has n — 1 negative eigenvalues. Thus Theorem 4.3.2 implies
Theorem 4.3.1.
Definition 4.3.2 A bipartite decomposition {G\, С?2> * * * »Gr} of a graph G may be viewed
as an edge coloring of E(G) with r colors, such that the edges colored with color i induce
the complete bipartite subgraph G{. A subgraph H of G is multi-colored if no two edges
of H received the same color.
Theorem 4.3.2 has been extended by Alon, Brualdi and Shader in [3]. We refer the
interested readers to [3] for a proof.
Theorem 4.3.3 (Alon, Brualdi and Shader, [3]) Let G be a graph with n vertices such that
A = A(G) has n+ positive eigenvalues and n- negative eigenvalues. Then in any bipartite
decomposition {G\, <32, • • • , G>}> there is a multi-colored forest with at least max{n+, n_}
edges. In particular, any bipartite decomposition of Kn contains a multi-colored tree.
Theorem 4.3.4 (Caen and Gregory, [44]) Let n > 2 and let K*n denote the graph
obtained from Kn>n by deleting edges in a perfect matching.
(i) If ИГ* has a bipartite decomposition {Gb • • • , Gr}, then r>n.
(ii) If r = n, then there exist integers p > 0 and 5 > 0 such that pg = n — 1 and each
Gi is isomorphic to Kp,q.
Proof Let {Л*,У} denote the bipartition of V(G*n), where X = {a?i,a?2»,,# >sn} and
У = O/bS/2,* • • ,t/n}- For each t with 1 < i < r, Gi has bipartition {Хг,У5}. Let G'{ be
the subgraph induced by the edge set E(Gi), and let Ai = -A(GJ) be the adjacency matrix
of G'i. Note that
7-/ = Л1+Л2, + -^ + Лг. (4.8)
Matrices in Combinatorial Problems
173
For each г with 1 < i < r, let
x, = (*»,*», • • • ,x$f алс! у, = (»»,»«, • • • ,yWf
such that for fc = 1,2, • • • , n,
,, fl if,fc6* andyW = (l *»*«
[ 0 otherwise [ 0 otherwise.
Therefore, Ai = х,у?\ 1 < * < r. Let Ax = (xi,x2,--- ,xn) € Bn>r and Ay =
(УьУ2, • * • ,Уп)т € Br,n. Then by (4.8),
J-I = AxAy. (4.9)
By (4.9), n = rank(J - J) < r, and so Theorem 4.3.4(i) follows.
By (4.9), for each г with 1 < i < r, yfx» = 0. For integers i,j with 1 < i,j < n,
define Г/ € Bn>n_i to be the matrix obtained from Ax by deleting Column i and Column
j from Ax and by adding an all 1 column as the first column of U; and define V 6 Bn_i,n
to be the matrix obtained from Ay by deleting Row i and Row j from Ay and by adding
an all 1 row as the first row of V. Then
UV = In+Xiyf + Xjyj
is a singular matrix. Let
It follows that
0 = det(UV) = det(Jn + UiVi) = det(/2 + ViUi)
= l-(yfx,)(yjx«),
and so for each г, J,
yf xj = yJxi = L
If r = ra, then by (4.9), we must have
AyAx = J-I, (4.10)
and so by (4.9) and (4.10),
U\ = (xi,Xj) and Vi
-($)•
Ax J = «/Ax, and Ay J = JAy,
174
Matrices in Combinatorial Problems
and so all the rows of Ax have the same row sum and all the columns of Ax have the same
column sum and so there exists an integer p > 0 such that Ax J = J Ax = pJ- Similarly,
there exists an integer q > 0 such that Ay J' = J Ay = qJ> It follows that
(n - 1) J = (J -1) J = (AxAy)J = Ax(AyJ) = Ax(qJ) = (pq)J,
and so Theorem 4.3.3(ii) obtains. []
Definition 4.3.3 Let mi,m2,--* >wi* be positive integers, and let G be a graph. A
complete (mi,m2,-'* ,mt)~decomposition of G is a collection of edge-disjoint subgraphs
{Gi, • • • , Gt) such that E{G) = и^-Е^С?,) and such that each G, is a complete m^partite
graph.
Another extension of Theorem 4.3.1 is the next theorem, which is first proposed by
Hsu [134].
Theorem 4.3.5 (Liu, [173]) If Kn has a complete (mi,m2, • • * ,m*)-decomposition, then
t
n < 5^(т» -1) +1.
Proof Suppose that {Gi, • • • ,Gt} is a complete (mi, • • • ,mt)-decomposition of G, where
Gi is a complete m$ partite graph with partite sets Л,,!, Ait2i • • • ,А^т{, (1 < г < t).
Let xi,X2, • • • ,жп be real variables and for t, j = 1,2, • • • , i, let
Lij= 23 Xk-
k€Aiti
Note that
t
i=l l<i<*<mt- l<i<i<mi
Consider, for each i with 1 < г < t, the system of equations
Г Lw=0
l **'
By contradiction, assume that n > 5^?=i(m* — 1) + 1- Then in the system there are more
variables than equations, and so the system must have a nonzero solution (x\, a?2, • • • ,xn).
Matrices in Combinatorial Problems
175
For such a solution,
0
= (x>)=2 e *<^+s^
\i=l / l<i<j<n t=l
= 2? y: bw^»+E^
»=1 l<j<fc<n i=l
1=1
a contradiction. []
Corollary 4.3.5 (Huang, [136]) If Kn has a complete (mi,m2,--- , m*)-decomposition
with mi = ТП2 = • • • = 7п^ = m, then
m — 1
Corollary 4.3.5 follows immediately from Theorem 4.3.5. When m = 2, Corollary 4.3.5
yields Theorem 4.3.1.
Definition 4.3.4 Let G be a simple graph and let xty € V(G). Let Р*(ж,у) denote a
collection of к internally disjoint (s,t/)-paths:
Рк(х,у) = {РиР2Г-,Рк},
where the paths are so labeled that \E(Pi)\ > \E(P2)\ > ••• > \E(Pk)\. The ^-distance
between x and t/ is
<fc(*fy) = min l|S(P*)|};
all possible Pjb(xty)
and the fc-diame?er of G is
dk(G)= max dk(x,y).
x,yeV(G)
The following problem was posed by Hsu [134]: Given two sequences of natural numbers
U = {lu hi * *' > h} and Dt = {di, cfe> • • • , d*}, is it possible to decompose a Kn (n > 2)
into subgraphs Fi, i<2> • • • , -Fi such that each Fi is fo-connected and such that d(. (Fi) < di,
1 < i < t. Such a decomposition, if exists, is called an (Lt, Dt)-decomposition of Kn.
Let /(?*, Dt) denote the smallest integer n such that Kn has an (Lti ^^-decomposition.
When h = fe = • • • = /t = / and di = d2 • • • = dt = d, we write /(/, d, ?) for /(?*, Dt).
Theorem 4.3.6 Let Lt = {/ь/2,*" ,/t}and A = {^1,^2,*-- ,*}, and let Af = ?)i=i&+
l)l«. Then
/(Lt,Dt) > |(1 + л/ГТШ). (4.11)
176
Matrices in Combinatorial Problems
Proof Suppose that Kn has an (L$, ?)t)-decomposition Fi, F2, • • • ,Ft. Then
(2) =Ei^i)i^|D^№)i^5E^+^ = f •
Therefore, n(n - 1) > M, and so (4.11) obtains. []
Corollary 4.3.6 /(I.**) > * + V1+4*(* +*),
Proof When h = J2 = • • • = /* = /,
t
Af = ?> + l№ = il(J + l)f
which implies Corollary 4.3.6. Q
Theorem 4.3.7 Let Lt = {Ji.fe»--- >h} and A = {di,6fe,*•• ,dt} with each d* > 1.
Then
t
/№*,Л*)<5> + 1- (4.12)
t=i
Proof Since a complete (/i + l)-partite graph is ^-connected, it suffices to decompose
Kn into t subgraphs Fi,F2, • • • ,Ft such that each Fi is a complete (k + l)-partite graph.
Thus (4.12) follows from Theorem 4.3.5. ?
By Theorem 4.3.6 and Theorem 4.3.7, we obtain the corollary below.
Corollary 4.3.6 Let M = ?t=i h(k + 1). Then
(i) (1 + УТ+Ш)/2 < f{LuDt) < YLi U + !•
(ii) (1 + v^ + W + 1))/2 ^ /(* Д *) < « + 1.
The upper bound in Corollary 4.3.6(H) can be improved by applying a result of Huang
[136].
Theorem 4.3.7 (Huang, [136]) Let 6, m, n be integers such that n = b(m -1) +m—(b-1)
and 2 < Ь < m — 1. Then itfn can be decomposed into 6+1 complete m-partite subgraphs.
Theorem 4.3.8 For 3 < t < I + 1 and d > 2,
f(l,d,t)<tl-t + $. (4.13)
4.4 Matrix-Tree Theorems
Let D be a digraph. Aside from the adjacency matrix A(D), there are other matrices
associated with D. The study of these matrices can reveal combinatorial properties of the
digraph D.
Matrices in Combinatorial Problems
177
Definition 4.4.1 Let Dbea digraph with n vertices and without multiple arcs and loops.
Let A(D) e Bn be the adjacency matrix of D. The path matrix of D is
P(D) = J?Ak{D)9
fc=i
where the multiplication and addition are Boolean.
Theorem 4.4.1 Let D be a digraph with V(D) = {vi, V2, • • • ,vn} and denote P{D) =
to).
(i) D is strongly connected if and only if P(D) = J.
(ii) Define
Pu P12P21 ••• PinPni
P(D)©Pr(D) =
P21P12 P22 '"' P2nPn2
PnlPln Pn2p2n '' *
If the nonzero entries in the ith row of P(D) 0 PT(D) is
PijiPjliiPiJ2Pj2ii''' iPijkPjkii
then D\ = D[{v,, t/^l, Vj2, • * * , % }]> tne subgraph of D induced by the vertices {vi, v^, Vj2, • •
is a maximal strong subgraph of D containing vi (that is, for any и € V(D) — V(Di),
D\V(Di) U {и}] is not strong).
Proof We only need to prove Part (ii).
Note that for each t = 1,2, • • • , fc, рць = pjti = 1. Therefore D has a directed (v,-, Vjt)-
path and a directed (vjt, Vi)-path, and so D has a closed walk Wo such that Wo contains
all vertices vi, v$x, • • ¦ , Vjh.
If Vj € У (Wo) — {^}, then D has a directed closed walk containing vi and u/, and so
Pij -Pji = 1. It follows that j e {ji,i2,• • • > j*}, and so Wq=D%.
Suppose that there exists a Vj € V(D) - F(D2) such that D[V(Di) U {v,}] is also a
strong subgraph of D. Then once again we have py = p# = 1, and so j € {ji,J2> * * * ><?*}>
a contradiction again. Q
Definition 4.4.2 Let D be a digraph. For a vertex v € V(D) and an arc e € ?(D), write
v — tail(e) if in D e is an out-arc of v\ and write v = head(e) if e is an in-arc of v.
The incidence matrix of D is B(D) = (6#) € Mnjin, defined in Definition 1.1.3. Let
Bf(D) denote a matrix obtained from B(D) by deleting a row of ?(D).
We can imitate the proof of Theorem 4.4.1 to obtain the following.
Proposition 4.4.1 Let с > 1 be an integer and let G denote the underlying graph of
D (that is, G is obtained from D by replacing each directed edge of D by an undirected
178
Matrices in Combinatorial Problems
edge). Then G has с components if and only if
r(B(D))=r(B,(D))=:n-c,
where r(B(D)) and r(Bf(D)) are the rank of B(D) and the rank of Bf(D), respectively.
Theorem 4.4.2 Let D be a digraph with n vertices and let G denote the underlying graph
of D. The arcs e^, Cj2, • • • , ejw_ j form a spanning tree of G if and only if the submatrix
of Bf(D) consists of the columns corresponding to these arcs has determinant 1 or — 1.
Proof Let #i denote the submatrix of В/(D) consists of the columns corresponding to
the arcs GjtiGfoi" • j^in-i* The subgraph D± induced by these arcs has n vertices and
n — 1 arcs, and B/(Di) = B\. If det(#i) € {1,-1}, then r(Bi) = n — 1, and so by
Proposition 4.4.1, D\ is a spanning tree in G.
Conversely, if Di is a spanning tree of G, then by Proposition 4.4.1, r{B\) — n - 1,
and so by Theorem 1.1.4, B\ is a nonsingular unimodular square matrix. It follows that
det(Bl)6{lf-l}.n
Definition 4.4.3 Let G be a connected labeled graph. Define r(G) to be the number of
distinct labeled spanning trees of G. If D is a weakly connected digraph, and if G is the
underlying graph of D, then define r(D) = r(G).
Theorem 4.4.3 (Matrix-TreeTheorem) KD is weakly connected, the number of spanning
trees of the underlying graph of D is
t(D)= d*(Bf(D).Dj(D)).
Proof By Binet-Cauchy formula and by Theorem 4.4.2, det(Bf(D) - DJ(D)) = r(D) •
(±l)2 = r(D).0
Theorem 4.4.4 (Cayley) Let n > 1 be an integer. Then r(Kn) = nn~2. Here Kn denotes
a labeled complete graph on n vertices.
Proof Let Bf(Kn) = (by). Then Bf(Kn)Bj(Kn) = %) € Afn-i,n-i, where for
z,i = l,2,— ,n-l,
n(n-l)/2
«
It follows that
Bf(Kn)BJ(Kn) =
n-l -1 ••- -1
-1 n-l ••• -1
-1 -1 ••• n-l
Matrices in Combinatorial Problems
179
and so by Theorem 4.4.3, r(Kn) = det(Bf(Kn)Bj(Kn)) = nn~2. Q
Definition 4.4.4 Let D be a digraph with V(D) = {vi,v2,- • • ,vn}. Let dt, df denote
the outdegree and the indegree of vi in D, respectively, where 1 < i < n. Define Mout =
diag(df,<#, • • • , d+) and M\n = diag(df, dj, - • • , d~)y and define
Cout = Mmt - A(D), and C7in = Afln - A(D).
Definition 4.4.5 Let D be a digraph and let v € V(D). A v-50«jnce tree is a weakly
connected subgraph in which v has indegree zero and every other vertex has indegree
exactly one. A v-sink tree is a weakly connected subgraph in which v has outdegree zero
and every other vertex has outdegree exactly one.
The Propositions below follow from Definitions 4.4.4 and 4.4.5.
Proposition 4.4.2 Each of the following holds.
(i) For each row of C7out> the row sum is zero.
(ii) Each column sum of Cout is zero if and only if D is eulerian. (That is, D has a
directed trail that uses each arc exactly once).
(iii) Each column sum of Cin is zero.
(iv) Each row sum of Cout is zero if and only if D is eulerian.
(v) Write C70ut = (c»i)- For each i with 1 < i < n, the cofactor of the element cy in
det(Cout) is equal to the cofactor of the element сц in det(C0ut)-
(vi) Write C|n = (cy). For each j with 1 < j < n, the cofactor of the element cy in
det(Cin) is equal to the cofactor of the element Cij in det(Cm).
Proposition 4.4.3 The underlying graph of a v-source tree or a v-sink tree is a tree.
Theorem 4.4.5 Let D be a digraph with V(D) = {vi,V2,-** ,vn}. Write Cout ^ (cij)
and Cin = (cy). Each of the following holds.
(i) For each j with j = 1,2, • • • ,n, the cofactor Cij of the element cy in det(C0ut) 1S
the number of spanning vi-sink trees of D.
(ii) For each j with j = 1,2, ¦ • • ,n, the cofactor C^ of the element cj4 in det(Cin) is
the number of spanning vi-source trees of D.
Sketch of Proof By duality, only Part(i) needs a proof.
Without loss of generality, assume that (vi,vi) € E(D). (The case when (vi,Vi) €
E(D) is similar). Let D1 and D" denote the digraphs obtained from D by deleting and
180
Matrices in Combinatorial Problems
by contracting (vi,vi), respectively. Then
Сц • • • Cit
Cout(D') =
Cnl
Cii-1
Cni
cm
Cm
Cnn
Since (vi,vi) is contracted, CovA(Dn) can be obtained from GQVLt(D) by deleting the eth
row and the ith column, and by replacing Сц by сц 4- сц — 1, c\j by сх<7- + c#, and Cj\ by
сд + cjU 2<j<n.
Let C(.Di) and C(D[) denote the cofactors of the (i, l)-element m-C0Ut(D) and CoutC^'))
respectively; and let C(D") denote the cofactor of the (1, l)-element in Cout(D"). Then
C{DX) =
C22
Ci2
C2i
Ctt-1
' •' c2n
'•• Cin
cnn
+
C22 •
0 •
Cn2 •
• c2i •
• 1 •
Cni
* c2n
• 0
Cnn
Cn2 * * * Cni
= C(D[)+CM).
Let T(Di) denote the number of spanning vi-sink trees in D. Given a spanning vi-sink
tree T, either Г is a spanning vi-sink tree in D' if (vi, vi) & E(T) or T\ obtained from T
by contracting (vi,vi), is a spanning vi-sink tree in D" if (v?,vi) € E(T). It follows that
T(D1)=T(Di) + T(D't).
With this reduction formula, Part(i) of Theorem 4.4.5 can now be proved by induction
on \E(D)\ to show that T(DX) = C{DX). Q
4.5 Shannon Capacity
The Shannon capacity 0(G) of a graph G, first introduced by Shannon [238], originates
from the theory of error correcting codes. The determination of 0(G) is very difficult even
for a graph with very few vertices. In 1979, Lovasz introduced a matrix method to study
0(G) and successfully solved the long lasting problem for determining 0(C$). We shall
introduce this method of Lovasz in this section.
Throughout this section, the vertices of a graph G will be letters in an given alphabet,
where two letters (vertices of G) are adjacent if and only if these letters can be confused.
Thus the maximum number of single letter message that can be sent without the danger of
Matrices in Combinatorial Problems
181
confusion is a(G), called the independence number of G, which is the maximum cardinality
of a vertex subset V С V (G) such that the vertices in V are mutually nonadjacent (vertex
subset with this property will be called an independent vertex set).
Definition 4.5.1 Let Hi and #2 be two graphs with Vx = V{HX) and V2 = V(#2). The
strong product of Hi and Hz, is the graph Hi*H2, whose vertex set if the product V\ x V2,
where two vertices (111,^2) and («1,^2) are adjacent if and only if one of the following
occurs:
(i) u± = vi and u2v2 € E(H2)\ or
(ii) u2 = v2 and U1V1 € E(H\); or
(iii) both U1V1 € E(Hi) and U2V2 € E(H2).
Let fc > 0 be an integer. For a graph G, define G^ = G, and G<*> = G(*-1> * G.
Example 4.5.1 Call two fc-letter words are confundable if for each 1 < i < k, their ith
letters are equal or can be confused. Thus in G^, vertices are fc-letters, and two fc-letter
words are adjacent in G^ if and only if they are confundable.
Definition 4.5.2 The Shannon capacity of G, is the number
0(G) = sup \/a(G(*>) = lim \/a(G(*>).
k V fc-юо V
By Definitions 4.5.1 and 4.5.2, it follows that
0(G) > a(G). (4.14)
Shannon in [238] showed that if a graph G is perfect (that is, x(?) = ^(G)), then (4.14)
holds. For other graphs, like the 5-cycle G5, Shannon only showed
V5<0(G5)<|. (4.15)
Recall that if u = (t*i,ti2, • • • >un)T and v = (vi,v2, • * • ,vm)T are two vectors, then
their tensor product is
Definition 4.5.3 Let G be a simple graph with vertex set {1,2, • • • , n}. An orthonormal
representation of G is a system of unit vectors {vi, v2, • • • , vn} such that v* and Vj are
orthogonal if and only if the vertices i and j are not adjacent.
The value of an orthonormal representation {vi, V2, • • ¦ , vn} is
с l<i<n (cTUf)2
182
Matrices in Combinatorial Problems
where с runs over all unit vectors. If с yields the nunimum, then с is called the handle of
the representation {vi,V2,-*- ,vn}. Let
0(G) = min{ value of {vb v2, • • • , vn}},
where the minimum runs over all orthonormal representation of G. The птптпптп yielding
representation {vi, V2, • • • , vn} is an optimal representation.
Proposition 4.5.1 Let G and H be graphs. Each of the following holds.
(i) Every graph G has an orthonormal representation.
(ii) If {ui, i*2, • ¦ • >u»} an<^ {vi»v2> * * * > vm} are orthonormal representations of G and
H, respectively, then the vectors {щ <g> vj : 1 < i < ra, 1 < j < m} is an orthonormal
representation of G * H.
(m)0(G*H)<0(G)0(B).
(iv) a(G) < (9(G).
Proof For (i), we can take an orthonormal basis of an n-dimensionaJ real vector space.
Proposition 4.5.1 (ii) follows from the following fact in linear algebra: If u,v,x,y are
vectors, then
(u (8) v)T(x (8) y) = (uTx)(vTy). (4.16)
Let {ui,U2,--« ,un} and {vi,V2,*-- ,vm} be optimal representations of G and Я,
with handles с and d, respectively.
By (4.16), с 0 d is a unit vector, and so by (4.16) again,
0(G * H) < max „ ^JV7V—-—rrx
= max, J- .2* .2=0(G)0{B).
i,j (стщ)2 (dTVj)2
This proves (Hi).
Without loss of generality, assume that {1,2, • • • , k} is a maximum independent vertex
set in G. Thus ui, • • • , щ are mutually orthogonal, and so
l = |cf>BcW>||f
Hence (iv) follows. Q
By Proposition 4.5.1, for each к > 0, a(G^) < 0(G<*>) < (0(G))*, and so by Definition
4.5.2, Theorem 4.5.1 below obtains.
Theorem 4.5.1 (Lovasz, [189])
9(G) < 0(G).
Matrices in Combinatorial Problems
183
Proposition 4.5.2 Let ui, u2, • • • , un is an orthonormal representation of G and vi, v2, • • • , vn
is an orthonormal representation of 6?c, the complement of G. Each of the following holds,
(i) If с and d are two vectors, then
f> 0 v,)T(c ® d) = ?(uf c)(vf d) < |c|2|d|2.
(ii) If d is a unit vector, then
0(G)>E(vfd)2.
(Hi) 9(G)6(GC) > n.
Proof By (4.16), the vectors щ <g> v», (1 < г < n) form an orthonormal basis and so
Proposition 4.5.2(i) follows from
n
\c®d\2>J2(*i®Vif(c®d)
i=l
and from (4.16).
Let с be the handle for an optimal representation ui, 112, • • • , un of G. Then
Proposition 4.5.2(ii) follows from Proposition 4.5.2(i).
Let d be the handle for an optimal representation vi,V2,* • • ,vn of Gc. Then
Proposition 4.5.2(iii) follows from Proposition 4.5.2(H). Q
Let G be a graph on vertices {1,2, • • • ,n}. A denote the set ofnxn real symmetric
matrix A = (a#) such that
Oij = 1 if i = j or if г and j are nonadjacent,
and let В denote the set of all n x n positive semidefinite matrices В = (bij) such that
b^ = 0 for all pairs of nonadjacent vertices (itj)
tr(B) = 1
Note that tr(BJ) is the sum of all the entries in ?.
Theorem 4.5.2 (Lovasz, [189]) Let G be a graph with vertices {1,2, • • • ,n}. Then each
of the following holds.
(i)e(G) = mm{Xm^(A)}.
(H)0(G)=max{tr(SJ)}.
184
Matrices in Combinatorial Problems
Proof Let {ui, U2, • • • , Un} be an optimal representation of G with handle с Define for
1 < hj < Щ
an = 1
and A = {aij)nXn. Then A€ A. Note that the elements in the matrix 6(G)I - Л are
It follows that 9(G)I — A is positive semidefinite and SO Ama3c (A) < 0(G).
Conversely, let A = (а^) e A and let A = Amax(A.). Then AJ — A is positive
semidefinite, and so there exist vectors xi,--- ,xn and a matrix X = [xi,— ,xn] such that
XTX = XI — A. Since A is an eigenvalue of At rankpf) < n, and so there exists a unit
vector с which is perpendicular to all the Xi's. Let
uj = -^(c + x<).
Then for 1 < i,j < n
Ы2 = i(l + |Xi|2) = l
ufuj = —(1 + xfxj) = 0, if i Ф j are not adjacent.
A
Therefore, {ui, • • • , un} is a orthonormal representation of G with
Hence 6(G) < A. This completes that proof for Theorem 4.5.2(i).
By Theorem 4.5.2(i), there exists annxn matrix A = (а#) € A such that Amax(A) =
0(G). Let В ев. Then by the choice of A and by the definition of #,
mb j) = E i>; = E Ea*6* = tr(^)>
t=i j=i «=i j=i
and so
$(G) - tr(BJ) = tr((0(G)/ - Л)Б). (4.17)
Matrices in Combinatorial Problems
185
It follows that both 9(G) I — A and В are positive semidefinite. Let At, Л2, • • • , An be the
eigenvalues of 2?, and let Wi, • • • , wn be mutually orthogonal eigenvectors corresponding
to Ai, • • • , An, respectively. Then
n n
tr((0(<3)J - A)B) = ?eT(0J - A)Bwi = ?A*wi*(w " ^)w* ^ °*
i=l t=l
This, together with (4.17), implies that 0(G) > тахвев tr(BJ).
Conversely, let 2?(С?) = {itjt : 1 < t < m}. Consider the (m + l)-dimensional vectors
h=(hhhh,-- ,himhjm,(?hi)2)T'
where h = (hi, /12, • • • , ЛП)Т ranges though all unit vectors, and let ti denote the set of all
such vectors h. Note that ti is a compact subset in the (m + l)-dimensional real space.
Claim Let z = (0,0,••• ,О,0(6?))Г. Then there exist vectors hi,h2,--- ,h/v € ti, and
nonnegative real numbers ci, C2, • • • , cjy such that
N
?* = 1, (4.18)
t=i
N
5>ь* = z- (4-19)
x=i
If not, then there exists a vector a = (ai,a2, • • • ,ат,у)т and a constant a such that
aTh < a, for all h € ti but aTz > a.
Note that for h = (1,0, • • • , 0)r, the corresponding h satisfies aTh < a, and so у < о.
On the other hand, that aTz > a implies 9(G)y > a, and so 9(G)y > а > t/. By Proposition
4.5.1(iv), 0(G) > 1, and so а > у > 0. We may assume that у = 1, and so 9(G) > a.
Now define A = (o^) with
Г §a* +1, if {i,j} = {*'*, J*}
^ 1 otherwise
then that aTh < a can be written as
n n
ЬТЛЬ = V^ Y^ aijhihj < a.
t=i i=i
Since Amax(^) = max{xTi4x : |x| = 1}, this implies that Атах(Л) < a. However, Ae A,
and so by Theorem 4.5.2(i), 9(G) < a, a contradiction. This proves the claim.
Therefore (4.18) and (4.19) hold. Set
hp = (hPil, hPt2, • • • , hPin)T
N
p=l
В = (by)
186
Matrices in Combinatorial Problems
Then В is symmetric and positive semidefinite. By (4.18) tv(B) = 1. By (4.19),
K>h = 0,(1 < Л <m)
tx(BJ) = 0(G).
Therefore В e B, and so 0(G) < max?€g tx[B J). This complete the proof of Theorem
4.5.201). ?
Corollary 4.5.2 There exists an optimal representation {ui, • • • ,Un} such that
0(G) =
(стщ)*
, 1 < i < n.
Theorem 4.5.3 (Lovasz, [189]) Let Vi, V2, ¦ • • , vn range over all orthonormal
representation of Gc, and d over all unit vectors. Then
n
0(G) = maxJ2(dTVi)2-
Proof By Proposition 4.5.2(h), it suffices to show that for some v^s and some d, 0(G) <
Eii(dTVi)2.
Pick a matrix В = (Ь#) € В such that tt(BJ) = 0(G), Since В is positive semidefinite,
there exists vectors wi, w2, • • • , wn such that
&ii=w?wi> l<*»i<«»
Since В € В,
Set
?|w?|2 = l, and
5>
= 0(G).
Vi = r-^-r, (l<i<n) and d :
lwi|
(l>)
E»«
Then the Vi's form a orthonormal representation of Gc, and so by Cauchy-Schwarz
inequality,
= d'^w, =
2
=
n
?w<
t=i
-*(G).
Matrices in Combinatorial Problems
187
This proves the theorem. []
Corollary 4.5.3 X(G) > 0(GC).
Proof Let vi, v2, • • • , vn be an orthonormal representation of G, d a unit vector. Suppose
that x(<3) = k and Vi, Угг • • , Vi be a partition of V(G) corresponding to a proper k-
coloring. Then by Theorem 4.5.3,
Thus the corollary follows. Q
Theorem 4.5.4 (Lovasz, [189]) Let G be a graph on vertices {1,2,— , n}. Д* denote the
set ofnxn real symmetric matrix A* = (oy) such that
a^ = 0 whenever i and j are adjacent.
Let Ax(A*) > A2(A*) > • • • > An(A*) be eigenvalues of an A*A*. Then
^maxjl-^l.
v ; A*eA*\ An(A»)J
Sketch of Proof Let A* — (oy) € A* and let f = (Д, /2, • • • , /n)T be an eigenvector of
Xi(A*) such that |f |2 = -1/Ап(Л*) (note that since tr(A*) = О, An(A*) < О).
Define the matrices F = diag(/b/2,— ,/n) and В = (by) = F(A* - \n(A*)I)F.
Then Б € В, and so by Theorem 4.5.2,
9(G) > tr(BJ) = ^^^M-A-(A*)E/'
= ?[Ax(^)/f - An(^)/f] = 1 - M?l.
Conversely, by Theorem 4.5.2, choose В 6 В so that 0(6?) = tr(2?J), and then follow
basically an inversion of the argument above. Q
Corollary 4.5.4 (Hoffman, [123]) Let G be a graph with A = A(G), and let Ax > A2 >
•• * > An be eigenvalues of A. Then
Proof This follows from Corollary 4.5.3 and Theorem 4.5.4. Q
Theorem 4.5.5 (Lovasz, [189]) Let G be a regular graph on n vertices and let Л1 > A2 >
•• • > An be the eigenvalues of A = A(G). Then
0(G) < ^~- (4.20)
188
Matrices in Combinatorial Problems
Equality holds in (4.20) if the automorphism group of G is edge-transitive.
Proof Let vt-, (1 < i < n) be eigenvectors corresponding to A», respectively. Since G is
regular, vi = j = (1,1, • • • , 1)T, and each v* is also an eigenvector of J.
Note that real number x, the matrix J — xA€ A, and so by Theorem 4.5.2, Amax(«/ -
xA) > 0(G). However, the eigenvalues of J - xA are n — x\i, — x\2i • • • , — x\ni and so
Amax(«/ — sA) is either the first or the last. Hence the optimal choice of x = n/(Ai - A„),
and so (4.20) follows from Theorem 4.5.2.
Assume now that the automorphism group Г of G is edge-transitive. Let С = (c#) 6 A
such that Amax(C) = 0(G). Note that each element in Г corresponds to a permutation
matrix. Define
Then we can verify that V € A and has the form J — xA. By Theorem 4.5.2, 0(G) =
Amax(C) and so equality holds in (4.20). [J
Corollary 4.5.5A For an odd integer n > 0,
. _ ncos(7r/n)
°{bn) - l + cos(7r/n)-
Corollary 4.5,5В 0(С5) = л/5\
Proof Applying Theorem 4.5.5 to G = Cn, we have Corollary 4.5.5A. In particular,
в(Сь) = л/5, and so by Proposition 4.5.1, 0(C5) < л/5. Thus Corollary 4.5.5B follows
from (4.15). Q
We conclude this section with an application of Shannon capacity, due to Lovasz [189].
For integers n, r with n > 2r > 0, let К(n, r) denote the graph whose vertices are r-subsets
of an n-element set 5, where two subsets are adjacent in K(n,r) if and only if they are
disjoint.
Theorem 4.5.6 (Lovasz, [189])
e(^(n)r))=^_i1j.
Proof For each s € 5, all the r-subsets containing s form an independent set in К(щт),
and so
e(tf(n,r))>a(tfO
-»* (;:;)•
Matrices in Combinatorial Problems
189
On the other hand, as the automorphism group of K(n, r) is edge-transitive, (4.20)
may be used to derive the desired inequality. Since K(n, r) is regular, j is an eigenvector
I 7b ~ T \
for the eigenvalue j 1 of К(n,r).
Let 1 < t < r. For each T С S with \T\ = t, let хт be a real number such that
for every UcS with \U\ = t - 1, ?) xT = 0. (4.21)
ист
There are j J — I j linearly independent I 1 -dimensional vectors of the
type (• • • , хт, • - • )• For each such vector, and for each Ac S with \A\ = r, define
TcA,\T\=t
Then there are j J — I J linearly independent j j-dimensional vectors of
the type
X=(.-,*A,-)- (4.22)
We shall show that every vector x of the form (4.22) is an eigenvector of the adjacency
(л — r _ i \
1.
r-t J
In fact, for any Aq С S with \Aq\ = r, and for each 0 < i < i, define
|ГпАо|=»
Then we have
|T|=t
For each Q < i < t, and for each J/ С S with |J7| = * - 1 and with \U П Aq\ = », by
(4.21), we obtain an recurrence relation for /%:
(i + l)A+i + (*-0A = 0,
which yields
A = (-!)'( j)ft.
190
Matrices in Combinatorial Problems
Therefore,
A> = (-i)*A = (-1)^ло,
as desired. Hence xa0 is an eigenvector of the adjacency matrix of K(n,r).
By this construction we have found
•¦?((:)-(-))-(:)
linearly independent eigenvectors of К(щг)> as eigenvectors belonging to different
eigenvalues are linearly independent. It follows that all the eigenvalues of K(n,r) are
and so the largest and the smallest are the ones with t = 0 and t = 1, respectively. Now
the proof for Theorem 4.5.6 is complete by applying (4.20). []]
Corollary 4.5.6A The Petersen graph, which is isomorphic to K(5,2), has capacity 4.
Corollary 4.5.6B (Erdos, Ко, Rado [82])
а(К(п,г)) = в(К(п,г)) =
4.6 Strongly Regular Graphs
In 1966, Erdos, Renyi and S6s proved the so called friendship theorem [83]: In a society
with a finite population, if every two people have exactly one common friend, then there
must be a person who is a friend of every other member in the society. The friendship
theorem can be stated in graph theory as follows, whose proof will be postponed.
Theorem 4.6.1 (Erdos, Renyi and Sos, [83]) Let G be a graph on n vertices. If for each
pair of distinct vertices x and y> there is exactly one vertex w adjacent to both x and y,
then n is odd and G has a vertex и 6 V(G) such that и is adjacent to every vertex in
V(G — u) and such that G — и is a 1-regular graph.
Definition 4.6.1 For a graph G with v ? V(G), let N(v) = Ng(v) denote the vertices
that are adjacent to v in G.
Let n, k, Л, fj, be non negative integers with n > 3. A fc-regular graph G on n vertices
is an (n, fc, Л, n)-strongly regular graph if each of the following holds:
(4.6.1A) If щ v € V(G) such that и and v are adjacent in <?, then \N(u) П N(v)\ = Л.
(4.6.1B) If it, v e V(G) such that и and v are not adjacent in G, then \N(u)nN(v)\ — \i.
(::;•
Matrices in Combinatorial Problems
191
Example 4.6.1
(i) The 4-cycle is a (4,2,0,2)-strongly regular graph,
(ii) The 5-cycle is a (5,2,0,l)-strongly regular graph,
(iii) If n > 6, the л-cycle is not a strongly regular graph,
(iv) The Petersen graph is a (10,3,0,l)-strongly regular graph,
(v) The disjoint union of two copies of K$ is a (6,2,l,0)-strongly regular graph,
(vi) For m > 2, the complete bipartite graph Кт,т is a (2m,m,0,m)-strongly regular
graph.
Proposition 4.6.1 Let G be a fc-regular graph with n vertices and let A = A(G). Then
G is an (n, fc, Л, /*)-strongly regular graph if and only if one of the following holds.
(i) A2 = kI + \A + p,(J -1 - A).
(ii) A2 - (\-ti)A- (k-fj)I = ftJ.
Proof By Proposition 1.1.2(vii), and by Definition 4.6.1, that G is an (n, fc, Л, p)-strongly
regular graph is equivalent to Proposition 4.6.1(i), and it is straightforward to see that
Proposition 4.6.1(i) and Proposition 4.6.1(ii) are equivalent. Q
Proposition 4.6.2 Let G be an (n, kt Л, ^)-strongly regular graph. Then each of the
following holds.
(i) k(k - Л - 1) = fi{n - к - 1)
(ii) The complement of6risan(n,n-fc — l,n-2fc+ji — 2,n — 2k + A)-strongly regular
graph.
(iii) \i = 0 if and only if G is the disjoint union of some Кь+\Ъ.
Proof This follows from Proposition 4.6.l(i) and (ii). [3
Theorem 4.6.2 Let G be a connected (n, fc, A, /x)-strongly regular graph, let I = n — к — 1
and let
d=(A-M)2+4(*-,x),
tf = (fc + /)(A-/x) + 2fc.
Then the spectrum of A — A(G) is
Spec(4):
where
о = 1 (A - и 4- \fd\ > 0.
(4.24)
P = \ (\-fJL + y/d) >0,
•a*->/3) <-i,
192
Matrices in Combinatorial Problems
and where
Proof Let Ai(A) > ••• > \n(A) denote the eigenvalues of A. By Corollary 1.3.2A,
Xi(A) = fc. Since G is connected, A is irreducible, and so the multiplicity of Xi(A) = к is
1.
By Proposition 4.6.1 (i),
(Л - &/)(A2 - (A - p)A -(к- p)I) = 0,
and so p and <r in (4.24) are the other eigenvalues of A.
If d = 0, then by A; > mu, A = ji = к. However, since G is a (n, A:, A, #)-strongly regular
graph, A < A: — 1, a contradiction. Hence d > 0, and so к > p > a. By (4.24), write
A = A; + p + с + pa, ц = к + pa.
Since A; > ^, we have p > 0 and /* < 0. If a = 0, then A = fc+p > A;, contrary to A < fc-1.
Hence a < 0.
Consider (2, the complement of G. By algebraic manipulation, we obtain the
corresponding parameters for Gc as follows:
d = d, p = — <г — 1, <f = — p — 1.
As for Gc, p > 0, we must have p > 0 and с < —1.
Finally, we note that if r and $ are multiplicities of p and a, respectively, then
{r + s = n — 1
fc + rp + so = 0
and by algebraic manipulation again, (4.25) obtains. Ц
Theorem 4.6.3 Let G be an (n, Aj, A, /z)-strongly regular graph, let Z = n — A: — 1, and
adopt the notations in (4.23), (4.24) and (4.25).
(i) If 5 = 0, then
X 4 » 1 П — 1
A = /a — l,A: = / = 2/x = r = s — —-—.
(ii) If S ф 0, then л/3, р, o" are integers. Moreover, if n is even, then y/d\6 but 2\/3 /f<5,
and if n is odd, then 2y/d\6.
Sketch of Proof If S = 0, then by (4.23), 2к/(ц - A) = A; +1 > A:, and so 0 < \i - A < 2,
which yields A = \i — 1. The other equalities follow from Proposition 4.6.2(ii) and (4.25).
Matrices in Combinatorial Problems
193
The conclusion when 6 ф 0 follow by (4.24) and (4.25). Q
A strongly regular graph satisfying Theorem 4.6.3(i) is also called a conference graph.
By Theorem 4.6.2, if G is a connected strongly regular graph, then G has exactly 3
distinct eigenvalues.
Theorem 4.6.4 Let G Ъе а connected regular graph. Then G is strongly regular if and
only if G has exactly 3 distinct eigenvalues.
We are now ready to apply Theorem 4.6.2 to present a proof, due to Cameron [45], for
Theorem 4.6.1.
Proof for Theorem 4.6.1 Let G be a graph satisfying the conditions of Theorem 4.6.1.
Claim 1 If и and v are not adjacent in G, then и and v must have the same degree.
Let u,v e V(G) be distinct non adjacent vertices. Then there exists a unique vertex
w such that w is adjacent to both и and v. Also, G has vertices x ф v and у Ф и such
that x is the only vertex adjacent to both и and w and у is the only vertex adjacent to v
and w.
If z ? {w,x} is a vertex adjacent to it, then there exists a unique z' ? {w,y} such
that z' is adjacent to both z and v. Note that we can exchange и and v to get the same
conclusion on v. Therefore, и and v must have the same degree.
Claim 2 If G is a fc-regular graph, then G = Ki, or G = K$.
If G is fc-regular, then G is an (n,fc, 1, l)-strongly regular graph. By Theorem 4.6.2,
s - r = 8/y/d = k/y/k — 1 is an integer, and so (k — l)|fc2- It follows that either к = 0 or
к = 2, and so <2 is either iiTi or ЛГ3.
By Claim 2, we may assume that G is not a regular graph. Let и and v be two vertices
with different degrees. Then by Claim 1, и and v must be adjacent. Let w be the only
vertex in G adjacent to both и and v, and renaming и and v if necessary, we may assume
that w and и have different degrees. Let x € V(G) — {u,v,iu}. Then by Claim 1 and by
the assumption that и and v have different degrees, x must be adjacent to either и от v.
Similarly, x must be adjacent to either и or w.
However, since и is the only vertex adjacent to both v and w, x must be adjacent to
м. Therefore, и is a vertex in G that is adjacent to every other vertex in (7, and each
component of G — и is a JRl2. Q
C. W. H. Lam and J. H. van Lint [149] considered a generalization of friendship theorem
to loopless digraphs, first proposed by A. J. Hoffman.
Definition 4.6.2 A loopless digraph D is a к-firiendship graph if for any pair of distinct
vertices u, v € V(P), D has a unique directed (u, v)-walk of length fc, and for every vertex
и е V(?>), D has no (u,u)-walk of length к.
194
Matrices in Combinatorial Problems
Note that if Л € Bn satisfying Ak = 3-1, then by Proposition 1.1.2(vii), D(A) is a k-
friendship graph. The converse of this also follows from Proposition 1.1.2(vii). Therefore,
to determine the existence of a fc-friendship graph, it is equivalent to showing that the
equation Ak = 3 — I has a solution.
Example 4.6.2 Let F2 denote the directed cycle of length 2. Then for any odd integer
к > 0, i*2 is a fc-friendship, (called a fish in [149]).
Proposition 4.6.3 Let D be a ^-friendship graph with n vertices, and let A = A(D).
Then each of the following holds.
(i)tr(A)=0.
(ii)A* = J-I.
(iii) For some integer с > 0, A3 = ЗА = c3. (Therefore, A has constant row and
column sums c; and the digraph D has indegree and outdegree с in each vertex.)
(iv) The integer с in (ii) satisfies
n = ck + 1. (4.26)
Proof Since Z? is loopless, tr(A) = 0. By Proposition 1.1.2(vii) and Definition 4.6.2,
Ak = 3 — I. Multiply both sides of Ak = 3 -1 by A to get
Ak+1=3A-A = A3-A,
which implies that A3 = JA = c3, for some integer c. Multiply both sides of Ak = J - J
by J, and apply Proposition 4.6.3(ii) to get
ck3 = Ak3 = 32-3^n3-3={n- 1) J,
and so c* = n — 1. []
Theorem 4.6.5 (Lam and Van Lint, [149]) If к is even, no ^friendship graph exists.
Proof Let к = 2/. Assume that there exists a ^-friendship graph Z> with n vertices. Let
Л = A(D) and let Ai = A1. By Proposition 4.6.3(i), A\ = J-J. Therefore by Proposition
4.6.3, n must satisfy n = c2 + 1 for some integer c. The eigenvalues of A must then be с
with multiplicity 1, and i and —i (where i is the complex number satisfying i2 = — 1) with
equal multiplicities. This implies tr(-A) = c, contrary to Proposition 4.6.3(i). []
For fc odd, a solution for A* = 3 — I is obtained for each n — c* + 1, where c> 0 is
an integer. Consider the integers mod n. For each integer v with 1 < v < c, define the
permutation matrix Pv = (p§?) by
1 if j = v - ci (mod n) . ^ . . ^ . ч
n л • (0<M<n-l).
0 otherwise
#-{
Matrices in Combinatorial Problems
195
and define
л=Х>
(4.27)
In fact, the matrix A of order n has as its first row (0,1,1, • • • , 1,0, • • • , 0,0) where there
are с ones after the initial 0. Subsequent rows of A are obtained by shifting с positions to
the left at each step. The matrix Ak is the sum of all the matrix products of the form
P P ... P
where (ai,a2,--- ,a*) runs through {1,2,-•• ,c}*, the set of all A; element subsets of
{1,2,—,c}.
The matrix PaiPa2 ' "^ak is a permutation matrix corresponding to the permutation
x H- (-c)kx + 53ai(-c)*~*' (mod n).
(4.28)
Theorem 4.6.6 (Lam and Van Lint, [149]) The matrix A defined in (4.27) satisfies Ak =
J - J for odd integer к > 1.
Proof Note that if (ai, «2, • • • , a*) € {1,2, • • • , c}*, then
К
5>H0"
<n-l
(which is obtained by letting the o^'s alternate between 1 and c). Similarly, if (ft, ft, • ¦ ¦ , ft) €
{1,2, • • • , c}* also, then by (4.26), c* = n — 1, and so
?<*i(-c)*--X>(-c)
¦*-<
<(c-l)][y-?=n--2.
It follows that
][>(-c)»-* = 5>(-e)»-' (mod n)
implies that the two sums are equal which is possible only if (a\, аг, • • • , <*k) = (ft > ft » *" > ft)-
Therefore if (ai,a^, • * • > a*) runs through 2, • ¦ • , c}*, the permutations in (4.28) form the
set of permutations of the form a:«-»a: + 7(l<7<n). This proves the theorem. Q
Theorem 4.6.7 (Lam and Van Lint, [149]) Let A be defined in (4.27) and let D = D(A).
Then the dihedral group of order 2(c +1) is a group of automorphisms of the graph D.
Proof In the permutation x i-> (—c)x + v which defines P„, substitute x = у + A(c* +
l)/(c + 1). The result is the permutation у «-> (—c)y + v. Hence for Л = 0,1,2, • • • , с, we
196
Matrices in Combinatorial Problems
find a permutation which leaves A invariant. These substitutions form a cyclic group of
order c.
In the same way it can be found that the substitution
s = l-2/ + A(c* + l)/(c+l)
maps Pv to the permutation у и> (—с)у + (с + 1 — v) and therefore leaves A invariant.
This, together with the cyclic group of order с above, yields a dihedral group acting on
D.Q
It is not known whether the solution of A* = J — I is unique or not. In [149], it
was shown that when A; = 3 and n = 9, the dihedral group of Theorem 4.6.7 is the full
automorphism group of the friendship graph D. However, whether the dihedral group in
Theorem 4.6.7 is the full automorphism group of D in general remains to be determined.
We conclude this section by presenting two important theorems in the field. Let
T(m) = L(Km) denote the line graph of the complete graph Kmi and let I^wi) =
L(Kmtm) denote the Une graph of the complete bipartite graph Km%m. Note that T(m) is
an (m(m — l)/2,2(ra — 2), m — 2,4)-strongly regular graph, and Ьг(яг) is an (m2,2(m -
2), m - 2,2)-strongly regular graph.
Theorem 4.6.8 (Chang, [51] and [52], and Hoffman, [126]) Let m > 4 be an integer. Let
G be an (m(m — l)/2,2(m — 2),m — 2,4)-strongly regular graph. If m ф 8, then G is
isomorphic to T{m)\ and if m = 8, then G is isomorphic to one of the four graphs, one of
which is T(8).
Theorem 4.6.9 (Shrikhande, [254]) Let m > 2 be an integer and let G be an (m2,2(m -
2),m — 2,2)-strongly regular graph. If m Ф 4, then G is isomorphic to Z/2(m); and if
m = 4, then G is isomorphic to one of the two graphs, one of which is ?2 (4).
4.7 Eulerian Problems
In this section, linear algebra and systems of linear equations will be applied to the study
of certain graph theory problems. Most of the discussions in this section will be over
(7^(2), the field of 2 elements. Let V(m,2) denote the m-dimensional vector space over
<2.F(2). Let B^m denote the matrices В € Bn>m such that all the column sums of
В are positive and even. For subspaces V and W of V(m,2), V + W is the subspace
spanned by the vectors in V U W. Let E = {ei,e2, • • • ^ещ} be a set. For each vector
x = (rri,0:2, • • • ,xm)T € V(m, 2), the map
x = (xi,x2i • • • ,xm)T <r> Ex = {si : where xi = 1, (1 < i < m)} (4.29)
Matrices in Combinatorial Problems
197
yields a bijection between the subsets of E and the vectors in V(m,2). Thus we also use
V(E,2) for V(m,2), especially when we want to indicate the vectors in the vector space
are indexed by the elements in E. Therefore, for a subset E' С Е, it makes sense to
use V(??', 2) to denote a subspace of V(??, 2) which consists of all the vectors whose ith
component is always 0 whenever ei € E — E', 1 < i < m.
For two matrices Bi,B2, write B\ С ?2 to mean that B\ is submatrix of ?2.
Throughout this section, j = (1,1, • • • , 1)T denotes the m-dimensional vector each of
whose component is a 1.
Definition 4.7.1 A matrix В € В* >m is separable if В is permutation similar to
\bu 0 1
[О B22 J '
where Вц € Bni>mi and B22 € ВП2>7П2 such that n = n\ +ri2 and m = mi+m2, for some
positive integers ni,n2,mi,m2. A matrix В is nonseparable if it is not separable.
For a matrix В € В* >m with rank(B) > n — 1, a submatrix 2?' of Б is spanning in В if
rank(B') > n — 1. Note that for every В € B^m, each column sum of В is equal to zero
modulo 2. Thus if Б € B*>m is nonseparable, then over GF(2), rank(B) = n — 1.
A matrix Б € B?m is even if Bj = 0 (mod 2); and Б is Eulerian if Б is both
nonseparable and even.
A matrix Б € Bn>m is simple if it has no repeated columns and does not contain a
zero column. In other words, in a simple matrix, the columns are mutually distinct, and
no column is a zero column.
Example 4.7.1 When G is a graph and Б = B(G) is the incidence matrix of G, G is
connected if and only if Б is nonseparable; every vertex of G has even degree if and only
if Б is even; G is a simple graph if and only if Б is simple; and G is eulerian (that is, both
even and connected) if and only if Б is eulerian.
Proposition 4.7.1 By Definition 4.7.1, Each of the following holds.
(i) If Bi,B2 € Bn,m are two permutation similar matrices, then B\ is nonseparable if
and only if Б2 is nonseparable.
(ii) Suppose that B± € Bn>m and Б2 € Bn>m/ are matrices such that B\ C52. If B\
is nonseparable, then B2 is nonseparable.
(iii) Suppose that Bi € Bn>m and Б2 € Bn>m/ are matrices such that Bi С B2» If Bi
has a submatrix В which is spanning in Bb then Б is also spanning in B2.
(iv) Let В = B(G) € Bn>m be an incident matrix of a graph G. If В is nonseparable,
then rank(B) = n — 1.
Proof The first three claims follow from Definition 4.7.1. If В = B(G) is nonseparable,
then G is connected with n vertices, and so G has a spanning tree T with n — 1 edges.
198
Matrices in Combinatorial Problems
The submatrix of Б consisting of the n — 1 columns corresponding to the edges of T will
be a matrix of rank n — 1. Q
Definition 4.7.2 Let А, В € B?>m be matrices such that А С В. We say that A is
cyclable in Б if there exists an even matrix A' such that А С А' С В; and that Л is
subeulerian in Б if there exists an eulerian matrix A' such that А С А' С Б.
A matrix Б € B?>m is supereulerian if there exists a matrix B" € B* m„ for some
integer m" < m such that Б" С Б and such that B" is eulerian.
Let (7 be a graph, and let Б = B(G) be the incidence matrix of G. Then <7 is
subeulerian (supereulerian, respectively) if and only if Б (G) is subeulerian (supereulerian,
respectively).
Example 4.7.2 Let G be a graph and Б = Б(6?) be the incidence matrix of G. Then
G is subeulerian if and only if G is a spanning subgraph of an eulerian graph; and G is
supereulerian if and only if G contains a spanning eulerian subgraph.
What graphs are subeulerian? what graphs are supereulerian? These are questions
proposed by Boesh, SufFey and Tindell in [12]. The same question can also be asked for
matrices. It has been noted that the subeulerian problem should be restricted to simple
matrices, for otherwise we can always construct an eulerian matrix B' with Б б В' by
adding additional columns, including a copy of each column of Б.
The subeulerian problem is completely solved in [12] and in [138]. Jaeger's elegant
proof will be presented later. However, as pointed out in [12], the supereulerian problem
seems very difficult, even just for graphs. In fact, Pulleyblank [214] showed that the
problem to determine if a graph is supereulerian is NP complete. Catlin's survey [48] and
its update [57] will be good sources of the literature on supereulerian graphs and related
problems.
Definition 4.7.3 Let Б € Вп>т, let E(B) denote the set of the labeled columns of B.
We shall use V(B72) to denote V(E(B),2). For a vector x € ^(Я(Б),2), let Ex denote
the subset of E(B) defined in (4.29). We shall write V(B -x, 2) for V(E(B) - Exi 2), and
write V(x,2) fov V(EX12).
Therefore, V (Б — x, 2) is a subspace of V(B, 2) consisting of all the vectors whose ith
component is always 0 whenever the ith component of x is 1, (1 < i < m), while V(x,2)
is the subspace consisting of all the vectors whose ith component is always 0 whenever the
**th component of x is 0, (1 < i < m).
For a matrix Б € Bn>m and a vector x € У(Б,2), we say that Column г of Б is
chosen by x if and only if the ith component of x is 1. Let Бх denote the submatrix of
Б consisting of all the columns chosen by x. If E' С Е(В), then by the bijection (4.29),
there is a vector x € V(B, 2) such that Ex = E'. Define Be» = Бх. Conversely, for each
Matrices in Combinatorial Problems
199
submatrix А С В with A € Bn>m, there exists a unique vector x € V(?,2) such that
Bx = A. Then denote this vector x as хд.
A vector x e V(B, 2) is a cycle (of B) if 2?x is even, and is eulerian (with respect to
B) if ?x is eulerian. Note that the set of all cycles, together with the zero vector 0, form
a vector subspace C, called the cycle space of B\ Cx, the maximal subspace in V(?,2)
orthogonal to C, is the cocycle space of B.
For x,y € V(m, 2), write x<yify-x>0, and in this case we say that у contains
x. Let Б € Bn>m be a matrix and let x € V(B, 2) be a vector. The vector x is cyclable in
В if there exists an cycle у € V(B, 2) such that x < y. Denote the number of non zero
components of a vector x € V(n,2) by ||x||o.
Theorem 4.7.1 Let В € B*m. A vector x is cyclable in В if and only if x does not
contain a vector z in the cocycle space of В such that ||z||0 is odd.
Proof Let С and Сх denote the cycle space and the cocycle space of B, respectively.
Let x € V(B, 2). Then, by the definitions, the following are equivalent.
(A) x is cyclable in B.
(B) there exists а у € С such that x < y.
(C) there exists а у € С such that x = y + (y + x)€C + V(B - x,2).
(D)x<=C + F(B-x,2).
Therefore, x is cyclable if and only if x e С + V(В - х, 2). Note that
[C + V(B - x, 2)]x = Cx П V(B - x, 2)x = Cx П V(x, 2).
It follows that x is cyclable if and only if x is orthogonal to every vector in the subspace
Cx П V(x, 2). Since x contains every vector in V(x, 2), and since for every nonzero vector
z e Cx, ||z||o is odd, we conclude that x is cyclable if and only if x does not contain a
vector z in the cocycle space of В such that ||z||0 is odd. []
Theorem 4.7.2 (Jaeger, [138]) Let A,B € B?>m be matrices such that А С В. Each of
the following holds.
(i) A is cyclable in Б if and only if there exists no vector z in the cocycle space of В
such that ||z||0 is odd.
(ii) If, in addition, Л is a nonseparable. Then A is subeulerian in Б if and only if there
exists no vector z in the cocycle space of В such that ||z||0 is odd.
Proof By Definition 4.7.2 and since A is nonseparable, A is subeulerian in В if and
only if the vector xa is cyclable in B. Therefore, Theorem 4.7.2(ii) follows from Theorem
4.7.2(i).
By Theorem 4.7.1, x^ is cyclable in В if and only if xa does not contain a vector z in
the cocycle space of В such that ||z||0 is odd. This proves Theorem 4.7.1(i). Q
200
Matrices in Combinatorial Problems
Theorem 4.7.3 (Boesch, Suffey and Tindell, [12], and Jaeger, [138]) A connected simple
graph on n vertices is subeulerian if and only if G is not spanned by a complete bipartite
with an odd number of edges.
Proof Let G be a connected simple graph on n vertices. Theorem 4.7.3 obtains by
applying Theorem 4.7.2 with A = B(G) and В = A(Kn) (Exercise 4.12). Q
Definition 4.7.4 A vector b € V(n,2) is an even vector if ||b|| = 0 (mod 2). A matrix
tm is collapsible if for any even vector b € V(n, 2), the system
#x = b,
has a solution x such that Ях is nonseparable and is spanning in Я, (such a solution x is
called a Ъ-solution).
Let n,m,ni,mi,Ш2 be integers with n > щ > 0, and m>mi,m2 > 0. Let Вц 6
Bni,roi,5i2 € ВП1>Ш2,Б22 € Bn_ni>m2 and Я € Bn_ni>m_(mi+m2). Let s$ denote the
column sum of the ith column of B22, 1 < i < тг, and let В € Bn>m with the following
form
Б =
Вц Bi2 0
0 Б22 Я
(4.30)
Define Я/Я € Bn-n2+i>m_m2 to be the matrix of the following form
B/H =
Вц В\2
0
v?
where vj e V(m,2) such that vj = (vmi+i,vmi+2,-
Si (mod 2), (1 < i < шг).
,vmi+m2) and such that vmi+i =
Proposition 4.7.2 Let Bi,B2 € Bn>m such that Bi is permutation similar to B2. Then
each of the following holds.
(i) B\ is collapsible if and only if Я2 is collapsible.
(ii) B\ is supereulerian if and only if B2 is supereulerian.
Proof Suppose that B\ = PB2Q- Let b € V(n,2) be an even vector. Then since b is
even, b; = P-1b € V(n, 2) is also even. Since Bi is collapsible, ?iy = b' has solution
у € V(m, 2) such that (?i)y is nonseparable.
Let x = Q^1y. Then
Pb = b' = В1У = PB2Qy = PB2x,
and so Ях = b has a solution x = Qy.
Matrices in Combinatorial Problems
201
Note that P~1(Bi)y = (B2Q)y = (B2)x. Therefore, Bx is nonseparable, by Proposition
4.7.1 and by the fact that {Bx)y is nonseparable. This proves Proposition 4.7.2(i).
Proposition 4.7.2(ii) follows from Proposition 4.7.2 (i) by letting b = 0 in the proof
above. Q
Proposition 4.7.3 If Я € В* m is collapsible, then Я is nonseparable, and гапк(Я) =
n-1.
Proof By Definition 4.7.4, the system Ях = 0 has a 0-solution x, and so ЯХ is non-
separable and spanning in Я, and so Proposition 4.7.3 follows from Proposition 4.7.1.
a
Theorem 4.7.4 Let Я be a collapsible matrix and let Б be a nonseparable matrix of the
form in (4.30). Each of the following holds.
(i) If B/H is collapsible, then В is collapsible.
(ii) If B/H is supereulerian, then В is supereulerian.
Proof We adopt the notation in Definition 4.7.4. Let b be an even vector, and consider
the system of linear equations
(;)-(Sb
where bi € V(ni,2),b2 € V(n - nb2), Xi € У(ть2),х2 € V(m2i2) and x3 € V(m -
ян — m2,2). Let
f0 ifbxiseven ^ fc, = / Ь, \
I 1 otherwise \ S J
ible,
CM*)-
Бц Б12 0
0 Б22 Я
Then b' is an even vector. Since B/H is collapsible,
ii Br
(B/N)x12 =
has a Ь'-solution xi2. Therefore
(G/H)X12 is nonseparable and spanning in G/Я. (4.32)
Since b is even, by the definition of St b2 — B22x2 is also even. Since Я is collapsible,
the system
Ях3 = b2 — B22x2
has a (b2 — B22x2)-solution X3. Therefore,
Яхз is nonseparable and spanning in Я. (4.33)
202
Matrices in Combinatorial Problems
Now let
We have
Bx =
Bu B12 0
О Б22 Я
ЯцХ1 + Bi2x2
Яг2х2 + Яхз
Hi)-
Thus, to see that x is a b-solution for equation (4.31), it remains to show that Bx is
nonseparable and is spanning in B.
Claim 1 Bx is nonseparable.
Suppose that Bx is separable. We may assume that
(4.34)
If
" X '
0
я* =
has a submatrix
J
submatrix
r 1
0
L °
0
0
Y J
, where X ф 0 and Y ф 0.
that is a submatrix of
1
that is a submatrix of
0
Я
x3
*i
0
Я
" 0 "
Я
, then
Гхя о
L °
K* .
, and if
0 1
У
j
has a
By (4.33), Яхз is nonseparable, and so we must have Хн = 0. By the definition of B? ro,
В has no zero columns, and so
the columns chosen by X3 are in the last m — (mi + шг) columns of B.
By (4.34) and (4.35),
X
0
has a submatrix
хв/н
0
that is a submatrix of
and
has a submatrix
0
Yb/h
that is a submatrix of
Яц Я12
0 Я22
(4.35)
B11 ?12
0 ?22
By (4.31)
and (4.33), Xb/h Ф 0. If Yb/h Ф 0, then (B/H)Xl2 is separable, contrary to (4.32).
Therefore, Yb/h — 0> ^d so
the columns chosen by X12 are in the first (mi + тг) columns of B.
(4.36)
By (4.34), (4.35) and (4.36), У = Яхз and X is the first nx rows of B/Hxi2. This implies
that the last row of Я/Ях12 is a zero row, and so Я/ЯХ12 is separable, contrary to (4.31).
This proves Claim 1.
Matrices in Combinatorial Problems
203
Claim 2 Bx is spanning in B.
It suffices to show that rank(Bx) = n - 1. Since (B/#)Xl2 spans in B/#, there exist
ii column vectors v1}V2,--- jV^ in the first mi columns of B, and fe column vectors
wi,W2, • • ¦ , wj2 in the middle m2 columns of В such that h + h = fU and such that
vi,V2,--- |Vjj,wi,W2,-«' ,wj2 are linearly independent over GF(2). Since HX3 spans
in Я, there exist column vectors щ,-* • ,un2-i hi the last m — (mi + m2) columns of
В such that ui,--« ,un_ni_i are linearly independent over GF(2). It remains to show
that Vi, v2, • • • , vit, wj, w2, • • • , wj2 and щ, • • • , un_ni _x are linearly independent. If not,
there exist constants c\, • • • , cit, c[ • • • , c[2, c", • • • , с?а_х such that
f>Vi+ ?>>< + ? c<4 = 0. (437)
*=1 t=l i=l
Consider the first ni equations in (4.37), and since vi,v2,»-- ,v/1,wi,W2,«-* ,wj2 are
linearly independent over GF(2), we must have c\ = • • • = cix = 0 and c[ = • • • = c{2 = 0.
This , together with the fact that ui, • • • ,un-ni-i are linearly independent, implies that
<? = ••» = cJJ_ni_1 = 0. Therefore rank(Bx) = n — 1, as expected. Q
Definition 4.7.5 Let В € B*>m. Let r(B) denote the largest possible number к such
that E(B) can be partitioned into к subsets J5?i, JSfe, • • • ,-E* such that each B^ is both
nonseparating and spanning in B, 1 < i < k.
Example 4.7.3 Let G he a graph and let В = B(G). Then r(B) is the spanning tree
packing number of G, which is the maximum number of edge-disjoint spanning trees in <?.
Proposition 4.7.4 Let В G B* m be a matrix with r(B) > 1. Then for any even vector
b e V(n, 2), the system Bx = b has a solution.
Proof We may assume that В 6 BJ>n_j and rank(B) = n — 1, for otherwise by tau(B) >
1, we can pick a submatrix B' of В such that B' is nonseparating and spanning in В to
replace B. Since b is even and since every columns sum of A is even, it follows that the
rank([B,b]) = n — 1 = rank(B) also. Therefore, Bx = b has a solution. Q
Theorem 4.7.5 Let В € В* >m be a matrix with т(В) > 2. Then В is collapsible.
Proof We need to show that for every even vector b € V(n, 2), Bx = b has a b-solution.
Since r(B) > 2, we may assume that for some B\ € B*1>m and B2 € В*_пьт, В =
[Bi, B2] such that each B» is nonseparable and spanning in B. Let Xi = (1,1, • • • , 1,0, • • • , 0)T €
V(n, 2) such that the first n\ components of xi are 1, and all the other components of xi
areO.
Write В = [BitB2) = [Bb0] + [0,B2]. Since Bi € B?1>m, [Bi,0]xx is even, and so the
vector b — [Bi,0]xi € V(n,2) is also even.
204
Matrices in Combinatorial Problems
Since t([0,?2]) > 1> by Proposition 47.4, the system [0,?2]x2 = b — [#i,0]xi has a
solution x2, such that the first n± components of x2 are 0.
Let x = xi + x2. Then since the last n — n\ components of xi are 0 and the first n\
components of x2 are 0, we have
Bx = [BbB2](xi+x2) = b.
By the definition of xx, Bx contains B\ as a submatrix, and so Bx is both spanning in В
and nonseparable, by Proposition 4.7.1. Q
Theorem 4.7.6 (Catlin, [47] and Jaeger, [138]) If a graph G has two edge-disjoint spanning
trees, then G is collapsible, and supereulerian.
We close this section by mentioning a completely different definition of Б ulerian matrix
in the literature. For a square matrix A whose entries are in {0,1, —1}, Camion [46] called
the matrix A Eulerian if the row sums and the column sums of A are even integers, and
he proved the following result.
Theorem 4.7.7 (Camion [46]) An m x n (0,1, —1) matrix A is totally unimodular if and
only if the sum of all the elements of each Eulerian submatrix of Л is a multiple of 4.
4.8 The Chromatic Number
Graphs considered in this section are simple, and groups considered in this section are all
finite Abelian groups. The focus of this section is certain linear algebra approach in the
study of graph coloring problems.
Let Г denote a group and let p > 0 be an integer. Denote by V(p, Г) the set of p-tuples
(0i,02>--- ,gP)T such that each gt € Г, (1 < i < p). Given g = (91,92,-" ,9p)T and
h = (hi, /i2, • • • , hp)T, we write g ^ h to mean that gi ф hi for every i with 1 < i < p. For
notational convenience, we assume that the binary operation of Г is addition and that 0
denotes the additive identity of Г. We also adopt the convention that for integers 1, —1,0,
and for an element g € Г, the multiplication (1)(#) = g, (0)(g) = 0, the additive identity
of Г, and (—1)0 = — g, the additive inverse of g in Г.
Let G he a graph, к > 1 be an integer, and let C(k) = {1,2, • • • , к} be a set of к
distinct elements (referred as colors in this section). A function с : V(G) «-> С (к) is a
proper vertex к-coloring if f(u) ф f(v) whenever uv € E(G). Elements in the set C(k)
are referred as colors. A graph G is k-colordble if G has a proper ^-coloring. Note that a
graph G has a proper fc-coloring if and only if V(G) can be partitioned into к independent
sets, each of which is called a color class. The smallest integer к such that G is A;-colorable
Matrices in Combinatorial Problems
205
k X(<2)> the chromatic number of G. If for every vertex v € V(G), x(G — v)< x(G) = k,
then G is k-critical or just critical.
Let G be a graph with n vertices and m edges. We can use elements in Г as colors.
Arbitrarily assign orientations to the edges of G to get a digraph D = D(G), and let
В = ?(?>) be the incidence matrix of D. Then a proper |r|-coloring is an element
с€У(п,Г) such that
where 0€ У(ш,Г).
Viewing the problem in the nonhomogeneous way, for an element b € У(т,Г), an
element с 6 V(n,T) is а (Г,Ь)-coloring if
BTc^b. (4.38)
Definition 4.8.1 Let Г denote a group. A graph G is Г-colorable if for any b € У(ш,Г),
there is always а (Г, b)-coloring с satisfying (4.38).
Vectors in V(|JE?(C?)|,r) can be viewed as functions from E(G) into Г, and vectors in
V(|V(G)|,r) can be viewed as functions from V(G) into Г. With this in mind, for any
b € V(|i2(G)|,r) and e € E(G), Ъ(е) denotes the component in b labeled with element
e. Similarly, for any с € V"(|V(G)|,r) and v € V(G), c(v) denotes the component in с
labeled with element v.
Therefore, we can equivalently state that for a function b € У(т,Г), а (Г, b)-coioring
is a function с € V(n, Г) such that for each oriented edge e = (ж, у) € E(G), c(x) — c(«/) ф
b(e); and that a graph G is Г-colorable if, under some fixed orientation of G, for ant
function b e У(т,Г), G always has а (Г, b)-coloring.
Proposition 4.8.1 If for one orientation D = D(G), that G is Г-colorable, then for any
orientation of G, G is also Г-colorable.
Proof Let D\ and D2 be two orientations of G, and assume that G is Г-colorable under
D\. It suffices to show that when Di is obtained from D\ by reversing the direction of
exactly one edge, G is Г-colorable under D2-
Let Bi = B(Di) and 2?2 = -В(Дг). We may assume that B\ and B2 differ only in Row
1, where the first row of B2 equals the first row of Bi multiplied by (—1).
Let b = (Ььбг,-- ,Ьт)Т € У(ш,Г). Then V = (-61,62,-•• ,6m)T € У(т,Г) also.
Since G is Г-colorable under Di, there exists а (Г,b'J-coloring c' = (ci,c2,-*- >Cn)T €
7(п,Г). Note that с = (-ci,c2,- • • ,Cn)T € V(n,T) is a (r,b)-coloring, and so G is also
Г-colorable under D2. ?
206
Matrices in Combinatorial Problems
Definition 4.8.2 Let G be a simple graph. The define the group chromatic number xi(G)
to be the smallest integer A; such that whenever Г is a group with |Г| > к, G is Г-colorable.
Example 4.8.1 (Lai and Zhang, [152]) For any positive integers m and k, let G be a
graph with (2m + k) + (m + k)m+k — 1 vertices formed from a complete subgraph Km on
m vertices and a complete bipartite subgraph KriyT2 with r\ = m+к and r<i — (m+fc)m+fc
such that
\V(Km)nV(Kri>r2)\ = l.
We can routinely verify that x(G) = "» and xi(G) =m + k (Exercises 4.19).
Immediately from the definition of Xi(p), we have
x(G)<Xi(G)- (4.39)
and
Xi(G') < Xi(G), if G' is a subgraph of G. (4.40)
More properties on the group chromatic number Xi(G) can be found in the exercises. We
now present the Brooks coloring theorem for the group chromatic number.
Theorem 4.8.1 (Lai and Zhang, [152]) Let G be a connected graph with maximum degree
A(G). Then
Xi(G)<A(G) + li
where equality holds if and only if G = Cn is the cycle on n vertices, or G = Kn is the
complete graph on n vertices.
The proof of Theorem 4.8.1 has been divided into several exercises at the end of this
chapter.
Modifying a method of Wilf [275], we can applied Theorem 4.8.1 to prove an
improvement of Theorem 4.8.1, yielding a better upper bound of Xi(G) in terms of \i(G), the
largest eigenvalue of G.
Lemma 4.8.1 Let G be a graph with Xi{G) = k. Then G contains a connected subgraph
G' such that xi(G) = к and 6(G') >k-l.
Proof By Definition 4.8.1, G is Г-colorable if and only if each component of G is Г-
colorable. Therefore, we may assume that G is connected.
By (4.40), G contains a connected subgraph G' such that Xi(<2) = A; but for any proper
subgraph G" oiG\ Xi(G") <k.Letn = \V(G')\ and m = |JS?(G')|.
Matrices in Combinatorial Problems
207
If S(G') <k-ly then G' has a vertex v of degree at most d < к—2 in G'. Note that by
the choice of G', Xi(G' ~ v) ^ * " !• By Proposition 4.8.1, we assume that G' is a digraph
such that all the edges incident with v are directed from v, and such that v corresponds
to the last row of В = B(G'). Let vi9 V2, • • • , v<j be the vertices adjacent to v in G', and
correspond to the first d rows of B, respectively; and let e* = (vtVi), (1 < » < d) denote
the edges incident with v in C?', and correspond to the first d columns of B, respectively.
Let Г be a group with |Г| = к — 1. For any b = (&i,&2>**- > &<f» bd+ъ • • * >bm)T €
7(т,Г). Let b' = (bd+i,— ,bm)T =€ V(m-d,r) SinceXi(<?' - v) < fc-1 = |Г|, there
exists а (Г,b')-coloring с' = (ci,C2, • • - ,Cn-i)T € V(n — 1,Г).
Note that |Г - {bi + ci,&2 + c2,--- ,b<* + cd}| > (fc - 1) - d > 0, there exists a
с* € Г- {bi +ci,62 + c2,-" ,&d + cd}. Let с = (ci,--,Cn-i,Cn)T € У(п,Г). Since
с» — Ci ф bi, 1 < % < d, с is а (Г, b)-coloring of (?'. As Г and b are arbitrary, it follows
that Xi(6?') < к - 1, contrary to the assumption that Xi(0') = fc. ?
Theorem 4.8.2 Let G be a connected graph and let Ai be the largest eigenvalue of A(G).
Each of the following holds.
0)
Xi(G)<l + Ai, (4.41)
where equality holds if and only if G is a compete graph or a cycle,
(n) (Wilf, [275])
X(G)<1 + Ab
where equality holds if and only if G is a compete graph or an odd cycle.
Proof By (4.39), and by the well know fact that x(Cn) < 3 for any cycle Cn on n > 3
vertices, with equality holds if and only n is odd, it is straightforward to see that Theorem
4.8.2(ii) follows from Theorem 4.8.2(i).
By Lemma 4.8.1, G has a connected subgraph G' satisfying Lemma 4.8.1. Thus
Ai(G) +1 > Ai(G') +1 > Xi{G). (4.42)
By Theorem 1.6.1, Ai(G') > S(G') > к - 1, and so (4.41) obtains. Assume that equality
holds in (4.41). Then
\1(G) = k-l^Xi(G)-l (4.43)
Hence equalities hold everywhere in (4.42). By Corollary 1.3.2A, G' is (k — 1) regular.
If к > 3, then by Theorem 4.8.1, G' = Kk. Denote
V(G) = {vi,--- ,vktVk+i,-~ >vn}
208
Matrices in Combinatorial Problems
such that V(G') = {vu • • • , vk}. Then
A = {ai>5) = A(G) =
A21 A22
We want to show that k — n and so G = (?'. If & < n, then let x = (1,1, • • • , l,c,0, • • • ,0)T
be a n-dimensional vector such that the first к components of x are 1, and the (k + l)th
component is с and all the other components are 0. By Theorem 1.3.2,
(Лх)тх *(*-!) +fellow.!
Ai(G) - -щ-= &т^ •
Note that ?jLi Oj,A;+i > 0. If ?*-i %-,*+! > 0, then choose e so that 2 ?jLi aj,fc+i >
e(& — 1), which results in Xi(G) > к - 1, contrary to (4.43). Therefore, ?*=i Qj}k+i = 0,
and so a,jtk+i = 0 for each j with 1 < ^' < к. Repeating this process yields that A& = 0,
and so A2i = Af2 = 0, contrary to the assumption that G is connected. Therefore, we
must have n = к, and so G = G' = -ЙТП-
With a similar argument, we can also show that when к = 2, С? = С?' = Cn is a cycle.
D
Corollary 4.8.2 Let G be a connected graph with n vertices and m edges. Then
Ы<?)<1 + ^рЯ (4.44)
Equality holds if and only if G is a complete graph.
Proof Let Ai, Л2, • • • , A„ denote the eigenvalues of G. By Schwarz inequality, by ?2=1 к =
0andi;iiAf = 2m)
A? = (-AX)2 = (? A,) < (n - 1) 2 A? = (n - l)(2m - A?).
\*=2 / t=2
Therefore, (4.44) follows from that (4.41).
Suppose equality holds in (4.44). Then by Theorem 4.8.2(i), G must be a complete
graph or a cycle. But in this case, we must also have Л2 = A3 = • • • = An, and so G must
be a Kn. (see Exercise 1.7 for the spectrums of Kn and Cn.) Q
The following result unifies Brooks coloring theorem and Wilf coloring theorem.
Theorem 4.8.3 (Szekers and Wilf, [258], Cao, [42]) Let f(G) be a real function on a
graph G satisfying the properties (PI) and (P2) below:
(PI) If Я is an induced subgraph of <3, then /(#) < /(G).
(P2) /(<?) > 6(G) with equality if and only if G is regular.
Then x(6r) < f(G) +1 with equality if and only if G is an odd cycle or a complete graph.
Matrices in Combinatorial Problems
209
We now turn to the lower bounds of x(G). For a graph G, o>(G), the clique number of
(7, is the maximum к such that G has Kk as a subgraph. We immediately have a trivial
lower bound for x(<2):
Xi(G)>x(0) >»(<*)-
Theorem 4.8.4 below present a lower bound obtained by investigating A(G), the adjacency
matrix of G. A better bound (Theorem 4.8.5 below) was obtained by Hoffman [123] by
working on the eigenvalues of G.
Theorem 4.8.4 If G has n vertices and m edges, then
Proof Note that G has a proper fc-coloring if and only if V(G) can be partitioned into к
independent subsets Vi,V2i • • • , V*. Let щ = |V*|, (1 < ? < к), we may assume that the
adjacency matrix A(G) has the form'
An A12 ••• Ai*
A21 Л22 ••• A2k
A(G) =
(4.45)
where the rows in [Aiu Ai2, • • • , -А**] correspond to the vertices in 1^, 1 < i < к. Since V{
is independent, Л^ = 0 € Bni, (1 < i < к), and so
2m = \\A(G)\\<n2-itnb (446)
It follows by Schwarz inequality that
к
t=l \i=rl /
and so Theorem 4.8.4 follows by (4.46). []
Lemma 4.8.2 (Hoffman, [123]) Let A be a real symmetric matrix with the form (4.45)
such that each Ац are square matrices. Then
к
Amax(A) + (k - l)Amin(A) < ]T Amax(A«)-
Theorem 4.8.5 (Hoffman, [123]) Let G be a graph with n vertices and m > 0 edges, and
with eigenvalues Ai > Л2 > • • • > An. Then
(4.47)
210
Matrices in Combinatorial Problems
Proof Let к = x(G)- Then V(G) can be partitioned into к independent subsets
Vw* ,14, and so we may assume that A(G) has the form in (4.45), where Ац — 0,
1 < i < k. By Lemma 4.8.2, we have
A! + (fc-l)An<0.
However, since m > 0, we have An < 0, and во (4.47) follows. Q
4.9 Exercises
Exercise 4.1 Solve the difference equation
Fn+3 = 2Fn+i +Fn+n,
JPbs 1,^1=0,^3 = 1.
Exercise 4.2 Let Sa(*,A;,v) be a ^-design. Show that
Exercise 4.3 Show that for г = 0,l,-«« ,t, a ^-design Sa(?,/;,v) is also an г-design
5д. (*,&,»), where
Exercise 4.4 Prove that 6fc = vr in BIBD.
Exercise 4.5 Prove Theorem 4.3.8.
Exercise 4.6 Let A = (ay) and Б = (by) be the adjacency matrix and the incidence
matrix of digraph D(V, E) respectively. Show that
\v\ \e\ \v\ \v\
?X>=0 and ?][>y = |S|-
*=i j=i i=i j=i
Exercise 4.7 For graphs G and Я, show that 0{G * H) = 6{G)9{H).
Exercise 4.8 If ?? has an orthonormal representation in dimension d, then 0(G) < d.
Exercise 4.9 Let G be a graph on n vertices.
(i) If the automorphism group Г of G ^s vertex-transitive, then both $(G)0(Gc) = n
and G(G)0(<2C) < n.
(ii) Find an example to show that it is necessary for Г to be vertex-transitive.
Matrices in Combinatorial Problems
211
Exercise 4.10 If the automorphism group Г of G is vertex-transitive, each of the following
holds.
(i)e(G*G<) = \V(G)\.
(ii) if, in addition, that G is self-complementary, then 0(G) = y/\V(G)\.
(Ш)0(С5) = л/5.
Exercise 4.11 Prove Proposition 4.6.2.
Exercise 4.12 Prove Theorem 4.7.3.
Exercise 4.13 (Cao, [42]) Let v be a vertex of a graph G. The fc-degree of v is defined
to be the number of walks of length A; from v. Let A*(G) be the maximum fc-degree of
vertices in G. Show that
(i) Д*((7) is the maximum row sum of Ak(G).
(ii) For a connected graph G,
x(G)<[^k(.G))1/k + h
where equality holds if and only if G is an odd cycle or a complete graph.
Exercise 4.14 Let Г be an Abelian group. Then a graph G is Г-colorable if and only if
every block of G is Г-colorable.
Exercise 4.15 (Lai and Zhang, [152]) Let Я be a subgraph of a graph G, and Г be an
Abelian group. Then (G,H) is said to be Г-extendible if for any b € У(|?((?)|,Г), and
for any (r,bi)-coloring ci of #, where bi is the restriction of b in E(H) (as a function),
there is а (Г, b)-coloring с of G such that the restriction of с in V(#) is ci (as a function).
Show that if (G, H) is Г-extendible and H is Г-colorable, then G is Г-colorable.
Exercise 4.16 (Lai and Zhang, [152]) Let G be a graph and suppose that V(G) can
be linearly ordered as t/i, tfe, • - * , v» such that cfc.fyt) < к (i = 1,2, • • • ,n), where G» =
G[{vi, v2, • • * , V{}] is the subgraph of G induced by {v\, V2, • • • , v»}. Then for any Abelian
group Г with |Г| > к +1, (Gi+i, G«) (i = 1,2, • • • , n — 1) is Г-extendible. In particular, G
is Г-colorable.
Exercise 4.17 (Lai and Zhang, [152]) Let G be a graph. Then
Xi(G)<m^{S(H)} + l.
Exercise 4.18 (Lai and Zhang, [152]) For any complete bipartite graph ifm>n with n >
mm, Xi(#m,n)=m + L
Exercise 4.19 (Lai and Zhang, [152]) For any positive integers m and к, there exists a
graph G such that x(G) = m and xi(G) =m + k.
212
Matrices in Combinatorial Problems
Exercise 4.20 Let G be a graph. Show that
(i) If G is a cycle on n > 3 vertices, then xi (O) = 3.
(ii) xi(<2) < 2 if and only if б7 is a forest.
Exercise 4.21 Prove Theorem 4.8.1.
4Л0 Hints for Exercises
Exercise 4.1 Apply Corollary 4.1.2B to obtain к = 3,r = l,a = 2,/? = l,6n = n,
Co = l,Ci = 0,C2 = 1.
Exercise 4.2 Count the number of ^-subsets in Sx(t, k, v) in two different ways.
Exercise 4.3 For any subset S С X with |5| = », the number of = ways of taking t-
subsets containing S from X is ( I, while each ^-subset belongs to Л of the X{S in
V'-*' /
an S\(t,к, v). Thus the number of X^s containing 5 is Л
On the other hand, the number of ways of taking ^-subset containing S from X is
f *-* "\
I I where S belongs to A» of the X^s. Hence the number of X^s containing S is
\t-i J
<*-.;)¦
Exercise 4.4 Count the repeated number of v elements in two different ways.
Exercise 4.5 Let m = I + 1 and b = t — 1 and apply Theorem 4.3.7. Then there exists a
complete graph Kn with n = b(m-1)+m- (6-1) = (t-1)1 + (J +1) - (*-2) = tl-t+St
which can be decomposed into t complete (/ + l)-partite subgraphs F\, F2i • • • ,Ft. Clearly
dk (Fi) < 2 < d, and so (4.13) follows.
Exercise 4.6 In the incidence matrix, every row has exactly a +1 and a —1, and so the
first double sum is 0. The second double sum is the sum of the in-degrees of all vertices,
and so the sum is |2?(I?)|.
Exercise 4.7 By Proposition 4.5.1, it sufiices to show that 6(G*H) < 0(G)9(H).
Let vi, • • • , vn, and wi, • • • , wm be orthonormal representations of Gc and #,
respectively, and let с and d be unit vectors such that
?(vfc)2= 0(G), f>Jd)» = 0(H).
Then the v* ® w^ >s form an orthonormal representation of Gc * #. Since Gc * H С G * #,
the Vi ® w/s form an orthonormal representation of G * H. Note that с <g> d is a unit
(::«¦
Matrices in Combinatorial Problems
213
vector. Hence
n m
<KG*H) > X^Kv^w^cSd))2
n m
= E(v^)2E(wJd)2-
Exercise 4.8
Let ui,"- ,un be an orthonormal representation of G in dimension d. Then щ ®
ui, • • • , un <8> un also form an orthonormal representation of (?. Let ei, • • • , e<* be an
orthonormal basis, and let
b = -7=(ei <g> ex + e2 <8> e2 H h е<* <g> erf).
vfl
Then |b| = 1 and
(щ®щ)тЪ = -д.
Hence 0(6?) < d follows by the definition of 0.
Exercise 4.9 (i). View elements in Г as n x n permutation matrices. By Theorem 4.5.2,
there exists а В б В such that ti(BJ) = 6(G) > and consider the matrix
'-«ч-йО^")-
Then as PJ = JP = J, we have В е # and tv(BJ) = 0(G). Since Г is vertex transitive,
5Й = 1/n. Imitate the proof of Theorem 4.5.3 to construct orthonormal representation
vi ,•••', vn and the unit vector d.
Note that in the proof of Theorem 4.5.3, equality in the Cauchy-Schwarz inequality
held, and so we have in fact (using the notation in the proof of Theorem 4.5.3)
(dTVi)2 = 0(<7)М2 = 0(в)Ъи.
Hence back to the proof of this exercise, we have
(dTv.)2 = №,
It follows by the definition of 0(<3C) that
d(Gc) < max
The other assertion of (i) follows from Theorem 4.5.1.
214
Matrices in Combinatorial Problems
(ii). Take G = #iin-i, for n > 3.
Exercise 4.10 It suffices to show (i). Note that the "diagonal" of G*GC is an independent
vertex set in G * Gc.Hence
0(G * Gc) > ol{G * Gc) > \V(G)\.
On the other hand, by Theorems 4.5.1 and 4.5.4 and by the previous exercise,
B(G * Gc) < 9{G * Gc) = 9(G)9(GC)).
Exercise 4.11 Let j = (1,1,-- ,1)T € Впд. Multiply both sides of the equation in
Proposition 4.6.1(i) from the right by j to get к2 = к+\к+ц{п-1—к), and so Proposition
4.6.2(i) obtains.
Let I = n — к — 1. Then Gc, the complement of G7 is Z-regular. By Proposition 4.6.1,
(J -1 - A)2 = /J + (I - к + fj, - 1)(J -1 - A) + (/ - к + Л + 1)A
This implies Proposition 4.6.2(ii), by Proposition 4.6.1.
If G is the disjoint union of some Kk+i\ then it is routine to check that G is an
(n, к, к -1,0)-strongly regular graph. Conversely, assume that G is an (n, к, Л, 0)-strongly
regular graph. By Proposition 4.6.2(ii) and since /4 = 0, A = fc—1, which implies that
each component of G is a complete graph.
Exercise 4.12 By Theorem 4.7.2 with B* = B(Kn), a simple nonseparable matrix А С
B(Kn) is subeulerian if and only if there exists no vector z in the cocycle space of B(Kn)
such that ||z||o is odd.
Exercise 4.13 (i) follows from Proposition 1.1.2(vii). For (ii), note that [Ak(G)]^k
satisfies properties (PI) and (P2) in Theorem 4.8.3.
Exercise 4.14 Let Г be an Abelian group. If a graph G is Г-colorable, then every subgraph
of G is also 7-colorable. In particular, every block of G is Г-colorable.
It suffices to prove the converse for connected graphs with two blocks. Let G be a
connected graph with two blocks G\ and 6?2 and assume that G\ and C?2 are Г-colorable.
Let v0 be the cut vertex of G. Then v0 € V(Gi) П V(G2).
Let m = \E(G)l гщ = \E(Gi)\ with 1 < i < 2, and let У(гщ,Г) denote the set of
mi-tuples whose components are in Г and are labeled with the edges in 6?*.
For any b € V(m,r), we can get two vectors bi € V(mbr) and b2 € V(m2,r).
Since Gi and Gi are Г-colorable, there exist a (r,bi)-coloring сг € V(|V(Cri)|,r) and
an (r,b2)-coloring c2 :€ V(|V(G2)|,r). Let Ci(v0) = 9u where 1 < i < 2, and for each
v € V(G2), let c2(v) = c2(v) + pi - ?2. Then
()=f ci(v), i?«€V(Gi)
1 <?(»), if«€V(C?a).
Matrices in Combinatorial Problems
215
It is routine to verify that с is а (Г, b)-coloring of G.
Exercise 4.15 For any b € V(|?7(<2)|,r), since Я is Г-colorable, Я has а (Г,btf)-coloring
ся : V(H) и* Г, where b# is the restriction of В in E(H). Since (G,H) is Г-extendible,
ся can be extended to а (Г, (r)-coloring.
Exercise 4.16 Let D be an orientation of E(Gi+i) such that every e = Vjxv& € E(G{+i)
is directed from Vjx to Vj2 if ji > J2 and from Vj2 to v^ otherwise. For any b €
y(jE((?i+i)|, Г) and any (Г, i)-coloring ci of G{t where bi is the restriction of b in E(Gi),
we define a function с : V (G«+i) н> Г as follows: Assuming that Vix vi+i, Vi2 v*+i, • ¦ • , v,r Vi+i
are all the edges joining v^+i (0 < r < fc) in G»+i, we let c(v) = ci (v) if v € V(G,), and let
c(vi+i) = g' such that y' € Г = r-{c(vip)+b(vipvi+i)|p = 1,2, • • • ,r}. Since |Г| > fc+1,
Г' ^ 0, and so с can be defined. It is routine to verify that с is а (Г, b)-coloring, and so
(Gi+i,Gi) is Г-extendible, where i = 1,2, • • • ,n — 1.
By Exercise 4.15 and since C?i is Г-colorable, it follows that G is Г-colorable.
Exercise 4.17 Let |V(G)| = n, к = тахяс<?{<*(#)} + 1, and vn be a vertex of degree at
most k. Put Яп_1 = G — {vn}. By assumption Hn~i has a vertex, say vn_i, of degree
at most к. Put Яп_2 = G — {vn,vn_i}. Repeating this process we obtain a sequence
vi,v2, • • • ,vn such that each v^ is joined to at most A; vertices preceding it. Now Exercise
4.17 follows from Exercise 4.16.
Exercise 4.18 Assume that Кт>п has the vertex bipartition (X, Y) with X = {xi, x%, • • • , xm}
and У = {yi, у2, • • * , Уп}- Let Г be an Abelian group with Г| < m and D be an orientation
of Е(Кт,п) such that every e = ar,t/j € ??(iTm>n) is directed from y$ to ж».
Denote the set of all functions с : V(Km,n) и- Г by C(Kmin, Г). For every function с €
С(Кт,п,Г), we can get a function cx : -X" «-> Г. Let С(Х,Г) = {с* : с € С(#т,п,Г)}.
Since |Г| < го, |С(Х,Г)| = т|г| < тт. Assume that С7(Х,Г) = {ci,c2,— ,cr}, where
г = m'rl. Now we define ft : E{Km>n) к* Г) (I = 1,2,--- ,r) as follows: Ifl^j, let
fi(?i2/j) = 0 for every г, and otherwise let fi(xiyi) = a^ € Г such that {ci(xi) + a^ : г =
1,2, • e • , m} = Г. Let f = ?J_X ft- Then for any function с : V{Km^n) «-> Г, there exists at
least one arc e = yjXi € Е(Кт,п) such that с(^)—c(x\) = f(e). Hence xi(i^TO,n) > m+1.
On the other hand, by Exercise 4.17, \i {Km,n) < m +1.
Exercise 4.19 Let G be the graph in Example 4.8.1 Since G contains a Kmi x(G) = m*
Apply Exercise 4.18 to show that Xi(6?) = m + fc.
Exercise 4.20 To see that if G contains a cycle, than Xi(<2) > 3, it suffices to show that
Xi(Cn) > 2 for any n > 3, where <7n denote a cycle on n vertices. Let Z2 denote the group
of 2 element. If Xi(Cn) = 2, then Cn is Z2-colorable. Denote V(Cn) = {vi,v2,- • • ,vn},
such that the orientation of G is {(vi,Vi+i) : i — 1,2,-•• ,n (mod n)}. Assume first
that n is even. Let b = (0,0,-•• ,0,1)T : E(Cn) н* Z2. (Note that b(vn,vi) = 1.) By
216
Matrices in Combinatorial Problems
the assumption that G is ^-colorable, G has а (Г, b)-coloring с : V(G) «-> Z2 such that
c(vi)—c(v»+i) Ф b(vi, Vi+i), where t = 1,2, • • • , n (mod n). If c(vn) = 1, then c(v2t+i) = 0
and c(v2i) = 1, and so c(vn) — c(vo) = 1 = b(v„,vi), a contradiction. (This shows that
Xi(Cn) > 2. Together with Exercise 4.17, the above implies that Xi(G) = 3. )
If n is odd, then choose b = 0, and a similar argument works also.
On the other hand, we can routinely argue by induction on |F(G)| to show that if G
is a tree, then Xi (O) < 2.
Exercise 4.21 If G is connected and not regular of degree A(G), then таа:#с<?Я(Д) <
A (6?) - 1 and so Xi(G) < A (6?). Without loss of generality, let G be 2-connected and
A(<3)-regular. If G is a complete graph, then xi(G) = |V(G)| = A(G) + 1.
К A(G) = 2, then G is a cycle and so by Exercise 4.20(i), Xi(G) = 3 = A(G) + 1.
If G is 3-connected and G is not complete, then there are three vertices vi,v2 and vn
(n = |V(Cr)|) in G such that vivn, v2vn € ?(G) and viv2 ? J5?(G). If C? is 2-connected, let
{vn,v'} be a cut set of G. Then there are two vertices v\ and v2 belonging to different
endblocks of G — vn. Now, we arrange the vertices of G - {t/i, v2} in nonincreasing order
of their distance from vn, say V3, V4, • • • , vn. Then the sequence vi, v2, • • • , vn is such that
each vertex other than vn is adjacent to at least one vertex following it, namely each vertex
other than vn is joined to at most A(<3) — 1 vertices preceding it.
Let D be an orientation of E(G) such that every e = ViVj € E(G) is directed from vi
to Vj if i > j and from Vj to Vi otherwise. For any b : E(G) н> Г, where |Г| > A(G),
we define с : V(G) и> Г as follows: Assign a\ € Г to c(vi) and a2 € Г to c(v2) such
that a\ + b(vivn) = a2 + b(v2vn); for t>j (3 < j < n), let v^vj^v^Vj,• • • ,t/^t/j € ?(<?)
(r < A(Ct) — 1 if j < n) be the edges joining Vj and having ip < j (p = 1,2, • • • , r), and
assign aj to c(vj) such that a,j € 1^- = Г — {c(v*p) + b(vipU;)|p = 1>2, • • • ,r}. If j < n,
then г < A(G) — 1 and so Г,- ф 0; if j = n, then Гп 9^ 0$ since a\ +b(vivn) = аг+b(v2vn).
It is now routine to verify that с is а (Г, b)-coloring.
Chapter 5
Combinatorial Analysis in
Matrices
5.1 Combinatorial Representation of Matrices and
Determinants
Definition 5.1.1 For a matrix A = (a#) € Afm>n, the weighted bipartite graph of Л,
denoted by К A, has vertex set V = Vi U V2 and edge set E, where Vi = {tii,U2, • • • ,um}
and V2 = {vi, V2, • * • , vn} such that гци? € ?? with weight ay if and only if ay ^ 0.
To represent a determinant by graphs, we adopt the convention to view К A as a
weighted complete bipartite graph Кт)П with partite sets Vi and V2, such that UiVj € E
with weight ay, for all иг- € Vi and tty € V2.
If A = (ay) € Mn, then we can extend the definition of D(A) by defining D(A) as the
weighted digraph of A such that V(D(A)) = {1/1,1/2,-*• ,*>л}, where (i/«,ity) € i?(D(-A))
with weight ay if and only if a^ ф 0.
For the convenience to interpret a determinant by digraphs, we can view D(A) as a
complete digraph on n vertices with a loop at every vertex by assigning ay to the arc
(vi, Vj) for every г, j = 1,2, • • • , n.
Example 5.1.1 For the matrix
4 =
2-300
0 1.2 0 -1
5 0 3-6
the weighted bipartite graph is
217
218
Combinatorial Analysis in Matrices
Figure 5.1.1
Example 5.1.2 Let A = (a#) € Mn be a square matrix. Let Кп>п denote the weighted
bipartite graph of A with partite sets V\ = {щ,и2,-" ,wn} and V2 = {vi,V2,"- ,vn}-
For any permutation тг in the symmetric group on n letters, the edge subset
«Rr = {(«1^(1)), (W2Vff(2)), • • • , («n^(n))}
is a perfect matching in КПъП. Therefore, this yields a one to one correspondence between
Sni the symmetric group on n letters, and Mn> the set of all perfect matchings of Kn>n.
For each n € <Sn> define
signer)
_f 1 if 7Г is
[ -1 if 7Г is
an even permutation
an odd permutation.
Let Wa(F*) = sign(7r) П(щ»•)€*¦» °»i- Then the determinant of A can be written as
det(A)= ? wa№)-
Example 5.1.3 Let A = (oy) € Afn be a square matrix. Let 1>(Л) denote the weighted
digraph of A with V(D(A)) = {vi, V2, • • • , vn}. For any permutation 7r in the symmetric
Combinatorial Analysis in Matrices
219
group on n letters, the arcs
F* = {(Vb^li)),^!),^!))),- ,}
form a subdigraph called a Ufactor in D(A). Therefore, this yields a one to one
correspondence between Sn, the symmetric group on n letters, and Vn, the set of all 1-factors
dD(A).
Note that each 1-factor Fn is a disjoint union of directed cycles in D(A). For a directed
cycle C, define
ИЪ(0 = - П <*> and^(F^)= П W^(Cf>-
(vi,Vi)€S(C) C€F*
Note that if A; denotes the number of disjoint directed cycles in FW9 then
(-1)* = (-1)"(-1)"-* = (-1)" signW.
Therefore, the determinant of A can be written as
det(A) = (-1)" ? WA(FW).
Fnevn
Definition 5.1.2 Two matrices AtB E Mn are diagonally similar if there is a non singular
diagonal matrix D = diag(di, d2, • • • , dn) such that DAD"1 = B.
Example 5.1.4 If A and В are diagonally similar, then D(A) = D(B), when weights are
ignored and zero weighted arcs dropped. However, it is possible that D(A) = D(B), but
A and В are not diagonally similar. Consider the example:
[ 0 2 '
[ 1 0 >
, and В =
"oil
1 0 J
Clearly D(A) = D(B). If there were a D=diag(di,d2) such that DAD"1 = ?, then
MidJ1 = 1
d2di1 = 1.
A contradiction obtains.
Theorem 5.1.1 (Fiedler and Ptak, [88]) Let A,B € Mn be two square matrices such that
A is irreducible. Then A and В are diagonally similar if and only if each of the following
holds:
(i) D(A) = D(B), and
(и) For each directed cycle С in D(A), WA(C) = WB(C).
220
Combinatorial Analysis in Matrices
Proof Assume first that A and В are diagonally similar. Then ац = О if and only if
bij - 0, for any ij = 1,2,— ,n, and so D(A) = D(B). Let D = D(A) = D{B). By
assumption, there is a D=diag(di, 0*2 > • • • , dn) with d» ^ 0 such that DAD'1 = ?. Thus,
diaydj1 s= &y> for any t, j = 1,2, • • • ,n.
If follows that for each directed cycle С = v^v^ • • • Vifcv,x,
Wb (C) = -bh ii2 bi2ii3 • • • 6|fcfil
= ~°ii,t2 a*2,*3 • • • °«Jb ,<г = ^A (C).
Conversely, assume that both (i) and (ii) hold. Since A is irreducible, D(A) is strongly
connected, and so by D(A) = D(B), В is also irreducible. We argue by induction on
|jE7(D(A))| (or equivalently, the number of non zero entries of A) to show that A is
diagonally similar to B.
Suppose first that D = V1V2 * * * vnv\ is a directed cycle. By assumption,
a1>2a2,3 • • • a„,i = -WA(C) = -WB(C) = 61,262,3 * • • &n,i.
Define
dx =
di+i =
1
diditi+i
bit*
i+i
, for i = 1,2, • • • , n — 1.
Let Л = diag(a\,d2, ¦ • • , dn). Then DAD'-1 = Б.
Now assume that D is obtained from a strong digraph .D' by adding a directed path
VfcVfc-i • • "U2V1 vn. (Thus D' may be viewed as D(A'), where A' is obtained from A by
changing the nonzero entries а*,*-1>*- ¦ ,fl2,i>fli,n to zeros. This can be done since D is
strong, and so every arc of D lies in a directed cycle of ?>). Therefore,
4 =
°i,i+l
a*,i;-i
°l.n
A' J
, and Б:
Gi,i+1
6*,*-l
Ь\,п
B'
where A',?' € Mn-k+i are irreducible, and, in A, only 04,4-1, • • • ,02,1, oi>n are nonzero
entries outside A'; and in ?, only bjb,*-i,*-« ,&2,i,&i,n axe nonzero entries outside ?'.
By induction, there is a nonsingular D' = diag(d*,- • • ,dn) such that D'A'{D')~l = ?'.
Define
— ^»+1°Й-1,г
* =
°i+l,i
, for each i = 1,2, • • • , fc — 1,
Combinatorial Analysis in Matrices
221
and let D = diag(di, • • • , dn). Then DAD"1 = B, and so A and В are diagonally similar.
D
Shao and Cheng [248] modified the conditions in Theorem 5.1.1(H) to obtain necessary
and sufficient conditions for matrices A and В which are not necessarily irreducible to be
diagonally similar. Interested readers are referred to [248] for further details.
5.2 Combinatorial Proofs in Linear Algebra
Combinatorial methods have been appHed to prove results in matrices. For example, the
Jacobi identity was studied combinatorially by Jackson and Foato ([89]). Brualdi gave
combinatorial proofs of the Jordon canonical form of a matrix ([20]) and he also showed
that the elementary divisors of a matrix can be determined combinatorially ([21] and
[22]). In this section, we present the combinatorial proofs of two matrix identities given
by ZeUberger ([280]).
Once again we adopt the following notational convention: For a matrix A, (A)ij denotes
the (i,j)-entry of A.
Theorem 5.2.1 (Cayley-Hamilton) Let A € Mn. Then xa{A) = 0.
Proof Fix an Л € Mn. Let
Xa(A) = det(AI - A) = An + oiA"-1 + • • • + ak\n~k + • • • + an-i A + on.
Therefore, it suffices to prove this matrix identity:
An + аг A71-1 + • • • + akAn~k + • • • + an-iA + anIn = 0. (5.1)
As in Example 5.1.3, let D(A) denote the weighted digraph of A with V(D(A)) =
{v\, V2, • • • , vn} (viewed as a weighted complete digraph on n vertices, where an arc (vi, Vj)
has weight a#), Vn the set of all 1-factors of D(A) and let ?>* denote the set of all 1-factors
of all subdigraphs of D(A). Then
det(-;i)= ? Wa(Fk)bdA det(Jn-A)= ? WA{F9).
Note that in (5.1), a* is the sum of the weights of all subgraphs of D(A) induced by к
element subsets of V(D(A))> and that the (г, j)-entry of An~k is the total weight of all
directed (v«, w/)-walks of length n — k.
Fix i and j, let A = A(i,j) denote the collection of such subgraph pairs (P,C7) in
D{A):
(Al) P is^a directed (vi,u/)-walk,
(A2) С is an arc disjoint union of directed cycles,
222
Combinatorial Analysis in Matrices
(A3) \E(P)\ + \E(C)\=n.
Let o(C) denote the number of cycles in С Then the weight of (P, C) can be defined as
follows.
W(P,C) = (-l)°W П а"'
(vktvt)€E(P)UE(C)
To verify (5.1), it suffices to verify both of the following claims.
Claim 1 The (i,j)-entry of the left hand side of (5.1) is
(P,C)eA(i,j)
Fix a A; with 0 < к < п. Suppose that \E(P)\ = n - A;. Then JJ ami is the
(t/m>V/)€?(P)
total weight of the directed (vi, Vj)-walk P, and the (?,y)-entry of An~k is the sum of the
total weight of all directed (v,,t^)-walk of length n — k. By (A3), |i?(C)| = fc, and so
E(C) corresponds to a A; element subset of V(D(A)). The total weight of these fc-element
subsets is equal to the sum of all к х к principal submatrices of (—A)> which is a*.. In
other words,
a»(A-*)u = ? П
Q>ml 22 JJ Q>ml
(p, c) e A(i, i) (vm M)eE(P) J
with \E(P)\ = n - Jb /
(P. C) € A(it j) (Vm,Vl)eE(C)
with |??(C)| = ft
Thus Claim 1 follows by summing up from Л = 0,1, • • • , n.
Claim 2 For each (i,j),
? W(P,C) = 0.
(P,C)€.4(i,j)
Fix a (P,C7) € Д(г,У). Starting from v$, P may revisit a vertex that is already in
P, in which case P contains a directed cycle C\\ or P will visit a vertex that is in C,
in which case P and a directed cycle C2 in С share a common vertex. Obtain a new
pair (P',C") € Л(г,^) as follows: In the former case, move C\ from P to C, and in the
latter case, move C2 from С to P. Note that W(P,C) = -^(P'jC"), and that the
correspondence between (P, C) and (P', C) is a bijection. Therefore, Claim 2 follows. Q
Theorem 5.2.2 Let A = (%¦),? = (by) € Afn. Then det(AB) = det(4) det(P).
Proof Let Sn denote the symmetric group on n letters. For each 7r € <Sn, define
u>a(*) = sign(7r)a1^(1)a2^(2) • • • ап,тг(п)>
wB (тг) = sign(7r)61,ff(1) b2yW(2)'• • bn>ir (n) •
Combinatorial Analysis in Matrices
223
Note the difference between the definitions of wa here and that of Wa previously. With
these notations,
det(A) = wA(Sn) = E «UM, and det(?) = wB(Sn) = E wbM-
neSn w€Sn
Note that
n
Thus we can introduce a digraph D = D(A,B) with V(D) = {vi, V2, • • • ,vn}, where there
are two parallel arcs from each v* to each Vj, one with weight a^ (denoted by v« -*a vj)
and the other with weight b# (denoted by Vi -*в Vj). With this model, we represent
uikhj by a path ViVkVj. This also motivates the following notation.
Let Z(n) denote the set of pairs (/,7г), where / is a function from {1,2, • • • ,n} into
itself and where n € Sn. Define
n
w(/,7r)= signfr) Д (Oi/(ob/«)ir(o)-
Note that
det(AB) = w{Z(n)) = 53 «>(/»*)• (5-2)
(/,7T)6Z(n)
ff / € Sn, then Z*-1*- € 5n, and so w(/,7r) = «иСЛювСГ"1*). К follows that
? «,(/,*) = E «иШадСГ1*) (5.3)
= E «*(Л E W*M = <*et(4)det(B).
By (5.2) and (5.3), it suffices to show that
E Ц/,7Г) = 0. (5.4)
Since / 0 <Sn, there exist 6,t,t' € {1,2,- •• ,n} such that f(i) = f(i') = 6, where г ^ i'.
Then, D has arcs v* -?a Щ and tv -*д v&. Choose a smallest 6 such that |/*"1(6)| > 2,
and after b is chosen, choose t, t' € f~l(b) such that г +1' is smallest.
If Vj and v^ are in the same cycle of тг, that is, n has a cycle
Vi -*A Vb ~*B V*{i) -*A >B Vi' ~*A Vb ->B *>*(*') ->Д • • • Vi,
then there is а тг' € <Sn, such that x is not in the cycle above, 7г'(а;) = 7г(л), and such that
the cycle above is broken into two cycles:
vi -*a Vb -*в */*(?) ->л »в V» and ужф -+a >в v? -*a vb ->в v^y
224
Combinatorial Analysis in Matrices
К Vi and vi* are not in the same cycle of 7Г, that is, тг has cycles
Vi -+A Щ ->B V*(i) "+A >B Vi and Vi» ->A Vb ~+В Vn(V) ->A >B V{>,
then there is a 7r' € Sni such that x is not in these two cycles, 7r'(a:) = ir(x)t and such that
these two cycles are combined into a cycle:
Vi -U Vb ->B V^i» ->A >B Vi» ->л Vb ~*B %(i') -+A-~ V^
Thus, (/,7r) <—? (/,я"0 is a one to one correspondence from the set {(/,7r) : f &Sn
and 7Г € <Sn} onto itself such that
Therefore, (5.4) must hold. Ц
5.3 Generalized Inverse of a Boolean Matrix
Definition 5.3.1 Let Bm>n denote the set of all m x n Boolean matrices. A generalized
inverse (or just a g-inver$e) of a matrix A € Bn,m is a matrix В € Bn>m such that
ABA = A.
A matrix A = (a#) € Bm,n can be represented by a bipartite digraph ?(#„»,Sn)>
called the bipartite digraph representation of A, where i^i = {tti,tt2, * * * >^m} and 5n =
{vi,V2,**- ,vn} such that (u^Vj) is an arc if and only if ац > 0. Conversely, given a
bipartite digraph B(Rm, Sn) whose arcs are all directed from a vertex in Rm to a vertex
in 5n, there is a matrix A € Bm>n, denoted by M(B(Rm,Sn)), whose bipartite digraph
representation is B(RmySn).
Note that in our notation, the arcs in a bipartite digraph B(Vi, V2) are always directed
from Vi to V2. Thus B(Rmt 5n) and B(5n, ^m) have identical vertex sets but the arcs are
directed oppositely.
If A € Bm>n has a bipartite digraph representation B(Rm,Sn) and if M(B(Sni Rm))
is the bipartite digraph representation of a generalized inverse of A, then B(Sn,Rm) is
called the g-inverse graph of A (or of B(Rmy Sn))-
If G = BORjn,Sn) U?(5n,Rm), then G is called the combined graph of B(Rm,Sn) and
Example 5.3.1 The bipartite digraph representation of the matrix
10 0
A =
Oil
111
Oil
is the bipartite graph in Figure 5.3.1.
Combinatorial Analysis in Matrices
225
B(#4,S3)
Figure 5.3.1
Example 5.3.2 (Combined graph) Let A be the matrix in Example 5.3.1 with
representation B{Ra, S3) and G = Б(#4,«SO U B(53, Л4). (See Figure 5.3.2). We can verify that
B\ = М(5з,Й4) is a p-inverse of A, where
*i =
10 0 0
0 0 0 1
0 10 1
226
Combinatorial Analysis in Matrices
R4
Sz
Figure 5.3.2
Example 5.3.3 (Nonuniqueness of ^-inverses) Each of the following is a ^-inverse of the
matrix A in Example 5.3.1.
B2 =
10 0 0*
0 0 0 0
0 10 0.
, ?3 =
1000"
0 0 0 0
0 1 0 1 e
, В4 =
10 0 0
0 0 0 1
0 0 0 0
Definition 5.3.2 The set of all ^-inverses of A is denoted by A~. A matrix В € A~ is
a maximum g-inverse of A and is denoted by max A*~, if В has the maximum number of
nonzero entries among all the matrices in A—; a matrix В € A~ is a minimum g-inverse
of A and is denoted by min A~, if В has the minimum number of nonzero entries among
all the matrices in A".
Combinatorial Analysis in Matrices
227
Note that both maxA~ and minA~ are sets of matrices. For notational convenience,
we also use max A" to denote a matrix in maxA~, and use min A~ to denote a matrix in
minA".
Example 5.3.4 Let A be the matrix in Example 5.3.1. Then max A" = Bi and both Bi
and В4 are minA~. In fact, Zhou [291] and Liu [167] proved that while min A" may not
be unique, max A" is unique as long as A~ Ф 0.
Theorem 5.3.1 Let A G Bm>n with a bipartite digraph representation B{Rm,Sn)- For a
graph B(Sn, Rm), the following are equivalent.
(i) B(SniRm) is a ^-inverse graph of A.
(ii) In the combined graph G = B(RmiSn) U B(Sn,Rm)> for each pair of vertices
(и*, vj) with щ 6 Rm and Vj € Sn) (u^vj) is an arc of G if and only if G has a directed
(iti, Vj)-walk of length 3.
Proof Denote M = [gi$) = M(B(Sn,Rm)) and A = (a^).
Suppose first that ?(5П, ftn) is a ^-inverse graph of A. Then AM A = A, and so for
each i, j,
^ 0>ip9pqa>qj = Oij. (5.5)
If (uj,Vj) is an arc in G with щ 6 i?m and v7- 6 5n, then сцу = 1, and so by (5.5), there
must be a pair (p,g) such that aiPgpqaqj = a^ = 1. Hence aiP = gpq = agj- = 1, which
implies that G has a directed (ui,Vj)-walk of length 3.
If (ui,Vj) is not an arc in G, then by (5.5), aiPgpqaqj = 0 for all choices of (p,#), and
so G does not have any directed (ttj,Vj)-walk of length 3, and so (ii) must hold.
Conversely, assume that (ii) holds. Then AM A = A follows immediately by (5.5), and
so (i) follows. [2
Definition 5.3.3 Let G = B(RmtSn) U B(SniRm) be a combined graph. For each pair
of vertices (u,v), if (u, v) € E(G) only if G has a directed (u, v)-walk of length 3, then we
say that the pair (u, v) has the (US) property; similarly, if G has a directed (u,v)-walk of
length 3 only if (u,v) € E(G), then we say that the pair (utv) has the (3-1) property.
For a vertex и € Rm, if for each v € Sn, (w, v) has the (1-3) property (or (3-1) property,
respectively), then we say that и is a vertex with the (1-3) property (or (3-1) property,
respectively).
If each vertex in Rm has the (1-3) property (or (3-1) property, respectively), then we
say that G has the (1-3) property (or (3-1) property, respectively).
With these terminology, Theorem 5.3.1 can be restated as follows.
Theorem 5.3.1' Let A € ВШ|П and let B(Rm,Sn) be the bipartite digraph representation
of A. Then a bipartite digraph B(Sn,Rm) is a p-inverse graph of Л if and only if the
228
Combinatorial Analysis in Matrices
combined graph G = B(Rm,Sn) U B(Sn,Rm) has both the (1-3) property and the (3-1)
property.
Corollary 5.3.1 A Suppose that Б(5п,Лт) is a ^-inverse graph of B(Rm9Sn)* Then
for every pair of vertices и € Rm and v € Sn in the combined graph G = B(Rm,Sn) U
B(Sn,Rm), either d(utv) = 1 or d(tt,v) = oo.
Proof Note that if d(u, v) = A; < oo, then fc must be an odd integer. By Theorem 5.3.1, if
к > 1, then к > 3. Take a shortest directed (it, v)-path P = VoVi • • • Vk in G, where vq = u
and Vfc = v. Then by Theorem 5.3.1, d(vo,vz) = 1, contrary to the assumption that P is
a shortest path. Q
Corollary 5.3.1B Suppose that B(SnyRm) is a.p-inverse graph of B(Rm,Sn). Then for
vertices щ,и2 € Rm and t/i,v2 € 5n in the combined graph G = B(Rm, Sn)UB(SniRm)i
if (t*i,vi), (u2,v2) € ?(<2), and if (щ,v2) ? E(G). then (vuu2) <? E(G).
Lemma 5.3.1 In the digraph G = B(Rm> Sn)l)B(Sni Rm), if for some и G Rm and v € 5n,
d+(n) = 0 or d~(v) = 0, then the pair {u,v} has (1-3) property and (3-1) property.
Proof G does not have a directed (it, v)-path of length 1 or 3. Q
Lemma 5.3.2 In the digraph G = B(Rm,Sn) U B(5n, #m), For any и € -Rm, if for any
v € «Sn, at least one vertex in {u,v} lies in a directed cycle of length 2, then и has (1-3)
property.
Proof By Definition 5.3.3, we may assume that (u, v) € E(G). If one of и or v lies in a
directed 2-cycle, then G has a directed (it, v)-walk of length 3. []
Given a combined graph G = ?(#„1,5,0 U B(Sn, Дщ), when («i, vi), (1x2^2) € ??((?)
and (tti, v2) g E(G), we say that the pair {v\, t^} is a forbidden pair. An arc (u, v) € 2?(6?)
with и € #m and v € Sn is called a stride arc if neither и not v lies in a directed cycle of
length 2.
We now present an algorithm to determine if a matrix A € Bm>ft has a «^-inverse, and
construct one if it does. The validity of this algorithm will be proved in Theorem 5.3.2,
which follows the algorithm.
Algorithm 5.3.1
(Step 1) For a given A € Bm>n, construct the bipartite digraph representation of A>
denote it by 2?(#т,5л).
(Step 2) Construct a bipartite digraph Bo = B(Sn, Rm) as follows:
For each pair of vertices и e Rm and v € 5n, an arc (v, u) € E(Bo) if and only if {v, u}
is a not a forbidden pair.
(Step 3) Let G = B(Rm, Sn) U B0.
Combinatorial Analysis in Matrices
229
If for each single arc (u,v) of G, the pair {u, v) has (1-3) property, then Bo is a g-
inverse graph of B(RmiSn)1 and M(B0) is the maximum ^-inverse of A; otherwise A does
not have a p-inverse.
Example 5.3.5
A =
Since G has no single arcs, M (Bo) is the maximum ^-inverse of A.
Lemma 5.3.3 The graph G = B{Rm> Sn) U B0 produced in Step 3 of Algorithm 5.3.1 has
(3-1) property.
Proof Pick и € Rm and v € Sn. Suppose that (7 has a directed (u,v)-walk uu'v'v
of length 3, but (u,v) ? E(G). Then {u',t/} is a forbidden pair, and so by Step 2,
(w'X) 02S(G), a contradiction.
Lemma 5.3.4 Let В'(?п,Ят) be a p-inverse graph of A, then B'(?n, Дщ) is a subgraph
ofB0.
Proof Let
G = B^Sn) UB0(Sn,.Rm), and G' = B(Rm,Sn) uB'(5n, ftn).
Let u € .Rm and v € Sn. J? (u,v) ? E(G), then {tx,v} is a forbidden pair, by Step 2 of
Algorithm 5.3.1. By Corollary 5.3.1B, and since B'(Sn,Rm) is a y-inverse of B(Rm,Sn),
wehave(u,v)0JE?(G'). ?
Theorem 5.3.2 Let A € BTO>n with a bipartite digraph representation B(jRm,<Sn), and
let Bo = Во(5п, Rm) be the bipartite digraph produced by Algorithm 5.3.1. The following
are equivalent.
(i) A has a ^-inverse.
(ii) In the combined graph G = B(#m, Sn) U B0, if for some и € Rm, v € 5n, («, v) €
B(G) is a single arc, then the pair {щ v) has (1-3) property.
Proof Assume first that В' = В'(5п,Вт) is ap-inverseof A, and let G' = BtB^S^UB'.
If Part(ii) is violated, then there exists an arc (u, v) € E(G') with it € #т and t/ € Sn
such that G' has not (u, v)-trail of length 3. By Lemma 5.3.2, (w, v) must be a single arc.
It follows that G1 does not have a (1-3) property, and so by Theorem 5.3.1', B' is not a
^-inverse of A, a contradiction.
10 11
10 11
0 0 0 1
1111
0 10 0
, M(B0) =
0 10 0 0
0 0 0 0 1
110 0 0
0 0 10 0
230
Combinatorial Analysis in Matrices
Conversely, by Theorem 5.3.2(H) and by Lemma 5.3.2, B0 has (1-3) property. By
Theorem 5.3.Г, by Lemma 5.3.3 and by the fact that B0 has (1-3) property, B0 is a
p-inverse of A. Q
Now we consider properties of a minimum ^-inverse of A. We have the following
observation, stated as Proposition 5.3.1. The straightforward proof for this proposition is
left as an exercise.
Proposition 5.3Л Let A € Bm>n. Each of the following holds.
(i) Let В 6 Bn,m be a matrix. If for some min A~, we have mm A" < В < maxA+,
then В is also a ^-inverse of A.
(ii) If Bo(SniRm) is а тахЛ4*, then a minium p-inverse B*(SniRm) of A can be
obtained from BQ(Sn,Rm) by deleting arcs such that G = B(Rm,Sn) U B*(SniRm) has
(1-3) property and such that B*(SntRm) has the minimum number of arcs among all
(/-inverses of A.
(iii) Let (v,u) with v 6 Sn and и € Rm be an arc in Bo(Sn,Rm)* If d^(u) = 0 or
d~(v) = 0 in G = B(Rm)Sn) U BQ(Sni Rm), then the arc (v,tt) can be deleted and the
resulting graph Bo - (v, u) is also a ^-inverse of A.
Theorem 5.3.3 Let B(Rm,Sn) be the bipartite representation of A, let B*(SniRm) be
a minimum ^-inverse of B(Rm,Sn), and let G* = B(Rm,Sn) U B*(SniRm)- If (u,v) is
a single arc of (?*, then G* must have a directed -ЙГг.г as a subgraph whose arcs are all
directed from Rm to Sni and such that (u,v) is an arc of this directed #2,2•
Proof Since B*(Sn, Rm) is a ^-inverse, (w,v) has (1-3) property. Since (uyv) is a single
arc, 6?* has a directed (tt,t))-path m>i«iv with и,щ € Rm and v,vi € 5n.
If (t*i,t/i) is in G*, then G* has a desirable #2,2¦ If (t*i,vi) is not an arc in 6?*, then
as (w, v — 1) has (1-3) property, G* has either a directed (u> vi)-path UV2U2V1 with u2 Ф «,
or a directed 2-cycle V1U2V1. In either case, since (и2,у) has (1-3) property, G* contains
(u21v)i and so a desirable #2,2 must exist. Q
By Theorem 5.3.3, we can first apply Algorithm 5.3.1 to construct a ^-inverse of
Bo(Sn,Rm)> and then obtain a minimum p-inverse by deleting arcs from Bo. Interested
readers are referred to [174] for details.
5.4 Maximum Determinant of a (0,1) Matrix
What is the maximum value of |det(<A)|, if A ranges over all matrices in Bn? What is
the least upper bound of |det(4)|, if A ranges over all matrices in Mnl The Hadamard
inequality (Theorem 5.4.1) gives an upper bound of |det(^)|, but determining the least
upper bound seems very difficult. This section will be devoted to the discussion of this
Combinatorial Analysis in Matrices
231
problem.
Theorem 5.4.1 (Hadamard, [111]) Let A = (o?i) € Mn. Then
№ЦЛ)|2<П?4.
Moreover, if each ац € {1,-1}, then
|det(^)|<n /^4<nt, (5.6)
i=i у i=i
where equality in (5.6) holds if and only if AAT = nln.
Definition 5.4.1 Let Afn(l, —1) denote the collection of all n x n matrices whose entries
are 1 or —1. A matrix H € Mn(l, -1) is a Hadamard matrix if HHT = nln.
Proposition 5.4.1 Suppose that there exists an n x n Hadamard matrix. Each of the
following holds.
(i) an = yfn*.
(ii) n = 1,2 or n = 0 (mod 4).
Proof (i) follows by Theorem 5.4.1.
Suppose that H = (h{j) is a Hadamard matrix. By the definition of a Hadamard
matrix, HHT = #r# = n/n. Hence, for n > 2,
n n
Since /&ij + /i2j = ±2,0 and Л^- + hzj = ±2,0, the left hand side of the equality above is
divisible by 4, and so (ii) holds. []
It has been conjectured that a Hadamard matrix exists if and only if n = 1,2, or n = 0
(mod 4). See [237].
For each integer n > 1, define
an = max{det(tf) : #€Mn(l,-l)},
/?n = max{ det(B) : В € Вл}.
When n 0 0 (mod 4), the value of an is determined by Ehlich [80]. Williamson [276]
showed that for n > 2, an = 2n_1^n. Therefore, we can study ^n hi order to determine
an.
When A belongs to some special classes of (0,1) matrices, the studies of the least upper
bound of |det(A)| were conducted by Ryser with an algebraic approach and by Brualdi
and Solheid with a graphical approach.
232
Combinatorial Analysis in Matrices
Example 5.4.1 Let A € Bn be the incidence matrix of a symmetric 2-design 5л(2, fc,n).
Then
It follows that
AAT = ATA =(k- A) Jn + AJn.
|det(^)| = fc(fc-A)^.
Note that the parameters satisfy A(n — 1) = к (к — 1). Ryser [224] found that the
incidence matrix of symmetric 2-design S\(2,k,n) yields in fact the extremal value of
|det(A)|, among a class of matrices in Bn with interesting properties.
Theorem 5.4.2 (Ryser, [224]) Let Q = fay) 6 Ъп with ||Q|| = ?. Let к > Л > 0 be
integers such that \(n — 1) = k(k - 1). If
t < kn and A < к — A, or if t > kn and к — A < A, (5.7)
then |det (Q)\ < к(к - А)1^1.
Proof For a matrix E € Bn, let E(x, y) denote the matrix obtained from E by replacing
each 1-entry of E by an x, and each 0-entry of E by a y. With this notation, set
fc-A
-> Qi=Q(-P,l) and Q =
p z
zT Qi
(5.8)
where zT = (^/p, д/р, • • • , y/p). Let 5» = Ej=i 0y> f°r eacn * ^*п 1 < * < л. By Theorem
5.4.1,
(5.9)
|det(Q)| < y/p* + np]I y/p + Si.
n
Note that ^ St = *P2 + fa2 - *) = *(p2 - 1) + n2, and that
2 /a-A + An\ *2(*-A)
p'+np-pl^^— j=-^2— •
n
It follows by (5.7) that ^ Si < kn(p2 -1)+n2. For each t, let 5» be a quantity such that
n
Si >?,¦,(! <*<n), and J2Si<kn(p2-l)+n2.
Thus
^(p + u) = to(p2-l)+n2 + np = nUp2 + ~ j1 J
= nkp(p +1) =
n(fc - A)fc2
A2
Combinatorial Analysis in Matrices 233
It follows
П(Р + 3.) < (j?> + *'>)" < (^^У- (5-10)
Combine (5.9) and (5.10) to get
idet(5)i < ^Sц^/^I•
By (5.8), we can multiply the first row of Q by —1/y/p and add to the other rows of ф to
get
\det(Q)\ =p|det(Q(-*M,0))| < (^y^) • (5.11)
Note that |det(Q(-fc/A,0))| = (k/\)n\ det(Q)|. It follows that
p|det(0)|<^(v^^A)n+1.
Therefore the theorem obtains. []
Theorem 5.4.3 (Ryser, [224]) Let Q = fay) € Bn be amatrix. If |det(Q)| - fcffc-A)2^,
then Q is the incidence matrix of a symmetric 2-design 5д(2, &,л).
Proof К |det (Q)\ = k(k - A)2^1, then
n+1
^,(.J,.)|.(wp)
Define О as in (5.8) and employ the notations in Theorem 5.4.2. By (5.11),
k n+1
|det(^)| = (^*EZ) ,
and so equality must hold in (5.10), which implies
, . (fc-A)fc2
p + 6i = Г2 , 1 < г < п.
It follows that Q(f = fc2(fc - A)/A2Jn+i, and so
QiQf = ^-A)Jn-pJn. (5.12)
234
Combinatorial Analysis in Matrices
For each г, let n = ??=i qy. By (5.12),
k2
р2г{ + {п-п) = —(&-A)-p
(р2-1)г, = ?(*-A)-p-n.
Hence r» = к, for each г with 1 < i < n.
For i ф j with 1 < г, j < n, let / denote the dot product of the tth row and the jth
row of Q. By (5.12),
fp2 - 2(k - f)p + n - 2fc + / = -p
f(p2 + 2p+l) = 2kp-p + 2k-n.
It follows that fk2/\2 = fc2/A and so / = A.
Therefore, Q is the incidence matrix of a symmetric 2-design 5д(2,&,п). Q
The following theorem of Ryser follows by combining Theorems 5.4.2 and 5.4.3.
Theorem 5.4.4 (Ryser, [224]) Let n>fc>A>0be integers such that A(n-l) = fc(fc-l).
Let Q 6 Bn with ||Q|| = t = foi. Then
IdetWJI^fcfA-A)2*1,
where equality holds if and only if A is the incidence matrix of a 2-design 5л (2, fc,n).
Definition 5.4.2 Let A € Bn. Define two bipartite graphs Go (A) and Gi(A) as
follows. Both Go (A) and Gi(A) have vertex partite sets U = {ui,u2,--- ,wn} and V =
{vi, V2, • • • jVn}. An edge г^ € 2?(Go(A)) (ищ € i?(Gi(A)), respectively) if and only if
dij = 0 (aij = 1, respectively). Note that Go (A) = Gi(Jn — A).
A matrix A is acyclic if Gi(A) is acyclic, and A is complementary acyclic if Go (A) is
acyclic.
A matrix A € Bn is complementary triangular if A has only l's above the its main
diagonal. For example, Jn — A is a triangular matrix.
For each integer n > 1, define
/n = max{| det(A)| : A € Bn and A is complementary acyclic}.
Example 5.4.2 Since an acyclic graph has at most one perfect matching, if A is acyclic,
thendet(A)€ {0,-1,1}.
Example 5.4.3 Suppose A is complementary acyclic, and let В be the matrix obtained
from A by permuting two rows of A. Then В is also complementary acyclic with det(B) =
— det(A). Therefore,
fn = max{ det(A) : A € Bn and A is complementary acyclic}.
Combinatorial Analysis in Matrices
235
Brualdi and Solheid successfully obtained the least upper bound of |det(A)|, where A
ranges in some subsets of Bn with the complementary acyclic property. Their results are
presented below. Interested readers are referred to [39] for proofs.
Theorem 5.4.5 (Brualdi and Solheid, [40]) Let n > 3 be an integer and let A € Bn be a
complementary acyclic matrix such that A has a row or column of all ones. Then
|det(A)|<n-2. (5.13)
For n > 4, equality in (5.13) holds if and only if A or AT is permutation equivalent to
Ln =
1 1
0
0
Jn-l — J„_i
(5.14)
For n = 3, equality in (5.13) holds if and only if A or AT is permutation equivalent to one
of these matrices
1 1 1
0 0 1
0 10
)
111
1 0 0
111
I
1 1 1
10 1
110
Definition 5.4.3 For a matrix A € Bn, the complementary term rank of A, pj-л, is the
term rank of Jn — A.
Theorem 5.4.6 (Brualdi and Solheid, [40]) Let n > 3 be an integer and let A € Bn be a
complementary acyclic matrix with pj-л = n — 1. Then
{n-2 if 3 < n < i
m 8,r» зл * ~o~
(5.15)
-y^J|«f*| ifn>8.
For n > 4, equality holds in (5.15) if and only if A or AT is permutation equivalent to Ln
as defined in (5.14) (when 4 < n < 8), or
where Z has at most one 0.
0T
Z
J
1
0
t/rn
J
гЧ_/Г«!
Pi J
(n>8),
Theorem 5.4.7 (Brualdi and Solheid, [40]) Let n > 2 be an integer and let A € Bn be a
complementary acyclic matrix with pj_a = n. Then
(n-2 ifn<
det(A)| < ^
I l^jr^l ifn>
(5.16)
236
Combinatorial Analysis in Matrices
Equality holds in (5.16) if and only if A or AT is permutation equivalent to Jn — /n, or
(n > 5).
0T 0 jr
J 0 Jr«^l1 - /Гп^11
More details can be found in [39]. For most of the matrix classes, the determination
of the maximum determinant of matrices in a given class is still open.
5.5 Rearrangement of (0,1) Matrices
The rearrangement problem of an n-tuple was first studied by Hardy, Littlewood and
Polya [114]. Schwarz [231] extended the concept to square matrices.
Definition 5.5.1 Let (a) = (ai,a2i * * * »un) be an n-tuple and let n be a permutation on
the set {1,2, • • • ,n}. Then (av) = (a*(i), a^), • • • aw(n)) is a rearrangement of (a).
A matrix A € Mn can be viewed as an n2-tuple, and so we can define the rearrangement
of a square matrix in a similar way.
Let 7Г be a permutation on {l,2,-«- ,n}, and let A = (ay) € Mn. The matrix
An = (oy) is called a permutation of A if a'^ = л»(«),1г0*)> for all 1 < 1,7 < n. Clearly a
permutation or a transposition of a matrix Л is a rearrangement of A. We call a
rearrangement trivial if it is a permutation, or a transposition, or a combination of permutations
and transpositions. Two matrices A\, A2 € Mn are essentially different if A2 is a nontrivial
rearrangement of A\.
For each A = (a^) € Mn, define \\A\\ = ?2=i ??=1 %•¦ Proposition 5.5.1 below
follows immediately from the definitions.
Proposition 5.5.1 For matrices Ai, A2 6 Mni each of the following holds,
(i) If Л1 is a rearrangement of A2i then ||Ai|| = ЦА2Ц.
(ii) If Ai is a trivial rearrangement of A2i then ||A2|| = \\А%\\.
Definition 5.5.2 Let
77 = max{||A2|| : A € Mn}, and N = min{p2|| : A € Mn}.
Let Z? = {Л € Mn : ||42|| = J\f} and U = {A € Mn : ||Л2|| = N}, let С denote the set of
matrices A = (o#) € Mn such that for each », o# > а#/ whenever 7 < j\ and such that
for each j9 ay > a*^ whenever г < г'; and let С denote the set of matrices A = (ay) € Mn
such that for each г, ay > ay whenever 7 < /, and such that for each 7, ay < a?j
whenever % < г'.
Combinatorial Analysis in Matrices
237
Theorem 5.5.1 (Schwarz, [231])
г7пс#0, шййпсфф.
Definition 5.5.3 For a matrix A € Mn, let Ai(A) and An(A) denote the maximum and
the minimum eigenvalues of A, respectively. Let
A = max{Ai(A) : A € Mn}, and
A = min{An(A) : AeMn})
and let
Ъ = {AeMn : A!(A) = A}and
В = {AeMn : An(A) = A}.
Theorem 5.5.2 (Schwarz, [231])
ВПСфЪ, and6nC^0.
Definition 5.5.4 For integer n > 1 and a with 1 < а < n2, let Un{&) = {A € Bn :
||j*|| = <t}. Let
Fn(<r) = max{||A2|| : АеКп(а)}, and
Nn(v) = min{p2|| : Л € %(*)}.
Let ?/n(o") denote the set of matrices A = (а#) 6 Wn(o") such that for each г, a# > a#'
whenever j < j', and such that for each j, a^ > a^- whenever % < г'; and let Un{a) denote
the set of matrices A = (a#) € Wn(cr) such that for each г, a^ > a#* whenever j < j', and
such that for each j, ay < a^j whenever г < i'.
Proposition 5.5.2 follows from Theorem 5.5.1 and the definitions.
Proposition 5.5.2 For integers n > 1 and a with 1 < a < n2, each of the following holds.
(i)iVrn(c7)=max{||A2|| : A € &«(*)}, and Nn(<r) = min{||A2|| : A?Un{a)}.
(ii) Let Л = (aij) € i7n(o"), let S{ = 5^JLX ау an<^ r* = !CiLi ai* denote the ith row
sum and the ith column sum of A, respectively. Then
jv«w > ич=|>, > i (±r?j (±s?j = ?.
Example 5.5.1
Г l l l "
110
[ 1 0 0 m
e U3{6) and
* 1 0 0 1
110
11 1 j
238
Combinatorial Analysis in Matrices
Aharoni discovered the following relationship between Nn((r) and Nn(n2 - a), and
between Nn(o) and Nn(n2 — <r).
Theorem 5.5.3 (Aharoni, [1]) Let n and a be integers with n > 1 and 1 < a < n2. If
A € Ип(а), then
(i)||A2|| = 2an-n3 + ||(Jn-^)2||.
(ii) Nn(a) = 2<m - n3 + JVn(n2 - <r).
(iii) iVn(o-) = Ion - n3 + iV^n2 - a).
Parts (ii) and (iii) of Theorem 5.5.3 follow from Part (i) of Theorem 5.5.3 and the
observation that if Л € Un(a), then Jn — A € Un(n2 - a). In [1], Aharoni constructed four
types of matrices for any 1 < a < n2, and proved that among these four matrices, there
must be one A such that N»(o-) = ||Л2||.
Theorem 5.5.3(ii) and (iii) indicate that to study ~Nn(p) and Nn(a), it suffices to
consider the case when a > ra2/2. The next result of Katz, points out that an extremal
matrix reaching Nn(a) would have all its 1-entries in the upper left corner principal
submatrix.
Theorem 5.5.4 (Katz, [142]) Let n, к be integers with n2 > k2 > n2/2 > 0. Then
Nn(a)=k3.
Corollary 5.5.4 Let n, к be integers with n2 >k2 > n2/2 > 0. Then
Nn(n2 - k2) = kz -2fc2n + n3.
To study iVn(o-), we introduce the square bipartite digraph of a matrix, which plays a
useful role in the study of ||Л2||.
Definition 5.5.5 For a A = (Aij) € Bn, let K(A) be a directed bipartite graph with vertex
partite sets (Vi,V2), where V\ = {ui,u2,--- ,ип} and V2 = {vi,v2,-- ,vn}, representing
the row labels and the column labels of Л, respectively. An arc (u^Vj) is in E(K) if and
only if aij = 1.
Let K\ and K2 be two copies of K(A) with vertex partite sets (Vi, V2) and (Vl^),
respectively, where V{ = {u'^u^ • - • ,u'n} and V2 = {v'ltv2, • • • , vJJ, and where (uritvfi €
E(K2) if and only if а# = 1. The square bipartite digraph of A, denoted by SB(A), is the
digraph obtained from K\ and #2 by identifying vi with ttj, for each i = 1,2, • • • , n.
The next proposition follows from the definitions.
Proposition 5.5.3 Let A € Bn. Each of the following holds.
(i) ||Л2|| is the total number of directed paths of length 2 from a vertex in Vi to a
vertex in Vi.
Combinatorial Analysis in Matrices
239
(ii) For each vi € V2 in SB (A), dr(vi) = s, is the ith row sum of A, and d+(vi) = n
is the ith column sum of A.
(Ш) ||A2|| = ?<T(t*)<**(««) = X>«"
Example 5.5.2 The square bipartite graph of the matrix Ai in Example 5.5.1 is as follows:
3 Vx
3 V2
Figure 5.5.1 The graph in Example 5.5.1
Example 5.5.3 The value ||M2|| may not be preserved under taking rearrangements.
Consider the matrices
10 0
0 1 0
0 0 1
and A2 =
1 1 0
1 0 0
0 0 0
Аг =
Then A\ and A2 are essentially different and ||Ai|| ф ЦАЦ).
Theorem 5.5.5 (Brualdi and Solheid, [38]) If а > n2 - [f J ГЦ, then
Nn = 2(rn-n3.
Moreover, for A € Un{o)^ ||A2|| = i\rn(o-) if and only if A is a permutation similar to
Jk X
Ji,k Ji
(5.17)
240
Combinatorial Analysis in Matrices
where X € Mkj is an arbitrary matrix, and where к > 0 and I > 0 are integers such that
к + I = n.
Sketch of Proof Construct a square bipartite digraph D = SB(A\) as follows: every
vertex in {щ,-- ,uj} is directed to every vertex in {vj+1,--- ,vn}, where / > 0 is an
integer at most n. By Proposition 5.5.3(i), \\АЦ\ = 0. Let A = Jn — A\. By Theorem
5.5.3(i) and by ||Л?|| = 0,
\\A2\\ = 2cm-n3 = Nn(v),
where * = ||Л|| = \\Jn - Аг\\ > n2 - Щ ГЯ-
By Theorem 5.5.3(i), if Л € Un{&) satisfies ||Л2|| = Ът - n3, then ||(Jn - Л)2|| = О,
and so by Proposition 5.5.3(i), SB(Jn—A) must be some digraph as a subgraph of the one
constructed above, (renaming the vertices if needed). Therefore, A must be permutation
similar to a matrix of the form in (5.17). Q
Proposition 5.5.4 Let A € Un{&) and let D = SB(A) with vertex set V\ U V2 UV^ using
notations in Definition 5.5.5.
(i) К for some i < n and j > 1, (uiyVj) € #(?>), then both (u^Vj^i) 6 2S(Z>) and
(щ+uvj) e E(D).
(ii) If a > I J, and if |[Л2|| = Nn(cr), then in D, that i > j implies that (щ, Vj) G
ад.
(iii) If o" > I ), and if Л € Un(<r) and ||A2|| = Nn(^), then every entry under the
main diagonal in Л is a 1-entry.
Proof Part (i) follows from the Definition 5.5.4 and Definition 5.5.5. Part (iii) follows
from Part (ii) immediately.
To prove Part (ii), we argue by contradiction. Assume that there is a pair p and q such
that p > q but (uPivq) ? E(D). Since а > n(n — l)/2 and by Proposition 5.5.4(i), there
must be an % such that (u^Vi) € E(D). Obtain a new bipartite digraph D\ = SB(Aq)
from D by deleting (щ, v«), (у^у'{) and then by adding (up,vq) and (vPiv'q). Note that
P2H - МЙ = (ГЫ - <ГЫ) + (<*+(«») - d+(t,,)) -1, (5.18)
where the degrees are counted in D. By Proposition 5.5.4(i) again,
dT{vi) > n - (i - 1), d+(vi) > i, <T{vv) <n-pt and d+(vq) >q-l. (5.19)
It follows by (5.18) and (5.19) that
P2IMI^II>P-?+l>2,
Combinatorial Analysis m Matrices
241
contrary to the assumption that ||Л2|| = Nn(v). Q
Theorem 5.5.6 (Brualdi and Solheid, [38]) If а = I П J, then
Moreover, if A € Un(a) and \\A2} = Йп(а), then A is permutation similar to Xn, the
matrix in Bn each of whose 1-entry is below the main diagonal.
Proof This follows from Proposition 5.5.4(iii). []
0)
To investigate the case when [ л ] < а < n — [—J f—1, we establish a few lemmas.
Lemma 5.5.1 (Liu, [175]) Let A = (а#) € Un(cr), let A(a 4- epg) denote the matrix
obtained from A by replacing a 0-entry Opg by a 1-entry, and let sp and rg denote the pth
column sum and the qth row sum, respectively. Then
\\A*(n + r UI-/ ИЛ211 + вР + г« ****
Л {0 + epq)\\ = <
( ||A2|| + sp + rg + l ifp =
Proof Note that SB(A(a+epq) is obtained from Si? (A) by adding the arcs (upi vq)t (vp) v'q).
If P Ф Qi the number of the newly created directed paths of length 2 from V\ to V% in
SB(A(<7 + epq) is с?*"(ид) + cT*(vp) = rq + sp; if p = g, an additional path ttpvpVp is also
created, and so Lemma 5.5.1 follows from Proposition 5.5.3(i). []
Lemma 5.5.2 (Liu, [175]) Let Ln be the matrix in Bn each of whose 1-entry is below the
main diagonal. An (i, j)-entry in Ln is called an upper entry if i < j. Let A denote the
matrix obtained from Ln by changing the upper entries at (ittji), where 1 < t < r, from
0 to 1. If all the it's are distinct and all the jt's are distinct, then
where
|И2и = (з)+Ел^>^
[ П-Zt+Ji if *t =J*.
Proof This follows immediately from Lemma 5.5.1 and Theorem 5.5.6. []
With Proposition 5.5.4(iii) and Lemma 5.5.2, it is not difficult to prove the following
theorem.
242 Combinatorial Analysis in Matrices
Theorem 5.5.7 (Liu, [175]) Let а = f ^ ) + k, where 1 < к < n, then
-0
Theorem 5.5.8 (Brualdi and Solheid, [38]) If о = I }, then
=(T).'
Moreover, if Л € ?/n(0") and ||Л2} = Nn(a), then Л is permutation similar to Z?, the
matrix in Bn each of whose 1-entry is on and below the main diagonal.
Proof This follows from Theorem 5.5.7 with к = га. ?]
=(т)
The case when а = I J + к with 1 < к < n — 1 can be studied similarly. With
the same arguments as in the proofs for Lemmas 5.5.1 and 5.5.2, we can derive the lemmas
below, which provide the needed arguments in the proof of Theorem 5.5.9 (Exercise 5.10).
Lemma 5.5.3 If а > I J, and if A € Un(&) and ||j42|| = Йп(а), then every entry
on or under the main diagonal in A is a 1-entry.
Lemma 5.5.4 Let L* be the matrix in Bn each of whose 1-entry is on or below the main
diagonal. Let A denote the matrix obtained from L* by changing the upper entries at
{hijt), where 1 < t < r, from 0 to 1. If all the it's are distinct and all the jt's are distinct,
then
||=(п^2)+|>+1-*<+*)-
(а)=(пГ)+*(п+2)'
_/n + l\ n
\\A<
Theorem 5.5.9 (Liu, [175]) Let а = \ '" ^ * ) + к, where 1 < к < [^J, then
N,
Theorem 5.5.10 (Brualdi and Solheid, [38]) If n > 2 is even and if а
then
Combinatorial Analysis in Matrices
243
Proof Apply Theorem 5.5.9 with к = n/2. Q
Conjecture 5.5.1 (Brualdi and Solheid, [38]) Let k, I, n and q be integers such that
1 < & < n, n = qk + l and 0 < I < fc. Let
Jn,k = ( «+1 Wn*,
and let
AnA
Jk
Jk
J Jk
where every entry of An,t below the mail diagonal is a 1-entry. Then
#„(*«,*) = |<4||.
Theorem 5.5.10 proved Conjecture 5.5.1 for the special case when к = 2 and n is even.
To further approach this conjecture, we introduce some notations.
Through the end of this section, let L* (Sr) be the matrix obtained from L* by changing
the 0-entries into l-entries at the positions (г, г 4-1), with г*о < г < г*о + г — 1, for some
1 < г'о < п — 1 (and call these newly added l-entries an Sr); let L* (Tr) be the matrix
obtained from L* by changing the 0-entries into l-entries at the positions (г, г + j), with
*o < г < *o + ** — 1 and 1 < j < r — (г — го), for some 1 < г*о < n — 1 (and call these newly
added l-entries a TV).
Let A(Sr) = ||(L;(Sr))2|| - ||(L;)1 and Д(ГГ) = ||(Ь;(ГГ))2|| - ||(L;)»||. Let ||Tr|| =
r(r + l)/2 denote the number of l-entries of a Tr and let ||Sr|| = r denote the number of
l-entries of a 5y.
Lemma 5.5.5
^>=(T)(»^)-
Proof By Lemma 5.5.1,
ДСП.) = «?j + ?j(j + i)
- (T)(-^)-
244
Combinatorial Analysis in Matrices
This proves Lemma 5.5.5. Q
Lemma 5.5.6 If ||Tr|| = ?*=1 ||Tr.|| for some t > 1, then A(Tr) > ?*i=sl A(Tri).
Proof By assumption and by r > r*,
It follows by Lemma 5.5.5 that A(Tr) > ?'=1 A(Tri). Ц
The next two lemmas can be proved similarly.
Lemma 5.5.7
A(Sr)=r(n + 3)-l.
Lemma 5.5.8 If ||5r|| = ЕЦ 11**11 for some t > 1, then A(Sr) > J2Ui A(sn)-
Theorem 5.11 Suppose that
/ n + 1 \ _ ,n. ,^rn + ln
"[ 2 ]+^У<*<Г-1-1.
Then
»~г / ч /n + 2 \ ,, ftN ,n-l,
ВД= 3 J+fc(n + 3)-L—J.
Proof Assume that A € Un{o) with ||Л2|| = Nn(o). By Proposition 5.5.2, we may assume
that A € Un(p), and so Z? is a submatrix of A. By Lemma 5.5.8, the minimum of ||A2||
can be obtained by putting A; — [—-—J of S2 and 2[——J — к of S\ above the main
diagonal of L*. Therefore,
*»w = 11(ь;)2и+ Y, A^+ ? A(*)
i=l i=l
/ 71 + 2 "\ ,. ft4 .П-1,
= ( з J+*(n + 3)-L-2-J.
This completes the proof. [J
Combinatorial Analysis in Matrices
245
5.6 Perfect Elimination Scheme
This section is devoted to the discussion of perfect elimination schemes of matrices and
graph theory techniques can be applied in the study.
Definition 5.6.1 Let A = (a#) € Mn be a nonsingular matrix. The following process
converting A into I is called the Gauss elimination process.
For each ?= 1,2,-•• ,n,
(1) select a nonzero entry at some (it,jt)-ce\l (called a pivot),
(2) apply row and column operations to convert this entry into 1, and to convert the
other entries in Row it and Column ц into zero.
The resulted matrix can then be converted to the identity matrix J by row permutations
only. The sequence (*i,ii), (*2>i2), • • • ,(in,jn) is called a pivot sequence.
A perfect elimination scheme is a pivot sequence such that no zero entry of A will
become a nonzero entry in the Gauss elimination process.
Example 5.6.1 For the matrix
"4111
110 1
10 10
10 0 1
The pivot sequence (1,1), (2,2), (3,3), (4,4) is not a perfect elimination scheme since the
0-entry at (3,2) will become a nonzero entry in the process. On the other hand, the pivot
sequence (4,4), (3,3), (2,2), (1,1) is a perfect elimination scheme.
Example 5.6.2 There exists matrices that does not have a perfect elimination scheme.
Consider
110 0 1
0 110 1
A=|0 1 1 1 0
10 110
10 0 11
Note that if for a given (i9j), there exist s,t such that asj ф 0, ац Ф 0 but ast = 0, then,
Oij cannot be a pivot in a perfect elimination scheme. With this in mind, we can easily
check that the matrix A in this example does not have a perfect elimination scheme.
246
Combinatorial Analysis in Matrices
Example 5.6.3 Matrices of the following type always have a perfect elimination scheme,
A =
* *
* * *
* *
0 *¦ *
* *
where * denotes a nonzero entry.
Definition 5.6.2 Let G be a simple graph, let и>(6?),х(6г),а((х) and k(G) denote the
clique number (maximum order of a clique), the chromatic number, the independence
number (maximum cardinality of an independence set), and the clique covering number
(minimum number of cliques that covers V((?)), respectively. For a subset А С V(G),
G[A] denotes the subgraph of G induced by A. A graph G is perfect if G satisfies any one
of the following:
(PI) u(G[A]) = X(G[A]), VA С V(G).
(P2) a(G[A]) = k(G[A]),VA С V(G).
(P3) u(G)a(G) > |A|,VA С V(G).
(The equivalence of that (PI), (P2) and (P3) is shown by Lovasz [190] in 1972.)
Definition 5.6.3 A graph G is chordal if G does not have an induced cycle of length
longer than three.
Given a graph G, a vertex v € V(G) is a simplicial vertex if G[N(v)] is a clique. If
[tfi»v2> • • * >Vn] is an ordering of V(G) such that v» is simplicial in G[{vt, • • • , vn}], for each
i = 1,2, • • • , n — 1, then [vi, • • • , vn] is a perfect vertex elimination scheme of just a perfect
scheme.
An edge e = xy in a bipartite graph Я is bisimplicial if the induced subgraph #[iV(a:)U
iV(y)] is a complete bipartite graph. Given an ordering [ei, e2, • • • , em] of pairwise nonad-
jacent edges in #, let Si denote the vertices in H that are incident with {ei,e2, • • • ,е*},
where 1 < i < m, and let So = 0- An ordering [ei,в2, • • • , em] of edges in Я is a partial
scheme if the ei's are pairwise nonadjacent edges in Я and if for each i > 1, e$ is
bisimplicial in Я — Sj_i. An ordering [ei,e2, • • • ,em] of edges in Я is a perfect edge elimination
scheme (or just a scheme) if it is a partial scheme and if Я — Sm is edgeless. A bipartite
graph Я possessing a scheme is a perfect elimination bipartite graph.
Theorem 5.6.1 (Dirac, [74]) Let G be a chordal graph. Then G has a simplicial vertex.
If G is not a complete graph, then G has two nonadjacent simplicial vertices.
Sketch of Proof This is trivial if G is a complete graph. Argue by induction on \V(G)\
Combinatorial Analysis in Matrices
247
and assume that G has two nonadjacent vertices и and v and a minimum vertex set S
separating и and v. Let Gu and Gv denote the connected components oiG — S containing
и and v, respectively.
Let G[V(GU) U 5] and G[V(GV) U S] denote the subgraphs of G induced by V(GU) U 5
and by V(GV) U 5, respectively.
By induction, either since G[V(GU) U S] contains two nonadjacent simplicial vertices,
whence one of these two vertices must be in Gv, as G[V (Gn)U5] is induced; or G[V(GU)US]
is complete. Apply induction to G[V(GV) U 5] as well, and so the theorem follows by
induction. Q
Theorem 5.6.2 (Fulkerson and Gross, [94]) Let G be a simple graph. The following are
equivalent.
(i) G is chorda!.
(ii) G has a perfect scheme such that any simplicial vertex of G can be the first vertex
in a perfect scheme.
(iii) Every minimal separation set of G induces a complete subgraph.
Proof (iii) =Ф- (i). Let u, a:, v, у и Уг» • * • > Уь & be a cycle of (7 with length fc+3 > 4. Note
that any vertex subset S separating и and v must contain ж, yi, • • • , у*, and so яу* € E(G)
is a chord of this cycle.
(i) =Ф- (iii). Let S be a minimal vertex set separating и and v in G. Let G« and Gv
be the components of G \ S containing и and v, respectively. Since S is minimal, each
s € S is adjacent to some vertex in Gu and some vertex in Gv. For each pair of distinct
vertices ж, у 6 5, there exists an (or, y)-path P whose internal vertices are all in GUi and
an (x,y)-path Q whose interna! vertices are all in Gv. It follows by (i) that xy € E{G),
and so 5 induces a complete subgraph of G.
(i) =ф. (И). Argue by induction. By Theorem 5.6.1, G has a simplicial vertex v, and
so G — v is also a chordal graph, which has a perfect scheme. The add v to this scheme to
get a perfect scheme of G with v being the first vertex.
(ii) =ф. (i). Let С be a cycle of G and let v € V(C) such that in a perfect scheme of
G, v is the first among all vertices in V(C). As \N(v) П V(C)\ > 2, that v is simplicial
implies that С has a chord. []
Theorem 5.6.3 below gives an inductive structural description of chordal graphs. A
proof of Theorem 5.6.3 can be found in [155].
Theorem 5.6.3 (Leukev, Rose and Tarjan, [155]) li G is a chorda! graph, then there
exists a sequence of chordal graphs Gu 0 < i < s, such that Go = G, Gs is a complete
graph and for each \<i<s — 1, Gi is obtained by adding a new edge from Gi-i.
Definition 5.6.4 The notions of associated digraph and the bipartite representation of a
248
Combinatorial Analysis in Matrices
(0,1) matrix will be extended. Let A — (ац) € Mn.
The associate directed digraph D(A) of A has vertex set {vi,V2,--* ,vn} such that
(v{, Vj) e E(D(G)) if and only if both ay ф 0 and i ф j. When A is symmetric, D(A) can
be viewed as a graph, and in this case, we write G(A) for D(A).
The bipartite representation 2?(Л) of A has vertex partite sets X = {х\,Х2,* • • ,a:n}
and У = {2/1,2/2, • • • ,2/n}> representing the rows and the columns of Л, respectively, such
that (xiyj) € E(B(A)) if and only if ay ^ 0. For each г, а^ and «/* are partners
corresponding to the vertex vi in -D(>1).
Some observations from the definitions and from the remarks in Example 5.6.2 are
listed in Proposition 5.6.1.
Proposition 5.6.1 Let A = (ay) € Mn.
(i) If Л is symmetric, then D(A) can be viewed as a graph. An entry ац is a pivot if
and only if vi is simplicial in D(A).
(ii) Suppose that A is symmetric such that each ац Ф 0. A perfect elimination scheme
of A with each ац as a pivot corresponds to a perfect vertex elimination scheme of G(A).
(iii) A bisimplicial edge of В (A) corresponds to a pivot in A\ and a perfect elimination
scheme of A corresponds to a perfect edge elimination scheme of В (A).
Theorem 5.6.4 (Columbic [60]) and Rose [218]) Let A = (ац) € Мп be a symmetric
matrix with ац Ф 0, 1 < i < n. Each of the following is equivalent.
(i) A has a perfect elimination scheme.
(ii) A has a perfect elimination scheme of A with each ац as a pivot.
(iii) G(A) is a chorda! graph.
Proof Part (ii) and Part (iii) are equivalent by Theorem 5.6.2. As (ii) trivially implies
(i), it suffices to show that (i) implies (iii).
By Proposition 5.6.1 (iii), we may assume that B(A) has a perfect edge elimination
scheme [ei,*** ,em].
Suppose G(A) has a chordless cycle vaiva2 • • • vapvai for somep > 4. Since each ац ф 0,
the induced subgraph Я = B(A)[{xai, xa2, • • • , xap, yai, ya2 > * * * > Vap}] is a 3-regular graph
with edge set
{(яа<Уа,+1) : 1<1<р-1}и{(ХарУа1)ЛУарУаг)}^
U {(yaixai+1) : l<i<p-l}U{xaiVai : 1<г<р}.
Since [ei, • • • ,em] is a perfect edge elimination scheme, there is a smallest j such that
Cj is incident with a vertex in V(H). The edge ej cannot be in E(H) since no edge in
E(H) is bisimplicial. Without loss of generality, we assume that ej = xaiySi for some
уs g. V(H). Denote x3 the partner of ys.
Combinatorial Analysis in Matrices
249
Since p > 4, in Я, N(xai) = {уа1,Уа2,Уар} and N(yai) C\N(ya2) C\N{yap) = {x0l}.
Since tj = a?ai«k is bisimplicial, V(H) П iV(ys) = {xai}. By symmetry, У"(Я) П N(xs) =
{2/ai}« Note that araiyai,a:st/s € 2?(Я(Л)) but ж5уа2 ? Е(В(Л)), contrary to the fact that
xaiys is bisimphcial. Therefore, p = 3 and G(A) must be chorda!. ?]
We conclude this section with two more results by Columbic and Goss [61] on the
properties of perfect elimination bipartite graphs. Interested readers are referred to [61]
for proofs.
Theorem 5.6.5 (Columbic and Goss, [61]) If Я is a perfect elimination bipartite graph
and if e = xy is bisimplicial in Я, then Я — {a:, y} is also a perfect elimination bipartite
graph.
Theorem 5.6.5 (Columbic and Goss, [61]) If a bipartite graph Я has no pair of disjoint
edges, the it is a perfect elimination bipartite graph.
5-7 Completions of Partial Hermitian Matrices
All the matrices considered in this section will be over the complex number field. Denote
by ~z the conjugate of a complex number z, and by A the conjugate of a matrix A with
complex entries. An n x n matrix Я is Hermitian if Я = Я* = Ят.
An n x n matrix A is positive definite Hermitian (positive semidefinite Hermitian^
respectively) if for any n-dimensional complex vector x ф 0, xTAx > 0 (> 0, respectively).
While all positive definite Hermitian matrices are positive semidefinite Hermitian, the
matrix Jn, when n > 2, is positive semidefinite Hermitian but not positive semidefinite
Hermitian.
A Hermitian matrix A = (a#) is a partial Hermitian matrix if some of the a^-'s are not
specified. These unspecified entries may be viewed as blank slots. Given a partial
Hermitian matrix A, is it possible to file the blank slots with certain complex number so that the
resulting matrix is positive semidefinite Hermitian? If the answer is affirmative, then the
resulting Hermitian matrix if a positive semidefinite completion of the partial Hermitian
matrix A. Results in this section are mostly from the work of Grone, Johnson, Sa and
Wolkowwicz [107]. Some of the facts and properties of positive semidefinite Hermitian
matrix are listed in the proposition below.
Proposition 5.7.1 Each of the following holds.
(i) Let A\, A2, • • • , Ak be positive semidefinite Hermitian matrices. If c\, c<i, • • • , c* are
nonnegative real numbers, then 52i=1 c%Ai is also positive semidefinite Hermitian.
(ii) Let A = (o^) be an n x n Hermitian matrix. Then each ац is a real number, for
i = 1,2,-•• ,n.
250
Combinatorial Analysis in Matrices
(iii) A is positive semidefinite Hermitian if and only if every eigenvalue of A is nonneg-
ative.
(iv) Let Л be a Hermitian matrix. Then A is positive semidefinite if and only if for
each г = 1,2, • • • , n, det(Ai) > 0, where Ai is an i x i principal submatrix of A.
(v) Let A — (а^) be a Hermitian matrix. Then
n
det(A)< Y[au (5.20)
Moreover, if an > 0 for each г = 1,2, • • • , n, then equality holds in (5.20) if and only if A
is diagonal.
Definition 5.7.1 Let G be a graph vertex set {vi> V2, • • • , vn}, and with loops permitted.
A G-partial matrix is a set of complex numbers, denoted (ау)а, where ay is defined if
and only if (viVj € E(G). (As C? is undirected, ay is defined if and only if aji is defined).
A completion of (ay)o is an n x n matrix M = (my) such that my = ay
whenever ViVj € E(G). We say that M is a positive completion (a nonnegative completion^
respectively) if and only if M is a completion of (ay) о and M is positive definite (positive
semidefinite, respectively).
Given a. graph G with V(G) = {vi, C2, • • • , vn}> the (^-partial matrix (ay)o is G-partial
positive (G-partial nonnegative^ respectively), if both of the following hold.
(5.7.1A) For all 1 < ij < n, ay = Щ, and
(5.7.IB) For any complete subgraph К of <3, the corresponding principal submatrix
{aij)viyvj€V{K) of (%*)g is positive definite (positive semidefinite, respectively).
Let G be a subgraph of J. A J-partial matrix (by)j extends a G-partial matrix (ay)
if 6^ = ay for every v^- € ?((?) С ??(J).
A graph G is completable , (nonnegative-completable respectively) if and only if any G-
partial positive (G-partial nonnegative, respectively) matrix has a positive (nonnegative,
respectively) completion.
Let LP(G) denote the set of vertices of G at which G has loops. Without loss of
generality, we assume that either LP(G) = 0 or LP(G) = {vi,V2,*** ,*>*.}, for some
1 < к < n. For notational convenience, we also use LP(G) to denote the subgraph of G
induced by LP(G).
Proposition 5.7.3 below indicates that the terms "nonnegative-completable" and
"completable" coincide.
Proposition 5.7.2 (Grone, Johnson, Sa and Wolkowicz, [107]) G is completable (nonnegative-
completable respectively) if and only if LP(G) is completable (nonnegative-completable
respectively).
Proof It suffices to show that completable case. If G is completable, then LP(G) is also
Combinatorial Analysis in Matrices
251
completable, since any complete subgraph must be contained in LP(G). For the converse,
denote
AG(x) =
An
where Ац is positive definite к х к (representing a positive completion of an LP (^-partial
positive matrix), and H is (n — к) х (n-k) Hermitian. Note that Ag(x) is positive definite
for sufficient large positive x. Q
Proposition 5.7.3 (Grone, Johnson, Sa and Wolkowicz, [107]) Let G be a graph with
G = LP(G). Then G is completable if and only if G is nonnegative-completable.
Proof Assume first that G is completable. For a G-partial nonnegative matrix (a^)e,
define, for each integer n > 0, Ak = (o>ij)g + ?/. Then each An is a G-partial positive
matrix, and so Лп has a positive completion Mn. Since G = LP(G)t the sequence ^4n is
bounded and so has a convergent subsequence with limit A, which will be a nonnegative
completion of (%)<?¦
Assume then G is nonnegative-completable, and let (а%)о be a (^-partial positive
matrix. Choose e > 0 so that (%•)<? - el is still a G-partial positive matrix. Then
(p>%j)g — ^I has a nonnegative completion A, which yields a positive completion A + c/ of
Definition 5.7.2 An ordering of a graph G is a bijection а : V(G) «-> {1,2,¦-• ,n},
and for vertices u,v € V(6?), we say that it follows v (with respect to the ordering a) if
a(v) < a (it). A graph G is a 6onrf ^ттарЛ if there exists an ordering a of 6? and an integer
m with 2 < m < n such that
tw € E(G) if and only if \a(u) — a(v)| < m — 1.
Example 5.7.1 Let G denote the graph with
V(G) = {^1,^2,^3,^4} and E(G) = {viv2,V2V3,V3V4,viV3,V2V4}.
Let a be the map defined by a(v{) = г, and let m = 3. Then we can check that G is a
band graph.
Note that every band graph is a chordal graph. But a chordal graph may not be a band
graph. Let H denote the graph obtained from the 3-cycle u\U2Uzui by adding two new
vertices гц and its such that щ is only adjacent to щ and us is only adjacent to «3. Then
H has only one 3-cycle and so it is chordal. If H were a band graph, then there would
exist a bijection a and an integer 2 < m < 5 satisfying the definition of a band graph.
Since H has a 3-cycle, m > 2. If m > 4, the vertex щ with а(гц) = 3 will have degree 4,
252
Combinatorial Analysis in Matrices
absurd. Now assume that m = 3. Then the vertices щ with а(щ) = 1 or а(щ) =¦ 5 will
have degree 2, whereas H has only one vertex of degree 2, absurd again.
Theorem 5.7.1 (Dym and Gohberg, [78]) Every band graph is completable.
Theorem 5.7.2 (Grone, Johnson, S& and Wolkowicz, [107]) A graph G is completable if
and only if G is chordah
With the remarks before Theorem 5.7Л, we can see that Theorem 5.7.2 generalizes
Theorem 5.7.1. The proof of Theorem 5.7.2 requires several lemmas and a new notion. A
cycle С in a graph G is minimal if С is an induced cycle in G. Note that any minimal
cycle is chordless. For an edge e = uv € E(G), G + e denotes the graph obtained from G
by joining и and v by the edge e.
Lemma 5.7.1 Let G be a graph. The following are equivalent.
(i) G has no minimal cycle of length exactly 4.
(ii) For any pair of distinct nonadjacent vertices щ v € V(G), the graph G + uv has a
unique maximal complete subgraph H with u,v € V(H).
Proof (i) =^ (ii). Let u,v € V(G) be distinct nonadjacent vertices and let H\ and Щ
denote two maximal complete subgraphs in G + uv with щ v € V{H\) П V(#2), but Щ
does not contain Hz^i as a subgraph. Then there exist Zi € V(Hi) — {u,v} such that
Z\Z2 & E(G + uv). But then, G[{zi1Z2iui v}] is a minimal 4-cycle of G, a contradiction.
(ii) =ф- (i). Suppose that (?[{^ь^2>^,г;}] is a minimal 4-cycle of G. Then uv ? j?((y)
and и ф v. Hence G + uv has a unique maximal complete subgraph Я containing uv.
Note that 21,22 € V(#), and so Z1Z2 € 12(G), absurd. Ц
Lemma 5.7.2 Let 6?' be a subgraph of G induced by V(G'). If 6? is completable, then
G' is also completable.
Proof Let (ау)а' be aG'-partial nonnegative matrix. Define a G-partial nonnegative
matrix (c4j)a as follows.
ar = / <J if ViVjeEiG')
%3 у 0 otherwise.
Then (dij)G has a nonnegative completion M. The principal submatrix M' corresponding
to rows and columns indexed by V(G') is then a nonnegative completion of (a^)c. Q
Lemma 5.7.3 If a A; x fc positive semidefinite matrix A = (a#) satisfies ay = 1 whenever
I* - il ^ I>tnen Л. = J*.
Proof We may assume that к > 4 since the case for к = 2,3 are easy to verify. If there
exists an ay =^ 1 for some 1 < i < j < k, then j — i > 2. Let A1 denote the principal
Combinatorial Analysis in Matrices
253
submatrix of A corresponding to the rows and columns t, i -f 1 and j. Then A' satisfies
the hypothesis of the lemma and so а# = 1, absurd. This completes the proof. Q
Proof of Theorem 5.7.2 Assume that G is completable but G is not chordaL Then
G has an induced cycle С of length at least 4. Without loss of generality, assume that
С = v\V2 • • 'VkV\. Note that С is an induced subgraph of G. Define a <7-partial matrix
(a'ij)c as follows.
, f 1 if|t-j|<l, and{i,i}#{l,*}
ij \ -1 if(i,j) = (l,*)or(U) = (M).
Then (ву)с is a C-partial nonnegative matrix (we need to check only the principal minors
of order 2). By Lemma 5.7.3, (а>у)с is not completable to a positive semidefinite matrix,
and so by Lemma 5.7.2, G is not completable either, a contradiction.
Conversely, assume that G is chorda! but not a complete graph. Let G = Go, (?i, • • • , Gs
be a sequence of chordal graphs satisfying the conditions of Theorem 5.6.3. Let A = (<Hj)e
be a G-partial positive matrix. We shall show that there exists a G\-partial positive
matrix A\ which extends A, and so the sufficiency of Theorem 5.7.2 will follow by induction
on s.
Let uv € E(Gi) — E(G). By Lemma 5.7.1, there exists a unique maximal complete
subgraph H of <ji with u,v e V(H). Without loss of generality, assume that V(H) =
{vi,V2,--- ,vp} with и = vi and v = vp. For any complex z, let Ai(z) denote the 6?i-
partial matrix extending A with the (l,p)-entry being z and the (p, l)-entry z. Let M{z)
denote the principal submatrix of A\{z) corresponding to the vertices in V(H). Then
A\(z) is a G\ partial positive matrix if and only if M(z) is a positive matrix. Thus it
suffices to show that there exists an zq such that M(zq) is positive definite.
However, with a : V(H) *-* {1,2,«• • ,p} defined by a(vi) = *, the edges in E(H) are
exactly the edges
{ущ : |*-Л<р-2,1<«<7<р}.
and so such a zq exists, by Theorem 5.7.1. Q
5-8 Estimation of the Eigenvalues of a Matrix
Throughout this section С denotes the field on complex numbers. All the matrices
considered in this section will be over С Let A = (a^) be an nxn matrix, D =diag(au, агг, • • • , (inn)
imdB-A-D. For a z € C, define Az = D + zB. ThenAo =i?andAi = ii Note that
the eigenvalues of A0 are оц, а22> • • • , ann. As the zeros of a polynomial vary continuously
with the coefficients of the polynomial, it is natural to guess intuitively that when \z\ is
254
Combinatorial Analysis in Matrices
small, the eigenvalues of Az will be close to ац,о22,- •• , or ann on the complex plane.
This is confirmed by Gersgorin.
Definition 5.8.1 Let A = (%•) be an n x n matrix, and let
n
Ri(A)= ]Г |<ц,|, l<*<n.
The matrix A is diagonal dominant if
Ы > Л (A), 1 < i < n.
К (5.21) is strict, then A is strict diagonal dominant.
(5.21)
Theorem 5.8,1 (Gersgorin, [98]) Let A = (a#) be an n x n matrix. Then all eigenvalues
of A lie in the region G(A), which is the union of the closed discs
G(A) = \J{zeC : \z^au\<Ri(A)}
(5.22)
Moreover, if the union of к of these n discs form a connected region on the complex plane
and if this connected region is disjoint from the other n — к discs, then this connected
region has exactly к eigenvalues of A.
Proof Let Л be an eigenvalue of A, and let x = (ffi,ff2>*** >#n)T be an eigenvector
belonging to Л. Pick a component xp such that
Ы > fall <i <n.
Since x ф 0, |xp| > 0. Thus
^xp — У ,avixh
i=i
This is equivalent to
P(A-app)= ]Г ар^-.
i = i
It follows that
MA-app)| =
]C ^i^i
i*p
< 5^ К>Я*1
i = i
i*p
< Ы Yl lawl= MRp-
3 = 1
Combinatorial Analysis in Matrices
255
This proves the first assertion of Theorem 5.8.1.
Let A = D-Ъ-В, where D =diag(an, a22, • • • > ann) and let A€ = D+e?, for some с > 0.
Note that Ri(At) = #i(c?) = cRi(B) = еК»(Л). Without loss of generality, assume that
the first A; discs
к
\J{zeC : |*-а«|<Д«(А)}
i=l
form a connected region Gu{A) on the complex plane, which is disjoint from other n — к
discs. Note that for any e with 0 < e < 1,
fc
G*(A€) = {J{zeC :\z- ац\ < eRi(A)}
i=l
lies in the region Gk(A), and so Gk(A€) is also disjoint from the other discs {z € С :
к - ац\ < Ri{A)}, к + 1 < i < п.
For each t, the continuous curve \{(Ай) with (0 < с < 1) lies in the disc {z € С :
|z — а«| < Ri(A)}. Hence 6?* (A) has at least A; eigenvalues of A. By the same reason,
UiLfc+i{* € С : |я — а«| < сйг(Л)} also contains at least n — к eigenvalues of A.
Since the region Gk(A) and UiL*+i{* e С : |я — a?i| < e#i(A)} are disjoint, and
since Л has at most n eigenvalues, the second assertion of Theorem 5.8.1 now obtains. []
Each of the closed discs in (5.22) will be called a Gersgorin disc. Applying Theorem
5.8.1, we can obtain the following theorem.
Theorem 5.8.2 Let A = (a#) be an n x n matrix such that A is strict diagonal dominant.
Then
(i) A is nonsingular.
(ii) Кай>0,1<г<п, then every eigenvalue of A is has a positive real part.
(iii) If Л is Hermitian, and if an > 0, where 1 < i < n, then all eigenvalues of A are
positive.
Example 5.8.1 A strict diagonal dominant matrix is nonsingular but a diagonal dominant
matrix may be singular. The following is an example.
[421]
Oil.
L о i i J
Theorem 5.8.3 Let A = (a^) be an n x n matrix, and let A be an eigenvalue of A
lying on the boundary of G(A), with an eigenvector x = (a?i, жг, • • * , xn)T. Let xp be the
component of x such that \xp\ = maxi<i<n \x{\. Each of the following holds.
(i) If for some к, |ж*| = |жр|, then |A — а**.| = Rk(A). (In other words, Л also lies in
256
Combinatorial Analysis in Matrices
the fcth Gersgorin disc.)
(ii) Suppose that for some к = 1,2, * • • , n, \xk\ = \xp\. If for some j ф к, ащ ф О, then
N = Ы-
Proof Since Л lies in the boundary of G(A), for each t = 1,2,• • • ,n, |A — ац\ > Ri(A).
It follows that when |а:*| = |жр|,
Ы|А-а**| =
X) аЫхз
< X 1**^1
< W X) la*il = NI X 1***1 = 1**1 Д*.
i = i i = l
3*k J * *
and so equalities must hold everywhere. Thus both (i) holds and
? M(M-N) = o
holds, and so by the fact that each |а*у|(|ж*| — \xj\) > 0, (ii) must follow as well. Q
Corollary 5.8.3 Let A = (a#) be an n x n matrix such that а# ф 0, 1 < »,j < n,
and let Л be an eigenvalue of A lying on the boundary of G(A), with an eigenvector
x = (хих2г-л >sn)T.
(i) Every Gersgorin disc contains A.
(ii) For 1 < ij < n, \xi\ = \xj\.
Brauer considered taking two rows when determining the radii of the Gersgorin discs
instead of just one row, and successfully extended Theorem 5.8.1.
Theorem 5.8.4 (Brauer, [14]) Let A — (o#) be an n x n matrix. Then all eigenvalues of
A lie in the region
(J {z e С : \z - aH\\z - aj5\ < Щ{А)Щ{А)}. (5.23)
»\ 3 = 1
i*3
Proof Let A be. an eigenvalue of A with an eigenvector x = (si,^,-- iXn)T. Let
|arp| = maxi<i<n \xi\ > 0. Since each an lies in the region (5.23), A must be there also
when x has only one nonzero component.
Now assume that x has two nonzero components. Let \xp\ >\xq\> \xi\ for all i with
Combinatorial Analysis in Matrices
257
i € {1,2, • • • , n} — {p, q}. As before, we have
|sp||A-app| =
which yields
]C °Pixi
i*P
< X) KilM
i = i
< \xq\ 53 м^ы J2 m^w^p»
i*p
IA-^I^BpEH-
(5.24)
However, we also have
К1|А-аи|
which yields
S) ачз*
3 = 1
3*4
< Yl KilM
i = 1
< i*pi X K>i = ta>i Y, Kii = i*pi^g.
i = i
i = i
i*p
|A-agg| <Ядт^-т.
(5.25)
Therefore the theorem follows by combining (5.24) and (5.25). ?]
Motivated by the success of Brauer, it is natural to consider more than two rows in a
time. Attempts were made by Brauer and by Marcus and Mine. Unfortunately, this does
not lead to a successful generalization of Theorem 5.8.1. (See comments in [23]). Brualdi
([23]) discovered new connection between the distributions of eigenvalues and closed walks
and connectivity in digraphs, and thereby finding a new extension.
Definition 5.8.2 A digraph D is cyclically connected if for any vertex v, there exists a
vertex w such that D has a directed (v,w)-walk and a directed (tu,v)-walk. Thus in a
cyclic connected digraph D, every vertex lies in a nontrivial directed closed walk (a trivial
directed closed walk is just a loop). We define a matrix A to be weakly irreducible if D(A)
is cyclically connected.
For each vertex v € V(D), let N+(v) to be the set of vertices и € V(D) — {v} such
that (v,u) € E(D). Note that if D is cyclic connected, then N+(v) # 0, Vv e V(D).
258
Combinatorial Analysis in Matrices
Throughout this section, the collection of all nontrivial directed closed walks of D(A)
is denoted by С (A). For a W = v^v^ • • • VikVikJhl € С (A) (where vik+l = t/^), write
к к
Vi€tV i=l t/<€W j=l
A pre-order on a set V is a relation •< satisfying
(POl) x •< x, Vs € V, and
(P02) i^y and «/ :< 2 imply that iXz, V#, y,zeV.
Theorem 5.8.5 (Brualdi, [23]) Let A = (a#) be an nxn matrix. If A is weakly irreducible,
then every eigenvalue of A lies in the region
(J (*€C : П \z-ou\< П A(^>V
eC(A) I view v«€W J
(5.26)
WeC(A)
Proof Let Л be an eigenvalue of A. If for some г, А = ац% then clearly Л lies in the region
(5.26). Thus we assume that \фац, Vi, and let x = (яьвд, • • • >Sn)T be an eigenvector
belonging to Л. Then define a pre-order on V(D(A)) a follows:
Vi <Vj <—+\xi\ <\Xj\.
Claim 1 Л lies in the region (5.26) if there exists a W € C(A) with these properties
(A) W = Vfct/fe • • • vifcVifc+1 with vix = vijb+1 and к > 2.
(B) For each j = 1,2, • • • ,k, vm ^ vi<+1 for all vm 6 #+(а^)
(C)Kl>o,i<ja.
If such a W exists, then by Ax = Ax, for j = 1,2, • • • , fc,
n
vm€N+(v4)
m = 1
Therefore,
|А-о^||*«,| =
vneJV+C^.)
< ]? tan» IM
It follows
t/«€JNT+(vv.)
П1л-а^1К1<П^к^|*
i=i i=i
(5.27)
(5.28)
Combinatorial Analysis in Matrices
259
Note that
к к
П1Л-0ь-ь-1= П 1Л-°"1> andn>,= П *•
j=l ViGV(W) Я=1 t/<€W
As vik+1 = Vix and so ж *fe+1 = ar^. Hence
Combine (5.28) and (5.29) to get
П |А-а«|< П ft' (5-3°)
view view
and so Л lies in the region (5.26).
Claim 2 A closed walk satisfying (A), (B) and (C) in Claim 1 exists.
Since x^O, there exists X{ ф 0. Note that
n
(Л - au)xi = 22 ^i^i = z2 aiix5-
3 = 1 v3eN+(vi)
3*i
This, together with \xi\ > 0 and Х-ацф 0, implies that among the vertices in N+(yi)t
there must be at least one Vj € N+(vi) such that Xj ф 0.
Let vix = v* and let v»2 G N(vit) such that for any v 6 N+(viJ, t; 4 t/i2. Note that
xi2 ф 0.
Inductively, assume that a walk v^v^ • - -v^tty, satisfying (B) and (C) in Claim 1,
has been constructed. Since Xi$ Ф 0, we can repeat the above to find V?i+1 € N+(vj) such
that for any v € N+(vj) v ^ v,i+1.
Since D(A) has only finitely many vertices, a closed walk satisfying (A), (B) and (C)
of Claim 1 must exists. This proves Claim 2, as well as the theorem. Q
Theorem 5.8.6 (Brualdi, [23]) Let A = (а#) be an n x n irreducible matrix and let Л be
a complex number.
If Л lies in the boundary of the region (5.26), then for any W € С (А), Л also lies in
the boundary of each region
IzeC : П \z-au\< Д *W)} • (5-31)
I view view J
Proof Note that an irreducible matrix is also weakly irreducible. All the argument in
the proof of the previous theorem remains valid here. We shall use the same notation as
260
Combinatorial Analysis in Matrices
in the proof of the previous theorem. Note that Claim 2 in the proof of Theorem 5.8.5
remains valid here.
Since Ri > 0, for each i. If Л = аи for some г, then Л cannot be in the boundary of
(5.26). Hence Л Ф a«, 1 < i < n.
Fix a W e C{A) that satisfies (A),(B) and (C) of Claim 1 in the proof of Theorem 5.8.5.
Since Л lies in the boundary the region (5.26), for each V{ € V(W), we have |A - ац\ > Я»,
and so
П l*-<*il> П **№' (5'32)
view vtew
By (5.30), we must have equality in (5.32), and so Л lies in the boundary of (5.31) for this
W.
Note that when equality holds in (5.32), we must have, for any j = 1,2, * • • , k, that
equalities hold everywhere in (5.27). Therefore, for any closed walk in C(A) satisfying
(A), (B) and (C) of Claim 1 in the proof of Theorem 5.8.5, for any v^ € V(W) and for
any ит€#+(^),
\xm\ = \xij+11 = C|i+1 is a constant. (5.33)
Define
К = {vi e V(D(A)) : \xm\ = a= constant, for any vm € N+(vi)}.
By Claim 2 in the proof for Theorem 5.8.5, К ф 0. If we can show that К = V(D(A)),
then for any closed walk W € С (A), W will satisfy (A), (B) and (C) of Claim 1 in the
proof of Theorem 5.8.5, and so Л will be on the boundary of the region (5.31) for this W.
Suppose, by contradiction, then some vq € V(D(A)) - K. Since D(A) is strongly
connected, D(A) has a shortest directed walk from a vertex in К to vq. Since it is shortest,
the first arc of this walk is from a vertex in AT to a vertex Vf not in K. Adopting the same
pre-order of D(A) as in the proof for Claim 2 of Theorem 5.8.5, we can similarly construct
a walk by letting vix = v/, v^ is chosen from N+iv^) so that for any v € iV+fyiJ,
v :< V{2. Since D(A) is strong, N+(vi) ф 0, for every v* € V(D(A)). Once again, such a
walk satisfies (B) and (C) in Claim 1 in the proof of Theorem 5.8.5.
In each step to find the next v^, we choose V{. ? К whenever possible, and if we have
to choose v^ € K, then choose Vi. € К so that v^ is in a shortest directed walk from a
vertex in К to a vertex not in K> Since \V(D(A)) — K\ is finite, a vertex v not in К will
appear more than once in this walk, and so a closed walk W € C(A) is found, satisfying
(A), (B) and (C) of Claim 1 in the proof of Theorem 5.8.5, and containing v. But then,
by (5.33), every vertex in W must be K, contrary to the assumption that v /nK. Hence
V(D(A)) = K. This completes the proof. Q
Combinatorial Analysis in Matrices
261
Corollary 5.8.6 Let A = (a#) be an n x n matrix. Then A is nonsingular if one of the
following holds.
(i) A is weakly irreducible and
П M > П **, for any W e C(A).
view vizw
(ii) A is irreducible and
П M * П *, for any W e C(A\
view view
and strict inequality holds for at least one W 6 С (A),
Proof In either case, by Theorems 5.8.5 or 5.8.6, the region (5.26) does not contain 0;
and when A is irreducible, the boundary of the region (5.26) фее not contain 0, either.
?
5.9 M-matrices
In this section, we will once again restrict our discussion to matrices over the real numbers,
and in particular, to nonnegative matrices. Throughout this section, for an integer p > 0,
denote (p) = {1,2, • ¦ • ,p}. For the convenience of discussion, a matrix A € Mn is often
written in the form
Л =
An A12
An A22
Api Ap2
Alq
A2g
(5.34)
where each block Ац € Mmi%1Xi and where тщ + m2 Л V mp = n = n\ + n2 H h nq.
In this case, we write A = (Aij),i = 1,2,••• ,p and j = 1,2,••• ,q. A vector x =
(xfjX^,••• ,xj)r is said to agree with the blocks of the matrix (5.34) if x* is an mi-
dimensional vector, 1 < i < p. When x = (xf,xj,••• ,xj)r, xf is also called the ith
component of x, for convenience.
Definition 5.9.1 Recall that if A > 0 and A € Mn, then A is permutation similar to its
262
Combinatorial Analysis in Matrices
PVobenius Standard from (Theorem 2.2.1)
B =
An
0
0
Art-i.i
^0+2,1
0
A22
0
...
0
0
Agg
Ag+i,g
*^$+2,9
0
Ag+i,g+i
^4-2,3+1
0
0
0
0
A5+2,
0 \
0
0
0
0
(5.35)
\ Ak,i •" M,g Aki9+i Akk )
By Theorem 2.1.1, each irreducible diagonal block An, 1 < i < fc, corresponds to a strong
component of D(A). Throughout this section, let pi = р(Ац), the spectral radius of An,
for each i with 1 < i < к.
Label the strong components of D(A) (diagonal blocks in (5.35)) with elements in (?),
and define a partial order < on (к) as follows: for г, j € (к), i ¦< j if and only if in D(A),
there is a directed path from a vertex in the jth strong component to a vertex in the ith
strong component; and i -< j means i X j but гф j.
The partial order *< yields a digraph, called the reduced graph R(A) of A, which has
vertex set (fc), where (г, j) € E(R(A)) if and only if i ¦< j. Note that by the definition of
strong components, R(A) is has no directed cycles.
If a matrix A has the form (5.35), then denote pi = р(Ац)у 1 < i < к. Let M = XI-A
be an M-matrix. Then the ith vertex in R(M) (that is, the vertex corresponding to An
in R(A)) is a singular vertex if Л = pi. The singular vertices of reduced graph R(M) is
also called the singular vertices of the matrix M.
For matrix of the form (5.34), define
f 1 ifi = jor АцфО
10 | 0 otherwise.
Also, let
Rij = max 7г/»7л/ • • • Ъз >
where the maximum is taken over all possible sequences {г, h, • •
,Q,J}>
Proposition 5.9.1 With the notation above, each of the following holds.
(i) If Л is a Rrobenius Standard form (5.35), then with the partial order ^, we can
equivalently write,
[ 0 otherwise.
Combinatorial Analysis in Matrices
263
GO
(Ш)
$3 RihRhj > Rij > RiiRij, 1<1<P
У2 HhRhj > Rij > max yihRhj, if гф .?¦
(5.36)
Example 5.9.1 Let
A =
10 0 0 0
-10 0 0 0
-a -1 1 0 0
-10 0 0 0
-6 -c -1 -1 1
where a, Ь, с are nonnegative real numbers. Then R(A) is the graph in Figure 5.9.1.
2 6
3 •
О singular vertex # nonsingular vertex
Figure 5.9.1
Definition 5.9.2 A matrix В = (bij) € Mn is an M-matrix if each of the following holds.
(5.9.2A) an > 0, 1 < i < n.
264
Combinatorial Analysis in Matrices
(5.9.2B) bij < 0, for i ф j and 1 < ij < n.
(5.9.2C) If Л ф 0 is an eigenvalue of ?, then Л has a positive real part.
Proposition 5.9.2 summerizes some observations made in [229] and [216].
Proposition 5.9.2 (Schneider, [229] and Richman and Schneider, [216]) Each of the
following holds.
(i) Л is an M-matrix if and only if there exists a nonnegative matrix P > 0 arid a
number p > p(P) such that A = pi — P, and A is a singular M-matrix if and only if
A = p(P)I-P.
(ii) If A = (Ay) is an M-matrix in the Probenius standard form (5.35), then the
diagonal blocks Ацу 1 < i < k, are irreducible M-matrices.
(iii) The blocks below the main diagonal, А#, 1 < j < i < k, are non-negative. In
other words, —Aij > 0.
Lemma 5.9.1 Let A = (Ay), i,j = 1,2,---к be an M-matrix in a Probenius Standard
form (5.35), and let x = (xf, x^, • • • , x?)T agreeing with the blocks of A. For an а € (к)
and for an h > o, let
х^ = 0 if Ria = 0
Xi » 0 if Ria = 1.
i = l,2r--,h-l. (5.37)
If
then
yi = 0 and
У* = ~~ 2-vj=i AijXj, г = 1,2y • • • , ky
( yft = 0 if Rha = Q
1ул>0 if ДЛа = 1.
(5.38)
(5.39)
Proof Since AhjXj > 0, we have ул > 0, and уЛ = 0 if and only if AhjXj = 0,
j = 1,2,— ,Л-1. By (5.37), yh = 0 if and only if
IhjRja =0, j = 1,2,• • • ,Л- 1. (5.40)
Since *yhj = 0 whenever h < j, we also have
h-1 к
y^lhjRja = У* IhjRjai and maxjhjRja =max<yhjRja.
Ash фа, it follows by (5.36) that (5.40) holds if and only if Rha = 0. ?
Theorem 5.9.1 (Schneider, [229]) Let A = (А#) be an Af-matrix in Probenius standard
form (5.35), and let a be a singular vertex of R(A). Then there exists a vector x =
Combinatorial Analysis in Matrices
265
(xf, xj, • • • , x%)T such that Ax = 0 and
х^ » 0 if Ria = 1 (that is, a-<i)
х* = О otherwise.
Proof Let x = (xf ,Хз\ • • • ,x?)T be given and let у = (yf,y2\ • • • ,yjOT be defined by
(5.38). Then Ax = 0 if and only if
АцХг=уи » = 1,2, ••-,*. (5.41)
Now x* = 0, for all i < a. Note that since Л is an M-matrix, the block matrix Aaa has
an eigenvector xa >> 0 belonging to the eigenvector 0. Since A is in Frobenius standard
form, we have Ria = 0, when i < a , and Raa = 1- Thus xi,X2, • • • ,xa satisfy (5.37). By
induction, assume that Xi, X2, • * • , хл-i satisfy (5.37), for some h > a. If yi, y2, • • - , Ун-г
satisfy (5.38), then yh also satisfies (5.39), by Lemma 5.9.1. Thus if Rha = 0, then уд = О;
and if Xh — 0, then x& satisfies (5.41) with i = h.
If Rha = 1? then у л > 0, and so as a is a singular vertex, we conclude that Ann is
nonsingular. Note that as the inverse of a nonsingular M-matrix, Aj^J » 0. Therefore,
хл = А^ун » 0. Thus Xft satisfies (5.41) with i = /i, and so the theorem follows by
induction. Q
Corollary 5.9.1 A A singular M matrix must have an eigenvector x > 0, belonging to
the eigenvalue 0.
Corollary 5.9.1B Let A be an Af-matrix, and let 71,72, • • • ,7« are singular vertices of
R(A). If R(A) has no singular vertex that can reach to another singular vertex, then A
has s linearly independent eigenvectors x^x2,»" ,xs which belong to the eigenvalue 0
and satisfy (5.37) (with 0 = 7,).
Example 5.9.2 Let A be the M-matrix
L 0 1 j
Then R(A) is edgeless and has two vertices, one singular and one nonsingular. The vector
x = (1,0)T is the unique unit eigenvector with x > 0.
Definition 5.9.3 Let Л be an M-matrix and let the Jordan blocks of A corresponding
to the eigenvalue 0 be Jni, Jn2, • • • , Jn,, where щ > пч > • • • > ns > 0. Then the Segre
characteristic of A is the sequence (ni,n2, • • • ,ns). The Jordan graph of A (with respect
to the eigenvalue 0) is an array consisting with s columns of ¦'s, where the jth column
(counted from the left to right) has щ *'s. The Wyre characteristic of Л is a sequence
(i/Ji, W2) - • • , wu), where wi is the number of *'s in the zth row (counted from the bottom
and up) of J(A). Note that wi > w2 > • • • > ws > 0.
266
Combinatorial Analysis in Matrices
The first element in the Segre characteristic of A is the index of A, denoted md(A),
Thus ind(A) = щ. We have these observations.
Proposition 5.9.3 Let A be a matrix with Segre characteristic (щ, пг, • • • , ns) and Wyre
characteristic (од, од, • • • , од). Then each of the following holds.
(i) ind(A) = и = ni.
(ii) The number 0 is an eigenvalue of A if and only if ind(A) > 0.
(iii) If ind(A) > 0, then од > од > • • • > ОД > 0.
(iv) For an integer к with 1 < A; < и, од + од Н h од is the dimension of Кег(А*),
the null space of Ak.
Example 5.9.3 If A has four Jordan blocks corresponding to eigenvalue 0 which are
of order 3, 2, 2, and 1, respectively. Then ind(A) = 3, the Segre characteristic of Л is
(3,2,2,1), and the Wyre characteristic of A is (4,3,1). The Jordan graph J(A) is
* * *
* * * *
Definition 5.9.4 Let A be an M-matrix with u = ind(A). The null space Ker(Aw) is
called the generalized eigenspace of A, and is denoted by E(A). For a vector x, if none of x,
(-A)x, • • •, (—А)*~хх is 0, but (—A)kx = 0, then the sequence x, (-A)x, • • •, (-A)*_1x
is a Jordan chain of length k. A Jordan basis of E(A) is a basis of E(A)> which is a union
of Jordan chains. A Jordan chain (or a Jordan basis) is nonnegative if each vector in the
chain (basis) is nonnegative.
Let R(A) denote the reduced graph of an M-matrix A in standard form (5.35). A
vertex i in R(A) is a distinguished vertex if in R(A), pi > pj whenever i 4 j. Thus a
singular vertex i is distinguished if and only if j is a nonsingular vertex whenever i -< j.
Let the singular vertices of R(A) be од, од, • • • , wg. The singular graph of Л is a graph
S(A) whose vertices are од,од, • • • ,wq, where од ^ од if and only if од ^ од in R(A). If
for each од in S(A), the vertices {w : w ^ од} with the order ^ is a linear order, then
S(A) is a rooted /ores*.
Let Ai denote the set of maximal elements (with respect to the order -<) in S(A). Note
that elements in Ai are distinguished vertices of S(A). For j = 2,3, • • •, let
j
Aj = { the maximal elements in S(A) \ M Ai}.
Put the vertices in Ai on the lowest level, and for j > 2, put vertices in Aj one level higher
than those in Aj_i. Then remove the directions by •<. The resulting graph, denoted
S*(A), is the level diagram of A. Label the levels of S*(A) from bottom up. The highest
Combinatorial Analysis in Matrices
267
level label is the high of S*(A). Let 7,- = |Aj|, j = 1,2, • • • , h, where h is the high of S*(A).
Then (71,72, • • * ,7л) is the level characteristic of A
For a subset Q С Л^, where 2 < j < ht A(Q) С A^_i is the subset consists of all the
vertices j such that for some i 6 Q, г ^ j.
Example 5.9.4 Let 5*(A) be a diagram given as follows:
I
Figure 5.9.2
Then Лх = {5,6,7,8}, A2 = {2,3,4}, Ax = {1}; Д(1) = {2,3} but 7 ? Д(1).
Д({2,3}) = {5,6}. The height of 5,(A) is h = 3, and the level characteristic of A is
(4,3,1).
Lemma 5.9.2 Let A = (Ay), 1 < i, j < A; be a singular M-matrix in standard form (5.35),
and let 7i,72, - • - ,ys be the singular vertices of A such that 71 < 72 < • • • < 7«. If A has
m linearly independent eigenvectors belonging to the eigenvalue 0, then for each integer
n < m, there exists an eigenvector x, belonging to the eigenvalue 0, such that for some
* < 7n+s-m> (xj)i> the **h component of xj, is nonzero.
Proof The conclusion is obvious if yn+s-m = &• Assume that 7n+s-m < &, and let
x1, • • • , xm be linearly independent eigenvectors of A belonging to 0, such that for i =
1,2, • • • , уп+s-m and for j = n, n + 1, • • • , m, xj = 0, where xf is the ith component of
x'\
Let /x = 7n+s_m+l. The vectors ((x?)T, • • • , (x^)T)T, j = n,n+l, • • • ,m are m—n+1
linearly independent eigenvectors of the matrix В = (Ay), г, j = ц, Ai+1> • • • , m, belonging
to the eigenvalue 0. However, the multiplicity of 0 in Б is the same as the number of
singular vertices in R(B), which is m — n, a contradiction. ?]
268
Combinatorial Analysis in Matrices
Lemma 5.9.3 Let A = (Ay), 1 < г, j < к be a singular M-matrix in standard form (5.35).
Let 7x < 72 < • • • < ys be the singular vertices of A. If A has s linearly independent
eigenvectors belonging to the eigenvalue 0, then there exist s eigenvectors x* = (xj,^, * * *)T>
1 < j < s, belonging to the eigenvalue 0, such that
f xif = 0 if г < 7,-
Proof Let zJ = (z\,z\, *' *)T» 1 < i < s be linearly independent eigenvectors belonging
to the eigenvalue 0.
Note that z\ = 0 for each г < 71 and each 1 < j < s. By Lemma 5.9.2 with m = s and
n = 1, we may assume that for some j, we have z\ Ф 0, if г = 71. This zJ can be chosen
as x1.
Inductively, assume that eigenvectors x1, x2, • • • , хл, zn+1, zn+2, • • • , zs have been found,
all belonging to the eigenvalue 0, such that
(A) (5.42) holds for j = 1,2, • • • , щ and
(B) For j = n + 1, n + 2, • • • jS} z^ = 0 whenever г < 7n.
Set a = 7n to get
ЛюХд = Aaaz? = 0, j = n + l,n + 2,--- ,5.
As the null space of an irreducible singular M-matrix is one dimensional, it follows that
Let y* = zJ* — Aj-xn, j = n +1, • • • , s. Then x1, • • • , xn, yn+1, • • • , y5 are linearly
independent eigenvectors belonging to the eigenvalue 0. Moreover, if г < 7n, then y\ = 0 for each
j = n +1, n + 2, • • • , s. By Lemma 5.9.2, there exists a j > n +1 such that when г = 7n+i,
y{ Ф 0. Choose this y* to be xn+1. Therefore,
(A) (5.42) holds for j* = 1,2, • • • , n, n + 1, and
(B) For j = n + 2, • • • , s, 2/J =0 whenever г < 7„.
Thus the lemma follows by induction. Q
Lemma 5.9.4 below can be easily proved.
Lemma 5.9.4 Let Л be an irreducible singular M-matrix and let x be a vector. If either
Ax > 0, or if Ax < 0, then Ax = 0.
Theorem 5.9.2 (Schneider, [229]) Let A = (Ay), 1 < i,j < к be a singular Af-matrix in
standard form (5.35). The following are equivalent.
(i) The Segre characteristic of A is (1,1, • • ¦ ,1).
(ii) In R(A)y no singular vertex of A can be reached from another singular vertex.
Combinatorial Analysis in Matrices
269
Proof Let S = {71,72,"• ,7s} be the set of all singular vertices of R{A) such that
7i <72 <••• <7«-
Note that the eigenvalue 0 has s linearly independent eigenvectors if and only if the
Segre characteristic of A is (1,1, • • • , 1). Therefore, by Corollary 5.9.IB, that (ii) implies
that the eigenvalue 0 has s linearly independent eigenvectors, and so (i) must hold.
Conversely, assume that (i) holds, and so the eigenvalue 0 has s linearly independent
eigenvectors x^x2,--- ,x*. By Lemma 5.9.3, we may assume that these s eigenvectors
satisfy (5.42).
By contradiction, we assume that for some distinct a, ft € 5, a x 0. Thus Rpa = !•
Choose such a pair of a, /9 € S such that
Rpa = 1,0 > a, and /3 - a < fi' - a',Va'/?' € S with а' ф ft' and Rpa, = 1. (5.43)
By (5.43), if a < a < S < /3, a, 6 € 5, then Rs<r = 0 except both a = a and 6 - /?.
Let Б — (-Aij), z,j = a,«" ,/? — 1. Let tfi < 8% < ••• < <J7 be singular vertices of
R(B). Then tfi = a = 7,-, for some j. By Corollary 5.9.1В, В has 7 linearly independent
eigenvectors zh, h = 1,2,-•• ,7, where each zA = ((z?)T,--- ,(zj^-.1)r)T satisfies (5.37),
h = 1,2, • • • ,7. Note that the multiplicity of the eigenvalue 0 of Б is 7, every eigenvector
of В belonging to 0 is a linear combination of zhi h = 1,2, • • • , 7.
As a = 7/, ((x?)T, • ¦ • , (x^_x)T)T is an eigenvector of В belonging to the eigenvalue
0. Therefore, (x^) = 2J=1 A^z^, i = 1,2, • • • , ft — 1. Since x? ^ 0, and since z? = 0 when
h = 2,3, • • • , 7, we have Ai ^ O.It follows that
7 7
^34 = ЦллУ^ wherey$ = -53A#zf, /i = 1,2,— ,7.
When t = 1,2, • • • , a — 1, set z? = 0, and apply Lemma 5.9.1 to get
y? > 0 if Rfr = 1
y$ = 0 if J*0T = 0
Thus
yj > 0, and yp = 0, for each h = 2,3, • • • ,7.
It follows that -А/9/зх^ = Aiy^, and so either
Appxfc > 0 or 0 > Appx?p,
contrary to Lemma 5.9.4. Therefore, if a, /3 € S, a -< 0, we must have ifya = 0. Q
Corollary 5.9.2 Let A = (Л#), 1 < i, j < к be a singular M-matrix in standard form
(5.35). Then S*(A) has the horizontal level form
* * *¦• •*
270
Combinatorial Analysis in Matrices
if and only if the Jordan graph J(A) has the same form.
Example 5.9.5 Let A be the matrix in Example 5.9.1. The both S*(A) and J(A) are
* *
Schneider also discovered a relationship between Wyre characteristic of a matrix A
and the singular graph S(A) of A, as follows. Interested readers are referred to [229] for
further details.
Theorem 5.9.3 (Schneider, [229]) Let A = (A#), 1 < i,j < к be a singular M-matrix in
standard form (5.35). The following are equivalent.
(i) The Wyre characteristic of A is (1,1, • • • , I).
(ii) The singular graph S(A) is linearly ordered.
Example 5.9.6 Let A be the JW-matrix
1
—a
-Ъ
—с
-d
0
0
-n
—v
—e
0
0
1
—w
-f
0
0
0
0
-9
where all the elements below the main diagonal are nonpositive, and where either uw > 0
or v > 0. Then S(A) is
i:
and so both Sm(A) and J (A) are
*
Therefore, the eigenvalue 0 has exactly one 2x2 Jordan block.
A generalization of Theorem 5.9.2 and Theorem 5.9.3, called Rothblum index theorem,
was obtained by Rothblum.
Theorem 5.9.4 (Rothblum, [220]) Let A = (Л^), 1 < г, j < к be a singular M-matrix
in standard form (5.35). Then ind(A) equals the height of the diagram S*(A), that i, the
length of a longest singular vertex chain in R(A).
Combinatorial Analysis in Matrices
271
We conclude this section with several open problems in this area, proposed by
Schneider, [228].
(1) What is the relationship between S(A) and J(A)?
(2) When does 5* (A) = J(A) hold?
(3) Given S(A), for an M-matrix By what conditions on J(B) will assure that S(A) —
5(B)?
(4) Given J (A), for an M-matrix B, what conditions on S(B) will assure J(B) = J (A)?
Some progresses towards these problems have been made. Interested readers are
referred to [13].
5.10 Exercises
Exercise 5.1 Show that A = (ay) and В = (by), where ay's are complex numbers and
where each b# € {0,1}, are diagonally similar if and only if there exist complex numbers
dud2, • • • ,dn , where dk ф 0 , i = 1,2, • • • ,n, such that a# = c^dj1 for every ay # 0.
Exercise 5.2 Given Л € Mn such that A is irreducible. What is the sufficient and
necessary condition for A to be diagonally similar to a (0,1) matrix?
Exercise 5.3 Give a counterexample to show that, in Exercise 5.2, the condition that A
is irreducible is necessary.
Exercise 5.4 Let M and A be the matrices defined in the proof of Theorem 5.3.1. Express
<7y, the entries of the matrix M, in terms of the entries of A by verifying each of the
following.
0)
_ j 0 if there exist x and у such that ax{ = ajy = 1 and axy = 0,
%0 1 1 otherwise.
(H)
9ij = JJ[1 - axiajy(l - axy)].
Exercise 5.5 Let A = (oy),A0 = (?y),a* = (ощ,ои,- ,а*п),& = (0ib02fc,-" >0nft)T
(as in the proof of Theorem 5.3.1). Let (cy) = (ay) ф (by) denote the matrix in which
each C{j = ay • Ъ^. Show that
(1) if at = a - «i + а»2 4 + aih in Д then A = /3^ Ф Аа Ф • • • Ф A* in Л0.
(2) If a* =ai? then/?* = &.
(3) If at = 0 then ft = (1,1,— ,1)T.
Exercise 5.6 Let A 6 Bn be a nonsingular matrix. Show that pj-л > n — 1.
272
Combinatorial Analysis in Matrices
Exercise 5.7 Let A € Bn be a complementary acyclic matrix with pj-a = n - 1. If Л
contains an all 1 row and an all 1 column. Then detA = ±1.
Exercise 5.8 Let M € Mn, and for i — 1,2, • • • ,n let n and si denote the ith row sum
and the tth column sum, respectively. Show that ||M2|| = ?«=i rvsv.
Exercise 5.9 Prove Theorem 5.5.7.
Exercise 5.10 Prove Theorem 5.5.9.
Exercise 5.11 Let Я be a bipartite graph with vertex bipartition sets V(H) = XuY. If
Я does not have a pair of disjoint edges, then each vertex z, where z is not isolated, is an
end point of a bisimplicial edge in Я.
Exercise 5.12 Prove Theorem 5.6.5.
Exercise 5.13 Prove Proposition 5.7.2 for the case when G is nonnegative computable.
Exercise 5.14 Prove Theorem 5.8.2.
Exercise 5.15 Prove Corollary 5.8.3.
Exercise 5.16 Let A = (oy) be an n x n diagonal dominant matrix such that A > 0.
Show that if there exists an i e {1,2, • • • ,n} such that \ац\ > JSJ. Then A is nonsingular.
Exercise 5.17 Prove Corollary 5.9.1 A.
Exercise 5.18 Prove Corollary 5.9.IB.
Exercise 5.19 Prove Lemma 5.9.4.
Exercise 5.20 For a stochastic matrix A, the order of each Jordon = block corresponds
to eigenvalue 1.
Exercise 5.21 Find an example to show that there exist matrices A and В with S(A) =
5(B) but J(A) ф J(B).
5.11 Hints for Exercises
Exercise 5.1 Apply ац = dibijdj1.
Exercise 5.2 By Theorem 5.1.1 and Exercise 5.1, the condition is Wa(C) = 1 for each
directed cycle С in D(A).
Exercise 5.3 Consider weighted digraph D, with V(D) = {1,2,3,4} and E — {ei, ег, е3, e^},
where ex = (l,2),e2 = (l,4),e3 = (2,3),e4 = (3,1),e5 = (3,4). Assign the weights as
follows: W{ex) = W(e3) = W{eA) = 1, W(e2) = 2 and W(eb) = 3. Then D satisfies
Wd(C) = 1. But A(D) is not diagonally similar to any (0,1) matrix.
Combinatorial Analysis in Matrices
273
Exercise 5.7 Suppose A =
Since В is complementary acyclic,
Exercise 5.4 Apply the definitions of M and A in the proof of Theorem 5.3.1.
Exercise 5.5 Without loss of generality, suppose that аз = ai + a2. We show that
A=A$A. If Q>iz = 0, then by Exercise 5.4(i), there exist ж, у such that аХ{ = озу = 1,
axy = 0. Let diy = 1. Since азу = Oiy+a2y, by Exercise 5.4(ii) pi$ = 0. Hence д& = 9i\'9i2-
Conversely let дц = 0. We have #3 = 0. Thus gi3 = дц • gi2. If at = a*, then ft — ft. If
a* = 0, а*у =s 0, у = 1 — n, then by Exercise 5.4(ii) дц = 1, г = 1 — п.
Exercise 5.6 Consider a set of lines including e rows and / = columns. Let
\ D Jn-e,n-f J
Since A is nonsingular, columns C/+i, • • • , Cn of A are linearly independent. But I J
has at most e+1 independent rows. Thus e+l>n — /,e+/>n — 1. By K5nig Theorem
the inequality follows.
/ i l-.-i \
i
: В
\ i ;
Jn_i — В is permutation equivalent to a triangular matrix. Thus В is permutation
equivalent to a complementary triangular T. Since pj-в = n — 1, T contains a main diagonal
with all zero and all entries above the main diagonal of T are 1. Thus det A = ±1.
Exercise 5.8 Let M = (т#). Then
n n
i,j=rl 1/^1
n n n
Exercise 5.9 This follows from Proposition 5.5.4(iii) and Lemma 5.5.2. To construct a
matrix A € Bn reaching this bound, we can add к 1-entries in the main diagonal of the
matrix Ln.
Exercise 5.10 This follows from Lemmas 5.5.3 and 5.5.4. To construct a matrix A € Bn
reaching this bound, we can add к 1-entries above the main diagonal of the matrix L*.
Exercise 5.11 If not, let z € Y and xqz e E. We can construct an infinite chain of
subsets of X as follows, Xo С Х\ С • • • С • * •, contrary to the finiteness of X. Suppose
Xk = {ar0,xi,--- ,xk} С X and Y* = {z,yuy2t ••• ,y*} С Y such that агэд € E if and
only if i < j for all 0 < ij < fc, and such that X{Z € E for 0 < г < fc.
274
Combinatorial Analysis in Matrices
Since XkZ is not bisimpliciai, there exist vertices x and у(ф z) such that Xky,xz ? E
but xy g E. Thus y$Y\.. Therefore xiyi+i and Xky are not pair of disjoint edges, which
implies xiy e E. But xy & E. Thus x g Xk* Let Xk+i = я* U {Ук+i}- The algorithm can
continue infinitely, and so a contradiction obtains.
Exercise 5.12 Apply Exercise 5.8 and Theorem 5.6.5.
Exercise 5.13 Imitate the proof for the completable graph case.
Exercise 5.14 If A is strict diagonal dominant, then does not lie in any of the Gersgorin
discs of A, and so 0 is not an eigenvector of A. Therefore, A is nonsingular.
When all an > 0, since A is diagonal dominant, each Gersgorin disc is lying on the
right half complex plane and so (ii) must hold.
By Proposition 5.7.1(ii), all eigenvalues of a hermitian matrix are real, and so (iii)
follows from (i) and (ii).
Exercise 5.15 Apply Theorem 5.8.3.
Exercise 5.16 If not, then 0 is an eigenvalue of A. Since A is diagonal dominant, 0 must
lie on the boundary of (7(A). By Theorem 5.8.3 every Gersgorin disc contains 0. But
\ац\ > R'i} the i-th disc does not contain 0, a contradiction.
Exercise 5.17 and 5.18 Corollary 5.9.1 A follows immediately from Theorem 5.9.1. For
Corollary 5.9.1B, let a = jj in Theorem 5.9.1. Then by Theorem 5.9.1, there exist
eigenvectors xx,x2, • • • ,x5 which belong to the eigenvalue 0 and satisfy (5.37). Assume that
Aix1 + A2x2 + • • • + Ллхл = О
Then for i = 1,2, • • •, к, Y?h=i А^х? = 0. Note that since a = fj is a singular vertex, if
/? = 7л, (h ф j), then x? = 0, and so Ajxj = 0. As xj ф 0, we must have \j = 0, and so
x1, x2, • • • , x5 are linearly independent.
Exercise 5.19 Since A is an irreducible M-matrix, there exists a vector u >> 0 such that
uTA = 0. Therefore, we have uTAx = 0. Since Ax > 0 (or Ax < 0), and since u » 0,
we must have Ax = 0.
Exercise 5.20 Note that all singular vertices in R(A) are endpoint (or start point). Apply
Theorem 5.9.2.
/ 0 0 0 0 \
Exercise 5.21 Example: Aid) =
W -1-10 0
\ -a -1 0 0 )
J(A(1)) ф J(A(2)).
, a > 0. 5(A(1)) = 5(A(2)). But
Chapter 6
Appendix
6.1 Linear Algebra and Matrices
Let F be a field and let n,m > 1 be integers. Then Mmtn(F) denote the set of all
m x n matrices over F, and Mn(F) = Mn>n(F). When F is not specified, or is the real
numbers field or the complex number field, we omit the field and simply write Mm>n and
Mn instead. For a matrix A = (ay) € Mm>n, and for 1 < % < m and 1 < j < n,
the symbol (A)ij denotes the (t,j)-entry of A, whereas Ац denote a block submatrix of
A. If v = (х\}Х2Г" >xn)T denotes an n-dimensional vector, then (v)i denotes the ith
component X{ of v.
For a matrix A = (ay) € Mm>n, we say that A is a positive matrix and write A > 0 if
ay > 0 for all i and j with 1 < i < m and 1 < j < n, but A^Q. If A = 0 is possible,
then A is a nonnegative matrix, and we write A > 0 instead. For an n dimensional vector
x = {x\, x2i • • • , жп)т, we similarly define x > 0 and x > 0 and call x a positive vector or a
nonn^attve vector, respectively. If, ay > 0 for all t and j with 1 < i < m and 1 < j < n,
then A. is strictly positive and we write A » 0. Similarly we define a strictly positive
vector x and write x » 0.
Let A e Mn- The characteristic polynomial of A is Xa(A) = det(A — A/n); and the
minimum polynomial of A, denoted тл(А), is the unique monic polynomial with the
minimum degree among all monic polynomials that annihilate A.
For Ai e Mn.t for each г with 1 < i < c, we write
diag(Ai,A2,--- ,AC) =
Ai 0
0 A2
0 0
.(A.1)
(6.1)
275
276
Appendix
When A{ = (ai) € Mi, A in (АЛ) becomes diag(oi,o2, • • • , oc), and is a diagonal matrix.
The trace of a matrix Л = (a*/) € Afn, is tr(A) = ?2=1 а«.
Certain facts about trace and determinant of a matrix are summarized in Theorem
6.1.1, while some of the useful facts in linear algebra and in the theory of non negative
matrices are listed in the theorems that follow.
Theorem 6.1.1 Let А, В € Mn with eigenvalues Ai, A2, • • • , An. Then
(i) A is nonsingular if and only if Ai ф 0 for each % = 1,2, • • • , ra.
(ii) Let Л и be a square matrix, and suppose that A has the form
A =
An A12
A21 A22
If Aii,A12,i4.2i,-A22 all have the same dimension and satisfy A11A21 = A2iAnt then
det(A) = det(^u^22 - A21A12). Furthermore, if An is nonsingular, then det(A) =
det(Au) det(A22 -A2iAulAi2).
Theorem 6.1.2 (Hamilton-Cayley Theorem) Let A € Mn. Then xa{A) = 0.
Theorem 6.1.3 (The Rayleigh Principle, see Chapter 6 of [91]) Let A € Mn be a real
symmetric matrix, let Ai = Ai(A) be the largest eigenvalue of A, and let An = \n(A) be
the smallest eigenvalue of A. Each of the following holds.
л\ л Та ИТЛи
(i) Ai = max u Ли = max . lo .
M=i H*> |u|2
/»\ л Та • иГЛи
(п) An = mm xx1 Ли = mm , lo .
|u|=i |u|#o |u|2
Theorem 6.1.4 (Chapter 6 of [91]) Let A = (oy) € Mn be a positive, and let Ai > A2 <
• • • < An be the eigenvalues of A, Then each of the following holds.
(i) Ai has multiplicity one.
(ii) If n > 2, then Ai > |A*| for all i with 2 < i < n.
Theorem 6.1.5 (Chapter 6 of [91]) Let A = (a#) be an n by n real matrix and let
A+ = (Ы). Then maxi<i<n{|A?(4)|} < maxi<i<n{|Ai(A+)|}.
Theorem 6.1.6 Let A = (а#) € M+ be such that if for any i ф j, either ац > 0, or there
exist *i, t2i • • • , tr such that aitl > 0, atlt2 > 0, • • •, atrj > 0, then (J + A)n_1 is positive.
Proof If Л is a (0,1) matrix, then the assumption says that D(A), the associated digraph
of A (see Definition 1.1.1), is a strongly connected digraph, and so for any pair of vertices,
there is a path from one to the other with length at most n—1, which proves the conclusion.
In general, for each r < n — 2, the (i,j) entry of Ar+1 is ?tltt2t— ,$r аИ1<Нхъ * * *0*rj>
Appendix
277
which is positive if and only if one of its terms is positive. Therefore,
d+i*)-i-E(n;1)^>o-
This proves the theorem. []
In Section 4.4, Cauchy-Binet formula is used to prove the Matrix-Tree Theorem. We
state this useful formula here. For a reference of this formula, see [133].
Theorem 6.1.7 (Cauchy-Binet Formula) For integers m > 0,n > 0 and r with 1 < r <
min{m,n}, let A € Mm>* and В 6 M&>m С = AB 6 Mm>n, and let a = (»i,t2,"« ,ir)
and /? = (ji,J29 •ф * >ir) be two r-tuples of indices such that 1 < i\ < ii < • • • < ir < m
and 1 < ji < J2 < • • • < jr < ^. Then
det(A[a|A) = X) det(A[a|7])det(^[7|/?]).
т
6.2 The Term Rank and the Line Rank of a Matrix
Definition 6.2.1 For a matrix A € Bm,n, a line of A is either a row or a column of A.
The line rank of A, denoted A^, is the minimum number of lines that contain all positive
entries of A. Two positive entries of A axe independent if they are not in the same line
of A. The term rank of A, denoted рл, is the maximum number of independent positive
entries in A.
The proposition below follows immediately from the definition.
Proposition 6.2.1 Let А, Б € Bn. Each of the following holds.
(i) If there are permutation matrices P, Q € Bn such that A = PBQ, then Ал = Ав
and pA = рв-
(ii) If A = BT, then Ал = Ав and pA = рв«
Theorem 6.2.1 Let A 6 Bm>n. The following are equivalent.
(i) \a < m.
(ii) pA < m.
(iii) For some integers p and q with 1 < p < m and 1 < q < n and with p + g = n + 1,
A contains a 0pXg as a submatrix.
Proof By Definition 6.2.1, (i) and (iii) axe equivalent. To see that (ii) and (iii) axe
equivalent, first observe that if m < n, then let
A=\ A }.
278
Appendix
It follows that pa < m ^=» рд<п and that A has a Opx(n-P+i) submatrix <=$ Л has a
OpX(n-p-{-i) submatrix. Therefore it suffices to prove that (ii) and (iii) are equivalent when
m = n.
Note that (ii) and (iii) are equivalent if m = n = 1. Assume that m = n > 1.
If A has a Opxg as a submatrix with p + q — m + 1, then the p rows containing this
Opxg submatrix has at most m — </ = p— 1 non zero columns, and so it is impossible for A
to have p positive entries among these p rows such that no two of these p positive entries
are in the same line. Hence pa < m.
Now assume that pA < rnt that (ii) and (iii) are equivalent for smaller values of m,
and that А ф 0.
Since А ф 0, we may assume that ац > 0 for some 1 < i,j < m. Let A(i\j) denote
the matrix obtained from A by deleting the row and column of A containing a#. Then
PA(i\j) < m — 1. By induction, A(i\j) has a 0plXqi as a submatrix, for some pi,gi with
P! + qx — m and 1 < Pi,^i < m — 1. By Proposition 6.2.l(i), we may assume that
A =
X 0
Z Y
where X € BPl>Pl, Y € Bm_Pl>m_Pl and Z € Bm_pliPl. Since рл < m, either p* < Pi
or py < m—pi. Without loss of generality, we assume that px < Pi- By induction, X
contains a 0p2Xg2 as a submatrix for some 1 <Р2,Ц2 <Pi with Р2 + ^2 = Pi 4-1. It follows
that A has a 0P2x(g2+m-pi) as a submatrix, where рг + (#2 + яг — p\) = m + 1. Thus the
equivalence between (ii) and (iii) now follows by induction. []
Theorem 6.2.2 (Konig, [148]) For any A fc &mtTi) Ал = рл-
Proof By Proposition 6.2.1(ii), we may assume that m < n.
If all positive entries of A are contained in \a lines, then each of these lines can contain
at most one independent positive entry of A, and so \a > Pa- Therefore, it suffices to
show \a < PA»
By Theorem 6.2.1, we may assume that Xa < m. Suppose that A has e rows and /
columns, with e + / = A^, which contain all the nonzero entries of A. By Proposition
6.2.1, we may assume that the first e rows and the first / columns of A contain all nonzero
entries of A, and so
A =
X Y
Z W
where X € Be>/, Y € Be,n-/, Z € Bm-e,/ and W =
If we can show py = e, then by Proposition 6.2.1(H), the same augment yields pz = /,
and so pA > Py + Pz — e + / = Ал, as desired. Thus we only need to show py = e.
Appendix
279
Suppose e > 0. Then e = \a - / < n — /. If py < e, then by Theorem 6.2.1, py < e.
As W = 0m_e>n_/ and by the definition of Aa> Xa < f + Ay < / + e, a contradiction. Q
6.3 Graph Theory
A graph G consists of a nonempty set V(G) of elements called vertices, and a set E(G)
of elements called edges, and a relation of incidence that associates with each edge e two
vertices и and v, called the ends of e. Sometimes a graph G with vertex set V = V(G) and
edge set E = E(G) is denoted G^iS), to indicate the vertex and edge sets. If an edge e
has ends u, v, then e is incident with it and v, and u and v are adjacent to each other. In
this case we write e = (гш) or e = uv. An edge with identical ends is a /oop, and one with
distinct ends is a link Two or more edges with the same pair of vertices as their common
ends are multiple edges. A graph G is simple if G does not have loops nor multiple edges.
Given graphs G and Я, if У(Я) С V(G), E(H) С #(G) and for each edge e € E(H),
the ends of e in Я are the same ends of e in G, then Я is a subgraph of G, and 6? a
supergraph of Я. К V(G) = У(Я) and Я С G, then Я is a spanning subgraph of G.
Let G = G(V,?7) be a graph, and 5 С .E(G) be an edge subset. The subgraph
Я = H(V, S) of G with V being the set of vertices in G that are incident with an edge
in S is the subgraph induced by the edge set 5, and will be denoted by G[S].
Let G = G(V,.E7) be a graph, and Я С V[G) be a vertex subset. The subgraph
Я = Я (Я, ??') of G with E' be the set of edges in G whose ends are in R is the subgraph
induced by the vertex set Я, and will be denoted by G[R].
Let ж and у be vertices of a graph G. An (re, y)-walk in G is a sequence
W = {voie1,Viie2iv2i-- ,Ук-1,ек,ьк},
where a: = vo, vi, • • • , vk = t/ are in V(G), ei, • • • ,e& are in ^(G), and Vf_i and Vi are the
ends of ei, 1 < i < к. The vertices vi, • • • ^-х are internal vertices of W. The /еш#Л of
Ж is the number of edges in W, namely, |??(W)| = к. We allow к = 0 and so vo itself is
a walk of length zero.
A walk W is a trail if the edges eb • • • ,е& are all distinct, and a jHztfi if all vertices
vo, • • • , v* are distinct. We then define (ar,«/)-irmfe and (x,y)-paths similarly. A trail with
vo = Vk is a c/osed trat/. A closed trail with the vertices vo = v*, vi, • * • , v*_i being distinct
is a cs/c/e. The girth of a graph G is the shortest length of a cycle of G.
The degree of a vertex v in a graph G denoted by do(v), is the number of edges in
G that are incident with v, where a loop counts as two edges. The maximum and the
minimum degree of the vertices of a graph G are denoted by A(G) and 6(G), respectively.
A graph G is r-regular if A(G) = 6(G) = r. Theorem 6.3.1 below follows by counting the
incidences of a graph in different ways.
280
Appendix
Theorem 6.3.1 ([115]) Let G be a graph, then
? dG(v) = 2\E(G)\.
veV{G)
A graph G is planar if G can be drawn on the plane so that no two edges intersect.
The next theorem can be derived from the Euler Polyhedron Formula and Theorem 6.3.1.
Theorem 6.3.2 ([115]) Let G be a simple planar graph. Then
|?(G)|<3|V(G)|-6.
A simple graph on n vertices is the complete graph on n vertices, denoted Kni if every
pair of distinct vertices are adjacent. A maximal complete subgraph Я of a graph G is
called a clique if Я is isomorphic to a complete graph. The clique number of a graph G,
denoted cj(G), is the maximum к such that G has Kk as a subgraph.
The chromatic number of a graph G, denoted x(G), is the minimum number A; such
that the vertices of G can be colored with A; distinct colors so that no two vertices with
the same color are adjacent in G. A subset X С V(G) is called an independent set of G
if no two vertices in X are adjacent in G. The independence number of G, denoted a((7),
is the maximum cardinality of an independent subset of G. Immediately following these
definitions, we have the following result.
Theorem 6.3.3 ([115]) Let G be a graph. Then
X(G)a(G) > |V(G)|, and a(G) = w(Gc).
Let G and Я be two vertex disjoint simple graphs. The (disjoint) union of G and Я,
denoted by G U Я, is the graph with vertex set V(G) U V(#) and edge set E(G) U ?(#).
The jVwn of G and Я, denoted by G V Я, is the simple graph obtained from G U Я by
adding all possible additional edges that join a vertex in G with a vertex in H.
A graph G is connected if V(G) has only one equivalence class. Note that G is connected
if and only if for every pair of vertices а:, у € V(G), G has an (ж, t/)-path.
A digraph (directed graph) D is obtained from a graph G by assigning each edge
e € ??(G) a direction. We call D an orientation of G. If e has w and v as ends and if e is
oriented from и (tatf) to v (head), then we denote the oriented e by (u,v). The oriented
edges in a digraph D are called arcs. We sometimes denote a directed graph D by D(V, E)
to indicate the vertex set V and the arc set E of D. Loops in a digraph are defined similar
to those in a graph. But two or more arcs with the same heads and the same tails are
multiple arcs. For a vertex v € V(D), we denote the number of arcs in D with v as a head
by dp(v), called the indegree of v in D. Similarly, the number of arcs in D with v as a tail
is denoted by d^(v), called the outdegree ofviaD. The sum of d^(v) and d^(v) is the
Appendix
281
degree of v in D, denoted by cfo(v). The subscript D may be omitted when the digraph
D is understood in the context. Similar to the undirected graph case, the following can
be obtained by counting |J5?(D)| in different ways.
Theorem 6.3.4 Let D be a digraph, then
E daM= E da(v) = \E(D)l
veV(D) v€V(D)
For ж, у € V(D), a directed (x, y)-waUz (or (ж, 2/)-diwalk) in D is a walk as defined above,
with an additional requirement that each e% be directed from Vi-i to V{. Sometimes we use
the notation T = v\ -* V2 -* •••-»• Vk to denote a directed walk T which starts from v\
and ends at v*, where ^ ->• v«+i indicates that the arc (viy vi+i) is in the walk Г. Directed
trails, paths, cycles in a digraph D are defined similarly.
A digraph D is strong if for any pair of vertices u, v € V(D), D has a directed (u, v)-
walk. A maximal strong subdigraph of D is called a sfrxm^ component of D. We also say
that a digraph D is weakly connected if the underlying graph of D, obtained from D by
erasing all the directions on the arcs of D, is a connected graph.
Index
(1-3) property 227
(3-1) property 227
1-factor 219
Г-colorable 205
Г-extendible 211
(r,b)-coloring205
(L*, ^-decomposition 175
(m, fc)-cycle 89
(r,$)-graph5
(v,fc,A)-BIBD 169
(v,M)-SBIBD169
acyclic 234
adjacency matrix 1
reduced 2
adjacent 279
admittance matrix 3
agree with the blocks of the matrix 261
arc 280
associated digraph 1
b-solution 200
balanced incomplete block design 169
band graph 251
BIBD 169
bipartite decomposition 171
bipartite digraph representation 224
bisimplicial 246
block 168, 261
irreducible 143
trivial 143
Boolean matrix 101
multiplication and addition 101
Boolean rank 150
branch 55
canonical transformer 104
characteristic
level 267
Segre 265
Wyre 265
characteristic equation 161
characteristic polynomial 4, 275
chordal 246
chromatic number 205, 280
circular period 127
clique 280
clique number 209, 280
cocycle space 199
collapsible 200
color class 204
column sum vector 71
combined graph 224
compact 81
companian matrix 161
complement 82
fully 82
complementary acyclic 234
complementary term rank 235
complementary triangular 234
completablc 250
283
284
Index
complete (mi, m2> • • • , mt )-decomposition
174
complete fc-equipartite 86
complete graph 280
completion 250
nonnegative 250
positive 250
conference graph 193
confundable 181
contraction 55
convergence
index 102
period 102
corresponding homogenous equation 161
cospectral graph 20
cospectrally rooted 22
cover 167
cyclable 198, 199
cycle 199, 279
cycle space 199
cyclic vertex 55
cyclically connected 257
cyclically d-partite 102
decomposable
nearly 58
partly 48
decomposition
{Lu Dt) 175
complete (m1,m2, • - • ,mt) 174
definite Hermitian 249
degree 279
maximum 279
minimum 279
density 57
design
t-design 168
balanced incomplete block design 169
symmetric balanced incomplete block
design 169
diagonal 49
nonzero 49
diagonal dominant 254
diagonally similar 219
difference equation 161
digraph 280
fc-cyclic 79
cyclically connected 257
Eulerian 80
minimally strong 54
primitive 107
square bipartite 238
strong 281
weakly connected 281
weighted 217
weighted associate 163
directed (rr,y)-walk 281
disjoint union 280
distinguished vertex 266
doubly stochastic matrix 77
doubly stochastic type 79
edge 279
end 279
equation
characteristic 161
corresponding homogenous 161
difference 161
equivalence normal form 52
essentially different 236
Eulerian 197, 204
Eulerian digraph 80
Eulerian vector 199
even 197
exponent
fully indecomposable 136
Index
285
Hall 142
primitive 107
strict fully indecomposable 137
strict Hall 142
weak fully indecomposable 145
weak Hall 145
weak primitive 145
extend 250
Extremal Matrix problem 111
fish 194
follow 251
forbidden pair 228
FVobenius normal form 50
Probenius number 99
Frobenius problem 99
fully complement 82
fully indecomposable 49
fully indecomposable exponent 136
strict 137
p-inverse 224
^-inverse graph 224
maximum 226
minimum 226
G-partial matrix 250
G-partial nonnegative 250
G-partial positive 250
Gauss elimination process 245
generalized composition 22
generalized eigenspace 266
generalized inverse 224
Gersgorin disc 255
girth 279
graph 279
band 251
chordal 246
combined 224
completable 250
complete 280
conference 193
connected 280
cospectral 20
directed 280
^-inverse 224
girth 279
Jordan 265
^-friendship 193
line 17
nonnegative-completable 250
perfect 181, 246
perfect elimination bipartite 246
planar 280
r-regular 279
reduced 262
rooted 22
singular 266
strongly regular 190
total 17
weighted bipartite 217
group chromatic number 206
Hadamard matrix 231
Hall exponent 142
strict 142
weak 145
Hall matrix 142
handle 182
head 280
Hermitian 249
high 267
homogenous solution 162
imprimitive 102
imprimitive parameters 144
imprimitive standard form 105
in-incidence matrix 19
incidence 279
286
Index
incidence matrix 2, 167
oriented 2
incident 279
indecomposable
fully 49
indegree 280
independence number 181, 280
independent 277
independent set 280
independent vertex set 181
index 266
index of convergence 102
index of imprimitivity 102, 105
index of maximum density 125
induced subgraph 279
interchange 74
internal vertex 55, 279
invariant 75
irreducible 48
irreducible block 143
join 280
Jordan basis 266
nonnegative 266
Jordan chain 266
nonnegative 266
Jordan graph 265
fc-colorable 204
fc-critical 205
^-cyclic digraph 79
A:-diameter 175
^-friendship graph 193
Kronecker product 24
kth lower multi-exponent of D 130
kth upper multi-exponent of D 130
Laplace matrix 3
Laplace matrix of a graph 3
length 56
length 279
level characteristic 267
level diagram 266
line 277
line graph 17
line rank 277
link 279
local switching in G with respect to тс 23
loop 279, 280
Af-matrix 263
majorized by 72
matching 167
matrix
G-partial 250
G-partial nonnegative 250
G-partial positive 250
Af-matrix 263
acyclic 234
adjacency 1
admittance 3
Boolean 101
companian 161
complementary acyclic 234
definite Hermitian 249
diagonal dominant 254
doubly stochastic 77
essentially different 236
Eulerian 197, 204
even 197
fully decomposable 49
Hadamard 231
Hall 142
Hermitian 249
imprimitive 102
in-incidence 19
incidence 2, 167
Index
287
irreducible 48
Laplace 3
maximal 72
nearly reducible 54
nonnegative 275
nonseparable 197
out-incidence 19
partial Hermitian 249
partly decomposable 48
path 177
permutation 1
positive 275
primitive 102
reducible 48
semidefinite Hermitian 249
separable 197
simple 197
spanning 197
stochastic 77
strict diagonal dominant 254
strictly positive 275
subeulerian 198
supereulerian 198
weakly irreducible 257
maximal matrix 72
maximum ^-inverse 226
maximum density 125
index 125
Maximum Index problem 111
minimal cycle 252
minimally strong digraph 54
minimum ^-inverse 226
minimum polynomial 275
Moore graph 5
multi-colored 172
multiple arcs 280
multiple edges 279
n-derangement 91
nearly decomposable 58
nonnegative completion 250
nonnegative matrix 275
nonnegative-completable 250
nonseparable 197
normal form
equivalence 52
Probenius 50
normalized class 75
optimal representation 182
ordering 251
orientation 280
oriented incidence matrix 2
orthonormal representation 181
value 181
out-incidence matrix 19
outdegree 280
partial Hermitian 249
partial scheme 246
partial transversal 167
particular solution 162
partly decomposable 48
partners 248
path 279
(ar,y)-path279
path matrix 177
perfect 246
perfect edge elimination scheme 246
perfect elimination bipartite graph 246
perfect elimination scheme 245
perfect graph 181
perfect scheme 246
perfect vertex elimination scheme 246
period of convergence 102
permanent 61
permutation 236
288
Index
permutation equivalent 1
permutation matrix 1
permutation similar 1
polynomial
characteristic 275
minimum 275
positive completion 250
positive matrix 275
positive semidefinite completion 249
pre-order 258
primitive 102
primitive digraph 107
primitive exponent 107
problem
Extremal Matrix 111
Probenius 99
Maximum Index 111
Set of Indices 111
Set of Matrices 112
Procedure Redirecting 51
product
Kronecker 24
strong 181
tensor 24
tensor 181
proper vertex fc-coloring 204
r xn normalized Latin rectangle 91
r-regular 30
reach 107
rearrangement 236
trivial 236
recurrence relation 161
reduced adjacency matrix 2
reduced associated bipartite graph 2
reduced graph 262
reducible 48
nearly 54
representation
bipartite digraph 224
optimal 182
orthonormal 181
root 22
rooted forest 266
rooted graph 22
row sum vector 71
SBIBD 169
scheme
partial 246
perfect 246
perfect edge elimination 246
perfect elimination 245
perfect vertex elimination 246
SCR 168
SDR 167
Segre characteristic 265
semi-definite positive 41
semidefinite Hermitian 249
separable 197
Set of Indices problem 111
Set of Matrices problem 112
Shannon capacity 181
simple 197, 279
simplicial vertex 246
single arc 228
singular graph 266
singular vertex 262
solution
homogenous 162
particular 162
source component 90
spanning 197
spanning subgraph 279
spectral radius 12, 24
spectrum 4
Index
289
square bipartite digraph 238
SR167
Steiner 169
stochastic matrix 77
strict diagonal dominant 254
strict fully indecomposable exponent 137
strict Hall exponent 142
strictly positive 275
strong component 281
strong product 181
strongly regular graph 190
subeulerian 198
subgraph 279
submatrix 47
sum vector
column 71
row 71
supercompact 84
supereulerian 198
supergraph 279
symmetric balanced incomplete block
design 169
system of common representatives 168
system of distinct representatives 167
system of representatives 167
^-design 168
tail 280
tensor product 24, 181
term rank 277
topological ordering 90
total graph 17
total support 53
totally unimodular 3
trace 276
trail 279
(rr,y)-trail279
closed 279
transversal
partial 167
tree
v-sink 179
v-source 179
trivial block 143
trivial rearrangement 236
union 280
disjoint 280
upper entry 241
v-sink tree 179
v-source tree 179
vector
nonnegative 275
positive 275
vertex 279
distinguished 266
simplicial 246
singular 262
vertex cover 167
walk 279
weak fully indecomposable exponent 145
weak Hall exponent 145
weak primitive exponent 145
weakly irreducible 257
weight function 62
weighted associate digraph 163
weighted bipartite graph 217
weighted digraph 217
whole chain 73
Wyre characteristic 265
Bibliography
[1] R. Aharoni, A problem in rearrangements of (0,1) matrices, Discrete Math., 30 (1980),
191-201.
[2] N. ALon, Eigenvalues and expenders, Combinatorica, 6 (1986), 83-96.
[3] N. Alon, R. A. Brualdi and B. L. Shader, Multicolored trees in bipartite decompositions
of graphs, J. Combin. Theory, Ser. B, 53 (1991), 143-148.
[4] S. A. Amitsur and J. Levitzki, Minimal identities for algebras, Proc. Amer. Math.
Soc, 1 (1950), 449-463.
[5] M. Behzad, G. Chartrand and E. A. Nordhaus, Triangles in line graphs and total
graphs, Indian J. Math., 10 (1968), 109-120.
[6] N. L. Biggs, Algebraic Graph Theory, Cambridge University Press, 2nd Edition, New
York, (1993).
[7] F. Bien, Constructions of telephone networks by group representatives, Notices Amer.
Math. Soc, 36 (1989), 5-22.
[8] G. Birkhoff, Tres observaciones sobre el algebra lineal, Univ. Nac. Tucuman Rev. Sor.
A, 5 (1946), 147-150.
[9] J. A. Bondy and U. S. R. Murty, Graph Theory with Applications, American Elsevier,
New York, (1976).
[10] R. C. Bose, Strongly regular graphs, partial geometries, and partially balanced designs,
Pacific J. Math., 13 (1963), 389-419.
[11] R. Bott and J. P. Mayberry, Matrices and trees, Economic Activity Analysis, O.
Morganstern, (1954), Wiley, 391-400.
[12] F. T. Boesch, С SufFey and R. Tindell, The spanning subgraph of eulerian graphs, J.
Graph Theory, 1 (1977), 79-84.
291
292 Bibliography
[13] R. Bru and R. Canto and Bit-Shun Tam, Predecessor Property, full combinatorial
column rank, and the height characteristic of an M-matrix, Linear Algebra AppL,
183(1993), 1-22.
[14] A. Brauer, The theorems of Ledermann and Ostrowski on positive matrices, Duke
Math. J., 24 (1957), 256-274.
[15] A. T. Brauer and B. M. Seflbinder, On a problem of partitions, II, Amer. J. Math.,
76 (1954), 343-346.
[16] L. M. Bregman, Certain properties of nonnegative matrices and their permanents,
Soviet Math. Dokl, 14 (1973), 945-949.
[17] R. L. Brooks, On colouring the nodes of a network, Proc. Cambridge Philos. Soc, 37
(1941), 194-197.
[18] W. G. Brown, On the non-existence of a type of regular graphs of girth 5, Canad. J.
Math, 19 (1967), 644-648.
[19] R. A. Brualdi, Some applications of doubly stochastic matrices, Linear and Multilin.
Algebra, 10 (1988), 77-100.
[20] R. A. Brualdi, The Jordan canonical form: an old proof, Amer. Math. Monthly, 94
(1987), 257-267.
[21] R. A. Brualdi, Combinatorially determined elementary divisors, Congressus Numer-
antium, 58 (1987), 193-216.
[22] R. A. Brualdi, Combinatorial verification of the elementary divisors, Linear Algebra
AppL, 71 (1985), 31-47.
[23] R. A. Brualdi, Matrices, eigenvalues, and directed graphs, Linear and Multilin.
Algebra, 11 (1982), 143-165.
[24] R. A. Brualdi, Matrices of zeros and ones with fixed row and column sum vectors,
Linear and Multilin. Algebra, 33 (1980), 159-231.
[25] R. A. Brualdi, Matrices permutation equivalent to irreducible matrices and
application, Linear and Multilin. Algebra, 7 (1979), 1-12.
[26] Brualdi, Introductory Combinatorics, Elsivier-North Holland, New York, (1977).
[27] R. A. Brualdi and P. M. Gibson, Convex polyhedra of doubly stochastic matrices, I,
J. Combinatorial Theory, Ser. A, 22 (1977), 194-230.
Bibliography
293
[28] R. A. Brualdi, J. L. Goldwasser and S. T. Michael, Maximum permanents of matrices
of zeros and ones, J. Combinatorial Theory, Ser. A, 49 (1988), 207-245.
[29] R. A. Brualdi and M. B. Hedrick, A unified treatment of nearly reducible matrices
and nearly decomposable matrices, Linear Algebra AppL, 24 (1979), 51-73.
[30] R. A. Brualdi and A. J. Hoffman, On the spectral radius ^of (0,1) matrices, Linear
Algebra AppL, 65 (1985), 133-146.
[31] R. A. Brualdi and Bolian Liu, A lattice generated by (0,1) matrices, Ars Combinatoria,
31 (1991), 183-^90.
[32] R. A. Brualdi and Bolian Liu, Fully indecomposable exponents of primitive matrices,
Proceedings of MAS, 112 (1991), 1193-1201.
[33] R. A. Brualdi and Bolian Liu, Generalized exponents of primitive directed graphs, J.
Graph Theory, 14 (1990), 483-500.
[34] R. A. Brualdi and Bolian Liu, Hall exponents of Boolean matrices, Czech. Math. J.,
40 (1990), 659-670.
[35] R. A. Brualdi, S. Parter and H. Scheider, The diagonal matrix, J. Math. Anal. AppL,
16 (1966), 31-50.
[36] R. A. Brualdi and J. A. Ross, On the exponent of a primitive nearly reducible matrix,
Math. Oper. Res., 5 (1980), 229-241.
[37] R. A. Brualdi and B. L. Shader, Matrix factorizations of determinants and
permanents, J. Combin. Theory, Ser. A, 54 (1990), 132-134.
[38] R. A. Brualdi and E. S. Solheid, Some extremal problems concerning the square of a
(0,1) matrix, Linear and Miltilin. Algebra, 22 (1987), 57-73.
[39] R. A. Brualdi and E. S. Solheid, On the minimum spectral radius of matrices of zeros
and ones, Linear Algebra AppL, 85 (1986), 81-100.
[40] R. A. Brualdi and E, S. Solheid, Maximum determinants of complementary acyclic
matrices of zeros and ones, Discrete Math., 61 (1986), 1-19.
[41] D. de Caen and D. G. Hoffman, Impossibility of decomposing the complete graph on n
points inton — 1 isomorphic complete bipartite graphs, SIAM J. Disc. Math., 2 (1989),
48-50.
[42] D. Cao, Bounds on eigenvalues and chromatic number, Linear Algebra AppL 270
(1998), 1-13.
29 4 Bibliography
[43] Da Song Cao and Hong Yuan, Graphs characterized by the second eigenvalue, J. Graph
Theory, 17 (1993), 325-331.
[44] D. de Caen and D. Gregory, On the decomposition of a directed graph into complete
bipartite subgraphs, Ars Combinatoria, 23B (1987), 139-146.
[45] P. J. Cameron, Strongly regular graphs, Selected Topics in Graph Theory, L. W.
Beineke and R. J. Wilson, 337-360, Academic Press, (1978).
[46] P. Caniin, Characterization of totally unimodular matrices, Proc. Amer. Math. Soc,
16 (1965), 1068-1073.
[47] P. A. Catlin, A reduction method to find spanning eulerian subgraphs, J. Graph
Theory, 12 (1988), 29-45.
[48] P. A. Catlin, Supereulerian Graphs: A Survey, J. Graph Theory, 16 (1992), 177-196.
[49] Cao, Dasong and Andrew Vince, The spectral radius of a planar graph, Linear Algebra
Appl., 187 (1993), 251-257.
[50] Cao, Ru-cheng and Liu, Bolian, A formula for solutions of linear homogeneous
recurrence with constant coefficients, Math. In Practice And Theory, 3 (1983), 80-82.
[51] Chang, li-Chien, The uniqueness and non-uniqueness of the triangular asssociation
scheme, Sci. Record Peking Math. (New Ser.) 3(1959), 604-613.
[52] Chang, li-Chien, Asssociation scheme of partially balanced designs with parameters,
Sci. Record Peking Math. (New Ser.) 4(1960), 12-18.
[53] C. Y. Chao, On a conjecture of the semigroup of fully indecomposable relations, Czech.
Math. J., 27 (1977), 591-597.
[54] С Y. Chao and M. С Zhang, On the semigroup of fully indecomposable relations,
Czech. Math. J., 33 (1983), 314-319.
[55] G. Chartrand and L. Lesniak, Graphs & Digraphs, Wadsworth, California, (1986).
[56] J. Chen, Sharp bound of the kth eigenvalue of trees, Discrete Math. 128 (1994), 64-72.
[57] Z. H. Chen and H.-J. Lai, Reduction Techniques for Supereulerian Graphs and Related
Topics - A Survey, Combinatorics and Graph Theory'95, (Ku Tlmg-Hsin ed), World
Scientific, Singapore, (1996) 53-69.
[58] F. R. K. Chung, Diameters and eigenvalues, J. Amer. Math. Soc, 2 (1989), 187-196,
Bibliography
295
[59] F. R. K. Chung, Diameters of graphs: odd problems and new results, Congressus
Numerantium, (1987).
[60] M. C. Coiumbic, A note on perfect Gaussian elimination, J. Math. Anal. AppL, 64
(1978), 455-457.
[61] M. C. Coiumbic and G. F. Goss, Perfect elimination and chordal bipartite graphs, J.
Graph Theory, 2 (1978), 155-163.
[62] L. Collatz and U. Sinogowitz, Spektren endlicher grafen, Abh. Math. Sem. Univ.,
Hamburg, 21 (1957), 63-77.
[63] W. S. Connor, Jr., On the structure of balanced incomplete block designs, Ann. Math.
Statist., 23 (1952), 57-71.
[64] C. A. Coulson and G. S. Rushbrooke, Note on the method of molecular orbitals, Proc.
Cambridge Phil. Soc, 36 (1940), 193-200.
[65] D. M. Cvetkovic, The generating function for variations with restrictions and paths
of the graph and self-complementary graphs, Univ. Beograd Publ. Elektrotehn. Fak.,
Ser. Mat. Fiz., 320-328 (1970), 27-34.
[66] D. M. Cvetkovic, Spectrum of the total graph of a graph, Publ. Inst. Math. (Beograd),
16 (30) (1973), 49-52.
[67] D. M. Cvetkovic, Spectra of graphs formed by some unary operations, Publ. Inst.
Math. (Beograd), 19 (33) (1975), 37-41.
[68] D. M. Cvetkovic", Spectra of graphs formed by some unary operations, Publ. Inst.
Math. (Beograd), 19 (33) (1975), 31-41.
[69] D. M. Cvetkovic, On graphs whose second largest eigenvalue does not exceed 1, Publ.
Inst. Math, (beograd) 31 (1982), 15-20.
[70] D. M. Cvetkovic, M. Doob, I. Gutman and A. Torgaser, Recent Results in the Theory
of Graph Spectra, Academic Press, New York, (1989).
[71] D. M. Cvetkovic, M. Doob and H. Sachs, Spectra of Graphs, Academic Press, New
York, (1980).
[72] D. Cvetkovic and S. Simic, On graphs whose second largest eigenvalue does not exceed
&±, Discerte Math. 38 (1995), 213-227.
[73] C. Delorme and P. Sole, Diameter, covering index, covering radius and eigenvalues,
Europ. J. Combin., 12 (1991), 93-108.
296
Bibliography
[74] G. A. Dirac, On rigid circuit graphs, Abh. Math. Sem. Univ. Hamberg, 25 (1961),
71-76.
[75] J. Donald, J. ELwin, R. Hager and P. Salomon, A graph theoretic upper bound on
the permanent of a nonnegative integer matrix, I, Linear Algebra Appl., 61 (1984),
178-198.
[76] J. Dinitz and D. Stinson, A Brief Introduction to Design Theory, in Contemporary
Design Theory, J. Dinitz and D. Stinson eds., John Wiley & Sons, New York (1992).
[77] A. L. Dulmage and N. S. Mendelson, Graphs and matrices, Graph Theory and
Theoretical Physics, F. Harary, 167-277, Academic Press, (1967).
[78] H. Dym and I. Gohberg, Extensions of band matrices with band inverse, Linear
Algebra Appl, 36 (1981), 1-24.
[79] G. P. Egorycev, A solution of Van der Waerden*s permanent problem, Dokl. Akad.
Nank SSSR (in Russian), 258 (1981), 1041-1044.
[80] H. Ehlich, Determinant nabshatzungen fur binare matrizen mit n = 3 mod 4, Math.
Zeitchr., 84 (1964), 438-447.
[81] M. Ellingham and X. Zha, The spectral radius of graphs on surfaces, J. Combin.
Theory, Ser. B, to appear.
[82] P. Erdos, С. Ко and R. Rado, Intersection theorems for systems of finite sets, Quart.
J. Math. Oxford, 12 (1961), 313-320.
[83] P. Erdos and A. Renyi and V. T. S6s, On a problem of graph theory, Studia Sci. Math.
Hungar., 1 (1966), 215-235.
[84] P. Erdos and H. Sachs, Reguldre graphen gegebener taillenweite mit minimaler knote-
nenzahl, Wiss. Z. Univ., Halle, 12 (1963), 251-257.
[85] D. I. Falikman, A proof of Van der Waerden's conjecture on the permanent of a doubly
stochastic matrix, Mat. Zametki (in Russian), 29 (1981), 931-938.
[86] D. G. Feingold and R. S. Varga, Block diagonally dominant matrices and
generalizations of the Gerschgorin circle theorem, Pacific J. Math., 12 (1962), 1241-1250.
[87] M. Fiedler and V. Ptak, Generalized norms of matrices and the location of the
spectrum, Czech. Math. J., 12 (1987), 558-571.
[88] M. Fiedler and V. Ptak, Cyclic products and an inequality for determinants, Czech.
Math. J., 419 (1969), 428-450.
Bibliography 297
[89] D. Foata, A combinatorial proof of JacobVs identity, Ann. Discrete Math., 6 (1980),
125-135.
[90] Т. Н. Foregger, An upper bound for the permanent of a fully indecomposable matrix,
Proc. Amer. Math. Soc, 49 (1975), 319-324.
[91] J. N. Franklin, Matrix Theory, Prentice Hall, Inc. Englewood Cliffs, New Jersey,
(1968).
[92] S. Frieland, The maximal eigenvalue of 0-1 matrices with prescribed number of 1 's,
Linear Algebra Appl., 69 (1985), 33-69.
[93] G. Frobenius, Uber matrizen aus nicht negativen elementen, Sitzber, Akad. Wiss.,
(1912).
[94] D. R. Fulkerson and D. J. Gross, Incidence matrices and interval graphs, Pacific J.
Math., 15 (1965), 835-855.
[95] D. Gale, A theorem onflows in networks, Pacific J. Math., 7 (1957), 1073-1082.
[96] F. R. Gantmacher, Application of the Theory of Matrices, Vol II, Interscience, New
York, (1959).
[97] A. M. H. Gerards, A short proof of Tutte's characterization of totally unimodular
matrices, Linear Algebra Appl., 114/115 (1989), 207-212.
[98] S. A. Ger sgorin, Uber die abgrenzung der Eigenwerte einer matrix, Izv. Akad. Nauk
SSSR Ser. Fiz-Mat., 6 (1931), 749-754.
[99] P. M. Gibson, A lower bound for the permanent of a (0,l)-matrix, Proc. Amer. Math.
Soc, 33 (1972), 245-246.
[100] D. Gregory, J. Shen and B. Liu, On the spectral radius of bipartite graphs, to appear.
[101] C. D. Godsil and B. D. Mckay, Constructing cospectral graphs, Aequat. Math, 25
(1982), 257-268.
[102] J. M. Goethals and J. J. Seidel, Strongly regular graphs derived from combinatorial
designs, Canad. J. Math., 22 (1970), 597-614.
[103] M. C. Golumbic, Algorithmic Graph Theory and Perfect Graphs, Academic Press,
New York, (1980).
[104] R. L. Graham and H. O. Pollak, On embedding graphs in squashed cubes, Lecture
Notes in Math. Vol 303, 99-110, Springer-Verlag, 1972.
298
Bibliography
[105] R. L. Graham and H. O. Pollak, On the addressing problem for loop switching, Bell
Syst. Tech. J., 50 (1971), 2495-2419.
[106] D.A. Gregory, S.J. Kirkland and N.J. Pullman, A bound on the exponent of a
primitive matrix using boolean rank, Linear Algebra Appl. 217 (1995), 101-116.
[107] R. Grone, С R. Johnson, E. M. Sa and H. Wolkowicz, Positive definite completions
of partial hermitian matrices, Linear Algebra Appl., 58 (1984), 109-124.
[108] M. Grotschel, L. Lovasz and A. Schrijver, The ellipsoid method and its consequences
in combinatorial optimization, Combinatorica, 1 (1981), 169-197.
[109] M. Grotschel, L. Lovasz and A. Schrijver, Polynomial algorithms for perfect graphs,
Topics on Perfect Graphs, С Berge and V. Chvatal, 99-110, North-Holland, (1984).
[110] Guo, Zhong, The primitive index set of a primitive matrix with positive diagonal
elements, Acta Math. Sinica, 31 (1988), 283-288.
[Ill] J. Hadamard, Resolution dune question relative and determinants, Bull. Sci. Math.,
17 (1993), 240-246.
[112] P. Hall, On representatives of subsets, J. London Math. Soc, 10 (1935), 26-30.
[113] M. Hall, Combinatorial Theory, (2nd edition), Wiley, New York, (1986).
[114] G. H. Hardy, J. E. Littlewood and G. Polya, Inequalities (2nd Edition), Cambridge,
London, (1952).
[115] F. Harary, Graph Theory, Addition-Wesley, London, (1969).
[116] H. B. Mann and H. J. Ryser, Systems of distinct representations, Amer. Math.
Monthly, 60 (1953), 397-401.
[117] R. E. Hartwig and M. Neumann, Bounds of the exponent of primitive which depend
on the spectrum and the minimal polynomial, Linear Algebra Appl., 184 (1993), 103-
122.
[118] D. J. Hartfiel, A simple form for nearly reducible and nearly decomposable matrices,
Proc. Amer. Math. Soc, 24 (1970), 388-393.
[119] B. R. Heap and M. S. Lynn, The structure of powers of nonnegative matrices, SIAM
J. Appl. Math., 14 (1966), 610-639.
[120] W. C. Herndon and M. L. Ellzey, Isospectral graphs and molecules, Tetrahedron, 31
(1975), 99-107.
Bibliography 299
[121] M. Hofemeister, Eigenvalues of trees, Linear Algebra AppL, 260 (1997), 43-59.
[122] A. J. Hoffman, On graphs whose least eigenvalue exceeds — 1 — y/2, Linear Algebra
AppL, 16 (1977), 153-165.
[123] A. J. Hoffman, — 1 - л/2, Combinatorial Structures and their Applications, 173-176,
Gordon and Breach, (1970).
[124] A. J. Hoffman, The eigenvalues and colorings of graphs, Graph Theory and Its
Applications, F. Harary, 79-91, Academic Press, (1970).
[125] A. J. Hoffman, On the polynomial of a graph, Amer. Math. Monthly, 70 (1963),
30-36.
[126] A. J. Hoffman, On the uniqueness of the triangular association scheme, Ann. Math.
Statist., 31 (1960), 492-497.
[127] A. J. Hoffman and J. B. Kruskal, Integral boundary points of convex polyhedra, Ann.
Math. Studies, Princeton University Press, Princeton, 38 (1956), 223-246.
[128] A. J. Hoffman, P. Walfe and M. Hofmeister, A note on almost regular matrices
Linear Algebra AppL, 226-228 (1996), 105-108.
[129] J. G. Holland and R. S. Varga, On powers of nonnegative matrices, Proc. Amer.
Math. Soc, 9 (1958), 631-634.
[130] Hong Yuan, On the spectra of unicycle graphs, J.of East China Normal
University (natural science edition), 1 (1986), 31-34.
[131] Hong Yuan, The kth largest eigenvalue of a tree, Linear Algebra AppL, 73 (1986),
151-155.
[132] Hong Yuan, Bounds on spectral radius of graphs, Linear Algebra AppL, 108 (1988),
135-139.
[133] Roger A. Horn and Charles R. Johnson, Matrix Analysis, Cambridge University
Press, Cambridge, (1985).
[134] D. F. Hsu, On disjoint multipaths in graphs, groups and networks, IEICE
Transactions on Fundamentals, (to appear),
[135] Huang Deode, On circulant Boolean matrices, Linear Algebra AppL, 136 (1990),
107-117.
[136] Huang Qingxue , On the decomposition of Kn into complete m-partite graphs, J.
Graph Theory, 15 (1991), 1-6.
300 Bibliography
[137] Luo Hua and Bolian Liu, A simple algorithm of the maximum g-inverse for a boolean
matrix, J. of South China Normal University (Sci. edition), 1 (1998), 6-11.
[138] F. Jaeger, A note on subeulerian graphs, J. Graph Theory, 3 (1979), 91-92.
[139] Jiang Zhiming and Shao Jiayu On the set of indices for reducible matrices, Linear
Algebra AppL, 148 (1991), 265-278.
[140] C. R. Johnson, Matrix completions problem: a survey, Matrix Theory and
Application, C. R. Johnson, 171-198, Amer. Math. Soc, (1990).
[141] W. B. Jurkat and H. J. Ryser, Matrix factorizations of determinants and permanents,
J. Algebra, 3 (1966), 1-27.
[142] M. Katz, Rearrangements of (0,l)-matrices, Israel J. Math., 9 (1971), 53-72.
[143] Ke Zhao, On the equation of ax + by + cz = n, J. of Sichuan University Math.
Biquarterly(natural science edition), 1 (1955), 1-4.
[144] K. H. Kim-Butler and J. R. Krabill, Circulant Boolean relation matrices, Czech.
Math. J., 24 (1974),
[145] H. H. Kim and F. W. Roush, On inverse of Boolean matrices, Linear Algebra AppL,
22 (1978), 247-262.
[146] G. Kirchhoff, Uber die auflosung der gleichungenm auf welche man bei der Unter-
suchung der Linearen verteUung galvanischer stroml gefuhrt wird, Ann. Phys. Chem.,
72 (1847), 497-508.
[147] D. Konig, Vonalrendszerek is detrimindnsok, Mat. Termeszettud. Ertestio., 33
(1915), 221-229.
[148] D. Konig, Theorie der Endlichen und Unendlichen Grahen, , New York, (1950).
[149] C. W. H. Lam and J. H. van Lint, Directed graph with unique paths of fixed length,
J. Combin. Theory, Ser. B, 24 (1978), 331-337.
[150] H. A. Laue, A graph theoretic proof of the fundamental trace identity, Discrete Math.,
69 (1988), 121-198.
[151] C. W. Lam, How reliable is a computer-based proof, The Math. Intelligence, 12
(1990), 8-12.
[152] H.-J. Lai and X. Zhang, Group chromatic number of a graph, submitted.
Bibliography 301
[153] H.-J. Lai and X. Zhang, Group chromatic number of a graphs without K$-minors,
submitted.
[154] C. G. Lekkerkerker and J. Boland, Representation of a finite graph by a set of
intervals on the real line, Fund. Math., 51 (1962), 45-64.
[155] G. S. Leuker, D. J. Rose and R. E. Tarjan, Algorithmic aspects of vertex elimination
on graphs, SIAM J. Computing, 5 (1976), 226-283.
[156] M. Lewin, On a diophantine problem of Frobenius, Bull. J. London Math. Soc, 5
(1972), 75-78.
[157] M. Lewin and Y. Vitek, A system of gaps in the exponent set of primitive matrices,
Illinois J. Math., 25 (1981), 87-98.
[158] M. Lewin, A bound for a solution of a linear diophantine problem, J. London Math.
Soc. II. Ser. (2), 6 (1972), 61-69.
[159] M. Lewin, Bounds for exponents of doubly stochastic primitive matrices, Math. Z. ,
137 (1974), 21-30.
[160] Li Ching, A bound on the spectral radius of matrices of zeros and ones, Linear
Algebra AppL, 132 (1990), 179-183.
[161] Q. Li and K. Feng, On the largest eigenvalue of Graphs, Acta Math. Appl. Sinica, 2
(1979), 169-175.
[162] J. H. Van Lint, Combinatorial Theory Seminar in Eind Hoven University of
Technology, Lecture Notes in Math Vol. 382, 47-49, Springer-Verlag, New York, 1970.
[163] Li Qiao, On the eight topics of matrix theory, Shanghai Sci.and Tech. Press,
Shanghai, (1988).
[164] Y. Lin and J. Yuan, The minimum fill-in number problem for matrices and graphs,
Oper. Res. Strategy, 1 (1992), 515-522.
[165] Lin Guoning and Zhang Fuji On the characteristic polynomial of directed line
graph and a type of cospectral directed graph, Kexue TongBao(Chines Sci. Bulletin),
22(1983), 1348-1350
[166] Lin Guolin and Zhang Fuji, On the characteristic polynomial of directed line graph
and a type of cospectral directed graph, Kexue TongBao (Chines Sci. Bulletin), 2107
(1996), 1996.
302
Bibliography
[167] Bolian Liu, Some asserting theorems for generalized inverse of boolean matrix, J. of
Math. (Chinese), 8 (1988), 189-190.
[168] Bolian Liu, On the distribution of exponent set of primitive matrix, Acta Math.
Sinica, 32 (1989), 803-809.
[169] Bolian Liu, A matrix method to solve linear recurrences with constant coefficients,
Fibonacci Quarterly, Feb. (1992), 1-9.
[170] Liu Bolian, On fully indecomposable exponent for primitive boolean matrices with
symmetric ones, Linear and Multilinear Algebra 31 (1992), 131-138.
[171] Bolian Liu, Weak exponent of irreducible matrices, J. of Mathematical Research and
Exposition, 14 (1994), 35-41.
[172] Bolian Liu, On sharp bounds of the spectral radius of graphs, Univ. Beograd Publ.
Electrotechn, Fak. Ser Mat. 9 (1998), 55-59.
[173] Bolian Liu, On the (Ktу Kt)-decomposed number, (to appear).
[174] Bolian Liu, A graphical method to find generalized inverse of Boolean matrices, (to
appear).
[175] Bolian Liu, On an extremal problem concerning (0,1) matrices, (to appear).
[176] Liu Bolian, On exponent of indecomposability for primitive boolean matrices, Linear
Algebra Appl. (to appear).
[177] Bolian Liu and B. D. Mckey and N. Womold and Zhang Kemin, The exponent set of
symmetric primitive (0tl)-matrices with zero trace, Linear Algebra Appl., 136 (1990),
107-117.
[178] Bolian Liu and Qiaoliang Li, On a conjecture of strictly completely irreducible index
of primitive matrix, Sci. In China, Series A, 25 (1995), 920-926.
[179] Bolian Liu and Qiaoliang Li, Exact upper bound of convergence index for boolean
matrices with non-zero trace, Advances in Math., 23 (1994), 331-335.
[180] Bolian Liu and Qiaoliang Li, On a conjecture about the generalized exponent of
primitive matrices, J. of Graph Theory, 18 (1994), 177-179.
[181] Liu Bolian, Li Qiaoliang and Zhou Bo, The distribution of convergent indices of
boolean matrices with d diagonal elements, J. Sys. Sci. & Math. Scis. 18 (1998), 154-
158.
Bibliography 303
[182] Bolian Liu and Shao, Jiayu, Completely description of the set of primitive extremal
matrix, Sci. Sinica (Sci. In China),Series A, 1 (1991), 5-14.
[183] Bolian Liu and Shao Jiayu, The index of convergence of boolean matrices with
nonzero trace, Advances in Math., 23 (1994), 322-340.
[184] Liu Bolian, Shao Jiayu and Wu Xiaojun, The exact upper bounds for index of
convergence of doubly stochastic matrices , Acta. Math. Sinica , 38 (1995), 433-441.
[185] Liu Bolian and Zhou Bo, A system of gaps in generalized primitive exponents,
Chinese Ann. Math. 18A (1997), 397-402.
[186] Liu Bolian and Zhou Bo, The kth upper multiexponents of primitive matrices, Graphs
and Combinatorics 14 (1998), 155-162.
[187] Bolian Liu and Bo Zhou Some results on the compact graph and supercompact graph,
(to appear).
[188] L. Lovasz, An Algorithmic Theory of Numbers, Graphs and Convexity, SIAM,
Philadelphia, (1986).
[189] L. Lovasz, On the Shannon capacity of a graph, IEEE Trans. Inform. Theory, 17-25
(1979), 1-7.
[190] L. Lovasz, A characterization of perfect graphs, J. Combin. Theory, Ser. B, 13 (1972),
95-98.
[191] L. Lovasz and M. D. Plummer, Matching Theory, Elsivier Science, , (1986).
[192] H. B. Mann and H. J. Ryser, Systems of distinct representatives, Amer. Math.
Monthly, 60 (1953), 397-401.
[193] Miao Zhenke and Zhang Kemin, The exponent set of undirected graph with minimum
odd cycle length r, J. Of Nanjing University Math. Biquarterly, 9 (1992), 29-36.
[194] H. Mine, Nearly decomposable matrices, Linear Algebra Appi., 5 (1972), 181-187.
[195] H. Mine, On lower bounds for the permanents of (0,l)-matrices, Proc Amer. Math.
Soc, 22 (1969), 117-123.
[196] H. Mine, Upper bounds for the permanents of (0,l)-matrices, Bull. Amer. Math.
Soc, 69 (1963), 789-791.
[197] H. Mine, Permanents, John Wiley & Sons, Reading, Massachusetts, (1978).
[198] H. Mine, Theory of Permanents, LAA., 21(1987) 109-148.
304 Bibliography
[199] H. Mine, Nonnegative Matrices, John Wiley & Sons, New York, (1988).
[200] P. Miroslav, On graphs whose second largest eigenvalue does not exceed y/2— 1, Univ.
Beograd, Publ. Elektrotechn, Fak. Ser Mat. 4 (1993), 73-78.
[201] B. Mohar, Laplacian Matrices of Graphs, Studia Scient. Math. Hung., 1 (1989),
153-156.
[202] B. Mohar, Laplacian Matrices of Graphs, Stud. Phys. Theoret. Chem. 63, 1-8,
Elsevier Science, (1989).
[203] B. Mohar, The laplacian spectrum of graphs, preprint ser., Dept. of Math, Univ. E.
K. Ljubljana, 26 (1988), 353-382.
[204] J.W. Moon and L. Moser, Almost all (0,l)-matrices are primitive, Studia Scient.
Math. Hung., 1 (1966), 153-156.
[205] J. W. Moon and N. J. Pullman, On the power of tournament matrices, J. Combin.
Theory, 3 (1967), 1-9.
[206] A. Mowshowitz, The group of a graph whose adjacency matrix has all distinct
eigenvalues, Proof techniques in Graph Theory, F. Harary , 109-110, Academic Press,
(1969).
[207] S. Neufeld and Shen Jian, Some results on generalized exponents, J. Graph Theory
28 (1998), 215-225.
[208] A. Neumaier, The second largest eigenvalue of a tree, Linear Algebra Appl., 46
(1982), 9-25.
[209] Pan Qun, The exponent set of class of nearly decomposable matrices, Appl. Math.
A J. of Chinese University, 6 (1991), 401-405.
[210] G, W. Peck, A new proof of a theorem of Graham and Pollak, Discrete Math., 49
(1984), 334-328.
[211] O. Perron, Zur theorie der matrizen, Math. Ann., 64 (1907), 248-263.
[212] R. J. Plemous, Generalized inverse of Boolean relation matrices, SIAM Appl. Math.,
20 (1971), 426-433.
[213] H. Poincar'e, Second complement a Idnalysis situs, Proc. London Math. Soc, 32
(1901), 277-308.
[214] W. R. Pulleyblank, A note on graphs spanned by eulerian subgraphs, J. Graph
Theory, 3 (1979), 309-310.
Bibliography
305
[215] R. Rado, A theorem on independence relations, Quart. J. Math. (Oxford), 13 (1942),
83-89.
[216] D. Richman and H. Schneider, On the singular graph and the Weyr characteristic
of an M-matrix, Aequationes Math., 17 (1978), 208-234.
[217] J. B. Roberts, Notes on linear forms, Proc. Amer. Math. Soc. 7 (1956), 456-469.
[218] D. J. Rose, Triangulated graphs and the elimination process, J. Math. Anal. Appl.,
32 (1970), 597-609.
[219] J. A. Ross, On the exponent of a primitive, nearly reducible matrix, П, SIAM J. Alg.
Disc. Math., 3 (1982), 359-410.
[220] U. G. Rothblmn, Algebraic eigenspaces of non-negative matrices, Linear Algebra
AppL, 12 (1975), 281-292.
[221] P. Rowlinson, Maximal index of graphs, Linear Algebra AppL, 110 (1988), 43-53.
[222] H. J. Ryser, Combinatorial Mathematics, MAA, Washington, (1963).
[223] H. J. Ryser, Combinatorial properties of matrices of zeros and ones, Canad. J. Math.,
9 (1957), 317-377.
[224] H. J. Ryser, Maximum determinants in combinatorial investigations, Canad. J.
Math., 8 (1956), 245-249.
[225] H. Sachs, Regular graphs with given girth and restricted circuits, J. London math.
Soc, 38 (1963), 423-429.
[226] H. Sachs, Beziehungen zwischen den in einem graphen enthaltenen Kreisen und
seinem charakeristischen polynom, Publ. Math. Debrecen, 11 (1964), 119-134.
[227] H. Sachs and Uber Teiler, Faktoren und charakteristische polynome von graphen, II,
Wiss, Z. Techn. Hochsch. Ilmenau, 13 (1967), 405-412.
[228] H. Schneider, The influence of the marked reduced graph of a non-negative matrix
on the Jordan form and related properties: a survey, Linear Algebra Appl., 83 (1986),
161-189.
[229] H. Schneider, The elementary divisors associated with 0 of a singular M-matrix,
Proc. Edinburg Math. Soc, 10 (1956), 108-122.
[230] A. Schrijver, A short proof of Minc}s conjecture, J. Combin. Theory, Ser. A, 25
(1978), 80-81.
306
Bibliography
[231] В. Schwarz, Rearrangements of square with non-negative elements, Duke Math. J.,
31 (1964), 45-62.
[232] S. Schwarz, The semigroup of fully indecomposable relations and Hall relations,
Czech. Math. J., 23 (1973), 151-163.
[233] S. Schwarz, On a sharp estimate in the theory of binary relations on a finite set,
Czech. Math. J., 20 (1970), 703-714.
[234] A. J. Schwenk, W. С Herndon and M. L. Ellzey, Jr., The construction of cospectral
composite graphs, Ann. N. Y. Acad. Sci., 319 (1979), 490-496.
[235] A. J. Schwenk and R. J. Wilson On the Eigenvalues of a Graph, In Selected Topics
in Graph Theory, Edited by L. W. Beineke and RJ.Wilson, Academic Press, 1978.
[236] J. J. Seidel, Graphs and two-graphs, In Proc. Fifth Southeastern Conference on
Combinatorics, Graph Theory and Computing, (Boca Raton, FL., 1974), Congressus
Numerantium, 319 (1974), 125-143.
[237] J. Seberry and M. Yamada, Hadamard Matrices, Sequences, and Block Designs, in
Contemporary Design Theory, J. Dinitz and D. Stinson eds., John Wiley & Sons, New
York (1992).
[238] С E. Shannon, The zero-error capacity of a noise channel, IRE Trans. Inform.
Theory, Vol. IT-2, 3 (1956), 8-19.
[239] Jian Shen, A problem on the exponent of primitive digraphs, Linear Algebra AppL,
244 (1996), 255-264.
[240] J. Shen, D. Gregory and S. Neufeld, Exponents of indecomposabUity, linear Algebra
Appl. 288 (1999), 229-241.
[241] Shen Jian and S. Neufeld, Local exponents of primitive digraphs, Linear Algebra
Appl., 268 (1998), 117-129.
[242] Shao Jiayu, On the indices of convergence of irreducible and nearly reducible boolean
matrix, Math. AppL (in Chinese), 5 (1992), 333-344.
[243] Shao Jiayu, The indices of convergence for reducible boolean matrices, Acta. Math.
Sinica, 33 (1991), 13-28.
[244] Shao Jiayu, Bounds on the kth eigenvalue of trees and forests, Linear Algebra Appl.,
149 (1991), 19-34.
Bibliography
307
[245] Shao Jiayu, On the set of symmetrical graph matrix, Sci. Sinica Series A, 9 (1986),
931-939.
[246] Shao Jiayu, Matrices permutation equivalent to primitive matrices, Linear Algebra
AppL, 65 (1985), 225-247.
[247] Shao Jiayu, On a conjecture about the exponent set of prijnitive matrices, Linear
Algebra AppL, 65 (1985), 91-123.
[248] Shao Jiayu and Chen Bo, Graph theoretical criteria for diagonal similarity of
matrices, J. Of Math. (Chinese), 17 (1997), 105-112.
[249] Shao Jiayu and Hu Zhixiang, The exponent set of primitive ministrong digraphs,
AppL Math. A J. of Chinese University, 6 (1991), 118-134.
[250] Shao Jiayu and Li Qiao, On the index set of maximum density for reducible Boolean
matrices, Discrete AppL Math., 21 (1988), 147-156.
[251] Shao Jiayu and Li Qiao, The index set for the class of irreducible Boolean matrices
with given period, Lin. Multilin. Alg., 22 (1988), 285-303.
[252] Shao, Jiayu and Li, Qiao, On the indices of convergence of irreducible Boolean
matrices, Linear Algebra AppL, 97 (1987), 185-210.
[253] Shao Jiayu, Wang Jianzhong and Li Guirong, Generalized primitive exponent and
completely characterize its extremal digraphs, Chinese Ann. Math. 15A (1994), 518-
523.
[254] S. S. Shrikhande, The uniqueness of the L^ association scheme, Ann. Math. Statsit.,
30 (1959), 781-798.
[255] J. H. Smith, Some Properties of the spectrum of a graph, Combinatorial Structures
and their Applications, , 403-406, Gordon and Breach, (1970).
[256] R. P. Stanley, A bound on the spectral radius of graphs with a edges, Linear Algebra
Appl. 87 (1987), 267-269.
[257] A. P. Street and D. J. Street, Combinatorial Experimental Design, MClaredon Press,
Oxford, (1987).
[258] G. Szekers and H. S. Wilf, An inequality for the chromatic number of a graph, J.
Combin. Theory 4 (1968), 1-3.
[259] L. Teirlink, Non-trivial t-designs without repeated blocks exist for all t, Discrete
Math., 65 (1987), 301-311.
308 Bibliography
[260] G. Tinhofer, Graph isomorphism and theorems of Birkhoff type, Computing, 36
(1986), 285-300.
[261] G. Tu, A formula for general solutions of homogeneous trinomial recurrences, Chin.
Ann. Of Math., 2 (1981), 431-436.
[262] W. T. Tutte, The dissection of equilateral triangles into equilateral triangles, Proc.
Cambridge Philos. Soc, 44 (1948), 463-482.
[263] H. Tverberg, On the decomposition of Kn into complete bipartite graphs, J. Graph
Theory, 6 (1982), 493-494.
[264] J. H. Van Lint, Combinatorial Theory Seminar, Lecture Notes' in Math. Vol. 382, ,
47-49, Springer-Verlag, (1970).
[265] R. S. Varga, Matrix Iterative Analysis, Prentice-Hall, Engelwood Cliffle, New Jersey,
(1962).
[266] B. L. Van der Waerden, Aufgabe 45, Jber. Deutsch Math. -Verein., 35 (1926), 117.
[267] Y. Vitek, Bounds for a linear diophantine problem of Frobenius, J. London Math.
Soc, 10 (1975), 79-85.
[268] Wan Honghui, Structure and cardinality of the class U(R, S) of (0,l)-matrices, Acta
Math. Sinica, 30 (1987), 183-190.
[269] Wang Boying, The exact number of matrices in the class U(R,S) of (0,l)-matrices,
Sci. Sinica (Sci. in China) Series A, 5 (1987), 463-468.
[270] Wang Jianzhong and Zhang Kemin and Wei E\iyi and Pan Jinxiao, Description
on the second primitive exponent of symmetrical primitive matrices, J. of Nanjing
University Math. Biquarterly, 2 (1994), 193-197.
[271] Wei Wandi, Combinatorial Theory I, Sci. Press, (1981).
[272] Wei Wandi, Combinatorial Theory II, Sci. Press, (1987).
[273] Wei Wandi, The class U{R,S) of (0,1) matrices, Discrete Math., 39 (1982), 301-305.
[274] H. Wielandt, Unzerlegbare, nicht negative matrizen, Math. Z., 52 (1950), 624-648.
[275] H. S. Wilf, The eigenvalue of a graph and its chromatic number, J. London Math.
Soc, 42 (1967), 330-332.
[276] J. Williamson, Determinants whose elements are 0 and 1, Amer. Math. Monthly, 53
(1946), 423-474.
Bibliography
309
[277] E. S. Wolk, A note on the comparability graph of a tree, Proc. AMS, 16 (1965), 17-20.
[278] Wu Xiaojun, Bounds of the eigenvalues of unicyclic graphs, J. of Tongji University,
19 (1991), 221-226.
[279] X-J.Wu and J-Y.Shao, The index set of reducible Boolean matrices, J. of Tongji
University, 19(1991), 3:333-340.
[280] D. Zeilberger, A combinatorial approach to matrix algebra, Discrete Math., 56 (1985),
61-72.
[281] Zhang Fuji, Generalized linear difference equation and its reverse question, Chinese
Sci. BuIletin(Kexue TongBao), 31 (1986), 492-494.
[282] Zhang Kemin, On Lewin and Vitek's conjecture about exponent set of primitive
matrices, Linear Algebra Appl., 96 (1987), 101-108.
[283] Zhang Kemin and B. Y. Hua, On the exponents set of primitive locally semicomplete
digraphs, submitted to Linear Algebra Appl..
[284] Zhang, Kemin, Wang, Hongde and Hong, Jizhi, On the set of index of maximum
density of tournaments, J. Of Nanjing University, Math. Biquarterly, 4 (1987), 9-14.
[285] Zhou Bo, Estimates on the indices of convergence of boolean matrices with s cycle
positive entries on exactly t rows, Math, in Practice and Theory 29 (1999), 19-23.
[286] Zhou Bo and Liu Bolian, On a conjecture of strictly Hall index of primitive matrix,
Chinese Sci. Bulletin(KeXue TongBao), 41 (1996), 2107.
[287] Zhou Bo and Liu Bolian, Characterization of the extreme matrices of convergent
index among boolean matrices with nonzero trace, Advances in Math. (China) 25
(1996), 540-547.
[288] Zhou Bo and Liu Bolian, Convergent indices of boolean matrices with s-cycle positive
elements on exactly t rows, Acta Math. Sinica 41 (1998), 517-524.
[289] Zhou Bo and Liu Bolian, On almost regular matrices, Untilitas Mat. 54 (1998),
151-155.
[290] Zhou Bo and Liu Bolian, Matrices with maximum exponents in the class of doubly
stochastic primitive matrices, Discrete Applied Math. 91 (1999), 53-66.
[291] Zhou Zhenhai, A sufficient an4 necessary condition for generalized inverse of boolean
matrix, Chinese Sci. Bulletin(Kexue TongBao), 29 (1984), 16.
310 Bibliography
[292] Zuo Guangji, Primitive matrix with minimal number of positive elements. Math.
AppL (in Chinese), 5 (1992), 31-37.