АКАДЕМИЯ НАУК УКРАИНСКОЙ ССР
ИНСТИТУТ ГИДРОМЕХАНИКИ
/И IXV
с
%2><p В. М. Сеймов
ДИНАМИЧЕСКИЕ
КОНТАКТНЫЕ
ЗАДАЧИ
г-*
ИЗДАТЕЛЬСТВО «НАУКОВА ДУМКА»
КИЕВ — 1976

531
C28
УДК 539.3:534.1
В монографии обобщен метод ортогональных многочленов
на динамические контактные задачи теории упругости и гидро-
гидроупругости, дана его численная реализация на ЭВМ, а также
решены новые нестационарные задачи о колебаниях жестких и
упругих штампов на упругом полупространстве, которые
применяются в гидротехнических сооружениях, фундаментах
промышленных установок и других конструкциях на упругом
основании. Изучено изменение распределения контактных
напряжений в зависимости от времени, составлены рекомен-
рекомендации по их расчету и вспомогательные таблицы.
Книга рассчитана на научных работников и инженеров,
занимающихся исследованием и проектированием динамически
нагруженных конструкций на упругом основании.
Ответственный редактор
д-р техн. наук Л. И. Дятловицкий
Рецензенты:
д-р физ.-мат. наук И. Т. Селезов,
д-р физ.-мат. наук А. Ф. Улитка
Редакция физико-математической литературы
С 20303-'86 224-76
М221 @4)— 78
(С) Издательство «Наукова думка», 1976
ОГЛАВЛЕНИЕ
Предисловие 5
Глава 1. Динамические перемещения упругой полуплос-
полуплоскости
§ 1. Произвольные нагрузки 11
§ 2. Равномерно распределенные нестационарные воздей-
воздействия 18
Импульсные нагрузки 18
Внезапно приложенные постоянные нагрузки ... 25
§ 3. Гармонические силы 28
§ 4. Полиномиальные разложения 37
Импульсные нагрузки 37
Внезапно приложенные гармонические нагрузки 50
§ 5. Перемещение внутренних точек 54
Глава 2. Колебания жесткого штампа на упругой полу-
полуплоскости
§ 1. Вертикальные нагрузки 60
§ 2. Воздействие симметричных упругих волн 75
§ 3. Горизонтальная и моментная нагрузки 79
§ 4. Воздействие антисимметричных упругих волн ... 90
§ 5. Колебания системы из двух штампов 93
§ 6. Колебания массивных плотин 104
Глава 3. Колебания полосы конечной жесткости на упру-
упругой полуплоскости
§ 1. Симметричные колебания ПО
Произвольная вертикальная нагрузка ПО
Частные виды вертикальной нагрузки 122
Нагрузка моментами 125
§ 2. Антисимметричные колебания 127
Произвольная вертикальная нагрузка 127
Частные виды вертикальной нагрузки 133
Нагрузка моментами 137
§ 3. Некоторые частные случаи колебаний Ш-

Оглавление
Глава 4. Колебания круглого и прямоугольного штампов
на упругом полупространстве
§ 1. Динамические перемещения упругого полупростран-
полупространства (осесимметричная задача) 147
§ 2. Вертикальные колебания круглого штампа .... 152
§ 3. Вертикальные колебания прямоугольного штампа 161
Глава 5. Гармонические колебания полосы на упругом
полупространстве под слоем жидкости (плоская задача)
§ 1. Колебания упругого полупространства 175
§ 2. Установившиеся колебания бесконечной полосы 184
§ 3. Симметричные колебания полосы конечной жест-
жесткости 188
§ 4. Антисимметричные колебания полосы конечной
жесткости 195
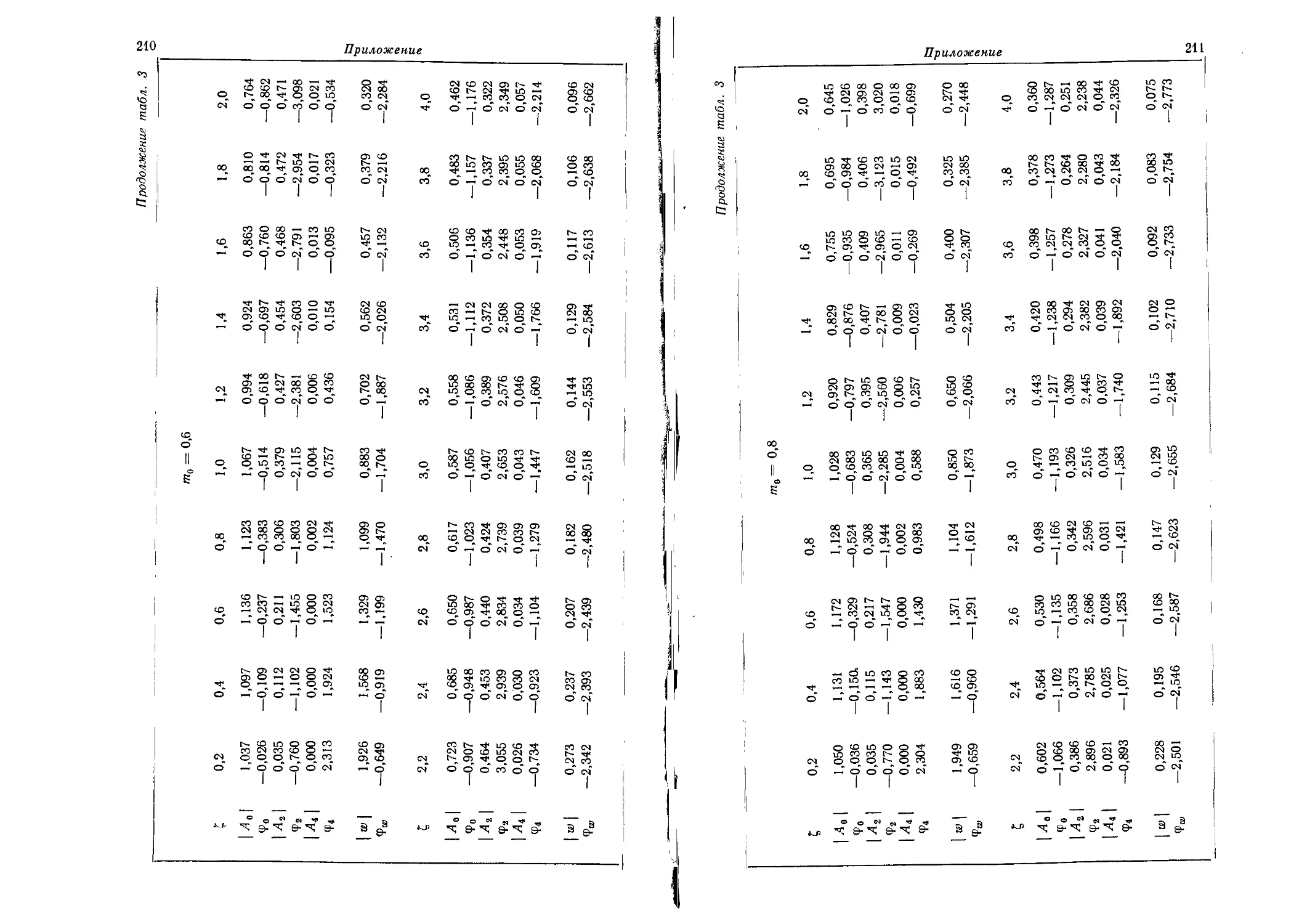
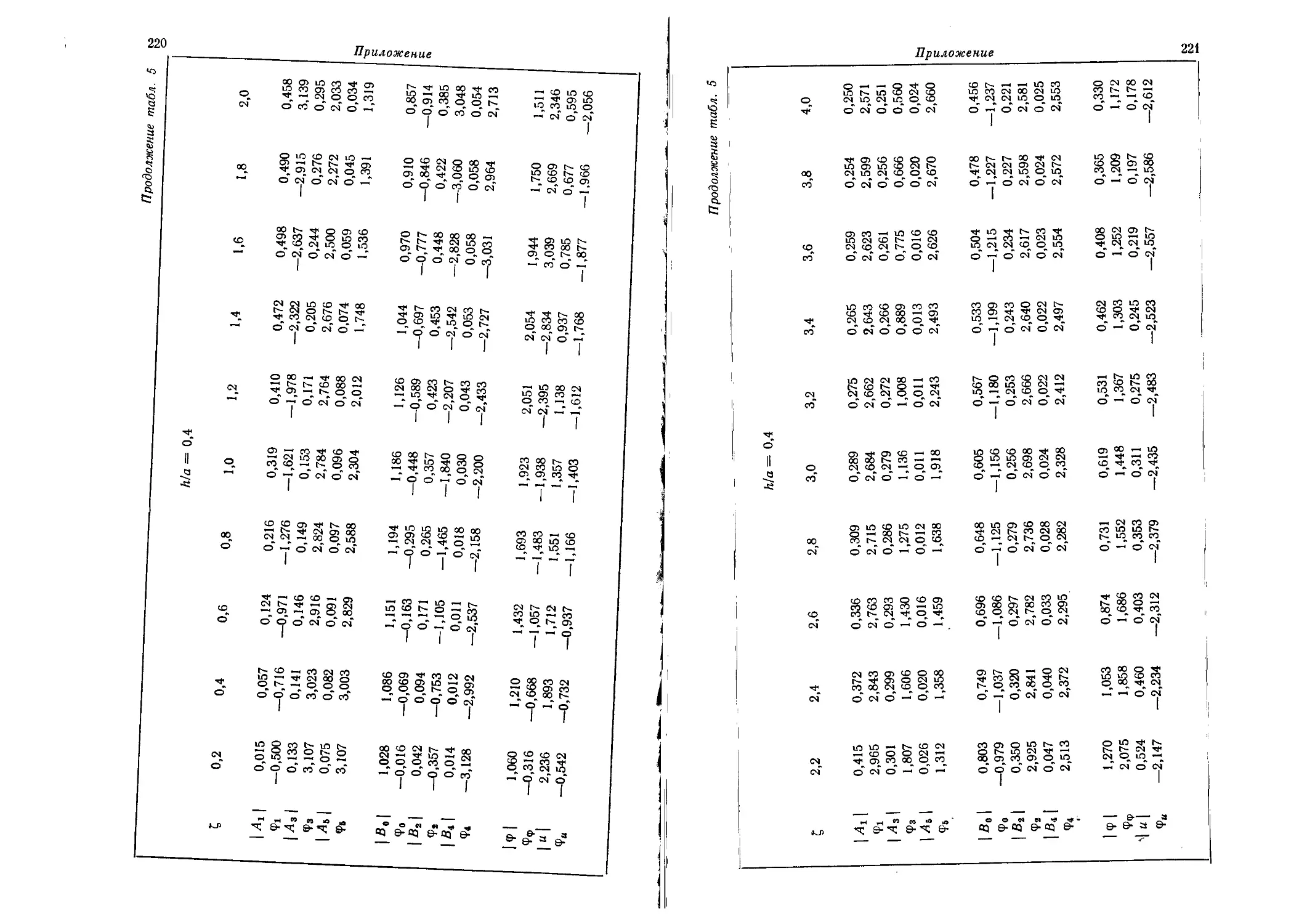
Приложение. Таблицы для расчета стационарных и не-
нестационарных колебаний жестких штампов на упругом
полупространстве 203
Литература 276
ПРЕДИСЛОВИЕ
В строительстве широко применяются конструкции в виде
массивов, плит и балок, расположенных на упругом основании.
С развитием техники увеличиваются динамические воздействия на
сооружения, повышаются требования к противовибрационной за-
защите. Этим определяется необходимость уточнения существующих
методов расчета таких сооружений.
Многие практически важные задачи о колебаниях сооружений
могут быть сформулированы как динамические контактные задачи
теории упругости, а при взаимодействии с жидкостью (в случае
гидротехнических сооружений) — как задачи гидроупругости. Урав-
Уравнения теории упругости описывают поведение оснований в реаль-
реальных условиях приближенно, однако при малых колебаниях, как
об этом свидетельствуют эксперименты Ф. Ричарта [135], О. Эрле-
ра [119], М. Новака [129], Р. Д. Филиппова и В. П. Гостева [100],
наблюдается удовлетворительное соответствие между опытом и тео-
теорией. В рамках модели упругого основания в виде упругого полу-
полупространства представляется возможным учесть инерцию основа-
основания, взаимодействие нескольких сооружений, распространение
упругих волн и рассеяние энергии вследствие излучения.
Для практических расчетов конструкций на упругом основании
при динамических нагрузках в качестве модели основания часто
применяются модель Винклера и модель с двумя упругими харак-
характеристиками (подробные рекомендации даны в работах Д. Д. Бар-
Баркана [6], Н. А. Кильчевского [45], Б. Г. Коренева, М. Н. Ручим-
ского и Е. И. Черниговской [49, 50], А. И. Цейтлина [104],
О. А. Савинова [75], в справочнике по динамике сооружений [98]).
Существенным недостатком этих моделей является их безынерцион-
ность. По данным И. Н. Годзевича [23], необходимая масса фунда-
фундамента при вынужденных вертикальных колебаниях может быть в
2—2,5 раза меньше, если учесть инерцию основания.
С развитием вычислительной техники стало возможным реше-
решение многих задач динамики конструкций на упругом основании в
более строгой постановке. А. П. Филиппов [99], И. А. Николаенко
[68], 3. М. Гершунов [22], Б. Г. Коренев [47], П. В. Крауклис,
Л. А. Молотков [52], А. Г. Ишкова [40] исследовали колебания не-

Предисловие
ограниченных плит на упругих безынерционном и инерционном
полупространствах. Возрос интерес к динамическим контактным за-
задачам теории упругости со смешанными граничными условиями,
решению которых предшествовали подробные исследования стати-
статических контактных задач [65].
В статье Н. М. Бородачева [17] приведен достаточно полный об-
обзор работ по динамическим контактным задачам, поэтому нет необ-
необходимости останавливаться на их разборе. Можно лишь отметить
три основных направления в разработке динамических контактных
задач и указать исследования, в которых рассмотрены плоские,
осесимметричные и пространственные динамические задачи о штам-
штампах со сплошным основанием на упругом полупространстве. К пер-
первому из них относятся, например, работы Е. Рейсснера, О. Я. Шех-
тер, Р. Арнольда, В. Байкрофта, В. А. Ильичева, в которых
принимаются некоторые допущения о характере распределения
контактных напряжений и контактное условие удовлетворяется
приближенно либо в одной точке, либо в среднем по площади.
В работах второго направления (Н. М. Бородачев, Ю. С. Яковлев,
В. Л. Лобысев и др.) задачи сводятся к парным интегральным урав-
уравнениям, которые преобразуются в интегральное уравнение Фред-
гольма II рода. Последнее решается приближенным методом. Третье
направление (В. М. Сеймов, М. Ойен) характеризуется сведением за-
задач к бесконечной системе линейных алгебраических уравнений
на основе разложения решения в ряд по специально выбранной
системе ортогональных многочленов.
Плоскую задачу о вдавливании штампа, движущегося с посто-
постоянной скоростью по границе упругой полуплоскости, впервые рас-
рассмотрел Л. А. Галин [21]. В работе В. А. Свекло [76] сформулиро-
сформулированы теоремы единственности и существования для динамической
контактной задачи. Начало движения штампа на упругой полуплос-
полуплоскости изучено Л. М. Флитманом [102]. Н. М. Бородачев исследовал
вертикальные [10] и горизонтальные [11] гармонические колебания
штампа путем сведения парных интегральных уравнений к инте-
интегральному уравнению Фредгольма II рода. Аводжоби [1] рассмотрел
напряжения под штампом при его вращательных гармонических
колебаниях. Карасудхи, Кир, Ли [44] изучили вертикальные, го-
горизонтальные и связанные горизонтально-вращательные колеба-
колебания штампа. Антисимметричные колебания штампа рассмотрены так-
также в работе Г. Пауля, Н. Матейли [131]. М. Ойен [130] нашел функ-
функции влияния, характеризующие взаимодействие штампа с упругой по-
полуплоскостью, разложив выражения для нормальных и касательных
напряжений под штампом в ряды по полиномам Чебышева 1. Асимпто-
Асимптотический метод исследования колебаний штампа применен В. Г. Бу-
1 Ранее полиномы Чебышева были использованы для решения
статических контактных задач в работах [46, 25, 26, 77—80], дина-
динамических — в работах [81, 82].
Предисловие
ряком [ 18], силы трения учтены в работе Ж. Луко и Р. Вестмана [62].
В указанных выше исследованиях численное решение задач дано
для малого диапазона частот. Приближенное решение задач о ко-
колебаниях штампа при больших частотах приведено в работе Аво-
Аводжоби [2].
Удар жесткой балки об упругую полуплоскость рассмотрен
Каватейта Кацуо [121]. Нестационарное движение жесткого штам-
штампа на упругой полуплоскости изучено Ю. С. Яковлевым и В. Л. Ло-
бысевым [111, 112, 61]. Задача сведена к интегральному уравнению
Фредгольма II рода. Исследована структура решения. Численное
решение дано для равнодействующей контактных напряжений.
Постановка задачи о горизонтально-вращательных нестационарных
колебаниях жесткого штампа под действием сейсмической волны в
предположении линейного закона распределения контактных напря-
напряжений сформулирована в работе Д. Бейли, Д. Рафтопулоса, Р. Ска-
вуццо [114].
Более подробно освещены в литературе исследования колеба-
колебаний круглого штампа на упругом полупространстве. Начало этим
исследованиям было положено Е. Рейсснером [134]. Он изучал вер-
вертикальные гармонические колебания штампа при равномерном
. распределении контактных напряжений. В аналогичной постановке
эта задача рассмотрена в работе О. Я. Шехтер [106], где указаны так-
также ошибки, допущенные Е. Рейсснером [134]. В дальнейшем [107,
108, 109] О. Я. Шехтер изучала гармонические колебания плиты ко-
конечной жесткости, высокочастотные колебания жесткого штампа.
В работах Р. Куинлэна [133], Т. Санга [137], Р. Арнольда, Ж. Бай-
Байкрофта, Ж-Варбуртона [ 113, 116], Ж. Торейми [139] при исследо-
исследовании колебаний штампов принимались различные законы распре-
распределения контактных напряжений (равномерный, параболический,
седлообразный). Действительное распределение напряжений не
находилось.
Задачи о гармонических колебаниях круглого штампа на упру-
упругом полупространстве в строгой постановке решены Н. М. Борода-
чевым [8, 9, 12—17]. Парные интегральные уравнения им сведены к
интегральному уравнению Фредгольма II рода, которое решалось
либо способом последовательных приближений, либо путем заме-
замены его системой линейных алгебраических уравнений. Кроме низ-
низкочастотных рассмотрены также высокочастотные колебания [16].
Несколько усложненные задачи (неплоская подошва штампа,
наличие сцепления) рассмотрены в работах В. Н. Закорко и
Н. А. Ростовцева [32, 33]. Зависимость распределения контактных
напряжений от частоты колебаний показана Ж. Лайсмером и Ф. Ри.
чартом [126, 127]. Метод конечных элементов для исследования вер-
вертикальных колебаний штампа применен К. Дансом [118]. Гармони-
Гармонические колебания штампа в общем случае рассмотрены С. Бозе
[115]. Расширенный диапазон частот исследован Ж. Луко, Р. Вест-

Предисловие
маном [125]. Т. К. Де [117] решена осесимметричная задача о перио-
периодических колебаниях штампа путем сведения ее к интегральному
уравнению Фредгольма II рода и применения аппроксимации ядра
функциями Бесселя и Ханкеля. Колебания жестких плит на водо-
насыщенном основании изучены в работе В. М. Лятхера, Б. И. Ди-
духа, М. Н. Бессонова, И. И. Борзенко [63].
Задачу о взаимном влиянии двух жестких штампов при их
гармонических колебаниях и равномерном распределении напря-
напряжений под штампами в приближенной постановке рассмотрела
О Я. Шехтер [НО]. Гармонические колебания штампа под действием
упругих волн, распространяющихся от силы, приложенной к по-
поверхности полупространства на большом расстоянии от штампа,
исследованы Г. Б. Муравским [66, 67]. Свободные вращательные
колебания штампа в приближенной постановке рассмотрены
В. Р. Дудиным [27].
Гораздо меньшее количество работ посвящено нестационарным
колебаниям круглого штампа. Удар жесткого цилиндра по упругому
полупространству рассмотрен М. Гутцвиллером [120]. Вертикальные
нестационарные колебания штампа [127] исследовались путем раз-
разложения уравнения движения в ряд по гармоническим колебаниям.
В. Б. Поручиков [74] изучил вдавливание жесткого штампа в упру-
упругое полупространство в начале движения. Ю. С. Яковлев, В. Л. Ло-
бысев, В. И. Сайгина [59—61] исследовали нестационарное движение
жесткого штампа и для равнодействующей контактных напряжений
получили приближенное простое выражение. Построению импуль-
импульсной переходной функции системы круглый штамп — полупростран-
полупространство в предположении статического закона распределения контакт-
контактных напряжений и изучению колебаний штампа при прохождении
упругих волн в полупространстве посвящены работы В. А. Ильи-
Ильичева [38, 39].
Наименее изучены колебания прямоугольных штампов.
В. А. Ильичевым [34, 36] рассмотрено действие импульсной нагрузки
на невесомый квадратный штамп и с помощью метода Б. Н. Жемоч-
кина определены контактные напряжения в ряде точек в заданные
моменты времени. Им же [35, 37] в приближенной постановке (в
предположении равномерного распределения контактных напряже-
напряжений и без учета горизонтальных и вращательных смещений) иссле-
исследованы нестационарные колебания двух массивов. В работах [138,
122] изучены гармонические вертикальные, горизонтальные, вра-
вращательные и крутильные колебания прямоугольного штампа на
упругом полупространстве при заданном законе распределения
контактных напряжений.
Вопросу о единственности решений интегральных уравнений ди-
динамических контактных задач посвящена работа В. А. Бабешко [51.
Некоторые динамические контактные задачи рассмотрены в рабо-
работах [41, 42, 56—58, 81—96].
Предисловие
Резюмируя, можно отметить следующее. Интенсивное развитие
исследований в области динамики штампов на упругом инерцион-
инерционном полупространстве относится к последним двум десятилетиям
(по нестационарным колебаниям — к последним шести — восьми го-
годам). Решение целого ряда задач динамики штампов на упругом
полупространстве, особенно относящихся к гармоническим коле-
колебаниям, уже найдено. Однако при изучении большинства из них
принимались упрощающие допущения о характере распределения
контактных напряжений, рассматривался ограниченный диапазон
частот колебаний. Многие вопросы требуют дополнительных иссле-
исследований. Часть из них рассмотрена в данной работе: изменение в
зависимости от времени распределения контактных напряжений
под штампами при нестационарных колебаниях, в более строгой
постановке (с нахождением эпюр действительного распределения
контактных напряжений) задача о стационарных и нестационарных
колебаниях штампов под действием упругих волн, распространяю-
распространяющихся в упругом полупространстве, и о колебаниях нескольких
штампов, нестационарные колебания плит и балок конечной жест-
жесткости (конечных размеров), расположенных на упругом инерцион-
инерционном полупространстве, колебания плит и балок, взаимодействую-
взаимодействующих с упругим полупространством и слоем жидкости, задача о
колебаниях прямоугольного штампа.
В монографии рассмотрены задачи динамики сооружений, ко-
которые сводятся к плоским, осесимметричным и пространственным
динамическим контактным задачам теории упругости и гидро-
гидроупругости. Для решения их применен метод ортогональных много-
многочленов. Эффективность метода показана на многих примерах.
В первой главе исследуются перемещения упругой полуплос-
полуплоскости при нестационарных и гармонических нагрузках, распреде-
распределенных на участке ее границы. Рассмотрено действие внезапно
приложенной гармонической силы. Вторая глава посвящена неста-
нестационарным колебаниям жестких штампов на упругой полуплоскос-
полуплоскости. Изучены вертикальные и горизонтально-вращательные колебания
штампов под действием нагрузок, приложенных к штампу и к
границе полуплоскости, колебания двух штампов и массивной пло-
плотины. В третьей главе рассматриваются неустановившиеся и уста-
установившиеся колебания полосы конечной жесткости, расположенной
на упругой полуплоскости. В четвертой — исследуются верти-
вертикальные нестационарные колебания круглого штампа на упругом
полупространстве, излагается методика решения задачи о неста-
нестационарных колебаниях прямоугольного штампа. Пятая глава по-
посвящена решению некоторых задач о взаимодействии упругой по-
полосы с упругой полуплоскостью и слоем жидкости при гармони-
гармонических колебаниях.
На основании изучения контактных напряжений установлено,
что при колебаниях штампов эпюра напряжений изменяется в

10
Предисловие
зависимости от времени и может быть или равномерной, или парабо-
параболической, или седлообразной, или промежуточной формы. Выявлены
некоторые характерные особенности системы штамп — упругое по-
полупространство, например немонотонность изменения частоты сво-
свободных колебаний такой системы в зависимости от массы штампа.
Расчеты колебаний плит конечной жесткости на упругом полупро-
полупространстве (плоская деформация) показали, что при действии крат-
кратковременных нагрузок колебания быстро затухают. Влияние слоя
жидкости над плитой при гармонических колебаниях малых частот
на величины изгибающих моментов несущественно, однако с ростом
частоты оно увеличивается.
Для большинства рассмотренных задач составлены программы,
по которым произведены вычисления на ЭВМ, и таблицы. Эта ра-
работа выполнена старшими инженерами Н. П. Ермоленко, Е. Д. Шев-
Шевченко, Л. В. Дюминой и инженером Т. Л. Ревой. Практические ре-
рекомендации и таблицы для расчета нестационарных и гармони-
гармонических колебаний жестких штампов на упругом полупространстве
при некоторых видах воздействий приведены в «Приложении».
Результаты исследования могут быть использованы для расче-
расчета конструкций на упругом основании при динамических воздей-
воздействиях в гидротехническом, промышленном и транспортном строи-
строительстве. Разработанная методика позволяет более экономно про-
проектировать такие конструкции, поскольку благодаря учету инерции
основания уменьшаются амплитуды колебаний, а при учете крат-
кратковременности действующих нагрузок коэффициенты динамичнос-
динамичности могут быть меньше единицы.
Значительную помощь автору при работе над книгой оказали
д-р техн. наук Л. И. Дятловицкий и д-р техн. наук В. Г. Чуднов-
ский, автор приносит им глубокую благодарность. Искрен-
Искреннюю признательность выражает автор также д-ру физ.-мат. наук
А. Ф. Улитко и д-ру физ.-мат. наук И. Т. Селезову за полезные
критические замечания при обсуждении рукописи.
Автор
Глава 1
ДИНАМИЧЕСКИЕ
ПЕРЕМЕЩЕНИЯ
УПРУГОЙ ПОЛУПЛОСКОСТИ
§ 1. ПРОИЗВОЛЬНЫЕ НАГРУЗКИ
При решении ряда задач о действии динамических нагрузок на
конструкции и сооружения на упругом основании возникает не-
необходимость в определении перемещений упругого основания, ко-
которое принимается в виде упругой полуплоскости, под действием
нагрузок, приложенных на границе и изменяющихся в зависимости
от времени и расстояния по сложным законам. Наиболее подробно
исследовано [70, 97, 123, 132] действие вертикальной сосредото-
сосредоточенной силы, изменяющейся в зависимости от времени в виде мгно-
мгновенного импульса. Перемещения упругой полуплоскости под дей-
действием нагрузки, изменяющейся по произвольному закону, могут
быть определены при помощи интегрирования по координатам х и t
(вычисление интегралов типа свертки). Однако выполнить такое
интегрирование трудно, так как под знаком интеграла находится
разрывная функция, соответствующая фронтам распространяю-
распространяющихся волн, и само вычисление интеграла типа свертки при слож-
сложных нагрузках является трудоемкой операцией, требующей боль-
большой памяти ЭВМ. Ниже приведено решение задач о действии
некоторых видов вертикальных и горизонтальных нагрузок, рас-
распределенных на участке границы. Решения задачи о мгновен-
мгновенной нагрузке получены в таком виде, что переход к другим на-
нагрузкам выполняется без затруднений. Кроме нагрузок простей-
простейшего вида, равномерно распределенных, исследовано воздействие на-
нагрузки на полуплоскость более общего характера. Это воздействие
может быть представлено произвольной функцией, допускающей
разложение в ряд по ортогональным многочленам. Найдены также
формулы для определения перемещений внутренних точек упругой
полуплоскости.
Рассмотрим так называемую задачу Лэмба [123], т.е. задачу о
динамических перемещениях упругой полуплоскости (плоская де-
деформация) при заданных нагрузках, изменяющихся вдоль границы
в зависимости от времени.
Пусть на границе упругой полуплоскости (рис. 1) приложена
вертикальная нагрузка, закон изменения которой описывается за-
заданной функцией р (х, t). Требуется найти вертикальные v (x, у, t) и
горизонтальные и (х, у, f) перемещения точек полуплоскости.

12
Глава 1. Динамические перемещения упругой полуплоскости
Для решения задачи воспользуемся дифференциальными урав-
уравнениями движения полуплоскости, которые при записи их в
перемещениях имеют вид
дхди *1~ Р ди* ~ Р ~д!*~ ' I
A.1)
где
дЧ
дх*
1/
У
'V
B
' 1
2
(\ fi2l
У1 Р J
1 — 2\
Е,
d*v .
дхду
Р ' дхду
'о
ду*
— R2
д*У
dt*
С» =
Ро
A + v0) (I - 2v0)
2(l+v0) '
Cj и с2 — скорости продольной и поперечной волн в упругом полу-
полупространстве; X, ц, Ео, v0 и р0 — соответственно постоянные Ла-
мэ, модуль упругости, коэффициент Пуассона и плотность материа-
материала полупространства; х = х/а, у = у/а, t = c2t/a — безразмерные
переменные; х, у, t — действительные переменные; а — произволь-
произвольный параметр, имеющий размерность длины (если нагрузка при-
приложена на участке конечной длины, то в качестве параметра а
У///////////////-
/РШ)
ш
'//////////////
У
Рис. 1.
удобно принять полудлину этого участка). Применяя к уравне-
уравнениям A.1) преобразование Лапласа по времени [97], при нулевых
начальных условиях получаем
дх*
п -
дхду
дх*
д*и d*v
~дхд~у"^~дуг
A.2)
где преобразования Лапласа функций и (x,y,t) и v (x,y,t) имеют
вид
и (х, y,s)=\u (х, у, t) e~stdt; v (x, y,s)=Jv (х, у, t) e~stdt A.3)
§ 1. Произвольные нагрузки
13
(s — безразмерный параметр преобразования Лапласа). Функции
по изображениям Лапласа находятся по формулам обраще-
обращения [97]
f "(х- У*s) e'$ds'
v(x,y, 0=
A.4)
_ \
j v(x, y,s)esds,\
c—ioo I
где интегрирование выполняется в комплексной плоскости вдоль
прямой, параллельной мнимой оси и расположенной на расстоянии
с от нее.
Для решения уравнений A.2) вводим функции ф (x,y,s) и ij; (x,y,s):
а дх ~^~ а ду ' ~~ а ду а дх У ¦ >
Уравнения A.2) удовлетворяются, если функции q>(x,y,s) и ¦ypix^.s)
находятся из решений волновых уравнений
дхг
A.6)
Применяя к уравнениям A.6) преобразование Фурье по коорди-
координате х [97], получаем
ду%
=0;
A.7)
где преобразования Фурье функций ф (x,y,s) и \|) (x,y,s) имеют вид
У&'У^^ТгтЕ \ Ф(х-^ s)e dx'
I, У, s) =
—оо
+ ОО
(х, j/, s)
A.8)
(^ — безразмерный параметр преобразования Фурье). Если извест-
известны преобразования Фурье, то сами функции находятся по следую-
следующим формулам обращения:
ay 2л
\ ф (g, y, s) e at,',
= -f== j" Ф (I, У,
A.9)

14
Глава 1. Динамические перемещения упругой полуплоскости
Учитывая условия на бесконечности, решения уравнений A.7)
выбираем в виде функций
Ф (g, y,s) = A (g, s) e-yVf+№"; o|) (g, y,s) = B (g, s) e-^'+s' ,A.10)
где коэффициенты Л (g,s) и В (g,s) находятся из граничных усло-
условий для нормальных оу (x,y,t) и касательных тху (x,y,t) напряжений:
ay(x,0,t)=~p(x,t) или ау(х, 0, s) = — р(х,
fXy (x, 0,t) = 0 или тхУ (х, 0, s) = 0.
Подставляя функции A.10) в формулы A.9), получаем
+°°
{U
Ф (х, у, s) = —L=r Г Л (g, s) ет»
ay 2л .1
о
—оо
ф (*, г/, s) = —i=- f В (g, s) е-
dg.
A.12)
Дифференцируя последние выражения по х и г/ и подставляя ре-
результат в равенства A.5), находим
v (х, у, s) = -fy= +f [A (I, s) VW
— ilB{l,s)e-y
и (х, у, s) — —~ f
v y ' а2 V 2я 3
g, s) е-»
A.13)
+ В (g, s) y'fqr^e-i/T^FP] g-'^dg.
Напряжения ст^ (x,y,t) и тед (x,y,t) определяются зависимостями
дх ~ ду I ' " а
или в изображениях Лапласа
к I ди , * 1 , п (»
dv
ди
Производные по л; и г/ выражений A.13) подставляем в формулы
A.15) и удовлетворяем граничным условиям A.11). В результате
получаем систему двух уравнений для определения неизвестных
A (l,s) и В (l,s):
(|2 + -i- s2j Л (?, s) - $ У |2 + * В (g, s) = ^ Д(g, s);
i? VTTWA (I s) + (Г + — s2J B F. s) = °.
A.16)
i. Произвольные нагрузки
i5
где двойное преобразование (Лапласа и Фурье) заданной функции
р (x,t) имеет вид
р (|, S) = -^ Г ^ р (Х, /) e'^-si dtdx. A.17)
Из системы A.16) очевидно, что
Л (I, s) = — 2| .^"s, p (g, s); В (|, s) = —— f /g s) S ^(^- s)>
Ц (S'SJ ' A.18)
где
A.19)
F (|, s) = B?2 + s2J — 4g2 у |2 + P2s2 К g2 + s2 .
Подстановка выражений A.18) в A.13) приводит к таким формулам
перемещений полуплоскости в изображениях Лапласа:
4- s2)
|, s)
+°о =
Г ^ (^' s) U2
— 2 /|2 + p»s» V I2 + s2 e-
Переходя к оригиналам, получаем
e~ix4l.
.20)
A.21)
v {x, y,t) =
C-j-JOO -J-OO
/ 2я
С—ioo —оо
g, s)
A.22)
-I-OO
С—ioo —oo
— 2
+ s
2 e-
A.23)
При у = О
п (x, 0, s) = i=-
/2
+OO
Гр{
(E,
x
A.25)

16 Глава 1. Динамические перемещения упругой полуплоскости
с4-1оо +оо
С—too —-оо
T
С—joo
— 2
A.26)
A.27)
Таким образом, задача сводится к вычислению двойных инте-
интегралов A.22) и A.23) или A.26) и A.27) (для границы) при извест-
известной функции р (x,t).
О
У
Рис. 2.
Далее рассмотрим задачу, аналогичную предыдущей, но при
действии на границе полуплоскости горизонтальной нагрузки
x(x,t) (рис. 2). Решение ищем при следующих граничных условиях:
au(x,0,t)=0
или а (х, 0, s) = 0;
Ххи (X, O,t) = —T (X, t) ИЛИ Тху (X, 0, S) = — Т(X, S).
A.28)
Неизвестные A (|,s) и Б (|,s) в ,этом случае определяем из системы
уравнений
|, s)-
Z, s) = 0;
% VI2 + P2s2 A (I, s) + (? + \ S2) В (I, s) =
решая которую находим
¦ т(I, s),
A.29)
где
1'
+00 О
Д {* (
Л -оо 0
A.30)
A.31)
§ 1. Произвольные нагрузки
17
Подставляя выражения A.30) в формулы A.13), в изображениях
Лапласа получаем
s} = 7?^
— B|2 + s2)
+ОО
П*& s)<
Оригиналы этих функций имеют вид
c—ioo
X
с+/оо _r_
c—ioo
При у = О
X
+oo _ -
p(.Y 0 A- -f
n-^
ts.
С—ioo —oo
xKrT^)^l+s^s;
c-\-ioo -\-cx>
A.32)
A.33)
A.34)
A.35)
A.36)
A.37)
A.38)

18
Глава 1. Динамические перемещения упругой полуплоскости
§ 2. РАВНОМЕРНО РАСПРЕДЕЛЕННЫЕ НЕСТАЦИОНАРНЫЕ
ВОЗДЕЙСТВИЯ
ИМПУЛЬСНЫЕ НАГРУЗКИ
Пусть в момент времени t = О на участке границы упругой
полуплоскости шириной 2а (рис. 3) приложена вертикальная на-
нагрузка вида
где q — интенсивность нагрузки. Требуется найти перемещения
v (х, О, I) и к (х, О, /). Эта задача исследована в работе [69]. Рас-
Рассмотрим несколько иной подход к вычислению двойных интегралов,
который распространяется на случай более сложных нагрузок.
Рис. 3.
Двойное преобразование функции A.40), определяемое форму-
формулой A.17), имеет вид
p(|)S) = ^iiiL. A.41)
ут i '
Подставляя это выражение в формулы A.24) — A.27), получаем
хЩ- A.42)
62s2 sin \
Ъ (х, 0, s) = -ЗЕ. j si"/(^ BБ« + * - 2
A.43)
v(x,0, t)=-
™ J J"
с—too 0
с-\-1оо оо
c—too 0
2 V |2 + pV V |2 + s2)
A.45)
2. Равномерно распределенные нестационарные воздействия
19
В двойном интеграле A.44) вводим новую переменную s = \p и
изменяем порядок интегрирования:
X
X
A-46)
Интегрирование в комплексной плоскости по переменной р про-
производим по контурам 1\ и Г2 (рис. 4). Подынтегральная функция во
Рис. 4.
внутреннем интеграле A.46) имеет следующие особые точки: р =
= ±t и р = ±f/p A/р > 1) — точки ветвления радикалов гх —
= Vl + р2 и г2 = У\ + р2р2; р = ±t?i — полюсы 1-го порядка.
Фиксируем ветви многозначных функций гх и г2 при условии,
что эти радикалы положительны на действительной оси, и тем са-
самым устанавливаем правило знаков (см. рис. 4).
Интегралы по контурам 1\ и Г2 соответственно равны суммам
интегралов
+ i/fl I О —I —ОД Ы
IJJ J J
too
Г,
i
\c-foo
1/Р
—ОД
1
—Ji
-«7р -/ о
J
од
_6j

20
Глава 1. Динамические перемещения упругой полуплоскости
которые равны нулю согласно теореме Коши о вычетах (интегралы
по дугам большой окружности равны нулю при стремлении радиуса
ее к бесконечности). Последние два слагаемые в A.47) и A.48) —
интегралы по малым полуокружностям около полюсов р = ±г?х-
Находя выражения для каждого из интегралов и суммируя ра-
равенства A.47) и A.48), получаем (при ? = 1/т])
Т
где
= Bт]2 — 1)» + 4т]2 K^
A.49)
A.50)
Соотношение A.49) подставляем в A.46) и находим интеграл по
переменной ?:
W4rl)dE=-J-In
xV —(л —о2
A.51)
В результате получаем выражение, удобное для вычисления пере-
перемещений на ЭВМ:
p
г
о
— я
' (тц)
ш
—С —
-Л2
1п
- (< + л)
^ — (t —
A.52)
из которого следует, что на фронтах релеевских волн есть разрывы
логарифмического вида. Второе и третье слагаемые непрерывны по
§ 2. Равномерно распределенные нестационарные воздействия 21
параметрам х и /; особенности подынтегральных функций в них
интегрируемы. Изображение Лапласа функции A.52) имеет вид
,A-53)
где
In
|* — С — ЧI
e~stdt =
-<!_*,гEj [A _x)z] + e-A+*)*Ei[(l+x)z] —
^1~^-г^^~^1~х)гЕ\[—A~хJ
A*1 <-i);
A.54)
zEi[— A + х) г] —,
1);
Ji[— (х— 1J] + е-(д:+1)г]
)zEl[~(x+l)z] — e- (x~l) гЕ\[(х — \) z]
1, 2 = STj).
Переходим к определению горизонтальных перемещений гра-
границы упругой полуплоскости. Выражение A.45) приводим к виду
X
2п(
I
Аналогично предыдущему внутренний интеграл записываем в виде
C+loo _ _ _ _л_____л__ .
1
2ш"
с—loo
A.56)

22
Глава 1. Динамические перемещения упругой полуплоскости
Подставляя A.56) в A.55) и учитывая значение интеграла [24]
получаем выражение
да
¦Y^k^lH{t~{l-X^l)~H(t~^ +х^гП
F (r\) f (r\)
A.58)
изображение Лапласа которого имеет вид
ц/* 0 s) = ч——\ " 2Т)^~1 (с~''
1
i
' (л) / (л)
(е~
— е
- A+*) sn
. A-59)
T(X,t) =
О
A.60)
где т — интенсивность нагрузки. Требуется найти перемещения
v(x,0,t) и и(х,0, t).
Рис. 5.
Рассмотрим, далее, задачу, в которой в момент времени t — О
на участке границы упругой полуплоскости (рис. 5) приложена
горизонтальная нагрузка вида
тб@ (|*| <1);
§ 2. Равномерно распределенные нестационарные воздействия
23
Двойное преобразование функции A.60) имеет вид
T(Es) = ?^-r- (L61)
Сравнивая формулы A.38) и A.27), видим, что вертикальные пере-
перемещения при горизонтальной нагрузке и горизонтальные переме-
перемещения при вертикальной нагрузке определяются аналогичными
формулами (отличающимися только знаком, если законы изменения
нагрузок одинаковы). Следовательно, чтобы получить формулы
для вертикальных перемещений при нагрузке A.60), достаточно в
выражениях A.58) и A.59) изменить знаки и вместо q подста-
подставить т:
v(x, 0, 0 =
Для определения горизонтальных перемещений при нагрузке
A.60) воспользуемся формулой A.39). Подставляя в нее выраже-
выражение A.61), делая замену переменной s = lp и изменяя порядок
интегрирования, получаем
2та р
2та С sin!

о
X
X
c+loo
2ш
I c-ioo
dg. A-64)
где внутренний интеграл, как и ранее, находим, пользуясь кон-
контурами 1\ и Г2:
2ш' J
с—loo

24 Глава 1. Д
инамические перемещения упругой полуплоскости
' (тц)
Sill
2 fyiZJrf .
I _ ' Pit-
я J i
о
P
-sin^E)*,.
r\F(r\)m
Подставляя A.65) в A.64) и интегрируя по |, получаем
и(*,0,/) = -^|-я-
A.65)
In
- (/ + тр»
In
Л, . A.66)
Преобразование Лапласа функции и(х,0,() имеет вид
.A-67) 1
J
где /j (x,sr\) определяется по формуле A.54).
При вычислении перемещений необходимо знать величины дей-
действительных корней т)! уравнения
Bт]2-1J —4т]2Кт]2^]
-1=0. A.68)
Это уравнение имеет два действительных корня (т) = :?¦%) и четыре
комплексных (при к Ф ц; если к = ц, то все корни действитель-
действительные). Полюсами подынтегральной функции в формуле A.46) и
функций, аналогичных ей, являются только величины р = ±i/f\u
где % — наибольший действительный положительный корень урав-
уравнения A.68) (остальные особые точки устранимы). Некоторые част-
частные значения величин т]х: ,<
v0 0 1/6 1/4 0,3 0,4 0,5 I
% 1,145 1.10475 1,08766 1,07827 1,06135 1,04678
Нами рассмотрено действие нагрузок, изменяющихся в зави- J
симости от времени по закону б-функции. Переход к нагрузкам, j
изменяющимся по другим законам, можно осуществить либо в об- |
§ 2. Равномерно распределенные нестационарные воздействия
25
ласти оригиналов — произвести свертку выражений A.49) или A.52),
A.56) или A.58), A.65) или A.66) с заданной функцией изменения
нагрузки в зависимости от времени, либо в области преобразова-
преобразований Лапласа — в исходные зависимости A.26), A.27), A.38) и
A.39) подставить соответствующие значения ~р (l,s) и т (g,s) и выпол-
выполнить интегрирование по контурам Гх и Г2, как это показано выше,
с учетом вычетов в полюсах функций р (|,s) и т (|,s).
ВНЕЗАПНО ПРИЛОЖЕННЫЕ ПОСТОЯННЫЕ
НАГРУЗКИ
Если в момент времени t — 0 на участке границы полуплос-
полуплоскости (см. рис. 3) приложена вертикальная нагрузка вида
,<*,о-{<Я('»
A.69)
то, произведя свертку выражения A.49) с функцией Хевисайда и
учитывая значение интеграла
4-[(!+*)
In
A + хГ - <Ут)«
A + *)•
+ -Lin
In
+
A.70)
нолучаем формулу для вертикальных перемещений:
J
A.71)
Это выражение является непрерывной функцией переменных х и t.
Ее изображение Лапласа имеет вид
v (х, 0, s)
Aqa 1
Г
- П F'l«\ /l (Х> STl) +
h (x. -**.
где функция ^(х, st]) определяется по формуле A.54).
A.72)

26
Глава 1. Динамические перемещения упругой полуплоскости
При отыскании выражения для горизонтальных перемещений
производим свертку функции A.56) с функцией Хевисайда и, при-
принимая во внимание, что
); A.73)
\ 2
получаем
х>0).
Преобразование Лапласа по времени функции и(х, О, t) имеет вид
_я_ 2т]| — 1 io_ , ,_,., STh ^ ^_ A+Je)
2
v ' ' ЯЦ S2
' М
T1.V
1
2Bц»-1)У ла-Р2УТ=1Г' .- 11_» 15Л _ -
F (Л) / (Л) ^
При возрастании ^ перемещения должны стремиться к стати-
статическим. Анализ формулы A.71) показывает, что вертикальные пере-
перемещения растут по закону In t{t-*- oo). Из решений статических
задач для упругой полуплоскости известно, что при равнодейству-.
ющей вертикальных нагрузок, не равной нулю, вертикальные пере-
перемещения определяются с точностью до постоянной. Переход к ста-
статике на основе формулы A.71) может быть осуществлен, если за
эту постоянную (не зависящую от координаты х) принять член,
содержащий 1п^(?->оо), и исключить его, найдя относительные
перемещения, как это делается при решении статических задач.
При кратковременных нагрузках затруднений в определении
перемещений не возникает. Так, если нагрузка имеет форму прямо-
прямоугольного импульса продолжительностью Т, то перемещения
v (х, 0, t)T определяются по формуле
S %0,t)-v{x,Q,t-T) (t>T)
§ 2. Равномерно распределенные нестационарные воздействия
27
(при t -*- сю перемещения равны нулю). Однако, чем больше Т,
тем большего максимума достигают вертикальные перемещения, в
пределе стремясь к бесконечности. Физически, разумеется, такое
явление не наблюдается. Следовательно, математический дефект
модели упругого основания в виде упругой полуплоскости, который
проявляется в статических задачах, есть и в динамических задачах,
хотя и носит ограниченный характер, так как при кратковремен-
кратковременных нагрузках по формуле A.76) получаются правильные резуль-
результаты.
Горизонтальные перемещения, описываемые формулой A.74),
при t -*- оо стремятся к статическим значениям, в чем можно убе-
убедиться с помощью непосредственного вычисления.
Аналогично решается задача, в которой к границе полуплоскости
(см. рис. 5) приложена горизонтальная нагрузка вида
тЯ(/)
О
A.77)
Выражения для вертикальных перемещений получаем на основе
формул A.74) и A.75), изменяя знак и подставляя т вместо ц:
та 1
n 2r\2\ — 1 ln- \ 1-х 1 sti, -
T n*F' (П.\ К
2Bт|«-1)/>-рг/1-тJ , - 11-х I
. ] м 79)
Для определения горизонтальных перемещений производим сверт-
свертку функции A.65) с функцией Хевисайда и учитываем значение
интеграла A.70). В результате находим

28
Глава 1. Динамические перемещения упругой полуплоскости
где функция fi(x,tlv\) определяется по формуле A.70). Изображе-
Изображение Лапласа функции A.80) имеет вид
х О «Л — 4та *
причем функция /х (х, st]) определяется по формуле A.54). Функция
A.80) при / -»- оо изменяется так же, как и функция A.71). Со-
Соображения, высказанные по этому поводу, справедливы и в случае
определения горизонтальных перемещений под действием гори-
горизонтальной силы.
§ 3. ГАРМОНИЧЕСКИЕ СИЛЫ
Рассмотрим случай, когда к границе полуплоскости (рис. 6)
приложена нагрузка вида
P(x,t)=*P8(x)H(t)elV,
A.82)
где ?" = aco/cjj — безразмерная частота колебаний; а — произволь-
произвольный параметр, имеющий размерность длины; со — круговая частота.
Двойное преобразование функции A.82) имеет вид
Учитывая, что преобразование Фурье по переменной х функции
A.82) отличается от преобразования Фурье равномерно распреде-
\PH(tJe&
Рис. 6.
ленной нагрузки на участке — 1 < х < 1 множителем sin ?/?, для
определения перемещений при указанной нагрузке используем фор-
формулы A.46) и A.55). Полагая в них sin ?/§ = 1, 2qa = Р, произ-
§ 3 Гармонические силы
29
водя свертку функций A.49) и A.56) с функцией A.82) и учитывая
значение интеграла
Б cos (-!-
-84)
для вертикальных перемещений нолучаем такое выражение:
где функция
, О*. ¦
A.85)
о
* -1 cos Ц- |) - Oft sin [i- |]
W ^
[cos
) ci
sin
si
-2. sin
~ J2ef [c
— cos (*n + t) I ci (xti + 0 ? — sin {xr\ + t)t, si (хт| + 0 ? —
— cos (xr\— t)?ci\xt\ — t\? — sm (xr\ — t) ? si (rr) — t) t, —
— я# (хц — t) sin (Схт)) cos (SO — nH(t — xri) cos (?xti) sin (^) —
— i [Sin (XT] + t) I Ci (XT] + 0 ? — COS (XT] + 0 ? Si (XT) + t)l —
~ sin (*n — 0 ci I xr\ — 111 + cos (xt) —¦ 0 ? si (xtj — /) ? —
— nH (t — XT)) cos (?xti) cos (?/) + яЯ (хц — t) sin (?jnj) sin (?/)]} A.86)
найдена с помощью таблиц [24]. Из структуры формулы A.85) видно,
что на фронте релеевской волны существует разрыв логарифми-
логарифмического вида.Поступая с формулой A.55) аналогично предыдуще-
предыдущему, получаем выражение для горизонтальных перемещений при
нагрузке A.82):
¦ 0-87)

30
Глава 1. Динамические перемещения упругой полуплоскости
Вычисление перемещений на ЭВМ по формулам A.85) и A.87)
для всего переходного процесса не представляет затруднений (кроме
значений на фронте релеевской волны), так как интегралы в них
собственные. При изменении фактической нагрузки по закону ко-
косинуса следует взять действительные части, по закону синуса —
мнимые. При значениях / ^> щ (случай установившихся колебаний)
формулы A.85) и A.87) упрощаются и принимают вид
о (*,<>,/) = -
2P/V
Kr,?-|
— Я ¦
F' (тц)
cos
ci
sin
si
+ i -f e-
] +
/P2-t)a
F (Л)
[cos (?xn) ci
sin
si
sin
si
1.88)
u(x,0,/) = —
2P&*
ЯЦ
4 %/=" (r)i)
A.89)
Чтобы выяснить характер волн, распространяющихся от источ-
источника возбуждения, рассмотрим точки границы полуплоскости,
расположенные на большом расстоянии от силы, х^> 1. Так как
интегральные синус и косинус являются функциями, убывающими
при росте аргумента, si х ~ — cos x/x; ci x ~ sin х/х (х -*• оо), то в
формуле A.88) в первом слагаемом, не содержащем интегралов,
и в интеграле на участке Р < Л < 1 ПРИ больших х можно прене-
пренебречь членами, содержащими указанные функции. Интеграл на
участке 0 ^ г\ <; р приводим к виду
р
"Г Й~'
3. Гармонические силы
31
A.90)
Второе слагаемое в последней формуле при л; -»- оо имеет более
высокий порядок малости, чем первое, так как интеграл является
убывающей функцией параметра х. Следовательно, в качестве при-
приближенного значения выражения A.88) при больших х можно при-
принять представление
0(*,O,/) -i
F' Ш
¦
!tx
dl
A.91)
Асимптотическое значение (главные члены) интегралов в этом пред-
представлении находим методом Лайтхилла [124]. В результате по-
получаем
и(х, 0, 0
"^ BP»-0« gpx)'/. ^ ••¦] ^^°°)- 0-92)
Аналогично находим асимптотическое выражение для горизон-
горизонтальных перемещений:
pel%t Г 1 2т)^-
ц I 2 tjjf i
Bр2 - 1K
(дс-»-оо). A.93)
Асимптотические разложения A.92) и A.93) совпадают с соответ-
соответствующими формулами, полученными Лэмбом A23) при решении

32
Глава 1. Динамические перемещения упругой полуплоскости
задачи об установившихся колебаниях. Как следует из этих фор-
формул, от источника возмущения распространяются волны трех ти-
типов (продольные, поперечные и волны Релея).
QH(t)ei(t
f////// /s/s
'///////7777
¦У
Рис. 7.
Пусть теперь к границе полуплоскости приложена горизонталь-
горизонтальная сила (рис. 7) вида
Q (х, t) = Q8 (х) Н @ e(v. A.94)
Вертикальные перемещения при этой нагрузке находим, пользуясь
формулой A.87):
v(x, 0, Qs-iiL. "
. A.95)
Выражение для горизонтальных перемещений получаем на основе
формулы A.64), полагая в ней 2ха = Q, sin ?/? = 1 и выполняя
свертку при помощи формулы A.84):
и(х, 0, 0
-Ц-1 -n-$Z±flixvk, t)
t
После переходного процесса (/ ^ хх\) устанавливаются переме-
перемещения, определяемые следующими выражениями:
4
Bч?-
в (*, 0. О - -
- я
[cos ftniJ ci Кль
,$ 5. Гармонические силы
33
+ sin
si
+ i -f e-^'] +
+ sin gxr]) si
cos «rr|) ci
BV
_ ,• Л±- g-'t«i dij +
cos (t,xrj) ci (?,хц) 4- sin (^хц) si
A.98)
Асимптотическое значение (при jc -»- сю) вертикальных переме-
перемещений определяется по формуле, аналогичной выражению A.93):
BP»-1)«(PW"" ' V" "'" vL99)
При отыскании асимптотического значения горизонтальных пере-
перемещений, как и ранее, исходим из приближенного выражения
лц
После соответствующих выкладок получаем
u(x,0,t)~-^
A.100)
i
^ / 2
-р^)] x
X
A.101)
Разложения A.99) и A.101) содержат слагаемые, соответствую-
соответствующие указанным выше трем типам волн, распространяющихся от
2 t —2880
гос. гу
БИБГ

34
Глава 1. Динамические перемещения упругой полуплоскости
источника возбуждения. Из асимптотических разложений A.92),
A.93), A.99) и A.101) следует, что формулы для перемещений
A.88), A.89), A.97) и A.98) удовлетворяют принципу излучения.
Выше формулы для установившихся колебаний упругой полу-
полуплоскости под действием внезапно приложенной гармонической
силы при / ^> хц получены путем предельного перехода. Для сра-
сравнения приведем решение задачи об установившихся колебаниях, в
которой переходный процесс исключается.
Пусть к границе полуплоскости приложена вертикальная сила
(см. рис. 6), изменяющаяся в зависимости от времени по гармони-
гармоническому закону при любых t:
P(t) = Pely. A.102)
Исходными при решении задачи по-прежнему являются уравнения
A.1). Введением функций ф (х, у, t) и г|з (х, у, t) эти уравнения, как
и в § 1, сводятся к волновым:
+ ¦
ду*
ду*
df-
A.103)
Так как при нагрузке A.102) колебания гармонические, то функ-
функции ф (х, у, /) и г|з (х, у, t) могут быть представлены в виде произве-
произведений ф (х,. у, t) = ф* (л;, у) ёУ\ г|з (х, у, t) = гр* (х, у)ёУ. Подставляя
эти выражения в соотношения A.103), получаем следующие урав-
уравнения эллиптического типа (уравнения Гельмгольца):
ау
дх2
ду1
+ Р2?2Ф* = 0;
= 0. A.104)
Решая их с помощью преобразования Фурье, аналогично тому,
как это сделано в § 1, и удовлетворяя граничным условиям для
напряжений, получаем
и (х, у, 0 =
X
X
B12 - С2J - Ч* VI2
(Ы05)
Ре^'
,
5. Гармонические силы
35
На границе (у = 0) эти выражения принимают вид
v(x, 0, 0=
Рек<
6
» -
A.107)
A.108)
При решении рассматриваемой задачи Лэмб показал [123], что
выражения A.107) и A.108) содержат как распространяющиеся,
1
1
. ?<
г
Рис. 8.
так и стоячие волны. Чтобы решение удовлетворяло принципу из-
излучения, т. е. содержало только распространяющиеся от источника
возмущения на бесконечность волны, необходимо выполнить ин-
интегрирование в комплексной плоскости по замкнутому контуру и
выделить стоячие волны.
Введем в формулу A.107) новую переменную | = —t,r\:
о-109)
Интегрируя по контуру (рис. 8), где подынтегральная функция
имеет четыре точки ветвления (г\ = ±р и г\ = ±1) и два полюса
^ = i^i). находя вычеты в полюсах на действительной оси и учи-
учитывая знаки радикалов sign (т) + 1) \fyf _ 1; sign(r] + р) |ЛJ — P2.J

36
Глава 1. Динамические перемещения упругой полуплоскости
получаем
, A.110)
откуда следует, что главное значение интеграла A.109), которому
равны вертикальные перемещения границы полуплоскости, имеет
вид
•<*¦<>¦ 4—
X VY=
2я/
. cos
A.1
где последнее слагаемое соответствует перемещениям стоячей вол-
волны. Для того чтобы формула A.111) содержала только распростра-
распространяющиеся волны, последнее слагаемое в ней следует исключить
В результате получаем
PeiZl
Эти соотношения удовлетворяют принципу излучения (в чем можно
уоедиться, применив асимптотическое разложение интеграла в
A.112) при х -> оо). v
Таким образом, установившиеся колебания упругой полуплос-
полуплоскости при действии вертикальной силы рассмотрены двумя спо-
сооами. При решении задачи первым способом предполагалось на-
§ 4. Полиномиальные разложения
37
личие переходного процесса. Формулы A.88) и A.89) справедливы
для случая, когда процесс уже установился. Решение уравнений
A.1) естественным путем привело к результатам, удовлетворяю-
удовлетворяющим всем условиям задачи. При использовании второго способа
с самого начала ставилась задача об установившихся колеба-
колебаниях. Формальное математическое решение приводит к резуль-
результату, не удовлетворяющему физическим условиям задачи, так
как оно содержит и распространяющиеся, и стоячие волны (см.
формулу A.111)), которых в упругой однородной полуплоскости
не может быть. Упругие волны, распространяющиеся от источника
возмущения, приложенного на границе, не встречают на своем
пути преграды или материала с другими свойствами, отразившись
от которых, они могли бы образовать стоячие волны.
Лэмб указал способ [123], как из формального решения по-
получить правильный результат с физической точки зрения. Выде-
Выделение членов, соответствующих стоячим волнам, и отбрасывание
их может показаться искусственной операцией. Однако следует
помнить, что сама постановка задачи о гармонических колебаниях
не вполне совершенна, так как в природе нет установившихся ре-
режимов без переходного процесса.
Более естествен первый способ решения рассматриваемой зада-
задачи, который к тому же приводит к формулам, не содержащим не-
несобственных интегралов. Сравнение формул A.88) и A.112) по-
показывает, что вычисления по второй формуле более трудоемки, так
как интеграл в ней несобственный не только из-за полубесконеч-
полубесконечного интервала интегрирования, но и из-за характера подынте-
подынтегральной функции, имеющей разрыв в точке г\ = %. При умень-
уменьшении частоты колебаний (? -»- 0) вертикальные перемещения, опи-
описываемые формулами A.88) и A.112), возрастают по закону 1п?,
т.е. переход к статистической задаче сопровождается появлением по-
постоянной (не зависящей от координат хну) бесконечно высокого
порядка, которая может быть исключена при вычислении относи-
относительных перемещений.
§ 4. ПОЛИНОМИАЛЬНЫЕ РАЗЛОЖЕНИЯ
ИМПУЛЬСНЫЕ НАГРУЗКИ
Рассмотрим более общий случай, когда на участке— 1 <; х < 1
действует вертикальная нагрузка, допускающая разложение в ряд
по полиномам Чебышева I рода TJx) = cos k arccos x с весом
A - *«)-•/.,
(x)
A.114)

38
Глава 1. Динамические перемещения упругой полуплоскости
где Ak(t) — заданные функции времени. Пусть
К @ = АкЬ (О,
т.е.
= 6
A.115)
A.116)
Преобразование Лапласа по переменной / и преобразование Фурье
по координате х функции A.116) имеет вид
оо кп
X?/~VM?), . A.117)
где 7^,A) — функция Бесселя I рода. Подставляя это выражение
в формулы A.26) и A.27), получаем
о(*,0, 9 =
__ ь-п с 4-too 4-oo
С—/ээ —со
A.118)
С-Ц'оо -f-oo
k—0
С—too —oo
— 2 V?TW Vl2 + s2) e~ixl+s'dlds. A.119) $
Если нагрузка p(x,t) A.114) представлена только четными по-
полиномами, то выражения A.118) и A.119) принимают вид
C-{-too оо
/ О
с-/оо О
A.120)
-/во 0
— 2 Ki2 + P2s2 V Е2 + s2) sin xle^dlds. A.121)
После введения новой переменной р = s/| и изменения порядка
интегрирования получаем
*=о
X
§ 4. Полиномиальные разложения
39
X
Г+io
' г
2ш J
С—loo
A.122)
и (дс, 0, t) = -| ^ (~
72* (I) si
sin xg X
X
¦ e'iPdp d\. A.123)
j
Подстановка значений внутренних интегралов из A.49) и A.56) и
интегрирование по | приводят к таким формулам:
j
A.124)
где
, t) = j 72* (E) cos xl sin Tgd? =
— Uik-x (x + т) + f/at—i (x —'
I
@ < т <. 1 — x);
V (x + t)» - 1 U + т + / (x + TJ - I]2* '
A--
/ (X + T)« - 1 (X + X + / (X + T)» - I]2*
1
(X - TJ — 1 [T — X + / (T — X? — I]2*
A + х<т,
+x)\
A.126)
1);

40 Глава 1. Динамические перемещения упругой полуплоскости
C2k (x, т) =
(- 1)*
2
,2*
(X + ТJ - 1 \Х + Т + / (X + ТJ - 1]
1
У (х - тJ - 1 \х - х + / (х - тJ - \fk '
k-i(x — т);
A.127)
(х + тJ - 1 [х + т + / (х + тJ - I]
2*
+
V (x-xf-\[x-
(х, г) = j 72* (?) sin x? sin (т|) dg =
о
(л: + т)
1 - (* + тJ '
A.128)
причем формула A.127) справедлива при х> 1; первая ее строка
соответствует переменным 0 ^ т ^. х — 1, вторая — х — 1 <; т <;
<; х + 1 и третья — 1 + х < т (т = tlry, T2k(x) = cos 2k arccos x;
U bin arccosx
k-\ (x) =
полиномы Чебышева II рода). Преобра-
Преобразования Лапласа по времени функций A.124) и A.125) имеют вид
Г Л/ 2 О2
, 0, s) = |L 2 (~
- я
С2А (х,
р
Г К р2 — т1
\ f(T[)
о
4ti2 (ri2 — б2) /1 — т]2
f 4ti2 (ri2
э
A.129)
4. Полиномиальные разложения
41
где
C2k(X, Z) =
т- cos л:?
sin xgdg (г = sr\).
A.131)
При вычислении последних интегралов @ <; х <. 1) используем
следующий прием. Разлагаем косинус в ряд по полиномам Чебыше-
Чебышева I рода:
со
(_ l)r72r(l)T2r(x)
Тогда
С (х z)-
za 7o (s)
Учитывая, что [24]
). A.132)
-dlT2r(x).
A.133)
Rez>0);
0 (k
получаем
C2k (х, z) = (- 1 )* \l2k (z) Ko (z) + 2I2k (z)
, z =
(г) Г2л
,.0-134)
A.135)
Где ^2*(г), /С2г(г) — модифицированные функции Бесселя соот-
соответственно I и II рода, или
4" Я*-и (fe) -
C2k (х, z) = (— 1)* ch xzK2k (z) - 4
W <*-') -»+i («) ^2Г W (| x |< 1). A.136)
причем полиномы Ломмеля определяются по формуле [7]
^ ' <- l)"BJfe-2r-«-l)IBJfe-/«- 1I
X
n=0
X
n\Bk-2r-2n-l)\Br
/ 9 \2 (А-л-п) - 1
D-) • 0-137)

42 Глава 1. Динамические перемещения упругой полуплоскости
Применяя преобразование Лапласа к равенству A.127), при ¦'
х > 1 получаем
C2h (х, z) =
2 1.1
ш
0 1-0
V (т + х)* - 1 [т + х + V (т + х? - \\
,2*
X—1 _ Х+1
J V {х-т)*-1[х-х+У (x-^-lf Т J
0 1
x+l
Y (т — xY — 1 [т — x + >/ (т —
). A.138)
Заменяя в этом выражении переменные, приводим его к виду
cbz(x-l)d\
-1 (I + >/F--ri)
.2*
ch zx
f
i
¦{«/«©.
h zg
A.139) ;
Первый интеграл в формуле A.139) не выражается в элементарных '•'¦
функциях, но после подстановки | = ch0 он принимает вид, удоб- ;
ный для вычисления по квадратурным формулам. Второй интеграл ¦
после указанной подстановки находится по формуле, приведенной '-.
в работе [128], третий — может быть выражен в элементарных ;
функциях. Таким образом,
Arch х
C2k (x, z) = (— 1 )* [— J e~m chz(x— ch 0) dQ +
/-I B* + r — 1)! / 2
8 jLi Bл — 1)! (k — r)\
x(^-Jlr+^(z^ (z = sr\>0; x>l); A.140)
, x> 1). A.141)
# 4. Полиномиальные разложения
43
Найдем теперь формулы для вычисления интеграла S2k(x,z) A.131).
При | х \ < 1 значение этого интеграла ищем в виде разложения
в ряд по полиномам Чебышева. Используя разложение
записываем
S2k (x, z) =
=0 i-o
- sin 2k arcsin.
= 0)
A.143)
Учитывая интегральное представление для произведения функций
Бесселя
л/2 л/2
72*(I) Ъг+i © = -tf- J j cos Br — 2k + 1) ф1 sin Bft + 2r + 1) ф2 X
о о
X sin Bg cos фх sin ф2) йф^фа, A.144)
получаем
= \ 1
0
. A.145)
При х > 1
S2k (х, z) = A j cos
Л/2
(z = sn). A.146)
Если функции A2k (t) изменяются по известному закону, то для
отыскания перемещений v(x,0,t) и u(x,0,t) нужно вычислить свертку

Глава 1. Динамические перемещения упругой полуплоскости
(U47)
dx, A.148)
где функция C2k (x,t/n]) определяется по формуле A.126) при
О ^ х < 1 и по A.127) при х > 1, а функция S2k (x,t/r\) — по
формуле A.128).
Рассмотрим случай, когда нагрузка A.114) представлена не-
нечетными полиномами Чебышева. Формулы A.118) и A.119) при-
принимают вид
C-|-fOO СО
*~°
4г f
С—/ео О
С—too О
— 2 К|2 + Р2«2 К t2 + s2) cos *ges
Поступая аналогично предыдущему, получаем
A.149)
A.150) \
4. Полиномиальные разложения
45
k=0
я Щ-1
2 n2F' In ^
; A.152)
S2*+l (X, Т) =
sin *g sin x|dg =
(- D*
@ < т < 1 — х);
+ U 2k (X — T)
(x
A—
(т - xf — 1 [t — x + V (т - «J - 1]2A+1
A.153)
1);
sin Tgdg =
_ (- 1)*
у
V
+ 1
У
(X
У
(х
ч
(X
+ тJ - 1 \х ¦
(х - тJ - 1
+ тJ — 1 \х -
(х-т);
+ тJ - 1 \х ¦
f т4
[х-
1
-f- т -f
1
4-т4
-У
1
¦У
-У
1
(х + тJ-1]2
У (х - тJ - 1Г"*"'
(X + Xf - l]2k+l
(х + тJ - 1]^-*-
A.154)
- хJ - 1 [г— х + V (т - ^J - 1]2А+1
(х, т) = j 72ft+i (|) cos xg sin x|d| =
У 1 - (Т + а:J
|т —л:
1
у l-(T-xJ '
A.155)

46
Глава 1. Динамические перемещения упругой полуплоскости
причем формула A.154) действительна при х > 1, первая ее стро-
строка соответствует переменным 0 < т <; х — 1, вторая — х— 1 <
<. т <; х + 1, третья —х + 1 < т. (т = t/ц). Преобразования Лап-
Лапласа по времени функций A.151) и A.152) имеют вид
(x, sr\) йц
S2k+i {x,
= -fr 2 (-
2
'STll)
1
a
— 1)
Сг
где
A.158)
При | х | ^ 1 значения последних интегралов, как и ранее, ищем
в виде разложения в ряд по полиномам Чебышева. Используя раз-
ложение A.142), получаем
9 V /_ 1Л
(Е)
S2k+i (x, z) =
I] 2k + 1
Учитывая, что [24]
(U59)
(z = 0).
(z)/C2r+1(z)
A.160)
4. Полиномиальные разложения
47
находим
f,z) = (-l)*2f2
|_л=0
(г) K2r+i (г) Г2л+1 (дг)
+ 2
r=k+l
или
z) I2r+i (z) T2r+i (x) ,
S2k+i (x, z) =
A.161)
= (— 1)* sh
где
9 k-l
r=0
A.162)
ft—r—1
я! B^ — 2г — 2л
1)! \ к
Применяя преобразование Лапласа к равенству A.154), получаем
_ / 1)*+' С ё~гх&1
S2k+l (х, z) = g )
\+х
: — xJ — 1 [T — X ¦
оо
V (х + х? - 1 [т + х + V (т + *J - 1]
2*+1
: • A-164)
Заменяя переменную интегрирования в этом выражении, приводим
его к виду
,z) = (-\)kl- f
1 о
Arch х
(—1)
; — г)! (k — л)!
r\ Bk — 2r-\- 1)!
X
X
(¦fr
- 1J*+'
0, x>\); A.165)
(z = 0,x>l). A.166)

48
Глава 1. Динамические перемещения упругой полуплоскости
Найдем формулы для вычисления интеграла С2к+\ (х,г) A.158).
При 0 <; х 4* 1 значение этого интеграла ищем в виде разложения
в ряд по полиномам Чебышева. Используя представление A.132),
получаем
Cik+i (x, г) =
/o.2*+i (г) + 2 2 (- 1)' Iwk+i (г) Т2г (х) (г > 0);
r=1 A.167)
Ьj^-sin [B/г + l)arccosA:] (z = 0), | x\ <; 1,
причем функции I2r,2k+\ (z) находим по формуле A.145) при соот-
соответствующей замене индексов. При х > 1
C2k+i (х, z) = A f sin B* + 1) ф^ф ] |51'П(\Г+У5Д:| dl =
о о
л/2
= — е~*г f sin Bk + 1) ф sh (г sin <p) йф = (— 1)*+I -y- /2ft+1 (z) е~хг.
A.168)
Пусть на участке — 1 < х ^ +1 границы упругой полуплос-
полуплоскости приложена горизонтальная нагрузка, представленная рядом
(х)
[ — *2
A.169)
где Вк — заданные коэффициенты. В соответствии с формулами
A.38) и A.39) для перемещений границы получаем зависимости
» 2Я1 J J F (|, s) (^ё +
2л
J
с—/оо —оо
+ s2 — 2 VF+W KlM7^5) «"'^"dgrfs; A.170)
С+!О
С—/со —оо
A.171)
Если нагрузка x(x,t) представлена только четными полинома-
полиномами, то последние выражения принимают вид
с—(ос О
§ 4. Полиномиальные разложения
49
__ 2 Yf 4- p2s2 /Е2 + s2) sin xlestdUs\ A.172)
C—foo 0
A.173)
Так как эти формулы аналогичны выражениям A.121) и A.120), то
для вертикальных перемещений получаем зависимость вида A.125):
(L174)
а для горизонтальных — вида A.124):
А=0
' т)йц + 3
Bti2 —1J/1—
^ /
A.175)
Последовательность выкладок при получении последней формулы
такая же, как и в § 2. Отличие заключается только в другом виде
двойного преобразования функции т(|, s), что обусловливает
появление функций С2*(х,—) вместо логарифмической A.66).
Если нагрузка A.169) представлена нечетными полиномами
Чебышева, то выражения A.170) и A.171) принимают вид
¦ (,, 0, о - f J (-
-±Г
с—(во 0
s2 — 2 VWTW2 Vl2 + s2) cos xlestd\ds\
A.176)
X
A.177)
с—/оо О

50
Глава 1. Динамические перемещения
т.е. эти формулы аналогичны зависимостям A.150) и A.149). После
интегрирования для вертикальных перемещений получаем соот-
соотношение вида A.152):
в
а для горизонтальных — вида A.151):
«<*. о. о
+ J W
-?
оо Г
2 <- о* ^ - -
М , . f Bti2
— ri2
A.179)
ВНЕЗАПНО ПРИЛОЖЕННЫЕ ГАРМОНИЧЕСКИЕ
НАГРУЗКИ
Рассмотрим случай, когда вертикальная нагрузка задана функ-
функцией
р (х, t) = Н (t) eV 2 Ak pf= , A -180)
где Ak — постоянные коэффициенты. Для отыскания перемещений
при этой нагрузке, описываемой только четными полиномами, не-
необходимо найти свертку выражений A.124) и A.125) с функцией
' с-». о -V
• i) *
Г
J
р
4т| (л2 - 0»)
—щ
tWt^1- П 18П
k=0
4. Полиномиальные разложения
51
X
я 2г1?~' Сдц-чо (у т
d.,82)
где интегралы по переменной т содержат элементарные функции
A.126) — A.128) и могут быть вычислены по квадратурным форму-
формулам. Как видно из формул A.181) и A.182), перемещения при на-
нагрузке вида A.180) в общем случае определяются через двойные
интегралы. При / ^> 1, когда переходный процесс заканчивается
и колебания происходят в установившемся режиме, эти формулы
несколько упрощаются. Методом Лайтхилла [124] находим асим-
асимптотическое значение интегралов
(x, %$; A.183)
= J ?2k (9 cos *&dg J S ('-x) sin U-
о о
j (9 sinx\d j
о о
) sin (-L
, ед, A.184)
т.е. при установившихся колебаниях перемещения описываются
формулами
k=0
«„. о, о —
V ifi — р2 _
A.185)
т -те

Комплексные функции С2к (x, /?т]) определяем по формулам A.136)
(| х | ^ 1) и A.140) (/ х \ > 1), а комплексные функции S2k (x,iZ,r\) —
по формулам A.143), A.145) (j х |< 1) и A.146) (| х | > 1),
полагая в них z = i ?г] и отделяя действительные и мнимые части.
Если нагрузка A.180) представлена только нечетными полиномами,
то необходимо произвести свертку выражений A.151) и A.152) с
функцией е'У. Опуская промежуточные выкладки, записываем
окончательные формулы для перемещений при t ^> 1 (случай уста-
установившихся колебаний):
v(x,0,i) =
A.187)
J
где комплексные функции S2k+\ (х,%ц) и C2k+i(x,i?,i\) находятся
соответственно по формулам A.162), A.167) (| х j < 1) и A.165),
A.168) (\х\>\) при г = Ц.
Рассмотрим, далее, случай, когда на участке границы упругой
полуплоскости (— 1 <; х ^ 1) внезапно прикладывается горизон-
горизонтальная нагрузка, заданная функцией
^. A.189)
Если нагрузка представлена только четными полиномами, необ-
необходимо произвести свертку выражений A.174) и A.175) с функцией
о(*,0,/) =
-?¦ 2 <-
§ 4. Полиномиальные разложения
53
A.191)
где функции С2к(х,—) и S2k(x,—) находятся по формулам A.126) —
A.128). При t ^> 1 (случай установившихся колебаний) интегралы
по переменной т в выражениях A.190) и A.191) определяются соот-
соответственно по формулам A.184) и A.183), а значения перемещений —
по формулам
„кп ll я 2л?-1 7 ,_,
f
k=0
Bт!2
Ь2
Р
х. «n) ^ +
"A.193)
где функции S2k{x,it,y\) и C2k (х,1^у\) определяются как и ранее.
При нагрузке A.189), представленной нечетными полиномами
Чебышева, находим свертку выражений A.178) и A.179) с функ-
функцией elV\
v(x,0, t) =
ft=0
„<Х«-х
BЛ2 - 1) V Л2 - ft2 /1 - Л2
п_Ч_
2 „2/7.
т
dx; A.194)

Глава 1. Динамические перемещения упругой полуплоскости
(случаи установившихся колебаний)
О, /) = _22LI Va
2/
; A.196)
J
где функции C2k+l(x>
j
A.197)
определяются как и ранее.
§ 5. ПЕРЕМЕЩЕНИЕ ВНУТРЕННИХ
ТОЧЕК
При решении некоторых задач кроме перемещений границы
упругой полуплоскости необходимо также знать закон распределе-
распределения перемещений по глубине под действием динамических нагрузок,
приложенных к участку границы. Рассмотрим задачу, изложенную
в § 2 (см. рис. 3), для случая у > 0.
Прежде чем перейти к нагрузке в виде функции Хевисайда, рас-
рассмотрим вспомогательную задачу о действии мгновенной нагрузки
A.40). Подставляя двойное преобразование (Лапласа и Фурье)
A.41) этой функции в формулы A.22) и A.23), получаем такие вы-
§ 5. Перемещение внутренних точек
55
ражения для изображений Лапласа вертикальных и горизонталь-
горизонтальных перемещений:
v(х, **) =
cos х
A.198)
'и (х, У,*)~
— 2 Vl2 + PV V I2 + s2 e~y^+s'] d?, A.199)
где F(l, s) определяется по формуле A.19). После применения фор-
формулы обращения выражение A.198) принимает вид
X
etsds. A.200)
Во внутреннем интеграле вводим новую переменную p—s/l:
__ 2qa f sin ? nns v? .
У'
Г x
X
С ICO
^-4/
. A-201)
Интегрирование в комплексной плоскости по переменной р произво-
производим по контурам 1\ и Г2 (см. рис. 4), аналогично тому, как это сде-
сделано в § 2. Опуская промежуточные выкладки, записываем функ-
функцию (
цию
в Биде
v(x, у, t) =
— 2оа С sin
X
X
8C—2p2) —
i—Q)e
X

56 Глава 1. Динамические
1/C
j
X
перемещения упругой полуплоскости
ГПГТ [B _ г?) e-yv^=^ -
! cos (y\
B - ?2J V~l
¦ _2_ Г B-g2) cos (у? /Р2С2 - 1) - 2 cos (yg \П?~ 1) т /
« J B-?«)» + 4Kp»t*-l^?»-l
1/8
U.
?-lx
A.202)
Эту формулу удобно использовать для вычисления перемещений
при нагрузках, изменяющихся в зависимости от времени по различ-
различным законам, выраженным аналитически, так как свертка может
быть произведена под знаком интеграла. Например, если нагрузка
изменяется в зависимости от времени как функция Хевисайда, то,
интегрируя выражение A.202) по / от нуля до t и делая подстановку
? = 1/т], получаем
где
Ф.
ф* (Р. х, у, t, х[) =
/,/,11): 1_ у ^-fpzITpi x
!.*,#, /,
I (Р. X, у, t, Г]) —
П) +
A.203)
(*= 1; 2);
A.204)
4-2Т|1п
; 1 — jc); A.205)
5. Перемещение внутренних точек
57
X In
[j/2 (Р2 - Л2) - г2т)а]а - ^2 (у У Р2 - г]2 - гт]J
[г/2 (Р2 - т]2) - г2т]2]2 - Р (у
г]2)
[г/2 (Р2 - п2) - г2г!2]2
(< + ЩJ ~ У2 (Р2 ~ Л2)
- гт]J - г/г (Р2 - Т]2)
A.206)
+ H(t-\4(l-x)-yV
_Н (t -\r](l + х) +
\) (t-\4(l + х)
\ -rf\) -
A.207)
Аналогично получаем выражение для горизонтальных переме-
перемещений под действием внезапно приложенной нагрузки, равномерно
распределенной на участке границы упругой полуплоскости,
и (х, y,t) = —
iqa
л2(х |8C-2р2) ц\-
-2 lAi?-|J2 V г]?- 1 ?хA, х, у, t, %)]-
+ 2 ур—^ут=$ % A, х, у, t,
+ 2
_ 1) ^ (Р, х, у, /, л) -
где
(Р. *. y,t,rH = —
A.208)
A.209)

58
Глава 1. Динамические перемещения уЛгругой полуплоскости
1
Х!пгта
(р\ г, у, t, г]) = -L-yVrf — |
[г/2 (Т12 — Р2) + Р — г2г]2]2 + 4г/2г2П2 (л2 — р2)
2гу(*ц / т]2 — р2
</2 (Т12 — Р2) — г2гJ] + [у2 (ri2 — Р2) +
„„„+„ г/2 (л2 - Р2) + г**) + гУ
— arct
A.210)
A.211)
+ (^1
(У
I г | т]J
Arctg -rr =
arctg -у (Y > 0);
arctg-?-+ sign X л (К<0),
A-212)
A.213)
причем arctg -rr — главное значение. Как следует из структуры
формул A.203) и A.208), определение перемещений v (x, y,t) и
и(х,у, t) сводится к вычислению элементарных функций и интегра-
интегралов от них в конечных пределах, причэм все функции непрерывны.
Полученные в этой главе формулы описывают распространяю-
распространяющиеся от источника возбуждения волны, хотя этот процесс и не
всегда представлен в явном виде в приведенных выражениях. На-
§ 5. Перемещение внутренних точек
59
пример, из формул A.74), A.87) следует, что описываемые ими
волны распространяющиеся, а из формул A.71), A.85) в явном
виде это не вытекает. Однако если найти асимптотическое разло-
разложение, как это сделано для функции A.88), то можно убедиться,
0,5
1,0
1,0
п п
2
У
4
\А
У
8
!
10
/
12
гт
16
18
t
ТТЛ .
гг
4
к
Рис. 9.
Рис. 10.
что волны действительно распространяющиеся. Вычисления пере-
перемещений в различных точках упругой полуплоскости показали
[30], что по формулам § 5 получаются нулевые (в пределах точности
вычислений на ЭВМ) значения перемещений до тех пор, пока в
данную точку не придет продольная волна.
На рис. 9 и 10 представлены графики соответственно вертикаль-
вертикальных и горизонтальных перемещений (в долях 1,75 да/ц) точки упру-
I 4 6
10 12 14 16 18 t
N
\
\
\
\
V
/
J
V
J
-t
i
-0,5
О
0,5
1,0
2
\
it
\
\
(
7
/
10
12
п
16
t
Рис. И.
Рис. 12.
гой полуплоскости с координатами х = 4, у = 0 под действием рав-
равномерно распределенной на участке границы нагрузки, изменяю-
изменяющейся в зависимости от времени в виде прямоугольного импульса,
продолжительностью Т = 2, на рис. 11 и 12 — аналогичные графи-
графики при х = у = 4. Вопрос о стоячих волнах возникает лишь при
исследовании периодических колебаний упругой полуплоскости без
учета переходного процесса (см. § 3).

Глава 2
КОЛЕБАНИЯ
ЖЕСТКОГО ШТАМПА
НА УПРУГОЙ ПОЛУПЛОСКОСТИ
§ \. ВЕРТИКАЛЬНЫЕ НАГРУЗКИ
Пусть на жесткую полосу шириной, равной единице, и длиной
1а (рис. 13), выделенную из балочной плиты, действует вертикаль-
вертикальная сила, изменяющаяся в зависимости от времени по заданному
закону P(t). Требуется найти нормальную реакцию основания
р (x,t) и вертикальное перемещение полосы w(t). Трение между
полосой и полуплоскостью не учитывается.
Для решения задачи воспользуемся дифференциальным урав-
уравнением движения полосы (в безразмерных переменных)
4 fiw @ = р (/)_
B.1)
полуплоскости A.1) и контактным условием
w(t) = v(x,0,t) (|х|<1), . B.2)
где Мо — масса полосы, R(f) — равнодействующая нормальной
реакции основания
R(t) =
B.3)
Применяя к уравнению B.1) преобразование Лапласа и учитывая
условие B.2), получаем
^-]*v(x,0,$ = P(s)—R(s) (U|<1). B.4)
Подстановка в последнее уравнение значения v(x,0,s) из формулы
A.24) и применение формулы обращения Фурье к равенству A.17)
приводят в области изображений к парному интегральному урав-
уравнению вида
l, s) cos
— R(s)
B.5)
§ 1. Вертикальные нагрузки
61
где
h — высота штампа; р — плотность его материала; функция F(\, s)
определяется по формуле A.19). Из уравнения B.5) находим изо-
изображение р(х, s) и переходим к оригиналу по формуле обращения
р (х, s) e4s. B.7)
с—ioo
Получить точное выражение для функции р (х, t) не представ-
представляется возможным, и поэтому оправдан поиск эффективных при-
приближенных решений. В работах 18, 10, 11, 13] уравнения вида B.5)
P(t)
Рис. 13.
применительно к установившимся колебаниям штампа решаются
методом сведения их к интегральному уравнению Фредгольма II ро-
рода, которое затем решается приближенно (численно или в рядах).
Аналогичный подход при неустановившихся колебаниях штампа
применен в работах [59—61]. Известны также способы непосред-
непосредственного сведения парных интегральных уравнений к алгебраи-
алгебраической задаче [71—73, 103] путем представления решения системой
ортогональных функций. В последнем случае для получения эф-
эффективного решения, обеспечивающего быструю сходимость, су-
существенно выявление особенностей искомой функции.
Чтобы установить характер особенностей функции р (х, f), к
уравнению B.5) (| * | < 1) применяем теорему о свертке для пре-
преобразования Фурье. В результате получаем интегральное уравне-
уравнение Фредгольма I рода
+1 °о
m0 VTn s* J р (х1, s) J Vfijt%* cos (х - х') Id^dx' = Р (s) — R(s),
-1 0
B.8)
ядро которого путем интегрирования в комплексной плоскости (см.
гл. 1, § 2) может быть приведено к виду

62 Глава 2. Колебания жесткого штампа на упругой полуплоскости
Ei
Ei<-sx^)}-
p
0
л ) F
- srn)| A,-
где
1 Ei («П) + ^ Ei (-
e~*Ei (г) + e2 Ei (— z) = 2 (С + In г) ch z + ch г
B-9)
~ Sh Z 2
2
= °'57722).
т. е. при s->0, что в области оригиналов соответствует большим
значениям ?, ядро B.9) может быть разложено в ряд, содержащий
степенные функцки и произведение логарифма и степенной функ-
функции. Интегральные уравнения Фредгольма I рода с ядрами, со-
содержащими логарифм, рассматривались (применительно к стати-
статическим контактным задачам) в работах [3, 4], где показано, что
решение их имеет особенность вида 1/]/ 1 — х2. Следовательно, и
функция p(x,t), по крайней мере при больших значениях t, имеет
э:у же особенность. При малых значениях / поведение реакции
р(х, t) (х ->- + 1, / -*- 0) описывается системой 4 ункций, сумма ко-
которых с определенной точностью может оказаться равной величине
У\ —л:2 и тогда особенность по краям штампа практически исчез-
исчезнет.
Независимо от вида колебаний (стационарных или нестацио-
нестационарных) и типа штампа (жесткого или упругого), решение для кон-
контактных напряжений ищем в виде разложения в ряд по полиномам
Чебышева I рода, ортогональным (с весом ^
A < < 1]) б
рда, ортогональным (с весом l/J/l —а:2 в интервале
1 < х < 1]) и образующим полную систему функций,
(X)
B.11)
где A2k(t)—неизвестные функции, зависящие от времени.
П. И. Клубиным установлена [46] эффективность использования
ортогональных полиномов для решения статических контактных
задач. Покажем, что метод ортогональных многочленов достаточно
эффективен при решении динамических задач.
§ 1. Вертикальные нагрузки
63
Двойное преобразование функции B.11) имеет вид
B.12)
2
k=o
Последнее выражение удовлетворяет уравнению B.5) при | х\ > 1.
Чтобы удовлетворить этому уравнению при | х | < 1, подставляем
в него значение p(l,s) из формулы B.12) и, учитывая, что
R(s) = naA0(s), B.13)
получаем
(- 1)*
i
X
) COS X%dl =
P(s)
na
B.14)
Интеграл в этом выражении в соответствии с формулами A.120)
и A.129) может быть записан в виде
i
к, sr\) йц
B.15)
причем функция C2k{x, si\) находится по формуле A.136) при / х\ <
< 1 и по формуле A.140) при \х\~>\. Используя разложение
в ряд по полиномам Чебышева A.135) функции С2*(х, srj), получаем
), B.16)
где
c2k,2r (s) = -M —
V Ti? - e2
F, (r]i)—
hk (sih) K
ir
3
); B.17)

64
Глава 2. Колебания жесткого штампа на упругой полуплоскости
при k <i r индексы у бесселевых функций I и II рода от мнимого?
аргумента следует поменять местами. Подставляем разложение!
B.16) в уравнение B.14):
оо Г °о "I —
Ао (s) + m0s2 2 A2k (s) c2k,0 (s) + 2 2 c2k,2r (s) T2r (x) =-- -^- B.18*?
Приравнивая в этом выражении коэффициенты при полиномах Че-
бышева одинаковых степеней, стоящих слева и справа от знака ра-
равенства, получаем систему алгебраических уравнений для опреде-
определения неизвестных А2и (s):
A2k(s)c2k,o(s) = D0(s);
*=0
откуда находим
=h 2, ...),
B.19)
где A(s) — определитель системы B.19); A2k(s) — определитель,
получающиеся при замене соответствующего столбца матрицы сво-
свободными членами
P(s)
D0(s) =
D2r(s) = 0 (/"=1,2, ...).
Изображение вертикальных перемещений штампа может быть
найдено из уравнения B.1):
s)}. B.21)
Применяя к выражению B.20) формулу обращения Лапласа, полу-
получаем
Аоь (t) =
Для вычисления интеграла в B.22) проанализируем особенности
подынтегральных функций в нем. Функции c2k,2r (s) B.17), как
следует из формулы A.134), определены при Res > 0, но при рас-
рассмотрении интеграла B.22) по комплексной переменной s могут
быть аналитически продолжены во всю плоскость изменения пере-
переменной s. Так как функции c2k,2r (s) содержат логарифм, то нуль
для них будет точкой ветвления. Выражение B.22) представляет
собой решение физической задачи, следовательно, при функции
P(t), ограниченной на бесконечности, в нем не будет слагаемых,
§ 1. Вертикальные нагрузки
65
растущих по экспоненциальному-закону, т.е. в определителе A(s)
не будет корней с положительной действительной частью. На
рис. 14 показан контур, с помощью которого можно вычислить инте-
интеграл B.22). На верхнем берегу разреза переменная s прини-
мает значения %е<п, а на ниж- /^
нем — %е-ш. Находя интеграл
по этому контуру и учиты-
учитывая, что интегралы вдоль дуг
большого радиуса в пределе рав-
равны нулю, получаем
1 с+!°° _
= ^ res [A
2*1
Рис. 14.
l, B.23)
где первое слагаемое — сумма
вычетов в полюсах, соответ-
соответствующих комплексным корням S/ = —? ± it, уравнения A (s,-) =
= 0 (! > 0), второе слагаемое — сумма вычетов в полюсах функции
~Р (s); Im A2k (|е'я) — мнимая часть неизвестных А2к(%ёл), которые
находятся из решения системы B.19) с комплексной матрицей (так
как функции c2k,2r{&n) комплексны); интеграл Лапласа может быть
вычислен по квадратурным формулам [54]. Функции c2k,2r (|е'я),
необходимые для вычисления значений 1тЛ2* (^я), находятся с
помощью выражения B.17). Учитывая, что
К2г Ш«) = Kir Ш - nil* (т?), B.24)
и подставляя s = &п в формулу B.17), получаем
c2k,2r {lein) = Re c2k,2r Це*) + i Im c2k,2r (&'% B.25)
где
B.26)
3 5—2880

66 Глава 2. Колебания жесткого штампа на упругой полуплоскости
Im c2k,2r (&?"•) = -2 [- я ' f!*j~p2 /я ОШ /* (%?) +
.
B.27
Корни sy = —I ± i? уравнения A (s,) = 0 находятся путем реше
.ния системы двух трансцендентных уравнений
ReA(—g
ImA(—
B.281
для чего может быть использован метод, изложенный в работ
[101]. При вычислении определителя A (s) от комплексного аргу*
мента s = —| -f- it, = r^fc, где
— arctg^ + я (?>0);
— arctg -| п (КО),
используем соотношения
|{ Д/
Re c2k,2r (гс А) = -|-{-я
[/» (%гс А)
+
Re[/
Re
{r<AtiI dT1); B-29)
Im
V
Im
Im
(геAn)j Л|
Im
. B.зо)
^ 7. Вертикальные нагрузки
67
Учитывая, что
/2Jk(z)
_ 1)" Bfe - 2л + 2пI Bг - п - 1)! /J_
^ п! BЛ — 2л + /г)! B* + я)! ^ 2
п=0
2 In-!-
2" 2 "я! B* + п)! B/- + яI- № + 2/- + я)!
, B.31)
где L =2гь Byfe + 2г + 2п + 1) - г|> (п + 1) - У Bk + п + 1) -
-- грBг + л + 1) — ^рB* + 2r + n + 1), получаем
Re
гф
1_ -v?
2 Zd п!
п=0
B* + п)! Bл + и)! Bk + 2л + я)!
х
Im 1Ыг]лсА)/ЫТСАI = 4
-4-2
¦l%\] = JL V (- 1)"B*-2л + 2я)!Bл-я-
П 2 Zi n\ Bk — 2л + га)! Bft + яI
n=0
2(ft—л+я)
X
B.32)
(— 1)" Bft - 2л + 2яI Bл — я - 1)!
я! Bk — 2л + га)! Bk + я)! Х
:—л + п)фс —
X
2
п=0
2(А—л+я)
я! Bk + я)! Bл + и)! Bft + 2л + П)!
X
B.33)
После определения полюсов s, вычеты в них находятся по формуле
-. , . s//. A2A (SPg Г9 34)
res [Л2А (S/) е ' | = А> (S/) • (Z'6V
где величина A' (sy) определяется путем численного дифференциро-
дифференцирования функции комплексной переменной.

68
Глава 2. Колебания жесткого штампа на упругой полуплоскости
Для большинства функций P(t), применяемых в расчетах ко-
колебаний конструкций, полюсы изображения Лапласа Р (s) нахо-
находятся легко, поэтому вычисление второго слагаемого в формуле
B.23) не представляет существенных затруднений. Перемещение
штампа определяется путем вычисления интеграла свертки на
основе равенства B.21):
Wit) —
J (' ~ т)[Р <т
B.35)
Из анализа выражения B.23) следует, что первое слагаемое в нем
представляет собой гармоническую функцию, затухающую в за-
зависимости от времени, причем характер изменения ее от аргумента
t не зависит от вида приложенной к штампу нагрузки, т. е. эта со-
составляющая функции A2k{t) соответствует свободным затухающим
колебаниям штампа. Величина ? есть не что иное, как безразмерная
частота свободных колебаний штампа на упругой полуплоскости,
а \ — коэффициент затухания, обусловленный излучением энер-
энергии на бесконечность. Второе и третье слагаемые в формуле B.23)
соответствуют вынужденным колебаниям, причем если последний
член имеет существенное значение в начальный период движения
штампа, стремясь к нулю с ростом t при любой не возрастающей на
бесконечности нагрузке, то второе слагаемое существенно зависит
от вида заданной нагрузки P{t) и при t -*¦ оо может принимать
различные значения.
Кроме формулы B.23) для вычисления интеграла B.22) может
быть использован следующий способ. Так как из физических условий
задачи следует что, определитель системы B.19) не имеет корней в пра-
правой полуплоскости (Re s> 0), то интеграл по прямой, параллельной
мнимой оси, можно заменить интегралом по мнимой оси и в этом
случае интеграл обращения преобразования Лапласа сводится к
интегралу Фурье [136]
@ = — 4 J
Im
sin
B.36)
Этот интеграл сходится медленнее, чем интеграл Лапласа в фор-
формуле B.23), но знание комплексных корней определителя не
требуется. Функция \mAok(it) при фиксированных значениях ? на-
находится из системы уравнений B.19) путем подстановки в нее зна-
значения s = it, и решения системы с комплексной матрицей, коэффи-
коэффициенты которой определяются с помощью выражений
Recikfir(i?)«_(_ l)k+r\-n
' Ш
§ 1. Вертикальные нагрузки
69
Mtf (ri2-
где Л^л (&п)—функция Неймана;
(k>r), B.37)
72»(?rhO2r«%) +
B.38)
Для получения оценок сходимости ряда B.11) и выяснения
возможности решения системы B.19) методом усечения матрицу
записываем в виде
l/m0s2+ coo(s) co2(s) coi(s) ...
C2U
ci0 (s)
|
c42 (s) c44 (s) ...
B.39)
При фиксированном действительном s > 0 находим сумму коэффи-
коэффициентов в каждой строке матрицы B.39):
2,= 2 \c^,2r(s)\ (/" = 0, 1,2, ...).
B.40)
Учитывая, что при s > 0 все функции, кроме /7'(rli). в B.17) поло-
положительные и что
C2k,2r(s)<iC*hk(z)K2r(z) @<Z<00), B.41)
где с* — положительная постоянная, величина которой несущест-
несущественна для общих оценок, B.40) можно заменить мажорантным
рядом S2r = 2 hk (z) K2r (z) (k > г, при k < г индексы у бесселе-
вых функций I и II рода от мнимого аргумента следует поме-
поменять местами). Так как [24]
то
/»(*) = ¦
= ±. [ch z
B.42)
far (г)], B.43)

70
Глава 2. Колебания жесткого штампа на упругой полуплоскости
т. е. сумма конечна при любых значениях z > 0 и г. Исследуем по-
поведение этой суммы при г — N + \, N + 2, ... Делим все коэффи-
коэффициенты в строке матрицы B.39) на диагональный член и находим
их сумму:
с г—\ и 17\ °° I <-Л
¦ — 1 = У т^тгг +
12г (г) К2г (г)
где
г-\
K2k (г)
К2г(г)
<г-
К2Г (г)
__
B.44)
B.45)
k=r+l
m=l
ге
r+m
2m
4m
16 (/-+1J
Следовательно,
). B.46)
I. B.47)
На основании равенства B.43) и асимптотической оценки B.47)
приходим к выводу, что система уравнений B.19) относится к классу
квазирегулярных систем [43], ее решение имеет вид A2k (s) < const.
Условия квазирегулярности системы B.19) соблюдаются и в том
случае, когда в ней делается подстановка A2k(s) = A2k{s)l(k + 1):
г2 In r
16г г
12г (г) К2г (г)
т. е. Alk(s)< a* = const; A\k(s)< {a*l(k + 1 )J или
оо со t
|ft(s)<(a*J
(г ->¦ оо),
B.48)
B.49)
k=0
Полученные оценки свидетельствуют о том, что бесконечная
система уравнений B.19) допускает решение методом усечения.
Так как функция A2k(t) может быть восстановлена по значениям
A2k (s) на действительной оси [53], то приведенные выше оценки для
вещественного s > 0 достаточны.
В качестве примера неустановившихся колебаний рассмотрим
действие вертикальной силы, внезапно приложенной к штампу:
Р (t) = РН @; Р (s) = P/s. B.50)
Подставляя значение Р (s) в систему B.19), находим величины
A2k (s). Для перехода к оригиналам используем формулу B.36), за-
§ 1. Вертикальные нагрузки
71
меняя интеграл суммой по методу Филона [97]. Применяя квадрат-
квадратную формулу с весовой функцией j/l — if [54], предварительно вы-
выделив логарифмическую особенность подынтегральной функции в
точке л = 0, вычисляем интегралы B.37) и B.38).
Результаты вычислений функции A2k (t) (в долях Plna) и w (/)
(в долях P/n\i) при коэффициенте Пуассона материала полуплос-
полуплоскости vo=0,3 и значении параметра т0 =0,4 представлены в
Таблица 2.1
«)
Л, it)
wit)
А„(<)
A, {
wit)
0,1
0,2
0,3
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
3,0
4,0
5,0
6,0
7,0
8,0
0,206
0,409
0,588
0,731
0,929
1,035
1,083
1,083
1,084
1,071
1,058
1,046
1,088
1,036
1,014
1,009
1,004
1,004
0,011
0,042
0,088
0,145
0,276 (
0,415 (
0,552
0,670
0,800
0,911
1,015
1,113
1,548
1,814
1,977
2,104
2,206
2,301
3,260
3,465
3,616
3,735
3,891
3,982
1,032
1,060
,076
,082
,085
,084
,063
,034
,016
,008
1,005
1,003
—0,168
—0,269
—0,313
-0,332
-0,307
—0,246
—0,167
—0,092
—0,028
0,026
0,068
0,096
0,083
0,046
0,025
0,013
0,007
0,004
0,011
0,041
0,084
0,137
0,262
0,398
0,537
0,672
0,802
0,925
1,039
1,144
1,557
1,816
1,987
2,117
2,225
2,320
0,261
0,465
0,615
0,734
0,891
0,983
1,032
1,060
1,075
1,081
1,084
1,083
1,062
1,031
1,017
1,008
1,005
1,003
—0,161
—0,265
—0,317
—0,340
—0,316
—0,246
—0,160
—0,083
—0,021
0,028
0,061
0,082
0,082
0,050
0,025
0,012
0,007
0,004
—0,025
-0,027
—0,014
0,002
0,019
0,022
0,018
0,010
—0,002
—0,011
—0,012
—0,005
0,000
0,002
0,000
0,000
0,000
0,000
0,011
0,041
0,084
0,137
0,262
0,398
0,537
0,672
0,802
0,925
1,039
1,145
1,557
1,816
1,988
2,117
2,225
2,321
табл. 2.1. В разложении B.11) последовательно удерживались
один, два и три члена ряда (в таблице — соответственно 1, 2, 3).
Функция A0(t) быстро стабилизируется, т.е. ее значения при двух
и трех членах ряда практически совпадают; близки друг к другу
и значения функции A2(f) при двух и трех членах ряда; величина
функции Л4(?) на порядок меньше величин функций A0(t) и
A2(t). При росте / функция A0(t) стремится к единице, а функции
Л2ц@ и Л4(*) — к нулю, т. е. распределение контактных напряже-
напряжений стремится к статическим значениям. Отсюда следует, что наи-
наибольшее число членов ряда B.11) требуется для описания контакт-
контактных напряжений в начальный период движения штампа.

72 Глава 2. Колебания жесткого штампа на упругой полуплоскости
Известно [102], что распределение контактных напряжений в
начальный период движения штампа равномерное. На рис. 15 и
16 показано, как изменяются эпюры контактных напряжений в
зависимости от числа членов ряда в разложении B.11) при т0 =1,0
0,95х
Рис. 15.
Рис. 16.
и mo= 0,4. Кривые 1, 2 и 3 соответствуют случаям, когда в форму-
формуле B.11) удерживались один, два и три члена ряда при t =0,1,
кривые 4, 5 и 6 — то же при t — 0,2. Из рисунков видно, что при
одном члене ряда (кривые / и 4)
0 02 0,4 0,6 0,8 0$ х распределение напряжений такое,
!/nn=u4l I I I как в статике, при двух членах
ряда (кривые 2 и 5) распределение
А,,
Рис. 17.
Рис. 18.
напряжений близко к равномерному и при трех членах ряда (кри-
(кривые 3 и 6) оно практически равномерное (за исключением малых
участков у краев штампа). При увеличении времени t эпюра кон-
контактных напряжений трансформируется из равномерной в седло-
седлообразную (рис. 17). Характер изменения A0(t) и A2(f) представлен
на рис. 18. Аналогичные результаты получаются и при других зна-
значениях параметра пг0.
На основании приведенных расчетов можно сделать вывод о
том, что для правильного описания динамических контактных на-
напряжений в любой момент времени t в разложении B.11) достаточно |
удержать два-три члена ряда. '
§ 1. Вертикальные нагрузки
73
Рассмотрим случай, когда к штампу внезапно прикладывается
вертикальная сила, изменяющаяся по гармоническому закону
P(t) PH(t)№ B.51)
g __ SOU безразмерная частота колебаний. Найдем напряже-
напряжения по контакту и вертикальное перемещение штампа при tj>l,
т е при установившихся колебаниях. Преобразование Лапласа
функции B.51)имеетвид J5(s) = Я/(8_ф. B.52)
В формуле B.23) первое и третье слагаемые стремятся к нулю при
t-+oo. Остается только член, соответствующий вычету в полюсе
s='?, т- е- Лй (*)=<#'А», B-53)
где комплексные коэффициенты A2k находятся при решении систе-
системы линейных алгебраических уравнений B.19), в которой следует
положить s = it,, а свободные члены умножить на (s — it):
Ао —
A2kc2k,2r(it) = 0 (г- 1, 2, ...).
2
А=0
B.54)
Коэффициенты c2k,2r (it) матрицы B.54) определяются по форму-
формулам B.37) и B.38).
Далее нормальная реакция основания находится по формуле
р(х, о =
k=0
где
14
*1
lmA
2k
arctg
Im A,
[2k
Re Л
[2k
(ReA2k>0);
±n (ReA2k<0),
B.55)
B.56)
B.57)
причем знак числа я определяется знаком мнимой части; равно-
равнодействующая реакция — по формуле
R = na\A0\ei{V+<f°), B.58)
вертикальное перемещение штампа B.21) — из выражения
где
w (/) = —Ч— у (Re Ао — Р/паJ + (Im Aof e 1У+Фш) t B.59)
v — сдвиг фаз между силой Р и перемещением штампа,
f arctg Dq ,1тЛ° (Re Ao - Р/па > 0);
arctg
Im An
B.60)
Re Ao — Р/ла
±n

74 Глава 2. Колебания жесткого штампа на упругой полуплоскости
Если приложенная сила изменяется по закону ccs?/, то в выра-
выражениях B.55), B.58) и B.59) следует удержать действительные час-
части, если по закону sin ?/, то —
мнимые. На рис. 19 показаны |
эпюры контактных напряжений
через Vie периода (пг0 — 0,4;
v0 == 0,3; ? = 1,0), которые сви-
свидетельствуют о том, что в про-
процессе колебаний периодически
происходит трансформация эпю-
эпюры напряжений из параболиче-
параболической в седлообразную и наобо-
наоборот.
Если в системе уравнений
B.54) положить Р — 0, то она
будет соответствовать свободным
колебаниям жесткого штампа
на упругой полуплоскости. Ис-
Исходя из физических условий,
Рис- 19- можно предположить (а рас-
расчеты подтверждают это), что при
действительных ? определитель A(i?) не равен нулю. В противном
случае свободные колебания полосы на упругой полуплоскости но-
§ 2. Воздействие симметричных упругих волн
75
0,2 Qfr 0,6
1.2
1,6 1,8
Ofi 1,0
Рис. 20.
сили бы характер устанозившихся, что невозможно, так как упругая
полуплоскость поглощает энергию вследствие излучения. Опреде-
Определитель A (s) может быть равен нулю только при комплексных зна-
значениях s =—1± /?, которые находятся из решения системы
трансцендентных уравнений B.28). Результаты решения этой си-
системы в случае определителей 2-го и 3-го порядков представлены
в табл. 2.2. Характер изменения коэффициента затухания \ и час-
частоты свободных колебаний ? от массы штампа показан на рис. 20,
Таблица 2.2
i
Определитель
порядка
%
2-го
С
Определитель
порядка
1
3-го
1
0
0,05
0,1
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
1,369
1,282
1,208
1,080
0,878
0,723
0,607
0,519
0,457
0,406
0,367
0,334
0,307
0,452
0,480
0,507
0,553
0,604
0,613
0,598
0,574
0,548
0,522
0,498
0,476
0,457
1,350
1,281
1,215
1,057
0,875
0,724
0,582
0,531
0,455
0,411
0,370
0,337
0,306
0,450 ,:
0,476
0,491
0,536
0,588
0,605
0,606
0,589
0,540
0,531
0,505
0,483
0,453
1
откуда видно, что при увеличении массы штампа от нуля частота
сначала растет до некоторого предела, а затем падает. Это можно
объяснить затуханием колебаний, которое резко возрастает при
малых значениях параметра пг0. Близкие значения | и? для опре-
определителей 2-го и 3-го порядков (см. табл. 2.2) подтверждают вывод
о быстрой сходимости ряда B.11).
§2. ВОЗДЕЙСТВИЕ СИММЕТРИЧНЫХ
УПРУГИХ ВОЛН
В некоторых случаях сооружения подвергаются воздействию
упругих волн, распространяющихся в основании от источника
возбуждения, расположенного на некотором расстоянии от соору-
сооружений. Рассмотрим колебания штампа под действием двух вер-
вертикальных сил Р (t), приложенных к границе полуплоскости
(рис. 21).
В уравнении движения штампа B.1) в этом случае нужно поло-
положить Р (t) =0, так как внешние силы к штампу не прикладываются.

76 Глава 2. Колебания жесткого штампа на упругой полуплоскости
Парное интегральное уравнение B.5) принимает вид
@<*<l); 1 B-61)
pit);
1
T
1
a
i
pin
Рис. 21.
где / = На — относительное расстояние от центра штампа до сил;
/ — действительное расстояние. Определяя контактные напряжения
с помощью разложения B.11), находим
Т> F, s)=a l/lr Jo(- *>* Л
Подставляя это выражение в B.61), получаем
cos
Л (s) + /По** 2 (- 1 f Л2, (S) J ^f + f2
А=0 о
cos хЩ =
Раскладывая обе части уравнения B.63) в ряды по полиномам
Чебышева и приравнивая коэффициенты при полиномах одинаковых
степеней, приходим к системе уравнений B.19), в которой свобод-
свободные члены находятся по формулам
па
{г =1,2, ...),
B.64)
§ 2. Воздействие симметричных упругих волн
77
где
2r (I, S) = (- 1)' 4 [- я
B.65)
причем Сг/-(/, si]) определяется по выражению A.140), в котором
вместо k следует подставить г, а вместо х — подставить /. Формула
Q(t)'
///////// S/S/////S//S// // / / f f/
Рис. 22.
B.65) аналогична выражению A.129), описывающему (при | х | >1)
перемещения границы упругой полуплоскости за пределами за-
загруженного участка, т.е. знания этих перемещений достаточно для
решения задачи о воздействии упругих волн на сооружение.
Функции A2k(t) вычисляются по формуле B.23) или B.36),
действительные и мнимые части функций C2r (I, it,r\) — соответствен-
соответственно по формуле A.140), где следует положить k = г, х = I, z =
= it,r\. Вертикальное перемещение штампа находим по формуле
B.35), которая для данного случая имеет вид
t
(t - т) Ао (т) dx.
B.66)
Под действием горизонтальных сил Q (/), направленных в разные
стороны (рис. 22), происходят только вертикальные колебания штам-
штампа. Уравнение колебаний штампа остается прежним — B.1) при
Р (t) =0. Учитывая на основе формулы A.36) вертикальные пере-
перемещения границы полуплоскости под действием горизонтальных
сил, получаем систему уравнений B.19) со свободными членами
D2r (s) =
(г = 1, 2, ...),
B.67)

а
з-
д п 2 Й 2J S SK "S оо со о 2S ою-. —
о г~- ^ о слюсосо ~^ ^f ~^ li; со со ю ю
О — — — О_ О О ¦* —i О, О О ©_ О « О О О О а>
—' О О О О CNOOOO со" О* о" о" О Ю О о" О О
«. Ills о, S| = S. о i§2cl . §§| =
о о о о" о —. о о о" о" cn о о о" о ч" о о о" о
ссЦЦ ooSi^i ool^l .!§§§
О О О О О — О О О О CN О О О О -** О О О О
,iisi ,|1|| ,РД| ri.§iS
о о о о о — о о о о" и" dodo" ¦*" о" о о* о
« iisi « ?$§.§ со i§2| „ §§§S
о о о о о _¦ о о о о <n о о о о- те" о о о* о
KS|2 Й88« SS82
о I I I I _: «|. о о о <n о о о о- V о о о о
оо 3 ? <n со со - <g ? оо © 3
f II II те "_ Ю О О * О NO™ СООООСО
<=>* " ? ° Т f N" f f f °" " °" f f °"
со § I si со ills e sill
л '"' л ~ CN О О О - CO* о" О О о"
- °<т
??
- ° ° 9 9 «"«?<?<=>",-? « о" о © o"
CO CO ^ «
°. -. Я. о
О О О о
, СО СО ^
& 8 ? 8
о" о" о" о
7
О О)
с- с- с-^.
ч"—' v-^' >*-' ^щш^
О « *f
¦* , ¦* со
N N О1 1Л
CN_ О — CN ¦*
со" о" © © о*
I I
^¦*> ^^« ?^.
в N ч.
"^ ^ ^
§ 3. Горизонтальная и моментная нагрузки
79
где
Ъгг (I, s) = (- 1У 4-
Г
J
2 r\iF'
S2r(l,
J
Рис. 23.
функция S2/- (/, st]) определяется поформуле A.146) при k = r,x =1.
Если к границе внезапно прикладываются симметрично по отно-
отношению к штампу две вертикальные Р (t) = РН (*)е'У или горизон-
горизонтальные Q{f) = QH(f)eV силы,
то при ^ ^> 1 (установившиеся
колебания) решение задачи B.23)
определяется вычетом функции
A-2k (s) fs' в полюсе s = it,, неиз-
неизвестные Ачи {t) находятся из
формулы B.53), а коэффициенты
A2k — с помощью решения си-
системы уравнений B.19) при s = it,
и свободных членах соответ-
соответственно B.64) и B.67), в которых
вместо Р (s) и Q(s) следует подста-
подставить Р и Q. Действительные и мнимые части функций С2г (/, it,r\) и
~S2r (I, i?,f\) находятся по формулам A.140) и A.146) при z = it,r\.
В качестве примера рассмотрим действие внезапно приложенных к
границе полуплоскости вертикальных сил Р (/) = PHl(t). Резуль-
Результаты вычислений функции А2к (t) (k = 0, 1,2) в долях 2Р/па и функции
w (t) в долях 2Р/лц при пг0 — 0,4, / =2 и v0 = 0,3 представлены
в табл. 2.3. Относительное расстояние от сил до штампа равно
единице. Продольная волна проходит это расстояние за безразмер-
безразмерное время t = 0,53. В интервале времени 0 < t <; 0,53 штамп
находится в покое.
На рис. 23 показан график функции Ао (t) (равнодействующей
нормальных напряжений по контакту), из которого следует, что
наибольшее влияние упругой волны на штамп соответствует време-
времени прихода волны Релея.
§ 3. ГОРИЗОНТАЛЬНАЯ И МОМЕНТНАЯ
НАГРУЗКИ
Под действием горизонтальной силы Q (f) и момента М (t)
(рис. 24) штамп совершает сложное движение, которое может быть
разложено на три простых вида; вертикальное и горизонтальное

80 Глава 2. Колебания жесткого штампа на упругой полуплоскости
перемещения центра тяжести штампа и поворот его относительно |
центра тяжести. Так как угол поворота штампа мал, то вертикаль- |
ное перемещение центра тяжести штампа — величина более высо-
высокого порядка малости, чем горизонтальное перемещение. Следова-
M(t)
Q(V
о\
Рис. 24.
тельно, из трех условий равновесия штампа достаточно рассмотреть
сумму проекций всех сил на ось х и сумму моментов относительно
центра тяжести штампа:
Ш*
B.69)
4
B.70)-
где н0 (t) — горизонтальное перемещение центра тяжести штампа;
w (x, t) — вертикальное перемещение точек штампа при его повороте
вокруг горизонтальной оси, проходящей через центр тяжести штам-
штампа; полярный момент инерции 70 массы полосы относительно ука-
указанной оси определяется по формуле
+ "Г" "Я ' <2-71>
— равнодействующая касательных контактных напряжений,
QR (t) = a J т (х, t) dx; B.72)
MR (/) — момент равнодействующей нормальных контактных на-
напряжений,
+.1
MR (/) = fl« j p (jc, 0
Учитывая, что
B.73)
B.74)
3. Горизонтальная и моментная нагрузки
81
где и (t) — перемещение середины подошвы штампа, уравнения
B.69) и B.70) приводим к виду
~ «о) [Q @ - Q« @1 - 4" "о 1^ @ - М« (/)];
B.75)
Q« Wi + м @ - м« (о,
B.76)
4-
где
/о =
fflo
, 1 Л2 1 .
ha Мо __ _3 h_
1 h2
B.77)
B.78)
Предполагается, что при колебаниях штамп от полуплоскости не
отрывается и в любой момент времени соблюдаются контактные
условия
и @ - и (х, 0, 0; w (х, t) = v (х, 0, 0 (| х\ < 1). B.79)
В области преобразований Лапласа уравнения B.75) и B.76)
записываются в виде
B.80)
u (s) = A + JL- n0) [Q (s) - QR (s)] -
-±-по[М (s) - MR (s)];
-g- na2\ij0s2w (x, s) = a\M (s) — MR (s)] л; —
.. -QR(s)]x. B.81)
Горизонтальные и (х, 0, t) и вертикальные v (х, 0, /) перемещения гра-
границы полуплоскости равны сумме перемещений, возникающих под
действием горизонтальных и вертикальных напряжений. В изо-
изображениях
и (х, 0, s) = ik (х, 0, s) + ир (х, 0, s);
у (х, 0, s) = щ (х, 0, s) + vp (x, 0, s),
или, с учетом формул A.37) и A.25), A.36) и A.24),
и (х, 0, s) =
1
B.82)

82 Глава 2. Колебания жесткого штампа на упругой полуплоскости
v (х, 0, s) =
= —-т=- f ттйг^ф^' s)^« s)-s*V?TWp'(t s
где
B.83)
Ф (?, s) = 2?2 + s2 — 2 Vl* + p2s21/g2 + s2 . B-84)
Удовлетворяя контактным условиям B.79), подставляем значения
перемещений B.82) и B.83) в уравнения B.80) и B.81), а к выра-
выражениям A.31) и A.17) применяем формулу обращения преобразо-
преобразования Фурье. В результате получаем (в изображениях Лапласа)
систему парных интегральных уравнений вида
т0У2я !
iL [s2 I/FT?" т (|, s) + ©D (?, s) J5 (?, s)] d? =
4 «о) Ю (s)-Q« (s)]--f no[M(s) -Af«(s)] (|*|< 1);
4-fl/o
X
= [M(S) - M^ (S)] X_ A ^ (
oo oo
j' т (?, s) cos jegdg = 0; J J> (I, s) sin 44 - 0
о о
1);
| * | > 1).
B.85)
Найти функции т (х, t)np (x, t) из системы уравнений B.85) труд-
труднее, чем при вертикальных колебаниях штампа. При учете каса-
касательных реакций особенности в напряжениях по краям штампа
сложнее и в условиях динамики выявить их в точном виде затруд-
затруднительно. Поэтому ищем приближенное решение системы уравнений
B.85) в виде рядов, сохраняя особенность A — х2)-'^:
Р (х, t) =
т (х, t) =
go A2k+1 (t) T2k+i (x); B.86)
со
2 B2k (t) T2k (x), B.87)
где A2b+\(t)n B2k(t) — неизвестные функции. Так как вертикаль-
вертикальное перемещение центра тяжести штампа не учтено, а нормальные
контактные напряжения при действии сдвигающей силы малы (это
§ 3. Горизонтальная и моментная нагрузки
83
из статики), то, чтобы не загромождать решение, в разло-
№п„„„ B.86) и B.87) удержаны соответственно только нечетные
и четные полиномы. В соответствии с формулами B.73) и B.72)
MR (t) = 4 яаМ1 О: Q* @ = яаВо @- B-88)
После двойного преобразования (Лапласа и Фурье) функции B.86)
и B.87) имеют вид
B.89)
x d, s) = a Y \ | (-
:(SKT»©.
Последние выражения удовлетворяют третьему и четвертому урав-
уравнениям в системе B.85). Чтобы удовлетворить первому и второму
уравнениям, подставляем в них функции B.89) и преобразования
Лапласа функций B.88):
±по)во (s) - пЛ (s) + mos 2
(~ 1)* J
X
X [s2
(s)
na
na?
±B0(s)x
X
x
(s) -
(s)] ds =
a na
B.90)
Первый интеграл, входящий в уравнения B.90), определяется на
основании формул A.173) и A.175) (в изображениях):
— Л
B.91)

84 Глава 2. Колебания жесткого штампа на упругой полуплоскости
второй — на основании формул A.176) и A.178):
(В
Г
J
2л (ih|» -
третий — на основании формул A.121) и A.130):
B.93)
четвертый — на основании формул A.149) и A.156):
f s2 Vl2 + B2s2 „ Л. . .. 2 Г 1/»]?
2
X
F' (тц)
P
{x' SX]l) + 1 V^FM^ ^2k+l (*> sr$ dr\ +
x
.* 4
где функции C2ft (.v, srj), C2ft+i (x, sti), S2k (x, sr\) и S2fe+i (x, sr\) при
|л:|<;1 находятся соответственно по формулам A.135), A.167),
A.143) и A.161).
Раскладывая выражения B.91) — B.94) в ряды по полиномам
Чебышева, получаем
со
J l<F(t'
0 '
И С 1);
*|< 1);
2 f gaki2r (s)T2r (х)
B.95)
B.96)
3. Горизонтальная и моментная нагрузки
85
7 .?Ф g'
.1 /" (S>
где
(I) sin ^d6 = - 2
r=0
sin 4d| = (_ i)*2 f cWr+l (s)
r=0
B.97)
B-98)
(sti) ^ (sti) dTi
-Г
X
X
B.99)
Re s > 0; ^ > г (при ^ < г индексы модифицированных функций
Бесселя I и II рода следует поменять местами);
2, (ft|« -
/2,2r+1 (srj)
B.100)
причем функция /2*2л+1 (sn) определяется по формуле A.145), а
значения функций d2k+i,2r (s) и c2A+i,2r+i (s) —соответственно по фор-
формулам B.100) при перестановке индексов /гиги B.17) при замене
индексов 2k + 1 вместо 2k и 2г + 1 вместо 2г. Далее подставляем
разложения B.95) — B.98) в систему уравнений B.90):
,o (s) B2* (s) -
±.п)в0 (s) - Мх (s)
О j
>2r (s) A2k+i (s)]

86 Глава 2. Колебания жесткого штампа на упругой полуплоскости
х
ОС ОО
X S 2 К-
ft=0 r=0
-JLbo(s)x + Ax (s) х
ft,2r+l (s)B2k(S) + C2k+\,2r+\ (S) A2k+l (S)] X
B.101) f
Приравнивая коэффициенты при полиномах Чебышева одинако-
одинаковых степеней, получаем систему линейных алгебраических урав-
уравнений
~ «о
mos2gOo (s)] Bo (s) - [пд + m^d1Q (s)\ Аг (s) +
ОО
+ "V2 2 lgik,o (s) B2k (s) — (— l)*4k+i.o (s) Ла+1 (s)j = Do (s);
oo
S f^2*,2r (S) 52* (S) — (— l)Ai/2ft+Ur (S) Л2*+1 (S)] = Dz, (S)
(r=l, 2, ...);
- 4 + 2/0s2d0I (s)] Bo (s) + [1 + 2/0Aru (s)] Лх (s) +
2/0s2 2 K- 1
u (s) Л2А+, (s)] = Д (s);
I] [(—
k=0
d2ft,l (s)B2fc(S)-
(s) B2A(s) + c2A+I,2A+, (s) Л2А+, (S)j = o2,+1 (s)
('= 1, 2, ...),
B.Ю2) I
где
¦r».)^-».
2M(s)
=1, 2, ...);
D, (s) =
^-i-^f-; ^+l(S) = 0 (r=l, 2, ...).J
B.103)
Решая эту систему, находим неизвестные B2k (s) и A2k+\ (s). Возврат
к оригиналам производится по формулам вида B.23) или B.36).
§ 3. Горизонтальная и моментная нагрузки
87
Изображения горизонтальных и угловых перемещений штампа
определяются из формул B.80) и B.81):
u(s) =
B.104)
оригиналы функций B.104) при найденных Во (t) и Аг (t) — путем
вычисления интегралов свертки:
B.105)
- -с)
B.106)
Рассмотрим установившиеся колебания. Пусть к штампу вне-
внезапно прикладываются гармонические нагрузки
Q @ = QH (t) Р ¦ M(t) = MH (t) eiV . B.107)
Найдем контактные напряжения и перемещения штампа при t ^> 1
(установившиеся колебания). Решение для данного случая полу-
получаем из системы уравнений B.102), подставляя в нее s = t? и ум-
умножая столбец свободных членов на s — f?:
- К - m
2Л1
.2r (Ю
(г =1,2, ...);
== О
B.108)

Глава 2. Колебания жесткого штампа на упругой полуплоскости
- 2jJ?cn (»Е)] А, -
- 2/„?8 g [(- 1L*, > (»?) В» + c2k+1A (CQ A2k+l] =
2Л1 h Q .
а яа
4=0
= О
= 1, 2, ...),
где g2k,2r №), d-2k+\,2r (*'?)» d2k,2r+i (Ю и c2ft+i,2r+i (t?) — комплексные
функции, действительные и мнимые части которых определяются
по формулам
Re
-J
I
-io9)
?2r (Ш
+ ) Vp~[r])yf -32k Ы Ъг Ы dr\ +
-J
B.1 io)
Re
Im
/
2*+1'2r
~ ') /n2 -
Im
3. Горизонтальная и моментная нагрузки
89
; B.112)
Re
x
(- l)n Г Bn
(?т)/2)
2п
Х Zi T(n + k + r+ 3/2) Г (п — г + k + 3/2) Г (п — А + г + !/„) X
гс=О
Im
X Hn-
•; B.113)
B.114)
Функции Red2fe,2r+i (t'O и Imd2fe,2/-+i (t?) определяются по формулам
B.111) и B.112) при перестановке индексов k и г, а значения вели-
величин Re c2fe+i,2r+i (»D и Im c2k+\,2r+\ Ю — по формулам B.37) и B.38)
при замене индексов цилиндрических функций 2k + 1 вместо 2k
и 2л + 1 вместо 2г.
После решения системы B.108) и определения комплексных
коэффициентов B2k и A2k+\ вычисляем контактные напряжения
B.115)
B.116)
(модули и аргументы комплексных чисел находим по формулам
вида B.56) и B.57)). Определяем равнодействующую касательных
и момент равнодействующих нормальных напряжений:
QR @ = па | Во | е ' ; М« @ = -L яа" И, | eW+">. B.117)
Для перемещений штампа (горизонтального и углового) справед-
справедливы выражения
u(t) =
V-Щ
2М
А _^_ _ в,
па
B.118)
B.119)
Если в системе уравнений B.108) положить Q = 0 и М = 0, то,
раскрывая определитель этой системы, можно найти собственные
частоты и коэффициенты затухания колебаний штампа при его
поступательно-вращательном движении.

90
Глава 2. Колебания жесткого штампа на упругой полуплоскости
В качестве примеров рассмотрим действие внезапно приложен-
приложенной горизонтальной силы<2(/) =QH(t)n момента М (t) = MH (t).
На рис. 25 показаны изменения угла поворота фундамента (в до-
долях от статического значения 2A —2v0) Q /пагц) в зависимости от
времени. Положительным принят
угол поворота по часовой стрел-
-г1
hja--
1
X
/ от,—
\
Q
Q
777777
ч .
t
Рис. 25.
ке. Видно, что сначала фундамент наклоняется влево, а затем
знак угла поворота изменяется и значение угла выходит на ста-
статическую величину. На рис. 26 приведены графики ф (/) (в долях
1,ЗМ/ла?ц) при действии на штамп внезапно приложенного мо-
момента.
§ 4. ВОЗДЕЙСТВИЕ АНТИСИММЕТРИЧНЫХ
УПРУГИХ ВОЛН
Рассмотрим колебание штампа под действием двух антисим-
антисимметричных вертикальных сил Р (t), приложенных к границе полу-
полуплоскости (рис. 27). В уравнениях движения B.75) и B.76) в дан-
данном случае следует положить Q (t) = 0 и М (t) = 0. Несколько
изменится система парных интегральных уравнений B.85), в кото-
которой Q (s) = 0 и М (s) = 0, а последнее уравнение следует записать
в виде
1& s)sinje&/g = ?(s)e(*-/) (|*|>1). B.120)
Двойное преобразование (Лапласа и Фурье) нормальных на-
напряжений по границе полуплоскости имеет вид
B.121)
s) = ia У-— S (-
+ i У-1-
Р (s) sin Ц
§ 4. Воядействие антисимметричных упругих волн
91
После подстановки р (?, s) B.121) и т (|, s) B.89) в систему интеграль-
интегральных уравнений B.85) приходим к системе линейных алгебраи-
алгебраических уравнений B.102), где
д, (s) = -
\ (s) = -
0(/, s); D2r(s) = -
(г = 1, 2, ...);
^- /^й! (/, s); D2r+, (s) =
г2г+1 (I, s) (r = 1, 2, ...);
\т (I, s) ],
B.122)
Ь2л (I, s) определяется по формуле B.68),
Ъ2г+1 (I, S) = (- 1)' -|-
' (ill)
B.123)
S2r+\(l,sr]) находится по формуле A.165). Функции A2k+\ (t) и В2к @
вычисляются по формулам вида B.23) или B.36). Действительные
-p(t)
Pit)
Q(t)
У
Рис. 27.
Рис. 28.
и мнимые части функций Ьъ (/, it,) и a2r+i (/, %) находятся по выра-
выражениям B.68) и B.123) с учетом зависимостей A.146), A.162) и
A.165). Перемещения штампа u(t)n(p(t) определяются по форму-
формулам B.105) и B.106), где следует положить Q(t) = 0 и М (t) ==0.
При действии на границе полуплоскости двух симметричных
горизонтальных сил Q (t) (рис. 28) третье уравнение в системе B.85)
принимает вид
У-^- J т (I, s) cos
о
= Q (s) б (х - I)
). B.124)

92 Глава 2. Колебания жесткого штампа на упругой полуплоскости
Используя представление B.87), получаем изображение Лапласа
и Фурье касательных напряжений по границе полуплоскости:
т(?, s)=a/|-2 (-l)kB2k(s)
B.125)
После подстановки т (?, s) B.125) и р (|, s) B.89) в систему интеграль-
интегральных уравнений B.85) получаем систему линейных алгебраических
уравнений B.102) со свободными членами
DQ (s) =
x (s) = -
2Q(s)
m0s2a0 (I, s);
(r = 1, 2, ...);
(I, s);
i B-126)
z>
'2Н-1 (S) = —
где
(/, s) = (- 1)г -L-
(
F' М
(/, sr\) йц +
С2г (/,
B.127)
b2r+] (I, s) = (- 1)' 4- [ - -f -^
2,+1
(/,
— ti2
функции С2гA, sr|) и C2r+i(/, st]) находятся по формулам A.140) и
A.168).
В случае установившихся колебаний в систему уравнений B.102)
и выражения B.122) и B.126) следует вместо s подставить t?, a
вместо P(s) и Q(s) записать Р и Q. Действительные и мнимые части
функций S2, (/, ily\),S2r+x(l, ttt)), C2a (/, i?n) и C2a+i (/, ^т)) находятся по
формулам A.146), A.162), A.140) и A.168), контактные напряже-
§ 5. Колебания системы us двух штампов
93
ния определяются по выражениям B.115) и B.116), а перемеще-
перемещения штампа — по формулам B.118) и B.119), в которых следует
положить Q = 0 и М = 0.
§ 5. КОЛЕБАНИЯ СИСТЕМЫ
ИЗ ДВУХ ШТАМПОВ
Пусть на границе упругой полуплоскости находится система
из двух жестких штампов, на которую действуют изменяющиеся в
зависимости от времени нагрузки (рис. 29). Колебания в этом слу-
случае симметричны в вертикальном направлении и антисимметрич-
антисимметричны — в горизонтальном. Движение штампов может быть разложено
\P(t) \P(t)
1 1
-Q(t)
а ' о
Рис. 29.
на поступательное вертикальное, поступательное горизонтальное
и вращательное вокруг центра тяжести штампа. Требуется найти
нормальные контактные напряжения штампов при их поступа-
поступательных и вращательных колебаниях и касательные контактные
напряжения штампов при их горизонтальных поступательных ко-
колебаниях. Касательные контактные напряжения штампов при их
поступательных вертикальных колебаниях не учитываются.
Исходя из симметрии, записываем уравнения движения для
одного штампа, расположенного справа от точки о @ < л;):
d*wi^ =P(f)-R(t) (U'|<1); B.129)
| а>' (х1,0
= M(t)-MH(f)-
_ qr (oi -
B.130)
-L. r0 [M (t) - mr
B.131)

94 Глава 2. Колебания жесткого штампа на упругой полуплоскости
или в изображениях
niim^w, (s) = P(s)-R(s)
(| х' | <. 1);
(л:', s) = [Ж (s) — Af* (s)l x' -
-J^IQ(s)-Qr(s)]x'
u (s) = A + — noj [Q (s)
(s)] -
B.132)
B.133)
B.134)
где w0 (t) — составляющая перемещения штампа при его поступа-
поступательном вертикальном движении; w'(x', t) — составляющая верти-
вертикальных перемещений точек подошвы штампа при его повороте
вокруг центра тяжести, и (t) — горизонтальное перемещение подо-
подошвы штампа. Суммарные вертикальные перемещения точек подо-
подошвы штампа w (x', t) = w0 (t) + w'(x', t) в соответствии с формула-
формулами B.132) и B.133) в области преобразований Лапласа опреде-
определяем по выражению
2 М (s) — Mr (s)
5 (*', s) = р (*)-«(*)
х —
h Q(s)-QR(s)
a яц/oS2
B.135)
Удовлетворяя контактным условиям
w (x1, s) = 'v(l + x', 0, s); и (s) = и (I + x', 0, s)
(I *'!<!) B-136)
и учитывая, что напряжения на границе полуплоскости вне штам-
штампов равны нулю, получаем систему парных интегральных уравне-
уравнений вида
[s2
nm0
- [Af (S) - MR (S)] X' - A
(s) - R (s)] +
lQ(s)-QR(s)]x';
B.137)
5. Колебания системы из двух штампов
95
X
- Qr (s)|
nm0
¦ ^-nolM(s)-MR(s)}
J p (?, s) cos (/ + *') Щ = 0 (| x' | > 1);
6
J т {I, s) sin (/ + *') Щ = 0 (| x' | > 1).
Решение уравнений для напряжений на границе полуплоскости
ищем в виде рядов
Р (х, 0 =
' т (х, t) =
Vl — ix—tJ
(/—1 <.«</+1);
B.138)
B2k(t) T2k(x - I)
Y\— (X— If ft=0
(/-1<х</+1); B.139)
при остальных значениях хр (х, t) — 0 и т (л;, t) = 0. Для определе-
определения касательных напряжений используются только четные полино-
полиномы, так как самоуравновешенные касательные напряжения под
штампом, возникающие при его вертикальных колебаниях, не учи-
учитываются .
Двойные преобразования функций B.138) и B.139) имеют вид
p (I, s) = a V2n 2 Ak (s) 'J
cos
(*T +
B.140)
т (I, s) = ai \'2n sin Щ 2 (— 1)* B2k (s) 72k (g).
После подстановки значений B.140) в систему B.137) получаем
C0S
1
Г
X
, s) sin
(s) 72A (g) Us =
J

96 Глава 2. Колебания жесткого штампа на упругой полуплоскости
X 1М (s) - -f a*\ (s)j х' А
5|П?Г*'6 [go (g, s)S 4(s)cosffe4 + /gW
f" VSi s) [_ A=o \ z / '
+ s* S (- \f B2k (s) 72* (g) sin /g! dg =
0 !
^«o [Q(s)-naB0(s)l-
B.141)
(изменение горизонтальных перемещений границы полуплоскости
в пределах штампа не учтено, так как не учтены самоуравнове-
самоуравновешенные касательные напряжения под штампом). Раскладывая в
этих уравнениях левые и правые части в ряды по полиномам Че-
бышева и приравнивая коэффициенты при полиномах одинаковых
степеней, получаем систему линейных алгебраических уравнений
,(O
а (s) + m0s2 S (- 1) {Л2к (s) [с$.о @, s) + <$„ (/, s)] -
fc0
(s) C2ft'+l,o (',
*,o (/, s)} =
2 (— l)ft {^2* (S) [42,2r @, S) + C2%2r (I, S)] —
— A2k+l (S) 4feVl.2r (/, S) + B2k (S) ^ar (/, S)} = 0
(r=l, 2, ...);
A Bo (s) + A, (s) - 2/0s2 2 (- 1)* {A2k (s) 42,i (/, s) -
— л2а+1 (s) [42+i,i @, s) — <
+ B2k (s) [42,1 (o, s) - 42,i (/, s)]} =
2M(s)
na2
'a
na
k=o
{A2k (S) СЙ.2Г
@, S) -
- 42+1.2Л+1 (/, S)] + B» (S) [42.2Л+1 @, S) -
1 + 4-n0 Bo (s) — tt<A (s) + mosa 2 (— 1)* {Аи (s) X
B.142)
§ 5. Колебания системы ив двух штампов
97
X
A, s)-A2k+l (s) I42+L0 @, s) -42+1,0 (/, s)l
— Пп
2М (s)
2 (— 1)* {A2k (s) 4Ьг (I, s) — A2k+x (s) [42+1,2, @, s) —
fe=0
$ (/, S)] + B2h (S) lgg.2, @, S) - ?$,2, (/, S)]} == 0
(r= 1, 2, ...),
где
» (/, s) = J
, (g) 7, (g) cos 2/gdg; B.143)
dg» (/, s) = J ^1'^ 7, (g) 7, (I) sin 2/^; B.144)
0
c,l (I, s) =
B.145)
В обозначениях функций B.143) — B.145) нижние индексы k, r
соответствуют порядкам функций Бесселя, стоящим под знаком
интеграла в правых частях этих равенств, верхние индексы с, s —
функциям cos 211 и sin 2/1. С помощью одного из способов, ука-
указанных в работе [48], приводим выражения B.143) — B.145) к виду,
4 5—2880

98
Глава 2. Колебания жесткого штампа на упругой полуплоскости
удобному для вычислений в комплексной плоскости переменной
s (рис. 30):
1
С Brf—lfV
J F (г]) f
X lk
Ir
(Л)
Ik (si,) lr
X
((k -+- г) четное);
B.146)
-2'ST1 ^ «ft + г) нечетное).
B.147)
Формула для ci!r^, s) при (& + г) четном имеет вид B.147), где
(-1);
^ Ik{sx])Ir{sr])
+ г) четное);
B.148)
следует вместо множителя (—IJ записать (—IJ и сум-
сумму (k + г) считать четной. Выражение для с?1{1, s) при (k + г) -к
нечетном имеет вид B.146), где следует вместо множителя (—IJ ь
взять (—IJ ' и сумму (k + г) считать нечетной.
Аналогично получаем
§ 5. Колебания системы из двух штампов
99
dic!r (I, s) =
= (-1)
+ /") нечетное).
B.149)
(S
Формула для d(S{l, s) при (k + г) четном имеет вид B.149), где
следует вместо множителя (—IJ' ' записать (—IJ и сум-
сумму (k + г) считать четной. Выражение для d{$}{l, s) при (k + г)
нечетном имеет вид B.148), где следует вместо множителя (—IJ
W-i;
взять (—IJ и сумму (k + г) считать нечетной.
И, наконец, выражение B.145) приводим к виду
В%A, «) = (-
х е
8$ (/, s) = (- 1)"
Р
((k + г) четное);
B.150)
a~2'sii ,
dr,
((k + г) нечетное).
Формула для g{s,l(l, s) при (k + г) четном имеет вид B.151), где
следует вместо множителя (—IJ записать (—IJ. и сумму
(k + г) считать четной. Выражение для gls.l(l, s) при (k + г) нечетном
4*

100 Глава 2. Колебания жесткого штампа на упругой полуплоскости
имеет
где следует вместо множителя
(—IJ
вид B.150),
взять (—IJ и сумму (k + г) считать нечетной.
Несобственные интегралы в формулах B.146), B.148) и B.150),
которые следует понимать в смысле главных значений, сходятся при
/ > 1, Re s > 0 или Re s = 0, | Ims | > 0. Функции (ffhAO, s),
cBk+i.2r+i @, s), dBk+h2r @, s) и gfktir @, s) определяются с помощью
)
cik2
)k+'
выражений, найденных ранее: cik,2r @, s) = (—\)k+'c2k,2, (s);
cfk+ur+i @, s) = (-lf+'+V2A+,,2,+I (s); d|S+i.2r @, s) = -da+,.2, (s);
g2k,2, @, S) = (— l)k+rg2k,2r (S), ГДе ВеЛИЧИНЫ C2Al2, (S), d2ft+l,2r (S) И
g2k,2r (s) находятся по формулам B.17), B.100) (при перестановке
индексов k и г) и B.99), значение с2*+1,й-+1 (s) — по формуле B.17)
при замене индексов 2k + 1 вместо 2k и 2г + 1 вместо 2г. Функция
№ @, s) находится по той же формуле, что и функция
+, @, s), при перестановке индексов k и г.
При использовании формулы B.36) для перехода от изображения
Лапласа к оригиналу необходимо знать значения коэффициентов
матрицы B.142) на мнимой оси. Эти величины находятся по фор-
формулам B.146) — B.151) при s = it,. Чтобы несколько упростить
при s = it, вычисление комплексных выражений B.146), B.148) и
B.150), содержащих интегралы от разрывных функций, преобра-
преобразуем их, интегрируя по контуру (см. рис. 30). Опуская промежу-
промежуточные выкладки, выписываем окончательный результат для функ-
функции B.146):
/ j\
I R2 /.
tP 'k
J Bi2 +1J - 4|2 VWTW
' (tit)
cos
r Ы cos
§ 5. Колебания системы из двух штампов
101
, (СП) cos B/Sn) dr,
B.153)
четное).
Несобственный интеграл от непрерывной функции в B.152) вычис-
вычислить проще, чем несобственный интеграл от осциллирующей при
\}-P(t) Ш
77 х,х'
Рис. 31.
s — it, разрывной функции в B.146). Аналогично преобразуются
выражения B.148) и B.150).
Теперь определяем реакции под штампом:
] ОО
Р (*'' 0 = у- тт S Ak (t) Tk(x');
V 1 — х ь=о
т(х', t) =
_
V \ — X'
@ Т2к(х'),
B.154)
и перемещения:
w (t) = —?_ f (/ — т)
J
2А1(т)
U —
- А, (х)]}
na
?—А^)-
{T)]\dT
B.155)
Рассмотрим, далее, движение двух жестких штампов, расположен-
расположенных на границе упругой полуплоскости, под действием нагрузок

102 Глава 2. Колебания жесткого штампа на упругой полуплоскости
(рис. 31). Колебания в данном случае антисимметричны в верти-
вертикальном направлении и симметричны — в горизонтальном.
Как и ранее, исследуем колебания правого штампа. Уравнения
движения B.129) — B.131) справедливы и для этого случая. Удов-
Удовлетворяя контактным условиям B.136) и учитывая, что напряже-
напряжения на границе полуплоскости вне штампов равны нулю, получаем
систему парных интегральных уравнений вида
_2_
' я
-igO>(g, s)x(i, s)]dg = -
M (s) - Мд (s) __, Л
nmn
a/0
я/0
B.156)
V
T(g,
Al(s)-
и \
Q Is) — QD (S)
ят0
(U'K
oo
J p (I, s) sin
0
= 0
eo
J T (g, S) COS (/ + X') № = 0 (I X' I > 1).
Напряжения на границе полуплоскости ищем в виде B.138) и
B.139). Двойные преобразования выражений для контактных на-
напряжений имеют вид
t, s) = ia
, s) = a
h (s)
cos/i J (-
sin (k ~
(g).
B.157)
Аналогично предыдущему эти выражения подставляем в систему
уравнений B.156), раскладываем функции переменной х' в ряды по
полиномам Чебышева и приравниваем коэффициенты при полино-
полиномах одинаковых степеней в левых и правых частях этих уравнений.
§ 5. Колебания системы из двух штампов
103
Рис. 32.
Получающаяся при этом система линейных алгебраических урав-
уравнений для определения неизвестных Ak(s) и B2k{s) совпадает с си-
системой уравнений B.142), в которой следует лишь поменять знаки:
в первом и втором урав-
уравнениях — у коэффициентов
C$2, (/, S), с?+1.2,(/, S) И
(Шл (I, s); в третьем и чет-
четвертом — у коэффициентов
C2k,2r+\ (/, S), C^.l,2r+1 (/, S) И
dBk,2r+\ (I, s); в пятом и шес-
шестом — у коэффициентов
dibr (I, s), dtSb-u» (I, s) и
§»,2а (I, s). Далее задача об
антисимметричных колеба-
колебаниях системы двух штам-
штампов решается с помощью
формул, приведенных при
рассмотрении случая сим-
симметричных колебаний.
В качестве примера рас-
рассмотрим колебания двух
штампов под действием вне-
внезапно приложенных по-
постоянных сил и моментов.
Решая задачу в первом при-
приближении, в разложениях
B.138) и B.139) удержива-
удерживаем по два члена ряда. На
рис. 32—34 показано, как
изменяются горизонталь-
горизонтальные перемещения u(t) в до-
долях P/n\i, углы поворота
штампов ф@ в долях Q/лац
и ф(^) в долях 2M/na?\i в
зависимости от времени
при v0 = 0,3, / = 3,0. Вы-
Вычисления проведены для
упрощенной схемы: в правых частях уравнений B.130) и B.131)
не учитывались слагаемые, содержащие высоту штампа h, что,
вообще говоря, допустимо при малых значениях h. Как видно
из рисунков, взаимодействие штампов носит сложный характер,
обусловленный отражениями волн от них. Вопрос о сходимости
рядов B.138) и B.139) приобретает особо важное значение. Для
точного описания процесса колебаний двух штампов потребуется
4 56
Рис. 33.
8 9 t
 5 6
Рис. 34.

104 Глава 2. Колебания жесткого штампа на упругой полуплоскости
большее число членов ряда, чем в случае одного штампа, и оно
может быть установлено путем численного эксперимента на основе
формул, приведенных в этом параграфе.
§ в. КОЛЕБАНИЯ МАССИВНЫХ ПЛОТИН
Плотины гидроузлов кроме статических нагрузок подвергаются
также динамическим воздействиям, обусловленным, например, ра-
работой гидроагрегатов, сбросом воды в нижний бьеф. При расчете
гравитационных бетонных плотин
на мягких грунтах важное значе-
значение имеет определение напряже-
напряжений по контакту плотины с ос-
основанием и перемещений ее в це-
целом. В этом случае плотина мо-
может рассматриваться как жесткое
тело на упругом основании. При
известных напряжениях по кон-
контакту напряжения в самой плотине
могут быть определены, например,
методом конечных разностей [31].
Пусть плотина схематизирова-
схематизирована в виде жесткого массива, рас-
расположенного на упругом полупро-
* странстве (плоская деформация),
и подвержена действию динами-
динамических нагрузок (рис. 35, 0' —
центр тяжести плотины, х0 и у0 —
расстояния от начала координат
до центра тяжести). Требуется определить контактные напряжения
р (х, t) и т (х, t), перемещения плотины w (t), и (t) и угол поворота
ее вокруг центра тяжести ф (t). Расчет плотины на статические на-
нагрузки с учетом давления воды может быть выполнен известными
методами [28]. Гидродинамическое давление на плотину и основа-
основание в излагаемом приближенном решении не учитывается. Некото-
Некоторые исследования [29], посвященные изучению влияния гидродинами-
гидродинамического давления на напряжения в плотине, свидетельствуют о
том, что это влияние незначительно. Как и в случае колебаний
штампов, симметричных относительно середины подошвы, рас-
рассматривается частичное сцепление плотины с основанием: при вер-
вертикальных колебаниях не учитываются касательные реакции, а
при горизонтальных — самоуравновешенные нормальные реакции.
Из трех уравнений движения массива — вертикальных коле-
колебаний, горизонтальных колебаний и вращения вокруг центра тя-
тяжести — первое уравнение решается способом, изложенным в § 1,
Рис. 35.
§ 6. Колебания массивных плотин
105
с учетом значения параметра т0 = М0/ла2р0, где Мо — масса пло-
плотины, приходящаяся на 1 п.м. Запишем два других уравнения дви-
движения плотины как жесткого тела:
70 -J- -^- = М (t) - MR (t) -~у0 [Q (t) - QR (t)],
B.158)
где u0 (t) — горизонтальное перемещение центра тяжести плотины;
ф (^ _ уГол поворота ее вокруг оси, проходящей через центр тя-
тяжести; Q (t) — равнодействующая заданных горизонтальных нагру-
нагрузок, приложенная у подошвы плотины; М (t) — момент заданных
нагрузок относительно центра тяжести плотины (кроме момента
горизонтальной силы, приложенной у подошвы сооружения);
qr (f) — равнодействующая касательных напряжений по контакту
плотины с основанием; MR(t) — момент контактных нормальных
напряжений относительно центра тяжести плотины; 70 — полярный
момент инерции массы плотины относительно оси, проходящей через
центр тяжести ее. Учитывая, что
где и (t) — горизонтальное перемещение подошвы плотины, уравне-
уравнения B.158) приводим к виду
2 ^ «о) [Q @ - Q* (О] -
B.160)
=M(t)- MR (t) - y0 [Q @ - QR @1,
где
„, Af0 . 27o .
27o
B.161)
Принимая подошву плотины плоской, записываем <р (t) =
= w (x, t)/a(xo + x), и уравнения B.160) в изображениях при-
принимают вид
n\im0s2 и (s) = A + 2уопо) \Q(s) — QR (s)] — *
B.162)
~na2iij0s2w (x, s) = a[M (s) - MR (s)] {x0 + x) —
— a2y0 [Q (s) — QR (s)] (x0 + x),

106
Глава 2. Колебания жесткого штампа на упругой полуплоскости
причем х0 = Хд/а, у0 = уо/а, w (x, t) — вертикальные перемещения
точек подошвы плотины при ее повороте вокруг центра тяжести.
Удовлетворяя контактным условиям
и (s) = и (х, 0, s); w (х, s) = v (x, 0, s) (| х\ < 1) B.163)
и учитывая, что напряжения на границе полуплоскости вне плоти-
плотины равны нулю, получаем систему парных интегральных уравне-
уравнений
+ОО
mns*
+ s2 т (|, s)] dl = A + 2yQnQ) [Q (s) - QR (s)] -
~-no[M (s)-MR(s)]
_L ai s2 1/-JL
+OO
[s2
g> s) -
B.164)
(I, s) x (I, s)] dl = [M (s) — MR (s)] (дс0 + дс) —
p{l, s)e~uldl = 0 (|дс|>1);
—oo
+OO
Выражения для напряжений по контакту плотины с основанием
ищем в виде рядов
р '
, 0 =
/1 —х*
2
k=0
Л, @ Г, (х);
т(х, 0 =
B.165)
В выражении для касательных напряжений взяты только четные
полиномы Чебышева, так как не учитываются самоуравновешен-
самоуравновешенные касательные напряжения, возникающие по подошве плотины
при повороте ее вокруг оси, проходящей через центр тяжести пло-
плотины и не совпадающей с серединой подошвы. Момент равнодей-
равнодействующей нормальных напряжений относительно центра тяжести
и равнодействующую касательных напряжений определяем по
формулам
MR (t) = 4 ла2 [2Vl0 @ + А, (/)]; QR (t) = паВ0(t). B.166)
§ 6. Колебания массивных плотин
107
Двойные преобразования (Лапласа и Фурье) функций B.165)
имеют вид
B.167)
Эти ряды удовлетворяют третьему и четвертому уравнениям в си-
системе B.164). Чтобы удовлетворить первому и второму уравнениям,
подставляем в них функции B.167) и изображения выражений
B.166) раскладываем левые части этих уравнений в ряды по поли-
полиномам Чебышева и приравниваем коэффициенты при полиномах
одинаковых степеней. В результате получаем в области преобра-
преобразований Лапласа бесконечную систему ли_нейных_алгебраических
уравнений для определения неизвестных Ak{s) и B2k(s), сходную с
системой B.102),
- 2п0х0А0 (s) -
(s)] A1(s)
*
+ m0s2g00 (s)] Bo (s) + m0s2 2 [(— I)
X A2k+1 (s) + g2k,o (s) B2k (s)] = A + 2tto#o)
„ 2M(s) ,
2/гог/о -
,o(s) X
Q(s)
na
2
k=0
2r (S) A2k+i (S) + g2k,2r(s) B2k(s)] = 0
(r=l, 2, ...);
[2x1 + j0s2c00 (s)] A0(s) + хД (s) — 2x0y0B0 (s) +
^- - 2хоУо
[i0 (s) A2k (s) = x0 -jjj
2 C2ft,2r(s)^2A(s) = 0 (r = 1, 2, ...);
k=i
oo
2л;0Л0 (s) + [1 + 2/0s2cu (s)] ^ (s) + [— 2г/0 + 2/oS2^oi (s)] X
CO
X Bo (s) + 2/0s2 2 [саи-i.i (s) ^2*+i (s) +
+ (- 1)* d»., (s) Btt.(s)] = -^ - 2^0 -1|L .
B.168)

108 Глава 2. Колебания жесткого штампа на упругой полуплоскости
Q +i (s) ^j*+i (s) + (— 1)*4г*,2г+1 (s) 5a (s)] = 0
(r=l, 2, ...),
где коэффициенты матрицы находятся по формулам, приведенным
в § 3. После решения системы B.168) возврат к оригиналам произ-
производится по формулам вида B.23) или B.36). Изображения переме-
перемещений плотины в соответствии с формулами B.160) принимают вид
^L-2x0A0(s)-A1(s)\\;
Ф (s) =
/о*2
~^L-2xoAo(s)-A1(s)-
\ B.169)
-2y0
Q(s)
na
- So (s)]} •
I
и угловое перемещения плотины вычисляются с
помощью интегралов свертки
2А1 (т)
яа2
Ф@ =
Vh
B.170)
В случае установившихся колебаний, когда на плотину дейст-
действуют нагрузки
Q @ = Qe'e'; M (t) = МеР , B.171)
решение задачи определяется системой B.168) при s = it,, Q(s) =
= Qe1^', M(s) = MelV. Действительные и мнимые части коэффициен-
коэффициентов матрицы находятся по формулам § 3. Выражения для контакт-
контактных напряжений при этом имеют вид
Т2к(х)
/1 — х2
B.172)
6. Колебания массивных плотин
109
причем комплексные числа Аи и Яг* находятся из системы B.168)
при s = it,. Момент равнодействующей нормальных напряжений
относительно центра тяжести и равнодействующая касательных
напряжений определяются по зависимостям
MR (t) =
= -у па2 V B*0 Re Ло + Re ЛхJ + Bх0 Im Ло + Im Л2)
Для перемещений плотины справедливы выражения
" @ = -^rW- ^(Re uf + (Im uf
Re и = A + 2поУо) (Re Во -
2M
ф@ =
+ "о 1"^" ~ 2x° Re Л« ~" Re AlJ ;
Im u = A + 2/г0г/0) Im Bo — n0 Bx0 Im Ao + Im
1 У (Re фJ + (Im фJ е
Q
ла
Refi0
Im ф = 2x0 Im Ло + Im Лх — 2г/0 Im.
B.173)
B.174)
B.175)
B.176)
Таким образом, приведенные выше зависимости полностью опре-
определяют решение задачи о неустановившихся и установившихся ко-
колебаниях плотины как жесткого тела на упругом основании.

Глава 3
КОЛЕБАНИЯ ПОЛОСЫ
КОНЕЧНОЙ ЖЕСТКОСТИ
НА УПРУГОЙ ПОЛУПЛОСКОСТИ
§ 1. СИММЕТРИЧНЫЕ КОЛЕБАНИЯ
ПРОИЗВОЛЬНАЯ ВЕРТИКАЛЬНАЯ НАГРУЗКА
Рассмотрим колебания полосы конечной жесткости, выделенной
из балочной плиты, под действием нагрузки q (х, t) (рис. 36),
которая может включать в себя и сосредоточенные силы, прило-
приложенные на произвольном расстоянии от начала координат Для
решений задачи необходимо найти нормальную реакцию основания
р (х, t), прогибы полосы w (x, t), углы поворота ф (л:, /), изгибаю-
изгибающие моменты М (х, t) и перерезывающие силы Q (*, t).
Учитывая, что скорости распространения упругих волн в по-
полосе, как правило, на порядок больше, чем в основании, соответ-
соответствующем мягким грунтам, исходим из приближенного неволново-
неволнового уравнения движения полосы. Приближенно можно считать,
что при действии динамической нагрузки все точки полосы одно-
одновременно приходят в колебательное движение, которое описы-
описывается уравнением
~дхг
-р(х, ОЬ
где
kt =(l/ac2)VD/ph ;
D — цилиндрическая жесткость плиты (полосы),
D = Eh3/l2 A — v2);
C.1)
C.2)
C.3)
Е, v и р — соответственно модуль упругости, коэффициент Пуас-
Пуассона и плотность материала полосы. Граничные условия для урав-
уравнения C.1):
ф (х, 0 =
dw
адх
\х=0
= 0;
0; Q(x, t) = —
d3w
l*=0
= 0;
= 0.
C.4)
Начальные условия принимаем нулевыми. Кроме того, должно
быть удовлетворено контактное условие
w(x, t) = v(x, 0, t) (|*| ^1), C.5)
§ 1. Симметричные колебания
111
me вертикальные перемещения границы полуплоскости v {x, 0, t)
определяются по формуле A.26). Найдем прогибы полосы.
Применяя к уравнению C.1) преобразование Лапласа по пере-
переменной /, получаем
d4a> (л, s)
dx*
— p"w (x, S) =
(x, s) - p {x, s)], C.6)
где
p = Vis/kl; C.7)
w {x, s),q (x, s), p {x, s) — соответственно преобразования Лапласа
функций w {x, t), q (x, t) и р (x, t). Распространяя на динамику спо-
способ представления реакций по контакту балочной плиты с упругим
Ж**)
т
Рис. 36.
полупространством, приведенный в работе [46], и используя ре-
результаты предыдущих глав, ищем решение задачи для нормальной
реакции р (х, t) в виде ряда
2 A2k(t)T2k(x),
k=0
р (х, 0 =
C.8)
где неизвестные функции Aik(t) определяются исходя из контакт-
контактного условия C.5). Уравнение C.6) записываем в виде
¦ р*а>{х, s) = ~ \q(x, s) —
x, s)
die*
у 1 —
A2k(s)T2k(x)
C.9)
Так как в данном случае рассматриваются нагрузки, симметричные
относительно начала координат, то при решении уравнения C.9)
применяем косинус-преобразование Фурье с конечными преде-
пределами [97] для правой половины полосы @ < х < 1). Косинус-
преобразованием Фурье с конечными пределами функции w (x, s)
является выражение
C.10)
wc (ft, s) = j w (x, s) cos nnxdx.

112
Глава 3. Колебания полосы конечной жесткости
Соответствующая формула обращения имеет вид
w (х, s) = щ (О, s) + 2 2 wc (ft, s) cos nnx. C.11)
n=l
Умножаем все члены уравнения C.9) на cos nnx и интегрируем в
пределах от нуля до единицы:
cos плхйх „ (_ 1Г
1 — AT2
(ft, s) = j G (л;, s) cos /шлхЬс;
о
cos nnxdx = (— 1)* -2- 72A (/гя).
C.13)
C.14)
па
(-l)nft2n2c2(s)
Удовлетворяя первым трем граничным условиям C.4) и обозначая
—J- т! ' = c2(s) (постоянная интегрирования), получаем такое
выражение для косинус-преобразования Фурье с конечными пре-
пределами функции w (x, s):
2 Dp* [Л°^ па J ltt ~ U^'
1 Г
?Л«. s) — C.15)
(п > 0),
где R (s) — преобразование Лапласа равнодействующей заданной
нагрузки q (x, t)
+}
R(s) = a ] q(x, s)dx. C.16)
—i
Применяя к выражению C.15) формулу обращения C.11), находим
ch px
shp
Fc (x, s)
A2k (s)
х, s)
C.17)
§ 1. Симметричные колебания
ИЗ
где
Fc(x, s)
[X, S) = (
C.18)
C.19)
Постоянную c2(s) находим, используя последнее условие C.4):
4 1 V (- 1)" n?qc (n, s)
2?" 2
я2р cthp + ctgp ^ ni — p*/ni
(— 1)* sh py2k (p) — sin pl2k (p)
+
ft=o
sinpchp + shpcosp
C.21)
После подстановки этого выражения в формулу C.17) получаем
+ F*e (x, s) + 2 Аы (s) Фа (х, s)
причем
К {x, s) = Fc (x, s) i-
C.22)
x, s) -
sin pch p+cos pshp
s'n P ch px — sh
Ф» A, s);
C.24)
(l, S) =
sh p
sin p
C.25)
Чтобы приравнять перемещения границы полуплоскости A.129) к
перемещениям полосы C.22), последнее выражение разлагаем в
ряды по полиномам Чебышева. Пользуясь представлениями
cos px = 70 (р) + 2 2 (- 1)' 72л (р) Т2г (х);
г=1
ch px = /0 (р) + 2
/¦=1
1),
C.26)

114
Глава 3. Колебания полосы конечной жесткости
получаем
а4
W (X, S) ?тг- \ —
где
R(s)
22 lc,2r (s) + S ~A2k (s) a2kt2r (s)I 7V (*)) > C.27)
r=l I k=0 J j
7 1А I IV 12
tc,2r (S) = (— 1) —р
(n, s)
п=1
1 sinp/2/. (р) — (— \)г sh pj2/. (p)
pa sin р ch p + cos p sh p
C.28)
^ ' ' p3
sin p/2f (p) — (— l/ sh
(p)
sin p ch p -f- cos p sh
C.29)
Выражения для вертикальных перемещений (в изображениях Лап-
Лапласа) границы полуплоскости на участке — 1 < х < 1 A.129) и
A.135) при нагрузке C.8) принимают вид
со со "j
V (X, О, S) = -?- 2 ^2* (S) С2*,0 (S) + 2 2 C2k,2r (s) Г2л (х) (| X \ < 1),
C.30)
где функции c2k,2r (s) определяются по формуле B.17). Приравни-
Приравнивая в разложениях C.27) и C.30) коэффициенты при полиномах
Чебышева одинаковых степеней, получаем систему алгебраических
равнений относительно изображений A2k(s) функций А^ЦУ
I]
Ао (s) + m0s2 2 A2k (s) [c2k,o (s) — koa2k,o (s)] = Do (s);
(s) \c2k,2r{s) — koa2k,2r (s)] = Dsr (s) (r = 1,2,...),
C.31)
где
os2/c,o (s);
c.2r(s) (r= 1, 2, ...);
C.32)
— показатель гибкости полосы,
+vQ).
C.33)
§ 1. Симметричные колебания
115
В частном случае, k0 = 0 (абсолютно жесткая полоса), система
уравнений C.31) совпадает с системой B.19). Возврат к оригина-
оригиналам A2k(t) можно производить по формуле B.36), где \mA2k(iQ —
мнимая часть неизвестных системы C.31), в которой следует положить
s = И, Р = iy, У = VVK
ь2г (to = (- i)r4-1 ^D"")^;я;й
1С,гг \ ь/ \ 'я4 ^4 и4 — Y /я4
+ K(i, «о 4_
f!=l
sh y cos y + sin y ch y
6 V
C.34)
n=\
sin
(~ ')" 9c (», '9
f!=l
sin (y)
sh (y)
C.35)
C.36)
C.37)
Изображения относительных прогибов полосы, углов поворота,
изгибающих моментов и перерезывающих сил находим соответст-
соответственно по следующим формулам:
ф (*, s) =
w0 [x, s) = w (x,
) - К (о, s) +1
аз I dT. (x, s)
w @, s) =
(s) [Фа (х, s)
6D
j
_ I d?F* (a;, s)
(,,*) =-a-
:(S)
A=0
C.38)
; C.39)
; C.40)
, C.41)
где функции F'c(x, s) и Ф2к(х, s) определяем по формулам C.23),
C.18) и C.24), C.19). Производные функций не выписываем, гак
как найти их просто. Отметим лишь, что дифференцирование ряда

116
Глава 3. Колебания полосы конечной жесткости
C.19), не выражающегося в элементарных функциях, ухудшает его |
сходимость. Поэтому для ускорения сходимости ряда ф'2к (х, s)
преобразуем его к виду
(х, s) = (-
-( IV*
(ия) cos /гяя
*1 iS
C.42) 1
Пользуясь интегралом Бесселя
я/2
/
12k (ял) = — J cos 2?ф cos (пя sin ф) йц>, C.43)
о
и формулой [24]
""Г
/1=1
-""„Г =4 ^х + ^-х2 @<.*<2я), C.44)
получаем сумму первого ряда в правой части C.42)
7
xi — х arcsin x —
А «2
(nn)
cos ппх =
_ | я Г я
— 4ft»-1 [~8~Т
+ (- 1)* -^ /Г=^
C.45)
т. е.
Фо (х, s) = 6
-(-
— хarcsin л:— Kl— х2 —
70 (ия) cos /гял
C.46)
§ 1. Симметричные колебания
117
cos /гя^
3.47)
(*=1, 2, ...).
Дифференцируя последние две функции по х, получаем
Ф0
)= -6(arcsm x - - х) + (-1)*-4
ппх
^ C.48)
X
72fe (ип) sin иял:
(~ l)k^Yx
=1, 2, ...).
C.49)
Обращение выражений C.38) — C.41) производим с помощью фор-
формулы B.36):
со
C.50)
Щ(х, 0 = х) ^mwo{x, it)si
о
и ей аналогичных для ф(х, t), M (x, t) и Q(x, t).
При вычислении подынтегральных функций в интегралах Фурье
в формулах C.38) — C.45), C.46)— C.49) и в системе уравнений
C.31) следует положить s = it,, p = iy, у = У tjk^. В частности,
¦=* ~Р I шу\ ' sin y ch ул:—^shYCOsY^ p"/1 TV C\ ^П
с\> ь/ с \ ) ь/ ^2 sin y ch y + sh y cos y c ' '
, Ю = -^- 2 J1^:
l
sin 7 ch
n=\
. Y4/
¦ cos
C.52)
C.54)
Анализ системы уравнений C.31) и выражений C.38) — C_.41) при
s_= it, показывает, что функции A?k (it,), w0 (x, it,), ф (х, it,), M (x, it,),
Q (x, it) непрерывны по переменной t,. При возникающих для ряда
значений ? неопределенностях вида 0/0 или оо — оо получаются ко-
конечные величины.
Воздействия, изменяющиеся в зависимости от времени по слож-
сложным законам, могут быть приближенно сведены к сумме постоян-
постоянных нагрузок, внезапно прилагаемых в различные моменты време-
времени. Поэтому в качестве основного вида неустановившейся нагрузки

118
Глава 3. Колебания полосы конечной жесткости
в дальнейшем будем рассматривать внезапно приложенную на-
нагрузку
q{x,t) = q{x)H{t). C.55)
Тогда в соответствии с формулами C.13) и C.16)
qc (n, s) = — ] q (x) cos nnxdx = qc (n) -i- ;
!
C.56)
C.57)
где R — равнодействующая нагрузки q(x). Столбец свободных чле-
членов в системе уравнений C.31) в этом случае содержит множитель
1/s. Следовательно, ее можно решать в долях от 1/s. Формулы для
вычисления оригиналов искомых функций B.36) и C.50) прини-
принимают вид
C.58)
wn
C.59)
в свободные члены системы C.31) и во все формулы для прогибов,
углов поворота, изгибающих моментов и перерезывающих сил сле-
следует подставить R вместо R(s) и qc(n) вместо ~qc(n, s). Для вычисле-
вычисления интегралов C.58), C.59) по-прежнему используем метод Фи-
Филона, заменяя интегралы суммами:
2 ( 1
= Т }Т Re A
— Р' - Y') я + 2Р'в] +
о,
Р
m=l
2m
Sln
m=0
C.60)
= 1Г "Г Re w° (х- °> К2 - Р' - Y')л + 2р'в]
Reou0(x, «X
т=!
N-1 „ —
2m
sin 2пгв
,
m=0
2m
+°,'r' sin Bт+1)9,
C.61)
§ 1. Симметричные колебания
119
r |
где6 = h't;h' —шаг интегрирования; Р' = 2
+ cos2 Э sin B6)
= 4
sin 0
cos 6
. Структура формул C.60) и C.61) такова,
что при t ^> 1 искомые функции стремятся к предельным значе-
значениям, соответствующим решению статической задачи, т. е. Л2* =
= КеЛг*@); w0 (х) = Re w0 (x, 0) при ^^>1. Статические значения
коэффициентов Л2* находим путем решения системы уравнений C.31)
при s = 0, где
1/8A -Р2)к (k = r>0);
^= 0 C-62>
Для определения коэффициентов а^,2г @) C.29) вычисляем сумму
Я/2 я/2
_4
я
о о
X
п=\
Я/2 Я/2
cosj2mxcosJLsnv$)= 2 л2 Г f cos 2 (Jfe ^ г) ф COS 2 (Л + г) г|з
X
X ['— 2 cos2 ф sin21|з + 4 cos3 ф sin3 г|з — 2 cos4 ф sin4 г|з
Учитывая, что [24]
\ sinv-
0
л/2
Г cosv-' ф cos
2
(-
•1
i
лГ
F(v)
ь\ г 1
(V)
я
(v + 1 Л
{ 2 k)
C.63)
окончательно получаем
\к+г
п=\
15Г A + А — /") Г A — ft + г) Г A + ft + /-) Г A — & — /")
2Г B + А — г) Г B — ft + г) Г B + ft + г) Г B — ft — г)
9

120
Глава 3. Колебания полосы конечной
жесткости
Так как
2ГC + к-г)ГC-Ь + г)Г('4 + к + г)ГC~к-г) [
~ (* = 0); -f л (k=l); 0F = 2; 3, . ..);
1
sin p ch р + cos p sh уэ
х (r==1); ° (' = 2, з,...),
то
@) =
64
105я
C.65)
64
64
:=2, r=l);
,2r @) =
! — Г
C.66)
Свободные члены системы C.31) определяем по формулам C.32) и
C.28), при s = 0
?40) =
(я)
(/"=1,2, ...).
C.67)
Конкретные значения qc(n) зависят от заданного распределения
нагрузки по ширине полосы:
1
qc (п) = J q (x) cos nnxdx.
о
C.68)
Статические значения относительных прогибов, углов поворота,
изгибающих моментов и перерезывающих сил полосы при s = 0
1. Симметричные колебания
121
находим по формулам C.38) — C.41), где
К (х, о) = -? 2 i#- [^J^ + (- i
' х C + 2л:2) arcsin x — ¦
5 ,3 _.„ ,
C.70)
Ф2* (дг,
X
16 "л ^ 20 v" ' "
з
+ -j- x arcsin л";
Зя 3 у'Г^?
C.71)
k)
— 8k2
3) U2k-x (x) —
(* = 2, 3, ...);
' — 9)
11л:2 —
^D+ 11 л2) К1
C.72)
C.73)
20
j-x arcsin ж;
C.74)
Зя
(х, 0) = Ф»(а-, 0) = ^^
3^Dfe2_9)[^(-8^2+8fe2-2-2-3^
X
+ Dk2x2 + Wx2 — \k2 4- 4)T2»W] (k = 2, 3, . . .), C.75)
-d®'o(dXx' 0) = -=-л:C + *2)-4(' + 2x2)arcsin x~TxУ1^2'
C.76)
d<D\(x, 0)
lie
— x2 1_arcsinx; C.77)

122
Глава 3. Колебания полосы конечной жесткости
, 0)
х, 0)
dx
dx
' 2 (k2 — 1) Dk2 — 1)
X
X
C.78)
d2G>*Q(x, 0) з ¦
j# = — л A + x2) — 6x arcsin x — 6]/l — x2; C.79) j
*, 0)
= — 2A — xJVl~ x2;
x, 0) сРФ2к(х, 0)
3 ^1 —
X
X 4-U2b-i(x)—2T2k(x)
= 2, 3, ...);
x, 0)
= Зях— 6 arcsin x;
x, 0)
— x2;
;, 0)
л:, 0)
C.80) :
j
1
C.81) |
C-82) I
"I
¦i
C.83) !
: = 2, 3, . . .).
C.84)
ЧАСТНЫЕ ВИДЫ ВЕРТИКАЛЬНОЙ
НАГРУЗКИ
Пусть изменение нагрузок в зависимости от времени имеет вид
функции Хевисайда. Для обращения преобразования Лапласа ис-
используем формулы вида C.58) и запишем функции с параметром :
Рис. 37.
s = it,- При равномерно распределенной нагрузке на части полосы
(рис. 37) справедливы выражения
q (х) = qH (хх + х) Н to — х)\ qc (n) = q
sin ппх-
1-- р —
пп
; R = 2qax1; C.85) |
Симметричные колебания
123
6 V* sin nnXy cos пял:
3n
@ <.
C.86)
При ^ = v = 0 (статическое приложение нагрузки)
Ft (x, 0) =
Kl)> C.87)
6 V 72r ("") Sin
+
J (-
sh y cos v + sin 7 ch v
, iQ
;чя
;>0);
C.89)
= 0; r=l, 2, ...)•
Значения функций C.86)-C.88) даны в долях 2<//я. Если нагрузка
приложена по всей длине полосы (хг = 1), то Fc (x, iQ U и
^2'вСсл7чае равномерно распределенной нагрузки на участках по
концам полосы (рис. 38),
ЦХ1-х)\; C-90)
R = 2qa(l — x1), C.91)

справедливы выражения C.86), C.87) и C.89), взятые с обратными
знаками; в формуле для Do (j?) C.88) вместо хх следует подставить
A - хх).
Две сосредоточенные силы, приложенные на произвольном рас-
расстоянии от центра (рис. 39) описываются выражениями
-?¦
— хх)\; ~Яс (п) = -? cos ппхц R = 2Р.
C.92)
Сравнивая C.92) и C.85), видим, что расчетные формулы для дан-
данного случая можно получить путем дифференцирования выражений
C.86) — C.88) по хх и замены q = PI a:
2 cos у A—
t жт
cos nnxt cos ппх
chv(l—
<•*«.!); (v>0);
C.93)
W
C-94)
Xi
§ 1. Симметричные колебания
125
(-1)'
); D2r(iQ = kofc.2r(iQ (r =
У2г (пя) cos пшх
, 2, . . .); C.95)
" 4- — (~')'"sh"'':72r(T)-sinT/2
{ V2 sh у cos y + sin y ch y
C.95)
i (C = 0; r=l, 2, ...).
Выражения C.93) — C.95) даны в долях 2Р/па. Если силы приложены
по концам полосы, то в формулах C.93) и C.94) следует пользовать-
пользоваться первыми выражениями, положив в них х± = 1; если сила 2Р
приложена в центре полосы, то — вторыми выражениями при х± = 0.
Производные соответствующих порядков, необходимые для опре-
определения углов поворота, изгибающих моментов и перерезываю-
перерезывающих сил, находим, дифференцируя по х функции C.86) и C.93),
причем третьи производные последней функции в точке х = хг из-
изменяются скачками на величину +3я, что соответствует измене-
изменению перерезывающей силы на величину Р.
НАГРУЗКА МОМЕНТАМИ
Пусть к полосе внезапно приложены постоянные моменты
(рис. 40). Применяя к уравнению C.9) косинус-преобразование Фурье
с конечными пределами и учитывая, что при х = хх функция М (х, s)
M(t)
i: 1
1 а °
а
У
Рис. 40.
терпит разрыв на величину M(s), а также, что в данном случае
q (х, /) = 0, записываем
И", s) =
{-If nWc2(s) +
х
C.97)
X «Я Sin ППХХ ?- 2 (- 1)* A2k (S) 12k {ПЯ)

126
Глава 3. Колебания полосы конечной жесткости
После применения к этому выражению формулы обращения C.11) I
и определения постоянной интегрирования c^(s) из последнего ус-
условия \ЗА) получаем
w (х, s) = "U _ ^р- Ао (s) + F'c (x, s) + 2 Л2* (s) Ф» (х, s) , C.
где
98)
, it,); C.99)
Зл ["sin y A — xt)
If [ sirpy ЧХ ~
Зя Г sinY*i /1
1м slnV^YO-
тч 6 V< n sin пяхх
sh y A — xx) г 1
C0S nitX =
sh y
a-chy(l —.
.(*. 0) =
]c.2r№ =
Y>0); C.100) 1
--Y A-^IA -xtf-l+ Здг2] @<х<х1);
C.101) 'I
"¦.o(i'0; D2r{iQ = k0Jc,2r{it) (r=l, 2, ...); C.102) j
, , > 6 V* nr (raIX)
(-Df-^2l W4_V4/JT4 «in
sin y ch Y +
C.103)
(Y=0; r=l, 2, ...).
Вторая производная функции C.100) в точке х — хх изменяется
скачком на +3я, что соответствует изменению изгибающего момен-
момента на величину М. Выражения C.100)—C.102) даны в долях 2М/даа.
Если моменты приложены по концам полосы (хх = 1), то Fe(x, it,) =
= F'c(x, »0 = К(х, Ц) = К(х, Ц) = 0, кроме Fc(l, %) = Зя.
§ 2. Антисимметричные колебания
127
§ 2. АНТИСИММЕТРИЧНЫЕ КОЛЕБАНИЯ
ПРОИЗВОЛЬНАЯ ВЕРТИКАЛЬНАЯ НАГРУЗКА
Рассмотрим колебания полосы конечной жесткости под дейст-
действием антисимметричной нагрузки q (x, t) (рис. 41), которая может
включать в себя и противоположно направленные сосредоточен-
сосредоточенные силы, приложенные на произвольном расстоянии от начала
координат.
о
Ч
Рис. 41.
При решении задачи, как и в § 1, исходим из приближенного
уравнения C.1) при граничных условиях
о»@,0 = 0; М@, t) = M(l, 0 = 0; Q(l, t) = 0. C.104)
Нормальные напряжения по контакту ищем в виде ряда по нечет-
нечетным полиномам Чебышева
р (х, 0 =
^2H~i @ T2k+i (x),
C.105)
где неизвестные функции Л2*4-1 @ по-прежнему определяются из
контактного условия C.5). Подставляя выражение C.105) в урав-
уравнение C.1), получаем
d*w , 1 d2at) a4 f , A 1 ~ . ,A T , Л
+ \4 (x 0 2/ @ Гй+i (X)
D
или в изображениях
C.106)
1
К1 — * k=a
C.107)
Последнее уравнение решаем, применяя синус-преобразование Фурье
с конечными пределами [97] для правой половины полосы @ «^ х <.
< 1). Синус-преобразованием Фурье с конечными пределами функ-
функции w (x, s) является выражение
1
ws(n, s)=
, s)sinnnxdx,
C.108)

128
Глава 3. Колебания полосы конечной жесткости
а формула обращения имеет вид
со
w (x, s) = 2 2 tt>s (n> s) s'n
C.109)
Умножаем все члены уравнения C.107) на sin nnx и интегрируем
в пределах от нуля до единицы:
4-
, cPw @, s)
[- (_ l)" n3n3w(\, s) — rtWay@, s) + n4jx%s («, s);
C.110)
C.111)
C.112)
(n, s)= \ q(x, s)s'mnnxdx;
6
sin nnxdx = (— 1)* -j- U
2k+i
Удовлетворяя первым трем условиям в C.104) и обозначая
3Dt«(l,s)/fl4 = Ci(s) (постоянная интегрирования), получаем выраже-
выражение для синус-преобразования Фурье с конечными пределами
функции w(x, s):
C.113)
К последнему соотношению применяем формулу обращения C.109),
а постоянную интегрирования c^s) находим из условия Q(l, s) =0.
В результате получаем
w (х, s) =
где
6D
Fs (X, S) + Сг (S) g (X, S) +
k=0
<7s (га, s)
(s)a>2*+i(*. s) ,
C.114)
C.115)
2. Антисимметричные колебания
129
' S)
2
, s) ; C.117)
C.118)
Используя представления
oo
sin px = 2 2 (- l)r ?2r+i (p) Г2Г+1 W;
r=0
C.119)
sh px = 2 2 hr+i (P) T2r+1 (x) (x < 1),
раскладываем выражение C.114) в ряд по полиномам Чебышева
w(x, s) = 2 ¦
где
r=0
А=0
(s) a2k+h 2r+1 (s) Г2г+1 (x),
C.120)
Fs" A, s) (-
P3
f sh p j2r+1 (p) + sin pl2r+l (p)
sin pch p — sh p cos p
oo
(гая) 72r+i(
C.121)
п=1
~ ')' sh p72r+[ (p) + sin p/2r+, (p)
C.122)
P3 sin p ch p — sh p cos p
Изображения вертикальных перемещений границы полуплоскости
на участке — 1 < х < 1 A.156) и A.161) при нагрузке C.105)
принимают вид
v(x, 0, s) = 2 -S- 2 2
s) С214-1.2Г+1 (s) T2r+i (х), C.123)
где функции C2k+i.2r+i(s) определяются по выражению B.17) при
соответствующей замене индексов. Приравнивая в разложениях
C.120) и C.123) коэффициенты при полиномах Чебышева одина-
одинаковых степеней, получаем систему алгебраических уравнений отно-
относительно изображений Лапласа A2k+i(s) искомых функций A2k+i(t):
2 A2k+\ (S) [C2*+l,2/-+l (S) — k<,a2k+\, 2Л+1 (S)] =
(r = 0, 1, 2, ...).
(s) C.124)

130
Глава 3. Колебания полосы конечной жесткости
После определения неизвестных A2k+i(s) перемещения полосы
находим по формуле C.114), а углы поворота, изгибающие момен-
моменты и перерезывающие силы — по выражениям
' s) = W \Fs <*' s> + ~ci (s) 8' (*• s) + 2 ^2ft+i (s) Ф2А+1 (x, s) ;
L A=0 J
C.125)
—,, _ °° _ _^ 1
К (x, s) + cx (s) g" (x, s) + 2 ^2ft+i (s) Ф2*+1 (x, s) ;
ft=O J
C.126)
-
Ф (х
M(x, s) = —
Q(x, s) = 2-
Fs (л;, s) + Cl (s) g"' (x, s) +
(x, s)\,
C.127)
которые содержат производные по х функций C.115), C.116) и
C.118). Для ускорения сходимости рядов Ф'^+i (х, s) и Ф2А+1 (х, s)
аналогично тому, как это сделано в § 1, приводим их к виду
Ф'[ (х, s) = 3 /arcsin х + х ]/ — х2 — -^- х) —
я6 ft?
(nn) sin плд;
C.128)
6 s2
„-5 «2(ra4
=l, 2, ...); C.129)
-; C.130)
(X, S) =
(гая) cos гаях
р ур () р ,, p y, у Wx,
где c2ft+i, 2/-+1 (Ю находим по формулам B.37) и B.38) при замене
= 1, 2, ...). C.131) :
Возврат к оригиналам A2k+i (t) производим по формуле B.36),
решая систему уравнений C.124) при s = it,, p = iy, у = W
(Ю ф B37) B38)
§ 2. Антисимметричные колебания
131
индексов цилиндрических функций 2k индексами 2k + 1 и 2г ин-
индексами 2г + 1;
an ( n*+'+' 6
n=l
A,
sin у/2г+1 (у) + (- l)r sh Т72г+1 (у) _
sjn у ch у — sh у cos у
C.132)
sin y/2r+1 (y) + (- l)f sh ycr2f+1 (Y) _ j
sin у ch у — sh у cos у '
U<\ 1
. C.134)
Обращение выражений C.114), C.125) — C.127) выполняем по
формулам вида C.50), полагая s — it, и учитывая, что
C.135)
sh yx . sinyx .
shy ' sin у '
C.136)
Как и в случае симметричных колебаний, в качестве основного
вида неустановившейся нагрузки рассматриваем внезапно прило-
приложенное воздействие вида C.55). В соответствии с формулой C.111)
1
S (n, s) = -j-^q (x) sin nnxdx = qs (n) -|-.
о
C.138)
Систему уравнений C.124) решаем в долях 1/s и для вычисления
оригиналов искомых функций используем выражения вида C.58)
и C.59), при этом в свободные члены системы и во все формулы
для прогибов, углов поворота, изгибающих моментов и перерезы-
перерезывающих сил подставляем qs (n) вместо qs (n, s). Интегралы Фурье
по-прежнему вычисляем по методу Филона, используя формулы
вида C.60) и C.61).
Статические значения коэффициентов A2k+i = Re Д&@) на-
находим путем решения при s = 0 системы C.124), которая в этом

132
Глава 3. Колебания полосы конечной жесткости
случае приводится к виду
оо
2 [C2k+l,2r+i @) — koa*2k+l,2r+l @)] = kjlir+l @) -f-
@) 4 (/-=1,2,...), C.139)
21
где
@) = (- 1)'
(/m);
1
2 [ Г B +/г — л) Г B — ft + г) Г C +/г + л) Г A — k — r)
9
2Г
-') Г
-4— k —
• C.143)
Выражение для коэффициента c*i =Rec1@) в этом случае
имеет вид
со
с\ = — 7s,i @) + 2 Л2*+1 [-^- с2к+1Л @) — а2к+хл @)]. C.144)
Статические значения прогибов, углов поворота, изгибающих мо-
моментов и перерезывающих сил полосы находим по формулам C.114),
C.125) —C.127) при s = 0. Функции Ф2к+\ (х, 0) и их первые про-
производные определяем по таким выражениям:
Ф,(х, 0) = ?-*(П-
+ -?-A3 +
Ф3(х, 0) = пг- x-\--q-arcsinx +
~
C.140)
C.141)
C.142)
2. Антисимметричные колебания
133
0) =
-л:2
Ф',(х, 0) = —п?-(П +
Bft-1) Bft+ 3)
+ Зх arcsin х + B + х2) ]/ — х2;
C.148)
_ + 2 A — х2J]/"! —х2; C.149)
Ф2А+! (х, 0) - 2jfe {ft + ,} Bk _ 1)Bfe + 3) X
X (- ЗхГ2,+1 (х) + ^тг. [D^2 + 4k + 3) х2- 4? (А + 1)] U2k (x)\
вторые и третьи производные — по формулам C.128) — C.131) при
s = 0.
ЧАСТНЫЕ ВИДЫ ВЕРТИКАЛЬНОЙ
НАГРУЗКИ
Как видно из формул C.115) и C.121), функции Fs (x, s) и сво-
свободные члены системы C.124) определяются заданными нагрузка-
нагрузками. Рассмотрим некоторые частные случаи приложения нагрузки
по ширине полосы. Изменение нагрузок в зависимости от времени,
-дЮ-
Alt)
Рис. 42.
У
Рис. 43.
как и ранее, принимаем в виде функции Хевисайда. Для обращения
преобразования Лапласа используем формулы вида C.58) и функ-
функции записываем с параметром s = it,.
При нагрузке, распределенной по линейному закону (рис. 42),
справедливы равенства
q X) =
C.151)

134
Глава 3. Колебания полосы конечной жесткости
. qQ sin плх1 — плх1 cos nnx1
> = ~x~; л^г ;
CO
9 V4 sin nnxl — mtxt cos nnx1 o-
яГ Zd n2 (л4 — v*/n4) Ot
C.152) 1
_ j
9я r/sinYx, \ sin y A—
_^ LJ д- cos yX \ U
4y4 [\ Y /
slnY
x
sh y A — x)
sh y
\ Y
; Y>0);
C.153)
— жх ch y*i^ X
, 0) =
Зя
C.154)
Sin ПЯД?! — OTJCt COS fOTXt
n=l
ij) sin Y/2r+1 (Y) + (-
(V)
fl,2r+l @) = (— 1)Г -^-
— njtJCl C0S njt^l) 72r+l («Jt)
G = 0).
C.156)
C.157)
Значения функций C.153) — C.157) даны в долях iqo/Зпх^ Если
нагрузка приложена по всей длине, то в формулах C.153) и C.154)
следует пользоваться первыми выражениями, положив в них хх= \.
При нагрузке, равномерно распределенной на части полосы
(рис. 43), получаем выражения
q{x) = q sign xH (Xl + x)H (Xl — х); C.158)
1^ C.159)
§ 2. Антисимметричные колебания
135
(X, ly —
n=\
„ („4 _
sin nnx —
Зя
sin y
sh y
= )
C.160)
- cos
,. - ch
C.161)
) Z
КA ¦ <0 sin yl2r+1 (Y) + (~ 1У sh Y72H-1 (V) (Y>0); C.162)
Y3 sh y ch y — sh y cos у
= 0); C.163)
C.164)
A, = x\ (Y = 0).
X, . , X,
-Pit)
Pit)
0
Рис. 44.
Рис. 45.
Значения функций C.160) — C.164) записаны в долях 2qln. В пре-
предельном случае, когда нагрузка приложена по всей длине полосы,
в формулах C.160) и C.161) следует пользоваться первыми выра-
выражениями, положив в них хг = 1.

136
Глава 3. Колебания полосы конечной жесткости
В случае нагрузки, равномерно распределенной на участках по \
концам полосы (рис. 44), \
q(x) = qsignx[\—H(x
x)H(Xl—x)]; C.165) \
=^-; C.166)
со
-9-\ 6 Х^ COS П71Х-, — (— 1)"
, «0 = -яг Z n(n*-vW) si
' Зя
— cos yA—
^-sinYx+ '-Chs;y-Xl) shT*]
_|
sinY
C.167)
; т>0);
f
-A x
C.168)
со
\г 6 V^ COS /HUi — (— 1)"
) -?Г 2 Я(Я«-^/я4)
F's" (I, ij) sin
Y3 sin y ch y — sh y cos у
/r>\ i iv 6 V cos пял:,— (— 1)"
S.2/-+1 @) = ( 1) —— > * '—
C.169)
n=\
2r+i (nn) {y = 0); C.170)
^=1 —*? (Y = 0). C.171)
Значения функций C.167) — C.171) записаны в долях 2qln.
Две сосредоточенные силы на произвольном расстоянии от на-
начала координат (рис. 45) можно записать в виде выражений
Ч(х) = -|-[— Ь(х + xj + 8(x — Xl)}; C.172)
qs (n) = -^- sin nnxv C.173)
§ 2. Антисимметричные колебания
137
Сравнивая соотношения C.159) и C.173), видим, что расчетные
формулы для данного случая можно получить путем дифференци-
дифференцирования выражений C.159) — C.164) по хх и замены q = Р/а:
. .„ 6
(x, iQ = -^r
sin nnx.
sinплх =
n=\
sin
.
sin
Xl) h
sh A_
inY(l— x)~
<1; y>0);
-3x2l + x])x~(l—x1)x3\ @<ж<жх);
C.174)
-f \xx A - л:2) A —x) - дсх A - xf\ (Xl < x < 1);
C.175)
sinпя^-
sin Y/2f+1(Y)+ (-!/sh
sin -y ch у — sh у cos у
v' /' \
@) = (- 1)' 4-
sin
(V =
C-177)
Лх = 2х! (т = 0). C.178)
Значения функций C.174) — C.178) записаны в долях 2Р/па. Третьи
производные функций C.174) и C.175) в точке х = хх изменяют-
изменяются скачком на величину +3я, что соответствует изменению перере-
перерезывающей силы на величину Р. Если силы приложены по концам
полосы (хх = 1), то функция Fs(x, t?) и ее производные по х равны
нулю, кроме F"s{\, it) = Зя.
НАГРУЗКА МОМЕНТАМИ
Пусть к полосе внезапно приложены постоянные моменты М
(рис. 46). Применяя к уравнению C.107) синус-преобразование
Фурье с конечными пределами и учитывая, что при х = хх изгибаю-
изгибающий момент М (х, s) терпит разрыв на величину М (s), получаем
W, (П, S)
D
Р- ПП COS ППХХ
а2
- Ь 1)" -
»—г2(-
fe=0
|
(яя) . C.179)

138
Глава 3. Колебания полосы конечной жесткости
Выполняя обращение по формуле C.109) и определяя постоянную ;!
интегрирования сх (s) аналогично тому, как это сделано выше, на- 1
ходим зависимость C.114), в которой при s = it,
Fs(x,it) = -±
I Зя [cos у 0 — *i) „;„ ..„
п cos плх-1
sin ппх =
,_*>. . x, ,
A/ft'
'//////////Y/////////////////j\
a °\ a
V/77, x
Рис. 46.
F, (*.<)) =
C.181)
Свободные члены в системе C.124) определяются в данном случае
по выражению
i;r\ I \\rJ
"(I, t?) sin T72r+i (V
sin y ch y — sh y cos y
U+. @) = (- Df+1 -I- 2 72г
cos
n=\
C.183)
C.184)
C.180) \
а остальные функции определяются по формулам C.116) — C.118). S|
В случае статического приложения нагрузки (? = y = 0)
(ЛЯ) —
(Y>0). C.182) I
При y = 0 свободные члены системы C.139) находятся по фор- «!
мулам !
3. Некоторые частные случаи колебаний
139
Значения функций C.180) — C.184) записаны в долях AMIna. Вто-
Вторые производные по х функций C.180) и C.181) в точке х = х1
изменяются скачком на величину +Зя/2, что соответствует изме-
изменению изгибающего момента на величину М. Если моментная на-
нагрузка, равная 2М, приложена в середине полосы, то в формулах
C.180) и C.181) следует пользоваться вторыми выражениями, по-
положив в них х1 = 0, при действии моментов по концам полосы —
первыми выражениями, положив х± = 1.
§ 3. НЕКОТОРЫЕ ЧАСТНЫЕ
СЛУЧАИ КОЛЕБАНИЙ
Пусть к полосе внезапно приложена гармоническая нагрузка
q(x, t) = q(x)H{t)(*U. C.185)
Тогда при t^ 1, т.е. в случае установившихся колебаний, реше-
решение задачи аналогично решению задачи о колебаниях жестких штам-
штампов и определяется комплексными функциями Ak (iQ (k = 0, 1, 2, ...),
Щ (•*> '01 Ф (х> '?)» М- (х. '?) и Q (х. '?). действительные части кото-
которых входят в формулы вида C.58). Используем такие обозначения:
где
C.186)
C.187)
arctg lmlfe№) + я (Re Ak (it,) < 0; Im Ak (iQ > 0); C.188)
Re Ak (iQ
, Im Ak (it)
arctg —_ ь
Re Ak Ю
arctg lm^(<D -я (ReAk(it)<0; 1тЛ,(^<0);
Re Ak (it,)
ReA2k(iQ, lm A2k(iQ и Re42ft+! (/?), \mA2k+l (it,) находятся из реше-
решения соответственно систем C.31) и=C.124) при s = it,, в свободных
членах которых вместо qc (n, s) и qs (n, s) записываются величины
ЯЛп) C.56) и qs(n) C.138);
х)\ C.189)

140
Глава 3. Колебания полосы конечной жесткости
где
\w
„ (х) | = V [Re w0 (х, it)}* + [Im w0 (x, iQ]2;
(Rewo(x, iQ>0);
C.190)
arctg Im^(x' 'g)
Re ш0 (х, iQ
фда (x) = j arctg f^-f + л (Re o»0 (x, iQ < 0; Im o»0 (ж, ф > 0);
Im
arctg Im *¦><*' g-ji
Аналогично записываются выражения для ср (х, t), M (x, t) и Q (x, t).
Действительные и мнимые части выражений для относительных
прогибов, углов поворота, изгибающих моментов и перерезываю-
перерезывающих сил при симметричных колебаниях в соответствии с формула-
формулами C.38)— C.41) имеют вид
C.192)
Rew0(x, it) = -^- \Fc (x, it)-Fc@, it
+ ^ReA2k(iQ[^lk(x, iQ—&2k@, iQ]
lmw0 (x, iQ = gg 2 Im Л2*(iQ [Фа(x, iQ — Ф» @, iQ];
Г ""* r\ °° ~* • '
iQ = -Err c-r— Ь 2 Re ~A2k (iQ 2k, *'
Ъ1 6D dx ^J v *' d>:
im ф (x, /D = -S- 2
»
C.193)
C.194)
ReQ(x, i0= —
:Ла(^
k=0
C.195)
§ 3. Некоторые частные случаи колебаний
141
действительные функции Fc (x, iQ, Ф2к (х, it) и их производные по
х определяются по формулам C.51)— C.54).
При антисимметричных колебаниях в соответствии с формула-
формулами C.114), C.125)-C.127)
Re w (х, iQ = -gH F, (x, iQ + Re cx (iQ g (x, iQ +
+ 2 Re Л2*+1 (t"S) 5>2*+i (x, iQ ;
fe=0 J
4 Г - - °° - -
Im w (x, it) = -go" Im cx (i?) g (x, iQ + 2q Im A2k+l (iQ Ф2к+1 (x, t?) I;
C.196)
Re ф (x, t'S) = -?r IK (x, iQ + Re ~cx (iQ~g' (x, iQ +
3
Im Ф (x, it) = gg
2 Re
1
(x, t?) ;
J
I
Im cx (»S) g' (x, it) + ^ Im A2k+X (iQ Ф2к+1 (х, i?)J;
C.197)
Re M (x, iQ = - \- \Fs (x, it) + Re cx (iQ g" (x, iQ +
+ 2 Re Л2*+1 (iQ Ф2*+! (х, t"S) ;
ImM(x, t'S) =
2 Г °°
^ — -|- Im Cj (t"S) g" (x, t'S) + 2 Im Л2й+! (tS) Ф»+1 (x, i'S) |;
I «=o
Re Q (x, iQ = - -g- [Fs' (x, ф + Recx (/s) /' (x, iS) +
1
-f 2 Re A2k+\ (iQ ФгА+1 (x, iQ ;
ft=0 J
Im Q (x, iS) = 1- Im cx (iS)?" (x, »S) +
+ 2 Im Л2^+1 (iQ Ф2к+1(х, iQ ;
ft=0 J
C.198)
(ЗЛ99)

142
Глава 3. Колебания полосы конечной жесткости
Re Ci (it) = —
Imq (it) = _
p- Fs(l,i® + ZRe.
Im
О, Ю ;
C.200)
действительные функции Fb (x, it,), g (x, it), Фг*+! (x, it,) и их произ-
производные по х определяются по формулам C.135) — C.137).
Таким образом, решение задачи о гармонических колебаниях яв-
является промежуточной операцией при решении задачи о неустано-
неустановившихся колебаниях под действием внезапно приложенных по-
постоянных нагрузок, если при этом используются формулы обраще-
обращения вида C.58). Иными словами, если некоторая комплексная
функция / (?), ограниченная при ? = 0, представляет собой реше-
решение задачи о гармонических колебаниях штампа на упругом полу-
полупространстве с частотой ?, то решение задачи о неустановившихся
колебаниях штампа под действием внезапно приложенной постоян-
постоянной нагрузки определяется интегралом Фурье:
C.201)
При действии на полосу нагрузки, изменяющейся в зависимости
от времени в виде прямоугольного импульса безразмерной продол-
продолжительностью Т, функции находим с помощью соотношений
Рт(х, 0 =
P(x, t)
p(x, t)-p(x, t-T)
C.202)
гдер(х, t) — решение задачи при действии внезапно приложенной
постоянной нагрузки.
В случае действия на полосу нагрузки, изменяющейся в зави-
зависимости от времени по произвольному закону, либо q (x, t) прибли-
приближенно заменяется ступенчатой функцией и тогда используется
формула C.202), либо вычисляется интеграл свертки
р*(х, Q-
. т)
C.203)
где р (х, t) — та же функция, что и в C.202).
Рассмотрим некоторые примеры.
Пусть полоса и полуплоскость имеют такие характеристики:
/1=1л;а = 5л;я, = 0,1884; k0 = 0,373; v0 = 0,3. Исследуем
!
в
3"
3
о"
© N CO О Ю
С? О г** &* г--
-" о" о о" о"
7
(~- — О> ¦*
о t^ (м (^
О р" р" р" р"
Г- СО
Р г-
О Р
О ОО CD О) 00
t-^ О I4- 00 (^
о" о* о* о" о
© Ю Tf W t-
О 00 О '"f 00
С?^ о 0О СО N
о" о о" о" о*
I I I
LO^ О 00 СО 00
о о о" о* о"
5 00 — ¦* СО
¦5- о оо га и
о" о о о" о
со t^ to со
г- оо оо о)
О 1С И N
рррр
Ю О1
Р Ю _. .
(N p_ Th —
о" р* р* р* р
_ N 0»01
S со f- «3 —
^- р CN p to
о из из о
о оо о ¦*
5 о оо со
оГ о" о" о
ю со — со
оо о ¦* оо
О 00 СО f4-
о" о" о" о*
Я. °. ^ эт. "Ч
со р" р" р" р"
7
°
ooo - о
«3 Ю — СО
оо о ч* oi
р 00 СО С-
-ррр
§^f 00 О) СО
00 00 СО СО
а о^ (^ со^ (-^
оГ о* о о* о
о ^ оо оо о^
0 оо оо со S
01 О О О О
§ СО 00 ^ 00
оо о ^* о
г— ож оо со^ оо_
-Г о" о" о о" см о о о о
8Tf !N ^f (N
00 СЛ СО СЛ
Г-- О f~- СО h-
" о
СО
00
5
^ ооо
= ОРР С ОООО
S о оо со f-
- 77°7
о оо о со g
:- oSoo
о об ел со t4-
СО О N СО h
- 77°7
(N СО «3 О
§ю о о> -
00 О СО 00
О ОО СО N
of о* о* о о
25 оо о ^* о^
¦^* О 00 СО Is-
(?i О*" о" о" О*
7
<S оо о ^ ел
СО О ОО СО N
оГ о" о о" о"
¦* ооо
о g f~ cq oo
со о" о" о" о"
I i°7
о
о
э
7
со
7 7°7
7
СО 00 t^ m
00 t"- О) Р-
О Г- СО С-
§ со ел оо о
00 f- CN 00
СО О О О о
СО (N 00 00
00 00 О) 00
5 оо оо о)
со о" о" о" о
^э оо оо со оо
со" о" о" о" о"
ооо
7
Tf (Л W О
00 00 О0 СЛ
77S
СО ОООО
О 00
й о_
со о" о о
— о) О J g со з
^* оо Р оо оо со оо
СО S (NO ^ СО^ t^
of о" о" о" о со о о о" о
о" о о о оГ о о о о со о о о о
8
— ю ¦* ю
00 1О *-* 00
О N П N
8^г оо со о
оо оо со оо
о о
7
^?
э-
о
с-
*
1
с
СУ
- 7
~ *
э-
о
с-
7
СУ
ст о
с-
о
о
<-.
8-
оо
^ СУ
со О
С
О
^.
э-
о
<?
о
с
СУ

а
з-
з
о й ЙЙ ~ © f- t"- сч ч" о toto- s о — о^ о о
OfOOjCNgJ О О) О СО Ю О О СО СО т}< О О1 СО СО *
о «о ю о я, Осле^оо) о cjtooN oootooo)
-о7оо оГ о7оо со О--ОО .-о7оо
о°ооооосо о со ю со со о m с~ — оо о о со о t~-
О 23 S~ ОО) — COCO OOtOCO^f О О> СО П СО
и, оо * о и О) о) s осч ел ел to о о) с» оо too n
о-о7оо ~- о7оо о)" о7оо со О--ОО
о m ¦* ю t~- ооосососл о n со и n ocnoooi
q О) СЛ О) СЛ О OI —i Л 1Л О О N СО Ю О СЛ "^ СО тг
й оо ^ о -¦ оо о> s о п оо ел to о <n оо оо со о о)
о о--оо -- о'7оо оГ о--оо со о7оо'
О О Ю СО Ol О © Tf CO CD OO^ftMOO О СО СО — СО
о <doo<m*-^ о со 1- со ю о -н(^-со^ о сртгсо^
S 00 Ю О W N Oi N О СЧ h О) tO О IM h CO tO О W
о О--ОО -- о7оо- « о7оо со о7оо
О <?> °0 f*" ^ Q Tf «• Tf 00 О N О М ^f OUO^fO--
О (N О) <N ^f О СОСОСОУЭ О ^ О СО Ю Q ai^CO^f
о" о" -н" о* о -* о" -н* о* о* <n* о" —* о" о" со о* —• о" о"
I I I I I I III III
О Ю1ПО)СЛ О СО СО ^ in О 1Л СО ^ ^ О СЛСО — (~-
Sino)O)— осоо)сосо оо) — coco о фюя*
юсл^оо) ю oit-оя юсл(— оо) юоосооо)
о о7оо - о7оо оГ О--ОО со ?-7-о-?-
о f * О) N ою^о)^г ooof-'*'* осо^о)о
о о) to — о оо)Осою оо) — coco ootocoin
5 01 (О О IN -ФСЛГ-ОО) ^f^f-OCN * CJtOOCI
о О--ОО - ^--оо «- о-Гоо- со о-7оо
о с^ >—I со со о со со со оо ooo^f^ о uo ^ -« n
О C-^-00-чЧЭ О ^ СО СО Ю Q COCn)CO<0 О О ^ СО ^
СО h СО О -4 ^ О) 45 О (М СО О N О W СО СЛЧЭОО)
о ?---о?- - о7оо оГ о7о?- со о-7оо
O^f-'S'CO О OI O1 И N О — СО 5 СО О t; IN ПО
О ООСООО О СОсОСО^ О СО CN СО tO О О N СО Ю
И * S о О CNoOcDOCN И 01 N О IN И о> <О О IN
°" 111°' ~ ii°'i w" ii°"i " f7°f
§ S§1S § sill § §g§g § §§13
00-000 - f f 00- oT o7oo- coo7oo
^c-^c- ^c*^^ ^c-^^ ^o^^
ёГ^су s°^^cy "" а°э^^су а°э^су
5. Некоторые частные случаи колебаний
145
колебания при действии внезапно приложенной в начале координат
постоянной силы, равной 2Р. Необходимые вычисления производим
на ЭВМ, пользуясь формулами § 1. Результаты расчетов от-
относительных прогибов полосы w0 (x, t) (в долях Pa3/3nD), углов
0,05
-1
0
0,2
0,6
0,Н
о,ь
м
I
v -177
\
0
\
V
\ \
\\
\\
\
/
7
/ /
//
1/
0,2 s
/t-O.i
/HZ
Л
Г/
^-
ОА^-
/
\2PH(t)
г—1—
""W"
m
Рис. 47.
поворота ф (х, t) (в долях Pa2/3nD), изгибающих моментов М (х, t)
(в долях Ра) и перерезывающих сил Q (x, t) (в долях Р) в зависи-
зависимости от времени t представлены в табл. 3.1 (для точки х = 0,2) и
«
ОЛ
0,2
0
0,1
/
/
/
0,1
Л
Ofi
\
\
0,6 0,8
4i?
1
о
^*~—
1,2
2№(t)-
1
У
«
mt-i)Jl
х |
—
;,б t
Рис. 48.
3.2 (для точки х = 0,8). Как видно из этих таблиц, колебания
быстро затухают. При t = 3-М расчетные величины мало изме-
изменяются и близки к статическим значениям (w0 @,2)ст = —0,082;
Ф @,2)ст = -0,766; М @,2)„ = 0,321; Q@,2)CT = -0,777; w0 @,8)CT =
= -0,876; Ф (О,^ = —1,606; М @,8)ст = 0,029; Q @,8)ст =
= —0,233 в долях, указанных выше). Максимальные значения рас-

146
Глава 3. Колебания полосы конечной жесткости
четных величин соответствуют времени t — 0,5. Коэффициенты ди-
динамичности равны примерно 1,1.
Изменение эпюры изгибающих моментов в полосе в зависимости
от времени показано на рис. 47. Видно, что в начале движения по-
полосы зпюра вдоль координаты х изменяет знак. При увеличении t
она постепенно трансформируется в статическую эпюру. На рис. 48
представлен график изменения максимального изгибающего мо-
момента в начале координат при действии нагрузки в виде прямо-
прямоугольного импульса продолжительностью Т = 0,5. С прекраще-
прекращением действия нагрузки изгибающий момент резко падает. Коэф-
Коэффициент динамичности может быть меньше единицы (при кратко-
кратковременных нагрузках).
Глава 4
КОЛЕБАНИЯ КРУГЛОГО
И ПРЯМОУГОЛЬНОГО
ШТАМПОВ НА УПРУГОМ
ПОЛУПРОСТРАНСТВЕ
§ 1. ДИНАМИЧЕСКИЕ ПЕРЕМЕЩЕНИЯ
УПРУГОГО ПОЛУПРОСТРАНСТВА
(осесимметричная задача)
Пусть к границе упругого полупространства (рис. 49) приложена
вертикальная осесимметричная нагрузка, закон изменения кото-
которой в зависимости от радиуса и времени описывается заданной
функцией р (г, t). Требуется найти вертикальные w (r, z, t) и радиаль-
радиальные и (г, г, it) перемещения полупространства.
Для решения задачи воспользуемся дифференциальными урав-
уравнениями движения полупространства
d2w
, 2
ди
d2w
дЧ
drdz
р.2 дЧ
— V Я*2 >
D.1)
где г ~ r/a, z = zla — безразмерные переменные; гиг — действи-
действительные переменные; а — параметр, имеющий размерность длины;
/ — безразмерное время. Вводя функции ср (г, г, t) и а|) (г, г, 0.
дг2 а2 г дг
иКг, г, (; = —— ^—^-^
приводим D.1) к волновым уравнениям
д2ф _1_ дф . д2ф _ а
дг2 "¦ г аг ~*~ дг2 Р
D.2)
D.3)
дг* ^ г дг ' dz2 ~~ dt2 '
которые в изображениях Лапласа при нулевых начальных условиях
имеют вид
¦ + -J-4 + 3--1»*-*
D.4)
дг*

146
Глава 3. Колебания полосы конечной жесткости
четных величин соответствуют времени t — 0,5. Коэффициенты ди-
динамичности равны примерно 1,1.
Изменение эпюры изгибающих моментов в полосе в зависимости
от времени показано на рис. 47. Видно, что в начале движения по-
полосы зпюра вдоль координаты х изменяет знак. При увеличении t
она постепенно трансформируется в статическую эпюру. На рис. 48
представлен график изменения максимального изгибающего мо-
момента в начале координат при действии нагрузки в виде прямо-
прямоугольного импульса продолжительностью Т = 0,5. С прекраще-
прекращением действия нагрузки изгибающий момент резко падает. Коэф-
Коэффициент динамичности может быть меньше единицы (при кратко-
кратковременных нагрузках).
Глава 4
КОЛЕБАНИЯ КРУГЛОГО
И ПРЯМОУГОЛЬНОГО
ШТАМПОВ НА УПРУГОМ
ПОЛУПРОСТРАНСТВЕ
§ 1. ДИНАМИЧЕСКИЕ ПЕРЕМЕЩЕНИЯ
УПРУГОГО ПОЛУПРОСТРАНСТВА
(осесимметричная задача)
Пусть к границе упругого полупространства (рис. 49) приложена
вертикальная осесимметричная нагрузка, закон изменения кото-
которой в зависимости от радиуса и времени описывается заданной
функцией р (г, t). Требуется найти вертикальные w (r, z, t) и радиаль-
радиальные и (г, г, it) перемещения полупространства.
Для решения задачи воспользуемся дифференциальными урав-
уравнениями движения полупространства
d2w
, 2
ди
d2w
дЧ
drdz
р.2 дЧ
— V Я*2 >
D.1)
где г ~ r/a, z = zla — безразмерные переменные; гиг — действи-
действительные переменные; а — параметр, имеющий размерность длины;
/ — безразмерное время. Вводя функции ср (г, г, t) и а|) (г, г, 0.
дг2 а2 г дг
иКг, г, (; = —— ^—^-^
приводим D.1) к волновым уравнениям
д2ф _1_ дф . д2ф _ а
дг2 "¦ г аг ~*~ дг2 Р
D.2)
D.3)
дг* ^ г дг ' dz2 ~~ dt2 '
которые в изображениях Лапласа при нулевых начальных условиях
имеют вид
¦ + -J-4 + 3--1»*-*
D.4)
дг*

штампов
148 Глава 4. Колебания круглого и прямоугольного
Применяя к ним преобразование Ханкеля [97] по переменной г,
получаем
_^-_№- + р-^ф = и; -^--(?2 + 52)г|; = 0, D.5)
где ф (?, г, s) и if (?, z, s) — преобразования Ханкеля функции
Ф (г, z, s) и ijj (r, z, s),
Г -
ф (I г, s)^a2 ¦ гц> (г, г, s) 70 (rg) dr;
r, 2,
D.6)
'""О
Рис. 49.
Соответствующие формулы обращения имеют вид
Ф(г, г, s) = -^
, г, S) = J-J^G, г, sKro(rg)dg.
D.7)
Учитывая условия на бесконечности, решение уравнений D.5)
выбираем в виде функций
| (I z, s) = A (I, s) е-*У&№'; f (|, 2, S) = 5 (g, s) е-**$+*, D.8)
где коэффициенты Л (?, s) и В (|, s) находятся из граничных условий
для нормальных az (r, z, t) и касательных xrz (r, z, t) напряжений:
а2 (г, 0, /) = — р {г, 0; ог (г, 0, s) = — р (г, s);
тгг (г, 0, 0 = 0; хп (г, 0, s) = 0. (
Подставаяем функции D.8) в формулы D.7):
со
Ф (г, г, s) = -L J |Л (g, S) r-
о
ОО
, г,
D.10)
§ 1. Динамические перемещения упругого полупространства 149
Дифференцируя эти выражения по г и г и подставляя результат
в соотношения D.2), получаем
И'. г- s) = -^-.\6l— a
|, s)
D.11)
+ В (I s) VWT^e-^^^] ¦31 {г\) dl D.12)
Напряжения az (r, z, t) и хгг (г, z, t) определяем по зависимостям
ОО
п(г, г, s) = ^т J I2 [- a A (I s) r^№-
о
WT^e-^^^] ¦31 {г\) dl
*г (Л г, 0
-^ + у-) и + (Я. + 2(г) ж ;
, ,. и / 5ш , ди
ди
D.13)
Производные по г и г выражений D.11) и D.12) подставляем в
формулы D.13) (предварительно переведя их в область изображе-
изображений) и удовлетворяем граничным условиям D.9). В результате по-
получаем систему двух уравнений для определения неизвестных
A {I, s) и В (I, s):
I2 + 4"
I, S) = —^-p(g, s);
= 0,
D.14)
где p (|, s) — двойное преобразование (Лапласа и Ханкеля) задан-
заданной функции р (г, t),
p(l, s) = a2 j J rp (r, t) 70 (rl) e-s<dtdr.
D.15)
о о
Из системы D.14) находим
D.16)
функция F (|, s), как и в плоской задаче, определяется по формуле
A.19). После подстановки выражений D.16) в равенства D.11) и

150 Глава 4. Колебания круглого v прямоугольного штампов
D.12) получаем
w (г, z, s) = JL
+ s2) r^W -
D.17)
«(г, г, s) =
Оригиналы этих выражений имеют вид
а» (г, г, 0 =
и (г, г, /) =
При г = 0
-Л
2ш
i
f f
J J
c—loo 0
^A, s)
fBg2 + 52) e-^
n ь -r i
2m'
с—^oo 0
4. ] 9)
D20)
s) 7o
u(r, 0, s) = ^
w(r, 0, 0 =
^
^55
C+/o
5- J
l
C—loo 0
«(r, 0, 0 =
D.22)
'D.23)
c-^-loo oo
= _i L I
ац 2ro J
^> S)
c—(oo 0
f (g, S)
О l/>2 I fl2s2 1/E2 I <;2\
X
X 7j (a© es'tt. D.24)
В качестве примера рассмотрим действие нагрузки, мгновенно
приложенной к границе полупространства по площади круга ра-
§ 1. Динамические перемещения упругого полупространства 151
диуса а и распределенной вдоль координаты 0 < г < 1 по закону,
который может быть представлен рядом полиномов Лежандра
P2k(V~l —г2) с весом A — г2)'1, соответствующим данному аргу-
аргументу,
р (г, t) =
A2kP2k (КТ=72) @ < г < 1), D.25)
У \-А fi,
где Ачь — коэффициенты разложения в ряд по полиномам Лежандра
заданной функции распределения нагрузки вдоль радиуса.
Двойное преобразование (Лапласа и Ханкеля) функции D.25)
имеет вид
P&s) = W
D.26)
Г(*+1) "«-t-'/.w-
После подстановки формулы D.26) в выражение D.21) получаем
(г, 0, s) =
Ж
Используя представление [24]
оо
7 Ш _ Л Г 2 V Bп + '/2)Г(п
D.27)
=^. D-28)
2
n=0
выражение D.27) разлагаем в ряд по полиномам Лежандра:
T:^J)) D.29)
w
(r, 0, s) = -2- 2 2
t1 fto n0
где
х
оо
о
, (I) dg.
D.30)
Для приведения несобственного интеграла D.30) к более про-
простому виду применяем к нему формулу обращения преобразования
Лапласа:
c-j-too оо
[ I
С—?оо б
C+tco
\
с—ioo
B + Л* - 4 К Г
1 +

152 Глава 4. Колебания круглого и прямоугольного
штампов
.,.о *»+•,.©[-2^;,
2 Г 4т) (т]2 — б2) /1 — Т1а
sin — I йц
D.31)
где при отыскании интеграла по комплексной переменной р ис-
использовано выражение A.49). Возвращаясь снова к изображению
Лапласа равенства D.31) и учитывая формулу [24]
+1
окончательно получаем
3
J' |/R2 „2
—то—
J
то—
2 O2\
v, (srl)
). D.33)
При k < я индексы модифицированных функций Бесселя I и II ро-
рода следует поменять местами.
§ 2. ВЕРТИКАЛЬНЫЕ КОЛЕБАНИЯ
КРУГЛОГО ШТАМПА
Рассмотрим действие силы Р (t) на круглый жесткий штамп
радиуса а и высоты h, расположенный на упругом полупростран-
полупространстве (рис. 50). Эта задача в случае гармонических колебаний рассма-
рассматривалась в работах [134, 108, 8, 9, 12—17]; равнодействующая
контактных напряжений при нестационарных колебаниях опреде-
определена в работах [59—61, 38]. Найдем распределение нормальных
реакций р (г, t) по контакту штампа с основанием и вертикальное
§ 2. Вертикальные колебания круглого штампа
153
перемещение его w0 (t) [88] (трение между штампом и основанием
не учитывается).
Исходными принимаем уравнения движения штампа
2navm1-^- = P(t)-R(t), D-34)
где m1 = /ip/2ap0; R (t) — равнодействующая нормальных кон-
контактных напряжений. В изображениях уравнение D.34) имеет вид
1s2wo(s) = F(s)— R~(s). D-35)
\P(t)
0\ф2а
Рис. 50.
Используя контактное условие
щ (s) = w(r, 0, s) @ <. г < 1), D.36)
где функция w (г, 0, s) определяется по формуле D.27), и учитывая,
что напряжения на границе полупространства за пределами штам-
штампа равны нулю, получаем в области изображений парное интеграль-
интегральное уравнение
F,
р (t s) 70 (rg) dg = Р (s) -R (s) @ < г < 1);
D.37)
где р (%, s)—двойноэ преобразование (Лапласа и Ханкеля) кон-
контактных напряжений р (г, t).
Решение задачи ищем в виде разложения в ряд по полиномам
Лежандра [46]
Р(г, 0 =
D.38)
где (по аналогии с плоской задачей) сохранена особенность вида
A — r2)~v\ характерная для статики; функции A2k (t) определяют-
определяются из уравнений D.37). Двойное преобразование разложения D.38)
имеет вид
р (I, s) = -^=-
(s)
1
Vl (I).
D.39)

154
Глава 4. Колебания круглого и прямоугольного штампов
Каждый член этого ряда удовлетворяет уравнению D.37) при г > 1.
Чтобы удовлетворить уравнению D.37) при /" <; 1, подставляем в
него значение р (|, s) D.39) и, учитывая, что
R (s) = 2na2A0 (s), D.40)
получаем
= W @^/¦<!)• D.41)
Используя формулу D.28), разлагаем обе части этого уравнения
в ряды по полиномам Лежандра и приравниваем коэффициенты при
полиномах одинаковых степеней. В результате получаем систему
алгебраических уравнений
Ао (s)
A2k (s)
2j л2* (s) c2A+.Ai 2n+Vi (s) = 0
=1, 2, ...),
D.42)
где коэффициенты c2k + <д. 2n +«/«(s) определяются по формуле D.33).
Отсюда находим
Л2* Cs) =
Т
с—loo
Здесь A(s)—определитель системы D.42); A2k (s)—определитель,
получающийся при замене соответствующего столбца матрицы сво-
свободными членами.
Проанализируем особенности подынтегральных функций в ин-
интеграле D.43) аналогично тому, как это сделано при рассмотрении
плоской задачи (гл. 2, § 1). Так как функции с2ь + ч„ 2п +»/, (s) не_ со-
содержат точек ветвления, то особыми точками выражений A2k(s)
являются полюсы, соответствующие комплексным корням S/ =
= — ? ± it уравнения A (s) = 0, и полюсы sp функции Р (s). Выра-
Выражение D.43) представляет собой решение физической задачи, сле-
следовательно, при функции Р (t), ограниченной на бесконечности, в
нем нет слагаемых, растущих по экспоненциальному закону, т. е.
определитель A (s) не содержит корней с положительной действи-
действительной частью. Контур интегрирования образован прямой, па-
параллельной мнимой оси, и дугой окружности, соединяющей концы
этой прямой в левой полуплоскости так, чтобы все полюсы находи-
находились внутри контура.
§ 2. Вертикальные колебания круглого штампа
155
Используя теорему о вычетах для функций Л2* (t), получаем
A2k @ = 2 res [A2h (s,) esf'\ + 2 res \A2k (sp) eV]. D.44)
Корни s, находятся из системы двух трансцендентных уравнений,
которая получается при раскрытии комплексного определителя
Д(—Н ± it) = 0- Первое слагаемое является гармонической функ-
функцией, затухающей в зависимости от времени. Характер изменения
ее от аргумента / не зависит от вида приложенной к штампу нагруз-
нагрузки, т. е. эта составляющая функции A2k (t) соответствует свободным
затухающим колебаниям штампа. Величина ? — безразмерная
частота свободных колебаний круглого штампа на упругом полу-
полупространстве; I > 0 — коэффициент затухания, обусловленный из-
излучением энергии на бесконечность. Второе слагаемое соответству-
соответствует вынужденным колебаниям, оно существенно зависит от вида
заданной нагрузки Р (t) и при ^->-оо может принимать различные
значения (нуль, константа, гармоническая функция и т. п.). Вычет
функции ~A2k (s) est в полюсе s,- = —| ± it, находится по формуле
f est при s^-Sj. Для определения A'(s) используется формула
дифференцирования функции комплексной переменной. Произ-
Производные находятся численно. Полюсы функций Р (s) обычно известны,
поэтому определение второго слагаемого в формуле D.44) не пред-
представляет затруднений. Кроме этой формулы для вычисления функ-
функций Aik (t) может быть использован интеграл Фурье B.36). Переме-
Перемещение штампа определяется интегралом свертки
D.45)
или интегралом Фурье
D.46)
Пользуясь формулой D.44), можно исследовать, в частности,
гармонические колебания штампа. Например, если к штампу вне-
внезапно приложена гармоническая сила Р (t) = PH (t) e'V, где Р —
амплитуда силы, t, — аа/с2 — безразмерная частота колебаний, то
P(s) = P/(s — iQ и при t ^> 1 (установившиеся колебания) реше-
решение задачи определяется вторым слагаемым в формуле D.44), если
положить sp = it,. Вычет функции A2k (s) е^ в полюсе s = it нахо-
находится из системы D.42), в которой следует положить s = it и за-
записать свободный член в первом уравнении в виде выражения
Pe'V/2na2. Действительные и мнимые части коэффициентов

156
Глава 4. Колебания круглого и прямоугольного
штампов
! + v,. in + i/2 (it) определяются соответственно по формулам
Re,
Г (* + О Г (я + 1)
' — Л2
72ft+V,
2,,+у,
X
С 4т]2 (гJ — ft2) |/i — лз
ten)
D.47)
Im
,. 2n+V, CO = —
M T(k + Va) r (n
X
11
:72"+'/2 (СП) ^Л
Л (St1) =Wv. ten) dn I, D.48)
3 J
где CT2fe+v2 (x) ^2n+v, W и 72A+v, (*) 72n+v,W —функции Бесселя и
Неймана полуцелого индекса и их произведения,
к+п
Г (~ m
2n - 2/п)!
— т)! Bп — тI Г Bk + 2n — т
, Г (т + »/«) Г BА + /я + 2) Г Bл + /я + 2) Г (J
(* < 1);
?2ft+v, (*) ^n+V, (X) =
(— 1)т Г Bfe + 2п + 2т + 2) (;
Г (/я + 1) Г Bft + 2п + 2т + 2) Г B/г +
m
D.50)
— . sin х У
2/п)!
Bт)!BА-2т)!Bх)*"
§ 2. Вертикальные колебания круглого штампа
157
ft—1
cos х
™0 Bт + 1)! B* — 2/я — 1) Bл:Jт+1 ]
= (- d"+1 VH-
D.51)
п—1
— sin х
% Bт)! Bя — 2т)! Bxfm
:-»ГР»+ .%»+«! 1 (х>1). D.52)
Bт + 1)! Bп - 2т - 1)! BxJm+l
Теперь исследуем сходимость решения.
Оценим сумму членов ряда в каждой строке матрицы D.42)
оо
52„ = 2 I C2ft+V,,2n+V, (s) I D-53)
при действительном s > 0. Запишем мажорантный ряд
п-1
S2« = 2 V^Vu IWv. (г) /Сги-v. (г) - /С2„+./а (г) /2ft+v, (г)] +
+ /Сгв-р/, (z) 2 '
/
a*+v.
@ < г< оо). D.54)
fe=0
Бесконечный ряд в D.54) сходится, что устанавливается, например,
путем сравнения его с выражением [24]
Bk +
, (г) = У Щ-<?.
D.55)
Следовательно, сумма Sin конечна при любых фиксированных зна-
значениях п и z.
Исследуем, далее, поведение S2n при я -»- оо. Предварительно
выражение D.54) приводим к виду
T(n+\)S2n
Г (п
г(я+1) у П^ + У2)^+./г(г)
Г(п + 72) ?{, Г(А+1)Л2п+1/,(г)
78)
D.56)
Используя асимптотические представления для функций /гп+v, (г) и
/C2n+v,(z) при я ->¦ оо, аналогично тому, как это сделано в § 1 гл. 2,
видим", что правая часть соотношения D.56) убывает и начиная с
некоторого значения я = N величина ее меньше единицы, т. е.

158
Глава 4. Колебания круглого и прямоугольного штампов
система уравнений D.42) квазирегулярна и допускает решение
методом усечения.
В качестве примера рассмотрим колебания жесткого фунда-
фундамента при действии внезапно приложенной силы/3 (t) = PH (t) и
Таблица 4.1
t
1
-МО
w{t)
2
Л (О
A,(t)
w, «)
3
4>«)
-МО
МО
о»о@
1
0
0,1
0,2
0,3
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
3,0
4,0
5,0
6,0
7,0
8,0
0
0,170
0,353
0,531
0,683
0,917
1,060
1,137
1,162
1,162
1,153
1,137
1,119
1,117
1,059
0,998
0,981
0,993
1,000
0
0,011
0,039
0,085
0,139
0,268
0,405
0,538
0,658
0,763
0,884
0,931
0,955
1,140
0,973
0,983
0,987
1,004
1,002
0
0,214
0,399
0,551
0,679
0,872
1,004
1,092
1,147
1,178
1,192
1,191
1,180
1,073
0,991
0,977
0,991
1,001
1,002
0
0,250
0,399
0,459
0,477
0,408
0,272
0,113
-0,026
—0,138
-0,221
-0,260
—0,285
-0,122
—0,001
0,029
0,015
—0,000
—0,004
0
0,010
0,038
0,081
0,133
0,258
0,394
0,530
0,659
0,773
0,872
0,954
1,017
1,124
1,057
0,997
0,985
0,993
1,000
0
0,214
0,398
0,549
0,678
0,873
1,006
1,092
1,146
1,178
1,191
1,191
1,181
1,073
0,990
0,977
0,991
1,001
1,002
0
0,238
0,395
0,469
0,492
0,417
0,265
0,095
—0,038
-0,141
-0,209
—0,240
—0,242
—0,114
0,001
0,028
0,013
-0,000
—0,003
0
-0,052
—0,051
—0,018
0,010
0,046
0,044
0,029
0,001
—0,026
—0,030
—0,013
0,009
0,002
—0,001
0
0
0
0
0
0,010
0,038
0,081
0,133
0,258
0,394
0,530
0,658
0,773
0,873
0,954
1,018
1,124
1,057
0,997
0,985
0,993
1,000
численным способом исследуем вопрос о необходимости и достаточ-
достаточном количестве членов ряда в разложении D.38).
Функции A2k (t) определяем по формуле B.36), используя ме-
метод Филона [97]. Величины функций A2k(t) в долях Р/2па2и w0 (/)
в долях статического перемещения Р A —vl)/2aE0 при v0 = 0,3 и
тх = 0,4 представлены в табл. 4.1. В разложении D.38) последо-
последовательно удерживались один, два и три члена ряда (в таблице
соответственно 1,2, 3). Как видно из таблицы, искомая функция Ао (t)
быстро стабилизируется, т. е. ее значения при двух и трех членах
ряда практически совпадают; значения функции Л2 (/) при двух и
трех членах ряда близки; величины функции Л4 (t) на поря-
порядок меньше величин функций Ао (t) и Л2 (/)• При t> 1 функции
Ао (/) и w0 (t) стремятся к единице, а функции Л2 @ и A4(t) — к ну-
нулю, т. е. распределение контактных напряжений и перемещение
штампа приближаются к статическим значениям. Отсюда следует,
§ 2. Вертикальные колебания круглого штампа
159
О 0,1 0,2 0,3 • ОЛ 0,5 0,6 0,7 0,8 0,9 г
что наибольшее число членов ряда D.38) требуется для описания
контактных напряжений в начальный период движения штампа,
которые распределены равномерно.
На рис. 51 показано изменение эпюры контактных напряжений
на участке 0 ^; г < 0,95 в зависимости от числа членов ряда в
разложении D.38) при т1 = 0,4. Напряжения вычислялись при
t = 0,1 и t = 0,2, в фор-
формуле D.38) удерживались
один, два и три члена ря-
ряда. Из рисунка видно, что
при одном члене ряда рас-
распределение напряжений
такое, как в статике; при
двух — близко к равномер-
равномерному и при трех — прак-
практически равномерное (за
исключением малых уча-
участков у краев штампа). При
росте t эпюра контактных
напряжений трансформиру-
трансформируется из равномерной в сед-
седлообразную, о чем можно
судить по характеру изме-
изменения функций Ло (t), Л2 @
и Л4@ (см. табл. 4.1).
Аналогичные результаты
получаются и при других
значениях параметра
0,2
0,4
Щ
0,8\
Р
'—^—
2
—.
—/_
^./
\\ 1
1 ?
t=0,1
5
N
\
s
\
Рис. 51.
1 2 3 4- 5 6 7 8 940 11 1~2 П'К t
Рис. 52.
На основании приведенных расчетов можно сделать вывод, что
для правильного описания динамических контактных напряжений
в любой момент времени t в разложении D.38) достаточно удержать
два-три члена ряда.
Изменение в зависимости от времени перемещения фундамента
при ту = 0,4, тх = 1,0 и mv = 2 показано на рис. 52 (во всех
случаях принято v0 = 0,3). При вычислении на ЭВМ интеграла
B.36) определялись КеЛ2&A'?) и lmA2k(iQ в дискретных значениях
переменной ? в интервале 0 < ? < 20, т. е. в указанном интервале
безразмерной частоты решалась задача о гармонических колеба-
колебаниях фундамента. Значения амплитуд колебаний в диапазоне
0 < ? < 1.5 совпадают с полученными в работе [13].
Для исследования свободных колебаний штампа решаем систе-
систему трансцендентных уравнений
ReA(—g+ »?) = 0; Im Д (—g + ф = 0.
Последовательно раскрываем определители 2-го и 3-го порядков
системы уравнений D.42). Искомые величины близки, что еще раз

160
Глава 4. Колебания круглого и прямоугольного штампов
свидетельствует о быстрой сходимости ряда D.38). Результаты вы-
вычислений безразмерных коэффициентов затухания | и частот сво-
свободных колебаний ? при v0 = 0,3 и ряде значений параметра тх
представлены в табл. 4.2.
§ 3. Вертикальные колебания прямоугольного штампа
161
V
\
:
0,4
0,2
77777777777777777 р '
ч
I
0,2 0,4- 0,6 0,8 1,0 1,2 1,k 1,6 1,8 m,
Рис. 53.
Рис. 54.
Графики изменений | и ? показаны на рис. 53. Как и в случае
плоской задачи, наблюдается увеличение до некоторого предела
частоты свободных колебаний штампа при росте его массы. Этот
результат соответствует характеру резонансных кривых, приве-
приведенных в работе [109]: при уменьшении массы штампа резонансный
пик смещается сначала вправо (в сторону увеличения резонансных
частот), а затем влево. „ , . „
Таблица 4.2
пг,
Определитель
порядка
1
2-го
1
Определитель
порядка
I
3-го
1
0,0
0,1
0,2
0,3
0,4
0,6
0,8
1,0
1,2
1.4
1,6
1,8
2,0
1,571
1,242
1,013
0,832
0,696
0,515
0,405
0,331
0,280
0,241
0,213
0,190
0,172
0,894
1,032
1,079
1,0787
1,051
0,974
0,899
0,835
0,782
0,735
0,696
0,663
0,634
1,578
1,243
1,004
0,820
0,694
0,508
0,404
0,327
0,266
0,242
0,211
0,190
0,176
0,899
1,036
1,081
1,081
1,051
0,971
0,902
0,839
0,780
0,735
0,698
0,663
0,629
При кратковременной нагрузке в виде прямоугольного импуль-
импульса продолжительностью Т = 2 колебания штампа быстро зату-
затухают (рис. 54, wo(t) дано в долях РA —vl)l2aE0; m1 = 0,6; v0 =
= 0,3).
§ 3. ВЕРТИКАЛЬНЫЕ КОЛЕБАНИЯ
ПРЯМОУГОЛЬНОГО ШТАМПА
Пусть на жесткий прямоугольный в плане штамп, располо-
расположенный на упругом полупространстве, действует вертикальная
сила P(t) (рис. 55), вызывающая поступательное движение его.
Необходимо найти распределение нормальных напряжений
р (х, у, t) по контакту штампа с основанием и его вертикальное пере-
перемещение wo(t). Переменные х = х/а, у = y/b, t =c2t/a по-прежне-
по-прежнему безразмерные. Уравнение движения штампа имеет вид
n2am2pi—^° — Р (/) — R(t), D-57)
где т2 = 4hbp/n2a2p0; 2а и 2b — длины сторон штампа; h — его
высота; R it) — равнодействующая контактных напряжений,
R(t) = ab\ \p{x, у, t)dxdy.
D.58)
6 5-2880

162
Глава 4. Колебания круглого и прямоугольного штампов
Уравнение D.57) необходимо решать вместе с уравнениями дви-
движения упругого полупространства при соблюдении контактного
условия
wo(t) = w(x,y,O, t) (И<1;|у|<1), D-59)
где w (х, у, z, t) — вертикальные перемещения полупространства.
Для отыскания значений w (х, у, О, t) при нагрузке р (х, у, /), рас-
распределенной по прямоугольной площадке, используем. формулу
Рис. 55.
D.21), которая в случае действия на границе основания сосредо-
сосредоточенной силы Р (t) имеет вид
W{
Чтобы придать этому выражению вид, более удобный для дальней-
дальнейших выкладок, рассмотрим интеграл
1 Г
2itt J
J
с—tea О
с—loo
¦sin
§ 3. Вертикальные колебания прямоугольного штампа
163
Применяя к нему преобразование Лапласа, получаем
J
D.62)
Учитывая значение интеграла [24]
-r %-k[I0(rk)-L0(rk)],
D.63)
г 2
где Lo (rk) — модифицированная функция Струве индекса нуль,
находим
w (г, 0, s) - У К (г, s), D.64)
где
К (г, s) = - л
-i -?- srh (/0
i) - Lo (rsriO)J +
(Л) / (л)
2_Tj n_s , ,_L ,
Illfi -Lst,^^) —
dt). D.65)
Перемещение границы полупространства под действием нагрузки
р (х, у, s) определяется с помощью интеграла свертки
4г аЪ
—1 —J
w (х, у, 0, s) =
^' s)^ (/^~^
(а = Ыа).
D.66)
6*

164 Глава 4. Колебания круглого и прямоугольного штампов
После подстановки D.66) в соотношение D.57) получаем интеграль-
интегральное уравнение для определения неизвестной функции р (х, у, s):
it it
m
+i +i _
abs* Г Г р(х', у', s) К (V(x - x'f + а? (у - y'f, s)dx'dy' =
-i -i
_
= P(s)>-R(s) (\x\<l, \y\<l). D.67)
Найти точное выражение для функции р (х, у, t) не представляе-
представляется возможным. Как известно, до сих пор не удалось еще получить
точное решение статической задачи о контактных напряжениях
прямоугольного штампа. Характер особенностей функции р (х, у, t)
у краев штампа и в углах неизвестен. Можно лишь утверждать,
что при увеличении отношения сторон штампа контактные напря-
напряжения в средней его части должны соответствовать напряжениям
в плоской задаче. Последнему условию можно удовлетворить, если
искать решение пространственной задачи в виде двойного ряда
Р (х, У, 0 = 2 2 А2п,2т @
о
2
о т=о
^JlfL , D.68)
— х У ^ — У
где А2п, чт @ — искомые функции. При увеличении длины сторо-
стороны штампа (например, Ь ^> а) у = у/Ь -*¦ 0, влияние корня A—#2)'/а
на конечных расстояниях от оси х мало. Равнодействующая кон-
контактных напряжений определяется по формуле
R(t) = atabA00(t). D.69)
Подставляя выражения D.68) и D.69) в уравнение D.67), получаем
оо оо
Ло (S) + m2S2 2, 2d A2n,2m (s) Ф2п,2т (X, у, S) = -Щ" D.70)
п=П т=П п а"
где
+1 +1
4>2п,2т (X, У, S) =
Т2п(*)Т2т(у)_ у ,J 3( у } d,d,
ii /1-*/я/1-*'» к D.71)
А2п,2m(s)—-изображения Лапласа искомых функций A2rii2m(t). Для
того чтобы удовлетворить уравнению D.70) в заданном прямо-
прямоугольнике, разлаг*аем функцию Ф2п, 2т (х, у, s) в двойной ряд по
полиномам Чебышева
п.2т (X, У, S) = -L
С
~11_ 4% (s) T
2p
+ -2" 2 да (s) Т2, (у) +
4—1
lT2p(x)T2q(y), D.72)
§ 3. Вертикальные колебания прямоугольного штампа
165
где
D.73)
]]
или
+Г
D.74)
-1 —1
/С (г, s) определяется по формуле D.65); г— Vkx" — x'f+ a2(y"—y'J.
Разложение D.72) подставляем в уравнение D.70) и приравниваем
в левой и правой частях его коэффициенты при полиномах Чебы-
Чебышева одинаковых степеней. В результате получаем бесконечную
систему линейных алгебраических уравнений относительно изо-
изображений Лапласа Л2п, 2m(s) неизвестных функций Лгп, 2m(t)'-
оо оо —
n=0 m=0
=1, 2, ...).
D.75)
2 2 42n,2m(s;
n=o m=0
Количество уравнений в этой системе должно соответствовать коли-
количеству членов ряда, удерживаемых в D.68). Например, если взять
четыре члена ряда (п = 0; 1; т = 0; 1), то матрица системы D.75)
будет иметь вид
- — гг .. — . „ Свободный
член
с00 (s)
22 v '
D-76)
Переходим к определению коэффициентов матрицы с2™'i2p(s). Вы-
Вычислить пятикратные интегралы в D.74) при заданном значении
s трудно. Поэтому преобразуем это выражение, чтобы понизить
кратность интегрирования и получить формулы, пригодные для
расчетов.
Представим значения искомых коэффициентов в виде суммы
п2т,2п |
С2п,2р '
5_ (] v ) Г2т'21 4-
— 9 V1 У0> L2n,2p ^
C2n,2p
D.77)

166 Глава 4. Колебания круглого и прямоугольного штампов
где первое слагаемое находим из решения статической задачи, |
-1 -1
+1 +1
X f f Taa(xl)Tam{y')dxrdy-dx'dy'
_J _J, У 1 -x'2/l — y'aV(*» —х'^ + аЧ^-Л2 ' '
или (см. формулу D.63))
Т г' ^w^fe'
1-1 -1 /Г^^УГ^
xdx'd/djrtfy'dE- D-79)
Второе слагаемое в D.77), определяемое из решения динамической
задачи, с учетом формулы D.63) имеет вид
)
X —:
(ED
?2 + |
dx"dy"dx'dy',
D.80)
где г = /(х" — х'J + а2 (У" ~ У'J.
Интегрирование в выражениях D.79) и D.80) сначала выпол-
выполняем по переменным х', у', х", у", а затем по |. Функция Бесселя
нулевого порядка с помощью формул сложения [55] разлагается
в ряды
70 (I V(x" - x'f + а* (у" - у')*) =
/=—со
5
i=—оо
3. Вертикальные колебания прямоугольного штампа
167
2 V2k+i(tx"O,{lx')]x
/=-со J
х[ 5 ^(«E/Wwl. D.81)
L г=—оо J
Учитывая значение интеграла [24]
С Т2р (х") уа
J
разложение D.81) подставляем в формулу D.79) и интегрируем
по х", у", х', у'. В результате получаем
« - 4 j J Д [7/+„ (i- в) 7;-л (i- б) 7/+р (I б) 7/-Р (т б)] X
х 2 7'+'« (т ag) 7i-m (т aE) 7'+" (т б) 7'-* (т
ОО Г ОО
+2 2 н iL 2 7,+/+„ D- б) 7ft+/^n D- б) 7/+р D- б)
&=1 1_ /"=—со
х vPD-б) || 2_
/= ОО
D.83)
Используя интегральные представления для произведений функций
Бесселя, суммируем ряды в D.83) по индексам / и- i:
2 ik+,+n D- б) ъ+/-п D- е) 7/+р D- б) 7/-р D- б) -
•= (~'Г Р J j 72П(IsinфО?2р(Бsinф^ х
о о
X 2 cos 2
/=—со
Фгcos
(~^" "
?2« (i sin
sin ф) cos
D.84)

168
Глава 4. Колебания круглого и прямоугольного штампов
Здесь использовано выражение бесконечного ряда косинусов через
б-функцию [20]:
2] cos kx = nb(x) 1к- @ < x < 2л). D.85)
С учетом суммы ряда D.84) разложение D.83) принимает вид
со С Г Я/2 -I
& = (- lf+p+m+< 4И ( 1 **. (g sin Ф) 72Р (g sin Ф) <*Ф
x
X
?
?
J 72m (ag sin ip) 72, (ag sin ip) dip
о
ГТ
+ 2 2 (— 1)» j 72n (g sin ф) 72р (g sin ф) cos
ft—1 о
х
X
Я/2
) 72m (ag sin ip) 72(? (ag sin
D.86)
Просуммируем последнее выражение по k с помощью формулы
2
D.87)
Подставляя значение этой суммы в D.86), находим
к> Я/2
4f
Пусть
X
О О
, (ag cos ф) 72, (ag cos
D.88)
X
X
Т2п(х')Т2т(у'
—i ^-i
(у') Г 7o(rl)
= (^_ цп+р+т+д _8_ г2 Г Г 72n(gsin
¦ sin ф)
о о
X 72q (agcos
) х
D.89)
(г = sn; r = К(х" — x'f + а2 (у" — у'J).
§ 3. Вертикальные колебания прямоугольного штампа
169
Тогда выражение D.80) запишется в таком виде:
D.90)
Слагаемые коэффициентов матрицы D.75), определяемые дву-
двукратным интегралом D.88), зависят только от соотношения сторон
штампа и могут быть протабулированы. Величину интеграла D.88)
можно представить рядом, содержащим степени и логарифм па-
параметра а. Заменяя переменные, приводим его к виду
& («) = (- \)n+p+m+q 4" \ 72m (at) 72Q (a?) dg
о
х 3 v^rw
х
D.91)
Произведение функций Бесселя от аргумента ? заменяем интеграль-
интегральным представлением [19] и выполняем интегрирование по пере-
переменной ?. В результате получаем
X
2яГ J
(— s) Г (— s — п — р) Г (s + п + р + 1) X
X Г2 (s + п + р + У2)
-ds x
x
(ag) 7a, (ag) d\.
D.92)
После интегрирования по переменной ? [24]
)
COS2
П Г Is + П + Р + -^- + fl/
X
sin3 ns П Г (s + 1 + bj) a2
, D.93)

170
Глава 4. Колебания круглого и прямоугольного штампов
где аг = 0; а2 = m + q; a3 = m — q; at = —m + q; аъ = —m — q;
bi=0; b2 = n + p; b3 = 2n; bx = 2p; Ьъ = 2n + 2p.
Подынтегральная функция в D.93) при п > р имеет полюсы
1-го порядка в точках s = — k (k = 2р + 1, 2р + 2, .... п + р),
2-го порядка — в точках s = — k (k = 1, 2, ..., 2р) и 3-го порядка —
в точках s = k(k = 1, 2, 3, ...). Деформируя путь интегрирования
так, чтобы все полюсы находились справа, замыкая контур в пра-
правой полуплоскости и находя вычеты, получаем
(а) = —т=— X
я4 у п
X
X
2(n+p-fc)+l
2p_ г (ft) П г
X
X
fe=l
/=2
5
X —21па —
/=2
ад +4-У—Н=^ —
J ftSy П г (k +1 + 6,-) a2(«+p+ft)+i
X
M3"-i+h:
12 5
D.94)
где ф'(й) — производная функции ty(k)
Выражение D.89) аналогично сводится к двойному ряду
& (г) - (- \)n+"+m+" ±- z*
3. Вертикальные колебания прямоугольного штампа
171
X
_8_ г2 Г
X
пГ J
Г (— s) Г B« + 2р + 2s + 1) ds
Г Bft + s + 1) Г Bр + s + 1) Г Bft + 2р + s + 1)
X
X
.*)
2(n+P+s)
; + i2 + z2)ys2 +
X
я.у'зг
2ш'
X
X
1
Г Bя + s + 1) Г Bр + s + 1) Г Bп + 2р + s + 1)
2(n+P+s)
X
X
K ' пу"я
X
( V
"Г/
\2(m+i?+ft)
Г (ft + 1) Г Bт + 1ц + ft + 1) Г Bт + ft + 1) Г B? + ft + 1) 2я;
X
X
(¦
—joo
Г Bл + s + 1) Г Bр + s + 1) Г Bл + 2р + s + 1)
•ds x
X
/ j
Ы
2(n+p+s)
1 3 га
p2(n+p+m+q+k+s)
D.95)
Последний интеграл в D.95) подстановкой х = >а --2- приводится
к табличному виду [24]
i, „
-i-; ¦§-;
= — Z2(n+p+m+q+k+s)+l \ x
0
0'
X

172 Глава 4. Колебания круглого и прямоугольного штампов
~\
ny^ г (
= 4 cos nsr A — n— p — s) Г (n + p + m + q + ft + s + 1)
Подставляем этот результат в выражение D.95):
Л2л,2р (Z) =
= 4
1 \ (az\2{m+^+k'> I z \2("+р)+'
k=0
Г (ft + 1) Г Bт + 2? + * + О Г Bт + ft + 1) Г Bq + /г + 1)
X
X
_
2т"
±]{±-j ds
—loo
cos nsT Bя + s + 1) Г Bр + s + 17ГBп + 2р + s + 1) X
D.97)
Подынтегральная функция в D.97) имеет полюсы 1-го порядка в
правой полуплоскости в точках s = 1/2 (I = 0, 1, 2, ...). Находя
вычеты, получаем
X
х
Г (k + 1) Г Bт + 2<? + k + 1) Г Bm + k + 1) Г Bq + /г + 1)
X
ХГ
Вычисление рядов D.94) и D.98) не представляет особой труд-
трудности.
Как видно из выражений D.94) и D.98), коэффициенты c^',%{s)
системы уравнений D.75) в плоскости комплексной переменной s
не содержат точек ветвления. Следовательно, как и в случае осе-
симметричной задачи, функции А2п, 2т@ могут быть найдены с по-
помощью вычетов:
, @ = 2 res [Л2„,2т I
где
+ 2 res [Л2„,2т (sp) eV], D.99)
D.100)
! 3. Вертикальные колебания прямоугольного штампа
173
A2n 2m (s) и A (s) — определители системы D.75). Корни уравнения
д (J_^ ± j?) = 0, как и ранее, находятся из системы трансцендент-
трансцендентных уравнений вида B.28), вычеты в полюсах s = —I ± it,—
численным дифференцированием определителя A (s) по комплексной
переменной. При отыскании корней определителя в формулах
D.98) следует подставить s = —? + it, и отделить действительные
и мнимые части:
= 4
Г (ft + 1) Г Bт + 2fr + ft + 1) Г Bт + * + 1) X
X
X
X
Г Bp + i-
D.101)
+ /+1. При вычислении действительной части функции
Kl™',24P(i]rei<e) нужно взять cos Л/ф, мнимой—sin Ncp.
После отыскания функции Лоо (t) находим вертикальное переме-
перемещение штампа:
t
' . f (/_т)Г-|^-_Лоо(т.Iб/т. D.102)
о
Вертикальные перемещения точек границы упругого полупростран-
полупространства за пределами штампа в соответствии с формулами D.66) и
D.68) могут быть найдены по формуле (в изображениях)
w (х, у, 0, s) =
X — Я
n=0 m=0
Р
n,2m (X, У,
DЛ03)

174
Глава 4. Колебания круглого и прямоугольного штампов
где
со +1 +1
К2
,2т (X, У, STl) = j \ \
п,2
X
X
О —1 -1
dxWdl D.104)
Аналогично предыдущему, пользуясь формулой сложения для
функции Бесселя D.81), разлагаем выражение D.104) в ряды по
произведениям цилиндрических функций, выполняем интегрирова-
интегрирование по переменным х' и у' и суммируем ряды. В результате полу-
получаем
К2п,2т(Х, У, Sr]) = (^l)n+hAnX
со л/2
f f ?2 cos (х\ sin op) _ ,,. . \ /f. \rr/f- \jj»
X \ \ ga I л^а 72<г (g Sin ф) COS @»/? COS ф) 72m («I COS ф) tftprfg.
& ё1 ё +(ет|} D.105)
Оригинал этой' функции имеет вид
оо Л/2
X J J I sin { —|j cos (*g sin ф) 72n (? sin ф) cos (ayl cos ф) х
n n
о о
X 72m (a| cos ф) dqjdg. D.106)
Вертикальные перемещения любой точки границы упругого полу-
полупространства в момент времени t находим по формуле
a» (*, y, 0, 0 = ^27
2 2
n=0 m=0
*
P" - Г K lr „ t
F{) A2n,2mU, </, —
<4-107)
Учитывая, что коэффициенты А2п, 2т @ выражаются элементарными
функциями D.99), свертку по t производим под знаком интеграла
в D.107), после чего при заданных координатах х, у, t вычисляем
перемещения на ЭВМ.
Глава 5
ГАРМОНИЧЕСКИЕ
КОЛЕБАНИЯ ПОЛОСЫ
НА УПРУГОМ ПОЛУПРОСТРАНСТВЕ
ПОД СЛОЕМ ЖИДКОСТИ
(плоская задача)
§ 1. КОЛЕБАНИЯ УПРУГОГО ПОЛУПРОСТРАНСТВА
Рассмотрим плоскую задачу о периодических колебаниях уп-
упругого полупространства, покрытого слоем сжимаемой невязкой
жидкости [105]. Пусть на границе полупространства и слоя жидко-
жидкости (рис. 56) на участке —1 < х< 1 действует распределенная на-
нагрузка р (х, t). Требуется найти перемещения полупространства,
скорости и гидродинамическое давление жидкости. В данном слу-
случае необходимо решить дифференциальные уравнения движения
полупространства A.1) и волновое уравнение для потенциала ско-
скоростей жидкости
дх
л г
ду2
_ c| ааф1
E.1)
где с — скорость звука в жидкости. Составляющие скорости vx
и vg и гидродинамическое давление жидкости рх (х, у, t) опреде-
определяются через функцию фх [51]:
E.2)
»--¦*¦: ^ =
аду '
E.3)
где рх — плотность жидкости. Граничные условия задачи: 1) на
свободной поверхности (у = —Я) при учете волнения
E.4)
дф1 (х, - Я, Q 4 Э2Ф1 (х, - Я, 0 _
Т — яЯ
где Н = Н/а — относительная высота слоя жидкости; Я — дей-
действительная высота; g — ускорение силы тяжести; 2) на границе
раздела упругого полупространства и слоя жидкости (у = 0)
(И>1);

176 Глава 5. Гармонические колебания полосы под слоем жидкости
,(x, 0, t) = 0 (—oo<*<oo);
, 0 _ Ф> (x, 0, Q
л7 (— oo<x<oo).
E.6)
E.7)
Учитывая, что при установившихся колебаниях р (х, t) = р* (х)е^{,
<Pi(*. У, t) = ф1 (л:, у)е®, уравнение E.1) записываем в виде
; = о,
где р\ = cjc, ? = аа/с2. Применяя к этому уравнению преобразо-
преобразование Фурье, получаем обыкновенное дифференциальное уравне-
уравнение 2-го порядка
E.9)
решение которого имеет вид
*ЛЬУ) = А1®/— + В1®е-уУ^\ E.Ю)
где Ах (?) и В1 (?¦) — постоянные, определяемые из граничных ус-
условий E.4), E.5). Обращаем E.10) и учитываем время:
E.11)
ф1 (х, у, t) == -L_ J [A, (g) eyV + В, (I) e
Удовлетворяя условию E.4), находим
Ах (I) e~"Vl!~^ (?» +
+ 5х (I) еНУ*~^ (?» -рз КЕ2-^2) = 0,
E.12)
.7. Колебания упругого полупространства
177
откуда
E.13)
+
Решая уравнения движения упругого полупространства A.1
так же, как это сделано в § 3 гл. 1, и удовлетворяя условиям E.5)
и E.6),' получаем
2ш р0
(l2~~ С2)
= 0,
E.14)
E.15)
где р* (?
E.7) получаем
преобразование Фурье функции р* (х). Из условия
- ^Аг (I) - V? - Ш2В, (I) = 0.
E.16)
Таким образом, матрица системы из четырех уравнений имеет вид
Свободный 1
:, В(Ь АЛ) й'(&> ЧЛеН "
ij2 Pi
2ш Ро
2Ш p»
0
E.17)
Решая эту систему, находим
X
(ej ~ 2ц
- p»?« D
; E-18)
iip
E.19)

178 Глава 5. Гармонические колебания полосы под слоем жидкости
а A) =
^Гу Р* (Б) .
где
4ц
E.21) 1
х
Ш'-i
i2 -
X
- h a2 - Pit2) th я
№2} + \ с4
-рЦ- E-2-2)
Подставляем E.20) и E.21) в E.11):
ашр0
г X
2
р, ch ь, (Я + у) -•¦?- sh |0 (Я
сь яь, -
+ у -g-1-
—Р!?"; ?2 = 1/?2-Р2?2; Ез^
f (g) = B|2 — С2J — 4?2 КЕ2—P2S2 Kl2
; E.24)
E.25)
Ha основании формул § 3 гл. 1 вертикальные перемещения полупро-
полупространства определяются через функции А (?) и В (I):
J [- Л (
v (х, у, t) = -?-=¦
Подставляя E.18) и E.19) в E.26), получаем
у, i)-
Если волнение на поверхности жидкости не учитывать, то ус-
условие E.4) следует заменить: ^
Pl(x, -Я, t) = _Pl-a.-^- = 0,
E.28)
-уЩ е-^Ч\. E.26) I
§ 1. Колебания упругого полупространства
179
а в в
ыражениях E.23) и E.27) следует положить р2 = 0:
Ф1
_
ашр0 /2S 3 Ь, ch
^- is- th Я§0
Ро So
E.29)
(Х у
Ро So
E.30)
Если с2 -С с< сжимаемостью жидкости можно пренебречь. Полагая
в E.29) и E.30) Рх = 0, 10 = I, записываем
ашр0 "
Ро S
х
0
^ (s) + S4 -g-
E.32)
Пусть нагрузка р (х, t) задана в виде ряда
Тогда выражения E.31) и E.32), удовлетворяющие принципу из-
излучения, при симметричной нагрузке примут вид
. У. t)—
-nt
Т|! Ch ЙЯ1Ц) F', (Т|!)
E.33)
2
ft=0

180 Глава 5. Гармонические колебания полосы под слоем жидкости
X
lBtl* ~
х
— В2
X cos Цхц) йц - ni —?—f- [Bл? - 1) е
E.34) J
при антисимметричной нагрузке —
- В2 sh [?(# +
E.35)
О (^- У. 0 =
X
X
X
У т? _ 82
X sm(?,xr$dx\ — ni ? X
X [Br,; -
72k+l (С%) sin
где
J
E.36)
= Bri8 - I)8 -
F\ (t|) = 8ti Bti2 — 1) —
E.37)
„ / /ri2 —1 . Ут]2—82\ ,
У2 1 /
/т]2 — В2
'5-38)
i. Колебания упругого полупространства
181
« — действительный положительный корень уравнения Fх (л) - 0.
Вертикальные перемещения границы упругого полупространства
(у = 0) находим по формулам
v{x> о, о = —
X
cos
- я t
cos
E.39)
ft=0
X
K^-B2
f ; (лх)
sin
E.40)
Разложения этих выражений в ряды по полиномам Чебышева при
UI < 1 имеют вид
v(x,0, O = _^L-2^'
\c2ki0 + 2 2 с2,,2,Г2, (x) j;
(x) j; E.41)
v(x, 0, 0 =
2 2 Л24+1с2,+1,2г+1Г2г+1 (jc),
ft=0 /-=0
E.42)
где
Re
° о
Гр+ ^_L(Tl2-_p2) th
x
X
D)
(СП)
5 E-43)
X

182 Глава 5. Гармонические колебания полосы под слоем жидкости
!-P2)ft2-l). E.46)
Коэффициенты C2k+i,sr+i находятся по формулам E.43) и E.44), в
которых следует заменить индексы 2k и 2г индексами 2k + 1 и
2г+ 1.
Разлагая выражение E.39) при х -»¦ оо в асимптотический ряд,
получаем то
»(*. о, о—-—2*(—
E.47)
где первое слагаемое соответствует поверхностной волне (у = 0),
распространяющейся со скоростью cs = c2/x\lt второе — попереч-
поперечной волне, распространяющейся со скоростью са> и третье — про-
продольной волне со скоростью сг. Из E.37) можно установить, что
г^ растет до некоторого предела при увеличении ? или Я, соответ-
соответственно скорость cs меньше скорости волн Релея. Так как при на-
наличии слоя жидкости r\lt а значит, и cs зависят от ? (частоты), то
происходит дисперсия поверхностных волн. Как видно из E.47),
амплитуды поверхностных и поперечных волн при наличии слоя
жидкости меньше, чем соответствующие амплитуды в отсутствие
слоя жидкости; от высоты слоя жидкости амплитуды продольных
волн и скорости продольных и поперечных волн не зависят. Со-
Согласно формуле E.3) при симметричной нагрузке
Pi (х, У, 0 = - -ir
fc=0
(x, у),
E.48)
§ 1. Колебания упругого полупространства
при антисимметричной нагрузке
где функции D. ,..,,,«,) =
183
х, у),
E.49)
— 1) V т|'— Ра + -^
Pi
— Р*) X
E-50)
J ю
! E-52)

184 Глава 5. Гармонические колебания полосы под слоем жидкости
Im C2k+\ (х, у) =
Р
Г
J
о
Sh
- г]2) /b=
sin
sh [?
E.53)
могут быть вычислены на ЭВМ. Согласно E.2) при симметричной
нагрузке
ic
k=0
-дГ
v,,=
при антисимметричной нагрузке
г. У)>
-j-C2h+i(x, у);
c2k+l (x, y).
E.54)
E.55)
E.56)
E.57)
Таким образом, найдено решение задачи, сформулированной в
начале параграфа. Интегралы E.43) и E.44) вычислены на ЭВМ
при следующих данных: Я = 0; 0,5; 1,0; 1,5; 2,0; ? = 0; 0,2;
0,4 2,0; р/р0 = 0,5; v0 = 0,3 (см. «Приложение», табл. 11). jj
§ 2. УСТАНОВИВШИЕСЯ КОЛЕБАНИЯ
БЕСКОНЕЧНОЙ ПОЛОСЫ
Рассмотрим периодические колебания слоистой среды: на уп-
упругой полуплоскости находится упругая бесконечная полоса вы-
высотой h, а над ней слой жидкости высотой Я.
Пусть к полосе на упругой полуплоскости (плоская деформа-
деформация), покрытой слоем жидкости, приложена сосредоточенная сила
(рис. 57), изменяющаяся по закону
Р Сх, 1) = Р8 (х) е>ш1, E.58)
§ 2. Установившиеся колебания бесконечной полосы
185
где р _- амплитуда силы; х, t — действительные переменные. Тре-
Требуется найти прогиб полосы w (x, t) и потенциал скоростей жидко-
жидкости «Pi (x, У, 0- Полагаем, что жидкость невязкая. Исходными
для решения задачи принимаем следующие уравнения: для жид-
жидкости — уравнение потенциала скоростей
для полосы — дифференциальное уравнение изгиба
D -^ + рй -^- = Р8 (х) ё* + Pl (х, - h, t) - р (х, t), E.60)
y77777777777
Рис. 57.
для полуплоскости — уравнения движения A.1). Граничные условия:
у = - (Я + Щ, Рг (х, - Я- А, 1) = 0; E.61)
-y=-h, y=^L. = -^L; E.62)
У у ду dt . У '
g = 0, w (х, Г) = v (х, 0, 7); оу (х, 0,1) = —р{х, 7);
тху (х, 0, t) = 0. E.63)
Уравнения E.59), E.60) и A.1) решаем с помощью преобразо-
преобразования Фурье [97]. Решая уравнение E.59) и удовлетворяя условиям
E.61) и E.62), находим
г, у) =
Рг
— tf/c2 ch (H Yl2 —
E.64)
E.65)
где_ф1(?, у), w* (I), p[(l, —h) — изображения Фурье функций
Ф* (х, у), w*(x) и р\ (х, —h), не содержащих переменной t. В ре-
результате решения уравнений E.60) и A.1) соответственно получаем
-Л)-?(Б)]; E.66)

186 Глава 5. Гармонические колебания полосы под слоем жидкости
Е 0)-- » ">'
E.67У
Щ. E.68))|
V"
Из уравнений E.65)—E.67) находим (с учетом формул обращения)
E.69I
§ 2. Установившиеся колебания бесконечной полосы
187
— Р* ch (©'Я' КтJ — PJ) Ф (л)
E.70)
w (х', i) =
Ре1*'
E.72)
Вычисляя на ЭВМ несобственный интеграл в этом выражении,
находим величины прогибов полосы, дифференцируя w (x'y t) по
х',— углы поворота, изгибающие моменты и перерезывающие силы.
Анализ функции E.71) показывает, что при увеличении плот-
плотности материала полосы р, плотности жидкости р1( частоты коле-
колебаний и (до некоторого предела) и высоты слоя жидкости Н значе-
значение т)! возрастает по сравнению со значением % в отсутствие поло-
полосы и жидкости, т. е. скорость волны Релея cR — с2/%, которая
E.71)
L = v^ZJ/ц. — приведенная длина бесконечной балки; ©' = Lft»/c2;
х' = ~x.lL; у' = ylL; Н' = HIL; h' = hIL — безразмерные парамет- I
ры (Pi < Р). На действительной оси при некоторых значениях па-
параметров функция Ф(т)) обращается в нуль (г\ — % > 1).
В выражении E.69) выделяем стоячую волну по способу Лэм-
ба [123]. В результате получаем выражение для прогибов, удовлет- |
воряющее принципу излучения,
в данном случае от частоты колебаний, уменьшается. При
жесткости балки и частоты колебаний (начиная с
^которого значения) ,,,-* 1, т.е. скорость волны Релея увели-
увеличивается до скорости поперечной волны. При этом Ф (г\) -»- °° и
Таблица 5.1
77, см
0
50
100
200
и
0,2
1,860
1,870
1,877
1,868
0,4
1,414
1,424
1,425
1,351
0,6
1,116
1,117
1,104
1,002
0,8
0,902
0,893
0,870
0,768
второе слагаемое в формуле E.72) исчезает. Значение параметра
и' = ио, при котором уже нет волны Релея, определяется из
трансцендентного уравнения
Таким образом, при 0 < со' < соо w@]
волны Релея существуют, при ft» >
>¦ шо их нет.
Для вычисления амплитуд по- 10
лосы E.72) на ЭВМ составлена
программа. Вычисления выпол-
выполнены для точки х' = 0 при сле-
следующих характеристиках поло- о,
сы, основания и слоя жидкости:
ft = 20 см, L = 100 см, сг =
= 10 000 см!сек, р/р0 = 1,2, рх/р0 =0,5,
В = 0 53 р\ = 0 077. Параметр со изменялся в пределах и,2 <
< со' < 0 8 с интервалом 0,2 (соответствующая частота в герцах
п- переделах 3,2 < п <. 12,8). Результаты вычислений ампли-
амплитуд прогибов w @) в долях Р/л\х при разных высотах слоя жидкос-
жидкости представлены в табл. 5.1. Как видно, влияние слоя жидкости
возрастает с увеличением частоты колебаний. Для оценки влияния
инерции полуплоскости на перемещения полосы при вычислениях
плотность материала полуплоскости условно уменьшена в четыре
раза, т. е. р/ро = 4,8, Pl/p0 = 2, р = 0,154. Результаты вычисле-
вычислений при п = 12,8 гц приведены на рис. 58. Видно, что роль инер-
инерции основания существенна.

188 Глава 5. Гармонические колебания полосы под слоем жидкости
§ 3. СИММЕТРИЧНЫЕ КОЛЕБАНИЯ ПОЛОСЫ
КОНЕЧНОЙ ЖЕСТКОСТИ
Рассмотрим задачу о колебаниях балочной плиты конечной
жесткости на упругом полупространстве под слоем жидкости при
действии периодической симметричной нагрузки. Пусть на полосу
конечной жесткости шириной, равной единице, и длиной 2а
(рис. t>y, а), выделенную из балочной плиты, действует нагрузка
§ 3. Симметричные колебания полосы конечной жесткости
189
q(x, /),изменяющаяся в зависимости от времени по гармоническо-
гармоническому закону
q(x, t) = q*(x)e'V, E.74)
где q* (x) — амплитуда нагрузки; ? — безразмерная круговая час-
частота. Требуется найти нормальную реакцию полуплоскости р (х, t)
(подошву полосы считаем абсолютно гладкой), прогибы полосы
w(x, t), потенциал скоростей жидкости <рх (х, у, t). При этом пред-
предполагается, что жидкость невязкая и несжимаемая, толщина слоя
жидкости Н значительно больше толщины полосы ft, волнением
поверхности жидкости и изменением гидродинамического давления
по высоте полосы можно пренебречь.
Для решения задачи воспользуемся приближенным уравне-
уравнением движения полосы
~ai д* . г- а, ар ~ = <7* (х) efV + Pl (x, -ft, 0 -p(x, О,
E.75)
уравнениями движения упругого полупространства, находящегося
в условиях плоской деформации A.1), и уравнением Лапласа для
потенциала скоростей жидкости
d2<Pi , d2<Pi
дх*
Граничные условия:
да> @, 0 _ п. д*и> (О, О
ду*
= 0.
Tx
_ d3w(l, t) _
l, t)
w(x, t) = v(x, 0, 0
y = ^H, Pi (x,
E.76)
); E.77)
E.78)
E.79)
E.80)
E.81)
т*»(*. О, 0 = 0 (— оо<х<оо). E.82)
Равнодействующую неизвестных нагрузок в правой части уравне-
уравнения E.75) — реакции полуплоскости р (х, t) и гидродинамического
давления жидкости на полосу рг (х, —ft, t) — обозначим через
Pr(x, t) и будем искать выражение для этой функции в виде ряда
у = и,
Pi(*. 0, 0 =
-Я, 0 = 0;
dv(x, 0, t)
dt
jp(x,t)
oy(x, 0, 0-(_pi(x> 0) t)
= P(x, t)-Pi(x, —h, t) =
E.83)
ft=0

190 Глава 5. Гармонические колебания полосы под слоем жидкости
где A2k — комплексные неопределенные коэффициенты. Полагая
при установившихся колебаниях
w(x, t) = w*(x)e<V; р(х, t) = р*{х)№\ ф1(*, у, t)=^(x
E.1
исключаем время из уравнения E.75):
СО
?*(*)-2
где у = V\,lkx, т. е. приходим к уравнению C.1), решение которо
как для неустановившихся, так и для установившихся колебан
приведено в гл. 3.
Определим теперь перемещения границы полуплоскости. „,,
ма нагрузок, действующих на границе полуплоскости, представ!
лена на рис. 59, б. Так как согласно E.83) р (х, t) = р^(х, t) щ
+ Pi(xt —К 0 й п0 предположению p-iix, —А, t) » рг (х, 0, Щ
можно считать, что эти нагрузки приближенно эквивалентны на\
грузкам, показанным на рис. 59, в. Следовательно, задача анало!
гична рассмотренной в § 1 задаче о колебаниях упругой полуплос|
кости под слоем жидкости при действии нагрузки E.83), npi
женной на участке —1 <. х <; 1 границы полуплоскости. Иско
перемещения находим по формулам E.39) и E.41).
Таким образом, решение рассматриваемой задачи определяе
из системы уравнений C.31) при s — it,. Коэффициенты Rec2k, & ;...
Im c2k, а- находятся соответственно по формулам E.43) и E.44),?
После отыскания из этой системы неизвестных А2и прогибы поло^
сы, углы поворота, изгибающие моменты и перерезывающие силь|
определяются по формулам § 1 гл. 3, гидродинамическое давление!
и скорости жидкости — по формулам E.48), E.54) и E.55), реак-
реакции полуплоскости — по формуле
(И<1). E.86)
Рассмотрим примеры. Пусть v0 = 0,3 и балочная плита имеет
такие характеристики: 1) А == 0,5 м, а — 5 м, т0 = 0,0942, k0 =
= 3; 2) h = 1 м, а = 5 м, т0 = 0,1884, k0 = 0,373. Исследуем
колебания ее под слоем жидкости высотой Я = 0,5 и Н = 1,0 при
действии на плиту сосредоточенной силы в центре, равной 2Ре1&.
Результаты решения системы C.31) (при котором использованы
данные табл. 11 приложения), свидетельствующие о характере
изменения коэффициентов A2k (в долях 2Р/ла) ряда E.83) в за-
зависимости от высоты слоя жидкости и частоты колебаний пред-
представлены в табл. 5.2 и 5.3. В табл. 5.4 приведены результаты рас-
расчета амплитуд относительных прогибов \wQ (x)\ (в долях Pa3/3nD)
CV1
I
ч
ча
а
lO CD ОО
со о оо
t-~ CN -^
°i °i °i
о о" о
lO ОО CN
о^ -^ со
о^ о^ о^
о" о" о
— со оо
<n ю а>
о о> го
— о" о"
^ О
CN О> —
О OlOl
-" о о
to ^,
со —<
о о
^ Ю СО 00
_ ГО 00 00
>Л сЬ CN —'
о 9. о. о,
II ~~~
о ^ о
S —< со
СО СО CN
О О О
о о о
CN О ГО
CN CN -1
О О* О
I I I
t-- t^- CO
СО СО 00
111
¦* ^ со
¦* О5 Ю
IN И IN
С-со
8 8 8
о о
(N 00 —<
СО t"~ О
СО СО to
о о о
ill
^ «Э (N
СО ^ 00
о_ о о
р" а о
о о. о^
о о о
СО СО 00 1Л CN ГО
00 t^- ГО 1С N О)
о го о t^- со ^
00 ^ 00 О -н «
777 111
00 Ю СО <N t>- Ю
с^ а со t^- со t*-
—. 00 СП
t— t— t~-
111
¦*¦*-.
о о ^«
en ^ io
777 Iff
00 ¦* f~- ~ ?2
со со О *—« —¦*
¦ ¦ ¦ "ff
_Г -Г -Г о
Q О СО ОО — со
CD CO CD <-< „ —'
—Г —Г —Г 9 9°
III IM
со о
1 777 111
sis ss.&.
* - _г о о о
I7 I ill
S S S о о о
§§§
CD СО СО О О О
<N
CN CN СО 1Д 1Л CN
СО 00 t^-
¦^ СО СО О О О
Ю CN
оо
о S
о о о о о о
— О 00 CN —< CN
^ cn — ^ ю ^-
^ СО CN <N CN —
"*. "*. " 9. 9 9
о" о" о" о о* о
t^- CD CO CO CO
¦* ¦* о о о
о о о
11
о о о о
°°°
со со со со ^^ о^
¦* СО СО CN СО СО
1Л 1С 1С О О О
о" о" о* о" о о
о оо го оо
t^» t~» 00 О^
О о о
1
о о
о о о о о о
Ом- —« -^ 1С
¦3<. со со о. 9. 9 !;
о* о" о" о* о о
Й S Й о о о
о" о* о"
ю о
о о „-
о
&>
о ю. °- a u
° о - ° с
О
1 °. о  °. о ю-
э — о - =>
« N ¦*
v В &
°- => S °

00 ¦* CO t- CD СП
—' Ю 00 CO 00 LO
CO О 00 CN 00 Ю
СП СП 00 СО CN CN
О о" О
2 ? § g 8
СО СП ^ __о ОО И OCD00 ОСПСП О —' ~
ОСПСП CNCNC4 t^t^^ СОСОСО —* О О ООО
ооо ооо ооо
CDC0C0 ОСПСО ¦* S3 —' —' Ю СО
(N •* Г- 00COCN * О 00 ОС0С0
СП t^ t4- СЛСОСО <N <N —* __—».-*
ЮЮЮ^ —<<N<N —. — ^ч ООО
о" о" о о" о" о
- • ¦ ¦ СП СО Ю СО - - — - - — — - « — - ч - - - -
S2C0CN СОСОСО OOt^cO ЮСОГ- СОСОСО ООО
Ооо ООО ЮЮЮ ООО — — "н ООО
— —' ООО
I I I
ооо
о
ооо
оо
ооо
Hi
ююю
CN <N <N
CN CN <N
CD CD CD
o" o'
1
ю ю S
со со со
ООО ~~L ~~- ~L ООО
ооо
а;
1
о
ю
о"
о
СО
О
о* —"
о
Е
о
ю
о"
CU
о_
о
о"
еч
О_
О
ю
о"
CU
о_
о
"i. °.
о" —"
§ 3. Симметричные колебания полосы конечной жесткости
193
и амплитуд изгибающих моментов \М (х)\ (в долях 2Ра/п) при
высоте слоя жидкости, равном полудлине полосы (Я = 1,0) и не-
некоторых значениях параметра у. Сравнение этих результатов с
данными расчета без слоя жидкости (табл. 5.5) показывает, что
Таблица 5.4
X
1 ю. (*) 1
\М(х)\
V
0,8
1,4 1,8
0,8
1,4
1,8
О
0,2
0,4
0,6
0,8
1,0
О
0,0415
0,1300
0,2333
0,3376
0,4417
О
0,0432
0,1376
0,2621
0,3629
0,4780
Я= 1,0; А = 0,5 м
О 0,4365
0,0424 0,1842
0,1452 0,0467
0,2458 0,0069
0,3597 0,0066
0,4738
О
0,4544
0,2058
0,0771
' 0,0426
0,0216
О
0,4423
0,2096
0,1059
0,0775
0,0276
О
\М(х)\
0,8
1.2
1.2
0
0,2
0,4
0,6
0,8
1,0
0
0,0878
0,3450
0,6032
0,9418
1,2949
Н = 1,0; h =
0
0,0765
0,2662
0,5208
0,8066
1,1023
1,0 м
0,8222
0,5436
0,3276
0,1679
0,05743
0
0,7323
0,4677
0,2726
0,1373
0,0481
0
влияние жидкости в рассмотренных примерах при низкочастотных
нагрузках (со <; 50 сект1) на колебания полосы на упругой полу-
полуплоскости незначительно (разница в максимальных относительных
прогибах и моментах не превышает 5—10%).
Как отмечалось выше, в приведенном решении не учитывается
сжимаемость жидкости. По-видимому, результат решения рас-
рассматриваемой задачи с учетом сжимаемости может существенно
отличаться, особенно в тех случаях, когда сжимаемость упругого
полупространства и сжимаемость жидкости — величины одного
порядка либо когда вторая превышает первую.
7 5—2880

»^^ t^^ ^^^ ^^^ t^4 ^^5 ^4^ ^^5 ^4^
• О OJtNOOOCOO'*'*
CO О О —'
О О
°i °. "I ^"V Я. "*. °. "*- "*•
со" —" q" —« o" o" o" o" o"
11
cSS .. ..
Oi rt OO rt О О rt Г^_
о о о" сГ о" о —" о"
CO 00 CO O5 О О 00
_ СО <N CD 00 О СО
О о ~ со О Ю О
eg -^^
°1, —. О О СО О 1E О_ ¦* ¦*
^^ СТ1 ^н ^^ if ^Э ^Э ^D ^Э ^Э
о
CD
СО
(N
Ю
О
S
cs t^ со
1Т1
СО (N СО
— СО ^
1
CD О
— О
79
о
00
о"
СО -i р -^ Р О О О о" [| О
л;
со — о — о о о
Mil
о — -рррор-о
OOltSOtOOOflOO О
w со ЛОООЮО^^ °° •.
О О О —' О
t^ -Г о о о о о"
t^» LO t4*" С^ 00 00 "^ СО
т О) -— ^нО^нсООС^СО
° 00* ^" о" -* О О О* О О*
III
^ CD ^ гн х <N N
О lO •-• ри о ^ ^
о" о* о" о" о" -^ о
о о
а и oi s
СО О О (N
ю о ¦* ¦*_
-^ о о р о о
р-оор
2 S §8
-" о" о" о
*5 co^^-t^-coolo
*Л о о «Л О *—i О N
СО "i О О Ю о
о d —Г сГ о" сГ
О w о о СО о —« о "-4 *^
—" р о" —" о"
Р- 3
f- 3
§ 4. Антисимметричные колебания полосы конечной жесткости 195
§4. АНТИСИММЕТРИЧНЫЕ КОЛЕБАНИЯ ПОЛОСЫ
КОНЕЧНОЙ ЖЕСТКОСТИ
Исследуем антисимметричные гармонические колебания полосы
под действием нагрузки q(x, t) = q*(x)e'V (рис. 60). Исходные
уравнения те же, что и в предыдущем параграфе. Равнодейству-
Равнодействующую неизвестных нагрузок — реакции полуплоскости р (х, t) и
гидродинамического давления жидкости на полосу рх (х, —A, t) —
в данном случае ищем в виде разложения в ряд по нечетным поли-
полиномам Чебышева
pR (х, t) = p {x, t) - Pl (x, -h, t)
2k+l
. E.87)
k=\
Решение задачи о прогибах полосы при наличии слоя жидкости
по виду не отличается от решения, полученного в § 2 гл. 3 для слу-
случая без слоя жидкости, а влияние последнего учитывается коэффи-
коэффициентами A2k+\. Перемещения границы упругой полуплоскости на-
находим по формулам E.40) и E.42).
Решение рассматриваемой задачи об антисимметричных коле-
колебаниях определяется из системы уравнений C.124) при s = t?.'Ко-
t?.'Коэффициенты Rec2ft+i, 2г+1 и Imc2A+i. ь+i находятся соответственно по
формулам E.43) и E.44) при замене индексов бесселевых функций
2k и 2г индексами 2k -\- 1 и 2г + 1, прогибы полосы, углы поворо-
поворота, изгибающие моменты и перерезывающие силы — по формулам
§ 2 гл. 3, гидродинамическое давление и скорости жидкости —
по выражениям E.49), E.56) и E.57), реакции основания —

Таблица 5.6
х и
г
I w (х) | О
фш (*) О
|ф(*)| 1,762
О
О
4>м (*) О
IQWI 0,195
О
\М(х)
0,2
0,354
О
1,785
О
—0,038
О
0,179
О
0,4
0,6
0,0
0,717
О
1,850
О
-0,069
О
0,126
О
1,096
О
1,945
О
—0,085
О
0,023
О
0,8
0,8
1,495
О
2,043
О
-0,072
О
0,168
О
1» (*I
Фш(«)
1 Ф (*) 1
¦ (*)
\М(х)\
Фм(*)
IQWI
Фе(*)
0
2,173
0,307
0
—
0,166
3,073
0,436
0,306
2,191
0,304
—0,032
—0,066
0,154
3,080
0,879
0,303
2,244
0,295
—0,060
—0,059
0,115
3,106
1,335
0,298
2,322
0,283
—0,075
—0,048
0,032
3,255
1,808
0,293
2,406
0,271
—0,067
—0,032
0,140
—0,078
1,0
1,910
0
2,096
О
О
О
0,785
О
2,295
0,287
2,454
0,265
О
0,015
0,785
О
О
2,330
0,610
О
0,146
2,784
0,2
0,4
0,6
0,8
0,4
1,2
0,467
0,608
2,340
0,604
—0,029
—0,344
0,137
2,826
0,937
0,602
2,370
0,587
—0,053
—0,304
0,106
2,971
1,416
0,593
2,419
0,564
—0,068
—0,240
0,044
3,533
1,905
0,583
2,478
0,541
—0,062
—0,152
0,122
—0,410
1,0
0
1,934
0,089
0
0,188
3,138
0,388
0,088
1,956
0,087
—0,037
—0,004
0,173
3,138
0,785
0,087
2,019
0,085
—0,067
—0,003
0,123
3,140
1,198
0,086
2,110
0,081
—0,083
—0,003
0,025
3,151
1,630
0,084
2,206
0,077
—0,071
—0,002 .
0,162
—0,004
2,077
0,082
2,258
0,075
0
0,001
0,785
0
2,405
0,573
2,516
0,530
О
0,066
0,785
О
ТЙУЧЯй г
Продолжение табл. 5.6
I w (х)\
фюМ
I ф (*) I
I M Ml
IQWI
о
2,341
0,782
О
0,155
2,566
0
I ф (*) I 2,187
Ч>(*) 1,128
IМ (х) I о
I Q (*) I 0,223
Фо (х) 2,336
5
I • М I
0,2
0,468
0,779
2,345
0,774
—0,030
—0,556
0,143
2,628
0,437
1,124
2,178
1,116
—0,043
—0,787
0,197
2,396
0,4
1,4
0,938
0,772
2,359
0,753
—0,055
—0,495
0,106
2,857
1,8
0,871
1,113
2,158
1,085
—0,075
—0,727
0,123
2,670
0,6
1,413
0,761
2,388
0,723
—0,069
—0,395
0,051
3,720
1,100
1,096
2,141
1,039
—0,087
—0,616
0,063
4,148
0,8
1,893
0,747
2,429
0,694
—0,062
—0,253
0,133
—0,650
1,727
1,076
2,143
0,993
—0,070
—0,428
0,199
—0,871
1,0
2,383
0,734
2,459
0,679
0
0,108
0,785
0
2,155
1,057
2,157
0,970
0
0,209
0,785
0
0
0
—
2,291
0,957
0
0,183
2,403
0
2,044
1,285
0
0,266
2,338
0,2
0,4
0,6
1,6
0,458
0,954
2,289
0,948
—0,035
—0,718
0,165
2,470
0,916
0,945
2,288
0,921
—0,063
—0,652
0,112
2,746
1,373
0,931
2,292
0,884
—0,076
—0,535
0,057
3,929
2,0
0,408
1,281
2,029
1,272
—0,051
—0,788
0,232
2,388
0,810
1,268
1,992
1,233
—0,088
—0,738
0,136
2,635
1,204
1,247
1,955
1,177
—0,100
—0,641
0,067
4,364
0,8
1,832
0,914
2,314
0,847
—0,065
—0,355
0,161
—0,814
1,591
1,223
1,939
1,121
—0,077
—0,465
0,239
—0,859
1,0
2,297
0,898
2,336
0,829
0
0,157
0,785
0
1,977
1,200
1,944
1,093
0
0,258
0,785
0

Таблица 5.7
Н = 1,0
X
г
\w (*) 1
фшМ
I ф (*) I
о
О
1,762
О
О
Ф.М М О
\Q(x)\ 0,019
Фп W О
I M (х) |
\w(x)\
фш(*)
I ф (*I
Фл<(*)
0,2
0,354
О
1,785
О
-0,038
О
0,179
О
0,4
0,6
0,0
0,717
О
1,850
О
—0,069
О
0,126
О
1,096
О
1,945
О
—0,085
О
0,123
О
0,8
0,8
1,459
О
2,043
О
—0,072
О
0,168
О
1,0
1,910
О
2,096
О
О
О
0,785
О
1,992
0,106
О
0,186
3,136
0,2
0,400
0,106
2,014
0,105
—0,036
—0,005
0,171
3,137
0,4
0,6
0,4
0,808
0,105
2,076
0,102
—0,066
—0,005
0,123
3,139
1,232
0,103
2,166
0,097
—0,082
—0,004
0,026
3,154
1,2
0,8
1,675
0,101
2,261
0,093
—0,071
—0,003
0,160
—0,006
1,0
2,134
0,099
2,313
0,091
О
0,001
0,785
О
0
2,316
0,399
0
0,157
3,028
0,464
0,398
2,332
0,395
—0,031
—0,110
0,147
3,041
0,935
0,394
2,379
0,384
—0,057
-0,097
0,112
3,086
1,148
0,388
2,450
0,370
—0,073
—0,077
0,036
3,307
1,915
0,381
2,528
0,355
—0,065
—0,050
0,132
—0,128
2,426
0,375
2,573
0,348
0
0,021
0,785
0
0
—
2,452
0,801
0
—
0,149
2,592
0,491
0,799
2,456
0,794
—0,029
—0,530
0,138
2,654
0,983
0,792
2,470
0,775
—0,054
—0,470
0,105
2,875
1,479
0,782
2,498
0,747
—0,068
—0,372
0,051
3,699
1,983
0,769
2,539
0,719
—0,061
—0,236
0,127
—0,626
2,493
0,757
2,568
0,705
0
0,087
0,785
0
Продолжение табл. 5.7
IФ W I
¦ (*)
I M (x) |
0,2
0,4
0,6
1,4
1,8
2,086
1,412
0
0,416
1,408
2,067
1,400
—0,052
—0,799
0,825
1,396
2,018
1,364
—0,091
—0,749
1,222
1,378
1,964
1,311
—0,103
—0,651
0,8
a» Ml
фюМ
ф(*)|
ФМ
М(х)\
QMI
фо (х)
0
—
2,398
1,016
0
—
0,180
2,390
0,479
1,013
2,394
1,008
—0,035
—0,830
0,162
2,460
0,957
1,005
2,387
0,983
—0,062
—0,661
0,111
2,744
1,434
0,992
2,387
0,983
—0,075
—0,541
0,059
3,902
1,912
0,976
2,403
0,948
—0,064
—0,356
0,158
—0,830
1,610
1,355
1,932
1,255
—0,079
—0,474
2,328
2,378
2,624
4,379 —0,868
1,0
2,394
0,961
2,422
0,912
0
0,136
0,785
0
1,994
1,332
1,930
1,227
0
0,231
1QWI 0,273 0,238 0,139 0,070 0,246 0,785
0
0
1,886
1,576
0
0,317
2,377
0,2
0,4
0,6
0,8
1,6
2,0
0,376
1,571
1,861
1,562
—0,061
—0,752
0,274
2,418
0,742
1,557
1,795
1,520
—0,104
—0,711
0,154
2,629
1,092
1,535
1,719
1,455
—0,117
—0,629
0,074
4,596
1,429
1,508
1,668
1,387
—0,087
—0,474
0,286
—0,810
1,0
0
—
2,268
1,223
0
—
0,225
2,316
0,453
1,220
2,256
1,213
—0,043
—0,807
0,198
2,377
0,901
1,210
2,227
1,183
—0,076
—0,746
0,124
2,658
1,343
1,194
2,199
1,139
—0,088
—0,632
0,065
4,145
1,780
1,175
2,189
1,094
—0,071
—0,439
0,202
0,891
2,218
1,156
2,198
1,071
0
0,186
0,785
0
1,758
1,481
1,658
1,352
0
0,267
0,785
0

\w(x)
I ф W I
I M (x) I
I Q (*) I
(*)
i Ф (*) I
IQWI
Таблица 5.8
0,2
0,4
0,6
0,8
Я= 2,0
1,0
0,0
0
0
1,762
0
0
0
0,195
0
0,354
0
1,785
0
—0,038
0
0,178
0
0,718
0
1,850
0
—0,069
0
0,126
0
1,096
0
1,945
0
—0,085
0
0,023
0
1,495
0
2,043
0
—0,072
0
0,168
0
1,910
0
2,096
0
0
0
0,785
0
0
.—
2,001
0,120
0
—
0,185
3,136
0,402
0,119
2,023
0,118
—0,036
—0,006
0,171
3,136
0,812
0,118
2,084
0,115
—0,066
—0,005
0,122
3,138
1,237
0,116
2,174
0,110
—0,082
—0,004
0,026
3,155
1,682
0,114
2,269
0,105
—0,071
—0,003
0,159
—0,006
2,142
0,112
2,321
0,103
0
0,002
0,785
0
0,8
0,2
0,4
0,6
0,8
0,4
1,2
1,0
0
—
2,282
0,424
0
—
0,157
3,019
0,457
0,422
2,298
0,420
—0,031
—0,118
0,147
3,033
0,921
0,418
2,344
0,408
—0,057
—0,105
0,112
3,081
1,397
0,412
2,414
0,392
—0,073
—0,083
0,036
3,321
1,887
0,405
2,491
0,377
—0,065
—0,054
0,132
—0,139
2,391
0,398
2,536]
0,369
0
0,022
0,785
0
0
—.
2,385
0,817
0
0,152
2,594
0,477
0,815
2,389
0,810
—0,030
—0,528
0,140
2,655
0,956
0,808
2,403
0,789
—0,054
—0,469
0,106
2,876
1,439
0,797
2,430
0,760
—0,069
—0,372
0,050
3,685
1,929
0,784
2,470
0,732
—0,062
—0,236
0,130
—0,620
2,426
0,771
2,500
0,717
0
0,086
0,785
0
Продолжение табл. 5.8
\w(x)\
фа; (Ж)
I ф (*) I
I M (х) |
Фл1 W
IQ W I
\w(x)\
Фа; W
I Ф (X) I
л1
0,2
0,4
0,6
1,4
0
2,331
1,027
0
—
0,181
2,402
0,466
1,024
2,327
1,018
—0,035
—0,718
0,163
2,470
0,930
1,015
2,320
0,992
—0,063
—0,651
0,112
2,748
1,394
1,002
2,320
0,956
—0,076
—0,533
0,058
3,910
1,8
0
2,033
1,417
0
0,273
2,335
0,405
1,412
2,014
1,404
—0,052
—0,791
0,238
2,386
0,804
1,400
1,966
1,367
—0,091
—0,741
0,139
2,632
1,191
1,381
1,912
1,312
—0,103
—0,644
0,069
4,383
0,8
1,858
0,985
2,336
0,919
—0,065
—0,352
0,160
—0,816
1,568
1,357
1,881
1,255
—0,079
—0,468
0,246
—0,859
1,0
2,327
0,970
2,355
0,900
0
0,134
0,785
0
1,942
1,334
1,879
1,226
0
0,226
0,785
0
0
2,206
1,230
0
0,226
2,328
0
1,842
1,580
0
0,315
2,383
0,2
0,440
1,227
2,194
1,220
—0,043
—0,794
0,199
2,389
0,367
1,575
1,816
1,565
—0,060
—0,746
0,273
2,424
0,4
0,6
1,6
0,876
1,216
2,166
1,189
—0,076
—0,735
0,124
2,664
1,306
1,200
2,138
1,143
—0,088
—0,623
0,064
4,154
2,0
0,724
1,561
1,751
1,522
—0,104
—0,705
0,154
2,635
0,066
1,538
1,676
1,456
—0,116
—0,623
0,073
0,8
1,731
1,180
2,129
1,097
—0,071
—0,433
0,202
—0,878
1,394
1,511
1,626
1,386
—0,087
—0,468
0,285
4,596 —0,803
1,0
2,156
1,161
2,137
1,073
0
0,182
0,785
0
1,714
1,483
1,616
1,350
0
0,261
0,785
0

202 Глава 5 Гармонические колебания полосы под слоем жидкости
по формуле
р (Х, t) = е®
• E.88) 1
В качестве примера приведем результаты вычислений амплитуд
перемещений, углов поворота, изгибающих моментов и перерезы-
перерезывающих сил при действии двух сил РеФ, приложенных по кон-
концам полосы. Характеристики полосы и основания: v = 0,167,
v0 = 0,3, с2 = 98 м/сек, р/р0 = 1,225, а = 5 м, h = 1 м, k0 =
= 0,372, tn0 = 0,156 при Я = 0 (табл 5.6), Я = 1,0 (табл 5.7),
Я = 2,0 (табл. 5.8). Частота нагрузки изменялась в пределах
0 < а» < 39 сект1 @ < ? <. 2) В разложении E.87) удерживались
три члена ряда. Амплитуды прогибов \а> (х)\ вычислялись в долях
2Pa3/3nD, углы поворота |ср (х)\ — в долях 2Pa2/3nD, изгибающие
моменты \Щх)\ — в долях 4Ра/л, перерезывающие силы \Q(x)\ —
в долях 4Р/л. Анализ показывает, что в дорезонансной зоне про-
прогиб при наличии слоя жидкости больший, а в послерезонансной
зоне — меньший прогиба в отсутствие жидкости. При низких час-
частотах влияние слоя жидкости невелико (изменение величин на
5—10%), по мере роста частоты колебаний оно увеличивается.
Приложение
ТАБЛИЦЫ
ДЛЯ РАСЧЕТА СТАЦИОНАРНЫХ
И НЕСТАЦИОНАРНЫХ КОЛЕБАНИЙ
ЖЕСТКИХ ШТАМПОВ
НА УПРУГОМ ПОЛУПРОСТРАНСТВЕ
Таблицы для расчета контактных напряжений и перемещений
ж-стких штампов на упругом полупространстве (плоская и осе-
симметричная задачи) при установившихся и неустановившихся
колебаниях составлены по данным вычислений на ЭВМ. Програм-
Программы для ЭВМ разработаны на основании изложенной в гл. 2 и 4
методики решения динамических контактных задач.
Диапазон изменения безразмерной частоты колебаний принят
0 < ? < 4, безразмерного времени — 0 < t < 5. Коэффициент Пу-
Пуассона материала основания равен 0,3. В качестве основной на-
нагрузки при неустановившихся колебаниях принята внезапно при-
приложенная постоянная сила (или момент). Для изучения других
случаев колебаний могут быть использованы интеграл свертки
или замена заданной функции изменения нагрузки в зависимости
от времени ступенчатой функцией. Предполагается, что при коле-
колебаниях штамп от основания не отрывается.
Значения функций Tk(x)lY 1 —х2 и функций Pk(\f\ —r2)/Vl—Л
используемые при вычислениях контактных напряжений, приведе-
приведены соответственно в табл. 1, 2.
Нормальные напряжения р(х, f) по контакту вытянутого в
плане массива (толстой плиты) с упругим полупространством, на-
находящимся в условиях плоской деформации, при действии верти-
вертикальной силы P(t) — Pel# (рис. 61) определяются по формуле
Р С*. 0 = 21 А» I -^ е"***, ? = асо/с, A)
равнодействующая нормальных контактных напряжений —
Я(*)=-яа|Л0|е«»-Нр»>, B)
вертикальное перемещение массива —
w{t) = \w[(?iV+vv). C)
В табл. 3 приведены значения модулей \A2k\ (в долях Р/ла),
\w\ (в долях Р/лр) и аргументов фг*, <рш комплексных коэффициен-
коэффициентов Л 2ft, ay в зависимости от параметров ? и ш0 = М/ла2р0 (М —
масса штампа). Если значения ? и т0 не совпадают с табличными,
производится линейная интерполяция. При действии на массив

204
Приложение
силы, изменяющейся в зависимости от времени по закону cos t,t или
sin t,t, в формулах A) — C) следует взять соответственно действи-
действительную или мнимую часть. Резонансная частота вычисляется по
формуле у . ...
т У «р = ?рс2/а, D)
где 1Р — определяемое по табл. 3 значение безразмерной частоты,
при которой значение модуля \А0\ (т. е. модуль равнодействующей
\R\) достигает максимума.
Нормальные напряжения р(х, t) по контакту массива с упругим
полупространством при действии внезапно приложенной верти-
вертикальной силы P(t) = PH(t) (см. рис. 61) определяются по формуле
2
Pit)
_ о
'S////SS//777
. a i
а
Рис. 61.
Рис. 62.
а их равнодействующая — по формуле R(t) = naA0(t). В табл. 4
представлены значения функций A2k(t) (в долях Plna) и w(f) (в
долях Pln\i) при заданных / и т0.
Нормальные р (х, /) и касательные т (х, t) напряжения по кон-
контакту массива с упругим полупространством при действии горизон-
горизонтальной периодической силы Q (/) = Qel& (рис. 62) определяются
по формулам
Р (х, t) = 2 | A
2k+1
ут=-
E)
ft—о у 1 - х-
момент равнодействующей нормальных и равнодействующая каса-
касательных контактных напряжений —
G)
(8)
угол поворота массива и горизонтальное перемещение его по-
Д0ШШ" — (9)
A0)
Приложение
205
В табл. 5 приведены значения модулей |Л24+1|, |5»| (в долях
Q/jtjx), |ф| (в долях 0,253 Qlna[i), \u\ (в долях Q/n[i) и аргументов
ф2/н-ь ф2*. Фф. Фи комплексных коэффициентов Л24+1, Вт, Ф, и в
зависимости от параметров ? и hla (при р/р0 = 1,4). Резонансные
частоты вычисляются по формуле D), где ?р — определяемые по
табл. 5 значения безразмерных частот, при которых значения мо-
модулей \Aj\, \B0\ (соответственно момент равнодействующей нор-
нормальных и равнодействующая касательных напряжений) и |<р|
достигают максимума (\АХ\, \В0\ — резонанс по равнодейству-
равнодействующим напряжений, |<р| — по угловому перемещению).
Нормальные р (х, t) и касательные т (х, t) напряжения по кон-
контакту массива с упругим полупространством при действии внезап-
внезапно приложенной горизонтальной силы Q (t) = QH (t) (см. рис. 62)
определяются по формулам
/»<*. 0-2^.@-5=^; (»)
ft=0 (/1-Х
2 , ,л T2k(x)
ft=o
момент равнодействующей нормальных и равнодействующая каса
тельных напряжений —
4
QH() 0(t). A4)
В табл. 6 даны значения функций Аы+i (О и B2k(t) (в долях Q/na),
Ф (t) (в долях 0,253 Q/na[i) и и (t) (в долях Q/n\i) в зависимости от
параметров t и hi а (при р/р0 == 1,4).
Нормальные р (х, t) и касательные т (х, t) напряжения по
контакту массива с упругим полупространством при действии перио-
периодического момента M(t) = М№ (рис. 63) определяются по формулам
E), F), момент равнодействующей нормальных и равнодей-
равнодействующая касательных напряжений, угол поворота массива и го-
горизонтальное перемещение его подошвы — соответственно по фор-
формулам G) — A0). В табл. 7 представлены значения модулей |Л2а+1|,
|Вг*| (в долях 2 М/па2), |<р| (в долях 1,354 М/ла?^), \и\ (в долях
0,253 М/ла\к) и аргументов ф2*+ь фг*, фф и фи комплексных чисел
^2fe+i, B-iu, Ф, и в зависимости от параметров ? и hi а (при р/р0 =
= 1,4). Резонансные частоты вычисляются по формуле D), где
?р — определяемые по табл. 7 значения безразмерных частот, при
которых значения модулей \А1, |50| (резонанс по равнодейству-
равнодействующим напряжений) и |<р|, \и (резонанс по перемещениям) до-
достигают максимума.
Нормальные р (х, t) и касательные т (л:, t) напряжения по кон-
контакту массива с упругим полупространством при действии внезапно

206
Приложение
приложенного момента M(t) = MH(t) (см. рис. 63) определяются
по формулам A1) и A2), момент равнодействующей нормальных и
равнодействующая касательных напряжений — по формулам A3)
и A4). В табл. 8 приведены значения функций A2k+i(t) и Бг*(/) (в
долях 2 М/па2), ср (t) (в долях 1,354 М/па?^), и (/) (в долях
0,253 М1па\х) в зависимости от параметров/ и hi а (при р/р0 = 1,4).
Pit)
S//7777S7K77
0 02а
У
Рис. 63,
Рис. 64.
Нормальные напряжения р (г, /) по контакту круглого в плане
массива (толстой плиты) с упругим полупространством (осесим-
метричная задача) при действии вертикальной силы P(t) = Ре®
(рис. 64) определяются по формуле
р (г, 0=2
(? = асо/с2), их равнодействующая — по формуле ^@=2яа|Л0|е
вертикальное перемещение массива — по зависимости w(t) =
= |uy|ew+V. В табл. 9 представлены значения модулей \Ащ
(в долях Р/2па2), \w\ (в долях статического перемещения
^A —vl)/2E0a) и аргументов q>2k, Ц>ш комплексных чисел A2k, w
в зависимости от параметров i и т1 — М/2ла2р0 (для цилиндра
тг = /гр/2ар0). Резонансные частоты вычисляются по формуле
Wp = ?рс2/а, где ^р — определяемые по табл. 9 значения безраз-
безразмерных частот, при которых максимума достигают значения либо
модуля \А0\ (соответственно модуля равнодействующей \R\) —
резонанс по равнодействующей напряжений, либо модуля \w\ —
резонанс по перемещениям.
Нормальные напряжения р (г, t) по контакту круглого в плане
массива (толстой плиты) с упругим полупространством при дей-
действии внезапно приложенной вертикальной силы P(t) — PH(t)
(см. рис. 64) определяются по формуле
р(г, 9 =
Приложение
207
а их равнодействующая — по формуле R(t) = 2яаМ0(/). В табл. 10
приведены значения функций А2к (/) (в долях Р/2ла2) и w(t)
(в долях Р(\ — vl)/2Eoa) в зависимости от параметров t n т1.
Для определения вертикальных перемещений участка границы
упругой полуплоскости при наличии слоя жидкости (см. гл. 5)
используются коэффициенты с*,,(%,), указанные в табл. 11 в за-
зависимости от параметров Hut,.
Таблица 1
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
0,95
1,0
Т„(х)
Y\ - х'
Т,(х)
Т,(х)
tax)
Ть(х)
Y\ — x*
1,0000
1,0050
1,0206
1,0483
1,0911
1,1547
1,2500
1,4003
1,6667
2,2941
3,2026
—1,0000
—0,9849
—0,9390
—0,8596
—0,7419
—0,5774
—0,3500
—0,0280
0,4667
1,4223
2,5781
oo
1,0000
0,9254
0,7071
0,3615
—0,0821
—0,5774
—1,0540
—1,3992
—1,4054
—0,5304
0,9481
oo
0,0
0,1005
0,2041
0,3145
0,4364
0,5774
0,7500
0,9802
1,3334
2,0647
3,0425
oo
0,0
—0,2975
—0,5797
—0,8303
—1,0300
—1,1547
—1,1700
—1,0194
—0,5867
0,4955
1,8559
oo
0,0
0,4826
0,8625
1,0471
0,9643
0,5774
—0,0948
—0,9395
—1,6619
—1,4502
—0,0548
oo
Таблица 2
Р„ {V 1 - Г' )
У\ — г'
Pt(Vl-r* )
Vl-r'
Pt (У 1 _ г2 )
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
0,95
1,0
1,0
1,0050
1,0206
1,0483
1,0911
1,1547
1,2500
1,4003
1,6667
2,2941
3,2026
oo
1,0
0,9899
0,9594
0,9068
0,8292
0,7217
0,5750
0,3711
0,0667
—0,4932
—1,1329
—oo
1,0
0,9952
0,8798
0,6137
0,3404
0,0271
—0,2913
—0,4547
—0,6800
—0,4119
—0,1632
oo

1ло|
Фо
м.
Фг
\At\
Ф4
Фо
M.I
Фг
М4
0,2
1,012
—0,008
0,034
—0,742
0,000
2,331
1,879
—0,631
2,2
0,982
—0,364
0,630
—2,684
0,035
—0,191
0,371
—1,799
0,4
1,031
—0,034
0,105
—1,027
0,000
1,999
1,474
—0,844
2,4
0,972
—0,394
0,643
—2,788
0,043
—0,368
0,336
—1,838
0,6
1,047
—0,072
0,194
—1,290
0,000
1,688
1,226
—1,034
2,6
0,961
—0,423
0,649
—2,884
0,051
—0,540
0,306
—1,874
0,8
1,054
-0,117
0,288
-1,537
0,002
1,390
1,031
-1,204
2,8
0,949
—0,452
0,652
—2,973
0,060
—0,708
0,280
—1,909
т0 = 0,2
1,0
1,051
—0,162
0,374
—1,764
0,004
1,110
0,870
—1,352
3,0
0,936
-0,481
0,650
-3,054
0,068
-0,872
0,258
-1,943
1,2
1,042
—0,203
0,447
— 1,967
0,007
0,850
0,735
— 1,473
3,2
0,923
-0,509
0,645
-3,129
0,077
-1,033
0,239
-1,976
1,4
1,029
—0,240
0,506
—2,146
0,011
0,611
0,626
— 1,570
3,4
0,909
—0,537
0,637
—3,084
0,085
— 1,191
0,222
—2,009
1,6
1,017
-0,274
0,551
-2,304
0,016
0,391
0,539
-1,646
3,6
0,895
-0,564
0,626
-3,021
0,093
-1,347
0,207
-2,040
1,8
1,005
-0,305
0,586
-2,445
0,021
0,185
0,470
-1,707
3,8
0,881
-0,589
0,615
-2,963
0,100
-1,501
0,193
-2,070
Таблица 3
2,0
0,993
—0,335
0,612
—2,570
0,028
0,007
0,416
—1,757
4,0
0,866
—0,613
0,602
—2,912
0,107
— 1,652
0,180
—2,099
Продолжение табл. 3
Ав |
\А 1
Ф.
Ф4
и
1
Фш
с
А,.
Фл
AL
Фг
А,
Ф4
Фш
0,2
1,024
—0,017
0,034
—0,751
0,000
2,322
1,902
—0,640
2,2
0,864
—0,678
0,554
—2,998
0,031
—0,505
0,327
—2,113
0,4
1,064
—0,070
0,108
—1,063
0,000
1,963
1,521
—0,880
2,4
0,835
—0,720
0,552
—3,115
0,037
—0,695
0,288
—2,165
0,6
1,093
—0,151
0,203
—1,369
0,000
1,609
1,279
—1,113
2,6
0,806
—0,761
0,545
3,060
0,043
—0,878
0,257
—2,212
0,8
1,097
—0,245
0,299
—1,666
0,002
1,261
1,074
— 1,333
2,8
0,778
—0,800
0,534
2,962
0,049
—1,055
0,230
—2,257
т0 = 0,4
1,0
1,076
—0,337
0,382
— 1,938
0,004
0,935
0,890
—1,526
3,0
0,750
—0,836
0,521
2,873
0,055
—1,227
0,207
—2,298
1,2
1,040
—0,415
0,446
—2,179
0,007
0,638
0,734
—1,685
3,2
0,723
—0,871
0,505
2,792
0,060
—1,394
0,187
—2,337
1,4
1,000
—0,481
0,491
—2,387
0,010
0,370
0,608
—1,811
3,4
0,697
—0,902
0,488
2,718
0,065
—1,556
0,170
—2,374
1,6
0,961
—0,537
0,521
—2,568
, 0,015
0,127
0,510
—1,909
3,6
0,672
—0,931
0,470
2,653
0,070
—1,715
0,155
—2,408
1,8
0,926
—0,587
0,540
—2,727
0,020
—0,096
0,434
—1,989
3,8
0,648
—0,958
0,452
2,595
0,074
—1,869
0,142
—2,439
2,0
0,894
—0,634
0,551
—2,869
0,025
—0,306
0,374
—2,055
4,0
0,625
—0,982
0,435
2,543
0,077
—2,021
0,130
—2,468
о
3
s
8
со

210
о
,764
о
,862
о
,471
о
,098
та
,021
о
,534
1
Приложение
О ч^
сч оо
со сч о
О CN TJ-
462
о
176
322
о
349
сч
057
о
214
сч
096 |
о
662
сч
о ¦)• и * n n oi <о
~-» •—' t-~ Ю -* CN t-~ -^
со » * * в о сз го_ сч
—* о" о о" cn" о" о" о" cn"
со
—¦ о
Л О 00 -< СО Ю t-~ СЧ
ю to со oi ~ oi юта
* ^ * s о о ¦* —¦
" * о" сч* о" о" " "
о
о
ТН 00 t~~ -н СО СО
ф ^ CN № О W
СЧ_ &1 СО_ * п О *
-* о" о о сч" о" о"
о
СЧ t
о СО
1~- 00
о" —'
со
о
t-~ ^ сп ю -^ i^-
СО -* t-~ -н О Ю
©_ q и п —«_ ©_ i~^
—* —* о о" cn" о" о"
I I
го -^
СО О
оо^ t->
о —*
I
оо fh
о --
СО СО СО СО С^ ^
<N 00 Q О О С1-)
m й оо о
о ^
(О N -
со и «
СО -н tN (N
О
о
О
СО ~
в -«fo-Го- -*о
с-, со ю р о го со
СО И П СО О м CN
С-^ о О О N О П Cf3
о" —Г о о о" о сч" «"
со"
Г- I— Ю Ю 00
Ю СО СП Ю СО
— со со о о
Ю СО
о" —" о" cn" о" in"
со оо
СЗ СО
on
CD СО * СО СО О) I— CO
О СО Ю * 1Я « -ч -*
СО Ю -н СО т(* О О) нч СО
о" сч" со" о -f о" сч* о -т4" о сч"
¦Ч- Г- ч1- СО О ¦* СЧСО
СЧ СП Ю О — Ю СОСЧ
•* О1_ СО ¦* со О - ЮО ¦*
—< о" о" о" сч" о" о" о" сч" со*
-" CN CN СО О СО О>
СО —« !-~ О Ю СО СЧ
1Л ^-* СО Ю СО ^ ^^
о1 —Г о* сч" о* -ч" о*
CN
со*
О
со"
сосо
Ю О
" "
о —" о" сч" о" •-" о сч"
1^сос^тата
1О о * СО О
Г " "
О
о —Г о" сч" о"
|тачспспсп
—¦ сч см та со i^
"?. ^ ^1 *~. Ч. 'i.
о" —Г о сч" о* —*
йоотнтатао Осо
со_ со_ сп ¦*_ оо_ о — сч_ ¦*
in ооосч'о— осч"
тоспосо t~-ro
т(<1птасосч сосп
сп ¦* сп _о^ сп cn со
cn" о о" о" сч" о" о" о" cn"
о"
ооросч «о сч о о о го о" о
cot— -*loco^; сосч
И О СО Ю« СО 1-~т(<
CN N О) * О О 1~^ CN_ CO
cn ооотаоо с"сч"
I I I
° о " и •» ч,
о « „ <*
а
с:
Приложение
211
LO (О 00 О 00
* CS О) М -
О OOCOOO
t>| О* « О СО О*"
SS —< 00 ¦* СО Ю СО
00 Ю ГО ¦* СЧ t— 1^
О СО_ СЧ_ СЧ_ CN О_ СО О t4-;
V о" —" о" сч* о" сч о" сч*
ю ¦**" со со ю сч юю оо со ¦**¦ о го 4* со ¦***
сп оо о сч ~* сп счоо t-~ t-~ со оо тн оо оо »л
СЮ СО_ СП ¦*_ — О^ ¦*_ СО ГО_ СО СО_ CN СЧ СЧ_ О -* О !-¦_
—* о" р" о со" о" о" о сч" го о" —" о" сч" о" сч" о" сч
о о со о о
I I
Ю Ю СП Ю —' СП
ю го о со — со
СО 1-^ СП -^ СП О СЧ
сп ю г- сч ¦*
СО ГО СЧ СЧ СО О
— о о о сч о
о о сч о о о см
о" сч со" о —" о" сч" о" сч о сч
ооо-^счспсч счо
СГ) СО Г*» *—' O*i СО ^ 1О
о^ t*- ^s оо сз с^ с> ^э -.
^ оо оо ^ n о о юс^ ^ т^с^
-Г о о" о" cn о" о" о" oi со о -н* 6 n о - о
О МО OON
SSSS8S
¦се — о ¦* го ¦* ^92
re CN СО **• О N —«СО
- о о о сч" о" о о" сч со" о" -" о сч о - о сч
о о со го сч р ^
—" —" о" о" сч" о" о" о —¦
со
So
ГО О
СП СЧ
о
О "¦* ^I П 1О О >О —
со" о^'^осчо*-* о
ОО^ООтНСЧСО TJ"C4 OOCDCNCD^-'— l^^j
CN СЧ О ^ О СО О^н СЛСО^СЛСОСЧ т^СЧ
со_ -¦ ю я сп о О) — со_ оо_ ¦&¦ — со ю о ¦*_ -ч со
о —Г о" о" —" о о" —* -" сч" о —« о" сч" о —" о сч"
еч cj n n оо ™ —
1>- W *1 ^ О СО 1-^СП
СО - СО N Ю О * СО СЧ_
о" -" О* О -7' О -" -" —"
- d ю со о со со о
СО Ю - * О СО —'СО
_; —i —i —i о со сосп
ю оо со ор со
-<fo-
-o- -
со ю о
та со t^
О О 1--
8 $
О —¦ О О О О СЧ —'О
сч" о" —" о сч о —• осч
t И СО Ю Ю N щ СО
ч SSfegо fe 2S
СЧ о -" О* CN О* -" О СЧ*
счсососо^^со оо^н
осоооспсчо счо
СЧ СО О СО 00 О_ 00 CN Ю
сч" о" -" о « о о осч
I I
^ ^?^?^? а ^э -
* а

212
-Л
I
&
t
Приложение
О1 ¦* 00 СМ СО N О СО
¦^ тН ГО О —' —' ЭТ CD
о ю — со О) о оо и ю
cn" о" —" о" см" о" о о cn
СО СП СП ¦* ЭТ I— ОО
сп о тн го — — оо —
оо. ю -•_ га о о, со, cn, ю,
—" о" —" о го" о" о" о см"
со оо n оо о cn ело
со со, о_ со, о, о, ¦*, го, ¦*
— о* — о" со о" о o"cn"
¦* i— — со op ю г- г-
_„ ЭТ — CD CN О СО ¦* ^
"*.. *~. Я та °1 Я  "*. т-
—¦" р" — о" cn" о" о" о* cn"
СО г~ 00 Р Ю 1"~ ОСО
га-^ю^^оо сп ~^
СМ 00, СП СО t4^ О_ —*, Ю, СМ,
— о" о" о cn" о" о" о" см"
о
""• 1-^С^т^СПгоЮ Р 1"~
ее со т*< га о со ocn
|| о, сп, со, эт ¦* Р, ¦*, оо_ Р,
о — o"Oo"cNo"P o"cN
s II I
p со со ^ см го t~~ »—'
— со о оо о ¦* сою
°°.  'Ч. га Я Я °°- Я. "^
о" -Г о о cn о" р —" —
Sfc^HSPJS ?)ЯЙ
CnCNcN^pCO О 00
СО - * и <О О Я TfCO
о --оо-о-- --г
сооэ?-оо©со ^Й
C0^?>t?>^O^ т^О
«ч S S 8 ? 8 8 S; S
о" —" о" о" о о" cn" -Г о"
^* СО Ю 00 tD Г-- —< Tt
СП 1О СЗ СО ГО СП СО Tt*
Р CNCOCN— ©СО ОСО
¦* О —" о" CN* о" CN о" CN
СЛ N Ю СО Ю 00 1^00
О * - О ГО Ю COCN
оо го со см_ cn o_ cn_ о оо
со о" —" о сч* о* см" о" cn"
ю^ооо-^оо ю -«
смгасмюга^-« i-^^<
со^ га со cn cn о — ооо
го" о" -" О* СМ* О CN о" (N*
¦^ О —' —< <N ^ -«j<*-4
T^<N-^orai^ оосп
^ гогоемгоосп о N
га о -" о* см" о —" о см"
ю n >t oi о ю -^о
-, СО О Ю Ю СО CN СП|^
<N го_ ЭТ^ (N_ ГО_ Р, 00_ Я, ^
го о" —* о" см* о" -* о" cn"
1-^ГОСПСООО-^ С^Ю
oooococniniS. о v
Р_ ТО_ СМ_ CN_ ¦*_ О С?) — 1^
га о" -н о" cn" о" —" о см"
го — га — coco cnoo
— СО 00 О CN — CN —
°°.  °! °1 ю Я ю. — i^
cn" о" —" о см" о" —" о" cn"
— СО 00 Ю СО ГО О1-^
со, 5 8^SSS 28
cn" о" — о cn* о — о" of
ГО00ГОО^-*ГО rocN
C^O^^OOCNOO СОЮ
¦*_ ¦*_ CN_ СО СО, О_ — — СО
cn" о" —" О CN о" -" о" CN
И I4- (О Ю М ^* CNro
О N CN 00 — О СГ> —
см_ ю, —;_ эт t^ Р, Р — со
cn" о" —" о cn" о" —" о" см"
Приложение
213
1
СО 1^
о со_
о о"
СПС^ЭТСМ ЮО — t~~ CDOO^t4
со о) о см м N оо оемдю
Я Я Я. Я "Ч ° о о_ о_ щ ©_ р о_ Р о
CN* — О* О —" ЭТ" —* О* О* ~" Ю* —" о" О СМ*
сп
о
см
го
о"
см
,02
о
.57
о
ЭТ СП О I—
сп о о о —
-* -" о" р" -
1
со ¦* — со
И N О S „
СП О О О 1О 00,
cn" — о о — ¦*
оо см о о
О <М О CN
—" О О" CN
ЭТ — [^ Ю ООГОтН С^СП^-"ГО СПЮО1^
*t Ol CN О ^СП^-'СМ CNC^O^ OcNOOO
00, О — О Ю ООООО^^ 00ООО,Ю СО, О О О СП
о —* о о* о" — —" о" о —" см" —" о" о" —" ¦* —" о" о" —"
CMI— СМСМ ГОСМООСМ О — — СО ОО OS
СОтРСОГО ¦* 00 — S СОСООО О СО О ^
г~ О СМ, О, ¦*_ г^ О, Р, Р, Р, I--, О, О, О, Ю, ¦*, О, О О СП
о — о о о — —" о" о" —" см —" о" о" —" ¦** —Г о о —"
СОСОСМСО ^^ГОСООО — -^ СО CM CN CN —' |-~
— О ГО Ю * N -. — ГО00О1— — ГО О О
СО ОГООГО СО 000,0 СО ООО,1^ CN ОООСЛ
о" —" о" о о —* — о" о" —" cn" —" о" о" —" ¦* — о" о —"
t^oroo гос^-со«* смоо-^ю госпгою
елг-смоо ¦* ю — со га оо о га — со о со
ю,спгоосч юрорсп юо,о,о,т^ о, о о о оо
о о" о" о" о —* —" о" о" о см* —" о* о" —" тг" — о" о —*
I I I
ю - о ю
¦^ СП ¦*, О_ CN_
о о" о" о" о"
CN
о"
СО Ю СП CN
ю см о го
оо ¦* о —
О О О Р
S8
о о
Ю N ^ СО
¦* т — р
о о о сп
—" — о
ГО СО
S5
i
CN
со
о"
* - О N
CN Р Р Р. 1^,
-Г -Г о" о о
^f 1^ СО СО
ГО 00 О СП
¦^< о о о го_
cn" —• о о —
Ю 00 ГО Ю
ГО 00 О Ю
ГО О О О СО
CN —" О" р —
•& ГО CD CM
(N О О_ Р, СО_
CN -<" Р" Р —"
Tj< Ю О "¦
0^ о О О 00^
го" -Г о" о" —"
00 СП CN ГО
СО о О О Is-
со" _Г о" о" "
о
сп со —• см
— ю о см
¦* о о о f-
со" -" о" о" -
о ю см сп
ю s -^ —
— <( N О О_
о* о"
—0
с- с сг
со S СП ^
— О О Р 1~-
—* —" о" о о
N (О О »
- 3.8 о. 8
cn" -Too"—'
СМ ГО — t^-
CN CD Q CD
CM О О О CD
ГО _." о" О" —

Продолжение табл. 4 ^2.
t
Aa(f)
A2it)
Atit)
wit)
t
Aoit)
AAt)
AAt)
wit)
t
Aoit)
AAt)
Atit)
wit)
t
Aoit)
AAt)
Atit)
wit)
0,1
0,260
—0,160
—0,025
0,010
1,1
1,048
—0,120
0,013
0,605
2,1
1,081
0,087
0,002
1,194
3,2
1,055
0,075
0,001
1,618
0,2
0,464
—0,265
—0,027
0,000
1,2
1,059
—0,083
0,009
0,672
2,2
1,079
0,089
0,002
1,242
3,4
1,049
0,068
—0,000
1,674
0,3
0,615
—0,317
—0,014
0,084
1,3
1,068
—0,049
0,004
0,738
2,3
1,078
0,089
—0,002
1,288
3,6
1,044
0,061
—0,001
1,726
0,4
0,733
—0,340
—0,002
0,137
1,4
1,074
—0,021
—0,002
0,802
2,4
1,077
0,090
—0,004
1,332
3,8
1,038
0,056
0,000
1,773
am ---
m0 = 0,4
0,5
0,824
—0,338
0,008
0,197
1,5
1,078
0,005
—0,007
0,864
2,5
1,074
0,092
—0,003
1,374
4,0
1,033
0,049
0,001
1,815
0,6
0,891
—0,316
0,017
0,261
1,6
1,081
0,027
—0,011
0,924
2,6
1,072
0,091
—0,003
1,414
4,2
1,029
0,042
—0,000
1,855
0,7
0,943
—0,284
0,021
0,329
1,7
1,083
0,045
—0,013
0,982
2,7
1,070
0,089
—0,002
1,452
4,4
1,025
0,037
—0,000
1,892
0,8
0,983
—0,245
0,021
0,398
1,8
1,083
0,061
—0,012
1,038
2,8
1,067
0,088
—0,000
1,488
4,6
1,022
0,032
—0,000
1,926
0,9
1,010
—0,202
0,020
0,467
1,9
1,083
0,073
—0,008
1,092
2,9
1,064
0,085
0,000
1,523
4,8
1,018
0,028
0,000
1,957
1,0
1,032
—0,160
0,017
0,538
2,0
1,083
0,081
—0,002
1,144
3,0
1,061
0,082
0,000
1,556
5,0
1,016
0,024
0,000
1,987
о
съ
3;
Продолжение табл. 4
t
An(t)
4 * 0 V/
A, it)
А4 it)
wit)
t
ABit)
A, it)
AAt)
wit)
t
An(t)
* 0 V *f
A» it)
Aiit)
wit)
t
Aoit)
A, it)
d * 2 V '
A 4 (/)
wit)
0,1
0,182
—0,112
—0,017
0,007
1,1
0,990
—0,157
0,013
0,517
2,1
1,113
0,058
0,000
1,128
3,2
1,097
0,081
0,000
1,602
0,2
0,339
—0,194
—0,020
0,028
1,2
1,016
—0,126
0,010
0,583
2,2
1,114
0,066
0,001
1,181
3,4
1,089
0,077
—0,000
1,665
0,3
0,468
—0,244
—0,012
0,061
1,3
1,038
—0,097
0,006
0,648
2,3
1,115
0,071
—0,001
1,231
3,6
1,081
0,072
—0,001
1,722
0,4
0,580
—0,275
—0,004
0,102
1,4
1,056
—0,069
0,001
0,713
2,4
1,116
0,076
—0,003
1,280
3,8
1,073
0,066
—0,000
1,774
m0 = 0,6
0,5
0,674
—0,287
0,003
0,151
1,5
1,071
—0,043
—0,002
0,776
2,5
1,115
0,080
—0,003
1,327
4,0
1,065
0,060
0,001
1,820
0,6
0,752
—0,283
0,010
0,205
1,6
1,083
—0,019
—0,006
0,839
2,6
1,114
0,083
—0,003
1,372
4,2
1,057
0,053
—0,000
1,863
0,7
0,818
—0,268
0,014
0,263
1,7
1,093
0,001
—0,008
0,900
2,7
1,112
0,084
—0,002
1,415
4,4
1,050
0,048
—0,000
1,001
0,8
0,874
—0,246
0,015
0,324
1,8
1,100
0,019
—0,008
0,960
2,8
1,110
0,085
—0,001
1,456
4,6
1,043
0,042
—0,000
1,936
0,9
0,920
—0,218
0,016
0,387
1,9
1,105
0,035
—0,006
1,018
2,9
1,107
0,085
—0,000
1.495
4,8
1,037
0,037
0,000
1,969
1,0
0,958
—0,188
0,015
0,452
2,0
1,110
0,048
—0,002
1,074
3,0
1,104
0,084
—0,000
1,532
5,0
1,032
0,032
0,000
1,998
>«
с
s>
о
съ
(N5
сл

216 Приложение
-I I7T7 17ZI Го^—I
г °. ?-.з1§ о §1.8.1 о. 5Ш§i о. ii§§
а — о о о" о сч — о" о" о" со" —" о" о" — ю —Г о" о" сч"
? I I 1
ад
а ¦* со сч оо t^ — ¦* — мюо * сосоооо
I о» S сч 5 Ц. о» 8 8 8.3. о» - & 8 3 со. 8 S 8 S
Т} О о" р о" О — — о" О* о" СЧ — О О —" ¦* —Г о о" —
a I ii
t!
? и 2 - S28S 3 ? S = ?888
°°. ¦"-.. °i Р <n оо qo_qco оо_ -оо* со о о о а>
о о р о о" — — о" о о" см" —Г о" о" —* ¦*" — о" о" —"
I ! I I I
О СО О г-~ О> СО Ю ^ СООСМ1Л hi к о ^t
— ¦* — —! (О СО О СЧ * N О 2 00 СО О —
n n cn о сч i^, о. о. о. оо г-^ — о. о со ¦*. о о о сп
о" о" о о" о" — —" о" о" о сч" —" о" о" —" ¦*" — о" о* —
— оо со t^ — со со cn — ю сч оо ¦* сч о —
со SS8.S «о SS.8.S о 2§_8_з « 8 11S5
о о" о" о" о — — о" о" о" сч — о" о" — ¦*" —" о" о" —"
оо
°" S 5 8 S3 8S8S 883S SS8S3
у ю ю. сч. о. -! ю. о. о о. со ю — о о сч о -ооа
о о о о" о" о" — —" о" о" о" сч" —" о" о" —" ¦*" Л о" о" —"
S I II I
сооою— cot-~co* ю со сч оо *счоо
^ n и о со ^ ото Л союо— — t^-ot^
¦* ¦* сч_ о_ о ¦* о_ О о_ со ¦* — о. р сч с» — о о 1^
о о" о" о о — —" о" о о сч" —* о" о" — со" *JГ о" о —"
t-~co — оо сл^-сосч осо-нсо сою-н —
l^Ol — ¦* „I— C4OI— Й 41 О «5 СЧр-О —
со. со — о о 'Я0' — P."?. n ".об-¦ to „ о § s
о о" о" о" о *" о" о" о" о" сч" — о о" — со" —Г о о" —"
со со to о n ю Ф cj те со о tN о n о to
сою — S ., ¦* Tf о О сч со 5 « пРо*
сч. сч_ —. о. о w сп —;_ о. ю сч_ -^ р_ о. —I * я о о to
о о" о" о" о — о" о" о" о" сч" — о" о" —" со —Г о" о" —'
рсосою cn о> — оо n оо о to с-~ооо*
* оо — о — со — * — сч о ю coP-ot^-
-^-^р.р.0 ^.t'i^HP.'^l ^.^.P.^^ сч-^оою
о о" о" о" о" — о" о" о" о" сч" — о" о — со —" о" о" —
СГ СГ СГ СГ СГ С~ СГ о С СГ СГ СГ СГ СГ СГ СГ
Приложение
217
1
—" ©' О О* ©
О
р р
CN —
—I
©
О
сч
О) О
о со"
о о ¦*
" о" о" —" "з
q
— о" о
О СП О Q2
о о о. о. о.
" о" о" cn"
СП 1^
о" о"
СО СО 00
сч о со
о о оо
со
о
7"
о" о - - о о о
и
о со о со
о ю о о
— — -„ -« °°» "Т. Р Р Р.
сч —' о о" — ¦*" — о" о" сч"
Hi CO QJ СО
00 СО СЧ О СЧ_ 00.
о о о о о
00 —
сч" -" о р -
—" —" о" о" о сч — о о
^^^ 77
о" о о о
ЮЮОО
—ж о_ Ои сг^
~Г О О —*
— О О —'
СЧ СЧ О 00
сч со о —
— О О О)
7
о Q о" о « ~ 9 9 °Л
7
О1 СО СЧ N СОСООС1
¦* * О 1О COCOOCD
CD —. О. О. СЧ. СЧ. —. О. О. 00_
сч —" о" о" —<" ¦*" — о" о •—"
о- . -оо
со сч о оо
n ело ет
о^ о_ о_ со_
"
о" о р
9 о" О* -" о" р О О СЧ - О О -
3§8| о§||2
|Г —• о о" —
* СО
. p.
"
СЧ ¦* Ю
О СТ1 О
¦* — о.
о" — о о о о
¦*СОСЛСП СЧ — CDC75
"-н CD О СО "^ СО СО ^^
СО. СО. —. О. О. СО. СП — О. Ю.
о" о"оо"о —' оооо
Ю О 00 О
сч м ^о о сч ^ ~1 о ч^
о о"р"р"о — оо"оо"
^ — W CS
С0С0ОЮ
-ч О О •—' 00 ,
^'оо- со -Г о" о
СОЮ
О О S
о" о ^
hi СЧ — t^
сч сч о gj
со —. О_ О. О.
сч" — о р —
— о" о —¦
77
Is
7 7
со со о —
сч - р. о. о. ¦* —. Р
CN — О О — СО— О
td t^ P —
— о со
7"
« - о о о - оо - Р ™.
о" о" р" р" о - о о о о
_§111 «§§|S
см" —" о" о" о" со - о" о —
СГ СГ СГ
с-сгсг

218
3
СМ
О
Приложение
о
<N
5
о"
cn"
5
CN
o"
CN
in
CN*
oo
Ю
о
о
уз та со со cn та
°.  * й о оо
" О о" N О* <N"
О
-w -* ч \л uj ¦«* сп со см о та cn
*Ol«MOn 00 CO CM — CN CN
сз <м* о" см* о" см" — 9 о cn" о" та"
О
оо
о"
СО
о"
О
»8«йа
-1 °. -1 00 О CN
о « о n о и"
Kg
~ °Ч  OJ, О СО
О -< О in" о" (N
§ s S S 8 =
™. Ч " О> О U5
О -. О (М о" CN
сп та —н о ю i^
t- ю ¦* |^ оо со
Я "Я ~1 СП О СО
о" -" сГ см" о* см"
сз^ "^ "^ сп о оо
о —« о <м* с* см*
ls.Ss.ll
О О О СО О* <N
о ? 2 8 5 g
о о о со о" со"
О ^ -^ — о —
О О о СО* о" СО
СМ Г-
CN СО
о о
О
S5 « ? 8 8 ?
"". п. ™ о о с»
- О О И о N
1Л — ^* N N о
cn со cn сп —. та
— <м та ^ о со
—< о о —" о" <м*
оо см ¦# cn ¦* -^
« сп со ю —. ю
-; -¦_ CN ю о 00
—' О о" —" о* <М*
8 $3 85 2 S
1 ". "". ". О О)
—< р о —" о" <м"
<N СО Ю С| та CN
•^ ^ та см -^ о
о о — о о —•
~р-о7*о-та
2 2 SJ
§ Я К 2 SJ
Я. о о г- о —
~ О О О о СО
2 §ЙЙ ?Й
о о о^ со^ о *-^
-«" Q О О о" Ю
2; s. со сч
88KS
О (N О —"
"З1 р та сп
с» 5 со ю
О та" О* -"
3 "¦ оо со
та оо cn сп
Я. ^ <"i ¦*
О CN О СО -^ СМ* С* ^
29 ¦* со ю
сп тн та оо
о эт_ о та
-1 см" —" —Г
О)
и ел м оо
- <N -* о»
— -н —. О
?¦ 00 СП CN
оо ¦* оо ¦*
О О Ю СО
2 NOCO
о со оо В
--О--О
Ю —, СО
о со w
-
е- 3 е-
о.
С:
Приложение
219
о
¦*"
оо
со"
СЛ СО CN — ¦*
СО CN ¦* CN <N
—¦|_ cn t>i —. о
о cn" о —' о
—. 00 CN СЧ_ ©_ Ю_
о cn" о —¦ о cn
О CN
^ оо со --* оо
- О) О) ^ О)
ел сож слж о^ —^
•Ч сп_
о о о
со_
то
сп
CN
О
оо
CN
ю
CN
О
CN
С^
сп
о
о
In
CN
¦*. я °, °.
' сз то о" cn
О — О CN
ю cn та оо
CN 00 ТО CN_
О -" О N
§3 5 5 та
CN 00 ТО CN
о - о" сч'
тг —_ СО_ CN ¦* О, О
го" о о" о —' о cn
со оо о та cn
cn ю —" о •—
оо оо ч^ ^, Я
о о" о го о
СО CN «?>
<О 00 N
w °°„ ^
о —<" о"
СО 1Л О -4 ^* ^
CN " U3 00 gj ?)
J СО tN 1О_ О О1
о п о - о -
ГО CN ¦* —' JO
CN ¦* «Э — Й
—. СО CN_ 1~-_ О_
о м" о -1 о
сп ю со I— г-
Ю CN —• —' О
оо_. °°. - ~"- -
с* о о го о
О Ю
I
cd см г-- о со ¦*
CN ТО СО 1О ТО CN
00 — 00_ CN 00_^ О_ 00_
CN О CN О —' О —
«О
CN
та с
— 0
о с
э оо с
Ч. °i <~
ч'о'с
< S ш
з со та
\ °. °°.
ч" о —
CN* О CN О CN О —¦
о" о о то о cn
о ю io ^f ^
Й ¦* CN 1^ О
о! t- f_ q o_
о" о о cn о
СО 00 00 CN СП ¦"*
СО СП СМ СП О ^г
СП CD ¦*_ 00_ О. ТО_
о о" сэ cn" о cn"
<м ^ ZZ S * t?
8 S 3 S о !?
J о О И о" И
I I
fe то - ^
та сп ¦* —i
о -" о' ет
* Ю N -
CD CN  00
то о ^ о^
О И* О «
in ^ CD Ф
то ¦* О —;
tf -н Ю О
"
о"
О CN
СП 1Л
ю_ сп.
о —'
сп та сп
.— СП ^^
CD ¦*_ СО
о" с* о
к! S ID N
« о ° и о
°
©¦""С ©¦
------*''? ©.^= ©¦

«Pi
Из
Фз
м.
Фв
Iй.
Фо
1*1
ф*
Ф4
|ф|
фф
|"|
ф«
0,2
0,015
—0,500
0,133
3,107
0,075
3,107
1,028
—0,016
0,042
—0,357
0,014
—3,128
1,060
—0,316
2,236
—0,542
—— -
0,4
0,057
—0,716
0,141
3,023
0,082
3,003
1,086
—0,069
0,094
—0,753
0,012
—2,992
1,210
—0,668
1,893
—0,732
0,6
0,124
—0,971
0,146
2,916
0,091
2,829
1,151
—0,163
0,171
—1,105
0,011
—2,537
1,432
—1,057
1,712
—0,937
м. —
0,8
0,216
—1,276
0,149
2,824
0,097
2,588
1,194
—0,295
0,265
—1,465
0,018
—2,158
1,693
—1,483
1,551
—1,166
— ..—__
Ма = 0,4
1,0
0,319
—1,621
0,153
2,784
0,096
2,304
1,186
—0,448
0,357
—1,840
0,030
—2,200
1,923
— 1,938
1,357
— 1,403
——
1,2
0,410
—1,978
0,171
2,764
0,088
2,012
1,126
—0,589
0,423
—2,207
0,043
—2,433
2,051
—2,395
1,138
—1,612
1,4
0,472
—2,322
0,205
2,676
0,074
1,748
1,044
—0,697
0,453
—2,542
0,053
—2,727
2,054
—2,834
0,937
— 1,768
—
1.6
0,498
—2,637
0,244
2,500
0,059
1,536
0,970
—0,777
0,448
—2,828
0,058
—3,031
1,944
3,039
0,785
— 1,877
—¦ »
Продолжение
1,8
0,490
—2,915
0,276
2,272
0,045
1,391
0,910
—0,846
0,422
—3,060
0,058
2,964
1,750
2,669
0,677
— 1,966
¦¦ .
табл. 5
2,0
0,458
3,139
0,295
2,033
0,034
1,319
0,857
—0,914
0,385
3,048
0,054
2,713
1,511
2,346
0,595
—2,056
-"¦ ¦¦—
Продолжение табл.
2,4
0,372
2,843
0,299
1,606
0,020
1,358
0,749
—1,037
0,320
2,841
0,040
2,372
1,053
1,858
0,460
—2,234
2,6
0,336
2,763
0,293
1,430
0,016
1,459
0,696
-1,086
0,297
2,782
0,033
2,295
0,874
1,686
0,403
—2,312
2,8
0,309
2,715
0,286
1,275
0,012
1,638
0,648
— 1,125
0,279
2,736
0,028
2,282
0,731
1,552
0,353
—2,379
hla = 0,4
3,0
0,289
2,684
0,279
1,136
0,011
1,918
0,605
—1,156
0,256
2,698
0,024
2,328
0,619
1,448
0,311
—2,435
3,2
0,275
2,662
0,272
1,008
0,011
2,243
0,567
—1,180
0,253
2,666
0,022
2,412
0,531
1,367
0,275
—2,483
3,4
0,265
2,643
0,266
0,889
0,013
2,493
0,533
—1,199
0,243
2,640
0,022
2,497
0,462
1,303
0,245
—2,523
3,6
0,259
2,623
0,261
0,775
0,016
2,626
0,504
-1,215
0,234
2,617
0,023
2,554
0,408
1,252
0,219
—2,557
3,8
0,254
2,599
0,256
0,666
0,020
2,670
0,478
-1,227
0,227
2,598
0,024
2,572
0,365
1,209
0,197
—2,586
4,0
0,250
2,571
0,251
0,560
0,024
2,660
0,456
-1,237
0,221
2,581
0,025
2,553
0,330
1,172
0,178
—2,612

Продолжение табл. 5 К
«Pi
\А3
Фз
Фб
Фо
\В2\
Фг
\В4\
Ф4
фф
1
0,2
0,034
—0,517
0,136
3,096
0,077
3,094
1,043
—0,025
0,048
—0,382
0,012
—3,067
1,127
—0,335
2,272
—0,551
0,4
0,132
—0,717
0,149
2,972
0,089
2,941
1,136
—0,111
0,118
—0,798
0,009
—2,455
1,471
—0,731
1,988
—0,777
0,6
0,305
— 1,104
0,159
2,790
0,103
2,660
1,233
—0,280
0,233
—1,222
0,021
—1,738
2,043
— 1,202
1,846
—1,063
0,8
0,543
—1,553
0,155
2,621
0,110
2,249
1,239
—0,526
0,374
—1,721
0,047
— 1,889
2,715
— 1,764
1,617
—1,418
hla = 0,6
1,0
0,752
—2,050
0,152
2,601
0,099
1,783
1,087
—0,755
0,474
—2,245
0,074
—2,291
3,143
—2,361
1,232
— 1,747
1,2
0,863
—2,503
0,182
2,607
0,075
1,368
0,897
-0,857
0,500
-2,705
0,092
-2,714
3,202
-2,906
0,867
-1,916
1,4
0,888
-2,893
0,233
2,449
0,051
1,044
0,793
—0,858
0,474
—3,077
0,100
—3,105
3,028
2,897
0,664
—1,926
1,6
0,847
3,051
0,278
2,183
0,031
0,837
0,764
—0,873
0,419
2,909
0,099
2,820
2,705
2,469
0,589
-1,929
1,8
0,757
2,770
0,303
1,891
0,018
0,823
0,746
—0,939
0,355
2,696
0,090
2,507
2,288
2,098
0,546
—2,009
2,0
0,650
2,560
0,309
1,622
0,010
1,093
0,709
-1,026
0,296
2,567
0,077
2,257
1,862
1,794
0,493
-2,128
Продолжение табл. 5
2,2
2,4
2,6
2,8
hla = 0.6
3,0
3,2
3,4
3,6
3,8
Ал
(Г)
Т1
А,
Л3
(Г)
Y3
/к
Фб
В.
"в
Фо
В. 1
 1
fnn
В, 1
°* 1
Ф4
Ф 1
т 1
Фф
1 и 1
1 " 1
Фи
| 0,552
2,418
| 0,302
1,394
| 0,008
1,524
| 0,658
—1,106
0,253
2,505
0,064
2,074
1,494
1,558
0,433
—2,245
0,473
2,332
' 0,292
1,204
0,008
1,869
0,604
—1,168
0,223
2,482
0,053
1,953
1,204
1,379
0,375
—2,345
0,414
2,285
0,281
1,044
0,008
2,127
0,553
—1,214
0,203
2,477
0,044
1,884
0,982
1,242
0,324
—2,426
0,371
2,262
0,272
0,904
0,009
2,335
0,509
—1,247
0,189
2,478
0,037
1,859
0,814
1,138
0,281
—2,491
0,341
2,252
0,264
0,779
0,011
2,490
0,471
—1,270
0,179
2,480
0,032
1,870
0,686
1,058
0,245
—2,543
0,319
2,247
0,258
0,663
0,013
2,585
0,438
—1,287
0,171
2,483
0,029
1,905
0,588
0,904
0,215
—2,585
0,303
2,243
0,252
0,555
0,015
2,625
0,411
— 1,299
0,165
2,486
0,028
1,946
0,511
0,943
0,190
—2,620
0,292
2,235
0,247
0,450
0,018
2,623
0,387
—1,307
0,160
2,489
0,027
1,980
0,449
0,901
0,169
—2,649
0,282
2,224
0,243
0,350
0,021
2,589
0,367
—1,313
0,157
2,492
0,027
1,994
0,400
0,866
0,152
—2,673
4,0
0,275
2,208
0,238
0,252
0,024
2,533
0,349
-1,319
0,154
2,493
0,027
1,984
0,359
0,834
0,137
-2,694

224
1
сч"
Приложение
—i ¦"? СЧ — N N
8 S 8 Я 8 5.
о" сч" о — о сч"
oo n
о" и
»eON
in ю о со
о* « о и"
Ю — СП СЧ NN
О Ю СЧ СП О О
О ¦* — СЧ ¦* СО
Ю О Ю СО СЧ СТ>
—< СП CN CN О CN
— — СЧ О СМ
О
о о"
N CN ¦* О
Jg сс и о
о - о и о" -
й со oi о « оо
<N ю I— СО О —'
N_ CT1_ СЧ_ СО_ —«_ —<__
О о" о" Сч" о" Сч"
со ю со оо о сп
СО — ю —| CN О
1~-_ 00_ СО_ Ю —«^ ¦*_
о о о и о" см"
¦* СО СЧ 00 CN СЧ
о -^ со N со со
СО^ N т^ N »-* N
о" о" о" сч" о" см"
СО СО ¦* СП
N -ч N СО
оо * ¦*
— -Г О CN
N СО N
СО Ю СП
00 00 О СЛ
сп ©и ^ оо
см" cn" о —"
оо о о —
—< СО СО СП
Ю ^ Ю СО
со" см" о —Г
«5
с:
СП
* о
014
сч
221
о
081
о
024
о
Приложение
425
302
357
127
сч © — еэ
475
027
718
СЧОч
,352
о
,649
о
,119
,734
о сч
225
00 W Ю СО ^ 00 00 СО 00 О) N ^
-л Is- <м с* f*- <n оо •—' ifl w со сч N
°Ч <N О CN «н © ^ СО СО ^ Th Ofc 1^;
00 О М О О О (N О* -н О <N О ~
ор ю ел оо ел со
СЧ О СЧ И Ов Лв
о и о" о" о" сч
-• П И 1Л N *
О CN СО СО - Ю
Й О N П О 1О
О CN О о" О CN
СО О СП О N О
СО 'Ф СЧ СО СЧ —«
со, со^ —_ *, ©_ s
о" -* о сч" о" ¦—
ю 3 со Ч" сч оо
со со ^ *т о шв
сГ — о* of d -^
см ¦* см ю
О) N СО —
И СО -• N
о о о" см
О СО N СО
5 S 2 S
о о о сч
8Й8^
N
со в со
N ^ СО
О О О CN
оо
о"
оо_
о"
СО
о"
о"
N тН СМ СМ О> СО
—• О О1 О ¦* 00
и о -< ^* о со
—" со" о см" о" о"
СО СО <7> N СМ ~
—I ю со —¦ оо ю
СМ^ Ю ^-н Ю О "•
—Г см" о" см" о" —"
ОО - Ю - NO
¦* СО ¦* N. —- СО
О О) *-" СО —< N
со —. сп сч ¦* оо
¦* со с» сч со сч
СО_ N ¦*_ —¦_ — —
о" о о" со" о" со"
О
I I
—< — о см о —<
— 00 Ю_ — О —i
—" о о" сч" о" см"
СО —• —:
СЧ О N
СО СО -¦
О N
СМ —<
Ю СО Ю —|
О ¦* СО О
со ¦* со ¦*
о —" о см о см"
СО СО О1 NN
ЮИЮОО)
CN 00 — О)_ О
* " "
— о о — о —
со со ю ^ ^
О) СО Ю 1О м
о сч о сч
<n о а> со pi оо
<?> СО СО 00 Г^- Is-
о^ ю •—• о о о
о* о* о* со о" со"
-> о о о о —
о *юо« я
СО СО Ю ^^ "^ тН
о о о ^ о_ о>
—Г о" о" о" о" см"
1
О О « N чр
од s-OQ э-OQ
дэ -Г .¦* 00
cn оо_ ю_ оо
со" см" о —~
со
N
N
О
00
СП
О
со
ю
о
со
N
СМ
со
сч
о
со
00
со
см
СП
сч
¦*"
J5
оо_
сч"
°°-
о"
N
о
о
сч"
ю » * ¦*
Ю О N т^
о ¦*, сп_ сч
СО ^Г* *"• *Т*
^ Й - со
сц со со ю
— е-
в- э-
a
е-
оо
о*
сч
со
ев
см
»/4 8 5—2880
N СО СО СО Ю CN
U, —• со со — ю
я о_ и *_ о, ю
о" сч" о о" о сч
О N СО СЧ СО —
^ О *J* N "¦ СЧ
со о on ю о ю
о" CN о" О о" CN
еч oi ел со сч с»
N О1 ^ 00 •""* со
СО Si СЧ СО О ¦*
о" —" <? о" о сч
5 8_ см_ ю_ о^ ¦*_
о сч" о о" о сч
¦* °. 'Ч °i °- •
о" сч" о" о о сч
сч_
сч"
о>
О
СО
О
сч
о со
об сч
сч —
о —
о
о
о
S
со
сч
_, » п л и,
е-"ч; е-^: е-
О —" О* (N О* —"
— ^с сп — 2С со
5 Я 2 5 о S
о —" о сч о" —
N СО Ю 00 О> СО
^ О ^ со со сэ
¦^ со —^ СО^ О, СО^
о —¦" о" сч о —<
о со ^ — со со
S N Ю СО ¦* —1
-ф (N ^- СО О СО^
О* « о" ON О* м
СЧ СО N
т). СО СО .. -
ю сч_ —_ со^ о_
о" -•" о" сч" о" "
со со см ю со
СЧ СО О1 СЧ N О>
SN СО СО СО Ю
— —• СО О N
о - о сч о -
о о « е*
со ©.аз e-i
о о о сч
— СП Ю N
г-^ СМ ^м СП
со *_ cs_ ю
О О* о" CN
N J1 Р fc
io N й 00
сп сп еч -*
о о о сч
Sis
„"- о сч
м (О ¦* Ю
К! см о с?
: сч. тг Л
«- о я
I I
&¦

226
I
Я.
СЧ
00
о"
со
o"
Приложение
— —< г- о ¦* оо
СО О СО * - CN
СО О) СЧ —> О Ю
о"- -I о -Г о" сч"
О СО 00 00 W СО
COIN SN- О
00 О <N СО О ТО
О W О « О И
Г
*-Г сч © -^ ©
гГ СО Ю М* О тН
^ М IO N О О r"t
«г* —Г oj ©" СЧ ©* **
t-» CO <N СО <N
00 О 00 CN О
оо oi со со сЭ
d d
8
— CN О СЧ О О
SIA 6 О О 1О
-" « о" N О 1*
SIO С4^ СО 00 СЧ
О С^ СО СО Ю
и В « я - о
- - О N О И
—. со сч со о> ю
¦* О t— СЧ О Ю
* oi « оо - s
о" О о" N о" И
en — со оо
* ю i^ оо
en со оо о
¦* ю i^ оо оо
О —" о" CN О*
°\
Л СО >и О) Ю СО
г- со r~ t*. тг сч
Г-_ СО^ СО_ **_ —• ¦*_
о" р" о" сч" о" сч
Ю WON N 1Я *
Ю Q 1Я 00 in О
(О Й ^ N ^ Ю
О* О О CN О CN
сч сч t~- — г- со
СО О) СЧ СЧ in I—
ifl СО й -ч -н О
о о" о со" о* со"
Ю О) Ю О) СЧ И
мл сд to to ^
t-~ О Ю Ю -*. 1Л.
о" « о сч" о ci
¦* СО СО -а СЧ
о> со 0Q О У>
— -. О
Ч* cfl -<_
-ггт
S СО — CM CN 00
CN CN CN O5 О СЧ
тН О СП О
4^4 СО СО ^f*
^. -г * «
-с - О CN
с; п о N "• N сч fc- сч —
га сч cn оо о со со оо со со
Г- О CN — -н ей СЧ СО Ю ©
о"~осч"еэ"-< сч"-^осч
О1*КО"*П
g. cS а н s s
о о о сч" о" сч
О) N Ю СО
LO О СО 1П
С>5 CN о" -f
— со —. оо
^Г (N о —
<N — m
2 s f<
C7i Tt* l-^
<N о -
й (О
So
я So оо
CT Ф Ol О
Ю CN о CN
о оо сч n
СО N о 1О
* " № ••
¦* -г" сч —'
-^ СП СМ О)
сч* р сч" о
S^ESSfiSJ05 ооч-соооооср ^сч^-сч
О * Ч1 Ю СО Ю N Tf CD СО О 00 П 0О й N
—I Ю_ >-н_ О О_ О^ О О О; ¦* О СО СО СО и Ю
о" о о" со* о со" -" о о" о о cj" —Г р" см р"
о о ¦« м
0Q э-OQ e
Приложение
22?
¦^ СО -^ О IN
ю о) о - и
(N_ Св_ CN_ O_ О_
о* —* о" р" о"
¦* 00 СО Ю СП Ю О)
¦* 1^ 00 — СО СЧ СО
го_ см го —< ¦*_ о_ ю_
см" о" -" о" tl о" ¦"" о" о" о" сч
-~ Ю (J> •*?
со со о со
Л Ю « N
" " "
со_
со"
И СП N 010 П
СО СП О СО CN О
IN 00 CN О О ч^
О — О о" О (N
CN СО Ю Ц5 1Я •"
О) СО — 35 CN 1^
CN СО —с ¦* О_ Ю
О" -« О CN О -<
со ю сч -^
о о" о сч
СМ СО •^
CN
СО •^ О 00 СО
00 CN — О *
О — о" о" о" CN
О) —¦ Ю СО СО ¦*
О ОО -ч Ю CS 1Й
й га -< * о ю
о" — о" CN о" —"
in _н со со
-; оо со сч
¦* Ю « !-¦_
о" о • о" см
4f N <*< Л CD N
op oo —« ю —* со
CN 00 CN CN_ О ¦*
о —" о о" о" см
СО 00 СО CN Г- СО
СЧ 1^ — ¦* IN CN
со со ^- ч* р in^
о « о сч о —*
— m со сч
t-~ О in О
-^ СО ¦—' 1^-
о" о о" сч"
см
со"
р СО 00 О) Ю Ю
О 1-^ ^^ тн ~^ СО
СО 00 CN СО О Ч^
о" — О О о" CN
IN CN 00 ¦* О> СО
in l-^ —< <N CN 00
со и — ¦* р. ¦*
О -" О CN О -
¦^rj ^ 1-^ 1-^
о о о см
о
со"
CN
о"
СВ Tf O1
¦* « эт
тГ О ¦*
CN
' О о О
О * О CN CN
об со сч о со
ГО СО — Ч|_ О_
о — о сч" о
о о" о сч"
со_
CN
i-^ ю го оо
сч irt —• О)
сч ю о го
т^ О> ^ ^ ^ t
— Щ СЧ 1^ СО СО
¦* со —_ со_ о_ ¦*
" " " " "
О — О О О СЧ о -" О N О «
тН СО СО О
Г- I— СЧ 1°
о о о" сч
СО
сч
ГО СП ^* О ГО О
ro_oqcN_copco
о" -" о" о" о" CN о" -f О сч" О —1
го со см
¦* оо сч
го
о
о — о о о сч
О1 — 00 СЧ СЧ СО
о «" о" см" о ~
00 0D_ СЧ_ Ю
о" о" о" сч
5Я
оо со ч1
о о" сч
см
еч
ю
о
3§ S?
оо сч
—¦ о
го
in
СП
о
го
о
о
со
СП
СО
сч
го
ю
о
со*
сч
сч
ю
о
,237
сч
со
о
о
in
ю
us e e ea
©¦ QQ 8-QQ
-" - О «N
е-

228
«о
з
з
I
Приложение
со en — ¦* ю cn ¦* cn * ю оо см ю <N сою
_ © СП СО — СО — ТГ СО СО — I— (DO—• CM CD
о сэ —1 о —__ о_ о_ о а о_ о — о о —„ о_ со со_
—Г О О о — О О О о (N О О © -Г о" о" О* —
ю ю * — U5CN те op со i— см Р га ю тг сп
* о о ю о со — — ю со — оо to- ю —
j СП^ О W О -^ О О О 00 СП О — ©^ ^Ч — О t-~ СО
о о о о — о о о о" —"о" о" о — о о" о —
ю со « сп оо со ¦* ~, © — со Pi^oo сп с~-
—. о ю г- ей — (о s со <n oo ten— i— со
оо о и о о о о oJS. оо о — © ©„ © © юю
°" 7" 7* 7~ ™ 7" 7" 7* °" ~ °" 7" 7* "" °" ?" °""~
о тн © о w ю — ?2 t-~ со en- ?х ^^ сгз оо ^-ч
«сод 53-*—. ofS cnc^oo oocn— а> —¦
h. О — О О « О_ —¦_ «5 t^ О — О О_ о, О Ю Ю
о* о о" о — о о" о о — о" о" о — о о" о —"
O0CNCN СООЮ Ю щ T(t Tf О m^Oi ¦^^'
Ч> Ю Ю О ОО - CN— (NCOQ? SoO— — Ю
СО О*-*© О'—'О ^-н1Я. СО О — О .О© ю 'Р
о о о" о" « о о о" о -^ о" о" о ~ о о о —
SCOCO I^OQCO CO00 ОСОО! СО(МО О)Ю
—' Ю COCN— CO2 CNT(<aj O|^c^ CN00
Ю О^^О 0>(NO "^^ ^ О —< О "^ОО тНСО
о" о" о* о* о" о о" о" о — о о" о" — о" о о —
III Ml II I
О СО * (NO— ©СО * « Ю и UJ -. 4>СО
00СОЮ THio— CO00 н )Л GO ~*IOCN ¦^'^ч
-тн ООО ОО^СЧ^О^ *^<-vl 44 О — С^ *^ОО COCO
о" о о о" о" о о о" о" — ооо — о" о о —*
cncncb о in со сооо О1*— 5?ооо» — ю '
О — СО CN00— О1^ — (О00 ~СО— COCO
СО_ — О_ О 1^ CN_ О — — СО_ О — О  О О_ Oj_ CN
о" о" о* о о" о" о о о —" ооо ~ о о" о" —
— л 00 •—tCOCO СО00 1-^00сО ?2а>Ю CN»-^
i-hOI^h IOCOCN СО00 О1"~1~- ««""^^ ООЮ
(N — ОО ЮСЧ_О_ ОО_ (N о — О .ОО_ "Т.~
о" о о" о ооо" о" о -Г о" о о ~ о" о" о* —
rococo i^qoo со-* сооо °Оюсо <J>Q
S Рэ Q g (с •-• CNCN о о) I— 2 *""' ОСО
о* сГ о" о о" о" о" о* о* — ооо — о о" о —"
с-с с- _л с-с-с- с с сг _ „
Приложение
229
— м t ™ t2 "^ ;S ° ©СОЮ ООСПЮ Q O>
г-, 3 — fc SSfe— C^S OMN OCO— Ю CN
Я. - - ~ © O_ ©_ ©_ — О О О — О ОО© О CN
т ° 7 ° "" ° ° "" М" "* °" °" 9 —о" О — (N
I <N|^ *
— <N t- (M
°~o p
см enco
— — OS
o T o>
СМ О О О — О О — —" СО О
CN Tt* СО О
О О О CN
' о" ©" — CN
© — оо - со ю —
CN <N P- CN 00 —
00^ р -^ О ООО
CN* ООО — О О
— Ю О Ю СО О •* тр 1~- —
— Ю Q CO h- _^-^— COC35
— СП « О-О. О О_ О О —
— — со оро —' о р — cn
77
со оо оо со сп о
" сч ор —
023
118
078
CN О О О
— о о"
§1Я — ¦* (N — I— 1Я CO-
COIN о rt s _,(>_- t~-r^
_cn r-_ o_— о ооо о —
— — СО О о" О — О" о" — «N
ЮЮСП COCN— CN* СО*1* CN — ¦*
(N — 1-^ СО СП —* СОСП OCOl-^ — |Л —
СО О — О ООО ООО СО О — О OOP
см о о о — о о
— — со орр — о о
I
1
CN
о со со см _
,, <N — оо со а _. _
[| ю о_ — р р о о_ р оо ю
J3
CN OOO — О
оо
1
— О О О О
~ — со о" о"
7 7 -°7
ю р
оо ю
— см*
я?
—* (N*
СО — 00 --
Tf О — О ООО О
СП — Г~
СП — CN
о ~
7
— Ю Ю 00 тГ СО
га t- — ю — о
¦* р —_ о pop — —
со о р" р" —" о" о" —" cn
77 "°7
¦* ¦* 00 ¦* (N О
со — со ¦* о —
со о —^ р р — р_
см* о о* о. — о о"
00— 1^О>^ СО — тг — ¦*
00СП О Й N ^ со —< — 00
сл.1^, со о — о ооо -о
о" —" со о о" о" —* о* о" — см*
со — га сп *— см оспоо i-^cora со
-. 00 ЮОО -*Ю — CN I- U.CO— —
СМ_ р-^_О р—_О С7> t— <N О —< О ООО ^^
сч орр — о* р" о— со" оо*р —"ор" -^см
— об ю о
— О О — а
77 -°
оо -^оо
I I I
со-^оо
СО — I-
о со—
00
cot— о> сп — см
— (N1^ = t— —
со^оо n ч о со cot о> сп — см ою
СО — I- 1ЯО— 00— — (N1^ =— t— — CNCO
О — О О— О СОГ- — О — О ООО "Т.0.
о" — (N
(N о О О — О
О О — О О
Я ООО — о" О
SSS SSS
ее
SSSSSS

Продолжение- табл. б g§
0,1
0,2
0,3
0,4
hla = 0,4
0,5
0,6
0,7
0,8
0,9
At(t)
AAt)
Ab(t)
в At)
в At)
BAt)
ф@
u(t)
t
AAt)
Ab(t)
BAt)
BAt)
BAt)
Ф@
u(t)
—0,101
0,048
0,002
0,180
—0,101
—0,012
—0,030
0,013
1.1
—0,095
—0,208
—0,053
1,056
—0,108
—0,023
—0,325
0,853
. -.
—0,171
0,064
—0,006
0,341
—0,170
—0,018
—0,086
0,052
1,2
—0,071
—0,205
—0,059
1,086
—0,086
—0,022
—0,255 •
0,949
—0,207
0,043
—0,023
0,477
—0,200
—0,020
—0,166
0,110
1,3
—0,047
—0,198
—0,065
1,110
—0,064
—0,022
—0,168
1,042
—0,220
0,002
—0,036
0,594
—0,208
—0,023
—0,247
0,183
1.4
—0,024
—0,189
—0,071
1,127
—0,041
—0,022
—0,066
1,132
—0,221
—0,043
—0,040
0,696
—0,208
—0,028
—0,315
0,266
1,5
0,000
—0,180
—0,078
1,140
—0,018
—0,020
—0,045
1,217
—0,212
—0,091
—0,040
0,784
—0,190
—0,032
—0,367
0,358
1,6
0,023
—0,170
—0,083
1,148
0,004
—0,019
0,167
1,298
—0,193
—0,136
—0,039
0,858
—0,183
—0,033
—0,403
0,454
1.7
0,043
—0,160
—0,086
1,153
0,024
—0,017
0,295
1,374
—0,170
—0,172
—0,039
0,920
—0,165
—0,031
—0,417
0,553
1.8
0,063
—0,151
—0,088
1,155
0,044
—0,016
0,426
1,446
—0,146
—0,193
—0,041
0,974
—0,147
—0,028
—0,406
0,654
1.9
0,081
—0,143
—0,088
1,155
0,062
—0,013
0,556
1,514
1,0
—0,121
—0,204
—0,046
1,020
—0,129
—0,025'
—0,375
0,754
2,0
0,096
—0,136
—0,086
1,152
0,078
—0,009
0,683
1,578
Продолжение табл. 6
t
ААО
AAt)
АьО)
ВАП
BAt)
Bt(f)
ф@
u(f)
t
AAt)
AAt)
As (t)
B0(t)
BAt)
Bt(t)
Ф@
u(t)
2,1
0,107
—0,130
—0,086
1,149
0,092
—0,006
0,805
1,637
3,1
0,094
—0,119
—0,089
1,089
0,125
—0,004
1,443
2,060
2,2
0,116
—0,125
—0,089
1,145
0,103
—0,004
0,919
1,693
3,2
0,085
—0,121
—0,089
1,083
0,121
^0,005
1,447
2,088
2,3
0,123
—0,122
—0,094
1,139
0,113
—0,003
1,024
1,745
3,3
0,075
—0,123
—0,087
1,077
0,115
—0,007
1,442
2,115
2,4
0,127
—0,118
—0,096
1,133
0,120
—0,003
1,118
1,794
3,4
0,065
—0,126
—0,086
1,071
0,109
—0,008
1,430
2,140
hla = 0,4
2,5
0,128
—0,114
—0,094
1,128
0,125
—0,003
1,201
1,840
3,5
0,056
—0,129
—0,084
1,064
0,103
—0,009
1,411
2,163
2,6
0,126
—0,113
—0,092
1,122
0,129
—0,002
1,271
1,883
3,6
0,046
—0,131
—0,083
1,059
0,097
—0,010
1,389
2,185
2,7
0,123
—0,113
—0,092
1,115
0,132
—0,002
1,328
1,923
3,7
0,037
—0,133
—0,080
1,053
0,089
—0,011
1,363
2,205
2,8
0,118
—0,113
—0,091
1,108
0,132
—0,002
1,374
1,961
3,8
0,029
—0,135
—0,079
1,048
0,083
—0,011
1,333
2,224
2,9
0,111
—0,114
—0,089
1,102
0,131
—0,003
1,409
1,996
3,9
0,022
—0,138
—0,079
1,042
0,076
—0,012
1,302
2,242
3,0
0,103
—0,116
—0,089
1,096
0,128
—0,003
1,431
2,029
4,0
0,015
—0,139
—0,079
1,037
0,069
—0,013
1,271
2,259
Si
о
с

232
3
a
Приложение
t~~ CO СО Ю СО —00
S И Oi CO 4*" Tt* CN
 P °Ч.  °. "Ч 
о" о" о" о" о"
(DON — CO t-~
CO CO t~~ Л О
О О
CO t
Л О •-
— О о
"
P
OOO
о
О О — О -» S О —_ тР
сч" о о" р" —ос> о" —
о
15.
Ю СО СП
сч ю сч
СП СО — О
о" - - -
сч сч ю ¦* о
— о
о р"
ооо ооо
— 00 I— СЧ I— СЧ
О СО 1~- СЧ — СЧ
сп о — о — о о
о о -"ооо --оо
N (О О>
„ СО СЧ СЧ
оо. эт — о
о" о о о
•ч -. р
ооо
о
со сч —-> ю ю
СО Ю 4J. N N
со ¦* оо о — о
ОО -" РРР
— оо i- оо
— со сч сч
— р р —
— р" р" р"
1
со.
о
о — сч ю со i— — сч —
СО СЧОО1* СП СО 00 00 I—
О t-~ — О Ю СО. t-~ Р " Р
о ооо оо —"
оо оо
СП Ю
ОО
— ю
t~- —
CN СЧ
111 °11
ооо — о о о
III II I
о — — спсо— coco оосо — оо со — оо
¦^тнсо ** оо -^ ооо счоосо оо t~~ со осо
СО СООО СО — О ЮСЧ СО — — О ООО ¦* —
о ооо ооо оо - ооо -?-о о--
¦* сч —
СЧ О СО
U5 СО_ О_ О
р- о о" о
ю о г-
_^ сп ¦* сч
¦* сч о о
о" о"
о о о
ю - о
POP
СП ¦*
Ю СП
со —
оо — ооо — о о"
I III II
CN
CN 1
§8
СО 00
lO О
р —
11 1
со ю оо
¦* сп сп
~ ¦*.  ™
о — р р
__ ю _
со сч Р
со оо со
р °
1— СО Р 00 Ю
1- CD СЧ СО 00
со — р — о со
о" о" р" о" о" р о" о —"
м '11 1
Of*- Oi ""^ О
СЛ ^ ^5 СО СО
1 о. о —i о^
о" о" -Г о о"
II II
со
1—
СП
о
— СП Ю —
СО СО 1— СП
— О СО 00
о" о'
СЧСО— ЮСОСО и О 001-~СЧ
., СП 1^ О COCO— О» ^ Ю О) *
CN — О. О, СЧ — О О О СЧ СЧ — О
о р" о о" р р- р" р" р —" о <э р-
СОЮО
роо ооо
со — ¦* оо 1^ Р
о ю о n n -
— — р р — о_ р
о ооо о р о
О Р Р р О
I
р р
р' р"
¦* о
оо ел
CN —
— Р О О
со — ¦*
СО Ю ¦* ¦*
О 1^
1 1
. ю ¦*
СП — Р
р- р
SSS
в « ^
oqqqQJ э- а
С
ю
о е, ч. —* ^
oq oq <Ч 8-а
Приложение
COI— 00 CO'l'O ЮСО COCOtJ- Рт(<— О1*
о ¦* —'ф со-*о cni^ *ЯО1 Ксоо оосч
СЧ_ — О — — О_ 1О СП О н-О —_ — Р. (^ СО
та о о о" — о о — — ¦* о" о" о -" о о — сч"
_ cni-^i-^ cot^-oo со^^ cn^t*1^ сооо ооо
СП СО — СП CDCOO ОСО ЮСОСП П * О — СП
СЧ* °1 ~1 Р "¦„ •". О_ 1О СП СП — — О —_ — О 00 СЧ_
о" о" р" —' о" о" — — со" о" р" о" — о о —" сч"
« п О) n счоо!-~ сотн ^ — ю счюсч счо
.со — сп сосчо споо t^cocn * ^ о m n
СЧ CN — О — — О И 00_ 00^ — — О_ — — О 00_ СЧ_
о" о о — о о —" — со" о" о о —" о" о —" сч"
— счео — оо ю о f споосо son юо
г-счечеп со — о i^co оосчо? * й о ¦* ^
^j, сч_ — р —_ — о сч_ оо_ г^ —;_ — р — —_ о оо_ сч_
о" о" о — о о —" —" со" о" о" о" — о" о —" сч"
.* to ю ^ спюсо coco союоо — сою оооо
щ. О CN О) ЮОО ТН00 ОСЧСП ЮЮО ^fO
сч °i. "". Р ~1 ~ Р "Т. ^ ^Ч. ^ ~1 Р "Т.  Р °Ч. ^
о" о" о" — о" о" —" —" со о" о" о* —• о о —" сч"
N OJ ^- СО-^О СПР ЮСОСП тНЮСО СП1^
ЮООСЧСП Ю ф О СПСО ^* СЧ О) ЮЮО СО N
w о" о" о — о" о" о — я ооо" —" о о — сч"
II II
_, * Ю И C0CD— 1Я-* СООО S Ш N 0000
' (О П а Ю1— О -^^ СЧСЧО 1ЯЮО — СО
сч ~1 "Т. Р - оо oq_ со ¦* сч — —__ •; ~ о оо_ —
о" о о — о о о — со" ооо —" о о" —" сч
сосчеп oi о ^ юсо тсспр о ю со -^о
со я ^ со vie о оо— со — о <оюо ооо
ооо" —" о" о о —" со" о" о р" — о" о" —" сч"
_, Ю N П tJ-CNI^ ОСО ОООО — СО СП Ю —
СЧ 0-^00 -^т^О СЧЮ Tf^-O СОЮО COCO
ооо — оо о— со" ооо — о о" — сч"
_ — СО 00 СПСОСЧ COCO П N О СЧОО СЧСП
. г- in f- сосч— юсп ¦* — о сойо t~- —
сч о_ —_ р, — о_ о со ¦* —_ (N —_ —i —i ~¦_ о_ со Ог
о" р" о — о" о о —" со" о о" о* —" о о — сч*
=с- g <с с-«г-с~ *-. ^ <* 2 **" ^ ^ ^ —- '-
233
8
15.
С:
со
о
8+8/4*

Продолжение табл. 6
0,1
0,2
0,3
0,4
hla = 0,8
0,5
0,6
0,7
0,8
0,9
1,0
AAt)
As(t)
A,(f)
BAt)
BAt)
BAt)
ф@
и@
t
AAt)
A3(t)
Ab(t)
BAt)
BAt)
BAt)
ф(*)
u(t)
—0,104
0,051
0,005
0,118
—0,067
—0,008
—0,028
0,009
1,1
—0,452
—0,163
—0,028
0,855
—0,177
—0,056
—1,024
0,639
—0,195
0,079
0,000
0,229
—0,116
—0,015
—0,089
0,034
1,2
—0,439
—0,175
—0,032
0,893
—0,173
—0,057
—1,057
0,719
—0,268
0,079
—0,012
0,329
—0,144
—0,020
—0,189
0,074
1,3
—0,421
—0,182
—0,035
0,927
—0,167
—0,057
—1,062
0,798
—0,328
0,059
—0,023
0,420
—0,159
—0,027
—0,308
0,124
1,4
—0,395
—0,186
—0,040
0,956
—0,159
—0,056
— 1,043
0,875
—0,376
0,028
—0,027
0,504
—0,169
—0,037
—0,433
0,184
1,5
—0,364
—0,187
—0,046
0,981
—0,147
—0,054
—0,999
0,951
—0,412
—0,009
—0,026
0,579
—0,175
—0,046
—0,559
0,251
1,6
—0,327
—0,187
—0,051
1,003
—0,134
—0,052
—0,929
1,024
—0,437
—0,051
—0,025
0,647
—0,177
—0,052
—0,683
0,324
1,7
—0,287
—0,184
—0,055
1,021
—0,119
—0,049
—0,836
1,095
—0,452
—0,090
—0,023
0,707
—0,178
—0,055
—0,796
0,400
1,8
—0,242
—0,180
—0,059
1,037
—0,103
—0,046
—0,721
1,164
—0,459
—0,021
—0,023
0,762
—0,179
—0,057
—0,891
0,478
1,9
—0,194
—0,176
—0,062
1,050
—0,085
—0,041
—0,588
1,230
—0,459
—0,145
—0,025
0,811
—0,179
—0,056
—0,968
0,558
2,0
—0,145
—0,171
—0,062
1,062
—0,067
—0,036
—0,438
1,293
>fc3
Й
0»
Продолжение табл. 6
t
AAt)
AAt)
Ab(t)
BAt)
BAt)
BAt)
Ф (t)
u(t)
t
AAt)
A3(t)
BAt)
ВАП
Ф(Л
u(t)
2,1
—0,095
—0,166
—0,064
1,072
—0,048
—0,029
—0,274
1,355
3,1
0,302
—0,123
—0,097
1,153
0,123
0,014
1,490
1,880
2,2
—0,045
—0,161
—0,068
1,081
—0,029
—0,023
—0,099
1,414
3,2
0,321
—0,122
—0,100
1,161
0,134
0,016
1,626
1,927
2,3
0,004
—0,156
—0,075
1,090
—0,010
—0,018
0,082
1,471
3,3
0,336
—0,121
—0,102
1,168
0,144
0,017
1,749
1,973
2,4
0,053
—0,150
—0,080
1,098
0,008
—0,013
0,270
1,527
3,4
0,347
—0,121
—0,103
1,174
0,153
0,019
1,857
2,018
hla = 0,8
2,5
0,099
—0,143
—0,082
1,106
0,027
—0,009
0,459
1,581
3,5
0,354
—0,123
—0,104
1,180
0,161
0,020
1,950
2,061
2,6
0,142
—0,138
—0,084
1,115
0,045
—0,004
0,647
1,633
3,6
0,357
—0,124
—0,105
1,186
0,167
0,020
2,028
2,104
2,7
0,182
—0,134
—0,087
1,122
0,063
0,000
0,831
1,685
3,7
0,356
—0,126
—0,105
1,191
0,171
0,020
2,092
2,146
2,8
0,218
—0,130
—0,090
1,130
0,080
0,004
1,010
1,735
3,8
0,352
—0,128
—0,105
1,194
0,174
0,019
2,141
2,187
2,9
0,250
—0,127
—0,092
1,138
0,095
0,008
1,181
1,784
3,9
0,345
—0,131
—0,105
1,197
0,176
0,019
2,176
2,226
3,0
0,278
—0,124
—0,094
1,146
0,109
0,011
1,341
1,833
4,0
0,335
—0,133
—0,106
1,199
0,176
0,018
2,198
2,264
•ъ
я
s»
с
S
СП

Продолжение табл. 6
t
A, it)
AAt)
АЪЦ)
BAt)
BAt)
BAt)
ф@
и it)
t
AAt)
AAt)
AbU)
Boit)
BAt)
BAt)
<P(Q
и it)
0.1
—0,098
0,048
0,004
0,108
—0,060
—0,008
—0,024
0,008
1,1
—0,565
—0,137
—0,024
0,811
—0,186
—0,066
— 1,178
0,596
0.2
—0,188
0,078
0,000
0,211
—0,106
—0,014
—0,082
0,031
1,2
—0,569
—0,151
—0,026
0,848
—0,186
—0,068
—1,254
0,672
0,3
—0,265
0,082
—0,010
0,305
—0,132
—0,019
—0,178
0,067
1,3
—0,566
—0,161
—0,028
0,880
—0,186
—0,069
—1,307
0,746
0,4
—0,333
0,067
—0,020
0,391
—0,148
—0,027
—0,298
0,114
1,4
—0,556
—0,167
—0,032
0,908
—0,182
—0,070
—1,337
0,819
h/a= 1,0
0,5
—0,392
0,042
—0,024
0,471
—0,159
—0,036
—0,429
0,170
1,5
—0,539
—0,172
—0,036
0,931
—0,176
—0,070
—1,343
0,889
0,6
—0,441
0,009
—0,024
0,543
—0,167
—0,046
—0,567
0,232
1,6
—0,514
—0,174
—0,040
0,951
—0,169
—0,069
—1,325
0,957
0,7
—0,481
—0,028
—0,023
0,609
—0,171
—0,054
—0,708
0,300
1,7
—0,484
—0,174
—0,044
0,967
—0,160
—0,067
—1,280
1,023
0.8
—0,513
—0,064
—0,021
0,668
—0,176
—0,059
—0,845
0,371
1,8
—0,448
—0,173
—0,047
0,980
—0,149
—0,065
—1,213
1,086
0,9
—0,537
—0,094
—0,020
0,721
—0,180
—0,062
—0,970
0,445
1,9
—0,406
—0,171
—0,049
0,991
—0,136
—0,061
—1,124
1,147
1,0
—0,555
—0,118
—0,021
0,769
—0,183
—0,064
—1,081
0,521
2,0
—0,360
—0,168
—0,049
1,001
—0,122
—0,056
—1,014
1,205
.,...™.„..,.- „,м.;
ило
H
n>
3
С
(b
Продолжение табл. 6
t
AAt)
ААП
Ab(t)
BAt)
BAt)
BAt)
9(9
u(t)
t
AAt)
AAt)
Ab(t)
в At)
BAt)
BAt)
v(t)
u(t)
2,1
—0,310
—0,165
—0,050
1,009
—0,107
—0,050
—0,884
1,260
3,1
0,209
—0,126
—0,085
1,082
0,063
0,005
0,924
1,732
2,2
—0,258
—0,162
—0,054
1,015
—0,091
—0,044
—0,737
1,313
3,2
0,240
—0,124
—0,088
1,092
0,078
0,009
1,104
1,776
2,3
—0,204
—0,158
—0,060
1,022
—0,074
—0,038
—0,577
1,365
3,3
0,285
—0,123
—0,091
1,102
0,093
0,012
1,276
1,820
2,4
—0,148
—0,153
—0,064
1,028
—0,057
—0,033
—0,404
1,414
3,4
0,318
—0,122
—0,094
1,113
0,107
0,016
1,437
1,864
h/a= 1,0
2,5
—0,092
—0,148
—0,067
1,034
—0,040
—0,028
—0,222
1,462
3,5
0,347
—0,122
—0,096
1,124
0,120
0,019
1,588
1,908
2,6
—0,037
—0,143
—0,069
1,041
—0,022
—0,022
—0,033
1,509
3,6
0,371
—0,122
—0,098
1,135
0,131
0,021
1,727
1,952
2,7
0,016
—0,139
—0,072
1,048
—0,004
—0,016
0,159
1,555
3,7
0,391
—0,123
—0,100
1,146
0,141
0,023
1,853
1,996
2,8
0,068
—0,135
—0,075
1,055
0,012
—0,010
0,353
1,600
3,8
0,408
—0,125
—0,101
1,157
0,151
0,025
1,967
2,041
2,9
0,118
—0,131
—0,078
1,064
0,029
—0,005
0,548
1,644
3,9
0,420
—0,127
—0,103
1,167
0,159
0,026
2,067
2,085
3,0
0,165
—0,128
—0,081
1,072
0,046
0,000
0,739
1,688
4,0
0,429
—0,129
—0,106
1,177
0,166
0,027
2,154
2,129
e
s»
0»
с
N5
CO

0,2
Таблица 7
0,4
0,6
0,8
hla = 0,2
1,0
1,2
1,4
1,6
1,8
2,0
Ф1
Л3\
Фз
*ь\
ф5
Sol
Фо
я.1
Фг
ВЛ
Ф4
Ф|
Фф
«1
Фи
1,003
—0,000
0,037
3,135
0,041
3,138
0,001
—0,203
0,256
—0,005
0,095
0,000
1,033
—0,023
1,029
0,342
1,015
—0,001
0,030
3,115
0,044
3,115
0,005
—0,429
0,275
—0,039
0,098
—0,001
1,090
—0,086
1,135
0,718
1,035
—0,007
0,015
—3,109
0,047
3,060
0,013
—0,675
0,301
—0,116
0,101
—0,010
1,150
—0,180
1,325
1,071
1,063
—0,020
0,011
—0,752
0,051
2,968
0,022
—0,940
0,330
—0,236
0,106
—0,034
1,203
—0,296
1,561
1,371
м mmatm
1,096
—0,044
0,047
—0,621
0,054
2,844
0,034
—1,217
0,355
—0,391
0,112
—0,078
1,240
—0,430
1,777
1,617
1,129
—0,079
0,095
—0,744
0,057
2,696
0,046
—1,501
0,374
—0,571
0,119
—0,141
1,258
—0,574
1,907
1,818
1,157
—0,125
0,151
—0,908
0,059
2,531
0,056
—1,783
0,383
—0,765
0,124
—0,220
1,255
—0,725
1,912
1,984
1,177
—0,179
0,213
— 1,088
0,059
2,357
0,063
—2,055
0,383
—0,967
0,127
—0,310
1,229
—0,880
1,790
2,115
1,184
—0,238
0,278
— 1,274
0,059
2,178
0,067
—2,307
0,373
—1,171
0,129
—0,405
1,180
—1^035
1,570
2,209
-.,4 -Х-л^Ль^яЖ
1,178
—0,298
0,340
— 1,460
0,058
1,996
0,067
—2,532
0,356
—1,373
0,128
—0,498
1,112
—1,185
1,300
2,263
SAaaafca
ю
СО
ОО
Продолжение табл. 7
hla = 0,2
Фз
\АЪ
Фо
В2\
ф2
\Bt\
Ф4
|Ф|
фф
|«1
Фи
2,2
1,160
-0,354
0,395
—1,639
0,056
1,814
0,064
—2,718
0,332
—1,568
0,126
—0,582
1,030
— 1,324
1,031
2,271
2,4
1,133
—0,403
0,442
—1,807
0,055
1,631
0,059
—2,857
0,305
—1,755
0,123
—0,654
0,942
— 1,449
0,804
2,232
2,6
1,103
—0,445
0,481
—1,961
0,053
1,447
0,053
—2,942
0,277
—1,932
0,120
—0,712
0,853
—1,557
0,633
2,150
2,8
1,072
—0,480
0,511
—2,102
0,052
1,262
0,048
—2,974
0,249
—2,100
0,117
—0,761
0,770
— 1,650
0,516
2,046
3,0
3,2
3,4
3,6
1,043
-0,509
0,535
-2,229
0,051
1,074
0,045
-2,960
0,222
-2,261
0,116
-0,803
0,694
— 1,727
0,439
1,943
1,017
—0,533
0,553
—2,345
0,051
0,883
0,044
—2,922
0,197
—2,416
0,115
—0,843
0,628
—1,791
0,387
1,860
0,994
—0,554
0,567
—2,451
0,052
0,691
0,044
—2,882
0,174
—2,568
0,116
—0,887
0,570
— 1,844
0,349
1,803
0,973
—0,574
0,578
—2,549
0,053
0,499
0,046
—2,858
0,152
—2,719
0,117
—0,935
0,521
—1,889
0,317
1,771
3,8
0,956
—0,592
0,586
—2,640
0,055
0,308
0,048
—2,856
0,133
—2,870
0,119
—0,990
0,478
—1,926
0,289
1,755
4,0
0,940
—0,611
0,592
—2,726
0,058
0,120
0,051
—2,874
0,115
—3,024
0,121
—1,053
0,441
-1,959
0,262
1,750

240
«2
Q.
C5
A/a
Приложение
о
CN
00
90S
273
695
7
583
о
343
о
292
о
790
7
544
7
CD CN
Ю 00
О Tf
О —
061
707
о —
193
о
204
о
019
7
760
CN
317
о
354
о
757
7
514
7
133
о
140
о
891
7
741
7
129
¦-и
251
—¦
566
7
366
7
729
"
493
CN
229
CN
245
cn
— —| О О —" О —'
Р СО СО CN СО Об
Щ. "Я "Т. °. °- 
_Г о о* —* о см"
CN CN CN CO О)
Ю 00 CD Tf t~
Tf_ CO CN —l Ю
CN* O* —* O* O*
00 Г-- 00 СО О —'
00 О СО О Tf CN
о cn" о" —" о* о*
Ю 00 00 Ю СО 00
¦ "¦ -1 00 CD CN
00 Ю О 00 3 00

О Tf
CN CO
CN —•
О
Ю
Tf
О
О
Ю
О CN
СО Tf
СО СО
о
00
7
Й
со
°7
СО 1О
°7
8.я
pop
OSlON
Ю О 00
°7°7°7
CD О Ю CN Ю CN
t^ 00 Ю О — t^-
О О СО СО —I О
о
ю
,08
о
CN
,02
о
00
,01
о
,03
о
,05
CN
S
о
о
,04
—0,
со
СО
о
СО
.31
—0,
Tf
О
СО
о
7
со
.0?
«ООСООП
7
СО lO CN СО Ю Ю
СО О СО СО Tf О
•—" о" о* со* о* со
7
о о о о р
00 00 Tf СО О
СО CN p p О
о о" о" о* р*
7
СО СО f О
о — о_ ~
о" со о" со*
со со г^ ю со о
О СО Ю О С7> О
О_ —_ CN О_ СЭ_ О_
о" о" о* о" о" о"
8-^ 9-*< 8- Щ S-0Q 8- Щ Э-
О5 W Ю Ю
СО LO О О5
^н* ~ CO* CN*
С0_ О) О
" СО" CN*
7
Tf — СО СО
о> со — со
СО t~- CN СЛ
" " * Г
п ю и s
-" р" со" -Г
00 CN О Tf
О> Ю Ю CN
— о со —*
CN — О
О СО Ю
CN
00 CN
О О СО Ю
55 CN CN_ CN_
—' о cn" —"
Ю CN Ю СО
— СО О 00
— О Ю 00
— р" -" о"
7
о о « »
—" о" —" о"
— е-— а
&• ь з е-
Приложение
241
S
Tf
OJ СО 00 О Tf —
t^. CN CN — Tf —
CO О Tf -и О СО
0---OCO-00
00 00 О
go ю
со о
S ^ N N
— t~. as со
co_ co_ —i oq
о" cn" о" cn" о" —* о cn о о
I
о
Tf
со"
<O О Tf_ О O_ "^
о —« о" со" о о
О — О CN О О
I I
CN 00 CN t^- О CN
Ю 00 СО Tf Tf О
t~. CO Tf_ 00_ О_ CN_
О* о" о" CN О О
CN
О СО CD
i- СО О_
"
СО
-<
Tf_
7
О CN О" CN* О -й
CN О Г^ Ю Ю О
О Ю t^ Tf 00 СО
^* со о Р о со
о" CN О* СО О —•
юмоп s о
О СО СО LO 00 СО
^^ со о^ р Ои со^
О CN* С? СО О —
СО
О) Ю ОО Og
СО « CN_ CO
о cn" о" о
00 CN CN Tf
СО СО CN О
к к •> •>
О (N О «
Tf СО — СО
5 & CN S
с? cn" о" —"
Tf
о"
CN_
со"
о
со"
Tf --^ СО
h- CO Tf
О Tf ^~
Ю
СО
О О О CN О О
I I
Tf Г^ 00 Ю
СО Ю CN СО
00 О) Tf СО
О CN
7
—< 00
Tf Tf
О lO
о" о"
О Tf Ю Р СО СО
О N о" И о" -
t~. 00 О) СО CN СО
= g2s 8 8
О (N О IN О ^;
5? §J. 8 55
О CN* О* —
Й -. « «
О" CN* О* —
СО
CN
CTi Ю Tf ¦—< CN 1-H
§ СО CN — Tf CN
и со ¦* Ч о n
О" о" О" CN О О
о" о" О CN О О
CN
cS
о_
Й
00_
о"
CN
О
Tf
о"
Tf
О
CN.
CN
т?
О_
о"
1
О
S N h- lO S lO
2 ff 2 S 8 §S
сГ сч о сч о -p
§ = S P S fc
-". °o  и. ~ 
О CN о" CN О -"
ОИО NO"
О Tf
Tf CD
СО О_
*
О5
СО
Ю
О CN О —
О « N (О
?. 8. S К
о cn" о" —<
О) СО СО О
1Д 00 tD N
00 °0ж t^ СО
о" -f о* —"
CN_
cn"
-" О О CN О —'
^Л т^
_< О CN_ СО —_ О_
О* СО* О* —" О* --" О
S 5 т?й
СО h- — —
^ щ°?<4 Э^«? 8^ 8-^3 8^

1
242
3
а;
СО_
о"
00
о"
о"
Приложение
8
О
s
о
s
CN
О
So
о
CN
Ю
Tf
О
О
8
о
Tf 00
t- CD
CN t-
О <N
CO
CN
О
о
CN
Ю
О
r~
Ю
CN
__,
s
СЛ
o"
CD
СЛ
Tf CD
ел ел
°i. *^
o" —'
I I
—* CN 00 СГ) ~ Tf
CO Tf CD — Ю —
— СЛ CN CO O_ CN
—* o" O* —" O* —"
00 N
Ю СО
О ^
— — О l~~
00 -ч CD 00 Ю
О О CN CD CN
cn со ел — о со
- - n in n gi
CO. O_ CN_ CO — ©^
о" со" o" —* o" —"
со f- n со о
CO Ю CN Ю Tf
"Я °1 "Я ю- 
o" cn" о —" о*
S 8 8 8 2. §
О CN* O* —" O* O*
g§2
—¦_ t- СЛ CN
—¦" —' —Г CN*
Ю СО СО О
|-~ CD CN CD
CN Tf CO CN
— -Г СО <N
IN CN 00 N
t^- "^ О СЛ
CO CN О —
—" —" Ю CN
..-.»°.o.
о о о о cn
Ю Tf Ю Tf —• Tf
П. ™. °. ¦*. °. П
—< о" о" о" о of
CN П CD O> N
t^- СО О CN CD
CN — О —• О
—i t~- 00 CN Tf Q
CO —_ CO_ О —l Й
O* CN* O* —" O* Q*
» Ol » N Ю
O> 5) CO CO CN
со ra n —< w
Ю CN Ю t^- CD CN
N 00 00 П CN CO
00 — CN О
И MN S
Tf_ СЛ_ CD O_
-<* o* cd" cn"
O> 00 О w
Ю И CO b
•* N Ю 00
" " T
IN N CO -
¦4- Tf Ю CD
— О О — О CN
CD Ю CN Ю Ю Tf
^^ О О 00 О о)
—" о о" cn" о" of
*—' Ю CD 00 Ci
*-< со to ^ оо
О О О О О
* О со" о" со"
ооо -о
— О CD ~
О ~^ СЛ ^^ CO CO
g s s sj q s
о" о о" о* о"
о -о
N О1 О ^
СЛ Tf о О)
IN IN CN CO
- о т»Г -Г
О
ооо
о о
°. °. я. ~ - ~1
—" о" о* п о со"
« Ю in
8- -ч; 8-
о о о о
О N ©J
8- "Q 8- '
СО СО СО 00
Ю О СО Ю
— —¦ CN О
-Г О* CN -
CD Tf -^ СО
Tf CN ю Ю
О О (N Ю
- о -Г о
Э- Э- 3 8-
Приложение
243
оо
СО
со
СО
CN
СО*
о
со"
00
CN*
CD
CN*
Tf
cn"
CN
CN*
Tf cn со ел
О —• CD Ю 00
—• Tf — Q Ю
— CN О 00 О
О —' О CN О О
О CN О —' О —
о — о со о
2 as ^ at?
Ю CN П -_ О_ <N_
о" —" о" со о" о
со о о
lOOCNll) O1
со со —I ю cn
Ю CN^ СО О_ О_
о — о* со" о"
°
о со тр ст> о
СО —< CD CN Ю
СЧ СО О)ж О О^
~+ сГ с4! о о
тГ OlOtOOO
о со — со cs о>
со сч со оо о^ —^
о" -^ о" сч" о" о"
о со со о —•
cn --j ио со 2;
СМ СО Is— О СО_
2 й
Г^ CN СО СО^ О^ Tf^
о" —Г о cn о о"
о — Tf ю ю с»
о ел — оо со со
00 — СО т? О_ СО
О* —* О* CN O* О
ио со ел cd ел Tf
со ^ о о со с^
о* —* о" cn* о о
« и « ю
О CN О CN О —
— CN О N О_ СО
о" о* о" cn" о —'
о" cn о" со" ° 
СО Tf Ю Tf И —
2 8 g о я. S8
о" см о" со" ° -Г
Tf CO CO Tf О CD
Tf — Г^ О CD Tf
-н CO О О) О Й
О* CN O* CN* О —<
CD Tf СО о -" t;
ю Tf ел ю t; см
F- СО О s О Ю
о" и о" еч о -
оо со оо t^ cn ел
t~. ел —¦ ел рг 2
О* CN* О* оГ О "Г
Tf —I ел оо оо —
О Г^ Tf СО 00 Ю
CN Tf ^ Tf Ол Tf^
О* CN О* CN* О —•
CD CN Г^ -^ ^^ Tt4
СО СЛ 00 СО О J--
о) ю_ -^ см_ -^ га
о и о и" о --
О о Я N ч* ¦*
щ е-ч в-ч е-
cn ел — en
CN 00 Ю t^-
CN Ю_ CN_ CN_
O* CN О* О*
«оЦ| 5 gg.SH. З.Ш
о cn" о" о
Ю CN Tf О
t^. Tf ел со
CN Ю CN П
о cn" о" о"
О N О —
iS — CN CD
CO >Л_ CO_ CO
o* cn" o" o"
со ^- оо —
lO N ^ О
со Tf_ ra_ Tf_
о cn" о" о"
CD CN Ю 00
о га r^ ю
Tf Tf CO_ ¦*
О CN О* О*
о см о о
00 СО Г^ —
Ю СО ^ N
О* CN* о" о"
CD О Tf CM
СО СМ_ Tf_ о_
О* CN о" —"
О W N
О 00 CD CO
00 О Ю Ю
О* <N О* -"
— е-— з
©• &¦ а е-

Продолжение табл. 7
Mil
q>l
\л3
<Ps
И. I
Фб
<fo
IB*I
ф2
I я* I
Ф4
|ф I
Фф
1«1
0,2
1,025
—0,001
0,039
3,129
0,043
3,134
0,012
—0,141
0,262
—0,007
0,097
—0,001
1,059
—0,026
1,482
0,692
0,4
1,118
—0,025
0,039
3,023
0,052
3,061
0,061
—0,407
0,305
—0,074
0,107
—0,021
1,213
—0,122
3,606
1,204
0,6
1,283
—0,134
0,035
2,610
0,067
2,809
0,173
—0,875
0,373
—0,292
0,124
—0,124
1,434
—0,344
8,460
1,512
0,8
1,378
—0,363
0,024
1,212
0,076
2,351
0,320
—1,541
0,403
—0,679
0,137
—0,348
1,515
—0,694
12,318
1,761
hla = 0,8
1,0
1,320
—0,566
0,053
—0,295
0,070
1,923
0,401
—2,151
0,362
—1,018
0,136
—0,561
1,397
—0,987
10,076
1,985
1,2
1,263
—0,722
0,102
—0,805
0,061
1,603
0,430
—2,617
0,321
— 1,267
0,135
—0,745
1,302
—1,215
6,780
2,167
1.4
1,204
—0,895
0,155
—1,327
0,054
1,314
0,430
-3,017
0,286
-1,517
0,132
-0,956
1,220
-1,465
4,122
2,273
1,6
1,095
-1,078
0,199
-1,709
0,046
1,038
0,399
2,914
0,245
—1,781
0,123
—1,183
1,089
-1,733
2,050
2,251
1,8
0,948
-1,230
0,224
-2,033
0,039
0,797
0,347
2,630
0,198
-2,023
0,107
-1,380
0,916
-1,975
0,793
1,897
2,0
0,803
-1,329
0,235
-2,290
0,032
0,604
0,293
2,426
0,154
-2,222
0,091
-1,523
0,747
-2,164
0,462
0.Й97
Продолжение табл. 7
Mil
Ф1
Из
Фз
к
Фб
Фо
|В,
Фг
|в«
Ч>4
М
фф
1
фц
2,2
0,685
— 1,382
0,238
—2,489
0,028
0,450
0,247
2,288
0,118
—2,382
i 0,077
—1,616
0,606
—2,304
0,537
0,367
2,4
2,6
2,8
hla =0,8
3,0
3,2
3,4
3,6
3,8
0,595
-1,403
0,237
—2,646
0,025
0,318
0,211
2,198
0,090
—2,514
0,066
—1,670
0,497
2,407
0,565
0,210
0,528
—1,406
0,326
—2,776
0,023
0,198
0,184
2,142
0,067
—2,631
0,058
—1,698
0,413
—2,483
0,544
0,152
0,478
—1,399
0,235
—2,887
0,021
0,080
0,163
2,108
0,049
—2,744
0,052
—1,710
0,349
—2,540
0,502
0,126
0,441
—1,388
0,233
—2,986
0,021
—0,039
0,148
2,088
0,034
—2,862
0,048
—1,714
0,298
—2,584
0,456
0,113
0,412
—1,376
0,232
—3,076
0,021
—0,162
0,136
2,076
0,022
—3,007
0,045
— 1,717
0,259
—2,619
0,412
0,105
0,389
—1,367
0,231
3,122
0,021
—0,289
0,127
2,068
0,012
3,041
0,043
—1,723
0,227
—2,647
0,372
0,100
0,370
—1,361
0,229
3,041
0,022
—0,419
0,120
2,062
0,004
2,241
0,042
—1,738
0,201
—2,670
0,337
0,095
0,355
—1,358
0,227
2,964
0,023
—0,551
0,114
2,054
0,007
0,670
0,041
—1,763
0,180
—2,689
0,307
0,090
4,0
0,341
—1,358
0,224
2,889
0,024
—0,686
0,109
2,045
0,013
0,289
0,041
—1,798
0,162
—2,707
0,281
0,084

<Рз
Фо
Фа
[fi.l
ЧР4
0,2
Продолжение табл. 7
0,4
0,6
0,8
hla= 1,0
1,0
1,2
1,4
1,6
1,8
2,0
1,040
—0,003
0,041
3,125
0,044
3,131
0,018
—0,140
0,266
—0,009
0,099
—0,002
1,076
—0,028
1,840
0,831
1,197
—0,051
0,046
2,957
0,058
3,014
0,101
—0,461
0,328
—0,107
0,114
—0,045
1,307
—0,156
6,197
1,320
1,441
—0,300
0,051
2,266
0,081
2,559
0,303
— 1,149
0,416
—0,488
0,139
—0,279
1,606
—0,534
17,020
1,610
1,329
—0,640
0,042
0,843
0,076
1,919
0,448
—2,000
0,367
—0,993
0,132
—0,608
1,419
—0,990
16,148
1,862
1,168
—0,788
0,062
—0,353
0,060
1,533
0,472
—2,554
0,291
— 1,241
0,122
—0,771
1,195
— 1,206
9,252
2,089
1,106
—0,930
0,101
—0,938
0,050
1,242
0,477
—2,967
0,253
—1,436
0,120
—0,944
1,114
— 1,407
5,256
2,261
1,028
—1,119
0,141
— 1,465
0,043
0,948
0,458
2,938
0,219
—1,676
0,114
— 1,173
1,027
— 1,671
2,516
2,330
0,894
—1,305
0,168
—1,865
0,035
0,673
0,404
2,612
0,177
—1,923
0,101
—1,405
0,880
—1,942
0,737
2,054
0,742
— 1,438
0,180
—2,179
0,028
0,454
0,339
2,367
0,135
—2,126
0,085
—1,586
0,714
—2,165
0,446
0,385
0,614
—1,511
0,183
—2,414
0,023
0,292
0,281
2,201
0,101
—2,273
0,070
—1,705
0,570
—2,330
0,685
0,013
"¦
?:
г»
о
и
5
... -".пц-ДЙЙТ-ДД
Продолжение табл. 7
Ф1
Л3\
Фз
Фо
Ifi.l
Фг
|fi*l
Ф4
М
фф
I " 1
Фи
2,2
0,517
—1,539
0,183
—2,594
0,020
0,169
0,235
2,094
0,074
—2,375
0,059
— 1,776
0,458
—2,447
0,728
—0,041
2,4
0,446
—1,541
0,181
—2,736
0,018
0,066
0,201
2,027
0,053
—2,445
0,050
-1,813
0,374
—2,531
0,685
—0,048
2,6
2,8
hla= 1,0
3,0 3,2
0,395
—1,528
0,180
—2,854
0,016
—0,026
0,176
1,987
0,038
—2,486
0,044
—1,828
0,310
—2,593
0,617
—0,043
0,357
—1,508
0,179
—2,956
0,016
—0,120
0,156
1,963
0,025
—2,491
0,039
— 1,829
0,262
—2,640
0,549
—0,036
0,329
—1,487
0,178
—3,048
0,015
—0,217
0,142
1,950
0,015
—2,422
0,036
—1,823
0,224
—2,677
0,486
—0,028
0,308
—1,468
0,177
—3,134
0,016
—0,319
0,130
1,943
0,007
—2,094
0,033
—1,817
0,195
—2,705
0,432
—0,022
3,л
0,291
—1,452
0,176
3,067
0,016
—0,426
0,121
1,939
0,005
—0,978
0,032
—1,815
0,171
—2,729
0,386
—0,016
3,6
0,277
—1,440
0,174
2,989
0,017
—0,539
0,114
1,935
0,010
—0,374
0,031
—1,821
0,151
—2,748
0,346
—0,012
3,8
0,266
—1,433
0,173
2,913
0,017
—0,657
0,109
1,931
0,015
—0,245
0,030
—1,838
0,135
—2,765
0,313
—0,009
4,0
0,256
—1,430
0,171
2,839
0,018
—0,777
0,104
1,926
0,020
—0,230
0,030
—1,867
0,122
—2,779
0,285
-0,007

t
0,1
Ax (t) 0,480
A3 (t) —0,236
Ab (ty —0,030
Bo (t) —0,030
B2 @ 0,022
BAO 0,011
<P(t)
"@
Ai@
A3(t)
BAO
u(t)
0,055
—0,026
1,1
1,107
0,109
—0,062
0,001
0,319
0,105
1,135
0,109
0,2
0,801
—0,336
—0,024
—0,044
0,040
0,032
0,155
—0,063
1,2
1,098
0,097
—0,064
0,002
0,339
0,105
1,180
0,182
0,3
0,953
—0,296
0,004
—0,040
0,056
0,061
0,296
—0,103
1,3
1,095
0,076
—0,065
0,004
0,351
0,105
1,209
0,261
0,4
1,027
—0,203
0,017
—0,031
0,076
0,090
0,445
—0,130
1,4
1,085
0,057
—0,060
0,006
0,357
0,105
1,228
0,345
h/a = 0,2
0,5 0,6
1,083
—0,116
0,003
—0,025
0,105
0,114
0,580
—0,136
1,5
1,066
0,043
—0,051
0,009
0,358
0,106
1,240
0,429
1,115
—0,035
—0,019
-0,018
0,141
0,129
0,705
—0,125
1,6
1,052
0,026
—0,047
0,012
0,355
0,106
1,242
0,514
0,7
1,117
0,041
—0,036
-0,011
0,178
0,133
0,822
—0,101
1,7
1,046
0,004
—0,045
0,013
0,350
0,106
1,236
0,599
0,8
1,114
0,092
—0,049
—0,006
0,217
0,127
0,924
—0,064
1,8
1,037
—0,012
—0,042
0,015
0,342
0,106
1,226
0,679
0,9
1,119
0,109
—0,059
—0,003
0,256
0,116
1,007
—0,014
1,9
1,021
—0,022
—0,043
0,017
0,333
0,105
1,213
0,754
Таблица 8
1,0
1,118
0,111
-0,062
—0,001
0,291
0,107
1,076
0,044
2,0
1,012
—0,033
—0,052
0,018
0,323
0,102
1,197
0,824
Пр
Продолжение табл. 8
t
АЛО
ААО
ААО
BAO
BAO
BAO
ф@
u(t)
t
АЛО
AsiO
Аъ@
B0(f)
BAO
BAO
Ф@
u{0
2,1
1,009
—0,044
—0,060
0,017
0,313
0,097
1,179
0,887
3,1
0,989
—0,053
—0,040
0,005
0,253
0,092
1,045
1,120
2,2
1,005
—0,049
—0,055
0,017
0,304
0,093
1,161
0,941
3,2
0,991
—0,053
—0,039
0,003
0,252
0,092
1,040
1,117
2,3
0,996
—0,050
—0,042
0,017
0,296
0,093
1,143
0,988
3,3
0,994
—0,053
—0,039
0,002
0,250
0,093
1,034
1,111
2,4
0,990
—0,054
—0,035
0,016
0,280
0,095
1,126
1,027
3,4
0,993
—0,049
—0,038
0,001
0,249
0,094
1,031
1,103
hi a = 0,2
2,5
0,990
—0,060
—0,038
0,014
0,282
0,096
1,109
1,059
3,5
0,992
—0,045
—0,038
0,000
0,248
0,094
1,029
1,095
2,6
0,990
—0,063
—0,042
0,012
0,275
0,095
1,094
1,083
3,6
0,995
—0,046
—0,040
0,000
0,247
0,094
1,026
1,086
2,7
0,988
—0,061
—0,043
0,011
0,269
0,093
1,082
1,100
3,7
0,999
—0,047
—0,043
—0,001
0,247
0,094
1,024
1,077
2,8
0,988
—0,060
—0,043
0,009
0,264
0,093
1,071
1,112
3,8
0,998
—0,043
—0,044
—0,001
0,246
0,093
1,023
1,068
2,9
0,990
—0,059
—0,045
0,007
0,260
0,092
1,060
1,119
3,9
0,995
—0,039
—0,041
—0,001
0,246
0,093
1,022
1,059
3,0
0,989
—0,056
—0,044
0,006
0,256
0,092
1,052
1,122
4,0
0,997
—0,039
—0,038
—0,001
0,247
0,094
1,021
1,051

Продолжение табл. 8
0,1
0,2
0,3
0,4
hi a =0,4
0,5
0,6
0,7
0,8
0,9
AAt)
AAt)
Ab(t)
B0(t)
в At)
BAt)
<P@
u(t)
t
AAO
A3(t)
AAt)
BAt)
BAt)
BAf)
<p(t)
u(t)
0,279
—0,139
—0,019
—0,039
0,025
0,007
0,029
—0,030
1,1
1,198
0,075
—0,054
—0,025
0,271
0,118
1,072
—0,325
0,511
—0,220
—0,018
—0,067
0,044
0,020
0,091
—0,086
1,2
1,207
0,079
—0,058
—0,014
0,299
0,119
1,145
—0,255
0,685
—0,232
—0,001
—0,080
0,057
0,039
0,189
—0,166
1,3
1,211
0,076
—0,062
—0,004
0,322
0,119
1,204
—0,167
0,820
—0,203
0,008
—0,083
0,070
0,062
0,305
—0,247
1,4
1,207
0,069
—0,062
0,005
0,340
0,119
1,251
—0,066
"'И—
0,930
—0,159
0,003
—0,082
0,089
0,084
0,425
—0,315
1,5
1,197
0,061
—0,059
0,015
0,352
0,119
1,286
0,045
1,015
—0,104
—0,008
—0,077
0,112
0,103
0,547
—0,367
1,6
1,184
0,049
—0,056
0,024
0,360
0,119
1,310
0,167
1,076
—0,045
—0,020
—0,068
0,140
0,116
0,670
—0,403
1,7
1,168
0,035
—0,055
0,032
0,364
0,118
1,323
0,294
1,121
0,005
—0,032
—0,057
0,171
0,121
0,786
—0,417
1,8
1,150
0,021
—0,052
0,039
0,365
0,117
1,327
0,426
1,157
0,039
—0,043
—6,047
0,205
0,120
0,891
—0,406
1,9
1,129
0,008
—0,052
0,045
0,362
0,116
1,324
0,555
m -
1,0
1,182
0,061
—0,050
—0,036
0,240
0,118
0,987
—0,375
2,0
1,108
—0,004
—0,057
0,050
0,358
0,113
1,313
0,682
Продолжение табл. 8
—
t
AAt)
AAt)
Ab(t)
B0(t)
BAt)
BAt)
q><0
u(t)
t
AAt)
AAt)
Ab(t)
B0(t)
BAt)
BAt)
<p@
u(t)
2,1
1,090
—0,017
—0,062
0,053
0,351
0,108
1,297
0,805
3,1
0,975
—0,066
—0,043
0,031
0,269
0,090
1,075
1,443
2,2
1,071
—0,026
—0,060
0,056
0,344
0,103
1,277
0,919
3,2
0,973
—0,065
—0,042
0,026
0,264
0,090
1,060
1,446
2,3
1,052
—0,033
—0,053
0,057
[ 0,335
0,100
1,255
1,023
3.3
0,973
—0,065
—0,041
0,021
0,259
0,090
1,046
1,442
2,4
1,035
—0,042
—0,048
0,057
0,327
0,100
1,231
1,117
3,4
0,973
—0,063
—0,040
0,017
0,254
0,090
1,035
1,430
hi a = 0,4
2,5
1,021
—0,051
—0,047
0,055
0,318
0,099
1,205
1,201
3,5
0,973
—0,060
—0,039
0,012
0,251
0,091
1,027
1,411
2,6
1,009
—0,057
—0,048
0,052
0,309
0,097
1,180
1,271
3,6
0,975
—0,058
—0,039
0,008
0,248
0,091
1,020
1,380
2,7
0,998
—0,061
—0,047
0,049
0,300
0,095
1,157
1,328
3,7
0,977
—0,056
—0,041
0,004
0,246
0,091
1,014
1,362
2,8
0,990
—0,064
—0,047
0,045
0,291
0,093
1,133
1,374
3,8
0,979
—0,053
—0,041
0,001
0,244
0,091
1,010
1,333
2,9
0,984
-0,067
—0,047
0,041
0,283
0,092
1,111
1,408
3,9
0,982
—0,049
—0,040
—0,001
0,242
0,091
1,008
1,302
3,0
G,979
—0,067
—0,046
0,036
0,276
0,091
1,092
1,431
4,0
0,984
—0,047
—0,039
—0,003
0,242
0,092
1,006
1,271
r-i
риложе
a
с
INS
СЛ

252
00
0
114
019
— «о
036
7
096
7
198
о
о
о
Приложение
Tf Tf
00 Ь- О
О О СМ
230
009
— о
060
7
052
о
358
125
о о
365
186
-| О
i
— см
со о
ел о ©
son —< ю
О Г- О Tf _J
О — ©
77 7
1 i .
о* о о"
•* о> ю
СП CN_ О_ О^
— — о" о*
ООО «О
ID
О*
ел cn « ю га cn ^ со
СЛСОСМ « Tf © COCO
00 Oi О О *-t чш* ~* COCO
о" о" о* о* о* о" о" о" о"
оо_ см_ о_ ©_ ©_ е\ —I сок
« « о" о* о" о* о* «
cn со —' см—-ел смел й п ю
t^ о> о о -« _ © юю г-- смоо
о" о~ " *
Tf О О CMCfrOO СМ О СО Tf l}S О СО CN 5>О
о* о" о о о" о" о" о" о* — « о" о* о" о" о" «
77
8§
7 1
§1 §
о о о
28 =
Т-о о
ОО ОО « « © © ООО «
CM CO IO « 00 Ю •—« t*- _
га со © « to Tf смел 1"тН
со « © —< © © смсм Tf смо
СОСОСО ОСМСО t^ CO Tfr^Tf СО О Ю COCO
¦^TfO CM00CO —«О 1Л Tf LO CM —н CM CN «
lO D ^ч Cj t—н ^5 ^Э CO ^ lO Cn СЭ ^Э О СО *"¦' CS Ю
o" o"o*o" o"o*o" o"o" —" «o*o* o"o"o" ""
° S CN
Tf CM_ O_ O_ O_ CM —j.
о" о" о о о" о" о" о" о" « -" о" о* о* о" о" ™
7
7
I
f 7
7 7
7
¦f
СО
7
7
^у Г** ^^ ^^ lO ^^ СО 00
СО Ю —'„ О_ О_ О_ О_ ~* —•__
о* о" о" о" о" о* о* о
о
^ ^ ОО ООО ^-<
7
00 Ю <N Ют^Ю C4<N СО тр К OCOh- «—«CO
LO LO ^** t4^ ^^ ^"^ ^ О CTi O^ ^d^ ^'^ t* lO ^^ 0^ 0^
о" о"о"о* о" о" о о" о" -* «оо о" о" о" ~Я>
OOTfCO « ю 1Л О5©
СО 51 - t CS О «СО
 "Т. Ч. °. °. ° °. ° °.
* о о" о" о
N 1Й « ^ N СО Ю
ю со ¦* со см « со
о о о о о
« «ОО ООО ОО
SSS SS
rt W щ о «
it ее с- с-
о « ч> N—' ^—•*
oq oq сц е- з
щ
о
со
043
062
с
>
054
о
094
о
313
о
098
о
Приложение
t*- ю
о ел
и ю о
975
о
059
—0
042
7
027
о
256
о
090
о
253
034
780
СО СО Ю 1ч — о СМСО СО«3 TfOO TfO
«сз по • -- ¦
\п ю т елсмо со о ^¦сотЛ сососл
ел о о о_ о га - см_ ю ел_ ел о о_ о cn о о_ оо_
см* «* о" о" о" о" о" -Г -Г га* о" о" о о* о* о «" «
СО
о"
ю со со
00 ООО
« --оо
со оо о
СП тр Ю
(^ ООО
« -*оо
о о" о" — —
О
S
CN
00 Tf 1Л СЧ ^
оо_ ел о Ок о «
га" о о" р о" о* о" «" «
7
^J lO lO ^^ f ^ »-*^ со i& (^j (Jj ^^
О) CO О CO N OOCO^1 ^ !D ф
О CO »—' (N СЧ h- CbO O^ О СЧ О
о" о" о" -^ —Г со" о* о о* о" о* о
00 Ю
CD Tf
О 00
7
(N СЧ Is- 00СЧ00 COCO
= 3
Ю N ^ 1ч Tf «
§т|-о О * СО CD 2 iO
га —I ra« сослоо о
СО 00
00 Tf
о оо
см«оо ооо «« га о
7
77
ООО —• -<
СО Tf N
со га ю
1О «_ О О__
см <—, о о
Ю 00 С^ СО СЛ
о" о" о" — о"
— 1ч СО
ел со З1
Ю СЛ_ О^ О_
га о* о* о ©~ ©~ о
Tt- ел
со h»
о сч
о
о
TfTfl4 ОСМСМ —' Ю
— W "
-^ —• о о
00 00 N ^СОСО 0000
ОэсО^ is оо ф у—< у—(
0) О О о ^ О •-< СО
CN -н о О ООО
о соооо ооо —• *ч
ю со
—_ о
7
ю со t
ел о со
— о О
^5 СО ^^ СО СО СО О
о о" о" «о* со —
ел оо см га оо Tf
О О CN S « t-
7
О ООО —¦ —•
^ СО N
о со_ —_
о _ _.
см -« со
ю см о
ю О
со ю
°
7
ооо «о со «о
7
Tf СЛ Tf © Ю
оо ел ел со га
СО СМ С^ "^ Г^-
о" о* о" -Г —
SS § S S S S
СО« COCO « ООО
СО Tf CM
8 2 So-
см « о о ооо
7
— о га —. р о
I
ООО —< —¦
С С С О 'СГ ¦•
CJ- С <С ОСГСГ ^^^
¦^'¦ч:-^' oq'cq'oq' е-з
9 5-2880

Продолжение табл. 8
t
Аг{0
A3(f)
Аъ@
Во@
В2@
В4@
Ф(О
u(t)
t
Ai(t)
A3(t)
Ab(t)
Bo@
Ba@
Bt(t)
«P@
"@
0,1
0,136
—0,068
—0,009
—0,041
0,024
0,004
0,014
—0,028
1,1
1,043
0,012
—0,030
—0,138
0,192
0,101
0,789
—1,025
¦iWn- -fc'Vi -'-и.
0,2
0,265
—0,115
—0,009
—0,076
0,042
0,011
0,045
—0,089
1,2
1,095
0,022
—0,035
—0,127
0,215
0,107
0,875
—1,057
0,3
0,383
—0,133
—0,000
—0,103
0,055
0,021
0,099
—0,189
1,3
1,141
0,027
—0,040
—0,114
0,237
0,112
0,956
— 1,062
0,4
0,492
—0,132
0,005
—0,123
0,065
0,034
0,166
—0,308
1,4
1,180
0,029
—0,043
—0,099
0,257
0,116
1,030
—1,043
hla = 0,8
0,5
0,594
—0,119
0,004
—0,139
0,076
0,049
0,243
—0,433
1,5
1,212
0,030
—0,044
—0,082
0,275
0,120
1,098
—0,999
0,6
0,687
—0,097
0,000
—0,149
0,090
0,063
0,328
—0,560
1,6
1,238
0,029
—0,046
—0,063
0,291
0,123
1,159
—0,930
0,7
0,772
—0,069
—0,006
—0,154
0,105
0,076
0,419
—0,684
1,7
1,257
0,025
—0,048
—0,044
0,305
0,126
1,211
—0,836
0,8
0,849
—0,041
—0,013
—0,155
0,124
0,085
0,512
—0,796
1,8
1,270
0,021
—0,049
—0,025
0,317
0,128
1,256
—0,722
0,9
0,920
—0,019
—0,020
—0,152
0,145
0,091
0,606
—0,892
1,9
1,277
0,015
—0,051
—0,005
0,327
0,129
1,294
—0,589
1,0
0,984
—0,001
—0,026
—0,146
0,168
0,096
0,698
—0,968
2,0
1,280
0,009
—0,056
0,013
0,335
0,129
1,324
—0,438
f
о
M
$=
Продолжение табл. 8
t
At(t)
A3 (i)
At,(t)
B0W
вг@
B4@
ф@
u(t)
t
Ai(t)
A3(t)
A6(t)
Bo @
в2 @
BAt)
ф@
u(t)
2,1
1,279
0,002
—0,060
0,031
0,342
0,128
1,346
—0,274
3,1
1,140
—0,057
—0,060
0,133
0,335
0,107
1,300
1,490
[2,2
1,273
—0,003
—0,062
0,049
0,346
0,126
1,362
—0,099
3,2
1,124
—0,061
—0,059
0,133
0,330
0,106
1,281
1,626
2,3:
1,264
—0,009
—0,060
0,066
0,349
0,124
1,372
0,082
3,3
1,109
—0,064
—0,058
0,132
0,326
0,104
1,262
1,749
2,4
1,252
—0,016
—0,059
0,080
0,352
0,123
1,376
0,270
3,4
1,095
—0,066
—0,057
0,129
0,320
0,102
1,243
1,857
hla =0,8
2,5
1,239
—0,024
—0,060
0,093
0,352
0,121
1,375
0,459
3,5
1,082
—0,067
—0,055
0,125
0,315
0,101
1,224
1,950
2,6
1,224
—0,031
—0,061
0,104
0,351
0,119
1,370
0,648
3,6
1,070
—0,068
—0,055
0,120
0,310
0,100
1,205
2,029
2,7
1,207
—0,037
—0,061
0,114
0,349
0,117
1,361
0,832
3,7
1,059
—0,069
—0,054
0,114
0,305
0,098
1,187
2,093
2,8
1,191
—0,043
—0,061
0,121
0,347
0,114
1,349
1,010
3,8
1,049
—0,068
—0,054
0,108
0,300
0,097
1,170
2,141
2,9
1,174
—0,049
—0,062
0,127
0,344
0,112
1,334
1,181
3,9
1,041
—0,067
—0,052
0,100
0,295
0,096
1,154
2,176
3,0
1,157
—0,054
—0,061
0,131
0,340
0,110
1,318
1,342
4,0
1,033
—0,066
—0,051
0,092
0,290
0,095
1,139
2,198
a
Cb
to
СЛ
O1

256
1
Приложение
о m оо s со сч —' —• мо о> оо ю со оо«
Ю Р •—¦ t— тр 00 0000 Ю О ^t CO О СЧ СЧ •—'
О 00 О О —' -^ O_ U5 O_ О NO, O_ O_ CO^ —_ C4_ O_
— о* о" о" о о о* о" —* сч" —" о" о" о" о о" —* ,-"
III I II I
O> S_ О O_ "I ~ °. ¦*. °i °i °i 4. P» P. ^  1 
о с? о" о" о о" о" о о — —" о о р" с? о —1 —
Ml I II !
ПО» Ю О О СО Ю S Tf — О) П N Q СО
—« Tf О S — S —< Tf « м i< N 00 (N CO —
00 S О О — —' О Tf 00 00_ IM_ О O_ °. ^ "^  ci.
о ooo ooo о о —" —" о о" ooo "" "Г
O) — CO о in N O) CO © CO O) CO о O) COO
CO (О О CO О) СО COO O) — CO СЛ S — 0000
Г-~ CDOO — О О CO S S ¦"¦** О О CJ CN *-< О CN
о о" о" о" о" о о о" о — — о" о о о о -Г -Г
^н м -. ОЭ СО — СО (^ Ю СО N ЮЮЮ S Ю
СО 00 О ЮНОЮ СО СО _ Ю—ifO -« Ю —< ?J?J
СО ЮОО -^"ОО СМЮ CD "-<ОО *^ СЧ^ »-^ О^ СО
о о" о о" ооо оо — —' о о роо —• «
о
" oot^-Tf Tf и о) сосл ооою ?3®о с2!2
[| Ю Tt*OO -*OO н ^< Ю ^^OO "^.C4^. &l ^
о о" о" о" о о о" о оо -" —> о о роо °
ОЮ* ю CN N -нОО Tft^-CO Ю СО Ю П N
0H0 CNCOCN П S t-. — CO TfCNO QJCO
Tf СО S о —' О О —• СЧ Ч<_ О_ О_ О_ —<„ CN_ --_ 00_ СО
о" ооо" о" о о о" о" — —" о" о ооо о" —¦
О) •* О — CM t- t^.00 ЮтСО W * О PS
0H0 О 1Л ^ t^-t^- CN*-^CO VOOO CNO
CO CN«O -^ ОО О— CO_ O_OO_ ~1 °i "Т. °°. °Я
о о" о" о" о"о"сГ °"р "^ — оо роо °"J*
TfOOCO СООф COCN — О СО tj-LOTf CO-*
О СО О s те О СО00 t^-^-CN Ю СО СП TfLO
СЧ CN С? О ООО ОО СЧ О"} Ол О, "^ ^ О^ ^ СЧ^
о ооо ооо do — о"оо ооо" °""Г
CO^Ht^. OOCOTf —* Tf СОСЧСЧ СОСООО СООО
ОЮО СОСЧО ^^СЧ ^н О CN t^-COOO CD N
—, ^-чОО ООО ОО -^ ООО^ ^.^.^. ^^1
о" о"о"р* о"сГо" о" р" ^ ооо ооо о—<
-¦^ — ч*-' ^-^ d- *3- ^-^ !С' tf~^ -»*» ^-' ^^ ^^ ч^-' '*-' ~—-' >^» >^
м « 1Я о « ч]< ^— ¦— ^H«ia ow^t —
тг,тг,тг, OQOQOQ е-3 "^"^'^ OQOQCQ 9.3
Приложение
О) N Tf CO to О) ЮО) ЮОО) Ю —' Ю C4Tf
TfTfCO СЧ Tf —1 COCO СО СО Ю TfC4O ЮЮ
o_ сч_ o_ o_ —¦_ co_ ~_ co_ t~- o_ —op —¦ co_ -4 сч -и
со —' о о" о" о" о" -о Tf -Г о" о о" о" с? —Г сч"
О")СЧСО t^-t^-^^ 0H0 ЮОО О)т^СО Ю N
Ю Tf СО ^Н^СЧ СОтр TfcOCO Tf CN О COCO
О)_ СЧ_ О_ О "Iе"!"™. СО Ю_ СЛ_ —_ О_ О_ —• СО_ —« СЧ О_
сч" —Г о о о" о" о" —« с? со" —<* о о о о" о —Г сч*
OOt^CN ЮСОСО О СО СО О) —1 СЧОООО О)^-
CDCOCO О Tf tN S Я ЮСОСО a) CN О SCO
°Ч. '-Ч °. °. "~1 °Я ~t и. °Я °°.  ° °. *"¦ m. ™ w °i
сч" -^ о о" о" о" о" —<* о со* —* о" о" ооо —Г —
СО — -Ч ^-иЮ'ч** ООСЪ t--O0C4 Tf —^ О СЧСО
N СО CD O)TfC4 СОЮ СОСОСО ЮСОО О> iO
"""¦ СЧ. °. °. Ч. и. ~1 'Я ~ ¦*! "" ° Р. — со — сч оо
сч" —" о" о" о" о" о •-" о" со" — о" о о" о о* —" —"
f- СО О CD CN Ю СЧСО ООСОСЧ ЮтfO ЮГ^-
ООСЧСО S Tf CN COCO P-CQCD ЮСО— ОСЧ
со_ сч_ о_ о_ о_ со — со о со — о о_ -i то —' п N
СЧ --чОО ООо" — р" со" —* о" О о" О* о" S ~
II ] II
ЮО00 О)О)С0 СЧСЧ OTfC4 Tf N CN 0000
00 CN Ю Ю П CN If) О* Ol CD CO Ю CO —< — 00
ю сч_ o_ p o_ co_ »- co_ сч ю —¦_ о o_ — со ~ со ю
сч" —" о" о о о" о* —¦" о" со —" о* о" о о" о* -" —"
II I II
СОСОСО — Tf CO OOTf СЧСЧСЧ СЧОСО OS
00—;Ю TfCOC4 COO О СО СО ЮтР_ COCO
Tf^ СЧ^рр Р.^^. CO^Tf Tf СЧОО рч СО « COTf
сч" — о" о" о о" о* —* о" со" —* о о о" о" о" —* —Г
Ю t СО СЧОСО COS TfO)CO CO СО Ю -"СО
00ОЮ СЧСЧСЧ — S —' Ю СО S.Tf-H TfS
со^ cn о о рсо^— сою со счоо — со —* сосч
сч —' о о ооо ^-о" со" —"о* о о"о"о" —* —'
SCOCO C4CNCO TfS СОЮСО COTfCO — Tf
ОЮ ОСЧСЧ О)СО СЧЮСО ^^^ ЮО
CN CN О О О СО_ — CN S_ CN CN О О — СО — СО —
сч — о" о о" о" о" —"о со" — о" о о о" о" —" --"
- •« Tf COTfCO Tfrf OO^^CO СОСООО O)Tf
(~ою —„.^ сооо союсо со-*— юсч
—i cn q о рсо_—_ СЧ°° ~ счоо — со — со о>
сч — оо ооо ^Р ^ -^о"о" о"о"о" —"о"
^ " "? ^ —м «Э О « ч*
т^т^тг; oqcqcq е-а "^"^"^ oqoqcq
257

258
ел
сз
а-
Приложение
СО
Ю
О
СО СО СО ™-< СП СЧ
Ю lO (D W Ю - СО
О О тР О СП О in Ю
CN —" О — О о" О* О
CN О 00 СМ О) Tf
MS О Л ПЮ
°°. г~". ~~i ~1 ^ °i
о" о" —* О О —*
cnoincoooto о со со со in сп о in
СО — СП СП СО Tf — Ь- 1П тГ СО t~- CS СП
СС ОтГСЛООР-_ СО 1П_ СО_ СО S - О N О
-* -Г р о" — о" о" О—*
О CN
to со
?2:
СО О О —¦ О О
— ¦* СО
ийо
СО_ —«_ СО СП_ _ _
— —" о о" ~* о~ о
о
Г~ тГ 00 О!
я о сп со
О_ СП СО ¦*,
~ о —
Ю 00 (N О N W
TfOOOOCN—«CO
— <N_ |~~ Ю О О|
-Г о о —" о" —"
о
о -j<
CS
о
¦ч}* 1П -ч«« ^f О О COCO
Uj -' CO CO — Ю г^ СП
CN -и IN [О S О 1С 00O
- -cfo-o- о-"
—« r- 00 Ю Ю CN
^ I>- —' О ^ ^
~• ^ q o^ oq oi
o* o* in о -
о о
О О W О N Ю СЧ
—I (ч ^. s о СО оо
00^ - О СО IN q - СП
О*" -н' О О W О IN О
© ю оо © © © оо
t4* СО Г*"- ^^ ^5 ""¦ ^5 ^5
CD О О - Ю О ^f O1^
о" —Г о" о" <n" о" <n ~S о"
о
СО О О) СЧ О N СО^О
СО « N СО О (О о W
о о о t^ о ^ о со
Т"
СО N
о о о
- о о
о cn —То
I I I
О CN
I
СО Tf N О -н СО COCD
1>- ~^ Ю © © СО СО©
CD 00 N 1-' © <N О <N*~1
СО* ©" ©" ~ ©* ©" © ©" <N
I I
S
сч
СО О О —' О О О
7
°|
Tf ^t lO G) О) О Ю t^
—' lO 00 N Ю О f-<N
СО О^ CD •—I —я ^ч CD oi ©
со © © — о о
о
о-
-3" СО СП СО СП
СО IN 00 N П
О СП СО_ —;I CN —<_
со" о" о" —" о" о" о
00 f~ СО CN о 0°
— со сп,
I °
^ CN 'ф «О О) ^ Г-.СО
Ю О) 00 00 « Ю СО ^
о ю ^ со^ —^ сч со сп
о" о" ^Г о" о" о о ~
СО —¦ ~ СЧ О Tf 00
Is— CD l>- О О t4* qo
CD СП Lf^ -^ Ю^ —^ О^ СО
о" о" —" о" о" о о"
Т " I
а з 8 s ^ 2 сЗ
1П —' CD О — ^ 00
о о — о о о
00 -^ О '—'
©ОтР
о"
— 00
О1^
—Г о" о" сч о" сч -о
I I
„ -N N ¦* •*
?^ 8--^ 8-
'-Ч
сч"
CD
CN
О
СП
¦ч-
о
СО
—«
CD
t*-
о
со
CD
О
о
СО
о
CD со
CD CO
о-
О о w (N
а ?
Приложение
259
о
CN
OCOincOTfCN
-мяо *о
оосъьпо^
О О О О О О
О
N Си
COCO
—^ 1П
о" —" о о" о" -" о и
III I
OOOCSOOLOtj-
СП 00 СП СО С5 СО
ооооо"о"
СО ^ О N tO ^ С5СП
gTf СО О CS О » Я
h~_ 00^ СП О_ CD_ CD_ 00_
—Г о о" о о о о-
TfCDLOCOCOCO
-Г „" о" о" — о" о* о ~~
о
СО — CN 00 00 СО 1П —<
оо_ Ю — h- т* —_ ¦* — in
со" о" •— о" о" о" —• o"cn
О
<О_ 1П
со "
О> СО f * N N
О ^ О) О СО СО CD
1П —^ t^- -^ —«СО ^^
""" *
ОО
CD—"
Ю
--ооо—
t^COTfCNCDCO r~t^-
CN Ol CN CN Я N t^t^.
Tt«_ CO О 00 CO —> —¦ "T.Tt"»
CO О —Г о" о" о" -<" «DCS
о"
88=:? 8S
't О СЯ ОСО
CD «
o о
СЛЮСЧЮЮ
OOCNCOCOOCD «t
о cNcomoooco оо
- -оо-о- --Г
о
мл и и •* и со
1П CD 1П CO —" —' СП
CS (О О CO W -^ О ^1
-" О* О
о —• о cn
ScoScSg^ go
© CD©00~4""~'00 ь>| ^Ч
со" о" -" о" о о" о о <n
CD0000C4C4CD ^f О
со s ^ n о со oj О)
СЧ СО -^ О О ON
о" —Г ©¦ ©" <n ©
I
I
о" -." о о" м* о «" —•
о
CN 00 CN
OOt^
о
'сГ
°
й§с?|л
00 N О СО О О
CN О" —* О" О О
о о —.00
to soioioo* «.n •¦¦i
CN 6" О" о" О О О О CS
Tf СО О) СП CS, О. Л ". °i
<N О" о" О* О О О О Cj»
CN
О
о о
— о
СП
о
о
CS
О N
8 §
О CS
¦^ е-
о
3
SJ
7
CN
СМ
(Л
in со
оо
¦ч: 8-
CN
СП
о
"ч;
,349
о
18
о
ш
7
э-
В
СО
1
8^ !

Продолжение табл. 9
Фо
МП
ИИ
Ч>4
\А9\
МП
Ф4
1*1
Фа.
0,2
1,026
—0,004
0,020
2,938
0,000
2,905
1,019
—0,160
2,2
0,666
—1,180
0,722
0,082
0,043
—0,375
0,303
—2,451
0,4
1,107
—0,034
0,084
2,708
0,000
2,643
1,075
—0,347
2,4
0,615
—1,199
0,706
—0,041
0,050
—0,557
0,254
—2,505
0,6
1,238
—0,123
0,206
2,4,21
0,000
2,322
1,157
—0,588
2,6
0,573
—1,218
0,688
—0,154
0,058
—0,731
0,216
—2,550
0,8
1,376
—0,300
0,387
2,050
0,002
1,914
1,218
—0,912
2,8
0,538
—1,237
0,668
—0,258
0,067
—0,899
0,187
—2,588
щ — 0,6
1,0
1,413
—0,553
0,584
1,607
0,006
1,433
1,167
— 1,304
3,0
0,507
— 1,257
0,645
—0,355
0,075
— 1,063
0,163
—2,622
1,2
1,292
-0,799
0,710
1,179
0,011
0,965
0,981
-1,677
3,2
0,479
-1,277
0,621
-0,443
0,083
-1,223
0,144
-2,652
1,4
1,106
-0,971
0,755
0,838
0,017
0,581
0,763
-1,960
3,4
0,453
—1,295
0,595
—0,524
0,091
—1,379
0,128
—2,679
1,6
0,943
-1,070
0,759
0,581
0,022
0,279
0,587
-2,154
3,6
0,429
-1,313
0,569
-0,598
0,098
-1,531
0,114
-2,704
0,821
-1,125
0,750
0,383
0,028
0,032
0,459
-2,287
3,8
0,407
-1,328
0,542
-0,664
0,105
-1,680
0,103
-2,727
2,0
0,732
—1,157
0,737
0,221
0,035
—0,181
0,368
—2,381
4,0
0,387
—1,341
0,516
—0,723
0,111
—1,825
0,093
—2,748
a
к
Продолжение табл. 9
тг = 0,8
\АЛ
Фо
\а,\
ф2
\At\
Ф4
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
1,035
—0,005
0,020
2,936
0,000
2,904
1,028
—0,162
1,148
—0,048
0,087
2,695
0,000
2,629
1,114
—0,360
1,338
—0,178
0,222
2,368
0,000
2,267
1,250
—0,643
1,520
—0,450
0,428
1,899
0,003
1,764
1,346
—1,063
1,465
—0,813
0,605
1,347
0,006
1,174
1,209
—1,564
1,198
—1,090
0,659
0,889
0,010
0,675
0,909
— 1,968
0,949
—1,235
0,648
0,573
0,014
0,317
0,655
—2,224
0,777
—1,299
0,625
0,352
0,018
0,049
0,483
—2,384
0,662
—1,325
0,605
0,183
0,023
—0,168
0,370
—2,488
2,0
0,583
—1,336
0,587
0,042
0,028
—0,360
0,293
—2,560
Чз
Мо|
Фо
\А,\
Ф2
Ф4
\W\
Фш
2,2
2,4
2,6
2,8
3,0
3,2
3,4
3,6
3,8
0,526
—1,342
0,570
—0,080
0,033
—0,538
0,239
—2,614
0,483
—1,349
0,554
—0,192
0,039
—0,707
0,199
—2,656
0,448
—1,358
0,537
—0,295
0,046
—0,872
0,169
—2,691
0,418
—1,369
0,519
—0,391
0,052
—1,032
0,145
—2,720
0,392
—1,382
0,500
—0,479
0,058
—1,188
0,126
—2,746
0,369
—1,395
0,479
—0,562
0,064
—1,341
0,111
—2,770
0,348
—1,407
0,458
—0,637
0,070
—1,491
0,098
—2,791
0,329
—1,419
0,436
—0,704
0,075
—1,638
0,088
—2,811
0,311
—1,429
0,415
—0,765
0,080
—1,781
0,079
—2,829
4,0
0,296
— 1,437
0,394
—0,819
0,085
—1,922
0,071
—2,845

Продолжение табл. 9
0,2
2,2
0,4
0,6
0,8
щ = 1,0
1,0
1,2
1,4
1,6
2,4
2,6
2,6
2,8
3,2
3,4
3,6
1,8
А„\
Фо
А*\
Фг
лл
Ф4
W |
1,045
—0,007
0,020
2,935
0,000
2,902
1,037
—0,163
1,191
—0,062
0,091
2,680
0,000
2,615
1,157
—0,374
1,450
—0,242
0,241
2,302
0,000
2,202
1,355
—0,707
1,647
—0,631
0,464
1,719
0,003
1,583
1,458
— 1,243
1,418
— 1,073
0,586
1,087
0,006
0,913
1,171
— 1,824
1,048
— 1,324
0,576
0,654
0,000
0,440
0,796
—2,202
0,795
— 1,424
0,543
0,384
0,012
0,128
0,549
—2,413
0,640
— 1,454
0,516
0,197
0,015
—0,105
0,399
—2,539
0,542
—1,457
0,495
0,051
0,019
—0,300
0,303
—2,620
3,8
Ао\
Фо
А2\
Фа
А*\
Ф4
W |
Фо>
0,429
—1,447
0,465
—0,185
0,027
—0,643
0,195
-2,719
0,392
—1,445
0,451
—0,288
0,032
—0,803
0,162
—2,752
0,363
—1,447
0,436
—0,384
0,037
—0,961
0,137
—2,780
0,339
—1,453
0,421
—0,474
0,042
—1,115
0,118
—2,803
0,317
—1,460
0,404
—0,558
0,047
— 1,266
0,102
—2,825
0,298
—1,469
0,387
—0,635
0,052
— 1,415
0,090
—2,844
0,281
— 1,477
0,369
—0,706
0,056
—1,561
0,079
—2,861
0,265
—1,485
0,352
—0,770
• 0,061
—1,703
0,071
—2,877
0,251
—1,491
0,334
—0,828
0,065
—1,843
0,063
—2,891
2,0
0,476
—1,452
0,479
—0,073
0,023
—0,476
0,240
—2,676
4,0
0,238
—1,497
0,317
—0,878
0,068
—1,981
0,057
—2,904
t
A0(t)
АЛО
АЛО
w(t)
t
АЛО
АЛО
АЛО
t
Ай@
АЛО
АЛО
t
АЛО
АЛО
АЛО
0,1
0,382
0,422
—0,089
0,020
1,1
1,110
—0,151
—0,004
0,691
2,1
1,062
—0,194
0,012
1,013
3,2
1,007
—0,029
—0,004
1,043
0,2
0,648
0,632
—0,074
0,066
1,2
1,108
—0,206
—0,024
0,743
2,2
1,056
—0,173
—0,012
1,025
3,4
1,002
—0,015
—0,001
1,036
0,3
0,810
0,658
—0,002
0,132
1,3
1,106
—0,244
—0,041
0,791
2,3
1,053
—0,156
—0,019
1,034
3,6
0,999
—0,003
0,005
1,029
0,4
0,926
0,613
0,044
0,205
1,4
1,105
—0,265
—0,054
0,833
2,4
1,046
—0,142
—0,008
1,041
3,8
0,996
0,005
0,006
1,022
т1 = 0,2
0,5
1,002
0,513
0,068
0,281
1,5
1,099
—0,280
—0,053
0,871
2,5
1,039
—0,127
0,001
1,046
4,0
0,995
0,012
—0,004
1,016
0,6
1,045
0,374
0,082
0,358
1,6
1,093
—0,284
—0,041
0,905
2,6
1,033
—0,108
0,004
1,049
4,2
0,995
0,012
—0,001
1,011
0,7
1,075
0,240
0,073
0,433
1,7
1,088
-0,275
-0,025
0,934
2,7
1,028
-0,091
0,007
1,050
4,4
0,994
0,012
0,004
1,007
0,8
1,095
0,117
0,051
0,504
1,8
1,082
—0,262
—0,004
0,959
2,8
1,022
—0,078
0,009
1,051
4,6
0,995
0,013
0,001
1,003
Таблица 10
0,9
1,102
0,002
0,036
0,571
1.9
1,075
-0,246
—0,019
0,981
2,9
1,018
—0,062
0,006
1,050
4,8
0,995
0,012
—0,000
1,001
1,0
1,107
—0,086
0,018
0,634
2,0
1,069
—0,220
—0,029
0,998
3,0
1,014
—0,049
0,002
1,048
5,0
0,996
0,009
—0,000
0,999

Продолжение табл. 10
t
AAt)
AAt)
Л4 (/)
w(f)
t
A0(t)
AAt)
Ai (f)
w(t)
t
ААП
AAt)
AAt)
w(t)
t
A0(t)
AAt)
AAt)
w(t)
0,1
0,214
0,238
—0,052
0,010
1,1
1,123
0,027
0,015
0,596
2,1
1,174
—0,233
0,004
1,043
3,2
1,050
—0,085
—0,002
1,117
0,2
0,398
0,395
—0,051
0,038
1,2
1,146
—0,038
0,001
0,658
2,2
1,165
—0,224
—0,007
1,065
3,4
1,031
—0,059
—0,001
1,105
0,3
0,549
0,469
—0,018
0,081
1,3
1,165
—0,092
—0,013
0,718
2,3
1,156
—0,214
—0,013
1,083
3,6
1,014
—0,036
0,002
1,089
0,4
0,678
0,492
—0,010
0,133
1,4
1,178
—0,141
—0,026
0,773
2,4
1,146
—0,204
—0,008
1,098
3,8
1,000
—0,015
0,004
1,073
mx = 0,4
0,5
0,785
0,473
0,031
0,193
1,5
1,187
—0,180
—0,032
0,825
2,5
1,134
—0,191
—0,003
1,109
4,0
0,990
0,000
—0,001
1,057
*
0,6
0,873
0,417
0,046
0,258
1,6
1,191
—0,209
—0,030
0,872
2,6
1,122
—0,176
—0,000
1,117
4,2
0,983
0,011
—0,000
1,041
0,7
0,946
0,346
0,049
0,325
1,7
1,193
—0,228
—0,024
0,915
2,7
1,110
—0,161
0,001
1,122
4,4
0,978
0,020
0,002
1,027
0,8
1,006
0,265
0,044
0,394
1,8
1,191
—0,240
—0,013
0,954
2,8
1,097
—0,146
0,003
1,125
4,6
0,976
0,025
0,001
1,015
0,9
1,053
0,179
0,038
0,463
1,9
1,187
—0,245
0,000
0,988
2,9
1,085
—0,130
0,003
* 1,126
4,8
0,976
0,028
0,000
1,005
1,0
1,092
0,099
0 029
0,530
2,0
1,181
—0,242
0,009
1,018
3,0
1,073
—0,114
0,002
1,124
5,0
0,977
0,028
0,000
0,997
о
сь
a
с
Продолжение табл. 10
t
AAt)
A2(t)
А АП
w(t)
t
A0(t)
AAt)
AAt)
w(t)
t
AAt)
A2(f)
AAt)
w(t)
t
A0(t)
A2(t)
AAt)
w(t)
0,1
0,149
0,166
—0,036
0,007
1,1
1,041
0,117
0,017
0,504
2,1
1,254
—0,196
0,002
1,022
3,2
1,145
—0,137
—0,002
1,191
0,2
0,285
0,285
—0,038
0,026
1,2
1,085
0,063
0,007
0,567
2,2
1,254
—0,200
—0,006
1,055
3,4
1,113
—0,113
—0,002
1,185
0,3
0,409
0,354
—0,017
0,058
1,3
1,123
0,012
—0,003
0,629
2,3
1,252
—0,202
—0,010
1,085
3,6
1,083
—0,088
0,007
1,172
0,4
0,521
0,391
0,001
0,098
1,4
1,156
—0,033
—0,013
0,688
2,4
1,247
—0,203
—0,007
1,110
3,8
1,054
—0,064
0,002
1,154
m1 = 0,6
0,5
0,623
0,396
0,017
0,145
1,5
1,183
—0,074
—0,019
0,746
2,5
1,239
—0,200
—0,004
1,132
4,0
1,028
—0,041
—0,000
1,132
0,6
0,714
0,374
0,029
0,198
1,6
1,205
—0,110
—0,019
0,801
2,6
1,229
—0,195
—0,002
1,150
4,2
1,006
—0,022
—0,000
1,109
0,7
0,796
0,336
0,034
0,255
1,7
1,223
—0,138
—0,017
0,852
2,7
1,218
—0,188
—0,000
1,164
4,4
0,988
—0,005
0,001
1,085
0,8
0,869
0,287
0,033
0,315
1,8
1,236
—0,161
—0,011
0,900
2,8
1,205
—0,180
0,001
1,175
4,6
0,973
0,009
0,001
1,062
0,9
0,933
0,231
0,030
0,378
1,9
1,246
—0,179
—0,001
0,945
2,9
1,191
—0,170
0,000
1,183
4,8
0,963
0,020
0,000
1,041
1,0
0,990
0,173
0,026
0,441
2,0
1,252
—0,190
0,005
0,985
3,0
1,176
—0,160
0,000
1,189
5,0
0,956
0,028
0,000
1,022
Sq
о
N
a
с

266
Q.
Приложение
— СО — СО
» О1 (N N
— о" о" о о cn"
и too о
со со о со
8 8 8
СО IN О W h- CO О >—• h-OOOO
i —" о* о" о* со <—" о" о' —Г ю" о* о" о —*
с^ оо сч о со
о" о* о" о" о
— — о
О (N IN О
оо о^ сч —• 8
о" cs —<* о" о"
I
О
О -—¦ СО О — Ю О
оо ass.s .о atg
о о о" о — — о" о" о* cn* —Г о" о"
(О (О 12? ОО
со со о <м
СО СО (N СО |*~ СО — t»
СП СО — t» О) ь О СО
—' О О h- h- CN — О —
О О О О О — — о" О о" CN —* о" о" —"
¦Y
00_ СП О О —
¦*" о" о" о" —
Г» t» О О
— CN О ^f
со_ о о о —
¦ч" — о" о" —
Ю Ю — 00
S S 8 2
— СО CN СО
о N О i1
t— С»— СП CNoOCOCO
со SSS? «28SS! со g?8^ с oS82
о о о о о - - о о" о" cn — о" о" -" Tt* —" о" о" —
оо
о
О-3- —
§8
И i1 О Ю N Ю IN N СО СО СО Ю
— СО •—' •—• (NO'—CD Ot»P —
Ю ЮСОО—• Ю — О О СО Ю СО *—< О -« ^^ ¦—^ч^ч-* t.N
о" о" о о" о" —" — о о" о" cn" —" о" о" —" ¦*" — р* о" —"
I
и и о s оо со о о осоооо # о о со
¦* •* п о о •* qooS -t со- о о со — — о см
о* о" о* о* о — -<" о" о" о* см* — о* о — со* — о* о" —
•* Tf Ю Ю СО о
CN СО — -^ ^* fc.
COCOtNOO СООО
соооою coisii coS^ii
о о о" о о" -Г - о" о" о" cn" - о" о* - со" - о" о* -"
CN
,222
о
,113
,222
о
,127
о
с-
,030
1
,028
Ч1
,020
о
,005
о
с-
со
as
cn as
— о
s
— СП
—. о
о
111
О
154
о
С4
008
о
016
о
с-
490
о
431
о
^^
3
00 CN
С -о
CD CN
-ИЗ
CN — О
с- с-
о «
004
о
001
о
С
012
971
о
3
со
CN
СО
215
246
—¦
с-
9
142
—0,
157
—0,
^^
CN Ю
8 S
1~
88
О CN
О —
?<с
Приложение
267
lOOOOOtN
00ОЭ — CN
N "" ° n.
СО О СО ^
СООООСО
°i. °. °. °°.
* " " "
ОСЛО —
СО И О (О
° ° °
—" о* О* О о" cn" —* о" о" о" со" —" о" О —" ю" — о" о —
о О
-~а>Р,о ¦* ся о f — со о оо cnlooco
CNtNSJf^ О On- Ч1 ЮОФ COTfOO)
oi sin о и в и о о as cn со_ —^ о_ —_ со о_ о о_ —_
о* о* о* о" о — — о" о о" cn" —* о" о" -^ Tt<" — о о* —"
^ (О О -
Ю LO ^ CN
С» СО CN_ О (N
о* о" о" о о*
CN — COtN
s Tf о (О
О О t
О
S W О СО
CTICOQCN
О_ О_ О_. CN_
" "
—* —" о* о* о cn" —" р* о -* ¦*" — о о —
о* о
о -* ¦*" — о о
СО to О) ю
СО N - N
ю w о —
" "
о* о" о* о" о" —'
СОГ^СЛСЛ
СО — ОО
— oot^- ^
— о о о и -
СП Q — Ю
СОЮО-*
co^'-^p—^
СО
^p^ ^
о"о"- ¦*" — о" о
СПоО^СО tD СО С) ^ TfLOCNTt*
о со — со фоою со^о—
LOtNO— СООООСО tD СО — О —
" " * " " " " " "
CNt^- — О
о о о" о" о* —" —" о" о о cn" —" о о —"
— cnooi^lo cot^.oooo
m Ж О О1 ЮСООО)
|| ю ^ cS p S in p d o_ in
м о о" о о о" —¦" — о" о" о"
S I
ю 2 со со
И СО О S
со — о о_
" "
^p
•* - о о —
— О
— о_
_ р
—' р р" —" Tt<" — р р
II II
_ — CN СО
1ft t» О СО
¦*_ СО CN_ O_ О_
о" о о р о
о о о_ ю
— о о" о
1
TfOTftN Ч1 00 О IN
— СО О * "CN0 01
¦Ч" СО — ОО 00 CN — О CN
е,- --оо-- Co" -"op--"
ООСО^СО COOCNCO 00OCD—
О^СО ЮОО00 СП О р
О о П СЛ
COOCNCO 00OCD
СОО^С ЮОО00 СП — О р
СО IN CN О_ о_ П СЛ ~ О_ -Ч<_ СО_ <N_ —_ О_ р
о" о" о" о" о" —¦" о о о" о" cn" —" о" о" -^
СООО
Г^.ч^О
СО_ CN_ — О
со" —* о" о
— CN Ю СО
cooocn—
TfOCNOO
оюог
. . . . . 1 .
о" о" о" о" о —" о" о* о о и
CNCOCOO О ^ СО СО TfO
on о со оооою ою
" * " о'о'о" со — о" о
ЮСОтРЮ
t< СО t
(NCO^
CHOCNO Tt< СО
— О — О_ О —_ 00_ —
" * * " " "
— CN
О -
О О)_
"
Ю lO IN
(NLOO
СО_ —_ О_
_ _ _ _ _ р _ _
о" о о о* о* —" о" о" о" о" cn —" о* о о" со" —
р _ _
о* о о" со" — о о
? ?
? ? ?

268
Приложение
lO — CD —' Г-~
о s -и мм*
- о о о о о
о" о" о* о" о"
оо to и о oi
сп со со ю •-•
on CQ — Ю |~~ 00
. о о о о о
~ о" о* о* о" о
МЛ 00 " О
«о fe g g 2 ~
" о о" о" с? о*
00 CN CN ТР 00
СП Г- И CN Ю
¦* 2 8 о 2_ =
~ о" с? о* о* о"
И !D Ю N S
lOfflCO-O
_, N Ю IN !D 00
°1 — о_ о_ еэ о
*¦* о о" о" о" о
Ю СО СО Ю l4^
CN Ю СО СО О
~ 00 Г-- 00 СО -н
Я; и - о о о
~ о о" о" о" о"
Mill
ф iO ф -н О
О CD О О 9
i tJ- CO IN N -
о o
Tf (N N N •*
тр ф Oi О ^
m CD О ^ 00 CO
ОД CD tO 1С Tf Tf
о <f «f <f <f cf
oo«mgi
Tf S О tO (N
_ 001OW S CO
¦*. o> o> o> со об
о о* о" о" о" о"
Mill
00 -4 О О О)
О О О) Г*» Ю
CS Ю Ю ^ Tf т(<
о т* Т ПГ Т "Т
—. CD
СО I4-
о о о
= S t « n
со
CN CN
О CD
111
о р р о о
Mill
о ¦* о ю со
<—' ^ »¦ О ^^
§§88
о р о о о
II I II
cd а о со
Г-- Г*- CN СО
СО т|« iO Ю
о о о о
ffff
О) Ю о. О
fff
ff
> о о о
> о о о
о о" о о о
о р о_ о_ о
о" сГ о" с? о"
о о о_ о о
о о* о" о" о"
о* о" о о" о"
—< О СО CN О
О CN ¦* СО СО
(М CN — — —
(N « И И И
fffff
о о р р р
о о о
I I I
CN h- тр СО СО
CN СО СО СО СО
CN CN CN CN CN
о" о о о о
Mill
h- Tf 00 00 Ю
CD СЧ —i О О
^^ CO CO CO CO
CN CN CN CN CN
1
О CN CN CN (N
CN_ CN CN_ CN_ (N
о" о о" о о"
тр — 00 h- lO
Ol С^ ^5 СЭ ^5
<—• CN CN CN CN
fffff
00 Tf Ю Ю
CD 00 00 00
СП СП СП СП
11111
|~~ 00 00
оо оо оо
о о о о о
II II I
1111
00
o"
СП CN СО СО СО
Ю О CD CD CD
Г-— t— Г— Г— Г—
1
о о о о
мм
E.0
¦Qo
о ю-°.
о -
E.0 00-
lO О
-^ cn"
ю о ю о
° о -" -Г CN
E.0 огз ay
° о
E?)
р
ю о_
—« CN*
р
CN
а
I
I
1
оо
о
Приложение
Ю 00 Ю Tt> Tf
.. .. 3 Tf Tf CDCOCOCOCO
— CN <M CN CN — CN CN CN CN
° ° ° ° Я ° ° ° ° °
СП Ю CD h- t*-
СО СО ^ ^Р ^Р
. » . . Я
о о" о о* о
. - .
о" о о о о
SSgg «go88
w „ _ „ . . CNCNCN
. °» °. °- Я. Я. °. Я. °. °- °.
-" о" о" о" о о о* о о о с?
Tf CO Tf
СП О О
Ю
О
I—^ I—^ I—^ I—^ 1***^
о" о" о о" о"
t^. 00 ¦* О СО
CN ¦* Ю Ю Ю
8 8 8 8 8
о" о" о" о" о
I
О 8 <=>
о
CN
о
СО Ю 00 00 00
о lo ю ю ю
р р р р р
о о о о о
О ~* '—' """• ^*
о о о о о
о о о о о
О —' СО Tt< Ю CN СО
— CN CN CN CN Й fc
8 8 8 8 8 8 8
—Г ооооо ооооо
Tf СП CN CN CN
СО Tf Ю Ю Ю
«" о* о о о о ооооо
CN CN СО СО СО
8 8 8 8 8
о" о о" о о
— Ю CD CO CD
^ о о о о о 8 8 § 8 8
о о с? о" о" о*
Ю СО I— t^. t^-
ооооо 88888
о о о" о* о о"
— CN CN CN CN
ооооо §8888
о о о о о
СП Ю CD CO CD
СП О О О О
11111
¦ч^ Tt< CD CO CO
СП О О О О
fffff
CN h- O> O5 СТ>
тр I>- I>- h- t--
8 8 8 8 8
fffff
Tf 00 О О О
CN Tf Ю СО Ю
8 8 8 8 8
fffff
8 CN CN CN CN
8 8 8 8 8
fffff
00 Q> О О О
00 О O> C? O5
fffff
00
о
CD CD CD СО
?п СП СП СП
р р р
о" о о о" о"
I М М
00
о
11111
fff
CD
00
о_
CD
00
о
CO
t-
00
р
1
CD
О
о
CD
t~-
с»
О
ffff
269
E.0 J!to
о
ю о
о" —"
E?) °*'
1Л
—
о_
CN
i
о ю- °.
° о -
E.0 ».
ю о
— CN
'эа
о ю- °-
° о -
E.0 ^
о
CN
I

E
E
©a
E
H
0
0,5
1,0
1,5
2,0
0
0,5
1,0
1,5
2,0
0
0,5
1,0
1,5
2,0
0,2
1,0835
1,1121
1,1427
1,1665
1,1891
—0,0040
—0,0042
—0,0044
—0,0047
—0,0049
0
0
0
0
0
0,4
1,0368
1,0902
1,1314
1,1595
1,1720
—0,0153
—0,0172
—0,0189
—0,0203
—0,0213
0,0003
0,0004
0,0004
0,0005
0,0005
0,6
0,9636
1,0257
1,0631
1,0707
1,0604
—0,0321
—0,0376
—0,0422
—0,0449
—0,0460
0,0001
0,0020
0,0024
0,0026
0,0028
0,8
0,8704
0,9284
0,9443
0,9291
0,9062
—0,0517
—0,0627
—0,0699
—0,0724
—0,0728
0,0047
0,0063
0,0076
0,0082
0,0084
1.0
0,7651
0,8060
0,7961
0,7674
0,7408
—0,0708
—0,0874
—0,0951
—0,0963
—0,0959
0,0107
0,0151
0,0179
0,0188
0,0190
1,2
0,6561
0,6722
0,6421
0,6084
0,5820
—0,0862
—0,1063
—0,1118
—0,1113
—0,1104
0,0205
0,0301
0,0347
0,0356
0,0357
1,4
0,5517
0,5422
0,5010
0,4648
0,4417
—0,0951
—0,1142
—0,1155
—0,1138
—0,1128
0,0344
0,0519
0,0580
0,0587
0,0587
1,6
0,4585
0,4294
0,3852
0,3522
0,3283
—0,0956
—0,1078
—0,1045
—0,1022
—0,1013
0,0524
0,0799
0,0866
0,0870
0,0869
Продолжение
1,8
0,3815
0,3431
0,3006
0,2689
0,2464
—0,0870
—0,0862
—0,0797
—0,0773
—0,0764
0,0736
0,1122
0,1184
0,1183
0,1182
табл. 11
2,0
0,3235
0,2871
0,2478
0,2173
0,1962
—0,0699
—0,0532
—0,0441
—0,0419
—0,0411
0,0967
0,1453
0,1560
0,1497
0,1495
270
илоз
сь
С
Продолжение табл. 11
1
с
Е
??
<¦*
Е
Н
0
0,5
1,0
1,5
2,0
0
0,5
1,0
1,5
2,0
0
0,5
1,0
1,5
2,0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,0001
0,0001
0,0001
0,0001
0,0001
0
0
0
0
0
0
0
0
0
0
0,0002
0,0003
0,0004
0,0004
0,0004
0
0
0
0
0
0
0
0
0
0
0,0007
0,0009
0,0011
0,0012
0,0012
—0,0001
—0,0001
—0,0001
—0,0001
—0,0002
0
0
0
0
0
0,0015
0,0021
0,0024
0,0025
0,0026
—0,0003
—0,0004
—0,0005
—0,0005
—0,0005
0
0
0
0
0
0,0027
0,0037
0,0042
0,0043
0,0043
—0,0007
—0,0012
—0,0014
—0,0015
—0,0015
0
0
0,0001
0,0001
0,0001
0,0040
0,0055
0,0060
0,0060
0,0060
—0,0016
—0,0028
—0,0034
—0,0034
—0,0035
0,0001
0,0002
0,0002
0,0002
0,0002
0,0051
0,0068
0,0070
0,0069
0,0069
—0,0033
—0,0059
—0,0068
—0,0069
—0,0069
0,0002
0,0005
0,0005
0,0006
0,0006
0,0056
0,0066
0,0063
0,0062
0,0062
—0,0061
—0,0110
—0,0121
—0,0123
—0,0123
0,0005
0,0011
0,0013
0,0013
0,0013
2,0
0,0050
0,0038
0,0030
0,0029
0,0028
—0,0101
—0,0184
—0,0199
—0,0199
—0,0199
0,0011
0,0024
0,0027
0,0027
0,0027
о

272
Приложение
Приложение
273
О LO Ю 00 —
00 N СО С) О)
CD 00 CD lO Ю
— О_ О_ О_ О
о* о* о" о* о"
СО 00 —¦ CN —<
N CN Ю О О
— Ю CN CN —
00 CN ¦— — — —.
—' о* о* о" о" о
О N *•* Tf О)
S СО Ю 00 (О
CD CN ОЭ 00 00
СО CN CN — — —
—' о о о о о"
t4» LO
00
о*
со
о"
— ooooo
СО СО Ю Tf ю
О> СО N 00 U3
сч со^ со со_ со со
-Г о о о" о" о
ч со со ю
N 00 N CD
со со со со
о о о о о
t4- Г*- lO CO 1>-
00 O> CJ> CJ> 00
CO CO CO CO CO
о о о о" о"
О (М —< Tf CO
CD N ^ О> N
8 ffi S 8 Я
о о" о о" о"
Tf 00 CN Ю CN
ooooo
ooooo
ю о ю о
О* — — CN
A0 «о
а?)
S8888
о о" о" о о"
N О> О) CN О
CD Ю — — —¦
ООООО
fffff
lO lO •—' СО ~->
—< CN CN CN CN
ООООО
fffff
О О CN Ю Tf
СО Ю Tf СО СО
— CN CN CN CN
ООООО
ООООО
СО CN CN CN —
—• CN CN CN CN
ООООО
fffff
ООООО
о* о о о о"
- О) О) О О)
00 О -1 W ^
ООООО
ООООО
8 8 8 8 8
fffff
О) Ю S СО О
—< CN CN CN <N
8 8 8 8 8
о" о" о о" о
ХО СО CD NN
ООООО
ю о ю о
О" -" ~ N
C.0 18
00 Ю СО л. N
t~- CN (М S! CN
Tf CD CO Jo «О
о" о" о" о о"
СО О СО og <N
Tf Ю Ю ю ^
о" о" о о" о"
11111
о о" о о о*
о г- оо S3 °5
СО СО СО СО ^
о" о" о" о о"
СО Ф 1Л 1Д Ю
CN СО СО СО ^
о" о о о" о
о о> со со со
СО Ю CD CD CD
CN CN CN CN CN
о" о о о о"
SCN Tf Tf Tt*
CN CN CN CN
CN CN CN CN CN
о" о о о" о
S CO N NN
00 С7> О) О О>
о" о о о" о"
ю о> о о о
NN 00 00 00
о* о" о о о
So о о о
NN NN
о" о о о" о"
О « — О4
а»)
«2
в
Е
I
о
о
of
СО Tf N NN
Ю
О
ff
о о
о о"
— ООООО
о о о о_ о
о о о о о"
— ООООО
« ООООО
— — CN CN CN
ООООО
о о о о_ о^
о" о о" о* о"
CD
о
Tt-
о"
CN_
о"
а;
C?) ^
о о|
ООООО
ООООО
ООООО
ю о ю о
о о- _г _- cn
A0
о о о _
о о о о
о" о о о
N 00 00 00
N N N N
еэ о о о
о о о о
" о
т
fllll
iliii
fffff
8 I 8 I 8
ooooo
CN 00 00 00 O>
88888
fffff
N — —' — CN
§8888
ooooo
^ CO
CN CO CO CO CO
11111
о о о о
о о о о
о о о о
ffff
lO О Ю О
о" „" — CN
E0'
— оо о а> оо
Ю N N N N
N NN NN
о о о_ о_ о
о о о" о о
о о ^- -^ —'
Tf О CD CD CD
N N N N N
о о_ о_ о о_
ООООО
—¦ CD CD CD CD
CO Tf Tf Tf T
t^ t^. t^- t^- t^
о о o_ о o_
о" о" о" о о
CN СО СО СО СО
N N N N N
о о о о о_
о* о" о" о" о"
О Tf Tf Tf Tf
—¦ CN CN CN CN
N NN NN
О O_ p_ O_ О
о" о о" о о
— CD О CD CD
J^! N f^ N N
о* о о о" о
N —• О О О
l^. t t t t
о о о o_ о
о о" о" о" о"
N
8S8
N NN NN
о о_ о_ о_ о
о о о" о" о
CN CO CN CN CN
ООООО
N NN NN
о о о, о_ о_
о" о о о" о"
ООООО
N NN NN
о о о о_ сэ
ООООО*
_ ю о ю о
о о- _- _- м-
E0'

274
•8
«о
о
CN
о"
A0
Приложение
о
CN
оо
s
CN
31
77
Ю
CD
CN
7
—
со1
о
о
a
°
CD
CO
1
00
8
7
CO
CO
о
Ю
CD
1
O>
CO
7
—
05
о
4"
s
о
CN
CO
s
о
s
о
о
со
ю
08
о
8
07
о
S
S
о
8
о
О)
о
о
о
о
о
—,
о
о
8
7
о>
ш
CN
о
о
со
1A
о
о
CN
о
7
о
о
7
00 00
CN CN
о о
77
о о
77
со со oi io со
СО СЧ СЧ СЧ СЧ
сч со со со со
77777
<N CD h- CM СО
t4- О) ^5 00 СО
СО О) " О О
oi oi со со со
о о" о" о* о*
I I I I I
CN CD CT> CN CD
О СО О '"** Оэ
I—^ if} f^. f^. СО
CN CN CN CN CN
О О О* О О
I I I I I
—н ^ СО '—" СО
СО Ю тр 00 t*-
Ю О) - ^ ^
— •—¦ CM t>i CN
ооооо
о со ю ю ю
о" о" о" о" о"
I I I II
О CD CO
S N И
t*4» 00 CTl
о о о
77
СО СО
7777
n S й ? *
ооооо
77777
•* О)
ооооо
ю о ю о
СЧ Ci СЧ СО СО
со ^ ю ю ю
о о ©^ о о
о" о* о" о" о
00 СО И N
^CN CD CD
CN
о" о" о" о" о"
CN CO — t~- t^-
СО О) CN CN CN
— -< СЧ W N
О О О O_ О
о о о о* о
О 00 О CN СО
N О1 « И IN
о_ 8_ о_ о_ о
о" о" о" о" о
8
о
О
8
о
5
8
о
со
8
о
й
8
о
ю
8
о
я
8
о
8
о
ю
8
о
00
8
о
сч со со со
ооооо
7777
8 8 8 8 8
о о* о о" о"
Mill
g2288
8 8 8 8 8
ооооо
ооооо
—. CN CN CN CN
ооооо
ооооо
ооооо
ООООО ООООО
ю о ю о
о —" « cn"
Приложение
275
о
cn"
СО Ю CD CD
8888S
ооооо
-н t^ О —• —
и га ч1 ч1 f
ооооо
ооооо
77777
—¦* l»N l»N l-Ч l-Ч
со 8 8 8 8 8
- 77777
CD О CN CN CN
^ I 8 8 8 8
^ о" о" о" о о
I I I I I
- 77777
CN CN CN CN
^э ^? ^2 ^^
О ^3 О ^Э
оооо
7777
— CN CN CN CN
^5 ^э ^? ^2 ^^
^5 О ^3 О ^Э
о ооооо
00
о
о о о
ооооо
8888 8
о* о" о" о о"
о" о" о" о" о
о о" о" о" о*
ооо||
§ о" о о
ооооо
7777
ооооо
ооооо
ооооо
ооооо
ооо°° ооооо
оо ооо°° ооооо
ооооо
ооооо ооооо ооооо
a;
A0 Ъ
_ ю о
° o"-
B0 "-
in о
— cn"
er> ^ ^
o"~"
A0 es-
in O.
—' cn"
о ю-
о
A0
О 1Л О
— — CN

ЛИТЕРАТУРА
1. Аводжоби. Гармонические колебания твердого прямоугольного тела на по-
поверхности упругого полупространства.— В кн.: Прикладная механика. Тру-
Труды Американского общества инженеров-механиков. Сер. Е, 33, 3. «JVnp», M.,
1966, 80—86.
2. Аводжоби. Приближенное решение задач о колебаниях жестких тел на
упругом основании при больших значениях коэффициента частоты.— В кн.:
Прикладная механика. Труды Американского общества инженеров-механи-
инженеров-механиков. Сер. Е, 38, 1. «Мир», М., 1971, 110—116.
3. Александров В. М. О приближенном решении одного класса интегральных
уравнений. — Изв. АН АрмССР, 1964, 17, 2, 3—8.
4. Александров В. М. О приближенном решении некоторых интегральных урав-
уравнений теории упругости и математической физики.— ПММ, 1967, 31, 6, 1117—
1131.
5. Бабешко В. А. О единственности решений интегральных уравнений динами-
динамических контактных задач.— ДАН СССР, 1973, 210, 6, 1310—1313.
6. Баркан Д. Д. Динамика оснований и фундаментов. Стройвоенмориздат, М.,
1948, 283 с.
7. Бейтман Г., Эрдейи А. Высшие трансцендентные функции. Функции Бессе-
Бесселя, функции параболического цилиндра, ортогональные многочлены. «Наука»,
М., 1966, 296 с.
8. Бородачев Н. М. О решении динамической контактной задачи для полупро-
полупространства в случае осевой симметрии.— Изв. АН СССР. Механика и машино-
машиностроение, 1960, 4, 141—144.
9. Бородачев Н. М. Динамическая контактная задача для круглой пластинки,
лежащей на упругом полупространстве.— В кн.: Теория пластин и оболо-
оболочек. Труды Всесоюзной конференции. Изд-во АН УССР, Киев, 1962, 280—
283.
10. Бородачев Н. М. Об определении напряжений под колеблющимся фунда-
фундаментом. — Основания, фундаменты и механика грунтов, 1962, 3, 4—7.
11. Бородачев Н. М. Колебания штампа, лежащего на упругом полупростран-
полупространстве, под действием горизонтальной гармонической силы.— Изв. вузов.
Строительство и архитектура, 1963, 9, 19—26.
12. Бородачев Н. М. Динамическая контактная задача для толстой плиты в
случае осевой симметрии.— В кн.: Труды IV Всесоюзной конференции по
теории оболочек и пластин, Ереван, 1962. Изд-во АН АрмССР, Ереван,
1964, 248—254.
13. Бородачев Н. М. Динамическая контактная задача для штампа с плоским
круговым основанием, лежащего на упругом полупространстве.— Изв.
АН СССР. Механика и машиностроение, 1964, 2, 82—90.
14. Бородачев Н. М. Вертикальные колебания круглого штампа на упругом
полупространстве.—Строительная механика и расчет сооружений, 1964, 5,
33-36.
Литература
277
18
22
15. Бородачев Н. М. Определение динамических напряжений, возникающих в
упругом полупространстве под штампом с плоским круговым основанием.—
Изв. АН СССР. Механика, 1965, 4, 158—162.
16. Бородачев Н. М. Высокочастотные колебания круглого штампа.— Строи-
Строительная механика и расчет сооружений, 1967, 6, 31—32.
17. Бородачев Н. М. Контактные задачи теории упругости при динамическом
нагружении.— В кн.: Контактные задачи и их инженерные приложения.
Доклады конференции. Изд. НИИМАШ, М., 1969, 160—168.
Буряк В. Г. Динамическая контактная задача для упругой полуплоскости. —
Изв. АН СССР. Механика твердого тела, 1972, 6, 155—159.
19. Ватсон Г. Н. Теория бесселевых функций. Т. 1. ИЛ, М., 1949, 798 с.
20. Виленкин Н. Я., Горин Е. А., Костюченко А. Г., Красносельский М. А.,
Крейн С. Г. и др. Функциональный анализ. «Наука», М., 1964, 424 с.
21. Галин Л. А. Контактные задачи теории упругости. Гостехиздат, М., 1953,
264 с.
Гершунов 3. М. Оценка инерционных сил упругого основания в задачах об
установившихся колебаниях балок и плит, лежащих на упругом полупро-
полупространстве.— В кн.: Исследования по динамике сооружений и расчету кон-
конструкций на упругом основании. Труды ЦНИИСК, 2. Стройиздат, М., 1961,
78—89.
23. Годзевич И. Н. Об экономическом эффекте учета инерции основания в задачах
динамики фундаментов.— Изв. вузов. Строительство и архитектура, 1972,
4, 28—29.
24. Градштейн И. С, Рыжик И. М. Таблицы интегралов, сумм, рядов и про-
произведений. Физматгиз, 1962, М., 1100 с.
25. Гудуишури И. И. Учет реактивных касательных напряжений при расчете
полосы конечной жесткости на упругой полуплоскости.— Сообщ. АН ГССР,
1957, 18, 1, 67-75.
Гудушаури И. И. Расчет фундаметных полос конечной жесткости с учетом
реактивных касательных напряжений.— Изв. АН СССР. Механика и маши-
машиностроение, 1959, 4, 77—83.
27. Дудин В. Р. Свободные вращательные колебания фундамента на полупро-
полупространстве.— В кн.: Материалы к предстоящей научно-технической конфе-
конференции. Секция строительного производства, 3. Изд. Сиб. металлург, ин-та,
Новокузнецк, 1972, 51—58.
28. Дятловицкий Л. И. Напряжения в гравитационных плотинах на нескальных
основаниях. Изд-во АН УССР, Киев, 1959, 340 с.
29. Дятловицкий Л. И., Ермоленко А. И., Лемберг Э. Д. Исследование нестацио-
нестационарных колебаний бетонной плотины, взаимодействующей с жидкостью.—
В кн.: Труды координационных совещаний по гидротехнике, 64. Динамика
гидросооружений. «Энергия», Л., 1972, 161—170.
30. Дятловицкий Л. И., Сеймов В. М., Ермоленко А. И., Кукленке Н. П. Со-
Сопоставление точного и разностного решений плоской задачи о распростране-
распространении упругих волн.— В кн.: Труды II Всесоюзной конференции по числен-
численным методам решения задач теории упругости и пластичности. Изд. СО АН
СССР, Новосибирск, 1971, 114—125.
31. Дятловицкий Л. И., Чудновский В. Г., Лемберг Э. Д. К вопросу о колеба-
колебаниях гравитационных плотин под действием кратковременных нагрузок.—
В кн.: Труды координационных совещаний по гидротехнике, 47. Сей-
Сейсмостойкость гидротехнических сооружений. «Энергия», Л., 1969, 132—
145.
32. Закорко В. Н. К динамической задаче о распределении давления на контакте
круглого штампа с упругим полупространством.— Физико-технические про-
проблемы разработки полезных ископаемых, 1965, 3, 3—13.
Закорко В. Н., Ростовцев Н. А. К динамической контактной задаче стацио-
» „—„„„тпацгтм _ пмм. 1965. 29, 3, 545—
26.
33.
ЗаКОрКО D. 11., гиыииоцсо it. ... -ч „
нарных колебаний упругого полупространства.
552.

278
Литература
34. Ильичев В. А. Действие импульсной нагрузки на массив, лежащий на упру-
упругом инерционном полупространстве.— Строительная механика и расчет
сооружений, 1964, 6, 32—37.
35- Ильичев В. А. К вопросу о передаче через грунт колебаний от одного фунда-
фундамента к другому.— В кн.: Доклады к Международному симпозиуму по ди-
динамике грунтов, 1967. Стройиздат, М., 1967, 53—70.
36- Ильичев В. А. К. решению нестационарной контактной задачи о квадратном
штампе, лежащем на инерционном полупространстве.— В кн.: Исследования
по теории сооружений, 17. Стройиздат, М., 1968, 223—235.
37. Ильичев В. А. Вертикальные нестационарные колебания массива под дей-
действием волн, возникающих в полупространстве при колебаниях другого мас-
массива.— В кн.: Динамика сооружений. Стройиздат, М., 1968, 106—123.
38. Ильичев В. А. К построению импульсной переходной функции систем
штамп—полупространство.— Изв. АН СССР. Механика твердого тела,
1973, 1, 107—119.
39. Ильичев В. А. Определение динамических напряжений под фундаментами
сооружений при прохождении упругих волн в грунте.— В кн.: Труды к
VIII Международному конгрессу по механике грунтов и фундаментострое-
нию. Стройиздат, М., 1973, 317—319.
40. Ишкова А. Г., Беэухова Н. Н. Вынужденные колебания пластинки, лежа-
лежащей на упругом полупространстве.— В кн.: Исследования по теории соору-
сооружений, 19. Стройиздат, М., 1972, 196—203.
41. Канарский В. Ф., Сеймов В. М. Динамический расчет плит креплений отко-
откосов на волновую нагрузку.-— В кн.: Труды координационных совещаний
по гидротехнике, 64, 2. Динамика гидросооружений. «Наукова думка», Киев,
1972, 77—86.
42. Канарский В. Ф., Сеймов В. М. Номограмма для расчета гибких откосных
плит на волновую нагрузку.— В кн.: Динамика гидротехнических соору-
сооружений. Труды V Всесоюзного совещания. Изд. Гидропроекта, М., 1972,
64—70.
43. Канторович Л. В., Крылов В. И. Приближенные методы высшего анализа.
Физматгиз, М.—Л., 1962, 696 с.
44. Карасудхи, Кир, Ли. Колебания тела, лежащего на упругой полуплоскости.—
В кн.: Прикладная механика. Труды Американского общества инженеров-
механиков. Сер. Е, 35, 4. «Мир», М., 1968, 80—89.
45. Кильчевский И. А., Фрадлин Б. Н., Сахновский С. М. О расчете балок, ле-
лежащих на упругом основании переменной жесткости.— Изв. Киевск. по-
литехн. ин-та, 1953, 12, 3—10.
46. Клубин П. И. Расчет балочных и круглых плит на упругом основании.—
Инж. сб., 1952, 12, 95—136.
47. Коренев Б. Г. Некоторые вопросы расчета балок и плит, лежащих на упругом
основании.— В кн.: Сборник трудов МИСИ им. В. В. Куйбышева, 14. Гос-
стройиздат, М., 1956, 145—168.
48. Коренев Б. Г. Введение в теорию бесселевых функций. «Наука», М., 1971,
288 с.
49. Коренев Б. Г., Ручимский М. Н. Некоторые задачи динамики балок на упру-
упругом основании. Госстройиздат, М., 1955, 44 с.
50. Коренев Б. Г., Черниговская Е. И. Рас*чет плит на упругом основании. Строй-
Стройиздат, М., 1962, 356 с.
51. Кочин И. Е., Кибель И. А., Розе И. В. Теоретическая гидромеханика. Ч. 1.
Физматгиз, М., 1963, 612 с.
52. Крауклис П. В., Молотков Л. А. О низкочастотных колебаниях пластины на
упругом полупространстве.— ПММ, 1963, 27, 5, 947—951.
53. Крылов В. И., Скобля Н. С. Справочная книга по численному обращению
преобразования Лапласа. «Наука и техника», Минск, 1968, 296 с.
54. Крылов В. И., Шульгина Л. Т. Справочная книга по численному интегриро-
интегрированию. «Наука», М., 1966, 372 с.
Литература
279
55. Кузнецов Д. С. Специальные функции. «Высшая школа», М., 1965, 424 с.
56. Кукленка Н. П., Сеймов В. М. Установившиеся колебания балочной плиты,
лежащей на упругом полупространстве.— Прикладная механика, 1968, 4,
7, 102—108.
57. Кукленко Н. П., Сеймов В. М. Вертикальные гармонические колебания
балочного фундамента на упругом полупространстве.— В кн.: Динамика
оснований и фундаментов. Труды II конференции, 3. Изд. НИИ оснований и
подземных сооружений, М., 1969, 11 — 19.
58. Кукленко Н. П., Сеймов В. М. Установившиеся антисимметричные коле-
колебания полосы конечной жесткости на упругой полуплоскости.— В кн.:
Труды координационных совещаний по гидротехнике, 64, 2. Динамика гид-
гидросооружений. «Наукова думка», Киев, 1972, 69—76.
59. Лобысев В. Л., Сайгина В. И., Яковлев Ю. С. К решению динамической за-
задачи о круглом штампе на границе с упругим полупространством.—
Физико-технические проблемы разработки полезных ископаемых, 1971, 2,
25—33.
60. Лобысев В, Л., Яковлев Ю. С. Осесимметричная динамическая задача теории
упругости со смешанными граничными условиями.— Изв. АН СССР. Ме-
Механика твердого тела, 1971, 4, 103—108.
61. Лобысев В. Л., Яковлев Ю. С. Динамический расчет сооружений на основе
плоской и осесимметричной задачи теории упругости со смешанными гранич-
граничными условиями.— В кн.: Труды координационных совещаний по гидротех-
гидротехнике, 64, 2. Динамика гидросооружений. «Наукова думка», Киев, 1972,
29-36.
62. Луко, Вестман. Динамика жесткого фундамента, соединенного с упру-
упругим полупространством.— В кн.: Прикладная механика. Труды Американ-
Американского общества инженеров-механиков. Сер. Е, 39, 2. «Мир», М., 1972,
211—219.
63. Лятхер В. М., Дидух Б. И., Бессонов М. Н., Борзенко И. И. Изучение ко-
колебаний жестких плит и массивов водонасыщенного грунта при действии ди-
динамических нагрузок.— В кн.: Труды координационных совещаний по гид-
гидротехнике, 64, 2. Динамика гидросооружений. «Наукова думка», Киев,
1972, 86—94.
64. Маделунг Э. Математический аппарат физики. Справочное руководство.
Физматгиз, М., 1961, 620 с.
65. Механика в СССР за 50 лет. Т. 3. Механика деформируемого твердого тела.
«Наука», М., 1972, 480 с.
66. Муравский Г. Б. О гармонических колебаних штампа на упругом изотроп-
изотропном полупространстве.— Строительная механика и расчет сооружений,
1969, 4, 39—43.
67. Муравский Г. Б. Гармонические колебания штампа на полупространстве при
действии силы, приложенной к поверхности полупространства.— Изв.
АН СССР. Механика твердого тела, 1969, 6, 134—139.
68. Николаенко И. А. Колебания неограниченной плиты, лежащей на упругом
полупространстве и упругом слое.— В кн.: Вопросы расчета плит на упру-
упругом основании. Стройиздат, М., 1958, 63—119.
69. Огурцов К- И., Климова Д. Н. Поле напряжений в полупространстве при
воздействии удлиненного и равномерно распределенного по ширине заряда. —
В кн.: Материалы Всесоюзного симпозиума по распространению упруго-
пластических волн в сплошных средах. Изд-во АН АзССР, Баку, 1964.
70. Петрашень Г. И., Марчук Г. И., Огурцов К- И. О задаче Лэмба в случае
полупространства.—Уч. зап. ЛГУ, 1950, 135, 21, 71—118.
71. Попов Г. Я- О методе ортогональных многочленов в контактных задачах
теории упругости.— ПММ, 1969, 33, 3, 518—531.
72. Попов Г. Я- Применение методов Винера—Хопфа и ортогональных много-
многочленов к контактным задачам.— В кн.: Контактные задачи и их инженерные
приложения. Изд. НИИМАШ, М., 1969.

280
Литература
73. Попов Г. Я- О сведении интегральных уравнений теории упругости к бес-]
конечным системам.— ПММ, 1972, 36, 4, 672—681.
74. Поручиков В. Б. Осесимметричная динамическая задача о штампе на упругом
полупространстве.— Вестн. Моск. ун-та. Математика. Механика, 1966, 6,
114—120.
75*. Савинов О. А. Современные конструкции фундаментов под машины и их рас-
расчет. Стройиздат, М., 1964, 346 с.
76. Свекло В. А. К решению динамической задачи теории упругости для
'полуплоскости при смешанных граничных условиях.— ПММ, 1959, 23, 2,
266—273.
77. Сеймов В. М. Розрахунок балочних плит на пружнш ochobi з урахуванням
сил тертя при вертикальному розподменому навантаженнь— ДАН УРСР,
1958, 10, 1058—1063.
78. Сеймов В. М. Розрахунок балочних плит на пруяопй ochobj при наванта-
женш горизонтальною силою.—ДАН УРСР, 1958, 12, 1308—1312.
79. Сеймов В. М. Розрахунок круглих плит на пружнш ochobj з урахуванням сил
тертя.— Прикладна мехашка, 1959, 5, 4, 379—390.
80. Сеймов В. М. Розрахунок балочних плит на пружшй ochobj з урахуванням
сил тертя по контакту. Вид-во АН УРСР, Ки'т, 1962, 108 с.
81. Сеймов В. М. Методика розв'язання динам1чно! контактно! задач1 для ба-
лочно'1 плити скшченно1 жорсткосп на пружному nienpocTopi.— Прикладна
механша, 1964, 10, 1, 96—99.
82. Сеймов В. М. Антисимметричные колебания жесткой полосы на упругой
полуплоскости.— Прикладная механика, 1965, 1, 8, 86—92.
83. Сеймов В. М. Вынужденные колебания полосы на упругой полуплоскости
при действии периодического момента.— В кн.: Труды координационных
совещаний по гидротехнике, 28. «Энергия», М.— Л., 1966, 245—252.
84. Сеймов В. М. О динамической контактной задаче для полосы на упругом
полупространстве.— В кн.: Аннотации докладов III Всесоюзного съезда по
теоретической и прикладной механике. «Наука», М., 1968, 271.
85. Сеймов В. М. О периодических колебаниях полосы на упругой полуплос-
полуплоскости под слоем жидкости.— В кн.: Распространение упругих и упруго-
пластических волн (материалы III Всесоюзного симпозиума). «Фан», Таш-
Ташкент, 1969, 162—170.
86. Сеймов В. М. О рекомендациях по динамическому расчету конструкций гид-
гидросооружений на упругом основании.— В кн.: Труды координационных
совещаний по гидротехнике, 64, 2. Динамика гидросооружений. «Наукова
думка», Киев, 1972, 8—29.
87. Сеймов В. М. Вертикальные неустановившиеся колебания жесткого штампа
на упругой полуплоскости.— В кн.: Труды координационных совещаний
по гидротехнике, 64, 2. Динамика гидросооружений. «Наукова думка»,
Киев, 1972, 53—60.
88. Сеймов В. М. Применение метода ортогональных многочленов к ди-
динамическим контактным задачам.— Прикладная механика, 1972, 8, 1,
69—77.
89- Сеймов В. М. Рекомендации по расчету напряжений по контакту массива с
упругой полуплоскостью при вертикальных гармонических и неустановив-
неустановившихся колебаниях.— В кн.: Динамика гидротехнических сооружений. Тру-
Труды V Всесоюзного совещания. Изд. Гидропроекта, М., 1972, 52—57.
90. Сеймов В. М. Рекомендации по расчету контактных напряжений и переме-
перемещений круглого массива на упругом полупространстве при вертикальных
гармонических и неустановившихся колебаниях.— В кн.: Динамика гидро-
гидротехнических сооружений. Труды V Всесоюзного совещания. Изд. Гидропроек-
Гидропроекта, М-, 1972, 58—63.
91. Сеймов В. М. О колебаниях прямоугольного штампа на упругом полупро-
полупространстве.— В кн.: Второй национальный конгресс теоретической и при-
прикладной механики. Резюме докладов. Изд. БАН, Варна, 1973, 173.
Литература
281
92. Сеймов В, М., Кукленка Н. П. К задаче о периодических колебаниях полу-
полуплоскости.— Прикладная механика, 1967, 3, 7, 96—103.
93. Сеймов В. М., Кукленко Н. П. Установившиеся колебания бесконечной по-
полосы на упругой полуплоскости подслоем жидкости.— В кн.: Труды коор-
координационных совещаний по гидротехнике, 54. Динамика гидротехнических
сооружений. «Энергия», Л., 1970, 205—209.
94. Сеймов В. М., Островерх Б. Н. О колебаниях пластины, защемленной в упру-
упругое полупространство, под действием нагрузки, внезапно приложенной к пло-
плотине и полупространству.— В кн.: Труды Гидропроекта, 20. Изд. Гидропроек-
Гидропроекта, М., 1971, 113—121.
95. Сеймов В. М., Островерх Б. Н. Расчет неустановившихся продольных коле-
колебаний пластинки, прикрепленной к границе полупространства.— В кн.:
Труды координационных совещаний по гидротехнике, 64, 2. Динамика гид-
гидросооружений. «Наукова думка», Киев, 1972, 61—69.
96. Сеймов В. М., Шевченко Е. Д. Расчет колебаний жесткого балочного фун-
фундамента на упругом полупространстве при действии периодического момен-
момента.— В кн.: Динамика оснований и фундаментов. Труды II конференции,
3. Изд. НИИ оснований и подземных сооружений, М., 1969, 20—27.
97. Снеддон И. Преобразования Фурье. ИЛ, М., 1955, 668 с.
98. Справочник по динамике сооружений. Под ред. Б. Г. Коренева, И. М. Ра-
Рабиновича. Стройиздат, М., 1972, 512 с.
99. Филиппов А. П. Колебания упругих систем. Изд-во АН УССР, Киев, 1956,
322 с.
100. Филиппов Р. Д., Гостев В. П. О распределении напряжений под подошвой
колеблющегося фундамента.— В кн.: Строительная механика и строитель-
строительные конструкции. Горький, 1972, 90—91.
101. Фильчаков П. Ф. Численные и графические методы прикладной математики.
«Наукова думка», Киев, 1970, 800 с.
102. Флитман Л. М. Динамическая задача о штампе на упругой полуплоско-
полуплоскости. - ПММ, 1959, 23, 4, 697—705.
103. ХенлЛ., Мауе А., Вестпфаль К- Теория дифракции. «Мир», М., 1964,
428 с.
104. Цейтлин А. И. Упруго-пластические деформации бесконечной балки при
импульсивной нагрузке.— В кн.: Исследования по динамике сооружений
и расчету конструкций на упругом основании. Труды ЦНИИСК, 2. Стройиз-
Стройиздат, М., 1961, 33—50.
105. Шерман Д. И. О распространении волн в жидком слое, лежащем на упру-
упругом полупространстве.— Труды Сейсмологического института, 1945,
115.
106. Шехтер О. Я- Об учете инерционных свойств грунта при расчете вер-
вертикальных вынужденных колебаний массивных фундаментов.— В кн.:
Вибрации оснований и фундаментов, 12. Стройвоенмориздат, М., 1948,
72—90.
107. Шехтер О. Я- О решении осесимметричных задач для круговых плит на
упругом основании.— Основания, фундаменты и механика грунтов, 1966,
5, 1—5.
108. Шехтер О. Я- Некоторые динамические и статические задачи расчета круг-
круглых плит на упругом основании.— В кн.: Сборник трудов НИИ осно-
оснований и подземных сооружений Госстроя СССР, 57. Стройиздат, М., 1967,
37—72.
109. Щехтер О. Я- Резонансные кривые вынужденных гармонических колеба-
колебаний жесткого круглого штампа на упругом полупространстве.— В кн.:
Основания, фундаменты и подземные сооружения. Сборник трудов НИИ
оснований и подземных сооружений Госстроя СССР, 58. Стройиздат, М.,
1969, 74—80.
ПО. Шехтер О. Я- О взаимном влиянии колебаний двух жестких круглых
штампов на упругом полупространстве при вертикальных осесимметричных

282
Литература
гармонических воздействиях.— В кн.: Основания, фундаменты и подзем-
подземные сооружения. Сборник трудов НИИ оснований и подземных сооружений,
62. Стройиздат, М., 1973, 3—10.
111. Яковлев Ю. С, Лобысев В. Л. О решении динамических задач теории упру-
упругости со смешанными граничными условиями.— В кн.: Труды Гидропроек-
Гидропроекта, 20. Изд. Гидропроекта, М., 1971, 65—80.
112. Яковлев Ю. С, Лобысев В. Л. Плоская задача о движении твердого тела на
границе с упругим полупространством под действием заданной системы
сил.— В кн.: Труды Гидропроекта, 20. Изд. Гидропроекта, М., 1971,
81—87.
113. Arnold R. N.. Bycroft G. N., Warburton G. B. Forced vibrations of a body
on an infinite elastic solid.— J. Appl. Mech., 1955, E22, 391—400.
114. Bailey J. L., Raftopoulos D. D., Scavuzzo R. J. Formulation of coupled lateral-
rotational foundation-soil interaction of building structures.— Nucl. Eng.
and Des., 1973, 24, 12.
115. Bose S. K. A generalised oscillatory Reissner-Sagoci problem. — Bull. Cal-
Calcutta Math. Soc, 1971, 63, 1, 27—38.
116. Bycroft G. N. Forced vibrations of a rigid circular plate on a semi-infinite elas-
elastic space and on an elastic stratum. — Phil. Trans. Roy. Soc. London, 1956,
A248, 948, 327—328.
117. De Т. К- Dynamic contact problem of steady periodic vibrations on an elas-
elastic half-space.—Z. angew. Math, und Mech., 1972, 52, 11, 549—551.
118. Duns С S. Vertical response of a rigid base to dynamic loading.— Civil
Eng. and Publ. Works Rev., 1969, 64, 760, 1091—1095.
119. Ehrler 0. Nonlinear parameters of vibrating foundations.—J. Soil Mech.
and Found. Div. ASCE, 1968, 94, 6, 1199—1214.
120. Gutzwiller M. C. Shock of the rigid circular cylinder upon elastic half-spa*
ce.—Phil. Trans. Roy. Soc. London, 1962, A255, 1053, 153—191.
121. Kawatate Kazuo. Stress distribution on the elastic plane with a rigid be-
beam.— In: Proceedings of the 19th Japanese National Congress on Applied
Mechanics, 1969, Tokyo, 1970, 199—203.
122. K,obori Takuji, Minai Ryochiro, Suzuki Tamotsu, K,ysakabe K,aoru. Dynamical
ground compliance of rectangular foundation.— In: Proceedings of the 16th
Japanese National Congress on Applied Mechanics, 1966, Tokyo, 1967, 301 —
306.
123. Lamb H. On the propagation of tremors over the surface of an elastic so-
solid.— Phil. Trans. Roy. Soc. London, 1904, A203, 1—42.
124. Lighthill M. J. Introduction to Fourier analysis and generalised functions.
Cambridge at the University Press, 1958, 79 p.
125. Luco J. E., Westmann R. A. Dynamic response of circular foetings.—J.
Eng. Mech. Div. ASCE, 1971, 97, 5, 1381—1395.
126. Lysmer J. Vertical Motion of Rigid Footings. Contract No DA-22-079-eng-
340. Report No 3-115. Vicksburg, 1965.
127. Lysmer J., Richart F. E. Dynamic Response of Footings to vertical Loa-
Loading.—J. Soil Mech. and Found. Div. ASCE, 1966, 92, 1, 65—91.
128. Miller G. F. On definite integrals in hydrodynamical problem.— Proc. Rov.
Soc., 1957, 243, 1232.
129. Novak Miles. Prediction of footing vibrations.—J. Soil Mech. and Found.
Div. ASCE, 1970, 96, 3, 837—861.
130. Oien M. A. Steady motion of rigid strip bonded to an elastic halfspace.—
In: Paper of the American Society of Mechanical Engineers. WA/APM-56,
1970, 1-7.
131. Paul H. S., Mathiyalu N. Sinusoidal rocking of a rigid rectangular body
on an infinite isotropic elastic plate.— Trans. ASME, 1969, E36, 3, 648—
649.
132. Pekeris С L. The seismic surface pulse.— Proc. Nat. Acad. Sci. USA, 1955
41, 7, 469—480.
Литература
283
133. Quinlan P. M. The elastic theory of soil dynamics.— In: ASTM Special
Technical Publication, 156. Symposium of Dynamic Testing of Soils, 1953,
3—34.
134. Reisner E. Stationare, axialsymmetrische, durch eine schuttelnde Masse er-
regte Schwingungen eines homogenen elastischen Halbraumes.— Ing. Arch.,
1936, 7, 6, 381—396.
135. Richart F. E., Whitman R. V. Comparison of footing vibration tests with
theory.-J. Soil Mech. and Found. Div. ASCE, 1967, 93, 6, 143—168.
136. Silverberg M. An efficient method for numerical Laplace transform inversion
based on error control.— IEEE Intern, conv. Rec, 1967, 15, 5, 117—120.
137. Sung T. Y. Vibrations in semi-infinite solids due to periodic surface loa-
loading.— In: ASTM Special Technical Publication, 156. Symposium of Dyna-
Dynamic Testing of Soils. Philadelphia, 1954, 35—63.
138. Thomson W. Т., Kobori Takuji. Dynamical compliance of rectangular foun-
foundations on an elastic half-space.—J. Appl. Mech., 1963, E30, 4, 116—121.
139. Toriumi G. Vibrations in foundations of machines.— Techn. Rep. of Osaka
Univ., 1955, 5, 146.