Текст
и*. .
СПРАВОЧНИК
ПРОЕКТИРОВЩИКА
б 9&(0 S3)
& ¥ I'M
ДИНАМИЧЕСКИЙ
РАСЧЕТ СООРУЖЕНИЙ
НА СПЕЦИАЛЬНЫЕ
ВОЗДЕЙСТВИЯ
Под редакцией профессоров
Б. Г. КОРЕНЕВА,\И. М. РАБИНОВИЧА
*
*£-£>6 Mb____________
[ Cih^-lHOTEKA
| Крли^ОГ. -ОСН0ГШ
it С. и *’* 'СТ*!ТуТЖ
МОСКВА
СТРОЙИЗДАТ
198 1
им-
Справочник по расчету сооружений на
специальные динамические воздействия
предназначен для инженеров-проектиров-
щиков. Являясь самостоятельным изданием,
этот справочник в то же время можно рас-
сматривать как продолжение (и дальнейшее
развитие) вышедшего в 1971 г. «Справоч-
ника по динамике сооружений».
В «Справочнике по динамике сооружений»
основное внимание было уделено расчету
сооружений на обычные эксплуатационные
динамические воздействия. Наиболее под-
робно излагался расчет сооружений на на-
грузки от машин; особенно детально изу-
чались гармонические воздействия и
пульсные нагрузки сравнительно неболь-
шой интенсивности; наряду с этим рассмат-
ривалось действие ветровых нагрузок и др.
В настоящем справочнике рассмотре-
ны воздействия, которые большей частью
возникают сравнительно редко, но учет
влияния которых тем не менее необходим.
Среди них большую роль играют нагрузки,
вызванные ударом и взрывом, а также сейс-
мические воздействия. Многие из них мо-
гут быть причиной разрушения или повреж-.
дений зданий и сооружений, влиять на со-
хранность оборудования и угрожать здоро-
вью и даже жизни людей. Поэтому учет
подобных воздействий имеет очень важное
значение.
Настоящий справочник посвящен не
только расчету сооружений на специальные
воздействия, но также вопросам виброза-
щиты сооружений и экспериментальным ме-
тодам исследования при учете указанных
воздействий.
В связи с тем что степень изученности
влияния рассматриваемых в справочнике
воздействий различна и далеко неодинакова,
то и степень обеспеченности нормативными
документами и даже характер освещения
существа самих расчетов на эти воздейст-
вия в монографической и учебной литера-
туре различны; поэтому неизбежны и раз-
личные подходы к изложению материалов,
положенных в основу тех или иных разде-
лов справочника. Например, при изложении
^вопроса о действии нагрузок, вызванных
пролетающими самолетами, нужно было
учитывать новизну и недостаточную раз-
работанность этой проблемы. Проблема
сейсмостойкости, наоборот, изучена деталь-
но и в соответствующем разделе приведены
основные положения расчета, имеющие
практический характер.
При рассмотрении виброзащиты с по-
мощью гасителей колебаний в раздел вклю-
чены многочисленные графики и таблицы.
Существо же вопроса об аэродинамических
методах подавления вибраций, степень его
изученности и наличие только лишь экспе-
риментальных данных в этой области были
причиной того, что соответствующий раздел
имеет иной характер. Таким образом, неко-
торая внешняя разностильность разделов
есть лишь отражение того факта, что раз-
личные воздействия изучаются с разных
позиций и что в этой связи учет их влия-
ния описывается по-разному.
Рассмотрим кратко содержание справоч-
ника. В первом разделе, посвященном расче-
ту сооружений на ударные и взрывные на-
грузки, эта проблема рассматривается под-
робно и в различных аспектах. Здесь даны
параметры воздушных ударных волн и волн,
возникающих в/грунте, расчетные схемы со-
оружений и их предельные состояния и на
основе этого изложены конкретные вопро-
сы расчета сооружений.
Второй раздел содержит специальные
данные по расчету сооружений на действие
внутренних взрывов, которые могут возни-
кать в зданиях взрывоопасных производств.
Здесь основное внимание уделено рассмот-
рению взрывной нагрузки, рекомендациям
по учету ее воздействия, а также мерам
по ее снижению.
В третьем разделе рассмотрен расчет со-
оружений на сейсмические воздействия. На-
ряду с практическими методами расчета и
проектирования зданий здесь излагаются
данные, относящиеся к учету неупругих де-
формаций, а также краткие сведения о при-
менении вероятностных методов.
Четвертый раз; (ел справочника в основ-
ном посвящен важной специальной пробле-
ме динамического расчета высоких соору-
жений на ветровые воздействия — их аэроди-
намической неустойчивости. Как это хоро-
шо известно из литературы, такие явления
как ветровой резонанс и галопирование бы-
ли причиной не только повышенных вибра-
ций, но и разрушений, и поэтому расчету
на подобные воздействия в справочнике
уделено достаточно большое внимание.
Далее, в пятом разделе * рассмотрен
другой вид аэродинамического воздейст-
вия — влияние ударных звуковых волн, воз-
никающих при полете сверхзвуковых само-
летов.
Шестой раздел посвящен инженерному
анализу динамических воздействий, переда-
ваемых мостовыми кранами. Его особенно-
стью является то, что наряду с горизон-
тальными силами инерционного происхож-
дения, связанными с явлениями торможе-
ния здесь рассматриваются так называемые
боковые силы, связанные с учетом перекоса
крана при его движении, а также непарал-
лельностью и искривлениями в плане крано-
вых путей; эти силы имеют большое значе-
ние и могут превосходить по величине тор-
мозные силы.
В седьмом разделе, по существу допол-
няющем соответствующий раздел «Справоч-
ника по динамике сооружений», приводятся
данные о некоторых специальных воздейст-
виях, возникающих при расчете фундамен-
тов под турбоагрегаты.
В связи с тем что задачи о расчете со-
оружений на динамические воздействия, пе-
редаваемые через грунт, возникают не
только при рассмотрении сейсмических яв-
лений, но и при учете влияния работы раз-
личных промышленных агрегатов, а также
при учете влияния движения поездов метро
/
и др. и что этот вопрос в справочной лите-
ратуре ранее не обсуждался, то этой проб-
леме посвящены четыре раздела настояще-
го справочника.
В восьмом разделе приводятся данные
о динамическом взаимодействии сооружения
и окружающего грунта.
В девятом разделе рассмотрена задача
о контакте жесткого сооружения — штампа
с грунтом, рассматриваемым как упругое
полупространство.
Десятый и одиннадцатый разделы по-
священы соответственно учету влияния по-
ездов метро и работы установок взрывной
штамповки.
В двенадцатом разделе изложен расчет
сооружений, оборудованных гасителями
колебаний. Поскольку при расчете сооруже-
ний, оборудованных гасителями, нельзя ог-
раничиваться рассмотрением защищаемых
объектов как систем с одной степенью сво-
боды н следует рассматривать наряду с
гармоническими и другие воздействия, то в
справочнике даны рекомендации и вспомо-
гательные материалы, необходимые для
проведения соответствующих расчетов.
В литературе, посвященной гашению
вызванных ветром колебаний гибких высо-
ких сооружений, наряду со способами, ос-
нованными па применении гасителей, боль-
шое внимание уделено использованию аэро-
динамических методов.
Последние два раздела содержат све-
дения о применении мелкомасштабного мо-
делирования и динамической фотоупруго-
сти.
Справочник в целом охватывает широ-
кий круг вопросов, связанных с динамиче-
ским расчетом сооружений на специальные
воздействия. При этом предполагается, что
читатель может в случае необходимости
почерпнуть необходимые сведения по нор-
мированию уровня вибраций, определению
форм и частот свободных колебаний и др.
из «Справочника по динамике сооружений»,
который в ближайшее время выйдет вторым
изданием.
В справочнике не приводятся данные,
относящиеся к расчету мостов и эстакад,
речных и морских гидротехнических соору-
жений и др.
Динамика подобных специальных со-
оружений во многих случаях связана с ины-
ми, не рассматривавшимися в обоих томах
справочника эксплуатационными нагрузка-
ми. Подобные сооружения, очевидно, име-
ют и иные расчетные схемы. В этой связи
намечается издание справочника «Динами-
ческий расчет специальных инженерных со-
оружений и конструкций», который явится
по существу третьей книгой общего спра-
вочника.
Авторский коллектив предлагаемого
справочника представлен специалистами тех
областей динамики, которые рассматривают-
ся в этом издании; в большинстве случа-
ев они являлись авторами соответствующих
нормативных и инструктивных документов.
Справочник в целом ориентирован на уста-
новившуюся практику расчета во всех тех
случаях, где это оказалось возможным.
Большую роль в формировании многих
из направлений, отраженных в справочнике,
сыграли работы члена-корреспондента АН
СССР, профессора, Героя Социалистическо-
го Труда И. М. Рабиновича — выдающего-
ся ученого, внесшего большой вклад в раз-
витие строительной науки. И. М. Рабинови-
чем осуществлено общее редактирование
справочника «Динамический расчет соору-
жений на специальные воздействия» совме-
стно с автором этого предисловия.
Б, КОРЕНЕВ
РАЗДЕЛ 1. РАСЧЕТ КОНСТРУКЦИЙ СООРУЖЕНИЙ НА
ДЕЙСТВИЕ ВЗРЫВНЫХ ВОЛН
(О. В. ЛУЖИН, И, Н. ПОПОВ, Б. С. РАСТОРГУЕВ)
Во многих случаях нагрузки, вызван-
ные действием взрывных волн, являются
для сооружений аварийными, и они значи-
тельно превосходят эксплуатационные ста-
тические нагрузки. К таким сооружениям
может быть предъявлено только требование
восприятия динамической нагрузки без об-
рушения. Тогда можно допустить развитие
пластических деформаций, учесть повыше-
ние прочностных характеристик материалов
при высокоскоростных деформациях, и в
итоге конструкция по расчету может обес-
печить защиту от интенсивных динамиче-
ских воздействий. Ниже приведены сведе-
ния о взрывных нагрузках на сооружения,
изложены общие принципы взаимодействия
волн с конструкциями и особенности их ра-
боты при интенсивных динамических нагруз-
ках. Даны методы расчета наиболее распро-
страненных в практике строительства желе-
зобетонных конструкций сооружений.
1.1. ВЗРЫВНЫЕ ВОЛНЫ
и
Взрывом называется процесс быстрого
выделения большого количества энергии,
вызванный внезапным изменением состоя-
ния вещества или его параметров [15]. Из-
менение состояния вещества обычно возни-
кает в результате быстропротекающей хими-
ческой (взрывчатые вещества, газо- или пы-
левоздушные смеси) или ядерной реакции.
Взрыв вследствие быстроты изменения па-
раметров вещества возникает при разруше-
нии паровых котлов, баллонов со сжатым га-
зом и т. п.
В результате взрыва в окружающей
среде распространяются ударные волны или
волны сжатия. На фронте ударных волн
происходит скачкообразное изменение дав-
ления, плотности, температуры, скорости
движения частиц среды. Для волн сжатия
характерно постепенное нарастание этих
параметров. Под давлением понимается из-
быточное давление, возникающее в среде
при прохождении взрывной волны, т. е. дав-
ление, отличающееся от нормального атмос-
ферного при взрыве в воздухе или от бы-
тового давления грунта при распростране-
нии волны в грунте. Параметры волн зави-
сят от источника энергии взрыва, окружа-
ющей среды (воздух, грунт, вода), расстоя-
ния от центра взрыва и других факторов.
Взрывные волны действуют на конст-
рукции сооружений как кратковременные
динамические нагрузки. В зависимости от
назначения сооружения и причин взрыва
кратковременные нагрузки могут быть эксп-
луатационными или аварийными. В первом
случае в конструкциях не должны возни-
кать деформации, приводящие к нарушению
нормальной эксплуатации сооружения. Во
втором случае в некоторых конструкциях
сооружения могуг быть допущены пласти-
ческие деформации и даже разрушение.
1.2. ПАРАМЕТРЫ ВОЗДУШНЫХ
УДАРНЫХ ВОЛН И
ИХ ВЗАИМОДЕЙСТВИЕ
С ПРЕГРАДОЙ [1, 2, з, 4, 9, 15]
Эффект действия воздушных ударных
волн на конструкции и сооружения разли-
чен при взрыве в воздухе, над поверхно-
стью земли — при воздушном взрыве или у
поверхности — наземном взрыве. Воздуш-
ная ударная волна состоит из фазы сжатия,
в котором давление выше атмосферного, в
фазы разрежения (рис. 1.1). Степень по-
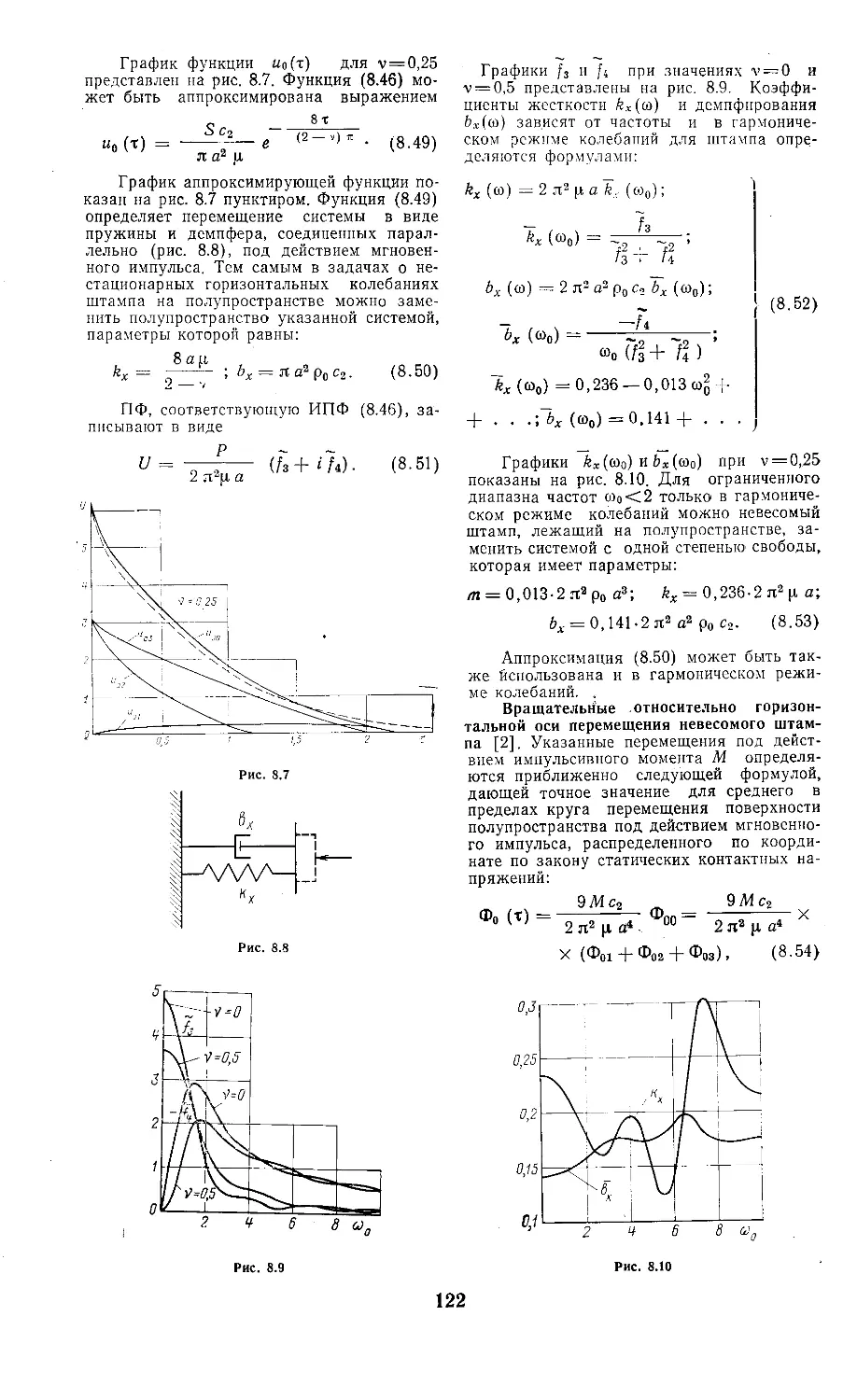
1.1. Изменение давления в фиксированной на
местности точке в зависимости от времени
Арф — избыточное давление на фронте; Др—•
максимальное давление разрежения; т_|_, т_ —
продолжительность фазы сжатия, разрежения
вреждения сооружения при действии удар-
ной волны в большинстве случаев опреде-
ляется давлением в фазе сжатия, посколь-
ку оно обычно значительно превышает дав-
ление в фазе разрежения. При определении
нагрузок, возникающих при действии удар-
ной волны на преграду, необходимо учиты-
вать условия ее взаимодействия с прегра-
дой (отражение, обтекание, затекание).
Основные параметры воздушной удар-
ной волны при распространении по воздуху
от центра взрыва (проходящая волна) оп-
ределяют по формулам:
а) при воздушном взрыве тротилового
заряда избыточное давление на фронте
ударной волны, МПа:
V— з— с
А Рф = 0,084 + 0,27 ^2 + 0) 7 ;
(1.1)
продолжительность фазы сжатия
g _ _
T+= 1,5- 10-3Z С v R с;
5
импульс давления в фазе сжатия, (МПа-с),
отнесенный к поверхности фронта волны
площадью 1
м2,
При расчетах сооружений на действие
воздушной ударной волны вместо функции
(1.9) можно использовать линейную за-
висимость давления от времени (прямая 2
на рис. 1.2)
>
А р (/) — А рф [ 1 ] ,
(1.Н)
б) при наземном
заряда
А рф=о,1
взрыве тротилового
= 1,7-KF3 v
3,---
И С2
1.2. Давление ударной волны
1 — действительное давление-, 2 — равновеликое
по импульсу; 3 — по касательной к действитель-
ному давлению
; МПа-с/м2;
в) при взрыве в
м2, неограниченной длины
штольне сечением S,
з
где 9 — эффективное время действия удар-
ной волны, определяемое из условия равен-
ства импульсов давлений, изменяющихся,
согласно законам (1.9) и (1.11), по фор-
муле
2т,
о-12’
(1-6)
где С — масса тротилового заряда, кг;
R — расстояние от центра взрыва, м.
Для других взрывчатых веществ (ВВ)
величину С, приведенную в формулах (1.1) —
(1.6), принимают равной весу заряда рас-
сматриваемого ВВ, умноженному на коэф-
фициент а, равный отношению удельной
энергии вещества к удельной энергии тро-
тила; для аммонитов а = 0,8—1,2, для гек-
согена а =1,4.
Для ядерного взрыва при определении
параметров воздушной ударной волны зна-
чение С принимают равным значению тро-
тилового эквивалента по ударной волне
(можно принимать, что тротиловый эквива-
лент по ударной волне равен половине пол-
ного тротилового эквивалента ядерного
взрыва £).
Максимальное давление разрежения и
продолжительность фазы разрежения при
воздушном и наземном взрыве при Арф{<
0,4 МПа равны:
Если полученное из расчета время до-
стижения конструкцией максимального пе-
ремещения значительно меньше (на поря-
док и больше) продолжительности фазы
сжатия т+, то целесообразно принять пря-
мую совпадающей с касательной к кривой
(1.9) в точке / = 0 (прямая 3 на рис. 1,2),
и в таком случае время 0 нужно опреде-
лять по формуле
0=—т,. (1.13)
П "Г
Ар_ = 0,03
(1.7)
т_ = 0,16 £с с. (1.8)
Изменение давления в фазе сжатия во
времени принимают по закону (кривая 1 на
рис. 1.2)
Др (/) = Дрф 1 —
(1.9)
ДРфТ+
При встрече проходящей волны с не-
подвижной преградой ограниченных разме-
ров происходит отражение волны и обтека-
ние сооружения волной (рис. 1.3). В мо-
мент отражения волны от преграды давле-
ние, действующее на преграду, скачкооб-
разно возрастает по сравнению с давлени-
ем в проходящей волне, а затем при обте-
кании уменьшается. График изменения дав-
ления во времени на переднюю стену пре-
грады показан на рис. 1.4. Характеризую-
щие этот процесс параметры приведены ни-
же.
Максимальное давление отражения
Аротр, действующее в начальный момент
времени на фронтальную плоскую прегра-
ду, которая нормально расположена к на-
правлению распространения волны, опре-
деляют по формуле
6 д Рф
Дротр —2Дрф+ • (1.14)
А Рф г 9,72
.где
(1.Ю)
Значения Ар$, т+, Лрот? при заданных
полном тротиловом эквиваленте Е и рас-
стоянии от преграды R можно определить
по номограмме, приведенной на рис. 1.5
[4].
6
1.3. Взаимо-
действие удар-
ной волны,
распространя-
ющейся от на-
земного взры-
ва, с сооруже-
нием
а — начало от-
ражения вол-
ны; б — обте-
кание соору-
жения волной;
мПа
ЛРотр
15
0,2 7 -77J
0,12
0,1
0,08
0,06
0,04
0,03
0,05
- 0,045
--0,075
- 0,025
-0,018
- 0,014
0,02 --0,01
отр
Схема пользования
Е,ТМС /
20000
8000 -
3000 -
900 -
400 -
100 -
40 ~
10 -
8 '
~ 1,5
- 1
в—установле-
ние режима
обтекания
R,KM S,KM* 2
~ 0,6
- 0,5
~ 0,2
- 0,25
- 0,2
70
65
60
40
13300
7900
5000
30 - 2860
22,5
700
255
0,6 -
0,46-
0,55-
0,01
0,008
-0,005
-0,004
i
-- 0,15
- 0,07
1.4. Среднее давление на
фронтальную стену преграды
конечных размеров (пунк-
тир — отражение от беско-
нечной преграды)
1.5. Номограмма для опреде-
ления параметров ударных
волн при наземном взрыве
1.6. Давление на тыльную
стену преграды
7
Время /обт от начала отражения до нача-
ла установления режима обтекания нахо-
дят по формуле (см. рис. 1.4)
ЗЯ*
^обт — р. » (1*15)
где Я* — меньшая из величин высоты Я
или половины ширины (Ь) передней стенки
преграды; Рф — скорость движения фронта
ударной волны;
Оф = 340 V1 +8,3 Дрф м/с, (1.16)
где Дрф, МПа.
Давление на переднюю стенку преграды
в момент установления режима обтекания
Дроб Т
Д Робт ~ Д Рф Д Рек 0,5 Д Ротр, (1.17)
где Дрек — давление, создаваемое скорост-
ным напором;
2.5 Д Рф
ДРск = —-------— (1.18)
Д Рф + 0,72
Максимальное значение давления на бо-
ковые стены, перекрытие и тыльную стену
преграды при обтекании можно принимать
равным значению давления во фронте
ударной волны Дрф [12]. Изменение во
времени давления на боковые стены и пе-
рекрытия такое же, как в проходящей вол-
не, а на тыльную стену преграды принима-
ют согласно рис. 1.6, где /бок==//ЯФ, /тыл-
время достижения максимального давления
на стыльной стенке, принимаемое равным
наименьшему из значений
t t (1 19)
‘ТЫЛ-- r-v » ‘ТЫЛ ---- п 9 к1*1'’)
Уф
где I — длина преграды в направлении
движения волны (см. рис; 1.3).
Полное давление на преграду равно
разности давлений, действующих на ее
фронтальную и тыльную стены.
1.3. ПАРАМЕТРЫ ВОЛН В ГРУНТЕ
И ИХ ВЗАИМОДЕЙСТВИЕ
С СООРУЖЕНИЕМ [2, 7, 11, 12]
Параметры волн, распространяющихся
в грунтах вследствие взрыва, существенно
зависят от расстояния до центра заряда и
от расположения заряда относительно по-
верхности земли (воздушный, наземный и
подземный взрывы).
При взрыве заряда в грунте или на его
поверхности в ближней к заряду зоне про-
исходит разрушение структуры и дробле-
ние грунта с образованием полости (кавер-
ны) при подземном взрыве или воронки
при наземном взрыве. За пределами кавер-
ны и воронки взрывные волны распростра-
няются в виде ударных волн или волн сжа-
тия. На больших расстояниях образуются
сейсмические волны различного вида (см.
разд. III). При наземном взрыве возникают
также волны в грунте вследствие распро-
странения над поверхностью грунта воз-
душной ударной волны (рис. 1.7). Парамет-
1.7. Взаимо-
действие вол-
ны сжатия в
грунте с со-
оружением
1 — упругая
волна; 2 —
то же, упру-
гопластиче-
ская
1.8. Диаграм-
ма деформа-
ций ст—е грун-
та
7 — динамиче-
ская; 2— ста.'
тическая; 3—
при разгруз-
ке
1.9. Расчет-
ная диаграм-
ма деформа-
ций грунта
Eq, Ei — мо-
дули дефор-
маций грун-
та при на-
грузке; Ер ~
модуль де-
формаций
грунта при
разгрузке;
&s — динами-
ческий пре-
дел упругости
грунта
ры этих волн сжатия в грунте определяют-
ся параметрами порождающей их воздуш-
ной ударной волны и характеристиками
грунта.
При плоском фронте волны в грунте
характеристикой грунта, определяющей
тип распространяющейся волны и ее интен-
сивности, является диаграмма сжатия: за-
висимость напряжения в от деформации е
(рис. 1.8). Если давление на фронте волны
соответствует начальному участку динами-
ческой диаграммы a—е, на которой d2a/
Ids2 С 0, то с ростом давления мгновенный
модуль деформации E=deldt и, следова-
тельно, скорость распространения волны
а=^Е)р (р — плотность грунта) уменьша-
ются. Вследствие этого увеличивается вре-
мя нарастания давления в волне, что при-
водит к образованию в грунте волны сжа-
тия. При больших давлениях, соответству-
ющих участку диаграммы, на котором
бР а
—— 2>0, с ростом давления увеличивается
а 8
скорость айв грунте распространяются
ударные волны. Уменьшение напряжения в
грунте при прохождении волны (разгрузка)
происходит в соответствии с участком 3 на
диаграмме (рис. 1.8).
При расчете параметров волнового по-
ля в грунте диаграмму а—е аппроксими-
руют обычно диаграммой Прандтля с уп-
рочнением (рис. 1.9). Скорости распростра-
нения волн упругих ао=УЕо/р и упруго-
пластических а^ — ^Е^р определяют из экс-
8
1.10. Волна сжатия в грунте
периментов [11]. Значения ав и для раз-
личных грунтов приведены в табл. 1.1
[12].
ТАБЛИЦА 1.1
Скорость распрост-
ранения волн, м/с
Г рунты
упругих
уПругО-
ПЛаСТИЧе-
СКИХ^!
Песок рыхлый
Песок ненарушенный
Суглинок, супесь
сыпные
Суглинок, супесь
нарушенные
Глина насыпная
Глина плотная
на- 200 500 250 100 250 150
не- 700 350
300 150
1500 500
Ниже приведены формулы, определяю-
щие давление в грунте на глубине 2 в про-
ходящей волне сжатия и при ее отражении
от преграды.
Параметры 8iApm волны сжатия в
грунте, возникающей при действии воздуш-
ной ударной волны на поверхности 2=0
грунта, находят по формулам (рис. 1.10):
/ 1 1 \
01 = г ----------- ; (1.20)
\ 01 Оо /
/ 0,5z\
Д рт=Д Рф 1--------— при£р=оо; (1.21)
\ 01 tj /
Дрт = Дрф
при £p = £q, (1.22)
где £Р — модуль деформации грунта при
разгрузке; 0—эффективное время действия
воздушной ударной волны, определяемое
согласно (1.11) — (1.13).
При встрече с преградой (конструк-
цией) волна сжатия отражается, что при-
водит к увеличению давления на преграде
по сравнению с давлением в проходящей
волне. Одновременно вследствие переме-
щения конструкции под действием этой вол-
ны происходит снижение давления на кон-
струкцию в зоне охваченной волной. В ито-
ге результирующее давление, которое дей-
ствует на точки конструкции (см. рис. 1.7),
1.11. График коэффициента отражения при
— 2 (о. — динамический предел упругости грун-
та)
расположенные в грунте на глубине г,
равно:
АРк (Л z) =йв Др (/, г) — р 01 оК) (1.23)
где &p(t, z) —давление в волне сжатия на
глубине z (см. рис. 1.10); ик — скорость
движения конструкции, определяемая при
расчете; kB — коэффициент взаимодействия.
Зависимость (1.23) использована при
построении графиков на рис. 1.17. Для кон-
струкций, поверхность которых нормальна к
направлению распространения волны, ко-
эффициент kB равен коэффициенту отраже-
ния &отр (см. ниже) и, если поверхность
параллельна направлению волны, Лв равен
коэффициенту бокового давления (см.
ниже). Для конструкций, нормаль к по-
верхности которой расположена под углом
<р к направлению распространения волны
сжатия, kQ определяют по формуле
/гв ~ &отр cos2 <р + sin2 ср. (1.24)
Коэффициент отражения &Отр при ди-
аграмме сжатия грунта в виде диаграммы
Прандтля (см. рис. 1.9) при n0/ai = 2 при-
нимают по графику, приведенному по
рис. 1.11. При произвольной диаграмме
о—е в области давлений, где d2o/de2<0,
&отР находят по формуле
Оот СТ (еОт
отр = а = Г
А Рт А рт
где бот — деформация грунта вблизи пре-
грады, определяемая из уравнения
А ОТ ъ /П
| а (е) d& = 2 I а (е) de,
о 6
Максимальную деформацию ет грунта»
в проходящей волне сжатия находят из
уравнения п(етп)=Арт, где Арт— макси-
мальное давление в грунте, опреде-
ляемое по формулам (1.21) или (1.22). При
давлениях в грунте, когда d2a/d&2>Qt воз-
никают чрезмерно большие нагрузки на
конструкцию и расчетные зависимости для
этого случая не приводятся.
Коэффициент бокового давления может
быть принят: для песка £б = 0,35; для супе-
си и суглинка k5 ==0,6; для глины k6 = 0,75;
для водонасыщенных грунтов &б = 1.
9
Расчет конструкций заглубленных соо-
ружений на действие взрывной волны, рас-
пространяющейся в грунт от взрыва тро-
тилового заряда, расположенного также в
грунте, можно проводить на эквивалент-
ную статическую нагрузку, величину кото-
рой, Н/м2, вычисляют по эмперической фор-
муле
(J — krp &заб ^2 to f (Р)» (1*25)
где &гр — коэффициент, зависящий от
свойств грунта, равный: для песка естест-
венной влажности 0,11, для насыщенного
водой песка 0,13; для глины естественной
влажности 0,14; йзаб — коэффициент, зави-
сящий от глубины заложения заряда: при
взрыве заряда на глубине 5го равен 1,
при взрыве на поверхности грунта — 0,2,
при взрыве заряда, заглубленного на его
высоту, — 0,5; С — масса заряда тротила, кг;
Я — расстояние от центра заряда до прегра-
ды, м; со — круговая частота первой формы
собственных колебаний преграды, вычисля-
емая без учета влияния прилегающего к ней
грунта 1/с; /(£)—коэффициент, учитываю-
щий зависимость нагрузки от угла р меж-
ду нормалью к преграде и направлением
.движения волны; принимают при 15го</?<^
25г0 равным 1, при /?>25го—f(P) =
= 0,3+0,7 cos р; Го — средний радиус тро-
тилового заряда, м;
г0 = 0,053 ^С.
Формула (1.25) справедлива при условии
где Т=2л/(о — период собственных колеба-
ний конструкции без учета грунта.
1.4. ДИНАМИЧЕСКИЕ НАГРУЗКИ
ОТ ВЗРЫВНЫХ ВОЗДЕЙСТВИЙ [12]
При динамическом расчете сооружения
действительные законы изменения нагрузок
во времени заменяют упрощенными, расчет-
ными. Наиболее часто используемые упро-
щенные законы изменения нагрузки во вре-
мени представлены на рис. 1.12, где p(t) —
погонная интенсивность нагрузки на конст-
рукцию, равная произведению избыточного
давления Др(/) на ширину участка, с кото-
рого собирается нагрузка на данную кон-
струкцию.
Эффективное время действия нагрузки
0 определяют по формулам (1.12) или
(1.13); времена 01 находят: для воздушной
ударной волны — по формулам (1.15) (для
рис. 1.12,6) или (1.19) (для рис. 1.12,в),
для волны сжатия в грунте — по формуле
(1.20). Для динамических нагрузок, соот-
ветствующим взрывным воздействиям, не
рассматриваемым в этом разделе, значения
0 и 01 имеются в литературе.
Принимаемые при расчетах функции
p(t) зависят от расположения конструкции
относительно направления движения фронта
волны, заглубления в грунт, а также зна-
чений ©О, (001, <й02, где (о — круговая часто-
та колебаний конструкции.
Зависимости, описывающие мгновенно
возрастающие, а затем убывающие нагруз-
ки видов, представленных на рис. 1.12,а, б,
применяют при расчете конструкций на дей-
ствие воздушных ударных волн (проходя-
щих и отраженных): нагрузки первого ви-
да (а) — для конструкций покрытий и боко-
вых стен сооружения, нагрузки второго (б)
для конструкций фронтальной стены (см.
рис. 1.3).
Нагрузка, изменение которой во вре-
мени показано на рис. (1.12,s), принимают
для расчета конструкций, находящихся на
тыльной стороне сооружения, в замкнутом
помещении при затекании в него волны че-
рез проемы, под слоем грунта. Эта же
функция аппроксимирует нагрузки, возника-
ющие также при взрыве газо- и пылевоз-
душных смесей. Зависимость третьего ви-
да вводят в расчет, если (O0i>l. Если
(001^1, то расчет на нагрузку, описывае-
мую зависимостью, представленной на
рис. 1.12,в, может быть заменен расчетом
на нагрузку, показанную на рис. 1.12,а.
При расчетах нагрузки можно прини-
мать постоянными во времени при t ^0i
(пунктирные прямые на рис. 1.12), если
<002^ 50 при расчете конструкции в упру-
гой стадии и соО?^ 300 при расчете в пла-
стической стадии. Если время действия ди-
намической нагрузки относительно мало,
так что (о9<бл/2, то конструкции можно
рассчитывать на действие мгновенного им-
0
пульса интенсивностью 1=^ p(t)dt,
о
При относительно большом времени
нарастания нагрузки, когда w0i 20, дейст-
вие динамической нагрузки на сооружение
практически эквивалентно действию стати-
ческой нагрузки интенсивностью р.
1.12. Законы изменения дина-
мической нагрузки во времени
10
1.5. ПРЕДЕЛЬНЫЕ СОСТОЯНИЯ
И РАСЧЕТ СЕЧЕНИЙ [2, 8, 9, 12, 14]
На действие кратковременных дина-
мических нагрузок конструкции рассчиты-
вают по двум группам предельных состоя-
ний в зависимости от эксплуатационных
требований.
Расчет по первой группе предельных
состояний обеспечивает: отсутствие разру-
шения конструкции, при этом в наиболее
напряженных сечениях железобетонных
конструкций деформации сжатого бетона
могут достигать предельных значений; в ар-
матуре изгибаемых и внецентренно-сжатых
с большими эксцентрицитетами элементах
могут развиваться значительные пластиче-
ские деформации;
отсутствие пластических деформаций в
конструкции; напряжения в растянутой
арматуре железобетонных конструкций мо-
гут достигнуть предела текучести.
Расчет по второй группе предельных
состояний обеспечивает выполнение допол-
нительных требований, предъявляемых к
конструкции, по чрезмерному раскрытию
трещин и по чрезмерным перемещениям
(прогибам, углам поворота). При этом ос-
таточные деформации в конструкции можно
допускать или не допускать.
Если при расчете по первой группе пре-
дельных состояний необходимо обеспечить
отсутствие разрушения, то за критерий при-
нимают предельные значения перемещений,
углов раскрытия трещин в шарнирах плас-
тичности, кривизн, деформаций бетона и
арматуры. Выбор нормируемых параметров
зависит от типа сооружений, напряженно-
деформированного состояния конструкции и
возможности получения соответствующих
величин существующими методами динами-
ческого расчета.
Если при расчете по первой группе пре-
дельных состояний необходимо обеспечить
отсутствие пластических деформаций в рас-
тянутой арматуре, то предельную несущую
способность определяют из условия появле-
ния в растянутой арматуре напряжений,
равных динамическому пределу текучести
в момент достижения конструкцией макси-
мальных перемещений.
При расчете конструкций по второй
группе предельных состояний за предель-
ные принимают значения перемещений или
раскрытия трещин, задаваемых условиями
эксплуатации сооружения.
Железобетонные элементы по прочно-
сти рассчитывают по нормальным и наклон-
ным сечениям согласно главе СНиП П-21-75
«Бетонные и железобетонные конструкции»
со следующими изменениями.
При определении предельных усилий в
сечениях принимают динамические расчет-
ные сопротивления, равные: для растянутой
арматуры R^~ ky R*a, для сжатой с=
= с, для бетона в сжатой зоне/?£р=
— ^уб) /?*р, для бетона в растянутой зо-
не R» = № R* где R\ с, R* -со-
J ** •• * W J*
противления, назначаемые в зависимости от
условий эксплуатации и требований к на-
дежное! и конструкций.
Коэффициент упрочнения для бетона при-
нимают =1,2. Коэффициент упрочне-
ния ky для арматуры определяют в зависи-
мости от средней скорости деформации &
и класса арматуры (рис. 1.13). Среднюю
1.13. Коэффициенты упрочнения для арматурных;
сталей
скорость деформации в случае использова-
ния условия отсутствия пластических де-
формаций в арматуре определяют по фор-
муле
• g (т)
8 Еаг ’
где о(т) —напряжения в арматуре, вызван-
ные динамической нагрузкой, в момент вре-
мени т достижения конструкцией макси-
мальных перемещений (см. п. 1.8); Ел —
модуль упругости арматуры.
При расчете конструкций, когда допус-
каются пластические деформации в арма-
туре, коэффициент упрочнения ky вычисля-
ют последовательным приближением. Вна-
чале задают величину по табл. 1.2.
ТАБЛИЦА 1.2
Класс арматуры A-I А-П A-III
ky 1,4 1,3 1,2
А(с) ЯУ 1,1 1,1 1,1
Зате^г находят среднюю скорость деформа-
ции:
4° *а
8 =
где т — время конца упругой стадии, най-
денное при усилиях, определенных при на-
пряжениях в растянутой арматуре
(см. п. 1.9).
По полученному значению е уточняют
ky согласно графикам, приведенным на
рис. 1.13.
Жесткость изгибаемых элементов при-
нимают:
при отсутствии трещин в растянутой
зоне
Bi — Еб Jп»
(1.26>
11
где J. — момент инерции приведенного се-
ления;
при наличии трещин в растянутой зоне
Mg-Mf
В =-------------г—- , (1.27)
(1/Ро) — (1/Р1)
где Mq —предельный момент внутренних
сил в сечении, определяемый . согласно
СНиП 11-21-75: при напряжениях в растя-
нутой арматуре R& в бетоне и сжа-
той арматуре 7?^ с 5 —момент в сече-
нии, соответствующий началу образования
трещин и равный
М* = RJ Гт;
— упругопластический момент сопротив-
ления по растянутой зоне, определяемый
согласно СНиП 11-21-75;
1/Р1 = мД/Ви
Bt вычисляют по формуле (1.26):
(1.28)
где
Значение принимается равным |т =
= 5 при g > 0,2 и £т = 0,1+0,5§ при |<
С0,2; значение у' находят по формулам
СНиП 11-21-75, в которых вместо | под-
ставляют gT. Здесь g=x//i0> где х— высота
сжатой зоны бетона в сечении при разру-
шении, определяемая из условия равнове-
сия внутренних сил при напряжениях в рас-
тянутой арматуре R^, в бетоне /?£р > в сжа-
той арматуре R% с , Ао — расчетная высота
сечения.
Жесткость изгибаемых элементов пря-
моугольного сечения можно определять по
формуле
В = 0,8£а^а (hQ — x) (h9 — 0,5 х),
где Fa — площадь поперечного сечения рас-
тянутой арматуры.
Для изгибаемых и внецентренно-сжа-
тых конструкций, рассчитываемых с учетом
пластических деформаций в растянутой ар-
матуре, необходимо соблюдение условия
£<£$. (1.29)
Здесь граничное значение относи-
тельной высоты сжатой зоны, определяемое
по СНиП П-21-75, но при динамических
сопротивлениях бетона и арматуры, как
показано ниже.
Для конструкций из тяжелого бетона
и арматуры классов A-I, А-П, А-Ш
—ту. ,,-30>
1 + 4000 V ~ 1,1 )
где £о= 0,85 - 0,0008 й<б) Rnp
7?пр — расчетные сопротивления, определя-
емые по СНиП 11-21-75.
Для железобетонных изгибаемых и вне-
центренно-сжатых с большими эксцентрици-
тетами конструкций в качестве нормируе-
мых параметров обычно принимают углы
раскрытия трещин в шарнирах пластично-
сти. Условие прочности конструкций, в ко-
торой образовалось п шарниров пластично-
сти, имеет вид:
(1.31)
где Ti — полученный из динамического
расчета угол раскрытия трещины в Лм шар-
нире пластичности; УИщ — предельный угол
раскрытия трещины в i-m шарнире пластич-
ности.
Предельный угол раскрытия Vn вычис-
ляют по формуле
Фп — ( 'j ^пл> (1-32)
\ Рп Ро /
где 1/ро определяют по формуле (1.28);
1 £а “F
Рп ^0
8а — деформация арматуры при разруше-
нии сжатого бетона, равная
где 8б — предельная деформация сжатого
бетона, равная 0,0025; § — характеристика
сжатой зоны бетона, определяемая так же
как в формуле (1.30); /Пл—длина пласти-
ческой зоны [14];
/ПЛ = С1С2 (/о/Ло)’/4йо, (1.33)
где /0 — длина примыкающего к шарниру
пластичности участка конструкции, на кото-
ром изгибающий момент сохраняет знак;
Ci — коэффициент, равный для пролетных
сечений Ci==0,9, для опорных сечений за-
щемленных и неразрезных балок С[ = 0,7;
С2— коэффициент, равный для изгибаемых
элементов Сг—1, для внецентренно-сжатых
элементов
С2 = 1 + 0,5 (1.34)
**пр
где N — продольная сила; Afnp — несущая
способность сечения при центральном сжа-
тии.
Для исключения возможности разрыва
растянутой арматуры изгибаемых элемен-
тов должны соблюдаться условия — для
арматуры класса А-Ш g 0,05, а для
A-I V и выше § > 0,1. (1.35)
1.6. РАСЧЕТНЫЕ СХЕМЫ
Взрывная волна может оказывать разру-
шающее действие только на отдельные эле-
менты сооружения (локальное действие)
12
или на все сооружение (общее действие).
В конструкциях сооружения в зависимости
от эксплуатационных требований допуска-
ются: а) только упругие деформации;
б) пластические деформации, сопровожда-
ющиеся в железобетонных и каменных кон-
струкциях значительным раскрытием тре-
щин; в) выход из строя отдельных элемен-
тов (например, наружных панелей) без раз-
рушения всего сооружения. Все эти факто-
ры влияют на выбор расчетных схем.
В зависимости от требований к точно-
сти расчета, технических возможностей вы-
полнения расчета и точности исходных
предпосылок некоторые конструкции рас-
считывают как изолированные или с учетом
их взаимного влияния. В первом случае со-
оружение расчленяют на отдельные про-
стейшие конструктивные элементы (балки,
плиты, колонны и т. п.), опорные закрепле-
ния которых (шарнирные, жесткие) прини-
мают исходя из конструкций сопряжения
элементов. Для каждой конструкции вы-
полняют динамический расчет. Во втором
случае рассчитывают все сооружение с уче-
том пространственной работы его элементов
или рассчитывают отдельные элементы, но
с учетом их взаимного влияния (упругие
или пластические закрепления опор, верти-
кальные смещения элементов и всего со-
оружения и т. п.).
1.7. ЭКСПЕРИМЕНТАЛЬНЫЕ
ЗАВИСИМОСТИ ДЛЯ ОЦЕНКИ
ДЕЙСТВИЯ ВОЗДУШНЫХ ВЗРЫВНЫХ
ВОЛН НА СООРУЖЕНИЯ [5]
Экспериментальные зависимости позво-
ляют оценить степень повреждения соору-
жений, удаленных на различные расстояния
от центра взрыва. Расстояния от центра
взрыва, м, на которых возникают повреж-
дения сооружений, определяют по форму-
лам:
r=feB]/‘C; г=Къ / С, (1.36)
где С — масса заряда ВВ, кг; kB, Кв — ко-
эффициенты, принимаемые по табл. 1.3 [5]
в зависимости от массы заряда, условий его
размещения и степени безопасности соору-
жений.
Коэффициент Кв используют для откры-
тых зарядов массой больше 10 т при 1-й,
2-й и 3-й степенях безопасности и для за-
рядов массой больше 20 т, заглубленных
на всю высоту, при 1-й и 2-й степенях без-
опасности; для всех других случаев — ко-
эффициент kB. Тип взрывчатого вещества
при расчете безопасных расстояний не учи-
тывают. Степень безопасности устанавлива-
ют в зависимости от значимости объекта.
Если взрывы производят в узких доли-
нах или проходах между стенами на ули-
цах, то значения г, найденные по (1.36), за-
тем должны быть удвоены. Если сооруже-
ние расположено за преградой (лесные на-
саждения, возвышенности), то значения г
могут быть уменьшены, но не более чем в
2 раза.
Минимальное расстояние, на котором дей-
ствие воздушной волны еще безопасно для
человека, определяют по формуле
Гмин = 15 с, (1.37)
где С — масса заряда ВВ, кг.
Эту формулу используют, когда по ус-
ловиям работ необходимо максимальное
приближение обслуживающего персонала
к месту производства взрывных работ. В
нормальных условиях это расстояние сле-
дует увеличивать в 2—3 раза.
Значения давлений в проходящей воз-
душной ударной волне большой продолжи-
тельности (т+>0,1 с), при которых в эле-
ментах сооружений происходят различные
разрушения, определяют по табл. 1.4.
ТАБЛИЦА 1.3
Степень безопас- ности Возможные повреждения Открытый заряд Заряд, заглубленный на вы- соту
G, т kB «в G, т йв хв
1 Отсутствие повреждений Меньше 10 Больше 10 50-^00 400 Меньше 20 Больше 2Ю 20—50 200
2 Случайные повреждения за- стекления Меньше 10 Больше 10 10—30 100 Меньше 20 Больше 20 5—12 50
3 Полное разрушение застек- ления, частичные поврежде- ния рам, дверей, наруше- ние штукатурки и внутрен- них легких перегородок Меньше 10 Больше 10 5—8 30-50 2—4 — '
4 Разрушение внутренних пе- регородок, рам, дверей, ба- раков, сараев и т. п. Независимо от С 2—4 1 1—2
5 Разрушение малостойких каменных и деревянных зданий, опрокидывание же- лезнодорожных составов Независимо от С 1,5-2 » 1 — 0,5—1 -—
13
ТАБЛИЦА 1.4
Здания и сооружения
Давление 0,1 МПа, при котором наступа-
ет разрушение
полное
сильное
слабое
Промышленные здания с металлическим или железобе-
тонным каркасом
Многоэтажные жилые дома с каменными стенами (бо-
лее трех этажей)
Малоэтажные (1—3 этажа) каменные дома с металли-
ческим каркасом
Деревянные дома
Укрытия простейшего типа
Подвальные убежища
Металлические и железобетонные мосты
Деревянные мосты
Частично заглубленные резервуары
Смотровые колодцы
Подземные стальные сварные трубопроводы диаметром
менее 340 мм
То же, диаметром более 350 мм
Водонапорные башни
Кабельные подземные линии
Воздушные высоковольтные линии электропередач______
0,5—0,8 0,3—0,5 0,05—0,2
0,3—0,4 0,2—0,3 0,05-0,1
0,35-0,45 0,25—0,35 0,07—0,15
0,2—0,3 0,12—0,2 0,06—0,08
0,15-0,2
1,5—2 —* 0,7—1
2—110 05-2
0,5—1 0,3—0,5 0,1—0,3
1 0,5 0,1—0,3
20 и более 15—20 6—10
20 и более 15—20 6—10
10 и более 6—10 2—3,5
0,5-1 0,3-0,5 0,1-0,2
10 и более 5—10 2-3
1 0,5 0,1—0,3
При полных разрушениях происходит
разрушение всех несущих конструкций, вос-
становление зданий и сооружений невоз-
можно. При сильных - - разрушение боль-
шей части несущих конструкций. В зданиях
сохраняются прочные подвалы, часть кар-
каса, стены нижних этажей. Восстановление
нецелесообразно и возможно лишь путем
нового строительства с использованием от-
дельных сохранившихся конструкций. При
слабых разрушениях частично разрушаются
отдельные части здания (сооружения): пе-
регородки, крыши, легкие пристройки, две-
ри и т. п. Для восстановления требуется
капитальный ремонт.
В подземных сетях коммунального хо-
зяйства при их полном разрушении разры-
ваются или раздавливаются трубы (кабе-
ли); при сильном происходят деформации
или разрывы трубопроводов в отдельных
местах; при слабом повреждаются стыки в
отдельных местах.
1.8. РАСЧЕТ КОНСТРУКЦИЙ
В УПРУГОСТИ СТАДИИ [2, 8, 9, 10, 12]
Ниже изложен метод, применяемый для
расчета в упругой стадии конструкций на
действие кратковременных динамических
нагрузок. Этот метод основан на приведе-
нии конструкции к системе с одной сте-
пенью свободы путем задания формы коле-
баний, совпадающей со статической формой
перемещения конструкции под действием
рассматриваемой нагрузки. Движение кон-
струкции может быть описано дифферен-
циальным уравнением
^2
L = p (t) f, (M), (1.38)
д
где ш(А1, i/)—перемещение точки ДИ кон-
струкции; L(w)—дифференциальный опе-
ратор, в который входят производные толь-
ко по пространственным координатам;
p(t)— pf(t); р — параметр, характеризую-
щий максимальную погонную динамическую
нагрузку; fi(M), f(t)—функции, характе-
ризующие изменение нагрузки по поверх-
ности конструкций и во времени соответст-
венно; т—погонная масса конструкции.
Динамическое перемещение конструкции
представляется в виде:
w (М, /) = pF (М) Т (/), (1-39)
где F(M)—функция от пространственных
координат (форма прогибов), описываю-
щая перемещения конструкций от действия
статической нагрузки интенсивностью fi(M).
Функцию F (М) определяют предвари-
тельно из решения дифференциального урав-
нения
L (М),
которое удовлетворяет граничным услови-
ям на контуре конструкции, зависящим от
вида контурных закреплений.
Функция динамичности T(t) описывает
изменения во времени перемещений конст-
рукций и как следствие усилий в ней. При-
менение метода Бубнова — Галеркина при-
водит к уравнению для функции
Т (/) + со2Г (/) =со2/ (/), (1.40)
где со — круговая частота собственных ко-
лебаний конструкции, соответствующая при-
нятой форме колебаний, совпадающей с
формой прогиба от заданной статической
нагрузки
Значение w определяют по формуле
С ft (М) F (М) dM
ш = -. (1.41)
m j Я (M) dM v *
Определив функцию T(t) из (1.40), на-
ходят перемещения конструкции w(M, t) в
любой момент времени по (1.39), а усилия
в ней вычисляют по статическим формулам
на основе известных теперь перемещений.
При расчетах значение со можно не вы-
числять по (1.41), а принимать равным кру-
говой частоте собственных колебаний кон-
струкции, соответствующей той форме ко-
лебаний, которая 'наиболее близка к стати-
ческой форме перемещений конструкции от
нагрузки fi(M). При расчете конструкций,
у которых аналитическое выражение для
14
статической на-
по поверхности
динамической и
величине. Наи-
статической формы перемещения громоздко
или не находится в замкнутом виде, дина-
мические усилия и перемещения определяют
умножением их соответствующих статиче-
ских значений, принимаемых по литератур-
ным или справочным данным, на функцию
динамичности T(t). Эти статические значе-
ния находят от действия
грузки, распределенной
конструкции аналогично
равной ее максимальной
большее значение функции динамичности
называется коэффициентом динамичности.
Он не является постоянной величиной и за-
висит от вида нагрузки и динамических
свойств (массы и жесткости) конструкции.
Изложенный подход неприменим для
расчета конструкций, напряженно-деформи-
рованное состояние которых представляет
собой результат наложения напряженно-
деформированных состояний, изменяющих-
ся во времени с существенно различными
периодами (например, открытая цилиндри-
ческая оболочка) и в случае действия ди-
намической нагрузки, распределение кото-
рой по поверхности значительно меняется
во времени (например, при набегании вол-
ны на конструкцию).
Ниже приведены функции динамичности
и коэффициенты динамичности для взрыв-
ных нагрузок наиболее распространенных
видов:
нагрузка вида
(см. рис. 1.12,а):
р (О =
д
Р
О
т (/) = 1-
при О
при
0;
нагрузка вида (см. рис. 1.12,в):
р (/) =
где
Р
О
р 1—
О
2
sin со /
О
2
sin СО t
со (Z — 9),
2
1
\ Л sin со 0
- sin со 02—------------
2/ СО 01
— + —— cos со 02 —
' 01 СО 02/
cos со 0
&д при со02<2ОО следует
максимум функции (1.46):
2 sin
1
при
вычислять как
2>200. (1.47)
sin со t
---Г— О
. Л 1 — cos со 0
где А = sin со 0 —-----------------
sin со 0
д
со 6
sin4
При
со О
со О
при
(1.43)
(1.44)
Значения kK для нагрузок вида (1.42),
(1.45) можно определять также по графи-
кам, приведенным на рис. 1.14, 1.15:
нагрузка вида (см. рис. 1.12,6):
Р (0 =
*
Pi
О
где 01 =
(0=11-
sin со t
(1.48)
д=
Р1
О
/
15
1.14. Коэффициенты динамичности при расчете
конструкций в упругой стадии для мгновенно
возрастающей нагрузки
коэффициент динамичности при на-
грузке на поверхности грунта вида (1.42)
при 9 = оо находят по графикам, приведен-
ным на рис. 1.17, на которых
to Н р аг
sn = , V) = ,
аг 2 со
где Н — толщина слоя грунта над конст-
рукцией; а\ — скорость распространения уп-
ругопластических волн в грунте (см. табл.
1.1); р — плотность грунта обсыпки; тх—
масса конструкции, приходящаяся на еди-
ницу площади загружаемой поверхности;
со — частота собственных колебаний конст-
рукции, определяемая без учета массы грун-
та над конструкцией.
В данном случае коэффициент дина-
мичности учитывает (кроме эффекта дина-
1.15. Коэффициенты дина-
мичности при расчете кон-
струкции в упругой стадии
для нагрузки с нарастани-
ем во времени
Л 1 — COS СО 01 Д
где 01 = sin со 0i — -------------------+ -
СО 01 (0 02
Л sin со 01
а2 = cos со 0i —--------=— ;
со 01
А — ах sin со 02 — а2 cos со 02;
В = — —— + ах cos со02 + аг sin 9г;
СО 02
£д следует вычислять как наибольшее зна-
чение функции (1.49);
/ arc tg со 01 \ .
I ~ёх I *
\ со 01 у
при co0j >]2 arctgco0I (при Д = 0,5 <00^
2,785).
Значение &д для нагрузки вида (1.48)
при 9 и Д = 0,5 может вычислять по графи-
ку, приведенному на рис. 1.16.
Для изгибаемых конструкций, располо-
женных под слоем грунта толщиной:
мического действия нагрузки) влияние от-
ражения волны сжатия от перекрытия и
свободной поверхности грунта.
Ниже приведены формулы для вычис-
ления прогибов и изгибающих моментов в
одно- и многопролетных балках, загружен-
ных равномерно распределенной статиче-
ской q и динамической р нагрузками. Ко-
эффициенты динамичности принимают по
приведенным выше формулам и графикам в
зависимости от закона изменения динами-
ческой нагрузки во времени. Максимальные
изгибающий момент и прогиб:
4^макс ~ Alp — Мд;
#макс — Ур кд~\~Уд> (1.50)
где Мр, ур —изгибающий момент и прогиб
от статического действия динамической на-
грузки интенсивностью р; Mq, yq — изгиба-
ющий момент и прогиб от действия стати-
ческой нагрузки интенсивностью q, опреде-
ляемые методами теории железобетонных
конструкций.
Для шарнирно-опертой балки пролетом I
Н
0,25 01
со
16
1.16. Коэффи-
циенты дина-
мичности при
расчете кон-
струкций в уп-
ругой стадии
для нагрузки
с отражением
1.17. Коэф-
фициент ди-
намичности
при расчете
заглубленных
$
а
где В — жесткость среднего сечения балки,
определяемая согласно п. 1.5.
При действии равномерно распределен-
ного мгновенного импульса интенсивностью i
4 I 1 f В
Ломакс = я т |/ tn + Q*
Унаке —
Для балки с защемленными концами:
для опорного сечения
= k1' ^n==nF*i: (I-51)
для пролетного сечения
р /2
мрр=-1Г <3-2й1);
(3 — 2^),
(1.52)
где ki — коэффициент, учитывающий пере-
распределение изгибающих моментов в же-
лезобетонных балках;
0,27 4-0,73Pi .
0,46 4- 0,54 р! ’
Воп
Рх=—; (1.53)
В°п, Впр — жесткость опорного и пролетно-
го сечений.
Прогиб середины пролета
р Z4 Vi
Ур “ 384 Вп₽ ’
где Vi = 1—0,32(^1—1) —
(1.54)
— 0,85 (Агх —0,407) 1 — — .
\ Pi /
Для балки с одним защемленным и дру-
гим шарнир но-опертом концом:
для сечения на защемленной опоре
^n = -V" П-55)
о * о
_ 0,26 4-0,74 р!
~ 0,58 4-0,42 Pi *
(1.56)
для пролетного сечения с координатой
Для неразрезных балок значения изги-
бающих моментов определяют по форму-
лам (1.51) (1.52) (1.55) (1.57) с заменой
fei и k2 на , fe” в соответствии с п. 1.9.
1.9. РАСЧЕТ БАЛОК
В ПЛАСТИЧЕСКОЙ СТАДИИ [2, 9, 12]
Если к конструкции предъявляется
только требование отсутствия разрушения,
то ее рассчитывают с учетом работы мате-
риала в пластической стадии. В этом слу-
чае для железобетонных конструкций дол-
жны удовлетворяться условия (1.29), (1.35).
Балка с шарнирно-опертыми концами
под действием равномерно распределенных
статической и динамической нагрузок. В
пластической стадии в середине пролета
образуется шарнир пластичности. Проч-
ность железобетонной балки по нормально-
му сечению (в середине пролета) рассчиты-
вают из условия
Тмакс = ,nPfD kv ¥п> (1.58)
где — коэффициент динамичности по
углу раскрытия трещины в шарнире плас-
тичности, равный
kn — коэффициент динамичности по пере-
мещениям; вычисляют в зависимости от ви-
да нагрузки по графикам рис. 1.18, 1.19,
1.20; — предельный момент внутренних
сил сечения, определяемый при динамиче-
ских сопротивлениях арматуры и бетона;
Тп — предельный угол раскрытия в шарни-
БИБЛИОТЕКА
К р G > : оз о оного
я «л к т ех н г1. ' с; <v г о к • уг и т ут 1
17
ре пластичности, принимаемый по форму-
лам (1.32) (1.33) при /0=А С2=1.
1.18. Коэффициенты динамичности для шарнир-
но-опертой балки при расчете в пластической ста-
дии для мгновенно возрастающей нагрузки
Максимальный прогиб балки находят
по формуле
5 р /4
#макс = 384 В “F Уд- (Ь59)
Расчет прочности по наклонному сече-
нию (на опорах) производят на действие
поперечной силы
Ниже приводятся аналогичные формулы
для расчета балки в случае действия рав-
номерно распределенного мгновенного им-
пульса интенсивностью Z:
#макс —
Г4Л*О Z*
л3 В
0,85Z2 5 \
Мд т / 4
(1.60)
Тмакс = 0.П
60Л4о
I2 (О2 I*
(1.61)
M0 = M$ — Mq.
1.19, Коэф-
фициенты ди-
намичности
для шарнир-
но-опертой
балки при
расчете на-
грузки с на-
растанием
в пластиче-
ской стадии
в упругой ста-
дии
1.20. Коэффициенты динамичности для шарнир-
но-опертой балки при расчете нагрузки с отраже-
нием
.......при расчете в упругой стадии
....... при расчете в пластической стадии
Балка с защемленными концами при
действии равномерно распределенной дина-
мической нагрузки, изменяющейся во вре-
мени по закону (1.42). Упругая стадия де-
формирования балки заканчивается после
образования двух шарниров пластичности
на опорах или одного шарнира пластично-
сти в пролете (упругопластическая стадия).
При дальнейшем увеличении прогиба воз-
можно образование всех трех шарниров
пластичности (пластическая стадия). Ниже
рассматривается только случай, когда вна-
чале шарниры пластичности возникают на
опорах. Этот случай имеет место при усло-
вии
М£пд — Л4°п 2
М"РД — < 3 — 2 6! ’
V If
где Mj°A, ЛГ£РД — предельные моменты
внутренних сил в опорном и пролетном се-
18
чениях балки соответственно, определяемые,
согласно СНиП 11-21-75, при напряжениях:
в растянутой арматуре в бетоне
^пр, в сжатой арматуре 7?а.с.
Расчет прочности по нормальным сече-
ниям ведут в следующей последовательно-
сти:
находят время Xi конца упругой ста-
дии; значение Xi является корнем уравнения
П (Тх)-С’ с1-62)
Если уравнение (1.64) имеет решение,
то балка в процессе деформирования дости-
гает пластической стадии; условия прочно-
сти по нормальным сечениям имеют вид:
шоп ____
1 макс
lFnP —
х макс
где Л (Т1) = 1 —
—COS €01 ^1 +
sin сох xr
to! 0 1
—-------ЛЯ?
192 вп₽
96 ВПР
цгол
п »
где = 8Т2 (т2) + 0,576 X
(1.67)
X (б-йм-—^—) s2 + 0,282raS; (1.68)
\ 3 (£>1 6 /
А^ = ^-8Т2 (х2) (1.69)
— жесткость пролетного сечения балки;
tn — погонная масса балки.
Определяют время х2 конца упругоплас-
тической стадии, значение х2 является кор-
нем уравнения
Т2 (та) =--~2й1- (С-^П). О-63)
о
где
м
м ^рд _
Л4рР
7’2 (т2) = Тг (/) при t = т2,
где Т2 (/) = С, sin ® (/ — Tj) —
— С2 cos и (t — т,) 4- 1 — &°п — (1.64)
и
Ci = 2,27г, v2 4----С2 = 1-й°п-
со 0
т, л2 I / Вп₽ '
—-g-; co = -jr У
1 — COS €01
И = sin 0)1 Т1 — --------------;
0)1 0
v2 == 0,184 — 0,13 ki -|-
+ (0,184^-0,071) — .
Pi
Если уравнение (1.63) не имеет реше-
ния, то шарнир пластичности в середине
пролета не возникает и балка работает
только в упругопластической стадии; в этом
случае условие прочности по нормульному
сечению балки имеет вид:
П"аке = 79^ (1-65)
где =8T2(tmi); значение tm\ находят
из выражения
tg -------9------- =
[Г2(х2) определяют по формуле (1.63)];
Г2 — Cl C0S 03 (Т2----- *1) +
1
+ С2 sin 0) (т2 — ti) — —"7 .
<о 0
Предельные углы раскрытия трещин в
шарнирах пластичности находят по форму-
лам (1.32) (1.33), в которых для при-
нимают Zo=O,25 I и для Чг”р —/о = 0,5/.
Расчет прочности балки по наклонным
сечениям на опорах ведут на действие по-
перечной силы
qt
где kq принимают:
при работе балки в упругопластической
стадии
при работе балки в пластической ста-
дии
Приведенные зависимости справедливы,
если максимальные перемещения балки
имеют место в течение времени действия
нагрузки: при т2 < 0, если балка работает
в уйругопластической стадии; при х2+
+ (s/o)i) <0ь если балка работает в пласти-
ческой стадии.
Для случаев, когда максимальные пе-
ремещения балки имеют место после окон-
чания действия нагрузки, расчетные зави-
симости здесь не приводятся.
Балка с одним защемленным и другим
шарнирно-опертым концом при действии
равномерно распределенной динамической
нагрузки (1.42). Ниже рассматривается
только наиболее часто встречающийся слу-
чай, когда шарнир пластичности возникает
вначале на опоре (упругопластическая ста-
дия), а затем в пролете (пластическая ста-
19
дня). Этот случай может быть при выпол-
нении условия
Л4дпд — М
оп
Я
мпрд _ мпр
(1.70)
Если система уравнений (1.71), (1.72)
не имеет решения, то шарнир пластичности
в пролете не возникает, и балка работает
только в упругопластической стадии; усло-
вие прочности по нормальному сечению име-
ет вид:
Прочность балки по нормальным сече-
ниям рассчитывают в следующей последо-
вательности.
Находят время п конца упругой ста-
дии из уравнения (1-62), в котором
Л4°п определяет по формулам (1.55):
15,45 1/
( р~ V -ггГ-
оп _____
2макс
рр
106,8 ВПР
W°n, (1.74)
где =4,45 T2(tmi).
Значение tmi находят из выражений
(1.66), (1.73).
Если система уравнений (1.71), (1.72)
имеет решение, то балка работает в пласти-
ческой стадии, и условия прочности по нор-
мальным сечениям имеют вид:
Из системы уравнений (1.71) и (1.72)
находят время т2 конца упругопластической
стадии и величину г), которая определяет
место образования шарнира пластичности
2х0
, где — расстояние от
/ «9 \
1 — —
\ 4 /
пролетного шарнира пластичности до шар-
нирной опоры;
оп ____
макс
ПГПр =
макс
рР
106,8 ВПР
р Р
43,8 ВПР
(1.75)
ХГ2(Т2)=^Р; (1.71)
р -Г k
!—Р
П =---------------------, (1.72)
W + Y + T2 (Т2)
где
Л1"рд — М"Р
ьпр_______«_______9—
м мпр
Л4"р, М"р определяют по формулам (1.57);
Л (Т2) == Т2 (/) при / = т2.
Выражение для T2(t) имеет такой же
вид, как (1.64), но с измененной величиной
С), равной
Ci = 1,57 Г1 v3 + , (1,73)
(о U
где v3 = 0,348—0,15&2 +
+ 10,196 —0,022 й2) -2- .
Pi
Решение системы (1..71), (1.72) целесо-
образно вести последовательными прибли-
жениями: задают величину 11=1, из урав-
нения (1.71) определяют 7г (т2); по формуле
(1.72) уточняют значение ц и, используя
его, находят из (1.71) уточненное значение
ТгСгз); затем определяется время т2. Далее
проверяют прочность балки.
Значения s, б, г2 вычисляют по форму-
лам (1.68), (1.69).
Предельные углы раскрытия в шарни-
рах пластичности определяют по формулам
(1.32), (1.33), в котором для "Ф'ц11 принима-
ют /о = 0,3/ и для —/о = О,7/.
Прочность балки по наклонным сече-
ниям рассчитывают на действие поперечных
сил:
на шарнирной опоре
на защемленной опоре
где kQ3 принимают равными:
при работе балки в упругопластиче-
ской стадии
21
при работе балки в пластической ста-
дии
= ------7-) С + Т’г
kQ з = (1 + -T-'l k« + Тг (t2)-
\ Т1 J
4. Неразрезные балки при действии рав-
номерно распределенной динамической на-
грузки (1.42). Неразрезные равнопролетные
балки приближенно можно рассчитывать
по вышеприведенным формулам для одно-
пролетных балок, если динамическая на-
грузка возникает одновременно во всех
пролетах. В этом случае неразрезная балка
представляется в виде системы однопролет-
ных балок с защемленными концами (сред-
ние пролеты) и с одним защемленным и
другим шарнирноопертым концом (крайние
пролеты, у которых одна опора шарнир-
ная). Коэффициенты k\ (1.53) и 62 (1.56)
следует изменить, так как соотношения
между изгибающими моментами на опорах
и в пролете неразрезных балок отличаются
от таковых в однопролетной балке. Поэто-
му вместо коэффициентов k\ и /г2 надо при-
нимать коэффициенты k\l , » которые в
зависимости от числа пролетов равны; при
трех пролетах для среднего пролета —
= 1,2 63; при четырех пролетах для второго
и третьего пролетов 61/ ~ 1,076]; при пяти
пролетах: для второго и четвертого пролета
=1,105 61, для третьего пролета 6”—
= 0,948 6Ь для крайних пролетов при шар-
нирной концевой опоре — для двухпролет-
ной балки 62 ==62; при числе пролетов
больше двух 6” = 0,8 62.
Если смежные пролеты и вычисленные
для них коэффициенты 6г (Z =1,2) взаимно
не равны, то при определении изгибающего
момента на промежуточной опоре следует
принимать средние величины пролетов и
коэффициентов 6t.
Углы раскрытия трещин в шарнирах
пластичности на средних опорах неразрез-
ной балки принимают равными сумме уг-
лов раскрытия трещин в шарнирах на опо-
рах соответствующих однопролетных балок
(с защемленными концами). При определе-
нии предельных углов раскрытия трещин в
шарнирах пластичности, согласно п. 1.5,
значение /0 принимают: для шарниров на
средних опорах /о = 0,5/, для шарниров в
пролетах — как для соответствующих одно-
пролетных балок.
1.10. РАСЧЕТ КОНСТРУКЦИЙ
С УЧЕТОМ ВЕРТИКАЛЬНЫХ
СМЕЩЕНИЙ ОПОР [2, 9]
При действии на сооружение верти-
кально направленной взрывной нагрузки
происходит смещение опор перекрытий, учет
которого может привести к выводу, что со-
оружение выдерживает большую нагрузку,
чем в предположении неподвижности опор.
Смещение опор вызывается разными при-
чинами: деформациями колонн, стен, сме-
щениями опорных конструкций и всего со-
оружения в целом вследствие деформации
грунта основания. В общем случае учиты-
вают все указанные факторы.
Для сооружений, расположенных на
мягких грунтах, наибольшее влияние на
смещение опор перекрытий оказывает по-
датливость грунтового основания. Влияни-
ем деформаций опорных конструкций (ко-
лонн, стен) можно пренебречь. Ниже для
этого случая излагаются два приближенных
метода расчета, основанных на следующих
предпосылках:
1) все сооружения рассматривают как
жесткое тело, для которого находят верти-
кальные перемещения, возникающие вслед-
ствие податливости грунта. Ускорения, ко-
торые соответствуют найденным перемеще-
ниям, являются причиной дополнительных
инерционных сил, возникающих при движе-
нии сооружения, которые вводят в расчет
отдельных конструкций;
2) часть сооружения (колонны, стены,
фундаменты) рассматривают как жесткое
тело, нагрузкой на которое являются силы
реакций от элементов покрытия. Величины
реакций определяют с учетом перемещений
этой жесткой части вследствие податливо-
сти грунта. Найденные таким путем силы
реакции под подошвой фундаментов исполь-
зуют при расчете несущей способности всех
элементов сооружения.
Второй метод более точный, но требует
трудоемких вычислений.
Степень влияния вертикальных переме-
щений сооружения на работу его конструк-
ций и выбор метода расчета зависят от
конструкции сооружения, вида грунта ос-
нования и динамической нагрузки. Ниже
рассматривается ячейка сооружения, состо-
ящая из колонны, фундамента и части пе-
рекрытия, с которой собирается нагрузка
на колонну (рис. 1.21). Перекрытие состоит
из ригелей, опирающихся на колонны, и
уложенных на ригели плит. Предполагает-
ся, что плиты деформируются вместе с ри-
гелями.
При действии нагрузки достаточно
большой продолжительности (со0 50) вли-
ННННН1Т1П
1.21. Расчетная схема сооружения с учетом по-
датливости основания
21
яние вертикальных перемещений следует
учитывать, если
So =
где
(1.76)
Qi
со D
(1.77)
9
czi — скорость распространения упругоплас-
тической волны в грунте основания, прини-
маемая по табл. 1.1; со — частота колебаний
ригеля перекрытия, определяемая без учета
смещения опор и с учетом массы опираю-
щихся на него плит перекрытия;
F$ — площадь подошвы фундамента.
Первый метод расчета можно исполь-
зовать при s0< 1, второй метод расчета —
при l<s9^3. При $о>3 конструкции со-
оружения можно рассчитывать без учета
вертикальных смещений опор.
Расчет конструкций сооружения на дей-
ствие давления (1.11) с учетом перемеще-
ния всего сооружения как жесткого тела.
Определение перемещений сооружения.
Уравнение движения сооружения (рис. 1.21)
как жесткого тела имеет вид:
р (t) + Мф (i) — ти (/) =0, (1.78)
где P(t) =Ap(t)Fn— динамическая нагруз-
ка на перекрытие; N$(t) — равнодействую-
щая напряжений под подошвой фундамен-
та; т=тп+.тк+тф — масса всего соору-
жения; Fn, тп — площадь и масса части
перекрытия, с которой собирается нагрузка
на колонну; тк, т$ — масса колонны и фун-
дамента соответственно; u(t) — вертикаль-
ное перемещение сооружения.
Выражение, определяющее силу N$(t),
записывается в виде:
Л^ф (О = — сйи при и > 0, (1.79)
„ Р
где Ci = р a, Рф\ с0 =------------- .
&
Выражение для определения перемеще-
ния сооружения:
Расчет ригеля перекрытия в упругой
стадии. Левую часть уравнения движения
ригеля записывают так же, как и левую
часть уравнения движения ригеля при не-
подвижных опорах, а правая часть уравне-
ния равна p(t)—MiQu(t), где p(t)~
==Ap(t)b— погонная динамическая нагруз-
ка на ригель \(Ь — расстояние между риге-
лями); те — погонная масса ригеля; и —
вертикальное ускорение опор, найденное из
решения уравнения (1.78). Максимальное
значение усилий и прогиба ригеля находят
по формулам (1.50), в которых коэффици-
ент динамичности йд равен наибольшему
значению выражения
+ Xi sin со t — Х2 cos со t -|-
+ — (di cos q2 co t + d2 sln 0 * ;
Si
(1.82)
. 1 Sg
где Xi = —- -[** (qi d2 — q2 di);
о t) Si
— 1 + d2;
Sl
2 qi q2 Si + (1 -j- — q%) A
1 U — ?2)3-F 4 <?2
__ Л~~~ (! +^1—^2)
2 (1 + *71 — *?f)2 + 4 77 i/g
(1.83)
При определении наибольшего значения
функции (1.82) следует учитывать возмож-
ность нескольких максимумов этой функ-
ции. Условия закрепления концов ригеля
учитывают при определении
Расчет в пластической стадии шарнир-
но-опертого ригеля. Пластическая стадия
работы ригеля начинается в момент време-
ни т, определяемый из уравнения
Т (т) =*м, (1.84)
Предположим, что после того, как пе-
ремещение сооружения u(it) достигло мак-
симального значения (в момент времени
определяемого из уравнения u(t) = Q),
дальнейшее движение сооружения прекра-
щается [при u(t) — u(fi)]. Это допу-
щение соответствует модели грунта, в ко-
торой разгрузка происходит при постоян-
ной деформации (£р=оо).
где Т(т) принимают, согласно (1-82), при
/=.т; JfeM = (Mg-M) МР, Mp=pZ2/8.
Условие прочности ригеля по нормаль-
ному сечению, выражения для прогибов и
усилия принимают по формулам, приведен-
ным в п. 1.9, в которых коэффициент дина-
мичности для перемещений равен наиболь-
шему значению функции
Ап —feM + 0,59 (1 — зше )Х
X (z - 2о)а+[1,28 Ri (гв) +l,18v£/1(z0)lx
X (1.85)
<71
22
где z0 = cdt; z —cd/;
s2
/?х (zo) ~ cos Zq + X2 sin Zq + X
si
X [ № <72 “ ^1 <71) cos g2 ?o —
— № 9i + 41 91) sin 92 Zo] e~ ’* г° — —;
CD U
S2
v = — ;
s0
Ui (z0) = (—— cos 72Zo+ f sin (?2г(Д X
\ co 9 qi )
n > 1
V д— Q\ 2o_______________ •
24 e л *
cd 0 qi
— <71 z.
sin q2 z e
U (z0) = U (z) при z = z0.
Расчет фундаментов и центрально-на-
груженной колонны. На подошву фундамен-
та со стороны грунта действует нормальная
сила, максимальное значение которой
Л/ф = ^т+ДРф^п*д.ф. (1.86)
где #фТ — продольная сила в колонне от
статической нагрузки; &д.ф — коэффициент
динамичности для усилия под подошвой
фундамента, принимаемый по графикам
рис. 1.22.
Площадь подошвы фундамента [уже
использовавшаяся в формулах (1.78)—
1.22. Коэффициенты динамичности для усилия
под подошвой фундамента
(1.81) и (1.86)], проверяют из условия, что
среднее давление под подошвой не превы-
шало расчетного, умноженного на коэффи-
циент динамического упрочнения &у —5, и
в любом случае не было больше 15 кгс/см2.
Максимальное значение продольной си-
лы в сечении колонны у верха фундамента
равно:
*К = Я"+ДРфА^д.к, (1.87)
где —продольная сила в сечении ко-
лонны от статической нагрузки; &д.к — ко-
эффициент динамичности для усилия в ко-
лонне, равный наибольшему значению фун-
кции
5 (О = 1~
q1 cd 9!
О
v ~ Lcos °z
sin q2(&t e Ш (1.88)
При расчете фундамента на продавли-
вание и при проверке прочности колонны
продольную силу принимают равной (1.87).
Расчет конструкций сооружений с уче-
том влияния деформаций перекрытия на его
перемещения. Рассматривается ячейка со-
оружения, изображенная на рис. 1.21. Ко-
лонна и фундамент предполагаются абсо-
лютно жестким телом. Приводятся уравне-
ния движения сооружения и ригеля пере-
крытия при его работе в упругой и пласти-
ческой стадиях.
Упругая стадия. Перемещения ригеля
при действии динамической нагрузки пред-
ставляют в виде суммы двух перемещений
у (х, Z)=u (t)+pF (X) Т (/), (1.89)
А Рф Fn
где и (/) =------- U (/)—перемещение
со
колонны; F(x)—функция, задающая форму
изгиба ригеля; T(t)t U(t) — функции дина-
мичности для ригеля и колонны соответст-
венно; р — максимальная погонная динами-
ческая нагрузка.
Уравнение движения колонны совмест-
но с фундаментом
2(2 + #ф — mtu1=0,
где гП1 = тк + тф;
р/
Q= " T(t)—опорная
реакция ригеля; тУф — усилие под подошвой
фундамента, принимаемое по формуле
(1.79).
Функции динамичности T(t) и U(t) яв-
ляются решениями системы дифференци-
альных уравнений, которые следуют из
уравнений движения колонны с фундамен-
том и ригеля перекрытия:
U[t)+r1U(t) +
(190)
117 (0 +7 (0 +
+ <о2 Т (О = <о2 f (/), ,
Cl с0 а>2 пг„
где г 1 — , Го — , Л — ,
Ш1 ГП1 Со
<0 — определяют как в (1.77); та — как в
(1.78); f(t) — закон изменения динамиче-
ской нагрузки во времени; начальные усло-
вия при t — Q: U = T—U=t=Q.
Пластическая стадия. Рассмотрим шар-
нирно-опертый ригель. Время т конца уп-
ругой стадии определим из уравнения
Т (т) = £м,
23
1.23. Коэффициенты динамичности для шарнирно-опертой балки с учетом податливости основания
------------- при расчете в пластической стадии; ------------при расчете в упругой стадии
Mq pl2
где k" = м~ ’
JL/
Остальные обозначения приведены в п. 1.9.
Перемещение ригеля в пластической
стадии представляют в виде суммы переме-
щений
у (х, t) =и (/) +pF (х) Т (т) +
ригеля при значениях параметров (1.77)»
si (1.81), s2 (1.83) и о>0, приведенных на
этом рисунке. Часть кривой &п, нанесенная
сплошной линией, соответствует работе ри-
геля в пластической стадии, а пунктирная —
работе ригеля в упругой стадии. Эти части
взаимопримыкают в точке с абсциссой 6мо-
Если йм0, то ригель работает в
упругой стадии и его максимальный прогиб
равен
+ ф (О Х-, (1.91)
#макс —
5pZ4
[384 В *д + Уя'
где ср(/) —угол поворота половины ригеля.
Дифференциальные уравнения движе-
ния колонны совместно с фундаментом и
ригеля перекрытия имеют вид:
пги (/) + Ci и (Z) + с0 и (Z) +
т& Z2 ..
+ -4— <р = (/);
4
3 24 Мр
Т и (0+ф (0= -^йгХ
X [f (О — *м]-
В момент начала пластической стадии
деформирования, т. е. при t—x, перемеще-
ния и скорость конструкции определяют
выражениями:
Со
(1.93)
. р Z3
го — 0; ф =-------- Т (т).
т т ЗОВ
Системы уравнений (1.90), (1.92) целе-
сообразно решать с применением ЭВМ.
Для частного вида нагрузки, а именно из-
меняющейся во времени по закону f(t) —
= 1 — (Z/0), Z<0, на рис. 1.23 приведены
графики коэффициентов динамичности по
перемещениям ka для шарнирно-опертого
где /?д=Лп — принимают по соответствую-
щим графикам при /гм^&мо.
Если ^м"<^мо, то в ригеле возникают
пластические деформации. Условие прочно-
сти имеет! вид
макс
19,2В
(1-92)
1.11. РАСЧЕТ ВНЕЦЕНТРЕННО-
СЖАТЫХ КОЛОН [9]
Рассмотрим железобетонные колонны
центрально-нагруженные продольной стати-
ческой силой W и поперечной динамической
нагрузкой интенсивностью p(t). В таких ус-
ловиях могут находиться крайние колонны
сооружения, воспринимающие горизонталь-
ную нагрузку от стен ограждения, на кото-
рые действует взрыв. В зависимости от со-
отношения продольной и поперечной нагру-
зок возможны два случая разрушения ко-
лонн:
случаи 1 —разрушение начинается с до-
стижения предела текучести в растянутой
арматуре и завершается раздроблением бе-
тона сжатой зоны при развитии пластиче-
ских деформаций ~ растянутой арматуре;
случай 2 — разрушение происходит
вследствие раздробления бетона при пол-
ностью сжатом или частично растянутом
сечении, но при отсутствии пластических
деформаций в растянутой арматуре.
В случае 1 расчет конструкции ведут с
учетом ее работы в пластической стадии, в
24
случае 2 конструкция работает только в
упругой стадии.
Случай 1 разрушения имеет место, если
(1.94)
где £ = х/йо — относительная высота сжатой
зоны при разрушении; для прямоугольного
сечения с размерами b%h значение £ равно:
N + R^Fa-RlcF’a
b h0
, (1.95)
— граничная высота сжатой зоны,
определяемая по формуле (1.30).
Расчет колонны по случаю 1 внецент-
ренного сжатия. Несущую способность ко-
лонны рассчитывают: а) при отсутствии
трещин в растянутой зоне; б) при наличии
трещин в растянутой зоне и при отсутствии
пластических деформаций в растянутой ар-
матуре; в) при развитии пластических де-
формаций в растянутой арматуре.
Расчет колонны при отсутствии трещин
е растянутой зоне
Дифференциальное уравнение движения
колонны, рассчитываемой как сжато-изогну-
тый стержень, имеет вид:
о д*У1 , „д2У1 , &У1 ,, ос,
+ + ^’(i.96)
Максимальные значения прогиба и изгиба-
ющего момента:
^хмакс — Р F i (^) йд1;
М1макс = (^) Йд1.
Функцию динамичности 7\(t) и коэф-
фициент динамичности йд1 определяют по
формулам, приведенным в п. 1.8 с заменой
со на coivi-
Ниже даны выражения для функций
прогиба Fx(z) и изгибающего момента
M\(z> t) при различных граничных услови-
ях колонн. Обычно колонны железобетон-
ных зданий рассматривают как упругоза-
щемленные. В этом случае для колонны с
одинаковыми закреплениями обоих концов
граничные условия имеют вид (начало ко-
ординат 2 = 0 помещено в середине высоты
колонны)
// д yi
при z=± — ^=0; Мг=±с (1.101)
z v о z
перемеще-
где Сф — жесткость опорного закрепления
колонны относительно угловых
ний; Н — высота колонны.
В этом случае:
г2
N
где В\ — жесткость на изгиб железобетон-
ной колонны без трещин, определяемая по
формуле (1.26); p(t)~pf(O- Начальные
д yi
условия: при t — 0 Ц1 = 0 ~~— =0. Гранич-
д t
ные условия принимают в соответствии с
закреплениями концов колонны.
Уравнение (1.96) решают методом за-
дания формы перемещения (п. 1.8) в виде
статической линии прогиба, т. е. динамиче-
ский прогиб колонны представляется в виде:
(г, /)=РЛ (г) Л (/), (1.97)
ф
CCx
A] Pi cos %i
eti
H2
8
(1.102)
где статическую форму прогибов Fi(z) и
функцию динамичности T\(t) определяют
соответственно из уравнений:
(г) + F\ (г) = 1;
Л (/) + аЦ Г, (О = <! f (t).
Круговую частоту колебаний co.vi мож-
но принимать равной
где (01 — круговая частота колебаний ко-
лонны, определенная при отсутствии про-
дольной силы и при жесткости Р^ =
=ji2Bi/Zq ; Zo — приведенная длина колонны.
Изгибающий момент в сечениях ко-
лонны
Ceti COS ki г
Pl COS X!
pH2
(1-ЮЗ)
Изгибающие моменты в опорном сече-
нии и в среднем сечении колонны
Mi (0, /) =
G1
pl COS *1
Для расчета колонны с шарнирно-опер-
тыми концами в формулах (1.101)— (1.104)
следует полагать
(г, /) = -рВх^ (г) 7\(/). (1.100)
сф = °'> ^i = 0; ai-=Pi=l.
25
Для расчета колонны с жестко заде-
ланными концами значения констант и из-
гибающего момента определяют по форму-
лам:
где В2 — жесткость сечения колонны с
трещинами, определяемая по формуле
%! №
D1 ~ fef tg -Л1 8
1
All (г, О = —т х
(1.105)
где
(1/ро) -(1/Pi)
(1.109)
Л1о№^₽^о (1-0,5 5) +
+^.с Р'Л - «') - N (°-5 А ; (1 • 1Ю)
g находят из выражения (1.95);
определяют по формуле (1.106);
——— cos^z—11^—Л (/).
sin /4 ।
Рассматривается случай, когда при дан-
ной нагрузке трещины в растянутой зоне
колонны не образуются; тогда для всех се-
чений колонны выполняется условие
м1макс (г) N ги + , (1.Ю6)
1 M*N
pl Bl ’
В\ вычисляют по формуле (1.26); на-
ходят по формулам fl.28), (L95).
Функция P2(z) является решением
уравнения (1.98), в котором Bi заменена
на В2.
Функцию динамичности находят из
уравнения
гг (t) + <42 Т, (О =
где гу — определяемое, согласно СНиП II-
21-75, расстояние от центра тяжести приве-
денного сечения колонны до ядровой точки,
наиболее удаленной от растянутой зоны;
= R* Wt,
* г
= ®лг2 4 4)-Л 4i)b (1.111)
где
где WT — момент сопротивления приведен-
ного сечения для крайнего растянутого
волокна с учетом неупругих деформаций
растянутого бетона, определяемый по
СНиП 11-21-75.
Если для некоторого пролетного сече-
ния, координата которого обозначена Zo,
будет
^1макс (2о) > «у,
то в средней части колонны возникают
трещины, влияние которых необходимо
учитывать при расчете.
Расчет колонны при наличии трещин
в растянутой зоне. Трещины в пролетном
сечении колонны с координатой z0 обра-
зуются в момент времени определяемый
из уравнения
В (го Ы = M*N.
(1.107)
(о2 — круговая частота колебаний ко-
лонны определенная при Лг=0 и жестко-
сти В2;
р(2) _ д2 ^2
кр /2
*0
Начальные условия для уравнения
(1.111):
Т2(Л)=0;
Я/2
( (z) dz
• Z
^2 (4) = н/2 41) —
f F2 (г) dz
о
Л . DrH Н3
ki sin X! + 2 + 48
~ a2 . D2H H3 T1 (Z1)-
fe2 sinz2+ 2 + "48~
Для условий (1.101) уравнение (1.107)
имеет вид (при z = 0, т, е. для сечения в
середине высоты колонны)
При динамической нагрузке вида
р(/)=р(1—функцию динамичности
и
T2(t) определяют выражением
Тъ (0 = Q sin wv2 (/ — /i) —
Перемещения колонны и изгибающие
моменты при находят по формулам:
У2 (2, t) — У\ (z, /i) +
+ р F2 (z) Г2 (?);
М2 (z, t) (z, /х) —
— р (О,
(1.108)
26
Функция Т2(/) достигает наибольшего
значения ТД/т) в момент tm, который на-
ходят из уравнения
7V2
Выражение (1.113) справедливо, если
Ли "’ч 6-
При упругой заделке обоих концов,
когда при
Н д и2
выражение для имеет вид (1.102),
в котором всюду вместо В[ нужно запи-
сать В2.
Изгибающий момент
М2 (z, I) —Л41 (г, /1) 2
а2 cos k2 z
₽2 COS 7-2
р//2
4
Г2 (/), (1.114)
где коэффициенты k2, «2, Рг находят
по формулам (1.102), в которых Bi замене-
но на В2.
Прочность колонны проверяют в сече-
нии z — zm, в котором изгибающий момент
M2(z, tm) достигает наибольшего по абсо-
лютной величине значения IM2(zm, /т)'|.
Обычно zm = 0 или zm = H/2.
Если
| Л42 (Zm,
(1.115)
то при данной нагрузке прочность колонны
обеспечена.
Если
^2 (zm, /т)
(1.116)
> Мо#,
то в растянутой арматуре возникают пла-
стические деформации и расчет колонны
следует продолжать в пластической стадии.
Расчет колонны в пластической стадии.
Рассмотрим колонну с одинаковыми упру-
гозаделанными концами при действии на-
грузки вида p(t)=p(l——-). Предполагает-
ся, что шарниры пластичности в опорных
и среднем сечениях образуются одновре-
менно. Это предположение допустимо, ес-
ли абсолютные значения изгибающих мо-
ментов в этих сечениях Л12(0, 0> М2
о
отличаются не более чем на 20%.
Момент времени т окончания упругой
стадии работы колонны находят из урав-
нения
М2 (г, т)
где M2(z, т) принимают по формуле (1.114)
для того сечения z = 0
или ?=Я/2, в котором /M2(z, /)/ име-
ет большее значение, a дг определяют
по формуле (1.110).
Дифференциальное уравнение движения
колонны в пластической стадии, т. е. при
/2>т, имеет вид:
mH3 .. NH р№ / t \
24 <Р— 2 <₽= 8 \ ~ 0 ) “
-AZ (1.118)
где ф — угол поворота половины колонны
вследствие ее пластического деформирова-
ния; Л1 qP (Mg11 ) — момент внутренних сил
относительно центра тяжести сжатого бе-
тона для пролетного (опорного) сечения;
/о *= pFi (0) Ti (ti) -ppF2 (0),T2 (т) — прогиб сред-
него сечения колонны в конце упругой
стадии; x = £ft0, где g определяют по фор-
муле (1.95)
Начальные условия: при /=т <р = 0
ф(О)=<ро,
8pr2(bN2
где фо = рр X
I А2 . DtH Н3\
х I— sin ха + —— + — ; (1.119)
\ #2 40 /
Г2 = Cl COS СОдг2 (т — Zj) +
+ С2 sin сОдг2
(1.120)
Решением уравнения (1.118) при на-
чальных условиях (1.119) является
ф (/) = С3 sh Л (/ — т) + С4 ch X (/ — т) —
2Мр / t \
-'лпН1-*2-т : (1.121)
, л/ ]2 N рР
где л — у mfl2 ; Мр — 8 ;
N (h-x~fa)+М^ ~ Mon
1 /. 2 Мр \
Сз = ~Т — NH9 J ’
2 ЛЕ? / т \
г. — ---— I 1 _ьп_—
NH V о / *
Угловая скорость
<р (/) — X [Сз ch X (Z — т) + С4 sh X (/—т) ] +
+ ЮТ-- (1J22)
Максимальный угол поворота колонны
Ф/п — Ф Um) >
где tm вычисляют из уравнения ф(/)=0.
Если при всех t ф(/)>0, то происхо-
дит разрушение колонны вследствие поте-
27
ри устойчивости. Прочность колонны будет
обеспечена при
Ч’макс —
'Скс = Ф/п *
-щпр.
пгоп
п »
(1.123)
где предельные углы раскрытия , ф°п
определяют согласно п. 1.5.
Расчет колонны по случаю 2 внецент-
ренного сжатия. Случай 2 разрушения
имеет место, если
д
Я •
Значение £ для колонны из бетона
маркц М 400 и ниже с арматурой классов
A-I, А-П, А-Ш определяют по формуле
N + С — /?а (Fa + F&)
^1,(1.124)
где
—находят по формуле (1.30).
Жесткость сечения колонны при отсут-
ствии и при наличии трещин в растянутой
зоне принимают Bi — E0Jn. Прогиб и изги-
бающие моменты в колонне определяют по
формулам (1.97) — (1.105).
Прочность колонны проверяют исхо-
дя из условия
А11макс — Р&1 ^Д1
44^ ,
(1.125)
где Mg# определяют по формуле (1.110),
в которой £ принимают согласно (1,124).
СПИСОК ЛИТЕРА ТУ РЫ
1. Бегун Ф. А., Станюкович К. П.,
Шехтер Б. И. Физика взрыва. М., 1959.
2. Боданский М. Д, и др. Расчет кон-
струкций убежищ./ Боданский М. Д., Гор-
шков Л. И., Морозов В. И., Расторгу-
ев Б. С. М„ 1974.
3. Власов О. Е. Основы теории дей-
ствия взрыва. М., 1957.
4. Ганушкин и др. Приспособление
подвалов существующих зданий под убе-
жища. М., 1971.
5. Единые правила безопасности л р/л
взрывных работах. М., 1972, 319 с.
6. Инструкция по расчету перекрытий
на импульсные нагрузки. М., 1966.
7. Ляхов Г, М. Основы динамики
взрыва в грунтах и жидких средах. М.,
1964.
8. Попов И. Н., Расторгуев ь. С. Ди-
намический расчет железобетонных конст-
рукций. М., 1974.
9. Покровский Г. И. Взрыв. М., 1973.
1'0. Рабинович И. М. и др. Расчет со-
оружений на импульсные воздействия. М.,
1970.
11. Руководство по расчету остаточных
деформаций грунтов при динамических
нагрузках. М., 1967.
12. Руководство по проектированию
строительных конструкций убежищ граж-
данской обороны. М.» 1974.
13. Справочник по динамике соору-
жений. М., 1972.
14. Тихий М., Ракосник И. Расчет
железобетонных рамных конструкций в
пластической стадии. М., 1976.
1’5. Яковлев Ю. С. Гидродинамика
взрыва. М., 1961.
РАЗДЕЛ 2. ЗАЩИТА ЗДАНИЙ ВЗРЫВООПАСНЫХ
ПРОИЗВОДСТВ ОТ НАГРУЗОК,
ВОЗНИКАЮЩИХ ПРИ ВЗРЫВНОМ ГОРЕНИИ
ГАЗОВОЗДУШНЫХ СМЕСЕЙ (ГВС) ВНУТРИ ПОМЕЩЕНИЙ
(Н. А. СТРЕЛЬЧУК, Г. Г. ОРЛОВ)
2.1. ОБЩИЕ СВЕДЕНИЯ
При проектировании зданий взрыво-
опасных производств конструктивное и
компоновочное решения должны быть та-
кими, чтобы в случае взрыва газовоздуш-
ной смеси (ГВС) внутри помещения по-
вреждения были минимальными. Для ре-
шения такой задачи важно знать возмож-
ный режим течения взрыва ГВС в произ-
водственных помещениях, так как величи-
на и интенсивность возникающих нагрузок
зависит от режима горения ГВС.
Согласно современным представлениям
[4, 7, 8, 15, 16, 17, 18] существуют три
характерных режима горения: нормальное,
неустойчивое (ускоряющееся) и детонаци-
онное. При нормальном и ускоряющемся
режимах горения фронт пламени распрост-
раняется с дозвуковой скоростью. Причем
поскольку при нормальном режиме горе-
ния отсутствуют причины, вызывающие ин-
тенсификацию горения, то пламя распрост-
раняется фактически с постоянной скоро-
стью, которая определяется выражением
Р ^вр
б/в — С;н п — Рц Л у" — ^нер, (2-1)
Ро 1 о
где — нормальная скорость горения
ГВС; р, ро — плотность продуктов сгора-
ния и исходной ГВС; тр—отношение из-
менения числа молекул до реакции в пла-
мени и по окончании горения; Гвр, То — со-
ответственно температура продуктов сгора-
ния и исходной смеси при постоянном дав-
лении; ер — степень расширения продуктов
горения при постоянном давлении.
Из выражения (2.1) можно определить
видимую скорость распространения фронта
пламени с учетом самопроизвольного дви-
жения газа, вызываемого расширением
продуктов горения. Это выражение спра-
ведливо для случая сферического фронта
пламени и для случая, когда фронт пла-
мени является плоским.
Нормальная скорость горения пред-
ставляет собой основную характеристику
ГВС. Она зависит от природы горючего
газа, соотношения горючего и окислителя
в ГВС, а также от начального состояния
(температуры и давления) смеси. В этом
случае при горении в открытой атмосфере
ГВС такого состава, при котором наблю-
дается наибольшая скорость реакции, нор-
мальная скорость горения составляет 0,3—
0,7 м/с. Только для горючих газов неко-
торых видов она может достигать 0,8—•
2,5 м/с (этилен, ацетилен, водород).
Важной характеристикой ГВС являет-
ся температура ее горения (Твр). Для га-
зовоздушных смесей стехиометрического
состава температура Гвр составляет 1500—
3150°С. Что касается значения т|, то оно
для реальных газов изменяется от 1,02 до
1,06 [7]. Видимая скорость пламени, рас-
считанная на основании приведенных дан-
ных по выражению (2.1), может быть 5—
15 м/с. Эта величина более чем на порядок
меньше скорости звука. В этом случае пе-
ред фронтом пламени имеется незначитель-
ное возмущение среды, а перепад давле-
ния перед фронтом и за фронтом пламе-
ни не превышает 1 Н/м2 [4]. Фронт пла-
мени, распространяющийся от точечного
источника поджигания, имеет форму
сферы.
При горении в нормальном режиме в
замкнутных объемах происходит адиаба-
тическое повышение давления по мере вы-
горания ГВС. Причем при сгорании при-
мерно V27 части объема давление увели-
чится не более чем на 4% [10]. В даль-
нейшем скорость нарастания давления все
более увеличивается по мере приближения
фронта пламени к стенкам. В замкнутом
объеме при полном сгорании ГВС давле-
ние может достичь 600—1200 кН/м2 [9].
В производственных помещениях при
наличии легкосбрасываемых конструкций
(ЛСК) горение ГВС происходит вначале
как в замкнутом объеме. При вскрытии
ЛСК в результате истечения газа через
образовавшиеся проемы давление будет
снижаться по сравнению с давлением, ко-
торое могло бы быть в случае горения
ГВС в замкнутом объеме. При этом интен-
сивность снижения давления будет зави-
сеть от скорости горения ГВС и от време-
ни вскрытия ЛСК, а также от величины
вскрываемых отверстий.
При определенных условиях возмож-
на интенсификация горения ГВС, которая
приводит к ускоряющемуся режиму горе-
ния. ^Интенсификация горения наблюдает-
ся при турбулизации ГВС перед фронтом
распространяющегося пламени. Кроме то-
го, на интенсификацию горения может
влиять повышение давления и температу-
ры перед фронтом пламени. В результате
турбулентности ГВС увеличивается эффек-
тивная поверхность фронта пламени, что
может привести к возрастанию видимой
скорости распространения фронта пламе-
ни [10].
На формирование поверхности фронта
пламени, помимо присущего ему явления
неустойчивости, влияют также технологи-
ческое оборудование, размещенное в зда-
нии, внутренние конструкции каркаса зда-
ния, принудительный воздухообмен.
29
При практических расчетах скорость
горения ГВС в ускоряющемся режиме
можно определять по формуле
t/B = a(/H8p. (2.2)
Как следует из выражения (2.2), коэф-
фициент а равен отношению скоростей
распространения пламени при рассматри-
ваемом ускоряющемся и нормальном режи-
мах горения ГВС. Этот коэффициент а
принято называть коэффициентом интенси-
фикации горения, его значение может быть
получено опытным путем. Согласно опыт-
ным данным [5], коэффициент интенсифи-
кации а —2. Следовательно, скорость ви-
димого горения ГВС может достигать 10^-
30 м/с. При указанных скоростях распро-
странения фронта пламени перепад давле-
ния перед фронтом пламени и за ним не
превышает 1—2 Н/м2 [4]. При больших
скоростях видимого горения ГВС перед
фронтом пламени могут образовываться
уже значительные по интенсивности волны
сжатия. Давление в волне сжатия по ме-
ре увеличения скорости пламени возрастает
и при достижении фронтом пламени скоро-
сти звука может быть значительным.
В отличие от перемещения фронта
пламени в дозвуковом режиме, характери-
зующимся распространением пламени по
горючей среде послойной передачей тепло-
ты при горении в результате молекулярной
теплопроводности, при детонации каждый
последующий слой газа нагревается не
вследствие теплопроводности, а путем бы-
строго адиабатического сжатия, достаточно
интенсивного, чтобы довести реагирующую
среду до воспламенения.
При детонации ГВС в окружающей
среде образуются воздушные ударные
волны. Давление на фронте ударной вол-
ны превышает давление при дефлаграцион-
ном горении ГВС в замкнутом объеме.
Кроме того, при взаимодействии ударной
волны с преградами может произойти
дальнейшее повышение давления в преде-
лах от 2 до 8 раз.
В условиях производственных помеще-
ний детонационный режим горения ГВС
практически не зафиксирован. Имевшие
место взрывы ГВС внутри помещений, при
которых разрушались соседние здания, не
могут служить доказательством детонаци-
онного горения ГВС внутри помещений.
Эти разрушения могли быть обусловлены
горением ГВС в ускоренном режиме, ког-
да образующиеся при этом волны сжатия
по мере их распространения преобразова-
лись в ударную волну.
Таким образом, при разработке меро-
приятий по обеспечению взрывозащиты
зданий взрывоопасных производств наибо-
лее характерными режимами горения ГВС
следует считать нормальный режим горе-
ния ГВС или ускоряющийся с коэффици-
ентом интенсификации, равным 2.
Анализ технических решений по обес-
печению взрывобезопасности показывает,
что традиционные решения, основанные
главным образом на разработке мероприя-
тий по технике безопасности, нередко при-
водят к тому, что при взрывном горении
ГВС в производственном помещении про-
исходит разрушение строительных конст-
рукций, которое может привести к гибе-
ли людей и материальному ущербу. Ис-
пользование ЛСК необходимой площади
для снижения давления в объеме помеще-
ния до заданной величины повышает
взрывозащиту зданий.
2.2. ОПРЕДЕЛЕНИЕ
ТРЕБУЕМОЙ ПЛОЩАДИ
Л ЕГКОСБРАСЫВАЕМЫХ
КОНСТРУКЦИЙ (ЛСК)
ИЗ УСЛОВИЙ ОБЕСПЕЧЕНИЯ
ВЗРЫВОЗАЩИТЫ
ПРОИЗВОДСТВЕННЫХ ЗДАНИЙ
Исходные предпосылки. Легкосбрасы
ваемые конструкции по характеру работы
при взрывном горении ГВС можно разде-
лить на две группы. К первой группе от-
носятся ЛСК, имеющие сравнительно не-
большую массу и разрушающиеся практи-
чески мгновенно. При расчете таких ЛСК
представляется возможным пренебречь
силами инерции, возникающими при дви-
жении ЛСК, а также считать, что вскры-
тие перекрываемых ими проемов происхо-
дит мгновенно. В связи с этим при опре-
делении значений давлений, образующихся
при взрывном горении ГВС, можно счи-
тать, что с момента вскрытия ЛСК исте-
чение газа из объема будет происходить
через полностью открытое сечение проема.
При достаточно большой площади образую-
щихся проемов можно обеспечить сниже-
ние давления с момента вскрытия ЛСК.
Ко второй группе относятся ЛСК, при
вскрытии которых нельзя пренебречь си-
лами инерции. Для этих ЛСК характерно
относительно медленное (не мгновенное)
вскрытие проемов в ограждающих конст-
рукциях. В результате этого в начальный
момент после вскрытия проемов независи-
мо от их площади нагрузка при взрывном
горении ГВС будет возрастать.
В настоящее время в качестве ЛСК
широко применяют остекление. Глухое ос-
текление по характеру разрушения может
быть отнесено к первой группе ЛСК, а по-
воротные остекленные переплеты — ко вто-
рой. Ко второй группе ЛСК относятся сте-
новые элементы, плиты покрытий.
При применении ЛСК первой группы
повышение давления в помещении, разви-
вающееся при взрывном горении ГВС, мо-
жет быть ограничено заданной величиной
путем выбора необходимой площади ЛСК.
Требуемую площадь ЛСК следует устанав-
ливать исходя из наиболее неблагоприят-
ных условий с точки зрения обеспечения
взрывозащиты зданий взрывоопасных про-
изводств, при которых может возникнуть
взрывное горение ГВС внутри помещений.
Такой подход к определению площади ЛСК
необходим для получения надежных ре-
зультатов по обеспечению взрывобезопас-
ности. Поэтому при определении требуемой
площади ЛСК применительно к нормаль-
ному или ускоряющемуся режимам горе-
ния ГВС, когда не задано количество
30
взрывоопасной смеси в объеме помещения,
следует принимать, что весь объем поме-
щения заполнен взрывоопасной ГВС. Кро-
ме того, во всех случаях также надо при-
нимать, что инициирование взрывного го-
рения ГВС происходит в центре объема.
При сферической форме помещения
(резервуара и т. и.) и инициировании
взрывного горения в центре фронт пламе-
ни при его распространении имеет форму
сферы. Сферический фронт пламени сохра-
няется и в помещении, имеющем кубиче-
скую форму, до подхода его к стенкам
[16]. Эксперименты, проведенные в поме-
щении объемом 196 м3 при взрывном го-
рении 4,4 %-ной концентрации пропановоз-
душной смеси, подтвердили, что сфериче-
ский фронт пламени сохраняется фактиче-
ски до момента касания им стенок [21].
При наличии ЛСК, когда давление в
помещении, возникающее при взрывном го-
рении ГВС, не будет превышать давления
50—70 кН/м2, при которых разрушаются
строительные конструкции, скорость распро-
странения пламени можно определить по
формуле (2.2). Поскольку в этих случаях
скорость распространения пламени по
крайней мере на порядок меньше скорости
звука, можно принять, что изменение дав-
ления в помещении будет квазистати-
ческим.
До момента вскрытия ЛСК повыше-
ние давления внутри помещения опреде-
ляют как в замкнутом объеме [4, 16, 10].
С момента вскрытия ЛСК при определении
давления необходимо учитывать наряду с
горением ГВС внутри объема также и исте-
чение газа из помещения через образовав-
шиеся проемы в ограждающих конструк-
циях. Истечение газа через проемы может
рассматриваться адиабатическим [14].
Если давление на ограждающие кон-
струкции, возникающее при взрывном го-
рении ГВС, ограничено допустимой на-
грузкой на основные несущие конструк-
ции, то задача расчета ЛСК сводится к
определению площади ЛСК. При этом для
ЛСК, выполняемых в виде остекления, мо-
жет быть принято равномерное располо-
жение проемов по площади ограждающих
конструкций.
Определение требуемой площади ЛСК.
Давление, действующее на ограждающие
конструкции при взрывном горении ГВС в
замкнутом объеме, определяют в зависи-
мости от массовой доли сгоревшей ГВС
следующим выражением, выведенным
Я. Б. Зельдовичем:
где Р — давление, возникающее при взрыв-
ном горении ГВС при сгорании доли т
ГВС; Pq — начальное значение давления в
помещении; Рв — давление, возникающее в
замкнутом объеме,' полностью заполненном
взрывоопасной ГВС при полном ее сгора-
нии; &v — степень расширения продуктов
говения при постоянном объеме.
Массовую долю сгорающей ГВС опре-
деляют формулой
УЛ
v п
где Ун — объем, который занимала сгорев-
шая часть ГВС до начала ее воспламене-
ния; Уп — объем помещения.
Объем Уг, занимаемый сгоревшей
смесью к моменту времени t:
vr=y лазуЗе^з. (2.5)
Значение Уг может быть представлено
также выражением
Уг = Уп<о, (2.6)
где со— доля объема помещения, занимае-
мая сгоревшей частью ГВС.
Из (2.4) следует
Ун = Упт. (2.7)
Используя (2.6) и (2.7), получим
Ун/Уг =
или
(2.8)
где К — поправочный коэффициент, учиты-
вающий расширение газа (К=ю/т).
Согласно (2.8), имеем
где y = CPICv\ здесь Ср — удельная тепло-
емкость при постоянном давлении, Cv —
удельная теплоемкость при постоянном
объеме.
Для начальной стадии распространения
пламени, когда ш<1, разлагая (2.9) в ряд
по малому т и ограничиваясь линейным
членом, получим
т
w(npH т^О) (ef 1)' (2-Ю)
Поскольку y^(TBV—Tq)/(T^p—Го), то,
формула (2.10) приводится к виду:
“(при гп-^0) ~ т П (2.11)
Такое увеличение объема сгорающего
газа может быть при свободном расшире-
нии продуктов горения. Это подтверждает
то, что сгорание в замкнутом объеме в
начальной стадии протекает в тех же ус-
ловиях, что и при Р = const.
Таким образом, при т-<1 можно при-
нимать
Ун Уг 4 л а3 и3„ &2п /з
* 1 Н. fJ
SpVn = зК
(2.12)
Используя зависимости (2.4), (2.8) и
(2.9), получим уравнение для определения
т при сгорании ГВС в замкнутом объеме:
/ Уг
1—т-= [ 1 — ——
\ Уп
С-1) mj1/v. (2.13)
31
Рис. 2.1. Зависимости V'r/Vn от массовой доли
сгорающей ГВС т, построенные по (2.12) и
(2.13); 7=1,4
значений, приводящих к разрушению основ-
ных несущих конструкций зданий, для оп-
ределения значения Р можно использовать
зависимости (2.3) и (2,12). Подставляя
(2.12) в (2.3), получим
л a3 Вд /3
н р
(2.14)
Выражение (2.14) рекомендуется ис-
пользовать при определении избыточного
давления при взрывном горении ГВС, тог-
да, когда оно не превышает 50—70 кН/м2.
В случае необходимости определение воз-
никающих давлений, больших, чем указан-
ные, а также при уточнении расчета сле-
дует уравнение (2.3) решать совместно с
уравнением (2.13).
При вскрытии ЛСК и образовании в
ограждении здания отверстий полная
энергия, выделяемая при взрывном горе-
нии ГВС, идет на повышение внутренней
энергии газа, на перемещение ЛСК и на
истечение газа через отверстие. В связи с
этим представляется возможным вывести
формулы для определения возникающих
нагрузок на ограждающие конструкции при
взрывном горении ГВС внутри помещения,
используя уравнение (2.14) —выражения,
определяющие расход газа и скорость его
истечения из помещения. Истечение газов
через открытые проемы представляет со-
бой расширяющийся поток, движущийся
с дозвуковой скоростью. Как показано в
работе [Г], объем истекающего газа будет
пропорционален площади проемов F, нахо-
дящихся под действием переменного давле-
ния Р за время от t—О до t, когда проем
открыт с начала горения ГВС, и от tp до
t когда проем вскрывается при достиже-
нии давления на ограждающие конструк-
ции, равного Рр.
В этом случае можно записать
t
Д V = TnCK Ф f (р) (2.15)
V
о
Рис. 2.2. Зависимости Р от Vr/Vn > построенные
по (2.3) с учетом (2.12) и (2.13)
Выражение (2.13), определяющее связь
между отношением Гг/Гп и массовой до-
лей сгорающей ГВС т к моменту времени
/, получено с учетом адиабатичности взрыв-
ного горения ГВС в замкнутом объеме.
Выражение (2.12) устанавливает связь
между Vt/Vh и т для процесса при
Р —const.
Графики зависимостей Гг/Кп от т,
построенные на основе выражений (2.12) и
(2.13) для разных значений е=ес = еР,
приведены на рис. 2.1. На основании рис.
2.1 с помощью выражения (2.3) получены
представленные на рис. 2.2 зависимости Р
от Vt/Vh. Как следует из рис. 2.2, исполь-
зование выражения (2.12) вместо (2.13)
для определения избыточного давления
АР — Р—Ро на основе формулы (2.3) при
ДР = 50 кН/м2 приводит к погрешностям,
не превышающим 10% при в=6; 8% при
£ — 8 и 6% при e=il0. Таким образом,
практически для всех возможных видов
ГВС, когда возникающие при взрывном го-
рении нагрузки не превышают предельных
где ДГ — объем газов, истекающих через
отверстие площадью 7"лсК’ ПРИ переменном
давлении Р; R — газовая постоянная;
— скорость истечения газа в отверстие;
ср — коэффициент истечения.
Тогда с учетом (2.14) и (2.15) можно
записать выражение для определения дав-
ления в помещении при взрывном горении
ГВС и одновременном истечении газа из
помещения:
1/п+ -у- (е„
Р = -------4--------у —
v п
t
— -FjlCK <Р° У dh
32
Вводя обозначения
После дифференцирования (2.17) по t
(2.18)
Это уравнение удовлетворительно опи-
сывает изменение давления в помещении с
открытыми проемами при взрывном горе-
нии ГВС.
В том случае, когда проемы закрыты
безынерционным ЛСК, при достижении
давления Рр в момент времени t элементы
ЛСК закрываются (например, разрушается
остекление), и изменение давления на ог-
раждающие конструкции можно найти из
уравнения
Р-Р.
аг /3
где время /р определяется из выражения
(2.14):
(2.20)
Согласно (2.19), давление внутри по-
мещения будет увеличиваться и после вскры-
тия ЛСК.
После окончания горения ГВС, когда
будет происходить истечение продуктов го-
рения при переменном (уменьшающемся)
давлении, в уравнении (2.19) член, учиты-
вающий горение tzr/3, можно положить рав-
ным нулю. С учетом этого выражение, оп-
ределяющее изменение давления во времени
внутри помещения, будет
или, продифференцировав по t, получим
На основании выведенных зависимо-
стей запишем выражение, определяющее
требуемую площадь ЛСК, которая мгно-
венно вскрывается при заданном значении
нагрузки Р — Рр
/?ТР
глск
(2.23)
Это выражение определяет требуемую
площадь ЛСК через коэффициент Ксбр, что
обусловлено терминологией нормативных
документов, где нормируемым значением
является /Себр, выраженный в ма/Ю0 м3.
Анализ зависимости (2.23) показывает, что
при Рр^-pQ требуемое значение КсбР->
-*-макс.
Формула (2.23) позволяет установить
требуемую площадь ЛСК для защиты ос-
новных конструкций зданий от разрушений
при взрывном горении с учетом скорости
горения взрывоопасной смеси, объема по-
мещения и допускаемой нагрузки на ос-
новные конструкции. Результаты вычисле-
ний по (2.23) приемлемы для случая, ког-
да вскрытие ЛСК происходит мгновенно
при достижении давления Р — Рр. Для дру-
гих случаев этот расчет выполняют при
предварительном определении площади
ЛСК с последующим их уточнением на ос-
нове определения нагрузок, возникающих
Рис. 2.3. Избыточное АР давление на ограждаю-
щие конструкции здания от взрывного горения
ГВС в зависимости от Kcgp по уравнению
(2.28)
------ 7/н—0,3 м/с; ---------=0,4 м/с;
—.—.— //„ = 0,6 м/с
н.
Зак 195
33
в помещениях с учетом конечного времени
срабатывания и конструктивных особен-
ностей ЛСК.
На рис. 2.3 приведены графики, по-
строенные по (2.23), с помощью которых
можно установить требуемые значения
Ксбр в зависимости от допускаемого дав-
ления на ограждающие конструкции, ско-
рости горения ГВС и объема помещения.
На основе анализа выражений (2.18) и
(2.23) получены следующие критерии по-
добия, которые позволяют на основании
экспериментов, проведенных в опытных ус-
тановках, устанавливать требуемые пло-
щади ЛСК для натурных объектов:
- (2.24)
нат
2.3. ОПРЕДЕЛЕНИЕ ДАВЛЕНИЯ,
ВОЗНИКАЮЩЕГО
ПРИ ВЗРЫВНОМ ГОРЕНИИ
ГАЗОВОЗДУШНОЙ СМЕСИ
В ПОМЕЩЕНИЯХ ЗДАНИЙ
ВЗРЫВООПАСНЫХ ПРОИЗВОДСТВ
Предпосылки к определению нагрузок
при взрывном горении ГВС. Для определе-
ния давлений, возникающих при взрывном
горении ГВС в случае применения ЛСК
первой группы (мгновенное вскрытие прое-
мов), могут быть использованы зависимо-
сти, приведенные в п. 2.2. Эти зависимости
позволяют найти значения давлений как
при требуемой площади ЛСК, так и при
площадях, отличных от последней. Следу-
ет иметь в виду, что при площадях ЛСК,
меньших требуемых, давление, возникаю-
щее при взрывном горении ГВС, будет
превышать по величине давление, до-
пускаемое на ограждающие конструкции.
При применении ЛСК второй группы
(относительно медленное вскрытие проемов)
нагрузки можно определять исходя из тех
же предпосылок, что и для первой груп-
пы. Однако при этом необходимо учиты-
вать увеличение отверстий проемов, свя-
занное с движением ЛСК после момента
их вскрытия. Поскольку в этом случае
площадь сечения отверстий возрастает мед-
ленно, то после вскрытия ЛСК давление
будет по-прежнему увеличиваться в тече-
ние некоторого промежутка времени даже,
тогда, когда общая площадь проемов, пе-
Рис. 2.4. Изменение давления в помещении при
взрыве горючей газо-воздушной смеси
1 — давление при взрыве в замкнутом объеме;
2 — то же, с отверстием в объеме; 3 — то же, в
помещении при мгновенном вскрытии легкосбра-
сываемых конструкций; 4 — то же, в помещении
с учетом конечного времени вскрытия легкосбра-
сываемых конструкций
рекрываемых ЛСК, будет не меньше тре-
буемой величины для ЛСК, относящихся к
первой группе.
Возможный характер нагрузок, воз-
никающих при применении ЛСК второй
группы, показан на рис. 2.4. Там же при-
ведены графики изменения давления во
времени в случае применения ЛСК первой
группы при обеспечении требуемой площа-
ди проемов (кривая 5), а также второй
группы (кривая 4). Как следует из этих
графиков, при применении ЛСК второй
группы наблюдается повышение давления
после вскрытия последних. Время и интен-
сивность повышения давления зависят от
площади проемов и от характеристик ЛСК.
Давление, возникающее при взрывном
горении ГВС в случае применения ЛСК
второй группы, определяют в результате
совместного решения уравнения движения
ЛСК с уравнениями, описывающими изме-
нение давления при взрывном горении ГВС
с учетом истечения газа через открываю-
щийся проем. При составлении уравнений
движения ЛСК необходимо учитывать кон-
структивные особенности последних.
Все виды ЛСК второй группы в зави-
симости от конструктивного исполнения
при составлении уравнений движения мо-
гут быть разделены на три подгруппы:
Г) смещаемые горизонтальные, которые
выполняют в виде облегченных плит, устраи-
ваемых в покрытии (рис. 2.5,а);
2) смещаемые вертикальные в виде
плит, устраиваемых в вертикальных ог-
раждающих конструкциях (рис. 2,5,6);
3) поворотные, которые представляют
собой плиты с шарнирным закреплением
одной из ее сторон, устраиваемые в верти-
кальном ограждении зданий (рис. 2.6).
Для каждой из указанных групп ЛСК
составляют уравнения движения (после
вскрытия ЛСК) под действием нагрузок,
возникающих при взрывном горении ГВС
внутри помещения.
34
Рис. 2.5. Расчетные схемы для определения на-
грузок на конструкции при взрыве ГВС в поме-
щении, в ограждении которого находятся сме-
щаемые ЛСК
а — легкосбрасываемые конструкции в горизон-
тальном ограждении; б — то же, в вертикальном
ограждении
Определение давления при использова-
нии смещаемых ЛСК в покрытии здания.
Рассмотрим работу ЛСК, входящей в со-
став покрытия, которая представляет со-
бой свободно лежащую плиту (см.
рис. 2.5,а). В интервале времени 0<7
нагрузка, действующая на конструкцию, из-
меняется по закону, определяемому выра-
жением (2.14). В интервале времени /РС
<Zt ^/макс будет происходить дальнейшее
нарастание давления внутри объема поме-
щения, где /макс соответствует моменту до-
стижения максимального давления на
ограждающие конструкции.
Для ЛСК, представляющей собой сво-
бодно опертую плиту площадью F, рас-
положенную горизонтально (например, в
покрытии здания), уравнение движения бу-
дет
х _____
т P—Po — mg, (2.25)
d /3
где Р — давление от взрыва ГВС на ЛСК;
Лиек_________________________
F (х) а b + 2 (а -ф b) х (t) *
F(х) =tz&-J-2(a+^)x(0 —эффективная пло-
щадь действия скоростного напора, созда-
ваемого газом, вытекающим через отвер-
стие на расстоянии х от последнего; х(/) —
закон перемещения элемента ЛСК; т—мас-
са ЛСК.
Возникающие нагрузки от взрывного го-
рения ГВС внутри помещения при исполь-
зовании смещаемой ЛСК можно устано-
вить при совместном решении уравнений
(2.19) и (2.25).
Выражение для скорости нарастания дав-
ления получим по аналогии с (2.18) диф-
ференцированием (2.19) по времени:
~ - ЗлгР0 (/ + /P)2-Bxx (/), (2.26)
В (2.26) время t отсчитывают от мо-
мента времени /р.
Pftl
Рис. 2.6. Расчетные схемы для поворотных лег-
косбрасываемых конструкций
а — поворотный элемент с горизонтальным (верх-
ним) шарниром; б — то же, с горизонтальным
(нижним) шарниром; в — то же, с вертикальным
шарниром
2* Зак. 195
35
Дифференцируя уравнение (2.25) по
времени и затем заменяя его правую часть
выражением (2.26), получим
х
т—~ = 3аг (Zp+Z)2P0-B1x (/); (2.27)
аг*
здесь также момент времени t = tp принят
за начало отсчета.
Уравнение (2.27) можно представить в
виде:
d:i х Вг 3 аг
—г+---------- ----~(/р + /2) /’о; (2.28)
d 1Л tn т
при начальных условиях / = 0, х(0)=0,
А-Л(0) =0, х"(0)=0
решение уравнения (2.25) будет
дг У I ( Big \
Х = В X2 I \ Заг — 2) Х
X 2 f — cos ~^~2— —
.__ У з” . \ / УД
+ J/ 3 sin —g— X t J — 2 X /р I cos —zy- У
X X t — 2 t + V 3 sin —— X —
— /р X2 z + 2 cos X ,) } +
3 av t2 3 ar 6 аг Zp
+-----+ —TT /2 + —ТГ <2-29)
tn X3 tn X3 т X3
где X = y'B1//n,
после чего можно получить следующие
формулы:
для скорости изменения давления
(2.30)
для определения давления на огражда-
ющие конструкции
75 <Z> = -2)х
X (2cos 3 Ь/ + е_’/гХ'-з) +
/х 1" 2 t
( __ СУ
+ /р X2 (/ 3 sin bt +
(2.31)
Определение давления при использова-
нии смещаемых ЛСК, расположенных в
вертикальном ограждении здания (вывод
нижеприведенных формул аналогичен и по-
этому здесь опущен).
Для скорости нарастания давления
* Р аг Л t/2 ,
dt ~ X2 е I
e-3/^t-y^s\n -X_L u)-)
Для определения давления на ограж-
дающие конструкции
Р (Z)=3ar/3D + -^e^/2x
4 7 г Р X3
Ь Zp X2 I \ 3 sin
X /+cos
- Ч + 2 /р X V Tsin -LL. X t -
J \
Определение давления при использова-
нии поворотных ЛСК в вертикальном ог-
раждении зданий. Уравнения движения по-
воротных ЛСК имеют вид:
с горизонтальным верхним шарниром
d2 <р I 12Ь
Jz ~ =—G — Sin ф+Р (/) — ; (2.34)
Cv II &
с горизонтальным нижним шарниром
d2 ф I bl2
Л -7^ =0 — sin<p+P (?) — ; (2.35)
vv L £ &
с вертикальным боковым шарниром
12Ь
(2.36)
где G — масса поворотного элемента; I —
высота поворотного элемента; b — ширина
поворотного элемента; /г — момент инер-
ции массы вращающейся плиты относи-
тельно оси вращения.
Скорость изменения давления находят
из выражения
•4Х=ЗагРо (/р + О2-В2<Р (<), (2-37)
/2 + b I
где В2 =---------------- ip X
У п
36
ф — коэффициент истечения;
раскрытия поворотной ЛСК; /р =
7?р — расчетное давление, при котором сра-
батывает замок поворотной ЛСК.
Совместное решение уравнения (2.37)
с уравнениями (2.34), (2.35) и (2.36) по-
зволяет получить следующие зависимости
для определения скорости изменения и дав-
ления, возникающего при взрывном горе-
нии ГВС при применении поворотных ЛСК:
с верхним горизонтальным шарниром
(2.38)
У 3 Г IT \
и COS —Щ t + у 3 Sin (Xi t
(2.41)
Р (/) = аг /р + 3 аг g t2 — 6 аг q2 t
г*
d P ar
dt “ a2
+]/ 3 sin
с вертикальным боковым шарниром
-J- У 3 sin
P (0=ar/p+~--5- ea//2
✓ О ЛО\
Зависимости (2r38) и (2.39), (2.40) и
(2.41), а также (2.42) и (2.43) позволяют
определять значения /макс и Рмакс ДЛЯ
ЛСК указанных видов.
с нижним горизонтальным шарниром
—~ — 6 аг g t — 6 аг q2 +
d t
37
2.4. ОПРЕДЕЛЕНИЕ
ОБЛАСТИ ПРИМЕНЕНИЯ
ЛЕГКОСБРАСЫВАЕМЫХ
КОНСТРУКЦИЙ
Применение ЛСК — надежный метод
защиты зданий от опасного повышения
давления на ограждающие конструкции
при взрывном горении ГВС. Эффектив-
ность применения ЛСК зависит от того, на-
сколько полно учтены параметры взрыво-
опасной ГВС при определении требуемой
площади ЛСК и выполнены необходимые
требования, предъявляемые к параметрам
ЛСК, исходя из величины взрывной на-
грузки, при которой обеспечивается нераз-
рушаемость основных несущих конструк-
ций.
Несущие конструкции эксплуатирумых,
а также строящихся зданий со взрыво-
опасными производствами имеют различ-
ную прочность. При решении вопросов
взрывозащиты зданий при применении ЛСК
в настоящее время не учитывают величину
и характер нагрузок, действующих на несу-
щие конструкции.
Использование ЛСК без учета нагру-
зок, действующих на основные несущие
конструкции зданий при взрывном горении
ГВС внутри производственного объема,
не обеспечивает требуемой взрывобезопас-
ности производств.
При проектировании зданий для взрыво-
опасных производств следует установить
области эффективного применения ЛСК
при условии, что уровень взрывобезопасно-
сти будет отвечать требуемому. Необходи-
мо выделить следующие области, в кото-
рых:
применение ЛСК обеспечивает необходи-
мую взрывобезопасность без ^проверки несу-
щей способности конструкций на действую-
щие нагрузки, когда нет необходимости в
дополнительном усилении основных несу-
щих конструкций; *
при использовании ЛСК требуется про-
верить несущую способность основных кон-
струкций, чтобы выявить необходимость
усиления, последних, а объем работ по уси-
лению несущих конструкций и возможность
использования ЛСК для обеспечения взры-
вобезопасности определяется уровнем эко-
номической целесообразности проводимых
мероприятий;
в связи со значительными динамиче-
скими нагрузками на строительные конст-
рукции и технологическое оборудование
применение ЛСК в некоторых случаях ста-
новится нецелесообразным.
Для определения областей эффективно-
го применения ЛСК необходимо установить
значения максимальных нагрузок, при ко-
торых выходят из строя (разрушаются) ос-
новные несущие конструкции. Оценка не-
сущей способности существующих конструк-
> ТАБЛИЦА 2.1
Типы и характеристика конструкций Несущая способность кон- струкций, кН/м2 Значение ДРр в зависимо- сти от конструктивной схе- мы зданий, кН/м2
О г I Стеновые однослойные панели из легкого бетона длиной 6 м, высотой 1,2—1,8 см серии 1.432-5 )а жда ю щ и е 5,6—7 5—7
Кирпичные стены толщиной 1,5 или 2 кир- пича 40—50 40-50
Железобетонные плиты размером 1,5X6 м для покрытия промышленных зданий се- рии 1.466-7 7—18
Остекление толщиной 4 мм стальных окон- ных панелей и переплетов промышленных зданий серий ПР-Об-бО/ЗТЗ и ПР-05-32 Не более 3,5 а
Участки ЛСЦ покрытия Не более 1,2
Ворота распашные промышленных зданий серии ПР-05-36.1, ПР-05-136.2, ПР^05-36.3 и ПР-05-36.4’ Давление, разрушающее уз- лы запорного устройства, 4,3 3,5—0,95
Двери промышленных зданий по ГОСТ <6629—74 'Сборные железобетонные колонны сплош- ного сечения 40X40 см для одноэтажных зданий с расчетной высотой 6,2 и 7,4 м се- рии КЗ-ОД-49 Давление, разрушающее уз- лы запорного устройства, 1,5 Несущие 150—200 1,1-1,8 При сплошной навеске сте- новых панелей 8—15. При остеклении 24—46
Сборные железобетонные предваритель- но-напряженные двускатные балки для покрытий зданий пролетами 12 и 10 м с шагом балок 6 м серии ПК-01-06 85—90 При отсутствии участков ЛСК покрытия 6—7. При наличии участков ЛСК по- крытия 18—20
38
ций промышленных зданий может быть
сделана на основании результатов исследо-
ваний, имеющихся в литературных источни-
ках [14, 15, 16, 17, 18, 19, 20, 21].
Имеющиеся данные о нагрузках, при
которых начинают разрушаться ЛСК, узлы
их крепления и запорные устройства, а так-
же несущие конструкции приведены в
табл. 2.1,
Нагрузки, при которых разрушаются
запорные устройства дверей, ворот и узлов
крепления легкосбрасываемого покрытия
меньше, чем нагрузки, при которых разру-
шается остекление. Но двери и ворота обыч-
но перекрывают незначительную часть про-
емов зданий и могут рассматриваться толь-
ко как дополнительные к остеклению лег-
косбрасываемые конструкции. Легкосбра-
ТАБЛИЦА 2.2
Вид конструкции Степень разрушения Избыточ- ное дав- ление взрыва, кН/м1
Остекление Частичное разрушение 1,5—2
Остекление Полное раз- рушение 3,5—7
Перегородки, двери, рамы Сильное раз- рушение 12
Промышленные зда- ния То же 17
Промышленные зда- ния со стальным и железобетонным кар- касами 53 4
Здания с массивны- ми стенами Среднее раз- рушение 70
Кирпичные и желе- зобетонные здания и сооружения Полное раз- рушение 100
сываемые участки покрытия обладают от-
носительно большим временем срабатыва-
ния, в течение которого взрывная нагрузка
могла превысить нагрузку, разрушающую-
остекление, в несколько раз. Согласно
табл. 2.1, разрушение основных ограждаю-
щих конструкций (например, стеновых па-
нелей) начинается при нагрузках ЛРр бо-
лее 5 кН/м2. В результате анализа имею-
щихся экспериментальных и расчетных
данных составлена табл. 2.2, где приведе-
на степень разрушения сооружений и от-
дельных конструкций в зависимости от
нагрузок.
Повреждения строительных конструк-
ций можно разделить на слабые, средние и
сильные (табл. 2.3). При слабых разруше-
ниях основные строительные конструкции
остаются целыми. Разрушается остекление,
отрываются двери, ворота, образуются тре-
щины на внутренних перегородках. Воз-
можны незначительное повреждение тех-
нологического оборудования, вентиляцион-
ных коробов, сдвиг незакрепленного обо-
рудования. Такие повреждения могут быть
при нагрузках до 5 кН/м2. Эксплуатация
здания при выполнении незначительного
ремонта допустима.
Если применение ЛСК обеспечивает сни-
жение нагрузок, действующих на огражда-
ющие конструкции при взрывном горении
ГВС до 5 кН/м2, то при этом обычно не
требуется проверка несущей способности
существующих основных конструкций. При
выборе типа ЛСК возможна экономическая
оценка вариантов ЛСК с учетом их конст-
руктивных решений и применяемого мате-
риала.
Средние разрушения характеризуются
частичным разрушением основных несу-
ТАБЛИЦА 2.3
Максимальное избы- точное давление при взрывном горении ГВС в случае приме- нения ЛСК АР, кН/м2 ДР<5 5<tAP<50 60<ДР<100 АР>100
Ожидаемый эффект воздействия нагрузок при взрывном горе- нии ГВС на конст- рукции в обычном исполнении Разрушение остекле- ния и легких пере- городок, вскрытие ЛСК, дверей, ворот Разрушение плит по- крытия, перекрытий, кровли, кирпичных стен толщиной до 51 см, бетонных стен толщиной до 26 см Разрушение зданий со стальным карка- сом, кирпичных стен толщиной до 64 см, бетонных стен до 36 см Полное раз- рушение кир- пичных и же- лезобетонных зданий
Области применения ЛСК Рекомендуется при- менение ЛСК. Не требуется проверка несущей способно- сти существующих конструкций Рекомендуется при- менение ЛСК с про- веркой прочности основных несущих конструкций и в слу- чае необходимости усиление отдельных конструкций в обыч- ном исполнении При максимально возможной площа- ди ЛСК необходимо усиление всех несу- щих конструкций или разработка но- вых конструкций, способных воспри- нять эти нагрузки Не рекомен- дуется при- менение ЛСК
Обоснование целесо- образности применя- емых решений Экономическая оцен- ка возможных вари- антов ЛСК (приме- няемого материала, конструктивных ре- шений и т. п.) Экономическая оцен- ка эффективного применения ЛСК с учетом усиления от- дельных конструк- ций Может быть реко- мендована защита в исключительных слу- чаях. Предел уси- ления несущих кон- струкций — уровень его экономической целесообразности —
39
щих строительных конструкций, разруше-
нием плит покрытия, дверей, перекрытий,
кровли и оборудования.
В несущих конструкциях появляются
остаточные деформации, разрушаются кир-
пичные стены толщиной до 51 см, шлако-
блочные и бетонные стены толщиной 24—
26 см. Эти повреждения вызываются на-
грузкой 5—50 кН/м2. После проведения
восстановительных работ эксплуатация
здания возможна. В некоторых случаях,
как видно из анализа разрушающих на-
грузок, целесообразно заблаговременно уси-
лить отдельные конструкции здания.
Если применение ЛСК обеспечивает
снижение нагрузок до 5—50 кН/м2, то сле-
дует проводить расчет прочности конструк-
ций, предусматривая при необходимости их
усиление. При этом необходима экономи-
ческая оценка эффективности применения
ЛСК с учетом усиления отдельных конст-
рукций.
Сильные разрушения характеризуются
разрушением несущих конструкций зданий,
сильным разрушением оборудования и ча-
стичным разрушением соседних зданий.
Так, при нагрузках 50—100 кН/м2 разру-
шаются промышленные здания со стальным
каркасом, кирпичные стены толщиной
64 см, бетонные и шлакобетонные стены
толщиной 25—36 см. При таких нагрузках
в случае использования ЛСК потребуется
усиление всех конструкций при максималь-
но возможной площади ЛСК и разработке
новых конструкций, способных воспринять
возникающие нагрузки. Защита зданий от
воздействия нагрузок в пределах 50—
100 кН/м2 может быть рекомендована в
исключительных случаях, а пределом уси-
ления несущих конструкций является уро-
вень его экономической целесообразности.
При нагрузках более 100 кН/м2 кир-
пичные и железобетонные здания разруша-
ются полностью, и защита зданий в обыч-
ном исполнении применением ЛСК не реко-
' мендуется.
Исходя из этих данных, можно ука-
зать области рационального применения
ЛСК для обеспечения защиты зданий от
действия взрыва ГВС внутри помещения и
оценить ожидаемый эффект воздействия на-
грузок при взрывном горении ГВС на кон-
струкции в обычном исполнении (табл. 2.3).
В случаях, когда возникает необходимость
в усилении несущих конструкций здания,
последние надо рассчитывать на нагрузки,
возникающие при взрывном горении ГВС
в условиях применения ЛСК.
СПИСОК ЛИТЕРА ТУ РЫ
1. Абрамович Г. Н, Прикладная газо-
вая динамика. М., 1976
2. Андреев К. К-, Беляев А. Ф: Теория
взрывчатых веществ. М., 1960.
3. Ганушкин В. И. и др. Приспособ-
ление подвалов существующих здании под
убежище. М., 1971.
4. Зельдович Я. Б., Воеводский В. В.
Тепловой взрыв и распространение пламе-
ни в газах. М., 1947.
5. Иващенко П. Ф., Румянцев В. С.
Конвективный подъем и скорости распро-
странения больших очагов пламени. —
Физика горения и взрыва, 1978, № 3.
6. Когарко С. М., Адушкин В. В.,
Лямин А. Г, Исследование сферической
детонации газовых смесей. — Научно-тех-
нические проблемы горения и взрыва, 1965,
№ 2.
7. Льюис Б., Эльбе Г. Горение, пламя
и взрывы в газах. Пер. с англ. М., 1968.
8. Маркштейн Л. Г. Нестационарное
распространение пламени, М., 1968.
9. Монахов В. Г. Методы исследова-
ния пожарной опасности веществ. М., 1972.
10. Розловский А, И. Научные основы
техники взрывобезопасности при раооте с
горючими газами и парами. М., 1972.
11. Садовский М. А, Механич^ ’
действие воздушных ударных волн взрыва
по данным экспериментальных исследова-
ний. Физика взрыва. —Сб. трудов № 1.
М„ 1952.
12. Савич П. Л, Динамика взрывных
волн. Ч. I и IE М., 1941.
13. Стрельчук И. А. Докторская дис-
серт. МИС}И им. В. В. Куйбышева, 1956.
14. Станюкович К. И. Физика взры-
ва. / Под ред. .К. П. Станюковича, М., 1975.
15. Франк-Каменецкий Д, А. Диффу-
зия и теплопередача в химической кинети-
ке. М„ 1967.
16. Хитрин Л, И. Физика горения и
взрыва. М., 1957.
17. Щелкин К. И. Неустойчивое горе-
ние и детонация в газах. — Успехи физи-
ческих наук, 87, вып. 2, 1965.
18. Щелкин К. И., Трошин Я. К. Га-
зодинамика горения. М., 1963.
19. Юрманов Ю. А. Защита сооруже-
ний от действия воздушной УВ. Записки
ЛГИ им. Плеханова, 1966, т. 52, вып. 1.
20. Яковлев В С. Гидродинамика
взрыва. fM., 1961.
21. Hellebrandt D. М. Explosionsavas-
tin. Teknick Tidskrift, 1958, v. 88, N 48.
РАЗДЕЛ 3. РАСЧЕТ ЗДАНИЙ И СООРУЖЕНИЙ
НА СЕЙСМИЧЕСКИЕ ВОЗДЕЙСТВИЯ
(Б. Е. ДЕНИСОВ, Л. Ш, КИЛ И МН И К,
Н. А. НИКОЛАЕНКО, С. В. ПОЛЯКОВ)
Современные методы расчета зданий и
сооружений на сейсмические воздействия
основаны на нескольких подходах, область
использования которых определяется пол-
нотой исходной сейсмологической информа-
ции, степенью детальности учета жесткост-
ных и диссипативных характеристик кон-
струкций и выбором критериев, обеспечи-
вающих надежную работу сооружений при
землетрясениях.
Практические способы расчета обычно
базируются на динамическом анализе со-
оружений как упругих систем (см. пп 3.1
и 3.2). При этом расчетные ускорения
грунта принимают меньше максимальных,
инструментально зарегистрированных при
сильных землетрясениях в данном расчет-
ном районе. Анализ последствий многих
землетрясений показал тем не менее, что
такой подход позволяет обеспечить надеж-
ность работы зданий и сооружений при
сейсмических воздействиях.
По мере накопления информации о па-
раметрах сейсмических 'воздействий и пове-
дении зданий и сооружений осуществляет-
ся переход к более полному учету несущей
способности сооружений благодаря образо-
ванию неупругих деформаций и одновре-
менно переход к моделям сейсмических воз-
действий, отражающих реальные значения
ускорений колебаний грунта и сооружений
(см. п. 3.3). Это позволяет разрабатывать
более обоснованные методы проектирова-
ния и строительства, повышать экономич-
ность зданий и сооружений при сохранении
требуемого уровня надежности. Поскольку
моменты времени, когда возникают земле-
трясения различной интенсивности в дан-
ном районе, распределены случайным обра-
зом в интервале, равном сроку службы со-
оружения, и,-кроме того, сейсмические воз-
действия и колебания сооружений могут
быть описаны случайными функциями вре-
мени, то наряду с детерминистскими полу-
чили развитие вероятностные методы рас-
чета сейсмостойких зданий и сооружений
(см. п. 3.4).
Понятие о предельных состояниях сей-
смостойких зданий и сооружений. Пре-
дельные состояния конструкций сейсмостой-
ких зданий и сооружений характеризуются
[34] потерей пригодности к дальнейшей эк-
сплуатации или потерей способности к обес-
печению безопасности людей и сохранности
ценного оборудования. При этом не всегда
экономически целесообразно требовать пол-
ной сохранности конструкций, в них может
допускаться некоторое развитие пласти-
ческих деформаций, отдельных поврежде-
ний, локальных хрупких разрушений, вы-
ключение внутренних связей и др., которые
не нарушат сохранности сооружения в це-
лом и могут быть исправлены при ре-
монте.
Сейсмостойкость зданий и сооружений
в целом и их отдельных элементов обес-
печивается: выбором благоприятной в
сейсмическом отношении площадки строи-
тельства; прочностью и устойчивостью
конструкций; способностью несущих и ог-
раждающих конструкций к диссипации
энергии и адаптации их к сейсмическому
воздействию; применением специальных
конструктивных мероприятий (здания
простой формы в плане, разделение анти-
сейсмическими швами на отсеки простой
формы, антисейсмические пояса и др.):
надлежащим качеством выполнения строи-
тельно-монтажных работ.
Способность сооружения или здания
противостоять сейсмическому воздействию
характеризуется следующими свойствами
их конструкций: прочностью при вязком,
хрупком и других видах разрушения; ус-
тойчивостью положения (в том числе про-
тив опрокидывания и сдвига) и формы де-
формирования; упругостью и пластично-
стью; диссипацией (поглощением энергии
сейсмического воздействия).
В настоящее время расчет конструкций
на сейсмические воздействия выполняют по
первой группе предельных состояний в со-
ответствии с требованиями главы СНиП
П-А. 10-71 [89].
3.1. РАСЧЕТ ЗДАНИЙ
КАК УПРУГИХ СИСТЕМ
1. Статический и динамический
методы определения
сейсмических нагрузок
В развитии теории сейсмостойкости со-
оружений можно выделить четыре этапа.
1. Статическая теория сейсмостойкости,
предложенная Ф. Омори и Сано [82], осно-
Bcfea на том, что сооружение колеблется с
теми же параметрами, что и грунт, иг
следовательно, сейсмические нагрузки мож-
но определять по формуле
S~-ma-KzQ, (3.1)
где m, Q—масса и вес сооружения; а—
максимальное ускорение поверхности грун-
та; Ac — a/g — коэффициент сейсмичности;
g — ускорение силы тяжести.
2. По динамической теории сейсмостой-
кости, предложенной Н. Мононобе [80],
сейсмические нагрузки определяют с учетом
деформируемости сооружений по формуле
S = Kc₽Q. (3-2)
41
где р — коэффициент динамичности;
= I — (Т2/?*) ’ (3’3)
где Т — период собственных колебаний со-
оружения по основному тону; То — период
колебания основания.
Формула (3.3) основана на предполо-
жении о том, что основание сооружений со-
вершает установившиеся гармонические ко-
лебания,
3. В 1927 г. К. С. Завриев [25] незави-
симо от Мононобе предложил рассматри-
вать сейсмические перемещения грунта как
незатухающие колебания, начинающиеся в
некоторый момент времени £=0 и соверша-
ющиеся по закону косинуса. Согласно это-
му предложению, коэффициент р равен:
1 - Ц2/^)
г. е. вдвое выше, чем у Н. Мононобе.
4. Спектральный метод расчета, пред-
ложенный в 1934 г. М. А. Био [70], харак-
теризует важный этап развития теории сей-
смостойкости. С использованием результа-
тов измеренных ускорений маятников, обла-
дающих разными периодами собственных
колебаний, был построен стандартный
спектр ускорений (рис. 3.1). Важными ра-
ботами, развивающими это направление,
являются исследования Г. Хаузнера, Г. Ка-
на, Р. Мартела и Дж. Алфорда [74, 76, 77].
Построение спектров реакций ускорений
[78] проводили с помощью аналогового вы-
числительного устройства, при этом коле-
бания системы с одной и несколькими
степенями свободы рассматривали с учетом
затухания. Многочисленные работы по изу-
чению спектров землетрясений послужили
основой для построения стандартной спек-
тральной кривой, принятой в Калифорний-
ских нормах [69] (рис. 3.2). Эта кривая
определяет зависимость между нормируе-
мыми ускорениями сооружения, моделируе-
мого системой с одной степенью свободы, и
периодом его собственных колебаний при
перемещении основания сооружения по за-
кону, отвечающему реальным землетрясе-
ниям. Сейсмическую нагрузку на нижнем
уровне определяют по формуле
S = CSQ, (3.4)
где С— коэффициент, зависящий от периода
собственных колебаний сооружения (рис.
:3.2) : S Q — вес всего сооружения.
Сейсмическую силу, действующую на
конструкцию в уровне к, имеющую вес QK
и расположенную на высоте hKl находят из
формулы
S Qk
Sk = ~ (3.5)
Qi
1
Этот метод определения сейсмических
-сил учитывает динамический характер воз-
действия и в некоторой степени динамичес-
кие параметры сооружения.
Рис. 3.1. Примеры спектров ускорений, построен-
ных по методу М. Био
— спектр ускорений в направлении северо-во-
сток в г. Ферндале (Калифорния) 11.9.1938 г.;
б — то же, в направлении юго-восток; в — то же,
в г, Монтана 3.10.1935 г., направление восток
Рис. 3.2. Стандартный спектр ускорений по про-
екту Калифорнийских норм
1 — для зданий; 2 — для сооружений
В работе А. Г. Назарова [40] был
предложен метод инструментального ин-
тегрирования дифференциальных уравнений
сейсмических колебаний и построения спек-
тральных кривых для линёйных осциллято-
ров с помощью много маятниковых сейсмо-
метров.
В работах И. Л. Корчинского [28, 29,
30, 31, 32? 33] спектральный метод расчета
получил значительное развитие. На основе
42
анализа сейсмограмм некоторых слабых
землятрясений, происшедших в нашей стра-
не, было предложено записывать закон дви-
жения грунта в виде суммы затухающих
синусоид:
п
Уо = 2 e~S01 * sin + <р^’ (3'6)
/=1
где т/0— перемещение грунта; — На-
чальная амплитуда; eoj— коэффициент за-
тухания колебаний грунта; coj—угловая
частота колебаний грунта; (pj —угол, опре-
деляющий момент вступления, соответству-
ющего слагаемого ряда; t — время [индекс
/ указывает, что каждая из приведенных
выше величин относится к слагаемому в
формуле (3.6), имеющему номер /].
При определении сейсмических нагру-
зок И, Л. Корчинский учитывал только одно
слагаемое в формуле (3.6), принимая при
этом различные значения угловой частоты
о), и рассматривал сооружение как систему
с п сосредоточенными массами. Приведем
полученную им итоговую формулу для сей-
смической силы, возникающей в точке k со-
оружения при его колебаниях по г-й фор-
ме:
п
пг~\
где Qm — вес, сосредоточенный в т-й точке
сооружения; Худ — отклонение k-й точки
сооружения при его колебаниях по i-й фор-
ме; pi — коэффициент, характеризующий
отклик динамической системы при движе-
нии ее основания [28, 30].
2. Определение сейсмических нагрузок
на здания и сооружения
по спектральным кривым
Основу методики расчета по спектраль-
ным кривым составляет назначение расчет-
ной спектральной кривой, ординаты кото-
рой используют при определении расчет-
ных сейсмических нагрузок. Эти кривые на-
Рис. 3.3. Рас-
четная схема
системы с од-
ной степенью
свободы
массы при приложении к ней горизонталь-
ной силы, равной 1); у — коэффициент не-
упругого сопротивления; i — мнимая еди-
ница; у*—перемещение, измеряемое отно-
сительно точки основания, которая в свою
очередь движется по закону Уд ; у* —
ускорение основания; значения у* и Y*Q —
комплексные. .
Для построения Уд (t) заданная функ-
ция Уо(/) должна быть разложена в ряд
Фурье; этот ряд и сопряженный ряд Фурье
образуют действительную и мнимую части
комплексной функции У* (/),
Действительная часть y(t) решения
комплексного уравнения (3.8) может быть
представлена в виде [40]:
У (О = е 2 (Ci sin X. t + С2 cos X t) —
/ у
1 Г 7 X “V X
— “Г J Y° e sin%(/—
0 (3.9)
где Х = 2л/Т— угловая частота собственных
колебаний с учетом рассеяния энергии; Т —
период собственных колебанию
При нулевых начальных условиях (на-
чальное смещение г/о = 0 и начальная ско-
рость ип = 0) постоянные интегрирования
Ci и С2 равны нулю, и общее решение диф-
ференциального уравнения (8.8) имеет вид:
у (О = —4
А
значают на основе анализа спектров реак-
ций происшедших сильных землетрясений
с привлечением других (макросейсмических)
данных о сейсмическом эффекте. За рас-
четные принимают огибающие ряда спек-
тральных кривых, построенных по записям
землетрясений для усредненных характе-
ристик затухания [28, 29, 30, 31, 32, 33, 35,
38, 3,9].
Определение сейсмических нагрузок в
системе с одной степенью свободы. Диффе-
ренциальное уравнение колебаний такой
системы (рис. 3.3) при учете рассеяния
энергии по теории неупругого сопротивле-
ния [62]
+ С^* = -/?гУ*0, (3.8)
где т — масса осциллятора; С=4/6 —ко-
эффициент жесткости (6 — перемещение
X sin % (/—т) dx. (3.10)
Под сейсмической нагрузкой для систе-'
мы с однбй степенью свободы понимают
силу инерции, деформирующую упругий
элемент, на котором закреплена масса. Эта
сила инерции
[S (/)=-т (Уо+ У). (З.П)
Дифференцируя дважды (3.10), под-
ставим в формулу (3.11) полученное вы-
ражение у и, учитывая, что значение у ма-
ло по сравнению с единицей, после преоб-
разований получим
$ (0 =-— a [t, у, Г), (3.12>
g
43
где Q = mg;
а (С Т, у)=-у-j Г» (г) е т X
О
X sin — (/ — т) d т. (3.13)
Из формул (ЗЛ1) и ЗЛ'2) видно, что
a(t,y, Т) представляет собой ускорение ко-
лебаний линейного осциллятора с периодом
собственных колебаний Т и коэффициентом
неупругого сопротивления у. Максимальное
значение сейсмической силы
макс S(/) = QCa (T)/g. (3.14)
Второй множитель формулы (3.14)
представляет собой функцию, описывающую
зависимость абсолютных значений макси-
мальных ускорений линейного осциллятора
от периода Т его собственных колебаний
при фиксированном коэффициенте неупру-
гого сопротивления у и заданном воздейст-
вии Уо(-О;
Са (Т) = макс< I а Т, Y) |. (3.15)
Указанную функцию называют спект-
ром ускорений1, а ее графическое изобра-
жение — спектральной кривой ускорений. В
названии «спектр ускорений» слово спектр
не соответствует точному значению этого
слова, принятому в математической физике,
однако, несмотря на условность, оно широ-
ко применяется в литературе по сейсмо-
стойкому строительству. В инженерной
практике и научных исследованиях при оп-
ределении сейсмических нагрузок пользу-
ются также понятием «спектры скоростей
и перемещений» со сделанной выше оговор-
кой относительно слова спектр. Скорость
колебаний линейного осциллятора выража-
ется при значениях у< 1 приближенной
формулой
V (t, Т, Y) = То (Т) е т х
»/
о
X sin—(/ — т) dx. (3.16)
Спектр скоростей определяется выра-
жением
Cv (Т) = макс^ | v (/, 71, у) |. (3.17)
Перемещение осциллятора после заме-
ны X в формуле (3.10) может быть пред-
ставлено в виде:
1 А. Г. Назаров [40] эту функцию называет
«спектром приведенных сейсмических ускоре-
ний» .
Спектр перемещений1 определяется за-
висимостью
Су (Т) == макс/ \ у (/, Г, у) |. (3.19)
Сравнивая выражения (3.13), (3.16) и
(3.18), замечаем, что между спектрами ус-
корений, скоростей и перемещений сущест-
вует следующая связь:
Са (Г) -jCc Су (7). (3.20)
Зависимости (3./2GI) позволяют выра-
зить максимальную сейсмическую нагрузку
через любой из этих спектров:
макс S (/)=— Са (Г) =
CV{T) =
(3.21)
В строительных нормах, принятых в
СССР, в основу расчета положен спектр
ускорений, который представлен в виде
[1,2]:
Са (Т') ^’сйР (Т), (3.22)
где К с — коэффициент сейсмичности, харак-
теризующий интенсивность сейсмической
нагрузки; его значения [4] определяют в
зависимости от балльности землетрясения,
которые равны 0,025; 0,05 и 0,1 при рас-
четной сейсмичности 7, 8 и 9 баллов соот-
ветственно; р(7) — коэффициент динамич-
ности.
Коэффициент динамичности представ-
ляет собой такую же функцию Т, как и
Са'(Т), но отличается от нее только посто-
янными множителями:
₽ (П Са (Т). (3.23)
Kcg
Кривая, характеризующая зависимость
коэффициента динамичности от периода
собственных колебаний сооружения, приня-
тая в нормах СССР [1], приведена на
рис .3.4. Эта кривая соответствует средним
значениям коэффициента у = 0,1. На основе
формул (3.21) и (3.22) расчетную сейсми-
ческую нагрузку, действующую на систему
с одной степенью свободы, в соответствии
с [1] определяют выражением
S = макс S (/) = Кс Р (Л <?. (3.24)
Определение сейсмических нагрузок в
системах со многими степенями свободы.
Динамические системы с конечным числом
степеней свободы часто используют в ка-
честве расчетных схем сооружения. Одна
из таких расчетных схем с точечными мас-
сами, расположенными в уровне перекры-
тий, представлена на рис. 3.5.
При учете рассеяния энергии по теории
неупругого сопротивления [62] система
д и ф фере нци а л ьн ы х ура вн ей и й д ви жен и я
1 С. В. Медведев [39] эту функцию называ-
ет «спектр действия».
44
Рис. 3.4. Коэффициент динамичности по СНиП
Н-А.12-69*
рассматриваемой механической модели име-
ет вид:
п
mk Ук (О + (1 л- i у) с*/ У*! (О =
7=1
= ~mkY*Q (/) (k = 1, 2, ... , n), (3.25)
где Cfcj — перемещение в точке
k при действии единичной силы в точке /;
коэффициент неупругого сопротивления у
здесь принимают ПОСТОЯ: ни ы м.
При нулевых начальных условиях
Уь (0) -0; yk (0)-=0 (Л>=1, 2, ... , и)
действительную часть решения дифференци-
ального уравнения (3.25) запишем в следу-
ющем виде [124]:
п п
Ук (0 = ytk (О — X-ik. Zt (О > 26)
/=1 z=l
где (?) = — (hfT} у); (3.27)
п
2 т! Xii
= ; (3.28)
2т'
/=1
Di — величины, называемые коэффициента-
ми разложения; аг(/, Т, у) определяют в
соответствии с формулой (3.13):
п
^ik=2т< х^6w
/=1
(А= 1, 2, ... , п). (3.29)
Рис. 3.5. Расчетная схема системы с п степеня-
ми свободы
Выражение (3,.26) представляет процесс
сейсмических колебаний каждой точки k
системы с п степенями свободы в виде сум-
мы п слагаемых yik (7=4,2, ...,п), каждое
из которых является произведением коэф-
фициента Xik на функцию времени (/).
Из формулы (3.29) видно, что значения
Xik [формы собственных колебаний (рис.
3.6)] представляют собой ординаты упру-
гой линии при действии на заданную меха-
ническую систему п сосредоточен-
ных сил, каждая из которых при-
ложена в одной из точек расположе-
ния сосредоточенных масс и пропор-
циональна произведению этой массы на ор-
динату упругой линии в этой же точке: ко-
эффициентом пропорциональности является
, где Хг — угловая частота собственных
колебаний системы, определяемая общими
методами вычисления частот для систем с
несколькими степенями свободы (см., на-
пример, [3]). Формы собственных колеба-
ний обладают свойством ортогональности:
п
2 mk XikXjk^O (3.30)
А=1
Сила инерции, действующая в точке k
с учетом всех форм собственных колебаний,
п
Sk (t)=-mk^lXikD£a£(t,T,у). (3.31)
1~\
Максимальные значения сил инерции
для t-й доставляющей при использовании
* Схарактеризует жесткость всего соору-
жения в рассматриваемом направлении.
Рис. 3.6, Формы собственных колебаний системы с пятью степенями свободы
45);
спектра ускорений и формулы (3.31) нахо-
дят из выражения
5/й = макс |SZA (/) | =
(3.32)
— tn^ Xtk Dj. Ca (T£ ).
Как видно из формулы (3.3(2), спек-
тральные кривые позволяют определить на-
ибольшие сейсмические нагрузки, соответст-
вующие отдельным формам колебаний при
сейсмических воздействиях. Между тем для
обеспечения безопасной работы сооружения
необходимо знать максимальные сейсмиче-
ские нагрузки, возникающие при колебани-
ях системы с учетом всех форм колебаний.
Спектральный метод не дает сведений о
моментах времени, когда появляются мак-
симальные сейсмические силы для отдель-
ных форм колебаний, в связи с чем на ос-
нове формул (3.31) и (3.32) можно полу-
чить только верхнюю оценку величины сей-
смических нагрузок:
п
~ (Тi) .
i— 1
(3.33
Таким образом, в рамках спектрального
метода максимальные значения сейсмичес-
ких нагрузок остаются неизвестными. На
практике расчетные значения сейсмических
нагрузок находят на основе дополнитель-
ных предположений, определяемых специфи-
кой нормативных требований разных стран.
Речь идет о том, чтобы уточнить оценку
(3.33) максимума сейсмической нагрузки,
исходя из некоторых инженерных сообра-
жений. Ниже приведены несколько из су-
ществующих методов определения усилий
Nt в элементах конструкций, соответствую-
щих сейсмическим нагрузкам Sik.
.1. Предполагается [24], что максимумы
ускорений по всем формам колебаний до-
стигаются одновременно, т. е. все функции
Qi(t) имеют максимум в некоторый момент
времени t+. В этом случае в качестве рас-
четной принимают сумму максимальных уси-
лий, соответствующих каждой форме коле-
бании:
(3.34)
2. Предполагается, что максимумы уси-
лий по каждой форме колебаний достига-
ются неодновременно и что при оценке проч-
ности данного элемента конструкции доста-
точно поочередно брать максимумы усилий
в нем по каждой форме, а усилиями по
другим формам колебаний пренебречь [24]
В этом случае
tfp = |A/z|. (3.35)
3Л В качестве расчетного принимают
среднеквадратическое из усилий по учиты-
ваемым (всем или нескольким) формам ко-
лебаний:
(3.36}
4. В строительных нормах СССР [1]
расчетные усилия в рассматриваемом сече-
нии конструкции от действия сейсмической
нагрузки при учете высших форм колеба-
ний определяют по формуле
/ п
*Р=]/ Скс + 0.5 2 *Ь(3-37)
где Л^р — расчетное значение усилий в рас-
сматриваемом сечении от действия сейсми-
ческой нагрузки; NMa«c — наибольшее зна-
чение усилия в рассматриваемом сечении,
вызываемого сейсмическими силами, соот-
ветствующими одной из форм колебаний
сооружения; Л/\ — значения усилий в том
же сечении, но для других форм колебаний
(кроме формы колебаний, для которой
ВЗЯТО Ломакс).
Приведем формулу (3.32) к виду, при-
нятому в нормах [1] : для этого достаточно
ввести обозначения, которые даны ниже,
Итак, максимальная сейсмическая нагрузка,,
действующая на массу номер k, при коле-
баниях i-й формы
Sik = QkKe?> (О) (3.38)
/г
где = -------- (3-39)
/=1
Для коэффициентов учитываемых форм
собственных колебаний трл справед-
п
ливо соотношение 5т]гА=1 (6=1,2..., п).
z’~l
Для жестких зданий со сложной конструк-
тивной схемой допускается [4] определять
коэффициента (для основного тона) по
приближенной формуле исходя из предпо-
сылок, что первая форма собственных коле-
баний имеет вид прямой:
(3.40, 3.41 >
где Xj —- высота расположения груза Qj над
точкой, относительно которой колеблется
сооружение^.
Коэффициент динамичности р(7\) при-
нимают по расчетной спектральной кривой
(см. рис. 3.4).
По поводу кривой р (7\) необходимо
заметить следующее!. Принятием единой
кривой для коэффициента динамичности
вводят предположение о сравнительно ма-
46
лом влиянии на спектральный состав коле-
баний оснований таких факторов, как вид
грунта, интенсивность землятрясения и т. д.
Постепенно с накоплением достаточно
большого количества записей землетрясе-
ний их, по-видимому, можно будет сгруп-
пировать для норм по сходным спектрам
и установить для расчета ограниченный вы-
бор спектральных кривых (3 (7\), учитыва-
ющий разные грунтовые условия и другие
факторы.
3. Распределение
сейсмической нагрузки
После определения сейсмической на-
грузки ее распределяют между отдельными
параллельно работающими вертикальными
несущими конструкциями здания (стенами,
рамами и т. д.). Перекрытия и покрытия
играют в здании роль горизонтальных ди-
афрагм, которые перераспределяют нагруз-
ку и обеспечивают пространственную работу
сооружения^
Методы, изложенные в работах [51,
52, 53, 54, 55, 56], позволяют исследовать
напряженное состояние элементов конструк-
ций. Приведенная в них методика примени-
ма, если в качестве исходной информации
о землетрясении задана запись ускорений
грунта — акселерограмма. В том случае,
когда имеются записи смещений или скоро-
стей колебаний грунта при реальных земле-
трясениях, т. е. сейсмограммы и велосиграм-
мы, дифференциальнные уравнения колеба-
ний системы должны быть преобразованы
соответствующим образом.
Учету пространственной работы соору-
жений посвящена работа [21] и др. Из-
ложенный в ней метод основан на расчле-
нении пространственной конструкции на
плоские элементы, а нагрузка основана на
части, позволяющие удовлетворить условия
совместности деформаций по линии сопря-
жений расчлененных частей здания. Взаимо-
действие между расчлененными плоскими
элементами моделируется упругими связя-
ми. Сейсмическую нагрузку по площади пе-
рекрытий принимают равномерно распре-
деленной. Эту методику удобно использо-
вать для конструкций, в которых можно
принять, что формы изгиба расчлененных
вертикальных элементов подобны. Практи-
чески точные результаты можно получить
для зданий с регулярно расположенными
конструкциями. В более сложных случаях
следует применять методику непосредствен-
ного определения форм и частот собствен-
ных колебаний сооружений из решения ве-
ковых уравнений с помощью ЭВМ для про-
странственных расчетных схем с сосредото-
ченными массами,
Расчетная схема сооружения может,
быть также представлена как перекрестная
система с дискретно расположенными мас-
сами [60]. Для определения матрицы по-
датливости системы применяют метод пере-
мещений, что позволяет расчленить рас-
пределенную систему на большое число
элементов и, как следствие, распределенную
массу — на большое число сосредоточенных
масс. Учет момента инерции этих масс мо-
жет потребоваться при расчете систем
сложной конфигурации, когда могут воз-
никать, кроме поступательных также и
вращательные колебания. Сейсмические на-
грузки находят после определения форм
собственных колебаний и соответствующих
им периодов по методике [1].
В работах [41, 42, 43] рассмотрен дру-
гой подход к расчету сооружений как про-
странственных систем. Он позволяет обна-
ружить качественно новые особенности ха-
рактера движения пространственной кон-
струкции. Расчетную модель принимают в
виде системы твердых тел, соединенных
упругими связями, которые моделируют
реальные жесткости сооружений. Упругое
основание может быть представлено раз-
личными моделями ।(.винклеровское осно-
вание, полупространство и др.). Движение
основания задано тремя компонентами по-
ступательного движения и тремя компонен-
тами вращения. Данная расчетная модель
не ограничивает рассчитываемых перемеще-
ний и углов поворота твердых тел и позво-
ляет проследить все стадии работы соору-
жений от упругой до разрушения.
Полученная система дифференциальных
уравнений движения [42] для общей моде-
ли при конечных значениях перемещений и
углов поворота содержит нелинейные пе-
рекрестные связи типа произведений обоб-
щенных координат и их скоростей, которые
можно трактовать как параметрические
возмущения и тем самым объяснить воз-
никновение колебаний в определенных на-
правлениях при действии внешнего возму-
щения по другим направлениям. Решения
этих задач необходимо выполнять на ЭВМ.
Для системы из двух упругосоединен-
ных тел, моделирующих массивные соору-
жения, такие, как одноэтажные здания, зда-
ния с первым гибким этажом и др., исполь-
зуя метод статистической линеаризации, по-
лучены замкнутые аналитические решения
данной нелинейной задачи. Рассматривае-
мый подход также позволяет рассчитывать
параметры упругих пространственных коле-
баний сооружений при малых перемеще-
ниях и углах поворота. Линеаризованные
уравнения движения [42] для малых ам-
плитуд колебаний интегрируют в замкну-
том виде. Эти решения могут служить ос-
новой для построения инженерных алгорит-
мов ^определения сейсмической нагрузки в
виде'главных векторов сейсмических сил и
моментов.
Рассмотрим упрощенный метод распре-
деления сейсмических нагрузок между вер-
тикальными и горизонтальными несущими
конструкциями одноэтажного здания. Схе-
му работы перекрытия такого здания в
горизонтальном направлении можно приб-
лиженно представить как неразрезную бал-
ку (рис. 3.7,а, б), опирающуюся на упругие
опоры, роль которых играют стены, рамы и
другие конструкции.
Если считать перекрытие в горизон-
тальном направлении абсолютно жестким,
то перемещения Дт всех упругих опор при
их симметричном расположении и симмет-
47
Рис. 3.7. Схемы работы балки-перекрытия на уп-
ругих опорах (стенах, рамах каркаса)
а — аксонометрия; б — в плане здания при =/
#= Д2...^ Дл; в — ю же, при ^ = А2 = ... — ^п ; г ~~
в предположении, что в пределах между двумя
опорами перекрытие работает по схеме простой
балки; / — перекрытие; 2 — стена
ричной нагрузке будут одинаковыми (рис.
3.7,в). При этом предположении реакция в
k-и опоре может быть найдена по формуле
п
S& ~ НА Вт, (3.42)
1
п
где^5т — равнодействующая горизонталь-
1
ной нагрузки на все перекрытие, найденная
по формуле (3.33):
= Bk =
Д + ^2 • • + В^ ... • Вп
Bk
= ----•> (3.43)
т~]
В[ — 1/61,...,/^= 1 /6* — жесткости опор пе-
рекрытия, имеющие номера 1,,..,/г; 61,...,
б/< — горизонтальные перемещения опор 1,
под действием силы Si = 1, ...;Sh ~ 1.
Если жесткости всех опор одинаковы
(Bt — Bk), то pk-= 1/л, где п — число опор.
В случае, если жесткость перекрытия
по сравнению с жесткостью опор очень ма-
ла или если горизонтальные связи между пе-
рекрытиями соседних пролетов имеют очень
малую жесткость по сравнению с жесткостью
самого перекрытия в горизонтальной плос-
кости, то с известным приближением пере-
крытия можно рассматривать как шарнир-
но-опертые простые балки (рис. 3.7,а). При
этом в каждой точке А-й опоры независимо
от ее жесткости реакция S& равна сумме
реакций двух смежных простых балок. В
этом случае сейсмическая нагрузка распре-
деляется между опорами по грузовым пло-
щадям.
В действительности соотношения жест-
костей перекрытий и опор, а также жест-
кости связей таковы, что возникающие в
опорах реакции имеют промежуточную ве-
личину между двумя установленными выше
пределами, что можно выразить формулой
S* = Vj Sl + vn SV- (3.44)
Принимая один из коэффициентов vi
или Yu равным нулю, а другой — единице,
можно получить один из рассмотренных вы-
ше предельных случаев. Промежуточные
значения vi и vu соответствуют тем или
иным реальным соотношениям жесткостей
перекрытий, опор и связей. В работе [20]
рекомендуется для монолитных перекрытий
принимать vi=0,9 и vu — 0,1; для сборных
перекрытий с монолитными обвязками —
\’г=0,6 и vi 1 = 0,4. а для деревянных —
vi — 0,1 и vu=0,9. Аналогичные рекомен-
дации сделаны в [8], хотя численные зна-
чения коэффициентов несколько отличаются
от приведенных выше.
Формула (3.44) получена применитель-
но к одноэтажным зданиям, однако ею
можно пользоваться для зданий высотой
до пяти этажей включительно, деформации
которых преимущественно определяются
сдвигом. Для зданий выше пяти этажей, а
также при не регулярных конструкциях
требуется расчет, основанный на более точ-
ных расчетных схемах,
ч
4. Расчетные схемы зданий
для оценки
сейсмических нагрузок
В качестве динамических расчетных схем
сооружений могут быть использованы кон-
сольные, плоские и пространственные рам-
ные системы (рис. 3.8, а,б,в). Для этих
систем могут быть приняты расчетные
схемы, представленные на рис. 3.9, а,б,в
[35]. Предполагается что записи сейсмичес-
ких колебаний получены для фундаментов
и расчет ведут с учетом одной компоненты
движения основания (например, горизон-
тальной).
48
Пространственные расчетные схемы
(рис. 3.9,6) целесообразно использовать
при расчете каркасных сооружений боль-
шой протяженности, длина которых соизме-
рима с шириной. Для определения сейсми-
ческих нагрузок на сооружения, представ-
ляемые указанными расчетными схемами,
существуют два основных метода: расчет
по спектральным кривым [1] и на основе
использования записей реальных землетря-
сений (см) п. ДЗ),
Определение сейсмических сил по СНиП.
Сейсмические нагрузки определяют на ос-
нове зависимости (3.38) для каждой i-й
формы собственных колебаний сооружения,
представленного расчетной (схемой, пока-
занной на рис. 3.8,а,6,в. При этом одномер-
ная консольная схема учитывает распреде-
ление масс и жесткостей по высоте соору-
жений, плоская расчетная схема (см. рис.
3.8,6)—по высоте и длине сооружений и
пространственная схема — по высоте, ши-
рине и длине сооружения. Две последние
расчетные схемы учитывают податливость
не только вертикально стоящих конструкций
(стен, рам и т. д.), но и горизонтальных
диафрагм жесткости (перекрытий). При ис-
пользовании этих расчетных схем необхо-
димо учитывать не менее трех-четырех пер-
вых форм колебаний. Коэффицент динамич-
ности Р (7\) В формуле (3.381) вычисляют
по графику, приведенному на рис. 3.4, в за-
висимости от периода Ti, соответствующе-
го i-й форме колебания и определяемого по
формуле __
Ti = 2 л v ц . О-45)
где характеристические числа %г
являются решением частотного
уравнения:
(6ц --Ti) 6|2 ^2 • * • тП
621 (622 ^2—7./) • ’ • ^2П —-
6rtl tTl\ 6j2
= 0.
(^пп mn Ti)
(3.46)
После решения этого уравне-
ния определяют также собствен-
ные векторы или ординаты формы
колебаний сооружения Xik [6].
Коэффициент формы находят по
формуле (3.39). Усилия в каждом
элементе конструкции от найден-
ных значений сейсмических сил
Sik суммируют по формуле (3.37).
5. Влияние
высших форм колебаний
на сейсмические нагрузки
Вклад высших форм колеба-
ний при определении сейсмической
нагрузки зависит от динамических
свойств сооружения и от вида
принятой расчетной спектральной
кривой. Погрешность, получаемая
вследствие игнорирования высших
форм, может быть значительной
при определении усилий в верх-
них сечениях, особенно для соору-
жений, масса и жесткость кото-
рых увеличиваются к основанию (например,
дымовые трубы).
При нахождении сейсмических нагру-
зок [1] для зданий с жесткой конструк-
тивной схемой (Л <0,35 с) достаточно учи-
тывать первую форму колебаний, для зда-
ний с гибкой конструктивной схемой (Т4>
>0,35 с) число форм колебаний, которые
необходимо учитывать, может достигать
3 и более. Способы определения усилий в
элементах конструкций в рамках спектраль-
ного метода при учете высших форм коле-
баний изложены в п. 2.
6. Учет податливости
основания при определении
сейсмических нагрузок
Учет упругой податливости основания
имеет наибольшее значение для жестких
сооружений (см. рис. 3.9). В зависимости
от свойств грунтов и конструкции фунда-
мента вклад в общую величину перемеще-
ний могут вносить упругое горизонтальное
перемещение фундамента и его упругий по-
ворот. Единичные перемещения bkj, входя-
щие в формулу (3.46), при учете только
сдвига по основанию определяют следую-
щим образом:
= (1//<Л), (3.47)
где —единичные перемещения, опреде-
ляемые без учета податливости основания;
Кх — Сх л /грр Ч~ Сz FC1K (3.48)
Рис. 3.8. Расчетные схемы сооружений при определении сей-
смической нагрузки по СНиП
а — консольная; б — плоская; в — пространственная
Рис. 3.9. Расчетные схемы сооружений при определении сей-
смической нагрузки на основе реальных записей землетрясе-
ний
а — консольная; б—плоская; в — пространственная
49
Кх — жесткость основания при горизонталь-'
ном перемещении фундамента; Сх=0,7;
Cz — коэффициент упругого равномерного
сжатия; его значения в зависимости от
расчетного сопротивления грунта приведе-
ны в табл. 3.1; F$— площадь подошвы
фундамента; Етр — площадь боковых по-
верхностей фундамента, по которым воз-
никают касательные напряжения; FCm—
площадь боковых поверхностей фундамен-
та, по которым происходит сжатие грунта.
Таблица 3.1
Расчетное сопротив- ление грунта R, МПа Коэффициент упругого равномерного сжатия С,, кН/м3
0,1 0,2 0,3 0,4 0,5 20 000 40 000 50 000 60 000 70 000 1
Рис. 3.10. Схемы возникновения в протяженных
зданиях усилий
а — продольных; б—вертикальных (заштрихова-
ны возможные графики распределения ускорений
по длине здания, стрелками показано направле-
ние действия инерционных сил)
Единичные перемещения при уче-
те только упругого поворота определяются
выражениями:
6a/ = 6W+J^-> (3.49)
где Xi, хк — координаты точек it k (высоты
этих точек над подошвой фундамента);
Кф = Сф + Сх ГТр /2р + Срх JTP (3.50)
— жесткость основания при повороте, где
Сф =2Сг — коэффициент упрогого нерав-
номерного сжатия; СфА.= 1,4CZ — коэффи-
циент упругого неравномерного сдвига;
/ф — момент инерции площади основания
фундамента относительно оси, проходящей
через центр тяжести; FtP, 1тр — соответ-
ственно площадь и расстояние до оси вра-
щения боковых поверхностей фундамента,
параллельных оси вращения; 7Тр — поляр-
ный момент инерции боковых поверхностей,
перпендикулярных оси вращения, относи-
тельно точки, находящейся на оси враще-
ния, равный сумме осевых моментов инер-
ции относительно взаимно перпендикуляр-
ных осей, проходящих через эту точку.
7. Крутильные колебания
и влияние протяженности
зданий в плане
Если расчетная схема сооружений
представлена в виде консоли, а центры
масс и жесткостей сооружения не нахо-
дятся на одной вертикали, то расчетную
схему следует усложнить и ввести в рас-
чет дополнительно эксцентрицитет между
центрами масс и жесткостей, значения мо-
ментов инерции масс и жесткость на кру-
чение всего сооружения в целом. Рекомен-
дации по учету крутильных колебаний на
основе приближенных схем изложены в
работах [2, 30]. Размеры зданий заметно
влияют на характер и значения сейсмиче-
ских нагрузок. Увеличение длины здания
может отрицательно сказываться на его
сейсмостойкости. Если длина здания соиз-
мерима с длиной сейсмической волны, то
крутящий момент может достичь большого
значения, и дополнительные усилия в кон-
струкциях в углах здания превысят соот-
ветствующие усилия, определенные без уче-
та кручения. Учет протяженности позво-
ляет выявить и другие эффекты. Поскольку
сейсмические волны проходят не мгновенно,
а с определенной скоростью зависящей от
плотности грунта и характеристик конст-
рукции, то различные участки основания
по длине здания колеблются несинфазно,
с разными ускорениями, что вызывает в
здании дополнительные продольные усилия
сжатия — растяжения '(рис. 3.10,а) и го-
ризонтального сдвига. Аналогичные рас-
суждения применимы к вертикальным коле-
баниям (рис. 3.10,6). С расчетом зданий
большой протяженности более подробно
можно ознакомиться в работах [20, ЗГ,
32, 33, 48]
3.2. ОСОБЕННОСТИ
МЕТОДОВ ПРОЕКТИРОВАНИЯ
ЗДАНИЙ РАЗЛИЧНЫХ
КОНСТРУКТИВНЫХ РЕШЕНИЙ
1. Здания
с несущими каменными
(кирпичными) стенами
Каменные здания высотой до пяти эта-
жей, применяемые в сейсмических районах,
отличаются сравнительно малыми периода-
ми собственных колебаний. Для таких со-
оружений СНиП П-А. 1:2-69 [1] разрешает
при определении сейсмических сил ограни-
чиваться учетом только первой (основной)
формы колебаний.
Сцепление — одна из основных харак-
теристик, определяющих сейсмостойкость
кладки. По этому признаку [1] делят все
кладки в зависимости от достигаемого в
них сцепления на три категории, приведен-
ные в табл. 3.2.
Обеспечить высокое сцепление можно
только при условии принятия мер, в зна-
чительной степени зависящих от местных
50
условий строительства. Некоторые рекомен- !
дации по этому вопросу изложены в рабо-
тах [23, 63].
Т А Б Л И Ц А Ъ
Категория кладки Нормальное сцепление МПа Р
минимум максимум
1 0,18
2 0,12 0,18
3 0,06 0,12
В зависимости от категории кладки оп-
ределяют область ее применения в сейсми-
ческих районах, вводят ограничения раз-
меров зданий или их отсеков и устанавли-
вают требования к размерам сечения про-
стенков, перемычек [1].
Глубину заложения фундаментов в
зданиях высотой до пяти этажей принима-
ют такой же, как и для несейсмических
районов. При слабых грунтах и высоких
зданиях'желательно заглублять фундамент,
устраивая подвалы. Фундаменты здания
(отсека) рекомендуется закладывать на
одном уровне. Под несущие стены следует
применять ленточные фундаменты. Одним
из наиболее уязвимых мест кирпичных стен
и стен из мелких камней являются места со-
пряжения стен взаимно пермендикулярного
Направления — углы и пересечения. Кроме
усиления связи этих стен антисейсмически-
ми поясами, которые выполняют при балль-
ности площадки строительства 7 и выше,
при расчетной сейсмичности 9 баллов тре-
буется армировать все сопряжения, а при
расчетной сейсмичности 7—8 баллов — уг-
ловые участки наружных стен и в местах
примыкания внутренних стен к наружным.
Кроме того, армирование можно применять
на сплошных участках кладки и в простен-
ках. В этом случае для увеличения несу-
щей способности кладки ее укладывают
также и на уровне подоконников и пере-
мычек?
Проемы, ширина которых больше пре-
дельной [1], должны быть обрамлены мо-
нолитной железобетонной замкнутой ра-
мой. Пример выполнения такого обрамле-
ния в оконном проеме показан на рис. 3.11.
В стенах крупноблочных зданий уста-
навливают вертикальную арматуру в пазах
между блоками или по граням простенков.
При многорядной разрезке (рис. 3.12) ар-
матуру в наружных и внутренних гранях
стен соединяют хомутами, укладываемыми
при монтаже в горизонтальные швы между
блоками. При двухрядной разрезке арма-
туру устанавливают без замкнутых хому-
тов. Для повышения сопротивления сдвигу
стенок блоков по антисейсмическим поясам
последние предложено устраивать со шпон-
ками, входящими над и под поясом в вер-
тикальные пазы между блоками, как это
показано на рис. 3.12. При выполнении
этих шпонок из уголков их можно исполь-
зовать для заанкерирования вертикальной
арматуры.
В кирпичных и блочных зданиях обыч-
но применяют многопустотные настилы из
3) ' /7
2 - 2 Ж
. '7?5с7/У:7''-,'17,(7 с
Рис. 3.11. Усиление граней проемов железобетон-
ной рамой
а — оконный проем; б — дверной проем; 1 — же-
лезобетонные сердечники; 2 — обвязка; 3 — желе-
зобетонная перемычка, объединенная с обвязкой;
4 — панели перекрытий
плит. Замоноличивают их согласно СНиП
П-А. 12-69 одним из следующих способов:
устройством железобетонных антисейсмиче-
ских поясов с заанкерированием в них па-
нелей перекрытий; устройством монолитных
обвязок *£ заанкерированием панелей пере-
крытий в обвязках и применением между
панелями связей, рассчитанных на сдвиг;
без устройства поясов или обвязок с исполь-
зованием между панелями, а также между
панелями и стенами связей, воспринимающих
усилия растяжения и сдвига.
Пример сопряжения перекрытий и на-
ружных стен показан на рис, 3.13. Обвязку
перекрытий в крупноблочных зданиях ус-
танавливают в пазах между плитами пере-
крытий и поясными блоками стен. Послед-
ние взаимосоединяются в непрерывный по-
яс специальными выпусками и закладными
деталями.
Антисейсмическим поясахМ отводится
большая роль в обеспечении сейсмостойко-
сти здания. Пояса укладывают по пери-
метру всех наружных и внутренних про-
51
Рис. 3.12. Усиление крупноблочных стен
а — вертикальной арматурой но граням простенков при четырехрядной разрезке стен; б — то же, при
двухрядной разрезке; в — пояс со шпонками для сопротивления сдвигу по горизонтальным швам;
1 — перемычечный блок; 2— стеновые блоки; 3 — горизонтальные хомуты; 4 — вертикальные стерж-
ня усиления; 5 — панели перекрытий; 6 — сварка стержней пояса и блока; 7 — отверстия для про-
пуска стержней
Рис. 3.13. Сопряжение перекрытий и наружных
стен
а — с устройством пояса; б — с железобетонной
обвязкой; 1 — анкерная обвязка; 2 — железобе-
тонный пояс; 3 — анкер диаметром 8 мм через
50—60 см; 4 — каркас обвязки; 5 — железобетон-
ная обвязка
дольных и поперечных стен под перекры-
тиями. Они представляют собой железо-
бетонную раму, связанную с перекрытиями.
Связь пояса с кладкой может быть усилена
выпусками арматуры или устройством же-
лезобетонных анкеров, заделываемых в
кладку (рис. 3.14). Пояса усиливают связь
между стенами, увеличивают их сопротив-
ление изгибу в плоскости стены, а также
повышают жесткость и монолитность пере-
крытия.
Мероприятия по усилению каменных
(кирпичных) стен, а также специфика оп-
ределения усилий в элементах конструкций
изложены в работах [49, 50].
2. Крупнопанельные здания
В настоящее время .крупнопанельные
здания строят на территории рсех союзных
республик СССР, расположенных в зоне
возможных сейсмических воздействий, и хо-
тя объем кирпичного строительства пока
еще сравнительно большой, соотношение
объемов строительства ежегодно изменяет-
ся в пользу крупнопанельного.
При проектировании крупнопанельного
здания рекомендуется принимать конструк-
тивную схему с несущими продольными и
поперечными стенами с шагом последних
до 4 м и с плитами перекрытий размером
на комнату, опирающимися на стену по
всему контуру. Можно использовать другие
конструктивные схемы, но при этом шаг
поперечных стен не должен превышать
6,5 м.
Необходимо стремиться к обеспечению
равномерного и симметричного распределе-
ния масс и жесткостей относительно обеих
осей здания в плане. Поперечные и про-
дольные стены должны быть сквозными на
всю ширину и длину здания. Оси стен
должны быть прямыми, без изломов и сме-
щений. В виде исключения при соответ-
ствующем обосновании в здании с шагом
поперечных стен не более 4 м допускается
Z-образный излом в плане здания (отсека)
осей не более двух поперечных стен. При
этом расстояние между параллельными
осями двух участков стены не должно
превышать 0,6 м, а в панели внутренней
продольной стены на участке излома осей
поперечной стены следует предусматривать
усиленное армирование. Максимальную дли-
ну крупнопанельных зданий назначают та-
кой же, как для несейсмических районов,
но она не должна превышать 60 м.
52
Рис. 3.14. Антисейсмические пояса
а — заанкеривание поясов в верхних этажах каменных стен; б — детали крепления перегородок к
перекрытиям и несущим стенам; в — детали устройства сборных железобетонных лестниц; / — пане-
ли перекрытия; 2 — конопатка войлоком; 3 —'металлические закрепы через 80 см; 4 — панель перего-
родки; 5 — стена; 6' — заерщенные костыли (три по высоте этажа); 7 — настилы перекрытий; 8 — пло-
щадка в уровне междуэтажного перекрытия; 9 — стержни железобетонного пояса, пропущенные че-
рез трубки; 10 — консоль для опирания маршей; 11 — анкерный стержень диаметром 10 мм; 12 —
промежуточная площадка; 13— распределительные балки; 14 — закладные детали; 15 — выпуск диа-
метром 12 мм; 16 — сварка
Рис. 3.15. Чертежи здания по проекту серии 1-464АС-15
«— фасад и разрез; б — план фундамента; в — план типового этажа; г — план перекрытия; д — се*
чение фундаментов
а
53
Рис. 3.16. Конструктивное решение стыковых со-
единений, принятое в проектах серии 1-464АС
а — стык панелей наружных стен; б — стык па-
нелей внутренних стен
Z-2
Фундаменты следует применять ленточ-
ные из монолитного железобетона (бетон
марки не ниже 100) или из сборных эле-
ментов (бетон марки не ниже 150). В зда-
ниях высотой более пяти этажей фунда-
ментные подушки надо выполнять из моно-
литного железобетона. При больших на-
грузках и слабых грунтах могут быть ис-
пользованы фундаменты в виде сплошной
монолитной железобетонной плиты под
всем1 зданием.
Панели внутренних стен следует изго-
товлять из тяжелого или легкого бетонов
размером на комнату с устройством, как
цравило, вертикальных стыков на участках
пересечения стен. Панели внутренних и
наружных стен (или несущие слои послед-
них) можно выполнять как из одного, так
и из разных материалов. При использова-
нии панелей из тяжелого бетона для внут-
ренних стен и из легкого бетона для на-
ружных стен предельную высоту здания
назначают как для здания из легкобетон-
ных панелей [8].
Стеновые панели сейсмостойких зданий
следует армировать двойной арматурой,
которую можно выполнять в виде прост-
ранственных каркасов или сварных арма-
турных стоек. При сейсмичности 7 баллов
в зданиях высотой не более пяти этажей
допускается применение одинарной арма-
туры при соблюдении требований [8]. Па-
нели и плиты перекрытий следует изготов-
лять из тяжелого бетона марки не менее
200. С точки зрения сейсмостойкости наи-
более эффективной конструкцией перекры-
тий являются сплошные плиты размером
на комнату. Более подробные сведения о
конструировании крупнопанельных зданий
изложены в работах [8, 49, 50], где имеют-
ся также рекомендации по определению
усилий в элементах вертикальных диаф-
рагм жесткости. ПриемУ проектирования
крупнопанельных зданий из ' виброкамен-
ных и виброкирпичных панелей даны в
работах [26, 49, 50]. Примеры различных
конструктивных решений конструкций круп-
нопанельных зданий приведены на рис. 3.15,
3.16, 3.17, 3.18, 3.19, 3.20.
20 20
Рис. 3.17. Конструк-
тивные решения сты-
ковых соединений,
принятые в проектах
серии 1-ТТЖ-464АС
а — горизонтальный
стык панелей попе-
речных внутренних
стен; б — то же, про-
дольных внутренних
стен; в — вертикаль-
ный стык пересече-
ния панелей внутрен-
них стен; г — со-
пряжения панелей
наружных и внутрен-
них стен в верхнем
и среднием уровнях
54
ишиLUJLLTTFEr 111 П-ЦМШД
Рис. 3.18. Пример конструкции внутренней
Узел 2
стеновой панели по проекту серии 1 -464ДС
Рис. 3.19. Чертежи здания по проекту серии 1-464АС-6
а — фасад; б план фундаме нта; в — план типового этажа; г — план перекрытия; д — сечения и
узел фундаментов
55
Для снижения сейсмических нагрузок
некоторыми авторами предлагается устраи-
вать в зданиях так называемый иервый
гибкий этаж. При таком решении первый
этаж здания выполняют каркасным без
заполнения, остальные вышележащие эта-
жи возводят из панелей в виде жесткой
коробчатой системы. Большие смещения
верха гибкой части здания могут быть при-
чиной необратимых деформаций в стойках
каркаса. При расчете конструкций гибкого
этажа следует обеспечить обратимость де-
формации стоек. В связи с этим стойки
должны быть рассчитаны на прочность по
упругой стадии, и их желательно выпол-
нять железобетонными с жесткой армату-
рой. Один из примеров конструктивного ре-
шения крупнопанельного! здания с пер-
вым каркасным этажом приведен на рис.
3.21.
Учитывая сравнительно небольшую ве-
личину затухания колебаний зданий с пер-
вым гибким этажом при расчете несущих
конструкций этого этажа, сейсмическую на-
грузку следует увеличивать при железобе-
тонных стойках в 1,5 раза. Строительство
таких зданий особенно противопоказано при
слабых грунтах, а в остальных случаях же-
лательно ограничивать высоту зданий пятью-
шестью этажами.
3. Каркасные здания
Здания с несущим каркасом получили
широкое распространение в строительстве.
Для большинства промышленных и обще-
ственных зданий, а также для зданий по-
вышенной этажности такая конструкция, с
точки зрения объемно-планировочных реше-
ний, рациональна. Элементы железобетон-
Рис. 3.20. Чертежи 12-этажного крупнопанельного дома по проекту серии 1-464ДС-8
а — фасад и разрез; б, в — планы технического подполья и типового этажа; г—детали усиленных
вертикальных стыков в первых трех этажах
56
ного каркаса конструируют и рассчитывают
согласно работам (1, 6, 71. По способу из-
готовления и возведения железобетонные
каркасы зданий, проектируемых для строи-
тельства в сейсмических .районах, ? могут
быть сборными, сборно-монолитными и мо-
нолитными. 4
При проектировании каркаса особо?
внимание должно быть уделено узлам, ко-
торые следует рассчитывать на прочность.
При недостаточной прочности узла .его на-
до усилить армированием по расчету. В
некоторых случаях прочность узла может
быть повышена использованием бетона бо-
лее высокой марки. Сетки косвенного ар-
мирования рекомендуется устанавливать
нормально к оси колонны (рис. 3.22). Если
по данным расчета косвенное армирование
в узле не требуется, то узел следует кон-
структивно армировать: если колонна сжа-
та — хомутами из стержней диаметром не
менее 8 мм, шагом* 70—100 мм; если ко-
лонна растянута — хомутами и дополни-
тельными вертикальными стержнями диа-
метром не менее 8 мм, устанавливаемыми
по периметру хомутов, шагом 70—100 мм
(рис., 3.23).
В ригелях и колоннах для повышения
несущей способности сечений, примыкаю-
щих к жестким узлам рам, следует на
участке по длине, равному высоте сечения,
но не менее 40 см от торца, примыкающего
к узлу элемента, устанавливать замкнутую
поперечную арматуру с шагом, вдвое мень-
шим, чем требуется по расчету, но не бо-
лее 10 см (рис. 3.24).
Для сборных железобетонных каркасов
используют несколько способов их разрезки
на монтажные элементы (рис. 3.25). При-
меры стыков при разном способе разрезки
приведены на рис. 3.26—3.35. Один из уз-
лов металлического каркаса показан на
рис. 3.36.
4. Опытные данные
и эмпирические формулы
по динамическим
Ч характеристикам зданий
\ В практике проектирования сейсмо-
стойких зданиях с жесткой конструктивной
схемой часто используют эмпирические
формулы для определения значения периода
Г, с, (первой формы собственных колебаний:
7ф = 0,0905 р. /7 ; (3.51)
Тф = ап, (3.52)
где b — размер здания в плане (ширина
или длина), м; где Н — высота
здания, м; п — число этажей; а — коэффи-
циент, зависящий от конструкции здания
и вида основания.
29,50
27,49
-----п
0,00
М* ТО^
260\,26
514 ,260
Рис. 3.21.
ный дом
а — фасад
этажа;
^3,00
Десятиэтажный крупнопанель-
с первым каркасным этажом
и разрез; б - план типового
в — план первого каркасного эта-
жа; г — план фундаментов
-4.50
6,04
ПОТО
57
Рис. 3.22. Армирование узла сетками, располо-
женными нормально к оси колонны
1 — колонна; 2 — поперечный ригель; 3 — про-
дольный ригель; 4 — сетки
1
Рис. 3.23. Армирование узла хомутами и допол-
нительными вертикальными стержнями
1 — колонна; 2 — поперечный ригель; 3— продоль*
ный ригель; 4 — хомуты; 5 — дополнительные вер*
тикальные стержни
Рис. 3.24. Армирование поперечной арматурой
участков колонн и ригелей, примыкающих к
узлу (армирование центральной зоны узла не по-
казано)
Рис. 3.25. Способы разрезки каркаса
а — все элементы стыкуются в узле; б — в узле
стыкуются только ригели (колонны высотой на
этаж); в —то же, колонны высотой на 2—3 эта-
жа; г—в узле стыкуются ригели только одного
направления; д — в узле стыкуются только ко-
лонны; е — в узле элементы каркаса не стыку-
ются
58
а) Оголобник ригеля б)
Рис. 3.26. Примеры стыков при первом способе разрезки
а — стык колонны с ригелем ЦНИИ общественных зданий; б — стык, использованный при строитель-
стве высотного здания гостиницы «Украина» в Москве; е — стык колонны с ригелем ЦНИИ промыш-
ленных зданий; / —сварные швы; 2 — накладка; 3 — колонна
Рис. 3.27. Примеры стыков, применяемых при
«тором способе разрезки каркаса и опытный
стык
а — стык с опиранием ригелей на консоли и про-
пуском верхней арматуры через отверстия (впо-
следствии инъектируются раствором) в колонне;
б — то же, но при верхней арматуре, проходя-
щей вне колонны; в — при отсутствии консолей
с монтажом ригелей на временных монтажных
столиках; г — опытные стыки
Рис 3.28. Стык колонн со стальными оголовни-
ками
а — с накладками из арматуры; б—без накладок
Рис. 3.29. Стык с металлическими скрытыми кон-
солями
1 — колонна; 2 — ригель; 3 — закладные детали
(отверстия для бетонирования не показаны); 4 —
сварные соединения арматуры; 5 — усиленный
арматурный выпуск
59
Рис 3.30. Стык без опорных консолей Рис. 3.31, Совмещенный железобетонный стык
J колонна, 2 ригели; 3 рифления; 4 — свар- 1 — колонна; 2 — ригель; 3 — бетон омоноличива-
ные соединения арматуры; 5 — заливка бетоном ния; 4 — выступы ригеля (усиление центральной
зоны дополнительным армированием не показа-
Рис. 3.32. Армирование продольного монолитного железобетонно-
го перекрытия
а — поперечный разрез ригеля у колонны; б — поперечный разрез
ригеля в середине его пролета; в — продольный разрез ригеля у
колонны; 1 — колонна; 2 — сборные железобетонные ригели; 3 —
сборные железобетонные плиты
60
ч
Рис. 3.33. Сопряжение сборных поперечныхх ригелей перекрытия со средней колонной
а — при опирании плит на полки ригелей; б — при опирании плит на ригели прямоугольного сече-
ния; / колонна; 2 — ригель; 3 — ванная сварка; 4 — выпуски арматуры в продольный монолитный
ригель
Рис. 3.34. Консольное сопряжение сборных попе-
речных и продольных ригелей с колонной
/ — колонна; 2 — поперечный ригель; 3 — про-
дольный ригель; 4 — опорная консоль; 5 — ван-
ная сварка; 6 — отверстия в колонне
Рис. 3.35 Сопряжения сборных поперечных и
продольных ригелей с колонной (при бесконсоль
ном опирании продольных ригелей)
а — узел поперечной рамы; б — узел продольной
армы; 1 — колонна; 2 — поперечный ригель; 3 —
продольный ригель; 4 — ванная сварка; 5 — свар-
ные сетки; 6 — хомуты; 7 — бетон марки на одну
ступень выше, чем бетон примыкающих сборных
элементов
61
ТАБЛИЦА 3.3
Число этажей Назначение здания, материал несущих стен или каркаса Число объек- тов Период собственных колебаний (средний) в направлении, с
поперечном продоль- ном
по опыту, То по форму- ле (3.52), ГФ Vro
по опыту
С несущими стенами
(кирпичными,
3
4
5
6
7
3
4
5
Жилые здания
То же
»
Школы, конторы и др.
То же
каменными, крупноблочными)
8 0,153 0, 168 1,1 0,16
4 0,24 0,224 0,93 0,221
4 0,264 0,28 1,07 0,22
2 0,333 0,336 1
1 0,435 0,448 1,03 0,435
2 0,22 0,195 0,89 0,21
4 0,307 0,26 0,85 0,278
2 0,325 0,325 1
Крупнопанельные здания
4 Жилые здания серии 1-464 2 0,165 0, 188 1,14 0,155
5 То же 1 0,3 0,235 0,79 0,22
9 Жилые здания из вибропрокатных пане- лей 1 0,4 0,423 1,06 0,32
Каркасно-панельные
(сборные) здания
14 (Жилые здания
16 |То же
0,86
0,76
0,76
а с н
Здания с нижними карк
анельными
к р у п н о п
ы м и и
этажа
верхними
м и
10
18
Жилые
этаже
То же
»
здания с магазином в
нижнем
0,28
0,64
1,14
0,3
0,4
1,05
к и р
я
п
и ч н
ы м з а
полнителе
м
Каркасные здани
12 Здание банка с монолитным железобетон- ным каркасом 1 0,96 — I.™ 0,89
12 Здание банка со стальным каркасом 2 1,175 1 - — 1,125
13 То же 1 1,149 ' « 1,24
/-Г
*алки
Более точные результаты дает фор-
мула (3.51). В табл. 3.3 н на графиках
рис. 3.37 приведены данные измерений пе-
риода основного тона собственных колеба-
ний, полученные по некоторым натурным
опытам Го и по формуле (3.52).
Здесь использованы следующие значе-
ния коэффициента а, полагая при этом, что
грунты основания имеют среднюю дефор-
мативность: жилые здания крупнопанель-
ные, а = 0,047; жилые здания с несущими
кирпичными, каменными и крупноблочными
стенами, а = 0,056; школьные и другие об-
щественные здания с кирпичными,, камен-
ными и крупноблочными стенами, а = 0,065;
каркас из монолитного железобетона с кир-
ТАБЛИЦА 3.4
Рис. 3.36. Узел каркаса в проекте 11-этажного
здания для строительства в Алма-Ате
Тип здания Значение ф
от До среднее
Каркасные здания с кирпичным заполнением .0,32 0,68 0,46
Крупнопанельный четы- рехэтажный дом серии 1-4164 0,44 0,54 0,49
Пятиэтажный дом с не- сущими стенами из мел- ких каменных блоков 0,4 0,76 0,58
Кирпичные здания вы- сотой 7—24 м 0,48 0,76 0,6
Крупноблочный четы- рехэтажный дом из кам- ня-ракушечника, раз- резка стен четырехряд- ная 0,5 0,78 0,64
62
Рис. 3.37. Опытные величины
периода и формы основного то-
на собственных колебаний зда-
ний
а — зависимость Т от высоты
здания со стальным каркасом;
б — то же, но с железобетон-
ным каркасом (п — номер верх-
него этажа); в — первые фор-
мы колебаний при изгибе и
сдвиге; г — формы колебаний
зданий с несущими стенами;
1 — кирпичного 4-этажного; 2 —
кирпично-блочного 4-этажного;
3 — из кирпичных шлакоблоков
5-этажного; 4 — крупнопанель-
ного 8-этажного; 5 — панельного
4-этажного; 7 — опытная кри-
вая; 7/— расчетная с учетом
сдвига; 777 — с учетом податли-
вости грунта
личным или легкобетонным заполнением
стен, а = 0,064; стальные каркасные с кир-
пичным или легкобетонным заполнением,
а = 0,08.
Данных по оценке характеристик зату-
хания собственных колебаний зданий пока
очень мало; в табл. 3.4 приведены коэф-
фициенты поглощения ф для некоторых
зданий, полученные по результатам натур-
ных измерений последних лет.
3.3. УЧЕТ РАЗВИТИЯ НЕУПРУГИХ
ДЕФОРМАЦИЙ И ИЗМЕНЕНИЯ
ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК
ЗДАНИЙ И СООРУЖЕНИЙ
ПРИ СЕЙСМИЧЕСКИХ ВОЗДЕЙСТВИЯХ
Общие сведения. Инструментальные
данные о характере работы сооружений
и результаты анализа последствий сильных
землетрясений указывают на то, что дей-
ствительные сейсмические нагрузки часто
превышают нормативные значения [16, 24,
30, 56, 69, 73, 74, 84—87]. При этом здания
и сооружения не могут работать только в
пределах упругости. В них развиваются ин-
тенсивные пластические деформации, воз-
никают повреждения, остаточные сдвиги и
т. п. [9, 10, 16, 19, 24, 27, 30, 34, 58, 71 —
74, 84—87].
Цель расчета зданий и сооружений на
сейсмические воздействия с учетом неупру-
гой работы конструкций — оценка их ди-
намических характеристик и напряженно-
деформированного состояния для более
полного отражения на стадии проектирова-
ния действительной работы сооружений
при интенсивных землетрясениях, корректи-
ровки объемночпланировочных и конструк-
тивных решений, определения показателей
их надежности. Такие расчеты базируются,
с одной стороны, на более полном учете
исходной информации о сейсмических про-
цессах и их проявлении на поверхности
земли (параметры, характеризующие интен-
сивность, повторяемость, спектральный со-
став и другие факторы), и, с другой сто-
роны, данных о механических явлениях в
сооружениях и их элементах при сейсмиче-
ских колебаниях вплоть до исчерпания не-
сущей способности (наступления предель-
ных состояний).
В табл. 3.5 приведены параметры предель-
ных состояний, используемые в настоящее
время в литературе по сейсмостойкому строи-
тельству [9, 10,( 16, 19-24, 27, 30, 34, 40,64,
66, 67, 69, 71, 72—75, 81, 83—87]. При
этом параметры с индексом «п» характе-
ризуют полные* перемещения, углы поворо-
та и деформации, а с индексом «у» — пре-
дельные значения в упругой стадии работы.
Все параметры разделяются на четыре
группы: прочностные, деформационные,
энергетические и параметры механических
и динамических характеристик. Дальней-
шая детализация параметров выполнена в
зависимости от характера нагрузок, а так-
же применительно к отдельным конструк-
тивным элементам, соединениям (сопряже-
ниям элементов), для зданий и сооружений
в целом. Это позволяет при установлении
их количественных значений использовать
результаты различных экспериментальных
исследований и инженерного анализа пос-
ледствий сильных землетрясений.
Коэффициенты п и х подразделяются
в зависимости от вида перемещений и де-
формаций (х, 0, е и др.), к которым они
относятся. Результаты исследований по-
казывают, что максимальные значения цД
для сооружений в целом можно принимать
равными соответственно 4—6 и 3—5 для
зданий со стальным и железобетонным
каркасом и 2—3 для связевых систем.
Коэффициенты Ц характеризуют способ-
ность конструкций к деформированию, а
коэффициенты х и их суммарные значе-
ния — накопление остаточных деформаций
и повреждений. Они могут быть использо-
ваны при нормировании предельных зна-
чений остаточных деформаций как парамет-
ров расчетных предельных состояний.
63
ТАБЛИЦА 3.5
Параметры расчет- ных предельных со- стояний Для отдельных конструктивных элементов и соединений Для сооружений при динамических (сей- смических) воздей- ствиях
при однократном нагруже- нии при циклическом нагруже- нии
Прочностные Параметры прочности: сдви- гающая сила Q; усилия в элементах М, N; относи- тельные параметры = = Q/Qy Максимальные значения сдвигающих сил усилий в элементах , Ммякг; относи- тельных параметров р у макс
Деформационные Абсолютные значения пе- ремещений х, углов поворо- та 0, деформаций е Максимальные значения пе- ремещений *макс» углов поворота 0макс- дефор- маций еМакс Максимальные зна- чения перемещений хмакс ’ сдвигов Дмакс и «Р-
Коэффициенты относитель- ных перемещений /х,у углов поворота Цд = = 0п/еу, деформаций = — Еп^еу Максимальные значения ко- эффициентов цхмакс. На , Ц 0 макс £ макс Максимальные зна- чения коэффициен- тов относительных перемещений Цдмакс
Коэффициенты остаточных перемещений, углов поворо- та, деформаций: = = гост^лу’ ~ %ст/9у’ % =Еост/8у Максимальные значения ко- эффициентов xXMaKc. V макс’ Ие макс Максимальные и суммарные значения коэффициентов ос- таточных перемеще- ний х А А макс SxA А макс
Суммарные значения коэф- фициентов остаточных пе- ремещений, углов поворота, деформаций: Xz EzQ л U > Хх е Отношения коэффи- циентов относитель- ных и остаточных перемещений для разных этажей, кон- струкций и т. п.
Энергетические
Коэффициенты расхода
энергии:
энергия условного уп-
ругого деформирования
потенциальная энергия
деформации
потенциальная энергия
___деформации
предельная энергия
упругого деформирова-
ния
Коэффициент диссипации:
расход энергии на ги-
стерезисные явления
предельная энергия уп-
ругого деформирова-
ния
Суммарные значения коэф-
фициентов расхода энергии
Суммарные значения коэф-
фициентов диссипации ES23
Отношения между
суммарными коэффи-
циентами ’ диссипа-
ции энергии для раз-
ных этажей, конст-
рукций и т. д.
Механические и ди- Коэффициенты изменения жесткости (отношение началь-
намические характе- ной жесткости и жесткости в предельном состоянии)
ристнки
Коэффициенты из-
менения жесткости
и мгновенных пе-
риодов (частот) сво-
бодных колебаний
Параметры изменения механических и
динамических характеристик позволяют ин-
тегрально описать нелинейную ряботу кон-
струкций и характеризуют суммарное из-
менение параметров жесткости за весь про-
цесс нагружения. Их удобно использовать
при оценке необратимых деформаций и по-
вреждений зданий и сооружений при ин-
женерном анализе последствий землетря-
сений.
Наряду с максимальными значениями
параметров ц, х, Q и др. широко исполь-
зуют их отношения, которые характеризу-
ют распределение необратимых деформаций
между отдельными этажами, отсеками, ра-
мами, диафрагмами и другими конструктив-
ными элементами.
Характерные зависимости типа восста-
навливающая сила—перемещение для от-
дельных конструктивных элементов и со-
оружений в целом. Экспериментальные и
теоретические зависимости восстанавливаю-
щая сила — перемещение, изгибающий мо-
мент - угол поворота (кривизна), напря-
жение— деформация и др., применяемые в
исследованиях по сейсмостойкости соору-
64
ТАБЛИЦА 3.6
Зависимость
График зависимости
Упруголинейная
Идеальная упругопластическая
Идеальная упругопластическая с упрочнением
Рамберга — ОсгуДа
i
Криволинейная параболическая
Экспоненциальная
Обобщенная
3 Зак. 193
65
ТАБЛИЦА 3.7
Зависимость
График зависимости
Упруголинейная с изменяющейся жесткостью
Линейная со скачкообразно изменяющейся жестко-
стью
То же
Нелинейно-упругая с изменяющейся жесткостью
Идеальная упругопластическая с изменяющейся
жесткостью
Экспоненциальные с изменяющейся жесткостью
Обобщенные
66
Рис. 3.38. Схема генери-
рования искусственных
сейсмограмм
жений [5, 9, 10, 16, 19, 24, 27, 30, 34, 64,
66, 67, 71—75, 84—87] для упругопластиче-
ских систем и систем с изменяющейся же-
сткостью, представлены соответственно в
табл. 3.6 и 3.7.
Нелинейность работы элементов опре-
деляется различным характером процессов
нагружения и разгрузки с появлением пе-
тель гистерезиса [5, 10, 19, 30, 56, 57, 62,
64, 65], нестационарность— изменением во
времени параметров жесткости и затуха-
ния колебаний [9, 10, 19, 41, 66]. Нели-
нейно-упругие системы характеризуются
нелинейной зависимостью сила — переме-
щение при совпадении графиков нагруже-
ние— деформация и разгрузка — деформа-
ция.
В настоящее время наиболее широко
используют зависимости типа диаграммы
Працдтля, билинейного и трилинейного ти-
па, зависимости Рамберга — Осгуда, с пере-
ходной параболической кривой между зо-
ной -упругих деформаций и стадиями те-
кучести или упрочнения. В некоторых слу-
чаях к удовлетворительным с практической
точки зрения результатам приводит исполь-
зование упрощенных моделей жесткопла-
стического тела (идеального и с упроч-
нением).
Экспоненциальные зависимости (в том
числе с нисходящей ветвью) позволяют
аппроксимировать весь процесс упругопла-
стического деформирования конструкций до
исчерпания несущей способности, при этом
для описания опытных кривых необходимы
лишь два-три параметра [10].
Обобщенные модели деформирования
неупругих систем предложены в работах
[37, 43]. Модель в [37] (см. табл. 3.6,
поз. 7) позволяет решать в статистической
постановке задачи для систем с существен-
ной нелинейностью. В этой модели учиты-
вается уровень нагружения (параметры
До и х0 зависят от нагрузок), а также эф-
фект упрочнения и повторного нагружения.
Обобщенные модели [45] (см. табл. 3.7)
предназначены для исследования динамиче-
ских систем с переменной структурой и
учитывают два вида разрушений — хруп-
кое разрушение и пластические деформации
материала (модель а) или изменение кине-
матической схемы системы с переменной
структурой (модель б).
Расчет конструкций на основе записей
реальных сейсмических колебаний грунта.
Особенности применения ЭВМ и АВМ.
Один из основных источников информации
о сейсмических воздействиях — данные сети
сейсмологических станций, регистрирующих
параметры движения грунта,
и станций инженерно-сейсмо-
метрической службы для за-
писи колебаний зданий и со-
оружений [16, 24, 27]. Записи
реальных сейсмических коле-
баний грунта используются
в графической форме в
виде осциллограмм (сей-
смограмм, велосиграмм и
акселерограмм) или в ви-
де цифровой последова-
тельности ординат, взятых с не-
котором шагом с осциллограммы, что удоб-
но для ^вода в ЭВМ.
Инструментальные записи обычно пред-
варительно обрабатывают, определяя ба-
зисную (нулевую) линию и корректируя
результаты оцифровки с учетом возможных
сбоев в работе считывающих, цифрующих
и других электронных устройств.
Наряду с записями реальных сейсмиче-
ских колебаний грунта используют искусст-
венные осциллограммы, генерируемые с
помощью АВМ на основе специальных ал-
горитмов, а также обобщения и анализа
данных сейсмических и инженерно-сейсмо-
метрических наблюдений [9, 24, 43]. На
рис. 3.38 представлена принципиальная схе-
ма генерирования искусственных сейсмо-
грамм [43].
Расчет зданий и сооружений на реаль-
ные сейсмические воздействия включает
следующие этапы: 1) выбор сейсмограммы
или совокупности сейсмограмм в качестве
расчетного сейсмического воздействия, при
этом может быть изменена его интенсив-
ность путем масштабирования; 2) выбор и
обоснование расчетной динамической моде-
ли сооружения; 3) выбор расчетных зави-
симостей, характеризующих прочностные,
деформационные й в некоторых случаях
энергетические свойства элементов конст-
рукций; 4) разработку методов определе-
ния динамической реакции расчетной мо-
дели на заданное воздействие; 5) реализа-
цию алгоритмов расчета на электронных
вычислительных или аналоговых машинах;
6) анализ результатов вычислений и выбор
расчетных значений усилий в элементах;
7) проверку прочности, деформативности
и параметров энергоемкости анализируемых
конструктивных схем, т. е. оценку их сей-
смостойкости.
В некоторых случаях расчет допол-
няют оценкой работы зданий и сооружений
с использованием методов теории надежно-
сти.
Интенсивность и продолжительность
сейсмических воздействий выбирают с уче-
том характера прогнозируемых землетря-
сений для отдельных регионов и строитель-
ных площадок, а также технических воз-
можностей используемых вычислительных
машин. За рубежом наиболее часто исполь-
зуют для этой цели записи землетрясений
Эль-Центро, 1934 и 1940 гг.; Олимпия,
1949 г.; Тафт, 4952 г.; Порт-Хьюним,
1957 г.; Паркфилд, 1966 г.; Мацуширо,
1966 г.; Токаши-Оки, 1968 г.; Сан-Фернан-
до, 1971 г., и др. Интенсивность воздей-
ствий задают с помощью коэффициентов
3* Зак. 195
67
Ud-Uj
Прогид 6 упруго
пластической
стадии.
и
Прогид 8 упругой Ц/
стадии
Рис. 3.39. Упругий и неупругий элементы рамы
Рис. 3.40. Диаграмма билинейного тжна
Т, с
Рис. 3.41. Спектр максимальных ускорений для
упругопластической системы
увеличения (уменьшения) ординат реальных
записей. В качестве расчетных моделей зда-
ний и сооружений при расчетах на основе
записей реальных сейсмических воздействий
чаще всего использую! обычные консоль-
ные системы с сосредоточенными и рас-
пределенными массами.
Наряду с этим, как отмечалось в п. 3.1,
рассматриваются расчетные модели зданий
в виде перекрестных систем [34], консоль-
ных пластин, плоских и пространственных
рам, систем материальных твердых тел,
соединенных различными связями [16, 30,
34, 44, 74, 81, 86, 87], которые более точ-
но отражают действительную работу конст-
рукций. В некоторых случаях применение
консольных расчетных моделей не позво-
ляет учесть сложный нелинейный характер
деформирования элементов, податливость
перекрытий, влияние моментов от осевых
усилий и других факторов.
Получает развитие расчет сейсмостой-
ких зданий и сооружений с использованием
метода конечных элементов. Он удобен
для анализа сложных систем, состоящих
из различных конструктивных элементов
(рамодиафрагмы) или разных по механи-
ческим свойствам оред (системы сооруже-
ние—фундамент—грунт), а также при изу-
чении напряженно-деформированного сос-
тояния сложных элементов ((диафрагмы с
проемами, подкрепленные элементы, узлы
каркасных зданий и т. п.) [8Г, 87].
После обоснования расчетной модели
сооружения составляют уравнение или сис-
тему дифференциальных уравнений, опи-
сывающих колебания этой модели. В слу-
чае нелинейно-упругих систем матрица ко-
эффициентов жесткости состоит из величин,
зависящих только от параметров реакции
системы. Для систем гистерезисного типа и
систем с переменной структурой коэффи-
циенты матрицы зависят также от времени.
В зависимости от того, кркие дополнитель-
ные факторы учитывают в расчете, в диф-
ференциальных уравнениях могут быть до-
полнительные члены, характеризующие гео-
метрическую нелинейность, нелинейную
инерционность системы, нелинейное затуха-
ние, а также возбуждение параметрических
колебаний [9, 19, 411.
Матрицы диссипативных сил составля-
ют с учетом пропорциональности затуха-
ния относительным скоростям движения
частей системы (гипотеза Фойхта), отно-
сительным перемещениям (гипотеза Е. С.
Сорокина) или с учетом обеих гипотез
(комбинированное затухание). 'Иногда учи-
тывают также сухое трение, возникающее
по границам взаимодействия колеблющих-
ся элементов. При расчетах нелинейных и
нестационарных систем влияние диссипатив-
ных характеристик (их величин в началь-
ном состоянии) на параметры реакции ме-
нее значительно, чем в случае линейных
систем, в связи с тем, что большая часть
энергии внешнего воздействия поглощается
в результате развития пластических дефор-
маций, хрупких разрушений и других ос-
таточных изменений во внутренней струк-
туре системы [16, 86, 87].
Для составления дифференциальных
уравнений колебаний используют основные
уравнения теоретической механики, а так-
же методы сил и перемещений, расчлене-
ние системы на составные части (этажи,
ярусы) или отдельные конструктивные эле-
менты. Применяют также метод двойных
жесткостей [16, 86], когда каждый эле-
мент рамы предполагается состоящим из
двух элементов — упругого и неупругого
68
(рис. 3.39). Матрицы жесткости состав-
ляют для указанных элементов с учетом
совместности их деформирования, реше-
ние дифференциальных уравнений "выпол-
няют в форме приращений.
Проиллюстрируем изложенное на стри-
мере системы с одной степенью свободы,
рис. 3.40 приведена широко используемая
диаграмма билинейного типа. Для одномас-
совой системы консольного типа при учете
затухания по гипотезе Фойхта уравнения
колебаний и их решение на различных
этапах деформирования конструкций име-
ют следующий вид [24]:
а) стадия упругой работы (участок
0—1):
у + 2ъу + 1%у = — Го;
т— sin 11
X
У =
к
е—е (t—t)
о
(3.53)
где Хо — угловая частота собственных ко-
лебаний системы без учета затухания; Х=
= Xq — е2; Уо(/)—акселерограмма зем-
летрясения; i/o и у о — соответственно пере-
мещение и скорость системы при /=0;
б) стадия упрочнения (участок 1—2):
*1 Ут
У :---------
Ут
cos Ух
X (/ /т) +
t
х I Уо (т) е-е sin X'(/ — т) dr,
4
(3.54)
где Xi — 1—(ki[k) — параметр упрочнения;
k — начальная жесткость; kt — жесткость в
стадии упрочнения; Хо*='(1“Xi) Xq ; Х'=
Xg* — e2; ут и у?—перемещение и ско-
рость в момент перехода от упругой
стадии работы к стадии упрочнения (точка
П;
в) стадия разгрузки (участок 2—2):
У "Т 2 е у + Хо У (#макс Ут) —
У— хХ (#макс #т)~М#макс Х1 (#макс #т)]Х
XCOS Хо (/ —/2) —
t
J ?0 Ц) е~ 8 х
X
X sin X (t — т) dr,
где i/макс — максимальное перемещение в
момент времени /=|/2.
Дальнейший расчет выполняют ана-
логично с учетом начальных условий.
По результатам расчетов с учетом со-
отношений (3.53—3.55) можно построить
спектры реакций упругопластических сис-
тем и сравнить их с соответствующими
аналогами для упругих систем. На рис.
3.41 для примера показан спектр макси-
мальных ускорений для упругопластической
системы с одной степенью свободы, полу-
ченный с помощью ЭВМ для записи зем-
летрясения Олимпия, 1949 г. При этом при-
нимали, что = 0,51/„а£с,коэффициент не-
упругого сопротивления у=2е/Х0—0,12 при
0,1 Т 1 с и у = 0,08 при Г> 1 с. Как
видноЧиз рис. 3.41, учет упругопластических
свойств системы намного снижает макси-
мальные ускорения по сравнению с ускоре-
ниями упругой системы (xi=0). При рас-
четах с использованием диаграммы
Прандтля (xi = 1) происходит заметное
снижение сейсмических сил.
Строгого соотношения между перемеще-
ниями упругопластических и упругих сис-
тем установить не удается.
Нелинейность работы конструкций
проявляется: а) в повышении диссипации
вследствие образованжя петель гистерезиса,
что уменьшает перемещения на всем диа-
пазоне частот; б) в изменении мгновенной
частоты колебаний системы, которое спо-
собствует увеличению или уменьшению пе-
ремещений в зависимости от соотношений
частотных характеристик воздействия и
сооружения. Соотношение между макси-
vn-пл vnn
мальными значениями ^макс и #макс оп*
ределяют в различных интервалах частот
преобладающим влиянием одного из ука-
занных факторов [16].
Совместный учет двух горизонтальных
составляющих сейсмического воздействия^
равно как учет вертикальных воздействий,
приводит к более раннему развитию не-
упругих деформаций, а кривые деформиро-
вания характеризуются большим числом
скачков (пластических сдвигов).
Учет совместного действия силовых фак-
торов при анализе напряженно-деформиро-
ванного состояния конструкций сейсмостой-
ких зданий и сооружений. Колонны кар-
касных зданий во время землетрясения
работают как внецентренно-сжатые или
сжато-изогнутые элементы. В зданиях с
гибким первым этажом, особенно в много-
этажных, крайние колонны могут оказаться
внецейтренно-растянутыми. При сейсмиче-
ских колебаниях вертикальные несущие
элементы испытывают изгиб в двух на-
правлениях. Кроме того, в железобетон-
ных колоннах каркасов при небольшой их
гибкости возникают значительные попереч-
ные силы, которые могут существенно сни-
зить прочность приопорных зон. Узлы ри-
гелей и колонн испытывают совместное
действие изгибающих моментов, продоль-
ных и поперечных сил. Диафрагмы бескар-
касных зданий в условиях сейсмических
воздействий работают на знакопеременные
усилия сдвига и растяжения-сжатия. В-
отдельных элементах зданий (простенки,
перемычки и др.) возникает сложное на-
69
Рис. 3.42. Влияние дополнительных моментов
РД на динамические реакции каркасных зданий
пряженное состояние: изгиб со сдвигом, вне-
центренное сжатие со сдвигом и т. п.
В большинстве случаев для оценки
прочности конструкций сейсмостойких зда-
ний приемлемы основные положения и
методы строительной механики, разработан-
ные для обычных условий нагружения [15,
18, 57; 81]. В исследованиях по теории
сейсмостойкости широко используют методы
теории предельного равновесия, анализа
механизмов разрушения и др. [34, 57, 73—
75, 81, 84—87]. Соотношения силовых фак-
торов в предельном состоянии элементов
определяют в соответствии с положениями
теории пластичности и теории прочности
[61]. При этом переменный характер уси-
лий учитывают с помощью поправочных
коэффициентов и оценивают с позиций
малоцикловой усталости [27, 30,
70]. Для практических расчетов внецент-
ренно-сжатых и сжато-изогнутых элементов
железобетонных и стальных каркасов со-
ставлены графики соотношений изгибаю-
щих моментов и продольных усилий в пре-
дельном состоянии для разных диапазонов
гибкостей, форм сечений, марок бетона и
стали [71, 83].
При анализе динамической реакции
каркасных зданий в случае интенсивных
сейсмических воздействий существенное
влияние на параметры напряженно-дефор-
мированного состояния, характер пре-
дельных состояний и деформирование ока-
зывают дополнительные моменты РД, воз-
никающие в деформированных колоннах
от вертикальных усилий (рис. 3.42). Эти
усилия вводят в канонические уравнения
равновесия системы, т. е. рассчитывают
конструкции по деформированной схеме
[34, 52, 67, 69—73, 75, 82—85].
Понятия об оптимальном проектирова-
нии сейсмостойких зданий и сооружений.
Понятие оптимальности в теории сейсмо-
стойкости объединяет три этапа рациональ-
ного проектирования зданий и сооружений:
1) определение приемлемой степени
сейсмического риска и оценка на ее основе
необходимых затрат на антисейсмические
усиления конструкций [9]. За минимизиру-
емую целевую функцию принимают сумму
первоначальных затрат на возведение зда-
ний и затрат на их восстановление с учетом
повторяемости землетрясений для различ-
ных регионов и ограничений по надежности
проектируемых объектов;
2) установление экономических крите-
риев оптимальности конструктивных реше-
ний и определение на их основе для соору-
жений разных классов регламентируемых
значений абсолютных и относительных пере-
мещений, деформаций и других параметров
предельных состояний [10];
3) определение оптимальных парамет-
ров конструктивных решений для отдельных
классов зданий и сооружений [34, 68, 73,
74, 87].
В качестве критериев оптимальности для
третьего этапа принимают условия дости-
жения минимального расхода материалов
на основные несущие конструкции; мини-
мальной стоимости конструкций; равномер-
ного распределения коэффициентов подат-
ливости ц или коэффициентов пластичности
х по высоте сооружений; равномерного рас-
пределения коэффициента сейсмической на-
грузки или сдвигающих усилий по высоте
зданий (принцип равнонапряженности);
равномерного распределения коэффициентов
диссипации энергии (принцип полного ис-
пользования энергетических резервов со-
оружения), а также критерии совершенства
механических систем [34]. Указанные за-
дачи решают применением классических ва-
риационных методов, методов линейного,
нелинейного и динамического программиро-
вания, принципа максимума Понтрягина.
В качестве ограничений используют ус-
ловия не превышения сейсмическими нагруз-
ками пределов прочности элементов, а пе-
ремещениями сооружения в целом или его
элементов — регламентируемых значений
перемещений (деформаций). В результате
могут быть получены распределения проч-
ностных, деформационных и энергетических
параметров предельных состояний элемен-
тов зданий и сооружений, обеспечивающие
оптимальные в принятом смысле технико-
экономические показатели конструктивных
решений.
Принципы проектирования систем с за-
данными параметрами предельных состоя-
ний. В последние годы в отечественной и
зарубежной литературе по сейсмостойкому
строительству были предложены и частич-
но реализованы в практике проектирования
и строительства новые принципы проектиро-
вания, обеспечивающие повышенную степень
сейсмозащиты зданий и сооружений. Повы-
шение сейсмостойкости достигается приме-
нением следующих конструктивных решений
зданий (методов активной" сейсмозащиты):
с каркасным нижним этажом («гибким»
первым этажом); -
с переменными динамическими харак-
теристиками (системы односторонних вы-
ключающихся и включающихся связей);
с заданными зонами развития пласти-
ческих деформаций;
с повышенными диссипативными харак-
теристиками (в том числе с упругофрик-
ционными соединениями);
с системами сейсмоизоляции;
с подвесными массами и технологиче-
ским оборудованием;
с подвесными этажами;
70
с регулируемыми напряжениями в не-
сущих конструкциях, в которых применя-
ют предварительно напряженные элементы.
Эти конструктивные решения разра-
ботаны исходя из целенаправленного ис-
пользования неупругих свойств конструк-
ций (развития пластических деформаций,
остаточных сдвигов, локальных разрушений,
диссипации энергии), эффектов сейсмоизо-
ляции и приспособляемости, а также уп-
равления схемами работы сооружения в
процессе его деформирования при земле-
трясении.
Каждое из указанных решений имеет
достоинства и недостатки. Поэтому на
практике, как правило, используют два или
несколько конструктивных решений, на-
пример сейсмоизоляция в уровне верха
фундаментов или первого этажа с включаю-
щимися упругими связями, системами по-
вышенного затухания и др. При этом уда-
ется достичь снижения сейсмических нагру-
зок на надземные конструкции здания в
зависимости от спектрального состава и
других особенностей сейсмического воздей-
ствия.
Целесообразность применения перечис-
ленных решений определяют на основе тех-
нико-экономического анализа и сопоставле-
ний затрат на специальные и традицион-
ные методы сейсмозащиты зданий и соору-
жений.
3.4. ВЕРОЯТНОСТНЫЕ МЕТОДЫ
РАСЧЕТА СООРУЖЕНИЙ
НА СЕЙСМИЧЕСКИЕ ВОЗДЕЙСТВИЯ
i
1. Стохастические модели
колебаний грунта
при землетрясении
Инструментальные записи колебаний
грунта и сооружений, сделанные во время
землетрясений, показывают, что движение
поверхности земли является типичным не-
стационарным случайным процессом. Опи-
сать это движение любым детерминирован-
ным законом невозможно. Существует об-
щепризнанное мнение, что одно из наиболее
перспективных направлений развития теории
сейсмостойкости'должно опираться на ве-
роятностные методы расчета сооружений, в
основе которых лежат методы теории слу-
чайных процессов.
Одна из первых попыток применить те-
орию вероятностей к расчету сооружений
на сейсмические воздействия была сделана
Г. Хаузнером [79] в 1947 г., предложившим
представлять движение грунта в виде се-
рии случайных некоррелированных импуль-
сов. Затем в 1958 г. последовало предло-
жение М. Ф. Барштейна [17] рассматри-
вать изменение во времени ускорения грун-
та при землетрясении как стационарный
случайный процесс, а движение конструк-
ции, сооружения изучать в переходном ре-
жиме. В 1959 г. В. В. Болотиным [14] бы-
ло предложено аппроксимировать те же ус-
корения грунта квазистационарным слу-
чайным процессом. В 1963 г. для расчета
нелинейных и параметрических систем
Н. А. Николаенко предложил рассматри-
вать процесс сейсмических колебаний грун-
та как 6<коррелированный. В последние го-
ды появились другие предложения по ве-
роятностному описанию (моделям) движе-
ния грунта при землетрясениях.
* В расчетах и исследованиях по теории
сейсмостойкости сооружений наибольшее
распространение получили расчетные мо-
дели сейсмического воздействия двух ви-
дов. Первая модель использует огибающие
максимальных ординат спектров динами-
ческих реакций линейных осцилляторов.
Другая модель использует акселерограммы
зарегистрированных землетрясений, осред-
ненные спектральные характеристики кото-
рых приближенно отражают свойства ин-
струментальных ^записей. Первая модель
неприемлема в расчетах нелинейных, пара-
метрических чи нестационарных динамиче-
ских систем. Вторую модель можно приме-
нять при расчетах и исследованиях любых
систем. Обе модели не отражают физиче-
ски возможного разнообразия спектраль-
ных и других характеристик сейсмических
колебаний грунта.
Обработка записей землетрясений дает
очень большое разнообразие форм спек-
тральных кривых, построенных по акселе-
рограммам сильных землетрясений, записан-
ных не только в различных регионах, но и
в одном сейсмическом районе. Это обстоя-
тельство объясняется многими факторами:
строением очага землетрясения, условиями
в точках наблюдения, условиями прохож-
дения сейсмических волн через напластова-
ния, имеющие различное геологическое
строение, координатами эпицентра и мно-
гим другим. Землетрясения, записанные на
одной и той же сейсмической станции, мо-
гут иметь различные доминантные частоты
и формы спектров. В этом и проявляется
случайный характер землетрясения.
Инженерная сейсмология в настоящее
время не располагает сведениями о стати-
стических характеристиках землетрясений
каждого района, тем более отдельных стро-
ительных площадок. Это приводит к необ-
ходимости создавать статистические моде-
ли сейсмических колебаний грунта в усло-
виях неполной информации.
Информация, которую можно получить
из сейсмограмм прошедших землетрясений,
является единственным исходным объектив-
ным материалом, на основе которого мож-
но рассчитывать сооружения на прочность
и устойчивость, но она очень ограничена,
так как число записей сильных землетрясе-
ний весьма мало. ъ
Все землетрясения можно условно раз-
делить на три типа.
Первый тип — кратковременные земле-
трясения импульсивного характера с не-
большой магнитудой (например, землетря-
сение в Агадире). Математической моделью
таких землетрясений является 6-коррелиро-
ванный процесс или его суперпозиция с
весьма узкополосным случайным процессом.
Второй тип — нерегулярные колебания
средней продолжительности. Они наблюда-
ются на плотных грунтах при средних рас-
стояниях от эпицентров. Примером такого
землетрясения является землетрясение в
71
Эль-Центро в 1940 г. Для этих землетрясе-
ний характерно преобладание высокоча-
стотных составляющих (10^16 Гц) на
близких расстояниях от эпицентров и повы-
шение роли низкочастотных составляющих
с увеличением расстояния от эпицентра.
Третий тип — землетрясения большой
продолжительности (2—4 мин), в которых
преобладают низкочастотные составляющие
(0,7—0,4 Гц), хотя продолжительность до-
минантной составляющей 10—30 с. Как от-
мечают отдельные авторы, колебания грун-
та этого типа есть результат прохождения
колебаний второго типа через толщи рых-
лых отложений. Примером может служить
землетрясение в Мехико-Сити, Д|957 г.
Существенная нерегулярность сейсми-
ческих колебаний грунта, обусловленная са-
мим механизмом образования сейсмических
волн в очаге и прохождением через нерегу-
лярные геологические образования, опреде-
лила переход от детерминированной модели
к трактовке сейсмического движения грун-
та как случайного процесса. В последние
20 лет был предложен ряд моделей (мате-
матическое описание) сейсмических колеба-
ний грунтов. Рассмотрим некоторые из этих
моделей.
Система случайных импульсов. Сейсми-
ческое движение основания представляется
в виде: последовательности импульсов по-
стоянной величины (последовательности
П-образных участков на графике ускоре-
ние— время), случайным образом распре-
деленных во времени [79]; случайной по-
следовательности импульсов синусоидаль-
ной формы [88] с равномерным распреде-
лением на фиксированном интервале.
Суперпозиция волн:
f п
xQ (t) = 2 cos (&/ t + Ф/)
./«1
(/) = 0 при ^0;; > °;
(3.56)
где Qj и Фj — независимые случайные величи-
ны, равномерно распределенные в интерва-
ле (1 ... 8) 2л 1/с и (О...2л) соответствен-
—a J
но. Множитель (te < ) отражает наблю-
дающиеся на акселерограммах переходные
эффекты в1 начале п роцесс а.
Случайный 6-коррелированный процесс
[39]. Используют для оценки максималь-
ной сейсмической реакции динамических си-
стем, исследования задачи о первом пере-
сечении заданного уровня и т. д. Эта мо-
дель требует минимальной информации о
вероятностных характеристиках сейсмиче-
ского процесса и ограничивает его только
по интенсивности.
Усеченный 6-коррелированный процесс
используют в тех случаях, когда процесс
ограничен по интенсивности и известны
крайние значения частот, в пределах кото-
рых заключена основная часть спектраль-
ной плотности. Эта модель отражает усло-
вия неполноты сейсмологической информа-
ции.
Стационарный случайный процесс [17].
Изменение ускорений грунта во времени
рассматривают как стационарный нормаль-
ный случайный процесс F(t), а движение
упругой системы исследуют в переходном
режиме при нулевых начальных условиях:
F (t) при t > 0;
0 при 7^0.
Для процесса F(t) на основе обработ-
ки ряда акселерограмм сильных землетря-
сений М. Ф. Барштейном предложена сле-
дующая корреляционная функция Д/т):
ГоК) =
Х(т) =В.. (0)е-“|т| cos 0 т, (3.57)
Aq
где (0)—дисперсия ускорения; зна-
хо
чения параметров аир рекомендованы в
пределах а = 6...8 1/с; р=14...2О 1/с.
Эта модель движения грунта во всех
случаях дает возможность определить верх-
нюю границу сейсмической нагрузки. Ряд
авторов для корреляционной функции про-
цесса F(t) предлагали другие зависимости.
Квазистационарный случайный процесс.
а) Квазистационарная модель В. В. Боло-
тина [14] состоит в том, что ускорение
грунта аппроксимируется произведением
детерминированной функции времени и ста-
ционарного случайного процесса
Хо (/) =
при 7 0;
при t < 0.
(3.58)
Константы Ло и 8 определяют при
аппроксимации колебаний.грунта.
б) Нестационарная модель типа [11]
" _ М (Л tt>z) ф (Л и, шг-) при t > 0;
0 при
(3.59)
представляет нестационарный мультипли-
кативный случайный процесс. Функция
qp (t, со, м;)—стационарный нормальный
случайный процесс; A(t, coj — огибающая,
принятая при фиксированных значениях
частот С0г в виде импульса Берлаге:
А (0 = А0/е-£»Н' - . (3.60)
Эта модель нестационарного процесса
характеризуется не одним спектром, а
множеством (расчетных спектров в задан-
ной области частот, ограниченной значени-
ями минимальных и максимальных наблю-
давшихся средних частот в диапазоне
доминантных частот, представляющем ин-
терес с точки зрения воздействия на соо-
ружение. Для расчета принимают огибаю-
щую всех спектров, соответствующих раз-
личным i(Oi.
Предложенные модели описывают го-
ризонтальную составляющую сейсмического
движения грунта и не относятся к верти-
кальной составляющей. Во многих случаях
вертикальные сейсмические силы могут иг-
рать определяющую (роль ;при разрушении
сооружений или значительно усугублять
разрушения, производимые горизонталь-
ными составляющими сейсмического воз-
действия.
72
Отметим, что для корректного расчета
сооружения как пространственной системы
сейсмическое движение грунта надо пред-
ставлять трехкомпонентным вектором по-
ступательного и вращательного движений
[42].
В работах [44, 45] приведена методика
расчета малых пространственных колеба-
ний сооружений и показано, как, опираясь
на волновую теорию распространения сей-
смических волн, можно получить всю не-
обходимую статистическую информацию о
компонентах вращательных движений осно-
вания по записям поступательных движе-
ний.
2. Стохастический метод
расчета сооружений
на сейсмические воздействия
Рассмотрим, механическую систему с
одной степенью свободы (рис. 3.43). Урав-
нение движения этой системы при задан-
ном движении ее основания, если для сил
Рис 3.43. Расчетная модель системы с одной сте-
пенью свободы при сейсмическом движении ос-
нования
затухания принять гипотезу Е. С. Соро-
кина, имеет вид:
-J- (// /у) соXi — — xq, (3.61У
где
где б — логарифмический декремент коле-
баний;
здесь — квазиупругий коэффициент;
/Hi — сосредоточенная масса. Функция вре-
мени хо является стационарным случайным
процессом с заданным нормальным зако-
ном распределения с известной дисперсией
и средним, равным нулю. Начальные усло-
вия системы считаем нулевыми [4].
Квадрат модуля комплексного коэф-
фициента передачи рассматриваемой сис-
темы, учитывая, что при у<С1 можно при-
нять и имеет вид:
IФ (i со, /) '2 - , Ф (Е со ) 2 х
f — ^2 и t
х 1 2е 2
X [cos (со — со!) t — (у/2) sin (со
[(of — (О2 (О2 — (01 со (со2 — со2)]
т2 (со4 — 2 и со2 со2 + wt)2
X sin (со — (Oi)Z, (3.62)
Рис. 3.44. График ко-
эффициента дина-
мичности для пере-
ходного режима
/ — = 20,94 1/С; 2 —
wi=6,27 1/с
Рис. 3.45. Графики
коэффициента дина-
мичности для стаци-
онарного режима
а — для железобе-
тонных конструкции;
б — для стальных
конструкций
73
где
1
[ Ф (l 0>) | 2 = --------------------------------—
! /n? (co4 — 2 и co? co2 + )
Максимальное значение Xi(t) в пере-
ходном режиме примерно в 1,4 раза боль-
ше значения хц в стационарном режиме.
Для расчета можно принять
Для определения дисперсии выхода
нестационарной системы, которая будет
функцией времени, воспользуемся извест-
ной формулой теории случайных процессов:
<Х1 (С >макс = (1,42) < xf > • (3.68)
где
СО
X f | Ф (г со, /) [2 G.. (со) d со, (3.63)
— QO
Если воспользоваться свойством узко-
полосности системы и считать, что спект-
ральная плотность G - (со) не имеет раз-
Xq
рывов и очень резких максимумов вблизи -
(Bi, то получим очень простую формулу
для стационарного значения дисперсии
Xi (0:
G" (со) = В- (0) х
Xq ' ' Xq ' '
(«1)
(3.69)
(3.64)
Спектральная плотность G- (со) про-
Xq
цесса xo(t) найдена в соответствии с фор-
мулой (3.64), определяющей корреляцион-
ную функцию этого процесса.
После всех вычислений получим еле-
дующую формулу для (t) > [4, 16]:
гл 2
Разница в величинах >, полу-
ченных по формулам (3.66) и (3.69), не
имеет, практического значения.
Величина £•• (0)/mj <о| равна дис-
хо
Персии статического перемещения <хст>,
тогда из (3.65) следует, что
< Z2 (/)>
<xf (t)>
(3.70)
, (0)
<*?(/)> = <£2(/)>- (3.65)
т{ coj
Для дисперсии коэффициента £(7) по-
лучается очень громоздкая формула, кото-
рую мы не приводим (см. работы [4, 17]).
На рис. 3.44—3.45 приведены графики ко-
эффициента £(t) для случая у==0,1; а=
= 7 1/с; р = 18 1/с; соi=20,94 1/с и 6,28
1/с, что соответствует статистическим дан-
ным сейсмических колебаний, грунта, а
значение у—0,1 соответствует железобетон-
ным конструкциям. Из этих графиков сле-
дует, что дисперсия выхода системы в пе-
реходном режиме имеет колебательный ха-
рактер вследствие биений между возмуща-
ющей частотой и частотой собственных ко-
лебаний системы.
При <x><Zxl(t)> стремится к
постоянному стационарному значению
В.. (0) а
Х° /1. (3.66)
«м W ~ «.О
tn2
+ 2 а (01 + —
Y
— 2 т2) «2 + 2 а у т2 cof + /п4
(3.67)
есть коэффициент динамичности.
Расчетное значение сейсмической на-
грузки
S — £ (^) ^1 /расч> (3.71)
где
/рас, = k.. У В: (0) (3.72)
Xq » Хф
определяет расчетное значение сейсмичес-
кого ускорения для данного района, кото-
рое выражается через коэффициент сей-
смичности kG:
/расч — 1/" (6) — S*
х$ Г . Хо
Тогда сейсмическая сила
S=1,4Q*cL
где Q = mig — значения £ берут по графи-
кам, приведенным на рис. '3.45, в зависи-
мости от материала конструкции.
В нормах по определению расчетной
сейсмической нагрузки [Г] коэффициент
Г,4 не фигурирует. При корректировании
графика коэффициента динамичности, при-
нятого в нормах, предполагалось, что име-
ется много неучтенных факторов, которые
снижают расчетную сейсмическую нагруз-
ку. К таким факторам, в частности, можно
отнести диссипацию энергии в конструктив-
ных соединениях, появление пластических
деформаций в отдельных элементах конст-
рукций и резкое увеличение диссипативных
сил при развитии пластических дефор-
маций.
74
3. Вероятностный метод -
расчета сооружений,
несущих резервуары
с жидкостью*
Рассмотрим простейшую расчетную
модель сооружения, несущего частично
заполненный резервуар. Считаем, что мас-
са сооружения сосредоточена на уровне, на
котором находится резервуар (см. рис. 3.46).
На рис. 3.46 показана инерциальная система
отсчета (х, у) и подвижная система отсчета
(хь yi), связанная с сооружением. Урав-
нения колебаний рассматриваемой одномас-
совой системы с полостью, заполненной
жидкостью, при сейсмическом движении
основания имеют вид?.
* •
-J"- (wj Z о) Q3 Xj
00
Значение Vi вычисляют по формуле
(для Йо>1)
vj = 5,98 Vth 1,84Л, -уу,
а у а
где vi — коэффициент кинематической вяз-
кости.
Решение системы уравнений (3.71) в
переходном режиме для определения дис-
персии X\(t) сопряжено с преодолением
больших вычислительных трудностей и
имеет только теоретическое значение, глав-
ным образом для того, чтобы проследить
развитие колебания системы в начальный
период. На рис. 3.47 для некоторых значе-
ний параметров системы показаны графики
%(t) коэффициентов динамичности в пере-
ходном режиме, который равен:
<5S(O> =------------(3.76)
fk + 2 ^kfk~V fk + ~ — xo.
где xo — ускорение движения основания
(сейсмическое ускорение); fk(t)— функция,
определяющая волнообразование на по-
верхности жидкости;
k ~~ В Bk
Q2 =-----,----; mk = — - ;
/п + тж М
т — масса конструктивных элементов и
i резервуара; — масса жидкости; В и
Вк -определяют в зависимости от формы
'резервуара.
Для резервуара цилиндрической формы
В = 2 л; a2 h р = 2 тж;
где
(3.77)
Значение коэффициента динамичности
в стационарном режиме для k—\ вычис-
ляют по формуле
М2 Q4
77Z] to2 \
-—G .. (со) d со
I2 — (07 / н
В4 = -~- — thxjfefto, (3.74)
«О yk
/?21 со4 \3
(О2—со? )
где h^—hja, h — высота налива жидкости
в резервуаре; а—радиус резервуара.
Для практических расчетов (с точно-
стью до 98%) достаточно ограничиться уче-
том только волны первой формы, т. е. при-
нять - k — 1, тогда [4]
где
ная
вания;
(3.78)
— нормированная спектраль-
плотность ускорения движения осно-
1 / 1,84
<01 = ]/ —1—th (1,84ft»);
V а
.. (со) =
НХ0
(со)
А0
в.. (0)
(3.79)
(3.75)
Вг = 0,227 4~ th (1,84 й0).
й0
Графики коэффициента £ для у=0,1;
0,05 и -а = 7 1/с; [3=18 1/с и различных
значений тх и coj приведены на рис. 3.48.
Анализируя графики, представленные
на рис. 3.47—3.48, можно сделать следу-
ющие выводы:
1) максимальное значение коэффициен-
та динамичности системы с жидким напол-
Риг. з.4б. Расчетная модель одномассовой систе-
мы при сейсмическом движении основания
нением в переходном режиме примерно в
1,3—1,4 раза больше соответствующего
значения коэффициента динамичности в
стационарном режиме;
2) стандарт коэффициента динамично-
сти для системы, если жидкость рассматри-
вать как твердое тело, больше соответст-
вующего стандарта £ с учетом подвижности
жидкости для /721 = 0,2 примерно в 1,2—
1,35 раза; для пи ==•(), 4 примерно в 1,6—
1,7 раза; для mt = 0,6 примерно в 2,5—
75
Рис. 3.47. График
коэффициента ди-
намичности в пе-
реходном режи-
ме для системы с
жидким напол-
нением
Рис. 3.48. Графики коэффициента динамичности
в стационарном режиме для железобетонных и
металлических конструкций
а — для железобетонных конструкций; б — для
стальных конструкций; 1 — /П1 = 0; 2 — mi=0,2,
3~ ш1=0,4; 4--/п; = 0,6; п: к см. (3.73); k = \
2,7 раза. Приблизительно такое же соотно-
шение имеет место и для коэффициентов
динамичности в стационарном режиме;
3) переходный режим в системе с жид-
ким наполнением значительно продолжи-
тельнее переходного режима системы, в ко-
торой жидкость можно рассматривать как
твердое тело. Это объясняется тем, что
собственные колебания маловязких жид-
костей затухают медленно. Колеблющаяся
жидкость в системе играет роль гармони-
ческого источника возбуждения с медленно
уменьшающейся амплитудой. Расчетное
значение сейсмической ецлы определяют по
формуле S = l,4Q&cL где Q — полный вес
всех конструктивных элементов и жидко-
сти; £ — стандарт коэффициентов динамич-
ности, который .находят по графикам на
рис. 3.47 или 3.48 в зависимости от собст-
венной частоты Q, значения т, и материала
несущих конструкций.
Таким образом, благодаря подвижно-
сти жидкости значительно уменьшаются
сейсмические силы от ее массы. При проек-
тировании сооружений с резервуарами сле-
дует стремиться к тому, чтобы значение
nii было большим. О расчете сооружений,
несущих несколько резервуаров, и много-
этажных сооружениях с резервуарами см.
[41.
СПИСОК ЛИТЕРАТУРЫ
1. СНиП II-A.12-69*. Строительство
в сейсмических районах. Нормы проектиро-
вания. М., 1970.
2. Инструкция по определению рас-
четной сейсмической нагрузки для 'зданий
и сооружений. М., 1962.
76
3. Справочник по динамике сооруже-
ний. Под ред. Б. Г. Коренева, И. М. Раби-
новича. М., 1972.
4. Рекомендации по расчету резерву-
аров и газгольдеров на сейсмические воз-
действия. М., 1969.
5. Рекомендации по расчету железо-
бетонных рамных каркасов на сейсмиче-
ские воздействия с учетом пластических
деформаций. Ташкент, 4972.
6. Руководство по проектированию
жилых и общественных зданий с железо-
бетонным каркасом, возводимых в сейсми-
ческих районах. М., 1970.
7. Руководство по проектированию
производственных зданий с каркасом из
железобетонных конструкций для сейсми-
ческих районов. М., 1972.
8. Инструкция по проектированию
конструкций панельных жилых домов
(ВОН 32Л7). М., 1978.
9. Айзенберг Я. М. О расчете адапти-
вных систем с выключающимися связя-
ми при неполной сейсмологической инфор-
мации .— В кн.: Сейсмостойкость зданий и
инженерных сооружений. / Под ред.
И. И. Гольденблата. М., 1972.
1'0 . Айзенберг Я. М., Дилимник Л, Ш.
О критериях оптимального проектирования
и параметрах предельных состояний при
расчетах на сейсмические воздействия. —
Строительная механика и расчет сооруже-
ний, 1970, № 6.
11. Айзенберг Я. М., Ульянов С. В.
Построение модели сейсмического воздей-
ствия и ансамбля аналоговых акселеро-
грамм для расчета сооружений. — В кн.:
Материалы к Всесоюзному совещанию по
проектированию и строительству сейсмо-
стойких зданий и сооружений. М., 1971.
12. Айзенберг Я. М. Вероятностная
спектрально-временная модель сейсмиче-
ских воздействий на сооружения. — па уч.
тр. J ЦНИИСК. М., 1974, вып. 33. Сейсмо-
стойкость зданий и инженерных сооруже-
ний.
13. Багманян А. Л., Ульянов С. В.
Использование АВМ в задачах моделиро-
вания динамических воздействий на соору-
жения. — Сейсмостойкое строительство,
1974, № 6.
14. Болотин В. В. Статистические ме-
тоды в строительной механике. Изд. 2-е.
М., 1965.
15. Болотин В. В., Гольденблат И. И.,
Смирнов А. Ф. Строительная механика.
Современное состояние и перспективы раз-
вития. Изд. 2-е. М„ 1972.
16. Баркан Д. Д., Бунэ В. И. и др.
Современное состояние теории сейсмостой-
кости и сейсмические конструкции (по ма-
териалам IV Международной конференции
по сейсмостойкому строительству. / Под
ред. С. В. Полякова. М., 1973.
17. Барштейн М. Ф. Приложение ве-
роятностных методов к расчету сооружений
на сейсмические воздействия. — Строитель-
ная механика и расчет сооружений, 1960,
№ 2.
18. Геммерлинг А. В. Расчет стержне-
вых систем. М., 1974.
19. Гольденблат И, И., Николаен-
ко Н. А. Расчет конструкций на действие
сейсмических и импульсивных сил. М., 1961.
20. Гросман Д. Б. Колебания протя-
женных сооружений при сейсмическом воз-
действии (G6. науч. тр.). / ТашЗНИИЭП,
Ташкент, 1964, вып. VI.
21. Егупов В. К., Домандрина Т. А.
Расчет зданий на сейсмические воздейст-
вия. Киев, 1969.
22. Егупов В. К. Расчет зданий на
прочность, устойчивость и колебания. Ки-
ев, 1965.
23. Бременом П. Л., Измайлов Ю. В.
Моноли^юсть и сейсмостойкость конструк-
ций из естественного камня. Кишинев,
1968.
24. Завриев Д. Q, Назаров А. Г, и др.
Основы теории сейсмостойкости зданий и
сооружений. Руководство по проектирова-
нию сейсмостойких зданий и сооружений,
т. 2. М., 1970.
25. Завриев Д. С. Расчет инженерных
сооружений на сейсмостойкость. — Изв.
Тифлисского политехи, ин-та, 1928.
26. Измайлов Я. А., Антонов А. В,
Крупнопанельные дома из виброкаменных
панелей. — В кн.: Исследования по сейсмо-
стойкости крупнопанельных и каменных
зданий. М., 1962.
27. Дарцивадзе Г. Н., Медведев С. В.,
Напетваридзе Ш. Г. Сейсмостойкое строи-
тельство за рубежом (по материалам Вто-
рой всемирной конференции по сейсмостой-
кому строительству в 1960 г. в Токио). М.,
1962.
28. Дорчинский И.' Л. Расчет соору-
жений на сейсмические воздействия. Науч-
ное сообщение ЦНИИПС, вып. 14. М.,
1954.
29. Дорчинский И. Л. и др. Основы
проектирования зданий и сооружений в
сейсмических районах. М., 1964.
80. Дорчинский И. Л. и др. Сейсмо-
стойкое строительство зданий. М., 1971.
311. Дорчинский И. Л. Приближенная
оценка сейсмических колебаний сооружений
большой протяженности (в плане). Иссле-
дования по сейсмостойкости здании и со-
оружений. М., 1961.
32. Дорчинский И. Л. Влияние протя-
женности (в плане) здания на величину
действующей на него сейсмической нагруз-
ки.— !В кн.: Сейсмостойкость промышлен-
ных зданий и инженерных сооружении. М.,
1962.
33. Д&рчинский И. Л., Шепелев В. Ф.
Расчет высотных зданий на сейсмические
воздействия с учетом их протяженности. —
Строительное проектирование промышлен-
ных зданий, 1965, № 2.
34. Дилимник Л. Ш. Методы целенапра-
вленного проектирования в сейсмостойком
строительстве. М., 1980.
35. Дириков Б. А., Золотов А. Б.
Расчет конструкций как пространственных
систем по записям землетрясений. — В кн.:
Сейсмостойкое строительство, № 5, М.,
1974.
36. Дричевский И. Я., Уланов Г. М.
Об одном обобщении теории накопления
отклонений.—"Прикладная математика и
механика, 1973, т. 36, вып. 5.
77
37. Макаров Б. П., Кириков Б. А.,
Новожилов А. В, О случайных колебаниях
упругопластических систем при сейсмиче-
ских воздействиях. — Науч. тр. / ЦНИИСК.
М., 1975, вып. 44. Сейсмостойкость зданий
и инженерных сооружений.
38. Медведев Q 5., Карапетян^ Б. К<,
Быковский В. А. Сейсмические воздействия
на здания и сооружения. М., 1968.
39. Медведев С, В. Инженерная сей-
смология. М., 1962.
40. Назаров А. Г. Метод инженерного
анализа сейсмических сил. Ереван, 1959.
41. Николаенко Н. А. Нелинейные ди-
намические задачи пространственных кон-
струкций в теории сейсмостойкости.—В кн.:
Сейсмостойкое строительство. № 5. М.,
1974.
42. Николаенко Н. А. Назаров Ю. П.
Динамика и сейсмостойкость пространст-
венных конструкций и сооружений. — В кн.:
Исследование по теории сооружений, вып.
23. М., 1977.
43. Николаенко Н. А., Ульянов С. В.
Статистическая динамика машинострои-
тельных конструкций. М., 1977.
44. Николаенко Н. А., Назаров Ю. П.
О пространственных колебаниях сооруже-
ний при сейсмических воздействиях. —
Строительная механика и расчет сооруже-
ний, 1979, № 3.
45. Николаенко Н. А., Назаров Ю. П.
Векторное представление сейсмического
воздействия.—'Строительная механика и
расчет сооружений, 1980, № 1.
46. Павлык В. С. Принцип проекти-
рования сейсмостойких зданий с повышен-
ными диссипативными свойствами. Мате-
риалы к Всесоюзному совещанию по про-
ектированию и строительству сейсмостой-
ких зданий и сооружений. Основные на-
правления исследования по сейсмостойкому
строительству. М., 1971.
47. Петров Б. Н., Уланов Г. М.,
Ульянов С. В., Хазен Э. М. Ценность ин-
формации. Семиотические аспекты инфор-
мационной теории управления и киоерне-
тики. — В кн.: Теоретическая кибернетика
(итоги науки и техники), т. 6, кн. 1. М/,
1975.
48. Петров А. А. Учет протяженности
зданий в расчетах на сейсмические воздей-
ствия.— В кн.: Ташкентское землетрясение
и .вопросы се йс м ост о йк о г о строительства.
М„ 1969.
49. Поляков С. В. и др. Проектирова-
ние сейсмостойких зданий, М., 1971.
50. Поляков C\f В. Сейсмостойкие кон-
струкции зданий. М., 1969.
51. Поляков С. B.t Денисов Б. Е.
Анализ работы крупнопанельных зданий на
действие ; горизонтальных (сейсмических,
ветровых) нагрузок с использованием пло-
ских пространственных моделей. — Строи-
тельство и архитектура Узбекистана, 1967,
52. Поляков С. В., Денисов Б. Е.
Распределение усилий в элементах стен и
перекрытий с учетом их совместной работы
при действии на здание горизонтальных
сил. — В кн.: Совершенствование методов
расчета и конструирования зданий и соору-
жений, возводимых в сейсмических райо-
нах, вып. 1. М., 1967.
53. Поляков С. В., Андреев О. О.,
Денисов Б. Е., Кириков Б. А. Упругопла-
стическая работа конструкций при несин-
хронном движении основания.—b кн.:
Сейсмостойкое строительство, вып. 1. М.,
1974.
54. Поляков С. В., Денисов Б. Е.,
Кириков Б, А. Об учете податливости пе-
рекрытий при оценке сейсмических на-
грузок на здания. — Строительная механи-
ка и расчет сооружений, 1973, № 6.
55. Поляков С. В., Кириков Б. А.,
Мозгалева М. Л. Анализ пространственных
форм колебаний сооружений, рассчитывае-
мых по реальным записям землетрясений. —
В кн.: Сейсмостойкое строительство, № 6.
М., 1974.
56. Поляков Q. В., Золотов А. Б.,
Кириков Б. А. О расчете конструкций зда-
ний с учетом деформативности перекрытий
по реальным записям землетрясений. —
Строительная механика и расчет сооруже-
ний, 1975, № 2.
57. Рабинович И. М., Синицын А. П.,
Лукин О. В., Теренин В. М. Расчет соору-
жений на импульсивные воздействия. М.,
1970.
58. Рассказовский В. Т. Основы физи-
ческих методов определения сейсмических
воздействий. Ташкент, 1973.
59. Ржаницын А. Р. Расчет сооруже-
ний с учетом пластических свойств мате-
риалов. М., 1954. I
60. Указания по определению расчет-
ной горизонтальной сейсмической нагрузки,
действующей на одноэтажное промздание
с мостовыми кранами. М., 1973.
61. Солодовников В. В. Техническая
кибернетика, т. I — II. / Под ред. В. В. Со-
лодовникова. М., 1967.
62. Сорокин Е. С. К теории внутрен-
него трения при колебаниях упругих си-
стем. М., 1960.
63. Степанян В. А. Нормальное сцеп-
ление раствора с камнем. Ереван, 1960.
64. Тян А. С. Исследование колебаний
упругопластических систем при сейсмиче-
ских воздействиях. —.Строительная механи-
ка и расчет сооружений, 1965, № 5.
65. Уланов Г. М, Динамическая проч-
ность и компенсация возмущений в систе-
мах автоматического управления. М., 1971.
66. Хачиян Э. Е. Сейсмические воз-
действия на высокие здания и сооружения.
Ереван, 1973.
67. Ципенюк И. Ф., Ржевский В. А.
О сейсмостойкости конструкций.—ртрои-
тельная механика и расчет сооружений,
1973, № 6.
68. Чирас А. А. Теория оптимизации
в предельном анализе твердого деформиру-
емого тела. Вильнюс, 1971.
69. Basic Design Criteria of the Re-
commended Lateral Force Requirements and
Commentary, Proc. ASCE, ST9. 1972.
70. Biot M. A. Mechanical Analysis
for the Prediction of Earthquake Stresses,
Bulletin of the Seis. Soc, of America, vol.
31, No. 2, 1941.
78
71. Blume J., Newmark N., Corning L.
Design of Multistorey Reinforced Concrete
Buildings for Earthquake Motions. Chicago,
1961.
72. Cicmigiu Al., Titaru Em., Vel-
kov M. Energetic Interpretation of the
Structure Behaviour during the Earthquake
of 26 July, 1967 in Scopje, 1967.
73. Earthquake Engineering, Proce-
edings of the Third European Symposium on
Earthquake Engineering, Sofia, Bulgaria,
Sept. 14—17, 1970. Sofia, 1971.
74. Earthquake Engineering, Proce-
edings of the Fourth European Symposium
on Earthquake Engineering, London, Sept.
5—7, 1972, Imperial College, Sofia, 1973.
75. Goel S. G., Berg G. V. Inelastic
Earthquake Response of Tall Steel Frames,
Pros. ASCE, v. 94, ST8, Aug. 1968.
76. Housner G. W.> Martel. R. R., Al-
ford J. L. Spectrum Analysis of Strong —
Motion Earthquakes, Bull, of the Seis. Soc.
of America, vol .43, No. 2, 1953.
77. Housner G. W. Behaviour of Stru-
ctures during Earthquake, Journ. of .;the
Eng. Meeh. Div. Proc, of American Soc. of
Civ. Eng., vol. 85 NEM 4, 1959.
78. Housner G. W., Me Cann G. C. The
Analysis of Strong Motion Earthquakes
with the Electric Analog Computer, Bull.
Seis. Soc. of America, v. 39, No. 1, 1949.
j 79. Housner G. W. Characteristics of
Strong Motion Earthquakes, Bull. Seis. Soc.
Am., vol. 37, No. 1, 1947, p. 291—312.
80. Mononobe N. Die Eigenschwingun-
gen eingespannter Stabe von veranderli-
chen Querschnitt, Zeitschrift fur Angewand-
te Mathematik and Mechanik, Band 1, Heft
6, 1921.
81. Muto K. et al. Structural Chara-
cteristics of Current High — Rise Practice,
Papers of the Annual Meeting, Arch. Inst,
of Japan, Nov. 1971.
82. Omori F. Seismic Experiments on
the Fracturing and Overturning of Columns,
Publ. Earthquake Inter. Comm, in Foreign
Languages, No. 4. Tokyo, 1900.
83.4PIastic Design in Steel, A. Guide
and Commentary, ASCE New York, 1971.
84- Proceedings of the Second World
Conference on Earthquake Engineering.
Tokyo, 1960, v. I —III.
85. Proceedings of the Third World
Conference on Earthquake Engineering, New
Zealand, Oakland — Wellington, 1965, v.
I —III.
86. Proceedings of the Fourth World
Conference on Earthquake Engineering, San-
tiago, Chile, 1965, v. I — III.
87. Proceedings of the Fifth World
Conference on Earthquake Engineering, Ro-
me, 1973.
88. Rascon O. A., Cornell C. A.,
Strong Motion Earthquake Simulation,
Cambridge, Massachusetts. MMT, 1968.
89. СНиП II-A. 1Ю-71. Строительные
конструкции и основания. Основные поло-
жения проектирования. М., 19*71.
РАЗДЕЛ 4. АЭРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ
ВЫСОКИХ СООРУЖЕНИЙ И ГИБКИХ КОНСТРУКЦИЙ1 * *
Ф. БАРШТЕИН)\
В практике эксплуатации высоких со-
оружений и гибких конструкций известны
случаи, когда системы, имеющие доста-
точную надежность при действии на них
расчетной ветровой нагрузки в направле-
нии потока ветра, обнаруживают в усло-
виях естественного ветра склонность к
раскачиванию поперек потока, т. е. стано-
вятся аэродинамически неустойчивыми. Не-
устойчивость такого рода есть результат
аэродинамического взаимодействия между
сооружением и потоком ветра.
Рассмотрим два вида аэродинамиче-
ской неустойчивости, типичных для высо-
ких сооружений. Первый — вихревое воз-
буждение сооружения; оно наблюдается
при колебаниях дымовых труб, радио-
мачт и тому подобных гибких сооружений
цилиндрической формы и объясняется вих-
реобразованием в аэродинамическом следе
за сооружением при обтекании его пото-
ком ветра. Второй вид аэродинамической
неустойчивости принято называть гало-
пированием.
Галопированию подвержены гибкие
конструкции с элементами, имеющими
плохообтекаемые поперечные сечения
(башни, мачты, монументы с квадратным,
прямоугольным и ромбовидным сечением),
'покрытые льдом провода антенно-мачтовых
систем и линий электропередачи, а также
конструкции опор ЛЭП из уголков и швел-
леров. Колебания такого типа определя-
ются формой и расположением тела отно-
сительно потока, его изгибной и крутиль-
ной жесткостями и, наконец, величиной
конструкционного демпфирования.
Эти явления в настоящее время еще
не изучены полностью. Имеются только
несколько эмпирических моделей аэроди-
намических сил, которые действуют на ко-
леблющуюся конструкцию. Соответствую-
щие теоретические модели достаточно на-
глядны, включают параметры, которые поз-
воляют сопоставить наблюдаемые особен-
ности аэроупругих явлений, однако не
раскрывают некоторых важных деталей
фактического взаимодействия конструкции
с потоком.
4.1. ВИХРЕВОЕ ВОЗБУЖДЕНИЕ
СООРУЖЕНИЙ
ЦИЛИНДРИЧЕСКОЙ ФОРМЫ
Особенности явления поперечных ко-
лебаний цилиндров в потоке ветра. Рас-
смотрим характерные черты колебаний,
возбуждаемых вихрями, на примере кру-
гового цилиндра. Главная трудность при
1 Основные понятия о сопротивлении тел,
обтекаемых потоком воздуха, приведены в рабо-
те [3].
исследовании этого явления состоит в
том, что нестационарные аэродинамические
силы, действующие как на неподвижный,
так и на колеблющийся цилиндр, сильно
зависят от чисел Рейнольдса Re=:vd/v и
не могут быть определены теоретически
(ц — скорость потока, d — диаметр ци-
линдра, v — кинематическая вязкость воз-
духа).
Хорошо изучена [7, 9, 14, 22, 24] кар-
тина обтекания неподвижного цилиндра
потоком воздуха. При R<10 ламинарный
поток еще плотно прилегает к цилиндру;
с увеличением числа Рейнольдса позади
цилиндра образуются два стационарных
вихря, которые растут и, наконец, отры-
ваются от основного потока при Re=40.
При Re>50 начинается попеременный от-
рыв вихрей. Область этого ламинарного
отрыва распространяется до Re=150; об-
разующийся вихревой след называется
вихревой дорожкой Бенара — Кармана.
Область между Re=150 и Re = 300
является переходной, поток в вихревой
дорожке становится турбулентным, а от-
рыв вихрей—нерегулярным. Начиная с
Re=300, в отрыве вихрей наблюдается
периодичность, причем на колебания пото-
ка, имеющего некоторую преобладающую
частоту, налагаются турбулентные флук-
туации. Этот процесс остается неизменным
до Re=2-105. Выше этого значения Re
пограничный слой на цилиндре становит-
ся турбулентным, вихри отрываются без
преобладающей частоты, нерегулярно. Это
состояние потока сохраняется до Re =
= 5-106. Измерения Чинкотта и других
[14] в так называемой транскритической
области чисел Рейнольдса Re>5-106 по-
казали, что в этом случае снова образуется
вихревой периодический след с почти по-
стоянным коэффициентом лобового сопро-
тивления сх и преобладающей частотой от-
рыва вихрей (рис. 4.1).
Для неподвижного цилиндра частота
отрыва вихрей определяется числом Стру-
халя:
v
где ns — частота отрыва вихрей.
Зависимость числа Струхаля от чисел
Рейнольдса показана на рис. 4.1.
Важная особенность вихревого воз-
буждения гибких цилиндров — возникнове-
ние интенсивных колебаний поперек пото-
ка при скоростях, находящихся в опреде-
ленных интервалах. Внутри каждого из
этих интервалов имеется скорость, именуе-
мая критической, для которой частота
вихрей Бенара — Кармана, определяемая
числом Струхаля (4.1), равна собствен-
ной частоте колебаний цилиндра.
80
Натурные и модельные
испытания круговых ци-
линдров-fl, 4, 6, 8, 12, 14,
16, 17, 21] показывают, что
колебания таких тел вдоль
и поперек потока происхо-
дят со случайной амплиту-
дой и фазой и с частотой,
близкой к собственной ча-
стоте колебаний в данном
направлении. Сложение
этих двух взаимно перпен-
дикулярных колебаний дает
траекторию, близкую к эл-
липсу, большая ось которо-
го перпендикулярна направ-
лению потока. Такой харак-
тер колебаний цилиндра
указывает на случайную
природу действующих на
0,6
0,5
0,2
0,6
Рис. 4.1.
речной
ламинарный погра- Турбулент- Транскритичес-
ничный слой ный погра - коя область
Докритичвсная об- ничный слой процесс со дер -
ласть /// нЗакрити-тжитпериода-
Турбулетная дик ре- че^с^б- чесюун^состаб-
г бая дорожка урроресс елцчийныи
й *i ///
'льющую
0,5
0,4
0,5
0,2
г
‘^5
- сз <
0L
10
15
У
10
Зависимость числа Струхаля Sh и коэффициента попе
силы с от чисел Рейнольдса для кругового цилиндра
Ст
. 0,5
г
него аэродинамических сил.
Из графиков, показанных на рис. 4.2,
видно, что колебания цилиндра поддержи-
ваются энергией потока даже при малых
скоростях. С увеличением скорости пото-
ка растут и амплитуды колебаний ци-
линдра. Это наблюдается как при лами-
нарном, так и при турбулентном обтека-
нии.
Так называемому кризису сопротив-
ления соответствует область резкого сни-
жения коэффициента поперечной силы су
(см. рис. 4.1) и значительное уменьшение
амплитуд поперечных колебаний цилиндра.
При скоростях потока, близких к кри-
тическим, колебания конструкции управ-
ляют процессом распространения вихрей
даже тогда, когда изменение скорости по-
тока должно сместить частоту отрыва вих-
рей ns от собственной частоты цилиндра.
Подобное действие механических колеба-
ний на отрыв вихрей называется захватом
[25]. В области захватывания (рис. 4.3)
частота срыва вихрей постоянная, а не
является линейной функцией скорости вет-
ра. Это явление имеет автоколебательный
Рис. 4.2. Изменение амплитуд колебаний цилинд-
ра d—0,8 м на упругих опорах в зависимости от
скорости потока при собственной частоте коле-
баний опор:
1 — п —3,8 ... 4 Гц; 2 — п = 5,5 Гц; 3— п — 5,4 Гц
линдра, которая возникает при критиче-
ской скорости ветра, когда аэродинамиче-
ское демпфирование становится отрица-
тельным и превышает потери энергии
вследствие конструкционного демпфирова-
ния в цилиндре (т. е. колеблющийся в воз-
душном потоке цилиндр получает энергию
из потока).
Аэродинамическое демпфирование. При
анализе аэродинамической неустойчивости
важную роль играет суммарный коэффи-
циент потерь гибкого сооружения, обус-
ловленный конструкционным демпфирова-
нием (внутренним трением в соединениях
и в материале сооружения) и аэродина-
мическим демпфированием, вызванным
движением сооружения в потоке ветра:
Усум = Ya + •Yk! У = 5/я-
Для некоторых сооружений (дымовых
труб, мачт и башен) имеются эксперимен-
тальные значения коэффициентов потерь,
характеризующих конструкционное демп-
фирование, однако число этих измерений
мало. Рекомендуемые в разделе «Ветро-
вые нагрузки» главы СНиП II-6-74 значе-
ния логарифмического декремента колеба-
ний дк следует рассматривать как величи-
ны первого приближения.
Силу аэродинамического демпфирова-
ния обычно представляют [26] в виде
суммы двух слагаемых, из которых первое
пропорционально динамическому переме-
*
Рис. 4.3. Изменение частоты отрыва вихрей в за-
висимости от скорости потока
81
Рис. 4.4. Диаграмма области аэродинамической
неустойчивости для жесткого цилиндра круглого
поперечного сечения
/ — т] Омакс относится к k (vtnd) для всех значе-
ний параметра демпфирования; 2 — область неус-
тойчивости
Рис. 4.5. Зависимость аэродинамического воз-
буждения цилиндра от приведенной скорости
v — v/nd для Т]о = О,О1; Re=l,2105
щению цилиндра, второе сдвинуто относи-
тельно перемещения на л/2 и пропорцио-
нально скорости колебаний:
Fa (t)=Hay + K!ly; у = у9еге>*. (4.2)
Безразмерные величины, пропорцио-
нальные у, и Ла, записывают в таком
виде:
У , с Ла
Т] = ; Пя =-----—— И «а —-------~— •
d , р d2 n2 р d2 п
Для выяснения поведения сооружения
в натуре можно использовать значения
ha и йа, полученные в модельных испыта-
ниях при соответствующих приведенной
скорости и безразмерной амплитуде.
Для системы с одной степенью сво-
боды
4 л2 ц ( Пл \ 2 ц 6а
Ъ =—зг — ;
р d2 \ п2 ) р dz
где ц — масса единицы длины сооружения;
п, По — частоты собственных колебаний в
потоке ветра и в вакууме; р — плотность
воздуха; 6а — логарифмический декремент,
соответствующий аэродинамическому демп-
фированию; d — характеристический раз-
мер.
Для большинства сооружений ветер
слабо влияет на частоту колебаний. В этом
случае плло, и первым слагаемым в (4.2)
можно пренебречь. Параметр k& (так же,
как и 6а) зависит от формы поперечного
сечения, приведенной скорости, амплитуды
колебаний и числа Рейнольдса. Если пара-
метр &а положителен, то коэффициент по-
терь при действии силы аэродинамическо-
го демпфирования уа снижает амплитуду
колебаний. В случаях, когда значение уа
отрицательно и его величина такова, что
|уа| >Ук, Усум становится отрицательным,
в сооружении наблюдаются нарастаю-
щие колебания. Отрицательное аэродина-
мическое демпфирование в данном случае
рассматривают как аэродинамическое воз-
буждение.
Диаграмма, показывающая область
аэродинамической неустойчивости для
жесткого цилиндра круглого поперечного
сечения при колебаниях, перпендикуляр-
ных ветровому потоку, представлена на
рис. 4.4. Из диаграммы видно, что макси-
мальные амплитуды возникают при приве-
денной скорости уг=5 для любых величин
конструкционного демпфирования. Зависи-
мость параметра k& от vT показана на
рис. 4.5.
Минимальное значение k& соответству-
ет уг = 5, но и при 4<иг<9,5 наблюдает-
ся аэродинамическое возбуждение. В ука-
занных пределах vr параметр kA зависит
от амплитуды п0. С уменьшением ампли-
туды колебаний параметр k& возрастает.
С. Скрутон [26] показал, что при vr = 5
зависимость от т)о гиперболическая:
По = 0,55. (4.4)
Связь между значением £а т]0 и коэф-
фициентом поперечной силы су имеет вид:
4 Л &а По
су= —----- 2 10 =0,27. (4.5)
vr
Это значение ’соответствует Re» 105.
Если для некоторых скоростей потока
известны максимальные амплитуды, то, ис-
пользуя выражение (уа+ук)по=О и диа-
грамму на рис. 4.3, можно также получить
для этих скоростей данные о параметре ka.
Влияние формы поперечного сечения,
параметров конструкции и потока ветра
[22]. Все поперечные сечения имеют свои
характеристические числа Струхаля, изме-
няющиеся в зависимости от положения се-
чения по отношению к направлению потока
и от чисел Рейнольдса. Для сечения с уг-
ловыми точками число Струхаля слабо
зависит от чисел Рейнольдса, так как точ-
ки отрыва потока фиксированы и совпа-
дают с угловыми. Вихреобразование будет
хорошо коррелировано по длине элемента,
так что аэродинамическое возбуждение бу-
дет сильным! и более согласованным, чем в
случае круглого сечения, в котором отрыв
потока будет определяться числом Рей-
нольдса.
Важным параметром формы попереч-
ного сечения является длина тела в на-
правлении потока, а также форма части
сечения, расположенной ниже точек отры-
ва, поскольку эта кормовая часть пред-
ставляет собой часть конструкции, непо-
средственно подвергающейся вихревому
возбуждению. Длинная кормовая часть
либо мешает вихреобразованию в следе,
либо способствует присоединению отделив-
шегося потока к поверхности, а затем но-
вому отрыву вниз по потоку. В любом слу-
чае этот параметр непосредственно влияет
на число Струхаля.
82
Число Рейнольдса является важной
характеристикой круглых сечений, для ко-
торых число Струхаля и размер кормовой
части определяются положением точек
отрыва вихрей, в свою очередь зависящим
от Re. Установлено [22], что в тех слу-
чаях, когда конструкционное демпфирова-
ние мало и имеют место колебания боль-
шой амплитуды, число Струхаля не зави-
сит от Re и равно 0,2.
Турбулентность потока и изменение его
скорости с высотой существенно влияют
на колебания при вихревом возбуждении:
1) частота срыва вихрей изменяется по вы-
соте цилиндра в зависимости от градиен-
та средней скорости; 2) турбулентность
потока нарушает регулярность распростра-
нения вихрей; 3) нарушается корреляция
вихрей вдоль цилиндра. Вследствие этого
аэродинамические силы приобретают ха-
рактер случайных функций времени, и
их действие на конструкцию становится
менее эффективным по сравнению с дей-
ствием установившегося потока.
В настоящее время может быть лишь
качественно описана взаимозависимость
турбулентности и вихревого возбуждения.
Количественная оценка этого эффекта воз-
можна на основании экспериментальных
данных.
Теоретический анализ вихревого воз-
буждения. Этой задаче посвящено много
исследований [1, 4, 5, 6, 7, 15, 27], тем
не менее в настоящее время мы еще не
располагаем достаточно обоснованной
теоретической моделью этого явления.
Лнализ отделившегося потока вокруг ко-
леблющихся тел все еще остается полуэм-
пирическим. Это обусловлено непригод-
ностью использовавшихся схематических
моделей для описания характеристик аэ-
родинамического следа, определяемого
телом и его движением.
Основной инструмент исследовате-
лей - испытание аэроупругих моделей. По-
следующий анализ колебаний исходит из
эмпирически установленных границ обла-
стей аэродинамического возбуждения рас-
сматриваемой системы.
Определять природу и оценивать вели-
чину возмущающей силы, которая дейст-
вует при отрыве вихрей, приходится по-
ка по приближенным зависимостям.
Принято значение интенсивности по-
перечной силы принимать равным
р V2
q (t)=cy (Re, Sh, t) d. (4.6)
Приведенные в литературе значения
коэффициента поперечной силы су для
кругового цилиндра в большинстве случаев
получены не непосредственным измерени-
ем поперечной силы в гладком потоке. В
главе СНиП П-6-74 коэффициент попе-
речной силы су для закризисной области
чисел Рейнольдса принят 0,25. Он соот-
ветствует полученному в экспериментах
значению су, умноженному на коэффици-
ент 0,8, учитывающий вероятность воз-
никновения плоскопараллельного потока
ветра по высоте сооружения. С. Скрутон
[26] получил для су значение 0,27 при
Рис. 4.6. Числа Струхаля и коэффициенты по-
перечной силы Су для прямоугольного сечения в
зависимости от отношения h/b
5)
Рис. 4.7. График функции М (<р, ф)
Re=105, К. Накагава [17] — су = 0,25- -
0,27. Для 40<Re<3-105 су = 0,6 [25].
Значения чисел Sh и коэффициента попе-
речной силы су для призмы с прямоуголь-
ным поцеречным сечением, рекомендуемые
нормативным документом ISO по ветро-
вым нагрузкам, приведены на рис. 4.6.
Модель осциллятора, возбуждаемого
поперечной силой [25]. Уравнение попе-
речных колебаний цилиндра можно запи-
сать так:
2 1 р v2 d
У + Ч®1У+ ®{У = -------(4.7)
1 т 2
где коэффициент поперечной силы су удов-
летворяет уравнению осциллятора с ха-
рактеристиками Ван-дер-Поля:
"си+ a, ci, + a2c®+ а3су = а1у. (4.8)
83
Уравнение (4.8) отражает аналогию
между изучаемой системой и осциллято-
ром Ван-дер-Поля, в котором малым
амплитудам соответствует слабое демпфи-
рование, большим амплитудам —сильное
демпфирование.
В работе [25] приведена решение урав-
нения (4.8), которое записано в таком виде:
X(aos Су— Ь ь^Су) =f as (у/d), (4.9)
где tDvs = 2л ns — струхалева круговая ча-
стота колебаний, определяемая уравнением
(4.1); а, Ь, с, сУо — параметры, определяе-
мые экспериментально; d — диаметр ци-
линдра.
Эмпирическая квазилинейная модель
[1]. Такая модель отражает некоторые
основные экспериментальные факты, на-
блюдаемые в области захватывания, когда
собственная частота колебаний цилиндра
контролирует систему цилиндр — ветровой
поток. В этой системе следует различать:
1) механическую колебательную систему —
цилиндр; 2) усилитель колебаний — вихри,
возникающие при обтекании цилиндра по-
током; 3) ограничитель нарастания колеба-
ний — нелинейная характеристика затуха-
ния в системе.
Колеблющийся цилиндр — это элемент
системы, задающий частоту автоколеба-
ний. При отсутствии ветра цилиндр спосо-
бен совершать только затухающие собст-
венные колебания. Вихри связывают меха-
ническую колебательную систему с внеш-
ним источником энергии—ветровым пото-
ком. При этом колебания цилиндра влия-
ют на образование вихрей, навязывая свой
период процессу в обтекающем потоке.
Такого рода обратное действие на источ-
ник энергии, характерное для всякой ав-
токолебательной системы, называют об-
ратной связью. Таким образом, установив-
шийся режим в системе цилиндр — поток
предопределяется скоростью потока и ха-
рактеристикой затухания колебаний ци-
линдра.
Рассмотрим задачу о колебаниях же-
сткого консольного цилиндра на упругой
опоре. Уравнение движения такой систе-
мы с одной степенью свободы имеет вид
J<p + P<p
(4.Ю)
где <р — угол поворота опоры цилиндра;
Р — коэффициент демпфирования; с — ко-
эффициент жесткости при повороте; J —
= ц(д24-г2)—момент инерции массы ци-
линдра относительно его опоры; b — рас-
стояние от центра тяжести цилиндра до
опоры; г—радиус инерции массы цилинд-
ра относительно оси, проходящей через
центр тяжести; q$ — амплитуда силы
#(х, 0 У свободного конца цилиндра; гра-
фик изменения силы f(t) представлен на
рис 4.7,tz; Af — момент относительно опо-
ры аэродинамических сил, распределенных
по образующей цилиндра.
Принято, что закон распределения
этих сил совпадает с формой собственных
колебаний механической системы, т. е. на-
грузка распределена по закону треуголь-
ника. В этой задаче момент Л1(ф, ф) явно
не зависит от времени и является функци-
ей положения и скорости колебаний само-
го цилиндра. Чтобы автоколебания были
возможны, знак момента должен совпа-
дать со знаком ср. Пространственное гра-
фическое изображение функции Л4(<р, <р)
приведено на рис. 4.7,6.
Приближенное решение задачи найде-
но методом, разработанным в работе
[11]. На основании этого решения полу-
чаем (о = (0ь т. е. в первом приближении
частота автоколебаний совпадает с часто-
той собственных колебаний системы:
где фо, А40 — амплитудные значения соот-
ветственно угла поворота и возмущающего
момента; c = Jo)12; —первая собствен-
ная угловая частота колебаний цилиндра;
6 — логарифмический декремент колеба-
ний.
Поперечные колебания упругого ци-
линдрического стержня [1]. Учитывая для
стержня только первую форму собственных
колебаний ai(z), его перемещения можно
записать: I
у (z, t) = a, (z) Pl (t), (4.12)
где pi(t) —обобщенная координата.
Тогда уравнение движения в обоб-
щенных координатах будет
Pi (O+Y®iPi (/)+®2 Р1 (t) = ~^. (4-13)
Об
Обобщенная сила
Qi (0 ~ J Q (z, О ai (^) dz. (4.14)
°
Обобщенная масса
Н
Мюб = Н I а2 (г) dz,
•7
О
где Я — высота стержня.
Примем, как и для жесткого цилинд-
ра на упругой опоре,
4
q (z, /) = — q0 ах (z) sin co /,
л
где to —< угловая частота колеба-
ний силы q(z, /); q$ — ордината эпюры
аэродинамической силы у свободного кон-
ца консоли.
Повторяя для уравнения (4.13) рас-
суждения, приведенные выше при рассмот-
рении уравнения (4.10), получим для пе-
ремещения конца стержня выражение
л 4 р0 л с ,.
Уо — . 2 — Я Уо > (4-
о л (ко' о и
84
где (/g — Fo/ц^—прогиб верхнего конца
стержня от статически приложенных аэро-
динамических сил. г
Колебания упругого стержня, имеюще-
го форму усеченного конуса, возбуждаемые
случайной поперечной силой. Эксперимен-
ты А. Рошко [24], И. Чинкотта [14] по-
казали, что в области за кризисом сопро-
тивления при числах Рейнольдса 1,4Х
X Ю64-3,5-106 действующая на цилиндр
поперечная сила случайна и имеет непре-
рывный спектр, при Re от 3,5-106 до 6-Ю6
процесс имеет узкополосный спектр, выше
Re —6-106 до Re =1,8-107 процесс случай-
ный, но содержит периодическую составляю-
щую (см. рис. 4.1). Основываясь на этих
экспериментах, У. Фынг [16], М. Новак
[18] рассматривают задачу о поперечных
колебаниях цилиндра как задачу о вынуж-
денных колебаниях упругого стержня,
возбуждаемого случайной поперечной си-
лой.
Поведение гибкой конструкции, имею-
щей форму усеченного конуса, рассмотрено
в работе [27]. Установлено, что при коле-
баниях по первой форме максимальные
амплитуды получаются тогда, когда часто-
та срыва вихрей, соответствующая диамет-
ру на уровне 2/3 высоты конструкции, сов-
падает с ее собственной частотой. При бо-
лее высоких скоростях потока при вихре-
вом возбуждении могут возникнуть одно-
временно первая и вторая формы собст-
* венных колебаний.
Для железобетонных дымовых труб
усилия, возникающие в направлении дей-
ствия ветра, являются преобладающими для
сечения ниже 2/3 высоты трубы; для
верхней части трубы расчетными могут
стать усилия, при вихревом возбуждении
соответствующие второй форме колебаний
конструкции.
Перемещение гибкого усеченного кону-
са при возбуждении случайной попереч-
ной силой можно записать так.
где ai(z) —i-я форма собственных колеба-
ний стержня; s — число учитываемых форм
собственных колебаний.
Тогда уравнение движения в обобщен-
ных координатах Pi(t) будет иметь вид
(4.13). Обобщенная масса Л410б =
И
= Jg.(z) a? (z)dz, где ц(г)—масса еди-
о
ницы высоты сооружения на уровне z,
н
Qz(f) = I q(z, t) &i(z)dz— обобщенная си-
о
ла; q(z, t)—интенсивность поперечной
силы.
Спектральная плотность обобщенной
силы
н и
~ J ^*^<7 *5(7 л) X
1 6 О
X R (г) az (zk) az- (27J dzk dzm. (4.17)
Следуя работе [27], примем на осно-
вании эмпирических данных для энергети-
ческого спектра интенсивности поперечной
силы следующее выражение:
s
где п2^----z-_ — средний квадрат коэф-
c^'/2pdv*
фйциента поперечной силы; l/s pdv2 — ско-
ростной напор, соответствующий средней
о
скорости ветра; В = —~——-—
У Л nsSq (ns)
— относительная ширина спектра; п3 — ча-
стота, соответствующая пику энергетичес-
кого спектра Sg(n); п — текущая частота,
Гц.
Нормированный коэффициент простран-
ственной корреляции
Rkm (') = COS
(4-19)
d(Zk) и d(zm) —диаметры стержня в точ-
ках k и т.
Подставляя в (4.17) выражения (4.18)
и (4.19), получим
sq. («) =
Пренебрегая взаимной корреляцией
между*/собственными формами колебаний
консольного стержня, средний квадрат его
перемещений можно записать
s ________
= 2 р? (П <4 (4-21)
Z—1
где средний квадрат обобщенной коорди-
наты
оо
Р? (О = J I Ф/ (i ®) I2 Sq, (<о) d® =
о
ac р аг (zKp) у
8 л2 Sh2 Mi J ’ (4‘22)
85
здесь | Ф{ (ted) |2 — квадрат модуля переда-
точной функции системы, соответствую-
щей ее f-й форме собственных колебаний;
00
L—^R(r)dz— масштаб турбулентности (в
о
Z
диаметрах стержня), е=аа“+т;аа— no-
ct
казатель в степенном законе, характери-
зующем изменения средней скорости ветра
по высоте.
Критическую скорость определяют для
сечения стержня диаметром d, для которо-
го величина tZi(z)d4(z) максимальна.
Н
Обобщенная масса стержня Mi= I ц(г) х
О
X aj(z)dz; Sh=0,22. (4.23)
Рекомендации по определению переме-
щений и усилий при вихревом возбуждении
сооружений, имеющих форму кругового
цилиндра и усеченного конуса. Для таких
сооружений кроме расчета на скоростной
напор в направлении потока ветра с уче-
том динамического действия его пульсаций
должны быть определены перемещения и
усилия при вихревом возбуждении. Для
сооружений цилиндрической формы и с
малой коничностью в качестве расчетного
принимают резонансный случай, возникаю-
щий при совпадении частот срыва вихрей
Бенара — Кармана с собственными часто-
тами колебаний сооружения.
Для железобетонных дымовых труб,
имеющих форму усеченного конуса, опре-
деляют перемещения и усилия, возникаю-
щие при вынужденных колебаниях соору-
жения под действием случайной попереч-
ной силы. В этом случае взаимодействие
потока с сооружением не учитывают. Та-
кой подход допустим, если расчетная ам-
плитуда колебаний сооружения не превы-
Щает 0,03 его верхнего диаметра.
Согласно указаниям, приведенным в
главе СНиП П-6-74 «Нагрузки и воздей-
ствия» [10]:
1)' проверку на резонанс сооружений
круговой цилиндрической формы произво-
дят в тех случаях, когда критическая ско-
рость ветра цКрг находится в пределах
О,64У^о^УкР1^25 м/с, где q0 — нормативный
скоростной напор ветра. При aKpi<;O,64y<7o
усилия в сооружении при резонансе всег-
да меньше усилий при расчете в направ-
лении действия ветра. Скорость 25 м/с
принята в качестве верхней границы кри-
тической скорости для всех географических
районов СССР;
2) критическая скорость ветра, вызы-
вающая резонансные колебания сооруже-
ния в направлении, перпендикулярном ве-
тровому потоку, определяют по формуле
°кр z = "гТяТ ’ (4'24)
где Ti—период собственных колебаний со-
оружения по t-й форме, с; для круга Sh=
=0,2, для сечений с угловыми точками
Sh = 0,15; d — диаметр сооружения, м;
для сооружений с малой коничностью (с
уклоном не более 0,01) диаметр его сече-
ния на уровне 2/3 высоты;
3) при проверке на резонанс ампли-
туду интенсивности динамической силы
7i(z), Н/м, на уровне z при колебаниях
сооружения по i-й форме находят по фор-
муле
Qi (г) = ?о i at (г) d, (4.25)
и
где qQi = cyqKPi — амплитуда интенсивно-
сти на уровне свободного конца сооруже-
ния консольного типа или в середине про-
лета трубчатой мачты на вантах. Для со-
оружения консольного типа учитывают
только первую форму собственных колеба-
ний; </Крг = 0,61 За 2р/—скоростной напор,
соответствующий критической скорости
акр1-; Су — коэффициент поперечной силы,
принимаемый 0,25 для сооружений круго-
вой цилиндрической формы и 0,5 для ци-
линдрических сооружений с поперечными
сечениями, имеющими угловые точки;
4) резонансные усилия и перемещения
сооружения в сечении с координатой z
определяют по формуле
лрез (2) = Л. Хс (г) ,
о
(4.26)
где Xе (z)—прогиб, изгибающий момент
или поперечная сила от статически прило-
женной нагрузки Fi(z); для мачт на ван-
тах в качестве расчетного* значения Fi(z)
принимают наибольшее из значений, вы-
численных для критических скоростей
акр1-, при этом число учитываемых форм
колебаний принимают не более четырех;
6 — логарифмический декремент колебаний,
принимаемый: 0,3 для железобетонных и
каменных сооружений; 0,15 для стальных
аппаратов на железобетонных постамен-
тах; 0,1 для мачт и стальных футерован-
ных дымовых труб; 0,05 для стальных со-
оружений и конструкций;
5) расчетную статическую составляю-
щую ветровой нагрузки по направлению
действия ветра q^p> Па, которая соответ-
ствует критическому скоростному напору
<7кр<, принимают постоянной по высоте
сооружения и равной
<7кр — 9кр i сх, (4-27)
где сх — коэффициент лобового сопротив-
ления, принимаемый по п. 14 табл. 8 гла-
вы СНиП П-6-74.
Динамическую составляющую ветро-
вой нагрузки по направлению действия
ветра Др, соответствующую q^i, опреде-
ляют в соответствии с указаниями, приве-
денными в пп. 6.11—6.14 главы СНиП
П-6-74, при этом коэффициент динамично-
сти для сооружений, указанных в под-
пунктах «а», «б», «в» п. 4, принимают по
графику 2 рис. 3 главы СНиП П-6-74;
6) при расчете на резонанс другие
кратковременные нагрузки допускается не
учитывать;
86
7) расчетные усилия и перемещения
сооружения при резонансе допускается
вычислять по формуле •
X (z) =
=у[Х₽ез (г) р + [Xе (z)+ X* (z)]2, (4.28)
где X₽e3(z)—перемещение, изгибающий
момент или поперечная сила, определяе-
мая по формуле (4.25); Xе (г); %д(г) —
то же, от нагрузок и > определяе-
мых по п. 5.
Для сечений конических железобетон-
ных дымовых труб, расположенных ниже
2/3 высоты трубы, расчетными будут уси-
лия, возникающие от статической и дина-
мической составляющих ветровой нагруз-
ки, приложенные по направлению действия
ветра. Для верхней части трубы расчет-
ными могут стать усилия при вихревом
возбуждении, соответствующие второй
форме собственных колебаний/
Для конической трубы критическую
скорость ветра определяют для сечения
диаметром для которого значение
а2(г) максимально. Здесь а2 (г)—орди-
ната второй собственной формы колеба-
ний трубы; zKp — высота, для которой
вычисляют критическую скорость
dKp
укр = зд > (4.29)
;где Т2 — период, соответствующий второй
собственной форме колебаний.
Расчетное значение обобщенной коор-
динаты, соответствующее второй собствен-
ной форме, вычисляют по формуле
где L=2 — масштаб турбулентности (в
диаметрах трубы) у = д/л—0,1; 0 =
— аа~ + г; аа=0,16; т— наклон образу-
ющей трубы к вертикальной оси; р =
= 1,29*10~3, т/м3 — плотность воздуха;
cv=0,25— коэффициент поперечной силы;
М2 определяют по формуле (4.23).
Расчетные перемещения и усилия в се-
чениях трубы вычисляют по формуле
^расч (г) — (г) Ррасч» (4-31)
где ррасч — расчетное значение обобщен-
ной координаты, принимаемое по формуле
(4.30); аДг) —коэффициенты распределе-
ния амплитуд перемещений, изгибающих
моментов и поперечных сил.
42. ГАЛОПИРУЮЩИЕ КОЛЕБАНИЯ
ГИБКИХ ПРИЗМАТИЧЕСКИХ
КОНСТРУКЦИЙ
Как уже отмечалось выше, галопиро-
вание, которое возникает в гибких приз-
матических конструкциях при определенных
скоростях ветра, связано с аэроупругой
неустойчивостью таких тел. Колебания та-
кого типа возникают в плоскости, перпен-
дикулярной направлению ветра, и сохра-
няют свою интенсивность даже при значи-
тельной турбулентности набегающего по-
тока. Это явление аэродинамического воз-
буждения изучали на основе квазистацио-
нарной модели Дж. П. Ден-Гартог [5],
Г. Паркинсон [23], М. Новак и А. Давен-
порт [19, 20].
Напомним, что при рассмотрении яв-
ления в рамках квазистационарной моде-
ли гЛшовенные аэродинамические силы,
действ^ощие на колеблющееся в потоке
ветра тело, принимают такими же, как
для неподвижного тела, обтекаемого по-
током с относительной скоростью, равной
геометрической сумме скорости установив-
шегося потока и скорости поперечных ко-
лебаний системы.
В настоящее время пока еще мало
экспериментальных и теоретических ис-
следований этого явления, поэтому мы рас-
смотрим здесь только такие вопросы:
1) галопирующие колебания призм в глад-
ком потоке ветра [19]; 2) особенности ре-
шения этой задачи для турбулентного
потока.
Особенность галопирования [22]. Это
явление возникает при формах поперечно-
го сечения, имеющих фиксированные точ-
ки отрыва. Так же, как и при вихревом
возбуждении, частоты галопирующих ко-
лебаний близки к собственным. Если при
вихревом возбуждении интенсивные коле-
бания возникают в определенных интер-
валах скоростей ветра, то галопирование
происходит при всех скоростях выше кри-
тических, определяемых конструкционным
демпфированием.
На рис. 4.8 показано квадратное се-
чение призматического тела в условиях
покоя и в условиях движения в направ-
лении, перпендикулярном направлению
ветрового потока. На рис. 4.86 тело
смещается вниз со скоростью dyjdt, при
этом относительная скорость потока цот
направлена под углом атаки, равном, на-
прцмер, а = 6°. Поток так же, как и в
условиях покоя рассматриваемого тела,
по-прежнему отрывается по углам 1 и 4
квадратного сечения, однако отделившие-
Рис. 4.8. Квадратное сечение призматического
тела в условиях покоя и в условиях движения в
направлении, перпендикулярном направлению
ветрового потока
87
Рис. 4.9. Коэффици-
енты С „ для пря-
Fy
моугольного сечения,
швеллера и двутав-
ра
Рис. 4.10. Схема действия аэродинамических
сил F
ся пограничные слои асимметричны, слои
с наветренной стороны располагаются
ближе к стороне 1, 2, а слой с заветренной
стороны — к стороне 3, 4. В результате
сторона 1, 2 испытывает больший отсос,
чем сторона 3, 4, и возникает сила Fy,
направленная в сторону движения. На рис.
4.8,в угол а увеличивается до 13°, и с на-
ветренной стороны поток вновь присоеди-
няется к сечению тела в точке 2, Fy при
этом угле достигает максимального зна-
чения.
Характер обтекания, показанный на
рис. 4.8, указывает на то, что повторное
присоединение отделившегося потока к
поверхности кормовой части является важ-
ной характеристикой галопирования. Как
видно из рис. 4.9, при малом отношении
сторон прямоугольного сечения hfb не воз-
никает поперечной силы и сечение будет
устойчивым в состоянии покоя.
Галопирование призм в гладком пото-
ке [19]. Если призма колеблется со ско-
ростью у поперек потока, имеющего ско-
рость v, то относительная скорость иот
вызывает аэродинамическую силу F, опре-
деляемую лобовым сопротивлением и попе-
речной силой (рис. 4.10).
Составляющая силы F в направлении
движения
Р6/1Иот- (4-32>
У £
где
у
^от = sec а, а = arctg — ;
Ср = — (Су + сх tg а) sec а; (4.33)
b — ширина наветренной стороны, призмы;
Н — высота призмы; сх и су— коэффици-
енты лобового сопротивления и попереч-
ной силы конструкции.
Уравнение движения призмы, рассмат-
риваемой как система с одной степенью
свободы, можно записать в таком виде:
- , 2
У + «I У — -др + Y* to! у = 0, (4.34}
где <О|, М — собственная угловая частота
системы и ее масса; у — коэффициент дис-
сипации энергии конструкции.
Из выражения (4,33) следует, что ес-
ли cF >-0 при осД>0, то в системе воз-
у
буждаются колебания. Первая производ-
ная коэффициента cF по а при а = 0
у
а
ё
Выполнение условия Л1>0 (критерий
Ден-Гартога) необходимо для возбужде-
ния колебаний. Однако оно не является
достаточным, так как суммарный коэффи-
циент диссипации энергии зависит также
от положительного конструкционного
демпфирования. На рис. 4.9 показано из-
менение cF в зависимости от угла атаки
у
для призм с квадратным и прямоугольным
поперечными сечениями, а также для
швеллера и двутавра [13].
Экспериментальную зависимость ко-
эффициента поперечной силы от угла ата-
ки можно приближенно аппроксимировать
полиномом вида:
(4.36)
где Ai — i-й член разложения.
Число учитываемых членов ряда зави-
сит от формы поперечного сечения приз-
мы. Для квадратного сечения i= 1, 3, 5,
7. Если функция cF асимметрична, то
используют и четные показатели степени.
Подставляя (4.36) в уравнение (4.34),
получим
У + У + 2 I — v Ai I у +
\ 2 b /
т , А *!
+ 2 ~ У ^7~2- = 0. (4.37)
/=з
88
ТАБЛИЦА 4.1
Форма еобственных колебаний Форма ко- лебаний ап <г> Тип .А (2) Ci С 2 Сз С5 С7 Примечание
1 1а ч 1 1 1 1 1 1 Жесткое тело на
с н \Ь /г Г/в 6 1 6 - 9 6 упругой опоре
\ 10 / 7 А 5
п=2 . п л Sin 2 2 1 1 8 3 5 35 Призматический
1 1 ь- Н ^3 Л 4 8 64 стержень, струна
ь 1 "ч Ч
Z За 1 1 3 3 3 1 Жесткая консоль
Н 4 5 7 3 на упругой опо-
н О**— _ I 4 36 М VA 18 3 18 18 18 ре
__J * \ ю J 19 4 29 35 49
/ 2 V/> 9 3 9 9
Зс -
\ ю У 10 4 ‘4 2 22
Z2 4а 1 1 т“ о 5 5 5 Упругая консоль
чО Н Н2 7 9 13 17 с распределенной
" 1 4 массой
.<1 J / 4b iz—Г/в 30 5 30 10 30
\ ю ) 31 7 53 25 97
4с Г/з 15 5 15 5 15
\ ю / 16 7 26 12 46
где =----------— параметр массы; Аг>0,
4 А1
знаки перед А/ изменяются, начиная с
+ ^з-
При ос->0 влияние членов, содержащих
степени у} исчезает, и характер движения
зависит только от знака коэффициента
перед у, т. е. от значения суммарного ко-
эффициента диссипации энергии. Если
этот коэффициент положителен, то ну-
левое положение устойчиво. Если он от-
рицателен, то нулевое положение неустой-
чиво и уравнение (4.37) описывает само-
возбуждающие колебания.
Приведем формулы для случая, когда
скорость ветра переменна по высоте приз-
мы. Пусть скорость ветра v (z) =;U0&i (z),
где Vo — скорость ветра на уровне 10 м;
k(z) — (z/10)a t — коэффициент, учитываю-
щий изменение средней скорости по высоте
сооружения; at — показатель степени для
местности типа t. Введем приведенную
скорость Vr=vl((iiib). Тогда стационарные
безразмерные амплитуды а—а/b могут
быть определены из алгебраического урав-
нения
н
J ki (г)2-L a (z)1-1 dz
где Ci = ---------77-----------------; (4.39)
j d2 (z) d z
о
a(z)—собственная форма колебаний кон-
струкции.
Для конструкции с распределенными
параметрами = р62/4ц, где ц— масса
единицы высоты призмы.
Для некоторых собственных форм ко-
лебаний квадратной призмы коэффициенты
а и AtCi приведены в табл. 4.1 и 4.2.
ТАБЛИЦА 4.2
Собствен- ная форма колебаний Л/ С1
А * Аг с2 Л3 As Сй А с
la 2,69 168 6 270 59 900
16 2,31 202 12 540 369 400
2 2,69 126 3 919 32 758
За 2,69 101 2 687 I 997
36 2,55 104,28 2 894 22 004
4а 2,69 93,33 2411 17 617
46 2,6 95,09 2 508 18 526
Условием начала автоколебаний явля-
ется
2 а*+—-А,С1=0, (4.38)
2nM vr
nMv л / о
4k «1 — —~ь— Л < о*
89
т. е. когда скорость ветра
2 yk Mi ц.
> ^Крит — , л
р b Al С1
(4.40)
Если критическая скорость ветра
больше, чем скорость в данном географи-
ческом районе с вероятностью превыше-
ния один раз в пять лет, то расчет кон-
струкции на аэродинамические силы, воз-
никающие при галопировании, можно не
производить.
Характер изменения амплитуд коле-
баний аэродинамически неустойчивой кон-
струкции (призмы) в зависимости от ско-
рости ветра показан на рис. 4.11. Как
видно, конструкция остается практически
неподвижной, пока скорость ветра не до-
стигнет критической приведенной скорости
vкрит- Дальнейшее увеличение скорости
ветра вызывает интенсивные поперечные
колебания. Каждой скорости соответст-
вует своя стационарная амплитуда коле-
баний, которая с увеличением скорости
ветра приближается к асимптоте, прохо-
дящей через начало координат. Асимптота
соответствует коэффициенту диссипации
энергии Ya = 0. Скорости vri и пГ2 опреде-
ляют границы, в пределах которых могут
происходить бифуркация или колебатель-
ный гистерезис.
Теоретический анализ [19) показывает,
что для всех конструкций, имеющих опре-
деленный вид поперечного сечения, оди-
наковые собственные формы, но произ-
вольную массу и затухание, стационарные
амплитуды могут быть описаны универ-
сальной кривой в плоскости
2 пм 2 пм
а -------------
Y Y
(см. рис. 4.11); координаты кривой не
зависят от аэродинамических постоянных
поперечного сечения конструкции. Благо-
даря этому на основе измеренных стацио-
нарных амплитуд колебаний аэроупругой
модели можно экспериментально построить
универсальную кривую реакции конст-
рукции, не определяя при этом аэродина-
мические постоянные поперечного сечения.
Аэроупругая неустойчивость призм в
турбулентном потоке [20]. Эту задачу, как
и приведенную выше, рассмотрим в ква-
рке. 4.11. Изменение амплитуд колебаний аэро-
динамически неустойчивой конструкции
зистационарной постановке. Представим
продольную (вдоль ветрового потока)
компоненту скорости ветра в виде:
v = v + vr (/) . (4.41)
Тогда уравнение поперечных колебаний
движения прямоугольной призмы как си-
стемы с одной степенью свободы будет
У + ©1 У +
= 4г (Z)+FB (01. (4.42)
где Еп(0 и Ев(/)—случайные силы, учи-
тывающие воздействие на призму попе-
речной компоненты пульсации скорости и
аэродинамической силы, возникающей
при вихревом возбуждении.
Уравнение (4.42) — неоднородное не-
линейное дифференциальное уравнение с
переменными во времени коэффициентами.
Малость пульсации продольной компонен-
ты скорости v'(t) по сравнению с ее сред-
ним значением v и случайный характер
пульсации позволяют считать, что дина-
мическая неустойчивость (параметриче-
ский резонанс) в этой системе проявится
слабо. Поэтому при анализе галопирова-
ния этот вопрос можно* не -рассматривать.
Следует отметить, что в турбулентном
потоке среднее время Г, в течение которо-
го призма неустойчива, изменяется не-
прерывно в зависимости от отношения
vKp[v. Поэтому в таком потоке существует
тенденция к появлению поперечных колеба-
ний и при средних скоростях, меньших
критической скорости. По той же причине
критическая скорость ветра не может быть
так четко выражена, как в гладком по-
токе. Можно также считать, что практиче-
ское влияние пульсации скорости на ус-
тойчивость призмы обычно' меньше, чем
влияние средней скорости потока. Отсюда
следует, что в левой части уравнения
(4.42) можно пренебречь влиянием пуль-
сации скорости на аэродинамическое демп-
фирование системы.
Упрощенное уравнение движения
призмы будет иметь вид (4.37). Однако
между этими уравнениями имеется суще-
ственное различие. В гладком потоке ко-
лебания не возникают при скорости пото-
ка, меньше критической, если не считать
колебаний, образующихся при вихревом
возбуждении. В турбулентном потоке по-
перечные колебания возникают даже в ус-
тойчивой области, так как общее эффек-
тивное демпфирование системы уменьшает-
ся в результате отрицательного аэродина-
мического демпфирования в призмах,
имеющих аэродинамические неустойчивые
поперечные сечения.
Таким образом, для решения задачи о
колебаниях типа галопирования в турбу-
90
лентном потоке необходимо знать спект-
ральные плотности и взаимные спектраль-
ные плотности пульсации поперечной ком-
поненты скорости и аэродинамических сил
при вихревом возбуждении. Коэффицией-
ты разложения Ai должны быть опреде- ч
лены для турбулентного потока.
В настоящее время пока еще мало
экспериментальных данных для построе-
ния статистических характеристик аэро-
динамических сил, действующих на кон-
струкцию при галопировании, поэтому оп-
ределять эти силы следует как для уста-
новившегося потока. Конструкции, для ко-
торых квазистационарная модель не может
быть использована, надо рассчитывать на
основе данных испытаний аэроупругих
моделей.
СПИСОК ЛИТЕРАТУРЫ
1. Барштейн М. Ф. Динамический рас-
чет высотных сооружений цилиндрической
формы. — В кн.: Исследования по динами-
ке сооружений. М., 1957.
2. Барштейн М. Ф. Некоторые вопро-
сы динамического расчета .высоких соору-
жений на действие ветра. — В кн.: Труды
конференции по аэродинамике и аэроупру-
гости высоких строительных сооружений.
М., 1974.
3. Барштейн М. Ф. Динамический
расчет высоких сооружений на действие
ветра. Справочник по динамике сооруже-
ний. / Под ред. Б. Г. Коренева и И. М.
Рабиновича. М., 1972.
4. Блюмина Л. X,, Захаров Ю. Г. Ко-
лебания цилиндрических тел в воздушном
потоке, — В кн.: Исследования по дина-
мике сооружений. М., 1957.
5. Ден~Гартог Дж, П. Механические
колебания. М., 1960.
6. Луговцов А, Н. Колебания типа
«.ветровой резонанс» цилиндрических кон-
струкций.— В кн.: Колебания зданий и
сооружений. М.» 1963.
7. Мэррис А. Обзор исследований по
вихревым дорожкам, периодическим сле-
дам и индуцированным явлениям вибраций.
Теоретические основы инженерных расче-
тов. Серия Д. т. 86, № 12, 1964.
8. Савицкий Г, А., Попов С. Г. Об
аэродинамических силах, действующих на
круговой цилиндр при его колебаниях в
потоке.—В кн.: Вопросы механики. М.,
1961.
9. Современное состояние гидроаэро-
динамики вязкой жидкости. / Под ред.
С. Гольдштейна. М., 1948.
10. Глава СНиП 11-6-74 «Нагрузки и
воздействия». М., 1976.
11. Теодорчик К, Ф. Автоколебатель-
ные системы. М., 1952.
12. Федяевский К. К., Блюмина Л. X.
Силы вихревой природы, действующие на
вынужденно колеблющийся цилиндр. —
В кн,: Труды конференции по аэродинами-
ке и аэроупругости высоких строительных
сооружений. М., 1974.
, 13. Фомин Г, М., Блюмина Л, X., Со-
колов А. Г., Беспрозванная И. М. Проблемы
исследования аэродинамических и аэроуп-
ругих характеристик высоких строительных
сооружений. — В кн.: Труды конференции
по аэродинамике и аэроупругости высоких
строительных сооружений^ М., 1974.
14. Cincotta J. J., Jones (j. W., Wal-
ker R. W. Experimental investigation of
wind — induced oscillation eltects on cy-
linders in two — dimensional flow at high
Reynolds numbers. Meeting on Ground
Wind Loa^l Problems in Relation to Leunch
Vehicles. NASA Langley Research Center,
1966.
15. Fdrsching H. Grundlagen der Aero.
elastik. Berlin, 1974.
16. Fung Y. C. Fluctuating lift and
drag action on a cylinder in a flow at
supercritical Reynolds numbers. J. of the
Aerospace Sciens, v. 27, 1960.
17. Nakagava K. and all. An experi-
mental study of aerodynamic devices for
reducing wind induced oscillatory tendencies
of stacks. Proq. Symp. Wind Effects on
Structures NPL. Teddington, 1965.
18. Novak M, A statistical solution
of the lateral vibrations of cylindrical stru-
ctures in air — flow. ACTA Technica, CSAV,
1967.
19. Novak M. Aeroelastic galloping of
rigid and elastic bodies. The University of
Western Ontario, BLWT3—68, 1968.
20. Novak M., Davenport A. Aeroela-
stic instability of prisms in turbulent flow.
J. of the Engineering Mechanics Division,
1971.
21. Novak M., Fischer 0. On the lift
forces on a cylinder vibrating in air flow.
ACTA Technica, CSAV, N 6, 1969,-
22. Parkinson G. V. Wind — induced
instability of structures. Phil. Trans. Roy.
Soc. London, A. 269. 1971(.
23. Parkinson G. V. Aeroelasic gal-
loping in one degree of freedom. Proc.
Symp. Wind Effects on Structures. NPL.
Teddington, 1965.
24. Roshko A. Experiments on the
flow past a circular cylinder at very high
Regnolds numbers. J(. of Fluid Meeh., v. 10,
1961.
25f . Sitnure E., Scanlan R. Wind effects
on structures. An Introduction to Wind
Engineering. New York, 1978.
26. ScMon C. On the wind — excited
oscillations of stacks towers and masts.
Proc. Sym. Wind Effects on Structures.
NPL. Teddington, 1965.
27. Vickery B., Clark A. Lift or ac-
ross — wind response of tapered stacks. J.
of the Structural Division., Jan., 1972.
28. Wooton L, R. The oscillations of
large circular stacks in wind. Proc, of the
Institution of civil engineers, vol. 43, Aug.,
1969.
РАЗДЕЛ 5. ДИНАМИЧЕСКИЕ ВОЗДЕЙСТВИЯ НА ЗДАНИЯ
И СООРУЖЕНИЯ ОТ СВЕРХЗВУКОВЫХ САМОЛЕТОВ
(А. И. ЦЕИТЛИН)
5.1. ОБЩИЕ СВЕДЕНИЯ
Использование сверхзвуковых самоле-
тов в пассажирской авиации выдвигает
ряд проблем, связанных с действием воз-
душной ударной волны (звукового удара)
на людей, животных, поверхность грунта,
здания, сооружения и различные техниче-
ские устройства. Наиболее важным воп-
росом является изучение влияния на лю-
дей систематических ударов при регуляр-
ных полетах самолетов, но не менее важ-
но и поведение зданий и сооружений при
воздействиях такого рода. Известны
многочисленные случаи, когда звуковой
удар от сравнительно легких самолетов
вызывал разрушение строительных конст-
рукций. Для примера можно привести по-
лет самолета F-104 на высоте 150 м в
аэропорту г. Оттавы (Канада), в резуль-
тате которого зданию аэровокзала был
причинен значительный ущерб (стоимость
ремонтных работ, в основном восстанов-
ления оконного застекления и перегоро-
док, составила 0,3 млн. долларов).
В связи с реализацией программ соз-
дания сверхзвуковых транспортных самоле-
тов типа ТУ-144 и «Конкорд» в СССР и
за рубежом были проведены широкие ис-
следования с целью изучения параметров
ударной волны, возбуждаемой самолета-
ми различного типа в режимах разгона,
крейсерского полета, маневрирования и
торможения, а также выяснения возмож-
ных последствий систематического дейст-
вия звуковых ударов на окружающую
среду и ограждающие конструкции зда-
ний и сооружений.
Рассматриваемые ниже вопросы мо-
гут представлять интерес и при изучении
действия на сооружения ударных волн,
порождаемых промышленными взрывами
или разрывом сосудов, находящихся под
давлением. Такие задачи возникают, в
частности, при расчете конструкций лабо-
раторных корпусов, в которых испытыва-
ют различные сосуды, например фюзеля-
жи самолетов. В случае разрыва сосуда
внутри здания распространяется воздуш-
ная волна, по своему характеру близкая
к iN-волнам, возбуждаемым сверхзвуковы-
ми самолетами, однако существенно боль-
шей интенсивности. При взрывном горе-
нии газо-, паро- и пылевоздушных смесей
(см. раздел 2 этого справочника) в не-
которых особых случаях также возмож-
но распространение N-образных ударных
волн.
5.2. РАСПРОСТРАНЕНИЕ
ЗВУКОВЫХ УДАРНЫХ
ВОЛН ПРИ ПОЛЕТАХ
СВЕРХЗВУКОВЫХ САМОЛЕТОВ
При движении самолета со сверхзву-
ковой скоростью в атмосфере возбужда-
ются ударные волны, достигающие земли
и создающие на ее поверхности кратко-
временный перепад давления.
Ударные волны порождаются отдель-
ными частями движущегося самолета
(носовой частью фюзеляжа, крыльями,
оперением), и потому эпюра давления
(т. е. график изменения давления во вре-
мени) имеет сложную форму (чаще с
двумя четко выраженными положительной
и отрицательной фазами), напоминаю-
щую по своей конфигурации латинскую
букву iN (отсюда и название для идеа-
лизированной эпюры давления N-волна).
Распространяющиеся ударные волны об-
разуют конус, в вершине которого нахо-
дится движущийся самолет, а ось конуса
совпадает с линией движения самолета
(рис. 5.1). Угол раствора конуса зависит
от высоты и скорости ^полета; при увели-
чении скорости он уменьшается.
Сечение конуса поверхностью земли
определяет зону действия звукового уда-
ра. Ширина этой зоны в направлении,
перпендикулярном линии полета, практи-
чески оказывается конечной из-за неодно-
родности атмосферы и постепенного отра-
жения расходящихся волн от нижних ее
слоев; она неодинакова для самолетов
различных типов и во многом зависит от
высоты полета: чем больше высота, тем
шире полоса вдоль трассы, подверженная
звуковому удару. Для типичных боевых
самолетов, совершающих полеты на вы-
соте 10—12 км, эта полоса имеет ширину
50 км. При крейсерском полете англо-
французского пассажирского самолета
«Конкорд» на высоте 17 км ширина по-
лосы достигает 80 км, а для американско-
кого самолета «Боинг 2707-300», который
должен летать на высоте 19 км, она со-
ставит 95 км,.
Эпюра давления на поверхности зем-
ли даже для одного и того же самолета
может иметь различную конфигурацию,
видоизменения которой зависят от высо-
ты полета, а также от турбулентности и
неоднородности атмосферы. Характерная
особенность ударных волн от самолета
ТУ-144 по сравнению с другими самоле-
тами — дополнительная ступень в поло-
жительной фазе (двухступенчатая волна),
вызванная ударной волной от крыла, на
сравнительно больших расстояниях. У
других самолетов ударная волна от кры-
ла достигает волну от носка фюзеляжа
92
быстрее, чем у ТУ-144; поэтому у них зо-
на, в которой распространяется двухсту-
пенчатая волна (так называемое ближ-
нее поле), значительно меньше.
На рис. 5.2 [2] показаны предельные
высоты полета самолета ТУ-144, после
превышения которых двухступенчатая
волна ближнего поля переходит в N-об-
разную волну (эта зона называется даль-
ним полем) для различной массы самоле-
та, соответствующей примерно началу и
концу крейсерского полета. С увеличени-
ем массы самолета и его скорости, выра-
женной в числах Маха1, граница между
ближним и дальним полем снижается.
При крейсерском полете на высоте более
18 км поверхность земли будет находить-
ся в зоне дальнего поля, и , следователь-
но, на нее будут падать N-волны.
Интенсивность звукового удара вдоль
трассы полета и поперек нее различна
(рис. 5.3). В крейсерском режиме полета
она постоянна вдоль трассы, а поперек
Рис. 5.1. Распространение ударных волн при по-
лете сверхзвукового самолета
полосы уменьшается от оси к краям при-
мерно вдвое. Однако при изменении ре-
жимов полета интенсивность звукового
удара вдоль трассы резко возрастает в
результате фокусировки. Так, при разгоне
самолета и переходе через скорость зву-
ка интенсивность звукового удара в ре-
зультате фокусировки может в несколько
раз превысить интенсивность ударных
волн, соответствующую крейсерскому по-
лету. Зона фокусировки при разгоне,
имеющая форму полумесяца, обычно не-
велика—около 10 км вдоль трассы, и
при регулярных полетах будет занимать
фиксированное положение на расстоянии
до 200 км от аэродрома. Определить поло-
жение этой зоны можно
лишь с точностью до не-
скольких километров, так
что полосы, где будет на-
блюдаться фокусировка,
протянутся на 20—22 км
вдоль трасс; эти участки
будут наиболее опасны.
При маневрах самолета
на сверхзвуковой скорости,
связанных с изменением
курса, также происходит
фокусировка, резко повы-
шающая избыточное давление на фронте
ударной волны (так называемая супер-
фокусировка). Известны случаи десяти-
кратного увеличения интенсивности звуко-
вого удара при виражах самолета, а также
двойные и тройные повторные удары, вы-
званные суперфокусировкой.
Предотвращение фокусировки при ус-
тановившемся вираже может быть достиг-
нуто непревышением некоторого предель-
ного угла крена самолета. Это предельное
значение угла крена слабо зависит от вы-
соты, но существенно — от скорости поле-
та. На малых сверхзвуковых скоростях
полета ТУ-144 фокусировка происходит
уже при весьма небольших углах крена.
Предотвращение фокусировки при разго-
tt9«H
18
16
/4
12
10
1,
Рис. 5.2. Предельные высоты
Ту-144, разделяющие дальнее
звукового удара на поверхности земли
полета самолета
и ближнее поле
Разгон до сверх-
звуковой ско-
рости
Сверхзвуковой полет
интенсивности звукового удара вдоль и по-
трассы сверхзвукового полета
взлет
Зона фокусирования
5.3. Изменение
перек
рнзра пикового давления
вдол') прассы
Эпюра пикового давления
поперек трассы
Торможение дозвуковой
скорости
—посадка
1 Числом Маха называется отношение ско-
рости полета самолета к скорости звука в воз-
духе.
не самолета, по-видимому, невозможно
'[2]. Отметим, что фокусировка может
быть также вызвана изменением скорости
звука и скорости ветра в приземном слое
атмосферы.
В работе р] даны результаты экспе-
риментальных исследований сооружений
различной формы, проведенных на моде-
лях, для изучения отражения и фокуси-
ровки N-образных волн в условиях город-
ской территории. Наибольшие значения
перепада давления по всему периметру
здания соответствуют углу падения вол-
ны а=45°, который имеет место при ско-
рости полета с числом Маха М= 1,41.
Кроме того, при этом угле падения сни-
жение давления в N-волне происходит
медленнее, так что при прочих равных ус-
ловиях импульс давления на здание ока-
зывается максимальным именно при М —
I
93
= 1,41. Наибольшее усиление давления
вследствие фокусировки для зданий прос-
тейшей конфигурации (в форме параллеле-
пипеда) для точки, находящейся вбли-
зи поверхности грунта, составляет 3—3,6
раза, причем большие значения соответ-
ствуют моделям высоких зданий. Эффект
дифракции в этом случае имеет локаль-
ный характер, так что у изолированных
зданий и у зданий, расположенных груп-
пой, усиление одинаково*. Наиболее не-
благоприятным случаем, при котором
усиление было больше пятикратного, ока-
залось симметричное падение N-волны на
внутренний угол Г-образного в плане вы-
сокого здания.
Кроме действия на ограждающие кон-
струкции здания, звуковой удар влияет
также и на внутренние конструкции —
прежде всего на легкие перегородки, под-
Время
1 нарастания
весные потолки, штукатурку. Проникно-
вение ударных волн через открытые окна
и двери может в некоторых случаях со-
провождаться значительным увеличением
давления, вызванным резонансом в замк-
нутом объеме внутренних помещений.
Комната с открытым окном при этом иг-
рает роль резонатора Гельмгольца, и если
период собственных колебаний такого ре-
зонатора близок к продолжительности зву-
кового удара, то происходит значительное
увеличение давления по сравнению с давле-
нием в наружном пространстве.
5.3. ХАРАКТЕРИСТИКИ
ЗВУКОВОГО УДАРА
Как уже указывалось, эпюра давле-
ния, характеризующая звуковой удар,
имеет сложную форму, зависящую от мно-
жества факторов, среди
которых прежде всего сле-
дует отметить тип самоле-
та, состояние атмосферы,
высоту полета, характер
отражения от препятствия.
На рис. 5.4,а показана наи-
более характерная эпюра
давления, близкая к iN-об-
разной. Давление в началь-
ный момент быстро воз-
растает до максимального
значения (пика давления),
причем время нарастания
т весьма мало, но конечно.
Идеальной -образной эпю-
ры со временем 'нарастания
т = 0 не наблюдается. За-
тем давление уменьшается
почти по линейному зако-
ну, при- этом минимальное
значение примерно равно
по абсолютной величине
пику давления, Продолжи-
тельность звукового удара
Т называется «периодом»
(рис. 5.4,а). Пик давления
и период Т в полной мере
характеризуют идеализиро-
ванную iN-волну.
Значение пика давления,
как и конфигурация всей
эпюры, зависит от типа
4
Рис. 5.5. Расчетная интенсивность звукового уда-
ра для самолета Ту-144 при весе 1600 кН
Рис. 5.6. Расчетная интенсивность звукового уда-
ра для самолета Ту-144 при весе 1100 кН
94
и массы самолета, скорости, высоты и ре-
жима полета, атмосферных условий и др.
Номинальное давление в N-волне Др оп-
ределяют как пик давления в волне, от-
раженной от поверхности земли с коэф-
фициентом увеличения, равным 2. Вдоль
центральной линии полосы звукового уда-
ра номинальное значение Др для
типичных боевых самолетов составляет
около 70 Н/м2, а для самолетов типа
«Конкорд» и «Боинг» — от 75 до 175 Н/м2,
Самолет ТУ-144, как показывают расче-
ты, вызывает звуковой удар примерно та-
кой же интенсивности, как и «Конкорд».
' На рис. 5.5—5.6 приведены результа-
ты расчета интенсивности звукового уда-
ра для сверхзвуковых самолетов весом
'<?= 1600 и 1100 кН. Здесь же показана
граница, разделяющая ближнее и дальнее
поле. Расчеты выполняли для стандартной
атмосферы; при изменении атмосферных
условий давление может намного увели-
читься. Вообще говоря, Др является слу-
чайной величиной. Имеются эксперимент
тальные результаты, характеризующие ве-
роятностны^ свойства этой величины. На
рис. 5.7 приведена [8] кривая распреде-
ления вероятностей Р значений
Дризм/Дррасч, построенная на основе дан-
ных 12406 измерений, проведенных во
время 1625 полетов сверхзвуковых само-
летов различного типа (В-70, SR-71,
F-101, F-104, В-58). Здесь ДрИЗм —
F=101, F=104, В = 58). Здесь Дризм —
пиковое давление, фиксируемое в экспе-
риментах; Дррасч — расчетные значения
пикового давления для нетурбулентной стра-
тифицированной атмосферы, соответству-
ющей американской стандартной модели
атмосферы 1962 г. Приведенное распреде-
ление близко к лог-нормальному, оно сви-
Рис. 5.7. Распределение вероятностей отношения
экспериментального значения интенсивности зву-
кового удара к его расчетному значению
&= 1600кН
Рис. 5.9. Расчетное
волны самолета
значение периода звуковой
Ту-144 при весе 1600 кН
Рис. 5.10. Расчетное значение периода звуковой
волны для самолета Ту-144 при весе 1100 кН
95
детельствует о возможности большого
превышения значения Лр вследствие ат-
мосферных факторов.
Изменение режима полета также су-
щественно влияет на значение пика дав-
ления. При подъеме и снижении Лр мо-
жет увеличиться в 1,5—2 раза по сравне-
нию с горизонтальным полетом. Кроме
того, резкое увеличение Др дает описан-
ное выше явление фокусировки, возника-
ющее при переходе через скорость звука
и маневрировании.
Эффекты, близкие к фокусировке,
могут наблюдаться и при падении звуко-
вых ударных волн на неплоские поверх-
ности. Таким воздействиям подвергаются
тупиковые участки долин с крутыми скло-
нами или улиц с высокими зданиями. От-
ражение волн от поверхности земли или
сооружений и их последующее взаимо-
действие с падающими волнами значи-
тельно меняет интенсивность и всю эпю-
ру давлений при звуковом ударе. Коэф-
фициент отражения звуковой волны от
плоской поверхности зависит от упругих
свойств преграды: для мягких материалов
он близок к 1, для абсолютно жестких
равен 2. Для зданий наиболее характерен
случай, когда ограждающие конструкции,
например оконные стекла, подвергаются
действию падающей и отраженной от зем
ной поверхности волны (рис. 5.8). Нё
этом же рисунке показаны типичные эпю-
ры давления при последовательном дей-
ствии двух N-волн одинаковой интенсив-
ности в различных по высоте точках со-
оружения.
Кроме пикового давления Др важней-
шим параметром N-образных волн явля-
ется их период Т (длительность звуково-
го удара). Поскольку iN-волна представ-
ляет собой идеализацию, то ее период не
соответствует отрезку времени между
максимумом и минимумом давления в ре-
альной звуковой волне. Однако время на-
растания давления так же, как и про-
должительность замыкающего скачка,
обычно невелико по сравнению с перио-
дом Т (в среднем это отношение J/25:
;1/зо)* так чт° в расчетах ими можно
пренебречь.
Номинальное (среднее) значение пе-
риода N-волны принимают для типичных
боевых самолетов 0,1 с; для «Конкорда»
Т — 0,25 с, для «Боинга» Т — 0,3 с. Расче-
ты, выполненные для самолета ТУ-144
[2], показывают, что период Т может из-
меняться в пределах 0,2...0,4 с. На рис.
5.9, 5.10 приведены результаты этих рас-
четов для самолетов с полетным весом
G=1600 и 0 = 1100 кН. Здесь также ука-
зана граница, разделяющая ближнее и
дальнее поле.
При фокусировке период волны уве-
личивается в среднем до 1,5 раза по
сравнению с номинальным значением, при-
чем резко меняется характер эпюры дав-
- ления. Увеличение длительности звуково-
го удара при суперфокусировке менее су-
щественно.
5.4. РАСЧЕТ СООРУЖЕНИЙ
НА ДЕЙСТВИЕ ЗВУКОВЫХ
УДАРНЫХ ВОЛН
Прогноз уровня колебаний строитель-
ных конструкций зданий и сооружений,
подвергающихся действию звукового уда-
ра, и оценка влияния этих колебаний на
прочность конструкций в значительной
мере затруднены из-за невозможности во
многих случаях достаточно обоснованно
определить характеристики конструктив-
ных элементов и их фактическое состоя-
ние. Как показывают экспериментальные
исследования, номинальные динамические
нагрузки от звукового удара не пред-
ставляют опасности для зданий и соору-
жений, по крайней мере для тех конструк-
тивных элементов, которые находятся в
нормальном или приемлемом с эксплуата-
ционной точки зрения состоянии. Возмож-
ность разрушения грозит лишь уже по-
врежденным конструкциям либо конструк-
циям, подвергшихся воздействиям, резко
увеличенным вследствие фокусировки или
резонансных явлений. Существен тот факт,
что при регулярных полетах сверхзвуко-
вых самолетов звуковой удар будет пред-
ставлять собой многократно повторяющееся
воздействие, так что известное влияние
на прочность могут оказать усталостные
явления.
Для расчета конструкций на дейст-
вие звукового удара может быть ис-
пользован спектральный подход, заклю-
чающийся в определении динамического
коэффициента для каждой формы собст-
венных колебаний рассматриваемой кон-
струкции. При этом под динамическим ко-
эффициентом понимают отношение макси-
мального по модулю перемещения (или
внутреннего усилия) для рассматриваемой
собственной формы к статическому значе-
нию того же параметра при действии
обобщенной силы, соответствующей равно-
мерному загружению конструкции нагруз-
кой с постоянной интенсивностью Лр.
Рассмотрим малые колебания конст-
рукции, упругие силы которой описыва-
ются некоторым оператором L. Посколь-
ку действие многократно (в течение срока
службы сооружения возможны тысячи и
десятки тысяч циклов деформирования),
то колебания системы должны ограничи-
ваться упругой стадией работы материа-
ла. В связи с этим практически для всех
ограждающих конструкций оператор L
может быть принят линейным; влияние
геометрической нелинейности даже для
таких относительно гибких конструкций,
как оконные стекла, незначительно и мо-
жет быть оценено величиной порядка
10%. С учетом частотно-независимого
вязкоупругого сопротивления уравнение
колебаний конструкции записывается в
следующем общем виде '[5]:
mz + у V tn L1^2 z +L z ~ Л p q (/), (5.1)
где z — перемещение; у — коэффициент
внутреннего неупругого сопротивления
(коэффициент потерь); m — масса конст-
96
рукции на единицу поверхности; Др —
пиковое давление; q(t)—закон изменения
давления во времени; точка означает
дифференцирование по времени.
В частности, для системы с одной
степенью свободны L—k (k— квазиупру-
гий коэффициент), и уравнение (5.1) име-
ет вид
г + укг + ^г = q (/), (5.2)
т
где Х=з Уk/m — круговая частота собст-
венных колебаний системы.
Учитывая, что у<^1, решение уравне-
ния (5.2) при нулевых начальных усло-
виях можно представить в следующей
форме:
о
X sin X (/ — т) dx. (5.3)
Для N-образной волны продолжи-
тельностью Т с точностью до малых вели-
чин второго порядка
Z (/о)
1 — 2Z0 То 1 +у (л То) 1 —
— ^1(4)—(/о) (^о^^о);
(Л) - то) -г1 Uo - То)-
—(Л))—2 2 (/о) (Т0<4),
Рис. 5.11. Динамические коэффициенты 64- и 6—
для системы с одной степенью свободы при дей-
ствии N-волны
z2 Со) = (Л Та)-1 е
X (— sin 2 л /о + Y cos 2 л /0) •
Динамические коэффициенты б+ —
2макс ^ст> и 6 ^макс ^ст’ соответству-
ющие наибольшему положительному и
наибольшему^ отрицательному перемеще-
ниям системы,^ приведены на рис. 5.11.
Как видим, для большинства строитель-
ных материалов значение динамического
коэффициента не превышает 2.
В случае отражения волны от поверх-
ности земли (см. рис. 5.8) на ограждаю-
щие конструкции здания действует на-
грузка
<71 (t) =
= \p[q(t) + k0G (/-Ti) q (/-n)], (5.5)
где k0 — коэффициент отражения: <г(/ —
—Ti)—единичная ступенчатая функция
Хевисайда; ti — интервал времени между
воздействиями падающей и отраженной
волн.
При этом перемещение будет
21 (0 =?(/) +&о<? (t — Ti) z (t—Xi), (5.6)
Г
T/Ts
Рис 5.12. Динамические коэффициенты 6+ и 6—
для системы с одной степенью свободы при дей-
ствии падающей и отраженной N-волны с ин-
тервалом = r
4(0,5) Зак. 195
97
ТАБЛИЦА 5.1
98
где z(t) определяется по формуле (5.4)
с учетом перехода к безразмерному вре-
мени /0.
На рис. 5.12 приведены графики ди-
намических коэффициентов для двух пос-
ледовательных звуковых ударов — падаю-
щего и отраженного от поверхности зем-
ли (с коэффициентом отражения &о— 1>
вычисленные по формуле (5.6) при Т1 =
= Т. В табл. 5.1 приведены максимальные
динамические коэффициенты для различ-
ных сочетаний падающей и отраженной
волн.
Уравнения колебаний конструкций,
рассматриваемых как системы с конечным
числом степеней свободы по аналогии с
(5.1), могут быть представлены в матрич-
ной форме:
MZ+ryM (М"‘ K)1/2Z + KZ =
= ApQi <?(/), (5.7)
где М— симметричная матрица инерци-
онных коэффициентов; К — симметричная
матрица квазиупругих коэффициентов;
Z —• вектор перемещений; Qi — вектор
внешних сил, элементы которого пропор-
циональны площади, воспринимающей
давление.
Полагая можно перейти к
уравнению
Ё+уС1й + Ви = \рГЛ~Ч‘ Qtq (О,
где
С! = м1/2 (м-‘ к)*Л м_1/2,
в = М“1/2 КЛГ,/!.
Для симметричной матрицы В спра-
ведливы спектральные представления
В = Ф0ЛФ^1, В*/г = Ф0Л1/2 Ф^1,
где Фо — ортогональная матрица собствен-
ных векторов матрицы В, расположенных
по столбцам; Л — диагональная матрица
собственных значений (квадратов собст-
венных частот).
Поскольку = В и, следовательно,
С1 = В ;/2, то, полагая U —Фоа, Qi =
= М*^2Ф0Ь и используя спектральные пред-
ставления матрицы В и ее квадратного
корня, получим
аг (О ar (/) + X? ar (t) =
= Д pbrq (/) (г= 1, 2................п). (5.8)
Решив уравнения (5.8), общее реше-
ние можно представить в виде суперпо-
зиции 7 = Фа, где Ф = {фг—матрица
собственных векторов матрицы М"1 К,
элементы которой представляют собой ор-
динаты форм собственных колебаний сис-
темы, причем Ф = М~ Фо.
Для N-волны решение уравнения (5.8)
записывается в виде
1 — 2 tr хг 1 + у (л хг) 1 —
> 2i (Zr) 22 (Zr) (^/>‘tr).
т Кг
где хг = —
Решение уравнения (5.7):
V п
zi аг (О <frj. (5.9)
Г=1
где j— номер массы или точки; г — но-
мер формы колебаний; п— число степе-
ней свободы: фгj — ординаты форм соб-
ственных колебаний; — частоты собст-
венных колебаний.
Внутренние усилия в системе (изги-
бающие моменты, поперечные силы) мо-
гут быть определены по формулам:
п
Му (/) = аг (/) Mryj
л
Q/ (О ~ аг (0 Qr/>
Г=1
• (5.10)
где Mrj, Qrj — изгибающий момент и по-
перечная сила в точке j при деформиро-
вании системы по r-й форме собственных
колебаний.
При расчете конструкций, рассматри-
ваемых как системы с распределенными
параметрами (балки, пластинки, оболоч-
ки), также используют метод разложения
по формам собственных колебаний. На-
пример, в случае шарнирно-опертой пря-
моугольной пластинки уравнение (5.1)
будет
D V V — у У rn D \/ z + mz~
= (5.11)
где D, m — цилиндрическая жесткость и
масса (на единицу площади) пластинки;
V = (д2/дх2) + (д2/ду2) — оператор Лапла-
са в декартовых координатах.
Разложение по формам собственных
колебаний
!Л1
Z (X, у, /) = 22“" Xr Xs
Г=1 S—1
(5.12)
приводит к уравнениям типа (5.7) отно-
сительно обобщенных координат
^rs “Ь Y ^rs &rs “b ^rs A Q (О >
(5.13)
где
brs = ) xr W dx | Xs (y) dy;
6 6
4*(0,5) Зак. 195
99
Xrs — круговые частоты собственных коле-
баний пластинки; Xr, Xs— нормированные
балочные функции для шарнирно-опертой
балки; /ж, 1У—длины сторон пластинки;
пь л2 — число учитываемых форм.
При других краевых условиях разло-
жения (5.12) по балочным функциям уже
не приводят к разделенным уравнениям
(5.13), решение которых выписывается в
виде, аналогичном (5.8), однако с доста-
точной для практических расчетов сте-
пенью точности можно прийти к этим
уравнениям, ограничиваясь диагональными
членами в получаемой системе. Следова-
тельно, приближенно для любых условий
закрепления краев пластинки решение
можно представить в виде, аналогичном
(5.12), с коэффициентами, определяемыми
из уравнений (5.13). Внутренние усилия
в пластинке можно найти по известным
формулам, связывающим перемещения
пластинки с изгибающими, крутящими
моментами и поперечными силами.
В большинстве случаев при расчете
конструкций на звуковой удар можно ог-
раничиться учетом только первой формы
собственных колебаний; высшие формы
возбуждаются весьма слабо вследствие
практически равномерного загружения
конструкции импульсивной нагрузкой и
из-за того, что периоды высших форм
собственных колебаний обычно бывают
много меньшими, чем продолжительность
удара. Ниже приведены формулы для
прогибов и наибольших изгибающих мо-
ментов в пластине.
При учете только первой формы коле-
баний
г (х, у, t)=auXi (х) X, (у). (5.14)
Вводя динамические коэффициенты
а1 макс Лг а1 макс
° " ьг Д'р ; ° = Ь~\р ’
(5.15)
определяемые по графикам, приведенным
на рис. 5.11, 5.12 и в табл. 5.1, наиболь-
шие во времени перемещения пластинки
можно представить в виде
. д± 6ц Л р
^акс =------*1 W *1 (У) • (5-16)
Наибольшие изгибающие моменты:
х макс
м~ =
у макс
[<(^) + vx; (%)].
При неплотном закреплении краев
пдастинки (например, оконных стекол),
как показано в {И], напряжения в ней
могут значительно возрастать, поэтому в
районах полетов сверхзвуковых самоле-
тов к элементам закрепления стекол дол-
жны предъявляться особые требования
в отношении плотности заделки.
5.5. ЭКСПЕРИМЕНТАЛЬНЫЕ
ИССЛЕДОВАНИЯ
При изучении воздействия звукового
удара на сооружения и отдельные эле-
менты ограждающих конструкций широко
используют модельные и натурные экспе-
рименты. Модельные эксперименты прово-
дят в ударных трубах и специальных ими-
таторах звукового удара. Ударная волна
в имитаторах генерируется либо последо-
вательным взрывом двух точечных заря-
дов со сдвигом по времени, равным про-
должительности звукового удара, либо
взрывом распределенного по длине трубы
набора зарядов ВВ, обеспечивающим за-
данный профиль (N-волны. В таких уст-
ройствах проводят испытания моделей или
отдельных элементов, например оконных
стекол.
Изучение действия звукового удара
на здания и сооружения проводилось в
натурных условиях главным образом в
США, Англии и Франции, причем типы
исследуемых сооружений были самыми
разнообразными. Так, в США основное
внимание уделялось сравнительно легким
зданиям, характерным для массовой заст-
ройки американских городов и поселков,
и, в частности, таким их конструктивным
элементам, как оконные стекла, детали
крыш, облицовка и т. п. В Англии и
Франции, где много старинных зданий и
исторических памятников, а также вет-
хих деревянных домов, подробно изуча-
лось влияние звукового удара на конст-
рукции подвесных потолков, витражей,
перегородок, кровель и других элементов
сооружений, в том числе находящихся в
плохом состоянии.
В Англии было проведено около 50
испытательных полетов самолетов «Кон-
корд», во время которых изучалось дей-
ствие звукого удара на население, живот-
ных и сооружения в обширном районе,
насчитывающем 1,5 млн. жителей. Воз-
действия оценивали по качеству жалоб и
претензий на возмещение ущерба, посту-
павших от населения. Анализ этих мате-
риалов показал, что наибольшее количест-
во из 384 удовлетворенных претензий
(около 84%) относилось к повреждениям
сооружений, причем большинство из них
было незначительным, и значительный
ущерб был нанесен лишь отдельным со-
оружениям, по-видимому, достаточно вет-
хим. При этом основные повреждения на-
блюдались в полосе шириной до 32 км,
хотя общая ширина полосы звукового
удара составляла 80 км. После проведе-
ния нескольких первых полетов число
жалоб и претензий намного снизилось.
Можно отметить также, что повреждае-
мость домов в густонаселенных районах
оказалась более высокой, чем в местности
с небольшой плотностью населения.
100
Отдельное исследование (при 10 по-
летах самолета «Конкорд») было посвя-
щено изучению реакции сооружений на
звуковой удар с помощью вибрризмерений.
Объектами исследования были четыре
собора, четыре служебных здания, два
дома, небоскреб и здание музея. Уста-
новлено, что вибрации с интенсивностью#
значительно большей, чем от обычных воз-
действий, возникают лишь в элементах
кровель, потолков и окон, причем относи-
тельный уровень этих вибраций выше для
крупных зданий. Существенных поврежде-
ний конструкций обнаружено не было; в
основном повреждения локализовались
вблизи имеющихся трещин или ранее
поврежденных участков. Аналогичные ис-
следования проводились во Франции.'
В США было проведено несколько се-
рий испытательных полетов военных само-
летов различного типа над городами и спе-
циальными полигонами. Всего было прове-
дено около 3000 полетов, из них в Оклахо-
ме и на полигоне Уайт Сендз — 2750 поле-
тов. По этому числу полетов еще нельзя
сделать окончательных выводов, однако их
достаточно для того, чтобы можно было
сделать предварительные выводы. В целом
результаты этих исследований хорошо сог-
ласуются с данными экспериментов, прове-
денных во время полетов самолета «Кон-
корд». Они свидетельствуют о том, что но-
минальное давление звукового удара Др=
= 100...150 Н/м2 не представляет опасности
для конструкций зданий, находящихся в
нормальном, неповрежденном состоянии.
Отмеченные случаи повреждений оконных
стекол и штукатурки относятся главным
образом к элементам с уже нарушенной
структурой.
Установленные в результате проведен-
ных различными авторами экспериментов
границы неразрушимости стекол, штукатур-
ки и кафеля приведены в табл. 5.2:
ТАБЛИЦА 5.2
Конструктивный элемент Макси- мальное давление, Н/м»
Штукатурка 500
Кафельная облицовка 400
Оконные стекла при от- ношении толщины к меньшему пролету 1/500 400
1/300 1000
1/100 10 000
Указанные цифры нельзя понимать как
абсолютный предел; они лишь оценивают
верхнюю границу давления, при котором
вероятность разрушения оказывается пре-
небрежимо малой. В целом же разброс зна-
чений разрушающего давления для ограж-
дающих конструкций весьма велик, для
остекления, например, этот разброс может
составлять ±200—300% •
СПИСОК ЛИТЕРАТУРЫ
1. Голобинский А. И., Соколов К. Б.,
Хитрук Т. С., Окунев Л. А. Исследования
(Отражения, дифракции и фокусировки N-
волны звукового удара на моделях раз-
личных сооружений. Труды ЦАГИ им. Жу-
ковского, вып. 1397, 17—~43. М., 1972.
2. Жилин Ю. Л. Звуковой удар от
сверхзвукового пассажирского самолета. —
Труды ЦАГИ им. Жуковского, вып. 1489,
41—87. М., 1973.
3. Труды ЦАГИ им. Жуковского, вып,
1397. М„ 1972.
4. Труды ЦАГИ им. Жуковского,
вып. 1489. М., 1973.
5. Цейтлин А. И. О линейных моде-
лях частотно-независимого внутреннего
трения. — Изв. АН СССР. Механика твер-
дого тела, 1978, № 2.
6. Acoust J. Soc. Amer., 39, N 5, part
2, 1966.
7. Acoust J. Soc. Amer., 48, N 3, part
3, 1970.
8. Acoust J,. Soc. Amer., 51, N 2, part
3, 1972.
9. Mater. Res. Stand., 4, 1964.
10. Sound J. and Vibration, 20, N 4,
1972.
11. Crandall S. H., Kurzwell Z. On the
rattling of windows by sonic booms. J. Aco-
ust, Soc. Amer., 44, N 2, 1968.
12. Newberry C. W. The Response of
Buildings to Sonic Boom. J. Sound and
Vibration, 6, 1967(.
13. Crocker M. J. Hudson R. R. Stru-
ctural Response to Sonic Boom, J. Sound
and Vibration, 9, 1969.
14. Clarcson B. L.t Mayes W. H. So-
nic— Boom—Induced Building Structur
Responses Including Damage. J. Acoust.
§oc. Amer. 51, N 2, 1972.
15. Sharpe R ,L., Garrison K. Structu-
ral response to sonic booms, J. Struct. Divi-
sion, 98, N 10, 1972.
4 Зак. 195
РАЗДЕЛ 6. КРАНОВЫЕ НАГРУЗКИ
CjAl. Ф. БАР ШТ ЕН Н\, А. Н. ЗУБКОВ)
Крановые нагрузки, действующие на
каркас промышленного здания, разделяют на
вертикальные и горизонтальные. К послед-
ним относятся силы торможения, развивае-
мые тележкой крана, и поперечные силы, воз-
никающие при движении мостового крана.
6.1. ВЕРТИКАЛЬНЫЕ
КРАНОВЫЕ НАГРУЗКИ
Вертикальные крановые нагрузки, пере-
даваемые колесами кранов на крановый путь,
принимают в соответствии с требованиями
ГОСТов на краны, а для нестандартных
кранов — в соответствии с данными, указан-
ными в паспортах заводов-изготовителей. Под
крановым путем понимают обе балки, несу-
щие один мостовой кран. Коэффициент пе-
регрузки для статических крановых нагру-
зок 1,2.
Мостовой кран передает на поддержи-
вающие конструкции вертикальные динами-
ческие нагрузки двух видов: первые из них
связаны с вертикальными колебаниями под-
крановых балок, крана и тележки вследст-
вие неровностей кранового пути и колес кра-
на. Эти нагрузки зависят от скорости дви-
жения крана, пролета балки и жесткости
конструкции моста; вторые — нагрузки, вы-
зываемые массой крана, тележки и груза,
движущейся по ровной поверхности упругой
весомой балки.
В настоящее время известны решения
ряда задач о движении силы или груза по
балке ф8].
В общем случае, когда учитывают инер-
цию балки и груза, точное решение задачи
получают с помощью сложных алгоритмов,
затрудняющих использование полученных
результатов в практических расчетах. По-
этому иногда при выводе уравнений колеба-
ний балки пренебрегают ее инерцией по
сравнению с инерцией движущегося груза
(задача Стокса). В [9] определены коэффи-
циенты динамичности для различных случа-
ев движения груза по балке. Однако этот
динамический эффект целесообразно учи-
тывать только при больших скоростях дви-
жения. Как показано в [7], для подкрано-
вых балок силы инерции, развиваемые мас-
сой груза и массой балки, невелики и прак-
тически не оказывают влияния на динами-
ческие силы. Поэтому для определения по-
следних вводят коэффициент динамичности,
равный отношению прогибов, возникающих
при движении груза по балке и при стати-
ческом действии сил. Экспериментально уста-
новлено, что коэффициент динамичности из-
меняется от 1 до 1,3. Чаще всего его значе-
ние не превышает 1,1—1,2. При указанных
условиях расчетная нагрузка от колеса кра-
на на рельсы может быть определена по
формупе, приведенной в работе [6]:
1,2 Г / — 0,9 у ]
Р = QK + 2 (QT -г Q) ’ ,
2m I
(6.1)
где Qk, Qt — вес кранового моста и тележ-
ки, указанный в паспорте крана; Q — грузо-
подъемность крана; I — пролет; m — число
колес с одной стороны; у — наименьшее рас-
стояние между тележкой крана и осью под-
кранового рельса, указанное в паспорте;
1,2 — коэффициент перегрузки.
Согласно главе СНиП II-6-74 «Нагрузки
и воздействия», расчетные вертикальные на-
грузки от кранов тяжелого и весьма тяже-
лого режимов работы находят с учетом ко-
эффициента динамичности, равного 1,1, если
в нормах проектирования конструкций не
приводится других данных.
При расчете подкрановых балок верти-
кальные нагрузки определяют от двух наи-
более неблагоприятных по действию мосто-
вых кранов. При наличии одного крана и при
условии, что второй кран не будет установ-
лен в течение периода эксплуатации соору-
жения, вертикальные нагрузки могут быть
вычислены от одного крана. При расчете
рам, колонн, фундаментов й оснований
многопролетных зданий с мостовыми крана-
ми, расположенными в каждом пролете на
одном ярусе, вертикальную нагрузку опре-
деляют на каждом крановом пути от двух
наиболее неблагоприятных по воздействию
кранов, а при учете совмещения в одном
створе кранов разных пролетов — от четы-
рех наиболее неблагоприятных по воздейст-
вию кранов. А
6.2. ГОРИЗОНТАЛЬНЫЕ СИЛЫ,
ВЫЗЫВАЕМЫЕ ТОРМОЖЕНИЕМ
ТЕЛЕЖКИ КРАНА
Природа возникновения этих сил, пове-
дение тележки в переходном режиме от
равномерного движения к торможению,
влияние упругого смещения каркаса и скру-
чивания вала между тормозным шкивом и
редуктором на силы торможения рассмотре-
ны в работе [4]. Показано, что механизм
возникновения сил торможения связан с при-
менением в современных конструкциях кра-
нов автоматических, нормально замкнутых
тормозов. Эти тормоза почти мгновенно соз-
дают полную величину тормозной силы
(время нарастания этой силы составляет
примерно 0,002 с ), что оказывает на соору-
жение динамическое действие. Высокоча-
стотные изменения тормозной силы в пере-
ходной период гасятся внутри систем
«мост — тележка», и их можно не учиты-
вать. На тормозные силы также мало влия-
ют упругие перемещения каркаса здания и
деформация валов трансмиссионной системы
тележки.
102
При гибком подвесе груза горизонталь-
ные силы, вызываемые торможением тележ-
ки, могут быть определены по формуле
т pW — m21, (6.2)
Р J1 \ J 2 /
где г — радиус колеса тележки; ц — переда-
точное число редуктора; L — общее сопро-
тивление тележки перекатыванию, включая
тормозной момент; М — масса тележки и
и груза; т2— масса груза;
2</к г*
А— А т ' о 2 №
р2 р2
г2 г3
А “ А --- т2 J j = J1 — ~ М,
р3 р-
где — момент инерции шкива и ротора
мотора; А — момент инерции колес редук-
тора и ведущих колес, приведенный к
тормозному шкиву; А- момент инерции хо-
дового колеса.
При жестком подвесе груза силу тормо-
жения вычисляют по формуле
М. (6.3)
р J1
Уменьшение сил торможения при заме-
не жесткого подвеса на гибкий} не превыша-
ет '25%.
По главе СНиП П-6-74 нормативную
горизонтальную нагрузку, направленную по-
перек кранового пути и вызываемую тормо-
жением тележки, принимают: для кранов с
; гибким подвесом 0,05 суммы номинальной
грузоподъемности крана и веса тележки; для
крана б жестким подвесом груза 0,1 той же
суммы.
Эту нагрузку учитывают при расчете
поперечных рам зданий и подкрановых балок.
При этом полагают, что она передается на
одну балку кранового пути, распределяется
поровну между всеми колесами крана и мо-
жет быть направлена как внутрь рассмат-
риваемого пролета, так и наружу.
Нормативную горизонтальную нагрузку,
направленную вдоль кранового пути, вызы-
ваемую торможением моста крана, прини-
мают! 0,1 нормативной вертикальной нагруз-
ки па тормозные колеса рассматриваемой
стороны крана.
6.3. ГОРИЗОНТАЛЬНЫЕ
ПОПЕРЕЧНЫЕ СИЛЫ (БОКОВЫЕ),
ВОЗНИКАЮЩИЕ
ПРИ ДВИЖЕНИИ КРАНА
При совпадении направления движения
крана с направлением качения колес и при
параллельности подкрановых путей попереч-
ные силы на ребордах колес не возникают.
Движению крана в этом случае препятст-
вуют лишь трение качения колеса по рель-
сам и трение в подшипниках. Такой случай
движения крана можно назвать идеальным.
Мостовые краны и подкрановые пути имеют
неправильности, которые приводят к тому,
что при движении крана возникают переко-
сы моста относительно подкрановых путей и
контакты реборд колес с рельсами, что вы-
зывает появление боковых сил.
Задача об определении этих сил, тесно
связанная с вопросом о дополнительных со-
противлениях передвижению крана при пе-
рекосах, давно привлекает внимание иссле-
дователей ,{4]. Однако проводившиеся в этой
связи работы имели в основном экспери-
ментальный характер.
В [10] взаимодействие мостового крана
и каркаса промышленного здания изучали
в производственных условиях, при этом по-
перечные силы определяли по записям пере-
мещений колонн и подкрановых балок. В
[1] на основании натурных измерений для
определения боковых сил предложена фор-
мула^
Т = 0,1 -у Р“акс, (6.4)
где I и. о — пролет и база крана; —
наибольшая вертикальная нагрузка, переда-
ваемая на рельс колесом.
Согласно главе СНиП П-6-74, действую-
щую поперек кранового пути нормативную
горизонтальную нагрузку, вызываемую пере-
косами крана (боковую силу), принимают
0,1 нормативной вертикальной нагрузки на
колесо. Эта нагрузка от всех колес одной
стороны крана может быть направлена как
внутрь здания, так и наружу. Ее учитывают
только при расчете подкрановых балок и их
креплений к колоннам в зданиях с кранами
весьма тяжелого режима работы, а также с
кранами тяжелого режима работы метал-
лургического производства. При этом на-
грузку, вызываемую торможением тележки,
не учитывают.
В работе 1[3] на основе эксперименталь-
ного изучения поперечных сил и характера
движения моста крана рассмотрена задача
о движении жесткого крана по подкраново-
му пути, который имеет отклонение от про-
ектного положения, и исследованы возни-
кающие при этом поперечные силы. Уста-
новлено, что преобладающее влияние на
образование перекоса оказывают случайные
отклонения подкрановых путей в горизон-
тальной плоскости от проектного положе-
ния. Неодинаковый диаметр ведущих колес
и перекос осей колес относятся к системати-
ческим неправильностям крана и способству-
ют образованию перекоса.
Изучение характера движения мостово-
го крана показывает, что его колеса поми-
мо поступательного движения совершают
неуправляемые непрерывные боковые сме-
щения.^ Такое движение моста похоже на
влияние вагонов поезда при движении
железнодорожного состава, когда реборды
колес набегают то на* один, то на другой
рельс.
В зависимости от поперечных смещений
колес движение моста может происходить
при отсутствии контакта реборд с рельсами
и при контакте рельсов с ребордами одного,
двух и даже трех колес крана. Могут воз-
никнуть и предельные случаи, когда вслед-
ствие значительного отклонения подкрано-
вых путей от проектного положения проис-
ходит заклинивание моста либо ребордами
ведущих или ведомых колес, либо реборда-
ми колес, расположенных по диагонали мо-
4* Зйк. 195
103
ста. Поперечные смещения колес крана
вследствие перекосов горизонтальной рамы
моста малы по сравнению1 с поперечным .сме-
щением колес при перекосе моста в целом
относительно подкрановых путей. Поэтому
при анализе движения крана деформации
горизонтальной рамы моста можно не учи-
тывать и мост рассматривать как абсолют-
ное твердое тело.
Траектория движения крана вследствие
нерегулярности отклонений подкрановых пу-
тей от проектного положения имеет случай-
ный характер. Мост крана при этом совер-
шает непрерывные нерегулярные поперечные
смещения и поворот в горизонтальной плос-
кости. Контакт реборд колес с рельсом ог-
раничивает движение крана в поперечном
направлении. Колесо следует за отклоне-
ниями подкранового рельса и кран как бы
«блуждает» по путям. Естественно, что и
поперечные силы, возникающие при движе-
нии крана, изменяются случайным образом.
В1 настоящее время отсутствует экспери-
ментальный материал о характере движе-
ния крана и о смещениях его колес, чтобы
решить поставленную задачу. Поэтому при
теоретическом анализе используют модель,
согласно которой рассматривается движение
жесткого моста по подкрановому пути,
имеющему в горизонтальной плоскости слу-
чайные отклонения от проектного положения
при непрерывном контакте рельса с одной
ребордой и реборд двух колес, расположен-
ных на одной концевой балке моста крана.
При решении указанных задач использо-
ваны гипотезы псевдоскольжения [5, 11,12]
и методы теории случайных функций.
Гипотеза псевдоскольжения. Суть этой
гипотезы, нашедшей широкое распростране-
ние при анализе движения железнодорож-
ных экипажей, состоит в следующем. При
движении колеса по рельсу наряду с каче-
нием наблюдается проскальзывание его в
сторону движения, если колесо ведомое, и
в противоположную сторону, если оно ве-
дущее, т. е. фактическая частота вращения
колеса при прохождении заданного пути не
равна частоте вращения, если исходить из
пройденного пути и радиуса колеса. Для ве-
дущего колеса она будет большей (s'>-0),
а для ведомого — меньшей (s'<0).
.Величину
s' Vo — ЮГ
S — --- = --------
^0 Оо
тде Vo — скорость перемещения центра ко-
леса; со— угловая скорость; г — радиус ко-
леса, Ф. Картер [10] называет крйппом,
У. Рокар [11]—псевдоскольжением,
А. Ю. Ишлинский i[12] — мерой кажущегося
проскальзывания.
В зоне контакта колеса с рельсом су-
ществует количественная зависимость между
псевдоскольжением и силой упругого про-
скальзывания, их вызывающими. Ф. Картер,
используя результаты решения контактной
задачи, полученные Герцем, и основываясь
на экспериментальных исследованиях, пред-
ложил следующую эмпирическую зависи-
Рис. 6.1
мость для определения сил упругого про-
скальзывания:
F — ks, (6.6)
где коэффициент k зависит только от вели*
чины опорной поверхности зоны контакта
колеса с рельсом и от нагрузки на колесо;
k = 2500 Д/> г,
где Р—нагрузка на колесо, Н; г—радиус
колес, м.
Зависимость (6.6) будет справедлива
до тех пор, пока значение F не превысит
силы сухого трения колеса о рельс. Коэф-
фициент k одинаков для случаев, когда уси-
лие действует вдоль рельсового пути и под
углом к нему.
Движение крана при контакте рельса
с ребордой ведущего колёса. Рассмотрим
картину силового взаимодействия между
колесами крана и подкранового пути. На
ведущие колеса крана (рис. 6.1) действуют
силы сцепления Т, равные разности сил
сцепления ведущих колес с рельсами Рф
(Р —нагрузка на колесо; ф— коэффициент
сцепления) и сил статического сопротивле-
ния. Последние силы складываются из сил
трения в подшипниках ведущих колес и сил
трения качения колес по рельсу. Помимо
сил Т при взаимодействии реборд колес
крана с рельсом в зоне контакта возникает
боковая сила Р и сопротивление от трения
реборды о рельс Rf (f = 0,2 — коэффициент
трения скольжения). Силы упругого про-
скальзывания на колесах крана, используя
зависимость (6.5), могут быть записаны
следующим образом:
= 44) = 0;
П" = г<2> =
где I, b — соответственно пролет и база кра-
на; хс и ус—обобщенные координаты цен-
тра инерции моста; ср — угол поворота.
104
Статистический анализ отклонений под-
кранового пути от проектного положения,
выполненный на основании данных гео-
дезической съемки состояния ряда‘ подкра-
новых путей, показал, что средний квадрат
отклонения 0^ = 2,5-Ю~5 м2, а корреля-
ционная зависимость удовлетворительно ап-
проке и м и р у е тся выражением
Л «о
X (cos₽o7.---— sinp0|z|), (6.8)
где a0 и p„— параметры корреляционной
функции; % — интервал корреляции, м.
Спектральная плотность, соответству-
ющая корреляционной функции, имеет вйд
4 а со2 сы
Su (со) = -----------------(6.9)
0 со4 + 2a со2 +
Здесь а —Уо а, р = Уоро, m2 = v2 (а2+
+р2 ), а = а2 — р2 (o = y0v, где со — угловая
частота; V — 2TIL — волновое число; L — дли-
на волны, м.
Дифференциальные уравнения движе-
ния моста крана:
Mb
0о
Ik
УотА
0о
(6.10)
k
2у0
системы
перемещение начала подвижной
координат у=ум + (6/2) ф, где М — сосре-
доточенная в центре инерции масса моста,
тележки и груза; I — момент инерции моста.
Остальные параметры системы приведены
выше.
Среднее значение и средний
боковой силы:
2J г И/24-262) ~
квадрат
г vQ(fl-b)
4Л
------- Ф2 4-
(f Z— 6)2 v
Vo (fj — b)2
выражаются через статистические характе-
ристики угла поворота
Оу т2(С1т2 + С1)
а=__£.------*------(6Л2)
(Cs - Cj m2)2 + С2
где Ci=-^- (/2 + 262-6//);
4
— (/2+ 462 _ 2bfl)\
о
С3-= 2k (f I— Ь); С4 =
м
{fl-by,
va
Так как у = у=у = 0, то ф = ф — ср’—О
и, следовательно, J? = 0. Средние квадраты
производных угла поворота равны:
Ф3 = т2 ф3, ф2 = zzz4 ф2.
Подставляя ф2, ф2 и ф2 в (6.II) и пре-
небрегая членами, содержащими т4 и т6,
получим выражение для среднего квадрата
боковой силы
= 16Л2 ml о2 .
V д/о
Из изложенного следует, что при кон-
такте рельса с одной ребордой колеса по-
перечное смещение моста происходит без
поворота, а боковая сила определяется на-
грузкой на колеса и статистическими ха-
рактеристиками подкранового пути и не
зависит от геометрических размеров крана.
Учитывая сказанное, средний квадрат силы
упругого проскальзывания может быть за-
писан следующим образом:
Движение при контакте рельса с ре-
бордами колес, расположенных на одной
стороне крана (рис. 6.2). На этом рисунке
Д1 и —боковые силы на первом и четвер-
том колесах крана. Обобщенные координа-
ты центра крана выражаются через попе-
речные смещения колес 1 и 4 следующим
образом:
1 , 1
У=~^~ (Ум + УыУ. ф = ~ (Ум — Ум),
где z/oi и Ум—отклонения подкранового пу-
ти в точках контакта / и 4 колес крана.
Дифференциальные уравнения движе-
ния крана:
Мх = 2Т — Rif + RJ-,
Ri — #4 = м у + — (у + 0о ф);
00
(6.11)
При неучете влияния у и ф выражения
для боковых сил имеют вид
— Ai у + Дг Ф 4~ Аз ф I
/?4 — -А У — А2 ф + Д5 ф,
л 1 Л 2k(f!±b)
где At = — Д3 = ------------
0о b
(6.14)
105
Рис. 6.2
k (l2~2b2)
2vq b
Статистические характеристики и R4
вычисляются следующим образом. Усредняя
по времени обе части систем (6.14), полу-
чим
я1 = /?4 = 0.
Возводя обе части системы в квадрат
я учитывая, что
Ф2 Оуо (1 — cos т г0);
т2 0 + cos тхйу,
ЧУ «
tn sin zn т0, где т0 = Z>/u0,
получим средний квадрат боковой силы R% :
fe2 wo
4b2
[Wq (Z2 262)2 +
(6.15)
Чтобы получить R4, следует в выраже-
нии (6.15), заменить на (fl — b).
Таким образом, боковые силы, возни-
кающие при взаимодействии с рельсом двух
реборд колес крана, в отличие от случая
движения крана при контакте с рельсом
одной реборды зависят и от соотношения
пролета крана к его базе. Аналогичные вы-
ражения для средних квадратов боковых
сил получаются для случая движения при
контакте рельс ребордами колес, располо-
женных по диагонали.
Расчетные значения боковых сил для
четырехколесных и многоколесных кранов
приведены в работе [3]. Там же вычисле-
ны боковые силы с учетом жесткости под-
крановой эстакады.
Краны с раздельным приводом. На па-
раметры движения кранов с раздельным
приводом при изменяющемся моменте сил
сопротивления заметное влияние оказывает
электромагнитная инерция двигателей. Как
показали исследования [2], при быстро ме-
няющихся (внешних нагрузках токи в обмот-
ках ротора и статора и -вращающий момент
не соответствуют частоте вращения ротора
в установившемся режиме. В связи с этим
двигатели крана развивают различные ди-
намические моменты, существенным обра-
зом влияющие на кинематику движения мо-
ста. При этом мост крана, обладая извест-
ной податливостью, начинает участвовать в
перераспределении тяговых усилий. Соот-
ветственно уменьшаются и боковые силы,
действующие на колеса крана. Задача изу-
чения степени участия моста во взаимодей-
ствии электродвигателей до настоящего вре-
- мени не рассмотрена.
СПИСОК ЛИТЕРАТУРЫ
1. Балашов В. П. Поперечные силы
при движении мостовых кранов с централь-
ным приводом. — Труды (Сб. тр., Науч,
тр.) / ВНИИПТМаш. М., 1960, № 2.
2. Балашов В. П. Боковые силы в
кранах мостового типа .в периоды пуска и
торможения.—Труды (Об. тр.,. Науч,
тр.) / ВНИИПТМаш. М., 1970, № 5.
3. Барштейн М. Ф., Зубков А. Н. Ис-
следование поперечных сил, возникающих
при движении мостового крана. — ь кн.:
Динамика сооружений. М., 1968.
4. Брусиловский А. И. Исследование
тормозных сил тележки’мостового крана.—
В кн.: Исследование по динамике соору-
жений. М., 1951.
5. Ишлинский А. Ю. О проскальзыва-
нии в области контакта при трении каче-
ния. — Изв. АН СССР, ОНТ 1956, №6.
6. Кикин А. И. Особенности проекти-
рования стальных конструкций зданий ме-
таллических цехов при учете условий экс-
плуатации.— В кн.: Вопросы применения
стальных конструкций в строительстве. М.,
1953.
7. Ручимский М. Н. О вертикальных
динамических усилиях, возникающих при
движении мостового крана по подкрановым
балкам.— В кн.: Исследование по динами-
ке сооружений. М., 1951.
8. Справочник по динамике соору-
жений. М., Стройиздат, 1970.
9. Филиппов А. П., Кохманюк С. С.
Динамическое воздействие подвижной на-
грузки на стержни. Киев, 1967.
10. Хохарин А. X. О боковых воздей-
ствиях мостовых кранов на каркас про-
мышленного здания. —'Промышленное
строительство, 196'1, № 9.
11. Carter F. W. Proceedings of the
Royal Society of London, v. 121, 1928.
\2. Rocard У. La Stabilite de Route
des Lokomotives. Paris, 1936.
РАЗДЕЛ 7. ОСОБЫЕ РЕЖИМЫ РАБОТЫ КОНСТРУКЦИЙ,
НЕСУЩИХ ЭНЕРГЕТИЧЕСКИЕ АГРЕГАТЫ
(И. С. ШЕЙНИН)
Особые (анормальные) режимы работы
энергетических машин возникают в резуль-
тате нарушения нормальной работы или
разрушения каких-либо элементов машины.
Образующиеся при таких режимах динами-
ческие нагрузки на строительные конструк-
ции, на которых установлены машины, от-
носятся к особому сочетанию нагрузок.
При проектировании этих строительных
конструкций необходимо представлять при-
роду анормальных режимов, характер яв-
лений, приводящих к их возникновению, и
располагать такими количественными харак-
теристиками динамических нагрузок, кото-
рые позволили бы провести расчет и обес-
печить надежность и экономичность строи-
тельных конструкций, поддерживающих ма-
шину.
7 1. ПРИРОДА ОСОБЫХ РЕЖИМОВ
И СООТВЕТСТВУЮЩИЕ
ИМ ДИНАМИЧЕСКИЕ НАГРУЗКИ
Наиболее распространены энергетиче-
ские машины двух видов — вертикальные
гидроагрегаты и паротурбоагрегаты.
Вертикальные гидроагрегаты [1, 3] со-
стоят из гидравлической турбины и гидро-
генератора, имеющих общий вертикальный
вал, вращающийся в двух или трех направ-
ляющих подшипниках, который передает
осевую составляющую нагрузки на подпят-
ник (рис. 7.1). Наиболее распространены
реактивные турбины — поворотно-лопаст-
ные и радиально-осевые (рис. 7.2). Генера-
торы с подпятником, расположенным выше
магнитной оси ротора (на верхней кресто-
вине), называют подвесными, а при распо-
ложении подпятника ниже магнитной оси
ротора (на нижней крестовине, на крышке
турбины или на специальной опоре)—зон-,
тичными. Статические нагрузки на подпят-
ник зависят от массы ротора, диаметра ра-
бочего колеса турбины и напора. Для наи-
более крупных агрегатов эти нагрузки мо-
гут достигать 35 МН. Частоты вращения
гидроагрегатов могут быть от 55—90 мин-1
при низких напорах, когда применяют по-
воротно-лопастные турбины, до 70—
200 мин-1 при более высоких напорах, ког-
да применяют радиально-осевые турбины
Для строительных конструкций, несу-
щих вертикальные гидроагрегаты, расчет-
ными являются особые режимы работы че-
тырех видов [2, 8].
1. При коротком замыкании на зажи-
мах генератора или на шинах генератор-
ного напряжения на ротор и статор дейст-
вует крутящий момент Л4к.з, кН-м, макси-
мальное значение которого
’60Хк.з (7.1)
/об Xj
Рис, 7.1. Расположение подпятника и направляющих подшипников в агрегатах с подвесными и зон-
тичными гидрогенераторами
а — три направляющих подшипника, подвесной генератор, верхний подшипник в общей масляной
ванне с подпятником; б — два направляющих подшипника, подвесной генератор, верхний подшипник
в общей масляной ванне с подпятником; в — три направляющих под шипника, зонтичный генератор,
подпятник спирается на нижнюю крестовину, средний подшипник в общей масляной ванне с подпят-
ником; г — два направляющих подшипника, зонтичный генератор, подпятник и верхний подшип-
ник в общей масляной ванне, подпятник с опорой на крышке турбины; д — три направляющих под-
шипника, зонтичный генератор, подпятник расположен на крышке турбины; е — два направляю-
щих подшипника, верхний под ротором, зонтичный генератор, подпятник расположен на крышке
турбины; ж— два подшипника, зонтичный генератор, единый вал, подпятник и верхний подшип-
ник в общей масляной ванне, подпятник с опорой на крышку турбины; 1 — направляющий подшип-
ник; 2 — подпятник; 3 — подпятник, объединенный с направляющим подшипником в общей масляной
ванне; 4 — верхняя крестовина; 5 — нижняя крестовина; 6 — опора подпятника; 7 — крышка турбины
107
Рис. 7.2. Реактивные турбины
а — поворотно-лопастная; б — радиально-осевая: в — подвод воды к турбине круглой металличе-
ской спиральной камерой; 1—направляющий аппарат; 2— рабочее колесо; 3 — отсасывающая тру-
ба; 4—статор турбины
где Лк.з — коэффициент, принимаемый в
зависимости от номинальной мощности ге-
нератора Л/ц, МВт, по следующей зависи-
мости: Мн — менее 320, 500, 1200; Лк.з—
1,4; 1,6; 1,9, а при промежуточных значе-
ниях Мн— по линейной интерполяции;
/об — частота вращения ротора, с-1 или
Гц, называемая также оборотной частотой;
х — сверхпереходная реактивность гене-
ратора по продольной оси, значение кото-
рой указывается в паспорте машины и
обычно находится в пределах 0,25—0,35 для
генераторов без демпферных обмоток и
0,15—0,25 для генераторов с демпферными
обмотками, а при отсутствии паспортных
данных принимают равным нижнему значе-
нию; тИн — номинальный крутящий момент,
кН - м.
Время нарастания этого момента от
нуля до максимального значения /к.3 зада-
ется заводом — изготовителем генератора и
находится обычно в пределах 0,005—0,01 с.
Для приближенных расчетов можно при-
нять, что закон нарастания близок к экс-
поненциальному:
Чез (О = Чсз.м~ (A4B>3.M-AfH)e-₽'.(7.2)
Если Р принять из условия, что при
/ = /к.з момент ЛГк.з будет достигать 95%
максимального значения, то
In 0,05
^к.з
(7.3)
Таким образом, для приведенных вы-
ше значений ^к.3 величина р лежит в пре-
делах 300—600 с-1.
Момент короткого замыкания практи-
чески полностью передается на подгенера-
торную конструкцию через опорные части
статора генератора.
2. При коротком замыкании половины
обмоток полюсов ротора генератора возни-
кает радиальная сила одностороннего тя-
жения ротора к статору, линия действия
которой вращается с оборотной частотой.
Максимальную амплитуду этой силы Рк.з.м,
кН, приближенно определяют по формуле
рк.з.м = 180Рг/Л (7.4)
где Di — диаметр расточки статора, м; It —
длина сердечника статора, м.
Вследствие высокой индуктивности об-
моток ротора генератора время /к.з нара-
стания этой силы велико и при мощностях
генераторов 40—500 МВт будет соответст-
венно от 1,5 до 2,5 с.
Таким образом, через направляющие
подшипники на подгенераторную конструк-
цию при таком коротком замыкании в мо-
мент времени t действует вращающаяся
сила, проекция которой на любую верти-
кальную плоскость
/ 3t \
Р (t) = р 1 р ^к.з х
х К.З V' К.З.М \1 — е
X sin (2л/об/ — фн), (7-5)
где фн — угол между плоскостью^ для ко-
торой определяют проекцию силы, и верти-
кальной плоскостью, проходящей через
равнодействующую сил одностороннего тя-
жения, в момент начала короткого замыка-
ния. Линия действия силы Рк.з(7) прохо-
дит через ось агрегата на высоте магнит-
ной оси ротора генератора. Равная ей по
величине и обратная по направлению сила
действует на сердечник статора и через не-
го на строительные конструкции.
3. При аварийном сбросе электрической
нагрузки или при аварийной потере возбу-
ждения генератором скорость вращения аг-
регата может возрасти до угонной Пу,
об/мин, указываемой обычно в паспорте аг-
регата, что соответствует частоте fy=ny/
/60 Гц. При этом амплитуда горизонталь-
ной возмущающей силы вследствие меха-
нического дебаланса достигает
Ру ~ Рц (/у//об) > (7*6)
где Рц — определяют по графику, приведен-
ному на рис. 7.3, в зависимости от мощно-
сти агрегата.
Линия действия этой силы проходит
через ось агрегата на высоте центра тяже-
сти ротора гидроагрегата.
4. При отрыве одной из лопастей по-
воротно-лопастной турбины внезапно воз-
никает сила механического дебаланса
Ротр—(2л fog)2 (7-7)
где тл, Гл—соответственно масса и рас-
стояние от оси агрегата до центра масс
лопасти.
108
Линия действия этой силы вращается
с оборотной частотой в горизонтальной
плоскости, лежащей на высоте центра масс
лопасти.
Для гидроагрегатов с радиально-осевой
турбиной проверку на отрыв лопасти не
проводят. Данные о значениях анормаль-
ных нагрузок на некоторых вертикальных
гидроагрегатов приведены в табл. 7.1.
Паротурбоагрегаты состоят из паровой
турбины, турбогенератора и возбудителя,
имеющих, как правило, один общий гори-
зонтальный вал (двухвальные турбины из-
готовляют значительно реже). Паровая тур-
Рис. 7.3. Зависимость амплитуды оборотной со-
ставляющей динамической нагрузки, возникаю-
щей в результате механического дебаланса, от
номинальной мощности вертикального гидроагре-
гата
бина большой мощности [11] представляет
собой набор отдельных турбин (цилинд-
ров) высокого, среднего и низкого давле-
ния, роторы которых объединены чаще все-
го в один общий валопровод с помощью
жестких или упругих муфт (рис. 7.4). Ста-
тор каждого цилиндра самостоятельно опи-
рается на фундамент и крепится к нему с
помощью дистанционных болтов. Послед-
ние допускают сравнительно небольшие
сдвиги лап статора по фундаментной раме
при тепловых деформациях турбины в про-
цессе прогрева во время пуска либо охлаж-
дения после остановки (подобные, но мень-
шие реформации происходят и при измене-
нии режимов работы турбины), но препят-
ствуют срыву машины с фундамента. В
конструкции статора предусмотрены одна
или несколько точек, зафиксированных от
сдвига по фундаменту. Эти точки называют
фикс-пунктами.
При обычных колебаниях в системе
турбоагрегат — фундамент упругие силы и
трение между лапами статора и фундамент-
ной рамой, как правило, обеспечивают сов-
местность их перемещений, в связи с чем
при динамических расчетах на нормальные
эксплуатационные нагрузки обычно счита-
ют смежные точки статора и фундамента
жестко связанными. Можно предполагать,
что при более сильных динамических воз-
Рис. 7.4. Энергетические паровые турбины мощностью
а — 300 МВт ЛМЗ; б — 300 МВт ХТГЗ; в — 500 МВт ХТГЗ; г — 500 МВт для атомных электростан-
ций ХТГЗ; д — 800 МВт ЛМЗ; е — условные обозначения; 1 — цилиндр высокого давления; 2 — ци-
линдр среднего давления; 3 — цилиндр низкого давления; 4 — генератор; 5 — упругая муфта; 6 —
жесткая муфта; 7 — подшипник опорный встроенный; 8 — то же, выносной; 9 — подшипник упорно-
опорный выносной; 10 — подшипник приставной; 11—впуск свежего пара; 12 — передача пара че-
рез промежуточный подогрев; 13 — выпуск пара в конденсатор
109
ТАБЛИЦА 7.1. ЗНАЧЕНИЯ АНОРМАЛЬНЫХ НАГРУЗОК
ОТ ВЕРТИКАЛЬНЫХ ГИДРОАГРЕГАТОВ1
Станция
Частота вра-
щения, об/
/мин
М
к.з.м
кН*м
Кегумская
Нарвская
Цимлянская
Павловская
Горьковская
Новосибирская
Каховская
Иркутская
Волжские
сходненская
Г юмушская
Мингечаурская
Червакская
Красноярская
Саяно-Шушенская
Диаметр
расточки
статора,
м
if
Длина
сердечника
статора
lt, м
II О В О Р ОТ Н О -лопает ными турбин а м и
26,3 107,1 300 6,48 1,53 0,23 240 1780 1180
52 88,2 180 9,69 1,63 0,20 660 2840 960
71,5 62,5 134 12,8 2,25 0,21 1210 5180 1240
103,5 83,3 167 10,96 2,30 0,26 1070 4540 1330
123,5 68,2 140 14,3 2,54 0,14 2900 6540 1500
С ради а л ь н с - о с е в ы ь ! И Т у р б 1 i н а м и
25 187,5 370 4,94 1,49 0,33 90 1320 580
66 375 600 3,86 2,60 0,21 188 1810 700
85,5 125 236 7,78 2,53 0,23 666 3540 1100
155 187,5 393 7,70 2,35 0,17 1090 3260 1650
500 93,8 190 16,1 1,75 0,30 4550 5070 1680
640 142,8 280 11,85 2,75 0,30 3957 5870 1600
[9] и по заводским проспектам.
1 Данные по гидроагрегатам приведены по
действиях, связанных с особыми режимами
работы агрегата, возможны перемещения
лап статора относительно фундамента.
Корпус статора генератора жестко кре-
пят к фундаменту, но сердечник статора в
большинстве мощных генераторов подвешен
к корпусу через виброизоляторы [2, 10],
благодаря чему вибрации корпуса и дина-
мические нагрузки от статора на фунда-
мент в обычных стационарных режимах
достаточно малы. Подшипники, в которых
вращается ротор, встроены в корпуса ста-
торов цилиндров либо вынесены из этих
корпусов и самостоятельно опираются на
фундамент. В последнем случае часть сил
взаимодействия между ротором и статором
замыкается через фундамент.
Природа возникновения анормальных
режимов в турбоагрегатах аналогична опи-
санной выше для гидроагрегатов.
1. При коротком замыкании на зажи-
мах генератора максимальный момент, дей-
ствующий на ротор и статор Мк.з.м, и за-
кон его нарастания во времени определяют
по тем же формулам (7.1) — (7.3), причем
время нарастания /к.з характеризуется те-
ми же величинами, что и для гидрогенера-
торов. Однако в некоторых случаях необ-
ходимо учесть и фактический закон изме-
нения момента короткого замыкания. Это
можно сделать по формулам, которые при-
водятся в книге [10]. Здесь необходимо
отмстить только, что математически этот за-
кон может быть описан суммой внезапно
возникшей постоянной и двух гармонических
составляющих, частоты которых равны f и 2/,
где f— частота переменного тока в сети.
Кроме того, иногда приходится различать
двухфазное и трехфазное короткое замы-
кание, характеризующиеся различными ко-
личественными оценками величин составля-
ющих.
В последние годы в отечественной и
зарубежной литературе [4, 5, б, 7, 12] по-
явились расчетно-теоретические работы,
указывающие на возможность достижения
еще большего значения крутящего момента
при коротком замыкании, "если оно окажет-
ся кратковременным либо быстро отклю-
чится короткозамкнутый фидер. При расче-
те низкочастотных фундаментов следует
учитывать, что из трех вышеупомянутых
составляющих закона изменения момента
внезапно возникшая постоянная составля-
ющая может оказаться большей в то вре-
мя, как переменные составляющие станут
меньшими, чем при коротком замыкании
без отключения.
Поскольку сердечник статора соединя-
ется с корпусом генератора через вибро-
изоляторы, то момент короткого замыкания
передается на фундамент в преобразован-
ном виде. Для приближенных оценок при-
нимают, что максимальный момент умень-
шается примерно в 1,5 раза, а время его
нарастания увеличивается в 1,5—2 раза.
2. При оасчете усилий от короткого
замыкания обмоток полюсов ротора гене-
ратора можно использовать те же соотно-
шения (7.4) и (7.5), что и для гидрогене-
раторов в те же данные о времени £к.з-
3. Фундаменты под турбоагрегаты не
рассчитывают на возможность возрастания
частоты вращения валопровода турбоагре-
гата при внезапном сбросе нагрузки или
потере возбуждения.
4. При отрыве одной или двух турбин-
ных лопаток внезапно возникающая сила
механического дебаланса может быть опре-
делена по формуле (7.7). При этом необ-
ходимо иметь в виду, что для каждого под-
шипника наиболее существенна сила, кото-
рая возникает при отрыве лопаток, бли-
жайшей к этому подшипнику ступени тур-
110
бины. Наибольшая сила возникает при
отрыве лопаток последней ступени низкого
давления, так как эти лопатки имеют наи-
большие размеры. Обычно эту силу и прИг
нимают в качестве расчетной при проверке
прочности фундамента. Поскольку ротор
низкого давления, равно как и весь вало-
провод турбоагрегата на рабочих оборотах,
нельзя считать жестким, то и силу, возни-
кающую при отрыве лопатки, можно рас-
пределять между подшипниками ротора
обратно пропорционально расстояниям до
них только в качестве первого приближе-
ния. Более точным является определение
сил, передающихся на подшипники, на ос-
нове расчета гибкого валопровода в стаци-
онарном режиме. Но вполне надежен толь-
ко расчет переходного процесса в системе
турбоагрегат — фундамент при внезапном
дебалансе. Данные о значениях некоторых
анормальных нагрузок от паротурбоагрега-
тов приведены в табл. 7.2,
ТАБЛИЦА 7.2. ЗНАЧЕНИЯ НЕКОТОРЫХ
АНОРМАЛЬНЫХ НАГРУЗОК
ОТ ТУРБОАГРЕГАТОВ
Тип 1 - .. Мощ- ность, МВт . 3 . м ’ кН -м Р - w о.л кН i
ВК-100-6+ТВФ-100-2 100 1920 261
К-200- 1.30+ТВВ-200-2 200 2150 366
К-300-240+ТВВ-.320-2 300 7680 632
K-500-1Q5+TBB-500-2 500 12 800 632
К-800-24-0+ТВВ-8СЮ-2 800 17 900 632
* Указаны значения расчетного момента для
фундаментов.
7.2. НЕКОТОРЫЕ СВЕДЕНИЯ
О РАСЧЕТЕ НА НАГРУЗКИ,
ВОЗНИКАЮЩИЕ
В ОСОБЫХ РЕЖИМАХ
Все нагрузки, возникающие в особых
режимах работы энергетических машин,
можно разделить на две группы: 1) быстро
нарастающий момент, который действует
на сердечник статора и передается от него
на поддерживающую конструкцию; 2) срав-
нительно медленно нарастающая или вне-
запно возникающая гармоническая сила,
которая передается от ротора через под-
шипники. Однако поскольку конструкции,
несущие гидро- и турбоагрегаты, неодина-
ковы, методы их расчета оказываются раз-
ными.
Конструкции, несущие гидроагрегаты,
обычно весьма массивны (рис. 7.5), а их
собственные частоты намного выше частот
вращения гидроагрегатов. Поэтому для
них основной является проверка на срав-
нительно быстро нарастающий момент ко-
роткого замыкания ПО1 (7.2).
Перед проведением точного расчета
следует выполнить сравнительно простую
оценку прочности конструкции на основе
статического расчета с применением верх-
ней оценки коэффициента динамичности по
рис. 7.6, вводимого в зависимости от отно-
сительной скорости нарастания нагрузки
•р//о, где fo — низшая частота, Гц, собствен-
ных крутильных колебаний системы, состо-
ящей из статора генератора, рассматривае-
мого как абсолютно твердое тело, и упру-
гой поддерживающей конструкции. Как
видно из рис. 7.6, при О,3/о момент
можно считать приложенным статически, а
при p^2Ofo практически Кд = 2. В неко-
торых случаях, если проверка с введением
Кд = 2 показывает достаточную прочность
поддерживающей конструкции, то нет не-
обходимости определять даже /о-
Что касается гармонических сил, пере-
дающиеся от ротора через подшипники
при коротких замыканиях в цепи ротора,
при угоне или при отрыве лопасти, то, по-
скольку собственные частоты колебаний
конструкций обычно намного превышают
оборотные частоты ротора, считают, что
достаточно, чтобы строительные конструк-
ции были равнопрочны с подшипниками,
которые на них опираются.
Фундаменты турбоагрегатов большой
мощности (135 МВт и более на 3000 об/
/мин) в настоящее время выполняют в ви-
де пространственной одноэтажной рамы,
опирающейся через массивную нижнюю
плиту на грунтовое основание (рис. 7.7).
Агрегат устанавливают на верхнее строе-
ние, а между колоннами фундамента раз-
мещают конденсаторы турбины, трубы, по
которым подают и отводят пар, конденсат
и охлаждающую воду, а также каналы с
шинами электрического напряжения и вспо-
могательное оборудование. Низшие собст-
венные частоты системы турбоагрегат —
фундамент — основание, как правило, в 7—
15 раз ниже рабочей (50 Гц) частоты вра-
щения ротора. Спектр собственных частот
весьма густ и вблизи рабочей частоты всег-
да существует несколько собственных. При
динамическом расчете системы на обычные
эксплуатационные нагрузки проверяют амп-
литуды колебаний на крышках подшипни-
ков и на фундаменте в местах опирания
подшипников. При такой проверке, если
фундамент запроектирован правильно, бли-
зость нескольких высших собственных час-
тот к рабочей оборотной частоте практиче-
ски не сказывается отрицательно, так как
на графиках частотных характеристик си-
стемы, построенных с учетом затухания в
материале фундамента, пики, соответству-
ющие этим частотам, не проявляются либо
проявляются весьма слабо.
Однако опыт расчетов на особые воз-
действия пока настолько мал, что не уда-
ется высказать на его основании какие-
либо соображения о возможных упрощени-
ях расчетной схемы системы и методов рас-
чета. Можно только отметить, что в таких
расчетах статоры цилиндров высокого и
среднего давления могут быть приняты как
абсолютно твердые тела, чего нельзя ска-
зать о статорах цилиндров низкого давле-
ния и генератора, которые имеют сравни-
тельно малую жесткость, так что низшие
собственные частоты этих элементов оказы-
ваются ниже оборотной частоты.
Корректная постановка задачи расчета
системы турбоагрегат — фундамент — осно-
111
Рис. 7.5. Поперечный
разрез здания Крас-
ноярской ГЭС на
Енисее с радиально-
осевой турбиной и
зонтичным генерато-
ром 500 МВт,
93,75 мин—1
1 — напорный тру-
бопровод; 2 — повы-
шающий трансфор-
матор; 3 — токопро-
воды от генератора
к трансформатору;
4 — спиральная ка-
мера
Рис. 7.6. Зависимость коэффициента динамично-
сти от относительной скорости нарастания на-
грузки
вание на особые воздействия связана с
построением алгоритмов и программ расче-
та на ЭВМ сложной системы, которая со-
стоит из пространственной рамы, взаимо-
действующей с элементами машины. При
спектральном подходе для построения час-
тотной характеристики системы каждую из
ее частей сначала рассчитывают самостоя-
тельно, а потом они соединяются по методу
динамических жесткостей или податливо-
стей. Такая постановка предполагает ли-
нейность системы.
Опыт расчета более простых конструк-
ций с учетом нелинейности позволяет за-
ключить, что расчеты переходных процес-
сов без учета нелинейных эффектов, возни-
кающих вследствие' проскальзывания в
элементах, сухого трения и больших дефор-
маций, идут в запас прочности. Качествен-
Рис. 7.7. Общий вид фундамента под турбоагрегат S00 МВт (по
проекту Харьковского отделения института Теплоэлектропроект)
112
ное соображение о том, что учет таких не-
линейностей ведет главным образом к уче-
ту дополнительной диссипации энергии, да-
ет возможность распространить этот вывод
и на более сложные системы,
а
СПИСОК ЛИТЕРАТУРЫ
1. Владиславлев Л. А. Вибрация гид-/
роагрегатов гидроэлектрических станций.
М., 1972.
2. Детинко Ф. М., Загородная Г. А.,
Фастовский В, М. Прочность и колеоания
электрических машин. Л., 1969.
3. Использование водной энергии. [
! Под ред. Д. С. Щавелева. Л., 1976.
4. Казовский Е, Я., Насибов В. А.,
. Ру бисов Г. В. Переходные процессы при
отключении кратковременных к. з. синхрон-
ных машин. — Изв. АН СССР. Сер. «Энер-
гетика и транспорт», 1972, № 5.
5. Казовский Е. Я., Рубисов Г, В.
Переходные процессы в синхронной маши-
не, работающей параллельно с сетью, при
отключении кратковременных коротких за-
мыканий.— Электротехника, 1975, № 12.
6. Казовский Е. Я., Рубисов Г. В. Пе-
реходные процессы при отключении несим-
метричных коротких замыканий генерато-
ра, включенного в мощную сеть. —Изв. АН
СС С Р. С ер. «Э нер гетика и тр а н спорт»,
1975, № 3,
7. Казовский Е. Я., Рубисов Г. В.
Скручивающий момент, действующий на
валопровод агрегата при внезапных изме-
нениях нагрузки и при отключении внезап-
ных коротких замыканий. — Изв. АН СССР.
Сер. «Энергетика и транспорт», 1975, № 4,
8. Рекомедации по определению ди-
намических нагрузок, передаваемых верти-
кальным гидроагрегатом на сооружение.
П14^73 / ВНИИГ. Л., 1974.
9. Турбинное оборудование гидро-
электростанций. Руководство по проекти-
рованию. / Под общей ред. А. А. Морозова.
М. — Л., 1958.
1'0. Турбогенераторы. Расчет и
струкция. / Титов В.
кий Г. М., Загородная Г. А. и др7 Под
ред. Н. П. Иванова и Р. А. Лютера. Л.,
1967.
И. Щегляев А. В. Паровые турбины.
М., 1976.
12. Loge К, Lambrecht D. Die Aus.
wirkung dreipoliger Netzkurzschlusse mit
Kurzschlussfortschaltung auf die mechani-
sche Beanspruchung van Turbosatzen.
ETZ —A, Bd 95, 1974, H. 10.
КОН-
, Ху торец-
РАЗДЕЛ 8. ДИНАМИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ
СООРУЖЕНИЙ С ОСНОВАНИЕМ И ПЕРЕДАЧА КОЛЕБАНИЙ
ЧЕРЕЗ ГРУНТ [ПРОМЫШЛЕННАЯ СЕЙСМИКА]
(В. А. ИЛЬИЧЕВ)
8.1. ОБЩИЕ СВЕДЕНИЯ
К проблеме, сформулированной в назва-
нии раздела, приводят многие практические
задачи: расчет и проектирование фундамен-
тов под традиционные машины повышенной
мощности, под новые машины и технологи-
ческое оборудование с динамическими на-
грузками, фундаментов испытательных виб-
ростендов, работающих в широком диапазо-
не частот, более точная оценка парамет-
ров колебаний строительных конструкций с
учетом податливости основания фундамен-
тов и излучения энергии в грунт, опреде-
ление уровня колебаний грунта, возбужда-
емых волнами напряжений, распространя-
ющимися от промышленных источников виб-
раций и транспортных средств, определение
уровня вибрации различных приемников
колебаний для сопоставления с допусти-
мым уровнем или для оценки требуемого
снижения фактического уровня вибраций;
последнее относится к фундаментам преци.
зионных станков и оборудования, к здани-
ям, предназначенным для длительного' пре-
бывания людей (жилые, общественные,
больничные и т. п.), и другим, расположен-
ным рядом с источниками колебаний. До-
стоверное определение динамических на-
пряжений на контакте подошвы фундамен-
та с грунтом, а также уровня колебаний
грунта необходимо для решения вопроса
о возможности изменения свойств грунтов
при вибрации, которое может привести к
возникновению длительных незатухающих
осадок фундаментов, главным образом зда-
ний, в которых размещено оборудование с
динамическими нагрузками.
Проблема динамического' взаимодейст-
вия сооружений с основанием и передачи
колебаний через грунт сложна и далека от
своего решения в том объеме, который оп-
ределяется требованиями практики. В на-
стоящее время пока имеется лишь ограни-
ченное число исследований, результаты ко-
торых могут быть использованы в инже-
нерной деятельности. Ряд задач и их прак-
тических приложений рассмотрен в книгах
[6, 20], а также в работах [3, 4, 5, 8, 14,
17] и др.
Для решения указанной проблемы необ-
ходимо изучить колебания сложной динами-
ческой системы, состоящей из трех различ-
ных подсистем: 1) сооружения или фунда-
менты—источники колебаний; 2) грунт;
3) сооружения или фундаменты — приемни-
ки колебаний, приняв некоторые упрощаю-
щие предположения. Основное из них—
линейная постановка задачи, возможность
использования которой следует из анализа
опыта эксплуатации промышленных зда-
ний. Чаще всего вибрации не вызывают по-
вреждений и пластических деформаций эле-
ментов правильно запроектированных и
возведенных зданий, и колебания таких
строительных конструкций происходят в
упругой стадии. Даже в тех немногих слу-
чаях, когда вибрации вызывают длительные
незатухающие осадки фундаментов, уровень
колебаний фундаментов и грунта можно
оценить удовлетворительно, исходя из ли-
нейной постановки, так как неупругая осад-
ка фундамента за один цикл колебаний,
как правило, на несколько порядков мень-
ше амплитуды колебаний фундамента или
окружающего грунта.
Во многих практических задачах в рас-
смотрение можно не вводить также и взаи-
модействие через грунт источника и прием-
ника колебаний. Например, для двух оди-
наковых круглых в плане фундаментов, рас-
стояние между которыми в свету превыша-
ет три диаметра, можно не учитывать их
взаимного влияния при нахождении ампли-
туд колебаний фундаментов, так как по-
грешность в определении исходных данных
сопоставима, с погрешностью пренебреже-
ния взаимнйм влиянием фундаментов.
Таким образом, с инженерной точки зре-
ния проблема может быть упрощена и раз-
бита на две относительно самостоятельные
задачи: о взаимодействии с основанием со-
оружений или отдельно стоящих фундамен-
тов как источников, так и приемников; о
распространении в грунте колебаний от за-
данных динамических воздействий.
Передаточные и импульсные переходные
функции для механических систем [15]. В
дальнейшем широко используются переда-
точные функции (ПФ) и импульсные пере-
ходные функции (ИПФ) для различных ме-
ханических систем. Свойства этих функций
определяются следующими соотношениями.
Пусть колебания некоторой механиче-
ской системы описываются векторным диф-
ференциальным уравнением
L (/) (8.1)
и соответствующими граничными и началь-
ными условиями.
Передаточная функция. Решение урав-
нения (8.1), которое удовлетворяет гранич-
ным условиям и описывает установившие-
ся гармонические колебания системы под
действием нагрузки
q (i) = Q eiat, (8.2)
имеет вид
о> (О = Q В (®) егИ? = Q [Л («) +
+ if2 (w)] eia>t, (8.3).
где со — угловая частота вынужденных ко-
лебаний; i— мнимая единица.
114
Функцию
/о (ю) = fl (®) + ^2 (со)
(8.4)
называют передаточной функцией, • а
fi(co) и /г(<о)—соответственно ее дейст-
вительной и мнимой частями.
Импульсная переходная функция. Реше-
ние уравнения (8.1) при принятых для (8.3)
граничных условиях и нулевых начальных
условиях при специальной правой части
q (О, (8-5)
где £(/) —дельта-функция Дирака, запишем
в виде
w (/) = qQwQ (/) при t > 0; ]
> (8.6)
to (/) — 0 при t < 0. J
Функция сС'о (f) является импульсной
переходной функцией для той же механи-
ческой системы.
Важно отметить, что нагрузки (8.2) и
(8.5) приложены в одних и тех же точках
данной системы и имеют одинаковые интен-
сивности и направления.
Связь между ПФ и ИПФ. Функции ПФ
и ИПФ взаимосвязаны преобразованием
Фурье:
со
’—00
о
(0 = --- I
Л
о
00
/2 (со) — — J ц>0 (/j) sin со /i d /i,(8.9)
о
ш0 (/) =
(О —
(8.10)
Функции /у (со) и ^г(со) выражаются од-
на через другую с помощью преобразова-
ния Гильберта:
А (со) =— I ~du; (8.11)
л J и — (О
-00
1 р fl (и)
f. (со) = — — du. (8.12)
л J со и
—оо
При вычислении интегралов в (8.10) —
(8.12) полезно учитывать, что функция
fi (со) четная, а /г (со) нечетная, что видно
из первых формул в (8.8) и (8.9). Из вы-
ражений (8.11) и (8.12) следует также, что
ЛФ определяется полностью, если известна
только либо ее действительная, либо ее
мнимая часть. Достаточно знать одну из
функций fi(<o), А(со) или о?0(0» чтобы по^
формулам (8.7) — (8.12) найти две другие, а
также функцию /о (со).
Перемещения механической системы при
действии произвольной нагрузки. Если на
рассмотренную выше динамическую систе-
му действует произвольная нагрузка q(t),
которая при /<0 отсутствует, то колебания
тех же точек системы, для которых постро-
ены ПФ или ИПФ, определяются формула-
ми:
при использовании ПФ
00
w (/) = J Q (ш) f0 (ш) (8.13)
—оо
(8.14)
при использовании ИПФ
w (/) = I q (/ —/Д ш» (/1) dit. (8.15)
о
Формулы (8.13) — (8.15) соответствуют
предположению, что динамическая система
находилась в покое при Ненулевые на-
чальные условия могут быть учтены этими
же формулами, если ввести в нагрузку q(t)
дельта-функции или их производные.
Функции /о (со) и Wo(t) можно рассмат-
ривать как динамический (соответственно
стационарный и нестационарный) аналог
коэффициентов влияния метода сил класси-
ческой строительной механики. Примени-
тельно к задаче о действии сосредоточен-
ной силы на плоскую поверхность упругой
среды, моделирующей упругое основание,,
указанные функции представляют собой яд-
ра для данной динамической модели осно-
вания.
8.2. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ
КОЛЕБАНИЙ СООРУЖЕНИЙ,
СИЛЫ РЕАКЦИИ ГРУНТОВОГО
ОСНОВАНИЯ, КОНТАКТНЫХ
НАПРЯЖЕНИЙ И ПАРАМЕТРОВ
КОЛЕБАНИЙ ОКРУЖАЮЩЕГО ГРУНТА
Возможны различные математические
формулировки задачи о совместных колеба-
ниях двух различных систем — сооружения
и грунтового основания: 1) использование
единой расчетной схемы, объединяющей обе
системы в одну, и решение задачи о коле-
баниях этой единой более сложной систе-
мы; 2) решение задач о колебаниях каж-
дой из систем без связи с другой и затем
использование условий совместности для ре-
шения задачи о связанных колебаниях, что
и отвечает смыслу слова «взаимодействие».
Первый путь часто применяют, когда
используют численные методы решения за-
дачи— конечных разностей, конечных эле-
ментов и др., и здесь не обсуждается. Вто-
рой путь используют при теоретическом и
инженерном анализе, поскольку он позво-
ляет лучше понять механическую картину
взаимодействия, изучить качественные осо-
115
Рис. 8.1
теристики фундамента — его масса и подат-
ливость в вертикальном направлении — вхо-
дят в Lc(tt’).
Система (8.16) может быть аналитически
решена применением преобразования Лапла-
са по времени, что оказывается практически
возможным для некоторых частных случа-
ев функции Worn (/) и простых операторов
Lc(w). Решение системы (8.16) можно так-
же получить численными методами, напри-
мер заменяя дифференциальное выраже-
ние конечно-разностным, а интеграл конеч-
ной суммой.
Примеры записи системы (8.16) для
различных сооружений. Расчетные схемы
сооружений приведены на рис. 3.2,а,б.
а) Массивный фундамент под машину,
жесткое сооружение, деформациями кото-
рого можно пренебречь по сравнению с его
перемещением:
Рис. 8.2
бенности и получить количественные резуль-
таты. Динамические свойства каждой из
систем могут быть описаны различными спо-
собами — линейными дифференциальными
уравнениями, заданием передаточных или
импульсных переходных функций и др. Вы-
бор способа описания динамических свойств,
а также условий совместимости колебаний
каждой из систем влечет за собой разно-
образие математических формулировок за-
дачи о взаимодействии.
Ниже приведена постановка задачи,
когда колебания сооружения определяют-
ся линейным дифференциальным выраже-
нием, а динамические свойства основания
описываются передаточной либо импульсной
переходной функцией. Постановка задачи
дана для вертикальных колебаний, а пояс-
няющая расчетная схема показана на
рис. 8.1. Сооружение опирается на основа-
ние через невесомый абсолютно жесткий
штамп, имеющий в плане две оси симмет-
рии.
Нестационарные колебания под дейст-
вием нагрузки q(t), />0. При t<ZO на-
грузка отсутствует, и сооружение находится
в состоянии статического равновесия. Коле-
бания сооружения определяются дифферен-
циальным выражением Lc(w). Вертикаль-
ное перемещение невесомого штампа, лежа-
щего на поверхности грунтового основания,
при действии на штамп в центре симмет-
рии мгновенного сосредоточенного единич-
ного импульса определяется ИПФ wom(/).
Совместные колебания сооружения и
основания описывают системой интегродиф-
ференциальных уравнений [7]:
С(®) — г (/);
t
f>
г (/ — /1) ш0Ш (6)
О
(8.16)
Начальные условия — нулевые. Неиз-
вестными являются перемещения w(t) и
сила реакции r(t) между сооружением и
грунтом. В (8.16) wm(0—перемещение по-
дошвы сооружения. Динамические харак-
d2 w
~dF
= я (0 — г (0;
т
(8.17)
t
w (0 = Jr (/ — /1) Е’ош (*1) dtl.
о
б) Виброизолированный фундамент под
машину, П-образная рама:
+ & ~ qi (/);
(8.18)
— k (кц — w2) =q2 (0 — r (/);
Гармонические колебания рассматрива-
емой системы определяются уравнениями
№
‘Царм (IT)=Q-R; )
foul (^) ’ J
где 4арм (^)=Zc(w)e - ПФ,
соответствующая ИПФ wom(t), и учтено,
что при гармонических колебаниях, вызван-
ных нагрузкой q(t)—Qeiai*:
г (/) = R e£<s>t;
а>шЧ) = • (8.20)
Из второго уравнения (8.19) можно
найти R, и тогда для определения переме-
щений получим уравнение
£гарм + f Q ь + £ (со) = Q,
(8.21)
где k (со) = , (8.22)
/1 (®) +f2 (®)
—ft (<>)
f\ (“) + fl (“)
(8.23)
116
Таким образом, при изучении взаимо-
действия сооружения с основанием в гар-
моническом режиме колебаний можно осно-
вание заменить упругой пружиной и вязким
демпфером, характеристики которых зави-
сят от частоты колебаний.
После определения перемещений соору-
жения, в том числе и перемещения ТГШ,
можно найти силу реакции Ж®) из второ-
го уравнения (8.19):
= [lab (a>Y+k (to)] Гш. (8.24)
Существует связь между системами
уравнений (8.19) и (8.16). Система (8.19)
получается из (8.16) применением к вы-
ражению (8.16) преобразования Лапласа по
времени t и последующей замены парамет-
ра преобразований Лапласа р на tto. Об-
ратная связь также верна. Если нужно оп-
ределить перемещения сооружения и его
основания при действии произвольной на-
грузки q(t), но с обязательным условием
использования /Ош(со), то решение системы
(8.19) можно рассматривать как ПФ и
перемещения под действием нагрузки q(t)
найти по формулам (8.13) и (8.14).
О передаточных и импульсных пере-
ходных функциях для невесомого штампа.
ПФ fОШ и ИПФ «Уош, предполагаемые из-
вестными при решении систем уравнений
(8.16) и (8.19), следует находить предва-
рительно из решения контактной задачи о
действии гармонической либо импульсивной
нагрузки на невесомый штамп, лежащий на
упругом основании, которое моделирует
грунт. В результате решения такой задачи,
кроме fom(to) и ьуош(0, должны быть так-
же определены контактные напряжения
о0(х, у, to) и сто (х^ у, t) соответственно при
единичной гармонической и импульсивной
нагрузках на невесомый штамп. Некоторые
точные решения контактных задач приведе-
ны в разд. 9. Приближенные выражения
для /ош (to) и а'Ош(П при вертикальных ко-
лебаниях, а также соответствующие функ-
ции при горизонтальных и вращательных
колебаниях штампа приведены ниже.
Распределение контактных напряже-
ний. При необходимости найти распределе-
ние контактных напряжений под подошвой
фундамента после решения задачи .о дина-
мическом взаимодействии сооружения с
грунтом можно использовать следующие
формулы, аналогичные формулам (8.13) и
(8.15):
ОС
а (х, у, t) = I R (<о) <т0 (х, у,со) х
V
— ас
X e''a,t dw, (8.25)
г (t) е d со;
(8.26)
Схема решения задачи о динамическом
взаимодействии сооружения с грунтом. Ис-
ходная информация. Известны расчетная
схема сооружения, т. е. его математическая
модель >Lc(w) и ИПФ пиОш(0 невесомого
штампа, совпадающего по форме с отпечат-
ком подошвы фундамента сооружения.
Функция «Уош (0 может быть получена тео-
ретически либо экспериментально в натурных
условиях. Нагрузка на сооружение q(t) за-
дана. Записывают систему уравнений (8.16),
в результате решения которой определяют
перемещения системы w(t) и силу реакции
грунтового основания г(/). Если в исходной
информации вместо доош(0 задана fom(/),
то записывают систему уравнений (8.19).
Из ее решения определяют комплексные
амплитуды колебаний и силы реакции по
подошве фундамента. Для произвольной
нагрузки q(t) решение в этом случае может
быть получено по формуле (8.13). При не-
обходимости распределение контактных на-
пряжений находят по формуле (8.25) или
(8.26).
Определение параметров колебаний
грунта, вызванных волнами напряжений,
распространяющимися от источников коле-
баний. Из предыдущего изложения извест-
но решение задачи о распределении кон-
тактных напряжений i<j(x, у, t) под подош-
вой фундамента сооружения или сила ре-
акции r(ty Пусть известно также решение
задачи о перемещении точек поверхности
упругой среды, моделирующей грунт, при
действии на поверхность сосредоточенного
импульса или гармонической силы. Обозна-
чим это решение через go(x, у, t), где под
go понимают перемещение в направлении
любой координатной оси. Тогда перемеще-
ния поверхности грунта, вызванные волна-
ми, которые распространяются от колеблю-
щегося сооружения, определятся формулой
t
g (х, у, t) = J ( J G (X —Хь у —Ух,
о й
t — ti) go (•*!. 7/i. Z1) dxi rf/i> (8.27)
где Q — область, занимаемая штампом.
Функции go(x, у, t) приведены в следу-
ющем пункте.
Формула (8.27) по структуре аналогич-
на формуле (8.15) и go(x, у, t) является
ИЦф или ядром рассматриваемой динами-
ческой модели основания. Иногда контакт-
ные напряжения представляют в виде
п
а (х, у, 0=2 Гк <8,28)
k=o
t
где гк (/) = г (t — /J (/J d (8.29)
6
4fK(x, у)—заданные функции, по которым
производят разложение; цк(/) — функция,
определяющая изменение во времени со-
ставляющей гРк(х, у) контактных напряже-
ний в задаче о действии импульса на неве-
сомый штамп.
117
Кроме того, пусть известна ИПФ hK(x, у,
О, которая определяет перемещение в неко-
тором направлении точки поверхности с
координатами х и у при действии распре-
деленной нагрузки у), изменяющейся
во времени как 6-функция. Тогда переме-
щение этой же точки в том же направлении
под действием волн от колеблющегося со-
оружения определится формулой *
п t
А=о о
Х/гк (х, у, /j) dtx.
(8.30)
Функции /гк(х, у, /) приведены ниже
для некоторых распределений у, t).
На некотором удалении от фундамента
сооружения детали распределения контакт-
ных напряжений мало влияют на колебания
грунта, поэтому закон распределения кон-
тактных напряжений можно принять одина-
ковым для всего процесса колебаний, на-
пример как ТХх, у). Тогда вместо (8:30)
можно использовать формулу
t
g (х, У, 0 = j г (/ — /1) /г0 (х, yt /г) dtx.
о
(8.31)
Для больших расстояний от фундамен-
та, превышающих несколько длин излучае-
мых волн, можно считать источник коле-
баний точечным и использовать для оценки
уровня вибраций формулу
t
g (*. У, t) = f г (t — ti) g0 (x, у,
0
/ — /г) d tx,
(8.32)
пульсные переходные функции, которые сле-
дует использовать в формулах, приведенных
в п. 8.2.
Для сооружений, опирающихся на фун-
даменты, деформативностью которых мож-
но пренебречь, при решении задач о взаимо-
действии с грунтовым основанием можно ис-
пользовать ПФ и ИПФ для жестких неве-
сомых штампов, опирающихся на упругое
основание. К числу таких сооружений отно-
сятся трубы, башни, силосы и т. п., а также
сооружения, которые имеют отдельно стоя-
щие фундаменты под колонны: каркасные
здания, промышленные здания и т. п. Точ-
ные решения соответствующих контакт-
ных задач даны в разд. 9. Ниже приведены
приближенные выражения для некоторых
ПФ и ИПФ, которые в некоторых случаях
применять предпочтительнее, поскольку
имеется аналитическая формула, а не число-
вые результаты, и иногда эта формула весь-
ма проста, так как задача о перемещении
штампа сведена к задаче о перемещениях
системы с одной или полутора степенями
свободы, параметры которой заданы.
Вертикальные перемещения круглого не-
весомого штампа [10]. Импульсная пере-
ходная функция для круглого штампа в
предположении, что его перемещение под
действием мгновенного импульса прибли-
женно равно среднеинтегральному переме-
щению поверхности полупространства в пре-
делах круга, загруженного нагрузкой, рас-
пределенной по координате по закону ста-
тических контактных напряжений и изменя-
ющейся во времени как 6-функция, опреде-
ляется формулой
S 1
Ц,о (Т) = — — -----------Woo; Woo =
л а3 р0 Cl q
= ^oi Ч- W? + ^оз• (8.33)
в которой go — та же функция, что и в фор-
муле (8.27).
Слагаемые представляются формулами:
8.3. ПЕРЕДАТОЧНЫЕ
И ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ
ФУНКЦИИ ДЛЯ ЗАДАЧИ
О ВОЛНОВОМ ВЗАИМОДЕЙСТВИИ
СООРУЖЕНИЯ С ГРУНТОВЫМ
ОСНОВАНИЕМ, МОДЕЛИРУЕМЫМ
ПОЛУПРОСТРАНСТВОМ
При теоретическом построении ПФ и
ИПФ для грунтового основания обычно ис-
пользуют модель грунта в виде однородно-
го изотропного идеально упругого полупро-
странства. Это простейшая модель в ряду
усложняющихся моделей, позволяющая опи-
сать возникновение и распространение в
грунте продольных, поперечных и поверхно-
стных волн. Можно применять и другие мо-
дели —слой на несжимаемом основании, си-
стемы слоев на упругом полупространстве
или на несжимаемом основании и др. Одна-
ко численные результаты получены главным
образом для упругого полупространства.
Ниже приведены формулы и графики, опи-
сывающие различные передаточные и им-
0 < х < 2&;
2Й < т;
0 < х < 2<у;
2q < т;
(8.34)
В формулах (8.33) и (8.34) введены
следующие обозначения: а — радиус штам.
па; ро — плотность материала полупростран-
ства; x—C2t/a; t — время; С2=Ур7ро, Ci =
=УХ+2ц/ро — скорости упругих продоль.
ных и поперечных волн в полупространстве;
118
Рис. 8.3
Рис. 8.4
X, р — константы Ляме; v — коэффициент
Пуассона; 5 — значение импульса;
О — корень уравнения;
(-1 — 2v2)2 —4v2 а2 р2 = 0; 1
Л0 = ₽яи 2(1- 28*) +
В2 ар
Ч- 2ар Рр + +
Рр
. &21Ы
ар
aR = —1; ₽я = V 82 — д2;
Ai (V) =₽! [(1 - 2u2)2 +
+ 4y2aiPi]“‘ , at =
= /n=V2, ₽1 = r^^;
A2 (v) = 4t>2 fj; <Xi [—16 (1 — q2) X
(8.35)
Xt>' + 8 (3 —2<?2) t>« —8v2+l]-1;
a2 = У t>2 — 1 ; p2 = K^2 — q2 •
Функция
S 1
e>e(0)= —----------; w0 (r) =0,r > 2 8.
л a2 p0 Ci
Графики функций ^оо(т) приведены на
рис. 8.3. Функция ьуо(т) (8.35) может быть
аппроксимирована выражением
Ио (Т) = — —------ (q п е q +
л а2 ро с2
+ Рте_₽х)- (8-36)
Значения констант даны в табл. 8.1.
V 0 0,25 0,5
1*. 1,6 1,79 2,12
D 4,29 4,22 5,54
Н 1,68 1,32 1,23
Функция (8.36) представляет собой пе-
ремещение верхней части механической си-
стемы, показанной на рис. 8.4,а, при действии
мгновенного импульса на эту верхнюю
часть. Отсюда следует, что при расчете со-
оружений на вертикальные колебания с
учетом волнового взаимодействия с грун-
том можно полупространство, моделирую-
щее грунт, заменить указанной механиче-
ской системой, параметры которой опреде-
ляются формулами:
bi = л а2 р0 Ci; ki~ 2 лар0С! —
Ро а3 =
2 л
Ро а3;
(8.37)
а2 ро с2.
Верхняя часть системы (см. рис. 8.4,а) —
невесомая пластина, пружина с жестко-
стью kt и демпфер bi моделируют эффект,
создаваемый продольными волнами. Пара-
метры kt и bi зависят от радиуса штампа,
плотности материала полупространства и
скорости продольных волн и не зависят от
коэффициента Пуассона и скорости попе-
речных волн. Нижняя часть системы соот-
ветствует вкладу, вносимому в динамиче-
ское поведение штампа поперечными и ре-
леевскими волнами. Параметры m2, b2, k2
также зависят от размеров штампа и плот-
ности среды, но в отличие от параметров
верхней системы зависят от v и Сг и не за-
висят от скорости продольных волн. Тем
самым в модели разделено влияние про-
дольных волн и поперечных, а также реле-
евских волн на движение штампа. Про-
дольные волны создают сопротивление дви-
жущемуся штампу (фундаменту), завися-
щее от его перемещения и скорости. Попе-
речные и релеевские волны создают также
и сопротивление, которое зависит от уско-
рения движения штампа, что нашло свое
отражение в появлении массы т2. При
119
ТАБЛИЦА 8.2
V 0,00 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4
Ti У2 1,215 1,094 1,207 1,113 1,200 1,132 1,195 1,149 1,193 1,163 1,197 1,173 1,211 1,177 •ч 1,243 1,169 1,317 1,141
v->0,5, что соответствует с4~>оо, коэффици-
енты ki и стремятся к бесконечности, и
рассматриваемая модель вырождается в
систему с одной степенью свободы, имею-
щую параметры т2> Ь2 и k2.
Для диапазона значений коэффициента
Пуассона Ch<v<0,4 функция (8.33) мо-
жет быть аппроксимирована еще проще, чем
в (8.36) [11]:
Ц>о(т) = — - ъе~УгХ, (8-38)
л а? р0 Ci
где у2 = Y1 —--------- .
Л (1 — ^)
Значения у! и у2 в зависимости от ко-
эффициента Пуассона даны в табл. 8.2.
Тем самым в указанном диапазоне v
штамп, лежащий на полупространстве, мо-
жет быть заменен параллельно соединен-
ными пружиной и демпфером, параметры ко-
торых следующие:
4 ц а ,
k = ------; b = л а2 ро ci у, =
1 — ч 1
а}
4 а2 Ро с2
у2 (1 — 'О *
(8.39)
Указанная механическая модель приве-
дена на рис. 8.4,6. Выпишем теперь переда-
точные функции, соответствующие импульс-
ным переходным функциям, определяемым
формулами (8.33), (8.36) и (8.38):
б)
Для представления (8.33) имеем [12]
(- 1)/-1 Ъ = A) G/ (<Оо ») + — X
Л
<7
X I А1 (у) G}- (w0 о) dv +
о
л
(8.41)
(8.40)
Рис. 8.5
Г . Л (о>о *)
где Gi («о х) = cos со0 х-------------- ;
<о0 х
{ Ji (<о0*)
О2 (w0 х) = sin to0 x -------------- ,
to0 x
0 co0 < oo;
Ji(y)—функция Бесселя; <o0 = toa/c2; ос-
тальные обозначения прежние.
Графики функций fi и }2, вычисленные
по (8.41) для коэффициентов Пуассона v =
= 0; 0,25 и 0,5, приведены на рис. 8.5,а, б, в.
Функции fi и f2 близки к нулю при too>3,
поэтому на этих же рисунках показаны
* г**
графики функции f=WG)ofj. Выражение
(8.41) справедливо в неограниченном диа-
пазоне частот 0^ too<°o. Для ограничен-
ного диапазона частот too <1,5 решение
имеется в работах [22, 24, 25].
В гармоническом режиме колебаний
штамп, лежащий на полупространстве, со-
противляется внешней нагрузке так же, как
пружина жесткостью /г (to) и демп-
Р
а р
(/1+^2).
120
Рис. 8.6
В этом случае коэффициент демпфирования
вычисляют по формуле
3,4а2р0с2
1 — •)
(8.45)
Горизонтальные перемещения круглого
невесомого штампа [2] приближенно опре-
деляют следующей формулой, полученной в
предположении, что это перемещение приб-
лиженно равно среднему в пределах круга
перемещению от нагрузки, распределенной
по координате по закону статических кон-
тактны^ напряжений и изменяющейся во
времени как 6-функция:
2 л2 а2 р. “°®
‘01 I I >
яС0(М(М)
при т <
И
(8.46)
где
«01 —
при т
О
фер с коэффициентом демпфирования 6(<о),
соединенные параллельно (8.22) и (8.23):
Q
(8-47)
«02 =
при т
при т
2
О
(8.42)
где fi и f2 вычисляют по формуле (8.41).
Графики функций для v = 0,25 показаны на
рис. 8.6 [12].
Передаточные функции, соответствую-
щие представлению (8.36), имеют вид:
Q
71 = л 1 |2 [(2/9)2 + о)2 ] 1 +
2
+ (₽2- “о)^(₽2 + шо)2/°г4;
— ?2=л 1 “о ((2/<?)2+
+ cog Г1 + 2 р ш0 [л (Р +
+ (O^/D)-1}).
(8.43)
«03 =
2
при Т
(8.48)
Для представления (8.38) передаточные
функции
(8.44)
При использовании формул (8.44) для
решения только задач о гармонических ко-
лебаниях в ограниченном диапазоне частот
со0<1,5 можно снять ограничение v<0,4 и
для всех значений коэффициента Пуассона
0<v<0,5 использовать формулы (8.39), по-
лагая в них 72= 1,177, что совпадает с пред-
ложением, изложенным в работах [28, 29].
О
при 2 q < ч
при 2
92“Л
Л2Г (а) = (2 а2 —I)2 а, [(2 а2 — 1)2 +
+ 16а2₽2г1.
Остальные обозначения те же, что в (8.35).
5 Зак. 195
121
График функции н0(т) для v = 0,25
представлен на рис. 8.7. Функция (8.46) мо-
жет быть аппроксимирована выражением
“о(т) = —~—е (2-'l)’t • (8.49)
л а2 [1
График аппроксимирующей функции по-
казан на рис. 8.7 пунктиром. Функция (8.49)
определяет перемещение системы в виде
пружины и демпфера, соединенных парал-
лельно (рис. 8.8), под действием мгновен-
ного импульса. Тем самым в задачах о не-
стационарных горизонтальных колебаниях
штампа на полупространстве можно заме-
нить полупространство указанной системой,
параметры которой равны:
8 а р
2 — v
; Ьх = л а2 р0 с2.
(8.50)
ПФ, соответствующую ИПФ (8.46), за-
писывают в виде
Графики f3 и f4 при значениях v = 0 и
v = 0,5 представлены на рис. 8.9. Коэффи-
циенты жесткости ^х(со) и демпфирования
Ьх((а) зависят от частоты и в гармониче-
ском режиме колебаний для штампа опре-
деляются формулами:
kx (со) = 2 л2 р a kx (соо);
(8.52)
Ьх (<») = 2 л2 а2 р0с2 Ьх (<оо);
kx (соо) = 0,236 — 0,013 со2 +
+ • • •; Ьх (ш0) = 0,141 + . .
Рис. 8.7
Графики ^х(й)о) и Ьх(соо) при v = 0,25
показаны на рис. 8.10. Для ограниченного
диапазна частот о)о<2 только в гармониче-
ском режиме колебаний можно невесомый
штамп, лежащий на полупространстве, за-
менить системой с одной степенью1 свободы,
которая имеет параметры:
fii = 0,013-2 л2 р0 a3; kx ~ 0,236-2 л2 р а;
Ьх = 0,141 -2 л2 а? ро с2- (8.53)
Рис. 8.8
Аппроксимация (8.50) может быть так-
же йспользована и в гармоническом режи-
ме колебаний. ,
Вращательные относительно горизон-
тальной оси перемещения невесомого штам-
па [2]. Указанные перемещения под дейст-
вием импульсивного момента М определя-
ются приближенно следующей формулой,
дающей точное значение для среднего в
пределах круга перемещения поверхности
полупространства под действием мгновенно-
го импульса, распределенного по коорди-
нате по закону статических контактных на-
пряжений:
9 М с2 л 9 М с2
Ф° (Т) = 2 л2 U а‘ °00 = 2 л2 ц а4 Х
X (Фо1 + Ф02 + ®оз)> (8.54)
Рис. 8.9
Рис. 8.10
122
Рис. 8.12
( л Со (О’) К (Т/'О*)
где Ф01 (t)= < при т<2 О;
[ О при т>2 О;
Для оценочных расчетов функция (8.54)
может быть заменена функцией
9 М с2
Фо (т) =
Ф02
(8.55)
X (До sin 'Г е Е1 х + е £1Г), (8.57)
Фоз
(у) К (т/у) d v
при т<2 q;
при т>2 q; ;
(8.55)
параметры которой приведены в табл. 8.3.
Функция (8.57) описывает перемещение под
действием мгновенного импульса механиче-
ской системы, показанной на рис. 8.12, пе-
ремещение которой надо понимать в смыс-
ле вращательных (угловых) перемещений
(табл. 8.3).
Безразмерные параметры этой системы:
2 Во
Xq йо
О при 2<т;
ei
- •
«1
(8.58)
(у) = v 1 Л
(a), А2В(у) = р2 1 А2(о).
ПФ, соответствующая (8.54),
быть представлена в виде
9М - 7
---Г (^ + ^в).
2 л2 р а3
может
(8.59)
Остальные обозначения прежние.
График функции (8.54) показан на
рис. 8.11 для v = 0.
Графики и fe показаны на рис. 8.13.
Коэффициенты жесткости (со) и демпфи-
рования бфСсо) для штампа в гармониче-
ТАБЛИЦА S.3
V 61 9 с 6 о Xq
0 1,745 4,998 1,257 0,723 2,44
0,05 1,698 5,131 1,317 0,746 2,479
0,10 1,645 5,286 1,183 0,77 2,522
0,15 1,583 5,517 1,100 0,704 2,563
0,2 1,511 5,842 1,149 0,8'39 2,607
0,25 1,425 6,312 1,156 0,889 2,654
0,3 1,319 7,016 1,178 0,951 2,704
0,35 1,1’85 8,366 1,223 1,028 2,762
0,4 1,007 10,056 1,389 1,123 2,8311
0,45 0,744 14,562 1,388 1,251 2,923
0,5 0 оо 1,531 1 1,444 3,037
5* Зак. 195
123
Рис. 8.13
равномерно распределенной по прямоуголь-
ной площади нагрузки, имитирующей пря-
моугольный штамп, построены в работах
[1, 26, 30] .
8.4. ПЕРЕДАТОЧНЫЕ И ИМПУЛЬСНЫЕ
ПЕРЕХОДНЫЕ ФУНКЦИИ
ДЛЯ ЗАДАЧИ
О РАСПРОСТРАНЕНИИ ВОЛН
В ГРУНТЕ ОТ КОЛЕБЛЮЩИХСЯ
СООРУЖЕНИЙ
Рис. 8.14
Рассмотрим ПФ и ИПФ для задачи сле-
дующего типа: задана нагрузка, действую-
щая на некоторый участок полупространст-
ва; нужно определить перемещение точек
поверхности полупространства вне области,
занимаемой нагрузкой. Полупространство
используют как модель грунта.
Плоская задача. На участок полупло-
скости шириной 2а приложена равномерная
вертикальная о и горизонтальная т нагруз-
ки (рис. 8.15,а, б), изменяющиеся во време-
ни как б-функция. Перемещение точек по-
верхности определяется формулами [20].
При действии вертикальной нагрузки:
вертикальное перемещение
а а [ - ?2
° °' = л2 ц L- Я ’ll(m) Х
X In [Я (x, t]i) ] +
p 1/ q2 — n2
+ f : (л) ’ 1П И (X’ 4)1 dT1 +
ском режиме колебаний зависят от частоты
и их графики, вычисленные по формулам:
/б
(8.60)
Л (Л2 — Q2) Kl — Ч2
F (4) f (4)
X In [W (x, T])] (8.62)
представлены на рис. 8.14 для v=0,25.
В гармоническом режиме колебаний
может быть также использована система,
показанная на рис. 8.12, с параметрами
(8.58). Для диапазона частот <Оо<1,5 и
только в гармоническом режиме можно за-
менить штамп, лежащий на полупростран-
стве, системой с одной степенью свободы,
которая имеет параметры? [29]:
горизонтальное перемещение
X [Я (/ -11-Х I ’ll)—Я (/-1 14-XI П1) ] j+
p 2 (2 T)2 — 1) ]A)a— Я2 1—-t]2
+ J f (л) f (n) x
0,18; k3 =
(8.61)
На низких частотах демпфированием в
первом приближении можно пренебречь.
Другие формы штампа и модели осно-
вания. ПФ для круглого штампа, лежащего
на слое, подстилаемым жестким основани-
ем, построены в приближенной постановке
задачи в работах [24, 25, 32]. ПФ, которые
определяют перемещение некоторых точек
поверхности полупространства при действии
X [H (t—|1—x|t))—H —|1—*1 4)] ^4-
(8.63)
При действии горизонтальной нагрузки:
вертикальное перемещение определя-
ется формулой (8.63), в которой заменить
о на т и изменить знак;
124
горизонтальное перемещение
« (х, О, О =
л2 р,
In [N (х, т]1)] +
В
У1 —л2
In IW, п)1^т1 +
о ’* у,,/
(2п2— 1) /Т—Г12
In [Л7 (х, Л) I dтр (8.64)
п^(п)л(п)
В формулах (8.62) — (8.64) обозначено:
— 4 Т]2 У Т|2 — д2 ]/ т]2 — [
торого V=0,25, представлен на рис. 8.16.
ПФ, определяющая перемещения поверхно-
сти полупространства при действии гармо-
нической во времени нагрузки, равномерно
распределенной на площади круга, найдена
в работах [16, 23].
Нагрузка, распределенная по прямо-
угольнику (рис. 8.17) [21]. Нагрузка ин-
тенсивностью р равномерно распределена
по поверхности полупространства по пло-
щади прямоугольника со сторонами 2а\2Ь
и изменяется во времени по гармоническо-
му закону. Комплексные амплитуды коле-
баний поверхности, соответствующие вкла-
ду релеевских волн, преобладающих на
больших расстояниях, определяются следую-
щими формулами:
для смешения в направлении радиуса-
вектора
(2Е+1) PG (£') X
(8.65)
N
X S (а. 6) —----------; (8.67)
Nt (х, g) = x42-(/ + £)2;
JV2 (х, g) =хЧ2-(/-£)2. ,
Я(£)—единичная ступенчатая функция
Хевисайда; тн— корень уравнения FCn) =
dF(i))
= 0; Г(тц) = —
dr] ^тц.
Перемещение полуплоскости от импуль-
сивных нагрузок, распределенных по поли-
номам Чебышева, рассмотрено в работе
[20].
Осесимметричная задача. Импульсивная
нагрузка распределена по площади круга
по закону
Фо (р) = (1 —
— р»)—*z«; <Pi(p) =(1-р2)’Л. (8.66)
ИПФ, определяющая соответствующие
вертикальные перемещения точек поверх-
ности полупространства вне круга p=rja>
>1, построена в работе [13]. График, ил-
люстрирующий распространение волн от на-
грузок фо и ф1 для полупространства, у ко-
для смещений в направлении, перпен-
дикулярном радиусу-вектору uQ = 0;
для смещений в направлении оси г
(вертикальных)
w = (2§' + 3)
Смещения в направлении оси х равны
u — ur cos 0, смещения в направлении оси г/
равны: v = wrsin0.
В формулах (8.67) и (8.68) обозначено:
7.г=1/с|, /i2=l/Cj;
Е (5) = (2g + D-
-4 (£+1) Vi ]A + -x2^ft2-; (8.69)
Л-
Рис. 8.17
Рис. 8.16
125
£(V)=0, I1 — 0,183 для случая Х=ц.
Скорость волны Релея:
X Ц ]/2~л (сох)’72]"1;
sin (aa cosO) sin (ba sinO)
sinO cosO
а = х<о /1 +6',
r — радиус-вектор.
Из вышеприведенных формул видно, что
линии равной фазы смещения иг или w,
представляя собой окружности, распростра-
няются в бесконечность с радиальной скоро-
стью волн Релея. Амплитуда этих смещений
неограниченно уменьшается с увеличением
радиуса линии равной фазы. Вдо'ль каждой
линии равной фазы амплитуда смещений из-
меняется в зависимости от угла 0 и, если
числа aa и Ьа достаточно велики, то для
ряда углов 0 эти амплитуды будут обра-
щаться в нуль, и в таком случае вся карти-
на распространения упругих волн по по-
верхности может быть уподоблена равно-
мерно расширяющейся секториальной шах-
матной доске, состоящей из неравных кле-
ток.
Если же числа aa и Ьа будут очень ма-
лыми, то вдоль линий равной фазы значе-
ния смещений не будут существенно зави-
сеть от угла 0 и формулы (8.67) и (8.68)
перейдут в обычные формулы распростране-
ния круговых волн Релея. Таким образом,
устанавливаемая формулами (8.67) и (8.68)
зависимость смещений ит и w от угла 0 объ-
ясняется конечными размерами области,
находящейся под нагрузкой.
Сосредоточенная сила, действующая
на поверхность полупространства. Принцип
взаимности [19]. Пользуясь принципом
взаимности, можно уменьшить число вычис-
лений и заменить один эксперимент другим.
Выберем по точке 0 и О' соответствен-
но на плоскостях z=0 и z —hp>0 и будем
считать, что в одной из них приложено воз-
действие, а в другой регистрируется состав-
ляющая поля смещений. Обозначим через
(?о(А), c0o(/i) смещения в точке О', которая
находится на плоскостивозбужден-
ные нормальной силой fklt приложенной к
6)
а)
0,2 -
0,2
I статическое
I состояние.
0,2
О
0,2
(Статическое
I состояние
р si* £*=//$
---------!₽:-----и------------
Pju rm
С2 /Г;=7/ 5 z п8Р {горизонтальная
сила)
S)
.2
С2!С, = 1/^ {вертикальная сила}
R
0,2
0S
Статическое
। состояние
г)
0,2
О
0,2
0S
Статическое
Н— —состояние
О
№
О
г
7/W
Sprp
' ЯS г w(c ОС 8)
С2/с, -{/Eposes (горизонтальная
сила)
Сj /Г;=7/ /Г {вертикальная сила)
у ТРр гр сг /С, 0,20 (Кортикальная сила]
С2/С, р25, cosO--1 {горизонтальная
сила)
Рис. 8.20
Рис. 8.19
в)
OS
С2 /G S,25, siiiH (горизонталь-
г)
0,2
о
наясила)
IСтатическое
\ состояние
Р ______________ Р
0,--------------------
126
точке 0, взятой на плоскости z=0. Через
^i(/t), Pi(h) и Wt(h) обозначим составляю-
щие смещения в точке О', возбужденного
касательной силой fit, приложенной в точке
О, а через ^о(О), wo(0) и ?i(0), Pi(0),
t0i(O) —составляющие поля смещений в точ-
ке 0, возбужденного приложенным!! в точ-
ке 0' соответственно нормальной fki и ка-
сательной fti силами (рис. 8.18).
Тогда оказываются справедливыми ра-
венства:
(А) = (0), 41 (Л) = <71 (0);
Pi (Л) = Pi (0);
?о W = — cos 0 i»i (0); Wi (А) =
= — cos 0 <70 (А),
(8.70)
где q, pr w — радиальная, тангенциальная и
вертикальная компоненты смещения.
Перемещения точек поверхности при
действии внезапно приложенной силы, ос-
тающейся затем постоянной [18]. Переход
к воздействию произвольного вида
и (Г, 2, I) =
= [ « (г, г, t-t,) Г (/1) dti, (8.71)
V
о
если u(rf z, t)—есть решения для воздей-
ствия
' (1,/>0;
10, t < 0.
Смещения на границе полупространства
обозначены: а) при действии вертикальной
силы: w — вертикальная составляющая;
q — горизонтальная составляющая; б) при
действии горизонтальной силы: w — верти-
кальная составляющая; q — горизонтальная
составляющая.
Формулы для указанных смещений по-
лучены в работе [18] для произвольных
значений коэффициентов Пуассона материа-
ла полупространства. Ниже приведены ча-
стные случаи формул, когда Х = ц, что со-
ответствует v = 0,25:
при
В формулах (8.72) — (8.74) обозначено:
g = r/c2/; Д1 = Ц2 /3-3 ;
_________ +
Л2 = V2 у 3 + 3 ; Д2=.2-(2//з’);
Д4 = 2 + (2/К 3 ). (8.75>
Результаты вычислений по формулам
(8.72) — (8.74) сведены в табл. 8, с. 182 ци-
тированной выше работы и представлены
на рис. 8.19. Кроме того, на рис. 8.20 даны
графики аналогичных функций при v =
= 0,467, что соответствует c2/ci = 0,25.
СПИСОК ЛИТЕРАТУРЫ
1. Аводжоби, Гармонические колеба-
ния твердого .прямоугольного тела на по-
127
верхности упругого полупространства.
Труды Американского общества инжене-
ров-механиков. —Прикладная механика
(рус. пер.), г. 33, сер. Е, № 3, 1966.
2. Аникьев А. В., Ильичев В. А. Не-
стационарные горизонтально-вращательные
колебания фундамента. — В кн.: Труды IV
конференции по динамике оснований и
фундаментов. Ташкент, 1977.
3. Баранов В. А. Поперечные колеба-
ния стержня, опертого на инертное полу-
пространство.— Труды (Об. тр., Науч,
тр.) / Воронежский инж.-строит, ин-т. Во.
ронеж, 1964, № 11>0 (вып. 1).
4. Баранов В. А. Продольные вы-
нужденные колебания призматического
•стержня на упругом инертном полупрост-
ранстве.— В кн.: Исследования по теории
сооружений, вып. XIII. М., 1964.
5. Баранов В. А. О расчете вынуж-
денных колебаний заглубленного фундамен-
та.— В кн.: Вопросы динамики и прочно-
сти, вып. 14. Рига, 1967.
6. Динамика сплошных сред в зада-
чах гидротехники. / Под ред. В. М. Лятхе-
ра, Ю. С. Яковлева. М., 1975.
7. Ильичев В. А. Вертикальные не-
стационарные колебания массива под воз-
действием волн, возникающих в полупро-
странстве при колебаниях другого масси-
ва.—В кн.: Динамика сооружений. / Под
ред. Б. Г. Коренева. М., 1963.
8. Ильичев В. А. Определение дина-
мических напряжений под фундаментами
сооружений при прохождении упругих волн
в грунте. Труды к VIII Международному
конгрессу по механике грунтов и фунда-
ментостроению. / Под ред. Н. А. Цытовича.
М„ 1973.
9. Ильичев В. А., Таранов В. Г. Экспе-
риментальное изучение динамического взаи-
модействия вертикально-колеблющегося
фундамента с основанием. — Основания,
фундаменты и механика грунтов, 1У75,
№ '5.
10. Ильичев В. А. К построению им-
пульсной переходной функции системы
штамп — полупространство. —Изв. АН
СССР. Сер. МТТ, 1973, № 1.
11. Ильичев В. А. О динамическом
расчете фундаментов. — Труды (Об. тр.,
Науч, тр) / НИИОСП. М, 1976 (вып.
67).
12. Ильичев В. А. Особенности вза-
имодействия с грунтом большеразмерных
фундаментов при сейсмических воздейст-
виях. — В кн.: Сейсмостойкое строительство
(вып. 2). М., 1975.
13. Ильичев В. А. Определение вер-
тикальных перемещений поверхности грунта
вне колеблющегося фундамента.—кн.:
Труды IV конференции по динамике осно-
ваний и фундаментов. Ташкент, 1977.
14. Коренев Б, Г., Ильичев В. А., Рез-
ников Л. М. Колебания башнеобразных со-
оружений с учетом инерции упругого осно-
вания. Fourth World Conference on Earth-
quake Engineering. Santiago, Chile, 1969.
15. Морс Ф. M., Фешбах Г. Методы
теоретической физики. М., 1958.
16. Муравский Г, Б. О гармонических
колебаниях -штампа на упругом изотроп-
ном полупространстве. — Строительная
механика и расчет сооружений, 1969, № 7*
17. Муравский Г. Б. Гармонические
колебания штампа на полупространстве
под действием силы, приложенной к по- •
верхности полупространства. — Изв. АН
СССР, сер. МТТ. 1969, № 6.
, 18. Огурцов К. И. Количественные
исследования волновых процессов в упру-
гом полупространстве при различных типах
воздействий. — Уч. записки ЛГУ, № 208.
Сер. мат. наук, вып. 30. Динамические за-
дачи теории упругости. Л., 1956.
19. Огурцов К. И., Успенский И. И.,
Ермилова И. И. Некоторые количествен-
ные исследования по распространению
волн в простейших упругих средах. — В
кн.: Вопросы динамической теории расп-
ространения сейсмических волн, № 1. Л.,
1957.
20. Сеймов В. М. Динамические кон-
тактные задачи. Киев, 1976.
21. Сретенский Л. Н. Упругие волны,
возникающие от нормальных напряжений,
приложенных к поверхности полупростран-
ства.— В кн.: Проблемы механики сплош-
ной среды. М., 1961.
22. Шехтер О. Я. Об учете инерцион-
ных свойств грунтов при расчете верти-
кальных вынужденных колебаний массив-
ных фундаментов. — В кн.: Вибрации ос-
нований и фундаментов, № 8. М., 1948.
23. Шехтер О, Я. О взаимном влия-
нии колебаний двух жестких круглых
штампов на упругом полупространстве
при вертикальных осесимметричных воз-
действиях— Труды (Об. тр., Науч, тр.) /
/НИИОСП. М., 1972, № 62.
24. Arnold R. N., Bucroft G. Я., War-
burton.G, В. Forced vibrations of a body on
an elastic solid. Journal of Applied Mecha-
nics. Transactions of the ASME, vol. 22,
No. 3, 1955.
25. Bycrojt G. V. Forced vibrations of
a rigid circular plate on a semi - infinite
elastic space and an elastic stratum. Philo-
sophical Transactions of the Royal Societ
of London. Ser. A, No 948, 1956.
26. Kobori T., Minai R., Suzuki T.,
Kysakabe K. Dynamical ground compliance
of rectangllar foundation. «Proc. 16th Japan
Nat. Congr. Appl. Meeh. Tokya, 1967, 1967.
27. Lamb H. On the propagation of
tremors over the surface of an elastic so-
lid. Phylosophical Transactions of the Roy-
al Society of London. Sen. A, vol. 203, 1904.
28. Lysmer Richart F. E. Dynamic
respons of footigs to vertical loading. J. of
SM and F Div. ASCE, vol. 92, No SMI,
1966.
29t . Richart F. E., Hall /. R., Wo-
ods R. D. Vibrations of Soils and Foundati-
ons. Prentice — Hall, Inc. Englewood Cliffs,
New Jersey, 1970.
30. Tomson W. T., Kobori T. Dynami-
cal compliance of rectangular foundations
on an elastic half — spacey Transactions, of
the ASME, Journal of Applied Mechanics,
vol. 30, ser. E, No 4. 1963.
31. Warburton G. B. Forced vibrations
of a body on an elastic stratum, Journal of
Applied Mechanics, vol. 24, 1957.
128
РАЗДЕЛ 9. ДИНАМИЧЕСКАЯ КОНТАКТНАЯ ЗАДАЧА ДЛЯ
ПОЛУПРОСТРАНСТВА
(И. М. БОРОДАЧ ЕВ)
К динамическим контактным задачам
теории упругости приводят проблемы рас-
чета фундаментов под машины, фундамен-
тов зданий и сооружений, воспринимающих
динамическую нагрузку, и оснований гидро-
технических сооружений. Например, при про-
ектировании фундамента, на котором уста-
новлена машина, создающая значительную
динамическую нагрузку, задача инженера
состоит в том, чтобы на основе динамиче-
ского расчета дать правильный прогноз
ожидаемого уровня колебаний фундамента.
Напряжения, возникающие в фундаменте,
и давления, передаваемые на грунт, не дол-
жны превосходить допускаемых [14].
Амплитуда колебаний фундамента или
сооружения и динамические напряжения,
возникающие в грунте под ними, во многих
случаях могут быть оценены в результате
решения динамической контактной задачи.
Массивный фундамент под машину или же-
сткое сооружение можно рассматривать как
жесткий штамп. Для определения напря-
женного состояния грунта и параметров ко-
лебаний фундамента обычно применяют
расчетную модель линейно-деформируемой
среды, основанную на предположении, что
можно использовать соответствующие ре-
шения теории упругости. В этой модели
грунт считают идеально упругим однород-
ным изотропным полупространством или
упругим слоем. Для практических
целей большое значение имеет рассмотрение
вопроса о действии на фундамент гармони-
чески изменяющихся во времени вертикаль-
ных и горизонтальных сил и пар сил.
Обзор работ, посвященных динамиче-
ской контактной задаче теории упругости,
приведен в монографии [16]. Однако во
многих опубликованных трудах результаты
представлены в форме, мало пригодной для
практического использования, и почти от-
сутствуют числовые примеры. Ниже приве-
дены результаты решения задач об уста-
новившихся гармонических колебаниях
штампа с плоским круговым или кольце-
вым основанием, расположенного на упру-
гом изотропном полупространстве. Наи-
больший интерес представляет рассмотре-
ние пространственной динамической кон-
тактной задачи для штампа более сложной
формы в плане (прямоугольной и т. п.).
Однако такая задача весьма сложна, и в
настоящее время пока нет ее точных реше-
ний. Поэтому задачу о штампе с плоским
круговым основанием можно рассматривать
как некоторую «эталонную» задачу. Имея
решение для штампа с круговым основани-
ем, можно, используя известные приемы,
получать приближенные решения для штам-
пов другой формы в плане. Один из таких
приемов изложен в работе [1]. Решения ря-
да динамических контактных задач, дове-
денных до числовых результатов, можно
найти в книге [17].
9.1. КОЛЕБАНИЯ ШТАМПА
С ПЛОСКИМ круговым
ОСНОВАНИЕМ ПОД ДЕЙСТВИЕМ
ВЕРТИКАЛЬНОЙ ВОЗМУЩАЮЩЕЙ
СИЛЫ
Штамп с плоским круговым основани-
ем расположен на упругом однородном
изотропном полупространстве z^ 0; здесь
приняла цилиндрическая система коорди-
нат (рис. 9.1). На штамп действует верти-
кальная сила (где Q и Р — посто-
янные), направленная по оси симметрии.
Под действием этой силы штамп будет со-
вершать гармонические колебания с ампли-
тудой Ьо относительно положения статиче-
ского равновесия. Считаем, что отрыв
штампа от упругого полупространства не
имеет места. Силы трения между штампом
и упругим полупространством не учитыва-
ются. Нагрузка на полупространство вне
штампа отсутствует.
Закон движения штампа в таком слу-
чае представится выражением
ь (О =&?T + W , (9.1}
где b(t)—полное вертикальное перемеще-
ние штампа, отсчитываемое от ненагружен-
ного состояния; Ь®т — статическое переме-
щение от силы Q; Ьо — амплитуда колеба-
ний штампа; <р — угол сдвига фаз между
перемещением штампа и возмущающей си-
лой; со — угловая частота колебаний.
При этом
ст 8 (1 — Р2) ’
„ / Ц VZ»
Чтпг) <9'2>
где X, ц — упругие постоянные Ламе; —
радиус основания штампа.
В работах [2, 3] найдено, что
Р ош и
6о = tg Ф =---------.
coso —х
(9.3>
129
ТАБЛИЦА 9.1
k Vo при значении v 6 при значении v
0,00 0,25 0,50 0,00 0,25 0,50
п оп 1 0000 1,00(00 1,0000 0,0000 0,0000 0,0000
0,25 1,0,139 1,0121 1,0097 0^21135 0,1968 0,2079
0,50 1,0579 1,04'98 1,0402 0,4235 0,3908 0,4141
0,75 1,1380 1Д .177 1,0948 0,6243 0,5774 0,61152
1,00 1,2608 4,2186 1,1776 0,8072 0,7526 0,8061
1,25 1,43,19 1,3646 1,2917 0,9627 0,9005 0,9812
1.50 1,6467 1,5469 1,4615 1,0885 11,0239 1,1166
определяют по первой формуле (9.2) с
заменой Q на Р. р — плотность материала
полупространства; т — масса штампа;
Дд— динамический коэффициент для пе-
ремещений.
Отрыва штампа от упругого полупро-
странства не будет, если
В формулы (9.3), (9.4) входят значе-
ния уо и 6. В табл. 9.1 приведены значения
Ye и б для некоторых коэфициентов Пуас-
сона v и параметра k.
Используя формулы (9.3), (9.4) и
табл. 9.1, определяем амплитуду колебаний
&о штампа и угол сдвига фаз <р.
С помощью (9.4) и табл. 9.1 можно
построить графики изменения динамическо-
го коэффициента Дд в зависимости от k
при фиксированных значениях v и т\ На
рис. 9.2 приведены графики для случая v =
'=0,25 и т* = 0, 5, 10, 20. На рис. 9.3 по-
казано изменение угла 4р в зависимости от
k для v = 0,25 и т*=0, 5, 10, 20.
Суммарные статические и динамические
нормальные напряжения на площадке
.контакта определяют по формуле
Ог (г, 0, /) = О^(СТ) (г, 0) +
+ стГ(ст) (г. °) а (г) е'1®*-™1,
(0^г</?), (9.5)
°? (ст)
(Ог==г<К);
(9.6)
Выражение для ог{ст) (г, 0) можно по-
лучить из (9.6) заменой Q на А В том
случае, когда на штамп действует сила
Рис. 9.2
Рис. 9.3
130
ТАБЛИЦА 9.2
k <Хо (Xi аз аз а* Р(1)
0,00 0,0000 0,0000 0,0000 0,0000 0,0000 1,0000
0,0000 0,0000 0,0000 0,0000 0,0000
0,25 0,0468 0,0001 —0,0001 0,0007 —0,0013 1,0079
—0,0026 —0,0003 0,0034 —0,0171 0,0169 0,1971
0,50 0,1872 —0,0006 —0,0186 0,06183 —0,0588 1,0323
—0,0212 0,0012 —0,0105 0,0336 —0,0275 0,3930
0,75 0И202 —0,0066 —0,0082 0,0189 —0,01212 1,0742
—0,0741 0,0010 0,0095 —0,0220 0,0152 0,5859
1,00 0,7345 0,01155 —1,0701 (3,7443 —+3,1036 1,1290
—0,1738 —0,0383 1,3073 —4,5654 3,7816 0,7766
1,25 1,11419 —0,0902 0,6695 —2,3336 2,0152 1,2166
—0,3760 0,0614 —0,5244 1,9128 — 1,65215 0,9501
1,50 1,5950 —0,0931 —0,4291 1,5936 —1,3966 1,3159
—0,6808 0,1025 —0,3660 1,3351 • л —1,1-874 1,1066
Q+Pcosg)^ в формуле (9.5) следует заме-
нить В** — (И] на cos [со/ — ^(г)].
Здесь of(CT) (г, 0) —нормальное напряже-
ние на площадке контакта при статическом
приложении силы Р; а (г)—динамический
коэффициент для напряжения о2; Т(г) —
угол сдвига фаз между напряжением и
приложенной силой. В табл. 9.2 приведены
значения комплексных чисел ап (при N =
=4) и р (1) для случая v = 0,25, причем
в верхних строках даны значения действи-
тельной части числа ап и р (1), а в ниж-
них — значения мнимой части. Более под-
робные таблицы этих значений приведены в
[4]. Для примера на рис. 9.4 построены
графики динамического коэффициента а(0)
при v = 0,25 и /п* = 0, 5, 10, 20.
Задача о колебаниях штампа с плоским
кольцевым основанием, расположенного на
упругом полупространстве, под действием
вертикальной возмущающей силы рассмот-
рена в работе [5], но до числовых резуль-
татов она не доведена.
9.2. КОЛЕБАНИЯ ШТАМПА
С ПЛОСКИМ КРУГОВЫМ
ИЛИ КОЛЬЦЕВЫМ ОСНОВАНИЕМ
ПОД ДЕЙСТВИЕМ
ГОРИЗОНТАЛЬНОЙ
ВОЗМУЩАЮЩЕЙ СИЛЫ
На упругом изотропном полупростран-
стве расположен штамп с плоским
кольцевым основанием. На штамп действу-
ет горизонтальная возмущающая сила
Те£®* (рис. 9.5). Внутренний радиус осно-
вания штампа наружный Р2. Высота
штампа предполагается малой по сравнению
с его наружным радиусом. В этом случае
под действием горизонтальной возмущаю-
Рис. 9.5
щей силы штамп будет совершать только
горизонтальные колебания. Предполагается
также, что нормальные напряжения о2 от-
сутствуют на площадке контакта штампа с
упругим полупространством и что поверх-
ность полупространства вне штампа сво-
бодна от усилий. Под действием приложен-
ной горизонтальной силы Те£ штамп бу-
Рис. 9.6
Рис. 9.7
131
ТАБЛИЦА 9.3. ЗНАЧЕНИЯ Vo И б ПРИ е=0
k V» при V б При V
0 0,25 0,5 0 0,25 0,5
0,00 0,25 4,0000 1,0111 ,1,0000 4,0000 1,0054 0,0000 0,0000 0,0000
1,0080 0,1712 0,1361 0,0994
0,50 1,0456 1,0323 1,0216 0,3889 0,2694 0,1966
0,75 1,1054 1,0738 1,0485 0,4982 0,39167 0,2894
1'00 1,1947 1,1330 1,0866 0,6430 (0,5140 0,3756
1,25 1,3124 1,2090 1,1315 . 0,7672 0,6180 0,4533
L5O 1,4554 1,2969 1,1839 0,8609 0,17062 0,5213
ТАБЛИЦА 9.4. ЗНАЧЕНИЯ Vo И б ПРИ е=0,5
k Vo При V б При V
0 0,25 0,5 0 0,25 0,5
0,00 0,9621 0,9621 0,9621 0,0000 0,0000 0,0000
0,25 0,9470 0,9706 10,9677 0,1652 ОД 314 0,0959
0.50 Ч ,0110 0,99164 0,9046 0,3263 0,2505 0,1894
0,75 1,0757 1,0403 1,0125 0,4779 0,3807 0,2780
1,00 1,1717 1,1031 1,0509 0,61136 0,4911 0,3593
1,25 1,3009 1,1840 1,0983 0,72615 0,5868 0,4312
1,50 1,4517 1,2804 1,1522 OJ81O9 0,6649 0,4927
ТАБЛИЦА 9.5. ЗНАЧЕНИЯ Vo И б ПРИ е=0,8
k Vo при v б При V
0 0,25 0,5 0 0,25 0,5
0,00 0,8733 0,8733 0,8733 0,0000 0,0000 0,0000
0,25 0,8858 0,8820 0,8769 0,1(500 0,1193 0,0871
0,50 0,9242 0,9084 0,8957 0,2939 0,2342 0,1712
0,75 0,9914 0,9531 0,9232 0,4248 0,3401 0,2492
1,00 1,0001 1,0162 0,9606 0,5343 0,4322 0,3184
1,25 1,2242 1,0967 1,0058 0,6126 0,5056 0,3767
1,50 1,3846 1,1901 1,0557 0,6502 * 0,5666 0,4230
дет совершать горизонтальные колебания
по закону doeZ (ш ~ ф), где d0 — амплитуда
горизонтальных колебаний штампа; <р —
угол сдвига фаз между колебанием штам-
па и возмущающей силой. Ниже приведе-
ны результаты для кольцевого штампа. По-
лагая в них Я1 = 0, получим соответствую-
щие результаты для кругового штампа.
Задача о горизонтальных колебаниях
штампа с плоским круговым основанием
рассматривалась Л. С. Сигаловым [18], а
кольцевого штампа — А. Н. Буряковым
[9]. Приводим основные результаты
ты [9]: г
da == > ^1 := о / t ой \ г* *
рабо-
Yo (1 — 2х cosд +х*)1/1 ’
sin б
tg <р=-----------;
cos о —- х
fea т* .
Х= 8 (1-Р2) Yo 1
I р . т
R* — : т =
\ Н / Р ^2
(9.8)
«где т — масса штампа. *
Численные значения и 6 для ряда
значений коэффициента Пуассона v, пара-
метров k и & приведены в табл. 9.3—9.5.
Случаю кругового штампа соответствует
е$=0.
На основании формул (9.8) и табл.
9.3—9.5 можно построить графики измене-
ния коэффициента К и угла сдвига фаз <р
в зависимости от k при различных v, е и
т*. На рис. 9.6 и 9.7 представлены такие
графики для v = 0,25; е = 0; 0,8 и т‘=0;
10. Определение касательных динамических
напряжений и тг 0 под штампом под-
робно рассмотрено (с доведением до чис-
ловых результатов) в работе [10].
9.3. КОЛЕБАНИЯ ШТАМПА
С ПЛОСКИМ КОЛЬЦЕВЫМ
ИЛИ КРУГОВЫМ ОСНОВАНИЕМ
ПОД ДЕЙСТВИЕМ
ВОЗМУЩАЮЩЕГО МОМЕНТА,
ПРИЛОЖЕННОГО В ВЕРТИКАЛЬНОЙ
ДИАМЕТРАЛЬНОЙ
ПЛОСКОСТИ ШТАМПА
На упругом изотропном полупростран-
стве 0 находится штамп с плоским коль-
цевым основанием (рис. 9.8). На штамп
действуют вертикальная статическая сила
Q и пара сил с возмущающим моментом
Mei ш f, приложенная в вертикальной диа-
132
12
Рис. 9.8
метральной плоскости штампа. Высота
штампа предполагается малой по сравне-
нию с его наружным радиусом. В этом слу-
чае под действием возмущающего момента
штамп будет совершать лишь угловые ко-
лебания. Предполагается также, что силы
трения между штампом и полупространст-
вом отсутствуют и что поверхность полу-
пространства вне штампа свободна от уси-
лий. Под действием приложенного момента
Me1 ® * штамп будет совершать угловые
колебания Фоег “ <Р), где ф0 — амплиту-
да угловых колебаний штампа; <р —• угол
сдвига фаз. Штамп не будет отрываться от
Ряс. 9.9
полупространства при выполнении условия
^т>Ф0/?2. Имеем [6]
= Y Q4u~RV) • (9’9)
Ч Ц /\2
График зависимости у от параметра 8
приведен на рис. 9.9. Основные результаты
ТАБЛИЦА 9.6. ЗНАЧЕНИЯ Vo И б ПРИ е=0
Vo при v б при V
Ь f 0 0,25 0,5 0 0,25 0,5
0,00 0,3330 0,3330 0,3330 0,0000 0,0000 0,0000
0,25 0,3264 0,3273 0,3273 0,0048 0,0038 0,036
0,50 0,3093 0,3122 0,3119 0,3414 0,0279 0,0263
0,75 0,2805 0,2940 0,2928 0,1005 0,0829 0,0783
1,00 0,2730 0,2777 0,2751 0,2011 0,11685 0,1601
1,25 0,2626 0,2664 <0,2613 0,3278 0,2786 0,2664
1,50 0,2595 0,2611 0,2528 0,4698 0,4046 0,38196
ТАБЛИЦА 9.7. ЗНАЧЕНИЯ Vo И б ПРИ е=0,5
k X Vo при v б При V
0 0,25 0,5 0 0,25 0,5
0,00 0,3291 0,3291 0,3291 0,0000 0,0000 0 оооо
0,25 0,3223 о;з2зз 0,3232 0,0047 0,00318 0 0035
0,50 0,3059 0,3087 0,3084 0,0341 0,0277 0 0261
0,75 0,0869 0,2912 0,2901 0,0996 0,0821 0 0776
1,00 0,2712 0,2757 0,2730 0,1995 0,167,1 0 1589
1,25 0,2616 0,2650 0,2600 01,3256 0,2765 0.2646
1,50 0,2593 0,2605 0,2522 0.4674 0,4021 0,3875
ТАБЛИЦА 9.8. ЗНАЧЕНИЯ Vo И б ПРИ 8=0,8
Vo при v б при V
0 0,25 0,5 0 0,25 0,5
0,00 0,3050 0,3050 0,3050 0,0000 0,0000 0 оооо
0,25 0,2994 0,3002 0,3002 0,0044 0,0035 0 оюзз
0,50 0,2857 0.2881 0,2878 0,0319 0,0259 0 0243
0,75 0,2702 0,2736 0,2726 0,0933 0,07619 О П72Я
1,00 0,2578 0,2613 0,2688 0,1873 0,15617 V * V 1 «О 0 14Q4
1,25 0,2514 0,2537 0,2489 0,3060 0,2596 0 24Q9
1,50 0,2508 0,2521 0,2440 1 0,4617 0,3776 0,3657
133
решения динамической контактной задачи
имеют вид [11]:
ЗМ
Фо-КФп 1- 16 (1_р2) g дз >
% Зу0 (1 — 2 у, cos6 + x2)1/a
sin S (9.10)
tg ф = —7------ ;
coso —x
_______fe2Q* _
* - 16 (l-₽a) Vo :
Q* = й/p 8 = Ri/R2,
где £2 — момент инерции массы тонкого
кольцевого штампа относительно диаметра.
Значение k определяют так же, как и
в (9.8). Значения у0 и входящих в фор-
мулы (9.10), для ряда значений коэффици-
ента Пуассона v и параметров k, е приве-
дены в табл. 9.6—9.8. Случай кругового
штампа получается при 4=0-
На основании формул (9.10) и табл.
9.6—9.8 можно построить графики измене-
ния коэффициента К и угла сдвига фаз ф
в зависимости от k при различных v, е и
г. Для примера на рис. 9.10 и 9.11 пока-
заны такие графики для v = 0,25; е — 0; 0,8
и Qf*=0; 2. Нормальные динамические на-
пряжения oz на площадке контакта можно
определить способом, предложенным А. Н.
Буряковым [10].
9.4. КРУТИЛЬНЫЕ КОЛЕБАНИЯ
ШТАМПА С ПЛОСКИМ
КОЛЬЦЕВЫМ (КРУГОВЫМ)
ОСНОВАНИЕМ
Штамп с плоским кольцевым основа-
нием сцеплен с упругим изотропным полу-
пространством 0. К штампу приложена
в горизонтальной плоскости (плоскости,
перпендикулярной оси г) пара сил с воз-
мущающим моментом Под дейст-
вием этого момента штамп будет совер-
шать колебания Vez °Z вокруг вертикаль-
ной оси z, где V — комплексная амплитуда
угловых колебаний штампа. Касательные
напряжения на границе полупространства
вне площадки контакта отсутствуют.
« Задача о крутильных колебаниях штам-
па с плоским круговым основанием, лежа-
щего на упругом полупространстве, рас-
сматривалась в [20, 21]. Формулы и чис-
ловые результаты, приведенные в этих ра-
ботах, позволяют определить закон движе-
ния штампа и динамические касательные
напряжения на площадке контакта.
В работе [7] изучался вопрос о кру-
тильных колебаниях штампа с плоским
кольцевым основанием. В частности, для
вычисления амплитуды Vo угловых пере-
мещений штампа получена формула
3 М
^о = КФ1; Ф1= —-----------
16 И #2
Определение коэффициента К подроб-
но рассмотрено в статье [7].
9 5. ДРУГИЕ ЗАДАЧИ
Выше были рассмотрены задачи об ус-
тановившихся колебаниях штампа примени-
тельно к случаю, когда возмущающая сила
(или пара сил) была приложена непосред-
ственно к штампу. Г. Б. Муравский [15]
изучал гармонические колебания штампа,
когда возмущающая сила была приложена
к поверхности полупространства (вне
штампа).
В последние годы появились работы по
динамическим контактным задачам теории
упругости, в которых рассматриваются не-
установившиеся колебания штампов, рас-
положенных на упругом полупространстве
134
(или упругом слое). В некоторых из них
решения доведены до числовых результа-
тов [8, 12, 13, 17]. Более подробный обзор
работ, посвященных нестационарным динаг
мическим контактным задачам теории уп-
ругости, содержится в монографии Д16].
СПИСОК ЛИТЕРАТУРЫ
1. Бородачев Н, М. Вынужденные ко-
лебания жестких плит и массивов, лежа-
щих на упругом полупространстве. — Ос-
нования, фундаменты и механика грунтов,
1966, № 1.
2. Бородачев И. М. Динамическая
контактная задача для штампа с плоским
круговым основанием, лежащего на упру-
гом полупространстве. — Изв. АН СССР.
Qep. «Мех. и машиностр»., 1964, № 2.
3. Бородачев Н. М. Вертикальные ко-
лебания кругового штампа на упругом по-
лупространстве. — Строительная механика
и расчет сооружений, 1964, № 5.
4. Бородачев И. М. Определение ди-
намических напряжений, возникающих в
упругом полупространстве под штампом с
плоским круговым основанием. — Изв. АН
СССР. Сер. «Механика», 1965, № 4.
5. Бородачев Н. М. Динамическая
контактная задача для штампа с плоским
кольцевым основанием, расположенного на
упругом полупространстве. — В кн.: Проч-
ность и пластичность. М., 1971.
6. Бородачев Н. М., Бородачева Ф. Н.
Вдавливание кольцевого штампа в упругое
полупространство. —- Инж* журнал, меха-
ника твердого тела, 1966, № 4.
'7 . Бородачев Н. АГ, Мамтеев Ю. А.
Крутильные колебания упругого полупро-
странства, вызванные поворотом кольцево-
го штампа.—Прикл. механика, 1970, т. 6,
вып. 3.
8. Бородачев И, М., Мамтеев Ю. А.
Неустановившиеся крутильные колебания
упругого полупространства. — Изв. АН
СССР. Сер. «Механика твердого тела»,
1969, № И.
9. Буряков А. Н. Горизонтальные ко-
лебания штампа с плоским кольцевым ос-
нованием, расположенного на упругом
полупространстве. — Изв. вузов. Сер.
«Строит, и архит»., 1971, № 12.
10. Буряков А. И, Некоторые динами-
ческие контактные задачи теории упругости
для кольцевого штампа. Дис. на соиск. уч.
ст. канд. физ.-мат. наук. Саратов, 1973.
11. Буряков А. И. Динамическая кон-
тактная задача об угловых колеоаниях
кольцевого штампа, расположенного на
упругом полупространстве. — Изв. вузов.
Сер. «Строит, и архит.», 1970. № 6.
12. Ильичев В. А. К решению неста-
ционарной контактной задачи о квадратном
штампе, лежащем на инерционном полу-
пространстве.— В кн.: Исследования по
теории уооружений, 1969, вып. 17.
13. Ильичев В, А. К построению им-
пульсной переходной функции системы
-штамп — полупространство. — Изв. АН
СССР. Сер. «Механика твердого тела»,
1973, № 11.
14. Коренев Б. Г, Предисловие к кни-
ге: Э. Рауш. Фундаменты машин, м., 1965.
15. Муравский Г, Б. Гармонические
колебания штампа на полупространстве при
действии силы, приложенной к поверхно-
сти полупространства. — Изв. АН СССР.
Сер. «Механика твердого тела», 1969, № 6.
16. Развитие теории контактных задач
в ССС-Р. / Отв. ред. Л. А. Галин. М., 1976.
17. Сеймов В. М. Динамические кон-
тактные задачи. Киев, 1976.
18. Сигалов Л. С. Горизонтальные
колебания штампа с плоским основанием на
упругом полупространстве. — В кн.: Дина-
мика гидротехнических сооружений, вып.
28. М. — Л., ,1966.
19. Сигалов Л. С. Изгибные колебания
штампа с плоским круговым основанием
на упругом полупространстве. — Изв. ву-
зов. Сер. «Строит, и архит»., 1966, № 6.
20. Уфлянд Я. С. О крутильных ко-
лебаниях полупространства. — Прикл. ма-
тематика и механика, 1961, т. 25, вып. 1.
21. Sagoci Н. F. Forced torsional os-
cillations of an elastic half — space. II.
Journ. of Appl. Phys., 1944, vol .15, N 9,
655—662.
РАЗДЕЛ 10. РАСЧЕТ ПАРАМЕТРОВ КОЛЕБАНИЙ ГРУНТА
И ЗДАНИЙ, ВЫЗЫВАЕМЫХ ДВИЖЕНИЕМ ПОЕЗДОВ
МЕТРОПОЛИТЕНА
(В. А. ИЛЬИЧЕВ)
Проблема защиты зданий от колеба-
ний, возникающих при движении поездов
метрополитена, приобрела особую актуаль-
ность в последние годы, когда при строи-
тельстве новых линий метрополитена нача-
ли прокладывать, как правило, туннели
мелкого заложения. Этот способ прокладки
туннелей имеет технико-экономические пре-
имущества по сравнению с прокладкой тун-
нелей глубокого заложения и в настоящее
время является основным. Однако при экс-
плуатации туннелей метрополитена мелкого
заложения в зданиях, главным образом
жилых, расположенных вблизи трассы, ко-
лебания достигают такого уровня, что ста-
новятся ощутимыми для людей, находя-
щихся в них. Для уменьшения этих коле-
баний необходимо их изучение, чтобы ра-
ционально выбрать или создать новые тех-
нические средства уменьшения уровня ко-
лебаний жилых зданий, строящихся или
построенных вблизи линий метрополитена
мелкого заложения.
В этом разделе приведены результаты
экспериментальных исследований по опре-
делению уровня колебаний туннелей, грун-
та, жилых зданий и других объектов, на-
ходящихся вблизи линий метрополитена,
даны методы расчетного определения уров-
ня колебаний грунта, а также сообщаются
сведения о важнейших способах уменьше-
ния вибраций.
10.1. ОБЩИЕ СВЕДЕНИЯ
О КОЛЕБАНИЯХ, ВОЗНИКАЮЩИХ
ПРИ ДВИЖЕНИИ ПОЕЗДОВ
МЕТРОПОЛИТЕНА,
И О СПОСОБАХ ИХ УМЕНЬШЕНИЯ
Параметры колебаний. Продолжитель-
ность колебаний в зданиях, вызванных од-
ним проходящим поездом метрополитена,
составляет примерно 10 с. В часы пик на
трассе метрополитена может проходить в
обоих направлениях 40 пар поездов в 1 ч
и более. Следовательно, продолжительность
воздействия колебаний может достичь 10—
20% общего времени, в течение которого
работает метрополитен.
Спектральный состав этих колебаний
достаточно широк 5—100 Гц, однако основ-
ная энергия колебаний сосредоточена в бо-
лее узком диапазоне — 35—60 Гц. Макси-
мальные амплитуды колебаний строитель-
ных конструкций зданий, находящихся
вблизи от туннелей метрополитена, равны
нескольким микронам, обычно же амплиту-
ды колебаний редко превышают 1 мкм.
Колебания такой интенсивности не влияют
на прочность строительных конструкций
зданий. В то же время скорость колебаний
может быть 0,5 мм/с, а ускорение колеба- •
ний — 20 см/с2. Колебания такой интенсив-
ности могут быть ощутимыми и раздража-
юще действовать на людей. Именно с этим
и связана актуальность рассматриваемой
проблемы.
Требования санитарных норм. Допусти-
мые уровни колебаний в жилых и общест-
венных зданиях установлены санитарными
нормами [7]. Согласно нормам [8] разреша-
ется размещать жилые здания не ближе чем
40 м от туннеля. При более близком рас-
положении уровень колебаний следует оп-
ределять расчетом и в случае необходимо-
сти разрабатывать виброзащитные меро-
приятия.
Меры борьбы с вибрациями. Виброза-
щитные мероприятия могут быть осуществ-
лены на. любом участке пути, по которому
распространяются колебания от источника
до приемника. Наиболее целесообразно по-
давлять колебания в самом источнике. Для
этого на метрополитенах ряда стран выпол-
няют различные мероприятия, направлен-
ные на совершенствование подвижного со-
става и рельсового основания. Перечислим
главные из них:
а) применение резинополимерных мате-
риалов в соударяющихся частях вагонов,,
создание малошумных двигателей и мотор-
компрессора, использование электротормо-
жения и дифференциальной передачи от
двигателя к колесу, улучшение «мягкой»-
подвески и применение «бесшумных» колес
(на пневматическом ходу или с резиновы-
ми вставками);
б) тщательная шлифовка сварных сты-
ков и верхней поверхности головки рельса,
установка подвижных крестовин, устране-
ние кривых малого радиуса, улучшение
качества рельсовых сталей, покрытие боко-
вой поверхности головки рельса специаль-
ной смазкой, установка амортизирующих
подкладок под рельсы, применение щебе-
ночно-асфальтового балластного основа-
ния, устройство балластного корыта на
амортизаторах и др. Кроме того, для умень-
шения вибраций туннельную обделку мож-
но устраивать более массивной или в виде
слоистой конструкции.
Помимо указанных мероприятий можно
использовать и другие, связанные: с устрой-
ством препятствий в грунте — ограждающие
стены и траншеи, вертикальные или гори-
зонтальные слои грунта между тоннелем и
зданием с измененными свойствами; с градо-
строительными архитектурно-планировочны-
ми решениями — удаление застройки от ли-
ний метрополитена с учетом дифференциа-
ции зданий (учреждения и общественные
здания, жилые здания, больницы и т. д.)„
136
ТАБЛИЦА 10.1
изменение трассы метрополитена; с установ-
кой защитных средств в здании — устройст-
во прокладок в фундаменте и на уровне
сопряжения фундамента и стены, вибро-
изоляция отдельных помещений, выбор ра-
циональной несущей конструкции здания.
Выбор средств, уменьшающих вибра-
ции зданий, которые находятся вблизи ли-
ний метрополитена, зависит от конкретных
условий и технико-экономических показа-
телей.
10.2. ЭКСПЕРИМЕНТАЛЬНЫЕ
ДАННЫЕ О КОЛЕБАНИЯХ
ТУННЕЛЕЙ, ГРУНТА, ЗДАНИЙ
И ДРУГИХ ОБЪЕКТОВ,
РАСПОЛОЖЕННЫХ ВБЛИЗИ
ЛИНИЙ МЕТРОПОЛИТЕНА
Описание экспериментов и их резуль-
татов, Ниже приведены в систематизиро-
ванном виде результаты экспериментальных
исследований вибраций, вызываемых дви-
жением поездов метрополитена, выполнен-
ные на десяти различных участках, отли-
чающихся глубиной заложения туннелей
(глубокого и мелкого заложения, назем-
ные трассы), конструкцией туннелей, грун-
товыми условиями, конструкцией зданий,
расстоянием зданий от туннеля и т. п. Све-
дения об экспериментальных данных необ-
ходимы для формирования общего пред-
ставления о явлении и для разработки ме-
тодов расчета параметров колебаний и
выбора рациональных средств борьбы с
повышенными вибрациями. Перечень объ-
ектов * обследования с их краткой техниче-
ской характеристикой и основными экспе-
риментальными данными приведены в
табл. 10.1. Описание объектов обследова-
ния под номерами, соответствующими но-
мерам в этой таблице, приведены ниже.
1. Пятиэтажное жилое здание, кирпич-
ное, с наружными и внутренней продоль-
ной несущими стенами. Перекрытия из
сборных железобетонных плит. Фундамен-
ты ленточные. Основанием являются супе-
си № = 0,25 МПа, ниже залегают пески
мелкозернистые, водонасыщенные. Туннели
мелкого заложения (ТМЗ).
2. Туннели метрополитена. Туннель
мелкого заложения выполнен из чугунных
тюбингов, шпалы рельсового пути втоплены
в бетон. Грунты те же, что в п. 1.
3. Девятиэтажное жилое здание. Зда-
ние кирпичное с наружными несущими сте-
нами и внутренним железобетонным карка-
сом. Имеется подвал. Фундаменты ленточ-
ные сборные. Основанием фундамента яв-
ляется мелкозернистый песок, ТМЗ.
4. Туннель метрополитена мелкого за-
ложения. Тупиковая часть туннеля, прямо-
угольного поперечного сечения, выполнена
из сборных железобетонных элементов.
Шпалы уложены на щебень; Грунты те
же, что и в п. 3, а ниже залегают суглинок
с редким гравием, песок мелкозернистый
глинистый.
5. Туннель метрополитена глубокого
заложения. Туннель выполнен из чугун-
ных тюбингов, шпалы рельсового пути
№ п.п. Расстояние в плане от объ- екта до тун- неля, м Вертикально или горизонтально Параметры колеба- ний объекта
преобла- дающая частота /, Гц наиболь- шая ам- плитуда А, мкм
1 1-7,5 Г 51 3,2
2 '1 М В 38 2,6
В 52 3,6
3 4,5-46,4 Г 55 3,6
4 — г . 40 2
в 55 4
5 —— в 50 0,8
60 1,6
6 12,5. 56 0,5
7 . в 50 1.5
д % 45 1,3
8 22,5 г 49 1,7
9 60—70 в 10 1,6
г 23 0,4
10 0,9
( 14 г 46 0,7
10 1 22 49 0,7
1 и 1 16 53 1,4
( 24 г 44 0,7
11 7 J' 48 1,5
12 14 в 30 1,2
г 35 8
13 50 в 30 0,9
г 35 1,2
14 20 в 37 1,7
в 8 . 1,4 5
г 40
г 8 1
15 0—20 в 37 9
в 8 1,3
г 40 2,5
г 7,5 1,2
16 — в 40 14
40 3,7
17 8—25 в 35 3,3
в 9 4
г 40 3,1
18 0—20 в 39 2,5
8 2
в 8 3,5
45 4,6
19 3 в 40 2,1
в 9 3
35 7
9 2,2
втоплены в бетон. Геологическое строение
вблизи туннеля: туннель расположен в из-
вестняках, выше — слой глины толщиной
9 м, суглинок толщиной 7 м, выше — супесь,
песок.
6. Вентиляционная шахта № 1. Шахта
железобетонная, внутренний диаметр 3 м.
Геологическое строение см. п. 5.
7. Туннель метрополитена глубокого за-
ложения. Туннель выполнен из чугунных
тюбингов, шпалы рельсового пути втопле-
ны в бетон. Геологическое строение вблизи
туннеля: туннель — в известняках, выше
туннеля — слрй известняка толщиной 7 м,
глина толщиной 12 м, выше — песок, су-
глинок, песок.
8. Вентиляционная шахта № 2. Шахта
имеет внутренний диаметр 6 м. Ствол шах-
ты выполнен из чугунных тюбингов. Гео-
логическое строение см. в п. 7. 9. Поверх-
ность грунта — измеряли колебания грунта
на участке, предназначенном для строи-
тельства производственного здания. Осно-
ванием фундаментов будут служить древне-
аллювиальные пески средней плотности,
водоносные. Наземная трасса метрополи-
тена.
137
10. Шурфы глубиной 3,5 м: а) шурф
№ Г, б) шурф № 2; в) шурф № 3; г) шурф
№ 4. Вибрации измеряли на дне шурфов,
выкопанных в пределах контура планов
проектируемых зданий. Грунты — суглинки,
тмз.
И. Восьмиэтажное жилое здание. Зда-
ние кирпичное с наружными и внутренними
несущими стенами, перекрытия сборные
железобетонные, фундаменты сборные же-
лезобетонные. Имеется подвал. Грунты см.
в п. 10. ТМЗ.
12. Шурф глубиной 1,8 м. Шурф выко-
пан на расстоянии, равном расстоянию от
проектируемого здания до линии метропо-
литена. Конструкция проектируемого зда-
ния и грунтовые условия те же, что и в
п. 13. ТМЗ.
13. Четырнадцатиэтажное общественное
здание. Здание имеет монолитный железо-
бетонный каркас. Стеновые панели наруж-
ных стен навесные, внутренние перегород-
ки кирпичные, фундаменты под колонны
монолитные железобетонные. Грунты —
пески. ТМЗ.
14. Девятиэтажное жилое здание. Зда-
ние крупнопанельное восьмисекционное с
подвалом. Наружные стены из керамзито-
бетона, внутренние — из бетонных панелей.
Фундаменты ленточные. Грунты — супеси.
ТМЗ.
15. Поверхность грунта. Измеряли ко-
лебания поверхности грунта на участке
между зданиями (п. 14) и туннелем метро-
политена.
16. Туннель метрополитена мелкого за-
ложения. Туннель выполнен из железобе-
тонных тюбингов, шпалы рельсового пути
втоплены в бетон. Туннель является источ-
ником колебаний грунта и здания, указан-
ных в пп. 14, 15.
17. 16-этажное жилое здание. Здание
крупнопанельное с несущим железобетон-
ным каркасом и поперечными железобетон-
ными диафрагмами жесткости. Наружные
панели навесные. Фундаменты свайные.
Грунты— суглинки. ТМЗ.
18. Поверхность грунта. Измеряли ко-
лебания певерхности грунта у торца зда-
ния (п. 17), ближайшего к линии метропо-
литена.
19. Четырехэтажное жилое здание. Зда-
ние с кирпичными наружными и внутрен-
ними несущими стенами. Фундаменты лен-
точные. Здание расположено на участке,
указанном в пп. 17 и 18. ТМЗ. В туннелях,
где проводили исследования, скрепления
(конструкция прикрепления рельса к шпа-
ле) раздельные маятникового типа. При-
меняют рельсы Р-50.
Источники колебаний. При движении
вагонов метрополитена возникает несколь-
ко источников колебаний. Это работа дви-
гателя, компрессора, тормозной системы
вагона и пр.; динамическое взаимодействие
подвижного состава, рельсо-шпальной ре-
шетки и основания пути <[5].
Вторая группа источнников колебаний
является доминирующей с точки зрения со-
здания вибраций туннеля, окружающего
грунта и зданий.
Колебания с частотой 35—50 Гц вызы-
ваются вертикальными колебаниями непод-
рессоренных масс вагонов (масса колесной
пары плюс масса букс, подшипников и
т. д.), вызываемых случайными неровно-
стями пути, выбоинами на колесе, стыками
рельсов и т. п. Колесную пару можно рас-
сматривать как систему с одной степенью
свободы, упругостью является упругость
рельсового основания. Собственная частота
такой системы составляет 40 Гц. Механизм
возникновения колебаний с частотой 50—
60 Гц более сложен, связан с горизонталь-
ными колебаниями неподрессоренных масс
вагонов. Гармоники с частотой 8—10 Гц
вызываются колебаниями подрессоренных
масс тележек вагонов.
Параметры колебаний зданий. Движе-
ние поездов метрополитена вызывает коле-
бания строительных конструкций зданий с
частотой 35—60 Гц и амплитудой от долей
микрона до 1—3 мкм. Преобладающими
являются горизонтальные колебания в на-
правлении поперек оси туннеля и здания
(здание параллельно туннелю). Вертикаль-
ные колебания имеют тот же частотный
состав и вдвое, втрое меньшую амплитуду.
Наибольшие амплитуды горизонтальных
колебаний наблюдаются в уровне пола
подвала здания. Здесь амплитуды колеба-
ний стен в 2—2,5 раза больше амплитуд
колебаний лестничной площадки первого
этажа. Выше первого этажа амплитуды ко-
лебаний могут изменяться как в направле-
нии уменьшения, так и в направлении не-
которого увеличения.
Записи колебаний, сделанные с по-
мощью вибрографов, установленных на
смежных этажах, на однрм этаже, но в
смежных секциях или на одном этаже, но
на наружных стенах (дворовый и уличный
фасад), не обнаруживают заметной взаи-
мосвязи. Это указывает на то, что при ука-
занных выше частотах колебаний перекры-
тия нельзя рассматривать как абсолютно
жесткие в горизонтальном направлении
диски.
10.3 . РАСЧЕТНАЯ ОЦЕНКА
УРОВНЯ КОЛЕБАНИЙ
ГРУНТА ВБЛИЗИ ТУННЕЛЕЙ
МЕТРОПОЛИТЕНА
Ниже приведены решения задач дина-
мической теории упругости, которые могут
быть использованы для оценки уровня ко-
лебаний грунта, окружающего туннель мет-
рополитена.
Расчетная схема. В качестве расчетной
модели грунта принята однородная изо-
тропная упругая среда, внутри которой
действует некоторый источник колебаний,
параметры которого известны. Необходимо
определить перемещения в упругой среде.
Поскольку длина поезда метрополитена до-
стигает 140 м, что превосходит длину обыч-
ного жилого дома или дДину его темпера-
турного блока, зачастую можно ограничить-
ся рассмотрением плоской задачи, т. е. счи-
тать, что в направлении оси туннеля па-
раметры колебаний не изменяются.
138
Рис. 10.1
M
71 — J1 (Ад f) -J- E J (*2 r) +
r«i
1
Л (V)Wi'(V);
u = —
rk±
M
Пространственная задача о колебаниях
туннеля и окружающего грунта при движе-
нии заданной периодической пульсирующей
нагрузки вдоль туннеля рассмотрена в ра-
боте [2]. В работе [3] предложен алгоритм
решения задачи об определении перемеще-
ний и напряжений в упругой полуплоско-
сти при действии заданного импульсивного
движения жесткой круглой шайбы, находя-
щейся под границей полуплоскости. Дан
пример определения перемещения точки
дневной поверхности, полученное решение
можно использовать как импульсную пере-
ходную функцию.
Определение амплитуд вынужденных
колебаний грунта в окрестности круглого
туннеля глубокого заложения. Туннель
предполагается недеформируемым и совер-
шающим поступательные колебания в на-
правлении поперек своей продольной оси.
Рассмотрим следующую задачу — опреде-
лить перемещения в изотропной упругой
плоскости, вызванные заданным гармони-
ческим движением круглой жесткой шайбы
(рис. ’10.1). Решение этой задачи может
быть применено для относительно заглуб-
ленных туннелей и для зданий, весьма
близко расположенных к туннелю, в тех
случая, когда влияние дневной поверхно-
сти грунта можно не учитывать.
Перемещение точек упругой плоскости
в направлении осей полярной системы ко-
ординат г и 0 определяют приведенными
ниже формулами, полученными в резуль-
тате преобразования выражений, найден-
ных в работах [4, 9]:
a Rki cos 0
С2 + D2
У Р2 + S2 X
X cos (со t — <рг);
a R ki sin 0
“0 = ~ С2 + D2
(ЮЛ)
E — CJ2 (*1 R) 4- DY2 (*1R),
G = DJ2 (kxR) —CY2 (kiR);
M = GJ2 (k2R)+DY2 (*aR);
N — DJ2 (k$R) — GY2 (*2R);
C = Rk1j'1 (k2R) J2 (k± R) —
R *1 ?i (*2 R) Y2 R) 4-
J2 (*2 E) Jl (*1 R) —
-Y2 (k2 R) Л (k± R);
D = RktJ2 (ktR) Y\ \k2R) +
+ R *1 J\ (*2 R) Y2 (*t R) +
4“ Jl (*1 R) ?2 (*2 R) +
+ Л (*2 R) ?i (*iR),
S U
tg <Рл = — —; tg ф0 - —
} (Ю-2)
Г1 = krr\ r2 = k2r,
где Ci, C2 — скорости продольных и попе-
речных волн в упругой среде; R, <о, а — ра-
диус, угловая частота и амплитуда колеба-
ний жесткой шайбы; г — радиус-вектор
точки, в которой определяют перемещение
упругой среды; t — время; /п(х), Уп(х) —
функции Бесселя и Неймана соответственно.
Амплитуды горизонтальных колебаний
точек упругой среды, вызванные вертикаль-
ными колебаниями шайбы (рис. 10.1), вы-
числяют по формуле
X Т/Г2 + U2 cos (со t — <р0),
<Р С2 + Sin 9 cos 9 Х
где Р = —— Л (ki г) + М X
rki
XJj (*1Г)+4-Г1 (й2г) +
1 rk2
+ NY[ 0V);
G
S == —- Ji (k2r) + N Jt (*ir) —
r*2
(йхг);
rk2 J
(10.2)
X у (P-T)2 + (S-U)2COS (<о/-ф^р),
(10.3)
где
Амплитуды горизонтальных колебаний,
вызванные горизонтальными колебаниями
139
шайбы
10.1,6):
(обозначения показаны на
рис.
и" — а
гор
Rkr
С2 + Р2
X V(P cos2 Ох + Т sin2 GJ2 + (S cos2 0i
+ U sin2Ox)2 cos (<d t — Фгор), (10-4)
где
IT S cos2 Ox + U sin2
tn®11 — —----------—-----------
^rop P cos2 0i+ T sin2 Ox
Угол 0 в (Ю.З), (10.4) отсчитывают от
вертикальной оси, направленной вниз; ра-
диус г отсчитывают от центра туннеля.
Примеры вычислений, приведенные ниже,
показывают, что амплитуды колебаний
грунта могут изменяться немонотонно по
мере удаления от туннеля.
Для больших значений параметра
kit2r формулы можно упростить, восполь-
зовавшись асимптотическими разложениями
бесселевых функций и удерживая чле-
ны, имеющие порядок 1/У&1,2г. Соответст-
вующие асимптотические формулы для
(10.1) имеют вид:
aRki /Л424- № У2cos G
ur rH .__ X
(С2 + D2) Yn Vki r
X cos (co t — <pr);
“0~
aRkx У ffi+G2 /2 sin 0
(C2 + z?2) Yn Y^r
(10.5)
X cos ((D t — Ф^) .
На рис. 10.2 представлены графики
функций иг и uq t построенные по форму-
лам (10.1), а также графики изменения
амплитуд горизонтальных колебаний грунта
вдоль вертикальной прямой, проходящей на
расстоянии четырех радиусов от оси тун-
неля. Для расчета приняты следующие ис-
ходные данные. Радиус туннеля /? = 3 м.
Амплитуды колебаний туннеля в верти-
кальном и горизонтальном направлении
даны ниже. Коэффициент Пуассона грунта
0,4, что соответствует суглинкам и глинам.
Параметры &х = 2,1 и А2=5,18, соответст-
вующий им набор значений частот и ско-
ростей Ci и С2 распространения упругих
волн в грунте, для которых справедливы
представленные графики, могут быть вы-
числены по формулам Й1—i(o/Ci и 62=
= <о/С2. Для некоторых частот такие вы-
числения сделаны и сведены в табл. 10.2.
ТАБЛИЦА 10.2
Частота колебаний, Гц 35 40 45 50 55 60
Ci, м/с 1000 1143 1286 1429 1571 1714
С2, м/с 425 486 546 607 668 729
Этими графиками можно пользоваться
для оценки уровня колебаний грунта при
удалении от туннеля по следующим на-
правлениям: вдоль горизонтальной и верти-
кальной прямых, проходящих через ось тун-
неля, и вдоль вертикальной прямой на рас-
стоянии 12 м от оси.
Примеры расчета и сопоставление с
экспериментами.
Пример 1. Поскольку от-
сутствуют экспериментальные данные о ко-
лебаниях точек внутри массива грунта, то
для сопоставления выбраны эксперимен-
тальные данные о колебаниях стволов двух
вентиляционных шахт, краткое описание
которых содержат пп. 5, 6, 7 и 8 табл. 10.1.
Для расчета амплитуд колебаний грун-
та, окружающего шахту № 1, на основа-
нии экспериментов приняты следующие ис-
ходные данные. Амплитуда вертикальных
колебаний основания туннеля ав=0,8 мкм,
амплитуда горизонтальных колебаний ат =
= 1,63 мкм. Частота колебаний по обоим
направлениям принята одинаковой 56 Гц.
Скорость продольных волн для расчета при-
нята для всего напластования грунтов по-
стоянной Ci=1600 м/с, что соответствует
плотным глинам '[8]. Скорость поперечных
волн С2 = 680 м/с.
На рис. 10.2 представлено поперечное
сечение туннеля вертикальной плоскостью,
проходящей через ось шахты № 1, и гра-
фики изменения амплитуд горизонтальных
колебаний упругой среды, вычисленные по
указанным формулам для точек, лежащих
на вертикальной и горизонтальной линиях,
которые проходят через центр сечения тун-
неля, и на вертикальной линии, удаленной
от туннеля на расстоянии, равном рассто-
янию до оси шахты. На этом же рисунке
показаны экспериментально зарегистриро-
ванные амплитуды колебаний стенок ство-
ла шахты. Результаты аналогичных вычис-
лений для шахты № 2 показаны на рис. 10.3.
При вычислениях приняты те же значения
параметров, что и для шахты № 1, за ис-
ключением ав=1,5 мкм и аг =1,3 мкм.
Здесь же приведены экспериментальные
данные.
Значения амплитуд по расчету оказа-
лись больше, чем зарегистрировано в экс-
перименте для шахты № 1, и меньше, чем
для шахты № 2. Поскольку условия экспе-
римента в значительной мере одинаковы,
то такое расхождение объясняется разли-
чием приемников колебаний — шахт, в пер-
вом случае железобетонная, а во втором
случае из чугунных тюбингов. В целом рас-
чет дал достоверную оценку уровня коле-
баний грунта вблизи тоннеля.
Расчет и эксперимент указывают на
незначительное уменьшение амплитуд коле-
баний грунта в довольно широком диапа-
зоне расстояний (до 30 м) от туннеля глу-
бокого заложения. Более того, из резуль-
татов вычислений следует, что возможно
увеличение амплитуд горизонтальных коле-
баний грунта в некотором диапазоне рас-
стояний при удалении от туннеля вдоль
вертикальной прямой, находящейся от тун-
неля на расстоянии 10—20 м. Эта особен-
140
ность волновой картины обнаружива-
ется также в эксперименте для шах-
ты № 2.
Пример 2. Приведем результаты
вычислений по формулам (10.1),
(10.3) и (10.4) и сопоставим их с эк-
спериментальными данными для фун-
даментов пятиэтажного здания (п. 1,
табл. 10.1). Примем следующие зна-
чения входящих в формулы парамет-
ров: R = 3 м, со=314 рад/с, что со-
ответствует / = 50 Гц, цв = Г8 мкм,
Crop =3,2 мкм.
Эти значения параметров несколь-
ко отличаются от значений, приведен-
ных в табл. 10.1, поскольку в ней по-
мещены максимальные амплитуды ко-
лебаний, а здесь дан расчет примени-
тельно к одной из конкретных реали-
заций записей колебаний, полученных
на данном объекте.
Сведения о скоростях распростра-
нения волн в грунте, окружающем
туннель, приняты по литературным
источникам i[l] для супеси: скорость
поперечных волн С2=300 м/с, ско-
рость продольных волн Ci = 600 м/с,
что соответствует коэффициенту Пу-
ассона v = 0,35.
Результаты вычислений амплитуд
колебаний фундаментов жилых зда-
ний, выполненных для грунта, нахо-
дящегося в уровне подошвы фунда-
ментов продольных несущих стен в
средней секции здания, приведены на
рис. 10.4. Следует отметить, что экс-
периментальное значение амплитуды
колебаний наиболее удаленной сте-
ны (ось В) соответствует не полу
подвала, как для/ Других стен, а уров-
ню цоколя, где амплитуды колебаний
примерно вдвое меньше. Наблюдает-
ся удовлетворительное согласование
расчетных и экспериментально полу-
ченных значений.
Определение амплитуд вынуж-
денных колебаний грунта, вызван-
ных колебаниями прямоугольного
туннеля мелкого заложения, с учетом
дневной поверхности. Ниже приведе-
ны графики, по которым можно опре-
делять амплитуды вертикальных ко-
лебаний точек поверхности грунта
для некоторого частного случая соот-
ношения геометрических и кинемати-
ческих параметров задачи. Графики
вычислены по формулам, дающим ре-
шение следующей задачи динамиче-
ской теории упругости 1[6]. Опреде-
ны перемещения и напряжения в уп-
ругой однородной изотропной полуплоско-
сти от действия гармонической во времени
нагрузки, равномерно распределенной по
площади прямоугольника, две стороны ко-
торого параллельны границе полуплоскости
(рис. 10.5). Главный вектор нагрузки ле-
жит в плоскости, совпадающей с плоскостью
рисунка. Здесь же приведены геометриче-
ские размеры, характеризующие положение
нагрузки, и показана принятая прямоуголь-
ная система координат.
/То расчету
метрополитена
12,5 м
Рис. 10.2
22,5м
V
zz Cm8on шахты 152
ч у
п/ *
a
• I
* Рис. 10.3
Равнодействующая вертикальной на-
грузки равна Р, интенсивность равномерно
распределенной нагрузки q=P/2a(b2—Ь4).
Комплексные амплитуды горизонтальных и
вертикальных колебаний границы упругой
полуплоскости определяются формулами:
“ = 2ц а (Ь2 — bi) lFs +‘ ’•
°=-*а£-Ь1) (Ю.6)
141
Амплитуды? мм
| |
расчет по формуле^. 3)
0,001 - ——с
----—=4=——
Рис. 10.7
колебаний
Рис. 10.4
Рис. 10.5
Рис. 10.0
Функции Fj, j=l, 2...4 зависят от
размеров и положения загруженной обла-
сти, частоты колебаний и упругих характе-
ристик материала полуплоскости.
Исходные данные, при которых приве-
дены вычисления, следующие. Нагрузка
равномерно распределена по площади квад-
рата со стороной 2а=5,28 м, что соответ-
ствует круглому тоннелю диаметром 6 м.
Условно принято, что расстояние от днев-
ной поверхности грунта до верха тоннеля
Z?4 = a=2,64 м, тогда 62 = 3а=7,92 м. Ско-
рость поперечных волн в грунте принята
С2 = 300 м/с, что соответствует средним
грунтовым условиям. Коэффициент Пуассо-
на грунта v = 0,25. Расчеты проведены при
двух значениях частоты колебаний тонне-
ля /1=50 Гц и /2=30 Гц. Тогда со-
ответствующее значение коэффициента
k=<j)/C2 = 1,05 и 0,63, а значение
параметра а=&а = 2,8 и 1,7 для каж-
дой из частот соответственно. Амплиту-
да колебаний поверхности с точностью до
постоянных множителей пропорциональна
величине Fo= ]/ F^-^Ff. Графики функ-
ции Fo представлены на рис. 10.6. На
рис. 10.7 приведены экспериментально за-
регистрированные амплитуды вертикаль-
ных колебаний грунта на различных рас-
стояниях до, оси тоннеля. Преобладающая
частота колебаний грунта находилась в ди-
апазоне 31—37 Гц. График на рис. 10.7 от
точки, находящейся на расстоянии 4 м от
оси туннеля, до точки на расстоянии 20 м
соответствует участку графика на рис. 10.6
от примерно х/а=1,5 до 8. Как видно из
сопоставления этих рисунков, приведенные
выше формулы дают результаты, качествен-
но согласующиеся с результатами экспери-
мента.
Практические расчеты по приведенным
выше материалам можно выполнять в сле-
дующей последовательности. Полагаем, что
туннель генерирует гармонические колеба-
ния грунта. Для расчета принимаем частот-
ный диапазон 35—60 Гц. По формулам
(10.3), (10.4) и (10.6) определяем ампли-
туду колебаний грунта в долях от амплиту-
ды колебаний туннеля. Амплитуду колеба-
ний туннеля принимаем по эксперимен-
тальным данным 1,5—15 мкм. Как прави-
ло, амплитуда колебаний туннеля может
быть принята в расчете 2—4 мкм, что со-
ответствует рельсовому пути со шпалами,
втопленными в бетон, на прямом участке
туннеля между станциями. Тем не менее
на одном и том же участке для вагонов
метрополитена одного типа возможно, как
показывают натурные эксперименты, уве-
личение амплитуд колебаний в 3—5 раз, что
зависит от состояния ходовой части, глав-
ным образом колес подвижного состава.
Туннель метрополитена генерирует случай-
142
ные колебания, параметры которых зависят
от многих факторов — геометрии колес и
головки рельсов, неоднородности рельсово-
го основания и т. п. Статистические зависи-
мости изучены недостаточно, однако при-
веденные формулы можно рассматривать
как соответствующие передаточные функ-
ции.
10.4 . ОЦЕНКА УРОВНЯ
КОЛЕБАНИЙ ЗДАНИЙ
В первом приближении можно считать,
что фундаменты здания совершают коле-
бания с теми же параметрами, что и грунт.
С некоторым запасом можно принять, что
в здании в целом будет наблюдаться такой
же уровень колебаний. Однако для много-
этажных зданий высотой пять и более эта-
жей амплитуды колебаний, начиная с пер-
вого этажа и выше, будут примерно в 1,5—
2 раза меньше, чем амплитуды колебаний
фундаментов. В высоких зданиях на верх-
них этажах возможно некоторое увеличе-
ние амплитуд колебаний по сравнению со
средней по высоте частью здания.
Динамические напряжения в строи-
тельных конструкциях от вибраций, вы-
зываемых движением поездов метрополи-
тена, невелики и имеют порядок несколь-
ких сотых МПа, и их можно не учитывать
при оценке прочности строительных конст-
рукций зданий.
СПИСОК ЛИТЕРАТУРЫ
Волин Л. П.> Жадин В, В., Лим-
бах Ю. И, Опыт определения упругих по-
стоянных грунтов в полевых условиях. — В
кн.: Вопросы динамической теории распро-
странения сейсмических волн, вып. 2. Л.,
1959.
2. Дашевский М. А. Излучение упругих
волн при движении пульсирующей нагрузки
вдоль тоннеля, проложенного в грунте.—
Строительная механика и расчет сооруже-
ний, 1971, №5.
3. Дашевский М. А. Распространение
волн при колебаниях тоннелей метро. —
Строительная механика и расчет сооружений,
1974, № 5.
4. Дашевский М. А. Дифракция упругих
волн на полости, подкрепленной кольцом
жесткости. — Строительная механика и рас-
чет сооружений, 1967, № 2.
5. Дорман И. Я. Борьба о вибрацией и
шумом, создаваемыми поездами метропо-
литена (обзор зарубежного опыта). М., 1973.
6. Ильичев В. А., Шехтер О. Я. Опреде-
ление динамических напряжений и переме-
щений в упругой полуплоскости от внутрен-
него источника, имитирующего воздействие
тоннеля метрополитена мелкого заложе-
ния.— В кн.: Динамика и сейсмостойкость
оснований и фундаментов. М., 1976.
7. Санитарные нормы допустимых ви-
браций в жилых зданиях (СН 1304-75). М.,
1975.
8. СНиП П-60-75. Планировка и за-
стройка городов, поселков и сельских на-
селенных пунктов. М., 1975.
9. Рао У. Я., Mow С. С. Dynamic stres-
ses concentration in an elastic plate with
rigid circular inclusion. Proc. of. the Fourth
U. S. Nat. Congress of Appl. Meeh., June.
1962.
143
РАЗДЕЛ 11. КОЛЕБАНИЯ ФУНДАМЕНТОВ УСТАНОВОК
ВЗРЫВНОЙ ШТАМПОВКИ И ГРУНТА
(В. А. ИЛЬИЧЕВ)
11.1. ОБЩИЕ СВЕДЕНИЯ
Штамповка взрывом — относительно
новый и широко распространяющийся в
промышленности вид технологии обработки
металлов давлением. Установки, в которых
осуществляется этот технологический про-
цесс, весьма разнообразны по своей конст-
рукции, и их конкретное исполнение зави-
сит от типа энергоносителя [взрывчатое ве-
щество (ВВ), электрический разряд и др.],
характера среды, передающей энергию удар-
ных волн от источника к заготовке (ваку-
ум, газообразная, жидкая и сыпучая среда
и др.), а также от других факторов [1, 2, 10,
12, 13, 16]. С точки зрения динамики соору-
жений установки взрывной штамповки (ВШ)
представляют собой весьма мощный источ-
ник колебаний.
В этом разделе приведены эксперимен-
тальные данные по колебаниям фундамен-
тов установок, грунта и окружающих зда-
ний, даны рекомендации по определению
параметров колебаний, возникающих при
работе установок ВШ (см. рисунок), пред-
назначенных для проведения технологиче-
ских операций холодной штамповки и ка-
либровки листовых деталей с помощью
энергии ударных волн, распространяющихся
в воде от взрыва заряда ВВ, Другие дина-
мические факторы, которые могут действо-
вать на строительные конструкции при ра-
боте установок ВШ, — воздушная ударная
волна и так называемый «султан воды»,
выбрасываемый вверх, здесь не рассмат-
риваются.
Технология гидровзрывной штамповки
состоит в следующем. Деталь или плоскую
заготовку, предназначенную для обработки,
вместе с матрицей опускают в резервуар с
водой, над заготовкой укрепляют заряд ВВ
и затем взрывают. Ударные волны, образу-
ющиеся в воде, деформируют заготовку, об-
жимая ее по форме матрицы. Точность из-
готовленных таким образом изделий весь-
ма высока и дополнительная обработка
практически не требуется.
Начальные сведения о подводном взры-
ве. При взрыве заряда ВВ, помещенного в
воду, образуется ударная волна, распрост-
раняющаяся со сверхзвуковой скоростью.
Давление в жидкости при прохождении
ударной волны от сферического заряда без
учета влияния дна и свободной поверхности
воды определяется формулой [4, 8,17]
р = рте е, (11.1)
где
рт =0,1А (G^'/r)1113 МПа;
t — время, отсчитываемое от момента при-
хода ударной волны в данную точку;
0 = (G,/s/r)0’24 G'/s• 10“4 с;
G — масса заряда ВВ, кг; г — расстояние, м,
от центра заряда до точки в жидкости, где
определяется давление;
Ai = yiA; Yz (Qz/Qt)0,376,
где Qi — удельная энергия данного ВВ,.
кДж/кг; QT = 4200 кДж/кг, удельная энер-
гия тротила; А = 533.
Время действия ударной волны состав-
ляет тысячные доли секунды. Поэтому для
расчетов строительных конструкций, имею-
щих периоды колебаний порядка сотых до-
лей и более, действие давления можно за-
менить действием мгновенного импульса, ко-
торый при использовании тротила равен:
00,63
Jo = Pm в = А—— 10“® . (Ц.2)
*U,oU
Из формулы (11.2) видно, что импульс
давления пропорционален массе заряда в
степени 0,63.
Газообразные продукты взрыва обра-
зуют^так называемый «газовый пузырь», ко-
торый, пульсируя, всплывает на поверх-
ность. Период первой пульсации Т, с, без
учета ограниченности объема бассейна на-
ходят по формуле [4, 8, 17]
(Л+10,3)5/‘
где 6=2,11 с-(м)^* /(кг)1^’ для тротила;
h — глубина, на которой размещен заряд, м;
G — масса заряда.
Давление газообразных продуктов взры-
ва передается на воду, достигая максиму-
ма при минимальном радиусе пузыря. Вре-
мя появления первого максимума опреде-
ляют формулой (11,3).
Установка взрывной штамповки
1 — цилиндрический резервуар; 2 — вода; 3 —
грунт; 4 — трубка к вакуум-насосу; 5 — железо-
бетонный фундамент; 6 — прокладка; 7 — матри-
ца; 8 — листовая заготовка; 9 — прижимное
кольцо; 10 — заряд ВВ
144
11.2. ЭКСПЕРИМЕНТАЛЬНЫЕ
ДАННЫЕ О КОЛЕБАНИЯХ,
ВЫЗЫВАЕМЫХ РАБОТОЙ
УСТАНОВОК ВЗРЫВНОЙ
ШТАМПОВКИ
Сложность процессов, происходящих
при взрывной штамповке, их неизученность
с точки зрения динамического воздействия
на окружающие здания и сооружения за-
ставляют обращаться к экспериментальным
данным, которые представляют основной
исходный материал для оценки уровня ко-
лебаний при проектировании фундаментов
установок ВШ и цехов, в которых они дол-
жны размещаться.
Результаты экспериментальных иссле-
дований, изложенные ниже, иллюстрируют
процессы колебаний установок ВШ и грунта
и могут быть использованы при проектиро-
вании. Сведения об установках ВШ, для
которых приведены экспериментальные дан-
ные, помещены в табл. 11.1 [5].
Колебания фундаментов установок ВШ
и поверхности грунта имеют ярко выра-
женный нестационарный характер. На за-
писях имеются повторяющиеся участки, та-
.кие, как если бы колебания вызывались дву-
мя импульсами, следующими с интервалом
/1. Первый импульс .есть результат воздей-
ствия ударной волны на дно бассейна, а
второй объясняется пульсацией газового
пузыря, что видно из табл. 11.2, в которой
приведены средние значения эксперимен-
тально зарегистрированных значений /1, с,
для различных масс заряда и значения Т, с,
подсчитанные по формуле (11.3). Результа-
ты оказываются достаточно близкими, осо-
бенно для тротила. Экспериментальные дан-
ные о колебаниях фундаментов установок
ВШ помещены в табл. 11.3 и 11.4.
Фундамент установки ВШ № 2 под
действием ударной волны и импульса дав-
лений, возникающего при первой пульсации
газового пузыря, совершает свободные ко-
лебания с частотой около 10,6 Гц.
ТАБЛИЦА 11.1
№ уста- новки ВШ ГШ г* Размеры бас- сейна, м Уро- вень воды, м Высота подвески заряда над дном, м Общая масса установки с водой, т Размеры подошвы фундамен- та, м Инженерно-геологи- ческие- условия пло- щадки Масса взрыва- емых зарядов ВВ G, кг
диа- метр высота
1 . 3,6 ipZ f 3,6 2,6 f 1,5 215 0 5,5 Пески мелкозернис- тые /?н=0,25 МПа. Уровень грунтовых вод ниже 8 м 0,05; 0,1; 0,2; 0,3
2 4 4 3 1,5 189 4,8X4,8 Суглинки 9,05; 0,1; 0,3; 0,6; 1
3 6,9 6,5 4,5 1,5 370 0 7,5 Чередующиеся на- пластования мелко- зернистых водопа- сыщенных песков и илов толщиной сло- ев 0,8—2 м; 7?н = = 0,1 МПа 0,075; 0,15; 0,5; 1; 2; 4; 7; 10
ТАБЛИЦА 11.2
№ установ- ки ВШ Масса заряда G, кг 0,05 0,075 0,1 0,15 0,2 0,3
1 Л (флегм, гексоген) 0,111 0,146 * 0,187 0.220
2 Л (тротил) 0,129 — 0,143 * Ч 0,197
3 /1 (аммонит) * » 0,146 0,166
3 Л (тротил) — 0,9 > 0,126
Т по формуле (11.3), с (тро- тил) 0,099 0,102 0,112 0,128 0,158 0,181
Продолжение табл. 11.2
№ установ- ки ВШ Масса заряда G, кг 0,5 0,6 1 2 4 7 10
1 /1 (флегм, гексоген) ——ч
2 /1 (тротил) 0,246 — —
3 Л (аммонит) 0,234 0,305 0,39 0,502 fc-чч
3 t\ (тротил) 0,192 0,23 0,303 — -—
4 Т по формуле (11.3), с (тро- тил) 0,193 0,227 0,242 0,307 0,386 0,484 0,515
145
ТАБЛИЦА 11.3
Масса заряда G, кгс Амплитуда колебаний фундамента установки ВШ № 2 Частота колебаний f мм
от дейст- вия удар- ной волны Aj , мм (экспери- мент) Расчет по формуле (11,9) при а = 0 А , мм макси- мальная зарегист- рированная (ударная волна и пульсация пузыря) А макс’ мм
0,05 — 0,63 1,69 9,6
0,1 0,79 0,73 1,31 П,9
0,3 0,9 1,16 1,16 п,о
0,6 2,19 2,38 11,0
1 2,52 2,01 9,7
дно резервуара установки ВШ № 3 и зна-
чения масс падающих частей молота Qo,
при ударе которых о шабот со скоростью
7 м/с возникает такой же импульс; при этом
принимали, что коэффициент восстановле-
ния скорости равен нулю. Значения >
импульса в табл. 11.5 вычислены по экспе-
риментальным данным о колебаниях фун-
дамента.
Значение импульса J в табл. 11.5 при-
ближенно пропорционально весу заряда в
степени 0,-63.
Колебания грунта. Наибольшие ампли-
туды колебаний имеют место при прохож-
дении поверхностной волны от источника.
Амплитуды колебаний грунта при увели-
чении расстояния до установок ВШ умень-
шаются вблизи фундамента обратно про-
ТАБЛИЦА 11.4
Масса заряда G, кг 0,075j 0,15 г* 0,5 1 2 4 7 10
Амплитуда колебаний фун- дамента установки № 3 от действия ударной волны Ai, мм 0,4 0,67 4,87 6,92 10,0 26,8 30,8 38,5
Частота колебаний f , Гц 11,2 7,96 5,21 4,5 4,3 4,12 4,07 3,91
Колебания фундамента установки ВШ
№ 3 значительно сложнее. При взрыве за-
рядов массой 0,075 и 0,15 кг фундамент со-
вершает 5—7 циклов периодических коле-
баний под действием пульсаций газового
пузыря. При увеличении веса заряда коле-
бания фундамента по своему характеру
все более отличаются от периодических и
приближаются к нестационарным свобод-
ным колебаниям. Для зарядов массой 0,5—•
4 кг влияние ударной волны и пульсации
газового пузыря хорошо различимы на ос-
циллограммах. Для зарядов массой 0,5 и
1 кг период пульсации близоок к периоду
свободных колебаний фундамента. Поэто-
му фундамент совершает колебания, напо-
минающие по своему характеру резонанс-
ные; их продолжительность больше, чем
для зарядов других весов. Это явление спе-
цифическое для установок ВШ, и его сле-
дует учитывать в расчетах. При взрыве за-
рядов массой 4 кг и выше газообразные
продукты взрыва сразу прорываются в ат-
мосферу, не образуя пульсирующего газо-
вого пузыря. При взрыве зарядов массой
1—2 кг и больше в основании фундамента
установки ВШ № 3 возникали пластические
деформации, что приводило к образованию
остаточной осадки фундамента.
В табл. 11.5 приведены ориентировоч-
ные значения импульса /, действующего на
ТАБЛИЦА 11J5
G, кг 0,5 1 2 4 7 10
J, Н-с 59500 84700 122 000 328 000 366 000 471 000
Qo, т 8,5 12 17,3 46,5 52 67
порционально расстоянию на расстоянии
свыше примерно трех диаметров фундамен-
та, а дальше обратно пропорционально- кор-
ню квадратному из расстояния.
При взрыве' заряда достаточно боль-
шой массы (для описанных установок 0,3—
0,5 кг), когда газообразные продукты
взрыва сразу прорываются в атмосферу и
влияние пульсации газового пузыря практи-
чески не сказывается, амплитуды колеба-
ний фундамента и поверхности грунта про-
порциональны весу заряду в степени 0,63.
Для относительно небольших зарядов массой
менее 0,3 кг амплитуды колебаний при-
мерно пропорциональны весу заряда в сте-
пени !/з. Например, для установки ВШ № 1
отклонение от этой зависимости не превы-
шает в среднем 8%.
11.3, ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ
КОЛЕБАНИЙ ФУНДАМЕНТОВ
УСТАНОВОК ВЗРЫВНОЙ
ШТАМПОВКИ
И ПОВЕРХНОСТИ ГРУНТА
Для определения параметров колеба-
ний фундаментов может быть принята рас-
четная схема в виде твердого тела, лежа-
щего на упругом основании и совершающе-
го вертикальные колебания.
Нагрузка. На дно резервуара действует
нагрузка от ударной волны и пульсаций
газового пузыря, закон изменения во вре-
мени которой зависит от выполняемой тех-
нологической операции. Рекомендации по
определению нагрузки от ударной волны на
дно резервуара имеются в [12]. Для ори-
ентировочных расчетов параметров колеба-
ний фундаментов установок ВШ можно
146
пользоваться следующими данными, соб-
людая указанные ниже ограничения.
Импульс ударной волны, вызывающий
колебания фундамента установки, можно
оценить для тротила по формуле
J = r (G) VT Ю5 н-с; (11.4)
0,0
при G > Go;
при
(П.5)
где G — масса заряда тротила, кг; R — ра-
диус резервуара, м, 1,75^7?=^3,5;
£ _ / 0,31 кг для резервуара радиусом 1,75 м,
0 10,5 кг длярезрвуара радиусом 3,5 м.
Формулы (11.4) и (11.5) являются при-
ближенными, основанными на эксперимен-
тальных данных [5], и могут быть исполь-
зованы при расчете невиброизолированных
фундаментов установок ВШ, имеющих ци-
линдрический резервуар, при высоте подве-
ски заряда ВВ~1,5 м над дном и уровне
воды 2,5—3 м при выполнении операций
штамповки и калибровки листовых деталей.
Действие на дно резервуара давления,
возникающего при первой пульсации газо-
вого пузыря в момент его наибольшего
сжатия, можно приближенно заменить дей-
ствием мгновенного импульса, приложенного
в момент времени зависящий от разме-.
ров резервуара, уровня воды, массы и поло-
жения заряда. Это допустимо делать в слу-
чаях, когда вторая пульсация газового пу-
зыря практически отсутствует. Для условий
эксперимента, описанного выше, можно
принять при использовании тротила, что
/1«Г, где Т вычисляют по (11.3). Значение
импульса равно а/, где а зависит от тех же
факторов. Значение а можно принимать
по табл. 11.6 [5] при сходных с экспери-
ментами условиях.
Расчетная схема и параметры колеба-
ний. Уравнение колебаний фундамента
m
-j— ct J 5 (/ — /j),
где 6(/) —дельта-функция.
Масса системы равна массе всей уста-
новки ВШ, включая воду. Коэффициент же-
сткости основания
kz = CzF, (11.7)
где F — площадь подошвы фундамента;
Cz — коэффициент упругого равномерного
сжатия [15].
Коэффициент демпфирования
* = (11.8)
где Ф — модуль затухания, следует прини-
мать по рекомендациям [14, ([15].
Колебания фундамента установки ВШ
совершаются по закону
w (/) — Ао [e~nt sin coj t + a x
X sin o)i (/ — Л) T) (/ — /i)], (П.9)
где T](/) —единичная ступенчатая функция;
T|(t) = 1 при OO и Ti(/)•== 0 при /<0.
Амплитуду колебаний фундамента
вследствие воздействия ударной волны оп-
ределяют приближенной формулой
П~
Аф =-------2“* . (Н.Н)
/П (01
Максимальная амплитуда колебаний с
учетом действия ударной волны и первой
пульсации газового пузыря может быть най-
дена с помощью графика функции w(/),
построенного по (11.9).
Нормирование параметров колебаний
фундаментов установок ВШ. Размеры фун-
дамента и его массу выбирают исходя из
того, чтобы параметры колебаний фунда-
мента не выходили из заданных пределов.
Технологический процесс не накладывает
ограничений на параметры колебаний фун-
дамента. При размещении установок ВШ в
цехах допускаемая амплитуда колебаний
фундаментов этих установок может быть
принята такой же, как для фундаментов
молотов [15], что обеспечит отсутствие ос-
таточных осадок.
Для установок, находящихся на откры-
тых площадках, особенно для временных,
можно допустить образование остаточных
осадок фундамента. Однако это обстоятель-
ство не должно мешать нормальному про-
ведению технологических операций, и по-
этому надо принять соответствующие конст-
руктивные меры: увеличить высоту стенки
резервуара, применять разборный рабочий
ТАБЛИЦА 11.6
ВШ № 1 Масса заряда Gt кг 0,05 0,1 0,2 0,3 ——
a 1,4 1,2 1 1 1 1
ВШ № 2 Масса заряда G, кг 0,05 0,1 0,3 0,6 1
a 2 1,5 1,2 1 0
ВШ № 3 Масса заряда G, кг 0,15 0,5 1 2 4—10
a 0,8 1,6 1 6,5 0
147
настил вокруг установки ВШ для того, что-
бы обеспечить возможность заполнения за-
зора между стенкой установки ВШ и грун-
том, и т. п.
Определение параметров колебаний
грунта. Амплитуду1 вертикальных колеба-
ний грунта находят по формуле
Лф —— е 0 гф> при гг^г0;
г*
(11.12)
где Гф — радиус подошвы фундамента; г0=
= 6<ф; гг — расстояние от оси фундамента
до точки на поверхности грунта; ip — коэф-
фициент, учитывающий поглощение энергии
волн в грунте, берут по рекомендациям [14].
Формула (11.12) применима, если Аф
не превышает допускаемой амплитуды ко-
лебаний для фундаментов под молоты [13].
Для оценки воздействия упругих волн,
распространяющихся в грунте на окружаю-
щие здания, сооружения и фундаменты чув-
ствительного к вибрациям оборудования,
можно принять '[6], что при прохожде-
нии поверхностной волны, имеющей наи-
большую амплитуду колебаний, движение
поверхности грунта в вертикальном направ-
лении определяется формулой (11.9), в ко-
торой следует положить
пл
А0 = Агре^. (11.13)
Для расстояний гг>(4...6)Гф перед
правой частью формулы (11.13) следует по-
ставить знак минус, имея в виду, что на
таком удалении от фундамента точки грун-
та при прохождении поверхностной волны
сначала движутся вверх. Можно принять,
что амплитуды горизонтальных колебаний
поверхности грунта примерно равны ампли-
тудам вертикальных колебаний и сами ко-
лебания совершаются по закону (11.9).
Сдвиг фазы между вертикальными и гори-
зонтальными колебаниями следует принять
наиневыгоднейшим для данного динамиче-
ского расчета^
Динамический расчет строительных кон-
струкций на воздействие волн, распростра-
няющихся в грунте, надо выполнять для раз-
личных зарядов, а не только максимально-
го по весу, так как наибольшие амплитуды
колебаний могут быть вследствие влияния
пульсации газового пузыря при зарядах
меньше максимально допустимого для дан-
ной установки.
Виброизоляция фундаментов установок
Для снижения динамических воздействий
на грунтовое основание и окружающие
здания и, сооружения можно применять виб-
роизоляцию, что экспериментально прове-
рено в работах [3, 9], где даны соответст-
вующие рекомендации. Виброизоляцию
рассчитывают так же, как и для молотов
[7, 11]. Основным требованием является
обеспечение прочности виброизоляторов при
колебаниях фундамента, вызванных дейст-
вием ударной волны на дно резервуара и
пульсацией газового пузыря. Целесообразно
использовать пружинно-рессорные вибро-
изоляторы.
СПИСОК ЛИТЕРАТУРЫ
1. Антоненков О. Д- и др. Штамповка
подводным взрывом. М.» 1967.
2. Вопросы теории «и практики гид-
ро взрыв ной штамповки (библиографиче-
ский указатель литературы 1У61—
1964 гг.)./ Под ред. В. Г. Степанова. Л.,
1965.
3. Воробьев Г. К. Результаты дина-
мических испытаний фундамента на вибро-
изоляторах. Материалы координационного
совещания по динамике строительных кон-
струкций и методам борьбы с вибрациями.
М., 1975.
4. Замышляев Б. В., Яковлев Ю. С.
Динамические нагрузки при подводном
взрыве. Л., 1967.
5. Ильичев В. А. Экспериментальное
изучение колебаний фундаментов установок
взрывной штамповки, грунта ,и зданий. —
Труды (Об. тр., Науч, тр.) / ЦНИИСК-
М., 1975. ’
6. Ильичев В. А. Вертикальные неста-
ционарные колебания массива под воздей-
ствием волн, возникающих в полупростран-
стве при колебаниях другого массива.—*
В кн.: Динамика сооружений. / Под ред.
Б. Г. Коренева. М., 1968.
7. Ильичев В. А. Расчет подшаботной
пружинно-рессорной виброизоляции моло-
тов.— Строительная механика и расчет
сооружений, 1973, № 4.
8. Коул Р. Подводные взрывы. М.„
1950.
9. Некоторые вопросы расчета бассей-
нов. О. В. Лужин, Б. С. Бегун, Г. К. Во-
робьев и др. — В кн.: Обработка металлов
взрывом, 4.1. М., 1971.
10. Пихтовников Р. В., Завьяло-
ва В. М. Штамповка листового металла
взрывом. М., 1964.
1'1 . Руководство по проектированию
виброизоляции машин и оборудования.
ЦНИИСК. М.; 1972.
12. Степанов В. Г., Сипилин П. М.,
Навагин Ю. С., Панкратов В. П. Гидро-
взрывная штамповка элементов судовых
конструкций. Л., 1966.
13. Степанов В. Г., Шавров И. А. Вы-
сокоэнергетические импульсные методы об-
работки металлов. Л., 1975.
14. Савинов О. А. Современные кон-
струкции фундаментов под машины и их
расчет. Л., 1964.
, 15. СНиП П-19-79. Фундаменты машин
с динамическими нагрузками. Нормы про-
ектирования.
16. Штамповка взрывом. Основы >ге-
ории. / Под ред. М. А. Анучина. М., 1972.
17. Яковлев Ю. С. Гидродинамика
взрыва. Л., 1961.
148
РАЗДЕЛ 12. РАСЧЕТ СООРУЖЕНИЙ, ОБОРУДОВАННЫХ
ДИНАМИЧЕСКИМИ ГАСИТЕЛЯМИ КОЛЕБАНИЙ
(Б. Г. КОРЕНЕВ, Л. М РЕЗНИКОВ)
12.1. ОБЩИЕ СВЕДЕНИЯ
В этом разделе рассмотрен расчет со-
оружений с динамическими гасителями ко-
лебаний (ДГК) при специальных воздей-
ствиях - сейсмических, взрывных и др., а
также при действии ветра и нагрузок от
машин. При правильном проектировании
и расчете ДГК являются надежным и эф-
фективным способом борьбы с вибрациями,
дополняющим другие известные методы.
Применение гасителей особенно целесо-
образно для высоких или протяженных в
плане гибких сооружений, выполненных из
металла, при ветровых, сейсмических и
взрывных воздействиях, когда использование
других способов уменьшения колебаний
затруднительно. В частности, гасители эф-
фективны при установке их на башенных
соружениях, мечтах с оттяжками, на-
земных трубопроводах, зданиях с метал-
лическим каркасом, гибких покрытиях в
виде мембран, пластинок, складок, оболо-
чек. В железобетонных сооружениях вслед-
ствие большего собственного демпфирова-
ния эффективность гасителей оказывается
ниже, чем в металлических.
ДГК уменьшают колебания, вызванные:
1) периодическими, в частности гармо-
ническими, воздействиями со стабильной
или нестабильной частотой, в особенности
если она близка к одной из частот свобод-
ных колебаний системы;
2) ветровым резонансом или галопиро-
ванием сооружений поперек ветрового по-
тока;
3) кинематическим воздействием одной
или пакета затухающих синусоид, переда-
ющихся на гибкую защищаемую конструк-
цию, опирающуюся на массивное сооруже-
ние или на жесткую конструкцию, которая
непосредственно подвергается действию
взрыва или землетрясения;
4) случайными воздействиями (пуль-
сации ветра, сейсмика), особенно если
спектр нагрузки является узкополосным
и частоты свободных колебаний сооруже-
ния попадают в указанную полосу;
5) действием кратковременных импуль-
сов непосредственно на защищаемую кон-
струкцию, когда гасители существенно
уменьшают время переходного процесса.
ДГК обычно выполняют в виде «мас-
сы», которую присоединяют к защищаемой
конструкции с помощью упругого элемен-
та и демпфирующего устройства (гасите-
ли с упругим элементом) либо подвеши-
вают на тросе или шарнирном стержне
(маятниковые гасители). Амплитуды коле-
баний массы гасителя, как правило, намно-
го превышают амплитуды колебаний за-
щищаемой конструкции, которые уменьшают-
ся вследствие действия упругих и дисси-
пативных сил со стороны гасителя. Масса
гасителя может представлять собой сталь-
ной, чугунный или железобетонный эле-
мент, в некоторых случаях — резервуар,
заполненный жидкостью.
Упругий элемент гасителя обычно вы-
полняют в виде стальной пружины или си-
стемы пружин, по конструкции близкой в
пружинному виброизолятору; для этого
можно применять также резиновые и пла-
стмассовые детали, консольные и двух-
опорные балки, пластинки и т. п.
Если ДГК находится в закрытом и
отапливаемом помещении, то в качестве
демпфирующих устройств можно исполь-
зовать вязкие демпферы, аналогичные тем,
которые применяют при вибропзоляцин
фундаментов под машины [42]. В гаси-
телях, размещенных на открытых площад-
ках или в условиях, не допускающих про-
ведения частых осмотров, ЦНИИСК им.
В. А. Кучеренко рекомендует использовать
внутреннее трение в упругом элементе. В
частности, в маятниковых ДГК, устанавли-
ваемых для уменьшения колебаний гибких
высоких сооружений, верхнюю часть троса
(можно закрепить так, чтобы при колеба-
ниях маятника возникало демпфирование
вследствие местного изгиба троса. При не-
обходимости одновременного гашения вер-
тикальных и горизонтальных колебаний
можно применять разработанную Урал-
промстройниипроектом конструкцию, пред-
ставляющую собой (маятник с нитью под-
веса, обладающей большой растяжимостью.
Расчет сооружения, оборудованного ДГК,
сводится к рассмотрению колебаний систе-
мы с присоединенными осцилляторами. Су-
щественной частью расчета является оп-
тимизация параметров гасителей — выбор
собственной частоты (настройки) и демп-
фирования при заданной массе гасителя
(иногда оптимизируются также его масса
и расположение). Иногда в расчете учиты-
вают конструктивные ограничения на ам-
плитуды колебаний динамического гасителя
(например, если маятниковый гаситель
колебаний размещен внутри свободного
пространства дымовой трубы, имеющей не-
сколько дымовых каналов).
Принятый критерий качества может
отражать условие прочности сооружений
при динамических воздействиях или соот-
ветствовать кинематическим характеристи-
кам (перемещения, скорости, ускорения и
др), назначаемым согласно санитарно-ги-
гиеническим и технологическим требова-
ниям. В первом случае гаситель должен
обязательно иметь надежность, близкую к
надежности защищаемых конструкций, и
быть постоянно готовым к работе. Жела-
тельно, чтобы и во втором случае гасители
удовлетворяли этим же условиям и по
возможности не требовали постоянного
ухода и частых ремонтов.
149
1
Основные результаты, получаемые по
теории ДГК одномассовой системы, мо-
гут быть полезны при решении задач о
гашении колебаний конкретных конструк-
ций, в частности для приближенного вы-
бора параметров и грубой оценки эффек-
тивности гасителя, даже если расчетная
схема защищаемой конструкции и не сво-
дится к системе с одной степенью свободы.
Краткие сведения о работе линейного ДГК
(упругий элемент обладает линейной ха-
рактеристикой), установленного на одно-
массовой системе, при различных воздейст-
виях изложены в п. 12.2; некоторые дан-
ные о многомассовых и нелинейных гаси-
телях приведены в п. 12.3. В последующих
двух пунктах обсуждается расчет дискрет-
ных и континциальных систем с присоеди-
ненными ДГК при гармонических и негар-
монических воздействиях; рассматриваются
задачи о гашении) продольных и поперечных
колебаний стержней, поперечных колеба-
ний пластинок, складок, оболочек; изложе-
ны результаты, относящиеся к виброгаше-
нию башен, мачт, трубопроводов при гар-
монических и случайных воздействиях.
Большинство результатов, представлен-
ных ниже, получено решением минимакс-
ных задач: оптимальные параметры ДГК
определены из условия минимума соответ-
ствующего критерия качества. Последний
в свою счередь найден как максимум по
одному из характерных параметров воз-
действия ((например, по частоте, которая
вследствие нестабильности может прини-
мать самое неблагоприятное значение и
вызывать резонансные колебания конструк-
ций). В формулах, таблицах, на рисунках
индексы ОПТ в обозначениях оптимальных
параметров ДГК и max в обозначениях
максимального расчетного значения кри-
терия качества применены только в тех
случаях, когда их отсутствие может выз-
вать недоразумение.
Если расчетная схема защищаемой кон-
струкции может быть представлена в виде
многоступенчатого стержня с присоединен-
ными упругодиссипативными связями на
границах отдельных участков и нет возмож-
ности непосредственно использовать при-
веденные ниже результаты, рекомендуется
выполнять расчеты с помощью программы,
помещенной в '[34].
12.2. ЛИНЕЙНЫЙ ДГК,
УСТАНОВЛЕННЫЙ НА СИСТЕМЕ
С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Теория динамического гасителя доста-
точно детально разработана для случая,
когда в защищаемой конструкции учитыва-
ется одна степень свободы, соответствую-
щая форме свободных колебаний (обычно
первой), которая дает наибольший вклад
в вынужденные колебания. При известных
круговой частоте со и форме у(х) свобод-
ных колебаний конструкции приведенные в
точку подвеса гасителя масса, квазиупру-
гий коэффициент и сила соответственно
равны:
М — vr 2J т (х) v2 (х) dx; К ~ (о2
X
Т ~ vr 11 q (х) v (х) d х,
(12.1)
X
где гп(х), q(x) — погонная масса конструк-
ции и нагрузка; уг — ордината формы ко-
лебаний в точке подвеса гасителя; % — об-
ласть изменения х.
Эффективность ДГК зависит от от-
ношения его массы m к величине М, назы-
ваемой далее главной массой, и повыша-
ется, как правило, при установке гасителя
в точке с максимальной ординатой соот-
ветствующей формы колебаний конструк-
ции.!
Далее определены оптимальные пара-
метры и эффективность гасителя при раз-
личных воздействиях. Влияние на колеба-
ния конструкции неучтенных форм, частоты
которых удалены от парциальной частоты
ДГК, можно принимать таким же, как
при отсутствии гасителя.
Гармонические воздействия
Рассматриваются кинематическое, а
также силовое возбуждение с амплитудой
То, постоянной или пропорциональной квад-
рату частоты. Если угловая частота ро
воздействия изменяется в небольших
пределах вне резонансных зон системы с
гасителем, то целесообразно устанавливать
ДГК без демпфера и в расчете пренебрегать
рассеянием энергии. При широкополосных
воздействиях, в особенности в резонансных
случаях, необходимо применять ДГК с
вязким или внутренним неупругим сопро-
тивлением. Оптимальные параметры гаси-
теля могут выбираться из условия мини-
мума таких критериев качества R: Хо, Ко,
IFo — амплитуды перемещения, скорости,
ускорения главной массы; Uq = Xq — ZQ —
амплитуды перемещения главной массы от-
носительно основания, где Zo — амплитуда
перемещения основания. Тип воздей-
ствия и принятый критерий качест-
ва определяют соответствующий расчетный
случай' (табл. 12.1).
ТАБЛИЦА 12.1. ОБОЗНАЧЕНИЯ
РАСЧЕТНЫХ СЛУЧАЕВ
Воздействие Критерий качества R
Хо w0 и0 Vo
Силовое (Т= а в а е
— const) Силовое (T~Pq) б д б ж
Кинематическое а в г е
ДГК без демпфирования. Для системы
с гасителем (рис. 12.1,а) безразмерные
амплитуды колебаний равны
150
Рис. 12.1. ДГК без демпфирования
а — схема гасителя колебаний; б — амплитудно-
частотные характеристики; / — без гасителя;
2 — с гасителем
Здесь v = m/M; /2 = /q/(d2 -относитель-
ная масса и настройка гасителя; Х = %о/хст;
V= Vo/хст ©о; 1Го/хст «о — амплитуды
перемещения, скорости и ускорения главной
массы; У=Уо/хСт, S = S0/xCT — амплитуды
перемещения массы и удлинения упругого
элемента гасителя; хСт = ^о— при кинема-
тическом, хст = То/К — при силовом воздей-
ствии, — при кинематическом или си-
ловом воздействии с постоянной ампли-
тудой То; с — р2— для инерционного воз-
буждения вращающимися дебалансами. При
кинематическом воздействии амплитуда от-
носительного перемещения главной массы
Из условия Л = 0 определяются собст-
венные частоты колебаний рассматривае-
мой системы:
“1,2= ]/0,5„ [ 1 + Р (1 + V)] ± 0,б5<
Э/И +f2 (1 + V)]2 —4/2.
Для того чтобы выбранный критерий
качества на границах частотного диапазона
Р==Р1 и р—р2 (рис. 12.1,6) не превышал
некоторого заданного значения А, следует
параметры гасителя назначать по форму-
лам:
2 2
Р2-Р1
v = ------------- ;
Pl Pl (ф2 — Ф1)
Р? Pl (Фа — Ф1)
? = —--------~’
Р2 Фа — Pi Ф1
где “
значения р для
разных расчетных случаев (см, табл. 12.1)
равны:
верхний знак соответствует tpi, нижний —
ф2. Прочность упругого элемента гасителя
можно проверить, определив S по форму-
лам (12.2). Расчетные случаи «а», «б» изу-
чены в [1]„
ДГК с вязким сопротивлением [8, 37].
Введение в гаситель неупругого сопротив-
ления позволяет уменьшать резонансные
колебания защищаемой конструкции. Под-
ход к оптимизации параметров здесь отли-
чается от случая ДГК без демпфирования,
так как определяются оптимальные зна-
чения настройки /2 и относительного коэф-
фициента вязкого сопротивления ц — рг/соо
при заданном значении v. Последнее наз-
начают исходя из обеспечения требуемого
значения критерия качества при соблюде-
нии условий прочности или ограничений
на амплитуду колебаний упругого элемен-
та гасителя. При выборе оптимальных па-
раметров гасителя обычно не учитывают
собственного демпфирования в защищаемой
конструкции (влияние этого фактора об-
суждается ниже). Это позволяет исполь-
зовать известное свойство независимости
критерия качества от значения ц при
совпадении частоты воздействия с инва-
риантными угловыми частотами ри, кото-
рые соответствуют точкам пересечения ам-
плитудно-частотных характеристик главной
массы при v = 0 и при v=/=0, ц=0. Вык-
ладки по определению /опт и Цент оказы-
ваются довольно громоздкими. Основные
результаты для указанных в табл. 12.1
расчетных случаев представлены в табл.
12.2. Для выбранных значений j2 и ц. без-
размерные амплитуды колебаний главной
массы и массы гасителя при (Произвольной
угловой частоте р можно найти по фор-
мулам (12.2), заменив в них f2 на f2A~tpp.
ДГК с внутреннем неупругим сопро-
тивлением, учитываемым по Е. С. Сорокину.
В этом случае в формулах (12.2) следует
•заменить'/2 на /2 где
*
4 - Y02 4уог
и2 =--------— ; = •------—
4 + Тог 4 + Y02
$
— константы, зависящие от коэффициента
Ус,2 неупругого сопротивления упругого
элемента гасителя. Выражение /2 (иг+
~Ну2) принимает вид /2(1+172), если по-
ложить
151
152
ТАБЛИЦА 12.2. РЕЗУЛЬТАТЫ ДЛЯ ОДНОМАССОВОЙ СИСТЕМЫ С ДГК ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ С НЕСТАБИЛЬНОЙ ЧАСТОТОЙ
ДГК с вязким или внутренним трением \ ' ДГК с вязким трением ДГК с внутренним трением
р2 ^макс f2 'опт Ц2 4эпт с макс V2 г2опт С макс
з у
(1 + V) (2 + v)
(3 — v8) v
2(1 — 2 V — V8)
2(1—2у) / 2
V I/ 3 (2 + v) X
Г Х(1 — 2,375 V)
V (3 + V) (1 + V)
[1-2V-V1] (2 +V)
4 (2 4 v) (1 +v)
1 4 0,5 у
(1 4 v)2
3 у
2 (1 4 v) X
X (1 4 1,25 V)
12 у (1 4 1.83 V)
.(У 8 4 5 у Т У у )2 2 ] / 1 3 у (1 4 0,25 у)
ж 2 (2 4 V)2 24 у г ' V 1 4 0,5 V 2
4 1, / 1 — 0,25 у Зу (1 4 0,83 у)2 4
(2 4 у) у 3 2 V (2 4 у) (1 4 0,58 у) Уз
Оптимальные значения р, уг подбираются
так же, как для гасителя с вязким тре-
нием. Значения /оПТ , > /?тах для обоих
типов гасителей совпадают, а коэффициен-
ты неупругого сопротивления и максималь-
ные амплитуды удлинения упругих элемен-
тов гасителей различаются (см. табл. 12.2).
Оптимальные значения у02 и /* находят
по (12.3), предварительно определив f2 и
у2 по формулам табл. 12.2,
Влияние отклонений параметров гасите-
ля от оптимальных значений на его эффек-
тивность. Отклонение от оптимума настрой-
ки в отличие от демпфирования заметно
сказывается на эффективности ДГК [37].
Относительное приращение критерия каче-
ства R по сравнению с его оптимальным
значением 7?0Пт вследсттвие отклонения на-
стройки составляет
гаситель
ротивлением
2
2
2(Р-0,5у1Ц)
(12.5)
внутренним неупругим соп-
2 (1 — Vi Ya)'
(1 + Д(1 —2Y1Y2 —Y1)
Ъ— Vi
1 — Yi Уг
2 .
(12.6)
(12.7).
причем коэффициент чувствительности а
для разных расчетных случаев равен:
l+0,625v
ж) 0,75+ —4;-------
здесь -yi~vi/wi== 4701/(4—^0! ). При опре-
делении оптимального коэффициента неуп-
ругого сопротивления гасителя можно не
учитывать демпфирование в основной кон-
струкции. Определяя f* , следует умно-
жить значения /2, найденные по формулам
(12.4) и (12.5), на коэффициент ]/1—Yp
а найденные по формулам (12.6) и (12.7) —
на коэффициент
Вероятностный подход к учету отклонений
параметров ДГК рассматривается в рабо-
тах [29, 36].
Учет демпфирования основной конст-
рукции [37]. Внутреннее неупругое сопро-
тивление конструкции влияет на расчетные
амплитуды колебаний, главным образом
резонансные, а следовательно, и на эффек-
тивность гасителя; в меньшей степени из-
меняются оптимальные параметры ДГК.
Об этом свидетельствуют результаты чис-
ленной оптимизации для расчетных слу-
чаев «а», «б» (табл. Г2.3), где yoi— коэф-
фициент внутреннего неупругого сопротив-
ления конструкции. Приближенно опти-
мальная настройка гасителя и расчетная
амплитуда колебаний главной массы оце-
ниваются! по формулам:
гаситель с вязким сопротивлением
1 Yi М-
а\ р -----------------bU-— •
11 (1+Ч2 2(1+11)’
. Амплитуды
1 — Y2
5 удлинения упругого элемента гасителя соот-
ветственно при вязком и внутреннем неуп-
ругом сопротивлении приближенно равны:
(12.4)
б) ? =
1+у| + 1,5у1Ц .
(l_Y1)a(l + ,)
*/i+yF2 •
Определение оптимальной настройки
ДГК при ограниченной величине внутрен-
него неупругого сопротивления. Если конст-
рукция ДГК не позволяет реализовать на
практике оптимальное значение затухания,
рекомендуется назначать оптимальную наст-
ройку, принимая в расчет реально существую-
щее значение у02> которое обычно меньше оп-
тимального.
Оптимальная настройка определяется
из условия* равенства резонансных ампли-
туд колебаний главной массы, соответст-
вующих частотам собственных колебаний
системы, оборудованной динамическим га-
сителем. Результаты вычислений для раз-
личных значений v и yoi приведены в [34].
В качестве примера на рис. 12.2 изображе-
ны зависимости (v=0,02; yoi=0,01) резо-
нансных амплитуд колебаний главной мас-
сы, найденные при условии, что частота
воздействия совпадает с первой (кривые
1) или второй (кривые 2) частотами соб-
ственных колебаний системы с гасителем
Ч Зак. 195
158
ТАБЛИЦА 12,3. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ДГК И РАСЧЕТНЫЕ АМПЛИТУДЫ КОЛЕБАНИЙ ГЛАВНОЙ МАССЫ
ПРИ ВОЗДЕЙСТВИИ ГАРМОНИЧЕСКОЙ СИЛЫ С ПОСТОЯННОЙ АМПЛИТУДОЙ («а») ИЛИ ИНЕРЦИОННОЙ СИЛЫ («б»)
— е „
V Yoi Гаситель с вязким трением Гаситель с внутренним неупругим сопротивлением
«а» «б» «а* «б»
X M- f1 И Р р ц Р
0,025 р Р 0 0,05 . 0,10 t • th/A did ' ч, Ир V - j r ( ( . 8,99 6,49 5,02 0,187 0,187 0,197 0,952 0,944 0,936 8,85 6.37 4,96 0,191 0,191 0,191 0,976 0,988 1,005 9,04 6,48 5,03 0,197 0,197 0,207 0,970 0,964 0,956 8,94 61,41 4,99 0,491 0,2011 0|,2011 0,994 ;1;,007 ,1,025 м •1 ( 1,
0,050 СИ IDO O 0*0 Ж ' r * 1 6,40 5,02 4,12 0,255 0,255 0,265 0,907 0,899 0,887 С, 21 4,87 4,01 0,267 0,267 0,267 * 0,952 0,969 0,990 6,48 5,06 4,15 0,265 0,280 0,285 0,941 0,934 0,924 6,34 4,96 4,06 0,277 0,277 0,282 0(,987 1,006 1,029
0,075 0 0,05 0,10 5,26 4,30 3,63 0,301 0,301 0,301 0,865 , 0,855 0,844 5,03 4,11 3,48 0,323 0,323 0,323 0,929 0,950 0,974 5,35 4,36 3,67 0,331 0,346 0,351 0,914 0,906 0,895 5Д9 4,23 3,57 0,333 0,333 0,333 0,982 1,006 1,033
0,100 0 0,05 0,10 4,59 3,84 3,31 0,336 0,336 0,336 0,827 0,816 0,803 4,31 3,62 3,13 0,369 0,369 0,369 0,906 0,929 0,958 4,69 3,92 3,36 0,376 0,381 0,391 0,888 0,879 0,868 4,50 3,76 3,23 0,379 0,384 0,389 Д 978 U.003 а ,озз
Сплошные линии относятся к случаю, ког-
да амплитуда силы не зависит от ее ча-
стоты, штриховые — когда амплитуда си-
лы пропорциональна квадрату частоты.
Оптимальные значения настройки гасителя
соответствуют абсциссам точек пересечения
кривых 1 и 2 для данного значения уог-
Прохождение
через резонанс [5, 35]
Оптимальные параметры ДГК с вязким
сопротивлением, установленного с целью
максимального снижения амплитуд неста-
ционарных колебаний конструкции при про-
хождении через резонанс под действием
силы с переменной угловой частотой p(t) —
= Pa+^t и амплитудой, пропорциональ-
ной p2(t), равны '[35]:
Р = Д— -- Д /2; ц ~
1 — у
(12.8)
где значения Л/2 даны в табл. 12.4. в кото-
9
рой е —е0/о>0 •—относительное угловое ус-
корение; ео — угловое ускорение в момент
прохождения через резонанс; h — коэффи-
циент неупругого сопротивления защища-
емой конструкции, учитываемого по Фойг-
ту.
Зависимости наибольших в процессе
Рис. 12.2. Влияние настройки на резонансные
амплитуды колебаний главной массы при
V—0,02; Voi —0,01
1 — частота воздействия совпадает с первой час-
тотой собственных колебаний системы с гаси-
телем; 2 — то же, со второй частотой собствен-
ных колебаний системы с гасителем
прохождения через резонанс
амплитуд колебаний глав-
ной мацсы X от v, А, 8 по-
казаны на рис. 12.3, причем
штриховая линия соответст-
вует параметрам гасителя
(12.8), сплошная — вариан-
ту Д/2 = 0.
Импульсивные воздействия
Периодические импульсы
[39]. Пусть частота повто-
рения импульсов близка к
частоте собственных коле-
баний инструкции. Тогда
оптимальные параметры
ДГК с вязким трением, ми-
рно. 12.3. Зависимость максимальных амплитуд колебаний главной
массы от углового ускорения при прохождении через резонанс
ТАБЛИЦА 12.4. ДОБАВКИ Др ДЛЯ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОЙ НАСТРОЙКИ
ГАСИТЕЛЯ ПРИ ПРОХОЖДЕНИИ ЧЕРЕЗ РЕЗОНАНС
V h е
—0,008 —0,004 —0,002 0 4.' 0,002 0,004 0,008
0,025 0,025 0,05 0,1 0,114 0,117 0,134 0,060 0,063 0,071 0,033 0,036 0,046 0,004 0,008 0,018 —0,019 —0,013 —0,001 —а,042 —0,030 —0,030 —0,055 —0,065 —0,055
0,05 0,025 0,05 0,1 0,090 0,095 0,108 0,049 0,055 0,069 0,029 0,035 0,050 0,005 0,010 0,023 —0,012 —0,005 0,009 —0,029 —0,020 —0,003 , —0,055 —0,055 —0,007
0,1 0,025 ; 0,05 0,1 0,080 0,087 0,108 0,048 0,055 0,072 0,027 0,035 0,051 0,006 0,013 0,030 —0,008 —0,001 0,017 —ао17 —0,011 0.006 —0,048 —0.032 —0,006
б5" Зак. 195
155
ТАБЛИЦА 12.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ГАСИТЕЛЯ И РАСЧЕТНЫЕ ОТКЛОНЕНИЯ
ГЛАВНОЙ МАССЫ ПРИ ДЕЙСТВИИ ПЕРИОДИЧЕСКИХ ИМПУЛЬСОВ
X h Случай «а> Случай «б»
Ц f2 X Ц f2
0,025 0 0,05 0,10 0,188 0,188 0,188 0,962 0,957 0,950 9,62 7,13 5j,74 0,190 0,190 0,190 ‘ 0,974 0,980 0,990 9,57 7,10 5,71
0.050 0 0,05 0,10 01,259 0,259 01,259 0,927 0,920 0,911 6t,99 5|,66 4,81 0,264 0,264 0,264 0,950 0,958 0,970 6,92 5,60 4,76
0,075 0 0,05 0,10 0,309 0,309 0,309 0,893 0,886 0,876 5,84 4,92 4,30 0,318 0,318 0,318 0,927 0,937 0,951 5,74 4,85 4,23
0,100 0 0,05 0,10 0,348 0,348 0,348 0,862 0,853 О'. 843 5,15 4,45 3,95 0,360 0,360 0,360 0,905 0,917 0,932 5,04 4,36 3,88
ТАБЛИЦА 12.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ГАСИТЕЛЯ
ПРИ ДЕЙСТВИИ ОДИНОЧНОГО ИМПУЛЬСА
Д ¥=0,025 ¥ = 0,05 ¥ = 0,075 v=0,l
Ц f2 б б О f2 б Ц f2 б
0 0,305 0,952 0,158 0,416 0,907 0,218 0,491 0,865 0,264 0,548 0,827 0,302
0,025 0,328 0,948 0,181 0,438 0,902 0,242 0,512 0,860 0,288 0,567 0,820 0,324
0,05 0,352 0,945 0,206 0,458 0,898 0,265 0,532 0,854 0,310 0,585 0,814 0,347
0,075 0,374 0,941 0,229 0,480 0,892 0,289 0,551 0,848 0,334 0,603 0,808 0,369
0,1 0,394 0,937 0,251 0,500 0,888 0,313 0,571 0,844 0,358 0,621 0,803 0,391
нимизирующие наибольшие перемещения
конструкции, определяются так:
а) в случае, если величина импульса
не зависит от частоты повторения, то
1 + 0,43 v — 0,19 Кй" [> +
+ (0,37/й + й) х
X (3 V + 4 h) ]
б) в случае, если величина импульса
пропорциональна частоте повторения, то
1 + йр, — (0,2 + 0,9 -/н ) X
X (1—2/7)(1 + 1,5w) X
X (0(5v+ft« + ft!*)
=----------1+v-ft* =
И= V (1 + Ж2 + Я
Оптимальные параметры гасителя и
расчетные отклонения главной массы при-
ведены в табл. 12.5.
Одиночный импульс. Величина первого
максимума перемещения главной массы
после приложения импульса слабо зависит
от параметров гасителя {47]. Основной эф-
фект от присоединения гасителя заключает-
ся в более быстром затухании колебаний.
Параметры ДГК, обеспечивающие скорей-
шее затухание переходного процесса, опре-
деляются из условия шах 6, где 6 — мо-
дуль наибольшей из вещественных частей
корней характеристического уравнения сис-
темы, которая определяет темп затухания
колебаний. Результаты оптимизации даны
в табл. 12.6.
Оптимальную настройку при ропт
можно найти по формуле
Р (1 — ч) 4-0,25 [р (1. + >) +
+ h]3 — /ip [р (1 + >) 4-h} — h
p (1 + ,)a — ft (1 — 0
Приближенное значение оптимальною
коэффициента затухания равно:
-> Г h
р = 2 I /-----------4--------------- •
V (1 4- ^)3 (1.01 + ^)3
Действие мгновенного импульса на мас-
сивную конструкцию, поддерживающую
гибкий конструктивный элемент значительно
меньшей массы [25]. В такой системе мож-
но пренебречь влиянием указанного гибкого
элемента на колебания поддерживающей
массивной конструкции и принять закон
движения основания гибкого элемента в
виде одной или суммы нескольких затуха-
ющих синусоид в зависимости от числа
степеней свободы поддерживающей кон-
струкции. В резонансной ситуации, когда
частоты колебаний гибкого элемента и под-
держивающей конструкции близки между
собой, установка ДГК на защищаемый гиб-
кий элемент позволяет снизить максималь-
ные амплитуды колебаний последнего и
156
6*
О 0,025 0,05 0,075 hK
Рис. 12.4. Влияние показателя затухания воздей-
ствия на эффективность ДГК
ускорить затухание колебаний в переход-
ном процессе.
Для одномассовых моделей защищае-
мого элемента и поддерживающей конст-
рукции коэффициент гашения Кг макси-
мальных нестационарных амплитуд коле-
баний защищаемого элемента при установ-
ке ДГК различной массы приведен на рис.
12.4, причем h и — соответственно без-
размерные коэффициенты вязкого трения
гибкого элемента и массивной конструкции.
Эффективность ДГК '(по уменьшению ам-
плитуд колебаний) хотя и ниже, чем при
гармоническом воздействии с нестабильной
частотой, однако при малых значениях h,
hh она все же достаточно велика. Безраз-
мерные оптимальные параметры гасителя,
отнесенные к частоте колебаний защищае-
мого элемента, можно определить по фор-
мулам:
~| [ 4 * f2 1 + 3,5 ц [h + hK)
ц = 1/ -------’ р =------------------•
F 2 + у 1 + у
Рис. 12.5. Зависимость среднеквадратичного отк-
лонения главной массы от параметров системы
и воздействия
2 — v=? 0,025; 3 — v —0,05; 4 — v = 0,075;
5 v —- 0.1
р,24- (1—f2)2+vf2
2vjll
Дисперсия относительного перемещения
главной массы при кинематическом воздей-
9 Р о
ствии равна: ~ Ч- ох , причем при
вычислении о?- , ординаты спектраль-
ной плотности белого шума приняты рав-
ными нулю вне частотного диапазона
{—Р» +р}.
Оптимальные параметры ДГК приведе-
ны в табл. 12.7. При учете вязкого трения
в защищаемой конструкции оптимальная
из условия miner2 настройка гасителя
равна [31]:
Стационарные
случайные воздействия
Воздействие белого шума. Если прене-
бречь демпфированием в конструкции, на
которой установлен ДГК с вязким сопро-
тивлением, то при силовом или кинемати-
ческом воздействии белого шума (с орди-
натой спектральной плотности 2л“1) дис-
персии абсолютного перемещения, скорости
и ускорения главной массы соответствен-
но равны:
Узкополосное воздействие [19]. Для
спектральной плотности воздействия
st (Ро) = 2 а0 (ад + ₽§)/rt I Ро —
(Po + «o‘)al2
стандарт отклонения главной массы при
оптимальных параметрах ДГК с .внутрен-
ним трением показан на рис 12.5. При
ТАБЛИЦА 12.7. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ГАСИТЕЛЯ
ПРИ ДЕЙСТВИИ БЕЛОГО ШУМА
Критерий
качества
Значение критерия
f2
И
2, О2 - ±
хи
0,75 V
О?
О?.
Р
V —V2) (1 —0,25 V)
V
1 — 0,5 v
(1 — 0,25 V)
1 — V — V8
0,75 V)
157
этом Yi — коэффициент неупругого сопро-
тивления защищаемой конструкции; а =
=а0/со0; значение [% принято из условия
2
максимума . Оптимальные параметры
ДГК приближенно равны:
1-1,25.40,1 [-(1,14
9 ') Yoi + (Г1
Чо2 =
3 Yoi) а] при а < 0,1
~ Vol + '4
1 — 0,8 > при 0,1 + Yoi
+ ч < а < 0,6;
1 — 0,6 '> при а > 0,6;
1 1,5-. {1 - [а/(0,1 +
+ 3.)][1 -0,75а/(0,1 +
— 3 ч]} при а < 0,13 4- 3
У >/(1 -- >) при а >
> 0,13 + 3 .
12.3. МНОГОМАССОВЫЕ
И НЕЛИНЕЙНЫЕ ДГК
ПРИ ГАРМОНИЧЕСКОМ
ВОЗДЕЙСТВИИ
Многомассовые гасители
Применение нескольких гасителей
'вместо одного (позволяет распределить ре-
акцию по конструкции, улучшить условия
транспортирования и монтажа. Если на
перекрытии находится много однотипных
машин, вызывающих горизонтальные коле-
бания здания, то можно установить группу
одинаковых ДГК, учитывая в расчете от-
клонения параметров гасителей от номи-
нальных значений I [27, 29]. При густом
спектре частот строительной конструкции
группа гасителей уменьшает колебания на
нескольких резонансных частотах (см.
п. 12.4). Для конструкций с разреженным
•спектром резонансные колебания можно
уменьшить, применяя как одиночные гаси-
тели с оптимальным демпфированием, так
и много гасителей с малым затуханием, на-
строенных на разные частоты в пределах
заданного диапазона.
При последовательном соединении п
гасителей (рис. L2.6) парциальные угловые
частоты колебаний п массового гасителя
[11] равны
(Причем диапазон
— (01 = 2
увеличивается пропорционально фп.
Эффективность группы параллельных
ДГК. Если квадраты парциальных угловых
частот гасителей одинаковой массы равно-
.мерно распределить в диапазоне от [2—а
Рис. 12.6. Параллельное и последовательное при-
соединение гасителей
Рис. 12.7. Зависимость расчетной амплитуды ко-
лебаний главной массы от относительной массы
группы параллельных ДГК при гармоническом
воздействии
до [2+а, то безразмерная амплитуда коле-
баний главной •• массы при гармоническом
воздействии равна:
/=1
(/2 — а 4- а/) (1 -И у2)
(Д — а + a j) (1 + i у2) — Р2
где а=2а/п; с=~- 1 и с = р2 — соответст-
венно для воздействия с амплитудой, по-
стоянной или пропорциональной квадра-
ту частоты; v — суммарная относительная
масса гасителей; yi, у2— коэффициенты
внутреннего трения упругих связей соответ-
ственно главной массы и гасителей.
Представление об эффективности ко-
нечного оптимального числа гасителей при
нестабильной частоте внешней силы дает
предельный случай п=оо, поскольку ре-
зультаты при ^опт и /i = oo весьма близки.
На рис. 12.7 показаны зависимости X
от v при с=1, у2=0,01 и оптимальных
значениях f2 и а. При с=р2 кривые ана-
логичны, однако [О2ПТ и аОдт существенно
отличаются от предыдущих. В обоих слу-
чаях /опт>1’ и значения [ 2ПТ — 1, аопт,
п возрастают при увеличении v. Уменьше-
ние амплитуд л примерно такое же, как
после установки одиночного гасителя мас-
сы v с оптимальным демфированием.
158
Однако перемещения масс гасителей
при малом демпфировании могут быть
большими. При гармоническом воздейст-
вии с угловой частотой р — —a-\-ai
амплитуда абсолютного перемещения мас-
сы /-го гасителя | Vj | « Х/у2, т. е. |УУ|«
100Х при уг —0,01. Поэтому группа
гасителей с небольшим демпфированием
в их упругих элементах применяется, если
амплитуды колебаний конструкций срав-
нительно малы.
Нелинейные ДГК
Исследованию нелинейных ДГК по-
священо много работ [1, 10, 32, 43J.
Изучены кусочно-линейные, а также из-
меняющиеся по кубическому закону или
по закону гиперболического синуса ха-
рактеристики упругого элемента гасителя.
Нелинейность упругой характеристики по-
зволяет получить в системе с двумя сте-
пенями свободы только одну резонансную
частоту с неограниченно возрастающими
амплитудами колебаний, поэтому колеба-
ния уменьшаются в более широкой поло-
се частот возмущающей силы, чем в слу-
чае линейного гасителя (также без демп-
фирования). Эффективность ДГК с нели-
нейной упругой связью и оптимальным
демпфированием близка к эффективности
линейного ДГК.
Практический интерес представляет
также учет нелинейности затухания гаси-
теля [12], поскольку в некоторых конст-
рукциях демпферов, применяющихся в
ДГК, неупругое сопротивление является
существенно нелинейным. Так как
оптимальные параметры нелинейных ДГК
зависят от уровня внешнего воздействия,
то для получения максимальной эффек-
тивности ДГК параметры следует назна-
чать по наибольшему ожидаемому уров-
ню воздействия.
Маятниковый гаситель. Маятниковые
динамические гасители применяются для
уменьшения крутильных колебаний конст-
рукций машин [43]. В последние годы
они стали использоваться для снижения
уровня колебаний башенных сооружений
при действии ветра [4, 12], Некоторые
варианты подвески маятника с дополни-
тельными упругими связями, позволяющи-
ми изменять настройку гасителя, пока-
заны на рис. 12.8.
Эффективность маятникового гасителя
с вязким демпфером (рис. 12.9, демпфер
не показан) при действии гармонической
силы с нестабильной частотой исследова-
на в i[38]. На рис. 12.10 даны зависимос-
ти коэффициента динамичности Кд для
главной массы и наибольшего угла откло-
нения маятника F от безразмерного пара-
пет <°о
метра нагрузки Т ~ -----— при оптималь-
ных параметрах гасителя. Сплошные ли-
нии соответствуют случаю =0, пунк-
тирные — / j = ОД/2; римскими цифрами
пронумерованы кривые для v = 0,025 (I);
0,05(11); 0,1(111); коэффициент вязкого
Рис. 12.8. Варианты установки маятникового га-
сителя
Рис. 12.9. Расчетная схема маятникового гасите-
ля
Рис. 12.10. Зависимости коэффициента динамично-
сти и наибольшего угла отклонения маятника от
безразмерного параметра нагрузки
/ —v=0,025; 2 — v = 0,05; 3 — v=0,l
тренйя главной массы принят равным
/г —0,05; g— ускорение силы тяжести;
<^=К1М-, /3 = /о/“о: fo = g/1’
fl = Kjm I coq.
При углах F<0,4 маятниковый гаси-
тель можно рассчитывать по линейной
теории, при 0,4</'<0,9 необходимо учи-
тывать влияние нелинейности на опти-
мальные параметры и снижение эффек-
тивности гасителя; режим с углами
>0,9 является нежелательным.
159
Рис. 12.11.
Подвеска ма-
ятникового га-
сителя
1
0 tir' 20 30 Ч-Q 50 А}шл
Рис. 12.12. Зависимости декремента коле-
баний от амплитуды
Рис. 12.13. Гаситель с предвари-
тельным натягом
Маятниковый гаситель с нелинейным
затуханием. Выбор конструкции демпфи-
рующего устройства гасителя, простого в
эксплуатации, достаточно надежного и
безотказно работающего при переменном
температурном режиме, — весьма слож-
ная задача. Одно из возможных конструк-
тивных решений представляет прост-
ранственную раму, к вершине которой на
многопрядевых тросах с жестким сердеч-
ником подвешен груз. Изменение расстоя-
ния а между опорами (рис. 12.11) позво-
ляет регулировать настройку и декремент
колебаний гасителя.
Экспериментальные зависимости дек-
ремента колебаний гасителя с грузом 2 т
от амплитуды показаны на рис. 12.12.
Кривые 7, 2, 3, 4 соответствуют гасителю
с тремя тросами длиной 2,25; 2,46; 2,66
и 2,8 м; кривые 5, 6, 7, 8— гасителю с
одним тросом длиной 0,8; 2,25; 2,46 и
2,66 м. При длине тросов от 2 до 3 м де-
кремент вначале растет с увеличением
амплитуды колебаний, затем уменьшается,
т. е. при относительно больших амплиту-
дах демпфирование в тросе определяется
силами сухого трения.
Динамический гаситель такой конст-
рукции, установленный на башне высотой
100 м, как показали натурные испытания,
уменьшил амплитуды колебаний башни в
3 раза. Теоретическое исследование
ДГК, неупругое сопротивление в котором
описывается степенной функцией скорос-
ти, выполнено в |[Г12].
Динамический гаситель с предвари-
тельным натягом [1.43]. Упругий элемент
гасителя (рис. 12.13) имеет симметричную
характеристику, определяемую тремя па-
раметрами: усилием предварительного на-
тяга £0, жесткостью пружины k зазором
между ограничителями 2b. Предваритель-
ный натяг позволяет получить в отсутст-
вие демпфирования конечные амплитуды
колебаний объекта при резонансных час-
тотах.
Наименьшие амплитуды колебаний
главной массы будут при параметрах га-
сителя:
_____________1___________
(а — 2) (0,432 а 4-0,566) ’
= (а-2) (а+1.316)
• ' (аЧ-0,315)а
+ _ 1_____________
Т ~ 0,432 а + 0,136 ’
ь
— = 0,863а (а +0,315),
*ст
где = ; а=Ддоп/-Хст; Ддоп— до-
пускаемая амплитуда колебаний главной
массы; соо — угловая частота колебаний
главной массы.
Эффективность ДГК с предваритель-
ным натягом и оптимальным вязким демп-
фированием [38] близка к эффективности
линейного гасителя с оптимальным зату-
ханием.
Об оптимальной нелинейной характе-
ристике упругой связи гасителя. По спо-
собу прямой линеаризации [6] нелиней-
ная характеристика R(s) заменяется ли-
нейной r(5)s, причем коэффициент r(S) =
s'
= 5S”5 I R(s)s3ds зависит от амплиту-
Г/
о
ды 5 удлинения упругого элемента гаси-
теля. Предположив отсутствие колебаний
главной массы в линеаризованной систе-
ме без демпфирования, можно определить
r(5o)=mpo , So = T(po)/mpo * гдс Р°’
Т(ро)—угловая частота и зависящая от
нее амплитуда гармонической возмущаю-
щей силы; m — масса гасителя.
Оптимальные зависимости г(5), R(s)
представлены в табл. 12.8, где Т(р)~ Т(ро)/
/Г(со); №=5о/хст; 5 = S q/.v с т: -^ct==7'(w)/K;
р —Ро/w; (о = УК/М. Для возмуща-
ющей силы Г(р)=р2 не удается подобрать
характеристику R (s), обеспечивающую пол-
ное гашение колебаний главной массы в ли-
неаризованной системе. Наибольший интерес
представляет случай 7'(р0) =Г(!Со), подробно
рассмотренный в1 [32], при этом найденная
характеристика R($)=0,8Г(co)gns реали-
зуется с помощью предварительного натя-
га упругого элемента очень малой жест-
кости.
Подобранные характеристики упругого
элемента гасителя обеспечивают уменьше-
ние колебаний главной массы при S^=0.
В случае Т(ро)=Т(<о) [32] при угловой час-
тоте pg (l+2,25v)“1 КМ~1 может быть
5 = 0, так как в гасителе сила инерции
160
ТАБЛИЦА 12.8,. ОПТИМАЛЬНЫЕ УПРУГИЕ ХАРАКТЕРИСТИКИ ГАСИТЕЛЯ
ДЛЯ РАЗЛИЧНЫХ СЛУЧАЕВ ЗАВИСИМОСТИ АМПЛИТУДЫ ВОЗМУЩАЮЩЕЙ СИЛЫ
ОТ ЧАСТОТЫ
Г(р) 1 р Р3 Р4
г 1 1 V3 52 v2 S
5 v S2
К (5)/Г«о) 0,8 sign s 0,6 V S 1,4 V3 S3 1,2 v2 s2 sign s
не превосходит усилия натяга 0,8Г(*й)). При
этом амплитуда колебаний главной массы
1 + 2,25,
1,25,
превышает соответствующее значение для
линейного гасителя с оптимальным зату-
ханием (см. табл. 12.2).
12.4. РАСЧЕТ И ГАШЕНИЕ
КОЛЕБАНИЙ СИСТЕМ
С РАСПРЕДЕЛЕННЫМИ
И ДИСКРЕТНЫМИ МАССАМИ
Расчет континуальных систем
с присоединенными
гасителями при гармонических
и случайных воздействиях [15]
Ниже кратко изложены известные
методы строительной механики примени-
тельно к рассматриваемым динамическим
задачам.
При гармоническом перемещении
Wseipt точки подвеса линейного гасителя
комплексная амплитуда силы, действую-
щей на систему со стороны гасителя в
точке 5, равна Xs = mspsWsf где ms —
масса гасителя; ps = p^~]~p^Rs; Rs = — р2+
или /?s = — р2 + (ид + it’s)/1 —
в зависимости от вида неупругого сопро-
тивления в гасителях. Принимая за неиз-
вестные амплитуды Xs (3=1, 2,..., k),
можно записать в матричной форме си-
стему уравнений метода сил:
(D — В) X — С; D =
Единичные bsi и грузовые Св переме-
щения при варьировании угловой частоты
р представляют собой частотные характе-
ристики системы без гасителей соответст-
венно от действия единичных гармониче-
ских сил и внешней гармонической на-
грузки. Часто их можно найти в замкну-
том виде с учетом распределения реак-
ций гасителей по некоторым стандартным
областям.
При разложении решения в ряд по
нормированным формам Wj собственных
колебаний системы без гасителей в слу-
чае сосредоточенных реакций Xs можно
получить:,
СО
i=i
00
Cs = 2 P'/Rh (12-l0>
/-1
где Pj — обобщенная сила, численно рав-
ная работе внешней нагрузки на пере-
мещениях Wj; Wsj — ордината формы
W’j в точке 3; = или
2_ в зависимости ОТ
вида неупругого сопротивления в системе.
Этот способ расчета удобен при k<Zn, где
п — число слагаемых, учитываемых в
(12.10).
При k>n целесообразно пользовать-
ся методом перемещений, в котором за
неизвестные принимаются комплексные
амплитуды обобщенных координат
Zje’*’*, соответствующих нормированным
формам U/j. В этом случае уравнения
имеют вид:
(/?-A)Z=P; R = Rn
При использовании смешанного мето-
да неизвестные Z?- и Хв находят из урав-
нений:
(12.11>
где , W$p — перемещения в основной
системе (система без гасителей, на кото-
161
рую наложены связи, устраняющие обоб-
щенные перемещения по п формам коле-
баний) от действия силы l-ez(oZ в точке
i и от нагрузки соответственно
при п->оо, в показателе экспонен-
ты i означает мнимую единицу).
При вычислениях целесообразно при-
менять приемы, повышающие сходимость
разложений, например выделение стати-
ческих составляющих i[15, 20J, или реше-
ния для системы с измененными гранич-
ными условиями; это особенно важно при
определении усилий.
Приведенные уравнения позволяют
найти частотные характеристики, которые
можно использовать при расчете системы
с ДГК на негармонические нагрузки. В
частности, при стационарных случайных
воздействиях дисперсии перемещений, ус-
корений, усилий в конструкции вычисля-
ются в виде интегралов от произведений
квадратов модулей соответствующих час-
тотных характеристик на спектральную
плотность воздействия.
Стержни
постоянного сечения
Продольные колебания. Формы и час-
тоты свободных колебаний стержня опре-
деляются выражениями
Wj = С sin а;- х + cos а/ х; со/ = а/
в которых р — плотность; Е — модуль уп-
ругости; характеристическое число а/ и
константа С находятся в результате под-
чинения IFj граничным условиям.
Эффективность гашения продольных
колебаний <[461 рассмотрим на примере
свободного стержня длиной 7, для которо-
/ Л X
го ]F/ = cos —/=1, 2,... Положим, что
It
один гаситель установлен на конце стерж-
ня в точке приложения гармонической
силы и настроен на низшую частоту ко-
лебаний стержня, другой гаситель располо-
жен в середине пролета и настроен на
вторую частоту.
Оценку эффективности и оптимизацию
параметров гасителей производят по наи-
большим амплитудам скоростей сечений
стержня при единичной амплитуде возму-
щающей силы. Значения оптимальных па-
раметров каждого из гасителей, отнесен-
ные к соответствующей резонансной час-
тоте (табл. 12.9), удовлетворительно сов-
падают со значениями, найденными при
учете лишь одной резонирующей формы
колебаний стержня с использованием фор-
мул (случаи «е», см. табл. 12.2). Приве-
денная масса стержня для каждой из
форм колебаний равна половине его мас-
сы М.
В этой и других подобных задачах
со сравнительно разреженным спектром
взаимное влияние гасителей, настроенных
на разные частоты, невелико. Это позво-
ляет часто ограничиваться рассмотрением
простейших расчетных моделей конструк-
ций — в виде систем с одной степенью
свободы. Применение ДГК при продоль-
ных колебаниях стержней снижает также
возможность возникновения параметриче-
ского резонанса, так как вследствие уве-
личения демпфирования системы размеры
областей динамической неустойчивости
уменьшаются [44].
Поперечные колебания. Как показано
выше, существенным этапом изучаемых
задач является рассмотрение вынужден-
ных колебаний системы без гасителей при
действии внешней нагрузки и единичных
сосредоточенных гармонических сил.
Здесь может быть весьма полезным раз-
ложение решения в ряд по формам соб-
ственных колебаний, однако часто удает-
ся построить решение в замкнутом виде,
например с помощью метода начальных
параметров. Приведем результаты решения
задачи о колебаниях консоли с двумя
ДГК |47], установленными в сечениях
х=0,5/=/1 и х=1. Эта задача представ-
ляет не только методический, но и прак-
тический интерес.
Формы и частоты свободных колеба-
ний консоли равны:
У] — ch а/ х — cos а/ х —
sh а/1 — sin а, I
ch а/1 + cos ау-1
9 . /'F7
X (sh а;х—sin а/ х); ©/ = I/ — ,
где EJ, т, I — соответственно жесткость
при изгибе, погонная масса и длина стер-
жня; «/7=1,8751; 4,69409; 7,85476...—
корни частотного уравнения cosa//chct// =
1.
При воздействии на свободный конец
консоли с гасителями гармонической силы
комплексная амплитуда перерезываю-
щей силы в заделке равна:
Q = [ ch а + cos а + ai Zi 6 X
*
X(ch0! —COS01]%~1.
ТАБЛИЦА 12.9, ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ГАСИТЕЛЕЙ
ПРИ ПРОДОЛЬНЫХ КОЛЕБАНИЯХ СТЕРЖНЯ
т М V Первый резонанс Второй резонанс Одномассовая система
f f ц f Ц
0,025 0,05 0,965 0,28 0,968 0,26 0,965 0,262
0,0333 0,0667 0,949 0,3 0j,960 0.29 0,953 01.294
0,05 0,1 0,931 0,34 0.942 0,34 01.932 0|,351
од 0,2 0,875 0,48 0,918 Q.44 b Q.874 Oi.447
162
Рис. 12.14. Амплитудно-час-
тотная характеристика пере-
резывающей силы в заделке
консоли с двумя гасителя-
ми
ТАБЛИЦА 12.10, ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ГАСИТЕЛЕЙ
ПРИ ПОПЕРЕЧНЫХ КОЛЕБАНИЯХ КОНСОЛИ
т/М f т Резо- нанс х=1 х — 1-2
f Ц 2 V* Ц* 2 f Н 2 V* f* U* 2
0,025 I II 0,92 0,90 0,18 0,16 0,1 0,91 0,17 0,99 0,95 0,07 0,13 0,011 0,051 0,99 0,95 0,06 0,13
0,05 I II 0,86 0,85 0,22 0,18 0,2 0,83 0,21 0,97 0,90 0,1 0,17 0,022 0, 102 0,98 0,91 0,09 0,17
0,1 I II 0,76 0,76 0,126 0,18 0,4 0,72 0,23 0,95 0,82 0,13 0,20 0,045 0,204 0,96 0,83 0,12 0,21
0,25 I II 0,55 0,55 0,25 0,16 1 0,5 0,22 0,89 0,64 0,18 0,22 0, 112 0,408 J 0,9 0,71 0,17 0,23
Здёсь
/- == — [ (ch a cos a -f- 1) + a Z (sh a cos а —
— ch a sin а) 4~ d a Zx ch ar cos ar —
aaiZZr^ ,
— “гл------;----------- ; Ф = — db x
b a + ch tZi -|- cos aY J
X (ch2 ai — cos2 czi) -j- (sh2 ax — sin2 ат) X
X (ch £Zi — cos ai) - 2d ch ax cos a* X
X [2b sh ax sin аг — (sh — sin аг) ];
b = sh аг + sin ai; d — sh a± cos аг —
— ch ai sin ах; a = I
Z и Z[ вычисляются по формуле
fo + 1 P
— P2 + ip V-л! m
в которой f0, go, m — параметры гасите-
лей, установленных соответственно в се-
чениях х~1 и Х~1\.
Амплитудно-частотная характеристика
Q(p) при оптимальных параметрах гаси-
телей, имеющих массы m = 0,05 Mf тг =
= 0,025 М (М — масса стержня), приве-
дена на рис. 12.14. Гаситель в сечении
x=i/ настраивается на первый резонанс,
а в сечении х=0,5 I — на второй.
Оптимальные параметры гасителей f
и ц/2, отнесенные к соответствующей ре-
зонансной частоте (табл. 12.10), удовлет-
ворительно согласуются со значениями
/*, ц*/2, вычисленными для эквивалентных
одномассовых систем по формулам «а» из
табл. 12.2. При нахождении значений v*
учтено, что приведенная масса стержня
для первой и второй форм свободных ко-
лебаний в сечении х=1 составляет по
0,25 Л4, в сечении х=0,5 / —соответст-
венно 2,15 М и 0,49 М.
Стержни
переменного сечения
Среди различных законов изменения
жесткости и массы стержня по длине
большой практический интерес, в особен-
ности при исследовании колебаний башен-
ных сооружений, имеют степенные за-
коны:
EJ — Е (x/R)n+2;
m — mR (*/R)n,
(12.12)
где n — действительное число (не обяза-
тельно целое)1; х — расстояние от вооб-
ражаемой вершины стержня до сечения;
R — координата более удаленного от вер-
шины конца стержня.
1 Если п — полуцелое число, решение полу-
чается в элементарных функциях.
163
Значение л —О соответствует «идеаль-
ному» двутавру с линейно-изменяющейся
высотой сечения; п—1 —клиновидному
стержню или тонкостенному конусу с по-
стоянной толщиной стенки; п—2 — кони-
ческому стержню. После сокращения на
множитель elpot можно получить уравне-
ние для амплитуд поперечных колебаний
стержней рассматриваемого класса:
терц W — q,
Используя эти функции, нетрудно за-
писать выражение для формы вынуж-
денных колебаний стержня с учетом
включений типа присоединенных сосредо-
точенных масс, упругих опор, динамиче-
ских гасителей.
Например, для стержня, опирающего-
ся в сечении x=R через штамп (момент
инерции массы /ф) на основание с ква-
зиупругим коэффициентом fei+f&s, форму
вынужденных колебаний можно записать
в виде
которое сводится [131 к системе двух не-
однородных уравнений Бесселя A(w)±
±?.' = TF/2, Здесь:
d2 t 1 d n2
Tp2 p dp " p2 ’
— , Pn R2
₽ = 26 | x ; b* = E-°—- ;
E JR
и =
Е J сс
2R (kt — ik2)
u = pnW; F = Rn (2b)2n q/mRp%$n.
Амплитуды перемещений и усилий связа-
ны с новыми переменными так:
W - Ц7°/|5Л ; <р = 26* <Р°/Р'г! 1;
М = EJR^2M«/Rn+2i (26)2";
Q^E JR$n+' Qa/Rn+28 (2b)-n--,
Функции метода начальных парамет-
ров, образующие при р = а единичную
матрицу для (р°, АГ, Q0, имеют вид
[18]:
Xi ,з = {- Yn (₽) 4+1 (“) *
4 (₽) 4+i (« + v 14 (Р) 4+1 («) +
+ 4(P)-4+i («)!};
—4 (Р) 4+2 (“) +
+ 4 (₽) 4+2 («) - VI14 (Р) 4+2 («)-
j -4 (Р)4+2 («))};
причем начальные параметры А1^ , в
точке a=2b^R находятся из условия
удовлетворения; граничным условиям на
другом конце стержня; аргументы цилинд-
рических функций в выражении для U
являются комплексными при учете внут-
реннего трения в стержне по Е. С. Соро-
кину, так как в этом случае E=Eq(u+Iv).
Формы свободных колебаний стержня
также удобно находить методом началь-
ных параметров, при этом следует
опустить в выражении для U
последнее слагаемое и принять А1^ =1;
й2 = 0; Е: — Еои.
При решении конкретных задач виб-
рогашения |[18—2Q] обычно применяют
разложение по формам собственных коле-
баний системы без гасителей и метод сил.
Допустим, что один из гасителей мас-
сой Шт установлен на верхнем конце
стержня при х~г и предназначен для
уменьшения колебаний по первой форме,
другой — массой шг установлен в сечении
х— £ (в частности, может быть £ = г) с
целью снижения колебаний по второй фор-
ме. Принимая за основную систему стер-
жень без гасителей и используя формулы
(12.9), (12.10), можно при вычислении
частотных характеристик найти амплиту-
ды прогибов сечений г и
— [ ( 1 - /Hg Р^ ^£^)
m
I PS br 1/A:
W? = [ (1 — mr pr brr)C^ —mr pr b?r СД /А;
а затем для произвольного сечения W =
СО
х^ — {— 4*(Р) 4 (а) 4-
4 1
/=1
где
+ 4 (Р) 4 (а) - ~ \Хп (Р) 4 (а)
Л
Pr pj blr;
In (Р) Кп (а)]}.
— пгг
164
~ I j tfx Wj d X -j- mr .rWrW ri —
\ r
+ "4
/ i
остальные обозначения соответствуют при-
нятым в формулах (12.9), (12.10).
При случайном воздействии, которое
можно представить в виде произведения
детерминированной функции qx и стацио-
нарной случайной функции времени z(t),
дисперсии перемещений (усилий) у в про-
извольном сечении равны:
со
FV) = */ (О (О Y W Y (Wi).
i. M
где V(U/j)—распределение перемещения
(усилия) у вдоль стержня, соответствую-
щее форме свободных колебаний Wj. Кор-
реляции обобщенных координат kj(t)ki(t)
находят численным интегрированием в
частотной области.
Вопросы гашения колебаний консоль-
ных стержней постоянного и переменного
сечения, вызванных перемещениями осно-
вания по закону затухающей синусоиды,
рассмотрены в [25]!,
Гашение колебаний
пластинок, складок, оболочек
Пластинки, складки, оболочки явля-
ются конструктивными элементами пере-
крытий и покрытий зданий и сооружений.
Они подвергаются воздействиям от не-
уравновешенных машин, от ветровых,
сейсмических и других специальных на-
грузок. Решение вопросов гашения коле-
баний таких конструкций в отличие от
вопросов виброгашения систем с несколь-
кими степенями свободы или стержней
требует проведения более тонких исследо-
ваний. Это связано с большей густотой
спектра собственных частот, а также с
необходимостью учета в отдельных слу-
чаях местных напряжений в зоне контак-
та, которые зависят от закона распреде-
ления внешней нагрузки и реакций гаси-
телей по поверхности конструкции и для
одномерных систем имеют меньшее значе-
ние; наконец, более трудным становится
выбор мест расположения гасителей.
При расчете пластинок, складок, обо-
лочек с присоединенными ДГК использо-
вание грубых моделей вряд ли допустимо.
В тех случаях, когда для оценки эффек-
тивности гашения все же оказывается
возможным расчетную схему конструкции
представить в виде системы с одной или
двумя степенями свободы, такие упроще-
ния должны быть обоснованы соответст-
вующими исследованиями.
Пластинки. При гармонической нагруз-
ке расчет пластинки с гасителями можно
производить по формулам (12.9), причем
решения для воздействий, распределенных по
окружности, кругу или кольцу, в некоторых
случаях удается построить методом компен-
сирующих нагрузок [42] в замкнутом ви-
де без использования разложений по фор-
мам колебаний. Такие решения [22] по-
лучены для круглой пластинки постоян-
ной толщины и с более жесткой круговой
вставкой (постамент машины) для случая,
если квазиупругие коэффициенты в гра-
ничных условиях являются заданными
функциями частоты колебаний, что позво-
ляет рассматривать пластинку как эле-
мент более сложной системы.
С использованием метода компенси-
рующих нагрузок была исследована эф-
фективность гашения колебаний квадрат-
ной жестко защемленной пластинки в за-
висимости от коэффициента у неупругого
сопротивления пластинки и радиуса /д
круглой площадки, по которой передают-
ся реакция гасителя, сила инерции присо-
единенной массы (0,1 от массы пластин-
ки) неуравновешенной машины и внешняя
гармоническая сила с частотой, близкой
к низшей собственной частоте пластинки.
Минимизировалась амплитуда А переме-
щения в центре пластинки при амплитуде
внешней силы, пропорциональной . На
рис. 12.15 сплошные линии соответствуют
случаю /д —0,01а, штриховые — п = 0,15а,
штрихпунктирные — эквивалентной систе-
ме с одной степенью свободы (а — сторо-
на пластинки, v — отношение массы гаси-
теля к приведенной массе пластинки). Хо-
тя здесь вклад высших форм колебаний
не был заметным, следует иметь в виду,
что при несимметричном расположении
гасителя и с увеличением частоты воздей-
ствия- влияние высших форм может ока-
заться существенным.
Усилия в меньшей степени, чем про-
гибы, уменьшаются, что объясняется боль-
шим влиянием на них высших форм ко-
лебаний. Тем не менее в режимах, близких
к резонансным, применение ДГК для
уменьшения напряжений является доста-
точно эффективным не только для плас-
тинок, но и для других конструкций.
Складки. Подъемистые складки сред-
ней длины обладают густым спектром
собственных частот, а формы их колеба-
ний, начиная с первой, имеют узловые
линии и пучности, которые могут совпа-
дать с ребрами складки. Сосредоточение
массы на ребрах при упрощении расчет-
ной схемы может привести к искажению
собственных частот и форм, поэтому в
расчете желательно учитывать распреде-
ление массы на гранях. При определении
частот и форм колебаний складок с onopj
ными диафрагмами, гибкими из своей
плоскости, целесообразно воспользоваться
методом перемещений [7].
Сложный характер первых форм ко-
лебаний складок затрудняет выбор мест
установки гасителей. С целью уменьшения
контактных напряжений обычно гасители
располагают в местах передачи внешних
сил или по ребрам складки.
Более густой, чем у пластинки, спектр
собственных частот приводит к необходи-
165
Рис. 12.15. Зависимости амплитуды колебаний пластинки от отно
сительной массы гасителя
Рис. 12.16. Эффектив-
ность и оптимальные па-
раметры гасителя для
складки
----------- -у = 0,05;---
-----------7=0,1
мости учета большего числа собственных
форм колебаний. Поэтому при исследова-
нии виброгашения складок, находящихся
под действием гармонических или случай-
ных сил, целесообразно использовать сме-
шанный метод (12.11).
Представление о гашении колебаний
пятигранной складки дают результаты
[14]. На рис. 12.16 показаны зависимости
от суммарной относительной массы v га-
сителей оптимальных параметров f2 и ц,
а также коэффициента k, равного отно-
шению квадратов характерных амплитуд
колебаний складки до и после установки
гасителей. Колебания складки вызывались
гармоническим воздействием вентилятора
с диапазоном изменения частоты (30—60)
с-1. Ширина диапазона частот воздейст-
вия и его положение в спектре собствен-
ных частот складки сильно влияют на k.
Так, при №0,0125, у=0,05 значения k
для прямо- и кососимметричных составля-
ющих воздействия соответственно равны
2,6 и 6,6. Объясняется это тем, что для
прямосимметричных форм низшая частота
была в 1,34 раза выше (около 47 с”1)
низшей частоты для кососимметричных
форм и воздействие оказалось более уз-
кополосным.
При расчете на стационарные случай-
ные пульсации ветра дисперсии характер-
ных перемещений складки при v —0,0125
уменьшались в 2,5 раза.
Основные особенности складчатых
покрытий (густота спектра и наличие не-
скольких узлов и пучностей у низших
форм колебаний) присущи также цилинд-
рическим оболочкам, которые при расче-
те часто заменяют складками. При боль-
шом числе установленных гасителей целе-
сообразно применять смешанный метод рас-
чета, при малом — удобнее метод сил.
Пологая сферическая оболочка. Для
оболочек с густым спектром применять
одиночный гаситель без демпфирования
нецелесообразно. Требуемое число гасите-
лей должно быть не меньше числа собст-
венных частот оболочки, попадающих в
заданный интервал частот воздействия.
Превышение минимально необходимого
числа гасителей несколько уменьшает их
эффективность. Нижняя оценка эффектив-
ности при установке оптимального числа
гасителей получается при рассмотрении
континуального гасителя '[15], реакция
которого равномерно распределена по по-
верхности оболочки.
Дифференциальное уравнение свобод-
ных 'колебаний пологой сферической обо-
лочки с присоединенным континуальным
динамическим гасителем без демпфирова-
ния после сокращения на
Д^ Д^ Г — = Д^ =
имеет вид
аа 1
а?2 + е х
(12.13)
где
Е, а, р, R, h — соответственно модуль уп-
ругости, коэффициент Пуассона, плотность
материала, радиус срединной поверхности
и высота оболочки; г\ — некоторый раз-
мер (для круглой в плане оболочки — ра-
диус внешнего контура); v и сог— отно-
сительная масса и парциальная частота
гасителя; со — частот свободных колеба-
ний оболочки с гасителем.
Для того чтобы вона частот Юн<со<сок
была без резонансной и амплитуды w при
этом не превышали статических перемеще-
ний для пластинки с теми же краевыми
условиями, следует удовлетворить условию
14С'0, т. е. параметры гасителя должны
быть равны:
со г — wH;
(*-1)
(А* + х) (А, + 1)
166
10 30 50 70 90 1Ш*
Рис. 12.17. Зависимости относительной массы га-
сителя от безразмерного параметра, характери-
зующего подъеммстость и густоту спектра пологой
оболочки
1 2'34 <5 6 7 8 9 10 11 12 13 14 15 16 X
Рис. 12.18. Оптимальные параметры гасителя и
соответствующие значения V* для круглой плас-
тинки
Здесь
12(1—a2) rf ш2
й2 R2 со;? — <о2
Н п
характеризует подъемисность оболочки и
косвенно густоту ее спектра; константа х =
X* — со2
= — ----__ — частотный диапазон
X* со„ — со2
«н<со<(Ок, где Хн, Хк соответствуют зна-
чениям сон, (Ок для V —0. При построении
зависимостей v от А* для круглой в плане
оболочки (рис 12.17) принято XH = Xi, где
Xi — наименьший корень уравнения (12.13);
номер корня Хк показан цифрами у кривых.
Рис. 12.19. Оптимальные параметры гасителя и
соответствующие значения т* для пологой обо-
лочки с защемленным краем
м “к
Отношение — --------------— можно наити
«2 + 1
с помощью значений X [42, с. 233]. Так, для
защемленной оболочки с А* = 50 при Хк=
—Х3 будет v=0,04, %=Г1,7, оо^ /а>н =
= 1,21; п ри Хк=Х4 — соответствен но v =
= 0,062, х='1б,4, (о* /(1)2=1^28.
Итак, при небольшом v можно получить
сравнительно узкую безрезонансную зону,
в которой при отсутствии гасителя находи-
лось несколько собственных частот оболоч-
ки.
[При достаточно широком диапазоне
частот воздействия целесообразно приме-
нять гасители с демпфированием, сущест-
венно повышающие логарифмические дек-
ременты колебаний системы. Пусть ц =
=|Цг/(Оо, f2 == со г/cDq —безразмерные пара-
метры гасителя; ш0 —низшая собственная
частота оболочки без гасителя и без демп-
фирования; у* — минимальное значение
Yj=6j-/n в заданной воне частот, характе-
ризуемой величиной %=X4/Xj ; / — номер
соответствующей частоты собственных ко-
лебаний оболочки с гасителем.
В частном случае круглой пластинки
(A*=iO) при заданных краевых условиях
можно для фиксированного числа п собст-
венных частот в диапазоне О<(о<сок най-
ти значение % и, пользуясь графиками (рис.
12. 18), определить оптимальные значения
ц, Д при которых у* будет максимальным.
На рис. 12.i 19 приведены зависимости оп-
тимальных значений у*, ц, f2 от А* для
круглой в плане оболочки с защемленным
краем при п=2 (оплошная линия), п — 4
(|штрих1пунктир), п = 10 (штриховая линия),
С увеличением подъемистости оболочки зна-
167
чение у* возрастает, а ц уменьшается, что
объясняется сужением диапазона частот
при фиксированном л.
Расчет систем
с присоединенными ДГК
при прохождении
через резонанс
Дискретные многомассовые системы.
При действии возмущающей силы с мед-
ленно изменяющейся частотой нестационар-
ные колебания системы с присоединенными
ДГК описываются дифференциальным урав-
нением
My + H9y + C0y = Q0 (/) t
где М, Но, Со — матрицы порядка п соот-
ветственно инерционных, диссипативных и
квазиупругих коэффициентов; у— вектор
обобщенных координат; —вектор
амплитуд возмущающих сил; cp(f) —пере-
менная фаза, пелинейно-зависящая от вре-
мени.
Полагая y=Ye1^^, у—Уе1^\ можно
исходную систему уравнений, решение ко-
торой быстро осциллирует, привести к двум
матричным уравнениям для нахождения
медленно изменяющихся амплитудных
функций:
V = — [^ + Z <р (/) Е] V—С У+ Q (0;
Y=V— i ф (/) Y.
Здесь Е— единичная матрица;
С=М~1С0; Введя обоз-
начения Y=Z2-\-iZ4; V~ Z1-j-iZ3;
получим матричное уравненние Z = OZ+g(Z)
Хотя порядок соответствующей системы
уравнений вдвое выше, чем исходной, чис-
ленно интегрировать ее проще ввиду -мед-
ленного изменения вектора Z. При возму-
щении^ Qo(t)cos^>(t) с произвольной на-
чальной фазой ф(0) огибающие колебаний
определяются модулями компонент векторов
Z2~YiZ^ и Z\-\-iZ%.
Континуальные системы. Дифференци-
альные уравнения движения системы с I
присоединенными ДГК имеют вид
mxw+ +h~\Lw = qxQ (/) ?<₽ «)_]_
I
+ 2 S (х ~ %г) (Hr Уг + % Уг) «г;
4=1
Й’г + Уг + Hr Уг + ft Ут = о
(г= 1, 2,
Здесь L — дифференциальный оператор по
координате х, характеризующий данную
континуальную систему; со, сог—прогибы
системы соответственно в произвольной точ-
ке х и в точке хг присоединения гасителя
с номером <п»; h, tnx, Qx— коэффициент
вязкого трения, погонные масса и действу-
ющая нагрузка, Q(Y), <р (0 — заданные
медленно изменяющиеся функции времени;
б (х — хг) — дел ьт а -фу нкц и я дира к а;
тг, цг, /г, уг — соответственно масса, коэф-
фициент вязкого трения, парциальная ча-
стота и относительное перемещение гаси-
теля с номером «г».
Представляя прогибы w в виде ряда
оо
и» = 2 IF/(х), (12.14)
/=1
по формам свободных колебаний системы,
удовлетворяющих однородному уравнению
LWj — tnx(£^ U7j = 0 и соотношению орто-
гональности j mxW ^Widx^0 ( j^i), можно
х
вместо исходного уравнения получить си-
стему, которая после подстановки
у = Л/е/ч)(О ; (0 =0/
Ут = Ут е£ Ф ('>; 0Г = 1|)Г ?*₽«)
приводится к виду
8/ = [— i <jp (/) — h toy] 8/ — (.Л х
I
+ /?/,-)+<*/Q С);
(12.15)
Q (/) cty Wj r — —
-РГУГ (r=l, 2........../),
где % — область изменения x;
Если в (12.14) удержать п членов,
учитывая положение интервала изменения
«
частоты ф(0 в спектре собственных частот
168
to?, то систему (12.15) можно записать в
матричной форме Z = <PZ-^Q(t)q.
Здесь
h Q —' Q Bp ВF
bx 0 0
hW' й Q b2 b3
0 E bt
a
0
9= W'a ’
fci = —1ф(/)£; Ь2--ц—W"3g; bz=-F—W'3F;
MM Д = ||'ф||; a=,[ a/
= || Р/ r > H ~ Mr, F = fr, ’ :—
/=1,2, . . ., n; г= 1, 2,
Далее нетрудно перейти к системе урав-
нений л ор яка 4n4~4Z относительно вещест-
вспЛых функций, которая 'численно инте-
грируется. Амплитудный вектор Z медлен-
но изменяется с течением времени в отли-
чие от быстро осциллирующих w и ут.
Расчет
многомассовых систем
при нестационарных
случайных воздействиях
Для анализа поведения многом а особых
систем при воздействиях стационарных слу-
чайных процессов с нулевым математиче-
ским ожиданием, модулированных детерми-
нированными функциями (времени, удобно
использовать метод моментов |9], основан-
ный на временном подходе.
Ори кинематическом действии нестаци-
онарного ‘белого шума F(t) ф(7) на систему
с п степенями свободы матричное уравнение
колебаний (после умножения на матрицу,
обратную матрице инерционных коэффици-
ентов)
х 4-Zfi + Cx = S1 -у Ц(/)ф (/)] +
а г
SF(t)ty (1)
приводится к виду
если принять
(12.16)
У (О =
Здесь Н, С — матрицы диссипативных и
кваз иу п р у пи х коэффициентов; F(t) — квад-
ратная т\т матрица детерминированных
модулирующих функций; Si,S—прямоуголь-
ные, числовые матрицы; ф(£)—век-
тор центрированных белых шумов с корре-
ляционной матрицей ф (0ФЛ (т) — Q6 (t — т);
Q — квадратная т\т матрица; б—функ-
ция Дирака; штрих-символ транспонирова-
ния; черта 'сверху означает усреднение по
ансамблю.
Применяя к уравнению (’12.16) извест-
ную процедуру метода моментов ]У[, полу-
чим диффер енци а л ьн ое уравнение от носи -
тельно искомой матрицы J (t)~y(t)y'(t)
корреляционных моментов координат си-
стемы
(t) =BJ (t)+J (t)B' +
+ DF(t)QF' (t) D', (12.17}
которое справедливо также и в случае,
если элементы матрицы В являются задан-
ными функциями времени и условие асимп-
тотической устойчивости системы не нару-
шается.
Численно интегрируя уравнение (12.17)
при заданных начальных условиях J(O),
можно определить элементы матрицы J(t)
в переходном режиме.
При воздействии на систему возмуще-
ний F(t)y(t), где ф(0 — т — мерный век-
тор стационарных случайных функций с
дробнорациональными спектральными плот-
ностями, следует дополнить уравнения ис-
ходной системы уравнениями формирую-
щего фильтра, преобразующего белые шу-
мы ф(£) в стационарные функции ф(/). Да-
лее можно воспользоваться уравнением
(12.17), причем начальные значения корре-
ляционных моментов для координат систе-
мы соответствуют заданным условиям при
/='0, взаимных корреляционных моментов'
координат системы и фильтра равны \улю,
корреляционных моментов координат филь-
тра рассчитываются для установившегося
режима [ввиду стационарности функций
ф(/)1 •
12.5. ГАШЕНИЕ КОЛЕБАНИЙ
КОНСТРУКЦИЙ И СООРУЖЕНИЙ
Ниже приведены теоретические и экспе-
риментальные данные об эффективности
виброгашения некоторых высоких (башни,
мачты) и протяженных (трубопроводы,
провода) одномерных конструкций, колеба-
ния которых вызываются в основном ветро-
выми, а также сейсмическими (в сейсмически-
активных районах) и другими специальны-
ми (воздействиями. Примшение ДГК для
уменьшения колебаний таких конструкций
особенно эффективно. Даны также краткие
сведения о применении ДГК в фундаментах,
под машины.
Башенные сооружения
Расчетная схема башенного сооружения
обычно принимается в виде стержня пере-
менного сечения. В ряде случаев можно*
169
ТАБЛИЦА 12.11, РЕЗУЛЬТАТЫ РАСЧЕТА РАДИОБАШНИ ПРИ ГАРМОНИЧЕСКОМ
ВОЗДЕЙСТВИИ
V Отношение массы гасителя к массе сооружения, %
0 0,5 1 1,5 2 0 0,5 1 1,5 2
Момент в заделке, кН-м Прогиб, СМ
0,05 2830 790 600 520 460 18,9 5,3 4,1 3,5 3,1
0,10 1420 630 510 450 ' 400 9,5 4,2 3,5 3 2,7
0,15 950 530 440 400 360 6,3 3,5 3 2,6 2,4
положить, что жесткость и погонная масса
стержня изменяются по степенным зако-
нам (121.1'2).
Виброгашение при ветровом резонансе.
Сооружения круглой формы в плане (а
иногда и при других формах сечения) при
определенных условиях могут колебаться
поперек ветрового потока. Частота этих ко-
лебаний обычно совпадает с одной из соб-
ственных частот, чаще всего с частотой ос-
новного тона. Простейшей моделью ветро-
вого воздействия в этом случае может слу-
жить га/рмоническая нагрузка с нестабиль-
ной частотой, принимающей наиболее не-
благоприятное значение в окрестности низ-
шей частоты колебаний сооружения (см.
разд. 4).
Представление об эффективности вибро-
гашения можно получить из табл. 12.11, в
которой даны результаты [181 расчета ра-
диобашни высотой 100 ад, общей -массой
50 т на действие равномерно распределен-
ной гармонической нагрузки ^=3|0Н/м с
нестабильной частотой. ДГК с вязким тре-
нием был установлен в верхнем сечении ба-
шни, внутреннее неупругое сопротивление в
башне учитывалось иго Е. С. Сорокину
(у — коэффициент неупругого сопротивле-
ния). Значения оптимальных параметров
гасителя хорошо соответствуют значениям,
полученным для системы с одной степенью
свободы с гасителем (ом. п. 12.2).
Результаты модельных и натурных ис-
пытаний свидетельствуют о высокой эф-
фективности ДГК при ветровом резонансе.
Для моделей сооружений с поперечным се-
чением в виде ромба и астроиды [4]
при -массе гасителя, составлявшей 0,01 (мас-
сы моделей, декременты собственных коле-
баний увеличились с 0,’01—0,035 до 0,12—
0,15. По данным натурных наблюдений,
после установки гасителя с массой, равной
0,017 массы реального сооружения (сечение
в виде ромба), декременты собственных ко-
лебаний сооружения высотой ЗЮ м повыси-
лись в 5 раз, максимальные амплитуды ко-
лебаний уменьшились в 3—5 раз.
Экспериментальное исследование 1451
показало, что маятниковый гаситель массой
800 кг, установленный на стальной башне
с железобетонным постаментом 4 в места
башни 88,5 м, масса 4266• 103 кг), увеличил
декремент колебаний с 0,0524 до 0,5.
При обтекании конструкций круглоци-
л индрической формы пот оком жидкости
ДГК существенно уменьшают амплитуды
колебаний поперек потока. В модельном
эксперименте [21 получено при установке
ДГК восьмикратное уменьшение амплитуд
автоколебаний консольного стержня в дос-
таточно широком диапазоне скоростей по-
тока.
Гашение колебаний при сейсмических
воздействиях [20]. Если воспользоваться
гипотезой стационарности сейсмического
воздействия [3], то сооружение с гасителя-
ми можно рассчитать методом сил (см. п.
Г2.4). При этом амплитудно-частотные ха-
р акт еристики относителен ых перем еще ни й
разлагаются в ряд по формам колебаний
сооружения с учетом реакций от гасителей.
Результаты вычислений свидетельству-
ют о том, что применение гасителей даже
небольшой массы достаточно эффективно.
На рис. 12.20 коэффициент К показывает
уменьшение дисперсий прогиба верхнего се-
чения радиобашни высотой 100 м (сплош-
ная линия) и изгибающего момента в за-
делке (штриховая линия) при установке
двух гасителей с оптимальными параметра-
ми. Отношение массы каждого гасителя к
массе сооружения обозначено v*. С увели-
чением п [показатель степени в формулах
(12.1'2)1 эффективность гасителей повыша-
ется.
Как показали расчеты |30], снижение
усилий в каркасных зданиях при сейсмиче-
ских воздействиях невелико, но все же со-
ставляет 30—40%.
Гашение автоколебаний поперек ветро-
вого потока. Для исследования галопирова-
ния сооружений с аэродинамически неус-
тойчивой формой сечения (прямоугольник,
ромб и т. л.) вполне приемлем квазиерати-
ческий подход. При этом коэффициент Сх
в выражении qx = 0,5CxpZixy^ погонной
аэродинамической силы, действующей на со-
оружение в сечении х (в направлении -попе-
рек потока, тип роксимиру етс я пол ином-ом
сх = 2 (-1)(/-1)/2х
7=1. 3, . . .
X А/ (wx/vx)' ,
где р—плотность -воздуха; hx — попереч-
ный размер сечения; wx — соответствен-
но скорости ветра и сооружения; коэффи-
циенты Aj находятся по экспериментальным
данным для конкретного сечения.
Оптимальные параметры гасителя, най-
денные из условия максимума критической
скорости потока [21], при которой возни-
170
Рис. 12.20. Эффективность гашения колебаний
башни при сейсмическом воздействии
Рис. 12.21. Зависимости стандартов перемещения
и скорости верхнего сечения обелиска от скоро-
сти ветра
кают автоколебания сооружения с частотой
основного тона, равны:
1/(1 + >); ц =
= V 2 (т 1 + -1)/(I + О /1 + ' .
(12.18)
ДГК с такими параметрами повышает кри-
тическую скорость ветра в (l+Vv/y) раз,
где у—коэффициент неупругого сопротив-
ления сооружения. Параметры гасителя
(12.18) оптимальны и при скоростях пото-
ка выше критической, так как им соответ-
ствуют наименьшие амплитуды автоколеба-
ний системы.
Случайные колебания поперек ветрово-
го потока. Для сооружений с аэродинами-
чески неустойчивыми сечениями под дейст-
вием внешних возмущений амплитуды вы-
нужденных колебаний поперек потока мо-
гут существенно возрастать при приближе-
нии скорости ветра к критическому значе-
нию. Исходя из того что порывистость вет-
ра имеет не только продольную, но и попе-
речную составляющую, можно рассмотреть
задачу о случайных колебаниях сооруже-
ния поперек потока [23]. Решение получено
путем статистической линеаризации аэро-
динамических- сил с последующим приме-
нением методов Бубнова — Г а лер кин а и
последовательных приближений. Исследова-
ны колебания стального пустотелого э&ели-
ска квадратного сечения |(2мХ^м) с толщи-
ной стенки 0,01 м. Параметры сооружения:
высота — 60 м, £Д = 2,24-10й Н-м2,. —
640 кг/м, у = 0,03, (01 = 5,8 с-1, со2 = 36,4с~1,
(о3=402 с"1. Зависимости стандартов пере-
мещения и скорости верхнего сечения обе-
лиска поперек потока от скорости ветра в
том же сечении показаны на рис. 12.21, при-
чем сплошные линии соответствуют соору-
жению без гасителя, пунктирные — сооруд
жению с гасителем массой 480 кг, парамет-
ры которого определены по формулам
(12.18). Таким образом, для сооружений с
аэродин амически неустойчивым сечением
ДГК существенно уменьшает случайные ко-
лебания поперек потока в докритической
зоне скоростей.
Мачтовые сооружения [16]
Исследуя колебания мачты при ветро-
вом резонансе, можно принять (расчетную
схему в виде стержня с линейно-упругими
опорами без учета массы оттяжек и дейст-
вующих на них аэродинамических сил.
Если при изменении скорости ветра в
заданном диапазоне ветровой резонанс воз-
никает лишь на одной низшей собственной
частоте мачты, то оптимизация параметров
ДГК по разным критериям качества приво-
дит к близким результатам. Для мачты с
одним ярусом оттяжек и ДГК на верхнем
конце (рис. 12.22) зависимости от |i, ко-
эффициент а гашения К и 'безразмерных оп-
тимальных параметров /2, ц гасителя с вяз-
ким трением приведены на рис. 12.23. При
этом принято: c = c0l3/EJ (с0— коэф-
фициент жесткости опоры, моделирующей
оттяжку; EJ — изгибная жесткость ствола
мачты); отношение массы гасителя к массе
ствола мачты v* = 0,615; коэффициент не-
упругого сопротивления мачты у = и,|ОЬ/л;
кривые, соответствующие оптимизации по
Критерию максимальных перемещений (из-
гибающих моментов), изображены сплош-
ными । (штриховыми) линиями.
Если ветровой резонанс возможен для
первых двух собственных частот мачты, то
эффективность гасителя заметно умень-
шается по рравнению с рассмотренным вы-
ше случаем. При этом оптимальные пара-
метры ДГК могут быть различными^ при
использовании разных критериев качества.
Результаты вычислений для мачты с шар-
нирно -опертым нижним концом при указан*
ных выше исходных данных приведены ча
рис. 12.24. Влияние жесткости упругой опо-
ры при фиксированном §1 = 0,7 показано на
рис. 12.25. Уменьшение эффективности ДГК
.при 51 а? 0,6 объясняется тем, что узел вто-
рой формы приближается к точке подвеса
гасителя; в подобных случаях следует из-
менить расположение гасителя или уста-
новить два гасителя в разных уровнях.
Проведенное исследование показало,
что при оптимизации по критерию макси-
мального перемещения мачты существенно
уменьшаются также и изгибающие момен-
ты, при оптимизации по критерию макси-
мального изгибающего момента терем еще-
171
Рис. 12.22.
Схема мачты
с гасителем
Рис. 12.23. Влияние па-
раметра на расчет
мачты с гасителем
Рис. 12.24. Расчет мач-
ты с шарнирно-опертым
нижним концом
при £i=0t7
мия мачты в случае резонанса на двух ча-
стотах уменьшаются в значительно меньшей
степени.
Трубопроводы [33]
Наземные трубопроводы обычно состо-
ят из большого числа температурных
юте оков, р азд е л енны х ко мп енсатор ам и. 1 и -
личная расчетная схема отсека — нор-аз-
резная балка, спектр собственных частот
которой имеет зоны сгущения, ограничен-
ные снизу значениями частот шарнирно-
опертой и сверху — защемленной однопро-
летной балки.
Вер хн я я граница ч аст отного д иа п а зон а
(предельная частота), в котором возможен
ветровой резонанс, равна соп — 2jwnSh/d,
где d — диаметр; уп—максимальная ско-
рость -ветра; Sh — число 'Струхаля, для
цилиндра Sh—0,2. Эффективность .вибро-
гашения можно 'Оценить отношением К
наименьших декрементов б в диапазоне ча-
стот 0<(о<Оп для системы с гасителями
и без них.
Алгоритм расчета. Значения ы=1тру
6 =—2nRep/Jmp определяются после на-
хождения комплексных корней р частот-
ного уравнения. Для стержня с неболь-
шим числом упруго податливых опор и
присбединенных гасителей удобно восполь-
зоваться методом начальных параметров.
Если неразрезной стержень имеет п
одинаковых симметричных пролетов дли-
ной L с присоединенными гасителями, то
корни р определяются из уравнения час-
тот для регулярной неразрезной балки:
г —cos (nS/n). Вещественная величина
z=4>klq>n в рассматриваемом случае равное
отношению углов поворота сечений в кон-
це и в начале характерного пролета стер-
жня (разрезанного и шарнирно-опертого),
возникающих от момента ept, приложен-
ного в конце этого пролета. Для стержня
•с шарнирно-опертыми концами значения
S=l, 2, п—1 и дополнительно в не-
четных зонах сгушения частот S—п, в чет-
ных — 3=0; при з а щ е м л енн ы х к онца х
стержня S==l, 2, ..., п— 1 и дополнитель-
но в нечетных зонах сгущения S = 0, в
четных — S = n.
Задаваясь последовательно значениями
(и~1тр и находя Rep из условия Jmz=0,
можно построить зависимости 2(G)) и
6(со). Точки пересечения кривой z(g)) с ro-
il 3
ризонталями cos определяют значе-
ния о) и д.
С увеличением п интервалы между соб-
ственными чдетотами в зонах (границам
зон соответствуют z=—1; +1) уменьша-
ются, зоны становятся почти непрерывны-
ми и мало зависят от условий закрепле-
ния концов стержня. При п-+ро качество
виброгашения определяется наименьшим
для —значением 6(g)).
Анализ результатов. Если предельная ча-
стота (Оп находится в интервале между
первой и второй зонами сгущения частот
трубопровода, то гасители целесообразно
устанавливать в середине каждого проле-
та.
Для бесконечного регулярного трубо-
провода с гасителями, зависимости у = 0/л
от безразмерной частоты а>* = о)/со0 устано-
вившихся колебаний в пределах первой
зоны сгущения частот показаны на рис.
12.26. Параметры гасителей: v =0,025;
f2 = 1,225; pt =0,56 >(кривая 7); ц = 0,8
(кривая 2); ц=1, 2 (кривая 5). Здесь v—
отношение массы гасителя к массе балки
в пределах пролета; настройка f' и коэф-
фициент вязкого трения ц отнесены к
собственной частоте о)0 колебаний одного
пролета трубопровода (разрезанного),
шарнирно-опертого по концам. Штриховая
линия соответствует значению у—Vi !В си-
стеме без гасителей.
С уменьшением п эффективность К га-
сителей повышается (рис. 12.27), причем
при п~4 параметры ц, f2 и К мало отли-
чаются от полученных для (было
принято v = 0,025, у1=0,|()1).
172
Рис. 12.26. Зависимости v от частоты установив-
шихся колебаний
tZZZZZZZZLVZZZ2ZZZ2
Рис. 12.29. Демпфер Стокбриджа
Рис. 12.30. Подвеска гасителя к канату оттяжки
>°2 J Ч 5 6 7 д 9 10 п
Рис. 12.27. Зависимости оптимальных параметров
и эффективности гасителей от числа пролетов
трубопровода
Рис. 12.28. Зависимости у от частот
Зависимости -у от частот со* в случае,
если сои несколько превышает верхнюю
границу .второй зоны сгущения частот при
v ОДУ025, Yi =0.01, показаны на рис. 1-2.128.
Кривые 1, 2 соответствуют двум гасите-
л я м, v ст ai11 он л ен j i ы м си ммет рично в к а-ж -
дом пролете на расстоянии L/3 друг от
друга, с одинаковыми парамепрам-и; ц —
= 1,25; Р-1,82; (1); цОД,8; f=2,5 (2).
Кривая 3 соответствует трем гасителям,
один из которых расположен в середине
пролета (ц—1,0; f2=il,l), а два других—
на расстоянии 0,3L от опор (р=4; р=ОД).
Рассмотренные примеры свидетельствуют
о высокой эффективности гасителей при
ветровом резонансе.
Провода и канаты
Действие ветра является основной при-
чиной колебаний проводов, канатов и дру-
гих подобных конструкций. Обычно разли-
чают два вида колебаний проводов: гало-
пирование и высокочастотную вибрацию.
Под галопированием понимают низкочас-
тотные (порядка нескольких герц) коле-
бания с большой амплитудой (до несколь-
ких метров). Явления галопирования про-
водов и канатов обычно (возникают при
гололедных образованиях или изморози,
когда сечение принимает аэродинамически
•неустойчивую форму, и при скорости вет-
ра (8—120) м-с11, направленной под неко-
торым углом к проводу. Чаще всего по
длине пролета образуется одна-две полу-
волны, т. е. возбуждаются низшие формы
собственных колебаний. Механизм таких
колебаний довольно подробно рассмотрен
Ден-Гартовом [8].
Высокочастотная вибрация проводов и
канатов в направлении поперек ветрового
потока наблюдается гораздо чаще, чем
галопирование. Такие колебания происхо-
дят с частотой до 100 Гц в диапазоне ско-
ростей ветра f(0,5—114) м-С”1; по длине
пролета может ^образоваться несколько
стоячих волн с ^большой амплитудой (до
н еок ол ьк и х ди ам етров).
Колебания оттяжек «мачт могут возни-
кать также из-з а устойчивых периодиче-
ских колебаний ствола мачты при действии
ветра [41].
Легкая возбуждаемость колебаний про-
водов и канатов является следствием их
сравнительно небольшого неупругого со-
противления. Поэтому один из основных
способов борьбы с колебаниями, в осо-
бенности с высокочастотными, заключается
в увеличении рассеяния энергии путем ус-
тановки демпферов и гасителей. Предот-
173
вращение галопирования значительно
сложнее и в основном сводится к Оорьбе
с образованием гололеда.
Из конструкций ДГК наибольшее распро-
странение получили так называемые демп-
феры Стокбриджа (рис, 12.29). Рассеяния
энергии при интенсивных колебаниях
сосредоточенных грузов происходит ©след-
ствие внутреннего трения в стальном тро-
се.
Раз р аб отан н ы е в п ос л ед ни е поды к он -
стр'укции гасителей колебаний проводов
ЛЭП [26], канатов оттяжек мачт
[41] незначительно отличаются от демп-
фера Стокбриджа. Схема подвески гасите-
ля <к канату оттяжки, рекомендуемая в
[41], показана на рис. 12.30. Обычно га-
сители размещают на расстоянии 1,Ъ—2
м от каждой опоры, что вызвано необхо-
димостью демпфировать различные формы
собственных колебаний. Наиболее эффек-
тивно демпфируется та форма колебаний,
на частоту которой настроен гаситель. При
более высоких частотах колебаний влияние
присоединенного гасителя выражается в
некотором увеличении рассеяния энергии.
Эффект, однако, снижается с возрастани-
ем отношения частоты колебаний к пар-
циальной частоте гасителя.
Учитывая воз1можн'0сть возникновения
колебаний в широком диапазоне частот,
иногда устанавливают по два гасителя
у каждой опоры, один из них настраива-
ется на низкую частоту* другой — на более
высокую. Ближе к опоре размещается вы-
сокочастотный гаситель. ДГК с двумя
степенями свободы эффективен в «более
широкой полосе частот [40], чем обычный
гаситель.
Фундаменты под машины
При проектировании 1ви.броизолирован-
ных фундаментов под машины примене-
ние гасителей колебаний является целесо-
образным в следующих случаях:
1) активная виброизоляция; ДГК мо-
гут эффективно уменьшить амплитуды
колебаний .при пускоостановочном резо-
нансе, ДПК настраиваются на частоту,
близкую к частоте свободных колебаний
фундамента на виброизоляторах, расчет
производится по формулам (Т2.8);
2) .противоударная виброизоляция; ДГК
могут подобно демпферам ускорить про-
цесс затухания колебаний при действии
н еп ериодич ески х уд аров;
3) пассивная виброизоляция; гасители
колебаний, настроенные на частоту, близ-
кую к частоте свободных колебаний, сни-
жают амплитуды колебаний, имеющих ука-
занную частоту (см. п. 12.2).
При невиброизолированных фундаментах
гасители могут существенно снизить амп-
литуды колебаний при сравнительн© ста-
бильной частоте воздействия [24].
СПИСОК ЛИТЕРА ТУ Р Ы
1. Алексеев А. М., Зборовский А. К.
Судовые виброгаоители. Л., 196Й.
2. Алексеев А. М., Сборовский А. К.
Исследование автоколебаний гидроупругой
системы с учетом сил сопротивления. —
В кн.: Рассеяние энергии при колебаниях,
упругих систем. Киев, 1968.
3. Барштейн AI. Ф. Приложение ве-
роятностных методов к расчету сооруже-
ний на сейсмические воздействия. — Стро-
ительная механика и расчет сооружений,.
1960, № 2.
4. Беспрозванная И. М. и др. О при-
менении демпфирующих устройств для га-
шения автоколебаний высоких сооружений
башенного типа. — Строительная механика,
и расчет сооружений, 1972, № 6.
5. Ван-Дао Н. Нестационарные коле-
бания динамической системы с гасителем. —
Изв. АН СССР. Механика, 1965, № 4.
6. Вибрации в технике. Спр., т. 2. Ко-
лебания нелинейных механических систем.
I Под ред. И. И. Блехмана. М., 1979.
7. Волоцкий М. Я. Гармонические ко-
лебания ортотропных складок. — строи-
тельная механика и расчет сооружений,.
1972, № 3.
8. Ден-Гартог Дж. П. Механические
колебания, М., 1960.
9. Казаков И. Е. Статистическая те-
ория систем управления в пространстве
состояний. М., 1975,
10. Каудерер Г. Нелинейная механика.
М„ 1961.
11. Кобелев В. М., Копелев Ю. Ф.
Ревва В. Ф. Демпфирование микроколеба-
ний в механических системах многомассо-
выми виброгасителями. — В кн.: Рассеяние
энергии при колебаниях механических си-
стем. — Киев, 1970.
12. Коренев Б. Г., Блехерман А. Н. К
расчету" динамического гасителя с нелиней-
ным сопротивлением. — Тр. ЦНИИСЗК, 1974*
вып. 34.
13. Коренев Б. Г. Некоторые задачи
теории упругости и теплопроводности, ре-
шаемые в бесселевых функциях. М., 1960.
14. Коренев Б. Г., Волоцкий М. Я.
Применение динамических гасителей для
уменьшения колебаний складчатых си-
стем.— Строительная механика и расчет
сооружений, 1973, № 1.
15. Коренев Б. Г., Волоцкий М. Я.г
Резников Л. М. Вопросы гашения колеба-
ний пластинок, складок, оболочек. — В сб.:
Исследования по теории сооружений, вып.
XXI. М., 1975.
16. Коренев Б. Г., Волоцкий М. Я->
Фукс О. М. О гашении колебаний мачто-
вых сооружений. — Строительная механика
и расчет сооружений, 1976, № 1.
17. Коренев Б. Г., Поляков В. С.
Оптимальные параметры динамического га-
сителя колебаний при воздействии типа
сейсмического.— Реферативная информа-
ция ЦИНИС, 1977, Сер. XIV, вып. 3.
18. Коренев Б. Г., Резников Л. М. О
жолебаниях башенных сооружений, обо-
рудованных динамическим гасителем. —
Строительная механика и расчет сооруже-
ний ,19*68, № 2.
19. Коренев Б. Г., Резников Л. М. О
колебаниях конструкций с динамическими
гасителями при стационарных случайных
воздействиях. — Строительная механика и
расчет сооружений, 1969, № 4.
174
20. Коренев Б. Г„ Резников Л. М. Га-
шение колебаний башенных сооружений
при сейсмических воздействиях. —Строи-
тельная механика и расчет сооружений,
1971, № 5.
21. Коренев Б. Г., Резников Л. М. О
гашении автоколебаний башенных соору-
жений при действии ветра.—Строительная
механика и расчет сооружений, 1971, № 6.
22. Коренев Б. Г., Резников Л. М.
Вынужденные колебания круглой и квад-
ратной пластинки с динамическим гасите-
лем при гармонических воздействиях. — В
кн.: Динамика сооружений. М., 1971.
23. Коренев Б. Г., Резников Л. М.
Случайные колебания поперек ветрового
потока башенных сооружений с аэродина-
мически неустойчивой формой сечения. —
Строительная механика и расчет сооруже-
ний, 1973, №2.
24. Коренев Б. Г., Сердобольский А. И.
Демпфирование колебаний жестких мас-
сивных конструкций, расположенных на
упругом основании. Деп. ЦИНИЦ, 1980.
25. Коренев Б. Г., Фишман Г. М. Ко-
лебания системы с линейным динамическим
гасителем при импульсивном воздействии
на поддерживающую их конструкцию. —
Строительная механика и расчет сооруже-
ний, 1977, № 6.
26. Либерман А. Я. Современное со-
стояние проблемы вибрации и защиты от
нее воздушных линий. — Тр. ЦНИЭЛ,
1956, т. 5.
27. Манапов А, 3., Пику лев IE А.
Оптимальные параметры группы ви&рога-
сителей при нестабильной частоте гармо-
нического воздействия. — Строительная ме-
ханика и расчет сооружений, 1975, № 1.
28. Пановко Я. Г. Присоединенные
динамические системы как гасители колеба-
ний.— В спр.: Прочность, устойчивость, ко-
лебания, т. 3. М., 1968.
29. Пику лев И. А., Эрделевский А. Н.
К вопросу проектирования группы виорога-
оителей с учетом расстроек.—Строительная
механика и расчет сооружений, 1971, № 5.
30. Поляков В. С. Эффективность ди-
намических гасителей для линейных систем
при землетрясениях типа Газлийского 17
мая 1976 г. — Реферативная информация
ЦИНИС, 1978, сер. XIV, вып. 2.
31. Попов В. И., Сиваков А. И. Гаше-
ние колебаний, вызванных случайной си-
лой.— В сб.: Динамика и прочность ма-
шин, 1975, вып. 21.
32. Потехин А. Ф. О выборе оптималь-
ной упругой характеристики нелинейного
гасителя колебаний. —Тр. Тамбовского
ин-та хим. машиностроения, 1970, вып. 4.
33. Рекомендации по методике расчета
вибротасителей и их применению для на-
земных балочных систем трубопроводов,
140—73. Всес. науч.-исслед. ин-т по строит-
ву магистральных трубопроводов, 1973.
34. Рекомендации по проектированию
гасителей колебаний для защиты зданий и
сооружений, подверженных горизонтальным
динамическим воздействиям от технологиче-
ского обрудования и ветра. М., 1978.
35. Резников Л. М. Выбор оптималь-
ных параметров динамического гасителя
при прохождении через резонанс. — 15 кн.:
Динамика сооружений, М., 1968.
36. Резников Л. М. Вероятностный
анализ системы с динамическим гасите-
лем.— Машиноведение, 1969, № 2.
37. Резников Л, М. Оптимизация па-
раметров динамических гасителей колеба-
ний с различными видами сопротивления. —
Проблемы прочности, 1970, № 9.
38. Резников Л. М, Анализ эффектив-
ности некоторых типов нелинейных дина-
мических гасителей при гармонических воз-
действиях.— iB кн.: Динамика сооружений.
М., 1971.
39. Резников Л. М., Фишман Г. А1.
Оптимальные параметры и эффективность
динамического гасителя при действии пе-
риодических импульсов. — Машиноведение,
1973. № 1.
40. Савицкий Г. А. Основы расчета
радиомачт. М., 1953.
41. Селезнева Е. Н. Защита оттяжек
мачт от вибрации. — В сб.: Материалы по
металлическим конструкциям, 1969, вып.
14.
42. Справочник по динамике соору-
жений. М., 1972.
43. Терских В. П. Расчеты крутильных
колебаний силовых установок. М., 1954.
44. Цвениашвили Д. X., Карамыш-
кин В. В, Области динамической неустой-
чивости консольного стержня с гасителем
колебаний. — Сообщения АН ГрузССР,
1969, т. 54, № 3.
45. Fisher О. Some experience with the
use of vibration absorbers on aerial masts. —
Acta technica CSAV, 1974, roc. 19, N 2.
46. Neubert V. H. Dynamic absorbers
applied to a bar that has solid damping. —
Journ. of the Acoust. Soc. of Amer., 1964,
v. 36, N 4.
47. Snowdon J. C. . Vibration and
shock in damped mechanical systems. New
York, 1938.
РАЗДЕЛ 13. АЭРОДИНАМИЧЕСКИЕ СПОСОБЫ ГАШЕНИЯ
КОЛЕБАНИЙ ВЫСОКИХ СООРУЖЕНИЙ В ВЕТРОВОМ ПОТОКЕ
(Л. X. БЛЮМИНА, М. Я. ГЕМБАРЖЕВСКИИ)
13.1. ФИЗИКА ЯВЛЕНИЯ
У (высоких сооружений (дымовые и вен-
тиляционные трубы, радиобашни и теле-
визионные башни, опоры линий электропе-
редач, аппараты колонного типа, (мону-
менты и тому подобные сооружения), име-
ющих в поперечном сечении плохосютекае-
мый профиль, который способствует отры-
ву потока, могут возникнуть опасные ко-
лебания (в ветровом потоке, 'Приводящие
к (разрушению конструкции'. Поэтому аэрю-
дин ам ячеек а я усто йчи вость таки х со ор у -
жений становится важным условием, ко-
торое необходимо соблюдать при проекти-
ровании. Колебания сооружений имеют
максимальную составляющую в направ-
л он ии, перл ендииул ярном н-ап р явлению
ветра; частота и форма их, как правило,
близки к частоте и форме собственных ко-
лебаний сооружения.
Сооружения, обладающие малым конст-
руктивным демпфированием и низкой соб-
ственной частотой, колеблются при дос-
таточно низких скоростях ветрового пото-
ка. Амплитуда и число циклов этих ко-
лебаний бывают значительными, что мо-
жет привести сооружение в аварийное со-
стояние. Аэродинамические способы гаше-
ния колебаний устраняют причину, вызы-
в ающу ю ин тенсивн ые кол еб а ни я, изм ен е -
нием характера обтекания сооружения воз-
душным потоком в сечении и по высоте
сооружения.
-Рассматриваемые колебания имеют ха-
рактер автоколебаний. Наиболее часто на-
блюдаются автоколебания высоких соору-
жений типа «ветровой резонанс» и «гало-
пирование». Колебания типа «ветровой ре-
зонанс» вызываются периодическим 'Сры-
вом вихрей с поверхности сооружения, в
результате которого появляется знакопе-
ременная циркуляция Г, а следовательно,
и знакопеременная поперечная (подъем-
ная) сила Р=риГ, где р — плотность воз-
духа; v — скорость потока.
При этих колебаниях происходит «за-
хват» частоты срыва вихрей частотой соб-
ственных колебаний сооружения (вихри
начинают срываться с частотой, равной
частоте собственных колебаний), в ре-
зультате происходит резкое возрастание
амплитуды колебаний. Ветровой резонанс
имеет место в достаточно узком диапазо-
не скоростей ветра. Для круглоцилиндри-
ческих сооружений ветровой резонанс на-
ступает примерно при такой скоп-ости
ветра, когда аэродинамическое число Стру-
халя Sh = nd!v становится равным кине-
матическому числу Струхаля Sh1=nirf/y,
при этом максимальные амплитуды коле-
бания сооружений наблюдаются уже при
Sh = Shi л; 0,2, где п—частота срыва вих-
рей; П\ — частота собственных колебаний
цилиндра, оп ира ющегос я на упругие оп о -
ры; d — диаметр круглого цилиндра; v —
скорость ветра.
Для высокого сплошного (нерешетчато-
го) сооружения, имеющего в поперечном
сеч ен ни многоуго л ьник, малой м а л ь н ы е
значения амплитуд в режиме ветрового
резонанса (отмечаются примерно при 5Ц —
— Shi = nb{v^ 0,14 ... 0,16, где b—проек-
ция максимальной по длине диагонали
(многоугольника на Плоскость, перпенди-
кулярную направлению ветра (так же как
для обтекания пластины, установленной
перпендикулярно направлению потока,
Sh^'0,14 ... 0,16).
Галопирующие колебания возникают
только в конструкциях, при обтекании
КОТ ор ЫХ ВОЗ Д уШ(Н ы-м пот оком ПОЛЕ ля ет с я
стационарная поперечная сила. Эти коле-
бания вызываются отрывом потока, в ре-
зультате которого значения коэффициен-
та поперечной силы в зависимости от ут-
ла атаки Cy=f (<z) резко уменьшаются
и становятся отрицательными, так что
у
ок аз ыв ае т ся бол ыпе к оэффици ен т а
лобового сопротивления Сх; иными (слова-
ми, необходимое условие возникновения
галопирующих колебаний имеет вид
d Су
d а
Сх < 0.
Характерной особенностью галопирую-
щйх колебаний является (рост амплитуды с
увеличением скорости ветра. Подробнее о
природе аэродинамических сил , действу-
ющих на сооружение, изложено ib разд. 4.
13.2. АЭРОДИНАМИЧЕСКИЕ
СПОСОБЫ ГАШЕНИЯ
КОЛЕБАНИЙ СООРУЖЕНИЙ
В СССР и за рубежом существует мно-
го аэродинамических способов гашения
колебаний. Для гашения колебаний тел
круглоцилиндрической формы были пред-
ложены разнообразные устройства. Из на-
иболее известных следует отметить навив-
ку проволоки по винтовой линии по вы-
соте сооружения [3, 4, 5, 7, 10, 19, 20, 21,
22], применение интерцепторов [8, 9, 12,
14], использование перфорированного ко-
жуха [22, 23], установку рассекателей для
трубопроводов [17, 18], устройство кана-
лов для протока воздуха вблизи угловых
точек [1, 2, 6, 7, 15]. Однако в работах за-
рубежных авторов отсутствуют сведения о
влиянии толщины количества и углов на-
мотки проволок, формы, размеров, коли-
чества и мест крепления интерцепторов,
176
размеров отзгрстий перфорированных ко-
жухов 1на эффективность уменьшения коле-
баний и о влиянии всех этих факторов на
лобовое 'Сопротивление сооружения. Кро-
ме того, не приведены зависимости амп-
литуд колебания сооружения со средства-
ми гашения колебаний и без них от ос-
новных критериев подобия—чисел Re и
Sh.
Ниже рекомендуются только те способ
гашения колебаний, которые прошли тща-
тельную экспериментальную проверку, по-
скольку каждый из них нужно применять
с большой осторожностью. Неправильное
использование того или иного способа мо-
жет не только не уменьшить колебания
высокого сооружения, но еще больше его
раскачать.
1. Все сооружения как с круглой фор-
мой сечения, так и с сечением, имеющим
Рис. 13.3
углов ы е точки, с л ед у ет по в оз м ожности
строить сужающимися по высоте. Б этом
случае амплитуды колебания у кониче-
ских сооружений существенно меньше, чем
у цилиндрических. Объясняется это тем,
что у вершины конического тела напря-
женность Г срывающихся вихрей меньше,
чем у вершин ы цилиндрического тела.
Следов а те л ьн о, значение периодической
силы вблизи вершины конического тела,
пропорциональное Г, .меньше, чем вблизи
вершины цилиндрического тела.
2. Для гашения колебаний цилиндриче-
ских и конических сооружений круглой
формы наиболее простым и проверенным
способом является намотка четырех про-
волок диаметром, равным 0,5% диаметра
цили н.д рич еск ого или кон и ч еского те л а у
его основания под углом 9—12° к оси те-
ла. Эти проволоки образуют четыре вин-
товые линии, отстоящие одна от другой
на 90°, считая по основанию цилиндра
или конуса. Намотанные проволоки созда-
ют сдвиг фаз в срыве вихрей по высоте
сооружения, т. е. .нарушают одновремен-
ность срыва вихрей, что уменьшает зна-
чение
На
силы.
/рис. 13.1,а приведена зависимость
относительной амплитуды a—ajd верхней
точки круглого цилиндра от кинематиче-
ского числа Струхаля Sh^njd/u при на-
личии н ам отанной проволоки и б ез нее.
Максимальное значение амплитуды коле-
баний круглого цилиндра соответствует
числу Струхаля Shi = Sh л; 0,2. Амплитуда
колебаний круглого цилиндра без намо-
т а ни о й проволоки н а много б ол ьше, а зо-
на ветрового резонанса примерно в 2 ра-
за шире, чем для цилиндра с намотанной
проволокой. Л о бовое сопр огив лен,ие ци -
линдр-а при наличии указанной проволоч-
ной намотки /р за кризисных режимах об-
текания увеличивается примерно на 35—
40% (рис. 134,6).
Как показали экспериментальные иссле-
дования в аэродинамической трубе ЦАГИ,
количество и угол намотки проволоки
значительно влияют на гашение колебаний
и на лобовое сопротивление. Так, при тол-
щине проволоки 1,2% диаметра цилиндра
коэффициент лобового сопротивления Сх
возрастает в 2 раза. На рис. 13.2 приве-
дены зависимости относительных ампли-
туд колебания a~a/D0CB верхней точки
ко 1 г и ч с с к ого круглого тела с прав Oi очно й
177
намоткой и без нее от чисел Рейнольдса.
Навивка, существенно уменьшая ампли-
туду колебания, увеличивает коэффициент
л обов ог о сопротивления в з акри тич еском
режиме примерно на 50% (рис. 13.3).
3. Для гашения колебаний круглых ци-
линдрических и конических сооружений
можно использовать интерцепторы, пред-
ставляющие С0160Й прямоугольные пласти-
ны. Эти пластины целесообразнее всего
располагать по спирали в верхней части
сооружения. Высота пластин от поверхно-
сти сооружен ия до лжи а сост ав л ять п ри -
мерно 5—4'2% диаметра основания. Опыт-
ные исследования, проведенные в аэроди-
намической трубе ЦАГИ, показали, что
они менее эффективны, чем проволочные
гасители (см. рис. 13.2).
4. Для гашения колебаний высоких со-
оружений, имеющих в поперечном сечении
угловые точки (например, трапеция, квад-
рат, треугольник и другие формы попереч-
ного сечения), навивка проволоки и при-
менение интерцепторов неэффективно, так
как наличие острых ребер делает харак-
тер обтекания таких сооружений отличным
от обтекания сооружений с круговым по-
перечным сечением. У таких тел острые
ребра фиксируют положение точки отрыва
вихрей при всех скор остях потока. Дру-
гая особенность таких тел — то, что при
их обтекании помимо силы лобового со-
противления возникает еще и стационар-
ная поперечная '(подъемная) сила. Это
об у сл овли в а ет вдаможность возникн овен и я
не только ветрового резонанса, но и гало-
пирования.
Для гашения колебаний сооружений,
им еющих в п о пер ечном сечении угловы е
точки, как показали систематические экс-
пер им ентал ыные послед ов амия в аэр ода -
намических трубах ЦАГИ и натурные
наблюдения, надежным средством являют-
ся каналы для протока воздуха, встроен-
ные вблизи угловых точек. Ути каналы
Представляют собой простой и эффектив-
ный способ для гашения колебаний типа
ветровой резонанс и галопирующих коле-
баний.
Большая эффективность действия кана-
лов объясняется тем, что проходящий че-
рез каналы воздушный поток снижает на-
пряженность периодически срывающихся
вихрей, т. е. уменьшает знакопеременную
раскачивающую силу, одновременно умень-
шая значения статических коэффициентов
попепечной силы С”и лобового сопротив-
ления Сх. Особенно уменьшается абсолют-
ная величина производной по углу ата-
ки а, которая в основном влияет на воз-
никновение галопирующих колебаний. Эф-
фект действия каналов показан на рис.
13.4—13.8 для сооружений, имеющих ром-
бическое поперечное сечение, сечение,
близкое к астроиде, и трапециевидное.
Каналы выполнены в верхней части со-
оружения на участке 0,4 высоты, ширина
каналов составляет 0,05—0,08 наибольше-
го линейного размера поперечного сече-
ния и отстоят на 0,07—0,42 (в том же из-
мерении) от ребер (рис. 43.4). Размеры
каналов и место расположения зависят
от конструкции, формы и размеров со
оружения «и в каждом отдельном случае
должны определяться испытанием в аэро-
динамических трубах жестко и упруго
закрепленных моделей.
Эффективность применения каналов для
гашения колебаний типа ветрового резо-
нанса показана на рис. 13.4,а, где приве-
дены результаты экспериментальных ис-
следований относительных амплитуд коле-
баний ~a = ajb, где Ь—наибольший попе-
речны й р азм ер ци л и н дрмчеоко й м одели,
имеющей ромбическое сечение. В этом
случае максимальные амплитуды колеба-
ния вблизи ветрового резонанса в диапа-
зоне углов 25°^а^40° уменьшаются в-
несколько раз благодар я устройству пр я-
моугольных сквозных каналов в верхней
ч асти модели на уч эстке протяженност ью
0,4 высоты.
На рис. 13.4,6 относительные амплиту-
ды колебаний а даны в зависимости от ки-
н ем а тич еск ого чис л а С тру х а ^я Shi. Здесь
же видно, что ветровой резонанс возни-
кает при Shi»0,14. Возникновение знако-
переменной поперечной силы, действующей
на сооружение с ромбическим поперечным
сечением (рис. 13.5,я), и влияние каналов
на обтекание потока показаны на рис.
13.5,6.
Н аглядн ое п р едет ав ление об эффект и в-
ности гашения галопирующих колебаний
модели с сечением, близким к астроиде, с
помощью устройства каналов дают рис.
13.6 и 13.7. На рис. 13.6 представлены аэ-
р один амически е х ар актери стики : коэф фи -
циенга поперечной силы Cy — t(a) и лобо-
вого сопротивления Cx=f(cc) и соответству-
ю ща я крив а я аэр од и нам и ч еской неу ст ой -
чивости, рассчитанная по Ден-Г ар тогу
(dCy/da)+Cx.
Кривые, приведенные на рис.^ 13,Д пока-
зывают, что значения Су и Сх для модели
с каналами значительно меньше, чем для
модели без каналов.
Как следует из кривой аэродинамиче-
ской неустойчивости, на рис. 13.6,6 у высо-
кого сооружения без каналов с сечением,
близким к астроиде, могут возникнуть га-
лопирующие колебания в диапазоне углов
атаки 34°^ДаД45°. Устройство каналов
исключает эти колебания.
Максимум кривой, приведенной _на
рис. 13.7,а, указывает на то, что макси-
мальная относительная .амплитуда а—
— 2а/Ь при постоянной скорости воздуш-
ного потока соответствует углу атаки
35°—40°.
На рис. 13.7,6 показано увеличение амп-
литуд колебания модели с возрастанием
скорости потока при наиболее неблаго-
приятном направлении ветра ос « 4LT, что-
характерно для галопирующих колебаний.
Наличие каналов ликвидирует аэродина-
мическую неустойчивость модели.
На рис. 13.8 иллюстрируется эффектив-
ность применения каналов для гашения
колебаний модели с трапециевидным се-
чением. Даже при наиболее опасных, с
точки зрения возможности возникновения .
178
V
Рис. 13.4
Зона Возникновения голапи-
рующих колебаний', ----
dCK „ sn
—— + С О
Рис. 13.6
без каналов
।
1
каналами
30° 00
без каналов
С каналами
00°
Рис. 13.5
без каналов
Рис. 13.7 ►
179
80° 160° a
—®— без каналов
Рис. 13.8
галопирующих колебаний, направлениях
воздушного потока (углах атаки) каналы
почти 1пол1ностью ликвидируют интенсив-
ные колебания.
СПИСОК ЛИТЕРАТУРЫ
1. А.с. 280807 (СССР). Сооружение
типа башни. / Блюмина Л. X., Гембаржев-
ский М. Я-, Гребенников В. Н., Соко-
лов А. К. — Заявл. Опубл, в БИ 1970,
№ 28.
2. Блюмина Л. X., Беспрозванная И. АГ.
Гембаржевский М. Я., Гребенников В. Н.,
Фомин Г. М. Аэродинамический способ
гашения колебаний высоких сооружений
башенного типа. — Строительная механика
и расчет сооружений, № 6, 197'1.
3. А.с. 305524 (СССР). Устройство
для гашения колебаний надземных трубо-
проводов. / Блюмина Л. X., Гребенников
В. Н., Казакевич М. И. Заявл. от 11/XII-
1970 г., № Опубл, в БИ, 1973, № 6.
4. Блюмина Л. X., Гребенников В. Н.
Экспериментальное исследование гашения
колебаний круглых консольных цилиндри-
ческих и конических тел в воздушном пото-
ке. —В кн.: Промышленная аэродинами-
ка, вып. 30. М., 1978.
5. Блюмина Л. X., Гребенников В. Н.,
Л шит в ан В. И. Исследование гашения ко-
лебаний круглых цилиндров на режиме вет-
рового резонанса. — Сб. статей по аэрогид-
родинамике. Труды ЦАГИ, вып. 1567,
1974.
6. Блюмина Л. X., Гембаржевский
AL Я-, Гребенников В. Н., Соловьева Е. В»
Аэродинамический способ гашения колеба-
ний высоких сооружений с поперечным се-
чением, имеющим угловые точки. — Цб.
статей по аэрогидродинамике. Труды ЦА-
ГИ, вып. 1567, 1974.
7. Гембаржевский М. Я-> Блюми-
на Л. X., Гребенников В. Н. и др- Исследо-
вания некоторых аэродинамических спо-
собов гашения колебаний сооружений. —
В кн.: Труды конференции по аэродинами-
ке и аэроупругости высоких строительных
сооружений. М„ 1974.
8. Луговцов А. Н. О способах умень-
шения интенсивности колебаний типа «вет-
ровой резонанс» цилиндрических конструк-
ций, — В кн.: Колебания зданий и соору-
жений. М., 1963.
9. Меир У., Маул Д. Плохообтекае-
мые тела и отрыв вихрей. Обзор докладов
на «Евромех-17». Сб.: Механика, 1972,
№ 2.
ГО. Новак М. Поперечные колебания
высоких конструкций с круглым сечением.
Русский перевод из «Inzenyrske stavby»,
1965, № 11.
11. Патент ФРГ № 1. 216. 515. кл.
37 f, 15/28, 1966.
12. А.с. 77097 (СССР). Цилиндриче-
ская строительная конструкция / Савиц-
кий Г . А. Заявл. Опубл, в БИ, 1940, № 12.
13. Савицкий Г. А. Основы расчета
радиомачт. М., 1953.
14. Фомин Г. М. Об одном способе
гашения колебаний плохообтекаемых тел,
находящихся в потоке жидкости и газа.—
Иэв. АН СССР, МЖГ, № 1, 1968.
15. Федяевский К. К., Блюмина Л. X.
Гидроаэродинамика отрывного обтекания
тел. М., 1977.
16. Baird R. С. Pipe — line bridge
vibrationcause and cure. The Petroleum
Engineer, y. 29, № 5, 1957.
17. Baird R. C. Wind induced vibration
of a pipe-line suspension bridge — and
its cure. Frans., ASME. v. 77. № 6, 1955.
18. Nakagava R., Fujino T., Arita У.,
Shima T. An experimental study of aerody-
namic devices for reducing windinduced
oscillatory tendencies of stacks. Proc, of
the -International Conference ot Wind Effect
on Buildings and Structures. Teddington,
London, 1965.
19. Price P. Suppression of the fluid —
induced vibration of circular cylinders.
I. Eng. mech. Div. Proc. ASME, v. 82,
№ 3, 1956.
20. Scruton C., Wais he D. E. L NPL,
Aero Report, № 3315, 1957.
21. Scruton C. A note on the device
for the suppression of the vortex — excited
oscillations of flexible structures of cir-
cular or near circular section with
special reference to its application to tall
stacks. NPL. Aero Report, N 1012, 1963.
22. Vickery B. J„ Walshe D. E. J.
NPL. Aero Report, № 1132, 1964.
23. Walshe D, E. I, Wootton A. R.
Preventing wind — induced oscillation of
structures. Proc. Inst. Civil Eng., v. 47,
1970.
РАЗДЕЛ 14. МАЛОМАСШТАБНОЕ МОДЕЛИРОВАНИЕ
ДИНАМИЧЕСКИХ ЯВЛЕНИЙ
(И. С. ШЕЙНИН)
i
Маломасштабное . моделирование —
это один из видов физического моделиро-
вания [39], осуществляемый на моделях
малого размера. Маломасштабное моде-
лирование экономично, не требует боль-
ших экспериментальных площадей и гро-
моздкого испытательного оборудования,
позволяет относительно быстро изготов-
лять и испытывать модели, благодаря че-
му может быть не только средством ре-
шения общих задач моделирования [39],
но и одним из средств вариантного про-
ектирования. При выполнении приведен-
ных ниже рекомендаций маломасштабное
моделирование позволяет добиться значи-
тельной точности получаемых результатов.
14.1 ОСОБЕННОСТИ
МЕЛКОМАСШТАБНОГО
МОДЕЛИРОВАНИЯ
Основными особенностями маломас-
штабного моделирования являются: 1) от-
каз от условий простого подобия; 2) при-
менение низкомодульных полимерных ма-
териалов для изготовления моделей и не-
обходимые в этой связи; 3) использова-
ние специальных методов и средств для
испытания этих материалов; 4) использо-
вание специальной технологии изготовле-
ния моделей; 5) применение специальных
средств возбуждения вибраций и измере-
ния деформаций; 6) привлечение теории
вязкоупругости к анализу законов моде-
лирования.
Эти особенности были выявлены при
отработке методики маломасштабного
моделирования и объясняются следующи-
ми соображениями.
1. В соответствии с существующей
практикой для изготовления и испытания
наиболее удобны модели, размещаемые
на столе, т. е. которые имеют максималь-
ный размер не более 1—2 м. В зависимо-
сти от размеров натурного сооружения и
моделируемого вместе с ним грунтового
массива (если моделируют взаимодейст-
вие сооружения с грунтовым массивом,
что важно, например, для фундаментов
под машины, высотных, подземных и гид-
ротехнических сооружений) линейный мас-
штаб модели обычно получается в пре-
делах
1/вооо "С а1 "С 1/15- (14.1)
Поскольку одна из основных измеря-
емых величин при изучении динамических
явлений в сооружениях — перемещения
элементов, которые и в натуре так малы,
что лежат вблизи пороговой чувствитель-
ности виброизмерительных приборов, а на
моделях при соблюдении простого подо-
бия будут в а^-1 раз меньше, то при ис-
пользовании маломасштабных Моделей
приходится отказываться от сохранения
такого простого подобия. При этом всю
интерпретацию результатов моделирова-
ния можно излагать на языке теории рас-
ширенного подобия [18, 32]. Однако в*
последние годы развился “ несколько иной
язык, базирующийся на требовании, что-
бы физическая модель и натура были
системами, преобразующими подобные ди-
намические воздействия (нагрузки) в по-
добные выходные процессы (процессы, ха-
рактеризуемые подобными законами изме-
нения перемещений, деформаций и напря-
жений), т. е. были системами, имеющими
одинаковые амплитудные, амплитудно-
частотные и фазо-частотные характерис-
тики, построенные в критериальных систе-
мах координат. Поскольку большинство
реальных сооружений и конструкций ра-
ботает в линейной стадии [39], ниже бу-
дут рассмотрены только вопросы модели-
рования в линейной постановке.
2. Необходимость применения низко-
модульных материалов объясняется рядом
причин. Во-первых, при отказе от просто-
го подобия деформации на модели во
столько раз больше, чем на натуре, во-
ные полимерные материалы — примерно до
сколько раз больше отношение перемеще-
ний к линейным размерам. Поэтому ес-
ли потребовать, чтобы абсолютные пере-
мещения на модели н в натуре были рав-
ны, с тем чтобы использовать вибродатчи-
ки одинаковой чувствительности, то де-
формации на модели 8М окажутся в а”1 раз
больше, чем £н в натуре. Однако если
бетон работает! в линейной стадии
примерно до i8H^ 10”4, то низкомодуль-
10-1, то с учетом запаса по дефор-
мациям в натуре и позволяет перекры-
вать весь диапазон масштабов (14.1).
Во-вторых, при одинаковых материалах
натуры и модели частоты колебаний уве-
личились бы обратно пропорционально
линейному масштабу, так что, например,
частотам в натуре до 100 Гц при масшта-
бах (14.1) соответствовали бы частоты
на модели 2,5—500 кГц. Это частоты зву-
кового и даже ультразвукового диапазо-
на, на котором вследствие больших по-
терь на излучение и ряда других причин
нарушается физическая природа изучае-
мых процессов и сильно затрудняется
возбуждение вибраций по заданному за-
кону и их измерение.
Учитывая, что в низко модульных по-
лимерных материалах скорости распростра-
нения упругих волн существенно (до 20
раз) меньше, чем в бетоне, удается в со-
ответствующее число раз снизить и час-
тоту. Необходимо, однако, отметить, что
промышленность не выпускает специаль-
181
ных низкомодульных полимерных матери-
алов для моделирования, в связи с чем
при изготовлении моделей приходится
подбирать рецептуру таких материалов с
использованием промышленных полуфаб-
рикатов. Рекомендации по подбору мате-
риалов приведены в п. 14.12.
3. Для моделирования динамических
явлений в сооружениях с помощью низко-
модульных полимерных материалов необ-
ходимо определять такие механические
характеристики материалов, как модули
упругости и сдвига в пределах линейных
деформаций, коэффициент внутреннего
неупругого сопротивления, а также зави-
симость этих величин от частоты колеба-
ний, температуры, влажности и других
факторов. Поскольку низкомодульные по-
лимерные материалы, выпускаемые про-
мышленностью, предназначены для дру-
гой цели и для них важны другие харак-
теристики, соответственно и приборы, се-
рийно выпускаемые для определения этих
характеристик, не могут быть использова-
ны для моделирования.
Методика определения механических
характеристик низкомодульных модельных
материалов и необходимые для этого при-
боры изложены в п. 14.4.
4. Необходимость специальной техно-
логии изготовления моделей связана с
требованиями к однородности материала
модели, необходимостью обеспечения до-
статочно низкого уровня начальных на-
пряжений и другими специфическими тре-
бованиями. Рекомендации по этим вопро-
сам приведены в п. 14.3.
5. Необходимость в специальных сред-
ствах возбуждения вибраций объясняется
электродинамические
жесткость
системы, соизмери-
ббльшую, чем
упругой
жесткость
тем, что обычные
возбудители имеют
подвески подвижной
мую или даже
модели, изготовленной из низкомодульно-
го материала, в связи с чем характерис-
тики механической системы вибровозбу-
дитель—модель значительно отличаются
от исходных для одной модели, причем
погрешность не всегда удается прогнози-
ровать и исключить. Применение специаль-
ных микрсвибраторов, описанных в п. 1.5,
позволяет избежать указанных ошибок.
Аналогично проволочные ' тензодатчики,
широко применяемые в настоящее время
для измерения деформаций в элементах
сооружений, оказываются непригодными
для материалов с модулем упругости ни-
же ГПа [21], так как, армируя эти мате-
риалы, изменяют исследуемую систему и
вносят погрешность в результаты измерений.
6. Поскольку низкомодульные поли-
мерные материалы являются типичными
вязкоупругими материалами, то для осу-
ществления моделирования на их основе
неооходимо было с помощью теории вяз-
коупругости установить, каким требовани-
ям они должны удовлетворять, чтобы
обеспечить заданную точность моделиро-
вания. Соответствующие рекомендации
приведены по ходу изложения.
to*1
14.2. ПОДБОР МОДЕЛЬНОГО
МАТЕРИАЛА
Материал, применяемый для изготовле-
ния маломасштабной модели, должен
иметь следующие механические характе-
ристики i[39]:
1) коэффициент Пуассона vM и лога-
рифмический декремент колебаний 5М
должны быть такими же, как и в нату-
рном материале: vH и 5Н- При моделиро-
вании сооружений из бетона и железо-
бетона рекомендуется принимать
0,17<чм<0,23;
0,15 < бм <к0,35;
(14.2)
(14.3)
2) модуль упругости материала £м
должен быть по возможности ниже, а
плотность рм должна быть по возможности
выше, чтобы максимально снизить скоро-
сти упругих волн. Однако не рекоменду-
ется применять материал с модулем упру-
гости меньше 10—20, так как иначе
могут сказаться эффекты армиру-
ющего действия даже тех специальных
средств измерения деформаций, которые
к настоящему времени разработаны. С
другой стороны, применение материала с
модулем упругости больше, чем 50—100,
или с плотностью меньше 0,8 г/см3
может вызвать нежелательное повышение
частот, на которых должно проводиться ис-
пытание модели. Кроме того, как показы-
вает опыт, при меньшей плотности пока
не удавалось добиться достаточно малого
затухания. Поэтому можно записать:
в качестве необходимых условия
10 ==s KM =с 100; (14.4)
0,8 г/см3е=рм; (14.5)
в качестве желательных
10<Ем=Сб0 ;
1,2 г/см3<рм;
условия
(14.4а)
(14.5а)
3) предел пропорциональности между
динамическими напряжениями и деформа-
циями должен составлять не менее 3%
модуля упругости
ап> 0,03 ем; О4-6)
желательно, чтобы он удовлетворял ус-
ловию
(Тп>0,05Ем; (14.6а)
4) механические характеристики, ука-
занные в п. 1 и 2, не должны зави-
сеть от частоты либо могут иметь зави-
симость от частоты, настолько слабую,
чтобы во всем диапазоне частот, на ко-
торых будут проводиться испытания мо-
дели, отклонения этих характеристик от
среднего значения не превзошли 5 %.
Это требование вызвано тем обстоятель-
ством, что низкомодульные материалы,
как уже упоминалось, могут проявлять
в своем поведении реологические свой-
ства в значительно более сильной степени,
чем обычные строительные материалы.
Поэтому следует решить вопрос о диапа-
зоне частот, в пределах которых модель-
182
ный материал идентичен по своим харак-
теристикам натурному. Очевидно, что эти
частоты не могут быть слишком низки-
ми, так как при увеличении значения пе-
риода колебаний до величин порядка ос-
новных значений времен релаксации роль
реологических свойств в модельном ма-
териале станет большей, чем в натурном.
Это выразится снижением приведенного
модуля упругости £”р =&о/&о, равного
отношению амплитуды напряжений к ам-
плитуде деформаций в гармоническом
процессе. В то же время на достаточно
высоких частотах начнет сказываться за-
висимость затухания от частоты колеба-
ний, не свойственная строительным мате-
риалам в зоне обычных частот динами-
ческих явлений.
Кроме того, этот материал должен
удовлетворять определенным технологи-
ческим требованиям, которые выявились
в результате сопоставления различных
технологических приемов изготовления мо-
делей:
1) допускать изготовление модели
или ее частей способом литья в заранее
приготовленные формы, ибо этот способ
значительно менее трудоемок, чем другие,
основанные на применении механической
обработки;
2) допускать приготовление литьево-
го состава в лабораторных условиях пу-
тем механического перемешивания, а за-
тем заливку и отверждение модели без
применения вакуумирования, термообра-
ботки или других процессов, требующих
специального оборудования;
3) допускать приготовление литьево-
го состава достаточно большими порци-
ями (замесами), желательно массой до
5 кг, при трудоемкости не более 1 чел.-ч
на 1 кг;
4) иметь жизнеспособность от момен-
та окончания перемешивания до момента
окончания укладки в формы не менее
25 мин при вязкости к моменту окончания
укладки не более 500 Па*с„ с тем, чтобы
производить укладку без захвата возду-
ха и образования пузырей;
5) иметь максимальную экзотермию
не более .0,01 Вт/г при коэффициен-
те теплоемкости см>1,2 Дж/(г-°С), ко-
эффициенте теплопроводности jXM ^10-s
Дж/(см-с-°С) и коэффициенте линейного
расширения сс<5*10-* (1/°С) для того,
чтобы не достигались недопустимые тем-
пературные деформации при отверждении;
6) иметь технологическую усадку за
весь процесс отверждения не более 1% без
изменения первоначальной формы детали;
7) легко отделяться от формы при
подготовке поверхности формы только
смазыванием каким-либо веществом при
комнатной температуре и без применения
специального оборудования;
8) допускать , экспериментальное оп-
ределение основных физико-механических
характеристик образцов, материала, от-
литых одновременно с моделью, доста-
точно быстро, но не позднее чем через
4 5 сут. Эти же характеристики для пол-
ностью отвержденных образцов следует
пересчитывать с помощью стабильных
коэффициентов;
9) полностью отверждаться не позд-
нее чем через 2—3 недели после заливки;
10) после полного отверждения дол-
жен сохранять стабильность [41] физико-
механических характеристик во времени,
обеспечивающую их отклонение от перво-
начальной величины не более 5% в тече-
ние месяца;
11) иметь слабую зависимость меха-
нических характеристик от температуры,
допуская их изменение не более чем на
0,5% на ГС в зоне температур от 15 до
25°С;
12) допускать склеивание отвержден-
ных деталей тем же материалом в тече-
ние не менее 1 мес с момента их отвер-
ждения без потери прочности места
склейки по сравнению с прочностью оста-
льных сечений деталей, а также приклеи-
вание металлических и резиновых датчи-
ков и других устройств, необходимых
для проведения испытаний моделей.
Допускается, а иногда может оказа-
ться даже полезным использование мате-
риалов с более сильными, чем указано
выше, температурными и частотными за-
висимостями, если изменение механичес-
ких характеристик с частотой может быть
скомпенсировано повышением температу-
ры, при которой проводятся испытания
(но не более чем до 50°С), т. е. если
выполняется одно из следующих условий:
1) модуль упругости и модуль сдвига из-
меняются пропорционально, так что ко-
эффициент Пуассона, зависящий от их от-
ношения, не изменяется, а логарифмический
декремент колебаний либо не изменяется,
либо уменьшается с повышением темпера-
туры, но увеличивается с повышением час-
тоты, либо, наоборот, увеличивается с
повышением температуры, но уменьшается
с повышением частоты; 2) логарифмичес-
кий декремент колебаний не изменяется,
а коэффициент Пуассона меняется при
повышении температуры в противополож-
ную сторону, чем при повышении частоты;
3) обе ^величины — и логарифмический
декремент колебаний, и коэффициент Пу-
ассона — изменяются с повышением тем-
пературы в одну сторону (т. е. обе уве-
личиваются либо обе уменьшаются) и
пропорционально друг другу, а с измене-
нием частоты в другую сторону и тоже
пропорционально друг другу.
В результате анализа всех основных
классов современных низкомодульных ма-
териалов [|2, 6, 31, 40, 41, 46], отбора тех
из них, которые по свойствам оказывались
ближе других к области указанных выше
требований, и последующего синтеза раз-
личных композиций из этих материалов
удалось создать несколько композиций [7,
19. 20, 24,, 25, 35, 36, 37, 38, 49, 50, 51, 52,
53], удовлетворяющих большинству из пере-
численных требований и довольно близких к
удовлетворению остальных. Ниже приво-
дятся данные об одной из таких компози-
ций [20, 38, 49], опыт использования кото-
183
рой уже довольно велик и нашел отраже-
ние в Технических условиях [19,52].
Композиция состоит из связующей осно-
вы и наполнителей. В качестве связующего
используют смесь олигодиенуретанэпоксида
марки ПДИ-ЗА и эпоксидно-анилиновой
•смолы марки ЭА. Олигодиенуретанэпоксид
иДИ-ЗА представляет собой весьма вязкий
при комнатной температуре каучук, содер-
жащий на концах молекулярных цепочек
эпоксидные группы, благодаря чему для
его отверждения не требуется горячая
вулканизация, а достаточно введение при
комнатной температуре обычного отвер-
дителя, применяемого для ;эпоксидных
смол, например полиэтиленполиамина
(ПЭПА). В отвержденном состоянии он
имеет модуль упругости порядка 20—
30 кгс/см. Перемешивание его с отверди-
телем и укладка в формы затруднены из-
за высокой вязкости.
Эпоксидно-анилиновая смола ЭА, на-
оборот, имеет малую вязкость при комнат-
ной температуре, а будучи отвержденной с
помощью одного из тех же отвердителей,
имеет модуль упругости довольно высо-
кий — более 4 ГПа.
Смесь ПДИ-ЗА и ЭА позволяет получить
продукт, достаточно удобный для укладки
в формы и имеющий подходящий модуль
упругости после отверждения. У этой сме-
си и логарифмический декремент колеба-
ний б близок к требуемому, но коэффици-
ент Пуассона слишком высок, а плотность
близка к нижнему пределу. Для снижения
эффективного коэффициента Пуассона в
смесь добавляют пробковую кргшку с раз-
мером частиц от 0,5 до 2 мм. Попада-
ние частиц меньшего размера не снижает
коэффициент Пуассона. Частицы большего
размера ухудшают однородность матери-
ала. Для компенсации снижения плотно-
сти от добавления пробки и для повыше-
ния плотности против начальной исполь-
зуют добавки минеральных наполнителей
в виде тяжелых порошков из веществ, хи-
мически не реагирующих с вяжущими, нап-
ример пылевидного кварца с размером час-
тиц менее 0,63 мм или железного порошка.
В Технических условиях на этот мате-
риал [19] приводятся требования к исход-
ным веществам, используемым для получа-
ния данного материала, описываются мето-
ды их подготовки и анализа, даются реко-
мендации по подбору соотношения исход-
ных веществ, необходимого для получения
характеристик модельного материала, по
технологии подготовки форм, приготовления
и укладки литьевого состава, а также по ме-
тодике приготовления и испытания конт-
рольных образцов.
Механические характеристики этого мо-
дельного материала практически не зави-
сят от частоты колебаний в пределах 20—
100 Гц и от температуры в пределах ком-
натной температуры 20±5°С. Исключением
является логарифмический декремент ко-
лебаний, для которого на частотах выше
120 Гц имеется сильная зависимость от
частоты, не компенсируемая изменением
температуры. На рис. 14.1. показан общий
характер изменения логарифмического дек-
ремента колебаний для одного из образ-
Рис. 14.1. Характер изменения логарифмического
декремента колебаний в зависимости от частоты
и температуры для одного из видов модельного
материала
цов такого материала в зависимости от
частоты и температуры.
В табл. 14.1 [20] для ориентации
приведены конкретные примеры некоторых
составов и соответствующие им механичес-
кие характеристики. Как видно, свойства
модельного материала зависят от соотно-
шения олигодиенуретанэпоксида ПДИ-ЗА
и эпоксидно-анилиновой смолы ЭА, их
вязкости, от количества и вида наполни-
теля. Чем выше их вязкость, тем ниже
модуль упругости материала. С увеличе-
нием количества эпоксидно-анилиновой
смолы в составе модельного материала
увеличивается значение модуля упругости
и логарифмического декремента колеба-
ний, а коэффициент Пуассона уменьшае-
тся. При получении модельного материала
в соответствии с требованиями к его ме-
ханическим характеристикам и в зависи-
мости от вязкостй ПДИ-ЗА подбирают со-
отношение ПДИ-ЗА и ЭА. Чем выше вяз-
кость ПДИ-ЗА, тем большее количество ЭА
вводят в состав модельного материала.
Значение модуля упругости и плотно-
сти материала можно увеличить введени-
ем в состав модельного материала боль-
шего количества минерального наполни-
теля, коэффициент Пуассона при этом не
изменяется. Снизить коэффициент Пуассо-
на можно введением в! состав материала
большего количества пробковой крошки.
Логарифмический декремент колебаний
можно подобрать изменением соотноше-
ния ПДИ-ЗА и ЭА и их вязкостью. Чем
меньше ЭА в модельном материале и вы-
ше вязкости ПДИ-ЗА и ЭА, тем ниже ло-
гарифмический декремент колебаний. От
количества наполнителя логарифмический
декремент колебаний модельного материа-
ла практически не меняется.
Еще более широкий диапазон физико-
механических свойств при большей доступ-
ности материалов имеют разработанные
в последние годы новые композиции [7,
24, 25, 34—36, 50—53 на основе смеси оли-
годиенуретандиэпоксида марки ПДИ-ЗАК с
различными эпоксидными смолами, в част-
ности ЭД-20 и ЭИС-1, и с эпоксидными
разбавителями, например полиоксипропи-
лентриэпоксидом ТЭ-1500 или ДЭГ-Ж с
применением пористых наполнителей, та-
ких, как активированный уголь и фенол-
формальдегидные микросферы БВ-01, а
также различных тяжелых наполнителей.
184
ТАБЛ И ЦА 14.1
Состав, вес. ч. Свойства
ПДИ-ЗА ЭА * ПЭПА проб- ковая крошка кварц пылевид- ный Е, Мпа V б р, г/ГСМ3
коли- чество вязкость при 50°С, Пь • с коли- чество кинемати- ческая вязкость при 25°С, мм2/с
100 7,6 30 667 8,6 13 52 19,1 0,24 0,32 0,93
100 7,6 40 667 11,0 14 56 30,0 0,22 0,35 0,94
100 7,6 50 667 13,5 15 60 38,0 0,20 0,33 0,94
100 7,6 60 667 16,4 16 64 50,0 0,16 0,41 0,94
100 24,0 30 667 8,7 13 52 17,1 0,23 0,27 0,93
100 24,0 40 667 11,0 14 56 20,0 0,23 0,26 0,93
100 24,0 50 667 13,6 15 60 г 25,4 0,20 0,32 0,94
100 24,0 60 667 16,4 16 64 30,4 0,16 0,35 0,94
100 24,0 70 667 18,5 17 68 43,5 0,13 0,38 0,95
100 7,6 40 667 11,0 21 56 31,0 0,15 0,35 0,85
100 7,6 40 117 12,5 14 56 53,0 0,20 0,30 0,95
100 9,6 50 117 15,0 15 100 46,0 0,18 - 0,32 1,00
1 100 7,6 50 133 15,0 15 60 63,0 0,16 0,30 0,98
hoo 7,6 25 667 11,0 14 56 27,0 . 0,23 0,30 0,98
14.3. ПРОЕКТИРОВАНИЕ
И ИЗГОТОВЛЕНИЕ МОДЕЛИ
И КОНТРОЛЬНЫХ ОБРАЗЦОВ
При проектировании модели обяза-
тельным является требование полного
геометрического подобия всех элементов
модели и натуры. Можно пренебречь лишь
единичными деталями типа выступов, ниш
или отверстий, максимальный размер ко-
торых не превышает 1/10 минимального
размера элемента, на котором они распо-
ложены.
При .проектировании следует найти
разумное соотношение между величина-
ми, входящими в уравнение
/м_____ам________
/н ^ман 4л
Ем Рн
Ен Рм
(И.7)
где f, I и а — соответственно частоты, на
которых проводят испытания, характер-
ный линейный размер и скорость распро-
странения продольной волны; остальные
обозначения те же, что и выше. При этом
исходят из соображений о наличии мате-
риалов, средств возбуждения вибраций и
желательных размеров модели.
Например, если требуется изготовить
и испытать модель пространственной же-
лезобетонной рамы, габаритные размеры
которой в натуре 80X20X20 м, сделанной
из бетона с £н = 3,15-104 МПа и рн =
= 2,4 г/см3, работающей в диапазоне час-
тот 15 Гц 60Гц, а из вибровозбуди-
тельных средств в наличии имеется микро-
вибратор (см. п. 14.5.), который устойчиво
работает на частотах 30 Гц<т/м^250 Гц,
то это сразу позволяет записать 0,24^
^(/н//м)=^0,5 и определяет соотношение
между масштабом и механическими харак-
теристиками материалов:
0,24 ЯмРц.
г ЕнРм 4l г 'EHpM^
(14.8)
Чем ниже £м и выше рм, тем меньше мо-
жет быть модель. Например, если£м=
= 21 МПа, рм=1 г/см3, то неравенство
(14.8.) примет вид
0,0096^-^^0,02. (14.9)
*н
Для удобства пересчета размеров ре-
комендуется в качестве масштаба выби-
рать одно из промежуточных значений,
определенных из двойного неравенства (14.
8), образующее правильную дробь с зна-
менателем, кратным десяти. При этом
если требования к точности результатов,
невелики, например при выборе вариантов
на ранних стадиях проектирования, то из
условия минимума затрат на моделирова-
ние рекомендуется выбирать наименьший
масштаб. При необходимости добиться мак-
симальной точности моделирования реко-
мендуется выбирать наибольший из масшта-
бов. Наряду с другими преимуществами для
точности это позволяет испытывать модели
на наиболее низких частотах, на которых
легче удается реализовать условие(14.3).
После выбора масштаба рекоменду-
ется проверить, не внесет ли больших пог-
решностей крепление вибродатчиков. Нап-
ример, если упомянутая выше рама имеет
наименьший элемент размером 0,7Х1Х6м,
то при масштабе 1/50 этот элемент на мо-
дели будет иметь массу 80 г, т. е. крепле-
ние на нем вибродатчика массой 2 г вне-
сет погрешность по его парциальной час-
тоте не более 5%, тогда как при масшта-
бе 1/100 масса элемента на модели сни-
зится до 10 г и крепление датчика массой
2 г вообще недопустимо.
Если требуется моделировать динами-
ческое взаимодействие сооружения с осно-
ванием, то такое основание может быть
изготовлено вместе с моделью в виде мас-
сива с размерами, в несколько раз пре-
восходящими размеры сооружения, с пе-
ресчетом механических характеристик ос-
нования по общим правилам. Если необ-
ходимо, чтобы в этом массиве не образо-
7 Зек. 195
185
Рис. 14.2. Размеры и
конструкция форм для
изготовления стандарт-
ных образцов
1 — поддон; 2 — центри-
рующие шпильки; 3, 4—
стяжные болты с контр-
гайками; 5,6 — полу-
формы
вывались стоячие волны, то его помещают
в оболочку из материала, имеющего вы-
сокую вязкость при значении волнового
сопротивления, близком к волновому соп-
ротивлению материала, моделирующего ос-
нование. Если достаточно учесть упругость
основания приближенно по схеме Винклера
при коэффициенте упругого равномерного
сжатия^ Сгм, то можно установить модель
на слой поролона толщиной
= EM0/Czm, (14.10)
где Ем.0 — модуль упругости поролона, оп-
ределяемый из опыта.
После нахождения масштаба и подбо-
ра состава материалов приступают к изго-
товлению модели. Если модель имеет слож-
ную конфигурацию, не позволяющую от-
лить ее в одну легко разбирающуюся фор-
му, то рекомендуется сначала отлить от-
дельные элементы простой конфигурации,
а затем собрать из них модель, склеивая
их с помощью того же материала. Формы
для заливки делают из любого, удобного
для этих целей материала, например из
оргстекла для моделей, имеющих плоские
поверхности, или из гипса для моделей,
имеющих криволинейные поверхности.
Одновременно с формами для заливки
модели готовят формы для контрольных
образцов (рис. 14.2), имеющих стандарт-
ные размеры. Перед укладкой материала
в формы последние тщательно очи-
щают и на них наносят один-два слоя
разделителя, обеспечивающего свободное
отделение формы после, отверждения мо-
дели. В качестве разделителя рекоменду
ется использовать раствор (7—10%) кау-
чука СК.ТВ (по ГОСТ 14680—79) в бензи-
не. После нанесения каждого слоя формы
сушат в течение 5—6 ч при комнатной
температуре.
Литьевой состав приготовляют отдель-
ными замесами, масса материала в каж-
дом из которых не должна превышать
5 кг, и определяется в зависимости от мас-
сы заливаемых из этого замеса элементов
модели и контрольных образцов с учетом
того, что при заливке массивных элемен-
тов толщина слоя, укладываемого из каж-
дого замеса, не должна превышать 25—30
мм. Для приготовления замеса исходные
вещества отвешивают в расчетной пропор-
ции, затем ПДИ-ЗА и ЭА тщательно пере-
мешивают (в случае высокой вязкости
ПДИ-ЗА ее предварительно нагревают до
40—50° С и при перемешивании с ЭА до-
водят до комнатной температуры), далее,
не прекращая перемешивания, вводят
ПЭПА, пылевидный кварц и пробковую
крошку. Каждое следующее вещество вво-
дят не ранее чем после введения предыду-
щего будет достигнута полная однородность,
но после введения ПЭПА до начала укладки
в формы должно пройти не более 5 мин,
а до окончания — не более 20 мин. Укла-
дывая материал в формы, необходимо сле-
дить за тем, чтобы не образовались пу-
зырьки воздуха. Следующий слой можно
укладывать только после того, как ранее
уложенный слой остынет до комнатной
температуры (через 3—4 ч).
Отверждение материала происходит
при комнатной температуре. Для обеспече-
ния однородности элементы модели с оди-
наковыми механическими характеристика-
ми должны быть изготовлены из одной
производственной порции исходных мате-
риалов.
Модель или ее детали извлекают из
форм не ранее чем через сутки. В слу-
чае необходимости модель склеивают из
деталей, устанавливают на подготовлен-
ном по проекту основании, крепят к ней
датчики и возбудители и проводят другую
работу, необходимую для подготовки ее к
испытаниям. При изготовлении модели из
материалов по рецептам ТУ [19. 52, 53],
датчики приклеивают клеем № 88.
14.4. ОПРЕДЕЛЕНИЕ
ФИЗИКО-МЕХАНИЧЕСКИХ
ХАРАКТЕРИСТИК
МОДЕЛЬНОГО МАТЕРИАЛА
Наиболее распространенные методы
определения физико-механических харак-
теристик модельного материала можно
разделить на две группы — методы мгно-
венного снятия нагрузки [9, 19, 47] и
резонансны^ методы [10, 11, 19, 52, 53].
Первые из них менее трудоемки, но
и менее точны, чем вторые, а кроме того,
не позволяют изучить частотные зависимо-
сти, в связи с чем применяются главным
образом, при моделировании, не требую-
щем высокой точности. В соответствии с
названием все эти методы базируются на
мгновенном снятии нагрузки с образца с
записью процесса его деформирования.
186
Выделяя упругую часть деформации, оп-
ределяют модули упругости (при предва-
рительном растяжении) и сдвига (при пред-
варительном скручивании круглого образца,
а по их отношению вычисляют коэффици-
ент Пуассона. По записи свободных зату-
t
Рис. 14.3. Общий вид установки для определе-
ния модуля упругости методом мгновенного сня-
тия нагрузки
а — установка в сборе; б — тензометрические хо-
муты; 1 — станина; 2 — шаровые опоры; 3 —• цан-
говые зажимы; 4 — образец; 5 — рычажная систе-
ма нагружения
хающих колебаний определяют характе-
ристики затухания.
Поскольку время реализации упругой
части деформации близко к четверти пе-
риода собственных колебаний, а основная
«собственная частота соответствует четверть-
волновой форме собственных колебаний, то
характерная длина волны, при которой реа-
лизуются механические характеристики, оп-
деляемые таким способом, равна четырем
длинам образца. Учитывая, что маломас-
штабные модели имеют максимальный раз-
мер от 50 до 150 см, а минимальный в
несколько раз меньше, так что характер-
ные длины волн, соответствующие их соб-
ственным частотам, могут быть в пределах
10—150 см, длину образца для определе-
ния механических характеристик следует
выбирать в пределах 2,5—40 см, среднее
геометрическое из которых 10 см. Стан-
дартные образцы, ранее предложенные для
испытаний полимерных материалов других
видов, имеют близкую к требуемой длину
12 см, в связи с чем их размеры приняты
в качестве стандартных и для испытаний
этих видов.
Методы мгновенного снятия нагрузки и
оборудование для их реализации подробно
описаны в статьях и Технических условиях
[9, 19, 47]. На рис. 14.3 и 14.4 показан
общий вид установок для определения мо-
дулей упругости и сдвига.
Резонансные методы базируются на
использовании кинематического возбужде-
ния продольных или крутильных колебаний
стержня из исследуемого материала, одним
концом прикрепленного к возбудителю и
имеющего груз на другом конце (рис. 14.5
и 14.6). С помощью пьезоакселерометров
определяют перемещения концов стержня
и по отношению этих перемещений и зна-
чению резонансной частоты определяют
модуль упругости £м или сдвига GM, ко-
эффициент внутреннего неупругого сопро-
тивления Ум и логарифмический декремент
колебаний 6М — яум:
Р юрЕ /2
Ci (?)
Со (?)
Vm ==-----
Рмро/2 .
с, (?) :
(14.11)
где (орв, соре — резонансная угловая час-
тота, измеряемая при определении соответ-
Рис. 14.4* Общий вид установки для определения
модуля сдвига методом мгновенного снятия на-
грузки
а — установка в сборе; б — тензометрические
хомуты
7* Зак. 195
187
4
Рис. 14.5. Общий вид установки для определения
модуля упругости и логарифмического декремен-
та колебаний резонансным методом
1 — возбудитель колебаний; 2 — образец; 3 —
пьезоакселерометры; 4 — набор сменных грузов
Рис. 14.6. Общий вид установки для определения
модуля сдвига резонансным методом
ственно Ем и GM; р, 4— плотность и дли-
на образца соответственно; 7? — отношение
амплитуд колебаний конца стержня с при-
крепленной массой и конца стержня, за-
крепленного на возбудителе, при первом
резонансе; q — отношение масс (при опре-
делении Е) или моментов инерции относи-
тельно продольной оси (при определении
G) груза и стержня; Сь Со —функции от
q (см. табл. 14.2*).
Применение образцов уменьшенной дли-
ны и набора грузов, имеющих различные
массы и момент инерции, позволяет полу-
чать значения механических характеристик
в достаточно широком диапазоне частот.
Образцы и модели испытывают одновре-
менно с тем, чтобы исключить влияние
времени и температуры при пересчете ре-
зультатов моделирования на натуру.
* Таблицу Д4.2 составил канд. техн, наук
А. И. Комаров по результатам вычислений, кото-
рые проводил инж. Б. В. Цейтлин.
14.5. СРЕДСТВА ВОЗБУЖДЕНИЯ
И ИЗМЕРЕНИЯ ВИБРАЦИЙ
МАЛОМАСШТАБНЫХ МОДЕЛЕЙ
Основным требованием к устройству
для возбуждения вибраций! и маломасштаб-
ных моделей является внесение минималь-
ных и обязательно поддающихся оценке
изменений в инерционные и жесткостные
характеристики модели. На основе анализа
оборудования для возбуждения вибраций
различных видов [12] установлено, что
этому требованию в наибольшей степени
соответствуют центробежные вибраторы,
так как на жесткостные характеристики
модели они вообще не влияют, а их влия-
ние на инерционные характеристики легко
поддается учету, поскольку массу вибрато-
ра определяют просто взвешиванием, а
имея малые размеры и будучи помещен-
ным б жесткий корпус, он в большинстве
случаев может быть принят за сосредото-
ченную массу. Для того чтобы массу, при-
соединяемую к модели, свести к миниму-
му, вибратор должен быть изготовлен из
легких материалов, по возможности ком-
пактно. Чтобы избавиться от механических
помех, обычно возникающих от трения в
шестернях и турбулентного движения мас-
ла в картере, следует применять
шестерни, изготовленные из специальных
«малошумных» материалов, не требующих
смазки, например из фторопласта. Отечест-
венная промышленность выпускает такие
шестерни, например, для электробритв.
Электродвигатель, вращающий ротор
вибратора, устанавливают на отдельной
подставке, не связанной с моделью, и сое-
диняют с вибратором с помощью гибкого
вала, выполненного из тросика, заключен-
ного в рукав. Такие рукава выпускаются
промышленностью, например, для привода
спидометров автомобилей и мотоциклов.
При этом массу двигателя отделяют от
модели и, кроме того, модель изолируют
от вредных вибраций двигателя.
Вибратор должен быть сконструирован
так, чтобы он спокойно работал на до-
вольно высоких оборотах (желательно —
12—15 тыс. мин.-1) и позволял устанавли-
вать достаточно большие дебалансные гру-
зы, чтобы создавать силу до 0,5—1,0 Н
при 600 мин-1. Тогда в совокупности с на-
бором электродвигателей или с одним
электродвигателем, но при использовании
редуктора можно возбуждать частоты от
10 до 200—300 Гц, т. е. практически все
частоты, необходимые для маломасштаб-
ного моделирования.
Указанным требованиям в значительной
мере отвечает микровибратор |44], общий
вид которого со снятой крышкой показан
на рис. 14.7. Его основные технические ха-
рактеристики:
Масса (вместе с крепежны-
ми хомутами)................. 100 г
Максимальная частота вра-
щения ....................15 000 мин-1
Диапазон статических мо-
ментов дебалансов .... 0,9—2,02 г-см
Соответствующий диапазон
максимальных значений воз-
мущающей силы . . . .21.7 — 48,0 Н
188
ТАБЛИЦА 14.2
О
0,02
0,04
0,06
0,08
0,10
0,12
0,14
0,16
0,18
0,20
0,22
0,24
0,26
0,28
0,30
0,32
0,34
0,36
0,38
0,40
0,42
0,44
0,46
0,48
0,50
0,52
0,54
0,56
0,58
0,60
0,62
0,64
0,66
0,68
0,70
0,72
0,74
0,76
0,78
0,80
< 0,82
0,84
2,471
2,3716
2,2816
2,1966
2,1167
2,0417
1,9709
1,9044
1,8414
1,7822
1,7263
1,6734
1,6233
1,5757
1,5309
1,4884
1,4479
1,4094
1,3728
1,3379
1,3091
1,2730
1,2427
1,2137
1,1861
1,1597
1,1342
1,1100
1,0865
1,0641
1,0426
1,0219
1,0020
О,9828
0,9643
О,9465
0,9293
0,9127
0,8967
0,8812
0,8662
0,8518
0,8378
1,273
1,273
1,271
1,267
1,265
1,262
1,258
1,254
1.249
1,245
1,240
1,236
1,231
1,226
1,222
1,217
1,213
1,209
1,205
1,201
1,197
1,193
1,189
1,185
1,182
1,178
1,175
1,172
1,169
1,166
1,163
1,160
1,157
1,154
1,152
1,149
1,147
1,145
1,142
1,140
1,138
1,136
1,134
0,86
0,88
0,90
0,92
0,94
0,96
0,98
1,00
1,05
1,10
1,15
1,20
1,25
1,30
1,35
1,40
1,45
1,50
1,55
1,60
1,65
1,70
1,75
1,80
1,85
1,90
1,95
2,00
2,05
2,10
2,15
2,20
2,25
2,30
2,35
2,40
2,45
2,50
2,55.
2,60
2,65
2,70
2,75
0,8242
0,8111
0,7983
0,7860
0,7740
0,7624
0,7511
0,7401
0,7141
О,6897
0,6670
0,6457
О,6257
0,6069
0,5892
0,5724
0,5566
0,5417
0,5273
0,5140
0,5012
0,4890
0,4774
О,4663
0,4558
0,4457
0,4360
0,4267
0,4178
0,4093
0,4011
0,3933
О,3857
О,3784
0,3714
0,3647
0,3582
0,3519
0,3458
0,3400
0,3343
0,3288
О,3235
132
130
128
126
124
122
121
119
115
108
105
102
999
096
091
084
082
080
078
076
075
073
072
070
069
067
066
065
064
061
060
059
058
057
056
054
2,80
2,90
3,00
3,40
3,60
4,00
4,20
4,40
4,60
5,00
6,00
6,50
7,00
7,50
8,00
8,50
9,00
9,50
10,0
10,5
12,0
13,0
14,0
15,0
16,0
17,0
18,0
19,0
20,0
21,0
0,3184
0,3134
0,3086
0,3039
О,2674
0,2416
О,2304
0,2203
0,2110
0,2025
0,1946
0,1873
0,1713
0,1578
0,1462
0,1363
0,1276
0,1199
0,1131
0,1071
0,1016
0,0967
0,0922
О,0844
0,0810
О,0779
0,0749
О,0697
О,0652
0,0612
О,0576
0,0517
0,0491
0,0468
0,0447
0,0428
0,0410
0,0394
1,053
1,051
1,050
1,0495*
1,047
1,044
1,042
1,040
1,038
1,036
1,034
1,031
1,026
1,024
1,023
1,021
1,020
1,019
1,018
1,017
1,016
1,0154
1,015
1,014
1,0135
1,013
1,0125
1,012
1,011
1,010
1,0096
1,009
1,0085
1,008
1,0078
1,0075
1,0071
1,0069
1,0066
Для измерения вибраций используют
миниатюрные пьезоакселерометры [12]
минимального веса, так как это единствен-
ные приборы, позволяющие проводить из-
мерения абсолютных ускорений и имею-
щие массу, приемлемую для маломас-
штабных моделей. Промышленность вы-
пускает пьезо акселерометры массой от 0,4 г
и выше.
Рис. 14.7. Микровибратор (крышка снята)
При отсутствии пьезо акселерометров с
достаточно малой массой можно приме-
нять различные бесконтактные методы из-
мерения относительных перемещений |12]г
например емкостные или индуктивные. Но
так как чувствительность соответствую-
щих датчиков существенно зависит от на-
чальных зазоров, которые меняются в хо-
де эксперимента из-за изменения темпе-
ратуры и других условий, то точность
этих методов ниже, чем при использова-
нии подходящих по массе пьезоакселеро-
м етр ов.
Рис. 14.S. Модель пространственной железобе-
тонной рамы, выполненная в масштабе 1 : 70, в
момент испытаний
189
Для измерения деформаций используют
тензор ез исто.р ы, котор ые отлич а юте я от
широкоизвестных проволочных тем, что в
них чувствительный элемент изготовляют
из электропроводящих резин 1'1, 3, 5, 15,
30, 33, 45, 48], имеющих низкий модуль
упругости. Для краткого обозначения та-
ких тензорезисторов предлагается термин
«эластор». Для снижения поперечной чув-
ствительности эласторов можно использо-
вал ь специально разработанную для этой
цели электропроводящую резину с орто-
тропной тенз очувствите л ьностью, т. е.
различной тензочувствительностью в двух
взаимно перпендикулярных направлениях.
Вторичная измерительная аппаратура ни-
каких особенностей связанных с мало-
масштабностью моделирования, не имеет.
14.6. ИСПЫТАНИЯ МОДЕЛЕЙ
Программа испытания моделей разраба-
тывается в зависимости от задачи, решае-
мой с помощью моделирования. Наиболее
типичная задача состоит в определении
заданного компонента перемещений ui>
скоростей uj, ускорений и, или деформа-
ций 8j в заданной точке (где /—номер,
присваиваем ый д айном у комп он ен ту в
данной точке) при воздействии определен-
ной комбинации дин амических нагрузок,
2РЛ(/), где k — номер, присваиваемый дан-
ному компоненту силы в данной точке,
причем в дальнейшем для краткости бу-
дем просто говорить «точка с ном ером /
или 6» или «точка /г», имея в виду, что
это понятие включает в себя также све-
дения и о компоненте.
Как известно, эта задача легко может
быть решена, если будут известны пере-
даточные функции динамической системы,
или, как их еще называют, гармонические
функции влияния:
(со) — | а^у (со) | , (14.12)
модуль которых равен амплитуде, а аргу-
мент— сдвигу фазы соответствующей оп-
ределяемой величины с номером / под дей-
ствием силы Рьее®*, имеющей единичную
амплитуду, приложенной в той же точ-
ке и имеющей ту же линию действия, что
и сила Pk(t).
Таким образом, задача может быть све-
дена к нахождению гармонических функ-
ций влияния (14J12).
При определении гармонических функ-
ций влияния вибратор устанавливают в
точку k, а во всех точках j устанавлива-
ют датчики. Затем проверяют линейность
модели. Для этого, медленно меняя обо-
роты вибрат ор а, проходят в есь ч астотны й
диап азон и по ближа йшему к вибратор у
датчику следят за амплитудой колебаний
с тем, чтобы определить, на какой частоте
/р эта амплитуда будет максимальной.
Затем увеличивают массу дебалансов виб-
ратора и опять, изменяя частоты, но в об-
ласти, близкой к fp, находят частоту и
амплитуду максимума. Если частота не
изменилась и амплитуда увеличивалась
пропорционально массе дебалансов, то
модель считают работающей в линейной
области.
Далее необходимо определить, доста-
точна ли динамическая сила для вычисле-
ния ahj в самой удаленной от вибратора
точке /. Для этого, меняя обороты вибра-
тора, проходят весь диапазон частот, про-
веряя, достаточны ли амплитуды выходного
сигнала с датчика j для надежного измере-
ния амплитуд и фаз. Если они достаточны,
то переходят к определению гармонических
функций влияния по всем датчикам; если
нет, то оценивают, нужно ли увеличивать
момент дебалансов или вообще эту гармо-
ническую функцию влияния можно считать
нулевой. Уровень сигнала, при котором
функцию (Zkj можно считать нулевой, за-
висит от характера решаемой задачи и не-
обходимой точности результатов. Если же
в конечном итоге надо будет просто про-
суммировать влияние равных по амплитуде
динамических сил, приложенных в разных
точках, то достаточно, чтобы отношение
амплитуд сигналов самого далекого и са-
мого близкого датчиков было близко к
V20 с тем, чтобы при меньшем отношении
считать сигнал нулевым при сохранении
максимальной точности моделирования.
Если сигнал нельзя считать нулевым,
но для надежного измерения необходимо
его увеличить в п раз ,то увеличивают мас-
су дебалансов тоже в п раз и опять про-
веряют линейность системы. Если система
оказывается линейной, то переходят к оп-
ределению akj по всем точкам /.
Возможен и другой путь проверки ли-
нейности системы, когда, повторяя опера-
цию увеличения массы дебалансов и изме-
рения сигнала ближайшего к вибратору
датчика, находят наибольшую динамиче-
скую силу, при которой система еще оста-
ется линейной, а затем при проведении ис-
п ыт аний стр ем ятся никогда не достиг а т ь
значения силы, превосходящей половину
от предельной.
Снятие гармонических функций влия-
ния можно производить параллельно сразу
во всех точках /, если исследователь рас-
полагает многоканальной аппаратурой с ре-
гистрацией не. менее чем / сигналов, либо
последовательно с непосредственным изме-
рением амплитуд и фаз сигналов не менее
чем от Д1ву£ датчиков, из которых один
считается базисным и не переключается от
измерения к измерению.
Частоту обычно меняют ступенями,
устанавливая величину шага в зависимости
от характера функции — реже на горизон-
та л ьн ы х уч астка х амп литудно -ч асто т н о й
характеристики моделей и чаще вблизи ре-
зонансных максимумов. При этом если пе-
реключение датчиков на регистрирующую
аппаратуру осуществляется вручную, то
обычно после каждого переключения сни-
мают сигналы на всех частотах, а при на-
личии автомата или полуавтомата пере-
ключения датчиков с автоматической реги-
страцией амплитуд и фаз в цифровом коде
пр оизвюдител ьнее оказыва ется енмм ат ь
сигналы со всех датчиков на каждой фик-
сированной частоте возбуждения. Считает-
190
ся, что гармонические функции влияния во
всех точках j сопоставимы, если сигналы
базисного датчика, замеренные при опреде-
лении каждой из них, окажутся тождест-
венными.
Для построения модуля гармонической
функции влияния значение амплитуды сиг-
нала, измеренной на каждой частоте, делят
на значение силы, развиваемой вибратором
на этой частоте, 'Переставляя вибратор во
все точки k, получают в конечном итоге
все значения гармонических функций влия-
ния. При одновременной регистрации сиг-
налов от всех датчиков можно также оп-
ределять формы колебаний модели. На
рис. 14.8 показана маломасштабная мо-
дель пространственной железобетонной ра-
мы с установленными на ней микровибра-
тором и пьез1оакселерометрами.
14.7. ПЕРЕСЧЕТ РЕЗУЛЬТАТОВ
МОДЕЛИРОВАНИЯ НА НАТУРУ
Результаты моделирования на натуру
пересчитывают по обычным правилам [39].
В частности, модули гармонических функ-
ций влияния (14.12) и ер есчитыв а ют по
формулам
I ан I — I ам | ; (14.13)
фазы пересчета не требуют, так как
Фн = фм- (14.14)
Частоты пересчитывают по формуле
(14.7). Например, для условий примера,
рассмотренного в п.З, если ai= 1/50, то
3,15-104-50 75 000
f __ f - Ал 1 / Рм _
/ н — / м , I/ c —
V Ph
1 */* 3,15-104-l
V - 21.2,4 =0'417^
Зная дармоничеакие функции влияния
для определенных величин в заданных точ-
ках сооружения, можно определить сами
эти величины при любой комбинации при-
ложенных сил. Например, если ajk — это
функция влияния для перемещений, то при
воздействии п гармонических сил
/(cof-j-Ф )
Eke перемещения в точках j могут
быть найдены по формуле
п
ui=^^k (14.15)
k=l
При воздействии п политармонических
сил, каждая из которых состоит из т гар-
моник
Pk (О = 2 Pkr е‘ ' (14.16)
Г—1
эти перемещения будут
п т
“/=22 ам pkrе' (и^+<₽^)-
£=1 г=1
(14.17)
При воздействии п сил, имеющих
— у £ф. (со)
спектр Рц(кд)е * , спектр перемещения
в точке j будет
п
й, (со) = У, a,fe (со) Tk (со) e^k <“>. (14.18)
А—1
В настоящее время маломасштабное
моделирование используется довольно ши-
роко для исследования динамических явле-
ний в сооружениях сложной конфигурации
и для обеспечения проектирования таких
сооружений [4, 8, 14, 16, 17, 22; 23; 26—29;
42, 43].
СПИСОК ЛИТЕРА ТУ РЫ
1. А.с. 248315 (СССР). Тензодатчик.
[Андреев В, Е., Шолухов В. Г, Заявл. №
1230314/25-28 Опубл, в БИ, 1969, № 28.
2. Григорьева Г. П„ Ляндзберг Г. Л,
Сирота А. Г. Полимерные материалы. М.,
1966.
3. Гутман Ф., Лайонс Л. Органические
полупроводники. М., 1970.
4. Гухман А. А. Введение в теорию
подобия. М., 1973.
5. Дулов А. А., Слинкин А. А. Орга-
нические полупроводники. М., 1970.
6. Каргин В. А., Слонимский Г. Л.
Краткие очерки по физико-химии полиме-
ров. М., 196-7.
7. Комаров А. И., Самсонова Т. И.,
Сафонов Г. В. Низкомодульный материал
для изготовления маломасштабных, моде-
лей. Тр. коорд. совещаний по гидротехнике,
вып. 109.—В кн.: Повышение надежности
системы тур боагрегат — фундамент — осно-
вание мощных энергоблоков. Л., 1976.
8. А. с. 629463 (СССР). Устройство
для динамических испытаний сооружений и
их моделей / Комаров А. И., Степанов Г.; IL
Опубл, в Б. И., 1987, № 39.
9. Комаров А. И., Цейтлин Б. В. Ком-
плект приборов для определения комплекс-
ных модулей упругости и сдвига полимер-
ных материалов. Информационный листок
№ 792—74. ЛЦНТИ, 1974.
10. Комаров А. И,, Цейтлин Б. В.
Определений динамических свойств поли-
мерных материалов методом вынужденных
колебаний. Изв. ВНИИГ, т. 104. Л., 1974.
11. Комаров А. И., Цейтлин Б. В.
Резонансный метод определения комплекс-
ного модуля упругости вязкоупругих ма-
териалов. Информационный листок
№ 0026—73. Сер. 18Б —10. Информэнерго,
1973.
12. Максимов Л. С., Шейнин И. С.
Измерение вибрации сооружений. Л., 1974.
13. Маломаспттабное моделирование
динамических явлений в фундаментах мощ-
ных турбоагрегатов. / Комаров А. И.»
191
Рабкин М. А., Самсонова Т. И., Степа-
нов Г. И. и др.)- Труды коорд. совещаний
по гидротехнике, вып. 109. — В кн.: Повы-
шение надежности системы турбоагрегат —
фундамент — основание мощных энергобло-
ков. Л., 1976.
14. Мастаченко В. Н. Надежность мо-
делирования строительных конструкций.
М., 1974.
15. А.с. 183995 (CQCP). Датчик для
измерения деформаций. / Мизякин С. Д.
и др. Опубл, в БИ, 1966, № 14.
16. Монахенко Д. В. Исследование
сейсмостойкости бетонных плотин на мо-
делях. Л., 1974.
17. Монахенко Д. В. Физическое мо-
делирование сейсмостойкости сооружений.
Л., 1975.
18. Назаров А. Г. О механическом по-
добии твердых деформируемых тел. Ере-
ван, 1965. "
19. Низкомодульный материал для из-
готовления моделей, предназначенных для
исследования динамических явлений в
строительных сооружениях и конструкци-
ях (ТУ 1— 74/ВНИИГ). Л., 1974.
< 20. Низкомодульный (материал для
моделирования динамических явлений в со-
оружениях. ] Балясов В. Н., Еремиче-
ва К- А., Комаров А. И., Микора Р. И. и
др.— Изв. ВНИИГ, т. 104, 1974.
21. О .влиянии жесткости проволочных
тензодатчиков на результаты определения
деформативных характеристик низкомо-
дульных материалов. / Степанов Г. Н.,
Комаров А. И., Балясов В. Н., Троянов
К- Л. Тр. коорд. совещ. по гидротехнике,
вып. 64, ч. II. Киев, 1972.
22. О динамических податливостях
фундаментов под турбоагрегаты, опреде-
ленных на моделях, теоретически и в на-
турных условиях. / Клебанов Б. В., Сте-
панов Г. Н., Троянов К. Л., Бабский Е. Г.,
и др. —В кн.: Динамика энергосооруже-
ний, вып. 4. Л., 1975.
23. Основы теории подобия и модели-
рования. Терминология. Вып. 88, М., 1973.
24. А. с. 633842 (СССР). Полимерная
композиция / Самсонова Т. И., Микора Р. И.,
Комаров А. И., Шейнин И. С., Нетребчен-
ко Г. И. Опубл, в Б. И., 1978, № 43.
25. А. с. 681078 (СССР) Полимерная
композиция для изготовления маломасштаб-
ных моделей бетонных сооружений / Сам-
сонова Т. И., Микора Р, И., Шейнин И. С.,
Нетребченко Г. И. Опубл, в Б. И., 1979
№ 31.
26. Поляков Л. П., Файнбурд В. М.
Моделирование строительных конструкций.
Киев, 1975.
27. Приборы и оборудование, исполь-
зуемые при маломасштабном моделирова-
нии динамических явлений в сооружениях. /
/ Егоров А. Н., Комаров А. И., Михе-
ев Л. Г. Степанов Г. Н., Шейнин И. С. — В
кн.: Методы и средства измерений в гид-
ротехнических исследованиях. Л. 1976.
28. Рабкин М. А. и др. Методика мо-
делирования динамических процессов в
конструкциях на моделях из вязкоупругих
материалов. Информационный листок
№ 0031—76. Сер. 18Б—11. Информэнерго,
1976.
29. Рабкин М. А. и др. О возмож-
ности моделирования динамических явле-
ний'<в конструкциях на моделях из вязко-
упругих материалов. — Изв. ВНИИГ, т. 107,
1975.
30. Резиновые датчики деформаций. /
/ Шейнин И. С., 'Комаров А. И., Чудако-
ва Р. М. Информационный листок № 640—
75. Сер. 40. ЛЦНТИ, 1975.
31. Розанов Н. П., Каганов Г. М. Низ-
комодульные материалы для моделей и
задачи их дальнейших исследований. — В
кн.: Моделирование строительных конст-
рукций. М., 1971.
32. Руководство по исследованию ме-
ханических свойств строительных конструк-
ций на моделях. Ленинакан, 1966.
33. Сажин Б. И. Электропроводность
полимеров. М., .1965.
34. Самсонова Т. И„ Комаров А. \И.,
Фальк Л. В. Влияние наполнителей на фи-
зико-механические свойства модельных ма-
териалов.— Изв. ВНИИГ, т. 113, Л., 1976.
35. А.с. 559938 (СССР). Эпоксидная
композиция. / Самсонова Т. И., Мико-
ра Р. И., Шейнин И. С. Опубл, в БИ, 1977,
№ 20.
36. А.с. 5(27457 (СС(СР). Состав для
маломасштабных моделей бетонных соору-
жений. / Самсонова Т. И., Сафонов Г. В.,
Шейнин И. С., Опубл, в БИ, 1976, № 33.
37. Самсонова Т. И. Полимерные ма-
териалы для изготовления маломасштаб-
ных моделей. Л., 1975ч
38. Самсонова Т. И., Сафонов Г. В.,
Микора Р. И. Низкомодульный полимерный
материал для мелкомасштабного моделиро-
вания. Информационный листок № 832—
75. ЛЦНТИ, 1975.
39. Справочник по динамике сооруже-
ний. / Под ред. Б. Г. Коренева и И. М. Ра-
биновича. М., 1972.
40. Справочник по пластическим мас-
сам. / Под ред. М. И. Г арб ар а, В. М. Ка-
таева, М. С. Акутина, т. 1. М., 1967; т. 2,
1969.
41. Старение и стабилизация полиме-
ров. М., 1964.
42. Степанов Г. Н., Троянов К. Л.
Исследование колебаний фундаментов мощ-
ных турбоагрегатов на моделях. — В кн.:
Динамика гидросооружений ГЭС, вып. 3.
Л., 1973.
43. Степанов Г. Н., Троянов К. Л.
К вопросу определения форм колебаний
стержневых систем.—'В кн.: Динамика
гидротехнических сооружений (Труды V
Всесоюз. совещ.). М., 1972.
44. Степанов Г. Н., Троянов К. Л.
Методика и аппаратура для исследования
динамики фундаментов мощных турбоаг-
регатов на мелкомасштабных упругих мо-
делях. — Изв. ВНИИГ, т. 98, 1972.
45. Степанов Г. Н., Чудакова Р. М.,
Шейнин И, С. Исследование на маломасш-
табных моделях динамических характери -
192
I
стик проектируемого фундамента турбоаг-
регата мощностью 1200 МВт. Труды коорд.
совещаний по гидротехнике, вып. 109.— В
кн.: Повышение надежности системы тур-
боагрегат — фундамент — основание мощ-
ных энергоблоков. Л., 1976.
46. Тагер А. А. Физико-химия поли-
меров. М., 1963.
47. Шейнин И. С., Комаров А. И.,
Балясов В. Н. Комплект измерительной ап-
паратуры для изучения механических ха-
рактеристик низкомодульных полимерных
материалов. — Тр. коорд. совещаний по
гидротехнике, вып. 64, ч. II. Киев, 1972.
48. Электропроводящие полимерные
материалы. / Гуль В. Е., Царский Л. И. и
др. М., 1968.
49. А.с. 34182'0 (СССР). Эпоксидная
композиция. / Балясов В. Н., Шейнин И. С.,
Степанов Г. Н., Эрлих И. М., Еремиче-
ва К. А. Опубл, в БИ, 1972, № 19.
50. А.с. 523915 (СССР). Эпоксидная
композиция. / Самсонова Т. И., Сафо-
нов Г. В., Микора Р. И., Шейнин И. С.
Опубл, в БИ, 1976, № 29.
51. А.с. 487096 (СССР). Эпоксидная
композиция. / Самсонона Т. И., Сафо-
нов Г. В., Микора Р. И., Шейнин И. С.
Опубл, в БИ, 1975, № 37.
52. Низкомодульные материалы для из-
готовления маломасштабных моделей, пред-
назначенных для исследования динамиче-
ских явлений в строительных сооружениях
и конструкциях: ТУ 34-9-2-78/Минэнерго
СССР. Л., 1978.
53. Рекомендации по маломасштабному
моделированию динамических явлений в
строительных конструкциях и сооружениях:
И 87-80. Л., 1980.
РАЗДЕЛ 15. ДИНАМИЧЕСКАЯ ФОТОУПРУГОСТЬ
(Н. А. СТРЕЛЬЧУК, Г. Л. ХЕСИН)
Поляризационно-оптический метод ис-
следования напряжений в конструкциях и
деталях (метод фотоупругости) включает
в себя в качестве составных частей стати-
ческую фотоупругость, термофотоупругость,
фотопластичность и фотоползучесть. Изу-
чение на моделях из оптически чувстви-
тельных материалов напряжений и дефор-
маций, возникающих под действием дина-
мически приложенной нагрузки, с последу-
ющим пересчетом на условия натуры со-
ставляет предмет метода динамической
фотоупругости. Методом динамической фо-
тоупругости в основном изучаются дина-
мические задачи, в которых главную роль
играют волны напряжений, возникающие
под действием взрыва, удара и др. Основы
метода динамической фотоупругости и при-
меры моделирования различных инженер-
ных задач изложены, например, в работе
[7].
15.1. ОСНОВЫ МЕТОДА
ДИНАМИЧЕСКОЙ ФОТОУПРУГОСТИ
Поляризационно-динамические установ-
ки. Основные схемы поляризационно-дина-
мических установок |(ПДУ), их особенно-
сти и области применения приведены в
табл. 15.1. Примеры картин полос т (х,
у, t) и т (х, t), полученных соответственно
в режимах покадровой съемки и фотореги-
стратора, приведены на рис. 15.1 и 15.2.
На рис. 15.3 приведен пример съемки сме-
щений и (х, t). Более подробное описание
различных схем] ПДУ имеется в работе [7].
Вопросы, посвященные применению различ-
ных источников света и высокоскоростных
камер, изложены в работах [4, 6].
Наряду с регистрацией волн напряже-
ний (картин полос) т (х, у, t) и переме-
щений Uij (х, у, I) в пределах области, ох-
ватывающей всю модель или ее часть, в
некоторых случаях (в частности, для опре-
деления компонентов тензора по/ при-
меняются фотоэлектрические способы ре-
гистрации оптической разности хода в от-
дельных точках модели [1].
Методы моделирования динамического
воздействия. Выбор способа генерирова-
ния динамической нагрузки определяется
с учетом критериев подобия и масштабов
моделирования, зависящих от рассматри-
ваемой задачи.
Способы генерирования динамических
нагрузок, а также основные сведения о
нагрузочных приспособлениях и получае-
мой в модели зависимости нагрузки от
времени приведены в табл. 15.2 и 15.3.
При изучении импульсивных воздейст-
вий, особенно таких, как взрыв, целесооб-
разно моделировать не сам источник воз-
мущения, а параметры волн напряжений,
которые создаются этим источником на
некотором расстоянии от него и затем рас-
пространяются в среде.
15.2. РАСШИФРОВКА
ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
Зависимость между оптическими и меха-
ническими величинами. Основная трудность
при установлении зависимостей между оп-
тическими т (х, у, t) и механическими
Oij (х} у, \t), е,ц (х, у, t) величинами за-
ключается в том, что большинство опти-
чески чувствительных материалов, даже
высокомодульных (Е>3-103 МПа), кото-
рые в условиях статического нагружения
ведут себя практически линейно-упруго,
в условиях импульсивного нагружения де-
формируются как упруговязкие динамиче-
ские системы.
Под воздействием механических напря-
жений в оптически чувствительном мате-
риале изменяется тензор его диэлектриче-
ской проницаемости и с некоторым приб-
лижением можно предположить, что компо-
ненты этого тензора линейно |(алгебраиче-
ски или операторно) связаны с компонен-
тами тензоров напряжений или деформа-
ций. Для описания двойного лучепрелом-
ления в оптически чувствительном материа-
ле необходимо установить временные за-
висимости между тремя тензорами второго
ранга: диэлектрической проницаемости, на-
пряжений и деформаций.
Если принять в качестве диэлектри-
ческого тензора тензор Дилла и записать
связь между оптическим и механическими
тензорами в виде линейных интегральных
операторов, полагая для упрощения, что
главные оси тензоров напряжений, дефор-
маций и диэлектрического тензора совпа-
дают и записывая относительную разность
хода 6 в порядках полос т, получим за-
висимости: .
где d — толщина модели в направлении
просвечивания; функции CJ"1 (t—т), C^(t—
—т) представляют собой реооптические мо-
дули соответственно по напряжениям и
деформациям.
194
Рис. 15.1. Кинограмма картин полос ?п(х, у, I) при взаимодействии волны напряжений с прямо-
угольным отверстием, полученная в режиме покадровой съемки с помощью поляризационно-дина-
мической установки по схеме 1, табл. 15.1 (частота съемки 2,5-106 кадров/с, ноле съемки 70X70 мм)
Рис. 15.2. Фотограммы картин полос т(х, t), полученные с помощью
установки по схеме 1 табл. 1, в режиме фоторегистратора, v
помощью поляризационно-динамической
р = 2,2 мм/мкс
?пйная Длиной 16 мм вдоль оси стержня; на торце стержня взрыв заряда азида
свилда у—30 мг; М — 2:1; б — прямолинейная щель, нормальная свободной поверхности- одновре-
менный взрыв трех накладных зарядов на поверхности пластинки, Л4=2:1
Из (15.1) и (15.2) по обобщенной
теореме о среднем получим
1
01 — О2 = —2 т (/), 81 —82 =
= (15.3)
где Са , Се 1 — значения функций С (t)
Cg (t) в некоторой точке интервала 0^
^т<т0 (То — длительность импульса).
Методика определения и в Я* °)
в условиях импульсивного нагружения.
В методе динамической фотоупругости ко-
эффициенты, которые входят в формулы
(15.3), обычно называют динамической
Рис. 15.3. Фотограммы смещений в стержне и
пластинке при импульсном воздействии (увели-
чение при съемке в 40 раз)
(2 смещение точки в центре поперечного се-
Чг?Н^?1 стержня, вызванное продольной волной,
р 1’6 мм/мкс; б вертикальные смещения сво-
бодной поверхности пластинки при действии
взрыва заряда ВВ у поверхности, с’ =1,5 мм/
/мкс
195
ТАБЛ ИЦА 15.1
№ п.п.
Схема и основные узлы
поляризационно-динамической установки
Назначение установки
Регистрирующая камера
тип камеры частота съемки, кадр/с время экспо- зиции, мкс размер кадра, мм общее число кадров Источник света; параметры блока питания
Тип материалов
для изготовления
моделей
Регистрация волн напряже-
ний в режимах покадровой
съемки и фоторегистратора
при нормальном просвечива-
нии в моделях из материа-
лов со скоростями волн:
= (1 ...3) 10- м/с
СФР, режим по- кадровой съемки 6,25-10® 2,5*10® 1,6 0,4 10X10 5X5 60 240 ИСШ-400; £7= = 1,4 кВ; = 75 мкФ ИСШ-10,0; U= = 4,5 кВ; С = =300 мкФ И ФК-20000; U — = 5,6 кВ; С— = 1350 мкФ На основе эпок- сидных смол (пп. 1, 2, 7, 8 табл. 15.4)
СФР, режим фо- торегистратора До 0,02 25X375 Оргстекло, сопо- лимеры диаллил- фталата (п. 10 табл. 15.4)
Скоростная кино- камера фирмы «Бекман и Уит- ли», модель 189, режим покадро- вой съемки 1,2-10® 0,5 18X24 25 Импульсная лам- па фирмы «Бек- ман и Уитли», модель 357; энер- гия вспышки £= = 200 Дж Полиэфирная смола (п. 3 табл. 15,4)., хомалит-100, колумбийская смола CR-39
Одновременная съемка ди-
намических процессов дву-
мя или несколькими каме-
рами, работающими в раз-
личных режимах: раздель-
ная регистрация порядков
полос и смещений при та-
рировке, одновременная по-
кадровая съемка и фоторе-
гнстрация, регистрация кар-
тин полос на черно-белую
и цветную пленки, съемка
процессов с различными
скоростями и т. д.
Применяют камеры различных типов, источники света и материалы моделей,
характеристики которых указаны в п.п. 1 и 3 этой таблицы
Регистрация волн напряже-
ний в режиме покадровой
съемки в моделях из низко-
модульных материалов со
скоростями волн Ср до
100 м/с
СКС-1М
ZL-1
Фастакс
4-Ю3 . 50 7,5X10,4 1000
4-104 20 4X4,4 10000
8*10* 25 7,5X10,4 2000
ДРШ-250; / =
= 9 ... 10 А; £7 =
= 110 В
£7=110 В
Полиуретановый
каучук СКУ-6,
СКУ-В, игдантин
(п. 9 табл. 15.4)
Хизол-4485 (п. 6
табл. 15,4)
Регистрация картин полос СФР, в режиме
при одновременном нор- фоторегистратора
мальном и наклонном про-
свечивании моделей из вы-
сокомодульных полимеров
'в задачах, связанных с раз-
делением напряжений
0,1 25X375 —— ИСШ-400; (7= На основе эпок-
= 1,4 кВ; С= сидных смол
= 75 мкФ (п. 1, 2, 15.4) табл.
Регистрация картин полос отдельными кадрами с раз- личным интервалом между ними Многоискровая камера типа Кранца — Шар- дина 3,3-10*— 0,8-10* 0,6 * 55
16 Воздушный иск- ровой разрядник с блоком пита- ния: (7 = 15 кВ; /= = 5 тА Полиэфирная смо- ла хомалит-100, колумбийская смола CR-39 (п. 3, табл. 15.4)
Покадровая регистрация
волн напряжений в моделях
из материалов со скоростя-
ми Ср — (2 . . . 4)103 м/с с
помощью
лазера
добротностью
Ждущая камера
с зеркальной раз-
верткой изобра-
жения
7,5-10*
0,02 18X24 20
Импульсный ла-
зер с модулиро-
ванной доброт-
ностью, лампа
Полиэфирная
смола хомалит-100
многоимпульсного
модулированной
Регистрация в режиме стро- Стандартная фо- 10—30 5000 24X36
боскопа картин полос в моделях при периодическом токамера 50—100 0,5 24X36
характере нагружения
накачки:
11,4 кВ
ИФК-20; U =
= 600 В; С=
= 4 мкФ
ИСП-5; (7=10 кВ;
С = 0,002 мкФ
Низкомодульные
оптически чув-
ствительные ма-
териалы.
Высокомодульные
оптически чувст-
вительные мате-
риалы
ТАБЛИЦА 15.2
Форма заряда и спо-
соб взрыва
Схема
График зависимости
порядков полос т
от времени
Количественные
соотношения
Цилиндрический за-
ряд в шайбе из ма-
териала модели
Одновременный
взрыв двух зарядов
Одновременный
взрыв нескольких за-
рядов для создания
периодической на-
грузки от волны Р
Цилиндрический за-
ряд в пластинке
Удлиненный заряд с
односторонним ини-
циированием
Удлиненный заряд с
двусторонним ини-
циированием
W = 10 ... 100 мг;
t__ = 4 ... 12 мкс:
т~/т+ = 1,25;
тмакс = 1 ’
W = 30 мг
W ~ 10 ... 100 мг:
= 4 ... 12 мкс;
гп^/т^ = 0,2;
/71макс = 1 *$’
U7 = 30 мг
макс . а ±
пгг= mr s 1 г. р t;
3 = 2 Л СрМ;
тмакс ~ 1 * * * ’5’
W = 30 мг
W — 30 мг;
макс
тг = тг --
Хе т t sin р /;
3 = 2 л с /К\
а = 0,578 (ЭД6-МА)
D '
а = arcsin-----:
с
Р
D • D
р ~ arcsin-----
2 — 2 т& cos 2 а ;
S гп 2 m sin 2 0:
S S
Способ возбуждения
интенсивных плоских
поперечных волн в
модели
При di = 5 мм;
d2 ~ 6 мм;
W = 70 мг
mnlmS * 0(1
р ь
Здесь: 1 — модель; 2—шайба,- 3 — электрод из фольги; 4 — капсюль из парафина для зарядов;
5— стержень из дюралюминия. Значение приведено на расстоянии г = 70 от заряда.
198
ценой полосы материала соответственно, по
напряжениям аод°> деформациям
В одномерной волновой задаче напря-
жения в линейном вязкоупругом мате-
риале могут быть найдены по формуле [14]
о (х,/) = р [с0 и (х, t) + с0 и (х, /) +
t
+ J с (/—т) и (х, т) d т], (15.4)
о
где Со — скорость распространения фронта
возмущения; со—производная по времени
от скорости распространения возмущения,
имеющая размерность ускорения; р — плот-
ность материала.
Показано, что для оптически чувстви-
тельных материалов типа ЭД6-МА, Э40-
МТГФА с точностью до (4—6) % в форму-
ле (15.4) можно ограничиваться только
первым членом.
Тарировочные эксперименты [8] про-
водятся на свободно подвешенных стерж-
нях размером 5X5X500 мм. Импульсивная
нагрузка создается взрывом торцевых за-
рядов азида свинца массой 15—100 мг.
При этом длина возмущенной зоны в
стержне составляет 45—80 мм. Порядок
интерференционных полос m(t) и смещения
u(t) одновременно регистрируются в одном
и том же сечении образца с помощью
двухпозиционной| поляризационно-динами-
ческой установки (ПДУ МИСИ, схема 2,
табл. 15.1) с 60-кратным увеличением при
записи смещений. Функции m(t) и u(t)
регистрируются по всей длине стержня в
сечениях, расположенных через 20 мм.
Значения Одд*0^ и 8дд°>в выбранногл се-
чении стержня для любого времени /ив
пределах возмущенной зоны определяются
по формулам
(1,0) _ Р с0 и < j. -(1,0) _
а0д — т (/) а' е0д —
нения возмущения в стержне; — ско-
рость развертки; а — угол наклона полосы
нулевого порядка к горизонтали в режиме
фоторегистратора (щель фоторегистратора
нормальна к фронту распространяющейся
волны) (рис. 15.2); М — геометрический
масштаб; u(t)—скорость смещения частиц,
определяемая графическим дифференциро-
ванием кривой u(t) (см. рис. 15.3,а);
m(t) — порядок полосы (см. рис. 15.2,а);
e(i/) =— u(t) — относительная деформация;
с
с—скорость продольной ВОЛНЫ; v — коэф-
фициент Пуассона, определяемый
муле j
по фор-
(15.6)
соответ-
в которой обозначено через сР, cs
ственно скорости продольных и поперечных
волн в образце. Для высокомодульных ма-
териалов типа! ЭД6-МА, Э40-МТГФА значе-
ние коэффициента Пуассона, определенное
по скоростям волн, практически совпадает
со значением, найденным из статического
опыта.
Для определения значений eff) и v
также применяется тензометрирование ма-
лобазными (1—2 мм) фольговыми датчи-
ками.
Для вязкоупругого материала в общем
случае !Одд и 8дд Смогут быть переменны-
ми в процессе прохождения волн напряже-
ний. Однако для материалов типа ЭД6-МА
кривые u(t), m(t) в безразмерном виде
совпадают и скорость распространения
возмущения практически постоянна, поэто-
му значения Одд и едд°^в пределах возму-
щенной зоны не изменяются и их можно
определять по максимальным значениям
/j m ГТ макс.
^макс> "ьмакс И
Здесь
(1 + у) е (/)
~ т (/) а
1
Co=^ptga — скорость
(15.5)
распростра-
(ПО) _
Од
Р цмакс . t
^макс
(1 + V) е”акс
-------------- d.
^макс
(15.7)
Рис. 15.4. За-
висимости оп-
тических ха-
рактеристик
материала
ЭД-6МА от
скорости де-
формирования
а Едд »
о- - 4’
а)
199
Метод генерирования
импульсной нагрузки
Схема нагружения
Копер со свободно падаю-
щим грузом
Механический
Копер с падающей кареткой
200
Маятниковый копер
Пневматиче-
ский
ТАБЛИЦА 15.3
Параметры нагрузочного устройства
и динамического воздействия
Область применения
Энергия удара A = Ph регулируется вы-
сотой падения бойка h и его весом Р.
Максимальная скорость соударения до
3 м/с. Длительность ударного импульса,
например, при ударе сферы радиусом R о
плоскую поверхность:
Исследование продольного и
поперечного удара по стерж-
ням и балкам, исследова-
ние бурового инструмента
л 1 — V1
где о =--------
Каретка в верхнем положении удержива-
ется электромагнитом, установленным на
траверсе, высота положения которой изме-
няется в пределах до 4 м. Максимальные
скорости удара v0 до 6—8 м/с
Исследование динамики ре-
зания и раскола
Параметры удара изменяются вследствие Исследование продольного
угла отклонения маятника а и различного и поперечного удара по
веса бойков. Заданный угол отклонения стержням и балкам
фиксируется электромагнитом, размыка-
ние цепи которого приводит в действие
копер. Максимальная скорость удара и0
до 1,2 м/с
Камера высокого давления Р— 1 МПа;
камера низкого давления Р=0Н МПа;
давление на фронте ударной волны ДР—
— 0,Л8 МПа; скорость фронта ударной вол-
ны v = 550 м/с; длительность фазы сжа-
тия Т_™. = 3,75 мс
Камерой низкого давления является ствол
ружья диаметром 5—12 мм; при открытии
диафрагмы стальной шарик приобретает
скорость о0, меняющуюся в диапазоне 20—
100 м/с в зависимости от его массы и дав-
ления газа или воздуха в камере
Создание плоских волн
большой продолжительно-
сти в плоских моделях из
низкомодульных материалов,
например СКУ-6,, Хизол-8705
Исследование свойств фото-
упругих материалов при
средних скоростях удара,
исследование динамических
напряжений и разрушений
в пластинках и объемных
моделях
Взрыв заряда азида свинца
в модели
1. Цилиндрический заряд в пластинке
2. Цилиндрический заряд в шайбе
3. Несколько цилиндрических зарядов для созда-
ния периодической нагрузки
4. Удлиненные заряды
5. Гейерирование плоских поперечных волн
(см. табл. 15.2)
Применяемая масса зарядов 117=10—
1 СЮ мг; плотность БВ 1,4 г/см3; ско-
рость детонации Д = 1200—2400 м/с; ини-
циирование заряда высоковольтным раз-
рядом (7=10—30 кВ; длина фазы сжатия
_6 >—
%cJK = /Сj г у W изменяется в моделях в
пределах 15—60 мм; периодическая на-
грузка создается в виде
(ПС \
---t I
1 I
Лсж /
Исследование различных
классов инженерных волно-
вых задач, связанных с
изучением сейсмического
действия взрыва, дифракции
волн и динамической кон-
центрации напряжений, мо-
делирование волн и источ-
ников различных типов
или с затухающей амплитудой
Использова-
ние химиче-
ских ВВ
удар каплей
жидкости
Ударный
взрывной
пер
ко-
макс —а/ .
т (О = mr е sin
Изменение скорости полета и диаметра
капли достигается установкой сменных ка-
мер с различным выходным отверстием и
применением различных по весу зарядов
ВВ во взрывном копре; диаметр сопла
0,2—2 мм; скорость капли =100 . ..
. . . 1000 м/с; длительность ударного им-
пульса т = 0,2 ... 5 мкс
Исследование напряжений в
специальных деталях и кон-
струкциях при высокоскоро-
стном соударении с капля-
ми жидкости
---------
удар твердым
телом
Применяют различные по весу и форме
бойки. Давление выделившихся при взры-
ве ВВ газов сообщает бойку скорость,
регулируемую массой бойка и весом ВВ.
При изменении массы бойка от 10 до 60 г
Моделирование ударных им-
пульсов в различных зада-
чах динамики
и U7=10. . . 100 мг получают скорости уда-
ра
оуд = 3 ... 30
м/с
Использова- Электрический разряд в
ние энергии жидкости
разряда кон-
денсаторов
Напряжение зарядов конденсаторов и0=
= 6 . . . 20 кВ; емкость конденсаторов С =
= 2 . . . 150 мкФ, запасаемая энергия
1Г0 =0,5 ... 5 кДж; длина разрядного
промежутка (=10. . . 30 мм, время фазы
сжатия тсж= 30 ... 90 мкс; максимальное
давление Р=10 ... 20 МПа
Создание волн напряжений
с фронтом цилиндрической
формы в плоских моделях
и стержнях из высокомо-
дульных материалов на ос-
нове эпоксидных смол
Метод генерирования
импульсной нагрузки
Схема нагружения
Электрический взрыв про-
волочки в жидкости
202
Использование
энергии раз-
ряда конден-
саторов
Электрический взрыв про-
водника (фольги), вклеенно-
го в модель
Магнитно-импульсное нагру-
жение моделей с помощью
магнитного индуктора
Продолжение табл. 15.3
Параметры нагрузочного устройства
и динамического воздействия
Область применения
Напряжение заряда конденсаторов Uq=
= 20... 40 кВ; С = 3 ... 6 мкФ; Wo=
= 2... 5 кДж; длина разрядного проме-
жутка /=100 ... 150 мм; тсж=ЗО. . .
. . . 40 мкс; Р — 5 ... 10 МПа (взрывающая-
ся проволочка 0 0,1 мм служит для ста-
билизации формы канала разряда)
Создание волн напряжений
с плоским фронтом в плос-
ких моделях из высокомо-
дульных материалов
Напряжение заряда конденсаторов (70 =
= 6. . .20 кВ; С=30. . .2400 мкФ; М—
= 2 ... 40 кДж; сечение проводника S’ =
= 0,5 . . . 4 мм2; длина /=100...150 мм;
Т =15...200 мкс; Р=10 . . . 50 МПа;
параметры волны сжатия приближенно
определяют зависимостями:
^сж — ^,4 L ;
Uzrk г
/ А X V/*
1g Р = 0,6 = 11,4 ----МПа,
\ си0 /
где С — емкость конденсаторов, мкФ;
L — индуктивность разрядной цепи; А —
поверхность взывающегося проводника,
см; и0 — напряжение
(70 = 6 . . . 20 кВ; С’= 150 ... 1200 мкФ;
lFo=5 . . .20 кДж; тсж=20 ... 100 мкс;
Р = Ю...2О МПа; магнитное давление
1 d L
Р =---- ---/2 где d Lid р — изменение
2 dp
индуктивности системы L при изменении
расстояния р между индуктором и токо-
проводящим слоем, нанесенным на мо-
дель
Создание интенсивных волн
напряжений большой про-
должительности с фронтом
плоской формы
Создание волн напряжении
с плоским и цилиндрическим
фронтом
В качестве основного параметра, с ко-
торым связано возможное изменение зна-
чений оОд,О) и &од 0), можно принимать
условную скорость деформации е, которая
определяется зависимостью
^макс
(15.8)
где tn — время, в течение которого скорость
смещения достигает максимального значе-
ния.
На рис. 15.4 приведены зависимости
е0д 0)=2Ф1 (е) и од °> —Фя('е)> полученные
по описанной методике для материала
ЭД6-М. Из графиков, в частности, видно, что
в интервале скоростей деформирования е —
200-2000 с-1 значения о^од и еод не
изменяются и на 30—40% превышают
соответствующие статические значения.
Определение напряжений и смещений
по картинам полос т (х, у, t). Непосред-
ственно по фотографиям картин полос т
(х, у, it), полученных в режиме покадровой
съемки (рис. 15.1), или т (х, t), получен-
ных в режиме фоторегистратора (рис. 15.2),
во (внутренних точках модели определяются
напряжения тМакс по формуле
/м _ (ql —q2) Z _ °.5m (О „(1,0)
тмаксП)— 9 -- , °од
(15.9)
На границах, свободных от нагрузки,
определяется контурное напряжение
°конт —
т (И „(1.0)
Л СТ0д
(15.10)
Скорости продольных Ср и поперечных
с3 волн вычисляются по формулам:
Ср, s
Д S(o
------— режим по кадро-
М и
вой съемки;
1
— vp tg а—режим фоторе-
(15.Н)
гистратора,
га
о
о
СП
га
о
га
S
га
га
и
О га *£
га га s
га
га
и
рч
>^:га
С о
|=:
о
га
S
га
CD
O’S
и л
о га
га
где со — частота съемки, к/с; Д5— переме-
щение полосы нулевого порядка; п — чис-
ло кадров в рассматриваемый интервал
времени; остальные обозначения прежние.
Различать продольные и поперечные
волны можно либо по вычисленной скорости
по формулам 15.11, либо путем специальной
съемки поля смещений в зоне возмущения,
вызванного интересующей волной.
Смещение Uij может быть найдено не-
посредственно при съемке риски (0,05—0,10
мм), нанесенной на модель в рассматрива-
емом месте, в режиме фоторегистратора с
увеличением 60—Л00 крат.
Перемещения точек модели в направ-
лении вдоль свободного от внешней нагруз-
ки прямолинейного контура L могут быть
Й ®
е к
<L>
Я
О
о
Я ф
и о о
га
S
203
вычислены по формуле (15.12), если извест-
на картина полос т(х> у):
u(L) = ±
„(1.0)
а0д
р с2 d
J т (L) dL. (15.12)
L
В случае падения под углом ip плос-
кой продольной волны (или цилиндриче-
ской волны для расстояний от заряда
г/го^7О) на свободный от внешней нагрузки
контур по известным из (15Д2) значениям
и полный вектор смещений и определяется
по формулам
и = и sin 1 р;
р = arcsin
sin р. (15.13)
Способы определения компонентов тен-
зора напряжений Oij (способы «разделения
напряжений»). Широко применяемые в ста-
тической фотоупругости методы разделения
напряжений, основанные на численном ин-
тегрировании дифференциальных уравнений
равновесия, не могут быть применены в
динамической задаче в связи с трудностя-
ми получения поля изоклин и определения
правой части дифференциальных уравнений
движения, в которую входят ускорения
и (х t), v (у, t).
Ниже (приведены формулы, позволяю-
щие определять компоненты тензора на-
пряжений и перемещения в плоской дина-
мической задаче фотоупруп
пространении в направлении
продольной волны р:
1 аод
— 1 _ V d тР
V стод’О)
= -jTZV —Г~ тр
при рас-
х плоской
оси
W
(15.14)
При этом перемещения вдоль прямой Lx
при нулевых начальных условиях определя-
ются по формулам
v — 0.
(15.15)
В плоской поперечной волне s, рас-
пространяющейся в направлении х, глав-
ные напряжения оь 02 направлены под
углом 45° к фронту волны и определяют-
ся из выражений
= — <т2 =
(1,0)
°Д ( ч
-а— W;
^макс — Т'ху —
(1.0)
о л ms (х) .
Перемещения вдоль прямой
нулевых начальных условиях
(15.16)
Lx при
и = 0.
(15.17)
1 + V
(1,0)
Од
В случае плоской осесимметричной за-
дачи для точечного источника импульсивно-
го возмущения j 1
1 + V аод 0)
ег= е0-—---------------j- т (г); (15.18)
Ел
Gr — ।____v2 (8r + v eo)»
En
сте= 1—va (e0 + v er). (15.19)
где r, 0 — полярные координаты.
В плоской динамической задаче при
наличии оси симметрии главные напряжения
в точках вдоль этой оси могут быть по-
лучены методом наклонного просвечивания
на установке, приведенной в табл. 15. Г, схе-
ма 4 [8].
Напряжения Oi и о2 в этом случае
определяются по формулам
ипо)
<У0д
a sin2 0
(тп— те cos9); (15.20)
0д0) cos б
а sin2 0
(тп cosO — /п0),
(15.21)
где 0 — угол между нормалью к пластинке
и осью наклонной ветви ПДУ; тп, —
порядок полос в рассматриваемой точке
соответственно при нормальном и наклон-
ном просвечиваниях. В формулах (15.20) и
(15.21) первый индекс у напряжения и
знак плюс соответствуют фазе сжатия в
зоне возмущения второй индекс у
напряжения и знак минус — фазе растя-
жения.
При отсутствии оси симметрии для
разделения напряжений необходимо осу-
ществить одновременное просвечивание по
трем направлениям, что связано с трудно-
стями технического порядка.
Для разделения напряжений в отдель-
ных точках модели используется электро-
тензометрирование с помощью малобазных
(1—2 мм) датчиков с одновременной съем-
кой поля т (х, у, t). В моделях, выпол-
ненных из материала с модулем £=5Х
XI О2 МПа (табл. 15.4), применяется метод
сеток [3]. Сетка изготовляется из резино-
вых нитей, обладающих малой жесткостью.
При использовании моделей из материалов
с модулем упругости £'=(25—35) 102 МПа
для определения поля перемещений
(х, у, t) и деформаций гц (х, у, t) применен
метод дифференциальных муаровых полос
[7].
Для построения поля суммы главных
напряжений! (поля изопах) может быть ис-
пользован трехпластинчатый интерферометр
ЛИТМОчМИСИ [10]. В связи с большими
потерями на полупрозрачных зеркалах ин-
терферометра в качестве источника света
204
необходим твердотельный лазер с модули-
рованной добротностью.
Разделение напряжений с помощью
фотоэлектрической и голографической ин-
терферометрии- Интерферометрические ме-
тоды измерений позволяют регистрировать
абсолютные разности хода поляризованного
света в модели Ai и Аг, которые непосред-
ственно связаны с главными напряжениями
<У1 и о2 соотношениями Фавра.
С целью разделения напряжений в
точке применяется [7] фотоэлектрическая
установка с трехпластинчатым интерферо-
метром ЛИТМО-МИСИ и Не—Ne лазером
в качестве источника излучения. Вопросы,
связанные с фотоэлектрической интерферо-
метрией в точке, изложены в работе [7].
Для разделения напряжений по полю
модели (в некоторой области модели) при-
меняется голографическая интерферометрия
[7, 15].
Вопросы теории подобия. Переход
от модели к натуре. Вопросы теории дина-
мического подобия и критериальные ком-
плексы подобия изложены в разд. ,14 спра-
вочника. Рассмотрим здесь лишь некоторые
специфические условия, характерные для
метода динамической фотоупругости.
Из условия Cp/cs^=idem вытекает необ-
ходимость Соблюдения УСЛОВИЯ Vh^Vm в
случае, когда натура и модель находятся
в одинаковом напряженном состоянии. При
исследованиях методом динамической фото-
упругости трехмерные конструкции, находя-
щиеся в условиях плоской деформации,
обычно изучаются на моделях, находящих-
ся в условиях обобщенного плоского на-
пряженного состояния. При этом должно
выполняться соотношение
(15.22)
При исследовании бетонных или скаль-
ных массивов (vh^0.2) на моделях, вы-
полненных из материалов типа ЭД6-МА
или 340-МТГФА (vM«0,35), условие
(15.22) уменьшает погрешность, вызванную
неравенством коэффициента Пуассона мо-
дели и натуры.
Для определения напряжений и пере-
мещений в натуре, при соблюдении в мо-
дели условий геометрического подобия и
подобия динамического воздействия, в
сходственных точках, находящихся на не-
котором удалении от места приложения
нагрузки, целесообразно пользоваться зави-
симостями:!
Ci н= ( ’l °он, н = I “j woh> (15.23)
\ (То /м \ wo /м
где (jihj Нгн — искомые напряжения и пере-
мещения в точке i натуры; (<л70о}м, (щ/
/но)м — соответственно отношения напряже-
ний и смещений в точках i и 0 модели;
сын, нон — напряжения и смещения в точ-
ке О натуры, которая выбирается так, что-
бы значения Оон, пон в ней можно было1
получить либо расчетным путем, либо из
натурных экспериментов (см. ниже пример
исследования по моделированию при алма-
атинском взрыве).
Точность метода. Оценка влияния вяз-
кости оптически чувствительных полимеров
на волновые поля напряжений. Точность
метода динамической фотоупругости, как
метода моделирования напряженного состо-
яния инженерных конструкций, определяет-
ся точностью нахождения напряжений в
модели и погрешностями, которые возни-
кают при переходе от напряжений в моде-
ли к напряжениям в натурных условиях.
Погрешности, связанные с переходом
от модели к натуре, существенно зависят от
вида заданного импульсивного воздействия
и соответствия физико-механических свойств
материалов модели и натуры. Для различ-
ных классов задач, которые правомочно
рассматривать в упругой постановке, эта
погрешность, по-видимому, может состав-
лять 8—20%. Следует иметь в виду, t что
большая точность навряд ли достижима и
на этапе перехода от реальной .проблемы к
расчетной схеме.
При оценке точности определения на-
пряжений для условий модели необходимо
иметь в виду два аспекта вопроса. При
определении по картинам полос т (х, у),
т(х, t) контурных напряжений и напряже-
ний Тмакс точность практически не отлича-
ется от точности метода полос в статиче-
ской фотоупругости и оценивается величи-
ной 3—6%. При разделении напряжений во
внутренних точках модели в зависимости
от применяемого метода погрешность может
достигать 8—15%. Однако наиболее важной
при моделировании динамической задачи
теории упругости является оценка влияния
вязкости оптически чувствительных матери-
алов на волновые поля напряжений.
Законы уменьшения амплитуд распрост-
раняющихся волн и изменение формы вол-
ны с расстоянием в оптически чувствитель-
ных материалах отличны от упругих сред,
что свидетельствует о проявлении вязкости,
так же как и различие статических и ди-
намических значений модуля упругости
Ел, цены полосы <?од °^ > е0д и ДРУГИХ ха‘
рактеристик материала. Отличие реальных
механических свойств материалов, исполь-
зуемых для изготовления моделей, от
свойств линейно-упругой среды приводит к
появлению погрешностей при решении уп-
ругих динамических задач поляризацион-
но-оптическим методом. Учет погрешностей
особенно затруднителен в случае сложных
динамических задач, связанных с возник-
нсивением в модели волн различных типов,
распространяющихся с различными скоро-
стями и создающих различные по характеру
распред едения напряжений и смещений и
обладающих различными закономерностями
уменьшения амплитуд с увеличением рас-
стояния до источника.
На рис. 15.5 показаны теоретическая
схема расположения фронтов волн, распро-
страняющихся в упругой полуплоскости
при действии вертикального мгновенного
импульса, приложенного на свободной гра-
нице, и экспериментальная картина полос
в модели из высокомодульного оптически
чувствительного материала при взрыве на-
кладного сосредоточенного заряда ВВ на
торце пластинки.
205
Т Л В Л И Ц А 15.4. ОПТИЧЕСКИ ЧУВСТВИТЕЛЬНЫЕ МАТЕРИАЛЫ, ПРИНИМАЕМЫЕ В
Статические характеристики
Материал ем О. J3 * ёД Щ см модуль упру- гости &ст, МПа коэффи- циент Пуассона V оптическая постоянная по напря- жениям „(ЙО) и0 сж» оптическая постоянная по деформа- циям Е(1,С) И J й
о? СТ МПах 0 сж’
Ч и К X Xсм/пол 1/пол
МЕТОДЕ ДИНАМИЧЕСКОЙ ФОТОУПРУГОСТИ
Динамические характеристики Область применения
модуль упру- гости Яд, МПа коэффициент Пу- ассона V скорость волны сжатия в стержне с, м/с оптическая постоянная по напря- жениям °0д > МПаХ Xсм/пол оптическая постоянная по деформа- циям е(1>0) е0 д ’ 1/пол
№
О
ЭД6-МА ЭД6-МТГФА CR-39* 1,22 1,22 1,2 3—3,5-фО? 3„1— 3,5-iLO3 1,4—2,1-10? 0,38 0,41 0,42
Оргстекло (листо- вое) 1,19 2,8—3,1 <103 0,37
О НС 1.2 3,1 —103 0,37
Хизол-4485 1,18 3—4,4 0,46—1,48
ЭПЭГК 40-50** 1,11 0,85-103 0,46
ЭПАСК Э66 1,29 3,5 0,5
Игдантин 1,18 ОД 0,5
Сополимеры ДАФ z ДАМ:
—100 : 0 1,29 3,5-103 0,39
—75 : 25 1,3 3.9-103 0,35
— 50 : 50 1,33 4,3-10? 0,33'
* Даны условно-мгновенные
1,0—1,3 0,4—0,5-10—3 3,6-4.3-103 0,36 1730
1,8—2 0,7—Д8-10—3 4,3—4,4-ЮР 0,39 1900
1,6 1,1—1,6-ю-3 4,8-Ю3 0,33 1900
13,5—20 7—8-Ю—3 5.5-103 0,36 2000
500 0,22 5-10? 0,36 2050
0,016 5—8-10)-3 4,5 0,46 60
0,2 2,7-Ю.-3 2- 2 -40? 0,44 1330
0,03 13-Ю-3 3,1-40? 0,46 1540
0,006 50-101-3 0,3 0,5 14,8
1,3 0,53-10—3 4,7-103 0,38 1900
1,3 01,47-10—з ' 5,4 •11О3 0,33 2050
1,9 0,59-10—3 5,7-103 0,3 2100
значения модуля упругости и оптических характеристик.
** Описываются уравнением: е (/) — ~
п
L~(t — т) <р (ст) d х с ядром L (t
Ji'
0
I—vft а -
0,5—0,6-101—3
0,7—0,9-10—3
0.Е 10—3
20 5-Ю-3
0,018 5-,10-3
0,5
0,6
0,014
1,9
2,6
3,7
Моделирование упругих вол-
новых полей напряжений
Изучение слоистых сред, ис-
следование дифракции волн
Исследование объемных мо-
делей
0.3-10-3
0,26-ЦО~3
0,08
0,57-10—3
0,6-10—3
0,77-10—3
4 Изучение волновых полей
I напряжений с помощью низ-
кочастотной регистрирующей
аппаратуры; изучение сло-
истых сред
1 Изучение волновых полей
} напряжений и процессов
) разрушения
ДАФ — диаллилфталат; ДАМ — диаллилмалеинат; ЭПЭГК — эпоксиполиэтиленгликолевые компаунды; ЭПАСК — эпоксидный
фамиламидом и модифицированный аллилкриламидом.
полимер
«ЭПОП-812», отвержденным суль-
Рис. 15.6. Экспериментальное (7) и теоретическое
(2) распределение динамических напряжений;
а у свободной поверхности от сосредоточенного
поверхностного источника
Рис. 15.5. Расположение фронтов волн в задаче
Лэмба
а — теоретическая схема (идеально упругая по-
становка); б — картина полос при взрыве поверх-
ностного заряда в пластинке из оптически-чув-
ствительного материала
Рис. 15.7. Картины полос, полученные на отра-
жательной поляризационно-динамической установ-
ке с однократной вспышкой в пластинках из
эпоксидной смолы с отражающим слоем
а — при ударной нагрузке; б — при взрывной на-
грузке
На основании решения [5] найдены
[7] напряжения (Jx(t) в точках свободной
границы упругой полуплоскости для сосре-
доточенной силы, изменяющейся во време-
ни по закону треугольника, что приближен-
но аппроксимирует колоколообразный им-
пульс в эксперименте. На рис. 15.6 показан
график изменения во времени напряжения
Gx(t) на фиксированном расстоянии от источ-
ника и экспериментально зарегистрированное
распределение порядков полос m(t) в соот-
ветствующей точке свободной поверхности.
Из приведенных данных видно, что для
рассмотренной задачи, характеризуемой на-
личием волн различного типа и сложным ха-
рактером распределения напряжений в про-
странстве и времени, при импульсном на-
гружении вязкие свойства применяемого
оптически чувствительного материала (ЭД6-
МА) не оказывают существенного влияния
на величины напряжений и характер их
изменения во времени на фиксированном
расстоянии от источника воздействия. Ана-
логичные выводы получены при рассмотре-
нии задачи о концентрации динамических
напряжений около отверстий [Ы].
Таким образом, исследования на мо-
делям из высокомодульных оптически-чув-
ствительных материалов методом динами-
ческой фотоупругости могут с достаточной
точностью применяться для решения упру-
гих задач. При этом в каждом случае сле-
дует учитывать возможную погрешность,
связанную с различием в законах затуха-
ния волн различных типов [1].
В экспериментальных исследованиях на
низкомодульных оптически чувствительных
материалах (полиуретановые резины, же-
латин и др.), вязкие свойства которых
проявляются сильнее, указанные погрешно-
сти могут возрасти, и возможность решения
упругой динамической задачи на таких мо-
207
делях требует специального обоснования.
В то же время эти материалы могут быть
использованы для исследования задач, в
которых ставится цель моделирования волн
напряжений в вязкоупругой постановке.
Исследование волн напряжений с по-
мощью оптически чувствительных покрытий.
Применение таких покрытий расширяет
возможности исследований и позволяет
изучать волновые процессы на изделиях, вы-
полненных из натурных материалов. Осно-
вы метода оптически чувствительных пок-
рытий изложены, например, в 11,7]. При-
мер картины полос, полученной в отражен-
ном свете, при динамическом нагружении
пластинки с зеркальным покрытием, кото-
рая наклеивается на исследуемую конст-
рукцию, приведен на рис. 15.7 (при удар-
ной нагрузке — вверху, при взрывной —
внизу).
Специфические особенности, которые
возникают при использовании оптически чув-
ствительных покрытий в динамической
фотоупругости, связаны с необходимостью
оценки влияния сложной картины волн на-
пряжений, возникающей за счет отраже-
ний от свободной и контактной поверхно-
стей покрытия, на интегральную величину
двойного лучепреломления; некоторые осо-
бенности в методике разделения напряже-
ний вызваны тем, что при динамическом
нагружении покрытие находится в услови-
ях объемного напряженного состояния.
Решение объемной задачи методом
динамической фотоупругости. Для исследо-
вания объемных динамических задач мето-
дом фотоупругости в основном применяют-
ся методы вклеенного полярископа и со-
ставных моделей <[12, 13].
В тех случаях, когда пространственная
конструкция состоит из тонкостенных эле-
ментов, каждый из них может просматри-
ваться на ПДУ в проходящем или отражен-
ном свете. При исследовании объемных
моделей часто встречаются случаи, когда
большой интерес представляют области, в
которых точки находятся в условиях
плоского напряженного состояния, однако
поле волновых напряжений в них форми-
руется с учетом пространственной работы
всей конструкции. В этих случаях в интере-
сующие области могут вклеиваться тонкие
пластинки с отражающим слоем, а измере-
ния производятся на ПДУ в отраженном
свете.
15.3. ПРИМЕРЫ ПРИМЕНЕНИЯ
МЕТОДА ДИНАМИЧЕСКОЙ
ФОТОУПРУГОСТИ
Метод динамической фотоупругости
применяется как для исследования отдель-
ных эталонных задач волновой механики,
так и для решения инженерных вопросов.
Рассмотрим два примера, характерных для
указанных выше постановок.
Пример 1. Исследование концентрации
напряжений в стержнях с ослаблениями и
в пластинках около отверстий при продоль-
ном импульсном воздействии. Концентра-
ция динамических напряжений исследова-
ние. 15.8. Изменение коэффициентов концентра-
ции максимальных напряжений в зависимости от
размеров отверстий (сплошные линии — динами-
ка, пунктир — статика)
/ — квадратные отверстия с диагональю, парал-
лельной оси стержня; 2 — квадратные отверстия
со стороной, параллельной оси стержня; 3 —
круглые отверстия
Рис. 15.9. Зависимость коэффициента концентра-
ции максимальных динамических напряжений от
относительного размера кругового отверстия
Направление выброса
437*
Поверхность задало
после дыдроса
5<V
/л/мнель
70м
7 Зарядная
номера
И-3680т
' .Qfi I Поверхность
!• отрыва пород
Рис. 15.10. Схема алма-атинского взрыва
лась на стержнях из материала ЭД6-МА
(4X20X400 мм) с центральными отверсти-
ями и симметричными выточками. Модели
нагружались по торцу однократным им-
пульсом давления (длина волн =4 00 мм)
с помощью электроразрядной установки с
использованием энергии импульсного маг-
нитного поля (табл. 15.3). Для примера на
рис. 15.8 представлены результаты иссле-
дований в виде графиков коэффициентов
концентрации максимальных динамических
напряжений на контуре ослаблений.
Зависимость максимальных значений
коэффициентов концентрации динамических
напряжений на контуре кругового отвер-
стия в безграничной пластинке от пара-
метра 2а/Хн представлена на рис. 15.9
208
Рис. 15.11. Кинограмма волн напряжений в пластинке при моделировании алма-атинского взрыва
(где Хн—длина участка нарастания дав-
ления до максимума в фазе сжатия за-
данного импульса давления). Эксперимен-
тальные значения К $ сравниваются с
теоретическими, которые получены с по-
мощью интеграла Дюамеля на основании
решения [15] для ступенчатой нагрузки,
определяемой функцией Хэвисайда.
Наиболее полно вопрос об исследовании
методом фотоупругости концентрации дина-
мических напряжений при импульсивных на-
грузках рассмотрен в монографии [7], где
приведены примеры решения задач о воз-
действии р и s волн на подкрепленные и
свободные отверстия различной формы в
пластинках.
Пример 2. Исследование волн напря-
жений при возведении алма-атинской селе-
защитной плотины с помощью направлен-
ного взрыва. При возведении селезащитной
плотины в районе Медео на реке Малая
Алмаатинка был произведен взрыв на выб-
рос заряда тротила массой w=3600 т. Для
оценки напряженного состояния водосбор-
ного туннеля, расположенного на противо-
положном берегу (рис. 15.10), при действии
волн напряжений были проведены иссле-
дования методом^ динамической фотоупруго-
сти [7, 12].
Решение этой сложной инженерной зада-
чи методом динамической фотоупругости с
полным соблюдением условий подобия моде-
ли и натуры в настоящее время не представ-
ляется возможным. Исходя из того что
длина туннеля и зарядной камеры значи-
тельно больше размера их поперечного се-
чения, исследования проводились в плоской
постановке (плоская деформация). В пред-
положении, что материалы натуры (грани-
ты серые крупнозернистые) и модели
(эпоксидная смола ( Э40-МА) являются
упругими, однородными и изотропными, по-
добие волновых явлений при равенстве
коэффициентов Пуассона модели и натуры
Рис. 15.12.
Эпюра рас-
пределения
контурных на-
пряжений в
водосбросном
туннеле
(сплошная ли-
ния — метод
динамической
фотоупруго-
сти; точки —
результаты
натурных из-
мерений)
и геометрическом подобии будет обеспече-
но в случае, если выполняется условие
(Х//)н=(Х//)м, (15.24)
где X и >/ — соответственно длина волны в
фазе сжатия и геометрический размер эле-
мента в натуре и модели.
При взрыве заряда массой 3600 т дли-
на волны Хн в фазе сжатия составляет
100 м (по данным ИФЗ АН СССР). Тогда
при выбранном масштабе геометрического
подобия ca=eH/eM = 5-103 надо, чтобы Хм
составляла 20 мм. Такая длина может быть
получена (см. табл. 15.2), если применить
сосредоточенный заряд азида свинца массой
w = 50 мг. *
Вследствие подобия волновых полей в
модели и натуре может быть записано со-
отношение!
(стг/а0)н= (сгг-/а0)м а; т^Шо, (15.25)
где яг- (Уо и mi, то — компоненты тензора
напряжений и порядки интерференционных
полос в сходственных точках i и 0 модели
и натуры. Откуда
т?
н == ^он • (15.26)
т0
209
Таким образом, для определения на-
пряжений Огн в произвольной точке натуры
достаточно знать соотношение порядков
полос niilmQ в сходственных точках подоб-
ной модели и напряжения сгОн в той точке
натуры, в которой они с достаточной уве-
ренностью могут быть получены расчетом
или из натурных наблюдений.
Формулы для определения наибольших
растягивающих и сжимающих напряжений
по контуру туннеля имеют вид:
где тр и та — порядок интерференцион-
ных полос в зоне расположения туннеля
соответственно для р и s; то — порядок
полосы в безграничной пластинке на уда-
лении от места взрыва, равном расстоянию
между зарядом ВВ и туннелем; огмакс—
радиальное напряжение для натурных ус-
ловий в неограниченном массиве на удале-
нии от заряда ВВ, равном расстоянию меж-
ду взрывной камерой и туннелем.
Значение о^макс=266 кг/см2 было най-
дено из теоретического решения Е. И. Ше-
мякина. Близкое значение (о?-макс”270 кгс/
/см2) дает эмпирическая формула ИФЗ АН
СССР, полученная после обработки данных
алма-атинского взрыва 21 октября 1966 г.
°?макс = 3.6 р С -6 R~1 -8, (15.28)
где ре — акустическая жесткость породы;
W— масса заряда ВВ; Д— расстояние от
заряда ВВ.
Величины порядков и интерференцион-
ных полос тРг ms и то берутся из кино-
грамм, полученных на установке ПДУ
МИСИ в режиме покадровой съемки или
фоторегистратора. На рис. 15.11 для при-
мера приведен монтаж картин полос т
(х, у, t) для различных моментов времени.
Исследование на модели позволило ус-
тановить общую волновую картину и необ-
ходимые количественные данные. В частно-
сти, было показано, что наибольшие рас-
тягивающие напряжения возникают в об-
делке туннеля от действия S волны и их
величина достигает 200 кгс/см2. Натурные
измерения, проведенные комплексной экспе-
дицией МИСИ им. В. В. Куйбышева и
НИС Гидропроекта во время алма-атинс-
кого взрыва, показали удовлетворитель-
ную сходимость результатов моделирова-
ния и натурных измерений (рис. 15.12).
К настоящему времени методом дина-
мической фотоупругости исследовано зна-
чительное количество задач. Не претендуя
на полноту, назовем некоторые основные
классы задач, решение которых осуществле-
но методом динамической фотоупругости.
Напряженное состояние балки при попе-
речном ударе; волны напряжений в плас-
тинках при различных источниках динамиче-
ского воздействия; волны напряжений у сво-
бодной поверхности полубесконечной плас-
тинки при сложной конфигурации границы,
волны напряжений в слоистых средах. Рас-
пространение трещин и дифракции волн
напряжений около стационарных трещин;
напряженное состояние гидротехнических
сооружений и их оснований при сейсмиче-
ских воздействиях. Решения указанных за-
дач приведены в работе [7]. Там же име-
ются необходимые ссылки на первоисточ-
ники.
СПИСОК ЛИТЕРАТУРЫ
1. Александров А. Я., Ахметзянов М- X.
Поляризационно-оптические методы меха-
ники деформируемого тела. М., 1973.
2. Барон, Мэтьюс. Дифракция волны
давления относительно цилиндрической по-
лости.— Прикладная механика, сер. Е,
№ 3, 1961.
3. Дюрелли А., Райли У. Введение в
фотомеханику. М., 1970.
4. Дубовик А. С. Фотографическая
регистрация быстропротекающих процессов.
М., 1975.
5. Климова Д. И., Огурцов К. И. Ко-
личественные оценки упругих волн напря-
жений в плоской задаче Лэмба. — В кн.:
Исследования по упругости и пластичности,
№ 5. Д., 1966.
6. Маршак И. С. Импульсные источ-
ники света. М., 1963.
7. Под общ. ред. Н. А. Стрельчука,
Г. Л. Хеоина. Метод фотоупругости, т. II.
М., 1975.
8. Методика и результаты тарировоч-
ных исследований оптически чувствитель-
ных высокололимеров на основе эпоксид-
ных смол при импульсных нагрузках / МИ-
СИ. М, 1970, №73. —Труды. / Хесин Г. Л.,
Костин И. X., Рождественский К- И., Шпя-
кин В. Н.
9. Методика и аппаратура для иссле-
дования динамических задач методом фо-
тоупругости. / Костин И. X., Славин О. К-,
Хесин Г. Л., Шпякин В. И. — В кн.: По-
ляризационно-оптический метод исследова-
ния напряжений. Л., 1966.
10. Определение суммы главных на-
пряжений с помощью интерферометра. /
/ Воронцов В. Л., Москалев В. А., Наги-
бина И. М., Омельченко Д. И., Хе-
син Г. Л.—В кн.: Поляризационно-опти-
ческий метод исследования напряжений. Л.,
1966.
Г1. Хесин Г. Л., Костин И. X., Зате-
ев В. Б. Исследование концентрации напря-
жений около отверстий в тонких пластин-
ках при воздействии волны давления. •—
Груды (Об. тр., Науч, тр.) / МИСИ., М.,
1970 № 73.
12. Хесин Г. Л., Костин И. X., Дмо-
ховский А. В„ Юренева Е. В. Исследование
210
напряжений от динамических воздействий
в моделях гидротехнических сооружений
методом фотоупругости. — Гидротехниче-
ское строительство, 1973, № 1.
13. Dally J. Г., Riley Г. Л Initial
studies in three— dimensional dynamic
photoelasticity Irans. ASME, 1967, Ё. 34,
№ 2, p. 405—410.
14. Hesin G. L., Kostin I. H., D mo how-
ski A. W. Die Spannungs optik als Losung-
smethode der elastichen Wellentheorie Be-
itrage zur Spannungsoptik, Verlag von De-
utsche Bauakademie, Berlin. 1973, p. 20—36.
15. Holloway D. C., Johnson R. H.
Advantements in holographic photoelasticity.
Exp. Meeh., № 2, 1971, <p. 57—63.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
При пользовании предметным указателем следует иметь в виду, что в рубриках, представляю-
щих собой сочетание прилагательного и существительного, применена инверсия — существительное
поставлено на первое место.
А
Автоколебания 176
Амплитуда колебаний
— штампа
----' поступательная 129
----угловая 133
— здания при движении поездов метрополитена
136, 138
Антисейсмические мероприятия 41, 50
Антисейсмический пояс 41, 51, 53
Аэродинамическая неустойчивость 80, 82, 90
Аэродинамические способы гашения колебаний
176
Аэродинамическое демпфирование 81, 82
В
Ветровой резонанс 149, 176
Взрыв
— газовоздушной смеси 5, 10, 29
— тротилового заряда 5
— ядерный 6
Взрывное горение 29
Вихревая дорожка Бенара—Кармана 80, 86
Вихревое возбуждение 80, 83, 85
Волны
— взрывные 5
— N-волны 92, 93
— разгрузки 8
— Релея 119, 126
— сейсмические 50
— сжатия 5, 9
— ударные 5, 92, 144
— — воздушная 5, 6
— — в грунте 8
----давления на преграду 5, 6, 7, 8, 9, 10
Г
Газовоздушные смеси 29
Галопирование 80, 87, 88. 149. 173
Д
Давление отражения 6
— избыточное 10
Демпфер Стокбриджа 174
Диаграмма
— билинейного типа 68, 69
— Прандтля с упрочнением 8
Динамическая контактная задача для полупро-
странства 129
Динамический гаситель колебаний (ДГК) 149
— многомассовый 158
— маятниковый 159
— с предварительным натягом 160
Диссипативные силы 68
Диэлектрический тензор 194
3
Захват частоты 81, 84
Защищаемая конструкция 150
Звуковой удар 92, 94, 95
Зона фокусировки 93
И
Импульс Берлаге 72
Импульсная переходная функция 114, 115
Интенсивность звукового удара 93
Интерцептор 178
Искусственные сейсмограммы 67
К
Картины полос 194, 195, 204
Кризис сопротивления 81
Критерий качества 150, 153
Критическая скорость ветра 80, 86, 87
Конструкционное демпфирование 81
Контактные напряжения 115, 130
Коэффициент
— бокового давления 19
— бытового давления 9
— взаимодействия 9
— демпфирования 147
— динамичности 15, 16, 17, 18, 23, 24, 44, 49, 73,
75, 96, 97, 100, 102
----для напряжений 131
----для перемещений 130, 131, 134
— жесткости 147
— интенсификации горения 30
— квазирующий 73
— кинематической вязкости 75, 80
— лобового сопротивления 80, 177, 178
— отражения 9
— поперечной (аэродинамической) силы 81, 83, 88,
170, 178
— пространственной корреляции 85
211
— сейсмичности 41, 44
— упрочнения 11
— чувствительности 153
Л
Ламинарный поток 80
Легко сбрасываемые конструкции (ЛСК) 30,31
Логарифмический декремент колебаний 73
М
Масштаб турбулентности 80
.Мгновенный модуль деформации 8
Мелкомасштабное моделирование 181
Метод
— наклонного просвечивания 204
— фотоупругости 194
Микровибратор 189
Минимаксная задача оптимизации параметров
ДГК 150
Н
Надежность ДГК 149
— защищаемых конструкций 149
Незатухающие осадки фундамента 114
О
Обобщенная масса 84
Оптическая разность хода 194
Оптически чувствительный материал 194, 199
Осциллятор Ван-дер-Поля 84
П
Параметры
-ДГК
----относительная масса 151
— — настройка 149, 151
----настройка оптимальная 153
----демпфирование 149, 151
—колебаний грунта 115
Передаточная функция 80, 114, 115
Период звукового удара 94
Петля Гистерезиса 68, 69
Пиковое давление ударных волн 96
Подводный взрыв 144
Поляризационно-динамическая установка 194, 196
Постоянные Ламе 129
Предельные состояния при расчете
— на действие взрыва 11
— на сейсмические воздействия 63, 64, 70
Прохождение через резонанс 155
Псевдоскольжение 104
Пульсация газового пузыря 144, 146
Р
Распределение сейсмической нагрузки 47
Реакция грунтового основания 115
Режим обтекания
— ламинарный 8
— турбулентный 8
Режим горения 29
Резонатор Гельмгольца 94
С
Сейсмическая нагрузка (сила) 41, 43, 44, 46, 47,
48, 49, 74
Скоростной напор 8, 85, 86
Скорость волны
— упругой 8, 9, 118. 140, 199, 203
— упругопластической 8. 9
Скорость деформации 203
Случайный процесс
— квазистационарный 72
— б-коррелированный 71
— нестационарный мультипликативный 72
— стационарный 72
----нормальный 72
— узкополосный 71
Спектр
— перемещений (действия) 45
— скоростей 44
— ускорений 42, 44
----для упругопластической системы 68
Спектральная кривая 43
— стандартная 41
Спектральный состав колебаний 136
Степень безопасности сооружения 13
— расширения продуктов горения при постоян-
ном объеме 31
Суперпозиция волн 72
Т
Теория сейсмостойкости
— динамическая 41
— статическая 4!
Гранекритическая область чисел Рейнольдса 80
Тротиловый эквивалент 6
Установка взрывной штамповки 144
Ф
Фаза
— сжатия 6
— разрежения 6
Фронт пламени 29
— ударной волны 5
Фронтальная стена 7
Функции динамичности 14, 15, 22, 25, 26
Функция Хевисайда 125
ц
Цикл деформации 96
Цилиндрические функции
— Бесселя 139
— Неймана 139
Ч
Частота срыва вихрей 80, 83
Число
— Маха 93
— Рейнольдса 80. 81, 83, 85
— Струхаля 80, 81, 83, 176, 178
Ш
Шарнир пластичности 12, 17, 18, 19, 20
Штамп с плоским
— круговым основанием 129, 131, 132
— кольцевым основанием 131, 132, 134
Э
Эмпирическая квазилинейная модель 84
Эффективное время действия воздушной ударной
голны 9
Эффективность ДГК 149, 150
ОГЛАВЛЕНИЕ
Раздел 1. Расчет конструкций сооружений на действие взрывных волн
(О. В. Лужин, Н. Н. Попов, Б. С. Расторгуев)
1.1,. Взрывные волны .................................................* ’ *
1.2. Параметры воздушных ударных волн и их взаимодействие с преградой [1, 2, 3, 4, J, loj
1.3. Параметры волн в грунте и их взаимодействие с сооружением [2, 7, 11, 12] . . .
1.4. Динамические нагрузки от взрывных воздействий [12]...........................
1.5. Предельные состояния и расчет сечений [2, 8, 9, 12, 14]......................
1.6. Расчетные схемы..............................................................
1.7. Экспериментальные зависимости для оценки действия взрывных волн на сооружения [о]
1.8. Расчет конструкций в упругой стадии [2, 8, 9, 10, 12] . . • • ................
1.9. Расчет балок в пластической стадии [2, 8, 9, 12]..............................
1.10. Расчет конструкций с учетом вертикальных смещений опор [2, 9]................
Список литературы
5
5
8
10
11
12
13
14
17
21
Раздел 2. Защита зданий взрывоопасных производств от нагрузок,
возникающих при взрывном горении газовоздушных смесей (ГВС)
внутри помещений (Н. А. Стрельчук, Г. Г. Орлов)
2.1. Общие сведения . . .........................................................
2.2. Определение требуемой площади легкосбрасываемых конструкций (ЛСК) из условий
обеспечения взрывозащиты производственных зданий ...................................
2.3. Определение давления, возникающего при взрывном горении газовоздушной смеси в по-
мещениях зданий взрывоопасных производств................................... 34
2.4. Определение области применения легкосбрасываемых конструкций............... 38
Список литературы . . .................................................. 40
Раздел 3. Расчет зданий и сооружений на сейсмические воздействия
(Б. Е. Денисов, Л. Ш. Килимник, Н. Н. Николаенко, С. В. Поляков)
3.1. Расчет зданий как упругих систем............................................... 41
3.2. Особенности методов проектирования зданий различных конструктивных решений . . 50
3.3. Учет развития неупругих деформаций и изменения динамических характеристик зданий
и сооружений при сейсмических воздействиях........................................... 63
3.4. Вероятностные методы расчета сооружений на сейсмические воздействия............ 71
Список литературы .................................................................. 76
Раздел 4. Аэродинамическая неустойчивость высоких сооружений и гибких конструкций
(М. Ф. Барштейн)
4.1. Вихревое возбуждение сооружений цилиндрической формы....................... S0
4.2. Галопирующие колебания гибких призматических конструкций............ . 87
Список литературы .............................................................. 91
Раздел 5. Динамические воздействия на здания и сооружения
от сверхзвуковых самолетов (А. И. Цейтлин)
5.1. Общие сведения . . . . ......................................................... 92
5.2. Распространение звуковых ударных волн при полетах сверхзвуковых самолетов ... 92
5.3. Характеристики звукового удара.................................................. 94
5.4. Расчет сооружений на действие звуковых ударных волн............................ |96
5.5. Экспериментальные исследования.................................................. 00
Список литературы.............................................*...................... Ю1
Раздел 6. Крановые нагрузки
(М. Ф. Барштейн, А. Н. Зубков)
6.1. Вертикальные крановые нагрузки..........................................
6.2. Горизонтальные силы, вызываемые торможением тележки крана...............
6.3. Горизонтальные поперечные силы (боковые), возникающие при движении крана . . .
Список литературы . .........................................................
Раздел 7. Особые режимы работы конструкций несущих энергетические агрегаты
(И. С. Шейнин)
7.1. Природа особых режимов и соответствующие им динамические нагрузки
7.2. Некоторые сведения о расчете на нагрузки, возникающие в особых режимах
Список литературы ...................................................... ::
102
102
103
106
107
111
113
213
Стр.
Раздел 8. Динамическое взаимодействие сооружений с основанием и передача колебаний
через грунт (промышленная сейсмика) (В. А. Ильичев)
8.1. Общие сведения . . . ...................,..................................... 114
8.2. Определение параметров колебаний сооружений, силы реакции грунтового основания,
контактных напряжений и параметров колебаний окружающего грунта.................... 115
8.3. Передаточные и импульсные переходные функции для задачи о волновом взаимо-
действии сооружения с грунтовым основанием, моделируемым полупространством . . 118
8.4. Передаточные и импульсные переходные функции для задачи о распространении волн
в грунте от колеблющихся сооружений................................................ 124
Список литературы................................................................ 127
Раздел 9. Динамическая контактная задача для полупространства (Н. М. Бородачей)
9.1. Колебания штампа с плоским круговым основанием под действием вертикальной
возмущающей силы................................................................... 129
9.2. Колебания штампа с плоским круговым или кольцевым основанием под действием
горизонтальной возмущающей силы.................................................... 131
9.3. Колебания штампа с плоским кольцевым или круговым основанием под действием
возмущающего момента, приложенного в вертикальной диаметральной плоскости штампа 132
9.4. Крутильные колебания штампа с плоским кольцевым (круговым) основанием .... 134
9.5. Другие задачи................................................................. 134
Список литературы.............................................................. 135
Раздел 10. Расчет параметров колебаний грунта и зданий,
вызываемых движением поездов метрополитена (В. А. Ильичев)
10.1. Общие сведения о колебаниях, возникающих при движении поездов метрополитена,
и о способах их уменьшения......................................................... 136
10.2. Экспериментальные данные о колебаниях туннелей, грунта, зданий и других объектов,
расположенных вблизи линий метрополитена.................................... . 137
10.3. Расчетная оценка уровня колебаний грунта вблизи туннелей метрополитена .... 138
10.4. Оценка уровня колебаний зданий.............................................. 143
Списоклитературы................................................................... 143
Раздел 11. Колебания фундаментов установок взрывной штамповки и грунта
(В. А. Ильичев)
11.1. Общие сведения.............................................................. 144
11.2. Экспериментальные данные о колебаниях, вызываемых работой установок взрывной
штамповки . . , . ........................................................ 145
11.3. Определение параметров колебаний фундаментов установок взрывной штамповки и
поверхности грунта ............................................................... 146
Список литературы ............................................................. 148
Раздел 12. Расчет сооружений, оборудованных динамическими гасителями колебаний
(Б, Г. Коренев, Л. М. Резников)
12.1. Общие сведения.............................................................. 149
12.2. Линейный ДГК, установленный на системе с одной степенью свободы............. 150
12.3. Многомассовые и нелинейные ДГК при гармоническом воздействии................ 158
12.4. Расчет и гашение колебаний систем с распределенными и дискретными массами . . 161
12.5. Гашение колебаний конструкций и сооружений ................................. 169
Списоклитературы.................................................................. 174
Раздел 13. Аэродинамические способы гашения колебаний высоких сооружений
в ветровом потоке (Л. X. Блюмина, М. Я. Гембаржевский)
13.1. Физика явления ............................................................ 176
13.2. Аэродинамические способы гашения колебаний сооружений....................... 176
Списоклитературы................................................................. 180
Раздел 14. Мелкомасштабное моделирование динамических явлений (И. С. Шейнин)
14.1. Особенности мелкомасштабного моделирования................................... 181
14.2. Подбор модельного материала.................................................. 182
14.3. Проектирование и изготовление модели и контрольных образцов.................. 185
14.4. Определение физико-механических характеристик модельного материала........... 186
14.5. Средства возбуждения и измерения вибраций мелкомасштабных моделей............ 188
14.6. Испытание моделей............................................................ 190
14.7. Пересчет результатов моделирования на натуру . 191
Списоклитературы................................................................... 191
Раздел 15. Динамическая фотоупругость (Н. А. Стрельчук, Г. Л. Хесин)
15.1. Основы метода динамической фотоупругости . . . ............................. 194
15.2. Расшифровка экспериментальных данных......................................... 194
15.3. Примеры применения метода динамической фотоупругости . ...................... 208
Список литературы.................................................................. 210
Грсдметный указатель.............................................................. 211
214
ТАБЛИЦА СООТНОШЕНИЙ МЕЖДУ НЕКОТОРЫМИ ЕДИНИЦАМИ ФИЗИЧЕСКИХ ВЕЛИЧИН,
ПОДЛЕЖАЩИМИ ИЗЪЯТИЮ, И ЕДИНИЦАМИ СИ
Наименование величины Единица Соотношение единиц
подлежащая изъятию СИ с
наименование обозначение наименование обозначе- ние
Сила; нагрузка; вес килограмм-сила тонна-сила грамм-сила кгс тс ГС 1 ньютон 1 кгс да 9,8 Нда 10 Н 1 тс да 9,8-103 Нда 10 кН 1 гсда9,8-10-3 Нда 10 мН
Линейная на- грузка Поверхностная нагрузка килограмм-сила на метр килограмм-сила на квадратный ) метр кгс/м кгс/м2 ньютон на метр ньютон на квадратный метр Н/м Н/м2 1 кгс/м да 10 Н/м 1 кгс/см2 да 10 Н/м2
Давление килограмм-сила на квадратный сантиметр миллиметр водя- ного столба миллиметр ртут- ного столба кгс/см2 мм вод. ст, мм рт. ст. > паскаль Па 1 кгс/см2 да 9,8-104 Па да да 105 ПадаОД МПа 1 мм вод. ст. да 9,8 Па да да 10 Па 1 мм рт. ст. да 133,3 Па
Механическое напряжение Модуль про- дольной упруго- сти; модуль сдви- га; модуль объем- ного сжатия килограмм-сила на квадратный миллиметр килограмм-сила на квадратный сантиметр кгс/м м2 кгс/см2 ► паскаль Па 1 кгс/мм2 да 9,8-10s Па да да 107 Па да 10 МПа 1 кгс/см2 да 9,84 Па да да 105 ПадаОД МПа
Момент силы; момент пары сил килограмм-сила- метр КГС’М ньютон-метр Н-м 1 кгс-м да 9,8 Н-м да да 10 Н-м
Работа (энер- гия) килограмм-сила- метр КГС’М джоуль Дж 1 кгс-мда 9,8 Дж да 10 Дж
Количество теп- лоты калория килокалория кал ккал | джоуль Дж 1 кал да 4,2 Дж 1 ккал да 4,2 кДж
Мощность килограмм-сила- метр в секунду лошадиная сила калория в секун- ду килокалория в час КГС-М/С л. с. кал/с ккал/ч J ► ватт Вт 1 кгс-м/сда9,8 Втда 10 Бт 1 л. с. да735,5 Вт 1 кал/с да 4,2 Вт 1 ккал/ч да 1,16 Вт
Удельная теп- лоемкость калория на грамм-градус Цельсия килокалория на килограмм-гр адус Цельсия кал/(г-°С) ккал/(кг-°С) i джоуль на кило- грамм кельвин Дж/(кг-К) 1 кал/(г-°С) да да4,2-103 Дж/(кг-К) 1 какл/(кг-°С) да да 4,2 кДж/(кг-К)
Теплопровод- ность калория в секун- ду на сантиметр- градус Цельсия килокалория в час на метр-гра- дус Цельсия кал/(с-см -°C) ккал/(ч-м-°С) ,1 ватт на метр- кельвин Вт/(м-К) 1 кал/(с-см-°С) да да420 Вт/(м-К) 1 ккал/(ч-м-°С) да да 1,16 Вт/(м-К)
Коэффициент теплообмена (теп- лоотдачи); коэф- фициент теплопе- редачи калория в секун- ду на квадратный сантиметр-градус Цельсия килокалория в час на квадрат- ный метр-градус Цельсия кал/(с-см2-еС) ккал/(ч-м2-°С) J 1 квадрат- ный метр- кельвин * Вт/(м*-К) 1 кал/(с-см2-°С) да да 42 кВт/(2-К) 1 ккал/(ч-м2-°С) да да 1,16 кВт/(м2-К)
215
ДИНАМИЧЕСКИЙ РАСЧЕТ СООРУЖЕНИЙ
НА СПЕЦИАЛЬНЫЕ ВОЗДЕЙСТВИЯ
СПРАВОЧНИК ПРОЕКТИРОВЩИКА
Редакция литературы по строительным материалам и конструкциям
Зав. редакцией П. И. Филимонов
Редактор Л. И. Круглова
Внешнее оформление художника Метчен i?o
Технический редактор В. Д. Павлова
Корректор Л. С. Лелягина
ИБ № 2938
Сдано в набор 18.02.81,. Подписано в печать 21.07.81. Формат 70X108!/i6
Бумага типограф. № 2 Гарнитура «Литературная» Печать высокая
Усл. печ. л. 18,9 Уч.-изд. л. 23,85. Тираж 25.000 экз. Изд. № А-Х-4736 Зак. № 195 Цена 1 р. 60 к:
Стройиздат, 101442, Москва, Каляевская, 23а
Подольский филиал ПО «Периодика» Союзполиграфпрома при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли
г. Подольск, ул. Кирова, 25
ББК 38.112
Д 46
УДК 624.042.8(031)
Рецензенты: проф. В. Г. Подольский, д-р техн, наук,
проф. Е. С, Сорокин_______
А в т о р ы: | М. Ф. Барштейн, |Я. М. Бородачев, Л, X. Блю-
мина, М. Я. Гембаржевский, Б. Е. Денисов, В. А. Ильичев,
Л. С. Килимник, Б. Г. Коренев, О. В. Лужин, И. А. Никола-
енко, Г, Г. Орлов, С. В. Поляков, Н. Н. Попов, Б. С. Растор-
гуев, Л. М. Резников, Н, А. Оррелъчук, Г. Л. Хесин,
А. И. Цейтлин, И. С. Шейнин.
Научный ре
Динамический расчет сооружений на
специаль-
46 ные воздействия / М. Ф. Барштейн, Н. М. Борода-
чев, Л. X. Блюмина и др.; Под ред. Б. Г. Коренева,
И. М. Рабиновича. — М.: Стройиздат, 1981.—
215 с.— (Справочник проектировщика).
Приведены сведения по прикладной динамике сооружений, отно-
сящиеся к расчету строительных конструкций на специальные динами-
ческие воздействия.. Рассмотрен расчет на сейсмические воздействия,
действие взрыва, нагрузки, возникающие при движении мостовых
кранов, вызываемые полетом сверхзвуковых самолетов и др. Включены
разделы по динамической фотоупругости и моделированию. Дан рас-
чет сооружений, оборудованных динамическими гасителями колебаний.
Для инженеров-проектировщиков и научных работников проект-
ных и научно-исследовательских организаций.
30205—315
—---------- 81—81.
047(01)—81
3202000000
ББК 38.112
6С1
© Стройиздат, 1981