Министерство сельского хозяйства
Российской Федерации
Новосибирский государственный
аграрный университет
А.Д. Дементьев, Л.А. Назаров, Л.А. Назарова
ПРИКЛАДНЫЕ ЗАДАЧИ
ТЕОРИИ УПРУГОСТИ
УЧЕБНОЕ ПОСОБИЕ
Новосибирск 2002

УДК 539.3
ББК 22.251
Д-302
Авторы: доктор физ. -мат. наук, проф., А.Д. Дементьев, доктор
физ. - мат. наук Л.А. Назаров, доктор физ. - мат. наук
Л.А. Назарова.
Прикладные задачи теории упругости./ Новосиб. гос. аграр. ун-т.
Авт. А.Д. Дементьев, Л.А. Назаров, Л.А. Назарова,-Новосибирск,
2002.- 224 с.
В учебном пособии авторы на основе общей классической
теории упругости дают многочисленные приложения решений
задач по анализу устойчивости и разрушения элементов
конструкций и природных объектов.
Учебное пособие предназначено для студентов
инженерных специальностей и аспирантов.
Рекомендовано Министерством сельского хозяйства
Российской Федерации в качестве учебного пособия для
студентов и аспирантов высших учебных заведений инженерных
специальностей.
Библиогр. 7. Ил. 66.
Рецензенты: Доктор физико-математических наук,
профессор АВ. Федоров.
Доктор физико-математических наук,
профессор А Ф. Ревуженко.
Издано при финансовом содействии ЗОА «Агрокомцентра»
ISBN 5-94477-022-8
©А.Д. Дементьев, Л.А. Назаров, Л.А. Назарова, 2002

ВВЕДЕНИЕ
Предмет теории упругости и ее место в механике
деформируемого твердого тела
Классическая теория упругости сохраняет своё почётное
место в ндуке о поведении деформируемого твердого тела. Её
исходные определения являются общими для всех разделов
этой науки, а методы и постановки, решения задач служат
образцами. Успехи и достижения теорий пластичности,
ползучести, упруго - вязкой среды, разрушения твёрдых тел не
заслоняют значения методов теории упругости для обоснования
приёмов расчёта напряженно-деформированного состояния в
строительных сооружениях и машинах, составляющих
существенную часть наук о сопротивлении материалов и
строительной механики.
Сопротивление материалов, теоретическая и
строительная механика и прочность конструкций развиваются
не изолированно от других дисциплин. И наиболее тесно они
связаны с теорией упругости. Влияние этой науки на развитие
прочностного цикла механики носит принципиальный характер.
Для теории упругости подчинённость аналитического
аппарата практическим целям не характерна, она не скована
необходимостью дать краткую сводку рекомендаций к расчёту.
з

Это позволяет провести более углублённую проработку не
только конкретных задач, но в первую очередь - общих задач и
методов.
Из сказанного не следует, конечно, что результаты,
полученные методами теории упругости, не могут без
надлежащей обработки получить практического применения. В
тех случаях, когда решение получено в достаточно простой и
общей форме, оно сразу может быть включено в арсенал
средств для практических расчётов. Достаточно вспомнить
такие классические задачи теории упругости, как контактная
задача, нашедшая прямое приложение, хотя бы в расчёте
шариковых подшипников, как задача о кручении
призматического бруса или задача определения напряжений
вблизи отверстий и выточек и многие другие.
Теория упругости богата не только множеством решённых
задач. Трудами Пуассона, Сен-Венана, Клебша созданы основы
механики деформируемых систем и заложены принципы,
соблюдения которых стало нормой во всех дисциплинах, прямо
или косвенно связанных с вопросами прочности.
Когда мы пользуемся, например, технической теорией
изгиба балок, то часто забываем, что её достоверность
обеспечена многочисленными исследованиями, проведенными
методами теории упругости. Именно эти исследования дают нам
ориентировку в таких вопросах, как пренебрежение вторичными
напряжениями, применимость или неприменимость гипотезы
плоских сечений, да и во многих других. Теория упругости, таким
4

образом, не только обогащает сопротивление материалов
новыми задачами и новыми постановками проблемы, но,
образно говоря, обеспечивает тылы в тех простейших методах,
которыми мы пользуемся повседневно. Можно смело сказать:
не будь теории упругости, сопротивление материалов
напоминало бы удручающий свод прочностных нормативов.
Среди наук, в области теории деформируемого твёрдого
тела, за последние десятилетия возникли и развились новые
дисциплины, такие как теория пластичности и теория
ползучести. Таким образом, дисциплин, занимающихся
вопросами механики деформируемых тел, очень много. По
степени теоретичности и прикладной направленности они
образуют целую гамму оттенков. Среди этих дисциплин теория
упругости занимает одно из основных мест.
Историческая справка
Теория упругости сформировалась, как один из важных
разделов математической физики в первой половине XIX века.
До этого времени трудами учёных XVII и XVIII веков - Галилея,
Мариотта, Гука, Бернулли, Эйлера, Кулона и других - была
довольно детально разработана теория изгиба тонких упругих
стержней. В начале XIX века Лагранжем и Софи Жермен было
дано решение задачи об изгибе и колебаниях тонких упругих
пластинок. Некоторые особенности таких тонких упругих тел
позволили значительно упростить постановку и решение задач о
5

деформировании под действием внешних сил, не вникая
особенно глубоко в существо явлений, происходящих в
материале. Начало XIX века ознаменовалось огромными
успехами математического анализа, обусловленными отчасти
множеством важных задач, возникших в физике, потребовавших
применения сложного математического аппарата и дальнейшего
развития его. Это и послужило основой для возникновения
особого направления в физике, названного математической
физикой. Среди множества проблем, вставших перед этой
молодой дисциплиной, необходимо отметить потребность в
глубоком исследовании свойств упругих материалов и в
построении математической теории, позволяющей возможно
полно изучать внутренние силы, возникающие в упругом теле
под действием внешних сил, а также деформацию тела, т.е.
изменение его формы. Этого рода исследования оказались
крайне необходимыми также для удовлетворения запросов
быстро развивающейся техники в связи со строительством
железных дорог и машиностроением. Запросы эти вызывались
необходимостью создать теоретические методы расчёта частей
сооружений и машин на прочность. Уже в 1825 г. крупный
французский инженер и учёный Навье выпустил "Курс лекций по
сопротивлению материалов", основанный на имевших к тому
времени экспериментальных данных и приближённых теориях.
В России аналогичный курс Н.Ф. Ястржембского появился в
1837 г.
6

Приоритет в создании основ теории упругости
принадлежит французским математикам и механикам Коши,
Навье и Пуассону, получившим основные дифференциальные
уравнения этой теории. Нельзя не отметить, что при разработке
её встретилась принципиальная трудность. Дело в том, что
математический анализ того времени был построен на понятии
непрерывного геометрического пространства, в котором можно
рассматривать бесконечно малые отрезки и на этой основе
ввести процессы дифференцирования и интегрирования. Между
тем общепринятая ньютоновская молекулярная теория
строения тел представляла их как дискретные среды,
состоящие из отдельных частиц, связанных между собой
силами взаимного притяжения и отталкивания. Оказалось
весьма трудным обосновать применимость к таким средам
аппарата математического анализа, который был существенно
связан с понятием о непрерывных функциях, способных
получать как угодно малые, т.е. бесконечно малые, приращения,
и с возможностью перехода к пределу при их суммировании, т.е.
при интегрировании. Вследствие этого первые работы по
математической теории упругости вызывали большие
дискуссии, и обоснованность подвергалась сомнениям. Однако
то обстоятельство, что даже в чрезвычайно малом объёме,
мысленно выделенном из тела, содержится огромное
количество молекул, навело исследователей на мысль
привлечь закон больших чисел и применить метод, который в
дальнейшем получил название статистического. Это позволило
7

перекинуть мост между непрерывным пространством
математического анализа и твёрдым телом, как дискретной
средой. Мощный аппарат математики стало возможным
применить к созданию новой области физики.
Важность приложений теории упругости в физике и
технике и выяснившаяся большая трудность решения
поставленных задач с точки зрения математического анализа
привлекли, к этой новой отрасли наук внимание крупнейших
исследований XIX и XX веков. Помимо названных основателей
теории упругости Коши, Навье и Пуассона, можно назвать таких
выдающихся учёных, как М.В. Остроградский, Ламе
(выпустивший в 1852 г. первый курс лекций по теории
упругости), Клайперон, Сен-Венан, Грин, Максвелл, В. Томсон
(лорд Кельвин), Релей, Мичелл, Матье, Ф.С. Ясинский,
СП. Тимошенко, Г.В. Колосов, Н.И. Мусхелишвили и многие
другие.
Бурный прогресс механики деформируемых сред в XX
веке резко отличается от более спокойного её развития в
предшествующем периоде. Разработанная математиками
(Коши, Пуассоном, Лагранжем и др.) и инженерами (Навье,
Ламе, Сен-Венаном и др.) теория упругости долгое время
рассматривалась как раздел математической физики, а не как
инструмент для практических расчётов. Например, решение
проблемы устойчивости стержня, полученное Эйлером ещё в
XVIII веке, считалось математическим парадоксом. Взамен
использовались грубо эмпирические формулы Бресса и др. Не
8

находили применение ни теория изгиба пластин и оболочек
Лагранжа - Кирхгофа, ни теория пластического течения Сен-
Венана-Леви. Для решения практических задач с успехом
создавались и использовались элементарные методы
сопротивления материалов.
Развитие промышленности и усложнение строительных
конструкций, машин, механизмов и их агрегатов потребовали от
инженеров создания уточнённых методов расчёта. Появляется
замечательная плеяда учёных-инженеров, свободно
пользующихся современным аналитическим аппаратом для
решения сложных технических проблем. В России это
А.И. Крылов, И.Г. Бубнов, В.Г. Галеркин, СП. Тимошенко,
Л.С. Лейбензон, П.Ф. Папкович и др., в Германии - Л. Прандтль,
его ученики и сотрудники - Т. Карман, Р. Мизес и др., в
Швейцарии - А. Стодола, в Австрии - Э. Мелан и т.д.
В предлагаемом учебном пособии авторы на основе
общей классической теории упругости дают многочисленные
приложения решений задач теории упругости к анализу
устойчивости и разрушения элементов конструкций и природных
объектов. Книга снабжена многочисленными иллюстрациями,
помогающими глубже понять механический смысл описываемых
процессов.
9

ГЛАВА 1
ОСНОВЫ ТЕОРИИ УПРУГОСТИ
§ 1.1. Теория напряжений
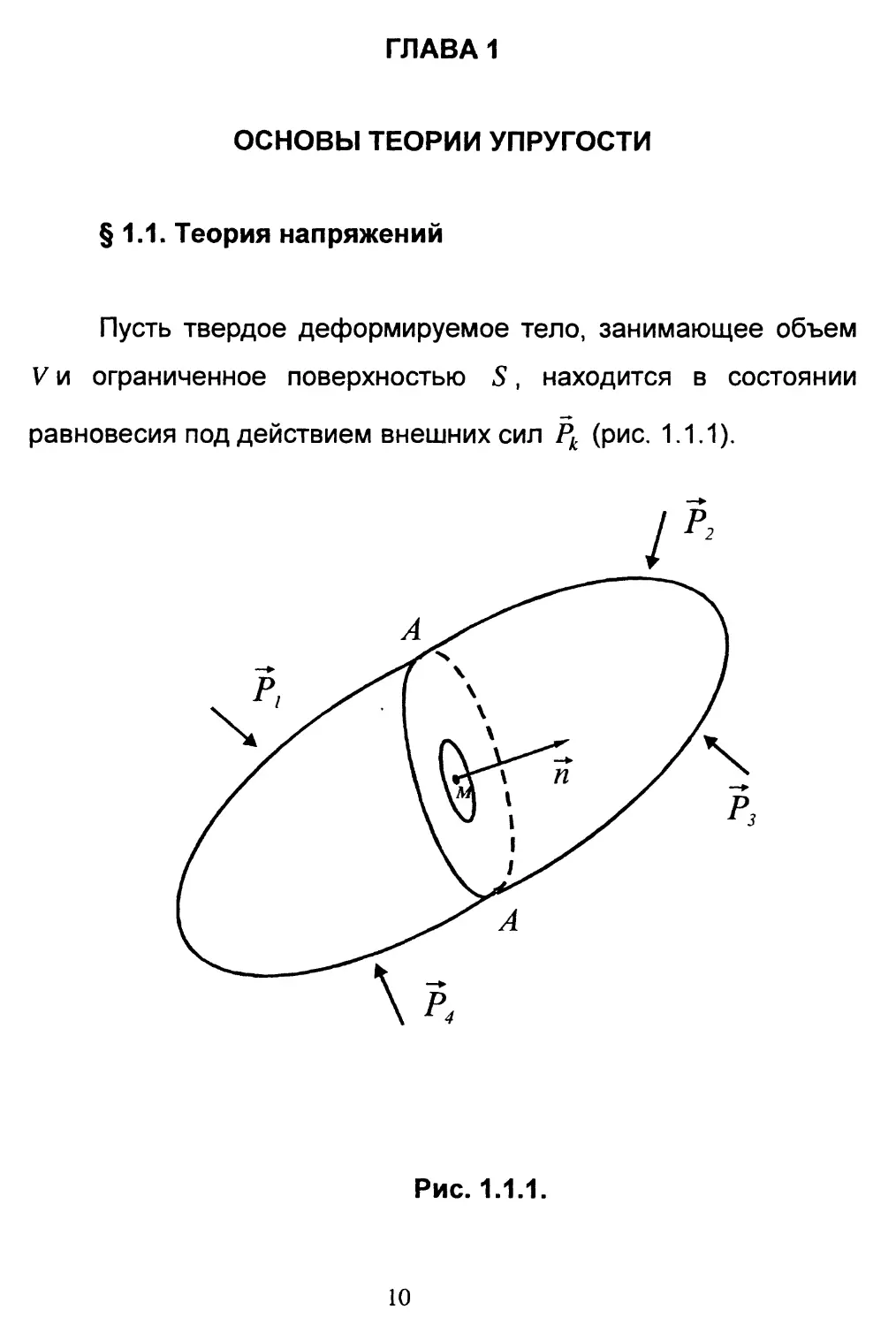
Пусть твердое деформируемое тело, занимающее объем
V и ограниченное поверхностью S, находится в состоянии
равновесия под действием внешних сил Рк (рис. 1.1.1).
Рис. 1.1.1.
ю

Под действием Рк в теле возникают внутренние силы
взаимодействия. Разделим мысленно тело на две части
поперечным сечением АА (рис. 1.1.1).
Рассмотрим одну из этих частей (рис. 1.1.2) Она находится
в равновесии под действием внешних и внутренних сил,
распределенных по сечению АА, которые представляют
действие материала отброшенной части объема на оставшуюся
часть V. Пусть эти силы распределены по сечению
непрерывным образом. Выделим в сечении АА в окрестности
стй(М,и)
Рис. 1.1.2.
некоторой точки М малую площадку AS с нормалью п.
Обозначим результирующую силу на этой площадке через AFn
Величина
и

AF
<7л(М,й) = lim n
(1.1.1)
Д5->о AS
называется вектором напряжений (иногда употребляют термин
"вектор усилий") на площадке с нормалью Я в точке М.
Очевидно, что величина и ориентация вектора дп зависят от
ориентации площадки AS , т.е. направления п (векторы дп и Я,
вообще говоря, не коллинеарны).
Рассмотрим объемный элемент, включающий точку М,
две грани которого параллельны и имеют нормали Я и -Я
(рис. 1.1.3).
п
п
Рис. 1,1.3.
12

Запишем закон движения этого элемента
4
(<тй + б_п)(Ы)2 + ФАЛ(А/)2 + ^fjAhM = ma, (1.1.2)
где Ф - массовые силы, действующие на каждый элемент тела,
fj - силы по другим граням параллелепипеда, т = pAh(Al)2 -
масса элемента, р - его плотность, а - ускорение центра
масс.
При стягивании элемента в бесконечно тонкую пластинку
(ДА —> 0) из (1.1.2) следует, что
<7„(М,-Я) = -а;ДМ,Я). (1.1.3)
Замечание. Так как через любую точку, лежащую внутри
объема, можно провести бесчисленное множество
элементарных площадок, то говорить о векторе усилий в точке
бессмысленно, нужно обязательно указать направление
нормали к площадке, на которой рассматривается вектор
напряжений дп (индекс п "идентифицирует" площадку).
Формула Коши
В декартовой системе координат рассмотрим объемный
элемент твердого тела AV , изображенный на рис. 1.1.4.
Пусть заданы вектора напряжений на трех взаимно
ортогональных площадках д_х, д_у и 6_z. Выясним, как связан
13

?а
Рис. 1.1.4.
с ними вектор напряжений дп на произвольно ориентированной
пло-щадке с нормалью Я. Составим уравнение движения
элемента AV:
_ AyAz _ AxAz _ Дх/Уу _ Ar -г AxAyAz _
сг —— + о_v + сг_7 - + сг„AS + Ф — = та, (1.1.4)
* 2 у 2 z 2 6
где т = pAxAyAz/6 - масса А V, AS - площадь наклонной
площадки с нормалью Я. Перенесем предпоследнее слагаемое
в левой части (1.1.4) в правую часть, воспользуемся (1.1.3) и
14

"стянем" элементарный объем (Ах —> 0, Ду —> 0, Дг —> 0) в
точку, что в пределе дает
_ AyAz - AxAz - AxAy
* 2AS у 2AS z 2AS
Из этого соотношения "выпали" члены та и ФДдДуДг/б,
поскольку они являются величинами третьего порядка малости
(оставшиеся члены имеют второй порядок малости). Из курса
аналитической геометрии известно, что
_ AyAz AxAz _ , AxAy
cos(n,x) = , cos(n,y)= , cos(w,z) = ,
2 AS 2 AS 2 AS
и мы получаем формулу Коши
6п = (Jxcos(n,x) + crycos(n,y) + (7zcos(H,z), (1.1.5)
с помощью которой вектор напряжений на произвольно
ориентированной площадке можно выразить через вектора
напряжений на трех взаимно ортогональных площадках.
Полученное векторное равенство (1.1.5) можно
спроектировать на оси декартовой системы координат
®пх ~~ ® хх^пх О ухСпу ~*~ ® zxCnz '
®пу ~ &хуСпх ~*~ & ууСпу ~*~ & zyCnz '
®nz ~ xzCnx "*~ ®yzCny ~*~ ®zzCnz '
Здесь и в дальнейшем символ стп означает косинус угла
между осями (направлениями) т и Я.
15

Величина опт, таким образом, имеет следующий
механический смысл - это проекция на ось т вектора
напряжений, действующего на площадке с нормалью п .
Величины аи (i = x,y,z) будем называть нормальными
напряжениями, а а у (i^j) - касательными. Положительные
направления компонент касательных напряжений на грани
кубического элемента принимаются совпадающими с
положительными направлениями координатных осей, если
растягивающие нормальные напряжения для тех же граней
совпадают с положительными направлениями осей и наоборот.
z t
°>у
i
i
\
G \
%
\
°>:
.<*=
i\
\ ''°Л
о»
1 1
aVY4
хх N
\
\
\]
У
\
Рис. 1.1.5.
16

На рис. 1.1.5 приведены положительные направления
напряжений для двух граней. На верхней грани положительные
направления совпадают с положительными направлениями
осей, на боковой грани - наоборот (из-за того что нормаль Я к
этой грани направлена в сторону отрицательных у).
Закон парности касательных напряжений
Составим уравнение движения объемного элемента,
вращающегося как абсолютно твердое тело вокруг оси,
проходящей через точку С, параллельной оси абсцисс
(рис. 1.1.6).
Считается, что нормальные напряжения приложены к
центру граней, т.е. они не дают вклад в уравнение для
моментов. Касательные напряжения на каждой грани,
умноженные на площадь, порождают силы, дающие момент
относительно оси, проходящей через точку С . Так что
J (о =
(\
(УуАУ
2 yz
AxAz-
(I Л
AxAz
(/ - момент инерции, со - угловое ускорение). При стягивании
элемента в точку левая часть уравнения имеет более высокий
порядок малости (т.к. /~((Ду)2 + (Дг)2^УуДг), чем члены в
правой части, т.е.
\°,£у
\
ДхДг-
(I Л
Л
AxAz = 0,
17

откуда а =<т
A z
vv
J*
а.
а.,.
f^z
L°*
УУ
У
Рис. 1.1.6
Аналогично можно получить два других равенства:
°yx=Gxy* °xz =Gzx-
Таким образом, для напряженного состояния справедлив
закон парности касательных напряжений Gtj = сгу7, и
количество напряжений, действующих на координатных
плоскостях, уменьшается до шести.
18

Преобразование компонент тензора напряжений
при повороте системы координат
Выясним, как изменяются компоненты ац при переходе от
одной декартовой системы координат к другой. Пусть задана
ориентация "новой" системы {X , У, Z) по отношению к "старой"
(х, у, z) через направляющие косинусы (Табл. 1.1).
Таблица 1.1.
X
Y
Z
X
сХх
CYx
CZx
У
СХу
сгу
CZy
Z
CXz
CYz
C2z
По формуле Коши (1.1.5) можно записать вектор
напряжений на площадке с нормалью, совпадающей по
направлению с осью X
°Х = °хСХх + °усХу + °zCXz •
(1.1.6)
Спроектируем это равенство на ось X
(°х)Х =(dx)xCXX^^y)xCXy^(^z)xCXz' (1-1-7)
В "старой" системе координат вектор ox = faxx,crXy,CTxz), тогда
его проекция на ось X
(°х )Х = °ххсХх + axyCXy + °xzCXz ' (1 ■1 8)
19

Аналогично:
(ду )х = аухсхх + °уусху + ayzcxz - С •1 -9)
fo )Х = С^СХх + °zyCXy + <?zzCXz ■ (1.1.10)
Подставляя полученные равенства в (1.1.7) и учитывая закон
парности, получаем
°ХХ = <*xAx + OyyCly + °,А. +
2ахуСХхСХу + 2<JxzCXxCXz + 2(JyzCXycXz
Теперь спроектируем векторное равенство (1.1.6) на ось Y
(°Х )у = (°х\сХх + {°у)уСХу + {°z\CXz •
Входящие сюда проекции можно выписать по аналогии с
(1.1.8) — (1.1.10)
(°х \ = °ххсУх + axyCYy + GxzCYz .
(*У X = аУ*С¥х + °УУСуУ + °УгСП '
(дг \ = <*zxCYx + azyCYy + azzCYz •
и, таким образом,
aXY = °xxCXxCYx + ayycXycYy + а zzCXzCYz +
OxyiCxjfYy +cYxcXy)+Vxz(CXxCYz +%cfc)+ (1.1.12)
Gyz(CXyCYz + cYycXz)-
По такой же схеме можно получить соответствующие
формулы для пересчета остальных компонент напряжений оп,
°zz> °xz и gyz - чеРез значения a{j в "старой" системе
20

(х, у , z). Закон преобразования компонент типа (1.1.11), (1.1.12)
можно представить в общем виде
°ki=cikcij°ij (ij = x,y9z; kJ = XJ,Z). (1.1.13)
В правой части (1.1.13) опущен знак суммирования по
повторяющимся индексам (правило Эйнштейна).
Набор величин, подчиняющихся закону преобразования
(1.1.13), называют тензором второго ранга. Компоненты
напряжений являются, таким образом, компонентами тензора
напряжений второго ранга, который удобно записать в
матричной форме
а =
где по диагонали стоят нормальные напряжения, а вне
диагонали - касательные. Матрица 8, вследствие парности
касательных напряжений, является симметричной.
Формула Коши, таким образом, представляет собой
скалярное произведение тензора напряжений а на вектор
нормали п = (cnx,cnrcnz)
бп=дп.
Соотношение (1.1.13) также можно представить в
'матричной нотации"
а, =А*(ТА, (1.1.14)
ахх
аху
к°хг
°ху
Оуу
°уг
°хг
ауг
° и)
21

где А -матрица, составленная из направляющих косинусов
(Табл. 1), звездочка означает транспонирование, бх -тензор
напряжений в системе координат (X,F,Z). Заметим, что А -
ортогональная матрица (А* = Л"1, det A = 1).
Главные напряжения
Найдем площадки (суть, нормали т), на которых вектор
напряжений дт коллинеарен т. Матрица д в этом случае
должна содержать только диагональные члены: проекции дт на
ортогональные к т направления по условию равны нулю, т.е.
нет касательных напряжений.
Итак, пусть существуют три взаимно перпендикулярных
направления таких, что на ортогональных им площадках,
отсутствуют касательные напряжения. Возьмем любое из этих
направлений, обозначим вектор усилий 6т и по формуле Коши
(1.1.5) запишем
°т = °хстх + °усту + °zCmz ' (1.1.15)
Спроектируем (1.1.15) на координатные оси, тогда
ПС = (7 С -\- (У С 4- СТ С
^ m^tnx w xx^mx ' ^ху^ту ' w xz mz '
amCmy = axyC,nx + °'yyCmy + GyzCmz < (1.1.16)
®mCmz ~~ xzCmx "*" ®yzCmy "*" ° zzCmz '
22

Система (1.1.16) имеет нетривиальное решение, если ее
определитель равен нулю
о
ху
ху
УУ
yz
yz
= 0
ИЛИ
где
<т:
№+^,-/з=0
(1.1.17)
!\ =<JXX+<JW+(J7J>
УУ
h = axxGyy + °xxGzz + GyyGzz -а1у- 0lz " a\z
h = GxxGyyGzz + 2GxyGxzGyz ~ GxxG)z ~ GyyGxz
2
zz^xy •
-CJ^G
Коэффициенты кубического уравнения (1.1.17) называются
инвариантами тензора напряжений, поскольку не зависят от
системы координат, в которой записан д. В этом можно
убедиться непосредственно, воспользовавшись (1.1.14).
Например,
deter, = det[A*&A)= det A*det(7det A = deter = /3
Напряжения ат, являющиеся корнями (1.1.17),
называются главными напряжениями (как правило,
обозначаются ох, сг2, сг3), а координатные оси базиса
(пространства /?3), в котором & имеет диагональный вид, -
главными направлениями тензора напряжений.
23

Заметим, что (1.1.17) всегда имеет три действительных
корня в силу симметрии а .
Таким образом, напряженное состояние в какой-либо
точке твердого тела можно описать либо с помощью шести
величин Oij в произвольной декартовой системе {x,y,z)> либо с
помощью трех значений главных напряжений стх, сг2, сг3 и
ориентации (т.е. трех направляющих косинусов) одного из
главных направлений (остальные два получаются
автоматически из условия ортогональности).
§ 1.2. Теория деформаций
Анализ параметров, характеризующих деформированное
состояние тела проведем последовательно для одно-, двух- и
трехмерной ситуаций. Сначала на простых моделях выясним их
физический смысл, а затем выпишем общую теорию. Отметим,
что такой анализ основан только на геометрических подходах,
не связан с напряженным состоянием и справедлив для любой
сплошной среды.
Одномерный случай. Пусть среда "расположена" вдоль
части оси х (рис. 1.2.1). Выберем две близкие точки М}(х) и
Д(х + Ах) на расстоянии Ах друг от друга. Приложим вдоль оси
некоторую силу F. Точка М{ под действием F получит
смещение их(х) и "перейдет" в точку М2(х + их(х)), а Л, - в
24

А2(х + Ах + их(х + Ах)). Расстояние M2A2 = Ax + Aux, где
Aux = ux(x + Ax)-ux(x) - приращение смещения.
Относительное изменение длины МХАХ можно представить в виде
х х+и(х) х+Ах х+Ах+и(х+Ах)
• • • • ►
Му М, А; А,
Рис. 1.2.1.
—^ — = —- = —±- + о(Ах), (1.2.1)
MXAX Ax dx
где остальные члены имеют более высокий порядок малости по
сравнению с Ах. Из (1.2.1) ясно, что функция их(х) должна
быть, по крайней мере, дважды непрерывно
дифференцируемой.
Назовем здесь мерой изменения формы {деформацией)
е^ предел относительного изменения длины МХАХ при
уменьшении его начального размера
Аих диг
hm —i = -rJL. (1.2.2)
'XX
Ах-^о Ах дх
Физический смысл индекса "хх" будет пояснен ниже.
25

Двумерный случай. Пусть твердое тело V занимает часть
плоскости Оху. Рассмотрим "волокно" МХСХ длины Дг,
ориентация которого задается углом ср (рис. 1.2.2) так, что
Ах = Arcoscp, Ay = Arsin(p. (12.3)
Выпишем координаты основных точек:
Мх(х9у), Ax(x + bx,y)t Вх(х,у + Ау), Сх(х + Ах,у + Ау).
i
в,
>s
<
У
их(х+Ах,у+Ау)
^>^С\
их(х,у+Ьу\^^
Г ~~г2
[ I с, 1
^
&
Н
а
■ш ж I
м2
/ v \л
^ \ф !
^ 1 1
А2
^
4
+
у+Ау)
+
а
X
[ ^
Mi
Ах
А,
Рис. 1.2.2.
26

Приложим к V некоторые нагрузки, в результате эти точки
"перейдут" в:
Мх -> М2(х + их(х,у),у + иу(х,у));
Ах -> А2(х + Ах + их(х + Ах, у), у + иу(х + Ах, у)) ]
Вх-> В2(х + их(х,у + Ау),у + Лу + иу(х,у + Ау))\
Сх-^С2(х + Ах + их(х + Ах,у + Ау), у + Ау + иу (х + Ах, у + Ау)),
где и^, иу - компоненты вектора смещений.
Определим, как и раньше, меру деформаций -
относительное изменение длины МХСХ
«.*.С-".С, (1.2.4)
Выпишем координаты векторов:
М2Л2 ^Дх + Д^и^Ди);
М2Я2=(Д",Ду + Дуиу); (1.2.5)
М2С2 =(Ах + Аих,Ау + Аи )
и, воспользовавшись соотношениями
Дх/=|^Дх + о(Дд:)|
Ayf = —Ay + o{Ay),
Af = AJ + Ayf,
27

получим
М2С2 = J(Ax)2+(Ay)2+2Sl+S2 ,
(1.2.6)
где
ди.
s'=17(Ax)+2
(диг ди Л ди
—± +—у- \АхАу + —^(Ау)2, (1.2.7)
ду дх I ду
S2 =
(диЛ
кдх;
(Ах)2+2
дих дих диу диу ~\
V
ш:Лу +
(ЪиЛ
дх ду дх ду
Теперь подставим (1.2.6), (1.2.7) в (1.2.4) и учтем (1.2.3)
v J j
(ЬуУ
e = ^\ + 2Sx+S2 -1,
— ди
s{ =
—-cos2 <р + —
дх 2
дих ди Л
—- +—-
ду дх
ди
sin фcosф + ——sin ф , (1.2.8)
ду
S2 =
(диЛ 2
COS ф +
дх
V J
3wv 3wv duv диЛ
~x "™x _|_. - У У
sin 2(p +
(duA
j
v J J
sin q>.
дх ду дх ду
Соотношения (1.2.8) - основные в теории деформаций.
Предположим, что все частные производные от смещений
малы
ды;
дх
«1,
ди;
ду
«1 (i = x,y)
и разложим (1.2.8)i в ряд Маклорена
(1.2.9)
(1.2.10)
28

Пусть "волокно" MlCl первоначально ориентировано по
оси х (ср = 0), тогда из (1.2.10)
ox
Аналогично для ориентации МХСХ по оси у (ф = л/2)
«««-if (1Z12)
Таким образом, деформация еп означает относительное
удлинение . (или укорочение) "волокна", изначально
ориентированного в направлении i, в том же направлении.
Условия (1.2.9) означают малость деформаций (т.е. мы
рассматриваем геометрически линейную теорию). Они
выполняются во многих ситуациях, возникающих на практике.
Оценим, например, величину вертикальной деформации е^
скального массива у подошвы горы высотой h = 1 км. Как будет
показано в §2.2, напряжение при этом равно ozz=pgh (p -
плотность, g -ускорение свободного падения), тогда на
основании закона Гука (§ 1.4)
е72 =^=0.0003,
zz E
если р=3000кг/м3, а модуль Юнга £,=100ГПа
{Приложение 4).
Выясним теперь, как изменяется величина изначально
прямого угла АХМХВ{ (между осями х и у) после деформации:
29

(
sin
7Г
\
--/A2M2B2
VZ J
M2A2-M2B2
11 2 2 -{при условии (1.2.9)}
M2A2
M2B2
-—£- +
71
^-^{угол мал!}--
ay дх 2
-ZA2M2B2.
Эту величину обозначим 2е и назовем сдвигом между
осями х и у. Здесь возникает вполне законное недоумение по
поводу термина "сдвиг", который подразумевает некоторое
движение (однокоренное слово!), т.е. величину размерности
длины. Можно предложить следующую интерпретацию.
У
1
1 ^
\
\
\
\
X
►
а
У
т" Ъ
—►
Рис. 1.2.3.
30

Пусть мы имеем штабель досок (рис. 1.2.3а). Сдвинем
каждую доску друг относительно друга на одинаковую величину
(рис. 1.2.36). Суммарный результат такой операции - изменение
ориентации (угла!) оси у .
Трехмерный случай. Пусть тело V занимает некоторую
область в пространстве. Рассмотрим "волокно" - вектор
МХСХ , проекции которого на координатные оси Ах, Ау и Az.
После нагружения V некоторыми силами МХСХ "перейдет" в
М2С2 ={Ax + Aux,Ay + Auy,Az + Auz),
где u=(ux,uy,uz) вектор смещений.
Предположим малость частных производных
«1 (i = x,y9z) 1.2.13)
\dui
дх
«1,
ди(
"э7
«1,
Эй,
и, пренебрегая их произведениями, вычислим
М2С2
2 (. „диЛ
1 + 2^^
дх
|(Дх)2 +
( диЛ
1 + 2—^-
ду
(Ау)2 +
(дих диЛ
—i + —I
ду дх .
(
ДхД;у +
диг ди, |
dz дх
|AxAz +
1 + 2^
dz
\
(Az)2 +
ГЭ"У диЛ
■ + ■
dz ду
AyAz,
или
M2C2
МХСХ
~2 1Х<А>А<г.
(1.2.14)
p,q=x,y,z
где
31

(дип ди.
р.+. *
dq dp
(1.2.15)
Можно показать, что величины epq имеют тот же
физический смысл, что в двумерном случае. Кроме того, из
(1.2.15) следует симметрия
epq=eqp (1.2.16)
по индексам.
Выясним, как изменяется epq при повороте системы
координат. Пусть "новые" координаты X,K,Z связаны со
"старыми" x9y9z посредством Табл. 1.1 § 1.1., тогда
АР= ^сРрАр, AQ= ^с^Ад(Р^ = Х^^). (1.2.17)
p=x,y,z q=x,y,z
Длина векторов не зависит от выбора системы координат,
поэтому из (1.2.14)
X еРд*Р*Я = S sPQAPAQ =
p,q=x,y,z P,Q=X,Y,Z
{учитывая (1.2.17)}= £ "ZcPpcQqePQ
\ApAq,
откуда
еря= Е
CPpCQq£PQ ■
P,Q=X,Y,Z
т.е. epq - тензор второго ранга - тензор деформаций, причем
на основании (1.2.16) - симметричный. Его можно записать в
матричном виде
32

£ =
^xx i xy i xz
' xy УУ ' У?-
У xz Y vz ezz
Ура = °'5eva ПРИ Р ф Я
РЯ
'РЯ
Условия совместности
Выпишем все компоненты е в явном виде
3wv
диЛ
Р =2 ~ Р — — Р
** дх ' уу ду ' г
duz
dz '
(1.2.18)
еху-2\
lfdu, диу^
■ + ■
ду дх
1.
xz 2
диг ди,
>£yz~2
\(duv диЛ
- + -
dz ду
dz дх
Видно, что они выражены через три смещения, поэтому
являются зависимыми. Непосредственной проверкой можно
убедиться, что имеют место соотношения
- +
ду2
д28
УУ
dz2
эч
дх2
д2е„
+
• + ■
дх2
^Ч
а/
д2е
уу _
= 2
д2е
*У
= 2-
дхду '
dydz '
д2е
хх _ 2 xz
dz2 dxdz
(1.2.19)
dydz dx
( деУ* | dE*z | дЕ*У
дх ду dz
33

д'вуу _д( де,
• + ■
де„, деЛ
'ху
yz
dxdz ду[ ду dz
д2е.
д( Эе„ _ деуг деЛ
дхду dz
-ху
dz
+ -
■ + -
дх ду
которые называются условиями совместности Сен-Венана
(тождествами Сен-Венана). Их легко запомнить, поскольку
получаются одно из другого круговой заменой индексов
jc I—> >^ I—> z i—> jc .
Движение тела как жесткого целого
Из курса теоретической механики известно, что
перемещение и любой точки M(x,y,z) абсолютно твердого
тела можно найти, зная перемещение й° его центра тяжести
M0(jt0,)>0,z0) и вектор поворота ю = (cox,coy,a)z) относительно
М0 по формуле
й = й° + гх(д, (1.2.20)
где г =М0М =(x-x0,y-y0,z-z0). Перепишем (1.2.20) в
развернутом виде
их = их + (у - y0)coz - (z - z0)coy,
иу = u°y + (z - z0)cox -(x- x0)o)z,
uz = u°z + О - x0)coy -(y- y0)cox,
34

и подставим в (1.2.18), тогда
£рд=0 (p,q = x,y,z).
Это значит, что движение тела как жесткого целого не меняет
его деформированное состояние.
§ 1.3. Уравнения движения
Несмотря на то, что предмет настоящей книги - статика
твердого деформируемого тела, выведем уравнения движения
элемента. Уравнения же равновесия получим как частный
случай.
35

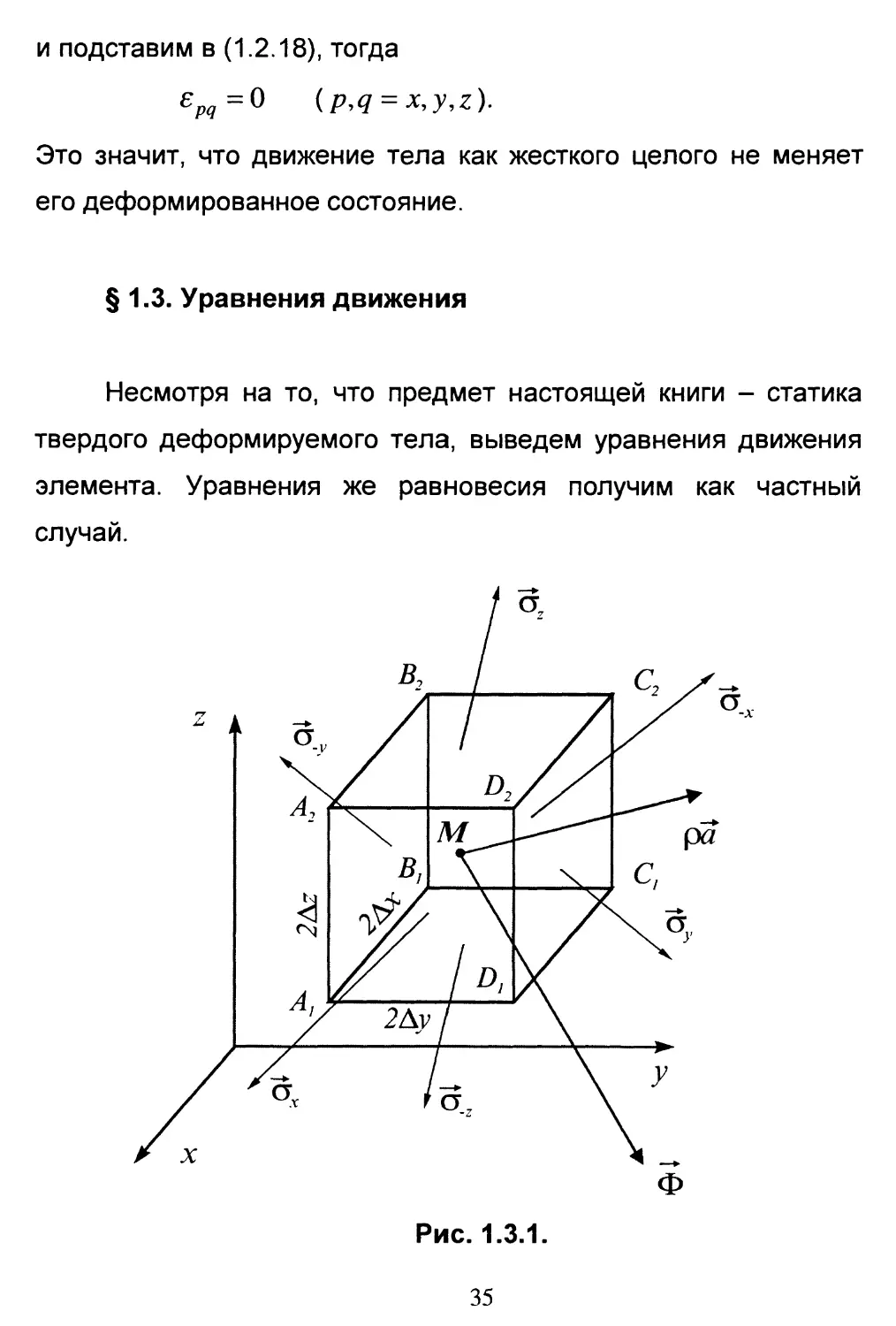
Введем, как обычно, декартову систему координат (x,y,z)
и рассмотрим элементарный объем AV - параллелепипед со
сторонами1 2Ах,2Ау и 2Az, центр которого расположен в
произвольной точке M(x9y,z). Напряженное состояние среды
определено тензором а^ (причем функции Оу(х9у,г^) должны
иметь непрерывные частные производные по пространственным
переменным; t- время), тогда на грани элемента AV действуют
следующие векторы напряжений, приведенные к центрам
соответствующих граней (рис. 1.3.1):
на AXBXCXDX o_z(x,y,z-AzJ)\
на A2B2C2D2 az(x,y,z + AzJ)]
на АХА2В2ВХ a_y(x,y-Ay,zJ)',
на CXC2D2DX dy{x,y + Ay,z,t)\
на СХС2В2ВХ a_x(x-Ax,y,z,t)\
на AXA2D2DX <Jx(x + Ax,y,z,t).
На AV действуют также массовые силы ФАУ
(AV = &AxAyAz - объем элемента) и силы инерции -apAV
{a = d2u/dt2 - вектор ускорений, й- вектор смещений). Для
равновесия AV необходимо, чтобы сумма всех сил,
приложенных к этому элементу, равнялась нулю:
\дх(х + Ах, у, z,0 + 6_х(х - Ах, у, z,t)\[AyAz +
[д Jx,y + &y,zJ) + 6 Jx,y-Ay,z,t)\[AxAz + (1.3.1)
36

[dzО, у, z + Дг,0 + <J_Z(х, у,z - Az,f )]4АхДу + ФАV - pa&V = 0 .
Поделим (1.3.1) на ДV, воспользуемся (1.1.3) и перейдем к
пределу при Ax-*0,A;y->0,Az->0, тогда
—— +—^ + —-^- + Ф = р—-. (1.3.2)
Эх Эу Эг Эг
Спроектируем (1.3.2) на оси координат:
дохх Эсг ЭсгГ7 _ д2их
—^ + —2- +—^- + ФГ = р—^,
Эх ду dz х Эг2
Эсг^ Эсг^ 3crv:r 32wv
—- +—- +—^+Ф=р—f, (1.3.3)
Эх ду dz у dt2
доХ7 до Эсг ^ д2и7
Эх Эу Эг z Эг2
Статические уравнения равновесия следуют из (1.3.3),
если положить, что смещения и напряжения не зависят от
времени, тогда в правой части (1.3.3) вместо сил инерции будут
нули.
§ 1.4. Закон Гука. Упругие константы материалов
Пусть один конец тонкого стержня (длина /0, радиус г0)
жестко заделан, а ко второму концу приложена сила F0,
равномерно распределенная по торцу (рис. 1.4.1). Тогда в
стержне возникают напряжения
37

G{ =
ТГГп
его длина изменяется (увеличивается, если F0 -
растягивающая, и уменьшается, если F0 - сжимающая),
становясь равной /. Р. Гук в 1660 г. экспериментально
установил (опубликовано только в 1678 г.), что между
относительным удлинением стержня
S^
2гл
!
F,
^1 =
А/
Рис. 1.4.1.
(Д/=/-/о),
и <т, существует линейная зависимость
а^Ее,, (1.4.1)
которая справедлива до определенных значений ох (см. §2.1)
для широкого класса твердых тел (от глин до металлов).
Коэффициент пропорциональности Е (измеряется в паскалях) в
38

(1.4.1), являющийся константой для конкретного материала,
впоследствии был назван модулем Юнга.
Если стержень однородный и изотропный, то укорочение
(удлинение) в направлении действия F0 вызывает его
расширение (сужение) в ортогональных направлениях (2 и 3)
так, что радиус становится равным г и имеют место
поперечные деформации
Аг
£2 =£з =— (Дг = г-г0),
го
причем знаки Аг и А/ различны.
Было экспериментально установлено, что между
деформациями существует прямо пропорциональная
зависимость
£2=£з=-^1> О-4-2)
где v - безразмерная константа материала, названная
коэффициентом Пуассона.
Выведем теперь закон Гука для трехмерного случая.
Рассмотрим объемный элемент AV - параллелепипед, грани
которого параллельны главным направлениям тензора
напряжений 1, 2 и 3. Тогда совместное действие трех главных
напряжений ох, ст2 и оъ "порождает" на основании (1.4.1) и
(1.4.2) в AV следующие деформации
Ол 0\ OV,
1 Е Е Е
39

e2= —-v-L-v-2-l (1.4.3)
2 E E E
0-> 0\ 0\
e, =—L-v—L-v—.
3 E E E
Соотношения (1.4.3) и есть искомый закон. Представим
(1.4.3) в форме, разрешенной относительно напряжений. Для
этого перепишем (1.4.3) в следующем виде
Ее, =ст1 -v(o2+o3),
Ее2 =cr2-v(cr1 + сг3), (1.4.4)
Ее3 = cr3-v(cr1 + сг2)
и сложим все уравнения
сг=ЗКе, (1.4.5)
где а = (ст1 + о2 + а3)/3 -среднее напряжение, е = е1+е2+е3
- объемная деформация,
3(1 -2v)
- модуль объемной упругости.
Соотношение (1.4.5) замечательно тем, что выполняется
не только для твердых тел, но и для многих жидкостей и газов.
Вспомним хорошо известный из курса общей физики закон
pV = RTt (1.4.6)
где р - давление газа, Т - температура, V - объем, R -
газовая постоянная. Пусть Т = const, найдем приращение (1.4.6)
А(рУ) = 0,
40

откуда
Ар = -ре,
в = AV/V - относительное изменение объема газа, роль
коэффициента пропорциональности играет текущее давление
Р-
Заметив, что на основании (1.4.5) ох+о2 =ЗКе-о3..., из
(1.4.4) получим
а{=Ле + 2ixex,
о2 =ЛЕ + 2/ле2, (1-4.7)
оъ = Хг + 2/ie3»
где Я =
■■ М =
- параметры Ламе.
(l+v)(l-2v) 2(1+ v)
Уравнения (1.4.7) записаны в системе координат, оси
которой совпадают с главными направлениями тензора
напряжений (и деформаций!). Выясним теперь, какой вид
примет (1.4.7) в произвольной системе координат (jc,)>,z). Пусть
А - матрица перехода от системы (1,2,3) к (x,y,z) (см. § 1.1,
Табл. 1.1). Перепишем (1.4.7) в "матричной" нотации
'1
О
<72
О О
о
(О
о
<73
= XeU + 2/м
8{ О 0 ^
О 82 О
О 0 г,
V
(1.4.8)
41

(U - единичная матрица), умножим (1.4.8) слева на Л и
справа - на А, тогда, учтя, что А* А = U , получим
б = Леи + 2/LL8
или в развернутом виде
°хх
ауу
°zz
°*У
°xz
°Уг
= Ле + 2/ле.
= Яе + 2/ле
= Ле + 2 fie.
= Z^xy ■
= 2/i£«,
= 2/ieyz,
в = Eja + вуу + £^ - первый инвариант тензора деформаций.
Соотношения (1.4.9) выражают закон Гука (уравнения
состояния линейно упругого тела) в произвольной системе
координат.
Определение упругих констант материалов
Опишем наиболее распространенный эксперимент,
позволяющий определить числовые значения упругих
характеристик горных пород £ и v.
Между двумя жесткими гладкими плитами Рх и Р2
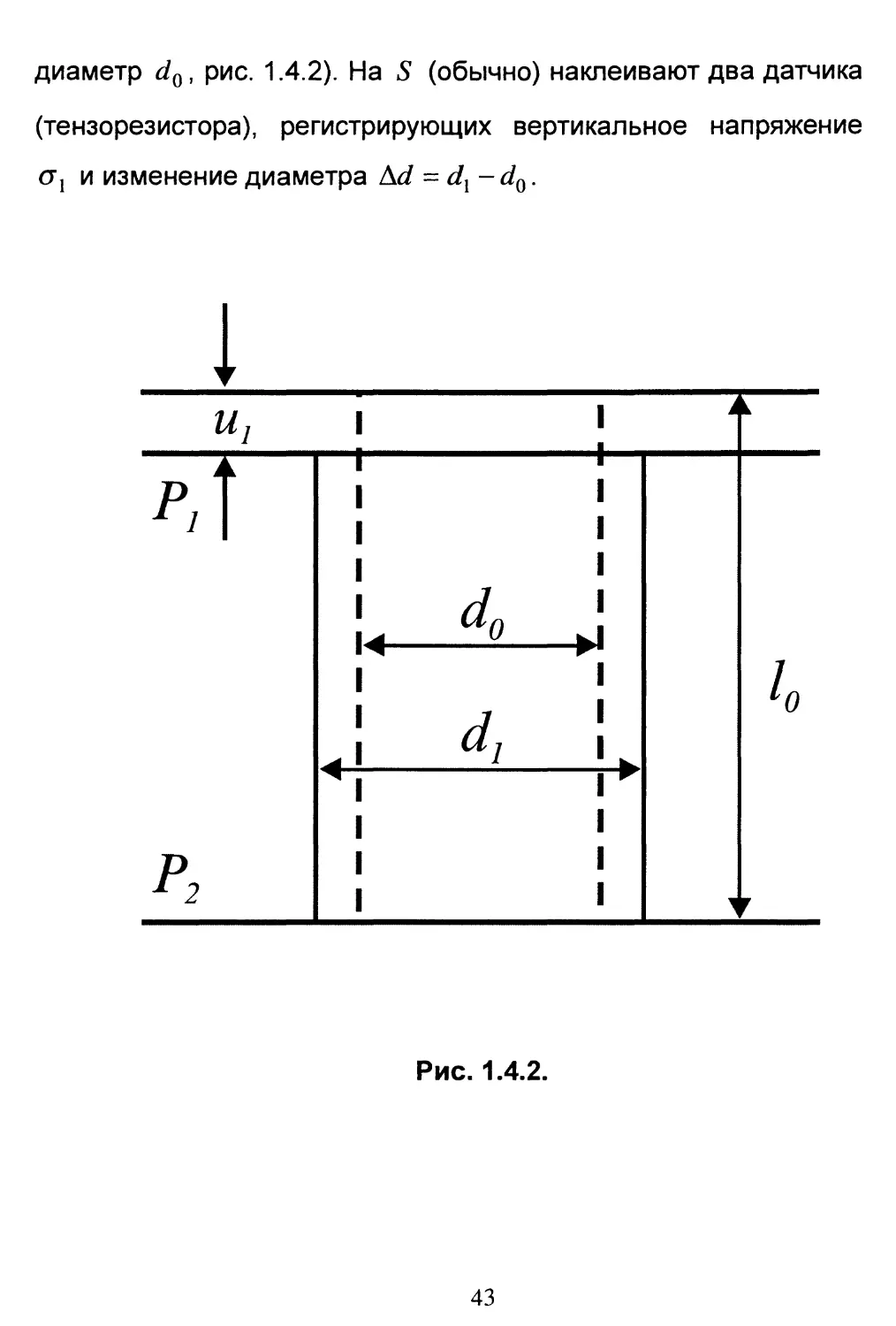
помещают вертикально цилиндрический образец S (высота /0,
42

диаметр d0, рис. 1.4.2). На 5 (обычно) наклеивают два датчика
(тензорезистора), регистрирующих вертикальное напряжение
ах и изменение диаметра Ad = d{-dQ.
i
Uj \ 1 i
^г
p2
! d0 \
! dj i
4 ■ i ^
^ i 1 ^
1
4
r
Рис. 1.4.2.
43

После этого с очень малой скоростью плиту Рх начинают
опускать, регистрируя смещение ux{ft)t t{ - параметр
нагружения. Одновременно фиксируются о"х (гг) и Ad(t()
Обработка данных состоит в вычислении:
• вертикальной sx(ti) = ux(ti)/lQ деформации;
• горизонтальной е2(^)= Д^(^) / ^о деформации;
• модуля Юнга Е( = стх(t()/sl(ti)\
• коэффициента Пуассона vt = -£2(01£\(Ь) •
Для упругих материалов (при определенном ограничении
сверху на величину их) значения Е{ и vt практически
неизменны.
§ 1.5. Полная система уравнений теории упругости и
постановка краевых задач
Приведем систему уравнений, описывающую объемное
напряженно-деформированное состояние твердого тела. В нее
входят:
уравнения равновесия
2 -^£! + фр=0 (1.5.1)
q=x,y,z дЯ
закон Гука
44

где
Я Л1 Р = Я
Pq JO P*q
-символ Кронекера, е = £pq8pq
выражения деформаций через смещения
8ря 21
\(дип дип}
(p9q = x9y9z) (1.5.3)
Е. + Г--Я-
J
dq dp
Всего 15 уравнений с 15 неизвестными {crpq,£pq1up}t
обозначим их набор для краткости U .
Замечание. Нетрудно убедиться, что если U{ \л U2 -
решения (1.5.1)—(1.5.3), то их линейная комбинация aUx+bU2
{а ,Ь-константы) тоже является решением, но для Ф = (а + Ь)Ф.
Для того, чтобы система (1.5.1)-(1.5.3) была полной,
необходимо доказать, что при заданных массовых силах и
внешних воздействиях ее решение существовало и было
единственным.
Рассмотрим в связи с этим основные краевые задачи,
которые могут быть сформулированы.
Пусть твердое тело занимает объем V, его граница
S = dV. Будем считать массовые силы Ф известными
функциями координат.
Первая краевая задача. Найти упругое равновесие тела,
если заданы смещения d на границе
45

ux=dx, uy=dyi uz=dz.
Вторая краевая задача. Найти упругое равновесие тела,
если заданы напряжения / на границе. По формуле Коши
орх cos(H, х) + ору cos(u, у) + apz cos(H, z) = fp, (1.5.4)
где Я - внешняя нормаль к 5 ; fx,fy,fz - известные функции -
проекции / на оси координат; р = jc, у, z .
Смешанная краевая задача. Аналогично двум
предыдущим, на части 5 заданы смещения, на остальной части -
напряжения.
Напомним, что смещения должны иметь непрерывные
производные, по крайней мере, до третьего порядка.
Докажем единственность решения задачи (1.5.1)—(1.5.4).
Вопрос о существовании мы оставим за рамками настоящей
книги, поскольку при доказательстве используются разделы
высшей математики (функциональный анализ и теория
интегральных уравнений, в частности), выходящие за рамки
программы подавляющего большинства ВУЗов. Примем как
факт, что решение существует.
Рассмотрим поверхностный интеграл
J=\\(fxux+fyuy+fzuz)dS (1.5.5)
s
и перепишем его с учетом (1.5.4)
J = jj(Qxcos(n,x) + Qycos(n,y) + Qzcos(H,z))dS , (1.5.6)
s
46

где
По формуле Грина
'-Ш
dQx , эа _ эа
^. + _^L + ^^
<ЛЛ
J*JI Эх ду dz
Преобразуем подынтегральное выражение к виду
dQx , dQy _ эа
«+-т+.
Эх Эу Эг
= 2
Эмг Эм
dx dy
p=x,y,z
ди.
danY допу, допЛ
рх
РУ
+ -
PZ
Эг
v
■ +
Эу Эг
*#>+
(1.5.7)
лгу
duY ЪиЛ
■ + ■
Эу Эх
+ 0\
Эиг Эм7 |
Эг дх
+ 0-
У*
3wv ЭмЛ
• + ■
dz ду
={учитывая (1.5.1) и (1.5.3)}=2W-(Фхих + Фуиу+Фм.)
Xю х У У
где
®хх^хх ~*~ ^yy^)^ "*~ ® zz^zz
={по (1.5.2)}=
Ме„ + £уу + еи)2 + 2ц(е1 + е^ + 4 + 24 + 24 + 2Ф ■
Значит W - положительно определенная квадратичная
форма от компонент тензора деформаций, т.е. она обращается
в ноль, если и только если epq = О.
Таким образом, из (1.5.5)-(1.5.7) окончательно имеем
47

5 ссс err (1-58)
JJJ (Ф А + Фуиу + ФЛ W = 2//JWW.
Пусть есть два различных решения Ux и U2 системы
(1.5.1)—(1.5.4), тогда U=Ul-U2 тоже ее решение при Ф = 0
(Замечание) и / = 0. Из (1.5.8) следует, что
jfjWdV = 0,
V
где Ж = W\[epq)x -(£pq)2)- Тогда, в силу положительной
определенности W, W = 0 и
т.е. доказано, что при заданных массовых силах и граничных
условиях деформации определяются единственным образом.
Смещения же, по известным е находятся с точностью до
движения тела как жесткого целого (§ 1.2).
Приведенное доказательство принадлежит Кирхгофу
(1858 г.), причем оно справедливо и для неоднородных сред,
т.е. в случае зависимости упругих характеристик среды от
координат.
Для существования решения второй краевой задачи (Ф и
f - известные функции), т.е. для корректной постановки,
должны быть выполнены два условия:
48

1) главный вектор F всех приложенных к V сил равен
нулю;
2) главный момент М равен нулю.
Эти условия могут быть выведены непосредственно из
уравнений равновесия. Действительно,
F = jjj&dV + jjfdS = jjfedV + $j& ■ ndS = {формула Грина}=
f- ^ ддЛ
-Щ*+2
v
V
P=x,y,z
P_
dp
\dV = {учитывая (1.5.1)}= 0.
Аналогично:
M = jjjrx^dV + jjrxfdS = jjjrxOdV^jjrxd ndS =
s
r
{Упражнение!} = fIT f x Ф + ^
v
до А
p
у p=x,y,z - j
dp
\dV=0.
В Главе 2 будет поставлено и решено много краевых
задач, в каждой из которых Условия 1) и 2) выполнены (в чем
читателю предоставляем убедиться самостоятельно). Здесь же,
в качестве примера, рассмотрим простую задачу о напряжениях
в верхней части земной коры. "Вырежем" в ней параллелепипед
V размерами 2LX, 2Lyt Lz так, что его верхняя грань
совпадает со свободной поверхностью. Введем декартову
систему координат (x,y,z), поместив начало в центр нижней
49

грани, ось z направим вертикально вверх и сформулируем
граничные условия на dV (рис. 1.1.6):
Gxz(x,y,Lz) = 0,Gyz(xyy,Lz) = 0, Gzz(x,y,Lz) = 0]
axz (x, )>,0) = 0, ayz (x, у ,0) = 0, uz (x, у ,0) = 0;
(Jxx(Lxy^) = ^xs(z)1CTxy(Lxy,z) = 01Gxz(Lxy,z) = 0] (1.5.9)
(Jxx(-Lxy^) = qA^^Xy(-Lxy^) = 01Gxz(-Lxy,z) = 0]
Gxy(x,Ly,z) = 0,(Tyy(x,Lrz) = qys(z),oyz(x,Lrz) = 0\
G^ix-Ly.z) = 0,Gyy(x-Ly,z) = qys(z) ,Gyz(x-Ly,z) = 0,
где s(z) = pgz - литостатическое напряжение; р - плотность
(считаем V однородным и изотропным); g -ускорение
свободного падения; qx и qy - коэффициенты бокового отпора,
характеризующие действие "отброшенной" части земной коры.
Массовые силы Ф = (ОД-pg) - гравитационные.
Непосредственной проверкой можно убедиться, что
напряжения
Gxx(x,y,z) = qxs(z), (Jyy(x,y,z) = qys(z), G^x.y.z) = s(z),
cr^Cx, y9 z) = 0, cr^O, y, z) = 0, oyz(x9 y, z) = 0,
удовлетворяют и уравнениям равновесия (1.5.1), и граничным
условиям (1.5.9), причем главный вектор и момент равны нулю.
50

Уравнения Ламе
Система (1.5.1)—(1.5.3) может быть сведена к трем
уравнениям в смещениях. Подставим (1.5.3) в (1.5.2) и затем в
(1.5.1)
где
juA^+U + AO —
ох
duY duv ди
\
■ + ■
■ + ■
juA" +(Я + АО
ду
дх ду dz
duY ди ди7
■ + -
/llAu. + (Я + /л)
dz
дх ду dz
3wv duv ди,
+ Ф*=0,
+ Ф =0,
■ + -
■ + ■
дх ду dz
+ Ф7 =0,
(1.5.10)
Д = -
■ + ■
■ + •
дх2 ду2 dz2
-оператор Лапласа (лапласиан). Функция /, удовлетворяющая
уравнению А/ = 0, называется гармонической.
Систему (1.5.10) в литературе часто называют
уравнениями Ламе, хотя, справедливости ради, надо заметить,
что для случая Я = jx она была получена Навье еще в 1821 г.
Если использовать известные в векторном анализе
операторы:
дивергенция
_ диг ди ди7
divu =^^ + —-2- + .
дх ду dz
51

градиент
_,, (df df df)
у дх ду dz J
то (1.5.10) можно представить в компактном виде
/иАи + (Л + ju)grad(div и )+ Ф = 0. (1.5.11)
Выведем одно важное следствие из соотношений
(1.5.1), (1.5.2).
Подставим соотношения закона Гука в уравнения
равновесия и продифференцируем: первое -по х, второе - по
у, третье - по z
а д2е . д
дх2 дх
д£хх д£*У
де
XZ
,д2еп д
Л—- + 2и —
ду2 ду
, д2е . д
Я—- + 2ц —
dz2 dz
дх
(де
ху
ду
де
дх
(де
I
+-
уу
+ -
dz
+ -
ЭФ,
дх
ду dz
у , деу* , дея
ЭФ,
+-
Э* ду dz
+ ■
ду
дФ^
dz
О,
= 0,
0.
Сложим все уравнения и учтем условия совместности
(1.2.19), тогда
ЭФ„ ЭФУ ЭФ
(3X + 6ju)Ae + -—^- + - +
Z _
о,
(1.5.12)
дх ду dz
Вспоминая, что е пропорционально а (1.4.5), из (1.5.12)
получим
52

ЗА + 2 и
Act =
A + 2,u
Гэф. эф, эфЛ (1513)
*. + —JL + y*z
У
Эх Э>> Эг
Если вектор массовых сил вихревого типа
(dGy 3G. 3G. 3GV 3Gr 3GV ^
ф = rotG =
У UKJz UKJz WVJx "^x У
. dz ду дх dz dy dz .
или просто нулевой, то из (1.5.12), (1.5.13) следует, что
изменение объема и среднее напряжение являются
гармоническими функциями.
§ 1.6. Двумерные модели: плоское напряженное
состояние, плоская деформация
Систему уравнений, описывающую объемное напряженно-
деформированное состояние вывели достаточно давно. Однако
аналитических методов ее решения не существовало, поэтому
исследователи упрощали эту систему, уменьшая размерность,
вводя различные гипотезы. Полученные более простые одно- и
двумерные задачи уже поддавались решению и, что было
гораздо важнее, позволяли проводить численные расчеты и на
этой основе делать практические выводы и давать
рекомендации. Но если следовать истории развития моделей,
то одно- и двумерные появились раньше трехмерной. В
качестве примера можно привести закон Гука.
Рассмотрим основные двумерные модели.
53

Плоское деформированное состояние
Пусть твердое деформируемое тело имеет форму
цилиндра произвольного сечения S, причем длина много
больше diamS. Предположим, что граничные усилия (и/или
смещения) одинаковы в любом поперечном сечении, массовые
силы и смещение в направлении оси цилиндра отсутствуют.
Описанная ситуация часто возникает на практике.
Например, в трубопроводах для транспортировки
углеводородного сырья, протяженных подземных горных
выработках, длинных железнодорожных тоннелях.
Выведем систему уравнений, моделирующую такое
состояние среды, взяв в качестве исходных соотношения
(1.5.1)-(1.5.3). Введем декартову систему координат (x,y,z),
направив ось z параллельно образующей цилиндра. В силу
введенных гипотез смещения их,иу не зависят от z , a uz = 0 и
Фг =0.
Тогда из (1.5.3) следует
а из закона Гука
cyxz=(jyz=0. (1.6.2)
Таким образом основная система (1.5.1)-(1.5.3) сводится
к восьми уравнениям с восемью неизвестными:
уравнения состояния
54

дет до"™
—^ +—2- + Фх=0, (1.6.3)
дх ду
дет дет
^■ + ——+ ФЛ, =0;
дх ду
закон Гука
оуу =Xe + 2ii£yy, (1.6.4)
<^=2^,
выражения деформаций через смещения
\(дир duq}
£ря 2
■ + •
(p,q = x,y). (1.6.5)
dq dp
Граничные условия на dS формулируются аналогично
трехмерному случаю.
Третье уравнение равновесия выполняется тождественно.
Соотношения (1.6.3) - (1.6.5) описывают плоское
деформированное состояние или плоскую деформацию.
На основании закона Гука и (1.6.1) ег^ = As. Складывая
(1.6.4)! и (1.6.4)2, получим о ж +&уу =2(A + jU)£ , поэтому
°zz=V(°xx+°yy) (1.6.6)
(напомним, что v= ), т.е. осевое напряжение отлично
2(А + jX)
от нуля и вычисляется после решения системы (1.6.3) - (1.6.5).
55

Функция напряжений
Рассмотрим важный для практики случай - отсутствие
массовых сил.
Уравнения равновесия примут вид
^ + ^ = 0, (1.6.7)
дх ду
дх ду
Выведем уравнения совместности Сен-Венана для
плоской деформации в терминах напряжений.
Для этого разрешим (1.6.4) относительно деформаций
2fiexx=(l-v)(jxx-V(jyyi
2fieyy =(l-v)ayy-v<yxx
2№Ху=°ху
и подставим в (1.2.19)!
ду2 дх2 дхду
(единственное оставшееся из шести уравнений совместности
(1.2.19), поскольку остальные выполняются тождественно в силу
принятых соглашений), тогда
d2aYY Э о д о
_?+_f_^+CTw)=2_^.
56

Отсюда, принимая во внимание, что о^+о- -гармоническая
функция (§ 1.5),
Э2сг 32crvv д2а^
^f- + ^ = 2 ^. (1.6.8)
ду дх дхду
Мы получили замкнутую систему трех уравнений
(1.6.7), (1.6.8) относительно трех компонент тензора
напряжений. Теперь, если на dS сформулирована вторая
краевая задача (задан вектор усилий), то решение не зависит
от деформационных характеристик среды {Е и v). Этот факт
будет неоднократно отмечен во второй главе.
Продифференцируем (1.6.7)i трижды по х, (1.6.7)2 трижды
по у и сложим результаты
э2 (э2а„ э2<0 э4<х„ э4<т
дхду
хх . УУ
2
J
ду2 дх
*> + ^ = 0,
дх4 ду'
откуда, учтя (1.6.8),
д4о„ д4сг„ д4ог/
Г^ + 2 , ^, + ?- = 0 (1.6.9)
дх4 дх2ду2 ду4
или
ДД<т„=0.
Аналогично можно получить такие же уравнения для о^ и с ^.
Введем теперь функцию *Р = ^(х,у) так, что
92^ Э2^ Э2¥ „,.<m
°*~W ^=^' ^=~55*? <1а10)
57

Уравнения равновесия (1.6.7) при этом выполнены
тождественно, а подставляя (1.6.10) в (1.6.8), получим
д4х¥ д4х¥ д4х¥
—г + 2—=—т + —г = 0. (1.6.11)
дх4 дх2ду2 ду4 V
Таким образом, apq можно выразить через одну
бигармоническую функцию, называемую функцией напряжений
или функцией Эри. Она играла важную роль при аналитическом
решении плоских задач во все время развития теории упругости
вплоть до 80-х годов прошлого столетия, т.е. до появления
быстродействующих компьютеров.
Плоское напряженное состояние
Рассмотрим пластинку толщиной 2h, ее верхняя и нижняя
поверхности - плоскости Рх и Р2. Нагружение осуществляется
только равномерно распределенными по торцам силами (и/или
смещениями), параллельными Рт. Потребуем, чтобы массовые
силы были также параллельны Рт а сами Рт свободны от
напряжений.
Выведем систему уравнений, описывающую напряженно-
деформированное состояние такой пластины. В качестве
исходной примем полную систему теории упругости (1.5.1)-
(1.5.3)
58

Введем декартову систему координат (x9y9z), плоскость
Оху которой совпадает со срединной плоскостью пластины, и
сформулируем граничные условия
axz U, у-К) = axz (х, у, К) = О,
ayz(x9y-h) = ayz(x9y9h) = 0, (1.6.12)
а^(х,у-К) = azz(x9y,h) = 0,
opqnq =fp на dS при -h<z<h (p9q = x9y,z),
где S - проекция на Оху области, занятой пластиной;
п = (пх9пу90) -внешняя нормаль к dS\ f = (fx,fy,0)
-заданная функция, не зависящая от z .
Для произвольной функции трех переменных w(x9y9z)
введем операцию осреднения
h
2h
1 h
w(x9y) = —\w(x9y9z)dz (1.6.13)
-h
и применим ее к уравнениям равновесия (1.5.1)i и (1.5.1)2
до ж да 1 \даХ7 . —
—— + - + — —^dz + Ф^ = 0,
дх ду 2й^Л dz
да да 1 \до
—^ +—^ + — —y-dz + Фv =0,
Эх ду 2Й Д dz y
откуда, учитывая граничные условия (1.6.1)i и (1.6.1)2,
doYY да
—— + —^ + Фх=0,
дх ду
59

^ + -т^ + ФГ°- О-6-14)
дх ду
Третье уравнение примет вид
доХ7 да Эсг
—^ + —— +—^ = 0
дх ду dz
и, поскольку axz(x,y,±h) = oyz(x,y,±h) = 0, то
acrzz(^y,±/i)_()
Эг
поэтому, принимая во внимание (1.6.12)3, можно считать, что
crzz(x,y,z) = 0 (1.6.15).
Из закона Гука
°zz =Mexx+eyy) + (X + 2fi)ezz
и (1.6.15) следует
'«-аТ^*»"»'- (1-616>
Подставим (1.6.5) в соотношения закона Гука для а^ и
ауу
ахх=\*£ + 2цеххУ (1.6.17)
(jyy =Л*е + 2цеуу,
60

Осредняя по z (1.6.17), соотношение для о^, выражения
деформаций через смещения, а также граничное условие
(1.6.12)4, получим
а^ =А*ё + 21*ёхх,
ауу =Л*Е+2/лёуу,
' ху
= 2/LlE
ху
(1.6.18)
(дй
£ря -2
р+эо
dq dp
{p,q = x,y)
in«=fP
на dS
(1.6.19)
ря я jp
Компоненты / имеют смысл удельного усилия на
единицу толщины пластины.
Уравнения (1.6.14), (1.6.18) с граничными условиями
(1.6.19) представляют собой полную систему (8 неизвестных
оpq,epqtup и 8 уравнений), сравнивая которую с аналогичными
формулами для плоского деформированного состояния,
убеждаемся, что они идентичны, если Я* заменить на Я.
Этот результат был опубликован Файлоном в 1900 г., а
позднее такую модель Ляв назвал "обобщенное плоское
напряженное состояние".
Качественное отличие ее от плоской деформации состоит
в том, что в первом случае после решения основной системы
вычисляется вертикальная деформация по (1.6.16), а во втором
- вертикальное напряжение по (1.6.6).
61

§ 1.7. Представление основных соотношений теории
упругости в различных системах координат
Настоящий параграф -справочный, в нем собраны
основные формулы линейной теории упругости для наиболее
употребительных систем координат: цилиндрической и
сферической, а также соотношения для одномерных и
двумерных моделей, получающихся из объемных при введении
соответствующих упрощающих гипотез, перечень которых дан в
каждом конкретном случае.
Уравнения Ламе в двух- и трехмерном случаях не
выписываются из-за их крайней громоздкости (мы оставляем
это читателям в качестве Упражнения). Их легко получить, если
воспользоваться векторным представлением (1.5.11) и
выражениями операторов дивергенции, градиента, ротора и
Лапласа, приведенными ниже. При этом лапласиан от
векторной функции вычисляется по формуле
Ай = gradydivu)- rotyrotu).
Цилиндрическая система координат
/. Общий случай.
Связь с декартовой системой координат
х = rcos#,
у - rsinO ,
62

z- z.
Вектор смещений й = (unue,uz).
Уравнения равновесия
дс„ о„ -стпп 1 дстГЙ дет
'гг , игг "ее ,
гв
г дв dz
+ Ф. =0,
дет- 2ет~ 1 дет™ дет{
гв | ^игв |
00
'0Z
г Эг Эг
+ Ф«=0,
Эг г г дв dz
Закон Гука
£ - £tftf + ^00 + £zz '
Выражение деформаций через смещения
диг
£вв ~
дг '
1 диЙ иг
- + —,
г дв г
Эй,
OZ
£гв =
' 1 Эиг Эи0 и0
г Э0 Эг г
63

Crz 2
1(dur du
dz
^+-
eez=-\
1 ( dua 1 du,
dz
■ + ■
Э0
Операторы:
градиент
I Эи> 1 Эи> dw\
дивергенция
,. _ dur ur 1 Эмд Эи7
or г г дв oz
ротор
/ _\ 1 ди7 дий
{rotu) =——5-—-£-,
(rotu)e =
диг duz
dz dr
1 Эи„
(rati) = ^_^L___
V '* Эг г г Э0
лапласиан от скалярной функции
Э w 1 3w 1 Э w д w
Aw = —- + ——— + ——=- + —=-,
Эг2 гЭг г2 дв2 dz2
64

//. Осевая симметрия:
1) смещения не зависят от полярного угла в;
2) тангенциальное смещение ие - О;
3) тангенциальная компонента массовых сил Фв = О.
Выражение деформаций через смещения
ди
V~ * £ее ~ » ezz ~ ~Т~'
dr r dz
егП - 8Й7 - 0 , £„ - —
диг ди7 1
—L +—7
dz дг
Из закона закон Гука следует, что
Уравнения равновесия
до„ ог-от до
°гв =°вг =°-
+ -
г г ^вв
дг г dz
Эсг_ от да
+ —^ + ФГ=0,
дг г
Операторы:
градиент
grad w ■
дивергенция
+ Ф_ -0.
(dw dw
— Л —
дг dz
,. _ диг иг ди7
div и = —- + —- + —-;
дг г dz
65

ротор
(rot u)r = (rot и) = О, (rotii)e = — -
dz
лапласиан от скалярной функции
d2w 1 dw d2w
дг2
+ + -
rdr dz'
HI. Плоская деформация:
1) смещения не зависят от переменной z ;
2) осевое смещение uz = 0;
3) осевая компонента массовых сил Фг = 0.
Выражение деформаций через смещения
диг 1 див иг
гв 2[гдв дг г ^
)
erz=eez=ezz:=0-
кона закон Гука следует, <-
(ТО
°п
= <*вг
= 0
Уравнения равновесия
дг
до
, агг~авв ,
Ida
гв
гв
la
гв
+ ■
Г Э0
1 Эсг,
+ ФГ=0,
'вв
+ Ф0=О.
Эг г г дг
Выражения компонент тензора напряжений через
функцию Эри Ч*
66

_ 1ЭУ 1 д2х¥
°rr~ г дг + г2дв2
°ев =
Э2У
Эг2
ОГг0="
1ЭУ
гЭ0
/V. Цилиндрическая симметрия:
1) смещения не зависят от 0 и z ;
2) смещения м0 = wz = 0; Ф0 = Фг = 0
3) компоненты массовых сил.
Выражение деформаций через смещения
_ диг _ иг
егг - ~Т~~ ' £вв ~ '
or г
£гв - erz ~ £6z ~ Ezz ~®-
Из закона закон Гука следует, что
Уравнение равновесия
дг г
Уравнение Ламе
(А + 2/Л —f + -
стг0 = <*« = (Т0г =0.
Эг2
г аг
+ ФГ=0.
Сферическая система координат
/. Общий случай.
Связь с декартовой системой координат
jc = /?sin<pcos0 ,
67

у = RsivKps'mG ,
z = Rcoscp.
Вектор смещений й = (uR, и^, uQ).
Уравнения равновесия
d°RR , 2aRR-aee-acP<p^CJR4>ctgq> t 1 daRQ . 1 daR
■ + -
- + -
dR R Rs'mcp дв R d(p
d°Rcp 3°яср+(°ее-°<р<р)с*8<Р , 1 do^ l da{
-+ф*=о,
ЭЛ
л
-+-
Л д(р Rsincp дв
+ Ф.=0,
д<тм , 3°Re+*req,ctgq> 1 Э<х0ф 1 давв+ф =()
■ + ■
■ + •
■ + -
Л Э<р /?sin<p Э0
ЭД R
Закон Гука
°ря =Хе5РЯ +2№Pq {p,q = R,<P,0)
8 — еДД + £<р(р + ^00 ■
Выражение деформаций через смещения
_ duR
£RR=~dR>'
~"вв
_ UR
+ ■
1 Э«0 "<р
/? Rsm(p дв R
_ uR 1 Эиф
+-f-rtg<p>
*w я + д Эф
'/ге
1 Эил Эм0 ив
Л
Rsinq) SO dR R
68

£R<p ~
£6<p -
1 duR du^ Uy
■ +
R dcp dR R
1 du 1 дий ut
- + ■
0 "0
/?sin<p Э0 Я Э<р Я
Cfg<j9
Операторы:
градиент
grad w =
дивергенция
' dw 1 Эи>
dR* Rdcp' Rsincp Э0
i ЭиЛ
duR 2uR 1
^ Я Я
divu = —L^^A-^ —
dcp
\
+ UcpCtg(p
1 Эм,
e .
Rsincp дв
ротор
(rotu)R =-
R
duQ
dcp
Л
+ uectgcp
1
dufi
V h Rsincp dO
dR R
Rsincp дв
( ^\ dw и 1 duR
V Ю dR R R dcp
лапласиан от скалярной функции
Aw =
Э2и> 2 3w 1 ( 32w dw
■ + ■
- + ■
ЭЯ2 /? Э7? Я2
f/. Осевая симметрия:
Л
- + —ctgcp
dcp dcp
1) смещения не зависят от угла в;
+ ■
1
d2w
R2sin2cpd0'
69

2) смещение ив = 0;
3) компонента массовых сил Фв = О.
Выражение деформаций через смещения
р — £L
RR dR '
Ы г» Ы п №ф
£,„,,, = —, £дя = — + —ctg(p,
я ее /г /г ^
"W
'Й0 _ °0<р
£fle> — " i £/?<» — _
/г «9
^1 duR duv ity ^
/г a<jo э/г /г
CT«e =cr0p =0-
Из закона Гука следует, что
Уравнения равновесия
d<yRR , 2crr ~авв -°щ, +<*R9ctg<p 1 daR(p
dR
R
• + •
/г э<р
+ ф«=о,
Э<тЛр 3<Тдф+(сг0е -(Tw)ctg<p 1 3crw ф =0
ЭЯ
Операторы:
градиент
gra<i w =
дивергенция
R
R д<р
<р
' dw 1 dw »
Э/г' /г Эф'
, _ Эмр 2м г, 1
(du„
dR
R R
д(р
■ + u(pctg(p
ротор
{rotu)R =(rotu)e = 0,
70

/ _\ 1 duR
(rot и) = -£-
V J(p Rs'mcp дО
' див Uq I
■ + ■
V
dR R
лапласиан от скалярной функции
d2w 2 dw 1 (d2w dw
■ + •
■ + ■
д(р2 дф
dR2 RdR R2
IL Сферическая симметрия:
1) смещения не зависят от углов ср и 9;
2) смещения и^ = ив = 0;
3) компоненты массовых сил Фф = Фв = О
Выражение деформаций через смещения
ctgcp
_ duR
£qxp — £вв
_UR
RR dR • w - Л
Из закона Гука следует, что:
1) °яв =<JR(p =С7в<р =0".
2) <rw = ове .
Уравнение равновесия
до
" £rR ~ £r<i> ~ £0в> ~~ " ■
'Rip
RR 2{°rr-0w>) . .
+ ^— + ФК = 0.
dR R
Уравнение Ламе
(А + 2/Л *. + ——*- Е.
\ dR2 R dR R2
+ ФЙ=0.
71

ГЛАВА 2
ПРИЛОЖЕНИЕ РЕШЕНИЙ ЗАДАЧ ТЕОРИИ УПРУГОСТИ
К ИССЛЕДОВАНИЮ УСТОЙЧИВОСТИ И РАЗРУШЕНИЯ
ЭЛЕМЕНТОВ КОНСТРУКЦИЙ И ПРИРОДНЫХ ОБЪЕКТОВ
§ 2.1. Понятие о прочности и критериях разрушения
твердых тел
В расчётах на прочность обычно предполагается, что
разрушение тела происходит, как только в некоторой его точке
определённая комбинация напряжений ctjl деформаций etj,
температуры и времени достигнет критического значения. При
этом сам процесс разрушения не рассматривается. Ясно, что
при таком подходе проблема прочности решается подбором той
или иной реологической модели и критерия разрушения.
Этот подход является прямым логическим следствием
принятого феноменологического рассмотрения в рамках
указанных параметров. Физически он оправдывается тем, что
развитие дефектов материала, приводящих к потере несущей
способности, весьма часто происходит в узкой
"околокритической" области, так что детальное знание самого
процесса разрушения имеет второстепенное значение. При
этом определяемый экспериментально критерий разрушения
отражает сложные микрофизические процессы разрушения,
происходящие в масштабе структурной ячейки вплоть до
72

молекулярного уровня и приводящие к образованию
макродефекта. Кроме того, поведение макродефекта
(понимаемого феноменологически как некоторый разрыв
смещения) зависит от типа разрыва. Например, образование
дислокаций и линий сложения, даже перерезывающих тело, как
правило, не приводит к его разрушению.
В качестве критериальной величины обычно берут
наибольшее главное напряжение, наибольшее главное
относительное удлинение, наибольшее главное касательное
или октаэдрическое напряжение, удельную энергию
формоизменения, полную удельную энергию деформации.
Каждый из критериев применим при вполне определённых
условиях для некоторого класса материалов. Правильное
использование этих критериев существенно зависит от
практического опыта исследователя. Накоплению такого опыта
посвящено большинство экспериментальных работ по
прочности.
Заметим, что в разное время этим критериям придавали
различное значение, иногда абсолютизируя тот или иной
критерий. Например, Ламе и Рэнкин принимали в качестве
критерия прочности наибольшее главное напряжение, а
Понселе и Сен-Венан - наибольшую деформацию.
Прочность материалов зависит от многих факторов:
структуры, условий нагружения, внешней среды, размеров и
формы образцов, длительности опытов и т.д. Поэтому
затруднительно указать какие-либо исчерпывающие
73

характеристики прочности материала. Проводятся обширные
исследования их механических свойств в различных условиях.
По результатам опытов оценивается сопротивление материалов
разрушению в зависимости от внешних факторов и структуры
самих материалов. Вопросы эти весьма сложные, им посвящено
огромное количество публикаций, касающихся различных
аспектов (физических, химико-технологических, механических и
т.д.) этой проблемы.
Поэтому рассмотрим, в основном, критерии
кратковременной прочности некоторых важнейших материалов
(металлов, бетона, горных пород и полимеров) в обычных
температурных условиях при достаточно простых, мало
изменяющихся во времени ("постоянных") нагрузках, т.е.
рассмотрим разрушение при относительно медленных
монотонных нагружениях и обычной температуре, когда можно
пренебречь ползучестью. При большом многообразии
материалов естественно и большое число критериев
разрушения. Мы не ставим здесь цели дать полный обзор,
отсылая читателя к соответствующей литературе. Остановимся
лишь на нескольких наиболее важных критериях.
Вопрос о том, что понимать под опасным состоянием,
решается по-разному, в зависимости от материала и
предъявляемых к нему требований. Это может быть состояние
на грани разрушения ("на пределе прочности"), подобное
состояние естественно учитывать для хрупкого материала.
Иногда опасным считается переход к пластическим
74

деформациям (состояние "на пределе текучести"), тогда
пластичные материалы в известной мере исчерпывают несущую
способность. При таком подходе критерии разрушения
аналогичны условиям пластичности.
В этом параграфе условимся помечать звёздочкой
постоянные, характеризующие опасное состояние, например,
сг*, £* и т.д.
Предельная поверхность
При одноосном напряжённом состоянии граница прочности
оценивается предельным ("опасным") значением напряжения.
При переходе к сложному напряжённому состоянию естественно
ввести простейшее обобщение этой картины - предельную
поверхность I в пространстве напряжений. Для изотропного
тела все направления эквивалентны, поэтому уравнение этой
поверхности должно быть инвариантным по отношению к
ориентации координатной системы, и, следовательно,
содержать лишь инварианты тензора напряжений
F(I?J%J°) = K* (2.1.1)
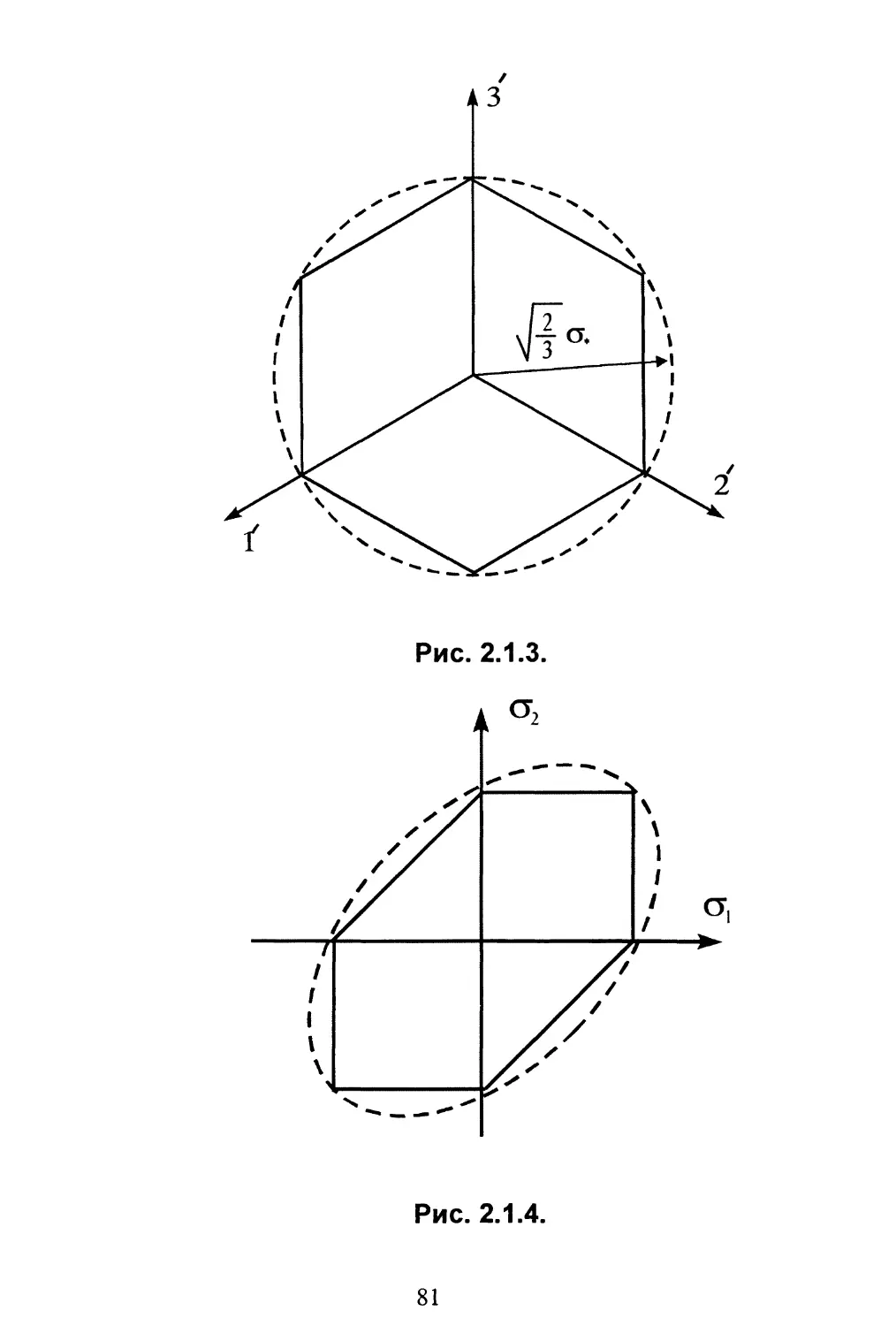
Можно рассматривать поверхность Е в пространстве
главных напряжений (рис. 2.1.1)
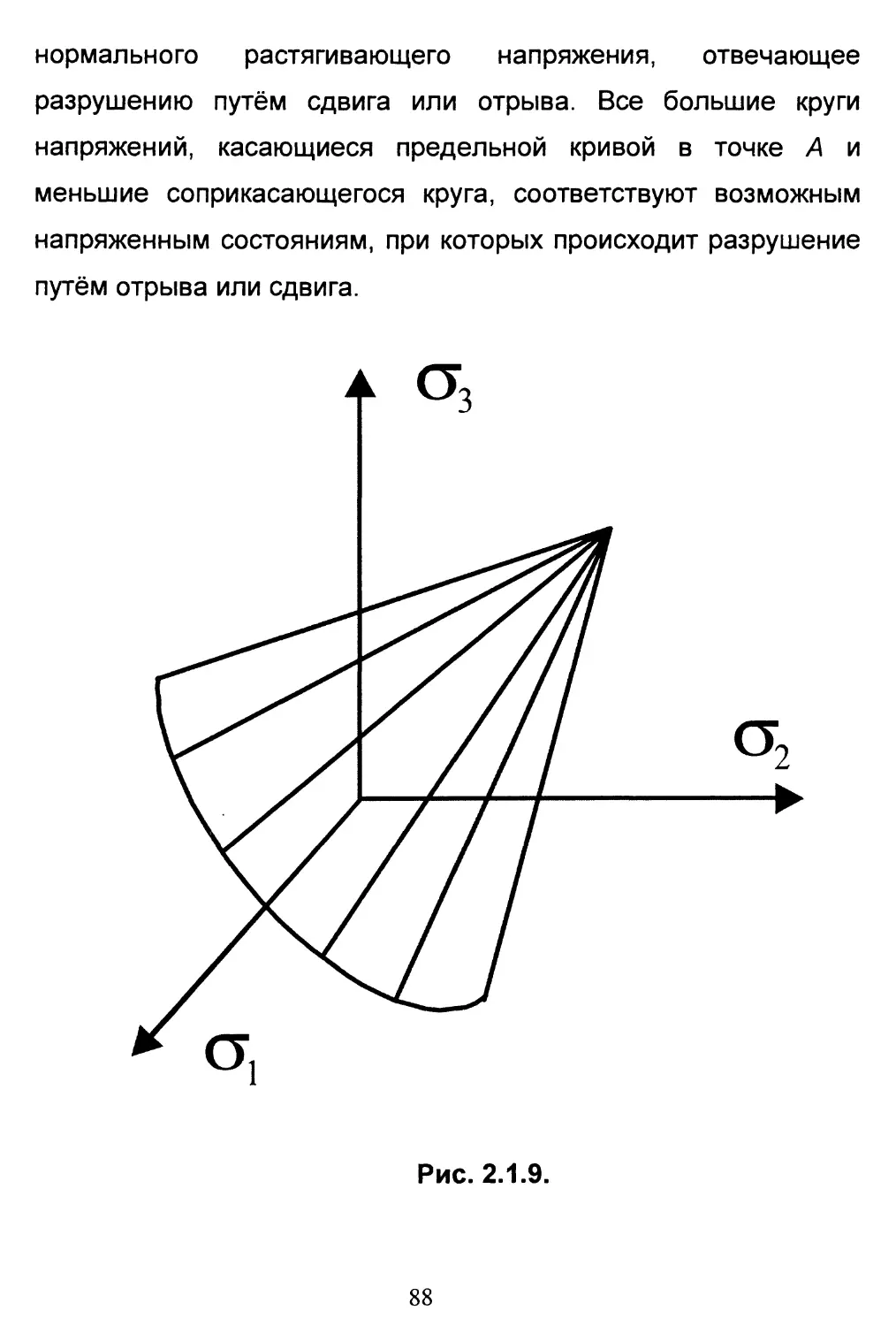
F(ov(J2,(J3) = AT* (2.1.2)
причём, вследствие эквивалентности всех направлений, F
должна быть симметричной функцией сг(.
75

Рис. 2.1,1.
Так как основными симметричными функциями тензора
напряжений д являются инварианты If, то уравнение (2.1.2)
может быть также представлено в форме (2.1.1). Вместо
выписанных в (2.1.1) инвариантов можно рассматривать любые
три независимые их комбинации.
При гидростатическом сжатии (о^. =-р8^, р -давление)
однородный материал не разрушается, в то же время
изменение гидростатического давления может оказывать
известное влияние на условия разрушения (для пластических
76

материалов это влияние меньше, чем для хрупких). В связи с
этим удобно ввести интенсивность касательных напряжений
и параметр Лоде - Надаи
_ 2g2-g1 -сг3
ах-оъ
которые не зависят от среднего давления а .
Теперь уравнение предельной поверхности может быть
представлено в виде
F(<y9T9fia) = K., (2.1.3)
а конкретизация этой зависимости приводит к тем или иным
критериям разрушения.
Гораздо реже в качестве критерия разрушения
используются ограничения, накладываемые на деформации; в
том случае в пространстве главных деформаций также имеется
некоторая поверхность, ограничивающая область безопасных
состояний.
Рассмотрим теперь некоторые критерии разрушения,
получившие распространение в инженерной практике.
Критерий наибольших нормальных напряжений
В опасном состоянии наибольшее главное напряжение
достигает предельного значения
77

Ртах = °* ' ^тах = тах (О\,02>°з) •
(2.1.4)
Предельная поверхность - куб со стороной 2сг* (рис. 2.1.2).
В простейшей форме изложенный критерий восходит ещё
к Галилею, позднее он получил развитие в работах Рэнкина.
Рис. 2.1.2.
Критерий (2.1.4) не всегда согласуется с основными
экспериментальными фактами. Так, при одноосном сжатии и
78

равномерном всестороннем сжатии граница прочности согласно
этому критерию будет одна и та же. Между тем хорошо
известно, что гидростатическое давление не приводит к
разрушению.
Для хрупких материалов при напряжённых состояниях,
близких к одноосным, критерий сгтах даёт более или менее
правильные результаты. Переход в пластическое состояние
рассматриваемым критерием описывается плохо.
Критерий наибольших удлинений
Некоторые опыты показывают, что разрушение путём
отрыва может происходить по сечениям, в которых нет
напряжений. В то же время удлинения по направлениям,
нормальным к указанным сечениям, имеются. Тогда
приобретает значение критерий наибольшего удлинения
(критерий Мариотта). При упругих деформациях можно при этом
получить условие, накладываемое на компоненты напряжений,
если воспользоваться законом Гука.
Критерий максимальных касательных напряжений
В опасном состоянии максимальное касательное
напряжение достигает предельного значения
*тах=1Г* (2.1.5)
79

где
(
rmax = max
\a\"a2\ \а\-аЪ\ Р2"а3
(2.1.6)
J
2 2 2
Иногда для удобства главные напряжения
упорядочивают по возрастанию оъ<о2<ох, тогда
* max *
Условие (2.1.6) в пространстве главных напряжений
определяет область, ограниченную поверхностью правильной
шестигранной призмы с осью ох = о2 = ст3, называемой
гидростатической осью, поскольку точкам этой прямой отвечают
гидростатические напряженные состояния. В нормальном
сечении призмы имеем правильный шестиугольник рис. 2.1.3.
Оси l',^ и 3' - проекции осей о",, о2 и оъ на плоскость,
перпендикулярную гидростатической оси. Очевидно, что
всестороннее сжатие (или растяжение) не приводит, согласно
(2.1.5), к разрушению и не изменяет условий разрушения.
В плоском напряженном состоянии (§1.5) предельное
условие определяется сечением призмы плоскостью <т3=0
(шестиугольник на рис. 2.1.4).
Критерий максимальных касательных напряжений, в
общем, правильно характеризует переход к пластическому
деформированию металлов, хотя и отмечаются некоторые
систематические отклонения. Так, согласно (2.1.5),
промежуточное главное напряжение не оказывает никакого
80

43
#«
i ЧС
Рис. 2,1.3.
Рис. 2.1.4.
81

влияния. В опытах, однако, такое влияние (хотя и небольшое)
наблюдается. Разрушения пластичных металлов, происходящие
путём среза, также удовлетворительно описываются критерием
ттах • Критерий наибольшего касательного напряжения
предложен Кулоном в 1773 г.
Условие (2.1.5), как условие наступления пластического
состояния (не разрушения!), позднее было использовано Треска
и Сен-Венаном.
Поведение хрупких материалов описывается критерием
ттах значительно хуже.
Заметим в заключение, что (2.1.5) является частным
случаем (2.1.3), не содержащего среднего давления.
Критерий наибольшей интенсивности
касательных напряжений
В опасном состоянии интенсивность касательных
напряжений достигает предельного значения
Т = ^= (2.1.7)
л/3
или в развернутой форме
(°\ ~°2? + fo ~°ъ? + fa -°\f = 2(У*2 • (2-1-8)
Это условие близко к критерию наибольшего касательного
напряжения. В пространстве главных напряжений условие
(2.1.7) соответствует поверхности кругового цилиндра с той же
82

гидростатической осью ох =о2 =ст3. При этом, как нетрудно
видеть, поверхность кругового цилиндра описана вокруг
шестигранной призмы Кулона. На рис. 2.1.3 пунктиром показано
нормальное сечение цилиндра, а на рис. 2.1.4 - сечение
цилиндра плоскостью о3 = О (плоское напряжённое состояние).
Условие (2.1.7) было предложено Хубером в 1904 г. в
качестве критерия прочности при а < 0 (объемное сжатие).
Несколько позднее (1913 г.) из других соображений (2.1.7) было
выдвинуто Р. Мизесом как условие пластичности. Как
выяснилось в последствии, (2.1.7) было сформулировано
Максвеллом в письме Кельвину ещё в 1856 г.
Величине интенсивности касательных напряжений можно
дать различную интерпретацию (октаэдрическое напряжение,
среднее по малой сфере, окружающей данную точку, и т.д.).
Поэтому критерий разрушения (2.1.7) можно истолковать по-
разному.
При чистом сдвиге {ох=-оъ, а2=0) интенсивность
Т = ттах = ох, поэтому предельное напряжение при сдвиге
т, =-г=сг*- (2.1.9)
Разрушения пластичных металлов, происходящие путём
сдвига (среза), удовлетворительно описываются (2.1.7). Вместе
с тем этот критерий, как и предыдущий, в общем, хорошо
фиксирует переход к пластической деформации в металлах, при
83

этом соотношение между пределами текучести (аналогичное
(2.1.9)) подтверждается экспериментами.
Разрушение хрупких материалов критерий наибольшей
интенсивности касательных напряжений описывает плохо.
Критерий Мора
Как уже отмечалось, ряд материалов (прежде всего -
хрупкие - бетон, стекло, горные породы и т.д.) различным
образом сопротивляются сжатию и растяжению, а именно,
прочность на сжатие ос выше прочности на растяжение at
(различие может быть в 5-8 раз). Этот факт можно учесть,
например, если принять, что величина касательного напряжения
тя, действующего на "площадке разрушения" (с нормалью К)у
зависит от величины нормального напряжения оп на той же
площадке
Условие (2.1.10) предложил О. Мор в 1900 г.
На плоскости (сгп,тп) соотношение (2.1.10) представляет
собой предельную кривую, ограничивающую область
безопасных состояний. Напряженное состояние здесь
характеризуется системой кругов Мора (рис. 2.1.5). Нетрудно
видеть, что наибольший круг напряжений должен касаться
предельной кривой. Действительно, если бы он пере-
84

а,
Рис. 2.1.5.
\/ // /П/ / П ///(////1 //////1 //1 /////// П //////11
а,
а,
а,
Рис. 2.1.6.
85

кал её, то для данного тп можно было бы указать касательное
напряжение, превышающее величину, вызывающую
разрушение. Таким образом, предельная кривая (2.1.10)
является огибающей наибольших кругов напряжений
(рис. 2.1.5).
Критерий максимального касательного напряжения
является частным случаем критерия Мора: предельная кривая
тогда вырождается в прямую линию, параллельную оси абсцисс
(рис. 2.1.6). При этом площадка, на которой достигается опасное
состояние, совпадает с площадкой, на которой действует ттах.
Следовательно, площадка разрушения наклонена под углом 45°
к площадке наибольшего и наименьшего главных напряжений.
В общем же случае, показанном на рис. 2.1.5, опасное
состояние достигается на площадке, образующей с названными
главными площадками углы, отличные от 45°.
Предельная кривая обычно "поднимается" в сторону
меньших нормальных напряжений (рис. 2.1.5.), что
соответствует меньшему сопротивлению материалов при
растяжении, чем при сжатии. На рис. 2.1.7 показан случай
прямолинейной огибающей, когда
г=к
(2.1.11)
На рис. 2.1.7. изображен частный вид предельной кривой,
пересекающей ось ап; при этом имеется наибольшее значение
86

А т«
ф£
а
Рис. 2.1.7.
Рис. 2.1.8.
87

нормального растягивающего напряжения, отвечающее
разрушению путём сдвига или отрыва. Все большие круги
напряжений, касающиеся предельной кривой в точке А и
меньшие соприкасающегося круга, соответствуют возможным
напряженным состояниям, при которых происходит разрушение
путём отрыва или сдвига.
Рис. 2.1.9,

Критерий Мора может быть также представлен некоторой
поверхностью в пространстве главных напряжений. Так, при
рассмотрении возможных шести случаев разных знаков и
соотношений между о(, нетрудно установить, что условие
(2.1.10) с прямолинейной огибающей приводит к шести
уравнениям плоскостей. Последние при ср = 30° (рис. 2.1.7)
образуют поверхность правильной шестигранной пирамиды
(рис. 2.1.9), которая вырождается в шестигранную призму при
переходе к критерию ттах (рис. 2.1.3).
По критерию Мора промежуточное главное напряжение <т2
не влияет на разрушение.
Форма предельной кривой должна быть построена по
экспериментальным данным для каждого материала.
Накопленные данные недостаточны для формулировки общих
закономерностей. Всё же можно считать, что промежуточное
напряжение а2 оказывает некоторое влияние на наступление
опасного состояния.
Критерий Шлейхера - Надаи
В известном смысле критерий Шлейхера - Надаи
аналогичен критерию Мора, но формулируется в терминах
интенсивности касательных напряжений Т и гидростатического
давления о: в опасном состоянии Т является функцией a,
характерной для данного материала
89

T = f{o) (2.1.12)
При f(a) = const = К* приходим к условию Мизеса. Заметим,
что первоначальная формулировка Шлейхера несколько
отличалась от приведённой. В пространстве главных
напряжений (2.1.12) определяет поверхность вращения
относительно гидростатической оси. В зависимости от вида
f(o) можно получить различные формы предельных
поверхностей.
Рис, 2.1.10.
90

На плоскости (7\сг) уравнение (2.1.12) определяет
некоторую предельную кривую - границу разрушения
(рис. 2.1.10)
Пунктирная прямая 1 соответствует условию наибольшей
интенсивности касательных напряжений ("пластическое
разрушение"), прямая 2 - условию наибольшего объёмного
растяжения ("хрупкое разрушение"). Общий случай
характеризуется некоторыми кривыми 3 и 4. Кривая 3 не имеет
резкого перехода от пластических разрушений к хрупким.
Наоборот, кривая 4 достаточно резко разграничивает два типа
разрушения. Заметим, что в формуле (2.1.12) вместо среднего
напряжения о иногда целесообразно взять наибольшее
значение из о{
T = f((J]). (2.1-13)
Заметим также, что для изотропного материала с
различными сопротивлениями на растяжение и сжатие критерий
разрушения должен в той или иной форме содержать
инварианты jxg и а.
Критерий Давиденкова - Фридмана
В литературе отмечаются два типа разрушения - путём
отрыва и путём сдвига (среза). В зависимости от условий опыта,
один и тот же материал может разрушаться хрупко или вязко.
При фиксированных температуре и скорости нагружения имеет
91

значение вид ("жёсткость") напряжённого состояния. Хорошей
иллюстрацией может служить известное образование чашечки
при разрыве шейки в экспериментах по определению прочности
металлических образцов.
На дне чашечки происходит разрушение путём отрыва,
поскольку в центральной части шейки возникает объёмное
напряжённое состояние, близкое к равномерному
всестороннему растяжению. Края чашечки разрушаются из-за
сдвига, ибо после разрыва дна напряжённое состояние в
периферийной части шейки будет типа одноосного растяжения.
Поэтому разделение материалов на хрупкие и пластичные
является достаточно грубой схематизацией.
Простейший способ учёта двойственного характера
разрушения заключается в одновременном рассмотрении
касательных и нормальных напряжений. Примерами такого
подхода являются критерии Мора и Шлейхера - Надаи. При
этом, однако, не учитываются деформационные характеристики
материала.
Предпринимались неоднократные попытки продвинуться в
этом направлении. В частности, ещё П. Людвиг связывал
условие прочности с кривыми пластической деформации.
Остановимся здесь на получившей известность схеме
Давиденкова - Фридмана.
Исходным является предположение о наличии у
материала двух характеристик предельной прочности:
92

сопротивления отрыву аг и сопротивления сдвигу (или срезу)
Величину аг для хрупких в обычных условиях материалов
можно трактовать как предел прочности при растяжении.
Значительно труднее определить эту характеристику для
пластичного материала. Иногда это удаётся сделать, испытывая
его при очень низкой температуре (когда материал становится
хрупким) или же нагружая образцы специального вида
(например, с тонкой прослойкой). При хрупких разрушениях в
опытах на сжатие обобщённое сопротивление отрыву
подсчитывается по критерию наибольшего удлинения на основе
закона Гука.
Сопротивление срезу ts можно найти, например, из
опытов скручивания полых трубок.
Учёт "жёсткости" напряжённого состояния осуществляется
посредством введения коэффициента
а = ^-, (2.1.13)
<*+
где ст+ - приведённое растягивающее напряжение,
определяемое по закону Гука для наибольшего удлинения е+:
ст+ - Ее+ .
Если а»1, т.е. имеются значительные касательные
напряжения при малых удлинениях (например, осевое сжатие,
гидростатическое давление), нагружение является "мягким".
93

Если а«1, т.е. имеются значительные упругие
удлинения при малых касательных напряжениях (например,
трёхосное растяжение, близкое к равномерному), нагружение
является "жёстким".
На плоскости (<т+,ттах тпак =т5) проведём "линию отрыва"
g+ =ar и "линию среза" (рис. 2.1.11). При пропорциональном
нагружении напряженное состояние на приведённой диаграмме
характеризуется лучом. Так, при равномерном растяжении луч
проходит по оси абсцисс (ттах =0). На рис. 2.1.11 пунктиром
показаны лучи, отвечающие одноосному растяжению (а = 0.5) и
одноосному сжатию (а = 0.5v ).
Рис. 2.1.11.
94

На рис. 2.1.11 луч растяжения пересекает линию отрыва, и
разрушение произойдёт путём отрыва. Однако, если
сопротивление отрыву для данного материала сравнительно
велико, тот же луч пересечёт линию среза, и разрушение будет
вязким.
Уязвимым местом теории Давиденкова - Фридмана
является использование далеко не универсального критерия
наибольшего удлинения и условного параметра жесткости
напряжения а.
Заключительное замечание
Имеются десятки примеров разрушения, предложенных
различными авторами. Условия их применимости изучены, в
общем, слабо. Обычно эти критерии содержат ряд
характеристик напряжённого состояния и дополнительные
константы.
В рассмотренных высших критериях подразумевалось, по
существу, простое (т.е. пропорциональное) нагружение.
Опытные данные о зависимости условий разрушения от пути
нагружения скудны, хотя этот вопрос имеет, вероятно, значение
для пластичных металлов. Сравнительно небольшие
предварительные пластические деформации не должны
заметно влиять на границу разрушения. Этого, в общем, нельзя
утверждать в случае больших пластических деформаций.
95

Формулировка критерия разрушения при сложном
нагружении требует, вообще говоря, использования
функционалов (по времени и параметру нагружения),
отражающих историю деформирования материала
(Л.М. Качанов "Основы механики разрушения", М.: "Наука"
1974 г.). При этом, разумеется, фиксированной предельной
поверхности не будет. Конкретизация критерия разрушения
возможна при наличии каких-либо концепций, касающихся
механизмов разрушения и основанных, в частности, на анализе
экспериментальных данных.
Заметим, что простейший вариант критерия разрушения
можно задать формулой
F(<rij9cl9c2...) = l
где с- - некоторые эмпирические параметры, характеризующие
накопления пластических деформаций и повреждений.
§ 2.2. Смещения и напряжения в однородных и
неоднородных нагруженных стержнях
Однородный стержень
Рассмотрим однородный тонкий стержень длины /,
стоящий вертикально на жестком недеформируемом основании.
Боковая поверхность свободна от напряжений. Плотность р и
96

модуль Юнга Е материала стержня постоянные. Необходимо
найти распределение смещений и напряжений.
Нетрудно понять, что решение будет зависеть только от
одной переменной х (§1.7), которую будем отсчитывать от
верхнего конца. Сформулируем граничные условия:
нижний конец неподвижен
их(1) = 0; (2.2.1)
верхний конец свободен от напряжений
<тЛ(0)=0. (2.2.2)
Имеют место:
уравнения равновесия
дет YY
—^ + pg=0] (2.2.3)
ox
закон Гука
°хх=Еехх] (2.2.4)
связь деформации со смещением
duY
exx=^L- (2-2.5)
ox
Подставляя (2.2.4) и (2.2.5) в (2.2.3), получим уравнение
д\ _ pg
дх2 Е '
после двукратного интегрирования которого найдем
(2.2.6)
их(х) = --^-х2+С1х + С2, (2.2.7)
2Е
97

где Сх и С2 неизвестные константы, подлежащие определению
из граничных условий.
Поскольку
ох
то из (2.2.2) сразу следует С, = 0. Подставляя (2.2.7) в (2.2.1),
PR 1
получим С2 =—2-г и, таким образом,
"» = ^|('2-*2). oxx(x) = -pgx (2.2.8)
Нетрудно видеть, что стержень укорачивается {их>0), а
максимальное напряжение pgl, как и следовало, ожидать,
достигается на его нижнем конце. Отметим, что второе
выражение в (2.2.8) в точности совпадает с законом Архимеда.
Полученное решение может быть использовано для
приближенных оценок напряжений в насыпных дамбах,
однородных массивах горных пород (см. § 2.4).
Неоднородный стержень
Многие природные объекты имеют слоистую структуру,
причем и плотность, и деформационные характеристики (в
частности, модуль Юнга) увеличиваются с глубиной.
Рассмотрим простейшую модель такой ситуации.
98

Пусть сформулирована задача (2.2.1)-(2.2.5), но р и Е
являются линейными функциями от х
р = р0(1 + а;с), Е = Е0(\ + ах) (2.2.9)
где р0 и Я0 -значения соответствующих величин "на
поверхности" (при х=0),а>0 - известная константа
(размерность м"1). Из (2.2.3) с учетом (2.2.9)
°хх (*) = ~Ро 8 \ С1 + Oix)dx =-p0g(x + 0.5ax2) + С,.
Используя граничное условие (2.2.2), найдем Q = 0. Тогда из
(2.2.4), (2.2.5) получим выражение
дих _ p0g 2x + ax2
дх 2Е0 1 + ах
интегрирование которого дает
Ро8
их{х) = -
2Et
^-ln(l + ajc) + —
+ С
2*
а а'
Теперь, определяя с помощью (2.2.1) константу С2, имеем
окончательно
Г1-х J.
и(х) =
Ро8
2Е(
а
, \ + ах 12-х2
— In —
-2 1 + а/
- + ■
(2.2.10)
cr^(x) = -p0g(x + 0.5ax ).
Переходя в (2.2.10) к пределу при а—>0, можно получить
(2.2.8). В этом мы предоставляем читателю убедиться
самостоятельно.
99

На рис. 2.2.1 показано распределение смещения -их/ы0
(и0 = 0.5p0gl21E0) при различных значениях безразмерного
параметра a =al.
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
Рис, 2.2.1.
Этот результат можно использовать при оценке оседания на
различной глубине насыпных сооружений. Видно, что с
увеличением плотности грунта осадка уменьшается.
100

Составной стержень
Пусть стержень состоит из двух жестко скрепленных между
собой частей с различными физическими свойствами: верхняя,
длины a, имеет плотность рх, модуль Юнга Ех; нижняя,
соответственно р2 и Е2. В обеих частях справедливо решение,
совпадающее по структуре с (2.2.7),
[их(х)\ = -Ахх2 +Схх + С2 (2.2.11)
[и^Сх)^ =-А2х2 +С3х + С4
где обозначено Д =0.5p/g/£'-. В (2.2.11) фигурируют четыре
неизвестные константы Су (7=1,...,4). Два условия (2.2.1) и
(2.2.2) для их определения нам уже известны. Два другие -
непрерывность смещений и напряжений на границе х-a
контакта верхней и нижней частей
[ux(a)\=[ux(a)]2 (2.2.12)
[^(4=^(4. (2.2.13)
Выпишем четыре уравнения для определения С,-:
(2.2.2) -> -гДх + С^О прих = 0
(2.2.1) —> -A2jc2+C3jc + C4 =0 прих = /
(2.2.12) -> -Дх2 + С1д: + С2 = -Л2д:2+Сзд: + С4 =0 при х = a
(2.2.13) -^ (-2А[х + С1)Е1 = (-2А2х + С3)Е2 при х = я
Решая эту систему, найдем
101

С х = О, С, = 2
V 2 J
\а (2.2.14)
у2
Г
\s л — -**2 3 ' 2 — I
еЛ
I--1
а2+С4
на чем, собственно, и заканчивается решение поставленной
задачи.
Нетрудно проверить, что если свойства частей стержня
одинаковы, то С3 =0, С2=С4 = Ах12 т.е. решение не зависит
от а, и мы приходим к (2.2.8).
Соотношения (2.2.12), (2.2.13) обычно называют
условиями сопряжения или "склейки".
Аналогичным образом можно найти решение для стержня,
составленного из нескольких частей.
§ 2.3. Упругий цилиндр под действием внутреннего
и внешнего давления
Вопросы сохранности подземных сооружений,
трубопроводов и цистерн высокого давления возникли очень
давно и продолжают оставаться актуальными до сих пор.
Приведенная ниже задача решена Ламе в 1859 году.
Рассмотрим длинный полый цилиндр, его внешний радиус
гх, внутренний г0. На соответствующих поверхностях
приложены постоянные давления рх и р0 (рис. 2.3.1).
102

Материал, из которого изготовлен цилиндр, будем считать
упруго-хрупким (параметры Ламе Я, /и; предел прочности на
растяжение at). Необходимо найти распределение напряжений.
Рис. 2.3.1.
Описанная ситуация позволяет использовать модель
плоской деформации (§ 1.6). В силу осевой симметрии решение
юз

зависит только от радиуса г, который отсчитывается от центра
поперечного сечения цилиндра.
Сформулируем граничные условия
°гг(г0) = -Ро> °rr(n) = -Pi' (2.3.1)
Имеют место:
уравнение равновесия (массовые силы отсутствуют)
(^та л э,. .. Л
(Я + 2/л
Э иг 1 диг и
*2 ~+г дг г2
= 0; (2.3.2)
и закон Гука, который запишем в виде (§ 1.7)
(Тгг=(Я + 2м)—^ + Я —'
dr r
dr r
(2.3.3)
Будем искать решение дифференциального уравнения
(2.3.2) в виде иг = гп. Подставляя это выражение в (2.3.2),
получим
(л2-1)г"-2=0.
Значит л= ±1, и (2.3.2) имеет решение
ur =Cxr + C2r~\ (2.3.4)
где константы Сх и С2 подлежат определению из граничных
условий. Используя (2.3.4), вычислим напряжения по (2.3.3)
G =(2Я + 2/|)С1-2^С2г"2,
rr ^ l ^ 2 (2.3.5)
овв =(2Л + 2/и)С1 +2/лС2г 2.
104

Подставляя в (2.3.1) выражение для агг, получим систему
линейных уравнений
(2A + 2/i)C, -2цС2гй2 =-р0,
(2А + 2/г)С, -2/лС2г1'2 =-рх,
решая которую, найдем
(2Х + 2ц)С1 =
/W-/W
г\ ~го
2\хСг =
rori2(Po~P\)
(2.3.6)
г\ ~го
Подставляя (2.3.6) в (2.3.5), окончательно имеем
°rr(r) = -Po +
гх (Ро ~ Р\)
(
1
а ев (г) = ~Ро +
г, -г,
о
ЛЛ
.2 Л
(2.3.7)
1 +
Обратим внимание, что напряжения не зависят от упругих
параметров А, /и,.
Проанализируем полученное решение. На рис. 2.3.2
показано распределение агг и стев для различных Р = рх1 р0
при г,/г0=5 (положительные значения - растяжение,
отрицательные - сжатие).
Можно видеть, что напряжения, максимальные на
внутреннем контуре, уменьшаются с приближением к внешнему.
С уменьшением Р в цилиндре появляются растягивающие на-
105

i.o A
P=O.OJ
Рис. 2,3.2.
пряжения, причем всегда овв>огг. Значит, в первую очередь
нужно ожидать (при высоком внутреннем давлении р0)
разрушений на площадках с нормалью по оси 9, т.е.
радиальных трещин.
На рис. 2.3.3 показано распределение огг и овв по
толщине цилиндра при Р = 0.02 и различных значениях
£ = гх I г0. Видно, что уменьшение толщины стенок цилиндра
увеличивает уровень растягивающих напряжений овв.
106

Рис. 2.3.3.
Оценим, какое предельное внутренне давление р0 может
выдержать цилиндр? Приравняем значение авв на внутреннем
контуре к пределу прочности материала на растяжение
°вв(Г0)= 2 2 = (Т"
тогда
Р* = Ро = ■
°ttf-r$) + 2r*Pl
(2.3.8)
г\ + го
107

Распределение /?* / рх в зависимости от £ при различных
значениях at показано на рис. 2.3.4.
Выведем теперь приближенную формулу оценки /?* для
тонкостенных труб. Пусть
rx=r0+ht (2.3.9)
Рис. 2,3.4.
108

h -толщина трубы,. h«r0. Подставим (2.3.9) в (2.3.8) и
разложим получившееся выражение в ряд Маклорена по /*,
оставив два первых члена
h (>-2Л
р* =2р1 +—а, +0\
го
*1
(2.3.10)
Таким образом, если мы хотим транспортировать жидкость
под давлением ЮМПа по стальной (сг,=500МПа) трубе
диаметром 2 м, то толщина стенок должна быть равна
h~kP*~2Pl r^2k см,
где А:-коэффициент запаса прочности.
§ 2.4. Круговая полость в безграничной упругой среде
Рассмотрим интересное приложение решения задачи
Ламе, полученного в § 2.3, к проблеме сохранности горных
выработок. Они могут быть расположены на больших глубинах в
недрах Земли и зачастую имеют поперечное сечение, близкое к
круговому;
Оценим сначала приближенно напряжения, которые имеют
место в массиве горных пород. Воспользуемся для этого
формулой (2.2.8),где глубина h = -x
oxx(h) = pgh. (2.4.1)
109

Плотность горных пород р варьируется в широком
диапазоне: от 1700 кг/м3 (уголь) до 3300 кг/м3 (базальт), тогда по
(2.4.1) на глубине 1км горное давлениерх-\8-30 МПа.
Заметим, что эта величина сравнима или даже превосходит
предел прочности ас на сжатие многих природных материалов
(например, для угля ос = 15+50 МПа, слабых
песчаников ос = 30+40 МПа, Приложение 4).
Итак, пусть круглое отверстие W (working - выработка)
радиуса г0 расположено в безграничной упругой плоскости.
Обозначим г расстояние от ее произвольной точки до центра
отверстия. На бесконечности действует постоянное радиальное
напряжение, численно равное горному давлению P\=pgh.
Контур W свободен от напряжений. Таким образом, можно
сформулировать краевую задачу
limarr(r) = -pl
г^°° (2.4.2)
<7„(Г0) = 0
Решение системы (2.3.1) - (2.3.3), (2.4.2) немедленно
получается из (2.3.7), если положить в нем р0=0 и перейти к
пределу при гх —> <ю
°гг=-Р\
( 2\
°ев = ~Р\
( 2\
(2.4.3)
Отметим два важных факта. Во-первых, максимальное
сжимающее напряжение достигается на контуре отверстия
по

авв(г0) = 2р], и именно это значение нужно сравнивать с
пределом прочности пород при проектировании выработок и
оценке их сохранности.
Во-вторых, ап,авв —» рх при г—»<», т.е. с удалением от
W напряжения приближаются к исходным значениям
(существовавшим в среде до образования отверстия): влияние
"возмущения", внесенного в массив выработкой, ослабевает (на
рис. 2.4.1 показаны эпюры агг Iрх и аев1 рх). Этот результат
служит хорошей иллюстрацией принципа Сен-Венана, который
в рассмотренной конкретной ситуации можно сформулировать
следующим образом: "любая неоднородность вносит
возмущение в существующее напряженно-деформированное
состояние среды, заметное лишь в достаточно малой
окрестности этой неоднородности".
Рис. 2.4.1.
111

Выясним теперь, что количественно означают слова
"достаточно малой"? Вычислим относительное отклонение
напряжений от их значения на бесконечности (из (2.4.3))
Kr+Pil'Pi = \°вв+Р\\/ Р\ =го/г2
и потребуем, чтобы они были меньше наперед заданной малой
величины £. Тогда, решая соответствующе неравенство,
найдем, что на расстояниях
г>г^9 г^=г0/^ (2.4.4)
поля напряжений в среде с отверстием и без него совпадают с
точностью £. Величина г% называется размером зоны влияния
выработки. Числовые оценки /£ необходимы при
моделировании напряженно-деформированного состояния
массива на ЭВМ. Дело в том, что вычисления всегда проводятся
в областях конечных размеров, и выбор их размеров имеет
решающее значение на время и точность расчетов.
Соотношение (2.4.4) позволяет a priori оценить этот размер. Так,
если задать £=0.01, то радиус круговой области, в центр
которой нужно поместить отверстие, равен 10 г0.
§ 2.5. Напряженное состояние вращающегося
однородного кольца
Многие детали машин и механизмов имеют форму тонких
дисков (сплошных или с отверстием). Скорость вращения таких
112

деталей может быть очень высока, поэтому встает вопрос об их
сохранности.
Рассмотрим задачу об определении напряжений во
вращающемся с постоянной угловой скоростью со однородном
диске плотностью р, внешний и внутренний радиусы которого
равны, соответственно, гх и г0. Контуры диска свободны от
напряжений.
Известно, что на каждую точку вращающегося тела
действует центробежная сила, пропорциональная расстоянию
от оси вращения, поэтому радиальная составляющая
потенциала массовых сил имеет вид Фг = ра>2г, а уравнения
равновесия (§ 1.7)-
1 дгг г дг г1 ,
V J
+ pft)2r = 0, (2.5.1)
где г-расстояние до центра диска.
Сформулируем очевидные граничные условия
<т„(г0) = 0, orr(rx) = Q. (2.5.2)
Из курса дифференциальных уравнений известно, что
общее решение (2.5.1) можно представить как сумму решений
однородного уравнения (уже найдено в § 2.3 - формула (2.3.4))
и частного решения и\ неоднородного, которое будем искать в
виде
и\{г) = Агп. (2.5.3)
Подставляя (2.5.3) в (2.5.1), получим
из

(Я + 2/г)(и2 -\)Агп-2 + ро)2г = О,
откуда п = 3, А = --
рсо
(2.5.5)
8(А + 2/г)
Таким образом, решение (2.5.1)
ur=Clr + C2r~l +Ar3, (2.5.4)
где неизвестные константы С, и С2 определяются из граничных
условий (2.5.2). Для этого по (2.5.4) с использованием закона
Гука (2.3.3), вычислим напряжения
агг =(2Л + 2ц)С1 -2цС2Г2 +(4Л + 6ц)Аг2,
авв = (2А + 2/л)С1 + 2цС2г~2 + {4А + 2ц)Аг2
и подставим в (2.5.2), тогда
(2А + 2/г)С, -2цС2Гъ2 + (4А + 6ц)Аг2 = О,
(2А + 2/г)С, - 2/iC2/i~2 + (4А + б^А^2 = 0.
Решая полученную систему, найдем
(2А + 2ju)C, = -(4А + 6/i)(r,2 + г02 )Л,
2/гС2 =-(4A + 6/i)r,2r02A
Теперь выражения для напряжений (2.5.5) примут вид
(
огЛг) = °о
Е2
Л
Z'
(
'ев
(г)
(2.5.6)
где введены обозначения
114

<У(\= * , P= —,
0 4(Я + 2/|) r02 2A + 3/i
(2.5.7)
Z = r/r0t ^=rx/r0.
Здесь, в отличие от §§ 2.3, 2.4, напряжения зависят от
физических свойств материала.
На рис. 2.5.1 показаны эпюры напряжений огг и авв вдоль
диска при различных значениях ^ и /? = 0.6. Можно видеть, что
все напряжения - растягивающие и овв>агг. Радиальное
напряжение агг достигает максимального значения а0(^-^{)
в точке г = д/^г, . Кольцевое напряжение овв, максимальное на
внутреннем контуре, монотонно убывает с удалением от него.
4.5 Г /г0
115

Оценим, каков может быть максимальный внешний радиус
диска при заданных свойствах материала, скорости вращения и
величине г0? Для этого решим относительно гх уравнение
гх =г0Л/0.5(сг,/<70+£-1).
Обратим внимание, что с учетом выражения для сг0
(2.5.7), гх пропорционален квадрату внутреннего радиуса
кольца г0.
§ 2.6. Полый шар под действием внутреннего и
внешнего давления
Указанная в заголовке задача моделирует поведение
сферических резервуаров высокого давления. Она также
решена Ламе в 1859 году.
Постановка и решение задачи идентичны таковым для
полого цилиндра (§ 2.3), поэтому будем отмечать лишь этапы и
выкладки, приводящие к искомому результату - распределению
напряжений в рассматриваемом объекте.
Граничные условия
<Гм(Ло) = -Ро. °rr(*\) = -Pi (2-6-1)
обеспечивают сферическую симметрию, поэтому поле
напряжений представлено тремя компонентами оRR,
116

авв = a(w > а поле смещений - одной uR (§ 1.7). Все они зависят
от переменной R - расстояния до центра шара.
Уравнение Ламе (§ 1.7)
(Я + 2рЛ
закон Гука
д uR 2 duR 2uR
dR2 R ЭЯ R:
= 0,
(2.6.2)
(Тй„=(Я + 2/|)^- + 2Я-^-,
dR
R
CT =A—^- + (2Я + 2и)-^-
вв dR R
(2.6.3)
Решение уравнения равновесия ищется в виде uR=R".
Подставляя это выражение в (2.6.2), получим
(n2+n-2)R"~2 = 0,
откуда п = 1, -2 и
uR(R) = ClR + C2R~2, (2.6.4)
где константы С, и С2 подлежат определению из (2.6.1).
Подстановка (2.6.4) в (2.6.3) дает
aRR =(ЗЯ + 2/|)С, -4/*С2/Г3,
сг«, =(ЗЯ + 2/г)С1 + 2цС2Я~3.
Подстановка (2.6.5)! в (2.6.1)
(ЗЯ + 2/*)С, -4/гС2/?о3 = -/V
(ЗЯ + 2/г)С, -4jiC2flf3 = -/>,.
Решение (2.6.6)
(2.6.5)
(2.6.6)
117

4 c ЩРо^РО
Окончательные выражения для напряжений принимают
вид
Orr (r) —Ро+ „з г,з
К1 _Л0
»«<*>~ft+*g4PJ
3,_ _чГ «ЗА
1 + ^L
(2.6.7)
V
tfJ
J
Здесь напряжения также не зависят от физических свойств
материала.
1.0-
-2.0-У
Р=0.01
!!!"::::sis::iiiii
0.5
1.2
1.5
1 1 1 1 1 1 1
1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.
Рис. 2.6.1.
118

На рис. 2.6.1 показаны эпюры oRR и овв при Rxl /?q = 5 для
различных значений Р = рх1 р0.
Качественно характер изменения напряжений
соответствует таковому для цилиндрической задачи (§ 2.3,
рис. 2.3.2), однако с увеличением R компоненты oRR, oQQ
уменьшаются быстрее, а их максимальные значения меньше,
чем огг и аве.
Рис. 2.6.2.
На рис. 2.6.2 показана зависимость oRR и авв от R при
Р= 0.02 и различных значениях £ = RxlR$. Здесь также имеет
119

место качественное соответствие с рис. 2.3.3, но абсолютные
величины напряжений меньше. Это говорит в пользу
сооружения сферических резервуаров.
Вычислим предельное внутренне давление /?0, (которое
может выдержать сферический резервуар), решив уравнение
aee(RQ) = (Tt или
откуда
_ _at(/?,3-/?03)+2/?,V,
(2.6.8)
fUUm
350-
300-
250-
200-
150-
100-
50-
0-
Ро /Р,
at /pI = 400^
' 300^~-
^^200^^
100
R,/Ro
1.5
2.0
Рис. 2.6.3.
2.5
3.0
120

Распределение р* I рх в зависимости от £ при различных
at показано на рис. 2.6.3.
Для тонкостенных резервуаров
R^R^+h (2.6.9)
{h-толщина стенок, h«R0). Подставляя (2.6.9) в (2.6.8) и
разлагая в ряд Маклорена по h, получим
h jh^
Р* = 2/7, + Gt + СА
2^ '
^2
Сравнивая это выражение с (2.3.10), можно заключить, что
при одинаковых размерах и толщине стенок сферический
резервуар может выдержать вдвое большее давление, чем
цилиндрический.
§ 2.7. Оценка напряжений в недрах Земли
Земля имеет форму эллипсоида, несколько "сплющенного"
с полюсов. Здесь мы этим пренебрежем и будем считать ее
радиус Rx постоянным, равным 6370 км. В центре Земли
расположено жесткое (недеформируемое!) ядро радиусом
RQ = 1215 км. Ядро окружено "жидким" слоем толщиной около
2270 км.
В верхних слоях земной коры плотность р~1500-
3000 кг/м3, скорость распространения сейсмических
121

(продольных) волн Vp ~ 2000-6000 м/с. С увеличением глубины
р и Vp существенно возрастают. По данным гравиметрической
и сейсморазведки средняя плотность Земли составляет
5500 кг/м3, а скорость волн 12000 м/с. Эти значения и примем
для расчетов.
Известно, что ускорение свободного падения g
уменьшается пропорционально расстоянию до центра
g~gRIRu
тогда потенциал сил гравитации, действующих на каждую точку
Земли равен
<bR=-pgR/Rl
(знак минус выбран потому, что силы действуют против
направления внешней нормали к поверхности Земли).
Не будем учитывать и атмосферное давление (0.1 МПа) на
дневной поверхности.
Итак, примем простейшую однослойную модель Земли и
определим, как распределены напряжения по ее толще.
Введенные гипотезы позволяют принять сферически
симметричную модель и использовать результаты § 2.6.
Сформулируем граничные условия
uR(Ro) = 01 стм(Л1) = 0. (2.7.1)
Уравнение равновесия (§ 1.7)
122

где R - расстояния до центра шара.
Общее решение однородного уравнения дается формулой
(2.6.4) с неизвестными константами С, и С2. Частное решение
неоднородного уравнения будем искать, как и раньше (§ 2.5), в
виде
uR(R) = ARn (2.7.3)
Подставляя (2.7.3) в (2.7.2), получим
(k + 2fi)(n2+n-2)ARn'2-pgR/Ri = 0,
откуда п = 3 и А = 2 .
10^ + 2/*)/?,
Таким образом, решение (2.7.2)
uR (R) = CXR + C2R~2 + AR3, (2.7.4)
Используя (2.6.3) вычислим напряжения по (2.7.4)
aRR = (ЗЯ + 2/i)Cx - 4fiC2R~3 + (5А + 6^)AR\ сч
(2.7.5)
авв = (ЗЯ + 2/г)Сх + 2^iC2R~3 + (5А + 2ц) AR2.
Теперь, подставив (2.7.4) и (2.7.5) в (2.7.1), получим
систему уравнений относительно С,, С2
CXR0 + С2Щ2 + А/^ = 0,
(ЗЯ + 2^)Q - 4fiC2R~3 + (ЗЯ + 2/1)Л/?!2 = 0,
решая которую, найдем
123

С, =-А
С2=А
jg2fl?+*o5
RlR3x{P2Rt-PxRl)
(2.7.6)
М3+Ло3
где введены обозначения
д _ ЗЯ + 2ц R 5Л + 6/Л
4/i 4/i
Подставляя (2.7.6) в (2.7.4) и (2.7.5) найдем окончательно
uR (К) = AR\
/Г-Л£ +
2 Rl{P2Rt-PxR20)
1 —
R
з\
/?J
стдд(/г) = -4И
СГда(Л) = -4/|Л
A*,3+/?3
(2.7.7)
iMi +*о
/г3
P2Rx2+(l-P2)R2 +
2 R30(P2R? ~ РхФ
R
V
-1
v2*3 у.
/М,3+д03
Заметим, что параметры /J, и /32 могут быть выражены
через коэффициент Пуассона v
ft =■
1+v
02 =
3-v
2(1-2v) 4 2(1-2v)
На рис. 2.7.1 для различных v показано распределение
смещении uR, отнесенных к и0
Р8Щ
Видно, что uR
достигает максимума на поверхности и слабо зависит от v.
124

4.0-
3.5-
3.0-
2.5-
2.0-
1.5-
1.0-
0.5-
0.0-
tin / ("П
0.2 0;
1 ■ 1
3000 4000
03
R, км
2000
5000
6000
Рис, 2.7.1.
Оценим количественно величину uR(R{). Для этого
воспользуемся известным соотношением из динамической
теории упругости (выходящей за рамки настоящей книги)
pVp =A + 2jU, связывающим деформационные и акустические
свойства среды. Тогда (рис. 2.7.1)
2R2
и (/?!>-3-2-Ц-« 845000 м,
125

т.е. под действием гравитационных сил поверхность
"опустилась" на 845 км, а радиальная деформация составила
RR
R, км
V.V"
-0.1-
-0.2-
-0.3-
-0.4-
-0.5-
-0.6-
-0.7-
п »-
Oee/PgR,
0.3
1
0.2 Л
^0.1
R, км
2000 3000 4000 5000 6000
2000 3000 4000 5000 6000
Рис. 2.7.2.
Рис. 2.7.3.
На рис. 2.7.2, 2.7.3 показаны эпюры oRR и авв (отнесены к
pgRx) для различных значений v. Как и следовало ожидать,
все напряжения - сжимающие, увеличиваются с глубиной,
причем oRR возрастает быстрее, чем овв. Они также слабо
зависят от v, хотя на поверхности при изменении v от 0.1 до
0.4 величина ствв увеличивается почти в два раза.
126

На контуре внутреннего ядра
VrrW в °-5 - °-8 PSR\=175 - 280 ГПа:
(7^(7^)^0.1 -0.6pgRx = 35-210 ГПа.
Для сравнения: модуль Юнга железа 200 ГПа, а
чрезвычайно твердого вольфрама - 360 ГПа.
В заключении отметим, что полученные в этом параграфе
оценки не являются точными, но позволяют судить о порядке
абсолютных значений напряжений, существующих в глубоких
недрах Земли.
Аналогичный подход можно применить и для других
планет, необходимо лишь знать их размеры, физические
свойства и ускорение свободного падения. Эту информацию
можно найти в астрономических справочниках. Единственная
сложность - величина R0, однако в первом приближении можно
полагать /?0=0» в (2.7.4) С2=0 и проигнорировать первое
условие (2.7.1).
§ 2.8. Поля напряжений в упругой полуплоскости,
создаваемые поверхностными нагрузками
Предварительные замечания
В этом и последующих параграфах будут рассмотрены
двух- и трехмерные задачи. Они гораздо сложнее одномерных,
127

но позволяют моделировать более широкий круг реальных
явлений и процессов и получать физические следствия.
Существует много способов решения неодномерных
задач. Некоторые требуют различных "ухищрений"
(представления Галеркина, Папковича) и носят оттенок
искусственности, другие требуют знаний специальных разделов
математики (теории функций комплексного переменного,
методов решения интегральных уравнений).
Мы остановимся на методе интегральных преобразований,
который является универсальным инструментом (применяется
во многих разделах механики и не только) и вполне "прозрачен"
для восприятия. Для его использования достаточно быть
знакомым с общим курсом математики ВТУЗов и прочитать
Приложения 1, 2 и Зв настоящей книге.
Пример применения интегрального преобразования
к решению краевой задачи.
Проиллюстрируем на примере методику решения с
помощью преобразования Фурье.
В полуплоскости у >0 необходимо найти функцию и(х,у),
удовлетворяющую гармоническому уравнению
й+г^=° <28-1»
Эх ду
граничному условию
128

u(x,0) =
2i 'X'-Z, (2.8.2)
[О |jc|>/
и исчезающую на бесконечности
и(х,у)-^0 при jc, у—><*>. (2.8.3)
Специфика (2.8.2) в том, что площадь под графиком этой
функции (21 *и0 /(2/) = и0) остается постоянной при изменении
размера области задания граничных условий /.
В силу (2.8.1) -(2.8.3) функция и четная по jc, поэтому
будем искать ее в виде
и(х, у) = —[щк, у)coskxdk , (2.8.4)
п о
где
оо
U {к,у) = \и(х, у) cos kxdx (2.8.5)
о
- образ Фурье, а к - параметр преобразования.
Подставляя (2.8.4) в (2.8.1), получим обыкновенное
дифференциальное уравнение
^L-k2U=0. (2.8.6)
ду
Теперь умножим (2.8.2) на coskx и проинтегрируем по х
от 0 до оо f тогда
U(k,0) = Jii(jc,0) cos kxdk = ^^L f (2.8.7)
129

т.е. получено начальное условие для (2.8.6). Общее решение
(2.8.6) имеет вид
и(к,у) = С1е~ку+ С2£^,
где Сх, С2 - неизвестные функции, зависящие, быть может, от
к. Из (2.8.3) следует, что U—>0 при у—>«>, поэтому С2=0.
Используя (2.8.7), найдем
1 21 к
и, наконец, по (2.8.4)
ио 1 ~kv sin kl cos kx „
u(Xy y) = -L\e *у dt. (2.8.9)
я* J к
Для вычисления (2.8.9) преобразуем подынтегральное
выражение к виду
±*-*
sin(x + /)£ sin(x - 1)к
и воспользуемся табличным интегралом
7 _ь sin/:*? g
в р dk = arctan g —.
Jo * P
Тогда
n^^rr-^fo -0 ), 0±=arctan^-. (2.8.10)
2nl у
Непосредственной проверкой можно убедиться, что
соотношения (2.8.1)- (2.8.3) выполнены (рис. 2.8.1, где
вертикальными стрелками показано граничное воздействие).
130

Получим одно важное следствие из (2.8.10). Перепишем
его в виде
Ну
и(х,у) = —-arctan-
2nl х2+у2-12
и, пользуясь правилом Лопиталя, найдем предел при / —» 0
и (х,у) =
У
п х2 +у2
\
Г 1
г 1
-/^\^
>
f Т Т
г 7
^
X
г ^
Рис. 2.8,1.
Функцию и будем называть фундаментальным решением
для сосредоточенной нагрузки:
1) и*удовлетворяет (2.8.1) и (2.8.3);
2) обращается в бесконечность при х = у = 0, но
131

г */ xj uo A
и (x, y)dx = — arctan —
J 71 V1
—oo У
="0;
3) в случае граничного воздействия произвольного
вида и(х,0) = f(x) распределение и во всей
полуплоскости можно найти по формуле
и(х,у) = — \f(t)u*(x-t9y)dt. (2.8.11)
"О-оо
В справедливости (2.8.11) для граничного условия (2.8.2)
можно убедиться непосредственным интегрированием с
последующим сравнением полученного результата с (2.8.10).
Действие вертикальной поверхностной нагрузки
на упругую полуплоскость.
Рассмотренная ниже задача опубликована Мичелом в
1903 году.
На поверхности упругой полуплоскости задана
вертикальная нагрузка амплитуды р0, равномерно
распределенная на отрезке [-1,1]. Необходимо найти поле
напряжений.
Поместим начало декартовой системы координат (лс,у) в
центр отрезка, направив ось ординат вниз, и сформулируем
граничные условия
132

Pq I -Ф *
10 I jc |> /'
<Tyy(x,0) = \„ ^ \ [ ,, (2.8.12)
cr^(;t,0) = 0.
Потребуем также, чтобы atj —> 0 при х, у —> °° (i,j = x,y).
Запишем систему уравнений Ламе для условий плоской
деформации при отсутствии массовых сил в виде
Э2и. Э2и. „ Э2м
—f + a—y + P—-тг- = 0,
Эд; Эу ЭхЭу
2 2 (2-8/13)
в Э2и_ Эй Зм
/3-—-+а—f+—f = 0,
дхду дх ду
где a =/i/(Я+ 2/i), /3 = l-a. Из (2.8.12) и (2.8.13) следует, что
их - нечетная функция по х, а иу -четная. Поэтому
представим их в виде синус-, а иу - косинус- преобразования
Фурье
их (х, у) = — Г Uх (к, у) sin kxdk,
' о
27
и у (х, у) = — J Uу (к, у) cos kxdk,
(2.8.14)
о
где
Uх (к, у) = J ux (х, у) sin kxdx,
о
оо
U у (к, у) = J и у (х, у) cos kxdx.
133

Подставляя (2.8.14) в (2.8.13), получим систему
обыкновенных дифференциальных уравнений
а-
d2U , dUv
Р
ac/v д2и
ду
(2.8.15)
■ + -
у -ak2U„ = 0.
ду ду2
Решение (2.8.15) будем искать в виде
Ux=Aesy,
Uy=Besy
(2.8.16)
(2.8.17)
с неизвестными А, В и s. Подставим (2.8.16) в (2.8.15)
(as2-k2]A-pksB = 0,
pksA + (s2-ak2)B = 0.
Система линейных уравнений (2.8.17) имеет
нетривиальное решение, если ее определитель равен нулю
|ш -к'
-pks
= 0 или
(5ks s2 -ak2\
(as2 -k2\s2 -ak2)+ /32k2s2 =0. (2.8.18)
Это уравнение с учетом соотношения « + /3=1 сводится к
биквадратному
s4-2k2s2+k4 =0,
которое имеет два корня s, = -к и s2 = к кратности 2.
Найдем частное решение (2.8.15), соответствующее
первому корню. Поскольку корень кратный, то оно имеет вид
134

("Л=(с,+ус2)*-*,
/ \ / X *, • (2.8.19)
где Сл = С„(£) - неизвестные функции (л = 1,...,4). Подставим
(2.8.19) в (2.8.15)i
(а(*2С! ~2/:С2 +А:2С2^)-^2(С, + С2у)-0к(-кС3 + С4 -i^y)]*'* =0,
откуда
С4=С2) С2=-^-к(С3-Сх). (2.8.20)
Я + 3/i
Подстановка (2.8.19) в (2.8.15)2 дает аналогичный
результат в силу (2.8.18).
Частное решение, соответствующее корню s2, имеет вид
(Ux\=(Dl+yD2)e*,
{uy)2=(D3+yD4)e^,
однако, поскольку при у-^°° напряжения должны исчезать, то
Ол=0(/1 = 1,...,4).
Итак, для четырех функций Сп(к) есть два соотношения
(2.8.20), два другие "дают" граничные условия (2.8.12).
Подставим (2.8.20^ в (2.8.19), затем - в (2.8.14). По полученным
выражениям для смещений и закону Гука вычислим касательное
напряжение
аху(х,у) = ц—\(-кС1 +C2-2kC2y)e~ky sinkxdk,
71 о
откуда, учтя второе граничное условие (2.8.12),
135

С2 =к(Сх+С3). (2.8.21)
На основании (2.8.20) и (2.8.21) можно выразить С2,С3 и
С4 через Сх
С2 =С4 = кСх,
_ Я + 2^и
С3 - Сх.
Теперь напряжения примут вид
Gxx(x,y)=^-(2A + 2ii)ikCx(l-ky)e-ky coskxdk %
о
a v(x,y) = ^(2A + 2ii)[kCx(l + ky)e-ky cos kxdk, (2.8.23)
0
2л °°
Crxv(jc,>;) = -^-(2A + 2/i)fA:2C1^^"^sinfcc^)
о
Умножим (2.8.12)! на cosfcc и проинтегрируем по х от 0 до
оо. Сравнивая полученный результат с (2.8.23)2 при у=0,
найдем
sin kl
(2Л + 2/иУсС{(к) = -р0
к
Подставляя это выражение в (2.8.23), имеем
136

a^(x9y) = -^f(l + ky)e-fy?^coskxdkt (2.8.24)
71 о k
a (jc, _y) = —- у Г e"^ sin kl sin fcxd/:.
^ 0
Вычисление интегралов типа (2.8.24) уже проводилось в
настоящем параграфе и не представляет сложности
cjxjc(X,y)=?<L(e_-o++s_-s+l
71
(Jyy(x,y) = ^(9_-e+-S_+S+), (2.8.25)
аху(х,у) = Щт_-Т+),
71
где
в± =arctan
У
у(х±1)
s+=-
(x±l)2 + y'
2
г.=. "
(х±1)2+у2
Обратим внимание, что напряжения не зависят от
физических свойств среды: плотности, модуля Юнга и
коэффициента Пуассона.
Непосредственной проверкой можно убедиться, что и
граничные условия, и уравнения равновесия выполнены.

На рис. 2.8.2, 2.8.3 показано распределение безразмерных
напряжений o(jl р0 в зависимости от £=x/l, r\-yll. Можно
видеть, что всюду в полуплоскости нормальные компоненты -
сжимающие, их концентрация наблюдается на границе области
приложения нагрузки. Еще одна отличительная особенность
поля напряжений состоит в том, что а^ затухает с глубиной
гораздо медленнее, чем о .
Рис, 2.8.2.
138

На рис. 2.8.4 показаны изолинии максимального
касательного напряжения
*тах =^{°хХ-°ууУ+4°2ху ■
В условиях всестороннего сжатия именно rm2LX указывает
на зоны возможных разрушений. Пусть задано некоторое
предельное значение т*, тогда там, где ттах>т* разрушения
могут иметь место (показаны тоном на рис. 2.8.5).
Рис. 2.8.3.
139

Рис. 2.8.5.
Действие вертикальной сосредоточенной
поверхностной нагрузки
Из (2.8.25) легко найти решение задачи Фламана (1892 г.).
Для этого используем уже известный прием: заменим р0 на
р0 II и перейдем в (2.8.25) к пределу при / —»0, тогда
140

Gxx(x,y) =
°*уу(х,у) =
°*ху(х>У) =
2p0 x у
n (x2+y2f
2p0 y3
71 (х2+У2)2'
_ 2p0 xy
" {x2 + y2j'
(2.8.26)
Рис. 2.8.6.
141

Полученные формулы дают фундаментальное решение, с
помощью которого может быть найдено распределение
напряжений в полуплоскости для любой вертикальной
поверхностной нагрузки. Пусть последняя задана в виде
о* (*,0) = f(x), тогда компоненты тензора напряжений в
полуплоскости
Рис. 2.8.6.
142

Рис. 2.8.7.
Изолинии сг*. /р0, а также т^ах/р0 показаны на рис. 2.8.5-
2.8.7. Они качественно соответствуют таковым в задаче Мичела.
Тоном на рис. 2.8.7 также показаны зоны возможных
разрушений при некотором критическом значении г* (выбрано
т* =0.1). Для перехода к анализу реальных полей напряжений
необходима информация о пределе прочности материала и
143

абсолютной величине р0. Линейность задачи позволяет
использовать решения (2.8.25) и (2.8.26) в качестве базовых.
§ 2.9. Действие вертикальной нагрузки на поверхности
упругого полупространства
Пусть на границе упругого полупространства приложена
вертикальная статическая нагрузка, распределенная по
некоторому известному закону. Необходимо построить поле
напряжений.
Задачи подобного рода возникают при моделировании
различных технологических процессов в горном деле (отбойка и
дробление породы, ударно-вращательное бурение),
машиностроении (оценка прочности и ударостойскости
элементов конструкций) и многих других отраслях
промышленности.
Постановка и решение выполнены впервые Буссинеском
(1885 г.), поэтому задача носит его имя.
С целью унификации изложения материала мы, в отличие
от автора, для решения используем метод интегральных
преобразований.
Введем цилиндрическую систему координат (r,0,z) и
остановимся сначала на способе задания граничной нагрузки.
Рабочий орган инструмента обычно имеет конечные размеры,
здесь же предположим, что воздействие:
1) осуществляется на всю поверхность z = 0;
144

2) симметрично относительно оси z ;
3) описывается функцией
F{r,m) = ~ ^——, (2.9.1)
2"(г2+т2У'2
2поо
где F0 = f f F{r,m)rdrdG -суммарная сила.
о о
Параметр т в (2.9.1) характеризует степень
"концентрированное™" воздействия. Действительно, пусть
ударник имеет форму окружности радиуса г0, а мы хотим, чтобы
большая часть (с) приложенной нагрузки была сосредоточена в
круге г < г0. Решим уравнение
27Г/0
cF0 = \ I F(r,m)rdrd9
о о
относительно т
т = г0^-1. (2.9.2)
На рис. 2.9.1 показана функция F(r,m)/pQ {pQ = F0/^r02 -
приведенное давление) при различных с<1. Видно, что
нагрузка имеет куполообразное распределение и с ростом с
концентрируется в начале координат.
В силу осевой симметрии смещения и напряжения не
зависят от угла 0, ив- 0, и на основании (§ 1.7) агв -ozQ =0.
Уравнения Ламе принимают вид (массовые силы отсутствуют)
145

10
F(r,m) /p,
с = 0.99
r/rr.
т
0.0 0.5 1.0 1.5 2.0
Рис. 2.9.1.
146

д2и. 1 Эы_ и. Э2и_ пд2и7
дг2
Эг2
drdz
Р
д (ди,
- + —
дг г
+ а
[ д2и7 1 ди7
- + -
дг2 г дг
+ ■
э2и
(2.9.3)
z _
dz:
= 0,
где « и Р определены в § 2.8.
Сформулируем также граничные условия для (2.9.3)
oa(r,0) = -F(r,m),
<тгг(г,0) = 0.
Будем искать решение (2.9.3) в следующей форме
(2.9.4)
ur(r,z) = ]ur(k,z)Jl(kr)dk,
о
оо
uz(r9z) = jUz(k9z)J0(kr)dk9
(2.9.5)
где J0,JX -функции Бесселя. Подставляя (2.9.5) в (2.9.3) и,
воспользовавшись соотношениями для бесселевых функций
(Приложение 2), получим зависящую от параметра
преобразования к систему обыкновенных дифференциальных
уравнений
а^-к2иг-Рк^ = 0,
Эг'
Эг
р^А-аЬЪ,
Эг
Э-2
= 0,
147

совпадающую с (2.8.15), если в ней заменить х на г, а у на z .
Этот примечательный факт и служит объяснением
использования метода интегральных преобразований для
решения.
Теперь можно воспользоваться результатами § 2.8 и сразу
записать
Ur=(Cx+zC2)e-k\
Uz=(c,+zC2)e-k\
(2.9.6)
C2=j^k{C3-C{). (2.9.7)
Учитывая (2.9.5), (2.9.6) и закон Гука
(диг ди7 i
Grz =Щ
■ + ■
Эг дг
вычислим касательное напряжение
оо
C7rz(r,z) = tij(C2-kCl-kC3-2kC2z)e-kzJl(kr)dk,
о
сравнивая которое с (2.9.4)2, найдем
С2=к(с1+С3) (2.9.8)
что совпадает с (2.8.21).
Теперь, выражая, как и раньше, С2 и С3 через Q с
помощью (2.9.7), (2.9.8), используя (2.9.5^ , (2.9.6) и закон Гука,
вычислим все напряжения
148

а„ (г, z) = (2А + 2ц )J [*(l - kz)J0(kr) -(у/- kz)Jx (кг) I к] С, (*)<ffe Л,
о
оо
Стда (г, z) = (2А + 2ju)J [(l - v)fc/0 (*r) + for - fe)7, (*г) / *] С, (£)e_fe Л,
о
оо
стя (г, г) = (2А + 2ц)\ к{\ + kz) С, (k)e'kzJ0 (kr)dk,
о
оо
(2.9.9)
где у/ = \i /(Я + ц).
Осталось определить С,. Представим функцию F в виде
интеграла Бесселя (Приложение 3)
F(r,m) = —\ke-k"lJ0(kr)dk
111
и сравним с (2.9.9)3 при z = О, откуда
(2А + 2/0С = -^£Г*"\
1 2/т
Теперь из (2.9.9) имеем окончательные формулы для
компонент тензора напряжений
тг °° Г" т f I \
(7rr(r,z) = -^{\k(\-kz)J0(kr)-(y/-kz)^y^
2п * |_ к
J (l-r^oCH + Cv-fe)^1^
<7ш О, z) = -
e~kpdk,
e'kpdk,
149

aa{r,z) = —^-\k(l + kz)e'kpJ0(kr)dk,
In
F
orz(r,z) = —°-z\k2e'kpJx(kr)dk,
(2.9.10)
In
где p = z + m.
При вычислении (2.9.10) нам понадобятся интегралы типа
Iin=\k[e-k4n{kr)dk,
выражения для которых приведены в Приложении 3.
Таким образом
arr(r,z) = --^
27Г
27Г
1
т Ъг z
— н w
R3 R5 R(R + z)
т
(
R3
1
Я(Я + z) R2
arz(r,z) = -
2л
Fo_3rzz
2л R
т Ър z
R3 R5
(2.9.11)
5 '
Л . -=2
где R = \r2 +z* .
Такое поле напряжений соответствует распределенной
нагрузке (с<1) и не имеет особенностей всюду в
полупространстве.
Переходя к пределу при т-^0 (суть, с-^1) в (2.9.11),
получим решение собственно задачи Буссинеска
150

crrr(r,z)
3r2z
In
R5
In
-iff
1
1
R(R + z)
R(R + P) R2
(2.9.12)
oa{r,z) = -
o*rz(r,z) = -
2n R5 '
^o 3rz2
In R5
(R = yr2+z2) для сосредоточенной в начале координат
нагрузки. Напряжения (2.9.12) при r,z—»0 имеют особенность
типа /Г2.
Как обычно, звездочка вверху означает фундаментальное
решение. Для произвольной вертикальной нагрузки
ста(г,0) = -/(г), (тгг(г,0) = 0
поле напряжений вычисляется по (2.9.12) с помощью интеграла
свертки
1 °°
Oij (r,z) = —j f(t)cr*j (r-t,z)dt.
О -с
Рисунки 2.9.2,2.9.3 иллюстрируют поведение
вертикальной компоненты о^1р$ при увеличении
"концентрированности" воздействия: можно отметить, что
незначительное увеличение с существенно изменяет картину
изолиний.
151

Рис. 2.9.2 Рис. 2.9.3.
Анализ поля напряжений
Проанализируем (2.9.11), (2.9.12) с позиции критериев
прочности. Вычислим главные значения тензора о^
0.5((T,+aJi0.5^-^)2+< , авв,
и в каждой точке полупространства упорядочим их по
возрастанию съ <о2 <ох. На рис. 2.9.4, 2.9.5 показаны изоли-
152

Рис. 2.9.4.
153

нии <У\/ро> о21Ро в безразмерных координатах
£ =r/r0lt] = z/r0 (сплошные линии - сжимающие напряжения,
штриховые - растягивающие), буквы а-г соответствуют
значениям с = 0.60, 0.75, 0.90 и 1. Видно, что распределенная
нагрузка либо не создает наиболее опасных для среды
растягивающих напряжений, либо их уровень относительно
невелик, а зоны возникновения расположены в глубине
полупространства. Эти же рисунки иллюстрируют, что весьма
незначительное увеличение параметра с и качественно (в
частности, происходит переход от преимущественного сжатия
по ох к растяжению), и количественно меняет характер
напряженного состояния.
С увеличением концентрации поверхностной нагрузки
(с =0.90, 1) картина распределения меняется: напряжение ох
становится растягивающим всюду, появляются зоны растяжения
и по о2. Таким образом, в конусе с вершиной в точке
приложения нагрузки элементы среды находятся в состоянии
двухосного растяжения (в радиальном и тангенциальном
направлениях) и сжатия по вертикали. Кроме того, в окрестности
поверхности также имеют место области растяжения по г и в.
В таких зонах можно ожидать появления радиальных и
кольцевых трещин. Это подтверждают и многочисленные
эксперименты по ударному разрушению горных пород и
металлов.
154

Рис. 2,9,5.
155

На рис. 2.9.6 (взят из [7]) показан результат вертикального
вдавливания заостренного индентора в глинистый грунт - на
поверхности ясно прослеживаются оба типа трещин. Этот факт
подтверждает, что упругие решения хорошо описывают
поведение широкого класса материалов на начальной стадии
нагружения, поскольку глины можно считать упругими весьма
приблизительно.
Рис. 2.9.6.
На рис. 2.9.7 представлены изолинии максимального
касательного напряжения
156

Рис. 2.9.7.
157

r =gi-g3
max ,-*
отнесенного к р0. Если ассоциировать возникновение зон
разрушения среды с выполнением условия ттах>т*, то эти
зоны состоят из двух частей: одна расположена под местом
приложения нагрузки (имеет близкую к сферической форму),
вторая - сравнительно небольшая - в окрестности поверхности.
Это качественно соответствует оценке возможных разрушений
по критериям ox=ot, a2-at, выполненной выше.
°\
1-
2-
3-
4-
1
1 1
Ч
\
0.1 /
/
//
*-V
2
я^^^^^—штт
озГ
3 4 с
1 ' ' ' 1
-^
от
// т
Рис. 2.9.8.
158

Рассмотрим еще один интересный аспект задачи: как
влияет коэффициент Пуассона v на форму и размеры зон
разрушения? Для этого построим изолинии ттах//?0 (рис 2.9.8) и
&\1Ро (рис 2.9.9, воздействие сосредоточенное - с=1) с
одними и теми же значениями при v = 0.15, 0.25, 0.35, что
охватывает практически все типы горных пород и металлов.
Рис. 2.9.9.
159

Область разрушения, определенная по критерию ттах = т*,
почти не меняется (за исключением окрестности свободной
поверхности). Если же использовать критерий ax=ati то с
увеличением v зоны, охватываемые одинаковыми изолиниями,
существенно уменьшаются. Заметим, что значения
v = 0.3-0.35 характерны для металлов.
§ 2.10. Распределение напряжений в окрестности
круглого отверстия
Пусть в безграничной упругой среде расположено длинное
цилиндрическое отверстие круглого сечения радиусом г0. Вдали
от него ("на бесконечности") ортогонально оси отверстия
действуют два взаимно перпендикулярных постоянных
напряжения величиной sx и s2. Необходимо найти напряженное
состояние вокруг отверстия.
Такая задача моделирует поведение массива горных
пород в окрестности протяженных подземных выработок (форма
поперечного сечения которых, как правило, близка к круговой) в
неравнокомпонентном поле внешних напряжений. Постановка и
решение впервые осуществлены Киршем в 1898 г., поэтому
задача носит его имя.
Введем цилиндрическую систему координат (r,0,z),
поместив начало в центр отверстия, ось z направим вдоль
образующих, и ориентируем луч 0=0 в направлении действия
160

II
1 1 1 1 I 1 1
6;/
/
/
/
' v^~
' /Ко
l ( ^4
\»
\
r ~ ч
s ч
-^ >< \
<^_ 1 1 b. ■
l ' ^^\ J X 1 \
\+^^^ V / '
* '
\ '
\ '
\ '
\ /
v '
ч ' \
ч ' \
N ^
^
^* —. —* 1
I 1 t ! ! t f
II
05
Рис. 2.10.1.
s2 (рис. 2.10.1). Описанная ситуация соответствует условиям
плоской деформации, поэтому будем рассматривать
произвольное сечение z = const, в котором тензор напряжений
представлен тремя компонентами агг, огв, овв, зависящими
только от г и в.
161

Сформулируем граничные условия
сггг(го,0) = О, (2.10.1)
<тгв(г0,6) = 0
(контур отверстия свободен от напряжений);
limcr (г,0) = -5,,
/•—>оо
1шктЛ(г,0) = -52, (2.10.2)
Г—>°°
Итст Гг,в) = 0
(напомним, что отрицательные напряжения - сжимающие); где
Gxx*axy>Gyy "" компоненты тензора напряжений в декартовой
системе координат, связанной с цилиндрической
соотношениями
х = rcosO ,
у = rsinO .
Специфика (2.10.1) - (2.10.2) состоит в том, что граничные
условия заданы в различных координатных системах.
"Переформулируем" (2.10.2), посредством введения временной
удаленной границы г-гх (гх>> г0) и пересчета на нее
напряжений (2.10.2) по формуле (1.1.14):
\°гв Свв
= А
(°хх °ху
ху
УУ
А,
(2.10.3)
162

где А =
( cos0 sin0^
-матрица перехода от координат (х,у)
-sin0 cos0
к (г,в) (рис. 2.10.1). Из (2.10.3) с учетом (2.10.2) получим
<тгг(гр0) = -sxcos20 - s2sin20 = S + Pcos20 , (2.10.4)
(Jre(rl,9) = -(sl -s2)sin0cos0 = -Psin20,
где 5 = -0.5(^ + s2), P = -0.5(^ - s2).
Из (2.10.4) следует, что поле напряжений можно
представить как сумму
где индекс "1" соответствует краевой задаче с условиями на
"временной" границе
<Jrr(rl90) = S, (2.10.5)
^(г1,0) = О|
а "2" - с условиями
crrr(r1,0) = Pcos20l (2.10.6)
агв(г1,в) = -Рьт2Э.
Первая из них уже решена в § 2.4, поэтому перейдем ко второй.
В § 1.7 приведены выражения компоненты тензора
напряжений через функцию Эри, которая удовлетворяет
бигармоническому уравнению
ДДЧР = 0. (2.10.7)
В цилиндрической системе координат оператор Лапласа имеет
вид (§1.7)
163

л э2 1 э 1 а2 /0<1Лвч
Эг гдг г■ дв
Для решения (2.10.7) воспользуемся методом разделения
переменных, т.е. исходя из вида граничных условий (2.10.6) и
соотношений (§ 1.7) будем искать функцию Эри в виде
4f(r,e) = y/(r)cosme, meN. (2.10.9)
Подставляя (2.10.9) в (2.10.7) и учитывая (2.10.8), получим
1 Э2 I д m2YaV 1ду/ т2 ^
хдг2 + гдг г2 .
■ + --тг- TW
cosm0=O. (2.10.10)
дг2 гдг г2
Функцию у/ ищем как степенную
у/ = га (2.10.11)
с неизвестным показателем а. Подставим (2.10.11) в (2.10.10)
(p2-m2)la-2f-m2]=0,
откуда
ах = m, сс2 = -т ,
а3 = 2 + m, а4 = 2-т.
В нашем случае т = 2, поэтому
vF(r,0) = (cir4+C2r2 + C3 + C4r"2)cos20, (2.10.12)
где неизвестные константы Сх, С2, С3 и С4 подлежат
определению из четырех граничных условий (2.10.1) и (2.10.6).
Для этого по формулам (§1.7) с учетом (2.10.12) вычислим
напряжения
164

, m 1ЭТ 1 д2х¥ (
агг(г,в) = -__ +—^-^ = -2
л
г дг г2 дО2
д2х¥
С-2+ 2 3 + 4 4
V Г Г J
cos20,
авв(г9в) = —т = 2\6Схг1 + С2+-^С4 cos20,
(2.10.13)
°ге(г,0) = -—\
\
1 ДчЛ /^ л 1 3
_^_ =2 Зг2С+С2—^С3—ГС4 |sin20
г Э0 ' ' х 2 2 3 4 4
У
J V
и, подставляя их в (2.10.1) и (2.10.6), получим систему линейных
уравнений
с2+4сз+4с4=о'
Зг02С1+С2- — С3-—С4=0,
(2.10.14)
г, 2
'1
'1
/, ^j
2 ^3 _4 ^4
2
Решение (2.10.14) имеет вид
С,=
1
(I-,2)5
с2=-
l + g2+4g4P
_I+iltilr2„ c _ 1 + g2 r.P
(2.10.15)
где g = r0/r{. Теперь в (2.10.15) перейдем к пределу при г, —»°°
(S->0)
165

с,=о,
с,=--
(2.10.16)
Подставим (2.10.16) в (2.10.13), учтем решение (2.4.3) (в
нем следует заменить - рх на S) для граничных условий
(2.10.5) и запишем окончательные выражения компонент
тензора напряжений в безразмерной форме
(
G(r,e) = S
агв(г,9) = Р
1-
_i
л
(
1-£2V
^
cos20,
1+?~?
^
sin 29,
(2.10.17)
<Jee(r,9) = -S
/
1 +
1
Л
+ Р
1 + -
^
cos 29,
где ^=о-|у/5,, £=r/r0, S=($ + l)/2, P=(q-l)/2, a
q = s2l sx - аналог коэффициента бокового отпора.
Проанализируем полученное решение. На всех
иллюстрациях приведены безразмерные напряжения (отнесены
к sx).
1. При q = 1 (sl=s2), т.е. в равнокомпонентном поле
внешних напряжений, (2.10.16) совпадает с (2.4.3), нормальные
компоненты ап и Oqq не зависят от полярного угла, а
касательное напряжение агв отсутствует.
166

2. На границе отверстия (£=1) только кольцевое
напряжение авв отлично от нуля
Рис. 2.10.2.
На рис. 2.10.2 показаны изолинии функции овв на
плоскости (0,#) при г = г0, которые позволяют оценить
167

устойчивость контура подземных выработок для известных
внешних нагрузок и, наоборот, оценить количественно величину
этих нагрузок, обследуя поверхность выработки.
Идея состоит в том, что горные породы слабо
сопротивляются растягивающим напряжениям. В
рассматриваемом случае в зонах, где кольцевые напряжения
положительны, можно ожидать появления радиальных трещин.
Решив неравенство
0^(1,0) > О,
найдем, что растяжение по ствв (рис.2.10.2) возможно:
при q > 3, если
\в\ < — arccos ;
1 ' 2 2(tf-l)
1
при q<-, если
\в\> arccos .
1 ' 2 2 2(1-4)
Таким образом, визуально определив в реальных условиях
границы зон радиальной трещиноватости 9} м 02, можно
оценить нижнюю границу коэффициента бокового отпора <у*
(штрихпунктирные линии на рис. 2.10.2).
3. На рис. 2.10.3 показано распределение радиальных агг
и кольцевых напряжений овв в окрестности отверстия при
q = 0.1. Они, за исключением небольших зон, прилегающих к
168

q = 0.1
0.5 1.0 1.5 2.0 2.5 3.0
О 0.5 1.0 1.5 2.0 2.5 3.0
Рис. 2.10.3.
169

кровле (верхняя часть выработки) и почве (нижняя часть),
сжимающие.
q = 0 q = 1.5
Рис. 2.10.4.
4. На рис. 2.10.4, 2.10.5 показаны изолинии максимального
ах и минимального о2 главных напряжений для различных q.
Видно, что о2 сжимающее всюду в среде практически для
170

любых реальных значений q. Зоны растяжения по ох, довольно
обширные при малых q, исчезают уже при q = 0.4 и возникают
снова при q>3.
q = 0
q = 1.5
q = 0.4
Ь\"
q = 3.5
/
i //
у /
1 * /
'* ' '■ 1—
/1
У>
/^ >^ [
■аашвр—^аш^^-.
Рис. 2.10.5.
171

q = 0.3
q = 1.0
Рис. 2.10.6.
5. На основании выводов предыдущего пункта можно
ожидать, что разрушение среды в окрестности отверстия будет
происходить, как правило, посредством сдвига, а не отрыва.
Поэтому рассмотрим изолинии максимального касательного
172

q = 1.5
q=2.5
q = 2.0
q = 3.0
напряжения
Рис. 2.10.7.
Tmax = -V{°rr -°ееУ+ 4°70
(рис. 2.10.6, 2.10.7) для различных q.
173

Зафиксируем некоторое (гипотетическое) предельное
значение ттах (выбрано 0.6) и посмотрим, как с изменением q
эволюционируют зоны с ттах<0.6. При q = 0 эта зона
достаточно далеко (на расстояние до двух размеров выработки)
распространяется вглубь массива. С ростом q, они заметно
уменьшаются. При q = l зоны, опасные по критерию ттах,
полностью охватывают контур и непрерывно увеличиваются с
дальнейшим возрастанием q.
Таким образом, наибольшую опасность для подземных
сооружений представляют поля внешних (естественных)
напряжений, в которых вертикальная и горизонтальные
компоненты сильно отличаются по величине. Один из
возможных методов "борьбы" с этим является выбор
оптимальной формы контура полости, так, чтобы
минимизировать величину ттах в ближней окрестности.
§ 2.11. Действие горизонтальной поверхностной
нагрузки на упругое полупространство
Ситуация, вынесенная в заглавие этого параграфа, часто
имеет место в реальных условиях, например, при торможении
автомобиля или буксировке по грунту тяжелых механизмов.
На поверхности z = 0 упругого полупространства z>0 в
направлении оси х действует касательное усилие,
174

распределенное по известному закону (на практике его можно
определить, зная размеры и вес объекта, а также коэффициент
трения). Необходимо найти поле напряжений. Это задача
решена Черутти в 1882 году и носит его имя.
Сформулируем граничные условия
oxz{x,y$) = -F(x,y,m),
<т^(;с,у,0) = 0, (2.11.1)
аи(х9у90) = 0,
где функция F определена формулой (2.9.1). Задача не имеет
симметрии и является, в отличие от § 2.9, "чисто" трехмерной.
Уравнения равновесия в смещениях при отсутствии
массовых сил принимают вид
(^
ей
д uY Э mv Э mv
(А
а\
где е =
3wv
дх2
Э\
дх2
V
дх2
дил,
-+■
-+■
ду2
д2иу
ь2
Э2м,
■+•
Эг:
Э2и.
•+■
Эг:
-+•
д2и.
(2.11.2)
Э/ Эг"
-+■
-+■
Эи7
дх ду dz
Для решения будем использовать метод интегральных
преобразований, и тогда встает вопрос: как определить четные
или нечетные неизвестные функции ux1uy1uz по переменным
175

х и у, т.е. какое преобразование Фурье применять к (2.11.2)
(синус- или косинус-)? Ответ дает граничное условие (2.11.1)-,,
которое, используя закон Гука и формулы из Приложения 3,
представим в виде
(диг ди7 _
я'
Щ
х_. "~z
J7
. = ^[[е-тк coskxxcoskvydkxdky (2.11.3)
dz Эх) ~2JJ у у
{к = Jkx +к*) откуда следует, что: их - четная функция по х и
у; иу - нечетная по х, четная по у , uz - нечетная по х и у .
Поэтому смещения ищем в виде следующих двойных
интегралов Фурье
оо оо
их (х, y,z) = jfux (kx 9ky9z) cos kxxcos ky ydkxdky ,
о о
оо оо
uy(x,y,z) = jjuy(kx,ky,z)sinkxxsmkyydkxdky , (2.11.4)
о о
uz(*,y,z) = jjuz{kx,ky,z)sinkxxcoskyydkxdky .
о о
Подставляя (2.11.4) в (2.11.2), получим
a^-fc+(*$)+ркхкуиу+0кх^ = О,
dz oz
a^-(ak2x+k2y)+l3kxkyUx-Pky^ = 0, (2.11.5)
oz oz
176

Э2£/,
Э(/,
ди.
-a(k2x+ak2)-fikx—±+Bky—?- = 0
Аналогично § 2.8 и § 2.9 решение (2.11.5) имеет вид
U =AeiZ,U=BeiZ,U =Cesz.
(2.11.6)
Подставим (2.11.6) в (2.11.5)
Р-К
к к
-kvs
кхку
k^s
^а\ (<^
p-kv -kvs
kys
p + s
В
„с,
о
(2.11.7)
где p = y/(s2 -к2), у/ = а//3 .
Однородная система линейных уравнений (2.11.7) имеет
нетривиальное решение, если ее определитель равен нулю,
откуда находим
2р3 =0 или (s2 -к2)3 = 0,
т.е. существует два корня кратности 3. Как обычно,
положительный корень отбрасываем, тогда решение (2.11.5)
принимает окончательный вид
Ux(kx9ky9z) = (Cl+zC2)e'kzt
Uy(kxyky,z) = (C3+zC4ykz, (2.11.7)
Uz(kx9ky9z) = (C5+zC6)e'kzt
где функции С, = С( (кх Д ) (/ = 1,...,6) подлежат определению.
Подставляя (2.11.7) в (2.11.5), после достаточно громоздких, но
177

очевидных выкладок, получим три соотношения, связывающих
Q
kyC2+kxC4=0t
kC2+kxC6=0t (2.11.9)
кхСх - куС3 + кС5 = (1 + 2у/)С6.
Еще три зависимости для С{ получим из граничных
условий: по (2.11.4), (2.11.7) и закону Гука вычислим axz, oyz,
сг^ и подставим в (2.11.1)
кСх - С2 + кхС5 = F0e~mk l{n2[i),
kC3-C4 + kyCs=0, (2.11.10)
кхС{-куС3+^(кС5-С6)=0.
Дальнейший ход решения полностью идентичен § 2.9: из
(2.11.9), (2.11.10) находим С,, подставляем в выражения (в виде
двойных интегралов Фурье) для напряжений и вычисляем
квадратуры. Это предлагается сделать читателям
самостоятельно в качестве Упражнения. Все необходимые
формулы даны в Приложении 3.
Мы же приведем окончательный результат
р
<jxx(x9y,z) = --L
2/Г
Зх
.3
#■-*
( х x(3x2-R2) 2хг Л
■ + —Ц Т- + -
R3 R3(R + z)2 R2(R + z)3
Ш

ayy(x,y,z) = -—-
In
Ъху2
R5
■щ
x x(y2-R2)
R
■ +
+ ■
2xy2
3 ' R\R + z)2 ' R2(R + zf
a„(x,y,z) = -
F0 3xzz
2n R5
(2.11.11)
axy(x,y,z) = ~
2n
3x2y
R5
-w\
ry(x2-R2)
R\R + z)2 ' R2(R + zf
+ ■
2x2y
axz(x,y,z) = -
ayz(x,y,z) = -
F0 3x2z
In R5 '
F0 3xyz
In R5
где z = z + m, R = ^x2 + y2 + z2
Решение же собственно задачи Черутти (сосредоточенное
поверхностное касательное воздействие) - фундаментальное
решение - получается из (2.11.11) переходом к пределу при
т —> 0. Формулы (2.11.11) сохраняют свой вид, но в них нужно
заменить г наг, тогда R = -^х2 + у2 + z2 ■
Проанализируем найденное поле напряжений в
вертикальном сечении полупространства плоскостью у = 0, где
проявляются все характерные особенности. На рисунках
показаны изолинии безразмерных напряжений а у I р0
(Ро = F0/(nrQ)) в безразмерных координатах %=х/г0,
V = z/r0.
179

Основной отличительной чертой поля напряжений при
касательном поверхностном воздействии является его резкая
дифференциация в зависимости от положения исследуемой
области по отношению к направлению приложения нагрузки: все
нормальные компоненты тензора напряжений -
антисимметричные функции от х.
с = 1.0
Рис. 2,11.1.
180

На рис. 2.11.1 показаны изолинии о^ при распределенном
(с = 0.6) и сосредоточенном (с = 1) воздействиях, v = 0.25.
Можно видеть, что если при х> 0 компонента аш сжимающая
(сплошныелинии), то при х<0 -растягивающая.
-у
= 0.6
-4
1
2
ЗА
4А
-3
л
"-<Ш--
• /
V*/ ''
с = 7.0
Рис. 2.11.2.
4 5
и-
./-
2-
3-
</-
^-
\ **— ** /III \
/ / 1
■
£^
<7/ |
4 5
а,
181

"Сосредоточение" нагрузки к начале координат
качественно не меняет картину изолиний (в отличие от
нормального воздействия, § 2.9): с увеличением параметра с
возрастают значения atj вдоль изолиний, форма же их остается
практически неизменной.
-5 -4 -3
04 . 1 . u
с = 0.6
-1 О У
T^^CZT—'—
Л
\
\
°°ъ>. _ -"
/
/
а,
с = 1.0
Рис. 2.11.3.
182

На рис. 2.11.2,2.11.3 показаны линии равного уровня
первого (jj и второго о2 главных напряжений. Здесь ох всюду
растягивающая, но при х<0 эта зона гораздо больше, чем при
х>0. Напряжение о2 сжимающее при х<0 и растягивающее
при х> 0.
Таким образом, основные разрушения по критерию
максимального напряжения можно ожидать:
• в той части полупространства, куда направлено
воздействие (по двум системам ортогональных
площадок);
• в противоположной части области нагружения -
появления системы трещин, близких к кольцевым.
На рис. 2.11.4 представлены изолинии максимального
касательного напряжения ттах. Они симметричны относительно
оси х = 0. Зоны, опасные с точки зрения возможных разрушений
по критерию ттах, состоят из двух полушарий, примыкающих к
поверхности. Зависимость ттах от параметра с аналогична
таковой для о-\ увеличение (при возрастании с) значений
вдоль изолиний без заметного изменения формы последних.
На наш взгляд, для прогноза зон возможных разрушений в
рассматриваемой ситуации критерий по ттах не подходит,
поскольку он нивелирует резкую несимметрию процесса (не
делает различия между растяжением и сжатием), что очень
важно при анализе разрушения и дробления горных пород.
183

-5 -4 -3 -2-/0 1
-ъ U
N ^<?«7. _ ^ ^ / -
ч ^ '
/
24
\ \
\
V,
"' -\ ^«*. _
/
/
^ Ч -^
Я
-.0.0^'
ъ V
и
'^
>*'
\
/
\
/
ч
ц - -
**/.
- TL
с = 0.6
-5
-3 -2
I... V,
/ I
t \
\ \ чл 'iv
\
\
N
л
40.0J
^ .4 \ч о- -
*««?. „
$
\
^.
*>'
/
/
\
^Ьы.
С = 7.0
Рис. 2.11.4.
184

§ 2.12. Наклонное воздействие на поверхности упругого
полупространства
На границе упругого полупространства действует
распределенная нагрузка, наклоненная под углом а к
поверхности. Необходимо найти поле напряжений.
/ 1 / ^
рг /У
/ ^ х
\ 1 *
I Z
Рис. 2.12.1.
Введем декартову систему координат (x,^,z), направив
ось z вертикально вниз, а ось х параллельно направлению
действия нагрузки (рис. 2.12.1). Спроектируем последнюю на
координатные оси
F=F sin a
X
Fy=0,
F=F cos a
(2.12.1)
185

где функция F = F(x,y,m) определена, как и раньше,
формулой (2.9.1). Теперь можно сформулировать граничные
условия
axz(x,yfi) = -Fxt
ст yz(x, у,0) = 0, (2.12.2)
an(*,;y,0) = -FZI
Поставленная задача - трехмерная.
В силу линейности краевых задач теории упругости по
граничным условиям (мы уже пользовались этим свойством в
§2.10) поле напряжений в полупространстве при воздействии
(2.12.2) может быть представлено в виде суперпозиции
°ij = {<Ju)vsina + ((Jij)Hcosa> (ij = x9y9z) (2.12.3)
где индекс "V" соответствует решению задачи Буссинеска
(вертикальное воздействие, § 2.9), а "Я" - решению задачи
Черутти (горизонтальное воздействие, §2.11). Таким образом,
(2.12.3) дает искомое распределение напряжений. Последний
шаг - переход от цилиндрической системы координат, в которой
найдены решения (2.9.11) и (2.9.12) во введенную декартову
систему по формуле
ху
G
XZ
ху
УУ
G
yz
О
yz
= АЩ
0
К°"
о
'ее
0
^ rz
о
А,
где матрица перехода имеет вид
186

А =
( cos0 sin0 О
-sin0 cos0 0
0 0 1
Тогда
(°Л = КЛ cos2 9 + КЛ sin2 в ■
(^Д ЧОк^Я+^Д COS20,
(а*у )к = (Кг )v " (°ео )v )cos0 sin 0 ,
(Ov = (Ovcos0.
(*Д =(Ovsin0.
Анализ поля напряжений, как и в §2.11, проведем в
вертикальном сечении у = 0. Проясним вопрос: как угол
наклона нагрузки влияет на зоны возможных разрушений?
На рисунках показаны изолинии безразмерных
напряжений (отнесены к F0 /яг02) в безразмерных координатах
£=x/r0, tl = z/rQ.
На рис. 2.12.2 представлен набор изолиний первого
главного напряжения ох =0.01 (растяжение) для различных а
при v = 0.25 (воздействие сосредоточенное, с = \). Здесь видно,
что чем меньше угол а, тем больше зона разрушения D, ее
основной "прирост" происходит в области х < 0,
187

Рис. 2.12.2.
противоположной направлению приложения нагрузки так, что
объем D максимален при а = 0.
На рис. 2.12.3 при тех же расчетных параметрах показан
набор изолиний rm2LX =0.05 для различных значений а. Здесь
можно проследить эволюцию зон возможных разрушений по
критерию тпшх. Если при а = 90° эта зона - практически шар
диаметра dv, то при а = 0° - это два полушария диаметром
dH, причем dyldH~\.2 (рис. 2.12.3). Тогда отношение
объемов Dv : DH =1.73: 2, т.е. разрушения при касательном
воздействии обширнее и по этому критерию.
188

-5 -4 -3 -2 -1 0 1 2 3 4 t,
Рис. 2,12.3.
Полученные результаты, на первый взгляд, говорят о
преимуществе пологого удара перед крутым. Однако это лишь
теоретический результат. Технически же реализовать пологое
воздействие на ровную поверхность весьма затруднительно.
Как уже отмечалось в § 2.11, это можно осуществить с помощью
сил трения, но коэффициент трения
поэтому и интенсивность касательного воздействия по
сравнению с нормальным будет, по крайней мере, в Ilk раз
меньше.
189

Приложение 1
Краткие сведения о преобразовании Фурье
Одномерное преобразование Фурье
I. Любая четная функция и(х), абсолютно интегрируемая
на [0,°°), т.е.
оо
j\u(x)\dx<oot (П.1.1)
о
может быть представлена в виде
u(x) = — [u(k)coskxdk, (П.1.2)
яо
где
оо
U(k)=ju(x)coskxdx. (П.1.3)
о
При этом (П.З) называется косинус-преобразование
Фурье, U{к) - образ Фурье функции и, а к - параметр
преобразования.
Замечание. Из (П.1.1) следует, что
limn(jc) = 0. (П. 1.4)
II. Если нечетная функция и(х), абсолютно интегрируема
на [0,°°), то она может быть представлена в виде
190

27
и(х) = — \U(к)sinkxdk ,
IT J
(П.1.5)
где
U(k) = \u(x)sinkxdx-
(П.1.6)
синус-преобразование Фурье.
III. Пусть четная функция и(х) имеет непрерывную,
абсолютно интегрируемую на [0,°°) производную, т.е.
ди(х)\
j
dx<oot
тогда
| sinkxdx = {интегрирование по частям}=
Ь дх
оо
= u(x)sinkx |~ -kju(x)coskxdx ={(П.1.3), (П.1.4)}= -kU(k).
Аналогично для нечетной функции
Г coskxdx= u(x)coskx Г +k\u(x)sinkxdx =
о "х о
= {и(0) = 0 т.к. и -нечетная, (П.1.4)} =kU(k).
191

IV. Пусть и(х) не является ни четной, ни нечетной
функцией, определена и абсолютно интегрируема на (-00,00).
Представим и в виде суммы
и(х) = и+(х) + и_{х),
и+(х) = — [и(х) + и(-х)],
и_(х) = —[и(х) - и(-х)\.
Очевидно, что и+ - четная функция, а и_ нечетная, и уже
для них можно использовать все результаты пунктов I - III.
Двумерное преобразование Фурье
I. Пусть четная по обеим переменным функция и(х, у)
абсолютно интегрируема на [0,<*>)х [0,оо)? т.е.
оооо
jj\u(x,y)\dxdy <оо, (П.1.7)
00
тогда она может быть представлена в виде двойного интеграла
Фурье
7?
и(х,у) = — \ \U(kx,ky)coskxxcoskyydkxdky
оо
где
192

U(kx,ky) = \ \u(xyy)coskxxcoskyydxdy.
00
Аналогично для нечетной по х и четной по у функции
и(х9у) = — \\U(kx,ky)smkxxcoskyydkxdky ,
оо
U(kx,ky) = J J u(x, y)sin kxxcos кyydxdy
oo
и так далее.
Здесь кх, к - параметры преобразования, U - образ
Фурье.
Замечание. Из (П. 1.7) следует
\imu(x,y) = 0, \imu(x,y) = 0.
Х—>оо у—>оо
II. Пусть четная по х и у функция и(х, у) имеет
непрерывную, абсолютно интегрируемую на [0, °°) х [О, °о)
частную производную по х, тогда
0000^ ( \
\\ L^— sin kxxcos кyydxdy = -kxU(kx,ky).
оо °х
Доказательство этой формулы проводится так же, как в
пункте III.
Аналогичные соотношения имеют место для частных
производных любого порядка, необходима лишь их абсолютная
интегрируемость.
193

Приложение 2
Функции Бесселя и их свойства.
Преобразование Бесселя.
Исторически сложилось так, что частный случай функции,
называемой сейчас функцией Бесселя, впервые рассмотрен
Д. Бернулли в 1732 г. Бессель же провел детальный анализ
свойств спустя почти сто лет.
Поставим задачу: найти решение уравнения
Аи = -к2и (П.2.1)
в цилиндрической системе координат (г,0). Уравнение типа
(П.2.1) описывают многие физические процессы, в частности,
колебания твердых деформируемых тел при периодических
внешних нагрузках.
Перепишем (П.2.1) в развернутом виде
д2и \ди 1 д2и у 2 /по ох
ТТ+~Т~+~^ = ~ku (nz2)
дг гаг г 69
и предположим, что граничные условия для функции и заданы
в виде
оо
и(г0,в)^^(апсо^пв +bnsinn9)1 (П.2.3)
тогда и будем искать в аналогичной форме
оо
u(r,0) = y£(Un(r)cosn9 +Vn(r)sinn9). (П.2.4)
194

Подставляя (П.2.4) в (П.2.2), получим, что ип и Vn должны
удовлетворять уравнению
d2Un 1 dU
■ + -
i + (^- )1/й=0|
дг2 г дг г
(П.2.5)
которое имеет два линейно независимых решения
Un(r) = Jn(kr), Un(r) = Nn(kr).
Функции Jп называют функциями Бесселя, a Nn -
функциями Неймана, а их общее название - цилиндрические
функции.
Из (П.2.5) можно найти представление Jn в виде
бесконечного ряда
Jn(r)
(Л
к2;
^
(-1)" (Л
и
K2J
(П.2.6)
i=0i\(i + n)l{
В связи с рассматриваемыми задачами (для областей,
содержащих начало координат) нас интересуют только функции
Бесселя, поскольку из (П.2.6) следует, что lim Jn (r) = 80п, в
г->0
тоже время limNJr) = °° [6].
г->0
Из (П.2.6) можно получить следующие свойства Jn :
1) —Jn(r) = Jn_l(r) + Jn+l(r)i
г
2) *JM = J ir)-ljir) = ljir)-j (г)]
dr r г
195

dr
4) ecM.r-.,^.
dr
В частном случае, при п = О из 2) следует
Функции Бесселя, как оказалось впоследствии, обладают
еще многими замечательными свойствами, Нам потребуется
здесь возможность их использования в качестве базовых для
интегральных преобразований (преобразований Бесселя).
Пусть функция и(г) четная, абсолютно интегрируема на
[0,°о) "свесом г", т.е.
оо
$ r\u(r)\dr< оо, (П.2.7)
о
тогда она может быть представлена интегралом Бесселя
оо
и(г) = jU(k)JQ(kr)dk . (П.2.8)
о
Найдем выражение U через и. Умножим (П.2.8) на rJ0(lr) и
проинтегрируем по г от 0 до оо
оо оо
jru(r)JQ(lr)dr = J] jU(k)J0(kr)dk \rJ0(lr)dr.
О 0^0 J
Сменим порядок интегрирования в правой части и
воспользуемся формулой [7]
196

оо
jrJ0(kr)J0(lr)dr = 8Ut
о
тогда
оо
£/(/) = jru(r)J0(lr)dr . (П.2.9)
о
Если и(г) - нечетная функция и имеет место (П.2.7), то
оо
u(r) = jU(k)Jl(kr)dk, (П.2.10)
о
оо
U(l) = jru(r)Jx(lr)dr. (П.2.11)
о
Сравнивая (П.2.8) и (П.2.9) с (П.1.2) и (П.1.3), а (П.2.10) и
(П.2.11) с (П. 1.5) и (П. 1.6), можно увидеть, что функция /0
"похожа" на косинус, a J{ - на синус.
197

Приложение 3
Несобственные интегралы от произведений
функций Бесселя и экспоненты
1. J e-kpJ0(kr)dk= —
о
оо
2. {ke'kpJ0(kr)dk=Ar
Ь R
3. fit2 e-kpJ0(kr)dk =^P---L
J0 /г5 /г3
оо
оо
5. [ke-kpJAkr)dk = -^r
0 iV
6. \к2 e-kpJAkr)dk=^P
1 R
R = i
5
r2 + p2
198

Несобственные двойные интегралы от произведений
тригонометрических функций и экспоненты
,-м
7Г 1
1. Г Г cos к rx cos к vydkYdkv =
00
2 R
71 р
2. \\е pkcoskxxcoskyydkxdky =——-
00 2 R
ОО ОО _ pj^
3. [Г kr sin krx cos kvydkrdkv = =-
J J к x x у j х у 2 r3
4. Г J кхку sin kxxsin kyydkxdky =
00
2 R°
5- Я*'"*** smkxxcoskyydkxdky = ^--^
00
2 tf3
a-r*
6. Г Г —— kx sin ^д: cos &y ydkxdky =
7Г Л
о о
2 /?(/? + z)
7- \ / "Г" ** cos *** cos *у^ A = T
о о
tf3 Л5
R = Jx2 + y2 + p2 , k = Jk2+k
2 , i.2
199

Приложение 4
Деформационные и прочностные свойства
некоторых металлов и природных материалов
Материал
Р
кг/м3
Е
ГПа
V
МПа
МПа
МПа
Металлы и сплавы
Алюминий
Железо
Золото
Медь
Никель
Свинец
Серебро
Цинк
Сталь
Чугун
Г
Известняк
Кварцит
Мрамор
Песчаник
Гранит
Базальт
Уголь
Дерево
2700
7880
19310
8930
8900
11350
10500
7150
7850
7250
72
267
81
125
206
17
81
78
175-220
60-120
0.343
0.280
0.420
0.348
0.309
0.446
0.339
0.212
0.26-0.29
0.15-0.17
Природные материалы и го
2300-3000
3000
2880
2100-2900
2800
2860
1200-1500
300-1050
40-70
40-100
60-90
5-50
50-90
90-120
35-60
10-12
0.19-0.22
0.15-0.09
0.34-0.40
0.19-0.21
0.10-0.31
0.24
0.14-0.16
0.1
90-120
180-250
100
150-200
400-450
20
180-300
150-250
350-700
160-240
оные по.
12
11-15
6-16
3-10
10-15
3-35
1.5-2.5
23-45
роды
90-120
290-300
60-190
30-150
100-250
30-400
15-50
50-100
18
15-21
24-31
23
10-90
17-45
9
-
Примечание. Для металлов можно с хорошей точность принять:
сгс = сг,, т*=0.5сг,.
200

Приложение 5
Поведение среды за пределом прочности
Материал, изложенный в этом разделе, выходит за рамки
заглавия настоящей книги, поэтому он вынесен в Приложение.
Тем не менее, мы считаем необходимым дать некоторое
представление о том, что выполнение того или иного критерия
разрушения не означает конец срока службы объекта. В
качестве иллюстрации рассмотрена задача о круглом
отверстии в условиях равнокомпонентного сжатия.
Не следует думать, что "разрушение" означает полную
потерю объектом функционального назначения. Мы будем
считать, что в области разрушения D среда потеряла часть
несущей способности, и приобрела иные (не упругие!) свойства
- наступила стадия запредельного деформирования.
Продолжим анализ напряженного состояния в окрестности
подземной выработки (начатый в § 2.4) и найдем области
возможных разрушений на основании различных критериев
прочности.
5.1. Критерий максимального касательного напряжения
Пусть разрушение наступает при выполнении условия
ттах =Т*- Поскольку о гг и о вв - главные напряжения, то
201

кг -(Jqq\
^max-' 2 '• (5.1-1)
Воспользуемся решением § 2.4 и вычислим
'о2
*max=Pl~ • (5.1-2)
г1
Откуда следует, что ттах возрастает с приближением к контуру
г = г0, поэтому при достаточном уровне внешних напряжений
область D должна охватывать выработку. Однако мы
совершим ошибку, попытавшись найти размер г* зоны
разрушения, приравняв выражение в правой части (5.1.2) к т*.
Дело в том, что рассматривается мгновенная ситуация: в
напряженной среде образуется выработка, а вокруг нее,
одновременно, - зона разрушения. Таким образом, поставлена
задача с неизвестной границей: необходимо найти
распределение напряжений в упругой зоне и в D, а также
размер г*.
В области D закон Гука "не работает" и вместо него -
условие разрушение (5.1.1), уравнение же равновесия (§ 1.7) то
же самое (закон природы!)
^+^-^=0. (5.1.3)
дг г
Решение системы (5.1.1), (5.1.3) имеет вид
crrr(r) = -2r*lnr + fi3.
202

где константа Въ определяется из граничного условия
стгг(г0) = 0
Въ = 2т* In r0,
тогда в области разрушения
г
ст (г) = -2тЛп-, (5.1.4)
cree(r) =-2т,
го
С Л
1 + 1п—
В упругой области г>г* напряжения уже найдены -
формулы (2.3.5), которые здесь запишем в более удобной
форме
°гЛг) = Вх+\, (5.1.5)
В?
г1
Поскольку \\marr(r) = -рх, то Вг = -рх.
г—>°°
На границе контакта D и упругой зоны должны
выполняться условия
• радиальное напряжение огг непрерывно;
• решение (5.1.5) удовлетворяет (5.1.1),
тогда
-2тИп-5. = -А+4. *L = Ua (5.1.6)
го г* г*
203

Решая (5.1.6), получим
г* = г0е
2т*
(5.1.7)
LJ'-) — Т*/* .
Из (5.1.7) следует, что по критерию ттах зона разрушения
появляется в среде (т.е. г* > г0) при
Pj>t*. (5.1.8)
Обратим внимание на экспоненциальную зависимость г*
от отношения внешнего напряжения к пределу прочности.
Замечание. Условие (5.1.8) можно получить и из упругого
решения (§ 2.4). Действительно, на контуре отверстия
°rr(ro) = °> °ве(го) = -2Р\>
тогда т^Оо) = рх, откуда и следует (5.1.8).
Приведем окончательные выражения компонент тензора
напряжений
г
°rr(r) =
-2т*1п-
м г}
-px+U —
г
Гп<Г<П
г* <г
°вв(г) =
-2т„
( Л
1 + 1п —
V
'о
r0<r<r*
•рх-т*— п<г
204

На рис. 5.1.1 показано распределение безразмерных
напряжений сггг/рх и oQelpx в зависимости от г/г0 для
различных значений рх/т*. Компоненты напряжений при г = п
непрерывны, но имеют разрывные производные: уравнение
равновесия выполняется не на гладких функциях. Сжатие в
тангенциальном направлении (напряжение авв) резко
возрастает с приближением к границе г = г*, а затем убывает до
"фонового" значения рх. Радиальное сжатие монотонно
возрастает от нулевых на контуре до рх.
Для сравнения на том же рисунке (штриховые линии)
приведено "упругое" распределение напряжений (§ 2.4). Можно
видеть, что с увеличением прочности среды (суть, т*), либо с
уменьшением внешней нагрузки (рх) разница между упругим и
неупругим решениями исчезает.
5.2. Критерий Кулона - Мора
Рассмотрим теперь другой критерий прочности Кулона -
Мора, согласно которому разрушение материала наступает при
выполнении условия
где k = tgq>, ф-угол внутреннего трения, тс -сцепление. В
нашем случае (круглая выработка, всестороннее сжатие):
205

Рис. 5.1.1.
206

• напряжения arr и авэ - главные;
• из упругого решения (§ 2.4) 0 > orr > oQQ,
поэтому предположим (а потом и проверим!), что и в области
разрушения выполняется то же самое неравенство. Тогда в
(5.2.1)
- =агг~°вв
^тах
i_ i arr+°ee
2 ' '" 2
Подставим (5.2.2) в (5.2.1) и выразим ат через <7Г
(5.2.2)
СУ ас, =■
1 + *
1-*
■стп--*тс
(5.2.3)
где s = 2/(1 - к). Из (5.2.3) следует
tfrr " <*«> = sorr + 5ТС. (5.2.4)
Уравнение равновесия (5.1.3) с учетом (5.2.4) примет вид
darr s s
г
s
дг г
—оп=—тс.
(5.2.5)
Решение (5.2.5)
arr(r) = B3rs+tc
содержит неизвестную константу Вг, которую найдем из
граничного условия orr(rQ) = 0
Значит в области разрушения
°n(r) = -*i
(5.2.6)
207

В упругой зоне (п. 5.1)
В,
Grr(r) = -Px+ 2
(5.2.7)
Г
г2
Таким образом, как и в п. 5.1, необходимо найти границу
раздела упругой и разрушенной зон г = г* и константу В2. Для
этого есть два условия:
1) непрерывность агг при г = г*
В,
У* 1
г0
У
= -pl+—■
г*
(5.2.8)
2) критерий (5.2.1) должен выполняться и для упругого
решения (5.2.7)
г»2
= кр1+тс
(5.2.9)
Решая совместно (5.2.8) и (5.2.9), найдем
г* = г0
^-а-к)
2
, в2 = (кР1+тс)г:
(5.2.10)
Теперь окончательно имеем
°гг(г) = \
-т*
Г/
Pi
1-
'0
J
V
А
r0<r<r*
r*<r
208

'ев
(r) =
f
1 + k rs ^
+1
1-* r„s
P\
1+
V
J _,
r0 <r<r*
r* <r
Из (5.2.10) можно найти условие возникновения зоны
разрушения, для чего решим неравенство п > г0, откуда
Рх>
\-к
(5.2.11)
Можно видеть, что с увеличением прочности среды
(параметры к и тс растут) возрастает и величина внешней
нагрузки, необходимой для начала разрушения. Однако для
ряда пород (например, базальтов) величина к ~ 1
(<р = 40° -45°), поэтому ни при каких внешних напряжениях рх
зоны разрушения не возникнут, т.е. в условиях всестороннего
равнокомпонентного сжатия выработки, проведенные в таких
породах, будут всегда устойчивы.
На рис. 5.2.1 представлено распределение напряжений в
зависимости от г/г0 при различных к и рх1тс = 20. Как и
следовало ожидать, качественно характер поведения компонент
тензора напряжений не изменился по сравнению с таковым
п. 5.1. Отличие состоит в более "медленном" росте г* при
увеличении р{.
На рис. 5.2.2 представлены изолинии размера зоны
разрушения, отнесенного к радиусу выработки. Тоном показана
209

p,/t=20 an/Pl\
■ 0.2
0.8
0.6
Рис. 5.2.1.
210

область изменения параметров к и рх1тс, при которых зона
разрушения не возникает (соответствует противоположному
(5.2.11) неравенству). Характерная особенность распределения
г* / г0 - очень медленный рост при увеличении к, если
значения параметра рх /тс мало отличаются от единицы.
211

УПРАЖНЕНИЯ
§1.1.
1. Найти компоненты матрицы перехода А, если система
координат {X,Y,Z) сначала повернута на угол <р
относительно оси z декартовой системы координат (;t,y,z),
при этом ось у "перешла" в ось ух, а затем на угол у/
относительно оси у{. Проверить условие ортогональности
для А.
§1.2.
1. Вывести выражения компонент тензора деформаций в
цилиндрической системе координат.
Указание. Квадрат элемента длины имеет вид
(Asf=(Arf + (rAOf+(Azf.
2. Проверить тождества Сен-Венана.
§1.4.
1. Вывести выражения модуля Юнга Е и коэффициента
Пуассона v через:
а) параметры Ламе Я и ji;
212

б) плотность р и скорости продольной Vp и
поперечной Vs волн, если Я + 2/л = pvj, ji = pVv2.
2. Вывести соотношения между коэффициентом Пуассона v и
отношением скоростей продольной и поперечной волн
Y = Vs/Vp.
§1-6.
1. Проверить формулы Эри для цилиндрической системы
координат.
§1.7.
1. Вывести уравнения Ламе в цилиндрической системе
координат для случаев I - IV.
2. Вывести уравнения Ламе в сферической системе координат
для случаев I - III.
§2.1.
1. Решить задачу о нагружении весомого стержня, состоящего
из трех частей с различными физическими свойствами.
2. Решить задачу о неоднородном весомом стержне, свойства
которого меняются по:
а) квадратичному закону
213

p = p0(l + ajc + /3;t2), £ = £0(l + ajc + j8jc2);
б) экспоненциальному закону
р = р0еах% Е = Е0еах.
§2.3.
1. Найти смещение иг в задаче Ламе, считая, что точки
внутреннего контура неподвижны.
Указание. По известным напряжениям и закону Гука
вычислить деформации егг и выполнить интегрирование.
2. Вычислить ттах. Считая известным предел прочности т*,
найти границу зоны разрушения г = г* в зависимости от /?0 и
рх. Когда задача имеет решение?
§2.5.
1. Найти смещение иг в задаче о вращающемся кольце,
считая, что точки внутреннего контура неподвижны в
радиальном направлении.
Указание. По известным напряжениям и закону Гука
вычислить деформации егг и выполнить интегрирование.
214

2. Вычислить ттах. Считая известным предел прочности т*,
найти границу зоны разрушения г = г* в зависимости от О).
Когда задача имеет решение?
3. Решить задачу о вращающемся кольце, если напряжения на
внутреннем и внешнем контурах не нулевые, а равны
соответственно р0 и рх.
§2.6.
1. Найти смещение uR в задаче Ламе, считая, что точки
внутреннего контура неподвижны.
Указание. По известным напряжениям и закону Гука
вычислить деформации eRR и выполнить интегрирование.
2. Вычислить ттах. Считая известным предел прочности т*,
найти границу зоны разрушения R- R* в зависимости от р0
и /?!. Когда задача имеет решение?
§2.8.
1. Найти распределение напряжений в "двухслойной" Земле.
Указание. На промежуточной границе R = Rm задать
непрерывность радиальных смещений uR и напряжений
G rr-
iis

§2.9.
1. Решить задачу Черутти для упругой полуплоскости
(сосредоточенная и равномерно распределенная нагрузка).
Указание. Смещения искать в виде
2 7
и (х,y) = — \U(k9y)coskxdk ,
27
uv(x,y) = — \U (k,y) sin kxdk.
У rr J У
2. Пользуясь фундаментальным решением, найти
распределение напряжений в задаче Фламана, если на
поверхности задано "куполообразное" усилие
a) Oyyixfl)
б) ауу(х,0) =
в) <7уу(х,0) =
Ро
О
( х2^
V J
Ро1
( г2\
О
V
V
J
»
|jc|>/
|х|>/
Ро
\л
О
1 ~т ]х]~1
3. Пользуясь фундаментальным решением задачи Черутти
(Упражнение 1), найти распределение напряжений в
216

полуплоскости, если касательная нагрузка на поверхности
задана в виде
а) ст^ОД)) =
б) аху(х,0) =
Ро
О
( х2^
V l J
Ро
О
I2
V J
jc|</ .
х\>1
| X |< / .
|х|>/
в) сг_,(*,0)
*УХ
(
Ро
1-J
h
V
/
[0 j jc |> /
а нормальные напряжения - нулевые а (х,0) = 0.
4. Получить выражения компонент тензора напряжений в
задачах Фламана и Черутти (сосредоточенное воздействие)
в цилиндрической системе координат
х = rsind ,
у = rcosO .
217

ИМЕННОЙ УКАЗАТЕЛЬ
Бессель (Bessel) 147,149, 195-198
Буссинеск (Boussinesq) 144,150,186
Гук (Нооке) 29, 37, 38, 42, 44, 52, 53, 54, 55, 60, 63, 65-70, 79, 93,
97, 104, 117, 135, 148,176, 178
Кирхгоф (Kirchhoff) 48
Коши (Cauchy) 13, 15, 19, 21, 22, 46
Ламе (Lame) 41, 51, 62, 67, 71,73, 102, 103, 109, 116, 117, 133,
145
Ляв (Love) 61
Мичел (Michel!) 132, 143
Навье (Navier) 51
Пуассон (Poisson) 39, 44, 124, 137, 159
Сен-Венан (Sent-Venant) 34, 56, 82
Файлон (Filon) 61
Фламан (Flamant) 140
Фурье (Fourier)M8, 129, 133, 176, 178,190-193
Черутти (Cheruti) 175, 178, 186
Эри (Airy) 58, 66, 163, 164
218

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Новожилов В.В. Теория упругости. - М.: Судпромгиз, 1958.
2. Рекач В.Г. Руководство к решению задач по теории
упругости.-М.: Высшая школа, 1977.
3. Снеддон И. Преобразования Фурье. - М.: ИЛ, 1954.
4. Тимошенко СП., ГудьерДж. Теория упругости.- М.: Наука,
1979.
5. Работнов Ю.Н. Механика деформируемого твердого тела. -
М.: Наука, 1979.
6. Градштейн И.С, Рыжик В.М. Таблицы интегралов, сумм,
рядов и произведений. М.: Наука, 1965.
7. Березанцев В.Г. Осесимметричная задача теории
предельного равновесия сыпучей среды. М.: ГИТТЛ, 1952.
219

СОДЕРЖАНИЕ
Введение
Предмет теории упругости и ее место в механике
деформируемого твердого тела 3
Историческая справка 5
Глава 1. Основы теории упругости 10
§1.1. Теория напряжений 10
§1.2. Теория деформаций 24
§1.3. Уравнения движения 35
§ 1.4 Закон Гука. Упругие константы материалов 37
§ 1.5. Полная система уравнений теории упругости и
постановка краевых задач 44
§ 1.6. Двумерные модели: плоское напряженное
состояние, плоская деформация 53
§ 1.7. Представление основных соотношений теории
упругости в различных системах координат 62
Глава 2. Приложение решений задач теории упругости
к исследованию устойчивости и разрушения
элементов конструкций и природных объектов 72
§ 2.1. Понятие о прочности и критериях разрушения
твердых тел 72
§ 2.2. Смещения и напряжения в однородных и
неоднородных нагруженных стержнях 96
220

§ 2.3. Упругий цилиндр под действием внутреннего и
внешнего давления 102
§ 2.4. Круговая полость в безграничной упругой среде 109
§ 2.5. Напряженное состояние вращающегося
однородного кольца 112
§ 2.6. Полый шар под действием внутреннего и
внешнего давления 116
§ 2.7. Оценка напряжений в недрах Земли 121
§ 2.8. Поля напряжений в упругой полуплоскости,
создаваемые поверхностными нагрузками 127
§ 2.9. Действие вертикальной нагрузки на
поверхности упругого полупространства 144
§ 2.10. Распределение напряжений в окрестности
круглого отверстия 160
§ 2.11. Действие горизонтальной поверхностной
нагрузки на упругое полупространство 174
§ 2.12. Наклонное воздействие на поверхности
упругого полупространства 185
Приложение 1. Краткие сведения о преобразовании
Фурье 190
Приложение 2. Свойства функций Бесселя.
Преобразование Бесселя 194
Приложение 3. Некоторые несобственные интегралы 198
Приложение 4. Физические свойства некоторых металлов
и природных материалов 200
Приложение 5. Поведение среды за пределом прочности 201
221

Упражнения 211
Именной указатель 212
Рекомендуемая литература 218
Содержание 219

Дементьев Александр Дмитриевич
Назаров Леонид Анатольевич
Назарова Лариса Алексеевна
ПРИКЛАДНЫЕ ЗАДАЧИ
ТЕОРИИ УПРУГОСТИ
Учебное пособие рекомендовано Министерством
сельского хозяйства Российской Федерации для студентов
и аспирантов высших учебных заведений инженерных
специальностей.
Редактор Н.К. Крупина
Лицензия № 020426 от 7 мая 1997 г.
Подписано к печати 27.05 2002 г. Формат 60x84 1/16.
Объем 14 печ. л. Тираж 200 экз. Заказ № 525.
Редакционно-полиграфическое объединение СО РАСХН, ротапринт.
630050, Новосибирская область, п. Краснообск