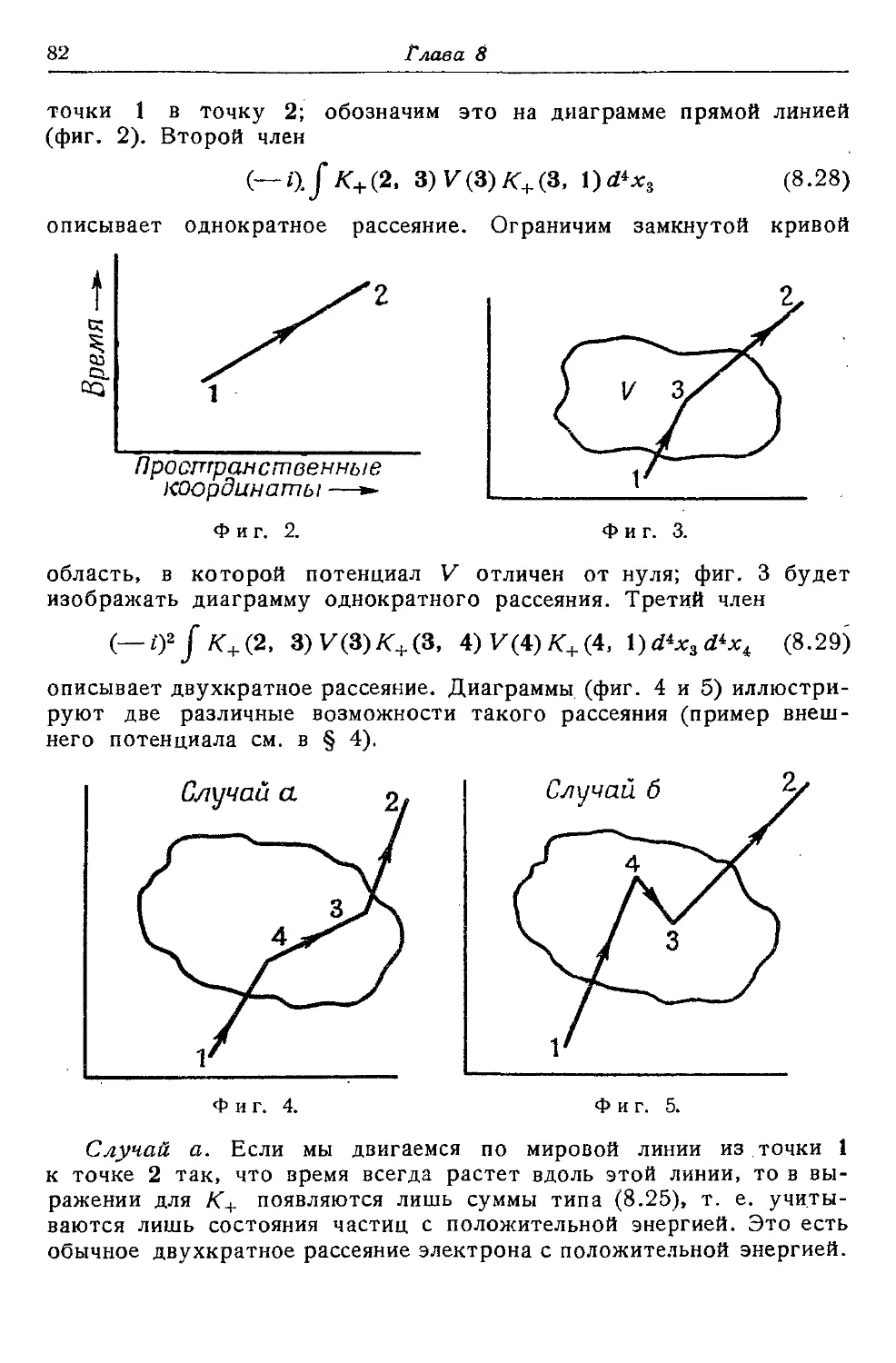
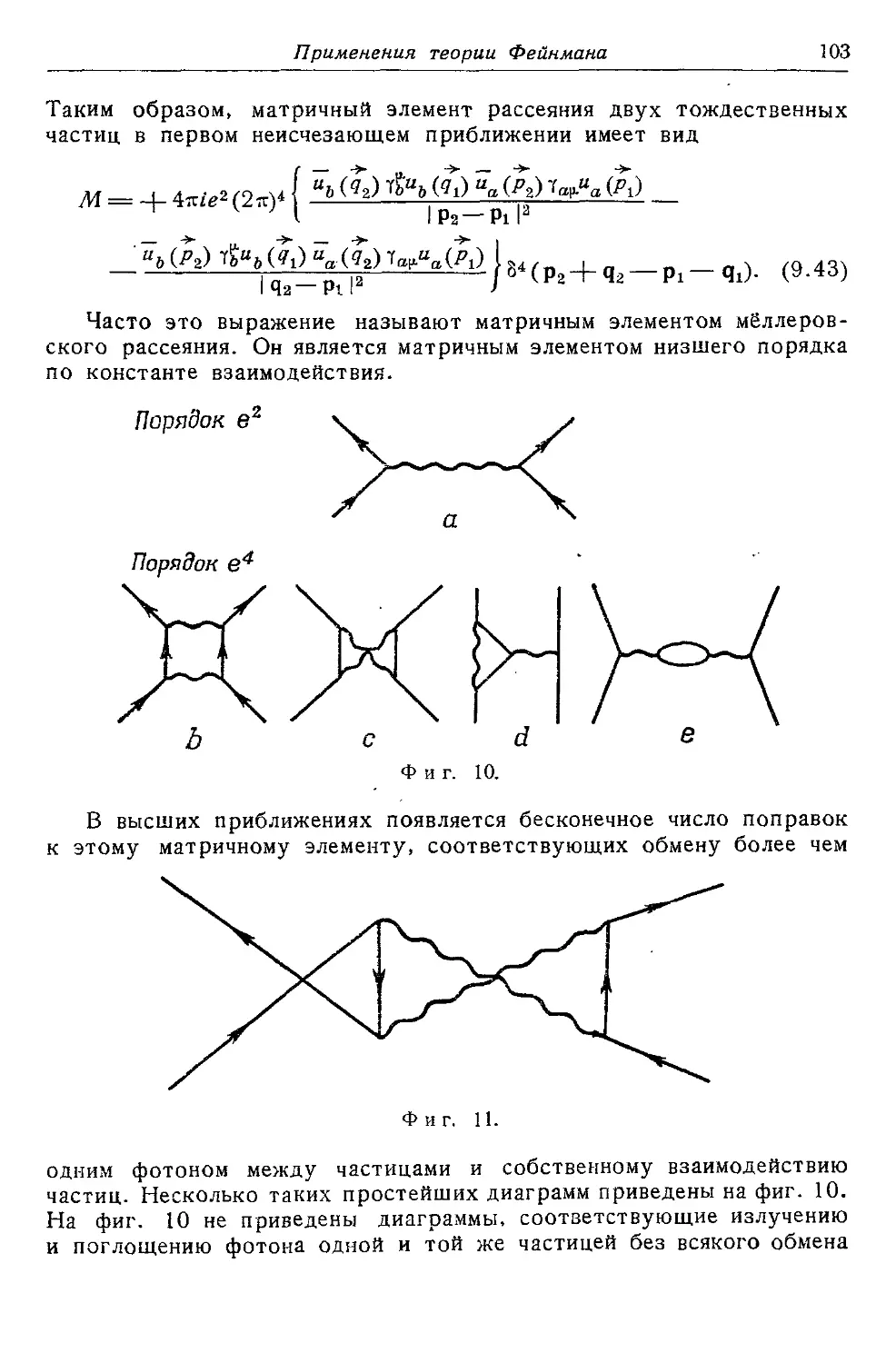
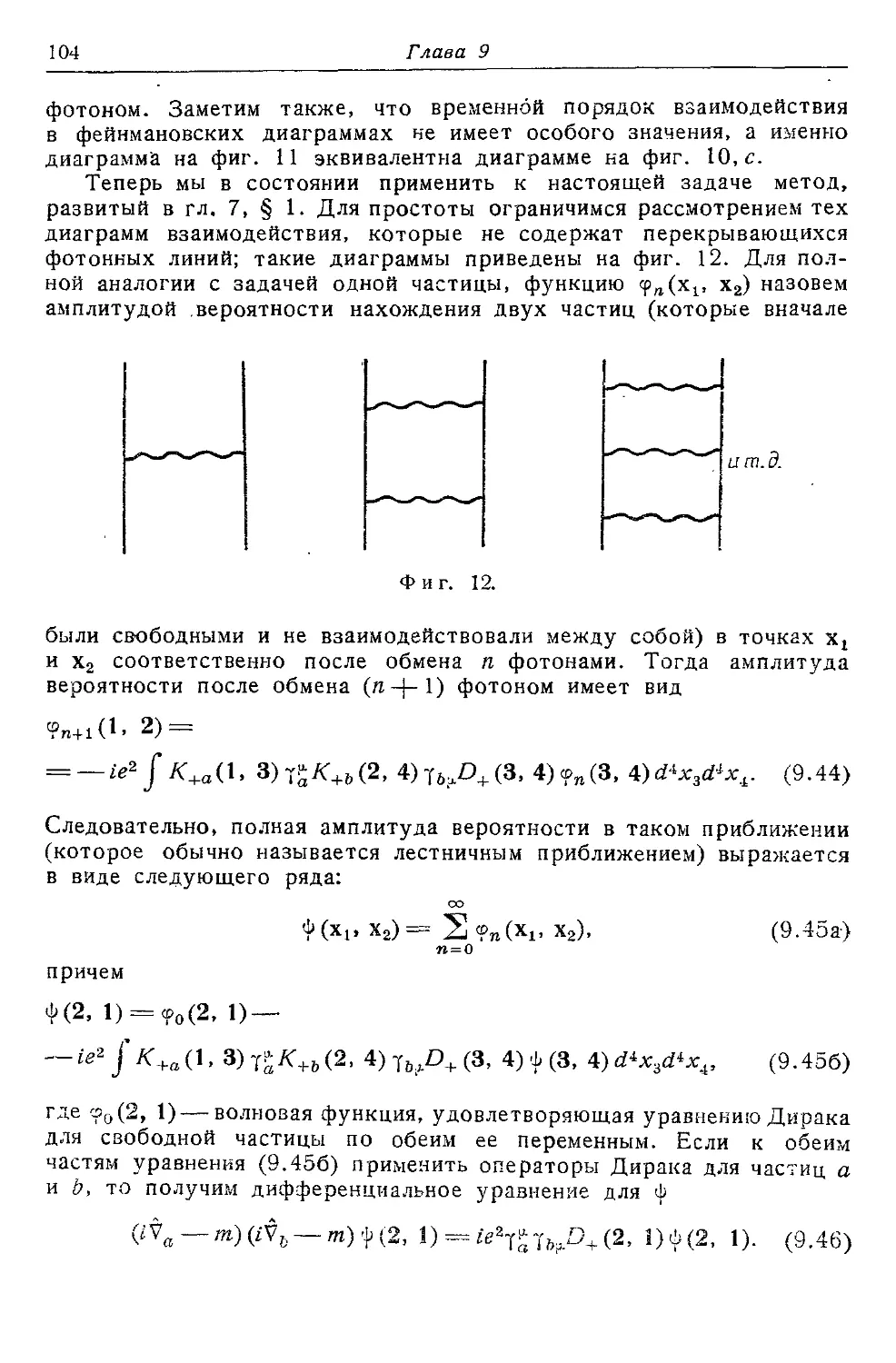
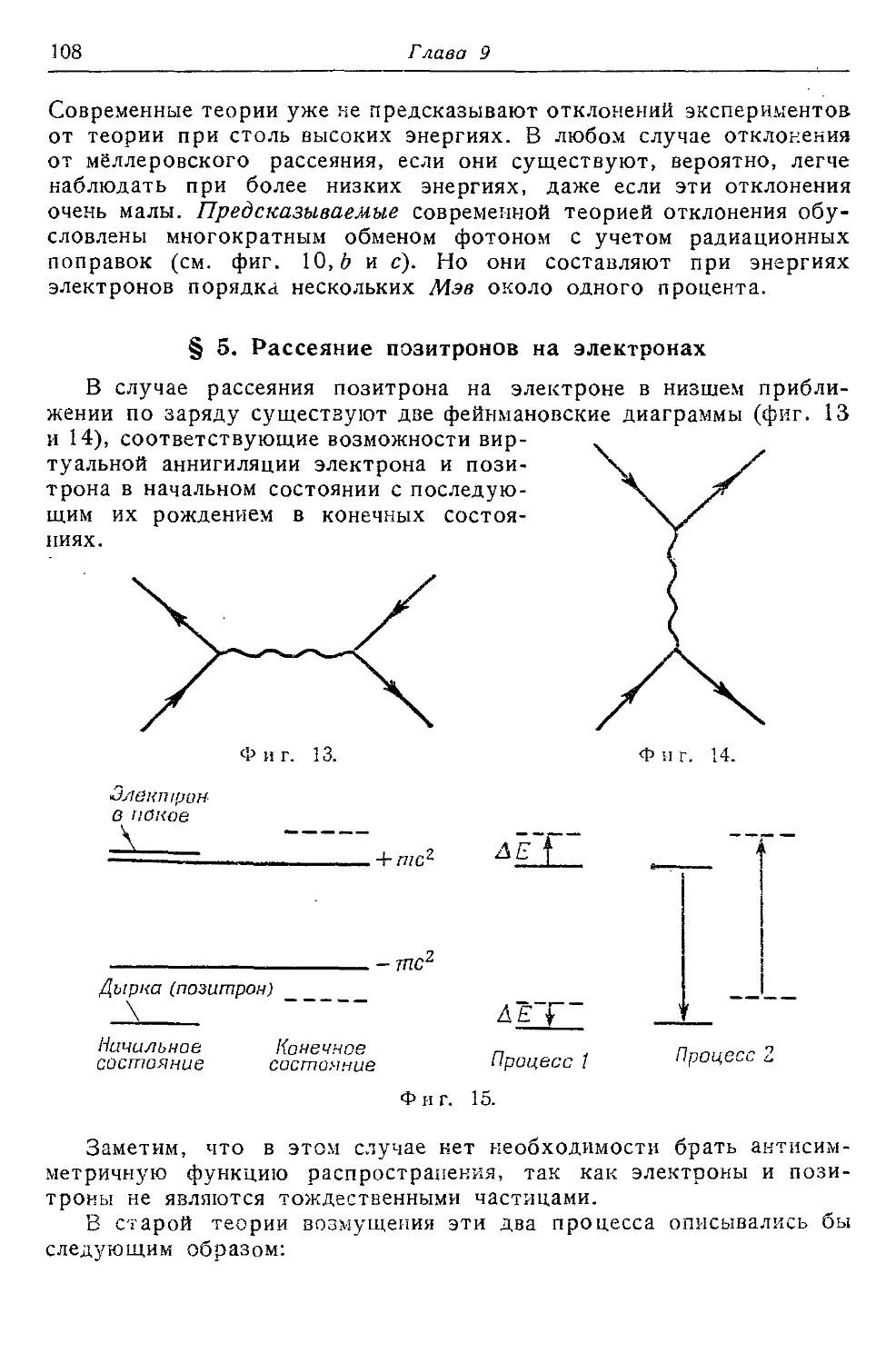
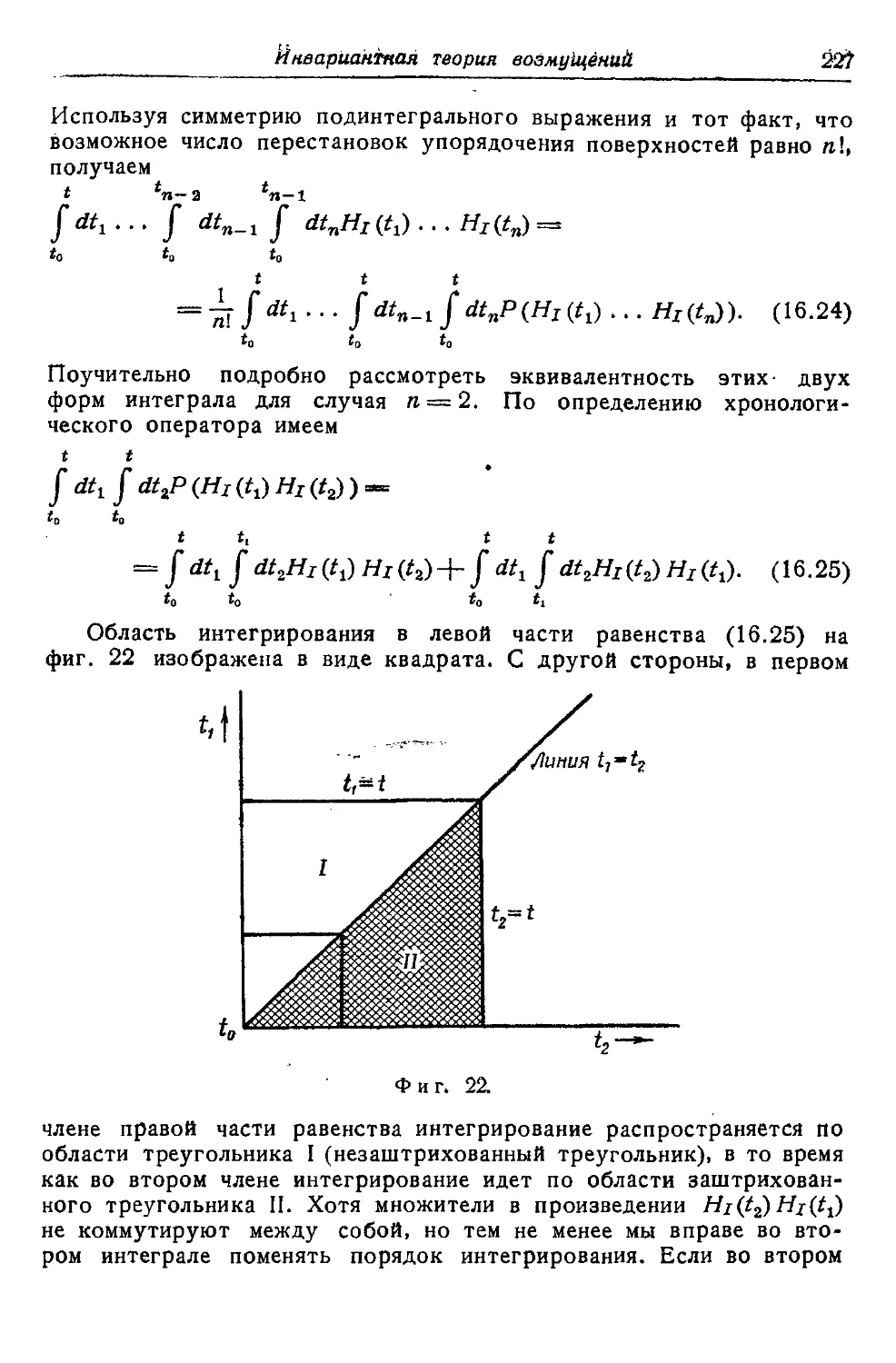
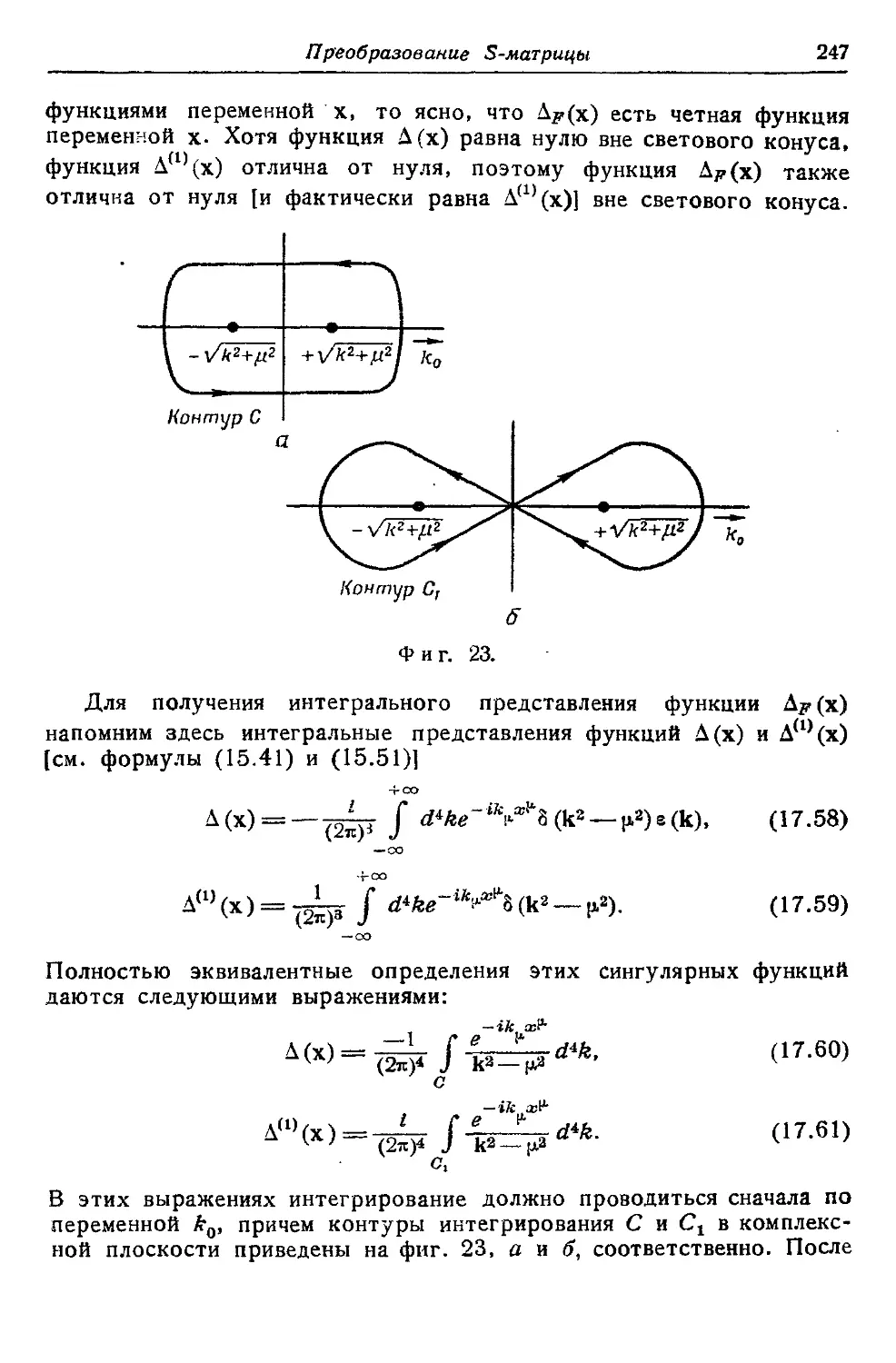
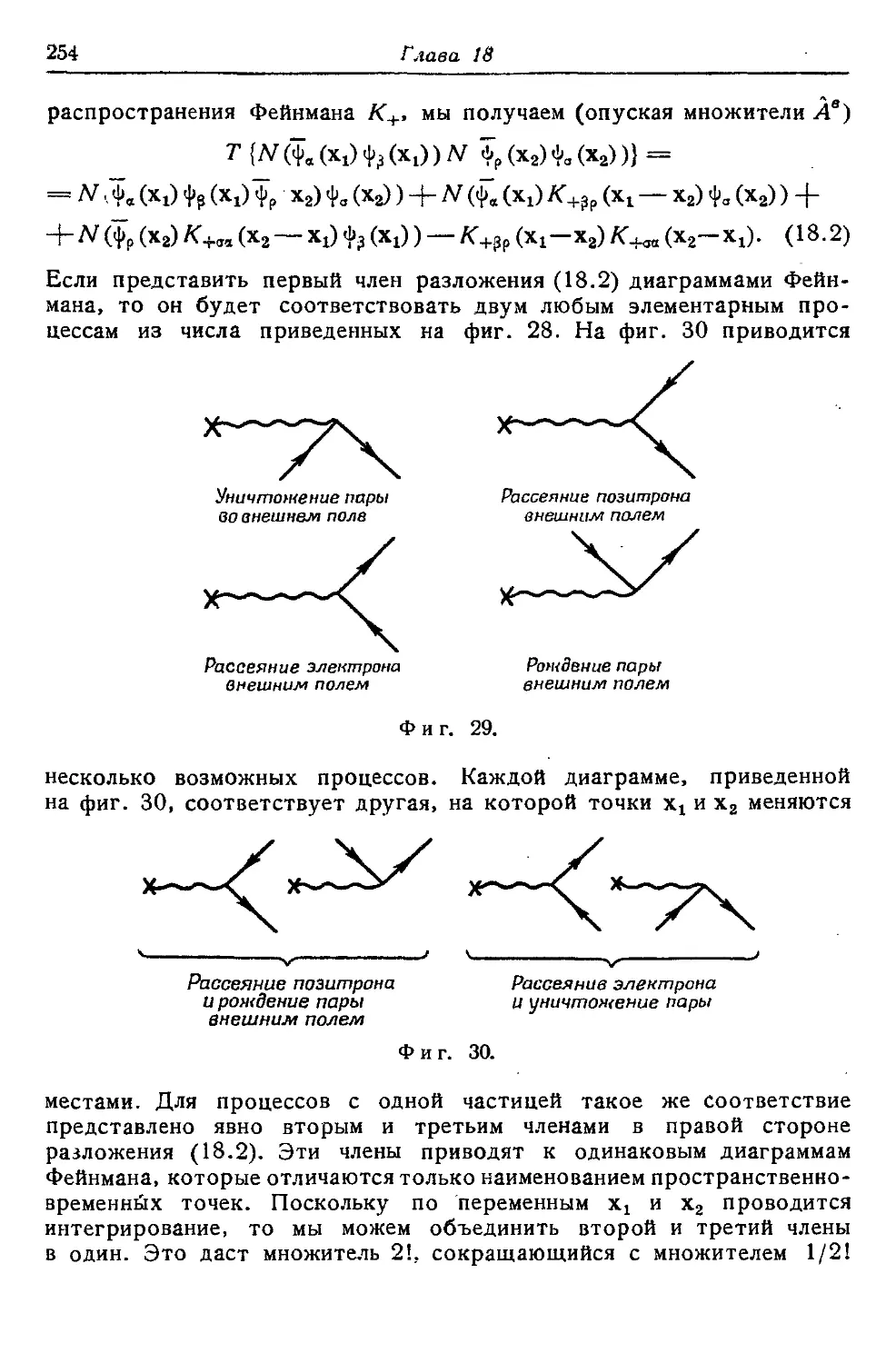
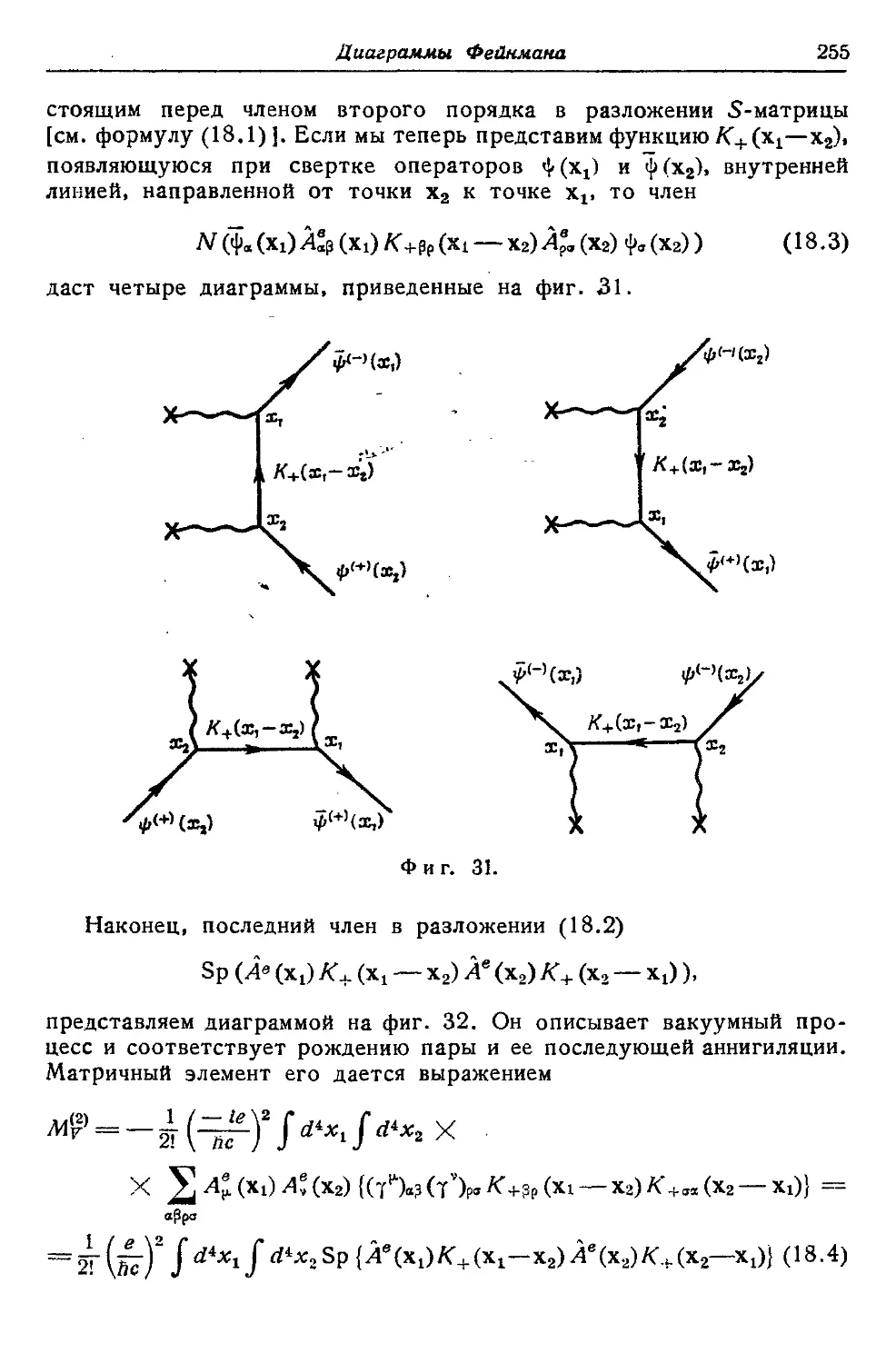
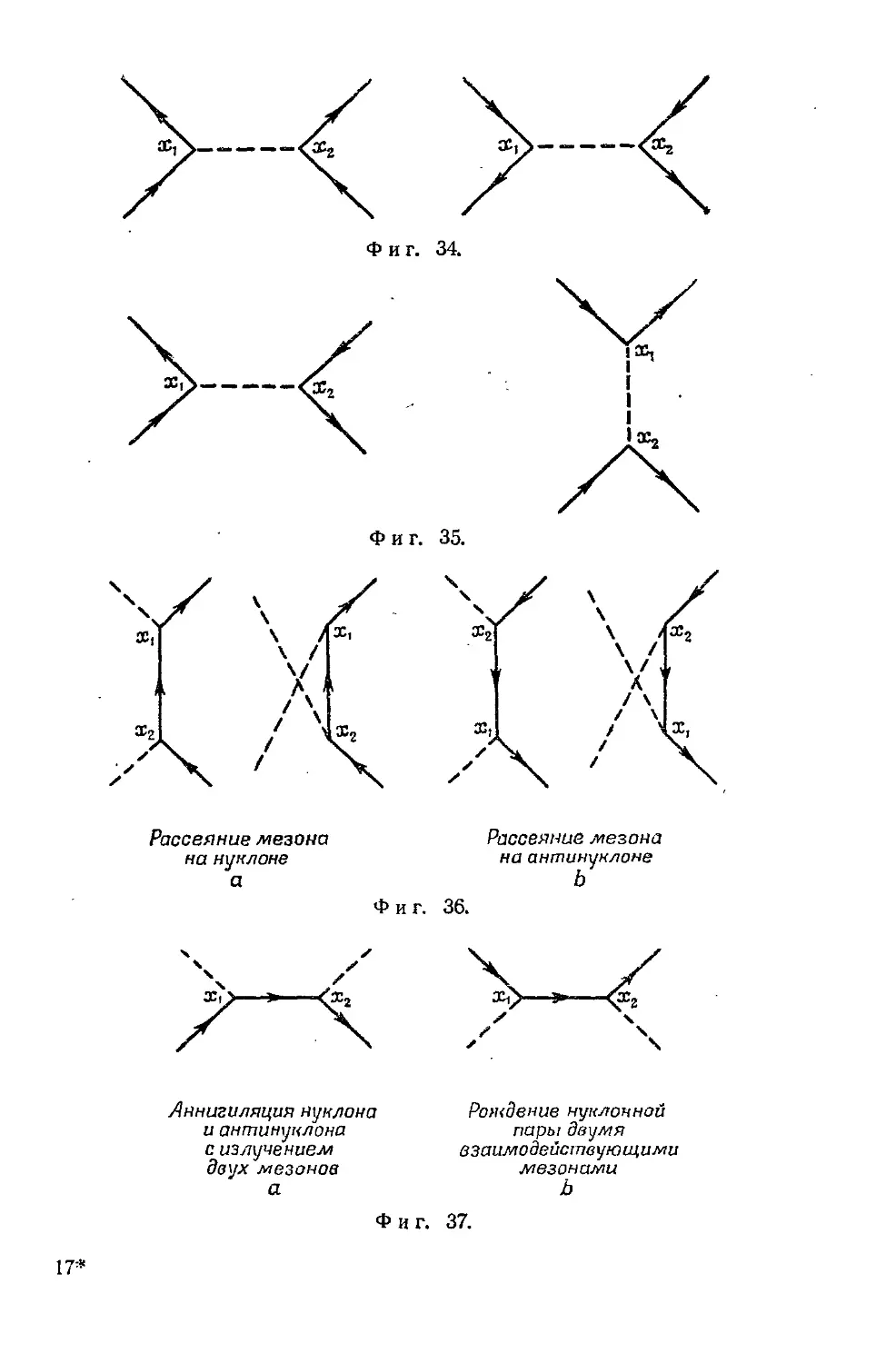
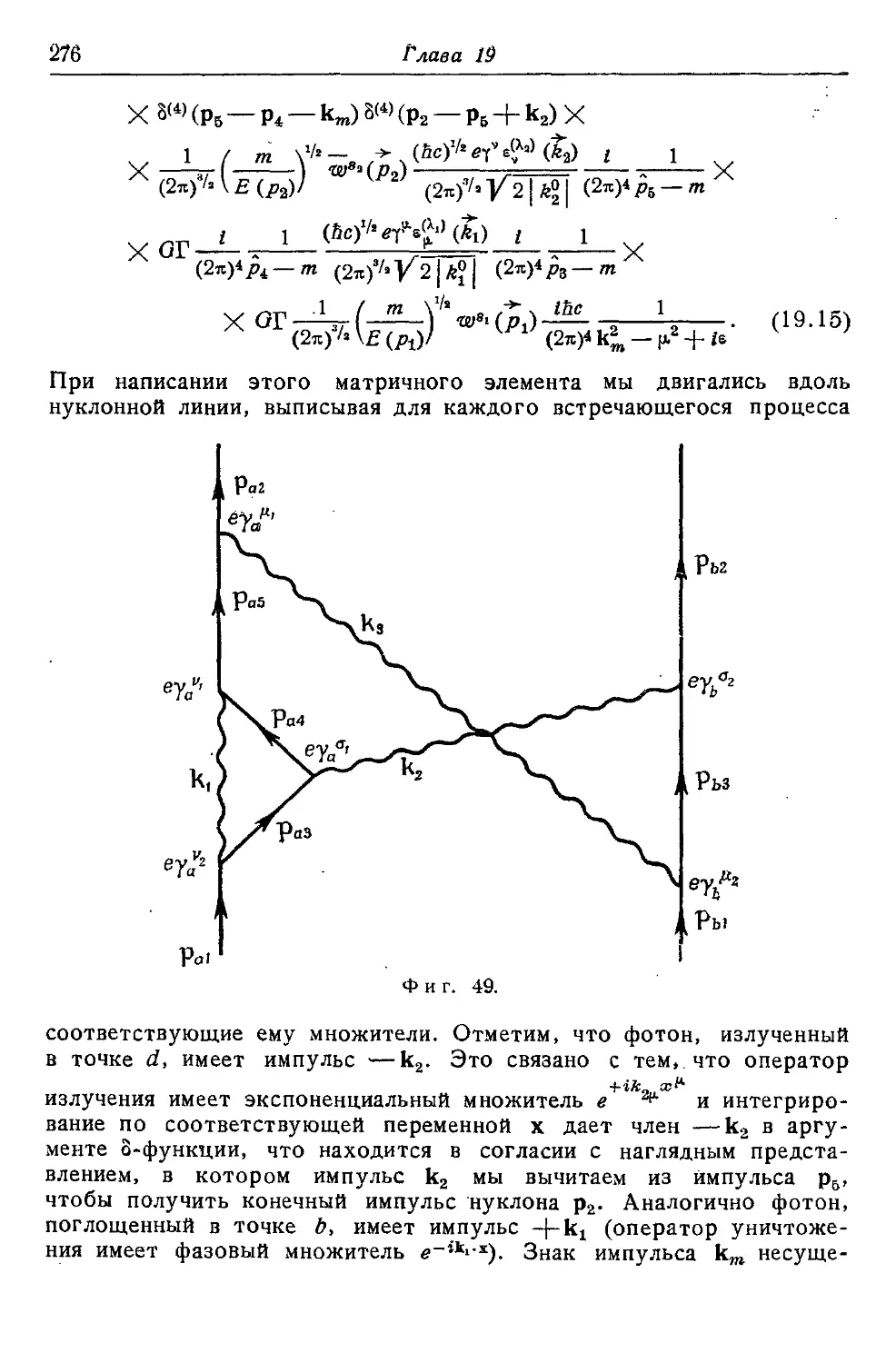
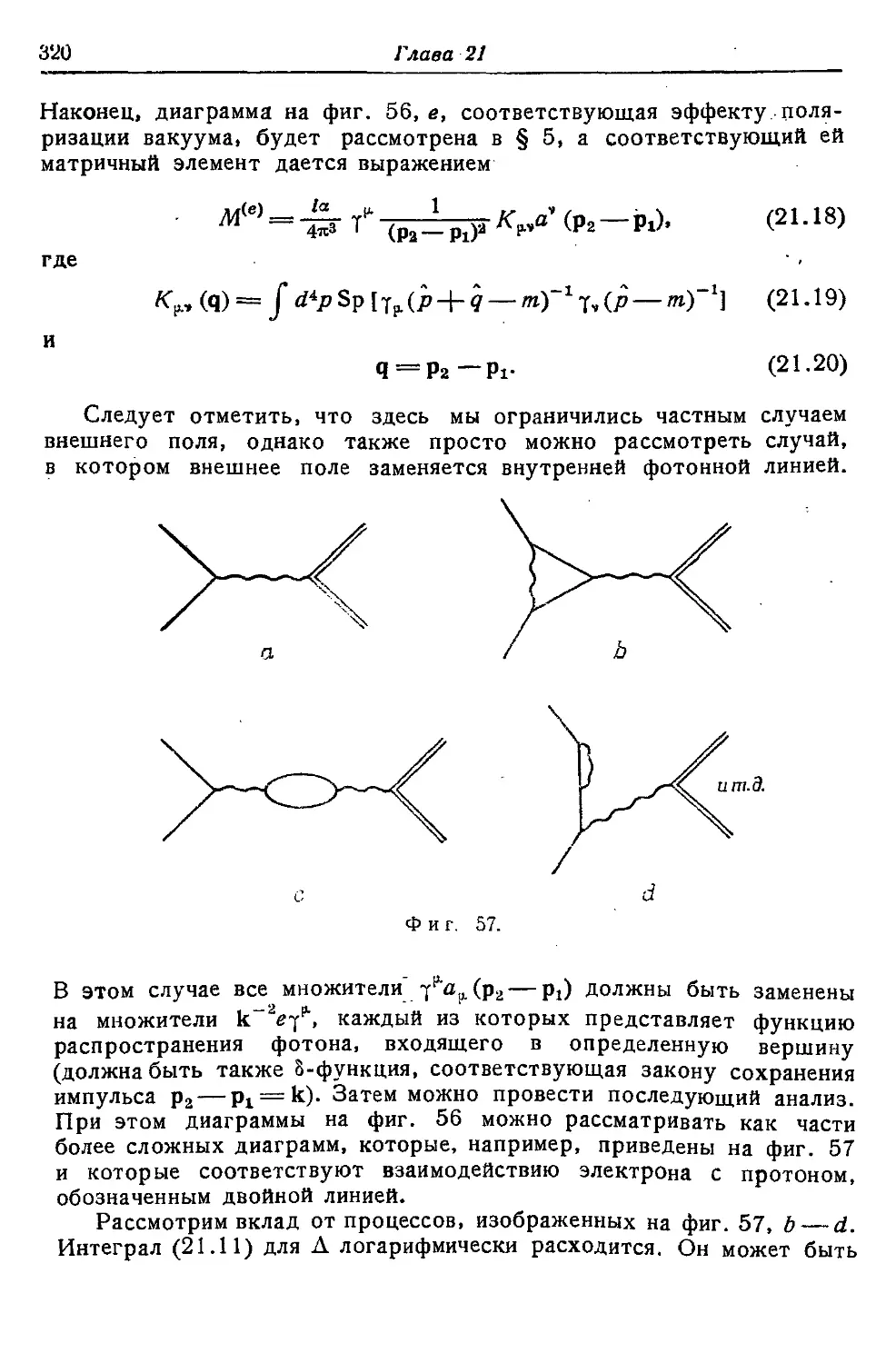
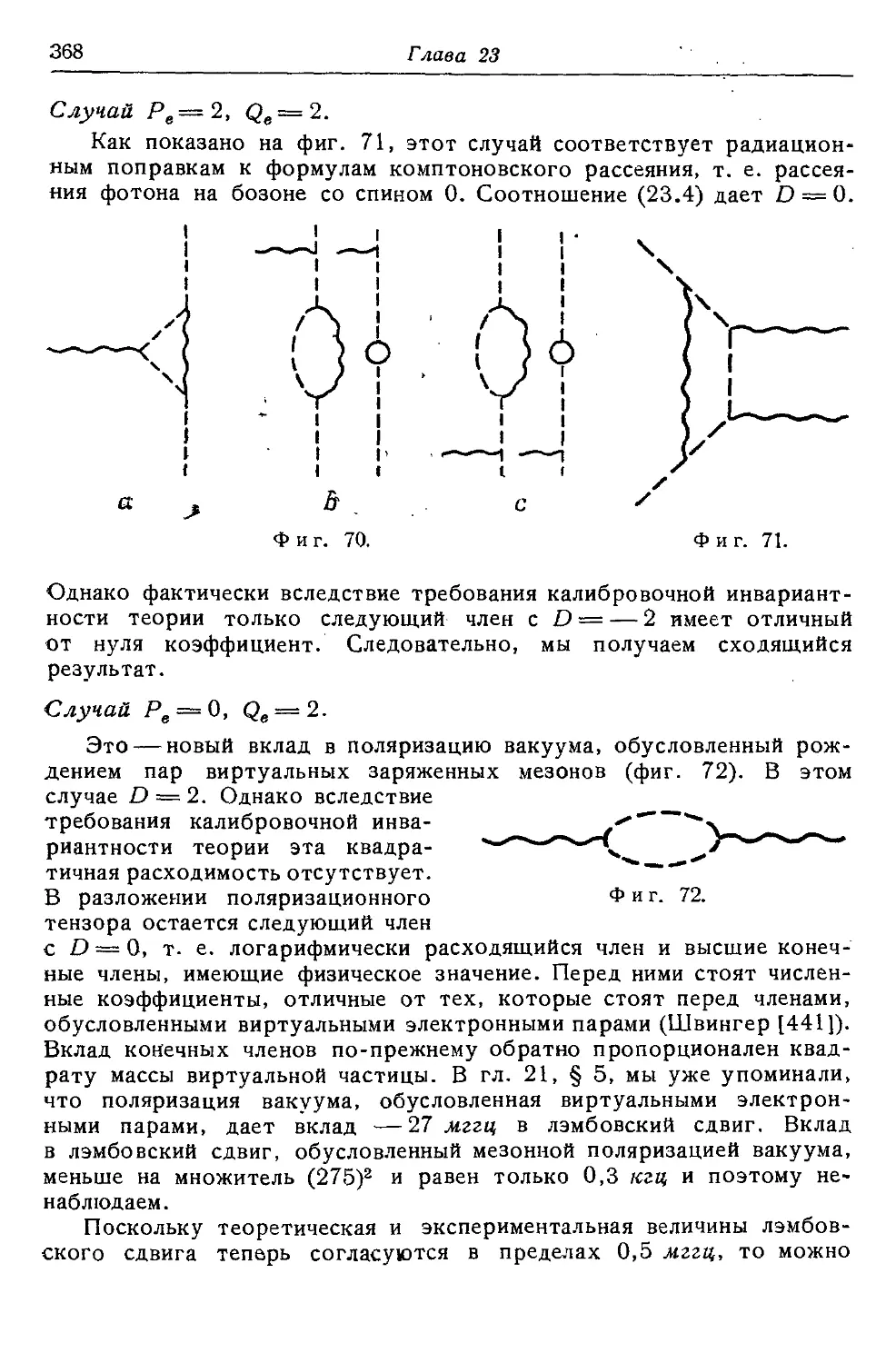
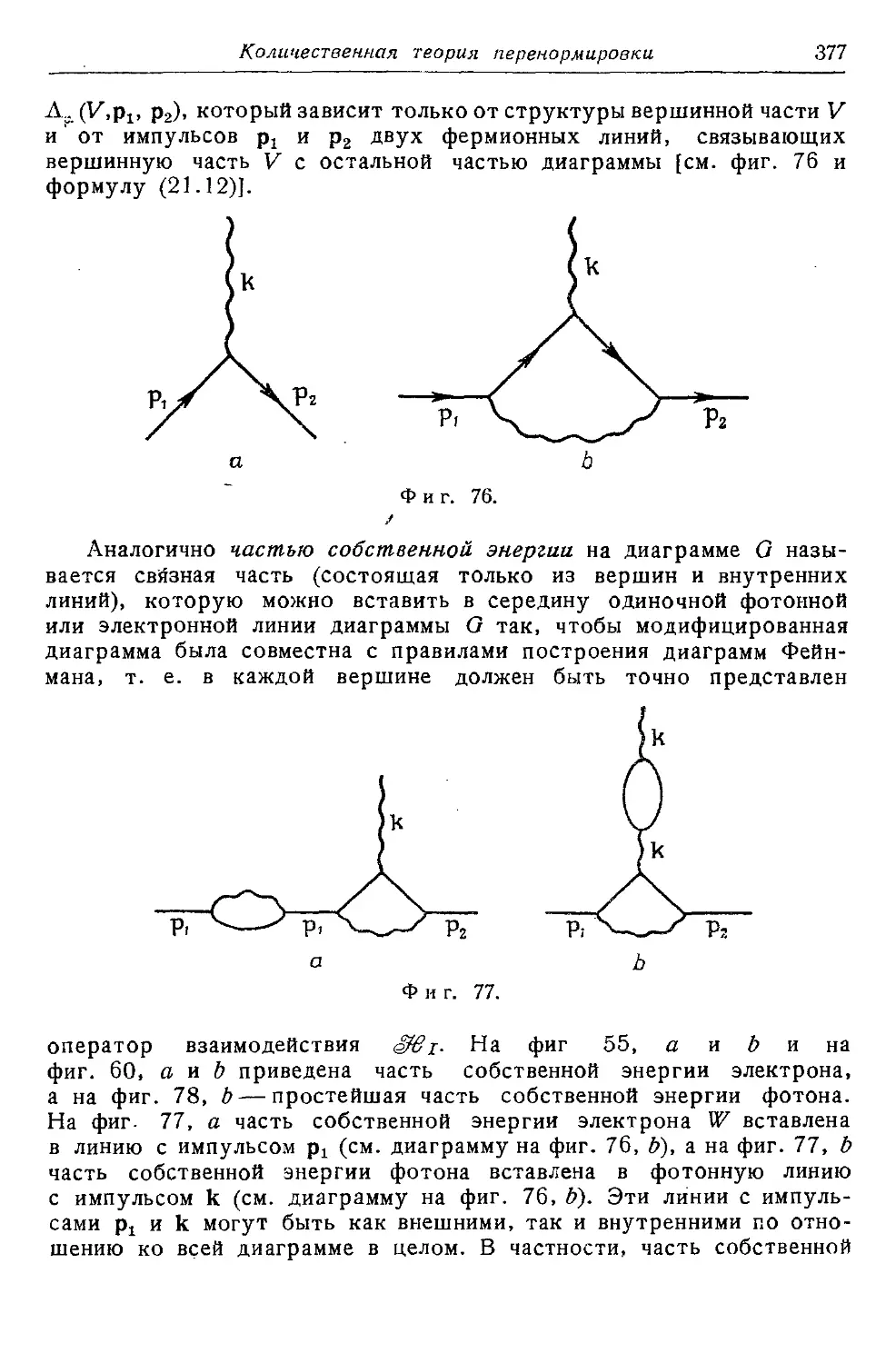
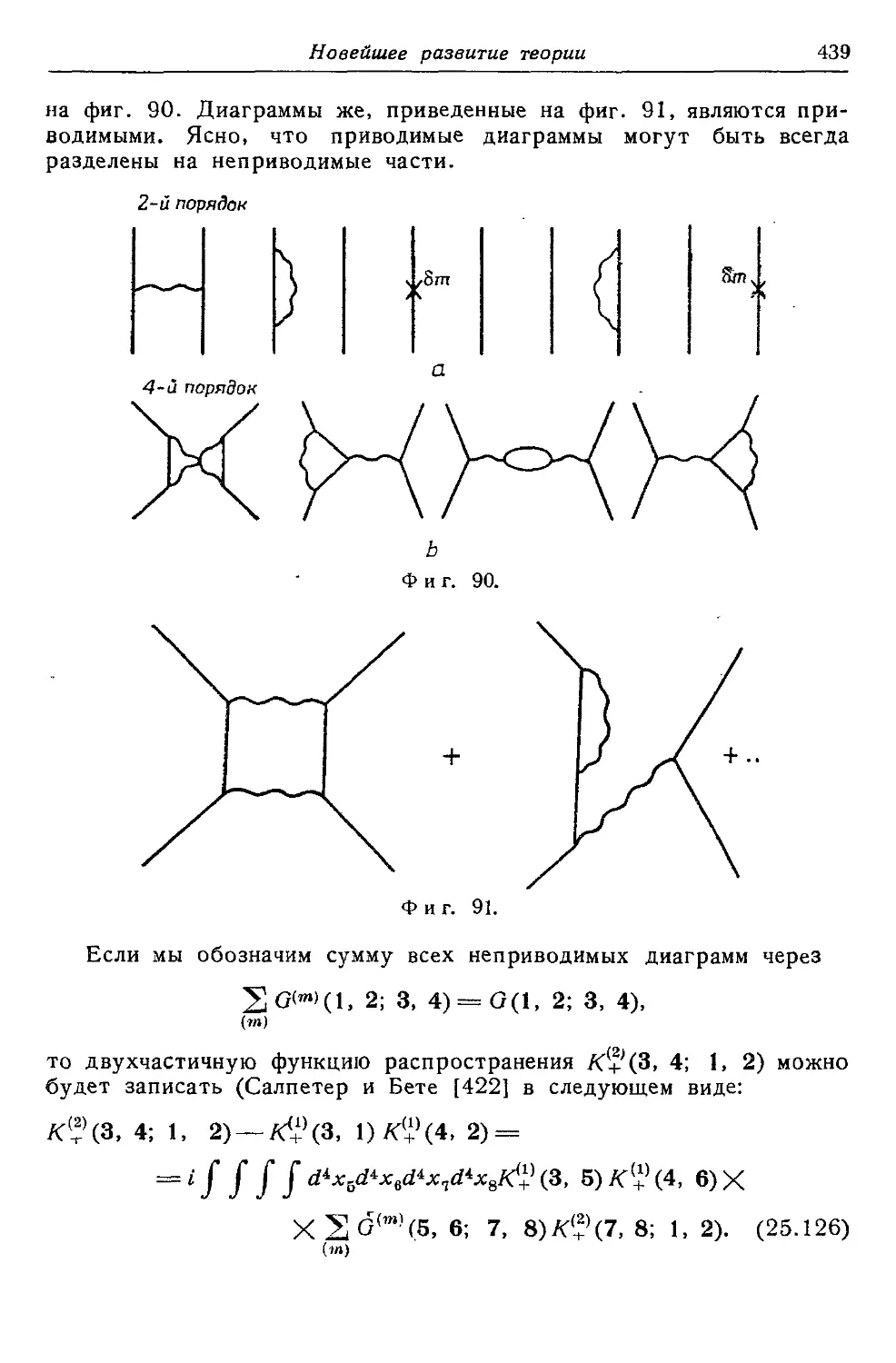
Текст
Volume
I
ELDS
Silvan S. Schweber
Associate Professor of Physics, Brande is Unioersity
Hans A. Bethe
Professor of Physics, Cornell University
Frederic de Hoffmann
Staff Member, Los Alamos Scientific Laboratorxj
ROW, PETERSON AND COMPANY
New York 19 5 5
С.ШВЕБЕР,Г. БЕТЕ, Ф.ГОФМАН
ТОМ
I
поля
ПЕРЕВОД С АНГЛИЙСКОГО
В. Н.БАЙЕРА, С. П. БАКАНОВ А
и А.А.РУХАДЗЕ
ПОД РЕДАКЦИЕЙ АКАДЕМИКА
И.Е.ТАММА
ИЗДАТЕЛЬСТВО
ИНОСТРАННОЙ ЛИТЕРАТУРЫ
МОСКВА 1957
ОГЛАВЛЕНИ Е
Предисловие к русскому изданию . . 5
Предисловие авторов 7
Глава 1. Введение. Мезонная физика и теория поля 11
Часть первая
РЕЛЯТИВИСТСКИЕ ВОЛНОВЫЕ УРАВНЕНИЯ ОДНОЙ
ЧАСТИЦЫ
Раздел I. Релятивистские волновые уравнения одной частицы
Глава 2. Уравнение Клейна — Гордона 18
§ 1. Уравнение для свободной частицы 18
§ 2. Физические свойства 19
§ 3. Взаимодействие с внешним электромагнитным полем ... 23
§ 4. Релятивистские обозначения 24
Глава 3. Уравнение Дирака 27
§ 1. Вывод уравнения. Выражение для тока 27
§ 2. Матрицы Дирака 30
§ 3. Ковариантная форма уравнений Дирака 33
§ 4. Релятивистская инвариантность 37
Глава 4. Свойства преобразований и значения операторов Дирака 44
§ 1. Свойства преобразований 44
§ 2. Значение операторов в нерелятивистском приближении . . 49
Глава 5. Свойства уравнения Дирака 54
§ 1. Спин 54
§ 2. Состояния с отрицательной энергией 55
§ 3. Уравнение Дирака с учетом внешнего поля 57
Глава 6. Применение уравнения Дирака 60
§ 1. Стационарные состояния 60
§ 2. Точная теория рассеяния при высоких энергиях 61
§ 3. Эффект, обусловленный структурой ядра 63
Глава 7. Вычислительная техника 66
§ 1. Вероятность перехода 66
§ 2. Нормировка и условия ортогональности 67
§ 3. Проекционные операторы 70
§ 4. Шпуры 72
Глава 8. Фейнмановская теория позитрона 75
§ 1. Нерелятивистская теория 75
§ 2. Релятивистская теория 79
§ 3. Импульсное представление 84
§ 4. Электромагнитное поле 87
§ 5. Бозе-частицы ...» 92
486 Оглавление
Глава 9. Применения теории Фейнмана 94
§ 1. Резерфордовское рассеяние 94
§ 2. Уравнения для связанных состояний 97
§ 3. Задача двух частиц 99
§ 4. Сечение мёллеровского рассеяния 105
§ 5. Рассеяние позитронов на электронах 108.
Часть вторая
ТЕОРИЯ ПОЛЯ
Раздел II. Поля и виды взаимодействий
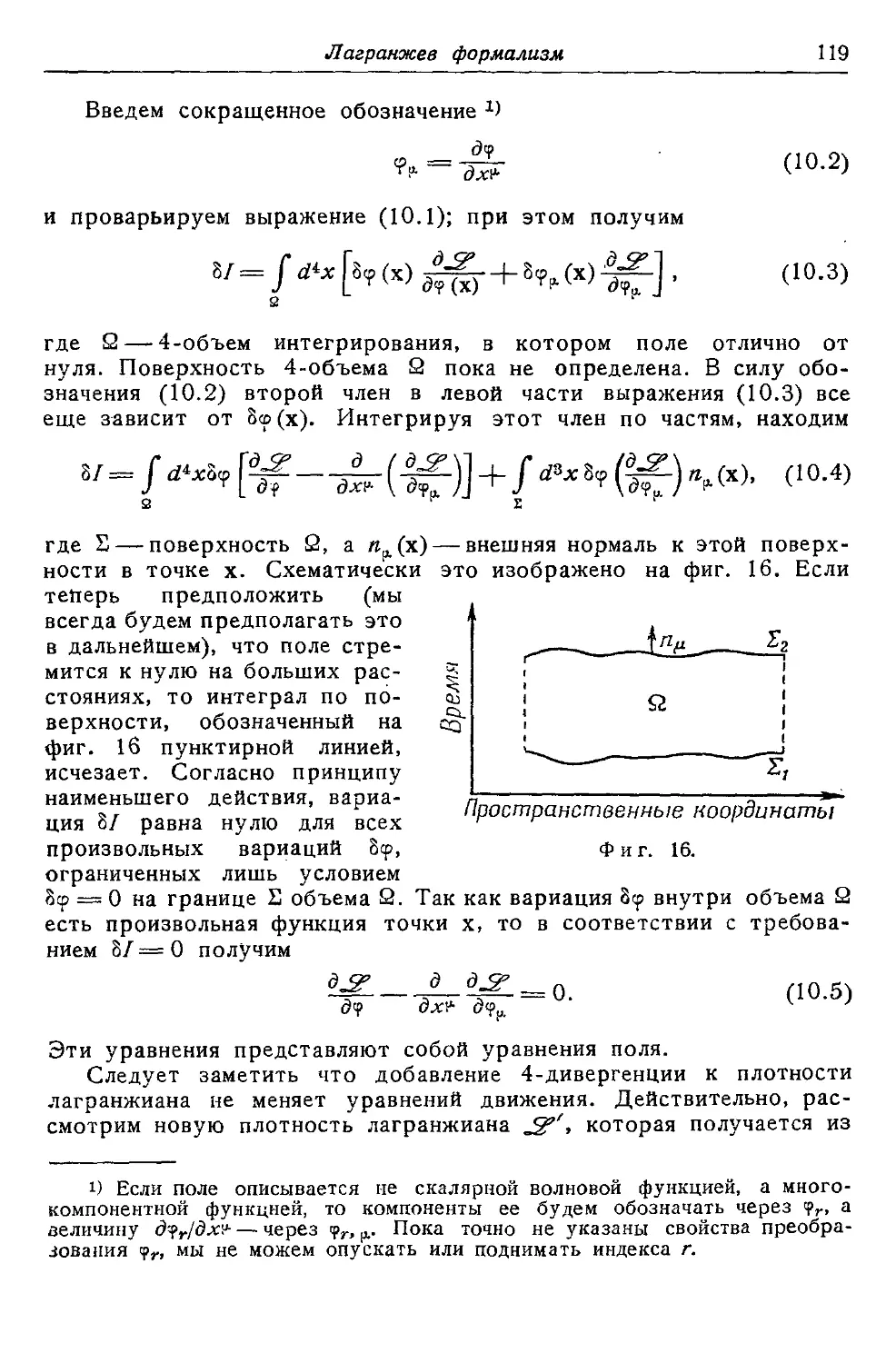
Глава 10. Лагранжев формализм 118
§ 1. Классическая теория 118
§ 2. Действительное однокомпонентное поле 123
§ 3. Комплексное скалярное поле 127
§ 4. Дираковское поле 129
§ 5. Максвелловское поле и векторное мезонное поле .... 131
Глава П. Взаимодействие между полями 135
§ 1. Прямые связи 135
§ 2. Связи с производной 136
§ 3. Более сложные типы связей 138
§ 4. Взаимодействие между двумя спинорными полями .... 141
§ 5. Взаимодействие и уравнения движения 142
Глава 12. Взаимодействие с электромагнитным полем 145
§ 1. Заряженное бозонное поле 145
§ 2. Дираковское поле 146
§ 3. Система трех полей 148
Раздел III. Квантовая теория полей
Глава 13. Квантование поля 150
§ 1. Представления Шредннгера и Гейзенберга 150
§ 2. Канонические перестановочные соотношения 152
§ 3. Импульсное представление и квантование скалярного поля 154
§ 4. Операторы числа частиц, нх рождения и уничтожения . . 159
§ 5. Квантование спинорного поля 164
§ 6. Зарядовое сопряжение 171
§ 7. Корпускулярно-волновой дуализм 173
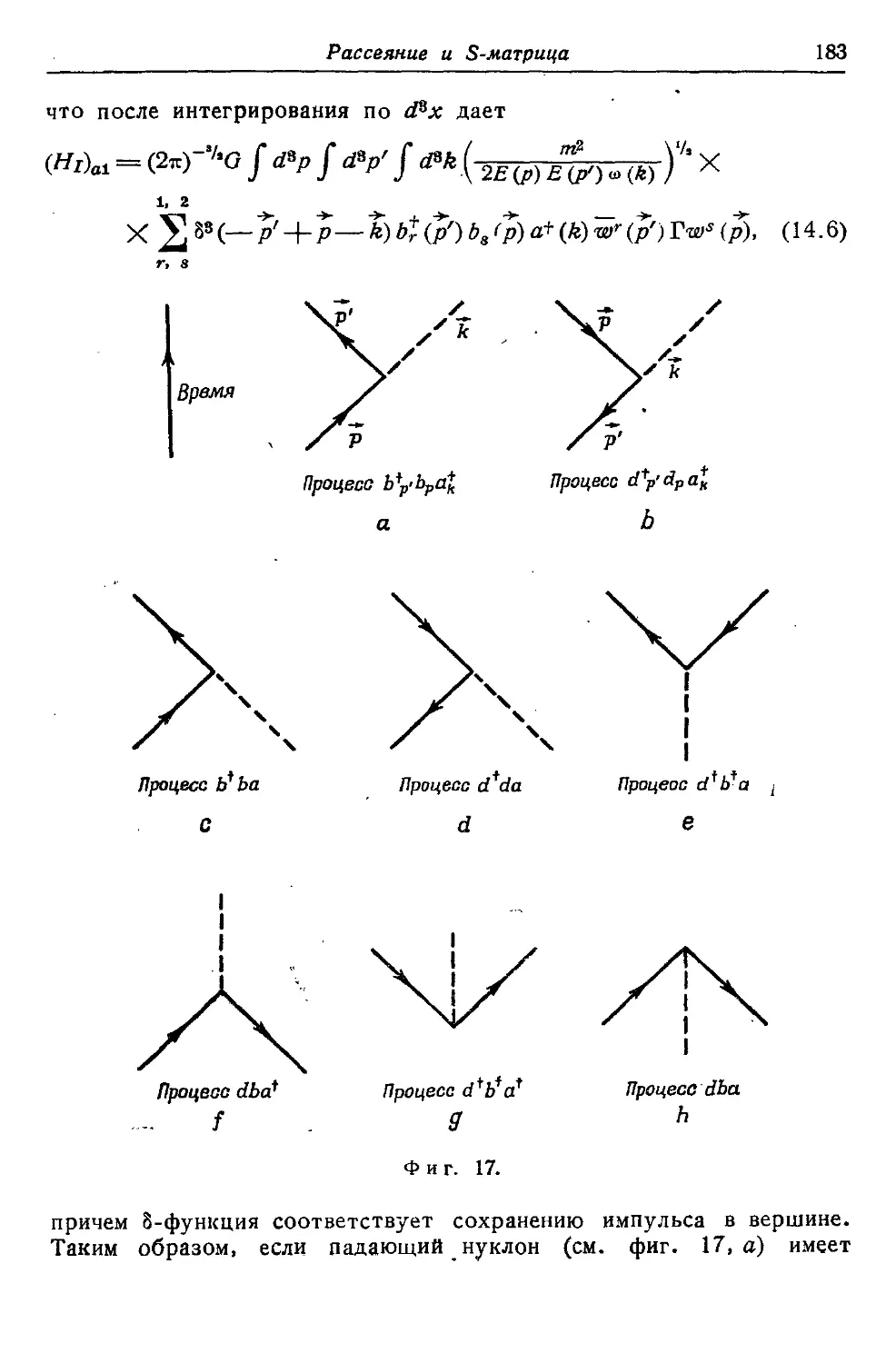
Глава 14. Рассеяние и 5-матрица 181
§ 1. Испускание и поглощение кванта 181
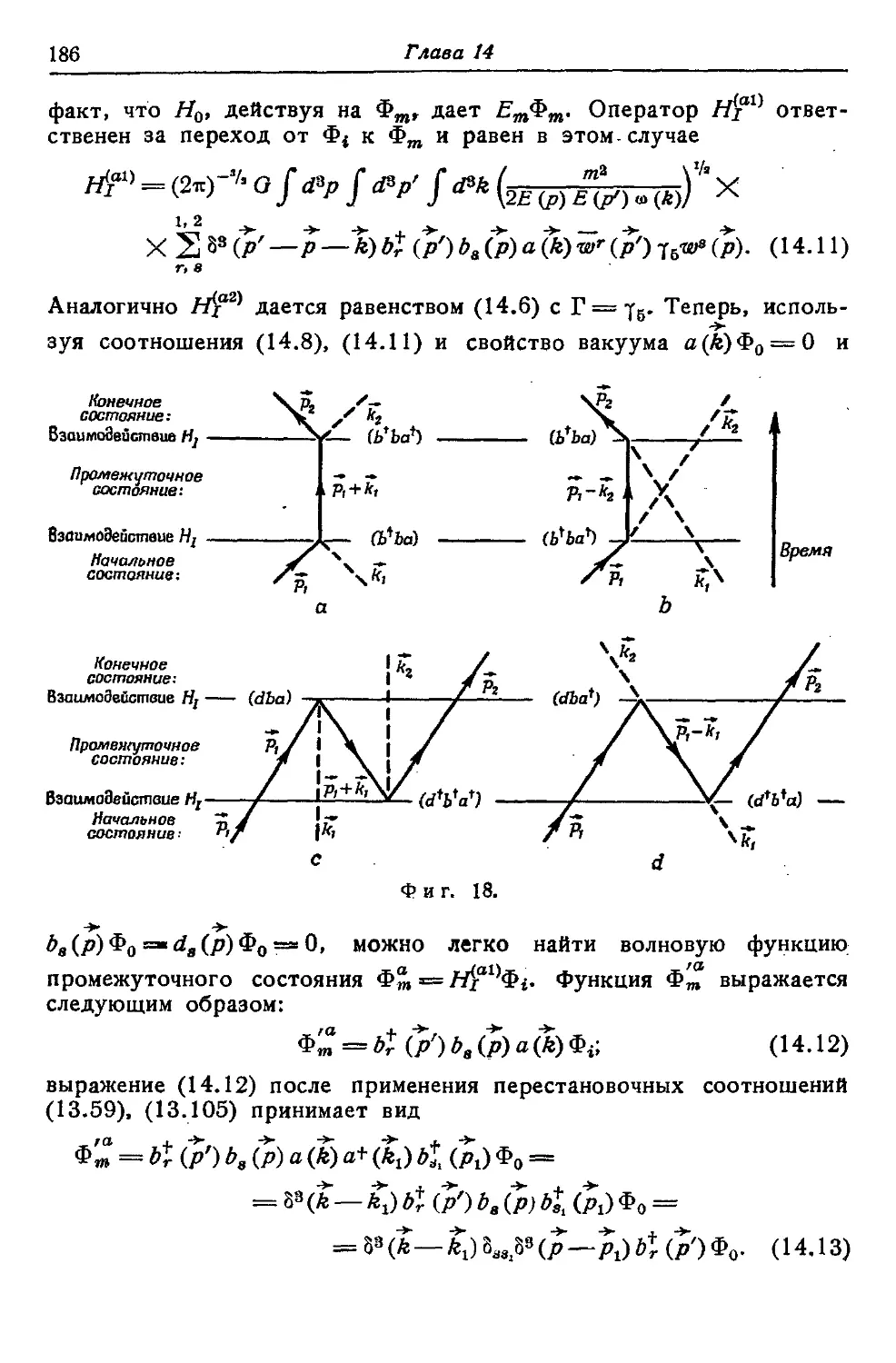
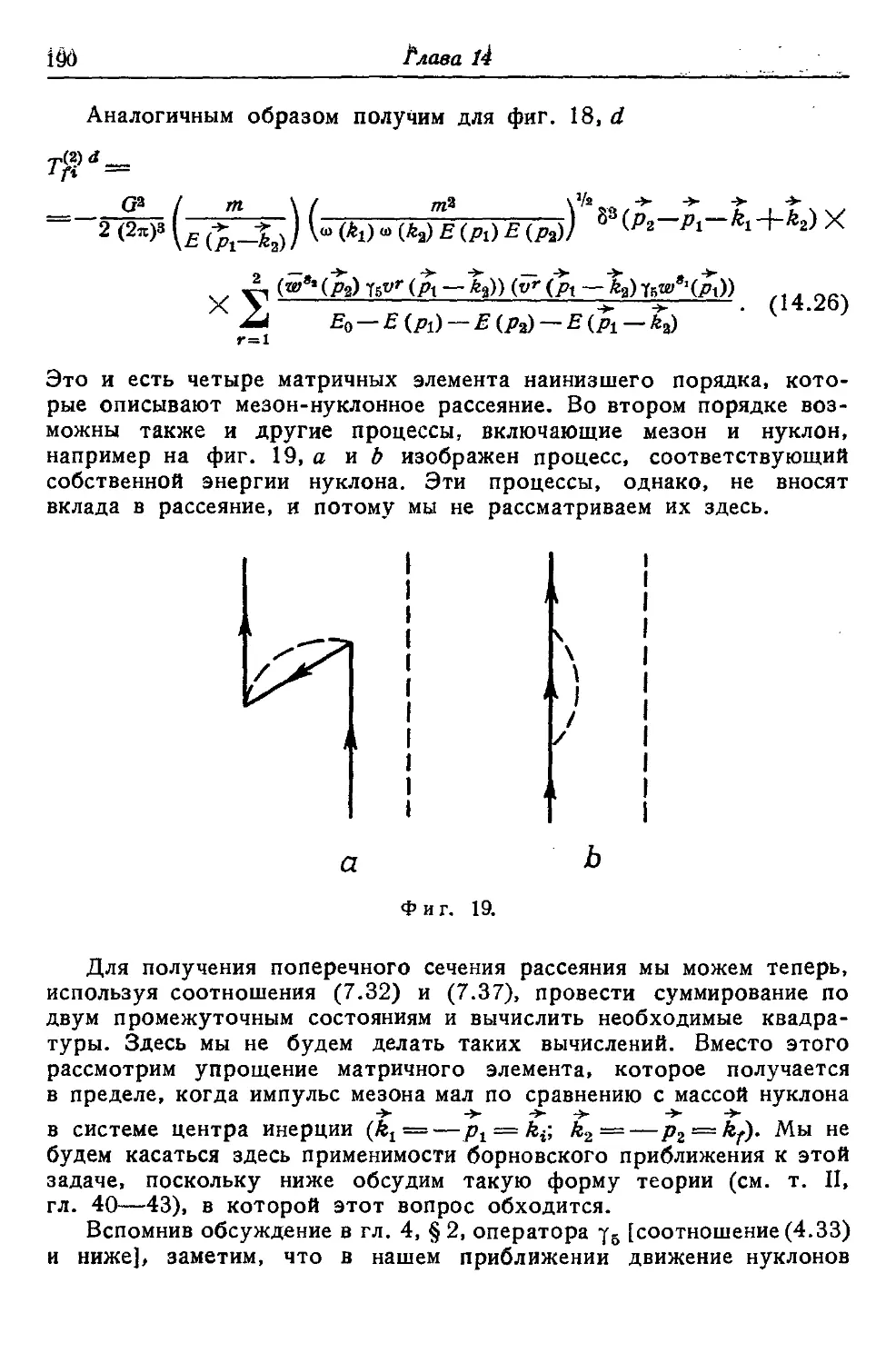
§ 2. Рассеяние незаряженных мезонов нуклонами 184
§ а 5-матрица 193
Глава 15. Ковариантный формализм 196
§ 1. Представление взаимодействия 196
§ 2. Ковариантные перестановочные соотношения 201
§ 3. Перестановочные соотношения для дираковских опера-
операторов 209
§ 4. Квантование электромагнитного поля 212
Глава 16. Инвариантная теория возмущений 224
§ 1. Теория 224
§ 2 Адиабатическая гипотеза 229
Оглавление 487
Глава 17. Преобразование S-матрицы 236
§ 1. Нормальное произведение 236
§ 2. Теорема Вика 240
§ 3. Применение к 5-матрице 244
§ 4. Представление инвариантных функций 246
Глава 18. Диаграммы Фейнмана 252
§ 1. Взаимодействие с внешним электромагнитным полем . . . 252
§ 2. Диаграммы Фейнмана в мезонной теории ..:..... 258
§ 3. Вакуумные амплитуды 261
§ 4. Правила для диаграмм Фейнмана 266
Глава 19. Импульсное представление 269
§ 1. Рассеяние двух фермионов 269-
§ 2. Собственная энергия нуклона 272
§ 3. Явная форма матричного элемента 273-
§ 4. Взаимодействие мезонов с электромагнитным полем . . . 278.
§ 5. Поперечные сечения: комптоновское рассеяние 281
Раздел IV. Перенормировка в квантовой теории поля
Глава 20. Собственная энергия фермиона 290'
§ 1. Степень расходимости 290
§ 2. Попытки сделать собственную энергию конечной 295
§ 3. Вычисление собственной энергии с помощью метода Фейн-
Фейнмана 302
Глава 21. Перенормировка 308.
§ 1. Перенормировка массы и нерелятивнстский лэмбовский
сдвиг 30&
§ 2. Радиационные поправки к формулам рассеяния 317
§ 3. Перенормировка волновой функции 323-
§ 4. Аномальный магнитный момент и лэмбозский сдвиг . . . 327
§ 5. Поляризация вакуума 331
§ 6. Перенормировка в мезоиной теории 338
§ 7. Применения 342
§ 8. Представление взаимодействия Фарри для связанных со-
состояний 347
Глава 22. Расходимости 354
§ 1. Общие положения 354
§ 2. Случаи, которые были уже рассмотрены 357
§ 3. Треугольные диаграммы 358
§ 4. Квадратные диаграммы 361
Глава 23. Перенормируемые н неперенормируемые теории .... 36&
§ 1. Взаимодействие бозониых полей 366
§ 2. Двухфотониое взаимодействие 369
§ 3. Связь с производными 370
§ 4. Высшие спины 373-
§ 5. Взаимодействие [S-распада 374
Глава 24. Количественная теория перенормировки 376
§ 1. Определения . 376.
§ 2. Отделение расходимостей из неприводимых диаграмм . . 38S
§ 3. Отделение расходимостей из приводимых диаграмм . . . 388
§ 4. Тождество Уорда 394
§ 5. Доказательство перенормируемости 397
§ 6. Смысл перенормировки заряда 404
488 Оглавление
§ 7. Общие замечания 406
§ 8. Перенормировка в представлении связанных состояний . . 409
Глава 25. Новейшее развитие теории 413
§ 1. Гейзенберговское представление 413
§ 2. Рассмотрение инвариантных свойств 421
§ 3. Средние значения в состоянии вакуума 427
§ 4. 5-матрица в гейзенберговском представлении 433
§ 5. Величина перенормировочных констант 434
§ 6. Проблема связанных состояний 437
§ 7. Многочастичные амплитуды 447
§ 8. Другие результаты, полученные в теории 448
Глава 26. Теорема эквивалентности 451
§ 1. Рассеяние свободных частиц 451
§ 2. Преобразование Дайсона 452
§ 3. Интерпретация 457
Приложения
Приложение А 459
Приложение Б 460
Литература 464
Предметный указатель 476
МЕЗОНЫ И ПОЛЯ
Том I
ПОЛЯ
Редактор Е. МАЙКОВА
Технический редактор С. Клименко
Сдано в производство 11/1 — 57г. Подписано к печати I5/VII 57 г. Бумага 60x92'/,,= 15,3 бум. л.
30,5 печ. л. Уч.-изд. л. 28,3. Изд. J* 2/3320. Цена 21 р. 80 к. Заказ J* 1784.
ИЗДАТЕЛЬСТВО ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва, Ново-Алексеевская, 52.
Министерство культуры СССР. Главное управление полиграфической промышленности
4-я тип. им. Евг. Соколовой. Ленинград, Измайловский пр., 29.
Редакция литературы по физике
Заведующий редакцией проф. А. А. СОКОЛОВ
ПРЕДИСЛОВИЕ
К РУССКОМУ ИЗДАНИЮ
Настоящий первый том двухтомной монографии „Мезоны и поля"
представляет собой законченное целое: он посвящен изложению
общих основ современной квантовой теории полей.
Эта монография предназначена для широкого круга физиков —
студентов, аспирантов и научных работников, — как изучающих тео-
теоретическую физику, так и ведущих научную работу в этой области
физики.
Как учебник и как справочное пособие эта книга, по моему
мнению, обладает рядом преимуществ по сравнению с другими
монографиями по тому же вопросу.
Во-первых, автору удалось удачно отделить основное от второ-
второстепенного и поэтому в относительно малом объеме изложить
основы теории так, чтобы, с одной стороны, это изложение было
достаточно строгим и последовательным в математическом отно-
отношении, а с другой стороны, основное физическое содержание теории
и общая качественная характеристика ее современного состояния
были выделены достаточно выпукло.
Во-вторых, в книге параллельно с изложением квантовой элек-
электродинамики излагается достаточно подробно и квантовая мезоди-
намика.
Наконец, в-третьих, очень удачна в книге библиография. Он
широко охватывает журнальную литературу не только по основным
вопросам, рассмотренным в книге, но и по многим проблемам
теории, которые за недостатком места только кратко упомянуты
в тексте. В американском издании библиография доведена до сере-
середины 1954 г.; при переводе мы ограничились добавлением ссылок
лишь на некоторые, наиболее важные работы последних двух лет.
Главы 1—16 переведены С. П. Бакановым и А. А. Рухадзе,
гл. 17—26 и Приложения — В. Н. Байером.
Академик И. Е. Тамм.
ПРЕДИСЛОВИЕ АВТОРОВ
В основе настоящей книги лежит курс лекций, прочитанных
одним из авторов (Г. Бете) в Корнельском университете весной
1953 г. Эти лекции были посвящены вопросам исследования про-
процессов при высоких энергиях. Второй автор (Ф. Гофман), посе-
посещавший Корнельский университет в течение 1953/54 учебного года,
подробно записал эти лекции. Его записи первоначально были рас-
распространены среди студентов и в небольшом количестве разосланы
в другие университеты физикам, интересующимся этими вопросами.
Ввиду огромного интереса к данному предмету было решено до-
дополнить эти записи и превратить их в книгу. При этом выясни-
выяснилось, что число экспериментальных и теоретических данных о полях
сильно возросло. Чтобы изложить их с единой точки зрения, необ-
необходимо было заново пересмотреть все экспериментальные резуль-
результаты. Кроме того, первоначальный материал значительно увеличился
благодаря включению гл. 38—51.
По первоначальному плану теоретическим основам посвящалась
первая часть книги, причем современную теорию поля предполага-
предполагалось описать лишь качественно. Однако в 1953/54 учебном году
третий автор (С. Швебер) прочитал курс лекций по современной
квантовой механике в Корнельском университете. Нам казалось, что
включение основной части этого курса сделает запланированную
книгу более полной, а излагаемую теорию — более количественной.
Теперь книга явно уже разделилась на две основные части.
Главы по теории поля, вероятно, будут представлять большой
интерес в основном для теоретиков, данные же по мезонам и их
интерпретация — для экспериментаторов. Было решено издать эти
части отдельно, хотя мы полагаем, что во всей книге в целом
найдутся вопросы, интересующие каждую из указанных групп
физиков.
Разделение книги на две части связано также с авторством:
первый том — преимущественно плод работы Швебера, второй же
том — Бете и Гофмана. Первый вариант нескольких глав первого
тома был написан Бете и Гофманом. Недостаток времени помешал
Гофману уделить достаточно внимания работе над первым томом
в ее конечной стадии. Поэтому Швебер по предложению Бете взял
на себя всю ответственность за переработку лекций.
Предисловие авторов
Первый том представляет собой в сущности учебник по совре-
современной теории поля. Мы старались вести изложение как можно
проще и придерживаться обычных понятий. Для этого в основу
нашего изложения мы положили работы Дайсона, написанные в 1949 г.,
а не более новые фундаментальные работы Швингера и Фейнмана,
опубликованные в 1950 и 1951 гг. Первый том можно изучать, не
обращаясь к ссылкам на второй том.
Второй том главным образом представляет собой попытку дать
перечень существующих экспериментов по тг-мезонам, не вдаваясь
в технику эксперимента, но освещая их физический смысл и взаим-
взаимную связь. Несколько глав (гл. 40—47) содержат элементарное
изложение существующих теорий тг-мезонных процессов. Главы
второго тома, посвященные экспериментальным, а также некоторым
теоретическим вопросам, могут быть поняты без чтения первого
тома. Знание первой части первого тома, в которой описываются
релятивистские волновые уравнения одной частицы, весьма жела-
желательно (почти все содержание этой части обычно излагается в боль-
большинстве университетских курсов квантовой механики).
Читателю-экспериментатору, желающему познать основы мезон-
ной теории, не вдаваясь глубоко в математику, мы рекомендуем
гл. 1—6, 8—12, 20, 21, 23 и 26 первого тома и все главы второго
тома, за исключением гл. 41—45. При чтении этих глав он встретит
ссылки на соотношения, выведенные в других главах, однако он
обнаружит, что эти ссылки несущественны для понимания.
Авторы второго тома — Бете и Гофман — благодарны третьему
автору — Швеберу — за переработку § 5 и 6 гл. 30, § 2—4 гл. 31
и § 1, 2 гл. 40, а также за помощь при унификации обозначений
второго и первого томов. Несмотря на то, что первый и второй
тома, по существу, независимы, мы не старались избегать взаимных
ссылок, сохраняя тем самым целостность предмета. Разумеется, были
приложены все усилия, чтобы не приводить неправильных сведений,
однако в книге все же, несомненно, имеются ошибки и несогласо-
несогласованности. Поэтому мы хотим заранее извиниться за них и надеемся,
что большое количество ссылок как на старую, так и на новейшую
литературу частично исправит эти ошибки.
Большую помощь в работе нам оказали наши коллеги, а также
ряд других лиц. Экспериментаторы любезно присылали нам резуль-
результаты опытов до их публикации. Ниже приводится далеко не полный
список групп и отдельных лиц, которым мы обязаны за сообщение
экспериментальных данных: Коллинс, Росс, Шатт и Торндайк (Брук-
хэйвенская национальная лаборатория); Бечер и Уокер (Калифорний-
(Калифорнийский технологический институт); Ашкин (Технологический институт
Карнеги); Ледерман и Стейнбергер (Колумбийский университет);
Коккони, Мартин, Сильверман и Вильсон (Корнельский университет);
Осборн (Массачусетский технологический институт); Дудзяк (Кали-
(Калифорнийский университет); Андерсон, Ферми, Гликсман, Орир и
Предисловие авторов
Розенфельд (Чикагский университет); Барнс, Роберте и Тинлот
(Рочестерский университет).
Мы также обязаны многим физикам-теоретикам, присылавшим
нам рукописи своих работ. Мы особенно благодарны тем нашим
коллегам, которые критически прочитали некоторые главы настоя-
настоящей книги и высказали ряд полезных замечаний, в частности Брюк-
неру, Кейсу, Далицу, Дайсону, Эдвардсу, Гольдбергеру, Конопин-
скому, Митра, Нелкину, Нойсу, Россу, Стейну, Сундаресану, Ватсону
и Вайтману. Мы также благодарны Юбераллю за проверку ссылок
к первому тому.
Наконец, мы очень благодарны Патриции Гофман за перепечатку
многих вариантов рукописи отдельных глав как первого, так и
второго томов. Мы также хотим поблагодарить Патрицию Мискол
за перепечатку первоначальных записей лекций и отчета Лос-Ала-
мосской научной лаборатории и, кроме того, Мильдрет П. Хозейт
за подготовку чертежей. Мы благодарим Мирну Швебер за редак-
редактирование большей части первого тома, а также Патрицию Гофман
за редактирование большей части второго тома. Мы обязаны Лос-
Аламосской научной лаборатории, которая, дала возможность раз-
размножить первоначальные записи лекций, а также оказывала всесто-
всестороннюю поддержку. Мы хотим поблагодарить доктора Герберта
Юбералля за проверку взаимных ссылок. Один из нас (Швебер)
хочет поблагодарить Национальное научное общество за дружескую
помощь во время написания книги. Наконец, мы благодарны работ-
работнику издательства Роу, Петерсон и К0, Мак-Ферсону за терпели-
терпеливое отношение к нашим изменениям текста книги.
Г. Бете,
Ф. Гофманг
С. Швебер.
Июнь 1954 г.
Глава I
ВВЕДЕНИЕ. МЕЗОННАЯ ФИЗИКА И ТЕОРИЯ ПОЛЯ
В настоящее время назрела необходимость создания книги по
мезонной физике. Проведено большое число количественных экспе-
экспериментов с тг-мезонами, в результате которых выяснены основные
свойства мезон-нуклонного взаимодействия. Так как в будущем
понадобится гораздо больше экспериментов и с большей точностью,
то представляет интерес выяснить, какого типа эксперименты наи-
наиболее подходящи для получения нужных сведений. В теории, оче-
очевидно, мы также еще слишком далеки от каких-либо количественных
предсказаний, однако мы можем качественно предсказать основные
свойства таких явлений, как рассеяние мезонов. В настоящее время
мы видим эти трудности теории и знаем ряд методов получения
приближенных решений.
Напомним кратко основные моменты развития мезонной физики
за последние 10 лет.
1. Открытие в 1947 г. Конверси, Панчини и Пиччиони [88] того
факта, что мезоны космического излучения ([х-мезоны), вопреки перво-
первоначальным предположениям, очень слабо взаимодействуют с нуклонами.
2. Открытие в 1947 г. Латтесом, Оккиалини, Пауэллом [299] того,
что мезоны, в изобилии встречающиеся в космическом излучении
([^-мезоны), являются вторичными частицами, возникающими при рас-
распаде других частиц — тг-мезонов, и того, что тс-мезоны сильно вза-
взаимодействуют с нуклонами.
3. Экспериментальное определение основных свойств свободного
тс-мезона освещено главным образом в работах Пановского, Стейн-
бергера и их сотрудников в Калифорнийском и Колумбийском
университетах (см. т. II, гл. 27).
4. Исследование взаимодействия между мезонами и нуклонами
при помощи экспериментов по рассеянию и фоторождению мезонов
на нуклонах.
5. Более глубокое обоснование квантовой теории поля путем
введения метода перенормировок.
6. Развитие некоторых теоретических методов изучения силь-
сильного взаимодействия в теории поля.
7. Открытие тяжелых мезонов и гиперонов.
Мы не будем детально рассматривать свойства [х-мезонов, тяжелых
мезонов и гиперонов. Мы лишь кратко опишем в т. II, гл. 50 и 51,
12 Глава 1
их известные свойства и обсудим, почему можно считать, что
а-мезоны, тяжелые мезоиы и гипероны не играют важной роли ни
в ядерных силах, ни во взаимодействии тг-мезонов с нуклонами при
не очень больших энергиях.
Обсудим все перечисленные выше моменты развития мезонной
физики, за исключением первых двух, которые мы считаем доста-
достаточно хорошо известными. В частности, полностью изложим совре-
современную теорию поля. Теория поля сама по себе является само-
самостоятельной дисциплиной и составляет содержание первого тома.
Читатель, интересующийся главным образом мезонами, а не теорией
поля, может опустить большую часть первого тома.
Достижения современной теории поля заключаются, во-первых,
в устранении расходимости при расчетах всех наблюдаемых эффек-
эффектов, во-вторых, в достаточно хорошем количественном согласии
теории с экспериментом. Однако это количественное согласие имеет
место только в атомной физике, где связь вещества с электромаг-
электромагнитным полем весьма слабая. Таким образом, удалось показать, что
теория, которая излагается в обычных учебниках (например, в учеб-
учебнике Шиффа [429]), является прекрасным приближением к действи-
действительности. Более того, с помощью этой теории были объяснены
такие тонкие эффекты, как лэмбовское смещение (см. работу Лэмба
и Резерфорда [295]), и было найдено (см. работу Салпетера [425]),
что вычисленная разность между уровнями 2Si/, и 2Р]/2 атома водо-
водорода, составляющая 1057,2 мггц, согласуется с экспериментом
Трибвассера и др. [487] с точностью до 0,6 мггц. Этим было уста-
установлено, что квантово-механические поправки к указанным уровням
и отклонения от закона Кулона в атоме водорода не превышают
одной миллиардной части. Аномальный магнитный момент электрона,
обусловленный радиационными поправками, был рассчитан Карплусом
и Кроллом [263] в четвертом приближении по е и оказался равным
■^-(^- — 2,973^-) =0,0011454 магнетонов Бора *>, A.1)
что находится в прекрасном согласии с самыми последними экспе-
экспериментальными данными.
Другим достижением теории перенормировок является то, что
предсказание теории позитрона о существовании поляризации ва-
вакуума подтвердилось как экспериментами по лэмбовскому смещению,
так и по сдвигу основного состояния позитрония. Вычисленная
разность уровней дуплета основного состояния позитрония равна
Дм = 2,0337 • 105 мггц (см. работу Карплуса и Клейна [266]);
половина этой величины обусловлена поляризацией вакуума. Экспе-
Экспериментальное значение этого сдвига равно B,037z±r 0,003)• 10б мггц-
У Это значение получено при подстановке величины а х =137,036 4 ±
± 0,0012, которая была установлена ранее.
Введение 13
Были также рассчитаны более сложные эффекты, как например
лэмбовское смещение сверхтонкой структуры, точная форма спек-
спектральной линии и т. д.
Поэтому мы будем полагать, что теорию перенормировок можно
считать в основном правильной и применимой к мезонной теории.
Конечно, теория перенормировок не устраняет бесконечностей
в собственной энергии, которые в течение многих лет были бичом
теории поля; однако она указывает, как обойти эти трудности и
вычислить оставшиеся после вычитания бесконечностей конечные
эффекты, чтобы получить согласие с экспериментом.
В первом томе дается описание новейшего развития теории поля,
включая теорию перенормировок. Первые девять глав посвящены
изложению теории Фейнмана. В них включен также обзор реляти-
релятивистских уравнений одной частицы, причем особое внимание уделено
физической интерпретации и обсуждению пределов применимости
этих уравнений. В последующих десяти главах излагается кванто-
квантование поля с современной точки зрения. При этом особое значение
придается теории рассеяния и главным образом 5*-матрице. В этих
главах, по существу, снова выводится формализм Фейнмана на осно-
основании классических работ Дайсона по теории поля. Следующие
пять глав излагают программу перенормировок, включая доказа-
доказательство перенормируемости квантовой электродинамики, данное
Дайсоном, Саламом и Уордом. Наконец, гл. 25 посвящается обзору
некоторых новейших достижений теории поля, таких, как вывод
уравнений связанных состояний и исследование уравнений поля без
применения теории возмущений.
Здесь не излагаются такие вопросы, которые, как мы полагаем,
являются содержанием обычных курсов элементарной квантовой меха-
механики; например, старое квантование поля излучения, испускание и
поглощение света и вообще такие вопросы, которые можно найти
в превосходном обзоре Ферми [155].
ОБОЗНАЧЕНИЯ
Обсудим некоторые обозначения, принятые в настоящей книге
(т. I и II).
Скаляры и векторы. Скаляры обозначаются обычным шрифтом.
Пространственные векторы (как в обычном пространстве, так и
в пространстве с изотопическим спином) обозначаются обычным
шрифтом со стрелкой сверху. Для обозначения 4-векторов приме-
применяется жирный шрифт. Скалярные произведения как 3-, так и
4-векторов обозначаются точкой между ними.
Обозначение Фейнмана и 4-векторы. Все компоненты наших
4-векторов действительны, т. е. х0 = ct (это подробно объясняется
в гл. 2, § 3). Смысл операторов Дирака ^ и их произведений
14 Глава 1
обсуждается в гл. 3, § 3, и в гл. 4. Символы Фейнмана вводятся
в гл. 8, § 3. Мы полагаем, что р = f°p°—~[ • Р-
Производные. В т. I использованы следующие сокращенные
обозначения (впервые введенные в гл. 10, § 1):
<Эч
~ШГ и
Изотопический спин. Мы обозначаем изотопический спин бук-
буквой Т. В некоторых случаях используется буква t для обозначения
изотопического спина отдельной частицы в системе. При чтении
гл. 30 (т. II) следует различать оператор t и собственное значение
оператора Т.
Единицы измерения ft и с. В обоих томах, особенно во втором,
мы часто полагаем Й = с=1, где Й—постоянная Планка (деленная
на 2тг) и с — скорость света. В этой системе единиц энергия,
импульс и масса имеют одинаковую размерность (обратную длине).
В тех случаях, когда мы не пользуемся этой системой единиц,
в частности в т. I, выбор системы единиц очевиден из самих урав-
уравнений.
Сдвиги фаз. Мы обозначаем сдвиги фаз символом 3.
Константа связи. Мы будем обозначать константу связи во вза-
взаимодействии без производных (гл. 11, § 1) через О, а константу
связи во взаимодействии с производными (гл. 11, § 2)—через Р/р,
где (j. — масса мезона. Как О, так и F безразмерные величины.
Мы будем часто использовать сокращенные обозначения: g2—G2/4iz
и f2=F2j4n. Вообще, когда употребляется термин „псевдоскалярное
взаимодействие" без дальнейших пояснений, то при этом подразуме-
подразумевается такая связь псевдоскалярного мезонного поля с нуклонным
полем, при которой член взаимодействия имеет вид ОФ^бФ? [выра-
[выражение A1.2)]. Аналогично под словами „псевдовекторное взаимодей-
взаимодействие" мы будем понимать такую связь указанных полей, при ко-
которой член взаимодействия [см. выражение A1.6)] имеет вид
IF -г , д<9
— П.тЛ»-^-
Библиография. Список литературы приводится в конце каждого
тома.
Конечно, в книге такого объема нельзя сохранить для каждой
физической величины только одно обозначение. Поэтому мы не
пытаемся дать исчерпывающего списка обозначений; указанные выше
обозначения предназначены лишь для общей ориентировки.
ЧАСТЬ ПЕРВАЯ
РЕЛЯТИВИСТСКИЕ
ЮЛНОВЫЕ УРАВНЕНИЯ
ОДНОЙ ЧАСТИЦЫ
РАЗДЕЛ I
РЕЛЯТИВИСТСКИЕ
ВОЛНОВЫЕ УРАВНЕНИЯ
ОДНОЙ ЧАСТИЦЫ
Несколько следующих глав посвящено рассмотрению релятивист-
релятивистских волновых уравнений для частиц, наиболее часто встречающихся
в физике, а именно: частиц со спином 0 и 1/2. Большее внимание
обращено на свойства и физическую интерпретацию этих уравне-
уравнений, чем на их применение к внутриатомным процессам. Мы пред-
предполагаем, что читатель достаточно хорошо знаком как с обычной
нерелятивистской квантовой механикой, так и с релятивистской клас-
классической механикой.
Зак. 1784. Мезоны и поля
Глава 2
УРАВНЕНИЕ КЛЕЙНА — ГОРДОНА
§ 1. Уравнение для свободной частицы
Нерелятивистское волновое уравнение для частицы в отсутствие
внешних сил можно получить из соотношения
Е=4г- С2-1)
с помощью замены
*-«-£. ■ B-2)
"/?-> — ifiV, B.3)
где V — оператор градиента. Эта операция приводит к уравнению
Шредингера для свободной частицы
Обычная физическая интерпретация этого уравнения следует из
определения плотности вероятности и тока в виде
р = ф'ф, B.5)
где через ф* обозначена величина, комплексно-сопряженная ф. Таким
образом, плотность вероятности р всегда положительно определена
и в силу уравнения B.4; удовлетворяет уравнению непрерывности
-^_ + div/=0. B.7)
Вскоре после того как Шредингер получил нерелятивистское
волновое уравнение B.4), он сформулировал [431] и соответствую-
соответствующее релятивистское уравнение. Одновременно аналогичное уравне-
уравнение было предложено независимо Гордоном [210] и Клейном [277]
(см. также работы Фока [180—182]j; если ввести операторы B.2)
и B.3), то оно вытекает совершенно естественным образом из реля-
релятивистского соотношения между энергией и импульсом для свобод-
свободной частицы
■§- = р*+тЧ*. B.8)
Уравнение Клейна — Гордона 19
Это приводит к следующему волновому уравнению:
которое известно как уравнение Клейна — Гордона.
Если мы потребуем выполнения уравнения непрерывности B.7),
->
то выражения для величин р и j должны принять вполне опреде-
->
ленный вид. В частности, мы можем выбрать j в виде B.6). В этом
случае на основании уравнения B.9)
Однако из соотношения B.10) видно, что величина р может
принимать как положительные, так и отрицательные значения. Это
следует из того, что dty/dt и ф могут меняться произво. ьным обра-
образом в некоторый момент времени t, ибо уравнение B.9) —второго
порядка. Так как величины ф и dty/dt являются функциями про-
пространственных координат х, то величина р может быть положитель-
положительной в одних областях пространства и отрицательной — в других.
По этой причине трудно рассматривать р как плотность вероят-
вероятности в обычном смысле. Даже если мы попытаемся изменить выра-
жение для у, все же р будет по-прежнему включать в себя как ф,
так и dty/dt. Эта трудность внутренне присуща теории и не зависит
от выбора у.
Из-за возможности отрицательных значений р уравнение Клейна —
Гордона не получало признания больше семи лет после своего появ-
появления. Однако в 1934 г. Паули и Вайскопф [371] х) предложили
новую интерпретацию этого уравнения: они рассмотрели его как
уравнение поля (в том же смысле, как уравнения Максвелла для
электромагнитного поля) и проквантовали его. Мы вернемся к этому
вопросу ниже, в гл. 13, § 3.
§ 2. Физические свойства
Волновая функция ф в уравнении Клейна — Гордона имеет только
одну компоненту. Поэтому при преобразованиях Лоренца функ-
функцию ф можно умножать только на комплексную постоянную. Из
условия нормировки B.16) следует, что этот множитель по модулю
должен равняться 1. Таким образом, функция <j> преобразуется как
скаляр при собственных преобразованиях Лоренца, т. е. без учета
отражений. Так как, конечно, не всякая волновая функция преоб-
преобразуется как скаляр при преобразованиях Лоренца, то указанное
См. также работу Паули [374].
20 t ■.-.■/■. Глава 2
трансформационное свойство дает нам весьма важные сведения
о частице (или поле), описываемой уравнением Клейна — Гордона.
Если у волновой функции больше одной компоненты, то число сте-
степеней свободы у частицы, которую она описывает, больше, чем
число степеней свободы перемещения. Эти дополнительные степени
свободы появляются за счет спина частицы. Таким образом, урав-
уравнение Клейна — Гордона описывает частицу со спином 0. Эксперимен-
Экспериментально установлено, что тс-мезон обладает спином 0 (см. т. II, гл. 28),
поэтому полагают, что уравнение Клейна — Гордона описывает
зг-мезоны.
Баргман и Вигнер [19] показали, что в общем уравнение дви-
движения и свойства преобразования волновой функции релятивистской
частицы почти однозначно определяются следующим требованием:
волновая функция должна описывать частицу с определенной и
конечной массой и спином и являться неприводимой. Последнее озна-
означает, что волновая функция должна преобразовываться по неприво-
неприводимому представлению группы Лоренца и поэтому являться реля-
релятивистски ковариантной. Неоднозначность возникает вследствие
существования состояний с отрицательной энергией (см. ниже) и
из-за произвола в выборе обратных операторов. Если мы имеем
дело со свободными частицами, то нет необходимости рассматривать
состояния с отрицательной энергией. Ниже обсудим вопрос о свой-
свойствах инверсии. Следовательно, можно сказать, что инвариантное
теоретическое рассмотрение вполне достаточно для определения
свойств волновых уравнений свободной частицы.
Волновая функция Клейна — Гордона преобразуется как скаляр
при собственных преобразованиях Лоренца; это означает теперь,
что величина р, определенная формулой B.10), представляет собой
временную компоненту 4-вектора, пространственные компоненты
которого определены соотношением B.6). Отсюда следует, что
интеграл |<28л:р является инвариантом по отношению к собственной
группе Лоренца. Кроме того, из уравнения непрерывности выте-
вытекает сохранение этого интеграла во времени. Это означает, что р
и j можно трактовать (как и делается в теории поля) как плот-
плотности заряда и тока соответственно. Следует отметить, что выра-
выражение B.10) в нерелятивистском приближении переходит в выраже-
выражение B.5). Это можно легко показать следующим образом. Пользуясь
заменой B.2), будем иметь
ih^ = Ety, B.11)
и, следовательно, выражение B.10) принимает вид
и при Е-^imc2 действительно переходит в выражение B.5).
Уравнение Клейна—Гордона 21
Посмотрим, однако, существуют ли релятивистские случаи,;
в которых вероятностная интерпретация все еще применима. Из
выражения B.12) следует ожидать, что если такие случаи суще-
существуют, то они должны представлять собой случаи свободной
частицы или частицы, движущейся в очень слабом внешнем поле.
Поэтому снова рассмотрим уравнение B.9). Оно имеет простое
решение в виде плоской волны, т. е.
ф — e-iEt/tgip .f/s> B.13)
где
£1 = =t"|/rc2j!?2-f-'ra2c4. B.14)
Оба знака квадратного корня отвечают решению уравнения, что
является характерной чертой релятивистской квантовой механики.
Для одной свободной частицы это не является проблемой. Частица
первоначально находится в состоянии с положительной энергией,
т. е. с энергией Е — -J-~\Ас2р2 -(- т2с*, и в отсутствие взаимодей-
взаимодействия всегда остается в этом состоянии. Кроме того, из выраже-
выражения B.12) видно, что для свободной частицы с положительной
энергией величина
Р>0 B.15)
и остается положительно-определенной во времени, согласно урав-
уравнению движения B.4). Таким образом, заключаем, что последова-
последовательная одночастичная теория может быть развита для свободных
частиц, если множество решений с положительной энергией мы
будем рассматривать как набор физически реализуемых состояний.
Это, однако, означает, что некоторые из операторов, которые
являются наблюдаемыми (как их обычно называют) в нерелятивист-
нерелятивистской квантовой механике, перестают быть наблюдаемыми в реля-
релятивистском смысле. Чтобы показать это, заметим, что из соотно-
соотношений B.10) и B.13) мы можем определить внутри множества
решений с положительной энергией следующее скалярное произ-
произведение1);
BЛ6)
До тех пор пока мы рассматриваем только волновые функции
состояний с положительной энергией, это скалярное произведение
является положительно-определенным, т. е. (ф, ф)^>0 и ((|>, ф) = 0
!) Обычно как скалярное произведение волновых функций [уравне-
[уравнение B.16)], так и фурье-образ волновой функции [соотношение B.17а)]
определяются без множителя тс2 и, следовательно, могут также использо-
использоваться при т = 0. Преимущество формул B.16) и B.17а) заключается
в том, что при от Ф 0 облегчен переход к нерелятивистскому пределу.
22 Глава 2
только при ф = 0. Оно сохраняется во времени1), согласно урав-
уравнению движения, если ф и <р подчиняются уравнению Клейна —
Гордона. В импульсном пространстве, когда
где
Ep = -{-cVp»-\-m.»c», B.176)
скалярное произведение имеет очень простой вид, а именно:
й- BЛ8>
Однако, как теперь легко проверить, оператор x — ihd/dp в этом
скалярном произведении уже не является эрмитовым, так как
U, ih A cp j = ih / |£- ф* (р) ± <р (р) =
)
B.19)
здесь опущен поверхностный интеграл. Иными словами, х нельзя
рассматривать как оператор положения, так как он неэрмитов и,
следовательно, ненаблюдаем. Отсюда вытекает весьма важное след-
ствие: волновую функцию Клейна — Гордона <p(JC, t) нельзя тракто-
трактовать как амплитуду вероятности обнаружения частицы в точке х
в момент t. Чтобы ответить на вопрос: „Какова вероятность обна-
ружения частицы Клейна — Гордона в некоторой точке д?", мы
должны найти, во-первых, эрмитов оператор, который строго может
быть назван оператором положения, и, .во-вторых, его собственные
функции Wa(x, t). Амплитуда вероятности обнаружения частицы
с волновой функцией <р (л;, t) в точке q в момент t выражается
в соответствии с общими принципами квантовой механики матрич-
ным элементом (Wq(x, t), w(x, t)).
V В противоположность, например, интегралу
X t) 9 (х, t).
Г
2> Множитель 1/£,„ введен дпя удобства. Если <Ь (х, t) — скаляр, то, так
как cPpjEp — инвариант, i> (p) — также скаляр.
Уравнение Клейна — Гордона 23
Ньютон и Вигнер [356] показали, что в релятивистском случае
оператор положения и его собственные функции (,локализованные
волновые функции"), по существу, определяются:
1) требованием, чтобы набор всех состояний, локализованных
->■ ■ ■
в точке q, образовывал линейное множество, инвариантное относи-
относительно вращения и отражения в пространстве и во времени;
2) естественным физическим требованием, чтобы после простран-
пространственного перемещения волновая функция ф состояния, локализо-
ванного в некоторой точке q, стала ортогональной к волновым функ-
функциям состояний, локализованных в точке q.
Оператор положения, который они получили для случая Клейна —
Гордона, имеет вид
£ =tfiA_ m P B.20)
ар
Его собственные функции не являются больше 3-функциями, как
в нерелятивистском случае, а размазаны по области порядка комп-
тоновской длины волны частицы. Причина этого заключается в том,
что мы допустили лишь волновые функции состояний с положи-
положительной энергией, а В-функции нельзя построить только из этих
функций. Отсюда следует, что эти локализованные волновые функции
лоренц-нековариантны. Они обладают только максимальной симме-
симметрией, соответствующей плоскости t = const в 4-пространстве.
§ 3. Взаимодействие с внешним электромагнитным полем
В присутствии электромагнитного поля (например, в случае
заряженного тг--мезона, движущегося по воровской орбите вокруг
ядра) мы должны видоизменить уравнение B.9), сделав обычную
калибровочно-инвариантную замену
Р-+Р—е-А, B.21)
£■->£■ — еср, B.22)
где А и ср — векторный и скалярный потенциалы электромагнитного
поля соответственно. Это ведет к уравнению
-Ж\1Ъ-*7 — е<?) Ф=(-Г V — -Т^М' + тсФ- B-23>
Шифф в своей книге [429] обсуждает решения этого уравнения.
В частности, он показывает, что в уравнении B.23) переменные г
и t разделяются, если потенциалы А и <р не зависят от времени.
В этом случае решение имеет вид
ф(л t)=u(jr)e-iEtlh. B.24)
24 Глава 2
Полученное дифференциальное уравнение для и можно решить
точно, когда Л = 0, а функция <р(г) обладает сферической сим-
симметрией и не слишком сингулярна. В частном случае кулонова
поля etp = — Ze2[r решение подробно дано Шиффом и приведено
в т. II, гл. 42, к которой мы и отсылаем читателя. Плотность
заряда становится в этом случае равной
<2-25б>
здесь мы использовали формулу B.11). Выражение B.256) переходит
в правильное нерелятивистское приближение (для Е > 0) во всей
области пространства, за исключением малых расстояний вблизи
г = 0, где движение является существенно релятивистским и одно-
частичная интерпретация теряет свой смысл, так как величина р
может стать там отрицательной. Величина тонкой структуры, тео-
теоретически предсказанная этим уравнением, больше наблюдаемой
экспериментально в спектре водорода. Действительно, для электро-
электронов, которые обладают спином 1/2, следует ожидать, что уравнение
Клейна — Гордона не имеет места. Однако величина тонкой струк-
структуры, предсказанная этим уравнением, должна быть правильной
для it--мезона, движущегося по воровской орбите вокруг ядра,
и ее можно наблюдать.
§ 4. Релятивистские обозначения
До сих пор мы не показали релятивистского характера уравне-
уравнения Клейна — Гордона. Иначе говоря, наши обозначения не подчер-
подчеркивали, например, 4-векторного характера р и у. В дальнейшем же
будет очень важно подчеркнуть ковариантный характер применяемых
физических величин. Для этой цели в настоящей книге используются
следующие релятивистские обозначения. Пространственно-времен-
Пространственно-временною координату обозначим через х9" (которая, как 4-вектор, будет
записываться буквой х). Примем x° = ct, х1 = х, х2~у и xb = z.
Мы будем использовать метрический тензор g^ со следующими
компонентами:
Л 0
о ~~о - ' -I B-26)
^0 0
(т. е. goo=l, gkk =—1 для fe=l, 2, 3 и g-?v==0 для {j. ф v)
и должны, следовательно, различать ковариантные и контрвариант-
Уравнение Клейна — Гордона 25
ные векторы. Контрвариантный вектор (который преобразуется как
координаты х, у, z, t) обозначается через v*", ковариантный вектор
(который преобразуется как градиент)—через v^. Аналогично
обозначаются тензоры. Вообще греческие буквы будут использо-
использоваться в качестве индексов для обозначения компонент @, 1, 2, 3)
пространственно-временного тензора, в то время как латинские —
для обозначения только пространственных компонент A, 2, 3).
Поднятие и опускание индексов производится с помощью метри-
метрического тензора
•о,. = 2 g^v\ B.27)
V* = 2 g*\. B-28)
где gv определяется уравнением
. = «, B-29)
причем 8J, есть символ Кронекера
{1 для и. = v
О для jj. Ф v.
Заметим, что поднятие или опускание индексов 4-вектора изменяет
знак пространственных компонент вектора, оставляя неизменной его
временную компоненту. Лоренц-инвариантное скалярное произведе-
произведение двух векторов р^, х?_ дается выражением
2 8*"Рг.х, = Цр»х^ = р • х, B.31а)
V И-
2 gvPfX, = ^0Р° — хгр1 — х2р2 — * V. B.316)
B.31в)
2 в"^*, = *°Р° — х-р. B.31 г)
Вектор называется времени-подобным, если
2^/>0, B.32а)
и-
пространственно-подобным, если
2«"он'<0, B.326)
и нулевым, если
5г»/ = 0. B.32в)
26 Глава 2
Если введем времени-подобный 4-вектор энергии-импульса, т. е.
то уравнение B.8) можно переписать в виде
2 = mV. B.34)
Соотношения B.2) и B.3) теперь можно объединить в одно:
р =ffi —. B.35)
У* дх* V
В связи с этим нужно отметить, что так как xf- является контр-
контрвариантным вектором, то djdx^- — ковариантный вектор и
дх*
д ( д
B'36б>
Следовательно, подставляя выражение B.35) в B.34), можно пере-
переписать уравнение Клейна — Гордона в инвариантной форме. В ре-
результате получим
или
— чи/ ■ v ^' }t(x) = O, B.37b)
где _ , ,
~~ " * B.38)
I»»
Аналогично, вводя 4-векторный потенциал
Л11={сР, X}, B.39)
можно переписать соотношения B.21) и B.22) в виде
р*.-+р,.— ±.А*, B.40)
а уравнение B.23) следующим образом:
U(x) = o. B.41)
Глава 3
УРАВНЕНИЕ ДИРАКА
§ 1. Вывод уравнения. Выражение для тока
Для устранения трудностей, связанных с отрицательными плот-
плотностями вероятности в уравнении Клейна — Гордона, Дирак предло-
предложил в 1928 г. новое уравнение, к изучению которого мы теперь
перейдем. В течение длительного времени считали, что уравнение
Дирака является единственно правильным релятивистским уравнением.
Это было действительно так до тех пор, пока Паули и Вайскопф
не предложили новой интерпретации уравнения Клейна — Гордона.
Но даже и теперь уравнение Дирака сохраняет особую важность,
так как оно описывает частицы со спином 1/2, а основные элемен-
элементарные частицы, включая электрон, протон и нейтрон, обладают
спином 1/2. Открытый в 1947 г. тт-мезон был первой частицей
с массой, отличной от нуля, и спином, равным нулю.
Чтобы избавиться от наличия отрицательных плотностей вероят-
вероятности, мы должны исключить производные по времени в выражении
для плотности вероятности р. Для этого необходимо, чтобы волно-
волновое уравнение содержало производные по времени только первого
порядка. Из симметрии, установленной теорией относительности,
между пространственными координатами х, у, z и временной коор-
координатой ct следует также, что волновое уравнение может содержать
пространственные производные волновой функции только первого
порядка. Таким образом, волновая функция Дирака ф должна удовле-
удовлетворять линейному дифференциальному уравнению первого порядка
по всем координатам 4-пространства1). Необходимо также, чтобы
она удовлетворяла уравнению Клейна — Гордона, так как последнее
просто означает, что выполняется соотношение B.8) и что при
больших квантовых числах справедлива классическая релятивистская
механика (принцип соответствия).
Аналогичное положение имеет место в элгктродинамике. Уравне-
Уравнения Максвелла являются уравнениями первого порядка и связывают
между собой определенные компоненты напряженностей электромаг-
->■ -*-
нитного поля й и ф. Волновое же уравнение в электродинамике
Ч Линейность требуется для выполнения принципа суперпозиции в кван-
квантовой механике.
28 Глава 3
является уравнением второго порядка; это означает, что фотоны
имеют массу покоя, равную нулю, как и требует релятивистская
теория для частиц, движущихся со скоростью света с. Волновому
уравнению удовлетворяет каждая компонента S и §, т. е. шесть
величин, описывающих поле. Это обстоятельство может быть исполь-
использовано в качестве руководящего принципа при получении уравнения
Дирака.
Предположим, что ф имеет N компонент фг, где число N пока
не определено (окажется, что оно равно 4). Самое общее линейное
уравнение первого порядка связывает производную по времени одной
компоненты с линейной комбинацией всех компонент и их простран-
пространственных производных. Оно имеет вид
3 N N
7Л+1 Д«г"д^+Пг2|М>« = 0( C.1)
fc= in п
где I, п=\, 2 ... N, множители т, с, Ъ введены из соображений
размерности, хк — пространственные координаты. Из однородности
пространства — времени следует, что afrt и ф1п — константы (безраз-
(безразмерные), не зависящие от пространственных координат х, у, z и
временной координаты t. Уравнения C.1) известны как уравнения
Дирака [102]. Естественный путь упрощения уравнений C.1) заклю-
заключается в использовании матричных обозначений, которые сводят эти
уравнения к одному матричному уравнению
T^==0. C.2)
Здесь ij) — столбец из N строк, а а1, а2, а3 и р являются iV-мер-
ными квадратными матрицами.
Найдем выражения для плотности вероятности и тока, которые
вытекают из уравнения C.2). Так как мы хотим сохранить обычное
определение плотности вероятности р, то положим
п п
или в наших матричных обозначениях
р= <|>+<|>, C.4)
где ф+ — величина, эрмитово-сопряженная ф, и, следовательно, пред-
представляет собой строку из N столбцов. Ясно, что плотность вероят-
вероятности C.3) является положительно-определенной величиной и тем
Уравнение Дирака 29
самым удовлетворяет основному требованию Дирака.. Величина <|>+
удовлетворяет уравнению, эрмитово-сопряженному уравнению C.2),
а именно:
Вообще а+ — матрица, комплексно-сопряженная и транспонированная
к а, т. е. матрица, у которой строки и столбцы взаимно переста-
переставлены и от каждого элемента взята комплексно-сопряженная вели-
величина, т. е.
tfn = fnl. C.6)
В соответствии с правилом умножения матриц следует всегда писать
<}+ слева, а ф — справа от матриц а и р (а+ и |3+).
Уравнение непрерывности можно теперь написать в виде
0' <3'7>
Уравнение такого вида можно получить, умножая уравнение C.2)
на '{/*" слева, а уравнение C.5) —на ^ справа и складывая получен-
полученные выражения. В результате имеем
/фTRm щТН~Ф) •— О. (о .о)
Для отождествления уравнений C.7) и C.8) мы должны приравнять
последние члены в уравнении C.8) нулю, так как они не содержат
производных. Это можно сделать, потребовав выполнения соотно-
соотношения
р = д, C.9)
т. е. потребовав, чтобы матрица ^ была эрмитовой (самосопряжен-
(самосопряженной). Для отождествления второго слагаемого в уравнении C.8)
с дивергенцией необходимо, чтобы
а+ = а. C.10)
Другими словами, а и J3 должны быть эрмитовыми матрицами. Это
можно также показать, переписав уравнение C.2) в гамильтоновой
форме
C.11)
30 Глава 3
Отсюда ясно, что если оператор Н является эрмитовым, то ак и $
также эрмитовы. Из сравнения уравнений C.7) и C.8) вытекает х>
. C.12)
§ 2. Матрицы Дирака
Для получения дальнейших сведений о свойствах матриц а и ^
выясним, какие условия налагаются на них следующим требованием:
функция <|> должна удовлетворять уравнению Клейна — Гордона.
Для этого умножим уравнение C.2) на оператор
i V, !р. (
с dt jiJ дх* Ъ v \
k~i
Это приводит к появлению в уравнении вторых производных по
координатам 4-пространства. Члены с djdt или смешанными про-
пространственно-временными производными уничтожаются, и мы полу-
получаем
Симметризация члена акл1 возможна, так как д/дхк и д/дхг коммути-
коммутируют между собой. Чтобы согласовать уравнение f3.14) с уравне-
уравнением Клейна — Гордона, необходимо привести правую часть C.14)
к виду
Это накладывает следующие условия:
-j~(a*a2-f а*а*) = 8». C.15)
as£-t-paft = O, C.16)
(а*J = ^2 = i. C.17)
Таким образом, мы видим, что все aft и 3 антикоммутируют между
собой и квадраты их равны единице. Вообще говоря, для решения
задач кет необходимости знать явный вид <хк и £j; достаточно»
J) Некоторые авторы, особенно в старой литературе, определяют выра-
выражение для тока C.12) со знаком минус. Это соответствует определению <хк с
обратным знаком, что неудобно. Раньше для обозначения дираковских матриц,
использовались разные символы, теперь же обозначение аир является обще-
общепризнанным. Общепринятое диракочское обозначение используется, напри-
например, в работе Мотта и Снеддона [347].
Уравнение Дирака 31
знать, что они эрмитовы и удовлетворяют соотношениям C.15)—C.17).
Но к этому выводу пришли лишь в 1931 г.
Тем не менее можно легко получить (не единичное) матричное
представление а* и р из спиновых матриц Паули
Эти матрицы антикоммутируют между собой и квадраты их равны
единице. Можно легко проверить, что нельзя найти четвертой 2-мер-
2-мерной матрицы, антикоммутирующей с ах, <зу и <jz1'>. Более того, мат-
матрицы а* и |3 нельзя построить из 3-мерных матриц. Это можно
показать несколькими способами. Самое простое доказательство
основано на свойствах определителей. Если мы перепишем соотно-
соотношение C.16) в виде
C.16а)
где множитель / — единичная матрица, то, приравняв определители
обеих сторон этого равенства, получим
(det p) (det afe) = (— 1 f (det a*) (det £) = (—-1 f (det ,3) (det a*), C.19a)
так как
det(— /).= (— if. C.196)
Следовательно,
(— lf= 1 C.19b
и мерность N должна быть четной.
Приведем несколько иное доказательство, основанное на исполь-
использовании свойства диагонализуемости эрмитовых матриц, так как
оно выясняет одно важное свойство матриц а* и £), а именно: след
этих матриц равен нулю. Выберем представление, в. котором мат-
матрица р диагональна. Заметим, что не все <хк и ft могут быть диаго-
нализованы одновременно, так как они антикоммутируют между
собой. В нашем случае матрица {3 имеет вид
'*,
C.20)
!) Это можно доказать следующим образом. Так как 2-мерные матрицы
имеют четыре элемента, то существует четыре и только четыре линейно не-
независимые 2-мерные матрицы. Три нз них представлены выше [см. C.18)].
Ясно, что единичная матрица („ .J является линейно независимой от этих
трех. Так как их всего четыре, то эта единичная матрица является един-
единственной 2-мерной матрицей, линейно не зависящей от аК Но единичная
матрица коммутирует, а не антикоммутирует с каждой из матриц ах, иу, оа.
32 Глава 3
Так как £J,= 1, то Ьг = 1 и &4 = ± 1 • (/ = 1, 2 ... Л/). Кроме
того, так как C2 = а|=1, каждая из этих матриц имеет обратную
матрицу, поэтому соотношение C.16) можно переписать в виде
aj1pafc = — р. C.21)
Взяв шпур обеих частей этого соотношения,! получим
Sp (ajr^a*) = Sp (WP) = Sp (P) = — Sp (?) C.22)
и, следовательно,
Sp(P) = O. C.23)
Аналогично
Sp(aft)=0. C.24)
Если в матрице C.20) m членов &4 = -|-1, а п членов #,= — 1, то
m-\-n = N. C.25)
С другой стороны, требование Spf3 = 0 означает, что
0 = 2&i='»—«» C.26)
i
т. е. т = п; поэтому
N = 2m C.27)
и, следовательно, as и р должны быть матрицами четной мерности.
Далее, можно показать, что мерность этих матриц кратна четырем
(см. работу Паули [373]). В частности, если мы обратимся к 4-мер-
4-мерным матрицам, то мы, действительно, сможем сконструировать
систему, основанную на том же самом принципе, который был
использован при написании матриц Паули. Если / означает единич-
единичную 2-мерную матрицу, то 4-мерные матрицы вида
и»
удовлетворяют всем нашим условиям. Они являются эрмитовыми и,
как можно показать, используя коммутационные свойства afe, анти-
коммутируют между собой. Это видно из примера
Выражения C.28) для матриц Дирака являются наиболее удоб-
удобными в тех немногих случаях, когда полезно использовать явный
вид этих матриц. Если матрицы имеют такой вид, то при скоростях
частицы, малых по сравнению со скоростью света с, две компо-
компоненты фх и <Ь2 функции <|> велики по сравнению с двумя другими
компонентами ф3 и ty*-
Уравнение Дирака 33
Так же, как и уравнение Клейна — Гордона, уравнение Дирака
в отсутствие взаимодействия допускает решение в виде плоской
волны. Для частицы с импульсом р и энергией Е функция ф(г, f)
имеет вид
<|> (У, t) = и(j?) e?p5ine-iEW, C.30)
где и(р) — 4-компонентный • столбец, называемый спинором. Спи-
нор и(р) удовлетворяет уравнению
(р). C.31)
Решения этого уравнения подробно обсуждаются Шиффом *>. Здесь,
как и в случае уравнения Клейна — Гордона, существуют решения
как с положительной, так и с отрицательной энергией Е. Но даже
после выбора знака Е все еще существуют два решения для ком-
понент и(р), соответствующие двум ориентациям спина частицы,
описываемой уравнением Дирака. Четыре независимых решения для
■> ■*■■*■■*■
данного импульса р будем обозначать через их(р), и2(р), и3(р) и
и*(р). Первые два из них отвечают двум различным спиновым состоя-
состояниям частицы с положительной энергией Е, два других — двум раз-
различным спиновым состояниям частицы с отрицательной энергией Е.
->-
Одно из них, и}(р), дается выражением D.24).
§ 3. Ковариантная форма уравнений Дирака
Нам осталось показать, что уравнение Дирака релятивистски
инвариантно. Под этим мы понимаем, что уравнение C.1) с теми же
самыми матрицами аА и р сохраняет свой вид в любой лоренцовской
системе координат; неизменными остаются также выражения для р
и у. Это не означает, однако, что в новой лоренцовской системе
координат не меняются компоненты волновой функции ф. Наоборот,
так же как ® и ф в электродинамике, компоненты функции ф выра-
выражаются друг через друга 2>.
Прежде чем подробно обсуждать лоренц-инвариантность уравне-
уравнения Дирака, полезно переписать его в форме, удобной для реля-
релятивистского рассмотрения. Для единой трактовки пространственных
координат xt = х, х2=у, х3= г и временной координаты t введем
величину
xfi = ct. C.32)
!) См. книгу Шиффа [429].
а) Эта точка зрения является естественной, если рассматривать уравне-
уравнение Дирака как уравнение поля. Некоторые авторы развивают теорию,
в которой компоненты <(* остаются постоянными, тогда как ад и {3 меняются.
34 Глава 3
Далее, пространственные производные в уравнении Дирака C.2)
в отличие от временной умножены на матрицы. Чтобы устранить это
различие, умножим уравнение C.2) на C слева. Используя величину
C.32), получаем
Вводя матрицы fi\ можно придать этому уравнению более симмет-
симметричный вид, причем -[V- определяется следующим образом:
Р = Т°» C-34)
рос" = yк (й=1, 2, о), ^ (о.оо)
или
£ а = f. C.36)
Следует отметить, что при таком определении только матрица j°
является эрмитовой, в то время как матрицы -j*—антиэрмитовы,
т. е. (-[fe)+ =—-fk, где (ffeJ =—1. Матрицы -р удовлетворяют
следующим перестановочным соотношениям:
~i^"C ~~\~ tv'Y'1 == 2g!>i'11> C.37а)
где /—единичная матрица. Поднятие и опускание индексов матрицы ^и-
производится так же, как у 4-вектора, т. е.
^ = 2g^r C-38)
V
и, следовательно,
Чр^+ТЛ^2^- C.376.)
Используя явный вид матриц aft и £>, находим
О t
п 1 C-39)
— а 0 /
Согласно таким определениям, уравнение C.33) принимает вид
C.40)
Это и есть уравнение Дирака в ковариантной форме, где простран-
пространственные и временные производные трактуются единым образом.
Чтобы уравнение C.40) выглядело еще проще, Фейнман [168] ввел
Уравнение "Дирака 35
следующее условное обозначение г>:
А = 2 Т'\= 2 1-.ЛУ-= у°Л° — .,? • Л. C.41)
A = 0 |*=0 '
В дальнейшем будем пользоваться системой единиц, в которой
с = й==1, как это принято в теории относительности2). При этом
т. Условимся также писать
В этих обозначениях уравнение C.40) принимает
b = Q, ■ . . . C.43)
где . .
V = -ro_^+^.^ C.43a)
Величины / и р также можно выразить с помощью матриц у:\ Умно-
Умножая выражение C.35) на C слева, получаем
рт* = а*, ' C.44)
так что формула C.12) перепишется в виде
-f- = ^\ C.45)
Если мы введем „сопряженную" волновую функцию
f*y>=t. . C.4&)
то уравнение C.45) примет вид
±- =*$•№- C-47)
Аналогично можно записать и р, именно:
ii = p = (jJ+ToTotj,== фт0ф. C.48)
!) В литературе часто пользуются другим обозначением, а именно букву,
обозначающую оператор, набирают жирным курсивом. [Авторы в оригинале
пользуются обозначением „А перечеркнутого „р перечеркнутое■•" и т. п.;
в переводе принято обозначение А, р и т. п. — Прим. перев.} ,
2) В литературе обратная комптоновская длина -волны /яе/Й часто обоз-
обозначается через тс Мы не пользуемся этим обозначением, потому что,.во-пер-
что,.во-первых, его легко спутать с k— импульсом фотона, во-вторых, трудно ввести
такого рода обозначения для масс различных частиц (электрона, протона,
нуклона) и, в-третьих, мы хотим подчеркнуть, что этот член связан с мас-
массой покоя частицы.
36 Глава 3
Уравнения C.46) и C.47) можно объединить
•л — [ "*)
i- = <Wi4b =Ь, 1Л. C.49)
Дифференциальное уравнение для ty+ есть уравнение C.5). Чтобы
придать ему более симметричный вид, умножим его на f0>[0 = 1
справа и воспользуемся соотношениями C.35), C.36) и C.46). При
этом очевидно, что сопряженное уравнение будет иметь вид
Следует обратить внимание на то, что хотя матрицы "[V- не эрми-
эрмитовы при у. =1,2,3, тем не менее часто применяемое произведение
(jifiMj) — эрмитово. Напомним, что
отсюда, согласно правилам коммутации, можно написать
(-jn)+ = ^о^^^о C.52)
и, следовательно,
OVV'V)+ = 1*+ (Т)+Ф + = 1*+ (Т)+ 7О4> — <V+7°T!>'!V ==^»Т^- C-53)
Уравнение Дирака удобно также записать в импульсном пред-
представлении. Для этой цели заменим ih д/дх^ на pv- [соотношение B.35)].
В результате уравнение C.40) примет вид
= 0, C-54а)
или в обозначениях Фейнмана
(р—тес)ф = О. C.546)
Такая форма весьма удобна для проверки выполнения основного
соотношения между энергией и импульсом. Мы покажем это, умно-
умножая выражение C.546) на оператор р; тогда будем иметь
р^ _ mCpb = (jncy ф. C.55)
Далее, пользуясь определением оператора р и соотношением
получаем, согласно правилам коммутации C.37),
*=р2=S—р2-C -56)
Уравнение Дирака 37
§ 4. Релятивистская инвариантность
Теперь мы в состоянии исследовать лоренц-инвариантность урав-
уравнения Дирака. Релятивистская инвариантность уравнения необходима
по следующим причинам: физические процессы, описываемые любыми
релятивистскими уравнениями, не должны зависеть от выбора лорен-
цовской системы координат. Следовательно, при правильном описании
физических процессов сами уравнения должны указывать иа инва-
инвариантность по отношению к выбору системы координат. Таким
образом, мы должны показать, что если написать уравнение Дирака
в разных системах координат, то существует линейное преобразо-
преобразование волновой функции, при котором новая волновая функция, по
нашему предположению, описывает то же состояние в новой си-
системе. Это линейное преобразование является, по существу, мате-
математическим выражением того факта, что наблюдатели в двух систе-
системах координат при проведении одинаковых экспериментов в своих
системах получат согласованные результаты.
Самое общее однородное лоренцовское преобразование, исключая
пространственно-временные перемещения, можно записать в виде
х'!Х= S в?*' C.57а)
v = 0
или в матричной форме
х'=ах, C.576)
где
Sa = 8I = Sa% C.58)
\h V-
Заметим, что лоренцовское преобразование линейно по всем
четырем компонентам и что коэффициенты а£ действительны. Вол-
Волновая функция ф' в новой системе координат получается из функ-
функции ф (в той же точке пространства—времени) с помощью линей-
линейного преобразования
ф' = 5ф, . C.59а)
где 5 — 4-мерная матрица, не зависящая от координат простран-
пространства— времени. Она имеет обратную матрицу S-1 и зависит только
от а<$, т. е.
Таким образом, преобразование C.59а) можно записать в явном
виде
4
фДх ,) == _2j оа^(а)фд(а-1х ). C.596)
Нужно подчеркнуть тот факт, что 5-матрица является 4-мерной не
потому, что существуют четыре компоненты пространства —
38 Глава 3 "
времени, а потому, что уравнение Дирака требует введения по
крайней мере 4-мерных матриц.
Напомним, что в ковариантной форме уравнение Дирака имеет вид
Потребуем, чтобы матрицы ^ оставались неизменными при пре-
преобразованиях Лоренца. При этом для инвариантности уравнения не-
необходимо, чтобы в новой системе координат выполнялось соотно-
соотношение
Используя выражения C.57) и C.59), можно переписать уравнение
C.40) в виде
так как
di> дх'х
д* &д'хд* 2uUv-drX'
дхдх
К X
Далее, поскольку а^ — числа, то S и af коммутируют. Следова-
Следовательно, умножая уравнение C.61) на 5 слева, получаем
C.63)
Таким образом, уравнение C.63) имеет форму уравнения C.40) при
условии, что
4 C.64) i)
Условие C.64) можно рассматривать как условие, накладываемое на
матрицу преобразования 5. Из условия C.64) и того факта, что
1) Паули отмечает [372, 373], что существование такой матрицы S уже
следует только из того факта, что 4-мерные матрицы f образуют неприво-
неприводимую группу. Так как матрицы -f^ = 2 а?Т* подчиняются тем же переста-
побочным соотношениям, что и матрицы f1, как это следует из соотноше-
соотношения C.58), то существует несингулярная матрица S, обладающая свойством
Y9" = S~1iv'S (см. также работу Паули [370]).
Уравнение Дирака 39
л£—=-действительные числа, следует
з
2
\ v
3
— а.Р"г°-4- 2 й£т& = (S^T^S) C 65)
так как матрица у0 эрмитова, а уй — антиэрмитова. Действительно,
мы убедились в том, что в нашем представлении для матриц у
справедливо соотношение
C.52)
Следовательно, умножая соотношение C.65) на у0 справа и слева,
получаем
Т°(«&Т°+ 2 ^Тй)т°= S <Г = 7°(S^S? T°, C.66а)
1)+T°. C.666)
0). C-66в)
так как
(тоГ1 = то.
з
Далее, 2 ^Т11' согласно условию C.64), равна S~1jv'S. Отсюда
(т°5+Т°) Т^ (Т0^!0) = S-'fS, C.67)
или
(«S7osY)-r|fc(ST0sV)~1 =т1'- C-68)
Нетрудно показать, что любая матрица, коммутирующая со всеми
матрицами -ff1, есть постоянная, умноженная на единичную матрицу.
Следовательно, в результате получаем
S-!0S+t°==bI, C.69)
где Ъ — константа, или
C.70а)
K C.706)
Так как матрица у0 эрмитова и левая часть выражения C.70а) также
эрмитова, то
Ь* = Ь. C.71)
40 Глава 3
Это означает, что константа Ь действительна. Кроме того, мы
можем нормировать матрицу 5 так, чтобы det5=l1).
В этом случае bi=l и, следовательно,
Ь = ±\. C.72)
Выясним, далее, когда Ь — -\-\ и когда Ь — — 1. Для этого рас-
рассмотрим следующее тождество:
5+5 = 5+Т°Т°5 = bfS-^S =
= b-f 2 Av = ba% ■ I— 2 balft* = * (a? . /— S a% a*). C.73)
Здесь использованы соотношения C.64) и C.70). Произведение
5+5 — произведение несингулярной матрицы на ее эрмитово-сопря-
женную имеет действительные и положительно-определенные соб-
собственные значения E=^=0), т. е.
SpE+5)>0. C.74)
Так как след ак равен нулю, то мы имеем
Sp5)-5 = 46a<>>0. C.75)
Таким образом, если а£<0, то Ь — —1, если же а°>0, то
6 = -f-l. Когда величина ag отрицательна, преобразование содержит
отражение во времени, т. е. f = —t (время меняет знак).
Далее, рассмотрим свойства преобразования сопряженного спи-
спинора ф = ф+7°- Так как
ф' = 5ф, C.59а)
то, взяв выражение, эрмитово-сопряженное этому равенству, полу-
получим
C.76)
Поэтому волновая функция ф', которая, по определению, равна
(так как матрицы f& не меняются при преобразованиях2)), согласно
формулам C.70), выражается в виде
. C.78)
Ч Заметим, что эта нормировка оставляет матрицу 5 неопределенной
с точностью до множителя У 1.
а) Отсюда следует, что выражение р неинвариантно при преобразова-
преобразованиях Лоренца и преобразуется по формуле.
if = S i>v = S iX;v = s 2 14s
V Jill f.
Уравнение Дирака > 41
Следовательно, ф/ = ф5~1 для тех преобразований, которые не ме-
меняют знака времени, в то время как ф' = — фЗ для преобразова-
преобразований, содержащих отражение во времени (а% < о).
Смысл формул C.70) можно несколько уяснить, если рассмотреть-
свойства преобразования тока
y> = <l)+7°Tllt- C.49>
Физические следствия уравнения Дирака должны быть одинаковы
во всех лоренцовских системах координат, поэтому необходимо
потребовать, чтобы ток у'1*" был 4-вектором и, следовательно, пре-
преобразовывался следующим образом:
/> = 2 <*£/* = 2 a*j>+TYi> = ty+fS-^v-Sty. C.79)
Получим теперь то же выражение для у'*\ используя волновые функ-
функции в штрихованной системе, но с теми же матрицами f
/>=(]/+7oTiy. C.80>
Согласно формуле C.76), мы можем переписать выражение C.80)-
в виде
Сравнивая выражения C.81) и C.79), видим, что должно удовлет-
удовлетворяться соотношение
. C.82>
которое совпадает с формулами C.70) при преобразованиях Лоренца,
не включающих отражения во времени. Однако из формул C.70>
следует, что в действительности у> является псевдовектором, так
как меняет знак при отражении во времени.
Выше были выяснены свойства матрицы преобразования S, теперь,
нужно еще показать, что при любом преобразовании Лоренца C.57у
можно найти матрицу S, удовлетворяющую соотношениям C.64) и*
C.70). Рассмотрим здесь только собственные преобразования Лоренца,,
для которых det (a£) = -f- 1 и а% > 0. В этом случае достаточно-
исследовать бесконечно малые преобразования, так как конечные
преобразования всегда можно получить из бесконечно малых путем.
многократного их повторения. При бесконечно малом преобразова-
преобразовании Лоренца для двух последовательностей координат х и у имеем
C.83а>
C.836)
42 Глава 3
или, другими словами,
a£ = 8£-|-Xe£, C.84a)
иначе
а = 1 + *е, C.846)
где X— бесконечно малая константа. Так как при преобразованиях
Лоренца скалярное произведение остается инвариантным, т. е.
2x^=2^4' C.85)
it ^ и-
то в первом порядке по X имеем
8^= — evi\ C.86)
Это соотношение является необходимым и достаточным условием
бесконечно малого лоренцовского преобразования.
В первом порядке по X матрицу 5 (а) можно записать в виде
=l + XT C.87а)
{1~}-Хе является аргументом, а не множителем) и
S-i=l— XT. C.876)
Для бесконечно малых преобразований соотношение C.64) можно
переписать в виде
^Y. C-88)
Следовательно, необходимо найти такую матрицу Т, чтобы
/7 — Tf*=2^TV- C.89)
Из уравнения C.89) следует, что Т определяется однозначно с точ-
точностью до аддитивной постоянной1). Кроме того, нормировка
4et 5=1 требует, чтобы
det(l-f- XT) = 1-f X Sp (Г) = 1
или чтобы
Sp(T) = O.
Так как путем выбора соответствующей аддитивной постоянной
всегда можно сделать Sp(T) = 0, то этот выбор определяет мат-
Ч Если существует два таких Т, то их разность коммутирует со всеми y^>
как это видно из соотношения C.89), и, следовательно, является постоянной
величиной, умноженной на единичную матрицу.
Уравнение Дирака 43
рицу Т однозначно и обеспечивает равенство det 5=1. Легко уста-
установить, что выражение
e'"<W.—ТЛц) C-90)
I»
удовлетворяет как соотношению C.89), так и требованию SpGI) = 0.
Эта матрица Т является искомой и однозначной.
Другое доказательство существования матрицы S для любого
лоренцовского преобразования было дано Дираком [115]. Он нашел
матрицу преобразования S, соответствующую трем конечным эле-
элементарным преобразованиям (именно вращению, перемещению и от-
отражению). Из этих трех элементарных преобразований можно по-
построить любое другое конечное преобразование.
Глава 4
СВОЙСТВА ПРЕОБРАЗОВАНИЙ И ЗНАЧЕНИЯ
ОПЕРАТОРОВ ДИРАКА
§ 1. Свойства преобразований
Из четырех матриц fV- можно образовать новые матрицы путем
перемножения двух или более матриц fv- между собой. Как видно
из соотношения C.37), произведение ff- на fi* дает единичную мат-
матрицу / со знаком плюс или минус. Таким образом, следует рассма-
рассматривать только такие произведения -у?-, в которых множители раз-
различны. Кроме того, из соотношения C.37) следует, что ^v-f =
= — fv7!"'> когда \ьфч. Поэтому изменение порядка множителей fV-
может привести лишь к изменению знака. Это означает, что суще-
существует всего только 16 независимых произведений, построенных
из f?-, а именно: одно произведение всех четырех fV-, четыре про-
произведения любых трех ft-, шесть парных произведений fV-, четыре
самих fV- и единичная матрица /.
Наличие точно 16 независимых матриц, построенных из матриц fV-,
следует также из того, что матрицы ft/- неприводимо представляются
4-мерными матрицами. Физический смысл нисколько не изменился бы,
если бы мы представили матрицу fV- в виде 8-мерных матриц, так
как последние всегда можно привести к (приводимому) виду
О 1
где fV- — 4-мерные матрицы. Это соответствовало бы написанию
двух несвязанных уравнений Дирака. Итак, 4-мерная матрица имеет
16 элементов, следовательно, в этом представлении существует 16
и только 16 линейно независимых матриц. Путем перемножения
матриц f* между собой можно образовать 16 независимых опера-
операторов; это показывает также, что для их представления необходимо
пользоваться по крайней мере 4-мерными матрицами.
В табл. 1 приведены 16 линейно независимых матриц. В ней
указаны свойства преобразования ковариантных величин, образован-
образованных умножением этих матриц на ф слева и на ф справа. Множи-
Множитель I введен в произведения ff-f и -fxf^Tv для тс>гс>> чтобы сделать
указанные ковариантные величины эрмитовыми. Квадрат любой мат-
матрицы, приведенной в табл. 1, равен =Ы. Всякую произвольную
4-мерную матрицу можно построить из 16 линейно независимых
матриц, приведенных в табл. 1.
Свойства преобразований и значения операторов Дирака
45
Таблица 1
Тип матрицы
/
Число линейно незави-
независимых матриц данного
типа
1
4
6
4
1
Свойство преобразования
Скаляр
Вектор
Тензор второго ранга
Псевдовектор
Псевдоскаляр
Прежде чем изучать свойства преобразования ковариантных вели-
величин, получаемых умножением матриц, указанных в табл. 1, на ф слева
и на ф справа, напомним кратко о различных классах преобразований.
Наиболее важным классом преобразований являются собственные
преобразования Лоренца, т. е. преобразования, которые могут
быть получены из единичного преобразования путем его непрерыв-
непрерывного изменения. По отношению к ним 4-объем является инвариан-
инвариантом, так как
dx0''dx1''dx2''dx?' = det | at \ dx°dx4x*dx*,
или
ибо
det |a 1=4-1.
D.1a)
D.16)
D.2)
Кроме того, для собственных преобразований Лоренца постоянная Ь
в соотношениях C.70) равна +1.
Далее, существуют несобственные преобразования Лоренца.
Они всегда могут быть построены как произведения собственных
преобразований Лоренца и простейших „несобственных" преобра-
преобразований, представляющих собой отражения пространственно-времен-
пространственно-временных осей. Эти отражения можно классифицировать следующим
образом.
/. Пространственные отражения:
Xго = х° D.3)
и одна из координат хк преобразуется согласно соотношению
тогда как остальные остаются неизменными.
2. Пространственная инверсия:
хг° = х°
D.4)
D.5)
46
и все хк преобразуются согласно соотношению
хГК'= — хк."~~ D.6)
Это — обычное определение, которое применяется при изучении чет-
четности в нерелятивистской квантовой механике.
3. Обращение знака времени:
х'° = — х°, - . D.7)
Xth = х*. D.8)
4. Обращение знаков времени и пространства:
л;'0 =— х°, ' D.9)
x'ft = — xk. D.10)
Напомним, что для первого и второго классов преобразований
£ = -j-l, в то время как для третьего и четвертого — 6 = —1..
Для первых трех классов преобразований имеет место равенство
det | а | = — 1, ' D.11)
тогда как для четвертого класса
det|a|=(—1)* = +1.
Заметим, что знак det|a| не является, следовательно, сам по себе
критерием того, с собственным или несобственным преобразова-
преобразованием Лоренца мы имеем дело. Для этого нам нужно еще опреде-
определить знак а°.
Для простоты исключаем из рассмотрения преобразования, кото-
которые содержат изменение знака времени, т. е. ограничиваемся слу-
случаями, когда 6 — -J-1. Пользуясь соотношением C.78), исследуем
теперь свойства преобразования ковариантных величин.
Запишем это выражение в виде .
фф = ф5~15ф = фУ- D.12)
Из соотношения D.12) следует, что фф — скаляр1) в отличие
от плотности вероятности р = Ф+ф, которая преобразуется как
временная компонента 4-вектора- - \.
Из соотношения C.81) следует, что ф-fNj ведет себя при пре-
преобразованиях, не включающих инверсии времени, как 4-вектор.
!) Заметим, однако, что если мы включим в рассмотрение инверсию
времени (Ь = — 1), то "'I' = —'/Yi т< е- "г1 в действительности ^является
псевдоскаляром при инверсии времени.
Свойства преобразований и значения операторов Дирака 47
Множитель i вводится для того, чтобы это выражение было
эрмитовым. Учитывая замечания, сделанные в начале этого пара-
параграфа, следует рассмотреть лишь шесть различных комбинаций при
v. Для этой цели введем матрицу
и рассмотрим свойства преобразования выражения фа^й. Используя
соотношения D.13) и C.54), получаем
- DЛ4>
p X
т. е. фа!"ф преобразуется как антисимметричный тензор второго-
ранга. Этот тензор иногда называют 6-вектором, так как он имеет
только шесть отличных от нуля независимых компонент. Он обла-
обладает теми же свойствами, что и тензор F^, построенный из напря-
женностей электромагнитного поля 6 и ф.
Такая аналогия используется для включения в уравнение Дирака
дополнительного* магнитного момента' частицы (помимо собственного
момента частицы, который дается самим уравнением) и для описания
ее взаимодействия с внешним электромагнитным полем (см. книгу
Паули [370] и гл. 12, § 2).
Произведение всех четырех матриц Дирака играет особо важную
роль в теории и поэтому имеет специальное обозначение
т. = т^тЧ2-)-3 С4.15>
■ О 1111* *• '
Мы умышленно написали у ув индекс внизу, чтобы подчеркнуть
тот факт, что этот индекс нельзя поднимать или опускать. Чтобы
подчеркнуть ковариантный характер матрицы "\ь, более правильно
определять ее следующим образом:
Te^irSwrrrV. DЛ6>
(ivXp
в зависимости от того, четным или нечетным
числом перестановок (транспозиций) могут быть приведены числа ja,
ч, \, р к последовательности 0, 1, 2,3, и равно нулю, когда какие-
48
Глава 4
либо два индекса совпадают. Определитель четвертого ранга
det [ а* | = det | a J можно записать с помощью тензора s jX в виде
det | а | з^в = 2
Кстати, последнее соотношение указывает на тензорный харак-
характер spi;lv и на тот факт, что компоненты е^^ инвариантны по отно-
отношению к лоренцовским преобразованиям. Поступая так же, как
при получении соотношения D.14), и используя выражения D.16) и
■D.17), получаем
. D.18)
DЛ9>
= det | о
-Следовательно, для собственных преобразований Лоренца
тогда как для преобразований первого и второго классов
Отсюда следует, что фт5ф преобразуется как скаляр при собствен-
собственных преобразованиях Лоренца и как псевдоскаляр — при простран-
пространственной инверсии *).
Здесь снова необходимо рассмотреть лишь четыре комбинации
с /. < [а < v. Можно легко установить, что
а"
Определитель в соотношении D.21) описывает преобразования тен-
тензора третьего ранга, антисимметричного по всем трем индексам.
У этого тензора имеется четыре отличных от нуля независимых
компоненты. Используя выражение D.15), их можно записать в виде
гФТбТ^Ф ((а = 0, 1, 2, 3). Такой же детерминант, как и в соотноше-
соотношении D.21), определяет преобразование элементов трехмерного
объема dxxdxzdx6 и т. д. 4-пространства. Четыре произведения
такого типа ведут себя во всех отношениях как компоненты 4-век-
Ц Термин псевдоскаляр будет означать, если это специально не огово-
оговорено, псевдоскалярность по отношению к пространственной инверсии.
Свойства преобразований и значения операторов Дирака 49
тора, ■ за исключением того, что в результате умножения их на
истинный 4-вектор (например, координатный вектор) получаются
не скаляры, а псевдоскаляры. Поэтому произведение трех fv-
называют псевдовектором (иногда называют также дуальным
вектором). Этим оправдано написание рассматриваемого тензора
в виде i'tYsT14}*-
Если нам известны свойства преобразования перечисленных ком-
комбинаций, то это дает возможность построить в дальнейшем инва-
инвариантные функции взаимодействия. Например, при построении таких
функций скаляр фф можно умножить на скалярную функцию у\ вы-
выражение фТбФ —на псевдоскалярную функцию ср, которая исполь-
используется для описания тс-мезонов; комбинацию ф-^Ф — на векторную
функцию Ар, которая может описывать, например, электромагнитное
поле. Взаимодействие с последним можно записать также в виде
ba^tyF^, где F^v — компоненты тензора электромагнитного поля.
Такое взаимодействие известно под названием взаимодействия Паули.
Необходимо заметить, что матрица у5 обладает некоторыми за-
замечательными свойствами. Она удовлетворяет соотношению
75^+^16 = ° D-22)
для любого [х., и квадрат ее равен —1, т. е.
— I- D-23)
Вообще fa — единственная матрица, которая коммутирует или
антикоммутирует с различными произведениями у^ в зависимости
от того, четное или нечетное число множителей jv- в этих произве-
произведениях. Она коммутирует со всеми компонентами антисимметричного
тензора второго ранга и антикоммутирует со всеми компонентами
антисимметричного тензора третьего ранга. Это свойство можно
легко понять, если вспомнить, что j5 является единственной матри-
матрицей, содержащей все четыре матрицы fV- и поэтому обладающей
свойствами каждой из них.
§ 2. Значение операторов в нерелятивистском приближении
Чтобы изучить матричные элементы фГф, где Г представляет
собой одну из 16 матриц, приведенных в табл. 1, удобно рассмо-
рассмотреть частный случай, когда ф является элементарным решением
уравнения Дирака для свободной частицы с импульсом р и энер-
гией ~\-Е [см. выражения C.30) и C.31)]. Используя матрицы а и
р, представленные в виде C.28), можно записать в следующей форме
(с точностью до нормирующего множителя) выражение для спи-
нора и(р), описывающего состояния с положительной энергией и
50
Глава 4
определенной ориентацией спина:
1
0
D.24)
J
В частности, мы можем рассмотреть случай, когда скорость частицы
мала по сравнению со скоростью света, т. е. нерелятивистский пре-
предел р<^тс. В этом случае две последние компоненты и будут
порядка vjc и, следовательно, малы по сравнению с единицей,
-)-
а нормирующий множитель будет порядка единицы. Величина -и (р)
-»■
обладает теми же свойствами, что и и(р), а именно: большие ком-
компоненты остаются большими, малые — малыми. В предельном случае
покоящейся частицы все четыре решения уравнения Дирака (уже
нормированные) имеют особо простой вид:
СПИН -4- -7Г
Спин—
Спин 4- -^
и* =
Спин =-
D.25)
Рассмотрим теперь выражения итТип, где тип могут прини-
принимать значение 1 или 2, т. е. состояния с положительной энергией
в предельном случае D.25). Тогда компоненты матрицы итТап равны
нулю или единице. Если же скорость частицы v мала, но конечна,
то равные нулю компоненты umYun для покоящейся частицы ста-
становятся в этом случае порядка vjc и потому остаются малыми по
сравнению с единицей. Компоненты же матрицы и>пТип, равные еди-
единице для покоящейся частицы, остаются большими и в общем
случае.
0 0 0)
D.26)
Свойства преобразований и значения операторов Дирака 51
т. е. эта величина велика.
Г = т*
По определению C.39), имеем
0
Таким образом, -у* связывает малые компоненты волновой функ-
функции D.24) с большими, и поэтому выражение ul^kul мало. В пре-
предельном случае покоящейся частицы [решения D.25)] оно равно
нулю.
По определению C.34), имеем
<7
т. е. аТи1 равно единице и, следовательно, оно велико.
г =
Если /, &, / образуют циклическую перестановку, то имеет
место равенство
/V 0
( D-29)
Если /=3, то иТи1 = 1 и и2Ги2 = —1; если же /=1 или 1 = 2,
то и^и1 по абсолютной величине равно единице. В каждом случае
имеется по крайней мере один большой по абсолютной величине
матричный элемент матрицы и'тТип, где m и п принимают значе-
значения 1 или 2.
о ). D.30).
т. е. и>пТип = 0 в предельном случае покоящейся частицы или по-
порядка v/c при конечном v.
Г = *7 Vt*
32 ' Глава 4
Здесь результат такой же, как и для ififk, т. е, иТи1 велико.
Г = д-1?2?3
D.32)
Это дает нуль для предельного случая покоящейся частицы с вол-
волновой функцией D.25).
Г = 75
/О /\
т»в-\/ о) D-33)
т. е. иТи1 = й~Ти2 = иТи1 = 0 для г» = 0.
Так как ~[ъ—псевдоскаляр, то даже при лоренцовском преобразо-
преобразовании к конечной скорости частицы v остается справедливым ра-
равенство итТип = 0. Следовательно, математическое ожидание ?5
в любом состоянии свободной частицы в точности равно нулю.
Эта особенность матрицы f6 отличает ее от „малых" операторов,
матричные элементы которых становятся порядка г»/с для малых,
но конечных скоростей частицы, так как различные компоненты
вектора, тензора и псевдовектора выражаются при лоренцовских
преобразованиях друг через друга, а среди них имеется по край-
крайней мере одна большая компонента.
Таким образом, мы показали, что из 16 матричных элементов
ttYu восемь являются большими и восемь — малыми для случая, когда
решение уравнения Дирака ф построено из одной или более пло-
плоских волн, описывающих состояния с положительной энергией.
Рассмотрим, далее, матричный элемент и+Ти±, где и+ означает
волновые функции и1 или и2 состояний с положительной энергией,
а и_ — волновые функции и8 или и4 состояний с отрицательной
энергией. Используя выражения D.25), находим, что
й_Тби+=1. D.34)
Отсюда видно, что оператор -]ь превращает волновую функцию
состояния с положительной энергией в волновую функцию состояния
с отрицательной энергией и обратно, т. е. оператор -|-б меняет
знак энергии частицы. Благодаря (псевдо) скалярному характеру j5
это утверждение остается справедливым для частиц любой ско-
скорости.
До сих пор мы рассматривали матричные элементы переходов
->-
между состояниями с одинаковым импульсом р. Рассмотрим теперь
->-
переход из состояния п с импульсом рх в состояние т с импуль-
импульсом р2. Матричный элемент оператора fs ПРИ таких переходах
Свойства преобразований и значения операторов Дирака 53
дается выражением
«m(P2O5»n(A)- D-35)
Напомним, что уравнение Дирака в импульсном пространстве
имеет вид
(А — /гас) и" = 0, D.36)
а сопряженное ему уравнение —
пт(р2—/гас) = 0. D.37)
Умножая уравнение D.36) на цт4ъ слева, а уравнение D.37) — на
'{ъип справа и складывая полученные выражения, находим
й й й5 D.38)
Так как оператор у5 антикоммутирует со всеми Уи.» т0 матрич-^
ный элемент рассматриваемого перехода имеет вид
11=0
Отсюда видно, что диагональные матричные элементы этого neper
хода, т. е. перехода с pj = р2, равны нулю, как уже отмечалось
выше. Для малых же изменений скорости между состояниями т и п
матричный элемент пропорционален разности скоростей. Вообще,
чем больше разность Pj— р2, тем больше матричный элемент пе-;
рехода. Если импульс р2 отрицателен, т. е. ит описывает состояние
с отрицательной энергией, то разность рх — р2 и соответствующий
матричный элемент особенно велики. Действие оператора f5(Pi—Рг)
можно уяснить себе, вспомнив, что справедливо равенство
(Pi — Рг>- D.40)
Второй член в правой части равенства D.40) можно записать в явном
виде, используя выражения D.27) и D.33),
* * *. . D.41а)
—«-(Pi—Ра)У
Если мы интересуемся только состояниями с положительной
энергией, то вклад в матричный элемент равен
■>■->- ->■
■—b.(Pl—p2), D.416)
т. е. равен скалярному произведению спина частицы на разность
ее импульсов. [Первый член в правой части равенства D.40) в не-
нерелятивистском приближении „мал".]
Глава 5
СВОЙСТВА УРАВНЕНИЯ ДИРАКА
§ 1. Спин
Понятие спина обсуждалось многими авторами (см., например,
книгу Дирака [115]); поэтому здесь мы ограничимся лишь основ-
основными положениями. Пусть/7 — произвольный эрмитов оператор. Он
является интегралом движения, если коммутирует с гамильто-
гамильтонианом Н
, [Н, /4 = 0. E.1)
Для случая дираковской частицы гамильтониан имеет вид
#=са.р-)-/гас2р. E.2)
Можно показать, что для уравнения Дирака орбитальный момент
£ — iS^XV E.3)
не является интегралом движения. Интегралом движения в этом
случае является величина J = L-\-1j2ha. Следовательно, мы припи-
приписываем дираковской частице собственный момент, равный 1/2Л. Это
означает, что частица имеет спин 1/2.
Для частиц с положительной энергией существуют два незави-
независимых состояния, соответствующие одному и тому же импульсу.
Они связаны с двумя возможными ориентациями спина. Согласно
квантовой механике, каждая такая пара физических состояний может
быть представлена в явном виде двумя векторами в гильбертовском
пространстве. Следовательно, излишне изображать эти векторы
четырехкомпонентными волновыми функциями, как обычно делается
в теории Дирака. Оказывается, можно найти такое преобразование,
которое приводит волновую функцию свободной дираковской
частицы с определенным импульсом к двухкомпонентной функции
типа функций, используемых в нерелятивистской теории спина
Паули [369]. Эта задача "была решена Беккером [24] с точностью
до члена порядка г»2/с2 и точно — Фолди и Ваутхейсеном [186].
В новом представлении физическое содержание уравнения Дирака
становится особенно наглядным. Например, в этом представлении
изменение во времени эрмитова оператора положения X (который
совпадает с оператором, полученным Ныфтоном и Вигнером [356]
Свойства уравнения Дирака 55
для частицы со спином 1/г) дается выражением р/Ер, т. е. скоростью
частицы (в противоположность старому представлению, где
оно равно сое). Кроме того, появляются новые операторы момента.
Выше мы видели, что в обычном представлении интегралом движе-
движения является сумма выражений г X Р и 7г^а (спиновый момент),
а не каждое в отдельности. В новом представлении, однако, вели-
величина Х~Х^р и новый спиновый момент £ каждый в отдельности
являются интегралами движения.
§ 2. Состояния с отрицательной энергией
Мы уже отмечали, что уравнение Дирака имеет решения, соот-
ззетствующие состояниям с отрицательной энергией. При физической
интерпретации этих решений возникают трудности; например, элек-
электрон с отрицательной энергией, если бы он существовал, ускорялся
бы в направлении, противоположном действующей силе. В 1930 г.
Дирак устранил эту трудность, предложив так называемую „теорию
дырок", которую он сформулировал в своей книге [103] следующим
образом: „Предположим, что почти все состояния с отрицательной
энергией заполнены, причем в каждом состоянии, согласно прин-
принципу Паули, находится один электрон. Незаполненное состояние
с отрицательной энергией проявляется как „нечто" с положительной
энергией, так как для уничтожения этого состояния, т. е. для его
заполнения, необходимо добавить к нему электрон с отрицательной
энергией". Когда Дирак впервые предложил свою теорию, он пола-
полагал, что мир построен только из протонов и электронов, и есте-
естественно было считать это „нечто" протоном. Вскоре такое пред-
предположение было отвергнуто Оппенгеймером [360] и Вейлем [527],
которые показали, что это „нечто" должно иметь массу, равную
массе электрона, и обладать отрицательной энергией. Так как
в 1931 г. позитроны (т. е. частицы с массой, равной массе элек-
электрона, и зарядом -(- е) еще не были обнаружены экспериментально,
Паули [370] рассматривал это предсказание как недостаток теории
Дирака.
Однако в 1933 г. к моменту выхода книги Паули из печати
теория уже получила подтверждение, так как Андерсон [5] экспе-
экспериментально доказал существование позитрона.
В первоначальной форме теории дырок Дирак считал, что мир
целиком заполнен электронами, причем в абсолютном вакууме все
состояния с отрицательной энергией заполнены, а с положительной
энергией свободны. В современной теории дырок, развитой Гейзен-
бергом [225, 226], Крамерсом [287] и другими авторами, ликвиди-
ликвидирована эта асимметрия заряда. Действительно, в новейшей форму-
формулировке теории дырок существует полная симметрия положительных
и отрицательных зарядов.
56 Глава 5
Теория дырок Дирака предсказывает возможность образования
пар в том случае, если энергия кванта достаточна для перехода
электрона из состояния с отрицательной энергией в состояние
с положительной энергией, т. е. если Av > 2mc2. В действитель-
действительности же, электромагнитный эффект проявляется даже в том слу-
случае, когда h-ч < 2тс2, так как электромагнитное поле может вызы-
вызывать перераспределение зарядов и тем самым „поляризовать вакуум".
Эффект поляризации вакуума можно обнаружить экспериментально
при изучении тонкой структуры основного состояния позитрония,
лэмбовского смещения и сдвигов уровней мезоатомов.
Позитронием называется связанное состояние электрона и пози-
позитрона, образованное под действием кулоновских сил. В основном
состоянии позитроний не обладает орбитальным моментом и благо-
благодаря наличию спинов электрона и позитрона может находиться
в триплетном E=1) или синглетном E = 0) состояниях. Согласно
теории Янга [541], Вольфенштейна и Равенхолла [540], две частицы
могут аннигилировать, испуская при этом два -(-кванта, только тогда,
когда они находятся в синг летном, а не в триплетном состоянии. Анни-
Аннигиляция частиц, находящихся в триплетном состоянии, возможна
с испусканием лишь трех у-квантов. Время жизни частиц в три-
триплетном состоянии примерно в тысячу раз больше времени жизни
в синглетном состоянии. Эти выводы были подтверждены экспери-
экспериментально Дейчем [100], Пондом и Диком [395]. Разность энергетиче-
энергетических уровней этих состояний равна примерно 9-10~4 эв (см. работу
Дёйча и Дулита [101], причем около половины величины указанной
разности обусловливается виртуальной аннигиляцией и последующим
рождением электронно-позитронной пары. Такой процесс может
происходить только в синглетном состоянии; он является обрат-
обратным эффекту поляризации вакуума, который представляет со-
собой рождение и последующую аннигиляцию электронно-позитронной
пары.
Выражение для лэмбовского смещения содержит член, обуслов-
обусловленный небольшим искажением электрического поля протона вслед"
ствие поляризации вакуума (как обсуждалось выше). Такое искаже-
искажение поля вызывает сдвиг уровня основного состояния атома водорода
примерно на 27 мгги, что было впервые вычислено Юлингом [488].
Так как теория и эксперимент согласуются с точностью до 0,6 мггц,
то это обстоятельство снова указывает на реальность поляризации
вакуума.
Этот факт был подтвержден в дальнейшем наблюдениями над
сдвигом уровней в мезоатомах, т. е. атомах, образованных it~- и
[А~-мезонами, движущимися по боровской орбите вокруг протона
или легкого ядра (см. также т. II, гл. 33, § 8, и гл. 50, § 6). Рассмот-
Рассмотрим систему тг--мезон — протон Р (ir-—Р). Также, как для атома
водорода, энергетические уровни данной системы будут смещены
относительно уровней, получаемых из уравнения Клейна — Гор-
Свойства уравнения Дирака 57
дона!) для частиц в кулоновом поле. Этот сдвиг обусловлен
в основном электромагнитными радиационными эффектами и в зна-
значительно меньшей степени конечными размерами нуклона и особенно
мезон-нуклонными взаимодействиями и т. п. Электромагнитные
радиационные поправки связаны с двумя эффектами: один из них
возникает из-за различия собственных энергий связанного и сво-
свободного тг--мезонов, второй — из-за поляризации вакуума нуклон-
ным полем. Поляризация вакуума в данном случае, как и вообще,
в действительности обусловлена рождением пар противоположно
заряженных частиц любого сорта, т. е., кроме электронно-позит-
ронных пар, рождением мезонных пар tz+-tz~ и [1+-[а~. Однако
в первом приближении эффект поляризации вакуума обратно про-
пропорционален квадрату массы частиц, образующих пару (тг*, ja*, e±),
поэтому основной вклад в наблюдаемый эффект дают электронно-
позитронные пары.
Для мезоатома вклад в сдвиг уровней, обусловленный поляри-
поляризацией вакуума нуклонным полем, в действительности гораздо
больше, чем вклад, обусловленный собственной энергией мезона
(отношение этих эффектов равно квадрату отношения массы мезона
к массе электрона). Кроме того, так как в мезоатоме мезон в сред-
среднем гораздо ближе к ядру, чем электрон в обычном атоме, то вели-
величина сдвига уровней, обусловленная поляризацией вакуума, также
значительно больше в первом случае. Так, для 1£"-уровня в системе
■к~-Р сдвиг уровня порядка 10 за (ср. со сдвигом приблизительно
10~2 за для атома водорода), а для системы w-Mg 15-уровень.
ниже на величину порядка 1,4 • 103 эв (сдвиг пропорционален Z2).
Наличие такого сдвига уровней в мезоатомах было обнаружено
недавно в институте Карнеги в прекрасных экспериментах Стирнса
и др. [457—459], снова подтвердивших реальность эффекта поля-
поляризации вакуума. Кроме того, эти экспериментальные результаты
ясно указали на характер взаимодействия электромагнитного поля
со всеми найденными в природе заряженными частицами.
Эффект поляризации вакуума при электростатическом взаимо-
взаимодействии заряженных частиц (например, двух протонов) также
указывает на существование отклонения от чисто кулоновского рас-
рассеяния. Весьма вероятно, что, когда экспериментальные данные по
рассеянию протонов на протонах при низких энергиях будут уточ-
уточнены, эти эффекты, несомненно, проявятся.
§ 3. Уравнение Дирака с учетом внешнего поля
Как было указано в случае уравнения Клейна — Гордона, чтобы
учесть внешнее электромагнитное поле, необходимо сделать калиб-
Соответствующее уравнение для тс-мезона.
58 Глава 5
ровочно-инвариантную замену
Pf.-^Pf.—jAy E.4)
Это приводит к уравнению
с[}) — ^-А^ = тсЧ, E.5)
или
{(Ро — в?) — a-(cj— eA) — $тс*}<Ь = О. E.6)
Уравнение E.6) можно привести к уравнению второго порядка,
по форме аналогичному уравнению Клейна — Гордона [см. уравне-
уравнение B.41)], умножив обе части уравнения E.5) на оператор
р — {ejс) А; в результате получим
i) = «Vf E.7)
Используя определение а^ [соотношение C.13)], левую часть пере-
перепишем в виде
[IV
'
Коммутатор в последней строчке можно легко вычислить, если вспо-
вспомнить, что
и, следовательно,
ieb (dAv-
__ ^Л ^l£_F E 9)
V дх' дх* J с ^'
Свойства уравнения Дирака . 59
Таким образом, окончательно получается следующее уравнение:
= (^J 6. E.10)
Дополнительный член
ЕИ^ = -т^-*-г-^ EЛ1)
соответствует взаимодействию спина 1/2йо с электромагнитным полем
->■■>■ ->-->-
(ф, S). Член ia • S соответствует спин-орбитальному взаимодействию.
Физический более наглядный метод получения уравнения второго
порядка был дан Фолди и Ваутхейсеном [186], к работе которых
мы отсылаем читателя для подробного ознакомления.
Глава 6
ПРИМЕНЕНИЕ УРАВНЕНИЯ ДИРАКА
§. 1. Стационарные состояния
Существует ряд задач, для которых уравнение Дирака E.6)
можно решить точно. Наиболее важными из них являются следующие
задачи:
1. Движение заряженной частицы в кулоновом поле (Дирак [102],
Дарвин [98], Гордон [211], Мотт [345]).
2. Движение частицы в однородном магнитном поле, охватываю-
охватывающем все пространство (Раби [398], Хафф [237], Заутер [427],
Джонсон и Липман [246]).
3. Взаимодействие частицы с плоской электромагнитной волной
(Волков [504]).
Эти задачи рассмотрены во многих учебниках (например, в книге
Мотта и Снеддона [347] и в книге Крамерса [288]).
Решение первой задачи имеет важные приложения, в частности
к определению энергетического спектра атома водорода и вычи-
вычислению энергий рентгеновских лучей при переходах К- и L-элек-
тронов тяжелых атомов.
В случае атома водорода уровни энергии характеризуются глав-
главным квантовым числом п и квантовым числом J, определяющим
собственное значение полного момента. Если определить матрицы
Дирака так, как это мы сделали в гл. 3, § 1, то „большие" ком-
компоненты волновой функции <|>j и ф2 будут описывать частицу
с орбитальным моментом /х ==у-|— х/2 (или / — 1J2), а „малые" <Ь3
и <bi— с орбитальным моментом I2 = j — V2 (или _/ —)—1/2)- Таким
образом, большие и малые компоненты имеют противоположные
четности, причем четность больших компонент равна (— 1)г" и является,
по определению, четностью состояния.
Наблюдаемая величина тонкой структуры водорода и водородо-
подобных атомов, в частности Не+, находится в хорошем согласии
с теорией Дирака. Вырождение уровней с одним и тем же j и раз-
различными / также хорошо согласуется с экспериментом, за исклю-
исключением одного случая, именно уровней Si/2 и Рц%. В этом случае,
как уже упоминалось выше, существует сдвиг уровней, найденный
Лэмбом [295]: терм 2Sy, лежит выше терма 2Pi/t примерно на
1058 мггц. Этот сдвиг теоретически объясняется с точностью до
0,6 мггц учетом радиационных поправок к обычной теории Дирака.
Применение уравнения Дирака 61
Теория рентгеновского спектра тяжелых элементов пока еще
далека от такого совершенства. Первый шаг для уточнения этой
теории был сделан Коэном [87]; он строго учел взаимную экра-
лировку электронов. Однако, как показал Зоммерфельд [456],
теория Дирака остается справедливой для состояний с релятивист-
релятивистскими энергиями даже в настоящем несовершенном виде. Чтобы
установить, например, релятивистскую часть радиационных поправок,
а также поправки, определяемые конечным размером ядра и т. д.,
необходимо провести подробные количественные вычисления.
§ 2. Точная теория рассеяния при высоких энергиях
В случае кулоновского рассеяния релятивистских электронов и
позитронов неэкранированным атомным ядром с зарядом Z наше
уравнение допускает разделение угловых и радиальных переменных.
Так как электрон обладает спином 1/2, то в результате рассеяния
часть электронов может изменить направление спина на обратное и
рассеянная волна будет описывать электроны со спинами обоих
направлений. Это ведет к несколько усложненной формуле для суммы
квадратов амплитуд рассеяния (см. книгу Мотта и Снеддона [347]),
которая не может быть выражена в замкнутой форме, а выражается
в виде ряда по угловым моментам.
Значительный вклад в теорию был сделан недавно Йенни, Равен-
холлом и Вильсоном [544], которые использовали представление
матриц у, удобное для изучения частиц высоких релятивистских
энергий. В этом представлении можно показать, что спин, перво-
первоначально параллельный направлению движения, остается таковым и
после рассеяния (что означает изменение его направления в про-
пространстве): Все вычисления при этом значительно упрощаются и
точность повышается.
Изучим теперь некоторые предельные случаи. Важнейший из них —
яерелятивистский предел, при котором полученная формула точно
совпадает с обычной формулой рассеяния Резерфорда. Даже в реля-
релятивистском случае, т. е. при больших скоростях электрона, для
малых углов рассеяния эта формула совпадает с формулой Резер-
Резерфорда
F.1)
(8/2) 4^2 sin4 F/2) '
Второе выражение более наглядно, чемпервое. Оно показывает, что
для малых углов рассеяния при использовании удобной переменной,
именно pv (т. е. произведения импульса частицы на ее скорость),
релятивистские поправки не меняют вида формулы. Величина pv
имеет размерность энергии. Она равна удвоенной кинетической
энергии при малом v и кинетической энергии при больших v.
62 Глава 6
Уравнение F.1) используется обычно для расчета многократного
рассеяния частиц в фотопластинках и определения pv из экспери-
экспериментов по измерению сечения этого процесса.
Для больших углов рассеяния б мы не можем, вообще говоря,
дать такой простой формулы. Однако для малых Z, т. е. для
Z/137<C]1. Мак-Кинли и Фешбах [316] (см. также статью Да-
лица [95]) получили следующее выражение для сечения в виде ряда
Мотта [345, 346] по степеням Z:
+^Ы!1)] F-2>
Второй член уже появляется в первом борновском приближении. Третий
член линеен по Z, что легко понять из его вида [величина {Е — V,z =
~ (Е— е®J была представлена в форме Е2— 2EV-\-V2]. Когда
величина Z положительна, т. е. при рассеянии электронов, V2 имеет
тот же знак, что и —2EV, и тогда третий член в выражении F.2)
складывается с главным (вторым) членом. При рассеянии же пози-
позитронов (отрицательные значения Z) этот член вычитается из главного
члена выражения F.2). При рассеянии электронов, когда значения Ь
и vjc не слишком велики, отношение <з/<зд становится больше
единицы. В книге Мотта и Месси [348] приводится расчет Барт-
летта и Ватсона [20—22] для случая однократного рассеяния
электронов и позитронов ядрами ртути1). Работа Мак-Кинли и
Фешбаха [316] содержит оценки для области энергий 1—4 Мэв.
Позднее в работе Фешбаха [164] был рассмотрен случай Е~^>тс2,
который имеет место для энергий, больших 4 Мэв. Более стро-
строгий расчет для случая высоких энергий был проведен Йенни и
др. [543, 544]. Как уже было указано выше [см. выражение F.2)], при
6 = 180° и v —> с сечение рассеяния стремится к нулю, т. е. очень
быстрые электроны или позитроны не рассеиваются в обратном
направлении.
Постановка экспериментов по рассеянию электронов связана
с рядом трудностей. Однако недавно такие эксперименты были
проведены и было получено Ван-де-Граафом и др. [500], а также
Бьюкнером и др. [72] хорошее согласие с теорией для энергий
2,25 Мэв для всех углов, за исключением очень малых. При очень
низких энергиях (ниже 245 кэв) Боте [63] измерил величину сечения
рассеяния электронов ядрами золота; она оказалась на 37%, ниже
теоретически предсказанного значения. По-видимому, при таких
низких энергиях теоретические оценки были проведены недостаточно
аккуратно. Липкин [306] наблюдал различие между сечениями рас-
рассеяния электронов и позитронов, которое следует из выражения F.2).
!) Их расчет более точен, чем соотношение F.2). Они фактически чи-
численно просуммировали ряд Мотта в интервале энергий от 0 до (vjc) = 1.
Применение уравнения Дирака
63
В 1929 г. Мотт [345, 346] указал на возможность осуществле-
осуществления эксперимента для определения эффектов поляризации частично
поляризованного пучка, обусловленных двойным рассеянием1). Рас-
Рассмотрим падающий неполяризованный пучок, т. е. пучок с беспо-
беспорядочно ориентированными спинами электронов. Пусть этот пучок
рассеивается сначала в точке А, а затем в точке В, как показано
на фиг. 1. Пусть aub — две амплитуды волновых функций, описы-
описывающих электроны со спинами, направленными вверх или вниз соот-
соответственно. При этом можно показать, что интенсивность пучка
в направлении / пропорциональна (а2-\-Ь2), а в направлении //—2ab,
А
I
Я
' 5
Фиг. 1.
Таким образом, интенсивность в направлении / больше, чем в на-
направлении //. Мотт показал, что при рассеянии электронов с энер-
энергией 400 кэв ядрами золота этот эффект должен быть порядка 10%.
До 1943 г. попытки найти такой эффект экспериментально не увен-
увенчались успехом. Однако в 1943 г. Шулл и др. [451], а несколько
позднее Крейн с сотр. [401] подтвердили наличие этого эффекта,
а также показали причину неудач предшествующих эксперимента-
экспериментаторов. При очень- высоких энергиях эффекты поляризации снова
становятся малыми, так как в процессе рассеяния спин «электрона
не меняет своей ориентации по отношению к направлению движе-
движения (см. замечание к теории Йенпи и др. в начале этого параграфа).
§ 3. Эффект, обусловленный структурой ядра
В области относительно низких энергий, где длина аолны элек-
электрона велика по сравнению с размерами ядра,, мы рассматривали
ядро как точечный рассеиватель. При более высоких энергиях
электрона такое рассмотрение уже незаконно, и можно предполагать,
что из экспериментов по рассеянию электронов высоких энергий
мы получим некоторые сведения о распределениях заряда и тока
в ядре.
*) Более подробно это'изложено в книге Мотта и Месси [348].
64 Глава 6
При энергиях электрона Е^> тс2 Фешбах [163] из общих теоре-
теоретических соображений показал, что сдвиг фаз при рассеянии зави-
зависит только от j и не зависит от / (так же как и уровни атома:
водорода). Этот факт был подтвержден численными расчетами, про-
проведенными для ряда частных случаев.
Недавно был проведен ряд экспериментов по рассеянию электро-
электронов достаточно больших энергий (Лайман и др. [315] использовали
15,7 Мэв, Пидд и др. [387] — 30—45 Мэв, Хофштадтер и др.
{234, 235] —84—186 Мэв).
Фешбах [163] также показал, что при условии, когда длина
волны электрона велика по сравнению с радиусом ядра, возмущение
кулонова поля, обусловленное конечными размерами ядра, действует
лишь на волну с _/ = i/2. Сдвиг ее фазы в этом случае пропорцио-
пропорционален объемному интегралу от разности между невозмущенным
кулоновским потенциалом и фактически имеющимся потенциалом
в присутствии ядра; последний в свою очередь пропорционален
среднему квадрату расстояния протонов от центра ядра.
Лайман и др., используя вычисления Фешбаха, проанализировали
свои экспериментальные результаты и установили, что радиус ядра
при предположении об однородном распределении заряда в ядре
равен 1,2 • 10~ А^ см, т. е. несколько меньше, чем принятый ранее
радиус 1,4- 10" А^см, полученный из экспериментов по рассея-
рассеянию быстрых нейтронов, по зеркальным ядрам и т. д. Величина
радиуса Лаймана была подтверждена экспериментами по рассеянию
электронов высоких энергий, а также измеренным Фитчем и Рейнуо-
тером [179] спектром рентгеновских лучей, испускаемых jx-мезонами
при переходах между квантовыми состояниями в атоме. Биттер и
и Фешбах [39], а также Бодмер [46] высказали дополнительные
теоретические соображения в пользу меньшей величины радиусов
ядер. Купер и Хенли [89], и особенно Янкович [241], показали,
как следует понимать прежние соображения в пользу больших
радиусов, 'полученных из экспериментов по зеркальным ядрам.
При энергиях электрона порядка фО Мэв и выше длина волны
электрона достаточно мала (порядка 2 • 10~18 см при 100 Мэв),
поэтому рассеяние должно зависеть от внутренней структуры ядра.
Смит [452, 453] и Шифф [430], используя борновское приближение,
изучали рассеяние электронов высоких энергий заряженными протя-
протяженными частицами с различным распределением зарядов по объему.
Однако почти для всех ядер, кроме самых легких, борновское при-
приближение неприменимо. Единственным надежным путем для вычи-
вычисления рассеяния электронов является численный метод. Он был
проведен с большой точностью Йенни, Равенхоллом и Вильсоном
[543, 544] с применением быстродействующей счетной машины;
значительного успеха добилась также Баранджер [14, 15], применив
полуаналитический метод. В частности, она показала, что полуана-
Применение уравнения Дирака 65
литический метод ВКБ1) можно применить для вычисления сдвига
фаз разных парциальных волн с точностью до 0,1е или лучшей.
Вычисления Йенни и др. находятся в прекрасном согласии
с экспериментами Хофштадтера и др., если подобрать подходящим
образом радиус ядра и распределение заряда в нем. И наоборот,
сравнение эксперимента с расчетами позволяет более точно опре-
определить уже известный радиус ядра. Оказывается, что он равен
A,2 =±г0,05)-10~18 л'/з см; это находится в полном согласии с резуль-
результатом, указанным выше. Кроме того, можно показать, что поверх-
поверхность ядер не может быть резко очерченной, т. е. что плотность
протонов в ядрах постепенно падает от центра к периферии, как
и требует квантовая механика. Расстояние, на котором плотность
протонов падает от 90 до 10% от плотности в центре, порядка
2 • 10~18 см и, по-видимому, не зависит от массового числа А.
Оказывается, что радиус ядра пропорционален А'/' вплоть до очень
малых А, включая даже Не*. Недавно в Стенфорде экспериментально
исследовали распределение заряда и измеряли величину магнитного мо-
момента протона; было получено, что размер протона порядка
0,7 ■ \0~13см.
') То есть метод Вентцеля, Крамерса, Брюллюэна.
Глава 7
ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
§ 1. Вероятность перехода
Рассмотрим систему с гамильтонианом Ji== Ho-\-V. Предпо-
Предположим, что нам известны собственные функции и собственные зна-
значения Но, т. е.
1
Далее, если система находилась первоначально в состоянии, описы-
описываемом собственной функцией ера оператора Но, то не зависящее от
времени возмущение 1^ вызовет переходы в другие состояния с той
же самой энергией. Если возмущение является очень слабым, то
число переходов в единицу времени из состояния а в состояние Ь
выражается хорошо известной формулой
| («р4, Wo) I2 S (Еь — Еа). G.2а)
Это есть первый член выражения для вероятности перехода. Его
обычно называют первым борновским приближением. Точное выра-
выражение для вероятности перехода дается соотношением
wa+b =2яй-1|0рь, Т<?а)\Ч(Еь — Еа), G.26)
где величина Т может быть разложена в ряд по степеням V, первым чле-
членом выражения G.26) будет тогда G.2а) (см., например, работу Снай-
дера [455]). Так как нас всегда интересует только переход в конечное
состояние, определяемое интервалом энергии от Еьло Eb-\- dEb и плот-
плотностью Pf, то вероятность перехода в единицу времени имеет вид
w = 2тгй-1 f dEb | (?6l Tfa)\4(Eb~Ea)Pf(Eb) =
). G.3)
Сечение перехода можно теперь получить, разделив w на соответ-
соответствующую относительную скорость.
В теории Дирака непосредственно применяется формула G.3).
Однако существует ряд методов, которые значительно облегчают
вычисления указанного сечения. Ниже опишем некоторые из этих
методов, как например нормировку функций, применение проекцион-
проекционных операторов и вычисление шпуров матриц.
Вычислительная техника 67
§ 2. Нормировка и условия ортогональности
Для упрощения расчетов наши волновые функции выгоднее нор-
нормировать на объем тс2/\Е\, а не на единицу объема1). Так как
единица объема в покоящейся системе испытывает в движущейся
системе лоренцовское сокращение в )/l—г>2/е2 = тс2/ | Е | раз, то
наша нормировка остается инвариантной.
Это условие делает нормировку с помощью сопряженных спи-
спиноров очень простой. Напомним, что уравнение Дирака в импульсном
пространстве имеет вид
тс2)и, G.4а)
G.46)
Умножая уравнение G.4а) на и+C слева, а G.46) на (За справа,
складывая их и учитывая антикоммутативность риг, получаем
2£и+ри = 2/гас2и+и. G.5)
Вспомнив, что и = и+13 и что, согласно нашей нормировке,
«^=!Ц, G-6)
найдем
uu=j§-{. G.7)
Таким образом, величина ии равна zt 1 в зависимости от знака
энергии. Обычно пишут
йи=е, G.8)
где s = dr 1.
Наша нормировка обладает также тем преимуществом, что делает
инвариантной относительно собственного преобразования Лоренца
и величину dpp так как плотность состояний в импульсном про-
пространстве для всех ориентации спина теперь равна
^ G-9)
Величина dsp = dpldp2dpb преобразуется при собственных преобра-
преобразованиях Лоренца как временная компонента 4-вектора, также
преобразуется и |£|. Следовательно, dpf — инвариант.
Рассмотрим условия ортогональности между спинорами. Если
-> -*■
ur(p)(r—l, 2) — два решения, соответствующие импульсу р и
положительной энергии частицы, то их всегда можно выбрать
Ч Ясно, что это возможно только в случае т ф 0 и, следовательно,
невозможно для случая нейтрино.
68 Глава 7
ортогональными друг к другу, так как они оба являются собственными
функциями одного и того же эрмитового оператора со. • р-\- рте2.
Условие их ортонормируемости гласит:
ЙЧР)И8(Р) = 3Г8 (г, s-1,2). G.10)
Далее, можно легко показать, что решения, отвечающие импульсу
— р частицы с отрицательной энергией, также ортогональны иг(р).
Рассмотрим уравнение Дирака для свободной частицы с положи-
положительной энергией
(р—/гас)и+(р) = 0. G.11)
Для спиноров, описывающих частицы с энергией —Е и импульсом
— р, р заменяется на —р, и уравнение принимает вид
Следует напомнить, что такая волновая функция описывает позит-
рон с импульсом -\~р, так как, согласно дырочной теории Дирака,
наличие позитрона с импульсом -\-р можно рассматривать как
отсутствие электрона с отрицательной энергией и импульсом —р
в зоне, заполненной электронами с отрицательной энергией. Умно-
Умножая уравнение G.11) на и_ (—р) слева, получаем
и_ (—р)ри+(р) = тси_ (~р)и+(р). G.13)
Взяв выражение, сопряженное G.12), и умножив его справа на
и+(р), получим
и- (—Р)ри+(Р) = — тси_ (—р) и+ (р). G.14)
Однако уравнения G.13) и G.14) только тогда могут быть совмест-
совместными, когда и_ (гр)и+(— р) = 0. Если два ортогональных решения,
соответствующих частице с отрицательной энергией и импульсом
— р, обозначить через vr(p), т. е. назвать волновыми функциями
позитрона функции V(p),
el (— p") = vr (р) (г = 1, 2), G.15)
то условия ортонормируемости, которым они подчиняются, в соот-
соответствии с условием G.7) примут вид
1) = — 8,а. G.16)
Вычислительная техника
Выпишем вместе все условия ортонормируемости
~пг(р)и*(р) = 8rs . (г, s = 1, 2), G.17а)
«•"(?)«•(>)= — К8 (/-,5=1,2). G.176)
vr (р) и* (р) =~п* (р) V(р) = 0 (г, s = 1, 2). G.17в)
Согласно згсловиям нормировки и ортогональности, решения для
частиц с импульсом р удовлетворяют соотношению
2 « Ср) Ц (Р) — vra (Р) ^(^) = -Н8^- G-! 8>
Знак минус в последнем соотношении возникает благодаря условию
нормировки G.7) для решений, соответствующих частицам с отри-
отрицательной энергией". Следует обратить внимание на порядок множи-
множителей в этом соотношении, т. е. на тот факт, что появляется ком-
комбинация аи, которая является 4-мерной матрицей, полученной путем
умножения столбца матрицы на строку. Аналогично из условий
ортонормируемости G.17а) и G.176) следует, что
2
2 (пг(р) и"(р) — Ъ-(р) vr (p)) = 4. • G.19)
Для облегчения дальнейшей работы введем следующие обозначения для
наших волновых функций:
->■ -*■
wr(p)= иг(р) для г= 1, 2,
(
p) для /-=1,2.
При этом условия ортонормируемости G.17) примут вид
w'ip)■&>&) = *%„ (г, 5=1, 2, 3, 4), G.21/
где
s«" = +l для г = 1, 2,
sr = _i для г = 3,4. G>22)
Соотношения G.18) и GЛ9) теперь записываются в виде
2 &rW{p)W(p)=I, G.23)
-* — ■>->.
2 ^^, G,24)
70 Глава 7
§ 3. Проекционные операторы
Часто возникает необходимость провести суммирование по про-
промежуточным спиновым состояниям; например, иногда нужно про-
провести такое суммирование только по тем промежуточным состоя-
состояниям, которые отвечают положительным энергиям частиц, либо
только по тем, которые соответствуют отрицательным энергиям
частиц. Пусть интересующая нас сумма имеет вид
2 _
Q = 2 (sQw*) Qw*Pr) =
t=i
1A^A, =SV
где Q И Р — операторы (призведения матриц 7). r и * — спиноры,
индекс t у знака суммы показывает, что суммирование необходимо
проводить только по двум состояниям wr, отвечающим положительным
энергиям частиц. Аналогично можно рассмотреть случай, когда про-
промежуточные состояния соответствуют отрицательным энергиям частиц.
Следовательно, необходимо найти проекционные операторы, кото-
которые можно ввести в левую часть соотношения G.23) таким образом,
чтобы проводить суммирование уже по всем четырем состояниям,
а не по двум wr(p)(r— 1, 2), как мы это делали раньше. При этом
для упрощения соотношения G.23) можно использовать условие G.21).
Мы хотим, чтобы проекционные операторы, о которых идет речь,
обладали определенным свойством: умножали спинор w на -f-1 для
состояний частиц с положительной энергией, и на нуль для состоя-
состояний частиц с отрицательной энергией. Такой оператор можно скон-
сконструировать, зная, что уравнение Дирака, выраженное в наших
спинорах да, при Й = с = 1 имеет вид
(р— m)wr(p) = Q для г =1,2, G.26)
(р + т)гг(й = 0 для г = 3,4. G.27)
Эти уравнения наводят на мысль определить проекционный опе-
оператор для состояний частиц с положительной энергией и импуль-
сом р в виде
Л+(Р) = "^- G-28)
так как благодаря уравнениям G.26) и G.27) он отвечает всем тре-
требованиям, предъявляемым к проекционному оператору, а именно:
для г=1,2,
^ G, 2У)
Д+ (р) wr(р) = 0 Для г = 3, 4.
Вычислительная техника 71
или
A+(/0w«-(J)==-5-(l+<)W(J5J- G.30)
Далее,
2т
так как для свободных частиц р2=р2 —/н2.
Принимая во внимание соотношения G.21) и G.29), легко находим
-(p). G.32)
Заметим, что величина A+sr обладает теми же свойствами, что и сам
оператор А+, так как для состояний частиц с отрицательной энер-
энергий, когда гг = —1, оператор А+, действуя на спинор wr, дает
нуль. Это позволяет нам записать формулу G.25) в виде
4 _
Q = 2 (sQA+^wt){wtPr). G.33)
t=i
Использовав соотношение G.23), перепишем формулу G.33) в виде
Q=(sQA+Pr); G.34)
таким образом, мы уже достигли поставленной цели — вычислили
сумму по всем промежуточным состояниям частиц.
Если нас интересуют только состояния частиц с отрицательной
энергией, то мы можем по аналогии определить проекционный
оператор в виде
Л_(Р) = ^-- G-35)
Он обладает следующими свойствами:
АЛР)^Ср) = ^{Р) Для г-3,4.
А_ (p)W'(p) = 0 для г==1,2,
(А_ (р)J = А_ (р) = — 2 ™г (Р) ^г (Д G-37)
Следует отметить, что сумма операторов А+ и А_ дает простой
результат
А+ (р)—|- А_ (р) = 1 G.38)
и что
(в) —0. G.39)
72 Глава 7
§ 4. Шпуры
Согласно выражению G.3), вероятность события, матричный эле-
элемент которого равен М = WfQwt, пропорциональна квадрату абсо-
абсолютной величины М, т. е.
| М |2 = М+М = (да Qw.) (wtQ+wf) = (w Qw.) (w.^°Q+'(°wf). G.40)
Здесь Q+ -—оператор, эрмитово-сопряженный (комплексно-сопряжен-
(комплексно-сопряженный и транспонированный) оператору Ql>. Введем
/V . „0о + «0 A А.\\
Тогда
| М |2 = (wfQWj) (WiQ'wf). G.42)
Во многих задачах нас не интересует спин частицы в конечном
состоянии. Поэтому выражение G.42) мы должны просуммировать
по двум конечным спиновым состояниям. С помощью методов, описан-
описанных в предыдущем параграфе, можно произвести такое суммирование,
вводя соответствующие проекционные операторы. Если мы имеем
дело с электронами, у которых начальные и конечные состояния
■*■ ■*"/
описываются спинорами wi(p) и wf(p), соответствующими положи-
„ ■*■ -*~,
тельной энергии и импульсам р и р , то мы получаем
4
г=1, 2 * г = 1 * +
где сумма | М |2 берется по всем конечным спиновым состояниям.
Если падающий пучок также неполяризован, то необходимо усред-
усреднить | М |2 по всем начальным спиновым состояниям и просуммиро-
просуммировать по конечным спиновым состояниям; в результате получим
2 4
1 чг-1 —.. .. J ^ ~г г , г г
= -я- У, [WiQ A+ (р ) QA+ (p) s tVi) =
1) Заметим, что, согласно соотношению C.52), та часть оператора Q,
которая содержит просто произведения матриц -f (назовем ее Q^), удовлетво-
удовлетворяет равенству "flQ^'fl =* Q%. В нематричной же части оператора Q комплекс-
комплексная единица -»I должна быть веюду заменена на /. '
Вычислительная техника 73
4
1 л , , 1 , ,
= ~2 2j (Я Л+ (p ) QA+(P))«* = -g- Sp (QA+ (p ) QA + (p)). G.44)
Обозначим
L = Q'A+(p')QA+(p). ■ G.45)
Оператор L можно представить с помощью линейной комбинации 16
линейно независимых матриц Г, о которых мы говорили выше:
16
L = 2 а{Сг = e1/-4-a37i+ • • • G-46)
г-i
Если взять шпуры обеих частей равенства G.46), то останется един-
единственный член, содержащий единичную матрицу, т. е.
SpL = 4al. G.47)
Практически полезны следующие два свойства шпура произведе-
произведения матриц т:
1. Шпур произведения нечетного числа матриц -у равен нулю.
Чтобы показать это, напомним элементарные свойства шпура
Sp (ABC) = Sp (CAB) G.48)
(то же справедливо при любой циклической перестановке). Далее,
как мы уже указывали, существует матрица y6, обладающая сле-
следующими свойствами:
Т5Т?.+ Т,Лб = ° <7-49)
или
ТбТр.. (Тб) = — Ts>.' G.50)
откуда
-i=(_l)nY T G.51)
Взяв шпуры обеих частей равенства G.51) и учтя свойство G.48),
приходим сразу к соотношению
(—l)»Sp(T|ll .. . Ъп) = Sp(TD . . . т,га), G.52)
т. е. шпур произведения нечетного числа матриц f равен нулю.
В частности, отметим, что
^ O. G.53)
Аналогично имеем
Sp yb «- — Sp \^Ь(Ь)"Ч - — Sp Ti- 0. G.54)
74 Глава 7
2. Если п — четное число, то с помощью перестановочных со-
соотношений шпур произведения матриц у всегда можно свести к вы-
выражению, содержащему лишь п — 2 множителя. Возьмем, например,
случай п = 2. Согласно перестановочным соотношениям
1^4-1,^=2^,, G.55)
имеем
= Sp (т„Та) =
=» -^ Sp G,7^-1- Т^ТО = fi^i Sp /= 4в(„, G.56)
так как
Sp/=4. G.57)
Аналогично легко показать, что
Sp (T^TvTpTc) = 4g^g-vp — ig^g9> + tgopgy.v G • 58)
Эти выводы означают, что если А и В коммутируют, то
Sp(AB) = 4AB = 42M£l\ G.59)
Sp(A) = 0 G.60)
и т. д.
Другие методы вычисления шпуров см. в работе Даффина [124],
Кайяньелло и Фубини [75].
Глава 8
ФЕЙНМАНОВСКАЯ ТЕОРИЯ ПОЗИТРОНА
В 1949 г. Фейнман [168] развил теорию, целью которой было
упростить все вычисления, связанные с учетом взаимодействия эле-
электронов и позитронов с внешними полями. Затем теория была
обобщена и на случай взаимодействия частиц между собой (Фейнман
[169]), причем она оказалась эквивалентной обычной теории поля
(Фейнман [170]). Кроме упрощения всех расчетов дырочной теории
Дирака, теория Фейнмана дала также совершенно новую физическую
трактовку процессов взаимодействия, которая позволяет наглядно
и понятно объяснить их. Здесь мы обсудим первую часть этой
теории, в которой рассматривается взаимодействие электронов
и позитронов только с внешними электромагнитными полями.
В гл. 15—19, введя квантование поля, мы рассмотрим общий случай
взаимодействий между частицами и докажем эквивалентность форма-
формализма Фейнмана и обычной теории. Ни один обзор работ Фейнмана
не может претендовать на такую ясность и простоту изложения,
как его оригинальные работы [168, 169]. Поэтому мы рекомендуем
читателям обращаться к последним.
§ 1. Нерелятивистская теория
Рассмотрим уравнение Шрёдингера
Ш^ = Щ. (8.1)
При решении дифференциального уравнения (8.1) обычно рас-
рассматривают ф (^i) как известную функцию и ищут изменение ф за
малый интервал времени Д^. Вместо этого Фейнман [168] предпо-
предположил, что при переходе к моменту t% волновая функция в точке
(/а, х.2) выражается через волновую функцию в точке (tv xt) (при
^а > ^i) следующим образом1):
*» *i. *i)<K*i. *i). h>h- С8-2)
1) Обозначение x^ принято для трех пространственных координат х, у,
г в момент t\. Дифференциал Фх означает интегрирование по обычному
пространству, d*x — по 4-пространству
dxo dJ(l dx* dx* = cdt dx dy dz = d*x.
76 Глава 8
Здесь К — функция Грина линейного уравнения (8.1). Предположим
далее, что Н—не зависящий от времени эрмитов оператор, т. е.
внешнее поле, которое мы хотим рассмотреть, постоянно во вре-
времени. В соответствии с принципом суперпозиции в квантовой ме-
ханике можно разложить d> (лг1( tO в ряд по полному набору орто-
нормируемых собственных функций ип (х) оператора Н с собствен-
собственными значениями Еп,
Нип = Епип, (8.3а)
onm, (8.36)
2 ип (*) ип (*') = S (% — Р). (8.3в)
п
Таким образом,
Ф(*1. y^S^AWr^^; (8.4)
п.
Величина сп получается обычно путем умножения равенства (8.4)
на ип(х1) и интегрирования по трехмерному пространству. В ре-
результате имеем
/. tJtPxy**»'^. (8.5)
Волновую функцию в момент t2 можно записать в виде
«|> (х2, t2) = S cnun(x2)e~iBn4n. (8.6)
п
Подставляя выражение (8.5) в формулу (8.6), меняя порядок сум-
суммирования и интегрирования и сравнивая с соотношением (8.2), по-
получаем
п
ИЛИ, ВВОДЯ
~£п(х< t) = an{x)e г п , (8.8)
получаем
■*■ ■> ж-1 ■*■ • ■*■
I/ (у + . у 4- \ >v (У + Лч (' V + \ (Я О\
1\ \™оу *2* 1 * 1у ^^Л /п \ 2' 2^ / W \ 1' I/* \ * /
П
Заметим, что для равных моментов времени tt — t2 = t равенство (8.7)
[согласно соотношению (8.3в)] дает
1\ \Х2» I, Х±, Z) = /j Un \X2) tin \pC-^) = о \Х% ЭС\I \у * *^/
п
это должно иметь место для обращения соотношения (8,2) в те
деетво при i% я» ^,
Фейнмановская теория позитрона 77
Так как нас интересуют лишь времена t2, большие tv то удобно
определить К только для ^ >- tt и положить К = 0 для t2 < *х.
Это граничное условие мы можем внести явно в определение К,
написав выражение (8.9) в виде
2( Ы&, УЙ^-/,), (8.11)
где b(t)—ступенчатая функция, определенная следующим образом:
b(t)= 1, если t > О,
9@=0, если t< 0. (8.12)
Из этого определения вытекает, что
~^ = 8@, (8.13)
Теперь уже весьма просто вывести дифференциальное уравнение,
которому удовлетворяет функция К- Так как функции уп являются
решениями уравнения Шредингера (8.1), то, согласно соотноше-
соотношениям (8.10), (8.11) и (8.13), мы получаем
l-^-~n(X2)JK(X2, Г2, Xlt fj —
— xt). (8.14)
При получении последней строки уравнения (8.14) мы снова вос-
воспользовались полнотой набора собственных функций ип(х) опера-
оператора Н. В общем случае, когда оператор Н не обязательно постоя-
постоянен во времени, можно еще определить К как решение уравнения
щ — Н(х2,
которое равно нулю для ^2 < ^i-
Покажем далее, что это определение (т. е. дифференциальное
уравнение и граничное условие К = 0 для t2 < £t), по существу,
эквивалентно интегральной форме (8.2). Иначе говоря, мы хотим
показать, что уравнение (8.15) вместе с требованием /<" = 0 для
t2 < tt ведет к соотношению
К(х2, t; xlt'f)=^b(x2 — *!>. (8.10)
78 Глава 8
Нетрудно установить и обратное, так как соотношение (8.2) тре-
требует, чтобы для t2=f=tx, согласно уравнению (8.1),
щ — Н(хг, *2)]tf(*8, t2; xlt tJ = O (8.15а)
и чтобы для tl — t2 — t
К(х2, *, *х; t) = bAc2 — xt). (8.10)
Если проинтегрировать теперь уравнение (8.15) по бесконечно ма-
малому интервалу времени от t2 = t1 — е до t2 = t1-\-z, то получим
( +
К(х2, *! + ■; xv tJ — KiXv t^ — г; xlt tl) = b(jct — x1) (8.16)
[второй член в левой части уравнения (8.15) исчезает в пределе
при s —> 0 только при условии, когда величина //конечна]. Однако
K(ti — е, 2'1) = 0, по определению, так как t2<C.tv поэтому в дей-
действительности получаем
,'lim K(x2, ^ + я; xlt ^) = К(.х2, tt\ xlt fx) = S (x3 — xj, (8.17)
что и требовалось.
Рассмотрим теперь теорию возмущений в формализме Фейнмана.
Предположим, что мы имеем дело с задачей, в которой Н —■ Но-\- V,
и что мы можем ее решить для случая Н — Но, т. е. когда V = 0.
Обозначим через Ко функцию Грина при V = 0, т. е. для свобод-
свободной частицы. Легко установить, что дифференциальное уравне-
уравнение (8.15) и граничное условие К = 0 для t2<it1 могут быть объ-
объединены в одно интегральное уравнение1):
+ ОО
КB, !) = /С0B, О —j^ jK0B, 3)VC)/CC, \)&{х3). (8.18)
Чтобы доказать это, умножим обе части уравнения (8.18) на опе-
оператор М-^зт ^оB) и> использовав уравнение (8.15), получим
следующее дифференциальное уравнение:
щ — Л0B)]*B, I) = rtS*B. \)+V{2)K{2, 1). (8.19)
Далее, если второй член в правой части перенести налево и сло-
сложить со вторым членом в левой части уравнения, то мы получим
дифференциальное уравнение (8.15) для К- Но, так как KqB, 1)
!) Здесь введены обозначения /С B, 1) = /С(аг3, £3; xlt t{); Ь* B, 1) =
= 5 (*2 — 'i) 5 (-*i — -*2)- Множитель с появляется в знаменателе, согласно
нашему определению d*x.
Фейнмановская теория позитрона 79
равно нулю, если t2<.tlt то отсюда следует, что и КB, 1) так же
равно нулю для t2 < tx.
Преимущество интегрального уравнения заключается не в том,
что оно содержит все граничные условия, а в том, что его легко
можно решить методом последовательных приближений или путем
разложения в ряд Неймана — Лиувилля
КB, 1) = *0B, !) + (=^)/<*ЗД>B, 3)^C)/СоC,
, 4)VD)КоD,
(8.20)
Правую часть выражения (8.20) можно интерпретировать следующим
образом. Первый член описывает распространение свободной ча-
частицы из точки 1 в точку 2. Второй член описывает распростра-
распространение свободной частицы из точки 1 в точку 3; в точке 3 проис-
происходит рассеяние, и частица снова распространяется свободно от
точки 3 к точке 2. Очевидно, необходимо провести интегрирование
по всем возможным точкам 3. Третий член описывает двухкратное
рассеяние, именно в точках 3 и 4 и т. д.
Для малого возмущения V часто можно получить хороший ре-
результат, взяв член только первого или второго порядка по V- Для
больших возмущений необходимо использовать много членов беско-
бесконечного ряда (8.20) или, еще лучше, решить интегральное уравне-
уравнение (8.18). Следует заметить, что бесконечный ряд такого типа,
как ряд (8.20), всегда можно преобразовать в интегральное урав-
уравнение. Так как переход от ряда (8.20) к уравнению (8.18) оказы-
оказывается здесь несколько тривиальным, то этот метод может в дей-
действительности служить для вывода либо интегрального, либо диф-
дифференциального уравнения для К в тех случаях, когда гамильто-
гамильтониан, или потенциал, нельзя написать целиком с самого начала.
Примерами таких случаев являются: а) взаимодействие электрона
с электромагнитным полем, включая все радиационные поправки;
б) релятивистская задача двух тел, когда взаимодействие между
ними является следствием взаимодействия каждого из них с полем
(гл. 25).
§ 2. Релятивистская теория
Обратимся теперь к релятивистским уравнениям в фейнмановском
формализме. Напомним, что в обозначениях Фейнмана уравнение
Дирака для свободной частицы имеет вид
GV — /и)ф = 0, (8.21)
где мы положили h = с = 1 (атомные единицы). Потребуем теперь,
как и в нерелятивистском рассмотрении, чтобы четырехкомпонентная
-> ■>
волновая функция ty(x2, t2) получалась из <b(xv tt) с помощью ядра
80 Глава 8
К (х2, t2', xlt t{), где К — 4-мерная матрица. Таким образом, мат-
матрица К должна также удовлетворять уравнению Дирака1), анало-
аналогичному уравнению (8U5),
(/Vj — m)KB, 1) = Й*B, 1). (8.22)
По аналогии с выражениями (8.4) и (8.6) функцию ф можно
разложить в ряд по полному набору собственных функций ип
[см. уравнение C.31)], т. е. набору, соответствующему как поло-
положительным, так и отрицательным энергиям. Для удобства вместо и*
мы будем применять сопряженные собственные функции и. Далее,
проведя преобразования, аналогичные тем, которые мы проводили
в нерелятивистском случае при выводе соотношения (8.7), найдем
частное решение уравнения (8.22) в виде
En-
S
Ко = 0 для t2 < tt.
Согласно требованию, функция ф разложена в ряд по полному
набору собственных функций ип, поэтому в решение (8.23) необхо-
необходимо включить также компоненты волновой функции, соответ-
соответствующие состояниям частиц с отрицательной энергией.
Однако такой выбор Ко [см. решение (8.23)] соответствует
скорее теории только для одних электронов, чем настоящей теории
дырок. Лучше всега можно это понять на следующем примере.
Рассмотрим электрон, который рассеивается потенциалом V, равным
нулю для t <—Г и для t^>T. В этом случае реальный электрон
имеет, конечно, только положительную энергию; следовательно, при
t <С—Т волновая функция падающего электрона соответствует
суперпозиции решений уравнения Дирака, описывающих свободную
частицу с положительной энергией. Однако при наличии потенциала V
выражение (8.20), примененное к этому случаю, приводит к тому,
что для t' ^> T волновая функция электрона будет, вообще говоря,
содержать компоненты, соответствующие как положительным, так
и отрицательным энергиям свободной частицы и тем самым показывать,
что существует конечная вероятность нахождения электрона в со-
состоянии с отрицательной энергией. Ясно, что это физически бес-
бессмысленно. Таким образом, решение (8.23) не является удовлетво-
удовлетворительным решением для К, и мы должны искать другое предста-
представление. При этом нужно учесть, что, согласно теории дырок, все
состояния с отрицательной энергией заполнены, и, следовательно,
Индекс 2 у оператора V означает дифференцирование по
Фейнмановская теория позитрона 81
электрон в результате рассеяния не может перейти ни в одно
из этих состояний. Это в свою очередь требует, чтобы для t2 >• ^1
функция К была суммой решений, соответствующих только поло-
положительным энергиям частицы. Однако, чтобы представление было
полным, функция К должна еще удовлетворять уравнению (8.22)
для всех моментов времени.
Чтобы удовлетворить этому условию, напомним, что, согласно
нашему предположению, частное решение (8.23) для К не содержит
решения однородного уравнения, соответствующего уравнению (8.15).
Член
Un(xi)Zn(x1)e-t*»lt'-t') (8.24)
представляет собой решение однородного уравнения для произволь-
произвольных tz. Следовательно, для того чтобы сделать
мы должны вычесть из решения (8.23) сумму всех членов (8.24) по
состояниям частиц с отрицательной энергией для всех моментов
времени. Эта сумма сокращается со второй половиной решения (8.23),
что приводит к следующей функции Грина К+ для случая свобод-
свободной частицы:
АГ+= S «пй)^»^-"»"'1' для '*>*» (8'25)
для £2 < tt функция К+ уже больше не равна нулю, а равна
К+=— S un(x3)un(xl)e-iE-{t^t') для t2<tv (8.26)
Еп<°
Таким образом, одно из изменений для получения правильной теории
дырок заключается в том, что условие К = 0 для 1г < tx заменяется
соотношением (8.26). Соотношение (8.26) удобно переписать в форме,
которая показывает, что в показателе экспоненты появляются лишь
положительные величины, именно
К+^- 2 un(x2)un(he-i{B-UU-ttl Для t2<tv (8.27)
Еп<й
При наличии потенциала можно написать интегральное уравне-
уравнение и его разложение в ряд, являющийся аналогом ряда (8.20).
В действительности, этот ряд идентичен с рядом (8.20), если
только К+ заменить на Ко, а V рассматривать теперь как 4-мерную
матрицу. Смысл членов полученного ряда лучше всего можно по-
понять, рассмотрев пространственно-временные диаграммы. Первый
член К+B, 1) описывает распространение свободной частицы из
82
Рлава 8
точки 1 в точку 2; обозначим это на диаграмме прямой линией
(фиг. 2). Второй член
+B, 8)VC)/C+C, l)d*xt (8.28)
описывает однократное рассеяние. Ограничим замкнутой кривой
с:
1
Пространственные
координаты —*-
Фиг. 2.
Фиг. 3.
область, в которой потенциал V отличен от нуля; фиг. 3 будет
изображать диаграмму однократного рассеяния. Третий член
(8.29)
описывает двухкратное рассеяние. Диаграммы (фиг. 4 и 5) иллюстри-
иллюстрируют две различные возможности такого рассеяния (пример внеш-
внешнего потенциала см. в § 4).
Случай а
Случай 6
Фиг. 4.
Фиг. 5.
Случай а. Если мы двигаемся по мировой линии из точки 1
к точке 2 так, что время всегда растет вдоль этой линии, то в вы-
выражении для К+ появляются лишь суммы типа (8.25), т. е. учиты-
учитываются лишь состояния частиц с положительной энергией. Это есть
обычное двухкратное рассеяние электрона с положительной энергией.
Фейнмановская теория позитрона 83
Случай б. При движении по мировой линии так, что при пере-
переходе из точки 4 в точку 3 мы возвращаемся во времени назад,
в выражении для К+ появляются суммы по состояниям частиц с отри-
отрицательной энергией. Эти суммы такого же типа, как (8.26). В фейн-
мановской интерпретации (см. также работы Штюкельберга [464, 465])
это соответствует распространению позитрона из точки 3 в точку 4.
Если считать, что время возрастает, то эту последовательность
событий можно интерпретировать следующим образом: в точке 3
рождается электронно-позитронная пара; электрон распространяется
в направлении к точке 2, в то время как позитрон аннигилирует
в точке 4 с приходящим туда электроном.
Заметим, что так как мы должны интегрировать по всем вре-
временам t3 и tv то оба случая описываются одним членом (8.29). Этот
член поэтому обычно изображается только одной диаграммой (фиг. 4),
а фиг. 5 считается идентичной, так как она может быть получена
из фиг. 4, если считать, что момент /3 следует раньше, чем t±. Более
того, заметим, что случай „б" протекает во времени точно так, как
представляет теория дырок: электрон с отрицательной энергией
переходит в состояние 2 с положительной энергией (конечное состоя-
состояние), т. е. рождается пара; затем дырка заполняется электроном,
находящимся в состоянии 1, т. е. происходит аннигиляция пары.
В результате наблюдаемый эффект сводится к следующему: электрон
рассеивается, переходя из состояния 1 в состояние 2, причем элек-
электрон' с положительной энергией заменяется одним из электронов
отрицательного фона. Следовательно, согласно принципу Паули,
матричный элемент должен иметь отрицательный знак. И, действи-
действительно, не пользуясь явно принципом Паули, мы получили выраже-
выражение (8.26) с отрицательным знаком. Таким образом, сам метод
построения функции распространения К+ дает отрицательный знак,
требуемый принципом Паули. Связь между спином и статистикой
(частицы со спином 1/2 подчиняются статистике Ферми) впервые была
установлена эмпирически при сопоставлении спинов и статистики
ядер (см. работу Бете и Бечер [31]). Паули [376]1) впервые уда-
удалось доказать, что частицы, описываемые уравнением Дирака, дол-
должны подчиняться статистике Ферми — Дирака.
Таким образом, ясно, что в методе Фейнмана мы всегда движемся
по мировой линии, даже если она- ведет нас во времени обратно.
Например, выше было описано виртуальное рождение пары и к одной
точке мы вынуждены были двигаться по времени обратно. Мы можем
также рассмотреть реальное рождение и аннигиляцию пар, пред-
представленные диаграммами на фиг. 6 и 7.
Важно отметить, что новая интерпретация Фейнмана дает в то же
время возможность развить теорию, которая может описывать очень
сложные процессы, не обращаясь к помощи старой теории дырок
См. также работу Паули [381].
84
Глава 8
с ее промежуточными состояниями. Метод Фейнмана дает, например,
возможность рассчитывать более простым путем, чем это делалось
раньше, такие процессы, как кулоновское рассеяние в высшем при-
приближении (см. работу Далица [95]). Как мы увидим ниже, его легко
также распространить на случай взаимодействия между частицами.
Вообще в старой теории процесс, включающий п промежуточных
состояний, требует вычисления 2й матричных элементов, каждый из
Рождение
Аннигиляция
Фиг. 6.
Ф и г. 7.
которых, вероятно, является гораздо более сложным, чем единствен-
единственное, заменяющее их фейнмановское выражение. Кроме того, при
расчете сложных процессов в старой теории легко потерять некоторые
из членов или ошибиться в знаке.
§ 3. Импульсное представление
В большинстве задач расчет значительно облегчается, если от
координатного пространства перейти к импульсному. Напомним, что
К+ — решение уравнения
(IV — т)К+B, 1) = г8*B, 1). ' (8.30)
Введем теперь фурье-образ функции К+, который обозначим че-
через S+(p), тогда
+ оо
К+B, 1) = f S+
(8.31)
где d4p = dp°dpl dp2 dp3. Вспомнив, что оператор (/V — т) можно
внести под интеграл в виде (р—т) и что 84-функцию можно напи-
написать в импульсном представлении
-1-СО
(8.32)
— оо
-1-СО
— *д = -щ* f e-b-<*-
получим следующее уравнение для S+ (p):
(р — /иM+(Р) = B<
(8-33)
Фейнмановская теория позитрона 85
или
5 (р) = —i— -^-i—. [ (8.34)
Это выражение можно переписать также следующим образом:
5 (р) = l l = l \ + тп l = l P + m (8 35)
+ BлL р — т Bкур + тр~т Bкур^~т^'
Мы уже показали, что
p2=^p^.=zp2_p2==p2> (8.36)
т. е. что знаменатель в выражении (8.35) не содержит больше мат-
матриц. С другой стороны, знаменатель в выражении (8.35) может быть
равен нулю. Эта возможность будет обсуждена ниже.
Если подставить теперь выражение (8.35) в (8.31), то получим
. (8-37)
Удобно определить интеграл /+B, 1) в виде
так как соотношение (8.37) можно тогда переписать следующим
образом:
АГ+B, l) = /(iV2 + /n)/+B, 1). (8.39)
Заметим, что интеграл /+ не содержит ни одного оператора Дирака,
а является просто функцией х2 и xt. Подставив выражение (8.39)
в (8.30), находим, что интеграл /+ удовлетворяет соотношению
(□ + «*')/+B, i) = _8*B, 1), (8.40)
где □ = V2. Это неоднородное уравнение Клейна — Гордона. Таким
образом, можно полагать, что интеграл /+ тесно связан с функцией
распространения бозе-частиц, т. е. частиц, спин которых равен
нулю.
Теперь мы должны проинтегрировать выражение (8.38), чтобы
получить интеграл /+ как функцию координат. Заметим, что при
этом необходимо интегрировать по каждой компоненте pv- в отдель-
отдельности. Записав отдельно пространственную и временную координаты
в показателе экспоненты, перепишем интеграл /+ следующим образом:
/ ±———*рар,. (8.41)
86
Глава 8
Подинтегральное выражение имеет полюсы при р1 — р*-\-тг = 0 или
при />0 = =t(/>2+ fft2)"^/2= =tЕр. По этой причине интеграл (8.41)
еще не определен. Чтобы определить его, Фейнман предложил рас-
рассматривать массу т как массу, имеющую бесконечно малую мнимую
отрицательную добавку, т. е.
т-+т— /8, S>0, (8.42)
и после устремить S к нулю.
Чтобы показать, что интеграл /+ теперь полностью определен,
проинтегрируем сначала по dp0, т. е. напишем
/+(х2 —Xl)-Bu) J
f
(8.43)
где, как и раньше, Ер = -\-(р%-\-/гс2I'2. Тогда соотношение (8.42)
означает, что Ер также имеет отрицательную мнимую добавку. Рас-
Рассматривая подинтегральное выражение в комплексной плоскости р0,
видим, что первый полюс ро = — Ер лежит теперь несколько выше
■ (- О
Ро
Ф и г. 8.
действительной оси (пути интегрирования), в то время как второй
полюс ро = -\-Ер — несколько ниже ее (фиг. 8). Проинтегрируем
выражение (8.43) по положительным значениям (t2— ^i). Это можно
проделать, замыкая контур интегрирования. Ввиду наличия экспо-
экспоненты такое замыкание нужно, очевидно, проводить ниже действи-
действительной оси. При этом полюс -\-Ер обходится по часовой стрелке.
Взяв вычет в этой точке, получим при интегрировании по р0
— =^— e~lEPl-t2~ti\ (8.44)
Если (i2 —1{) < 0, то мы должны замкнуть контур выше действи-
действительной оси, обходя при этом полюс —Ер против часовой стрелки.
В результате получим
"" '*~Ч" (8.45)
Фейнмановская теория позитрона 87
Заметим, что величина Ер, по определению, положительна, и, сле-
следовательно, показатель экспоненты опять отрицателен. Таким обра-
образом, интеграл /+, а значит, и функция К+ ведут себя согласно
формулам (8.25) и (8.26), а именно: при (t2 — ^i) > 0 играют роль
только положительные энергии, а при (t2 — ^i) <C 0 — только отрица-
отрицательные. Можно легко показать, что знак минус перед формулой (8.26)
является верным и, таким образом, условие (8.42) эквивалентно
нашему прежнему определению А'+1)-
Другая функция К получается, если вместо условия (8.42) по-
потребовать, чтобы величина р0 имела мнимую положительную добавку
. (8-46)
т. е. если интегрировать по пути, параллельному действительной
оси, и считать массу m действительной. При этом существуют два
полюса, лежащие ниже действительной оси, и при (t2 — tt)^> 0 играют
роль как положительные, так и отрицательные энергии, в то время
как при (t2 — у<0 внутри контура вообще нет полюсов. Следо-
Следовательно, К — импульсное представление функции распространения
в дираковской теории только для одних электронов, как это опре-
определяется формулой (8.23). Таким образом, различие между теорией
только для одних электронов и теорией дырок заключается лишь
в способе определения интеграла (8.41); эти теории одинаково
просты. Однако фейнмановская теория дырок имеет то преимущество,
что она является ковариантной, так как мнимая величина вводится
в инвариант т, в то время как в теории электронов — в компо-
компоненту р0 (в результате она становится отличной от других компонент).
Для несвободных электронов формализм теории позитрона, со-
совершенно аналогичный уже описанному, имеет смысл до тех пор,
пока внешний потенциал, во-первых, является достаточно слабым и,
во-вторых, достаточно медленно меняется. В связи с первым усло-
условием рассмотрим, например, случай кулонова поля, для которого
V = i°Ze2lr. Функция распространения в этом внешнем поле может
быть определена аналогично функциям (8.25) и (8.26), однако теперь
ип заменены на фп, являющиеся решениями уравнения Дирака в куло-
новом поле. Пока Z < 137, решения, соответствующие положительным
и отрицательным энергиям, имеют ясный смысл. Однако для Z > 137
эти решения больше не разделяются в энергетическом спектре щелью,
и различие в смысле положительных и отрицательных энергий ста-
становится неясным (см. работу Салама и Мэттьюса [421]).
§ 4. Электромагнитное поле
Предположим теперь, что рассматриваемый электрон взаимодей-
взаимодействует с внешним электромагнитным полем. В частности, выберем
!) Теперь, когда мы имеем интегральное представление (8.41) с усло-
условием (8.42), нет необходимости принимать во внимание отрицательный знак
в формуле (8.26).
88 Глава 8
электромагнитное поле таким, чтобы потенциал взаимодействия имел
вид
^еА; (8.47)
здесь мы подразумеваем, что по повторяющимся индексам произ-
производится суммирование. Уравнение Дирака теперь имеет вид
(iV — m)ty=eAty, (8.48)
а функцию распространения K't в этом внешнем поле можно опре-
определить как функцию, удовлетворяющую дифференциальному уравнению
(/V — eA — m)KiB, \) = itB, 1) (8.49)
и учитывающую только положительные энергии при t2 >■ tt, т. е.
в прошлом, и только отрицательные — при t2 < tx, т. е. в будущем.
Она удовлетворяет, таким образом, также интегральному уравнению
KfB, \) = K+B, \) — iefK+B, 3)АC)К + C, l)d%, (8.50)
которое уже включает указанные граничные условия. Разложение
этого интегрального уравнения по степеням потенциала возмущения
приводит к следующему ряду:
— ie JV*3/C+B, 3) AC)K+ C,
— ie? / d*x3 f d*XiK+ B,3) A C) K+ C, 4) A D) K+ D, 1) + . . .
(8.51)
В релятивистском случае связь между волновыми функциями ф B)
в точке х2 и фA) в точке Xj по аналогии с соотношением (8.2)
имеет вид (см. Приложение А)
£B, 1)^A)^, (8.52)
где d^x1 — элемент объема трехмерного пространства при фиксиро-
фиксированном времени tv а ф —решение уравнения (8.48). В нерелятиви-
нерелятивистском случае это последнее уравнение имеет вид
где й>0 — решение уравнения Дирака для свободной частицы. Заметим,
что мы выбрали такую функцию распространения, которая описывает
распространение частиц с положительной энергией по времени вперед,
а распространение частиц с отрицательной энергией — назад. В ре-
результате волновую функцию можно получить из уравнения (8.52)
только в том случае, когда компоненты, соответствующие частицам
с положительной энергией, определены на гиперповерхности, отве-
отвечающей некоторому раннему моменту времени, а компоненты, соот-
Фейнмановская теория позитрона 89
ветствующие частицам с отрицательной энергией, — на поверхности,
отвечающей несколько более позднему моменту времени. Поэтому
область интегрирования в выражениях (8.52) и (8.53) представляет
собой две плоские поверхности с постоянным временем t, между
которыми лежит пространственно-временная точка х2- Более точно
мы можем написать
фB)= / К+B, I)^(l)rf3*i— / К+B, Г)РФAО<*"*1'. (8.54)
tl<ta h>h
где в первый интеграл {tl < t2) входят лишь компоненты функции ф A),
соответствующие частицам с положительной энергией, а во второй —
компоненты функции фA), соответствующие частицам с отрицатель-
отрицательной энергией. Необходимость отрицательного знака перед вторым
интегралом видна из следующего: если волновая функция ф содержит,
например, только компоненты, соответствующие частицам с отрица-
отрицательной энергией, то формула (8.54) должна давать фB)->фA')>
а так как t2 лежит раньше tu то это может быть только в том
случае, если мы выберем отрицательный знак. Фейнман записал фор-
формулу (8.54) в более компактной и общей форме (см. Приложение А):
Х!), (8.54а)
где интегрирование производится по двум пространственно-подоб-
пространственно-подобным поверхностям о1), содержащим точку 2, а пх — внутренняя
нормаль к пространственно-подобной поверхности в каждой точке.
Если поверхность выбрана плоской (постоянное время t, причем
<1з(xt) = йьхг), как это было сделано выше, то нормаль пг напра-
направлена в положительном направлении t для более ранней поверхности,
соответствующей t\, и в отрицательном направлении t для более
поздней поверхности, соответствующей t'[.
Далее, в теории Фейнмана компоненты, соответствующие части-
частицам с положительной энергией, рассматриваются как амплитуды
вероятности того, что электрон имеет обычный отрицательный
заряд, в то время как компоненты, соответствующие частицам
с отрицательной энергией, рассматриваются как амплитуды вероят-
вероятности обнаружения позитрона с энергией —Е > 0. Таким образом,
чтобы определить волновую функцию в некоторый момент времени,
необходимо знать позитронную компоненту в последующий момент
времени и электронную компоненту в предыдущий момент времени.
Иными словами, амплитуда вероятности того, что один заряд нахо-
дится в пространственно-временнбй точке лг2, t2, не определена,
J) Пространственно-подобная поверхность — это поверхность, любые две
точки х, у которой не могут быть связаны световым сигналом, т. е. всегда
(х-уJ<0,
90 Глава 8
если известна только амплитуда вероятности обнаружения электрона
(или позитрона) в более ранний момент времени. Хотя позитрон не
мог присутствовать в более ранний момент времени, пара могла
родиться при самом акте измерения, которое дает амплитуду
вероятности обнаружения позитрона в будущем.
Амплитуда вероятности перехода электрона из некоторого со-
->
стояния с волновой функцией фоС*^- ^1) частиц с положительной
->
энергией в момент tt в состояние с волновой функцией <ро(х2, У
частиц с положительной энергией в момент t2 > tx дается теперь
выражением
М = f <fo(x2, t2)K+(x2, t2; xv ^)^o(*i. t1)d*x1dsx2 =
J . (8.55)
Если внешний потенциал еА действует между моментами времени
tt и t2, то функция К+ заменяется на функцию АГ+. Поэтому ампли-
амплитуда вероятности перехода в первом приближении в соответствии
с разложением (8.51) равна
. (8.56)
Однако соотношения (8.52) и (8.53) дают теперь возможность про-
-> ->
вести интегрирования по хг и х2, так как имеют место соотно-
соотношения
fK+C, 1){%(')<*3*1 = ФоC). (8.57)
/То B) Р/С.,. B, 3) d»x2 = То C); (8.58)
таким образом, равенство (8.56) принимает вид
Мх = — le f d*x&0 C) А C) % C). (8.59)
Предположим теперь, что начальная волновая функция соответ-
соответствует электрону, находящемуся в состоянии с положительной энер-
энергией и 4-импульсом pj, а конечная волновая функция — электрону
с 4-импульсом р2; следовательно,
Фо 00 = «(л)'■*''" (8-б0)
Ф0(х) = п(^2)г+^-х, (8.61)
где и — введенные выше спиноры, соответствующие свободным
частицам с положительной энергией. Если теперь ввести фурье-образ
Фейнмановская теория позитрона 91
функции Лр_(х), определенный следующим образом:
(8.62)
то подстановка выражений (8.60) —(8.62) в равенство (8.59) по-
позволит провести интегрирование по х3, так как эта переменная
появится теперь только в показателях экспоненты. Таким образом,
мы получаем
М1= — ie BтсL J* йЧгЪ* (р2 — к — рх) п(р2) а (к) а (рг) =
— -> ->
== — ie BтгL а (р2) а (р2 — рг) а (рг), (8.63)
что может быть истолковано как обусловленный внешним полем
вклад величины к = р2 — р1 в энергию-импульс частицы, причем
энергия-импульс всей системы (включая внешнее поле) при взаимо-
взаимодействии сохраняется [множитель 84(р2 — k — pt)].
Аналогичным образом, матричный элемент перехода от р1 к р2
во втором приближении получаем в виде
М2 = (— ief J d*x3 f d'xtf0 C) A C) K+ C, 4) A D) ф0 D); (8.64)
эта формула после подстановки фурье-образа функций А и К+
"[см. формулы (8.62) и (8.37)] и амплитуд [см. формулы (8.60)
и (8.61)] сводится к выражению
Мг = — ie* Bit)* J d*p J d*k, j rf**28* (pa — kx — p) 8* (Pl + k2 — p) X
~ "*" ' (Pi)' (8.65)
(p2 — Pl — k)-^—-1 a(k)«(^). (8.66)
p\ -f-« — /к
Выражение для М8 можно интерпретировать следующим обра-
зом. Электрон, имевший сначала импульс рх [множитель и^)],
взаимодействует с внешним полем [множитель а (к)] и получает от
него импульс к. Далее, он распространяется с импульсом
1
[множитель {Px~\-k — m)] и снова взаимодействует с внешним
потенциалом,* получая от него импульс р2 — pj — к; в результате
в конечном состоянии импульс электрона становится равным р2-
Так как возможны любые значения к, то нужно проинтегрировать
по ним. Ясно, что аналогичным образом можно выписать и члены
более высокого порядка, не выводя их явно.
Только что развитый метод можно легко использовать для рас-
расчета вероятности рождения пары во внешнем поле. В этом случае,
однако, временная компонента, соответствующая позитрону, отри-
отрицательна, а компонента, соответствующая электрону, положительна.
92 Глава 8
§ 5. Бозе-частицы
Бозе-частицы, подчиняющиеся уравнению Клейна—Гордона, также
могут трактоваться с помощью метода Фейнмана [169]. В атомных
единицах й = с = 1 уравнение Клейна-^Гордона имеет вид
(□-Ь™2)ф = 0, (8.67)
или, введя оператор импульса р^ = 1д/дх", можно написать
( — р2+/гс2)ф = 0. (8.68)
В данном случае функцией распространения частицы является функ-
функция /+, введенная нами ранее [см. формулу (8.38)]. Она удовлетво-
удовлетворяет следующему неоднородному уравнению:
(□+я*2)/+B, 1) = — S*B, 1). (8.69)
Если существует взаимодействие с внешним электромагнитным
полем, то р^ в уравнении (8.68) следует заменить на р?—еА^,
в результате уравнение Клейна—Гордона примет вид
{ЬГ—еА*){Р9.— еА^ — т*L1 = О. . (8.70)
Уравнение для функции распространения при наличии взаимодей-
взаимодействия с внешним полем записывается теперь следующим образом:
{(р*—еА*)(Р9.— еА,) — т*}3ХB, 1) = — S4B, 1). (8.71L
Если мы выберем калибровку внешнего потенциала так, чтобы
дАр/дх^ = 0, то р^ и А^ будут коммутировать, и уравнение (8.70)
можно переписать в виде
(pS — m2)/.fB, 1)= —34B, i)+{2«Aj^ — e\A^nli{2, 1); (8.72)
последнее уравнение в свою очередь можно преобразовать в сле-
следующее интегральное уравнение:
/+B. 1) = /+B, 1)— //+B, 3) {2еА..C)$ —
— е2А...C) А*C)} /+ C, 1)cfx^. (8.73)
Действуя на него оператором р2 — тг, мы можем снова получить
уравнение (8.72). Уравнение (8.73) включает, однако, граничное
условие: /+ содержит лишь положительные частоты при t2 > t1
(tx следует раньше t2) и отрицательные частоты при t2 <C tx (tt сле-
следует после t2). Это последнее интегральное уравнение также можно
разложить в степенной ряд, в котором появится член А2, соответ-
соответствующий двухкратному взаимодействию с внешним полем. Мы не
!) Индекс 2 у скобки и у оператора р^. = ihdjdx^ означает, что соответ-
соответствующие операторы действуют на функции точки 2,
Фейнмановская теория позитрона 93
будем обсуждать здесь член этого типа, так как снова встретимся
с ним при рассмотрении взаимодействия ir-мезона с квантованным
электромагнитным полем (см. гл. 19), тогда мы и проанализируем
этот тип взаимодействия.
Здесь же только заметим, что уравнение, соответствующее
уравнению (8.52), для случая бозе-частиц имеет вид (см. Приложе-
Приложение А)
Л^> ^ (8-74)
причем интегрирование ведется по двум плоским поверхностям,
между которыми лежит пространственно-временная точка 2. Для
времен, предшествующих времени 2, дают вклад только компо-
компоненты" ф с положительной частотой, а для времен, следующих за
временем 2, — только компоненты ф с отрицательной, частотой.
В прямой аналогии с дираковским полем их можно интерпретиро-
интерпретировать как волновые функции положительно и отрицательно заряжен-
заряженных бозонов. Скалярное произведение двух волновых функций
бозонов дается выражением A.16).
Глава 9
ПРИМЕНЕНИЯ ТЕОРИИ ФЕЙНМАНА
§ 1. Резерфордовское рассеяние
В гл. 6 мы рассмотрели теорию рассеяния электронов высокой
энергии кулоновым полем. В частности, мы написали ряд борнов-
ского приближения F.2) с точностью до членов первого порядка
по Za. к первому релятивистскому борновскому приближению.
В качестве примера применения формализма Фейнмана получим
теперь релятивистскую формулу рассеяния в первом борновском
приближении.
В предыдущей главе был написан матричный элемент, предста-
представляющий собой в первом порядке амплитуду рассеяния электрона
внешним потенциалом при переходах электрона из состояния, опи-
-*•
сываемого спинором и {р^), в состояние, описываемое спинором
•>
и(р2). Он имеет вид
(
М2 = (— 1е) B*)* а (£2) а (р2 — рО а (рг) (9.1)
и соответствует диаграмме Фейнмана, представленной на фиг. 3.
Если рассматриваемое нами внешнее электромагнитное поле является
кулоновым полем ядра с зарядом Ze(A° = V = Ze/r), то
«(q) = щг / «*"хт4 <х) dix =
&V (?) = -g- ± 5 (q0) Т" D. (9.2)
В этом случае амплитуда вероятности перехода имеет вид
М2 = — 2**8 (Ех — Е2) \и (р2) JnZl2 fu (pS\ , (9.3)
!) Здесь мы используем нерационализированную гауссовскую систему
единиц, в которой
— 4-nZeo (/•) и а = ^- =
Применения теории Фейнманй 95
где Е\ = Е2 = Е—энергия электрона. Вероятность перехода опре-
определяется квадратом модуля М2, т. е.
_ -»•
" Ог) — 5: Т°"
1 1»
(9.4)
Сразу ясно, что это выражение равно бесконечности из-за наличия
множителя S @), так как [S (Et — Е2)]2 =b(Et — Е2) 8 @). Однако
множитель S @) можно истолковать следующим образом:
+ Г/2
8@)= lim lim ~ С e^dt= lim ^-, (9.5)
где Т — время взаимодействия. Таким образом, вероятность пере-
перехода в единицу времени, ie/i^.2» в заданное конечное состояние,
->
описываемое спинором и(р2), имеет вид
■T°«(A)
—Е2). (9.6)
\P2— Pi I2
По форме это выражение совпадает с общим выражением G.2) для
вероятности перехода в заданное конечное состояние.
Так как нас не интересует ориентация спина электрона в ко-
конечном состоянии и так как падающий пучок электронов рассма-
рассматривается как неполяризованный, то выражение для | М212 должно
быть просуммировано по конечным и усреднено по двум начальным
ориентациям спина электронов. В соответствии с гл. 7 выраже-
выражение (9.6) при этом примет вид
w = * l.— 4Z2£4
1 s (A + m „pt + m \
2 ' 2m 2m '
Здесь под w подразумевается полная вероятность перехода в еди-
единицу времени в группу конечных состояний с плотностью конечных
состояний, равной dnfjdE = pf [см. соотношение G.3)]. Используя
свойства шпуров матриц ^ (см. гл. 7, § 5), можно легко вычислить
шпур в выражении (9.7). Вспомнив, что шпур от нечетного числа
матриц у равен нулю, и использовав соотношение G.58), получим
sp [Ч^ ^ЧР °)
> • Pi + "i2) = 2^ (Е* +р2 • рх + т*). (9.8)
Так как внешнее поле не зависит от времени, то энергия частицы
сохраняется, т. е.
Е = Ег = Ег = (р\ + mj* = {pl+mT. (9.9)
96 Глава 9
Отсюда следует, что сохраняется также величина трехмерного
импульса частицы. Если 6 — угол рассеяния, то
|ll|8e .10)
где |Л| = |^|=:р.
Кроме того, из релятивистской механики известно, что
= £, или ^-=1—^2 (9.11)
,£2 V >
где v—скорость частицы; таким образом, выражение (9.8) можно
переписать следующим образом:
~v>sm*±). (9.12)
Аналогично в силу сохранения величины трехмерного импульса
частицы имеет место соотношение
I?!— £2|=2/>sini-. (9.13)
Таким образом, для вероятности перехода w получаем
ЫЬ (9Л4)
так как /?/£ = •» как в нерелятивистской, так и в релятивистской
области энергии. Для получения дифференциального сечения выра-
выражение для w нужно разделить на плотность падающего потока,
которая равна vE/m= р/гп. (так как мы нормировали спинорные
волновые функции одной частицы на величину m/Е). Вспомним, что
плотность конечных состояний на единицу энергии [см. соотноше-
соотношение (9.9)] имеет вид
ЕB
так как
окончательно получаем
sin* A
Применения теории Фейнмана 97
Это выражение совпадает^ с выражением F.2) с точностью до попра-
поправочного члена Za. В следующем приближении, т. е. с учетом двой-
двойного рассеяния, расчет был проведен Далицом [95], который под-
подтвердил результаты Мак-Кинли и Фешбаха [316], а также выяснил
некоторые ошибки предыдущих авторов в высших борновских при-
приближениях теории поля.
Рассеяние частиц со спином 0 можно рассмотреть аналогичным
образом с учетом лишь члена А^р?- в выражении (8.73). При этом
формула для сечения будет совпадать с формулой (9.17), за исклю-
исключением множителя 1—v2 sin2 (Й/2), который как раз и возникает
из членов, зависящих от спина частиц. Случай рассеяния частиц
со спином 1 был рассмотрен в работе Месси и Корбена [325],
причем формула для сечения рассеяния отличается от формулы Ре-
зерфорда множителем (* ~Ь ^ ("^) sin2OJ.
§ 2. Уравнения для связанных состояний
До сих пор мы изучали лишь задачу рассеяния. Однако, исполь-
используя формализм Фейнмана, можно также изучать задачу связанных
состояний. Ясно, что в этом случае следует рассматривать частицу
как испытывающую постоянное воздействие заданного потенциала.
Определим поэтому величину К"^ B, 1) как амплитуду вероятности
перехода частицы из точки 1 в точку 2 при и-кратном рассеянии
заданным не зависящим от времени потенциалом А. Тогда выраже-
выражение для амплитуды вероятности перехода частицы из точки 1 в точку 3
при (п-\- 1)-кратном рассеянии имеет вид
/С'+ЧЗ, 1) = — ief K+C, 2)ДB)/С» B, \)d*xr (9.18)
Отсюда следует, что функция распространения частицы из точки 1
в точку 3 при произвольном числе рассеяний должна выражаться
в виде ряда
со
/Cf C, 1) = 2/С+C, 1). (9.19)
Проведя суммирование по всем п. в обеих частях соотношения (9.18),
получим уравнение
К±(% 1) —/С+C, 1) = — te /к+C, 2)AB)K$B, l)d*x3, (9.20)
которое совпадает с полученным выше интегральным уравнением
для ядра во внешнем поле.
Аналогичное рассуждение можно применить к функции a>n(l),
которая представляет собой амплитуду вероятности того, что
98 Глава 9
электрон с начальной волновой функцией ср0 перейдет в точку 1,
испытав при этом я-кратное рассеяние. Вспомнив, что
2т»B), (9.21)
напишем уравнение, соответствующее уравнению (9.20), в виде
<|> B) = ср0 B) — ie f K+ B, 3) А C) <|» C) d*xs. (9.22)
Это есть не что иное, как интегральная форма уравнения Дирака
при наличии внешнего поля. Действительно, применив оператор
Дирака (/V — т.) к обеим частям уравнения (9.22), получим
(iV2 — /*)фB) = еЛB)фC), (9.23)
так как
—/и)сроB) = О. (9.24)
Кроме того, здесь мы воспользовались соотношением (8.22). Решая
дифференциальное уравнение (9.23), можно, несомненно, получить
решения как задачи рассеяния, так и задачи связанных состояний
в зависимости от граничного условия, налагаемого на волновую -функ-
-функцию. Для задачи рассеяния волновая функция ф должна иметь сле-
следующий асимптотический вид:
(9-25)
где ф4—падающая плоская волна, а ф8—расходящаяся рассеянная
волна. Это выражение для волновой функции ф по форме в точно-
точности совпадает с уравнением (9.22), в котором <роB)—падающая
плоская волна. (Так как здесь мы рассматриваем потенциалы, умень-
уменьшающиеся с расстоянием быстрее, чем г, то о фазовых множи-
множителях в падающей волне можно не заботиться.) Таким образом,
уравнение (9.22) представляет собой интегральную форму уравнения
для задачи рассеяния. Интуитивно чувствуется, что волновая функ-
функция связанных состояний должна удовлетворять однородному инте-
интегральному уравнению
ф B) = — ie J K+ B, 3) А C) ф C) Фх3, (9.26)
так как оно не содержит падающей волны. Это в действительности,
так. Отсутствие <р0 можно лучше всего уяснить себе, если вспо-
вспомнить, что энергия связанного состояния всегда меньше т. Волно-
Волновая же функция ср0 характеризует свободную частицу с энергией,
большей или равной т. Следовательно, пока »0 ф 0, мы не в со-
состоянии удовлетворить уравнению (9.22) функцией типа
ф(х) = и(х)е-«* (Е<т), (9.27)
которая характеризует связанное состояние.
Применения теории Фейнмана 99
§ 3. Задача двух частиц
В качестве третьего примера применения формализма Фейнмана
рассмотрим взаимодействие двух частиц посредством электромагнит-
электромагнитного поля. При этом мы будем близко следовать работам Мёллера
[339, 340].
Если выбрать лоренцовскую калибровку, то уравнение Максвелла
для потенциалов примет вид
ПА, = 4*Д. (9.28)
Полученное уравнение можно решить с помощью функции Грина D+,
которая, по определению, удовлетворяет уравнению
□ 2£>+B, 0 = 4*8B, О: (9-29)
функцию Грина D+ можно представить в интегральной форме (с фейн-
мановским обходом полюсов), т. е.
-Ьсо
По существу, это выражение совпадает с выражением (8.38) для /+,
когда масса m равна нулю. Теперь можно написать равенство
A)<***!; (9.31)
в нем отсутствует однородный член. Это соответствует граничному
условию: в моменты времени t = ± оо нет свободного излучения
(т. е. отсутствуют решения А^ уравнения □^|?>=0).
Рассмотрим, далее, случай двух заряженных фермионов. Каждая
из частиц является источником электромагнитного поля, которое
оказывает влияние на движение другой частицы. Следовательно,
в результате взаимодействия частицы рассеиваются друг другом.
Используя квазиклассическую теорию излучения, запишем выражение
для тока, соответствующего переходу электрона а из состояния
-*■ ■*■
ua(Pi)e~iVi'x в состояние ua(p2)e~'lv*'*, в виде
этот ток в соответствии с равенством (9.31) создает в простран-
пространственно-временной точке х поле с потенциалом
А» (х) = е J d*x'D+ (х — х')
Pi) «a(P2
Этот потенциал теперь действует на движение второго электрона Ь.
С одной стороны, согласно соотношению (8.59), матричный элемент
100 Глава 9
первого порядка, соответствующий переходу (обусловленному ука-
указанным потенциалом) электрона b из состояния qx в состояние q2,
имеет вид
М = — le f а*хпь (£,) е+иь-*$А^ (х) иь 4) e~i<1'-* =
(9.34)
С другой стороны, вместо непосредственной записи матричного
элемента взаимодействия мы могли бы рассмотреть (как в случае
одной частицы) функцию распространения системы двух частиц.
В нерелятивистском приближении система двух частиц описывается
•> ->•
волновой функцией Шредингера ф (ха, хъ, Г), и мы совершенно точно
можем определить функцию распространения К(ха, xb, t\ xa, xb, t );
она представляет собой амплитуду вероятности того, что частица а
->■ ->
из точки ха в момент г перейдет в точку ха в момент t, тогда
■*■» ■*"
как частица b из точки хь в момент t' перейдет в точку хь в момент t.
Если частицы не взаимодействуют между собой, то
К(ха, хь, t; х'а, х'Ь' *') = КОа{ха, t; x'a, t') Коь(хь, t; х'ь, f), (9.35)
где КОа — функция распространения свободной частицы а. Далее,
в случае отсутствия взаимодействия можно определить более общую
функцию распространения, когда времена этих частиц в начальном
и конечном состояниях не совпадают. Так, мы можем определить
функцию
/Со(8, 4; 1, 2) = /СоаC, 1)/СобD, 2), (9.36)
которую можно интерпретировать как функцию распространения
частицы а из точки 1 в точку 3, а частицы b из точки 2 в точку 4.
Когда частицы взаимодействуют, то функцию распространения
системы можно определить только в том случае, если предположить,
что взаимодействие между частицами в интервалах времен от t1 до t.2
и от t3 до t± равно нулю. Физически это часто не осуществляется.
Несмотря на это, мы будем предполагать, что можно пренебречь
эффектами взаимодействия между частицами в интервалах времени
tx—12 и ti—13 по сравнению с эффектами взаимодействия в более
длительных интервалах времени t.^ —11 и Г4 —12. В задаче рассеяния
такое пренебрежение вполне оправдано, так как в начальном и ко-
конечном состояниях системы частицы настолько отдалены друг от друга,
что взаимодействием между ними в этих состояниях (т. е. в интер-
интервалах времени t2 —11 и t^ —13) вполне можно пренебречь.
По аналогии с соотношением (8.63) можно рассматривать выра-
выражение (9.34) как матричный элемент, возникший из поправки пер-
Применения теории Фейнмана 101
вого порядка /С*1* к функции распространения двух свободных
частиц, причем
Л™ (8, 4; 1, 2) =
=-ie2 Г frf**5d%/e+eC, S)tS^+o(S. 1)£>+(Б,6)/С+ьD,6)Тб.*+й(е,2).
(9.37)
Как и выше, мы можем представить выражение (9.37) диаграм-
диаграммой Фейнмана (фиг. 9); множитель D+ в этом выражении следует
рассматривать как функцию распространения виртуального фотона
Фиг.
(на фиг. 9 она указана волнистой линией). Выражение (9.37) факти-
фактически является основой фейнмановской электродинамики. Оно опи-
описывает эффект, при котором два заряда обмениваются одним фото-
фотоном. Хотя вышеприведенный вывод недостаточно удовлетворителен,
так как мы не квантовали электромагнитного поля, однако можно
показать (см. работы Фейнмана [170] и Дайсона [126, 127]) и мы,
действительно, покажем ниже (см. гл. 17), что, несмотря на это,
он верен: теоретический вывод, основанный на релятивистском кван-
квантовании поля, в первом борновском приближении дает то же самое
выражение (9.37).
Следует отметить, что матричный элемент является релятивистски
инвариантным. Так как суммирование идет по \х, то матричный
элемент учитывает продольные и поперечные волны релятивистски
симметричным образом. В импульсном пространстве матричный элемент
можно переписать в несколько более привычной форме, если вспо-
вспомнить, что потенциал А^, определенный соотношением (9.31), должен
удозлетворять условию Лоренца, dAJdxa = 0, для того чтобы взаимо-
взаимодействие носило правильный электромагнитный характер. Таким
образом, дифференцируя выражение (9.33) по х и учитывая условия
Лоренца, получаем
па (Р2) Т&Ма (Рд = «а Ш (т£*° — 1а "
102 Глава 9
Это соотношение в действительности имеет место, так как из-за
наличия S-функции k = pz—pv a u1(p2)n м1(/?1) являются спинорами
свободных частиц; следовательно,
МЛ) (А — А)«(а)=»(а)Ка- — и) — (А — «)]и(А) = 0. (9.39)
Таким образом, всюду, где в выражении (9.34) встречается ма-
матрица у0, можно воспользоваться соотношением
и заменить у° величиной 7crf(*/^o)> T- е-
где fj — матрица у в направлении распространения k (заметим, что
k0 ф \k\, так как мы имеем дело с виртуальным фотоном). Из этого
результата следует, что фотон поляризован перпендикулярно к напра-
направлению своего распространения. Соотношение (9.41) в действитель-
действительности имеет место для обеих частиц, так как с таким же успехом
можно считать, что частица b излучает фотон, а частица а погло-
поглощает его. Таким образом, обозначив поперечные компоненты через t^,
получим
_=
Jn t. t.
,0..O Zj ~alb
-i5L-TF-- (9-42)
Первый член этого выражения характеризует мгновенное взаимо-
взаимодействие и соответствует кул©новскому потенциалу, так как он
является фурье-образом кулоновского потенциала. Второй член учи-
учитывает лишь поперечные кванты, которые обусловливают обычное
запаздывающее магнитное взаимодействие частиц.
До сих пор не принимался во внимание тот факт, что рассма-
рассматриваемые частицы тождественны и подчиняются принципу Паули.
Учет этого обстоятельства приводит к требованию антисимметрич-
антисимметричности волновой функции системы частиц, что обеспечивается введе-
введением функции распространения АГC, 4; 1, 2) — КD, 3; 1, 2) для
перехода двух частиц из точек I и 2 в точки 3 и 4 соответственно.
Применения теории Фейнмана
103
Таким образом, матричный элемент рассеяния двух тождественных
частиц в первом неисчезающем приближении имеет вид
I Pa—Pi Is
_M£>J^^^
(9.43)
Часто это выражение называют матричным элементом мйллеров-
ского рассеяния. Он является матричным элементом низшего порядка
по константе взаимодействия.
Порядок е2
Порядок е4
\
с d
Фиг. 10.
В высших приближениях появляется бесконечное число поправок
к этому матричному элементу, соответствующих обмену более чем
Фиг. 11.
одним фотоном между частицами и собственному взаимодействию
частиц. Несколько таких простейших диаграмм приведены на фиг. 10.
На фиг. 10 не приведены диаграммы, соответствующие излучению
и поглощению фотона одной и той же частицей без всякого обмена
104
Глава 9
фотоном. Заметим также, что временной порядок взаимодействия
в фейнмановских диаграммах не имеет особого значения, а именно
диаграмма на фиг. 11 эквивалентна диаграмме на фиг. 10,с.
Теперь мы в состоянии применить к настоящей задаче метод,
развитый в гл. 7, § 1. Для простоты ограничимся рассмотрением тех
диаграмм взаимодействия, которые не содержат перекрывающихся
фотонных линий; такие диаграммы приведены на фиг. 12. Для пол-
полной аналогии с задачей одной частицы, функцию fn.(x1, x2) назовем
амплитудой вероятности нахождения двух частиц (которые вначале
и т.д.
Фиг. 12.
были свободными и не взаимодействовали между собой) в точках xt
и х2 соответственно после обмена п фотонами. Тогда амплитуда
вероятности после обмена (я-j-l) фотоном имеет вид
?я+1A, 2) =
, 4)T6,D+C, 4)сриC,
(9.44)
Следовательно, полная амплитуда вероятности в таком приближении
(которое обычно называется лестничным приближением) выражается
в виде следующего ряда:
оо
4>(xlt x2)= 2 фя(х„ х2),
(9.45а)
причем
= сооB,
—is* / К+а С1 - 3) ПК+Ь B, 4) Тй;)£>+ C, 4) ф C, 4) d*x3d*x4, (9.456)
где 'foB, 1) — волновая функция, удовлетворяющая уравнению Дирака
для свободной частицы по обеим ее переменным. Если к обеим
частям уравнения (9.456) применить операторы Дирака для частиц а
и Ь, то получим дифференциальное уравнение для Ф
i m)'}!B, 1) = ie^ilh^D+B, 1)фB, 1). (9.46)
Применения теории Фейнмана 105
Это уравнение впервые было получено Бете и Салпетером [422]
(см. также работы Намбу [351]), Швингера [442], Гелл-Манна и Лоу
[203] и Кита [275]).
Уравнение (9.46) рассматривается в гл. 25, там же проводится
его обобщение на более сложные случаи взаимодействия, чем при-
приведенные выше, и исследуются вопросы связи этого уравнения
с теорией поля, а также физическая интерпретация волновой
функции.
§ 4. Сечение мёллеровского рассеяния
Введем для матричного элемента (9.43) мёллеровского рассеяния
двух частиц следующее обозначение:
М= —Bir)*flR8<(Pl + qi^p2—q2). (9.47)
Тогда вероятность перехода будет определяться величиной \M\Z,
и выражение для вероятности перехода в заданное конечное состоя-
состояние в единицу времени и объема будет иметь вид1)
+ q1 — р2 — Qa)- (9-48)
Число конечных состояний равно
Однако так как в силу закона сохранения импульс частицы b опре-
определен в конечном состоянии, если известен импульс частицы а, то
следует принимать во внимание лишь фазовый объем одной конеч-
конечной частицы, или, другими словами, мы должны вести интегрирова-
интегрирование по трехмерному объему cPq, в результате чего выпадает трех-
трехмерная 8-функция. Таким образом, полная вероятность перехода
в единицу времени и объема выражается следующим образом:
"W (З^тЙттет*8^*3' (9'50)
а сечение рассеяния
*,=-*Щ±-. (9.51)
1) Аргументация при этом аналогична приведенной в § 1. Однако соот-
соотношение (9.5) здесь заменяется 4 мерной 8-функцией и поэтому необходимо
положить о4 @) -*■ Bл)~4 VT, где V—объем, в котором происходит взаимо-
взаимодействие.
106 Глава 9
■> ■>
где V — нормирующий множитель, (т/Е), a vl — v2 — относительная
скорость частиц1).
Если один из электронов до столкновения покоился, а второй —
имел энергию Е (где Е = ~{тс2) в лабораторной системе координат,
то угол рассеяния 6* (величины, относящиеся к системе центра
инерции, снабжены звездочкой сверху) будет связан с углом 9 со-
соотношением
cos0 — 2 + G-l)sin»6- (Э>52)
Вычислив матричный элемент М и множители, входящие в выраже-
выражение (9.51), Мёллер [339, 340] получил следующую формулу для
дифференциального сечения рассеяния:
2*. (9) sin « М = 4*
где
x = cos6*. (9.54)
Эта формула пригодна для всех углов рассеяния. Для малых углов
рассеяния первый член в скобках выражения (9.53) переходит в обыч-
обычное релятивистское выражение Резерфорда
1 (9.55)
sin*(8/2) '
ибо для малых углов 0*?» F/2).
Что касается энергетической зависимости, то легко показать,
что импульс каждого электрона в системе центра инерции опреде-
определяется величиной
р = т.7, Т (9.56)
/2( + 1)
и, следовательно, множитель перед скобками в выражении (9.53)
равен
(^)\ (9.57)
D Если предположить, что частица 2 закреплена, то поток падающих
частиц 1 будет равен \v± — Va\IVi, так как плотность частиц 1 равна 1/Vt.
Сечение рассеяния есть число актов рассеяния в единицу времени и объема,
деленное на падающий поток частиц и на число частиц в единице объема
рассеивателя A/V2). Это определение ведет к формуле (9.51). Выражение (9.51)
инвариантно по отношению к лоренцовским преобразованиям в направлении
-> ■>•
относительного движения частиц vi — v%.
Применения теории Фейнмана 107
т. е. в точности совпадает с соответствующим множителем в реля-
релятивистской формуле Резерфорда (9.17). Можно показать, что член
| 4 \
т 1 Х2 )
обусловлен спином электрона1). Второй же член в выражении (9.53)
связан с наличием обменного члена в матричном элементе.
Формула (9.53) была экспериментально подтверждена Пейджем
[362, 363] при изучении рассеяния р-частиц в тонких бериллиевых
мишенях в интервале изменения f от 2 до 4,5 и углов рассеяния
вплоть до 90° в системе центра инерции. При угле, равном 90°,
основной вклад в формулу рассеяния (9.53) дает спиновый член, что
было подтверждено указанными экспериментами. Эксперименты по
рассеянию (Скотт и др. [450]) электронов с энергией 15,7 Мэв
электронами находятся в хорошем согласии с мёллеровской форму-
формулой (9.53) в интервале углов от 70 до 105° в системе центра инерции.
Когда после войны были спроектированы ускорители высокой
энергии, многих физиков интересовал вопрос, пригодна или непри-
непригодна формула (9.53) для электронов высокой энергии. В частности,
из соображений классической физики можно было ожидать, что для
падающих электронов с длиной волны % порядка классического
радиуса электрона ег/тс2 будет иметь место отклонение от формулы
точечного рассеяния. В этом случае электрон должен обладать энер-
энергией 137тс2 в системе центра инерции; такую энергию сравнительно
легко можно реализовать при рассеянии электронов на протонах,
так как энергия электрона в лабораторной системе в этом случае
почти такая же, как и в системе центра инерции, т. е. 137/тгс2,
а электроны такой энергии легко получить ускорением их в син-
синхротроне. С точки зрения чисто классической физики рассеяние
электронов на протонах очень удобно для изучения „размеров"
электрона, так как радиус протона в классической электродинамике
равен е2/Мс2, т. е. значительно меньше радиуса электрона. Однако
в действительности вокруг протона имеется облако виртуальных
—in 1
мезонов с радиусом Й/^с—1 ,4 • 10 см = -~-е2/тс2. Поэтому, есте-
естественно, его нельзя считать точечным зарядом. Для исследования
границ применимости электродинамики нужно изучать рассеяние
электронов на электронах (возможно также изучение (х-мезоиов,
однако их слишком мало в нашем распоряжении). В этом случае
величине -[•*= 137 в системе центра инерции соответствует, согласно
выражению (9.57), ■[■ = 2 ■ 1372^ 40 000, или в лабораторной системе —
энергия электрона порядка 20 Бэв. Даже сегодня i получение элек-
электронов таких высоких энергий — дело далекого будущего. Однако
в 1946 г. выяснилось, это эта задача потеряла свое значение.
См. книгу Мотта и Месси [348].
108
Глава 9
Современные теории уже не предсказывают отклонений экспериментов
от теории при столь высоких энергиях. В любом случае отклонения
от мёллеровского рассеяния, если они существуют, вероятно, легче
наблюдать при более низких энергиях, даже если эти отклонения
очень малы. Предсказываемые современной теорией отклонения обу-
обусловлены многократным обменом фотоном с учетом радиационных
поправок (см. фиг. 10, & и с). Но они составляют при энергиях
электронов порядка нескольких Мэв около одного процента.
§ 5. Рассеяние позитронов на электронах
В случае рассеяния позитрона на электроне в низшем прибли-
приближении по заряду существуют две фейнмановские диаграммы (фиг. 13
и 14), соответствующие возможности вир-
виртуальной аннигиляции электрона и пози-
позитрона в начальном состоянии с последую-
последующим их рождением в конечных состоя-
состояниях.
Фиг. 13.
Ф и г. 14.
в гюкое
\
.+тсг
Дырка (позитрон)
\
Ничильное
состояние
Конечное
состояние
Процесс 2
Ф и г. 15.
Заметим, что в этом случае нет необходимости брать антисим-
антисимметричную функцию распространения, так как электроны и пози-
позитроны не являются тождественными частицами.
В старой теории возмущения эти два процесса описывались бы
следующим образом:
Применения теории Фейнмана 109
Процесс 1. а) Электрон переходит в энергетическое состояние,
которое выше первоначального на величин}' энергии Д£\ б) Дырка
заполняется электроном с отрицательной энергией, который нахо-
находился в энергетическом состоянии выше этой дырки на величину
энергии Д£. При этом создается новая дырка, или позитрон, но
уже с меньшей кинетической энергией.
Процесс 2. а) Электрон заполняет дырку, б) Электрон с отри-
отрицательной энергией переходит в состояние с положительной энер-
энергией, создавая при этом пару — электрон и дырка (позитрон).
Эти процессы иллюстрируются на фиг. 15.
Процессам 1 и 2 соответствуют матричные элементы Мг и М2-
Согласно принципу Паули, полный матричный элемент равен Мх — М>.
Баба [37] *> в результате вычислений получил формулу для сечения
рассеяния позитрона на электроне, которая имеет такую же струк-
структуру, как формула Мёллера для рассеяния электрона на электроне,
и отличается от нее лишь незначительно.
Экспериментальная проверка формулы Баба является также про-
проверкой всей теории дырок и, в частности, указанных выше двух
возможных процессов. Ашкин [11, 12] подтвердил правильность
формулы Баба экспериментами по рассеянию позитронов в интер-
интервале энергий от 0,6 до 1 Мэв и вплоть до углов 90°. Как и выше,
обменный член в формуле Баба существенен для получения согласия
теории с экспериментом.
Подробности см. в книге Росси [414].
ЧАСТЬ ВТОРА.Я
ТЕОРИЯ ПОЛЯ
РАЗДЕЛ II
ПОЛЯ
И ВИДЫ ВЗАИМОДЕЙСТВИЙ
До сих пор мы имели дело в основном с электронами и позит-
позитронами, взаимодействующими лишь с заданными внешними полями,
но не взаимодействующими между собой. В гл. 9, § 3, мы кратко
коснулись взаимодействия частиц, причем использовали квазиклас-
квазиклассическую теорию излучения. Однако правильное квантово-механи-
ческое описание взаимодействий частиц возможно лишь на основе
квантовой теории поля. Часть вторая данной книги посвящена именно
этому вопросу. Прежде чем приступить к его количественному рас-
рассмотрению, полезно качественно описать основные задачи и след-
следствия квантования поля.
Для этого рассмотрим электромагнитное поле, описываемое урав-
уравнением Максвелла — Лоренца. Хорошо известно (см., например,
работу Ферми [155]), что посредством преобразования Фурье дина-
динамическое описание поля можно свести к динамическому описанию
бесконечного набора гармонических осцилляторов. В случае отсут-
отсутствия зарядов и токов эти осцилляторы не связаны между собой,
и полная энергия поля
есть сумма энергий всех осцилляторов. Квантово-механическое опи-
описание такой системы осцилляторов хорошо известно каждому сту-
студенту, изучавшему основы квантовой механики. Кроме того, приме-
применение законов квантовой механики к этой задаче кажется естественным,
ибо электромагнитное поле обычно рассматривают как классическое
поле *).
1) Несколько отличная и более глубокая причина необходимости кванто-
квантования электромагнитного поля заключается в том, что если проквантованы
механические параметры (координаты и импульс) частиц, то следует кванто-
квантовать и поле, которое связано с ними. Это обусловливается тем фактом, что
принцип неопределенности Гейзенберга, по-видимому, нельзя применять к части
природы. Так, если бы принцип неопределенности не был применим к полям,
то, как показали Бор и Розенфельд [47] (см. также работу Гейзенберга [224]),
можно было бы поставить мысленный эксперимент, который позволил бы
в принципе точно измерить одновременно импульс и положение частицы,
наблюдая поля, создаваемые частицей. Таким образом, необходимость кван-
квантования электромагнитного поля есть прямое следствие квантовой механики
частицы.
8 Зак. 1784. Мезоны и поля
114
Однако можно также рассматривать уравнение Шредингера одной
частицы как уравнение движения для классического нерелятивист-
нерелятивистского поля, которое описывает отрицательно заряженное матери-
материальное поле. (С этой точки зрения наличие постоянной h несущест-
несущественно.) Измеряемыми характеристиками этого поля являются плот-
плотности заряда р(лг), тока j(x) и энергии поля £$ (х), которые можно
выразить с помощью волновой функции ф следующим образом:
ой
Такое классическое поле нужно рассматривать как классическую
систему с бесконечным числом степеней свободы, которую следует
квантовать так же, как любую другую классическую систему.
Теперь мы в состоянии развить для такого поля лагранжев
формализм, который позволит ввести канонически-сопряженные
переменные поля и гамильтониан системы (см. гл. 10). Налагая
условия квантования (т. е. условия, при которых канонически-со-
канонически-сопряженные переменные становятся операторами, удовлетворяющими
определенным перестановочным соотношениям), находим, что пере-
переменные поля (ф, ф*) превращаются в операторы, подчиняющиеся
определенным перестановочным соотношениям (см. гл. 13, § 1).
Далее, разумный выбор представления (см. гл. 13, § 2 и 3) дает
возможность описывать квантованную систему поля с помощью
„частиц", или, более точно, с помощью „квантов" поля, которые
являются носителями энергии и импульса (и заряда) поля. Если
операторы поля коммутируют между собой, то указанный рецепт
квантования ведет к частицам (квантам поля), подчиняющимся ста-
статистике Бозе —Эйнштейна. Если же частицы поля подчиняются
статистике Ферми — Дирака, то операторы поля антикоммути-
руют.
Эти соображения также применимы и к полям, описываемым
релятивистскими уравнениями, например к полю Клейна — Гор-
Гордона. Случай дираковского поля (и вообще любого описываемого
волновым уравнением поля с полуцелым спином) требует особого
рассмотрения, так как энергия поля в этом случае не является
положительно-определенной и квантование следует проводить со-
согласно антикоммутационным соотношениям (см. гл. 13, § 5). Ниже
мы убедимся в том, что квантование таких свободных полей также
позволяет описывать поле с помощью квантов, которые являются
носителями энергии-импульса поля (и заряда в случае комплексных
амплитуд поля).
115
Лагранжев формализм позволяет также рассматривать взаимо-
взаимодействие полей. Это достигается весьма просто путем введения
в лагранжиан системы члена взаимодействия (см. гл. 11 и 12).
Хотя канонический формализм при этом все еще позволяет кванто-
квантовать систему сравнительно простым способом, однако уяснить
смысл квантовой теории становится уже гораздо труднее. Это
особенно проявляется в случае взаимодействия релятивистских
полей: в теории появляются бесконечности, и задача еще больше
затрудняется. Однако ниже мы увидим, что некоторые интересные
результаты можно получить, пользуясь теорией возмущений (см.
гл. 14). Наконец, методы перенормировок (см. гл. 20 и 24) укажут
нам способ, с помощью которого можно обходить трудности, свя-
связанные с бесконечностями.
Существует также другой подход к теории поля, который
исходит из нерелятивистской теории Шредингера «-взаимодейст-
«-взаимодействующих частиц. Иордан, Клейн, Вигнер [247, 249] и Фок [183]
показали, что такую теорию можно сформулировать, вводя опера-
операторы а1е и а%, представляющие собой соответственно операторы
уничтожения и рождения частицы в &-ом квантовом состоянии.
В гл. 13, § 7, будет изложена эта теория, а также
новейшее ее развитие и связь с обычной теорией поля. В теории
Иордана — Клейна — Вигнера операторы ак и at служат для опи-
описания переходов частицы из одного квантового состояния в дру-
другое. Однако после того, как эти операторы определены, они допу-
допускают естественное обобщение на случай, когда частицы могут
реально рождаться и аннигилировать, т. е. когда общее число
частиц N перестает быть интегралом движения.
К счастью, именно такое положение имеет место в релятивист-
релятивистских квантовых теориях взаимодействующих полей и должно соот-
соответствовать тому, что в действительности наблюдается экспери-
экспериментально. Например, в случае электромагнитного поля квант света
может как излучаться, так и поглощаться; то же самое имеет
место и для других бозонов, например тс-мезонов. В случае элек-
электронов возможны рождение и аннигиляция позитронно-электрон-
ных пар. Все эти процессы удобно и точно описываются в теории
поля операторами рождения и уничтожения. Эти операторы слу-
служат также для краткого и точного описания взаимодействия двух
частиц (например, двух электронов), в результате которого излу-
излучается квант поля (квант света) одним из электронов и погло-
поглощается другим.
В операторной теории Иордана — Клейна — Вигнера, которая
была кратко описана выше, определяются, кроме того, операторы
числа частиц Nk = а£ак, показывающие, сколько частиц данного
сорта (нуклонов, мезонов, электронов, фотонов и т. д.) находится
в данном квантовом состоянии, например в состоянии с определенным
116
импульсом, энергией и направлением спина. Величина N = ^Nk
к
есть оператор полного числа частиц данного сорта. В самом общем
виде (т. е. при наличии взаимодействия) теорию поля можно рас-
рассматривать как обобщение обычной теории Шредингера для многих
частиц, на случай, когда оператор N не коммутирует с гамильто-
гамильтонианом.
Пусть ик(х) — нерелятивистская волновая функция частицы, на-
находящейся в состоянии k. Тогда мы можем определить оператор
4 (*) = 2 <**"*(*);
он является оператором уничтожения частицы. Можно показать,
что оператор ф удовлетворяет уравнению движения, тождественно
совпадающему по форме с уравнением Шредингера для одной
частицы:
где Н—гамильтониан одной частицы. Таким образом, можно уста-
установить связь с квантовой теорией поля, которая рассматривает ф
как оператор, полученный квантованием классической нерелятиви-
нерелятивистской волновой функции <!*• описывающей (отрицательно заряжен-
заряженное) материальное поле, и в которой ty*ty [соотношение B.5)] пред-
представляет собой плотность заряда, a j [соотношение B.6)] — плот-
плотность тока.
Хотя мы излагаем новейшее развитие релятивистской квантовой
теории системы полей, тем не менее в педагогических целях для
облегчения понимания вводим понятия, основывающиеся на старых
гамильтониановских методах, которые изложены, например, в книге
Вентцеля [525]. Мы отсылаем читателя к этой книге для ознаком-
ознакомления с историей развития теории поля. Полный список старой литера-
литературы (до 1947 г.) можно найти в работе Тиомно и Уилера [483]
(перечень литературы по физике элементарных частиц).
Первым известным в физике полем было электромагнитное поле,
однако впоследствии оказалось, что оно значительно сложнее дру-
других, так как для того, чтобы выполнялись уравнения Максвелла,
потенциал А должен удовлетворять не только волновому урав-
уравнению
но также и условию калибровки
•> 1 д<?
(Такое условное суммирование используется во всей второй части.)
Условие калибровки вызывает затруднения как в старой теории
117
поля, описанной в работе Вентцеля [525], так и в новейшем ее
развитии (см., например, статьи Швингера [438—440]). Таким об-
образом, электромагнитное поле дает примерное представление о тех
сложностях, которые имеют место в теории поля. С другой сто-
стороны, поле Клейна — Гордона (мезонное) характеризуется спином 0,
и поэтому волновая функция поля имеет всего лишь одну компо-
компоненту и не удовлетворяет условию калибровки. Связь поля Клейна —
Гордона с дираковским (нуклонным) полем также значительно проще
связи электромагнитного поля с полем частиц, со спином 1/2. По-
Поэтому сначала рассмотрим такое мезонное поле и его квантование.
Глава 10
ЛАГРАНЖЕВ ФОРМАЛИЗМ
§ 1. Классическая теория
Для простоты рассмотрим действительное поле, описываемое
одной переменной поля <р, которая является функцией координат
пространственно-временной точки л;„. Обычно изложение теории
поля начинают с определения плотности лагранжиана поля,
J3'=:J2'(<?> ду/дХу), подобранной так, что при варьировании инте-
интеграла действия по переменной <р получаются уравнения поля.
В частности, интеграл действия / определяется следующим обра-
образом:
f( £) (ЮЛ)
Далее, потребуем, чтобы интеграл действия / обладал экстремумом
при произвольных вариа'циях ср, удовлетворяющих условию
Ц(х, ^)=.8«р(ж, *а) = 0,
где tt и t2 — пределы интегрирования по временив формуле A0.1).
Этот принцип наименьшего действия является естественным обоб-
обобщением принципа Гамильтона в классической механике, так как
совокупности величин ср и ср можно сопоставить соответственно
координаты Qs и скорости Qs, встречающиеся в обычной механике.
В дальнейшем мы кратко обсудим этот вопрос.
Так как интеграл действия имеет фундаментальное значение
в теории, то потребуем, чтобы он был лоренц-инвариантным. По-
Поскольку элемент 4-объема d*x является псевдоскаляром, то функ-
функция Jg должна быть или скаляром, или псевдоскаляром. Мы будем
считать ее скаляром *). Из дальнейшего будет ясно, что такой
выбор обусловлен требованием — плотность энергии должна быть
положительно-определенной. При этом интеграл действия будет
псевдоскаляром.
У Если включены отражения вэ времени, то требование скалярности
функции Л2? обосновано для частиц с целочисленным спином.
Лагранжев формализм
119
Введем сокращенное обозначение
и проварьируем выражение A0.1); при этом получим
A0.2)
A0.3)
где 2 — 4-объем интегрирования, в котором поле отлично от
нуля. Поверхность 4-объема 2 пока не определена. В силу обо-
обозначения A0.2) второй член в левой части выражения A0.3) все
еще зависит от §<р(х). Интегрируя этот член по частям, находим
!-^
где S — поверхность Q, а п^(х)—-внешняя нормаль к этой поверх-
поверхности в точке х. Схематически это изображено на фиг. 16. Если
теперь предположить (мы
всегда будем предполагать это
в дальнейшем), что поле стре-
стремится к нулю на больших рас-
расстояниях, то интеграл по по-
поверхности, обозначенный на
фиг. 16 пунктирной линией,
исчезает. Согласно принципу
наименьшего действия, вариа-
2
о.
Я
Пространственные координаты
Фиг. 16.
ция 8/ равна нулю для всех
произвольных вариаций 8ср,
ограниченных лишь условием
Зср = 0 на границе S объема 2. Так как вариация 8ср внутри объема 2
есть произвольная функция точки х, то в соответствии с требова-
требованием 8/= 0 получим
A0.5)
Эти уравнения представляют собой уравнения поля.
Следует заметить что добавление 4-дивергенции к плотности
лагранжиана не меняет уравнений движения. Действительно, рас-
рассмотрим новую плотность лагранжиана jg?', которая получается из
1) Если поле описывается не скалярной волновой функцией, а много-
многокомпонентной функцией, то компоненты ее будем обозначать через <pr, a
величину d<fr/dxv- — через ч/г, р.. Пока точно не указаны свойства преобра-
преобразования (рп мы не можем опускать или поднимать индекса г.
120 Глава 10
плотности лагранжиана _g" добавлением к последнему 4-дивер-
генции:
где Fv-— 4-векторная функция переменных поля. Член
A0.7)
в интеграле действия может быть преобразован по теореме Гаусса
в интеграл по поверхности S, поэтому его вариация тождественно
равна нулю. Если Fv- зависит от cpv, то сказанное остается спра-
справедливым при условии, что J3^ не зависит от вторых производ-
производных. Хотя физическое содержание двух лагранжианов, отличаю-
отличающихся друг от друга 4-дивергенцией, одинаково, соответствующие
им гамильтонианы и, следовательно, канонический формализм для
них будут, вообще говоря, различными.
Обратимся теперь к вопросу эквивалентности соотношения A0.1)
и принципа Гамильтона. Ясно, что трудность, в силу которой это
соответствие перестает быть самоочевидным, вызывается тем об-
обстоятельством, что мы имеем дело с бесконечным множеством не-
непрерывных переменных, так как наши поля определены бесконеч-
бесконечным числом координат ср (х, у, г, t) в каждой точке 4-простран-
ства. Существует несколько способов преодоления этой трудности.
В каждом из них бесконечное множество непрерывных координат
заменяется бесконечным, но уже дискретным множеством. Одним из
таких способов является фурье-анализ или — более общий способ—
разложение поля в ряд по ортогональной системе функций.
Другой способ заключается в разбиении непрерывного трехмер-
трехмерного пространства на ячейки Злг8==Д3, столь малые, что изменение
физических величин внутри такого куба можно считать несуще-
несущественным (Ми [336], Гейзенберг и Паули [222]). Среднее значение <р
в кубе cps можно рассматривать как координату Qs. Таким образом,
в ячейке s координата Qs отождествляется с cps, Qa—с cps (и пространст-
пространственная производная Vcpg заменяется разностью (Qs+1 — <2S)/A)« Лагран-
Лагранжиан всей системы L при этом можно рассматривать как функцию всех
Qs и Qs и записать как сумму по всем ячейкам
^x,. A0.8)
где J5?s соответствует плотности лагранжиана _g* в ячейке s. Инте-
Интеграл действия при этом выражается следующим образом:
Qv ...; Qlt Q2 ...)-> J dt &х£*(у,-Цр}. A0.9)
Лагранжев формализм 121
Первая часть выражения A0.9) в действительности точно соответ-
соответствует принципу Гамильтона с лагранжевой функцией L, зависящей
от обычных координат, Qs, Qs. Для записи второй части A0.9)
воспользуемся выражением A0.8) и перейдем от суммирования
к непрерывному интегрированию; таким образом,
Величина L уже не является релятивистски инвариантной, так как
мы разделили пространство и время.
В классической механике с помощью лагранжевой функции L
можно определить канонически-сопряженный импульс. Аналогичным
образом можно определить здесь величину
dQs
Так как Qs содержится лишь в _2%, то, согласно выражению A0.8)
получим
/>s=ApL8xs. A0.12)
dQs
„Плотность" канонически-сопряженного импульса обычно опреде-
определяют в виде
7rs=AS-, A0.13)
т. е.
Ps = bxsTV3. A0.14)
Используя такой метод разбиений, мы должны помнить, что класси-
классический интеграл действия определяется как интеграл по времени от
лагранжиана системы [это показано в первой части выраже-
выражения A0.9)]. Поэтому сравнение нашего рассмотрения с этим мето-
методом возможно лишь в том случае, когда выбранная в соотноше-
соотношении A0.4) поверхность Е является плоской, т. е. поверхностью
постоянного времени /. В этом случае вектор п^ является единич-
единичным вектором в положительном или отрицательном направлении
времени, и поверхностный интеграл в соотношении A0.4) сво-
сводится к виду
- Г ) d3x 3cps ( —=#- J, A0.15)
где cps показывает, что значение величины ср берется на поверх-
поверхности Б. Согласно формуле A0.13), это выражение приводится
к виду
j (Px ScpsTtj, A0.16)
S
122 Глава 10
что в точности аналогично выражению
в классической механике частицы.
Возвращаясь опять к общим, поверхностям (см. фиг. 16), пред-
предположим, что тс в наиболее общем виде можно записать следующим
образом:
^ A0.18)
здесь уже не требуется, чтобы 4-поверхность была плоской. Впер-
Впервые произвольную 4-поверхность ввел в теорию Вейсс [512—514].
Таким образом, ему удалось развить релятивистски инвариантную
теорию в гамалыпоновой форме. Его работы легли в основу совре-
современной теории поля (см. работы Томонага [486], Дирака [116],
Швингера [438]). Единственным ограничением в выборе поверхно-
поверхностей Ej и Б2 является следующее требование: поверхности должны
быть пространственно-подобными, т. е. световой сигнал не может
распространяться от одной точки поверхности к другой точке той
же поверхности. Это приводит к тому, что функция ср (х) в любой
точке поверхности может быть определена независимо от функции
ср (хО в другой точке. Мы не будем излагать здесь эту теорию,
которая допускает варьирование не только оср, но также и гранич-
граничных поверхностей1).
Вместо этого изложим гамильтонов формализм и по аналогии
с механикой частицы определим плотность гамильтониана
3V = v:<? — Jg> A0.19)
и функцию Гамильтона
f A0.20)
Так же, как и в классической механике, можно получить при этом
обычные классические канонические уравнения движения
() "**<">• A0.21)
где о/8ср означает функциональное дифференцирование2).
Гамильтонов формализм дает удовлетворительные результаты
при рассмотрении простейших задач теории поля. Но этот метод
становится неудовлетворительным для более сложных задач из-за
1) См., например, работу Борна [54].
2) См. книгу Шиффа [429], а также работу Гейзенберга и Паули [222].
Лагранжев формализм 123
того, что релятивистские теории поля содержат расходимости, на-
например типа собственной энергии. Хотя эти расходимости могут
быть устранены с помощью рецептов вычитания (перенормировок),
которые будут обсуждаться ниже (гл. 21—24), однако получить
надежные результаты для конечных остаточных эффектов из неко-
вариантного формализма, подобно гамильтонову, очень трудно.
Успешное решение задач, требующих перенормировки, достигается
с помощью новейшего ковариантного формализма.
Ниже мы кратко рассмотрим некоторые примеры полей, встре-
встречающихся в физике, и выпишем их лагранжианы.
§ 2. Действительное однокомпонентное поле
Плотность лагранжиана записывается в виде
где |j. — постоянная, имеющая размерность обратной длины. Этот
лагранжиан инвариантен, если ср является скаляром или псевдоска-
псевдоскаляром. В любом из этих случаев <?2— скаляр, величина ср^?11 как
квадрат 4-вектора также является скаляром. Дифференцируя урав-
уравнение A0.22), получаем
^ = — р,2«р A0.23)
dtp r T v '
Следовательно, согласно уравнению A0.5), уравнение движения
имеет вид
_!Х2ср_^т^ = 0. A0.25)
Замечая, что второй член есть —□?> имеем
□ <Р + р-2<Р = 0- A0.26)
Это уравнение в точности совпадает с уравнением Клейна — Гор-
Гордона, если положить
;л = ^, A0.27)
т. е. если jj. есть обратная величина комптоновской длины волны
частицы с массой т, соответствующей квантованному полю.
Исходя из соотношения A0.13), определим далее сопряженный
импульс
^? A0-28>
124 Глава 10
Гамильтониан, соответствующий нашему лагранжиану, выраженный"
через ср и тс, согласно определениям A0.19) и A0.28), имеет вид
^^тсг + у^+^чО8' . A0.29)
где V — символ обычного трехмерного градиента. Выражение A0.29)
является положительно-определенным; полагают, что оно представ-
представляет собой плотность энергии. Это есть следствие выбора отрица-
отрицательного знака в выражении A0.22).
Полный гамильтониан Н, определенный равенством A0.20),
представляет собой полную энергию поля. Если лагранжиан _g"
в выражении A0.19) явно не зависит от времени, то dHjdt = 0, и
полная энергия системы сохраняется. Это полностью аналогично
утверждению классической механики: если величина I Ldt инвари-
инвариантна по отношению к перемещению по оси t, то энергия системы
сохраняется. Аналогично, если величина i Ldt инвариантна по от-
отношению к перемещению по оси х, то сохраняется х-компонента
импульса системы. (Для подробного ознакомления с вопросом о связи,
инвариантности Jg' по отношению к различным группам преобра-
преобразований с законами сохранения в теории поля отсылаем читателя
к работам Розенфельда [410], Белинфанте [27, 28], Паули [378],
Хилла [233], а также к Приложению Б.)
Далее, полную энергию поля можно написать в виде
(Ю.30)
где Г00 — @, 0)-компонента канонического тензора энергии-импульса,
определяемого следующим соотношением:
74" = <fV- 4=2. — J?gv. A0.31)
Благодаря уравнениям движения и тому факту, что J^f явно не
зависит от 4-координат*), этот тензор обладает свойством
= 0, A0.32)
х) Если _2" явно зависит от внешних координат, то это соответствует
наличию внешних полей, с которыми <р взаимодействует. В этом случае
уравнение A0.32) заменяется соотношением
Лагранжев формализм 125
дх-<
Интегрируя выражение A0.32) по всему (трехмерному) простран-
пространству, получаем
£f'2f£ 0. A0.34)
Если теперь Т^к исчезает на бесконечности (что имеет место в слу-
случае, когда сами поля исчезают на бесконечности), то второй член
этого равенства, который может быть преобразован по теореме
Гаусса в интеграл по поверхности, будет равен нулю. Таким обра-
образом, мы получаем четыре закона сохранения
A0.35)
Первый из них для ja = O соответствует сохранению энергии. Дру-
Другие три закона — сохранению трех величин:
Jk3 A0.36)
которые представляют собой три компоненты полного импульса
лоля. Далее, если Jg является скаляром, то 7>v будет тензором
второго порядка. Отсюда следует, что четыре величины
- = J
7>° dsx A0.37)
преобразуются как 4-вектор энергии-импульса поля. Определение
канонического тензора энергии-импульса A0.31) справедливо и
в более общем случае, когда поле описывается многокомпонентной
функцией. При этом в первом члене выражения A0.31) произво-
производится суммирование по всем компонентам функции срг, описывающей
поле (см. Приложение Б).
По аналогии с выражением A0.20) можно определить плотность
импульса поля как вектор с компонентами Тк0. При этом естест-
естественным определением плотности момента поля относительно начала
координат будет
A0.38)
причем полный момент поля выражается в виде I dzxmki0 =
126 Глава 10
Далее, чтобы величина Mki, являющаяся пространственной частью
тензора момента
Ж„ = f d*x (xj^ — xj^o), A0.39)
сохранялась, мы должны потребовать, чтобы
т ° С1
так как в этом случае по тем же соображениям, которые привели?
нас к равенству A0.35), обеспечивается сохранение величины
С dsxm^0. Но величина (д/дх?) т,^р, согласно выражению A0.32),.
равна
щ "Vp = -щ (^7vp x<,Tw) = Tv?. Тр.*- A0.41)
Следовательно, тензор М^ будет сохраняться, если Т = Tvs_, т. е.
если тензор энергии-импульса является симметричным. Свойства
симметрии тензора энергии-импульса, вообще говоря, не следует
из его определения A0.31). Однако этот тензор всегда можно сим-
метризовать (см. работы Белинфанте [27, 28]), так как к лагран-
лагранжиану системы всегда можно добавить 4-дивергенцию, не изменив
при этом физического содержания теории. Другими словами, плот-
плотность энергии, например, определяется не однозначно, в то время
как полная энергия поля определяется вполне однозначно.
Три пространственные компоненты (к, I) антисимметричного тен-
тензора момента М^ характеризуют момент системы, в то время как
три пространственно-временные компоненты @, k) связаны с цент-
центром инерции системы (см. работы Мбллера [343, 344], Прайса [397]).
Для случая нулевого спина тензор энергии-импульса имеет вид
Tv» = <р^-Ь i g*v(l*V— <Px<Px)- A0.42)
Очевидно, этот тензор уже симметричен. Это обстоятельство свя-
связано с тем, что поле Клейна — Гордона не обладает собственным
моментом, т. е. имеет спин, равный нулю (см. Приложение Б).
Представляет интерес исследовать, насколько однозначно опре-
определен данный лагранжиан. Мы уже отметили, что к плотности лаг-
лагранжиана всегда можно добавить 4-дивергенцию, не изменяя при
этом физического содержания теории. Оставляя пока эту произ-
произвольность в стороне, покажем, что, исходя из разумных физиче-
физических требований, можно однозначно определить лагранжиан системы
(см., например, работу Баба [38]). Первое из требований—это
требование релятивистской инвариантности лагранжиана. Ниже, при.
изучении электромагнитного поля, мы будем также требовать, чтобы
лагранжиан обладал калибровочной инвариантностью. В случае не-
Лагранжев формализм 127
взаимодействующих полей можно требовать выполнения принципа
суперпозии полей, что накладывает на лагранжиан системы следую-
следующее требование: он не должен содержать переменных поля выше,
чем во второй степени1).
Если мы потребуем существования решения задачи с заданными
начальными условиями, или задачи Коши, для наших гиперболиче-
гиперболических уравнений поля, то это приведет к тому, что в лагранжиане
появятся производные только конечного порядка по времени от
переменных поля. Согласно требованию релятивистской инвариант-
инвариантности, лагранжиан должен содержать производные по координатам
от переменных поля того же порядка, что и производные по вре-
времени. Большинство уравнений поля в физике — уравнения второго
порядка. Если мы ограничимся рассмотрением теорий таких полей,
то лагранжиан системы может содержать лишь ду/дх^, т. е. про-
производные первого порядка от переменных поля по 4-координатам.
Наконец, лагранжиан системы должен быть действительным, что
необходимо в квантовой теории поля для обеспечения его эрмито-
вости.
Таким образом, лагранжиан действительного однокомпонентного
поля обязательно содержит только <р2 и (да/дх^J. Единственная
произвольность в формуле A0.22) остается в выборе коэффициен-
коэффициентов при этих членах. Коэффициент (а должен иметь размерность
обратной длины, (а = mc/h; остается произвольность в выборе его
величины, т. е. массы т. частицы. Множитель */г в формуле A0.22)
может быть выбран произвольно, но, как мы уже видели, такой
выбор ведет к ■к = ср без числовых коэффициентов. Знак минус
в формуле A0.22), как уже обсуждалось выше, введен для того,
чтобы обеспечить положительную определенность гамильтониана
системы.
§ 3. Комплексное скалярное поле
Обобщение лагранжева формализма на этот случай, естественно,
следует из разделения комплексного поля на действительную и мни-
мнимую части:
^ A0.43)
В случае комплексного поля лагранжиан можно написать не только
как функцию cpW и ср<2) и их производных, но и, согласно выражению
A0.43), как функцию <р и ср* и их производных. В частности,
можно варьировать „24<р, <р ; ср*, ср*) независимо по со и ср*, что
!) Такое требование нельзя предъявлять к лагранжиану в случае взаи-
взаимодействующих полей, так как при этом были бы невозможны все реаль-
реальные взаимодействия. Линейной заменой переменных можно было бы такие
поля всегда отделить друг от друга.
128 Глава 10
эквивалентно варьированию ^(<рA), <р£>; <рB)> Т(^2)) по ТA) и
<рB) соответственно. В результате получаем следующие урав-
уравнения поля:
^ ^-^ = 0 A0.44а)
Щ 1^? = о. A0.446)
Лагранжиан комплексного скалярного поля получается из лагран-
лагранжиана действительного поля заменой ср2 на ср*ср, причем множитель
х/г писать уже не следует, так как в лагранжиане уже нет члена ф2
и, следовательно, при дифференцировании не возникает численного
множителя 2. Таким образом, лагранжиан комплексного скалярного
поля имеет вид
-2* = — (|*V<P — ?>")■ A0-45)
Канонически-сопряженные импульсы при этом записываются в виде
i*, A0.46а)
A0.466)
так что плотность энергии поля выражается следующим образом:
^?=iC9-{-icV — ^ = TC*7r + (V<y*)-(Vcp)-j-t).2<p*cp. A0.47)
Так же, как и в случае действительного поля, можно определить
канонический тензор энергии-импульса и из него получить полную
энергию и полный импульс поля, которые образуют 4-вектор.
Согласно свойству A0.32), эти величины будут сохраняться.
Если мы желаем, чтобы наше поле описывало распределение
заряда, то мы должны требовать выполнения закона сохранения пол-
полного заряда и найти дифференциальный закон сохранения заряда и
тока. Это означает, что в каждой точке 4-пространства существует
4-вектор j\, дивергенция которого равна нулю, т. е.
Ц=о- A0-48)
4-вектор ух может быть образован из функций поля <х>(*) и оB> сле-
следующим образом:
(^^) (.0.49)
где е — постоянная. Нетрудно установить соотношение
^ A0.50)
Лагранжев формализм 129
Так как каждая из функций срШ и срB) удовлетворяет уравнению
Клейна —Гордона, то из соотношения A0.50) находим, что у> дей-
действительно сохраняется.
Таким образом, комплексное скалярное поле может описывать
заряженные частицы (например, заряженные тг-мезоны). Выразив
соотношение A0.49) через ср и ср*, найдем для плотностей заряда и
тока следующие выражения:
р = — /е(шр— тс'ср*), A0.51)
или, выразив через плотность лагранжиана, получим
<10-53)
Можно показать [см. Приложение Б, соотношения (Б. 15)—(Б. 18)],
что существование 4-вектора плотности тока у> [выражение A0.53)]
в действительности есть следствие инвариантности лагранжиана по
отношению к „калибровочному" преобразованию первого рода, при
котором
ср -* е*«<р,
<P*-+e-V. A0.54)
где е — действительная константа. Закон сохранения у> следует из
уравнений движения A0.44). В дальнейшем мы покажем, что 4-век-
тор /> действительно играет роль вектора тока в уравнениях Макс-
Максвелла. Из выражения A0.53) следует, что в случае действительного
поля ср* = ср и ток у> тождественно равен нулю, т. е. действительная
функция ср может описывать только нейтральное, незаряженное поле.
§ 4. Дираковское поле
Выше были рассмотрены некоторые вопросы, связанные с полями,
описываемыми многокомпонентными функциями. Например, поле дира-
ковских частиц (частиц со спином 1/2) описывается четырехкомпо-
нентным спинором фв, который при преобразованиях Лоренца пре-
преобразуется согласно соотношению C.59). Рассмотрим эти четыре
компоненты спинора (])„ как независимые динамические переменные.
Главное отличие лагранжиана дираковского поля от лагранжианов
рассмотренных выше полей заключается в том, что он является
функцией первого порядка отЩ/дх^, что приводит к дифферен-
дифференциальному уравнению первого порядка для (рв. Поэтому необходимо
несколько изменить гамильтонов формализм. -
j=g Плотность лагранжиана~ выражается в виде
laO Глава JO .
Величина, обратная комптоновской длине волны дираковской частицы,
в выражении A0.55) обозначается через т. Этим обозначением мы
будем пользоваться и в дальнейшем, чтобы отличать дираковскую
частицу от бозе-частицы, для которой соответствующую величину
будем обозначать, как прежде, через \х. Уравнения движения полу-
получаются варьированием лагранжиана независимо по ф и ф. Так как
j<—*V+m)<|. — i-тф, .A0.56)
—!/V^, A0.57)
2 Y K J
то с помощью уравнения A0.5) получаем уравнение Дирака
)<|i = 0. A0.58)
Уравнение для сопряженного спинора получается аналогично путем
варьирования лагранжиана по (р. Отметим, что совершенно случайно
_g* обращается в нуль, если волновая функция <р удовлетворяет
уравнению движения.
Используя общее выражение для 4-вектора плотности тока,
соответствующее соотношению A0.53) для случая заряженного
бозе-поля, получаем для вектора тока в случае дираковского поля
следующее выражение:
у>==е^ф. A0.59)
Согласно уравнению движения, этот вектор сохраняется. В частности,
из закона сохранения dj'P-fdxv- = 0 следует, что
A0.59а)
это соответствует тому, что полный заряд поля сохраняется.
Линейная зависимость Jg от dty/dt приводит к тому, что кано-
канонически-сопряженный импульс уже зависит от переменных поля <р
и ф1). Однако можно обойти эту трудность, вспомнив, что все вели-
величины, представляющие физический интерес, можно получить, исходя
из тензора энергии-импульса [см. выражение A0.31)], который
в нашем случае, т. е. при _2" = 0, имеет вид
. (Ю.60)
Этот тензор не является симметричным, но он легко может быть
симметризован (см., например, работу Паули [370]). Однако тензор
!) Поэтому канонический лагранжев формализм уже неприменим и пере-
переход к гамильтониану не удается.
Лагранжев формйлиш
A0.60) дает такое же выражение для 4-вектора энергии-импульса,
как и симметризованный тензор, а именно:
Последняя строка соотношения A0.61) получается путем инте-
интегрирования по частям, причем поверхностные члены для ja=1, 2, 3
опускаются, а для ja=O используется соотношение A0.59а). Таким
образом, используя уравнения движения, получаем следующее выра-
выражение для полной энергии поля или гамильтониана поля:
Н = Р° = J Т°° dsx = f dsxty(— % • V + m)<p =
— to.- V-fpOT)<|». A0.62)
§ 5. Максвелловское поле и векторное мезонное поле
Калибровочно-инвариантный лагранжиан для электромагнитного
поля выбирается в виде О
4
где F'**—тензор электромагнитного поля, связанный с потенциа-
потенциалами поля следующим соотношением:
= ^*_^i'. A0.б4)
дх., дХр, к '
Здесь Л|1 = ((р, А), так что Fok = d,k, где & — вектор электриче-
электрического поля, a Fkl=feJ, где •§•?' — вектор магнитного поля и
_27 = —^(®2 — &2)- Варьируя соотношение A0.63) по потенциалам,
получаем уравнения Максвелла
= 0, A0.65)
!) В дальнейшем всюду в этой книге мы будем пользоваться системой
единиц Хевисайда — Лоренца, в которой (е2/4яйс) = о = i/t37. Потенциалы
в этой системе отличаются от потенциалов в гауссовской системе, использо-
использованной выше в теории Фейнмана, множителем 1/ "|/тс. В гауссовской системе
единиц лагранжиан A0.63) имеет вид
1з2 f лава id
или, выражая F7 через потенциалы, находим
0 x
A0.66)
В классической теории мы можем выбрать лоренцовскую калибровку
X — 0; тогда уравнения Максвелла примут вид Q/4l'=0.
Указанный выбор лагранжиана приводит к характерной труд-
трудности: импульс %°, канонически-сопряженный А0, тождест-
тождественно равен нулю, и поэтому гамильтонов формализм требует
улучшения. В квантовой теории, где А0 и it0 становятся операто-
операторами, удовлетворяющими определенным перестановочным соотноше-
соотношениям, то обстоятельство, что величина ■к0 равна нулю, вызывает
дальнейшие осложнения.
Преодолением этой трудности мы обязаны Ферми [153—155],
который предложил выбирать лагранжиан электромагнитного поля
в следующем виде:
■*—■r"^-i(s
Этот лагранжиан сейчас часто применяется в теории электромагнит-
электромагнитного поля. Он не является калибровочно-инвариантным, так как
содержит член %2. Однако очевидно, что он является релятивистски-
инвариантным. Варьируя этот лагранжиан по А^, получаем следую-
следующие уравнения движения:
))eo. A0.68a)
dxj дх,\дх»)
или
ПЛ' = 0. A0.686)
Эти уравнения неэквивалентны уравнениям Максвелла. Чтобы их
сделать эквивалентными, достаточно наложить на ^ дополнительное
условие:
^ = 0 при t = 0,
и
% — 0. при /-=0. A0.69)
Тогда, согласно уравнениям движения A0.68), ■/_ = 0 для всех мо-
моментов времени. Ниже мы обсудим роль этого дополнительного
условия в квантовой теории.
Лагранжиан A0.67) можно переписать в виде
Лагранжев формализм 133
или, если положить -^ = 0 и пренебречь членом, содержащим дивер-
дивергенцию, в виде
A0.71)
Из лагранжиана A0.71) можно получить канонически-сопряженный А.^
импульс
A0.72)
и, следовательно, плотность гамильтониана
з
Таким образом, мы видим, что энергия электромагнитного поля по
своей структуре аналогична суперпозиции четырех скалярных полей,
но она уже не является положительно-определенной1). Это произошло
потому, что мы еще не использовали нашего дополнительного усло-
условия. Воспользовавшись этим условием, можно придать гамильтониану
положительно-определенную (см. работу Гупта [216], а также
гл. 15, § 4) хорошо знакомую форму, а именно
Следует отметить, что все наше рассмотрение было основано
на использовании потенциалов в качестве переменных поля. В кван-
квантовой теории это обстоятельство становится источником ряда труд-
трудностей, так как потенциалы А^ определены неоднозначно; наблю-
наблюдаемой величиной является лишь 4-ротор А?>ч— -^v>(i> T- е- элек-
электрическое и магнитное поля. Поэтому при использовании только
потенциалов А^ для описания поля мы можем, не изменяя фактиче-
фактического содержания теории, провести калибровочное преобразование
вида
i A0-74)
так как тензор электромагнитного поля F^ инвариантен по отно-
отношению к калибровочному преобразованию. В выражении A0.74)
Л—произвольная функция, которая, согласно дополнительному
условию х = 0> удовлетворяет уравнению ДД = 0. Требование ка-
калибровочной инвариантности, таким образом, означает инвариант-
инвариантность всех наблюдаемых физических величин по отношению к пре-
преобразованию A0.74).
Рассмотренное нами максвелловское поле является частным слу-
случаем векторного поля (р^, когда масса частиц jj. равна нулю. Если же
Компонента (а = 0 вносит отрицательный вклад в гамильтониан
134 Глава 10
масса частиц отлична от нуля, то мы имеем дело с векторным ме-
зонным полем (см. работы Прока [396], Вентцеля [525], гл. III),
которое удовлетворяет следующим уравнениям движения:
дР„в
ЪГ = ~№« />=?„, — «Р^-
р
Дифференцируя эти уравнения по лг„, получаем у* = 0, т. е.
дополнительное условие выполняется автоматически, так как Z7 , =
= — Fv?. Уравнения движения A0.75) можно получить, исходя из
лагранжиана (для случая заряженного поля):
_Г = — jf;/^- Р2тУ- (Ю.76)
Дополнительное условие срхх = 0 приводит к тому, что только три
компоненты <р являются линейно независимыми. Число три тесно
связано с тем обстоятельством, что спин частицы, описываемой век-
векторным полем, равен единице и, следовательно, может принимать
25+ 1=3 возможных ориентации в пространстве. Временная ком-
компонента, которая не является линейно независимой, соответствует
полю со спином 0; это поле, однако, вносит отрицательный вклад
в полный гамильтониан системы [см. соотношение A0.73)]. Благо-
Благодаря дополнительному условию временная компонента, как и для
случая электромагнитного поля, исключается.
До сих пор мы ограничивались рассмотрением полей, описываю-
описывающих частицы со спином 0, */2 и 1. Теории полей, описывающих
частицы с произвольным целым или полуцелым спином (для случая
частиц с нулевой массой покоя даже с непрерывным спиномI), раз-
развивались многими авторами, как например Дираком [109], Фирцем
[172, 173], Паули [376], Паули и Беленфанте [377], Вигнером [537,
538], Крамерсом и др. [289], Хариш-Чандра [220], Баргманом и Вигне-
Вигнером [19] и многими другими. Здесь мы не будем излагать этих теорий 2>.
Заметим лишь, что так как скалярное поле описывает частицы со спи-
спином 0, а векторное поле — со спином 1, то, следовательно, можно
предполагать, что частицы с произвольным целым спином должны опи-
описываться тензорным полем порядка 5. С другой стороны, мы видим, что
частицы со спином 1/2 описываются спинорным полем. Частицы
с произвольным полуцелым спином можно описать с помощью общего
спинорного анализа, развитого Ван дер Верденом [501, 502] (см.
также работу Баде и Джела [13]).
*) Это значит, что существует бесконечное число различных состояний
поляризации, которые могут быть описаны непрерывной переменной (см. ра-
работы Вигнера [538], Баргмана и Вигнера [19]).
%) См„ например, книгу Вентцеля [525], гл. VI.
Глава 11
ВЗАИМОДЕЙСТВИЕ МЕЖДУ ПОЛЯМИ
Перейдем теперь к изучению взаимодействия полей и, в част-
частности, в первую очередь — связи между спинорным и бозонным по-
полями. Требование релятивистской инвариантности члена взаимодей-
взаимодействия в лагранжиане значительно ограничивает выбор возможных
связей между полями.
Условимся писать член взаимодействия двух полей в виде АВ,
где А соответствует первому полю, а В— второму полю. Будем
различать „локальное" взаимодействие, когда А(х) и В(х) берутся
в одной и той же пространственно-временной точке х, и „нело-
„нелокальное", когда это условие не выполняется. Кроме того, будем
называть взаимодействие „прямым" взаимодействием или „прямой"
связью, если ни А(х), ни В х) не содержат производных волновых
функций. В случае, когда А(х) и В(х) содержат производные вол-
волновых функций, будем называть взаимодействие полей „связью
с производной".
Волновые функции поля нормированы с помощью выражения для
лагранжиана свободных полей. Величина члена взаимодействия в ла-
лагранжиане будет, следовательно, определяться значением действи-
действительно мультипликативного множителя, называемого константой взаи-
взаимодействия. Обозначим константу прямой связи через G, а константу
связи с производной — через F. Кроме того, мы часто будем поль-
пользоваться сокращенными обозначениями g2 = О2/4тг и /2 = F2/4tc.
Так как в квантовой теории поля взаимодействие должно быть
эрмитовым, то будем проверять каждый раз эрмитовость произве-
произведения АВ. Ниже покажем это для псевдоскалярной прямой связи.
§ 1. Прямые связи
Рассмотрим простейший тип локальных прямых связей. Термин
„простейший" указывает на то, что одно из полей входит линейно
в член взаимодействия.
Скалярное поле. Взаимодействие скалярного поля со спинорным
полем (р имеет очень простой вид. Положим А = <$> и образуем ска-
скалярное произведение B—btyl1; инвариантный член взаимодействия
можно при этом записать в виде
i С11-1)
Ч Напомним читателю, что трансформационные свойства ковариантных
выражений tyTfy рассмотрены в гл. 4
136 Глава 11
Псевдоскалярное поле. В этом случае мы комбинируем А = <р,
где <р — псевдоскалярная функция, с псевдоскалярным ковариантным
выражением В = фТбФ' В результате получаем ФТбФТ== (})+РТб(!)<Р*
Далее, (tyt$)f = ^уврф = «рТбФ* так как Тб—антиэрмитова матрица,
и, следовательно, эрмитовый инвариантный член взаимодействия
имеет вид
Функция ср может описывать, например, поле нейтральных те-мезо-
нов, а ф — поле нуклонов. Если мы хотим рассмотреть взаимодей-
взаимодействие как заряженных, так и нейтральных мезонов с нуклонами, то
мы должны обобщить наш формализм, вводя <р*', где k=l, 2, 3
для положительных, отрицательных и нейтральных тс-мезонов соот-
соответственно1). Компоненты поля с индексами 1 и 2 идентичны с функ-
функциями ср<1} и (рв), представляющими собой компоненты комплексного
поля [соотношение A1.43)].
Векторное поле. Рассмотрим далее связь векторного поля <Рц
со спинорным полем ф. В этом случае ср^ комбинируем с ковариант-
ковариантным векторным выражением фу^ф» в результате получаем
где, как обычно принято в релятивистской теории, подразумевается
суммирование по р. Этот тип связи точно совпадает со связью
электромагнитного поля с зарядами в классической электродинамике,
а именно с A^fr, где _/> = фу1ч|».
Псевдовекторное поле. Обозначим компоненты поля через ср^ и
составим комбинацию <р^ и эрмитовой ковариантной псевдовектор-
псевдовекторной величины fy"[b~(V-ty, в результате получим
С11-4)
§ 2. Связи с производной
Обратимся теперь к локальным связям с производной. Для этого
случая взаимодействия скалярного (или псевдоскалярного) поля <р
со спинорным полем <|> будем полагать А = df/дх^, а для В возь-
возьмем векторное (или псевдоскалярное) ковариантное выражение, обра-
образованное из ф. Константу связи будем писать в виде F/(i, где [а —
масса частиц поля <р; при этом F — безразмерная константа. В этом
случае мы имеем следующие типы взаимодействия.
Скалярное поле. Взаимодействие выражается в виде
Подробно это будет рассмотрено в т. II, гл. 30 н 31.
Взаимодействие между полями 137
Псевдоскалярное поле (псевдоаекторная связь). Связь с про-
производной известна в этом случае как псевдовекторное взаимодей-
взаимодействие и имеет вид
??| (п.6)
Свойства, вытекающие из такого взаимодействия, можно изучить
более полно, выделив в выражении A1.6) пространственные и вре-
временные компоненты, т. е.
Согласно определениям D.27) и D.33), первый член выражения
A1.7) приводится к виду
+ -£ф+аф-У<р. A1.8)
Второй же член выражения A1.7) в том смысле, о котором мы го-
говорили в гл. 4, в нерелятивистском приближении „мал". Выражение
A1.8) имеет преимущество по сравнению с выражением A1.2), так
как содержит только хорошо известный оператор а для ферми-ча-
стиц (нуклона), который в нерелятивистском приближении велик.
Выражение A1.2) содержит необычный оператор у5, который в не-
нерелятивистском приближении мал. Можно показать (см. гл. 26),
что в первом порядке обе эти связи дают одинаковый результат;
в высших же порядках псевдоскалярная связь оказывается предпо-
предпочтительной.
Векторное поле (тензорная связь). В этом случае член связи
полей содержит производные ду^дх^. Предположим, что бозонное
поле является полем такого же типа, как максвелловское поле и
линейное векторное поле, рассмотренное в гл. 10, § 5, т. е. урав-
уравнения поля являются уравнениями первого порядка и включают
только антисимметричный тензор F^v, определенный выражением
A0.64). Разумно ввести этот тензор F^ B член взаимодействия со
спинорным полем. Для этой цели комбинируем Т7^ с ковариантным
антисимметричным тензорным выражением фа ф и в результате по-
получаем
i) Ф (TJ T)^ A1 -9)
Взаимодействие A1.9). можно использовать, например, для опи-
описания дополнительного взаимодействия (в дополнение к взаимодей-
взаимодействию Л^7>) дираковских частиц (т. е. нуклонов) с электромагнит-
электромагнитным полем 1К В этом случае компоненты тензора 'Ft-4 представляют
О См. книгу Паули-{370]. ....
138 Глава И
собой компоненты поля, а именно компоненты магнитного поля,
если [а и v являются пространственными индексами, и электрического
поля, если [а или v равны нулю. Следовательно, энергию взаимодей-
взаимодействия A1.9) можно рассматривать как взаимодействие электромагнит-
электромагнитного поля с „моментом" электрона, причем уйуг(А, 1=1, 2, 3) =
= — <3j(j^k=£l) соответствует магнитному моменту, a foTfc — элек-
электрическому. По этой причине взаимодействие A1.9) известно как
моментное взаимодействие Паули. Оно может быть использовано
для описания в нерелятивистской области взаимодействия (в первом
приближении) электрона, протона или нейтрона с внешним электро-
электромагнитным полем, обусловленного тем обстоятельством, что магнит-
магнитный момент этих частиц не точно совпадает с магнетоном Бора
eb/2mc (где е и т соответственно заряд и масса частицы). Однако
в квантовой теории поля это приводит к бесконечным выражениям
в высших приближениях теории возмущений, как и все взаимодей-
взаимодействия с производной. Что касается низшего порядка, то в этом
случае получается хотя и конечный, но не точный результат для
электронов и нуклонов высоких энергий. Это обусловлено тем, что
аномальный магнитный момент (свыше магнетона Бора) не является
внутренней характеристикой дираковской частицы и обусловлен
взаимодействием ее с внешним полем (с электромагнитным — в слу-
случае электрона, с мезонным — в случае нуклона), а это взаимодей-
взаимодействие с полем зависит от частоты, т. е. изменяется с ускорением
дираковской частицы.
§ 3. Более сложные типы связей
Связи, которые содержат члены типа ср2 или более высокой сте-
степени, конечно, также возможны. Такое взаимодействие имеет место,
например, между бозонным и электромагнитным полями. Иногда
даже неясно, является ли это взаимодействие взаимодействием пер-
первого или более высокого порядка по полю. Например, Дайсон [125]
и Нельсон [353] показали, что линейное псевдовекторное взаимодей-
взаимодействие A1-6) псевдоскалярного поля с дираковским полем может
быть преобразовано с помощью канонического преобразования
в псевдоскалярное, содержащее мезонное поле <р в показателе ком-
компоненты (см. гл. 26). В целом же нелинейные взаимодействия пока
еще не используются, в основном, из-за математических сложностей,
за исключением взаимодействия бозонов с электромагнитным полем
(в котором, однако, константа связи мала). То же самое относится
к связям с производными более высокого порядка. Это было иссле-
исследовано Пайсом и Уленбеком [366], а также Борном [60], Гри-
Грином [213] и др. Пайс и Уленбек подробно рассмотрели случаи,
когда член, характеризующий взаимодействие, имеет вид /(Ц])<р
(□—деламбертьян), причем /(□) может даже иметь трансцендент-
трансцендентные корни, т. е. /(□) может иметь вид ехр(—XQ). Они показали,
Взаимодействие между полями 139
что в квантовой теории поля очень трудно, в действительности
почти невозможно, одновременно удовлетворить следующим условиям:
1) в теории не должны появляться бесконечности;
2) энергия системы должна быть положительно-определенной;
3) должно существовать решение задачи Коши (задачи с началь-
начальными условиями) для уравнений с взаимодействием.
Теории, в которых имеется связь с производными более высо-
высокого порядка, могут быть рассмотрены как частный случай теорий
с нелокальным взаимодействием. В таких теориях член, характери-
характеризующий взаимодействие бозонного поля с фермионным, имеет вид
j d±xf j d^xT f dW'ty (x') ty (x") <? (xm) F (x, x', x", x'"). A1.10)
т. е. взаимодействие распространяется по 4-объему и характери-
характеризуется ядром F, которое называется форм-фактором. Такие взаимо-
взаимодействия были введены в надежде устранить расходимости, прису-
присущие всем современным релятивистским теориям с локальным взаимо-
взаимодействием (Ватагин [510]). Существует целый ряд ограничений,
налагающихся на форм-фактор F:
1. Форм-фактор должен быть инвариантным по отношению ко
всем преобразованиям Лоренца и, следовательно, должен быть функ-
функцией только от (х —х'J. (х' — х"J и (х"— х'"J-
2. В пределе, когда расстояния велики по сравнению с фунда-
фундаментальной длиной L, которая вводится форм-фактором, взаимодействие
должно сводиться к своему „локальному" виду. Поэтому функция F
должна достаточно быстро спадать при больших |х — х'| незави-
независимо от того, является ли расстояние х — х' пространственно- или
времени-подобным.
3. Хотя микроскопическая причинность и нарушается введением
форм-фактора F, однако нарушение макроскопической причинности
при этом не должно обнаруживаться. Зависимость величин поля от
времени t в более поздний момент t-\-x должна поэтому быть огра-
ограничена до -z^siLjc. Вообще принцип причинности требует, чтобы
форм-фактор в импульсном пространстве был гладкой функцией и
обладал несколькими ограниченными производными. Достаточным
условием выполнения принципа причинности является аналитичность
функции F.
Пайерлс и Мак-Манус [383], Блох [42,43], Кристенсен и Мёллер [291 ]
и др. исследовали такие нелокальные взаимодействия Ч. Паули [382]
Ч Нелокальные взаимодействия исследовались также в работах М. А. Мар-
Маркова [см. М а р к о в М. A., Journ. Phys. USSR, 2, 452 A940); М а р к о в М. А.,
ДАН СССР, 40, 18 A943); Марков М. А., ЖЭТФ, 25, 527 A953); Мар-
Марков М. A., Nuovo Cimento, Suppl., 4, 760 A956)].
В последних двух работах рассматривался вопрос о так называемом
„динамически деформируемом" форм-факторе, т. е. о форм-факторе, который
не является абсолютно жестким и может деформироваться при взаимодей-
взаимодействиях. — Прим. пере в.
140 . Глава 11
показал, что для определенных классов нелокальных взаимодействий все
еще применим канонический гамильтонов формализм. Мак-Манус [317]
(следуя некоторым идеям Пайерлса), Фейнман [165] и др. исследовали
такие взаимодействия для частного случая электромагнитного поля.
Они показали, что из теории можно устранить бесконечность, соот-
соответствующую собственной энергии спинорной частицы. Однако бес-
бесконечности, обусловленные поляризацией вакуума, все еще остаются
в квантовой теории.
Рассмотренные выше теории нелокальных взаимодействий обла-
обладают тем свойством, что, хотя взаимодействие нелокально, пере-
переменные поля ф (х), <р (х) остаются полностью . локальными. Юкава
[546—549] попытался рассмотреть нелокальные поля, т. е. системы,
в которых переменные поля нелокальны. В этом случае переменная,
поля <р(х) зависит уже не от одной пространственно-временной
точки, а от многих. Такая система является достаточно общей. Дли
дальнейшего развития своей теории Юкава воспользовался принци-
принципом взаимности Борна [53, 55—58, 60], который гласит:
«Законы природы симметричны в отношении пространства-вре-
пространства-времени и энергии-импульса, или, более точно, по отношению к преоб-
преобразованиям
х-*р, (П-11)
р->х A.1-12)
они инвариантны».
В частности, соотношению
р2 = т2 A1.13)
соответствует соотношение
•■i3 x2 = L2, (Н-14)
где L — характерная длина. Однако Фирц [174, 175] показал, что
в отсутствие взаимодействия теория Юкавы эквивалентна теории,
рассматривающей некоторую суперпозицию локальных полей. Более
того, Блох [43] показал, что даже при наличии взаимодействия эту
теорию можно интерпретировать как теорию с нелокальным взаимо-
взаимодействием с некоторым форм-фактором F.
Из всего сказанного видно, что существуют различные описа-
описания возможных взаимодействий полей. Многие из них были исполь-
использованы в мезонной теории за последние 15 лет, при этом обнару-
обнаружилось, что некоторые особенно удобны для расчетов или для
простого объяснения экспериментальных фактов. Благодаря таким
частичным успехам, а также сложности экспериментальных наблю-
наблюдений теоретики пока не склонны отбрасывать какие-либо из этих
возможностей.
Мы придерживаемся иной точки зрения. Мы уверены в том, что
законы природы весьма просты, но нет оснований полагать, что
ими особенно легко пользоваться для расчетов. Более того, мы уве-
Взаимодействие между полями
рены, что должен существовать принцип отбора, на основании ко-
которого определенные типы взаимодействий предпочитаются другим.
Действительно, ниже мы найдем такой принцип при обсуждении пере-
перенормировки квантовой теории поля (см. гл. 24). Оказывается, что
определенные типы взаимодействий допускают перенормировку, т. е.
они ведут к конечным значениям всех физических величин после
конечного числа перенормировок. Для других типов взаимодействий
это сделать невозможно. Мы полагаем, что в настоящее время
указанное обстоятельство является достаточной причиной для того,
чтобы отбросить взаимодействия последнего типа в пользу первого.
Мы считаем, что ограничение числа „возможных" взаимодействий
(и в некоторой степени возможных полей) с помощью такого прин-
принципа отбора, как перенормировка (даже если это окажется времен-
временным и, возможно, будет заменено в будущем конечной теорией),
всячески следует приветствовать.
§ 4. Взаимодействие между двумя спинорными полями
До сих пор, рассматривая спинорное поле, мы всегда выбирали
билинейную комбинацию фГф. Действительно, использование одной
функции <|> или ф или нечетного числа таких функций привело бы
к физически неопределенным выражениям, у которых, например,
в результате поворота системы координат на 360° изменялся бы
знак. Следовательно, в выражения для А и В должны входить или
билинейные комбинации, или четное число функций спинорного поля.
Примером взаимодействия двух спинорных полей является про-
процесс ^-распада1). Одним спинорным полем является нуклонное поле,
другим—поле ^-частиц и нейтрино. (Эти последние частицы обычно
называют „лептонами".) Для описания этого процесса Ферми [156]
предложил следующий вид взаимодействия:
где фд. — волновая функция нуклона, у_в — электрона, а уп — ней-
нейтрино; обе матрицы Г одинаковы. Взаимодействие A1.15) даже
сегодня лежит в основе теории [3-распада. Оно было выбрано Ферми
по аналогии с взаимодействием заряженных частиц с электромаг-
электромагнитным полем. Поле ~£п удовлетворяет уравнению Дирака, описы-
описывающего частицу с массой, равной нулю. В качестве оператора Г
можно взять одно из известных пяти выражений, приведенных
в табл. 1, т. е.
Г = /, Та- ПУЬ> 'ТбТа- Тв- (И-16)
1) Для общего ознакомления с р-распадом отсылаем читателя к работам
Конопинского [285, 286], а также к книге Блатта и Вайскопфа [40], гл. ^13.
Обзор экспериментальных работ и новейшую библиографию можно найти
в работе Фейнгольда [151].
142 ]\ава И
В действительности возможна любая линейная комбинация взаимо-
взаимодействия типа A1.15) с такими матрицами Г. Какая из этих форм
или комбинаций является правильной, должен определить экспери-.
мент; в этом и заключается основная задача изучения р-распада.
В 1935 г. Конопинский и Уленбек [283, 284] предложили для
описания ^-распада связь с производной в виде
Результаты этой теории были подтверждены экспериментальными
наблюдениями спектра ^-распада, которые, как позднее было пока-
показано, оказались ошибочными. К моменту появления обзорной статьи
Конопинского [285] в 1943 г. эксперименты окончательно отвергли
связь с производной A1.17).
В той же статье [545], в которой Юкава предложил мезонную
теорию ядерных сил, он предложил также рассматривать [3-распад
как процесс, обусловленный двумя последовательными взаимодей-
взаимодействиями, а именно взаимодействием нуклонного поля с мезонным,
описываемый членом взаимодействия
ОфдГф^. A1.18)
и взаимодействием мезонного поля с лептонным (поле [3-частиц и
нейтрино) в виде
где <р — волновая функция мезона. В этой теории мезон является
виртуальным, ибо он рождается, а затем поглощается в промежу-
промежуточном состоянии. В этих формулах мы умышленно написали G
и gn, чтобы указать, что величина константы связи в A1.18) велика,
а в A1.19) — мала. Нам кажется, что реальный тс-мезон не соот-
соответствует этой теории; распад тс-мезона на электрон и нейтрино
экспериментально еще не наблюдался. Таким образом, эксперимен-
экспериментально нам известна верхняя граница gn, которая ниже, чем это
требуется для р-распада по теории Юкавы. По-видимому, некоторые
из недавно открытых тяжелых мезонов можно использовать в тео-
теории Юкавы.
§ 5. Взаимодействие и уравнения движения
Лагранжиан, описывающий поля с взаимодействием, равен сумме
лагранжианов свободных полей и лагранжиана взаимодействия. Так,
для случая взаимодействия спинорного поля со скалярным бозонным
полем посредством прямой связи лагранжиан системы полей имеет вид
(П-20)
Взаимодействие между полями 143
где
(П-22)
A1.23)
Варьируя _g* по ф, получаем следующее уравнение движения для
поля <|>:
A1.24)
Правая часть этого уравнения соответствует взаимодействию
с мезонным полем. Варьируя по ср, получаем уравнение движения
для поля <р
? A1.25)
Таким образом, фГф является источником бозонного поля <р, так же
как в случае уравнений Максвелла ток является источником элек-
электромагнитного поля.
В 1935 г. Юкава [545] изучил уравнение A1.25) при Г=1,
предположив, что масса нуклона значительно больше массы мезона.
Это предположение позволяет (даже в квантовой механике) локализо-
локализовать нуклон в малой области пространства, например в начале
координат. Правая часть уравнения A1.25), которую можно считать
пропорциональной плотности нуклонов, в таком случае переходит
в пространственную 8-функцию. Так как источник не зависит от
времени, то существуют решения уравнения A1.25), также не зави-
зависящие от времени, поэтому □ можно заменить на V2. [Разумеется,
к этим решениям можно добавить решения однородного уравнения,
которые, как и в электродинамике, соответствуют распространению
свободной (без взаимодействия) мезонной волны в пространстве;
здесь мы не будем касаться этих решений.] Уравнение для мезон-
ного поля, таким образом, принимает вид
(V2 — fi2) <р = + G8 (г). A1.26)
Решение этого уравнения легко можно получить с помощью разло-
разложения обеих частей уравнения в ряд Фурье. При этом легко уста-
установить, что решение имеет вид
Таким образом, отвлекаясь от множителя 1/г, мы видим, что мезонное
поле убывает в е раз на расстоянии, равном комптоновской длине
волны мезона {i-1. Это мезокное поле может взаимодействовать
со вторым нуклоном; таким образом осуществляется взаимодействие
144 Глава II
между двумя нуклонами, которое будет зависеть от расстояния,
согласно формуле A1.27). Скорость спадания с расстоянием
„потенциала Юкавы" согласуется с требованием феноменологиче-
феноменологического описания ядерных сил. Используя наблюдаемую массу тс-мезона,
получаем, что „радиус" ядерных сил 1/ja равен 1,4. 10~13 см; эта
величина имеет нужный порядок для объяснения наблюдаемых ядер-
ядерных взаимодействий. В т. II, гл. 47, мы вернемся к задаче ядерных
сил и обсудим ее значительно подробнее.
Гамильтонов формализм, развитый в предыдущей главе, может
быть также применен к задаче взаимодействия полей. Другими сло-
словами, мы можем определить канонический тензор энергии-импульса,
причем интеграл по трехмерному пространству от компоненты Г00
будет соответствовать полной энергии или гамильтониану системы.
В случае взаимодействия скалярного бозонного поля со спинорным
посредством прямой связи эта процедура дает
A1.28)
где Но — сумма гамильтонианов свободных дираковского и мезон-
ного (Клейна — Гордона) полей [соотношения A0.62) и A0.29), соот-
соответственно], а Нх — энергия их взаимодействия
#, = + GJd3x фГфср- A1.29)
Глава V2
ВЗАИМОДЕЙСТВИЕ С ЭЛЕКТРОМАГНИТНЫМ ПОЛЕМ
Взаимодействие заряженного поля с электромагнитным опреде-
определяется уже требованием калибровочной инвариантности. Для учета
этого взаимодействия, как мы уже видели, необходимо заменить рх
на Ръ-\-е\А^ (где ех — заряд частицы), так что при действии на
переменную поля <р оператор д/дх* заменяется следующим образом:
JJJfl-Л.^Л. A2.1)
'1С *
При действии же на переменную поля <р* оператор д/дх1- заменяется
на оператор D*, который является комплексно-сопряженным D^, т. е.
D*= ——Ь — А.. A2.2)
& дх* ас г *- >
При действии оператора д/дх^ на действительное поле оч остается
неизменным. В дальнейшем поэтому мы не будем касаться таких
полей.
§ 1. Заряженное бозонное поле
В качестве иллюстрации к вышесказанному рассмотрим взаимо-
взаимодействие заряженного поля Клейна — Гордона с максвелловским
полем. Раньше мы уже отметили, что лагранжиан такого поля
имеет вид
J2?m = — (f*2?*? — (?*f^)> A2.3)
где индекс т у _g* указывает на то, что лагранжиан относится
к мезонному полю. Согласно изложенному выше, для получения
правильного лагранжиана взаимодействия заряженного бозонного
поля с максвелловским полем необходимо заменить в выраже-
выражении A2.3) оператор д/дх^ в соответствии с соотношениями A2.1)
и A2.2) и добавить к JS?m лагранжиан максвелловского поля.
В результате для полного лагранжиана системы получим следующее
выражение:
Л А -\ ми г\ * 1 -\ _ .
,A2.4)
~* 2 дх., дх-> r T
где е — заряд электрона.
10 Зак. 1784. Мезоны и полл
146 Глава 12
При варьировании £? по А^ получаем уравнения Максвелла
тогда как при варьировании по ср и по ср* получаем уравнение
Клейна — Гордона с учетом электромагнитного поля. Уравнения A2.5)
указывают, что ток как источник электромагнитного поля опреде-
определяется выражением
^f A2.6)
которое для данного случая можно представить следующим образом:
Определенный таким образом ток, согласно уравнениям движения,
сохраняется. Выражение A2.7) при А^ = 0 совпадает с вышеопре-
вышеопределенным выражением для тока A0.52). Это оправдывает предполо-
предположение о том, что выражение A0.52) действительно представляет
собой 4-Еектор тока в случае отсутствия электромагнитного поля.
Лагранжиан A2.4) обычно записывают в форме
-2* = -2^+-2%+ .2^. A2-8)
где JS'q -— лагранжиан свободного электромагнитного поля,
a J2>i—лагранжиан взаимодействия, т. е.
Этот лагранжиан можно представить в виде —j ,.А?, где вели-
величина j^ определяется соотношением A2.7), т. е. представляет собой
ток в присутствии электромагнитного поля. Появление члена е2А2ср*ср
характерно для взаимодействия бозонного поля с электромагнитным.
В нерелятивистском пределе он соответствует члену А2 в уравне-
уравнении Шредингера с учетом электромагнитного поля.
Мы можем здесь также развить гамильто.чов формализм, вос-
воспользовавшись методами гл. 10. Однако импульс канонически-
сопряженный ср теперь уже будет зависеть от электромагнитного поля.
§ 2. Дираковское поле
Лагранжиан системы взаимодействующих дираковского и элек-
электромагнитного полей имеет вид
Jg = — ——-—^— -——- <1)-|"-А ( \- ieA. ) Ф -f- 1ш<Ь<Ь -j—
Л OX*i OX"* J.L [_ \ дх^" '"/ J
1.., A2.10)
Взаимодействие с электромагнитным полем 147
где J2?n — лагранжиан свободного дираковского поля. При варьиро-
варьировании J2? по потенциалам электромагнитного поля получаем
. A2.11)
Аналогично при варьировании Jg по ф и Ф получаем уравнения
Дирака с учетом электромагнитного поля для фиф
А0, A2.12а)
) = 0. A2.126)
Из уравнения A2.11) следует, что ток при наличии электромагнит-
электромагнитного поля определяется выражением
которое формально идентично выражению для тока A0.59) в случае
свободного поля. Однако, по существу, это не так, ибо фиф
в выражении A2.13) подчиняются уравнениям A2.12), в которых
присутствуют потенциалы электромагнитного поля, в то время как
в выражении A0.59) ф подчиняется уравнению свободного поля.
В отсутствие электромагнитного поля (А^ = 0) оба эти выражения
совпадают.
Вышеизложенные теории инвариантны по отношению к калибро-
калибровочным преобразованиям, т. е. когда
?-*1;-~ A2Л4)
и одновременно
A2Л5)
где Л — произвольная функция координат, удовлетворяющая урав-
уравнению □ А = 0. Ясно, что этому удовлетворяет функция Л = const,
которая, как отмечалось выше, уже достаточна для сохранения
4-вектора тока.
В том специальном случае, когда заряженное поле взаимодей-
взаимодействует с внешним электромагнитным полем Л£(х), варьирование
по л£ уже не является произвольным. Таким образом, правильное
описание такой системы возможно с помощью следующего лаг-
лагранжиана:
A2.16)
где J^m — лагранжиан заряженного материального поля, а под уУ
подразумевается соответствующее выражение для тока этого поля
Ш Глава 12
в присутствии внешнего электромагнитного поля, т. е. соотноше-
соотношение A2.7) с заменой А^—^-А^ для случая бозе-поля и соотноше-
соотношение A2.13) для случая дираковского поля.
§ 3. Система трех полей
В заключение рассмотрим одновременное взаимодействие нуклон-
ного поля, заряженного бозонного и электромагнитного полей.
Сначала рассмотрим взаимодействие нуклонного поля с заря-
заряженным бозонным полем. Мы должны быть при этом осторожны,
чтобы не нарушить закона сохранения полного заряда. Позднее
рассмотрим возможные типы взаимодействия, при которых полный
заряд системы еще сохраняется. Ограничимся здесь только замеча-
замечанием, что для прямой связи взаимодействие опять будет иметь
вид ффср и фф?*- Следовательно, в этом случае введение электро-
электромагнитного поля будет снова осуществляться заменой A2.1) и A2.2)
в лагранжианах свободных материальных полей. Однако в случае
связи с производной, которая будет иметь, как и выше, вид
^L ^1 A2.17)
дх*
мы должны произвести замену A2.1) и A2.2) также и в лагран-
лагранжиане взаимодействия A2.17). Это приведет к члену связи, вклю-
включающему три поля
ф-^фА^. A2.18)
В псевдоскалярной мезонной теории этот член имеет вид
, A2Л9>
причем в основном он ответственен за процессы рождения заряжен-
заряженных мезонов f-лучами (см. т. II, гл. 35 и 37).
РАЗДЕЛИ!
КВАНТОВАЯ ТЕОРИЯ
ПОЛЕЙ
Глава 13
КВАНТОВАНИЕ ПОЛЯ
Гамильтонов формализм, развитый в гл. 10, дает нам возмож-
возможность проквантовать поле обычным способом, заменив скобки Пуас-
Пуассона коммутаторами; при этом система переменных превращается,
вообще говоря, в некоммутирующие операторы. Но прежде чем
приступить к квантованию поля, напомним кратко различные пред-
представления обычной квантовой механики.
§ 1. Представления Шредингера и Гейзенберга
В шредингеровском представлении состояние системы в заданный
момент времени t определяется полным набором всех возможных
измерений над системой в этот момент времени. Эти данные содер-
содержат вектор состояния системы 4!"s@' Дальнейшее развитие системы
описывается зависимостью от времени вектора состояния, которая
определяется уравнением Шредингера
W^(t)A3.1)
В этом представлении операторы Fs физически наблюдаемых вели-
величин не зависят от времени; это означает, что для всех моментов
времени они одинаковы, т. е. dFs/dt^=0. Однако математическое
ожидание оператора
(Я) = (Wa(t), FsWs(t)), A3.2)
вообще говоря, будет зависеть от времени, причем
ib±(Fs)^(Ws((), [Fs, He]Wa(t)). A3.3)
Назовем оператором Fs в представлении Шредингера такой опера-
оператор, для которого выполняется соотношение
Совершим, далее, над вектором состояния Ws(t) унитарное, завися-
зависящее от времени преобразование V(t), которое переводит его в вектор
состояния
фф-^ЮФаЮ. A3.5)
= v1"(оv(o=»i, v*(t=v-\f). A3.6)
Квантование поля 151
Используя уравнения A3.1) и A3.5), находим, что вектор состоя-
состояния Ф {£) подчиняется теперь следующему уравнению:
A3.7)
Поэтому, если мы выберем унитарный, завис^щчЯ от времени опе-
оператор V(t) так, чтобы он удозлетзорял уравнению
^ A3.8)
то преобразованный вектор состояния Фя не будет зависеть от вре-
времени. Поскольку оператор V(f) является унитарным, математическое
ожидание оператора Fs будет теперь выражаться в виде
A3.9)
Определим Fs(f) следующим образом:
Fn{t) = V(t)FsV-l(t). A3.10)
Тогда, согласно этому определению, зависящий от времени опера-
оператор Fs(t) имеет такое же математическое ожидание по векторам
состояния Фя, какое имеет опеэатор Fs по векторам состояния 4rs.
Дифференцируя соотношение A3.6) по времени, получаем
^+@+т^ = о. (i3.li)
Полученное уравнение вместе с уравнением П3.8) и его эрмитово-
сопряженным приводит к следующей зависимости оператора
от времени:
dV , dVf l
—wVfFB{t) + Fa{t)V _ = _
= ilHS, Fs(t)]- A3.12)
Уравнение A3.12) и независящий от времени вектор состояния,
который подчиняется соотношению
дФтт
-дг = 0, A3.13)
определяют представление Гейзенберга. Вектор состояния не зависит
от времени и одинаков для всех моментов времени. С другой стороны,
операторы Fir(t) зависят от времени. Вектор состояния Фя определяет
теперь всю историю системы, т. е. результат всех возможных измере-
измерений, производимых над системой за всю ее историю. Однако если про-
провести реальное измерение над системой, то вектор состояния изменится.
Хотя гейзенберговский вектор состояния Фя не зависит от времени,
его можно определить по тем результатам, которые он предсказывает
для некоторых измерений в заданный момент времени. Таким образом,
мы можем определить Фя как вектор состояния, который при t = 0
переходит в шредингеровский вектор состояния Ws@).
152 Глава 13
§ 2. Канонические перестановочные соотношения
Напомним, что квантование классической механической системы
состоит в замене скобок Пуассона для канонических переменных
перестановочными соотношениями. Эти перестановочные соотношения
для системы с п степенями свободы имеют вид
\Яг' Яз) = 1Рп Ps] = 0.
1Чт> /».]='«„, A3.14)
s, r — 1, 2 ... п.
В этих перестановочных соотношениях время как параметр, во всех
переменных одинаково. В случае сеточной схемы, где можно ото-
отождествить Qs(t) и fa(t), Ps(t) и ZxsKs(t), мы можем непосредственно
применить перестановочные соотношения (IS. 14), в результате полу-
получим
[Qs(Q. Qr(Щ = IP.@. Pr@1 = о. A3.15а)
lQa(t).Pr(t)] = lbiar. A3.156)
Последний коммутатор, выраженный через тсг, имеет вид
[Q.@. «г «)! = ** Йг- A3-16)
Переход к континууму производится путем суммирования A3.16)
по всем ячейкам 8л:г, причем
2 5xs [Qr (О, *s (/)] = Г [Т (Je, t), тс (J, 01 d3^' = ih, A3.17)
в J
откуда следует, что
[ср (х, t), тс (xr, t)] = ihb (x — Р). A3.18)
Агалогично соотношение A3.15а) для континуума переписывается
в виде
[<р(х, t), cp(x', 0] ==[«(*. 0. «(*'• 01=0- A3.19)
Соотношения A3.18) и A3.19i являются фундаментальными соотно-
соотношениями квантовой теории поля. Они показывают, что в квантовой
теории переменные поля и канонически-сопряженные им импульсы
становятся некоммутирующими между собой операторами. Поэтому
при перестановке переменных должна соблюдаться известная осто-
осторожность. Заметим, однако, что в силу соотношения A3.19) пере-
переменные одного сорта, т. е. два тс или два ср, в разных простран-
пространственных точках, но в один и тот же момент време-ш, коммутируют
между собой. Это соответствует тому, что динамические переменные,
относящиеся к различным степеням свободы, коммутируют между
собой,
Квантование поля 153
Развитый выше формализм легко обобщается на случай много-
многокомпонентных полей. Так как различные компоненты поля относятся
к разным степеням свободы системы, то мы получаем следующие
перестановочные соотношения:
[?г(*. О. *.(£. 01 = /«„&(* — х'),
A3.20)
где и:г — канонически-сопряженный срг импульс, причем г= 1, 2 .. .л;
п — номера компонент оператора поля.
Эти перестановочные соотношения не определяют представления,
в котором мы работаем (Гейзенберга или Шредингера). Для опре-
определения представления необходимо найти зависимость от времени
как вектора состояния системы, так и операторов поля.
Рассмотрим скалярное мезонное поле. В представлении Шредин-
Шредингера вектор состояния для такой системы будет удовлетворять сле-
следующему уравнению движения:
If > >
J ^{«W+IVWhVWIT A3.21)
Операторы тс(х) и f(x) при этом не зависят от времени и могут
быть определены в виде
п(х)= к (х, 0), A3.22а)
( = ср(х, 0), A3.226)
причем
[f(x), iz(x')] = ihb(x — x/). A3.23)
Унитарный оператор, преобразующий шредингеровское предста-
представление в гейзенберговское, записывается в явном виде следующим
образом:
Шт A3.24)
Это есть требуемое унитарное преобразование, которое непосред-
непосредственно следует из соотношения A3.8), так как Hs не зависит от
времени. Из выражения A3.24) следует (скорее, чем из exp {iffsft—£0)}),
что гейзенберговское представление выбрано так, что в момент t = 0
оно соответствует шредингеровскому представлению. Это находится
в согласии с соотношениями A3.22).
Вектор состояния системы Фя теперь уже постоянен во времени,
т. е,
154 Глава IS
Однако операторы поля зависят теперь от времени и подчиняются
следующим уравнениям движения:
^ | £ A3.26)
g £ . A3-27)
где
Я @ = в+«га*/*Явв-«Ъ*/* = tfs =
= 1 ]>*{*»(£ OH-[V?(jT. OP + pVC^ 0} A3.28)
« (х, О = еш^\ (х)«"**«*/*, A3.29)
<Р(*, О = еш**1*?$),-**&*. A3.30)
Используя перестановочные соотношения A3.20), легко можно уста-
установить, что уравнения A3.26) и A3.27) эквивалентны уравнению
Клейна — Гордона для оператора поля ср (х, t).
§ 3. Импульсное представление и квантование
скалярного поля
Выше мы ввели лишь перестановочные соотношения для переменных
поля, которые должны выполняться в квантовом случае. Теперь наша
задача заключается в установлении следствий наложения этих кван-
квантовых условий. В первую очередь мы проквамтуем действительное
скалярное поле ср, поскольку оно является наиболее простым. (Наше
рассмотрение с таким же успехом применимо и к псевдоскалярному
полю.) Мы будем работать в шредингеровском представлении, так
что операторы не будут зависеть от времени.
Следствия квантования значительно легче уяснить, если пользо-
пользоваться бесконечным числом дискретных переменных. Для этого раз-
•> ■-*■
ложим переменные поля <р (jc) и тс(х) в ряды Фурье, нормируя функ-
функцию на объем V = LS,
<р (х) = V~'h 2 Чье+й-*, A3.31)
к
тс(х) = V~'h 2 Рке-**-£. A3.32)
к
Суммирование проводится по всем k{ A = 1, 2, 3), которые удо-
удовлетворяют граничному условию на границе объема V (т. е. кото-
которые кратны величине 2ir/L). При этом мы допустили здесь обычное
условие периодичности [ср(*» + £) = Хср(х^; |Х|2 = 1], разбивая тем
Квантование поля 155
самым непрерывное А-пространство на ячейки. Знак минус в экспо-
экспоненте формулы A3.32) выбран умышленно; такой выбор приводит,
как это мы увидим вскоре, к упрощению расчетов.
Так как ср и тс являются в классическом пределе действительными
функциями, то в квантовом случае они должны быть эрмитовыми
операторами, т. е.
cp(*) = cpt(*), A3.33)
w(jc) = TC+(je), A3.34)
где, как обычно, а+ — оператор эрмитово-сопряженный а. Следо-
Следовательно, для коэффициентов разложения р и q мы должны иметь
<7_*=<7£. A3.35)
Р-ь=Р\- A3.36)
Не зависящие от времени операторные коэффициенты рк и qk
на том же основании, как Ps и Qs, следует рассматривать как дина-
динамические переменные. Действительно, если мы рассмотрим коммута-
коммутатор величин ср и тс, то, согласно соотношениям A3.14), для рк и qk
получим
[ср (х), тс (*')] =Г'22 [qk. Pv] е&*е-&-2 =
к к'
= ihV~l S Д-<*-£>; A3.37)
к
это соотношение в пределе при V —> оо переходит в уже известное
нам перестановочное соотношение для ср и тс
[ср(х), тс(х')] = *й§(£— Р). A3.38)
С другой стороны, если известно перестановочное соотноше-
соотношение (kl.23), то перестановочное соотношение для р]е и qk получается
способом, обратным тому, который ведет к соотношению A3.38).
Так как рк и qk выражаются через ср и тс в виде
A3.39)
A3.40)
то их коммутатор, согласно соотношению A3.23), равен
[Рн, ЧнЛ = V'1 f &х f <Рх' [тс (х), ср (%')} eitxe-it'.P в
__г-йу-1 Г dsxei №-?)■?=,_ ihbm,, A3.41)
156 Глава 13
Аналогично получаются соотношения
[рк, pv\ = [qk ,qv\ = 0. A3.42)
Далее, гамильтониан рассматриваемого поля имеет вид
A3.43)
Рассмотрим член f <p2d3;t. Используя выражение A3.31), получаем
Г <р2 Ле = К С 2 2 qt.e*£*qk,e&-*d*x. A3.44)
ft К
2
ft К
Проведя интегрирование, найдем
Вводя сокращенное обозначение
«"а^ + УРЧ1^ A3.46)
и используя соотношения A3.37) и A3.38), легко проверить, что
Это выражение по форме аналогично гамильтониану набора гармо-
гармонических осцилляторов, который известен нам из обычной квантовой
механики, за исключением того, что вместо qlqk и р%рк там стоят
q\ и р\. Если наши комплексные операторы рк и qk разделить
на сумму действительной и мнимой частей, то Н можно тогда пред-
представить в форме, содержащей лишь квадраты действительных вели-
величин. Однако если мы хотим выразить Н в форме, более удобной,
чем форма A3.Ч|,), то это легче всего сделать с самого начала,
рассматривая действительные коэффициенты разложения (как это
было сделано, например, Ферми [155J):
ср (%) = V~lh 2 qkl sin к. х+ qk2 cos к- х; A3.48)
/С
аналогичное разложение имеет место для тс(х). В методе Ферми
при разложении в ряд Фурье вместо двух волн с волновыми векто-
рами k и —k вводятся стоячие волны k\ и k2. В результате полу-
получается гамильтониан, представляющий собой сумму обычных гамиль-
гамильтонианов осцилляторов и содержащий величины как q\x и рк1, так
и д\2 и />|2. Удобнее всего его можно трактовать с помощью эле-
Квантование полк
is?
ментарной матричной квантовой механики. Стационарным является
состояние, в котором энергия осцилляторов равна Ьи>ы(пы~\-1/2), где
rijci означает число квантов состояния ki (I = 1 или 2). Операторы q^
представляются при этом матрицами, общий член которых обозна-
обознаA3.49)
Заметим, что общий член qkl обозначается через пк1, а д—че-
д—через пкг, причем пк1 и пк2 — не зависящие друг от друга квантовые
числа.
Матрицы qk и у+, которые нужны для диагонализации выраже-
выражечается через nki. Можно i
Як = У 2^
"[оказать, что дк1
0
УТ
0
0
УТ
0
У2
0
0
У2
0
Уз
имеет
0 .
0 .
Уз .
0 .
ния A3.47), можно построить из матриц qk
kl
однако мы не
будем подробно останавливаться на этом. Такое построение соот-
соответствует каноническому преобразованию от стоячих к бегущим
волнам. Вместо этого, следуя Вентцелю [255J, непосредственно напишем
A3.51)
где ак — матрица, т. е.
■** =
0
0
0
0
VI
0
0
0
0
У2
0
0
0 .
0 .
Уз .
0 .
A3.52)
общий член этой матрицы называется квантовым числом пк. Общий
член матрицы а_к называется независимым квантовым числом п_к.
Очевидно, что выражения A3.50) и A3.51) удовлетворяют усло-
условиям эрмитовости A3.35) и A3.36). Более того, они подчи-
подчиняются перестановочным соотношениям A3.41) и A3.42), что можно
увидеть, рассматривая матричные элементы A3.52). Так как кван-
квантовые числа пк и п_к независимы друг от друга, то матрица ак
описывает переходы, при которых изменяется пк, а матрица а_к —
158 Глава i3
переходы с изменением п_к. Действительно, единственными исчезаю-
исчезающими матричными элементами являются
(...пг...пк— 1...\ак\...щг...пк. ..) =VnuSnzV---. A3.53)
(.. .лг. . .пк... | at\. . .nv. . .пк—\.. .) = УчК}п1/ ■ • ■ A3.54)
Матричное умножение соотношения A3.53) на соотношение A3.54)
дает
(.. .пк. .. | акаЦ. . .пк.. .) = («*+ l)8WiV.. . A3.55)
аналогично
(.. .пк. ..\а\ак | .. .пк. . .) = (nk)bnjnjr.*. A3.56)
Разность между соотношениями A3.55) и A3.56) представляет со-
собой элемент единичной матрицы, т. е.
Ц, 4] = /. A3.57)
Кроме того,
[ак, av\ = [at, аЭД = 0 A3.58)
и
[ак, at] = lut'. A3.59)
Соотношения A3.58) и A3.59) показывают, что величины рк и дк,
определенные формулами A3.50) и A3.51), удовлетворяют пере-
перестановочным соотношениям A3.41) и A3.42).
Выражая гамильтониан в переменных а, получаем
A3.60)
к
Используя A3.55) и A3.56), мы видим, что величина полной энер-
энергии Е равна
A3.61)
к
Аналогично полный импульс поля можно выразить в виде
Р = fd3XK (х) V <р (л:), A3.62)
или, в переменных а,
^=2й*(ге*+т)- A3.63)
к
Соотношения A3.63) и A3.61) ясно указывают, что пк следует рас-
рассматривать как число частиц с импульсом k и энергией йш7с. Таким
образом, квантование поля выявляет корпускулярную сущность по-
последнего.
Квантование поля 159
Когда пк = 0, т. е. в поле нет частиц, то нулевая энергия
бесконечно велика. Так как изменение начала отсчета энергии с фи-
физической точки зрения несущественно, то обычно отбрасывают эту
нулевую энергию и определяют энергию следующим образом:
Е = 2йюАп.4 = 2й(В&айай- A3.64)
к ' к
Это изменение в определении энергии может быть в действительно-
действительности оправдано тем, что при переходе от классической теории
к квантовой порядок операторов определен лишь с точностью до
члена порядка Ъ (Розенфельд и Соломон [411]). С другой стороны,
нулевой импульс исчезает благодаря симметрии.
§ 4. Операторы числа частиц, их рождения и уничтожения
Содержание квантовой теории можно уяснить, подробно рассмо-
рассмотрев эрмитовский оператор Nk — акак, называемый оператором чи-
-»-
ела частиц в состоянии k. Выберем, как и выше, представление,
-»•
в котором все операторы Nk (т. е. для каждого Щ диагональны.
Это возможно благодаря коммутации операторов Nk при различ-
различных k, т. е.
[Nk, Nk,] = [atak, a\.aki\ =
= ак[ак, ак,]ак-\- ai>[at, akr]ak = 0. A3.65)
Исследуем теперь действие операторов ак в представлении,
в котором операторы Nk диагональны. Для этого укажем на сле-
следующие перестановочные соотношения между Nk и операторами ак
и at:
\ак, Nk\ = [ak, atak\ = ak, A3.66)
[at, iVu]= — at A3.67)
Пусть Фх и X — собственная функция и собственное значение опе-
оператора Nk, соответственно, т. е. ЛАлФх = лФI. Тогда а^Ф». — соб-
собственная функция оператора Nk с собственным значением X—1.
В этом легко убедиться, так как благодаря перестановочным соот-
соотношениям A3.66)
Nk (акФО = (akNk — ак) Фх = (X — 1) (айФх), A3.68)
что и требовалось доказать. Аналогично акФх является собственной
функцией оператора Nk с собственным значением X-J- 1.
160 Глава /3
Покажем далее, что собственные значения оператора Nk—не-*
отрицательные целые числа. Заметим, что если подействовать т раз
оператором ак на Фх, то мы получим собственную функцию с соб-
собственным значением X— т, где т — положительное целое число.
Таким образом, либо N обладает отрицательными собственными
значениями (величина X— т может быть сделана отрицательной при
достаточно больших т), либо одна из собственных функций должна
обратиться в нуль. Однако оператор Nk положительно определен
(^ 0), так как он представляет собой произведение оператора вре-
мени на его эрмитово-сопряженный. Иными словами, его собствен-
собственные значения должны быть положительно определены (^> 0). Про-
Произведение акак также поэтому неотрицательно и, следовательно,
для произвольного, не равного нулю вектора состояния
(Ф, Л^Ф)>0, где (Ф, Ф)>0. A3.69)
Знак равенства имеет место лишь для состояния Фо, для которого
акФ0 = 0. Следовательно, Фо описывает самое низкое состояние.
Так как МкФ0 = Х0Ф0, то мы имеем
(Фо> МкФ0) = \0(Ф0, Фо) = (Фо> 4%Ф0) = 0. A3.70)
Далее, так как (Фо, Фо) > 0, то в качестве наименьшего собствен-
собственного значения необходимо принять величину
Х0 = 0. A3.71)
Таким образом, мы установили, что собственные значения опера-
оператора Nk действительно неотрицательные целые числа.
Более того, из формулы A3.64) следует
//==2^^- A3.72)
к
Аналогичным образом можно записать и полный импульс Р
^ A3.73)
к
Следовательно, Nk обладает всеми свойствами оператора числа ча-
частиц. Его собственные значения являются положительными целыми
числами, а из формул A3.72) и A3.73) видно, что в отсутствие
взаимодействия каждая частица с импульсом к вносит свой вклад bk
в полный импульс поля и энергию Ьшк = Ъ Y b? -\- ^ в полную
энергию.
Оператор N = 2 Nk можно интерпретировать как оператор пол-
к
ного числа частиц. Действуя на вектор состояния Ф, он дает пол-
полное число частиц, присутствующих в поле. В нашем представлении,
Квантование поля 161
в котором оператор д/^ с собственными значениями пк, пк, . . ., диа-
гонален, т. е. ф
Щ A3.74)
соотношение A3.66) можно написать в явном виде
(n'k— пк+\){пк\ак\пк) = 0. A3.75)
Таким образом, величина (пк\ак\пк) отлична от нуля, только когда
пк=пк— 1 [вспомним соотношение A3.53)]. Мы можем поэтому
рассматривать ак как оператор уничтожения частицы. Действительно,
это уже было очевидно из равенства A3.68), так как ак, действуя
на вектор состояния Ф с числом частиц пк в состоянии k, приво-
приводит к состоянию, в котором имеется лишь пк—1 частиц. Анало-
Аналогичным образом можно переписать и соотношение A3.67)
(пк—пк—\)(пк\а1\ п'к) = 0, A3.76)
т. е. а\ — оператор рождения частицы.
Фундаментальную роль в теории играет состояние, которое
описывается функцией Фо и для которого ЫкФ0 = 0 при всех k.
Это такое состояние поля, в котором нет ни одной частицы. Оно
называется вакуумом. Согласно формулам A3.72) и A3.73), оно
имеет нулевую энергию и импульс и фактически представляет собой
состояние с наинизшей энергией. Кроме того, оно обладает свой-
свойством инвариантности. Всем наблюдателям вакуум представляется
одинаковым.
Как уже указывалось выше, мы можем сконструировать все ба-
базисные вектора теории, действуя последовательно операторами рож-
рождения, частиц на волновую функцию вакуума. Так, функция
A3-77)
соответствует, состоянию, в котором имеется один мезон с энергией
й(ол и импульсом hk. Аналогично
44'Ф0 ■ A3.78)
описывает состояние с двумя мезонами, и, наконец, ак . .. а\/Ф0
(с п множителями а+) есть волновая функция состояния с п мезо-
мезонами. Заметим, что волновая функция n-мезонного состояния орто-
ортогональна /ге-мезонной волновой функции при п ф гп, так как они
соответствуют различным собственным значениям эр'митового опера-
оператора полного числа частиц.
Из общих принципов квантовой механики следует теперь, что
волновая функция W произвольного состояния может быть разложена
162 Глава 13
обычным образом в ряд по базисным векторам
ЧГ = с0Ф0
Q+... A3.79)
Перейдем в этом последнем выражении к непрерывному спектру k.
При этом перестановочные соотношения для ак, например, примут,
вид
[ак, at,) = b(k—%'). A3.80)
В выражении A3.79) неоператорные функции c1(k), c2(k, k') и т. д.
играют роль, аналогичную коэффициентам разложения в обычной
квантовой механике. Их физический смысл легко установить. Он
заключается в следующем: амплитуда вероятности того, что в со-
состоянии ¥ нет ни одной частицы, очевидно, выражается матричным
элементом (<&0-,VP), где Фо — базисный вектор, соответствующий от-
отсутствию частиц. Эта величина в соответствии с выражением A3.79)
равна с0, так как волновая функция Фо ортогональна волновым
функциям всех состояний, в которых имеются частицы. Аналогично
-*-
амплитуда вероятности обнаружения одного мезона с импульсом р
в состоянии, описываемом вектором состояния W, дается матричным
элементом типа
куда снова не входит никаких других волновых функций ввиду их
ортогональности. В дальнейшем нам необходимо вычислить правую
часть соотношения A3.81). Напомним, что из определения эрмитово-
сопряженного оператора следует
(Ф, дф') = (а+ф, Ф');
таким образом, учитывая, что c1(k) — неоператорная функция, можно
написать
, J d^kc, (ЛLФ0) = f ^д.С1(|)(ф0, ар4Ф0). A3.82)
Используя перестановочное соотношение A3.80) и свойство вакуума,
а именно, что арФо==0, можно вычислить" теперь выражение
(Фо, flp
В результате получим
(Фо, ара1Ф0) = (Ф0, {4ар+3(р — *)} Ф„) =
= Ь(р— Л)(ФО, Фо). A3.83)
Квантование поля 163
Если мы предположим, что вакуумное состояние нормировано так,
что (Фо, Фо) = 1, то получим
(а1Фа,Ч) = сх(р). A3.84)
Мы видим, таким образом, что коэффициенты разложения cQ, c1 (k),
с2 (k, k') и т. д. можно интерпретировать как амплитуды вероят-
вероятности, соответственно, отсутствия мезонов, обнаружения одного ме-
зона с импульсом k, двух мезонов с импульсами k и к' и т. д.
в состоянии, описываемом вектором состояния W. Наконец, следует
отметить, что в соотношение A3.79) мы включили нормирующие
множители l/]/l!, 1/У~2\ 1/|/"п! при определении одно-, двух-
и n-мезонных состояний соответственно. Это означает, что мы нор-
нормировали волновую функцию W следующим образом:
(W, W) = | с0 |а + f d»k | сг (k) p + J d*k f d*k' | c2 (k, k') |
+...=1 A3.85)
и тем самым обеспечили правильную нормировку амплитуд вероят-
вероятностей сп (kt, ..., kn).
Необходимо отметить еще одно свойство коэффициентов разло-
жения сг(/г), с2(/г, k') и т. д. Из их определения в соотношении
A3.79) и того факта, что все операторы рождения частиц а\, а\г
и т. д. коммутируют между собой, следует, что амплитуды вероят-
->• ->-
ностей cn(ky, . . ., k^ являются симметричными функциями координат
->- •>
kv ...,кп. Следовательно, они описывают систему п частиц, под-
подчиняющихся статистике Бозе—Эйнштейна (см. также работы Иор-
Иордана и Клейна [247], Фока [183] и § 7).
Совершенно аналогичным образом может быть проведено и кван-
квантование комплексного скалярного поля. Впервые это квантование
было проведено Паули и Вайскопфом [371, 374]. Квантованное ком-
комплексное скалярное поле описывает заряженные частицы. Операторы
числа частиц, заряженных положительно и отрицательно, Nu и
N{k_\ могут быть определены независимо. Физически наблюдаемые
величины, именно полная энергия, заряд и импульс, выражаются
с их помощью следующим образом:
Н = 2
к
О3-86)
164 Глава 13
§ 5. Квантование спинорного поля ,
Квантование спинорного дираковского поля со спином а/2 можно
провести так же, как и квантование поля со спином 0. В этом слу-
-> —>
чае операторы поля ф (х) и 6 (х) в шредингеровском представлении
разлагаются в ряд по полному набору собственных функций wn(x)
уравнения Дирака для свободной частицы. Индекс п у wn(x) ука-
указывает на полный набор коммутирующих наблюдаемых величин,
а именно на энергию, импульс и спин частицы. Эти функции wn (x)
являются спинорами wr(p), r=\ ... 4, введенными в гл. 7 с по-
помощью соотношений G.20), умноженных на функцию, соответствую-
щую плоской волне exp(ip-x); таким образом, они имеют вид:
wr(p)e3>-% при г=1, 2,
^ .^^ A3.87)
wr(p)e-iP'x при г = 3, 4.
-> _ ■>
Разложение операторов ф (а:) и Ф (а;) записывается следующим об-
образом1):
й^И/^-й' A3-88а)
£l *^и (^' A3-886)
причем сумма распространяется на все состояния как с положитель-
положительной, так и с отрицательной энергией. Множитель (т/\Еп\у/2 обу-
обусловлен нашей нормировкой спиноров: twa» = e.
Рассмотрим теперь гамильтониан поля, который, согласно A0.62),
имеет вид
Н= fdsxty(—£; • V + ot)<|>. A3.89)
Подставляя разложения A3.88) в Н и используя соотношения A3.87),
получаем
H=^bfmbmEm\ A3.90)
здесь символы £m означают собственные значения оператора Ди-
■*■ -*■
рака а. • р-\- $т. Квантование этого поля по схеме, развитой в пре-
предыдущем параграфе, приводит к двум, связанным между собой
трудностям.
1) Черта сверху над оператором i> означает, что нужно взять сопряжен-
сопряженную величину неоператорного спинорного множителя w и эрмитово-сопря-
женную операторного множителя Ь.
Квантование поля 165
Во-первых, если мы будем интерпретировать bfb как оператор
числа частиц, то энергия поля может быть как положительной, так
и отрицательной, поскольку собственные значения Еп могут быть
как положительными, так и отрицательными {bfb~^- 0). Действи-
Действительно, если собственные значения операторов числа частиц пред-
представляют собой любые положительные целые числа, какими они.
должны быть, согласно перестановочным соотношениям A3.58) и
A3.59), то допустимы состояния с произвольно большой отрица-
отрицательной энергией, что не имеет никакого физического смысла.
Во-вторых, из эксперимента известно, что электроны подчи-
подчиняются принципу Паули, т. е. что в любом состоянии m не может
находиться более одного электрона (число m характеризует энер-
энергию, импульс и спин частицы). Поэтому квантование с помощью
коммутаторов, ведущих к статистике Бозе, является неверным, так
как последняя допускает присутствие в одном состоянии любого
числа частиц.
Разрешим сначала вторую трудность. Схема квантования, экви-
эквивалентная принципу Паули (т. е. требованию антисимметричности
волновых функций), была развита Иорданом и Вигнером [249]. В их
схеме операторы удовлетворяют не коммутационным, а „антикомму-
„антикоммутационным" соотношениям:
[*». bm]+ = [bt btn]+ = O, A3.91)
lbn. bl\+=bnm, A3.92)
где значок „ + " в нижнем индексе означает операцию х>
[А, В)+=АВ-\-ВА. A3.93)
Оператор числа частиц в состоянии m имеет теперь вид
Nm = bfmbm. A3.94)
Далее, из перестановочных соотношений A3.91) и A3.92) следует,
что для квадрата оператора числа частиц справедливо равенство
Д4 = btnbmbtbm = *2. A — bfmbm) bm = bibm = Nm, A3.95)
так как, согласно соотношению A3.91), bmbm = bmbm — Q- Таким
образом, N*n=Nm, а это означает, что число частиц в данном
состоянии может быть либо нулем, либо единицей в полном согла-
согласии с принципом Паули. То, что более одной частицы не может
1) Иногда в литературе для антикоммутатора используется обозначение
{А, В}.
166 Глава 13
находиться в одном состоянии, уже видно из перестановочного
соотношения A3.91), которое показывает, что результат действия
двух операторов рождения частицы на волновую функцию одного
состояния (с одним и тем же т) обращается в нуль.
Хотя мы удовлетворили принципу Паули с помощью соотноше-
соотношений антикоммутации, тем не менее перед нами осталась еще труд-
трудность, а именно гамильтониан не является положительно-определен-
положительно-определенным. Ее можно обойти, используя идею Дирака о том, что в вакуума
все состояния с отрицательной энергией заняты. Если мы напишем
в явном виде индекс /га, т. е. (р, г), где г отвечает четырем реше-
решениям, соответствующим данному импульсу /?(г=1, 2 для положи-
положительных энергий и г = 3, 4 для отрицательных), то при переходе
к непрерывным значениям р разложение функции <j> A3.88а) при-
примет вид
('Z A3.96)
r=3
ИЛИ
A3.97)
Если переписать операторы числа частиц в виде
N*r\p)= b$(p)br(p) для г=1, 2, A3.98а)
Ni~\—р)=£++2(— P)br+2( — р) для г=1, 2, A3.986)
то гамильтониан примет вид
2
H=f d*p 2 Ер { N(r+)(p) — Л/jT' (р)) ■ A3.99)
Аналогичным образом с помощью операторов числа частиц можно
выразить полный заряд:
2
Q = e.f dsxty (x) f°4> (x) = е С dap V {^+) (р) + Ni~} (р) }. A3.100)
Согласно дираковской теории дырок, вакуум определяется теперь
тем, что все состояния с отрицательной энергией заняты, т. е.
I—) * "*■
Ny (/7)=1 для всех р и всех г, а все состояния с положитель-
Квантование поля 167
кой энергией свободны, т. е. N\■ (/?) = О для всех р и всех г.
Энергия и полный заряд вакуума равны, следовательно,
A3.101)
г=1
Ясно, что эти величины бесконечно велики. Но они, согласно гипо-
гипотезе Дирака, ненаблюдаемы. Наблюдаемыми являются лишь разности
между Н и Ео, Q и Qo. Поэтому Н и Q дадим следующее новое
определение:
2 2
г=1
A3.102)
Q' = Q — Qo = е J d3p ^ {М+)(Р)— [1 — М-'Чр)]} • A3.103)
г
Соотношения A3.102) и A3.103) представляют собой математи-
математическое выражение того, о чем мы говорили выше, обсуждая теорию
дырок. Они явным образом показывают, что вклады в полный заряд
и энергию состояний с отрицательной энергией имеют место лишь
тогда, когда ЛЛ~)(р)=0, т. е. когда эти состояния не заполнены.
Вклад в заряд Q свободных состояний с отрицательной энергией
имеет знак (—е), противоположный знаку вклада состояний с поло-
положительной энергией. Вклад же в гамильтониан Н незаполненных
состояний р с отрицательной энергией равен -\-Ер; следовательно,
величина Н' является теперь положительно-определенной. Таким
образом, отсутствие частицы в состоянии с отрицательной энергией
соответствует наличию ее (с обратным знаком) в состоянии с по-
положительной энергией. Эта частица называется „позитроном" для
случая электронов, в общем же случае—„античастицей".
Следует подчеркнуть, что теория дырок Дирака и процедура
вычитания, к которой она приводит, являются возможными лишь
благодаря квантованию с помощью соотношений антикоммутации,
приводящих к тому, что каждое состояние с отрицательной энер-
энергией занято лишь одной частицей. Трудность с положительным
определением энергии в классической теории присуща всем теориям
163 ' Глава 13
полей с полуцелым спином. Связь между спином и статистикой,
можно установить, если вместе с Паули [376] на квантовую теорию
наложить следующие физические требования: 1) операторы двух
физических наблюдаемых величин, относящихся к пространственно-
временным точкам, разделенным пространственно-подобным интер-
интервалом, коммутируют (условие причинности) и 2) энергия системы
положительно определена.
Первый постулат оправдан тем, что в квантовой теории отсут-
отсутствие коммутации двух операторов наблюдаемых величин приводит
к невозможности измерить их одновременно с произвольной сте-
степенью точности. Однако измерения в точках, разделенных про-
странственно-подобньши интервалами, никогда не влияют друг на
друга, так как принцип причинности в теории относительности
требует, чтобы сигналы (энергия) не могли передаваться со ско^
ростью, большей скорости света. Следовательно, коммутатор физи-
физически наблюдаемых величин, относящихся к точкам, разделенным
пространственно-подобным интервалом, должен быть равен нулю.
Второй же постулат самоочевиден.
Можно теперь показать (Паули [376], Паули и Беленфанте
[377]), что квантование поля с целым спином с помощью антиком-
антикоммутационных соотношений Иордана — Вигнера (ведущих к статис-
статистике Ферми —Дирака) нарушает первый постулат, в то время как
квантование поля с полуцелым спином с помощью коммутационных
соотношений Бозе (ведущих к статистике Бозе — Эйнштейна) нару-
нарушает второй постулат.
Обычно дают другое определение операторов для состояний
с отрицательной энергией, т. е.
*г+2(— Р) = 4(/>) (г =1,2),
г+2К ю гкн) > A3.104I)
bt+2( — p)=dr(p) (г=1, 2)
и перестановочные соотношения A3.92) теперь имеют вид
Можно переписать их с помощью оператора числа частиц
А/*."'' (р) = 1 — Л#-> ( — р) == 1 — bt+г (— р) br+2{ — p) =
P~). A3.106)
!) Такое определение возможно, так как операторы удовлетворяют
антикоммутационным соотношениям, а последние остаются инвариантными
при замене Ь на Ь^ и.обратно.
Квантование поля 1 "9-
Операторы d+ и d являются теперь операторами рождения и уни-
чтожения античастиц, a Nr (p) (в дальнейшем мы будем отбрасы-
отбрасывать штрих) представляет собой оператор числа античастиц. Раз-
Разложение оператора <j>. имеет теперь вид
A3.107)
-*■
где, как и в гл. 7, мы обозначили wr+2(p) через vr(p); vr {р'
представляет собой спинор, описывающий частицу в состоянии с
->
отрицательной энергией и импульсом —р. Наше первоначальное раз-
->
ложение по ортогональным спинорам wr(p) обеспечивает то, что
оператор dj.(p) рождает позитрон с амплитудой вероятности vr(p),
как и должно быть в действительности для позитрона. Таким об-
->-
разом, (|) (х) является оператором рождения позитронов и в то ж&
время оператором уничтожения электронов. При такой формули-
формулировке дырочной теории вектор состояния вакуума Фо характери-
характеризуется условием
N(r+)(p)<l>0 = N(r~)(p)O0 = 0 для всех г и />? A3.108)
т. е. вакуум обладает нулевой энергией, зарядом и импульсом,,
не содержит ни одной частицы и представляет собой состояние:
с наинизшей энергией. Это состояние является инвариантным по
отношению ко всем лоренцовским преобразованиям. Другими сло-
словами, его можно характеризовать равенством
*г(р)Фо = <*г(Р)фо = О. A3.109)
Заметим, что эта формулировка не содержит больше понятия „за-
„заполненной зоны".
Метод 1>, аналогичный развитому для случая мезонного поля,
можно использовать и здесь для того, чтобы построить базисный
вектор в представлении, в котором операторы числа частиц диаго-
!) Заметим, что перестановочные соотношения между операторами числа
частиц JV'+' (р) и операторами Ь и А+ идентичны случаю Бозе [соотноше-
[соотношения A3.66) и A3.67)], даже несмотря на то, что операторы Ъ и 6+ удовле-
удовлетворяют антикоммутационным соотношениям. То же имеет место для опера-
операторов N^~)(p) и d. Заметим также, что оператор 7V(+) (p) коммутирует с по-
зитронными операторами d и df. Также коммутируют и операторы
170 Глава 13
нальны. Так, б£(/?)Ф0 описывает состояние с одним электроном ,оо
"*■ + "*" + "*■
■спином s и импульсом р; Ьа1(р1)Ьвг(р2)Ф0 — двухэлектронное со-
состояние и т. д. Однако амплитуды разложения с0, сх (ps),
-с2 (Pisi> Pzsz) являются теперь антисимметричными функциями своих
переменных, какими и должны быть амплитуды, описывающие ча-
частицы, подчиняющиеся статистике Ферми — Дирака (см. также
работы Фока [183] и Жана [245]).
Наконец, рассмотрим перестановочные соотношения в конфигу-
— ->■
рационном пространстве. Так как разложение <j> (х) в ряд имеет вид
2
-\-drfavrU>)e+i*'*}
то антикоммутатор фиф равен
X 2 S {[*r (P).
s]+ 2гГа(р) vl(p')} . A3.111)
Используя перестановочные соотношения и равенства G.32) и
■G.37), можно привести правую часть соотношения A3.111) к сле-
следующему виду:
с —*')• A3.112)
Выраженное с помощью эрмитово-сопряженного оператора ф+(л:) =
перестановочное соотношение имеет вид
A3.113)
Для изучения нерелятивистского предела квантовой теории полей
со спином 7г следует обратиться к статье Осборна [361].
Квантование поля 171
§ 6. Зарядовое сопряжение
Следует заметить, что развитая выше теория позитронов инва-
инвариантна относительно одновременной замены (Фарри [200])
Эту инвариантность обычно называют „инвариантностью по отно-
отношению к зарядовому сопряжению" (Крамере [287]); она наводит на
мысль, что можно сформулировать теорию дырок, используя как
для позитронов, так и для электронов лишь волновые функции,
описывающие частицы с положительной энергией. Действительно,
эта возможность следует из существования унитарной матрицы С,
имеющей свойства
— t^t=c-itpC> A3.114а)
С+С = СС+=1, A3.1146)
. Ст = — С, A3.114b)
где верхний индекс Т относится к транспортированной матрице
Существование матрицы С является следствием того, что ма-
матрицы — ^т удовлетворяют тем же самым антикоммутационным
соотношениям, что и fi*. Так как представление с помощью 4-мер-
4-мерных матриц является неприводимым, то существует преобразование
подобия, которое преобразует любую матрицу f^ в матрицу — ^т.
Более того, эта матрица преобразования С всегда может быть
выбрана унитарной. Теперь легко установить, что [это следует из
выражения A3.114а)] СтС~г коммутирует со всеми -\v-, и, следова-
следовательно, СтС~1 = а1, где а — константа. Взяв обратные и сопряжен-
сопряженные величины обеих частей этого соотношения, найдем (помня, что
матрица С является унитарной), что а= ztl. Можно показать,
что в действительности а=—1 (Паули [373, 378], Майорана [319],
Крамере [287]).
Рассмотрим теперь уравнение Дирака, описывающее частицу
в электромагнитном поле:
г — я) ф = П^р.ф. A3.115а)
.^7) = — ефтма- A3.1156)
(
Заметим, что если транспонировать уравнение A3.1156) и заменить
1^т в соответствии с выражением A3.114а) на f^ т0 мы получим
следующее уравнение:
~ — т\С^т = — e^A^cY- A3.116)
172 Глава 13
Таким образом, если <1> описывает движение частицы с зарядом в,
—т
то Сф описывает движение частицы с зарядом —е. Обычно
функцию Сф2" называют зарядово-сопряженной волновой функцией
и обозначают через Фс, т. е.
фс = СфУ. A3.117)
Рассмотрим теперь свойства зарядово-сопряженных спиноров,
описывающих свободные частицы. Из предыдущего мы знаем, что
электрон описывается волновой функцией и (р), которая в импульсном
пространстве подчиняется уравнению
(р—т)и(р) = 0. A3.118)
Аналогичным образом позитрон с энергией-импульсом -(-р описы-
описывается спинором г;(р), соответствующим частице с отрицательной
энергией и импульсом -—р, т. е. волновой функцией электрона,
отсутствию которого (в зоне состояний с отрицательной энергией)
он соответствует. Эта функция удовлетворяет уравнению
(— /?— m)v(p) = 0, A3.119а)
или
p — m) = 0. A3.1196)
Транспонируя уравнение A3.1196) и используя выражение A3.114а),
находим, что спинор
CvT(р) = ис (р) A3.120а)
удовлетворяет уравнению {р — т) ис(р)=0. Следовательно, этот
зарядово-сопряженный спинор относится к частице с энергией-им-
энергией-импульсом -f-p. Используя свойство матрицы .С, можно написать
соотношение, обратное A3.120а), т. е.
v(p) = C[u°(p)]T. A3.1206)
На основании этого соотношения мы можем заменить спинор vr(p),
соответствующий частице с отрицательной энергией и появившийся
в разложении ф [соотношение A3.107)], функцией С[ис(р)]Т. Отсюда
следует, что ф относится теперь лишь к частицам с положительной
энергией.
Таким образом, мы видим, что при зарядовом сопряжении
каждая частица превращается в свою „античастицу". Обратно,
требование инвариантности теории по отношению к зарядовому
сопряжению означает, что частица и соответствующая ей антича-
античастица должны иметь равные и противоположные заряды и магнитные
моменты, но одинаковые массу и спи::.
Квантование поля 173
Зарядовое сопряжение можно применить также и к нейтральным
частицам, что ведет к делению этих частиц на два класса. Первый
класс нейтральных частиц обладает тем свойством, что при зарядо-
зарядовом сопряжении содержащиеся в нем частицы превращаются сами
в себя. В современной теории тс°-мезон и фотон являются примерами
бозонов, которые ведут себя подобным образом. В действительности
же такой первой исследованной частицей был фермион, изученный
в связи с возможным описанием нейтрино (Майорана [319]; см. также
работы Паули [378], Мишеля [334]). В теории поля такие частицы
описываются эрмитовыми операторами для случая бозе-частиц и
самосопряженными операторами (т. е. фе = ф) для случая ферми-
частиц.
Второй класс нейтральных частиц характеризуется тем, что
входящим в него частицам соответствуют (нейтральные) античастицы,
отличающиеся от них самих. Современное описание нейтрона предпо-
предполагает, что нейтрон является как раз такой частицей. „Антинейтрон"
должен был бы иметь магнитный момент противоположного знака,
чем знак момента нейтрона. Для выяснения места, которое занимают
эти различия при описании нейтральных частиц в теории (З-распада,
отсылаем читателя к статье Мишеля [334].
§ 7. Корпускулярно-волновой дуализм
Выше мы проквантовали два поля, наиболее важных в современ-
современной физике. При этом мы видели, что можно построить квантовую
теорию поля с помощью частиц конечной массы, которые переносят
заряд, энергию и импульс поля. В отсутствие взаимодействия число
частиц поля является интегралом движения. Следовательно, это обстй-
ятельство должно вытекать из обычного уравнения Шредингера для п
частиц. И, наоборот, можно исходить из уравнения Шредингера для п.
частиц и построить операторный формализм, который только что был
описан. Покажем теперь, что Это действительно можно сделать.
Для этой цели рассмотрим систему, состоящую из п одинаковых
нерелятивистских частиц, описываемых уравнением Шредингера *'
, Х2, ..., Хп, 0^
— ~V\ + V{xk). A3.121)
Чтобы проанализировать содержание этой теории, введем пол-
полный набор нормированных волновых функций п частиц. Они могут
быть сконструированы из полного ортогонального набора волновых
!) Получающийся при этом формализм легко обобщить, включая взаимо-
взаимодействие между частицами (см., например, работу Фока [183]).
174 Глава 13
t
функций одной частицы. Так, если {их(х)} является таким набором,
причем
(их, Uf) = f &хи*х(х)и^х) = Ъх? A3.122)
(интегрирование содержит здесь также суммирование по спиновым
индексам, которые включены в х), то несимметризованную волновую
функцию п частиц можно образовать прямым перемножением п
функций одной частицы. Обозначим такую функцию через
Ux1xax3...xn(xv *2. •••> *п) = "л, (*i) их, 0*2) ••• %(*«)• A3.123)
Собственно говоря, симметризованные или антисимметризованные
волновые функции можно получить, действуя оператором
5 = A/и!J-Р или А —A/»!J ^?Р на U (см-> например, работу
Корсона [93]). Здесь Р—оператор перестановки, который пере-
переставляет номера координат хк, Ьр — четность перестановки Р; сум-
суммирование производится по всем п\ перестановкам номеров п.
Вместо того чтобы определить U с помощью набора {\, Х2,
Х3, .... Хп}, можно определить эту функцию, указав, сколько соб-
собственных значений Х1, Х2, ... повторяется, насколько часто и какие.
Следовательно, мы определим U с помощью бесконечной последо-
последовательности целых чисел nv n2, ..., которые называются „числами
заполнения": пх есть число появлений их в U (независимо от аргу-
аргумента). Ясно, что если мы имеем п частиц, то
2их = «- A3.124)
Заметим, однако, что последовательность чисел заполнения не опре-
определяет однозначно U, так как функция PU, где Р—произвольный
оператор перестановки хг .. . хп, будет иметь точно такие же
числа заполнения, определяющие ее. Однако последовательность
nv n2, ... должна однозначно определять, строго говоря, симметрич-
симметричность или антисимметричность U, т.е. либо SU (для симметричного
случая), либо ALJ (для антисимметричного случая).
Теперь можно разложить 47 в ряд по симметризованным должным
образом функциям
W= 2 (»; •*!> х2, ..., хп\п1г nv ...)£(«!, п2, ...; t), A3.125)
и,па...
где
(и; xv хг, .... хп\пи п2, ...) = | j£
= <U,... (*i. Х2 хп), A3.126)
причем Л== 5 = A/я!J Р в симметричном случае и А == А =
в антисимметричном случае. В последнем случае
Квантование поля 175
правая часть написанного выше уравнения сводится к обычному
определителю Слетера, и щ всегда -^ 1. Множитель n\jnx\n2\ ...
есть нормировочная постоянная, так что
l f d*x2 ... f <РхпФ*П1ЩПз . (xlt x2 xn) X
;- <13Л27>
Величины c(nv n2, -..; t) являются теперь „волновыми функциями"
в новом представлении, т. е. в представлении чисел заполнения.
Они представляют собой амплитуды вероятности обнаружения пх
частиц системы в момент t в состоянии 1, гаа частиц — в состоянии
2 и т. д.
В симметричном случае введем, следуя Иордану и Клейну [247]*
операторы аг и at, определяемые соотношениями
.nj+i... (*i. хг, .... хп, хп+1), A3.128а>
■ • ■ ' хп) ==
... nt-x... (*i, *2. • • ■• хп-х)- A3.1286)
Легко показать, что в скалярном произведении A3.127) аг и а[
являются в действительности эрмитово-сопряженными друг другу..
Оператор at называется оператором рождения, так как, действуя
на волновую функцию п. частиц, превращает ее в волновую функцию.
(п-\- 1) частиц. Точнее, он увеличивает число частиц в /-ом состо-
состоянии на единицу. Наоборот, оператор аг называется оператором,
уничтожения: он уменьшает число частиц в /-ом состоянии на еди-
единицу. Если теперь ввести оператор Л/^ = d\ai, то легко установить*
что
N^nk.-.n.... =aUi&nL. --п.... =л,ф£1...«,...; A3.129>
оператор Л/j называется оператором числа частиц в состоянии г„
так как, действуя им на Ф,"п п . мы находим число частиц.
в этом состоянии. Далее, мы можем ввести оператор полного числа
частиц
W = 2 N» = 2 afo. A3.130).
г г
который указывает, сколько всего частиц имеется в системе.
По определению, оператор \
перестановочным соотношениям:
По определению, операторы аг и а\ удовлетворяют следующим.
[ait а,\ = [а\, a\\ =
176 ■ . Г лаз и 13
Теперь легко показатьх> (см. работы Иордана и Клейна [247],
Фока [183]), что можно выразить полный гамильтониан с помощью
этих операторов следующим образом:
1...> A3.132)
где
tj) = J d3xul(x) H(x) uj (x). A3.133)
Введем далее операторы 2>
ф (лг) = 2 «г W ^i A3.134a)
и
4»f(*) = 2*4(*L. A3.1346)
которые в соответствии со свойствами операторовда|удовлетворяют
следующим перестановочным соотношениям:
[ф (х), 4>f {х')\ = 2 Iai> 4] иг (х) и*з (х') =
= 2 из (х> "У (х') = S(jc— л:'). A3.135)
где мы воспользовались полнотой набора {их(х)} (замкнутостью).
Аналогично
= 0. A3.136)
Выразив полный гамильтониан с помощью этих операторов, мы мо-
можем переписать его в виде
2
= / а*х B щ (х) 4) # (*) B «^ (*) <ъ-) =
A3.137)
а оператор полного числа — в виде
N = J d3x4»+ (*) ф (х) = ]У] ata;. J йзхи* (Х) ^ (x) ^ ^ а+а._ A3.138)
-1) Напомним, что
3) В связи с этим см. работу Пирена [388].
Квантование поля 177
Волновую функцию п. частиц в теории Шредингера можно теперь
охарактеризовать следующим образом: она является решением урав-
уравнения
НФ == (J* «Р*ф+(*)//(*) ф (*)) Ф == a 2J, A
в котором 47 есть собственная функция оператора N с собствен-
собственным значением п, т. е.
\ = n.W. A3.140)
Такое рассмотрение возможно, так как для задачи, которую мы
исследуем,
[Н, М] = 0. A3.141)
Вектор состояния, описывающий такую систему, представляет собой
некоторую линейную комбинацию Ф^ с фиксированным п. Этот
формализм проходит почти без изменения для случая, когда ча-
частицы подчиняются статистике Ферми — Дирака и, следовательно,
описываются антисимметричными волновыми функциями. Однако
в этом случае операторы а и а+ удовлетворяют антикоммутацион-
антикоммутационным соотношениям (см. § 5, а также работу Иордана и Виг-
нера [249]). Последние же обеспечивают условие: ни одно состоя-
состояние /, у, ... не занято более чем одной частицей.
Поскольку уравнение, описывающее изменение рассматриваемых
операторов во времени,
йф (jc) = [ф (jc), Н1=Л/(*)ф(ж) A3.142)
формально идентично уравнению Шредингера для одной частицы,
то описанный выше формализм часто называют „вторично кванто-
квантованной" теорией, а сам процесс „вторичного квантования" рассмат-
рассматривают как превращение волновой функции Шредингера в оператор,
удовлетворяющий определенным перестановочным соотношениям.
Хотя вышеизложенный формализм получен при рассмотрении
случая, когда число частиц остается постоянным, должно быть
ясно, что он допускает непосредственное обобщение на гамильто-
гамильтонианы, для которых N (т. е. полное число частиц) не является
!) В этом уравнении действие операторов ф на W можно определить,
возвращаясь к разложению ф по операторам рождения и уничтожения [соот-
[соотношение A3.134)], а Ф" — по Ф(п) [соотношение A3.125)], так как действие
операторов а и а1" на Ф(Л' нам известно. Таким путем можно раз и навсегда
определить действие операторов ф и ф+ на произвольную функцию W, т. е.
определить представление этих операторов (см. работу Фока [183]).
i?8 Глава iS •'
больше интегралом движения. Таким образом, этот формализм по-
позволяет рассматривать такие состояния, в которых частицы рож-
рождаются и аннигилируют, например [3-распад, рождение мезона
при нуклон-нуклонных столкновениях и т. д. В этих процессах
вектор состояния W должен быть линейной комбинацией Ф<п> с
й = 0, 1, 2, ...
Это рассмотрение также можно применить к любой релятивист-
релятивистской теории поля1^, например поля Клейна — Гордона. В § 3 мы
видели, что в случае свободного поля одной из особенностей кван-
квантовой теории поля является лаконичное и формальное квантово-
механическое описание системы п независимо действующих релятиви-
релятивистских частиц. Чтобы показать это с точки зрения настоящего
параграфа, применим описанный выше формализм к частицам Клейна—
Гордона в нерелятивистском приближении (Дирак [112], Швебер [433],
Лопес [308]). Так как физически реализуемые состояния релятиви-
релятивистской частицы со спином 0 содержат множество решений уравне-
уравнения Клейна—Гордона, соответствующих частицам с положительной
энергией (напомним рассуждения § 2 гл. 2), то набор волновых
функций одной частицы { их (х)} является здесь весьма многознач-
многозначным2). Соотношение B.16) является теперь скалярным произведением
и Ф*£' (Xi> х2, ..., хя)—симметризованные произведения их(х),
т. е. решения уравнения Клейна—Гордона, отвечающие положи-
положительным энергиям. Соотношения A3.128а) и A3.1286) снова опре-
определяют операторы а и af; выводы, вытекающие из этих соотношений,
остаются справедливыми и для рассматриваемого случая. Однако,
если мы введем операторы
?(+)(х) = 5>п(х)яп, A3.143а)
П
?(-»(x) = 2^(xL, A3.1436)
я
]+ A3.143в)
*) Релятивистская теория поля в конфигурационном пространстве рас-
рассмотрена в работе Вайтмана и Швебера [535].
2) Чтобы удовлетворить условию релятивистской ковариантности, вклю-
включим временную координату и, следовательно, напишем х. Функция их(х)
имеет вид [2Bw)8]-1/sexp(—гк • х), где йо = + V № + ^2. а индекс \ опре-
определяет энергию и импульс. Действительно, необходимо образовать волновые
пакеты так, чтобы получить нормированные волновые функции. Так как при
этом мы имеем дело лишь с решениями для частиц с положительными
энергиями, то можем записать уравнение Клейна — Гордона следующим
образом:
^1
2 ж**) = 2 Y-
Квантование поля 1?9
[соответствующие равенствам A3.134а) и A3.1346) в нерелятивист-
нерелятивистском случае], то, поскольку набор {и^(х)} не является полным
(для полноты нужно включить в него решения, отвечающие отри-
отрицательным энергиям), мы не можем больше пользоваться свойством
полноты, а поэтому у(+Цх) и qp(-)(xO будут удовлетворять не
перестановочному соотношению с 8-функцией, а соотношению
n; E+
_ 1 Г «"* e-ili-(K-K')
T^2)- A3.144)
Сумма
)))(х) A3.145)
представляет собой оператор квантованного поля, описываемого
уравнением Клейна — Гордона, в гейзенберговском представлении и
удовлетворяет уравнению
(П-Ь^2)?(х) = 0. A3.146)
Таким образом, мы снова получили, что квантование свободного
поля позволяет описывать систему с помощью квантов, носителей
энергии и импульса (а также заряда в случае комплексного поля).
На примере квантованного поля, подчиняющегося уравнению Клей-
Клейна— Гордона, видно, что теория квантованного поля не имеет
трудностей, связанных с отрицательными энергиями: энергия поля
является всегда положительно-определенной, так как каждый квант
вносит положительную энергию в полную энергию поля1'. Однако
операторы, квантованного поля в гейзенберговском представлении
(в котором они зависят явно от времени) будут содержать как
положительные, так и отрицательные частоты (энергии), причем на
этот раз отрицательные частоты соответствуют операторам рожде-
рождения9'. Корпускулярная картина квантовой теории поля является,
однако, лишь одной стороной физического содержания теории.
Другой ее стороной является волновая картина. По Бору, эти две
стороны являются дополнительными (и исключающими друг друга).
Чтобы пояснить это, снова рассмотрим случай квантованного электро-
электромагнитного поля. Корпускулярная точка зрения соответствует опи-
1) Это верно также н для теории поля со спином Va если принять
новую дираковскую интерпретацию вакуума.
2) Для рассмотренного выше уравнения Клейна — Гордона см. соотно-
соотношения A3.1436) и A3.145); напомним, что и^ есть решение, отвечающее от-
отрицательной энергии, если их соответствует положительной энергии.
180 Глава 13
санию поля с помощью полного набора физически наблюдаемых
величин, связанных с частицей, т. е. с помощью определенного
числа фотонов с заданными импульсами и поляризациями. Волновая
же картина соответствует описанию поля с помощью полного на-
набора физически наблюдаемых величин, связанных с полем, т. е.
с помощью некоторого числа операторов интенсивности квантован-
квантованного поля, математические ожидания которых соответствуют изме-
измеряемым интенсивностям поля. Эти два набора, однако, не комму-
коммутируют между собой. Следовательно, точное знание числа фотонов,
присутствующих в поле, исключает возможность точного нахожде-
нахождения интенсивностей поля. Таким образом, даже в вакууме (т. е.
в состоянии, где нет ни одного фотона) среднеквадратичные интен-
интенсивности поля не равны нулю. Эти флуктуирующие интенсивности
поля вакуума реально проявляются при измерениях. Например,
спонтанное излучение атома в возбужденном состоянии можно рас-
рассматривать как излучение под действием флуктуации вакуума. Дру-
Другой эффект, за который также ответственны флуктуации вакуума,
есть флуктуация положения заряда в пространстве; этот эффект
вносит вклад в собственную энергию частицы (Вайскопф [518]).
Уменьшение энергии связи несвободного электрона, обусловленное
флуктуациями его положения, объясняет большую часть лэмбов-
ского смещения уровня (УЭлтон [520], Вайскопф [519]).
В случае материальных полей этот корпускулярно-волновой
дуализа и дополнительность проявляются в флуктуациях заряда и
плотности тока в некотором конечном 4-объеме, когда число ча-
частиц строго определено. Таким образом, становится очевидным, что
квантовая теория полей, даже в случае свободного поля, является
более полной и плодотворной, чем корпускулярное рассмотрение
теории поля. Только рассматривая систему с обеих точек зрения
(корпускулярной и волновой), можно получить о ней правильное
представление.
Глава 14
РАССЕЯНИЕ И S-МАТРИЦА
§ 1. Испускание и поглощение кванта
Рассмотрим взаимодействие спинорного (нуклонного) поля и не-
незаряженного поля Клейна — Гордона (мезонного) посредством ло-
локальной прямой связи СфГфср (х) (где Г = / или f5). При этом
гамильтониан системы имеет вид
H = H0 + HIt A4.1)
где
#о = / tPxif* (*) { о • р+ §т } ф (
-Ь i- J rf»* { ^ (*)+ [Vcp (J)]2 + fiAp E*} A4.2)
*). A4.3)
В квантовой теории поля взаимодействие вызывает переходы между
состояниями, определяемыми гамильтонианом свободных полей Но.
Если предположить, что взаимодействие является слабым, то можно
применить методы обычной теории возмущений.
Рассмотрим подробно член взаимодействия, причем сначала рас-
смотрим его спинорную часть ф(дг)Гф(дг). Подставим в это выраже-
— ■> ->
ние разложения ф (х) и ф(х) по операторам рождения и уничтоже-
уничтожения. Эта подстановка покажет, что существуют четыре типа
взаимодействия, которые представлены членами:
1) член bp/bp соответствует уничтожению нуклона с импуль-
импульсом р и последующему рождению нуклона с импульсом р', т. е.
соответствует рассеянию нуклона;
2) член dpdpr соответствует рассеянию антинуклона;
3) член bpdpr соответствует аннигиляции нуклона и антинуклона,
т. е. уничтожению пары;
4) член ЬЩрг соответствует рождению пары.
Аналогично разложение мезонного поля по операторам рождени я
и уничтожения приводит [с учетом выражений A3.31), A3.50) и
182 Глава 14
Й = с = 1 ] к соотношению
<р (х) = <р+ (х) = V-*
1/s 2 (£)*<«*+«-*> •-**• <14-4>
к
Отсюда следует, что член взаимодействия Нх приводит к восьми
элементарным процессам, соответствующим:
а) испусканию бозона при 1) рассеянии нуклона, 2) рассеянии
антинуклона, 3) аннигиляции пары, 4) рождении пары;
б) поглощению бозона при тех же четырех нуклон-антинуклон-
ных процессах.
Эти процессы можно изобразить графически с помощью упоря-
упорядоченных во времени фейнмановских диаграмм. Если изображать
бозон пунктирной линией, направленной в сторону возрастания вре-
времени, а антинуклон — сплошной линией, направленной в сторону
убывания времени, то процесс „а" A), соответствующий испусканию
бозона при рассеянии нуклона, можно представить диаграммой на
фиг. 17, а. Время возрастает в направлении, показанном на этой
диаграмме стрелкой. В противоположность ранее рассмотренным
фейнмановским диаграммам (см. гл. 8 и 9) диаграмму на фиг. 17, а
нельзя топологически изменить. Это и означает .упорядоченность
во времени". Аналогичным образом процесс „а" B) может быть
представлен на фиг. 17, Ь, другие процессы — на фиг. 17, с — h.
Интегрирование оператора взаимодействия Hi no d3x приводит
к тому, что импульс сохраняется в каждой вершине (соответствую-
(соответствующей акту взаимодействия). Рассмотрим, например, процесс „а" A),
соответствующий фиг. 17, а. Часть Hi, ответственная за этот про-
процесс, равна для непрерывных значений р и ft1»:
= G (?«) -8/" f d*x f d*j/ f d*p f cPk X
r=la—i
X "wr(pr) Tw* (jo) e-w'-Ze +**■ яе-&-*, A4.5)
*) Начиная с этого места, обозначим а^ для непрерывного случая через
а (к). Аналогично напишем Е{р)= Y рЬ-\-т? и ш (#) = y.Aa_j-jj,2, Однако,
чтобы не было возможных недоразумений, мы будем писат^.
1K
3 + т* = Vp + 2р ■ £+ № + т*.
Рассеяние и S-матрица
183
что после интегрирования по d?x дает
= Bтг)-3/'О / d»p f d*p' f d
rrfi
2E(p)E<j/)<»(
X
i. г
)' (! 4 •
Время
Процесс dfp'dpaK
b
Процесс d da
d
I
I
Процеос dfbfa
е
Процесс dbcf
f
Процесс d^tf
g
Фиг. 17.
I
Процесс dba
h
причем 8-функция соответствует сохранению импульса в вершине.
Таким образом, если падающий нуклон (см. фиг. 17, а) имеет
184 Глава 14
импульс р, рассеянный нуклон — импульс р , то эти импульсы свя-
заны между собой соотношением р'=р — k, где k—импульс испу-
испущенного мезона.
Теория возмущений применяется теперь таким же образом, как
и в случае обычной квантовой механики. Если мы ограничимся
процессами второго порядка х>, то матричный элемент процесса
t-*f будет иметь вид
где Ф^, Фг и Фот обозначают соответственно конечную, начальную
и промежуточную волновые функции состояния системы. (Они
являются собственными функциями гамильтониана Но.) Суммирова-
Суммирование производится по всем промежуточным состояниям, отличным от
начального состояния (с энергией £). Вероятность перехода дается
соотношением G.3).
§ 2. Рассеяние незаряженных мезонов нуклонами
В качестве иллюстрации приведенных выше замечаний вычислим
здесь матричные элементы низшего порядка, описывающие рассеяние
незаряженного мезона нуклоном, для случая псевдоскалярной мезон-
ной теории с псевдоскалярной связью.
Рассеяние двух частиц происходит через следующие состояния.
Начальное состояние. Начальное состояние содержит мезон
->■ ->
с импульсом kx и нуклон с импульсом рх и спином slt т. е.
Промежуточные состояния. Благодаря взаимодействию Hi суще-
существуют следующие четыре возможности, которые определяют воз-
возможные промежуточные состояния (второго порядка):
а) Нуклон поглощает мезон (это соответствует члену b^ba
в гамильтониане взаимодействия НТ), так что в промежуточном
состоянии присутствует только лишь один нуклон с импульсом
pi=pl-\-kl и энергией Yp\-\~m2-
б) Нуклон испускает мезон с импульсом k2, соответствующил« конеч-
конечному состоянию (член взаимодействия &+Ьа+), так что в промежу-
Ц Никаких процессов первого порядка в действительности происходить
не может, так как при этом не могут одновременно сохраняться энергия и
импульса
Рассеяние и S-матрица 185
точном состоянии имеется два мезона с импульсами kx и k2 и один
нуклон с импульсом рх — k2.
в) Рождаются пара'нуклон — антинуклон и мезон (d+b+a*), так
что в промежуточном состоянии присутствуют два нуклона, один
антинуклон и два мезона. Нуклон и мезон, которые родились при
этом процессе, находятся в конечном состоянии.
г) Мезон, находящийся в начальном состоянии, рождает пару и,
таким образом, „аннигилирует" (d*bfa); следовательно, в промежу-
промежуточном состоянии имеется два нуклона и один антинуклон и нет ни
одного мезона.
Конечное состояние. Наконец, повторное действие оператора Hi
в соотношении A4.7) приводит теперь к конечному состоянию,
->
в котором присутствует один мезон с импульсом k2 и один нуклон
.->
со спином s2 и импульсом р2, т. е.
$/• = **,(#>) а+(£2)Фо- A4.9)
Конечное состояние достигается следующим образом:
а) нуклон в промежуточном состоянии испускает мезон, соот-
соответствующий конечному состоянию, и переходит в свое конечное
состояние (член взаимодействия №Ьа*);
б) нуклон в промежуточном состоянии поглощает мезон, соот-
соответствующий начальному состоянию (член взаимодействия b^ba);
в) антинуклон, рожденный в промежуточном состоянии, анниги-
аннигилирует с нуклоном, находящимся в начальном состоянии, и погло-
поглощается мезон, соответствующий начальному состоянию (dba);
г) антинуклон, рожденный в промежуточном состоянии, анниги-
аннигилирует с нуклоном, находящимся в начальном состоянии, и испускается
мезон, соответствующий конечному состоянию (dba+).
Эти процессы соответствуют упорядоченным во времени фейн-
мановским диаграммам, представленным на фиг. 18.
Рассмотрим сначала вклад в Tf\ от процесса „а". Полезно пере-
переписать матричный элемент A4.7) для этого случая в виде
, (НЛО)
где Ео = Е(p1)-\-(o(k1) — энергия начального состояния ^. Пере-
Переписывая матричный элемент в форме A4.10), мы можем использовать
полноту набора собственных функций Фот гамильтониана Но и тот
О Точнее говоря, необходимо включить в соотношение A4.10) множи-
множитель A — g"), где $ — проекционный оператор (проектирующий на началь-
начальное состояние). Однако (Ф.,
186
Глава 14
факт, что Яо, действуя на Фто, дает ЕтФт. Оператор Я/а1) ответ-
ответственен за переход от Ф$ к Фт и равен в этом случае
' f
2Е
X
1.2
г, а
. A4.11)
Аналогично
дается равенством A4.6) с Г = Тб- Теперь, исполь-
используя соотношения A4.8), A4.11) и свойство вакуума а(&)Ф0 =
Конечное
состояние:
ВзаинюЗейсшвие Hj -
Промежуточное
состояние:
ВзоимоЭейстлвие Иг -
Начальное
состояние:
— (Ь'ЪсЬ
Конечное
состояние:
ВзаимоЭействие Я; (с/к)
Промежуточное
состояние:
Взаимодействие Н,-
Н
Началъное _
состояние •• п.
7
Фиг. 18.
Ьа (р) Фо =- d8 (р) Фо = 0, можно легко найти волновую функцию
промежуточного состояния Ф™ = /$в1)Ф*. Функция Фот выражается
следующим образом:
Ф« = *г Ср') Ь8 (?) в (ft) Ф4; A4.12)
выражение A4.12) после применения перестановочных соотношений
A3.59), A3.105) принимает вид
Фот = #г (/»') bs (p) a (k) a+ (kt) bX (pt) Фо =
= 88 (A — ftj) * % (p') bs (p) bt (Pi) Фо =
= 58 (ft — K) 8^88 (P—Pi) bl (p') Фо- A4.13)
Рассеяние и S-натрица 187
Следовательно, согласно выражению A4.11),
А ( J" У X
£ Си)
Л 4- *i) Тб^81 (Л) *г (Л + *1) Фо. A4-14)
так что Фад описывает состояние с одним нуклоном с импульсом
pt-\-kt (в выражении присутствует член bt (PiЧ~*i)Фо)- Опера-
Оператор 7/0, действуя теперь на эту функцию, дает
поэтому (£0 — Яо), действуя на Ф^, дает
Далее, применяя описанные выше методы, легко показать, что
оператор Hj^, действуя на последнее выражение, дает
'/гх
(А + *i —"fe) ТбИ""(А + £)) («>r (A + ^i) 1*™"' (А»
_ —
X *J (pi+ *i —
Наконец, чтобы получить 7/>?а, мы должны вычислить матричный
элемент (Фг, Ь+а*Ф0). Это легко сделать, вспомнив определение
сопряженного оператора, именно:
(а+Ф, Ф) = (Ф, aW), A4.16)
так что
(Фл *J (Pi 4-*i — *)af (*) фо) =
£ о. *J (Pi 4" *i
*)88B — *)• A4.17)
188 Глава 14
Следовательно,
\ (
j 1»
Х
X V (^ (^а) Г5ауГ (^ + ^}) (^Г & + *1> Тб»*1 (А)) A4.18)
Наличие 8-функции соответствует сохранению в этом процессе пол-
полного импульса.
Ясно, что можно интерпретировать полученный матричный эле-
элемент следующим образом. Множитель
>
соответствует поглощению мезона с импульсом &t [множитель
1/VBtc)8cb(A1)] нуклоном, который находится в начальном состоя-
нии с импульсом рх и переходит при этом в состояние с импуль-
импульсом р' [множитель GIBK)b(m?IE(pl)E(p')jhmr(j>'Lbwai(p1)}. По-
Поскольку импульс в этом процессе сохраняется, то возникает мно-
множитель
' £*)
Аналогично множитель
соответствует матричному элементу перехода нуклона из состоя-
ния (р г) в конечное состояние (PzS2) с испусканием мезона с импуль-
импульсом k2. Импульс снова сохраняется, следовательно, снова необхо-
необходимо ввести множитель
Наконец, согласно теории возмущений, мы должны просуммировать по
всем промежуточным состояниям (что соответствует здесь
после того, как разделим это выражение на Ео — Еил> причем в нашем
примере Е?м = Е{р'). Это, действительно, снова приводит к равен-
равенству A4.18).
Используя указанные выше соображения, мы можем теперь сразу
выписать матричный элемент, соответствующий фиг. 18, Ь. Здесь
Рассеяние и S-матрица 180
нуклон, находящийся в начальном состоянии, испускает мезон с им-
импульсом k2, соответствующим конечному состоянию, и, следова-
тельно, переходит в состояние с импульсом рх — к%. В промежу-
промежуточном состоянии мы имеем, таким образом, два мезона и один
нуклон, так что энергия этого состояния равна
— %2). A4.21)
Поэтому матричный элемент TJ>fЪ имеет вид
m \ (
(Л) £ (/»>)
w yi (У'(?2) Тв^г (Pi —18)) (да»-(рл —
2
Процедура, аналогичная описанной выше, показывает, что множи-
множитель, соответствующий испусканию мезона (с импульсом k2) при
->-
рождении пары, когда нуклон характеризуется переменными (p2s2)'
а антинуклон — {р'г), имеет вид
?^ & A4-23)
Аналогично множитель, соответствующий аннигиляции пары (нуклон
->. *■ ■>
p^s^ антинуклон р'г) с поглощением мезона (с импульсом ftt), запи-
записывается в виде
A4.24)
Матричный элемент, соответствующий упорядоченной во времени
фейнмановской диаграмме (фиг. 18, с), равен поэтому
™<2) С __
() (^ГЛА^Ь х
Д, (ш (р2) Т5" (рг + ^)) (" Срх +%) Tow Ш) ..,„.
\/ \ ^ ^- . A1.ZD)
Zi Ео — Е (Л) — «> (к{) — Е (р2) — ш (Аа) — Е (Л + *i)
Знак минус перед матричным элементом следует из принципа Паули.
Рлава l4
Аналогичным образом получим для фиг. 18, d
т \ (
nfi
-%)) (vr (A -
14
Это и есть четыре матричных элемента наинизшего порядка, кото-
которые описывают мезон-нуклонное рассеяние. Во втором порядке воз-
возможны также и другие процессы, включающие мезон и нуклон,
например на фиг. 19, а и b изображен процесс, соответствующий
собственной энергии нуклона. Эти процессы, однако, не вносят
вклада в рассеяние, и потому мы не рассматриваем их здесь.
ч
а
Фиг. 19.
Для получения поперечного сечения рассеяния мы можем теперь,
используя соотношения G.32) и G.37), провести суммирование по
двум промежуточным состояниям и вычислить необходимые квадра-
квадратуры. Здесь мы не будем делать таких вычислений. Вместо этого
рассмотрим упрощение матричного элемента, которое получается
в пределе, когда импульс мезона мал по сравнению с массой нуклона
в системе центра инерции (kt =—р1 = kt; k2——р2==*/>)* ^ы не
будем касаться здесь применимости борновского приближения к этой
задаче, поскольку ниже обсудим такую форму теории (см. т. II,
гл. 40—43), в которой этот вопрос обходится.
Вспомнив обсуждение в гл. 4, § 2, оператора fs [соотношение D.33)
и ниже], заметим, что в нашем приближении движение нуклонов
Рассейниё и S-матриЦа 1§1
в системе центра инерции является нерелятивистским, поэтому мат-
матричный элемент
*»r (Pi + К) Тб^8' (pi) = ^ (°) l5w*' (— *i)
мал, так как он описывает переход между состояниями с положи-
положительной энергией частиц, импульсы которых мало отличаются друг
от друга. Согласно выражению D.41 б), величина его равна to-kJ2m,
где о описывает спин нуклона (теперь уже 2-мерная матрица). Ана-
логично матричный элемент w8'(P2)'[b'Wr(p1-\~kl) в системе центра
инерции равен в нашем приближении — ic • kfj2m. Форма io ■ kj2m
матричного элемента, соответствующего испусканию или поглоще-
поглощению мезона нуклоном при переходе нуклона из состояния с поло-
положительной энергией в состояние с положительной энергией, отра-
отражает некоторые важные особенности псевдоскалярной связи: 1) при
таком переходе мезон поглощается или испускается в Я-состоянии
и 2) взаимодействие ослаблено, поскольку оно содержит „малый"
оператор уь (см. гл. 4, § 2). Таким образом, диаграммы на фиг. 19, а
и b соответствуют процессам, ведущим главным образом к рассея-
рассеянию Я-волны мезона. В пределе при k<^m энергетический зна-
знаменатель в выражении A4.18) имеет вид (в системе центра инерции)
о—£ (л+£) =
A4.27)
т. е. матричный элемент A4.18) принимает теперь вид, отвлекаясь
от 8-функции,
rB) a
G2
2 B*
9t
2m
я)« [ш {ki) ф {kr)]'l* ш (A,)
n4
Второе выражение для матричного элемента показывает связь этого
матричного элемента с матричными элементами для псевдоскалярной
связи; это мы обсудим в гл. 26. Аналогично матричный элемент,
представленный диаграммой на фиг. 19, Ь, в нашем приближении
примет вид
■>■■*■■>■■>■
гB)й /6М2__1 (J • kj) (д • kf)
С другой стороны, матричные элементы A4.25) и A4.26), опи-
описывающие рождение пары, велики, как это было указано в гл. 4,
§ 2. В нашем приближении эти матричные элементы являются
192
Глава 14
сферически симметричными, так что диаграммы на фиг. 18, с и d
изображают процессы, которые в первую очередь ответственны
за рассеяние 5-волны. В т. II, гл. 41 и 42, мы увидим, что более
точное рассмотрение задачи рассеяния без использования борнов-
ского приближения показывает, что сечение рассеяния S-волны
значительно занижено по сравнению с сечением, вычисленным
в борновском приближении, в то время как сечение Р-рассеяния
завышено.
В заключение этого параграфа обсудим качественно, следуя
Чу [81], почему в пределе при k<k^m диаграммы на фиг. 18, а и b
Нуклон
Медленный
нуклон
Четность
положительная
(но определению)
Четность мезона отрицательная
Q
Фиг. 20.
Конечное
состояние
является
нечетным
изображают главным образом Р-рассеяние, а диаграммы на фиг. 18, с
и d—5-рассеяние. Причина, по существу, заключается в следую-
следующем. В системе центра инерции нуклон движется весьма медленно
по сравнению с мезоном, обладающим энергией ш (&) <^ т. Поэтому
в первом приближении можно полностью пренебречь движением нук-
нуклона. Рассмотрим теперь, как выполняются законы сохранения угло-
углового момента и четности в применении к двум различным типам
процессов поглощения мезонов, соответствующим фиг. 20, а и Ь.
Если считать совершенно произвольно внутреннюю четность ну-
нуклона в 5-состоянии положительной, то четность антинуклона будет
отрицательной. Поэтому четность системы после поглощения мезона
будет положительной в случае рассеяния нуклона (фиг. 20, а) и
отрицательной—в случае рождения пары нуклон — антинуклон. Если
рассматриваемый мезон является псевдоскалярным, то четность си-
системы перед поглощением будет положительной или отрицательной
в зависимости от того, находится мезон в Р- или 5-состоянии
соответственно. Поэтому псевдоскалярный мезои может быть по-
поглощен только в нечетном состоянии в случае, изображенном на
фиг. 20, а, и только в четном — в случае, изображенном на фиг. 20, Ь.
Далее, поскольку нуклон находится в 5-состоянии (фиг. 20, а) как
Рассеяние и S-матрица 193
до, так и после поглощения мезона, то поглощаемый мезон должен
находиться в Р-состоянии. Аналогично (фиг. 20,Ь) мезон должен по-
поглощаться, находясь в 5-состоянии (с отрицательной четностью).
§ 3. S-матрица
В предыдущем параграфе был вычислен матричный элемент рассея-
рассеяния мезона нуклоном в наинизшем приближении. Можно спросить,
как должен выглядеть матричный элемент Ti}, в высших приближе-
приближениях, т. е. когда рассматривается несколько промежуточных со-
состояний. В дальнейшем мы будем интересоваться и существенно
более сложными процессами, такими как рассеяние бозона несколь-
несколькими фермионами. Таким образом, представляло бы значительный
интерес построение матрицы (так называемой 5-матрицы), элементы
которой между определенными начальным и конечным состояниями
соответствовали бы вероятностям перехода между этими состоя-
состояниями. Такая матрица рассеяния впервые была введена Уилером [528]
при рассмотрении структуры ядра и задачи рассеяния. Она была
снова подробно исследована Гейзенбергом [230, 231] в связи с по-
попыткой построения теории элементарных частиц.
Соображения, которые привели Гейзенберга к рассмотрению 5-мат-
рицы (Гейзенберг [223, 229]), связаны с тем, что, по его убеж-
убеждению, трудность с расходимостью, присущая всем релятивистским
теориям поля, может быть устранена введением новой фундамен-
фундаментальной постоянной, имеющей размерность длины. Эта гипотеза
о фундаментальной длине была постулирована Гейзенбергом [223],
Амбарцумяном и Иваненко [4], а также Марчем [320—324] и др.
Гейзенберг полагал, что эта новая постоянная сыграет ту же роль
в ограничении квантовой теории поля, какую сыграла постоянная
Планка в ограничении применения обычной квантовой механики
к атомным системам.
В обычной квантовой механике атомная система полностью опре-
определена гамильтонианом Н системы. Однако наличие гамильтониана,
который фигурирует в уравнении Шредингера HW = ihW, означает
возможность непрерывного смещения волновых функций во времени,
что, по-видимому, противоречит существованию фундаментальной
длины. Поэтому Гейзенберг вынужден был отказаться от уравнения
Шредингера и понятия гамильтониана. Пытаясь выяснить, какого
типа операторы и функции должны заменить эти понятия, он при-
пришел к вопросу, какие величины в нынешней формулировке теории
поля останутся физически наблюдаемыми в будущей „правильной"
теории, т. е. какие из физически наблюдаемых величин не зависят
от существования минимальной длины. В частности, Гейзенберг рас-
рассматривал следующие физически наблюдаемые величины, которые
обязательно должны описываться любой теорией:
1) энергию и импульс свободной частицы;
194 Глава 14
2) дискретные уровни энергии стационарной замкнутой системы;
3) асимптотическое поведение волновых функций в процессах
рассеяния, испускания и поглощения, и, следовательно, вероятность
этих процессов, т. е. их поперечные сечения.
Чтобы положить поперечные сечения процессов и другие физи-
физически наблюдаемые величины (которые можно легко вычислить
из гамильтониана, если он существует) в основу новой теории,
Гейзенберг ввел некоторую унитарную матрицу 5 (характеристи-
(характеристическую матрицу), из которой, по его мнению, можно получить ве-
вероятности перехода и положения связанных состояний. В своей ори-
оригинальной статье он определил 5-матрицу с помощью решения
стационарной задачи рассеяния. Обычное решение \F стационарной
задачи в этом случае асимптотически ведет себя следующим обра-
образом:
lira <F = W1-f-<F2,
Г-> со
где Wt — функция, описывающая падающую волну, а Ф^ описывает
рассеянную волну. Тогда 5-матрица определяется как оператор,
который, действуя на функцию, описывающую падающую волну,
превращает последнюю в функцию, которая описывает рассеянную
волну, т. е.
Гейзенберг полагал, что в будущей теории 5-матрица примет на
себя роль, которую играет теперь гамильтониан. Гейзенберговская
теория 5-матрицы была развита дальше Мёллером [341, 342],
Штюкельбергом [467—470] и др.г' Связь между .S-матрицей в обыч-
обычной квантовой теории и 5-матрицей, используемой для вычисления
сечения и других физически наблюдаемых величин, обсуждалась во
многих работах, в частности Липманом и Швингером [307]. Пре-
Превосходный обзор применений 5-матрицы к теории рассеяния дали
Гелл-Манн и Гольдбергер [205].
На сегодняшний день, вообще говоря, ясно, что теория, содер-
содержащая только 5-матрицу, не является достаточно полной. В част-
частности, время не должно было бы больше появляться в этой теории,
а это является уже довольно сильным ограничением выводов, полу-
получаемых из теории. Далее, с практической точки зрения, мы не мо-
можем больше рассматривать введение фундаментальной длины как
метод исключения расходимости, принимая во внимание успех тео-
теории перенормировок. Тем не менее 5-матрица играла центральную
роль в развитии и успехах теории поля за последнее время.
Таким образом, фейнмановская квантовая электродинамика (Фейн-
ман [168, 169]) представляет собой типичную теорию 5-матрицы.
I) Обсуждение и ссылки, относящиеся к периоду до 1946 г., см. в статье
Вентцеля [524].
Рассеяние и S-матрица 195
Однако она обладает многими преимуществами по сравнению с ее
прежней формулировкой, данной Гейзенбергом и др. Самое важное
из них заключается в том, что эта теория не просто дает опреде-
определение свойств 5-матрицы, а описывает рецепт для реального вы-
вычисления ее и показывает, что такое вычисление может быть прове-
проведено в большинстве случаев. Кроме того, она много дает нам для
понимания строения релятивистской теории поля. Далее, так как
все матричные элементы этой теории ковариантны, то устранение
расходимостей можно провести легко и однозначно.
Связь фейнмановского формализма 5-матрицы с более обычной
формой релятивистской квантовой теории описана в двух статьях
Дайсона [126, 127], а также самого Фейнмана [170, 171] на основе
лагранжевой формулировки квантовой механики. Чтобы уяснить фор-
формализм Фейнмана—Дайсона, мы рассмотрим сначала основные черты
ковариантного формализма.
Глава 15
КОВАРИАНТНЫЙ ФОРМАЛИЗМ
§ 1. Представление взаимодействия
Дайсоновское доказательство эквивалентности двух форм теории
основано на переходе к представлению взаимодействия (//?). Это
представление, впервые введенное Штюкельбергом [461, 466, 467]
и широко применявшееся Томонага [486] и его сотрудниками (Коба
и др. [279, 280], Канэсава [261, 262]) и Швингером [438, 439], можно
получить унитарным преобразованием обычного уравнения Шредин-
гера
^^ A5.1)
Здесь Но—гамильтониан невзаимодействующих полей, Hi— гамиль-
гамильтониан, описывающий взаимодействие между этими полями. Как
указывалось выше (гл. 13 и 14), вектор состояния Ф в отсутствие
взаимодействия (//j = 0) описывает распространение в пространстве
заданного постоянного числа свободных частиц с определенным
импульсом и спином, не взаимодействующих между собой. Опера-
Оператор Hi описывает взаимодействие этих частиц друг с другом и
самих с собой.
Напишем теперь
ИЯ'» A5.2)
Используя равенство A5.1) и A5.2), легко убедиться в том, что
Ч?"@ удовлетворяет следующему уравнению:
A5.3а)
= H(iZB) @ W(f), A5.36)
где
■—оператор энергии взаимодействия в новом представлении. Этот
оператор явно зависит от времени в противоположность шредин-
геровскому оператору Hi, который от времени не зависел. Вообще
оператор Qm(t) в представлении взаимодействия связан со шредин-
геровским оператором Qs следующим образом:
Qib @ = eiSJI"Qse-iBMh. A5.4)
Ковариантный формализм 197
Отсюда следует, что в представлении взаимодействия зависимость
операторов от времени определяется гамильтонианом свободного
поля, так как, дифференцируя равенство A5.4), получаем
Л g =[Qni(.t), Ho] A5.5)
(заметим, что Но = Hq). Таким образом, в представлении взаимо-
взаимодействия операторы поля удовлетворяют уравнениям, описывающим
свободные поля, в то время как зависимость от времени вектора
состояния W(t) определяется, согласно соотношению A5.36), лишь
энергией взаимодействия HiB(t).
Если мы рассмотрим, например, скалярную мезонную теорию
с простой прямой связью, то в шредингеровском представлении
гамильтониан свободных полей будет иметь вид
y}, A5.6)
а гамильтониан взаимодействия
HZ=G f d*xty(х)Гф(х)ср (х). A5.7)
После перехода к представлению взаимодействия операторы поля
фхд (х, t), срхд (дг, f) удовлетворяют следующим уравнениям:
(— ^ + т)фхл(х) = 0, A5.8)
(П4-Р2).ФХЛ(Х)=О, A5.9)
и соотношение A5.3) теперь гласит
A5.10)
т. е. в скалярной мезонной теории гамильтониан взаимодействия
в представлении взаимодействия имеет вид
(х)<рм(х). A5.11)
Все операторы в правой части равенства A5.11) написаны в пред-
представлении взаимодействия и поэтому явно зависят от времени.
Преимущество представления взаимодействия обусловлено тем,
что операторы поля удовлетворяют уравнениям свободного поля,
поэтому инвариантные перестановочные соотношения можно написать
для всех моментов времени. Это представление позволяет обобщить
уравнение A5.3), сделав его ковариантным. Как было установлено
198 Глава 15
выше, уравнение A5.3) не является ковариантным, так как при
определении входящей в него производной по времени djdt преду-
предусматривается выбор специальной лоренцовской системы координат.
Указанное обобщение содержится во введении понятия произволь-
произвольной пространственно-временной поверхности вместо „плоской" по-
поверхности t = const. Единственное условие, которому должна удо-
удовлетворять указанная поверхность, заключается в том, что нормаль
к ней в любой точке х, л-Дх) является времени-подобной, т. е.
п.р(х)п^ (х) > 0. Это означает, что никакие две точки поверхности
не могут быть связаны световым сигналом, или, другими словами,
любые две точки на этой поверхности разделены пространственно-
подобным интервалом. Обозначим такую поверхность символом а.
Далее, каждой точке х на этой поверхности можно сопоставить
время t(x), называемое локальным временем точки. В пределе, когда
поверхность становится плоской, все точки имеют одинаковое время t,
равное координате плоскости t = const. Теперь мы в состоянии
естественным образом обобщить и Ч?"@> записав эту функцию в виде
W[t(x)]. Далее, мы можем рассматривать основное уравнение
^ A5.12)
как результат суммирования бесконечного ряда уравнений, получен-
полученных введением локального времени для каждой точки пространст-
пространственно-подобной поверхности. Если гамильтониан взаимодействия
в общем случае выразить как сумму по малым трехмерным ячейкам ДV
пространственно-подобной поверхности а, т. е.
tfi = 2^x(x)AV, A5.13)
то уравнение, которое имеет место в малой ячейке вокруг простран-
-> ->
ственно-временной точки х, t(x), можно записать в виде
A5.14)
dt(x)
Полученное уравнение представляет собой обобщение уравне-
уравнения A5.12). Итак, если вариация W(t), соответствующая жесткому
бесконечно малому перемещению поверхности t = const как целого,
определяется интегралом f e7&i(x)d5x, то становится очевидным,
t
что вариация Ч?"[^(лг)] относительно точки х будет определяться
плотностью энергии взаимодействия ет$?.г(х)ДУ в бесконечно малом
интервале вокруг х.
Ковариантный формализм. 199
->
Далее, поскольку произведение AVAt(x) является инвариантом,
то напрашивается следующая инвариантная процедура дифференци-
дифференцирования. Рассмотрим функцию пространственно-подобной поверх-
поверхности W \t (х)] = W (а). Сравним затем величины этих функций на
4-объем Q."
Фиг. 21.
двух пространственно-подобных поверхностях а и а', которые отли-
отличаются на бесконечно малую величину в окрестности пространст-
пространственно-временной точки х (см. фиг. 21). Определим теперь инвариант-
инвариантную операцию 8/оа (х) как
iim t'wr^wj-j I'WJ t A5.15a)
с j
AV
A5.156)
S°(x) AtAF^O e&t<X)bV
-:—-—r-\F(a)= Iim — о /—\—^~^ • A5.15b)
00 (x) 2 (x) ->. 0 ^ W s
Здесь Q (x) — объем, заключенный между поверхностью а и а', при-
причем а' означает пространственно-подобную поверхность, полученную
малой деформацией а вблизи точки х. В пределе Q (х) стягивается
в точку х. Поэтому уравнение A5.14) можно переписать в виде
i»F(a). A5.16)
Это уравнение уже ковариантно, так как оператор &€i—инвариант
в случае связи без производной (см. ниже замечания для случая
связи с производной) и так как при определении пространственно-
подобной поверхности не требуется какой-либо определенной лорен-
цовской системы отсчета. Поэтому уравнение движения системы
можно переписать без указания системы координат, к которой оно
относится. Уравнение A5.16) обычно называют уравнением Томо-
нага — Швингера.
200 Глава 15
Для существования решений уравнения A5.16) должно удовле-
удовлетворяться следующее условие интегрируемости:
8о(хMо(х/) во(х')8а(х) ~~ U-
Это условие, по существу, представляет собой ограничение области
изменения поверхности а(х). Кроме того, условие A5.17) означает,
что
I3&z(x), SffI(xf)] = 0 A5.18)
для точек х и х', лежащих на пространственно-подобной поверхно-
поверхности а. В последующих параграфах мы покажем, что инвариантные пере-
перестановочные соотношения для операторов поля таковы, что соотно-
соотношение A5.18) автоматически удовлетворяется для всех взаимодей-
взаимодействующих полей со связью без производной. Когда плотность лагран-
лагранжиана взаимодействия содержит производные по времени потенциалов,
описывающих поле (как в случае взаимодействия заряженного бозон-
ного поля с электромагнитным), то необходимо некоторое обобщение
описанных выше методов. В этом случае, чтобы удовлетворялось
условие интегрируемости (см., например, работу Кролла [293] и
Мэттьюса [326]), плотность гамильтониана взаимодействия должна
явно зависеть от поверхности. Вообще, условие интегрируемости
и вытекающее из него соотношение A5.18) означают, что решение
существует только тогда, когда поверхность а является простран-
пространственно-подобной, так как, вообще говоря, соотношение A5.18) не
выполняется, если х и х' разделены времени-подобным интервалом.
Кроме того, они обеспечивают условие: когда пространственно-
подобная поверхность является плоской (t = const), то любое реше-
решение уравнения A5.16) является также решением уравнения A5.12).
В нашей работе мы не будем пользоваться явным видом этих
поверхностей. Во многих случаях указанные пространственно-подоб-
пространственно-подобные поверхности не применяются, хотя, конечно, они являются
физически более реальными, чем плоские пространственно-подобные
поверхности t = const. Физически маловероятным является предпо-
предположение, что эрмитовские операторы поля, определенные точно
в пространственно-временной .точке, существуют и'могут быть изме-
измерены в обычном кванТово-механическом смысле. Действительно, Бор
и Розенфельд [47, 48] в своих классических работах по вопросу
измеримости электромагнитных полей уже показали, что измеримыми
являются лишь средние по малому объему 4-пространства значения
операторов поля. Связь между этими ограничениями измеримости
и проблемой расходимостей собственного заряда и собственной
энергии в релятивистских теориях поля до сих пор еще не уста-
установлена. Однако известно (Гейзенберг [227], Штюкельберг [475},
Штюкельберг и Грин [476], Коринальдези [91, 92]), что в теорию
вводятся еще и „граничные расходимости", если пространственно-
Ковариантный формализм 201
временной объем Q, в котором происходит рассеяние или произво-
производится измерение флуктуации поля или распределения заряда — тока,,
имеет резкие пространственно-временные границы.
§ 2. Ковариантные перестановочные соотношения
Большой прогресс, достигнутый за последние годы при изучении
релятивистских теорий полей, обязан, в частности, тому, что все
расчеты удалось провести таким образом, что в каждой стадии
проявлялась релятивистская инвариантность теории. Это дало воз-
возможность ввести представление взаимодействия и вместе с ним —
инвариантные перестановочные соотношения. Здесь мы кратко их
изучим.
Рассмотрим в первую очередь случай скалярного бозонного поля.
В гл. 13 мы видели, что в шредингеровском представлении незави-
->
сящий от времени оператор поля ср (лг) разлагается в интеграл па
->■ •>
операторам рождения и уничтожения частиц aJ(k) и a (k) следующим.
образом:
fix)^-^- f-^-(af(t)e-^^~\-a(%)e^-\ A5.19)
Bл) '' •> у 2o>fc
где
[a(k), a+(i0] = B(£ — P), A5.20a)
[а{к), а(!')] = [а+(А), а+(й')] = 0. A5.206)
Соответствующие операторы поля в представлении взаимодействия
tpJi2 (х, t) имеют вид
срхл (х) = еш"*ср (лг) е-«Ч A5.21>
где
24 A5.22)
o 2
к
Мы снова вернулись к дискретным значениям k, чтобы упростить
->
дальнейшее изложение. Для получения оператора <?1В (х, t) в пред-
представлении взаимодействия мы должны вычислить члены вида.
exp (iHot) (at + a_ft) exp (— 1Щ).
^.Рассмотрим оператор уничтожения и напишем
а'к=^еш^аке-ш"К A5.23).
Далее, ак коммутирует с а1'ак- при кфК'. Следовательно, доста-
достаточно рассмотреть выражение
ct-jc = e к к к аке lc h к . Aо.24>
202 Глава 15
Чтобы вычислить оператор а'к, представим его в виде
ак(Х) = eiafeafe°>feaaA.e~iaftafe'ofe*x, A5.25)
так что
ак{\) = ак A5.26)
и есть интересующий нас оператор, причем
а'к@) = ак. A5.27)
Дифференцируя равенство A5.25) по ~к, получаем
= — ш^ак(к), A5.28)
так что
ak(l)=afk(O)e~i"'ktt A5.29а)
или
ak = ake~imkt. A5.296)
Аналогичное вычисление, проведенное для оператора рождения частицы,
приводит к соотношению
akf = ale+ia>kt, A5.30)
так что
A5.31)
1/ Vm>
К> о
В форме A5.31), как указано, величина k0 = со^ = -j- у k2 -\~ рг
положительна. Поэтому заметим, что зависимость операторов рож-
рождения и уничтожения, входящих в оператор ®Ii2(x), от частоты
различна. Оператор рождения частицы а% умножается на его>й , т. е.
зависит от отрицательных частот, в то время как оператор уни-
уничтожения частицы зависит от положительных частот. Это различие
между ними лоренц-инвариантно. Действительно, оно позволяет
инвариантным образом разложить оператор ^^(х) на части, соот
ветствующие положительным и отрицательным частотам 1)
A5.32)
У Начиная с этого места, мы больше не будем писать индекса IR у опе-
операторов в представлении взаимодействия, поскольку зависимость этих опе-
операторов от х уже указывает на выбор представления. Кроме того, все
последующее изложение вплоть до гл. 25 ведется лишь в представлении
взаимодействия.
Ковариантный формализм 203
где
L Г **«(*)«,-*•* A5.33а)
Г
7Г^7 ^ A5.336)
а также
(Т(-)(х))+ = ср(+)(х). A5.34)
Оператор ср(+)(х) является оператором уничтожения, а оператор
ср(~>(х) — оператором рождения частицы.
Вакуум, который мы раньше характеризовали следующим усло-
-»-
вием: а(£)Фо=0 при всех k, теперь обладает свойством
ср(+)(х)Фо = О. A5.35)
Мы можем пользоваться одинаковыми символами для обозначения
вакуума свободного поля в обоих представлениях, поскольку в шре-
дингеровском представлении функция Фо была собственной функ-
функцией гамильтониана Но с собственным значением Ео = 0, поэтому
exp (iHot) Фо = Фо, т. е. Фо описывает вакуум также и в предста-
представлении взаимодействия.
Теперь легко написать перестановочные соотношения для опе-
операторов в представлении взаимодействия, используя перестановочные
соотношения A5.20а) и A.5.206)
/ J X
X {[a (ft), a+ A')] eik' ■ *'e-ik •x + [a+ A). a (ft') ] X
откуда
[«P(x), <р(х'I=у(^-в /^(в-*-(х-х')_в*.(ж-х')), (i5.37a)
*o>O
[<p(x), со (x')l = the ~ J ^««■(«'-^sinfto^o — jca), A5.376)
fco>0
при этом всюду Дг0 = —(— ш&.
!) Для удобства читателя мы включили сюда множитель {lief1-, на кото-
который умножается разложение A5.19), если не пользоваться системой атомных
единиц, где Й = с = 1.
204 Глава 15
Если определить величину Д(х — х') равенством
Д(х — х') = — ~~^ / ^(г«'С^-^-^, A5.38)
то перестановочные соотношения можно переписать в виде
[ср(х), ср (х'I = ЛсЬ. (х — х')- A5.39)
Функция Д — инвариантна относительно замены (х—»-x-j-l), так
как она является функцией лишь разности х — х'. Кроме того, ра-
равенство A5.38) можно переписать в форме, в которой более явно
видна инвариантность Д(х — х') по отношению к однородным ло-
ренцовским преобразованиям. Для этого напомним, что
^ o — (о*)}, A5.40)
поэтому равенство A5.38) можно написать в виде
4- со
A5.41)
где e(k) = ko/\ kQ\, и поэтому равно -(-1 при k0 > 0 и —1 при
k0 < 0. В последнем выражении k0 пробегает как положительные,
так и отрицательные значения. Множитель s(k), являющийся скаля-
скаляром, введен для того, чтобы при интегрировании равенства A5.41)
по k0 в выражении A5.38) между двумя экспоненциальными множи-
множителями появлялся нужный знак (минус). Поэтому правая часть выра-
выражения A5.41) инвариантна относительно всех собственных преобра-
преобразований Лоренца, поскольку к • х, к2 и d4k являются скалярами.
Следовательно,
Д(х) = Д(ах), A5.42)
где (а)^ == aij- — однородное лоренцовское преобразование.
Далее, соотношение A5.37) показывает, что при хо= Xq, т. е.
для равных моментов времени, этот коммутатор равен нулю. Это
и требуется, так как мы помним, что в квантовой механике отсут-
отсутствие коммутации двух эрмитовых операторов означает, что соот-
соответствующие им две физические величины невозможно одновременно
измерить с произвольной степенью точности. С другой стороны,
равенство коммутатора нулю позволяет одновременно диагонализо-
вать эрмитовы операторы, и, таким образом, становится возможным
одновременно точно измерить физически наблюдаемые величины,
соответствующие этим операторам. Конечно, измерения величин,
соответствующих эрмитовым операторам поля ср (jc, t) и ср (х', t),
не могут влиять друг на друга, поскольку, согласно теории отно-
относительности, две пространственно-временнйе точки х и х' невозможно
Ковариантный формализм 205
связать никаким сигналом. Принимая во внимание сказанное, ясно,
что функция Д(х) равна нулю не только для интервала хо = 0, но
также и для любого пространственно-подобного интервала, т. е.
при х2 < 0. Это следует из релятивистской инвариантности, по-
поскольку подходящим выбором лоренцовского преобразования всегда
можно преобразовать пространственно-подобный вектор х так, что
его образ х' в новой системе будет иметь компоненту х'0 = 0. Из
соотношения A5.42) теперь следует, что функция Д(х) обязательно
равна нулю в пространственно-подобных точках х, если она равна
нулю при х0 = 0.
Выражение A5.37) также указывает, что Д(х) является нечетной
функцией х. Но так и должно быть, поскольку функция Д пропор-
пропорциональна коммутатору; далее, мы имеем
[ср(х), <р(х')]= — [?(х')> ?(хI, A5.43а)
и поэтому
Д(х — х') = — Д(х' — х). A5.436)
Указанные свойства функции Д(х) можно объединить, написав
0, если х2 соответствует пространственно-подобному интервалу,
=^ е(х)/(х2) внутри светового конуса (х2 соответствует времеии-по-
( добиому интервалу).
Функция Д внутри светового конуса определяется следующим тре-
требованием: она должна быть нечетной и инвариантной. Единственными
инвариантами, которые можно построить из координат х, являются
х~— скалярная длина и е(х) — знаковая функция времени (заметим,
что функция s(x) определена и имеет смысл лишь внутри свето-
светового конуса!). Последнее соответствует утверждению, что абсолютное
прошлое и абсолютное будущее имеют инвариантный смысл. Следо-
Следовательно, единственная нечетная инвариантная функция координат
внутри светового конуса имеет вид е(х)/(х2).
Заметим далее, что рассмотренные нами ранее перестановочные
соотношения в шредингеровском представлении для тг(лг) и ср(лг)
включены в соотношение A5.37). Поскольку, согласно выраже-
выражению A5.21), шредингеровское представление и представление взаимо-
взаимодействия совпадают при / = 0 и, учитывая, что
имеем
, =й(|Д(х — х')} , =
= тЙ f d*keM-<*-Zfkosk0(x0 — х'о) t = —tf8(£ —2). A5.44)
206 Глава 15
Ясно, что в это соотношение также включены и перестановочные
соотношения A3.18) для равных моментов времени, поскольку ре-
результат A5.44) получен лишь при одном условии хо — х'о.
Наконец, из выражения A5.41) видно, что функция Д(х — х')
удовлетворяет уравнению Клейна — Гордона
— [i2)8(k2 — [i2)s(k) = 0, A5.45)
так как л:В(л:) = О. Это должно иметь место также и потому, что
действуя на левую часть равенства A5.39) оператором (Пх + ^2)»
мы получаем
—х0 = 0, A5.46)
так как ср(х) удовлетворяет уравнению Клейна — Гордона.
Поскольку функция Д(х) удовлетворяет гиперболическому диф-
дифференциальному уравнению второго порядка, то она однозначно
определяется дифференциальным уравнением
= 0 A5.47а)
и двумя начальными условиями при л:0=0:
а) А(х, л:0 = 0) = 0, A5.476)
/dJjZjti) =__8(^). A5.47в)
Функцию Д(х) можно выразить с помощью известных функций,
вычисляя интеграл в равенстве A5.376) (Дирак [107], см. также
книгу Шиффа [429]). Положив |л:| = ги k0 = -\-y~k2-\- jj,2, найдем
егк 'x sin koxo =
. L Г
2*2 J
1 1 д Г dk и ■ и
= тг-5 — г- • , - cos кг sin «nxn =
Ковариантныи формализм 207
Делая замену k = \>.shy, получаем ^
( -\-Ja{y.Vxl — г2) при хо>г,
= \ 0 при — г < х0 < г, A5.486)
I —JofaVxl — г2) при хо<—г.
Проведя указанные в соотношении A5.48а) дифференцирования,
мы можем написать функцию Д (х) в форме, в которой явно про-
проявляются как ее ковариантные свойства, так и сингулярность (см.
также дополнение к статье Швингера [439]):
^^} A5.49а)
где 8(_у) = 1 при _у>0 и 6(j/) = 0 при у < 0. Для малых х2 вблизи
границы светового конуса имеет место следующее разложение 2):
Д(х) = — 1S(X){S(X2L-^9(X2) + . . .}, A5.496)
в нем опущены члены, исчезающие при х2 —*■ 0; следовательно, функ-
функция Д(х) обладает 3-образной сингулярностью, а также конечным
разрывом (скачком) на границе светового конуса.
Существует другая инвариантная функция Д'1), которая также
удовлетворяет уравнению Клейна — Гордона, однако является четной.
= ДA)(х), A5.50а)
АA>(х) = 0. A5.506)
Ее интегральное представление имеет вид
J
+ 0O
— jx2). A5.51)
J) Напомним, что
+оо
J0(z) = — Г s
тс ^7
—оо
а) Напомним, что функция Бесселя разлагается в степенной ряд
г=о
208 Глава 15
Проделывая выкладки, аналогичные описанным выше для функ-
функции Д(х), легко убедиться в том, что
А«(*. xJ-l-L&F^r. x0), A5.51а)
где
\ -\-No(\>.Vx2o — r2) при|хо|>г,
I — гМ1' (*ц V г2 — 4) при т > | х01.
Отсюда следует, что Д'1' не исчезает вне светового конуса. На
больших пространственно-подобных расстояниях (т. е. при г^>х0)
Д падает экспоненциально. Функцию Д можно также записать
в форме, аналогичной равенству A5.49а) (см. дополнение к статье
Швингера [439]). Здесь мы приведем лишь ее представление вблизи
светового конуса, чтобы показать присущие ей сингулярности:
A5.51в)
где символ Р означает, что при интегрировании этой функции вокруг
сингулярной точки следует брать главное значение интеграла, и
7 = 0,577 .. . означает постоянную Эйлера. Здесь снова опущены
•члены, исчезающие в пределе при х2 —*■ 0.
В последующем изложении мы будем использовать перестано-
перестановочные соотношения между ср(+'(х) и ср(-)(х')- Согласно соотноше-
соотношениям A5.20) и A5.33), они имеют вид
= [?<->(х), ср<-)(х')] = О A5.52)
= г-ЙсД(+)(х — х'). A5.53)
и
[ср(->(х), ^ooi—^ /^«м-жо-
Й0>0
= ihcA(-)(x — x'). A5.54)
11 Напомним, что
N0(z) — |
п J
Ковариантный формализм 209
где в соответствии с прежним условием мы определили функцию
как зависящую от положительных частот часть функции Д(х — х')-
Аналогично
a (x x; —2B^K j k0
Из определений A5.55) и A5.56) следует, что
A5.57)
Подобным же образом
^|^« A) A5.58)
или, переписав несколько иначе,
Д(+)(х) =4 [Д(х) — /ДA)(х)], A5.59а)
Д(")(х)=^-[Д(х)+гДA)(х)]. A5.596)
Функция ДA) появляется, когда вычисляют среднее по вакууму
величины [ср(х), <р(у)]+- А именно, используя определение волновой
функции вакуума [соотношение A5.35)] и соотношение A5.34),
находим
(Ф0,{ср(х)ср(уН-ср(у)ср(х)}Ф0) = 2(Ф0, {<р(х)ср(у)}Ф0) — /ЛсД(х-у) =
= 2(ср(-)(х)Ф0, <р<-)(у)Ф0)-ЙсД(х-у) =
=-2(Ф0, ср(+)(х)ср(-)(у)Ф0)-^сД(х-у)=
(+)(х — у) — Д(х — у)] =
—у). A5.60)
§ 3. Перестановочные соотношения для дираковских операторов
Аналогичное рассмотрение может быть проведено для дираков-
дираковских операторов. Оно приводит к следующему выражению для этих
операторов в представлении взаимодействия:
X 2 {br(P)™r(P)e-iv*+4(p)vr(P)e+iv*}. A5.61)
r=l
210 Глава 15
Ковариантные перестановочные соотношения имеют вид
№«(*). Vx')}.= (—V* + fm)eiiA(x —x'; m) = — *Sep (х — х'), A5.62)
где Д(х; т.) дается равенством A5.41) с заменой ;j, на т, а функ-
функция S определяется соотношением
S(x —х') =—(iVx-4-m)A(x —х'; т). A5.63)
Следовательно,
*', 0) = (—T°g|-A(x— х')) , = + Т°з£— *')> A5-64)
■"о** о
как это и вытекает из рассмотренных выше перестановочных соот-
соотношений в шредингеровском представлении [равенство A3.112)].
Далее, поскольку функции tya(x) удовлетворяют уравнению Дирака,
мы должны получить уравнение
(iVx— m)S(\ — x') = 0, A5.65)
которое удовлетворяется тождественно, так как, согласно соотно-
соотношениям A5.63), A5.65) и A5.47),
(iV — m)(iV+m)A(x) = — (D+m2)A(x)=0. A5.66)
Как и в случае бозонного поля, части операторов, зависящие от
положительных и отрицательных частот, отвечают операторам уни-
уничтожения и рождения частиц соответственно. Однако здесь
br(p)W (p) e *P'X A5.67)
Po>O '" " r=l, 2
— оператор уничтожения фермиона, а
" l'r(p)vr (p)eiv'x A5.68)
оператор рождения антифермиона. Аналогично
v ' р >о r=i, 2
— оператор рождения фермиона, а
р.,>0 »•=!, 2
Ковариантный формализм 211
— оператор уничтожения антифермиона1^. Волновая функция ва-
вакуума Фо определяется теперь следующим образом:
ф(+)(х)Фо="ф(+)(х)фо==О- A5.71)
Перестановочные соотношения для операторов рождения и уничто-
уничтожения гласят:
A5.72)
f **
X 2 S &r fa, bt (p')]+ wra (р) Ц
r=ls=l
L X ) ЛЬ) • ■
= — /5^}(х — x')- A5.73)
При выводе последнего выражения мы использовали равенства G.32),
A3.91) и A5.55). Аналогичная процедура для операторов античастиц
приводит к соотношению
[<|Л~'(х), ^(8+'(х')] = — iS(~'(x — х'). A5.74)
где
Д(~'(х— х'; т). A5.75)
Заметим, что из соотношений A5.67) — A5.70) следует, что
Кроме того, если ввести зарядово-сопряжениыи оператор
то операторы рождения и уничтожения античастиц можно выразить с по-
помощью зарядово-сопряженных операторов:
212 Глава 15
При выводе равенств A5.74) и A5.75) мы использовали определение
проекционных операторов для решений уравнения- Дирака G.37),
отвечающих состояниям с отрицательными энергиями.
§ 4. Квантование электромагнитного поля
Если пользоваться лагранжианом Ферми A0.71), то электро-
электромагнитное поле будет описываться 4-потенциалом Аа(х), который
удовлетворяет следующему уравнению:
□ ^00 = 0. A5.76)
Пока не наложено условие Лоренца, электромагнитное поле можно
рассматривать как суперпозицию четырех скалярных полей, соот-
соответствующих различным [а, причем массы квантов полей равны
нулю [напомним, однако, что компонента ]>■ == 0 дает отрицательный
вклад в гамильтониан A0.73)J. Поэтому мы можем воспользоваться
разложением скалярного поля A5.31) (помня при этом, что каждому
трехмерному импульсу к соответствуют четыре независимых реше-
решения уравнения электромагнитного поля) и написать
*•*}, A5.77)
>=o
где sM(k) — единичные векторы поляризации, которые можно вы-
выбрать так, чтобы они образовывали ортонормированную систему
s(X)s(x')[i. __ о**'. A5.78)
[Вспомним случай частиц со спином 1/2; см. также соотношение
A5.100).] Величина gxr в выражении A5.78) представляет собой
метрический тензор B.26). Сумма по (к) в соотношении A5.77) есть
обычная сумма (а не лоренц-инвариантное скалярное произведение)
по четырем решениям, соответствующим различным поляризациям.
В квантовой теории а'х>(£) становится оператором уничтожения
-> ->■
фотона с импульсом k и поляризацией (к), а(х)+ (k) — оператором
-»- ->■-»■
рождения такого же фотона, а Мх'(£) — а№* (ft) c№ (k) — операто-
оператором числа фотонов с импульсом k и поляризацией \.
В дальнейшем мы не будем иметь дела с состояниями с различ-
различной поляризацией. Поэтому мы будем пользоваться лишь величинами
A5.79a)
At (k) = 23 "w (*) af»+ (ft), A5.796)
* f»+ (ft)
Ко вариантный формализм 213
причем в классической теории условие поперечности волн
ограничивает физически возможные состояния двумя состояниями,
соответствующими поперечным волнам.
В представлении Шредингера импульс, канонически-сопряжен-
канонически-сопряженный оператору А^(х), имеет вид
^(£) = _^M>(£} __(£££).) . A5.80)
Следовательно, канонические перестановочные соотношения гласят
( — P)K, A5.81)
, 0. (АЛР, t)])to. A5.82)
') = — ihb(x — *'
Рассуждения, аналогичные тем, которые привели нас к перестано-
перестановочным соотношениям A5.39) для скалярного поля, теперь показы-
показывают, что ковариантные перестановочные соотношения для потен-
потенциалов электромагнитного поля имеют вид
[АДх), /4v(x')]= — ihcg^D(\ — x'). A5.83)
где функция D(x — х') равна Д(х — х') при [а = 0. Отметим отли-
отличие в знаках в правой части соотношения A5.83) у временной и
пространственных компонент этой-функции.
В явном виде при |jt|=r функция D(x) выглядит следующим
образом (см. работы Иордана и Паули [248]):
1
B*)»
Й0>0
= —
+ «
1
-->■ ,
оо
•/
0
sin /
k
sin
0
kr sin
kr
A5.84)
214 Глава 15
а сингулярная функция DA) (x)г) —
U W ~~ BяK J *о ° °"~
&„>0
со
1 Г sin kr cos kx^
Tr
о
г—
_L_ I _
где символ Р означает, что при интегрировании этого выражения
вокруг сингулярной точки х2 = 0 следует брать главное значение
интеграла. Нетрудно проверить, что операторы A^(k) в соотноше-
соотношении A5.79) удовлетворяют следующим перестановочным соотноше-
соотношениям:
\\(k), Л+(£')] = — g,-fi(k — P); A5.86)
при этом другие коммутаторы равны нулю.
В классической теории поля условие Лоренца Л£'(х) = 0 обеспе-
обеспечивает соответствие уравнений A5.76) уравнениям Максвелла, а также
положительную определенность полной энергии поля. В квантовой
теории, однако, условие Лоренца нельзя накладывать в виде опе-
операторного условия, так как это противоречило бы перестановочным
соотношениям A5.83), ибо
,(x')]= —
ihc
дх''
Чтобы обойти эту трудность, соотношения A5.83) и A5.86) писали
до 1949 г. раздельно для пространственных и временной компо-
компонент А„. Таким образом, используя дополнительное условие Л^'1Г=О
для физически возможных состояний lF поля, можно исключить
продольную и времени-подобную компоненту вектора Ау Роль
динамических переменных будут играть оставшиеся поперечные
компоненты 4-потенциала; только они и квантуются. При наличии
Заметим, что
_ 1 ,. 1 — cos kx
Р —= lim ,
или, что эквивалентно,
со
/1
ехр (— ikx) dk = Р \-lr& (x).
х
Ковариантный формализм 215
зарядов это соответствует отделению мгновенного кулоновского
взаимодействия от запаздывающего поперечного электромагнитного
взаимодействия. Однако такая процедура не является релятивистски
инвариантной, поскольку для движущегося наблюдателя кулоновское
взаимодействие (продольные волны) и поперечные волны снова
смешиваются.
Совсем недавно Гупта [216] и Блейлер [41] развили метод,
который основан на использовании одинаковым образом всех четы-
четырех потенциалов и, следовательно, всегда остается явно реляти-
релятивистски инвариантным. Самым важным в этом методе является
выяснение того обстоятельства, что рассмотрение дополнительного
условия
Л£'(х)»Р = 0 A5.87)
как уравнения является слишком жестким. Действительно, если мы
наложим дополнительное условие A5.87) и будем рассматривать его
как уравнение, то не найдется таких состояний, волновые функции W
которых удовлетворяли бы этому условию. Согласно условию A5.87),
определенные сорта фотонов не только не могут присутствовать
в поле, но, более того, эти фотоны не могут также и излучаться.
Последнее обстоятельство несколько трудно для понимания. Гупта
и Блейлер предложили изменить условие Лоренца так, чтобы оно
содержало лишь оператор уничтожения частицы, т. е.
для любого физически реализуемого состояния W электромагнитного
поля. Это является достаточным для того, чтобы обеспечить попе-
поперечную поляризацию фотонов и не нарушить соответствия с клас-
классической электродинамикой. Далее, если обозначить амплитуду
вероятности обнаружения в состоянии W одного фотона с импуль-
сом k = {k0, k) (при k^k1 = 0) и поляризацией jj. через
/£>(£) = (Фо. А,. <%) W), A5.89)
то, согласно дополнительному условию A5.88), получим
kiLf<£)(k) = O. A5.90)
Это обеспечивает поляризацию фотонов перпендикулярно к на-
направлению движения, что можно показать следующим образом.
Напомним, что описание электромагнитного поля с помощью потен-
потенциалов является неоднозначным, т. е. можно всегда произвести
калибровочное преобразование
216 Глава 15
причем
DA(x) = O, A5.92)
где Л—числовая, неоператорная функция. Если фурье-образ функ-
функции Л(х) обозначить через Л (к), т. е.
Л(к) = JV/feA(x)e-ik-*, A5.93)
то Л (к) будет в действительности функцией лишь ft, так как,
согласно выражению A5.92), фурье-образ Л(к)=0 при к2 = 0.
Преобразование A5.91) в импульсном пространстве записывается
в виде
Инвариантность по отношению к калибровочному преобразованию
означает, что, если к функции /J;(ft) добавить произведение ft.^A(ft),
то полученная функция f^\k)~\-k,^A(k) будет описывать то же
самое физическое состояние, что и функция f\. (ft). Другими сло-
словами, состояния, описываемые функциями f^ (ft) и f\/(ti)-\-ft^A(ft),
эквивалентны (и неразличимы). Но если это так, то с помощью
калибровочного преобразования
f?(t)^fil\k)—^-rt\t) A5.95)
\k\
(т. е. Л(&) = —fo\ft)/fto) всегда можно получить однофотонную
амплитуду с нулевой временной компонентой, описывающую, однако,
то же самое физическое состояние1). Для такой амплитуды условие
поперечности волн A5.90) теперь уже гласит
2 К№ (А) = 0 = % ■ /A)(*) (!5■ 96)
и означает, что векторный потенциал (волновая функция), соответ-
соответствующий состоянию с одним фотоном, является поперечным, т. е.
ft ■ f (k) = 0. Ясно, что доказательство поперечности можно про-
провести совершенно аналогично и для re-фотонного состояния.
Неоднозначность в определении однофотонной амплитуды под-
подчеркивается соотношением A5.94), а именно эквивалентность ампли-
амплитуды f(?])(ft)~\-k?_A(ft) амплитуде f^\k) означает, что любую
амплитуду, пропорциональную ft?, можно положить равной нулю
(так как ее можно исключить выбором калибровки). Таким образом ,
^ В классической теории эти утверждения соответствуют тому, что
калибровку поля излучения, divA=0, у = 0, можно получить из условия
Лоренца # = 0 с помощью калибровочного преобразования,
Ковариантный формализм 217
физический смысл имеет та часть амплитуды f$\k), которая ортого-
ортогональна k^ (благодаря дополнительному условию), а не пропорцио-
пропорциональна kp (благодаря калибровочной инвариантности), т. е. ее
пространственно-подобная часть. Поэтому мы можем выбрать (и этот
выбор является простейшим) в качестве представителя класса функций,
эквивалентных однофотонным амплитудам, амплитуду
т. е. амплитуду, временная компонента которой равна нулю и для
которой выполняется соотношение k •//A>(/fe) = 0. Такой выбор
обеспечивает положительную определенность нормы волновой функ-
функции физически реализуемого однофотонного состояния W (состояния,
описываемого волновой функцией, единственная отличная от нуля,
амплитуда которой равна /^ (А)), т. е.
/т \р\.— Г /узь/'С1)* /и\ f ' (^ Р-/ьл ~> о
причем знак равенства имеет место только лишь при /'<1> = 0. Ана-
Аналогичные утверждения можно сделать и для и-фотонных амплитуд.
С помощью операторов в импульсном представлении 4-вектор
энергии-импульса поля выражается в виде
P?-^—fhk»At(t)Av(k). A5.97)
Покажем далее, что выражение — At (k) A1 (k) является, действительно,
положительно-определенным. Для этого выберем такую специальную
систему координат, в .которой различные векторы поляризации
eM(/fe) удовлетворяют условиям
k?S(V $) = k^f (к) = 0, A5.98а)
й ЗЛ, (ft) = —г- Й Sn \К)- \AO.yoOJ
В частности, например, этим условиям можно удовлетворить, повер-
повернув систему координат таким образом, чтобы k° = j k |, k1 — | k \
~ ~ ^ = |А|A, 1, 0, 0) A5.99)
и
Л = A, о, о, о),
==@, 0, 1, 0),
A5.100)
==@, 0, 0, 1),
«№>(£)—@, 1, 0, 0).
е
218 Глава 15
При таком выборе единичных векторов поляризации и при усло-
условии, что
рДЯ^ = j£j £[!, (к) п («)» ^lO.lUlJ
X
условие Лоренца A5.88) принимает вид
A5.102а)
или
a(°)(k) — aC>(k) = 0. A5.1026)
Следовательно, используя соотношения A5.78) и A5.102) и свой-
свойства действительности векторов поляризации, получаем
(
— 4 (*) А9ф) = — 2
XX'
= a<Ot (k) a<4 (X) -f- aB)+(£) aB) (А), A5.103)
т. е. фактически вклад в физические процессы дают только лишь
поперечные фотоны.
Таким образом, мы видим, что благодаря дополнительному усло-
условию A5.102) 4-вектор энергии-импульса, действительно, является
положительно-определенным. Этот результат станет более прозрач-
прозрачным, если заметить, что в системе координат, определенной соот-
соотношениями A5.98), дополнительное условие A5.1026) ограничивает
допустимые состояния системы такими состояниями, которые содер-
содержат равное число продольных и времени-подобных фотонов с оди-
одинаковыми импульсами. Далее, времени-подобные фотоны дают отри-
отрицательный энергетический (и импульсный) вклад в полную энергию
(и импульс) поля, так что этот вклад взаимно уничтожается с вкла-
вкладом продольных фотонов.
Однако в изложенной теории все еще остается одна трудность,
которая является результатом того, что мы описываем электрома-
электромагнитное поле с помощью потенциалов А^, а не с помощью физи-
физически наблюдаемых величин — напряженности поля F . Эта труд-
трудность заключается в следующем. Хотя мы и показали, что для
состояний, содержащих только лишь поперечные фотоны, норма вол-
волновой функции W является положительно-определенной, однако
это уже не имеет места для таких состояний, которые содержат
времени-подобные фотоны, как видно из того факта, что среднее
по вакууму оператора A (k)Ai(k), т. е.
(Фо> Д, (к) At (*') Фо) = (А$ (к) Фо, At $') Фо) = — g^b $~ P),
A5.104)
при j>, = v = O отрицательно, в то время как произведение А0А%
является положительно-определенным, если оператор Ло(&) эрмитов,
Ковариантный формализм 219
Таким образом, в самой теории имеется непоследовательность. Те-
Теперь уже невозможно исключить из теории состояний, содержащих
времени-подобные фотоны, так как последние необходимы для пра-
правильного математического определения оператора Л0(х).
Следовательно, мы должны найти такой способ определения ска-
скалярного произведения волновых функций, чтобы оно было положи-
положительно-определенным для тех состояний, которые содержат только
лишь поперечные фотоны, и могло быть неположительно-опреде-
неположительно-определенным или неопределенным для тех состояний, которые содержат
нефизические, т. е. времени-подобные и продольные фотоны. Это
все, что мы должны требовать, поскольку для состояний, реализую-
реализующихся в природе, указанное скалярное произведение является поло-
положительно-определенным.
Формулировка квантовой теории электромагнитного поля, кото-
которая решает эту задачу, была дана Гупта [216] и Блейлером [41].
Используя неопределенную метрику, введенную в совершенно дру-
другой связи Дираком [114] (см. также работу Паули [379]), они по-
новому определили скалярное произведение таким образом, что ма-
математическое ожидание оператора теперь выражается в виде
(F (х)) = OF, -nF (x) W), A5.105)
где t\—эрмитов оператор метрики
Т1+ = Ч1, A5.106)
причем он выбран так, что удовлетворяет равенству
т)г=1. A5.107)
Далее, потребуем, чтобы оператор т\ коммутировал с Ак(х)
(fe=l, 2, 3) и антикоммутировал с ^40(х), т. е.
[Лй(х), -ч] = 0, A5.108а)
ИоОО. 11+=0. A5.1086)
Эти условия могут быть удовлетворены в специальной системе ко-
координат, определенной соотношениями A5.98)—A5.100), если т] вы-
выбрать так, чтобы
-п¥ = П(—1)у@)(%, A5.109)
к
или в представлении, в котором диагональны не только операторы
&) но и -f\, причем
@) ->
= 8уП(—1)" <*>, A5.110)
к
где re'0' (k) — число времени-подобных фотонов с импульсом k в со-
состоянии у.
220 Глава 15
Исследуем, далее, в системе координат, определенной соотно-
соотношениями A5.98)—A5.100), векторы состояний, которые допускаются
дополнительным условием A5.1026). Для простоты ограничимся со-
стояниями с импульсом k и обозначим собственные функции опера-
операторов ЛЛХ>(&) (X = 0, 1, 2, 3) в пространстве чисел заполнения че-
через \п{'Г>, яB>, яC), я(°) >. Теперь легко проверить, что волновые
функции состояний
= |«W, геB>, 0, 0>,
, 1, 0> + |ге<1>, иB), 0, 1 >,
, 2, 0>+]A2|re(i>, ге<2>, 1, 1> +
0, 2>, A5.111)
г=1
обладают свойством а>
(а(8) (I) — а<°) (!)) ¥("*) = 0, A5.112)
т. е. все они удовлетворяют дополнительному условию. Более того,
скалярное произведение двух волновых функций, согласно Гупта,
выражается в виде
()^)
Г = 0 8 = 0
Х(—l)s<reW, re'2', /к —г, г | red)', дB)', д — s, s> =
r = 0
o- A5.113)
Последняя строка в этом равенстве получается, если при разложе-
разложении бинома
п
(g + *)»=Srt(n"!-r)i аП'ГЬГ A5.П4)
положить
в=1, Ь=—\.
'' Напомним, что
а| п. > = -|ЛГ | п — 1 >,
Ковариантный формализм 221
Из наличия множителя 8,^ в скалярном произведении A5.113)
следует, что в формализме Гупта векторы состояния W@) и \F@) -f-
+ 5 с(Л ^(Л эквивалентны: они ведут к одним и тем же физически
3 = 1
наблюдаемым следствиям. Эквивалентность состояний W1 ' и Ч/"(°) -\-
точно соответствует неоднозначности, которая лежит
в определении амплитуд /<"•> (Л1, &2 kn) (благодаря инва-
риантности по отношению к калибровочному преобразованию), но
теперь уже выраженной с помощью векторов состояний W.
Чтобы убедиться в этом более явно, вычислим математическое
ожидание оператора -^(х) по эквивалентным состояниям f и Ф,
где
W = П | я<Ц (к), nW(k), 0, 0>, A5.115)
к
), 0, l>}=ip-f-W'. A5.116)
Поскольку ^4„,(х) является оператором рождения или уничтожения
частицы, то, очевидно,
(W, тИ„(х)Ч0 = 0. A5.117)
С другой стороны, используя соотношения A5.77), A5.101) и A5.110),
находим
(Ф,
с* (ft) D3) (ft) + е(;> (ft")) e'k-x}. A5.118)
Далее, согласно соотношениям A5.99) и A5.100), в специальной
системе координат, в которой мы работаем,
^>(Л) + 4?(*)=-^г. A5-119)
Следовательно,
A5.120)
где
Д(х) = —V Г /% {c(t)g-ik-x4-<f(fe)gik-x). A5.121a)
v у Bя)/» J Y^W\3
2i>2 Глава 15
причем
□А(х) = О. A5,1216)
Таким образом, эквивалентность векторов состояний W и W-\-W
отражает тот факт, что описание поля с помощью потенциалов
всегда оставляет произвольность с точностью до калибровочного
преобразования, при котором А?—> А,^-\-(д/дх^) Д. Однако скаляр-
скалярное произведение A5.110) приводит к тому, что эквивалентные вол-
волновые функции соответствуют одинаковым физическим результатам.
Мы можем, если это нужно, выбрать волновую функцию W состоя-
состояния, не содержащего времени-подобных и продольных фотонов,
в качестве представителя эквивалентного класса функций. Это, од-
однако, соответствует выбору определенной калибровки.
Таким образом, формализм Гупта обладает тем преимуществом,
что он включает ^состояния, содержащие времени-подобные и про-
продольные фотоны, причем в математической схеме теории эти состоя-
состояния определены достаточно однозначно [как это и должно быть
при определении операторов А^(х)], на тем не менее они не дают
вклада в физически наблюдаемые величины.
Заметим, что формализм Гупта допускает также нужную нор-
нормировку волновых функций этих состояний1'. Норма волновой функ-
со
ции \F(°) -|- 2 с<ЛЧР"Ш, согласно формуле A5.113), тождественно
равна (\F(°), W(°)). Более того, соотношение A5.104) теперь уже
выполняется для р = 0 строго, так как
fiAt (Р)Фо) = (~1)Ь(%—%'). A5.122)
Состояние А% (fe) Фо в системе координат, определенной соотноше-
соотношениями A5.98)—A5.100), есть состояние с одним времени-подобным
фотоном; причем в формализме Гупта—Блейлера вакуум опреде-
определяется соотношением
4+)(x)*0 = 0, [j. = 0, 1, 2, 3, A5.123)
означающим, что вакуум есть состояние, в котором отсутствуют
фотоны любого сорта. Однако следует подчеркнуть, что определе-
определение A5.123) соответствует выбору определенной калибровки при
описании вакуума. На самом деле существует столько же физически
эквивалентных состояний вакуума, сколько существует возможно-
возможностей выбора калибровки [см. выше соотношение A5.111) при reW =
= иB) = 0J. Несмотря на это, при вычислении математического ожи-
ожидания калибровочно-инвариантной величины [как например F^y(\)
U Это было невозможно до введения неопределенной метрики. Волновая
функция „эквивалентного" состояния, содержащего бесконечное число вре-
времени-подобных и продольных фотонов, была ненормируема. В этой связи см.
работы Ма [318], Белинфанте [29], а также Кестера и Яуха [85].
Ковариантный формализм 223
или энергии-импульса поля] для всех различных состояний вакуума
получим один и тот же результат.
В заключение этой главы выпишем перестановочные соотношения
для напряженностей поля
Для ознакомления с применениями этих перестановочных соотноше-
соотношений к совместным измерениям компонент электрического и магнит-
магнитного полей в малой области 4-пространства мы отсылаем читателя
к классическим работам Бора и Розенфельда [47, 48], а также к об-
обзорной статье Коринальдези [92].
Глава 16
ИНВАРИАНТНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
§ 1. Теория
По аналогии с развитой в гл. 8 теорией возмущений напишем
уравнение Томонага — Швингера A5.12) в виде интегрального урав-
уравнения
4
W(t) = W(t0) — \ f dt'Hr(.nW(t'). A6.1)
to
Легко проверить, что решение уравнения A6.1) удовлетворяет также
и уравнению Томонага — Швингера A5.12). Однако, кроме того, ин-
интегральное уравнение A6.1) включает еще и начальное условие: при
t = t0 функция W сводится к вектору состояний W (t0). В действи-
действительности в полной аналогии с выражением (8.2) можно написать
to)W(to), A6.2)
t, to)W(t), A6.3)
причем
U(t0, to) = l, A6.4)
где U(t, t0) — унитарный оператор (для сохранения нормировки),
который, действуя на функцию W(t0), дает W(t). Оператор
£/(+оо, —oo)=5 A6.5)
является S-матрицей (Штюкельберг [466—468], или, как назвал
его Швингер [438], оператором столкновения), которая определяет
всевозможные изменения состояний системы в результате взаимодей-
взаимодействия. Этот оператор тождественно совпадает с S-матрицей Гей-
зенберга, так как, по определению,
vF(-f-oo)=5»F(— со), A6.6)
а Ф(—оо) и ^(-j-oo) являются асимптотическими формами падаю-
падающей и расходящейся волн соответственно.
Оператор U (t, t0) удовлетворяет следующему дифференциаль-
дифференциальному уравнению:
==Hl(t)U(t> h) A67)
Инвариантная теория возмущений 225
Из уравнения A6.7) вытекает, что
— ih Ш1^М. = w (t, t0) Hi (t), A6.8)
поскольку оператор Hx(t) является эрмитовым; следовательно, с по-
помощью обычной процедуры можно получить уравнение
^ (£/+(*, to)U(t, to)) = 0, A6.9)
откуда, согласно формуле A6.4), имеем
W(t, to)U(t, to)=l. A6.10)
Это, однако, еще не означает унитарности оператора U. Чтобы
оператор U был унитарным, должно выполняться равенство
U(t, to)U+(t, to)=l. A6.11)
Условие (l6.ll) выполняется в том случае, если оператор U удо-
удовлетворяет групповому свойству
U(tt tdU(tlt to)^U(t, tQ). A6.12)
Соотношение A6.12) действительно выполняется, так как, если
tJ = U(tv to)W(to)t
то имеем
= иу, WU(tv t0)W(t0), ' A6.14)
что и требуется для выполнения группового свойства A6.12). Если
в соотношении A6.12) положить t = t0, то получим
U(tot tJ^U-1^, t0). A6.15)
Далее, из равенства
U(t0, tdU(tv *o)=l. A6-16)
умножая его слева на Uf (t0, tt) и используя формулу A6.10), сле-
следует, что
U(tv to) = Uf(to, Ь)=и-1(!0, tt), A6.17)
что и требовалось доказать.
Непосредственным следствием группового свойства A6.12)
является то, что оно позволяет выразить любое конечное преобра-
преобразование в виде произведения последовательных бесконечно малых
преобразований
U(t, t') = U(t, tt)U(tv t^.-.U{tn_v tn)U(tn, f), A6.18)
где U (tj, tjhl) — бесконечно малое преобразование от момента вре-
времени tj к моменту tj+1. Далее, интегральное уравнение, которому
226 Глава 16
удовлетворяет U(t, t'), имеет вид
t
U(t, t/)=\—jfdxHI(x)U('z, t'); A6.19)
с
поэтому, если разность (tj — tj+1) бесконечно мала, то
. ti+l) = 1 — 1J dxHx (x) и (т, tj+1) да
A6.20)
Неограниченно увеличивая число интервалов и группируя члены,
получаем
U (t, to)=l+(=±)f dt.Hj {t,) -f-(^J f dtx f dt2Hjft
t, ■
f dt*HI {tl) HI {ti) Ht ^ + • • • A6-21)
t t,
t0
Рассмотрим, далее, л-й интеграл
J dt, f dt2 ... / dtnHx (tO Hx (t2) ... HT (tn\ A6.22)
t0 t0 t0
Дайсон [126, 127] заметил, что, по существу, интегрирование ведется
по всему интервалу времени от tQ до t с тем ограничением, что
момент времени /у лежит раньше момента tj_t (j^.n). Это ограни-
ограничение можно устранить введением хронологического оператора Р,
который обладает тем свойством, что, действуя на произведение
операторов, зависящих от времени, располагает последние в хроно-
хронологическом порядке, т. е. оператор с большим значением времени
в произведении стоит слева
. .. Hi(td)=* HjQd Hr(tt) . .. Hi(tJ, A6.23)
при ti > tf ... > tk.
Ц Формулу A6.21) можно также получить последовательной итерацией
уравнения A6.19), т. е. формула A6.21) представляет собой разложение Ней-
маиа — Лиувилля интегрального уравнения A6.19).
Инвариантная теория возмущений
22}
Используя симметрию подинтегрального выражения и тот факт, что
возможное число перестановок упорядочения поверхностей равно «!,
получаем
/Г Г
dtx ... I dtn_1 I dtnHi(t^ .. . Hj(tn) =
*Q Cg Iq
t t t
/I! J J J v 1/ ■* \ 7*/ / \ /
to *o to
Поучительно подробно рассмотреть эквивалентность этих- двух
форм интеграла для случая « = 2. По определению хронологи-
хронологического оператора имеем
t t
f dtl f dt2P (Hi (tt) Hi (t2)) —
ft, tt
Область интегрирования в левой части равенства A6.25) на
фиг. 22 изображена в виде квадрата. С другой стороны, в первом
Фиг. 22
члене правой части равенства интегрирование распространяется по
области треугольника I (незаштрихованный треугольник), в то время
как во втором члене интегрирование идет по области заштрихован-
заштрихованного треугольника II. Хотя множители в произведении Hi{t^Hi(t^)
не коммутируют между собой, но тем не менее мы вправе во вто-
втором интеграле поменять порядок интегрирования. Если во втором
Ш Глава IS • .
интеграле мы будем вначале интегрировать по tlt то пределы инте-
интегрирования изменятся, и мы получим
t U
fat2 f d^HiVJ HiitJ. A6.26a)
Если теперь произвести замену переменных tt -*■ t2 и t2 —*■ tv то
выражение A6.26а) примет вид
t tt
f dtx f dtjii (*i) Hz (*2), A6.266)
*0 «0
так что
t t t tt
f dtx f dtJP(Hz(tO #i(t2)) = 2! f dt, f dt2Hj(tt) Hi (t2), A6.27)
t0 t0 to t0
что доказывает справедливость равенства A6.24) для случая « = 2 1>.
Мы можем поэтому переписать разложение A6.21) следующим
образом:
t
и(t, y-i+i(—-) f dtj>(Hi(to)-b
to *o
ю п i t
()
Ш (ir) 5 dt^ Sdt2'-'.f dt«p№Ы • ■ ■ Н1(-^' A6'28)
t t t
t0
или, просуммировав ряд,
-jr>)f Hl(t')dt'\.
U(t. to) = p\exp(—-jr>)f Hl(t')dt'\. A6.29)
Проверим, является ли ряд A6.28) в действительности решением
уравнения A6.7). Для этой цели продифференцируем равенство A6.28)
по времени t; в результате получим
t ta ta
X пНх (t) P (Hi (tO Hj. (tO ...H!(tn_O). A6.30a)
Ц Читателю, интересующемуся этим вопросом, рекомендуем начертить
диаграмму л-го порядка, чтобы доказать это равенство для случая п пере-
переменных интегрирования.
Инвариантная теория возмущений 229
При написании правой части соотношения A6.30а) мы воспользова-
воспользовались симметричностью подинтегрального выражения, а также тем
обстоятельством, что оператор Hj(t) всегда зависит от момента вре-
времени t, более позднего, чем моменты времени £t . .. tn_1. Поэтому
мы вынесли оператор Hi(t) за знак Р-произведения и написали его
левее всех остальных множителей. Теперь соотношение A6.30а)
можно переписать следующим образом:
n=0 t0 t0
= Hi(t)U(t, t0); A6.306)
отсюда вытекает, что U (t, t0), действительно, является решением
уравнения A6.7). Вспомнив, что
Яг@ =
можно переписать соотношение A6.28) в форме, более явно указы-
указывающей на его ковариантность:
со t t t
SI /\ 1 i* г* л ■
I l , . i d^x> I и jc I d x ?C
nsO t0 t0 tQ
так как
;*/*—;?•
Теперь понятие упорядочения во времени уже имеет инвариантный
смысл. Таким образом, если мы обобщим соотношение A6.31) так,
чтобы пределы интегрирования представляли собой пространственно-
подобные поверхности о и о', то U (о, о') будет инвариантом, так
как e№i (x) = йФ (х) Гф (х) <р (х) является скаляром и элемент 4-объема
d^x является инвариантом. Соотношение A6.31) лежит в основе
современной ковариантной теории возмущения.
§ 2. Адиабатическая гипотеза
В действительности в расчетах прибегают к адиабатической гипо-
гипотезе (см., например, работу Дайсона [129]). Это достигается устре-
устремлением начального момента времени t§ к — оо и усреднением всех
230 Глава 16
членов, зависящих периодически от t0. Аналогично конечный момент
времени t устремляется к -(-со, и все осциллирующие члены усред-
усредняются. Однако при применении этой процедуры следует проявлять
известную осторожность, так как, например, для члена n-го порядка
существует п\ способов перехода к пределу to =— оо, поскольку
по времени производится л-кратное интегрирование. Для устранения
этих трудностей Дайсон [130—133] ввел так называемое „промежу-
„промежуточное представление взаимодействия" (или сглаженное представле-
представление взаимодействия), которое заключается, по существу, в умноже-
умножении гамильтониана взаимодействия на сходящийся множитель вида
e-M'l; затем после всех вычислений берется предел X—>0. Такой
сходящийся множитель устраняет неоднозначность при переходе
к пределам £ = =too. Это эквивалентно усреднению по всем п\ воз-
возможным переходам к пределу.
Приняв адиабатическую гипотезу, можно считать волновые функ-
функции начального и конечного состояний собственными функциями опе-
оператора Но (так как при £ = ztoo Hi = Q), которые обычно назы-
называются функциями состояний „голых" частиц. Мы можем поэтому
рассмотреть процесс рассеяния следующим образом:
1. В момент £ — — оо система находится в состоянии, описывае-
описываемом функцией Ф (собственной функцией оператора Н0У, в этом
состоянии находится заданное число частиц с определенными спином
и импульсом, причем частицы отделены друг от друга и не взаимо-
взаимодействуют между собой (Hj = 0). Заметим, что поэтому вектор Ф
является постоянным, не зависящим от времени вектором состояния
в представлении взаимодействия.
2. Далее, адиабатически включается взаимодействие, и состояние
с волновой функцией Ф переходит в состояние с волновой функ-
функцией W(to)—U(to, —оо)Ф, которое (как считают) соответствует
реальному состоянию физических („одетых") частиц с теми же импуль-
импульсом и спином. Здесь также предполагается, что частицы все еще
достаточно отделены друг от друга и не взаимодействуют между
собой. Однако изменение состояния соответствует тому, что Hi
обеспечивает собственное взаимодействие, в результате которого
„голые" частицы приобретают „шубу" с полным набором виртуаль-
виртуальных квантов и пар. Этот процесс обычно называют „одеванием"
частицы. „Голая" частица с виртуальным квантом соответствует
в представлении взаимодействия физически реальной частице, если
импульс и энергия частицы в этом состоянии удовлетворяют соот-
соотношению р2 = /те2.
3. Далее, частицы взаимодействуют между собой и благодаря
этому взаимодействию рассеиваются. По прошествии достаточно
большого времени Т = t — t0 частицы снова расходятся, но уже
находясь теперь в состоянии, описываемом волновой функцией
x¥(t, = U(t, to)W(to); это состояние соответствует физически реаль-
реальным („одетым") частицам после рассеяния,
Инвариантная теория возмущений 231
4. Далее, взаимодействие адиабатически выключается, и состояние
с волновой функцией xV(t) переходит в состояние с волновой функ-
функцией Ф'; такое состояние соответствует „голым" частицам после
рассеяния, причем Ф' = U(oo, t)W(t).
Таким образом, мы изменили реальную задачу рассеяния f^g) —> W(t)
„эквивалентной" задачей, вводя в рассмотрение „голые" частицы
при t — z+zoo. Далее,
ЧГ@ = £/(*, to)W(to); A6.32)
следовательно, это соотношение можно переписать в виде
U~l(oo, *)Ф'= £/(*, to)U(to, — оо)Ф. A6.33)
Отсюда, согласно второму и четвертому положениям, имеем
Ф' = £/(+оо, t)U(t, to)U(to, — оо)Ф =
= t/D-oo, —оо)Ф==5Ф; A6.34)
это означает, что Ф' при t = -\-oo действительно является волно-
волновой функцией состояния „голых" частиц, в которое они переходят
в результате рассеяния из состояния, описываемого функцией Ф
при t = — оо.
Мы можем несколько уяснить и уточнить выше перечисленные
положения, подробно рассмотрев вектор состояния
Hm U(t, и)Фа, A6.35)
где Фо — волновая функция состояния „голых" частиц, т. е. соб»
ственная функция оператора Но с собственным значением Еа.
Для дальнейшего анализа оказывается полезным получить явный
вид оператора U(t, tQ). Для этого напомним, что зависимость от
времени вектора, состояния Ws(t) в шредингеровском представлении
выражается в виде
ЧГ *в«щг A6.36)
где Н—не зависящий от времени полный гамильтониан системы.
При этом предполагают, что Н есть сумма двух частей HQ и Hi,
Н=Н0-{-Н1. A6.37)
причем каждая- из частей является не зависящим от времени опера-
оператором в шредингеровском представлении. Предполагают также,
что Но обладает только непрерывным спектром, причем
Я0Фа = ЕаФа,в A6.38а)
(Фа, Фь) = 5о6> A6.386)
и.^кроме того, предполагают, что Н обладает тем же непрерывным
спектром, что и //„. Будем обозначать „сходящуюся" и „расхода-
232 Глава 16
шуюся" волны (собственные функции Н), соответствующие Фа,
через Wa и Ч?"а соответственно. Эти функции удовлетворяют урав-
уравнениям Липмана — Швингера [307]
глГГе* A6.39а)
WZ = Фа+ lim -в \з j- HiWa, A6.396)
=£вЧГ*- A6.39в)
„Сходящаяся" волна ЧР"а является таким решением уравнения для
задачи рассеяния, в котором содержится падающая плоская волна
[соответствующая члену Фа в уравнении A6.39а)] и расходящаяся
рассеянная волна [представленная вторым членом в правой части
уравнения A6.396)]. Величина -\-is в знаменателе уравнения A6.39а)
обеспечивает существование только расходящихся рассеянных волн
(Дирак [115]). Аналогично Ч?а является таким решением, в котором
содержится плоская волна и сходящиеся рассеянные волны. Гамиль-
Гамильтониан Н может, кроме того, обладать собственными функциями,
соответствующими связанным состояниям (обозначенным греческими
индексами),
№? = E9Wr A6.40)
Положим, что энергия этих состояний меньше, чем энергия любого
собственного состояния гамильтониана Но, характеризуемого теми же
квантовыми числами. Из эрмитовости гамильтониана Н следует, что
волновые функции связанных состояний ортогональны волновым
функциям сплошного спектра, т. е.
(Тр. f*) = 0. A6.41)
Набор функций {W —j— ЧР*э} является полным набором. Заметим
также, что
(ЧВГ+, Wt) = bab. A6.42)
Возвратившись к соотношению A6.36), заметим, что если заме-
заменить шредингеровский вектор состояния Ws вектором состояния
в представлении взаимодействия W и воспользоваться соотношением
W(t) = eiB^8{t), A6.43)
то получим
W(t) = еш^-^(*-*о)е-^н«(*)ф(^о). A6.44)
Таким образом, из соотношения A6.2) следует
U{t, t0) = еш^е-ш^-^е-т^. A6.45)
Легко убедиться в том, что выражение A6.45) удовлетворяет диф-
дифференциальному уравнению A6.7).
Инвариантная теория возмущений . 233
Исследуем теперь выражение
lim U@, tQ)$a= lim еш*'е~*в**Фа. A6.46)
*„-» -со fu~» -оо
Если разложить Фа по полному набору собственных функций опе-
оператора Н, т. е.
Фа = J rfcWc+ (\FC+, Фа) + ^ *р С*"?. фа). A6-47)
где символ Г dc означает интегрирование (а также и суммирование)
по всем величинам, характеризующим собственные функции ЧР^~, то
в результате получим
U @, t0) Фа = f dc «■* (Вс-Еа) f»W+ (Wc+, Фа) +
^(VE«){°(^. Фв)^р. A6.48)
Если, теперь подставить выражение A6.39а) в матричный элемент
(Ч1"^", Фа), то, согласно соотношению A6.386), найдем
= 5C0 + iim E _^ _u (We, Я/Фа). A6.49)
Следовательно, соотношение A6.48) можно переписать в виде
U @, ^0)фа=^+ lim J dc' jdEc * _°E °_ u QV2,Hi&a)> XK +
H-S«'(V-B*)tllDPrp, Фа)ЧР-г A6.50)
В этом соотношении из интеграла по всем физическим величинам,
характеризующим соотношения, описываемые функциями W£, явно
выделено интегрирование по энергии (Ватсон [511],). Далее,
о
lim т- = 1 lim Г eis"e~*^\dx, A6.51)
откуда для фиксированного t0
^ш f —Е ы ===
= 1 lira feil
s "* 0+ -со
==f lim [ eUEc-Ea)ze-°[z~tAdx, A6.52)
8-»0 +
234 Глава 16
так что в пределе при /0-> — оо второй член в правой части соот-
соотношения A6.50) исчезает [величину е оставляют конечной до тех
пор, пока не вычислен предел при £0-> — оо. Заметим, что в пре-
пределе при £<,->•+оо мы получили бы 2таВ(£0—Еа)].
Член, обусловленный связанными состояниями [третий член в пра-
правой части соотношения A6.50)], при tQ —>— оо осциллирует; следо-
следовательно, если оператор Н имеет собственные функции, соответст-
соответствующие связанным состояниям частиц, то предела выражения A6.50)
при tQ-+— °°> вообще говоря, не существует. Из изложенной выше
адиабатической гипотезы, которая, по существу, определяет функ-
функцию U(t, —оо) в виде (Гелл-Манн и Гольдбергер [205])
о
U(i. — co) = 'lim t[ CdTe^U(t, Г), A6.53)
1i->0 -о,
следует, что вклад от члена, обусловленного связанным состоянием,
также равен нулю. Таким образом, наложение адиабатической гипо-
гипотезы, или математически эквивалентного ей условия A6.53), изба-
избавляет нас от рассмотрения таких начальных конфигураций, которые
содержат связанные состояния частиц. Окончательно получим формулу
lim £/@,/о)Фа = Ф+, A6.54)
*„->-00
которая указывает на то, что волновая функция состояния „голых"
частиц Фа при t0 —> — оо переходит в момент £ —0 в функцию W^,
описывающую рассеянную волну.
Аналогично можно показать, что если определить '(см. работу
Гелл-Манна и Гольдбергера [205])
со
U(oo,t)= lim т] CdTe-4TU(T, t) A6.55)
и разложить Фа по полному набору {^1 —|— ЧР}, то получим
Иш 1/@, *0)Ф. = «Вр", A6.56)
или
lim U~l@, to)Wb=$b. A6.57)
t0-»+oo
Таким образом, мы показали, что приведенные выше качественные
соображения можно обосновать в некотором смысле несколько более
строго. Заметим, кстати, что
Заъ = (фа. 5Фь) = (Фа, £/(+оо, — оо)Фь), A6.58а)
5о6 = (Фа. £/(+оо, 0I/@, — оо)Фь), A6.586)
Sab = (U@, +оо)Фа, U @, — оо)Ф6), A6.58b)
5„ь = (ЧГа, Щ)- * A6.58г)
Инвариантная теория возмущений 235
Соотношения A6.58) являются в действительности определением
S-матрицы в стационарном (не зависящем от времени) формализме
рассеяния (Гелл-Манн и Гольдбергер [205]).
Строго говоря, изложенный выше формализм неприменим в кван-
квантовой теории поля, так как оператор взаимодействия Hi также
вызывает в этом случае сдвиг уровня, причем невозмущенный энер-
энергетический уровень Еа переходит под влиянием взаимодействия Нх
в уровень Еа-\-кЕа, где АЕа—„собственная энергия" состояния а.
С измененным формализмом, который применим также и в кванто-
квантовой теории поля, читатель может познакомиться в статьях Пиренни
[388, 390] и Гелл-Манна и Гольдбергера [205].
Что касается практических выводов из расчетов квантовой элек-
электродинамики, то адиабатическая гипотеза привела к результатам,
прекрасно согласующимся с экспериментом. Это обстоятельство
является весьма удивительным, так как совершенно ясно, что невоз-
невозможно выключать (адиабатически или каким-либо иным образом)
взаимодействие между полями. В действительности именно в этом
отношении квантовая теория поля сильно отличается от обычной
квантовой механики. В последней мы имеем дело с потенциалами
конечного радиуса действия 1~>, так что в задаче рассеяния волновые
функции начального и конечного состояний действительно являются
свободными (невозмущенными волновыми функциями). В теории же
поля взаимодействие всегда присутствует, и, следовательно, никогда
нельзя в действительности говорить о невозмущенных невзаимодей-
невзаимодействующих состояниях. И уж, конечно, нельзя пользоваться адиаба-
адиабатической гипотезой при рассмотрении связанного состояния.
В настоящее время все еще остается не вполне решенным вопрос
о том, как обойтись без адиабатической гипотезы (в той или иной
ее форме). В этой связи следует упомянуть работы Фридрикса [192]
и в особенности Снайдера [455]. Они показали, что если заменить
разложение A6.47) разложением по „волновым пакетам", то при-
применение адиабатической гипотезы становится ненужным и излишним.
Мы будем рассматривать их работы как оправдание применения
адиабатической гипотезы. Кстати, нет сомнения в том, что самые
неприятные черты современных релятивистских теорий поля, а именно
наличие расходимостей, присущи им вне всякой связи с какой-либо
адиабатической гипотезой.
1) За исключением того случая, когда присутствует также кулоново
поле, имеющее бесконечный радиус действия. Но в этом случае иачальиые
и конечные состояния можно охарактеризовать точными волновыми функ-
функциями кулонова поля,
Глава 17
ПРЕОБРАЗОВАНИЕ S-МАТРИЦЫ
§ 1. Нормальное произведение
Каждому члену разложения в степенной ряд A6.31) могут соот-
соответствовать различные процессы, как виртуальные, так и реальные.
Дайсон [129—131] и Вик [531] показали, как выразить P(J^'/(x1) . . .
. . . $?вjfrjj)) в форме, в которой все виртуальные процессы представ-
представлены явно. Это так называемое разложение хронологического произ-
произведения на сумму нормальных произведений. Последний тип произ*
ведения определяется как такое произведение операторов рождения
и уничтожения свободных частиц, в котором все операторы рожде-
рождения стоят слева от всех операторов уничтожения. Тогда, если в
любом начальном и любом конечном состояниях задано некоторое
число частиц с определенными импульсами и спинами в каждом со-
состоянии, то существует одно и только одно нормальное произведе-
произведение, матричный элемент которого, соответствующий переходу между
этими состояниями, отличен от нуля. Таким образом, разложение
5-матрицы на сумму нормальных произведений эквивалентно пере-
перечислению всех матричных элементов 5-матрицы в представлении,
диагональном по числам заполнения свободных частиц. Диаграммы
Фейнмана оказываются просто конкретным способом представления
нормального произведения.
Здесь мы проведем преобразование 5-матрицы к нормальной
форме, следуя алгебраическому методу Вика [531]. Рассмотрим сна-
сначала простое произведение операторов в представлении взаимодей-
взаимодействия Q, какое возникает в разложении A6.21). Разложение такого
произведения на сумму нормальных произведений, в которых все
операторы рождения стоят слева от операторов уничтожения *),
можно получить с помощью перестановочных соотношений между
множителями Q. Последние представляют операторные тождества,
не зависящие от тех конкретных состояний, которые нас могут
интересовать. Введем оператор N, который, действуя на произве-
произведение операторов рождения и уничтожения, записывает это произ-
произведение в нормальной форме, подразумевая при этом, что пере-
перестановка операторов должна производиться так, как если бы все
коммутаторы и антикоммутаторы были равны нулю. Однако операция
О Отметим, что из самого определения следует, что для нормального
произведения операторов в представлении взаимодействия среднее значение
ПО вакууму равно нулю [см., например, формулу A7.6)].
Преобразование В-матри^и 23?
N включает в себя изменение знака, возникающее при переста-
перестановке операторов антикоммутирующих полей. Таким образом, для
произведения двух множителей имеем
Л^(?(-)(У)?(+)(х))==^(?(+)(х)?(-)(У)) = 9(-)(у)9(+)(х). A7.1)
и аналогично
= _ф<-'(у)ф(+>(х), A7.2)
N (ф<+> (х) ф(+) (у)) = — N (ф(+) (у) ф(+) (х)) =
)(х). A7.3)
По определению, для операции нормального произведения имеет силу
дистрибутивный закон, т. е.
<р(->B)). A7.4)
Поэтому из перестановочных соотношений [см. особенно фор-
формулу A5.74)] и определения нормального произведения следует, что
разложение произведения ф(х)ф(у) на сумму нормальных произве-
произведений может быть выполнено следующим образом:
?. (*) Ь (у) = ($<+H0 + V."'00) D+) (у) + Ф^ (у)) =*
Ф^+) (У) +^+) (х) ф&-> (у) +
) (х) 4+) (У) +?-"} (х) ^"} (у) =
&+) (У) — ^"> (у) V.+)(x) — ISf»? (у — х) +
\х) ^+) (у) +"ф!-) (х) ф^"' (У) =
) (х) ф(р+) (у) ) + ЛГ (ф1+) (х) ф'Г' (У)) +
> (х) фЬ+) (у)) + Л^ С?."» (х) ф^~' (у)) —
р — /4а'(У — х). A7.5)
При получении последнего равенства в формуле A7.5) мы исполь-
использовали дистрибутивный закон. Используя аналогичные алгебраиче-
алгебраические операции, легко получить
Ф« (х) фр (У) = Л^ (ф. (х) фр (у)) — *S$> (х — у),
A7-6)
(х) я> (У) = ^ (<р (х) я> (У)) + ''йсД(+) (х — у),
238 Глава 17
Теперь введем хронологический оператор Вика Т, который опре-
определяется так же, как хронологический оператор Дайсона Р, с той
лишь разницей, что оператор Т, по определению, включает в себя
знак перестановки электронно-позитронных множителей, т. е.
Т (UV .. . Z) = bpXY . . . A7.7)
Другими словами, оператор Т, действуя на произведение зави-
зависящих от времени операторов UV .. . Z, переписывает его в хроно-
хронологическом порядке XY ... (оператор, зависящий от наиболее позд-
позднего времени, стоит последним слева), причем все произведение имеет
знак плюс или минус (Ьр) в зависимости от того, является ли пере-
перестановка фермионных множителей при переходе от левой стороны
к правой стороне соотношения A7.7) четной или нечетной. Или, по
определению, оператор Т, переписывая все множители в хронологи-
хронологическом порядке, действует так, как если бы все коммутаторы и
антикоммутаторы были равны нулю. Таким образом, в случае двух
множителей получаем
71(Ф(х)ф(У)) = + ф(х)ф(у), если хо>уо> A7.8а)
0>л:0. A7.86)
В силу перестановочного соотношения [ф, ф]+ = 0 правую часть
соотношения A7,8) можно для обоих случаев записать в виде
A7.9)
Аналогично имеем
7"(«Кх)ф(у))' = + ф(х)ф(у), если хо>уо,
Т (ф (х) ф"(у)) = — ф (у) ф (х), если уо>хо,
т (<Р (х) ? (У)) = <Р (х) ? (У), если х0 > у0,
если,уо>*о. С ' }
Теперь вернемся к основной проблеме: выражению хронологиче-
хронологического произведения через сумму нормальных произведений. С этой
целью для описания коммутаторов или антикоммутаторов, которые
появляются при переходе от хронологического произведения двух
множителей к нормальной форме, введем понятие свертки (contraction)
двух множителей. Свертку мы будем обозначать точками, стоящими
сверху справа у соответствующих множителей. Она определяется
формулой
V = U'V'-\-N(UV), A7.12)
где U'V — свернутые множители. Вычислим их для некоторых про-
простых случаев. Из формулы A7.12) следует, что
A7.13)
Преобразование S-матрицы 239
Из определений Т- и /V-произведений, используя формулу A5.53),
для случая л:0 > у0 имеем
?(+>- (х) ср(-)- (у) = <р<+> (х) ср(-) (у) — ср(-) (у) <р(+) (х) =
= [<Р(+)(х), т<-)(у)] =
= 1ЙсД(+)(х —у), если хо>уо. A7.14)
Аналогично
ср(+)-(х)?<-)-(у) = О, если .у0 > *0. A7.15)
В более общем случае получаем
?' (х) ср- (у) = Т (<р (х) ср (у)) — N(<? (х) 9 (у)) =
= + ^сД(+)(х —у), если хо>уо, A7.16)
= — ibc A(-) (х — у), если у0 > х0.
Функцию, обладающую свойствами, указанными в правой части
соотношенияA7.16), обозначим, следуя Дайсону, через 1/2 5сДр(х—у).
Аналогично, используя формулу A7.12) и правила антикоммута-
антикоммутации, получим для фермионных множителей
— У), если хо>уо>
?)(х —у), если уо>хо,
S( — у). A7.17)
Таким же образом из определения N- и Г-произведений следует
Ь (у) 4** (х)=—¥* (Ю Фр (у) =
-= + y5^(x—У)- A7Л8>
Отсюда ясно, что
ф*9' = ф'?' = ф>ф' = ф'<]7* = 0. A7.19)
Итак, если свернутое произведение не равно нулю, то порядок
множителей в нем является существенным. Так как
— ^&)(х — у) = (Ф0, фа(х)фр(у)Фо) A7.20а)
и
— ^»(х —у) = (Ф0, Фр(у)ФЛх)Ф0), A7.206)
то можно написать
«|>; (х) фр (у) = (Фо, Т («|»а (х) фр (у)) Фо) =
l — у). A7.21)
•J4Q Рлава 17
Аналогично имеет место
— У)- A7-22)
Эту функцию иногда обозначают Д° и называют каузальной функ-
функцией по Штюкельбергу (см. работу [474]), отметившему, что она
представляет собой функцию Грина, которая обеспечивает правиль-
правильную каузальную последовательность событий во времени в квантовой
теории (см. также статью Фирца [176]),
§ 2. Теорема Вика
В § 1 мы видели, что свернутая пара множителей представляет
собой с-число. Определим теперь нормальное произведение, внутри
которого имеется одна или большее число свернутых пар множите-
множителей, так как это упрощает дальнейшие расчеты. Чтобы отличать
различные свернутые пары, мы будем обозначать их двумя точками,
тремя и т. д., стоящими сверху справа у соответствующих множи-
множителей пары. Пусть UV ... XYZ— операторы рождения или уничто-
уничтожения; введем тогда следующее определение:
N{U'V" ... R ... X"YZ') =
= ±z(U'Z-)(VX")N(... R ... Y), A7.23)
причем знак плюс или минус должен быть взят в зависимости от
того, является ли перестановка фермионных множителей при пере-
переходе от левой стороны к правой четной или нечетной.
Теперь докажем одну очень полезную вспомогательную теорему.
Теорема.
Если Z — оператор, зависящий от времени, предшествующего
каждому из времен, для которых заданы операторы UV . .. XY,
то
N(JUV . . . XY)Z = N(UV . . . XY'Z')-\-N(UV . . . XYZ')-^-
+ ... +AT(t/"V ... XYZ')-\-
-\-NQLJV ... XYZ). A7.24)
Поскольку для операции нормального произведения имеет место
дистрибутивный закон, то ясно, что достаточно доказать соотно-
соотношение A7.24) для случая, когда каждый из множителей U, V. . .X, Y
является либо оператором рождения, либо оператором уничтожения.
Кроме того, согласно нашему определению нормального произведе-
произведения, соотношение A7.24) остается правильным и при перегруппи-
перегруппировке множителей UV .. . XY, если в обеих сторонах соотношения
сделана одна и та же перегруппировка. Поэтому можно предпо-
Преобразование S-матрицы 241
ложить, что операторы UV . . . XY расположены в нормальном по-
порядке, т. е. все операторы рождения стоят слева от операторов
уничтожения.
Докажем теорему, предполагая, что Z является оператором
рождения, а все операторы UV ... XY—операторами уничтожения.
Этого, очевидно, достаточно. Если все UV ... XY являются опера-
операторами уничтожения и Z— оператором рождения, то можно доба-
добавить любое число операторов рождения во всех членах в обеих
сторонах соотношения A7.24) слева от всех множителей под знаком
iV-произведения, не нарушая справедливости нашей теоремы, так
как свертка двух операторов рождения дает нуль. Если, с другой
стороны, Z— оператор уничтожения и UV ... XY—операторы
рождения и уничтожения, то соотношение A7.24) сводится к три-
тривиальному тождеству, поскольку свертка двух операторов уничто-
уничтожения дает нуль, а свертка операторов рождения и уничтожения
также дает нуль, если время, от которого зависит оператор уни-
уничтожения, предшествует времени, от которого зависит оператор
рождения [см., например, формулу A7.15)]. Таким образом, в этом
случае в правой стороне формулы A7.24) остается лишь последний
член и соотношение сводится к тождеству.
Доказательство теоремы проводится методом индукции. Ясно,
что теорема верна для случая одного множителя под знаком iV-npo-
изведения, так как при этом (напомним, что время, от которого
зависит оператор Z, предшествует времени, от которого зависит
оператор К, по определению)
N(Y)Z= YZ = T(YZ), A7.25)
а Г-произведение, по определению A7.12), равно
T(YZ)=Y'Z' -\-N(YZ). A7.26)
Предположим теперь, что соотношение A7.24) верно для п множи-
множителей, и умножим его еще на один оператор уничтожения D слева,
считая, что время, от которого зависит оператор D, более позднее,
чем время, от которого зависит оператор Z. Тогда
DN{UV ... XY)Z =
= N(DUV ... XY'Z')-\- ... -\-N{DU'V ... XYZ')-\-
-\-DN(UV .. . XYZ), A7.27)
так как оператор D может быть внесен под знак N-произведения
во всех членах, где оператор Z свернут. Однако, по определению,
поскольку оператор Z является оператором рождения, а все
UV .. . —операторами уничтожения, то
W {UV . . . XYZ) = ipZUV ... XY, A7.28)
242 Глава If
где 8р — знак четности перестановки фермионных множителей; итак
мы имеем
DN(UV . . . XYZ) = ipDZUV . .. XY. A7.29)
С другой стороны, поскольку Z зависит от времени, предшествую-
предшествующего времени, от которого зависит оператор D, то
A7.30)
и, следовательно,
DZUV . . . XY = D'ruV . .. XY + IqZDUV ... XY. A7.31)
Далее, в силу нашего определения нормального произведения со
свернутыми множителями внутри него
D'Z'UV . . . XY = bPN{D'UV . . . XYZ'). A7.32)
Аналогично
ZDUV ... XY = ЪфрКЦриУ ... XYZ); A7.33)
в результате получаем
DN(UV .. . XYZ) = bpDZUV .. . XY=aFN(D'UV .. . XYZ')-\-
~bo|SpiV (DUV . . . YZ). A7.34)
Так как о| = ор=1, то мы доказали нашу теорему A7.24) для
случая п-\-1 оператора уничтожения и, следовательно, методом
индукции дано общее доказательство теоремы.
Эту теорему можно без труда обобщить. Умножим соотноше-
соотношение A7.24) слева на множитель R"S"; тогда благодаря определе-
определению A7.23) мы можем придать соотношению A7.24), например,
следующий вид:
M(UR"V . ..
-\-N(UR"V .. . S'XYZ). A7.35)
Аналогично можно умножить соотношение A7.24) на несколько
таких свернутых множителей. Таким образом, теорема A7.24)
остается верной и в том случае, когда внутри произведения
UV ... XY проделано любое число сверток (но, конечно, одних и
тех же в каждом члене).
Теорема Вика формулируется следующим образом:
Г-произведение может быть однозначно представлено в виде
суммы нормальных произведений
T(UV . . . XYZ) = N(UV ... XYZ)-{-N{U'V . . . XYZ)-\- . . . +
" ... X"YZ')-\- ... 4-
-\-N{U'V'W ... X"'Y'Z'"), A7.36)
Преобразование S-матрицы 243
где сумма в правой стороне включает в себя все возможные
свертки.
Доказательство снова проводим методом индукции. Теорема
верна для одного множителя. Она верна и для двух множителей,
как это видно из формулы A7.12). Предположим, что соотноше-
соотношение A7.36) верно для п множителей. Затем умножим его справа на
оператор 2, предшествующий во времени всем остальным множи-
множителям
Т {UV . . . XYZ) Q = Т (UV ... XYZQ). A7.37)
Члены в правой части соотношения A7.36), имеющие теперь форму.
N(UV ... XYZ)Q, могут быть сведены к нормальным произведениям
с помощью теоремы A7.24). Таким образом, теорема A7.36) верна
для д-f-l множителя, если 2 предшествует по времени UV.. .XYZ.
Последнее ограничение может быть, однако, легко устранено. Когда
оператор Q вносится под знак Т- и Л/^-произведений, мы можем
изменить порядок операторов, так как, по определению Т- и
iV-произвёдений, соотношение A7.36) инвариантно по отношению
к одной и той же перегруппировке множителей в обеих сторонах
соотношения. Таким образом, теорема доказана в общем случае для
га-f-l множителя.
Можно выписать также правила, аналогичные приведенным выше,
для разложения простого произведения операторов на сумму нор-
нормальных произведений (Дайсон [129, 130]). В этом случае символ
свертки обозначается линией, соединяющей соответствующие мно-
множители, а сама свертка может быть определена с помощью соот-
соотношения A7.6) следующим образом:
Q = — iSip (х — xQ = (Фо, ф«(х)фг(х')Фо). A7-38)
ФрООФ.'х) = — iSfaj>(х — х') = (Фо, фр(X')фа(х)Фо). A7.39)
у (х) <p(xQ = tA(+) (х — х') = (Фо, <р(х)?(х')Ф0). A7-40)
<? (х) ф (У) = ф (х) <|> (у) = у (х) ф (х) = со (х) ф (х) = 0. A7.41)
Теорема разложения, которая легко может быть доказана методом
индукции, в этом случае формулируется так:
UV ... XYZ=N(UV . . . XYZ)-\-N(UV . . . XYZ)-\-
-+-... N{UV . .. XYZ) -+-..., A7.42)
I 1
I 1
где сумма в правой стороне скова включает в себя все возможные
типы сверток.
244 Глава 17
§ 3. Применение к S-матрице
Только что доказанные теоремы не могут быть непосредственно
применены к преобразованию S-матрицы по следующим причинам:
во-первых, в разложение S-матрицы входит хронологический опе-
оператор Дайсона Р, а не оператор Вика Т; во-вторых, 5-матрица
содержит некоммутирующие операторы, зависящие от одного и
того же времени, и 7"-оператор не может определить их порядок.
В квантовой электродинамике, где член взаимодействия имеет
вид
вторая трудность может быть устранена, если учесть, что выра-
выражение для плотности тока
У^(х)=«ф(х)Т|1ф(х) A7.43)
фактически неверно. Действительно, рассмотрим среднее значение
тока в состоянии вакуума
Д (х) > о == « Ит 2 (Фо, ф. (х)
= — ie lim 2 4« > (х — х') (ТДр =
) A7.44)
Выражение A7.44) бесконечно. Уже в 1934 г. Гейзенберг [225, 226]
знал об этой трудности. Он отметил, что бесконечность среднего
значения тока в состоянии вакуума обусловлена „фоном" (т. е.
полностью заполненными состояниями с отрицательной энергией).
В связи с этим он предложил переопределить 4-вектор плотности
следующим образом:
у; (х)
в этом случае
(Фо, у;(х)Ф0) = 0. A7.46)
Это выражение получается при симметризации теории относительно
частиц и античастиц. Можно легко показать (Вик [531]), что этот
симметризованный ток (мы теперь опускаем штрих) можно записать
как нормальное произведение
Ур.Сх) —вЛ^(ф(х)Тр.ф(х)), A7.47)
поэтому, когда ток j^(x) встречается в хронологическом про-
произведении, нормальное произведение упорядочивает множители
Преобразование S-матрицы 245
в выражении для тока ./^(х). Итак, S-матрицу в квантовой элек-
электродинамике можно записать следующим образом:
+ СО +ОО
J rf**! j <1*<Хг . . .
П=0 —со — со
+ QO
, A7.48)
где множитель Л мы включили в нормальное произведение, так как
относительный порядок множителей ф (х) уР-ф (х) и Л„ (х) несуществе-
несущественен, потому что они коммутируют. Кроме того, мы переписали
разложение Дайсона A5.28), заменив Р-оператор 7"-оператором, так
как между ними теперь нет разницы, поскольку фермионные мно-
множители всегда встречаются парами, в которых оба множителя зави-
зависят от одного и того же времени.
Мы будем называть Г-произведение, в котором имеются нормаль-
нормальные произведения, смешанным Г-произведением. Вик обобщил
теорему A7.36) и на такие смешанные Г-произведения. Эта теорема
формулируется так:
Смешанное Г-произведение можно разложить согласно фор-
формуле A7.36), если опустить свертки между ^/-упорядоченными мно-
множителями.
Доказательство теоремы основывается на следующем приеме.
Предположим, что мы использовали дистрибутивный закон для све-
сведения смешанного Г-произведения типа A7.48) к сумме таких
смешанных Г-произведений, каждое из которых содержит только
операторы рождения и уничтожения XYZ (т. е. только матрицы А ,
ф(+), ф(-) и т. д., а не операторы А, ф, ф). Тогда мы можем рас-
рассматривать смешанное Г-произведение
T(M(RST) ... N(XYZ))
(где все три множителя RST XYZ под знаком каждого iV-произ-
ведения зависят от одного и того же времени) как предел Г-произ-
оедения, т. е.
T(RST . .. XYZ),
где время, от которого зависят операторы рождения внутри каждого
из произведений RST, ..., XYZ, на бесконечно малую величину
позднее времени, от которого зависят операторы уничтожения.
Теперь можно применить теорему A7.36). Поскольку свертки, которые
должны быть опущены по теореме для смешанного Г-произведения,
фактически равны нулю [оператор уничтожения зависит от времени,
предшествующего времени, от которого зависит оператор рождения,
см., например A7.15)], то теорема доказана.
246 Глава 17
В псевдоскалярной мезонной теории, где
Set (х) = G^ (х) 1-5Ф (х) ? (х), A7.49)
также не нужно проводить свертку множителей t|> (x) и ф (х) внутри
каждого оператора S^I(ji)> так как в этом случае
К 00 (Тб)аЭ ¥9 (х) = Ит {1 Sp (Ts
«4-Hm {Sp[(iV5 —/п)Т51ДР(§)} = 0, A7.50)
z 5 о
поскольку
SpT5=0,
S?^T+TT) O. A7.51)
Вследствие же соотношения A7.51) и правил антикоммутации для ф
и ф можно написать
^?1(х) = ^-О[ф(х)-1'5, ф(х)]9(х)=ОЛГ(ф(х)Т5?(х)ф(х)), A7.52)
что сводит S-матрицу для этого случая к форме, аналогичной рас-
рассмотренной в квантовой электродинамике.
§ 4. Представление инвариантных функций
Мы определили функцию Ар, возникающую при свертке двух
бозонных множителей следующим образом [см. выражение A7.22j):
() для х >0
A7.53)
для д:0<0.
Напомним теперь [см. формулы A5.57), A5.59)], что
<+) (")(х) A7.54)
ДA)(х)], A7.55)
уA)(хI. A7.56)
Функции Д, ДA) и Д'т) были уже определены в гл. 15. Функцию Д^
можно выразить тогда в следующем виде:
ДЯх) = ДA)(х) + Их)Д(х), A7.57)
где функция е (х) — х°/1 хР | указывает знак времени. Так как Д (х)
является четной функцией переменной х, а Д(х) и s(x) — нечетными
Преобразование S-матрицы
247
функциями переменной х, то ясно, что Д^(х) есть четная функция
переменной х- Хотя функция Д(х) равна нулю вне светового конуса,
функция ДA)(х) отлична от нуля, поэтому функция Др(х) также
отлична от нуля [и фактически равна ДA)(х)) вне светового конуса.
Контур С
Контур
Фиг. 23.
Для получения интегрального представления функции (
напомним здесь интегральные представления функций Д(х) и ДA)(х)
[см. формулы A5.41) и A5.51)]
+ о
Д(х) = ——^ f
—со
-f со
(i7.58)
A7.59)
Полностью эквивалентные определения этих сингулярных функций
даются следующими выражениями:
iW=i/W^' A7>60)
A7.61)
В этих выражениях интегрирование должно проводиться сначала по
переменной £0, причем контуры интегрирования С и Сх в комплекс-
комплексной плоскости приведены на фиг. 23, а и б, соответственно. После
248
Глава 17
этого должно выполняться интегрирование по вещественным пере-
переменным k1, k% и
Таким образом, поскольку
Й„>0
то для х0 > 0 будем иметь
A7.62)
A7.63)
где контур интегрирования С+ идет по вещественной оси k0 от -)-оо
до —со, обходя полюс в точке ko — -\-wk сверху, а полюс в точке
Контур С+ для
а
Контур С_ для жо< О
6
Фиг. 24.
&0 = —"J/Ofe2 -f- p.2 = — u)fc снизу, и замыкается большой полу-
полуокружностью в нижней полуплоскости (фиг. 24, а). Если х0 <С О,
то для функции Д*~'(х) имеет место следующее представление:
дС"} (х)=тй
для х°< 0:
A7-64)
контур интегрирования С_ приведен на фиг. 24, 5. Тогда, исходя
из определения A7.53) функции Д^-, можно написать
-т«
A7.65)
где Ср—контур интегрирования, приведенный на фиг. 25. В самом
деле, если х0 > 0, то можно замкнуть контур в нижней полупло-
полуплоскости, и тогда, согласно формуле A7.63),
i для л;0> 0. A7.66)
Преобразование S-матрицы
249
Аналогично, если х0 < 0, то мы получаем, замыкая контур в верхней
полуплоскости,
для лго<О,
A7.67)
что находится в согласии с предыдущим определением A7.53).
Тот же результат, который получается при интегрировании
по контуру Ср, можно получить при интегрировании по веществен-
вещественной оси k0 от —оо до -|-оо, если добавить к массе jx малую
отрицательную мнимую величину, которую следует устремить к нулю
после выполнения интегрирования. В этом случае знаменатель в выра-
выражении A7.65) получает вид (к2 — jx2-|-ts). Добавление к массе ^
Контур Ср
Фиг. 25.
малой отрицательной мнимой величины приводит к смещению полю-
полюсов. Теперь они оказываются в точках
гг3", A7.68)
так что полюс —и>к сдвигается вверх, а полюс -f- и>й — вниз, как
и должно быть.
Для полноты мы здесь приведем еще опережающую и запазды-
запаздывающую сингулярные функции Д^ (х) и Дд (х), которые определяются
следующими интегральными представлениями:
где контуры интегрирования Cj. и Сд приведены на фиг. 26. Если
хо 7> 0> то можно замкнуть контуры по большой полуокружности
250
Глава 17
в нижней полуплоскости, тогда мы получим
0 для лго> 0,
=— д(х) для л;0>0.
A7.71)
Аналогично, если х0 < 0, то контур можно замкнуть в верхней
полуплоскости, так что
Ьа (х) = Д (х) для х0 < 0.
Дд (х) = 0 для х0 < 0;
A7.72)
Контуры Сд и СК
Ф и г. 26.
отсюда и наименования для этих сингулярных функций: попережающая"
и „запаздывающая". Из самих определений следует, что
= Д4(х) —Дд(х),
= Дл(— х).
A7.73)
A7.74)
Симметричная во времени сингулярная функция Д (х) определяется
выражением
A7.75)
1
так что
или
Д(х)== —
для х0 < О,
для л;0> О,
д(х) =—i«
A7.76а)
A7.766)
A7.77)
Функции Д и ДA) широко использовались Швингером [436, 438—-440].
Преобразование S-матрицы 251
Функции Д^х), Д(х), Ад(х), Ая (х) удовлетворяют неоднород-
неоднородному уравнению Клейна — Гордона с 8*(х) в качестве функции
источника в правой части; функции же Д(±'(х), Д(х), Д (х) удовлет-
удовлетворяют однородному уравнению Клейна — Гордона.
Соотношение между функциями Sp и Д^? снова дается выражением
Sf(x)=—(tf + /»Lp(x), A7.78)
так что
fе-***1* d*p A7.79)
Таким образом, —1/г ^i? (x) = К+ (х) представляет функцию рас-
распространения Фейнмана, рассмотренную раньше в связи с позитрон-
ной теорией Фейнмана. Функции S<1). 5*+), 5д, Sr и т. д. связаны
с соответствующими функциями Д , Д , Дд, Дд и т. д. соотно-
соотношениями вида A7.78J.
Глава 18
ДИАГРАММЫ ФЕЙНМАНА
Чтобы освоиться с формализмом S-матрицы и иметь возможность
выписывать матричные элементы, не прибегая каждый раз непо^
средственно к теореме Вика, мы рассмотрим несколько примеров,
которые помогут нам вывести некоторые правила.
§ 1. Взаимодействие с внешним электромагнитным полем
Вначале рассмотрим случай взаимодействия электронно-позитрон-
ного поля с заданным внешним электромагнитным полем. Тогда,
энергия взаимодействия е%?1(х)=/*'(х) Л£(х)и S-матрица получает вид
wj~k f diXi f dix*T {N (*(Xi) A в (Xi) ф (Xi)} x
ХЛ/(ф(х2)Ле(х2)ф(х2))}+... A8.1)
Рассмотрим член первого порядка
Нормальное произведение спинорных множителей было уже выписано
ранее [см. выражение A7.5)]. Теперь операторы рождения и уничто-
уничтожения в нормальных произведениях представим прямыми: для элек-
электронов— со стрелкой, направленной вверх (в направлении возрастания
времени), для позитронов — со стрелкой, направленной вниз (в напра-
направлении убывания времени). Тогда:
1. Оператор ф(~'(х), соответствующий рождению электрона
в пространственно-временной точке х, представляется направленной
прямой, выходящей из точки х вверх (фиг. 27, а).
2. Оператор ф(+)(х) (уничтожение электрона в точке х) пред-
представляется направленной вверх прямой, кончающейся в точке х
(фиг. 27, Ь).
3. Оператор ф(+)(х) (уничтожение позитрона в точке х) пред-
представляется направленной вниз прямой, выходящей из точки х
(фиг. 27, с).
Диаграммы Фейнмана
253
4. Оператор ф<->(х) (рождение позитрона в точке х) предста-
представляется направленной вниз прямой, кончающейся в точке х (фиг. 27, d).
На пространственно-временных диаграммах, как это видно из
фиг. 27, время растет по направлению вверх, так что предлагаемое
Пространственные
координаты
b
Фиг.
27.
направление стрелок для позитронных множителей находится в согла-
согласии со взглядом Фейнмана на позитроны — как на электроны, дви-
двигающиеся в направлении убывания времени.
Видно, что при таком описании операторы ф представляются
линиями, выходящими из точки х (вверх или вниз), а опера-
операторы ф — линиями, заканчивающимися в точке х; далее, линии
с положительными частотами лежат ниже точки х, а линии с отри-
отрицательными частотами — выше точки х (позднее во времени). Тогда,
Фиг. 28.
при этих условиях, член первого порядка в разложении S-матрицы
можно представить четырьмя диаграммами Фейнмана, приведенными
на фиг. 28. Подразумевается, что внешнее поле должно действовать
в точке xt. Иногда это изображается явно путем представления
внешнего потенциала волнистой линией с крестом на конце. Исполь-
Используя последнее условие, можно изобразить все так, как показано
на фиг. 29.
Рассмотрим следующий член второго порядка. Используя теорему
Вика и выражая свертку двух спинорных множителей через функцию
254
Глава 18
распространения Фейнмана К+, мы получаем (опуская множители Ав)
T{N (фв (%0 % (xt)) N 6р (х2) фо (х2))} =
= N, фв (Xl) фр (xj% х2) фо (х2)) + N (Ф~. (хх) АГ+Эр (xt — х2) фо (х2) ) +
(х2) К+т (х2 — Xl) ф3 (хх)) — К+99 (Xi-x2) /C+oa (x2-Xl). A8.2)
Если представить первый член разложения A8.2) диаграммами Фейн-
Фейнмана, то он будет соответствовать двум любым элементарным про-
процессам из числа приведенных на фиг. 28. На фиг. 30 приводится
Уничтожение пары
во внешнем пола
X >
Рассеяние электрона
внешним полем
Рассеяние позитрона
внешним полем
Рождение пары
внешним полем
Фиг. 29.
несколько возможных процессов. Каждой диаграмме, приведенной
на фиг. 30, соответствует другая, на которой точки xt и х2 меняются
Рассеяние позитрона
и рождение пары
внешним полам
Рассеяние электрона
и уничтожение пары
Фиг. 30.
местами. Для процессов с одной частицей такое же соответствие
представлено явно вторым и третьим членами в правой стороне
разложения A8.2). Эти члены приводят к одинаковым диаграммам
Фейнмана, которые отличаются только наименованием пространственно-
временных точек. Поскольку по переменным хх и х2 проводится
интегрирование, то мы можем объединить второй и третий члены
в один. Это даст множитель 2!, сокращающийся с множителем 1/2!
Диаграммы Фейнмана
255
стоящим перед членом второго порядка в разложении S-матрицы
[см. формулу A8.1)]. Если мы теперь представим функцию /С+(хх—х2),
появляющуюся при свертке операторов ^(х^ и ф(х2), внутренней
линией, направленной от точки х2 к точке xt, то член
A8.3)
— х2) А", (х2) ф„ (х2) )
даст четыре диаграммы, приведенные на фиг. 31.
Х-
V—^-*- V?1 зс\ -** (ж2
C+)(=C) Я
Фиг. 31.
Наконец, последний член в разложении A8.2)
Sp (Ав (xt) К + (xt — х2) Ае (х2) К+ (х3 — xt)),
представляем диаграммой на фиг. 32. Он описывает вакуумный про-
процесс и соответствует рождению пары и ее последующей аннигиляции.
Матричный элемент его дается выражением
(х2 — xi)} =
256 Глава 18
и должен быть интерпретирован как амплитуда вероятности того,
что вакуум остается вакуумом, т. е. вероятности того, что ни
в начале, ни в конце нет частиц. Если вычислить этот матричный
элемент, то оказывается, что он имеет бесконечную мнимую часть.
Позднее (в § 3) мы увидим, как можно устранить эту труд-
трудность.
Из этих примеров ясно, что существует одно-однозначное соот-
соответствие между разлржением на сумму нормальных произведений и
диаграммами Фейнмана при условии, что две диаграммы Фейнмана,
различающиеся только индексами вершин, считаются отличными друг
от друга. Отметим, что нужно выбирать правильный знак матричного
элемента, соответствующего каждой диаграмме, который фактически
автоматически получается правильным при
Д^1 _rij_ д-,__^_^{ использовании разложения Вика.
В качестве примера рассмотрим ампли-
амплитуду рассеяния позитрона внешним полем
в низшем приближении. Пусть начальное
состояние есть
Wi = dl(p1)<&0 (IS.5)
и нас после рассеяния интересует состояние
Фиг. 32. *Р/. = 4а(р2)Ф0. A8.6)
Амплитуда вероятности (первого порядка по внешнему потенциалу)
для этого процесса равна
M=(Wf, [l-f-S^llV). A8.7)
Рассмотрим член
<*«.<**> Ф°' N ft (х^
При разложении нормального произведения вклад дает только член
— фр~)(х)^+)(х): оператор ф^+) (х) уничтожает позитрон в начальном
состоянии, а оператор ф^~' (х) рождает позитрон в конечном состоя-
состоянии. Далее, согласно соотношениям A5.68) и A5.70), имеем
,_ L_ f
A8-9)
Диаграммы Фейнмача
257
Следовательно,
1, 2
X
<) d ( 4
«. fpz) 4 <J>) ds (p') 4 (Л) Фо) X
x
Если ввести обозначение
то матричный элемент получает вид
A8.11)
(P2 Pl)vSt(Pz)- A8.12)
Это как раз тот матричный элемент, который мы должны были бы
написать в теории Фейнмака. Отметим, однако, что здесь матричный
элемент Mr j имеет знак плюс; в слу-
случае рассеяния электронов матричный
элемент М имеет знак минус. Мно-
Множители (т/ЕI'2 являются точными
нормировочными множителями вол-
волновых функций начального и конеч-
конечного состояний.
Соотношение A8.12) показывает,
что если мы чертим диаграммы Фейн-
мана в импульсном пространстве,
то понятия „начальный" и „конеч-
„конечный" относятся к последователь-
последовательности явлений вдоль пути частицы.
Другими словами, если мы имеем
дело с позитроном, то конечное со-
состояние (если время растет снизу ввгрх) находится внизу диаграммы,
как это показано на фиг. 33.
Если применить только что описанный метод к диаграммам,
содержащим две электронные или две позитронные линии, то авто-
автоматически будет включен правильный обменный член, обусловленный
принципом Паули. Для практических цглей, когда рассматриваются
тождественные частицы (все электроны, а также все позитроны
Фиг. 33.
258 Глава 18
тождественны), необходимо только из матричного элемента прямого
рассеяния вычесть такой же самый матричный элемент, в котором
конечные состояния частиц переставлены [напомним также соотноше-
соотношение (9.43)].
Таким образом, мы установили связь между формализмом теории
поля и гораздо более простым формализмом Фейнмана, развитым
в гл. 8 на основе интуитивных соображений.
§ 2. Диаграммы Фейнмана в мезонной теории
Рассмотрим теперь псевдоскалярную мезончую теорию с псевдо-
псевдоскалярной связью, для которой
J^I(x) = O(fr^cp,(x). A8.13)
В этом случае матричный элемент первого порядка St равен нулю,
поскольку энергия и импульс не могут сохраняться при излучении
или поглощении свободного мезона свободным нуклоном. Поэтому
рассмотрим член второго порядка
ХТ(сР(х1)ср(х2))}. A8.14)
Мы записали отдельно Т-произведение для нуклонных и мезонных
множителей, потому что они коммутируют между собой. Ранее было
показано, что свертка ф ТьФ' равна нулю [см. выражение A7.50)].
Поэтому разложение Г-произведения фермионных множителей на
сумму нормальных произведений фактически тождественно разложе-
разложению A8.2). Таким образом, необходимо рассмотреть только мезонные
множители. Используя теорему Вика, мы получаем для них
^ ? (Х2) )== ЛГ (? W ?(Х2)) + -±-***(*! ~ Х^ A8Л5>
Если свертку двух бозонных множителей <p(xi)> <р (х2) представить
пунктирной линией, соединяющей точки xt и х,, оператор рождения
мезона <p(~'(xi) — пунктирной линией, выходящей из точки xt и
направленной вверх, и оператор уничтожения мезона <р(+)(х!) — пунк-
пунктирной линией, направленной к точке xt, то диаграммы на фиг. 34—41
будут представлять матричные элементы второго порядка, входящие
в S"'. Рассмотрим отдельно эти диаграммы и соответствующие им
матричные элементы.
1. N ($<$$) N (<р<р).
Этот член равен (Sr ) и не дает вклада, так как энергия и импульс
не сохраняются.
Фиг. 34.
Фиг. 35.
\ /
X
•x,
x ЖТ
\ /Г
\/
A
/ \
\
/
Xo 3»t / \X,
x A -' x
Рассеяние мезона Рассеяние мезона
на нуклоне на антинунлоне
а Ь
Фиг. 36.
ч • 4
<?2
Аннигиляция нуклона
и антинуклона
с излучением
двух мезонов
а
Рождение нуклонной
пары двумя
взаимодействующими
мезонами
Ь
Фиг. 37.
17*
260 Глава 18
2.
Это выражение соответствует обмену бозонами между двумя
фермионами и, следовательно, аналогично выражению для мёллеров-
ского рассеяния нуклонов. Для взаимодействия тождественных частиц
следует взять не только две диаграммы на фиг. 34, но и еще две,
в которых точки xt и х2 переставлены. Это справедливо для каждой
диаграммы в данном параграфе, за исключением диаграммы на фиг. 40,
соответствующей флуктуациям вакуума. Если сложить матричные
элементы, соответствующие этим топологически эквивалентным диа-
диаграммам, то при этом как раз сокращается множитель 1/2! в разло-
разложении по теории возмущений. Обменное рассеяние будет автомати-
автоматически учитываться при вычислении матричного элемента между
начальным и конечным состояниями.
ТХ,
I
Фиг. 38. Ф и г. 39. Фиг. 40.
Рассеянию антинуклона на нуклоне соответствуют две диаграммы
на фиг. 35. Вторая возникает благодаря возможности аннигиляции
двух частиц с испусканием виртуального бозона, который рождает
частицы в конечном состоянии.
Только что рассмотренные процессы соответствуют наличию
в начальном и конечном состояниях двух фермионов.
3.
Матричный элемент 6Ч2) содержит также ряд членов, соответ-
соответствующих различным процессам с одним бозоном и одним фермионом
в начальном и конечном состояниях. Диаграммы этих процессов
приведены на фиг. 36. Кроме того, член NtyK+ty)N(cpcp) может при-
привести к процессам, указанным на фиг. 37,
4. М(ф)С+ф)<рУ.
Член N(tyK+ty) <р'<р' соответствует случаю, когда в начальном и
конечном состояниях имеется один фермион и ни одного бозона и
представляет собственную энергию фермиона, которая будет весьма
подробно рассмотрена ниже. Диаграммы собственной энергии при-
приведены на фиг. 38.
Диаграммы Фейнмана
261
5.
Аналогично член K+K+.N (<р<р) соответствует случаю, когда в на-
начальном и конечном состояниях имеется один бозон и ни одного
фермиона, и представляет собственную энергию бо-
бозона, диаграмма которой приведена на фиг. 39.
6. K+K+^f-
Наконец, член К+К+кр, диаграмма Фейнмана ко-
которого приведена на фиг. 40, отвечает случаю,
когда в начальном и конечном состояниях нет /
частиц. Он соответствует флуктуациям вакуума и
будет рассмотрен в § 3.
Следует, по-видимому, еще раз подчеркнуть, что
так же, как и в исходной позитронной теории Фейн-
Фейнмана (см. гл. 8) последовательность времен в проме-
промежуточных состояниях несущественна. Поэтому диа-
диаграмма на фиг. 41 представляет частный случай Фиг. 41.
диаграммы на фиг. 38, если л^ < хйг Другими сло-
словами, мы можем произвольно деформировать диаграммы Фейнмана,
но так, чтобы сохранялось правильное направление внешних линий,
т. е. конечного и начального состояний.
§ 3. Вакуумные амплитуды
Теперь обратимся к исследованию вакуумных матричных элемен-
элементов высшего порядка. Рассмотрим вначале случай электронно-пози-
тронного поля, взаимодействующего с внешним электромагнитным
полем. Среднее значение по вакууму матричного элемента 5 , соот-
соответствующее вкладу третьего порядка в амплитуду перехода вакуума
в вакуум под влиянием внешнего поля, дается выражением
И)* ЗТ J
/
X
Фо). A8.16)
В этот матричный элемент дадут вклад только те нормальные произ-
произведения в разложении 7"-произведения, в которых все фермионные
множители свернуты. Имеются два таких нормальных произведения,
которые соответствуют двум следующим возможностям свертки:
(Xi) A8.17a)
— f (Xl)f (x,)f (x,)f ■ (x2)f • (x2)f" (x,). A8.176)
Эти члены соответствуют двум диаграммам, приведенным на фиг. 42,
причем электромагнитное поле действует в точках 1, 2, 3.
262 Глава 18
Следует обратить внимание на знак минус перед выражениями
A8.17 а) и A8.17 б). Он обусловлен тем, что при свертывании первого и
последнего фермионных множителей мы всегда должны переставить
свертываемый множитель с нечетным числом множителей <J> или ф.
Итак, знак минус появляется по той же причине, что и перед послед-
последним членом в правой стороне соотношения A8.2). Вообще перед
матричным элементом любой замкнутой диаграммы Фейнмана стоит
множитель — 1.
а
Фиг. 42.
Следовательно, матричный элемент, соответствующий диаграммам
на фиг. 42, имеет следующий вид:
X!Sp(i(x1)/C+(x1 — x2)A(x2)K+(x2 — х3)Л(х3)/С+(х3-х1)+
4- Sp (A (Xl)K+ (х, — х3) А (х3) К+ (х3 — х2) X
ЛАГ+(Х2 —Xl))}. A8.18)
Хогя второй член можно сделать по форме тождественным первому
с помощью замены переменных, тем не менее мы оставим My
в форме A8.18) по причинам, которые вскоре выяснятся.
Покажем теперь, что матричный элемент A8.18) фактически равен
нулю. Для этого проведем следующее доказательство. Рассмотрим
матрицы -j-. подчиняющиеся перестановочным соотношениям
. A8.19)
Если мы будем транспонировать это соотношение, то получим
Итак, транспонированные матрицы -[ удовлетворяют тем же пере
становочным соотношениям, что и сами матрицы -(. Поэтому суще-
существует преобразование подобия, которое переводит матрицу fV-
Диаграммы Фейнмана 263
гп
в матрицу (т*1) (см. гл. 13, § 6). Если обозначить матрицу пре-
преобразования через С, то
A8.21)
Напомним, что матрицу С можно выбрать унитарной и антисиммет-
антисимметричной, т. е.
С+С = СС+=1, A8.22)
Ст = — С. A8.23)
Это свойство антисимметрии эквивалентно утверждению, что суще-
существует такое представление матриц -;, в котором все матрицы «f яв-
являются чисто мнимыми, т. е. t-j^ вещественно для [i = 0, 1, 2, 3
(Майорана [319], Рака [399], Фарри [201]). Связь между существо-
существованием преобразования подобия A8.21) и общими свойствами сим-
симметрии при перестановке положительных и отрицательных зарядов
в квантовой электродинамике рассматривалась Фарри [200], Крамер-
сом [287], Пайсом и Йостом [367], Вольфенштейном и Равенхол-
лом [540] (см. также гл. 13, § 6 и гл. 25, § 2).
Если подставить в первый член в формуле A8.18) под знаком
шпура множитель С~*С — I, то получим
Sp( ) = Sp [СА(хг)С~1СК+ (Хх — х2)С^СА(х2)С~1СК+ (х2— х3) X
11(х3 — xJC~1].' A8.24)
Далее, из формулы A8.21) следует, что
СК+ (Xl - х^С-1 = -^ / =£±£- .-*■(*-
/^s^-xl)- A8-25)
Поэтому шпур в выражении A8.24) можно переписать в следующем
виде:
Sp( ) = (— l)sSp(ir(Xl)^(x2 — х1)Л^(хг)^^(х3 — х2)Х
Х^(х3)^(х,-^)) =
=-Sp (К+ (xt-x3) А (х3) К+ (х3-х i
ХА(х,)К+(х2 — хО • A8.26)
так что два члена в выражении A8.18) сокращаются и, действи-
действительно, Мр = 0. Фактически уже каждый член в отдельности равен
нулю, поскольку заменой переменных можно преобразовать выра-
264 Глава 18
жение A8.26) к исходной форме [см. левую сторону выражения
A8.24)]; при этом оказывается, что выражение для шпура меняет
знак.
Взаимному сокращению двух членов в выражении A8.18) можно
дать следующее физическое толкование: первый член, соответствую-
соответствующий диаграмме на фиг. 42, а, может рассматриваться как описываю-
описывающий движение электрона по одному пути, тогда как второй член,
соответствующий диаграмме на фиг. 42, Ь, — как описывающий дви-
движение электрона по другому пути. Однако при изменении направле-
направления движения электрон ведет себя как позитрон, т. е. изменяется
знак его заряда и, следовательно, знак каждого взаимодействия
с потенциалом. Поэтому сумма матричных элементов, соответствую-
соответствующих двум таким диаграммам, равна нулю. В общем случае матрич-
матричный элемент, соответствующий замкнутой петле с нечетным числом
вершин, по аналогичным причинам равен нулю. Эта теорема принад-
принадлежит Фарри [200].
Обозначим, следуя Фейнману, сумму матричных элементов всех
диаграмм с замкнутыми петлями через L, т. е.
24" = -i, A8.27)
п
где зчак минус подчеркивает тот факт, что мы имеем дело с зам-
замкнутыми петлями. Кроме этих одиночных петель, возможно рожде-
рождение двух независимых пар, каждая из которых может сама анниги-
аннигилировать. Вклад таких пар петель равен L2/2\, поскольку в L2
каждая пара петель учитывается дважды. Поэтому полная амплитуда
перехода вакуума в вакуум есть
(Фо, 5Ф0)=1— L+f — £+...=е~ь. A8.28)
Величина L имеет бесконечную мнимую часть, соответствующую
собственной энергии вакуума; однако эта бесконечность не влияет
на нормировоч ую константу, так как вероятность того, что вакуум
останется вакуумом, дается выражением
Ь.Фо. 5Ф0)|2=ехр(—2ReL); A8.29)
вещественная часть L, вообще говоря, конечна.
Рассмотрим теперь рассеяние электрона в третьем порядке.
Кроме троекратного взаимодействия с внешним полем (фиг. 43, а),
возможно появление однократного рассеяния электрона вместе с не-
несвязанным с ним вакуумным процессом, как это показано на фиг. 43, Ь.
Матричный элемент, соответствующий переходу из состояния с им-
импульсом р в состояние с импульсом q, для диаграммы Фейнмана
на фиг. 43, b можно записать в следующем виде:
(q | S№) \p) = (q\ RW\p)@ | SW\ 0), A8.30)
Диаграммы Фейнмана 265
где {q\Rw\p)—первое борновское приближение для матричного
элемента, соответствующего однократному рассеянию, т е.
" — ■*■ ^ •>
u(q)a{q — р)и(р), A8.31)
и @ | 5B' | 0) — среднее значение матричного элемента второго порядка
5-матрицы по вакууму. Отсутствие связи между двумя частями
диаграммы на фиг. 43, b проявляется в том, что матричный эле-
элемент A8.30) представляет произведение двух множителей, не имею-
имеющих общих переменных.
"V"
ъ
Фиг. 43.
Аналогично в случае процессов более высокого порядка мы
получаем однократное рассеяние вместе с любым возможным вакуум-
вакуумным процессом. Поэтому полную амплитуду перехода из состояния
с импульсом р в состояние с импульсом q можно записать в сле-
следующем виде:
(q\S\p)^(q\R\p)@\S\0)^(q\R\p)e^, A8.32)
где @1 51 0) — среднее значение 5-матрицы по вакууму, предста-
представляемое вакуумными диаграммами Фейнмана, тогда как (q\R\p)
представляется только связанными диаграммами для процесса рас-
рассеяния, т. е. диаграммами, на которых нет несвязанных вакуумных
процессов. Величину (q\S\p) Фейнман [168] назвал абсолютной
амплитудой вероятности перехода, а величину (q\R\p)— относи-
относительной амплитудой вероятности перехода.
На деле для задачи электронов, двигающихся во внешнем поле,
мы должны вычислить L только 1 раз для заданного поля и рас-
рассматривать только матричные элементы рассеяния связанных диаграмм
[матрица R в выражении A8.32)]. Тогда абсолютная амплитуда
вероятности для данного процесса дается относительной амплитудой
вероятности | (р\ R | q) |2, умноженной на вероятность перехода
вакуума в вакуум [ехр(—2ReL)].
266
Глава 18
Аналогичная ситуация имеет место и в общем случае теории
полей. Вакуумные процессы соответствуют диаграммам, приведенным
на фиг. 44. Их матричный элемент дается выражением
(Ф0|5|Ф0> = в-в. A8.33)
В случае отсутствия внешнего поля величина L является чисто мни-
мнимой, так что вероятность перехода в вакуум равна единице.
Таким образом, если мы сосредоточиваем наше внимание на любом
реальном процессе, например на процессе, приведенном на фиг. 34,
с матричным элементом М, то в высших порядках эти же диаграммы
будут появляться вместе с несвязанными вакуумными процессами.
\ " /
\ /
\/ 1
/' \
\ /
1 f
/ \
и т.д.
Фиг. 44.
Суммирование по всем вакуумным процессам сводится к простому
умножению матричного элемента М на ехр(—L), т. е. на фазовый
множитель, по абсолютной величине равный единице. Поэтому
в дальнейшем мы можем не рассматривать все несвязанные диаграммы.
§ 4. Правила для диаграмм Фейнмана
В предыдущих параграфах мы установили одно-однозначное
соответствие между матричными элементами п-го порядка 5-матрицы
(нашими нормальными произведениями) и диаграммами Фейнмана
с п вершинами, если совпадают пространственно-временные точки
xt ... х„. Так как разложение Г-произведения включает в себя все
возможные свертки, то подобным образом существует одно-одно-
одно-однозначное соответствие между всеми возможными диаграммами с дан-
данным числом п вершин (с совпадающими точками) и нормальным
разложением Sn.
Это последнее обстоятельство и есть причина того, что концеп-
концепция диаграмм Фейнмана оказалась весьма полезной. На практике
выписываются все возможные топологически различные диаграммы*)
в соответствии с членом энергии взаимодействия. Если последний
имеет вид фГ'["р, то в каждой вершине должны встречаться две
фермионные и одна бозонная линии. Матричный элемент, соответ-
соответствующий любой диаграмме re-го порядка, можно получить,
выписывая следующие множители:
Ч Диаграммы, отличающиеся только перестановкой индексов вершин,
не рассматриваются как различные.
Диаграммы Фейнмана 267
1. (—i/hc)n из разложения по теории возмущений.
2. (GDsp в каждой вершине.
3. ll2Uckp(Xj—хг) для внутренней бозонной линии, соединяющей
точки х^- и хг.
4. [— 42Sp (хг — х/)Ц = [К+ (хг— х^)],р для внутренней фермион-
ной линии, направленной от точки Xj к точке хг. Предполагается,
что вершине хг соответствует множитель (ОГ)аа, а вершине Xj —
множитель (GDps-
5. Соответственно выбранные операторы уничтожения и рожде-
рождения ^^'(x), <>(±)(х). ?(±)(х) для каждой внешней свободной фермион-
ной или бозонной линии, выходящей из точки х или приходящей
в точку х.
6. (— 1) для каждой внутренней замкнутой фермионной петли.
7. После этого необходимо провести интегрирование по пере-
переменным xt, хг, ..., х„.
Если квантованное бозонное поле есть электромагнитное поле,
которое представляется волнистыми линиями, то множитель, отме-
отмеченный в п. 2, заменяется на следующий:
2- (вТ11)^ в каждой вершине,
а множитель, отмеченный в п. 3, — на
3. —lJ2bcDp(Xj — *i) gp.* для внутренней фотонной линии, соеди-
соединяющей ТОЧКИ Xj И Хг.
Предполагается, что множители (е^) и (е^) имеются в соответ-
соответствующих вершинах. Суммирование проводится по поляризационным
индексам (i и v.
Аналогично в п. 4 величина GT заменяется на величину е-{^, и
в п. 5 функция <р — на А.у где индекс ji совпадает с индексом мат-
матрицы fV-, действующей в той же вершине. Отметим, что мы опустили
множитель 1/ге!, поскольку рассматриваются только топологически
различные диаграммы. Ясно, что имеется п\ перестановок точек
xt ... хп между собой, которые оставляют диаграммы топологически
неизменными и различаются только индексами вершин. Это послед-
последнее замечание неприменимо к флуктуациям вакуума.
Строго говоря, если рассматривается электромагнитное поле, то
необходимо принимать во внимание дополнительное условие для
потенциалов. В представлении взаимодействия в присутствии элек-
электрических зарядов это условие можно взять (Блейлер [41)] в виде
-0. A8.34)
Однако если мы ограничиваемся рассмотрением задач рассеяния,
в которых в начальном и конечном состояниях заданы „голые"
частицы при t = =tco, то можно в целом использовать формализм,
развитый в гл. 15, § 4, поскольку эволюция системы описывается
268 Глава 18
через состояния „голых" частиц. Поэтому для задач рассеяния нет
нужды в введении какой-либо модификации дополнительного условия
(в связи с этим см. работу Кестера и Яуха [85]).
В приведенном выше рассмотрении не использовалось то, что
при отсутствии внешних полей полная энергия и импульс системы
при столкновениях не меняются. Поэтому следует ожидать, что мы
получим существенное упрощение, если перейдем в импульсное
пространство;
Глава 19
ИМПУЛЬСНОЕ ПРЕДСТАВЛЕНИЕ
§ 1. Рассеяние двух фермионов
Для иллюстрации методов, используемых в импульсном пред-
представлении, рассмотрим снова рассеяние двух фермионов. Согласно
правилам, установленным в предыдущей главе, оператор, соответ-
соответствующий диаграмме на фиг. 45, можно легко написать в простран-
пространстве координат. Он дается следующим выражением:
)Х
. x^AHxi — х2Жх2)Г<|>(х2)). A9.1)
Здесь мы еще не разложили операторы фермионного поля на опе-
операторы рождения и уничтожения. Отметим снова, что множитель 1/2!
в формуле A9.1) опущен, поскольку
имеется 2! диаграмм указанного типа,
а именно диаграмма на фиг. 45 и такая же
диаграмма с переставленными xt и х2. Если
мы рассматриваем рассеяние нуклона на Х1^ <^Сг
нуклоне, то ф должно быть оператором
рождения и ф—оператором уничтожения
нуклона. Величина 5да поэтому должна
иметь форму N(bfbb+b). Для написания Фиг. 45.
последней формулы мы использовали раз-
разложение операторов рождения и уничтожения, согласно формулам
A5.67) и A5.69). Для получения амплитуды вероятности рассматри-
рассматриваемого процесса нужно взять матричный элемент S'nn между началь-
начальным и конечным состояниями Ф1 и Ф^, соответственно. Определим
эти состояния следующим образом:
hf In Л <Ь
A9.2)
где .pjSji Ч\ГХ и J92S2> ?2r2 — импульсы и спины нуклонов соответ-
соответственно до и после столкновения. Тогда рассмотрение, аналогичное
проведенному в гл. 18 [см. формулы A8.5) — A8.12)], показывает,
2?0 Глава 19
что действие величины ф(х1)Гф(х1) сводится к уничтожению частицыf
характеризующейся переменными p1s1 в состоянии с волновой функ-
функцией w^ (р{) в исходном состоянии, и рождению частицы p2s2
->
с волновой функцией w"'(p2). Оператор $(х2)Г^ (х2) дает то же
->■
самое для частиц, характеризующихся переменными qr. Кроме того,
S'2' дает также матричный элемент обменного рассеяния, в котором
волновые функции двух частиц в конечном состоянии переставлены.
С другой стороны, мы можем в выражении A9.1) сразу заменить
операторы ty(x) и 6(х) соответствующими амплитудами свободных
частиц, которые они рождают или поглощают,
где р2 = /и2 и po = E(p)=Y p+
Тогда матричный элемент необменного рассеяния (мы сохраняем
множители hue) получает следующий вид:
he)
J d X* J d k [
X
Матричный элемент обменного рассеяния получается перестановкой
в элементе — М волновых функций конечных состояний двух частиц,
так что часть с волновыми функциями получает вид
'^-^-V"»-*»-*. A9.6)
Выполняя указанные интегрирования по переменным xt и х2, мы
получаем для матричного элемента М следующее выражение:
— 4i — k)X
X [«5 (Pg) Го«J (px)] [w% (q2) Fb w% (^)] X
i' Чтобы различать две частицы, мы используем при соответствующих
им волновых функциях дополнительные индексы а и Ь.
Импульсное представление
Мы специально оставили матричный элемент в форме A9.7), в кото-
которой его можно легко интерпретировать. Представим себе (фиг. 46),
что падающий нуклон а с импульсом pt и спином sx [волновая
функция w% (Pj)] излучает (множитель ОГ) бозонный квант с импуль-
импульсом к и затем двигается в конечном состоянии с импульсом р2
->■
[волновая функция да*а(/72)].
Дельта-функция Bic)*8W(p2— рх —[— к), возникающая при интегри-
интегрировании по переменной xt, указывает, что при излучении сохраняется
энергия и импульс. Итак, нуклон продолжает двигаться с импульсом
Рг = Pi — к. Аналогично нуклон Ъ с импульсом qt [волновая функ-
функция wr^'q{\ поглощает квант (множитель ОГ), испущенный нукло-
нуклоном а, и затем продолжает двигаться в конечном состоянии [волно-
вая функция •wr^{q^\. Благодаря на-
наличию 8-функции
— 4l — k)
энергия и импульс при этом процессе
снова сохраняются1). Функция рас-
пространения для бозе-квантов имеет
вид
1*>с 1 Фиг. 46.
причем необходимо провести интегрирование по всем виртуальным
квантам, т. е. по внутренним линиям. Величина
mi \'A
представляет нормировочные множители нуклонных волновых функ-
функций. Наконец, все выражение умножается на множитель (—i/hcJ,
возникающий при разложении на основании теории возмущений.
В данном примера мы можем выполнить интегрирование по к и
получить окончательное выражение для нашего матричного элемента
М = — Т 4^Гс 8'4> (Pi + 4i — Ра — Чг) (£ (л) £ {™)Е Ш Е (qj
х Кчр2)годаа(А)] В'^г,*;' 4)] [(q2—4iJ—
1) В старой теории возмущений энергия не сохранялась в промежуточ-
промежуточных состояниях, хотя импульс и масса сохранялась. В теории возмущений
Фейнмана и Дайсона энергия и импульс сохраняются, но масса (являющаяся
инвариантом теории) не сохраняется. В этом источник инвариантного харак-
характера теории возмущений Фейнмана. См. также работы Умэдзавы и Кавабе
[489, 493].
272 Глава 19
Выражение A9.8) с точностью до нормировочного множителя сов-
совпадает с выражением (9.43), полученным прежде; это подтверждает
правильность вывода, проведенного в гл. 9. Дельта-функция 8№
снова выражает сохранение полной энергии и импульса в данном
процессе.
§ 2. Собственная энергия нуклона
В качестве второго иллюстрационного примера рассмотрим соб-
собственную энергию нуклона. Ей соответствует диаграмма Фейнмана,
приведенная на фиг. 38, и, следовательно, следующий оператор:
S(;& = (- 0 / d*Xl I d*x2N [ф (Xl) Г (— -i 5, (Xl — x2)) X
—x2); A9.9)
матричный элемент этого оператора в импульсном пространстве при
использовании соотношения A9.3), A9.4), A7.65), A7.79) принимает
следующий вид:
"* !**• f
<
х -s <л>г
= i (-Щ-)) f ^k f d*q№ (p2 - q — k) 8W (Pl — k — q) X
X ~ (h Г jgjfe> Г- (ft) k2 _ ;2 + u (E ipZ*E (pf ■ A9.10)
Этот матричный элемент можно снова легко интерпретировать
с помощью диаграммы Фейнмана в импульсном пространстве (фиг. 47).
. Нуклон с импульсом pt (множитель
*<-'—n ws (Pt)) испускает бозон (множи-
^ тель ОГ) с импульсом к. Дельта-
Р ФУНКЦИЯ sD) (Pi — k — Ч) указывает,
что ПРИ этом процессе энергия
_ т^ и импульс сохраняются, так что
* * после излучения мезона нуклон
Фиг. 47. движется с импульсом q = рг—к.
Функция распространения для него
(обратный оператор Дирака) есть (q — m)~l. Виртуальный мезон
с импульсом к, функция распространения которого (обратный опе-
оператор Клейна — Гордона) есть (к2 — р-2). поглощается затем нукло.-
ном (множитель ОГ), причем снова сохраняются энергия и импульс
[&(*)(р2 — q — k)]. Далее, необходимо провести интегрирование по всем
Импульсное представление 273
виртуальным квантам (внутренним линиям), т. е. по переменным q и к.
Выполняя интегрирование по q, получаем
Функция 8D)(Pi—Р2) снова соответствует сохранению полной энер-
энергии и импульса. Энергия и импульс нуклона до и после процесса
одинаковы, иначе матричный элемент был бы равен нулю. Поэтому суще-
существует только диагональный элемент, для которого р—>р. Этот
единственный, отличный от нуля элемент можно переписать в не-
несколько иной форме, если учесть, что в данном случае операторы
рождения и уничтожения рождают и уничтожают частицы с оди-
одинаковыми энергиями и импульсами, так что в формуле A9.9) можно
сделать подстановку:
A9.12)
Интегрирование по переменным xt и х2 можно заменить на инте-
интегрирование по переменным xt — х2 и xt-l-x2, причем последнее
интегрирование дает величину VT, равную пространственно-вре-
пространственно-временному объему, по которому проводится интегрирование. При
этом мы получаем следующее выражение для нашего матричного
элемента: ■
4я3\4яйс/ BяK Е (р)
X^ЙЛ7
J
ыГ к*-
Пропорциональность матричного элемента М объему V обусловлена
тем, что спинорные волновые функции были нормированы в беско-
бесконечном пространстве. Если бы мы нормировали их на объем V, то
множитель V/Btc,3 не появился бы, и матричный элемент был бы
просто пропорционален времени Т. Значение указанной зависимости
от Т мы рассмотрим кратко при обсуждении собственной энергии
в гл. 20.
§ 3. Явная форма матричного элемента
Из рассмотренных выше примеров следует, что нет необходи-
необходимости сначала выписывать матричный элемент в пространстве коор-
координат. Он может быть сразу написан в импульсном пространстве.
274
Глава 19
В качестве примера рассмотрим более сложную диаграмму Фейнмана
(фиг. 48). Физически эта диаграмма представляет поправку к комп-
тоновскому рассеянию на протоне, обусловленную излучением вир-
виртуального нейтрального мезона. Вначале фермион (протон) находится
-э>-
в свободном состоянии iP8'(j91), потом рассеивается в точке а с излу-
излучением виртуального мезола, поглощает падающий световой квант
в точке Ь, поглощает обратно вир-
туальный мезон в точке с, наконец,
излучает световой квант в точке d
и затем продолжает двигаться в сво-
бодном состоянии ws*(pz). Таким
образом, диаграмма содержит четыре
Время внешних линии, которые не оканчи-
оканчиваются на диаграмме. Эти линии
соответствуют фермиону и фотону
в начальном и конечном состояниях.
Диаграмма имеет также четыре вну-
внутренних линии, а именно ab, be, cd
и ас, из которых три первых ли-
линии соответствуют распространению
фермионов, а последняя линия —
распространению виртуального ме-
мезона. Диаграмма имеет четыре вер-
вершины и, следовательно, соответ-
соответствует процессу четвертого порядка, который можно получить из
матричного элемента SD); причем последний задается формулой
Фиг. 48.
hi i f
X
,))}. A9.14)
Напомним, что на фиг. 48 не следует уделять внимания направ-
направлению во времени внутренних фермионных и бозонных линий. Однако,
чтобы выписать матричный элемент, мы должны обратить внимание
на порядок, в котором отдельные процессы встречаются вдоль
фермионной линии (причем этот порядок не обязательно должен
совпадать с последовательностью их во времени). С какого конца
диаграммы (по времени) мы должны начать, зависит от договорен-
договоренности. Оказывается, удобно начать с конечного состояния и затем
двигаться назад вдоль фермионной линии.
Напомним следующие правила, выведенные нами в предыдущих
примерах. Выпишем множители:
для каждой внутренней нуклонной линии с импуль-
1.
сом p
— т
Импульсное представление '276
2. 72~пка_ а2 для каждой внутренней мезонной линии с импуль-
импульсом к.
^' — ?2лЯк2^' для Каждой внутренней фотонной линии с им-
импульсом к, соединяющей вершины, в которых имеются матрицы fv-
и -fv-
4. е^ для излучения или поглощения в вершине виртуального
(внутреннего) фотона заряженным фермионом.
5. GY для излучения или поглощения в вершине виртуального
(внутреннего) мезона нуклоном.
,,. -> (heI/3 \
6. еу (k)-—'-jr = для каждой внешней фотонной линии, ко-
B%)/а у 2 | *01
торая излучается или поглощается в вершине (в которой имеется
матрица fty. е<х)(&)—4^-вектор поляризации (а^ =—1) излучаемого
или поглощаемого фотона с вектором энергии-импульса k [kQ = | k\;
отметим также, что A^eW (&) = 0] и поляризацией X.
1 (йсI/*
7. тг , Для каждого внешнего мезона с энергией иь, =
B«)'« уа5
"!112' который излучается или поглощается нуклоном в вер-
вершине (в которой действует оператор ОГ).
J I——— ■>
8. -q-Л/ . w8(p) для каждой внешней нуклонной линии
шульсом р i
с импульсом р и спином s, выходящей из диаграммы.
■w*(p) для каждой внешней нуклонной линии
>•
с импульсом р и спином s, входящей в диаграмму.
10. BтгL 8<*> (р — p'=tk) в каждой вершине, что соответствует
сохранению энергии-импульса для всех линий, сходящихся в эту
вершину; р и р' — импульсы фермионных линий и к — импульс вну-
внутренней или внешней фотонной или мезонной линии, кончающейся
в этой вершине.
П. (—1) для каждой замкнутой нуклонной петли.
12. (—ifhcj1 в соответствии с ге-ым членом разложения по теории
возмущений.
Далее, необходимо проинтегрировать по импульсам всех внутрен-
внутренних линий.
Применяя эти правила, мы можем сразу выписать матричный
элемент, соответствующий диаграмме на фиг. 48. Он имеет сле-
следующий вид:
М = (— Ш) f dik™ f dip* f dip* f dip* X
X [Bu)*l* 8<« (Pl — p3 — km) 8<*> <p4 — p3 — k,) X
276
Глава
X SD> (p6 — P4 — к*) SD) (Pa — P5 + k2) X
1 / m у/*—. /
X
X
(л)'
X
x
. A9.15)
При написании этого матричного элемента мы двигались вдоль
нуклонной линии, выписывая для каждого встречающегося процесса
Рьг
Рьз
'ы
Фиг. 49.
соответствующие ему множители. Отметим, что фотон, излученный
в точке d, имеет импульс —к2. Это связано с тем, что оператор
излучения имеет экспоненциальный множитель е ^ и интегриро-
интегрирование по соответствующей переменной х дает член —к2 в аргу-
аргументе 3-функции, что находится в согласии с наглядным предста-
представлением, в котором импульс к2 мы вычитаем из импульса р5,
чтобы получить конечный импульс нуклона р2. Аналогично фотон,
поглощенный в точке Ь, имеет импульс H-kt (оператор уничтоже-
уничтожения имеет фазовый множитель е~г^х). Знак импульса кт несуще-
Импульсное представление 277
ственен, если он последовательно используется в 8-функции.
Если предположить, что мезон излучается в точке а, то его импульс
в этой вершине будет + km, так что Pi = p3 + km'> тогда в вер-
вершине с мезон поглощается и, следовательно, p4-r-km = p5.
Ясно, что в нашем примере благодаря наличию 8-функций можно
провести три интегрирования по внутренним импульсам. Остаю-
Остающаяся 8-функция снова выражает сохранение полной энергии и им-
импульса для внешних линий.
Рассмотрим теперь случай двух заряженных фермионов, электро-
электромагнитно взаимодействующих между собой, как это показано на
диаграмме фиг. 49. При выписывании матричного элемента, соот-
соответствующего этой диаграмме, мы снова будем следовать вдоль
каждой фермионной линии от конечного состояния к начальному.
С какой частицы мы начнем, не играет роли, так как операторы,
относящиеся к различным частицам, коммутируют между собой.
Однако существенным является тот факт, что фотонные линии к2
и к3 пересекаются. Это означает, что следует обратить особое
внимание на правильный порядок вершинных операторов е^, так
как мы должны затем провести суммирование по их поляризацион-
поляризационным индексам. (Порядок вершинных операторов был бы несуще-
несущественен, если бы рассматривалось мезонное взаимодействие нуклонов,
для которого в этом случае вершинным оператором является
матрица ~F.) Применяя найденные выше правила, получаем следую-
следующее выражение для матричного элемента процесса [операторы
(матрицы у) Для двух частиц различаются с помощью индексов а и Ь\:
={— jLJ f d^k, j d*k2 j d^k3 f diPa3 f d*Pai f d*Pab f d*Pb3 x
X [B*)Чв w (кг + Po3 — Pal) 8W (Pa4 4- k2 — Pa3) x
X SD) (Раб — P«4 — kl) 8D) (P«2 — Р«Б — ks) X
X S<4> (p62 — p63 — k2) 8W (p63 + k3 — P&1) X
B)i-ma ia B7z)ipa3-ma a Bit)'*\E(py J
.'«,,2 ■ - X
""к' + И
-—тел i
'"•kfTft- A9Л6)
278 ' Глава 19
Здесь подразумевается суммирование по повторяющимся индексам,
а это означает суммирование по поляризациям виртуальных фото-
фотонов. Знак, который мы приписываем импульсам kj, k2, k3, снова
является несущественным. Однако надо быть последовательным при
рассмотрении сохранения импульса, т. е. рассматривать один конец
линии кванта как излучение кванта и второй конец—как его погло-
поглощение.
§ 4. Взаимодействие мезонов с электромагнитным полем
В гл. 12 мы видели, что взаимодействие заряженных бозонов
с электромагнитным полем описывается следующей плотностью
лагранжиана Л*г.
\х)9(х), A9.17)
где ср при рассмотрении квантованных полей являются операторами
поля. Если, как и в предыдущих случаях, перейти к представлению
взаимодействия и ковариантному уравнению Томонаги — Швингера,
то оказывается, что плотность гамильтониана взаимодействия, полу-
получаемая при прямом применении канонического формализма, не удо-
удовлетворяет условию интегрируемости A5.17). Канэсава и Томо-
нага [261, 262] (см. работы Неймана и Фарри [354], а также Кино-
Киносита [274], Киносита и Намбу [274]) показали, что правильное ко-
вариантное обобщение плотности гамильтониана взаимодействия
дается выражением
; а) = _ te
— « V (х) 9 (х) (^ (х) А^ (х) + [»„ (х) A» (x)f) =
х;а), A9.18)
где п^ — нормаль к пространственно-подобной поверхности а
в точке х. Отметим, что этот гамильтониан явно зависит от поверх-
поверхности а. Он сводится к обычному гамильтониану взаимодействия
в случае плоской поверхности t = const или /^ = A, 0, 0, 0). Зави-
Зависимость гамильтониана @%?i(x) от пространственно-подобной поверх-
поверхности является характерной чертой для всех видов связи с произ-
производными.
Теперь, так же, как и в гл. 16, можно ввести 5-матрицу, исполь-
используя в качестве гамильтониана взаимодействия 3%?i выражение A9.18).
Однако можно показать (Мэттьюс [327]), что при вычислении 5-мат-
рицы в этой теории зависящие от нормали члены всегда точно сокра-
сокращаются с некоторыми сингулярными выражениями, возникающими при
учете эффектов высших порядков для не зависящей от нормали
Импульсное представление 279
части гамильтониана e?t?i- В действительности, при правильном рас-
рассмотрении нужно полностью пренебречь частью, зависящей от нор-
нормали, и в то же время использовать для представления взаимодей-
взаимодействия простые правила, развитые в гл. 18. Таким образом, гамиль-
гамильтониан, который необходимо использовать, имеет вид
(х) = - le [?t (х) Ц& _ *£& 9 (х)] А- (Х) _
-«VWf(x)A'(x)^(x), A9.19)
и мы должны применять следующие выражения для сверток двух бо-
зонных множителей, содержащих производные х):
hcdhF(x-x')
• (х) д^■ (хр _ /ф -(д? (х) д^ (х') \ - \ _
~ дхг ~ \ о> \"ц; ^р ф°;"
. A9.206)
Если использовать эти формулы, то развитые раньше гра-
графические методы можно непосредственно обобщить и на данный
случай. Член порядка е в гамильтониане £?в' (х) приведет к диа-
диаграммам взаимодействия, содержащим две мезонные линии (ко-
(которые будут теперь представляться направленными пунктирными
линиями, чтобы указать знак заряда!) и одну фотонную линию
в каждой вершине, как показано на фиг. 50, а. Член взаимодей-
взаимодействия 9* (х) 9 (х) А^А* (х) приведет к одновременному излучению или
поглощению двух фотонов в вершине, как показано на фиг. 50, Ь.
Правила для получения матричного элемента, соответствующего
диаграмме л-порядка (т. е. диаграмме, содержащей п вершин), можно
снова получить с помощью применения теоремы Вика к разложению
5-матрицы для гамильтониана взаимодействия A9.19) (см. работу
Рорлиха [405], где это проведено детально). Отметим, что в дан-
данном случае вклад «-порядка в ^-матрицу содержит члены всех
порядков между еп и еш.
По полученным правилам в импульсном пространстве выписы-
выписываются следующие множители:
^ Согласно приведенным правилам, опускаются сингулярные выражения,
возникающие при дифференцировании сингулярных функций (Мэттьюс [327] и
Рорлих [405]).
280 Глава 19
1. —е{Р9.~\~р'9) в каждой одиночной вершине, где р^ и р'—им-
р'—импульсы мезонной линии для входящего и выходящего из вершины
мезона соответственно.
2. Bк)*3D'(р — p'rtk) в каждой одиночной вершине, где р и
р' — импульсы соответствующих мезонных линий и к — импульс
внутренней или внешней фотонной линии, кончающейся в этой вер-
вершине (знак плюс или минус берется в зависимости от того, излу-
излучается фотон или поглощается).
3. е2 B-irL gj^SW (р — p'rtkztk') в каждой двойной вершине
(т. е. вершине, в которой поглощаются или излучаются две фотон-
фотонные линии с поляризациями jx и v). Каждому фотону, излучаемому
или поглощаемому в двойной вершине, придается соответствующий
ему множитель (см. правила 4 и 6).
Фиг. 50.
^' —Bд^ кз"&?■'> для Каждой внутренней фотонной линии с им-
импульсом к, соединяющей вершины, в которых имеются множители
(р-\-р'У и (р-\-р'У для каждой одиночной вершины, множители gv-P
и g™ в случае двойной вершины (индексы р, а относятся ко вто-
второму фотону, излучаемому или поглощаемому в двойной вершине)
и множители (p-\~p')v-vi g1? в смешанном случае.
5. 2 2 2 для каждой внутренней мезонной линии с им-
импульсом р.
(X) ■*■ (heI!* 1
6. гу(к) —^— для каждой внешней фотонной линии, ко-
торая излучается или поглощается в одиночной или двойной вер-
шине; &р. (k) — 4-вектор поляризации [8^=—1, k^(k) = 0] излу-
излу\
8^^
чаемого или поглощаемого фотона с энергией ko = \k\, импуль-
импульсом к и поляризацией X.
EсI'1 1
7. '— для каждой внешней мезонной линии с импуль-
_^B«)/« Y^ic
сом k и энергией шк = Y~k2-\-p2, входящей или выходящей из диа-
диаграммы.
Импульсное представление 281
8. (—i/hc)n из разложения по теории возмущений.
Наконец, следует проинтегрировать по всем внутренним им-
импульсам и умножить интеграл на весовой множитель w = 2§Ё, где
g=d — а — Ь\
здесь d—число двойных вершин на диаграмме, а — число замк-
замкнутых фотонных линий (соответствующих тому случаю, когда один
и тот же фотон излучается и поглощается в двойной вершине) и b —
число пар двойных вершин, соединенных двумя фотонными линиями.
§ 5. Поперечные сечения: комптоновское рассеяние
Правила, выведенные в этой главе, дают нам возможность вы-
выписать матричный элемент, соответствующий любой заданной диа-
диаграмме Фейнмана, а следовательно, и вычислить 5-матрицу. Матрич-
Матричный элемент ^-матрицы между заданными начальным и конечным
состояниями является амплитудой вероятности перехода из дан-
данного начального состояния в данное конечное состояние. Запишем
эту амплитуду перехода в следующем виде:
M'\a), A9.21)
где мы явно выписали 8-функции, соответствующие сохранению
полной энергии и импульса во время процесса (£ро— 4-импульс
всех падающих частиц, £р6—4-импульс всех выходящих частиц).
В гл. 9 был уже рассмотрен случай не зависящего от времени
внешнего поля. В этом случае импульс не сохраняется, так что
амплитуда перехода имеет следующий вид:
ТЬа = — 2кЙ« (Е роа — Е pob) (b\M'\a). A9.22)
Способ получения поперечных сечений для этих случаев был кратко
описан в гл. 9, поэтому мы рассмотрим только положение, в кото-
котором отсутствует внешнее поле.
Вероятность перехода из состояния а в состояние Ь, очевидно,
дается выражением
|7"»в12 = B*У»8(*>(О)8(*>(Ерь —ЕРа) \{Ъ\М'\а)\\ A9.23)
Причина того, что эта вероятность бесконечна [множитель §<*> @)],
связана с тем, что наши волновые функции не нормируемы. Для
выхода из этого положения необходимо построить волновой пакет
для падающих и выходящих частиц (Снайдер [455]). Вместо этого
мы, следуя Липману и Швингеру [307], снова заменим множи-
множитель §<4) @) на соответствующий множитель Bir)-4VT, где V—
(большой) объем и Т — (длительное) время, в течение которого
происходит процесс рассеяния. Вероятность перехода в единицу
282 Глава 19
времени в единице объема в некоторую совокупность конечных
состояний, плотность которых р6, дается тогда следующим выра-
выражением:
/ р6 — £ Ра) | (* | М' | а) |». A9.24)
Поперечное сечение можно получить из величины wba, если разде-
разделить ее на поток падающих частиц, пересекающих единичную пло-
площадь в 1 сек.
Для иллюстрации применения формулы A9.24) вычислим попе-
поперечное сечение рассеяния фотона на свободных электронах (компто-
новское рассеяние) в низшем приближении теории возмущений.
Имеются две диаграммы Фейнмана *), дающие вклад в низшее
приближение. На первой из них электрон в состоянии p1sl погло-
погло(k)
щает фотон с импульсом kj и вектором поляризации e'Xi> (kj) и из-
излучает второй фотон с импульсом к2 и поляризацией eP*>(k2)t пере-
переходя при этом в конечное состояние с импульсом р2 и спином s2.
Во втором процессе акт излучения конечного фотона предшествует
акту поглощения начального фотона. Используя правила, выведен-
выведенные в § 3, легко проверить, что матричный элемент, соответствую-
соответствующий этим диаграммам Фейнмана, имеет следующий вид:
Pi— kt) (p2s2, к2е21 М' | РЛ, к^); A9.256)
здесь (поскольку не возникает неясностей) мы записали в^)^) как
et и «(Aj) как ш1; аналогично для е2, w2 и ^j, £2. В формуле
A9.25а) г0 есть классический радиус электрона е2/4птс2. Этот
множитель получен следующим образом: если применить правила
§ 3, то в формуле A9.25а) возникнет численный множитель а/2ти;
если нормировочный множитель волновой функции фотона
\\
фу ф ||
выразить через энергию фотона hc\k\, то при этом мы получим
в числителе дополнительный множитель йс, который вместе с мно-
множителем т переводит величину а в величину г0. Множитель т2
в числителе появился следующим образом: один множитель т воз-
возник из нормировочного множителя волновой функции электрона,
второй — при переходе от величины а к величине г0. Поскольку мы
!' Эти диаграммы приведены на фиг. 36, а для случая взаимодействия
мезона и нуклона,
Импульсное представление 283
приняли систему" единиц, в которой Ь = с = 1, йсо — энергия фотона
обозначается через ш = | k |.
Множитель в фигурных скобках в формуле A9.25а) обозначим
через R. Величину R можно упростить, если учесть, что электрон
и фотон являются свободными, т. е.
р? = р^ = от2, A9.26)
а также
k? = k2 = 0, A9.27а)
кх ■ s1 = k2'-e2 = 0. A9.276)
Мы достигнем дальнейшего упрощения результатов, если выберем
систему координат, в которой электрон вначале покоился, т. е.
в которой р1 = (/ге, 0, 0, 0). Выберем также такие векторы поля-
поляризации, которые имеют только пространственные компоненты;
этого всегда можно достичь с помощью подходящего калибровоч-
калибровочного преобразования (см. гл. 15, § 5). Вследствие такого выбора
калибровки имеем
Pl-e1 = p1.e2 = 0, A9.28)
поскольку вектор р1 имеет только временною компоненту, а век-
векторы 8 — только пространственные компоненты. Наконец, отметим,
что оператор R действует справа на дираковскую волновую функ-
функцию, являющуюся собственной функцией оператора ру с собствен-
собственным значением т. Используем перестановочные соотношения для
матриц -у
■^ _|_ .рр = 2gt", . A9.29)
чтобы написать
(Y • Pi)(T ' Bi) = — (Y • »i)(T • Pi) + 2pi • V A9.30)
Однако второй член равен нулю вследствие соотношения A9.28).
Аналогично можно показать, что произведение у ■ Pi антикоммути-
рует с произведением у • ^г- Используя эти результаты, можно ис-
исключить члены Pi-\-m, встречающиеся в выражении R. Наконец,
используя формулу A9.276), мы можем написать
(p2+.k2_Pl-kl) _
Для получения вероятности перехода необходимо возвести вели-
величину ТЬа в квадрат. Если нас не интересует спин электрона в ко-
конечном состоянии и мы ограничиваемся случаем, в котором в началь-
начальном состоянии имеются неполяризованные электроны, то, как бы-
ло видно в гл. 9, суммирование величины | ■до8а(/>?) Rw3^(pl)\2 по
284 Глава 19
индексу s2 и усреднение по индексу Sj соответствует вычислению
некоторого шпура. Несколько громоздкие вычисления приводят
тогда к следующему результату:
T A9.32а)
A9.326)
A9.32b)
A9.32r)
где при переходе от формулы A9.32в) к формуле A9.32г) мы ис-
использовали то, что в лабораторной системе координат рх = (т, 0, 0, 0),
а в есть угол между направлениями поляризации падающего и
излученного фотона. Выражение A9.32г) представляет существенную
часть формулы Клейна — Нишины (Клейн и Нишина [278], Ни-
шина [358], Тамм [478], см. также книгу Гайтлера [232]).
Для вычисления поперечного сечения процесса мы должны знать
плотность падающих частиц. Последнюю можно получить при рас-
рассмотрении плотности 4-мерного тока в начальном состоянии элек-
тронно-позитронной системы и вектора Пойтинга в случае электро-
электромагнитного поля. Рассмотрим среднее значение оператора 4-мерного
тока в начальном состоянии &£ (pt) Фо, в котором имеется один
электрон с импульсом pt и спином st:
Ясно, что при разложении входящих в ток операторов по опера-
операторам рождения и уничтожения для определенных импульсов и спи-
спинов вклад в матричный элемент A9.33) будут давать только члены,
пропорциональные bfb, откуда следует, что
( U (х)) = * (bt, (Pi) Фо. ¥* (х l *
A9-34)
где v^ — скорость падающей частицы. Следовательно, плотность
падающих электронов равна 1/Bя)8; эта величина является стан-
стандартным весовым множителем при нормировке на 5-функцию. Ана-
Аналогично легко показать, что плотность падающих фотонов также
равна 12K
Импульсное представление 285
Величина wba, даваемая формулой A9.24), является вероятно-
вероятностью перехода в единице объема в единицу времени для полученной
выше плотности падающих частиц. Для получения вероятности на
единицу плотности падающих частиц мы должны разделить вели-
величину wba в данном случае на величину 1/BтсN. Вероятность пере-
перехода в некоторую совокупность конечных состояний, плотность
которых
*P A9.35)
дается поэтому выражением
«1 ■» 2 = rl J d*k2 J d?PiW> (р2 + k2 — Pl — kt) E™^ F. A9.36)
(Множители 2тс сокращаются следующим образом: величина | ТЬа |а,
согласно формуле A9.31), дает вклад Bтс)-10; величина wba, со-
согласно формуле A9.24), имеет множитель Bir)* и падающий ток —
множитель BяN.)
Проведя интегрирование по dsp2, мы можем теперь исключить
8-функцию, зависящую от импульсных переменных, так что
F, A9.37)
где Ei~Pio~\-kio — полная энергия системы в начальном состоянии
и \£/.=р2о+k20 — полная энергия системы в конечном состоянии.
Запишем элемент импульсного пространства в следующем виде:
dEf. A9.38)
Теперь можно выполнить интегрирование по dEf и, таким образом,
устранить последнюю оставшуюся 8-функцию, зависящую от энер-
энергии. Наконец, мы получаем
Отметим, что интегрирование по dsp2 определяет импульсы частиц
в конечном состоянии через импульсы частиц в начальном состоянии
с помощью закона сохранения импульса; аналогично интегрирование
по dEf определяет полную энергию в конечном состоянии с по-
помощью закона сохранения энергии.
Выполним теперь дифференцирование, указанное в выражении
A9.38). Учитывая, что в лабораторной системе координат
Ef = u>2 -j- E2 = о)! + Ег = ю2 -f Vp\ -|- от2 =
= иJ-|-угш2—2u>lU>2 cos cp + ш|+ /га2, A9.40)
и используя соотношение Комптона
u^w^l—cos cp) = m (coj — oJ), A9.41)
286 Глава 19
мы получаем
dEf <О2 — <°i cos 9 £2 + m2 — °>i cos 9
1Н
— cosy) __т wx П9 42)
Вероятность перехода, при котором рассеянный фотон излучается
в телесный угол dQ с энергией о>2, дается тогда выражением
AJM3)
Дифференциальное поперечное сечение da определяется как вероят-
вероятность перехода, деленная на падающий поток (с=1) и на число
рассеивателей в единице объема [т/Е(рх)]. Следовательно, оно
дается выражением
da = rU^Jm2F dQ; A9.44)
это хорошо известная формула Клейна—Нишины.
Рассмотрим здесь только поперечное сечение в нерелятивист-
нерелятивистском пределе, т. е. в случае, ' когда а>1=ш2<^от и Pi = P2 =
= (/к, 0, 0, 0). В этом пределе формула A9.32г) сводится к сле-
следующей:
и дифференциальное поперечное сечение получает вид
danr = r\ cos2 QdQ; A9.46)
это есть классическая формула Томсона для рассеяния излучения
с малой энергией на статическом заряде. Дифференциальное попе-
поперечное сечение для неполяризованного света можно получить, про-
просуммировав по двум поляризациям фотона в конечном состоянии
и усреднив по двум начальным состояниям. Это суммирование
может быть легко выполнено 1); оно дает следующий результат:
l A9.47)
О Напомним, что 3-векторы еA) (А), еB) (А), А/1 ft | являются взаимно ор-
ортогональными, так что для них имеет место соотношение
V (*) £>
где индексы г, s = 1, 2, 3 означают комповенты векторов. Мы можем
поэтому написать
2
£<*> (fa е(Х) (% — 3 — -^*2.
Таким же образом легко проверить, что
Импульсное представление 287
где ср — угол между векторами kt и k2, т. е. угол рассеяния. Пол-
Полное поперечное сечение теперь получается путем интегрирования по
телесному углу dQ и равно
а = 4^го\ A9.48)
В гл. 24 мы увидим, что формула A9.48) (формула томсоновского
рассеяния) играет важную роль в понимании перенормировки заряда.
В заключение этой главы отметим, что вследствие унитарности
S-матрицы имеют место определенные соотношения между ее чле-
членами различного порядка. Так, если мы разложим S-матрицу в сте-
степенной ряд по константе связи, как это имеет место в случае раз-
разложения Дайсона, т. е.
S=\-\-eS1-\-esS2-\- ..., A9.49)
то условие унитарности S-матрицы получает вид
tSx -4- S^ -
+ «* (Sfs8 4- sts2 4- stsx + st 4- 5 j
+ ... A9.50)
и каждое выражение в круглых скобках должно равняться нулю.
Полученные соотношения между величинами Sn оказываются очень
полезными при проведении расчетов (см., например, работу
Йоста и др. [253]).
- ^ [>) (X) .T<w (M = 1
где <р — угол между векторами At и А2, т. е. угол рассеяния.
РАЗДЕЛ IV
ПЕРЕНОРМИРОВКА
В КВАНТОВОЙ ТЕОРИИ
ПОЛЯ
19 Зак. 1784. Мезоны "и поля
Г л а в а 20
СОБСТВЕННАЯ ЭНЕРГИЯ ФЕРМИОНА
§ 1. Степень расходимости
При разложении 5-матрицы мы видели, что один из возможных
процессов второго порядка соответствует излучению, а затем по-
поглощению фермионом виртуального бозона. Диаграмма Фейнмана,
соответствующая этому процессу, вновь приведена на фиг. 51.
Фиг. 52.
Фиг. 53.
Матричный элемент такого процесса был уже выписан ранее A9.13);
он имеет вид
М =
4-iztic
Г /и
■„ , , w
Е(р)
'<?>/
ХГгг
1
,_^ + /./- V". B0Л)
где волновые функции нормированы на объем V. Обозначим через
следующий оператор:
G2
. Г г 1
•» п — к — 1
B0.2)
Может случиться так, что диаграмма на фиг. 51 является частью
некоторой большой диаграммы, так что две внешние фермионные
линии будут соответствовать фактически функциям распростра-
распространения фермиона. Множители, соответствующие такой внутренней
части, даются тогда выражением
--*— £B) (р) -^— •
р — т
Собственная энергия фермиднй
Чрезвычайно важно понимать, что диаграмму на фиг. 51 всегда
можно рассматривать как модификацию функции распространения
свободной частицы (р — /и) (фиг. 52) с помощью добавления
дополнительного члена, который соответствует диаграмме на фиг. 51.
Модифицированная функция распространения тогда соответствует
диаграмме на фиг. 53 и аналитически дается множителем
B0.4)
р — m р — m 4я3 р —
Согласно теории Фейнмана, в случае свободной частицы функ-
функция распространения B0.4) должна описывать изменение волновой
функции частицы во времени. Мы знаем также, что волновая функ-
функция свободной частицы зависит от времени только через множи-
множитель ехр [—lE(p)t], где Е(р) = YР2 + "^- Таким образом, изме-
изменение волновой функции свободной частицы, обусловленное опера-
оператором SB), может соответствовать только изменению величины Е(р).
Далее, если матричный элемент B0.1) эквивалентен эффекту собст-
собственной энергии, т. е. изменению энергии частицы на величину АЕ,
то амплитуда перехода из начального состояния в конечное изме-
изменится на множитель ехр( — iAET) или в первом порядке на вели-
величину —1АЕТ. Поэтому имеем
— tAET = ^-sT^w(p) £<2> (р) w (р)
или
Д£ = -Ьщ, ™(^} IB) (p) w fpy B0>5)
Конечно, эффекты собственной энергии возникают не только из
простого дополнительного члена B0.2), но и из более сложных
диаграмм. К этому вопросу мы вернемся в следующей главе.
Вычислим теперь величину АЕ. Здесь для наших целей доста-
достаточно применить нековариантное рассмотрение, в котором при
интегрировании выражения B0.1) сначала выполняется интегриро-
интегрирование по dk0.
Ниже в этой главе мы вычислим выражение B0.1) с помощью
более современных методов, данных Фейнманом [169]. Для выпол-
выполнения интегрирования перепишем интеграл B0.2) в следующем
виде:
£B, (р) = ga Г
*г *<+■„• B0-6)
где ^ = G2/45
Глава
Кроме того, величина
— АJ + т2 B0.7)
представляет энергию нуклона в промежуточном состоянии, так что
знаменатель функции распространения нуклона в формуле B0.6)
имеет вид
""*" " ' -ko]2 — is. B0.8)
Аналогично можно написать
B0.9)
ь
X
а
х
X
а
X
с
Фнг. 54.
эта величина представляет энергию мезона в промежуточном состоя-
состоянии, так что знаменатель функции распространения мезона имеет
вид
Ш2ф-) — ьг. B0.10)
Таким образом, интеграл B0.2) можно переписать в следующей
форме:
р —к + т
» — к) — (&о — Е (р) J — /е] [со" (к) — к — it]
XV dsk dk f20 1я\
Если выполнять интегрирование в комплексной плоскости k0, то
необходимо учесть, что имеются четыре полюса, показанные на
фиг. 54. В частности, мы имеем:
Для полюса а: А0 = -(-ш(&) — is,
d: kQ = E(p) — E(p —
Собственная энергия фермиона 293
Если мы интегрируем по вещественной оси k0, то мы можем зам-
замкнуть контур интегрирования либо в верхней полуплоскости, либо
в нижней. Оказывается более удобно выбрать нижнюю полупло-
полуплоскость, т. е. обходить полюса awe. Поскольку выражение B0.2)
ведет себя при больших k0 как &J, то вклад в интеграл дают
только вычеты в полюсах. В явном виде вклад полюса а пропор-
пропорционален величине
4 = +Г~ + ^~+ ' B0.11)
2ш (ft) [Е (р-к) + «"(*) - Е (р)] [Е 0> — ft) — «(ft) + Е (р)]
а вклад полюса с пропорционален величине
B0.12)
Если написать
B0.13)
то выражение для £<2> можно переписать в следующей форме:
1B) = 2та^ J d3kJ = 2Ttig-2 J (jt _(_. y2 _ уз) d3A> B0.14)
где
*} B0.15)
*)]/„}. B0.16)
Чтобы показать поведение величины £<2) в простом случае, рас-
рассмотрим в дальнейшем случай Г= ^5 и предположим также, что
фермион покоится, т. е, р = 0. Предположение Г = f5 ведет к тому,
что член J1 в матричном элементе. wiP^ts} равен нулю. Это можно
показать следующим образом: матрица у5 антикоммутирует со
всеми матрицами ~(?, встречающимися в операторе р, поэтому мы
можем написать
«ЧР)Т
(
m)w(p). B0.17)
Поскольку рассматриваемая частица является свободной, то
(р—/re) w {р) = 0 и, следовательно, соотношение B0.17) равно нулю.
Кроме того, так как матрица -fs антикоммутирует с матрицей у>
можно написать
шТв* • АТбш = 0»Т°>)' & Тб = — 1- B0.18)
Однако из нашего рассмотрения в гл. 4 мы знаем, что величина
— ->-->■ -> -*-
w (p) fw (р) равна нулю, если /7 = 0, Итак, предположение р — 0
294 Глава 20
ведет к тому, что член J2 в матричном элементе wl?w будет также
равен нулю. Таким образом, для рассматриваемого специального
случая вклад дает только член J3. В частности, матричный элемент
wJ3w равен
wj,w = _ {о, (Л) /а + \Е (р) + Е (р — %)] /а) ^Tow. B0.19)
>
Так как Wfo'22'— *> если р = 0, то, используя простые дроби, можно
переписать выражение B0.19) в следующем виде:
= __1 Г
4£ (р-1) IE (р-
*) + <■> (Л) — ^ (Р) £ (Р - 2) —
B0.20а)
■даУдте; = ^—^г- —^—-+ ^—+ •
4E(p-ft) lE(p-k) + «>(k)-E(p) E(p-k) + E(p) + «>(k)]
B0.206)
Появление множителя l/E(p — k) следовало ожидать. В старой
теории он возникал вследствие использования проекционных операторов
для разделения состояний с положительной и отрицательной энергией;
фактически множители в выражении B0. 20 6) непосредственно связаны
со старой теорией возмущений. Мы уже отмечали, что Е(р-—к)
есть энергия фермиона в промежуточном состоянии и со(&) — энергия
мезона в промежуточном состоянии. Следовательно, величина
[Е (р—k)-\-o>(k)\ есть полная энергия системы в промежуточном
состоянии, а величина [Е{р — k)~\-a>(k) — Е(р)] — разность энергий
промежуточного и начального состояний; именно этот вид знаменателя
и следовало ожидать. Члены, которые сократились в выражении B0. 20),
•> +■
содержали величину [<»(£) — Е{р—k) — Е(р)] в знаменателе, т. е.
относились к частицам с отрицательной энергией в промежуточном
состоянии. Необходимо рассмотреть также член с \Е{р — k)-\-E{p)-\-
-j- о) (£)]. Он представляет переход из состояния с отрицательной
■*■■*■
энергией —Е (р — k) в промежуточное состояние, в котором имеется
нуклон с энергией Е(р) и мезон с энергией а>(£); в этом случае
знаменатель
Этот член должен был бы представлять в выражении для соб-
собственной энергии абсолютный вакуум. Однако в действительности
Собственная энергия фермиона 295
промежуточное состояние, в котором нуклон имеет энергию -\-Е(р),
уже занято реальным нуклоном. Таким образом, этот специфический
переход не может иметь места, и собственная энергия вакуума в
итоге уменьшается, что и дает знак минус перед соответствующим
членом в формуле B0. 20).
Для получения величины Ь.Е нужно [см. выражение B0. 14)] еще
выполнить интегрирование по трехмерному пространству к, т. е.
взять интеграл / J3kzdk. Этот интеграл расходится. При больших k
.->-»--»-•>■-
величины Е(р — k) и [Е(р — k)-\-u>(k) — Е(р)\ возрастают как пер-
-> -»-
вая степень к, а величина [Е(р — k)—со(k)-\-E(p)] стремится к по-
постоянному значению Е(р). Таким образом, наиболее сильная рас-
расходимость могла бы возникнуть из членов с отрицательной энергией
в выражении B0. 20), которые имелись бы в однонуклонной теории,
но сокращаются в теории дырок. Тем не менее оставшиеся члены
ведут себя как (k2/k2)dk при больших k, что приводит к линейной
расходимости. Однако два оставшихся члена в выражении B0.20)
имеют противоположные знаки, так что в действительности интеграл
оказывается расходящимся не линейно, а логарифмически. Следова-
Следовательно, в теории дырок собственная энергия расходится логариф-
логарифмически.
То, что собственная энергия должна быть бесконечной, было
выяснено давно — уже в 1929 г. Тогда Гейзенберг и Паули [222, 223]
указали на .это, а Валлер [505], Оппенгеймер [359], Розенфельд [412]
и др. вычислили собственную энергию электрона в теории Дирака
для одного электрона и нашли, что его собственная энергия рас-
расходится квадратично. В 1934г. Вайскопф [515,516] произвел новый
расчет собственной энергии электрона, используя теорию дырок Ди-
Дирака, и нашел, что расходимость является только логарифмической.
Большинство выполненных ранее расчетов собственной энергии
были более сложными, чем приведенные в данной главе (ср. работы
Умэдзавы и Кавабе [489, 492] и Гупта [217]). В частности, при расчете
электромагнитной собственной энергии обычно разделяли электро-
электромагнитное поле на вклад статического кулонова поля и поперечных
электромагнитных волн1', что возможно в нерелятивистском пределе,
где вклад статической части преобладает. Поэтому было опубли-
опубликовано много работ, в которых вычислялись вклады отдельных
частей поля в собственную энергию и обсуждался их физический
смысл (см., например, работу Вайскопфа [518]).
§ 2. Попытки сделать собственную энергию конечной
Важно сравнить собственную энергию, встречающуюся в кванто-
квантовой электродинамике, с собственной энергией, встречающейся в кла.о
См., например, книгу Гайтлера [232].
296 Глава 20
сической теории излучения 1\ и понять различие между ними.
Простейшим путем введения собственной энергии в классическую
электродинамику является отождествление ее с электрической и маг-
магнитной энергией собственного поля электрона. В другом подходе
учитывается то, что собственное поле электрона делает более
затруднительным ускорение электрона во внешнем поле; это экви-
эквивалентно появлению у электрона дополнительной массы (Лоренц
[309, 310]). Эта собственная масса дается выражением, аналогичным
выражению для собственной энергии, однако между ними имеется
определенное различие, которое вызывает значительные затрудне-
затруднения в классической теории собственной энергии. В классической
теории собственная энергия (с точностью до численного множителя)
равна e2jr0, где г0—„радиус" электрона. Таким образом, точечный
электрон имеет бесконечную собственную энергию.
Если приписать электрону конечный радиус, то выражение для
взаимодействия поля с электроном будет содержать форм-фактор,
который будет существенно отличаться от единицы тогда, когда
длина волны % будет приблизительно равна радиусу. г0- Положив
B0.21)
мы увидим, что классическая собственная энергия е2/гс пропорцио-
пропорциональна величине АМакс> т. е. мы получаем линейную расходимость
по k. О величине kM&R0. обычно говорят как об обрезании.
Очень широко распространенная в свое время теория при-
приписывала внутреннюю массу электрона энергии взаимодействия
(Абрагам и Беккер [1]). В этом случае электронный радиус равен
'; B0-22)
эту величину обычно называют .классическим радиусом электрона"
(.см., однако, работы Пуанкаре [392—394], где рассмотрены недо-
недостатки этой модели).
В лротивоположность классической теории собственная энергия,
вычисленная на основании теории дырок Дирака, пропорциональна
величине
Ч^) - B0-23)
т. е. расходится только логарифмически. Кроме того, в квантовой
теории собственная энергия зависит от массы покоя электрона т,
тогда как в классической теории величина т вообще не входит
в выражение для собственной энергии. Это важное различие вновь
указывает на то, что проблема собственной энергии в квантовой
теории имеет совсем другую природу, чем в классической теории.
1) См., например, обсуждение в книге Гаитлера [232].
Собственная энергия фермиона 297
Серьезные отклонения от классического поведения начинаются уже
на расстояниях порядка комптоновской длины волны t/mc, что
является наиболее важным. Классический радиус электрона в 137 раз
меньше, чем комптоновская длина волны электрона. Таким образом,
если мы будем рассматривать все более и более малые расстояния,
то необходимо принимать во внимание квантовые эффекты прежде,
чем скажутся возможные эффекты классического радиуса электрона;
поэтому маловероятно, что решение классической задачи собствен-
собственной энергии окажется или необходимым, или достаточным для реше-
решения квантово-механической задачи.
Если в теории дырок Дирака мы припишем большую часть массы
электрона его собственной энергии, то, согласно формуле B0.23),
мы должны постулировать радиус обрезания порядка
*„*>. =-Ш'-™' B0-24)
Следует принять во внимание, что на расстояниях, гораздо больших,
чем даваемое формулой B0.24), а именно на расстояниях порядка
комптоновской длины волны мезона й/|лс, могут рождаться вирту-
виртуальные мезоны, которые в свою очередь могут сильно взаимодей-
взаимодействовать с виртуальными нуклонами. Таким образом, квантовая
электродинамика может оказаться неприменимой гораздо раньше,
чем будут достигнуты энергии, соответствующие расстояниям,
вычисляемым по формуле B0.24). Отметим, что причиной неприме-
неприменимости квантовой электродинамики может быть то, что начинают
играть роль не только электромагнитное и электронно-позитронное,
но и другие поля.
Несмотря на различие между классической и квантовой теориями,
были предприняты многочисленные попытки найти такую формули-
формулировку классической теории Максвелла-Лоренца в присутствии точечно-
точечного заряда, в которой не было бы расходимостей. Существовала
надежда, что "если бы удалось построить классическую электро-
электродинамику, в которой не было бы трудностей с бесконечной собствен-
собственной энергией и конечными собственными натяжениями (разрывающийся
электрон), и если бы эту теорию удалось проквантовать, то проблема
построения внутренне последовательной квантовой электродинамики
могла бы быть решена. Было много успешных попыток построить
такую классическую теорию, но ни одна из них ничего не внесла
в решение квантовой задачи.
Так, например, Вентцель [522,523] *) пытался рассматривать
точечный заряд как предельный случай, в котором пространст-
пространственно-подобный вектор (радиус электрона) стремится к нулю.
С другой стороны, Дирак [ПО, 111] 2> пытался использовать сущест-
1) См. также его книгу [525].
2) См. также работу Елизера [146], где дан обзор предыдущих работ.
298 Глава 20
вование у уравнений Максвелла запаздывающих и опережающих
решений. Он определил „собственное" и „внешнее" поля как полу-
полусумму и полуразность соответственно запаздывающего и опережаю-
опережающего полей. Это разделение полей является инвариантным. ■ Он
допустил, что теория Максвелла-Лоренца описывает поле вплоть
до точечного электрона, и показал, что члены, которые приводят
к бесконечностям, можно вычесть лоренц-инвариантным способом.
Это соответствует вычитанию собственного поля из полного поля
для получения силы, действующей на данный электрон. Способ
вычитания не нарушает никаких законов сохранения; кроме того,
правильно принимается во внимание реакция поля излучения на дви-
движение электронов. Однако в этой классической теории Дирака сво-
свободный электрон может двигаться самоускоренно. Поэтому эта тео-
теория является неудовлетворительной.
Другой возможной в классических рамках теорией, тесно связан-
связанной с приведенной выше классической теорией Дирака, является
теория действия на расстоянии, предложенная Уилером и Фейнманом
[529, 530]. В этой теории электромагнитное поле снова инвариантно
разбивается на собственное и внешнее поля. Однако постулируется,
что собственное поле данного электрона не действует обратно на
частицу, которая его порождает. Поэтому в этой теории не суще-
существует понятия собственной энергии частицы. Формализм развит как
теория .действия на расстоянии, в которой поля являются просто
вспомогательными понятиями, не имеющими собственных степеней
свободы. Авторы проинтегрировали уравнения движения частиц, так
что поля явно не проявляются. В этой теории требуется, чтобы
взаимодействие между частицами осуществлялось полусуммой запаз-
запаздывающего и опережающего полей. С этой точки зрения, реакция
излучения возникает вследствие действия статистического механизма
(в отличие от чистой электродинамики) в мире, в котором все
испущенное излучение в конце концов поглощается.
Другой очень интересной теорией точечного электрона является
теория Штюкельберга [462, 463], в которой получается не только
конечная собственная энергия, но и равное нулю внутреннее натяже-
натяжение. Вследствие кулоновского отталкивания точечный заряд стре-
стремится разорваться, что ведет к бесконечной собственной энергии и
конечным собственным натяжениям. Идея Штюкельберга состоит
в том, что в дополнение к электромагнитному взаимодействию суще-
существует другое взаимодействие, характеризуемое „новым" (т. е. ме-
зонным) зарядом; эффект этого взаимодействия проявляется в при-
притяжении одинаковых зарядов, полностью уничтожающем кулоновское
отталкивание. Он постулировал взаимодействие электрона с коротко-
короткодействующим скалярным полем, в случае которого две одинаковые
частицы притягиваются друг к другу. Короткий радиус действия
новых сил необходим для того, чтобы не было наблюдаемых эф-
эффектов при взаимодействии расположенных далеко друг от друга
Собственная энергия фермиона 299
зарядов. Если константа связи со скалярным полем равна /, то
Штюкельберг нашел, что при е2=/2 полная классическая собствен-
собственная энергия конечна, а собственное натяжение равно нулю.
Бопп [49], Ланде и Томас (см. работы [296 — 298]) развили теорию,
аналогичную теории Штюкельберга, но вместо скалярного поля они взя-
взяли векторное. Хотя векторное поле приводит к отталкиванию между
частицами одного заряда, они предположили, что следует вычитать
полную энергию векторного поля из полной энергии электрона.
При этом компенсация возможна, но энергия не является более
положительно-определенной.
Фактически первой релятивистски и калибровочно инвариантной
теорией, дающей конечное собственное натяжение и конечную соб-
собственную энергию в классическом случае, была теория Борна [51,
52, 54] и Инфельда. В этой теории уравнения Максвелла заме-
заменены системой нелинейных уравнений, которые переходят в уравне-
уравнения Максвелла в пределе слабых полей. Квантование в этой теории
становится почти невозможным из-за ее нелинейности. Кроме того,
все же остаются сингулярности в величинах, описывающих поле
в присутствии точечных- зарядов.
Нелинейные унитарные теории поля -1) были предложены Ми 2\
Розеном(см. работы [407—409]), Джелом(не опубликовано, 1947/48 г.),
Финкельштейном(см. работы [177, 178]) и Дреллом [122]. В унитарной
теории поля частицы возникают не как сингулярности, а как малые объ-
объемы, в которых сконцентрированы энергия и заряд поля. В такой теории
уравнения движения частиц следуют из уравнений поля.. Именно
в этом отношении унитарная теория отличается от теории, в ко-
которой частицы представляются сингулярностями поля. В последнем
случае уравнения поля становятся неприменимыми в этих сингуляр-
ностях, и поэтому вообще нельзя определить движение частиц.
Унитарная теория должна быть обязательно нелинейной, поскольку
одна частица не может действовать на другую, если уравнения
линейны. Если в этой теории мы фиксируем заряд частицы, то от-
отсюда будет однозначно следовать дискретный спектр масс. Розен
(см. работы [407, 408]) и Джел (не опубликовано) показали, что
в некоторых известных классических теориях поля, таких как теория
дираковского поля, взаимодействующего с полем Клейна — Гордона
с помощью скалярной связи, возможно существование статических и
сферически симметричных решений, которые могут быть интерпрети-
интерпретированы как частицы. Эти решения повсюду свободны от сингуляр-
ностей и являются квадратично интегрируемыми, так что классиче-
классические бесконечности не могут возникнуть. Квантование унитарных тео-
теорий поля было формально исследовано Финкельштейном [177].
1) Мы не рассматриваем здесь общую теорию относительности Эйнштейна
или его единых теорий, которые являются первоклассными унитарными те-
теориями.
а) См. книгу Паули [368], в которой дан обзор этой работы.
300 Глава 20
Недавно Дирак [118—121] развил классическую теорию .непре-
.непрерывно распределенных зарядов, которые двигаются согласно урав-
уравнениям движения Лоренца. Характерной чертой этой теории являет-
является то, что в ней встречается только отношение заряда к массе efnt,
а не заряде и масса т отдельно. По-видимому, в современной формули-
формулировке теории можно ввести только отношение е/т. Дирак надеялся,
что можно будет найти новый метод квантования этой теории,
который ввел бы постоянную Л и в то же время объяснил то, что
электрический заряд встречается только кратным величине е. Это
дало бы соотношение между величинами е и Ь и, таким образом,
определило бы величину постоянной тонкой структуры вг/4тгйс.
Многие другие классические теории имели своей целью введение
радиуса электрона релятивистски инвариантным способом. Трудности,
которые встречались на этом пути, состоят в том, что необходимо
определить распределение заряда таким образом, чтобы это было
совместно с релятивистской интерпретацией причинности. Рассмот-
Рассмотрим, например, поведение абсолютно жесткого электрона под дей-
действием пакета электромагнитных волн. Как только пакет достигнет
края распределения заряда, электрон как целое придет в движение.
Таким образом, импульс внутри электрона распространяется мгно-
мгновенно, что находится в противоречии с релятивистскими законами
причинности. Поэтому были сделаны попытки добиться того, чтобы
эти нарушения причинности происходили в достаточно малых про-
пространственно-временных интервалах, и, таким образом, не возникало
противоречия с опытом (в связи с этим см. работу Кретьена и
Пайерлса [82]).
Такие линейные теории с протяженным источником были развиты
только недавно; в случае классической теории лучшими среди них
являются теории Боппа [50], Пайерлса и Мак-Мануса [317] и Фейн-
мана [165]. Мак-Манус [317] предположил нелокальное взаимодей-
взаимодействие типа, указанного в гл. 11, § 3. В явном виде он предложил
взаимодействие типа
/// (хО F [(х — х'J] А., (х) d*-x d*x', B0.25)
что соответствует усреднению по пространственно-временной обла-
области. Функция F является релятивистски инвариантной, поскольку она
зависит только от инвариантного 4-мерного расстояния между двумя
точками. Требуется, чтобы функция F достаточно быстро убывала,
когда величина R2 = | х — х' |2 становится большой; таким образом,
должно удовлетворяться следующее соотношение:
fF(x2)d*x= 1; B0.26)
это соотношение необходимо для того, чтобы полный заряд был
конечен и равен е. Такую функцию F можно получить, если рас-
рассматривать 4-мерный фурье-образ F(R2), определенный следующим
Собственная энергия фермиона 30l
образом:
fiK B0.27)
с подходящей функцией g(K2)- Такую функцию g можно, например,
определить так:
К* 1
^, Ко = -. B0.28)
° г0 К }
Таким образом, конечный радиус электрона г0 вводится релятивист-
релятивистски инвариантным образом. Эта теория Мак-Мануса, в которой
заряд электрона распределен в пространстве и во времени, дает
конечную собственную энергию электрона.
Фейнман [165] ввел конечный радиус электрона непосредственно
во взаимодействие между двумя электронами, а не во взаимодействие
между электроном и электромагнитным полем, поскольку он фор-
формулировал свою теорию как теорию действия на расстоянии. Затем
было последовательно показано, что теории Мак-Мануса и Фейнмана
являются эквивалентными для определенного класса функций F.
Большим преимуществом этих теорий является то, что они могут
быть проквантованы (Фейнман [166]) и фактически дают конечную
собственную энергию в низшем порядке теории возмущений.
Однако в квантовой теории существуют также и другие расхо-
расходимости, которые не встречаются в классической теории, а именно
обусловленные поляризацией вакуума. Этот процесс соответствует
рождению пары электромагнитным полем и последующей аннигиляции
этой пары. Чтобы устранить возникающие расходимости в нело-
нелокальной теории, мы должны рассмотреть лагранжиан взаимодействия
следующего вида:
А.(х"')/7(х — х', х —х", х — х'")Х
. B0.29)
В этом случае нельзя больше говорить о токе Ja в одной 4-точке,
поскольку выражение для тока содержит как переменную х, так и
переменную х'. В действительности, хотя полный заряд сохраняется,
мы не имеем больше локального уравнения непрерывности для элек-
электрического заряда, поскольку взаимодействие B0.29) не является
калибровочно инвариантным. Кретьен и Пайерлс [83] попытались
дать формулировку нелокальной электродинамики, в которой
удовлетворялось бы требование калибровочной инвариантности. Хотя
им и удалось построить такую теорию, они все же не смогли уст-
устранить в ней расходимости, связанные с вакуумной поляризацией.
Ш Рлава 26 ■ ___^
§ 3. Вычисление собственной энергии с помощью метода
Фейнмана
Несмотря на то, что классические попытки получить конечную
собственную энергию не были особенно успешными, они все же
используются в большом числе работ по квантовой теории поля
в качестве полезных методов для формального устранения расходи-
мостей из квантовой теории. Обычно удобно ввести обрезание типа,
предложенного Фейнманом f166J; оно делает собственную энергию
конечной, но зависящей от параметра обрезания X. Это обрезание
может рассматриваться как частный случай взаимодействия в форме
B0.29), в котором множитель
■j AF (х — у) = ер1 (Х) ф* (у),
появляющийся при обычной локальной формулировке теории поля,
заменяется на новую функцию
h (X — у) = J Vx' f d'?F (x — *')F (У — у') ?' (хО ер" (у'). B0.30)
Выбрав подходящие функции F, можно сделать функцию /р (х — у)
плавной функцией аргумента (х — уJ, не имеющей сингулярностей.
Ясно, что имеется много возможностей выбора функций /р (х), соот-
соответствующих различным функциям F; простейшей из них, по-види-
по-видимому, является функция, предложенная Фейнманом [166], которая заме-
заменяет функцию распространения бозона (к2—(а2) на величину
л B0.31)
о
Величина О зависит от переменной X, большой по сравнению с ве-
величинами т и р., и нормирована так, что
оо'
J G(X)rfX= 1. B0.32)
о
Следовательно, если не проводить интегрирование по X, то в пре-
пределе X —*- оо мы вернемся обратно к локальной теории. Каждый
интеграл по промежуточным бозонным квантам, который раньше
содержал множитель (к2 — р.2I, теперь получает дополнительный
улучшающий сходимость множитель С (к2), причем
со
С(к2) = — j Х2(к2 — |j.2 — X2) G(к)dl; B0.33)
о
Собственная энергия фёрМадна ЗбЗ
этого множителя достаточно, чтобы сделать сходящимися все ин-
интегралы по виртуальным бозонным квантам. Полюса по-прежнему
определены в смысле Фейнмана, т. е. масса р. имеет малую отрица-
отрицательную мнимую часть.
В качестве примера современной ковариантной техники интегри-
интегрирования ') проведем снова расчет собственной энергии нуклона,
используя метод обрезания Фейнмана. Если интегрирование по dk
будем проводить в конце расчета и учтем, что
X"
1 1 г 1
кз — ^ — кз — ,а2_\а =~ J dL (кз_,х2_/,)а • B0.34)
о
то интеграл собственной энергии [см. выражения B0.2), B0.5)]
получит вид
Рассмотрим сначала интеграл по переменной к. Благодаря обрезанию
этот интеграл теперь сходится. Поскольку мы имеем дело со сво-
свободными частицами (р2 = /я2), то знаменатель фермиона (р — кJ — ш2
можно упростить
р2 — 2р-к + к2 — т* = к2 — 2р • к. B0.36)
Далее, мы объединим знаменатели, чтобы получить знаменатель,
являющийся функцией только к2, используя для этого замечатель-
замечательную формулу Фейнмана
B
!) См. статью Фейнмана [169], особенно дополнение.
2) Эту формулу можно получить, если учесть, что
JL 1 (l l\ = ( M }dx
аЪ Ъ — а\а Ъ) \Ь — a) J х*
а
н ввести в последний интеграл новую переменную x = az-}-b{l—z). Соот-
Соотношение B0.37) справедливо для всех значений а и Ь. Если, однако, а и Ъ
имеют противоположный знак, то г необходимо рассматривать как ком-
комплексную переменную, и путь интегрирования должен отклоняться от веще-
вещественной оси, чтобы обойти сингулярность в точке г = Ь\(Ь — а). Фактически
можно выбрать любой путь интегрирования, соединяющий точки г = 0 и
г = 1 (но не проходящий через сингулярность), поскольку вычет подинте-
304 Глава 20
Поскольку в нашем примере имеется множитель (к2 — р.2—--L) , то
используем формулу
[аг+Ь(Т-г)Г B0-38)
о
которая получается из формулы B0.37) дифференцированием по а.
Объединенный знаменатель тогда принимает вид
(k2 — p.2 — L)z + (k2 — 2p-k)(l— z) =
= к2 — 2р-кA— z)-— (p.2 + L)z =
= [к — рA— z)]2 — /и2A— zf — (ji»+L)z, B0.39)
где мы снова использовали соотношение р2 = /и2. Введем теперь
переменную к'=к— рA—z), тогда интеграл можно записать сле-
следующим образом:
2 fdzz fd*k' rQz-£r + m)
J J [k/2 —m2(l —гJ —(^2
Теперь знаменатель является функцией к2 (мы опустили штрихи),
поэтому интеграл
равен нулю вследствие симметрии. Вообще из свойства симметрии
следует, что
J d4k (нечетное число множителей &^)/(к2) = 0, B0.41)
Jik*) = — i-^ J rfW/(k2). B0.42)
трального выражения в точке сингулярности равен нулю. Интеграл Фейнмана
B0.37) фактически представляет частный случай следующей общей формулы:
1 , ,.. Г Г dzx ... dzn
- ... +anzn]n
Для вычисления последнего интеграла необходимо ввести функцию
/ п \
В1 2 2i—1 ) в подинтегральное выражение (см. также книгу Гурса и Гед-
рика [212]). Интеграл можно записать также в форме
1 z, zn-2
— =(л-1I fdzr fdz2... Г dzn-rX
• • "те J J J
X [anzn~i + an-x (*„_ a
Собственная энергия фермиона 305
Поэтому член с k в интеграле B0.40) равен нулю, что эквивалентно
в случае отсутствия обрезания сведению расходимости интеграла
от линейной к логарифмической.
Таким образом, мы должны вычислить интеграл
+ОО
= J" d* (у-c + f.). ■ <20-43>
где С=тгA — zJ-f-Ср.2-f- L)z— положительно-определенная вели-
величина. Как уже указывалось, при интегрировании по вещественной
оси k0 полюса смещаются при прибавлении добавки Фейнмана — is
к массам частиц. Однако мы можем повернуть путь интегрирования
в комплексной области на 90° так, чтобы интегрирование велось
по мнимой оси от —/со до -{-/оо. Это возможно, потому что
при вращении контур нигде не пересекает сингулярностей; последние
расположены выше отрицательной вещественной оси и ниже поло-
положительной вещественной оси. Следовательно, можно ввести новую
переменную интегрирования k0 = ikit так что интеграл B0.43) пре-
преобразуется в интеграл в 4-мерном эвклидовом пространстве:
+ ОО +10О +ОО
+
— С tfk С dk° ■ I С
Если ввести четырехмерные сферические координаты, элемент объема
в которых равен 2iz2k3dk, то наш интеграл /, наконец, получит вид
Отметим, что величину такого рода интегралов с различными сте-
степенями в знаменателе можно получить из величины / с помощью
интегрирования или дифференцирования по параметру С.
Таким образом, собственная энергия равна (опуская интеграл Г dk\
\
G2
Е (р) 4тсйс 4
о
X I dbw (р) [Г (pz -f- т.) Г]
306 Глава 20
Если мы снова остановимся на случае Г = Тб и учтем, что
pw (р) = m-w (p), то получим
1
о
Интегрирование по переменной L тогда дает
V B°-47)
В пределе X—>• со можно пренебречь в числителе логарифма членами
|х22+/ге2A—zJ по сравнению с членом \2z. Если, кроме того, мы
будем пренебрегать массой [а по сравнению с массой т, то получим
Величина Д£ расходится логарифмически в пределе X—*со. Отметим,
что при вычислении этого выражения для собственной энергии мы
->-
не делали предположения /7 = 0. Интеграл B0.48) можно вычислить
без всяких приближений, тогда он равен
2~Т~ mZ^~ Z\m) V 2m*) Ш от
Интересно отметить (см., например, работу Энацу [147]), что
собственная энергия в скалярном случае расходится также логариф-
логарифмически, но имеет противоположный по сравнению с псевдоскаляр-
псевдоскалярным случаем знак, так что Д£ Cg2/4iz) In \/m. Знак собственной
энергии во втором порядке для электрона в квантовой электроди-
электродинамике такой же, как и в псевдоскалярном случае, причем
ДЕ'—(Зе2/2п)\пк/т. Поэтому, если принять идею Штюкельберга
о компенсации расходимости, то можно сделать собственную энергию
электрона второго порядка конечной, если в дополнение к электро-
электромагнитному полю предположить, что электрон взаимодействует со
скалярным полем с константой связи g2 = 2е2 (Саката [415], Пайс
[364], см. также обзорную статью Саката и Умэдзавы [416]) х>.
У Обсуждение проблем, связанных с собственным натяжением для фер-
миона в квантовой теории, рассмотрено в работах Пайса и Эпштейна [365],
Рорлиха [404], Вилларса [503J, Боров ица и Кона [62].
Собственная энергия фермиона 307
Метод обрезания Фейнмана, который мы только что описали,
может рассматриваться как частный случай общего формального
ковариантного метода рассмотрения расходящихся интегралов, дан-
данного Паули и Вилларсом [380] J). Их метод известен как метод
„регуляризации". Он состоит в том, что сначала проводится регуля-
регуляризация всех сингулярных выражений, а затем выполняется пре-
предельный переход. Таким образом, если
I(m) = f J(m)d*k B0.50)
есть расходящийся интеграл по внутренней линии с массой ш, то
регуляризованный интеграл /д (т) определяется выражением
где Со = 1 и то^=т.
Некоторые ограничения, накладывающиеся на величины Сц и т^
достаточны для того, чтобы сделать интеграл B0.51) сходящимся.
В электродинамике для достижения поставленной цели требуется
наложить следующие условия:
= 0, B0.52а)
i
2 Сгт\ = 0. B0.526)
г
Предельный переход состоит в том, что вспомогательные массы /и
(/ = 1, 2, ...) следует устремить к бесконечности.
Условия B0.52) обеспечивают отсутствие сингулярностей на све-
световом конусе у функций Д и ДA' в отличие от нерегуляризованных
функций [напомним соотношения A5.496) и A5.51в) и отметим, что
условия B0.52) как раз устраняют сингулярности]. Условий B0.52)
также достаточно, чтобы получить сходящееся выражение для соб-
собственной энергии электрона, если только проводится регуляризация
всего выражения как целого, а не отдельных его частей. После
выполнения конечного предельного перехода снова возникает лога-
логарифмическая расходимость.
Приведенная выше методика является, по терминологии Паули и
Вилларса, „формалистической" теорией, в которой даны чисто фор-
формальные рецепты для вычисления расходящихся интегралов, в отличие
от „реалистических" теорий, в которых математическая схема, обе-
обеспечивающая сходимость, получается в результате учета взаимодей-
взаимодействия с другими полями (см., например, работу Пайса [364]).
1) См. также работы Штюкельберга [472, 473] и Ривьера [403].
Глава 21
ПЕРЕНОРМИРОВКА
§ 1. Перенормировка массы
и нерелятивистский лэмбовский сдвиг
В гл. 20, § 3, была вычислена собственная энергия свободной
частицы. При наблюдении свободной частицы единственными ее из-
измеримыми характеристиками являются энергия Е и импульс р. Из
них можно образовать», только одну инвариантную величину Е2 —р2,
а именно массу частицы
Е2—р2 = тг. B1.1а)
Если мы имеем релятивистски инвариантное взаимодействие с полем,
то влияние этого взаимодействия на свободную частицу может
привести только к изменению ее массы, скажем, на величину Ьт.
Изменение энергии свободной частицы дается тогда выражением
B1.16)
Разлагая последнее выражение по Ьт, получаем
—2—j~—J" , т Ьт
М Р ~*~ Vm^-H
Итак, в первом порядке
Д£ = ^. B1.1г)
с.
Другими словами, в инвариантной теории собственная энергия
в первом порядке определенным образом зависит от импульса частицы,
а именно: она должна быть обратно пропорциональна У^т2-\-р2.
Обратно пропорциональную зависимость собственной энергии от
Е — исходной энергии свободной частицы, определил уже Вайскопф
при рассмотрении собственной энергии в теории дырок с помощью
развитой им теории возмущений.
Полученная нами в псевдоскалярной мезонной теории формула
B0.49) для свободной энергии первого порядка имеет требуемый
вид. Так как для нуклона ■Ш'Ш = 1, то
B1.2а)
Перенормировка 309
Поэтому для изменения массы мы получаем
Таким образом, в ковариантной теории Фейнмана явно выражено
то обстоятельство, что собственная энергия соответствует изменению
массы. Утверждение, согласно которому собственная энергия сво-
свободной частицы, может привести только к изменению ее массы,
лежит в основе современного способа разрешения трудностей, свя-
связанных с расходимостями. Впервые такого рода предложение было
сделано Крамерсом [290] в 1947 г. для случая классической элек-
электродинамики. Он указал, что мы никогда не можем экспериментально
наблюдать т0 — массу „голого" электрона, а можем наблюдать
только (то-\-Ът) — наблюдаемую массу электрона, которую мы
обычно обозначаем через /к, т. е.
т = т0-\-от. B1.3)
Поэтому Крамере предложил обратиться к исходной точке зрения
Гейзенберга на квантовую механику, согласно которой только на-
наблюдаемая величина т, а не отдельно величины т^ или Ьт, должна
рассматриваться в теории. Этот принцип известен как принцип пе-
перенормировки массы. Крамере готов был допустить, что изменение
массы электрона может быть бесконечным (надеясь, однако, что
в будущей теории оно будет конечно и мало), но не считал это
обстоятельство существенным, так как физически наблюдаемые ве-
величины, например уровни энергии или поперечные сечения, конечны,
если их выразить через наблюдаемую массу т. Этот принцип на
практике оказался чрезвычайно плодотворным и в последние годы
привел к успешному развитию квантовой электродинамики и псевдо-
псевдоскалярной мезонной теории.
Впервые принцип перенормировки массы был применен к задаче
о лэмбовском сдвиге, решение которой мы и приведем в качестве
примера. Когда в 1947 г. Крамере предложил этот принцип, Лэмб
и Ризерфорд [295] как раз измерили смещение уровня 25 водорода
по отношению к уровню IP. Следуя идее Крамерса, Бете [33] ин-
интерпретировал сдвиг уровней как эффект взаимодействия электрона
с полем излучения. В действительности Бете просто рассчитал соб-
собственную энергию электрона, связанного в атоме. Однако, согласно
идее Крамерса, большая часть этой собственной энергии уже при-
принимается во внимание, если мы используем в расчетах наблюдаемую
массу электрона т вместо массы „голого" электрона т0. Таким
образом, истинный сдвиг уровней есть разница между собственными
энергиями связанного и свободного электронов.
В нерелятивистском приближении, которое использовал Бете
в 1947 г., необходимо рассматривать только взаимодействие эле-
электрона с поперечными электромагнитными волнами. Гамильтониан,
310 Глава 21
описывающий электрон, движущийся в некотором поле с потенциа-
-»-
лом V(x) и взаимодействующий с полем излучения, должен быть
взят в виде
где
B1.4а)
B1.46)
Н* = ~^Р'А&>- B1В)
Здесь выбрана радиационная калибровка div A = 0, так что поле
излучения описывается только вектором-потенциалом А и ($ =
•*■ ■> ■*■
= —дА/дх°, a $ = rot/4. В шредингеровском представлении разло-
■*■ -*■
жение квантованного поля А(х) по операторам рождения и уничтоже-
уничтожения фотонов с импульсом k и поляризацией X имеет вид
2
V С
j=-x
X e^ (ft) (cx (&) e*^-* + ct (ft) e-^-*). B1.5a)
Отметим, что суммирование по поляризационному индексу X
ведется здесь только от 1 до 2, т. е. по двум поперечным напра-
■*■ ■>■>■->■
влениям, а поскольку div А = 0, то ех(&).& = 0 (Х=1, 2). Пере-
Перестановочные соотношения для операторов поля имеют обычный вид
= 0.
cj. (ft')] = 8»'8W (ft — ft'). B1-56)
4 В дальнейшем нас будут интересовать только эффекты собственной
энергии, обусловленные членом Hiat Поэтому мы опускаем член порядка А2,
который появляется при калибровочно инвариантном введении взаимодей-
взаимодействия заряженной частицы с полем излучения, получаемом при замене рг ->
->-Pj-—(eje) Aj-. Член А* дает в собственной энергии частицы несуществен-
несущественную константу (т. е. константу, не зависящую от импульса частицы). Однако
этот член играет большую роль в проблемах, в которых рассматривается
рассеяние излучения на заряженных частицах, и, конечно, в калибровочной
инвариантности теории.
Перенормировка 311
— оператор числа фотонов с импульсом k и поляризацией X и
= he 2
где (в& = | А|.
Гамильтониан B1.4) описывает взаимодействие точечной нереля-
нерелятивистской частицы с полем излучения. Однако вследствие наличия
члена взаимодействия Hi заряженная частица может, например, ис-
испустить виртуальные фотоны со сколь угодно большим импульсом
и при этом приобрести столь большой импульс отдачи, что ее дви-
движение не может больше рассматриваться нерелятивистски. Таким
образом, строго говоря, гамильтониан B1.4) является внутренне
непоследовательным. Эту трудность можно частично обойти, если
рассматривать частицу с распределенным зарядом и члену взаимо-
взаимодействия придать вид
где функция F (х) описывает форму распределения заряда. Далее,
если а — радиус распределения заряда (a ^h/mc), то волны с дли-
длиной, меньшей а, не будут взаимодействовать с частицей; другими
словами, только те величины k, для которых hk < me, будут да-
давать вклад в разложение B1.5а).
Рассмотрим теперь свободный электрон; в этом случае V(x) =0.
Если бы Hz было равно нулю, то собственные функции оператора Н
были бы и собственными функциями оператора Но, т. е. произве-
произведениями собственных функций операторов р2/2т0 и НТ&&. Если мы
положим, что связь между частицами и полем излучения мала и по-
поэтому применима теория возмущений, то член Hj даст сдвиг невоз-
невозмущенных собственных значений энергии. Рассчитаем это изменение
энергии во втором приближении для невозмущенного состояния,
->■
в котором имеется только один электрон с импульсом р и нет фото-
фотонов, т. е. для состояния, волновая функция которого
где V—нормировочный объем для электронной волновой функции
и Фо описывает вакуум поля излучения, так что сх(&)Ф0 = 0. Отме-
Отметим, что энергия этого состояния Ео равна p2j2m0, т. е. кинетиче-
кинетической энергии электрона.
Проводя вычисления таким же образом, как и в гл. 14, § 1,
легко получить, что сдвиг уровня энергии, обусловленный излуче-
излучением и последующим поглощением фотона электроном, во втором
312 Глава 21
приближении х> дается следующим выражением:
Х(Ф0. Cx(*)cx'(*O*o). B1-6в)
/ra2c22B7t)sj l^
.6г)
Отметим, что поскольку р\тй является скоростью частицы v, то
первый член в знаменателе в выражении B1.6г) будет порядка v[c
по сравнению с членом bck. Поскольку мы проводим расчет в не-
нерелятивистском приближении, то будем пренебрегать этим членом
по сравнению с членом bck. Кроме того, следует помнить, что функ-
ция F (k) обрезает вклад больших &(£>1/а) в интеграле, входя-
входящем в выражение B1.6г). Поэтому мы можем также пренебречь
членом b2k2l2m0 по сравнению с членом bck. Наконец, принимая во
■*■ ->■-*■
внимание, что k и ех (k) взаимно ортогональны, получаем
Х=1
Теперь мы можем выполнить интегрирование по угловым перемен-
->■
ным в выражении B1.6г), выбрав вектор р в качестве полярной
оси; тогда получим
оо
- — т^-4-а^-(—) fdk\F(k)\2. B1.бд)
2тп0 Зл 4теяс \7ЯОс / J i \ / i
о
Ч Член р ■ А не дает вклада в первом приближении, так как (*0) р X
X AWq) = 0; однако в этом приближении член Л2 дает постоянный член.
Перенормировка 313
Отсюда следует, что для точечного заряда, для которого F (k) = 1,
величина Д£B> расходится линейно. Важно, что полученный вклад
в собственную энергию фактически пропорционален р2/2т0 (кине-
(кинетической энергии частицы), поэтому энергия частицы во втором
приближении дается выражением
B1.7а)
где
оо
Sm^ + ^y fdk\F(k)\2. B1.7г)
о
Теперь примем точку зрения Крамерса. Определим Ьт как эле-
электромагнитную массу, которую частица приобретает (сверх „голой"
механической массы) вследствие взаимодействия с полем излучения.
Однако наблюдаемой массой является только то-\-Ьт, поскольку
не существует экспериментов, которые могли бы выделить из массы
заряженной частицы часть, имеющую электромагнитное происхожде-
происхождение, и часть, имеющую механическое происхождение. Поэтому вели-
величину то-\-Ьт мы отождествим с наблюдаемой экспериментальной
массой т. (Имеются, конечно, электромагнитные вклады в т0 выс-
высших порядков, и, строго говоря, следует взять сумму всех этих
вкладов плюс т0 и приравнять полученную величину т.) Так как
в нашей теории с обрезанием величина Ьт мала (порядка а), то
соотношение B1.7в) мы можем рассматривать как член второго по-
порядка, возникающий в разложении выражения
Ьт ,
Поэтому, если выразить теперь энергию через наблюдаемую вели-
величину т, то результат расчета по теории возмущений покажет, что
энергия частицы фактически равна Е = р2/2т и, таким образом,
имеет определенный смысл. Отметим, что при формальном подходе
к перенормировке массы безразлично, является ли величина Ьт ко-
конечной или бесконечной.
Рассматриваемая до сих пор теория еще неудовлетворительна
в одном отношении: в исходном гамильтониане встречается „голая"
масса. Применим снова принцип Крамерса, чтобы переписать гамиль-
гамильтониан в следующем виде:
\ PA
314 Глава 21
здесь мы пренебрегли членом порядка е3. Теперь мы будем расс'ма-
•*■ ■*■
тривать как возмущение не только член (е/тс) (р • А), но и член
(Ът/т)(р2/2т), где величина §/и берется равной
Если мы сделаем это, то в е2-приближении энергия одноэлектрон-
ного состояния будет точно равна р2/2гп. Обратно, мы могли бы
определить величину Ь/п в е2-приближении из требования, что энер-
энергия частицы должна равняться р2/2ш. Член (Ът/т)(р2/2т) обычно
называют контрчленом перенормировки массы.
Рассмотрим теперь случай электрона, связанного с протоном и
движущегося по воровской орбите, т. е. случай, когда V(x) =
= — Ze2l\x\. Гамильтониан для этой системы должен быть взят
в виде
где величина 5/и задается выражением B1.7г). Исходя из того, что
будут рассматриваться только связанные состояния электрона, можно
существенно упростить этот гамильтониан. Для связанных состоя-
состояний величина координаты электрона х всегда будет порядка боров-
ского радиуса. Поэтому, поскольку функция F (k) обрезает импульсы,
большие тс, и следовательно, k-x^znx, то мы можем пренебречь
экспоненциальными множителями в разложении B1.5а), т. е. заме-
заменить их единицами. Такого рода приближение известно как диполь-
ное. Оно эквивалентно пренебрежению эффектами запаздывания
и отдачи в процессе излучения и поглощения фотона электроном.
Другими словами, рассматривается взаимодействие электрона только
с такими длинными волнами, что можно пренебречь переносимым
•> •>
ими импульсом [множитель exp(ik • х)]. Следовательно, разложение
■*■ ■>•
вектора-потенциала А (х) в этом приближении имеет вид
2
АМ = \2ТШ f ~^2u4(k)(cAk) + cUk)-). B1.5в)
Применяя снова теорию возмущений, но выбирая теперь в каче-
качестве невозмущенных собственных функций собственные функции
гамильтониана
Перенормировка 315
получаем (Бете [33]) для сдвига уровня электрона, находящегося
в состоянии т, следующее выражение:
где индекс я, характеризующий энергетические состояния электрона,
пробегает все значения, a v — оператор скорости электрона. Далее,
мы можем написать
1 1 Еп — Ет
En-En
благодаря чему выражение B1.8а) можно переписать в виде
оо
г, 12 _1_ 5/П I Р2 1тт |
B1-8б)
Принимая во внимание, что
== I v \тт<
отмечаем, что первый член в выражения B1.86) представляет как
раз собственную энергию электрона, имеющего кинетическую энер-
энергию, соответствующую состоянию т. Следовательно, этот член
точно сокращается с контрчленом — вторым членом в выражении
B1.86). Таким образом, сдвиг уровней дается выражением
к
\Е 2а
En-E
где К — энергия обрезания (/С-—тс2). Предполагается, что эта
величина велика по сравнению со всеми разностями энергий Еп — Ет
в атоме.
Бете в своей работе [33] фактически не использовал контрчлена
и не рассматривал электрон как частицу, имеющую конечные раз-
размеры порядка комптонозской длины волны. Вместо этого он дока-
доказал, что при перенормировке необходимо вычесть из собственной
энергии связанного электрона поправку к кинетической энергии,
обусловленную собственной массой. При этом степень расходимости
собственной энергии связанного электрона уменьшается от линейной
316 Глава 21
к логарифмической [ср. К->-\-оо в выражении B1.8г)]. Бете затем
предположил, что в теории дырок этот же принцип приведет
к сходящемуся результату (поскольку там собственная энергия рас-
расходится только логарифмически), и поэтому ввел в нерелятивистской
теории обрезание для энергии фотона порядка тс2. При этом усло-
условии он получил формулу для сдвига уровней B1.8г), вычисление1)
по которой дает для 25-состояния (Бете [33], Бете и др. [35]) величину
сдвига уровней 1040 мггц, что находится в удивительно хорошем
согласии с наиболее поздними экспериментальными данными (Трибвассер
и др. [487])— 1057,77ztr0,10 мггц.
Последующие релятивистские расчеты подтвердили предположе-
предположение о сходимости выражения для сдвига уровней, рассчитанного
с помощью принципа перенормировки Крамерса. Эти релятивистские
расчеты были проделаны Швингером и Вайскопфом [437], Френчем
и Вайскопфом [191], Кроллом и Лэмбом [292], Фейнманом [166],
Швингером [438] и Бете [34, 35]; в результате был получен сдвиг
1) Вычисление проводится следующим образом: поскольку аргумент
логарифма в выражении B1.8г) в нерелятивистском приближении будет доста-
достаточно велик, то удобно записать
(Еп - Ет) | Рпт Р In
Ry
In
Ry
n
Приведенное соотношение есть определение величины (Е — ЕтH^. Было найде-
найдено (Бете и др. [35], что для 25-уровня атома водорода (Е — £гз)ср ~16,6 Ry.
Для атома водорода с
легко получить, что
п - Ет) | рпт Р = у <[р.
f
@) I3.
В этом приближении сдвиг уровней имеется только в S-состояниях. Так
как для S-состояния с квантовым числом п
(где а—боровский радиус), то выражение для сдвига уровней получает
вид
Оно дает для 2S-coctohhhh 1040?мггц.
Перенормировка 317
уровней, равный 1052 мггц. Дальнейшие уточнения расчета, осо-
особенно при учете компонент с большими импульсами для электрона
в 25-состоянии (Баранджер [16—18],
Карплус и др. [268]), привели к теорети-
теоретической величине, которая с точностью до
0,5 мггц совпадает с экспериментальной.х)
Перенормировку массы можно включить I \ А-8л
в полностью релятивистскую теорию сле-
следующим образом. Лагранжиан свободного
поля содержит член /гаофф, где т0 — масса
свободной частицы. Этот член можно запи-
сать в виде /гаф'Ь — о/гафй. Затем член — bmtyty
рассматривается как часть энергии возму- Фиг. 55.
щения, связанной со взаимодействием между
частицей и полем излучения. Точнее говоря, этот член должен
всегда рассматриваться вместе с диаграммой собственной энергии,
с вкладом которой он сокращается в случае свободной частицы.
Другими словами, мы всегда должны рассматривать вместе диа-
диаграммы, изображенные на фиг. 55, добавляя диаграмму b к диа-
диаграмме а; маленький кружок на диаграмме 55, Ь является предста-
представлением оператора —Ьт. Расходящаяся величина Ьт должна быть
определена так, чтобы вклад диаграмм собственной энергии типа а
точно сокращался с вкладом диаграмм типа Ь, если нуклон является
свободным, т. е. чтобы масса свободной частицы была равна т.
Поэтому величина Ьт будет задаваться разложением в степенной
ряд по константе связи при вычислении 5-матрицы. Величина. В/гаB>
была уже вычислена для случая нейтральной псевдоскалярной мезон-
ной теории с прямой связью и дается формулой B0.6).
§ 2. Радиационные поправки к формулам рассеяния 2>
Чтобы проиллюстрировать методику перенормировки (см. работы
Льюиса [305], Эпштейна [148]), рассмотрим теперь детально рассея-
рассеяние электрона на внешнем электромагнитном поле, включив радиа-
радиационные поправки к формулам рассеяния. Для этого случая плот-
плотность гамильтониана взаимодействия дается выражением
3Vi(x) = eN [h^\ (x)] + eN WfWl 001 — 8"*W 00- B1 -9)
1) В настоящее время существует расхождение между теоретической
величиной лэмбовского сдвига и его экспериментальным значением, равное
0,6 мггц; только 0,1 мггц из этой величины может быть объяснена объем-
объемным распределением заряда протона, определенным в опытах по рассеянию
быстрых электронов протонами. См., например, работы Хофштадтера [Н о f-
stadter, Rev. Mod. Phy,-\, 28, No. 3 A956)] и Пенни и Леви, Равенхолла
[Yennie D., Leby M., Raven hall D., Rev. Mod. Phys., 29, 144 A957).—
Прим. перев.
a) Полуклассическое рассмотрение радиационных поправок, которое
допускает простое физическое толкование, было проведено Уэлтоном [520]
и Коба [281]. См. также прекрасную обзорную статью Вайскопфа [519].
318
Глава 21
Первый член представляет взаимодействие электронно-позитрон-
ного поля с квантованным полем излучения, второй член — взаимо-
взаимодействие с внешним полем и третий член — контрчлен, дающий
перенормировку массы. Вклад в рассеяние дают те члены третьего
порядка в разложении 5-матрицы, диаграммы которых приведены
на фиг. 56. На фиг. 56, согласно условию, принятому раньше,
действие внешнего поля изображается волнистой линией с крестом
на конце.
Матричный элемент, соответствующий диаграмме на фиг. 56, а,
был исследован раньше. Для перехода из состояния с импульсом рх
Йеренормировка 3l9
в состояние с импульсом р.г он дается следующим выражением
= — 2та(р.2)М(а)а(}1), B1.10а)
еа(р2 — Pl). B1.106)
Мы опустили здесь нормировочные множители [т/Е (р)]'/г. Исполь-
Используя установленные выше правила, получаем для оператора М^К
соответствующего диаграмме Фейнмана на фиг. 56, Ь, следующее
выражение:
М
ia Г л. а. 1 - ,
= 2^5- I a k~\ —; x ea (p3 — pt) X
г). B1-12)
где а = £2/4тсйс = ^=- (величина электрического заряда е берется
в рациональной системе единиц). Диаграмма на фиг. 56, Ъ называется
вершинной диаграммой, и Л(р2, pt) является вершинным оператором
порядка а. В формуле B1.11) мы заменили функцию распростране-
распространения фотона к~2 на величину (к2 — Х^,,.) для того, чтобы изба-
избавиться от расходимости, поязляющейся при малых к. Интерпретация
этого приема будет рассмотрена в дальнейшем.
Аналогичным образом можно выписать операторы, соответствую-
соответствующие диаграммам на фиг. 56, cl и dl; они имеют следующий вид:
&± (P2-Pl), B1.13)
Рч—
где I* (р) — оператор собственной энергии второго порядка; в слу-
случае электродинамики он дается выражением
Диаграммы на фиг. 56, с2 и d2 представляют поправку к массе и
даются выражениями
М(с2) = еЪпг ~—а(р2—р,), B1.16)
Pi — m
2 — Pi)-^—. B1.17)
Pi — я»
3'20
Глава 21
Наконец, диаграмма на фиг. 56, е, соответствующая эффекту поля-
поляризации вакуума» будет рассмотрена в § 5, а соответствующий ей
матричный элемент дается выражением
где
^(.Ф = f
= p2— pi-
B1.18)
B1.19)
B1.20)
Следует отметить, что здесь мы ограничились частным случаем
внешнего поля, однако также просто можно рассмотреть случай,
в котором внешнее поле заменяется внутренней фотонной линией.
Фиг. 57.
В этом случае все множители т^ц (Ра — Pi) Должны быть заменены
на множители к"ге^, каждый из которых представляет функцию
распространения фотона, входящего в определенную вершину
(должна быть также 8-функция, соответствующая закону сохранения
импульса р2 — pt = k). Затем можно провести последующий анализ.
При этом диаграммы на фиг. 56 можно рассматривать как части
более сложных диаграмм, которые, например, приведены на фиг. 57
и которые соответствуют взаимодействию электрона с протоном,
обозначенным двойной линией.
Рассмотрим вклад от процессов, изображенных на фиг. 57, b d.
Интеграл B1.11) для Л логарифмически расходится. Он может быть
Перенормировка 321
вычислен 1), если использовать метод регуляризации Фейнмана (см.
дополнение В в работе Фейнмана [169]). Для этой цели функция
распространения фотона (к2—^Lra.) заменяется в выражении B1.11)
на величину
(к2-**».) —(к'-Л!*)-1;
здесь М'—большая „регуляризующая масса". Регуляризованное вы-
выражение можно записать в следующей форме:
Величина A[xc(q) представляет собой интеграл, сходящийся при
больших импульсах к (но расходящийся в пределе Хмшг. -> 0). Он
был вычислен Фейнманом для случая 0^q2^4ffi2 и р2 = р2=/и-2,
причем были отброшены члены, обращающиеся в нуль при переходе
к пределу Хмин.->0 и М->оо. Если ввести величину 6 с помощью
соотношения sin2 6 = q2/4/ra2, то при сделанных предположениях
выражение для А^с получит вид
Для малых q величина Л^с(Я) имеет форму
Все эти выражения имеют силу только в том случае, если частицы
в состояниях pt и р2 являются свободными, т. е. р2 = р2 = т2.
Следует отметить, что выражения B1.22) и B1.23) стремятся
к нулю, если величина приращения импульса q стремится к нулю,
и что расходящийся первый член выражения B1.21) не зависит
от q. Другими словами, только та часть Л^, которая остается, если
q —>- 0 или если р2 стремится к pt, содержит расходящийся инте-
интеграл.
В том, что это действительно так, можно убедиться следующим
образом (Фейнман [169]). Положим, что величина pt фиксирована,
и разложим величину Л^, определенную выражениями B1.11) и B1.12),
1) Три знаменателя могут быть объединены либо при повторном исполь-
использовании формулы Фейнмана B0.37), либо с помощью формулы
1 1
(abe)-1 = 2 Г dx х С dy [а A — х) + Ъху -f сх A — у)]'3.
322 Глава 21
в ряд по степеням разности р2 — pt, вернее по степеням компонент
этого 4-вектора. При этом разлагается выражение [р.г — k — m\~x,
а именно [ср. с формулой B1.29)]
1 1 1
i — a — m
= 1 (Pi — Pi)- \ h ••• B1.23a)
Px — k — m px — k — m
Ясно, что первый член имеет порядок 1/А при больших k, второй
член — порядок \\kz и т. д. Итак, если разложение B1.23а) под-
подставить обратно в интеграл B1.11), то только первый член его
приведет к логарифмически расходящемуся интегралу по k; во вто-
втором члене подинтегральное выражение будет вести себя как dkjk2,
и, следовательно, интеграл будет сходиться, а все последующие
члены содержат еще лучше сходящиеся интегралы; член, пропор-
пропорциональный (р2—pt)n, будет содержать интеграл, подинтегральное
выражение которого имеет форму dk/kn+l. Это доказывает наше
предыдущее утверждение, что только A^pi, pt) расходится [т. е.
зависит от регуляризующей массы М, как в выражении B1.21)],
а величина
p2) = A,1(p1, p2)— Ajjpp Pl) B1.236)
конечна (т. е. представляется интегралом, сходящимся по k, и не
зависит от регуляризующей массы). Поэтому выражение B1.236)
может рассматриваться как определение исправленной, конечной
части Л^, которую в выражении B1.22) мы обозначили как Л^с (по
крайней мере для случая, когда частицы в состояниях pt и р2
являются свободными).
Принцип перенормировки с помощью вычитания [аналогичный
примененному в выражении B1.23)] в чрезвычайно общей форме
используется в теории перенормировки. Разлагается оператор,
в нашем случае Л[Х(р1, р2), в степенной ряд по некоторой величине,
относящейся к внешним переменным, в нашем случае р2—-pt. Тогда,
только первый член (или несколько первых членов) разложения
будут содержать расходящиеся интегралы по внутренним перемен-
переменным (в нашем случае по k). Такие члены затем отбрасываются
релятивистски инвариантным образом. Для обоснования этого в не-
некоторых случаях отмечается, что они являются ненаблюдаемыми,
как например при перенормировке массы (см. § 1) или при пере-
перенормировке заряда (см. § 5), или что они сокращаются с другими
расходящимися величинами, как это будет показано в следующем
параграфе для случая ЛA; в некоторых случаях они сокращаются
со специальными членами, вводимыми в исходный лагранжиан, на-
например в случае, рассмотренном в гл. 22, § 4. Конечные члены,
Перенормировка 323
остающиеся после применения этой методики, берутся затем как
перенормированные выражения для операторов. С этой методикой
мы снова встретимся при перенормировке заряда в § 5 и во многих
местах в конце этого тома, особенно в гл. 24.
§ 3. Перенормировка волновой функции
Теперь приступим к исследованию выражений B1.13) и B1.14).
Появление в них множителей (р — т) создает трудности, так как
матричные элементы Л4(о1' и М должны быть взяты с двумя вол-
волновыми функциями свободных частиц, в результате чего знамена-
знаменатели обращаются в нуль. Правда, сумма числителей М * и N^cS)
также сокращается, но это ведет только к результату 0/0, кото-
который является неопределенным. Для получения однозначного резуль-
результата мы должны явно ввести затухающие множители, которые не-
необходимы для правильного определения начального и конечного
„голых" состояний (см. гл. 16, § 2). В нашем случае неоднознач-
неоднозначность существенно связана с предельным процессом, при котором
начальное и конечное время матрицы U (t, t0) устремляется к ztroo.
Предельный переход может нарушить унитарность 5-матрицы, если
не уделить этому специального внимания. Фейнман [169] и Дай-
сон [127, 130]!' показали, как преодолеть эту трудность. Если
явно ввести затухающую функцию g(t), которая автоматически
включает и выключает взаимодействие между полями, то гамильто-
гамильтониан взаимодействия заменяется на выражение 2)
i®i (x) -> eg(t)j^ (х) А* (х) — 8»ф (х) ф (х) \g{t)f. B1.24)
Предполагается, что время Т, в течение которого изменяется g(t),
очень велико по сравнению с длительностью процесса рассеяния.
Если фурье-образ g(t) обозначить через О(Г0), то
6 0) = / О(Г0)е-ЪЫТ0^{ G(T0)e-*-*dT0, B1.25)
— со
где вектор Гц имеет компоненты
Г = (Г0, 0, 0, 0).
Нормировка выбирается следующей:
=l. B1.26)
1) См. также стр. 542 в работе Карплуса и Кролла [263].
2) Член В/я, представляющий собственную энергию, будучи радиацион-
радиационным эффектом второго порядка, должен умножаться на [g (t)]2.
324
Глава 21
и предполагается, что функция G(T0) ведет себя почти как 8-функ-
ция, т. е. является большой только тогда, когда величина Го' не
превышает 7*-1.
Если гамильтониан взаимодействия B1.24) подставить в разло-
разложение 5-матрицы, то, например, выражение B1.14) заменится сле-
следующим:
'
X
^-g-f Га(р2-Р1-Г-Г0
X ^2\Pl-\~T)G(T0)G(Го)dV0dTo. B1.27)
Если Г-»со, то и Го->0 и Го^О и подинтегральное выражение
может быть разложено. Тогда функция распространения электрона
получает вид
1■
(Г+г')а
р-\-т
B1.28)
где мы использовали соотношение для свободной частицы р^ = тпг.
Аналогично, если разложить £2(р), используя следующее общее
разложение, верное для двух любых операторов А я В (Фейн-
ман [169])
А
B1.29)
. А + В "А
то можно также оставить только члены порядка Г в выраже-
нии £B):
£B)(р,+Г) = а Г
J
— а^(Р1)Гт, B1.30)
где /'(p) — логарифмически расходящийся интеграл. Используя соот-
соотношение B1.30), мы можем записать подинтегральное выражение
в формуле B1.27) в следующем виде:
B1.31)
Перенормировка 325
Теперь, если ввести таким же образом затухающий множитель g(t)
в выражение B1.17) для M(da\ то получим
MiaJ) =
J J
X G (Го) G (Го) йГ0 dY'o. B1.32)
Так как £B)(p2 = m2), по существу (т. е. с точностью до множи-
множителя— i/4ir3), определяется как 8/га, то ясно, что матричный эле-
элемент M{ds) сокращается с частью матричного элемента Л4(<|1), содер-
содержащей S (pt). Это фактически является перенормировкой массы.
Поэтому получаем
*№>+*<*> = ££//я-оДГоО(ту оайх :
/"(РОГ,- B1.33)
Далее, релятивистская инвариантность требует, чтобы вели-
величина Г (р) при преобразованиях Лоренца преобразовывалась как
4-вектор, и, следовательно, она должна иметь вид
Г (Pi) = Ad (Р?) т" + 7B) (Pi) (Pi — та) т" + As) (Pi) Т" (Pi — m) +
4- /D) (Pi) (Л — та) т" (Л — ^) + • • • , B1.34)
где Ai)> 7B), ... — функции инварианта р2.иТак как Г (pt) — оператор,
действующий на дираковский спинор, описывающий свободную ча-
частицу с импульсом pj, то вклад дают только первые два члена.
Кроме того, второй член, очевидно, дает результат порядка Г и
поэтому им можно пренебречь. Следовательно, необходимо рассма-
рассматривать только первый член. Для р2 = т2 можно написать следую-
следующее выражение:
B1.35)
где /A) = /(!)(/те2) является здесь константой. Теперь будем симметри-
зовать множитель 1\, входящий в формулу B1.33), написав
Г—>-1/2(Г-)-Г')- Принимая во внимание, что оператор B1.33) дей-
действует на дираковский спинор, описывающий свободную частицу,
можно добавить к Г оператор 1/2(/> — tti)\ тогда соотношение B1.33)
получает вид
= U j dY0 dY'oG (То) О (Го) а (р2 - Pl — Г - Г') X
т]. B1.36)
326 Глава 21
В пределе Го—»• 0 получим
| g _ pi)i B j ;37)
где на множитель 1/г следует обратить особое внимание. Аналогич-
Аналогичным образом можно рассмотреть выражения B1.13) и B1.16); при
этом получается следующее соотношение:
M(c*>+M(ca> = i-g^(P2-Pi)'<i)- B1-38)
Величина Av(p2, pt) в выражении B1.12), как легко видеть,
в пределе р2—>pt переходит в величину /v(Pi), определяемую выра-
выражением B1.30). Далее, в конце § 2 было показано, что только та
часть величины Л\ которая остается при переходе к пределу
Рг—*Pi» может быть расходящейся. Поэтому, используя выраже-
выражение B1.35), расходящуюся часть Л1F> [формула B1.12)] можно за-
записать в виде
М(ЬУ=А-'(р1, Pl)gav(p2 —Pl)=—ga(p2 —Pl)/A). B1.39)
Поэтому, хотя каждый из матричных элементов, представленных
диаграммами на фиг. 56, Ь, с и d, в отдельности расходится, сумма
их конечна и фактически равна следующей величине:
M=eA,c(pz, Р!)аЧР2 —Pi)- B1-40)
где Ачс определяется формулой B1.22). Далее, в гл. 24 мы пока-
покажем, что такое сокращение расходимостей между частями собствен-
собственной энергии и вершинными частями имеет место в квантовой электро-
электродинамике во всех порядках; это является следствием требования
калибровочной инвариантности теории (Уорд [506, 507]).
Чтобы понять физический смысл расходимости в сумме двух
матричных элементов, соответствующих диаграммам на фиг. 56, cud,
проведем следующее рассмотрение. Вычислим эффект взаимодействия
электрона с внешним полем вплоть до порядка е'6. Для случая пер-
первого порядка по е мы должны рассмотреть диаграмму на фиг. 56, а,
где представлено взаимодействие электрона только с внешним полем.
Для случая третьего порядка по е необходимо сделать два изме-
изменения. Во-первых, вероятность Р того, что электрон будет .взаимо-
.взаимодействовать с внешним полем, когда около него имеется виртуальный
фотон, отлична от нуля. Это описывается диаграммой на фиг. 56, Ь.
Во-вторых, вероятность того, что электрон взаимодействует с внеш-
внешним полем, когда около него нет виртуального фотона, теперь уже
не равна единице, а равна 1—Р, т. е. уменьшается на величину
вероятности нахождения виртуального фотона около электрона (это
выполняется автоматически, если 5-матрица унитарна, так как уело?
Перенормировка 327
вие унитарности гарантирует сохранение полной вероятности). Упо-
Упомянутая вероятность Р дается выражением
|/A), B1.41)
где величина a(k) — амплитуда вероятности того, что имеется вир-
виртуальный квант с импульсом k.
Уменьшение вероятности обнаружения электрона, не окруженного
виртуальными квантами, эквивалентно изменению нормировки вол-
волновой функции электрона. Поэтому диаграммы, представленные на
фиг. 56, с и <2, часто относят к перенормировке волновой функции.
Диаграмма на фиг. 56, с есть перенормировка падающей волновой
функции. Диаграмма на фиг. 56, d относится к перенормировке ухо-
уходящей волновой функции. Волновая функция, т. е. амплитуда ве-
вероятности, должна быть перенормирована на множитель A—Pfl*,
так что поправка первого порядка есть 11гР, что и объясняет мно-
множитель У2 в выражении B1.38).
§ 4. Аномальный магнитный момент и лэмбовский сдвиг
В последнем параграфе мы видели, что после перенормировки
массы сумма вкладов от процессов, изображенных на фиг. 56, Ь, с и d,
конечна, и соответствующий им матричный элемент дается выраже-
выражением B1.40). Смысл этих радиационных поправок, по-видимому,
легче всего понять, если рассматривать их как „эквивалентный"
потенциал, в котором движется электрон. Таким образом, мы можем
рассмотреть выражение B1.10) вместе с выражением B1.40)
M = e[TV+Ac(p2. P1)la,(p2 —Pi) B1.42)
и принять, что М является оператором, который в первом прибли-
приближении, как это определяется выражением B1.9), возмущает движе-
движение свободного электрона и вызывает рассеяние его из состояния pt
в состояние р2.
Предположим теперь, что электрон, кроме собственного магнит-
магнитного момента eh/2mc, обусловленного зарядом е и спином 1/2 (на-
(напомним, что это рассматривалось в гл. 5, § 3), имеет дополнитель-
дополнительный магнитный момент Aji (eh/2mc). Если электрон имеет такой допол-
дополнительный магнитный момент, то его гиромагнитное отношение больше
не будет точно равняться 2. Ту часть магнитного момента, которая
делает величину гиромагнитного отношения отличной от 2, часто
называют „аномальным" магнитным моментом. Дополнительное взаимо-
взаимодействие электронно-позитронного поля с внешним электромагнит-
электромагнитным полем, обусловливающее появление такого дополнительного
момента, может быть учтено добавлением члена
± £L * (х) B1Л
328 Глава 21
к плотности функции Лагранжа A2.16), описывающей электронно-
позитронное поле, взаимодействующее с внешним полем F^(x). Этот
член даст следующий вклад в плотность энергии взаимодействия
(мы положили й = с=1):
(^Iф(х)а'1>(х)^(х). B1.436)
В первом порядке вклад e%?i(x) в рассеяние электрона дается тогда
выражением
или, более подробно, для рассеяния, при котором электрон совер-
совершает переход1) из состояния pt в состояние p2 = Pi4-q2> мы полу-
получаем следующее выражение!
АЛ ' ( l\ I " I —___^_ J //4: -V"e^P2*^ О — ^Pl*^ ^v''
IVI • I " Ir J I л I ,n w. I U- ЛС * С * y\^
Xw^j^F^WwiPi)- B1.44a)
M' = — 2icta» (J2) Г~2е^ "j o!*"'/:'piv (q)l«»(Pi). B1 • 446)
M'= — 2Kiw(p2)l^±a^ {q^a (q) — ?.e,(q)}]«(A). B1.44b)
Ai' = — liclw (pz) [^— /1^ в^да (q)J да (^). B1.44r)
При получении выражения B1.44г) из выражения B1.44в) мы исполь-
использовали антисимметрию величины о^, а именно о = — а .
Сравним этот матричный элемент с выражением B1.23), спра-
справедливым для малых q = р3 — pt, т. е. для полей, которые медленно
меняются в пространстве и времени. Последнее утверждение стано-
становится ясным, если учесть, что в координатном пространстве д„ач(ц)
соответствует dAt(x)/dxf- и аналогично q2 соответствует □• По-
Поэтому в выражении B1.23) мы будем пренебрегать высшими произ-
производными. Тогда первый член выражения B1.33) может быть пере-
переписан в следующем виде:
B1.23b)
Вспомним, что
и, следовательно,
, (X) = f cfiqe-^Fv,, (q) = - I f <Иде~^х (^ D) - V» <Ч)
Перенормировка 329
Если сравнить выражения B1.23в) и B1.44г) [напомним также
выражения B1.10) и B1.12)], то ясно, что для слабых полей вклад
B1.23) в радиационные поправки второго порядка к рассеянию может
быть интерпретирован как следствие наличия у электрона аномального
магнитного момента, величина которого равна
Д|* = й' B1.45а)
Итак, радиационные поправки приводят к тому, что в нереляти-
нерелятивистском приближении (мадые q) при взаимодействии с магнитным
полем электрон ведет себя так, как будто он обладает магнитным
моментом, равным l-f-(a/2it) магнетонов Бора.
Существование этого аномального магнитного момента впервые
экспериментально обнаружили в 1947 г. Нейф, Нельсон и Раби [349],
Нагл, Джулиан и Захариас [350]. Брейт [64—66] первый указал,
что наблюдаемый эффект мог бы быть объяснен наличием у элек-
электрона малого дополнительного спинового магнитного момента.
Швингер [436] впервые показал, что часть радиационных поправок
в квантовой электродинамике соответствует дополнительному маг-
магнитному моменту, который связан со спином электрона и величина
которого равна а/2тс [см. также работу Люттингера [312]]. Карплус
и Кролл [263], используя формализм Дайсона — Фейнмана, вычислили
радиационную поправку четвертого порядка к магнитному моменту
электрона. Она равна —2,973 a2/ir2 магнетонов Бора, так что маг-
магнитный момент квазисвободного электрона равен в этом прибли-
приближении следующей величине:
Ш:\1 +!;~2'973 Й= !'001145 магнетонов Бора. B1.456)
Величина магнитного момента электрона была наиболее точно экспе-
экспериментально измерена в 1952 г. Кбнигом, Проделом, Кушем [282];
она равна l,001145zt0,000013 магнетонов Бора.
Аналогично лэмбовский сдвиг можно получить при рассмотрении
второго члена формулы B1.23). Строго говоря, электронная линия
на фиг. 55 в этом случае не является больше свободной (т. е.
р^фт2), так как электрон связан в атоме. Но если пренебречь по-
поправками, возникающими при учете того, что р2Фтг, то сдвиг
уровня будет просто средней величиной второго члена формулы
B1.23) для рассматриваемых состояний атома водорода. Последнее
утверждение не вполне точно, так как второй член формулы B1.23)
стремится к бесконечности, если фиктивную массу кванта Хмин-
устремить к нулю. Такая „инфракрасная катастрофа" должна быть
ложной, и, действительно, она не встречается в лэмбовском сдвиге
уровней связанных электронов.
В этом можно убедиться из нерелятивистского рассмотрения
лэмбовского сдвига, данного в § 1г где мы предполагали, что све-
330 Глава 21 ,
товые кванты имеют равную нулю массу покоя и что электрон
связан. Поскольку только состояния с пфт дают вклад, т. е. при-
приводят к множителю Еп— Ет в числителе, выражение B1.8'в) для
лэмбовского сдвига имеет резонансный знаменатель Еп— Em-\-k,
который не равен нулю для световых квантов нулевой энергии
(& = 0).
Затем можно провести следующее рассмотрение. Пусть нереля-
нерелятивистский лэмбовский сдвиг вычислен для световых квантов с рав-
равной нулю массой покоя по формуле B1.8в), а потом вычислен снова
для фотонов с массой покоя ~куат.. В последнем расчете величина k
в знаменателе B1.8в) должна быть заменена на величину
<"* = (£2 + 4ин.I/!. B1.45b)
Разность между результатами этих двух вычислений представляет
разность между лэмбовскими сдвигами связанного электрона, взаимо-
взаимодействующего с поперечными квантами, имеющими нулевую и ко-
конечную массу покоя соответственно. Эта разность равна
к
LE @) — LE (W) = з^з / dk 2 | vmn I* (En — Em) X
A Bl-45r)
_] +kE -E +(
Интеграл в выражении B1.45г) сходится как на нижнем пре-
пределе Aj = O, так и на верхнем пределе k—K', поэтому величину К
можно заменить на оо. Кроме того, существенный вклад в выра-
выражение B1.45г) дают только значения й<[Хмяя_, поэтому, если мы
выберем ^мин. <^С тс2, то все важные промежуточные состояния (п., k)
в формуле B1.45г) будут нерелятивистскими; следовательно, при-
приближения, использованные в § 1, включая и дипольное приближе-
приближение, являются оправданными.
Теперь к формуле B1.45г) добавим среднее значение второго
члена формулы B1.23) для рассматриваемых состояний атома водо-
водорода, оставляя массу фотона Хмн„. конечной. В самом деле, для того
чтобы оправдать использование оператора лэмбовского сдвига сво-
свободного электрона B1.23) для рассматриваемой задачи связанных
состояний, мы выберем величину ~kvam, большой по сравнению с ве-
величиной энергии связи в атоме водорода, т. е. выберем ~кшт.^> lRy-
Это условие, очевидно, совместимо с требованием Хмин.<^С те2. Вы-
Вычисление показывает, что в сумме выражения B1.45г) и среднего
значения выражения B1.23) сокращается член 1пХмия., и, как и сле-
следовало ожидать, результат не~ зависит от фиктивной массы фотона.
Френч и Вайскопф [191] указали, что следует учесть также вклад про-
продольных и временно-подобных фотонов в нерелятивистскую часть фор-
формулы B1.45г). Если это сделано, то результат эквивалентен сумме
Перенормировка 331
выражения B1.8г) и среднего значения второго члена формулы B1.23)
при условии, что j.
1пХмия. = 1п2/С — j . B1.45д)
Из только что описанных вычислений для лэмбовского сдвига
получается ранее упоминавшийся результат— 1052 мггц (после вклю-
включения эффектов поляризации вакуума). С уточнением этих вычисле-
вычислений и обсуждением высших приближений читатель может ознако-
ознакомиться в статьях Баранджера, Бете и Фейнмана [18], Карплуса и
др. [268], Салпетера [425] *>.
Теперь вернемся к обсуждению значения Х^,,. для проблем, свя-
связанных с рассеянием свободных электронов. Тот факт, что выра-
выражения B1.23) и B1.40) расходятся логарифмически- при >.„„. —>-0,
принято называть „инфракрасной расходимостью". Вышеописанный
метод, позволяющий устранить инфракрасные расходимости в слу-
случае связанных электронов, неприменим в случае свободных элек-
электронов. В то же время ясно, что нельзя вычислять поперечные сече-
сечения рассеяния непосредственно из выражений B1.23), B1.40), положив
в них Хини. —>-0. Эта трудность устранится, если учесть, что невоз-
невозможно указать эксперимент, в котором можно было бы гарантиро-
гарантировать, что электрон в течение процесса рассеяния не излучает ни
одного фотона. При постановке эксперимента в лучшем случае можно
добиться того, что если электрон и излучает фотон, то энергия
фотона меньше, чем некоторая величина k0, которая определяется
точностью измерительных приборов. Оказывается, что дифферен-
дифференциальное поперечное сечение для рассеяния с излучением фотона
(тормозное излучение) с энергией, меньшей k0, также содержит
инфракрасную расходимость и что эта расходимость точно сокра-
сокращается с аналогичной расходимостью в радиационных поправках
(см. фиг. 56, Ь). В общем случае инфракрасные расходимости всегда
сокращаются, если рассматривать все возможные процессы (включая
и излучение реальных квантов) в данном приближении. С общим
рассмотрением этой проблемы читатель может ознакомиться в статьях
Блоха и Нордсика [45], Паули и Фирца [375], Бете и Оппенгей-
мера [32], Йоста [250, 251], Брауна и Фейнмана [71] и Яуха и Рор-
лиха [242] (см. также § 8).
§ 5. Поляризация вакуума
До сих пор мы не рассматривали член, соответствующий диа-
диаграмме на фиг. 56, е. Для интерпретации этого члена представим,
что замкнутая электронно-позитронная петля производит ток
А(Ч) = Х5*„(Ч)«ЧЯ); B1-46)
1) Кроме того, см. работы Кролла и Поллока [294], а также Карплуса и
Клейна [267], где вычислены радиационные поправки к сверхтонкой структуре.
332 Глава 21
этот ток является источником фотона с импульсом q, который
взаимодействует с электроном и рассеивает его. Требование инва-
инвариантности этого индуцированного тока по отношению к калибро-
калибровочному преобразованию
а-->-а' + ?'Л B1.47)
приводит к соотношению
^v(q)<74 = 0. B1.48)
Аналогично для сохранения величины J^Cq) необходимо, чтобы удо-
удовлетворялось уравнение непрерывности
VU (Я) = УК^ (q) = 0, B1.49)
что эквивалентно соотношению B1.48), так как тензор К^ симме-
симметричен. Оператор К^(ф обычно называют поляризационным тен-
тензором. Если тензор K^(q) мы запишем в форме
^v(q) = K(i)(q2) V^+q^Cq2)^,. B1-50>
где вследствие релятивистской инвариантности K(i) и К{2) являются
функциями только инварианта q2, то соотношение B1.48) экви-
эквивалентно условию
^(i)(q2) = — KB)(q2). B1.51)
Таким образом, ток /^(q) в выражении B1.46) должен иметь вид
U Jj М ^ id (q2) a- (q), B1.52а)
или
U (q) = £ Кы (q2) 4 (q). B1.526)
где величина JJ(q) — ток, производящий внешнее поле ^(q). Для
получения формулы B1.256) мы использовали уравнения Максвелла для
внешнего поля, а именно
—|^— = j£(x); B1.53а)
в импульсном пространстве эти уравнения имеют вид
(ч?Яч—ё?.*ч2)а* (q)= 4 (q) B1.536)
и связывают внешнее поле с производящим его током.
Выражение Кф можно вычислить следующим образом:
B1.54а)
, (q) = j dz J d*p j^q^J I q2,z_'22\ _OT2i2• B1 -546>
о
Перенормировка 333
При получении выражения B1.54в) из B1.546) мы сместили начало
координат области интегрирования р—>р — qz. Поскольку постоян-
постоянная т имеет малую отрицательную мнимую часть, мы можем снова
повернуть контур интегрирования так, чтобы интегрирование по
переменной р0 производилось от —/оо до -f-ioo. Если мы вычислим
шпур в выражении B0.54в), принимая во внимание соотношения G.56)
и G.57), а также то, что шпур от нечетного числа матриц -j- равен
нулю, и если опустим члены, нечетные по переменной р [фор-
[формула B0.41)] и используем соотношение симметрии B0.42), то
получим
1
= 4j dz) d'p
B1.54г)
Это выражение для /Cv(q) квадратично расходится, поскольку
в подинтегральном выражении в числитель входит шестая степень
переменной интегрирования р (т. е. p2d*p), а в знаменатель — только
четвертая. Однако если мы потребуем, чтобы соотношение B1.54г)
было калибровочно инвариантным [формулы B1.50), B1.51)], то
в результате получим
-q«(* —*■)—-g-
J
d*P [р2 + чз(г — г*) — отар =°-
Хотя полученный интеграл, строго говоря, не имеет смысла, так
как он расходится, мы используем это выражение Ч (являющееся
результатом физического требования калибровочной инвариантности)
для того, чтобы переписать выражение B1.54г) в следующем виде:
1
К.ЛФ = — 8 (Я,Ч, — gavQ2) Г dz(z — г*) Г d*p [р2 + ч»(г_^)-«2]-г,
о B1.54д)
К*. (Я) = (W* — S",vq2) Kw (q2). B1 -54e)
Если величину Кщ (q2) разложить по степеням q2/m2:
2)
(Я2) = *(?} +Е<)+•••> B1-55)
то ясно, что величина k\i) расходится логарифмически, но все осталь-
остальные члены конечны. В этом можно убедиться следующим образом.
Разложение по q2 снижает степень переменной интегрирования р,
причем уменьшение показателя степени р равно увеличению показа-
показателя степени внешней переменной q, что было показано в конце § 2.
1) При несколько более удовлетворительном рассмотрении нужно было бы
первоначально „регуляризировать" выражение B1.54г) по электронным мас-
массам (см. дополнение С в работе Фейнмана [169], а также работу Паули
и Вилларса [380]).
334 Глава 21 ■■
Таким образом, член в выражении для Кщ, не зависящий от вели-
величины q2, умножается на интеграл по р, подинтегральное выражение
которого имеет нулевой порядок (т. е. dpjp); этот интеграл дает
логарифмическую расходимость для К$). Следующий член в выраже-
выражении для К(х) имеет порядок q2 и умножается на сходящийся интеграл,
подинтегральное выражение которого ведет себя при больших р,
как dp/ps; следовательно, к[[] и все высшие члены в разложении B1,55)
будут сходящимися интегралами по р. Теперь можно снова исполь-
использовать метод, примененный при получении выражения B1.236),
а именно из величины /СA) (q2) вычесть ее величину при q2 = О
и таким образом получить конечный результат. Ниже покажем, что
идея перенормировки заряда указывает как раз на то, что именно
остающаяся конечная часть /СA) (q2) — /СA) @) описывает наблюдаемые
эффекты поляризации вакуума.
Используя метод, который уже применялся при ковариантном
вычислении собственной энергии электрона (см. гл. 20, § 3), мы
можем вычислить (см. дополнение С в работе Фейнмана [169]) выра-
выражение для К^ (q); при этом получается следующий результат:
(q) = 4iA {q& — g,,q2) [— -g- ^ Hm 1 n A-
где q2=4/re2 sin2 9. Расходящийся логарифмически член—(8it2i/3) In (Х//и)
соответствует члену К(оу
Если на внешнее поле наложить условие Лоренца, имеющее
следующий вид:
и использовать формулу B1.55), то матричный элемент B1.18)
можно переписать в следующем виде:
№• <21-б6>
Теперь можно объединить первый член в правой части этого
выражения с матричным элементом B1.10), соответствующим диа-
диаграмме на фиг. 56, а. Тогда, хотя член (/а/4тс8)Кщ фактически рас-
расходится, мы можем рассматривать его просто как постоянный
множитель, уменьшающий величину внешнего поля. Это дает не-
ненаблюдаемую перенормировку внешнего поля. Из соотношения B1.526)
видно, что расходящаяся часть индуцированного заряда y«(q) точно
пропорциональна индуцирующему внешнему заряду Jp(q). Поэтому
Перенормировка 335
перенормировку можно рассматривать как такую методику, при
которой перенормируется плотность внешнего 4-мерного тока J^(q),
а тем самым и заряд в целом.
Отметим общие черты перенормировки заряда и массы. В обоих
случаях расходимость связана с ненаблюдаемыми явлениями. Так, при
перенормировке массы расходимость Ьт изменяет только т0— меха-
механическую массу электрона. Поскольку наблюдаемой является только
то-{~Ьт = т, то расходимость исчезает, если результат записать
через наблюдаемую массу. Это же имеет место и при перенорми-
перенормировке заряда. Внешний 4-мерный ток 7^ невозможно экспериментально
отделить от пропорционального ему индуцированного тока. Действи-
Действительно, точно так же, как вокруг электрона всегда имеется облако
виртуальных фотонов (и поэтому мы всегда измеряем т), так и
внешний ток всегда поляризует вакуум, и во всех измерениях вне-
внешнего тока (и заряда) измеряется не величина У£(х), а величина
B1.57)
где ijLs (х)— я перенормированная" плотность 4-мерного тока.
Поэтому, если результат записать через наблюдаемую плотность
внешнего тока J^r(x) (вместо У*), то он будет конечным, а именно
^ . . B1.58)
Следовало бы также перенормировать и остальные члены
ряда B1.58), но в том порядке, который мы рассматриваем, они уже
перенормированы. Однако диаграммы высших порядков приводят
к перенормировке этих членов.
Из сделанных выше замечаний достаточно ясно, что даже при
отсутствии бесконечностей, мы должны были бы перенормировать
теорию. Происхождение перенормировки связано с тем, что состояние
системы описывается с помощью невозмущенных „голых" волновых
функций, хотя в реальном физическом мире мы никогда не можем
выключить взаимодействие между полями. Поэтому появляются
поправки к „голому" заряду и массе. Однако так как на опыте
могут наблюдаться только „голая" масса („голый" заряд) плюс
поправки к ней, то мы всегда должны выражать наблюдаемые вели-
величины через перенормированные константы. Поэтому в некотором
смысле вопросы расходимостей и перенормировки разделены. Тем
не менее, поскольку все локальные релятивистские теории поля
со взаимодействием расходятся, мы будем использовать понятие
„перенормировки", чтобы выразить то обстоятельство, что расхо-
расходимостей не возникает, если наблюдаемые величины выражены через
перенормированный заряд и массу.
336 Глава 21
Вычисление члена /СA> может быть проведено непосредственно;
тогда первый порядок по q2//re2 индуцированного тока дается
выражением
24(я)- B1.59I)
Итак, электростатический потенциал между двумя классическими
пробными зарядами в вакууме теперь больше не дается точно зако-
законом Кулона, а изменяется под влиянием поляризации вакуума. Это
известно как эффект Юлинга [488], который впервые вычислил
отклонения от закона Кулона (т. е. коэффициент K\i) и т. д.) сразу же
после первого обсуждения поляризации вакуума Дираком [106, 107]
и Гейзенбергом [225, 226] 2>.
Эффект Юлинга дает поправку к лэмбовскому сдвигу, рав-
равную— 27 мггц. Так как расхождение между экспериментом и теорией
в настоящее время не превышает 0,5 мггц, то это является прямым
доказательством того, что поляризация вакуума является реальным
эффектом. . ,;
Сам эффект поляризации вакуума существенно размазывает эффек-
эффективный заряд точечных зарядов на расстояниях порядка Ь/тс [см.
разложение B1.58)]. Физическую картину, происходящую в поля-
поляризационных явлениях, можно представить следующим образом.
Заряд QQ в результате взаимодействия с электронно-позитронным
полем окружает себя облаком из электронов и позитронов; часть
из них, имеющая полный заряд SQ (того же знака, что и Qo), уходит
на бесконечность (см. дополнение к статье Швингера [440]), а часть
с полным зарядом — SQ остается в облаке, непосредственно связан-
связанном с пробным телом, т. е. на расстояниях, меньших h/mc. При
наблюдении заряда тела на больших по сравнению с h/mc расстоя-
расстояниях мы измеряем эффективный заряд Q — Qo — SQ. Однако при
наблюдении с расстояний, много меньших h/mc, наблюдался бы
заряд Qo.
Эффекты поляризации вакуума высших порядков в случае вне-
внешнего поля были рассмотрены в работах Челена [254, 255],
1) Отметим, что разложение B1.56) и, следовательно, B1.59) верно только
в том случае, если qa <[ /я2. Когда q2 > B/яJ, внешнее поле может рождать
реальные пары; тогда матричный элемент М^ будет иметь как веществен-
вещественную, так н мнимую части. Мнимая часть соответствует убыванию во времени
амплитуды вероятности того, что будет происходить только чистый процесс
рассеяния (без рождения реальных пар). С другой стороны, будет соот-
соответственно возрастать во времени амплитуда вероятности перехода в конеч-
конечное состояние, в котором имеется некоторое число (реальных) электронно-
позитронных пар. Возрастание и соответствующее убывание этих совокупно-
совокупностей матричных элементов таково, что полная вероятность перехода из
начального состояния равна единице н S-матрица унитарна (в связи с этим
см. работу Далица [96]).
2) Обзор этих работ см. в статье Вайскопфа [517]; см. также статьи
Валатина [496, 497].
Перенормировка 337
Фарри[202], Швингера [441], Умэдзавы и Камефучи [494] и др. В кван-
квантовой электродинамике поляризация вакуума в четвертом приближении
была проанализирована в работах Йоста и Люттингера [252], а также
Баранджера и др. [18], Дайсона, Салпетера. В последней работе вы-
вычислен вклад поляризации вакуума в лэмбовский сдвиг. В общем
случае замкнутые петли, содержащие больше двух фотонов или
взаимодействий с внешним полем, сходятся.
Положение, аналогичное рассмотренному выше, получается и
в случае, когда мы рассматриваем не взаимодействие с внешним
полем, а взаимодействие двух зарядов. Обусловленные поляризацией
вакуума поправки низшего порядка к рассеянию Мёллера предста-
представлены на диаграмме фиг. 57, с. В этом случае мы можем рассмотреть
радиационные поправки, заменяя функцию распространения фотона
(l/k2)^, в матричных элементах рассеяния Мёллера на величину
(с точностью до постоянных множителей)
«-p^v(k)-p. B1-60)
где /Ср.» — тензор поляризации B1.46). Тензор К^, как и в фор-
формуле B1.54), можно снова разложить, и постоянный расходящийся
член можно включить в перенормировку заряда е2, который встре-
встречается в матричном элементе низшего порядка, соответствующем
диаграмме рассеяния Мёллера.
Отметим, наконец, что тензор К^(к) в случае к2=0 описывает
в низшем приближении „собственную энергию" фотона, которая
в данном случае возникает вследствие рождения виртуальных элек-
тронно-позитронных пар и их последующей аннигиляции. Весьма
удовлетворительным представляется то, что величина К^(к)р(к)
равна нулю [здесь/v(k)—4-мерный потенциал, описывающий фотон
с вектором энергии-импульса к, для которого к2 = 0 и &v/v(k) = 0].
В этом можно убедиться из соотношения B1.54е). Вследствие этого
собственная энергия фотона равна нулю; это есть результат требо-
требования калибровочной инвариантности теории. Из соотношения B1.46)
следует также, что движущийся в пространстве одиночный фотон
не индуцирует токов в вакууме. Несколько другим путем можно
установить, что эффекты поляризации вакуума не имеют места при
свободном распространении электромагнитных волн. Однако послед-
последнее утверждение верно только в случае рассмотрения эффектов
в низшем порядке по внешнему или радиационному полю. Если же
рассматривать нелинейные эффекты во внешнем поле (т. е. квадра-
квадратичные члены и члены высших порядков по Ае), то, как мы увидим
в гл. 22, § 4, становится возможным наблюдать такие процессы,
как рассеяние фотона внешним полем. Аналогично в высших поряд-
порядках возможно рассеяние фотона на фотоне вследствие процессов
вакуумной поляризации высших порядков (замкнутые петли).
338 Глава 21
Перенормировка заряда, обусловленная поляризацией вакуума,
требуется не только вследствие виртуального рождения электронных
пар, но также и заряженных мезонных пар, нуклонных пар и т. д.
Фактически заряженные частицы любого вида дают вклад в поля-
поляризацию вакуума, и вклады различных частиц будут просто скла-
складываться (Фельдман [152], Умэдзава и Кавабе [490, 491, 493], Умэд-
зава и Камефучи [494]). Таким образом, указанная перенормировка
заряда может быть применена к заряду любой частицы, которая
может взаимодействовать с электромагнитным полем. Другими сло-
слов-ми, если предположить, что неперенормарованные заряды всех
частиц равны, то будут равны также и перенормированные заряды,
независимо от специфических форм взаимодействия, дающих вклад
в поляризацию вакуума.
До сих пор мы рассматривали только радиационные поправки
низшего порядка к формулам рассеяния на внешнем поле (см.
фиг. 56, а). Ясно, что в высших порядках возникают гораздо более
сложные диаграммы, чем приведенные на фиг. 56. Мы вернемся
к ним в гл. 24 при общем рассмотрении перенормировки.
§ 6. Перенормировка в мезонной теории
Соображения, использованные нами в электродинамике, могут
быть без труда перенесены в мезонную теорию. Рассмотрим диа-
диаграммы от b до е на фиг. 58, которые представляют радиационные
поправки низшего порядка к элементарной вершинной части (фиг. 58, а),
соответствующей рассеянию нуклона на мезоне. Мы не лредполагаем,
что нуклон или мезон являются свободными. Соответствующие
им линии могут быть частями более сложных диаграмм. В этом
случае диаграмме, изображенной на фиг. 58, а, будет соответство-
соответствовать множитель
B1.61)
Отметим, что в случае мезонной теории имеется на одну диаграмму
больше, чем в случае электродинамики; эта „лишняя" диаграмма
приведена на фиг. 58, е2. Это связано с тем, что мезон имеет массу
покоя. Диаграмма на фиг. 59 (являющаяся частью диаграммы на
фиг. 58, el) соответствует оператору (мы опускаем постоянные
множители)
l> f/^\1.62)
к2—
fd«pSp/r-* г Г-^—\1 . B1
J y v\ p + k — m p — m /J k2— (j.2
Если падающий мезон свободен, то мезонные функции распростра-
распространения в формуле B1.62) следует опустить. Рассмотрим именно этот
случай. Для вычисления интеграла применим регуляризацию.
p2
Pi
С/ С2
el
f I 6-Sm
Pi
I Pi
I
-Sm
d\
-V2
O-
dZ
Фиг. 58.
-v
к
p+K
Фиг. 59.
22*
340 Глава 21 ' .
Это будет выполнено следующим образом. Объединим два зна-
знаменателя в формуле B1.62), используя формулу Фейнмана
1
(aby1 = Jdz[az-\-(l—z)b]~2, B1.63)
о
так что наш интеграл B1.62) получит следующий вид (введены
регуляризирующие массы нуклонов):
M'=-g* fdz fd'pYCi SP[T (p + k + m^Vip+m,)]
0 J i (Pa + 2*p.k + *k2-/^ + /eJ
Полученный интеграл, очевидно, является функцией только к2, в чем
можно убедиться, смещая начало координат переменной интегриро-
интегрирования и используя свойство симметрии
В случае Г = fs матричный элемент, по существу, имеет форму
Очевидно, V представляет квадратично расходящийся интеграл. Мы
можем разложить V около точки к2 = jjl2 так же, как разлагали
тензор поляризации; тогда мы получим
K(k2) = V@) + (k2 — j*2)VA) + (k2— j/)V2)+ ••• B1.66)
Разложение в ряд Тейлора соответствует дифференцированию подин-
тегрального выражения и, следовательно, возрастанию степеней зна-
знаменателя в выражении B1.65), так что УA) расходится только лога-
логарифмически, а V и все высшие члены сходятся.
Теперь мы можем рассматривать первый член ряда B1.66) как
поправку к массе мезона вследствие взаимодействия с нуклонным
полем. В самом деле, если имеется поправка к массе бозона, то
в лагранжиане свободного поля „голую" массу бозона [х2 можно
заменить на величину [х2 — Sjjl2, где \х. — экспериментальная масса
бозона. Возмущение — §[А2ср2(х) должно тогда использоваться вместе
с любым членом поляризации вакуума типа, представленного на
фиг. 59. Член —8(jL2cp2(x) в гамильтониане взаимодействия приводит
к тому, что к величине М [формула B1.62)] необходимо добавить
выражение
которое сокращается с членом V в разложении B1.66), если
выбрать 8(jl2==^(O).
Перенормировка 341
Аналогичный член не встречается в электродинамике, так как
вследствие калибровочной инвариантности не может появиться член
вида А2, а это и приводит к тому, что масса фотона равняется нулю.
Для свободного бозона (k2 = (jl2), согласно формуле B1.66), имеет
место только перенормировка массы. Для процессов, в которых
участвует виртуальный (к2 Ф jjl2), а не свободный бозон, мы должны
принять во внимание и другие члены разложения B1.66). Поэтому
рассмотрим матричный элемент, соответствующий диаграмме на
фиг. 58, el. Если эта диаграмма лежит внутри некоторой большей
диаграммы, то ей соответствует следующий множитель (опускаем
постоянные множители):
{е1)^1V(k2)8*(р —Pi —k)- B1.68)
МО^ГV(k)
Рг—т pi — m ка-^ к 'к2—м
Аналогично диаграмме 58, е2 соответствует множитель
V2 S'(P2 — Pi — к). B1.69)
г к» jj2
V2
— тп
Если величину У(к9) в формуле B1.68) разложить согласно фор-
формуле B1.66), то первый член с И0) точно сокращается с М<ей)
(перенормировка массы). Рассмотрим член с И1'; он дает следующий
вклад в матричный элемент М^01)-.
= о -Л— Г -^ '1— И1» (к2 — tx2) —i
^ Г. 8(Р2 —Pi —к). B1.70)
Ръ — т. р1 — /я к2 — [А2
Полученная величина равна (бесконечной) константе, умноженной на
матричный элемент М(а\ Если выписать постоянные множители, тс и
т. д., то матричный элемент м[1р точно равен
At$=V*1)jrfa\ B1.71)
Поэтому можно объединить величины М^ и mffi и рассматривать
[1 +VA)] О как новую перенормированную и наблюдаемую константу
связи. Отметим, что величина VW совсем не зависит от процесса
рассеяния. Последний член \Д2> конечен и представляет наблюдаемую
радиационную поправку к матричному элементу М .
Рассмотрим следующую диаграмму, изображенную на фиг. 58, Ъ;
она представляет собой вершинную часть. Рассмотрение, аналогич-
аналогичное проведенному в квантовой электродинамике, приведет к тому,
что матричный элемент М ' может быть получен из матричного
элемента Ж(а* заменой в последнем оператора Г на оператор
Г->СГ-1-Д(р,, Pi). B1.72)
342 Глава 21 -.
где С — расходящаяся константа. Фактически, если мы рассматри-
рассматриваем только нейтральные мезоны, расходимость С сокращается
с двумя членами, соответствующими диаграммам на фиг. 58, cl и
dl. Однако в дальнейшем мы должны также рассматривать и заря-
заряженные мезоны, например в случае изменения состояния нуклона
(нейтрон переходит в протон) при излучении или поглощении мезона;
при этом упомянутое сокращение расходимости больше не имеет
места. Мы можем, однако, интерпретировать эту расходимость как
перенормировку константы связи (см., однако, работу Челена [2бО],
где рассмотрена неоднозначность такой перенормировки; см. также
т. II, гл. 44, § 4). Теперь рассмотрим диаграмму на фиг. 58, с, ей
соответствует оператор
()
где
Micl) = ^— 2(p2)M(a). B1.74а)
Р%— т
М(сг) = —, 1 ЬтМ(а). B1.746)
Рг — т
Здесь 2 — инвариантный матричный оператор (точнее инвариантом
является ф 2 ф)> поэтому оператор 2 (Р) можно разложить около
точки р== т следующим образом:
)SP). B1-75)
где от и В—расходящиеся константы. Так как оператор
линейно расходится1), то оператор 20(р)—сходится. Как и раньше,
мы определим
2(р2 = от2) = 8/ге. B1.76)
Поэтому можно написать
L B1-77)
Теперь снова можно объединить член ВМ с матричным элемен-
элементом М * и переопределить величину константы связи,
§ 7. Применения
В предыдущих параграфах было дано краткое описание совре-
современных методов обращения с расходимостями, которые возникают
в высших членах разложения в степенной ряд решений уравнений
1) Эта линейная расходимость случайно сводится к логарифмической
вследствие приблизительного взаимного сокращения членов, происходящих
от состояний с положительной и отрицательной энергией.
Перенормировка 343
движения в релятивистской теории поля. Эти методы были приме-
применены для расчета радиационных поправок низшего порядка для наи-
наиболее элементарных процессов рассеяния, в которых принимают
участие электроны и фотоны.
Первым таким процессом, для которого были вычислены радиа-
радиационные поправки (кроме лэмбовского сдвига — для него необхо-
необходимо рассматривать проблему связанных состояний), был процесс,
рассмотренный нами при исследовании методики перенормировки,
т. е. кулоновское рассеяние электронов. Радиационные поправки
к формуле рассеяния Резерфорда (см. гл. 9, § 1) в низшем прибли-
приближении были впервые вычислены Швингером [440]. Расчет прово-
проводился в первом борновском приближении как по отношению к куло-
нову полю, так и по отношению к полю излучения. Расчет имеет
силу, если отдельно выполняются соотношения г<С1 и Za<dl
(Z — заряд ядра). Поперечное сечение рассеяния для этого процесса
(включая и радиационные поправки) может быть получено обычным
путем из квадрата амплитуды перехода
Т = — 1-кГа (р2) Ми (рх), B1.78)
где величина М дается формулой С21.40) х>. Использование формулы
B1.40) не является полностью корректным, так как матричный эле-
элемент М из формулы B1.40) содержит инфракрасную расходимость
в пределе Хмин. -*■ 0.
Способ устранения этой трудности был уже указан раньше,
в конце § 4. Он основывается на том, что параллельно рассеянию
без излучения имеется отличная от нуля (и фактически бесконечная)
вероятность того, что электрон при рассеянии испустит один фотон.
Во втором порядке имеются две такие диаграммы: на одной элек-
электрон сначала рассеивается внешним полем, а затем испускает фотон;
на второй имеет место обратный процесс — сначала испускается
фотон, а затем электрон рассеивается. Матричные элементы, соот-
соответствующие этим двум диаграммам, можно легко выписать, если
использовать правила гл. 19, § 3. Для перехода рх —>р2 с испуска-
->-
нием фотона с энергией-импульсом к и поляризацией s<x>(&) [напо-
->-
мним, что к-е(х>(А) = 0] матричные элементы этих диаграмм имеют
вид
«(pi), B1-79)
B1.79а)
См. также вывод формулы Резерфорда в гл. 9, § 1.
344 Глава 21
Тг = - 2*/« (р2) [ее (р2 — Pl + к) {*ZipJ?,0 X
11 (
X g y • eW AI a (p.), B1.80)
^ 1/2B71K^ l *- 'J ^ v
^(p1). B1.80a)
Рассмотрим случай, когда излучаемый фотон является очень мягким,
т. е. когда &0<^/ге и A0«^|Pil« |Рг1- Принимая во внимание, что
q B1.81)
и что для рассматриваемой задачи
к2 = 0, B1.82а)
(Л —»)Я(Л)=О; р? = т2, B1.826)
п(р2)(рг — т) = 0; р! = /ге2, B1.82в)
мы можем получить следующее выражение:
B1.83а)
B1,83б)
где Т(а)(р1, р2) дается формулой B1.10). Вероятность того, что
электрон при рассеянии из состояния pt в состояние р2 испустит
один фотон (энергия которого лежит в пределах 0 и d
а поляризация произвольна), дается тогда выражением
з лв з ав
x=oo x=oo
X
Pa
i. P2)l2- B1-84)
Из формулы B1.84) видно, чго эта вероятность логарифмически
расходится на нижнем пределе.
Если, кроме этого, изменение импульса электрона мало, т. е.
q\z=\pt — p2\<s^m, то этот результат можно упростить, переходя
Перенормировка 345
к системе координат, в которой электрон, по существу, покоится
как в начальном, так и в конечном состояниях. В этой системе
рх -k = p2 ■k=mk0. B1.85a)
Множитель под знаком абсолютного значения в интеграле B1.84)
имеет тогда числитель
Если принять во внимание только поперечные кванты (а только
такие кванты могут фактически излучаться) и усреднить по всем
->■
направлениям вектора k, то получим
2
< 2 (q ■ «w (*) J > = —| q2- B1 -856)
x-i
Простые алгебраические выкладки приводят к следующему резуль-
результату:
з ае
|g() nft-M-, B1.86)
если нижний предел интегрирования по переменной k в интеграле
B1.84) заменить на ймия. • Величина АЕ относится к той системе
координат, где электрон, по существу, покоится. Кроме этой вели-
величины, все остальные множители релятивистски инвариантны. Расчеты
для случая произвольного изменения начальных энергии и импульса
электрона см. в работах Йоста [250, 251], Швингера [439], а также
Блоха и Нордсика [45].
Вероятность того, что электрон рассеивается из состояния и (рх)
в состояние а (р2) без излучения фотона, дается квадратом выраже-
выражения B1.78), или в явной форме:
| Т |* = | — 2*/« (р2) [М(а) + еА^о (р2, Pt) a" (p2 — Pl)] и (£) |« =
= l^o)(Pi. P2)|2 —
— 2wT(o)+(Pl, p2)a(p2)eAvC-(p2, Pl) а-(р, — рх) и (pt) +
Pl)a4P2 — Pi)«(Pi))Va)(P2. Pi). B1-87)
где мы пренебрегаем членами порядка ei. Из соотношения B1.23)
следует, что часть величины Avcr, которая имеет инфракрасную рас-
расходимость и которую мы обозначим A'G, дает следующий вклад
346 Глава 21
в соотношение B1.87):
— ■> г ■*■
— 2таи {р2) еА,с (р2> Pi) а" (р2 — pt) и ( pj
(мы снова предполагаем, что изменение импульса q мало). Тогда,
выделяя расходящуюся инфракрасную часть второго и третьего чле-
членов, можем переписать соотношение B1.87) в следующем виде:
B1.89)
Сравнивая выражения B1.86) и B1.89) можно видеть (см. также
работу Бете и Оппенгеймера [32]), что сумма | Т \г и J | Tt -f- T212,
т. е. полное поперечное сечение всех возможных процессов рассея-
рассеяния до порядка е8, конечна и свободна от расходимостей в пре-
пределе &МШ1_, Хми„. —>0. Однако полное поперечное сечение зависит от
энергии Д£, соответствующей энергии, ниже которой реальные фо-
фотоны не могут быть выделены в экспериментах по рассеянию. Вели-
Величина Д£ определяется разрешением по энергии детектора, исполь-
используемого в эксперименте.
Швингер [440] г> вычислил поперечное сечение для упругого рас-
рассеяния (упругое фактически является неупругим, но потери энергии
меньше, чем Д£) в предельно релятивистском, а также в промежу-
промежуточном и нерелятивистском случаях. Читатель может ознакомиться
с деталями вычислений и дальнейшей дискуссией в статье Швингера.
Здесь мы приведем только поперечное сечение в нерелятивистском
пределе, которое содержит вклад поляризации вакуума под дей-
действием внешнего поля [формула B1.56,]; в этом случае имеем
/19 . .
(+1п
где (dsfdQ)^ — резерфордовское поперечное сечение, даваемое фор-
формулой (9.17) (смысл величин v и Й такой же, как в упомянутой
формуле).
Позднее, в 1953 г., Ньютон [355] вычислил поправку порядка Zee
к результату Швингера. При этом он рассмотрел все диаграммы,
которые содержат до двух взаимодействий с кулоновым полем, но
только один виртуальный фотон. Они могут также рассматриваться
как радиационные поправки к формуле Мак-Кинли — Фешбаха F.2).
Радиационные поправки четвертого порядка к формулам рассеяния
электрона на внешнем поле (т. е. вклад от диаграмм, содержащих
1) См. также работу Фукуда и др. [193].
Перенормировка 347
два виртуальных фотона, но только одно взаимодействие с внешним
полем) были вычислены в работе Уинсара, Берсона и Кролла [521].
Второй задачей рассеяния, для которой вычислены радиацион-
радиационные поправки, является комптоновское рассеяние фотона на частице
со спином 0 или У-2- В работе Коринальдгзи и Йоста [90] были
вычислены радиационные поправки в случае рассеяния фотона на
частице со спином 0, а Шафрот [428] дал формальное, хотя чи-
численно неверное (см. работу Толла [485]), рассмотрение поправок
к формуле Клейна—Нишины. Браун и Фейнман [71] вычислили все
радиационные поправки низшего порядка и получили поперечное
сечение до порядка е6 как в нерелятивистском, так и в ультрареля-
ультрарелятивистском пределах. В их статье читатель может ознакомиться
с ясным и подробным изложением практической вычислительной
техники, применяемой при вычислении радиационных поправок.
В гл. 24, § 6 мы покажем, что в пределе стремящейся к нулю
энергии фотона все радиационные поправки к формуле комптонов-
ского рассеяния стремятся к нулю. Мы рассмотрим там этот факт,
являющийся важным для принципа перенормировки заряда (Тирринг
[480]).
Мы уже упоминали о выполненном Карплусом и Кроллом [263]
расчете радиационных поправок четвертого порядка к величине маг-
магнитного момента электрона. Читатель может ознакомиться в их
статье с выделением расходимостей в собственной энергии и вер-
вершинной части для случая, когда р2фт2, т. е. когда все линии
являются внутренними.
Следующим процессом, для которого были вычислены радиацион-
радиационные поправки низшего порядка, является внутреннее рождение пар
(Далиц [96]). Радиационные поправки к формулам тормозного излу-
излучения были вычислены Митра [337].
В общем эти электромагнитные радиационные поправки к фор-
формулам процессов рассеяния довольно малы A% и ниже), так что
даже в наиболее благоприятных условиях их трудно наблюдать.
Тем не менее успех теории в предсказании правильной величины
смещения уровней в лэмбовском сдвиге оставляет мало сомнений
в том, что эти эффекты действительно имеют место.
В мезонной теории радиационные поправки низшего и в некото-
некоторых случаях более высокого порядка были рассмотрены многими
авторами. Эти вопросы будут детально изложены во втором томе
(см. т. II, гл. 39 и 47, а также гл. 44 и 46).
§ 8. Представление взаимодействия Фарри
для связанных состояний
В § 4 мы встретились с некоторой трудностью при получении
формулы лэмбовского сдвига для связанных электронов из ранее
выведенных формул (см. § 2 и 3) радиационных поправок для сво-
348 Глава 21 :.
бодных электронов. Строго говоря, все результаты, полученные до
настоящего параграфа, применимы только к задачам рассеяния в тех
случаях, когда все частицы в начальном и конечном состояниях сво-
свободны. Имеется, однако, широкий класс интересных экспериментов
по рассеянию, при которых электрон связан в атоме (например,
релеевское рассеяние) и для рассмотрения которых описанные выше
методы непригодны.
В 1951 г. Фарри [202] указал, как можно обобщить формализм
Фейнмана-—Дайсона на такие случаи, когда электрон находится в свя-
связанном состоянии. Ясно, что эта задача может быть рассмотрена
в рамках шредингеровского представления, если в качестве невоз-
мущенного гамильтониана электронно-позитронного поля выбрать
следующий оператор:
Яо = j d*xty+ (х) {— t* ■ V + т) ф (х) ~\- J d3x^ (х) V(х) <]» (х), B1.91)
где V (х) описывает внешний статический потенциал, в котором элек-
электрон находится в связанном состоянии. Гамильтониан взаимодейст-
взаимодействия, описывающий взаимодействие между веществом и излучением,
дается формулой
±f$$ (ж), B1.92)
где А^(х) — квантованный электромагнитный потенциал в шредин-
геровском представлении. Собственные функции гамильтониана Но
являются векторами состояния систем с определенным числом (не-
(невзаимодействующих) электронов и позитронов в (одночастичных)
состояниях, описываемых решениями уравнения Дирака с потенциа-
потенциалом V(x). Точнее говоря, можно показать, что рассмотрение, про-
проведенное в гл. 13, § 5, может быть использовано аналогичным
образом и для гамильтониана B1.91), если разлагать встречающиеся
в нем операторы поля ф (х) и ф+ (х) по полной системе решений
уравнения Дирака во внешнем потенциале V(x).
Точно такая же методика была применена в первых релятивист-
релятивистских вычислениях лэмбовского сдвига (см., например, работы Френча
[191], Кролла и Лэмба [292]). Однако такое рассмотрение является
нековариантным, и выделение расходимостей далеко от однознач-
однозначности (см., например, работу Кролла и Лэмба [292]).
В методе Фарри упомянутое выше выделение расходимостей
производится в рамках ковариантного формализма, причем эффекты
внешнего потенциала включены в переменные поля.
Рассмотрим снова уравнение движения вектора состояния в пред-
представлении взаимодействия
j , B1.93)
Перенормировка 349
где J^j(x) — плотность энергии взаимодействия, задаваемая фор-
формулой B1.9). Здесь мы написали уравнение Томонага—Швингера
для случая плоской пространственно-подобной поверхности, урав-
уравнение которой имеет вид
п^ = %, B1.94)
где п^ — постоянный единичный вектор нормали к плоскости т.
Если п=A, 0, 0, 0), то х— гиперплоскость t= const и da = dsx;
тогда уравнение B1.93) сводится к более знакомой формуле
ih ^m _ j dSx j_i [ф (x) т^ (
|? ^ ) . B1.94a)
B1.946)
Так же, как и Фарри, проведем следующее унитарное преобразо-
преобразование вектора состояния
B1.95)
Вектор состояния Wp удовлетворяет уравнению
^ °¥M B1.96)
Если унитарный оператор У(У+ = У-1) выбирать так, чтобы он
удовлетворял уравнению
ИЛИ
= — VX @ / <Рх f [ф (х) /, <(• (х)] Ле, (х) V@, B1 -97а)
£C0=i
й ^Ш. = f d*x -f [ф (х) f, ф (х)] Ле, (х) К @, B1.976)
то вектор состояния 4?V будет подчиняться уравнению
р (х) ф^Ц ¥р @, B1.98)
где преобразованные операторы ф^ и AF определяются следующим
образом:
xo = t, B1.99)
xo = t. B1.100)
350 Глава 21
Выведем уравнения движения, которым удовлетворяет оператор
фр(х). Для этой цели продифференцируем соотношение B1.99) по
xo — ct и, использовав уравнение B1.97), получим
). B1.101)
Вычисление коммутатора в формуле B1.101) дает следующее выра-
выражение:
i- J dsX'[w(x')f, <|>(х'I, <КхХК(х') =
= / J cPx'S (x — x') i*A% (x') <|i (xO =
= —Т°Т^(х)ф(х), B1.102)
так как —iS(x — x') для t = t' равно -f°8<s> (x — xr) [см. формулу
A5.64)]. Тогда, принимая во внимание, что ф(х) является операто-
оператором в представлении взаимодействия и, следовательно,
^М=(_то^. у —гу>/и)ф(х), B1.103)
после приведения членов получаем, что оператор фр подчиняется
следующему уравнению:
^^T^WMx), B1.Ю4)
т. е. он удовлетворяет уравнению Дирака в присутствии внешнего
электромагнитного поля A^fx). Аналогично, поскольку операторы
Л„(х) и ф(х) коммутируют между собой, мы находим, что
А^х). B1.105)
Представление, характеризуемое уравнениями B1.98), B1.104) и
соотношением B1.105), известно обычно как представление взаимо-
взаимодействия Фарри для связанных состояний, поскольку с его помощью
могут быть рассмотрены задачи для связанных состояний.
В этом можно убедиться следующим образом. Пусть ?и(х)
является решением уравнения B1.104) в неоператорном смысле, где
индекс п определяет квантовые числа состояния (как связанные
Перенормировка 351
состояния, так и состояния рассеяния). Если оператор ф^,(х) разложить
по функциям срп(хI), а именно
Ых>= 2*«т»(х)+ 2 <йр„(х), B1.Ю6)
п, Я+ и, Е—
где в первый член включены только решения с положительной энер-
энергией (Е-j-), а во второй член—только решения B1.104) с отрица-
отрицательной энергией, тогда оператор Ь% будет являться оператором
рождения электрона в состоянии п. Состояние п может быть свя-
связанным состоянием электрона во внешнем поле, так что наше утвер-
утверждение доказано. Отметим, что в данном случае зависимость функ-
функций tpn(x) от времени не такая, как для свободных частиц, ибо
в выражении ехр (— 1Епх°) значения Еп равны энергиям в состояниях п.
Решение уравнения B1.98) можно снова представить в виде
*"* ih) = Vjf V» *i) ЧР (<i). B1 • 107)
где оператор Up{tz, tt) дается разложением Дайсона
и* (*.. to = £ (- ^)и ij. fd*Xl fd*xt...
»=o «, t,
U
... j d*XnT {sePi (Xl) &eF1 (x2)... зеш (хи), B i . 108)
SMbi(x)={«[фл-(x)•[*, <S?f (x)] A^(x) — 8mf^ (x)i|*, (x). B1.109)
Рассмотрим теперь вектор состояния Фо = ^оФро связанной си-
системы, описывающий состояние, в котором имеется один „голый"
электрон в некотором связанном состоянии а и нет фотонов. Энер-
Энергия этого состояния равна Еа—собственному значению энергии урав-
уравнения Дирака, соответствующего собственной функции <рв во внешнем
поле. Однако вследствие взаимодействия J^p-j(x) энергия этого
состояния изменяется. Фактически имеется полная аналогия со слу-
случаем, рассмотренным в гл. 20, § 1, и изменение энергии Д£"а в состоя-
состоянии Фа дается выражением
е-гдяа(*а-*1)==(фа) Ur^ ^)фа)> B1.110)
где разность времен tz — tx должна быть взята большой и необхо-
необходимо провести усреднение по положениям концов интервала tz и tv
J) Это разложение имеет смысл только в случае достаточно слабых полей,
для которых существует щель между собственными значениями с положи-
положительной и отрицательной энергией. Если это ие так, то не существует ста-
стабильного вакуумного состояния Ф?о. См. работы Снайдера и Вайнберга [454],
Фарри [202], Салама и Мэттьюса [421].
352 Глава 21 '■'.
зависимость от которых выражения B1.117) имеет осциллирующий
характер. (Вспомним обсуждение в гл. 16, § 2; его легко можно
обобщить на настоящий случай,, т. е. случай, когда Но имеет связан-
связанные состояния.)
Величина Д£"а имеет как вещественную, так и мнимую части.
Вещественная часть соответствует сдвигу уровня, обусловленному
взаимодействием с полем излучения. Мнимая часть Д£"а отрицательна
и соответствует распаду состояния Фа, при котором электрон пере-
переходит в более низкое энергетическое состояние; этот переход сопрово-
сопровождается излучением одного или большего числа фотонов. Итак, мни-
мнимая часть Д£а дает время жизни (или ширину уровня) в состоянии а.
Эта мнимая часть АЕа равна нулю для основного состояния.
Оператор Up (t2, tt) можно снова проанализировать с помощью
диаграмм Фейнмана. Приведенное рассмотрение и анализ в предста-
представлении взаимодействия свободных частиц различаются только сверт-
сверткой двух фермионных множителей, которая в данном случае дается
выражением
— у Sp (х2, xt) = (Ф^о, Т (<|^(х2) Фр (xt)) Ф^о) =
= +2 ?»(х2)?„(х1) для *20>х10,
п, Е+
= — 2 ?«(х2)<ри(х1) для х10>х20 B1.111)
п, Е-
и не является больше функцией разности пространственно-временных
координат, а есть функция переменных хх и х2 в отдельности и
разности t2 — tt в случае статического поля. Кроме того, в дан-
данном случае среднее значение тока в состоянии вакуума не равно
больше нулю, т. е.
4 е (Фя>. [ф, (х) TfL, tyF (х)] Ф*о) = Jp (х) Ф 0, B1.112)
а соответствует току, индуцированному в вакууме вследствие
наличия внешнего поля, и, следовательно, содержит вклад всех
явлений поляризации вакуума. Поскольку ток не равен нулю,
разложение 7-произведения в формуле B1.108) на сумму нор-
нормальных произведений должно включать свертки множителей [фрСх^т^,
которые встречаются в выражении для SPfi-
Именно в представлении взаимодействия Фарри для связанных
состояний были проведены последние и наиболее удовлетворительные
расчеты радиационных поправок второго порядка к уровням энер-
энергии в связанных состояниях.
Читатель может ознакомиться с деталями этих вычислений, в част-
частности с ковариантным выделением расходимостей (ультрафиолетовой
и инфракрасной) в задаче связанных состояний, по очень ясным статьям
Перенормировка 353
Кролла и Поллока [294], Баранджера, Бете и Фейнмана [18]. Кролл
и Поллок исследовали влияние радиационных поправок на разделение
сверхтонкой структуры. Это чрезвычайно важно, потому что наи-
наиболее точное численное значение постоянной тонкой структуры а
получается из определения разделения сверхтонкой структуры в водо-
водороде. В свою очередь Баранджер, Бете и Фейнман вычислили лэм-
бовский сдвиг уровней и получили поправки от больших импульсов
к ранее упоминавшимся расчетам лэмбовского сдвига, выполненным
Бете, Френчем, Вайскопфом, Лэмбом и Кроллом, Фейнманом. Про-
Проблема естественной ширины линий в представлении Фарри была рас-
рассмотрена Лоу [311].
Радиационные поправки к сверхтонкой структуре и к уровням
энергии связанных электронов были вычислены также Карплусом,
Клейном и Швингером (см. работы [268, 269]). В этих более фор-
формальных вычислениях использовалась новая техника расчетов, разви-
развитая Швингером [441, 442], которую из-за ограниченности объема мы
не можем привести в этой книге. Мы указываем читателю главным
образом статьи, написанные- в духе такого аспекта теории поля, ко-
который представлен в данном томе. В статьях Кролла, Поллока, Баранд-
Баранджера и др. используется метод Фейнмана—Дайсона; кроме того, они,
по-видимому, имеют то преимущество, что физический смысл вычи-
вычислений и приближений становится яснее, чем при более формальном
подходе Карплуса, Клейна и Швингера.
Представление Фарри было также использовано для вычисления
релеевского рассеяния. Это — рассеяние фотона на связанном- элек-
электроне. В общем виде эта задача для современных методов слишком
сложна, даже во втором приближении. Схема расчетов была развита
Брауном, Пайерлсом и Вудуордом (см. работы [69, 70]; там имеются
также ссылки на более ранние работы).
Представление взаимодействия для связанных состояний не является
строго говоря, полностью ковариантным, поскольку внешнее поле
выбирается в выделенной системе координат. (Однако в связи с этим
см. работы Эддингтона [136, 137], Дирака, Пайерлса, Прайса [113].)
Другими словами, протон при описании атома водорода берется
бесконечно тяжелым. Обсуждение полностью ковариантного описания
системы двух тел отложим до гл. 25.
Глава 22
РАСХОДИМОСТИ
До сих пор мы рассматривали некоторые простые расходящиеся
матричные элементы. Однако необходимо еще исследовать, не рас-
расходятся ли матричные элементы, соответствующие некоторым дру-
другим типам диаграмм, кроме тех, которые мы уже рассмотрели.
Другими словами, мы должны рассмотреть в более общем виде,
какие из диаграмм ведут к бесконечностям.
§ 1. Общие положения1)
Рассмотрим общий вид диаграммы, содержащей как бозонные,
так и фермионные линии, причем одни из них являются внутренними,
а другие— внешними. Если мы вычисляем 5-матрицу по теории
Фейнмана, то могут возникнуть три типа расходимостей, которые
можно, согласно Дайсону [126] классифицировать следующим обра-
образом:
1. Сингулярности, вызванные совпадением двух или большего
числа полюсов в подинтегральном выражении.
2. Расходимости при малых импульсах, связанные с наличием
в подинтегральном выражении множителя 1/р2.
3. Расходимости при больших импульсах, обусловленные недо-
недостаточно быстрым убыванием всего подинтегрального выражения
на бесконечности.
Расходимости первого типа могут возникнуть, например, при
рассмотрении многочастичного процесса рассеяния, если для некото-
некоторых специальных значений импульса частицы этот процесс может
быть разделен на ряд независимых процессов, в которых участвуют
различные группы частиц (обсуждение такого типа расходимостей
см. в статье Идена [138]J). Расходимости второго типа называются
обычно „инфракрасной катастрофой" (см. гл. 21, § 4).
1) По существу все выводы этого параграфа относятся к так называемым
связным диаграммам (определение их см. в гл. 24 на стр. 376).— Прим. перев.
а) Если представить S-матрицу в виде функции импульсов и энергий
падающих частиц, то, начиная с определенных значений энергии, становится
отличной от нуля вероятность рождения новых частиц. При пороговой энер-
энергии матричные элементы содержат сингулярности первого типа, которые
соответствуют точкам ветвления.— Прим. перев.
Расходимости 355
Здесь мы не будем останавливаться на расходимостях первого
или второго типа, а сконцентрируем наше внимание на действительно
вызывающих наибольшие трудности расходимостях третьего типа,
примеры которых в нескольких частных случаях были рассмотрены
в предыдущих главах.
Рассмотрим теперь общий вид диаграммы. Известно, что инте-
интегрирование необходимо проводить по всем внутренним импульсам pj
независимо от того, являются ли они импульсами бозонов или фер-
мионов. Итак, мы должны проинтегрировать по dipj = dpRdpjdpjdpp
Дайсон [127] показал, что для исследования возможных расходимо-
стей можно повернуть контур интегрирования по переменной р®
так, чтобы интегрирование по ней проводилось по мнимой оси в
комплексной плоскости р° (см. гл. 20). Он, кроме того, показал
[127]'), что это всегда возможно и не вносит новых расходимостей.
Такого рода преобразование имеет то преимущество, что после
выполнения его все четыре компоненты можно рассматривать едино-
единообразно, а именно, если положить jfi = ipj, где р^ вещественно,
обычные (рационализованные) знаменатели получают вид
2 2 22+/7г2-). Q2 Л)
Форма B2.1) является отрицательно-определенной, так что все вы-
выражение можно проинтегрировать в эвклидовом 4-пространстве р.
После этого преобразования легко рассмотреть интеграл, соответ-
соответствующий определенной диаграмме Фейнмана, и установить степень
его расходимости.
Если число импульсных множителей в числителе меньше, чем
в знаменателе, то мы получим сходящийся результат. В противном
случае, если число импульсов в числителе больше или равно числу
импульсов в знаменателе, то можно получить (но не обязательно
во всех случаях) расходящийся результат. Определим „размерность"
интеграла как разность полного числа импульсов в числителе и пол-
полного числа импульсов в знаменателе и обозначим ее через D; тогда
достаточным условием для сходимости является условие D < 0,
a D;>0 — условием, при котором может появиться расходимость.
Вначале рассмотрим взаимодействие фермионного и бозонного
полей для случая прямой связи. В дальнейшем кратко обсудим и
случай связи с производными. Из проведенного нами ранее рассмо-
рассмотрения следует, что для случая прямой связи в каждой „вершине"
произвольной диаграммы встречаются одна бозонная и две фермион-
ные линии. Для описания диаграмм примем следующие обозначения:
F—число фермионных линий,
В — число бозонных линий,
С — число вершин,
См. также его работу [130].
356 Глава 22
Fe— число внешних фермионных линий,
Ве — число внешних бозонных линий,
Fi — число внутренних фермионных линий,
Вг — число внутренних бозонных линий.
Задав определенное число и вид внешних линий, можно описать
физически наблюдаемый процесс. Задание определенных значений для
рг и Вг указывает, в каком приближении мы рассчитываем процесс;
при этом можно произвольно выбрать относительное взаимное рас-
расположение внутренних линий.
В случае прямой связи оператор взаимодействия Г (где Г равно
Тр., Yo или -0 не содержит импульса ни одной из участвующих в про-
процессе частиц. Внешние линии также не влияют на возможность поя-
появления расходимостей, так как по ним не проводится интегрирование.
Следующие факторы, однако, влияют на число импульсов, появляю-
появляющихся в числителе и знаменателе подинтегрального выражения:
1. Каждая внутренняя фермионная или бозонная линия дает четыре
импульса в числитель как вклад элемента интегрирования d^p. Это
дает вклад в величину D, равный 4(/7i-}-Bi).
2. В каждое интегрирование по всему 4-пространству в каждой
вершине дает вклад 4-мерная 8-функция. Это эквивалентно включе-
включению четырех импульсов в знаменатель. Напомним, однако, что одна
из этих 8-функций выражает просто сохранение полного импульса
в начальном и конечном состояниях процесса и поэтому не приводит
к уменьшению размерности подинтегрального выражения. Итак, вер-
вершины дают вклад в величину D, равный —4(С—1).
3. Каждая внутренняя фермионная линия дает одну степень р
в знаменатель, так как соответствующая ей функция распространения
имеет вид (р—т). Это дает вклад в величину D, равный —Ft.
4. Каждая внутренняя бозонная линия дает две степени р в знаме-
знаменатель, так как ей соответствует функция распространения (р2—ц2).
Это дает вклад в величину D, равный — 2В^. Поэтому D дается
выражением
D = 3Fi+2Bi—4(С—1). B2.2)
Мы можем выразить эту величину через число внешних линий,
если учесть, что число вершин связано с числом фермионных и бозон-
бозонных линий. В частности, так как в каждой вершине сходятся две
фермионные линии, то число концов фермионных линий равно удвоен-
удвоенному числу вершин. Поскольку каждая внутренняя фермионная линия
имеет два конца, а каждая внешняя — один, то
2Ft-\-Fe = 2C. B2.3)
Аналогично в каждой вершине кончается одна бозонная линия, и,
следовательно, число концов бозонных линий равно числу вершин,
т. е.
= С. B2.4)
Расходимости 357
Подставляя соотношения B2.3) и B2.4) в B2.2), получаем
D = 4 — J-Fe — Be. B2.5)
Существенным оказывается то, что коэффициент при члене С равен
нулю. Это означает, что в любой теории с прямой связью степень
расходимости не зависит от числа вершин на диаграмме1).
В дальнейшем мы рассмотрим важный класс расходящихся диа-
диаграмм, которые характеризуются тем, что если любую из их внутрен-
внутренних линий разрезать и заменить двумя внешними линиями, то
матричный элемент, соответствующий им, будет сходиться2). Такого
рода диаграммы мы назовем примитивными расходящимися диаграм-
диаграммами (Дайсон [127]). Они представляют собой базисные радиацион-
радиационные поправки, из которых могут быть получены (с помощью соот-
соответствующих вставок) все остальные расходящиеся радиационные
поправки. Теперь перечислим основные расходящиеся диаграммы.
В связи с этим напомним, что фермионная линия нигде не может
закончиться обрывом, поэтому число Fe всегда должно быть четным.
§ 2. Случаи, которые были уже рассмотрены
Случай Fe=2, Ba=0.
Простейшая (и только примитивно расходящаяся) диаграмма соб-
собственной энергии фермиона приведена на фиг. 60, а. Существуют,
а
Фиг. 60.
конечно, и другие (непримитивно расходящиеся) диаграммы собствен-
собственной энергии, содержащие больше одного виртуального бозона; при-
пример такой диаграммы приведен на фиг. 60, Ь. Из формулы B2.5)
следует, что D=l, т. е. возможно появление линейной расходи-
расходимости. Фактически, как было показано в гл. 20, расходимость яв-
1) Следует отметить, однако, что условие сходимости или расходимости
(ZJ 0) является достаточным, но не необходимым. Так, диаграммы низшего
порядка (не содержащие радиационных поправок), которые предста-
представляют возможный процесс, и все диаграммы высшего порядка (содер-
(содержащие, радиационные поправки и поэтому, возможно, приводящие к расхо-
димостям в зависимости от расположения внутренних линий) имеют одно
и то же условие для D.
2) Так как известно, что матричный элемент, соответствующий им, схо-
сходится, когда одна из переменных pj фиксирована и интегрирование прово-
проводится по всем остальным переменным; сходимость всего выражения гаран-
гарантирована прн условии, что Z)<J1.
358
Глава 22
ляется только логарифмической и соответствует случаю D = 0.
По-видимому, должно существовать общее правило (которое, однако,
не доказано), что если D является нечетным, то фактически появ-
появляется только следующая меньшая четная расходимость по сравнению
с максимально возможной.
Случай Fa^=0, Ba = 2.
Это случай собственной энергии бозона, которую мы уже довольно
подробно рассмотрели в гл. 21, § 5 и 6. Из формулы B2.5) мы
получаем, что D = 2. Эта квадратичная расходимость, в самом деле,
имеет место в случае мезонов; в случае фото-
фотонов, как мы видели, имеет место только лога-
логарифмическая расходимость, что является след-
следствием калибровочной инвариантности теории.
Случай Fe = 2, Ве = 1.
Диаграмма типа лэмбовского сдвига (фиг. 61)
является простейшим примером диаграмм такого
рода. В этом случае D = 0 и в принципе воз-
возможна логарифмическая расходимость. Однако,
как мы доказали в гл. 21, § 3, в случае элек-
электромагнитного поля и нейтрального псевдоска-
псевдоскалярного мезонного поля эта расходимость точно
сокращается с расходимостями, возникающими
в матричных элементах, соответствующих двум
диаграммам собственной энергии. В более
общих случаях эта диаграмма на самом деле приводит к логарифми-
логарифмической расходимости. Более сложные типы вершинных диаграмм
будут рассмотрены в гл. 24.
§ 3. Треугольные диаграммы
Случай Fe=0, Вв = Ъ.
В этом случае D== 1 и мы можем иметь линейную расходимость.
Характерная диаграмма такого типа приведена на фиг. 62. По очевид-
очевидным причинам эти диаграммы часто называют треугольными. В зави-
зависимости от конкретной природы фермионного треугольника при
взаимодействии с одним или большим числом бозонных полей воз-
возможно много различных видов этой диаграммы. Рассмотрим сначала
случай одного бозонного поля, в частности случай одного электро-
электромагнитного поля, т. е. диаграмму на фиг. 62. При вычислении ока-
оказывается, что вместо расходящегося интеграла мы получаем нуль.
Этот случай можно рассмотреть, обобщая метод, примененный
при исследовании внешнего поля (см. гл. 18, § 3). Получающийся
результат можно понять следующим образом. Фермионные линии
представляют положительные или отрицательные электроны. Пред-
Фиг. 61.
Расходимости
359
положим, например, что заряды приведены на фиг. 63. Тогда диа-
диаграмму на фиг. 63, b можно получить из диаграммы на фиг. 63, а
обращением направления электронных линий, после чего необходимо
сложить вклады обеих диаграмм, чтобы получить полный вклад
в б'-матрицу. Итак, если соответствующие матричные эле'менты
обозначить через М(а) и Ж(й), то нужно взять Ж(а) -)- Ж(й). Однако
обратное направление линий'заряженного фермиона попросту означает
обратный знак заряда. Поэтому матричный элемент М(й) отличается от
а
Ф и г. 62.
Фиг.
матричного элемента М только множителем (— 1K = — 1, следова-
следовательно, М(а) -)- М(Ь) = 0. В общем случае любой замкнутый многоуголь-
многоугольник из электронных линий (замкнутая петля), имеющий нечетное число
вершин, дает в электродинамике вклад, равный нулю. Эта теорема
была впервые сформулирована и доказана Фарри [200].
Если продолжить рассмотрение бозонного поля, взаимодействую-
взаимодействующего с фермионным, и предположить, что это псевдоскалярное
мезонное поле, то диаграмма по-прежнему даст нуль, что вытекает
из природы оператора взаимодействия 75 (Салам [418, 419]). Это
можно показать так. Предположим, что три внутренних импульса
фермиона есть рх, р2 и р3. Тогда матричный элемент пропорцио-
пропорционален величине
B2-6)
Pi — m />2 — m ps — m
Если проведем рационализацию знаменателя и учтем, что опера-
операторы -f5 и уа, встречающиеся в р, антикоммутируют между собой,
то числитель выражения B2.6) примет следующий вид:
Тб (Pi Г "*) ( р2 г "^i (г 3 Г "'/• \AA.I)
Чтобы получить элемент S-матрицы, мы должны взять шпур от
выражения B2.6), так как импульсы и спины фермионов произвольны.
В связи с этим напомним, что
Sp (Та) =
Т,
Тв) =
= Sp (Тб) = 0,
B2.8)
360 Глава 22
поскольку TsT^Tv == — И^мТ'Т'- Аналогично
p „р vTp) = 0- B2.9)
Таким образом, благодаря свойствам операции шпура, действительно,
шпур выражения B2.6) равен нулю и треугольные диаграммы не дают
вклада в случае псевдоскалярной мезонной теорииХК Непосредствен-
Непосредственным физическим следствием этого является невозможность распада
тяжелого псевдоскалярного мезона на два (или, в общем случае, на
четное число) более легких псевдоскалярных мезона.
Теперь рассмотрим бозонное поле, являющееся скалярным мезон-
ным полем. Каждый из трех операторов взаимодействия есть в дан-
данном случае Г=1, и выражением, соответствующим B2.7), является
(>1 + »)(>2+»ХЛ+«)- B2-Ю)
Если взять шпур этого выражения, то те члены, которые содержат
одну матрицу у или три матрицы -у> дадут нуль; однако будут не-
неравные нулю члены, либо содержащие две матрицы -f> либо вообще
.их не содержащие, так что в итоге мы
получаем отличный от нуля результат. Факти-
Фактически, поскольку величина D нечетная, мы
снова получим логарифмическую расходи-
расходимость, т. е. расходимость порядка D — 0,
а не максимально возможную расходимость
D=l. Введение члена ауь в лагранжиан,
где с—бесконечная величина, позволяет
избавиться от этой расходимости.
Допустим теперь, что имеются два раз-
различных бозонных поля; например, допустим,
что имеются два взаимодействия с фотонами
и одно с мезоном (Штейнбергер [460]), как это показано на фиг. 64
Эта диаграмма описывает физический процесс распада мезона на два
фотона (Янг [541], см. также т. II, гл. 27). В этом случае константа
связи е встречается только дважды, т. е. четное число раз, и поэтому
теорема зарядового сопряжения Фарри неприменима. Кроме того,
причина, приводящая к равенству нулю шпуров, больше не действует
независимо от того, Г—1 или Г=у5- В частности, в нашем
случае матричный элемент пропорционален величине
B2.11)
J) Это утверждение может быть доказано в псевдоскалярной теории
в общем случае замкнутой петли с нечетным числом вершии, если использо-
использовать свойство инвариантности S-матрицы по отношению к пространственным
отражениям (см. стр. 223 в работе Салама [418]). Общие правила отбора,
которые являются следствием теорем, аналогичных теореме Фарри для про-
процессов с участием нуклонов и антинуклонов, приведены в работах Фукуды,
Хайякавы и Миямото [196, 197], Пайса и Иоста [3671, Вольфенштейна и Равен-
холла [540].
Расходимости 361
Если Г=1, то отличный от нуля вклад дают члены, содержащие
четное число матриц у- Если же Г = уб, то в дополнение к мат-
матрице у5мы имеем больше четырех операторов, включающих f, с их.
помощью можно получить еще одну матрицу у5, что даст 7J? = —Ь
Поэтому и в случае псевдоскалярной мезонной теории мы получаем
отличный от нуля результат.
Если приходящий мезон на фиг. 64 является скалярным, то коррект-
корректное использование условия калибровки (Фукуда и Миямото [194, 195],.
Швингер [441]), аналогичного примененному при рассмотрении поляри-
поляризации вакуума (см. гл. 21, §5), показывает, что, хотя D= 1, в разложе-
разложение дает вклад фактически только член, имеющий размерность D = — 1»
и поэтому результат сходится. В случае псевдоскалярного мезоннога
поля матричный элемент, соответствующий диаграмме на фиг. 64,
также является калибровочно инвариантным и сходящимся. Распад,
нейтрального псевдоскалярного тг-мезона наблюдается эксперимен-
экспериментально.
Наконец, рассмотрим случай, когда два бозонных поля являются
мезонными полями. В этом случае получается отличный от нуля резуль-
результат для распада скалярного мезона на два псевдоскалярных мезона,
§ 4. Квадратные диаграммы
Случай £е=4, /% = 0.
В этом случае из формулы B2.5) мы получаем D=0. Рассмотрим
сначала рассеяние света на свете. Диаграмма Фейнмана для этого»
процесса приведена на фиг. 65. В резуль-
результате этого процесса два падающих фотона ^ ^
с импульсами кх и к3 рассеиваются друг на
друге и дают два выходящих фотона с импуль-
импульсами к2 и к4. Процесс, представленный на
фиг. 65, добавляет к лагранжиану член чет-
четвертого порядка по электромагнитному полю-
Таким же образом он добавляет к уравне-
уравнениям электромагнитного поля некоторые
члены третьего порядка по полю.
Как это было установлено еще в 1934 г.
(Халперн [219]), рождение виртуальных пар Фиг. 65.
в вакууме приводит к нелинейным взаимо-
взаимодействиям между электромагнитными полями. Эйлер (см. работы [149,.
150]) и Гейзенберг (см. работу [228]) пытались рассмотреть эту проб-
проблему в 1936 г., но вследствие трудности расчетов четвертого порядка
в старой теории смогли провести вычисления только в пределе малых
энергий фотонов. Поперечное сечение рассеяния двух фотонов с равной.
и очень малой энергией (йш <z^ me2), как показал Эйлер [150], возрастает
как шестая степень энергии. Однако последующие вычисления Ахиезе-
ра [2] показали, что в предельно релятивистском случае поперечное се-
362 Глава 22
чение убывает как(йш)~2. Полностью проблема была решена только в со-
современной квантовой электродинамике Фейнманом (см. дополнение D
к статье [169]), Карплусом и Нейманом [264, 265] *). Они получили,
что матричный элемент процесса не содержит логарифмической расхо-
расходимости, поскольку в действительности вклад дает только . член
с размерностью D= — 42), и поэтому матричный элемент процесса
быстро сходится.
Когда Гейзенберг рассматривал эту проблему в 1936 г., он
высказал предположение, что сходимость квантовой электродинамики
может быть получена с помощью введения сильной нелинейности
уравнений поля при больших энергиях фотонов, а также, что рас-
рассеяние света на свете может наблюдаться на звездах. Однако рас-
расчеты Карплуса и Неймана показали, что даже в наи-
наиболее благоприятном случае, когда энергия квантов
равна 2/гес2 (или около 1 Мэв), т. е. когда энергии
достаточно для рождения реальных пар, поперечное
сечение имеет порядок только 3 • 10~30 см2 h Этот
эффект трудно наблюдать в космических масштабах,
поскольку даже в межзвездном пространстве рас-
рассеяние излучения на межзвездном водороде (и пыли)
много больше рассеяния света на свете.
•Предметом экспериментального исследования мо-
Ф и г. 66. жет быть также другой электромагнитный про-
процесс, для которого Ba = 4, Fe = 0. Это — рассея-
рассеяние света на электростатическом поле во втором порядке4).
Изображая взаимодействие со статическим полем на диаграммах
■Фейнмана с помощью крестиков, мы можем представить этот про-
процесс так, как показано на фиг. 66. В частности, процесс может
наблюдаться в сильном кулоновом поле тяжелого ядра с зарядом Z.
Взаимодействие, изображенное крестиком, дает вклад Ze2 вместо
У См. также работу Уорда [506].
2) Это снова обусловлено требованием калибровочной инвариантности
теории, согласно которому любой дополнительный член четвертого порядка
к лагранжиану электромагнитного поля должен содержать (Р, ф* и т. п.,
а не АК Поскольку напряженность электрического поля @ пропорциональна кА,
то матричный элемент, соответствующий диаграмме на фиг. 65, должен содер-
содержать четвертую степень к, или, точнее говоря, произведение четырех опре-
определенных компонент волновых векторов от ki до к±. Как мы видели при
рассмотрении поляризации вакуума, это уменьшает высшую степень элек-
электронного импульса в подинтегральном выражении на четыре единицы.
3) Порядок величины поперечного сечения можно, очевидно, получить,
•если учесть, что есть четыре взаимодействия е, каждое из которых дает
вклад е/У~?>с в матричный элемент. Это означает, что поперечное сечение
должно быть порядка (е2/йсL (й/отсJ-.-4 • 10~30 см2.
4) В первом порядке рассеяние на статическом поле дает вклад,
равный нулю, так как этот порядок описывается треугольной диаграммой,
ж которой применима теорема Фарри; фактически теорема Фарри была
«олучена именно для этого случая.
Расходимости 363
вклада квантового взаимодействия е. Это дает в поперечное
сечение дополнительный множитель (Z2e2/hcJ по сравнению с тем,
что получается для сечения рассеяния света на свете. Тогда для Z
порядка 100 поперечное сечение будет около 0,5- 104 • 3 • 10~30 =
= 1,5 • 10~26 см2, или 15 мбарн.
Этот тип рассеяния был впервые предложен в 1933 г. Дель-
Дельбрюком [99] и поэтому часто называется „рассеянием Дельбрюка".
Оно было рассчитано Ахиезером и Померанчуком [3], Кеммером и
Людвигом (см. работы [271,272]) для некоторых предельных случаев еще
до появления современной квантовой электродинамики. Рассеяние Дель-
Дельбрюка для простого случая рассеяния фотона вперед, когда его
импульс практически не меняется, было
вычислено Рорлихом и Глюкштерном [406],
причем они использовали как само при-
приближение Фейнмана, так и метод анали-
аналитического продолжения.
Метод аналитического продолжения
был использован Толлом 1\ который также
вычислил поперечное сечение рассеяния
вперед, и Рорлихом и Глюкштерном Фиг. 67.
[406]2); этот метод состоит в следующем.
Предположим, что известно полное поперечное сечение процесса
реального образования пар в частном случае кулонова поля. Диа-
Диаграмма этого процесса приведена на фиг. 67. Тогда, если такой
процесс поглощения имеет место, то должен происходить также
дисперсионный процесс, который является рассеянием Дельбрюка.
С помощью одной из оптических теорем (см., например, работу
Лакса [300]) можно установить соотношение между связанной с по-
поглощением (мнимой) частью амплитуды рассеяния Дельбрюка вперед
и полным сечением процесса поглощения, представленного на фиг. 67.
Аналитические свойства матрицы рассеяния используются затем для
нахождения дисперсионной (вещественной) части этой амплитуды;
получаемые результаты имеют вид, аналогичный обычным диспер-
дисперсионным соотношениям3). Было найдено, что дифференциальное
поперечное сечение рассеяния Дельбрюка вперед продолжает непре-
непрерывно возрастать с ростом энергии у-квантов. Это один из неболь-
небольшого числа процессов, для которых имеет место такого рода непре-
непрерывный рост.
Менее точные расчеты, чем расчеты Рорлиха и Глюкштерна,
были выполнены Бете и Рорлихом [36] с целью получения углового
1) Toll J. S., Ph. dissertation, Princeton University, 1952.
2) См. также работы Йоста, Люттингера и Слотника [253], Гелл-Манна,
Гольдбергера и Тирринга [206].
3) Связь между причинностью и дисперсионными соотношениями рас-
рассматривалась в работе Гелл-Манна и др. [203], где даны также ссылки на более
ранние работы.
364 Глава 22
сечения рассеяния Дельбрюка для малых углов порядка 6 да тсг/Ьиу
и меньше. К сожалению, до сих пор не проведены расчеты рассея-
рассеяния Дельбрюка для углов и энергий, представляющих эксперимен-
экспериментальный интерес, а именно для больших углов и энергий в не-
несколько Мэв.
Последние экспериментальные исследования (Вильсон [539]) пока-
показывают, что вероятность существования рассеяния Дельбрюка несколько
больше 50%. Экспериментальные проверки существования такого
рода процессов с замкнутыми петлями все еще остаются желатель-
желательными, но уже не столь крайне необходимыми, как раньше, поскольку»
как уже указывалось, вклад эффектов вакуумной поляризации,
в лэмбовский сдвиг, равный —27 мггц, является реальным и наблю-
наблюдается на опыте.
До сих пор мы рассматривали в качестве бозонного поля только
электромагнитное поле. Можно исследовать также рассеяние мезо-
мезонов на мезонах, учитывая диаграммы рассмотренного типа (Салам
[418, 419]). В этой случае калибровочная инвариантность не может
быть применена для уменьшения порядка расходимости, и факти-
фактически как в случае скалярных, так и в случае псевдоскалярных
мезонов получается расходящийся результат. Это первый (и един-
единственный) процесс в псевдоскалярной теории, который приводит
к расходимости, не устраняющейся перенормировкой массы или кон-
константы связи. В духе развиваемой теории необходимо устранить
расходимость в рассеянии мезона на мезоне с помощью подходя-
подходящей перенормировки. Для этой цели в исходный лагранжиан нужно
ввести член Хер4 с соответственно выбранным (бесконечным) коэффи-
коэффициентом \.
Член с ср4 не является полностью инородным в теории. При
взаимодействии скалярных или псевдоскалярных мезонов с электро-
электромагнитным полем мы также встречаемся с членами типа ср срЛ^Л1*"
в лагранжиане взаимодействия, т. е. с членами четвертого порядка
по бозонным волновым функциям. Конечно, то, что коэффициент X
должен быть бесконечным для компенсации бесконечности, возни-
возникающей в матричном элементе четвертого порядка рассеяния мезона
на мезоне, представляет нечто новое. Неизвестно, может ли вели-
величина X, кроме бесконечной части, иметь также и конечную часть,
т. е. может ли комбинация Хер4 и матричного элемента, соответ-
соответствующего диаграмме на фиг. 65, давать также и конечные эффекты.
в пределе малых энергий мезонов.
Диаграмма рассеяния мезона на мезоне может представлять собой
часть других, более сложных диаграмм. Как показал Салам [418, 419],
это не ведет к каким-либо внутренним трудностям теории.
На этом мы заканчиваем рассмотрение диаграмм, которые ведут
к расходимостям при взаимодействии фермионов и бозонов. Боль-
Большинство из этих расходимостей может быть устранено перенорми-
перенормировкой массы и константы связи. Конкретнее говоря, мы имеем:
Расходимости 365
В электродинамике перенормировка массы и константы связи
устраняет все расходимости.
В псевдоскалярной мезонной теории перенормировка массы и
константы связи устраняет все расходимости, кроме той, которая
обусловлена квадратной диаграммой и для устранения которой не-
необходимо вводить в лагранжиан член Хер4.
В скалярной мезонной теории как треугольные, так и квадрат-
иые диаграммы приводят к расходимостям, которые не могут быть
устранены перенормировкой массы и константы связи; для устране-
устранения этих расходимостей необходимо вводить в лагранжиан члены
лср3 и йср4.
В случае теории нескольких мезонных полей со спином О
члены, которые должны быть введены в лагранжиан, имеют тот же
вид, как и в скалярной и псевдоскалярной теории.
Из этого заключения следует, что, с точки зрения теории поля,
теория псевдоскалярного мезонного поля несколько проще, чем
теория скалярного мезонного поля.
Глава 23
ПЕРЕНОРМИРУЕМЫЕ И НЕПЕРЕНОРМИРУЕМЫЕ
ТЕОРИИ
§ 1. Взаимодействие бозонных полей
Теперь обратимся к рассмотрению расходящихся диаграмм для
случая взаимодействия двух бозонных полей. Мы по-прежнему будем
рассматривать только прямую связь. В частности, рассмотрим взаимо-
взаимодействие заряженных бозонов1 со спином 0 (т. е. заряженных те-ме-
зонов) с электромагнитным полем (т. е. с фотонами). Пусть С — число
вершин, Р—число линий бозонных
частиц (мезонов), Q—число фотонных
линий на соответствующих диаграм-
диаграммах и индексы i и е снова служат
У ^^ для обозначения внутренних и внеш-
т них линий соответственно. Выражение
для величины D (Рорлих [405]) мы
Фиг. 68. можем получить с помощью метода,
использованного в гл. 22. Прежде чем
приступить к этому, сделаем одно ограничение: мы будем рассматривать
только взаимодействие вида р^А^ (где р^ обозначает импульс бозон-
ной частицы), а не взаимодействие Av-A^. Это говорит о том, что
будут рассматриваться только диаграммы с вершинами, предста-
представленными на фиг. 68, а, а не диаграммы с вершинами, представлен-
представленными на фиг. 68, Ь. При этом ограничении импульсы вводятся в под-
интегральное выражение следующим образом:
1. Каждая внутренняя линия частицы или кванта дает вклад d*p
в числитель. Это дает полный вклад в величину D, равный
2. Каждой вершине соответствует В4-функция. Это эквивалентно
введению четырех импульсов в знаменатель. Одна В4-функция выра-
выражает закон сохранения полного импульса. Таким образом, вклад
вершин в величину D равен —4(С—1). Кроме того, в каждой
вершине имеет место взаимодействие. В нашем случае мы допускаем
только взаимодействие р*М„. Тогда это дает дополнительный вклад
в величину D, равный -\-С.
3. Каждая внутренняя линия частицы дает в знаменатель вклад
второй степени по р, так как функция распространения ее имеет вид
(р2 — (*2)~1. Это дает вклад в величину D, равный —2Р,.
4. Каждая внутренняя фотонная линия дает в знаменатель вклад
второй степени по р, так как функция распространения фотона.
Перенормируемые и неперенормируемые теории 367
имеет вид 1/р.2. Это дает вклад в величину D, равный —2Q^. Сле-
Следовательно, для D получается следующее выражение:
D = 2Pi+2Qi —3C+4. B3.1)
Мы можем выразить эту величину через число внешних линий с по-
помощью соотношений
2Qi+Qe = C, B3.2)
2Pi-\-Pe=2C. B3.3)
Подставляя соотношения B3.2) и B3.3) в B3.1), получаем
D=4 — Pe — Qe. B3.4)
Так же, как и в случае взаимодействия между бозоном и фермионом,
коэффициент при величине С оказывается равным нулю и степень
расходимости не зависит от числа вершин.
Теперь мы перечислим все те диаграммы, которые приводят
к расходимостям. При этом мы должны учесть, что линия частицы
нигде не может закончиться обрывом (вследствие сохранения заряда),
так что величина Ре всегда должна быть четной.
Случай Ре = 2, Qe = 0.
На фиг. 69 приведена простейшая диаграмма для этого случая.
Величину D = 2 можно получить из формулы B3.4). Эта квадра-
квадратичная расходимость собственной энергии бозона со спином 0 фак-
фактически имеет место. Напомним, что для фермиона собственная
р-К
Фиг. 69.
энергия, обусловленная взаимодействием с фотонами, расходится
логарифмически, тогда как в классической теории собственная энер-
энергия электрона расходится линейно. Это ясно указывает на то, что
мы не можем доверять любой классической оценке собственной
энергии как бозона, так и фермкона.
Случай Ре=2, Qe=l.
Это — лэмбовский сдвиг для бозона. Как и в случае фермиона,
имеются три диаграммы этого процесса, они приведены на
фиг. 70, а — с. Матричный элемент каждой диаграммы в отдель-
отдельности расходится с D = 1, т. е. имеет место линейная расходимость,
но сумма матричных элементов, соответствующих всем трем диа-
диаграммам, конечна.
368
Глава 23
Случай Ре=2, Qe=2.
Как показано на фиг. 71, этот случай соответствует радиацион-
радиационным поправкам к формулам комптоновского рассеяния, т. е. рассея-
рассеяния фотона на бозоне со спином 0. Соотношение B3.4) дает D = 0.
О
а
Фиг. 70.
Фиг. 71.
Однако фактически вследствие требования калибровочной инвариант-
инвариантности теории только следующий член с D = — 2 имеет отличный
от нуля коэффициент. Следовательно, мы получаем сходящийся
результат.
Случай Ре = 0, Qe = 2.
Это — новый вклад в поляризацию вакуума, обусловленный рож-
рождением пар виртуальных заряженных мезонов (фиг. 72). В этом
случае D = 2. Однако вследствие
требования калибровочной инва-
риантности теории эта квадра-
тичная расходимость отсутствует. "
В разложении поляризационного Фиг. 72.
тензора остается следующий член
с D = 0, т. е. логарифмически расходящийся член и высшие конеч-
конечные члены, имеющие физическое значение. Перед ними стоят числен-
численные коэффициенты, отличные от тех, которые стоят перед членами,
обусловленными виртуальными электронными парами (Швингер [441]).
Вклад конечных членов по-прежнему обратно пропорционален квад-
квадрату массы виртуальной частицы. В гл. 21, § 5, мы уже упоминали,
что поляризация вакуума, обусловленная виртуальными электрон-
электронными парами, дает вклад —27 мггц в лэмбовский сдвиг. Вклад
в лэмбовский сдвиг, обусловленный мезонной поляризацией вакуума,
меньше на множитель B75J и равен только 0,3 кгц и поэтому не-
ненаблюдаем.
Поскольку теоретическая и экспериментальная величины лэмбов-
ского сдвига теперь согласуются в пределах 0,5 мггц, то можно
Перенормируемые и неперенормируемые теории 369
заключить, что не существует никаких заряженных частиц, которые
могли бы рождаться парами и имели бы массу, меньшую семи элек-
электронных масс.
Случай Ре = 0, Qe = 4.
Это — рассеяние света на свете; квадрат из внутренних линий на
соответствующей диаграмме будет образован линиями бозонов со
спином 0. Поскольку D = 0, то эта диаграмма приводит к сходящемуся
результату, так как из калибровочной инва-
инвариантности теории вытекает, что вклад дает
только следующий член с D = — 4, а также
члены высших порядков.
Случай Ре = 4, Qe=0.
Этот случай соответствует рассеянию
двух бозонных частиц друг на друге вслед-
вследствие электромагнитного взаимодействия
между ними; диаграмма процесса приведена
на фиг. 73. Поскольку D=0 и, так как
условие калибровочной инвариантности не Фиг. 73.
приводит к уменьшению степени расходи-
расходимости, фактически имеется логарифмическая расходимость. Так же
как и в случае рассеяния мезона на мезоне, обусловленном виртуаль-
виртуальными нуклонными парами (см. гл. 22), мы можем избавиться от этой
расходимости, вводя в исходный лагранжиан член Хер4, где коэффи-
коэффициент ). бесконечен.
§ 2. Двухфотонное взаимодействие
Вернемся теперь к диаграмме на фиг. 68, Ь, на которой два
фотона одновременно взаимодействуют в вершине. С таким положе-
положением мы уже встречались на фиг. 50, Ь. Размерность D подинтег-
рального выражения может быть получена обычным путем. В этом
случае мы рассматриваем вклад в подинтегральное выражение, обу-
обусловленный взаимодействием А^А9" в каждой вершине, и таким обра-
образом имеем
D = — 4C-T-4-|-2Pi-|-2Qi. B3.5)
Далее,
2Pi-\-P==2C B3.6)
= 2C. B3.7)
Следовательно, подставляя соотношения B3.6) и B3.7) в формулу
B3.5), получаем
D = 4— Pe — Qe. B3.8)
Так как формулы B3.8) и B3.4) идентичны, то двухфотонное взаи-
взаимодействие не призодит к дополнительным усложнениям. Диаграммы,
370 Глава 23
на которых один конец внутренней фотонной линии попадает в вер-
вершину со взаимодействием однофотонного типа (см. фиг. 68, а),
а второй конец—в вершину со взаимодействием двухфотонного типа
(см. фиг. 68, Ь), не приводят к внутренним трудностям.
§ 3. Связь с производными
Теперь рассмотрим связь с производными и сравним этот случай
со случаем прямой связи для взаимодействия фермиона и бозона.
В гл. 11 было показано, что для связи с производными в случае
скалярной или псевдоскалярной теории взаимодействие в вершине
определяется величиной Т^^д/дх^, где про-
производная действует на мезонный оператор.
Это приводит к тому, что в подынтегральное
выражение вводится дополнительный импульс
д/дХр_ —> k[>' в каждой вершине и, следователь-
следовательно, член -\-С— в величину D. Итак, в отли-
отличие от всех рассмотренных до этого пара-
Ф и г. 74. графа теорий величина D зависит от вели-
величины С и имеется бесконечное число типов
расходящихся диаграмм. Таким образом, если мы попытаемся приме-
применить принципы перенормировки к рассматриваемому взаимодействию,
то, чтобы сделать теорию конечной, потребуется бесконечное число
перенормировочных констант. Поскольку в современной формули-
формулировке теории перенормировки требуется один эксперимент для опре-
определения каждой перенормированной константы, то, чтобы сделать
теорию имеющей смысл, необходимо проделать бесконечное число
таких экспериментов, а это невозможно и не имеет физического
смысла.
Таким образом, эта теория не перенормируема. В заблуждение
вводит то, что в низшем порядке в случае связи с производными
мы получаем конечный результат. Например, матричный элемент,
соответствующий диаграмме на фиг. 74, для случая связи ьр.д/дх^
не только конечен, но фактически точно совпадает с матричным
элементом в случае прямой связи y6- Примерно до 1947 г. все вычи-
вычисления проводились только в этом порядке, поскольку вообще не
существовало методов обращения с расходимостями. Поэтому в ран-
ранних вычислениях, казалось, не было различия между трудностями
теорий с прямой связью и со связью с производными. Фактически
в случае псевдоскалярной теории связь с производными предпочти-
предпочтительней, потому что оператор ЧьТр. имеет большую величину в нере-
нерелятивистском пределе (см. гл. 4, § 2).
Мы уверены, что невозможность перенормировки теории является
достаточной причиной для того, чтобы отказаться в настоящее
время от всех типов связи с производными. С современной мето-
методикой это необходимо. Конечно, возможно, что с помощью некоторой
^_ Иеренормируёмые и неперенормируемые теории 371
искусной переформулировки теории удастся сделать перенорми-
перенормируемыми некоторые типы теорий связи с производными. Но если
это возможно, то структура теории должна быть фундаментально
изменена, и тогда результаты, получаемые в низшем порядке в этой
переформулированной теории, будут полностью отличаться от тех
результатов, которые получаются теперь в теории связи с произ-
производными без переформулировки. Каким бы ни было' окончательное
мнение о сходимости теории со связью с производными, результаты,
получаемые в ней с помощью современных методов в низшем порядке,
не будут законными ни в одном случае.
Более того, мы можем с уверенностью рассматривать как благо-
благоприятное обстоятельство тот факт, что некоторые теории, которые
на первый взгляд кажутся приемлемыми, не выдерживают проверки
на перенормируемость. Когда была открыта релятивистская электро-
электродинамика, то оказалось, что только уравнения Максвелла совместны
с требованием релятивистской инвариантности и микроскопической
причинности и что нет других уравнений поля такого типа, сов-
совместных с этими требованиями; это рассматривалось как большой
триумф теории. Этот же принцип позволил нам в гл. 10, в сущности,
однозначно найти лагранжианы свободных полей. Существование
требований, которые позволяют выбрать очень небольшое число воз-
возможных лагранжианов свободного поля, всегда рассматривалось как
очень ценное качество теории.
Требований микроскопической причинности и релятивистской
инвариантности недостаточно для существенного ограничения числа
возможных лагранжианов взаимодействия, в чем мы убедились в гл. 11.
Поэтому можно ожидать, что должен существовать некоторый прин-
принцип, ограничивающий число возможных выражений для лагранжиана
взаимодействия. Мы уверены, что в настоящее время, пока не созданы
сходящиеся релятивистские теории поля, такого рода принципом
является требование перенормируемости теории. В самом деле, сле-
следует ожидать, что правильное заключение о приемлемости взаимо-
взаимодействия может быть сделано только в том случае, когда результаты
этого взаимодействия исследуются во всех приближениях, а это как
раз точно то, что пытаются сделать в перенормируемой теории.
Вероятно, теория перенормировок не является окончательным
решением проблемы расходимостей, которые присущи релятивистским
теориям квантованных локальных полей. Мы надеемся, что будущая
правильная теория не только не будет содержать расходимостей,
но, кроме того, даст спектр масс элементарных частиц, величину
константы связи, а также величину постоянной тонкой структуры х<
1) В начале развития теории перенормировки существовала надежда,
что величину постоянной тонкой структуры можно будет получить, исходя
из следующего требования: расходимости, встречающиеся в последовательных
порядках теории возмущений, должны сокращаться^друг с другом. Эта идея
была предложена Паули. Однако было показано (Йост и Люттингер [252]),
372 Глава 23
(величины, которые в настоящее время берутся из эксперимента).
Несомненно, что многие стороны теории перенормировок будут
включены (или будут присутствовать) в будущую правильную теорию.
Точно так же вполне вероятно, что в будущей теории вопросы
взаимного отношения и одновременного сосуществования всех „эле-
„элементарных" частиц (таких, как электроны, нуклоны и т. д.) будут
являться существенной частью теории. Существует надежда, что
с помощью изучения современной формы перенормированной кванто-
квантовой электродинамики и перенормируемых мезонных теорий можно
выяснить, без чего в современных теориях можно обойтись, что
именно является следствием таких весьма общих принципов, как
релятивистская инвариантность и причинность, и что, следовательно,
будет присутствовать в будущей теории. Может даже случиться
так, что такого рода изучение позволит получить другую формули-
формулировку теории, в которой мы будем иметь дело только с конечными
величинами и которая прольет свет на вопросы, перечисленные выше.
Возражения против связи с производными, вытекающие из пере-
перенормируемости, имеются не только в случае псевдоскалярной мезон-
ной теории с псевдовекторной связью и скалярной мезонной теории
с векторной связью, но и для тензорной связи векторного поля.
Мы напомним читателю соотношение A1.9), где было указано, что
взаимодействие вида 'ia^diF1 может быть использовано для описания
дополнительного взаимодействия дираковской частицы (электрона
или протона) с электромагнитным полем. Указанный тип связи с про-
производными также расходится.
Это может показаться весьма удивительным, если учесть,
что электрон, и в особенности протон, имеют магнитный момент,
отличающийся от даваемого теорией Дирака. В любом медленно
меняющемся магнитном поле взаимодействие с дополнительным магнит-
магнитным моментом может быть описано на практике с помощью члена a^F^.
Однако этот член не может рассматриваться как часть фундамен-
фундаментального взаимодействия между электромагнитным полем и электро-
электроном или протоном, поскольку это привело бы к неперенормируемым
расходимостям. Наоборот, дополнительный момент возникает из
радиационных поправок, получающихся, если исходить из простого
фундаментального дираковского взаимодействия ^..А^. В случае элек-
электрона (Швингер [436, 440], Люттингер [312]) мы видели, что эти
радиационные поправки в самом деле дают наблюдаемый дополни-
дополнительный магнитный момент (см. гл. 21, § 4); в случае протона
что такая компенсация не имеет места. Так, вклад в поляризацию вакуума
имеет расходимости одного и того же знака во втором и четвертом поряд-
порядках. Такого же рода идея, рассматривающая конечность и сходимость вкла-
вкладов в собственную энергию, была сформулирована Рака [400], но опроверг-
опровергнута Франком [188] с помощью явного вычисления вклада четвертого порядка
в собственную энергию фермиона.
Перенормируемые и неперенормируемые теории 373
(Люттингер [313, 314], Кейс [78, 79], Ривьер [403], Боровиц иКон [61])
должно быть верно то же самое, если принять во внимание радиа-
радиационные поправки, связанные с виртуальным испусканием мезонов
(см. также т. II, гл. 46). Поскольку дополнительный магнитный
момент не является внутренне присущим частице, а обусловливается
радиационными поправками, можно ожидать, что он зависит от
частоты внешнего магнитного поля, и, вероятно, эта зависимость
от частоты может быть наблюдаема (Томпсон [482]). Было бы,
конечно, ошибочным рассматривать взаимодействие
дополнительный магнитный момент) как часть взаимодействия
электрона (или протона) с электромагнитным полем и рассчитывать,
например, вклад этого взаимодействия в формулы рассеяния элек-
электронов или нуклонов большой энергии на электромагнитном поле.
Такие расчеты дали бы очень большое поперечное сечение, которое
должно было бы рассматриваться как ложное.
§ 4. Высшие спины
Спины, более высокие, чем х/2, дают большие степени импуль-
импульсов в подинтегральное выражение. Обычно это обусловлено появле-
появлением производных в лагранжиане взаимодействия. Все они ведут
к неперенормируемым расходимостям в теории, за исключением только
нейтральных мезонов со спином 1. В последнем случае теория пол-
полностью аналогична электродинамике (отличие заключается в конеч-
конечности массы мезона, что исключает калибровочную инвариант-
инвариантность). Неизвестно, однако, существуют ли такие нейтральные
мезоны со спином 1. В случае взаимодействия с нуклонами нейтраль-
нейтральных мезонов со спином, большим 1, мы получаем расходимости.
Здесь мы исключили из рассмотрения заряженные мезоны со
спином 1, потому что член взаимодействия их с электромагнитным
полем содержит дополнительные производные, и поэтому теория
становится неперенормируемой. По аналогичным причинам теория
взаимодействия заряженных мезонов со спином 1 с нуклонами также
является неперенормируемой. В этом случае трудности связаны с тем,
что источник поля заряженных мезонов изменяется, когда излучается
заряженный мезон; протон может испустить заряженный мезон, но
после этого процесс не может повториться. Исключением из этого
общего правила является, по-видимому, смешанная теория Бете и
Бирда [23], в которой как псевдоскалярные, так и псевдовекторные
мезоны связаны с нуклоном с помощью псевдовекторной связи. При
такой формулировке теории, которая развита в этой статье, расхо-
расходимости не возникают. Однако общее исследование до сих пор не
проведено. Во всяком случае, поскольку взаимодействие заряженных
мезонов со спином 1 с электромагнитным полем является непере-
374 Глава 23
нормируемым, смешанную теорию Бете и Бирда не следует рас-
рассматривать серьезно.
В этой книге мы не будем рассматривать никаких частиц со
спином, большим 1, или заряженных частиц со спином 1. Хотя
лагранжиан для таких случаев и может быть выписан, вычисление
взаимодействий ведет к принципиальным трудностям. Поскольку
нам неизвестны способы, с помощью которых можно было бы обойти
трудности с расходимостями в этих неперенормируемых теориях и
которые не нарушали бы микроскопической причинности, мы не
будем рассматривать такие теории.
§ 5. Взаимодействие ^-распада
Методы, предложенные Ферми и Юкава для расчета взаимодей-
взаимодействия между нуклонами и лептонами (общее наименование р-частиц
и нейтрино), были уже рассмотрены в гл. 11. Обозначим лептоны
на диаграммах Фейнмана с помощью пунктирных линий. Тогда взаи-
взаимодействие Ферми будет представляться диаграммой, изображенной
на фиг. 75. Определим размерность D подинтегрального выражения
с помощью метода, который неоднократно применялся. В частности,
£> = — 4C-f 4-)-ЗР»Н-3^, B3.9)
где L — означает число лептонных линий. Кроме
того,
гГг-\-Не — ZC {Z6.10)
и
2Li-{-Le=2C. B3.11)
Тогда, подставляя соотношения B3.10) и B3.11)
в B3.9), получаем
Фиг. 75. \ J> у
D = 2C-\-4 — ~Pe — -jLe. B3.12)
Итак, чем больше вершин, тем больше D, и, следовательно,
теория Ферми является неперенормируемой. Возможно, конечно, что
взаимодействие Ферми не имеет места при очень больших энергиях
и что следует проводить обрезание при энергиях, сравнимых с мас-
массой нуклона. Поскольку явление ^-распада происходит при малых
энергиях, обрезание не делает незаконным рассмотрение его с помощью
взаимодействия Ферми. Это просто означает, что, когда энергия
сравнима с массой нуклона, явление становится более сложным и не
описывается больше взаимодействием Ферми. Если интегралы по
импульсам лептонов обрезать на энергии, равной массе нуклона, то
взаимодействие, представляемое диаграммой на фиг. 75, очень слабо.
Существует и другая возможность: р-распад может являться
двухступенчатым процессом, как его впервые рассматривал Юкаэа.
Перенормируемые и неперенормируемые теории 375
Вначале нуклон излучает бозон
N-+N'-\-B, B3.13)
который затем распадается на два лептона
B^s_|_v, B3.14)
где s — электрон, v — нейтрино. Известно, что В не может являться
тг-мезоном, так как последний не распадается на электрон и нейтрино
(см. т. II, гл. 27). Однако некоторые типы /С-мезонов (частицы с массой
около 1000), по-видимому, распадаются на электроны и другие
частицы (см. т. II, гл. 51) и, может быть, являются В-частицами,
постулированными в теории Юкавы.
Глава 24
КОЛИЧЕСТВЕННАЯ ТЕОРИЯ ПЕРЕНОРМИРОВКИ
Мы теперь покажем, что с помощью перенормировки массы и
заряда действительно можно устранить все ультрафиолетовые рас-
расходимости в разложении 5-матрицы в квантовой электродинамике.
В гл. 22 мы видели, что интеграл, соответствующий определен-
определенной диаграмме, может расходиться только в случае, если
где Fe и Ве — число внешних фермионных и бозонных линий, со-
соответственно. Из приведенного неравенства следует, что существует
конечное число типов диаграмм, которые могут вносить расходи-
расходимости в теорию. Причиной этого является то, что степень расхо-
расходимости интегралов, соответствующих этим диаграммам,1 не зависит
от порядка диаграмм. Перенормировка состоит в том, чтобы
с помощью вычитательной методики устранить бесконечности,
а также в теоретическом оправдании такой методики. Мы будем
излагать здесь методы перенормировки квантовой электродинамики,
следуя близко двум статьям Дайсона [126, 127]. Общее доказатель-
доказательство перенормируемости дадим согласно Уорду [508—509].
§ 1. Определения
Вначале определим понятия связной, приводимой и неприводимой
диаграмм, а также вершинной части и части собственной энергии.
Диаграмма называется связной (connected), если любая ее часть
связана с остальной частью диаграммы по меньшей мере двумя
линиями. Вершинная часть определяется как свйзная часть (состоя-
(состоящая только из вершин и внутренних линий), соединенная с осталь-
остальной частью диаграммы двумя фермионными и одной бозонной
линиями. На фиг. 76, а приведена простейшая вершинная часть.
Имеются также вершинные части V высших порядков (см., напри-
например, фиг. 76, Ь), которыми можно заменить любую из вершин
в диаграмме G, причем модифицированная таким образом диаграм-
диаграмма О' будет иметь определенный физический смысл. Матричный
элемент, соответствующий диаграмме G', можно получить из мат-
матричного элемента, соответствующего диаграмме О, заменой опера-
оператора fj, для данной рассматриваемой вершины на оператор
Количественная теории перенормировки
377
Л„ (V.pj, p2), который зависит только от структуры вершинной части V
и' от импульсов рх и р2 двух фермионных линий, связывающих
вершинную часть V с остальной частью диаграммы [см. фиг. 76 и
формулу B1.12)].
Фиг. 76.
,t
Аналогично частью собственной энергии на диаграмме G назы-
называется связная часть (состоящая только из вершин и внутренних
линий), которую можно вставить в середину одиночной фотонной
или электронной линии диаграммы О так, чтобы модифицированная
диаграмма была совместна с правилами построения диаграмм Фейн-
мана, т. е. в каждой вершине должен быть точно представлен
оператор взаимодействия S&I- На фиг 55, а и b и на
фиг. 60, а и Ь приведена часть собственной энергии электрона,
а на фиг. 78, b — простейшая часть собственной энергии фотона.
На фиг. 77, а часть собственной энергии электрона W вставлена
в линию с импульсом р! (см. диаграмму на фиг. 76, Ь), а на фиг. 77, b
часть собственной энергии фотона вставлена в фотонную линию
с импульсом к (см. диаграмму на фиг. 76, Ь). Эти линии с импуль-
импульсами pj и к могут быть как внешними, так и внутренними по отно-
отношению ко всей диаграмме в целом. В частности, часть собственной
378 Глава 24
энергии электрона W может состоять только из одной точки,
соответствуя члену — Зягф (х) ф (х) в гамильтониане взаимодействия
Определим, следуя Дайсону, импульсные фурье-образы опера-
операторов (|) и А следующим образом:
B4.1)
(k)d*k B4.2)
и аналогично во всей этой главе определим Sf(p) и Di?(k) как фурье-
образ функций Sf(x) и Dp(x) соответственно. В явном виде
±ib i^ B4.3)
2я р— m
Если диаграмму G, модифицированную вследствие любой из
указанных выше вставок, обозначить теперь через G', то с помощью
выведенных нами ранее правил для выписывания матричного элемента
можно найти, что матричный элемент, соответствующий диаграмме G',
может быть получен из матричного элемента, соответствующего
диаграмме G, если сделать следующие изменения:
а) для внешней электронной линии с импульсом рг
<KPi)-* SHPi) [£ (W. Pi) —2irf3m]<J.(Pl), B4.4)
Ф (Pi) -> ф (Pi) [S (W, Pl) — 2w 8m] S, (Pl); B4.5)
б) для внутренней электронной линии с импульсом pt
■bV(p1)->5/,(p1)[S(Wr, Pl) — 2«i8m]S,(p1); B4.6)
в) для внешней фотонной линии с импульсом к
А^ (к) -> А,, (к) П (ИГ, к) DF(к); B4.7)
г) для внутренней фотонной линии с импульсом к
Df (к) -> DF(к) П (W, к) DF (к); B4.8)
д) вершинный оператор -[-,,. заменим на
р1>Р2). B4.9)
Здесь операторы S (или П) зависят только от структуры
диаграмм W (или W") и от импульсов pt (или к), но не от осталь-
остальной части диаграммы. В пунктах „а" и „б" добавлен член—2та'8/л,
который представляет вклад от члена —йтгафф, согласно предыду-
предыдущему рассмотрению в гл. 21. Для оператора II собственной энер-
энергии фотона не нужно вводить такой контрчлен, поскольку собствен-
собственная энергия фотона равна нулю вследствие требования калибровоч-
калибровочной инвариантности теории. [Однако для мезонов член перенормировки
Количественная теория перенормировки
379
массы мезона является необходимым (см. гл. 21, § 6).] Аналогично
вершинная часть A^(V, рг, р2) зависит только от структуры диа-
диаграммы V и от импульсов pt и р2, соответствующих двум связан-
связанным с ней фермионным линиям. Отметим, что любой из операторов
Л^, Е и П может быть вычислен независимо от остальной части
диаграммы, и полученный результат будет иметь общий.характер.
Это может быть использовано в различных приложениях.
Фиг. 78.
Если из диаграммы G исключить все части собственной энергии,
а также вершинные части1), то мы получим приведенную диаграмму GQ,
которая называется остовом G. Диаграмма, совпадающая со своим
остовом, называется неприводимой. Части собственной энергии
второго порядка W и W на фиг. 78 являются единственными при-
примерами неприводимых частей собственной энергии. Части собствен-
собственной энергии высших порядков являются приводимыми, т. е. не
неприводимыми, и могут быть получены с помощью вставок частей
собственной энергии и вершинных частей в линии и вершины диа-
диаграмм W и W на фиг. 78. Однако вершинные части более высоких
Фиг. 79.
порядков, чем второй (пример вершинной части высших порядков
приведен на фиг. 76, Ь), могут быть как приводимыми, так и не-
неприводимыми. Вершинная часть, или часть собственной энергии,
называется собственной, если она не может быть разделена на две
части, соединенные одиночной линией; в противном случае она назы-
называется несобственной. На фиг. 79 приведен пример несобственной
части собственной энергии фермиона.
Теперь мы можем получить приводимую диаграмму О опреде-
определенного порядка, скажем порядка п, вставляя независимо и всевоз-
всевозможными путями части собственной энергии и вершинные части
требуемых порядков в различные линии и вершины неприводимой
диаграммы О0 низшего порядка. Эти диаграммы G образуют хорошо
определенный класс L и поэтому могут быть точно перечислены.
У Однако так, чтобы при этом диаграмма не выродилась в прямую
линию. — Прим. перев.
380 Глава 24
Предположим, что Мо—матричный элемент диаграммы Go. Тогда
любой матричный элемент М из класса L будет давать дополнитель-
дополнительные вклады в процесс, которому соответствует матричный эле-
элемент 5-матрицы Мо. Обозначим сумму всех вкладов, включая и Мо,
через Ms- Вследствие независимости всех вставок, сделанных в раз-
различные вершины и линии диаграммы Go, сумма Ms может быть
получена из матричного элемента Мо, если модифицировать в нем
множители следующим образом:
Каждый множитель Sp(p) в матричном элементе Мо, соответ-
соответствующий внутренней электронной линии диагрмммы Go, заменяется
на выражение
S*(p) = SF(p)~\-SF(p) E*(P) S'F(p) B4.10)
(доказательство будет дано ниже). Аналогично, для каждой внешней
электронной линии необходимо сделать замену
B4.11)
*(Р). B4.12)
Для фотонных линий сделаем следующие замены:
DF (k) -> Dp (к) = DF (к) + DF (к) П* (к) DF (к), B4.13)
Af, (к) -> Л; (к) = А,, (к) + А^ (к) П* (к) DF (к). B4.14)
И наконец, вершинный оператор ту должен быть заменен на оператор
Гр(Pi, P2)=TF + VPi-P2)- B4Л5)
Здесь Е*(р) и П*(к) представляют суммы операторов £(W, p) и
П {W', р) только по собственным частям собственной энергии.
Предполагается, что в сумму Е* включен вклад контрчленов соб-
собственной энергии. Аналогично АA(р1, р2) есть сумма всех собствен-
собственных вершинных частей A^V, tt, £2), поскольку, если вершинная
часть является несобственной, она состоит из собственной вер-
вершинной части плюс одна или большее число частей собственной
энергии, а последние уже включены в величины SF и Dp.
Несобственные части являются неперекрывающимися комбинациями
собственных частей, которые уже учтены в неявном определении
функций 5^? и DF, данном выше. В этом легко убедиться: напри-
например, несобственная диаграмма типа диаграммы, приведенной на
фиг. 79, уже включена в определение
Sp (p,W) = SF (p) 4- 5, (р) Е (р, W) SF (p, W), B4.16а)
где W соответствует оператору собственной энергии фермиона
(см. диаграмму на фиг. 78, а). Если разрешить это уравнение
Количественная теория перенормировки
■ 381
относительно функции SF, то получим
1
■Sp(p) =
■ SF (p) £ (Pi, W)
= SF (p) + SF (p) E (p. WO SF (p) +
+ SF(p)S(p, W)SF(p)-L(p, W)Sr(p)-\-...; B4.166)
графическим представлением выражения B4.16а) является диаграмма
на фиг. 80.
Приведенное выше формальное преобразование можно принять
лишь с оговорками, поскольку мы оперировали с расходящимися
Фиг. 80.
величинами. При практическом применении всегда используют регуля-
регуляризацию, так что все интегралы становятся конечными, хотя и зави-
зависящими от регуляризации. Величины, которые являются конечными
и при отсутствии обрезания, остаются неизменными, в то время
как логарифмически расходящиеся вгличины становятся конечными
логарифмическими функциями регуляризующих масс.
Матричный элемент 5-матрицы будет вычисляться правильно,
если включить только вклады от неприводимых диаграмм, после
того как сделаны замены B4.10) — B4.15) в каждом матричном
элементе, соответствующем остову (неприводимым диаграммам).
Уравнения B4.10) — B4.15) являются интегральными уравнениями.
Например, в координатном пространстве уравнение B4.10) имеет
вид
S'P(x — y) =
= Sp (х — у) + J <***' J d*ysF (x — х') S* (x' — у') S'p (у' — у).
B4.17)
Уравнению B4.15) соответствует в координатном пространстве
замена
Та5D) (х — х') 5<4) (х' — х") -^ Г, (х — х'; я
х"). B4.18)
382 Глава 24
Для вычисления операторов Л^, Е* и П* необходимо выписать
в явном виде интегралы в импульсном пространстве, соответствую-
соответствующие каждой части собственной энергии W и вершинной части V.
Для процессов высших порядков части W и V часто являются при-
приводимыми (W и W всегда приводимы) и содержат внутри себя вер-
вершинные части и части собственной энергии. В этом случае снова
удобно опустить приводимые части V и W и, сделав подстановку
B4.10)—B4.15), включить их вклад в интегралы, соответствующие
неприводимым частям V и W. Тогда получаются интегральные урав-
уравнения для Л^, Е* и П*.
Следует отметить, однако, что приводимые части собственной
энергии должны получаться при вставке вершинных частей только
в одну, а не в две вершины неприводимых частей собственной энер-
энергии, представленных на фиг. 78, а и Ь\ в противном случае одна
и та же часть собственной энергии может учитываться больше
1 раза. Принимая во внимание это обстоятельство, мы можем прак-
практически сразу выписать интегральные уравнения, которым удовле-
удовлетворяют функции S* и П* (а -— постоянная тонкой структуры):
Е*(х —х') =
2ы j d*y f dY^S'F (x — у) i; (у — x', у — у') D'p (у' — х),
B4.19)
/ d*y f dy Sp [T^ (x — у) Г, (у — х', у — у') ^ (У' — хI •
B4.20)
С другой стороны, для функции Л не удается выписать замкну-
замкнутое выражение через функции Г, Sp и Dy. Однако можно выписать
интегральное уравнение для вершинного оператора Г в виде сте-
степенного ряда; в импульсном пространстве это уравнение имеет сле-
следующий вид (Швингер [442], Эдварде [144]):
IV (Pi, P2)sT!i + A!lt(Pi, р2) =
Pl — kM^(Pl — к)Г1,.(р1 — к, Р2 — к)Х
—к)Г,(Р2 —к, p2)Di(k)<***4---. B4.21)
Другими словами, чтобы получить интегральное уравнение для функ-
функции Г., мы должны начертить все неприводимые вершинные диа-
диаграммы и в матричный элемент, соответствующий каждой из них,
подставить Sp вместо Sf, Г^ вместо у р. и Др вместо Dp. Тогда
получается полный ряд функции 1\.
Теперь обратимся к задаче отождествления расходимостей, встре-
встречающихся в теории, и выработке рецептов их устранения.
Количественная теория перенормировки 383
§ 2. Отделение расходимостей из неприводимых диаграмм
Следуя Дайсону, мы будем называть примитивным расходящийся
матричный элемент М, если при фиксированном значении- одного
из 4-векторов импульса в подинтегральном выражении интегрирова-
интегрирование по всем остальным переменным дает сходящийся результат.
Фиксирование четырех переменных интегрирования р\. означает за-
замену внутренней линии на соответствующей диаграмме на две внеш-
внешние линии. Пусть О есть примитивная расходящаяся диаграмма,
имеющая Fe внешних фермионных линий, Вв внешних фотонных ли-
линий; тогда, как мы показали в гл. 22(см. примечание 2 на стр. 357), диа-
диаграмма может расходиться при условии, если 3/2Fe-|-5e < 5.
Поэтому единственно возможными примитивными расходящимися
диаграммами являются диаграммы, перечисленные нами в гл. 22,
а именно:
1) часть собственной энергии электрона (Fe = 2, Be = 0);
2) часть-собственной энергии фотона Ee=2, Fe = 0);
3) вершинная часть (Fe=2, £?e=l);
4) рассеяние света на свете (Ве = 4, Fe — 0).
Благодаря теореме Фарри треугольные диаграммы можно не рас-
рассматривать. Кроме того, как мы установили ранее, матричный эле-
элемент рассеяния света на свете фактически
сходится благодаря требованию калибро-
калибровочной инвариантности теории.
Отметим, что большинство диаграмм
не удовлетворяет следующему условию:
соответствующие им интегралы должны
сходиться, если в подинтегральном выра-
выражении фиксировать один из внутренних
импульсов. Фактически по самому опреде-
определению расходящиеся матричные элементы
приводимых диаграмм не могут быть при-
примитивно расходящимися. Следовательно, Рт
примитивные расходимости соответствуют Фиг. 81
неприводимым диаграммам, т. е. остовам,
которые перечислены выше (в п. 1—4). Имеется только одна неприво-
неприводимая часть собственной энергии электрона или фотона (см. фиг. 78),
однако могут быть неприводимые вершинные части любого порядка.
Одна такая возможная неприводимая вершинная часть высшего по-
порядка приведена на фиг. 81.
Дайсон[127] предложил однозначный метод разделения прими-
примитивных расходящихся интегралов на конечную и бесконечную части.
Это в каждом случае достигается с помощью разложения подинте-
грального выражения в ряд Тейлора по внешним импульсам [вспом-
[вспомним формулы B1.23а), B1.29), B1.54), B1.66) и в особенности
рассуждения, следующие за формулой B1.23)]. Итак, если /?(р, t)
384 Глава 24
представляет подинтегральног выражение, в котором р и t — внеш-
внешний и внутренний импульсы соответственно, то мы можем написать
B4.22)
Каждое дифференцирование увеличивает разность степеней внут-
внутреннего импульса t числителя и знаменателя на единицу. Поэтому
логарифмически, линейно или квадратично расходящиеся интегралы
дают разложения R, в которых расходятся только один, два или
три первых члена. Вид расходящихся членов можно получить из
соображений релятивистской инвариантности. Рассмотрим теперь вы-
выделение расходимостей из неприводимых расходящихся диаграмм.
Часть собственной энергии электрона
Единственную неприводимую часть собственной энергии элек-
электрона можно представить в виде интеграла
2(W, p) = /#в(р, k)d*k, B4.23)
который линейно расходится
Разложение в ряд Тейлора дается выражением
tfe(p. k) = /?e@, к) + РA ^(P. k))p_o + fl.c(p, к). B4.24)
Поскольку интеграл 2 расходится линейно, член Rec представляет
сходящийся интеграл (подинтегральное выражение содержит две
дополнительные степени переменной k в знаменателе по сравнению
с Re(p, k)). Поэтому выражение B4.33) можно записать в виде
'* p), B4.25)
где А' и В' — расходящиеся матричные операторы, не зависящие от
величин р. Вследствие ковариантности мы должны иметь
Zc(W, Р)=Я1(Р2)+Я2(Р2)Р B4.26)
и
S; = B'V B4-27)
Так как интеграл Ее сходится, то его можно записать однозначно
в форме 1)
р*)= А"-+-В"{р — т) + {р — т.)SC(W, p), B4.28)
х) На практике это достигается разложением функции SF (p — к) в под-
интегральном выражении Re согласно формуле
(A -f ВГ1 = А~х — A~lBA~x + А~ХВ (А + ВУ1ВА~1,
полученной из формулы B1.29), если положить Л = & и В—р — т.
Количественная теория перенормировки 385
где функция Sc (W, р) равна нулю для случая свободных электронов,
т. е. если удовлетворяются соотношения р = /га и р2 = /га2. Если
положить
Л' + Л"+/Я5' = Л(Ж\ B4.29а)
Br~\-B"=B{W) B4.296)
и включить вклад члена —bmtyty, то после суммирования по всем
неприводимым диаграммам (имеется только одна!) мы получим сле-
следующее выражение:
mp) = AI—2K&mI-\-BI(p — m)-\-{p — n)ScV, p); B4.30)
это выражение представляет вклад неприводимых (индекс /) диа-
диаграмм собственной энергии в функцию £*(р). В выражении B4.30)
мы обозначили
) = Л(ТГ) = Л1_ B431)
В выражении B4.31) суммирование проводится по неприводимым W*.
Аналогично B^W) = Bi и т. д. Перенормировка массы определяется
так, что для р = т, т. е. для свободного электрона масса должна
точно равняться т. Поэтому
, р)ф(р)=О, если р=т, B4.32)
откуда следует, что
B4.33)
Часть собственной энергии фотона
Неприводимая часть собственной энергии фотона W, изображен-
изображенная на фиг. 78, Ь, может быть представлена в виде интеграла
R{W', k) = f Rp(k, q)diq; B4.34)
этот интеграл расходится квадратично, так как в подинтегральном
выражении имеются только две функции Sf- Поэтому в данное
случае мы напишем
dRv @, q)
Rp(k, q) = /?p@ ) + *V ^
+t № д1С^ + Rpc (kl q)' B4-35)
Поскольку у знаменателя подинтегрального выражения инте-
интеграла /?рс(к, q) имеется три дополнительные степени q по сравнению
с интегралом /?р(к, q), то Rpc(k, q) представляет сходящийся инте-
интеграл по переменной q. Проводя рассмотрение таким же образом,
386 Глава 24
как и в случае собственной энергии электрона, мы получаем на
основании ковариантности следующее выражение:
' '', к). B4.36)
где А1г В^ и С^ являются постоянными тензорами с одними и
теми же компонентами во всех системах отсчета, отсюда
■В1A = 0, . B4,37)
<?,» = £«,»■ B4.38)
Кроме того, из требования калибровочной инвариантности следует,
что появление члена с константой Лх запрещено, поэтому его нужно
положить равным нулю. Следовательно, поскольку С W"=Ck2,
то мы можем написать
", k)+C'k2, B4.39a)
где
DC(W'. Ю = 0 для k2=0 B4.396)
и константа С включена в константу С. Наконец, так как суще-
существует только одна неприводимая часть собственной энергии фотона,
то мы получим
IlJ(k) = k2Cr-|-k2£>c(/, к2), B4.40)
где константа С обозначена через Сг- Величина П/(к) снова пред-
представляет вклад в П* всех неприводимых диаграмм собственной энер-
энергии фотона.
Вершинная часть
Вклад вершинной части, в крайнем случае, может расходиться
логарифмически. Поэтому при разложении в ряд Тейлора подинте-
грального выражения Л^ для вершинной части не требуется членов
с производными, следовательно,
SP Pl, p2), B4.41)
где L^ J—постоянный расходящийся оператор, а Л^с — сходящийся
интеграл, равный нулю при Pi = P2 = 0- Требование ковариантности
приводит к тому, что
L<r>=L(V B4.42)
Кроме того, если рг = ра и р± удовлетворяют соотношению р1 = т,
то оператор Л^с сводится к постоянной, умножаемой на опера-
оператор 7(i> и может быть включен в член L-j-^. Поэтому можно пред-
предположить, что оператор А^с в выражении B4.41) равен нулю не
только в случае р1==Р2 = 0> но также и в случае рх = р2 = т.
Физический смысл этого следующий: величина Л^с дает вклад, рав-
равный нулю, в постоянном электромагнитном потенциале, так как
последний сообщает частице импульс, равный нулю. Это должно
Количественная теория перенормировки 387
быть так, потому что постоянный электромагнитный потенциал
всегда можно устранить с помощью калибровочного преобразования.
Далее, поскольку величина ф-^-^ф представляет 4-вектор тока элек-
электрона без радиационных поправок, величина фГ^ф может быть интер-
интерпретирована как 4-вектор тока электрона с включением радиацион-
радиационных поправок. Поэтому в выражении B4.41) подразумевается, что
весь статический заряд включен в член Lfp., так как для свобод-
свободного электрона Ap.c(V> Pi> РгI^^ и> следовательно, <\>Тр$ == ^•ФТр.Ф"
Суммируя выражение B4.41) по всем неприводимым вершинным
частям, получаем
S-dyCV*. pt, р2) = Лг^(р1, Р2) = /-П!1+-Л^(р1. р2). B4.43)
где Li—расходящаяся константа, а суммирование проводится по
всем неприводимым V*.
Соотношения B4.30), B4.40) и B4.43) являются основными для
отделения расходящихся членов в матричных элементах, соответ-
соответствующих неприводимым диаграммам. Укажем, что в статье Кар-
плуса и Кролла [263] отделение расходимостей проведено в явном
виде для диаграмм собственной энергии и вершинных диаграмм низ-
низших порядков. Вышеуказанный метод идентичен методу, приведен-
приведенному в гл. 21, где мы рассматривали перенормировку радиационных
поправок низшего порядка, используя, однако, метод регуляри-
регуляризации.
Теперь необходимо вывести формулы, аналогичные форму-
формулам B4.30), B4.40) и B4.43), которые давали бы вклад приводи-
приводимых собственных диаграмм в функции 2*, П* и Г^ и в которых
конечная и бесконечная части были бы снова разделены релятивистски
инвариантным и однозначным образом. Только из соображений
инвариантности ясно, что эти функции должны иметь вид
- 2i«b/?i) -\-B{p — n
n*(k) = Ck2-f-k2D
(Pi> Рг)= ^-ТцН-А*
) = Лр.с(р, p) = 0,
DG(k2) = 0, если
*)-Ь
c(k2)
если
k2 =
Sc(v)(P — "
P2).
p = m.
= 0,
i), B4.44)
B4.45)
B4.46)
B4.47)
B4.48)
где
где А, В, С и L являются расходящимися константами.
Однако формулы B4.44) — B4.46) представляют только оконча-
окончательную форму этих выражений. Для данной приводимой диаграммы
мы должны сначала показать, как можно провести отделение расхо-
расходящихся величин так, чтобы получить однозначный, ковариантный
и сходящийся результат.
388 Глава 24
§ 3. Отделение расходимостей из приводимых диаграмм
В § 2 мы рассмотрели инвариантный метод Дайсона отделения
расходимостей из неприводимых диаграмм. Чтобы показать возмож-
возможность перенормировки теории в целом, необходимо рассмотреть
диаграммы всех возможных типов и всех порядков как приводимые,
так и неприводимые. Поэтому покажем, как отделяются расходи-
расходимости из приводимых диаграмм.
р р-k, р-к,-к2 р-к2 р
Фиг. 82.
Диаграммы G, получаемые из неприводимой диаграммы Go путем
вставки частей V, W и W в различные линии и вершины диа-
диаграммы О0, могут быть разделены на три широких класса:
1) диаграммы с полностью неперекрывающимися вставками;
2) диаграммы, в которые сделаны вставки такого рода, что одна
из них полностью содержится внутри другой;
3) диаграммы с перекрывающимися вставками.
В первых двух классах расходимости могут быть устранены
с помощью инвариантного метода Дайсона отделения расходимости,
Р а р-К Ь р
Фиг. 83.
приведенного в § 2. В неперекрывающихся вставках отделение рас-
расходимостей может быть проведено независимо в каждой вставке.
Во вставках второго типа можно последовательно устранить расхо-
расходимости с помощью описанного выше метода, начиная с самой вну-
внутренней вставки и кончая расходимостью, которую дает сама диа-
диаграмма G. Аналогично комбинация двух первых типов расходимостей
не представляет трудности. Однако для перекрывающихся вставок
метод Дайсона недостаточен, так как в таких случаях мы одновре-
одновременно встречаемся с интегралами больше чем от одной переменной,
которые расходятся и остаются расходящимися, если интегрирова-
интегрирование проводится по любой одной переменной, в то время как все
остальные переменные фиксированы. Этим третий тип вставок отли-
отличается от первого и второго типов, в которых мы имели каждый
Количественная теория перенормировки 389
раз только по одной переменной и для которых фактически удава-
удавалось отделить расходимости с помощью формулы B4.22).
Пример такого рода перекрывающихся расходимостей приведен
на фиг. 82. На ней представлена диаграмма собственной энергии
электрона, которую можно получить вставкой вершинной части V
в вершину а или b диаграммы, изображенной на фиг. 83. Диаграмме
на фиг. 82 соответствует следующий матричный элемент:
2 (W2, Р) = *4 / / d^dW- (p, kt) О,„ (р, kt, k2) № (p, k2), B4. 49)
где
№ (Р. к2) = -L /
к£ (р
Расходится не только двойной интеграл по переменным kx и k2 (ли-
(линейная расходимость), но расходится (логарифмически) также и лю-
любой из интегралов по kx или k2, если интегрирование проводить по
одной из этих переменных, а другую фиксировать.
Фиг. 84.
Аналогично рассмотрим вставку вершинной части в вершину а
диаграммы собственной энергии фотона второго порядка, предста-
представленной на фиг. 84, а. Эта вставка может в то же время рассма-
рассматриваться и как вставка в другую вершину b (фиг. 84, Ь). Вообще,
вклады приводимых диаграмм (см. фиг. 84, Ь) в величины П* (или S*)
представляют собой интеграл, который включает в себя расходимо-
расходимости, соответствующие каждому способу, с помощью которого эта
диаграмма может быть построена вставками вершинных частей в лю-
любую или обе вершины исходной неприводимой диаграммы (фиг. 84, а).
Дайсон назвал их „£-расходимостями".
Эти „^-расходимости" приводят к трудностям, потому что ста-
становится возможным рассматривать приводимую часть собственной
энергии как построенную из неприводимой многими различными спо-
способами; при этом вершинная часть может рассматриваться как вставка
390 Глава 24
в одну или другую вершину неприводимой диаграммы второго по-
порядка, и каждый возможный способ фактически вносит свой собст-
собственный вклад в получающиеся расходимости.
Чтобы рассмотреть этот случай, Дайсон A949 г., не опублико-
опубликовано) и Салам [418, 419] дали однозначные правила для отделения
расходимостей из перекрывающихся диаграмм, которые сводятся
к правилам, данным в § 2 для неперекрывающихся диаграмм. Эти
правила позволяют отделить из перекрывающихся расходящихся ча-
частей однозначные, ковариантные и абсолютно сходящиеся части.
Следует, по-видимому, подчеркнуть, что трудности в получении
правильных рецептов для отделения расходимостей из перекрываю-
перекрывающихся диаграмм связаны только с трудностью нахождения такого
правильного способа перечисления всех расходящихся частей, кото-
который позволил бы строго интерпретировать все вычитательные
операции как перенормировку и однозначно выделить конечную часть.
Доказано, что это является очень сложной задачей, так как при
этом необходимо анализировать чрезвычайно сложные многократные
интегралы, для которых не существует адекватной системы обозна-
обозначений. (По предложенному Саламом определению, адекватной систе-
системой обозначений называется система, которая „кажется краткой и
понятной по крайней мере двум лицам, одно из которых, по-види-
по-видимому, является ее автором".) Впервые такого рода система обозна-
обозначений была дана Саламом в его важной статье [418], в которой на
ясной и строгой основе дан полный анализ перенормировки. Теперь
кратко, не входя в детали, изложим метод Салама.
Рассмотрим re-кратный интеграл /п> получающийся из диаграммы
с такими п. „базисными" импульсами tit что векторы распростране-
распространения, относящиеся к другим линиям, могут быть выражены как ли-
линейные комбинации выбранных импульсов tt (и импульсов, соответ-
соответствующих внешним линиям). Различные множители Sp и Dp, появляю-
появляющиеся в интеграле /та, могут быть функциями как одной перемен-
переменной tit так и функциями двух или большего числа переменных.
Интеграл B4.49) является примером интеграла /„для случая ге =.2.
По терминологии Салама, интегрирование по меньшему, чем п, числу
переменных, когда оставшиеся переменные фиксированы, называется
субинт<;грироваиием. Сходимость при каждом субинтегрировании
можно определить, вычисляя степень переменной tj (по которой про-
производится интегрирование) в числителе и знаменателе подинтеграль-
яого выражения (см. гл. 22, § 1). При вычислении степеней все
переменные интегрирования должны считаться равноправными. Именно
при этом мы приходим к заключению, что двойной интеграл по
переменным kt и k2 B4.49) расходится линейно, поскольку имеется
одиннадцать степеней к в числителе и только десять в знаменателе.
Для сходимости интеграла /„ в целом необходимо, чтобы сходилось
не только окончательное интегрирование по переменным tt . . . tn,
яо и все возможные субинтегрирования по меньшему числу базисных
Количественная теория перенормировки 391
переменных, т. е. по tit t^tj, ..., tjtj ... tn_v когда эти базис-
базисные переменные выбраны всеми возможными способами. Возможен
случай, когда некоторые интегралы сходятся (что определяется
с помощью вычисления степеней tj), а некоторые субинтегрирования
расходятся. В таком случае говорят, что интегралы являются по-
поверхностно-сходящимися.
Чтобы сделать интеграл /„ сходящимся, нужно вычесть из подин-
тегрального выражения ряд расходящихся членов, прежде всего тех,
которые соответствуют всем возможным субинтегрированиям по ба-
базисным переменным от одного интегрирования до (и—1) интегри-
интегрирования, и, наконец, тех, которые соответствуют конечному инте-
интегрированию по всем п переменным. Расходящиеся члены вычитаются,
согласно приведенным ниже правилам.
Сначала зафиксируем все переменные в подинтегральном выра-
выражении, кроме переменной tv и вычтем расходящиеся члены, соот-
соответствующие субинтегрированию по переменной tlt согласно прави-
правилам, данным Дайсоном [формула B4.22)]. При этом в вычитаемых
членах остаются неизменными те множители, которые не содержат
переменной tv а переменным t2, t3, . .., tn и внешним импульсам
в множителях, содержащих переменную tl3 придаются значения им-
импульсов для свободных частиц. Такое же вычитание должно быть
сделано соответственно каждому субинтегрированию по любой дру-
другой одиночной переменной t2, .. ., tn. Во вновь получаемом подин-
подинтегральном выражении следует зафиксировать все переменные, кроме
перемгнных tl и t2, и вычесть расходящиеся члены, соответствую-
соответствующие субинтегрированию по переменным t1t2. Эти члены выделяются
из нового подинтегрального выражения; в них сохраняются неизмен-
неизменными множители, не содержащие переменных tl и t2, а в тех мно-
множителях, в которых имеются переменные tl и tt, либо и t1 и t2,
импульсам t3, ti tn (и внешним импульсам) придаются значения
импульсов свободных частиц. Такое же вычитание должно быть сде-
сделано и для всех других возможных комбинаций переменных tj-p
взятых попарно. Таким же образом необходимо вычесть расходя-
расходящиеся члены, соответствующие субинтегрированиям по переменным
titjth, . . ., ttt2 . . . tn_v причем, прежде чем проводить вычитание рас-
расходящихся членов, соответствующих некоторому субинтегрироваиию,
из подинтегрального выражения должны быть вычтены расходящиеся
члены, которые соответствуют всем возможным субинтегрированиям
предыдущего низшего порядка. „Истинная расходимость" по неко-
некоторому субинтегрированию может быть теперь определена как рас-
расходящаяся часть, которую нужно вычесть из „модифицированного"
подинтегрального выражения (определенного выше), чтобы субинте-
субинтегрирование давало сходящийся результат.
После того как таким же образом вычтены истинные
расходимости во всех субинтегрированиях вплоть до порядка п—1,
должно быть проведено окончательное вычитание для отделения
392 Глава 24
истинных расходимостей при интегрировании по всем п переменным.
И наконец, если во время этой вычитательной процедуры окажется,
что некоторое субинтегрирование является поверхностно-сходя-
поверхностно-сходящимся, то соответствующее вычитание делать не нужно.
Вся изложенная выше методика может быть математически пред-
представлена в следующей форме:
/,=JS Я (!«)*& ... Ъ_А+1 ... tn)
* 4-2 я ft,
ij
4- • • • + D(tt ... tn)+ /c(ti ... tn)- B4.53)
Здесь D^tjtj ...)—„истинные расходимости", соответствующие суб-
субинтегрированиям по переменным tjtj ..., множитель „R" называется
„приведенным интегралом", величина £)(^2 ... tn) представляет
„истинную расходимость" при окончательном интегрировании но
всем п переменным. Салам [419] показал, что такая вычитательная
методика в перенормируемой теории поля позволяет, фактически,
однозначно выделить абсолютно сходящийся член /д.
Отметим, что если интеграл /„ не содержит перекрывающихся
сомножителей, то его можно представить в виде
U = (/ ^i (ti) d4t) (/ F2 (t2) d42) ...(_/>„ (tn) d4n ). B4.54)
В этом случае можно применить метод Дайсона отделения расхо-
расходимостей по каждой переменной отдельно, тогда мы получим, что
сходящаяся часть выражения B4.54) примет вид
—Д.(tr)} d4r), B4.55)
где Dr(tr) — член, дающий истинные расходимости при интегрирова-
интегрировании по переменной tr.
Если определить истинную расходимость D и приведенный инте-
интеграл R, так же как и в формуле B4.53), то в случае неперекры-
неперекрывающихся расходимостей из формул B4.54) и B4.55) получим
a
+ (_l)»-iD(t1 .. . tn)+Io{tv t2, . .., tn). B4.56)
Здесь в отлияие от формулы B4.53) члены имеют попеременно то
положительный, то отрицательный знаки.
Количественная теория перенормировка 393
Теперь выражения B4.53) и B4.56) можно применить для вывода
соотношений B4.44) — B4.46). Затем, если функции SFl, DFl и Г^
являются конечными, имеющими физический смысл частями функций.
SF, Df, Тр. и получаются из последних отбрасыванием расходя-
расходящихся частей функций Е*, П* и Л^, то можно показать, что после
подходящей перенормировки массы конечные и соответствующие им
бесконечные функции связаны следующим образом:
S'F (e) = Z2SF1 (в)),
B4-57)
где Zv Z2, Z3 — расходящиеся константы, a e1 = Zr1Z2ZI3'!e—-пере-
Zr1Z2ZI3'!e—-перенормированный заряд.
Мы не будем приводить здесь этого доказательства. Оно содер-
содержится в статьях Салама [418, 419], где имеется также доказательство
перенормируемости мезонных теорий, не содержащих связей с произ-
производными (см. также работу Такеда [477]). Вместо этого приведем
видоизмененную вычитательную методику, данную Уордом [509], в ко-
которой удалось обойти построение приводимых частей собственной,
энергии. Это достигается с помощью выведенного им [507] формаль-
формального тождества, которое мы приведем в следующем параграфе.
.В заключение этого параграфа следует отметить, что при рас-
рассмотрении приводимых частей собственной энергии использование
приведенных выше правил Салама является необходимым, если мы
хотим правильно представить вычитание с помощью множителя Z,
Только в случае если приняты эти (однозначные) правила для отде-
отделения расходимостей, можно провести доказательство перенормируе-
перенормируемости теории в рамках, указанных Дайсоном [127]. Однако для прак-
практических приложений правильная конечная часть может быть полу-
получена с помощью изложенного ниже более „наивного" приближения,
которое мы рассмотрим на примере перекрывающейся диаграммы,,
изображенной на фиг. 82.
Эта диаграмма может рассматриваться как полученная при вставке
вершинной части Л^(р — к, р) в вершину b (или а) диаграммы, пред-
представленной на фиг. 83. Далее, этот оператор может быть разделен,
согласно формуле B4.43), на сходящуюся и расходящуюся части,
следующим образом:
Л^(р —к, p) = LTll + A,G(p —к, р). B4.58)
Расходящийся множитель Lf может быть включен в перенорми-
перенормировку заряда матричного элемента, диаграмма которого приведена
на фиг. 83, если объединить матричные элементы, соответствующие
диаграммам на фиг. 82 и 83. Другая возможность состоит в отбрасы-
394
Глава 24
вании расходящихся членов, при этом неявно подразумевается, что
вклад этих членов сводится (это всегда можно считать) к умножению
матричного элемента диаграмм низшего порядка на некоторую по-
постоянную, т. е. к переопределению заряда (константы связи), входя-
входящего сомножителем в этот матричный элемент. Если мы вставим
вершинную часть A|iC(p — к, р) вместо оператора -^ в вершину а
{или Ь) на диаграмме, приведенной на фиг. 83, то конечная часть
величины 2 (соответствующая диаграмме на фиг. 82) может быть
вычислена с помощью вычитания расходящихся частей, согласно фор-
формуле B4.30); точно такой же конечный результат получается с по-
помощью правил Салама. Однако раходящиеся члены (если их сохранить)
получаются в этих двух методиках неодинаковыми. Фактически, если
принять эту „наивную" методику, то не удается доказать пере-
перенормируемость теории, так как в этом случае расходимости не могут
быть должным образом интерпретированы с помощью множителей Z,
которые перенормируют заряд е одним и тем оке способом в мат-
матричном элементе любой диаграммы.
§ 4. Тождество Уорда
Если мы продифференцируем тождество
SF(p)Spl(p)=\
ло переменной ру то после приведения членов мы получим
dSF(p)
dp»
= —5P(p)-
1 (p)
др*
B4.59)
Если явно подставить выражение для Sf (p) [формула B4.3)], то
соотношение B4.59) получает вид
dSF(p)
B4.60)
Правая часть соотношения B4.60) пред-
представляет множитель, точно соответствующий
простейшей вершинной диаграмме (фиг. 85),
на которой импульс внешнего фотона равен
нулю. Таким образом, формальное диффе-
дифференцирование функции распространения S& (р)
по переменной р^ соответствует вставке
в электронную линию внешней фотонной линии с равным нулю
импульсом.
Рассмотрим теперь диаграмму собственной энергии W, предста-
представленную на фиг. 78, а. Ей соответствует оператор
Фиг. 85.
k)TvDp(k).
B4.61)
Количественная теория перенормировки 395
Если мы продифференцируем оператор S(p, W) по переменной р ,
то, используя соотношение B4.60), получим
р, W)
= + е* f d^-SF (p — к) Т(^(р — к) bDp(к). B4.62)
dp*-
Однако с точностью до множителя (—2-х) это — оператор A(V, p, р),
соответствующий вершинной диаграмме, приведенной на фиг. 76, Ь,
если положить импульс к внешнего фотона равным нулю1).
Очевидно, что собственная вершинная диаграмма Л (V) может быть
получена из собственной диаграммы собственной энергии E*(W, p)
с помощью вставки внешней фотонной линии в любую электронную
линию диаграммы W. Однако, как мы видели, вставка в электрон-
электронную линию фотонной линии с импульсом, равным нулю, формально
соответствует дифференцированию функции распространения этой
линии по компоненте внешнего импульса pv-. Таким образом, диф-
дифференцирование выражения для собственной энергии E(W, p) по
переменной р^ эквивалентно вставке фотонной линии в каждую 2>
электронную линию диаграммы W, если импульс электрона на этой
линии есть р. Поэтому, если просуммировать все собственные диа-
диаграммы собственной энергии, а затем продифференцировать сумму
по переменной р, то мы получим все собственные вершинные диа-
диаграммы и, следовательно,
==д
1) Численный множитель —2а получается в выражении B4.61), если
учесть, что величина Б (р, V), согласно формуле B1.13), определяется как
соответствующий V матричный элемент, умноженный на величину 2/Bте)-!.
Кроме того, отметим, что А^ (рь р2, V) определяется как такой оператор;
который заменяет -^ на простейшей вершинной диаграмме, приведенной на
фиг. 78, а; этой диаграмме соответствует оператор
i-Pa ± k> 72^ 5^;Р) V, —у SF (p2) -^ Dp (к),
так что новый вершинный оператор соответствует вершинной части V. Сле-
Следовательно, оператор А,., соответствующий вершине на фиг. 76, б, имеет вид
\. (Pv Р2. V) = - 2а J d*kt4SF (рг — k) T(iSF (р2 — к) гDp (к).
[См. правила, выведенные в гл. 19, а также определения функций Sp(p)
и DF (k), т. е. формулу B4.3).]
21 Следует отметить, что замкнутые петли не дают вклада в собственную
часть собственной энергии 2*. Это можно показать следующим образом:
в случае замкнутой петли в качестве переменной интегрирования мы можем
взять tp — импульс всех электронных линий на этой петле; вставка фотонной
линии с импульсом, равным нулю, в такую петлю Может быть получена с по-
помощью дифференцирования подинтегрального выражения по переменной t^.
Тогда интегрирование полученного подинтегральиого выражения по перемен-
переменной интегрирования t^, очевидно, даст нуль (Уорд [506] ).
396 Глава 24
Это соотношение между функциями Е* и Л было впервые выведено
Уордом [506, 507].
Несколько другой вывод этого тождества, указывающий на связь
его с требованием калибровочной инвариантности теории, использует
то обстоятельство, что постоянный внешний электромагнитный потен-
потенциал передает импульс, равный" нулю. Рассмотрим собственный опе-
оператор собственной энергии £*(р) (фиг. 86) в присутствии постоян-
постоянного потенциала а^ и обозначим его в этом случае через Е„(р)
(импульс р не изменяется!). Теперь разложим величину Е„(р) в ряд
Фиг. 86.
по степеням числа раз действий внешнего потенциала. Тогда получим
.. B4.64)
Однако вследствие требования калибровочной инвариантности теории
оператор 2*(р) должен определяться выражением
Еа(р)=£*(р — ел) =
—■ - ^ \Р/ —™ ^** [ '' ' ) —г— — 6 а а ( —————— j . —*— , . . j i ^тг.оо^
V др* /в=() 2! ^др* др1 'а,= о
поэтому, сравнивая разложения B4.64) и B4.65), получаем
3"*М=Д11(р, р)> B4.66)
2я Эр11
^•"•\ = E (р> р). B4.67)
Bя>а dpv-др'
Здесь S^ — оператор комптоновского рассеяния для фотонов с нуле-
нулевой энергией.
Отметим [это немедленно следует из тождества B4.63)], что
в выражениях B4.44) и B4.46) мы должны иметь £?-j-2tcL=0; это
доказывает взаимное сокращение расходимости в лэмбовском сдвиге
Количественная теория перенормировки 397
и расходимости при перенормировке волновой функции (см. гл. 22)
во всех порядках квантовой электродинамики.
С помощью тождества B4.63) можно получить следующее соот-
соотношение между функциями Sp и Г^. Из выражения B4.10) следует, что
( — m— 2^Е*(Р))- B4.68)
Следовательно,
. P> —Г,(р. Р)- B4.69)
Это — другая возможная форма тождества Уорда.
§ 5. Доказательство перенормируемости
Приведенное ниже доказательство перенормируемасти в квантовой
электродинамике принадлежит Уорду [509]. При его выводе широко
используется формальное тождество B4.63).
Интегрируя соотношение B4.63), находим
р
Е*(Р) — £*(Р') = — 2tz f dqvA^q, q), . B4.70a)
p'
p», p*). B4.706)
о
Вторую форму B4.706) мы получили с помощью замены переменных
B4.71)
Здесь определена величина р' как импульс свободного электрона,
так что после интегрирования величину р'2 нужно положить равной т2,
а оператор р' — равным т, где т — экспериментальная масса элек-
электрона. Тогда в член Б*(р) автоматически включена перенормировка
массы, так как величина £*(р') для р'=т, по определению, равна
величине Ьт. В дальнейшем не будем выписывать члена £*(р')> пред-
предполагая, что член с величиной Ьт включен в определение опера-
оператора Е*(р)- Как видно из уравнения B4.21), мы можем правильно
получить значение оператора Л^, если на каждой неприводимой вер-
вершинной диаграмме Фейнмана заменим каждую матрицу f^ на вели-
величину Гц, каждую функцию Sp на функцию Sp, каждую функцию Dp
398 Глава 24
на функцию Dp и просуммируем полученный ряд. Кроме того, на
диаграмме А^ нет перекрывающихся частей, поскольку она построена
из неприводимых диаграмм.
Аналогично определим оператор Д.А с помощью соотношения
— ~^^- = К(^ к). B4.72)
следовательно,
к 1 .
П* (к) = — 2тг f dq* Д, (q, q) = — 2тг f dy k% (ку, ку), B4.73)
о о
где собственную энергию фотона П*@) мы положили равной нулю
вследствие требования калибровочной инвариантности теории.
Необходимо ясно понимать, что сделанные выше определения
с помощью дифференцирования по сути являются неявными опреде-
определениями, причем при вычислении функций Е и Af используются не-
неприводимые диаграммы. Фактически необходимо определить функцию
;к, к), B4.74>
которая связана с функцией Dp соотношением, аналогичным B4.69)*
а именно
W^(k) = -——[Dp(k)]~x, B4.75)
так что
i 1
[Dp(k)]~1 = 2v: j dy k^W^ky). B4.76)
Из соотношения B4.76) следует, что расходящаяся функция W^
может встречаться в интегральных уравнениях, определяющих функ-
функции Dp, П* и т. д.
Если найденный результат выразить с помощью диаграмм Фейн-
Фейнмана, то величина W^ будет предста-влять вклад всех неприводимых
диаграмм, получаемых из диаграмм собственной энергии фотона
вставкой во внутреннюю электронную линию внешней фотонной
линии, содержащей переменные внешнего фотона (фиг. 87).
В этом случае при получении матричного элемента из матричного
элемента, соответствующего исходной диаграмме Фейнмана, мы опять
должны сделать замену
Количественная теория перенормировки 399
Тогда первые два члена, а именно член 2lk^ и член, соответ-
соответствующий простейшей „пузырьковой" диаграмме, даются выражением
X Г, (р + k. p) S'F(P)} <?p+ ... B4.77)
Следующий за ними член соответствует „пузырьковой" диаграмме
с двумя пересекающимися фотонными линиями внутри нее (см. фиг. 87).
фиг. 87.
Имеются также члены более высоких порядков. Итак, теперь и вели-
величина Л^, и величина W^ определены как суммы вкладов неприводи-
неприводимых диаграмм.
Здесь мы можем дать схему для определения с помощью последо-
последовательных приближений конечных частей функций Гр.. Sp и Dp, ко-
которые должны быть подставлены в матричный элемент остова для
вычисления суммы всех вкладов в матричный элемент.
Чтобы сделать это, вспомним, что оператор Г^ логарифмически
расходится, следовательно, оператор Г„х, определенный с помощью
соотношения
1> р2) — Др.(р', р'), B4.78)
где р' — снова 4-импульс свободного электрона (т. е. р' = т), яв-
является конечным. Аналогично величина Д^ расходится линейно, так.
как величина П* расходится квадратично. [Фактически, ковариант-
ковариантность снижает эту расходимость до логарифмической, потому что
не существует инвариантного —4-вектора, т. е. величина Дц.(О, 0)
в формуле B4.79) равна нулю.] Поэтому величина
Д,ОЛс, ЛО-ДДО. O)-(jfc),(-3^57)ko B4.79)
сходится. Введем, следуя Уорду, вычитательную методику, с помощью
которой можно сделать ядра в уравнениях B4.10) — B4.15) конеч-
400 Глава 24
ными. Решениями этих новых уравнений будут конечные функции
DFl и Г,^. Итак, мы можем написать
B4.80)
i
(k) = DF (k) — 2kDfQs) f dyk»X
о
— ДДО, 0) —
P2) — Vp', РГ)- B4-82)
Функции 5yi, D^ и Г^.1, определяемые этими интегральными урав-
уравнениями, являются теперь конечными. Покажем далее, что эта моди-
модификация исходных интегральных уравнений B4.10) — B4.15) с по-
помощью вычитания бесконечных членов эквивалентна перенормировке
заряда. Иначе говоря, мы покажем, что конечные и соответствующие
им бесконечные функции, определяемые уравнениями B4.10), B4.13)
и B4.15), связаны следующими соотношениями:
B4.83)
== Z3DF1 (в1), B4.84)
1 B4.85)
где Zv Z2, Z3 — (бесконечные) константы, которые должны быть
определены, и
e1 = ZT1Z2Zfe. B4.86)
С помощью этих соотношений, впервые выписанных Дайсоном [127],
можно интерпретировать вычитание бесконечных постоянных как
выделение бесконечных постоянных множителей.
В правильности соотношений B4.83)—B4.85) можно убедиться,
подставив выражения B4.83)—B4.85) для функций SF, DF, Г^.
в исходную систему интегральных уравнений, определяющих эти
функции, а именно:
SfF = SF±SFZ*S'F, B4.87)
D + DU*DF, B4.88)
*), B4.89)
Количественная теория перенормировка 401
где величины 2* и П* задаются выражениями B4.19) и B4.20) соот-
соответственно, а суммирование проводится по неприводимым V*. Далее,
в уравнении B4.21) для функции Га в каждом члене с коэффи-
коэффициентом (е2)" содержится точно п функций Dp, 2п функций S'p и
Bre-j-1) функций Г. Следовательно, если в этих уравнениях
величину е заменить на величину ev согласно соотношению B4.86),
и функции Dp, Sp и Гр — соответствующими конечными выраже-
выражениями, с которыми они связаны соотношениями B4.83)—B4.85), то
получим
Ар(е, Га, SF, Dp) — Zr1A^(e1, Га1, Spu DF1). B4.90)
Аналогично в выражении для величины Д^ [формула B4.77)] каждый
член с коэффициентом (е2)п содержит B«-)-1) функций Г и Sp и
(п—1) функций Dp, так что, если мы снова заменим величины е
на elt Sp на SFl, Dp на Dpi, Г^ на Г^, то получим
ДA(е, Г^, Sp, Dp) = Zr1Z31Z2^(e1, T,^, SFl, DFl), B4.91a)
или
W (е Г s'w D'v\ = Z~^Z Z^VP (e V 5р D'w) B4 916}
Поэтому, используя выражения B4.70) и B4.73), получаем
B4.92)
, yk; ev Гх, 5л, Од). B4.93)
Если выразить интегральные уравнения B4.87)—B4.89) через
величины B4.92) и B4.93), то найдем
lZ2 f dxipv—p^A^ip», p^; eu Vv SPU D
0 B9.94)
Z3D'F1 (e{) =
= Dp — 2tzDfZT1Z2 j dyk?^ (yk, yk; ex, Yx, SF1, DF1) DF1 (ej, B4.95)
о
Zr^M^^ + Z^A^e» rt, Sk. On)- B4.96)
Эти уравнения должны быть идентичны интегральным уравнениям
B4.80)—B4.82) для конечных операторов Spi, Dpi и Г^. Две
402 Глава 24
системы уравнений будут фактически тождественны, если в фор-
формулах B4.82) и B4.96)
Если этот результат подставить в уравнение B4.80), то мы получим,
что уравнения B4.94) и B4.80) будут идентичны при условии
Z1=Z2, B4.98)
и, наконец, уравнения B4.81) и B4.95) совпадают, если
С. ку)ч
/к=о'
и
или, иначе, если
Z3==l + -^-Cav) B4.100а)
где
При получении соотношения B4.99) мы полагали в формуле B4.81)
Ар, (О, 0) = 0; последнее вытекает из требования ковариантности.
Наконец, из требования ковариантности опять-таки вытекает, что
Ca.v—Cea.v> следовательно,
Z3=l+C, B4.101)
а величина Cg^ дается формулой B4.1006).
Таким образом, мы показали, что соотношения B4.83)—B4.85)
правильны, если величина е1 дается формулой B4.86) и если мно-
множители Z определяются соотношениями B4.97), B4.98), B4.100).
Отметим, что из уравнений B4.80) и B4.81) получаются сле-
следующие результаты для свободного электрона:
im = ^(p), B4.102)
ГрлСРх, P2)li,=^m = T,; B4-103)
для свободного фотона
^=0= £>Ик)- B4.104)
Из этих соотношений видно, что во всех порядках по константе
связи не существует наблюдаемых радиационных поправок к фор-
формулам движения свободного электрона или фотона. Фактически
соотношения B4.102)—B4.104) могут рассматриваться как опреде-
определение перенормировки массы и заряда, согласно которому свободный
(физический) электрон должен обладать определенной массой /га
Количественная теория перенормировки 403
(экспериментальная масса электрона) и определенным зарядом ех
(экспериментальный заряд электрона), а свободный фотон должен
без возмущений распространяться в свободном пространстве с равной
нулю массой покоя.
Обратимся теперь к уравнению B4.11). Принимая во внимание,
что р соответствует импульсу свободного электрона, и используя
соотношения B4.102) и B4.68), легко показать, что если р = т, то
^ B4.105а)
m); B4.1056)
поэтому
¥ (Р) = Ф (Р) + 2* (Z2 — 1) SP (р) Ср — т) ф (р). B4.106)
Соотношение B4.106) неопределенно, так как, если оператор (р — т)
действует на функцию ф(р), то в результате получается нуль, если
же этот оператор действует на функцию Sp(p), то в результате
получается константа (l/2ir).
Таким образом, в зависимости от порядка, в котором произво-
производится вычисление, функция <]/(р) равна либо ф(р), либо Z2^(p).
В гл. 21 мы видели, что эта неоднозначность может быть устранена,
если при вычислении S-матрицы принять особые меры, с помощью
которых можно было бы гарантировать унитарность ее на каждом
этапе вычислений. Фактически мы там уже указали, что правильная
перенормировка волновой функции дается выражением
f(p) = Z^(p), B4.107)
так как из формул B4.97) и B4.98) и нашего рассмотрения в гл. 21
следует, что постоянная Z2 может быть интерпретирована как вероят-
вероятность нахождения „голого" электрона (см. также работы Карплуса
и Кролла [263]). Аналогичные рассуждения приводят к тому, что
ф'(р) = 4Аф(р) B4.108)
и что
Al(k) = zfAy.(k). B4.109)
Рассмотрим теперь неприводимый матричный элемент рассеяния М.
Пусть на диаграмме, которой соответствует матричный элемент М,
имеется: Fe внешних электронных линий, Ве внешних фотонных
линий и п вершин. Тогда, согласно анализу, проведенному в настоя-
настоящей главе, матричный элемент М будет содержать п множите-
множителей Г„, Fe множителей ф или ф, Ве множителей A, Fj множите-
множителей Sp, соответствующих Ft внутренним электронным линиям, и В^
множителей Dp для внутренних фотонных линий. Напомним, что
404 Глава 24
число внутренних и внешних линий связано соотношением
n^^Fe + Fi = Be + 2Bi. B4.110)
Следовательно, если в матричном элементе М заменить функции Г ,
Sp и Dp на соответствующие им конечные выражения Г^, Spi и Dplt
с которыми они связаны соотношениями B4.83)—B4.85), то множи-
множители Z будут встречаться в матричном элементе только в комбинации
Этого множителя как раз достаточно, чтобы перевести множи-
множитель еп, на который умножается матричный элемент М, в множи-
множитель е™. Таким образом, из матричного элемента М выпадают как
величина е, так и множители Z, остаются только конечные опера-
операторы r,ll(ei), Dpiiej), Spi(ej) и перенормированный заряд ех. Наконец,
;если мы отождествим величину ех с конечным наблюдаемым зарядом
электрона, то выражение для матричного элемента М не будет
больше содержать расходимостей. Поскольку для матричного эле-
элемента М мы выбрали наиболее общую формулу, то мы тем самым
полностью завершили устранение ультрафиолетовых расходимостей
из 5-матрицы1'.
В заключение этого параграфа отметим, что из соотношения B4.98)
Снова следует, что расходимость в перенормировке волновой функ-
функции точно сокращается с расходимостью в вершинной части во всех
порядках. Это прямое следствие тождества Уорда и, следовательно,
калибровочной инвариантности. Поэтому единственная истинная рас-
расходимость в квантовой электродинамике связана с собственной энер-
энергией фотона, т. е. с явлениями поляризации вакуума, и включена
в расходящуюся константу Z3.
§ 6. Смысл перенормировки заряда
Чтобы выяснить смысл перенормировки заряда, рассмотрим комп-
Тоновское рассеяние фотонов с очень низкой частотой на свободном
электроне (Тирринг [480]). Имеется два типа неприводимых диа-
диаграмм, дающих вклад. Первый тип представлен двумя диаграммами
на фиг. 88. Второй тип можно получить с помощью вставки двух
фотонных линий в оператор S\ как это показано на фиг. 89. Если
рассмотреть предельный случай фотонов с частотой, равной нулю,
то диаграммы на фиг. 88 дадут следующий оператор (в который
включены все радиационные поправки):
М(а) = BфЦ' (р) {F (p, p) Si- (р) Г (Р. Р) +
-т-Г(р, p)S;(p)r"(p, р)}'Ъ'(рL+)А[{~\ B4.111)
1) Инфракрасные расходимости и нх сокращение при выполнении про-
программы перенормировки рассмотрены Яухом и Рорлихом [242].
Количественная теория перенормировки
405
где р — импульс электрона, а А'(+\ А'( )—операторы рождения
и уничтожения для фотонов с частотой, равной нулю, включающие
и радиационные поправки [формула B4.14)]. Вспоминая приведенное.
5'F(p)
Фиг. 88.
Фиг. 89.
выше рассмотрение (см. § 4), видим, что диаграмме на фиг. 89
соответствует матричный элемент
М(Ь) = еЦ> (р) / ^S* j у (р) а1+)а}~\ B4.112)
Используя тождество
SF
B4.113)
и соотношение B4.69), легко получить
■ SF (р) F (р, р) SF (р) Г (р, р) SF (р)} + SF (p) g-^-} S'F (p). B4.114)
406 Глава 24
Поэтому мы можем написать полный матричный элемент М в виде
М = *<•>+ Ж<»> = еЦ' (р) { Sfl 00-^7 Sf> (р) } f (p) ^+Ч(-'.
14 * . B4.115)
Если использовать соотношения B4.105) и B4.107)—B4.109) и
выполнить указанные внутри скобок в выражении B4.115) операции,
то оказывается, что все множители Z2 сокращаются и матричный
элемент М получает вид
М = Z3^(p) {rSP(р) Г + Tv^(р) тЧ ф (Р) 4+)Л<->. B4.116)
Если положить Z3e2 = е^, то матричный элемент М будет в точ-
точности равен матричному элементу второго порядка для рассеяния
фотонов с частотой, равной нулю. Следовательно, в этом пределе
все радиационные поправки исчезают. Матричный элемент М при-
приводит тогда к хорошо известной формуле Томсона
Ы B4Л17>
(вывод см. в гл. 19, § 5, а также см. работу Брауна и Фейн-
мана [71], где рассмотрены и радиационные поправки).
Итак, мы видим, что перенормировка заряда может рассматри-
рассматриваться как экспериментально определяемая так, чтобы комптоновское
рассеяние при малых частотах давалось формулой Томсона. Это
определяет экспериментальный заряд электрона ех.
Физически такое утверждение может быть сделано потому, что
томсоновское рассеяние представляет .чисто классический эффект и
зависит только от полного заряда. В этом случае длина волны
фотона так велика, что детали распределения заряда в рассеивателе
являются несущественными. Поскольку вследствие закона сохранения
заряда радиационные поправки не могут изменить полный заряд, мы
можем непосредственно использовать формулу Томсона для опреде-
определения экспериментального заряда электрона ех.
Можно было бы определить заряд и из другого требования,
а именно: закон Кулона должен иметь силу на больших расстояниях
при взаимодействии двух покоящихся электронов. Это определение
привело бы к той же самой величине заряда е1. Фактически можно
показать (Челен [258, 260]), что перенормировка заряда определяется
в квантовой электродинамике существенно однозначно вследствие
закона сохранения заряда.
§ 7, Общие замечания
До сих пор мы рассматривали проблему перенормируемости
спинорной квантовой электродинамики. Салам [420] доказал пере-
перенормируемость теорий заряженных скалярного и псевдоскалярного
Количественная теория перенормировки 407
мезонных полей, взаимодействующих с электромагнитным полем.
В этом случае помимо перенормировки массы и заряда в лагранжиан
нужно еще добавить контрчлен 8Хср+2ср2 (величина 8). — бесконечна)
для того, чтобы последовательно сократились все расходимости,
появляющиеся при рассмотрении мёллеровского рассеяния одной бес-
бесспиновой частицы на другой (см. гл. 23). Доказательство перенор-
перенормируемости, т. е. существования соотношений типа B4.57), в этом
случае гораздо более сложно, чем в спинорной электродинамике,
ввиду наличия более сложных перекрывающихся диаграмм. Уорд [509]
обобщил свой метод, приведенный в § 5, и на этот случай. Однако,
как и в случае спинорной электродинамики, метод Салама более
прозрачен и дает более ясную физическую картину перенормировки,
чем более простой, но более формальный и неявный метод Уорда.
Доказательство перенормируемости теории поля мезонов, взаимо-
взаимодействующих с нуклонами, если оператор взаимодействия не содер-
содержит производных, также было дано Саламом [418, 419]. В случае
псевдоскалярных мезонов необходимо снова добавить к гамильто-
гамильтониану бесконечный контрчлен SXcg+2<p2 для заряженных мезонов и 8Х<р*
для нейтральных. В случае скалярных мезонов, как указывалось
в гл. 22, к члену с ср* необходимо добавить член 8^ср3 для того,
Чтобы сократились расходимости, которые дают части диаграмм с тремя
внешними мезонными линиями. Было найдено, что можно перенор-
перенормировать без каких-либо существенно новых усложнений комбини-
комбинированное взаимодействие мезонных, нуклонных, фотонных и элек-
трокно-позитронных полей (Мэттьюс [328—330], Салам [417],
Уорд [509]).
Приведенные в этой главе методы вычитаний основываются
на использовании обычного представления взаимодействия и с их
помощью , рассматривается только устранение расходимостей из
5-матрицы. Существуют другие методы устранения этих расходи-
расходимостей. Например, для сокращения эффектов, связанных с перенор-
перенормировкой заряда в лагранжиан можно ввести другие контрчлены
(такие же, как член перенормировки массы). Тогда все с самого
начала можно выразить через перенормированный заряд (как и через
перенормированную массу). Такая формулировка теории была дана
Гупта [218]. Формализм Гупта фактически описывает перенорми-
перенормировку заряда как перенормировку единиц, в которых измеряется элек-
электромагнитное поле, а не как перенормировку константы связи. Такеда
[477] использовал один из вариантов метода Салама для получения тре-
требуемых контрчленов. Прекрасное изложение этих методов дано в
статье Мэттьюса и Салама [333], где также ясно и просто рассматри-
рассматриваются задачи мезонных взаимодействий. Все эти методы, в конеч-
конечном счете, эквивалентны, т. е. они могут быть связаны друг с Дру-
Другом с помощью (неограниченных) „унитарных" преобразований.
Наконец, рассмотрим кратко пределы применимости теории пере-
перенормировок, с которой мы имели дело до сих пор. Первым и наи-
408 Глава 24
более важным является то, что приведенные выше соображения
(т. е. анализ Дайсоном расходимостей с помощью примитивных рас-
ходимостей) существенно зависят от разложения S-матрицы по сте-
степеням константы связи. Таким образом, предполагалось, что степен-
степенной ряд разложения 5-матрицы сходится после того, как выполнена
перенормировка. В гл. 16, § 2, мы видели, что ряд может и не схо-
сходиться в задачах, включающих связанные состояния. Это в явном
виде было показано Феррети [157—161]. Он рассматривал унитар--
ный оператор
'„
\T /ОЯ/(О^ \. B4.118)
п=0 У tn+l J
где tv ..., tn — последовательность времен в интервале от —оо
до t, которые в пределе становятся бесконечно близкими друг к
другу. Оператор V(t) диагонализирует полный гамильтониан H0-\-\Hi,
т. е. V есть такой оператор, что величина
E(k) = V~1(H0-lrlHi)V B4.119)
является диагональной в представлении, в котором диагоналей гамиль-
гамильтониан Но. В выражение для оператора Феррети явно ввел адиабати-
адиабатическую гипотезу, положив, что константа связи X является функцией
времени и очень медленно растет от величины Х = 0 при t' = — оо
до величины X = 1 при t' = t. Как мы установили раньше, это необхо-
необходимо для того, чтобы оператор V (t) сделать полностью определен-
определенным.
Далее, если произведение V(t) формально разложить в степенной
ряд по константе связи (см. гл. 16), то мы получим следующий
результат:
п t tn-l
() // > Hl d> • • • X ('«) Hl <'»>■ <24- * 20>
Затем Феррети рассмотрел, при каких условиях оператор V(t) равен
оператору S(t). В довольно общем виде он показал, что это равен-
равенство несправедливо, если полный гамильтониан H0-\-~kHi имеет
дискретные собственные значения. Это верно даже в том случае,
когда дискретные собственные значения могут быть вычислены
с помощью теории возмущений. При наличии связанных состояний
5-матрица не стремится к какому-либо определенному пределу,
когда скорость вариации величины X делается бесконечно медленной
(см. также обсуждение в гл. 16, § 2). Собственно говоря, Феррети
удалось показать, что в случае существования дискретных собствен-
собственных значений ряд для оператора S(t) фактически расходится (см.
также работу Глазера и Циммермана [208]). Поэтому, если даже
Количественная теория перенормировки 409
не рассматривать вопроса о сходимости, перенормировка S-матрицы
в том виде, в котором она была проведена в данной главе, строго-
говоря, применима только к чистым процессам рассеяния свободных
частиц.
Сходимость S-матрицы для процессов рассеяния была исследована,
в работах Херста [239, 240], Тирринга [481], Петермана [385, 3861
и др. Они доказали расходимость разложения теории возмущений
(опуская члены перенормировки) в случае скалярной мезонной тео-
теории с нелинейным взаимодействием в виде Хер3. Кроме того, Тирринг
и Петерман в своей работе фактически показали, что включение
перенормировки не меняет положения. Дайсон [134] О выдвинул ряд.
аргументов в пользу того, что подобным же образом разложение
S-матрицы в замкнутой квантовой электродинамике должно рассма-
рассматриваться только как асимптотическое разложение. Если это дей-
действительно так, то успех теории существенно зависит от малости
константы связи.
Феррети [161, 162] пытался дать формулировку теории, в кото-
которой удалось бы избежать разложения по степеням константы связи X,
Он предложил найти сначала дифференциальные уравнения, которым
бы удовлетворяли физически наблюдаемые величины, являющиеся
функциями величины X. Затем по программе, выдвинутой Феррети,
величина Q(X-j-SX) должна была выражаться через данную наблю-
наблюдаемую величину Q(X) и другие наблюдаемые величины. Ему удалось
доказать, что можно перенормировать величину Q(X-(-8X) в первом
порядке по 8Х. Аналогичные идеи были выдвинуты независимо в ра-
работах Фейнмана [170, 171], Томонага (не опубликовано, 1951) и
Швингера [442, 443]. Недавно Кайяньелло [76, 77] дал явное ком-
компактное выражение для общего вида матричного элемента n-го по-
порядка S-матрицы и, таким образом, продвинулся в направлении,
которое позволит обойти разложения в степенной ряд.
Однако наибольший успех в формулировке теории поля без раз-
разложения в степенной ряд был до сих пор достигнут в рамках гей-
гейзенберговского представления. Именно этому представлению посвящен
ряд вопросов, которые мы рассмотрим в гл. 25.
§ 8. Перенормировка в представлении связанных состояний
Доказательство перенормируемости, приведенное в данной главе,
может быть легко распространено на проблемы рассеяния, вклю-
включающие внешние поля, и в более общем виде на проблемы, рассма-
рассматриваемые в представлении взаимодействия Фарри для связанных
состояний (см. гл. 21, § 8). Следует напомнить, что принципиальное
различие между представлением взаимодействия частиц в свободных
состояниях и представлением взаимодействия частиц в связанных
См. также работы Хори [236] и Риддела [402].
410 Глава 24
состояниях состоит в том, что в последнем представлении свертки
электронных операторов определяются выражением
—jSeP(x., у)=(Фл>. 7"(<Ых)Му))ФЛ), B4.121)
где операторы фу, фу удовлетворяют уравнению Дирака в присут-
присутствии внешнего поля Ле(х). Функция —1/zS^(\,y) тождественна
с функцией распространения Фейнмана во внешнем поле К*, кото-
которую мы рассматривали в гл. 8, § 4. Как следует из уравнений
движения для операторов фу, фу и определения B4.121), она удо-
удовлетворяет следующим уравнениям:
, y) = — 2iSD)(x — у), B4.122а)
—у). B4.1226)
■Функция 5<*)(х—у) в правой стороне уравнения B4.122) возникает
при дифференцировании по времени соотношения B4.121). Чтобы
показать это, запишем Г-произведение в виде
Т(фу(х)фу(у)) = -i-[фу (х), фу(уI + \*(х — у) [фу(х), Ф
' B4.123)
Если оператор i-[°d/dx° действует на выражение B4.123), то при
действии его на функцию г(х — у) мы получаем функцию 2/f °5(')(jc0—yQ).
Благодаря наличию этой зависящей от времени 8-функции мы можем
лспользовать канонические' правила антикоммутации для операто-
операторов фу и фу, что дает функцию у°§<8> (х —у), тогда
> у)=
= (Фор, Т ( (*т? -^ + /у • V — e-fAl (х) — я») фу (х) фИу)) ^
— у) = го<4)(х — у), B4.124)
где при получении последнего равенства мы использовали уравнение
движения для оператора фу(х). Уравнения B4.122а) и B4.124) иден-
идентичны. Вывод уравнения B4.1226) можно провести таким же обра-
образом.
Количественная теория перенормировки 411
Если ввести фурье-образ
Sf (х, у) = ]>/>! f d%e-ip^e+i»>-*--SeF(Pl> p2), B4.125a)i>
^^— • B4.1256)
m
то уравнения B4.122а) и B4.1226) могут быть легко преобразованы
в импульсное представление. С помощью одной итерации из ком-
комбинации этих уравнений можно получить следующее точное уравне-
уравнение:
Sf(pv Pa) = Sf(Pi) 5D) (Pl — p2) —
ea (Pl — p2)
X ea (q) SF(Pl-q, p2 + q')ea (q')] SF(p2). B4.126)
Отметим теперь, что, используя уравнение B4.126), мы можем
выразить любое расходящееся выражение, в котором содержатся
функции Sp в представлении взаимодействия Фарри для связанных
состояний, через расходящиеся выражения, содержащие только функ-
функции Sp, и конечные выражения, в которых содержатся функции Sp
(член, содержащий функции 5у в правой стороне уравнения B4.126),
конечен, поскольку в этот член введены по крайней мере две допол-
дополнительные внешние линии, соответствующие двум множителям a(q)].
Первые два члена в правой стороне уравнения B4.126) представляют
собой начало разложения функции 5^ во внешнем поле. Ясно, что
первый член приведет ко всем диаграммам в представлении взаимо-
взаимодействия свободных частиц и может быть перенормирован согласно
методам, изложенным в настоящей главе. Член Sp(pl)a(q)Sp(p2)
приведет к диаграммам, рассмотренным в гл. 21, § 2. Там было
показано, что только диаграмме внешней поляризации вакуума соот-
соответствует истинная расходимость, тогда как сумма всех остальных
членов дает конечный вклад. Фактически, как только с помощью
!) Если внешнее поле не зависит от времени (этот случай наиболее инте-
интересен с точки зрения практических применений), то в формуле B4.125а)
функция S|i(p1,. р2) должна быть заменена на
5A)(^o-^o)Sf(Pi-Р2)-
412 Глава 24
перенормировки напряженности внешнего поля устраняется расхо-
расходимость, соответствующая поляризации вакуума внешним полем
во втором порядке, внешнее поле больше не вносит расходимостей1);
все вклады высших порядков в поляризацию вакуума внешним полем
являются конечными (см. работы Лоу [311], Кролла и Поллока [294],
Баранджера [16—18], где расходимость, связанная с поляризацией
вакуума внешним полем выделена в явном виде).
О Остаются, конечно, расходимости, обусловленные полностью разъединен-
разъединенными диаграммами флуктуации вакуума, приводящими к множителю ехр (—L),
на который множится любой матричный элемент. Раньше уже указывалось,
что расходящаяся (мнимая) часть величины L не приводит к каким-либо
трудностям, потому что если мы вычисляем вероятность какого-либо про-
процесса, то вклад дает только вещественная часть величины L. Ясно, что по-
последний множитель должеи быть включен в вычисляемое поперечное сечение.
Глава 25
НОВЕЙШЕЕ РАЗВИТИЕ ТЕОРИИ
До сих пор мы концентрировали свое внимание главным обра-
образом на описании чистых процессов рассеяния между начальным и
конечным состояниями свободных частиц. Именно для рассмотрения
такого рода процессов был развит формализм 5-матрицы. Этот
формализм позволяет описать результаты измерений поведения всей
системы в целом (т. е. дать суммарное описание во всем простран-
пространстве-времени (Фейнман [168, 1691). Существует, однако, другой
класс наблюдаемых величин, которые не могут быть описаны, если
известна только 5-матрица. Так, например, 5-матрица не позволяет
определить связанные состояния системы (Йост [251]) и не позволяет
описать результаты возможных локальных измерений, таких как из-
измерение плотности тока или напряженности поля в какой-либо про-
пространственно-временной области (Бор и Розенфельд [47, 48]). Для
описания такого рода случаев необходимо обобщить рассматривав-
рассматривавшийся до сих пор формализм. Мы увидим, что именно гейзенбер-
гейзенберговское представление хорошо подходит для описания такого рода
случаев.
§ 1. Гейзенберговское представление
Гейзенберговское представление, как было показано в гл. 13,
§ 1, определяется тем, что в нем вектор состояния системы постоя-
постоянен, а все взаимодействие включено в операторы. Поэтому в случае
электродинамики операторы1) удовлетворяют следующим уравнениям
движения:
ll(xL'(x), B5.1)
!1 |)V ф(х)Ь B5.2)
а вектор состояния ЧГ не зависит от времени
^ = 0. B5.3)
!) Во всей этой главе для обозначения операторов и векторов состояния
в гейзенберговском представлении применяется жирный шрифт.
412 Глава 24
перенормировки напряженности внешнего поля устраняется расхо-
расходимость, соответствующая поляризации вакуума внешним полем
во втором порядке, внешнее поле больше не вносит расходимостей1);
все вклады высших порядков в поляризацию вакуума внешним полем
являются конечными (см. работы Лоу [311], Кролла и Поллока [294],
Баранджера [16—18], где расходимость, связанная с поляризацией
вакуума внешним полем выделена в явном виде).
О Остаются, конечно, расходимости, обусловленные полностью разъединен-
разъединенными диаграммами флуктуации вакуума, приводящими к множителю exp (-^L),
на который множится любой матричный элемент. Раньше уже указывалось,
что расходящаяся (мнимая) часть величины L не приводит к каким-либо
трудностям, потому что если мы вычисляем вероятность какого-либо про-
процесса, то вклад дает только вещественная часть величины L. Ясно, что по-
последний множитель должен быть включен в вычисляемое поперечное сечение.
Глава 25
НОВЕЙШЕЕ РАЗВИТИЕ ТЕОРИИ
До сих пор мы концентрировали свое внимание главным обра-
образом на описании чистых процессов рассеяния между начальным и
конечным состояниями свободных частиц. Именно для рассмотрения
такого рода процессов был развит формализм 5-матрицы. Этот
формализм позволяет описать результаты измерений поведения всей
системы в целом (т. е. дать суммарное описание во всем простран-
пространстве-времени (Фейнман [168, 169]). Существует, однако, другой
класс наблюдаемых величин, которые не могут быть описаны, если
известна только S-матрица. Так, например, 5-матрица не позволяет
определить связанные состояния системы (Йост [251]) и не позволяет
описать результаты возможных локальных измерений, таких как из-
измерение плотности тока или напряженности поля в какой-либо про-
пространственно-временной области (Бор и Розенфельд [47, 48]). Для
описания такого рода случаев необходимо обобщить рассматривав-
рассматривавшийся до сих пор формализм. Мы увидим, что именно гейзенбер-
гейзенберговское представление хорошо подходит для описания такого рода
случаев.
§ 1. Гейзенберговское представление
Гейзенберговское представление, как было показано в гл. 13,
■§ 1, определяется тем, что в нем вектор состояния системы постоя-
постоянен, а все взаимодействие включено в операторы. Поэтому в случае
электродинамики операторы1) удовлетворяют следующим уравнениям
движения:
(/V — т) ф (х) = Ът$ (х) -+- е^^ (х) ф (х), B5.1)
x) = j,1(x) = |-[4(x)V ф(хI, B5.2)
а вектор состояния ЧГ не зависит от времени
^ = 0. B5.3)
!) Во всей этой главе для обозначения операторов и векторов состояния
в гейзенберговском представлении применяется жирный шрифт.
414 Глава 25
Уравнения B5.1) и B5.2) могут быть получены из следующей плот-
плотности функции Лагранжа:
ц. (х) dAv- (х)
[ф
(х) ф (х) = 8иг + Sd + 2/. B5.4)
Мы видим, что невозможно выписать перестановочные соотно-
соотношения для гейзенберговских операторов, которые имели бы силу
для всех времен. Это требует знания решений уравнений движения
B5.1) и B5.2) для всех времен, что фактически и является задачей,
которую мы должны решить. Однако из приведенного лагранжиана
можно получить канонические перестановочные соотношения, кото-
которые верны для операторов, зависящих от одного и того же вре-
времени :),
( ?(£ 9 8( — *0. B5.5а)
д*, о. дХ"{ft' i)]= — ihcg^b&—^>' B5-5б>
тогда как все остальные коммутаторы (антикоммутаторы) равны нулю.
Эти перестановочные соотношения можно обобщить на случай про-
произвольного пространственно-подобного интервала (Швингер и Вай-
скопф [437]); тогда они будут иметь вид
[ф(х), ф(хО]+= — iS(x — x'), B5.6а)
[АДх), Av(x0]= — ihcg^D(x — x'), B5.66)
[ф(х), ф(хО1+ = [ф(х), ф(хО]+ = О, B5.7а)
[ф(х), А^(х)] = [ф(х), А11(х)]=0, B5.76)
если (х^ — x'^f < 0.
Зная лагранжиан, можно также построить тензор энергии-им-
энергии-импульса Т^ (см., например, работы Швингера [441, 444, 445, 447J),
из которого можно определить полный 4-вектор энергии-импульса
поля Р^. Временная компонента его Ро есть гамильтониан системы,
который может быть выражен через переменные поля и сопряженные
им импульсы. При отсутствии внешних полей эрмитовские операторы
энергии-импульса удовлетворяют соотношениям
[Р^. PJ = 0; B5.8)
!) Более современные методы получения перестановочных соотношений
можно найти в статьях Пайерлса [384], Швингера [443, 444, 447], Бертона
и Таушека [73, 74], Чини [84].
Новейшее развитие теории 415
эти соотношения выражают сохранение полной энергии и полного
импульса поля. Оператор Р^ есть оператор пространственно-вре-
пространственно-временного смещения в следующем смысле:
^ B5.9>
В последнем соотношении F(x) — произвольный гейзенберговский
оператор, который зависит от переменной х только через опера-
операторы Av(x) и фОО-
Поскольку операторы Р^ коммутируют друг с другом, мы мо-
можем выбрать представление, в котором каждый вектор состояний
есть собственная функция всех операторов РЛ с собственным зна-
значением р„, т. е.
РД« = Р(,?ЧГ«- B5.10>
Тогда каждый вектор состояния ¥ будет описывать стационарные
состояния с определенной энергией и импульсом. Должно быть ясно,
что задание определенных энергии и импульса не характеризует.
однозначно состояние. В этом представлении, используя соотноше-
соотношение B5.10), можно написать матричный элемент выражения B5.9)
в виде
= /(P£> — p<*>)(¥a> F(x)¥b) =
= £(ЧГа, F(x)¥b). B5.11)
Отсюда
^»'*')-*, B5.12)
где F @)—оператор F(x), вычисленный в точке х=0. Соотноше-
Соотношение B5.12) выражает зависимость от координаты х матричного
элемента произвольного гейзенберговского оператора в представле-
представлении, в котором операторы Р^ диагональны. Этим представлением
мы будем пользоваться во всей данной главе.
Чтобы иметь возможность построить теорию, обычно делается
два физических предположения (которые, однако, до сих пор не
доказаны) (Челен [256], Вайтман, не опубликовано, 1952):
1. Собственные значения р<а> представляют собой временно-по-
временно-подобные или равные нулю (световой конус) векторы, т. е. р<а»р^)а>> 0.
Это чрезвычайно правдоподобное предположение требует, чтобы
полная масса системы была всегда вещественной. Однако полная
масса может равняться нулю в случае, когда имеются только фо-
фотоны. Данное предположение можно выразить также иначе: не су-
существует решений уравнения B5.10) с пространственно-подобными
импульсами.
2. Существует состояние с наинизшим собственным значением,
временной компоненты р0, т. е. полной энергии. Это состояние*
416 Глава 25
по определению, называется вакуумом и характеризуется волновой
функцией ЧГ0. Поскольку энергию вакуума можно всегда сделать
равной нулю с помощью добавления подходящей константы к опе-
оператору Ро, то в дальнейшем мы будем считать, что энергия вакуума
равна нулю. Итак, по этому предположению собственные значения
оператора Ро для любого состояния таковы, что р^га)^>0 для всех п.
В квантовой электродинамике требования р^0' = 0 недостаточно
для однозначного определения вакуумного состояния, потому что
остается еще свобода по отношению к калибровочным преобразо-
преобразованиям. В гл. 15, § 4 мы установили, что фактически имеется бес-
бесконечное число вакуумных состояний, отличающихся только выбо-
выбором калибровки. В дальнейшем примем специальную калибровку
{Челен [256]), для которой
(¥0, г,А!1(х)¥0) = 0. B5.13)
Предполагается, что соотношение B5.13) не противоречит второму
постулату.
Из соображений удобства мы определим гейзенберговский век-
вектор состояния так, чтобы он совпадал с вектором состояния в пред-
представлении взаимодействия в момент времени t = 0 (вспомним рас-
рассмотрение в гл. 13, § 1). Если в представлении взаимодействия
вектор состояния W(t) есть решение уравнения
d^ B5.14)
-то соответствующий ему гейзенберговский вектор состояния ¥ опре-
определяется следующим образом:
U(t, 0)¥ = W(f), B5.15)
где унитарный оператор U(t, 0) удовлетворяет уравнению
. dU (t, 0)
dt
с граничным условием
0) B5.16а)
U{0, 0)=1. B5.166)
Соотношение между операторами в представлении взаимодей-
взаимодействия и соответствующими им операторами в гейзенберговском пред-
представлении получается, если потребовать, чтобы средние величины,
выраженные через соответствующие векторы состояний, были оди-
одинаковы. Таким образом, по определению,
(¥, F(xL) = CF@. F(x)¥@), B5.17)
где время t, от которого зависит вектор состояния 1Р@> совпадает
со значением времени х0, от которого зависит оператор F(x).
Новейшее развитие теории 417
Тогда, используя соотношение B5.15), получаем
(¥, F(x)f) = (y(/, 0)¥, F(x)U(t, 0)¥) =
= (¥, U~l(t, 0)F(x)U(t, 0)¥), B5.18а)
ИЛИ ' ;
F(x) = {/-*(*. O)F00U(t, 0), B5.186)
где снова ^ = лг0.
Явное представление для оператора U можно получить следую-
следующим способом. Вспомним, что мы можем перейти |от шредингеров-
шредингеровского представления, в котором вектор состояния \Рд удовлетво-
удовлетворяет уравнению
i — (H* -4- HA Wo (f\ = HWa (f\ f 25 1 °>\
G4
(//0 и Hi — не зависящие от времени операторы), к представлению
взаимодействия с помощью унитарного преобразования
W (t) = e+iHot4>'s (t). B5.20)
Оба представления совпадают в момент времени t — 0. Далее,
принимая во внимание, что оператор Н= Но-\- Нх не зависит от
времени, можно прямо перейти от шредингеровского представления
к гейзенберговскому с помощью унитарного преобразования
\р __ giBt\]rs(f\ /25 21)
Ясно, что вектор состояния ¥ действительно удовлетворяет урав-
уравнению B5.3). Подставляя в выражение B5.21) вектор состояния
4t"s(t), задаваемый формулой B5.20), находим
W = etHte-iB'tW(t). B5.22)
Сравнивая формулы B5.15) и B5.22), получаем следующее пред-
представление оператора U:
U (t, 0) = е + ш»*е-шК B5.23)
Во всей этой главе мы будем много раз использовать „истин-
„истинное" вакуумное состояние ¥0 для взаимодействующих полей. Чрез-
Чрезвычайно важно иметь возможность выразить вектор состояния ¥0
через вектор состояния Фо — вакуумное состояние свободных частиц.
Чтобы сделать это, отметим, что ¥0 — собственное значение опера-
оператора Н с наинизшей энергией р^ = 0, тогда как Фо — собственная
функция оператора Но с собственным значением е0 = 0. Имеются
два стандартных метода рассмотрения проблемы (Гелл-Манн и Лоу
[203]). Первый из них состоит в введении представления взаимодей-
взаимодействия в момент времени t=—со, а не в момент времени ^=0,
как мы делали. Затем предполагается, что верна адиабатическая
гипотеза, так что в момент времени t=—оо константа связи равна
4i8 Глава 25
нулю и операторы Н и Но совпадают. Тогда в момент времени
t = —' оо, W (— со) = Фо и с точностью до фазового множителя мы
можем написать (вспомним обсуждение в гл. 16, § 2)
Wo^U@, — оо)Ф0. B5.24а)
Поскольку состояние вакуума является устойчивым, т. е. 5Ф0 = ХФ0
(X—константа, по модулю равная единице), то с точностью до кон-
константы, по модулю равной единице, можно также написать
= £/@, — oo)U(— оо, +оо)Ф0 =
= £7@, +оо)Ф0. B5.2.46)
Второй метод — теория возмущений для стационарных состояний.
Рассмотрим в момент времени £ = 0 функции Wo = W0(t =.0) = ЧГ0
и Фо в представлении взаимодействия, которые удовлетворяют урав-
уравнениям Шредингера
Я0Ф0 = е0Ф0, B5.25)
{Нй+Нт @)} <F0 = £0ЧГ0. B5.26)
В этих уравнениях мы сохраним обозначения Ео и е0 для собствен-
собственных значений. Уравнение B5.26) можно переписать в несколько иной
форме
(Яо —ео)¥о = (Ео — е0— tfz@))¥0. B5.26а)
Теперь введем проекционный оператор §0 на состояние Фо, кото-
который, действуя на функцию произвольного состояния ч7, обладает
свойством
§0У = аФ0. B5.27а)
где а — константа. Этот оператор удовлетворяет также следующим
соотношениям:
#S = #o. B5.276)
Фо» Д>] = 0. B5.27b)
Если мы теперь применим оператор $0 к обеим сторонам урав-
уравнения B5.26а), то получим тождество
= 0. B5.266)
Другими словами, вектор состояния (£0 — е0—Hr@))Wo всегда
ортогонален вектору состояния Фо. Поэтому, используя тождество
B5.266), мы можем переписать уравнение B5.26а) в следующем
виде:
(Яо — з0) Wo = A — §о) (£0 — е0 — Нт @)) ЦГ0. B5.26в)
Правая сторона уравнения B5.26в) обладает таким свойством, что
если на нее действует оператор (Яо — е0), то результат не равняется
Новейшее развитие теории 4Ш
нулю. Следовательно, если переписать B5.26в) в виде интегрального
уравнения (Липман и Швингер [307]), т. е. разделить его на опера-
оператор (Яо— е0), то получим
— s0 — HX(P))WO B5.28a)
и поэтому
CWO = [1 — (Яо — eo)-i(l— 8J(EO — е0 — Я/@))]-1Ф0, B5.286)
где с и с' — нормировочные константы.
Гелл-Манн и Лоу (см. дополнение к статье [203]) дали нестрогое
доказательство того, что уравнение B5.286) можно заменить фор-
формальным уравнением B5.24); точнее говоря, они показали, что можно
написать
,г . Ц@, ±оо)Ф0 т
С*° — (Фо, U @, ±оо) Фо) — CW°-
Как в числителе, так и в знаменателе формулы B5.29) имеются
бесконечные фазовые множители (соответствующие флуктуациям
вакуума, см. гл. 18, § 3), которые сокращаются в частном.
Доказательство очень похоже на то, которое мы кратко изло-
изложили в гл. 16, § 2, но несколько более сложно, вследствие наличия
сдвига уровней £0 — е0. В самом деле, если, следуя Гелл-Манну.и
Лоу, включить в оператор Я/ затухающий множитель ехр(—а|^|),
необходимый для придания строгого смысла оператору U @, —оо),
и определить U^(t, 0) как решение уравнения B5.16а), в котором
оператор Hit заменен на /fz(^)exp(—а|^|), т. е.
i dU*£ 0) = Hi(f)e—\*lил(t, 0), B5.16в)
и, кроме того, до конца этой главы обозначить
WQ(a) = U:\-~оо, 0)Ф0 = £/в@, — оо)Ф0, B5.29а)
то легко проверить, что благодаря уравнениям B5.25) и B5.29а)
имеет место уравнение
0, —oo)—Ua@, — оо)Я0}Ф0 =
= ЯД0<<х) — ео¥0(<х) =
= [Я0, иа@, — оо)]Ф0 =
0
Jdtl...
n = О —со — оо
и
х 2 37Г Р {Hl {tl) ■■Hl {tn)) Ф°: B50)
г=1
420 Глава 25
последнее равенство в уравнении B5.30) есть следствие того, что
в представлении взаимодействия Яо есть оператор смещения во вре-
времени, т. е.
ЦН0. F(x)]=^gi. B5.31)
Вследствие симметрии подинтегрального выражения уравнение B5.30)
можно переписать в следующем виде:
со О
(Яо — s0)Wo(a) = — ^ (~^"У
П — 0 -со
О
... f dtne*(t'
0
п — 0
... f dtne*^+t'+ ■- +tn>7>(Hl(t{) . . . Hz(tJ)\ Фо =
-оо )
| B5.32)
где второй член в правой стороне уравнения B5.32) получен
с помощью теоремы Эйлера в предположении, что оператор Я/ зави-
зависит только от величины О (но не от О2). Следовательно, мы имеем
{Яо+ Нт@) — е0} %(«) = teO ^q • B5.32а)
Теперь мы можем проверить (ср. с работой Гелл-Манна и др. [206]),
что член в правой стороне действительно представляет сдвиг уровня,
так как
( ^>) , Wo). B5.33)
Это доказывает исходное предположение, что выражение B5.29)
есть решение уравнения B5.26).
В дальнейшем в этой главе мы будем широко использовать выра-
выражение B5.29). Однако сначала исследуем некоторые трансформацион-
трансформационные свойства операторов и состояний в гейзенберговском представ-
представлении.
Новейшее развитие теории 421
§ 2. Рассмотрение инвариантных свойств
Большинство результатов, которые мы сформулируем в этом
параграфе, есть следствие инвариантности теории по отношению
к преобразованиям Лоренца и сделанных предположений о физиче-
физических состояниях системы полей. Следовательно, эти результаты
применимы также к любой релятивистской инвариантной теории
поля.
Прежде чем углубляться в математические детали, следует напо-
напомнить еще раз, что означает лоренц-инвариантность теории. С этой
целью рассмотрим две системы координат S и S'', связанные неодно-
неоднородным преобразованием Лоренца,
B5.34)
где /,, — постоянный 4-вектор смещения. Наблюдатель в системе 5
будет' иметь определенный набор наблюдаемых величин, соответ-
соответствующих им операторов и полную систему собственных функций;
то же будет иметь и наблюдатель в системе S'. Далее, для того
чтобы теория имела физический смысл, необходимо, чтобы существо-
существовал набор правил, с помощью которых наблюдатель в системе 5
может проверить эксперименты, сообщенные ему наблюдателем
в системе S'. Существование этого набора правил дает возможность
наблюдателю в системе S' выразить операторы и собственные функ-
функции в системе S через соответствующие величины в своей системе.
С точки зрения математического аппарата наличие этих правил
подразумевает, что существует унитарный оператор V, который
зависит от величин а^ и I . Этот оператор такой, что если Q и
W— операторы и собственные функции в системе S, то W — vW
и Q'=vQv~1 представляют соответствующие величины в системе 5'.
Кроме того, если теория должна быть лоренц-инвариантной, то все
физические законы должны иметь одинаковый вид, когда их выра-
выражают через операторы и собственные функции как в системе S,
так и в системе 5'.
Рассмотрим сначала случай невзаимодействующих полей; для
определенности возьмем поле Дирака со спином lj2 и выясним,
каковы должны быть трансформационные свойства операторов и
состояний системы, чтобы теория в самом деле была лоренц-инва-
лоренц-инвариантной.
Для невзаимодействующих полей (//z=0) представление взаимо-
взаимодействия идентично гейзенберговскому представлению. Чтобы избе-
избежать в дальнейшем путаницы, мы не будем использовать здесь
жирный шрифт для обозначения величин в представлении взаимо-
взаимодействия, которые, как установлено, фактически являются величи-
величинами в гейзенберговском представлении свободных полей.
Для упрощения выкладок рассмотрим случай одной частицы.
Этот случай описывается вектором состояния Ф^, причем един*
422 Глава 25 _
ственная неравная нулю амплитуда есть
Л(х) = (Ф0, ф.(х)Ф(ц). B5.35)
Это, очевидно, следует из свойств оператора ф(х) и вектора вакуум-
вакуумного состояния Фо. Оператор ф (х) есть оператор уничтожения элек-
электрона. Следовательно, при действии на вектор одноэлектронного
состояния ФA) он уничтожает имеющийся в нем электрон и в ре-
результате получается вакуумное состояние. Величина /а(х) должна
быть интерпретирована как амплитуда вероятности нахождения одного
электрона (вспомним, однако, что она не дает вероятность нахождения
частицы в точке х). Поскольку функция ф(х) удовлетворяет урав-
уравнению свободного поля
^) B5-36)
то,* подействовав на обе стороны выражения B5.35) оператором
(р— т), получим, что величина /(х) также удовлетворяет уравне-
уравнению Дирака
+ »)/00=0. B5.37)
Таким образом, можно заключить, что функция /(х) по сути
представляет „одночастичную" дираковскую „волновую функцию",
которая была детально рассмотрена в гл. 4. Имеется, однако, одно
существенное различие, являющееся следствием того, что вакуум
есть состояние с наинизшей энергией. Поэтому требуется, чтобы
ф<+>(х)Фо=0, или Ьг(р)Фо=0,
"ф<+)(х)Ф0=0, или dr(p)<&0 = 0, B5.38)
так что если выражение B5.35) переписать, используя формулы
A5.61) и B5.38), то получим
Л (х) = BЛ)-5'= У\ Г d*p г/ £ (Фо, Ьг (р)-ФA)) W (Р) «-*••«. B5.39)
r-i Ер
Следовательно, мы видим, что /(х) есть суперпозиция решений
уравнения Дирака, относящихся к состояниям с положительной
энергией в отличие от случая, рассмотренного в гл. 4, где a priori
допускалось, что функция /(х) может быть решением уравнения Ди-
Дирака, относящимся как к положительной, так и к отрицательной
энергиям. Это различие, хотя и важное для физического понимания
теории, не существенно для обсуждения инвариантности теории.
Далее, в гл. 5 мы видели, что если при однородном преобра-
преобразовании Лоренца
х'у = а^х^, или х' = ах B5.40)
Новейшее развитие теории 423
„волновая функция" /(х) преобразуется по следующим правилам:
2 V), B5.41)
где 5 — несингулярная 4-мерная матрица, действующая на спинорные
индексы а функции / и удовлетворяющая требованиям
S~"Y-S = «V. B5.42)
detS=l, B5.43)
то уравнение Дирака для одной частицы в самом деле имеет инва-
инвариантную форму, т. е. функция /' удовлетворяет тому же уравнению
в штрихованных координатах, которому удовлетворяет функция /
в нештрихованных.
Теперь определим трансформационные свойства операторов поля
и векторов состояния так, чтобы соотношение B5.41) имело силу
для одночастичной амплитуды. Тогда, в случае, когда имеется п
свободных, невзаимодействующих частиц, описываемых вектором
состояния Ф(п) и амплитудой
Л,... *„(Xi. • • •. хп) = (Фо, N (ф., (Xl) . . . ф.я(хя))Ф(п)), B5.44)
мы автоматически получаем, что амплитуда /«,... а (xv ..., л:п)
будет преобразовываться (как и следовало ожидать) непосредственно
как произведение одночастичных волновых функций, т. е.
/„' ... „' (xi х^)= 2 S..S5, . .. S*npnA... ^(a^xi, . . ., я^х'п).
1 " ^■•р» B5.45)
Как и в случае, рассмотренном в гл. 5, мы применим преобразова-
преобразование шредингеровского типа, при котором преобразуются волновые
функции (здесь векторы состояний), но один a mom оке набор опе-
операторов используется наблюдателями как в системе S, так и в си-
системе S'. Далее, результаты возможных экспериментов в системе,
содержащей одну частицу, будут описываться наблюдателем в си-
системе 5' с помощью амплитуды
'' ' B5.46)
тогда как наблюдатель в системе 5 опишет те же эксперименты
в своей системе с помощью амплитуды
/(х)=(Ф0, <Кх)ФA,). • B5-47)
Эти две амплитуды связаны между собой соотношением B5.41).
С другой стороны, как мы указывали выше, векторы состояний
связаны между собой соотношением
B5.48)
424 Глава 25
являющимся математической формулировкой тех правил, которыми
по условию определяется, какие из проведенных в различных системах
отсчета экспериментов должны считаться идентичными друг другу.
Чтобы связь между амплитудами B5.41) имела место, должно выпол-
выполняться соотношение
(Фо, 5(аL(х)ФA)) = (Ф; <Кх')Ф,'„\ B5.49)
Вспомнив, что оператор У является унитарным, мы можем выразить
трансформационные свойства этого оператора в следующем виде:
7"(а) 4 (х) Т(а) = 5 (а)'1*!*(х') = S (а)"Ч (ах). B5.50)
Приведенные выражения B5.48) и B5.50) дают схему преобразова-
преобразования операторов и векторов состояния в теории поля. Лоренц-инва-
Лоренц-инвариантность теории теперь очевидна, поскольку при описании теории
поля с помощью величин /„, (xt), /«.«.(x^ х2) и т. д. уравнения, кото-
которым подчиняются преобразованные амплитуды /' в штрихованных
координатах, могут быть просто получены, если поставить штрихи
в уравнениях, которым подчиняются амплитуды /.
Так как вакуум должен быть одинаковым для всех наблюдателей,
то он характеризуется выражением
7°Ф0 = фо, B5.51)
т. е. кроме того, что он является состоянием с няинизшей энергией,
он является также инвариантным.
Обратимся теперь к гейзенберговскому представлению для случая
взаимодействующих полей. Можно определить трансформационные
свойства операторов и состояний так, чтобы они были простыми и
соответствовали соотношениям B5.48) и B5.50) в случае свободных
полей. Итак, при неоднородном собственном преобразовании Лоренца
x' = ax + L B5.52)
преобразованное гейзенберговское состояние дается формулой
W = ©(a, L)W, B5.53).
тогда как преобразованные операторы, например, в случае скалярной
мезонной теории даются выражениями ^
•о{a., L)?(x)©(a, L)" = ?(ax + L), B5.54)
г» (а, Ь)ф(х)©(а, L) = S(a) ф (ax-f L). B5.55)
1) Отметим, что случай бесконечно малых смещений, описываемый соот-
соотношением B5.9), включен в соотношения B5.54) и B5.55), потому что при
чистом переносе (а = 1)
где Р — оператор эн«ргии-импульса поля. Если L соответствует бесконечно
малому смещению в пространстве-времени, т, е. L = -rjf, где т\ — бесконечно
Новейшее развитие теории 425
Вакуум в случае взаимодействующих полей опять является инвариан-
инвариантом, характеризуется соотношением
w(a, L)W0 = W0 B5.56)
и по сделанному нами предположению является состоянием с наиниз-
наинизшей энергией. Ясно, что формула B5.56) описывает состояние
с равными нулю зарядом, импульсом и моментом количества дви-
движения.
Трансформационные свойства, описанные до сих пор, относятся
только к собственным преобразованиям Лоренца. Трансформационные
свойства операторов (особенно спинорных операторов) при отра-
отражениях пространства и времени несколько более запутаны и требуют
дальнейшего рассмотрения. В частности, при отражении во времени
оператор v не является больше унитарным (Вигнер [536]). С пре-
преобразованиями отражения читатель может ознакомиться в исчерпы-
исчерпывающей статье Вайтмана и Швебера [535] ^.
В случае электродинамики инвариантность теории по отношению
к зарядовому сопряжению может быть сформулирована аналогичным
способом (Пайс и Йост [367], Вольфенштейн и Равенхолл [540],
Мишель [335]). Напомним, что зарядовое сопряжение представляет
операцию изменения знака заряда е всех частиц на обратный, причем
все остальные характеристики, например импульсы или спины, остаются
неизменными.
Унитарный оператор зарядового сопряжения vc, который осуще-
осуществляет эту операцию в электродинамике, дается выражениями
= С^(х), B5.57)
фс(х) = vc~$ (х) v^1 = (С-1*!* (x)f, B5.58)
где индекс Т означает транспонированную величину по отношению
к спинорным индексам. Здесь С — матрица, с которой мы встре-
малая величина, то из соотношения B5.54) следует, что
v ад 9 (х) v-t- (V) = 9 (х + У) да
да A + щ1 • Р) ? (х) A — li\l • Р) да
д?(х)
'»(*) + *Уц [Р*. 9 (х)] » 9 (х) + -^
I [РЛ. 9 (х)] =
Последнее соотношение совпадает с соотношением B5.9). Аналогично мы
можем написать для однородного преобразования Лоренца (L = 0)
где КУЛ = — Ж1^ — тензор момента количества движения системы полей.
Ч В связи с этим см. также работу Внка, Вайтмана и Вигнера [532].
426 Глава 25
чались уже в гл. 13, § 6 и в гл. 18, § 3. Она действует на спи-
норные индексы, обладает следующими свойствами:
С-\С = —£, B5.59)
СтС~1 = — \ B5.60)
и определяется с точностью до константы, по модулю равной еди-
единице. Инвариантность квантовой электродинамики по отношению
к зарядовому сопряжению будет гарантирована, если
— АДх). B5.61)
Действительно, если мы подействуем на уравнение B5.1) операто-
оператором <v0 слева и оператором г^Г1 справа, то, используя соотношение
B5.61) и умножая справа на матрицу С, мы получим точное урав-
уравнение движения для сопряженного спинора ф
^|JV х). B5.62)
Аналогично такая же операция над уравнением спинора ф Дает урав-
уравнение движения для спинора ф- Наконец, поскольку
^(х)^-1-— j,(x), B5.63)
то из соотношения B5.61) следует, что уравнение B5.2) инвариантно
по отношению к зарядовому сопряжению. Это завершает доказа-
доказательство инвариантности электродинамики по отношению к зарядо-
зарядовому сопряжению.
Далее, оператор ч>а оставляет инвариантными перестановочные
соотношения операторов поля и коммутирует с оператором Ро,
гамильтонианом поля. Поэтому он представляет интеграл движения.
Кроме того, поскольку два последовательных зарядовых сопряжения
любого вектора состояния приводят к этому же вектору состояния,
оператор <оа имеет два собственных значения: -f-1 и —1. Из соот-
соотношения B5.63) следует, что оператор vc антикоммутирует с полным
зарядом и, следовательно, операторы <ос и Q могут быть одновре-
одновременно приведены к диагональному виду только для состояний с рав-
равным нулю зарядом. Вакуум в дальнейшем мы можем характеризовать
еще и тем, что он инвариантен по отношению к зарядовому сопря-
сопряжению, т. е.
vBW0^W0. B5.64)
Соображения, аналогичные рассмотренным выше, могут быть приме-
применены и в случае заряженных мезонных полей и мезонных взаимо-
взаимодействий. Мы отсылаем читателя к статьям Пайса и Йоста [367],
Вольфенштейна и Равенхолла [540] и Мишель [335], в которых он
сможет ознакомиться с обсуждением этих случаев.
Новейшее развитие теории 427
§ 3. Средние значения в состоянии вакуума
Обратимся теперь к изучению средних значений гейзенберговских
операторов в состоянии вакуума.
Рассмотрим сначала среднее значение хронологического Г-произ-
ведения двух бозонных операторов в состоянии вакуума. Обозна-
Обозначим этот матричный элемент через
R{xt. x2) = (W0> T(<t<xJ4(xJ)W0) B5.65)
и рассмотрим, например, следующую последовательность времен
х10 > х20. Если гейзенберговские . операторы и векторы состояния
в правой стороне формулы B5.65) выразить теперь через соответ-
соответствующие величины в представлении взаимодействия, используя фор-
формулы B5.15), B5.18) и B5.24а), то получим для х10 > х20
R(xlt x2) = (t/@, +«э)Ф0, U~\tv 0)<?(x1)U(tv 0)X
^ 2, 0)f/@, — оо)Ф0). B5.66)
Мы опустили знаменатель в выражении B5.29); это означает
что если мы вычисляем выражение B5.66) с помощью диаграмм
Фейнмана, то необходимо опустить все несвязанные диаграммы
с вакуумными замкнутыми петлями. Далее, оператор U — унитарный
и обладает следующими групповыми свойствами [вспомним формулы
A6.9) —A6.17)]:
t,, tt)U(ta, t2) = U{tv tz) B5.67)
tO- B5.68)
Следовательно,
U~l (tv t2) U (tv *,) = U (t2, /,), B5.69)
причем оператор U(i, t') удовлетворяет уравнению
L?¥-i^- = HI(t)U(t, f), B5.70a)
где
Hi @ == C? J da (x) N (ф (x) Г<1> (х) cp (x)),
и граничному условию
U(t, t)= 1. B5.706)
Решение уравнения B5.70), как мы видели в гл. 16, может быть
представлено в виде
от t t
U (f. O= S(—0я^г jdt,. . . fdt*nHz{t0 ■ • • Hi(tj). B5.71)
rs-0 Г t/
428 Глава 25
Поэтому матричный элемент R можно переписать, в следующем
виде:
R(xv х2) = (Ф0> {/-'(О.+оо)*/-1^, 0)<р(х1)Х
X U (tlt t2) ср (х2) U(t2, — со) Фо), B5.72а)
R(xv х2) = (Ф0, T(t/(+oo, ^(x^f/ft, '2)<p(x2)^2> — оо))Ф„),
B5,726)
х, х2)=(Ф0, Г(*7(+оо, — <х))ср(Х1)?(х2))Ф0). B5.72b)
Очевидно, введение хронологического оператора в формуле B5.726)
вполне законно. Этот оператор позволяет затем переставить со-
сомножители под знаком Г-произведения и получить формулу B5.72в).
Оператор в последней формуле можно выписать в явном виде
T(U (+ оо, — от) ср (Xl) ср (х2)) =
СО -г СО -f- ОО
= 2 Цг~ / diyi ■■ f а4УпТ(^1(уд ■ • • ^7(УП>? (х1)ср(х2)).
"=° -от -°° B5.73)
Легко проверить, что выражение B5.73) верно при произволь-
произвольных временах д;10 и х20. С помощью теоремы Вика мы можем вы-
выписать матричный элемент R(xv x2) в виде разложения в степенной
ряд. Первые члены этого ряда имеют вид
А(х1—х2) =
J
d*yt Д, (xt — У1) Sp (Г6> (У1 — у2) Г X
—х2)+... B5.74)
Если выразить полученный результат с помощью диаграммы Фейн-
мана, то ясно, что матричный элемент R(xv x2) соответствует
простой бозонной линии и всем возможным вставкам в нее частей
собственной энергии и вершинных частей. Именно такую функцию
в гл. 24 мы назвали штрихованной бозонной функцией распростра-
распространения
Я(Х1, x2) = i-Akx1> x2) = (¥0, 74?(Xl)?(x2))W0). B5.75)
Таким же образом легко показать, что
i^ ^ B5.76a)
; B5.766)
Новейшее развитие теории 429
в формуле B5.766) вместо оператора U(-\-oo, —со) мы написали
5-матрицу. Если использовать трансформационные свойства вакуум-
вакуумного состояния и операторов поля, а также первое и второе пред-
предположения о состояниях полевой системы, сделанные в § 1, то
можно получить некоторые общие свойства функций Ду и Sp
(Челен [256])!). В дальнейшем предполагается, что мы имеем дело
с перенормированными гейзенберговскими операторами ф и ¥ (см-
также следующий параграф). Сингулярные функции Д' и S', рас-
рассматриваемые ниже, будут поэтому также перенормированными и
связанными с неперенормированными сингулярными функциями с по-
помощью обычных множителей Z.
Сначала рассмотрим бозонную функцию распространения
^p(xv x2). Поскольку оператор v, дающий собственное преобразо-
преобразование Лоренца, является унитарным, выражение B5.75) можно пе-
переписать в виде
i^ B5.77а)
у 0). B5.776)
Затем, используя формулу B5.55) и инвариантность вакуума [фор-
[формула B5.56)], получаем
у A*(xv х2) = (¥„, vT(f (Xl) f (x2))s-'f0) =
= (ЧГ0, 7'(?(ax1 + L)?(ax2+L))W0). B5.78)
Рассмотрим теперь случай чистой трансляции (а = I). Тогда из
формул B5.78) и B5.77 а) следует, что
t!jf (xv x2) = Д'Р (Xl + L, x2 + L). B5.79)
Поскольку это соотношение имеет место при произвольных L, то
ясно, что Д^(х1, х2) может быть функцией только разности коор-
координат хх и х2, т. е.
Д^ (xv x2) = Д^(Xl — x2). B5.80)
Аналогично, если мы рассмотрим собственное однородное преобра-
преобразование Лоренца, то получим, что
l — х2) = Д'р (a (Xl — x2)); B5.81)
поэтому Др может быть функцией только инварианта (xt — х2J.
Далее, следовало бы рассмотреть свойства матричного элемента при
отражениях пространства и времени. Однако, поскольку соответ-
соответствующие трансформационные свойства ранее не рассматривались,
здесь мы этого делать не будем.
См. также работу Лемана [301].
430 Глава US
Обратимся теперь к свойствам функции Д?, вытекающим из на-
наших базисных предположений о состояниях системы. Рассмотрим
снова случай х10 > х20. Используя полноту состояний Wn, формулу
B5.75) можно переписать в следующем виде:
1 t — х2) = (Wo, <р (Xl) ? (х2) Wo) =
?(x2)W0). B5.82)
Используя затем формулу B5.12), мы можем переписать выражение
B5.82) в виде
х - х2) = ^ (ЧГ0. ? (О) ^п)(^»> ? (О)
n
^o. ? @) Wn) |2 e-i^-Cx.-xJ. B5.83)
Если ввести теперь функцию плотности состояний, то суммирова-
суммирование по индексу п можно заменить интегрированием по переменной р.
Тогда можно написать
1д'Р(Х1— х2) = JVppCP2)*-1*-'*'-^ для xl0>x20, B5.84)
где
P(P2) = 2'|OFo. ?@)Wn)|2>0. B5.85)
Сумма, определяющая функцию р(р2I), берется по всем состояниям,
принадлежащим собственному значению р^. Замена суммы на инте-
интеграл возможна потому, что р(оп)>0 и (p(">J^ 0. Из последнего
условия следует, что не существует состояний Wn с пространствен-
пространственно-подобными импульсами, а также подразумевается, что функция
р(р2) равна нулю, если р2 < 0. А это достаточные условия для
замены суммы интегралом. Далее, функцию Д? можно переписать
в следующем виде:
t— x2) = ]
J для x1Q > x20, B5.86a)
J
О Ра>0
Д' /„ „ \ , .
F vxl Х2^ =
^-х») для х10<х20. B5.866)
J
!) Из требования инвариантности B5.81) следует, что р есть функция
только р2.
Новейшее развитие теории 431
В правой стороне этих выражений имеются интегралы по перемен-
переменной р, которые, очевидно (с точностью до множителя —BтсL),
представляют собой сингулярные функции Д(+> и ДЯ (но не штрихо-
штрихованные) для частиц с массой м. Поэтому функцию Др можно, нако-
наконец, выразить (вспомним гл. 17, § 4) в виде следующего интеграла:
+ ОО
2) = J" dm2p(m2)^p(x1 — x2■,m). B5.87)
Аналогичный результат справедлив и для сингулярных функций Д'(±)
и Д'*1) с той же самой весовой функцией р. Например,
Д' (хх — х2) = — I (Wo, [? (Xl), ? (х2)] ЧГ0) =
= J dm2p (/и2) Д (xt — х2; т). B5.88)
Итак, мы установили, что функцию Ду (а также другие сингу-
сингулярные функции) можно выразить в виде интеграла Стильтьеса по
массам. Этот факт имеет важное значение, так как из него вытекают
многие аналитические свойства функции Д^ (см. гл. 8 в книге Вид-
дера [534] и гл. 5 в книге Титчмарша [484]). Эти свойства
можно проще всего выразить с помощью фурье-образа функции
Ду(х), т. е.
оо
да+
О
Можно показать, например, что Д^(к2) есть регулярная функция
в верхней полуплоскости. Могут быть сделаны также некоторые
общие утверждения об ее асимптотическом поведении (Виддер [534]).
В частности, из выражения B5.89) следует, что функция Др(к2),
никогда не может быть меньше (даже асимптотически), чем функ-
функция Др(к2).
В случае свободного бозонного поля с массой (х ясно, что
функция плотности р имеет вид
р (т2) = 8 (т2 — (J.2), B5.90)
так что выражение B5.87) сводится к функции распространения
свободной бозе-частицы. В общем случае дискретные собственные
значения оператора Р2 приводят к появлению о-функций в функции
плотности р. Эти дискретные собственные значения выражают тогда
стабильные состояния полевой системы.
Аналогичное рассмотрение можно провести и в случае спиноров
(Леман [301]). Так, рассмотрим, например, матричный элемент
)W0). B5.91)
432 Глава 25
Из требования инвариантности при однородных преобразованиях
вытекает, что
Q-P (У) = S SS1 (a) S«p (a) Qsx (ay), где у = хх — х2. B5.92)
5т
Мы можем затем разложить величину Qa^(y) по шестнадцати линейно
независимым матрицам Г*, рассмотренным в гл. 4. Тогда получим
(Д> (у) +1 (ТбТ% QlA) (уН-
). B5.93)
где 5, V, Г ... означают скаляр, вектор, тензор, аксиальный век-
вектор и псевдоскаляр. Если использовать свойство шпуров матриц Г
и соотношения
S-1(a)T[lS(a)=a?Tv, B5.94)
S""l(a)oltvS(a)=a^cip'c и т. д.,
то можно прийти к следующему заключению: требование B5.92),
а также требование инвариантности по отношению к отражениям и
зарядовому сопряжению подразумевает, что величина Q выражается
в виде
Q(y2) = QlS) (У2)+ fQ'P(y2)- B5-95)
Написав Q = Q(y2) в формуле B5.95), мы тем самым в явной
форме представили инвариантность по отношению к однородным
преобразованиям Лоренца. Проводя вычисления таким же образом,
как в случае бозонных полей, можно прийти (Леман [301])х' к выводу,
что
со
) S'(+)( ) J d*(*)St+>(xl — x2; m*) +
— x2; m2), B5.96)
CO
J
где pj и р2 положительно-полуопределенные (positive semidefinite)
функции плотности в мезонной теории, которые могут быть, однако,
отрицательными в квантовой электродинамике (Челен [256]). Такой
же результат получается для сингулярных функций 5', S'F и т. д.
с теми же самыми весовыми функциями рх и р2.
Выражения B5.87) и B5.96) дают общее представление функций
распространения, в которые включены все радиационные поправки.
Ч См. также работу Гелл-Манна и Лоу [207].
Новейшее развитие теории - 433
Они могут быть получены из общих соображений инвариантности
и некоторых весьма правдоподобных предположений о свойствах
состояний системы.
§ 4. S-матрица в гейзенберговском представлении
После этих предварительных формальных соображений мы можем
теперь проанализировать некоторые из рассмотренных нами ранее
проблем и получить ряд новых результатов. Ограничимся областью
квантовой электродинамики, хотя ясно, что аналогичные утвержде-
утверждения могут быть сделаны и в случае перенормируемых мезонных
теорий (см. § 8).
Сначала рассмотрим определение S-матрицы в гейзенберговском
представлении (Янг и Фельдман [542], Челен [255]). С этой целью
проинтегрируем уравнения движения B5.1), B5.2), используя функ-
функции Грина Db, Sr и S^, определенные в гл. 17, § 4. Тогда мы
получим (опуская член с 8/и)
A(l(x)=AJ?(x)+ f Од(х — xOMxOrf**'., B5.97)
— СО
+ СО
ф (х) = 4>ln(x)+■ / 5д(х — хО^А'Чх'Жх')'*4*'; B5.98)
— СО
+ СО
е4»(х')т!1А[1(х'Mд(х/ — x)d*x'. B5.99)
Эти уравнения могут рассматриваться как определения приходящих
(incoming) гейзенберговских полей ф'" и Аш. Если использовать
предельные процессы, в которых мы предполагали, что взаимодей-
взаимодействие при переходе к пределу х0 —>■ — оо может быть включено
адиабатически [т. е. е—»-еехр(—а|хо|)], то мы получим, что опе-
операторы ф и фш> а также A(i и Ajf совпадают в момент времени
х0 = — со. [Обсуждение см. в работах Челена [259], Циммер-
Циммермана [550] и Кита [276]. В последней работе показано, почему
решение уравнений B5.97) —B5.99) в виде степенного ряда никогда
не даст связанных состояний. Можно установить связь этого заме-
замечания с замечаниями, сделанными нами в конце гл. 6 и 24, если
учесть, что такое решение в виде степенного ряда дает 5-матрицу;
см. ниже]. Операторы поля с индексом „in" удовлетворяют одно-
однородным уравнениям свободных полей и, следовательно, перестано-
перестановочным соотношениям для свободных полей, т. е.
№ (х). Фэ° (х')]+ = —*S.p (х — х'). B5.100)
[А? (х), AlQ (х')] = — ig^D (х — х'). B5.101)
434 Глава 25
Мы можем выписать также другую систему решений, проводя
интегрирование от -|-со до t и используя опережающие функции
Грина Sa и Da
+00
f DA(x
— CO
-foo
B5.102)
j SA(x — x')eTaAll(x'L»(x')d4x', B5.103)
' — x)d4jc', B5.104)
где снова операторы с индексом „out", определяемые уравнениями
B5.102)—B5.104), удовлетворяют уравнениям свободных полей и
перестановочным соотношениям
ЬС*(х), АГ'(х')] = — igavD(x —х'), B5.105)
[<ГЧх), ф°а4(х')]+ = — /S(x — x'). B5.106)
Поскольку операторы „приходящего" и „уходящего" (outgoing)
полей удовлетворяют одним и тем же перестановочным соотноше-
соотношениям, должно существовать следующее унитарное преобразование:
B5.107)
B5.108)
B5.109)
Можно показать, что оператор S тождественно равен S-матрице
(Янг и Фельдман [542], Челен [255]), которую мы рассматривали в
предыдущих главах. Преимуществом настоящего метода является
отсутствие связи его с какой-либо пространственно-подобной поверх-
поверхностью и нормалями к ней1).
§ 5. Величина перенормировочных констант
Челен в своей недавней важной работе [256], использовав фор-
формулировку квантовой электродинамики в гейзенберговском пред-
представлении, смог получить замкнутые выражения для перенормиро-
перенормировочных констант Zx, Z2, Z3 и Ьт. Здесь мы изложим кратко резуль-
результаты его анализа, следуя работе Лемана [301].
J) Формулировку теории рассеяния через операторы с индексами „in"
и „out" и связь их с операторами в представлении взаимодействия см.
в статье Швебера [435].
Новейшее развитие теории 435
В § 3 мы видели, что все штрихованные величины, введенные
в гл. 24, можно выразить через соответствующие гейзенберговские
операторы. Поэтому, используя соотношения B4.107) — B4.109),
можно определить перенормированные гейзенберговские переменные
(отмечаемые индексом 1) и наблюдаемый заряд ех с помощью со-
соотношений
4» = Z^X) B5.110)
3=Z^lt B5.111)
Aa = Z^A!li> B5.112)
е = Z^xZ^heu B5.113)
Z1(e1)=l—L(e1), B5.114)
), B5.115)
где расходящиеся величины L, В, С были определены ранее
[см. B4.97) B4.98) B4.100) и B4.101)].
Уравнения движения B5.1) и B5.2) можно записать для пере-
перенормированных операторов (мы опускаем индекс 1) в виде
(+ Л7 — щ) ф (х) = S/mJ> (Х)+ ег1гг\А'-(х) ф (х), B5.116)
Ф(х)]- B5.117)
Перенормированные операторы теперь удовлетворяют следующим
перестановочным соотношениям на пространственно-подобной поверх-
поверхности, т. е. для (х — х'J < 0;
[А.(х), Av(x')]= — ig^Z^Dix — x'), B5.118)
[ф(х), ф(х')]+= — jZ2-x5(x — x'). B5.119)
Используя эти соотношения, а также формулу B5.96) и соотноше-
соотношение, аналогичное B5.88) для электродинамики (т. е. среднее значе-
значение по вакууму для перенормированных операторов), получаем
) dp.2, B5.120)
о
со
Z2""x = J Ptim^dm2 B5.121)
о
(в случае электродинамики функция рх может быть отрицательной).
Выражение B5.120) можно получить, дифференцируя выражения
B5.118) и B5.88) по переменной xQ, полагая затем xQ = х'о и
сравнивая получающиеся выражения. [Напомним, что дА.(х)/дх0 для
хо = 0 равно —8(х); см. -формулу A5.49 а)]. Аналогично соотно-
436 Глава 25
шение B5.121) можно получить, сравнивая для равных времен
хо — х'о формулу B5.119) с выражением
(Wo> [ф(х). ?(х/)]+ЧГ0) = — iS'{x — х') B5.96а)
[здесь функция S' получена из правой стороны соотношения B5.96)
с помощью простой замены Д и S на Д и S соответственно].
Напомним, что для xo — Q, S(x) = f°b(x) и Д(х) = 0.
Поскольку р положительно-определенная функция, то из фор-
формулы B5.120) следует, что Z3 > 0. Кроме того, если предполо-
предположить, что в теорию включено описание физического состояния одного
бозона с массой [х((а=0 в случае электродинамики), то функция
р(/ге2) должна иметь вид
р (/те2) = 8 (/те2 — р2)-\-р'(тг)з B5.90а)
где p'(ffi2) — снова положительно-определенная функция. Поэтому
величина Z^1 должна быть положительной и больше единицы. Так
как, весьма вероятно, величина Z^ может быть бесконечной (Челен
[257]), то, по-видимому, соотношение B5.118) указывает на то, что
перестановочные соотношения для равных времен для перенормиро-
перенормированных полей фактически расходятся более сильно, чем 8-функция.
Однако прежде чем делать этот вывод, необходимо было бы про-
провести строгое исследование соотношений типа B5.88), B5.96), при-
причем расходимость интеграла
j р[(/ге2) dm2
должна была бы быть рассмотрена в свете теории распределения
Шварца [432].
Замкнутые выражения можно также получить для величин Ьт и
Zx (или L) (Челен [256]) 1К С помощью указанного метода можно
провести программу пергнормировки, не прибегая к теории возму-
возмущений. Кроме того, Челен показал, что функция плотности встре-
встречается в фэрмулах для наблюдаемых величин в виде
Этот интеграл должен быть конечным, если теория последовательна.
Челену [257] недавно удалось доказать замечательную теорему о том,
что по крайней мере одна (а возможно, и все) перенормировочная
константа (L, С, В) должна быть бесконечной.
См. также работу Мэттыоса и Салама [333].
Новейшее развитие теории 437
§ 6. Проблема связанных состояний
До сих пор в этой главе мы рассматривали только задачи рас-
рассеяния и не рассматривали задач, в которые включены связанные
состояния. Сейчас мы кратко опишем некоторые успешные попытки,
которые были сделаны при рассмотрении проблем связанных состоя-
состояний в теории поля.
К проблеме связанных состояний можно подойти двумя тесно
связанными путями. Один из них состоит в обобщении понятия
функций распространения Фейнмана на системы многих частиц
(Фейнман [168, 169], Швингер [442], Салпетер и Бете [422], Гелл-
Манн и Лоу [203], Нисидзима [357], Фрезе [189, 190] и др.). Другой —
в рассмотрении непосредственно амплитуды. Мы приведем оба метода.
Рассмотрим одну частицу. В случае свободного поля можно
интерпретировать матричный элемент
— \ SF (х — хО = (Ф„. Т (ф (х) фУ)) Фо) =
= (ф (х) ТоФо. Ф(х') Фо). если Хо > Хо B5.122)
как амплитуду вероятности нахождения электрона в точке х, если
в момент времени х'о электрон находился в точке х'. (Это, строго
говоря, не совсем верно, поскольку мы не можем интерпретиро-
интерпретировать х как собственное значение оператора положения.)
При наличии взаимодействия (предположим, что применима адиа-
адиабатическая гипотеза) можно дать следующее описание проблемы:
„голый" электрон рождается в момент времени £ = — со. При этом
вектор состояния есть ф(х')Фо- Этот вектор состояния может быть
получен во все последующие моменты времени с помощью опера-
оператора U (t, —со), так что вероятность найти электрон в состоянии
ф(х)Ф0 в момент времени t = х0=~\-оо (т. е. во время, гораздо
более позднее, чем х0 ——оо) с точностью до множителя fo ICM-
формулу B5.76)] дается выражением
(Фо, ф (х) 5ф (х') Фо) = (Фо, Т (S4» (х) ф (х')) Фо) =
= — ~S'F(x — х')- B5.123)
Теперь выражение B5.123) можно обобщить на произвольные точки
пространства-времени х, х'. Кроме того, поскольку несвязанные
диаграммы не должны рассматриваться в выражении B5.123), то,
используя формулу B5.33), можно написать
1 с' rv v/4 (Фо. Т (Зф (х) I (xQ ) Фо) __
— yOjlx — X)— (ф0) 5Ф0)
= (W0, 74$(x)?(x'))W0) =
= *W(x —х') B5.124)
438 Глава 25
и рассматривать это выражение как определение функции распро-
распространения Фейнмана (в которую включены радиационные поправки)
для случая одной частицы. Швингер [442] назвал эту функцию К{+
функцией Грина одночастичной системы. В недавней серии своих
работ, озаглавленной „Теория квантованных полей", [441, 442,
444—446, 448, 449],он развил общую теорию функций Грина в теории
полях). Она основывается на лагранжевой формулировке квантовой ме-
механики (см. гл. 6.33 в книге Дирака [108], а также работу Фейнмана
[167]. Данное им определение функции Грина для одно- и двухчастич-
двухчастичных систем совпадает (с точностью до множителя /) с определениями
B5.124) и B5.125). Он вывел также неоднородные дифференциаль-
дифференциальные уравнения, которым удовлетворяют эти функции Грина, и опре-
определил соответствующие однородные уравнения как волновые уравне-
уравнения для амплитуд. Мы не будем излагать здесь эту теорию, а будем
исходить из более интуитивного и менее формального рассмотрения
Салпетера — Бете [422] и Гелл-Манна и Лоу [203]. Связь швинге-
ровского метода функций Грина и приближения Фейнмана — Дай-
сона рассмотрена в статье Утияма и др. [495].
Функцию распространения для системы двух частиц мы можем
определить так же, как и для одной частицы, а именно:
* v ■ v ,1 _ (Фр, Т Eф (ха)ф (х4) ф (xt)
(х3, х4, хх, х2) —
v ,1
хх, х2) — (Фо, 5
К{г2 (х„ х4; хх, х2) = (¥„, Т (ф (х3) ф (х,)ф (хх) ф (х2)) ЧГ0). B5.1256)
Если выражение B5.125а) разложить в степенной ряд, то стано-
становится ясным, что функция К+ идентична двухчастичной функции
распространения, которая была рассмотрена в гл. 8. Теперь про-
продолжим начатый там анализ и рассмотрим более сложные диаграммы,
следуя рассмотрению Салпетера и Бете [422].
Понятия приводимых и неприводимых диаграмм для случая двух
частиц определим таким же образом, как мы это делали в гл. 24.
Назовем диаграмму приводимой, если ее можно разделить на две
несвязанные части, проводя при этом линию так, чтобы она вообще
яе пересекала бозоиной линии, а каждую из двух фермионных линий
пересекала только 1 раз. Неприводимые диаграммы могут быть упо-
упорядочены в соответствии со степенью константы связи, встречаю-
встречающейся в матричном элементе, отвечающем данной диаграмме. Непри-
Неприводимые диаграммы до четвертого порядка включительно приведены
*) Аналогичные вопросы исследовались также в следующих работах:
Ф рад к ии Е. С, ЖЭТФ, 26, 751 A954) и 29, 121 A955); Галанив А. Д.,
И оффе Б. Л., П омера ичу к И. Я., ДАН СССР, 98, 361 A954). — Прим.
перее.
Новейшее развитие теории
439
на фиг. 90. Диаграммы же, приведенные на фиг. 91, являются при-
приводимыми. Ясно, что приводимые диаграммы могут быть всегда
разделены на неприводимые части.
2-й порядок
4-й порядок
•8т
Ъ
Фиг. 90.
Фиг. 91.
Если мы обозначим сумму всех неприводимых диаграмм через
21. 2; 3, 4)=ОA, 2; 3, 4),
(да)
то двухчастичную функцию распространения К(+(Ь, 4; 1,2) можно
будет записать (Салпетер и Бете [422] в следующем виде:
К™ (9, 4; 1, 2) — К™C, 1)^+44, 2) =
= if f f f
, 6)X
E, 6; 7, 8)/C<?G, 8; 1, 2). B5.126)
440 Глава 25
Хотя это интегральное уравнение содержит бесконечный ряд 5jG(m),
ясно, что оно имеет гораздо меньше членов, чем исходное уравне-
уравнение. Однако этот ряд еще не сходится (Херст [238]). Если прове-
провести итерацию по Нейману — Лиувиллю для уравнения B5.126), то
станет ясным, что приводимые диаграммы также правильно вклю-
включены в рассмотрение с помощью интегрального уравнения. В этом
известное преимущество теории, в которой константа связи мала и
разложение 2 О т) может рассматриваться как асимптотический ряд.
(т)
Например, большая часть энергии связи между протоном и электро-
электроном может быть получена при повторном учете диаграммы, при-
приведенной на фиг. 90, а. Преимущество, достигаемое при использо-
использовании уравнения B5.126) с ядром GA), такое же, как если бы мы
решали уравнение Шредингера с потенциалом, вместо того чтобы
рассматривать этот потенциал как возмущение (ср. с гл. 40).
В низшем порядке функция взаимодействия О*1' в электродина-
электродинамике дается выражением
00E, 6; 7, 8) = + e2DH5, 6)S^)E, 7)SWF, 8)ТЬТ^. B5.127)
где индексы а и Ь относятся к двум фермионам. Следует отметить,
что в формуле B5.126) можно опустить все члены, соответствую-
соответствующие частям собственной энергии фермионов, так как их влияние
было уже учтено в выражении для G<m>, поскольку каждая фермион-
ная линия представляется множителем
Связь ядра К+ со свойствами стационарных состояний системы
двух нуклонов может выражаться следующим образом (Гелл-Манн
и Лоу [203]). Пусть tv t2 > t3, tit тогда, используя полноту системы
стационарных состояний ЧГП, выражение B5.125 б) можно перепи-
переписать в следующем виде:
. 2; 3, 4)=S(W0, 7^(х1)ф(х2))^й)(^й, Т(ф(х3)ф(х4))Wo)=
= 2У,п (хх, х2) Тп(х„ х4), B5.128)
где
Х« (xi, х2) = (ЧГ0, Т (ф (хх) ф (х2)) ЧГП) B5.129а)
и
ум(хг, х4) = (ЧГ0, Г(ф(х,)ф(х4))*„)*■£•$. B5.1296)
Здесь оператор Т упорядочивает операторы в обратном хронологи-
хронологическом порядке по сравнению с оператором Т, т. е. оператор, за-
зависящий от более позднего времени, стоит справа от оператора,
зависящего от более раннего времени. Таким образом, мы видим,
Новейшее развитие теории 441
что функция распространения двух частиц может быть построена
с помощью „двухчастичных амплитуд" точно так же, как была по-
построена соответствующая функция (8.25) в случае одной частицы.
Весьма возможно, что полное знание этой функции распространения
достаточно для определения уровня энергии связанного состояния
двух частиц.
Чтобы представить эту возможность более подробно, отметим,
что движение центра инерции может быть исключено следующим
образом. Поскольку векторы состояния Wo и Wn являются собствен-
собственными функциями оператора Р^ с собственными значениями pj* и £
соответственно, то, используя формулу B5.9), можно написать
(р("} — рГ) (w0. т (Ф СО Ф (х2)) чг„) =
= (Р^— р£0))х»(*1. х2) =
= (W6, [Т (ф (хх) ф (х2)), P^J Wn) =
n(xv x2). B5.130)
Последнее уравнение выражает с помощью амплитуды Xn(xi> хг)
свойства симметрии состояний Wn и Wo. Кроме того, поскольку при
пространственно-временной трансляции L вектор состояния ЧГП пре-
преобразуется согласно формуле
инвариантность матричного элементаB5.129) при такого рода тран-
трансляции требует, чтобы выполнялось соотношение
X» (Xi. х8) = («»(L) ЧГ0> о (L) Т (ф (Xl) ф (х2))«»-1 (L) о (L) WJ =
= (ЧГ0, 7- (ф (хх + L) ф (х2 + L)) WJ е+^ (Р<»)-рО»>. ь =
^)(°)-ь. B5.132)
Это—интегральная форма выражения B5.130).
Соотношение B5.132) должно быть верным для произвольного
смещения пространства-времени L. Поэтому можно написать (с точ-
точностью до нормировочной константы)
X«(xi. x^e-^'-^-Vnto, B5.133)
где
442 Глава 25 ■
— координата центра инерции1', а х = хх — х2—относительная
координата двух частиц.
Теперь по аналогии со случаем одной частицы мы можем напи-
написать [см. выражения (8.52) и (8.53)] уравнение распространения для
амплитуды уA, 2), причем ядром уравнения является функция
if'+ЧЗ, 4; 1, 2), а именно:
X C, 4) = / f Кг] C, 4; 1, 2) тоаТ°ьХA, 2) ^х^х2. B5.134)
Здесь интегрирование по переменным хх и хг должно снова прово-
проводиться по замкнутой трехмерной поверхности, причем простран-
пространственно-временные точки 3 и 4 должны лежать внутри этой поверх-
поверхности.
Чтобы получить уравнение для амплитуды связанных состоя-
состояний уа, Гелл-Манн и Лоу отметили, что, если опустить случайное
вырождение, энергия связанного состояния Ха, для которого
рЫрМ» <(,па-\-тьу, B5.135)
будет различной в каждом состоянии, характеризуемом теми же
самыми значениями других констант движения (таких, как простран-
пространственные компоненты полного импульса, четность, внутренний мо-
момент количества движения и т. д.); таким образом, функция уа будет
иметь характеристическую зависимость от времени, которая будет
■отличаться от зависимости в каждом другом состоянии. Поэтому
они ввели предельный процесс, в котором при Т —> — сю все осцил-
осциллирующие члены должны быть взяты стремящимися к нулю. Как
пример такого предельного процесса они дали следующее выраже-
выражение:
т
Hm g(T)= lim -i fg(-z)dx. B5.136)
Т-> — оо 2"->—со ' .•£_
22"
Если теперь выражение B5.133) подставить в правую часть вы-
выражения B5.134) и использовать формулы B5.126), B5.128), B5.129)
и выражение B5.136), то можно получить следующее уравнение для
амплитуд ух (Гелл-Манн и Лоу [203]):
у.Л 1, 2) = — i f f f f d'x^x^x^x^ X
^B, 6)GE, 6; 7, 8)/aG, 8). B5.137)
l) Выражение для Х справедливо в нерелятивистском случае; для реля-
тивистских систем X = {Е\Г^ -f- E^r^j(E\ + £2) [см., например, Широ-
Широков Ю. М., ЖЭТФ, 21, 748 A951)]. — Прим. перев.
Новейшее развитие теории 443
Точно такое же уравнение было выведено Салпетером и Бете, ко-
которые использовали несколько более интуитивные аргументы, осно-
основывающиеся на адиабатическом включении взаимодействия. Для про-
проблем рассеяния левая сторона формулы B5.137) должна быть заменена
на разность
Хп(Ь 2) —?яA, 2),
где функция срп — произведение двух дираковских волновых функ-
функций для свободной частицы; она может рассматриваться как падаю-
падающая плоская волна.
Дифференциальное уравнение, пригодное как для рассмотрения
процесса рассеяния, так и для исследования свойств связанных со-
состояний, может быть получено, если учесть (см. гл. 24), что
и что
-\-fd*yf d*y'SF(x — У) 2* (у — У) S'P(у' — х'). B5.138)
Тогда, применяя оператор Дирака к уравнению B5.138), получаем
= 2/8<*> (х — х') + / d^ylf (x — у) S'p (у — х')- B5.139)
Если мы применим дифференциальный оператор — i^v- (д/дх?-)-\~ m
для каждой частицы в уравнении B5.137), то получим
= — I f J dix^d*xsG(xv x2; xT, х8)-/„(*,,. х8) —
X ( 2* (хх — у) 1 SF (у — хб))а E1* (х2 - у') \ SF (у' — х.) \ X
X О(хв, х6; х7, х3)ул(х1, х8). B5.140)
Если в уравнении B5.140) опустить части собственной энергии фер-
миона, то оно приобретет особенно простую форму, поскольку вы-
выпадет последний член в правой стороне. Если в дополнение
к этому мы ограничимся низшим порядком взаимодействия, который
дается формулой B5.127), то уравнение B5.140) будет точно сов-
совпадать с уравнением „лестничного приближения", которое мы напи-
написали в гл. 9.
444 Глава 25
Наиболее существенным результатом, полученным нами, является
полностью релятивистское волновое уравнение для системы двух
тел B5.140). Однако этого удалось достичь ценой уменьшения ясно-
ясности физической интерпретации амплитуды. В частности, до сих пор
физически не объяснена зависимость амплитуды от относительного
времени х10—-х20. Неясно также, какое граничное условие должно
быть наложено на амплитуду при бесконечных значениях относитель-
относительного времени. Кроме того, до сих пор не сформулирована связь этой
амплитуды с характеристиками возможных экспериментов над си-
системой двух тел. [См., однако, работу Блоха [44], где дан анализ
и объясняются измерения в старом многовременном формализме Ди-
Дирака, Фока и Подольского (см. работы [104, 105]); уравнение,
полученное на основании его, имеет сходство с уравнением Бете —
Салпетера]. Последняя трудность связана с отсутствием положи-
положительно-определенной нормы для амплитуды.
Недавно удалось достигнуть значительных результатов (Вик [533]
и Куткоский [94]) в выяснении некоторых непонятных черт уравне-
уравнения Бете — Салпетера. Вик указал, что дополнительное условие для
амплитуды Бете —Салпетера может быть получено из ее определе-
определения B5.129), если добавить простые условия стабильности.
Итак, из формулы B5.133) следует, что для покоящейся си-
-»-
стемы, т. е. для р(я'= 0, двухчастичная амплитуда ^(х^ х2) имеет
вид
7а(Хх, х^ = *-"«•/„(х), B5.141)
где Е—полная энергия системы, а Т—„время" координаты центра
инерции; здесь х снова является относительной координатой двух
частиц, т. е. х = х1 — х2- Если ввести энергию связи связанного
состояния В, то
Е = me + mp — В < me+ mp, B5.142)
где me и mp — массы покоя электрона и протона. Если мы выпи-
выпишем формулы B5.129а) для случая х10 > х20, т. е.
7«(*i. X2) = S@|*e(xi)l»)(»|*P(x2)|«), B5.143)
п
то состояния п, дающие не равный нулю вклад, будут принадле-
принадлежать к определенному классу. Ясно, что соответствующие волновые
функции должны быть собственными функциями оператора полного
заряда с собственным значением — е. Кроме того, в системе коор-
координат, в которой полный импульс равен нулю, они должны быть
собственными функциями полного момента количества движения
с собственным значением 1/2й. Далее, все известные в природе со-
состояния, для которых полный заряд равен — е, момент количества
движения равен —j—1/2Й, удовлетворяют неравенству
En— pl>m2e, B5.144)
Новейшее развитие теории 445
где Еп и рп—полная энергия и импульс в состоянии п. Знак ра-
равенства имеет место только для физического одноэлектронного со-
состояния, т. е. состояния, в котором имеется один и только один
реальный (лабораторный) электрон. Вик назвал это неравенство
условием стабильности для электрона. Затем он предположил, что
физическое одноэлектронное состояние [для которого в формуле
B5.144) нужно взять знак равенства] есть состояние, с наинизшей
энергией из числа тех, которые дают вклад в сумму B5.143).
Аналогичным образом, когда относительное время t отрица-
отрицательно, можно показать, что состояния п', дающие вклад в ампли-
амплитуду, характеризуются, в частности, тем, что собственные значе-
значения энергии и импульса удовлетворяют неравенству
El'—pl,>ml; B5.145)
это неравенство Вик назвал условием стабильности для протона.
Три неравенства B5.142), B5.144) и B5.145) легли в основу даль-
дальнейшего рассмотрения. С помощью формул B5.143) и B5.133) можно
легко показать, что для £>0 амплитуда /а(х) имеет следующий
вид:
Л(х) = 2@|фв@)|«)(»|ф,@)|а)в V mv+m* ! , B5.146)
п
где pW — 4-импульс в состоянии а. Используя неравенства B5.142),
B5.144) и B5.145), можноsполучить
{п) ^__ о») m B5.147)
^и тпр + тпе *"> ^ тпр + тпв ^ v '
Следовательно, для t >> 0 амплитуда /а(х) имеет только положи-
положительные частоты. Аналогично из формулы B5.133) и приведенных
выше неравенств следует, что для t < 0 амплитуда /а(х) предста-
представляет собой суперпозицию членов только с отрицательной частотой.
Таким образом, амплитуда /а(х) имеет свойства функции распро-
распространения Фейнмана.
Поэтому для t >> 0 мы можем написать
+оо
/(х) == J d?p С dmg (р, ш) ехр (ip ■ х — Ш), B5.148)
"•мин.
где
(^) 2>me. B5.149)
Если амплитуду /(х) рассматривать как функцию комплексной пе-
переменной t, то она может быть аналитически продолжена в нижнюю
полуплоскость, в область, где 0>-arg^>—тс. Аналогично, начи-
начиная с отрицательной вещественной оси, можно аналитически про-
446 Глава 25 '
должить функцию /(х) в верхнюю полуплоскость, в область, где
7t>>arg^>0. Кроме того, поскольку В > 0, функция /(х) стре-
стремится к нулю, когда t —*■ оо в любом направлении в верхней или ниж-
нижней полуплоскости, отличном от вещественной оси.
Если перейти в импульсное пространство и написать
/()Л() + /2(),
где /1(х) = 0 для £<0 и /2(х) = 0 для t > 0, то при
Ti (Р> Ро) = ^ / ^хе~ *Р% f dt eip*f (x), B5.150а)
о
о
о
с5,(р, Ро)~7тг-Га I dsxe-iP'x I dte^'fCx), B5.1506)
— CO
используя выражение B5.147), легко получить, что
+ ОО
?i(Р> Ро) = -^a / ё(Р> <")(<"— Ро — ieyT-du, B5.150b)
шмин.
где s — бесконечно малая положительная константа. Из теории пре-
преобразований Стильтьеса следует, что <р1(р, р0) — аналитическая функ-
функция переменной р0 на всей комплексной плоскости, в области
2* > argO?o— (омин.) > 0. B5-151)
Аналогичное утверждение может быть сделано относительно функ-
функции ср2. Можно также показать, что функция ср (р) = ср (р, р0) = срх—^—ср2
определена во всей комплексной плоскости р0 с двумя разрезами
от и)мин. до -f- со и от —со до шмаке, где
— «We. = (~ + те) В + {m% -+- р2) Vl — т B5.152)
\mi> I
Следовательно, функция может быть продолжена аналитически иа
верхней полуплоскости в нижнюю через щель между двумя разре-
разрезами, существование которой зависит от того, является ли В>0
или нет.
Эти аналитические свойства волновой функции могут быть
использованы для преобразования уравнения Бете — Салпетера (с по-
помощью вращения пути интегрирования в комплексной плоскости)
в уравнение, в котором переменная р0 чисто мнимая (или относи-
относительное время чисто мнимое). При этом можно проводить вычисле-
вычисления в эвклидовом пространстве, что значительно упрощает матема-
математический аппарат.
Вику и Куткоскому, после того как было выполнено преобра-
преобразование к эвклидовому пространству, фактически удалось получить
Новейшее развитие теории 44Т
полную систему решений для связанных состояний в „лестничном
приближении" уравнения Бете — Салпетера в случае двух скалярных
бозонов, взаимодействующих через скалярные фотоны. С деталями
читатель может ознакомиться в их статьях (см. также работы Хайяск
и Мунаката [221], а также работы Гольдштейна [209]).
§ 7. Многочастичные амплитуды
Хотя уравнение B5.140) и может быть использовано при рассмо-
рассмотрении задач связанных состояний, однако оно имеет ограниченную
применимость. Это следует из того, что мы вывели уравнение B5.140)
с помощью функции распространения, в которой в начальном и
конечном состояниях могут находиться только два фермиона. По-
Поэтому, строго говоря, уравнение описывает только основное состоя-
состояние рассматриваемой связанной системы, поскольку возбужденные
состояния могут распадаться (например, с излучением фотона), что
приводит к конечному состоянию, в котором имеются, кроме двух
фермионов, и другие частицы. В уравнении для двух тел, которое
мы до сих пор рассматривали, мы пренебрегали возможностью рас-
распада и предполагали, что рассматриваемое связанное состояние ста-
стабильно.
Ясно, что мы сможем охватить все случаи, если включим в рас-
рассмотрение амплитуды, аналогичные jn{\lt х2), но соответствующие
наличию не только двух фермионов, но и других частиц. Эти выс-
высшие амплитуды можно определить с помощью формул, аналогичных
формулам B5.129).
Если W — вектор состояния рассматриваемой системы, например
атома водорода, то двухчастичную амплитуду Фейнмана у_A, 2)
можно определить, как и раньше, з виде
Х(Хх. х2) = (ЧГ0, Г(фв(х1)фр(х2))ЧГ), B5.153)
где индексы е и р относятся соответственно к операторам элек-
электрона и протона. Одночастичные амплитуды
или Х(х2)
тождественно равны нулю, так как векторы состояния W и ЧГа
описывают состояния с зарядом, равным нулю (т. е. являются соб-
собственными функциями оператора полного заряда Q с собственным
значением 0), тогда как вектор состояния ^(Х!)^ описывает состоя-
состояния с зарядом ±е и поэтому ортогонален к вектору состояния Wo.
Амплитуда Фейнмана для двух фермионов и одного бозона имеет вид
X(Xlx2; zlV.1) = (V0, 7'(фв(х1)фр(х2)А1),B1))ЧГ); B5.154)
аналогично амплитуда, соответствующая наличию двух бозонов и
двух ферминов, задается выражением
Г). B5.155)
448 Глава 25
Выбор этих амплитуд не является однозначным. Они соответствуют
одному возможному способу описания состояния с помощью системы
амплитуд. Так, например, амплитуды
()ф()I!1Г) B5.156)
и т. д.,
определенные через нормальные произведения операторов, дают дру-
другое возможное описание (Мэттьюс и Салам [332, 333], Фрезе [189]).
Мы можем также вернуться к представлению взаимодействия и описы-
описывать систему с помощью совокупности амплитуд
A(Xl, x2) = 0Fo(O, WOKxO.Kx^TW) и т. д., B5.157)
где W (f) — вектор состояния двухчастичной системы в представле-
представлении взаимодействия, xF0(t) — вектор вакуумного состояния для взаимо-
взаимодействующих полей и 44xi) и Ф (хг) — операторы в представлении
взаимодействия, удовлетворяющие уравнениям свободных полей.
Амплитуды %, в, / и т. д. определяют различные корпускуляр-
корпускулярные аспекты теории поля (Вайтман и Швебер [535]). Корпускуляр-
Корпускулярный аспект квантованной теории поля представляет собой полное
описание системы поля через наблюдаемые частицы, т. е. амплитуды,
которые дают вероятность нахождения в некоторый момент времени
определенного числа частиц с определенными свойствами. Этими
свойствами могут быть, например, импульсы и спины частиц.
В последнее время было проведено широкое обсуждение такого
рода различных амплитуд и соотношений между ними (Гелл-Манн
и Гольдбергер [204], Фрезе [189, 190], Мэттьюс и Салам [332],
Дайсон [135], Швебер [434], Идеи [143], Кестер [86] и др.).
Описание системы с помощью амплитуд позволяет построить
естественную теорию возмущений, в которой состояние описывается
конечным числом амплитуд (см. т. II, гл. 40). Уравнение движения
для рассмотренной выше двухчастичной амплитуды x(xi> хг)> полу-
получаемое с помощью такого приближения, тесно связано с уравне-
уравнением Бете — Салпетера (Идеи и Рикейзен [141], Идеи [143]).
§ 8. Другие результаты, полученные в теории
В заключение этой главы о современном развитии теории мы
хотим принести извинения авторам ряда важных работ, содержание
которых не приведено в этой книге ввиду ограниченности объема.
По-видимому, наиболее существенными из этих работ являются
работы Дирака [116], Фейнмана [170,171], Швингера [442—446,
448, 449], Пайерлса [384], Эдвардса и Пайерлса [145], Намбу [352]
и др., в которых рассматриваются основные положения теории поля,
базирующиеся на лагранжевой формулировке квантовой механики.
Мы также, по-видимому, недостаточно подчеркнули трактовку
релятивистских теорий поля в конфигурационном пространстве
Новейшее развитие теории 449
С этими вопросами читатель может ознакомиться в статьях Фока
[183—185], Дирака [112], Беккера и Лейбфрида [25, 26], Брауна и
Равенхолла [67], Жана [243—245], Лопеса [308], Сато [426], Дирака
[117], Швебера [433], Гюнтера [214, 215], Мэттьюса и Салама [331],
Вайтмана и Швебера [535] (в последней работе см. ссылки на дру-
другие работы) и многих др. Использование конфигурационного про-
пространства лежит в основе таких методов, как метод Тамма— Данкова
(Т-амм [479], Данков [97], Леви [303, 304]), который будет детально
рассмотрен во втором томе (гл. 40—44).
Следует упомянуть также современные расчеты тонкой структуры
спектра водорода и позитрония, основывающиеся на уравнении
Бете — Салпетера для двух частиц и использующие теорию возмуще-
возмущений (Салпетер и Бете [422], Швингер [442]). В частности, работы Сал-
Салпетера [424], Салпетера и Ньюкомба [423], Брауна [68] и Арно-
вита [10], в которых рассматривается массовая поправка к тонкой
и сверхтонкой структуре спектров атома водорода, и Карплуса
и Клейна [269], где рассматривается то же для позитрония1', должны
быть приняты во внимание. В работах Идена [139, 140, 142]2) было
обобщено уравнение Бете—Салпетера на случай распада возбужден-
возбужденных состояний и вообще на случай эффектов связанных состояний,
что позволяет вычислить время жизни возбужденных состояний*
исходя из ковариантного уравнения для частиц.
Теория ширины линий и связанных с этим явлений была рассмо-
рассмотрена в рамках ковариантной формулировки квантовой электродина-
электродинамики в работах Арноуса, Блейлера, Зинау,Гайтлера[6—9]иЛоу[311].
В связи с программой перенормировки следует сослаться на недав-
недавние работы Валатина [496—499]. Он переопределил уравнения для
функций распространения Sp и Dp, включив в них предельный пере-
переход, который является обобщением предельного перехода, предло-
предложенного в работах Дирака [107] и Гейзенберга [225, 226]. Эти
переопределения уравнения дают конечные (перенормированные)
функции распространения без появления расходящихся интегра-
интегралов. Затем Валатин показал, что в случае разложения в степенной
ряд имеется одно-однозначное соответствие с результатами, получен-
полученными Дайсоном [126, 127].
Гелл-Манн и Лоу [207] исследовали перенормированные функции
распространения Dpi и Sp\ для импульсов, много больших, чем масса
электрона (т. е. для малых пространственно-временных интерваловK).
Они нашли, что вследствие перенормируемости теории степенные
Ч См. также работу Фултона и Мартина [199].
2) См. также работы Идена и Рикейзена [141], Фултона и Карплуса [198].
3) Асимптотическое поведение перенормированных функций распростра-
распространения при больших импульсах (на малых расстояниях) было исследовано
также в квантовой электродинамике [см. работы: Ландау Л. Д., Абри-
Абрикосов А. А. и Халатников И. М., ДАН СССР, 95, 497, 773, 1177; 96,
261 A954); Фрадкии Е. С, ЖЭТФ, 28, 750 A955)] и в псевдоскалярной
450 Глава 25 "
ряды, определяющие функции DF1 и SPl (в асимптотической области),
удовлетворяют определенным функциональным уравнениям. Одним
из наиболее интересных заключений, к которым пришли эти авторы,
является то, что в перенормируемой теории форма распределения
поляризационного заряда, окружающего находящийся в вакууме
пробный заряд, не зависит на расстояниях, меньших,, чем h/mc, от
перенормированной константы связи (точнее, от этой константы
зависит только масштабный множитель). Эти же авторы исследо-
исследовали также вопросы, касающиеся величин перенормировочных кон-,
стант, которые подобным же образом связаны с поведением функций
распространения при больших импульсах (см. работу Челена [260]),
но в этом случае.они получили менее характерные результаты. Им,
однако, удалось показать, что неперенормированная константа
связи е\, встречающаяся в теории возмущений в виде степенного
ряда по перенормированной константе связи е^ с расходящимися
коэффициентами, может быть или а) действительно бесконечной,
как указывает теория возмущений, или б) конечной величиной, не
зависящей от значения константы е\. На основании своей работы
они не могут исключить случай „б".
мезонной теории [см. работы: Абрикосов А. А., Г а л а н и н А. Д.,
■Халатников И. М., ДАН СССР, 97, 793 A954); Фрадкин Е. С,
ЖЭТФ, 29, 377 A955); см. также Бог олюбов Н. Н. и Широков Д. В.,
УФН, 55, 149 A955); 57, 3 A955)]. — Прим. перев.
Глава 26
ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ
Исследуем здесь степень, в которой псевдоскалярную и псевдо-
псевдовекторную связи можно считать эквивалентными. Из рассмотрения,
проведенного в гл. 23, мы знаем, что эти два вида связи являются
фундаментально различными, так как псевдоскалярное взаимодействие
перенормируемо, тогда как псевдовекторное — неперенормируемо.
Тем не менее покажем, что до определенного порядка эти два вида
связи дают схожие результаты. В этом легко убедиться на простом
примере.
§ 1. Рассеяние свободных частиц
Рассмотрим мёллеровское рассеяние двух нуклонов, обусловлен-
обусловленное обменом мезоном. В нейтральной мезонной теории с псевдо-
псевдоскалярной связью
этому рассеянию соответствует матричный элемент
Mvs = (т) £ (a (pt) Ts а (рД, (и (р'2) 1ьи {р[)\ X
X МР2 — р,) 8D) (Pt + Р; — р2 — Р;>, B6.1)
где индексы а и b относятся к двум нуклонам. В случае псевдо-
псевдовекторной связи
P-r d
матричный элемент имеет вид
М1Ч= («О E^3) (« (Л) То (к — Рг) " (Л))а X
X (« Ср'2) Тб (Р'2 —Р[) « (р'Л Д /Р2 — Pt) S<4» (Pt + Р[ — Pa — Pj). B6.2)
Поскольку начальное и конечное состояния являются состояниями
свободных частиц, то,„используя тот факт, что матрица f6 анти-
коммутирует со всеми матрицами -у?-, мы можем написать
«"(Л) Тб (А — А) «(Л) = 2Me"(pl) Тб« (.Pi)' B6-3)
где Ж — масса нуклона.
29*
452 Глава 26 :
Поэтому в этом порядке оба матричных элемента совпадают,
если
О = — F. B6.4)
Для ^-мезонов [A = 0,15Af, так что F = 0,075 О.
В дальнейшем мы исследуем, в какой мере эти виды связей экви-
эквивалентны в высших порядках. Обычным методом рассмотрения этой
проблемы является метод канонических преобразований (Дайсон [125],
Кейс [80], Фолди [187]).
§ 2. Преобразование Дайсона
Рассмотрим гамильтониан мезонного и нуклонного полей, свя-
связанных прямой псевдоскалярной связью,
Н = f d*xp (а- р + Й) <К *) + ^ f (Рх {тг2 (х) + (V ср(х)J +
4-HV (х)} -+- Of <*9*ф+рТвср<К х). B6.5)
Мы опять рассматриваем случай нейтрального мезонного поля. Обобще-
Обобщение на случай симметричной мезонной теории может быть проведено
непосредственно.
Теперь проведем унитарное преобразование гамильтониана
H' = eieHe-is, B6.6)
где оператор 5 должен быть определен так, чтобы член с псевдо-
псевдоскалярной связью был устранен, а на его месте оказался бы член
с псевдовекторной связью. Это преобразование упрощает переход
к нерелятивистскому гамильтониану при рассмотрении нерелятивист-
нерелятивистских проблем. Во всей этой главе, за исключением мест, где это
будет специально оговорено, мы будем использовать шредингеров-
ское представление.
Предположим (Дайсон [125], Фолди [187], Бергер и др. [30]),
что эрмитовский оператор 5 может быть выбран в следующем виде:
f pstyPx =
где
s = /T5^(tp(x)); B6.8)
здесь w — функция только ср, а матрица Т5==Т°Т1Т2Т3 — антиэрмитова
и квадрат ее равен —1. Отметим, что 5 не является матрицей,
а является с-числом в спиновом пространстве и поэтому коммути-
коммутирует с любой из дираковских матриц.
Теорема эквивалентности 453
Чтобы вычислить выражение B6.6), проделаем следующую опе-
операцию, которая была уже использована в гл. 15. Определим
<|/(х, \) = еЩ(х>~ж. B6.9)
Тогда оператором, который мы хотим вычислить, является ¥(х, 1),
а непреобразованным оператором — ¥(х, 0). Далее
-« = i [S, f(x, £)]. B6.10)
Припоминая, что перестановочные соотношения
^ — х'), B6.1
инвариантны по отношению к унитарному преобразованию B6.6) и
что операторы ср и ф коммутируют между собой, получаем, исполь-
используя выражение B6.7),
^J рР Р^ ' У ~~SY ^> У- (.-лО. 1^_)
9
Уравнение B6.10) имеет теперь вид
dif' (*' £) = — isY (х, £) B6.13)
и после интегрирования дает
у (х, %) = е-**ьу (х, 0). B6.14)
При получении формулы B6.14) мы использовали начальное усло-
условие: у (х, 0) является непреобразованным оператором. Преобразо-
Преобразованный оператор тогда дается выражением
-у-
eiS<b(x)e-is =e-is^(x). B6.15)
Поскольку оператор s, задаваемый формулой B6.8), является эрми-
эрмитовым, то, взяв эрмитово-сопряженное от последнего выражения,
получим следующее соотношение:
eisb+(x)e-is =^(х)е+ь* = ^(х)е+™, B6.16)
30 Зак. 1784. Мезоны и поля
454 Глава 26 .
Убедимся в том, что при вычислении выражения B6.6) окажется
весьма полезной следующая формула:
eiSQe~iS = Ч;-Гчо, vj-rrjf
+ ir[5, [5, [5, Q]]]+ ... B6.17)
Это соотношение легко доказать, если разложить exp (iSX) Q ехр (
в ряд Тейлора около точки к = 0.
Кроме того, отметим, что, поскольку операторы <?(х) и ®(х')
коммутируют так же, как и оператор 5, с любой дираковской
матрицей
£. B6.18)
где индексы а, р означают, что рассматривается a£ матричный эле-
элемент матриц «с (эти матричные элементы являются числами!). По-
Поэтому, используя формулы B6.15), B6.16) и B6.18), получаем
ор
(^)) е-йф (^). B6.19)
Далее, припоминая, что матрицы р и у6 антикоммутируют, мы можем
преобразовать множитель [Зехр(—is) следующим образом:
со
= 2 3 (Тб)п5 =
;_1)»р^==в*.р. B6.20)
»=о
Аналогично
$Чье~™ = eisPf6. B6.21)
так что выражение B6.19) можно записать в виде
Нх = Г d3^ (J) e2is (РЛ4 + G^Ts? W) "> W- B6.22)
To же получим и для члена
= J dsx^+ W ?ist • pe-fs6(J). B6.23)
Теорема эквивалентности 455
Дальнейший перенос множителя ехр (—is) невозможен, так как
->• ->
операторы р =— iV и ср не коммутируют. Однако, учитывая, что
матрицы а и ^5 коммутируют, и используя формулу B6.17), мы
можем написать
ег8а ■ pe~ls = еиае-** ■ elspe~ls = а • etspe~ls —
= (а- 'р— a- Vs). B6.24)
В этом месте удобно ввести 4-мерную матрицу а$, которая связана
с матрицами а* и fs следующим образом:
»« = + 'Тб«1- B6-25)
Таким образом, выражение B6.23) можно переписать в виде
Нг = J d8^1- (х) а • рф (?) — Г dsx^ (x) t ■ Vwty (x). B6.26)
Наконец, мы должны вычислить
))9 + ^а92(х)) е-^. B6.27)
Для вычисления этого члена предположим, следуя Дайсону [125],
что неизвестная функция w((f) имеет вид
•у-
w (ср) == Хер (х), B6.28)
где X — константа, которая должна быть определена. Поскольку
■*" ■*■/
операторы <?(х) и ср (jc ) коммутируют, мы должны вычислить только
величину
е™ъ(х)е-^ = ъ'(х). . B6.29)
Используя формулу B6Л7), получаем
г/ (х) = «(*) + Л f cPx' [ф+ (>)/Твф(хО<р (^). *(*)]; B6.30)
все высшие члены (повторные коммутаторы) равны нулю благодаря
перестановочному соотношению между операторами ср {х) и тт (х).
[?D те (*01 = Й (Jc —«0, B6.31)
которое представляет с-число.- Следовательно,
я' (л) = тг (£)— Дф+ (J) ТьФ (*). B6.32)
30*
456 Глава 26
и формула B6.27) получает вид
\ / т/2 (х
V (*)) — a
• B6.33)
Приводя члены, получаем следующее выражение для преобразо-
преобразованного гамильтониана:
^f Ac) (S • р + рЛ1) ф (ж) + -g- J>* (^2 + (VcpJ + цV)
f (х) (е2« — 1) рЖф (х)+ J d*xbf (х) еш GpT&cp (х) ф (х) —
— X J й3л;ф+ (х) (t • Vcp (х)) d) (J) — a j* ds^d/+ (J) Тбф (J) я (jT) —
— T X2 (/ rfS^+ W ТбФ (*)/ • B6-34)
Хотя формула B6.34) является точной, однако мы не можем
подобрать величину X так, чтобы полностью устранить псевдоска-
псевдоскалярную связь. Это является следствием нашего предположения B6.28).
Если оставить функцию w произвольной (Бергер, Фолди и Осборн [30])
до тех пор, пока не будет завершено вычисление выражения B6.6),
то функция w может быть затем определена таким образом, чтобы
в преобразованном гамильтониане не осталось псевдоскалярной
связи.
Если в выражении B6.34) разложить экспоненциальный множи-
множитель и оставить члены, квадратичные по ср, и если выбрать
— Х=2^, B6.35)
то псевдоскалярная связь будет фактически в этом порядке устра-
устранена, и преобразованный гамильтониан получит вид
Н = Яд- + Нш + Hi, B6.36а)
где
СА
СА г
Ш J
- B6.366)
Теорема эквивалентности 457
§ 3. Интерпретация
Сейчас мы кратко проанализируем преобразованный гамильтониан
B6.36). Первый член в выражении B6.366) имеет обычную форму
члена связи с производными в мезон-нуклонном гамильтониане. На-
-*■
помним, что оператор тс (х), по существу, равен d<p/dt, так что этот
член взаимодействия можно записать в следующем виде:
&|*; B6-37)
— это обычное выражение для псевдовекторного взаимодействия.
Таким образом, мы показали эквивалентность псевдоскалярного и
псевдовекторного взаимодействий в первом порядке по константе
связи. Константа связи для связи с производными F/jj, связана с кон-
константой связи О соотношением
ТГ-2Й- B6-38>
„Двухмезонный член"
^/W B6.39)
аналогичен квадратичному члену (е2/2т) А2, который встречается
в нерелятивистской теории излучения. Он возникает при устранении
переходов, связанных с виртуальными парами. Он дает (в теории
возмущений) большой, не зависящий от спина вклад в ядерные силы
(см. статью Лепора [302], в которой использовано представление
взаимодействия). Важность этого члена в любом расчете мезон-
нуклонного рассеяния была подчеркнута в работе Дрелла и Хенли
[123], где было показано, что этот член приводит к сильному от-
отталкиванию для 5-волны при взаимодействии мезонов с нуклонами.
Важность этого эффекта видна из того, что член псевдовекторной
связи пропорционален константе FJ\x., тогда как член с <р2 пропор-
пропорционален величине M(Fj\bJ. Этот член будет подробно рассмотрен
во втором томе, гл. 39, 44 и 47.
Наконец, контактный член
всегда присутствует в гамильтониане для связи с производными.
Если лагранжиан Jg содержит член связи с производными B6.37),
то импульс, сопряженный полю ср> будет равен
458 Глава 26
Устранение члена с <р из гамильтониана приводит тогда к контакт-
контактному члену
Эквивалентность псевдоскалярной и псевдовекторной связей может
быть наиболее ясно доказана с помощью преобразования Фолди
(Фолди [187], Вентцель [526], Бергер и др. [30]), в котором опе-
оператор 5 дается выражением
/ d*x^ & ЪФ (*) агс Ц^1) B6•41)
С помощью этого канонического преобразования можно полностью
устранить псевдоскалярную связь. Однако член псевдовекторной
связи в этом случае появляется с нелинейным коэффициентом.
Наиболее общая форма теоремы эквивалентности была устано-
установлена в работе Молдауэра и Кейса [338], где показано, что в пер-
первом порядке по константе связи все возможные линейные взаимо-
взаимодействия между скалярными (или псевдоскалярными) мезонами и
нуклонами либо дают нуль, либо эквивалентны скалярной (псевдо-
(псевдоскалярной) связи.
Теорема эквивалентности в присутствии внешнего электромагнит-
электромагнитного поля была доказана в работах Кейса [80], Дрелла и Хенли
[123]. Чрезвычайно изящный способ вывода теоремы эквивалентности,
который использует произвольность выбора лагранжиана с точностью
до 4-мерной дивергенции, был дан в работе Келли [270].
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ. А
Здесь мы дадим несколько более строгий вывод формулы (8.54),
основанный на использовании теоремы Грина, которая в 4-простран-
стве имеет вид
здесь S — поверхность, охватывающая пространственно-временнбй
объем V, п? — внешняя нормаль к элементу поверхности й?з(х)
в точке х. Предположим, что функция ф(х) — решение уравнения
Дирака в форме волнового пакета
,^ «Ф(х) = О. (А.2)
Пусть функция F^(x'), входящая в (АЛ), равна К+(х — х')Х
X Tji'K*')' где х и х' — пространственно-временные точки внутри
объема. Тогда получим
/ £-, (К+ (х — хО т,Ф (х')) = (* dK+fx~X'} Ъ, + "iK+(x — х')\ ф(х'Н-
+ /Г+(х — х')
Второй член равен нулю, согласно уравнению (А.2). Тогда, под-
подставляя формулу (А.З) в формулу (АЛ) и учитывая, что
. дК+(х-х') ^^тК (Х_х') = — Й<*> (х —хО, (А.4)
получаем
ф (х) = — JK+ (х — хО ТAф (х') п* (хО do (x'), (A.5)
s
где п? — внешняя нормаль. С другой стороны, мы можем написать
ф (х) = fK+ (х — х') т,4- (х') п* (хО dz (хО. (А.6)
458 Глава 26
Устранение члена с <р из гамильтониана приводит тогда к контакт-
контактному члену
Эквивалентность псевдоскалярной и псевдовекторной связей может
быть наиболее ясно доказана с помощью преобразования Фолди
(Фолди [187], Вентцель [526], Бергер и др. [30]), в котором опе-
оператор 5 дается выражением
~ / &х^ (х) Тбф (*) агсЦ^У^-). B6.41)
S = ~ Ц)
С помощью этого канонического преобразования можно полностью
устранить псевдоскалярную связь. Однако член псевдовекторной
связи в этом случае появляется с нелинейным коэффициентом.
Наиболее общая форма теоремы эквивалентности была устано-
установлена в работе Молдауэра и Кейса [338], где показано, что в пер-
первом порядке по константе связи все возможные линейные взаимо-
взаимодействия между скалярными (или псевдоскалярными) мезонами и
нуклонами либо дают нуль, либо эквивалентны скалярной (псевдо-
(псевдоскалярной) связи.
Теорема эквивалентности в присутствии внешнего электромагнит-
электромагнитного поля была доказана в работах Кейса [80], Дрелла и Хенли
[123]. Чрезвычайно изящный способ вывода теоремы эквивалентности,
который использует произвольность выбора лагранжиана с точностью
до 4-мерной дивергенции, был дан в работе Келли [270].
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ. А
Здесь мы дадим несколько более строгий вывод формулы (8.54),
основанный на использовании теоремы Грина, которая в 4-простран-
стве имеет вид
(АЛ)
здесь 5 — поверхность, охватывающая пространственно-временной
объем V, пр — внешняя нормаль к элементу поверхности da (x)
в точке х. Предположим, что функция ф(х)— решение уравнения
Дирака в форме волнового пакета
Пусть функция F^(x'), входящая в (АЛ), равна К+(\ — х')Х
X ТцФ (х')> гДе х и х' — пространственно-временные точки внутри
объема. Тогда получим
i jp (К+ (х — х') ^ (х')) = (I dK+fx~X'} Г, + яАГ+(х — х')\ ф(х'Н-
— mif(x')\. (A.3)
Второй член равен нулю, согласно уравнению (А.2). Тогда, под-
подставляя формулу (А.З) в формулу (АЛ) и учитывая, что
. <ЦГ+(х-х0 T[i + пК+ (х _ х0 = _ д D) (Х _ ху (А 4)
получаем
(|)(x)=— I A'+(x— x') т^ОО л1Чх')rfo (*')• (A.5)
s
где «I1 — внешняя нормаль. С другой стороны, мы можем написать
')Л(хО. (А. 6)
460 Приложения
но теперь мы должны интерпретировать п? как внутреннюю нор-
нормаль. Если ф(х) — решение в форме волнового пакета, то вклад
в выражение (А.6) будут дазать только пространственно-подобные
поверхности, охватывающие объем V. Тогда выражения (А.6) и
(8.54) будут тождественны.
Аналогичный вывод годится и для уравнения Клейна—Гордона.
В этом случае теорема Грина (АЛ) записывается в форме
f
(A.7)
если предположить, что функция F^ равна
dQ дН
Выбрав функцию Н равной,/+(х — х') и функцию G равной бозон-
ной волновой функции J> (х), где точки х и х' лежат внутри обла-
области V, мы получим выражение (8.74), приведенное в тексте.
Аналогичное применение теоремы Грина в случае трех измерений
позволяет получить формулы для нерелятивистского случая [формулу
->■ ->■
(8.2)], если учесть, что в этом случае К (х2, t2; xv tt) = 0 при
ПРИЛОЖЕНИЕ Б
При выводе формулы A0.3) мы видели, что приращение плот-
плотности лагранжиана при вариации по переменной <р>- можно пред-
представить в виде
так что если мы имеем систему полей, удовлетворяющих уравнениям
движения A0.5), то приращение Ъ£? будет задаваться выражением
•■*-?£(&»•
Это выражение позволяет вывести законы сохранения, рассматривая
различные частные вариации переменной поля <рг.
Рассмотрим сначала случай, когда лагранжиан J3? не содержит
явно пространственно-временных координат, а вариация представляет
собой бесконечно малое смещение в пространстве-времени
х-»■ х + А.а = х', (Б.З)
при котором
Приложения 461
Тогда, оставляя только члены первого порядка по величине X, мы
получаем
(дч>'\ л
3?Дх)=(ж^=о = а,— срДх). (Б.5)
Аналогично при этой операции происходит приращение лагранжиана
(Б.6)
Тогда из формулы (Б.2) следует, что
Поскольку величина а* произвольна, то в формуле (Б.7) подразуме-
подразумевается, что
B?) т-^ = °- (Б-8>
dxv
Последнее выражение есть закон сохранения канонического тензора
энергии-импульса т£„. Таким же образом, как это было сделано в тексте
[формулы A0.34) — A0.36)], из соотношения (Б.8) может быть вы-
выведено постоянство во времени полной энергии и импульса полевой
системы. Отметим, что тензор энергии-импульса, получаемый из
формулы (Б.8), не должен быть симметричным.
Рассмотрение, аналогичное проведенному выше, может быть сде-
сделано, в случае, когда вариация переменной срг вызывается бесконечно,
малым преобразованием Лоренца
х' = ах
при котором вследствие линейности преобразования Лоренца
<рг(х)-»<р;(х')=2#(а)<р8(х). (Б. 10а)
Для случая бесконечно малого преобразования можно написать
Вг (а) яь §г ~~\~ "о" ~^br siiv- (Б. 1 Об)»
Лоренц-инвариантность лагранжиана означает, что он сохраняет при.
преобразовании Лоренца свой функциональный вид, т. е.
(х), ?Г; v_ (х)), (Б. 11 а)
или
). (Б. 11 б)
462 Приложения
Из соотношения (Б.2) тогда следует, что определенный тензор т' ■ ,
где
удовлетворяет уравнению
1? = °- (БЛЗ)
Белинфанте [27] показал, как переопределить канонический тен-
тензор энергии-импульса Т "" так, чтобы новый тензор Г" был всегда
симметричным и таким, чтобы
_^! = !!^ = 0. (Б. 14)
Кроме того, тензор момента количества движения определяется
из последнего тензора с помощью соотношения
ш^9=х9Тч? — х,Т„ (Б. 15)
я имеет следующее свойство:
_^Vvp = _^Vp = 0 (Б.16а)
дх9 дх?
•из которого вытекает
(Б.166)
Из выражения (Б.166) видно, что тензор т^? приводит к тем же
самым физическим следствиям, что и тензор »^vp) т. е. дает шесть
тех же самых констант движения.
Отметим, что если ср —скалярное поле, то Ь*У = 0, и из фор-
формул (Б.12) и (Б. 13) следует, что канонический тензор энергии-
импульса всегда симметричен.
Наконец, рассмотрим случай, когда лагранжиан J? описывает
комплексное поле. Поскольку лагранжиан _2" вещественен (эрмитов
в теории квантованных полей), то ясно, что в лагранжиане может
встречаться только комбинация <р*срг. Поэтому лагранжиан _2* является
инвариантом по отношению к преобразованию
?,. (Б. 17)
Приложения 463
где s — вещественная бесконечно малая константа.. Таким образом,
при преобразовании (Б.17)
8_2" = 0 (Б. 18)
(Б. 19а)
8ср; = — *£в; (Б. 196)
тогда из формулы (Б.2) следует, что
=0. (Б.206)
Последнее соотношение выражает собой закон сохранения заряда.
ЛИТЕРАТУРА
1. Abraham M., Becker R., Theorie der Electrizitat, Leipzig, 1933."
(Имеется перевод: А б р а г а м М., Б е к к е р Р., Теория электри-
электричества, изд. 2, M. — Л., 1939.)
2. Ахиезер A., Phys. Zs. Sowjetunion, 11, 263 A937).
3. Ахиезер А., Померанчук И., Phys. Zs. Sowjetunion, 11, 478 A937).
4. А м б а р ц у м я н В., Иваненко Д., Zs. f. Phys., 64, 563 A930).
5. Anderson C. D., Phys. Rev., 41, 405 A932).
6. Arnous E., Zienau S., Helv. Phys. Acta, 24, 279 A951).
7. Arnous E., Bleule г К., Helv. Phys. Acta, 25, 581 A952).
8. Arnous E., Helv. Phys. Acta, 25, 631 A952).
9. Arnous E., He i tier W., Proc. Roy. Soc, 220A, 290 A953).
10. Arnowitt R., Phys. Rev., 92, 1002 A953).
11. As hk in A., Ph. D. dissertation, Cornell University, 1952.
12. A s h k i n A., Page L. A., W о о d w а г d W. M., Phys. Rev., 94, 357 A954).
13. В a d e W. L., J e h 1 e H., Rev. Mod. Phys., 25, 714 A953).
14. В a ranger E. U., Phys. Rev., 93,1127L A954). (Имеется перевод в сбор-
сборнике „Проблемы современной физики", № 5, ИЛ, 1956.)
15. Bar anger E. U., Ph. D. dissertation, Cornell University, 1954.
16. Baranger M., Ph. D. dissertation, Cornell University, 1951.
17. Baranger M., Phys. Rev., 84, 866 A951).
18. Baranger M., В e t h e H. A., F e у n ra a n R. P., Phys. Rev., 92, 482 A953).
19. В a rgm ann V., Wigner E. P., Proc. Am. Acad. Arts. Sci., 34, 211 A948).
20. Bartlett J. H., Watson R. E., Phys. Rev., 56, 612 A939).
21. В a r 11 e 11 J. H., Watson R. E., Proc. Am. Acad. Arts. Sci., 74, 53 A940).
22. Bartlett J. H., Welt on T. A., Phys. Rev., 59, 281 A941).
23. В eard D. В., В e t h e H. A., Phys. Rev., 83, 1106 A951).
24. BeckerR., Gdttinger Nachrichten, 1945.
25. BeckerR., L e i b f r i e d O., Phys. Rev., 69, 34 A946).
26. Becker R., Leibfried O., Zs. f. Phys., 125, 347 A948).
27. В e 1 i n f a n t e F. J., Physica, 6, 887 A939).
28. Belinfante F. J., Physica, 7, 305 A940).
29. Belinfante F. J., Phys. Rev., 76, 226 A949).
30. В e r g e r J. M., F о 1 d у L. L., О s bo r n R. K., Phys. Rev., 87, 1061 A952).
31. Bethe H. A., Bacher R. F., Rev. Mod. Phys., "8, 82 A936). (Имеется
перевод: Бете Г., Б е ч е р Р., Физика ядра, т. I, Устойчивые состояния
ядер, Харьков, 1938.)
32. Bethe Н. А., О р р е п h e i га е г J. R., Phys. Rev., 70, 451 A946).
33. В е t h e H. A., Phys. Rev., 72, 339 A947). (Имеется перевод в сборнике
„Сдвиг уровней атомных электронов", ИЛ, 1950.)
34. В е t h e H. A., Report to the Eighth Solvay Congress on Elementary Par-
Particles, Solvay 1948.
35. Bethe H. A., Brown L. M., Stehn J. R., Phys. Rev., 77, 370 A950).
36. Bethe H. A., R о h r 1 i с h F., Phys. Rev., 86, 10 A952).
37. В h a b h a H. J., Proc. Roy. Soc, 154A, 195 A936).
38. Bhabha H. J., Rev. Mod. Phys., 21, 451 A949).
39. Bitter F., F e s h b а с h H., Phys. Rev., 92, 837L A953). (Имеется перевод
в сборнике „Проблемы современной физики", № 5, ИЛ, 1956.)
Литература 465
40. Blatt J. M., Weisskopf V., Theoretical Nuclear Physics, New York,
1952. (Имеется перевод: Блатт Дж., Вайскопф В., Теоретическая
ядерная физика, ИЛ, 1954.)
41. Bleuler К., Helv. Phys. Acta, 23, 567 A950).
42. В 1 о с h С, Kgl. Dansk. Vidensk. Selsk., Math.-Fys. Medd., 26, No. 1 A950).
43. В loch C, Kgl. Dansk. Vidensk. Selsk., Math.-Fys. Medd., 27, No. 8 A952).
44. В I о с h F., Phys. Zs. Sowjetunion, 5, 301 A934).
45. Bloch F., Nordsieck A., Phys. Rev., 52, 54 A937).
46. Bodmer A. R., Proc. Phys. Soc, 66A, 1041 A953).
47. Bohr N., RosenfeldL, Kgl. Dansk. Vidensk. Selsk., Math.-Fys. Medd.,
12, No. 8 A933).
48. Bohr N.. Rosenfeld L., Phys. Rev., 78, 794 A950).
49. Bopp F., Ann d. Phys., 38, 345 A940).
50. Bopp F., Ann d. Phys., 42, 573 A942/43).
51. Born M., Proc. Roy. Soc, 143A, 410 A934).
52. Born M., Infeld W., Proc. Roy. Soc, 144A, 425 A934).
53. Born M., Nature, 136, 952 A935).
54. Born M., Ann. Inst. Poincare, 7, 155 A937).
55. Born M., Proc. Roy. Soc, 165A, 291 A938).
56. Born M., Proc Roy. Soc, 166A, 552 A938).
57. Born M., Proc. Ind. Acad. Sci., 8, 309 A938).
58. Born M., Proc. Roy. Soc. (Edinburgh), 59, 219 A938).
59. Born M., Green H. S., Proc. Roy. Soc. (Edinburgh), 62, 470A949).
60. Born M., Rev. Mod. Phys., 21, 463 A949).
■61. BorowitzS, Kohn W., Phys. Rev., 76, 818 A949).
62. В о г о w i t z S., Kohn W., Phys. Rev., 86, 985 A952).
63. В о t h e W., Zs. f. Naturforsch., 4A, 88 A949).
64. В re it O., Phys. Rev., 72, 984L A947).
65. Breit Q., Phys. Rev., 73, 1410L A948).
«6. Breit O., Phys. Rev., 74, 656 A948).
«7. Brown О. Ё., Raven hall D. Q., Proc. Roy. Soc, 208A, 552 A951).
68. Brown G. E., Proc. Roy. Soc, 215A, 371 A952).
69. Brown O. E., Woodward J. В., Proc. Phys. Soc, 65A, 977 A952).
70. Brown Q. E., Peierls R. E., Woodward J. В., Proc. Roy. Soc,
227A, 51 A954).
71. Brown L. M., Feynman R. P., Phys. Rev., 85, 231 A952).
72. Buechner W. W., Burrill A. E., Sperduto A., V a n de О г a a f f
R. J., Feshbach H., Phys. Rev., 72, 678 A947).
73. Burton W. K., Touschek B. F., Phil. Mag., 44, 161 A953).
74. Burton W. K., Touschek B. F., Phil. Mag., 44, 1180 A953).
75. Ca i a n i e 11 о E. R., F u b i n i S., Nuovo Cimento, 9, 1218 A952).
76. Ca i a n i e 11 о Е. R., Nuovo Cimento, 10, 1634 A953).
77. С ai a niello E. R., Nuovo Cimento, 11, 492 A954).
78. Case К. М., Phys. Rev., 74, 1884L A948).
79. Case K. M., Phys, Rev., 76, 1 A949).
80. Case К. М., Phys. Rev., 76, 14 A949).
81. Chew O., Proceedings of the Third Rochester Conference on High Energy
Nuolear Physics, New York, 1952.
82. С h г ё t i e n M., P e i e r I s R. E., Nuovo Cimento, 10, 668 A953).
83. Chretien M., P e i e r 1 s R. E., Proc Roy. Soc, 223A, 468 A954).
84. С in i M., Nuovo Cimento, 9, 1025L A953).
85. С oe s t e r F., J a u с h J. M., Phys. Rev., 78, 149 A950).
86. Coester F., Phys. Rev., 95, 1318 A954).
87. Cohen S., Ph. D. dissertation, Cornell University, 1954.
88. С о n v e r s i M., P a n с i n i E., P i с с i о n i O., Phys. Rev., 71, 209L A947).
89. Cooper L. N., H e n 1 e у Е. M., Phys. Rev., 92, 801 A953). (Имеется
перевод в сборнике „Проблемы современной физики", № 5, ИЛ, 1956.)
466 ■ ' • Литература
90. С о г i n a I d e s i E., J о s t R., Helv. Phys. Acta, 21Д183 A948).
91. Corinaldesi E., Nuovo Cimento, 8, 494 A951). "
92. Corinaldesi E., Nuovo Cimento, Suppl., 10, No. 2, 83 A953). '
93. Corson E. M., Perturbation Methods in Quantum Mechanics of n-Electron
System, New York, 1951.
94. Cutkosky R. E., Phys. Rev., 96, 1135 A954).
95. Dal itz R. H., Proc. Roy. Soc, 206A, 509 A951).
96. Dalit z R. H., Proc. Roy. Soc, 206A, 521 A951).
97. D a n с of f S. M., Phys. Rev., 78, 382 A950).
98. Darwin С. О., Proc. Roy. Soc, 118A, 654 A928).
99. Delbrflck M., Zs. f. Phys., 84, 144 A933).
100. D e u t s с h M., Phys. Rev., 82, 455L A951).
101. D e u ts с h M., D u I i t E., Phys. Rev., 84, 601L A951).
102. Dirac P. A. M., Proc. Roy. Soc, 117A, 610 A928).
103. DiracP. A. M., Proc. Roy. Soc, 126A, 360 A930).
104. Dirac P. A. M., Proc. Roy. Soc, 136A, 453 A932).
105. Дирак П. A. M., Фок В., Подольский Б., Phys. Zs. Sowjetunion
2, 468 A932).
106. D irac P. A. M., Rapports du 7e Conseil Solvay 1933, Brussels, 1934.
107. D irac P. A. M., Proc Cambr. Phil. Soc, 30, 150 A934).
108. Dirac P. A. M., The Principles of Quantum Mechanics, 2nd ed., Oxford,
1935. (Имеется перевод: Дирак П. А. М, Основы квантовой меха-
механики, изд. 2, М. —Л., 1937.)
109. Dirac P. A. M., Proc. Roy. Soc, 155A, 447 A936).
ПО. Dirac P. A. M., Prop. Roy. Soc, 167A, 148 A938).
111. D irac P. A. M., Ann. Inst. Poincare, 9, 13 A938).
112. Dirac P. A. M., Proc. Roy. Soc, 180A, 1 A942).
113. Dirac P. A. M., P e i e r I s R. E., Pryce M. H. L., Proc. Cambr. Phil.
Soc, 38, 193 A942).
114. Dirac P. A. M., Comra. Dublin Inst for Advanced Studies, A, No. 1 A943).
115. Dirac P. A. M., The Principles of Quantum Mechanics, 3rd ed., Oxford,
1947.
116. Dirac P. A. M., Phys. Rev., 73, 1092 A948).
117. Dirac P. A. M., Ann. Insf. Poincare, 11, 15 A949).
118. Dirac P. A. M., Proc. Roy. Soc, 209A, 291 A951).
119. Dirac P. A. M., Ann. Inst. Poincare, 13, 1 A952).
120. Dirac P. A. M., Proc. Roy. Soc, 212A, 330 A952).
121. Dirac P. A. M., Proc. Roy. Soc, 223A, 438 A954).
122. Drell S. D., Phys. Rev., 79, 220 A950).
123. Drell S. D., Henley E. M., Phys. Rev., 88, 1053A952).
124. D uf f i n R., Phys. Rev., 77, 242 A950).
125. Dyson F. I, Phys. Rev., 73, 929 A948).
126. Dyson F. J., Phys. Rev., 75, 486 A949). (Имеется перевод в сборнике
„Сдвиг уровней атомных электронов", ИЛ, 1950.)
127. Dyson F. J., Phys. Rev., 75, 1736 A949). (Имеется перевод в сборнике
„Новейшее развитие квантовой электродинамики", ИЛ, 1954,^стр. 205.)
128. Dyson F. J., Phys. Rev., 77, 420 A950).
129. Dyson F. J., Advanced Quantum Mechanics, Cornell University, 1951.
130. Dyson F. J., Phys. Rev., 82, 428 A951).
131. Dyson F. J., Phys. Rev., 83, 608 A951).
132. Dyson F. J., Proc Roy. Soc, 207A, 395 A951).
133. Dyson F. J., Phys. Rev., 83, 1207 A951).
134. Dyson F. J., Phys. Rev., 85, 631 A952).
135. Dyson F. J., Phys. Rev., 91, 1543 A953).
136. Eddington A., Proc. Cambr. Phil. Soc, 35, 186 A939).
137. Eddington A., Proc. Cambr. Phil. Soc, 38, 201 A942).
138. Eden R. J., Proc. Roy. Soc, 210A, 388 A952).
Литература 467
139. Eden R. J., Proc. Roy. Soc, 215A, 133 A952).
140. Eden R. J., Proc. Roy. Soc, 217A, 390 A953).
141. Eden R. J., Rickayzen Q., Proc. Roy. Soc, 219A, 109A953).
142. Eden R. J., Proc. Roy. Soc, 219A, 516 A953).
143. Eden R. J., Proc. Cambr. Phil. Soc, 50, 592 A954).
144. Edwards S. F., Phys. Rev., 90, 284 A953). (Имеется перевод в сбор-
сборнике „Новейшее развитие квантовой электродинамики", ИЛ, 1954,.
стр. 378.)
145. Е d wars S. F., Peierls R. E., Proc Roy. Soc, 224A, 24 A954).
(Имеется перевод в сборнике „Проблемы современной физики", № 3„
ИЛ, 1955, стр 112.)
146. Е 1 i ezer С. J., Rev. Mod. Phys., 19, 147 A947).
147. Enatsu H., Progr. Theor. Phys., 6, 643 A951).
148. Epstein S. Т., Phys. Rev., 73, 177L A948); Phys. Rev., 73, 630L A948).
149. Euler H., К о с k e 1 В., Naturwiss., 23, 246 ,A935).
150. Euler H., Ann. d. Phys., 26, 398 A936).
151. Feingold A. M., Rev. Mod. Phys., 23, 10 A951).
152. F el dm an D., Phys. Rev., 76, 1369 A949).
153. Fermi E., Atti. Accad. Lincei., 9, 881 A929).
154. Fermi E., Atti. Accad. Lincei., 12, 431 A930).
155. Fermi E., Rev. Mod. Phys., 4, 87 A932).
156. Fermi E., Zs. f. Phys., 88, 161 A934).
157. Ferretti В., Nuovo Cimento, 7, 79 A950).
158. Ferretti В., Nuovo Cimento, 7, 375 A950).
159. Ferretti В., Nuovo Cimento, 7, 783 A950).
160. Ferretti В., Nuovo Cimento, 7, 899 A950).
161. Ferretti В., Nuovo Cimento, 8, 108 A951).
162. Ferretti В., Nuovo Cimento, 10, 1079 A953).
163. Feshbach H., Phys. Rev., 84, 1206 A951).
164. Feshbach H., Phys. Rev., 88, 295 A952).
165. Feynman R. P., Phys. Rev., 74, 939 A948).
166. Feynman R. P., Phys. Rev., 76, 1430 A948).
167. Feynman R. P., Rev. Mod. Phys., 20,367 A948).
168. Feynman R. P., Phys. Rev., 76, 749A949). (Имеется переводе сборнике
„Новейшее развитие квантовой электродинамики", ИЛ, 1954, стр. 138).
169. Feynman R. P., Phys. Rev., 76, 769 A949). (Имеется перевод в сборнике
„Новейшее развитие квантовой электродинамики", ИЛ, 1954, стр. 161.)
170. Feynman R. P., Phys. Rev., 80, 440 A950).
171. F е у n m a n R. P., Phys. Rev., 84, 108 A951). (Имеется перевод в сборнике
„Проблемы современной физики", № 3, ИЛ, 1955.)
172. Fierz M., Helv. Phys. Acta, 12, 3 A939).
173. Fierz M., Pauli W., Proc. Roy. Soc, 173A, 211 A939).
174. Fierz M., Phys. Rev., 78, 184L A950).
175. Fierz M., Helv. Phys. Acta, 23, 412 A950).
176. Fierz M., Helv. Phys. Acta, 23, 731 A950). (Имеется перевода сборнике
„Новейшее развитие квантовой электродинамики", ИЛ, 1954, стр. 239.)
177. Finkelstein R. J., Phys. Rev., 75, 1079 A949).
178. Finkelstein R. J., LeLevierR., RudermanM., Phys. Rev., 83,
326 A951).
179. F i t с h .V. URainwaterJ., Phys. Rev., 92, 789 A953).
180. Фок В. (не опубликовано).
181. Фок В., Zs. f. Phys., 38, 242 A926).
182. Фок В., Zs. f. Phys., 39, 226 A926).
183. Фок В., Zs. f. Phys., 75, 622 A932).
184. Фок В., Compt. Rend. (СССР), 1, 267 A933).
185. Фок В., Phys. Zs. Sowjetunion, 6, 425 A934).
186. Foldy L. L., Wouthuysen S. A., Phys. Rev., 78, 29 A950).
468 • Литература
187. Fold у L. L, Phys. Rev., 84, 168 A951).
188. Frank R. M., Phys. Rev., 83, 1189 A951).
189. Freese E., Zs. f. Naturforsch., 8a, 776 A953).
.190. Freese E., Nuovo Ciraento, 11, 312 A954).
191. French J. В., Weiss ко pf V., Phys. Rev., 75, 1240 A949). (Имеется
перевод в сборнике „Сдвиг уровней атомных электронов", ИЛ, 1950.)
192. Friedrichs К. О., Comm. on Pure and App. Math., 1, 361 A948).
193. Fukuda H., Miyamoto Y., Tomonaga S., Progr. Theor. Phys., 4,47,
121 A949).
194. Fukuda H., Miyamoto Y., Progr. Theor. Phys., 4, 347 A949).
195. Fukuda H., Miyamoto Y., Progr. Theor. Phys., 4, 392 A949).
196. Fukuda H., HayakawaS., Miyamoto Y., Progr. Theor. Phys., 5,
283 A950).
197. Fukuda H., HayakawaS., Miyamoto Y., Progr. Theor. Phys., 5,
352 A950).
198. Fulton Т., Karplus R., Phys. Rev., 93, 1109 A954).
199. Fulton Т., Martin P. C, Phys. Rev., 93, 903 A954).
200. Furry W. H., Phys. Rev., 51, 125 A937).
201. Furry W. H., Phys. Rev., 54, 56 A938).
202. Furry W. H., Phys. Rev., 81, 115 A951).
203. О ell-Mann M., Low F.. Phys. Rev., 84, 350 A951).
204. Q ell-Mann M., Qoldberger M. L., Phys. Rev., 87, 218A A952).
205. Oell-Mann M., О о 1 d b e r g e r M. L., Phys. Rev., 91, 398 A953).
206. Oell-Mann M., Ooldberger M. L., T h i r r i n g W., Phys. Rev., 95,
1612 A954).
207. Oell-Mann M., Low F., Phys. Rev., 95, 1300 A954). (Имеется перевод
в сборнике „Проблемы современной физики", № 3, ИЛ, 1955,стр. 145.)
208. О 1 a s e r W,, Zimmerman W, Zs. f. Phys., 134, 346 A952).
209. Goldstein J. S., Phys. Rev., 91, 1516 A953).
210. Gordon W., Zs. f. Phys., 40, 117 A926).
211. Gordon W., Zs. f. Phys., 48, 11 A928).
212. Goursat E., Hedrick E. R., A Course in Mathematical Analysis, 1,
Boston, 1904.
'213. Green H. S., Proc. Roy. Soc, 197A, 73 A949).
214. G unther M., Phys. Rev., 88, 1411 A952).
215. G п n t h e r M., Phys. Rev., 94, 1347 A954).
216. Gupta S. N., Proc. Phys. Soc, 63A, 681 A950).
217. Gupta S. N.. Phys. Rev., 77, 294L A950).
218. Gupta S. N.. Proc. Phys. Soc, 64A, 426 A951).
219. Hal pern O., Phys. Rev., 44, 855 A934).
220. H aris h-Chand ra, Proc Roy. Soc, 192A, 195 A948).
221. Hay as hi С, М u n a k a t a Y., Progr. Theor. Phys., 7, 481; 8, 142A952).
222. Hei sen berg VV., P a u 1 i W., Zs. f. Phys., 56, 1 A929).
223. H e i s e n b e r g W., Zs. f. Phys., 65, 4 A930).
224. Hei sen berg W., The Physical Principles of Quantum Theory, Chicago,
1930. (Имеется перевод: Гейзенберг В., Физические принципы
квантовой теории, М. —- Л., 1932.)
225. Не is en berg W., Zs. f. Phys., 90, 209 A934).
226. Hei sen berg W., Zs. f. Phys., 92, 692 A934); 98, 714 A936).
227. Hei sen berg VV., Leipziger Ber., 86, 317 A934).
228. Heisenberg W., Euler H., Zs. f. Phys., 98, 714 A936).
229. Heisenberg W., Ann. d. Phys., 32, 20 A938).
230. Heisenberg W., Zs. f. Phys., 120, 513 A943).
231. Heisenberg W., Zs. f. Phys., 120, 673 A943).
232. Hei tier W., The Quantum Theory of Radiation, 2nd ed., Oxford, 1944.
(Имеется перевод: Гайтлер В., Квантовая теория излучения,
М. —Л., 1940).
Литература 469
233. Hill E. L, Rev. Mod. Phys., 23, 253 A951).
234. Hofstadter R, Fechter H. R., M с 1 n t у г e J. A., Phys. Rev., 92,
978 A953).
235. Hofstadter R., H a h n В., К n u d s e n A. W., M с I n t у г е J. A.,
Phys. Rev., 95, 512 A954). (Имеется перевод в сборнике „Проблемы
современной физики", № 5, ИЛ, 1956.)
236. Hori S., Progr. Theor. Phys., 8, 569 A952).
237. Huff L. D., Phys. Rev., 38, 501 A931).
238. Hurst С A., Phys. Rev., 85, 920L A952).
239. Hurst С A., Proc. Roy. Soc, 214A, 44 A952).
240. Hurst C. A., Proc. Cambr. Phil. Soc, 48, 625 A952).
241. J a n с о v i с i В. Q., Phys. Rev., 95, 389 A954).
242. J a u с h J. M., R о h г 1 i с h F., Helv. Phys. Acta, 27, 613 A954).
243. Jean M., Compt. Rend., 232, 1183 A951).
244. Jean M., Compt. Rend., 232, 1291 A951).
245. Jean M., Ann. d. Phys., 8, 338 A953).
246. Johnson M. H., Lippraann B. A., Phys. Rev., 76, 828 A949).
247. Jordan P., К I e i n O., Zs. f. Phys., 45, 751 A927).
248. Jordan P., P a u 1 i W., Zs. f. Phys., 47, 151 A928).
249. Jordan P., Wigner E. P., Zs. f. Phys., 47, 631 A928).
250. Jost R., Phys. Rev., 72, 815 A917).
251. Jost R., Helv. Phys. Acta, 20, 256 A947).
252. Jost R, Luttinger J. M., Helv. Phys. Acta, 23, 201 A950).
253. Jost R., L u 11 i n g e г J. M., S 1 о t n i с k M., Phys. Rev., 80, 189 A950).
254. Kail en Q., Helv. Phys. Acta, 22, 637 A949).
255. Kallen O., Ark. f. Phys., 2, No. 37, 371 A950).
256. Kallen O., Helv. Phys. Acta, 25, 417 A952).
257. Kallen O., Kgl. Dansk. Vidensk. Selsk., Matti.-Fys. Medd., 27, No. 12
A953).
258. Kallen O., Helv. Phys. Acta, 26, 755 A953).
259. Kallen O., Physica, 19, 850 A953).
260. Kallen O., Nuovo Cimento, 12, 217 A954).
261. KanesawaS., Tomonaga S., Progr. Theor. Phys., 3, 1 A948).
262. Kanesawa S., Tomonaga S., Progr. Theor. Phys., 3, 101 A948).
263. Karplus R., К roll N. M., Phys. Rev., 77, 536 A950).
264. Karplus R., Neuman M., Phys. Rev., 80, 380 A950).
265. Karplus R., Neuman M., Phys. Rev., 83, 776 A951).
266. Karplus R., Klein A., Phys. Rev., 86, 257L A952).
267. Karplus R., Klein A., Phys. Rev., 85, 972 A952). (Имеется перевод
в сборнике „Новейшее развитие квантовой электродинамики", ИЛ,
1954, стр. 284.)
268. Karplus R., Klein A., S с h w i n g e r J., Phys. Rev., 86, 288^ A952).
(Имеется перевод в сборнике „Новейшее раззитие л квантовой элек-
электродинамики", ИЛ, 1954, стр. 305.)
269. Karplus R., Klein A., Phys. Rev., 87, 848 A952).
270. Kelly E. J., Phys. Rev., 79, 399 A950).
271. Kemmer N.. Helv. Phys. Acta, 10, 112 A937).
272. Kemmer N.. L u d w i g O., Helv. Phys. Acta, 10, 182 A937).
273. Kinoshita Т., Progr. Theor. Phys., 5, 473 A950).
274. Kinoshita Т., N a m b u Y., Progr. Theor. Phys., 5, 749 A950).
275. Kit a H., Progr. Theor. Phys., 7, 217 A952).
276. Kita H., Progr. Theor. Phys., 10, 231 A953).
277. Klein O., Zs. f. Phys., 41, 407 A927).
278. Klein O., N i s h i n a Y., Zs. f. Phys., 52, 853 A929).
279. Koba Z., Tati Т., Tomonaga S., Progr. Theor. Phys., 2, 101 A947).
280. Ко ba Z., Tat i Т., Тот onaga S., Progr. Theor. Phys., 2, 198 A947).
281. Koba Z., Progr. Theor. Phys., 4, 319 A949).
470 " Литература
282. К о е n i g S. Н., Р г о d e 11 А. О., К u s с h P., Phys. Rev., 88, 191 A952).
283. Konopinski E. J., U h 1 е n b е с к О. Е., Phys. Rev., 48, 7 A935).
284. Konopinski E. J., U h 1 e n b e с к G. E., Phys. Rev., 48, 107L A935).
285. Konopinski E. J., Rev. Mod. Phys., 15,209A943).
286. Konopinski E. J., Langer L. M.,, Annual Review of Nuclear Science,
2, Stanford, 1953.
287. Kramers H. A., Proc. Kgl. Ned. Acad. Wet., 40, 814 A937).
288. Kramers H. A., Quantentheorie des Elektrons und der Strahlung, Lei-
Leipzig, 1938.
289. Kramers H. A.. Bel infante F. J., LubanskI J. K., Physica, 8,
597 A941).
290. Kramers H. A., Rapports du 8e Conseil Solvay 1948, Brussels, 1950,
p. 241. .
291. Kris tensen P., Miller C, Kg!. Dansk. Vidensk. Selsk., Math.-Fys.
Medd., 27, No. 7 A952).
292. К roll N. M., Lamb W. E., Phys. Rev., 75, 388 A949).
293. Кто 11 N. M., Phys. Rev., 75, 1321A A949).
294. К roll N. M., Pollock F., Phys. Rev., 86, 876 A952),
295. Lamb W. E., Retherford R. C, Phys. Rev., 72, 241 A947).
(Имеется перевод в сборнике „Сдвиг уравнений атомных электронов".
ИЛ, 1950.)
296. L a n d ё A., Phys. Rev., 60, 121 A941).
297. L a n d ё A., Thomas L., Phys. Rev., 60, 514 A941).
298. Lande A,, Thomas L., Phys. Rev., 65, 175 A944).
299. L a t t e s С M. G., Occhialini С P. S., P о w e 11 С F., Nature, 160,
453, 486 A947).
300. Lax M., Phys. Rev., 78, 306 A950).
301. Lehmann H., Nuovo Cimento, 11, 342 A954). (Имеется перевод в
сборнике „Проблемы современной физики", № 3, ИЛ, 1955, стр. 133.).
302. Lepore J. V., Phys. Rev., 88, 750 A952).
303. Levy M. M., Phys. Rev., 88, 72 A952).
304. Levy M. M., Phys. Rev., 88, 725 A952).
305. Lewis H. W., Phys. Rev., 73, 173 A948).
306. Lipkin H. J., Phys. Rev., 85, 517 A952).
307. Lippmann B. A., Schwinger J., Phys. Rev., 79, 469 A950).
308. Lopes L., An. Acad. Brazil. Ciena, 23, 39 A951).
309. Lorentz H. A., The Theory of Electrons, Leipzig, 1916. (Имеется пере-
перевод: Лорентц Г., Теория электронов, М.—Л., 1934.)
310. Lorentz H. A., The Collected Pepers of Lorentz, Hague, 1937.
311. Low F., Phys. Rev., 88, 53 A952).
312. Luttinger J. M., Phys. Rev., 74, 893 A948). (Имеется переводе сбор-
сборнике „Сдвиг уровней атомных электронов"., ИЛ, 1950.)
313. L a 11 i n g e r J. M., Phys. Rev., 75, 309L A949).
314. Luttinger J. M., Phys. Rev., 75, 1277L A949).
315. L у m a n E. M., Hanson A. O., ScottM.B., Phys. Rev., 84, 626 A951).
316. M с К i n 1 e у W. A., F e s h b а с h H., Phys. Rev., 74, 1759 A948).
317. McManus H., Proc. Roy. Soc, 195A, 323 A948).
318. MaS. Т., Phys. Rev., 75, 535 A949).
319. Majorana E., Nuovo Cimento, 14, 171 A937).
320. March A., Zs. f. Phys., 104, 93 A936).
321. March A., Zs. f. Phys., 104, 161 A936).
322. March A., Zs. f. Phys., 105, 620 A937).
323. March A., Zs. f. Phys., 106, 49 A937).
324. March A., Zs. f. Phys., 106, 291 A937).
325. M a s s e у H. S; W., С о r b e n H. C, Proc. Carabr. Phil. Soc, 35, 463
A939).
326. Matthews P. Т., Phys. Rev., 75, 1270 A949).
Литература . 471
327. Ma t thews P. Т., Phys. Rev., 76, 684L, 1419L A949).
•328. Matthews P. Т., Phys. Rev., 80, 292 A950).
329. Matthews P. Т., Phil. Mag., 42, 221 A951).
■330. Matthews P. Т., Phys. Rev., 81, 936 A951).
331. Matthews P. Т., Sal am A., Phys. Rev., 86, 715 A952).
■332. Matthews P. Т., Sal am A., Proc. Roy. Soc, 221 A, 128 A954).
333. Matthews P. Т., S a 1 a m A., Phys. Rev., 94, 185 A954).
•334. Michel L., Proc. Phys. Soc, 63A, 514 A950).
■335. Michel L., Nuovo Cimento, 10, 319 A953).
■336. Mie O., Ann. d. Phys., 85, 711 A928).
.337. Mitra A., Nature, 169, 1009 A952).
•338. Moldauer P., Case К. М., Phys. Rev., 91, 459A A953).
•339. Miller C, Zs. f. Phys., 70, 786 A931).
340. Miller C, Ann. d. Phys., 14, 531 A932).
•341. Miller C, Kgl. Dansk. Vidensk. Selsk., Math.-Fys. Medd., 23, No. 1
A945).
•342. M Ф11 e г С, Kgl. Dansk. Vidensk., Selsk. Math.-Fys. Medd., 26, No. 19
A946).
-343. Miller C, Comm. Dublin Inst. for Advanced Studies, 4, No. 5 A948).
•344. Miller C, Ann. Inst. Poincare, 11, 251 A949).
345. Mott N. F., Proc. Roy. Soc, 124A, 425 A929).
346. Mott N. F., Proc. Roy. Soc, 135A, 429 A932).
■347. Mott N.F, Sneddon I.N., Wave Mechanics and its Application, Oxford,
1948.
-348. Mott N. F., M a s s e у Н. S. W., Theory of Atomic Collisions, 2nd ed.,
Oxford, 1949. (Имеется перевод: Мотт Н. и Месси Г., Теория атом-
атомных столкновений, М. — Л., ИЛ, 1951.)
•349. Nafe J. E., Nelson E. В., R a b i I. I., Phys. Rev., 71, 914 A947).
(Имеется перевод в сборнике „Сдвиг уровней атомных электронов",
ИЛ, 1950.)
-350. N a g I e D. E., Julian R. S., Zacharias J. R., Phys. Rev., 72, 971
A947).
351. Nambu Y., Progr. Theor. Phys., 5, 614 A950).
352. Nambu Y., Progr. Theor. Phys., 7, 131 A952).
-353. Nelson E. C, Phys. Rev., 60, 830 A941).
354. Ne um an M., Furry W. H., Phys. Rev., 76, 1677 A949).
355. Newton R. Q., Ph. D. dissertation, Harvard University, 1953.
356. Newton T. D., Wigner E. P., Rev. Mod. Phys., 21, 400 A949).
357. N i s h i j i m a K., Progr. Theor. Phys., 10, 549 A953).
358. N i s h i n a Y., Zs. f. Phys., 52, 869 A929).
359. Oppenheimer J. R., Phys. Rev., 35, 461 A930).
360. Oppenheimer J. R., Phys. Rev., 35, 939 A930).
361. О s b о r n R. K., Phys. Rev., 86, 340 A952).
362. Page L. A., Ph. D. dissertation, Cornell University, 1950.
-— - L. A., Phys. Rev., 81, 1062L A951).
A., Verh. Kgl. Acad. (Amsterdam), 19 A947).
A., Epstein S. Т., Rev. Mod. Phys., 21, 445 A949).
A., Uhlenbeck G. E., Phys. Rev., 79, 145 A950).
A., Jost R., Phys. Rev., 87, 871 A952).
i W., Enz. der Math. Wiss., 5, 539 A921). (Имеется перевод:
Паули В., Релятивистская теория элементарных частиц, ИЛ, 1947.)
369. Pa uli W., Zs. f. Phys., 43, 601 A927).
•370. P a u 1 i W., Handbuch der Physik, Bd. 24, 1, Berlin, 1933. (Имеется пере-
перевод: Паули В., Общие принципы волновой механики, М. — Л., 1948.)
371. Pa uli W., Weisskopf V., Helv. Phys. Acta, 7, 709 A934).
.372. Pa uli W., Zeeman Verhandlungen, Hague, 1935, S. 31.
-373. Pa uli W., Ann. Inst. Poincare, 6, 137 A936).
.363. P
364. P
-365. P
366. P
367. P
368. P
a
a
a
a
a
a
ge
i s
is
is
is
uli
472 Литература
374. Р a u 1 i W., Ann. Inst. Poincare, 6, 196 A936).
375. P a u 1 i W., F i e г z M., Nuovo Cimento, 15, 167 A938).
376. Pauli W., Phys. Rev., 58, 716 A940).
377. Pauli W., В el infante F. J., Physica, 7, 177 A940).
378. Pauli W., Rev. Mod. Phys., 13, 203 A941).
379. Pauli W., Rev. Mod. Phys., 15, 175 A943).
38a Pauli W., Villars F., Rev. Mod. Phys., 21, 434 A949). (Имеется
перевод в сборнике „Сдвиг уровней атомных электронов", ИЛ 1950)
381. Pauli W., Progr. Theor. Phys., 5, 526 A950).
382. Pauli W., Nuovo Cimento, 10, 648 A953).
383. P e i e г 1 s R. E., M с M a n u s H., Phys. Rev., 70, 795A A948).
384. Peierls R. E., Proc. Roy. Soc, 214A, 143 A952).
385. P e t e г m a n n M. A., Helv. Phys. Acta, 26, 291 A953).
386. Petermann M. A., Archives des Sciences Physiques et Naturelles
(Geneve), 6, 5 A953).
387. P i d d R. W., H a m m e r C. L., R a k a E. C, Phys. Rev., 92, 436 A953).
(Имеется перевод в сборнике „Проблемы современной физики", № 5,
ИЛ, 1956.)
388. Pirenne J., Helv. Phys. Acta, 21, 226 A948).
389. Pirenne J., Physica, 15, 1023 A949).
390. Pirenne J., Phys. Rev., 86, 395 A952).
391. P о d о 1 s k у В., см. Д и р а к П. А. М., Фок В, Подольский Б.
Phys. Zs. Sowjetunion, 468 A932).
392. Poincare H., Compt. Rend., 40, 1504 A905).
393. Poincare H., Rend. Palermo, 21 A906).
394. Poincare H., La Mechanique Nouvelle, Paris, 1924.
395. P о n d T. A., D i с k e R. H., Phys. Rev., 85, 489L A952).
396. Pro с a A. L., Journ. Phys. et radium., 7, 347 A936).
397. Pryce M. H. L., Proc. Roy. Soc, 195A, 62 A948).
398. R a b i I. I., Zs. f. Phys., 49, 507 A928).
399. Racah G., Nuovo Cimento, 14, 322 A937).
400. Racah G., Phys. Rev., 70, 406 A946).
401. R a n d e 1 s R. В., С h а о К. Т., С г a n e H. R., Phys. Rev., 68, 64 A945).
402. Riddell R. J., Phys. Rev., 91, 1243 A953).
403. R i v i e r D., Helv. Phys. Acta, 22, 265 A949).
404. Rohrlich F., Phys. Rev., 77, 357 A950).
405. Rohrlich F., Phys. Rev., 80, 666 A950).
406. Rohrlich F., Glue k stern R. L., Phys. Rev., S6, 1 A952).
407. Rosen N., Phys. Rev., 55, 94 A939).
408. Rosen N., Menius A., Phys. Rev., 62, 436 A942).
409. Rosen N., Rosens toe k H. В., Phys. Rev., 85, 257 A952).
410. Rosenfeld L., Ann. Insf. Poincare, 2, 25 A931).
411. Rose nf el d L., Solomon J., Journ. phys. et radium., 2, 139 A931).
412. Rosenfeld L., Zs. f. Phys., 70, 454 A931).
413. Rosenfeld L., Memoires de l'Academie Royale de Belgique, 6, 30
A940).
414. Rossi В., High Energy Particles, New York, 1952. (Имеется перевод:
P о с с и Б., Частицы большой энергии, М., 1955.)
415. Sakata S., Progr. Theor. Phys., 2," 145 A947).
416. Sakata S., U m e z a w a H., Progr. Theor. Phys., 5, 682 A950).
417. S a 1 a m A., Phys. Rev., 79, 910 A950).
418. Salam A., Phys. Rev., 82, 217 A951).
419. Salam A., Phys. Rev., 84, 426 A951).
420. Salam A., Phys. Rev., 86, 731 A952).
421. Salam A., Matthews P. Т., Phys. Rev., 90, 690 A953). (Имеется
перевод в сборнике „Проблемы современной физики", № 3, ИЛ, 1-955,
стр. 122.)
Литература 473
422. Sai peter E. E., В e t h e H. A., Phys. Rev., 84, 1232 A951). (Имеется
перевод в сборнике „Новейшее развитие квантовой электродинамики",
' ИЛ, 1954, стр. 334.)
423. Salpeter E. E., Newcomb W. A., Phys. Rev., 87, 150 A952).
424. Salpeter E. E., Phys. Rev., 87, 328 A952). (Имеется перевод в сбор-
сборнике „Новейшее развитие квантовой электродинамики", ИЛ, 195*4,
стр. 352)
425. S а I р.е t е г Е. Е., Phys. Rev., 89, 92 A953).
426. Sato I., Sci. Rep. of Tohoku Univ., ser. 1, 34, 75 A950).
427. Saute г F., Zs. f. Phys., 69, 742 A931).
428. Schafroth R., Helv. Phys. Acta, 22, 392 A949).
429. Schiff L. I., Quantum Mechanics, New York, 1949. (Готовится русский
перевод 2-го издания.)
430. Schiff L. L, Phys. Rev., 92, 988 A953). (Имеется перевод в сборнике
„Проблемы современной физики", № 5, ИЛ, 1956.)
431. SchrOdinger E., Ann. d. Phys., 81, 109 A926).
432. Schwartz L., Theorie des Distributions, Actualites Scientifiques et
Industries, Nos. 1091, 1122, Paris, 1950/1951.
433. Schweber S. Ph. D. dissertation, Princeton University, 1952.
434. Schweber S., Phys. Rev., 94, 1089 A954).
435. Schweber S., Nuovo Cimento, 11 A955).
436. Sch winger J., Phys. Rev., 73, 416L A948).
437. Schwinger J., Weiss kopf V., Phys. Rev., 73, 1272A A948).
438. Schwinger J., Phys. Rev., 74 1439 A948). (Имеется перевод в сборнике
„Новейшее развитие квантовой электродинамики", ИЛ, 1954, стр. 12.)
439. Schwinger J., Phys. Rev., 75, 651 A949). (Имеется перевод в сборнике
„Новейшее развитие квантовой электродинамики", ИЛ, 1954, стр. 40.)
440. Schwinger J., Phys. Rev., 76, 790 A949). (Имеется перевод в сборнике
„Новейшее развитие квантовой электродинамики", ИЛ, 1954, стр. 78.)
441. Schwinger J., Phys. Rev., 82, 664 A951). (Имеется перевод в сборнике
„Новейшее развитие квантовой электродинамики", ИЛ, 1954, стр. 254.)
442. Sc h winger J., Proc. Am. Acad. Arts. Sci., 37, 452 A951). (Имеется
перевод в сборнике „Проблемы современной физики", № 3, ИЛ, 1955,
стр. 2&)
443. Schwinger J., Phys. Rev., 82,914 A951). (Имеется перевод в сборнике
„Новейшее развитие квантовой электродинамики", ИЛ, 1954, стр. 115.)
444. Schwinger J., Phys. Rev., 91, 713 A953). (Имеется перевод: Ш в и н-
гер Ю., Теория квантованных полей, М., 1956, гл. I.)
445. Schwinger J., Phys. Rev., 91, 728 A953). (Имеется перевод: Ш вин-
re р Ю., Теория квантованных полей, М., 1956, гл. II.)
446. Schwinger J., Phys. Rev., 92, 1283 A953). (Имеется перевод:
Ш вин гер Ю., Теория квантованных полей, М., 1956, гл. III.)
447. Schwinger J., Phil. Mag., 44, 1171 A953). (Имеется перевод: III в и н-
гер Ю., Теория квантованных полей, М., 1956, Приложение.)
448. Schwinger J., Phys. Rev., 93, 615 A954). (Имеется перевод: Ш вин-
re р Ю., Теория квантованных полей, М., 1956, гл. IV.)
449. Schwinger J., Phys. Rev., 94, 1362 A954). (Имеется перевод:
Ш в и н г е р Ю., Теория квантованных полей, М., 1956, гл. V.)
450. Scott М. В., Н a n s о п А. О., L у m a n E. M., Phys. Rev., 84, 638 A951).
451. Shall С. G., Chase С. Т., Meyers F. E., Phys. Rev., 63, 29 A943).
452. Smith J. H., Ph. D. dissertation, Cornell University, 1950.
453. Smith J. H., Phys. Rev., 95, 271 A954).
454. S n у d e r H. S., Weinberg J., Phys. Rev., 57, 307 A940).
455. Snyder H. S., Phys. Rev., 83, 1154 A951).
456. Sommerfeld A., Atombau und Spektrallinien, Bd. 2, 1931 — 1939.
(Имеется перевод: Зоммерфельд, Строение атома и спектры, т. 2,
М., 1957.)
31 Зак. 1784. Мезоны и поля
Литература
457. Stearns М., S t e a r n s M. В., D e В e n e d e 11 i S., Leipuner L,
Phys. Rev., 93, 1123L A954).
458. Stearns M., Phys. Rev., 95, 1353L A954).
459. Stearns J., Phys. Rev., 96, 804L A954).
460. Steinberger J., Phys. Rev., 76, 1180 (.1949).
461. Stuck el berg E. С G., Ann. d. Phys., 21, 367 A934).
462. Stiickelberg E. С G., Nature, 144, 118 A939).
463. Stuckelberg E. C. G., Helv. Phys. Acta, 14, 51 A941).
464. Stuckelberg E. C. G., Helv. Phys. Acta, 14, 321 A941).
465. Stuckelberg E. С G., Helv. Phys. Acta, 14, 588 A941).
466. Stuckelberg E. С G., Helv. Phys. Acta, 17, 43 A944).
467. Stuckelberg E. C. G., Nature, 153, 143 A944).
468. Stuckelberg E. C. G., Arch. Sci. Phys. et Naturelles (Geneve), 61,
155 A944).
469. Stuckelberg E. С G., Helv. Phys. Acta, 18, 21 A945).
470. Stuckelberg E. C. G., Helv. Phys. Acta, 18, 195 A945).
471. Stuckelberg E. C. G., Phys. Cambr. Conference Rep., 1947, p. 199.
472. S tuck el berg. E. C. G., RiVier D., Phys. Rev., 74, 218 A948).
473. Stuckelberg E. С G., R i vi er D., Phys. Rev., 74, 986 A948).
474. Stuckelberg E. С O., Rivief D., Helv. Phys. Acta, 22, 265 A949).
475. Stuckelberg E. C. G., Phys. Rev., 81, 130 A951).
476. S t й с к е 1 b e r g E. С. О., Green Т. A., Helv. Phys. Acta, 24, 153 A951).
477. T а к е d a G., Progr. Theor. Phys. (Japan), 7, 359 A952).
478. T а м м И., Zs. f. Phys., 62, 545 A930).
479. T а м м И., Journ. of. Phys. (СССР), 9, 449 A945).
480. Thirring W., Phil. Mag., 41, 1193 A950).
481. Thirring W., Helv. Phys. Acta, 26, 33 A953).
482. Thompson R., Ph. D. dissertation, Cornell University, 1950.
483. T i о m n о J., Wheeler J. A., Am. Sci., 37, April and July A949).
484. Titch marsh E. C, Introduction to the Theory of Fourier Integrals,
Oxford, 1937. (Имеется перевод: Титчмарш Е. Введение в теорию
интегралов Фурье, М., 1948.)
485. Toll J. S., Phys. Rev., 90, 372A A953).
486. Tomonaga S., Progr. Theor. Phys., 1, 27 A946). (Имеется перевод в сбор-
сборнике „Новейшее развитие квантовой электродинамики", ИЛ, 1954, стр. 1.)
487. Triebwasser S., D а у h о f f E. S., Lamb W. E., Phys. Rev., 89,
98 A953).
488. Ue h 1 i ng E. A., Phys. Rev., 48, 55 A935).
489. Umezawa H.,Kawabe R., Progr. Theor. Phys., 4, 420 A949).
490. Umezawa H., Kawabe R., Progr. Theor. Phys., 4, 423 A949).
491. Umezawa H., Kawabe R., Progr. Theor. Phys., 4, 443 A949).
492. Umezawa H., Kawabe R., Progr. Theor. Phys., 4, 461 A949).
493. Umezawa H., Kawabe R., Progr. Theor. Phys., 5, 266 A950).
494. Umezawa H., KamefuchiS., Progr. Theor. Phys., 6, 543 A951).
495. Utiyama R., Sunakawa S., Imamura Т., Progr. Theor. Phy;.,
8, 77 A952). (Имеется перевод в сборнике „Проблемы современной
физики", № 3, ИЛ, 1955, стр. 80.)
496. V а 1 a t i п J. G., Proc. Roy. Soc, 222A, 93 A954).
497. V a 1 a t i n J. G., Proc. Roy. Soc, 222A, 228 A954).
498. V a 1 a ti n J. G., Proc. Roy. Soc, 225A, 535 A954).
499. Va latin J. G., Proc. Roy. Soc, 226A, 254 A954).
500. Van de Graaff R. J., Buechner W. W., Feshbach H., Phys.
Rev., 69, 452 A946).
501. Van der Waerden B. L., Cottinger Nachrichten, 1929, S. 100.
502. Van der Waerden B. L., Die Gruppentheoretische Methode in der
Quantenmechanik, Berlin, 1932. (Имеется перевод: Ван дер Верден
Б., Метод теории групп в квантовой механике, Харьков — Киев, 1938.)
Литература 475
503. V.tliars F., Phys. Rev., 79, 122 A950).
504. V о 1 к о w D. M., Zs. f. Phys., 94, 250 A935).
505. Waller I., Zs. f. Phys., 62, 673 A930).
506. W ard J. C, Phys. Rev., 77, 293L A950).
507. Ward J. C, Phys. Rev:, 78, 182L A950).
508. Ward J. C, Proc. Phys. Soc, 64A, 54 A951).
509. Ward J. C, Phys. Rev., 84, 897 A951).
510. Wataghin G., Zs. f. Phys., 88, 92 A934).
511. Watson K. M., U. S. Atomic Energy Commission document, AEC-U,
2765, 1953.
512. Weiss P., Proc. Roy. Soc, 156A, 192 A936).
513. Weiss P., Proc. Roy. Soc, 169A, 102 A938).
514. Weiss P., Proc. Roy. Soc, 169A, 119 A938).
515. Weiss kopf V., Zs. f. Phys., 89, 27 A934).
516. Weiss ко pf V., Zs. f. Phys., 90, 817 A934).
517. Weiss kopf V., Kgl. Dansk. Vidensk. Selsk., Math.-Fys. Medd., 14,
' No. 6 A936).
518. W e i s s к о р f V., Phys. Rev., 56, 72 A939).
519. Weisskopf V., Rev. Mod. Phys., 21, 305 A949). (Имеется перевод в
сборнике „Сдвиг уровней атомных электронов", ИЛ, 1950.)
520. We It on T. A., Phys. Rev., 74, 1157 A948).
521. W е п е s е г J., В е г s о h n R., К г о 11 N. М., Phys. Rev., 91, 1257 A953).
522. W e n t z e 1 G., Zs. f. Phy?., 86, 479 A933).
523. W e n t z e 1 G., Zs. f. Phys., 87, 726 A934).
524. W e n t z e 1 G., Rev. Mod. Phys., 19, 1 A947).
525. Wentzel G., Quantum Theory of Fields, New York, 1949. (Имеется
перевод: Вентцель Г., Введение в квантовую теорию волновых по-
полей, М. — Л., 1947.)
526. Wentzel G., Phys. Rev., 86, 802 A952).
527. Weyl H., Gruppentheorie und Quantenmechanik, 2nd ed., Leipzig, 1931.
528. Wheeler J. A., Phys. Rev., 52, 1107 A937).
529. Wheeler J. A., F e у n m a n R. P., Rev. Mod. Phys., 17, 157 A945).
530. Wheeler J. A., F e у n m a n R. P., Rev. Mod. Phys., 21, 425 A949).
531. Wick G. C, Phys. Rev., 80, 268 A950). (Имеется'перевод в сборнике
„Новейшее развитие квантовой электродинамики", ИЛ, 1954, стр. 245.)
532. W i с k G. С, W i g h t m a n A. S., W i g n e r E. P., Phys. Rev., 88,101 A952).
533. Wick G. C, Phys. Rev., 96, 1124 A954).
534. Widder D. V., The Laplace Transform, Princeton, 1946.
535. Wight man A. S, Schweber S. S., Phys. Rev., 93, 812 A955).
536. Wigner E. P., G6ttinger Nachrichten, 31, 546 A932).
537. Wigner E. P., Annals of Mathematics, 40, 149 A939).
538. Wigner E. P., Zs. f. Phys., 124, 665 A947).
539. Wilson R. R., Phys. Rev., 90, 720L A953).
540. Wolfenstein L., R a v e n h a 11 D. G., Phys. Rev., 88, 279 A952).
541. Yang С N., Phys. Rev., 77, 242 A950).
542. Yang C. N.. F e 1 d m a n D., Phys. Rev., 79, 972 A950).
543. Y e n n i e D. R., W i 1 s о n R. N.. R a v e n h a 11 D. G., Phys. Rev., 92,
1325L A953).
544. Yennie D. R., R a v e n h a 11 D. G., Wilson R. N., Phys. Rev., 95,
500 A954). (Имеется перевод в сборнике „Проблемы современной
физики", № 5, ИЛ, 1956.)
545. Yukawa H., Proc Phys.-Math. Soc. Japan, 17, 48 A935).
546. Yukawa H., Phys. Rev., 76, 300 A949).
547. Yukawa H., Phys. Rev., 76, 1731 A949).
548. Yukawa H., Phys. Rev., 77, 219 A950).
549. Yukawa H., Phys. Rev., 77, 849 A950).
550. Zimmerman; W., Zs. f. Phys., 135, 473 A953).
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адиабатическая гипотеза 229—235
определение истинного ваку-
вакуума 419, 420
перенормировка волновой функ-
функции 323, 403
связанные состояния 234, 235,
408
S-матрица 230—235, 407, 408
Амплитуды вероятности, интерпрета-
. ция векторов состояний в теории
поля 162—164
уравнений Клейна—Гордона
22
— состояний частицы в одночастич-
ной теории 421
теории поля 161, 216, 422,
447
Аннигиляции оператор; см. Уничто-
Уничтожения оператор
Антикоммутации 'соотношения для
перенормированных операторов 432,
435
~ различных времен 211
совместность 168, 169
статистика Ферми — Дирака
165—168, 170
Антинуклон 181
Антисимметричные волновые функ-
функции, связь с квантованием полей
173—178
спин 168
статистика Ферма — Дирака
170
Античастицы 55, 56, 167, 171
Бета-распада теория, возможные виды
связи 141, 142
перенормируемость 374, 375
Бете — Салпетера уравнение; см. Ре-
Релятивистское волновое уравнение
для связанных состояний
вывод с помощью теории поля
437—447
граничные условия 444, 445
решения 445, 446
Бете — Салпетера уравнение, теория
Фейнмана 104
Бозе — Эйнштейна статистика, пере-
перестановочные соотношения Иор-
Иордана — Клейна 162
симметрия волновой функции
частицы 163
спин 168
Бозон; см. Частица со спином 0, ча-
частица со спином 1
— рассеяние на фермионе 184, 260
Борна — Инфельда теория 299
Борна приближение для кулоновского
рассеяния электронов 94—97
разложение S-матрицы 184, 287
теория рассеяния 64
Ь- расходимости 389—394
Вакуум, амплитуды 160, 261
— поляризация; см. Поляризация ва-
вакуума
— процессы 261, 266
Вектор состояния вакуума 161
для взаимодействующих по-
полей 418—420, 425, 426
свойства преобразований
161, 424, 426
скалярного поля 161, 203
— спинорного поля 169, 211
— — — электромагнитного поля 222
Вероятность перехода 66
Вершинная диаграмма 319, 358
— часть диаграммы 377
Вершинные поправки в квантовой
электродинамике 319, 321, 322, 386
мезонной теории 341
лэмбовский сдвиг 329—331
Вершинный оператор, отделение
бесконечной части в вершинном
операторе 321, 322, 386, 387,
398
Взаимодействие между бозонным и
фермионным полями 135—141
— —■ двумя фермионнымн полями,
141, 142
Предметный указатель
477
Взаимодействие между заряженным
полем и электромагнитным полем
145—147
— — полями, правила для диаграмм
Фейнмана 267, 275
уравнения поля 142—144
— — формализм Лагранжа 135—
142
— с электромагнитным полем 87—91,
145—147
— частиц Дирака с электромагнитным
полем 57—59
Клейна — Гордона с электро-
электромагнитным полем 23, 24
Взаимодействия представление для
системы полей мезон — нуклон
197—199, 246
квантовой электродинамики
244
полей 209—223
скалярного поля 201—209
определение 196—200
Вика теорема 240, 245
Водорода атом, лэмбовский сдвиг
309—316, 329—331, 353
уравнение Дирака 60, 61
уровни энергии 60
Волновая функция; см. также Век-
Вектор состояния
для частиц со спином @, у,, 1)
18, 27, 132, 373, 374
локализованная 23
— — перенормировка 323
полевой системы 153
Вычисление шпуров 72—74
Вычитательные процедуры в класси-
классической электродинамике 296
перенормировка теории 322,
384—394, 398
— — собственная энергия фермиона
317, 342, 384—394
Гамильтона принцип 118—120
Гамильтониан взаимодействия 181, 197
— — для вещественного скалярного
поля 124, 156, 160
взаимодействующих полей
144
■г- — — комплексного скалярного
поля 128, 163
— нерелятивистского лэмбов-
ского сдвига 310
— — —- поля со спином 2/г 131
■ — системы бозон — фермион
181, 197
частиц со спином L/2 29, 30
электромагнитного поля 133,
217, 218
Гамильтониан взаимодействия, кано-
канонические переменные 121, 122
— — определение из лагранжиана
плотность 122
формализм 121—123
Гамма-матрицы, свойства 34, 44, 45,
• 73, 171
Гейзенберговское представление 413,
414, 433—435
определение 150, 151
уравнения движения для опе-
операторов 151, 153, 154, 415
штрихованная функция распро-
распространения 427—432
Грина теорема 459, 460
— функции; см. Функция распро-
распространения, Инвариантные сингул-
лярные функции
— — для системы двух частиц
438—444
— частиц Дирака 80—82, 437
Клейна — Гордона 92, 93
интегральное представление 84,
246—251
— — нерелятивистского уравнения
Шредингера 75—79
Гупта формализм; см. Квантование
поля электромагнитного
Дайсона преобразование 451—456
Дальнодействие, электромагнитная
теория 298
Дельбрюка рассеяние 362—364
Диаграммы; см. также Фейнмана
диаграммы
— неприводимые 379
— несобственные 379
— остов 379
— приводимые 379
— примитивные 357, 383
— связные 376
— собственные 379
Дирака матрицы, свойства 30—33, 44,
45, 171
— уравнение 27—43; см. также
Уравнения частицы со спином 1/2
в теории поля 129, 146, 164
— —- инвариантность 37—43
ковариантная форма 33—36
Дифференциальное поперечное сече-
сечение для кулоновского рассеяния
электронов 61, 62, 96, 346
мёллеровского рассеяния
106
— рассеяния
нуклонах 190
мезонов на
478
Предметный указатель
Дифференциальное поперечное сече-
сечение, определение 66, 282
Дополнительное условие в квантовой
электродинамике 214, 267
Дырок теория 55—57, 80, 83, 84;
см. также Позитронов теория
квантование поля со спином Va
164—169
рассеяние позитронов на элек-
электронах 108, 109
Заряда перенормировка 334—338, 400
404
в квантовой электродинамике
335, 400, 403—406
мезонной теории; см. Кон-
Константа связи
— — калибровочная инвариантность
в квантовой электродинамике 396,
404
комптоиовское рассеяние
404—406
мёллеровское рассеяние 337
смысл 404—406
эффекты поляризации вакуума
331—338, 404, 412
— сохранение, калибровочная инва-
инвариантность лагранжиана 462, 463
Зарядовое сопряжение 171—173
инвариантность квантовой элек-
электродинамики 425, 426
эффекты замкнутых петель
в квантовой электродинамике 262,
263, 358, 359
Излучения теория 311—315
Измеримость, перестановочные соот-
соотношения 168, 204
Импульс канонический 121
— как переменная в теории поля 121,
414, 424
— сохранение импульса во времени-
упорядочеиной фёйнмановской диа-
диаграмме 183
— тензор энергии-ямпульса 124
Импульсное представление по Гей-
зенбергу 414, 415
квантование поля 155—169
фейнмановских диаграмм 91,
269—282
фёйнмановской теории пози-
позитрона 84—87, 94, 92
Инвариантность; см. также Лоренц-
инвариантность, Преобразований
свойства
— волновые функции частиц 20
— интегралы движения 126, 460—463
Инвариантность квантозой электро-
электродинамики относительно зарядового
сопряжения 425, 426
— локализованные волновые функ-
функции 23
— формализм Лаграижа 124, 125.
460—463
Инвариантные сингулярные функции;
см. Грина функции, Функция рас-
распространения
интегральное представление
246—251
перестановочные соотноше-
соотношения 204—211
свертка пары операторов
239, 240
Инверсия времени, теория Дирака
40, 45
Интегралы движения в теории Ди-
Дирака 54, 55
инвариантность 460—463
Инфракрасные расходимости 321, 329,
354
рассеяние 343—345
связанные состояния 329—331
Испускание квантов 181, 258
Испускания оператор; см. Рождения
оператор
Калибровочная инвариантность, вер-
вершинный оператор 385, 386
квантование электромагнитного
поля 215—222
классическая электромагнитная
теория 133
рассеяние света на свете 361, 369
собственная энергия фотона
332, 337, 369, 385, 386
тождество Уорда 396
уравнения Максвелла 134
формализм Лагранжа 145—148
4-вектор тока 129, 145—148
Калибровочные преобразования 129,
145, 147
Канонические переменные поля 121
Квадратные диаграммы, рассеяние
света на свете 361, 362, 368
степень расходимости 362, 368
устранение расходимости 365
Квантование в ограниченном кубе 154
— классической системы 153
— перестановочные соотношения
113—115, 151—153, 159—163
— поля 152—170
— — ковариантный формализм
196—223
скалярного 155—163, 201—210
Предметный указатель
479
Квантование поля спинорного 163—
173,- 210—213
-—— электромагнитного 213, 223
Квантовая электродинамика в пред-
представлении взаимодействия 244, 317
Гейзенберга 412—415,
431—435
. Фарри 348—353, 409—411
калибровочная инвариантность
148, 216—218, 220—222,396, 397, 404
лагранжиан 146, 412
— — нелинейные эффекты 362—364
— — перенормнровочные константы
364, 393, 400, 402—404, 434—435
расходимости 317—337, 357—365,
383—393
уравнения движения 147, 148
устранения расходимостей
317—337, 383—412; см. также
Перенормировка
Клейна — Гордона уравнение; см.
Уравнение частиц со спином 0
— — оператор тока 19, 24
релятивистские обозначения 26
решения 21—23
— — трансформационные свойства 20
Комптоновское рассеяние 282—288
диаграммы Феннмана 274, 282,
404, 405
— — перенормировка заряда в кван-
квантовой электродинамике 405—406
Константа связи, обозначение 135
определение 135
перенормировка в мезоиной
теории 341, 342
Константы перенормировки
величина 434—436
определение 308, 317, 335, 393,
402—406
Контрчлены в теории перенормиро-
перенормировок, собственная энергия бозона 340
фермиона 313, 317
эффекты замкнутых пе-
петель в мезонной теории 364
Корпускулярная интерпретация тео-
теории поля 114, 179, 448, 449
Корпускулярно-волновой дуализм
173—180
Кулоновское рассеяние заряженных
мезонов 97
электронов 61, 94—97, 317—338,
342—346
Лагранжиан векторного мезонного
поля 133
— взаимодействующих полей 134, 143,
144
Лагранжиан в квантовой электроди-
электродинамике 145, 413
— действительного скалярного поля
123
— комплексного скалярного поля 128
— максвелловского поля 131
— плотность 118
— свойства преобразований 118
— спинорного поля со спином i/г 129
Лестничное приближение 104—106,
444, 447
Лоренца преобразования бесконечно
малые 41
неоднородные 421
— — несобственные 44, 45
однородные 37
— — собственные 44
Лоренц-инвариантность, взаимодей-
взаимодействия 135—141
— лагранжиана системы 118
— свойства преобразований опера-
операторов в теории поля 421—423
— сингулярных функций 204, 207,
429, 430, 431
— уравнения Дирака 37—55
— — Клейна — Гордона 20
Лоренцовская калибровка 101, 216
Лэмбовский сдвиг, величина в атоме
водорода 314, 331
— — вершинный оператор 330—332,
353
перенормировка массы 306—314
Магнитный момент заряженной ча-
частицы со спином 1/2 59
— — радиационные поправки
327—329, 372, 373
— — электрона, аномальная часть
327—329
Максвелла уравнение, калибровочное
преобразование 132
Матричное представление алгебры
Дирака 51
■ оператора рождения 157, 161
— уничтожения 157, 161
Матричный элемент оператора рож-
рождения 157, 161
уничтожения 157, 161
перехода 66, 184
полученный из фейнмановской
диаграммы 91, 188, 269—280
Мезоатомы 56
Мезон как псевдоскалярная частица
181
— рассеяние на нуклоне 184—192,
260, 261
— ядерные силы 143, 144, 457
480
Предметный указатель
Метрический тензор 24
Мёллеровское рассеяние 105—108, 337
Момент количества движения; см.
Спин
в теории Дирака 54, 55
— поля 126, 425, 462, 463
Нейтрино 142, 173, 375
Нерелятивистский предел матричных,
элементов в теории Дирака 49
— — уравнений Дирака 52
Клейна — Гордона 20, 23
Нормальное произведение, определе-
определение 23f
амплитуд состояний частицы
422, 447
представленное в виде фейн-
мановских диаграмм 252—256,
259—263
Нормировка векторов состояний
в теории поля 163
— дираковских волновых функций 67
Нулевой уровень импульса поля 158
энергии поля 159
Обменное рассеяние 102, 103, 270
Обозначения для производных от
переменных поля 115, 159
символа Фейнмана 34
— релятивистские 24
Оператор импульса 125, 424
— момента 54, 125, 424, 463
— определение 115, 159
— полной энергии 125, 144
— положения 22, 54
— проектирования 70, 417, 418
— рождения 115, 158, 168, 200, 210
— свойства 159—163, 169
— уничтожения 115, 159, 200, 210
— числа частиц 159, 163, 167—169,
213
для антифермионов 165—169
— бозонов 159
фермионов 165—169
фотонов 213
Паули принцип, антикоммутационные
соотношения Иордана — Вигнера
165—168
— — рассеяние двух фермионов 102,
103, 269
собственная энергия фермиона
290
спин 168
функция распространения Фейн-
Фейнмана 83
Перекрывающиеся расходимости
392—397
Перенормировка в квантовой элек-
электродинамике 317—338, 366—369,
376—405
— — мезонной теории 338—342
— — теории р-распада 374, 375
— волновой функции 323—-326
— заряда 332—339, 404—406
— константы связи 338—342
— контрчлены в лагранжиане системы
311—317, 360—364, 407
— массы 308—316, 324
Перестановочные соотношения; см.
Аитикоммутации соотношения
канонические 152, 414
ковариаитные для различных
времен 201—209
Периодическое граничное условие 155
Плотность вероятности тока и заряда
18—30, 35, 36, 129, 130, 146, 147,
462, 463
Поглощение кванта 181, 182
Поглощения оператор; см. Уничто-
Уничтожения оператор
Позитрон, рассеяние позитронов во
внешнем поле 252—258
на электронах 108, 109
Позитроний 55
Позитронов теория 75—87; см. также
Дырок теория
Полноты соотношения для векторов
состояния в теории поля 430, 440,
444
— дираковских спиноров 69
решений уравнения Шре-
дингера 76, 232
Поляризация вакуума 55, 331—337,
354, 369, 370
лэмбовский сдвиг 337, 370
перенормировка заряда 335,
404, 411
Представление; см. Матричное пред-
представление
— взаимодействия 196—200
— Гейзенберга 150, 152, 413—415
— импульсное 154, 414
— соотношения между различными
представлениями 150—152, 232,
415—417
— Фарри 347—352
— числа частиц (чисел заполнения)
159—162, 173—178
— Шредингера 150, 151
Преобразований свойства; см. Ло-
Лоренца преобразования, Релятивист-
Релятивистская инвариантность
векторов состояний вакуума
161, 169, 424, 426
Предметный указатель
481
Преобразований свойства, величина
орераторов Дирака 44, 49
—'— волновой функции Дирака 37
Клейна — Гордона 18
операторов и векторов состоя-
состояний 420—422
— при зарядовом сопряжении
422, 423
уравнение движения 20
Примитивные расходимости в бозон-
ной электродинамике 366—369
квантовой электродинамике
357—365, 383
мезонной теории 357—365
определение 356, 383
Принцип соответствия 140
Причинность 139, 140, 168, 301, 363, 371
Промежуточное состояние 184
Пространственно-подобная поверх-
поверхность 89, 122, 198
Процессы с замкнутыми петлями; см.
Собственная энергия бозона, ваку-
вакуума
Радиационные поправки, адиабатиче-
адиабатическая гипотеза 323, 326, 403, 404, 408
в квантовой электродинамике
317—338
мезонной теории 339—344
рассеяние электронов в куло-
новом поле 317—347, 409—411
Разложения коэффициенты, интер-
интерпретация вектора состояния в тео-
теории поля 162, 422
Рассеяние бозона на фермионе
184—192, 258
— борновское приближение 66, 184
— двух фермионов 269—272
— как поглощение и излучение кванта
180
— Комптона 281—286
— Мёллера 105—108, 338
— позитронов во внешнем поле 256,
257
на электронах 108, 109
— Резерфорда 61, 94—97, 317—337,
340—344
— Рорлиха 353
— света в кулоновом поле 363
на свете 361, 369
— S-матрица 181—184, 230, 233,
252—287, 317—338, 340—345,
348—350
Расходимости; ем. Перенормировка
— 6-расходимости 388—394
— в квантовой электродинамике
376—404
Расходимости в псевдоскалярной ме-
мезонной теории 338—342, 358—365
разложении S-матрицы по тео-
теории возмущений 317, 376—412
скалярной мезонной теории.
361—365,
-— вакуумных процессов 261—267
— вершинного оператора 322, 341;.
358, 386—387, 390
— инфракрасные 321, 330, 331, 343„
354
— общий анализ 354—366
— отделение 322—342, 383—394, 399„
400
— примитивные 357, 383
— собственной энергии бозона 340,.
341, 358
фермиона 290—307, 317, 358,.
384, 388
фотона 336—338, 385, 389
— теория перенормировки 322—404
Резерфорда — Мотта формула 62, 96
Релятивистская инвариантность; см.
Лоренц-инвариантность
Релятивистское волновое уравнение
19—26, 26—41, 131—134
• для связанных состояний'
97—99, 103, 104, 437—447
инвариантное рассмотрение 20*
Решение уравнения Дирака 33, 55,
58, 59
Клейна—Гордона 21, 23
Рождение пары в фейнмановскок
теории позитрона 82
рассеяние света на свете 361
Рождения оператор, графическое
представление 181, 252, 253, 258, 267
— — для квантов со спином @, 1/в> 1)
159, 161, 165, 168, 202, 203, 210,
211, 212, 310
определение 115, 158—161
Свободного поля уравнения; см. Ре-
Релятивистское волновое уравнение
Связанные состояния; см. Релятиви-
Релятивистское волновое уравнение для свя-
связанных состояний
сходимость S-матрицы 234, 407
теория рассеяния 231—235
Связь между полями; см. Взаимо-
Взаимодействие между полями
— — — локальная 135
нелокальная 139, 300, 301
прямая 135
псевдовекторная 136
——— — псевдоскалярная 136
— скалярная 135
482
Предметный указатель
Связь между полями
ными 136
Симметричные волновые функции,
квантование поля 115
спин 167
статистика Бозе—Эйнштейна
163
Система координат центра инерции
в бозон-фермионном рассеянии 190
для релятивистской си-
системы двух тел 442
•Скобки Пуассона 152
6-матрица, адиабатическая гипотеза
229-235, 322—326, 407—410
— в представлении взаимодействия
224, 225, 232—235
Гейзенберга 431—433
— диаграммы Фейнмана 252—287
— определение 193, 224
— расходимости в теории поля
290—296, 302—308, 317—412
— связанные состояния 233—235,
409—412
— сходимость ряда теории возмуще-
возмущения 408, 409
— теория рассеяния 193—195,
229—231, 252—287, 317—338,
340—345, 348—350
— унитарность 224, 322, 407
Собственная энергия бозона 338—340,
357, 367
вакуума 265, 419, 420
в теории Фейнмана 408—412
— — массы 302—311, 320
оператор 290, 379—382
отделение бесконечности 340,
383—395
перенормировка константы связи
338—340
степень расходимости 290—295,
357
фермиона 291—295, 357
фотона 335—337
Собственные значения оператора за-
заряда 163, 166, 167
— — — импульса 158, 163, 415
— положения 22, 23
числа частиц 159, 165
энергии 158, 163, 166, 167,
415
— функции оператора заряда
166—169, 445
— импульса 160, 415
положения 22, 23, 54
— числа частиц 159—163
полнота 69, 77, 232, 430,
440
с производ- Соотношения
ортогональности для
векторов состояний в теории поля
162, 230—232
дираковских волновых функ-
функций 66
нерелятнвнстских волновых
функций 76, 174
Состояния с отрицательной энергией
20—23, 32, 55—57, 164, 180, 415
Сохранения теоремы для заряда 18,
29, 129, 130, 146, 147, 462, 463 '
— тензора момента количества
движения 126, 462
энергин-импульса 125,
460, 461
инвариантные принципы 124,
460—463
Спнн дираковскон частицы 54
— перенормнруемость 373, 374
— свойства преобразований 20
— статистика 83, 167
— частицы Клейна — Гордона 20
Спиновые матрицы Паули 30
Спинор 27
— свойства преобразований 37
Спонтанная эмиссия 179
Средние значения, амплитуды частиц
422, 447, 448
интерпретация вектора состоя-
состояния в теории поля 162, 256, 422,
440
Статистика Бозе — Эйнштейна 163
— Фермн — Дирака 165
Статистическая интерпретация век-
вектора состояний в одночастичной
теории 22
теории поля 162
Сходимость разложения S-матрнцы
406—409
— ядра уравнения Бете — Салпетера
440
S-функции; см. Грина функция, Функ-
Функция распространения
Теория возмущений инвариантная
224—229
ряды Неймана — Лиувиля 79
стационарная 65
функции Грина 78, 81—83
Тока 4-вектор для комплексного ска-
скалярного поля 99, 147
— спинорного поля со спнном
1Ы 147
уравнения Днрака 29, 35
Клейна — Гордона 19, 20
— — определение с помощью плот-
плотности лагранжиана 129, 146, 462,463
Предметный указатель
483
Томонага — Швннгера уравнение 198,
199, 348
Томсоновское рассеяние 287
перенормировка заряда 404
Тонкой структуры постоянная 319,
353, 371
Треугольные диаграммы 262, 358
Унитарные теорнн поля 300
Уничтожения оператор, графическое
представление 181, 182, 252, 253,
258, 267
для квантов 115, 116, 157,
159—163, 165, 168, 203, 210—212
определение 115, 116, 159—163
Уорда тождество 394—396
калибровочная инвариантность
396—397
Уравнение частиц со спином 1 128—132;
см. также Фотон, Максвелла урав-
уравнение
0; см. Клейна — Гордона
уравнение
в присутствии элек-
электромагнитного поля 23, 26
как операторное урав-
уравнение 197
ковариантная форма 26
Va! CM- Дирака уравнение
в присутствии элек-
электромагнитного поля 58, 59
как операторное урав-
уравнение 197
ковариантная форма
32-35
Уравнения движения; см. Релятиви-
Релятивистское волновое уравнение
— — взаимодействующих полей
142—144
вывод из плотности лагран-
лагранжиана 118, 119
операторов в гейзенберговском
представлении 151, 413
представлении взаимо-
взаимодействия 197
Фарри теорема 262, 263, 359
— представление для связанных со-
состояний 347—353, 409—412
Фейнмана диаграммы 82, 84, 252—268;
см. также Диаграммы
в квантовой электродинамике
253, 254, 267
мезонной теории 258—261
правила для получения матрич-
матричного элемента нз диаграмм Фейн-
Фейнмана 266—268, 275
Фейимана диаграммы, разложение
5-матрицы 252—268
упорядоченные во времени
181—186
— теория позитронов; см. Позитро-
Позитронов теория, Дырок теория
Ферми — Дирака статистика, антнком-
мутационные соотношения 165—
170
антисимметрия волновых функ-
функций 170
спин 83, 168
Фолдн — Ваутхейсена преобразование
57—59
Фолдн-преобразованне 458
Форм-факторы 139, 300—302
Фотон; см. Квантование поля элек-
электромагнитного
— комптоновское рассеяние 281—287,
369
— рассеяние 361, 370
Дельбрюка 363
— собственная энергия 338, 370,
386—388
Функции К; см. Инвариантные син-
сингулярные функции
Функция распространения; см. Грнна
функция
для бозе-частнц 92, 93
двух взаимодействующих ча-
частиц 99—104, 437—439
днраковских частиц 79—81,
252, 436—438
представление 76—80, 84,
247—252
— — теория Фейнмана 76—93
Хронологическое произведение опе-
операторов, определение амплитуд ча-
частиц 447, 448
Хронологический оператор по Вику
238
Дайсону 226
Частица со спином 0, нерелятнвист-
ское уравнение 18
релятивистское уравне-
уравнение 19
статистика 168
1/2 волновая функция 27, 37,
59, 421
релятивистское уравне-
уравнение 35—59, 421
. свойства 55—59, 444
статистика 83, 167
1 131, 373—374; см. также
Фотон
484
Предметный указатель
Четность 59, 192
4-вектор, обозначение 25
Ширина линий 352, 353, 449
Шредингера представление 150
— уравнение; см. Томонага—Швин-
гера уравнение
— — для нерелятнвнстской системы
18
системы бозон—фермион 180
Эквивалентности теоремы 451—458
Электромагнитное поле, коварнант-
ное квантование 212—223
— — корпускулярный аспект 212
лагранжиан 131
уравнение Дирака 57—59
Клейна— Гордона 23, 24
уравнения движения 131, 132
Электроны, рассеяние на внешнем
поле 87—92, 94—97, 317—338,
342—347
Электроны, рассеяние на ядрах 63—65-
— свободные 164—170, 209—212
— собственная энергия 290—317, 378,
384
Энергии-импульса оператор, диаго-
диагональное представление 415—417
— — для поля частиц со спнном.
х/, 130
скалярного поля 124, 125
электромагнитного поля 134,
217
Энергия-нмпульс, закон сохранения
124, 125
— сохранение на диаграммах Фейн-
мана 91, 271
— частицы 18, 26
Юкавы теория 143, 144
Юлинга эффект 56, 336
Ядерные силы 143, 144, 457
Ячеек метод в теории поля 120
— — нормировка спиноров 273