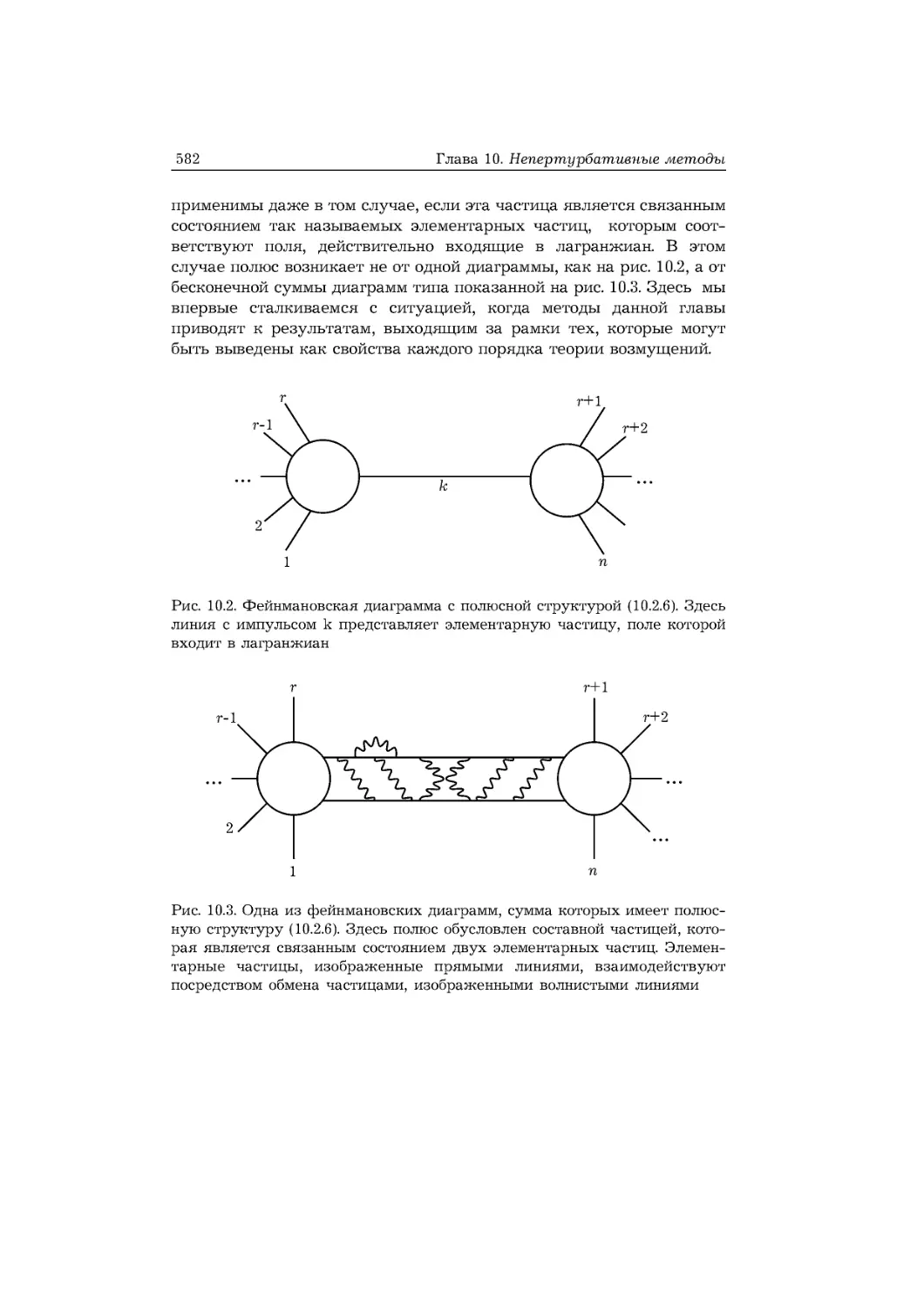
Текст
Стивен Ваинберг
КВАНТОВАЯ
ТЕОРИЯ ПОЛЕЙ
Том 1
Основы
Главы
1 -14
Перевод на русский язык А. В. Беркова
под редакцией Б.Л.Воронова
с исправлениями на 03.03.2001
с издания
The Quantum Theory of Fields
Volume I
Foundations
Steven Weinberg
University of Texas at Austin
CAMBRIDGE UNIVERSITY PRESS
© Steven Weinberg 1995
This book is in copyright. Subject to statutory exception
and to the provisions of relevant collective licensing agreements,
no reproduction of any part may take place without
the written permission of Cambridge University Press.
First published 1995
Reprinted 1996 (with corrections), 1998 (with corrections), 1999 (with corrections)
Содержание
Предисловие xv
Обозначения xxi
1. Историческое введение 1
1.1. Релятивистская волновая механика 3
Волны де Бройля. Волновое уравнение Шредингера—Клейна—Гордона.
Тонкая структура. Спин. Уравнение Дирака. Отрицательные энергии.
Принцип исключения. Позитроны. Пересмотренный взгляд на уравне-
уравнение Дирака.
1.2. Рождение квантовой теории поля 19
Квантованные поля Борна, Гейзенберга, Иордана. Спонтанное излу-
излучение. Антикоммутаторы. Квантовая теория Гейзенберга-Паули.
Квантование дираковского поля методом Фарри-Оппенгеймера. Кван-
Квантование скалярного поля методом Паули-Вайскопфа. Ранние вычис-
вычисления в квантовой электродинамике. Нейтроны. Мезоны.
1.3. Проблема бесконечностей 40
Бесконечно большие сдвиги энергии электрона. Поляризация вакуума.
Рассеяние света на свете. Инфракрасные расходимости. Поиск аль-
альтернатив. Перенормировка. Конференция в Шелтер Айленде. Лэм-
бовский сдвиг. Аномальный магнитный момент электрона. Формализ-
Формализмы Швингера, Томонаги, Фейнмана и Дайсона. Почему не раньше?
Библиография 51
Список литературы 53
2. Релятивистская квантовая механика 63
2.1. Квантовая механика 6 3
Лучи. Скалярные произведения. Наблюдаемые. Вероятности.
* Разделы, отмеченные звездочками, лежат несколько в стороне от основной линии
изложения и могут быть опущены при первом чтении.
iv Содержание
2.2. Симметрии 65
Теорема Вигнера. Антилинейные и антиунитарные операторы. На-
Наблюдаемые. Групповая структура. Представления с точностью до
фазы. Правила суперпозиции. Группы Ли. Структурные констан-
константы. Абелевы симметрии.
2.3. Квантовые преобразования Лоренца 72
Преобразования Лоренца. Квантовые операторы. Инверсии.
2.4. Алгебра Пуанкаре 76
jw и рц Свойства преобразований. Коммутационные соотношения.
Сохраняющиеся и не сохраняющиеся генераторы. Конечные транс-
трансляции и вращения. Свертка Иноню—Вигнера. Галилеевская алгебра
2.5. Одночастичные состояния 82
Правила преобразований. Бусты. Малые группы. Нормировка.
Массивные частицы. Безмассовые частицы. Спиральность и поля-
поляризация.
2.6. Пространственная инверсия и обращение времени 98
Преобразование J*™ и Рц. Унитарный оператор Р и антиунитарный
оператор Т. Массивные частицы Безмассовые частицы. Крамеров-
ское вырождение. Электрические дипольные моменты.
2.7. Проективные представления* 108
Два-коциклы. Центральные заряды. Односвязные группы
В группе Лоренца нет центральных зарядов. Двусвязность группы
Лоренца. Накрывающие группы. Пересмотренные правила супер-
суперотбора.
Приложение А. Теорема о представлении симметрии 120
Приложение В. Групповые операторы и гомотопические классы... 127
Приложение С. Инверсии и вырожденные мультиплеты 133
Задачи 139
Список литературы 140
3. Теория рассеяния 142
3.1. Ин- и аут-состояния 143
Многочастичные состояния. Волновые пакеты. Асимптотические
условия в начальный и конечный моменты времени. Уравнения Лип-
пмана-Швингера. Главные значения и дельта-функции.
3.2. ^-матрица 150
Определение ^-матрицы. Т-матрица. Борновское приближение.
Унитарность ^-матрицы.
3.3. Симметрии ^-матрицы 154
Лоренц-инвариантность. Достаточные условия. Внутренние симмет-
симметрии. Электрический заряд, странность, изоспин, ??7C). Сохранение
четности. Внутренние четности. Четность пиона. Несохранение чет-
четности. Инвариантность по отношению к обращению времени. Теоре-
Теорема Ватсона. Несохранение РТ. С, СР, СРТ. Нейтральные К-мезоны.
Несохранение СР.
3.4. Вероятности и сечения 178
Вероятности в ящике. Вероятности распадов. Сечения. Лоренц-
инвариантность. Фазовое пространство. Диаграммы Далица.
3.5. Теория возмущений 188
Старая теория возмущений. Теория возмущений, зависящих от времени.
Хронологически упорядоченные произведения. Ряды Дайсона. Лоренц-
инвариантные теории. Борновское приближение искаженных волн.
3.6. Следствия унитарности 195
Оптическая теорема. Дифракционные пики. СРТ соотношения
Вероятности распадов частиц и античастиц. Кинетическая теория.
Я-теорема Больцмана.
3.7. Разложения по парциальным волнам * 201
Дискретный базис. Разложение по сферическим гармоникам.
Полные упругие и неупругие сечения. Фазовые сдвиги. Пороговое пове-
поведение: экзотермические, эндотермические и упругие реакции. Длина
рассеяния. Упругие и неупругие сечения при больших энергиях.
3.8. Резонансы * 211
Причины появления резонансов: слабая связь, барьеры, комп-
комплексность. Энергетическая зависимость. Унитарность. Формула Брей-
та-Вигнера. Виртуальные резонансы. Фазовые сдвиги в резонансе.
Эффект Рамзауера-Таунсенда.
Задачи 220
Список литературы 221
4. Принцип кластерного разложения 225
4.1. Бозоны и фермионы 226
Перестановочные фазы. Статистика Бозе и Ферми. Нормировка для
тождественных частиц.
4.2. Операторы рождения и уничтожения 230
Операторы рождения Вычисление сопряженного оператора. Вывод
соотношений коммутации и антикоммутации. Представления общих
операторов. Гамильтониан свободной частицы. Лоренцовские преобра-
vi Содержание
зования операторов рождения и уничтожения. С, Р, Т свойства опера-
операторов рождения и уничтожения.
4.3. Кластерное разложение и связные амплитуды 236
Отсутствие корреляции удаленных экспериментов. Связные ампли-
амплитуды. Подсчет дельта-функций.
4.4. Структура взаимодействия 243
Условия кластерного разложения. Графический анализ. Двух-
Двухчастичное рассеяние порождает трехчастичное рассеяние.
Задачи 252
Список литературы 253
5. Квантовые поля и античастицы 254
5.1. Свободные поля 254
Поля рождения и уничтожения. Лоренцовские преобразования коэф-
коэффициентных функций. Построение коэффициентных функций Исполь-
Использование кластерного разложения. Причинность как следствие лоренц-
инвариантности. Античастицы как следствие причинности. Нормальное
упорядочение.
5.2. Причинные скалярные поля 266
Поля рождения и уничтожения. Требование причинности. Скаляр-
Скалярные поля описывают бозоны. Античастицы. Р, С, Т преобразования. 7С°.
5.3. Причинные векторные поля 275
Поля рождения и уничтожения. Спин нуль или спин единица.
Векторные поля описывают бозоны. Векторы поляризации. Требование
причинности. Античастицы. Масса нуль. Р, С, Т преобразования.
5.4. Дираковский формализм 283
Представление Клиффорда алгебры Пуанкаре. Преобразование матриц
Дирака. Размерность дираковских матриц. Явный вид матриц. Матрица
у5. Псевдоунитарность. Комплексное сопряжение и транспонирование.
5.5. Причинные дираковские поля 292
Поля рождения и уничтожения. Дираковские спиноры. Требование при-
причинности. Дираковские поля описывают фермионы. Античастицы. Про-
Пространственная инверсия. Внутренняя четность пар частица-античастица.
Зарядовое сопряжение. Внутренняя С-фаза пары частица-античастица.
Майорановские спиноры. Обращение времени. Билинейные коварианты.
Взаимодействие при бета-распаде.
5.6. Общие неприводимые представления
однородной группы Лоренца 305
Изоморфизм группе ?17B) ® SUB). (А, В) представление знакомых
Vll
полей. Поле Рариты-Швингера. Пространственная инверсия.
5.7. Общие причинные поля * 310
Построение коэффициентных функций. Скалярные плотности гамиль-
гамильтонианов. Требование причинности Античастицы Общая связь меж-
между спином и статистикой. Эквивалентность различных типов полей.
Пространственная инверсия. Внутренняя четность произвольных пар
частица-античастица. Зарядовое сопряжение. Внутренняя С-фаза
античастиц. Зарядово-самосопряженные частицы и соотношения дей-
действительности. Обращение времени. Проблемы высших спинов.
5.8. СРТ теорема 326
СРТ-преобразование скалярного, векторного и дираковского полей.
СРТ-преобразование скалярной плотности взаимодействия. СРТ-
преобразование общих неприводимых полей. СРТ-инвариантность
гамильтониана.
5.9. Поля безмассовых частиц 328
Построение коэффициентных функций Отсутствие векторных полей
со спиральностью + 1. Необходимость калибровочной инвариантнос-
инвариантности. Антисимметричные тензорные поля со спиральностью + 1. Сум-
Суммы по спиральностям. Построение причинных полей со спиральнос-
спиральностью + 1. Гравитоны. Спин > 3. Общие неприводимые безмассовые
поля. Единственность спиральностей для полей (А, В).
Задачи 340
Список литературы 341
6. ФЕЙНМАНОВСКИЕ ПРАВИЛА 344
6.1. Вывод правил 345
Спаривания. Теорема Вика. Правила в координатном представле-
представлении. Комбинаторные множители. Знаковые множители. Примеры.
6.2. Вычисление пропагатора 363
Полином в числителе. Фейнмановский пропагатор для скалярных
полей. Дираковские поля. Общие неприводимые поля. Ковариант-
ные пропагаторы. Нековариантные слагаемые в хронологически упо-
упорядоченных произведениях.
6.3. Правила в импульсном представлении 371
Переход в импульсное представление. Фейнмановские правила. Под-
Подсчет независимых импульсов. Примеры. Петлевые множители.
6.4. Выход с массовой оболочки 379
Токи. Амплитуды вне массовой поверхности являются точными мат-
матричными элементами операторов в гейзенберговском представлении.
viii Содержание
Доказательство теоремы.
Задачи 384
Список литературы 385
7. Канонический формализм 386
7.1. Канонические переменные 387
Канонические перестановочные соотношения. Примеры: действитель-
действительное скалярное, комплексное скалярное, векторное, дираковское поля
.Гамильтонианы свободных частиц. Лагранжианы свободных частиц.
Канонический формализм для взаимодействующих полей.
7.2. Лагранжев формализм 395
Уравнения движения Лагранжа. Действие. Лагранжиан. Уравнения
Эйлера~Лагранжа. Действительность действия. От лагранжианов к
гамильтонианам Новый подход к скалярному полю. Переход от пред-
представления Гейзенберга к представлению взаимодействия. Вспомога-
Вспомогательные поля. Интегрирование по частям в действии.
7.3. Глобальные симметрии 406
Теорема Нетер. Явное выражение для сохраняющихся величин.
Явное выражение для сохраняющихся токов. Квантовые операторы
симметрии. Тензор энергии-импульса. Импульс. Внутренние сим-
симметрии. Коммутаторы токов.
7.4. Лоренцевская инвариантность 418
Токи M№V . Генераторы J^v . Тензор Белинфанте. Лоренц-инвари-
Лоренц-инвариантность ^-матрицы.
7.5. Переход к представлению взаимодействия. Примеры 424
Скалярное поле со связью с производными. Векторное поле. Дира-
Дираковское поле.
7.6. Связи и скобки Дирака 433
Первичные и вторичные связи. Скобки Пуассона. Связи первого и
второго рода. Дираковские скобки. Пример: действительное вектор-
векторное поле.
7.7. Переопределения полей
и несущественные константы взаимодействия * 442
Лишние параметры. Переопределение полей. Пример: действи-
действительное скалярное поле.
Приложение. Вычисление скобок Дирака
из канонических коммутаторов 444
Задачи 450
Список литературы 451
IX
8. Электродинамика 453
8.1. Калибровочная инвариантность 454
Необходимость константы для сохраняющегося тока. Оператор за-
заряда. Локальная симметрия. Действие для фотона. Уравнения поля
Калибровочно инвариантные производные.
8.2. Связи и калибровочные условия 459
Первичные и вторичные связи. Связи первого рода. Фиксация ка-
калибровки. Кулоновская калибровка. Решение для А0.
8.3. Квантование в кулоновской калибровке 463
Остающиеся константы относятся ко второму роду. Вычисление ди-
раковских скобок в кулоновской калибровке. Построение гамильто-
гамильтониана. Кулоновское взаимодействие.
8.4. Электродинамика в представлении взаимодействия 468
Гамильтонианы свободного поля и взаимодействия. Операторы в кар-
картине взаимодействия. Разложение по нормальным модам.
8.5. Фотонный пропагатор 472
Полином в числителе. Отделение нековариантных слагаемых. Со-
Сокращение нековариантных слагаемых.
8.6. Правила Фейнмана для спинорной электродинамики 475
Диаграммы Фейнмана. Вершины. Внешние линии. Внутренние
линии. Разложение по а/4л. Круговая, линейная и эллиптическая
поляризация. Поляризация и суммы по спинам.
8.7. Комптоновское рассеяние 484
^-матрица. Дифференциальное сечение. Кинематика. Суммы по
спинам. Следы. Формула Клейна-Нишины. Поляризация при том-
соновском рассеянии. Полное сечение.
8.8. Обобщение: калибровочные поля как р-формы 494
Обоснование, р-формы. Внешние производные. Замкнутые и точные р-
формы. Калибровочные поля в виде р-форм Дуальные поля и токи в D
пространственно-временных измерениях. Калибровочные поля в виде
р-форм эквивалентны полям в виде (D — р — 2)-форм. В четырех изме-
измерениях нет ничего нового.
Приложение. Следы 498
Задачи 502
Список литературы 503
9. Методы функционального интегрирования 504
9.1. Общая формула для функционального интеграла 507
Амплитуды перехода для бесконечно малых интервалов. Амплиту-
Содержание
ды перехода для конечных интервалов. Интерполирующие функции.
Матричные элементы хронологически упорядоченных произведений.
Уравнения движения.
9.2. Переход к ^-матрице 517
Волновая функция вакуума. Добавка гг.
9.3. Лагранжева формула для функционального интеграла 523
Интегрирование по импульсам. Скаляры со связью с производными.
Нелинейная сигма-модель. Векторное поле.
9.4. Вывод фейнмановских правил
с помощью функциональных интегралов 531
Выделение действия для свободных полей. Гауссово интегри-
интегрирование. Пропагаторы: скалярные, векторные поля, связь с произ-
производной.
9.5. Функциональные интегралы для фермионов 536
Антикоммутирующие с-числа. Собственные векторы канонических
операторов. Суммирование по состояниям с помощью интегрирова-
интегрирования по Березину. Замена переменных. Амплитуды перехода для
бесконечно малых интервалов Амплитуды перехода для конечных
интервалов. Вывод фейнмановских правил Фермионный пропага-
тор. Вакуумные амплитуды как детерминанты.
9.6. Функциональная формулировка квантовой электродинамики... 557
Функциональный интеграл в кулоновской калибровке. Новое введе-
введение а0. Переход к ковариантным калибровкам.
9.7. Разные статистики * 563
Приготовление ин- и аут-состояний. Правила композиции. В про-
пространствах с числом измерений больше 3 — только бозоны и фермионы.
Анионы в двух измерениях.
Приложение. Многократные гауссовы интегралы 567
Задачи 571
Список литературы 572
10. Непертурбативные методы 574
10.1. Симметрии 575
Трансляции. Сохранение заряда. Теорема Фарри.
10.2. Полология 579
Полюсная формула для общей амплитуды. Вывод полюсной форму-
формулы. Обмен пионами.
10.3. Перенормировка поля и массы 588
Редукционная формула Лемана-Симанчика-Циммермана. Перенор-
XI
мированные поля. Полюсы пропагаторов. Во внешних линиях нет
радиационных поправок. Контрчлены в собственноэнергетических
частях.
10.4. Перенормированный заряд и тождества Уорда 597
Оператор заряда. Перенормировка электромагнитного поля. Пере-
Перенормировка заряда. Тождество Уорда—Такахаши Тождество Уорда.
10.5. Калибровочная инвариантность 604
Поперечность многофотонных амплитуд. Швингеровские члены.
Калибровочные слагаемые в фотонном пропагаторе. Структура фо-
фотонного пропагатора. Перенормированная масса фотона равна нулю.
Вычисление Z3. Радиационные поправки к выбору калибровки.
10.6. Электромагнитные форм-факторы и магнитный момент 610
Матричные элементы J0. Форм-факторы Jm: спин 0. Форм-факто-
Форм-факторы J^: спин 1/2 . Магнитный момент частицы спина 1/2. Измерение
форм-факторов.
10.7. Представление Челлена—Лемана * 618
Спектральные функции. Условия причинности. Спектральное пред-
представление. Асимптотическое поведение пропагаторов. Полюсы. Ог-
Ограничение на константу перенормировки поля Z = 0 для составных
частиц.
10.8. Дисперсионные соотношения * 624
История. Аналитические свойства амплитуды рассеяния вперед для
безмассового бозона. Вычитания. Дисперсионное соотношение. Крос-
Кроссинг. Теорема Померанчука. Реджевское асимптотическое поведе-
поведение. Рассеяние фотонов.
Задачи 634
Список литературы 635
11. Однопетлевые радиационные поправки
в квантовой электродинамике 638
11.1. Контрчлены 639
Перенормировка поля, массы и заряда. Контрчлены в лагранжиане.
11.2. Поляризация вакуума 640
Однопетлевой интеграл для фотонной собственноэнергетической части.
Параметры Фейнмана. Виковский поворот Размерная регуляриза-
регуляризация. Калибровочная инвариантность. Вычисление Z3. Сокращение
расходимостей. Поляризация вакуума при рассеянии заряженных
частиц. Эффект Юлинга. Мюонные атомы.
xii Содержание
11.3. Аномальные магнитные моменты и зарядовые радиусы 655
Однопетлевая формула для вершинной функции. Вычисление форм-
факторов Аномальные лептонные магнитные моменты порядка а
Аномальные магнитный момент мюона порядка a2ln(m^/me). Заря-
Зарядовый радиус лептонов.
11.4 Собственная энергия электрона 666
Однопетлевая формула для электронной собственноэнергетической
части. Перенормировка массы электрона. Сокращение ультра-
ультрафиолетовых расходимостей.
Приложение. Некоторые интегралы 671
Задачи 673
Список литературы 673
12. Общая теория перенормировок 675
12.1. Индексы расходимости 676
Индекс расходимости. Размерный анализ . Перенормируемость.
Критерий действительной сходимости.
12.2. Сокращение расходимостей 683
Вычитание путем дифференцирования. Программа перенор-
перенормировки. Перенормируемые теории Пример: квантовая электроди-
электродинамика. Перекрывающиеся расходимости Рецепт перенормировки
Боголюбова-Парасюка-Хеппа-Циммерманна. Выбор точки норми-
нормировки: теория ф4.
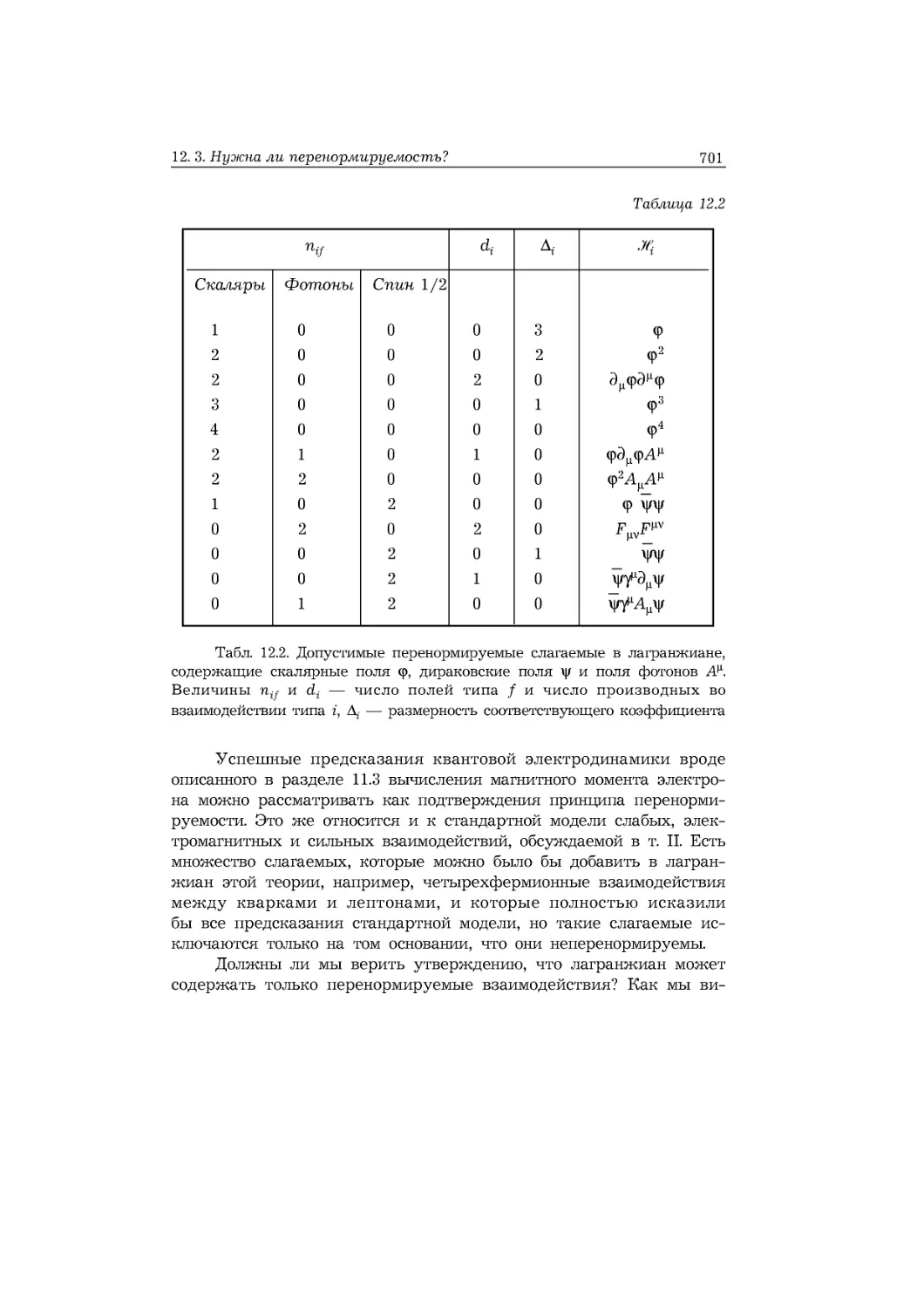
12.3. Нужна ли перенормируемость? 699
Список перенормируемых взаимодействий. Не существует перенор-
перенормируемых теорий тяготения. Сокращение расходимостей в неперенор-
мируемых теориях. Подавление неперенормируемых взаимодействий.
Пределы на новые масштабы масс. Проблемы с высшими производ-
производными. Детектирование неперенормируемых взаимодействий. Низко-
Низкоэнергетические разложения в неперенормируемых теориях . Пример:
скалярное поле с одной связью через производную. Насыщение или
новая физика? Эффективные теории поля.
12.4. Плавающее обрезание 711
Подход Вильсона . Уравнения ренормализационной группы . Теоре-
Теорема Польчинского . Притяжение к стабильной поверхности . Сравне-
Сравнение плавающего обрезания и перенормировки.
12.5. Случайные симметрии * 716
Общая теория перенормировок для заряженных лептонов . Пере-
Переопределение лептонных полей . Случайное сохранение лептонных
хш
ароматов, Р, С и Т.
Задачи 720
Список литературы 720
13. Инфракрасные эффекты 723
13.1. Амплитуды испускания мягких фотонов 724
Испускание одиночного фотона. Пренебрежение испусканием с внут-
внутренних линий. Лоренц-инвариантность требует сохранения заряда.
Испускание одиночного гравитона. Лоренц-инвариантность требует прин-
принципа эквивалентности. Многофотонное излучение. Факторизация
13.2. Виртуальные мягкие фотоны 730
Эффекты, связанные с мягкими виртуальными фотонами. Радиационные
поправки во внутренних линиях
13.3. Реальные мягкие фотоны. Сокращение расходимостей 737
Сумма по спиральностям. Интегрирование по энергиям. Сумма по
числу фотонов. Сокращение инфракрасных обрезающих множите-
множителей. Аналогичное сокращение для гравитации
13.4. Произвольные инфракрасные расходимости 741
Безмассовые заряженные частицы. Общее рассмотрение инфракрас-
инфракрасных расходимостей. Струи. Теорема Ли-Науенберга
13.5. Рассеяние мягких фотонов * 748
Полюсы в амплитуде. Соотношения сохранения. Универсальность
низкоэнергетического предела
13.6. Приближение внешнего поля * 752
Суммы по перестановкам фотонных вершин. Нерелятивистский пре-
предел. Перекрестный лестничный обмен
Задачи 759
Список литературы 760
14. Связанные состояния во внешних полях 762
14.1. Уравнение Дирака 763
Дираковские волновые функции как матричные элементы поля. Ан-
Антикоммутаторы и полнота. Собственные состояния с заданной энер-
энергией. Волновые функции с отрицательной энергией. Ортонорми-
рованность. «Большие» и «малые» компоненты. Четность. Спиновая и
угловая зависимость. Радиальные волновые функции. Энергии.
Тонкая структура. Нерелятивистские приближения
14.2. Радиационные поправки во внешних полях 774
Пропагатор электрона во внешнем поле. Неоднородное уравнение
xiv Содержание
Дирака. Эффекты радиационных поправок. Сдвиги энергии.
14.3. Лэмбовский сдвиг в легких атомах 781
Разделение больших и малых энергий. Слагаемое, соответствующее
большим энергиям. Низкоэнергетическое слагаемое. Влияние пере-
перенормировки массы. Полный сдвиг энергии. 1 = 0. I Ф 0. Численные
результаты. Сравнение теории и эксперимента для классического
лэмбовского сдвига. Сравнение теории и эксперимента для сдвига Is
состояния.
Задачи 802
Список литературы 803
Авторский указатель 805
Предметный указатель 810
ОГЛАВЛЕНИЕ ТОМА II
15. Неабелевы калибровочные теории
16. Методы фонового поля
17. Перенормировка калибровочных теорий
18. Методы ренормгруппы
19. Спонтанно нарушенные глобальные симметрии
20. Операторные разложения
21. Спонтанно нарушенные локальные симметрии
22. Аномалии
23. Протяженные полевые конфигурации
Предисловие к первому тому
Зачем нужна еще одна книга по квантовой теории поля? Сегод-
Сегодня любой студент, изучающий этот предмет, имеет на выбор ряд
прекрасных книг, многие из которых вполне современны. Еще одна
книга будет иметь ценность, только если она содержит что-то новое
или открывает новые перспективы.
Если говорить о содержании предлагаемой книги, то хотя она и
содержит довольно много нового материала, все же главное отличие
от других книг заключается в общности изложения: я пытался везде,
где возможно, обсуждать вопросы в максимально общем виде. Отчас-
Отчасти это связано с тем, что квантовая теория поля нашла применения в
областях, весьма далеких от сферы ее первых успехов — квантовой
электродинамики, но главным образом — с тем, что, по моему убеж-
убеждению, эта общность позволяет выявить главные моменты, не дав им
раствориться в технических деталях конкретных теорий. Конечно, для
иллюстрации общих положений я часто использую конкретные при-
примеры, выбранные из современной физики частиц, ядерной физики и
квантовой электродинамики.
Однако главное, что побудило меня написать эту книгу, было не
столько ее конкретное содержание, сколько общий замысел. Я поста-
поставил своей целью изложить квантовую теорию поля так, чтобы дать
читателю максимально ясное представление о том, почему эта теория
приняла такую форму, которую она имеет, и почему именно в этой
форме она так хорошо описывает реальный мир.
Начиная с первых работ Гейзенберга и Паули по общей кванто-
квантовой теории поля, традиционный подход заключался в том, что суще-
существование полей принималось как данное, что находило подтвержде-
подтверждение в нашем опыте описания электромагнетизма. Затем поля
«квантовались», т. е. правила канонического квантования или интегри-
интегрирования по траекториям применялись к нескольким простым полевым
теориям. Некоторые замечания по поводу такого традиционного под-
подхода читатель найдет в историческом введении в гл. 1. Вне сомнения,
xvi Предисловие
такой путь позволяет быстро войти в суть дела, но мне кажется,
что он оставляет вдумчивого читателя наедине со слишком боль-
большим числом вопросов, не имеющих ответа. Почему нам следует
доверять правилам канонического квантования или интегрирования
по траекториям? Почему мы должны принимать за истинные про-
простые уравнения поля и лагранжианы, которые пишутся в литера-
литературе? Кстати, а почему вообще нужны поля? Мне кажется непра-
неправильным апеллировать к нашему опыту - в конце концов, наша
цель в теоретической физике заключается не просто в том, чтобы
описать окружающий нас мир, но и объяснить с помощью неболь-
небольшого числа фундаментальных принципов, почему этот мир таков,
каков он есть.
Точка зрения, проповедуемая в этой книге, состоит в том, что
квантовая теория поля такая, какая она есть, потому что (если не
принимать во внимание теорий типа теории струн, в которых уча-
участвует бесконечно большое число типов частиц) это единственный способ
совместить принципы квантовой механики (включая свойство клас-
кластерного разложения) и теории относительности. Этой точки зрения я
придерживаюсь много лет, но в последнее время она получила новую
поддержку. Мы научились в последние годы рассматривать успешно
работающие квантовые теории поля, в том числе и квантовую элект-
электродинамику, как «эффективные теории поля», являющиеся низко-
низкоэнергетическими приближениями к более глубокой теории, которая,
может быть, является даже не теорией поля, а совсем другой теори-
теорией, скажем, теорией струн. С этой точки зрения, причина, почему
квантовые теории поля описывают физику при доступных энергиях,
заключается в том, что любая релятивистская квантовая теория выг-
выглядит при достаточно низких энергиях как квантовая теория поля.
Поэтому важно понять основы квантовой теории поля с помощью прин-
принципов квантовой механики и теории относительности. Кроме того, в
наши дни изменилась точка зрения на некоторые проблемы кванто-
квантовых теорий полей, например, на неперенормируемость и «тривиаль-
«тривиальность», которые тревожили нас в те годы, когда мы рассматривали эти
теории как истинно фундаментальные. В книге отражены эти измене-
изменения. Мое намерение было написать книгу по квантовой теории поля
эры эффективных теорий поля.
Самыми непосредственными и очевидными следствиями теории
относительности и квантовой механики являются свойства состояний
частиц, поэтому частицы появляются сразу — уже в гл. 2 они введены
Предисловие xvii
как объекты в представлениях неоднородной группы Лоренца в гиль-
гильбертовом пространстве квантовой механики. В гл. 3 подготавливает-
подготавливается почва для ответа на фундаментальный вопрос динамики: если
состояние в далеком прошлом задано как некоторая совокупность
свободных частиц, как будет выглядеть эта совокупность в буду-
будущем? Зная генератор трансляций во времени, т. е. гамильтониан,
мы можем ответить на этот вопрос, записав разложение по теории
возмущений множества амплитуд перехода, известного как S-мат-
рица. В гл. 4 мы привлекаем принцип кластерного разложения для
того, чтобы описать построение генератора временных трансляций
— гамильтониана с помощью операторов рождения и уничтожения.
Затем в гл. 5 мы возвращаемся к лоренц-инвариантности и показы-
показываем, что как следствие этой инвариантности операторы рождения
и уничтожения группируются в причинные квантовые поля. В до-
дополнение мы доказываем СРТ теорему и теорему о связи спина и
статистики. Этот формализм используется в гл. 6 для вывода фейн-
мановских правил для вычисления элементов 5-матрицы.
Только в гл. 7 мы подходим к лагранжиану и каноническому
формализму. Идея заключается в том, чтобы ввести эти понятия не
потому, что они оказались полезными в других областях физики (та-
(такое объяснение всегда не слишком удовлетворительно), а потому,
что этот формализм позволяет ввести гамильтонианы взаимодействия,
для которых 5-матрица удовлетворяет различным предполагаемым
симметриям. В частности, лоренц-инвариантность лагранжиана обес-
обеспечивает существование десяти операторов, удовлетворяющих со-
соотношениям алгебры группы Пуанкаре, а это, как мы показываем
еще в гл. 3, является необходимым условием для доказательства
лоренц-инвариантности 5-матрицы. Наконец-то, в гл. 8 появляется
квантовая электродинамика. В гл. 9 рассмотрено интегрирование по
траекториям, которое используется для обоснования полученных в
гл. 8 методом размахивания руками фейнмановских правил кванто-
квантовой электродинамики. Такое позднее введение интегралов по траек-
траекториям несколько противоречит сегодняшней моде. Однако мне ка-
кажется, что хотя интегралы по траекториям, несомненно, являются
лучшим способом быстрейшего вывода фейнмановских правил для
заданного лагранжиана, они несколько затемняют квантово-механи-
ческие основания подобных вычислений.
Первый том завершает серия глав 10-14, в которых излагается
введение в основы вычисления радиационных поправок в общих поле-
xviii Предисловие
вых теориях, включая петлевые поправки. Здесь также последова-
последовательность изложения несколько необычна: мы начинаем с главы, посвя-
посвященной непертурбативным методам. Отчасти это сделано потому, что
полученные результаты помогают понять необходимость перенорми-
перенормировки массы и заряда независимо от того, содержатся ли в теории
бесконечности или нет. В гл. 11 представлены классические однопет-
левые вычисления в квантовой электродинамике, дающие возмож-
возможность, с одной стороны, объяснить полезные вычислительные при-
приемы (фейнмановские параметры, виковский поворот, размерная
регуляризация и регуляризация Паули-Вилларса), а с другой сто-
стороны, демонстрирующие перенормировку в действии. Опыт, приоб-
приобретенный в гл. 11, распространяется в гл. 12 на все порядки теории
возмущений и на теории общего вида. Здесь же обсуждается совре-
современный взгляд на неперенормируемость, связанный с эффективными
теориями поля. Гл. 13 содержит изложение ряда специальных про-
проблем, возникающих для безмассовых частиц низких энергий или с па-
параллельными импульсами. Уравнение Дирака для электрона во внеш-
внешнем электромагнитном поле, исторически появившееся на самой заре
развития релятивистской квантовой механики, рассматривается только
в гл. 14, посвященной проблемам связанных состояний. Причина зак-
заключается в том, что это уравнение следует рассматривать не как ре-
релятивистскую версию уравнения Шредингера (как это делал Дирак),
а как приближение к истинной релятивистской квантовой теорий
полей фотонов и электронов. Глава заканчивается рассмотрением лэм-
бовского сдвига и сопоставлением вычислений с современными экспе-
экспериментальными данными.
У читателя может возникнуть ощущение, что некоторые вопросы,
особенно в гл. 3, могли бы быть с большим основанием содержаться в
учебниках по ядерной физике или физике элементарных частиц. Да,
вероятно это так, но по моему мнению, эти разделы обычно либо вообще
не освещаются, либо освещаются очень скупо, с использованием конк-
конкретных динамических моделей, а не общих принципов симметрии и кван-
квантовой механики. Я встречал теоретиков — специалистов по теории струн,
которые никогда не слышали о связи инвариантности относительно обра-
обращения времени со сдвигами фаз в конечном состоянии,
и специалистов по ядерной физике, которые понятия не имели, почему
резонансы описываются формулой Брейта-Вигнера. Таким образом,
в первых главах я попытался скорее перебрать, чем недобрать.
Предисловие xix
Во втором томе речь пойдет о достижениях последних лет,
которые оживили квантовую теорию поля: неабелевые калибровоч-
калибровочные теории, ренормализационная группа, нарушенные симметрии,
аномалии, инстантоны и т. п.
Я попытался дать ссылки как на классические работы по кванто-
квантовой теории полей, так и на полезные источники по вопросам, упомя-
упомянутым, но недостаточно подробно изложенным в книге. Я не всегда
знал, кто ответствен за изложенный материал, так что отсутствие
ссылок не следует считать утверждением, что представленные выво-
выводы и рассуждения оригинальны. Однако, некоторые все же обладают
этим свойством. Надеюсь, что мне удалось в ряде мест исправить из-
изложение в оригинальных статьях или стандартных учебниках, напри-
например, в доказательстве, что операторы симметрии либо унитарны,
либо антиунитарны, в обсуждении правил суперотбора, в анализе
вырождения частиц, связанном с нестандартными представлениями
отражений, в использовании принципа кластерного разложения, в
выводе редукционной формулы, в выводе приближения внешнего поля,
и даже в расчете лэмбовского сдвига.
К каждой главе, кроме первой, подобраны задачи. Некоторые из
них рассчитаны просто на закрепление технических приемов, описан-
описанных в главе. Другие нацелены на расширение результатов главы на
более широкий класс теорий.
Занимаясь преподаванием квантовой теории поля, я убедился,
что каждый из томов этой книги содержит достаточно материала для
одногодичного курса лекций для старшекурсников. Полагаю, что кни-
книга должна быть доступна студентам, знакомым с нерелятивистской
квантовой механикой и классической электродинамикой. Кроме того,
я предполагаю знакомство читателей с основами анализа в комплекс-
комплексной области и матричной алгебры. Сведения из теории групп и тополо-
топологии объясняются по ходу дела.
Эта книга не годится для студента, который хочет немедленно
начать вычислять с помощью диаграмм Фейнмана эффекты в стан-
стандартной модели сильных, электромагнитных и слабых взаимодействий.
Книга не подойдет и тем, кто ищет высокий уровень математической
строгости. На самом деле, некоторые части книги изложены на таком
уровне строгости, который вызовет слезы на глазах математически
настроенного читателя. Все же, я надеюсь, что книга будет полезна
тем физикам - ученым и студентам, которые хотят понять, почему
квантовая теория поля такая, какая она есть. Прочтя ее, они будут
хх Предисловие
подготовлены к любым новым открытиям в физике, выходящим за
рамки нашего сегодняшнего понимания.
Большую часть того, что изложено в книге, я узнал за годы
взаимодействия со многими другими физиками, число которых слиш-
слишком велико, чтобы их всех здесь перечислить. Но я должен выра-
выразить особую признательность Сидни Коулмену и моим коллегам по
Техасскому университету Арно Бому, Луи Бойа, Филу Канделасу,
Брайсу де Витту, Сесиль де Витт-Моретт, Жаку Дистлеру, Вилли
Фишлеру, Джошу Фейнбергу, Иоакиму Гомесу, Вадиму Каплу-
новскому, Джо Польчинскому и Полю Шапиро. Приношу благодар-
благодарность Джерри Холтону, Артуру Миллеру и Сэму Швеберу за по-
помощь в подготовке исторического введения. Я благодарю также Элис
Вилсон, которая сделала рисунки и печатала исходные файлы
LATEX до тех пор, пока я не научился делать это сам, а также
Терри Рили за помощь в поиске бесчисленного количества книг и
статей. Моя благодарность многочисленным студентам и коллегам,
особенно Хидеаки Аояме, Кевину Кехиллу, Амиру Кашани-Пуру,
Мичио Масуджиме, Фабио Стринго и Сан Фу Туану, за исправле-
исправление многочисленных опечаток в первом издании этого тома. Я при-
признателен Маурин Стори и Элисон Вулатт из издательства Кембрид-
Кембриджского университета за помощь в подготовке рукописи к изданию,
и особенно моему редактору Руфусу Нилу за полезные дружеские
советы.
СТИВЕН ВАЙНБЕРГ
Остин, Техас.
Октябрь 1994
Обозначения xxi
Обозначения
Латинские индексы i, j, к и т. д. принимают обычно значения
1, 2, 3 и нумеруют пространственные координаты.
Греческие индексы ц, V и т. д. принимают в большинстве случаев
значения 1, 2, 3, 0 и нумеруют пространственно-временные
координаты, причем х° — временная координата.
По повторяющимся индексам подразумевается суммирование,
если это не оговорено особо.
Пространственно-временная метрика г)^ диагональна, причем
Ли = Л22 = Лзз = 1. Лоо = - 1-
Даламбертиан определяется как С = Г|ЦЛ,Э2/дх^дху = V2 - d2/dt2,
где V2 = d2/dxldxi — лапласиан.
Тензор Леви-Чивита е^Р0 определяется как полностью
антисимметричный тензор с ?0123 = + 1.
Пространственные векторы обозначаются буквами, набранными
полужирным шрифтом.
Шляпка над любым вектором обозначает соответствующий
единичный вектор. Так, v = v/| v .
Точка над любой величиной обозначает производную этой
величины по времени.
Матрицы Дирака уц определены так, что уду + уд^ = 2^^. Кроме
того, у5 = гумУзУз и р = if.
Ступенчатая функция 6(s) равна +1 при s > 0 и - 1 при s < 0.
xxii Обозначения
Комплексное сопряжение, транспонирование и эрмитовое
сопряжение матрицы или вектора А обозначается как А", Ат и Af = А*т
соответственно. Эрмитово сопряженный оператор к оператору О
обозначается О\ за исключением случаев, когда используется
звездочка, чтобы подчеркнуть, что вектор или матрица операторов
не транспо-нируется. Символы + э. с. или + к. с. в конце уравнения
означают добавление слагаемых, эрмитово сопряженных или комп-
комплексно сопряженных предыдущим.
За исключением гл. 1, мы используем систему единиц, в которой
постоянная Планка Ь и скорость света с приняты равными единице.
Везде -е — заряд электрона, измеренный в рациональных единицах,
так что а = е2/Dл) = 1/137.
Числа в скобках в конце приводимых числовых данных показы-
показывают неопределенность в последних знаках приведенного числа. Если
это не оговорено особо, все экспериментальные данные взяты из
справочника:
Review of Particle Properties, Phys. Rev., 1994, D50, p. 1173.
Историческое введение
Мы настолько погружены в дела сегодняшней физики, что
нам трудно понять многие проблемы, стоявшие перед учеными
всего лишь несколько лет назад, или извлечь пользу из их опыта.
К тому же знание истории физики — это благо, имеющее и обо-
оборотную сторону: оно может помешать осуществить представ-
представляющуюся совершенно необходимой логическую реконструкцию
физической теории.
В этой книге я попытался представить квантовую теорию по-
полей в логической последовательности, подчеркивая дедуктивные вы-
выводы из физических принципов частной теории относительности и
квантовой механики. Такой подход с неизбежностью увел меня
в сторону от пути, по которому шло реальное развитие. Приведу
один пример. Исторически квантовая теория поля частично возник-
возникла из изучения релятивистских волновых уравнений, в том числе,
уравнений Максвелла, Клейна-Гордона и Дирака. По этой причине
вполне оправдано, что в учебниках и монографиях по квантовой
теории поля эти уравнения вводятся в самом начале, и им придает-
придается большое значение. Тем не менее, мне уже давно кажется, что
значительно лучшей отправной точкой является вигнеровское оп-
определение частиц как представлений неоднородной группы Лорен-
Лоренца, несмотря на то, что работа Вигнера была опубликована только
в 1939 году и еще долгое время после этого не оказывала сущест-
существенного влияния на развитие предмета. В этой книге мы начинаем
с частиц и только позднее переходим к полям.
Это совсем не означает, что частицы более фундаментальны,
чем поля. Уже в течение многих лет, начиная с 1950-х годов, приня-
принято считать, что законы природы имеют форму квантовой теории
Глава 1. Историческое введение
полей. Я начинаю в этой книге с частиц не потому, что они более
фундаментальны, а потому, что наши знания о частицах более опре-
определенны, более непосредственно выводимы из принципов квантовой
механики и теории относительности. Если бы оказалось, что какая-
то физическая система не может быть описана квантовой теорией
поля, это было бы сенсацией; но если бы оказалось, что система не
подчиняется законам квантовой механики и теории относительно-
относительности, это было бы катаклизмом.
На самом деле, точка зрения о фундаментальности квантовой
теории поля недавно подверглась сомнению. Фундаментальная тео-
теория может оказаться не теорией полей или частиц, а, возможно,
теорией чего-то совершенно иного, например, струн. С этой точки
зрения, квантовая электродинамика и другие квантовые теории по-
поля, которыми мы так гордимся, оказываются всего лишь эффек-
эффективными теориями поля, низкоэнергетическими приближениями
к более фундаментальной теории. Причина, по которой наши поле-
полевые теории так хорошо работают, заключается не в том, что они
фундаментальны, а в том, что любая релятивистская квантовая
теория выглядит как теория поля, если применять ее к взаимодей-
взаимодействию частиц при достаточно низких энергиях. Таким образом, ес-
если мы хотим узнать, почему квантовые теории поля таковы, како-
каковы они есть, нам следует начать с частиц.
Но мы не должны делать это ценой забвения своего прошлого.
Поэтому в данной главе описана история квантовой теории поля
с ранних времен до 1949 года, когда эта теория приняла современ-
современную форму. В остальной части книги я буду стараться уберечь исто-
историю от вторжения в физику.
Одна из проблем, с которой я столкнулся при написании этой
главы, заключается в том, что история квантовой теории поля с
самого начала была неразрывно связана с историей самой кванто-
квантовой механики. Поэтому читатель, знакомый с историей квантовой
механики, может встретить уже знакомый материал. Особенно это
касается первого параграфа, где я обсуждаю ранние попытки со-
соединить квантовую механику с частной теорией относительности.
Я могу только посоветовать такому читателю перейти к менее зна-
знакомым страницам.
С другой стороны, читатели, ранее незнакомые с квантовой
теорией поля, могут посчитать некоторые куски этой главы слиш-
слишком краткими, чтобы быть еще и понятными. Призываю таких чи-
1.1. Релятивистская волновая механика
тателей не тревожиться. Данную главу не следует рассматривать
как замкнутое введение в квантовую теорию поля, и она не нужна
для понимания остальной части книги. Некоторые читатели могут
предпочесть начать со следующей главы и вернуться к истории позд-
позднее. Однако для многих история квантовой теории поля может по-
послужить хорошим введением в саму эту теорию.
Должен добавить, что эта глава не является оригинальной ра-
работой по истории науки. Я писал ее, пользуясь книгами и статьями
настоящих историков, а также прочитанными мною некоторыми ис-
историческими воспоминаниями и оригинальными статьями по физи-
физике. Большинство из них упомянуто в библиографии в конце главы
и в списке литературы. Читатель, желающий более глубоко позна-
познакомиться с историческими деталями, должен обратиться к указан-
указанным трудам.
Несколько слов об обозначениях. Чтобы сохранить аромат про-
прошлых времен, я в этой главе буду явно выписывать множители
Ь и с (и даже К), но, чтобы облегчить сравнение с современной
физической литературой, я буду использовать более современную
рационализованную электростатическую систему единиц, в кото-
которой постоянная тонкой структуры а ~ 1/137 записывается как
е2/Dлйс). В последующих же главах я буду в основном использовать
«естественную» систему единиц, полагая Й = с = 1.
1.1. Релятивистская волновая механика
Волновая механика начиналась как релятивистская теория. Дей-
Действительно, как мы увидим далее, основоположники волновой ме-
механики Луи де Бройль и Эрвин Шредингер во многом вдохновля-
вдохновлялись в своих трудах идеями теории относительности. Только позднее
стало понятно, что релятивистская волновая механика как реляти-
релятивистская квантовая теория систем с фиксированным числом частиц
просто невозможна. Таким образом, несмотря на множество успе-
успехов, релятивистская волновая механика в конце концов уступила
дорогу квантовой теории поля. Тем не менее релятивистская волно-
волновая механика сохранилась как важная часть формального аппарата
квантовой теории поля. Кроме того, воспроизведение успешных ре-
результатов релятивистской волновой механики всегда было вызовом
для теории поля.
Глава 1. Историческое введение
Гипотеза о том, что материальные частицы могут описываться,
как фотоны, в виде волн, была впервые высказана Луи де Бройлем г
в 1923 году. Помимо аналогии с излучением, важнейшим аргумен-
аргументом было условие лоренц-инвариантности: если эти частицы описы-
вают-ся волной, фаза которой в точке х в момент времени t име-
имеет вид 2л(к-х —Vt), и если эта фаза должна быть лоренц-инвариантной,
тогда вектор к и частота V должны преобразовываться как х и t,
а следовательно, как р и Е. Чтобы это было возможно, величины
к и v должны зависеть от скорости так же, как р и Е, т. е. должны
быть пропорциональны этим величинам с одной и той же константой
пропорциональности. Для фотонов верно соотношение Эйнштейна Е
= hv, поэтому вполне естественным было предположение, что для
материальных частиц, как и для фотонов,
k = p/h, v = E/h . A.1.1)
Групповая скорость волны 3v/3k оказывается при этом равной ско-
скорости частицы, так что действительно частицам могут быть сопос-
сопоставлены волновые пакеты.
Предположив, что любая замкнутая орбита содержит целое чис-
число длин волн частицы А. = 1/|к|, де Бройль сумел вывести старое
правило квантования Нильса Бора и Арнольда Зоммерфельда, ка-
казавшееся до этого загадочным, хотя и приводившее к хорошим ре-
результатам при расчете атомных спектров. Далее, сам де Бройль и
Вальтер Эльзассер 2 предположили, что волновая теория де Бройля
может быть проверена, если поискать интерференционные эффекты
при рассеянии электронов в кристаллах. Несколькими годами спустя
эти эффекты были обнаружены Клинтоном Джозефом Дэвиссоном и
Лестером Джермером 3. Однако оставалось неясным, каким образом
следует изменить соотношения де Бройля A.1.1) для несвободных час-
частиц, например, электрона в произвольном кулоновском поле.
Следующим этапом в истории квантовой механики, отодви-
отодвинувшим в сторону волновую механику, было развитие в 1925—1927
годах матричной механики 4 в трудах Вернера Гейзенберга, Макса
Борна, Паскуаля Иордана и Вольфганга Паули. По крайней мере,
частично это развитие вдохновлялось убеждением, что теория долж-
должна включать только наблюдаемые величины, например, уровни энер-
энергии или вероятности испускания или поглощения. Работа Гейзен-
Гейзенберга 1925 года начинается с манифеста: «В настоящей работе дела-
1.1. Релятивистская волновая механика
ется попытка установить основы теоретической квантовой механи-
механики, опираясь исключительно на соотношения между величинами,
которые в принципе наблюдаемы». Подобный позитивизм периоди-
периодически проявлялся на разных этапах истории квантовой теории по-
поля, например, при введении Джоном Уилером и Гейзенбергом по-
понятия ^-матрицы (см. гл. 3) и при возрождении дисперсионной тео-
теории в 1950-х годах (см. гл. 10), однако современная квантовая теория
поля весьма далека от этого идеала. Мы слишком отклонимся от
нашего предмета, если будем сколько-нибудь детально описывать
здесь матричную механику.
Как всем известно, волновая механика была возрождена Эрви-
ном Шредингером. В серии статей 1926 года 5 вначале было предложе-
предложено знакомое всем нерелятивистское волновое уравнение, и на его ос-
основе воспроизведены результаты матричной механики. Только позднее,
в шестом разделе четвертой статьи предлагалось релятивистское вол-
волновое уравнение. Согласно Дираку6, история была совсем другой: сна-
сначала Шредингер вывел релятивистское уравнение, затем разочаровался
в нем, так как уравнение приводило к неправильной тонкой структу-
структуре уровней водорода, и, наконец, через несколько месяцев осознал,
что нерелятивистское приближение к релятивистскому уравнению са-
само по себе имеет смысл, даже если релятивистское уравнение невер-
неверно! К тому времени, когда Шредингер решился опубликовать свое ре-
релятивистское волновое уравнение, оно было уже независимо открыто
Оскаром Клейном 7 и Вальтером Гордоном 8, так что обычно его назы-
называют уравнением Клейна-Гордона.
Релятивистское волновое уравнение Шредингера было выве-
выведено на основе замечания, что для «лоренцовского электрона» с мас-
массой т и зарядом е, находящегося во внешнем поле с векторным
потенциалом А и кулоновским потенциалом ф, функция Гамильтона
Н и импульс р связаны соотношением *
0 = (Я + ефJ - с2(р + еА/сJ - т2с4 . A.1.2)
Для свободной частицы, которая описывается плоской волной
ехр{2ти(кх — Vt)}, соотношения де Бройля A.1.1) могут быть получены
* Это лоренц-инвариантное выражение, т. к. величины А и ф преобразуются
так же, как ср и Е. На самом деле, Шредингер записал Я и р через частные
производные функции действия, но для нашего обсуждения это несущественно.
Глава 1. Историческое введение
путем замен:
р = hk -» - ittV, E = hv -» ittd/dt,
A.1.3)
где h — введенное позднее Дираком удобное обозначение для
величины h/B%). Используя формальную аналогию, Шредингер пред-
предположил, что электрон во внешних полях А, ф будет описываться
волновой функцией \|/(х, t), удовлетворяющей уравнению, полу-
полученному с помощью тех же замен в формуле A.1.2):
0 =
* о 1 9 f * ^ еА
in — + еф -с2 \-inV + —
dt У с
\|/(x,t). A.1.4)
В частности, для стационарных состояний атома водорода А = 0
и ф = е/Dлг), а \|/ зависит от времени как ехр(—zEt/Й), так что A.1.4)
принимает вид:
0 =
4лг
-с2Й2У2-ш2с4
A.1.5)
При разумных граничных условиях можно найти собственные
значения энергии 9
= тс2
1-
2п2 2п4
п
A.1.6)
где а = е2/Dлйс) — постоянная тонкой структуры, примерно равная
1/137; п — положительное целое число, а I — орбитальный угловой
момент в единицах Й, равный целому числу, лежащему в пределах
0 < I < п -1. Слагаемое, пропорциональное а2, хорошо описывает
основные черты водородных спектров (серии Лаймана, Бальмера и
т. д.). По Дираку, именно это согласие подтолкнуло Шредингера к рас-
рассмотрению нерелятивистского волнового уравнения. С другой сторо-
стороны, слагаемое, пропорциональное а4, приводило к тонкой структуре
1.1. Релятивистская волновая механика
спектров, противоречившей уже существовавшим аккуратным изме-
измерениям Фридриха Пашена.
Полезно сравнить результат Шредингера с тем, который был полу-
получен Арнольдом Зоммерфельдом 10 по правилам старой квантовой теории:
Е = тс2
a2
2n2 2n4U 4
A.1.7)
Здесь к — целое число между 1 и п, которое в теории Зоммерфельда
выражается через орбитальный момент Ift в виде к = I + 1. Это
приводит к тонкому расщеплению, находящемуся в согласии с экс-
экспериментом. Например, для п = 2 из A.1.7) получаем два уровня
(к = 1 и к = 2), расщепление которых равно наблюдаемой величине
a4mc2/32 или 4,53 X 10~5 эВ. В противоречии с этим, результат Шре-
Шредингера A.1.6) дает при п = 2 величину расщепления уровней тон-
тонкой структуры a4mc2/12, что значительно больше наблюдаемой ве-
величины.
Шредингер правильно понял, что источником этого расхож-
расхождения было пренебрежение спином электрона. Расщепление атом-
атомных уровней щелочных атомов некулоновскими электрическими и
слабыми внешними магнитными полями (так называемый аномаль-
аномальный эффект Зеемана) показало, что мультиплетность состояний
больше, чем предсказываемая теорией Бора-Зоммерфельда. Это по-
побудило Джорджа Уленбека и Сэмюела Гаудсмита и предположить
в 1925 году, что электрон обладает внутренним угловым моментом
Й/2. По известной величине зеемановского расщепления 12 им уда-
удалось установить, что магнитный момент электрона равен
еП
2тс
Было ясно, что спин электрона должен взаимодействовать с
его орбитальным моментом, так что релятивистское уравнение Шре-
Шредингера и не могло привести к правильному значению тонкого рас-
расщепления.
К 1927 году уже несколько авторов 13 сумели показать, что спин-
орбитальное взаимодействие ответственно за расхождение между резуль-
результатом Шредингера A.1.6) и опытом. На самом деле, здесь играют роль два
эффекта: один из них — прямое взаимодействие магнитного момента
A.1.8) и магнитного поля, действующего на электрон, движущийся
Глава 1. Историческое введение
в электростатическом поле атома; второй эффект — релятивистская
«томасовская прецессия», связанная (даже в отсутствие магнитного мо-
момента) с круговым движением вращающегося электрона 14. Вместе эти
два эффекта приводят к подъему уровня с полным угловым моментом
j = I + 1/2 до значения, определяемого формулой Зоммерфельда A.1.7)
при к = I + 1 = j + 1/2, в то время как уровень с j = I — 1/2 опускается до
значения, даваемого той же формулой при к = I = j + 1/2. Таким обра-
образом, оказалось, что энергия зависит только от п и j, но не от I отдельно:
Е = тс2
1
1
a2
2n2
a4
2n4
(
j
n
+
1
—
2
3
4
A.1.9)
По случайности теория Зоммерфельда давала правильную ве-
величину расщепления в водороде (j + 1/2 принимает, как и к, толь-
только целые значения от 1 до п), однако совершенно неправильным
образом приписывала различным уровням значения орбитального
момента I. Кроме того, в согласии с экспериментом предсказыва-
предсказывалась мультиплетность уровней тонкой структуры в водороде, рав-
равная 2 для j = 1/2 и 2Bj + 1) для j > 1/2 (в соответствии со значениями
I, равными j ± 1/2).
Несмотря на эти успехи, все еще не существовало последова-
последовательной релятивистской теории, с самого начала включавшей спин
электрона. Такую теорию построил в 1928 году Поль Дирак. Однако
он не пытался просто создать релятивистскую теорию вращающего-
вращающегося электрона. Дирак подошел к задаче, поставив вопрос, кажущийся
в наши дни очень странным. В начале своей статьи 1928 года 15 он
спрашивает, «почему Природа выбрала именно эту модель электро-
электрона, вместо того, чтобы удовлетвориться точечным зарядом». Для нас
сегодня это звучит примерно так же, как вопрос о том, почему бак-
бактерия состоит из одной клетки. Спин Й/2 — просто одно из свойств,
определяющих именно электрон, и отличающее эту частицу от мно-
множества других известных в наши дни частиц с разными спинами.
Однако в 1928 году не возбранялось верить, что все вещество состоит
из электронов и похожих на них частиц, но с положительным заря-
зарядом, входящих в состав атомного ядра. Поэтому в духе того времени
можно так переформулировать вопрос Дирака: «Почему фундамен-
фундаментальные составляющие вещества должны иметь спин Й/2?»
1.1. Релятивистская волновая механика
Для Дирака ключом к ответу на этот вопрос было требование
положительности вероятностей. Было известно 16, что плотность ве-
вероятности для нерелятивистского уравнения Шредингера равна |\|/|2,
причем она удовлетворяет уравнению непрерывности вида:
—(I vl2) -—v • (y*vy - yvy*) = о,
3tv ; 2т v ;
так что интеграл от |\|/|2 по пространству не зависит от времени. С
другой стороны, единственные выражения для плотности вероят-
вероятности р и плотности тока J, которые можно построить из решений
релятивистского уравнения Шредингера, и которые удовлетворя-
удовлетворяют закону сохранения
Эр
^ + V-J = 0, A.1.10)
at
имеют вид
Wl , A.1.11)
at n J
J = iVc2Imy V + \|/, A.1.12)
где N — произвольная константа. Невозможно считать р плотно-
плотностью вероятности, так как и при наличии, и в отсутствие внешнего
потенциала ф плотность р не имеет определенного знака. Процити-
Процитируем воспоминания Дирака 17 по этому поводу:
«Вспоминаю, что как-то в Копенгагене Бор спросил меня, над
чем я работаю, и я рассказал, что пытаюсь построить удовле-
удовлетворительную релятивистскую теорию электрона. Бор отве-
ответил: "Но ведь это уже сделали Клейн и Гордон!" Поначалу такой
ответ меня крайне обескуражил. Казалось, что Бор вполне удовле-
удовлетворен решением Клейна, меня оке оно совершенно не устраивало
из-за возникающих при этом отрицательных вероятностей. Но
я не сдался и продолжал поиск теории, в которой были бы только
положительные вероятности».
Как утверждает Георгий Гамов 18, Дирак нашел решение про-
проблемы однажды вечером в 1928 году, когда он сидел, уставившись
10 Глава 1. Историческое введение
в огонь камина в колледже св. Иоанна в Кембридже. Дирак понял,
что уравнение Клейна-Гордона (или релятивистское уравнение Шре-
дингера) приводит к отрицательным вероятностям потому, что плот-
плотность р в уравнении закона сохранения A.1.10) содержит производ-
производные волновой функции по времени. Это, в свою очередь, вытекает
из того, что волновая функция удовлетворяет дифференциальному
уравнению второго порядка по времени. Задача, таким образом,
заключалась в том, чтобы заменить это волновое уравнение другим
уравнением, куда бы входили производные по времени первого по-
порядка, как в нерелятивистском уравнении Шредингера.
Предположим, что волновая функция электрона является мно-
многокомпонентной величиной \|/п(ж), удовлетворяющей волновому урав-
уравнению вида
гП^- = .Ж\]?, A.1.13)
at
где Ж — некоторая матричная функция пространственных произ-
производных. Поскольку уравнение линейно по производным по времени,
то для построения лоренц-инвариантной теории мы должны пред-
предположить, что оно также линейно и по пространственным произ-
производным, иными словами, Ж имеет вид
Ж = -ihca- V + oc4mc2, A.1.14)
где а1( а2, а3 и а4 — постоянные матрицы. Из A.1.13) можно полу-
получить уравнение второго порядка:
-й2 —^ = jr\|/ = -й2с2а^а3-
Э2\|/ 9 ,,
3t2
- ihmc {aiai + a4aj) h m^c^al^i.
(Здесь принято соглашение о суммировании по повторяющимся ин-
индексам: г, j принимают значения 1, 2, 3 или х, у, z.) Но это уравне-
уравнение должно согласовываться с релятивистским уравнением Шре-
дингера для свободного поля A.1.4), выражающим просто релятиви-
релятивистскую связь между энергией и импульсом. Поэтому матрицы а и а4
должны удовлетворять условиям:
1.1. Релятивистская волновая механика
11
Ц = 2ЪЦ1,
осгос4 + ос4осг = О,
A.1.15)
A.1.16)
A.1.17)
где Ъц — символ Кронекера A при г = j; 0 при г Ф j), a I — единичная
матрица. Дирак нашел набор матриц 4x4, удовлетворяющих этим
соотношениям:
0 0 0 1
0 0 10
0 10 0
10 0 0
ос, =
ос, =
ос, =
0 0 1 0"
0 0 0-1
10 0 0
0-100
ос, =
0
0
0
г
1
0
0
0
0
0
—г
0
0
-1
0
0
0
г
0
0
0
0
1
0
—г
0
0
0
0
0
0
-1
A.1.18)
Чтобы доказать лоренц-инвариантность развитого формализ-
формализма, Дирак умножил A.1.13) слева на ос4, так что уравнение стало
возможным записать в виде:
Э А
+ тсА К|/ = 0, A.1.19)
A.1.20)
у = -гос4сс , у0 = -гос4.
(Греческие индексы ц, V, и т. д. принимают значения 1, 2, 3, 0, при-
причем х° = ct. Дирак использовал в своей работе ж4 = ict и поэтому
у4 = 0С4.) Матрицы уц удовлетворяют следующим соотношениям
антикоммутации:
+1,
-1,
0,
ц = V = 0,
ц Ф V.
A.1.21)
12
Глава 1. Историческое введение
Дирак заметил, что эти соотношения являются лоренц-инва-
риантными в том смысле, что матрицы Л^У, где Л — произвольное
преобразование Лоренца, также им удовлетворяют. Отсюда Дирак
сделал вывод, что Л^У должны быть связаны с у1 некоторым преоб-
преобразованием подобия
Следовательно волновое уравнение оказывается инвариантным, ес-
если при преобразовании Лоренца жц —» A|1vxv волновая функция под-
подвергается матричному преобразованию \|/ —» 6"(Л)\|/. (Более подробно
эти вопросы обсуждаются в гл. 5 с несколько иной точки зрения.)
Для изучения поведения электронов в произвольном внешнем
электромагнитном поле Дирак воспользовался «обычной процеду-
процедурой», сделав те же замены
¦* Э ¦+ Э
in > in
at at
еф,
e
с
A.1.22)
что и в A.1.4). В результате уравнение A.1.13) принимает вид:
ih — + еф К|/ = -ittV + - А • ос\|/ + mc2oc4\|/. A123)
3t ) \ с
С помощью этого уравнения Дирак показал, что условие сохране-
сохранения углового момента в центральном поле имеет вид
[Ж-гПт х V + Па / 2] = О,
A.1.24)
где Ж - матричный дифференциальный оператор A.1.14), а 0
4х4-обобщение спиновых матриц, ранее введенных Паули 19:
о =
'0010
0 0 0 1
10 0 0
0 10 0
\
а.
A.1.25)
1.1. Релятивистская волновая механика 13
Так как каждая компонента о имеет собственные значения, рав-
равные ± 1, то наличие дополнительного слагаемого в A.1.24) показы-
показывает, что электрон обладает внутренним угловым моментом Й/2.
Дирак также квадрировал уравнение A.1.23) и получил урав-
уравнение второго порядка. Оказалось, что оно имеет тот же вид, что
и уравнение Клейна-Гордона A.1.4), за исключением двух дополни-
дополнительных слагаемых в правой части:
[-еПса • В - iehca • Е]\|/. A.1.26)
В случае медленно движущегося электрона доминирует пер-
первое слагаемое, соответствующее магнитному моменту, значение ко-
которого согласуется с найденным Уленбеком и Гаудсмитом п значе-
значением A.1.8). Как заметил Дирак, такое значение магнитного момен-
момента с учетом релятивистской структуры теории приводит к правиль-
правильной структуре тонкого расщепления в согласии (с точностью до ОС4тс2)
с результатами Гейзенберга, Иордана и Чарльза Г. Дарвина 13. Чуть
позднее Дарвин 20 и Гордон 21 вывели «точную» формулу для уров-
уровней энергии атома водорода в рамках теории Дирака:
Е = тс2
,-1/2
1 + -
а2
Первые три слагаемых в разложении этого выражения в ряд по
степеням ОС2 согласуются с приближенным выражением A.1.9).
Построенная теория удовлетворяла требованиям, выдвинутым
Дираком: формализм должен быть релятивистским, а вероятно-
вероятности — существенно положительными. Из A.1.13) и A.1.14) можно
вывести уравнение непрерывности:
Эр
-^ + V-J = 0, A.1.28)
at
р = |?|2, J = cy+ccy, A.1.29)
так что положительную величину |\|/|2 можно интерпретировать как
плотность вероятности, причем полная вероятность равна интегралу
„ , Г| |2 ,3
от квадрата модуля волновой функции J|\|/| ax.
14 Глава 1. Историческое введение
Однако возникла новая проблема, которую Дирак не сумел
сразу разрешить.
При заданном импульсе р волновое уравнение A.1.13) имеет
четыре решения в виде плоских волн:
\|/осехрU-(p-x-Et) . A.1.30)
Два решения с Е = +VP2c2 + то2с4 соответствуют двум спиновым со-
состояниям электрона с проекциями спина + Й/2. У двух других ре-
решений Е = —^/р2с2 + 7п2с4 , и они не имеют ясной физической ин-
интерпретации. Как отметил Дирак, эта же проблема возникает и для
релятивистского уравнения Шредингера: при каждом р существу-
существуют два решения вида A.1.30), одно — с положительным, другое —
с отрицательным значением Е.
Конечно, даже в классической физике релятивистское соотно-
шение Е2= р2с2 + ш2с4 имеет два решения: Е = ±yj-p2c2 +m2ci ¦ Одна-
Однако в этом случае можно просто предположить, что физическими яв-
являются только те частицы, у которых Е положительно. Так как у
положительных решений Е > тс2, а у отрицательных Е < — тс2,
между этими решениями существует щель конечной величины, при-
причем никаким непрерывным воздействием невозможно перевести
частицу из состояния с положительной энергией в состояние с
отрицательной энергией.
В релятивистской квантовой механике проблема с отрицатель-
отрицательными энергиями представляется значительно более серьезной. Как
заметил Дирак в работе 1928 года, взаимодействие электрона с из-
излучением может привести к переходам, в которых электрон с поло-
положительной энергией переходит в состояние с отрицательной энер-
энергией, а избыточная энергия уносится двумя или более фотонами.
Почему же тогда вещество стабильно?
В 1930 году Дирак предложил необычное решение проблемы.
Оно было основано на принципе запрета, так что уместно сказать
несколько слов об истории этого принципа.
Изучение периодической таблицы элементов, а также систе-
систематика рентгеновских спектров выявили определенные закономер-
ности заполнения электронами энергетических уровней атомов .
максимальное число электронов Nn на оболочке, характеризующейся
главным квантовым числом п, вдвое больше числа различных орби-
орбитальных состояний с данным п:
1.1. Релятивистская волновая механика 15
l) = 2n2=2, 8, 18,... (LL3i)
г=о
В 1925 году Вольфганг Паули высказал предположение, что
подобную структуру можно понять, если считать, что Nn равно пол-
полному числу возможных состояний на n-ой оболочке, и кроме того
существует некий таинственный принцип запрета, запрещающий
более, чем одному электрону находиться в данном состоянии. Пау-
Паули приписал загадочный множитель 2 в A.1.31) «необычной, класси-
классически необъяснимой двойственности» электронных состояний, что,
как мы видели, чуть позднее было связано со спином электрона п.
Принцип запрета дал ответ на вопрос, остававшийся неясным
в старой теории Бора и Зоммерфельда: почему все электроны в
тяжелых атомах на падают на оболочку с наименьшей энергией?
Затем принцип запрета Паули был формализован рядом авторов 25
как требование, чтобы волновая функция многоэлектронной систе-
системы была бы антисимметричной по пространственным и спиновым
координатам всех электронов. Энрико Ферми 26 и Дирак 27 включи-
включили этот принцип в статистическую механику, так что частицы, под-
подчиняющиеся принципу запрета, стали называть общим термином
фермионы, в то время, как частицы типа фотонов, для которых
волновая функция симметрична и которые подчиняются статистике
Бозе и Эйнштейна, получили название бозонов. Принцип запрета
сыграл важнейшую роль в теории металлов, белых карликов и ней-
нейтронных звезд и т. п., а также в химии и атомной физике, но обсу-
обсуждение этих вопросов уведет нас слишком далеко от основной темы.
Гипотеза Дирака состояла в том, что электроны с положи-
положительными энергиями не могут перейти в состояния с отрицатель-
отрицательной энергией, так как «все состояния с отрицательной энергией
заняты, быть может, за исключением нескольких состояний
с малыми скоростями». Эти вакантные состояния или «дырки»
в море электронов с отрицательными энергиями ведут себя как
частицы с противоположными значениями квантовых чисел: поло-
положительной энергией и положительным зарядом. Единственной час-
частицей с положительным зарядом, известной к тому времени, был
протон, и как позднее вспоминал Дирак 27а, «вся научная атмо-
атмосфера в те времена противилась введению новых частиц». Поэто-
Поэтому Дирак отождествил свои дырки с протонами; действительно,
16 Глава 1. Историческое введение
его статья 1930 года 22 так и называлась — «Теория электронов и
протонов».
Теория дырок немедленно столкнулась с серьезными трудно-
трудностями. Одна очевидная проблема была связана с бесконечной плот-
плотностью заряда вездесущих электронов с отрицательной энергией:
где же тогда создаваемое ими электрическое поле? Дирак предло-
предложил интерпретировать плотность заряда, входящую в уравнения
Максвелла, как «отклонение от нормального состояния электриза-
электризации мира». Другая проблема была связана с колоссальной разницей
наблюдаемых значений масс и взаимодействий электронов и прото-
протонов. Дирак надеялся, что кулоновские взаимодействия между элек-
электронами каким-то образом объяснят такую разницу, но Герман
Вейль 28 показал, что теория дырок полностью симметрична по от-
отношению к отрицательным и положительным зарядам. Наконец, Ди-
рак предсказал существование процесса электрон-протонной ан-
аннигиляции, в котором электрон с положительной энергией взаимо-
взаимодействует с дыркой в море электронов с отрицательной энергией, и
попадает на этот незанятый уровень, испуская пару гамма-квантов.
Само по себе это не создавало дополнительных трудностей для тео-
теории дырок. Более того, высказывались надежды, позднее не оправ-
оправдавшиеся, что таким образом удастся объяснить источник энергии
звезд. Однако вскоре Юлиус Роберт Оппенгеймер и Игорь Тамм
отметили 29, что электрон-протонная аннигиляция в атомах будет
происходить со скоростью, несовместимой с наблюдаемой стабиль-
стабильностью обычного вещества. По этим причинам в 1931 году Дирак
изменил свою точку зрения и решил, что дырки должны прояв-
проявляться не как протоны, а как новый сорт положительно заряжен-
ных частиц с массой, равной массе электрона .
Вторая и третья проблемы были устранены после того, как Карл
Андерсон, по-видимому ничего не знавший о предсказании Дирака,
открыл позитрон 30. 2 августа 1932 года в камере Вильсона, помещен-
помещенной в магнитное поле индукцией 15 кГс, был зарегистрирован не-
необычный трек от частиц космического излучения. Этот трек был ис-
искривлен в направлении, свидетельствовавшем о положительном за-
заряде частицы, причем его протяженность была по меньшей мере в
десять раз больше, чем можно было ожидать для протона!
И кривизна, и удельная ионизация трека были совместимы с гипоте-
гипотезой, что это след новой частицы, отличающейся от электрона только
знаком заряда, как и ожидалось для одной из дираковских дырок.
1.1. Релятивистская волновая механика 17
(Еще ранее это же открытие было сделано П. М. Блеккетом, однако
он его не опубликовал сразу же. Андерсон цитирует сообщения прес-
прессы о полученных Блеккетом и Джузеппе Оккиалини свидетельствах
существования положительно заряженных частиц в треках космиче-
космических лучей.) Так оказалось, что Дирак был не прав только в своем
первоначальном отождествлении дырок с протонами.
Открытие более или менее предсказанного позитрона, а так-
также предыдущие успехи уравнения Дирака в объяснении магнитного
момента электрона и тонкой структуры спектров водорода подняли
теорию Дирака на пьедестал, на котором она находится уже более
шести десятилетий. Хотя и нет сомнений в том, что теория Дирака
в какой-то форме выживет в любой будущей физической теории,
все же есть серьезные основания быть неудовлетворенными ее ис-
исходными посылками.
1. Проделанный Дираком анализ трудностей с отрицатель-
отрицательными вероятностями, возникающими при рассмотрении реляти-
релятивистского волнового уравнения Шредингера, казалось, исключа-
исключает существование любых частиц с нулевым спином. Но даже в
1920-х годах такие частицы были известны — например атом во-
водорода в основном состоянии или ядро гелия. Конечно, можно
было пытаться возражать, что атомы водорода и альфа-частицы
не являются элементарными и поэтому не должны описываться
релятивистскими волновыми уравнениями. Однако, не было ясно
(и продолжает оставаться неясным), как включить идею элемен-
элементарности в формализм релятивистской квантовой механики. В на-
наши дни известно большое число частиц со спином нуль — л-мезо-
ны, К-мезоны и т. д., которые не менее элементарны, чем протон
или нейтрон. Нам известны также частицы со спином единица —
W± и Z0, столь же элементарные, как электрон или любая другая
частица. Наконец, если не принимать во внимание эффекты силь-
сильного взаимодействия, в наши дни мы бы рассчитывали тонкую
структуру уровней «мезоатомов», состоящих из бесспиновых от-
отрицательно заряженных ж- или К-мезонов, связанных с атомным
ядром, исходя из стационарных решений релятивистского урав-
уравнения Клейна-Гордона-Шредингера! Итак, трудно согласиться с
тем, что релятивистское уравнение для частиц со спином нуль
содержит в себе что-то фундаментально неправильное, что вы-
вынуждает обратиться к уравнению Дирака — дело просто в том,
что спин электрона равен Й/2, а не нулю.
18 Глава 1. Историческое введение
2. Насколько нам сейчас известно, каждому сорту частиц
соответствует своя «античастица» с той же массой и противопо-
противоположным зарядом. (Некоторые истинно нейтральные частицы, вроде
фотона, являются античастицами для самих себя.) Однако, как
же мы можем интерпретировать античастицы заряженных бозо-
бозонов, например, % ± или W±, как дырки в море состояний с отри-
отрицательной энергией? Ведь для частиц, квантованных по прави-
правилам статистики Бозе-Эйнштейна, принцип исключения не дей-
действует и ничто не препятствует частице с положительной энер-
энергией перейти в состояние с отрицательной энергией, независимо
от того, занято оно или нет. Но если теория дырок неприменима
для бозонных античастиц, почему, спрашивается, ей следует до-
доверять в случае фермионов? Я расспрашивал Дирака в 1972 году,
что он думал в свое время по этому поводу. Он ответил, что не
воспринимал бозоны типа пиона или W± как «существенные». Не-
Несколькими годами спустя, в лекции 29а Дирак отметил, что «мы
не имеем более картины вакуума, в котором состояния с отрица-
отрицательной энергией заполнены», и подчеркнул, что в этом случае
«вся теория становится более сложной». В следующем разделе
мы покажем, как в результате развития квантовой теории поля
интерпретация античастиц как дырок стала ненужной, несмотря
на то, что до сих пор она, к сожалению, просачивается на стра-
страницы многих учебников. Процитируем Джулиана Швингера 30а:
«Картина бесконечного моря электронов с отрицательной энер-
энергией рассматривается сейчас в лучшем случае как историче-
исторический курьез и прочно забыта».
3. Одним из больших успехов теории Дирака было правильное
предсказание величины магнитного момента электрона. Оно особен-
особенно поражало потому, что магнитный момент A.1.8) оказался вдвое
больше, чем можно было бы ожидать в случае орбитального движе-
движения заряженной частицы с угловым моментом Й/2. Этот множитель
2 оставался загадкой вплоть до создания теории Дирака. Однако, на
самом деле, в линии рассуждений Дирака нет ничего, что безогово-
безоговорочно приводит именно к такому значению магнитного момента. Ко-
Когда мы включаем в волновое уравнение A.1.23) взаимодействие с
электрическим и магнитным полями, мы можем с успехом добавить
«паулиевское слагаемое» 31
A.1.32)
1. 2. Рождение квантовой теории поля 19
с произвольным коэффициентом к. (Здесь F^ — обычный тензор
напряженности электромагнитного поля, причем F12 = В3, F01 = Еъ
и т. д.) Такое слагаемое можно получить, добавив предварительно в
уравнение свободного поля слагаемое, пропорциональное выра-
выражению ['fbf]{d2/dx^dxv)\\f, которое, конечно, равно нулю, а затем
совершить, как и ранее, подстановку A.1.22). Более современный
подход заключается просто в замечании, что слагаемое A.1.32) удов-
удовлетворяет всем принятым принципам инвариантности, включая ло-
ренц-инвариантность и калибровочную инвариантность, так что нет
причин, почему такое слагаемое не должно включаться в волновые
уравнения (см. раздел 12.3.). Такое слагаемое будет приводить к до-
дополнительному вкладу в магнитный момент электрона, пропорцио-
пропорциональному к, так что, если не принимать во внимание возможное
требование чисто формальной простоты, нет никаких оснований ожи-
ожидать, что в теории Дирака магнитный момент электрона имеет ка-
какое-то определенное значение.
Как мы увидим далее, все перечисленные проблемы были в
конце концов решены (или, по крайней мере, разъяснены) в про-
процессе развития квантовой теории поля.
1.2. Рождение квантовой теории поля
Фотон — единственный пример частицы, которая до своего
открытия была известна как поле. Поэтому неудивительно, что раз-
развитие формализма квантовой теории поля прежде всего было свя-
связано с излучением, и только позднее он был применен к другим
частицам и полям.
В 1926 году в одной из основополагающих работ по матрич-
матричной механике Борн, Гейзенберг и Иордан 32 применили свои новые
методы к свободному полю излучения. Для простоты они игнори-
игнорировали поляризацию электромагнитных волн и рассмотрели про-
пространственно одномерную задачу, причем координата х изменя-
изменялась от 0 до L. Если потребовать, чтобы поле излучения и(х, t)
обращалось в нуль на концах интервала, то оно будет иметь вид,
совпадающий с величиной смещения точек струны с закрепленны-
закрепленными при х = 0 и х = L концами. По аналогии со случаем струны
для полного электромагнитного поля гамильтониан был выбран
в виде
20 Глава!. Историческое введение
ди
Чтобы свести это выражение к сумме квадратов, поле и было
представлено как сумма фурье-компонент при условии, что и = 0
при х = 0 и ж = L:
(L2.2)
fc=i V с У
fc /. A.2.3)
В результате
7EK() fc^D A-2.4)
4 fc=i
Таким образом, струна или поле ведет себя как сумма незави-
независимых гармонических осцилляторов с угловыми частотами cofc, как
и предвидел за 20 лет до этого Пауль Эренфест 32а.
В частности, «импульс» Pfc(t), канонически сопряженный к q^(t),
определяется, как и в механике частиц, условием, что если Н вы-
выражено как функция р и д, то
dpk(t)
Отсюда получается, что импульс
L
pk(t) = — qk(t), A.2.5)
и можно записать канонические перестановочные соотношения:
:-^-§fcr A-2.6)
[qk(t),qj(t)] = 0. A.2.7)
1. 2. Рождение квантовой теории поля
21
Кроме того, временная зависимость qk(t) определяется уравнением
движения Гамильтона
•• - 2 • - _ 2 ЭН 2
к L k L dqk{t) k k ' (L2'8)
Явный вид матриц, определяемых уравнениями A.2.6)—A.2.8),
был уже известен Борну, Гейзенбергу и Иордану из предыдущей
работы по гармоническому осциллятору. Для g-матрицы получается
выражение
Leo
к
ак exp(-zwfci) + a\ exp(+zwfci)], (L2.9)
t
где ак — не зависящая от времени матрица, а ак' — ее эрмитово
сопряженная матрица, удовлетворяющие перестановочным соот
ношениям
A1 =5W, A.2.10)
A.2.11)
Строки и столбцы этих матриц помечены набором неотри-
неотрицательных целых чисел щ, п2, ..., каждое из которых соответствует
нормальной моде. Матричные элементы равны
A.2.12)
A.2.13)
Для единственной нормальной моды эти матрицы можно вы-
выписать в явном виде:
а =
о VI о о
0 0 V2 0
0 0 0 V3
0 0 0 0
v ¦
/ 0 0 0 0
VI о о о
0 V2 0 0
0 0 V3 0
22 Глава 1. Историческое введение
Можно непосредственно убедиться, что матрицы A.2.12) и A.2.13)
удовлетворяют перестановочным соотношениям A.2.10) и A.2.11).
Физическая интерпретация вектора-столбца с целыми компо-
компонентами щ, п2, ... заключается в том, что он представляет состоя-
состояние с пк квантами в каждой нормальной моде к. Матрицы ак или а^,
действующие на такой вектор-столбец, будут соответственно умень-
уменьшать или увеличивать пк на единицу, оставляя неизменными все щ
с1фк. Поэтому можно интерпретировать эти матрицы как операто-
операторы уничтожения или рождения одного кванта в к-ой нормальной
моде. В частности, вектор со всеми пк = 0 представляет вакуум;
действие на него любого оператора ак дает нуль.
Дальнейшая интерпретация связана с рассмотрением функции
Гамильтона. Подставляя A.2.9) и A.2.10) в A.2.4), находим:
н = l^cofcDafc+|). A.2.14)
к
Таким образом, гамильтониан диагоналей в п-представлении:
= Y
Видно, что энергия состояния есть просто сумма энергий tm>k
каждого кванта в данном состоянии плюс бесконечная нулевая энер-
энергия Ео = з E^cofc. В применении к полю излучения этот формализм
подтвердил разработанный Бозе метод подсчета состояний излуче-
излучения по числу пк квантов в каждой нормальной моде.
Борн, Гейзенберг и Иордан использовали такой формализм при
выводе выражения для среднеквадратичных флуктуации энергии
в излучении черного тела. (Для этой цели они, в действительности,
использовали только коммутационные соотношения A.2.6)—A.2.7).) Од-
Однако вскоре такой подход был применен к исследованию более акту-
актуальной проблемы — вычислению вероятностей спонтанного излуче-
излучения.
Чтобы понять возникшие здесь трудности, необходимо вер-
вернуться немного назад. В одной из первых работ по матричной меха-
механике Борн и Иордан 33 высказали предположение, что атом, пере-
перескакивая из состояния C в более низкое по энергии состояние ос,
должен испускать излучение подобно классическому заряженному
осциллятору, смещение которого дается выражением
1. 2. Рождение квантовой теории поля 23
r(t) = rpa exp (-2%ivt) + Гра exp B%ivt), A.2.16)
hv = Ep-Ea, A.2.17)
а Гра — (За матричный элемент матрицы, связанной с координатой
электрона. Энергия Е такого осциллятора равна
Е = |m(r2 + B:wJr2) = 8jrW|rpa|2. A.2.18)
Непосредственное классическое вычисление позволяет теперь
найти излученную мощность, а после деления на энергию hv одного
фотона — вероятность испускания фотона
.,_ . 16Ji3e2v3 l2
Аф^а)= |rpa|2. A.2.19)
Однако оставалось совершенно непонятным, почему при рас-
рассмотрении спонтанного излучения следовало таким образом обра-
обращаться с формулами для излучения классического диполя.
Несколько позднее Дирак 34 дал более убедительный, хотя еще
менее прямой вывод этих соотношений. Рассматривая поведение
квантованных атомных состояний в осциллирующем классическом
электромагнитном поле плотностью энергии и, приходящейся на
единичный интервал частот в окрестности частоты A.2.17), он су-
сумел вывести формулы для вероятностей поглощения uB(a—>|3) или
индуцированного испускания иВф —> ос):
2л2е2
В(а ^ Р) = В(Р ^ а) = —^|гра|2. A.2.20)
(Отметим, что выражение в правой части этого равенства симмет-
симметрично по отношению к состояниям а и C, так как rap равно г$а\)
Эйнштейн 34а уже показал в 1917 году, что возможность теплового
равновесия между атомами и излучением черного тела требует
выполнения определенного соотношения между вероятностью
Аф —» а) спонтанного излучения и вероятностями иВ индуцирован-
индуцированного испускания или поглощения:
а) = {^ W -> а).
24 Глава 1. Историческое введение
Подстановка формулы A.2.20) в это соотношение немедленно
приводит к результату Борна и Иордана A.2.19) для вероятности
спонтанного излучения. Тем не менее, представляется неудовле-
неудовлетворительным, что термодинамические аргументы должны исполь-
использоваться для вывода формул, описывающих процессы, происходя-
происходящие с одиночными атомами.
Наконец в 1927 году Дирак 35 сумел представить строгое кван-
тово-механическое рассмотрение спонтанного излучения. Векторный
потенциал А(х, t) был разложен на нормальные моды, как в форму-
формуле A.2.2), и было показано, что коэффициенты удовлетворяют пере-
перестановочным соотношениям типа A.2.6). Соответственно, каждое со-
состояние свободного поля излучения было задано набором целых чи-
чисел пк, по одному на каждую нормальную моду, а матричные эле-
элементы энергии электромагнитного взаимодействия приняли вид сум-
суммы по нормальным модам, причем матричные коэффициенты оказа-
оказались пропорциональными матрицам ак и ак\ определенным в A.2.10)-
A.2.13). Главное в этих результатах — появление множителя в урав-
уравнении A.2.13). Вероятность перехода, в котором число фотонов в нор-
нормальной моде к увеличивается от пк до пк + 1, пропорционально
квадрату этого множителя, т. е. пк + 1. Но в поле излучения с пк
фотонами в нормальной моде к плотность энергии и на единичный
интервал частот равна:
так что вероятность испускания излучения в нормальной моде к
пропорциональна
8%hv3k
Первое слагаемое интерпретируется как вклад индуцированно-
индуцированного испускания, а второе - как вклад спонтанного излучения. Таким
образом, без всякого обращения к термодинамике Дирак смог заклю-
заключить, что отношение вероятностей индуцированного испускания иВ
и спонтанного излучения А удовлетворяет соотношению Эйнштейна
(.2.21). Используя свой же более ранний результат A.2.20) для В, Ди-
Дирак сумел заново вывести формулу Борна-Иордана 33 A.2.19)
1. 2. Рождение квантовой теории поля 25
для вероятности спонтанного излучения А. Несколько позднее анало-
аналогичные методы были использованы Дираком при квантово-механиче-
ском рассмотрении рассеяния излучения и времени жизни возбуж-
возбужденных атомных состояний 36, а также Виктором Вайскопфом и Юд-
Юджином Вигнером при детальном анализе формы спектральных ли-
линий 36а.
Дирак в своей работе разделил электромагнитный потенциал
на поле излучения А и на статический кулоновский потенциал А0,
что в результате нарушило явную лоренцовскую и калибровочную
инвариантность классической электродинамики. Позднее эти проце-
процедуры получили более солидное обоснование в известной работе Энрико
Ферми 266. В 1930-е годы многие физики изучали квантовую электро-
электродинамику по обзору Ферми 1932 года.
Использование канонических перестановочных соотноше-
соотношений для операторов q и р или а и а^ также поставило вопрос о
лоренц-инвариантности квантованной теории. В 1928 году Иордан
и Паули 37 сумели показать, что коммутаторы полей в разных про-
пространственно-временных точках являются на самом деле лоренц-
инвариантными. (Эти коммутаторы вычисляются в гл. 5.) Несколь-
Несколько позже Бор и Леон Розенфельд 38 использовали ряд остроумных
мысленных экспериментов для того, чтобы показать, что эти пе-
перестановочные соотношения выражают ограничения на нашу спо-
способность производить измерения полей в пространственно-времен-
пространственно-временных точках, разделенных времениподобными интервалами.
Вскоре после успешного квантования электромагнитного поля
эта же техника была применена к другим полям. Поначалу такую
технику называли «вторичным квантованием»: те поля, которые под-
подвергались квантованию, были волновыми функциями, используемы-
используемыми в одночастичных задачах квантовой механики, например, дира-
ковской волновой функцией электрона. По-видимому, первый шаг в
этом направлении был сделан в 1927 году Иорданом 39. В следующем,
1928 году Иордан и Вигнер 40 сделали важные дополнения. Они заме-
заметили, что принцип запрета Паули не позволяет числам заполнения
электронов пк в любой нормальной моде к (учитывающей как коор-
координатные, так и спиновые переменные) принимать значения, отлич-
отличные от 0 или 1. Следовательно, электронное поле нельзя представить
как суперпозицию операторов, удовлетворяющих перестановочным
соотношениям A.2.10), A.2.11), так какэти соотношения требуют, чтобы
п^ принимало любые целые значения от 0 до °о. Чтобы выйти из
26 Глава 1. Историческое введение
положения, они предположили, что электронное поле должно раз-
разлагаться на сумму операторов ак и ак\ удовлетворяющих антиком-
мутационным соотношениям
aka)+a)ak=bjk, A.2.22)
+a;-afc =0. A.2.23)
Эти соотношения могут быть удовлетворены матрицами, по-
помеченными последовательностью целых чисел щ, п2, ..., по одному
для каждой моды, причем эти целые числа могут принимать только
два значения — нуль и единица:
fl, n'k = 0, nk = 1, n'j = rij для j Ф k,
(ak) = < Ц2 24)
ni' "ь,- о для остальных индексов,
l, n'k = 1, nk = 0, n'j = Uj для j Ф k,
для остальных индексов.
Например, для одной нормальной моды матрицы ак и а^ со-
содержат ровно два столбца и две строки, соответствующие значени-
значениям п и п', равными 0 и 1. Матрицы а и а^ имеют вид:
1 0' 0 0
Читатель может убедиться, что матрицы A.2.24) и A.2.25) дей-
действительно удовлетворяют антикоммутационным соотношениям
A.2.22) и A.2.23).
Интерпретация вектора-столбца, задаваемого целыми числа-
числами щ, п2, ..., заключается в том, что, как и для бозонов, он пред-
представляет состояние с пк квантами в каждой нормальной моде. Раз-
Разница, конечно, в том, что, поскольку каждое число пк может
принимать только два значения 0 или 1, в каждой моде может быть
не более одного кванта, как и требуется принципом запрета Паули.
Оператор ак уничтожает квант в нормальной моде к, если он там
уже был, или действие этого оператора дает нуль; аналогично,
1. 2. Рождение квантовой теории поля 27
оператор а^ порождает квант в нормальной моде к, если только в
ней не присутствует уже один квант, в противном случае опера-
оператор а^ действует нулем. Много позже Фирц и Паули показали4Оа,
что выбор между коммутационными и антикоммутационными соот-
соотношениями диктуется только значением спина частицы: коммута-
коммутаторы следует использовать для частиц с целым спином вроде фото-
фотона, антикоммутаторы — для частиц с полуцелым спином вроде
электрона. (Иным способом это показано в гл. 5.)
Общая теория квантовых полей была впервые изложена в
1929 году в двух исчерпывающих статьях Гейзенберга и Паули41.
Исходным пунктом их работы было применение канонического фор-
формализма к самим полям, а не к коэффициентам нормальных мод, со-
содержащихся в этих полях. Гейзенберг и Паули рассмотрели лагран-
лагранжиан L как интеграл по пространству от локальной функции полей и
их пространственных и временных производных. Уравнения поля оп-
определялись из принципа стационарности действия { Ldt при варьиро-
варьировании полей, а коммутационные соотношения определялись из пред-
предположения, что вариационная производная лагранжиана по любой из
производных поля по времени ведет себя как сопряженный этому по-
полю «импульс» (для фермионных полей коммутационные соотношения
превращались в антикоммутационные). Гейзенберг и Паули примени-
применили общий формализм к электромагнитному и дираковскому полям и
исследовали различные инвариантности и законы сохранения, вклю-
включая законы сохранения заряда, импульса и энергии, а также лорен-
цовскую и калибровочную инвариантность.
Формализм Гейзенберга-Паули фактически совпадает с тем,
который описан в гл. 7, так что сейчас можно ограничиться одним
примером, который пригодится далее в этой главе. Лагранжиан сво-
свободного комплексного скалярного поля ф(х) имеет следующий вид:
Г Г 2
L = \d3x фЧ-с2(УфI -(Уф)-[тс2/п) ф!ф
A.2.26)
Если подвергнуть ф(ж) бесконечно малой вариации 8ф(ж), то
лагранжиан изменится на величину
8L = Г(?3а;[ф+8ф + фбф+ - c2V<p+ • Убф - с2Уф • Убф*
2 2 A.2.27)
-{mc2/hj ф*8ф -{mc2/hj ф5ф+].
28 Глава 1. Историческое введение
При использовании принципа наименьшего действия предпо-
предполагается, что вариации полей исчезают на границах пространст-
пространственно-временной области интегрирования. Таким образом, при вы-
вычислении изменения действия { Ldt можно сразу же проинтегриро-
проинтегрировать по частям и записать:
d4aW(п - (mc2/hf \ + 8<р(п - (mc2/hf V1.
Но это выражение должно обращаться в нуль при любых 8ф и
^, так что поле ф должно удовлетворять знакомому релятивист-
релятивистскому волновому уравнению
B/ф = 0 A.2.28)
и ф^-сопряженному уравнению. «Импульсы», канонически сопря-
сопряженные полям ф и (pt, даются вариационными производными
функции Лагранжа L по ф и ф +, которые легко находятся из A.2.27):
8L .+
л <Р . A.2.29)
8ф
8L
A-2.30)
Эти полевые переменные удовлетворяют обычным перестано-
перестановочным соотношениям с дельта-функцией вместо дельта-символа
Кронекера:
[jc(x,t),<p(y,t)] = [л+(х,{),ф+(у,?)] = -гЙ53(х -у), (L2.31)
[л(х,{),ф+(у,{)] = [л+(х,{),ф(у,{)] = 0, A.2.32)
[jt(x,t),Jt(y,t)] = [jt+(x,t),Jt+(y,t)] = [jr(x,t),JT+(y,t)] = 0, A.2.33)
[<p(x,t),<p(y,t)] = [ф+(х,{),ф+(у,{)] = [ф(х,{),ф+(у,{)] = 0. A.2.34)
Здесь (как и в механике частиц) функция Гамильтона дается
«суммой» всех канонических импульсов, умноженных на производ-
производные по времени соответствующих полей, минус функция Лагранжа:
1. 2. Рождение квантовой теории поля 29
Н = jd3x[ny + %*^]-L, A.2.35)
или, после подстановки A.2.26), A.2.29) и A.2.30),
Я = Jd3x[jrtJi + c2(V(p)f(V(p) + (т2с4//г2)(р4] . A.2.36)
После основополагающих работ Гейзенберга и Паули оставал-
оставался еще один вопрос, который необходимо было разрешить, прежде
чем квантовая теория поля смогла достичь окончательной предво-
предвоенной формы. Это было решение проблемы состояний с отрицатель-
отрицательной энергией. В предыдущем разделе мы видели, что в 1930 году,
как раз в то же время, когда появились работы Гейзенберга и Пау-
Паули, Дирак предположил, что все состояния электрона с отрица-
отрицательной энергией заполнены, а наблюдаемыми являются не сами
эти электроны, а дырки в море состояний с отрицательной энерги-
энергией. После того, как в 1930 году идея Дирака была наглядно подтвер-
подтверждена открытием позитрона, его «теория дырок» была использова-
использована для вычисления ряда процессов в низшем порядке теории
возмущений, в том числе, процессов рождения электрон-позитрон-
ных пар и рассеяния электронов и позитронов на электронах.
В то же время было затрачено много усилий на развитие фор-
формализма, лоренцовская инвариантность которого была бы очевидной.
Попыткой, оказавшей наибольшее влияние на дальнейшее разви-
развитие, был «многовременной» формализм Дирака, Владимира Фока
и Бориса Подольского 42, в котором вектор состояния был представ-
представлен волновой функцией, зависящей от пространственно-временных
и спиновых координат всех электронов как с положительной, так и с
отрицательной энергией. В рамках этого формализма сохраняетсется
по-отдельности полное число электронов с положительной и отрица-
отрицательной энергией; например, рождение электрон-позитронных пар
описывается как возбуждение электрона с отрицательной энергией с
переходом в состояние с положительной энергией, а аннигиляция
электрона и позитрона описывается как обратный процесс. Такой мно-
многовременной формализм имел то преимущество, что был явно ло-
ренц-инвариантным, но имел и ряд недостатков. В частности, была
глубокая пропасть между описанием фотона в терминах квантован-
квантованного электромагнитного поля и описанием электронов и позитронов.
Правда, не все физики считали это неудобством; электронное поле,
30 Глава 1. Историческое введение
в отличие от электромагнитного, не имело классического предела,
так что были сомнения относительно его физического смысла. К тому
же Дирак 42а рассматривал поля как средства наблюдения частиц,
так что он и не рассчитывал, что частицы и поля будут описываться
одинаково. Хотя мне неизвестно, тревожило ли это кого-нибудь в те
годы, но ведь в многовременном формализме был и более практиче-
практический недостаток: этот формализм было трудно использовать при опи-
описании процессов типа C-распада ядра, в котором рождаются элек-
электрон и антинейтрино без сопровождающих позитрона и нейтрино.
Осуществленное Ферми 43 успешное вычисление энергетического спек-
спектра электронов в C-распаде следует расценивать как один из первых
триумфов квантовой теории поля.
Ключевая идея, необходимая для демонстрации эквивалентно-
эквивалентности дираковской теории дырок и квантовой теории поля электрона,
была высказана в 1933-1934 годах Фоком43а, а также Уэнделлом
Фарри и Оппенгеймером 44. Чтобы представить суть этой идеи с бо-
более современной точки зрения, предположим, что мы пытаемся по-
построить электронное поле по аналогии с электромагнитным полем
или полем Борна-Гейзенберга-Иордана A.2.2). Так как электрон об-
обладает зарядом, мы не можем, по-видимому, смешивать операторы
уничтожения и рождения, и должны попытаться записать поле в
виде:
Щх) =
k
где щ{х)г~гтк1 представляют полный набор ортонормированных
решений уравнения Дирака A.1.13) в виде плоских волн (индекс к
теперь несет информацию о трехмерном импульсе, спине и знаке
энергии):
Jfuk=hakuk, A.2.38)
Ж = -гПса ¦ V + a4mc2, A.2.39)
= bkl, A.2.40)
а ак — соответствующие операторы уничтожения, удовлетворяющие
антикоммутационным соотношениям Иордана-Вигнера A.2.22)—A.2.23).
В соответствии с идеями «вторичного квантования» или канонической
1. 2. Рождение квантовой теории поля 31
процедуры квантования Гейзенберга и Паули 41 гамильтониан стро-
строится путем вычисления «среднего значения» Н, причем «волновая
функция» заменяется на квантованное поле A.2.37):
Н =
п(»какак ¦ A.2.41)
к
Конечно, трудность заключается в том, что этот оператор не
положителен — половина значений cofc отрицательны, в то время
как произведение а^ау. может принимать только положительные
значения 0 и 1 (см. формулы A.2.24) и A.2.25)). Для того, чтобы выле-
вылечить эту болезнь, Фарри и Оппенгеймер воспользовались идеей Ди-
Дирака 42, что позитрон можно интерпретировать как отсутствие элек-
электрона с отрицательной энергией. Соотношения антикоммутации сим-
симметричны по отношению к операторам рождения и уничтожения,
так что они определили операторы рождения и уничтожения пози-
позитрона как соответствующие операторы уничтожения и рождения
электронов с отрицательной энергией:
Ъ1=ак,Ък= 4 (для cofc < 0), A.2.42)
где индекс к у Ъ означает позитронную моду с импульсом и спином,
противоположными этим величинам в электронной моде к. Дира-
ковское поле A.2.37) можно теперь записать в виде
Щх) = ? {+)акик(х) + ? нЪ*кик(х), A.2.43)
к к
где символы (+) и (-) означают суммы по нормальным модам к с
энергиями wfc > 0 и cofc < 0, соответственно, а ик{х) =uk(x)e~i(ukt¦
Аналогично, используя соотношения антикоммутации для опе-
операторов Ъ, можно переписать оператор энергии A.2.41) в следующем
виде:
Я = ? ^tuokakak + ? (">Й| rafc| bfkbk + Ео, A.2.44)
к к
где Ео — бесконечное с-число
32 Глава 1. Историческое введение
Для того, чтобы подобное переопределение стало чем-то боль-
большим, чем простой формальностью, необходимо уточнить, что фи-
физический вакуум — это состояние Ч^, не содержащее электронов
или позитронов с положительной энергией:
ak%=0 (a>fc>0), A.2.46)
Ък%=0 (a>fc<0). A.2.47)
Таким образом, из формулы A.2.44) вытекает, что энергия
вакуума равна Ео. Если измерять все энергии относительно энергии
вакуума Ео, то физический оператор энергии равен Н — Ео; из A.2.44)
следует, что это оператор положителен.
Проблема состояний с отрицательной энергией для заряжен-
заряженных частиц со спином нуль была также разрешена в 1934 году Пау-
Паули и Вайскопфом 45 в работе, написанной отчасти как вызов дира-
ковской картине заполненных состояний с отрицательной энергией.
Операторы рождения и уничтожения удовлетворяют в этом случае
соотношениям коммутации, а не антикоммутации, поэтому невоз-
невозможно просто поменять роль этих операторов, как это было сдела-
сделано для фермионов. Вместо этого следует вернуться к каноническому
формализму Гейзенберга и Паули41 с тем, чтобы решить, какие
коэффициенты в разных нормальных модах являются операторами
рождения или уничтожения.
Паули и Вайскопф разложили свободное заряженное скаляр-
скалярное поле на плоские волны в кубическом пространственном объеме
A.2.48)
с волновыми числами, ограниченными условиями периодичности:
величины kjL/B%) должны быть при j = 1, 2, 3 набором трех поло-
положительных или отрицательных целых чисел. Аналогично канониче-
канонически сопряженная величина A.2.29) разлагается в виде
?p(kt)e-*-x (L249)
k
Здесь в показателе экспоненты поставлен знак минус, так что
A.2.29) принимает вид
1. 2. Рождение квантовой теории поля 33
,t) = g+(k,t). A.2.50)
Формулы фурье—обращения имеют вид
A.2.51)
р(к, t) = -j^l d3x л(х, t)e+ik'x . A.2.52)
Поэтому для всех g и р выполняются канонические коммута-
коммутационные соотношения A.2.31)—A.2.34):
[p(k, t), g(l, t)] = —\ d3xe*xe-ilx = -гй5к1, A.2.53)
V J
[p(k, t), g+(l, t)] = [p(k, t), p(l, t)] = [p(k, t), р+A, t)] =
[g(k, t), g(l, t)][g(k, t), д+A, t)] = 0, (L2M)
а также соотношения, получающиеся отсюда для эрмитово сопря-
сопряженных величин. Подставляя A.2.48) и A.2.49) в формулу A.2.36)
для функции Гамильтона, можно выразить этот оператор через ве-
величины р и д:
A.2.55)
<в| ее с2к2 + (mc2/hf . A.2.56)
Производные по времени величин р определяются из уравне-
уравнения Гамильтона
Р(М) = - = -<в|д+(М) A.2.57)
3g(k,t)
(и ему сопряженного). С учетом A.2.50) этот результат в точности
эквивалентен волновому уравнению Клейна-Гордона-Шрединге-
ра A.2.28).
34 Глава 1. Историческое введение
Мы видим, что, как и в случае модели Борна, Гейзенберга
и Иордана 4 1926 года, свободное поле ведет себя как бесконеч-
бесконечное число связанных гармонических осцилляторов. Паули и Вай-
скопфу удалось построить операторы р и д, удовлетворяющие
коммутационным соотношениям A.2.53)—A.2.54) и «уравнениям дви-
движения» A.2.50) и A.2.57), введя операторы уничтожения и рожде-
рождения а, Ъ, а^ и Ь^ двух разных типов, соответствующих частицам
и античастицам:
g(k, t) = i I [a(k) exp(-zcokt) - b+(k) exp(zcokt)], A.2.58)
p(k,t) = -a^[b(k)exp(-zcokt) + a+(k)exp(zcokt)], A.2.59)
V h
для которых
+(l)] = 5kl, A-2.60)
[a(k),a(l)] = [b(k),b(l)] = 0, A.2.61)
[a(k),b(l)] = [a(k),b+(l)] = [a+(k),b(l)] =[a+(k),b+(l)] = 0. A.2.62)
Можно непосредственно убедиться в том, что эти операторы
действительно удовлетворяют соотношениям A.2.53), A.2.54), A.2.50)
и A.2.57). Поле A.2.48) можно записать как
, t) = —j= ^ I [a(k) ехр(гк • х -
VV \2ш
(
- bf (-к) ехр(-гк • х + i(okt)],
а функция Гамильтона A.2.55) принимает вид
Я = Y, -Ь<»к [bf (k)b(k) + b(k)bf (k) + af (k)a(k) + a(k)af (k)],
2
k 2
или, используя A.2.60)-A.2.62),
1. 2. Рождение квантовой теории поля 35
Я = ?йсок[Ь+(к)Ь(к) + а+(к)а(к)] + Ео , A.2.64)
к
где Ео — бесконечно большое с-число
Существование двух разных типов операторов а и Ъ, равно-
равноправно входящих в гамильтониан, показывает, что построенная
теория описывает два сорта частиц одной и той же массы. Как под-
подчеркнули Паули и Вайскопф, эти две разновидности можно рас-
рассматривать как частицы и соответствующие античастицы, которые
(если они заряжены) имеют противоположные заряды. Таким обра-
образом, как мы отмечали выше, бозоны со спином 0, так же, как
и фермионы со спином 1/2, могут иметь свои античастицы, кото-
которые для бозонов невозможно интерпретировать как дырки в море
частиц с отрицательной энергией.
Теперь можно выяснить, какие из операторов а и Ъ или а) и W
являются операторами уничтожения, взяв среднее значение от ком-
коммутационных соотношений в состоянии вакуума Ч*о. Например, ес-
если а\ были бы операторами уничтожения, то при действии на ва-
вакуумное состояние они давали бы нуль, так что среднее по вакууму
от A.2.60) равнялось бы
-||а(к)^0||2 = (?0,[а(к),а+(к)рР0) = +1, A.2.66)
в противоречии с требованием, чтобы левая часть равенства была
отрицательной. Таким способом можно установить, что оператора-
операторами уничтожения являются а^ и Ъ^, и поэтому
= 0. A.2.67)
Это условие находится в согласии со всеми коммутационными
соотношениями. Итак, канонический формализм вынуждает заклю-
заключить, что коэффициент при e+im в выражении для поля A.2.63) дол-
должен быть оператором рождения, как это получается и в формализ-
формализме Фарри—Оппенгеймера 44 для частиц со спином 1/2.
Из уравнений A.2.64) и A.2.67) вытекает, что Ео есть энергия
вакуумного состояния. Если измерять все энергии относительно Ео,
36 Глава 1. Историческое введение
то физическим оператором энергии станет оператор Н - Ео, причем
из A.2.64) следует, что он положителен.
Как же обстоит дело с проблемой отрицательных вероятно-
вероятностей, которая стала отправной точкой в исследованиях Дирака?
Как заметил Дирак, единственная плотность вероятности р, кото-
которую можно построить из решений свободного скалярного волново-
волнового уравнения Клейна-Гордона-Шредингера A.2.28) и которая удов-
удовлетворяет закону сохранения в форме A.1.10), должна быть
пропорциональна величине
и поэтому не обязательно положительна. Аналогично, во «вторично-
квантованной» теории, где ф определяется уравнением A.2.63), р не
является положительным оператором. Так как оператор <рЦх) не ком-
коммутирует с оператором ф(х), формулу A.2.68) можно записать по-
разному, причем все выражения будут отличаться на бесконечно боль-
большие с-числа. Оказывается удобным записать плотность р в виде
Р =
Эф + Эф1'
—-ф+ —
dt dt
ф
A.2.69)
Интеграл по пространству от этого оператора легко вычисля-
вычисляется и равен
= Jp dsx = ?(af(k)a(k) - bf(k)b(k)).
k
Очевидно, что он имеет собственные значения обоих знаков.
Однако в определенном смысле такая же проблема возникает и
в квантовой теории поля частиц спина 1/2. Дираковский оператор
плотности Х|/^Х|/ действительно положительный, но чтобы построить
физическую плотность, мы должны вычесть вклад заполненных элек-
электронных состояний. В частности, пользуясь разложением на плоские
волны A.2.43), можно записать оператор полного числа частиц:
N = jd3xу V =? (+)a+(k)a(k) + ? (-»Ь(к)Ь+(к).
к к
Соотношения антикоммутации для операторов Ъ позволяют
переписать это выражение как
1. 2. Рождение квантовой теории поля 37
JV - ЛГ0 = ? <+V(k)a(k) - ? (-V(k)b(k), A.2.71)
к к
где ЛГ0 - бесконечная постоянная,
Wo=EHl- A.2.72)
к
Согласно A.2.46) и A.2.47) величина ЛГ0 есть число частиц
в вакууме, поэтому Фарри и Оппенгеймер сделали вывод, что опе-
оператор числа физических частиц есть ЛГ - ЛГ0 и он может, как для
поля спина нуль, иметь и положительные, и отрицательные собст-
собственные значения.
Предлагаемое квантовой теорией поля решение этой пробле-
проблемы заключается в том, что ни величины \|/ у Фарри и Оппенгейме-
ра, ни ф у Паули и Вайскопфа не являются амплитудами вероятно-
вероятности, которые должны определять сохраняющиеся положительные
плотности вероятности. Вместо этого физическое гильбертово про-
пространство разлагается на состояния, определенные как состояния с
заданным числом частиц и/или античастиц в каждой моде. Если Фп
есть полный ортонормированный набор таких состояний, то изме-
измерение числа частиц в произвольном состоянии Ч* приведет к веро-
вероятности обнаружения системы в состоянии Фп, равной
Рп = \{Фп,Ч)\2, A-2.73)
где (Ф^Ч*) есть обычное скалярное произведение в гильбертовом про-
пространстве. Таким образом, для любого спина даже не возникает во-
вопрос о возможности отрицательных вероятностей. Волновые поля
\|/, ф, и т. д. — совсем не амплитуды вероятности, а операторы,
рождающие или уничтожающие частицы в различных нормальных
модах. Было бы хорошо, если бы вводящий в заблуждение термин
«вторичное квантование» постепенно ушел бы на покой.
В частности, операторы ЛГ и ЛГ - ЛГ0 в A.2.70) и A.2.71) должны
интерпретироваться не как полные вероятности, а как операторы
числа частиц, точнее, числа частиц минус число античастиц. Для
заряженных частиц сохранение заряда приводит к тому, что опе-
операторы заряда пропорциональны операторам числа частиц, так что
знак минус в A.2.70) и A.2.71) позволяет немедленно прийти
к выводу, что заряды частиц и античастиц противоположны. В таком
38 Глава 1. Историческое введение
теоретико-полевом формализме взаимодействия соответствуют сла-
слагаемым в гамильтониане третьего, четвертого или более высоких
порядков по полевым переменным, а вероятности различных про-
процессов получаются использованием этих операторов взаимодейст-
взаимодействия в зависящей от времени теории возмущений. Концепции, изло-
изложенные в предыдущих кратких замечаниях, будут служить осно-
основой для большей части материала этой книги.
Несмотря на очевидные преимущества, квантовая теория поля
не сразу вытеснила теорию дырок. Обе точки зрения некоторое вре-
время сосуществовали, а при вычислениях вероятностей физических ре-
реакций использовались разные комбинации теоретико-полевого и ды-
дырочного подходов. Этот период ознаменовался расчетами в низшем
порядке по степеням е2 сечений разных процессов: е~ + у —> е~ + у
A929 год, Клейн, Нишина 46); е+ + е" -> 2у A930 год, Дирак47);
е" + е" -> е" + е~ A932 год, Меллер 48); e~+Z->e~+y+Z
иу + Z—>e+ + e~ + Z (здесь Z означает кулоновское поле тяжелого
атома) A934 год, Бете, Гайтлер49); е+ + е~ —» е+ + е~ A936 год, Ба-
Баба 50). (Правила вычисления таких процессов сформулированы в гл. 8
и подробно проиллюстрированы на примере рассеяния фотона на элек-
электроне.) Эти вычисления в низшем порядке теории возмущений дава-
давали конечные результаты, находившиеся в разумном согласии с экс-
экспериментальными данными.
Тем не менее, в 1930-е годы нарастало ощущение неудовле-
неудовлетворенности квантовой теорией поля (с учетом или без учета тео-
теории дырок). Одной из причин была очевидная неудача квантовой
электродинамики при расчете проникающей способности заряжен-
заряженных частиц в ливнях космического излучения, отмеченная в 1936
году Оппенгеймером и Франклином Карлсоном 50а. Другой причиной
неудовлетворенности, оказавшейся связанной с первой, было по-
постоянное открытие новых сортов частиц и взаимодействий. Мы уже
упоминали электрон, фотон, позитрон, нейтрино, и, конечно, яд-
ядро атома водорода — протон. В 1920-е годы было распространено
мнение, что более тяжелые ядра состоят из протонов и электронов,
однако было трудно понять, как легкая частица вроде электрона
могла удерживаться внутри ядра. Еще одна серьезная трудность,
связанная с такой картиной, была отмечена в 1931 году Эренфе-
стом и Оппенгеймером 51: для того, чтобы ядро обычного азота 14N
имело атомный номер 7 и массовое число 14, оно должно было со-
состоять из 14 протонов и 7 электронов и поэтому быть фермионом,
1. 2. Рождение квантовой теории поля 39
что противоречило полученному методами молекулярной спектро-
спектроскопии 52 выводу, что 14N — бозон. Эта (и другие) проблема реши-
решилась после открытия в 1932 году нейтрона 53 и гипотезы Гейзенбер-
га 54, что ядра состоят из протонов и нейтронов, а не из протонов и
электронов. Было очевидно, что для удержания ядра между ней-
нейтронами и протонами должны действовать большие неэлектромаг-
неэлектромагнитные короткодействующие силы.
После успеха фермиевской теории C-распада ряд авторов 54а
высказывал предположения, что в рамках этой теории ядерные
силы можно было бы объяснить как результат обмена электрона-
электронами и нейтрино. Несколькими годами спустя, в 1935 году Хидеки
Юкава предложил совершенно новую квантовую теорию поля для
описания ядерных сил 55. В рамках полностью классического опи-
описания он нашел, что взаимодействие скалярного поля с нуклонами
(протонами и нейтронами) должно было бы порождать нуклон-ну-
клонные потенциал, зависящий от расстояния между этими час-
частицами как
V(r) ос -ехр(-Хг), A.2.74)
г
а не как 1/г в случае кулоновского потенциала между электриче-
электрическими зарядами. Величина А, была введена в уравнение скалярного
поля Юкавы как параметр; проквантовав это поле, Юкава обнару-
обнаружил, что оно описывает частицы массой ti/(kc). Взяв наблюдаемый
радиус сильного взаимодействия между нуклонами, Юкава сумел
оценить, что ti/(kc) порядка 200 масс электрона. В 1937 году такие
«мезоны» были обнаружены в опытах с пузырьковыми камерами 56
Сетом Неддермейером и Андерсоном, а также Джабезом Карри
Стритом и Эдвардом Карлом Стивенсоном. По общему мнению, это
и были гипотетические частицы Юкавы.
Открытие мезонов подтвердило, что в космическом излучении
заряженными частицами могут быть не только электроны, и поэтому
проблема, тревожившая Оппенгеймера и Карлсона, была снята.-
Однако это открытие породило новые трудности. Лотар Нордхейм 56а
отметил в 1939 году, что те же самые сильные взаимодействия, за
счет которых мезоны множественно рождаются в верхних слоях атмо-
атмосферы (и которые требуются теорией Юкавы) должны приводить к
поглощению мезонов в нижних слоях атмосферы, что противоречило
наблюдавшемуся большому количеству этих мезонов на малых
40 Глава 1. Историческое введение
высотах. В 1947 году в эксперименте Марчелло Конверси, Этторе Пан-
чини и Оресте Пиччиони 57 было показано, что те мезоны, которые
преобладают в космическом излучении на малых высотах, на самом
деле слабо взаимодействуют с нуклонами и поэтому не могут быть
сопоставлены частицам Юкавы. Эта загадка разрешилась после теоре-
теоретического предположения 58, а затем и экспериментального подтвер-
подтверждения 59 Чезаре Латтеса, Оккиалини и Сесила Пауэлла, что на са-
самом деле существуют два типа мезонов с несколько различающимися
массами: более тяжелый (его сейчас называют л-мезоном или пионом)
способен сильно взаимодействовать и выполняет роль переносчика ядер-
ядерных сил, предсказанную Юкавой; более легкий (называемый сейчас
мюоном) способен только к слабым или электромагнитным взаимодей-
взаимодействиям и преобладает в космическом излучении на уровне моря, воз-
возникая как результат распада пионов. В том же 1947 году в космиче-
космическом излучении были найдены совершенно новые типы частиц, из-
известные сейчас как К-мезоны и гипероны (Джордж Рочестер и Клиф-
Клиффорд Батлер 60.) С 1947 года и вплоть до наших дней продолжается
открытие ужасающего количества частиц все новых разновидностей,
однако продолжение рассказа об этом увело бы нас далеко в сторону
от предмета рассмотрения. Все эти открытия ясно показали, что лю-
любая концептуальная основа, ограниченная фотонами, электронами и
позитронами, была бы слишком узкой для того, чтобы серьезно рас-
рассматриваться как фундаментальная теория. Но еще более важной ока-
оказалась чисто теоретическая проблема бесконечностей.
1.3. Проблема бесконечностей
Квантовая теория поля имеет дело с полями Х|/(ж), уничто-
уничтожающими и рождающими частицы в пространственно-временной
точке х. Предыдущий опыт обращения с классической теорией элек-
электрона предупреждает, что точечный электрон обладает бесконеч-
бесконечной собственной электромагнитной массой. В случае поверхност-
поверхностного распределения заряда по сфере радиусом а эта масса равна
е2/Fжас2) и расходится при а —> 0. К сожалению, та же проблема
с еще большей остротой встала в первые же дни существования
квантовой теории поля, и хотя ее удалось в значительной степени
смягчить последующими улучшениями теории, она так и остается
с нами по сей день.
1.3. Проблема бесконечностей 41
Проблема бесконечностей в квантовой теории поля была, по-
видимому, впервые отмечена в работах Гейзенберга и Паули 1929-
1930 годов41 Вскоре появление бесконечностей было подтверждено
при вычислениях электромагнитной собственной энергии связанно-
связанного электрона Оппенгеймером 61 и свободного электрона Айваром Вал-
лером 62. Они использовали обычную теорию возмущений второго
порядка с промежуточными состояниями, включавшими электрон
и фотон. Например, сдвиг энергии электрона Еп на n-ом энергети-
энергетическом уровне атома водорода определяется формулой:
=
где суммы и интеграл берутся по всем промежуточным состояниям
электрона т, спиральностям фотона А, и импульсам фотона k, a
Н' - слагаемое в гамильтониане, описывающее взаимодействие из-
излучения и электронов. Подобное вычисление дает формально беско-
бесконечную собственную энергию; более того, если устранить эту бес-
бесконечность путем отбрасывания всех промежуточных состояний с
волновыми числами фотонов большими 1/а, то собственная энергия
при а —> 0 ведет себя как 1/а2. Бесконечности такого рода часто
называют ультрафиолетовыми расходимостями, так как они возни-
возникают от промежуточных состояний, содержащих частицы очень ко-
коротких длин волн.
Во всех таких вычислениях электрон рассматривался по прави-
правилам первоначальной теории Дирака без заполненных состояний
с отрицательной энергией. Несколькими годами спустя Вайскопф по-
повторил вычисления собственной массы электрона в рамках новой ды-
дырочной теории с полностью занятыми состояниями с отрицательной
энергией. В этом случае во втором порядке теории возмущений
возникает дополнительное слагаемое, которое на языке теории без
дырок может быть описано как возникающее от процессов, в кото-
которых электрон в конечном состоянии сначала рождается из вакуума
вместе с фотоном и позитроном, а последний затем аннигилирует с
начальным электроном. Сначала Вайскопф получил зависимость 1/а2
от величины обрезания волнового числа фотонов 1/а. В то же время
(по предложению Бора) аналогичные вычисления были сделаны Карл-
Карлсоном и Фарри. Увидев результаты Вайскопфа, Фарри понял, что
хотя Вайскопф и учел то электростатическое слагаемое, которым
42 Глава 1. Историческое введение
пренебрегли он и Карлсон, но допустил ошибку при вычислении вкла-
вклада магнитной собственной энергии. Узнав об этом от Фарри, Вай-
скопф исправил свою ошибку и обнаружил, что все члены порядка
1/а2 в полном сдвиге массы сократились! Однако, несмотря на это
сокращение, бесконечность сохранилась: при обрезании по волново-
волновому числу величиной 1 /а собственная масса оказалась равной 63
За ( П )
2л \mcaj
A.3.2)
Ослабление зависимости от обрезания, принявшей вид In a
по сравнению с классической зависимостью 1/а или ранней кванто-
квантовой зависимостью 1/а2, было воспринято в свое время как обнаде-
обнадеживающий признак и оказалось очень важным позднее при разви-
развитии теории перенормировок.
В 1933 году, по-видимому, Дирак64 обнаружил возникнове-
возникновение бесконечности совсем другого типа. Он рассмотрел влияние внеш-
внешнего статического заряда почти однородной плотности ?(х) на ваку-
вакуум, т. е. на электроны с отрицательной энергией, находившиеся в
рамках теории дырок в заполненных энергетических состояниях.
Кулоновское взаимодействие между е(х) и плотностью заряда элек-
электронов отрицательной энергии приводит к «поляризации вакуума»
с индуцированной плотностью заряда
Pi \2
V2? + ... A.3.3)
тс)
Константа В конечна и порядка а. В то же время, константа А
логарифмически расходится как a In а, где 1/а - величина обреза-
обрезания по волновому числу.
Похоже, что бесконечности возникали и в связанной с преды-
предыдущей задаче рассеяния света на свете. Ганс Эйлер, Бернард Ко-
кель и Гейзенберг 65 показали в 1935-1936 годах, что эти бесконеч-
бесконечности можно устранить, используя более или менее произвольное
предписание, ранее предложенное Дираком 66 и Гейзенбергом 67. Они
вычислили эффективную плотность лагранжиана для нелинейных
электродинамических процессов, порождаемых виртуальными элек-
трон-позитронными парами,
1.3. Проблема бесконечностей 43
справедливую при частотах v <ЗС тес2/Н. Вскоре Николас Кеммер
и Вайскопф 68 высказали соображения, что в этом случае бесконеч-
бесконечности фиктивны, и что выражение A.3.4) можно вывести без всяких
вычитательных предписаний.
Ярким лучом в борьбе с бесконечностями было успешное рас-
рассмотрение инфракрасных расходимостей, возникающих не от вы-
высокоэнергетической, а от низкоэнергетической области интегриро-
интегрирования. В 1937 году Феликс Блох и Арне Нордсик показали 68а, что
эти бесконечности сокращаются, если учесть процессы с излучени-
излучением произвольного числа фотонов низкой энергии. В современных
терминах эта проблема будет обсуждаться в гл. 13.
Наконец, еще одна бесконечность возникла в 1939 году в вы-
вычислениях Сидни Майклом Данковым 69 радиационных поправок
к рассеянию электрона статическим кулоновским полем атома. Вы-
Вычисление содержало ошибку (было пропущено одно слагаемое),
но это стало понятно только позднее .
В 1930-е годы все эти бесконечности не воспринимались лишь
как неудачи конкретных вычислений. Скорее, они указывали на
пробел в понимании фундаментальных основ релятивистской кван-
квантовой теории поля, что только подчеркивалось упомянутыми в пре-
предыдущем разделе проблемами с космическим излучением.
Одним из симптомов этого непреходящего пессимизма было
продолжавшееся все 30-е и 40-е годы использование альтернатив-
альтернативных схем. Как вспоминал позднее Джулиан Швингер 696, «основ-
«основным занятием больгиинства вовлеченных в эти проблемы физи-
физиков был не анализ и тщательное применение известной
релятивистской теории взаимодействующих электронного и
электромагнитного полей, а попытки изменить ее». Так,
в 1938 году Гейзенберг 70 предположил существование фундамен-
фундаментальной длины L, аналогичной фундаментальному кванту дейст-
действия Ь и фундаментальной скорости с. По предположению, теория
поля была применима только на расстояниях, больших L, так что
все расходящиеся интегралы эффективно должны были обрезать-
обрезаться на расстояниях порядка L, или на импульсах порядка h/L. Что-
Чтобы придать теории поля нелокальную структуру, было высказано
несколько специальных предположений. Некоторые теоретики стали
подозревать, что формализм векторов состояний и квантовых
полей должен быть заменен на другой, основанный исключи-
исключительно на наблюдаемых величинах, типа введенной в 1937 году
44 Глава 1. Историческое введение
Джоном Арчибальдом Уилером 71 и Гейзенбергом 72 5-матрицы, эле-
элементы которой равны амплитудам различных процессов рассея-
рассеяния. Как мы увидим, понятие .^-матрицы стало жизненно необхо-
необходимой частью современной квантовой теории поля, а для некоторых
теоретиков чистая теория .^-матрицы стала идеалом, особенно как
возможное решение проблем сильных взаимодействий 73. Рассуж-
Рассуждая в несколько ином направлении, Уилер и Ричард Фейнман 74
попытались в 1945 году исключить электромагнитное поле, выво-
выводя электромагнитные взаимодействия из действия на расстоянии.
Им удалось показать, что полностью запаздывающий (или опере-
опережающий) потенциал можно получить, если учесть не только взаи-
взаимодействие между источником и пробными зарядами, но и между
этими зарядами и всеми другими зарядами во вселенной. Возмож-
Возможно, наиболее радикальной модификацией квантовой механики,
предложенной в эти годы, было введение Дираком 75 состояний с
отрицательной вероятностью как средства сокращения бесконеч-
бесконечностей в сумме по состояниям. Эта идея индефинитной метрики
в гильбертовом пространстве получила развитие и в квантовой тео-
теории поля, хотя и не в оригинальной форме.
В 1930-е годы в воздухе носилась и более консервативная идея
о том, как обращаться с бесконечностями. Возможно, все эти беско-
бесконечности могли быть поглощены в переопределении или перенор-
перенормировке параметров теории. Например, уже было известно, что в
любой лоренц-инвариантной классической теории электромагнит-
электромагнитные собственная энергия и собственный импульс электрона должны
иметь форму поправок к массе электрона. Отсюда, бесконечности в
этих величинах можно было сократить с «голой» неэлектромагнит-
неэлектромагнитной массой электрона, получив конечную измеримую «перенорми-
«перенормированную» массу. Кроме того, уравнение A.3.3) показывает, что по-
поляризация вакуума изменяет заряд электрона от величины, равной
интегралу е = J d3x-?, до величины
'полный
A.3.5)
Поляризация вакуума приводит к конечным результатам в низ-
низшем порядке, если наблюдаемые величины типа сечений рассеяния
выражены через еполный, а не через е. Вопрос заключался в том, все
ли бесконечности в квантовой теории поля можно устранить подоб-
подобным образом. В 1936 году Вайскопф 76 предположил, что дело обстоит
1.3. Проблема бесконечностей 45
именно так, и на ряде простых примеров убедился, что известные
бесконечности могут быть устранены перенормировкой физических
параметров. Однако при существовавшей тогда вычислительной тех-
технике было невозможно показать, что бесконечности всегда можно
устранить подобным образом, а пример Данкова 69, казалось, под-
подтверждал, что этого сделать нельзя.
Другим результатом, связанным с появлением бесконечностей,
стала тенденция полагать, что всякий эффект, который оказывался
бесконечным в рамках квантовой теории поля, на самом деле не име-
имеет места. В частности, в дираковской теории 1928 года предсказыва-
предсказывалось полное вырождение уровней 2s1/2-2p1/2 атома водорода во всех
порядках по а. Всякая попытка расчета расщепления этих двух уров-
уровней в рамках квантовой электродинамики сводилась к проблеме бес-
бесконечной собственной энергии связанного электрона. Поэтому реаль-
реальное существование такого расщепления не воспринималось всерьез.
Позднее Бете 80 вспоминал, что «этот сдвиг оказывался бесконеч-
бесконечным во всех существовавгиих теориях и поэтому просто игнориро-
игнорировался». Такое отношение сохранялось даже в конце 1930-х годов, ко-
когда спектроскопические эксперименты стали давать прямые указа-
указания на существование расщепления 2s1/2-2p1/2 уровней порядка 1000
МГц. Заметным исключением стал Эдвин Альбрехт Юлинг 78, кото-
который понял, что упомянутый выше эффект поляризации вакуума дол-
должен приводить к расщеплению уровней 2s1/2-2p1/2. К сожалению,
как мы увидим в гл. 14, этот вклад в расщепление много меньше 1000
МГц и к тому же имеет неправильный знак.
Туман, окутывавший квантовую теорию поля, начал рассеи-
рассеиваться вскоре после второй мировой войны. В течение 1—4 июня 1947
года в местечке Шелтер Айленд, штат Нью Йорк, проходила конфе-
конференция по основам квантовой механики, на которую собрались как
физики-теоретики, работавшие над проблемами квантовой теории
поля еще в 30-е годы, так и ученые молодого поколения, начавшие
научную работу во время войны. Что особенно важно, среди участни-
участников было и несколько физиков—экспериментаторов. Лидерами дис-
дискуссии стали Ганс Крамере, Оппенгеймер и Вайскопф. Один из
экспериментаторов (или, скорее, теоретик, ставший эксперимента-
экспериментатором), Уиллис Лэмб, рассказал об убедительном опыте по измере-
измерению сдвига уровней энергии 2s1/2-2p1/2 в водороде 79. Пучок ато-
атомов водорода от источника, содержавший много атомов в 2s- и
2р-состояниях, направлялся на детектор, чувствительный только
46 Глава 1. Историческое введение
к атомам в возбужденном состоянии. Атомы в 2 р-состояниях очень
быстро распадались, переходя в основное Is состояние с испускани-
испусканием одного фотона (ос—линия Лаймана), в то время, как 2§-состояния
могли только медленно распадаться с испусканием двух фотонов.
В результате детектор измерял число атомов в метастабильном 2s
состоянии. Пучок проходил через магнитное поле, благодаря которому
к любому имеющемуся сдвигу уровней 2s1/2-2p1/2 добавлялся извест-
известный зеемановский сдвиг. Кроме того, на пучок накладывалось микро-
микроволновое электромагнитное поле с фиксированной частотой V ~ 10 ГГц.
При определенной напряженности магнитного поля наблюдалось рез-
резкое уменьшение сигнала детектора, свидетельствовавшее о том, что
микроволновое поле породило резонансные переходы из метастабиль-
ного 2§-состояния в 2р-состояние, а затем — в основное состояние за
счет быстрого перехода с испусканием лаймановской ОС-линии. При
заданной величине магнитного поля полное расщепление уровней 2s—
2р, включавшее зеемановское расщепление и собственно сдвиг меж-
между уровнями, должно было равняться hv. Отсюда можно было из-
извлечь величину расщепления уровней. Было объявлено предвари-
предварительное значение сдвига, равное 1000 МГц и находившееся в согла-
согласии с более ранними спектроскопическими измерениями 77. Послед-
Последствия этого открытия нашли отражение в изречении, которое я слы-
слышал в Копенгагене в 1954 году, когда проходил там аспирантуру:
«Не следует говорить, что нечто равно нулю только потому, что
оно равно бесконечности!»
Открытие лэмбовского сдвига вызвало глубокий интерес у тео-
теоретиков, собравшихся в Шелтер Айленде, тем более, что многие
из них уже работали над улучшением формализма расчетов в кван-
квантовой электродинамике. Крамере доложил свою работу о перенор-
перенормировке массы в классической электродинамике протяженного элек-
трона , в которой показал, что трудности, связанные с расхо-
расходимостью собственной энергии в пределе нулевого радиуса, не воз-
возникают в явном виде, если записать теорию в виде, где массовый
параметр отождествлен с экспериментально наблюдаемой массой
электрона. Швингер и Вайскопф (до которых уже дошли слухи о
результате Лэмба) обсуждали ситуацию по дороге в Шелтер Ай-
ленд и высказали предположение, что поскольку, как было из-
известно, учет промежуточных состояний, включающих позитро-
позитроны, уменьшает расходимость выражений для сдвигов уровней энер-
энергии с 1/а2 до In а, то не может ли случиться, что учет этих проме-
1.3. Проблема бесконечностей 47
жуточных состояний сделает разности сдвигов атомных уровней
конечными. (На самом деле, в 1946 году, еще до того, как Вай-
скопф узнал об опыте Лэмба, он предложил эту задачу своему
аспиранту Брайсу Френчу.) Почти сразу же после конференции, в
поезде, идущем в Скенектеди, Ганс Бете 80 проделал нерелятиви-
нерелятивистское вычисление, все еще не учитывавшее эффекты, связанные
с наличием позитронных промежуточных состояний, но использо-
использовавшее для устранения бесконечностей простой метод обрезания
импульсов виртуальных фотонов величиной порядка тес. Бете по-
получил вселявшее надежду приближенное значение сдвига, равное
1040 МГц. Вскоре рядом авторов 81 были выполнены полностью ре-
релятивистские вычисления, использующие для устранения беско-
бесконечностей идею перенормировок. Эти вычисления привели к бле-
блестящему согласию с экспериментом.
На конференции в Шелтер Айленде был доложен и другой
взволновавший всех экспериментальный результат Исидора Раби.
Проведенные в его лаборатории измерения сверхтонкой структуры
водорода и дейтерия показали , что магнитный момент электрона
отличается от предсказываемого дираковского значения eh/2mc на
множитель, равный примерно 1,0013. Последующие измерения
гиромагнитных отношений в натрии и галлии привели к еще более
точному значению 83
eh
ц = A,00118 ± 0,00003).
2тс
Узнав об этих результатах, Грегори Брейт предположил 83а,
что отклонения возникают в результате радиационных поправок
порядка ОС к магнитному моменту электрона. На конференции и
Брейт, и Швингер доложили о своих попытках рассчитать эту
поправку. Вскоре после конференции Швингер успешно завершил
расчет величины аномального магнитного момента электрона 84,
получив значение
ц = -^A + -^) = -?*-.1,001162,
2тс 2% 2тс
находившееся в прекрасном согласии с экспериментом. Этот результат
наряду с расчетом лэмбовского сдвига, выполненными Бете, убедили
наконец физиков в реальности радиационных поправок.
48 Глава 1. Историческое введение
Применявшиеся в это время математические методы вычис-
вычислений представляли собой дикую смесь концепций и формализмов.
Один из подходов, развитый Швингером 85, был основан на оператор-
операторных методах и принципе наименьшего действия. Этот подход был
доложен на последовавшей за Шелтер Айлендом конференции в
Поконо Манор в 1948 году. Другой лоренц-инвариантный оператор-
операторный формализм был еще раньше построен Синитиро Томонагой 86
с сотрудниками в Японии, но эта работа сначала не была известна
на Западе. Еще в 1930-е годы Томонага столкнулся с бесконечностями
в мезонной теории Юкавы. В 1947 году он и его коллеги все еще на-
находились вне общего круга научных связей: об опыте Лэмба они
узнали из статьи в журнале Newsweek.
Внешне совершенно иной подход был предложен Фейнманом 87.
Он коротко доложил о нем на конференции в Поконо. Вместо того,
чтобы вводить квантовополевые операторы, Фейнман представил S-
матрицу в виде функционального интеграла от exp(zW), где W — ин-
интеграл действия для совокупности дираковских частиц, взаимодей-
взаимодействующих с классическим электромагнитным полем, взятый по всем
траекториям дираковских частиц, удовлетворяющим при t —> + °° оп-
определенным граничным условиям.
Одним из результатов работы Фейнмана, получившим необы-
необычайное практическое значение, была формулировка системы графи-
графических правил для вычисления элементов S—матрицы в любом
желаемом порядке теории возмущений. В противоположность старой
теории возмущений 1920—1930 годов, эти фейнмановские правила
автоматически учитывали одновременно процессы рождения частиц
и аннигиляции античастиц и приводили к результатам, которые на
каждом этапе вычислений были лоренц-инвариантными. На примере
вычисления Вайскопфом собственной энергии электрона 63 мы уже
видели, что природа возникающих бесконечностей становится понят-
понятной только, когда частицы и античастицы рассматриваются на
равных основаниях.
Наконец, в двух статьях 1949 года Фримен Дайсон 88 показал,
что операторные формализмы Швингера и Томонаги приводят к тем
же самым графическим правилам, которые нашел Фейнман. Дайсон
проанализировал также бесконечности, возникающие в произволь-
произвольных диаграммах Фейнмана, и наметил доказательство того, что все
они относятся к тому типу, который может быть устранен при пере-
перенормировке. Одним из самых поразительных результатов, вытекав-
1.3. Проблема бесконечностей 49
ших из анализа Дайсона, был критерий того, какие квантовые тео-
теории поля относятся к разряду «перенормируемых», в том смысле,
что все бесконечности могут быть поглощены переопределением ко-
конечного числа констант связи и масс. В частности, взаимодействие
паулиевского типа A.1.32), которое могло бы привести к изменению
предсказываемого значения магнитного момента электрона, нару-
нарушило бы перенормируемость квантовой электродинамики. С выхо-
выходом в свет статьи Дайсона наконец-то появился единый системати-
систематический формализм, который мог быть легко изучен физиками и
обеспечивал общий язык для последующих приложений квантовой
теории поля к задачам физики.
Я не могу расстаться с рассказом о бесконечностях, не упомя-
упомянув об одном удивительном аспекте этой истории. Еще в 1930 году
Оппенгеймер заметил, что основная ультрафиолетовая расхо-
расходимость в собственной энергии связанного электрона сокращается,
если взять разность сдвигов двух атомных уровней энергии. Позднее,
в 1934 году Вайскопф нашел, что большая часть расходимости
собственной энергии свободного электрона сокращается, если
включить в рассмотрение промежуточные состояния, содержащие
позитроны. Уже в 1934 году было вполне естественным полагать,
что включив позитронные промежуточные состояния и находя
разность сдвигов уровней для пары атомных состояний, можно
полностью устранить ультрафиолетовую расходимость в относи-
относительном сдвиге уровней энергии *. Были и экспериментальные
свидетельства 77 существования сдвига уровней 2s1/2-2p1/2, равного
примерно 1000 МГц. Так почему же никто из теоретиков до 1947
года не попытался численно оценить эту разность уровней энергии?
Строго говоря, одна такая попытка была в 1939 году88а, но
внимание было сфокусировано не на той части задачи на вычисле-
вычислении зарядового радиуса протона, что весьма мало влияет на уровни
энергии атома водорода. Расчет привел к грубому согласию с ранни-
ранними экспериментами77. Однако, как в 1939 году показал Лэмб, это
было ошибкой.
* На самом деле, такая догадка неверна. Как обсуждается в разделе
14.3, радиационные поправки к массе электрона влияют на сдвиг атомных
уровней не только через сдвиг энергии покоя электрона, который одинаков
для всех уровней, но и через изменение кинетической энергии электрона,
меняющейся от одного уровня к другому.
50 Глава 1. Историческое введение
Полностью релятивистское вычисление лэмбовского сдвига,
учитывающее позитроны в промежуточных состояниях, можно было
бы сделать и в 1930-е годы, используя старую нерелятивистскую
теорию возмущений. Пока удерживаются все слагаемые до данного
порядка, старомодная теория возмущений приводит к тем же резуль-
результатам, что и строго релятивистские расчеты с помощью форма-
формализмов Фейнмана, Швингера и Томонаги. На самом деле, первый
после работы Бете точный расчет лэмбовского сдвига, выполнен-
выполненный в США Френчем и Вайскопфом и Норманом Кроллом и Лэм-
бом, был сделан именно таким способом, хотя группа Томонаги 81
уже применяла ковариантные методы расчетов для решения этой и
других задач.
То, чего нехватало ученым, — это уверенности в схеме пере-
перенормировок как средства обращения с бесконечностями. Как мы ви-
видели, перенормировки широко обсуждались в конце 30-х годов. Но
в это время считалось общепринятым (такую точку зрения особенно
подчеркивал Оппенгеймер 89) что при энергиях, превышающих
100 МэВ, квантовую электродинамику нельзя воспринимать все-
всерьез, и что решение ее проблем может быть найдено с помощью
совершенно новых неожиданных идей.
На конференции в Шелтер Айленде произошло несколько со-
событий, изменивших такую точку зрения. Одним из них было сооб-
сообщение, что обсуждавшиеся в предыдущем разделе проблемы, ка-
касающиеся космического излучения, находят свое разрешение: Роберт
Маршак высказал гипотезу 58 о существовании двух мезонов с близ-
близкими массами — мюонов, которые и наблюдались на опыте, и пио-
пионов, ответственных за ядерные силы. Еще важнее было получение
достаточно точных значений лэмбовского сдвига и аномального маг-
магнитного момента электрона, что заставило физиков внимательно
обдумать всю проблему радиационных поправок. Возможно, не ме-
менее существенным было и то, что на конференции собрались теоре-
теоретики, имевшие свои оригинальные взгляды на перенормировку как
решение проблемы бесконечностей. Когда в конце 1940-х годов слу-
случилась революция, она была совершена в основном молодыми фи-
физиками. Несмотря на возраст, эти ученые сыграли консервативную
роль, отказавшись от поисков радикальных решений, которыми
занимались их предшественники.
Библиография 51
Библиография
Aramaki, S. Development of the Renormalization Theory in Quantum
Electrodynamics. Historia Scientiarum, 36, 97 A989); ibid. 37, 91
A989).[Раздел 1.3]
Beyer, R.T., ed. Foundations of Nuclear Physics (Dover Publications,
Inc., New York, 1949). [Раздел 1.2]
Brown, L. Yukava's Prediction of the Meson. Centauros, 25, 71 A981).
[Раздел 1.2]
Brown, L.M. and Hoddeson, L., eds. The Birth of Particle Physics
(Cambridge University Press, Cambridge, 1983). [Разделы 1.1-1.3]
Cao, T.Y. and Schweber, S.S. «The Conceptual Foundations and the
Philosophical Aspects of Renormalization Theory». Synthese, 97, 33
A933). [Раздел 1.3]
Dirac, P.A.M. The Development of Quantum Theory (Gordon & Breach
Science Publishers, New York, 1971). [Раздел 1.1]
Fermi, E. Quantum Theory of Radiation. Rev. Mod. Phys. 4, 87 A932).
[Разделы 1.2 и1.3]
Gamov, G.A. Thirty Years that Shook Physics (Doubleday and Co.,
Garden Sity, New York, 1966). [Раздел 1.1]
Jammer, M. The Conceptual Development of Quantum Mechanics.
(McGraw Hill Book Co., New York, 1966). [Раздел 1.1] (Имеется рус-
русский перевод: Джеммер М. Эволюция понятий квантовой механи-
механики. М., Наука, 1985.)
Mehra, J. «The Golden Age of Theoretical Physics: P.A.M. Dirac's
Scientific Work from 1924 tO 1933», in: Aspects of Quantum Theory,
ed. by A. Salam and E.P. Wigner (Cambridge University Press,
Cambridge, 1972). [Раздел 1.1]
52 Глава 1. Историческое введение
Miller, A.I. Early Quantum Electrodynamics — A Source Book (Cambridge
University Press, Cambridge, UK, 1994). [Разделы 1.1, 1.2, 1.3]
Pais, A. Inward Bound (Clarendon Press, Oxford, 1986). [Разделы 1.1,
1.2, 1.3]
Schweber, S.S. «Feynman and the Visualization of Space-Time
Processes», Rev. Mod. Phys., 58, 449 A986). [Раздел 1.3]
Schweber, S.S. «Some Chapters for a History of Quantum Field
Theory: 1938-1952», in: Relativity, Groups, and Topology II, ed. by
B.S. DeWitt and R.Stora (North-Holland, Amsterdam, 1984).[Раз-
делы 1.1, 1.2, 1.3]
Schweber, S.S. «A Short History of Shelter Island I», in: Shelter Island
II, ed. by R. Jackiw, S. Weinberg, and E. Witten (MIT Press, Cambridge,
MA, 1985). [Раздел 1.3]
Schweber, S.S. QED and the Men Who Made It: Dyson, Feynman,
Schwinger, and Tomonaga (Princeton University Press, Princeton, 1994).
[Разделы 1.1, 1.2, 1.3]
Schwinger, J., ed., Selected Papers in Quantum Electrodynamics (Dover
Publications Inc., New York, 1958). [Разделы 1.2 и 1.3]
Tomonaga, S.-I. The Physicist's Conception of Nature (Reidel,
Dordrecht, 1973). [Разделы 1.2 и 1.3]
Weinberg, S. «The Search for Unity: Notes for a History of Quantum
Field Theory», Daedalus, Fall 1977. [Разделы 1.1, 1.2, 1.3]
Weisskopf, V.F. «Growing Up with Field Theory: The Development of
Quantum Electrodynamics in Half a Century», 1979 Bernard Gregory
lecture at CERN, published in: L. Brown and L. Hoddeson, op. cit.
[Разделы 1.1, 1.2, 1.3]
Wentzel, G. «Quantum Theory of Fields (Until 1947)», in: Theoretical
Physics in the Twentieth Century, ed. by M. Fierz and V.F. Weisskopf
(Interscience Publishers Inc., New York, 1960). [Разделы 1.2 и 1.3]
Список литературы 53
Whittaker, E. A. History of the Theories of Aether and Electricity
(Humanities Press, New York, 1973). [Раздел 1.1]
Список литературы
1. de Broglie, L., Comptes Rendus, 177, 507, 548, 630 A923); Nature,
112, 540 A923); These de doctorat (Masson et Cie, Paris, 1924);
Annales de Physique, 3, 22 A925) [reprinted in English in: Wave
Mechanics, ed. by G. Ludwig (Pergamon Press, New York, 1968)];
Phil. Mag., 47, 446 A924).
2. Elsasser, W., Naturwiss., 13, 711 A925).
a Davisson, С J. and Germer, L. H., Phys. Rev., 30, 705 A927).
4. Heisenberg, W., A. Phys., 33, 879 A925); Born, M. and Jordan, P.,
Z. /. Phys., 34, 858 A925); Dirac, P. A. M., Proc. Roy. Soc, A109,
642 A925); Born, M., Heisenberg, W., and Jordan, P., Z. /. Phys.,
35, 557 A925); Pauli, W., Z. /. Phys., 36, 336 A926). Эти работы
перепечатаны в книге: Sources of Quantum Mechanics, ed. by B. L.
van der Waerden (Dover Publications, Inc., New York, 1968).
5. Schrodinger, E., Ann. Phys., 79, 361, 489; 80, 437; 81, 109 A926).
Эти статьи перепечатаны в переводе на англ., к сожалению, в
несколько сокращенном варианте, в книге Wave Mechanics (см. [1]).
Кроме того см.: Collected Papers on Wave Mechanics, trans, by J. F.
Schearer and W. M. Deans (Blackie & Son, London, 1928).
6. См., например: Dirac, P. A. M., The Development of Quantum
Theory (Gordon & Breach, New York, 1971). Кроме того, см. не-
некролог Дирака о Шредингере: Dirac, P. A. M., Nature, 189, 355
A961), и статью: Dirac, P. A. M., Scientific American, 208, 45
A963).
7. Klein, О., Z. /. Phys., 37, 895 A926). См. также: V. Fock, Z. /.
Phys., 38, 242 A926); ibid, 39, 226 A926).
8. Gordon, W., Z. /. Phys., 40, 117 A926).
54 Глава 1. Историческое введение
9. Детали вычислений см., например, в книге: Schiff, L.I., Quantum
Mechanics, 3rd edn (McGrow Hill, Inc., New York, 1968), Section 51.
(Есть рус. пер.: Шифф Л. Квантовая механика. М., ИЛ, 1957).
10. Pashen, F., Ann. Phys., 50, 901 A916). Эти эксперименты ре-
реально были выполнены с использованием ионов Не+, поскольку
расстояние между уровнями тонкой структуры у них в 16 раз
больше, чем у водорода. Впервые тонкая структура спектраль-
спектральных линий была обнаружена в интерферометрических опытах:
Michelson, A.A., Phil. Mag., 31, 338 A891); ibid, 34, 280 A892).
10a. Sommerfeld, A., Miinchner Berichte 1915, pp. 425, 429; Ann. Phys.,
51, 1, 125 A916). См. также: Wilson, W., Phil. Mag., 29, 795
A915).
11. Uhlenbeck, G.E. and Goudsmit, S., Naturwiss., 13, 953 A925);
Nature, 117, 264 A926). Спин электрона был ранее введен из
других соображений в работе: Compton, A.H., J. Frank. Inst.,
192, 145 A921).
12. Общая формула для зеемановского расщепления в одноэлектрон-
ных атомах была эмпирически установлена в работах: Lande, A.,Z. /.
Phys., 5, 231 A921); ibid., 7, 398 A921); ibid., 15, 189 A923); ibid., 19,
112 A923). В те времена дополнительный неорбитальный угловой мо-
момент, входящий в эту формулу, считался угловым моментом атом-
атомной «сердцевины»: Sommerfeld, A., Ann. Phys., 63, 221 A920);
ibid., 70, 32 A923). Только позднее было установлено, что допол-
дополнительный угловой момент связан со спином электрона (см. п).
13. Heisenberg , W. and Jordan, P., Z. /. Phys., 37, 263 A926);
Darwin, C.G., Proc. Roy. Soc, A116, 227 A927). Дарвин утверж-
утверждает, что несколько авторов сделали эту работу одновременно,
в то время как Дирак цитирует только Дарвина.
14. Thomas, L.H., Nature, 117, 514 A926). См. также: Weinberg, S.,
Gravitation and Cosmology (Wiley, New York, 1972), Section 5.1.
15. Dirac, P.A.M., Proc. Roy. Soc, A117, 610 A928). По поводу при-
применения этой теории к вычислению эффектов Зеемана и Паше-
Список литературы 55
на~Бака, а также относительных интенсивностей линий внут-
внутри мультиплетов тонкой структуры см. также Dirac, ibid., All8,
351 A928).
16. По поводу вероятностной интерпретации нерелятивистской
квантовой механики см.: Born, M., Z. /. Phys., 37, 863 A926);
ibid., 38, 803 A926); Wentzel, G., Z. /. Phys., 40, 590 A926);
Heisenberg, W., Z. /. Phys., 43, 172 A927); Bohr, N., Nature,
121, 580 A928); Naturwissenschaften, 17, 483 A929); Electrons
et Photons — Rapports et Discussions du Vе Conseil de Physique
Solvay (Gauthier-Villars, Paris, 1928).
17. Беседа между Дираком и Дж. Мехрой 28 марта 1969 года, цити-
цитируется в книге: Mehra, J., Aspects of Quantum Theory, ed. by A.
Salam and E.P. Wigner (Cambridge University Press, Cambridge,
1972).
18. Gamow, G., Thirty Years that Shook Physics (Doubleday and Co.,
Garden City, NY, 1966), p. 125.
19. Pauli, W., Z. /. Phys., 37, 263 A926); 43, 601 A927).
20. Darwin, C.G., Proc. Roy. Soc, A118, 654 A928); A120, 621 A928).
21. Gordon, W., Z. /. Phys., 48, 11 A928).
22. Dirac, P.A.M., Proc. Roy. Soc, A126, 360 A930); см. также [47].
23. Stoner, E.C., Phil. Mag., 48, 719 A924).
24. Pauli, W., Z. /. Phys., 31, 765 A925).
25. Heisenberg, W., Z. /. Phys., 38, 411 A926); 39, 499 A926); Dirac,
P.A.M., Proc. Roy. Soc, A112, 661 A926); Pauli, W., Z. /. Phys.,
41, 81 A927); Slater, J.C., Phys. Rev., 34, 1293 A929).
2d Fermi, E., Z. /. Phys., 36, 902 A926); Rend. Accad. Lined, 3, 145 A926).
27. Dirac, P.A.M., [25].
56 Глава 1. Историческое введение
27а. Dirac, P.A.M., First W.R. Crane Lecture at the University of
Michigan, April 17, 1989, неопубликовано.
28. Weyl, H., Theory of Groups and Quantum Mechanics, translated
from the second A931) German edition (Dover Publications, Inc.,
New York), Ch. IV, Section 12. См. также: Dirac, P.A.M., Proc.
Roy. Soc, A133, 61 A931).
29. Oppenheimer, J.R., Phys. Rev., 35, 562 A930); Tamm, I., Z. /.
Phys., 62, 545 A930).
29a. Dirac, P.A.M., Proc. Roy. Soc, 133, 60 A931).
30. Anderson, CD., Science, 76, 238 A932); Phys. Rev., 43, 491 A933).
30a. Schwinger, J., A Report on Quantum Electrodynamics, in:
The Physicist's Conception of Nature (Reidel, Dordrecht, 1973), p.
415.
31. Pauli, W., Handbuch der Physik (Julius Springer, Berlin, 1932-
1933); Rev. Mod. Phys., 13, 203 A941).
32. Born, Heisenberg, and Jordan, [4], Section 3.
32a. Ehrenfest, P., Phys. Z., 7, 528 A906).
33. Born and Jordan, [4].
34. Dirac, P.A.M., Proc. Roy. Soc, A112, 661 A926), Section 5. Более
понятный вывод дан в книге: Schiff, L.I., Quantum Mechanics, 3rd
edn. (McGrow-Hill Book Company, New York, 1968), Section 44.
34a. Einstein, A., Phys. Z., 18, 121 A917).
35. Dirac, P.A.M., Proc. Roy. Soc, A114, 243 A927).
36. Dirac, P.A.M., Proc. Roy. Soc, A114, 710 A927).
36a. Weisskopf, V.F. and Wigner, E.P., Z. /. Phys., 63, 54 A930).
Список литературы 57
36b. Fermi, E., Lincei Rend., 9, 881 A929); 12, 431 A930); Rev. Mod.
Phys., 4, 87 A932).
37. Jordan, P. and Pauli, W., Z. /. Phys., 47, 151 A928).
38. Bohr, N. and Rosenfeld, L., Kon. dansk. vid. Selsk., Mat.-Fys.
Medd., XII, No. 8 A933); Phys. Rev., 78, 794 A950).
39. Jordan, P., Z. /. Phys., 44, 473 A927). См. также: Jordan, P. and
Klein, O., Z. /. Phys., 45, 751 A929); Jordan, P., Phys. Zeit, 30,
700 A940).
40. Jordan, P. and Wigner, E., Z. /. Phys., 47, 631 A928).
40a. Fierz, M., Helv. Phys. Acta, 12 A939); Pauli, W., Phys. Rev., 58,
716 A940); Pauli, W. and Belinfante, F.J., Physica, 7, 177 A940).
41. Heisenberg, W. and Pauli, W., Z. /. Phys., 56, 1 A929); ibid, 59,
168 A930).
42. Dirac, P.A.M., Proc. Roy. Soc, A136, 453 A932); Dirac, P.A.M.,
Fock, V.A., and Podolsky, В., Phys. Zeit. der Sovjetunion, 2, 468
A932); Dirac, P.A.M., Phys. Zeit. der Sovjetunion, 3, 64 A933). См.
также Rosenfeld, L., Z. /. Phys., 76, 729 A932).
43. Fermi, E., Z. /. Phys., 88, 161 A934). Ферми цитирует неопуб-
неопубликованную работу Паули, где выказывается предположение,
что наряду с электроном в C-распаде испускается новая ненаб-
ненаблюдаемая нейтральная частица. Эта частица была названа ней-
нейтрино, чтобы отличить ее от недавно открытого нейтрона.
43а. Fock, V., С. R. Leningrad, 1933, р. 267.
44. Furry, W.H. and Oppenheimer, J.R., Phys. Rev., 45, 245 A934).
В этой статье используется формализм матрицы плотности, раз-
развитый в работе: Dirac, P.A.M., Proc. СатЪ. Phil. Soc, 30, 150
A934). См. также: Peierls, R.E., Proc. Roy. Soc, 146, 420 A934);
Heisenberg, W., Z. /. Phys., 90, 209 A934); Rosenfeld, L., Z. /.
Phys., 76, 729 A932).
58 Глава 1. Историческое введение
45. Pauli, W. and Weisskopf, V., Helv. Phys. Ada, 7, 709 A934). См.
также: Pauli, W., Ann. Inst. Henri Poincare, 6, 137 A936).
46. Klein, O.andNishina, Y., Z. /. Phys., 52, 853A929); Nishina,
Y., ibid., 869 A929). См. также: Tamm, I., Z. /. Phys., 62,
545 A930).
47. Dirac, P.A.M., Proc. Camb. Phil. Soc, 26, 361 A930).
48. M0ller, C, Ann. d. Phys., 14, 351, 568 A932).
49. Bethe, H. and Heitler, W., Proc. Roy. Soc., A146, 83 A934); см. также
Racah, G., Nuovo Cimento, 11, 7 A934); ibid., 13, 69 A936).
50. Bhabha, H.J., Proc. Roy. Soc, A154, 195 A936).
50a. Carlson, J.F. and Oppenheimer, J.R., Phys. Rev., 51, 220 A937).
51. Ehrenfest, P. and Oppenheimer, J.R., Phys. Rev., 37, 333 A931).
52. Heitler, W. and Herzberg, G., Naturwiss., 17, 673 A929); Raset-
ti, F., Z. /. Phys., 61, 598 A930).
53. Chadwick, J., Proc. Roy. Soc, A136, 692 A932).
54. Heisenberg, W., Z. /. Phys., 77, 1 A932); см. также: Curie-Joliot,
I. and Joliot, F., Compt. Rend., 194, 273 A932).
54a. По поводу ссылок см. в работе: Brown, L.M. and Rechenberg,
Н., Hist. Stud, in Phys. and Bio. Science, 25, 1 A994).
55. Yukawa, H., Proc. Phys.-Math. Soc. (Japan) C) 17, 48 A935).
56. Neddermeyer, S.H. and Anderson, CD., Phys. Rev., 51, 884 A937);
Street, J.C. and Stevenson, E.C., Phys. Rev., 52, 1003 A937).
56a. Nordheim, L. and Webb, N.. Phys. Rev., 56, 494 A939).
57. Conversi, M., Pancini, E., and Piccioni, O., Phys. Rev., 71, 209L
A947).
Список литературы 59
58. Sakata, S. and Inoue, Т., Progr. Theor. Phys., 1, 143 A946);
Marshak, R.E. and Bethe, H.A., Phys. Rev., 77, 506 A947).
59. Lattes, C.M.G., Occhialini, G.P.S., and Powell, C.F., Nature, 160,
453, 486 A947).
60. Rochester, G.D. and Butler, C.C., Nature, 160, 855 A947).
61. Oppenheimer, J.R., Phys. Rev., 35, 461 A930).
62. Waller, I., Z. /. Phys., 59, 168 A930); ibid., 61, 721, 837 A930);
ibid., 62, 673 A930).
63. Weisskopf, V.F., Z. /. Phys., 89, 27 A934). Электромагнитная
собственная энергия в этой работе вычислена только в низшем
порядке по а. Доказательство того, что расходимость имеет ло-
логарифмический характер во всех порядках теории возмущений
было дано в работе: Weisskopf, V.F., Phys. Rev., 56, 72 A939).
64. Dirac, P.A.M., XVII Conseil Solvay de Physique, p. 203 A933).
Последующие вычисления, основанные на менее ограничитель-
ограничительных предположениях: Heisenberg, W., Z. /. Phys., 90, 209
A934); Sachs. Akad. Wiss., 86, 317 A934); Serber, R., Phys.
Rev., 43, 49 A935); Uehling, E.A., Phys. Rev., 48, 55 A935);
Pauli, W. and Rose, M., Phys. Rev., 49, 462 A936). См. также:
Furry and Oppenheimer, [44]; Peierls, [44], Weisskopf, [63].
65. Euler, H. and Kockel, В., Naturwiss., 23, 246 A935); Heisenberg,
W. and Euler, H., Z. /. Phys., 98, 714 A936).
66. Dirac, P.A.M., Proc. Camb. Phil. Soc, 30, 150 A934).
67. Heisenberg, W., Z. /. Phys., 90, 209 A934).
68. Kemmer, N. and Weisskopf, V.F., Nature, 137, 659 A936).
68a. Bloch, F. and Nordsieck, A., Phys. Rev., 52, 54 A937). См. также:
Pauli, W. and Fierz, M., Nuovo Cimento, 15, 167 A938).
69. Dancoff, S.M., Phys. Rev., 55, 959 A939).
60 Глава 1. Историческое введение
69а. Lewis, H.W., Phys. Rev., 73, 173 A948); Epstein, S., Phys. Rev.,
73, 177 A948). См. также: Schwinger, J., [84] ; Koba, Z. and
Tomonaga, S., Progr. Theor. Phys., 3/3, 290 A948).
69b. Schwinger, J., в книге: The Birth of Particle Physics, ed. by L.
Brown and L. Hoddeson (Cambridge University Press, Cambridge,
1983), p. 336.
70. Heisenberg, W., Ann. d. Phys., 32, 20 A938).
70a. Wentzel, G., Z. /. Phys., 86, 479, 635 A933); 87, 726 A934);
Born, M. and Infeld, L., Proc. Roy. Soc, A150, 141 A935); Pauli,
W., Ann. Inst. Henri Poincare, 6, 137 A936).
71. Wheeler, J.A., Phys. Rev., 52, 1107 A937).
72. Heisenberg, W., Z. /. Phys., 120, 513, 673 A943); Z. Naturforsch.
1, 608 A946). См. также: M0ller, С, Коп. Dansk. Vid. Sel..,Mat.-
Fys. Medd., 23, No. 1 A945); ibid., 23, No. 19 A946).
73. См., например: Chew, G., The S-Matrix Theory of Strong
Interactions (W.A. Benjamin, Inc., New York, 1961) (есть рус.
пер.: Дж. Чу. Теория S'-матрицы. М.: Мир, 1965).
74. Wheeler, J.A. and Feynman, R.P., Rev. Mod. Phys., 17, 157 A945);
ibid., 21, 425 A949). Дальнейшие ссылки и обсуждение примене-
применения теорий действия на расстоянии в космологии см. в книге:
Weinberg, S., Gravitation and Cosmology (Wiley, 1972), Section
16.3 (есть рус. пер.: Вейнберг С. Гравитация и космология. М.:
Мир, 1976).
75. Dirac, P.A.M., Proc. Roy. Soc, A180, 1 A942). Критические за-
замечания см. в работе: Pauli, W., Rev. Mod. Phys., 15, 175 A943).
Обзор классических теорий этого типа, а также других попы-
попыток разрешить проблему бесконечностей см. в статье: Peierls,
R.P., in: Rapports du 8me Conseil de Physique Solvay 1948 (R.
Stoops, Brussels, 1950), p. 241.
76. Weisskopf, V.F., Kgl. Dansk. Vidensk. Selskab,Mat.-Fys. Medd.,
Список литературы 61
14, No. 6 A934), особенно с. 34 и с. 5-6. См. также: Pauli and
Fierz, [68a]; Kramers [79a].
77. Pasternack, S., Phys. Rev., 54, 1113 A938). Это предложение
было основано на экспериментах: Houston, W.V., Phys. Rev.,
51, 446 A937); Williams, R.C., Phys. Rev., 54, 558 A938). Сооб-
Сообщения о противоположных данных: Drinkwater , J.W.,
Richardson, O., and Williams, W.E., Proc. Roy. Soc, 174, 164
A940).
78. Uehling, E.A, [64].
79. Lamb, W.E. and Retherford, R.C., Phys. Rev., 72, 241 A947).
79a. Kramers, H.A., Nuovo Cimento, 15, 108 A938); Ned. T. Natwink.,
11, 134 A944); Rapports du 8me Conseil de Physique Solvay 1948
(R. Stoops, Brussels, 1950).
80. Bethe, H.A., Phys. Rev., 72, 339 A947).
81. French, J.B. and Weisskopf, V.F., Phys. Rev., 75, 1240 A949);
Kroll, M. and Lamb, W.E., ibid., 75, 388 A949); Schwinger, J.,
Phys. Rev., 75, 898 A949); Feynman, R.P., Rev. Mod. Phys., 20,
367 A948); Phys. Rev., 74, 939, 1430 A948); 76, 749, 769 A949);
80, 440 A950); Fukuda, H., Miyamoto, Y., and Tomonaga, S.,
Progr. Theor. Phys. Rev. Mod. Phys., 4, 47, 121 A948).
82. Nafe, J.E., Nelson, E.B., and Rabi, I.I., Phys. Rev., 71, 914 A947);
Nagel, D.E., Julian, R.S., and Zacharias, J.R., Phys. Rev., 72,
973 A947).
83. Kush, P. and Foley, H.M., Phys. Rev., 72, 1256 A947).
83a. Breit, G., Phys. Rev., 71, 984 A947). Швингер включил в работу
[84] исправленный вариант результатов Брейта.
84. Schwinger, J., Phys. Rev., 73, 416 A948).
85. Schwinger, J., Phys. Rev., 74, 1439 A948); ibid., 75, 651 A949);
62 Глава 1. Историческое введение
ibid., 76, 790 A949); ibid., 82, 664, 914 A951); ibid., 91, 713
A953); Proc. Nat. Acad. Set, 37, 452 A951).
86. Tomonaga, S., Progr. Theor. Phys. Rev. Mod. Phys., 1, 27 A946);
Koba, Z., Tati, Т., and Tomonaga, S., ibid., 2, 101 A947);
Kanesawa, S. and Tomonaga, S., ibid., 3, 1, 101A948); Tomonaga,
S., Phys. Rev., 74, 224A948); Ito, D., Koba, Z., and Tomonaga, S.,
Progr. Theor. Phys., 3, 276 A948); Koba, Z. and Tomonaga, S.,
ibid., 3, 290 A948).
87. Feynman, R.P., Rev. Mod. Phys., 20, 367 A948); Phys. Rev., 74,
939, 1430 A948); ibid., 76, 749, 769 A949); ibid., 80, 440 A950).
88. Dyson, F.J., Phys. Rev., 75, 486, 1736 A949).
88a. Frohlich, H., Heitler, W., and Kahn, В., Proc. Roy. Soc, A171,
269 A939); Phys. Rev., 56, 961 A939).
88b. Lamb, W.E., Jr., Phys. Rev., 56, 384 A939); 57, 458 A940).
89. Цитируется Р. Сербером в книге: The Birth of Particle Physics,
[69b], p. 270.
Релятивистская квантовая механика
Точка зрения, принятая в этой книге, такова: квантовая
теория поля такая, какая она есть, потому что (с определенными
оговорками) это единственный способ совместить квантовую меха-
механику с частной теорией относительности. Поэтому нашей первой
задачей будет изучение того, как в квантовых построениях возни-
возникают симметрии вроде лоренцовской инвариантности.
2.1. Квантовая механика
Сначала хорошее известие: квантовая теория поля основана
на той же квантовой механике, которая была создана Шрединге-
ром, Гейзенбергом, Паули, Борном и др. в 1925-1926 годах и с тех
пор используется для расчетов в атомной, молекулярной, ядерной
физике и физике твердого тела. Предполагается, что читатель
знаком с квантовой механикой. В этом разделе дается лишь самое
краткое изложение принципов квантовой механики в обобщенной
дираковской формулировке Ч
A) Физические состояния задаются лучами в гильбертовом
пространстве. Это один из видов комплексного векторного простран-
пространства. Иначе говоря, если Ф и Ч* есть векторы в этом пространстве (их
часто называют «векторами состояния»), то таковым является
и вектор ^Ф + ti^P, где ?,, ц — произвольные комплексные числа.
Гильбертово пространство снабжено скалярным произведением *:
Мы часто будем использовать дираковские скобочные обозначения и
вместо (х?1, Ч*2) писать <l|2>.
64 Глава 2. Релятивистская квантовая механика
любой паре векторов сопоставляется комплексное число (Ф,Ч*),
причем выполнены следующие условия:
(Ф,ЧГ) = (Ч,Ф)\ B.1.1)
(Ф,^1+^2) = ^1(Ф,^1) + ^(Ф,Ч'2), B.1.2)
^)- B.1.3)
Норма (Ч^Ч*) удовлетворяет также условию положительности:
(Ч^Ч*) > 0, причем норма обращается в нуль, если и только если
Ч* = 0. (Есть еще ряд технических предположений, позволяющих
совершать предельные переходы для векторов внутри гильбертова
пространства.) Луч — это множество нормированных векторов
(т. е. (Ч?, Ч?) = 1), причем Ч? и Ч? принадлежат одному лучу, если
Ч*' = ^Р, где Ъ, — произвольное комплексное число с |^| = 1.
B) Наблюдаемые представляются эрмитовыми операторами.
Это отображения Ч! —» АЧ! гильбертова пространства в себя, линей-
линейные в том смысле, что
+ Г|Ф) = ^АЧ1 + цАФ, B.1.4)
и удовлетворяющие условию вещественности А^ = А, где для
любого линейного оператора А сопряженный ему оператор А^
определяется условием
B.1.5)
(Есть также и некоторые технические предположения о непрерыв-
непрерывности АЧ* как функции Ч*.) Состояние, представленное лучом №,
имеет определенное значение а наблюдаемой, оператор которой
есть А, если векторы Ч*, принадлежащие этому лучу, являются
собственными векторами А с собственными значениями ос:
АЧ1 = аЧ>. B.1.6)
Элементарная теорема утверждает, что если А — эрмитов
оператор, то собственные значения а действительны, а собствен-
собственные векторы, отвечающие разным ОС, ортогональны.
2. 2. Симметрии 65
C) Если система находится в состоянии, представленном
лучом №, и проводится эксперимент по проверке того, является
ли это состояние одним из различных состояний, представлен-
представленных взаимно ортогональными лучами №х, '.Ш2, ... (например, путем
измерения одной или более наблюдаемых), то вероятность обна-
обнаружить систему в состоянии, описываемом лучом '.Шп, равна
Р(;й _> ;дп) =|(?,Ч')|2, B.1.7)
где Ч1 и *РП — любые векторы, принадлежащие лучам № и №п,
соответственно. (Пара лучей называется ортогональной, если ска-
скалярные произведения векторов из двух лучей равны нулю.) Другая
элементарная теорема утверждает, что если векторы состояний Ч*п
образуют полную систему, то полная вероятность равна единице:
'(tf->tfn) = l. B.1.8)
2.2. Симметрии
Преобразование симметрии — это такое изменение нашей
точки зрения, которое не меняет результатов возможных экспе-
экспериментов. Если наблюдатель О видит систему в состоянии, пред-
представленном лучами Ш или ,'fib !'Л2, —, то эквивалентный наблю-
наблюдатель О', исследующий ту же самую систему, будет видеть
ее в другом состоянии, представленном лучами Ж или Жъ Ж2,
..., соответственно, однако оба наблюдателя должны обнаружить,
что соответствующие вероятности не изменились:
РО» -> Яп) = Р(Ж -> <). B.2.1)
(Это лишь необходимое условие того, чтобы преобразование лучей
было симметрией; дальнейшие условия обсуждаются в следующей
главе.) Важная теорема, доказанная Вигнером в начале 1930-х
годов, утверждает, что для любого преобразования лучей '.Ш —» Ж
можно определить в гильбертовом пространстве оператор U,
причем, если Ч1 принадлежит лучу '.Ш, то U4? принадлежит лучу
Ж, а сам оператор U является либо унитарным и линейным:
66 Глава 2. Релятивистская квантовая механика
(иФ,ЦЧ>) = (Ф,Ч>), B.2.2)
Щ%Ф + цЧ?) = %иФ + ц1Г?, B.2.3)
либо антиунитарным и антилинейным:
(иФ,1Г?) = (Ф,Ч)*, B.2.4)
B.2.5)
В аргументации Вигнера пропущены некоторые этапы. Более полное
доказательство дано в Приложении А к этой главе.
Как уже отмечалось, оператор, сопряженный линейному опе-
оператору L, определяется равенством
(Ф,1/Ч') = (ЬФ,П B.2.6)
Это условие не может быть выполнено для антилинейного операто-
оператора, так как в этом случае правая часть соотношения B.2.6) была бы
линейна по Ф, в то время как левая часть - антилинейна. Вместо
этого оператор, сопряженный антилинейному оператору А,
определяется равенством
(Ф, А*Ч<) ее (А?, Ф)* = (?, АФ). B.2.7)
Если принять это определение, то условия унитарности или анти-
антиунитарности имеют одинаковый вид
Uf = U~\ B.2.8)
Всегда существует тривиальное преобразование симметрии
iil—ь'М, которому соответствует единичный оператор 17=1. Этот
оператор, конечно, унитарный и линейный. Теперь из соображений
непрерывности можно заключить, что любая симметрия (типа враще-
вращения, трансляции или лоренцовского преобразования), которая может
быть сделана тривиальной путем непрерывного изменения некоторых
параметров (углов поворота, расстояний или скоростей), должна
представляться не антилинейным и антиунитарным оператором, а
только линейным унитарным оператором U. (Симметрии, пред-
2. 2. Симметрии 67
ставляемые антиунитарными антилинейными операторами, менее
известны в физике; все они включают обращение направления
течения времени. Подробнее см. раздел 2.6.)
В частности, преобразование симметрии, бесконечно близкое
к тривиальному, можно представить линейным унитарным операто-
оператором, бесконечно близким к единичному:
U = 1 + Ш , B.2.9)
где ? — действительное бесконечно малое число. Для того, чтобы
этот оператор был унитарным и линейным, оператор t должен
быть эрмитовым и линейным. Поэтому t является кандидатом на
то, чтобы быть наблюдаемой. Действительно, большинство (если не
все) наблюдаемых в физике, вроде импульса или углового момента,
возникают подобным образом из преобразований симметрии.
Множество преобразований симметрии обладает свойствами,
позволяющими установить, что оно является группой. Если Т1 —
преобразование, переводящее лучи №п в Жп, а Т2 — другое
преобразование, переводящее Жп в Ж'п, то результат последо-
последовательного осуществления обоих преобразований является тоже
преобразованием симметрии, переводящим РЛп в Ж'п, которое мы
записываем как T2TV Кроме того, преобразованию симметрии Т,
переводящему лучи РЛп в Жп, соответствует обратное преоб-
преобразование Т, переводящее Жп в '.Шп. Наконец, существует тож-
дественное-преобразование Т = 1, оставляющее лучи неизмен-
неизменными.
Унитарные или антиунитарные операторы U(T), соответ-
соответствующие этим преобразованиям симметрии, отражают груп-
групповую структуру преобразований, но с тем усложнением, что в
противоположность самим преобразованиям симметрии операторы
U(T) действуют не на лучи, а на векторы в гильбертовом простран-
пространстве. Если Т1 переводит '.Шп в Жп, то ЩТ^, действуя на вектор *РП
из луча iitn, превращает его в вектор U(T1L'n из луча Жп. Далее,
если Т2 переводит Жп в Ж'п, то, действуя на ЩТ^Ч^ получаем
вектор ЩТ2)ЩТ1)Ч1п из луча Ж'п. Однако ЩТ2Т1)Ч1п также при-
принадлежит этому лучу, так что два вектора могут отличаться
только фазой фп(Т2, Тг):
1)Ч'я. B.2.10)
+4>B) = ЩТ2)ЩТ1)(Ч>А+Ч>В)
= U(T2)U(T1L>A+U(T2)U(T1L>
68 Глава 2. Релятивистская квантовая механика
Далее, за одним важным исключением, из линейности (или
антилинейности) U(T) вытекает, что эти фазы не зависят от
с о с т о -
яния *РП. Приведем доказательство. Рассмотрим два различных
вектора Ч?А, Ч*в, не пропорциональные друг другу. Применяя
B.2.10) к состоянию ^Ав = ^А + *РВ, получим
Всякий унитарный или антиунитарный оператор имеет обратный
оператор (сопряженный исходному), который также унитарен или
антиунитарен. Умножая B.2.11) слева на 17~1(Т2Т1), находим, что
B.2.12)
причем верхние или нижние знаки соответствуют унитарному или
антиунитарному оператору U(T2T1). Так как *РА и *^в линейно
независимы, это возможно лишь при условии, что
егфАВ =егфА =егфв_ B.2.13)
Таким образом, как и утверждалось, фаза в B.2.10) не зависит от
вектора состояния *РП, так что само соотношение можно записать
как операторное равенство
B.2.14)
При ф = 0 говорят, что U(T) реализует представление группы
преобразований симметрии. При произвольных фазах ф(Т2, Тг)
мы получаем то, что называется проективным представлением
или «представлением с точностью до фазы». Структура группы
Ли сама по себе не может указать, реализуют ли физические
векторы состояний обычное или проективное представление,
однако, как мы увидим, эта структура может указать, имеет ли
группа хотя бы одно внутренне ей присущее проективное
представление.
2. 2. Симметрии 69
В цепочке рассуждений, приводящих к B.2.14), есть одно
узкое место: может оказаться, что нельзя приготовить систему
в состоянии Ч?А + Ч^. Например, считается общепризнанным, что
невозможно приготовить систему в виде суперпозиции двух состо-
состояний, полные угловые моменты которых, соответственно, целые
и полуцелые. В таких случаях мы говорим, что между разными
классами состояний действуют «правила суперотбора»3, и фазы
ф(Т2, 1\) могут зависеть от того, на какие классы действуют
операторы U{T2)U{Tl) и U{T2,TX). В разделе 2.7 мы обсудим эти
фазы и проективные представления несколько подробнее. Как бу-
будет видно, всякая группа симметрии, имеющая проективные
представления, всегда может быть расширена (без какого либо
другого изменения ее физических приложений) таким образом, что
все ее представления можно будет определить как не- проективные
с ф = 0. Будем считать, что это уже доказано, и положим ф = 0 в
B.2.14).
Для физики особенно важны группы, носящие название
связных групп Ли. Это группы преобразований ТF), задаваемые
конечным набором действительных непрерывных параметров 6а,
причем каждый элемент группы можно связать с единичным
элементом некоторым путем, лежащим внутри группы. Закон
группового умножения принимает вид
т(ё)Т(9) = т(/(ё,е)), B.2.15)
где /а@,6) — функция 6 и 6. Полагая координаты единичного
элемента равными 6а = 0, мы должны иметь
/а(е,о) = /а(о,е) = еа. B.2.16)
Как уже отмечалось, преобразования таких непрерывных
групп должны представляться унитарными (но не антиунитарными)
операторами 17(ТF)) в физическом гильбертовом пространстве.
Для групп Ли эти операторы могут быть представлены (по крайней
мере, в окрестности единичного элемента) степенным рядом
ЩТ(9)) = 1 + г6% +-eb6ctbc +..., B.2.17)
где ta, tfc = tcb и т. д. — эрмитовы операторы, не зависящие от 6.
70 Глава 2. Релятивистская квантовая механика
Предположим, что 17(ТF)) реализует обычное (т. е. не проективное)
представление этой группы преобразований, иными словами
ЩТ(9))[7(Т(9)) = ЩТ(/(9,9))). B.2.18)
Посмотрим, как выглядит это соотношение, если разложить
его в ряд по степеням 6а и 6а. Как следует из B.2.16), разложение
/аF,6) до второго порядка должно иметь вид
/а(б,е) = еа + еа + /аьсеьес +..., B.2.19)
где /а5с — действительные коэффициенты. (Наличие любых слага-
слагаемых порядка б2 или б2 будет нарушать соотношение B.2.16).) Тогда
уравнение B.2.18) принимает вид:
+ ге\ + \ еье%с +... 1 х \л
B.2.20)
Слагаемые порядка 1,6, 6, б2 и б2 автоматически сокращаются
в обеих частях B.2.20), однако, собирая слагаемые с 6 6, находим
нетривиальное условие:
*Ьс=-*ь*с-*/аЬс*а- B.2.21)
Оно показывает, что если нам задана структура группы, т. е.
функция /F,6) , а следовательно, и ее квадратичные коэффициенты
/ а5с,мы можем вычислить слагаемые второго порядка в 17(ТF)),
зная генераторы ta, возникающие в слагаемых первого порядка.
Однако, должно выполняться условие самосогласованности:
оператор t^ должен быть симметричным по 5 и с (так как он равен
второй производной 17(ТF)) по 6Ь и 6е), так что из B.2.21) следует,
что
[tb,tc] = iCabcta, B.2.22)
где
2. 2. Симметрии 71
CV = -Ac + /acb B.2.23)
представляет набор действительных констант, называемых
структур-ными константами. Такой набор коммутационных
соотношений определяет алгебру Ли. В разделе 2.7 мы докажем,
что коммута-ционные соотношения B.2.22) — единственное
условие, необходимое для того, чтобы процесс разложения мог
быть продолжен: весь степенной ряд для 17(ТF)) можно вычислить
с помощью бесконечного набора соотношений типа B.2.21), если
нам известны слагаемые первого порядка, т. е. генераторы ta. Это
не обязательно означает, что знание ta однозначно определяет
операторы 17(ТF)) для всех 6а, однако, по крайней мере, в
конечной окрестности координат 6а = 0 единичного элемента
17(Т[6)) определяются однозначно в том смысле, что если 6, 6 и
/(б, б) заданы в этой окрестности,
то удовлетворяется уравнение B.2.18). Распространение этих резуль-
результатов на все 6а обсуждается в разделе 2.7.
Важным является частный случай, к которому мы будем
вновь и вновь обращаться. Пусть функция /@,0) (возможно, лишь
для некоторого подмножества координат 6а) является просто
суммой
/аF,ё) = 6а+1а. B.2.24)
Сюда относятся трансляции в пространстве—времени или
вращения вокруг фиксированной оси (но не вокруг двух по
очереди). Тогда коэффициенты fabc в B.2.19) и структурные
константы B.2.23) обращаются в нуль. Все генераторы коммути-
коммутируют друг с другом:
[tb,tc] = O- B.2.25)
Такая группа называется абелевой. В этом случае легко
вычислить 17(ТF)) для всех 6а. При любом целом N находим из
B.2.18) и B.2.24):
Г (
ЩТ(9)) = U\ Т
72 Глава 2. Релятивистская квантовая механика
Переходя к пределу N —> °° и удерживая только слагаемое
первого порядка в U(T(Q/N)), получаем
Г г "Г
ЩТ(9))= lim 1 + -9% ,
откуда
?7(Т(9)) = ехр(йа9а). B.2.26)
2.3. Квантовые преобразования Лоренца
Эйнштейновский принцип относительности утверждает
эквивалентность «инерциальных» систем отсчета. Он отличается
от галилеевского принципа относительности, которому подчи-
н я -
ется механика Ньютона, видом преобразования, связывающего
координаты в разных системах отсчета. Если жц — координаты
в одной инерциальной системе (ж1, ж2, ж3 — декартовы простран-
пространственные координаты, х°=t— временная координата, скорость
света положена равной единице), то координаты х'^ в любой
другой инерциальной системе должны удовлетворять соотноше-
соотношению:
^dx'v-dx = ^dx^dx" B.3.1)
или эквивалентно:
Здесь Г[^у — диагональная матрица, элементы которой равны
Ли = Л22 = Лзз = +1> Лоо = -1- B-3-3)
Принято правило суммирования по немым индексам: подразуме-
подразумевается сумма по любому индексу типа ц или V в формуле B.3.2),
появляющемуся в одном и том же слагаемом дважды, один раз
вверху, другой — внизу. Эти преобразования обладают тем специ-
2. 3. Квантовые преобразования Лоренца 73
альным свойством, что скорость света одинакова во всех инер-
циальных системах отсчета (в выбранных единицах она равна 1).
Действительно, световая волна, распространяющаяся с единичной
скоростью, удовлетворяет условию |dx/dt| = 1 или
= dx2 - dt2 = 0,
откуда следует, что и ц^йх'Ых^ = 0, т.е. |dx'/dt'| = 1*.
Всякое преобразование координат жц —» ж/ц, удовлетворяю-
удовлетворяющее B.3.2), линейно За:
x'V=A\xv+aV, B.3.4)
где а^ — произвольные константы, а постоянная матрица Л^у удовлет-
удовлетворяет условию:
VAVVa=V. B.3.5)
Для дальнейшего полезно записать условия лоренцовских преобра-
преобразований в иной форме. Матрица г\^ имеет обратную,обозначаемую
г\^, которая имеет те же компоненты, т. е. она диагональна и г|00 = -1,
ГI1 = ГJ2 = ГK3 = +1. Умножая выражение B.3.5) на г^Л*,. и группируя
множители, имеем
Умножая это равенство на матрицу, обратную Лцу^р' получаем:
ЛУаЛ\Г|стт =T|VK. B.3.6)
Эти преобразования образуют группу. Если сначала осуще-
*Существует более широкий класс преобразований координат, известных
как конформные преобразования, для которых rj^dx'^dx^ пропорционально,
хотя в общем случае не равно, r\ilvdxild,xv, и которые также оставляют
инвариантной скорость света. Показано, что конформная инвариантность в
двух измерениях имеет огромное значение в теории струн и статистической
механике, но физический смысл таких конформных преобразований в
четырехмерном пространстве—времени до сих пор неясен.
74 Глава 2. Релятивистская квантовая механика
ствить лоренцовское преобразование B.3.4), а затем второе ло-
ренцовское преобразование ж/ц —» х"^, так что
х"* = Х^рх'Р + а» = X
то результат эквивалентен лоренцовскому преобразованию
жц —> ж//ц, причем
х'^ = (A%Apv)xv + (Л%аР + av). B.3.7)
(Заметим, что если обе матрицы Л^у и А\ удовлетворяют B.3.5),
то это же верно и для Л^рДРу, так что это действительно
преобразование Лоренца. Черта используется здесь только для
того, чтобы отличить одно лоренцовское преобразование от дру-
другого.) Пре-образования Т(А,а), действующие на физические со-
состояния, удовлетворяют поэтому правилу композиции
а + а). B.3.8)
Беря детерминант от обеих частей B.3.5), находим, что
(DetAJ = 1, B.3.9)
так что А\ имеет обратную матрицу (A)vp, в силу B.3.5) равную
(Л-УУ = Л/ = л^ЛраЛ^а. B.3.10)
Как следует из B.3.8), обратное преобразование к Т(А,а) имеет
вид Т(Л,-Ла), причем тождественное преобразование равно
В согласии с тем, о чем шла речь в предыдущем разделе,
преобразования Т(Л, а) индуцируют унитарные линейные преобразо-
преобразования векторов в физическом гильбертовом пространстве
Операторы U удовлетворяют правилу композиции
17(Л,аI7(Л,а) = ЩЛЛ,Ла + а). B.3.11)
2. 3. Квантовые преобразования Лоренца 75
(Как уже отмечалось, чтобы избежать появления фазового мно-
множителя в правой части уравнения B.3.11), необходимо в общем
случае расширить группу Лоренца. Соответствующая процедура
описана в разделе 2.7.)
Вся группа преобразований Т(А,а) обычно называется неоднород-
неоднородной группой Лоренца или группой Пуанкаре. Она имеет много важ-
важных подгрупп. Во-первых^преобразования с аI = 0, причем
Т(Л,0)Т(Л,0) = ЩЛЛ,0). B.3.12)
очевидно образуют подгруппу, называемую однородной группой
Лоренца. Кроме того, из B.3.9) следует, что либо Det Л = +1, либо
Det Л = —1. Ясно, что преобразования с Det Л = +1 образуют
подгруппу как однородной, так и неоднородной группы Лоренца.
Далее, выписывая 00-компоненты уравнений B.3.5) и B.3.6), имеем:
(Л%J = l + AVVo =1 + Л°гЛ°г. B.3.13)
где проводится суммирование по индексу г, принимающему значе-
значения 1, 2, 3. Видно, что либо Л°о > +1, либо Л°о < -1. Преобразования
с Л°о > +1 образуют подгруппу. Действительно, если А\ и А\ —
две таких матрицы Л, то
(ЛЛ)°о = Л°оЛ°о +A°iA1o +Л°2Л2о +Л°3Л3о.
Но из уравнения B.3.13) вытекает, что 3-вектор iA}0^A20, Л30)
имеет длину ((Л%J - lI^2» аналогично 3-вектор (Л 1,Л 2, Л з) имеет
длину ((Л%J -1I/2» поэтому скалярное произведение этих двух
3—векторов ограничено условием
Л°2Л2о + Л°3Л3о|< л/(Л°оJ-1л/(ЛооJ-1, B.3.14)
так что
(ЛЛ)% > Л%Лоо - V(A°oJ-lV(A°oJ-l> 1.
Подгруппа преобразований Лоренца с Det Л = +1 и Л°о > +1
носит название собственной ортохронной группы Лоренца. Так
как невозможно с помощью непрерывного изменения параметров
перескочить от преобразования с Det Л = +1 к преобразованию
с DetA= -1,или от преобразования с Л°о > +1 к преобразованию
76 Глава 2. Релятивистская квантовая механика
с Л°о < -1, то всякое лоренцовское преобразование, которое
может быть получено из единичного преобразования путем не-
непрерывного изменения параметров, должно иметь Det Л и Л°о
того же знака, что и само единичное преобразование, т. е.
должно принадлежать собственной ортохронной группе Лоренца.
Всякое преобразование Лоренца — либо собственное и
ортохронное, либо может быть записано как произведение эле-
элемента собственной ортохронной группы Лоренца и одного из
дискретных преобразований if, У или if.T, где if — матрица про-
пространственной инверсии, ненулевые элементы которой равны
д>\ = 1, &\ = oj>22 = oj>33 = _1; B.3.15)
a J— матрица обращения времени с ненулевыми элементами
,Г°о = -1, J\ = J\ = iTh = I- B-3.16)
Таким образом, изучение всей группы Лоренца сводится к изуче-
изучению собственной ортохронной подгруппы, а также пространствен-
пространственной инверсии и отражения времени. Мы рассмотрим простран-
пространственную инверсию и отражение времени отдельно в разделе 2.6.
До этого будем изучать только однородную или неоднородную
собственную ортохронную группу Лоренца.
2.4. Алгебра Пуанкаре
Как мы видели в разделе 2.2, многое о любой группе симмет-
симметрии, являющейся группой Ли, можно узнать, изучая групповые
элементы вблизи единицы. В случае неоднородной группы Лоренца
единицей является преобразование Л^у = 5%, аУ* = 0, так что
следует изучать преобразования, имеющие вид
Л% =6%+ю%, а^ =е»\ B.4.1)
с инфинитезимальными параметрами (#v и е^. Условие B.3.5)
можно записать как
2.4. Алгебра Пуанкаре
= Л ap +«ap+«pa+C)(«2)-
Здесь использовано соглашение, которое будет далее приме-
применяться во всей книге, что опускание и подъем индексов осуще-
осуществляются сверткой с Г1„у или ц^у:
Удерживая только слагаемые первого порядка по со в
условии B.3.5), находим, что это условие сводится к требова-
требованию антисимметрии со^:
«V = -«V- B-4.2)
Антисимметричный тензор второго ранга в четырехмерном про-
пространстве имеет DхЗ)/2 = 6 независимых компонент, так что с
учетом четырех компонент ?^ неоднородное преобразование Лорен-
Лоренца определяется 6 + 4 = 10 параметрами.
Так как 17A, 0) переводит всякий луч в себя, этот оператор
должен быть пропорционален единичному оператору и может быть
сделан равным ему путем выбора фазы *. Для инфинитезимального
преобразования Лоренца B.4.1) оператор 17A + со, ?) должен быть
суммой единичного оператора 1 и слагаемых, линейных по сорст и ?р.
Запишем это в виде
17A + ю, ?) = 1 + - гюрстJP° - г?рРР +.... B.4.3)
Здесь JpCT и Рр — не зависящие от со и ? операторы, а
многоточие соответствует слагаемым более высокого порядка по со
и/или ?. Для того, чтобы оператор 17A + со, ?) был унитарным,
операторы JpCT и Рр должны быть эрмитовыми:
* При отсутствии правил суперотбора возможность, что коэффициент
пропорциональности зависит от состояния, на которое действует ?7A, 0),
может быть исключена с помощью тех же рассуждений, которые
использовались в разделе 2.2, чтобы исключить возможную зависимость фаз
проективных представлений групп симметрии от состояний, на которые эта
симметрия действует. Если же действуют правила суперотбора, может
оказаться необходимым переопределить ?7A, 0), включив фазовые множители,
зависящие от сектора, в котором действует этот оператор.
78 Глава 2. Релятивистская квантовая механика
jpaf = jpa^ ppf = рр_ B.4.4)
Так как С0рст — антисимметричный тензор, коэффициенты JpCT
можно также выбрать антисимметричными:
JpCT=-JCTp. B.4.5)
Как будет видно, Р1, Р2 и Р3 являются операторами компонент
импульса, J23, J31 и J12 — операторами компонент вектора момента
импульса, а Р° — оператором энергии или гамильтонианом*
Исследуем свойства лоренцовских преобразований операто-
операторов JpCT и Рр. Рассмотрим произведение
где А\ и ац - параметры нового преобразования, не связанные с со
или ?. Согласно B.3.11), произведение ЩЛ, -ЛаI7(Л, а) равно
17A,0), так что ЩЛ, -Л-1а) — оператор, обратный U(A, а). Тогда из
B.3.11) следует, что
17(Л, аI7A + со, ?)L7 (Л, а) = 17(ЛA + со)Л-1, Аг - AcoA-1a). B.4.6)
В первом порядке по со и ? имеем
-?рРрI/-1(Л,а)
^^ - (Ле - ЛсоЛ-М^Р^1-
Приравнивая коэффициенты при С0рст и ?„ в обоих частях этого
равенства (и пользуясь формулой B.3.10)), находим:
17(Л,a)JpaU-\A, а) = Л/Л/(^ - a^Pv + avP^), B.4.8)
* Определение генераторов момента импульса (углового момента) диктуется
коммутационными соотношениями для J^v. Однако они не позволяют выбрать
между операторами Р^ и —Р*1, так что знак слагаемого ерРр в B.4.3) является
предметом соглашения. Совместимость B.4.3) с обычным определением га-
гамильтониана Р° показана в разделе 3.1.
2.4. Алгебра Пуанкаре 79
t7(A,a)PPt/-1(A,a) = A/P*. B.4.9)
Для однородных преобразований Лоренца (ац = 0) из этих выра-
выражений просто следует, что J^v есть тензор, а Рц — вектор. Для
чистых трансляций (A^v = 6%) из этих формул следует, что Рр
является трансляционно-инвариантной величиной, а Jpo — нет. В
частности, изменение пространственно—пространственных ком-
компонент Jpo в результате пространственной трансляции соответ-
соответствует обычному изменению углового момента за счет переноса
начала координат, по отношению к которому вычисляется угло-
угловой момент.
Далее, применим правила B.4.8), B.4.9) к преобразованию,
которое само является бесконечно малым. Иначе говоря, выберем
матрицу А*\, = 5% + со^, ац = ?ц, где бесконечно малые величины оУ\,
и Е11 не связаны с предыдущими сои ?. Пользуясь формулой B.4.3) и
сохраняя только слагаемые первого порядка по аУ\, и е^, находим,
что формулы B.4.8) и B.4.9) принимают вид:
+ ?СТРР, B.4.10)
B.4.11)
Приравнивая коэффициенты при со^ и ?ц в обеих сторонах
этих равенств, находим коммутационные соотношения
-r|«>JVCT -nCT^JPv +r|(JVJP^, B.4.12)
B.4.13)
B.4.14)
Они определяют алгебру Ли группы Пуанкаре.
В квантовой механике особую роль играют те операторы,
которые сохраняются, т. е. коммутируют с оператором энергии
Н = Р°. Из формул B.4.13) и B.4.14) следует, что такими оператора-
операторами являются 3-вектор импульса
Р = {Р1,Р2,Р3}, B.4.15)
80 Глава 2. Релятивистская квантовая механика
3-вектор момента импульса
J = {J23,J31,J12} B.4.16)
и, конечно, сам оператор энергии Р°. Остающиеся генераторы
образуют так называемый 3-вектор буста
K = {J1O,J2O,J30}. B.4.17)
Эти генераторы не сохраняются, и поэтому мы не приписываем
физическим состояниям собственных значений К. В трехмерных
обозначениях коммутационные соотношения B.4.12), B.4.13) и B.4.14)
можно записать в виде:
[Ji,Jj] = i?ijkJk,
B
B
B
B
B
B
B
.4
.4
.4
.4
.4
.4
.4
.18)
.19)
.20)
.21)
.22)
.23)
.24)
полностью
где г, j, k принимают значения 1, 2, 3, а ?ф
антисимметричный тензор с ?ш = +1. Видно, что коммутационные
соотношения B.4.18) совпадают с коммутационными соотношения-
соотношениями для компонент оператора углового момента.
Чистые трансляции ТA, а) образуют подгруппу неоднородной
группы Лоренца с вытекающим из B.3.8) правилом группового
умножения
1,а) = ТA,а + а). B.4.25)
Оно аддитивно в том же смысле, что и B.2.24), так что,
используя B.4.3) и повторяя рассуждения, приведшие к B.2.26),
2.4. Алгебра Пуанкаре
находим, что конечные трансляции представляются в физичес-
физическом гильбертовом пространстве в виде
Щ1,а) = ехр(-гР^). B.4.26)
Точно так же можно показать, что вращение i?e на угол |9|
вокруг направления 9 представляется в физическом гильбертовом
пространстве как
0) = exp(zJ-9). B.4.27)
Представляет интерес сравнить алгебру Пуанкаре с алгеб-
алгеброй Ли группы симметрии ньютоновской механики — группы
Галилея. Можно вывести эту алгебру, начав с законов преобра-
преобразования группы Галилея и повторив ту процедуру, которую мы
использовали для вывода алгебры Пуанкаре. Однако, так как
уже выведены соотношения B.4.18)—B.4.24), легче получить ал-
алгебру Галилея как предел алгебры Пуанкаре при малых скорос-
скоростях с помощью приема, который известен как контракция Ино-
ню-Вигнера4> 5. Следует ожидать, что для системы частиц с
типичными массой т и скоростью v операторы импульса и мо-
момента импульса порядка Р ~ тх, J ~ 1 . С другой стороны,
оператор энергии Н = М + W, где полная масса М ~ т и энергия,
не связанная с массой (кинетическая и потенциальная), W ~ mv2.
Из уравнений B.4.18)-B.4.24) следует, что в пределе при v <^. 1
коммутационные соотношения принимают вид:
[Ji,Jj] = Щ^ъ [Ji,Kj] = Щккъ [Ki,Kj] = 0,
[Ji,W] = [PitW] = Q, [KitW] = -iPit
[JitM] = [PitM]= [KitM] = [W,M] = Q,
где К ~ l/v. Произведение трансляции х —» x + а и «буста»
x —> x + vt должно быть преобразованием х —> х + vt + а, но это
неверно для действия указанных операторов в гильбертовом
пространстве:
ехр(гК • v) ехр(-гР • а) = ехр(гМа • v / 2) ехр(г(К • v - Р • а)).
82 Глава 2. Релятивистская квантовая механика
Появление фазового множителя exp(zMa-v/2) показывает,
что это проективное представление с правилом суперотбора,
запрещающим суперпозицию состояний с разными массами. В
этом отношении математика группы Пуанкаре проще, чем груп-
группы Галилея. Однако нет никаких причин, препятствующих фор-
формальному расширению группы Галилея путем добавления одного
или более генераторов в ее алгебру Ли, которые коммутировали
бы со всеми другими генераторами и имели бы собственные
значения, равные массам различных состояний. В этом случае
физические состояния реализуют обычное, а не проективное
представление расширенной группы симметрии. По-видимому,
разница проявляется лишь в обозначениях, не считая того, что
при подобной интерпретации группы Галилея нет нужды в пра-
правиле суперотбора по массе.
2.5. Одночастичные состояния
Рассмотрим теперь классификацию одночастичных состоя-
состояний в соответствии с тем, как они преобразуются под действием
преобразований неоднородной группы Лоренца.
Все компоненты 4-вектора энергии-импульса коммутируют
друг с другом, поэтому естественно выражать физические векторы
состояний через собственные векторы 4-импульса. Вводя метку а
для обозначения всех других степеней свободы, рассмотрим векто-
векторы состояний Ч'рд, удовлетворяющие условию
Р^р>а = р^р>а. B.5.1)
Для произвольных состояний, описывающих, например, не-
несколько несвязанных частиц, метка о сама может включать как
непрерывные, так и дискретные метки. Примем как часть опреде-
определения одночастичного состояния, что метка о может быть только
дискретной, и ограничимся пока что рассмотрением такого случая.
(Однако конкретное связанное состояние двух или более частиц,
например, низшее энергетическое состояние атома водорода, следу-
следует рассматривать как одночастичное состояние. Оно не является
элементарной частицей, но различие между составными и эле-
элементарными частицами нам сейчас не важно.)
2.5. Одночастичные состояния 83
Из уравнений B.5.1) и B.4.26) следует, что состояния Ч*
преобразуются под действием трансляций по закону
Рассмотрим теперь, как преобразуются эти состояния под
действием однородных преобразований Лоренца. Из формулы B.4.9)
следует, что в результате действия квантового однородного преоб-
преобразования Лоренца 17(Л, 0) = ?7(Л) на состояние *Рр>а возникает
собственный вектор 4-импульса с собственным значением Лр:
Поэтому U(AL?pa должно быть линейной комбинацией векторов
СОСТОЯНИЙ Ч*Лр,с>':
В общем случае подходящим выбором линейных комбинаций *Рра
можно так выбрать метки а, чтобы матрица СО'О(Л, р) стала блоч-
но-диагональной, т. е. совокупность *Рра с меткой а, принимающей
значения внутри одного блока, сама была бы представлением не-
неоднородной группы Лоренца. Естественно сопоставить состояния
частицы конкретного типа с компонентами представления неодно-
неоднородной группы Лоренца, которое неприводимо в том смысле, что
его нельзя далее разложить указанным способом.
Конечно, разные сорта частиц могут соответствовать изоморф-
изоморфным представлениям, для которых матрицы СО'О(Л, р) либо тожде-
тождественны, либо совпадают с точностью до преобразования подобия.
В некоторых случаях удобно определить типы частиц как неприво-
неприводимые представления более широких групп, включающих неодно-
неоднородную собственную ортохронную группу Лоренца в качестве
подгруппы; например, как мы увидим, для безмассовых частиц,
взаимодействия которых сохраняют симметрию по отношению
к пространственным отражениям, принято рассматривать все ком-
компоненты неприводимого представления неоднородной группы
84 Глава 2. Релятивистская квантовая механика
Лоренца, включая пространственную инверсию, как один тип час-
частиц.
Наша задача заключается в исследовании структуры коэф-
коэффициентов СО'О(Л, р) для неприводимых представлений неодно-
неоднородной группы Лоренца. Для этого заметим, что единственными
функциями р^, остающимися инвариантными по отношению ко
всем собственным ортохронным преобразованиям Лоренца A^v, яв-
являются квадрат этого 4-вектора р2 = Ц^р^р* и знак р° при р2 < 0.
Таким образом, для каждого значения р2 и (при р2 < 0) определен-
определенного знака р° можно выбрать «стандартный» 4-импульс № и выра-
выразить любой 4-вектор р^ из этого класса в виде
B.5.4)
где I/v — стандартное преобразование Лоренца, зависящее от
р^ и неявно от выбора стандартного импульса №. Затем можно
определить состояния Ч'рд импульса р как
?р>о = Ы^ЩЦр))^ , B.5.5)
где N(p) — числовой нормировочный множитель, который будет
далее установлен. До этого момента мы ничего не говорили о том,
как метки а связаны с разными импульсами. Уравнение B.5.5) за-
заполняет этот пробел.
Действуя на B.5.5) произвольным однородным преобразовани-
преобразованием Лоренца ?7(Л), находим:
ЩЛ)?р>а = N(p)U(AL(p)L>ka
= Щр)ЩЦАр))ЩЬ-1(Ар)АЦр))Ч<Ка . B-5-6)
Суть последнего шага — в том, что преобразование Лоренца
L~1(Ap)AL(p) переводит к в L(p)k = р, затем в Лр и назад в к, так что
это преобразование принадлежит подгруппе однородной группы
Лоренца, состоящей из лоренцовских преобразований W^v оставля-
оставляющих № инвариантным:
W^yky = k^. B.5.7)
Эта подгруппа называется малой группой5. Для любого W,
удовлетворяющего B.5.7), имеем:
2.5. Одночастичные состояния 85
^' ¦ B.5.8)
Коэффициенты D(W) являются представлением малой группы, т.
е. для любых элементов W, W
a = U(W)U(WL>Ka
и поэтому
? B.5.9)
В частности, можно применить соотношение B.5.8) к преобразо-
преобразованию малой группы:
W(A, p) = L(Ap)AL(p), B.5.10)
после чего B.5.6) принимает вид:
а'
или, вспоминая определение B.5.5),
' ¦ B-5.11)
Помимо вопросов нормировки, задача определения коэффици-
коэффициентов Со'о в законе преобразования B.5.3) была сведена к задаче
нахождения представлений малой группы. Такой подход, заключа-
заключающийся в получении представлений какой-то группы типа неодно-
неоднородной группы Лоренца из представлений малой группы, носит
название метода индуцированных представлений 6.
В таблице 2.1 приведен удобный выбор стандартного импуль-
импульса к^ и соответствующей малой группы для 4-импульсов разных
классов. Из этих шести классов 4-импульсов только для случаев
а, в и е известна какая-то интерпретация в терминах физичес-
86
Глава 2. Релятивистская квантовая механика
Таблица 2.1
а
в
е
е
/? = - Л?<0, я, > 0
/? = - Л?<0, Л)<0
У = 0, Л)>0
У - 0, л, < 0
У=Л*>0
Стандартный
импульс к11
@,0,0,^
@,0,0,М)
@,0,к,к)
@,0,к,-к)
@,0,^0)
@,0,0,0)
Малая
группа
хЩЗ)
хЩЗ)
^Щ2)
^Щ2)
^2,1)
хЩЗД)
Табл. 2.1. Стандартные импульсы и соответствующие малые группы для
разных классов 4-импульсов. Здесь к — произвольная положительная энер-
энергия, например, 1 эВ. Тип малых групп почти очевиден: SOC) — обычная
группа вращений в трех измерениях (не содержащая пространственных
инверсий), поскольку вращения — это единственные собственные ортохрон-
ные преобразования Лоренца, оставляющие частицу с нулевым импульсом в
состоянии покоя. Группы ?0B,1) и ?0C,1) — группы Лоренца в B +1) и
C + 1) измерениях, соответственно. Группа 1?0B) — группа евклидовой
геометрии, состоящая из вращений и трансляций в двух измерениях. Появ-
Появление этой группы в качестве малой группы для случая р2 = 0 объяснено
в основном тексте.
ких состояний. Нет нужды много говорить здесь о случае е, когда
р^ = 0. Он соответствует вакууму, который инвариантен по
отношению к действию ?7(Л). В последующем изложении мы будем
рассматривать только случаи айв, соответствующие частицам
с массой М > 0 и М = 0.
2.5. Одночастичные состояния 87
Полезно сделать паузу и сказать несколько слов о норми-
нормировке таких состояний. Пользуясь обычной квантово-механичес-
кой процедурой ортогонализации и нормировки, можно выбрать
состояния со стандартным импульсом к^, ортонормированными
в том смысле, что
(^к',о',^к,о) = 53(k'-kMCT,CT . B.5.12)
(В этом соотношении возникла 6-функция, так как Ч^о и Ч^'о'
являются собственными состояниями эрмитова оператора с соб-
собственными значениями к и к', соответственно.) Отсюда вы-
вытекает, что представление малой группы в B.5.8) и B.5.11) долж-
должно быть унитарным *:
D\W) = D~l{W). B.5.13)
Что можно сказать о скалярных произведениях для произ-
произвольных импульсов? Используя унитарность оператора U(A) в
соотношениях B.5.5) и B.5.11), получаем, что скалярное произ-
произведение равно
= N(p)N*(p')D(W(L-1(p), p')aa'83(k' - k),
где к' = L~1(p)p/. Кроме того, к = L~1(p)p, и дельта-функция
53(к- к') пропорциональна 53(р - р'). При р' = р преобразование
малой группы тривиально, W(L-1(p), р) = 1, так что скалярное
произведение равно
(%>'>%,J = I N(p) p 6^63(к'- к). B.5.14)
Остается выяснить, чему равен коэффициент пропорци-
пропорциональности между 63(к — к') и 63(р — р'). Заметим, что лоренц—
* Малые группы ?0B,1) и ?0C,1) для р2 > 0 и р^ = 0 не имеют нетривиальных
конечномерных унитарных представлений. Поэтому, если бы существовали
состояния с данным импульсом р^ при р2 > 0 или р^ = 0, которые бы
нетривиальным образом преобразовывались под действием элементов малой
группы, то таких состояний должно было быть бесконечно много.
Глава 2. Релятивистская квантовая механика
инвариантный интеграл от произвольной скалярной функции /(р)
по 4-импульсам с -р2 = М2 > 0 и р° > 0 (т. е. для случаев а и в в
таблице) равен
J dAp 6(p2 - М2) 9(р° )/(р) = J d3pdp° 8((р° J - р2 - М2) 9(р°) /(р, р°)
,з /(Р,Ур2+М2)
о р , =—
2д/р2 + М2
F(р°) - ступенчатая функция: 6(ж) = 1 при х > 0, 6(ж) = 0 при
ж < 0). При интегрировании «на массовой поверхности» р2 + М2 = 0
инвариантный элемент объема есть
+М2. B.5.15)
Дельта-функция определена равенством
F(p) = fF(p') 63(p - p')d3p' = |>(р')[л/р'2+М263(р' - рI dV ,
J J L jVp/2+m2
откуда инвариантная дельта-функция равна
Л/р/2+М263(р/-р) = р°63(р/-р). B.5.16)
Так как р' и р связаны соответственно с к' и к лоренцовским
преобразованием L(p), имеем:
p°63(p'-p) =
и поэтому
(%>',%!a)=|iV(p)|26^^J63(p'-p). B.5.i7)
Иногда выбирают нормировочный множитель N(p) просто равным
единице, N(p) = 1, но в этом случае нужно следить за множителя-
множителями р°/к° в скалярных произведениях. Я предпочитаю более при-
привычное соглашение
N(p) = ,Jk°/p° , B.5.18)
2.5. Одночастичные состояния 89
при выборе которого
3р). B.5.19)
Рассмотрим два представляющих физический интерес слу-
случая: частицы с массой М > 0 и частицы нулевой массы.
Случай положительной массы
В данном случае малой группой является трехмерная группа
вращений. Ее унитарные представления могут быть разложены в
прямую сумму неприводимых унитарных представлений 7 D^) (R)
размерности 2j + 1, где j = О, 1/2, 1, ... Последние можно
построить из стандартных матриц бесконечно малых вращений
Rik = bik + &ik, где &ik = —®ki — бесконечно малые величины:
l + ®) = ba,a+±®ik(J$)a,a, B.5.20)
B.5.21)
(J^)a'a=(A]X'a=0b&a. B.5.22)
Здесь а пробегает значения j, j - 1, ..., —j. Для частицы массой М > 0
и спина j уравнение B.5.11) принимает вид:
B.5.23)
где элемент малой группы W(A, p) (вигнеровское вращение 5) опреде-
определяется формулой B.5.10):
W(A,p) = L-\Ap)AL(p).
Чтобы рассчитать результат этого вращения, следует выбрать «стан-
«стандартный буст» L(p), который переводит 4-импульс № = @, 0, 0,
М) в 4-импульс рц. Удобно выбрать его в виде
90
Глава 2. Релятивистская квантовая механика
B.5.24)
/М.
Очень важно, что если Л^у есть произвольное трехмерное
вращение .'>?, вигнеровское вращение W(A, p) совпадает с .'>? для
всех р. Для доказательства заметим, что можно записать буст
B.5.24) в виде
где К(р) - вращение (стандартная форма его определена ниже
уравнением B.5.47)), переводящее ось г вдоль направления р, а
1 0
0 1
о о
о о
о
о
Y
0
0
Тогда для произвольного вращения '.Ш
Однако в результате вращения К~1(;йр);йК(р) ось z оказы-
оказывается направленной сначала вдоль р, затем вдоль .^/?р, и наконец,
опять возвращается в исходное состояние, так что в совокупности
получается просто вращение на некоторый угол 6 вокруг третьей оси:
2.5. Одночастичные состояния
91
cose sine о о
-sine cose о о
О 0 10
О 0 0 1
Так как R(Q) коммутирует с В(|р|), получаем:
и отсюда
(M, р) = 31,
что и требовалось доказать.
Таким образом, состояния движущейся массивной частицы
(а следовательно и многочастичные состояния) преобразуются
по отношению к вращениям так же, как и в нерелятивистской
квантовой механике. Это еще одно хорошее известие, поскольку
весь аппарат сферических гармоник, коэффициентов Клебша-
Гордана и т. п. можно целиком перенести из нерелятивистской
квантовой механики в релятивистскую теорию.
Масса нуль
Прежде всего, следует установить структуру малой группы.
Рассмотрим произвольный элемент малой группы W^v, где W^vfcv =
№ и № = @,0,1,1) - стандартный 4-импульс для данного случая.
Действуя на времениподобный 4-вектор № = @, 0, 0, 1), это
лоренцовское преобразование должно дать 4-вектор Wt, длина
которого и скалярное произведение с вектором Wk = к такие же,
как и для вектора t:
Любой 4-вектор, удовлетворяющий второму условию, может быть
записан в виде
(Wtf =(a,p,U + O,
92
Глава 2. Релятивистская квантовая механика
и тогда из первого условия получаем соотношение
B.5.25)
Отсюда вытекает, что действие
лоренцовского преобразования
на tv совпадает с действием
1
0
a
-a
0
1
P
-P
-a
-P
i-C
-c
a
P
С
1 +
B.5.26)
Это не означает, что элемент W равен 5(а,Р), однако S 1(a,P)W
является лоренцовским преобразованием, не меняющим времени-
подобный вектор @,0,0,1), т. е. простым вращением. Кроме того,
S^v, как и W^v, оставляет инвариантным светоподобный 4-вектор
@,0,1,1), так что преобразование /S'~1(a,P)W должно быть вращением
на некоторый угол 6 вокруг третьей оси:
B.5.27)
cose sine о о
-sine cose о о
0 0 10
0 0 0 1
Поэтому наиболее общий вид элемента малой группы таков:
WF, a, P) = S(a, P)KF). B.5.28)
Что это за группа? Заметим, что преобразования с 6 = 0 или
с a = Р = 0 образуют подгруппы:
B.5.29)
B.5.30)
щёщв) = щв + е).
2.5. Одночастичные состояния
93
Эти подгруппы абелевы, т. е. все их элементы коммутируют друг
с другом. Более того, подгруппа с 6 = 0 является инвариантной в
том смысле, что ее элементы преобразуются в другие элементы
той же подгруппы под действием любого элементы всей группы:
B.5.31)
С помощью соотношений B.5.29)-B.5.31) можно найти произведение
любых элементов группы. Читатель узнает в этих правилах умно-
умножения те, которые принадлежат группе ISOB), состоящей
из трансляций (на вектор (а, C)) и вращений (на угол 6) в двух
измерениях.
Те группы, у которых нет инвариантных абелевых под-
подгрупп, обладают рядом простых свойств, и по этой причине
их называют полупростымии. Как мы видели, малая группа
ISOB), как и неоднородная группа Лоренца, не является по-
полупростой, что приводит к интересным усложнениям. Прежде
всего, посмотрим на алгебру Ли группы ISOB). Если считать 6,
СИ, C бесконечно малыми, то общий групповой элемент можно
представить в виде
О 6 -а а
-е о -р р
а р О О
-а -р О О
Из B.4.3) следует, что соответствующий оператор в гильбер-
гильбертовом пространстве равен
l/(WF, a, P)) = 1 + гаА + фВ +
где А и В — эрмитовые операторы:
А = -J13 + J10 = J2+Kx,
В = - J23 + J20 = - J, + К2 ,
B.5.32)
B.5.33)
B.5.34)
94 Глава 2. Релятивистская квантовая механика
и, как и ранее, J3 = J12. Либо из соотношений B.4.18)-B.4.20),
либо непосредственно из формул B.5.29)-B.5.31) видно, что ком-
коммутаторы этих генераторов равны
[J3,A] = +iB, B.5.35)
[J3,B] = -iA, B.5.36)
[А,В] = 0. B.5.37)
Так как А и В являются коммутирующими эрмитовыми оператора-
операторами, они (как и операторы импульса в неоднородной группе
Лоренца) могут быть одновременно диагонализованы на состо-
состояниях ?
Проблема заключается в том, что если будет найден один такой
набор ненулевых собственных значений А и В, то мы автоматичес-
автоматически получим континуум таких значений. Из B.5.31) имеем:
i/[K(e)]Ai/-1[i?(e)] = a cos e - в sm e,
ЩЩв)]Ви-1[Щв)] = A sin 6 +В cos6.
так что при произвольном 6
Согласно экспериментальным данным безмассовые частицы не обла-
обладают какой-либо непрерывной степенью свободы вроде 6. Чтобы
избежать появления подобного континуума состояний, мы должны
потребовать, чтобы физические состояния (называемые теперь Ч^д)
были собственными векторами АиВс а = Ъ = 0:
АЧ>ка=ВЧ>ка=0. B.5.38)
2.5. Одночастичные состояния 95
Эти состояния различаются собственным значением оставшегося
генератора
J3?fciO = оЧ>ка . B.5.39)
Так как импульс к определяет направление в трехмерном про-
пространстве, а равна компоненте углового момента в направлении
движения, иначе, спиральности частицы.
Теперь можно установить свойства лоренцовских преобра-
преобразований произвольных безмассовых состояний. Заметим, во-первых,
что с помощью общих соображений, приведенных в разделе 2.2,
уравнение B.5.32) обобщается для конечных а и В, принимая вид
U(S(a, В)) = ехр(гоА + гВВ), B.5.40)
а для конечных 6 — вид
). B.5.41)
Произвольный элемент малой группы W можно записать в виде
B.5.28), и поэтому
кга = ехр(шА +
так что из B.5.8) находим:
D&a(W) =
где 6 — угол, определенный так же, как в B.5.28). В результате
правило лоренцовского преобразования для безмассовой частицы
произвольной спиральности задается уравнениями B.5.11) и B.5.18)
и принимает вид
ехР(га6(Л,р))?Лр>а , B.5.42)
где 6(Л, р) определяется из равенства
W(A, р) = L (Лр)ЛЬ(р) = S(a(A, p), В(Л, р))Н(9(Л, р)). B.5.43)
96
Глава 2. Релятивистская квантовая механика
В разделе 5.9 будет показано, что электромагнитная калибро-
калибровочная инвариантность возникает из той части малой группы,
которая параметризована с помощью а и C.
До этого момента не было приведено никаких аргументов,
запрещающих спиральности безмассовой частицы о принимать лю-
любое действительное значение. Как мы увидим в разделе 2.7, суще-
существуют топологические соображения, ограничивающие разрешен-
разрешенные значения а целыми или полуцелыми числами, как и для
массивных частиц.
Для вычисления элемента малой группы B.5.43) для заданных
Л и р (а также для вычисления в следующем разделе действия
операций пространственной инверсии и отражения времени на эти
состояния), нам необходимо зафиксировать соглашение о виде
стандартного лоренцовского преобразования, которое переводит
вектор W1 = (О, О, К, к) в р*1. Удобно выбрать его в виде
B.5.44)
= K(p)B(|p|/K),
где В(и) — чистый буст в направлении третьей оси:
В(и) =
10 0 0
0 10 0
0 0 (м2 + 1) / 2м (м2 - 1) / 2м
0 0 (м2-1)/2м (м2+1)/2м
B.5.45)
а К(р) - чистое вращение, переводящее третью ось по направле-
направлению единичного вектора р. Например, пусть р определяется по-
полярным и азимутальным углами 6 и ф :
р = (sin 6 cos ф, sin 6 sin ф, cos 6).
B.5.46)
Тогда можно рассматривать К(р) как вращение на угол 6 вокруг
второй оси, переводящее @, 0, 1) в (sin 6, 0, cos 6), и последующее
вращение на угол ф вокруг третьей оси :
17(К(р)) = exp(«pJ3)exp(zeJ2), B.5.47)
где 0 < 6 < ж, 0 < ф < 2л. (Мы приводим ЦЩр)), а не Я(р),
2.5. Одночастичные состояния 97
указывая одновременно интервал изменения 6 и ф, поскольку
сдвиг 6 и ф на 2л определяет то же самое вращение К(р),
однако изменяет знак 1/(К(р)) при действии на состояния с полу-
полуцелым спином.) Так как B.5.47) — вращение, переводящее тре-
третью ось к направлению B.5.46), любой другой выбор К(р) будет
отличаться от приведенного не более чем на начальное враще-
вращение вокруг третьей оси, соответствующее просто переопреде-
переопределению фазового множителя для одночастичного состояния.
Заметим, что спиральность лоренц-инвариантна; безмассовая
частица заданной спиральности о выглядит одинаково (не считая
импульса) во всех инерциальных системах отсчета, и можно рас-
рассматривать безмассовые частицы с заданными различными значе-
значениями спиральности как разные сорта частиц. Однако, как будет
показано в следующем разделе, частицы противоположной
спиральности связаны симметрией относительно пространствен-
пространственного отражения. Так, поскольку электромагнитные и гравитаци-
гравитационные силы удовлетворяют требованию симметрии по отноше-
отношению к пространственной инверсии, обе безмассовые частицы со
спиральностями ±1, связанные с электромагнетизмом, носят на-
название фотонов, а две безмассовые частицы со спиральностями
±2, которые считаются связанными с тяготением, называются
гравитонами. С другой стороны, предполагаемые безмассовые
частицы со спиральностями ±1/2, испускаемые при C-распаде
ядер, при взаимодействиях не сохраняют симметрию по отно-
отношению к пространственной инверсии (если не считать тяготе-
тяготения), поэтому такие частицы называются по-разному: нейтрино
в случае спиральности +1/2, и антинейтрино — в случае
спиральности —1/2.
Хотя спиральность безмассовых частиц является лоренц-
инвариантной характеристикой, сами состояния частиц не обла-
обладают этим свойством. В частности, из-за зависящего от спираль-
спиральности фазового множителя ехр(шб) в уравнении B.5.42),
состояние, образованное как линейная суперпозиция одночас-
тичных состояний с противоположными спиральностями, перей-
перейдет в результате лоренцовского преобразования в другую супер-
суперпозицию. Например, общее однофотонное состояние с заданным
4-импульсом можно записать в виде
98
Глава 2. Релятивистская квантовая механика
а4
а_
= 1.
Наиболее общим является случай эллиптической поляризации,
когда оба коэффициента |оу не равны нулю и различны. Предельны-
Предельными частными случаями является циркулярная (круговая) поляриза-
поляризация, когда один из коэффициентов а+ или а_ обращается в нуль, и
линейная поляризация, когда |а+| = |а_|. Общая фаза а+ и а_ не
имеет физического смысла и в случае линейной поляризации мо-
может быть выбрана так, что а_ = а+*. Однако относительная фаза
важна. Действительно, в случае линейной поляризации с а_ = а+*
фазу (Х+ можно сопоставить с углом между плоскостью поляриза-
поляризации и некоторым фиксированным опорным направлением, перпен-
перпендикулярным вектору р. Из формулы B.5.43) следует, что под дей-
действием лоренцовского преобразования Л*\, этот угол изменяется на
величину 6(Л, р). Плоскополяризованные гравитоны можно опреде-
определить аналогичным образом, при этом следствием соотношения B.5.42)
будет то, что под действием лоренцовского преобразования Л
плоскость поляризации повернется на угол 26(Л, р).
2.6. Пространственная инверсия и обращение времени
В разделе 2.3 было показано, что всякое однородное преоб-
преобразование Лоренца является или собственным и ортохронным (т. е.
Det Л = +1 и Л°о > +1), или произведением собственного орто-
хронного преобразования и одного из преобразований kP, J'или :Ж?,
где ёРж 'J— преобразования пространственной инверсии и обращения
времени:
-1
0
0
0
0
-1
0
0
0
0
-1
0
0
0
0
1—1
' ' v ~
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
-1
Всегда считалось самоочевидным, что фундаментальное
правило умножения элементов группы Пуанкаре
ЩЛ, а)ЩЛ, а) = ЩАА, Ла + а)
2.6. Пространственная инверсия и обращение времени 99
выполняется и в том случае, если Л и/или Л включают множи-
множители if, J или :,'?J. В частности, считалось, что существуют
операторы, соответствующие самим ИР и ;Т,
такие, что
PU(A,a)P~1 = Щ&АР-1, Щ, B.6.1)
"Ш(Л,а)Т-1 = U(:fA:f-\,fa) B.6.2)
для любого собственного ортохронного преобразования Лоренца
А\ и любой трансляции аУ*. Эти законы преобразования содержат
в себе большую часть того, что принято понимать под словами
о «сохранении»величин Р и Т.
В 1956-1957 годах стало понятно8, что для Р это верно толь-
только в приближении, когда мы пренебрегаем эффектами слабых
взаимодействий, типа тех, которые обусловливают C-распад.
Инвариантность по отношению к обращению времени «прожила»
еще некоторое время, пока в 1964 году не появились косвенные
свидетельства9, что эти свойства Т также верны лишь приближен-
приближенно (см. раздел 3.3). В последующем изложении мы примем, что
операторы Р и Т, удовлетворяющие соотношениям B.6.1) и B.6.2),
действительно существуют, но будем держать в памяти, что это
утверждение носит приближенный характер.
Рассмотрим B.6.1) и B.6.2) для случая инфинитезимальных
преобразований, т. е. положим
А% = 5% + <в% , а^ = ?^ ,
где &V, = — Сйуц и ?„ — бесконечно малые величины. Пользуясь
соотношением B.4.3) и приравнивая коэффициенты при соро и ер в
B.6.1) и B.6.2), найдем свойства преобразования генераторов группы
Пуанкаре по отношению к Р и Т:
l = ipppojv» > B.6.3)
= i&vpv-, B.6.4)
100 Глава 2. Релятивистская квантовая механика
, B.6.5)
B.6.6)
Во многом эти соотношения напоминают формулы B.4.8) и B.4.9),
если не считать того, что мы не сократили множители г в обеих
частях этих уравнений, так как еще не приняли решения, считать
ли Р и Т линейными и унитарными или антилинейными и анти-
антиунитарными операторами.
Решение принимается очень просто. Полагая р = 0 в формуле
B.6.4), находим:
РгЯР = гЯ,
где Н = Р° — оператор энергии. Если бы Р был антиунитарным и
антилинейным оператором, то он антикоммутировал бы с г, так что
РЯР = -Я. Но в этом случае для любого состояния Ч* с ? > О
существовало бы другое состояние P"lxP с энергией —Е < 0. Однако
не существует состояний с отрицательной энергией (т. е. энергией,
меньшей энергии вакуума), так что мы вынуждены выбрать другую
альтернативу: оператор Р — линейный и унитарный и он комму-
коммутирует с оператором Я.
С другой стороны, полагая р = 0 в B.6.6), имеем
ТгЯТ = -гЯ.
Если предположить, что Т — линейный и унитарный оператор,
можно просто сократить все г, так что ТЯТ = —Я, и в
результате мы опять приходим к губительному выводу, что для
любого состояния Ч* с энергией Е существует другое состояние
Т*!* с энергией —Е. Чтобы избежать этого, мы вынуждены
заключить, что Т является антилинейным и антиунитарным
оператором.
Поскольку мы решили, что оператор Р линеен, а Т антилинеен,
можно переписать соотношения B.6.3)-B.6.6) в трехмерных обозна-
обозначениях через генераторы B.4.15)—B.4.17):
B.6.7)
B.6.8)
2.6. Пространственная инверсия и обращение времени Ю1
ррр-1=_Р) B.6.9)
B.6.10)
B.6.11)
ТРТ = -Р B.6.12)
и, как показано выше,
РЯР = ТЯТ = Я. B.6.13)
С физической точки зрения важно, что Р должен сохранять знак
J, так как по крайней мере орбитальная часть J есть векторное
произведение г X р двух векторов, каждый из которых меняет
знак при инверсии пространственных координат. С другой стороны,
оператор Т меняет знак J, так как после обращения времени
наблюдатель видит все тела вращающимися в другую сторону.
Заметим попутно, что B.6.10) совместно с перестановочными соотно-
соотношениями для компонент углового момента J X J = iS, поскольку Т
меняет знак не только J, но и г. Читатель может без труда
проверить, что B.6.7)—B.6.13) совместны со всеми перестановочными
соотношениями B.418)-B.4.24).
Рассмотрим действие операторов Р и Т на одночастичные
состояния.
Р: М> О
Одночастичные состояния 4*fe о определены как собственные
векторы операторов р, Я и J3 с собственными значениями 0, М и а,
соответственно. Из соотношений B.6.7), B.6.9) и B.6.13) следует,
что это же верно и для состояния P*Pfe а, и потому, чтобы исключить
вырождение, такие состояния могут отличаться только фазой:
причем фазовый множитель (|т|| = 1) может как зависеть, так и не
зависеть от проекции спина а. Чтобы показать, что Г|о не зависит от
а, заметим, что из B.5.8), B.5.20) и B.5.21) следует формула
, ± iJ2)?fc>a = V(j + a)(j±a + l)^CT±1, B.6.14)
102 Глава 2. Релятивистская квантовая механика
где j — спин частицы. Действуя оператором Р на обе части этого
равенства, имеем
Ла = Лс±1 .
так что Г|о действительно не зависит от о. Поэтому можно записать
P4>kG = r\4>kG , B.6.15)
где фазовый множитель г| носит название внутренней четности,
зависящей только от типа частицы, на волновую функцию которой
действует оператор Р.
Чтобы перейти к состояниям с конечным импульсом, следует
подействовать на состояние унитарным оператором U(L(p)),
соответствующим «бусту» B.5.24):
Заметим, что
РВДР = L(Pp),
Рр = (-p,Vp2 + M2).
так что, пользуясь B.6.1) и B.6.15), находим:
или
Р^ ^,а • B-6.16)
Т: М >0
Из уравнений B.6.10), B.6.12) и B.6.13) следует, что действие
Т на одночастичное состояние с нулевым импульсом *Pfea приводит
к состоянию со следующими свойствами:
2.6. Пространственная инверсия и обращение времени ЮЗ
так что
где ^о — фазовый множитель. Применяя оператор Т к B.6.14) и
вспоминая, что Т антикоммутирует не только с J, но и с г,
находим:
(-J, ± V2Ka4Ka
Снова используя в левой части равенства соотношение B.6.14),
видим, что квадратные корни сокращаются и
Ъа = Ъа±1•
Решением последнего уравнения является ^о = ?,(—У~а , где ? —
некоторый другой фазовый множитель, зависящий только от типа
частицы:
ТЧк,с=^-У-ах?к,-о- B-6.17)
Однако в противоположность «внутренней четности» Г| фазовый
множитель операции обращения времени ^ физически несущест-
несущественен. Этот вывод следует из того, что всегда можно переопределить
одночастичные состояния, изменив их фазу:
так что фазовый множитель ^ исчезает из закона преобразования:
В последующем изложении мы сохраним произвольный фазовый
множитель ? в B.6.17), чтобы не ограничивать возможности выбора
фазы одночастичных состояний. Однако следует помнить, что эта
фаза на самом деле не имеет значения.
Чтобы построить состояния с конечным импульсом, вновь
действуем «бустом» B.5.24). Заметим, что
104 Глава 2. Релятивистская квантовая механика
(Это означает, что изменение знака каждого элемента A^v с
нечетным числом временных индексов эквивалентно изменению
знака эле-ментов с нечетным числом пространственных индексов.)
С помощью B.6.2) и B.5.5) находим:
ТРр>а = С(-ГаЧ%,_а • B.6.18)
Р: М = О
Действуя на состояние Ч^о, определенное как собственный
вектор оператора Рц с собственным значением № = @,0,к,к)
и собственный вектор оператора J3 с собственным значением о,
оператор четности Р переводит это состояние в состояние
с 4-импульсом (,Jky = @,0,-к,к) и J3 = о. Таким образом, состояние
со спиральностью (проекцией спина на направление импульса) а
переводится в состояние со спиральностью —о. Как отмечалось
выше, это показывает, что существование симметрии относительно
пространственной инверсии требует, чтобы каждый тип безмассовых
частиц с ненулевой спиральностью обязательно имел партнера с
противоположной спиральностью. Так как Р не оставляет инва-
инвариантным стандартный импульс, удобно вместо этого рассмотреть
оператор и"(К2~1)'э> гДе ^2— вращение, также переводящее к в ИРк.
Его удобно выбрать как вращение на угол -180° вокруг оси у:
= exp(-mJ2). B.6.19)
Так как U(R2~1) меняет знак J3, находим:
1а=цаЧК_а, B.6.20)
где Г|о — фазовый множитель. Операция R2~1^ коммутирует
с лоренцовским «бустом» B.5.45), а $Р коммутирует с вращением ,
поворачивающим ось z в направлении р, так что, действуя
оператором Р на B.5.5), получаем для произвольного 4-импульса рц
2.6. Пространственная инверсия и обращение времени Ю5
Заметим, что R(j>)R2 — это вращение, поворачивающее ось г в
направлении-р, но U(R(p)R2) не в точности равно 17(К(-р)). Согласно
формуле B.5.47)
ЩК(-р)) = ехр(г(ф ± тс) J3) ехр(г(тс - 0) J2),
где азимутальный угол выбран как ф + тс, если 0 < ф < тс, или ф — тс,
если тс < ф < 2тс, с тем чтобы он оставался в интервале от 0 до 2тс.
Тогда
= ехр(-г(тс - 9)J2)
х ехр(-г(ф ± тс)J3) ехр(гф,73) exp(z0J2) exp(-zTcJ2)
= ехр(-г(тс - 0) J2) exp(+zTcJ3) ехр(-г(тс - 0) J2).
Но вращение на угол ±180° вокруг оси z меняет знак J2, так что
ЩК(р)К2) = l/(K(-p))exp(±zTcJ3). B.6.21)
Кроме того, R(-p)B(|p|/fc) есть просто стандартный буст L{i'Pp) в
направлении ,'fp = (—р, р°). Поэтому окончательно
_а
B.6.22)
где фаза равна -тса или +тса в зависимости от того, положительна
или отрицательна у—компонента вектора р. Это необычное изменение
знака в результате операции инверсии для безмассовых частиц
полуцелого спина связано с принятым в B.5.47) соглашением для
вращения, которое использовалось для определения состояний
безмассовых частиц с произвольным импульсом. Поскольку группа
вращений не является односвязной, подобные нарушения непрерыв-
непрерывности неизбежны.
Т: М = О
Действуя на состояние ^ка, являющимся собственным для
операторов Рц и J3 с собственными значениями W = @, 0, к, к) и а,
соответственно, оператор обращения времени Т переводит его в
состояние с 4-импульсом {ifky- = @, 0л -к, к) и J3 = -а. Таким
образом Т не изменяет спиральность J • к, и поэтому ничего нельзя
сказать о том, имеются ли у частиц со спиральностью о партнеры
106 Глава 2. Релятивистская квантовая механика
с противоположной спиральностью —о. Поскольку Т, как и Р, не
оставляет инвариантным стандартный 4-импульс, удобно рас-
рассмотреть генератор 17(К2~1)Т, где R2 — вращение B.6.19), который
также переводит к в (ijJk). Это преобразование коммутирует с J3,
так что
U(R^)J4>ka=i;a4>kta, B.6.23)
где С,с — другая фаза. Так как R2~1T коммутирует с бустом B.5.45),
а Т коммутирует с вращением, то, действуя оператором Т на
состояние B.5.5), получим:
С помощью B.6.21) находим окончательно:
V?pa = ^ ехр(±йсо)^>а . B.6.25)
Как и ранее, верхний или нижний знак в этой формуле соответ-
соответствует положительному или отрицательному знаку у-компоненты
вектора р.
Любопытно, что квадрат оператора обращения времени Т2
очень просто действует на одночастичные состояния как массив-
массивных, так и безмассовых частиц. Пользуясь B.6.18) и вспоминая, что
Т — антиунитарный оператор, получаем, что для одночастичных
состояний массивных частиц
или иначе
Т2хР ст = (-Jj4> ст . B.6.26)
Для безмассовых частиц мы получаем такой же результат. Если у—
компонента вектора р положительна, то у-компонента й?р отрица-
отрицательна и наоборот, поэтому из B.6.25) находим:
2.6. Пространственная инверсия и обращение времени Ю7
Если спиральность о — целое или полуцелое число, этот резуль-
результат можно записать в виде:
Т2^рст=(-J1а1^Р;СТ. B.6.27)
Под «спином» безмассовой частицы обычно понимают абсолютное
значение ее спиральности, поэтому B.6.27) эквивалентно B.6.26).
Этот результат приводит к интересному следствию. Когда Т2
действует на любое состояние Ч* системы невзаимодействующих
массивных или безмассовых частиц, он порождает множитель (-JJ
или (—J° для каждой частицы. Поэтому, если состояние содержит
нечетное число частиц с полуцелыми спином или спиральностью (и
дополнительно любое количество частиц с целыми спином или
спиральностью), мы получим общее изменение знака:
Т2Ч' = -Ч'. B.6.28)
Если теперь «включить» различные взаимодействия, этот ре-
результат сохранится, при условии, что эти взаимодействия, нару-
нарушая, быть может, вращательную инвариантность, не нарушают
инвариантность относительно обращения времени. (Например,
приведенные рассуждения применимы в том случае, когда систе-
система подвергается воздействию статических гравитационного и элек-
электрического полей.) Предположим теперь, что Ч1 есть собствен-
собственное состояние гамильтониана. Так как Т коммутирует
с гамильтонианом, состояние "РР также будет собственным со-
состоянием гамильтониана. Будет ли это то же самое состояние?
Если так, то "РР может отличаться от Ч1 только фазовым множи-
множителем:
но в этом случае
Т2хР = Т(^) = СТЧ* =| SI2 Ч< = Ч<,
что противоречит B.6.28). Мы видим, что если у оператора
108 Глава 2. Релятивистская квантовая механика
энергии есть собственное состояние, удовлетворяющее B.6.28),
то обязательно имеется другое состояние с той же энергией.
Этот факт известен как вырождение Крамерса 10. Конечно, вывод
тривиален, если система инвариантна относительно вращений,
так как полный угловой момент j любого состояния этой системы
должен быть полуцелым, и поэтому каждый энергетический уро-
уровень будет 2j + 1 = 2, 4, ... -кратно вырожден. Удивительно, что
даже в случае, когда инвариантность относительно вращений
нарушена внешними полями, например, электростатическим по-
полем, до тех пор, пока эти поля инвариантны относительно Т,
сохраняется по крайней мере двукратное вырождение. В частно-
частности, если бы любая частица имела электрический или гравитаци-
гравитационный дипольный момент, то статическое электрическое или гра-
гравитационное поле полностью снимало бы 2j + 1-кратное
вырождение по спину, так что подобные дипольные моменты
запрещены инвариантностью по отношению к обращению времени.
Для полноты изложения следует отметить, что Р- и Т-
преобразования могут действовать на мультиплеты частиц одной
массы более сложным образом. Эта возможность рассмотрена в
Приложении В к данной главе. Примеры ее использования в
физике неизвестны.
2.7. Проективные представления *
Вернемся к возможности, указанной в разделе 2.2, когда груп-
группа симметрии может действовать на физические состояния_ проек-
тивно, иначе говоря, когда элементы группы симметрии Т,Т и т. д.
могут быть представлены в физическом гильбертовом пространстве
операторами U(T), U(T) и т. п., удовлетворяющими правилу компо-
композиции:
ЩТ)ЩТ) = ехр(гф(Т,Т))ЩТТ), B.7.1)
с действительной фазой ф. (Черта здесь используется только для
того, чтобы отличать один оператор симметрии от другого.) Основ-
* Этот раздел лежит несколько в стороне от основной линии изложения и
может быть опущен при первом чтении.
2.7. Проективные представления 109
ное требование, которому должна удовлетворять любая фаза ф
в B.7.1), вытекает из условия ассоциативности
ЩТ3)(ЩТ2 )?7CZ\)) = (ЩТ3)ЩТ2 ))?7CZ\).
Оно имеет следующий вид:
ф(Т2,Т1) + ф(Т3,Т2Т1) = ф(Тз,Т2) + ф(Т3Т2,Т1). B.7.2)
Конечно, каждая фаза вида
ф(Т,Т) = а(ТТ)-а(Т)-ос(Т) B.7.3)
автоматически удовлетворяет B.7.2), но проективное представ-
представление с такой фазой можно заменить на обычное представление,
заменив оператор U(T) на
ЩТ) = ЩТ)ехр(га(Т)),
для которого
ЩТ)ЩТ) = п(ТТ).
Всякое множество функций ф(Т,Т)( удовлетворяющих B.7.2) и от-
отличающихся только на функции Аф(Т,Т) вида B.7.3), называется
2 -^коциклом. Тривиальный коцикл содержит функцию ф = 0,
и поэтому состоит из функций вида B.7.3), которые можно устра-
устранить переопределением U(T). Нас интересует вопрос, допускает ли
группа симметрии существование нетривиальных коциклов, иными
словами, может ли эта группа иметь представление на физичес-
физическом гильбертовом пространстве, которое внутренне проективно
в том смысле, что фаза ФС^Т1) %е может быть устранена описан-
описанным выше образом.
Чтобы ответить на этот вопрос, полезно рассмотреть сначала
влияние фазы ф в B.7.1) на перестановочные соотношения генера-
генераторов бесконечно малых преобразований. Если Т или Т - единич-
единичный элемент группы симметрии, фаза ф очевидно должна рав-
равняться нулю:
ф(Т,1) = фA,Т) = 0. B.7.4)
Если оба элемента Т и Т близки к единичному элементу, фаза
110 Глава 2. Релятивистская квантовая механика
должна быть мала. Используя для параметризации элементов
группы координаты 0а (см. раздел 2.2), причем Т@) = 1, находим,
что вследствие B.7.4) разложение в окрестности 0=0 = 0
должно начинаться со слагаемых порядка 0 0 :
ф(Т@),Т@)) = /аЬ0а0Ь+..., B.7.5)
где /аЬ - действительные числовые константы. Подставляя это разло-
разложение в степенное разложение соотношения B.7.1) и повторяя
шаги, которые привели к B.2.22), получаем:
[tb,tc] = zCabcta + zCbcl, B.7.6)
где СЬс — антисимметричный коэффициент,
Cbc = "/be +/cb • B-7.7)
Появление в правой части перестановочных соотношений слагае-
слагаемых, пропорциональных единичному элементу (так называемых
центральных зарядов), является для алгебры Ли прямым анало-
аналогом наличия фаз в проективном представлении группы.
Постоянные СЬс, так же, как СаЬс удовлетворяют важным огра-
ограничениям, вытекающим из тождества Якоби. Вычисляя коммута-
коммутатор B.7.6) с td и добавляя аналогичные выражения, в которых
индексы Ъ, с, d заменены на с, d, Ъ и d, Ъ, с, убеждаемся, что
сумма всех трех двойных коммутаторов тождественно обращается
в нуль, откуда
CabcCead + CacdCeab + CadbCeac = 0, B.7.8)
а также
СаЪсСас[ + CacdCab + CadbCac = 0. B.7.9)
Уравнение B.7.9) всегда имеет один очевидный класс ненулевых
решений для СаЬ:
СаЬ=СеаЬфе, B-7.10)
где фе — произвольные действительные постоянные. Для этих реше-
решений можно устранить центральные заряды из B.7.6) переопреде-
переопределением генераторов:
2.7. Проективные представления 111
Новые генераторы удовлетворяют перестановочным соотношениям
без центральных зарядов:
(ib,tc] = iCabcta. B.7.12)
Данная алгебра Ли может либо допускать, либо не допускать
существование решений уравнения B.7.9), отличных от B.7.10).
Теперь сформулируем ключевую теорему, определяющую
возможность или невозможность существования внутренне проек-
проективных представлений. Фаза любого представления U(T) данной
группы может быть выбрана так, что ф = 0 в B.7.1), если выпол-
выполнены два условия:
а) генераторы группы в этом представлении могут быть
переопределены так же, как в формуле B.7.11)), с тем, чтобы
устранить из алгебры Ли все центральные заряды;
б) группа является односвязной, т. е. любые два элемента
группы могут быть связаны путем, целиком лежащим внутри
группы, а любые два таких пути могут быть непрерывным образом
преобразованы друг в друга. (Эквивалентно, любая петля, начина-
начинающаяся и кончающаяся на каком-то групповом элементе, может
быть непрерывным образом стянута в точку.)
Доказательство теоремы дано в Приложении Б к этой главе.
Там же комментируется случай неодносвязных групп. Согласно
этой теореме существуют ровно две причины (причем одна не
исключает другую), по которым могут возникать внутренне проек-
проективные представления: алгебраическая, когда представление груп-
группы проективно уже в окрестности единицы, или топологическая,
когда группа неодносвязна, и поэтому путь из 1 в Т и затем из Т
в Т не может быть непрерывно продеформирован в некоторый
другой путь из 1 в ТТ. В последнем случае фаза ф в B.7.1) зависит
от конкретного выбора стандартных путей, ведущих из единичного
элемента к различным элементам группы и используемых для
определения соответствующих операторов U.
Рассмотрим теперь каждую из этих возможностей по очереди
применительно к частному случаю неоднородной группы Лоренца.
(А) Алгебра
С учетом центральных зарядов перестановочные соотношения
112 Глава 2. Релятивистская квантовая механика
для генераторов неоднородной группы Лоренца будут иметь вме-
вместо B.4.12)-B.4.14) вид:
B.7.13)
B.7.14)
B.7.15)
Очевидно, что константы С удовлетворяют также условиям анти-
антисимметрии:
B.7.17)
B.7.18)
ср,ц = _сц,Р_ B.7.19)
Покажем, что у всех этих констант есть дополнительные алгеб-
алгебраические свойства, позволяющие устранить их переопределением
J^v и Р^ путем сдвига на постоянные слагаемые. (Это соответствует
переопределению фазы операторов U{A,a).) Чтобы вывести указан-
указанные свойства, используем тождества Якоби
O, B.7.20)
0, B.7.21)
= 0. B.7.22)
(Тождество Якоби с тремя Р удовлетворяется автоматически и
поэтому не содержит дополнительной информации.) Подставляя
B.7.13)—B.7.16) в B.7.20)-B.7.22), находим алгебраические соотноше-
соотношения, которым удовлетворяют константы С:
0 = г1УРС^а - if pCv'a - if^'P + ifaCv'p, B.7.23)
2.7. Проективные представления 113
ц i ц ц^у , B.7.24)
^ i . B.7.25)
Сворачивая B.7.23) с r|vp, получаем:
O° = 0. B.7.26)
С другой стороны, константы О1'^1 и CP°>|1V не обязательно равны
нулю, но их алгебраическая структура достаточно проста, что
позволяет устранить эти константы переопределением Р^ и J^v,
соответственно. Свертка B.7.24) с r|vp дает
, B.7.27)
Сх=|лрУСр>. B.7.28)
Аналогично, сворачивая B.7.25) с r(vp , получаем:
?\ю,\г] = ^1]\iqXc! _ ^X\iQr]G + ^аХ?Г}\1 _ ^1}c:qX\l ^ B.7.29)
С^ = ^4vpCXv'aP . B.7.30)
(Эти выражения автоматически удовлетворяют соотношениям B.7.24)
и B.7.25), так что из тождеств Якоби уже нельзя извлечь допол-
дополнительной информации.) Теперь видно, что если константы С не
равны нулю, их можно устранить, определяя новые генераторы
Р^^Р^+С^, B.7.31)
B.7.32)
114 Глава 2. Релятивистская квантовая механика
и тогда перестановочные соотношения примут вид, который они
должны иметь для обычного представления:
B.7.33)
B.7.34)
B.7.35)
Мы всегда будем записывать перестановочные соотношения в
виде B.7.33)—B.7.35), но с опущенными тильдами.
Между прочим, заметим, что отсутствие центральных за-
зарядов в случае алгебры, порождаемой J^v, можно немедленно
вывести из того факта, что эта алгебра относится к типу полу-
полупростых. (Полупростые алгебры Ли не имеют инвариантных
абелевых подалгебр, порождаемых коммутирующими друг с дру-
другом генераторами, коммутаторы которых с любыми другими ге-
генераторами алгебры также принадлежат этой подалгебре.) Име-
Имеется общая теорема11, согласно которой любые центральные
заряды в случае полупростых алгебр Ли всегда можно устра-
устранить переопределением генераторов, как в B.7.32). С другой сто-
стороны, полная алгебра Пуанкаре, порождаемая коммутаторами
J^v и Р*1, не является полупростой (генераторы Р11 образуют
инвариантную абелеву подалгебру), и требуются специальные
аргументы, чтобы показать, что ее центральные заряды можно
устранить тем же способом. В самом деле, неполупростая алгеб-
алгебра Галилея, обсуждавшаяся в разделе 2.4, допускает существо-
существование центрального заряда — массы М.
Итак, неоднородная группа Лоренца удовлетворяет первому
из двух условий, необходимых для исключения внутренне проек-
проективных представлений. Что можно сказать о втором условии?
(Б) Топология
Чтобы исследовать топологию неоднородной группы Лоренца,
весьма удобно представить однородные лоренцовские преоб-
преобразования 2x2 комплексными матрицами. Действительно, любой
действительный 4-вектор V^ можно использовать для построения
эрмитовой 2x2 матрицы
2.7. Проективные представления 115
Vi + lY2 yoysj' B-7.36)
где ац - обычные матрицы Паули, причем а0 = 1. Обратно, всякая
2x2 эрмитова матрица может быть записана в этом виде и поэтому
определяет действительный 4-вектор V^.
Свойство эрмитовости будет сохраняться при преобразованиях
v -> XvXf, B.7.37)
где X — произвольная 2x2 матрица. Кроме того, инвариантный
квадрат 4-вектора равен
V^yv- =(V1J +(V2J +(V3J -(V0J = -Detu, B.7.38)
и этот детерминант сохраняется при преобразовании B.7.37), если
выполнено условие
|DetX|=l. B.7.39)
Каждая комплексная 2x2 матрица X, удовлетворяющая B.7.39),
определяет таким образом действительное линейное преобразо-
преобразование V^, оставляющее инвариантным выражение B.7.38), т. е.
однородное преобразование Лоренца A(k):
^ a]l. B.7.40)
Далее, для двух таких матриц X и X
так что
А(ХХ) = А(Х)А(Х). B.7.41)
Однако две матрицы X, отличающиеся только общей фазой,
одинаково действуют на г? в B.7.37) и поэтому соответствуют
одному и тому же лоренцовскому преобразованию. Поэтому удобно
116 Глава 2. Релятивистская квантовая механика
настроить фазу матриц X так, чтобы
l, B.7.42)
что совместимо с B.7.41). Комплексные 2x2 матрицы с детерминан-
детерминантом, равным единице, образуют группу, называемую SLB, С). (Сим-
(Символ SL означает «специальная линейная», причем слово «спе-
«специальная» соответствует единичному детерминанту элементов
группы, а С означает «комплексная».) Групповые элементы зависят
от 4 -1 = 3 комплексных параметров или шести действительных
параметров, т. е. от того же числа параметров, что и группа
Лоренца. Однако группа SLB, С) не тождественна группе Лоренца:
если X — матрица из SLB,C), то и —X принадлежит этой группе,
причем как X, так и —X соответствуют одному и тому же преобра-
преобразованию Лоренца в B.3.37). Действительно, легко видеть, что мат-
матрица
(е*/2 0 ^
отвечает лоренцовскому преобразованию Л(Х@)), представляю-
представляющему вращение на угол 0 вокруг оси z, так что X = -1 соответ-
соответствует вращению на угол 2%. Таким образом группа Лоренца не
совпадает с SLB,C), а равна SLB,C)/Z2 *, которая представляет
группу комплексных 2x2 матриц с единичным детерминантом и с
отождествлением пар элементов X и —X.
Какова же топология группы Лоренца? В силу теоремы о
полярном разложении 12 всякая комплексная несингулярная матри-
матрица X может быть представлена в виде
X = ueh,
где и — унитарная матрица, ah — эрмитова матрица,
и*и = \, hf =h.
* Группа Z2 состоит из двух элементов +1 и —1. В общем случае, когда мы
пишем G/H, где Я — инвариантная подгруппа группы G, подразумевается,
что в группе G отождествлены элементы д и gh, где д е G и h e H. Подгруппа
Z2 тривиально инвариантна, так как ее элементы коммутируют со всеми
элементами SLB, С).
2.7. Проективные представления 117
Так как Det и является фазовым множителем, a Det (exp К) =
= ехр (Тг К) действителен и положителен, то из условия B.7.42)
вытекает одновременно, что
Det и = 1, Tr h = 0.
(Множитель и соответствует подгруппе вращений группы Лоренца:
если и — унитарная матрица, то Tr (uvul) = Tr v, так что V0 =
5 Tr v остается инвариантным под действием А(и).) Далее, это
разложение однозначно, так что группа SLB,C) топологически
является просто прямым произведением (т. е. множеством пар
элементов) пространства всех матриц и и пространства всех
матриц h. Всякая эрмитова 2x2 матрица h со следом, равным
нулю, может быть представлена в виде
( с а — гЬ\
Н ъ
уа + гЪ -с )
где а, Ъ, с действительны, но в остальном произвольны, так что
пространство всех h топологически эквивалентно обычному трех-
трехмерному плоскому пространству R3. С другой стороны, всякая
унитарная 2x2 матрица с единичным детерминантом может быть
представлена в виде:
( d + ie f + ig}
u = \ ,
\-f + ig d- ie)
где d, e, f, g удовлетворяют единственному нелинейному ограни-
ограничению
d2+e2+/2+g2=l,
так что пространство SUB) всех и топологически эквивалентно
пространству Ss — трехмерной поверхности сферы в плоском
четырехмерном пространстве. Таким образом SLB,C) топологичес-
топологически эквивалентна прямому произведению R3xS3. Эта группа являет-
является односвязной: всякая кривая, соединяющая две точки из i?3 или
S3, может быть продеформирована в любую другую, и то же верно
для прямого произведения. (Все сферы Sn за исключением окруж-
окружности S1 являются односвязными.) Однако нас интересует не SLB,C),
а группа SLB,C)/Z2. Отождествление 1 и —1 эквивалентно отожде-
отождествлению унитарных множителей и и —и (так как eh всегда поло-
положительно), так что топология группы Лоренца — это топология
118 Глава 2. Релятивистская квантовая механика
R3xS3/Z2, где S3/Z2 — трехмерная сферическая поверхность с
отождествленными противоположными точками. Эта группа не
является односвязной; например, на S3 путь из и в и' нельзя
непрерывно продеформировать в путь из и в —и', тогда как в
S3/Z2 эти два пути соединяют одни и те же точки. Фактически,
S3/Z2 — двусвязная группа: пути между любыми двумя точками
разделяются на два класса, в зависимости от того, включают ли
они инверсию и —> —и, и каждый путь из одного класса можно
продеформировать в другой путь того же класса. Эквивалент-
Эквивалентным является утверждение, что двойная петля, дважды прохо-
проходящая один и тот же путь из какого-то элемента обратно в него
же, может быть непрерывным образом сжата в точку. (Как пока-
показано в Приложении Б, математически это выражается в утвер-
утверждении, что для группы S3/Z2 фундаментальная или первая
гомотопическая группа есть Z2.) Аналогично, неоднородная груп-
группа Лоренца имеет ту же топологию, что и группа RixR3xS3/Z2, и
поэтому она также двусвязна.
Так как группа Лоренца (однородная или неоднородная)
неодносвязна, она имеет внутренне проективные представления.
Однако поскольку двойная петля, дважды проходящая путь из 1
в Л, из Л в Л Л, и обратно в 1, может быть сжата в точку, мы
должны иметь
[[/(Л)[/(Л)[/-1(ЛЛ)]2 = 1,
и поэтому фаза е1^ ' является просто знаковым множителем:
U Щи (К) = ±ЩЛЛ). B.7.43)
Аналогично для неоднородной группы Лоренца
ЩА, а)ЩА, а) = ±ЩАА, Ла + а). B.7.44)
Нам знакомы такие «представления с точностью до знака»:
это состояния с целым спином, для которых знаки в B.7.43) и B.7.44)
всегда равны +1, и состояния с полуцелым спином, для которых эти
знаки равны +1 или -1 в зависимости от того, можно ли сжать в
точку путь от 1 к Л, затем к Л Л, и назад к единице. Это различие
обусловлено тем, что вращение на угол 2л; вокруг оси z, действуя
на вектор состояния с проекцией углового момента на ось z, равную
2.7. Проективные представления 119
О, дает фазовый множитель е2й1СГ, и поэтому никак не влияет на
состояние с целым спином и изменяет знак вектора состояния с
полуцелым спином. (Два этих случая соответствуют двум неприво-
неприводимым представлениям первой гомотопической группы Z2.) Итак,
B.7.43) и B.7.44) выражают правило суперотбора: мы не должны
смешивать состояния с целым и полуцелым спином.
Для случая конечных масс ограничения целым или полуце-
полуцелым спином были ранее выведены чисто алгебраическими метода-
методами из хороню известных представлений генераторов малой группы,
которые в данном случае есть просто матрицы углового момента
J^ с целым или полуцелым значением j. С другой стороны, для
нулевых масс действие малой группы на физические одночастич-
ные состояния сводится к вращению вокруг направления им-
импульса, так что поэтому здесь нет алгебраических причин огра-
ограничиваться целыми или полуцелыми значениями спиральности.
Однако существует топологическая причина: вращение на угол
4л вокруг направления импульса можно непрерывным образом
продеформировать в тождественное преобразование, так что мно-
множитель ехрDлго) должен равняться единице, и поэтому величи-
величина а должна быть либо целой, либо полуцелой.
Вместо того, чтобы иметь дело с проективными представлени-
представлениями и накладывать правила суперотбора, можно расширить группу
Лоренца, взяв ее равной SLB,C), а не SLB,C)/Z2, как ранее. Обычная
инвариантность по отношению к вращениям запрещает переходы
между состояниями с целым или полуцелым полным спином, так что
единственной разницей будет теперь то, что группа односвязна и
имеет поэтому только обычные, а не проективные представления,
так что теперь нельзя потребовать выполнения правил суперотбора.
Это означает не то, что теперь можно реально приготовить физи-
физическую систему в виде линейной комбинации состояний целого и
полуцелого спина, а лишь то, что наблюдаемая в природе лорен-
цовская инвариантность не может быть использована для того, что-
чтобы доказать невозможность таких суперпозиций.
Такие же соображения применимы к любой группе симмет-
симметрии. Если алгебра Ли этой группы допускает существование
центральных зарядов, всегда можно расширить такую алгебру,
включив в нее генераторы, которые коммутируют с любым
элементом алгебры и собственными значениями которых явля-
являются центральные заряды. Именно так мы действовали, когда
120 Глава 2. Релятивистская квантовая механика
добавили оператормассы к алгебре Ли группы Галилея в конце
раздела 2.4. Расширенная алгебра Ли теперь, конечно, свободна
от центральных зарядов, так что часть группы в окрестности
единицы имеет только обычные представления, и никаких пра-
правил суперотбора не требуется.
Аналогично, даже если группа Ли G не является односвяз-
ной, ее всегда можно представить в виде С/Я, где С — односвяз-
ная группа, которую называют универсальной накрывающей
группой группы G, а Н — инвариантная подгруппа * группы С.
В общем случае, можно взять в качестве группы симметрии
вместо G группу С, так как нет никакой разницы в следствиях
этого выбора, за исключением того, что G налагает правило
суперотбора, а С — нет. Короче говоря, проблема правил супе-
суперотбора есть нечто ирреальное: может быть, и можно пригото-
приготовить физическую систему в виде произвольной суперпозиции
состояний, но нельзя решить, так это или нет, ссылаясь на
принципы симметрии, поскольку какую бы ни группу симмет-
симметрии мы не приписывали природе, всегда существует другая
группа, приводящая к тем же следствиям, но без правил супе-
суперотбора.
Приложение А. Теорема о представлении симметрии
В этом приложении мы дадим доказательство фундамен-
фундаментальной теоремы Вигнера2, утверждающей, что всякое преоб-
преобразование симметрии может быть представлено в гильбертовом
пространстве физических состояний линейным и унитарным или
антилинейным и антиунитарным оператором. При этом главным для
нас будет то, что преобразования симметрии являются преобразо-
преобразованиями Т лучей, сохраняющими вероятности переходов в том
смысле, что если ^ и ^ — векторы состояний, принадлежащие
лучам !'Л1 и ;Й2, то любые векторы состояний Ч?\ и xP/2, принадлежа-
* Первая гомотопическая группа С/Я есть Я. Мы видели, что накрывающая
группа однородной группы Лоренца есть SLB, С), а накрывающая группа
трехмерной группы вращений есть ?17B). Подобная связь групп SL и SU
справедлива для случая трех, четырех или шести измерений. Для общего
случая d измерений накрывающая группа SO(d) носит специальное
наименование Spin(d).
Приложение А 121
щие преобразованным лучам Т'.Ш^ и Т;'Л2, удовлетворяют условию
Мы требуем также, чтобы преобразование симметрии имело
обратное преобразование, сохраняющее вероятности переходов
в указанном выше смысле.
Для начала рассмотрим некоторую полную ортонормированную
систему векторов состояний *Pfe, принадлежащих лучам ;Лк, причем
(Ч>к,Ц) = Ьк1. B.A.2)
Пусть х?к — некоторая произвольная выборка векторов состояний,
принадлежащих преобразованным лучам Т.'Як. Из B.А.1) имеем:
Но величина D*^,4^) автоматически действительна и положи-
положительна, так что отсюда вытекает, что она должна иметь значе-
значение, равное единице. Поэтому
(%,4>{) = 5ы. B.А.З)
Легко видеть, что преобразованные состояния Ч? \ также обра-
образуют полную систему, так как если бы существовал какой-ни-
какой-нибудь ненулевой вектор состояния Ч*', который был бы ортогона-
ортогонален ко всем Ч?\, то луч, полученный обратным преобразованием
луча, к которому принадлежит W, состоял бы из ненулевых
векторов Ч1", для которых
|2|^,^')|2 = О
для всех к. Это невозможно, так как предполагалось, что Ч?к
образуют полную систему.
Теперь следует принять соглашение о фазах для состояний
Ч?\. С этой целью выделим одно из состояний *Pfe, например, *Р1( и
рассмотрим векторы состояний
^ = ^№+^), B.А.4)
принадлежащие некоторым лучам .9^ с к Ф 1. Любой вектор
122
Глава 2. Релятивистская квантовая механика
состояния Т'к, принадлежащий преобразованному лучу ТУк, мо-
может быть разложен по векторам состояний *Р'г:
Из B.А.1) следует, что
а для I Ф к и I Ф 1
1
= 0.
Ясно, что для любого данного к подходящим выбором фаз двух
векторов состояний Т'к и Ч?\ можно так настроить фазы двух
ненулевых коэффициентов скк и ск1, чтобы они равнялись \j-j2- С
этого момента векторы состояний Т'к и Ч*^, выбранные подобным
образом, будут обозначаться UTfe и U4fk. Как было показано,
B.А.5)
Однако нужно еще определить U4? для произвольных векторов
состояний Ч1.
Рассмотрим произвольный вектор состояния Ч1, принадле-
принадлежащий произвольному лучу ill, и разложим его по Ч?к:
B.А.6)
Любой вектор состояния Ч1', принадлежащий преобразо-
преобразованному лучу Т'.Ш, может быть аналогичным образом разложен
по полной ортонормированнои системе векторов U4?k:
чг = ? ект?к.
B.А.7)
9 9
Из равенства величин (Ч?к,Ч?) и (U4?k,4?') вытекает, что для
всех к (включая к = 1)
П I2 I Г" 2 fo A R\
Приложение А
123
в то время как из равенства |(Yfe ,Ч?)\ и
(UTk ,*Р') вытекает, что
для всех к Ф 1
Ск+С1\2=\Ск+С[
Разделив B.А.9) на B.А.8), получаем соотношение
Re(Ck/C1) = Re(Ck/C[),
а с учетом B.А.8)
Поэтому либо
либо
Irn(Ck/C1) = ±Irn(Ck/C[).
С/с / C-i =Ск / Сх,
B.А.9)
B.А.10)
B.А.11)
B.А.12)
B.А.13)
Далее можно показать, что при всех к выбор должен быть один и
тот же. (Этот этап доказательства был пропущен Вигнером.) Для
этого предположим, что при некотором к имеем Ск/С1 = С'к/С\, а
при некотором I Ф к, напротив, Сх/Сг = {С\/С\)*\ Предположим
также, что оба отношения комплексны, так что мы рассматриваем
действительно два разных случая. (Это изначально требует, чтобы
к Ф 1 и I Ф 1, а также к Ф I.) Покажем, что такое невозможно.
Определим вектор состояния Ф = (^ + 4>к + Ч*г) / 7з . Так как
все отношения коэффициентов в этом векторе состояния действи-
действительны, мы должны получить те же отношения в любом векторе
состояния Ф', принадлежащем преобразованному лучу:
Ф'= -?=
где а — фазовый множитель, |а| = 1. Но тогда из равенства
вероятностей перехода
и
(Ф',Ч*') вытекает, что
1 + ^г +
С[ С[
1 +
124
Глава 2. Релятивистская квантовая механика
и поэтому
Это возможно только в том случае, если
или, иными словами, если
=0.
Отсюда, в противоречии с нашими предположениями, либо Ск/
С1( либо Ci/Cx должны быть действительны для любой пары к, I.
Видим, что для заданного преобразования симметрии Т, приме-
примененного к данному вектору состояний, для всех к должно быть
выполнено либо условие B.А.12), либо условие B.А.13).
Вигнер исключил вторую возможность B.А.13), поскольку, как
он показал, всякое преобразование симметрии, для которого эта
возможность реализуется, должно включать обращение времени, а в
представленном доказательстве он рассматривал только симметрии
типа вращений, не влияющие на направление времени. Мы изучаем
здесь симметрии, включающие обращение времени на равных основа-
основаниях с другими симметриями, так что нам следует считать, что для
каждого преобразования симметрии Т и вектора состояния E^Qc*^
выполнены либо BА.12), либо BА.13). В зависимости от того, какая из
этих альтернатив выполняется, определим U4? как тот из векторов
состояний *F, принадлежащих лучу Т.% фаза которого выбрана так,
что либо Сг = С\, либо Сг = С\\ Тогда либо
B.А.14)
либо
B.А.15)
Приложение А
125
Осталось доказать, что для данного преобразования сим-
симметрии мы должны сделать тот же выбор между формулами
B.А.14) и B.А.15) в случае произвольных значений коэффициен-
коэффициентов Ск. Предположим, что B.А.14) выполнено для вектора состо-
состояния ?fcAfe1Pfe, a B.A.15) — для вектора состояния ЕкВкЧ!к. Тогда из
инвариантности вероятностей переходов вытекает, что
к
2
=
к
или эквивалентно
B.А.16)
ы
Нельзя исключить, что B.А.16) выполнено для пары векторов
состояний LfcAfc^Pfc и LfcBfc^Pfc, принадлежащих разным лучам. Од-
Однако для любой пары таких векторов состояний, у которых ни
Ак, ни Вк не имеют все одинаковой фазы (так что B.А.14) и
B.А.15) не одинаковы), всегда можно найти третий вектор состо-
состояния, для которого *
B.А.17)
kl
и также
B.А.18)
kl
* Если для какой-то пары к, I и А*кАь и В*кВ1 комплексны, выбираем все
С равными нулю, за исключением Ск и Сг, а эти коэффициенты выбираем с
разными фазами. Если для какой-то пары к, I величина А*^ комплексна, а
В*кВг действительна, то должна существовать другая пара т, п (либо т,
либо те, но не оба сразу, могут при этом равняться к или Г), для которой
В*тВп комплексна. Если к тому же А*тАп комплексна, выбираем все С равными
нулю, за исключением Ст и С„, а у этих коэффициентов выбираем разные
фазы. Если А*тАп действительна, то выбираем все С равными нулю, за
исключением Ск, Сь Ст и С„, а у этих четырех коэффициентов выбираем
разные фазы. Случай, когда В*кВ1 комплексна, a A"fkAl действительна,
разбирается аналогично.
126 Глава 2. Релятивистская квантовая механика
Как мы видели, из B.А.17) следует, что для Е^А^^. и Ии^к^к
должен быть сделан выбор между B.А.14) и B.А.15), а из B.А.18)
следует, что один и тот же выбор должен быть сделан и для
Efe-Bfe^fe и LfcCfe4V Таким образом, один и тот же выбор между
B.А.14) и B.А.15) должен быть сделан для двух исходных векто-
векторов состояния LfcAfc^Pfc и YtkBk^k- Итак, показано, что для данного
преобразования симметрии Т все векторы состояний удовлетво-
удовлетворяют либо B.А.14), либо B.А.15).
Теперь нетрудно доказать, что квантово-механический опе-
оператор U может быть либо линейным и унитарным, либо анти-
антилинейным и антиунитарным. Сначала предположим, что для всех
векторов состояний удовлетворяется B.А.14). Любые два вектора
состояния Ч* и Ф можно разложить по полной системе:
соответственно, используя B.А.14), получаем:
РФ) = С/? {аАк + |3Bfc L>к =? {аАк + |3Bfc )W>k
к к
Вновь используя B.А.14), находим:
B.А.19)
так что оператор U линеен. Пользуясь B.А.2) и B.А.З), находим, что
скалярное произведение преобразованных состояний равно
kl
и, следовательно,
D',<P), B.A.20)
так что оператор U унитарен.
Приложение Б 127
Случай симметрии, которая удовлетворяет B.А.15) для всех
векторов состояний, разбирается во многом аналогично. Возможно,
читатель сам, без посторонней помощи воспроизведет доказатель-
доказательство. Однако, поскольку антилинейные операторы могут быть не
слишком привычны, все же приведем здесь необходимые детали.
Пусть B.А.15) удовлетворяется для всех векторов состояний LfcCfe4V
Любые два вектора *Р и Ф могут быть разложены как и ранее, так что
РФ) = t7?(ocAfc + fU3kL!k =
к к
Вновь пользуясь B.А.15), находим:
* * B.А.21)
так что U антилинеен. Используя B.А.2) и B.А.З), получаем, что
скалярное произведение преобразованных состояний
kl к
и поэтому
(Ч?,Ф)*, B.А.22)
так что оператор U антиунитарен.
Приложение Б. Групповые операторы
и гомотопические классы
В этом приложении мы докажем упомянутую в разделе 2.7
теорему, согласно которой фазы операторов ЩТ) для конечных
преобразований симметрии Т можно выбрать так, чтобы эти
операторы образовывали представление группы симметрии, а
не проективное представление, если только: а) генераторы груп-
группы можно определить так, чтобы в алгебре Ли не было цент-
128 Глава 2. Релятивистская квантовая механика
ральных зарядов; б) сама группа односвязна. Кроме того, обсу-
обсудим проективные представления для неодносвязных групп и связь
этих представлений с гомотопическими классами группы.
Для доказательства теоремы вспомним метод, с помощью
которого были построены операторы, соответствующие преоб-
преобразованиям симметрии. Как описано в разделе 2.2, для парамет-
параметризации этих преобразований мы вводим набор действительных
переменных 6а, так чтобы сами преобразования удовлетворяли
закону композиции B.2.15):
Мы хотим построить операторы ?7(Т(9)) = Щ9], удовлетво-
удовлетворяющие соответствующему условию *:
Чтобы сделать это, проведем произвольные «стандартные» пути ©q(s)
в пространстве групповых параметров, идущие из начала в каждую
точку 9, причем ©q@) = 0, ©qA) = 9a, и определим t/e(s) вдоль каж-
каждого такого пути с помощью дифференциального уравнения
и() itt7()hg(®())^ B.Б.2)
с начальным условием
?7в@) = 1, B.Б.З)
где
>а(9,9)~
дрь _ • B.Б.4)
. ои Je=o
Мы намерены в конце концов отождествить операторы [/[9] с
?/еA), но прежде следует выяснить некоторые свойства ?/e(s).
* Здесь и далее квадратные скобки используются для того, чтобы отличать
операторы U, построенные как функции групповых параметров, от операторов,
являющихся функциями самих групповых преобразований.
Приложение Б 129
Чтобы проверить закон композиции, рассмотрим две точки
Q1 и 62, и определим путь if, идущий из 0 в 91( а затем в /F2, б^:
J®gBS), 0<s<l/2,
В конце первого отрезка пути мы попадаем в точку, где опера-
оператор U!PB) = UqiA). Чтобы вычислить UJ,s) вдоль второго отрезка
пути, нам нужно знать производную от /а(®е Bs — V),($i). Для
этого используем фундаментальное условие ассоциативности
tfi))- B.Б.6)
Сравнивая коэффициенты при 6С3 в пределе 63 —> 0, находим
э/а(е2,е:к
эе2ь
B.R7)
Таким образом, дифференциальное уравнение B.Б.2) для l/3/(s)
вдоль второго отрезка совпадает с дифференциальным уравнением
для UqBs — 1). Начальные условия для этих величин различны,
однако Ut(s)Uq A) удовлетворяет тому же дифференциальному
уравнению, что и U/Bs-l), но вдобавок удовлетворяет и тому же
начальному условию: при s = г обе величины равны единице.
Отсюда мы заключаем, что для \ < s < 1
и, в частности,
17.^A) = 1/е2AI/в1A). B.Б.8)
Однако из этого не следует, что t/e(l) удовлетворяет желаемому
правилу композиции B.Б.1), так как, хотя путь ®Дя) идет из 6а =
О в 6а = /аF2, 6^, он в общем случае не будет совпадать с тем
выбранным нами «стандартным» путем ©у(ев), который идет
сразу из 0а = о в еа = fa^ ед Чтобы отождествить [/[6] с [7еA),
нужно еще доказать, что t/e(l) не зависит от пути из 0 в 6.
130 Глава 2. Релятивистская квантовая механика
Для этого рассмотрим вариацию Ш оператора Ue(s),
порожденную вариацией 8©(s) пути из 0 в 6. Беря вариацию
B.Б.2), приходим к дифференциальному уравнению
ds '
где h?c = dhb / Э@с . Используя коммутационные соотношения ал-
алгебры Ли B.2.22) (без центральных зарядов) и совершая пере-
перегруппировку слагаемых, получаем
as as
wrsic / \ B.Б.9)
+ ги-\т®ъ *±- (кь -habc + c\dhthdc
as
Однако переходя к пределу 63, 62 —> 0 в условии ассоциативности
B.Б.6), находим для всех 6
h{Q)b,c = -fadeh(Q)th(Q)ec. B.Б.10)
где /^ - коэффициент, определенный формулой B.2.19). Антисим-
Антисимметризация по Ъ и с показывает, что последнее слагаемое в B.Б.9)
обращается в нуль:
Кь ~ Чс + CaedhlK = 0- B.Б.11)
Таким образом, из B.Б.9) следует, что величина
постоянна вдоль пути 6(s). Отсюда следует, что оператор t/e(l)
стационарен при любой бесконечно малой вариации пути, оставля-
оставляющей закрепленными конечные точки 0@) = 0 и 0A) = 6 (а также
U"e@) = 1). Однако из предположения б) вытекает, что любой путь
от 0@) = 0 до 0A) = 6 можно непрерывно деформировать в любой
другой путь, так что теперь можно рассматривать t/e(l) как не
зависящую от пути функцию только переменной 6:
B.Б.12)
Приложение Б 131
В частности, так как путь ИР приводит из 0 в /F2, 9Д имеем
е1)], B.Б.13)
а тогда B.Б.8) показывает, что [/[6] удовлетворяет закону груп-
группового умножения B.Б.1), что и требовалось доказать.
Мы построили непроективное представление ?7[9], и осталось
показать, что любое проективное представление Щ9] той же груп-
группы с теми же генераторами представления ta может отличаться от
[/[6] только фазой:
U[9] = eiamU[Q],
так что фаза ф в законе умножения для U[Q]
U[Q']U[Q] = em&'e)
может быть устранена простым изменением фазы ?7[9]. Чтобы пока-
показать это, рассмотрим оператор
Операторы U[Q] и Щ9] имеют одни и те же генераторы, поэтому
производная левой части по 9 'а обращается в нуль при 9 ' = 0 и
0 =
где
6'=o
Дифференцируя полученное равенство по 9е и выполняя антисим-
антисимметризацию по Ъ и с, получаем сразу же
0=Эфь(9) Эфс(9)
Э9С Э9Ь
Согласно известной теореме13 из предыдущего равенства следу-
следует, что в односвязном пространстве фь есть просто градиент
132 Глава 2. Релятивистская квантовая механика
некоторой функции C:
Эр(9)
Фь(в) = ¦
эеь
Таким образом величина U"[6] 1U[Q]et^^ является на самом деле
постоянной по 6. Полагая эту величину равной ее значению при 6 =
О, видим, что U просто пропорционально U:
что и утверждалось выше.
Приведенный выше анализ дает некоторую информацию о
природе фазовых множителей, которые могут появляться в группо-
групповом законе умножения в случае, когда алгебра Ли не допускает
центральных зарядов, но группа не является односвязной. Предпо-
Предположим, что путь ;/из нуля в 6, а затем в /F,6) нельзя продеформи-
ровать в выбранный нами стандартный путь из 0 в /F,6), иными
словами, предположим, что петля из нуля через 6 в /F,6) и
обратно в нуль не может быть непрерывно продеформирована в
точку. Тогда выражение U"~1(/F2,61))U"F2)t/F1) может являться
фазовым множителем ехр(гфF2,61)) Ф 1, но / — одной и той же для
всех других петель, в которые можно непрерывно продеформиро-
вать данную петлю. Множество, состоящее из всех петель, начина-
начинающихся и кончающихся в нулевой точке, которые могут быть не-
непрерывно продеформированы в данную петлю, носит название
гомотопического классаи данной петли. Таким образом, мы ви-
видим, что /F2, 6г) зависит только от гомотопического класса
петли, идущей из нуля через 6 в /F,6) и затем обратно в нуль.
Множество гомотопических классов образует группу: «произведе-
«произведение» гомотопических классов для петель Я1.-^ и Я^ есть гомотопичес-
гомотопический класс петли, получающейся обходом по Я!г, а затем по Я^,
«обратный» гомотопический класс петли Я, есть гомотопический
класс петли, получающейся обходом Я в противоположном на-
направлении; «единицей» является гомотопический класс петель,
Приложение В 133
которые можно продеформировать в начальную точку. Эта группа
называется первой гомотопической или фундаментальной груп-
группой обсуждаемого пространства. Легко показать, что фазовые
множители образуют представление этой группы: если обход по
петле 1', дает фазовый, множитель ег^г а обход по петле 1', —
фазовый множитель е1^, то обход по обеим петлям дает фазовый
множитель ег^е1^. Поэтому можно составить каталог всех возмож-
возможных типов проективных представлений данной группы <<j (без цент-
центральных зарядов), если известны одномерные представления пер-
первой гомотопической группы пространства параметров группы ((j.
Более подробно гомотопические группы обсуждаются в т. П.
Приложение В. Инверсии и вырожденные мультиплеты
Обычно предполагается, что инверсии Т и Р переводят одно-
частичные состояния в другие одночастичные состояния того же
сорта, возможно, с зависящими от сорта частиц дополнительными
фазовыми множителями. В разделе 2.6 мы мельком обратили вни-
внимание на то, что на вырожденные мультиплеты одночастичных
состояний операторы инверсии могут действовать и более сложным
образом. Эта возможность, по-видимому, была впервые отмечена в
1964 году Вигнером 15. В данном Приложении рассматриваются
обобщения операторов инверсии, в которых вместо фаз инверсии
появляются конечные матрицы. При этом не делается ряда ограни-
ограничительных предположений, использованных Вигнером.
Начнем с обращения времени. Вигнер ограничил возможное
действие операторов инверсии, предположив, что их квадраты
пропорциональны единичному оператору. Так как Т - антиунитар-
антиунитарный оператор, легко видеть, что множитель пропорциональности
для Т2 может быть равен ±1, возможно, с разными знаками для
подпространств, выделенных правилами суперотбора. В том слу-
случае, когда знак Т2 на пространстве состояний с четными или
нечетными значениями 2j противоположен знаку (-lJ-', найденно-
найденному в разделе 2.6, физические состояния должны реализовывать
более сложные, чем предполагалось до сих пор, представления
оператора Т. Если мы хотим принять такую гипотезу, уже не
видно достаточных оснований для сохранения условия Вигнера,
что Т2 пропорционален единице. Обращение к структуре расши-
расширенной группы Пуанкаре неубедительно. Единственное полезное
134 Глава 2. Релятивистская квантовая механика
определение любого из операторов инверсии должно обеспечи-
обеспечивать точное или приближенное сохранение этого оператора. Од-
Однако такое определение может противоречить условию, что Т2
пропорционален единичному оператору.
Чтобы рассмотреть более общие возможности для операто-
оператора обращения времени, предположим, что он действует на мас-
массивное одночастичное состояние по правилу
где р, j и о — импульс, спин и z-компонента спина, а п, т —
индексы, которыми нумеруются члены вырожденного мульти-
плета частиц. (Появление множителя (-l)-7 и изменение знака р
и о выводятся так же, как в разделе 2.6.) Мы ничего не знаем о
матрице ,Ттп кроме того, что в силу антиунитарности Т матрица ,Т
должна быть унитарной.
Посмотрим теперь, как можно упростить это преобразование
подходящим выбором базиса одночастичных состояний. Опреде-
Определяя новые состояния с помощью унитарного преобразования:
*^p,ct,ti = У, '^тя^р,я,т > получаем то же преобразование B.В.1) с
изменившейся матрицей ,Ттп:
j' = ?/-!,Я>/ . B.В.2)
В общем случае с помощью такого выбора базиса одночастичных
состояний не удается сделать ,? диагональной, как это было бы
возможно в случае унитарного оператора Т. Однако можно сделать
эту матрицу блочно-диагональной, причем блоки имеют вид либо
1x1 фазовых множителей, либо 2x2 матриц вида
о
[e-iW2 о J'
где ф — различные действительные фазы.
(Приведем доказательство. Во-первых, заметим, что из фор-
формулы B.В.2) следует
Приложение В 135
Это унитарное преобразование, и его можно выбрать так, что-
чтобы диагонализовать унитарную матрицу :ЖТ. Считая, что это
сделано, и опуская индексы, имеем
,f = D;rT, B.B.4)
где D — унитарная диагональная матрица, имеющая на главной
диагонали фазы гг^п. Немедленным следствием этого является то,
что диагональная компонента ,Тпп обращается в нуль, за исключе-
исключением случая ег^" = 1. Далее, пусть ег^" = 1, но ег^т ф 1. Тогда из
B.В.4) следует, что .Ттп = .Тпт = 0. Перебирая сначала все строки и
столбцы, для которых ег^п = 1, приводим матрицу .'У к виду
J =
B.В.5)
где .:.</ — симметричная и унитарная матрица, а у ,93 все диаго-
диагональные элементы равны нулю. Так как Л симметрична, она может
быть представлена как экспонента от симметричной анти-
антиэрмитовой матрицы, поэтому ее можно диагонализовать преоб-
преобразованием B.В.2), действующим только на </, причем соответству-
соответствующая подматрица матрицы V/ действительна и потому ортогональна.
Поэтому достаточно рассмотреть подматрицу ,93, связы-
связывающую строки и столбцы, для которых ег<^" ф 0. Для значений
п Ф т из B.В.4) имеем ,Тцт = ег^.Гтп и ;Гтп = е^™;Гпт, так что
•Jnm е е ''ш и ''mn . . 'ymn- ^1<-ЮДс1 ,Jnm ,Jmn U,
только не выполнено ег^пег^т = 1. Если сначала перебрать все
строки и столбцы <Ю с данной фазой е 1 ф 1, затем все строки и
столбцы с противоположной фазой, затем все строки и столбцы
с какой-то другой фазой е ф 1, не равной е , строки и
столбцы с противоположной фазой и т. д., то матрица УЗ при-
примет блочно-диагональный вид:
щ о ...л
о щ ...
B.В.6)
где
136 Глава 2. Релятивистская квантовая механика
BН7)
Далее, унитарность матрицы .'^ а следовательно и .99, требует,
чтобы V'^'i = (('i ^'i = 1, откуда ?^ - квадратная и унитарная матри-
матрица. Если применить преобразование B.В.2) с матрицей V/, которая
блочно—диагональна в том же смысле, что и ,Т, причем матрица в
n-ом блоке имеет вид
(V, 0^
0 W, Г
с унитарными матрицами Vt и Wt, то подматрицы Щ подвергнутся
преобразованию <^ —> V^^W/. Отсюда ясно, что можно выбрать
это преобразование так, чтобы Щ = 1. Этим устанавливается соот-
соответствие между парами отдельных строк и столбцов внутри каждо-
каждого блока с фазами е^г' и е~г^г'. Чтобы привести матрицу :jf] к блочно-
диагональному виду с 2x2 блоками вида B.В.З), необходимо всего
лишь перегруппировать строки и столбцы с фазами ег<" поперемен-
попеременно с соответствующими строками и столбцами с фазами е *"".)
Важно подчеркнуть, что если ег<^ ^ 1, невозможно выбрать
состояния так, чтобы диагонализовать преобразование обращения
времени. Если даны два состояния Ч*ра±, на которые оператор Т
действует матрицей B.В.З), то
^Нф-^-р-а,? ¦ B-В.8)
Результатом действия преобразования обращения времени
на произвольную линейную комбинацию этих состояний будет
Для того, чтобы выражение c+4>pG+ + с_*Рр>а>_ под действи-
действием Т приобрело фазу X, необходимо, чтобы
Комбинируя эти уравнения, имеем е±г1^/2с'+ = \Х\2 с'+еТг1^/2, что
невозможно, если не выполнено хотя бы одно из двух условий:
Приложение В 137
либо с+ = с_= 0, либо ег^ = 1. Таким образом, при ег^ Ф 1 инва-
инвариантность по отношению к обращению времени требует дву-
двукратного вырождения этих состояний, не считая того, которое
связано с их спинами.
Конечно, если имеется дополнительный оператор «внутрен-
«внутренней» симметрии S, под действием которого состояния преобразу-
преобразуются по закону
Cm _ „±гф/2щ
°™р,ст,± ~ е -р,а,+ '
можно переопределить оператор обращения времени как Т' = S~1T,
и такой оператор не будет перемешивать состояния 4^0+ друг с
другом. Только при отсутствии внутренней симметрии можно при-
приписать удвоение состояний частиц самому обращению времени.
Вернемся к вопросу о квадрате Т. Вторичное применение
преобразования B.В.8) дает
B.В.9)
Если, следуя Вигнеру, предположить, что Т2 пропорциона-
пропорционален единичному оператору, мы должны иметь е1^ = е~^, и так как
отсюда следует, что фаза действительна, она может равняться
только +1 или — 1. Выбор ег^=-1 все еще будет требовать дву-
двукратного вырождения одночастичных состояний, помимо того
вырождения, которое связано с их спином. В рамках гипотезы
Вигнера все частицы должны проявлять такое удвоение числа
состояний. Однако нет оснований не взять произвольную фазу ф в
B.В.8), которая могла бы равняться нулю для одних частиц, и
быть отличной от нуля для других. Поэтому тот факт, что для
наблюдаемых частиц не выявлено дополнительное двукратное
вырождение, не исключает возможности, что для каких-то дру-
других частиц это вырождение существует.
Можно также рассмотреть возможность более сложных
представлений оператора четности Р, для которого
Р*Р = V °? Ч1 „piп\
р,а,п /^ 'упт х-р,ст,т > (AB.IU)
т
где матрица if унитарна и в остальном произвольна. В противо-
противоположность обращению времени, всегда можно диагонализовать
138 Глава 2. Релятивистская квантовая механика
эту матрицу с помощью выбора базиса для состояний. Однако
такой выбор базиса может оказаться не тем, в котором опера-
оператор обращения времени действует просто, так что в принципе
операторы Р и Т совместно могут привести к дополнительным
вырождениям, которые не требуются операциями Р или Т по-
отдельности.
Как обсуждается в гл. 5, всякая квантовая теория поля
считается удовлетворяющей симметрии СРТ, действующей на
одночастичные состояния по правилу
где пс обозначает античастицу (или зарядово-сопряженную части-
частицу) к частице п. В этом преобразовании не допускаются никакие
фазы или матрицы (хотя, конечно, всегда можно ввести фазы или
матрицы, объединив СРТ с подходящими внутренними симметрия-
ми). Отсюда вытекает, что
(CPTJ?p>a>n = (-iJj4pp>_a>n , B.B.12)
так что предложенная Вигнером возможность появления знака
-(-IJ-7 при действии оператора (СРТJ в квантовой теории поля
не реализуется.
Пока Т является хорошей симметрией для некоторого класса
явлений, такой же хорошей симметрией является и комбинирован-
комбинированная инверсия СР = (СРТ)Т. Для состояний, обычным образом пре-
преобразующихся под действием Т,
%,,n « ?-Pl-a,n . B-B.13)
оператор СР также действует обычным образом:
СРЧ>р^п~Ч>_рапС, B.В.14)
Тогда оператор С = СРР просто заменяет частицы на античас-
античастицы и наоборот:
СХ*Р,°,п~\с,пС- B-В.15)
С другой стороны, если Т имеет нестандартное представление
B.В.8), из B.В.11) имеем:
Задачи 139
P;CJ;Tc. B.B.16)
В частности, возможно, что вырождение, отмеченное значками
±, может быть тем же самым, что и вырождение частица-
античастица, так что античастица (определенная посредством
СРТ) состояния *Р± есть *PT . В этом случае СР имело бы необыч-
необычное свойство не менять частицы на античастицы и обратно. До
тех пор, пока рассматриваются подобные частицы, СР и Т имеют
тот же смысл, который обычно имеют Р и СР. Но это не просто
вопрос определения — на другие частицы СР и Т действовали бы
обычным образом.
Неизвестны примеры частиц, реализующих нестандартные
представления инверсий, и мы далее такие возможности рассматри-
рассматривать не будем. Начиная с этого момента, будем считать, что инвер-
инверсии действуют так, как было принято в разделе 2.6.
Задачи
1. Пусть наблюдатель 0 видит W-бозон (спин 1 и масса т Ф 0) с
импульсом р, направленным вдоль оси у, и z-компонентой
спина а. Второй наблюдатель 0' движется относительно перво-
первого со скоростью v в направлении оси z. Как наблюдатель ()'
опишет состояние W-бозона?
2. Пусть наблюдатель 0 видит фотон импульсом р в направлении
оси у и вектором поляризации в направлении оси z. Второй
наблюдатель 0' движется относительно первого со скоростью v
в направлении оси z. Как ()' опишет состояние фотона?
3. Получите перестановочные соотношения генераторов группы
Галилея непосредственно из закона группового умножения
(не используя результаты для группы Лоренца). Включите
наиболее общий набор центральных зарядов, которые не
могут быть устранены переопределением генераторов группы.
4. Покажите, что операторы Р^ и W^W11, где 1УЦ =
коммутируют с операторами лоренцовских преобразований
ЩА, а).
140 Глава 2. Релятивистская квантовая механика
5. Рассмотрите физику в двух пространственных и одном вре-
временном измерении, предполагая инвариантность по отноше-
отношению к «группе Лоренца» 50B,1). Как можно было бы описать
спиновые состояния отдельной массивной частицы? Как эти
состояния вели бы себя по отношению к преобразованиям
Лоренца? Что можно сказать об инверсиях Р и Т?
6. Как и в задаче 5, рассмотрите физику в двух пространст-
пространственных и одном временном измерениях, предполагая инвариант-
инвариантность по отношению к «группе Лоренца» 50B,1). Как можно было
бы описать спиновые состояния отдельной безмассовой частицы?
Как эти состояния вели бы себя по отношению к преобразованиям
Лоренца? Что можно сказать об инверсиях Р и Т?
Список литературы
1. Dirac, P.A.M. The Principles of Quantum Mechanics, 4th edn
(Oxford University Press, Oxford, 1958) (есть рус. пер.: Дирак
П.А.М. Принципы квантовой механики. 2-е изд. М.: Наука, 1980).
2. Wigner, Е.Р. Gruppentheorie und ihre Anwendung auf die Quanten-
mechanik der Atomspektren (Braunschweig, 1931), pp. 251-253.
Для безмассовых частиц см.: Wigner, E.P., in Theoretical Physics
(International Atomic Energy Agency, Vienna, 1963), p. 64.
3. Wick, G.C., Wightman, A.S., and Wigner, E.P., Phys. Rev., 88,
101 A952).
За. См., например, в книге: S. Weinberg, Gravitation and Cosmology
(Wiley, New York, 1972), Section 2.1.
4. Inonii, E. and Wigner, E.P., Nuovo Cimento, 9, 705 A952).
5. Wigner, E.P., Ann. Math., 40, 149 A939).
6. Mackey, G.W., Ann. Math., 55, 101 A952); 58, 193 A953); Ada
Math., 99, 256 A958); Induced Representations of Groups and
Quantum mechanics (Benjamin, New York, 1968).
Список литературы 141
7. См., например, книги: Edmonds, A.R. Angular Momentum in
Quantum Mechanics (Princeton University Press, Princeton,
1957), ch. 4 (есть рус. пер.: Эдмондс А. Угловой момент
в квантовой механике. М.: Атомиздат, 1968); Rose, M.E.
Elementary Theory of Angular Momentum (John Wiley & Sons,
New York, 1957), ch. 4; Ландау Л.Д., Лифшиц Е.М. Квантовая
механика. Нерелятивистская теория. Изд. 3-е. М.: Наука,
1974, § 58; Wu-Ki Tung. Group Theory in Physics (World
Scientific, Singapore, 1985), Sections 7.3 and 8.1.
8. Lee, T.D. and Yang C.N., Phys. Rev., 104, 254 A956); Wu, C.S. et
al, Phys. Rev., 105, 1413 A957); Garwin, R., Lederman, L.,
and Weinrich, M., Phys. Rev., 105, 1415 A957); Friedman, J.J.
and Telegdi, V.V., Phys. Rev., 105, 1681 A957).
9. Christenson, J.H., Cronin, J.W., Fitch, V.L., and Turlay, R.,
Phys. Rev. Letters., 13, 138 A964).
10. Kramers, H., Proc. Acad. Sci. Amsterdam, 33, 959 A930); см.
также: Dyson, F.J., J. Math. Phys., 3, 140 A962).
11. Bargmann, V., Ann. Math., 59, 1 A954), Theorem 7.1.
12. См., например, книгу: Turnbull, H.W. and Aitken, A.C. An
Introduction to the Theory of Canonical Matrices (Dover Publi-
Publications, New York, 1961), p. 164.
13. См., например, книгу: Flanders, H. Differential Forms (Academic
Press, New York, 1963), Section 3.6.
14. Введение в теорию гомотопических классов и групп см., напри-
например, в книгах: Hocking, J.C. and Young, G.S. Topology (Addison-
Wesley, Reading, MA, 1961), Chapter 4; Nash, С and Sen, S.
Topology and Geometry for Physicists (Academic Press, London,
1983), Chapters 3 and 5.
15. Wigner, E.P., in: Group Theoretical Concepts and Methods in
Elementary Particle Physics, ed. by F. Giirsey (Gordon & Breach,
New York, 1964), p. 37.
Теория рассеяния
Общие принципы релятивистской квантовой механики, изло-
изложенные в предыдущей главе, применялись нами до сих пор
только к состояниям отдельных стабильных частиц. Такие одночас-
тичные состояния сами по себе не очень интересны. Что-то нетри-
нетривиальное может случиться только в том случае, когда две или бо-
более частицы взаимодействуют друг с другом.
Однако реальные эксперименты в общем случае не описыва-
описываются простой последовательностью взаимодействий частиц. Поэто-
Поэтому (по крайней мере, в ядерной физике и физике элементарных
частиц) рассматривается базисный модельный эксперимент, в ко-
котором несколько частиц сближаются друг с другом с макроскопиче-
макроскопически больших расстояний и взаимодействуют в микроскопически
малой области, после чего продукты взаимодействия вновь разле-
разлетаются на макроскопические расстояния.
Физические состояния до и после соударения образованы час-
частицами, столь удаленными друг от друга, что их можно считать
невзаимодействующими, так что эти состояния можно описывать
прямыми произведениями обсуждавшихся в предыдущей главе од-
ночастичных состояний. В таком эксперименте измеряемой величи-
величиной является распределение вероятностей, или «сечения», для пе-
переходов между начальным и конечным состояниями удаленных друг
от друга фактически невзаимодействующих частиц.
В данной главе описан формализм \ использующийся для вы-
вычисления этих вероятностей и сечений.
3.1. Состояния ин и аут 143
3.1. Состояния ин и аут
Если состояние образовано несколькими невзаимодейству-
невзаимодействующими частицами, можно считать, что под действием преобразо-
преобразований неоднородной группы Лоренца оно преобразуется как пря-
прямое произведение одночастичных состояний. Чтобы пометить
одночастичные состояния, будем использовать их 4-импульсы р^ и
2-компоненты спина (или спиральности для безмассовых частиц) а.
Кроме того, поскольку мы будем иметь дело с несколькими сорта-
сортами частиц, введем дополнительную дискретную метку п, отмечаю-
отмечающую тип частицы и включающую описание ее массы, спина, заря-
заряда и т. д. Общий закон преобразования имеет вид
a| C.1.1)
Лр1,<Т1,П1;Лр2,С12,И2>"- '
где W(A,p) — вигнеровское вращение B.5.10), a D^(W(A,р)) — из-
известные Bj + 1)-мерные унитарные матрицы представления трех-
трехмерной группы вращений. (Такое правило верно для массивных час-
частиц; для любой безмассовой частицы матрица заменяется на
5СТ'СТ ехр(га0(Л, р)), где 0 — угол, определенный формулой B.5.43).)
Состояния нормированы, как в B.5.19):
- C.1.2)
± перестановки,
причем включено слагаемое «+ перестановки», чтобы учесть воз-
возможность того, что произведена некоторая перестановка частиц п\,
п2, ..^принадлежащих такому же сорту, что и частицы пь п2, - (Как
подробнее обсуждается в гл. 4, если эта перестановка включает не-
нечетную перестановку частиц с полуцелым спином, следует брать
знак «минус», во всех остальных случаях — знак «плюс». В данной
главе все это несущественно.
144 Глава 3. Теория рассеяния
Мы часто используем сокращенное обозначение, заменяя весь
набор р1( о1; щ; р2, о2, п2, ... какой-нибудь одной греческой бук-
буквой, например, ОС. Приняв такие обозначения, можно записать C.1.2)
в виде:
(?„,,?„) = 8«х'-а), C.1.3)
где 5(ос' — ос) является суммой произведений дельта—функций и кро-
некеровских символов, стоящих в правой части C.1.2). Кроме того,
при суммировании по состояниям принимается, что
Ct(X...— / i w ^ w /^v... /n ч j4
В частности, соотношение полноты для состояний, нормирован-
нормированных как в C.1.3), имеет вид:
? = J da ?„(?„, 40. C.1.5)
Закон преобразования C.1.1) может быть справедлив только
для частиц, которые по тем или иным причинам не взаимодейству-
взаимодействуют. Если положить Л/ = 6ЦУ и ац = @, 0, 0, х), то ЩА,а) = ехр(гНх),
и среди прочего из C.1.1) вытекает, что *Ра должно быть собствен-
собственным состоянием энергии:
НЧ>а=ЕаЧ>а, C.1.6)
причем энергия есть просто сумма энергий отдельных частиц:
Я«=Р10+Р2°+-. C-1.7)
без каких-либо членов взаимодействия, т. е. слагаемых, которые
определяли бы связь между несколькими частицами.
С другой стороны, закон преобразования C.1.1) применим для
процессов рассеяния в моменты времени t —> +°°. Как пояснялось
в начале этой главы, в типичном опыте по рассеянию начальные
частицы в момент времени t —> -°° находятся так далеко друг от друга,
что их можно считать еще не взаимодействующими, а в конеч-
конечном состоянии при t —> +°° они разлетаются так далеко, что уже
не взаимодействуют. Поэтому имеется не один, а два набора
3.1. Состояния ин и аут 145
состояний, преобразующихся по закону C.1.1): ин-состояния ХР(Х+ и
аут-состояния Ч?а~ — это такие состояния, что если
над ними произвести наблюдения при t —> —°о и t —> °°, соответ-
соответственно *, то будут обнаружены частицы, описываемые
меткой а..
Поясним это определение. В том формализме, который ис-
используется здесь, для сохранения строгой лоренц—инвариантности
векторы состояний не меняются со временем, т. е. вектор состояния
Ч* описывает всю пространственно—временную историю системы час-
частиц. (Такое описание известно как гейзенберговская картина, в про-
противоположность шредингеровской картине, в которой операторы по-
постоянны, а состояния меняются со временем.) Таким образом, мы
не утверждаем, что Ч*^ являются пределами зависящего от време-
времени вектора состояния 4*(t) при t —> +°°.
Однако в определении состояний неявно присутствует выбор
инерциальной системы отсчета, из которой наблюдается система;
разные наблюдатели видят эквивалентные векторы состояний, но
не один и тот же вектор. В частности, предположим, что стан-
стандартный наблюдатель б устанавливает свои часы так, что значение
t = 0 соответствует какому-то моменту времени, когда происходит
процесс соударения. Другой наблюдатель С/, покоящийся относи-
относительно первого, устанавливает часы так, что t' = 0 соответствует t
= х, иными словами, временные координаты двух наблюдателей
связаны соотношением t' = t — т. Тогда, если наблюдатель б видит
систему в состоянии Ч*, то наблюдатель б' видит систему в состоя-
состоянии 1/A,-т)Ч/ = ехр(-гЯт)Ч/. Таким образом, то, как выглядит
состояние системы в состоянии задолго до или намного позже со-
соударения (какой бы базис не использовал бы наблюдатель б) опре-
определяется применением оператора трансляции во времени ехр(—iHx),
взятом при t —> —°° или при t —> +°°, соответственно. Конечно, если
состояние действительно является собственным состоянием опера-
оператора энергии, оно не может быть локализовано во времени — при-
применение оператора ехр(—iHx) приводит к появлению несуществен-
несущественного фазового множителя ехр(-гЕат). Поэтому мы должны
рассматривать волновые пакеты, т. е. суперпозиции состояний,
* Индексы «+» и «-» для ин- и аут-состояний могут показаться перепу-
перепутанными, но это дань традиции. Такой выбор определяется знаками в
формуле C.1.16).
146 Глава 3. Теория рассеяния
с ненулевой амплитудой gf(oc), медленно изменяющейся в некотором
интервале значений энергии АЕ. Состояния ин и аут определяются
так, что суперпозиция
exp(-zHT)Jdag(ocL'a± =
при х « —1 / АЕ или х » +1 / АЕ имеет вид соответствующей су-
суперпозиции состояний свободных частиц.
Чтобы конкретизировать сказанное, предположим, что гене-
генератор временных трансляций Я можно разбить на два слагаемых —
гамильтониан свободных частиц Яо и гамильтониан взаимодей-
взаимодействия V:
H = H0+V, C.1.8)
причем собственные состояния Фа гамильтониана Яо описываются так
же, как и собственные состояния XJ*<X+ и Ч^" полного гамильтониана:
Я0Фа=ЕаФа, C.1.9)
'а). C.1.10)
Подчеркнем, что спектр оператора Яо предполагается совпа-
совпадающим со спектром полного гамильтониана Я. Из этого следует,
что массы, входящие в Яо, должны быть реально измеряемыми
физическими массами, которые не обязательно совпадают с «голы-
«голыми» массами, входящими в Я. Разница, если она существует, долж-
должна быть включена не в Яо, а в гамильтониан взаимодействия V.
Кроме того, все возможные связанные состояния в спектре Я долж-
должны быть введены в Яо так, как будто они являются элементарными
частицами *.
Теперь ин- и аут-состояния могут быть определены как собст-
собственные состояния не Яо, а Я:
* В нерелятивистских задачах можно включить потенциальную энер-
энергию связи в Но. Приложение такого метода к «соударениям с перестрой-
перестройкой», когда некоторое связанное состояние присутствует только в началь-
начальном, но не в конечном состоянии, или наоборот, требует различного раз-
разбиения Н на Яо и V в начальном и конечном состояниях.
3.1. Состояния ин и аут 147
№^=?„4^, C.1.11)
удовлетворяющие условию:
Jdae-^gCa)^* ^ J da е^Е«тд(а)Фа C.1.12)
при х —> — °° или х —> +оо, соответственно.
Формулу C.1.12) можно переписать как требование, что
exp(-zHx)Jda g(a)xPa± -» exp(-zHox)Jda д(а)Фа
для х —» —оо или х —> +оо, соответственно. Иногда это соотношение
переписывают как формулу для ин- и аут-состояний:
4>а± = П(+оо)Фа , C.1.13)
где
s ехр(+Шх) ехр(-гЯох). C.1.14)
Однако следует иметь в виду, что П(+°о) в C.1.13) приводит
к осмысленным результатам, только действуя на гладкую суперпо-
суперпозицию собственных состояний оператора энергии.
Немедленным следствием определения C.1.12) является то, что
ин- и аут-состояния нормированы точно так же, как состояния сво-
свободных частиц. Чтобы увидеть это, заметим, что поскольку левая
часть в C.1.12) получена действием унитарного оператора ехр(—iHx)
на не зависящее от времени состояние, его норма не зависит от
времени и поэтому равна норме своего предельного значения при
х —» оо, т. е. норме в правой части формулы C.1.12):
J da d|3 ехр(-г(Еа - Ер )х) g(a) g ф) (Ч>^, ?„*)
= J da d|3 ехр(-г(Еа - Ер )х) д(а) д* ф) (Фр, Фа).
Так как это равенство предполагается выполненным для всех
гладких функций g(a), то скалярные произведения должны быть
равны друг другу:
148 Глава 3. Теория рассеяния
СРр*,^*) = (Фр,Фа) = 8(Р - а). C.1.15)
Для ряда приложений полезно получить явное, хотя и фор-
формальное решение уравнения C.1.11) на собственные значения энер-
энергии, удовлетворяющее условиям C.1.12). Запишем уравнение C.1.11)
в виде
Оператор Еа — Но не является обратимым; он дает нуль при
действии не только на свободное состояние частиц Фа, но и на кон-
континуум других состояний свободных частиц Фр той же энергии. Так
как при V —> 0 ин- и аут-состояния как раз равны Фа, представляется
естественным записать формальное решение как сумму Фа и сла-
слагаемого, пропорционального V:
?„* = 0a+(Ea-Ho±iE)-1V4fa±. C.1.16)
Иначе, производя разложение по полному набору состояний
свободных частиц:
C.1.18)
где ? - положительная бесконечно малая величина, введенная для
того, чтобы придать смысл оператору, обратному к Еа - Но. Полу-
Полученные уравнения носят название уравнений Липпмана-Швингера 1а.
Мы используем C.1.17) в конце следующего раздела, чтобы полу-
получить несколько более строгое доказательство ортонормированности
ин- и аут-состояний.
Остается показать, что уравнение C.1.17) с добавками +г?
и —г? в знаменателе удовлетворяет условию C.1.12) для ин- и аут-
состояний, соответственно. Для этого рассмотрим суперпозиции
, C.1.19)
3.1. Состояния ин и аут 149
. C.1.20)
Мы хотим показать, что при t —> -°° и ( ^ +°° ^ +(t) и *^д~№
стремятся соответственно к Ф9(?). После подстановки C.1.17) в C.1.19)
получаем:
Не задумываясь, поменяем местами порядок интегрирования и рас-
рассмотрим сначала интегралы
+ г,
За = da
Р J
(Еа - Ев ± ie)
При t —> — °° можно замкнуть контур интегрирования по энер-
энергетической переменной Еа большой полуокружностью в верхней
полуплоскости, причем вклад в интеграл от этой полуокружности
обращается в нуль благодаря множителю exp(-iEat), который экс-
экспоненциально мал при t —> — °° и 1тЕа > 0. Поэтому интеграл равен
сумме вкладов от особенностей подынтегрального выражения в верх-
верхней полуплоскости. В общем случае, можно ожидать, что функции
д(ос) и Та^ имеют особенности при значениях Еа с положительными
мнимыми частями, но, так же, как и для большой полуокружно-
полуокружности, их вклад экспоненциально подавляется при t —> —°°. (Конкрет-
(Конкретно, значение —t должно быть много больше, чем временная неопре-
неопределенность волнового пакета д(ос) и длительность соударения; именно
эти величины определяют, соответственно, положение особенно-
особенностей g(a) и Tfy* в комплексной плоскости Еа.) В результате остается
особенность в (Еа - Eg ±i?)~1, которая лежит в верхней полуплос-
полуплоскости для .%", но не для .%+. Отсюда мы заключаем, что .%+ обраща-
обращается в нуль при t —> —°°. Точно так же, при t —> +°° следует замкнуть
контур интегрирования в нижней полуплоскости, и в этом пределе
./р~ обращается в нуль. Мы приходим к выводу, что Ч* ~(?) стремятся
к Ф„(?) при t—>±°°, в согласии с основным условием C.1.12).
150 Глава 3. Теория рассеяния
В дальнейшем удобно использовать следующее представле-
представление множителя (Еа — En ± ге) в C.1.17). В общем случае
E), C.1.22)
Е
?2 ' C.1.23)
C.1.24)
При |Е| » ? функция C.1.23) ведет себя как 1/Е, и обращается
в нуль при Е —» 0, так что при ? —» 0 она ведет себя как «главное
значение» ,У/Е. Это позволяет придать смысл интегралам от произ-
произведения 1/Е на любую гладкую функцию от Е, исключив бесконеч-
бесконечно малую окрестность точки Е = 0. При |Е| 3> ? функция C.1.24)
порядка ?, и при интегрировании по всем Е дает единицу, так что
в пределе при ? —> 0 она ведет себя как всем знакомая 5-функция
5(Е). С учетом этого обстоятельства можно опустить метку ? в пра-
правой части C.1.22) и записать просто
'-?
(Е ± гЕ) = — + тб(Е). C.1.25)
h,
3.2. д^-матрица
В общем случае экспериментатор приготовляет при t —> -°° со-
состояние, содержащее определенный набор частиц, и затем измеря-
измеряет, во что превратится это состояние при t —> +°°. Если при t —> —°°
состояние приготовлено так, что содержит набор частиц ОС, то оно
есть ин-состояние Ч*а+; если обнаружено, что при t —> +°° состояние
содержит набор частиц C, то оно есть аут-состояние ^r". Амплитуда
вероятности перехода а —» C дается скалярным произведением
V)- C.2.1)
Этот набор комплексных амплитуд известен как 5-матрица 2.
Если взаимодействие отсутствует, ин- и аут-состояния совпадают,
3.2. S-матрица 151
и Spa = 5(ос - C). Таким образом, вероятность реакции а —»C пропор-
пропорциональна |^ра - 5(а - C)|2. В разделе 3.4 мы детально рассмотрим
связь Saa с измеряемыми вероятностями и сечениями.
Видимо, следует подчеркнуть, что ин- и аут-состояния живут
в двух разных гильбертовых пространствах. Они отличаются только
своими метками, тем, как они выглядят соответственно при
t —> — °° и t -) +°°. Всякое ин-состояние можно разложить по аут-
состояниям, причем коэффициентами разложения и будут элемен-
элементы .^-матрицы C.2.1).
Так как S$a — матрица, связывающая два набора ортонорми-
рованных состояний, она должна быть унитарной. Чтобы подробнее
показать это, применим условие полноты C.1.5) к аут-состояниям и
запишем
Используя C.1.15), находим:
5a), C.2.2)
или короче S^S = 1. Аналогично, используя полноту ин- состояний,
получаем:
Jdp57P5;p = 5(Y-a) C.2.3)
или иначе SS^ = 1 *.
Часто удобно вместо .^-матрицы иметь дело с оператором S,
для которого по определению матричные элементы между состоя-
состояниями свободных частиц равны соответствующим элементам
.^-матрицы:
= 5ра. C.2.4)
Явное, хотя и крайне формальное выражение C.1.13) для ин-
и аут-состояний позволяет получить формулу для оператора S:
* Альтернативное доказательство приведено в конце этого раздела. От-
Отметим, что для бесконечных матриц условия унитарности SfS — 1 и SSf— 1
не эквивалентны.
152 Глава 3. Теория рассеяния
S = П(оо)+П(-оо) = Ц"(+°о,-оо); C.2.5)
где
Щт,т0) = ВД+П(т0) = ехр(гЯот)ехр(-гЯ(т-то))ехр(-гЯото). C.2.6)
Мы используем это выражение в следующем разделе для про-
проверки лоренц-инвариантности .^-матрицы, и в разделе 3.5 при вы-
выводе формулы для ^-матрицы в зависящей от времени теории воз-
возмущений.
Методы предыдущего раздела можно применить для вывода
полезной альтернативной формулы для S-матрицы. Обратимся вновь
к формуле C.1.21) для ин- состояния Ч*+, перейдя на этот раз к
пределу t —> +°°. Теперь следует замкнуть контур интегрирования
по Еа в нижней полуплоскости. Хотя, как и ранее, особенности в
Тра+ и д(а) не дают вклада при t —> +°°, следует учесть вклад сингу-
сингулярного множителя (Еа — Е$ + ге). Контур идет по действительной
оси от Еа = — °о до Еа = +°о, и замыкается по большой полуокружно-
полуокружности в нижней полуплоскости, так что контур обходит особенность в
направлении по часовой стрелке. Согласно известной формуле тео-
теории вычетов вклад в интеграл по ^„определяется значением подынте-
подынтегрального выражения в точке Еа = Eg — г?, умноженному на (—2лг).
Иными словами, в пределе ? —» 0+ и t-> +°° интеграл по а в C.1.21)
асимптотически ведет себя как
и поэтому при t —> +°°
Однако разложение выражения C.1.19) для Ч/д+ по полному
набору аут-состояний дает:
Так как S$a содержит множитель 5(Ер - Еа), это можно пере-
переписать в виде:
3.2. S-матрица 153
после чего, используя определяющее свойство C.1.12) для аут- со-
состояний, находим асимптотическое поведение при t —> +°°:
4>g+(t) -
Сравнивая с нашим предыдущим результатом, находим:
a = дф) - 2мс| dad(Ea - Яр) д(а) Тр+а
или иначе
Spa = 8(Р - а) - 2мс8(Еа - Ер)Тра+. C.2.7)
Эта формула позволяет установить простое приближенное вы-
выражение для .^-матрицы. В случае слабого взаимодействия V можно
пренебречь разницей между ин- состояниями и состояниями сво-
свободных частиц в C.1.18), так что C.2.7) принимает вид:
). C.2.8)
Формула C.2.8) известна под названием борновского приближения 3.
Поправки более высокого порядка обсуждаются в разделе 3.5.
Уравнения Липпмана—Швингера C.1.16) для ин- и аут- состоя-
состояний можно использовать для доказательства 4 ортонормированно-
сти этих состояний и унитарности S—матрицы, а также для вывода
формулы C.2.7), не используя при этом предельных переходов
к t —> +°°. Во-первых, подставляя соотношение C.1.16) по очереди
слева и справа в матричный элемент (Ч'р*, УЧ?^) и приравнивая
результаты, находим, что
= (Фр, Wa±) + (^±,V(Ep -Ho +ie)-1V4>a±).
Суммируя по полному набору промежуточных состояний Ф^ при-
приходим к уравнению:
Глава 3. Теория рассеяния
-J
i-l г_ _ _ . i-l
C.2.9)
Для доказательства ортонормированности ин- и аут- состоя-
состояний, разделим C.2.9) на Еа — Е$± 2г?. Получим:
Т.
±
Sp - Еа ± 2г?
1 а^
Е„
- ER ± 2г? J
Т.
±
- Еу ± г?
Т.
±
уа
Е„ - Е„ ± г?
Слагаемые 2? в знаменателях левой части можно заменить на
?, так как главное в этих слагаемых - то, что они положительные
бесконечно малые величины. Теперь видно, что величина
5(Р-а)+ Тр"
(Еа-Ер±г?)
унитарна. С учетом C.1.17) это соответствует утверждению, что Ч1^
образуют два ортонормированных набора векторов состояний. Уни-
Унитарность ^-матрицы можно доказать аналогично, умножив C.2.9)
не на (Еа - Ер ± 2г?)"\ а на 5(Ер - Еа).
3.3. Симметрии S-матрицы
В этом разделе мы рассмотрим, во-первых, что означает инва-
инвариантность б'-матрицы по отношению к различным симметриям, и,
во-вторых, каковы условия, которые накладываются на гамильтони-
гамильтониан, чтобы обеспечить эти свойства инвариантности.
Лоренц^инвариантность
Для любого собственного ортохронного преобразования Лоренца
х —» Лж + а можно определить унитарный оператор U(A,a), задав
правило его действия на ин- или аут-состояния в соответствии с
формулой C.1.1). Когда говорится, что теория лоренц-инвариантна,
подразумевается, что один и тот же оператор U(A,a) действует по
формуле C.1.1) как на ин-, так и на аут-состояния. Поскольку
оператор U{A,a) унитарен, можно записать:
3.3. Симметрии S-матрицы 155
откуда, используя C.1.1), получаем свойство лоренц—инвариантности
(на самом деле, ковариантности) 5-матрицы: для произвольных
преобразований Лоренца Л% и преобразования трансляций ац S-
матрица преобразуется по правилу:
0 0 /0/0
Р1Р2-Р1 V2
C.3.1)
e
(Штрихи отличают конечные частицы от начальных; черта над
индексом указывает переменные, по которым идет суммирование.)
В частности, поскольку левая часть этого выражения не
зависит от ац, это же должно быть верно и для правой части, поэтому
.^-матрица обращается в нуль, если не выполнен закон сохранения
4-импульса. Следовательно, та часть .S-матрицы, которая описывает
реальные взаимодействия между частицами, может быть представ-
представлена в виде
- а) = -2тиМра54 (рр - ра). C.3.2)
(Однако, как будет видно в следующей главе, амплитуда Мра сама
содержит слагаемые, включающие новые множители с дельта-
функциями.)
Формулу C.3.1) следует рассматривать не как теорему, а как
определение того, что мы понимаем под инвариантностью 5-матри-
цы, т. к. только для ряда специально выбранных гамильтонианов
Глава 3. Теория рассеяния
существует унитарный оператор, действующий на ин- и аут-
состояния по формуле C.1.1). Следует сформулировать условия,
которым должнен удовлетворять гамильтониан, чтобы обеспечить
инвариантность 5-матрицы. Для этого удобно будет работать с
оператором S, определенным формулой C.2.4):
По определению состояний свободных частиц Фа из гл. 2, эти
состояния реализуют представление неоднородной группы Лоренца,
так что всегда можно определить унитарный оператор U0(A,a),
индуцирующий на этих состояниях преобразование C.1.1):
(лР1АлР2)°...
v <T)
Таким образом, формула C.3.1) будет верна, если этот унитарный
оператор коммутирует с оператором S:
UQ(A,ay1SUQ(A,a) = S.
Это условие можно выразить и с помощью инфинитезимальных
преобразований Лоренца. Как и в разделе 2.4, должен существовать
набор эрмитовых операторов — импульс Ро, угловой момент Jo и
генератор бустов Ко — который, действуя вместе с Но на состояния
свободных частиц, порождает бесконечно малые неоднородные
преобразования Лоренца. Формула C.3.1) эквивалентна утвержде-
утверждению, что .^-матрица при таких преобразованиях не изменяет-
изменяется, или что оператор S коммутирует со всеми генераторами:
[H0,S] = [P0,S] = [J0,S] = [K0,S] = 0. C.3.3)
Так как операторы Яо, Ро, Jo и Ко порождают инфинитези-
мальные преобразования Лоренца состояний Фа, они автоматически
удовлетворяют коммутационным соотношениям B.4.18)—B.4.24):
3.3. Симметрии S-матрицы 157
г ji т}-\ — л9 тк (-о q 4.\
г тг zrJ-\_.-P zrk ir> q n
L П? (lJ — iilc П ' ^o.u.u/
г p pi] _ 7-p р/с /о о 7^
L" П ? 0 -I iilc 0 ' ^«j.o. i /
ri<-i pJi_ _;n 5 (ЯЗЯ1
[JS,H0] = [PJ,H0] = [Р*,Р*] = 0, C.3.9)
rifi и i _ _,-pi C 3 101
где г, j, /с и т. д. принимают значения 1, 2, 3, а е^ — полностью
антисимметричный тензор, ?123 = +1-
Аналогично можно определить набор «точных генерато
ров» — операторов Р, J, К, которые вместе с полным гамильто-
гамильтонианом Н порождают преобразования C.1.1) при действии, скажем,
на ин- состояния. (Как уже отмечалось, не очевидно, что те же
операторы, действуя на аут-состояния, порождают те же преобра-
преобразования.) Исходя из структуры группы, получаем, что эти точные
генераторы удовлетворяют тем же самым перестановочным соот-
соотношениям:
[J\JJ] = i?ijkJ , C.3.11)
C.3.12)
с, C.3.13)
C.3.14)
C.3.15)
[J\H] = [P\H] = [P\Pj] = 0, C.3.16)
[К\Н] = -гР*. C.3.17)
Глава 3. Теория рассеяния
Практически во всех известных теориях поля эффекты взаимо-
взаимодействий сводятся к добавлению слагаемого V в гамильтониан, без
изменения импульса и углового момента:
H = H0+V, Р = Р0, J = J0. C.3.18)
(Единственным известным исключением являются теории с тополо-
топологически твистованными полями, например, теории с магнитными
монополями, в которых угловой момент состояний зависит от взаи-
взаимодействия.) Из соотношения C.1.18) вытекает, что удовлетворяются
перестановочные соотношения C.3.11), C.314) и C.3.16), если счи-
считать, что оператор взаимодействия коммутирует с операторами им-
импульса и углового момента свободных частиц:
[V,P0] = [V,J0] = 0. C.3.19)
Теперь из уравнения Липпмана—Швингера C.1.16) или, экви-
эквивалентно, из C.1.13) легко получить, что операторами, генерирую-
генерирующими трансляции и вращения при действии на ин- (и аут-) состоя-
состояния действительно являются операторы Ро и Jo. Кроме того, видно,
что Ро и Jo коммутируют с оператором U{t, t0), определенным фор-
формулой C.2.6), а следовательно и с .^-оператором U(°°, —°°). Далее, мы
уже знаем, что .^-оператор коммутирует с Яо, так как в обоих сла-
слагаемых в C.2.7) содержатся дельта-функции, выражающие закон
сохранения энергии. Таким образом, остается показать, что гене-
генератор буста Ко коммутирует с оператором S.
С другой стороны, нельзя приравнять генератор буста К его
аналогу для свободных частиц Ко, так как в этом случае из C.3.15)
и C.3.8) будет следовать, что Н = Но, что очевидно неверно при
наличии взаимодействий. Таким образом, добавляя взаимодействие
V к Но, мы должны добавить также и поправку W к генератору
буста Ко:
K = K0+W. C.3.20)
Из оставшихся перестановочных соотношений остановимся на
C.3.17), которое теперь принимает вид
[K0,V] = -[W,H]. C.3.21)
3.3. Симметрии S-матрицы 159
Само по себе соотношение C.3.21) бессодержательно, так как
для любого V можно всегда определить W, задав его матричные
элементы между собственными состояниями *Ра и *Рр гамильтониана
Я в виде —(xilp,[K.0,V]xila)/(Ep — Ea).. Напомним, что ключевым мо-
моментом для лоренц—инвариантности теории является не то, что обя-
обязательно должен существовать набор точных генераторов, удов-
удовлетворяющих соотношениям C.3.11)—C.3.17), а то, что эти операторы
должны одинаково действовать на ин- и аут- состояния. Просто найти
оператор К, удовлетворяющий C.3.21), недостаточно. Это соотно-
соотношение становится существенным, если добавить требование, что
матричные элементы W должны быть гладкими функциями энер-
энергий, в частности, не должны иметь особенностей вида {Ea —Eg)'1.
Докажем теперь, что из C.3.21) и подходящего условия гладкости
W действительно вытекает оставшееся условие лоренц—инва-
лоренц—инвариантности [Ко,6"] = 0.
Чтобы показать это, рассмотрим коммутатор Ко с оператором
U(t, t0) при конечных t и t0. Используя формулу C.3.10) и тот факт,
что Ро коммутирует с Я, получим:
[К0,ехр(гЯ0?)] = -tP0 ехр(гЯ0?),
В то же время из перестановочного соотношения C.3.21) (или,
эквивалентно, из C.3.17)) вытекает:
[К,ехр(гЯ?)] = -?Рехр(Ш?) = -tP0
В коммутаторе Ко с U операторы импульса сокращаются, так
что
, C.3.22)
где
W(t) = exp(iHot)W exp(-iHot). C.3.23)
Если матричные элементы W между собственными состояниями
Яо являются достаточно гладкими функциями энергии, матричные
элементы W(t) между гладкими суперпозициями собственных состоя-
состояний энергии обращаются при t —> ±°° в нуль, так что из C.3.22) в
результате получается
Глава 3. Теория рассеяния
0 = [К0,Щоо-оо)] = [К0,5], C.3.24)
что и следовало доказать. Этот результат очень важен: соотношение
C.3.21) совместно с условием гладкости матричных элементов W,
обеспечивающих обращение в нуль W(t) при t —> +°°, является
достаточным условием лоренц-инвариантности ^-матрицы. Условие
гладкости довольно естественно, так как оно весьма напоминает
условие на матричные элементы V, необходимое для того, чтобы
V{t) обращалось в нуль при t —>±°°, как и требуется для подкрепления
самой идеи ^-матрицы.
Формулу C.3.22) при t = 0 и t0 = +°° можно использовать для
доказательства того, что
1Ш(+°о) = П(+°о)К0, C.3.25)
где П(±°о) является согласно C.1.13) тем оператором, который
переводит состояние свободной частицы Фа в соответствующее ин-
или аут-состояние Ч^*. Кроме того, из C.3.18) и C.3.19) тривиально
следует, что это же верно для импульса и углового момента:
0, C.3.26)
0. C.3.27)
Наконец, так как все Фа и Ч^* являются собственными состояниями
Яо и Я, соответственно, с одним и тем же собственным значением
Еа, то
C.3.28)
Из формул C.3.25)-C.3.28) следует, что в рамках наших пред-
предположений ин- и аут-состояния действительно преобразуются под
действием преобразований Лоренца так же, как и состояния сво-
свободных частиц.
Кроме того, поскольку это преобразования подобия, мы ви-
видим, что точные генераторы К, Р, J и Я удовлетворяют тем же
перестановочным соотношениям, что и Ко, Ро, Jo и Яо. Именно по-
поэтому при доказательстве лоренц—инвариантности S—матрицы не
требуется использовать другие включающие оператор К переста-
перестановочные соотношения C.3.12), C.3.13) и C.3.15).
3.3. Симметрии S-матрицы 161
Внутренние симметрии
Существуют различные симметрии, например, симметрия
относительно взаимной перестановки нейтронов и протонов в ядер-
ядерной физике или симметрия относительно операции «зарядового
сопряжения» для частиц и античастиц, не имеющие никакого пря-
прямого отношения к лоренц—инвариантности и, более того, выглядя-
выглядящие одинаково во всех инерциальных системах отсчета. Подобное
преобразование симметрии Т действует в гильбертовом простран-
пространстве физических состояний как некоторый унитарный оператор U(T),
который индуцирует линейные преобразования по индексам, отме-
отмечающим сорта частиц:
<— ~ ' • «1% ^ ' «2n2 ' Pioi%;p2o2n2;...' C.3.29)
В соответствии с общей дискуссией в гл. 2, оператор U(T)
должен удовлетворять групповому правилу умножения
U{f)U{T) = U{TT), C.3.30)
где ТТ — преобразование, полученное сначала действием преоб-
преобразования^ Т, а затем другого преобразования Т. Действуя опера-
оператором U(T) на C.3.29), видим, что матрицы CJ) удовлетворяют тому
же правилу:
%Т)%Т) = %ТТ). C.3.31)
Кроме того, беря скалярное произведение состояний, полу-
полученных действием оператора U(T) на два разных ин- или аут-
состояния, и используя условие нормировки C.1.2), находим, что
матрица У)(Т) должна быть унитарной:
3t(T) = ®-1(T). C.3.32)
Наконец, вычисляя скалярное произведение состояний,
полученных действием оператора U(T) на одно аут- и одно ин-
состояние, получаем, что CJ)(T) коммутирует с .^-матрицей в том
смысле, что
IQ2 Глава 3. Теория рассеяния
C.3.33)
JV; ~ ^р[с{п[;р'2с'2п'2;...;р1с1п1;р2с2п2;... ¦
Это есть определение того, что подразумевается под словами:
«теория инвариантна по отношению к преобразованиям внутренней
симметрии Т», так как для вывода C.3.33) все еще следует показать,
что один и mom же унитарный оператор U(T) индуцирует преобра-
преобразование C.3.29) как ин-, так и аут-состояний. Это будет выполнено,
если существует «невозмущенный» оператор преобразования U0(T),
индуцирующий такие преобразования состояний свободных частиц,
и коммутирующий как с гамильтонианом свободных частиц, так
и с гамильтонианом взаимодействия:
170-1(Т)Я0170(Т) = Я0, C.3.35)
Uq1{T)VU0{T) = V. C.3.36)
С помощью уравнения Липпмана-Швингера C.1.17) или
формулы C.1.13) находим, что оператор U0(T) индуцирует преоб-
преобразования C.3.29) ин- и аут-состояний, а также состояний сво-
свободных частиц, так что можно вывести формулу C.3.29), взяв U0(T)
вместо оператора U(T).
Очень важным с физической точки зрения частным случаем
является преобразование симметрии, описываемое однопараметри-
ческой группой Ли, когда Т — функция одного параметра 6, причем
Т(ё)Т(9) = Т(9 + 9). C.3.37)
Как показано в разделе 2.2, в этом случае соответствующие опера-
операторы в гильбертовом пространстве должны иметь вид:
17(Т(9)) = exp(zQ6), C.3.38)
где Q — эрмитов оператор. Аналогично, матрицы У)(Т) имеют вид
3.3. Симметрии S-матрицы 163
%n(TF)) = 8Я,Я ехр(гдп6), C.3.39)
где qn — набор действительных, зависящих от сорта частиц чисел.
В этом случае из формулы C.3.33) следует, что q сохраняются:
матричные элементы S$a обращаются в нуль, кроме случая, когда
Чп[+Aп'2+--- = Чп1+Чп2+--- C.3.40)
Классическим примером такого закона сохранения является
сохранение электрического заряда. Кроме того, во всех известных
процессах сохраняются барионное число (число барионов, т. е. про-
протонов, нейтронов и гиперонов, минус число их античастиц) и леп-
тонное число (число лептонов, т. е. электронов, мюонов, т-лепто-
нов и соответствующих нейтрино, минус число их античастиц).
Правда, как мы увидим в т. II, считается, что эти законы сохра-
сохранения выполняются лишь с очень хорошей степенью приближе-
приближения к реальности. Существуют и другие аналогичные законы со-
сохранения, определенно являющиеся приближенными. Примером
может служить сохранение величины, названной странностью,
которая была введена для объяснения относительно большого вре-
времени жизни ряда частиц, открытых в космических лучах Рочесте-
ром и Батлером 5 в 1947 году. Так, мезонам, называемым сейчас
К+ и К0, приписывается значение странности +1, а гиперонам Л°,
Е+, Е°, Е~ - значение -1, а у более привычных протонов, нейтро-
нейтронов и л-мезонов (пионов) странность считается равной нулю *. Со-
Сохранение странности в сильных взаимодействиях объясняет, по-
почему странные частицы рождаются всегда вместе, например, в
реакции %+ + п —» К+ + Л°, в то время, как относительно медлен-
медленные распады странных частиц в нестранные, например, Л° —> р + ж+
и К+ —» %++%° свидетельствуют, что взаимодействия, не сохраня-
сохраняющие странность, очень слабы.
Классическим примером «неабелевой» симметрии, генераторы
которой не коммутируют друг с другом, является симметрия относи-
относительно преобразований изотопического спина, предложенная в
* Верхние индексы указывают на электрический заряд частиц в
единицах абсолютного значения заряда электрона. «Гипероном» называют
любую частицу, обладающую ненулевым значением странности и
барионным числом, равным единице.
Глава 3. Теория рассеяния
1937 году 6на основании эксперимента 7, показавшего существование
сильных протон-протонных взаимодействий, аналогичных взаимо-
взаимодействиям протонов с нейтронами. Математически группой сим-
симметрии является группа SUB), совпадающая с накрывающей группой
для группы трехмерных вращений. Генераторы группы SUB) обозна-
обозначаются tj, г = 1, 2, 3, и удовлетворяют перестановочным соотно-
соотношениям, аналогичным B.4.18):
В ситуациях, когда имеет место симметрия по отношению
к преобразованиям изотопического спина, частицы образуют вырож-
вырожденные мультиплеты, характеризующиеся целым или полуцелым
числом Т, причем каждая из BТ + 1) компонент такого мультиплета
отличается значением t3, как в случае вырожденных спиновых
мультиплетов, существование которых требуется инвариантностью
относительно вращений. Такими мультиплетами являются: нуклоны
р и п с Т = 1/2 и t3 = 1/2, -1/2; пионы ж+, л°, 7Г с Т = 1 и t3 = 1, 0, -1;
Л°-гиперон с Т = 0 и t3 = 0. Эти примеры иллюстрируют соотношение
между электрическим зарядом Q, третьей компонентой изото-
изотопического спина t3, барионным числом В и странностью S:
B + S
Это соотношение было первоначально выведено на основании на-
наблюдавшихся правил отбора, однако Гелл-Манн и Нееман в 1960 году
показали, что оно есть следствие того, что изоспин Т и «гиперза-
«гиперзаряд» Y = В + S «погружаются» в алгебру Ли более широкой, но и
более сильно нарушенной неабелевой внутренней симметрии, осно-
основанной на неабелевой группе SUC). Как мы увидим в т. II, в наши
дни в рамках современной теории сильных взаимодействий — кван-
квантовой хромодинамики — изоспиновая и SUC) симметрия восприни-
воспринимаются как случайные следствия, вытекающие из малых значений
масс двух или трех легчайших кварков.
Следствия изотопической симметрии для реакций между сильно
взаимодействующими частицами могут быть получены теми же зна-
знакомыми методами, которые были развиты для вывода следствий
инвариантности относительно вращений. В частности, для двухча-
двухчастичной реакции А + В —» С + D таз формулы C.3.33) вытекает, что
3.3. Симметрии S-матрицы 165
.^-матрица может быть представлена в виде (опущены все индексы,
кроме изотопических):
где С- ¦ (jo;OiO2) — обычный коэффициент Клебша-Гордана для
образования состояния со спином j и третьей проекцией о из состо-
состояний со спинами jl и j2 и третьими проекциями с^ и G2', ST — «приве-
«приведенная» .^-матрица, зависящая от Т и от всех опущенных импульс-
импульсных и угловых переменных, но не от третьих проекций изоспина
^4з> ^вз> ^сз> ^оз- Конечно, это и все другие следствия изотопической
инвариантности являются только приближенными, т. к. изотопичес-
изотопическая симметрия не сохраняется в электромагнитных (и других) вза-
взаимодействиях, о чем свидетельствует то, что различные члены од-
одного изоспинового мультиплета, например, р и п, имеют разные
электрические заряды и немного отличаются по массе.
Четность
Если принять, что симметрия относительно преобразования
х —» -х действительно имеет место, то должен существовать уни-
унитарный оператор Р, под действием которого как ин-, так и аут-
состояния преобразуются как прямые произведения одночастичных
состояний:
где г\п — внутренняя четность частиц сорта п, а $Р меняет знак
у пространственных компонент р^. (Это правило верно для массивных
частиц; модификация для безмассовых частиц очевидна.)
Условие сохранения четности для .^-матрицы принимает вид
(о. о.
Как и в случае внутренних симметрии, оператор Р, удовлет-
удовлетворяющий C.3.41), действительно существует, если оператор Ро,
Глава 3. Теория рассеяния
который, по определению, точно так же действует на состояния
свободных частиц, коммутирует с V и Яо.
Фазы г\п могут быть найдены либо из динамических моделей,
либо из эксперимента, но при этом их невозможно однозначно оп-
определить, так как всегда можно переопределить оператор Р, скомби-
скомбинировав его с любым сохраняющимся оператором внутренней сим-
симметрии. Например, если Р сохраняется, то это же верно и для
оператора
Р' = Р ехр(гаВ + фЬ + iyQ),
где В, L и Q — барионное число, лептонное число и электрический
заряд, соответственно, а, C, у - произвольные действительные фазы;
таким образом и Р, и Р' можно считать операторами четности. Ней-
Нейтрон, протон и электрон обладают разными комбинациями значе-
значений В, L и Q, так что подходящим выбором фаз ОС, C и у можно
определить внутренние четности этих трех частиц равными +1. Од-
Однако, как только это сделано, внутренние четности других частиц,
например, заряженного пиона (который может быть испущен в пе-
переходе п —> р + ж~) уже не могут быть произвольными. Кроме того,
внутренняя четность любой частицы типа нейтрального пиона %°,
не характеризующейся никакими сохраняющимися квантовыми чис-
числами, всегда имеет смысл.
Предыдущие замечания позволяют понять, почему внутрен-
внутренние четности должны всегда иметь значения ±1. Легко видеть, что
оператор пространственной инверсии Р удовлетворяет закону груп-
группового умножения Р2 = 1; однако сохраняющийся оператор четнос-
четности может не совпадать с ним, а отличаться некоторым фазовым
преобразованием. В любом случае, выполнено или нет условие Р2 = 1,
оператор Р2 ведет себя как оператор преобразования внутренней
симметрии:
Р2Ч>± = л2 л2 Ч>±
р1а1п1;р2а2п2',... in1 in2"' PiCJ1n1;p2cJ2rt2'"-'
Если эта внутренняя симметрия есть часть непрерывной груп-
группы симметрии фазовых преобразований, подобных группе умноже-
умножения на фазу ехр(гаВ + zCL + iyQ) с произвольными значениями а, C
и у, то обратное преобразование — квадратный корень 1Р — тоже
должно входить в эту группу, причем JP2P2 = 1, [IP, P] = 0. (Напри-
(Например, если Р2 = ехр(гоВ + ...), то IP = exp(-^iaB + ...).) Теперь можно
3.3. Симметрии S-матрицы 167
определить новый оператор четности Р' = Р1Р, для которого Р'2 = 1.
Этот оператор сохраняется не в меньшей степени, чем Р, поэтому
нет никаких причин, по которым его нельзя назвать настоящим
оператором четности. В этом случае внутренние четности могут иметь
только значения +1.
Единственный тип теорий, в которых не всегда возможно оп-
определить четность таким образом, чтобы все внутренние четности
имели значения ±1, это тот, в котором существует некоторая дис-
дискретная внутренняя симметрия, не являющаяся составной частью
какой-то непрерывной группы симметрии фазовых преобразова-
преобразований 10. Например, как следствие закона сохранения углового мо-
момента, полное число F всех частиц с полуцелым спином может
изменяться только на четное число, так что сохраняется оператор
внутренней симметрии (-1)F. У всех известных частиц полуцелого
спина сумма В + L барионного и лептонного чисел принимает не-
нечетные значения, поэтому, насколько мы знаем, (-1)F = (-1)в + L.
Если это верно, то (—1)F есть часть непрерывной группы симмет-
симметрии, состоящей из операторов ехр(г(Х(В + L)) с произвольным дей-
действительным ос, причем оператор обратного квадратного корня есть
ехр(-мг(В + L)/2). В этом случае, если Р2 = (-1)F, то Р можно пере-
переопределить так, чтобы все внутренние четности равнялись +1. Од-
Однако, если когда-нибудь будут открыты частицы полуцелого спи-
спина с четным значением В + L (например, так называемые
майорановские нейтрино, у которых j = \ и В + L = 0), то можно
будет построить оператор Р2 = (—1)F, не имея при этом возможно-
возможности переопределить сам оператор четности так, чтобы его соб-
собственные значения равнялись только +1. Конечно, в этом случае
Р4= 1, так что все частицы имели бы внутренние четности либо
+1, либо +г (как у майорановских нейтрино).
Из формулы C.3.42) следует, что если произведение внутрен-
внутренних четностей в конечном состоянии равно произведению внутрен-
внутренних четностей в начальном состоянии или этому произведению, взя-
взятому со знаком «минус», то S—матрица должна быть соответственно
четной или нечетной по отношению к замене знаков у всех 3-им-
пульсов. Например, в 1951 году наблюдалось11, что пион может по-
поглощаться дейтроном из основного состояния %~d атома с I = 0
в реакции %~ + d —> п + п. (В разделе 3.7 мы покажем, что квантовое
число I орбитального углового момента можно использовать в реля-
релятивистской физике так же, как и в нерелятивистской квантовой
Глава 3. Теория рассеяния
механике.) Полный угловой момент начального состояния j' = 1 (спи-
(спины пиона и дейтрона равны нулю и единице, соответственно), так
что конечное состояние должно иметь орбитальный угловой момент
(=1 и суммарный спин нейтронов s = 1. (Другие возможности:
1= I, s = 0; I = 0, s = 1; I = 2, s = 1, разрешенные законом сохране-
сохранения углового момента, запрещены требованием антисимметрии ко-
конечного состояния относительно перестановки двух нейтронов.) Так
как I = 1 в конечном состоянии, матричный элемент нечетен отно-
относительно изменения направления всех 3-импульсов, так что можно
сделать вывод, что внутренние четности частиц в этой реакции дол-
должны быть связаны соотношением
Известно, что дейтрон является связанным состоянием прото-
протона и нейтрона с четным угловым моментом (в основном, I = 0), и,
как мы видели, протону и нейтрону можно приписать одинаковую
внутреннюю четность, так что v\d = r|n2. Отсюда можно сделать вы-
вывод, что Ц%- = ~1, т. е. пион является псевдоскалярной частицей.
Было показано, что %+ и %° также имеют отрицательную внутрен-
внутреннюю четность, как и следует ожидать, исходя из симметрии между
этими частицами (изотопической инвариантности).
Наличие у пиона отрицательной внутренней четности приво-
приводит к некоторым удивительным следствиям. Частица со спином нуль,
распадающаяся на три пиона, должна обладать внутренней четно-
четностью г\%3 = — 1, так как в инерциальной системе, в которой распада-
распадающаяся частица покоится, в силу инвариантности по отношению к
вращениям матричный элемент может зависеть только от взаим-
взаимных скалярных произведений импульсов пионов, которые все чет-
четны относительно изменения знака всех импульсов. (Смешанное ска-
скалярное произведение р1-(р2 X Рз), построенное из трех импульсов
пионов, обращается в нуль, так как рх + р2 + р3 = 0.) По той же
причине частица со спином нуль, распадающаяся на два пиона,
должна иметь внутреннюю четность х\^ = +1. В частности, среди
странных частиц, открытых в конце 1940 годов, казалось, обнару-
обнаружились две разные частицы с нулевым спином (что было установ-
установлено по угловому распределению продуктов их распада). Одна из
частиц, названная х, была идентифицирована по распаду на три
пиона, и поэтому ей была приписана четность —1, а другая частица
3.3. Симметрии S-матрицы 169
6 была обнаружена по распаду на два пиона, и ей была приписана
четность +1. Открытие превратилось в проблему, так как более де-
детальное изучение свойств х и 6 все яснее показывало, что эти час-
частицы имеют одинаковые массы и времена жизни. После многих пред-
предлагавшихся решений этой загадки, Ли и Янг в 1956 году разрубили
гордиев узел и предположили, что х и 6 представляют одну и ту же
частицу (известную сейчас как К*), но в слабых взаимодействиях,
ответственных за распад этой частицы, просто не сохраняется чет-
четность 12.
Как мы детально покажем в следующем разделе этой главы,
вероятность физического процесса а —» C (где а Ф C) пропорцио-
пропорциональна |*S*p(X|2, причем коэффициенты пропорциональности инвари-
инвариантны относительно изменения знака всех 3-импульсов. До тех пор,
пока состояния а и C содержат определенное число частиц каждо-
каждого типа, фазовые множители в C.3.42) несущественны при вычис-
вычислении |б"ра|2, и из C.3.42) вытекает, что вероятность процесса
ОС —> C инвариантна по отношению к изменению знака всех 3-им-
3-импульсов. Как мы видели, для распадов К-мезона на два или три
пиона это свойство — тривиальное следствие инвариантности по
отношению к вращениям, но в более сложных процессах оно дает
нетривиальные ограничения на вероятности. Так, следуя тео-
теоретическим предложениям Ли и Янга, By вместе с группой иссле-
исследователей из Национального Бюро стандартов США измерила
угловое распределение электронов в конечном состоянии в C-рас-
паде поляризованных ядер Со60 —> Ni60 + е~ + V 13. (Импульсы
антинейтрино или ядра никеля в этом эксперименте не измерялись.)
Обнаружилось, что электроны предпочтительно вылетают в на-
направлении, противоположном направлению спина распадающего-
распадающегося ядра, что было бы невозможно, если бы вероятность процесса
была инвариантной относительно замены всех 3-импульсов на про-
противоположные. Похожий результат был получен при изучении
распада положительного мюона (поляризованного в процессе обра-
образования в реакции ж+ —> ц+ + v) на позитрон, нейтрино и антиней-
антинейтрино 14. Таким образом, стало ясно, что четность действительно
не сохраняется в процессах слабого взаимодействия, ответствен-
ответственного за эти распады. Тем не менее, по причинам, обсуждаемым
в разделе 12.5, четность сохраняется в сильных и электромагнит-
электромагнитных взаимодействиях и поэтому продолжает играть важную роль
в теоретической физике.
270 Глава 3. Теория рассеяния
Обращение времени
Мы видели в разделе 2.6, что оператор обращения времени Т,
действуя на одночастичное состояние Ч*р>С;П, дает состояние
Ч'лэ-ап с перевернутыми спином и импульсом, умноженное на фазу
С,п(—1У~С. Многочастичное состояние, как обычно, преобразуется как
прямое произведение одночастичных состояний, не считая того, что
поскольку речь идет о преобразовании обращения времени, следу-
следует ожидать, что ин- и аут- состояния поменяются местами:
р1а1п1;р2а2п2;... ^щу ' ^>п2У ' ••• ¦Тр1-а1п1;.Тр2-а2п2;...' (о.о.ъо)
(Опять же, это верно для массивных частиц; необходимые для
безмассовых частиц модификации очевидны.) Далее будет удобно
записывать эту формулу кратко в виде
РР* = ч?а , C.3.44)
где ,Т содержит в себе изменение знака 3-импульсов и спинов,
а также умножение на фазовые множители, выписанные в C.3.43).
Так как Т — антиунитарный оператор, то
(XV— Щ+4) — (ТУЦ+ ТШ~1 14 Ч 4R\
I Ip , Т^у I — I I T^y , I Ip I , I UiOiU I
и условие инвариантности 5-матрицы по отношению к обращению
времени принимает вид
"В а = ^.j/a .j/f> > C.3.46)
или, подробнее,
с
ир[с[п{;р2с'2п2;...,р1с1п1;р2с2п2;...
= ?>п'1(-1У1 ^Сп^-1K2 °2..-С пД-1K1 Ol^n2(-1K2 °2-.. C.3.47)
W С*
Рр1-о1п1;Рр2-о2п2;..:,Рр'1-о'1п'1;Рр2-а2п2;... •
Заметим, что в дополнение к обращению импульсов и спинов поме-
поменялись местами начальные и конечные состояния, как и следовало
ожидать для симметрии, включающей обращение времени.
3.3. Симметрии S-матрицы 171
5-матрица будет удовлетворять этому закону преобразования,
если оператор То, индуцирующий преобразования обращения вре-
времени на состояниях свободных частиц,
Т0Ф« = Ф.лх C.3.48)
коммутирует не только с гамильтонианом свободных частиц (что
выполняется автоматически), но и с гамильтонианом взаимодей-
взаимодействия:
VHoTo = Яо , C.3.49)
T0-1VT0=V. C.3.50)
В этом случае можно положить Т = То и воспользоваться соотноше-
соотношением C.1.13) или C.1.16), чтобы показать, что преобразования обра-
обращения времени действуют именно так, как утверждается в C.3.44).
Например, действуя оператором Т на уравнение Липпмана—Швин-
гера C.1.16) и пользуясь C.3.48)-C.3.50), имеем
где из-за антиунитарности Т изменен знак у фактора ±ге. Это уравне-
уравнение Липпмана-Швингера для Ч*|а, что и подтверждает формулу
C.3.44). Аналогично, поскольку Т — антиунитарный оператор, он из-
изменяет знак i в экспоненте в выражении для ?l(t), так что
и опять получается формула C.3.44).
В противоположность сохранению четности, условие инвари-
инвариантности относительно обращения времени C.3.46) не говорит нам в
общем случае, что вероятность процесса а —» C совпадает с вероят-
вероятностью процесса ,Ти —> ,Tfi. Однако нечто подобное имеет место в
случаях, когда .^-матрица имеет вид
где матричные элементы S^ малы, а матричные элементы S^ для
какого-то конкретного процесса равны нулю, хотя в общем случае
Глава 3. Теория рассеяния
они много больше, чем матричные элементы S^\ (Например, можно
рассмотреть процесс ядерного C-распада N —» N' + е~ + V, причем
?@) — та часть 5-матрицы, которая определяется сильным ядер-
ядерным и электромагнитным взаимодействиями, а слагаемое S^ — по-
поправка к .^-матрице, целиком обусловленная слабыми взаимодей-
взаимодействиями. Вразделе 3.5 показывается, как можно в этих случаях
получить выражение для .^-матрицы в виде C.3.51) с помощью «бор-
новского приближения искаженных волн». В некоторых случаях S^
— просто единичный оператор.) В первом порядке по S^ условие
унитарности для .^-оператора записывается в виде
Используя равенство нулевого порядка S^S^ = 1, получаем для
S^ условие действительности:
SW=-SmS^Sm. C.3.52)
Если матрица S^\ так же, как и S^°\ удовлетворяет условию обра-
обращения времени C.3.46), соотношение C.3.52) можно представить в
следующем виде:
Поскольку S^ — унитарный оператор, вероятности процессов
а-)ри ,Уа —»,УC оказываются одинаковыми, если просуммировать
по наборам ./ и 3- начальных и конечных состояний, являющихся
полными по отношению к S^°\ (Под словом «полный» здесь подразу-
подразумевается, что если матричные элементы S ) не равны нулю и либо
а, либо а' принадлежат ./, то оба состояния принадлежат ./; анало-
аналогичное утверждение верно и для ,?.) В простейшем случае «полные»
наборы ./ и -J содержат каждый одно состояние; это означает, что
как начальное, так и конечное состояния являются собственными
векторами S^ с собственными значениями е г а и е р, соответ-
соответственно. (Величины 5а и бп называются «сдвигами фаз»; они дей-
действительны, так как S^ унитарна.) В этом случае формула C.3.53)
принимает простой вид
3.3. Симметрии S-матрицы 173
откуда ясно, что абсолютная величина .^-матрицы для процесса
а —» C такая же, как и для процесса ,У(Х —» ,Ур\ Именно так обстоит
дело в ядерном C-распаде (в приближении, когда можно прене-
пренебречь сравнительно слабым кулоновским взаимодействием между
электроном и ядром в конечном состоянии), поскольку и началь-
начальное, и конечное состояние являются собственными состояниями S-
матрицы сильного взаимодействия (с 5а = 5р = 0). Отсюда, если при-
принимается инвариантность относительно обращения времени,
дифференциальная вероятность C-распада не должна изменяться,
если изменить знаки импульсов и z-компонент о спинов всех час-
частиц. Это предсказание не противоречило экспериментам, проведен-
проведенным в 1956 году 13>14, в которых было обнаружено несохране-
несохранение четности; так, инвариантность относительно обращения време-
времени совместима с наблюдением, что электроны от распада ядра
Со60 —> Ni60 + е~ + V преимущественно испускаются в направлении,
противоположном направлению спина ядра Со60. Как описано ниже,
в 1964 году было получено косвенное подтверждение нарушения
инвариантности относительно обращения времени, но она остается
полезной приближенной симметрией в слабых, а также в сильных
и электромагнитных взаимодействиях.
В ряде случаев можно использовать базис состояний, для ко-
которых ,Уа = а и ,УC = C и формула C.3.54) принимает вид
Лра - е Лра ' (d.d. 55)
откуда следует, что i»Sl^ имеет фазу 5а + 5п по модулю ж. Это утвер-
утверждение известно как теорема Ватсона 15. Фазы, входящие в C.3.54)
и C.3.55), можно измерить в процессах, где наблюдается интерфе-
интерференция между разными конечными состояниями. Например, в распа-
распаде гиперона Л со спином 1/2 на нуклон и пион конечное состояние
может иметь орбитальный угловой момент, равный только 1 = 0 или
I = 1; угловое распределение пиона относительно направления спина
гиперона Л включает интерференцию этих состояний, и поэтому в
силу теоремы Ватсона зависит от разности фаз 5S - 5р.
РТ
Хотя эксперименты 1957 года по несохранению четности не
исключили инвариантности относительно обращения времени, они
Глава 3. Теория рассеяния
ясно показали, что произведение РТ не сохраняется. Если бы этот
оператор сохранялся, он должен был быть антиунитарным по тем
же причинам, что и оператор Т, так что в процессах типа ядерного
C-распада следствия такой инвариантности имели бы вид соотно-
соотношений, аналогичных C.3.54):
где преобразование !ЖТ изменяет знаки всех г—компонент спина, но
не компонент импульсов. Пренебрегая кулоновским взаимодействи-
взаимодействием в конечном состоянии, получим, что электрон в C-распаде
Со60 —» Ni60 + е~ + V не может иметь преимущественного направле-
направления вылета по отношению к спину Со60, что противоречит наблюде-
наблюдениям.
С, СР и СРТ
Уже отмечалось, что существует преобразование внутренней
симметрии, называемое зарядовым сопряжением, которое заменя-
заменяет частицы на античастицы и наоборот. Формально это требует су-
существования унитарного оператора С, который следующим обра-
образом действует на многочастичные состояния:
¦¦¦ p^nf ;p2o2n|;... C.3.56)
где пс — античастица к частице типа п, а ^п - еще одна фаза. Если
это верно как для ин-, так и для аут- состояний, то ^-матрица
удовлетворяет условиям инвариантности
с
IJp'1c[n'1;p2c2n2;...,p1c1n1;p2c2n2;...
-V.V. t t s C-3-57)
^п^п2 ¦ ¦ ¦ Ъп{г>п2 ¦ ¦ ¦ p'1c'1n'1c;p2c'2n'2c;...,p1c1n[;p2c2n2;...
Как и в случае других внутренних симметрии, 5-матрица бу-
будет удовлетворять этим условиям, если оператор Со, действующий
на состояния свободных частиц так, как указано в C.3.56), комму-
коммутирует с гамильтонианом взаимодействия V и со свободным гамиль-
гамильтонианом Яо; в этом случае полагаем С = Со.
3.3. Симметрии S-матрицы 175
Фазы ^п называются зарядовыми четностями. Как и в случае
обычных четностей г\п, величины ^п в общем случае определены
неоднозначно, так как для любого оператора С, удовлетворяющего
C.3.56), можно найти другой такой оператор с другими \п, умножив
С на любое фазовое преобразование внутренней симметрии, на-
например, на ехр(гаВ + zCL + iyQ). Зарядовые четности могут быть
индивидуально измерены только для полностью нейтральных час-
частиц вроде фотона или нейтрального пиона, которые не характери-
характеризуются никакими сохраняющимися квантовыми числами и совпада-
совпадают со своими античастицами. В реакциях, в которых участвуют
только полностью нейтральные частицы, в силу C.3.57) произведе-
произведения зарядовых четностей в начальном и конечном состояниях дол-
должны быть равны. Например, как будет далее показано, в кванто-
квантовой электродинамике требуется, чтобы фотон обладал зарядовой
четностью т|у = ~1, так что из наблюдения распада нейтрального
пиона л° —» 2у вытекает, что г^ = +1; отсюда же следует, что
процесс л° —» Зу должен быть запрещен, что и наблюдается на са-
самом деле. Для двух рассмотренных частиц зарядовые четности дей-
действительны и равны +1 или —1. Как и в случае обычной четности,
это будет всегда так, если все внутренние симметрии фазовых пре-
преобразований являются членами непрерывных групп фазовых пре-
преобразований, потому что тогда можно переопределить оператор С,
умножив его на обратный квадратный корень внутренней симмет-
симметрии, равной С2, так что после этого новый оператор С будет удов-
удовлетворять условию С2 = 1.
Для произвольных реакций из формулы C.3.57) вытекает, что
вероятность некоторого процесса равна вероятности того же про-
процесса, в котором все частицы заменены на соответствующие анти-
античастицы. Это утверждение непосредственно не противоречило экс-
экспериментам по несохранению четности, выполненным в 1957 году
(еще долго придется ждать, прежде чем кто-нибудь сумеет наблю-
наблюдать C-распад ядер антикобальта), однако эксперименты показа-
показали, что С не сохраняется в теории слабых взаимодействий, пред-
предложенной Ли и Янгом 12 для того, чтобы учесть несохранение
четности. (Ниже будет доказано, что наблюдаемое нарушение
сохранения ТР влечет нарушение сохранения С в любой полевой
теории слабых взаимодействий, а не только в том ее варианте,
который рассмотрели Ли и Янг.) Сейчас уже стало понятно, что как
С, так и Р не сохраняются в слабых взаимодействиях, ответственных
Глава 3. Теория рассеяния
за процессы типа C-распада или распадов пиона и мюона, однако и
С, и Р сохраняются в сильных и электромагнитных взаимодей-
взаимодействиях.
Хотя ранние эксперименты по несохранению четности показа-
показали, что ни С, ни Р не сохраняются в слабых взаимодействиях,
оставалась все же возможность, что их произведение СР универ-
универсально сохраняется. В течение нескольких лет ожидалось (хотя и не
с полной уверенностью), что будет экспериментально доказано уни-
универсальное сохранение СР. Такой закон сохранения приводит к осо-
особенно важным следствиям в отношении свойств нейтральных К-
мезонов. В 1954 году Гелл-Манн и Пайс 16 отметили, что поскольку
К0 не совпадает со своей античастицей (К0 обладает ненулевым
значением приближенно сохраняющейся величины, названной стран-
странностью), то частицами с определенным временем жизни будут не
К0 и К0, а их линейные комбинации К0 ± К0. Сначала это объясня-
объяснялось с помощью утверждения о сохранении С, но когда обнаружи-
обнаружилось, что зарядовая четность С не сохраняется в слабых взаимо-
взаимодействиях, аналогичные аргументы были повторены на основе
сохранения СР. Если произвольно определить фазы оператора СР
так, что в состояниях К0 и К0
к° = к" ' к" = к" '
то можно определить зарядово-самосопряженные одночастичные
состояния
^ ^ ]^
к
? =
имеющие собственные значения СР, равные +1 и —1, соответствен-
соответственно. Наименьшее время жизни имеют эти частицы относительно рас-
распада на два пиона, однако сохранение произведения СР позволяет
это только* для состояния Къ но не К2. Таким образом, следует
ожидать, что К2 распадается по более медленным модам в три пио-
*Спин нейтральных К-мезонов равен нулю, так что двухпионное ко-
конечное состояние имеет I - 0, а следовательно Р = +1. Далее, для двух п°
С = +1, так как С = +1 у отдельного п°, и для состояния п+п~ с I - 0 также
С = +1, так как С переставляет два пиона.
3.4. Сечения и вероятности 177
на или в пион, мюон (электрон) и нейтрино. Тем не менее, в 1964
году Фитч и Кронин обнаружили, что долгоживущий нейтральный
К-мезон с малой вероятностью все же распадается на два пиона 17.
Вывод заключался в том, что в слабых взаимодействиях СР не со-
сохраняется строго, хотя степень сохранения много больше, чем у С
и Р по отдельности.
Как мы увидим в гл. 5, есть серьезные основания полагать,
что, хотя С и СР не сохраняются по отдельности, произведение
СРТ строго сохраняется во всех взаимодействиях, по крайней мере,
в любой квантовой теории поля. Именно СРТ обеспечивает строгое
соответствиствие между частицами и античастицами, в частности,
из того факта, что СРТ коммутирует с гамильтонианом, вытекает
строгое равенство масс стабильных частиц и их античастиц. Так как
оператор СРТ антиунитарен, это преобразование связывает
5-матрицу произвольного процесса с 5-матрицей обратного про-
процесса, в котором изменен знак всех третьих проекций спина и час-
частицы заменены на античастицы.
Однако в случае, когда .^-матрица может быть разделена на
малое слагаемое SA^, определяющее данную реакцию, и большое
слагаемое S^°\ действующее в начальном и конечном состояниях,
можно использовать те же доводы, что и при рассмотрении сохра-
сохранения Т, чтобы показать, что вероятность всякого процесса равна
вероятности того же процесса, в котором частицы заменены на ан-
античастицы и перевернуто направление третьей компоненты спина,
если при этом проведено суммирование по наборам начальных и
конечных состояний, полным по отношению к S(Ol В частности, хотя
парциальные вероятности распада частицы в два конечных состоя-
состояния Pi и C2 с <S"n n =?0 могут отличаться от парциальных вероятнос-
вероятностей распада античастицы в два соответствующих конечных состоя-
состояния cP,J'J$l и (&:?.Т$2> мы увидим в разделе 3.5, что (без всяких
приближений) полная вероятность распада любой частицы равна
полной вероятности распада ее античастицы.
Теперь можно понять, почему опыты 1957 года по несохране-
несохранению четности можно было интерпретировать в рамках существую-
существующей теории слабых взаимодействий как свидетельство сильного на-
нарушения сохранения С и Р, но не СР. Все рассматривавшиеся теории
были теориями поля и поэтому автоматически сохраняли СРТ. Экс-
Эксперименты показали, что в ядерном C-распаде сильно нарушается
РТ, но не Т, поэтому любая совместимая с этими экспериментами
178 Глава 3. Теория рассеяния
теория, сохраняющая СРТ, должна включать несохранение С, но
не СР.
Аналогичное наблюдение в 1964 году малого нарушения зако-
закона сохранения СР в слабых взаимодействиях совместно с предпола-
предполагаемой инвариантностью всех взаимодействий относительно СРТ сра-
сразу же привело к выводу, что слабые взаимодействия не сохраняют
Т строго. Более детальное изучение системы К0 — К0 подтвердило
этот вывод, но до сих пор не удалось найти других прямых свиде-
свидетельств нарушения инвариантности относительно обращения вре-
времени.
3.4. Сечения и вероятности
Элемент .^-матрицы Saa является амплитудой вероятности
перехода а —» C. Как связана эта величина с теми вероятностями и
сечениями, которые измеряют экспериментаторы? В частности, из
C.3.2) видно, что S$a содержит множитель 54(рр - ра), обеспечи-
обеспечивающий сохранение полных энергии и импульса. Что должны мы
делать с множителем [54(рр - ра)]2 в вероятности перехода l^pj2?
Правильный способ разрешения этих проблем заключается в том,
чтобы понять, как реально ставятся эксперименты, используя для
этого волновые пакеты, описывающие локализованные вдали друг
от друга частицы перед соударением, а затем прослеживая эволю-
эволюцию во времени таких суперпозиций многочастичных состояний.
Ниже мы вместо этого используем быстрый и простой способ вывода
основных результатов, который скорее является даже не выводом,
а мнемоническим правилом для запоминания. Извинением является
то, что (насколько я знаю) разбирательство тонкостей, связанных с
этими вопросами, не является необходимым для решения ни одной
из интересных нерешенных физических проблем.
Пусть вся наша система физических частиц заключена в боль-
большой ящик макроскопического объема V. Например, можно рассматри-
рассматривать этот объем как куб с отождествленными точками на
противоположных гранях, так что из требования единственности
пространственной волновой функции вытекает квантованность им-
импульса:
2%
p = -j-(n1,n2n3), C.4.1)
3.4. Сечения и вероятности 179
где nt — целые числа, a L3 = V. Тогда все трехмерные дельта-функции
можно записать в виде
^JW<PP>*^V,P. C.4.2,
где 8р'р — обычный дельта-символ Кронекера, равный единице,
когда индексы совпадают, и нулю, когда они разные. Из условия
нормировки C.1.2) следует, что для используемых нами состояний
скалярные произведения в ящике не равны просто суммам произ-
произведений кронекеровских дельта-символов, а содержат дополни-
дополнительный множитель [V/BjrK]w, где N — число частиц в состоя-
состоянии. Чтобы вычислить вероятности переходов, нужно использовать
состояния с единичной нормой, поэтому введем нормированные
в ящике состояния как
хрящик = [Bnf/Vf*/2x?a, C.4.3)
норма которых
(^ик,ЧТик) = 8ра, C.4.4)
где 8ар — произведение кронекеровских дельта-символов для всех
3-импульсов, спинов и индексов сортов частиц плюс слагаемые с
переставленными частицами. Соответственно, можно записать
5-матрицу в виде
S^ = [VlB%KfNV+N«)/2S^m , C.4.5)
где Sp^"K вычисляется по состояниями C.4.3).
Конечно, если оставить частицы в ящике навсегда, то каждый
возможный переход будет повторяться вновь и вновь. Чтобы вы-
вычислить разумную вероятность перехода, следует заключить сис-
систему и в «ящик по времени». Предположим, что взаимодействие
включается только на время Т. Отсюда немедленно следует, что
дельта-функция, выражающая закон сохранения энергии, заме-
заменяется на
1 гт/2 / \
5Т (Еа - Ер) = — \_т/2 ехр(г(Еа - Ер )t) dt. C.4.6)
180 Глава 3. Теория рассеяния
Вероятность того, что многочастичная система, находившаяся
до включения взаимодействия в состоянии а, окажется после выклю-
выключения взаимодействия в состоянии В, равна
Р«Х -» В) = |^рик|2 = [B7tOv](JVa+JVp)|spa|2 . C.4.7)
Это выражение представляет вероятность перехода в одно кон-
конкретное состояние В в ящике. Число одночастичных ящичных
состояний в заданном элементе объема импульсного пространства
d3p равно Vd3p/BjrK, т. к. это есть число тех троек целых числе щ,
п2, ns, для которых импульс C.4.1) попадает в элемент объема
импульсного пространства d3p в окрестности р. Можно определить
интервал конечных состояний dB как произведение d3p для каждой
конечной частицы, так что полное число состояний в этом интер-
интервале
dip =[V/B7tK]WpdB. C.4.8)
Отсюда полная вероятность того, что система окажется в интер-
интервале dB конечных состояний, равна
dP(a -» В) = Р(ос -» B)d (р = [BтсK /v]^" ^^|2 dp. C.4.9)
В этом разделе мы ограничимся рассмотрением таких конечных
состояний В, которые не только отличаются (хотя и немного) от
начального состояния ОС, но и удовлетворяют более жесткому
ограничению, заключающемуся в том, что ни одно подмножество
частиц в состоянии В (отличное от всего множества) не имеет точно
того же 4-импульса, что и соответствующее подмножество частиц в
состоянии ос. (На языке, который будет введен в следующей главе,
это на самом деле означает, что мы рассматриваем только связную
часть 5-матрицы.) Для таких состояний можно определить не
содержащий дельта-функций матричный элемент Мра:
C.4.10)
Введение ящика позволяет интерпретировать квадраты дельта-
функций в I^RcJ2 при В Ф ос следующим образом:
3.4. Сечения и вероятности 181
Рр - Pa)f = 8^(РР - Ра)8^@) = 53v(pp - ра)У/BтгK ,
[8Т (Ер - Еа )f = 5Т (Ер - Еа )8Т @) = 5Т (Ер - Еа )Т /B%),
так что из C.4.9) имеем дифференциальную вероятность перехода
dP(OC -» Р) = B7tJ[B7tK/v]Wa(T/27t)|Mpa|2
53, (pp-paMT (Ep-Ea)d|3.
х
Если считать V и Т очень большими, произведение дельта-
функций можно рассматривать как обычную четырехмерную дельта-
функцию 84(рз - ра). В этом пределе вероятность перехода пропор-
пропорциональна времени Т, в течение которого включено взаимодействие,
причем коэффициент пропорциональности можно интерпретировать
как дифференциальную вероятность перехода
dF(a -» Р) s dP(a -^ Р) / Т
= (гя^-^у^-^^б^рр -Pa)dp, (ЗАП)
где теперь
. C.4.12)
Это основная формула, применяемая для интерпретации
вычислений элементов S—матрицы в терминах предсказаний для
реальных экспериментов. Ниже в этом разделе мы еще вернемся к
интерпретации множителя 84(рр - pa)d$.
Два случая особенно важны.
JVa = 1. В этом случае объем V в формуле C.4.11) сокращается,
и получается вероятность распада одночастичного состояния ОС в
произвольное многочастичное состояние C:
dF(a -» P)= Bтг)|Мра|284(рр -pa)d|3. C.4.13)
Конечно, эта формула имеет смысл только в случае, если время Т,
в течение которого происходит взаимодействие, много меньше
среднего времени жизни ха частицы ОС, поэтому нельзя перейти
182 Глава 3. Теория рассеяния
к пределу Т —> °° в 5т(Еа - Ер). В этой дельта-функции остается
неустранимая ширина АЕ — 1/Т > 1Аа, так что формула C.4.13)
применима только в случае, когда полная ширина распада 1 /та много
меньше, чем любая характерная энергия процесса.
JVa = 2. В этом случае вероятность C.4.11) пропорциональна
1/V, иными словами, плотности какой-то из частиц в том месте,
где находится другая. Экспериментаторы предпочитают измерять
не вероятность, деленную на плотность, а вероятность, отнесенную
к потоку частиц, или сечение. Поток каждой частицы в том месте,
где находится другая, определяется как произведение плотности
1/V и относительной скорости иа:
Фа=иа/У. C.4.14)
(Общее определение иа дано ниже; пока что ограничимся частным
случаем: если одна из частиц покоится, то иа определяется как
скорость другой частицы.) Таким образом, дифференциальное се-
сечение равно:
da(a -» Р) = dF(a -» Р) / Фа = B7гLм-1|мра|284(рр - pa)d|3 . C.4.15)
Хотя наиболее важны случаи Na = 1 и Na = 2, в принципе
измеримы и вероятности переходов для Na > 3, причем некоторые
из них играют важную роль в химии, астрофизике и т. п. (Например,
в одной из основных реакций с высвобождением энергии на Солнце
два протона и электрон превращаются в дейтрон и нейтрино.)
В разделе 3.6 приведены примеры использования основной формулы
для вероятностей переходов C.4.11) в случае произвольного числа
начальных частиц Na.
Обсудим теперь вопрос о свойствах лоренцовских преобра-
преобразований вероятностей и сечений. Это поможет дать более общее
определение относительной скорости иа в C.4.15). Правило
лоренцовского преобразования C.3.1) для .^-матрицы усложнено
наличием зависящих от импульса матриц, связанных со спином
каждой частицы. Чтобы обойти это усложнение, рассмотрим квадрат
модуля C.3.1) (выделив предварительно лоренц-инвариантную
дельта-функцию согласно C.4.12)) и просуммируем по всем спинам.
3.4. Сечения и вероятности 183
Тогда из унитарности матриц D- (W) (или их аналогов для частиц
аа
нулевой массы) следует, что, если не считать энергетических
множителей в C.3.1), такая сумма лоренц-инвариантна. Иными
словами, величина
2^МРа 11 ?11Е = КР« C.4.16)
спины Р а
является скалярной функцией 4-импульсов частиц в состояниях
а и р. (Символы произведений ПаЕ и Пр-Е означают произведение
энергий рО _ /„2 + т2 всех частиц в состояниях а и р.)
Теперь можно записать просуммированную по спинам веро-
вероятность распада C.4.13) в виде
- pa)dp / Пр
Множитель dP/Пр-Е представляет произведение лоренц-инвари-
антных элементов объема B.5.15) в импульсном пространстве, поэто-
поэтому он сам лоренц-инвариантен. Также инвариантными являются
множители Кра и 84(рр - ра), и остается единственный неинвариант-
неинвариантный множитель 1/Еа, где Еа — энергия единственной начальной
частицы. Отсюда можно сделать вывод, что под действием
лоренцовских преобразований вероятность распада частицы пре-
преобразуется как 1/Еа. Конечно, это обычное релятивистское
сокращение времени — чем быстрее частица, тем медленнее она
распадается (с точки зрения неподвижного наблюдателя).
Аналогично, формула C.4.15) для просуммированного по спинам
сечения может быть записана в виде
da(a - Р) = B%fu-%%%a5Hpa ~ Pp)dP /ЦЕ,
где Elvs.E2 — энергии двух частиц в начальном состоянии ОС. Принято
определять сечение (после суммирования по спинам) как лоренц-
инвариантную функцию 4-импульсов. Множители Raa, 84(рр — ра) и
dP/Пр-Е уже лоренц-инвариантны, поэтому такое условие означает,
что нужно так определить относительную скорость иа, чтобы в
произвольной инерциальной системе отсчета произведение иаЕ1Е2
было скаляром. Ранее отмечалось, что в инерциальной системе
184 Глава 3. Теория рассеяния
отсчета, в которой одна из частиц (например, первая) покоится, иа
есть просто скорость другой частицы. Это однозначно определяет
вид иа в произвольных инерциальных системах отсчета *:
ЕгЕ2, C.4.17)
где р1( р2 и m1( m2 — 4-импульсы и массы двух частиц в начальном
состоянии а.
Попутно заметим, что в «системе центра масс», в которой
полный 3-импульс равен нулю,
Pi = (р, Ег), р2 = (-р, Е2)
из C.4.17) получаем:
I pICEi + En) Di Do
C.4.18)
как и следовало ожидать для относительной скорости. Однако в такой
системе отсчета иа не является физической скоростью; в частности,
из C.4.18) видно, что для ультрарелятивистских частиц эта величина
может достигать значения 2.
Обратимся к интерпретации множителя 84(рр - pa)d$, называ-
называемого фазовым объемом. Он появляется в общей формуле C.4.11)
для вероятностей переходов, а также в формулах C.4.13) и C.4.15)
для вероятностей распадов и сечений. Ограничимся случаем лорен-
цовской системы центра масс, в которой полный 3-импульс началь-
начального состояния равен нулю:
ра= 0. C.4.19)
(Для Na = 1 это отвечает случаю распада покоящейся частицы.)
Если импульсы частиц в конечном состоянии равны р'1( р'2, ..., то
*Из C.4.17) очевидно, что иаЕ1Е2 — скаляр. Кроме того, когда части-
частица 1 покоится, то pj = 0, Ег - тъ и рг-р2 = - 'т1Е1, так что из C.4.17)
следует:
J
- т
что есть просто скорость частицы 2.
E2 =|Р2|/Я2,
3.4. Сечения и вероятности 185
54(рр - pa)d$ = 53(Р; + р?+...)8(Я; + E/2+...-E)d3p{d3p/2..., C.4.20)
где Е = Еа — полная энергия начального состояния. Каждый из
интегралов по p'fe, скажем, по р'1( может быть тривиально взят,
если просто опустить дельта—функцию от импульсов:
54(рр - Pa)d$ -» b{E{+E'2+...-E)d3p2... C.4.21)
понимая при этом, что, где бы не появился импульс j>\ (например,
в Е[), его следует заменить на
Аналогично можно использовать оставшуюся дельта-функцию
для вычисления еще одного любого из оставшихся интегралов.
В простейшем случае, когда в конечном состоянии находятся
две частицы, формула C.4.21) принимает вид
84(Рр - Pa)dP -» 8(Е( + Е'2 - E)d3p2 .
Подробнее, расписывая d?p\ в сферических координатах в импульс-
импульсном пространстве и выражая энергии частиц через модули их им-
импульсов и массы, получим:
^2 - Е)\р{\2 d\p{\d?l,
C.4.23)
где р'2 = - р\ и dQ. = sin6 dQ d<p — дифференциал телесного угла для
р\. Выражение C.4.23) можно упростить, пользуясь стандартной
формулой
где /(ж) - произвольная действительная функция с одним простым
нулем в точке х = х0. В нашем случае аргумент дельта-функции
Е\+ Е'2 — Ев C.4.23) имеет единственный нуль при \р\\ = к', где
к' = yl(E2 - т[2 - т22J - 4,т[2т22 / BЕ), C.4.24)
186
Глава 3. Теория рассеяния
_ If ^
Е'2 =
2E
p2 '2 , '2
т22 =
2Е
C.4.25)
C.4.26)
а производная равна
d
_ /с' /с' _ fc'E
'22 -Е)
C.4.27)
Таким образом, можно опустить дельта-функцию и диф-
дифференциал d\p\\ в C.4.23), разделив на C.4.27):
—>
Е
C.4.28)
и понимая при этом, что к', Е\ и Е\ везде далее задаются форму-
формулами C.4.24)-C.4.26). В частности, дифференциальная вероятность
C.4.13) распада одночастичного состояния с нулевым импульсом
и энергией Е на две частицы равна
dF(a
2%k'E[E2
C.4.29)
а дифференциальное сечение двухчастичного рассеяния 12 —> 1'2'
дается формулой C.4.15) в виде
ЕгГа
2_B%)ik%E'2E1E2
l ~ Е2к
' pal
где к =
р2
Рассмотренный случай JVp = 2 особенно прост, но есть и один
красивый результат для Л/р = 3, который стоит упомянуть. Формула
C.4.21) при JVp = 3 принимает вид
3.5. Теория возмущений
187
Запишем элемент объема в импульсном пространстве как
d3p'2d3p'3 =| р2|2 d\ P2II p3|2 d| p31 dQ.3dq>23d cos623 ,
где d?l3 — дифференциал телесного угла для р 3, а 623 и ф23 - полярный
и азимутальный углы р'2 относительно направления р'3. Ориентация
плоскости, в которой лежат векторы р'2 и р'3, определяется углом
ф23 и направлением р'3, а остающийся угол 623 фиксируется законом
сохранения энергии:
р2|2+2| р'2| | р3| cose
23
= E.
Производная аргумента дельта-функции по cos 623 равна
=|р211Рз1
3cos623
так что можно взять интеграл по cos 623, просто опустив дельта-
функцию и разделив на эту производную:
S4 (
Pa
V21 d| V2
P31
Заменив импульсы на энергии, получим окончательно
+ E{E2E'3dE2dE3dQ.3d($>23 .
C.4.31)
Вспомним теперь, что величина C.4.16). полученная суммиро-
суммированием
Mr
по спинам и умножением на произведение энергии,
является скалярной функцией 4-импульсов. Если приближенно заме-
заменить этот скаляр константой, то из C.4.31) следует, что для фикси-
фиксированного начального состояния распределение событий на плоско-
плоскости Е'2, Е'3 однородно. Всякое отклонение реально наблюдаемого
распределения событий от однородного — важное указание на
динамику процесса распада, включая возможные центробежные
барьеры или резонансные промежуточные состояния. Картинка этой
188 Глава 3. Теория рассеяния
плоскости с нанесенными на ней точками экспериментальных событий
носит название диаграммы Далица 19. Именно Далиц впервые
использовал ее в 1953 году для анализа нелептонного распада
К+ -» ж+ + ж+ + ж~:
3.5. Теория возмущений
Исторически наиболее полезной техникой для вычисления эле-
элементов ^-матрицы оказалась теория возмущений, т. е. разложение
по степеням взаимодействия V в гамильтониане Н = Но + V. Урав-
Уравнениями C.2.7) и C.1.18) .^-матрица задается в виде:
Spa = 8(Р - а) -
где W^ удовлетворяет уравнению Липпмана-Швингера C.1.17):
Т+Ф
= ф + \ dy У« У
Подействовав на это уравнение оператором V и взяв скаляр-
скалярное произведение с Фр, получим интегральное уравнение для Т+:
где
Ряд теории возмущений для Тра+ получается из C.5.1) с помощью
итераций:
3.5. Теория возмущений 189
Метод расчета, основанный на формуле C.5.3) и преобладав-
преобладавший при вычислениях 5-матрицы в 1930-х годах, называется сей-
сейчас старой теорией возмущений. Очевидным недостатком этого
метода является то, что энергетические знаменатели в C.5.3) мас-
маскируют лоренц-инвариантность .^-матрицы. Все же метод иногда
применяется в тех случаях, когда необходимо выяснить, каким об-
образом различные промежуточные состояния порождают сингуляр-
сингулярности ^-матрицы. В большей части этой книги мы будем опирать-
опираться на видоизмененную версию формулы C.5.3), известную как
зависящая от времени теория возмущений и обладающую тем пре-
преимуществом, что лоренц-инвариантность становится более очевид-
очевидной, хотя несколько затемняется вклад отдельных промежуточных
состояний.
Простейший способ вывода хронологически упорядоченного
разложения по теории возмущений заключается в использовании
формулы C.2.5), согласно которой оператор S равен
S = Щоо -оо),
Щх,х0) = ехр(гЯох)ехр(-гЯ(х-хо))ехр(-гЯохо).
Дифференцируя это выражение по х, получаем дифференциальное
уравнение
г — U(x,xo) = V(x)l/(x,xo), C.5.4)
V(t) = exp(iHot)Vexp(-iHot). C.5.5)
(Говорят, что операторы с такой зависимостью от времени опреде-
определены в картине взаимодействия, чтобы отличить их временную
зависимость от зависимости OH(t) = ехр(гЯ?)Онехр(-гЯ?), предписы-
предписываемой гейзенберговской картиной в квантовой механике.) Как урав-
уравнение C.5.4), так и начальное условие 1/(х0, х0) = 1 очевидно удов-
удовлетворяются решением интегрального уравнения
Щх, х0) = 1 - г Г dtV(t)U(t, x0). C.5.6)
•Ч
Итерируя это интегральное уравнение, получаем разложение
1/(х,х0) по степеням V:
190 Глава 3. Теория рассеяния
С7(х,хо) = 1-г[ dtiY^) + (-iJ [ dt1\1dt2V(t1)V(t2)
^0 0 0
, rT r*i rh C.5.7)
+ (-гK dtJ dt2 dt3V(t1)V(t2)V(t3)+...
•*Tn JTn JTn
Полагая x = °° и x0 = —oo, находим разложение в ряд теории возму-
возмущений для оператора S:
S = 1 - г Г dtjfih) + (-гJ Г dtx \Ч
л°= rt, ft, C.5.8)
+ (-гK ]_ dti ]_ dt2 ]_ dt3 V{tx )V(t2 )V(t3)+...
Это выражение можно также вывести с помощью разложения
по старой теории возмущений C.5.3), если воспользоваться фурье-
представлением энергетических знаменателей:
(Еа -Еу+ гг) = -iJ°° dx ехр(г(Еа - Еу )т), C.5.9)
понимая при этом, что интегралы должны вычисляться путем вклю-
включения обеспечивающего сходимость множителя е~ст в подынтеграль-
подынтегральное выражение с последующим устремлением 8 —> 0+.
Существует способ представления C.5.8) в виде, который очень
полезен при проведении явно лоренц-инвариантных вычислений.
Определим хронологически упорядоченное произведение любых за-
зависящих от времени операторов как произведение, в котором мно-
множители расположены в таком порядке, что тот, который отвечает
самому позднему моменту времени, располагается левее всех, сле-
следующим располагается множитель, отвечающий следующему мо-
моменту времени и т. д. Например,
T{V(t)} = V(t),
e(t! - t2)V(t1)V(t2) + e(t2 -
и т. д., где 6(т) — ступенчатая функция, равная +1 при х > 0 и 0 при
х < 0. Хронологически упорядоченное произведение п множителей
V есть сумма по всем п! перестановкам V, каждая из которых дает
3.5. Теория возмущений 191
тот же интеграл по всем tb..., tn. Поэтому можно переписать выра-
выражение C.5.8) в виде
S = l~<- L—^r)_ooaiiai2---ain1{vVi)---vVn)}- C.5.10)
n=l
Иногда это выражение называют рядом Дайсона 20. Если все V(t) в
разные моменты времени коммутируют, ряд можно просуммиро-
просуммировать, и тогда
( г° "\
S = exp -i dtV(t) .
V J— )
Ясно, что обычно так не бывает; в общем случае C.5.10) даже не
сходится и является в лучшем случае асимптотическим разложени-
разложением по степеням входящей в V константы связи.
Однако иногда C.5.10) записывают формально в виде
S = Т ехр( -гJ°° dtV(t)\
где символ Т указывает, что вычисление этого выражения следует
производить, разложив его в ряд и хронологически упорядочив каж-
каждый член разложения.
Теперь можно сразу же указать один большой класс теорий,
для которых 5-матрица явно лоренц-инвариантна. Так как ее элементы
являются матричными элементами оператора S между состояниями
свободных частиц Фа, Фр и т. д., все, что требуется, это чтобы S-one-
ратор коммутировал с генераторами 170(Л,а): Яо, Ро, Jo и Ко.
Чтобы удовлетворить этому требованию, предположим, что V(t)
можно записать как интеграл по трехмерному пространству:
V(t) = jd3x.7f(*,t), C.5.11)
где .Ж(ж) — скаляр в том смысле, что
1 + а). C.5.12)
(Приравнивая коэффициенты при а0 в бесконечно малых преобра-
преобразованиях, можно убедиться, что зависимость .У({?) от времени со-
совместима с C.5.5).)
192 Глава 3. Теория рассеяния
Теперь можно записать S как сумму четырехмерных интег-
интегралов
S = 1
'/¦ C.5.13)
n=l
Все выражение стало явно лоренц-инвариантным, если не считать
процедуры хронологического упорядочивания произведения опера-
операторов.
Хронологическое упорядочивание двух мировых точек хъ х2
лоренц-инвариантно, если только разность х± — х2 не является про-
странственноподобной, т. е. если (х1 — х2J > 0. Таким образом, хро-
хронологическое упорядочивание в C.5.13) не приводит к выделению
специальной лоренцовской системы отсчета, если (хотя это и не
единственное условие) все .Щх) коммутируют на пространственно-
подобных или светоподобных расстояниях *:
[Ж{х), Ж{х')\ = 0 при (х - x'f > 0. C.5.14)
Результаты раздела 3.3 можно использовать для того, чтобы полу-
получить формальное, не основанное на теории возмущений доказатель-
доказательство, что взаимодействие C.5.11), удовлетворяющее C.5.12) и C.5.14),
действительно приводит к .^-матрице с правильными свойствами
относительно лоренцовских преобразований. Для бесконечно малого
буста из C.5.12) имеем
г[К0, Ж{к, t)] = t- V./(f(x, t) + х • ^- Ж{к, t), C.5.15)
так что, интегрируя по х и полагая t = 0, получаем:
[K0,V] = [к0, Jd3xJf(x,0)] = [Ho,W], C.5.16)
где
W = jd3xx.7f(x,0). C.5.17)
* Мы записываем условие на х и х в виде (х: — х2J > 0, а не (х: — х2J > 0,
поскольку, как будет показано в гл. 6, лоренц-инвариантность может быть
нарушена неприятными особенностями при х = х'.
3.6. Следствия унитарности 193
Если (как это обычно имеет место) матричные элементы .Ж(х, 0)
между собственными состояниями Яо являются гладкими функция-
функциями собственных значений энергии, то это же верно как для V, что
необходимо для справедливости теории рассеяния, так и для W,
что необходимо для доказательства лоренц-инвариантности. Другие
условия лоренц-инвариантности — перестановочные соотношения
C.3.21) — также выполнены, если и только если
0 = [W, V] = Jd3xJd3yx[.7r(x,0),.7r(y,0)]. C. 5. 18)
Это условие, конечно, следует и из условия «причинности»
C.5.14), но само по себе дает менее ограничительное достаточное
условие лоренц-инвариантности 5-матрицы.
Теории такого класса — не единственные лоренц-инвариант-
ные теории. Однако и самые общие теории не слишком от них
отличаются. В частности, всегда должно быть выполнено переста-
перестановочное соотношение, похожее на C.5.14). Оно не имеет аналога в
случае нерелятивистских систем, для которых хронологическое упо-
упорядочивание всегда инвариантно по отношению к преобразованиям
Галилея. Именно это условие столь жестко ограничивает возмож-
возможность соединения лоренц-инвариантности с принципами кван-
квантовой механики.
Методы, описанные в данном разделе, полезны лишь в том
случае, когда оператор взаимодействия достаточно мал. Однако суще-
существует модифицированная версия такого приближения, известная
под названием борновского приближения искаженных волн и приме-
применимая в том случае, когда оператор взаимодействия содержит только
два слагаемых
V = VS+VW, C.5.19)
причем Vw мало, a Vs велико. Можно определить Ч^ как те ин- и
аут-состояния, которые были бы в случае, если бы взаимодействие
описывалось только слагаемым Vs:
р+а = (Фр, У^а+)= ([Ч'-р - (Ер -Щ
194 Глава 3. Теория рассеяния
?±а = Фа + (Еа -Но± ггу1 У
Теперь можно переписать C.1.16) в виде
-Щ- re) Vs^
р (р[ p -Щ +гг
так что
%=(Чф^Ю + (Чф,У5фа)- C-5.21)
Второе слагаемое в правой части как раз совпадает с оператором
Tga+, который должен был бы получиться при наличии только силь-
сильных взаимодействий:
sp,У8Фа). C. 5. 22)
(Для доказательства следует при выводе C.5.21) просто опустить
везде Vw.) Формула C.5.21) наиболее полезна в ситуации, когда
это второе слагаемое обращается в нуль, т. е. когда процесс a —> C
не может быть обусловлен только сильными взаимодействиями.
(Например, в C-распаде ядер именно слабые ядерные силы пре-
превращают нейтроны в протоны, хотя и нельзя игнорировать нали-
наличие сильных ядерных сил, действующих как в начальном, так и
в конечном состояниях.) Для подобных процессов матричный эле-
элемент C.5.22) обращается в нуль, и уравнение C.5.21) принимает
вид
^+а=0^Л+). C.5.23)
До сих пор все делалось точно. Однако подобный способ пере-
переписывания Т-матрицы становится весьма полезным, когда опера-
оператор Vw настолько мал, что можно пренебречь влиянием этого взаи-
взаимодействия на состояние W^ в C.5.23) и заменить Ч*а+ на состояние
v^/sa+> учитывающее только сильное взаимодействие Vs. В этом при-
приближении уравнение C.5.23) принимает вид
T&-(^sp,Vw4?). C.5.24)
3.6. Следствия унитарности 195
Эта формула верна в первом порядке по Vw, но во всех поряд-
порядках по Vs. Такое приближение очень часто используется в физике;
например, элемент ^-матрицы для C- или у-распада ядер вычисля-
вычисляется с помощью формулы C.5.24), где Vs — сильное ядерное взаи-
взаимодействие, Vw — слабое ядерное или электромагнитное взаимо-
взаимодействие, соответственно, а ^ф~ и Ч1^ — конечное и начальное
состояния ядер.
3.6. Следствия унитарности
Условие унитарности 5-матрицы позволяет получить интерес-
интересное и полезное соотношение, связывающее амплитуду Маа рассея-
рассеяния вперед для произвольного многочастичного состояния а с пол-
полной вероятностью всех реакций в этом состоянии. Напомним, что в
общем случае, когда состояния C и а могут как совпадать, так и не
совпадать, 5-матрица может быть записана в виде C.3.2):
Тогда условие унитарности принимает вид
5(у - a) = J dpsfySpa = 8(у - а) - 2ти54 (Ру - Ра )Муа
+ 2ти54(ру - Ра)М*ау + 4л2 JdC54(pp - руM4(рр - P
Сокращая 8(у - а) и множитель 2л84(ру - ра), находим, что при
Ру= Ра
О = -гМуа + iM'ay + 2%l d|354(pp - ра)М;уМ$а. C.6.1)
уа + iMay
Это соотношение особенно полезно в частном случае a = у, когда
оно принимает вид
ImMaa = -7tjd|354(pp -pa)|Mpa|. C.6.2)
Используя C.4.11), это выражение можно представить в виде фор-
формулы для вероятности всех реакций, вызываемых данным началь-
начальным состоянием ос в объеме V:
196
Глава 3. Теория рассеяния
Г„ ЕЕ dP
dp
- Pa)
м,
ра
C.6.3)
В частности, если а -двухчастичное состояние, можно пере-
переписать последнюю формулу как
ТтМ = -
167Г3
C.6.4)
где иа— относительная скорость C.4.17) в состоянии ОС и оа — пол-
полное сечение в этом состоянии, определяемое формулой C.4.15) как
aa = Jd|3da(a -» Р) / dp = BлL u Jdp|Mpa|254(pp - Pa). C.6.5)
Обычно эта формула записывается несколько иначе с помо-
помощью амплитуды -рассеяния /(ос —> C). Из формулы C.4.30) следует,
что дифференциальное сечение двухчастичного рассеяния в систе-
системе центра масс равно
dD.
B%)ik%E2'E1EA M 2
кЕ2
C.6.6)
где к' и к — величина импульсов начального и конечного состояний.
Поэтому определим амплитуду рассеяния следующим образом *:
/(СС-»Р)ЕЕ
4л2
Е V к
так что дифференциальное сечение записывается просто как
C.6.8)
* Заметим, что фаза / условна и выбирается в соответствии с интерпрета-
интерпретацией / в рамках волновой механики 21 как коэффициента при расходящейся
волне в решении стационарного уравнения Шредингера. Использованная нами
нормировка / несколько отличается от общепринятой для неупругого рассея-
рассеяния. Обычно / определяют так, что в выражении для дифференциального се-
сечения появляется отношение конечной и начальной скоростей.
3.6. Следствия унитарности 197
В частности, для упругого двухчастичного рассеяния
^-MRra. C.6.9)
С помощью выражения C.4.18) для относительной скорости иа мож-
можно переписать условие унитарности C.6.4) в виде
к
Im /(ос —> а) = —- а„. C.6.10)
4л; а
Такая форма записи условия унитарности C.6.4) носит название
^. 99
оптической теоремы .
Можно получить любопытное следствие оптической теоремы,
говорящее многое о картине рассеяния при высоких энергиях. Сле-
Следует ожидать, что амплитуда рассеяния / есть гладкая функция
угла, так что должен существовать некоторый телесный угол АП,
в пределах которого величина |/|2 почти равна (например, с точнос-
точностью до множителя 2) своему значению при рассеянии вперед. От-
Отсюда полное сечение ограничено величиной
c^>{\f\2dO>l\f(a^afAO>l
С помощью C.6.10) находим верхний предел на АО.:
АО <32ж2/к2оа. C.6.11)
Как мы увидим в следующем разделе, обычно полные сечения яв-
являются при больших энергиях постоянными или медленно растут с
энергией. Поэтому из C.6.11) вытекает, что телесный угол вокруг
направления вперед, в пределах которого дифференциальное сече-
сечение примерно постоянно, сужается по меньшей мере как 1/к2 при
к —> оо. Этот все более узкий пик в направлении вперед при больших
энергиях называется дифракционным пиком.
Возвращаясь к общему случаю реакций с участием произволь-
произвольного числа частиц, можно использовать C.6.2) совместно с СРТ ин-
инвариантностью, чтобы установить связь полных вероятно-
вероятностей взаимодействия частиц и античастиц. Так как оператор СРТ
198 Глава 3. Теория рассеяния
антиунитарен, его сохранение не приводит в общем случае к ка-
каким-то простым соотношениям между процессом а —> C и процес-
процессом, в котором все частицы заменены на свои античастицы. Однако
из этой инвариантности следует связь между процессом и обрат-
обратным процессом с участием античастиц. Используя те же аргумен-
аргументы, что и при выводе формулы C.3.46) из условия инвариантности
по отношению к обращению времени, можно показать, что СРТ
инвариантность требует, чтобы 5-матрица удовлетворяла условию:
S$,a = ^го>л,го>./р > C.6.12)
где WfJ означает, что мы должны перевернуть все z-компоненты
спинов, заменить все частицы на соответствующие античастицы и
умножить матричный элемент на разные фазовые множители для
частиц в начальном состоянии и на комплексно сопряженные мно-
множители для частиц в конечном состоянии. Так как из СРТ инвариан-
инвариантности следует, что массы частиц и соответствующих античастиц
равны, это же соотношение выполняется и для коэффициента, сто-
стоящего при Ъ\ра - рр) в S$a:
C.6.13)
В частности, когда начальное и конечное состояния одинаковы,
все фазовые множители сокращаются и C.6.13) принимает вид
М
' р1ст17г1;р2ст27г2;...;р1ст17г1;р2ст27г2;...
= м C-6.14)
Pj—<31ni;p2—ст2п2;...;р1—<31ni;p2—ст2п2;...'
где верхний индекс суп означает античастицу для п. Теперь из
обобщенной оптической теоремы C.6.2) следует, что полная веро-
вероятность процесса из данного начального состояния, содержащего
определенный набор частиц, равна полной вероятности процесса, в
начальном состоянии которого содержатся соответствующие
античастицы с противоположными значениями проекций спинов:
^р1о1п1;р2о2п2;... ~ р1-ст1п1с;р2-ст2п|;...' C.6.15)
Применяя это утверждение к одночастичным состояниям,
видим, что вероятность распада любой частицы равна вероятности
3.6. Следствия унитарности 199
распада античастицы с противоположной проекцией спина. Инвари-
Инвариантность по отношению к вращениям не позволяет вероятностям
распада зависеть от z-компоненты спина распадающейся частицы,
поэтому частным случаем общей формулы C.6.15) является
утверждение, что нестабильные частицы и их античастицы имеют
строго равные времена жизни.
Те же рассуждения, которые от условия унитарности S^S = 1
привели к формуле C.6.2), позволяют использовать другое условие
унитарности SS^ = 1, чтобы получить соотношение
ImMaa =-JiJd|354(pp -ра)|мар|2. C.6.16)
Объединяя его с C.6.2), приходим к соотношению обратимости
pp -ра)|мра|2 = Jd|354(pp -ра)|ма/. C.6.17)
или иначе
dr(P -» a)
где ca =[V / B%) ] a. Этот результат можно использовать при выводе
наиболее важных соотношений кинетической теории 23. Если Pad(X
— вероятность обнаружить систему в объеме doc пространства
многочастичных состояний Фа, то скорость уменьшения Ра за счет
переходов во все другие состояния равна PaJdpPndr(P —> a) / da,
а скорость увеличения Ра в результате переходов из всех других
состояний равна интегралу JdpPpdr(P —> a) / da; поэтому полная
скорость изменения Ра
dPa _ Г агф -* а) (P)
J dpP PJ dP C-6-19)
a _ Г агф -* а) Г
Г-J dpPP da P«J
200
Глава 3. Теория рассеяния
Отсюда немедленно вытекает, что )Pad(X не зависит от времени.
(Для доказательства достаточно переобозначить переменные
интегрирования во втором слагаемом C.6.19).) С другой стороны,
скорость изменения энтропии - J d(XPa ln(Pa / са) равна
i
^Ч = - da dBlnp*--
da
¦-Р„
d|3
Меняя обозначения переменных интегрирования во втором слага-
слагаемом, можно записать это выражение как
¦—
dt
da
In
a
a)
acp J
Далее, для любых положительных вероятностей ж и у функция
у\п(у/х) удовлетворяет неравенству *
у1п\ — \>у-х.
Поэтому скорость изменения энтропии ограничена:
¦- daP.ln^a da dp
PP Pa
dF(P -^ a)
da
Меняя обозначения переменных интегрирования во втором
слагаемом, находим
dt
daPaln(^4> da
a)
dF(a -^ P)
da
* Разность левой и правой частей при х —> у стремится к положительной
величине (х — уJ/2у и имеет производную по х, которая положительна или
отрицательна при всех х > у или х < у, соответственно.
3. 7. Разложения по парциальным волнам 201
Но из условия унитарности C.6.18) (в котором переставлены
а и C) следует, что интеграл по а в правой части обращается в
нуль, поэтому можно заключить, что энтропия всегда возрастает:
ijln(t)sa C-6-20)
Это соотношение носит название «Н^теоремы» Больцмана.
В учебниках по статистической механике ее часто выводят, либо
используя борновское приближение, в котором |MpJ2 симметрично
по а и C, так что cpdF(|3 —> a)/da = cadT(a —> P)/dC, либо предпола-
предполагая инвариантность относительно обращения времени, из которой
следует, что Маа2 не изменяется, если поменять местами ос и C,
одновременно обратив направления всех импульсов и спинов. Ко-
Конечно, ни борновское приближение, ни инвариантность относительно
обращения времени не являются точными , поэтому тот факт, что
для вывода Н-теоремы нужно только условие унитарности C.6.18),
является хорошей новостью.
Рост энтропии прекращается, если вероятность Ра становится
функцией только сохраняющихся величин, таких, как полная
энергия и заряд, умноженные на са. В этом случае из законов
сохранения вытекает, что производная dF(|3 —> a)/da обращается в
нуль всегда, кроме случая, когда выполнено равенство PJca =
= Рр/ср, так что в первом слагаемом C.6.19) можно заменить Рр на
Pacp/ca. Вновь используя C.6.18), видим, что в этом случае Ра не
зависит от времени. Опять же, для этого вывода нам понадобилось
не борновское приближение или инвариантность по отношению к
обращению времени, а только условие унитарности C.6.18).
3.7. Разложения по парциальным волнам *
Часто удобно работать с .^-матрицей в базисе состояний свобод-
свободных частиц, где все переменные, кроме полного импульса и полной
энергии, дискретны. Такое описание возможно, поскольку компо-
компоненты импульсов р1( ..., рп n-частичного состояния с определенными
* Этот раздел лежит несколько в стороне от основной линии изложения и
может быть опущен при первом чтении.
202 Глава 3. Теория рассеяния
полным импульсом р и энергией Е заполняют (Зп — 4)-мерное
компактное пространство. Так, в случае п = 2 в системе центра масс
р = 0 этим компактным пространством является двумерная
поверхность сферы.
Любая функция на таком компактном пространстве может быть
разложена в ряд по обобщенным «парциальным волнам» типа сфери-
сферических гармоник, обычно используемых для представления функций
на 2-сфере. Поэтому можно определить базис таких п-частичных
состояний, который дискретен, за исключением непрерывных
переменных р и Е.
Запишем состояния свободных частиц в этом базисе как Фери>
причем индекс N включает все спиновые переменные и метки сортов
частиц, а также те индексы, которые отмечают обобщенные
парциальные волны. Удобно выбрать состояния нормированными так,
что их скалярные произведения равны
р W C-7.1)
Матричные элементы оператора S в этом базисе имеют вид
(E,p), C.7.2)
где SN'N — унитарная матрица. Аналогично оператор Т, матричные
элементы которого (Фр, ТФа) совпадают с величинами Тра+,
определенными формулой C.1.18), может быть согласно C.4.12)
записан в новом базисе в виде
(фЕ'Р'м''ТФЕРы) = 63(p/-p)MJv;jv(E,p), C.7.3)
так что соотношение C.2.7) становится обычным матричным выра-
выражением:
SN%N (E, р) = б^д - 2%iMN%N (E, р). C.7.4)
В следующем разделе мы используем этот общий формализм, но
пока что рассмотрим реакции с двумя частицами в начальном
состоянии.
Например, рассмотрим состояние из двух нетождественных
частиц сортов п1м.п2с отличными от нуля массами М1 и М2 и произ-
произвольными спинами s1; s2. В этом случае состояния можно пометить
3. 7. Разложения по парциальным волнам 203
их полным импульсом р = Pi + р2, энергией Е, метками соротов
частиц щ, п2, 2-компонентами спинов а1( G2, и парой целых чисел
I и т (где т < I), которые задают зависимость состояния от направ-
направления, скажем, вектора рг. В качестве альтернативы можно пост-
построить удобный дискретный базис, объединив два спина в полный
спин s с 2-компонентой ц с помощью коэффициентов Клебша-Гор-
дана9, а затем, вновь используя эти коэффициенты, сложить спин
с орбитальным угловым моментом I с третьей проекцией т, полу-
получив полный угловой момент j с третьей проекцией о.
Так мы приходим к базису состояний ^Epjaisn («индекс канала»
п отмечает сорта двух частиц щ и п2), которые определяются их
скалярными произведениями с состояниями, имеющими определен-
определенные значения импульсов и третьих проекций спина отдельных час-
частиц:
^3 - Pi - Р2)
C.7.5)
)
)8Я>
где Y;m — обычные сферические гармоники 24. Дополнительный мно-
множитель (|р1|Е1Е2/-Е)^2 включен для того, чтобы эти состояния были
правильно нормированы в системе центра масс:
= 83(р')83(Е' - ЯN;Л;.8а>8в.1в8п>. C.7.6)
Чтобы избежать двойного счета для тождественных частиц, следу-
следует брать интеграл только по половине двухчастичного фазового объе-
объема в импульсном пространстве, так что в скалярном произведении
C.7.6) следует поделить на множитель v2.
В системе центра масс матричные элементы любого сохраня-
сохраняющего импульс инвариантного относительно вращений оператора
О должны иметь вид
C.7.7)
(Диагональность по j а о следует из перестановочных соотношений
О с J2 и J3, а тот факт, что коэффициент при 5ОО' не зависит от а,
204 Глава 3. Теория рассеяния
следует из равенства нулю коммутатора оператора О с J1 ± zJ2-
частный случай общего утверждения, известного в литературе как
теорема Вигнера-Эккарта 25.) Применяя полученные формулы к
оператору М, матричные элементы которого равны Мра, получаем:
f{ko1,-ko2,n -> к'о^-к'о'^п)
4л2
L C()C(i) C-7.8)
х CeIej (s', ц'; а;, &2 )С1У (j, а; т', ц') Y^'(к')Y-* (k)M^n,>bn (?).
Дифференциальное сечение рассеяния равно |/|2. Выберем
направление начального импульса к вдоль третьей оси, тогда
C.7.9)
Интегрируя |/|2 по направлению конечного импульса к', а также
суммируя и усредняя по конечным и начальным проекциям спина,
получаем полное сечение* перехода из канала п в канал п'\
*При выводе этой формулы мы используем стандартные правила сумми-
суммирования коэффициентов Клебша—Гор дана 9: во-первых,
и то же самое со штрихованными величинами;
?C(s(j,a;m,a)C(s(j,a;m,a)
и наконец
3. 7. Разложения по парциальным волнам 205
о(п -> п; Е) = — У Bj + 1)
/2B+l)B+l)^W
C.7.10)
ГЧ ГЧ ГЧ ^™- *} , ^ч v
X
Суммирование C.7.10) по всем двухчастичным каналам дает полное
сечение всех упругих или неупругих двухчастичных реакций:
У о{п -» п; Е) = — У Bj + 1)
C.7.11)
Для сравнения, с помощью формул C.7.8), C.7.9), C.7.4) и правил
сумм для коэффициентов Клебша-Гордана получаем усредненную
по спинам амплитуду рассеяния вперед:
2/cBSl+l)BS2+l)
jls
Тогда с помощью оптической теоремы C.7.10) находим полное
сечение:
C.7.12,
Если во входном канале п при энергии Е открыты только двух-
двухчастичные каналы, то матрица S^(E) (или по крайней мере ее
подматрица, включающая канал п) унитарна, и поэтому
lsn =2Re[l-SHE)]lsnMn, C.7.13)
так что выражения C.7.12) и C.7.11) совпадают. С другой стороны,
если открыты каналы, включающие три и более частиц, то разность
выражений C.7.12) и C.7.11) определяет полное сечение рождения
дополнительных частиц:
206 Глава 3. Теория рассеяния
; Е) =
^ + + ц
J C.7.14)
которое должно быть положительно.
Разложение по парциальным волнам особенно полезно для про-
процессов, у которых соответствующая часть 5-матрицы диагональна.
Это имеет место, если, например, входной канал п содержит ровно
две бесспиновые частицы, а все прочие каналы при данной энергии
закрыты, как в процессах %+%+ или %+%° рассеяния при энергиях
ниже порога рождения дополнительных пионов (электромагнитны-
(электромагнитными и слабыми взаимодействиями пренебрегаем). Для пары бесспи-
бесспиновых частиц j = I, и благодаря сохранению углового момента S-
матрица диагональна. Может быть и так, что .^-матрица диагональна
в определенных процессах с участием частиц со спином. Так, в пион-
нуклонном рассеянии полный момент системы может принимать зна-
значения j = I + 1/2 и j = I — 1/2, но при заданном j эти два состояния
имеют противоположную четность и не могут быть связаны ненуле-
ненулевыми матричными элементами 5-матрицы. В любом случае, если
для некоторых п и Е все элементы .^-матрицы SN'jlsn{E, 0) обраща-
обращаются в нуль, кроме случая, когда N' — это двухчастичное состояние
j, I, s, n, то из условия унитарности следует, что
4s'n',isnW = exp[2t5^n(E)]5n5s,s5nVl, C.7.15)
где 8^п(Е) — действительная фаза, обычно именуемая фазовым
сдвигом. Эта формула часто используется и в случае, когда
двухчастичная часть S—матрицы диагональна, но открыты каналы,
содержащие три и более частиц. В таких случаях фазовый сдвиг
должен иметь положительную мнимую часть, чтобы обеспе-
обеспечить положительность C.7.14). В случае действительных фазовых
сдвигов упругое и полное сечения определяются из C.7.10) и C.7.12)
в виде
4тг
" ' - ' -- ¦ " - -- C.7.16)
k2Bs1 + l)Bs2 +1)
jls
3. 7. Разложения по парциальным волнам 207
Этот известный результат обычно выводится в рамках нереля-
нерелятивистской квантовой механики путем исследования в координат-
координатном пространстве поведения волновой функции частицы в заданном
потенциальном поле. Представленное здесь доказательство имеет
целью, во-первых, показать, что разложение по парциальным вол-
волнам применимо для упругого рассеяния и при релятивистских ско-
скоростях, и, во-вторых, подчеркнуть, что оно не зависит от конкрет-
конкретных динамических предположений, а вытекает из условия унитар-
унитарности и принципов инвариантности.
Часто полезно ввести фазовые сдвиги и в задачах, когда не-
несколько открытых каналов образуют неприводимые представления
какой-то внутренней группы симметрии. Классическим примером
является изотопическая симметрия, при наличии которой индекс
канала п включает значения изоспинов Т1( Т2 двух частиц и треть-
третьих проекций изоспина tv t2- Состояния в канале п можно выразить
в виде линейных комбинаций неприводимых представлений со зна-
значением полного изоспина Т и третьих проекций ^причем коэффи-
коэффициенты разложения определяются знакомыми коэффициентами
Клебша-Гордана CT^(T,t;t1,t2). Предположим, что для интересую-
интересующих нас каналов при заданной энергии 5-матрица диагональна по
I, s, j, T, t. Условие унитарности и требование изотопической сим-
симметрии позволяют записать .^-матрицу в виде:
si's-T't',UTt = exP[2*6jkT(E)]SrA'A'T8t't> C. 7. 17)
где bj i sT(E) — действительный фазовый сдвиг, который в соответствии
с теоремой Вигнера-Эккарта не зависит от t. С помощью C.7.10)
можно вычислить парциальные сечения, а из C.7.12) следует, что
полное сечение
4л
х ?Bj + l)CTiT2(T,t;t1,t2J sin2 5jlsT(E).
jlsT(
jlsTt
Например, в пион—пионном рассеянии отличны от нуля фазо-
фазовые сдвиги ЬцОТ(Е) при Т = 0 и Т = 2 для каждого четного I и при
Т = 1 для нечетного I, а в пион—нуклонном рассеянии — фазовые
сдвиги 5 с Т = 1/2 или Т = 3/2.
208 Глава 3. Теория рассеяния
Ряд полезных сведений о пороговом поведении амплитуд рас-
рассеяния и фазовых сдвигов можно получить из рассмотрения их ана-
аналитических свойств, которые почти не зависят от любых дина-
динамических предположений. Если отсутствуют особые обстоятельства,
порождающие сингулярности в импульсном пространстве, можно
ожидать, что матричный элемент Щ'^-к'а^п'М^-к^п процесса дол-
должен быть аналитической функцией * 3-импульсов к и к' в окрестно-
окрестности к = 0 или к' = 0 (при упругом рассеянии к = к' = 0).
Обращаясь к разложению C.7.8) амплитуды М по парциальным
волнам, заметим, что комбинация /c*Yrm(k) есть простая полиноми-
полиномиальная функция 3-вектора к. Поэтому, для того, чтобы
амплитуда ^k'o'1-k'o'2n',ko1-ko2n была аналитической функцией 3-им-
3-импульсов к и к' в окрестности к = 0 или к' = 0, коэффициенты Mj,s,n, lsn
или эквивалентно &i'fis's^n'n ~ ^Vs'n lsn должны вести себя как
/сг+1'2/с'г+1'2 при к или к', стремящихся к нулю. Отсюда, для малых к
и/или к' существенный вклад в амплитуду рассеяния дает только низ-
низшая парциальная амплитуда в начальном и/или конечном состоянии.
Возможны три случая.
Экзотермические реакции
В этом случае к' стремится к конечному значению при к —> 0,
и в таком пределе 5n<Vs5n'n ~ ^I's'n lsn веДет себя как kl+1. Сечение
C.7.11) ведет себя как к21'1, где I — наименьший орбитальный угло-
угловой момент, при котором идет реакция. Чаще всего 1 = 0, так что
сечение реакции ведет себя как 1/к. (Именно так ведет себя, напри-
например, сечение поглощения медленных нейтронов сложными ядрами
или сечение аннигиляции электронно-позитронных пар в фотоны
при низких энергиях, если отбросить эффекты более высокого по-
порядка, связанные с кулоновскими силами.) Вероятность реакции
равна сечению, умноженному на поток, пропорциональный к, так
*Например, в борновском приближении C.2.8) амплитуда М пропорци-
пропорциональна фурье-образу матричных элементов взаимодействия в координатном
пространстве и поэтому аналитична при нулевом импульсе, если только эти
матричные элементы достаточно быстро убывают на больших расстояниях.
Главным исключением является рассеяние, обусловленное дальнодейству-
ющими силами типа кулоновских.
3. 7. Разложения по парциальным волнам 209
что при к —> 0 вероятность экзотермической реакции ведет себя как
константа. Однако вероятность поглощения при прохождении пучка
через мишень заданной толщины определяется именно сечением, а
не вероятностью реакции, так что для ряда веществ типа бора на-
наличие множителя \/к в сечении приводит к очень большой вероят-
вероятности поглощения медленных нейтронов.
Эндотермические реакции
В этом случае реакция запрещена, пока к не достигнет опреде-
определенного порогового значения, при котором к' = 0. В области чуть
выше порога 8;';5g/g5n/n - S^n, lsn ведет себя как (k')l+1. Сечение C.7.11)
в этом случае ведет себя как {k'Jl+1, где V — наименьший угловой
момент состояния, которое может возникнуть на пороге. Чаще всего
V = 0, так что сечение реакции растет над порогом как к', т. е. как
JE - Епорог . (Именно так обстоит дело в реакциях ассоциативного
рождения странных частиц или образования электронно-пози-
тронных пар при рассеянии фотонов.)
Упругие реакции
В этом случае к = к', так что обе эти величины стремятся
к нулю. (Так бывает в случае п' = п, или в случае, когда состояние
п' содержит частицы из того же изоспинового мультиплета, что и
п.) В упругом рассеянии всегда участвуют парциальные волны
с I = X = = 0, так что в пределе к —> 0 амплитуда рассеяния C.7.8)
стремится к константе:
f{k,o1,-k,o2,n -> k',ol-k',o'2,n') ->
^is^o^C^o^lo'^in -» п), C.7.19)
где а — постоянная величина, известная как длина рассеяния и
определяемая как предел
210 Глава 3. Теория рассеяния
при к = к' = 0. Суммируя 4л|/|2 по спинам конечных частиц и усредняя
по спинам начальных частиц, находим полное сечение перехода
п —> п' при к = к' = 0:
о(п -> п'; /с = 0) = BS+1^2s+1)I> + 1)а.2(п ">
. (з.7.21)
Классическим примером использования этой формулы явля-
является нейтрон-протонное рассеяние, когда существуют две длины
рассеяния, причем синглетная по спину длина рассеяния а0 суще-
существенно больше триплетной по спину длины av
Разложение по парциальным волнам можно использовать
и для грубой оценки поведения сечения при больших энергиях. Можно
ожидать, что с уменьшением длин волн рассеяние все более долж-
должно описываться на классическом языке: прицельный параметр час-
частицы с импульсом к и орбитальным угловым моментом I должен
равняться l/к, так что при рассеянии частица попадает в диск ра-
радиусом R, если I < kR. Это можно интерпретировать как утвержде-
утверждение, что матричные элементы 5-матрицы
O, I « kRn
, l»kRn> (ЗЛ.22)
где Rn — нечто вроде радиуса взаимодействия для канала п. При
заданном I » s существуют 2s + 1 значений j, причем все эти зна-
значения достаточно близки к I, так что приближенно 2j + 1 — 21 + 1,
и сумма по j и s в C.7.12) сводится к множителю порядка
B j + 1) = B1 + 1) ? Bs
js s
Поэтому полное сечение при к 3> l/Rn определяется из C.7.12) как
l<kRn
Совершенно аналогично из соотношения C.7.10) находим упругое
сечение рассеяния
o(n^n;E)^%R2n. C.7.24)
3.8. Резонансы 211
Разница между C.7.23) и C.7.24) равна неупругому сечению
лКп2, что и следовало ожидать при столкновениях с непрозрачным
диском радиуса Rn. (Несколько удивительное появление упругого
сечения рассеяния яКп2 связано с дифракцией на диске.) С другой
стороны, если предположить в соответствии с C.7.22), что Slsn lsn
комплексны только для значений прицельных параметров l/к в ма-
малой области шириной Ап « R в окрестности l/k = Rn, то, исполь-
используя неравенство Im(l — Sisnlsn)\ < 2, получаем с помощью такого же
анализа ограничение на действительную часть амплитуды рассея-
рассеяния вперед:
|Re /(n; Е)\ < 2/сК„А„«|1т /(п; Е)\. C.7.25)
Малая величина действительной части амплитуды рассеяния вперед
при больших энергиях подтверждается экспериментом.
До сих пор мы ничего не сказали о том, может ли радиус
взаимодействия Rn сам зависеть от энергии. Для очень грубой оцен-
оценки предположим, что Rn есть расстояние, на котором множитель
ехр(-цг) в потенциале Юкавы A.2.74) принимает значение, пропор-
пропорциональное некоторой неизвестной степени Е. В этом случае Rn ве-
ведет себя как 1пЕ при Е —> °о, а сечение пропорционально AпЕJ. На
основе очень общих предположений было строго показано26, что
полное сечение не может расти быстрее, чем AпЕJ при Е —> °°.
И действительно, наблюдаемое полное сечение протон-протонного
рассеяния растет при больших энергиях по закону, близкому к AпЕJ,
так что представленная грубая картина рассеяния при больших энер-
энергиях по-видимому имеет отношение к действительности.
3.8. Резонансы*
Часто бывает так, что частицы, принимающие участие в
многочастичном соударении, могут образовать промежуточное
состояние, состоящее из одной нестабильной частицы R, которая
затем распадается на частицы в конечном состоянии. Если полная
* Этот раздел лежит несколько в стороне от основной линии изложения и
может быть опущен при первом чтении.
212 Глава 3. Теория рассеяния
вероятность распада R мала, сечение при значении энергии в ок-
окрестности промежуточного состояния R очень быстро изменяется
(обычно появляется острый максимум), проявляя резонансное по-
поведение.
Мы увидим, что поведение сечений вблизи резонанса доста-
достаточно хорошо определяется только одним условием унитарности.
Это хорошее известие, поскольку механизмы образования почти
стабильных состояний весьма различны.
а) Простейшая возможность заключается в том, что гамиль-
гамильтониан можно представить в виде суммы двух слагаемых: «сильно-
«сильного» гамильтониана Но + Vs, причем частица R является собственным
состоянием этого гамильтониана, и слабого возмущения Vw, за счет
которого R распадается по разным каналам, включая начальное и
конечное состояния а и C рассматриваемого процесса соударения.
Например, существует нейтральная частица Z0 с j = 1 и массой
91 ГэВ, которая была бы стабильной в отсутствие электрослабых
взаимодействий. Эти взаимодействия позволяют Z0 распадаться на
электрон-позитронные пары, мюон-антимюонные пары и т.д.,
однако полная ширина распада много меньше массы Z0. В 1989 году
частица Z0 наблюдалась как резонанс * в электрон-позитронных
соударениях в ЦЕРНе и Станфорде в реакциях аннигиляции
е+ + е" -> Z°-> е+ + е", е+ + е" -> Z0 -> ц+ + ц" и т. п.
б) В ряде случаев частица имеет большое время жизни, пото-
потому что существует потенциальный барьер, не позволяющий состав-
составным частям разлететься. Классическим примером является
альфа-распад ядер: энергетически допустим вылет из ядра альфа-
частицы (ядра атома Не4), однако сильное электростатическое от-
отталкивание между альфа-частицей и ядром образует запрещенную
область вокруг дочернего ядра, в которой по классическим законам
альфа-частица находиться не может. Распад тем не менее происхо-
происходит за счет квантово-механического подбарьерного перехода и экс-
экспоненциально мал. Такое нестабильное состояние проявляется как
* Между прочим, этот пример показывает, что резонансное состояние
должно распадаться всего лишь относительно медленно. Время жизни
Z°-6o3OHa равно 2,6 х 10~25 с, и этого времени не хватает даже на то, чтобы
Z0, двигаясь почти со скоростью света, пересек атомное ядро. Важно то, что
скорость распада в 36 раз меньше, чем скорость осцилляции Й/М2 волновой
функции Z0 в системе покоя.
3.8. Резонансы 213
резонанс при рассеянии альфа-частицы на дочернем ядре. Напри-
Например, наинизшее по энергии состояние ядра Be8 нестабильно по от-
отношению к распаду на две альфа-частицы и проявляется как резо-
резонанс в Не4-Не4 рассеянии. (Помимо кулоновского барьера,
существуют центробежные барьеры, позволяющие продлить время
жизни альфа-, бета- и гамма-нестабильных ядер большого спина.)
в) Сложные системы могут быть почти стабильными по чисто
статистическим причинам, в отсутствие каких-то потенциальных
барьеров или слабых взаимодействий. Например, возбужденное
состояние тяжелого ядра способно распасться только в случае, ког-
когда из-за статистической флуктуации основная часть энергии
сконцентрируется на отдельном нейтроне. Такое состояние
проявляется как резонанс при рассеянии нейтронов на дочернем
ядре.
Описанные механизмы образования долгоживущих состояний
весьма различны. Поэтому поистине счастливым обстоятельством
является то, что большинство свойств резонансов следует только
из условия унитарности безотносительно к динамическому механиз-
механизму, приводящему к образованию данного резонанса.
Прежде всего, рассмотрим энергетическую зависимость
матричного элемента реакции вблизи резонанса. Зависимость от
времени волнового пакета doc д(ос)Ф+ exp(-iEat) из ин-состояний
определяется формулой C.1.19):
+e-*E«t = J
Как было отмечено в разделе 3.1, полюс функции Т$а+ в нижней
полуплоскости комплексной плоскости Еа дает вклад во второе
слагаемое, которое экспоненциально затухает при t —> °°. Конкретно,
полюс в точке Еа = ER — гГ/2 приводит к слагаемому в амплитуде,
ведущему себя как ехр(—iERt — Ft/2). Оно отвечает некоторому
состоянию, вероятность которого уменьшается со временем по
закону exp(-Tt). Мы заключаем отсюда, что долгоживущее состоя-
состояние с энергией ER и шириной Г соответствует слагаемому в амплитуде
рассеяния, меняющемуся как
214 Глава 3. Теория рассеяния
тр<х+ ~ (?<х - er + гГ/2) + const. C.8.1)
Далее будет удобно использовать в качестве базиса обсуждавшиеся
в предыдущем разделе ортонормированные дискретные многочастич-
многочастичные состояния ФрЕ№ здесь р и Е — полные импульс и энергия, N —
индекс, принимающий только дискретные значения (хотя их может
быть бесконечно много). В этом базисе S—матрица может быть
записана в следующем виде:
Sp>e>n>,pen = S3(P' - Р)8(Я' - E)SN,N(p,E), C.8.2)
Мы считаем, что вблизи резонанса амплитуда в системе центра
масс S@, Е) = ,ЦЕ) имеет вид
<PN,N{E) S SN,N{0,E) = ffON,N + Е_*™гТ/2, C.8.3)
где ,9q и ill примерно постоянны, по крайней мере, в относительно
узкой области энергий |Е - Ек| < Г.
В таком базисе условие унитарности S—матрицы принимает
вид обычного матричного уравнения
<f(E)f<f(E) = l. C.8.4)
Подстановка формулы C.8.3) показывает, что нерезонансная фоновая
5-матрица унитарна:
а матрица вычетов Ш удовлетворяет двум условиям:
У>1» - tfbf0 = 0, C.8.6)
+ ЖГЖ = О. C.8.7)
Эти условия можно записать в более ясной форме, полагая
.fl = -iT,4S0. C.8.8)
3.8. Резонансы 215
В терминах А вышеприведенные условия унитарности имеют
простой вид
J = 4, А2 = А. C.8.9)
Любая такая эрмитова идемпотентная матрица называется
проекционной матрицей. Эти матрицы всегда можно выразить в
виде суммы диад из ортонормированных векторов и^:
N'UN > ]_,UN UN - °rs- C.8.10)
r JV
Тогда дискретная часть S—матрицы имеет вид
JV"
и(г)и(г)*
UN'UN"
PON"N- C.8.11)
Можно считать, что каждое слагаемое в сумме по г возникло от
отдельного резонансного состояния, причем все эти состояния имеют
одни и те же значения ER и Г.
Какое отношение эти выражения имеют к вероятностям и сече-
сечениям?
Для простоты не будем сначала учитывать нерезонансное фоно-
фоновое рассеяние, положив .%N<N равным 6^^. К общему случаю мы
вернемся чуть позже. Тогда для описанных в предыдущем разделе
двухчастичных дискретных состояний в системе центра масс
формула C.8.11) принимает вид
_v Е У и(г) и(г)* C.8.12)
Е - ER + i Г/2 ^ afe'l's'n'ajGlsn-
Во всех случаях метка г включает индекс oR, задающий z—
компоненту полного углового момента резонансного состояния; для
состояния с полным моментом jR величина OR принимает 2jR + 1
значение. Если нет других вырождений, индекс г сводится к значению
R,
И
216 Глава 3. Теория рассеяния
%isl = 5,R ARj(jWbn, C.8.13)
где uisn — набор комплексных амплитуд (по теореме Вигнера-Эккарта
не зависящих от а). Представление C.8.12) задает амплитуду Si,
определенную формулой C.7.7):
sl's'n',lsn(E) = &vfis's&n'n ~ ^j,jR е-Е—+ г Г/2 L^Ul's'n'u'lsn' C.8.14)
г Г/2
Формула C.8.10) теперь принимает вид
2
U
Isn
+...= 1,
C.8.15)
Isn
где точки означают положительный вклад любых состояний,
содержащих три и более частиц. Как мы увидим, величины |w;sn2
имеют смысл относительных вероятностей распада резонансного
состояния в различные возможные двухчастичные состояния.
Теперь формула C.7.12) дает полное сечение всех реакций в
канале п:
%{2jR +1) ГГ
„
где
г = rV 2
п /_^ isn C.8.1 /)
Это одна из форм записи знаменитой формулы Брейта-Вигнера для
одного уровня 27.
Те же результаты можно использовать и для вычисления
сечения резонансного рассеяния из начального двухчастичного канала
п в конечной двухчастичный канал п'. Подстановка формулы C.8.14)
в C.7.10) дает:
+ 1) (Е - If, Г»/4 • <3-8'18>
Отсюда видно, что вероятности распада резонансного состояния
в любой из конечных двухчастичных каналов п' пропорциональны
3.8. Резонансы 217
Гп'. Согласно C.8.15) сумма всех Гп (включая вклады от конечных
состояний, содержащих три и более частицы) просто равна полной
вероятности распада Г, поэтому можно заключить, что Гп есть веро-
вероятность распада резонансного состояния по каналу п.
Из формул C.8.16) и C.8.18) следует, что у соответствующих
величин имеется характерный резонансный пик при значении энер-
энергии ER с шириной (т. е. полной шириной пика на половине его высо-
высоты), равной вероятности распада Г. (Индивидуальные Гп часто на-
называют парциальными ширинами.) Так как Гп < Г, полное сечение
в пике резонанса, грубо говоря, ограничено квадратом длины вол-
волны B%/кJ. Это правило, что в области отдельного резонансного пика
сечение ограничено квадратом длины волны, универсально и при-
применимо даже в классической физике (где роль условия унитарности
выполняет закон сохранения энергии), например, при резонансном
взаимодействии звуковых волн с пузырьками воды в море, или гра-
гравитационных волн с гравитационной антенной. (В последнем случае
относительный вклад колебаний в любой лабораторной массе, при-
приводящих к потере энергии за счет гравитационного излучения, очень
мал, поэтому даже в резонансе сечение неизмеримо меньше квад-
квадрата длины волны 28.)
Наконец, часто бывает, что резонанс регистрируется, но из-
измерения энергии недостаточно точны, чтобы разрешить его шири-
ширину. В этом случае экспериментально измеряется интеграл от полно-
полного сечения по области в окрестности резонансного пика. Для полного
сечения это равно
Таким образом, подобные эксперименты могут определить только
парциальную ширину распада резонансного состояния в состояние
начальных частиц, но не полную ширину или относительные веро-
вероятности распадов.
Изложенный формализм можно применить и тогда, когда ре-
резонансные состояния с данным значением z-компоненты спина обра-
образуют мультиплет, связанный с какой-то группой симметрии. На-
Например, если имеет место изоспиновая симметрия, то для резонан-
резонанса с полным изоспином TR индекс г, нумерующий резонансные со-
состояния, включает не только z-компоненту ак углового момен-
момента, но и третью проекцию изоспина tR, принимающую значения
218 Глава 3. Теория рассеяния
—TR, —TR + 1, ..., TR. В этом случае предыдущие результаты для
полного и парциальных сечений не изменяются, так как каждый
двухчастичный канал п имеет определенные значения tlt t2 z-ком-
понент изоспина двух частиц и поэтому резонансное состояние, воз-
возникающее в этом канале, может иметь единственное значение tR =
tx + t2. Парциальные ширины Гп зависят от значений t1 и t2 только
через множители Ст т (TR,tR;t1,t2J.
Наличие резонанса проявляется в характерном поведении фа-
фазовых сдвигов вблизи резонанса. Если вернуться к общей формуле
C.8.11) (продолжая считать .% = 1), то из C.8.10) видно, что для
каждого отдельного резонансного состояния г существует собствен-
собственный вектор матрицы ffN>N(E) с собственным значением
т—'
ехрBгб(г)(Е)) = 1-г-
Е - ER + г Г/2 '
или иначе
Г/2
j±2~. C.8.20)
Видно, что в интервале энергий порядка Г вокруг резонансного значе-
значения «собственная фаза» Ь^Г\Е) скачком меняется от значения v% (v —
положительное или отрицательное целое число) ниже резонанса до
значения (V + 1)л выше резонанса. Однако чтобы с помощью этого
результата что-то узнать о вероятностях реакций, нужно знать соб-
собственные векторы и$, которые, в общем случае, имеют компо-
компоненты с произвольным числом частиц с разными импуль-сами, спи-
спинами и другими характеристиками.
Полученные результаты оказываются значительно более полез-
полезными в тех частных случаях, когда частицам в некотором канале N
запрещен (обычно законами сохранения) переход в любой другой
канал. Отсюда нетрудно включить в общую формулу C.8.11) эффекты
нерезонансного фона, связанные с матрицей рассеяния Уо. Чтобы
#jv3v обращались в нуль при некотором N и всех N' Ф N, необходимо,
чтобы это же было верно для .%N>N , а также для и$ при всех г,
для которых и$ Ф0- Из условия унитарности C.8.5) следует, что
для такого N
•/jon'n = e
3.8. Резонансы 219
а из уравнения C.8.10) вытекает, что
UN UN ~ urs>
так что в C.8.11) может быть только одно значение г, при котором
и$ Ф 0. В этом случае из C.8.11) находим:
гГ 1
expBz80JV) = bN>N expBz8w(E)).
с полным фазовым сдвигом
bN(E) = 50JV -arctgf^ j. C.8.21)
Видно, что в интервале энергий порядка Г вокруг значения
резонансной энергии ER фазовый сдвиг bN(E) совершает скачок от
значения 80JV ниже резонанса до значения 80JV + ж выше него. Как мы
видели в предыдущем разделе, указанные предположения выполня-
выполняются для различных двухчастичных реакций типа пион-пионного или
пион-нуклонного рассеяния при энергиях ниже порога рождения до-
дополнительных пионов. В этих случаях индекс N включает полный
и орбитальный угловые моменты j, l (для пион-пионного рассеяния
j = I), 2-компоненту полного углового момента о, а также
полный изоспин Т и его третью проекцию t. В силу теоремы Вигнера-
Эккарта фазовые сдвиги могут зависеть только от j, I и Т, но не от о
или t. В указанных каналах имеются знаменитые резонансы: в пион-
пионном рассеянии при энергии 770 МэВ имеется резонанс, называ-
называемый р, с j = I = 1, Т = 1 и Г = 150 МэВ ; в пион-нуклонном рассея-
рассеянии при энергии 1232 МэВ имеется резонанс, называемый А, с j = |,
I = 1, Т = | и шириной Г = 110-120 МэВ.
Из формул C.7.12) или C.7.18) следует, что когда резонансный
фазовый сдвиг проходит через значение к/ 2 (или нечетное кратное
л/2), полное сечение достигает максимума. Нерезонансные фазовые
сдвиги обычно довольно малы, так что при энергии, близкой к ER,
когда фазовый сдвиг 8г проходит через ж/2, сечение ototal имеет
острый максимум. Однако иногда случается, что нерезонансный
фоновый фазовый сдвиг 80JV близок к ж/ 2, и в этом случае, когда
220 Глава 3. Теория рассеяния
фазовый сдвиг проходит через значение ж в окрестности ER, в
сечении появляется узкий провал, обязанный деструктивной
интерференции между резонансной и нерезонансной амплитудами.
Подобные провалы впервые наблюдали в 1922 году Рамзауер и
Таунсенд при изучении рассеяния электронов на атомах благородных
газов.
Задачи
1. Рассмотрим теорию с сепарабельным взаимодействием, для
которого
(Фр,УФа) = *
где д — действительная константа связи, э. иа — набор комплекс-
комплексных величин, удовлетворяющих условию
|2
II
= 1.
i ^ i
а
С помощью уравнения Липпмана-Швингера C.1.16) найди-
найдите явные решения для ин- и аут-состояний и постройте
5-матрицу.
2. Предположим, что в реакции е+е~-рассеяния при полной энер
гии 150 ГэВ обнаружен резонанс со спином 1, причем сечение
(в системе центра масс, усредненное по начальным и просум-
просуммированное по конечным спинам) упругого е+е~—рассеяния в пике
резонанса равно 10~34 см2. Чему равна относительная вероятность
распада резонансного состояния R по каналу R —> е+ + е"? Чему
равно полное сечение е+е~-рассеяния в пике резонанса? (При
ответе на оба вопроса не учитывайте нерезонансного фонового
рассеяния.)
3. Выразите дифференциальное сечение двухчастичного рассея-
рассеяния в лабораторной системе (где одна из начальных частиц
покоится) через кинематические переменные и матричный
элемент Маа. (Получите формулу непосредственно, не используя
результаты, полученные в этой главе для дифференциального
сечения в системе центра масс.)
Список литературы 221
4. Выведите разложение по теории возмущений C.5.8) непосред-
непосредственно из формулы C.5.3) старой теории возмущений.
5. Можно определить состояния «стоячих волн» Ч?а° с помощью
модифицированной версии уравнения Липпмана—Швингера
4>о = ф +
Покажите, что матрица
эрмитова. Покажите, как можно выразить S—матрицу через К—
матрицу.
6. Выразите дифференциальные сечения упругого %+р- и %~р-
рассеяния через фазовые сдвиги состояний с определенными
значениями полного углового момента, четности и изоспина.
7. Покажите, что состояния Фер,О8П, определенные формулой C.7.5),
правильно нормированы, так что их скалярные произве-дения
даются формулой C.7.6).
Список литературы
1 Более подробно см.: Goldberger, M.L. and Watson, K.M. Collision
Theory (John Wiley & Sons, New York, 1964) (имеется рус. пер.:
Гольдбергер М.Л., Ватсон К. Теория рассеяния. М.: Мир, 1967); New-
Newton, R.G. Scattering Theory of Waves and Particles, 2nd edn (Springer
Veriag, New York, 1982) (имеется рус. пер. первого издания: Ньютон
Р. Теория рассеяния волн и частиц. М.: Мир, 1972).
la. Lippman, В. and Schwinger, J., Phys. Rev., 79, 469 A950).
2. Wheeler, J., Phys. Rev., 52, 1107 A937); Heisenberg, W., Z. /.
Phys., 120, 513, 673 A943).
a Born, M., Z. Phys., 37, 863 A926); 38, 803 A926).
222 Глава 3. Теория рассеяния
4 Moller, С, Kgl DanskeVidenskab.Mat.Fys.Medd., 23, No. 1A945);
22, No. 19 A946).
5. Rochester, G.D. and Butler, C.C., Nature, 160, 855 A947). Истори-
Исторический обзор см. в статье: Rochester, G.D., in: Pions to
Quarks — Particle Physics in the 1950s, ed. by L.M. Brown, M.
Dresden, and L. Hoddeson (Cambridge University Press, Cambridge,
UK, 1989).
6. Breit, G., Condon, E.U., and Present, R.S., Phys. Rev., 50, 825
A936); Cassen, B. and Condon, E.U., Phys. Rev., 50, 846 A936);
Breit, G. and Feenberg, E., Phys. Rev., 50, 850 A936).
7. Tuve, M.A., Heydenberg, N., and Hafstad, L.R., Phys. Rev., 50,
806 A936).
8. Gell-Mann, M., Cal. Tech. Synchrotron Laboratory Report CTSL-20
A961); Phys. Rev., 125, 1067 A962); Ne'eman, Y., Nucl. Phys., 26,
222A961).
9. См., например: Edmonds, A.R., Angular Momentum in Quantum
Mechanics (Princeton University Press, Princeton, 1957), Ch. 3 (где
CJiJ2{jm;m1m2) обозначено как UiJ2JMhmiJ2m2)) (есть рус. пер.:
Эдмондс А. Угловой момент в квантовой механике. М.: Атомиздат,
1968); Rose, M.E., Elementary Theory of Angular Momentum (John
Wiley & Sons, New York, 1957), Ch. 3 (где CJiJ2(jm;m1m2)
обозначено как C{jlj2j;mlm2m)).
10. Feinberg, G. and Weinberg, S., Nuovo Cimento, Serie X, 14, 571
A959).
11. Chinowsky, W. and Steinberger, J., Phys. Rev., 95, 1561 A954); см.
также: Ferretti, В., Report of an International Conference on
Fundamental Particles and Low Temperatures, Cambridge, 1946
(The Physical Society, London, 1947).
12. Lee, T.D. and Yang, C.N., Phys. Rev., 104, 254 A956).
13. Wu, C.S. et al., Phys. Rev., 105, 1413 A957).
Список литературы 223
14. Garwin, R, Lederman, L., and Weinrich, M., Phys. Rev., 105, 1415
A957); Friedman, J.I. and Telegdi, V.L., Phys. Rev., 105, 1681 A957).
15. Watson, KM., Phys. Rev., 88, 1163 A952).
16. Gell-Mann, M. and Pais, A., Phys. Rev., 97, 1387 A955); см. также:
Pais, A. and Piccioni, O., Phys. Rev., 100, 1487 A955).
17. Christenson, J.H., Cronin, J.W., Fitch, V.L., and Turlay, R, Phys.
Rev. Letters, 13, 138 A964).
18. Schubert, K.R. et al., Phys. Lett, 31B, 662 A970). В этой работе, не
предполагая С РТ-инвариантности, анализируются данные по
распадам нейтральных каонов. Показано, что та часть СР-
нарушающей амплитуды, которая сохраняет СРТ и нарушает Т,
имеет отличные от нуля действительную и мнимую части в
пределах пяти стандартных отклонений, в то время как
сохраняющая Т и нарушающая СРТ часть амплитуды равна нулю
в пределах одного стандартного отклонения.
19. Dalitz, R.H., Phil. Mag., 44, 1068 A953); Fabri, E., Nuovo Cimento,
11, 479 A954).
20. Dyson, F.J., Phys. Rev., 75, 486, 1736 A949).
21. См. например: Schiff, L.I., Quantum Mechanics, 1st ed. (McGrow
Hill, New York, 1949), Section 19 (есть рус. пер.: Шифф Л.
Квантовая механика. М.: ИЛ, 1957).
22. Впервые это было доказано в классической электродинамике. См.
например: Kramers, H.A., Atti Congr. Intern. Fisici, Como, 1927.
Квантово-механическое доказательство см.: Feenberg, E., Phys.
Rev., 40, 40 A932); Bohr, N., Peierls, RE., and Placzek, C, Nature,
144, 200 A939).
23. Более общее доказательство было дано в конце 1960-х гг. в
неопубликованной работе Ч. Н. Янга и Ч.П. Янга. См. также: Aharo-
ny, A., in: Modern Developments in Thermodynamics (Wiley, New
York, 1973), pp. 95-114.
224 Глава 3. Теория рассеяния
24. См., например: Edmonds, A.R., Angular Momentum in Quantum
Mechanics (Princeton University Press, Princeton, 1957), Ch. 2 (есть
рус. пер.: Эдмондс А. Угловой момент в квантовой механике. М.:
Атомиздат, 1968); Rose, M.E., Elementary Theory of Angular
Momentum (John Wiley & Sons, New York, 1957) , Appendix III;
Ландау Л.Д., Лифшиц Е.М. Квантовая механика. Нереляти-
Нерелятивистская теория. М.: Наука, 1974, §28, 31.
25. Wigner, E.P., Gruppentheorie (Friedrich Vieweg and Sohn, Braun-
Braunschweig, 1931) (есть рус. пер.: Вигнер Г. Теория групп.
М.: ИЛ, 1972); Eckart, С, Rev. Mod. Phys., 2, 305 A930).
26. Froissart, M., Phys. Rev., 49, 1053 A961).
27. Breit, G. and Wigner, E.P., Phys. Rev., 49, 519 A936).
28. См. например: Weinberg, S., Gravitation and Cosmology (Wiley,
New York, 1972), Section 10.7 (есть рус. пер.: Вейнберг С.
Гравитация и космология. М.: Мир, 1974).
29. Kollath, R., Phys. Zeit., 31, 985 A931).
Принцип кластерного разложения
До этого момента мы почти что не говорили о детальной
структуре оператора Гамильтона Н. Этот оператор можно опреде-
определить, задав все его матричные элементы между состояниями с
произвольным числом частиц. Эквивалентно, как будет показано
ниже, любой такой оператор можно выразить как функцию опре-
определенных операторов, уничтожающих и рождающих отдельные
частицы. В гл. 1 мы видели, что такие операторы рождения
и уничтожения впервые появились на ранней стадии развития
квантовой механики в схеме канонического квантования электро-
электромагнитного поля и других полей. Возник естественный формализм
для теорий, в которых могут рождаться и уничтожаться как фото-
фотоны, так и массивные частицы, первой из которых в начале 1930-х
годов стала теория C-распада Ферми.
Однако есть и более глубокая причина построения гамильто-
гамильтониана из операторов рождения и уничтожения, выходящая за
рамки нужд квантования любой существовавшей до этого теории
поля типа электродинамики и не имеющая отношения к тому, могут
ли частицы реально рождаться и уничтожаться. Существенным
преимуществом этого формализма является то, что если мы запи-
запишем гамильтониан как сумму произведений операторов рождения
и уничтожения с подходящими несингулярными коэффициентами,
то .^-матрица будет автоматически удовлетворять ключевому фи-
физическому требованию, а именно, принципу кластерного разложе-
разложения \ сводящемуся к тому, что результаты удаленных друг от
друга экспериментов не коррелируют. Именно по этой причине
формализм операторов рождения и уничтожения широко исполь-
используется в нерелятивистской квантовой статистической механике,
226 Глава 4. Принцип кластерного разложения
где в типичной ситуации число частиц фиксировано. В релятивист-
релятивистских квантовых теориях принцип кластерного разложения играет
решающую роль в той системе рассуждений, которая делает тео-
теорию поля неизбежной. Было много попыток сформулировать реля-
релятивистски инвариантную теорию, не являющуюся локальной тео-
теорией поля. Действительно, можно построить теории, не являющие-
являющиеся теориями поля, и тем не менее приводящие к лоренц-инвари-
антной 5-матрице для двухчастичного рассеяния2, но все эти
попытки сталкиваются с трудностями в секторах с более чем двумя
частицами: либо трехчастичная .^-матрица оказывается неинвари-
неинвариантной по отношению к лоренцовским преобразованиям, либо на-
нарушается принцип кластерного разложения.
В этой главе мы обсудим сначала базис состояний, содержа-
содержащих произвольной число бозонов и фермионов, затем определим
операторы рождения и уничтожения, и наконец покажем, как
использование этих операторов облегчает построение гамильтониа-
гамильтонианов, приводящих к .^-матрицам, удовлетворяющим принципу кла-
кластерного разложения.
4.1. Бозоны и фермионы
Гильбертово пространство физических состояний натянуто на
состояния, содержащие 0, 1, 2, ... свободных частиц. Это могут быть
состояния свободных частиц, либо ин- или аут-состояния. Для опре-
определенности будем рассматривать ниже состояния свободных частиц
(^>р1о1п1,р2о2п2,...) но все результаты будут применимы и для ин- или
аут-состояний. Как обычно, индекс а отмечает z-компоненты спина
(или спиральности для безмассовых частиц), а п отмечает сорт
частиц.
Нам предстоит рассмотреть вопрос, который был опущен в
гл. 3, а именно, установить свойства симметрии таких состояний.
Насколько мы знаем, все частицы являются либо бозонами, либо
фермионами. Разница между ними состоит в том, что при переста-
перестановке двух тождественных бозонов вектор состояния не изменяет-
изменяется, а при перестановке двух тождественных фермионов вектор
состояния меняет знак. Именно,
ф , , = +ф , , (А 1 11
...рст...р о п... — ...р о п...реп... к^-^-^/
4.1. Бозоны и фермионы 227
причем верхний или нижний знак отвечает, соответственно, бозону
или фермиону, а многоточием отмечены другие частицы, которые
могут присутствовать в данном состоянии. Эти два случая часто
называются статистикой Бозе или Ферми. В следующей главе мы
увидим, что статистики Бозе или Ферми — единственно возможные
случаи для частиц целого или полуцелого спина, соответственно.
Однако сейчас эта информация нам не понадобится. В данной главе
мы дадим нестрогое доказательство того, что все частицы должны
быть либо бозонами, либо фермионами, а затем установим условия
нормировки многобозонных и многофермионных состояний.
Заметим, во-первых, что если две частицы со спинами и
импульсами р, аи р', о' относятся к одному сорту п, то векторы
состояний Ф...рст...р'су'п... и Ф...р'а'п...рст... представляют одно и то же
физическое состояние. Если бы это было не так, то частицы можно
было бы различить по тому, в каком порядке расставлены индексы
в векторе состояний, т. е. первая из указанных частиц была бы не
тождественна второй. Так как два вектора состояний физически
неразличимы, они должны принадлежать одному лучу, так что
...рап...р а п... п ...р а п...pan... y±.i..&)
где ап — комплексное число, по модулю равное единице. Можно
считать эту формулу частью определения того, что мы подразуме-
подразумеваем под тождественными частицами.
Суть вопроса в том, чтобы решить, от чего может зависеть
фазовый множитель ап. Если он зависит только от индекса сорта
частиц, то мы почти у цели. Вновь меняя местами две частицы в
D.1.2), получаем
Ф / / = а Ф / /
...р<ТП...р <Т П... П ...р<ТП...р <Т П...
так что ап2 = 1, откуда и возникают только две возможности в D.1.1).
От чего же еще может зависеть ап? Этот коэффициент мог бы
зависеть от числа и сортов других частиц в состоянии (отмечено
многоточием в D.1.1) и D.1.2)), однако это привело бы к нежелатель-
нежелательному результату, что симметрия векторов состояний относительно
перестановки частиц здесь, на Земле, зависела бы от нали-
наличия частиц где-нибудь в другой части Вселенной. Подобное
свойство исключается принципом кластерного разложения,
228 Глава 4. Принцип кластерного разложения
который обсуждается ниже в этой главе. Фаза <хп не может нетри-
нетривиальным образом зависеть от спинов тех двух частиц, которые
переставляются местами, поскольку такие зависящие от спина
фазовые множители должны реализовать представление группы
вращений. Однако известно, что не существует нетривиальных
одномерных представлений трехмерной группы вращений, т. е.
представлений в виде фазовых множителей. Фаза ап могла бы
существенным образом зависеть от импульсов обмениваемых час-
частиц, однако из требования лоренц-инвариантности следует, что ап
может зависеть только от скаляра Р1^р2^- Этот скаляр симметричен
относительно перестановки частиц 1 и 2, поэтому такая зависи-
зависимость оставляет в силе предыдущие рассуждения, приводящие к
заключению, что ап2 = 1.
Логический пробел в приведенной выше аргументации состо-
состоит в том, что состояния Фр1СТ1п,р2ст2п,...(хотя это и не отражено
в обозначениях) могут содержать фазовый множитель, зависящий
от пути в импульсном пространстве, по которому импульсы частиц
получают значения р1( р2, и т. д. В этом случае двойной обмен
местами пары частиц може изменить состояние на фазовый множи-
множитель, причем ап2Ф 1. Мы увидим в гл. 9.7, что в двумерном случае
такая возможность реальна, но это невозможно в случае трех
и более пространственных измерений.
Как обстоит дело с перестановкой частиц разных сортов?
Если угодно, можно снять проблему, просто согласившись с самого
начала помечать вектор состояния, перечисляя сначала все им-
импульсы и спиральности фотонов, затем все имульсы и проекции
спина на ось z электронов, и так далее по всей таблице элементар-
элементарных частиц. Альтернативно, можно принять, что метки частиц
расположены в любом порядке, и определить векторы состояний с
произвольно расположенными метками частиц равными вектору
состояния со стандартным образом расположенными метками, ум-
умноженному на фазовые множители, зависимость которых от пере-
перестановки частиц разных сортов может быть любой.
Чтобы иметь дело с симметриями типа изоспиновой инвари-
инвариантности, которые связывают частицы разных сортов, удобно при-
принять соглашение, обобщающее D.1.1):
вектор состояния будет считаться симметричным по отноше-
отношению к перестановке бозонов или любого бозона с любым фермионом,
и антисимметричным при перестановке двух фермионов во всех
4.1. Бозоны и фермионы 229
случаях, независимо от того, принадлежат ли частицы одному
сорту или нет *.
Нормировка этих состояний должна быть определена в согла-
согласии с указанными условиями симметрии. Чтобы сделать запись
более компактной, будем использовать метку g для обозначения
всех квантовых чисел отдельной частицы: ее импульса р, z—компо-
z—компоненты спина (или спиральности в случае безмассовых частиц) о и
сорта п. Таким образом, JV-частичное состояние будет обозначать-
обозначаться <^>q1...qJV (вакуумному состоянию Фо отвечает N = 0). Для случаев N
= 0 и N = 1 вопрос о симметрии не возникает, поэтому
(Ф0,Ф0) = 1, D.1.3)
(Фд,,Фд) = 5(д'-д), D.1.4)
где 8(д' - д) есть произведение всех дельта-функций и кронекеров-
ских дельта—символов для квантовых чисел частиц:
D.1.5)
С другой стороны, для N = 2 состояния ®q[,q'2 и Фд^ физически
одинаковы, поэтому здесь следует положить
i - g2). D-1-6)
причем знак «минус» берется в случае, если обе частицы — фер-
фермионы, а знак «плюс» — во всех остальных случаях. Очевидно, что
* На самом деле, по тем же соображениям чисто условной является сим-
симметрия или антисимметрия вектора состояния при перестановке частиц од-
одного сорта, но разных спиральностей или третьих проекций спина. Действи-
Действительно, мы с самого начала можем договориться перечислять первыми им-
импульсы всех фотонов со спиральностью +1, затем импульсы всех фотонов со
спиральностью —1, затем импульсы всех электронов с проекцией спина на
ось z, равной +2, и т. д. Мы принимаем соглашение, что вектор состояния
симметричен или антисимметричен при перестановке тождественных бозо-
бозонов или фермионов разных спиральностей или г-компонент спина с целью
облегчить использование инвариантности относительно вращений.
230 Глава 4. Принцип кластерного разложения
это совместимо с установленными выше свойствами симметрии
состояний. В более общей форме
D.1.7)
Сумма здесь берется по всем перестановкам if целых чисел 1, 2, ..., N.
(Например, в первом слагаемом в D.1.6) перестановка if совпадает с
тождественным преобразованием, if\ =1, l-j?2 = 2, а во втором слагае-
слагаемом kPl = 2, f?2 = 1.) Кроме того, bf— знаковый множитель, равный
—1, если /включает нечетную перестановку фермионов (т. е. нечетное
число перестановок пар фермионов), и +1 во всех остальных случаях.
Легко видеть, что D.1.7) обладает желаемыми свойствами симметрии
или антисимметрии по отношению к перестановке как qt, так и q ^.
4.2. Операторы рождения и уничтожения
Операторы рождения и уничтожения можно определить по их
действию на нормированные многочастичные состояния, обсуждав-
обсуждавшиеся в предыдущем разделе. Оператор рождения aJ(q) (или под-
подробнее a^(p,G,n)) определяется как оператор, который просто добав-
добавляет частицу с квантовыми числами q спереди в списке всех частиц
в данном состоянии:
^ к- D.2.1)
В частности, JV-частичное состояние можно получить, действуя на
вакуум N операторами рождения:
а|(д1)а|(д2)...а|(д„)Ф0 =Фад2^. D.2.2)
Этот оператор обозначают af(q) чисто условно; сопряженный ему
оператор, который обозначается a(q), можно вычислить, исходя
из D.1.7).
Как мы сейчас покажем, a(q) удаляет частицу из любого
состояния, на которое он действует, так что поэтому его называ-
называют оператором уничтожения. В частности, если частицы qqi-.qN
являются все либо бозонами, либо фермионами, то
4. 2. Операторы рождения и уничтожения 231
N
a(q)<\q2...qjv = ?(±)r+15(q - qr)%v..qr_iqr+v..qN, D.2.3)
r=l
где знаки +1 или —1 берутся, соответственно, для бозонов или
фермионов.
(Вот доказательство. Мы намерены вычислить скалярное про-
произведение а((?)Фд1(з2...(зЛ, с произвольным состоянием Фд^.д^. Исполь-
Используя D.2.1), находим:
Теперь воспользуемся формулой D.1.7). Сумма по перестановкам if
чисел 1, 2, ..., N может быть записана как сумма по целому числу г,
которое переставляется на первое место, т. е. ,'?г = 1, та по отображе-
отображениям й? остальных целых чисел 1, ..., г-1, г+ 1, ..., N в 1, ..., N - 1.
Далее, знаковый множитель равен
где верхний и нижний знаки относятся соответственно к бозонам и
фермионам. Отсюда, второй раз используя D.1.7), получаем:
N М
r=l ?f 1=1
N
r=l
Таким образом, обе части D.2.3) имеют одинаковый матричный
элемент с любым состоянием, и поэтому равны друг другу, что и
требовалось доказать.)
Как частный случай D.2.3), отметим, что и для бозонов, и
для фермионов оператор a(q), действуя на вакуум, дает нуль:
а(д)Ф0 = 0. D.2.4)
232 Глава 4. Принцип кластерного разложения
Так определенные операторы рождения и уничтожения удов-
удовлетворяют важным соотношениям коммутации или антикоммута-
антикоммутации. Применяя оператор а(д') к состоянию D.2.1) и используя D.2.3),
получаем:
r=l
(Знак во втором слагаемом равен (±)г+2, так как qr находится на
(г+1)-м месте в &qqv..qN.) С другой стороны, применяя оператор af(q)
к D.2.3), находим:
г=1
Вычитая или складывая, получаем
[a(q')a\q) + at(q)a(q')]oqi...Cjv = 8(g'
Но это верно для всех состояний (и, как нетрудно показать, верно
также для состояний, содержащих и бозоны, и фермионы). Поэто-
Поэтому отсюда вытекает операторное соотношение
a(q)a\q) + a\q)a(q) = 5(q' - q). D.2.5)
Кроме того, из D.2.2) немедленно следует, что
\W 4Wq') = 0, D.2.6)
а также
= O. D.2.7)
Как всегда, верхний и нижний знаки относятся к бозонам и фер-
мионам, соответственно. Согласно обсуждавшимся в предыдущем
разделе условиям, операторы рождения и/или уничтожения для
4. 2. Операторы рождения и уничтожения 233
частиц двух разных сортов коммутируют, если частицы — бозоны,
и антикоммутируют, если обе частицы — фермионы.
Приведенные рассуждения можно воспроизвести в обратном
порядке (и в большинстве учебников именно так и делается). Иными
словами, можно было бы начать с коммутационных или антикомму-
антикоммутационных соотношений D.2.5)—D.2.7), выведенных путем канониче-
канонического квантования некоторой полевой теории. Затем следовало бы с
помощью D.2.2) определить многочастичные состояния и из соотно-
соотношений коммутации или антикоммутации вычислить их скалярные
произведения D.1.7). В сущности, как обсуждалось в гл. 1, такой
подход был бы значительно ближе к тому, по которому историче-
исторически развивался этот формализм. Мы следуем не по историческому
пути, так как хотим быть свободными от любой зависимости от
существовавших до этого теорий поля и стремимся понять, почему
эти теории такие, какие они есть.
Докажем теперь фундаментальную теорему, сформулирован-
сформулированную в начале этой главы: любой оператор Ф можно представить как
сумму произведений операторов рождения и уничтожения:
n=om=o D.2.8)
X a\q[)...a\qN)a{qM)...a{ql)CNM{q[...qNql...qM).
Иными словами, мы хотим показать, что можно выбрать коэффи-
коэффициенты CNM так, чтобы матричные элементы этого выражения
приняли бы любое желаемое значение. Докажем это по индукции.
Во-первых, тривиально доказывается, что при должном выборе Соо
можно придать матричному элементу (Ф0/?Ф0) любое значение,
независимо от значений CNM при N > 0 и/или М > 0. Для этого
нужно только воспользоваться формулой D.2.4) и убедиться, что
среднее по вакууму от D.2.8) равно
(Фо,0Фо) =
'00-
Предположим теперь, что это же верно для всех матричных эле-
элементов О между JV-частичными и М-частичными состояниями с
N < L, М < К или N < L, М < К. Иначе говоря, эти матричные
234 Глава 4. Принцип кластерного разложения
элементы получают определенные желаемые значения путем под-
подходящего выбора соответствующих коэффициентов CNM. Чтобы по-
показать, что это же верно для матричных элементов () между
любыми L-частичными и К-частичными состояниями, используем
D.2.8) для вычисления матричного элемента
+ слагаемые, содержащие CNM с N < L,M < К, либо N < L,M < К.
Какие бы значения не имели коэффициенты CNM с N < L, М < К или
N < L, М < К, ясно, что при определенном выборе CLK этот
матричный элемент может принять любое значение.
Конечно, оператор не обязательно должен иметь вид D.2.8),
где все операторы рождения стоят слева от операторов уничтоже-
уничтожения. (Часто говорят, что в этом случае операторы записаны в
нормальном порядке.) Однако, если в формуле для разложения
какого-то оператора по операторам рождения и уничтожения они
записаны в каком-то ином порядке, можно всегда с помощью
многократного использования соотношений коммутации или анти-
антикоммутации перетащить операторы рождения налево от операто-
операторов уничтожения, приобретая за счет этого новые слагаемые от
дельта-функции в D.2.5).
Рассмотрим, например, аддитивный оператор Ф любого типа
(импульс, заряд и т. п.), для которого
*%...,„ = (/(q1)+...+/(qJV))Oqi...qjv. D.2.9)
Такой оператор можно записать в виде D.2.8), используя только
одно слагаемое с N = М = 1:
F = Jdgat(g)a(g)/(g). D.2.10)
В частности, гамильтониан свободных частиц всегда имеет вид:
Яо = Jdgaf(g)a(g)E(g), D.2.11)
4. 2. Операторы рождения и уничтожения 235
где E(q) — энергия отдельной частицы:
+т2п.
Нам потребуются свойства преобразования операторов рождения
и уничтожения по отношению к различным симметриям. Во-пер-
Во-первых, рассмотрим неоднородные собственные ортохронные преобра-
преобразования Лоренца. Напомним, что под действием лоренцовских пре-
преобразований JV-частичные состояния преобразуются по закону:
(А а)Ф - е-^лР1)ае-*(Лр2)а (ApJ (Лр2)
о„О
Pi T>2 ¦
g? (W(A, Pl ))Dg2 (W(A, p2))
X
Здесь рл — трехмерная часть Лр, D^' (R) — то же самое унитар-
унитарное представление со спином j трехмерной группы вращений,
которое использовалось в разделе 2.5, a W(A, p) — специальное
вращение
где L(p) — стандартный «буст», переводящий частицу массой m из
системы, где она покоится, в систему, где она имеет 4-импульс рц.
(Конечно, m и j зависят от индекса сорта частиц п. Все это относится
к случаю m Ф 0; безмассовые частицы мы обсудим в следующей
главе.) Эти состояния можно записать, как в D.2.2), в виде
,... = а|(р1а1п1)а|(р2а2п2)...Ф0,
где Фо — лоренц—инвариантное вакуумное состояние,
[70(А,а)Ф0=Ф0.
Для того, чтобы состояние D.2.2) преобразовывалось должным об-
образом, необходимо и достаточно, чтобы оператор рождения преоб-
преобразовывался по правилу:
236 Глава 4. Принцип кластерного разложения
x > D^L(W(A,v))a p.an. D.^.1^)
Аналогично можно установить, что под действием операторов С, Р
и Т, реализующих преобразования зарядового сопряжения, про-
пространственной инверсии и обращения времени на состояниях сво-
свободных частиц *, операторы рождения преобразуются по законам:
= ), D.2.13)
-^ЛпЛ-роп), D.2.14)
Tampan)!" = ^n(-l)j~a af (-p -on), D.2.15)
Как отмечалось в предыдущем разделе, хотя мы и рассматривали
операторы, рождающие и уничтожающие частицы в свободном
состоянии, весь формализм может быть применен к ин- и аут-
состояниям. В этом случае можно ввести операторы ain и aout,
действие которых на такие состояния определяется совершенно
аналогично. Эти операторы подчиняются закону лоренцовских пре-
преобразований вида D.2.12), но с заменой оператора преобразования
U0(A,a) свободных частиц на истинный оператор лоренцовского
преобразования U(A,a).
4.3. Кластерное разложение и связные ампдитуды
Одним из самых фундаментальных принципов физики
(а, может быть, и всей науки) является утверждение, что результа-
* Мы опустили индекс 0 у этих операторов, так как практически во всех
случаях, когда С, Р и/или Т сохраняются, операторы, реализующие эти преоб-
преобразования на «ин» или «аут» состояниях, совпадают с операторами, определен-
определенными аналогично на состояниях свободных частиц. Для непрерывных преобразо-
преобразований Лоренца это не так, и следует различать операторы ЩА,а) и U0{A,a).
4.3. Кластерное разложение и связные амплитуды 237
ты экспериментов, выполненных на достаточном удалении друг от
друга, являются независимыми. Вероятности различных соударе-
соударений, измеренные в Лаборатории им. Э. Ферми, не должны зависеть
от того, какие эксперименты в это время проводятся в ЦЕРНе. Если
этот принцип неверен, мы никогда не смогли бы предсказать резуль-
результаты какого-либо эксперимента, не зная все про всю Вселенную.
В теории .^-матрицы принцип кластерного разложения утвер-
утверждает, что если многочастичные процессы щ —» C1; а2 —» C2, ...,
а , —» C , изучаются в .А" удаленных друг от друга лабораториях, то
элемент ^-матрицы для всего процесса факторизуется. Иначе говоря *,
'S'p1+P2+...+P).,a1+a2+...+a ,. ~* <S'p1a1'S'p2a2---'S'p ,.a.,. > D.3.1)
если для всех i Ф j все частицы в состояниях а, и C, находятся на
большом пространственном удалении от всех частиц в состояниях
<Xj и Cj. Такая факторизация элементов 5-матрицы обеспечит фак-
факторизацию соответствующих вероятностей переходов, отвечающих
некоррелированным экспериментальным результатам.
Существует комбинаторный трюк, позволяющий более на-
наглядно записать формулу D.3.1).
Определим связную часть 5-матрицы Saa формулой:
pa = i^i (—) Pi<Xi P2a2'" ' D 3 2)
PART
Здесь сумма берется по всем различным способам разбиения
частиц в состоянии а на кластеры ос1( Щ, ..., и частиц в состоянии |3
на кластеры Р1( Р2> •••> причем не считаются различными разбие-
разбиения, отличающиеся только порядком частиц внутри данного кла-
кластера или перестановкой самих кластеров. Знак + или — соответст-
соответствует тому, совершается ли при перегруппировках а Ф а^... и |3 Ф
PjP2... четное или нечетное число перестановок фермионов. Термин
связная часть соответствует обсуждаемой в следующем разделе
интерпретации на языке фейнмановских диаграмм, представляющих
* Мы возвращаемся здесь к обозначениям гл. 3. Греческие буквы а и [3
отвечают множеству частиц с указанием значений импульса, спина и сорта
каждой частицы. Кроме того, сумма щ + а2 + ... + а ,. обозначает состояние,
образованное комбинацией всех частиц в состояниях <ху, о^,..., ос, (аналогично
238 Глава 4. Принцип кластерного разложения
разные вклады в ряд теории возмущений .
Данное определение является рекуррентным. Для каждого а
и C сумма в правой части D.3.2) содержит слагаемое Saa и сумму
Yj' произведений двух и более элементов 6"с-матрицы с полным
числом частиц в каждом состоянии а и C-, которое меньше числа
частиц в состояниях а и C:
PART
Предположим, что элементы Sc—матрицы в этой сумме уже
выбраны так, что формула D.3.2) удовлетворяется для состояний
C, а, содержащих вместе меньше, чем, скажем, N частиц. Тогда,
независимо от того, какие значения элементов S—матрицы в сум-
сумме Y/ получены таким способом, всегда можно выбрать оставшее-
оставшееся слагаемое S?a так, чтобы формула D.3.2) выполнялась для
состояний а, C, содержащих всего N частиц **. Таким образом,
* Это разложение было использовано Урселлом, Майером и др. в классической
статистической механике, и Ли, Янгом и др.3 в квантовой статистической механике.
Кроме того, Голдстоун 4 и Гугенгольц 5 применяли его для вычисления энергий
многочастичных основных состояний. Во всех этих приложениях целью выделения
связных частей функций Грина, функций распределения, резольвент и т. п является
желание иметь дело с объектами, простым образом зависящими от объема Эта цель
совпадает и с нашей, поскольку ниже будет показано, что ключевым свойством
связных частей S—матрицы является то, что они пропорциональны единственной
дельта-функции сохранения импульса, а в ящике дельта-функция превращается в
кронекеровский дельта-символ, умноженный на объем Формально кластерное раз-
разложение похоже на то, которое используется в теории шума 6 для разложения кор-
корреляционной функции нескольких случайных переменных на «кумулянты». Если слу-
случайная переменная получает вклады от большого числа N независимых флуктуации,
то каждый кумулянт пропорционален N.
** Следует отметить техническую деталь. Рассуждение верно только в том слу-
случае, когда мы пренебрегаем возможностью, что для одного или более связных
элементов S—матрицы в D.3.2) состояния о^- и |3;- оба вообще не содержат частиц
Поэтому мы должны определить связный элемент между состояниями вакуума
Sq о равным нулю. Мы не используем формулу D.3.2) для матричного элемента
S—матрицы между состояниями вакуума So 0, который в отсутствие меняющихся
во времени внешних полей просто определяется равным единице, Soo = 1. Мы
расскажем несколько больше об амплитудах перехода вакуум—вакуум во внешних
полях в т. П.
4.3. Кластерное разложение и связные амплитуды 239
формула D.3.2) не содержит никакой информации. Это есть просто
определение Sc.
Если каждое из состояний а и C является одночастичным с
квантовыми числами q и q', соответственно, то единственным ос-
остающимся в правой части D.3.2) слагаемым будет Sna, так что для
одночастичных состояний
S$q=Sq,q=8(q'-q). D.3.3)
(Если не считать возможных вырождений, пропорциональность
Sq'q дельта-функции 5(g - q') следует из законов сохранения.
Отсутствие в D.3.3) какого-то коэффициента пропорциональности
связано с подходящим выбором относительной фазы «ин» и «аут»
состояний.) Мы предполагаем здесь, что одночастичные состояния
стабильны, так что переходы между этими состояниями и любы-
любыми другими, например, вакуумным, отсутствуют.
Для переходов между двухчастичными состояниями формула
D.3.2) принимает вид
2 " 92) ± 5(9i " ъШъ " Qi)-D.3.4)
(Здесь использована формула D.3.3)). Знак «минус» берется
в случае, если обе частицы — фермионы, во всех остальных
случаях берется знак «плюс». Обратим внимание, что слагаемые с
двумя дельта-функциями просто добавляются к норме D.1.6), так
что Sna в этом случае равна (S - 1)ра.
Общий случай более сложен.
Для переходов между трехчастичными состояниями формула
D.3.2) имеет вид:
S" = S^
414243.414243 4i4243.4i4243
+8(gi - Qi)^,^ ± перестановки D35)
3 ~ 9з)± перестановки,
В случае же четырехчастичных состояний
240 Глава 4. Принцип кластерного разложения
41424з44.414г4з44
'?„' г, г, S^'' „ „ + перестановки
4i42.4i42 4з44.4з44 г
+ перестановки
D.3.6)
+ перестановки
8(Qi ~ Qi)8(Q2 ~ 9г)8(9з ~ 9з)8(?4 ~ 4i) — перестановки.
(Учитывая все перестановки, всего получаем 1 + 9 + 6 = 16 слагае-
слагаемых в D.3.5) и 1 + 18 + 16 +72 + 24 = 131 слагаемое в D.3.6). Если
отказаться от предположения о стабильности одночастичных состоя-
состояний, число слагаемых станет еще больше.) Как объяснено выше,
определение является рекуррентным: мы используем D.3.4), опре-
определяя S?a для двухчастичных состояний, затем используем это
определение в D.3.5), где определяются Saa для трехчастичных
состояний, наконец, используем оба эти определения в D.3.6), где
определяются S?a в случае четырехчастичных состояний, и т. д.
Суть такого определения связной части 5-матрицы заключается
в том, что принцип кластерного разложения эквивалентен требова-
требованию обращения в нуль Saa, если одна или более частиц в состояниях
C и/или а находятся на большом расстоянии от других частиц *.
Чтобы увидеть это, предположим, что частицы в состояниях
C и а сгруппированы в кластеры C1; C2, ... и а1( а2, ..., и что все
частицы из набора (Хг + C^ находятся на большом расстоянии от всех
частиц из набора ос;- + C;- для всех j Ф г. Тогда, если 6"?а. обращается
в нуль, когда любые частицы в |3' и а' далеки друг от друга, этот
матричный элемент обращается в нуль, если любые частицы в
указанных состояниях принадлежат разным кластерам, так что из
определения D.3.2) следует
* Чтобы придать смысл словам «на большом расстоянии», следует осуще-
осуществить фурье—преобразование Sc, так что каждая метка р трехмерного им-
импульса заменяется трехмерным вектором координаты х.
4.3. Кластерное разложение и связные амплитуды 241
где Е(^ - сумма по всем разным способам разбиения кластеров В? и
Щ на субкластеры В?1, Bj2, ... и ОСд, а?-2, - Возвращаясь назад к D.3.2),
видим, что это и есть желаемое свойство факторизации D.3.1).
Например, предположим, что в четырехчастичной реакции
вида 1234 Ф 1/2'3/4/ частицы 1, 2, 1' и 2' находятся очень далеко от
частиц 3, 4, 3' и 4'. Тогда, если Saa обращается в нуль, когда
любые частицы в В и/или ОС далеки от других частиц, единствен-
единственные остающиеся в D.3.6) слагаемые (в еще более компактных
обозначениях) имеют вид:
с ч с-С оС
°1'2'3'4',1234 ~~* °1'2',12°3'4',34
+ (83'384'4±83'484'зMГ2',12
+ FГ162,2 ± 8i'282'l)(83'384'4 ± 83'484'з)-
Сравнение с D.3.4) показывает, что это и есть требуемое свойство
факторизации D.3.1):
Мы сформулировали принцип кластерного разложения в ко-
координатном пространстве как условие обращения в нуль S&a, если
любые частицы в состояниях В или ОС находятся далеко от любых
других частиц. Для дальнейшего удобно переформулировать это в
импульсном пространстве. Пространственные матричные элементы
определены как фурье-образы
4' хх = fd3p;d3p2...d3Pld3p2...^v dd
Xpf.2 "'»^1^2"' J P1P2 •"jPlP2'"
, , , , D.3.8)
x eiPl Xl егР2 X2... e~iPl xi е~гРг Xa.
(Мы временно опустили спиновые индексы и метки сортов частиц,
которые сопровождают пространственные или импульсные индек-
индексы.) Если величины | Spp> p p J ведут себя достаточно хорошо
(точнее, если они интегрируемы по Лебегу), то согласно теореме
Римана-Лебега 7 интеграл D.3.8) должен обращаться в нуль, если
242 Глава 4. Принцип кластерного разложения
любая комбинация пространственных координат стремится к беско-
бесконечности.
На самом деле, это слишком сильное требование. Из трансля-
трансляционной инвариантности следует, что связная часть .^-матрицы,
как и сама .^-матрица, может зависеть только от разностей векто-
векторов координат и поэтому вообще не изменяется, если все хг и ж'
изменяются совместно, так что их разность остается постоянной.
Отсюда вытекает, что элементы Sc в импульсном пространстве,
как и аналогичные элементы S, должны быть пропорциональны
трехмерной дельта-функции, обеспечивающей сохранение импульса
(в результате чего I ^p;, ...,PlP2.. .1 становится неинтегрируемой по
Лебегу), а также дельта-функции, отвечающей закону сохранения
энергии. Таким образом, можно записать:
x5(E[ + E'2+...-E1-E2-...)
Казалось бы, нет никаких проблем: принцип кластерного
разложения требует лишь, чтобы величина D.3.8) обращалась в
нуль, когда разности некоторых координат Xj и/или х'- становятся
большими. Однако если сама величина С в D.3.9) содержит дополни-
дополнительные дельта-функции от линейных комбинаций трехмерных
импульсов, этот принцип не будет удовлетворяться.
Например, пусть в С имеется дельта-функция, требующая,
чтобы сумма р у и -р; обращалась бы в нуль для некоторого подмно-
подмножества частиц. Тогда выражение D.3.8) не будет изменяться, если
все x'j и х?- для частиц в этом подмножестве будут изменяться с
постоянной разностью и удаляться от всех других значений x'fe и хг,
что противоречит принципу кластерного разложения. Грубо говоря,
этот принцип утверждает, что в отличие от самой S-матрицы ее
связная часть содержит только одну дельта-функцию закона
сохранения импульса.
Чтобы сделать это утверждение более точным, можно ска-
сказать, что коэффициентная функция в D.3.9) является гладкой
функцией своих импульсных меток. Но насколько гладкой? Проще
всего было бы потребовать, чтобы Cpjp'2 ....р^... была аналитической
функцией всех импульсов при р\ = р'2 = ... = рх = р2 = ... = 0. Такое
требование действительно гарантировало бы, что Cp'lP2....p^... экспо-
4.4. Структура взаимодействия 243
ненциально быстро убывает, если любые х и х' очень далеки от
любых других х и х'. Однако экспоненциальное убывание Sc не
является существенной частью принципа кластерного разложения,
а требование аналитичности выполняется не во всех теориях. Осо-
Особенно это проявляется в теориях с безмассовыми частицами, где
Sc может иметь полюса при определенных значениях р и р'.
Например, как будет видно в гл. 10, если безмассовая части-
частица может испускаться в переходе 1 —> 3 и поглощаться в переходе
2 —> 4, >Sir412 будет содержать слагаемое, пропорциональное мно-
множителю 1/(р! - РзJ- После преобразования Фурье такие полюсы
породят в S^' ' __ слагаемые, убывающие лишь как отрицатель-
отрицательная степень разности координат1. Нет нужды формулировать прин-
принцип кластерного разложения столь жестко, чтобы исключить по-
подобное поведение. Таким образом, условие «гладкости» Sc следует
понимать так, что допускаются различные полюсы и разрезы при
определенных значениях р и р', но не столь серьезные сингулярно-
сингулярности, как дельта-функции.
4.4. Структура взаимодействия
Зададимся вопросом, какого типа гамильтониан приводит
к 5-матрице, удовлетворяющей принципу кластерного разложения.
Именно здесь полностью раскрывает свои возможности формализм
операторов рождения и уничтожения. Ответ может быть сформу-
сформулирован в виде следующей теоремы.
.^-матрица удовлетворяет принципу кластерного разложения,
если (и насколько я знаю, только если) гамильтониан может быть
записан в виде разложения D.2.8):
dq[...dqNdql...dqM
jv=om=o D 41)
где коэффициентные функции hNM содержат единственную дель-
дельта-функцию закона сохранения трехмерного импульса (мы на ко-
короткое время используем более развернутые обозначения):
244 Глава 4. Принцип кластерного разложения
hNM (
DA2)
x hNM(p[o[n{...p^a^n^,р^щ...pMaM%),
причем hNM не содержит дельта-функций. Подчеркнем, что фор-
формула D.4.1) сама по себе бессодержательна — мы видели в разделе
4.2, что любой оператор можно представить в такой форме. Только
когда формула D.4.1) объединяется с требованием, что коэффици-
коэффициентные функции hNM содержат единственную дельта-функцию,
выписанную в D.4.2), можно гарантировать, что .^-матрица удовле-
удовлетворяет принципу кластерного разложения.
Справедливость этой теоремы в рамках теории возмущений
станет очевидной, когда мы в гл. 6 разовьем формализм фейнманов-
ских диаграмм. Доверчивый читатель может предпочесть пропустить
остаток данной главы и перейти к рассмотрению приложений этой
теоремы в гл. 5. Однако доказательство содержит ряд поучительных
моментов и поможет понять, в каком смысле теория поля, обсуждае-
обсуждаемая в следующей главе, является неизбежной.
Для доказательства теоремы используем теорию возмущений
в форме, явно зависящей от времени. (Одним из преимуществ
зависящей от времени теории возмущений является то, что намно-
намного яснее становится содержащаяся в формулировке принципа кла-
кластерного разложения комбинаторика; если Е — сумма энергий
отдельных частиц, то e~iEt есть произведение функций от отдель-
отдельных энергий, в то время как для (Е - Еа + ге) это неверно.)
Формула C.5.10) определяет ?—матрицу в виде *
f f
b • J —О
^ f D.4.3)
тг=О
где функция Гамильтона разделяется на функцию Гамильтона
свободных частиц Но и взаимодействие V, причем
* Мы принимаем соглашение, что для п — 0 хронологическое произведе-
произведение в D.4.3) рассматривается как единичный оператор, так что слагаемое с п
- 0 в сумме просто соответствует слагаемому 8(C - а) в S^,.
4.4. Структура взаимодействия 245
V(t) = exp(iHot)V exp(-zHoi). D.4.4)
Состояния Фа и Фп можно представить, как и в D.2.2), в виде
произведения операторов рождения, действующих на вакуум Фо, а
оператор V{t) сам есть сумма произведений операторов рождения и
уничтожения, так что каждое слагаемое в сумме D.4.3) можно
записать как сумму средних по вакууму от произведений операто-
операторов рождения и уничтожения. Используя соотношения коммутации
или антикоммутации D.2.5), можно переместить по очереди каж-
каждый оператор уничтожения направо, так, чтобы он оказался пра-
правее всех операторов рождения. При каждой перестановке операто-
оператора уничтожения правее оператора рождения возникают два слагае-
слагаемых, что видно, если записать D.2.5) как
Перемещение других операторов рождения правее оператора унич-
уничтожения в первом слагаемом порождает все больше новых слагае-
слагаемых. Однако из формулы D.2.4) следует, что любой оператор унич-
уничтожения, переместившийся до конца направо, действует на Фо, что
дает нуль, так что в конце концов останутся только слагаемые с
дельта-функциями. Таким образом, среднее по вакууму от произ-
произведения операторов рождения и уничтожения дается суммой раз-
различных слагаемых, каждое из которых равно произведению дель-
дельта-функций и знаков +, происходящих от коммутаторов или анти-
антикоммутаторов. Отсюда следует, что каждое слагаемое в D.4.3) мож-
можно представить как сумму членов, каждый из которых является
произведением дельта-функций и знаков ±, происходящих от ком-
коммутаторов или антикоммутаторов, а также тех множителей, кото-
которые вносят операторы V(t), проинтегрированным по всем време-
временам, а также проинтегрированным и просуммированноым по им-
импульсам, спинам и сортам частиц в аргументах дельта-функций.
Каждое возникающее таким образом слагаемое можно симво-
символически изобразить в виде диаграммы. (Это еще не полный форма-
формализм диаграмм Фейнмана, поскольку мы еще не собираемся сопос-
сопоставлять элементам диаграмм конкретные числовые величины.
В данном контексте мы используем диаграммы только как способ
проследить за возникающими дельта-функциями от 3-импульсов.)
Нарисуем п точек, называемых вершинами, по одной для каждого
246 Глава 4. Принцип кластерного разложения
оператора V{t). Для каждой дельта-функции, возникающей при про-
протаскивании оператора уничтожения, находящегося в одном из опе-
операторов V(t), направо через оператор рождения, отвечающий со-
состоянию Фа, нарисуем линию, идущую снизу и входящую в соответ-
соответствующую вершину диаграммы. Для каждой дельта-функции, воз-
возникающей при протаскивании оператора уничтожения, отвечающе-
отвечающего состоянию, сопряженному конечному состоянию Фа, направо
через оператор рождения в одном из операторов V(t), нарисуем
линию, исходящую из соответствующей вершины и идущую наверх.
Для каждой дельта-функции, возникающей при протаскивании опе-
оператора уничтожения из одного V{t) через оператор рождения в
другом V(t), нарисуем линию между соответствующими вершинами.
Наконец, для каждой дельта-функции, получающейся при протас-
протаскивании оператора уничтожения, отвечающего сопряженному ко-
конечному состоянию, через оператор рождения в начальном состоя-
состоянии, нарисуем линию, идущую снизу вверх прямо сквозь диаграмму.
Каждая из дельта-функций, связанных с одной из этих линий,
выражает равенство импульсов пары операторов рождения и унич-
уничтожения, отвечающих этой линии. Кроме того, есть по крайней мере
одна дельта-функция, которую вносит каждая из вершин и которая
выражает сохранение полного 3-импульса в вершине.
Подобная диаграмма либо связна (каждая точка связана с
другой точкой системой линий), либо несвязна, но может быть
разбита на некоторое число связных кусков. Оператор V(t), ассоции-
ассоциированный с вершиной в какой-то связной компоненте диаграммы,
фактически коммутирует с оператором V(t), ассоциированным с
любой вершиной в любой другой связной компоненте, поскольку для
такой диаграммы отсутствуют какие-либо члены, отвечающие тому,
что оператор уничтожения в одной вершине уничтожает частицу,
порожденную оператором рождения в другой вершине - в противном
случае эти две вершины оказались бы в одной связной компоненте.
Итак, матричный элемент в D.4.3) можно выразить как сумму произ-
произведений вкладов от каждой связной компоненты диаграммы:
%%с D.4.5)
разбиение j=l
на кластеры
4.4. Структура взаимодействия 247
Здесь сумма берется по всем способам разбиения начальных и
конечных частиц и операторов V(t) на V кластеров (включая сумму
по V от 1 до п). Каждый j-ый кластер включает п?- операторов
V{tji),...V(tjn) и некоторые подмножества начальных частиц а; и
конечных частиц C,. Конечно, это означает, что
п = щ + ... + Пу,
а также что множество ос есть объединение всех частиц в подмно-
подмножествах а1( а2, ..., ОЦ,, и аналогично для конечного состояния. В
некоторых кластерах в D.4.5) может вообще не быть вершин, т. е.
rij = 0. Тогда необходимо, чтобы соответствующий множитель в
матричном элементе D.4.5) обращался в нуль всегда, кроме слу-
случая, когда Cj и щ являются одночастичными состояниями (и тогда
сам множитель есть просто дельта-функция 5(а; - C;)), так как
единственные связные диаграммы без вершин имеют вид прямых
линий, идущих снизу вверх через всю диаграмму. Самое важное:
индекс С в D.4.5) означает, что мы исключаем любые вклады,
соответствующие несвязным диаграммам, т. е. такие вклады, в
которых какой-то оператор V(t) или любая начальная или конеч-
конечная частица не связана с каждой другой последовательностью
рождений и уничтожений частиц.
Подставим теперь D.4.5) в сумму D.4.3). Интеграл по каждой
временной переменной берется в пределах от -°° до °°, так что не
имеет значения, как переменные tb t2, ..., tn рассортированы по
кластерам. Сумма по разбиениям на кластеры дает множитель
nl/n^.n^.-nyl, равный числу способов разбиения п вершин на V
кластеров, в каждом из которых содержится щ, п2, - вершин:
п\
щ !n? !...nv !
1 А v PART nv..nv j=l
248 Глава 4. Принцип кластерного разложения
Первая сумма здесь берется по всем способам разбиения частиц в
начальном и конечном состояниях на кластеры ах ... 0Cv и C1... CV
(включая сумму по числу кластеров V). Множитель п! сокращается
с множителем 1/п! в D.4.3), а множитель (—г)" в ряде теории
возмущений D.4.5) можно записать как произведение (—г)...(—z)"v,
так что вместо суммирования по п и последующего отдельного
суммирования по щ, ..., гц, ограниченного условием щ + ... + гц = п,
можно просто независимо суммировать по п1( ..., nv. Оконча-
Окончательно
PART j=l ni=0 ' -oo
Сравнивая это выражение с определением D.3.2) связных матрич-
матричных элементов, мы видим, что эти матричные элементы равны как
раз множителям под знаком произведения:
jdt1...dt^,T{V(t1),...V(tn^a)c. D.4.6)
п=0
(Индекс j опущен у всех tun, так как теперь это просто перемен-
переменные интегрирования и суммирования.) Итак, Saa вычисляется по
очень простому рецепту: эта величина есть сумма всех связных
вкладов в S-матрицу, т. е. отбрасываются все слагаемые, в ко-
кторых любая начальная или конечная частица или любой опера-
оператор V(t) не связаны со всеми другими некоторой последовательно-
последовательностью рождений и уничтожений частиц. Этим объясняется
прилагательное «связная» для матрицы Sc.
Как мы видели, в каждой вершине и вдоль каждой линии
импульс сохраняется, поэтому он сохраняется по-отдельности и в
связных частях S—матрицы, т. е. S^a содержит множитель 53(рп — ра).
Мы хотим доказать, что Sna не содержит других дельта-функций.
Предположим, что коэффициентные функции hNM в разложе-
разложении D.4.1) функции Гамильтона по операторам рождения и уничто-
уничтожения пропорциональны единственной трехмерной дельта-функ-
дельта-функции, обеспечивающей сохранение импульса. Это автоматически
выполняется для свободной функции Гамильтона Яо, и поэтому
4.4. Структура взаимодействия 249
в силу высказанного предположения верно и для оператора взаимо-
взаимодействия V. Возвращаясь к использованной выше графической
интерпретации матричных элементов, это означает, что каждая
вершина вносит одну трехмерную дельта-функцию. (Другие дель-
дельта-функции в матричных элементах V^g просто сохраняют неизмен-
неизменным импульс любой частицы, не рождающейся и не уничтожаю-
уничтожающейся в соответствюущей вершине.) Далее, наличие большей части
этих дельта-функций сводится к фиксации импульсов промежуточ-
промежуточных частиц. Единственные импульсы, остающиеся незафиксиро-
незафиксированными этими дельта-функциями, — это импульсы в петлях из
внутренних линий. (Всякая линия, разрезание которой оставляет
диаграмму несвязной, несет импульс, который фиксирован зако-
законом сохранения как некоторая линейная комбинация импульсов
линий, входящих или выходящих из диаграммы. Если у диаграммы
L линий, которые можно одновременно разрезать, и при этом сама
диаграмма не становится несвязной, то говорят, что в диаграмме
содержится L независимых петель и, соответственно, имеется L
импульсов, не зафиксированных законом сохранения.) В диаграмме
с V вершинами, I внутренними линиями и L петлями имеется V
дельта-функций, из которых I — L требуются для фиксации внут-
внутренних импульсов, а остающиеся V — I + L дельта-функций связы-
связывают импульсы входящих и выходящих частиц. Однако хорошо
известное топологическое тождество * утверждает, что для любой
диаграммы, состоящей из С связных кусков, число вершин, внут-
внутренних линий и петель связано соотношением
V - I + L = С. D.4.7)
Отсюда в связном матричном элементе типа Saa, возникающим от
диаграмм с С = 1, содержится только одна трехмерная дельта-
функция 53(рр - ра), что и требовалось доказать.
* У диаграммы, состоящей из одной вершины, V=l,L=0nC=l. Если
добавить V — 1 вершину с ровно таким количеством внутренних линий, чтобы
диаграмма осталась связной, то I = V-l, L = 0 и С = 1. Все добавочные
внутренние линии, проведенные (без появления новых вершин) в той же связ-
связной диаграмме, дают равное количество петель, так что I — V + L — 1 и С = 1.
Если несвязная диаграмма состоит из С таких связных частей, то суммы I, V
и L от каждой связной части будут удовлетворять равенству ?7 = YV + L-L — С.
250 Глава 4. Принцип кластерного разложения
В приведенном рассуждении было несущественно, что произ-
производится интегрирование по временным переменным от -°° до °о.
Таким образом, можно использовать те же аргументы, чтобы
показать, что, если коэффициенты hN>M в гамильтониане содер-
содержать ровно одну дельта-функцию, то U(t,t0) также можно разло-
разложить на связные части, в каждой из которых будет содержаться
одна дельта-функция, выражающая закон сохранения импульса.
С другой стороны, связная часть .^-матрицы содержит также
дельта-функцию, отвечающую сохранению энергии. Когда в гл. 6
мы подойдем к диаграммам Фейнмана, будет видно, что Sc$a
содержит лишь одну дельта-функцию закона сохранения энергии
5(Ер - Еа), в то время, как U(t,t0) вообще не содержит дельта-
функций, отражающих закон сохранения энергии.
Следует подчеркнуть, что требование, чтобы hNM в D.4.1)
содержало лишь одну дельта-функцию, отражающую закон сохра-
сохранения трехмерного импульса, весьма нетривиально и приводит к
далеко идущим выводам.
Например, предположим, что V имеет неисчезающие матрич-
матричные элементы между двухчастичными состояниями. Тогда в формуле
D.4.1) должно содержаться слагаемое с N = М = 2 и коэффициентом
(Мы временно опустили индексы спинов и сортов частиц). Но тогда
матричный элемент взаимодействия между трехчастичными со-
состояниями равен
D 4 9)
(P1P2' Р1Р2 )8 (Рз ~ Рз)± перестановки.
В начале главы отмечалось, что можно попытаться постро-
построить релятивистскую квантовую теорию, не являющуюся теорией
поля, выбрав v2j2 так, чтобы двухчастичная 5-матрица была
лоренц-инвариантной, и подобрав оставшийся гамильтониан так,
чтобы в состояниях с тремя или более частицами не было рассея-
рассеяния. Поэтому следует выбрать v3 3 так, чтобы сократить другие
слагаемые в D.4.9):
4.4. Структура взаимодействия 251
*>з,з(Р1Р2Рз»Р1Р2Рз) = -'u2,2(PiP2'PiP2)83(P3 ~ Рз) + перестановки.
D.4.10)
Однако это означало бы, что каждое слагаемое в vs 3 содержит два
дельта-функционных множителя (напомним, что v2 2(p'iP/2>PiPi) уже
содержит множитель 53(р\ + р 2 - Pi - Рг)). что нарушает принцип
кластерного разложения. Итак, в теории, удовлетворяющей этому
принципу, существование процессов рассеяния с участием двух
частиц делает неизбежным существование процессов рассеяния с
участием трех и более частиц.
Обращаясь к решению задач трех тел в квантовых теориях,
удовлетворяющих принципу кластерного разложения, следует за-
заметить, что слагаемое vss в формуле D.4.9) не причиняет особого
беспокойства, но дополнительные дельта-функции в других слагае-
слагаемых осложняют непосредственное решение уравнения Липпмана—
Швингера. Проблема заключается в том, что появление дель-
дельта-функций делает ядро [Еа - Ер + ie]~1Vpa этого уравнения
квадратично неинтегрируемым, даже если исключить все дельта-
функции, отражающие общий закон сохранения импульса. Как
следствие, ядро нельзя аппроксимировать конечной матрицей да-
даже очень большого ранга. Чтобы решить задачу взаимодействия
трех или более частиц, необходимо заменить уравнение Липпмана-
Швингера таким уравнением, которое содержало бы связную пра-
правую часть. Подобные уравнения для рассеяния трех или более
частиц были построены 8>9, и их удалось рекурсивно решить для
ряда задач нерелятивистской теории рассеяния, но эти уравнения
оказались мало пригодными в релятивистских теориях. Поэтому мы
их здесь не будем рассматривать.
Такая переформулировка уравнения Липпмана-Швингера ока-
оказывается полезной в другом отношении. Наши рассуждения в этом
разделе основывались на теории возмущений. Мне неизвестно ка-
какое-либо непертурбативное доказательство основной теоремы этого
раздела. Однако было показано 9, что переформулированные не-
пертурбативные динамические уравнения совместимы с требовани-
требованием, что Uc{t,t0) (а следовательно и Sc) должны содержать требуемую
252 Глава 4. Принцип кластерного разложения
принципом кластерного разложения единственную дельта-функ-
дельта-функцию закона сохранения импульса, если только гамильтониан удов-
удовлетворяет условию, что каждая коэффициентная функция hN}M
тоже содержит лишь одну такую дельта-функцию.
Задачи
1. Определим производящие функционалы для 5-матрицы и ее
связной части:
?—l— \v{qi)...v{q'N)v{qi)...v{qM)
М=1 iV -M-J
JV=1 М=1
х ^...qj,,qi...qMdq[... dQ«dQi-dqM,
i
JV=1M=1
Выведите формулу, связывающую F[v] и Fc[t;]. (Можно рас-
рассмотреть чисто бозонный случай.)
2. Рассмотрим взаимодействие
V = gjd3p1d3p2d3p3d3p463(p1 + р2 - р3 - р4)
xaf(p1)af(p2)a(p3)a(p4),
где д — действительная константа, а а(р) - оператор уничтоже-
уничтожения бесспинового бозона массой М > 0. С помощью теории
возмущений найдите матричный элемент 5-матрицы для рас-
рассеяния этих частиц в с. ц. и. в порядке д2. Чему равно соответст-
соответствующее дифференциальное сечение?
3. Когерентное состояние Ф^ определяется как собственное со-
состояние операторов уничтожения a(g) с собственными значе-
значениями X(q). Постройте такие состояния как суперпозицию мно-
многочастичных состояний Фд1д2...д№.
Список литературы 253
Список литературы
1. Принцип кластерного разложения в квантовой теории поля,
по-видимому, впервые был явно высказан в работе:
Wichmann, E.H. and Crichton, J.H., Phys. Rev., 132, 2788 A963).
2. См., например: Bakamijan, В. and Thomas, L.H., Phys. Rev., 92,
1300 A953).
3. Ссылки можно найти в работе: Lee, T.D. and Yang, C.N., Phys.
Rev., 113, 1165 A959).
4. Goldstone, G., Proc. Roy. Soc. London, A239, 267 A957).
5. Hugenholtz, N.M., Physica, 23, 481 A957).
6. См., например: Kubo, R., J. Math. Phys., 4, 174 A963).
7. Titchmarsh, E.C., Introduction to the Theory of Fourier Integrals
(Oxford University Press, Oxford, 1937), Section 1.8.
8. Faddeev, L.D., Zh. Eksper. i Teor. Fiz., 39, 1459 A961); Dokl.
Akad. Nauk SSSR, 138, 565 A961); 145, 30 A962).
9. Weinberg, S., Phys. Rev., 133, B232 A964).
Квантовые поля и античастицы
Теперь у нас есть все необходимое, чтобы обосновать введе-
введение квантовых полей.1 В процессе этого построения мы увидим
наиболее примечательные и универсальные следствия союза тео-
теории относительности с квантовой механикой: связь спина и статис-
статистики, существование античастиц, различные соотношения между
частицами и античастицами, включая знаменитую СРТ-теорему.
5.1. Свободные поля
В гл. 3 было показано, что если взаимодействие можно запи-
записать в виде
V(t) = Jd3x.yf(x,i), E.1.1)
где Ж— скаляр в том смысле, что
ио(Л,арГ(а:)?7о1(Л>а) = .ЩЛх + а), E.1.2)
удовлетворяющий дополнительному условию
[Ж{х), Ж{х')] = 0 для (ж - ж'J > 0, E.1.3)
то .^-матрица оказывается лоренц-инвариантной. Мы увидим да-
далее, что существуют и более общие возможности, но все они мало
отличаются от этой. (Оставляем пока что открытым вопрос,
5.1. Свободные поля 255
ограничены ли преобразования Л собственными ортохронными пре-
преобразованиями Лоренца, или они могут включать пространствен-
пространственные отражения.) Чтобы легче было удовлетворить принципу кла-
кластерного разложения, мы собираемся строить Ж(х) из операторов
рождения и уничтожения. Однако здесь мы сталкиваемся с пробле-
проблемой. Как следует из формулы D.2.12), в результате преобразований
Лоренца каждый такой оператор умножается на матрицу, завися-
зависящую от того импульса, который несет этот оператор. Как нужно
объединять такие операторы, чтобы получить скаляр? Решение
заключается в том, чтобы строить Ж(х) из полей уничтожения
У^(х) и рождения щ(х):
^2 J,a, n)a(p,cj, гг), ^ЛЛ^
с коэффициентами * щ(х; p,a,n) и vx{x; p,a,n), выбранными так,
чтобы под действием лоренцовских преобразований каждое поле
умножалось бы на матрицу, не зависящую от координат:
(В принципе, можно было бы написать для полей уничтожения
и рождения разные матрицы D±, однако мы увидим, что всегда
можно выбрать поля так, что эти матрицы будут одинаковыми.)
Применяя вторично преобразование Лоренца Л, получаем
) = Д(ЛЛ)),
так что, обозначив Лг = (Л) и Л2 = ( Л), видим, что D-матрицы
реализуют представление однородной группы Лоренца:
* Напомним, что индексы те и а нумеруют соответственно типы частиц и
г-компоненты их спинов.
256 Глава 5. Квантовые поля и античастицы
DiAJDiAz) = DiA^). E.1.8)
Существует много таких представлений, в том числе, скаляр D(A) = 1,
вектор D(Af-y = Л*\, и уйма тензорных и спинорных представлений. Все
они неприводимы в том смысле, что с помощью выбора базиса невоз-
невозможно привести все D(A) к одной и той же блочно-диагональной
форме с двумя или более блоками. Однако мы пока что не требуем,
чтобы D(A) была неприводимой; в общем случае это блочно-диаго-
нальная матрица с произвольным набором неприводимых представле-
представлений в каждом блоке. Иными словами, индекс I включает метки,
различающие типы описываемых частиц и неприводимые представле-
представления в разных блоках, а также индекс, нумерующий компоненты
отдельных неприводимых представлений. Ниже мы разделим такие
поля на неприводимые, так что каждое поле будет описывать один
единственный сорт частиц (и античастиц) и преобразовываться по
неприводимому представлению группы Лоренца.
Раз уж мы научились строить поля, удовлетворяющие зако-
законам преобразования Лоренца E.1.6) и E.1.7), то теперь можно
построить и плотность гамильтониана взаимодействия в виде
jvm i[...vN iv..iM
E.1.9)
x\|/j/(x)...\|/j' (x)\|/^(x)...\|/^ (ж)
причем это выражение будет скаляром в смысле E.1.2), если посто-
постоянные коэффициенты Qi[...i'N,iv..iM выбраны лоренц-ковариантными,
т. е. для всех Л
У Yd,-v(A-1)...dv!,(A-1)d-(A-1)...d - (Л-1)
f-*t *-* Ml lNlN Ml lMlM
1"'JV1'"M E.1.10)
В принципе, задача нахождения коэффициентов 9i[...i'N,\..лм > Удов-
Удовлетворяющих E.1.10), ничем не отличается (и ничем не сложнее на
практике) от использования коэффициентов Клебша-Гордана для
объединения разных неприводимых представлений трехмерной груп-
группы вращений в скаляры по отношению к вращениям. Ниже мы
5.1. Свободные поля 257
сумеем объединить поля уничтожения и рождения так, чтобы
плотность гамильтониана коммутировала сама с собой в точках,
разделенных пространственноподобным интервалом.
Как выбрать коэффициентные функции щ(х; p,tf,n) и иг(х; p,G,n)?
Уравнение D.2.12) и сопряженное ему уравнение определяют зако-
законы преобразования * операторов уничтожения и рождения:
170 (Л, Ь)а(р, а, п)Щ1 (Л, Ъ) = ехр(г(Лр) • b)V(ApH / р°
,o,n), E.1.11)
170 (Л, b)af (р, а, п)^ (Л, Ъ) = ехр(-г(Лр) • b)V(ApH / р°
-1(A,p))a+(pA,a,n), E.1.12)
где jn — спин частицы типа п, а рл — трехмерная компонента
4-вектора Лр. (Чтобы привести E.1.11) и E.1.12) к указанному виду,
мы использовали условие унитарности матриц вращения D — ¦)
Кроме того, как мы видели в разделе 2.5, элемент объема d3p/p°
лоренц-инвариантен, так что можно заменить d3p в формулах
E.1.4) и E.1.5) на d3(Ap)p°/(Ap)°. Объединяя все это, находим:
170 (Л, Ь)?+(х)ио1 (A,b) = Y,jd3 (Лр) щ (х; р, а, п)
х ехр(г(Лр) • b)D(^\w-\A,р))^р° / (Лр)°а(рл,а,п)
Uo (Л, b)vf (х)^ (Л, Ь) = ^ J d3 (Лр) иг (х; р, а, п)
can
х ехрН(Лр) • tyD^flW-HA,p))Vp°/(Ap)°a+(pA,o, n).
Для того, чтобы поля удовлетворяли законам лоренцовских преоб-
преобразований E.1.6) и E.1.7), необходимо и достаточно, чтобы
*Эти законы приведены для массивных частиц. Случай нулевой массы
рассмотрен в разделе 5.9.
258 Глава 5. Квантовые поля и античастицы
-1 (Л, р)) ехр(+г(Лр) • Ъ)щ (х; р, а, п),
)
)п(А )^(Лх + Ь;рл,а,п)
т~1 (Л, р)) ехр(-г(Лр) • Ь)иг (х; р, а, п),
или в несколько более удобной форме
= Vp°/(Ap)°? Dji(A) ехр(г(Лр) • Ь)иг(х; р, а, п), E-1.13)
Iг{А) ехр(-г(Лр) • b)vx (x; р, а, п). @.1.14)
г
Эти фундаментальные требования позволяют определить коэффи-
коэффициентные функции щ и vx через конечное число свободных па-
параметров.
Мы используем формулы E.1.13) и E.1.14) в три этапа, рас-
рассматривая по очереди три разных типа собственных ортохронных
преобразований Лоренца.
Трансляции
Сначала рассмотрим формулы E.1.13) и E.1.14) при Л = 1 и
произвольном Ъ. Сразу получаем, что мг(х;р,а,п) и т;г(х;р,а,п) имеют
следующий вид:
5.1. Свободные поля 259
щ(х;р,о,п) = BтгГ3/2е^мг(р,а,п), E.1.15)
иг(х;р,а,п) = B%r3/2e-iPxvl(p,o,n), E.1.16)
так что поля являются преобразованиями Фурье:
,n))
а,п
(Множители Bтг)~3/2 можно было бы включить в определение щ и vb
но принято выписывать их явно перед интегралами.) С учетом
E.1.15) и E.1.16) получаем, что условия E.1.13) и E.1.14) удовлетво-
удовлетворяются, если и только если для произвольного преобразования
Лоренца Л
, E.1.19)
x (рЛ,о, n)D^r(W(A,р)) = Vp°AAP)°Z Dji(A)yi(p,a, n). E.1.20)
Положим теперь р = 0 в E.1.19) и E.1.20). Пусть Л — стандарт-
стандартный буст L(g), переводящий частицу массой т из состояния покоя в
состояние с некоторым 4-импульсом ср. Тогда L(p) = 1 и
W(A,p) = L(Ap)AL(p) = L-l{q)L{q) = 1.
Отсюда в этом частном случае из формул E.1.19) и E.1.20) получаем
i@,a,n), E.1.21)
260 Глава 5. Квантовые поля и античастицы
E.1.22)
Иными словами, если нам известны величины щ@,<5,п) и г>г@,а,п)
для нулевого импульса, то для заданного представления D(A)
однородной группы Лоренца мы знаем и функции мг(р,а,п) и г>г(р,а,п)
для всех р. (Явные выражения матриц D^(L(g)) для произвольных
представлений однородной группы Лоренца будут выписаны в раз-
разделе 5.7.)
Вращения
Далее, положим р = 0, но будем теперь считать, что Л —
преобразование Лоренца с рл = 0. Иными словами, будем рассмат-
рассматривать Л как чистое вращение R. Очевидно, что W(A,p) = R, так что
формулы E.1.19) и E.1.20) принимают вид
их @, о, n)D^\R) = ? D-n(R)Ul@,<y, n), E.1.23)
E.1.24)
или эквивалентно
E.1.25)
E.1.26)
где J^ и JT — матрицы углового момента в представлениях D^(R) и
D(R), соответственно. Если Л ограничены вращениями R, то любое
представление ?>(Л) однородной группы Лоренца очевидно стано-
становится и представлением группы вращений. Тогда из формул E.1.25)
и E.1.26) следует, что если поле \|/j~(x) должно описывать частицы
5.1. Свободные поля 261
определенного спина j, то это представление D(R) должно содер-
содержать среди своих неприводимых компонент отвечающее спину j
представление D^\R), причем коэффициенты щ@,<5,п) и г>г@,а,п)
описывают то, каким образом представление группы вращений со
спином j погружено в D(R).
В разделе 5.5 мы увидим, что каждое неприводимое представ-
представление собственной ортохронной группы Лоренца содержит любое
заданное неприводимое представление группы вращений не более
одного раза, так что если поля У?(х) и уЦх) преобразуются по
неприводимому представлению, то они единственны с точностью до
общего масштабного множителя. В более общей форме утверждает-
утверждается, что число свободных параметров в полях уничтожения или
рождения (включая их общие масштабные множители) равно числу
неприводимых представлений, входящих в поле.
Непосредственной проверкой можно убедиться, что коэффи-
коэффициентные функции U;(p,G,n) и t>;(p,G,n), определяемые формулами
E.1.21) и E.1.22), причем щ@,<5,п) и г>г@,о,п) удовлетворяют соотно-
соотношениям E.1.23) и E.1.24), автоматически удовлетворяют и более
общим требованиям E.1.19) и E.1.20). Мы оставляем проверку этого
утверждения читателю.
Вернемся к принципу кластерного разложения. Подставляя
E.1.17) и E.1.18) в E.1.9) и интегрируя по х, находим, что гамильто-
гамильтониан взаимодействия равен
NM" a\...a'N ст1...стм n[...n'N nv..nM
xa\p[,o[,n{)...a\pN,o'N,n'N)a{pM,oM,nM)...a{p1,o1,n1)
E.1.27)
причем коэффициентные функции даются выражением
з / / / / > E.1.28)
= 5 (p1+...-p1-...)TWM(p1,a1,n1...,p1,a1,n1...)
где
262 Глава 5. Квантовые поля и античастицы
xu!i(Pllo1)n1)...UjM(pM,aM,nB). E.1.29)
Это взаимодействие имеет точно такую форму, которая га-
гарантирует, что .^-матрица удовлетворяет принципу кластерного
разложения: TNM содержит единственную дельта-функцию, а ко-
коэффициент TNM имеет (по крайней мере в случае конечного числа
сортов частиц) не более чем точки ветвления при нулевых импуль-
импульсах частиц.
На самом деле, утверждение можно обратить. Всякий опера-
оператор можно представить в виде E.1.27), и из принципа кластерного
разложения вытекает, что коэффициент TNM можно записать в
виде E.1.28) как произведение единственной дельта-функции на
гладкую коэффициентную функцию. Любая достаточно гладкая
коэффициентная функция (не содержащая дополнительных дель-
дельта-функций) может быть записана в виде E.1.29) *. Итак, из прин-
принципа кластерного разложения совместно с лоренц-инвариантно-
стью естественно вытекает, что плотность гамильтониана
взаимодействия должна быть построена из полей рождения и
уничтожения.
Если бы все, что нам требуется, сводилось к построению
скалярного гамильтониана взаимодействия, удовлетворяющего прин-
принципу кластерного разложения, то мы могли бы скомбинировать
операторы уничтожения и рождения в произвольные полиномы
E.1.9), коэффициенты которых 9i'vj'N,lv..lM подчинялись бы только
условию инвариантности E.1.10) (и подходящему условию действи-
действительности). Однако для лоренц-инвариантности 5-матрицы необхо-
необходимо также, чтобы гамильтониан взаимодействия удовлетворял
коммутационному соотношению E.1.3). Для произвольных функций
от полей рождения и уничтожения это условие не выполняется,
поскольку
*В общем случае индексы I и Г могут изменяться в бесконечных пределах.
Ограничение конечным интервалом изменения I и V связано с обсуждаемым в
гл. 12 принципом перенормируемости.
5.1. Свободные поля 263
E.1.30)
(знак + соответствует выбору коммутатора или антикоммутатора,
если частицы, уничтожаемые или рождаемые компонентами \|/^ и
Х|/^, являются бозонами или фермионами, соответственно), и в
общем случае это выражение не обращается в нуль даже для
пространственноподобных х — у. Очевидно, эту проблему не удает-
удается разрешить, если построить плотность гамильтониана взаимо-
взаимодействия только из полей рождения или уничтожения по отдельно-
отдельности, так как в этом случае взаимодействие не будет эрмитовым.
Единственный путь преодоления трудности — в том, чтобы образо-
образовать линейные комбинации полей рождения и уничтожения
\\fl(x) = Kl\\f^(x) + 'kl\\fi(x), E.1.31)
подобрав константы к и А. и любые другие произвольные константы
в полях так, чтобы при пространственноподобных интервалах х — у
= 0. E.1.32)
Ниже в этой главе мы покажем, как это можно сделать для разных
полей, преобразующихся по неприводимым представлениям. (Вклю-
(Включив в явном виде константы к и А. в E.1.31), мы сохраняем свободу
выбора общего масштабного множителя для полей рождения и
уничтожения в любой удобной нам форме.) Плотность гамильтониа-
гамильтониана Ж{х) будет удовлетворять перестановочным соотношениям E.1.3),
если она будет построена из таких полей и им сопряженных,
причем будет входить четное число любых компонент полей, унич-
уничтожающих и рождающих фермионы.
Условие E.1.32) часто называют условием причинности, т. к.
если х — у является пространственноподобным интервалом, ни
один сигнал из х не может попасть в у, и измерение \|/г в точке х не
может интерферировать с измерениями \рг> или \|/^ в точке у.
Подобные соображения приемлемы для электромагнитного поля,
поскольку, как показано в классической работе Бора и Розенфель-
да2, в данной пространственно-временной точке может быть изме-
измерена любая его компонента. Однако нам предстоит иметь дело с
полями типа дираковского поля электрона, которые не кажутся
264 Глава 5. Квантовые поля и античастицы
измеримыми ни в каком смысле. Точка зрения, принимаемая в этой
книге, заключается в том, что соотношение E.1.32) необходимо для
лоренц-инвариантности .^-матрицы без дополнительных предполо-
предположений об измеримости или причинности.
Есть еще одно обстоятельство, связанное с построением полей
E.1.31), удовлетворяющих условию E.1.32). Может оказаться так,
что частицы, уничтожаемые и рождаемые полями, обладают нену-
ненулевыми значениями одного или болеее сохраняющихся квантовых
чисел типа электрического заряда. Например, если частицы типа п
обладают значением q{n) электрического заряда Q, то
[Q,a{p,o,n)] = -q{n)a{p,o,n),
[Q, a) (p,c,n)] = +q{n)a} (p, а, п).
Для того, чтобы Ж(х) коммутировал с оператором заряда Q (или
другими генераторами симметрии), необходимо, чтобы он был
построен из полей, имеющих простые коммутационные соотноше-
соотношения с оператором Q:
E.1.33)
Тогда можно построить Ж(х), который будет коммутировать с Q,
взяв его как сумму произведений полей УцУ^--- и сопряженных
полей \|/т \|/т ..., причем
Однако соотношение E.1.33) выполняется для некоторой конкрет-
конкретной компоненты \\ff поля уничтожения, если и только если все
типы частиц п, уничтожаемые этим полем, несут один и тот же
заряд q(n) = qx; аналогично, оно удовлетворяется для конкретной
компоненты \|/^~ поля рождения, если и только если все сорта
частиц п, рождаемые этим полем, несут заряд q(n) = —qx. Мы
видим, что для того, чтобы такая теория сохраняла квантовые
числа типа электрического заряда, необходимо удвоение числа
сортов частиц с ненулевыми значениями этих квантовых чисел:
если конкретная компонента поля уничтожения уничтожает части-
частицу типа п, то та же компонента поля рождения должна рождать
5.1. Свободные поля 265
частицы сорта п, которые называются античастицами к частицам
типа п и обладают противоположными значениями всех сохраняю-
сохраняющихся квантовых чисел. В этом заключается обоснование сущест-
существования античастиц.
Если представление D(A) приводимо, можно использовать
базис для полей, в котором D(A) разбивается на блоки вдоль
главной диагонали, причем поля, принадлежащие разным блокам,
не переходят друг в друга при преобразованиях Лоренца. К тому же
преобразования Лоренца не влияют на тип частиц. Поэтому вместо
рассмотрения одного большого поля, содержащего много неприво-
неприводимых компонент и много типов частиц, можно с этого момента
ограничиться рассмотрением полей, которые уничтожают только
один определенный тип частиц (при этом индекс п будем опускать)
и рождают только соответствующие античастицы. Такие поля пре-
преобразуются по неприводимому представлению группы Лоренца (как
отмечалось выше, это представление может как включать, так и не
включать пространственное отражение). Следует понимать, что
в общем случае нужно рассматривать много разных полей такого
типа, причем некоторые из них могут быть образованы из произ-
производных других полей. В последующих разделах мы собираемся
завершить определение коэффициентов мг(р,а) и г>г(р,о), зафикси-
зафиксировать относительные значения констант к и А. и вывести соотноше-
соотношения, связывающие свойства частиц и античастиц, проделав это
последовательно для полей, принадлежащих простейшим неприво-
неприводимым представлениям группы Лоренца — скалярному, векторно-
векторному и дираковскому спинорному. После этого мы повторим анализ
для совершенно произвольного неприводимого представления.
Сделаем замечание по поводу уравнений поля. Как следует из
формул E.1.31), E.1.17) и E.1.18), все компоненты поля данной
массы т удовлетворяют уравнению Клейна-Гордона:
0. E.1.34)
Некоторые поля удовлетворяют одновременно и другим уравнениям
поля, в зависимости от того, превышает или нет число компонент
поля число независимых состояний частицы. Традиционно в кванто-
квантовой теории поля сначала рассматривают полевые уравнения или тот
лагранжиан, из которого они могут быть получены, а затем выводят
разложение полей по одночастичным операторам уничтожения
266 Глава 5. Квантовые поля и античастицы
и рождения. В излагаемом ниже подходе мы начинаем с частиц и
выводим вид полей, исходя из требований лоренц-инвариантности.
При этом уравнения поля возникают почти случайно как побочный
продукт такого построения.
Следует отметить одно техническое обстоятельство. Согласно
теореме, доказанной в разделе 4.4, условие, гарантирующее, что
теория будет удовлетворять принципу кластерного разложения,
заключается в том, что взаимодействие можно представить в виде
суммы произведений операторов рождения и уничтожения, распо-
расположенных так, что все операторы рождения находятся левее всех
операторов уничтожения. При этом коэффициенты разложения
содержат только одну дельта-функцию закона сохранения импуль-
импульса. Поэтому взаимодействие должно быть записано в «нормальной»
форме
V = jd3x:ЩЩх),\|/f (х)):, E. 1. 35)
где двоеточия означают, что выражение между ними должно быть
переписано так, чтобы все операторы рождения стояли левее опе-
операторов уничтожения (игнорируя при этой перестановке все нену-
ненулевые коммутаторы или антикоммутаторы, но учитывая знаки
минус от перестановки фермионных операторов). С помощью соот-
соотношений коммутации или антикоммутации полей всякая такая
нормально упорядоченная функция полей может быть записана и
как сумма обычных произведений полей с с-числовыми коэффици-
коэффициентами. После такого переписывания :.'/: становится очевидным, что
несмотря на нормальное упорядочивание, :.Д\|/(х),\|/^(х)): будет ком-
коммутировать с :.Ц\\г{у),\\гЦу)): при пространственноподобных х-у,
если эти функции построены из полей, удовлетворяющих E.1.32), и
содержат четное число любых фермионных операторов.
5.2. Причинные скалярные поля
Рассмотрим сначала однокомпонентные поля уничтожения и
рождения ф+(х) и ф~(х), преобразующиеся по простейшему из
5.2. Причинные скалярные поля 267
возможных скалярному представлению группы Лоренца с D(A) = 1.
Если ограничиться вращениями, то такое представление будет
скалярным представлением группы вращений с JT = 0, так что
уравнения E.1.25) и E.1.26) не имеют других решений, кроме j = О,
в этом случае о, о могут принимать только нулевые значения.
Таким образом, скалярное поле может описывать только частицы с
нулевым спином. Предполагая на время, что поле описывает лишь
один сорт частиц, не имеющих отличных от самих себя античас-
античастиц, и опуская индекс сорта п, спиновый индекс о и индекс поля I,
находим, что величины щ@,<5,п) и г>г@,а,п) равны числам м@) и г>@).
Общепринято подбирать общий масштаб полей уничтожения и
рождения так, чтобы обе эти константы имели значение Bт)~1//2.
Тогда из формул E.1.21) и E.1.22) находим:
и(р) = Bр°Г1/2, E21)
Отсюда в скалярном случае поля E.1.17) и E.1.18) равны
, E.2.3)
Ф"(х) = Jd3pB7t)-3/2Bp°)-1/2at(p)e-ipa; = (p+t(x). E.2.4)
Гамильтониан Ж (х), построенный как полином по полям ф+(х)
и ф~(х), будет автоматически удовлетворять требованию E.1.9), т. е.
будет скаляром. Остается удовлетворить другому условию лоренц-
инвариантности .^-матрицы — коммутации Ж(х) и Ж (у), взятых
в точках, разделенных пространственноподобным расстоянием
х — у. Если бы Ж(х) был полиномом только по ф+(х), то не возника-
возникало бы никаких трудностей. Все операторы уничтожения либо ком-
коммутируют, либо антикоммутируют, так что ф+(х) коммутирует или
антикоммутриует с ф+(у) для всех х и у, в соответствии с тем,
является ли частица бозоном или фермионом:
[ф+(х),ф+(у)]т = 0. E.2.5)
Поэтому любой оператор Ж(х), являющийся полиномом по ф+(х)
(для фермионов он должен быть четным), будет коммутировать
268 Глава 5. Квантовые поля и античастицы
с Ж{у) при всех х и. у. Проблема, конечно, в том, что Ж{х) должен
быть эрмитовым, а для этого должен содержать наряду с ф+(х) и
поле ф+^(х) = ф~(х). Но ф+(х) не коммутирует или антикоммутирует
с ф~(у) в точках, разделенных пространственноподобным расстоя-
расстоянием. Используя соотношения коммутации (для бозонов) или анти-
антикоммутации (для фермионов) D.2.5), находим:
что сводится к одному интегралу
[ф+(х), ф"(у)]+ = А+(х - у), E.2.6)
где А+ — стандартная функция
E.2.7)
Эта функция явно лоренц-инвариантна, поэтому при пространст-
венноподобных х она может зависеть только от инварианта х2 > 0.
Можно вычислить А+(х) для пространственноподобных х, выбрав
систему координат так, чтобы
х° =0, |х|= л/ж2".
Тогда выражение E.2.7) можно представить в виде
р dp sin(pVx )
2д/
р2+ш2
2д/
р2 +т2
Заменяя переменную интегрирования на и = р/т, находим
E.2.8)
5.2. Причинные скалярные поля 269
или, используя стандартную функцию Ганкеля,
rK^myfx2). E.2.9)
Это выражение не равно нулю. Что же с ним делать? Заме-
Заметим, что хотя А+(х) и не равна нулю, но при х2 > 0 эта функция
четна по хц. Попробуем построить Ж{х) не из одних полей ф+(х), а
из линейной комбинации полей
= кф+(х) + Хф"(х).
Используя E.2.6), имеем при пространственноподобных х — у
=|к|2
[ф(х),ф(у)]т =кХ([ф+(х),ф"(у)]_
Оба эти выражения будут обращаться в нуль тогда и только тогда,
когда частица является бозоном (т. е. когда берется верхний знак),
а величины к и А. равны:
|к| = \Х\ .
Относительную фазу к и А. можно изменить путем переопределения
фаз состояний, так что а(р) —» егаа(р), а^(р) —» е~гаа^(р), откуда
к -^ кег<х, X -^ Хе~г<х. Выбирая а = Arg(X/K)/2, можно таким образом
сделать равными фазы к и X, а следовательно, и сами эти величины.
Переопределяя ф(х), чтобы поглотить общий множитель
к = X, имеем окончательно
ф(х) = ф+(х) + ф++(сс) = ф+ (х). E.2.10)
Итак, гамильтониан взаимодействия .Ж'(х) будет коммутировать с
.Ж'(у) на пространственноподобных расстояниях х — у, если он
будет построен как нормально упорядоченный полином по самосо-
самосопряженному скалярному полю ф(х).
270 Глава 5. Квантовые поля и античастицы
Хотя выбор относительной фазы двух слагаемых в E.2.10) есть
вопрос соглашения, но приняв его, мы должны использовать это
соглашение везде, где бы не появилось скалярное поле данной
частицы в плотности гамильтониана взаимодействия. Например,
предположим, что плотность гамильтониана взаимодействия вклю-
включает не только поле E.2.10), но и другое скалярное поле такой же
частицы
ф(х) = eia(p+(x) + e-ia(p+t(x) .
где ОС — произвольная фаза. Поле ф, как и ф, будет причинным в том
смысле, что ф(х) коммутирует с ф*(у) на пространственноподобных
растояниях х -у, но ф(х) не будет при этом коммутировать с ф(у).
Поэтому в одной теории не могут появиться оба таких поля.
Если частицы, уничтожающиеся и рождающиеся полем ф(х),
обладают некоторым сохраняющимся квантовым числом типа элек-
электрического заряда, то Ж{х) будет сохранять это число только в том
случае, если каждое слагаемое в Ж(х) содержит равное число
операторов а(р) и a(p)t Но это невозможно, если Ж{х) построен как
полином по полю ф(х) = ф+(х) + ф+^(х). Иными словами, для того,
чтобы Ж(х) коммутировал с оператором заряда Q (или каким-то
другим генератором симметрии), необходимо, чтобы оператор взаи-
взаимодействия был построен из полей, имеющих простые перестано-
перестановочные соотношения с Q. Это верно для ф+(х) и сопряженного ему
поля, для которых
Но это не выполняется для самосопряженного поля E.2.10).
Выход из положения заключается в том, чтобы предположить
существование двух бесспиновых бозонов одинаковой массой т, но
зарядами +q и —q, соответственно. Пусть ф+(х) и ф+с(х) — поля
уничтожения для этих двух частиц, так что *
* Индекс «с» означает «зарядовое сопряжение». Следует помнить, что час-
частица, не несущая никакого сохраняющегося квантового числа, может как
быть, так и не быть своей собственной античастицей с ас(р) = а(р)
5.2. Причинные скалярные поля 271
Определим ф(х) как линейную комбинацию
имеющую явно тот же коммутатор с Q, как и отдельное поле ф+(х):
]_ =-дф(х).
Тогда на пространственных расстояниях коммутатор или антиком-
антикоммутатор ф(х) с сопряженным ему полем равен
к|2
[ф+с'(х),ф+с(у)]_
в то время как ф(х) и ф(у) автоматически коммутируют или анти-
коммутируют друг с другом для всех х и у, так как ф+ и (p+ct
уничтожают и рождают разные частицы. При получении этого
результата мы молчаливо предполагали, что массы частиц и анти-
античастиц одинаковы, так что коммутаторы или антикоммутаторы
содержат одну и ту же функцию А+(х - у). Случай статистики
Ферми снова исключается, так как ф(х) может антикоммутировать
с ф^(у) на пространственноподобных расстояниях только при к = А. =
= 0, а при этом поля обращаются в нуль. Таким образом бесспино-
бесспиновая частица должна быть бозоном.
В случае бозе—статистики, для того, чтобы комплексное поле
ф(х) коммутировало с ф^(у) на пространственноподобных расстояни-
расстояниях, необходимо и достаточно, чтобы к|2 = \Х\2 и массы частиц
и античастиц были бы одинаковы. Переопределяя относительную
фазу состояний этих двух частиц, снова можно сделать равными
фазы к и X, и тогда к = X. Этот общий множитель можно исключить
переопределением поля ф, так что
272 Глава 5. Квантовые поля и античастицы
или, подробнее,
<Р(а?)= з/2 о 1/2 ИР)е +а (Р)е ¦ E.2.11)
J BтгK/2Bр°I/2 L \ ^ )
Мы построили единственно возможное причинное скалярное поле.
Эта формула годится как в случае полностью нейтральных бесспи-
бесспиновых частиц, совпадающих со своими античастицами (тогда
ас(р) = а(р)), так и в случае, когда частица и античастица не
совпадают (тогда ас(р) Ф а(р)).
Для будущих применений заметим, что коммутатор ком-
комплексного скалярного поля со своим сопряженным равен
[(p(x),(pf(y)] = Л(х-у), E.2.12)
где
Д(х-у) = Д+(х-у)-Д+(у-х) = [ ^3 2 оИ^-е-'Р^)].
E.2.13)
Рассмотрим теперь действие на это поле разных преобразований
инверсии. Во-первых, из результатов раздела 4.2 можно сразу
получить, что действие оператора пространственной инверсии на
операторы уничтожения и рождения имеет вид *:
= л*а(-р), E.2.14)
=цсас\-9), E.2.15)
где ц и Г|с — внутренние четности частиц и античастиц, соответст-
соответственно. Применяя эти формулы к полю уничтожения E.2.3) и к полю,
зарядовосопряженному к полю рождения E.2.4), а также меняя
переменную интегрирования р на -р, находим, что
* Мы опускаем здесь индекс 0 у операторов инверсии Р, С и Т, так как
практически во всех случаях, когда эти инверсии являются хорошими сим-
метриями, одни и те же операторы индуцируют преобразования инверсии
как ин- и аут-состояний, так и состояний свободных частиц.
5.2. Причинные скалярные поля 273
Рф+(х)Р = цу+{<Рх), E.2.16)
^ * E.2.17)
где, как и ранее, .Ух = (—к, х°). Таким образом, действие простран-
пространственной инверсии в общем случае переводит скалярное поле ф(х) =
ф+(х) + ф+с1'(х) в другое поле фР = г|*ф+ + r|<4p+ct. Оба поля по
отдельности являются причинными, но если допустить, что ф и фР^
входят в одно взаимодействие, то возникают трудности, так как
эти поля в общем случае не коммутируют на пространственнопо-
добных расстояниях. Единственный способ не нарушить лоренц—
инвариантность, сохранение четности и эрмитовость взаимодейст-
взаимодействия заключается в требовании, чтобы фР было пропорциональным
ф, откуда
Г|с = Г|*. E.2.18)
Итак, внутренняя четность Г|Г|С системы, состоящей из бесспи-
бесспиновой частицы и ее античастицу<ы, равна +1 (другими словами,
такая система является четной). Теперь
Рф(х)Р"х = г|*ф(;Лг). E.2.19)
Эти результаты применимы и в случае, когда бесспиновая частица
совпадает со своей античастицей. В этом случае г|с = т|, откуда
следует, что внутренняя четность такой частицы действительна,
Л = ±1.
Рассмотрение зарядового сопряжения во многом аналогично.
Из результатов раздела 4.2 имеем
^Vtp), E.2.20)
=^ca+(p), E.2.21)
где t, и ^с — фазы, связанные с зарядовым сопряжением одночас-
тичных состояний. Отсюда следует, что
Сф+С+ (х)С = ^сф++ (х). E.2.23)
274 Глава 5. Квантовые поля и античастицы
Поле Сф(х)С-1 должно быть пропорционально полю ф(х), с которым
оно коммутирует на пространственноподобных расстояниях. Оче-
Очевидно, для этого необходимо, чтобы
t,c = ^ . E.2.24)
Как и в случае обычной четности, внутренняя зарядовая четность
^с состояния, содержащего бесспиновую частицу и ее античастицу,
является четной. Теперь
1=%*ч\х). E.2.25)
Как и выше, эти результаты применимы в случае, когда частица
совпадает со своей античастицей, и Е,с = Е,. Зарядовая четность
должна быть при этом действительна, Ъ, = +1.
Обратимся, наконец, к обращению времени. Из результатов разде-
раздела 4.2 находим:
1 = ^а(-р), E.2.26)
H,H {Ъ.2.21)
Вспоминая, что оператор Т антиунитарен, и вновь меняя перемен-
переменную интегрирования р на —р, находим:
E-2.28)
фМ ?V( E.2.29)
Чтобы Тф(х)Т-1 было простым образом связано с полем ф в обра-
обращенной по времени точке —.Ух, должно выполняться равенство
?с = ?*, E. 2.30)
и поэтому
E.2.31)
5.3. Причинные векторные поля 275
5.3 Причинные векторные поля
Рассмотрим следующее по простоте поле, преобразующее-
преобразующееся как четырехмерный вектор, т. е. по простейшему нетривиаль-
нетривиальному представлению однородной группы Лоренца. В современной
физике элементарных частиц все большую роль играют массив-
массивные частицы W± и Z0, которые при низких энергиях описываются
такими полями. Поэтому наше рассмотрение представляет не
только педагогический интерес. (Кроме того, хотя мы и рассмат-
рассматриваем массивные частицы, в квантовой электродинамике воз-
возможен подход, при котором фотон описывается как массивное
векторное поле в пределе очень малой массы.) Сначала будем
считать, что векторное поле описывает только один тип частиц
(опуская при этом индекс п). Затем мы учтем возможность
того, что поле описывает как частицу, так и соответствующую
античастицу.
В 4-векторном представлении группы Лоренца строки и столб-
столбцы матриц представления D(A) помечены индексами ц, V и т. д.,
принимающими четыре значения, причем
D(A)% = A%. E.3.1)
Части векторного поля, отвечающие уничтожению и рождению
частиц, записываются в виде:
^. E 3.3)
Коэффициентные функции м^(р,а) и г)ц(р,а) при произвольном им-
импульсе с помощью формул E.1.21) и E.1.22) выражаются через эти
же функции при нулевом импульсе:
E.3.4)
E.3.5)
276 Глава 5. Квантовые поля и античастицы
(здесь используется стандартное соглашение о суммировании по
повторяющимся пространственно-временным индексам ц, V и т. д.).
Кроме того, коэффициентные функции при нулевом значении им-
импульса подчиняются условиям E.1.25) и E.1.26):
=/%uv@,g), E.3.6)
* =/»W@,a). E.3.7)
В 4-векторном представлении генераторы вращения определяются
с помощью E.3.1) в виде
(/fc)°o=(/fc)°i= 0^0=0, E.3.8)
=-е^, E-3.9)
где индексы г, j, к принимают значения 1, 2, 3. Отметим в
частности, что/2 принимает вид:
(/2)°о=(/)°г=(/2Го=О, E.3.10)
(/2)S-=28V E.3.11)
Из формул E.3.6) и E.3.7) следует тогда, что
=0, E.3.12)
E.3.13)
E.3.14)
E.3.15)
5.3. Причинные векторные поля 277
Напомним к тому же известную формулу: (J^')|a = j(j + 1)Ь-^а. Из
формул E.3.12)—E.3.15) вытекает, что существуют две возможности
для значений спина частицы, которая описывается векторным
полем: либо j = 0, и тогда при р = 0 только и0 и v° отличны от нуля,
либо j = 1 (и j (j + 1) = 2), и при этом при р = 0 отличны от нуля
только пространственные компоненты иг и v%.
Рассмотрим эти возможности детальнее.
Спин нуль
Подходящим выбором нормировки полей можно записать един-
единственные ненулевые компоненты 4-векторов и^@) и ^(О) в обще-
общепринятом виде:
@) = -i(m / 2I/2.
(Индекс s принимает в этом случае единственное значение нуль и
поэтому опущен.) В случае произвольного импульса из формул
E.3.4) и E.3.5) следует:
°1/2 E.3.16)
E.3.17)
Векторные поля уничтожения и рождения в данном случае являют-
являются не чем иным, как производными от скалярных полей уничтоже-
уничтожения и рождения для рассмотренных выше бесспиновых частиц:
ж). E.3.18)
Очевидно, что причинное векторное поле для скалярной частицы
есть производная причинного скалярного поля:
E.3.19)
Таким образом, этот случай можно далее не рассматривать.
278
Глава 5. Квантовые поля и античастицы
Спин единица
Из формул E.3.6) и E.3.7) сразу же следует, что при а = О
векторы иг@,0) и г>г@,0) направлены вдоль третьей оси. При подхо-
подходящей нормировке полей можно выбрать эти векторы в виде
"о"
= BшГ1/2
E.3.20)
где 4-компоненты перечислены в порядке 1, 2, 3, 0. Чтобы найти
другие компоненты, используем формулы E.3.6), E.3.7) и E.3.9) и
вычислим результат действия повышающих и понижающих опера-
операу
торов Jx +iJ2 нами v. Получим:
1
= -г/@-1) = —1ГBт
л/2
Г1/2
E.3.21)
—= Bт)-1/2
V2
E.3.22)
С помощью формул E.3.4) и E.3.5) находим:
где
E 3.23)
E.3.24)
1
V2
1
+ i
0
0
l
- i
0
0
E.3.25)
5.3. Причинные векторные поля 279
Теперь поля уничтожения и рождения принимают вид
^ E 3.2б)
Конечно, поля ф+|1(х) и ф+у(у) коммутируют (или антикоммутируют)
для всех ж и у. Но это не относится к полям ф+|1(ж) и ф~у(у).
Коммутатор (для бозонов) или антикоммутатор (для фермионов)
этих полей равен
^ E.3.27)
где
n^v (р) = ? е^ (р, a)ev* (p, a). E.3.28)
Непосредственное вычисление с помощью E.3.25) показывает, что
ГР^О) является проекционной матрицей на пространство, ортого-
ортогональное направлению временной оси. Тогда из E.3.24) следует, что
n|iv(p) есть проекционная матрица на пространство, ортогональное
4-вектору рц:
№v (р) = гГ + pV / m2. E.3.29)
Коммутатор (или антикоммутатор) E.3.27) можно выразить через
функцию А+, которую мы определили в предыдущем разделе:
E.3.30)
т
2
Важное свойство этого выражения заключается в том, что оно не
обращается в нуль при пространственноподобных х — у и четно
относительно х — у. Поэтому можно повторить рассуждения преды-
предыдущего раздела для построения причинного поля. Образуем линей-
линейную комбинацию полей уничтожения и рождения
280
Глава 5. Квантовые поля и античастицы
для которой при пространственноподобных х — у
т
А+(х-у),
m
A+{x-y).
Для обращения в нуль обоих выражений при пространственноподоб-
пространственноподобных х — у необходимо и достаточно, чтобы частицы со спином едини-
единица были бозонами, и |к| = \Х\. Подходящим выбором фазы одночастич-
ных состояний можно добиться, чтобы к и X имели одинаковую
фазу, так что к = X, а затем устранить общий множитель к,
переопределив общую нормировку поля. В результате причинное
векторное поле массивной частицы со спином единица имеет вид:
E.3.31)
E.3.32)
Однако если частицы, которые описываются этим полем, обладают
ненулевым значением какого-то сохраняющегося квантового числа
Q, то невозможно построить из такого поля сохраняющее Q взаимо-
взаимодействие. Следует предположить, что существует другой бозон той
же массы и спина, обладающий противоположным значением Q, и
построить причинное поле как
Заметим, что поле действительно:
E.3.33)
или, подробнее,
E.3.34)
е+(
, а)ае+(р,
5.3. Причинные векторные поля 281
где верхний индекс «с» отмечает операторы, рождающие античас-
античастицу, которая зарядово сопряжена к частице, уничтожаемой по-
полем ф+|1(ж). Полученное поле причинно, но более не действительно.
Эта же формула применима и в случае полностью нейтральной
частицы со спином единица, совпадающей со своей античастицей,
если положить ас(р) = а(р). В любом случае коммутатор векторного
поля и сопряженного ему поля равен
^v _
т
2
E.3.35)
где А(х -у) — функция E.2.13).
Построенные нами для массивной частицы со спином едини-
единица действительные и комплексные поля удовлетворяют интерес-
интересным полевым уравнениям. Во-первых, так как рц в экспоненте в
формуле E.3.26) удовлетворяет условию р2 = —т2, поле удовле-
удовлетворяет такому же, как и для скалярного поля, уравнению Клей-
Клейна-Гордона
0, E.3.36)
Кроме того, поскольку из E.3.24) следует, что
е^(р,а)р^=0, E.3.37)
имеем еще одно уравнение:
Э^(х) = 0. E.3.38)
В пределе малой массы уравнения E.3.36) и E.3.38) превращаются в
уравнения электродинамики для 4-вектора потенциала в так назы-
называемой калибровке Лоренца.
Однако никакая теория массивных частиц со спином единица
при устремлении массы к нулю не превращается в электродинами-
электродинамику. Причину этого можно увидеть, рассмотрев вероятность образо-
образования частицы со спином единица за счет взаимодействия с плотно-
плотностью гамильтониана Ж = JyP^, где J^ — произвольный 4-вектор тока.
Возводя матричный элемент в квадрат и суммируя по проекциям
282 Глава 5. Квантовые поля и античастицы
спина частицы на ось z, получаем, что вероятность пропорциональ-
пропорциональна величине
Jv
где p — импульс испускаемой частицы со спином единица, а <^м> —
матричный элемент тока (взятый, скажем, при х = 0) между
начальным и конечным состояниями всех других частиц. Слагаемое
p^pv /т2 в n|iv(p) приводит в общем случае к бесконечному возраста-
возрастанию вероятности процесса при т —> 0. Единственный способ предот-
предотвратить катастрофу — предположить обращение в нуль произведе-
произведения <JA>p|1. В координатном пространстве это сводится к сохранению
тока J^ в том смысле, что д^ = 0. На самом деле, необходимость
сохранения тока можно увидеть после простого подсчета числа
состояний. У массивной частицы со спином единица имеется три
спиновых состояния, которые можно считать состояниями со спи-
ральностью +1, 0 и -1. В то же время любая безмассовая частица со
спином единица типа фотона может иметь только две спиральности
+1 и —1. Условие сохранения тока как раз и гарантирует, что в
пределе нулевой массы частицы со спином 1 в состояниях с нулевой
спиральностью не будут излучаться.
Преобразования инверсий можно рассмотреть во многом ана-
аналогично случаю скалярного поля. Чтобы вычислить результат дей-
действия преобразования пространственной инверсии, нужна формула
для ец(-р,з). Используя равенство 1/у(-р) = ^vLP-^p^v и формулу
E.3.24), находим
е^ (-р, а) = -;^vev (p, а). E.3.39)
Далее, чтобы вычислить результат действия операции обращения
времени, нужна формула для (~1) +ае^ (-р,-а). Используя равенст-
равенство е^\-о) = -ец(а) и предыдущую формулу для A|1v(-p), получаем
(-1I+сте^*(-р,-а) = ;^\,ev(p,G). E.3.40)
С помощью этих формул и свойств преобразования операторов
уничтожения и рождения, выписанных в разделе 4.2, можно непо-
непосредственными вычислениями найти законы преобразования полей
5.4. Дираковский формализм 283
уничтожения и рождения под действием преобразований инверсии.
Мы вновь обнаруживаем, что для того, чтобы причинные поля
преобразовывались бы в другие поля, с которыми они коммутируют
на пространственноподобных расстояниях, необходимо, чтобы внут-
внутренние фазовые множители, отвечающие пространственной инвер-
инверсии, зарядовому сопряжению и обращению времени для частиц со
спином единица и их античастиц, были связаны соотношениями:
Г|е=Г|*, E.3.41)
Zf = Z,', E.3.42)
?е = ?*. E.3.43)
(В частности, в случае, когда частицы со спином 1 совпадает со
своей античастицей, все фазы должны быть действительны.)
С учетом этих условий на фазы находим, что причинное векторное
поле E.3.34) обладает следующими трансформационными свойства-
свойствами относительно инверсий:
, E.3.44)
E.3.45)
). E.3.46)
В частности, знак «минус» в E.3.44) означает, что векторное поле,
преобразующееся как полярный вектор без дополнительных фаз
или знаков, связанных с матрицей ;'^v, описывает частицу со
спином 1 и внутренней четностью Т| = — 1.
5.4. Дираковский формализм
Среди всех представлений однородной группы Лоренца су-
существует одно, играющее особую роль в физике. Как мы видели
в разделе 1.1, это представление было впервые рассмотрено Дираком
в теории электрона3. Но, как часто случается, оно было уже
известно математикам4, так как при любом числе измерений это
284 Глава 5. Квантовые поля и античастицы
представление лежит в основе одного из двух больших классов
представлений группы вращений или группы Лоренца (точнее, их
накрывающих групп; см. раздел 2.7). Согласно рассматриваемому
здесь подходу, структура и свойства любого квантового поля дикту-
диктуется тем представлением однородной группы Лоренца, по которому
это поле преобразуется. Поэтому для нас более естественно сначала
описать дираковский формализм в том виде, как он возник в матема-
математике, а не так, как его ввел Дирак.
Представлением однородной группы Лоренца мы называем
множество матриц D(A), удовлетворяющих закону группового ум-
умножения
D{A)D(A) = D{AA).
Как и для унитарных операторов U(A), можно изучать свойства
этих матриц, рассматривая бесконечно малые преобразования
Л%=5%+ю%, E.4.1)
ronv = -«V» E-4.2)
для которых
ДЛ) = 1 + |со^/^, E.4.3)
где JT^V = ~/V|1 — множество матриц, удовлетворяющих коммута-
коммутационным соотношениям B.4.12):
rivP/^CT - ri№/VCT - г\ар- fpy + Т1ОТ /№. E.4.4)
Чтобы найти эти матрицы, предположим, что сначала мы построи-
построили матрицы у1, удовлетворяющие соотношениям антикоммутации,
{f,f} = 2гГ , E.4.5)
и попробуем определить
-\[^,Г\ E.4.6)
С помощью E.4.5) нетрудно показать, что
5.4. Дираковский формализм 285
Отсюда вытекает, что E.4.6) действительно удовлетворяет требуе-
требуемому коммутационному соотношению E.4.4). Предположим далее,
что матрицы у„ неприводимы. Это означает, что не существует
собственного подпространства, остающегося инвариантным под
действием всех этих матриц. В противном случае можно было бы
выбрать меньшее количество компонент поля, которые преобразо-
преобразовывались бы по формулам E.4.3) и E.4.6) с неприводимым набором
матриц уц.
Всякий набор матриц, удовлетворяющих соотношению вида
E.4.5) (или его евклидовому аналогу, в котором ri^ заменено на
кронекеровский дельта-символ), называется алгеброй Клиффорда.
Важность этого представления однородной группы Лоренца (точ-
(точнее, ее накрывающей группы) связана с тем, что наиболее общее
неприводимое представление группы Лоренца является тензором
либо спинором, преобразующимися по формулам E.4.3), E.4.6), или
прямым произведением спинора и тензора (доказательство приве-
приведено в разделе 5.6).
Смысл перестановочного соотношения E.4.7) заключается в
том, что ур является вектором, т. е. с учетом формулы E.4.3)
выполнено равенство
ACTpyCT. E.4.8)
Точно так же единичная матрица тривиально является скаляром:
D(A)ID~1(A) = 1, E.4.9)
и из E.4.4) следует, что/рст есть антисимметричный тензор:
D(A)/PaD(A) = А/А//^. E.4.10)
С помощью матриц у*1 можно построить другие полностью антисим-
антисимметричные тензоры
ут]) E.4.11)
уТуЛ1 _ E.4.12)
286 Глава 5. Квантовые поля и античастицы
Квадратные скобки в этих выражениях являются стандартным
обозначением того, что производится суммирование по всем пере-
перестановкам индексов внутри скобок, а знаки «плюс» или «минус»
определяются четностью перестановки. Например, формула E.4.11)
есть сокращенная запись выражения
//Рт = уРустут — уРутуст — устуРут 4- утуРуст + устутуР — утустуР
Многократно используя формулу E.4.5). можно записать любое
произведение у-матриц как сумму антисимметризованных произве-
произведений у-матриц, умноженных на произведение метрических тензо-
тензоров, так что полностью антисимметричные тензоры образуют пол-
полный базис множества всех матриц, которые можно построить из
матриц Дирака.
Этот формализм автоматически содержит преобразование чет-
четности, которое принято выбирать в виде
Р = гу°. E.4.13)
В применении к матрицам Дирака имеем:
(Зу^Р = -у\ (Зу°р-1 = +у° . E.4.14)
(Индексы выбраны так, что ц пробегает значения 0, 1, 2, ...) Такое
же преобразование подобия, примененное к любому произведению
у-матриц, приведет к появлению дополнительного знака «плюс» или
«минус» в зависимости от того, содержит ли произведение четное или
нечетное число у-матриц с пространственными индексами. В частности,
№Ч~1=Г, E-4-15)
Р/^Р =-/*°. E.4.16)
Все, что до сих пор говорилось в этом разделе, применимо для
любого числа пространственно-временных измерений и для любой
«метрики» tlv. Однако в четырехмерном пространстве—времени суще-
существует дополнительное ограничение, что ни один полностью антисим-
антисимметричный тензор не может иметь более четырех индексов, так что
последовательность тензоров 1, у, /рст, -/рсгт,... обрывается на тензоре
5.4. Дираковский формализм 287
E.4.12). Далее, каждый из этих тензоров преобразуется по-разному
под действием преобразований Лоренца и/или четности, так что все
они линейно независимы *. Число линейно независимых компонент
этих тензоров равно единице для 1, четырем для ур, шести для г/рст,
четырем для -/рот, и единице для ^W7, т. е. всего шестнадцать
компонент. (По общему правилу полностью антисимметричный тензор
с п индексами в пространстве d измерений имеет число компонент,
равное биномиальному коэффициенту d\/n\(d-n)\) Существуют не
более чем V2 независимых V X V матриц, так что наши матрицы должны
иметь не меньше, чем V16 = 4 строк и столбцов. Матрицы Дирака
минимальной размерности с необходимостью неприводимы; если бы
это было не так, то подпространство, оставляемое инвариантным
этими матрицами, реализовало бы представление меньшей размерно-
размерности. Поэтому примем, что у*1 есть матрицы 4x4.
(В более общем случае, при любом четном числе d простран-
пространственно-временных измерений, можно построить антисимметрич-
антисимметричные тензоры с 0, 1, ... , d индексами и с общим числом независимых
компонент, равным
^n\(d-n)\
Тогда у-матрицы должны иметь как минимум 2d//2 строк и столбцов.
Для пространства или пространства-времени нечетной размер-
размерности полностью антисимметричные тензоры ранга пи d — п могут
быть связаны линейными условиями
при г = 1, 2, ..., d—1, где e^2"^d — полностью антисимметричный
тензор, а при г = 0 левая часть равна единичной матрице. При
* То, что эти матрицы линейно независимы, можно показать другим
способом, заметив, что они образуют ортогональное множество со скаляр-
скалярным произведением двух матриц, определенным, как след от их произведе-
произведения. Заметим, что ни одна из матриц не может равняться нулю, т. к. каждая
компонента каждого тензора пропорциональна произведению разных у-мат-
риц, а квадрат такого произведения равен с точностью до знака произведе-
произведению соответствующих квадратов, т. е. равен +1.
288
Глава 5. Квантовые поля и античастицы
таких условиях * есть только 2d 1 независимых тензоров, откуда
минимальная размерность у-матриц равна 2(d~1^2).
Возвращаясь к четырехмерному пространству-времени, вы-
выберем явно набор 4x4 у-матриц. Удобным является следующий
выбор:
у°=-г
0 1
1 О
у = -г
О о
-а О
E.4.17)
где 1 — единичная 2x2 матрица, а компоненты вектор-матри-
вектор-матрицы а — обычные матрицы Паули
E.4.18)
(Матрицы oi как раз являются 2x2 у-матрицами в трех измерени-
измерениях.) Можно показать5, что любой другой неприводимый набор
у-матриц связан с этими матрицами преобразованием подобия.
С помощью формул E.4.17) без труда вычисляются генераторы
группы Лоренца:
1
~?Eijk
0
E.4.19)
riO _
Г=+:
О -с
E.4.20)
* Это ограничение не мешает включению пространственной инверсии в
дираковское представление группы Лоренца в нечетномерном пространстве-
времени, т. к. тензор eMiM-2-M-d четен по отношению к инверсии пространствен-
пространственных координат. Если нас не заботит пространственная инверсия, можно по-
построить 2'<г~2'/'2-мерные неприводимые представления собственной ортохрон-
ной группы Лоренца в пространстве-времени четного числа измерений, на-
наложив упомянутые выше ограничения, связывающие антисимметризован-
ные произведения г и d - г матриц Дирака. Примером могут служить подмат-
подматрицы в нижеприведенных формулах E.4.19) и E.4.20)
5.4. Дираковский формализм 289
(Здесь Eyk — полностью антисимметричный тензор в трех измере-
измерениях, причем ?123 = +1.) Заметим, что они блочно-диагональны,
так что матрицы Дирака реализуют приводимое представление
собственной ортохронной группы Лоренца, являющееся прямой
суммой двух неприводимых представлений с JT*3' = +?j,-fc/fc0-
Удобно записать полностью антисимметричные тензоры
E.4.11) и E.4.12) в несколько более простом виде. Матрица E.4.12)
полностью антисимметрична, следовательно, пропорциональна
псевдотензору еР11!, определенному как полностью антисиммет-
антисимметричная величина с е0123 = +1. Полагая индексы р, а, т, г\ последо-
последовательно равными 0, 1, 2, 3, видим, что
у5, E.4.21)
где
у5 = _^оу1у2уз_ E.4.22)
Матрица у5 является псевдоскаляром в том смысле, что
E.4.23)
Аналогично, -/рсгт должна быть пропорциональна тензору gP0^, свер-
свернутому с некоторой матрицей 4Ц. Полагая индексы р, а, т по очереди
равными 0, 1, 2, или 0, 1, 3, или 0, 2, 3, или 1, 2, 3, находим:
4?ах =3!геРотт1у5утг E.4.25)
Шестнадцать независимых 4x4 матриц могут быть поэтому выбра-
выбраны как компоненты скаляра 1, вектора У, антисимметричного
тензора /рст, «аксиального» вектора УдУ^ и псевдоскаляра у5. Легко
видеть, что квадрат матрицы у5 равен единице:
Y52 = 1, E.4.26)
а сама эта матрица антикоммутирует со всеми у*1:
°- E.4.27)
290 Глава 5. Квантовые поля и античастицы
Обозначение у5 особенно удобно, т. к. соотношения антикоммутации
E.4.26) и E.4.27) вместе с формулой E.4.5) показывают, что у0, у1, у2,
у3, у5 реализуют алгебру Клиффорда в пяти пространственно-
временных измерениях. В конкретном 4x4 представлении у-
матриц E.4.17) матрица у5 имеет вид
E.4.28)
Удобство такого представления состоит в том, что в нем jTpcT и у5
имеют б л очно—диагональный вид. Мы увидим далее, что это свой-
свойство окажется особенно полезным при рассмотрении частиц в
ультрарелятивистском пределе, когда v —> с. (Однако, это пред-
представление не совпадает с тем, которое описано в разделе 1.1 и
которое ввел Дирак, поскольку он интересовался, главным обра-
образом, поведением атомных электронов, для которых v <^ с. В этом
случае удобнее использовать представление, в котором диагональна
не матрица у5, а матрица у0.)
Построенное здесь представление однородной группы Лорен-
Лоренца не унитарно, т. к. не все генераторы jfрст являются эрмитовыми
матрицами. В частности, в представлении E.4.17) матрицы jT*3' эрми-
эрмитовы, но jTl° антиэрмитовы. Условия действительности удобно запи-
записать в явно лоренц—инвариантной форме, введя матрицу C = гу°
E.4.13), которая в представлении E.4.17) принимает вид
E.4.29)
V-1- и7
Из E.4.17) следует, что
Pyp y > E.4.30)
откуда
P/patP = /pa. E.4.31)
Следовательно, хотя матрицы D(A) не унитарны, они удовлетворя-
удовлетворяют соотношению псевдоунитарности:
. E.4.32)
5.4. Дираковский формализм 291
Далее, у5 эрмитова и антикоммутирует с C, так что
PyJP = -y5 , E-
откуда следует, что
Матрицы Дирака и связанные с ними матрицы обладают рядом
важных свойств симметрии. Из формул E.4.17) и E.4.18) вытекает,
что у„ симметричны при ц = 0, 2 и антисимметричны при ц = 1, 3,
так что
у? = _<ру^<р-1) E.4.35)
где Т означает транспонирование, и
W = у2р = -г . E.4.36)
V 2 /
Отсюда сразу же следует, что
/? = -^/nv^' E.4.37)
E.4.38)
E.4.39)
Полученные знаки окажутся важными, когда мы в следующем разде-
разделе будем рассматривать свойства разных токов по отношению
к зарядовому сопряжению. Конечно, можно объединить полученные
результаты для сопряжения и транспонирования, и получить правила
комплексного сопряжения дираковских и связанных с ними матриц:
E.4.40)
292 Глава 5. Квантовые поля и античастицы
у* = -№&-% E.4.42)
5.5. Причинные дираковские поля
Мы хотим теперь построить поля уничтожения и рождения частиц,
преобразующиеся по обсуждавшемуся в предыдущем разделе ди-
раковскому представлению группы Лоренца. Эти поля имеют общий
вид, задаваемый формулами E.1.17) и E.1.18):
(х) = Bл)/2 ? J d3p иг (р, а)е"^ае* (р, а)
(метка сорта частиц опущена). Чтобы вычислить входящие в эти
формулы коэффициентные функции мг(р,а) и г;г(р,а), необходимо
сначала использовать E.1.25) и E.1.26) и найти мг и f; для нулевого
импульса, а затем с помощью E.1.21) и E.1.22) вычислить их для
произвольных импульсов. В обоих случаях -Dj-j(A) следует брать как
4x4 дираковское представление однородной группы Лоренца.
С помощью E.4.19) условия при нулевом импульсе E.1.25) и E.1.26)
принимают вид *
* Мы опустили индекс сорта частиц п и заменили 4-компонентный индекс
I на пару индексов: принимающий два значения индекс т, нумерующий
строки и столбцы подматриц в E.4.19) и E.4.20), и второй индекс, принимаю-
принимающий значения + и отмечающий строки и столбцы суперматрицы в E.4.19)
и E.4.20).
5.5. Причинные дираковские поля
293
O> СВ-
СВсловами, если рассматривать ит+{0,о) и vm+{0,о) как т,о
элементы матриц U+ и V+, то в матричных обозначениях
E.5.3)
E.5.4)
Далее, Bj + 1)-мерные матрицы Jy) и -Jy)*, а также 2x2
матрицы о/2 реализуют неприводимые представления алгебры Ли
группы вращений. Общая теорема теории групп, известная как
лемма Шура6, утверждает, что если матрица вида 17+ или V+
связывает два таких представления, как в E.5.3) и E.5.4), эта
матрица должна либо равняться нулевой матрице (случай, не
представляющий интереса), либо быть квадратной и несингуляр-
несингулярной. Поэтому дираковское поле может описывать только частицы со
спином j = з (так что 2j + 1 = 2), а матрицы JA/2) и -Jt1/2)* должны
совпадать с о/ 2 с точностью до преобразования подобия. На самом
деле, в стандартном представлении генераторов вращений B.5.1)
и B.5.2) матрицы JA/2) = \о и -Jt1/2)* = 5G2O02- Тогда получаем, что
17+ и V+G2 должны коммутировать с О, следовательно, они должны
быть пропорциональны единичной матрице:
= c+5
Иначе говоря,
v(o,h =
±"тст>
О
c_
О
О
d+
О
d_
E.5.5)
0
c_
d+
0
294 Глава 5. Квантовые поля и античастицы
и спиноры при конечном импульсе равны
м(р, а) = *Jm/p°D(L(p))u@, а), E.5.6)
и(р, а) = ylm/p°D(L(p))v(O, а). E.5.7)
Остается выяснить, чему равны константы с+ и d+. Вообще говоря,
они совершенно произвольны — можно даже выбрать с_ и d_ или
с+ и d+ равными нулю, так что дираковское поле будет иметь лишь
две отличные от нуля компоненты. Единственное физическое усло-
условие, которое может как-то определить относительные значения с+
и d+, это сохранение четности. Напомним, что в результате про-
пространственной инверсии операторы уничтожения частиц и рожде-
рождения античастиц подвергаются преобразованию
-1 = Va(-p,a), E-5-8>
Pae+(p,a)P-1 = ifae+(-p,G), E.5.9)
так что
Кроме того, из формул E.4.16), E.1.21) и E.1.22) следует, что
м(-р,а) = Л/т/р°(ЗО(Ь(р))(Зм@,а), E.5.12)
E.5.13)
(Поскольку (З2 = 1, мы более не делаем различия между C и (З.) Для
того, чтобы оператор четности переводил поля уничтожения и
рождения в точке х в нечто, пропорциональное этим полям в точке
ifx, необходимо, чтобы (Зм@,а) и C?;@,а) были бы пропорциональны
м@,а) и v{0,o), соответственно:
5.5. Причинные дираковские поля
295
Рм(О, а) = Ъии(О, а), Ри(О, а) = Ь^@, а),
E.5.14)
где Ъи и Ь„ — знаковые множители, квадраты которых равны
единице, Ъи2 = bv2 = 1. В таком случае поля будут простым образом
преобразовываться при пространственной инверсии:
E.5.15)
E.5.16)
Подбором общего масштаба полей можно добиться, чтобы коэффи-
коэффициентные функции при нулевом импульсе имели вид
м@,-) = 4=
и@,—)
E.5.17)
v(oA) = -i=
о
1
о
Aj
-1
E.5.18)
Попробуем теперь объединить поля уничтожения и рождения в
линейную комбинацию
(ж),
E.5.19)
которая коммутирует или антикоммутирует сама с собой и с сопря-
сопряженной величиной в точках, разделенных пространственноподобным
интервалом. Прямое вычисление дает:
= Jd3p[|K|
E.5.20)
296 Глава 5. Квантовые поля и античастицы
где
^() ?.г(р,а)г^(р,а), E.5.21)
E.5.22)
Используя либо условия на собственные значения E.5.14), либо явные
формулы E.5.17) и E.5.18), находим, что при нулевом импульсе
Тогда из E.5.6) и E.5.7) получаем:
m +
^(р) = ^T ВДР^1 + b«P]D (L(P))' E.5.24)
Zp
M(p) = -^-D(L(P))[1 + bv|3]D+(L(p)). E.5.25)
Из условия псевдоунитарности E.4.32) следует:
D(L(p))PDt(L(p)) = p,
D(L(p))Dt(L(p)) =
Напомним также, что Р = ~tf, так что с помощью закона лоренцов-
ского преобразования E.4.8) находим:
D(L(p))PD(L(p)) = -iLjipYfV- = -ip^ I т. E. 5. 26)
Собирая результаты, получаем *:
* Иногда в дираковские спиноры включают дополнительный множитель
(р°/тI/'2, так что в знаменателях формул суммирования по спинам E.5.27) и
E.5.28) появляется т вместо р°. Используемое здесь условие нормировки имеет
то преимущество, что оно выдерживает плавный переход к случаю т — 0.
5.5. Причинные дираковские поля 297
[^V+bum]l3> E.5.27)
zp
т[р%и]|
zp
Подставляя в формулу E.5.20), находим окончательно:
, ??(У)Ь = AКГ [~У% + bum] |ЗА+(х - у)
где Д+ — введенная в разделе 5.2 функция
Г dzp
Д+(ж) = — -
+ J 2р°BлK
В разделе 5.2 было показано, что при пространственноподобных
х — у функция А+(х — у) является четной, поэтому, конечно, ее
первые производные — нечетные функции х — у. Отсюда, для того,
чтобы и обе производные, и слагаемые, не содержащие производ-
производных, в коммутаторе или антикоммутаторе обратились бы в нуль на
пространственноподобных расстояниях, необходимо и достаточно,
чтобы
к|2 = +|Х|2, E.5.30)
|K|2bu=±|X|2bv. E.5.31)
Ясно, что условие E.5.30) будет выполнено только, если выбрать
нижний знак «плюс». Иными словами, частицы, описываемые дира-
ковским полем, должны быть фермионами. Отсюда с необходимо-
необходимостью следует, что |к|2 = \Xf и Ъи = ~bv. Как и в случае скалярного
поля, можно переопределить относительную фазу операторов унич-
уничтожения и рождения так, чтобы отношение к/Х стало действитель-
действительным. В этом случае к = X и подбором общего масштабного множите-
множителя и фазы поля \|/ можно выбрать
к = X = 1. E.5.32)
298
Глава 5. Квантовые поля и античастицы
Наконец, при желании можно заменить \|/ на у5\|/, что одно-
одновременно меняет знаки у Ъи и bv, так что можно всегда выбрать
Ъи = -Ь„ = +1.
E.5.33)
Для будущих применений выпишем окончательный вид дираков-
ского поля:
уг (х) = Bл)-3/2 ? J d3p[Ul (p, o)eip'xa(p, а) + vt (p, о)е"*р'хас+(р, а)],
E.5.34)
где коэффициентные функции при нулевом импульсе равны:
E.5.35)
1
О
-1
-1
о
1
о
E.5.36)
Суммирование по спинам осуществляется по формулам
2ри р
zp
так что антикоммутатор E.5.20) имеет вид:
E.5.37)
E.5.38)
}uА(х - у).
E.5.39)
5.5. Причинные дираковские поля 299
Вернемся теперь к требованию, что в результате пространственной
инверсии поле Х|/(ж) должно переходить в нечто, пропорциональное
\|/(;йс). Чтобы это было возможным, фазы в формулах E.5.15) и E.5.16)
должны быть равны друг другу, откуда внутренние четности частиц
и их античастиц должны быть связаны соотношением:
Г|с = -ц. E.5.40)
Иными словами, внутренняя четность Г|Г|С системы, состоящей
из частицы со спином 1/2 и ее античастицы, равна -1. Именно по
этой причине мезоны с отрицательной внутренней четностью, та-
такие как р° и J/\|/, можно интерпретировать как s-волновые связан-
связанные состояния кварк-антикварковых пар. Из формул E.5.15)
и E.5.16) находим закон преобразования дираковского поля в
результате пространственной инверсии:
Р\\/{х)Р~1 = г|*р\|/(;Лс). E.5.41)
Прежде чем переходить к другим инверсиям, уместно заметить,
что формулы E.5.14), E.5.33) и E.5.26) показывают, что w(p,s) и
u(p,s) являются собственными векторами оператора —гр^Уи /тс
собственными значениями +1 и —1, соответственно:
(Ф^Уц + т)и{р, о) = 0, (-грцуц + m)v{p, о) = 0. E.5.42)
Отсюда вытекает, что поле E.5.33) удовлетворяет дифферен-
дифференциальному уравнению
(у^ + т)Щх) = 0. E.5.43)
Это знаменитое уравнение Дирака для свободной частицы со спином
1/2. С принятой здесь точки зрения, уравнение Дирака для свобод-
свободной частицы есть не что иное, как лоренц—инвариантная запись
использованного нами условия, чтобы объединение двух неприво-
неприводимых представлений собственной ортохронной группы Лоренца
давало поле, простым образом преобразующееся при пространст-
пространственной инверсии.
Чтобы установить свойства дираковского поля по отношению
к преобразованиям зарядового сопряжения и обращения времени,
300 Глава 5. Квантовые поля и античастицы
нам нужны выражения для комплексно сопряженных коэффици-
коэффициентных функций миг;. При нулевом импульсе эти функции дейст-
действительны, но чтобы получить коэффициентные функции при ко-
конечном импульсе, мы должны умножить их на комплексную матри-
матрицу D(L(p)). Из формулы E.4.41) следует, что для произвольных
действительных со^
так что, в частности,
D(L(p)Y = р
Заметим также, что (^1|Зг(,@,а) = -г>@,а) и (?^1(Зг;(О,а) = -и@,а), так
что
р,о), E.5.44)
f (Р> а) = -$Ш1 (р, а). E.5.45)
Для того, чтобы поле, получающееся при зарядовом сопряжении,
коммутировало бы с исходным полем на пространственноподобных
расстояниях, нужно, чтобы зарядовые четности частицы и анти-
античастицы были бы связаны соотношением
^ = К ¦ E-5.46)
В этом случае поле преобразуется по правилу
)С = -%$<exf\x). E.5.47)
(Мы обозначаем эрмитово сопряженное поле в правой части \|/*, а
не уу\ с тем чтобы подчеркнуть, что это все еще вектор-столбец, а
не строка.)
Мы все время различали частицы и их античастицы, но не
исключена возможность, что они на самом деле тождественны.
Подобные частицы со спином 1/2 называются майорановски-
ми фермионами. Рассуждая по той же схеме, которая привела
5.5. Причинные дираковские поля 301
к E.5.47), получаем, что дираковское поле такой частицы должно
удовлетворять условию действительности:
\|/(x) = -pW\|/*(x). E.5.48)
Внутренняя пространственная четность майорановских фермионов
должна быть мнимой, ц = +г, а четность относительно зарядового
сопряжения — действительной, Е, = ±1.
Существует важное различие между фермионами и бозонами,
касающееся внутренней фазы, возникающей при зарядовом сопря-
сопряжении состояний системы, состоящей из частицы и ее античастицы.
Такое состояние имеет вид
Ф = ? J d3pj с*У х(р, а; р', а V (Р, c)act (р', а')Ф0,
а,а'
где Фо — вакуумное состояние. При зарядовом сопряжении такое
состояние преобразуется в
СФ =
? f d3p f dVx(p,o;p',o>ct(P,o)at(p/,o>0.
Меняя местами переменные интегрирования и суммирования и
используя соотношения антикоммутации операторов рождения и
формулу E.5.46), можно переписать последнее выражение как
СФ ее - ? J d3pj d3p/x(p/, a'; p, a)a+(p, a)ac+(p', о')Ф0 •
a,a'
Отсюда находим, что внутренняя зарядовая четность системы,
состоящей из частицы, описываемой дираковским полем, и ее
античастицы, равна —1. Это означает следующее: если волновая
функция X состояния четна или нечетна по отношению к перестанов-
перестановке импульсов и спинов частицы и античастицы, то оператор зарядо-
зарядового сопряжения при действии на такое состояние дает соответствен-
соответственно -1 или +1. Классическим примером использования этих правил
является позитроний, связанное состояние электрона и позитрона.
Два низших энергетических состояния являются почти вырожден-
вырожденными s-волновыми состояниями с полным спином s = 0 и s = 1.
302 Глава 5. Квантовые поля и античастицы
Их называют соответственно пара- и ортопозитронием. Волновая
функция обоих состояний четна по отношению к перестановке им-
импульсов, и нечетна или четна при перестановке z-компонент спина,
так что парапозитроний и ортопозитроний имеют зарядовую чет-
четность С = +1 иС= — 1, соответственно. Такие значения решающим
образом влияют на возможные моды распада позитрония: парапози-
парапозитроний быстро распадается на пару фотонов (у каждого из которых
С = -1), а ортопозитроний может только значительно медленнее
распадаться на три или более фотонов. Точно так же, одиночные
мезоны р° и со0 рождаются как резонансы при аннигиляции электрон-
позитронных пар больших энергий через однофотонное промежуточ-
промежуточное состояние, так что у этих мезонов должно быть С = — 1. Это
совместимо с интерпретацией таких мезонов как кварк-антикварко-
вых связанных состояний с нулевым орбитальным моментом и сум-
суммарным спином кварков, равным единице.
Перейдем, наконец, к обращению времени. Напомним свойст-
свойства преобразований операторов уничтожения частиц и рождения
античастиц (формула D.2.15)):
= C(-D1/2-aa(-p,-G), E.5.49)
" =^c(-lI/2-aact(-p,-a). E.5.50)
Тогда при обращении времени поле E.5.34) преобразуется как
-1 = Bл)/2
а
х [C<(p,
Чтобы записать это выражение в такой же форме как \|/, следует
заменить переменные интегрирования и суммирования на -р и -а,
так что нам нужны формулы, связывающие u{(—p,—s) и иг*(—р,—s)
с W;(p,s) и Uj(p,s), соответственно. Для этого можно использовать то,
чтог/'° антикоммутирует с C и коммутирует с у5. С учетом предыду-
предыдущего выражения для D(L(p))* можно записать:
D*(L(-p)) = Y5pD*(L(p))py5 = у
5.5. Причинные дираковские поля 303
Далее, из формул E.4.36) и E.5.35)-E.5.36) следует
у ^-4@,-0) = (-1I/2-°м@, а),
так что
), E.5.51)
)_ E.5.52)
Итак, чтобы операция обращения времени перевела дираковское
поле в нечто, пропорциональное самому себе в обращенной по
времени точке (причем чтобы эти поля антикоммутировали на
пространственноподобных расстояниях), необходимо, чтобы внут-
внутренние фазовые множители, возникающие при обращении време-
времени, были связаны соотношением
^ = С E.5.53)
В этом случае
E.5.54)
Рассмотрим вопрос о том, как построить скалярные плотности
гамильтониана взаимодействия из дираковских полей и сопряжен-
сопряженных им полей. Как отмечалось, дираковское представление не
унитарно, так что Х|/^Х|/ не является скаляром. Чтобы обойти эту
трудность, удобно определить новый тип сопряженной величины:
\J7 = \|/+p. E.5.55)
Используя условие псевдоунитарности E.4.32), видим, что ферми-
онные билинейные комбинации, построенные с помощью \J7, под
действием преобразований Лоренца изменяются по закону
E.5.56)
304 Глава 5. Квантовые поля и античастицы
Кроме того, при пространственной инверсии
Р[Щх)МЩх)]Р~1 = Щ&х)$М$у(&х). E.5.57)
Беря матрицу М в виде 1, Y\ jT^, y5Y\ у5, получаем билинейные
комбинации \j/M\|/, преобразующиеся как скаляр, вектор, тензор,
аксиальный вектор и псевдоскаляр, соответственно. (Слово «акси-
«аксиальный» и приставка «псевдо» означают, что эти комбинации преоб-
преобразуются по отношению к пространственным отражениям противо-
противоположно тому, как преобразуются векторы и скаляры: четность
псевдоскаляра отрицательна, а пространственные и временная ком-
компоненты аксиального вектора имеют, соответственно, положитель-
положительную и отрицательную четности.) Эти результаты сохраняются,
если два фермионных поля в билинейной комбинации принадлежат
частицам разных сортов, не считая того, что в этом случае возни-
возникает отношение внутренних четностей.
Например, в первоначальной теории C-распада Ферми рас-
рассматривалась плотность гамильтониана взаимодействия, пропор-
пропорциональная Х|/руц\|/п\|/еуц\|/у. Позднее стало понятно, что наиболее
общее лоренц-инвариантное, сохраняющее четность и не содержа-
содержащее производных взаимодействие в C-распаде имеет вид линейной
комбинации произведений указанного вида, в которых у„ заменено
на любой из пяти ковариантов, образованных с помощью 4x4
матриц 1, у1, jT^v, УдУ1, или у5. (Как обсуждалось в гл. 2, оператор
пространственной инверсии определен так, что внутренняя чет-
четность протона, нейтрона и электрона равна +1. Если нейтрино не
имеет массы, то его четность также можно принять равным +1,
заменив при необходимости поле нейтрино на У5Х|/Г) Когда в
1956 году Ли и Янг усомнились в справедливости закона сохранения
четности, они расширили список возможных взаимодействий без
производных, включив в него десять слагаемых, пропорциональ-
пропорциональных \j7pM\|/n\j7eM\|/v, а также \j7pM\|/n\j7eMy5\|/v, где М — одна из
матриц 1, У1, jT^v, y5Y\ у5. Определенный интерес представляют
свойства этих билинейных комбинаций по отношению к зарядовому
сопряжению. Используя формулы E.5.47) и E.5.35)-E.5.39), имеем:
= ±\j/M\|/,
5.6. Общие неприводимые представления ... 305
где в последнем выражении берется знак + для матриц 1, у5уц и у5,
и знак — для у„ и Xv. (Знак «минус» в первой строчке возникает за
счет статистики Ферми. Мы игнорируем с-числовой антикоммута-
антикоммутатор.) Таким образом, бозонное поле, взаимодействующее с током
\j/M\|/, должно иметь С = +1 для скаляров, псевдоскаляров и
аксиальных векторов, и С = -1 для векторов и антисимметричных
тензоров. Это — один из способов понять, почему л° (взаимодейст-
(взаимодействующий с псевдоскалярным или аксиальным током нуклонов) имеет
С = +1, в то время как у фотона С = -1.
5.6. Общие неприводимые представления однородной
группы Лоренца *
Перейдем от частных случаев векторного и дираковского полей к
общему случаю поля, преобразующегося по общему неприводимо-
неприводимому представлению однородной группы Лоренца. Все поля могут
быть построены как прямые суммы таких неприводимых полей.
Общее представление собственной ортохронной однородной группы
Лоренца (точнее, ее инфинитезимальной части) реализуется мно-
множеством матриц JLV, удовлетворяющих тем же коммутационным
соотношениям E.4.4), что и генераторы группы:
\-J\iv Jpa i ~ Hc/pv^lqi + с/щэЛуст ~~ сАтуЛрц ~~ с/цстЛур" E.0.1)
(Конечно, j^v = — Д,ц и индексы в j^v поднимаются и опускаются, как
обычно, сверткой с тензорами ц^ и T|mv) Чтобы понять метод
построения таких матриц, разделим сначала шесть независимых
компонент Xv на два 3-вектора: матрицу углового момента
к = /23 > h = /si. h = S12 E-6-2)
и буст
•*l=/lO> -«2 =/20. ^3=/ЗО- E-6-3)
* Этот раздел лежит несколько в стороне от основной линии изложения и
может быть опущен при первом чтении.
306 Глава 5. Квантовые поля и античастицы
Тогда формула E.6.1) может быть записана в виде:
[?,#] = «Wfe, E.6.4)
[gi,.Xj] = i?ijk.Xk, E.6.5)
[.Xi,.Xj] = -i?ijkfk, E.6.6)
где г, j, к принимают значения 1,2,3, а ?ф — полностью антисиммет-
антисимметричная величина с ?ш = +1. Формула E.6.4) указывает на то, что
матрицы (f являются генераторами представления подгруппы вра-
вращений группы Лоренца, а формула E.6.5) отражает тот факт, что .X
есть 3-вектор. Знак «минус» в правой части формулы E.6.6) возника-
возникает из-за того, что г|00 = —1. Этот знак играет в дальнейшем
решающую роль.
Очень удобно заменить матрицы (f и .X двумя независимыми
спиновыми 3-векторами, записав
\ E.6.7)
E.6.8)
Легко видеть, что коммутационные соотношения E.6.4)—E.6.6) экви-
эквивалентны равенствам
[^,^] = ieijk,Jk, E.6.9)
[.Щ,.Щ] = ггф.%, E.6.10)
[Лг,Щ] = 0. E.6.11)
Матрицы, удовлетворяющие соотношениям E.6.9)—E.6.11), можно
найти так же, как это было сделано для матриц, представляющих
спины пары невзаимодействующих частиц, т. е. в виде прямой
суммы. Иначе говоря, отметим строки и столбцы этих матриц парой
целых и/или полуцелых чисел а, Ъ, пробегающих ряд значений
а = -А, -А + 1,..., +А, E.6.12)
5.6. Общие неприводимые представления ... 307
Ъ = -В, -В + 1,..., +В E.6.13)
и примем
где J^ и J'B^ — стандартные спиновые матрицы для спинов А и В:
± z4A))a,a = ба>±1Л/(А + а)(А±а + 1), E.6.17)
(аналогично для J'B^). Представление отмечается значениями поло-
положительных целых или полуцелых чисел А и В. Таким образом,
представление (А, В) имеет размерность BА + 1)BВ + 1) *.
Конечномерные представления однородной группы Лоренца
не унитарны, т. к. -Л и :JD эрмитовы, и поэтому (f эрмитова, но Ж
антиэрмитова. Причиной является присутствие г в формулах E.6.7)
и E.6.8), что требуется наличием отрицательного знака в E.6.6). Все
это вытекает из того, что однородная группа Лоренца — не четы-
четырехмерная группа вращений 50D), которая компактна, а неком-
некомпактная группа SOC, 1). Только компактные группы имеют конеч-
конечномерные унитарные представления (если не считать представле-
представлений, в которых некомпактная часть представлена тривиальной
единицей). Однако при работе с неунитарными представлениями не
возникает особых проблем, т. к. нас интересуют не волновые функ-
функции, а поля, которые не обязаны иметь лоренц-инвариантную
положительную норму.
* Существует альтернативный формализм 8, основанный на том факте,
что представление группы вращений со спином j можно записать как симмет-
ризованное тензорное произведение 2j представлений со спином 1/2, т. е. как
симметричный тензор группы ?17B) с 2j двузначными индексами. Поэтому
можно записать поля, принадлежащие представлению (А, В), с помощью 2А
двузначных индексов представления A/2,0) и 2?> двузначных индексов
представления @,1/2), снабженных точками, чтобы отличать их от первой
пары.
308 Глава 5. Квантовые поля и античастицы
Напротив, группа вращений имеет унитарные представле-
представления, генераторы которых являются эрмитовыми матрицами
g = cA + 3&. E.6.18)
С помощью обычных правил сложения векторов можно убедиться,
что поле, преобразующееся по представлению (А, В) однородной
группы Лоренца, имеет компоненты, преобразующиеся при вра-
вращениях как объекты со спином j, причем
j = А + В, А + В-1, ..., \А-В .
Этого достаточно, чтобы отождествить представления (А, В)
с, по-видимому, более знакомыми тензорами и спинорами. Напри-
Например, поле @, 0) является скаляром с единственной компонентой
j = 0. Поля (з, 0) или @, \) могут иметь только j = \; они соответству-
соответствуют двум верхним (т. е. у5 = +1) и двум нижним (у5 = —1) компонен-
компонентам дираковского спинора. Поле {\, \) имеет компоненты с j = 1 и
j = 0, соответствующие пространственной части v и временной
компоненте v° 4-вектора гЛ В общем случае поле (А, А) содержит
слагаемые только с целыми спинами 2А, 2А—1, ..., 0, и соответству-
соответствует бесследовому симметричному тензору ранга 2А. (Заметим,
что число независимых компонент симметричного тензора ранга 2А
в четырех измерениях равно
4-5...D + 2А-1) _ C + 2А)!
BА)! 6BА)!
и условие бесследовости сводит это число к
C + 2А)! A + 2А)!
6BА)! ~6BА-2)! '
как и следует ожидать для поля (А, А).) Еще один пример: поля
A, 0) и @, 1) могут иметь только компоненты j = 1 и соответствуют
антисимметричным тензорам F^v, удовлетворяющим дополнитель-
дополнительным, обеспечивающим неприводимость, условиям «дуальности»
5.7. Причинные поля. Общий случай 309
соответственно; такие тензоры называются соответственно «само-
«самодуальными» и «антисамодуальными». Естественно, что разделение
антисимметричного тензора F^v с двумя индексами на подобные
«самодуальную» и «антисамодуальную» части возможно только в
случае четырех измерений.
Произвольный тензор ранга N преобразуется как тензорное
произведение N 4-векторных представлений (з, г)- Поэтому путем
подходящих симметризации, антисимметризации и вычитания следа
можно разложить его на неприводимые части (А, В), где
А = N/2, JV/2-1,... и В = N/2, JV/2-1,... Таким способом можно
построить любое неприводимое представление (А, В), для которого
А + В является целым числом. Спинорные представления, у кото-
которых А + В — полуцелое, могут быть построены аналогичным
образом из тензорных произведений тензорных представлений и
дираковского представления (з, 0) © @, \). Например, тензорное
произведение векторного представления (з, \) и дираковского пред-
представления (з, 0) © @, \) дает спин-вектор У\ преобразующийся по
приводимому представлению
& h ® [E,0) © @i)] = (il) © (i0) © (li) © @i).
Величина у^х^ преобразуется как обычное дираковское поле {\, 0) © @, \),
так что можно выделить представление * (з, 1) © A, г)> потребовав вы-
выполнения условия Y^xi/11 = 0. Это поле Рариты-Швингера9.
До сих пор в этом разделе мы рассматривали только представ-
представления собственной ортохронной группы Лоренца. В любом представ-
представлении группы Лоренца, включающей пространственную инверсию,
должна существовать матрица C, изменяющая знаки тензоров с
нечетным количеством пространственных индексов. В частности
1 = +/, W1 = -X. E.6.19)
* Согласно E.6.18), такое поле преобразуется под действием обычных вра-
вращений как прямая сумма двух компонент с j — 3/2 и двух компонент
с j = 1/2. Удвоение компонент устраняется требованием, чтобы выполнялось
уравнение Дирака [/Эу + т]\|# = 0, а оставшаяся компонента с j - 1/2 устра-
устраняется наложением условия Э^\|# = 0. При таких условиях поле описывает
одну частицу со спином j — 3/2.
310 Глава 5. Квантовые поля и античастицы
Записывая это равенство через матрицы E.6.7) и E.6.8), имеем
Таким образом, неприводимое представление (А,В) собственной ор-
тохронной однородной группы Лоренца является представлением
группы Лоренца, включающей пространственную инверсию, только
в случае А = В. Как мы видели, такие представления (А, А) являются
скалярами, векторами и симметричными тензорами со следом нуль.
При А Ф В неприводимые представления группы Лоренца, включаю-
включающей пространственную инверсию, являются прямыми суммами
(А, В) © (В, А) с размерностью 2BА+1)BВ+1). Одним из них является
дираковское представление {\, 0) © @, \), обсуждавшееся в разделе
E.4). Для этого представления матрицей C является 4x4 матрица
E.4.29). Другой знакомый пример — представление A,0) ©@,1),
которое, как мы видели, есть антисимметричный тензор второго
ранга, содержащий как самодуальную, так и антисамодуальную
части.
5.7. Причинные поля. Общий случай *
Попытаемся построить причинные поля, преобразующиеся по опи-
описанному в предыдущем разделе общему неприводимому представ-
представлению (А,В) группы Лоренца. Индекс I заменен ниже парой индек-
индексов а, Ъ, принимающих значения в интервале E.6.12), E.6.13), так
что поля можно записать в виде
E.7.1)
где к и X — произвольные константы. Мы оставляем открытой
возможность, что такая частица совпадает со своей античастицей и
ac(p,a) = a(p,a).
* Этот раздел лежит несколько в стороне от основной линии изложения и
может быть опущен при первом чтении.
5.7. Причинные поля. Общий случай 311
Первоочередной задачей является нахождение коэффициент-
коэффициентных функций с нулевым импульсом uab@,G) и г;аЬ@,а). Основопола-
Основополагающие условия E.1.25)—E.1.26), которым подчиняются и@,о) и
v(Q,g), принимают вид:
а,Ъ
а а,Ъ
или, после использования соотношений E.6.14)—E.6.15),
E.7.2)
E.7.3)
Но соотношение E.7.2) есть не что иное, как условие, определяющее
коэффициенты Клебша-Гордана С^Цо^Ьу. Действительно, эти ко-
коэффициенты определены требованием, что если *Pab — состояния,
преобразующиеся при бесконечно малых вращениях по правилу
то под действием тех же вращений состояние
аЪ
преобразуется по правилу
Рассмотрение формулы E.7.2) показывает, что коэффициенты
маЬ@,а) удовлетворяют этому требованию, и поэтому uab@,a) равны
312 Глава 5. Квантовые поля и античастицы
с точностью до возможного коэффициента пропорцио-
пропорциональности. Принято выбирать эту константу так, что
иаЬ@,о) = Bm)-1/2CAB(jo;ab). E.7.4)
Этот результат единственен, поскольку каждое неприводимое пред-
представление {А,В) однородной группы Лоренца содержит данное пред-
представление группы вращений со спином j не более одного раза.
Аналогично, изучение формул E.6.16)—E.6.17) показывает, что ком-
комплексно сопряженные матрицы углового момента равны
-J<? = (-1Га'.Г^_а,. E.7.5)
Таким образом, если записать формулу E.7.3) через (—iy~Gvab(Q,—G),
она примет тот же вид, что и формула E.7.2). После подбора
постоянного множителя единственное решение для и@,а) принима-
принимает вид
иоЬ@,о) = (-1)>"+<Хь@-о). E.7.6)
Чтобы вычислить коэффициентные функции при конечном им-
импульсе, следует совершить преобразование буста. Для заданного
направления р = р/| р| буст B.5.24) можно представить как функцию
параметра 6, определенного равенствами
ch6 = Vp2 +m2 /m, sh6=|p|M
и писать 1Д,F) вместо Ь^(р):
E.7.8)
L% = ch 6.
Преимущество такой параметризации заключается в том, что
L(e)L(9) = L(e + 9). E.7.9)
5.7. Причинные поля. Общий случай 313
В случае бесконечно малых 6 [LF)]|1V —» 6ЦУ + @%, где сог0 = со0, = р{ 6
и сог = со°0 = 0. Следуя тем же рассуждениям, которые привели от
формулы B.2.24) к формуле B.2.26), получим:
D(L(p)) = ехр(-гр • Жв). E.7.10)
Это верно для любого представления однородной группы Лоренца.
Для неприводимых представлений (А,В) из формул E.6.7) и E.6.8)
следует, что
iJC = J-m, E.7.11)
а так как .-4 и °М -коммутирующие матрицы, то
D{L{p)) = ехр(-р • с^б) ехр(+р • SBQ). E.7.12)
Подробнее, используя E.6.14) и E.6.15), имеем:
D(L(p))aVab = (ехр(-р • j(A)e))a,a(exp(+P • J(BN))yb. E.7.13)
Тогда из формул E.7.4) и E.7.6) следует, что коэффициентные
функции при конечном импульсе равны
E.7.14)
г;аЬ(р,а) = (-1)^+ямоЬ(р-о). E.7.15)
Эти формулы дают явные выражения для поля при заданном типе
преобразования (А,В), так что поле E.1.31) этого типа единственно с
точностью до выбора постоянных множителей к и X.
В рамках такого формализма очень легко построить плотности
гамильтониана взаимодействия, являющиеся лоренцовскими ска-
скалярами. Представление (А,В) однородной группы лоренца есть пря-
прямое произведение представлений (А,0) и @,В), так что общие
формулы преобразований Лоренца E.1.6) и E.1.7) принимают вид
?lbaV). E.7.16)
а'Ъ'
314 Глава 5. Квантовые поля и античастицы
Далее, из формул E.6.14) и E.6.15) следует, что матричные генера-
генераторы представлений (А,0) и @,В) являются просто спиновыми мат-
матрицами для спинов А и. В, соответственно. Таким образом, можно
построить скаляры вида
Е Е 5'а1а2...аи,Ь1Ь,..Ьи?й1(Ж^а2)Ь2(^-<)Ьи(^. E-7.17)
взяв 0а1а2...аи,ь1ь2...ьи как произведение коэффициентов объединения
спинов Аг, А2,..., Ап в скаляр и спинов Вг, В2, ... , Вп — в другой
скаляр. (Хотя мы и не рассматриваем явно взаимодействия, содер-
содержащие производные, подобным способом можно построить наибо-
наиболее общее взаимодействие п полей, так как производная поля типа
(А,В) всегда может быть разложена на поля других типов без
производных.) Например, самый общий лоренцовский скаляр, по-
построенный из произведения трех полей, преобразующихся по пред-
представлениям (Aifii), (A2,B2) и (AS,BS), имеет вид
А А2 A3YB1 В2 В
и содержит единственный свободный параметр д. Это самое общее
трехполевое взаимодействие. (Скобки в E.7.18) обозначают З^'-сим-
волы Вигнера 10:
J2 js ] = у с- ¦ (j3m'3 тгт2)С- ¦ @0 т>3)
которые определяют связь трех спинов, образующую скаляр по
отношению к вращениям.)
Для того, чтобы .^-матрица была лоренц-инвариантной, недоста-
недостаточно, чтобы плотность гамильтониана взаимодействия .Ж(ж) была
скаляром типа E.7.18). Другим необходимым условием является
то, что ,У({х) должна коммутировать с .Ж(у) на пространственнопо-
добных расстояниях х — у. Чтобы увидеть, как можно удовлетво-
удовлетворить такому условию, рассмотрим коммутатор или антикоммута-
антикоммутатор двух полей частиц одного сорта: поле \|/ типа (А,В) и сопря-
сопряженное поле \j/t к полю \j/ типа (А,В). Находим:
5.7. Причинные поля. Общий случай 315
= Bл)/2 Jd3pBp°r1 V-g
х [ккУр(*-у) + ХХ*е-^(х-у)], E.7.19)
где л(р) — сумма по спинам:
)() Y()(V,O), E.7.20)
и, как обычно, верхние и нижние знаки отвечают, соответственно,
бозонам и фермионам. (Мы допускаем другие коэффициенты к и А.
в поле \j/.) Более подробно:
а'Ь' а'Ъ' а
Функция л(р) была вычислена явно. п Нам важно сейчас, что она
оказывается равной значению на массовой оболочке некоторой
полиномиальной функции Р от р и р°:
E-7.22)
и эта функция Р четна или нечетна в зависимости от того, четно
или нечетно целое число 2А + 2 В ;
ё E-7-23)
Проверим здесь это равенство лишь для одного конкретного на-
направления вектора р. Выбирая р вдоль третьей оси, имеем из
E.7.21)
жаь,аь(р) = L Сав(& аЪ)сАв№>й^) ехр([-а + Ъ - а + Ь]б).
316 Глава 5. Квантовые поля и античастицы
Коэффициенты Клебша—Гордана отличны от нуля только при зна-
значениях с = а+Ъис= п + Ъ, так что можно сделать замену
-а + Ъ-а + Ъ = -2а + о + 2Ъ - о = 2Ъ - 2а.
Выражение ехр(±6) можно записать как (р° ± р3)/т, так что
i2b-2a
||(pu +p°) / m
x
(a>W
Г, n Qs / п2Ь—2a ,C" _ .
J[(p° +p3)/m] (b > a)
где рО = yj-p2 + га2 ¦ Видим, что л(р) действительно можно записать
как значение полинома Р(р,р°) на массовой оболочке. Кроме того,
2Ъ - 2а равно 2В + 2А минус четное целое число, так что полином
удовлетворяет условию отражения E.7.23).
Всякий полином по р и (р2 +Ж2I/2 можно записать в виде,
линейном по (р2+тп2I/2 (выразив четные степени (р2+гп2I^2
через р), так что л(р) можно записать в виде
p), E.7.24)
где теперь Р и Q - полиномы только по р, причем
Р(-р) = (-JА+2ёР(р), E.7.25)
Q(-P) = -(-JA+2eQ(P)- E.7.26)
Для пространственноподобных промежутков х - у можно выбрать
лоренцовскую систему отсчета, в которой х° = у0, и записать
E.7.19) в следующем виде:
ab;5Sx - у,0)
[кк* ± (-JА+2~ВХХ*Ю h -Л-гУM3(х - у).
5.7. Причинные поля. Общий случай 317
Чтобы это выражение обращалось в нуль при х^ у, должно выпол-
выполняться равенство
кк*=±(-1JА+2ВМ*. E.7.27)
Рассмотрим частный случай одинаковых \|/ и \j), так что А = А
и В = В. (Подобные коммутаторы или антикоммутаторы неизбежно
появляются в [,Ж{х),,Ж(г/)], т. к. из эрмитовости гамильтониана выте-
вытекает, что если ,Ж(х) содержит \|/, он обязательно содержит и х^.)
В этом случае из E.7.27) следует, что
Такое возможно тогда и только тогда, когда
±(-1JА+2В = +1, E.7.28)
|к|2=|А,|2. E.7.29)
Конечно, 2А + 2В отличается от 2j на четное целое число, так что
из E.7.28) следует утверждение: рассматриваемая частица явля-
является бозоном или фермионом в зависимости от того, четно или
нечетно число 2j. Этим устанавливается общая связь между спином
и статистикой.12 Мы видели, как выполняется эта связь на частных
примерах частиц, описываемых скалярными, дираковскими и век-
векторными полями.
Вернемся к общему случаю разных полей \|/ и \j/. Деля обе
части E.7.27) на к = |Х| , получаем:
()С)
1С
Отсюда вытекает, что для любого поля
X = (-1JВск, E.7.30)
где с — один и тот же множитель для всех полей данной частицы.
Далее, из E.7.29) следует, что с есть просто фазовый множитель,
с\ = 1. Поэтому можно устранить с для всех полей, переопределив
318 Глава 5. Квантовые поля и античастицы
относительную фазу операторов а(р,а) и ас^(р,а) так, чтобы с = 1,
откуда X = (-JВк. Наконец, множитель к для каждого типа поля
можно устранить переопределением общего масштаба поля. Таким
образом, приходим к формуле для преобразующегося по представ-
представлению (А,В) поля данной частицы, которое единственно с точно-
точностью до общего масштабного фактора:
ггр-х
E.7.31)
Для данной частицы разные поля реально не отвечают физически
различимым возможностям. Например, для j = 0 возможными
являются поля типа (А, А) (поскольку из неравенства треугольника
А — В| < j < А + В в данном случае следует А = В). Начав со
скалярного @,0) поля ф, можно без труда построить поля (А, А)
с помощью 2А-ой производной:
{^••Л^Ф, E.7.32)
здесь фигурные скобки {} обозначают бесследовую часть, напри-
например,
(Напомним, что бесследовый симметричный тензор ранга N преоб-
преобразуется по представлению (N/2,N/2).) Однако формула E.7.31)
представляет единственное причинное поле (А,В) для частицы
данного спина j, так что для j = 0 поля (А,А) E.7.31) могут быть
только линейными комбинациями 2А-ых производных E.7.32) ска-
скалярного поля.
В более общей формулировке любое поле (А,В) для данной
частицы со спином j может быть представлено как дифференциаль-
дифференциальный оператор ранга 2В, действующий на поле фст(х) типа {j, 0) (или
дифференциальный оператор ранга 2А, действующий на поле @, j)I3.
Чтобы увидеть это, рассмотрим поле
{Э^...Э^в}фст. E.7 33)
5.7. Причинные поля. Общий случай 319
Оно преобразуется как тензорное произведение представлений {В,В)
и (j,0), поэтому по обычным правилам векторного сложения это поле
можно разложить по полям, преобразующимся по всем неприводи-
неприводимым представлениям (А,В), где \j — В\ < А < j + В, или эквива-
эквивалентно \А — В < j < А + В. Так как для данной частицы со спином
j формула E.7.31) описывает единственное поле типа (А,В), оно
может быть только * полем (А,В), полученным с помощью производ-
производных E.3.33).
Рассмотрим поведение построенных полей относительно ин-
инверсий. Начнем с пространственной инверсии. Как следует из ре-
результатов раздела 4.2, свойства операторов уничтожения частиц и
рождения античастиц по отношению к пространственной инверсии
выражаются формулами
Ра(р,о)Р-1 =ца(-р,о), E.7.34)
=Tfact(-p,a), E.7.35)
где Г) и Г)с — внутренние четности частицы и античастицы, соответ-
соответственно. Следовательно, общее причинное (А,В) поле E.7.31) преоб-
преобразуется под действием оператора четности Р следующим образом:
= Bл)-3/2_
E.7.36)
;(-JВас+(-р,а)е-Р-г;4в(Р,а)].
* Единственный пробел в этом рассуждении связан с гипотетической воз-
возможностью, что некоторые полученные таким способом поля (А,В), на самом
деле, обращаются в нуль. Но в этом случае поле (ро, отвечающее представлению
(j,0) должно удовлетворять полевому уравнению ?о Мо(Э/Эх)(ро(х) = 0 ,
следовательно, для каждого а должно быть ?о Мо(гр)ио(р, а) = 0.. Для
представления (j,a) коэффициент Клебша-Гордана Cj0 (jo; GO) равен просто
кронекеровскому дельта-символу 85ст, откуда ?о M(,{ip)D(,(,'{L{p)) = 0 . Но
это возможно только, если все Ma(ip) = 0, т. к. D(A) имеет обратную матрицу
D(A~1). Таким образом, поля (ро(х), отвечающие представлению (j,0), могут
удовлетворять только уравнению Клейна-Гордона (? - т2)фо(ж) = 0 • Сле-
Следовательно, ни одно из полей (А,В), полученных с помощью E.3.33), не мо-
может быть равным нулю.
320 Глава 5. Квантовые поля и античастицы
Мы хотим сделать замену переменной интегрирования р на —р,
а для этого нужно вычислить и,аЬ(-р,о) и г;аЬ(-р,а). Чтобы получить
необходимые выражения, достаточно вернуться к формулам E.7.14)
и E.7.15) и использовать свойство симметрии коэффициентов Клеб-
ша-Гордана14
CAB{jo;ab) = (-)А+вчСВАи<у;Ъа). E.7.37)
Находим:
иАъв(-р,о) = HA+B-iugA(V,o), E.7.38)
E.7.39)
так что
Р\\1Аъв(х)Р~1 = ^ J
E.7.40)
х
где, как и ранее, ,'fx = (-х, ж0). Мы получили причинное поле \\fBA(x),
взятое в точке .Ух, если не считать того, что коэффициенты при
слагаемых с операторами уничтожения и рождения могут отличать-
отличаться от тех, которые выписаны в E.7.31). Однако эти коэффициенты
должны быть теми же самыми, что и в E.7.31), с точностью до
общего постоянного множителя, так как формула E.7.31) представ-
представляет с точностью до масштаба единственное причинное поле любого
типа. Отсюда отношение коэффициентов при двух слагаемых в E.7.40)
должно быть таким же, как и в E.7.31) (с заменой В на А, так как
предполагается, что E.7.40) дает (В, А) поле):
цсН2В/ц*=Н2Аш E.7.41)
Однако разность А — В отличается от спина j только на целое число,
так что
Tf =rf(-Jj- E.7.42)
5.7. Причинные поля. Общий случай 321
Частные случаи этого равенства мы анализировали в разделах 5.2,
5.3 и 5.5 для j = О, j = 1 и j = 1/2. Теперь видно, что результат имеет
общий характер: внутренняя четность Г|сг| пары частица-анти-
частица-античастица равна +1 для бозонов и -1 для фермионов. Подставляя
E.7.42) в E.7.40), получаем окончательно для пространственной
инверсии:
Рх^аОР = Tl*(-l)A+B-JVbaA(-X,*0). E-7-43)
Рассмотрим применение этой формулы к дираковскому полю. Для
верхних (j, 0) и нижних @, з) компонент дираковского поля знак
(—1)А+В~з равен +1, так что оператор четности просто переводит х в
—х, меняет местами верхние и нижние компоненты и умножает
поле на rf. Замена верхних компонент на нижние у дираковского
поля осуществляется матрицей C в E.5.41).
Рассмотрим теперь операцию зарядового сопряжения. Дейст-
Действие С на операторы уничтожения частиц и рождения античастиц
определяется формулами
C =^ac(p,a), E.7.44)
Cac+(p,a)C-1=Sca+(p,a), E.7.45)
где t, и ?,с — зарядовые четности частицы и античастицы, соответ-
соответственно. Применяя это преобразование к полю E.7.31), находим:
ст E.7.46)
х [§V(р,о)е^х + Ъ,с(-1JВа+(р,-а)(-1^^]
Полезно сравнить эту формулу для зарядово-сопряженного поля к
полю (А, В) с формулой сопряженного (В, А) поля той же частицы:
E.7.47)
x If—Г'" ---•¦¦•'¦- - •'¦'¦••• ¦ - - •'¦'¦••• ¦
322 Глава 5. Квантовые поля и античастицы
Чтобы вычислить и , используем предыдущий результат:
Коэффициенты Клебша-Гордана в E.7.14) действительны, так что
^ J(B)(e))_b_b,
X —1
Используем свойство отражения для коэффициентов Клебша-Гор-
дана14:
СВАи,-о;-Ъ,-а') = CAB(jo; a'V) E.7.48)
и то, что эти коэффициенты равны нулю во всех случаях, кроме
а + Ъ' = о. Тогда
и^_а{р,-а)* = (-l)a+b"CTMfbB(p,a). E.7.49)
Отсюда сопряженное поле E.7.47) принимает вид (мы делаем заме-
замену а —> -а, Ъ —> -Ъ, о —> -а):
+(
х [(-1JА{-1У+аас(р,о)е*гх + а+(р,
Используя соотношение между знаками (-1) 2А i = (—1JВ+3', получа-
получаем:
E.7.50)
х [с()^х (l)'a+2Bt()iPa:]
Для того, чтобы поле С\|/аЬ (х)С~ коммутировало или антикомму-
тировало со всеми обычными полями на пространственноподобных
5.7. Причинные поля. Общий случай 323
расстояниях, необходимо, чтобы оно было пропорционально \|/_ь_а,
так как это поле сопряжено к единственному причинному полю
типа (А, В). Сравнивая E.7.50) с E.7.46), видим, что это возможно
только в случае, если зарядовые четности связаны соотношением
Г = ^с E.7.51)
и тогда
СуГИС = Г(-1)-2А-а-Ь-3?ВьА-аИ- E-7-52)
Мы уже обсуждали соотношение E.7.51) для спинов 0, 1 и 1/2 в
разделах 5.2, 5.3 и 5.5, а также рассмотрели некоторые применения
этого правила для анализа состояний электрон-позитронных и кварк-
антикварковых пар.
В частности, для частицы, совпадающей со своей античасти-
античастицей, в формуле E.7.52) следует опустить оператор зарядового
сопряжения в левой части и множитель ?, в правой:
<ьв(х) = (-1Г2А-а-ь-^в^_а(х). E.7.53)
Пример такого условия действительности уже рассматривался в
разделе 5.5. для майорановских частиц.
Перейдем, наконец, к обращению времени. Действие на опе-
операторы уничтожения частиц и рождения античастиц имеет вид
Я-1 = С(-1Гаа(-р,-а), E.7.54)
Та^р.а)"!" =Cc(-l)j~CTact(-p,-G). E.7.55)
Отсюда неприводимое поле E.7.31) преобразуется по правилу
E.7.56)
х [С*с()^х ^c(lJBct()^х]
Чтобы вычислить комлексно сопряженные коэффициентные функ-
функции, используем E.7.14) и стандартную формулу 14
CAB(j,o;a,b) = (-l)A+B-iCAB(j,-o;-a,-b), E.7.57)
324 Глава 5. Квантовые поля и античастицы
Тогда
$? +ь+а+А+в^4%). E.7.58)
Меняя переменные интегрирования и суммирования в E.7.56) на —р
и -а, находим, что для того, чтобы поле (А, В) при обращении
времени преобразовывалось в поле, пропорциональное другому
(А, В) полю, необходимо выполнение условия
Сс = С, E-7.59)
и в этом случае
$f 1 +ь+А+в2^>^_ь(х,-х0). E.7.60)
Следует отметить, что время от времени сообщается о разных
трудностях в теории частиц со спином > 3/2 15. В общем случае они
проявляются при изучении распространения полей с высшими
спинами в присутствии с-числового внешнего поля. В зависимости
от деталей теории, возникающие трудности включают отсутствие
причинности, несовместность уравнений, нефизические массовые
состояния и нарушение унитарности. Я не собираюсь подробно
анализировать эти проблемы, поскольку мне кажется, что они не
имеют отношения к той расчетной схеме, которая описана в данной
главе, по следующим причинам.
1. Поля Х|/а{,(ж) были построены здесь непосредственно из опе-
операторов уничтожения и рождения физических частиц, так что не
может возникать никаких вопросов о несовместимости с уравнения-
уравнениями или о нефизических массовых состояниях. Построенные поля
свободны, но включив их в плотность гамильтониана взаимодейст-
взаимодействия в картине взаимодействия, мы можем использовать теорию
возмущений для расчета элементов 5-матрицы, автоматически
удовлетворяющих принципу кластерного разложения. До тех пор,
пока гамильтониан взаимодействия эрмитов, не будет никаких
трудностей с унитарностью. В рамках теории возмущений гаранти-
5.7. Причинные поля. Общий случай 325
рована и лоренц-инвариантность, пока мы добавляем в плотность
гамильтониана подходящие локальные, пусть и нековариантные
слагаемые. Хотя строгое доказательство этого отсутствует, нет
оснований сомневаться в том, что это всегда возможно. Таким
образом, любые трудности с высшими спинами могут возникать
только при попытках выйти за рамки теории возмущений.
2. Как обсуждается в разделе 13.6, решение полевых уравне-
уравнений в присутствии с-числового фонового поля (именно в подобных
задачах были обнаружены все проблемы с высшими спинами)
действительно требует выхода за рамки теории возмущений, так
как результаты соответствуют суммированию бесконечного под-
подмножества слагаемых в ряде теории возмущений. Это частичное
суммирование обосновано, даже в случае слабых внешних полей,
только если поля достаточно медленно изменяются, причем ма-
малость энергетических знаменателей компенсируется слабостью по-
полей. Но полученные таким способом результаты зависят от всех
деталей взаимодействия частицы с большим спином с внешними
полями — не только от мультипольных моментов частицы, но и от
возможных слагаемых во взаимодействии, которые нелинейны по
внешним полям. Проблемы с высшими спинами 15 возникали только
для таких частиц больших спинов, у которых произвольно предпо-
предполагалось очень простое взаимодействие с внешними полями. Никто
не доказал, что при учете произвольных взаимодействий проблема
сохранится., а как мы увидим в гл. 12, следует ожидать, что
частицы с высшими спинами обладают всеми возможными взаимо-
взаимодействиями, которые дозволены принципами симметрии.
3. На самом деле, есть серьезные основания полагать, что
проблемы с высшими спинами исчезнут, если взаимодействие
с внешними полями будет достаточно сложным. С одной стороны,
нет ни малейших сомнений в существовании частиц с высокими
спинами, в том числе, различных стабильных ядер и адронных
резонансов. Если и существует какая-то проблема, связанная
с большим значением спина, она может касаться только «точечных»
частиц, т. е. тех частиц, которые особенно просто взаимодействуют
с внешним полем. Следует не забывать, что требование простоты
зависит от сделанного нами выбора того поля, которое представля-
представляет частицу с высшим спином. Напомним, что любые типы свобод-
свободных полей для данной частицы могут быть записаны как результат
действия оператора производной на любые другие типы полей,
326 Глава 5. Квантовые поля и античастицы
так что в картине взаимодействия всякое взаимодействие с внеш-
внешними полями можно записать с помощью любого желательного нам
типа поля. Однако взаимодействия, выглядящие просто в случае
использования поля одного типа, могут выглядеть сложно, если
выразить их через поля другого типа. По этой причине требование
простоты, похоже, не имеет никакого реального содержания.
4. Наконец, как многомерные теории типа Калуцы—Клейна, так
и теории струн дают примеры самосогласованных теорий массив-
массивных заряженных частиц со спином 2, взаимодействующих
с фоновым электромагнитным полем 16. (Показано, что согласован-
согласованность теории зависит от предположения о реалистичных внешних
полях, удовлетворяющих полевым уравнениям. Этот момент не учи-
учитывался в ранних работах.) Если переформулировать такие теории в
картине взаимодействия, то частица со спином 2 представляется
свободным A,1) полем. Однако, как отмечено выше, взаимодействия
можно выразить в этой картине с помощью любого поля типа (А, В),
содержащего представление группы вращений с j = 2.
5.8. СРТ-теорема
Мы видели, что сочетание требований теории относительно-
относительности и квантовой механики приводит к необходимости существова-
существования античастиц. Однако необходимо не только то, что каждая
частица имеет свою античастицу (в частном случае истинно ней-
нейтральные частицы совпадают со своими античастицами). Существу-
Существует точное соотношение между свойствами частиц и античастиц,
которое может быть сформулировано в виде утверждения, что при
подходящем выборе фаз произведение СРТ всех инверсий сохраня-
сохраняется. Это знаменитая СРТ-теорема *.
* Первое доказательство этой теоремы принадлежит Людерсу и Паули 17.
Строгое доказательство было дано в рамках аксиоматической теории поля 18.
В нем предположения о коммутативности использовались для того, чтобы
расширить лоренцовскую инвариантность теории до комплексной группы Ло-
Лоренца, затем с помощью комплексных преобразований Лоренца доказать свой-
свойства вакуумных средних от произведений полей относительно отражений, и,
наконец, используя эти свойства, вывести существование антиунитарного
оператора, индуцирующего СРТ-преобразования полей.
5.8. СРТ-теорема 327
В качестве первого шага в доказательстве рассмотрим, как
произведение СРТ действует на свободные поля разных типов. Из
результатов разделов 5.2, 5.3 и 5.5 для скалярного, векторного
и дираковского полей получаем:
СРТ ф(х) [ОРТ] = СТлУ (-х), E-8.1)
СРТ ф^(х) [СРТ]-1 = -СТлЧ(-я), E-8.2)
Нс). E-8.3)
(Конечно, фазы С,, ?, и Г| зависят от сортов частиц, описываемых
каждым полем.) Мы выбираем фазы так, чтобы для всех частиц
С^Л = 1- E-8.4)
Тогда всякий тензор Фц1...ци, образованный любой совокупностью
скалярных и векторных полей и их производных, преобразуется как
СРТф^1...^(х)[СРТГ1 = (-1)^ ...^(-х). E.8.5)
(Так как СРТ — антиунитарный оператор, то всякий комплексный
численный коэффициент, возникающий в этих тензорах, преобра-
преобразуется в комплексно сопряженный.) Нетрудно показать, что такое
же правило преобразования применимо для тензоров, построенных
из билинейных комбинаций дираковских полей. Применяя к ним
формулу E.8.3), находим:
t E.8.6)
(Знак «минус» от антикоммутации C и у5 компенсируется знаком
«минус» от антикоммутации фермионных операторов.) Если били-
билинейный ковариант есть тензор ранга п, то М равно произведению п
по модулю 2 дираковских матриц, так что У5Му5 = (—1)"М, и
поэтому билинейный ковариант удовлетворяет соотношению E.8.5).
Эрмитова скалярная плотность гамильтониана взаимодейст-
взаимодействия ,У({х) должна строится из тензоров с четным полным числом
пространственно-временных индексов, поэтому
328 Глава 5. Квантовые поля и античастицы
СРТ Ж{х) [СРТ] = Ж{-х). E.8.7)
Более общее (и в чем-то более легкое) доказательство теоремы
можно дать для эрмитовых скаляров, построенных из полей ?аь (ж),
принадлежащих одному или нескольким общим неприводимым пред-
представлениям однородной группы Лоренца. Собирая результаты пре-
предыдущего раздела для результатов инверсии таких полей, получаем
= (-lJB?^Bt(-x). E.8.8)
(Для дираковского поля множитель (~1JВ в E.8.8) сопровожда-
сопровождается матрицей у5.) Чтобы образовать скаляр Ж{х) из произведений
^аЬ 1(х№а% 2(ж)--ч необходимо, чтобы как А1 + А2 + ..., так и В1 +
В2 + ... были целыми, так что (—iJBi+2B2+- = 1, и эрмитов скаляр
Ж'{х) будет автоматически удовлетворять соотношению E.8.7).
Из этой формулы немедленно вытекает, что СРТ коммутиру-
коммутирует с оператором взаимодействия V = \ d3x Jf(x,0):
СРТ V [СРТ] = V. E.8.9)
Кроме того, в любой теории СРТ коммутирует с гамильтонианом
свободных частиц Жо. Таким образом, оператор СРТ, который был
определен здесь своим действием на операторы свободных частиц,
действует на ин- и аут-состояния так, как описано в разделе 3.3.
Физические следствия этого принципа симметрии уже обсужда-
обсуждались в разделах 3.3 и 3.6.
5.9. Поля безмассовых частиц
До сих пор мы рассматривали только поля массивных частиц.
Для некоторых из них, например, для скалярного или дираковского
полей, не возникает никаких проблем при переходе к пределу
нулевой массы. С другой стороны, в разделе 5.3. мы видели, что для
векторного поля частицы со спином 1 такой переход действительно
сопряжен с трудностями: по крайней мере один из векторов поляри-
поляризаций в таком пределе обращается в бесконечность. Мы увидим
ниже, что все неприводимые поля (А,В), которые могут быть по-
построены в случае конечной массы, нельзя построить из операторов
5.9. Поля безмассовых частиц 329
рождения и уничтожения физических безмассовых частиц со спином
j > 1. Такое любопытное ограничение на типы полей естественно
приведет нас к понятию калибровочной инвариантности.
Как и для массивных частиц, попытаемся записать произволь-
произвольное свободное поле безмассовой частицы как линейную комбинацию
операторов уничтожения а(р,а) частиц с импульсом р и спирально-
стью о и соответствующих операторов рождения ас^(р,о) для анти-
античастиц *:
уг(х) = Bл)-3/2
E.9.1)
где теперь р° = |р|. Операторы рождения преобразуются так же, как
одночастичные состояния в B.5.42):
U(A)af(V,o)U-1(A) = ^- ехр(гае(р,Л)К(рл,а), E.9.2)
t/(A)act(p,a)t/-1(A) = 1^- exP(za6(p,A))act(pA,a), E.9.З)
и поэтому
U(A)a(V,o)U-1(A) = l^j- exP(-za6(p,A))a(pA,a), E.9.4)
где рл = Лр, а угол 6 определен формулами B.5.43). Таким образом,
если мы хотим, чтобы поле преобразовывалось по некоторому
представлению D(A) однородной группы Лоренца,
* Мы рассматриваем только один сорт частиц и опускаем соответствующую
метку те. Кроме того, к и X — постоянные коэффициенты, которые
определяются из требования причинности при некотором подходящем выборе
нормировки коэффициентных функций щ и vt.
330 Глава 5. Квантовые поля и античастицы
E.9.5)
мы должны потребовать, чтобы коэффициентные функции и и v
удовлетворяли вместо E.1.19) и E.1.20) соотношениям
М;(рЛ,а)ехр(гае(р,Л)) = ——-^Щ^щ^с), E.9.6)
р
г;;(рл,а)ехр(-га6(р,Л)) = l-—_2^I^I(A)ui(p,o). E.9.7)
V (Ар)
(Вновь рл = Лр.) Как и в случае массивных частиц, этим требовани-
требованиям можно удовлетворить, положив (вместо E.1.21) и E.1.22)), что
E.9.8)
E.9.9)
где к — стандартный импульс, например, @,0,к), а ${р) — стан-
стандартное преобразование Лоренца, переводящее безмассовую час-
частицу из состояния с импульсом к в состояние с импульсом р. Кроме
того, вместо E.1.23) и E.1.24) коэффициентные функции при стан-
стандартном импульсе должны удовлетворять соотношениям
M;(k,a)exp(za6(/c,W)) = ?О;г(ТУ)иг(к,о), E.9.10)
г
Uj(k,o)exp(-io9(fc,W)) = ?Dn(W)^(k,a), E.9.11)
где W^ — произвольный элемент «малой группы» для 4-импульса к
= (к, |к|), т. е. произвольное преобразование Лоренца, оставляющее
этот 4-импульс инвариантным.
5.9. Поля безмассовых частиц
331
Суть формул E.9.10) и E.9.11) можно понять, рассмотрев отдельно
два типа элементов малой группы в формуле B.5.28). Для вращения
КF) на угол 6 вокруг оси z, которое дается формулой B.5.27),
яме) =
находим из E.9.10) и E.9.11)
cose -sine о о
sine cose о о
0 0 10
0 0 0 1
E.9.12)
E.9.13)
Для комбинации S((X, C) вращений и бустов в плоскости х—у,
даваемых формулой B.5.26),
10 -a a
0 1 -p p
a p 1-у у
a p -y 1 + y
у = (а2 +P2)/2.
из формул E.9.10) и E.9.11) получаем
E.9.14)
E.9.15)
Формулы E.9.12)—E.9.15) представляют условия, определяющие
коэффициентные функции и и v при стандартном импульсе к.
332 Глава 5. Квантовые поля и античастицы
Тогда формулы E.9.8) и 95.9.9) определяют их при произвольных
импульсах. Уравнения для v являются комплексно сопряженными к
уравнениям для и, так что при подходящем выборе постоянных к и
X можно отнормировать коэффициентные функции так, чтобы
Ui(p,o) = Mi(p,o)*. E.9.16)
Проблема в том, что для произвольных представлений однородной
группы Лоренца не удается найти щ удовлетворяющие E.9.14). Более
того, это не удается сделать даже для тех представлений, для которых
при т Ф 0 можно построить поля частиц данной спиральности.
Чтобы понять, в чем сложность, попробуем построить
4-векторное поле E,5) для безмассовой частицы со спиральностью
±1. В 4-векторном представлении имеем просто:
Принято записывать коэффициентные функции через «вектор по-
поляризации» ец:
^ /2е^(р,о), E.9.17)
так что из формулы E.9.8) получаем
e^(p,a) = ^(p)^vev(k,a). E.9.18)
Далее, формулы E.9.12) и E.9.14) принимают вид:
e k,a), E.9.19)
,G). E.9.20)
Из E.9.19) следует, что с точностью до константы, которую можно
включить в коэффициенты к и X,
l) = (l,±z,0,0)/V2. E.9.21)
Но тогда из E.9.20) вытекает, что одновременно а ± гC = 0, что
невозможно для произвольных действительных ОС и C. Поэтому
5.9. Поля безмассовых частиц 333
мы не можем удовлетворить фундаментальному требованию E.9.14)
или E.9.10). Вместо этого имеем:
D%(WF,a,P))ev(k+l) =
= ехР(±г6)je^(k +1) + ^р кА. E-9-22)
Таким образом, мы приходим к выводу, что невозможно построить
4-векторное поле из операторов уничтожения и рождения частицы
нулевой массы со спиральностью +1.
Закроем временно глаза на эту проблему, и попробуем про-
продвинуться далее, используя формулы E.9.18) и E.9.21) для опреде-
определения вектора поляризации при произвольном импульсе и записав
поле в виде
)/2
V Г I \ iv-x I \ I \* —ip-x cf ( \1 E 9 23)
ст=±1
Позднее мы вернемся к вопросу о том, как можно использовать
такое поле в качестве составной части физической теории.
Поле E.9.23) очевидно удовлетворяет уравнению
) = 0. E.9.24)
Другие свойства поля вытекают из свойств вектора поляризации.
(Эти свойства понадобятся нам позднее при изучении квантовой
электродинамики.) Заметим, что лоренцовское преобразование Л(р),
переводящее импульс к безмассовой частицы в импульс р, может
быть записано как «буст» Щ\р\) вдоль оси z, переводящий энергию
частицы |к| в |р|, и стандартизованное вращение К(р), переводящее
ось z в ось, направленную вдоль р. Поскольку ev(k,±l) является
чисто пространственным вектором, имеющим только х- и у-компо-
ненты, он не изменяется при бусте вдоль оси z, так что
,±l) = K(p)^vev(k,±l). E.9.25)
334 Глава 5. Квантовые поля и античастицы
В частности, е°(к, ±1) = 0 и к-е(к,±1) = 0, поэтому
е°(р+1) = О E.9.26)
р-е(р,±1) = 0. E.9.27)
Отсюда
а°(х) = 0 , E.9.28)
V-a(x) = 0. E.9.29)
Как мы увидим в гл. 9, этим условиям удовлетворяет вакуумный
вектор-потенциал электродинамики в так называемой кулоновскои
или радиационной калибровке.
Обращение в нуль а0 во всех лоренцовский системах отсчета
ярко показывает, что ац не может быть 4-вектором. Из E.9.22)
следует, что для произвольного импульса р и произвольного преоб-
преобразования Лоренца Л мы вместо E.9.6) получаем
,±1)ехр(±ге(р,Л)) = D^v(A)ev(p,±l) + р^±(р,Л), E.9.30)
так что при произвольном преобразовании Лоренца
U{A)ayL{x)U-1{A) = rtivav{Ax) + dyLQ.{x,A), E.9.31)
где ?1(х,А) — линейная комбинация операторов уничтожения и
рождения, точный вид которой нам не важен. Как будет детальнее
показано в гл. 8, поле типа а^(х) можно включать в состав лоренц-
инвариантных физических теорий, если взаимодействие поля а^ с
другими полями будут не только формально лоренц-инвариантны
(т. е. инвариантны относительно формальных преобразований Ло-
Лоренца, при которых ац —» А^аУ), но инвариантны и относительно
«калибровочных» преобразований а^ ^> а^ + д^О.. Это достигается,
если эти взаимодействия брать в виде а^, где j^ — 4-вектор тока,
для которого д^ = 0.
Хотя не существует обычного 4-векторного поля безмассовых
частиц со спиральностью +1, нетрудно построить для таких частиц
антисимметричное тензорное поле. Из формулы E.9.22) и условия
инвариантности к}1 относительно малой группы немедленно получаем:
5.9. Поля безмассовых частиц 335
,a,P))DVCT(WF,а,P))(fcPeCT(k+1) - кае?(к+1))
l)) E'9-32)
Это показывает, что коэффициентная функция, удовлетворяющая
соотношению E.9.6) для антисимметричного тензорного представле-
представления однородной группы Лоренца при подходящем выборе норми-
нормировки имеет вид
[] E.9.33)
где ец(р,±1) дается формулой E.9.25). Используя это равенство вме-
вместе с E.9.23), получаем произвольное антисимметричное тензорное
поле безмассовой частицы со спиральностью ±1 в виде
Uv = 3nav " 3van • E.9.34)
Заметим, что эта комбинация является тензором даже в том слу-
случае, когда а^ не является 4-вектором, поскольку лишнее слагаемое
в E.9.31) выпадает из E.9.34). Заметим также, что из формул
E.9.34), E.9.24), E.9.28) и E.9.29) следует, что f» удовлетворяет
вакуумным уравнениям Максвелла
Э^=0, E.9.35)
е^Эа/^ = 0. E.9.36)
Для того, чтобы установить коммутационные соотношения для
тензорных полей, нам нужны формулы суммирования по спираль-
ностям билинейных форм e^ev*. Используя явную формулу E.9.21),
получаем
ст=±1
откуда с помощью E.9.25) находим:
|к|2'
' (V,v)k-(v,v) - v{j y- E.9.37)
ст=±1 P
336 Глава 5. Квантовые поля и античастицы
Непосредственными вычислениями убеждаемся, что
х Jd3pBp°)-:[|к|2 е^х-\Х\2 е~^
E.9.38)
Очевидно, что это выражение обращается в нуль при ж0 = у0 тогда
и только тогда, когда
к|2=|Х|2. E.9.39)
В этом случае, поскольку /^ — тензор, коммутатор обращается
в нуль для всех пространственноподобных интервалов. Из формулы
E.9.39) следует также, что коммутатор ац обращается в нуль при
равных временах. Как будет видно в гл. 8, этого достаточно, чтобы
получить лоренц-инвариантную .^-матрицу. Относительные фазы
операторов рождения и уничтожения можно подобрать так, чтобы
к = 1. Тогда в случае, когда частицы совпадают со своими зарядово-
сопряженными, как у фотона, поля становятся эрмитовыми.
Почему при построении теорий безмассовых частиц со спином 1
желательно использовать поля типа аЦх), а не ограничиться полями
типа /^v(cc) с простыми свойствами лоренцовских преобразований?
Наличие производных в E.9.34) означает, что плотность гамильто-
гамильтониана взаимодействия, построенная только из /„v и его производ-
производных, будет иметь матричные элементы, более быстро убывающие
при малых энергиях и импульсах безмассовых частиц, чем те,
которые построены с помощью векторного поля ац. Соответственно,
взаимодействия в такой теории будут убывать на больших расстоя-
расстояниях быстрее, чем по обычному закону обратных квадратов. Такое
вполне возможно, однако калибровочно-инвариантные теории, ис-
использующие векторные поля для описания безмассовых частиц со
спином 1, представляют более общий класс теорий, включающий
те, которые в действительности реализуются в природе.
Аналогичные замечания применимы к гравитонам — безмас-
безмассовым частицам со спиральностью ±2. Из операторов уничтожения
и рождения таких частиц можно построить тензор КцУрс; с алгебраи-
алгебраическими свойствами тензора кривизны Римана-Кристоффеля:
антисимметричностью по перестановкам внутри пар ц, V и р, о,
5.9. Поля безмассовых частиц 337
и симметрией относительно перестановок самих этих пар. Однако,
чтобы включить обычные гравитационные взаимодействия по зако-
закону обратных квадратов, необходимо ввести поле h^, преобразую-
преобразующееся как симметричный тензор с точностью до калибровочных
преобразований, относящихся к типу, связанному в общей теории
относительности с произвольными преобразованиями координат.
Таким образом, чтобы построить теорию безмассовых частиц со
спиральностью ±2, включающую дальнодействие, необходимо, чтобы
эта теория обладала симметрией, похожей на общую ковариант-
ковариантность. Как и в случае электромагнитной калибровочной инвариант-
инвариантности, этого можно добиться, введя взаимодействие поля 7г„у
с сохраняющимся «током» 6^, теперь уже несущим два пространст-
пространственно-временных индекса и удовлетворяющим условию Э„6^у = 0.
Единственным таким сохраняющимся тензором является тензор
энергии-импульса, если не учитывать возможные слагаемые, имею-
имеющие вид полной производной и не влияющие на поведение порож-
даемыхподобным взаимодействием сил на больших расстояниях. *
Поля безмассовых частиц со спином j > 3 должны были бы взаимо-
взаимодействовать с сохраняющимися тензорами с тремя и более про-
пространственно-временными индексами. Однако таких тензоров не
существует, если не считать полных производных, поэтому без-
безмассовые частицы с большими спинами не могут порождать
далънодействующие силы.
Проблемы, с которыми мы столкнулись при построении 4-векторных
полей для спиральностей +1 и симметричных тензорных полей для
спиральностей ±2, являются частными случаями более общих огра-
ограничений. Чтобы увидеть это, рассмотрим проблему построения полей
* Если 0M-1-M-W — тензорный ток, удовлетворяющий условию Э^ б^1"^™ = 0,
то Jd3a: 9Ц1"'Ц" — сохраняющаяся величина, преобразующаяся как тензор
ранга N — 1. Единственными сохраняющимися тензорами такого рода явля-
являются скалярные «заряды», связанные с различными непрерывными симмет-
риями, и 4-вектор энергии-импульса. Сохранение любого другого 4-вектора
или любого тензора более высокого ранга исключило бы возможность рассея-
рассеяния на любые углы, кроме нулевого.
338 Глава 5. Квантовые поля и античастицы
безмассовых частиц, принадлежащих произвольным представлени-
представлениям однородной группы Лоренца. Как мы видели в разделе 5.6, всякое
представление D(A) однородной группы Лоренца можно разложить
на BА+1)BВ+1)-мерные представления (А,В), для которых генера-
генераторы однородной группы Лоренца представляются в виде
(/io)a'b',ab = ~4
^k ^а'а^Ь'Ь+(^к )
^'^Ъ'Ъ~(^ )b
где J^ — матрицы углового момента для спина j. Для бесконечно
малых 6 имеем D(R(Q)) = 1 + iJ23®> так что из формул E.9.12) и
E.9.13) получаем
aiiab(k,G) = (a + b)uab(k,a),
-ovab(k,o) = (a + b)vab(k,o).
Таким образом, iiab(k,G) и uab(k,a) должны обращаться в нуль
во всех случаях, кроме о = а + Ъи.о = -а-Ъ. Далее, полагая а и C
в E.9.14) бесконечно малыми, находим:
= DА) + ij{A))aa,ua,b(k,o) + DВ) - zJ<B))bb^ab,(k,a),
= (-J[A) + tii,A))aa,ua,b(k,o) + (-J[B) - iji,B))wuaV(k,o),
или проще
Отсюда следует, что uab(k,a) обращается в нуль, кроме случаев
а = -А, Ъ = +В, E.9.40)
и это же очевидно верно для uab(k,a). Собирая вместе эти результа-
результаты, видим, что поле типа (А,В) можно построить только из операторов
Задачи 339
уничтожения безмассовой частицы со спиральностью о и операторов
рождения античастицы со спиральностью -а, где
О=В-А. E.9.41)
Например, компоненты (з, 0) и @, \) дираковского поля безмасовой
частицы могут только уничтожать частицы со спиральностью
—5 и +з и, соответственно, рождать античастицы со спиральностью
. 1 1т-»
+2 и —2- -D «двухкомпонентнои» теории нейтрино рассматриваются
только поле {\, 0) и сопряженное ему поле, так что в этой теории
спиральность нейтрино равна —з> а спиральность антинейтрино
равна +5-
Теми же методами, что и в разделе 5.7, можно показать, что
(j, 0) и @, j) поля безмассовых частиц со спином j (т. е. со спирально-
спиральностью +j) коммутируют друг с другом и со своими сопряженными на
пространственноподобных расстояниях, если коэффициенты у сла-
слагаемых с операторами уничтожения ии рождения в E.9.1) удовле-
удовлетворяют соотношению E.9.39). После этого можно так подобрать
относительную фазу операторов уничтожения и рождения, чтобы
эти коэффициенты стали равными. Легко видеть, что поля безмас-
безмассовых частиц со спином j типа (А, А + j) или (В + j, В) являются
просто производными порядка 2А или 2В полей типа @, j) или (j, 0),
соответственно, так что нет нужды рассматривать здесь такие
более общие поля.
Теперь можно понять, почему нельзя построить векторное
поле для безмассовых частиц со спиральностью ±1. Векторное поле
преобразуется по представлению {\, \), поэтому согласно E.9.19)
может описывать только спиральность нуль. (Конечно, можно
построить векторное поле для нулевой спиральности — для этого
достаточно просто взять производную Эцф безмассового скалярного
поля ф.) Простейшее ковариантное безмассовое поле для спираль-
спиральности ±1 преобразуется по представлению A, 0) © @, 1).
Иными словами, это антисимметричный тензор /„v. Анало-
Аналогично, простейшее ковариантное безмассовое поле для спи-
спиральности ±2 преобразуется по представлению B, 0) © @, 2), т. е.
это тензор четвертого ранга, который, как тензор кривизны
Римана—Кристоффеля, антисимметричен при перестановке внут-
внутри каждой пары индексов и симметричен при перестановке
самих этих пар.
340 Глава 5. Квантовые поля и античастицы
Обсуждение операций инверсий Р, С, Т, проведенное в пре-
предыдущем разделе, с очевидными модификациями переносится на
случай нулевой массы.
Задачи
1. Покажите, что если коэффициентные функции при нулевом
импульсе удовлетворяют условиям E.1.23) и E.1.24), то коэф-
коэффициентные функции E.1.21) и E.1.22) для произвольного
импульса удовлетворяют определяющим условиям E.1.19) и
E.1.20).
2. Рассмотрите свободное поле л\/?(х), которое уничтожает и рож-
рождает зарядово самосопряженные частицы со спином 3/2 и
массой т Ф 0. Вычислите коэффициентные функции ifj^p,a),
на которые умножаются операторы уничтожения а(р,а) в вы-
выражении для этого поля, при условии, что под действием
лоренцовских преобразований поле преобразуется как дира-
ковское поле Щ с дополнительным 4-векторным индексом ц.
Каким полевым уравнениям, алгебраическим условиям и ус-
условиям действительности удовлетворяет это поле? Найдите
матрицу Р^у(р), которая при р2 = ~т2 определена равенством
Каковы коммутационные соотношения для этого поля? Как оно
преобразуется под действием инверсий Р, С и Т?
3. Рассмотрите свободное поле Н^{х), удовлетворяющее усло-
условиям Н^(х) = hVii(x) и ЬУ-у^х) = 0, которое уничтожает и
рождает частицу спина 2 и массой т Ф 0. Вычислите коэффи-
коэффициентные функции 11^^,0), на которые умножаются опера-
операторы уничтожения а(р,о) в выражении для этого поля, чтобы
под действием лоренцовских преобразований поле преобра-
преобразуется как тензор. Каким полевым уравнениям удовлетворя-
удовлетворяет это поле? Найдите функцию Р^'к\р), определенную ра-
равенством
Список литературы 341
Каковы коммутационные соотношения для этого поля? Как оно
преобразуется под действием инверсий Р, С и Т?
4. Покажите, что для безмассовой частицы со спином j поля типа
(A,A+j) или (B+j,B) являются производными порядка 2А или 2В
полей типа (Oj) или (j,0), соответственно.
5. Выясните трансформационные свойства полей типа 0,0) + (Oj)
безмассовых частиц со спиральностью +j под действием опера-
операций инверсии Р, С и Т.
6. Рассмотрите обобщенное дираковское поле у, которое преобра-
преобразуется по представлению (j,0) + (Oj) однородной группы Ло-
Лоренца. Перечислите тензоры, которые можно образовать из
произведений компонент \|/ и \f\ Проверьте результат, сравнив
1
с наиденными нами выражениями для j = з-
7. Рассмотрите обобщенное поле \|/аЬ, описывающее частицы со
спином j и массой т Ф 0, которое преобразуется по (А,В)
представлению однородной группы Лоренца. Предположим,
что гамильтониан взаимодействия этого поля имеет вид
V =
где Jab — внешний с-числовой ток. Каково асимпототическое
поведение матричных элементов испускания этих частиц с
энергией Е »т и определенной спиральностью? (Предполо-
(Предположите, что фурье-образ тока при разных а, Ъ имеет значения
одного порядка величины и не зависит сильно от Е.)
Список литературы
1. Подход, излагаемый в этой главе, был представлен в серии
работ: Weinberg, S., Phys. Rev., 133, D1318 A964); 134, В882
A964); 138, В988 A965); 181,1893 A969). Аналогичный подход был
342 Глава 5. Квантовые поля и античастицы
изложен в неопубликованных лекциях Ю. Вихмана.
2. Bohr, N. and Rosenfeld, L., Kgl. Danske Vidensk. Selskab. Mat.-Fys.
Medd., No. 12 A933) (перевод в сборнике: Selected papers of Leon
Rosenfeld, ed. by R.S. Cohen and J. Stachel (Reidel, Dordrecht,
1979)); Phys. Rev., 78, 794 A950).
3. Dirac, P.A.M., Proc. Roy. Soc. (London), A117, 610 A928).
4 Cartan, E., Bull. Soc. Math. France, 41, 53 A913).
5. См., например, Jauch, J.M. and Rorlich, F. The Theory of Photons
and Electrons (Addison-Wesley, Cambridge, MA, 1955), Appendix
A2; Georgi, H. Lie Algebras in Particle Physics (Benjamin-Cummings,
Reading, VA, 1982), pp. 15, 198. Исходная ссылка: Schur, I., Sitz.
Preuss. Akad., p. 406 A905).
6. См., например, Georgi, H. Lie Algebras in Particle Physics (Benjamin-
Cummings, Reading, VA, 1982), pp. 15, 198. Исходная ссылка:
Schur, I., Sitz. Preuss. Akad., p. 406 A905).
7. Lee, T.D. and Yang, C.N., Phys. Rev., 104, 254 A956).
8. См., например, Van der Waerden, B.L. Die Gruppentheoretische
Methode in der Quantenmechanik (Springer Verlag, Berlin, 1932);
Любарский, Г.Я. Теория групп и ее применение в физике (М.:
Гостехиздат, 1957).
9. Rarita, W. and Schwinger, J., Phys. Rev., 60, 61 A941).
10. См., например, Edmonds, A.R., Angular Momentum in Quantum
Mechamics (Princeton University Pree, Princeton, 1957), Chapter
3 (есть рус. пер.: Эдмондс, А. Угловой момент в квантовой
механике. М.: ИЛ, 1968).
11. Weinberg, S., Phys. Rev., 181, 1893 A969); Section V.
12. Fierz., M., Helv. Phys. Ada, 12, 3 A939); Pauli, W., Phys. Rev.,
58, 716 A940). He основанные на теории возмущений доказа-
Список литературы 343
тельства в аксиоматической теории поля были даны в работах:
Liiders, G. and Zumino, В., Phys. Rev., 110, 1450 A958); Burgoyne,
N., Nuovo Cimento, 8, 807 A958). См. также: Streater, R.F. and
Wightman, A.S. PCT, Spin & Statistics, and All That (Benjamin,
New York, 1968) (есть рус. пер.: Стритер Р., Вайтман А. РСТ, спин
и статистика и все такое. М.: Мир, 1970).
13. Поля в представлении (j,0) + @j) были введены в работе: Joos,
Н., Fortschr. Phys., 10, 65 A962); Weinberg, S., Phys. Rev., 133,
B1318 A964).
14. Edmonds, A.R. [10], или Rose, M.E. Elementary Theory of Angular
Momentum (Wiley & Sons, New York, 1957), Chapter III.
15. Velo, G. and Zwanziger, D., Phys. Rev., 186, 1337 A969); 188, 2218
A969); Wightman, A.S., in: Proceedings of the Fifth Coral Gables
Conference on Symmetry Principles at High Energy, ed. by T.
Gudehus, G. Kaiser, and A. Perlmutter (Gordon and Breach, New
York, 1969); Schroer, В., Seiler, R., and Swieca, A., Phys. Rev.,
D2, 2927 A970) и другие ссылки в этих работах.
16. Nappi, C.R. and Witten, E., Phys. Rev., D40, 1095 A989); Argyres,
P.C. and Nappi, C.R., Phys. Lett, B224, 89 A989). Вывод согласо-
согласованной теории частиц со спином j = 3/2 во внешних полях из
теории Калуцы-Клейна см. в работах: Rindani, S.D. and Sivakumar,
М
J. Phys. G: Nucl. Phys., 12, 1335 A986); J. Phys. C: Particles &
Fields, 49, 601 A991).
17. Liiders, G., Kgl. Danske Vidensk. Selskab. Mat.-Fys. Medd., 28, 5
A954); Ann. Phys., 2, 1 A957); Pauli, W., Nuovo Cimento, 6, 204
A957). Когда Людерс впервые рассмотрел вопрос о том, как
связаны инверсии, считалось общепризнанным, что Р сохраняет-
сохраняется, так что его теорема утверждала, что сохранение С эквива-
эквивалентно Т-инвариантности.
18. Jost, R., Helv. Phys. Acta, 30, 409 A957); Dyson, F.J., Phys. Rev.,
110, 579 A958). См. также книгу Стритера и Вайтмана [12].
6
Фейнмановские правила
В предыдущих главах использование ковариантных свобод-
свободных полей для построения плотности гамильтониана мотивирова-
мотивировалось требованием, чтобы б'-матрица удовлетворяла условиям
лоренц-инвариантости и кластерного разложения. Если мы по-
построили таким способом плотность гамильтониана, уже не имеет
значения, какую форму теории возмущений использовать для
вычисления .^-матрицы. Результаты будут автоматически удовле-
удовлетворять указанным условиям в каждом порядке по плотности
гамильтониана взаимодействия. Тем не менее, очевидны практи-
практические преимущества использования такого варианта теории воз-
возмущений, в котором лоренц-инвариантность и свойства кластер-
кластерного разложения ^-матрицы явно сохраняются на каждом этапе
вычислений.
В той теории возмущений, которую использовали в 1930-е
годы и которая сейчас известна под названием «старой» (мы описа-
описали ее в начале раздела 3.5), указанные свойства не выполнялись.
Большим достижением Фейнмана, Швингера и Томонаги
в конце 1940-х годов было развитие такой техники теории возму-
возмущений для вычисления .^-матрицы, в которой на каждом шаге
прослеживались лоренц-инвариантность и свойства кластерного
разложения.
В этой главе мы опишем диаграммную технику вычислений,
впервые предложенную Фейнманом на конференции в Поконо в
1948 году. Фейнман пришел к этим диаграммным правилам, раз-
развивая предложенный им подход, основанный на функциональном
интеграле. Этот подход будет рассмотрен в гл. 9. Здесь же мы
воспользуемся подходом, предложенным в 1949 году Дайсоном 1.
6.1. Вывод правил 345
Вплоть до 1970-х годов именно он был основой любого анализа
теории возмущений в квантовой теории поля, да и до сих пор этот
подход позволяет дать особенно ясное введение в фейнмановские
правила *.
6.1. Вывод правил
Исходной для нас является формула для ^-матрицы, полу-
полученная объединением дайсоновского ряда C.5.10) с выражением
D.2.2) для состояний свободных частиц:
?J d*x1... d4xw (Фо,... a(v'2o'2n'2 )a(p[o[n[)
«=o ^! F.1.1)
х^.-.Н (ж„)}а+(р1а1п1)а+(р2а2п2)...Ф0).
Напоминание: метки р, о и п отмечают импульсы частиц, их
спин и тип; штрихи относятся к меткам частиц в конечном состоя-
состоянии; Фо — вакуумное состояние свободных частиц; а и а) —
операторы уничтожения и рождения; Т означает хронологическое
упорядочивание, располагающее все Ж(х) в таком порядке, что
аргументы х° уменьшаются слева направо; Ж(х) — плотность га-
гамильтониана взаимодействия, рассматриваемая как полином по
полям и сопряженным полям,
гЩ(х), F.1.2)
г
причем каждое слагаемое .Щ является произведением определенно-
определенного числа полей и им сопряженных полей каждого типа. Поле
* Мы используем современную версию функциональный интеграл русского
перевода английского термина path intergral, предпочитая ее первоначальным
и до сих пор используемым версиям «интеграл по путям» или «интеграл по
траекториям». Это отвечает более широкому современному содержанию
понятия. — Прим. ред.
346 Глава 6. Фейнмановские правила
частицы типа п, преобразующееся по определенному представле-
представлению однородной группы Лоренца (с учетом или без учета простран-
пространственных инверсий), дается выражением
Щх) = ?Bл)-3/2|сг3р[г1г(р,а,п)а(р,а,п)е^
а F.1.3)
Здесь пс — индекс античастицы типа п, а в показателе
ехр(±гр-ж) компонента р° равна Jp2 + m2 .Коэффициентные функ-
функции щ и vx зависят от свойств поля по отношению к преобразова-
преобразованиям Лоренца и от спина частицы, которая описывается этим
полем. Эти функции были вычислены в гл. 5. (Например, в случае
скалярного поля коэффициент щ для частицы с энергией Е равен
BЕ)/2, а для дираковского поля щ и vx — нормированные дираков-
ские спиноры, введенные в разделе 5.5.) Индекс I у поля следует
понимать как указатель типа частицы и того представления груп-
группы Лоренца, по которому поле преобразуется. Кроме того, в него
включается бегущий индекс, отмечающий компоненты поля в
данном представлении.
Нет нужды рассматривать отдельно взаимодействия, содержа-
содержащие производные полей; с нашей точки зрения, производная поля
F.1.3) есть просто другое поле, описываемое той же формулой, но с
другими коэффициентами щ и vv Ниже мы будем делать различие
между некоторыми типами частиц, которые мы произвольно будем
называть «частицами», например, электроны, протоны, и т. д., и
типами частиц, которые будем называть «античастицами» (позитро-
(позитроны, антипротоны и т. д.). Полевые операторы, уничтожающие части-
частицы и рождающие античастицы, будут называться просто «полями»;
сопряженные им операторы, уничтожающие античастицы и рож-
рождающие частицы, будут называться «сопряженными полями». Ко-
Конечно, у некоторых типов частиц, вроде фотона и л°-мезона, анти-
античастицы тождественны частицам. В этом случае сопряженные поля
пропорциональны самим полям.
Начнем перемещать все операторы уничтожения в формуле
F.1.1) направо, используя на каждом шаге соотношения коммута-
коммутации или антикоммутации:
а(р a n)af (p'a'n') = ±af(p'a'n>(p a n) +63 (р'-р)б^б,, F.1.4)
6.1. Вывод правил 347
а(р а п)а(р' а' п') = ±а(р' а' п')а(р а п), F.1.5)
а+(рап)а+(р'а'п') = ±af (p'o'nOo^pon). F.1.6)
(аналогично для античастиц). При этом из знаков + справа выбира-
выбирается знак «минус» , если обе частицы п, п' — фермионы, и знак
«плюс», если одна или обе частицы — бозоны. Как только оператор
уничтожения оказывается крайним справа (или оператор рожде-
рождения — крайним слева), соответствующий вклад в F.1.1) обращается
в нуль, так как действие этих операторов на вакуумное состояние
дает нуль:
а(рап)Ф0=0, F.1.7)
,У F.1.8)
Ненулевые вклады в F.1.1) возникают от слагаемых с дельта-
функциями в правой части F.1.4), после того, как каждый оператор
рождения и уничтожения в начальном или конечном состоянии или
в плотности гамильтониана взаимодействия спарится с каким-то
другим оператором уничтожения или рождения.
Таким образом, вклад в F.1.1) данного порядка по каждому из
слагаемых ,У(\ в полиноме ,У?(\((х),\(Цх)) дается суммой по всем
способам спаривания операторов рождения и уничтожения2, каж-
каждый член суммы являтся интегралом от произведений множителей,
которые находятся по следующим правилам.
а) Спаривание конечной частицы с квантовыми числами
р', а', п' с сопряженным полем \|/г (ж) в .Щх) дает множитель
'п). F-1.9)
б) Спаривание конечной античастицы с квантовыми числами
р', а', пс' с полем \|/г(ж) в ,Щ(х) дает множитель
&n). F.1.10)
в) Спаривание начальной частицы с квантовыми числами
р, а, п с полем щ(х) в .Щх) дает множитель
348 Глава 6. Фейнмановские правила
. F.1.11)
г) Спаривание начальной античастицы с квантовыми числами
р, о, пс с сопряженным полем \|/г (ж) в Ж'^х) дает множитель
). F.1.12)
д) Спаривание конечной частицы (или античастицы) с кванто-
квантовыми числами р', а', п' с начальной частицей (или античастицей) с
квантовыми числами р, о, п дает множитель
[а(р'а'п'),а+(роп)]т =63(р'-рN^6пЧ. F.1.13)
е) Спаривание поля щ(х) в .Щх) с сопряженным полем ?т(У) в
ЖАу) дает множитель *
[^]Агт(х, у),F.1.14)
где \|/+ и \|/" - слагаемые в \|/, которые уничтожают частицы и
рождают античастицы, соответственно:
), F.1.15)
(ж) = Bjr)-3/2Jd3p^^(pan)e-ipa;af(panc), F.1.16)
Напомним, что 6(ж — у) — ступенчатая функция, равная +1
при ж0 > у0 и нулю при ж0 < у0. Такие ступенчатые функции
возникают в F.1.14) из-за хронологического упорядочивания в F.1.1);
спаривание поля уничтожения \|/+(ж) в Ж(х) с полем рождения
\|/+^(у) в Ж(у) можно учитывать, только если Ж(х) изначально
находится левее Ж(у) в формуле F.1.1), т. е. если ж0 > у0. Аналогич-
* Если взаимодействие Ж{х) записано в нормальной форме, как в E.1.33),
то отсутствует спаривание полей с сопряженными полями в одном и том же
операторе взаимодействия. В противном случае необходима некоторая про-
процедура регуляризации для придания смысла величине А!т@).
6.1. Вывод правил 349
но, мы учитываем спаривание поля уничтожения \|/~^(у) в Ж(у) с
полем рождения Х|Г(ж) в Ж(х), только если Ж{у) изначально нахо-
находится левее Ж{х), т. е. если у0 > х°. (Знак ± во втором слагаемом в
F.1.14) будет объяснен чуть ниже.) Выражение F.1.14) называется
пропагатором и вычисляется в следующем разделе.
5-матрица получается путем перемножения всех этих множите-
множителей с учетом дополнительных численных множителей, обсуждаемых
ниже, затем интегрирования по х1 . . . xN, суммирования по всем
спариваниям и затем по числу взаимодействий каждого типа.
Прежде чем погружаться в детали, удобно описать диаграммный
формализм, позволяющий проследить за всеми этими спариваниями.
Правила вычисления ^-матрицы удобно сформулировать на
языке фейнмановских диаграмм (рис. 6.1). Диаграмма содержит
точки, называемые вершинами, причем каждая вершина соответ-
соответствует одному из операторов .Щ(х), и линии, каждая из которых
соответствует спариванию операторов рождения и уничтожения.
Сформулируем правила более подробно.
а) Спаривание конечной частицы с сопряженным полем в
одном из операторов Ж'{х) изображается линией, идущей вверх из
вершины, соответствующей данному Ж(х), и имеющей стрелку,
направленную вверх.
б) Спаривание конечной античастицы с полем в одном из
операторов Ж\х) также изображается линией, идущей вверх из
вершины, соответствующей данному Ж(х), но со стрелкой, на-
направленной вниз. (Для частиц типа у и %°, совпадающих со своими
античастицами, стрелки на линиях не указываются.)
в) Спаривание начальной частицы с полем в одном из опера-
операторов Ж(х) изображается линией, входящей снизу в вершину,
соответствующую данному Ж\х), и имеющей стрелку, направлен-
направленную вверх.
г) Спаривание начальной античастицы с полем в одном из
операторов Ж(х) также изображается линией, входящей снизу в
вершину, соответствующую данному Ж(х), но имеющей стрелку,
направленную вниз.
д) Спаривание конечной частицы или античастицы с началь-
начальной частицей или античастицей представляется не связанной ни
с какими вершинами линией, проходящей снизу вверх через всю
диаграмму, со стрелкой направленной вверх или вниз для частиц
и античастиц, соответственно.
350
Глава 6. Фейнмановские правила
р',о',те'
I, х
Bл)
3/2
р',о',те'с
У\ i,
Bл)
3/2
i, х
а)
Bл)
3/2
в)
р,о,п(
б)
Bл)
г)
3/2
р',о',те'
или
Р,О,71
i, X
I, X
т, у
-гА1т(х,у)
е)
Рис. 6.1. Графическое изображение спариваний операторов, возникающих
при вычислении S-матрицы в координатном представлении. Выражения
справа — множители, отвечающие каждой линии фейнмановской диа-
диаграммы, которые должны включаться в подынтегральное выражение ко-
координатного представления S-матрицы
6.1. Вывод правил 351
е) Спаривание поля в Ж\х) с сопряженным полем в Ж (у)
представляется линией, соединяющей вершины Ж(х) и Ж {у), и
имеющей стрелку, направленную от у к ж.
Обратим внимание, что стрелки всегда указывают направле-
направление движения частицы, и противоположны направлению движения
античастицы. (Как отмечено выше, для частиц типа фотона, совпа-
совпадающих со своими античастицами, стрелки следует опустить.) На-
Направление стрелки в правиле е) совместимо с этим соглашением,
так как сопряженное поле в ЖАу) может либо рождать частицу,
уничтожаемую полем в Ж'Ах), либо уничтожать античастицу, рож-
рождаемую этим полем. Заметим также, что поскольку каждое поле
или сопряженное поле в Ж'Ах) должно с чем-нибудь спариться,
полное число линий в вершине типа г, соответствующей слагаемо-
слагаемому Ж'Ах) в F.1.2), в точности равно полному числу полей или
сопряженных полей в Ж'Ах). При этом число линий со стрелками,
направленными в вершину или из нее, равно, соответственно,
числу полей или сопряженных полей в соответствующем члене
взаимодействия.
Чтобы вычислить вклад в 5-матрицу данного процесса
в данном порядке Nt по каждому из членов взаимодействия Ж\(х)
в F.1.2), нужно проделать следующие операции.
1. Следует нарисовать все фейнмановские диаграммы, содер-
содержащие Ni вершин каждого типа г. Эти диаграммы должны иметь
линии, входящие в них снизу, и отвечающие каждой частице и
античастице в начальном состоянии, линии, выходящие вверх
и отвечающие каждой частице или античастице в конечном состоя-
состоянии, и такое число соединяющих вершины внутренних линий,
чтобы к каждой вершине подсоединялось нужное число линий.
Стрелки на линиях выбираются по указанным выше правилам
в направлении либо вверх, либо вниз. Каждая вершина помечается
индексом типа взаимодействия г и пространственно-временной ко-
координатой х^. Каждая внутренняя или внешняя линия помечается
на том конце, который соединен с вершиной, индексом типа поля I
(что соответствует полям Х|/;(ж) или \|/^(ж), рождающим или уничто-
уничтожающим частицу или античастицу в этой вершине). Кроме того,
каждая внешняя линия помечается на конце, откуда она входит в
диаграмму или выходит из нее, квантовыми числами р, а, п или
р', о', п' начальной или конечной частицы (или античастицы).
352 Глава 6. Фейнмановские правила
2. Каждой вершине типа i следует сопоставить множитель
—г (он возникает из множителя (—i)N в F.1.1)) и множитель gt
(константа связи, на которую умножается произведение полей
в Жг(х)).* Каждой линии, выходящей вверх из диаграммы, сопос-
сопоставляется множитель F.9.9) или F.9.10) в зависимости от направ-
направления стрелки на линии. Аналогично, каждой линии, входящей в
диаграмму снизу, сопоставляется множитель F.1.11) или F.1.12),
опять же, в зависимости от направления стрелки. Каждой линии,
проходящей снизу вверх насквозь через диаграмму, сопоставляет-
сопоставляется множитель F.1.13). Наконец, каждой внутренней линии, соеди-
соединяющей две вершины, сопоставляется множитель F.1.14).
3. Следует произвести интегрирование произведения всех
этих множителей по координатам хъ х2, ¦ ¦ ¦ всех вершин.
4. Результаты, полученные таким образом для каждой фейн-
мановской диаграммы, следует сложить. Полное выражение ряда
теории возмущений для ^-матрицы получается сложением вкла-
вкладов от каждого порядка теории возмущений по каждому из типов
взаимодействий (реально мы ограничиваемся тем порядком, кото-
который в состоянии вычислить в данный момент).
Заметим, что мы не включили в эти правила множитель 1/JV!
из F.1.1), так как хронологически упорядоченное произведение
в F.1.1) является суммой по N\ перестановкам координат хгх2 ¦ ¦ .xN,
дающим одинаковый вклад в окончательный результат. Чтобы по-
понять это другим способом, заметим, что фейнмановская диаграмма
с N вершинами есть одна из N] идентичных диаграмм, отличающих-
отличающихся только перестановками меток в вершинах. Учет этого дает множи-
множитель N1, сокращающийся с 1/NI в F.1.1). (Из этого правила существу-
существуют исключения, обсуждаемые ниже.) По этой причине далее мы не
будем рассматривать более одного набора фейнмановских диаграмм,
отличающихся только перестановкой меток в вершинах.
В ряде случаев возникают добавочные комбинаторные множите-
множители или знаки, которые следует учитывать в отдельных диаграммах.
* Мы сохранили авторские обозначения. Надеемся, что читатель в дальнейшем
не перепутает индекс г, нумерующий тип вершин взаимодействия, с мнимой
единицей, входящей как множитель в каждую вершину взаимодействия. —
Прим. пер.
6.1. Вывод правил 353
5. Предположим, что взаимодействие Ж'^х) содержит (помимо
других полей и сопряженных полей) произведение М одинаковых
полей. Пусть каждое из этих полей спаривается со своим сопряжен-
сопряженным полем в другой вершине взаимодействия (причем другой для
каждого спаривания), а также в начальном или конечном состоя-
состоянии. Первое из сопряженных полей можно спарить с любым из М
тождественных полей в Ж'^х), второе — с любым из оставшихся М—
1 тождественных полей, и так далее, что приводит к дополнитель-
дополнительному множителю М! Для компенсации этого множителя принято
определять константу связи g; так, чтобы в каждом .Ж-(х), содержа-
содержащем М тождественных полей (или сопряженных полей), явно воз-
возникал множитель 1/М!. Например, взаимодействие М-ого порядка
по скалярному полю ф(ж) следует записывать как дфм/М!. (В более
общем случае, часто выписывают явный множитель 1/М!, когда
взаимодействие содержит сумму М произведений полей из одного
мультиплета внутреннней группы симметрии, или когда по этой
или любой другой причине константа связи полностью симметрична
или антисимметрична относительно перестановки М бозонных или
фермионных полей.)
Однако такое сокращение множителя М! не всегда бывает
полным. Например, рассмотрим фейнмановскую диаграмму, в ко-
которой М тождественных полей в одном взаимодействии Ж\(х) спари-
спариваются с М соответствующими сопряженными полями в единствен-
единственном другом взаимодействии .Щу) (рис. 6.2). Следуя изложенному
выше, мы находим только М! разных спариваний (поскольку нет
никакой разницы, какое из сопряженных полей мы назовем пер-
первым, вторым и т. д.). В результате, сокращается только один из
двух множителей 1/М! в разных взаимодействиях. В этом случае
лишний множитель 1/М! следует «руками» включать во вклад
такой диаграммы.
Другие комбинаторные множители возникают в ситуации,
когда перестановки вершин не влияют на диаграмму. Выше отмеча-
отмечалось, что множитель 1/JV! в ряде F.1.1) обычно сокращается из-за
суммирования N1 диаграмм, отличающихся только переобозначе-
переобозначением индексов у N вершин. Однако такое сокращение неполно, если
при переобозначении вершин мы не получаем новой диаграммы.
Чаще всего это происходит при вычислении матричных элементов
5-матрицы между вакуумными состояниями в теории с квадратич-
квадратичным взаимодействием Ж = \|/^M;;'\|/;', где М может зависеть от
354 Глава 6. Фейнмановские правила
Рис. 6.2. Пример диаграммы, вклад которой в S-матрицу содержит допол-
дополнительный комбинаторный множитель. Если, например, в вершине взаи-
взаимодействия имеются три множителя, содержащих какое-то поле (наряду
с другими полями), то в гамильтониан взаимодействия обычно включают
коэффициент 1/3!, чтобы сократить множители, возникающие от сумм по
способам спаривания этих полей с сопряженными им полями в других
вершинах. Однако в приведенной диаграмме имеются два таких коэффи-
коэффициента 1/3! и лишь 3! различных спариваний, поэтому остается лишний
множитель 1/3!
Рис. 6.3. Диаграмма восьмого порядка амплитуды перехода вакуум-ваку-
вакуум-вакуум, когда частицы взаимодействуют только с внешним полем.
В этой диаграмме внешнее поле представлено волнистыми линиями. Суще-
Существует 7! таких диаграмм, отличающихся только переобозначением вер-
вершин, причем те переобозначения, которые приводят к простому повороту
кольца, не считаются различными. Поэтому множитель 1/8! в формуле
Дайсона F.1.1) сокращается не полностью, и остается множитель 1/8
внешних полей. (Физическое значение таких диаграмм вакуумных
флуктуации детально обсуждается в т. II). Фейнмановская диаграм-
диаграмма N-ото порядка по .Ж'есть замкнутое кольцо с N углами (рис. 6.3). В
этом случае имеется только (iV-1)! разных диаграмм, поскольку
перестановка индексов, передвигающая каждый из них к следую-
6.1. Вывод правил 355
щей вершине по кольцу, приводит к той же диаграмме. Поэтому
подобная диаграмма должна приводить к множителю
(N - 1)! 1
-ЦГ'Т FЛ-17)
6. В теориях с фермионными полями использование формул
F.1.4)-F.1.6) для перемещения операторов уничтожения и рожде-
рождения направо и налево приводит к появлению дополнительных зна-
знаков «минус» во вкладах разных спариваний. Конкретно, мы получа-
получаем отрицательный знак каждый раз, когда перестановка операто-
операторов в F.1.1), необходимая для того, чтобы собрать все спариваемые
операторы рядом друг с другом (помещая при этом операторы
уничтожения слева от спариваемых с ними операторов рождения),
включает нечетное число перестановок фермионных операторов.
(Это происходит потому, что при вычислении вклада конкретного
спаривания, можно сначала переставить все операторы в F.1.1)
так, чтобы каждый оператор уничтожения оказался слева от спа-
спариваемого с ним оператора рождения, игнорируя при этом все
коммутаторы или антикоммутаторы с неспариваемыми оператора-
операторами, а затем заменить каждое произведение спаренных операторов
на их коммутатор или антикоммутатор.) Из этого правила немед-
немедленно вытекает появление относительного отрицательного знака
между двумя слагаемыми в выражении F.1.14) для фермионного
пропагатора. Какая бы перестановка не переводила содержащую
операторы уничтожения часть \|/+(ж) поля в Ж(х) налево от содер-
содержащей операторы рождения части \|/+^(у) сопряженного поля в
Ж(у), перестановка, переводящая содержащую операторы уничто-
уничтожения часть \\/~Цх) сопряженного поля налево от содержащей
операторы рождения части \|/~(у) поля включает одну лишнюю
перемену мест фермионных операторов, что и приводит к отрица-
отрицательному знаку перед вторым слагаемым в F.1.4) для фермионов.
Наконец, отрицательные знаки могут возникать во вкладе всех
фейнмановских диаграмм. Например, рассмотрим теорию, в которой
единственно возможное взаимодействие фермионов имеет вид:
Ж{х) = ?gimfcy;f(x)ym(x)(pfc(x), F.1.18)
Irak
где gimk — произвольные константы, Щ(х) — совокупность комплекс-
комплексных фермионных полей, а фт(ж) — совокупность действительных
356 Глава 6. Фейнмановские правила
бозонных (не обязательно скалярных) полей. (Не только квантовая
электродинамика, но и вся «стандартная модель» слабых, электро-
электромагнитных и сильных взаимодействий имеет фермионные взаимо-
взаимодействия, которые можно привести к указанному виду.) Рассмот-
Рассмотрим сначала процесс фермион-фермионного рассеяния 12 —» Г2' во
втором порядке по Ж. В слагаемом второго порядка в F.1.1) ферми-
фермионные операторы возникают в следующем порядке (сделаны оче-
очевидные упрощения формы записи):
аB>A V (*)V(*)V+ (у)Щу)а* A)а+ B). F.1.19)
В данном порядке существуют две связные диаграммы, отве-
отвечающие спариваниям
[аA')у\х)][аB')у\у)][Щу)а\1)][Щх)а\2)] F.1.21)
(рис. 6.4). Для перехода от F.1.19) к F.1.20) необходима четная
перестановка фермионных операторов. (Например, можно переста-
переставить \|/(ж) направо с тремя операторами, а затем переставить аA')
через один оператор направо.) Таким образом, во вкладе спарива-
спаривания F.1.20) не возникает никакого дополнительного знака «минус».
Само по себе это не имеет значения; общий знак .^-матрицы не
влияет на вероятности переходов и в любом случае зависит от
соглашений о знаках для начальных и конечных состояний. Сущест-
Рис. 6.4. Связные диаграммы второго порядка для фермион-фермионного
рассеяния в теории с взаимоденйствием F.1.18). Сплошные линии соответ-
соответствуют фермионам, пунктирные — нейтральным бозонам. Вклады этих
диаграмм отличаются знаком, который возникает от дополнительной пе-
перестановки фермионных операторов в спариваниях, соответствующих
второй диаграмме
6.1. Вывод правил 357
венно то, что вклады спариваний F.1.20) и F.1.21) имеют противопо-
противоположный знак. Легче всего это видно, если заметить, что единствен-
единственной разницей между двумя спариваниями является перестановка
двух фермионных операторов аA') и аB'). На самом деле, относи-
относительный знак «минус» требуется статистикой Ферми: при таком
знаке амплитуда рассеяния становится антисимметричной относи-
относительно перестановки частиц 1' и 2' (или 1 и 2).
Однако не следует думать, что все знаки можно так просто
связать с антисимметрией конечных или начальных состояний
даже в низшем порядке теории возмущений. Чтобы стало ясно, о
чем идет речь, рассмотрим фермион-антифермионное рассеяние
12е —» 1'2'с во втором порядке теории возмущений по тому же
взаимодействию F.1.18). Фермионные операторы следующим обра-
образом входят в слагаемое второго порядка в F.1.1):
а(Гс )аA V (х)Щх)^ (у)Щу)а (l)af Bе). F.1.22)
В этом порядке имеются две диаграммы Фейнмана (рис. 6.5), отве-
отвечающие спариваниям:
[('\][Щ\][\\2сI F.1.23)
2с)] . F.1.24)
Г
1 2е
Рис. 6.5. Связные диаграммы второго порядка для фермион-антифермион-
ного рассеяния в теории с взаимоденйетвием F.1.18). Сплошные линии
соответствуют фермионам или антифермионам в зависимости от направ-
направления стрелок, пунктирные — нейтральным бозонам. Вклады этих диаг-
диаграмм снова отличаются знаком, который возникает от дополнительной
перестановки фермионных операторов в спариваниях, соответствующих
второй диаграмме
358 Глава 6. Фейнмановские правила
При переходе от F.1.22) к F.1.23) требуется совершить четную
перестановку фермионных операторов (например, переместить \|/(ж)
через два оператора налево, а \|/^(у) через два оператора направо),
так что во вкладе от спаривания F.1.23) не возникает никакого
лишнего знака «минус». С другой стороны, переход от F.1.22) к
F.1.24) требует нечетной перестановки фермионных операторов
(такой же, как в F.1.23), и дополнительной перемены местами
\\>Цх) с \|/^(у)). Поэтому вклад от этого спаривания входит с до-
дополнительным отрицательным знаком *.
Дополнительные знаки возникают при рассмотрении вкладов
более высоких порядков. В теориях рассматриваемого здесь типа,
где все взаимодействия фермионов имеют вид F.1.18), фермионные
линии в произвольной фейнмановской диаграмме образуют либо
цепочки линий, проходящих через всю диаграмму, с произвольным
числом взаимодействий с бозонными полями (рис. 6.6), либо образу-
образуют фермионные петли типа показанной на рис. 6.7.
Рассмотрим результат добавления к фейнмановской диаграм-
диаграмме любого процесса фермионной петли с М вершинами. Это соответ-
соответствует спариванию фермионных операторов:
[Щхг Щх2)] [Щх2 Щх3)]... [Щхм Щхг)]. F.125)
С другой стороны, эти операторы возникают в F.1.1) в сле-
следующем порядке:
Щхг )Щх1Щх2 )Щх2)... \|7(хм )Щхм). F.1.26)
* На самом деле, появление этого знака имеет некоторую связь со стати-
статистикой Ферми. Одно и то же поле может уничтожать частицу или рождать
античастицу, так что существует соотношение, известное как «кросс-сим-
«кросс-симметрия» между процессами, в которых начальные частицы или античастицы
обмениваются местами с конечными античастицами или частицами. В част-
частности, амплитуды процесса 12е —> 1'2'с связаны с амплитудами кросс-процес-
кросс-процесса 12' —> 1'2; два спаривания F.1.23) и F.1.24) соответствуют двум диаграм-
диаграммам, отличающимся перестановкой 1 и 2' (или 1' и 2), так что антисимметрия
амплитуды рассеяния относительно перестановки начальных (или конечных)
частиц естественно требует наличия знака минус в относительном вкладе
этих спариваний. Однако кросс-симметрия не является обычной симметрией
(она включает аналитическое продолжение по кинематическим переменным),
так что для произвольных процессов ее трудно использовать с какой-то
определенной точностью.
6.1. Вывод правил
359
2'
Рис. 6.6. Связные диаграммы второго порядка для бозон-фермионного
рассеяния в теории с взаимодействием F.1.18). Прямые линии — фермио-
ны, пунктирные — нейтральные бозоны
Рис. 6.7. Связная диаграмма низшего порядка для бозон-бозонного рассея-
рассеяния в теории с взаимодействием F.1.18). Подобные диаграммы с фермион-
ными петлями приводят к дополнительному знаку «минус», возникающе-
возникающему от перестановок спариваемых фермионных полей
Чтобы перейти от F.1.26) к F.1.25), необходимо совершить нечет-
нечетную перестановку фермионных операторов (передвинуть \у(хг) напра-
направо через 2М-1 оператор). Поэтому вклад каждой такой фермионной
петли сопровождается дополнительным отрицательным знаком.
Эти правила приводят к полной .^-матрице, включающей
вклады от процессов, в которых взаимодействуют далеко разнесен-
разнесенные в пространстве и времени различные кластеры частиц. Как
обсуждалось в гл. 4, для вычисления той части 5-матрицы, которая
не содержит указанных вкладов, нужно рассматривать только
связные фейнмановские диаграммы. В частности, это исключает
проходящие насквозь через диаграмму без взаимодействия линии,
которым соответствуют множители F.1.13).
360 Глава 6. Фейнмановские правила
Чтобы полностью прояснить фейнмановские правила, вычис-
вычислим вклады низшего порядка в .^-матрицу для рассеяния частиц в
двух разных теориях.
Теория I
Рассмотрим теорию фермионов и зарядово самосопряженных
бозонов с гамильтонианом взаимодействия F.1.18). Связные диа-
диаграммы низшего порядка для фермион-бозонного рассеяния пока-
показаны на рис. 6.6. Следуя перечисленным на рис. 6.1 правилам,
получаем матричный элемент ^-матрицы:
6
k'l'm'klm
xjd4x
jd4 J
F.1.27)
(Индексы 1 и 2 используются здесь для обозначения фермионов
и бозонов, соответственно.) Для фермион-фермионного рассеяния
также есть две диаграммы второго порядка, показанные на рис. 6.4.
Им соответствует матричный элемент .^-матрицы
2^ * ^' 9m'mk'9l'lk
k'l'm'klm
х ^(p220^(pJJOm(p222)i(p111)
(D.l.^o)
хахауе е е е ^ г)ак'к(х, у) [i <^ л \,
6.1. Вывод правил 361
причем последнее слагаемое означает вычитание предыдущего вы-
выражения с перестановкой частиц 1' и 2' (или 1 и 2). В такой теории
не существует диаграмм второго порядка для бозон-бозонного рас-
рассеяния. Простейшими являются диаграммы четвертого порядка
типа показанных на рис. 6.7.
Более конкретные примеры использования формул F.1.27) и
F.1.28) будут приведены в разделе 6.3, после того, как мы вычис-
вычислим пропагаторы и перейдем в импульсное пространство.
В предыдущем примере все три поля в гамильтониане взаимо-
взаимодействия F.1.18) различны. Полезно рассмотреть пример также с
трилинейным взаимодействием, но в котором все три поля одина-
одинаковы или, по крайней мере, входят симметричным образом.
Теория II
Пусть плотность гамильтониана взаимодействия есть сумма
слагаемых, трилинейных по действительным бозонным полям
фг(х):
•^И = —
Iran
где gf;mn — действительная полностью симметричная константа
связи.
Пусть мы хотим рассмотреть процесс рассеяния 12 —> 1'2' во
втором порядке по этому взаимодействию. К каждой из двух
вершин должны быть подсоединены по две из четырех внешних
линий. (Единственная другая возможность - в том, чтобы к одной
вершине была подсоединена одна из внешних линий, а три
другие были подсоединены ко второй вершине. Но в этом случае
у вершины с тремя внешними линями не останется больше
линий, чтобы соединить ее с первой вершиной, т. е. получится
несвязная диаграмма.) Третья линия при каждой вершине долж-
должна соединять вершины друг с другом. Имеются три диаграммы
такого типа (рис. 6.8), отличающиеся тем, какая внешняя линия
подсоединена к той же вершине, что и линия 1. Это могут быть
линии 2, 1' или 2'.
Следуя сформулированным правилам, запишем вклад в
.^-матрицу от этих трех диаграмм:
362
Глава 6. Фейнмановские правила
1\ ,2'
\ /
\ /
Y
I
i
.2' 2'
1/
Рис. 6.8. Связные диаграммы второго порядка для бозон-бозонного рассеяния
в теории с взаимодействием F.1.29)
с
= (-гJBл)-6 ? grrgWm~Jd4xJd4y(-zArm~(*,y))
IlT'mm'm"
F.1.30)
Более того, если бозоны в этой теории — бесспиновые частицы
одного типа, то взаимодействие F.1.29) имеет вид
,^ = д(р3/3! F.1.31)
и матричный элемент F.1.30) рассеяния скаляра на скаляре равен:
-,2
PiP2.PiP2
гд2
[ехр(-г(рх + р2) • х) ехр(г(рх + р2) • у)
+ ехр(г(рх - Pi) • х) ехр(г(р2 - р^) • у)
+ ехр(г(рх -р2)-х)ехр(г(р2 -р[)-у)]
6.2. Вычисление пропагатора 363
где AF(x — у) — пропагатор скалярного поля, вычисленный в сле-
следующем разделе. В этой теории не существует вкладов третьего
или любого нечетного порядка по Ж{х).
6.2. Вычисление пропагатора
Перейдем к вычислению пропагатора F.1.14). Пропагатор —
существенная составляющая фейнмановских правил, возникающая
в результате спаривания поля \|/г(х) с сопряженным полем \(тЦу).
Подставляя F.1.15) и F.1.16) в F.1.14) и пользуясь соотношениями
коммутации и антикоммутации для операторов уничтожения и
рождения, находим:
-iAlm(х,у) = 6(х - у)Bл)-3/2 Jй3р^Щ(рап)и
Вычисляя в гл. 5 коммутаторы и антикоммутаторы, мы показали,
что
-1
т 1_ /__2 , 2 \
F.2.2)
^(роФ1(роп) = ±B^/р2 + т\) Pim(-P-Vp2+W«). F.2.3)
где P;m(p,co) - полином по р и со. (Здесь, как и в F.2.1), верхние и
нижние знаки относятся, соответственно, к бозонным и фермион-
ным полям.) Например, если \|/г(х) и Х|/т^(у) - скалярные поля ф(х) и
ф(у) частицы спина 0, то
Р(р) = 1. F.2.4)
Если \|/;(х) и Х|/т^(у) - дираковские поля частицы спина 1/2, то
(б.2.5)
364 Глава 6. Фейнмановские правила
где I, m — принимающие четыре значения дираковские индексы.
(Матрица C возникает здесь потому, что мы рассматриваем спари-
спаривание Щх) и \|/mt(y). При спаривании \|/г(х) с \|/(у) = \утЦу)$ она не
появляется.) Если \|/г(х) и \|/т(у) - векторные поля V^x) и Vv(y)
частицы спина 1, то
В более общем случае, если \|/г(х) и \|/т(у) - компоненты полей
\|/аЬ(х) и \|/ag(y) частицы спина j в неприводимых представлениях
(А,В) и (А, В) однородной группы Лоренца, то
РаЪ,~аЪ
а'Ъ' а'Ъ' а
х
[ехр(-6р • JA) I [ехр(+6р
L Jaa'L
где sh 0 = |p|/m, а индексы a, b, a, b так же, как и индексы а', Ь',
а',Ъ', по которым идет суммирование, пробегают через единицу
значения от —А до +А, от -В до +В, от - А до + А и от —В до +В,
соответственно.
Подстановка формул F.2.2) и F.2.3) в F.2.1) приводит к следу-
следующему выражению:
-гА1т (х, у) = 0(х - y)Plm f -г — 1а+(х - у)
( Э > F.2.8)
+ 0(у-х)Ры1-г—1А+(у-х),
где А+(х) - введенная в гл. 5 функция
А+(х) = {2%)-3jd3p{2p°r1eipx , F.2.9)
в которой р° = + д/Р + т ¦
Чтобы продвинуться далее, необходимо сказать несколько
слов о том, как расширить определение полинома Р(р). Формулы
6.2. Вычисление пропагатора 365
F.2.2) и F.2.3) определяют Р{р) только для 4-импульсов «на массо-
массовой оболочке», т. е. при значениях р° = ± Jp2 + т2 ¦ Любая полино-
полиномиальная функция таких 4-импульсов всегда может рассматри-
рассматриваться как линейная по р°, так как любая степень (p°Jv или (p°Jv+1
может быть записана как (р2 + m2)v или р°(р2 + m2)v, соответст-
соответственно. Поэтому можно определить полином P^L\q) условиями, что
),
F.2.1U)
P(L) (q) = Р@) (q) + g°PA) (q) (для произвольных q^),
где Р^0'1) - полиномы, зависящие только от q. Теперь можно вос-
воспользоваться соотношениями
(x° -у0) = - А-9G/° -х°) = 5(х° - у0) F.2.11)
(напомним, что 0(х) имеет единичный скачок при х° = 0 и постоянна
в остальных точках), и переставить операторы производных в
F.2.8) и 6-функциии:
5(х° - y°)P^(-zV)[A+(x - у) - А+(у - х)],
F.2.12)
+(у - х)],
где AF — фейнмановский пропагатор, равный
-zAF(x) = 6(х)А+(х) + 0(-х)А+(-х). F.2.13)
Однако при х° = 0 функция А+(х) четна по х, так как замена
х —» -х в F.2.9) может быть скомпенсирована заменой р —» -р
переменной интегрирования. Поэтому можно опустить второе сла-
слагаемое в F.2.12) и записать просто
— JAF(x-y). F.2.14)
Полезнее всего использовать выражение для фейнмановско-
го пропагатора в виде интеграла Фурье. Ступенчатые функции
366 Глава 6. Фейнмановские правила
в F.2.13) имеют следующее фурье-представление *:
со
exp(-ist)
s + ге F-2.15)
Это выражение можно объединить с интегралом Фурье F.2.9)
для А+(х). Введем в этом интеграле в F.2.13) новые переменные
интегрирования q = р, д° = р° + s, тогда
xllg0--
Комбинируя знаменатели и переходя к четырехмерным обо-
обозначениям, находим:
ч-4 Г 74 ехр(гд-х)
) 4 сГд yv ч
... /о ч-4 Г 74 ехр(гдх)
AF(x) = Bл) 4 сГд yv ч , F.2.16)
J д^ + тЛ - ге v '
где g2 = q2 - (д0J. (В знаменателе мы заменили 2?^2 + га2 на е,
так как все, что требуется от этой величины — это быть положи-
положительной и бесконечно малой.) Теперь, между прочим, видно, что AF
является функцией Грина дифференциального оператора Клейна-
Гордона, в том смысле, что
(П-т2)Д?(х) = -54(х), F.2.17)
и граничные условия определяются добавкой —г'? в знаменателе.
Как следует из F.2.13), функция AF(x) при х° —> +°° или х° —> -°°
* Чтобы доказать это, заметим, что при t > 0 контур интегрирования можно
замкнуть большим полукругом в нижней полуплоскости, двигаясь по часовой
стрелке, так что вклад в интеграл от полюса в точке s = —ге равен —2лг. Если же
t < 0, контур можно замкнуть большим полукругом в верхней полуплоскости,
двигаясь против часовой стрелки, но в верхней полуплоскости подьштегральная
функция не имеет особенностей, и поэтому интеграл равен нулю.
6.2. Вычисление пропагатора 367
содержит только положительно- или только отрицательно-частот-
ные слагаемые ехр(-гх°7р2 +т2) или ехр(+гх°д/р2 +т2), соот-
соответственно.
Подстановка F.2.16) в F.2.14) приводит к выражению для
пропагатора:
Аы(х,у) = B7Г)-4 d4g \ (Ч> 2 . . F.2.i8)
В связи с этим выражением возникает одна очевидная проблема.
Полином Р(р) лоренц-ковариантен, когда р находится на массовой
оболочке, р2 = -т2, но интегрирование в F.2.18) производится по всем
ф, не ограниченным массовой оболочкой. Полином P(L^(g) определен
для произвольных q^ таким образом, что он линеен по д°. Очевидно,
это условие не лоренц-ковариантно, если только полином не линеен и
по каждой пространственной компоненте qi. Однако всегда можно
определить расширение полинома Р(р) на произвольные 4-импульсы
ф, которое мы обозначим просто P(q), таким образом, чтобы при
любых q^ полином P(q) был явно лоренц-ковариантен:
где A^v — общее преобразование Лоренца, a D(A) — соответствующее
представление группы Лоренца. Например, для скалярного, дира-
ковского и 4-векторного полей эти ковариантные расширения полу-
получаются очевидной заменой р^ на произвольный 4-вектор q^ в F.2.4),
F.2.5) и F.2.6). Для скалярного и дираковского полей полиномы уже
линейны по д°, и в этих случаях нет разницы между P^L\q) и Р(д):
Р^{q) = Plm{q) (скалярное и дираковское поля). F.2.19)
В то же время для векторного поля частицы спина 1
00-компонента ковариантного полинома P^v(g) = Лцу + т~2%Ч\ квад-
квадратична по д°, так что в этом случае есть разница:
= v +т [ад -&№Ж -q -mz)]
F.2.20)
368 Глава 6. Фейнмановские правила
(Здесь дополнительное слагаемое определяется двумя условиями:
оно должно компенсировать слагаемое (д0J в Р00(д) и должно обра-
обращаться в нуль, если q^ находится на массовой оболочке.) Подста-
Подстановка последнего выражения в F.2.18) приводит к следующему
виду пропагатора векторного поля:
Г Р (a)eiq<x~y)
4 \^p^254
J q + m - гг
F.2.21)
Первое слагаемое явно ковариантно, а второе, хотя и нековари-
антно, но локально, так что его можно компенсировать добавле-
добавлением локального нековариантного слагаемого в плотность гамиль-
гамильтониана. Конкретно, если взаимодействие V^x) с другими полями
описывается слагаемым У^(х)^(х) в ,Ж(х), то наличие второго
слагаемого в F.2.21) сведется к появлению эффективного взаимо-
взаимодействия
-1Жэфф(х) = -[-zJ^(x)][-zJv(x)][-zm-25°50].
(Множители —г всегда сопровождают вклады вершин и пропагато-
ров. Множитель j необходим потому, что возможны два способа
спаривания других полей с ,Ж;эфф(х), отличающиеся перестановкой
J11 и «Л.) Итак, вклад нековариантного второго слагаемого
в F.2.21) можно компенсировать, добавив к ,Ж(х) нековариантное
слагаемое
[JV)]2 F.2.22)
Именно сингулярность одновременных коммутаторов век-
векторных полей на малых расстояниях заставляет использовать
более широкий класс взаимодействий, чем те, которые описыва-
описываются скалярной плотностью. Детальное непертурбативное доказа-
доказательство лоренц-инвариантности .^-матрицы в этой теории будет
дано в следующей главе.
Не нужно думать, что описанное явление связано только со
спинами j > 1. Рассмотрим, например, векторное поле, связанное
с частицей спина j = 0 и равное (как обсуждалось в гл. 5) производ-
6.2. Вычисление пропагатора 369
ной Э^ф(х) скалярного поля. Для спаривания этого поля со скаляром
Ф^(у) полином Р(р) на массовой оболочке равен
Рх(р) = гРх, F.2.23)
в то время, как спаривание Э^ф(х) с Э^ф^х) приводит к полиному
F.2.24)
Для произвольных 4-импульсов q^ вне массовой поверхности
ковариантные полиномы получаются подстановкой q^ вместо р^ в
формулы F.2.23) и F.2.24). Полином Рг(д) уже линеен по д0, так что в
этом случае не возникает никакой разницы между Рг(д) и
Однако в случае F.2.24) разница есть:
= PM(g) + (g2 + m2M°5° , F.2.25)
поэтому пропагатор равен
Ам(х, у) = Bл)-4 Гd4g^f+T1^2_"?+ 5°5054(x - у). F.2.2б)
Как и выше, нековариантные вклады от второго слагаемого
можно сократить, добавив к взаимодействию нековариантное сла-
слагаемое
VW F.2.27)
где ^(х) — в данном случае ток, на который умножается Эцф(х) в
ковариантной части ,Ж(х).
Должно быть ясно, что (по крайней мере для массивных
частиц) вклады нековариантных частей пропагатора всегда могут
быть сокращены описанным способом путем добавления нековари-
нековариантных локальных слагаемых в плотность гамильтониана. Это
происходит потому, что числитель Pim^L\q) в пропагаторе должен
равняться ковариантному полиному Plm(q), когда дц находится на
массовой оболочке, поэтому разность между P;m(L)(g) и PimiQ.)
должна содержать множитель д2 + т2. Этот множитель сокращает
знаменатель (д2 + т2 - ге) во вкладе этой разности в F.2.18),
370 Глава 6. Фейнмановские правила
поэтому выражение F.2.18) всегда равно сумме ковариантного
слагаемого и слагаемого, пропорционального дельта-функции
54(х - у) или ее производным. Вклад последнего слагаемого можно
компенсировать добавлением во взаимодействие слагаемого, квад-
квадратичного по токам, с которыми связаны спариваемые поля, или
по их производным.
Далее мы будем молчаливо предполагать, что подобное слагае-
слагаемое уже было включено во взаимодействие, и использовать ковари-
антный полином Ргт(д) в пропагаторе F.2.18), опуская индекс L.
Может показаться, что такая процедура достаточно произ-
произвольна. К счастью, в обсуждаемом в следующей главе канониче-
каноническом формализме те нековариантные слагаемые в плотности га-
гамильтониана, которые нужны для сокращения нековариантных
добавок в пропагаторах, возникают автоматически. На самом деле,
это является одной из причин введения канонического формализма
Прежде чем завершить этот раздел, полезно отметить неко-
некоторые другие определения пропагатора, эквивалентные F.2.1), ко-
которые часто встречаются в литературе. Во-первых, взяв среднее по
вакууму от F.1.14), имеем:
-iAlm(x,y) =
(Здесь (АВ...H означает среднее по вакууму (Фо, АВ . . . Фо).) Как
\|/^~(х), так и \|/^+(у) при действии на вакуум дают нуль, поэтому
реально в пропагатор дает вклад только одно слагаемое в каждом
коммутаторе или антикоммутаторе:
-zAim(x,y) = 0(x-y)(^(x),^f(y))o±0(y-x)(^f(y),^(x))o. F.2.29)
Далее, \\Т^ и \|/+ будут давать нуль, действуя на вакуум
справа, а \|/~ и \\t+1; будут делать то же самое слева, поэтому везде в
F.2.29) можно заменить \|/+ и \|Г на полное поле \|/ = \|/+ + \\г:
6.3. Правила в импульсном представлении 371
-гА1т(х, у) = 0(х - у)(щ(х),у*т(У)H ± 0(У - *)(Vm(У),?г(*))„¦ F.2.30)
Часто эту формулу записывают в виде:
-iAlm(x,y) = (т{щ(х)у*т(у)})о , F.2.31)
где Т — хронологическое произведение, определение которого
распространено * теперь на все поля с учетом знака «минус» для
любой нечетной перестановки фермионных операторов.
6.3. Правила в импульсном представлении
Изложенные в разделе 6.1. фейнмановские правила указывают,
как вычислить вклад в 5-матрицу данной диаграммы JV-ro порядка,
который представляется в виде интеграла по N пространственно-
временным координатам от произведения зависящих от этих коор-
координат множителей. Линии конечной частицы (или античастицы) с
импульсом p/fl, выходящей из вершины с пространственно-времен-
пространственно-временной координатой х^, отвечает множитель, пропорциональный ехр(—
г р'-х). Линии начальной частицы с импульсом р^, входящей в верши-
вершину с координатой хц, отвечает множитель ехр(+гр-х). В разделе 6.2
мы показали, что множитель, отвечающий внутренней линии, иду-
идущей от точки х к точке у, можно записать как интеграл Фурье по 4-
импульсам (f вне массовой поверхности, причем под интегралом
стоит множитель ехр(гд-(х — у)). Величину q^ можно понимать как 4-
импульс, текущий вдоль внутренней линии в направлении стрелки
от у к х. Таким образом, интеграл по пространственно-временной
координате в каждой вершине приводит к множителю
где Ер' и Ер означают полный 4-импульс всех конечных или началь-
начальных частиц, выходящих или входящих в вершину, а Е</ и Eg обозна-
обозначает полный 4-импульс всех внутренних линий со стрелками,
* Это не противоречит предыдущему определению хронологически упоря-
упорядоченных произведений плотностей гамильтониана в гл. 3, так как эти плот-
плотности могут содержать только четное число фермионных полей.
372 Глава 6. Фейнмановские правила
направленными от вершины и к вершине, соответственно. Конечно,
вместо интегралов по хц теперь необходимо брать интегралы по фурье-
переменным ф для каждой из внутренних линий.
Эти соображения приводят к новому набору фейнмановских
правил для вычисления вклада в .^-матрицу в виде интегралов по
импульсным переменным (рис. 6.9).
1. Следует нарисовать все фейнмановские диаграммы желае-
желаемого порядка, как описано в разделе 6.1. Однако вместо того, чтобы
помечать каждую вершину пространственно-временной координа-
координатой, нужно пометить каждую внутреннюю линию 4-импульсом вне
массовой поверхности, текущим, по соглашению, в направлении
стрелки (или в любом направлении для линий нейтральных частиц
без стрелок).
2. Каждой вершине типа i следует сопоставить множитель
-гBлL д -б4 (Ер + Eg - Ер' - Eg'), F.3.2)
где суммы по импульсам имеют тот же смысл, что и в F.3.1). Дельта-
функция обеспечивает сохранение 4-импульса в любой точке диаграммы.
Каждой внешней линии, выходящей вверх из диаграммы, сопостав-
сопоставляется множитель Bл)~3/2г(,г*'(р'а'п') или множитель Bл)~3/2г;г(р'а'п')
в зависимости от направления стрелки вверх или вниз. Каждой внеш-
внешней линии, входящей снизу в диаграмму, сопоставляется либо мно-
множитель Bjt)~3/2U;(pGn) , либо множитель Bл)~3^2г;г*(рап), также в
зависимости от направления стрелки вверх или вниз. Каждой внут-
внутренней линии, концы которой помечены индексами I и т, причем
стрелка направлена от т к I, и которая несет 4-импульс gm, сопостав-
сопоставляется множитель, равный подынтегральному выражению в интегра-
интеграле фурье-представления F.2.18) для iAlm(x,y):
-гBлГ4 Plm (g) / (д2 + mf - ге). F.3.3)
Напомним, что для скаляров или антискаляров с 4-импульсом g
величины и и v равны просто Bд0)/2, а полином Р(д) равен единице.
Для дираковских спиноров с 4-импульсом р и массой М величины и и
v равны нормированным дираковским спинорам, описанным в разде-
разделе 5.5, а полином Р(р) равен матрице (-гуцрц + М)C.
6.3. Пуавила в импульсном пуедставлении
373
р',о',те'
У\ I, х
I, x
р',о',те'с
t, x
I, x
Р ,о ,п
Р,о,п
р',о',те'с
-г
т,у
Ры(ч)
BлL g2 + mf - гг
Рис. 6.9. Графическое изображение спариваний операторов при вычисле-
вычислении S-матрицы в импульсном представлении. Выражения справа — те
множители, которые отвечают каждой линии фейнмановской диаграммы в
импульсном представлении
3. Произведение всех указанных множителей интегрируется
по 4-импульсам всех внутренних линий и суммируется по всем
полевым индексам I, т и т. д.
4. Результаты, полученные таким образом для каждой фейн-
фейнмановской диаграммы, следует сложить.
374 Глава 6. Фейнмановские правила
Могут понадобиться дополнительные комбинаторные множи-
множители и связанные с фермионами знаки; соответствующие правила
перечислены в пунктах 5 и 6 раздела 6.1. Примеры использования
этих правил мы приведем в конце раздела.
Каждой внутренней линии соответствует 4-импульс, по кото-
которому проводится интегрирование. Однако многие из этих интегриро-
интегрирований снимаются дельта-функциями, отвечающимис вершинам. Так
как энергия и импульс сохраняются для каждой связной части
фейн-мановской диаграммы по-отдельности, то в диаграмме с С
связными частями останется С дельта-функций. Отсюда в диаграмме
с I внут-ренними линиями и V вершинами число независимых 4-
импульсов, не зафиксированных дельта-функциями, равно I — (V —
С). Очевидно, этому же равно число L независимых петель,
L = I-V + C, F.3.4)
которое определяется как максимальное число внутренних линий,
которые можно разрезать, оставляя связной каждую связную часть
полной фейнмановской диаграммы, поскольку любым таким и только
таким внутренним линиям можно приписать независимый 4-им-
4-импульс. Можно считать, что независимые импульсные переменные
характеризуют импульсы, циркулирующие в каждой петле. В ча-
частности, древесная диаграмма не содержит петель. В такой диа-
диаграмме после учета всех дельта-функций не остается интегралов по
импульсам.
Например, в теории с взаимодействием F.1.18) матричный
элемент F.1.27) фермион-бозонного рассеяния согласно правилам
Фейнмана в импульсном представлении будет иметь вид
р[а[п[ р'2а'2п'2,р1а1п1 р2ст2п2
? (-iJB%fgVm,k,glmkuv(V[o[ni)ul(Vlo1n1)
k'l'm'klm
Jd4g -
q2+m2m-ie)
+ uk(p2o2n'2)uk,(p2o2n2Mi(p2 - pr + qMi(p1 - p2, - q)],
где индексы 1 и 2 относятся к фермионам и бозонам, соответственно.
6.3. Пуавила в импульсном пуедставлении
375
Интеграл по импульсам в данном случае тривиален, так что
= гBлГ254(р1+р2-рг-р2,)
р2а2п2, р1а1п1 р2а2п2
k'l'm'klm
(Pl+P2)
F.3.5)
(Pl-P2')
и
Аналогично, матричный элемент F.1.28) фермион—фермион-
ного рассеяния в той же теории равен
>^
PiCTjnJp'2CT'2n2,p1CT1n1p2CT2n2
О (Pi + Р2 ~ Pi' ~ P2')
Х
llk То 2 ^с о c^
fc'I'm'fclm (Pl-prJ+m|-Z? F.3.6)
хи1п,{р'2о'2п'2)щ,{р[о[п[)ит{р2о2п2)и1{р1о1щ)-[Г ^ Г].
Из вида этих результатов вытекает необходимость более ком-
компактных обозначений. Можно определить фермион-бозонную мат-
матрицу констант связи
Матричные элементы F.3.5) и F.3.6) для фермион-бозонного и
фермион-фермионного рассеяния соответственно переписываются
в матричных обозначениях следующим образом:
,р1а1п1 р2ст2п2
к'к
2 ^!2 .
(Р1+Р2) 2+М2-г?
+
к'
(Pl - ргу + М2 - гг
376 Глава 6. Фейнмановские правила
° (Pi + V2 ~ Pi' ~ Р2')
F-3-9)
[l/фф 2'],
где М2 и т2 — диагональные массовые матрицы фермионов
и бозонов в формулах F.3.8) и F.3.9). Общее правило состоит в том,
что при использовании матричных обозначений следует выписы-
выписывать коэффициентные функции, матрицы констант связи и пропа-
гаторы в порядке, который определяется движением вдоль линий
против направления, указанного стрелками. В тех же обозначени-
обозначениях 5-матрица для бозон-бозонного рассеяния в этой теории будет
даваться суммой однопетлевых диаграмм, показанных на рис. 6.7:
° (Pi + Р2 ~ Pi' ~ P2')
(q + prJ + M2 - гг
F.3.10)
хГ
где многоточие в конце означает слагаемые, получающиеся пере-
перестановкой бозонов 1', 2' и 2. Знак минус перед всем выражением
справа связан с числом фермионных петель.
Отметим, что после снятия интегрирований с помощью дель-
дельта-функций остается только один интеграл по импульсам, как
и должно быть для диаграммы с одной петлей. В гл. 11 мы увидим,
как вычисляются подобные интегралы по импульсам.
Приведем еще один конкретный пример. Рассмотрим теорию,
в которой дираковское спинорное поле Х|/(х) массой М взаимодей-
взаимодействует с псевдоскалярным полем ф(х) массой т, причем гамильтониан
6.3. Плавила в импульсном представлении
377
взаимодействия имеет вид - гд\|/у5\|/ф. (Множитель —г включен для
того, чтобы гамильтониан взаимодействия был эрмитовым при
действительных константах связи д.)
Напомним, что для скаляра полином P(q) равен единице, а
для спинора он равен [—гу„д^ +М]C. Кроме того, множитель и для
скаляра с энергией Е равен BЕ)/2, а для спинора и есть обычным
образом нормированный дираковский спинор, рассмотренный в
разделе 5.5.
Из формул F.3.8)—F.3.10) в низшем порядке получаем:
X
(Pi +T>2> +m гг
-, г г, -пЛр\
u(v[a[)y5-—^
(
r
- гг
(фермион-бозонное рассеяние);
PlCTl Р2СТ2 .
-[!'<=> 2'],
(фермион-фермионное рассеяние);
1
(Pi-Pr) +mz -гг
P1P2.P1P2
х
f
^ у г,
[
д2+М2-г?
р2
-iy
ргJ+М2-г?
-^ц(д + Pr - Pi)" + M -zY^(g - pa,)" + M
у — у
5 (g + pr - p:J + M2 - ге 5 (g - p2,J + M2 - ге
378 Глава 6. Фейнмановские правила
(бозон-бозонное рассеяние), где в последней формуле многоточие
означает сумму по перестановкам частиц 2, 1' и 2'. Множители C в
числителях фермионных пропагаторов были использованы для то-
того, чтобы заменить v) на и.
Еще один полезный топологический результат выражает не-
нечто вроде закона сохранения линий. Представим, что все внутрен-
внутренние и внешние линии рождаются в вершинах и затем уничтожают-
уничтожаются парами в центрах каждой внутренней линии и поодиночке на
концах каждой внешней линии. (Это не имеет отношения к направ-
направлению стрелок на линиях.) Приравнивая число рождающихся и
уничтожающихся линий, получаем
где I и Е - числа внутренних и внешних линий, Уг — число вершин
разных типов г, а щ — число линий, подсоединенных к каждой
вершине. (Это выполняется и по-отдельности для полей каждого
типа.) В частности, если все взаимодействия содержат одинаковое
число пг = п полей, то
2I + E = nV, F.3.12)
где V — полное число вершин. В этом случае можно исключить I из
F.3.4) и F.3.11) и получить, что для связной (С = 1) диаграммы
число вершин дается формулой
2L + E-2
V = . F.3.13)
п - 2
Например, для трилинейного взаимодействия диаграммы про-
процесса рассеяния (Е = 4) с L = 0, 1, 2, ... имеют V = 2, 4, 6, ... вершин.
В общем случае разложение по степеням констант связи есть
разложение по увеличивающемуся числу петель.
6.4. Выход с массовой оболочки 379
6.4. Выход с массовой оболочки
В фейнмановских диаграммах, отвечающих любому матрич-
матричному элементу ^-матрицы, все внешние линии находятся «на мас-
массовой оболочке». Иначе говоря, связанный с внешней линией 4-
импульс частицы массой т удовлетворяет условию р^р^ = —т2.
Однако часто необходимо рассматривать фейнмановские диаграм-
диаграммы «вне массовой оболочки». Для них энергии, отвечающие внеш-
внешним линиям, как и энергии, сопоставляемые внутренним линиям,
являются свободными параметрами, не связанными жестко с ка-
каким-то трехмерным импульсом. Например, подобные ситуации воз-
возникают, когда диаграммы являются частями большей фейнманов-
ской диаграммы. Так, петля на некоторой внутренней линии диа-
диаграммы может рассматриваться как диаграмма с двумя внешними
линиями, находящимися вне массовой оболочки.
Конечно, если мы вычислили вклад данной фейнмановской
диаграммы вне массовой оболочки, нетрудно вычислить и соответ-
соответствующие элементы 5-матрицы, совершив переход на массовую
оболочку, т. е. положив компоненты текущего по линии 4-импульса
р^, который входит в диаграмму, равными р° = (р2 + т2I^2 для
частиц в начальном состоянии и р = -(р +т ) ' для частиц
в конечном состоянии, и включив необходимые множители для
внешних линий: Bж)~5^2щ и B%)~s^2v{ для начальных частиц или
античастиц, и Bж)~5^2щ и Bл)~3/2г;г для конечных частиц или анти-
античастиц. Когда мы перейдем к обсуждению в гл. 8 подхода, основан-
основанного на функциональных интегралах, будет видно, что проще всего
сначала вывести фейнмановские правила для диаграмм, все внеш-
внешние линии которых лежат вне массовой оболочки, а затем получить
матричные элементы 5-матрицы, устремив импульсы внешних
линий к их значениям на массовой оболочке.
Фейнмановские диаграммы с линиями вне массовой оболочки
являются частным случаем более общих фейнмановских правил,
учитывающих эффекты различных возможных внешних полей. Пред-
Предположим, что мы добавили к гамильтониану сумму слагаемых,
включающих внешние поля ?а(ж), так что взаимодействие V(t),
входящее в дайсоновское разложение C.5.10) для .^-матрицы, заме-
заменяется на
380 Глава 6. Фейнмановские правила
«Токи» oa(t) зависят от времени так, как полагается в пред-
представлении взаимодействия:
oa{t) = exp(zH0t)oa@) exp(-zH0t), F.4.2)
но в остальном являются вполне произвольными операторами.
5-матрица для любого перехода а —» C становится в этом случае
функционалом Sab[e] от с-числовой функции ea(t). Фейнмановские
правила для вычисления этого функционала определяются
очевидным обобщением обычных правил Фейнмана. В дополнение
к получаемым из V(t) вершинам, следует включить новые верши-
вершины: если оа{х) есть произведение па полевых множителей, то всякая
вершина оа с координатой х и с па подсоединенными к ней линиями
соответствующего типа согласно правилам Фейнмана в координат-
координатном представлении дает вклад, равный —г?а(х), умноженный на
содержащиеся в оа{х) числовые факторы. Отсюда следует,
что r-ая вариационная производная S^a[e] по ?а(х), ?ь(у) ... при ? = 0
дается в координатном представлении диаграммами с г дополни-
дополнительными вершинами, к которым подсоединены соответственно па,
пь, ... внутренних линий, а внешние линии отсутствуют. Указанные
вершины имеют координаты х, у, ..., по которым не производится
интегрирование. Вклад каждой такой вершины равен произведению
—г на тот числовой фактор, который содержится в соответствую-
соответствующем токе оа.
В частности, если все токи представляют собой поля, т. е.
VE (t) = V(t) + ? J d3x ?a (x, t)oa (x, t),
то r-ая вариационная производная ^„[е] по ег(ж), ?т(у), ... при ? = 0
изображается в координатном представлении диаграммами, имею-
имеющими г дополнительных вершин с координатами х, у, ..., причем к
каждой из них подсоединена одна единственная внутренняя линия
типа I, т, ... Такие линии можно рассматривать как внешние линии
вне массовой оболочки, с той только разницей, что их вклад в
матричный элемент равен не коэффициентной функции типа Bл)/
2мг(р,а)егр'х или Bл)/2г(,г'в(р,а)е"гр':г, а пропагатору, умноженному
на множитель —г от вершины в конце линии. В импульсном пред-
представлении фейнмановская диаграмма с частицами на массовой обо-
6.4. Выход с массовой оболочки
381
лочке в состояниях ОС и C иг внешними линиями типа I, т, ... с
импульсами р, р', ..., получается из вариационной производной
5?г(х)б?т(у)...]Е=о
путем отбрасывания пропагаторов на каждой из линий вне массо-
массовой оболочки, взятия соотвтствующего фурье-образа и умножения
на коэффициентные функции щ, щ и т. д., а также на (-г)г.
Во многих случаях полезным оказывается простое соотноше-
соотношение между суммой вкладов всех диаграмм теории возмущений для
любой амплитуды вне массовой поверхности и матричным элемен-
элементом между собственными состояниями полного гамильтониана от
хронологически упорядоченного произведения соответствующих опе-
операторов в гейзенберговском представлении. Это соотношение выте-
вытекает из теоремы3, утверждающей, что во всех порядках теории
возмущений *
б?а(ж)б?ь(у)...
(бАЗ)
8 = 0
где Оа(х) и т. д. являются аналогами оа(х) в гейзенберговоском
представлении:
Oa{x,t) = exp(zHt)oa(x,0)exp(-zHt) =
~\t), F.4.4)
F.4.5)
а *Ра+ и *Рр — собственные «ин» и «аут» состояния полного гамильтониа-
гамильтониана.
Дадим доказательство. Из формулы C.5.10) следует, что левая
часть F.4.3) равна
*Для единственного оператора О это утверждение составляет швингеров-
ский принцип действия 4.
382
Глава 6. Фейнмановские правила
5eai(x1)...5ear(a;r)
8=0
JV=0
N\
z1...dx
N
X
F.4.6)
Для определенности положим ж° > ж° > ... > ж° • Тогда все х,
большие жД можно обозначить ^oi- ¦ ¦ xojvo > все х между х^ и х20 —
<Сц-"%1, и т. д. Наконец, все х, меньшие хг°, можно обозначить
xrl...xrJV . После этого F.4.6) принимает вид:
6eai(a:1)...5ear(a:r)
И)
JV+r
8=0
/VI
JV=O JV • JVnJV,...JVr
dx01...
dxn... dx1Wi... j^ dxrl...
o Ц dxn... dx1Wi
rl.
X
...oar(xr)T{v(xrl)...V(xrWr)}oa).
iV0!iV...iVr!
Множитель N\/N0\N1\...Nrl равен числу способов рассортировать
N переменных х по г+1 подмножествам, содержащим No, Nv . . ., Nr
этих переменных. Вместо суммирования по No, Nb . . .,Nr
с учетом условия N0 + N1 + ... + Nr = N,a затем суммирования по N,
можно просто суммировать независимо по No, Nb . . ., Nr, полагая N
в множителе (—i)N равным No + N1 + . . . + Nr Получаем:
где
= (-г)г(фр,[/(оо,х1°)оа1(х1)
Je=0 F.4.7)
t(x2)U(x°2,x°3)...oa (хг)[/(х°,-оо)Фа),
-.JV /
dx1...dxwT{V(x1)...V(xw)}. (бА8)
JV=O
6.4. Выход с массовой оболочки
383
Оператор U(t',t) удовлетворяет дифференциальному уравнению
— U(t',t) = -iV(t')U(t',t)
dtf
с очевидным начальным условием
U(t, t) = 1.
Оно имеет решение
U(t', t) = exp(iHot') exp(-iH(t' - t)) exp(-zHot) =
F.4.9)
F.4.10)
F.4.11)
где ?1 дается формулой F.4.5). Подставляя F.4.11) в F.4.7) и пользу-
пользуясь формулой F.4.4), находим:
Je=O
F.4.12)
При получении этой формулы было сделано предположение,
что х® > х® ^ • • • ^ хйг , поэтому произведение операторов справа
можно заменить на хронологически упорядоченное произведение
Je=O
= (-г)г(П(оо)фр,Т{Оа1(х1)...Оаг(хг)}П(-оо)Фа).
F.4.13)
Но теперь обе стороны равенства полностью симметричны
(или антисиммметричны в случае фермионов) по а и ж, так что это
соотношение выполняется при любом порядке следования моментов
времени х-^...х®. Кроме того, в разделе 3.1 мы видели, что
F.4.14)
(в смысле соотношения C.1.12)). Таким образом, формула F.4.13) и
есть желаемый результат F.4.3).
384 Глава 6. Фейнмановские правила
Задачи
1. Рассмотрите теорию действительного скалярного поля ф со
взаимодействием
V = — fd3x(p(xK
3!J
(в представлении взаимодействия). Вычислите связный эле-
элемент ^-матрицы для скаляр-скалярного рассеяния во втором
порядке по д, взяв все интегралы. Используя этот результат,
вычислите дифференциальное сечение скаляр-скалярного рас-
рассеяния в с. ц. и.
2. Рассмотрите теорию, включающую нейтральное скалярное по-
поле ф(ж) для бозона В и комплексное дираковское поле Х|/(ж) для
фермиона F, взаимодействующих по закону
V = igj й3хЩх)у5\\1(хЩх).
(в представлении взаимодействия). Нарисуйте все связные фейн-
фейнмановские диаграммы в порядке д2 и вычислите соответствую-
соответствующие матричные элементы 5-матрицы для процессов Fc + В —>
Fc + В, F + Fc^F + FcvlFc+F^B+B (здесь Fc -
античастица F). Вычислите все интегралы.
3. Рассмотрите теорию действительного скалярного поля j(x) со
взаимодействием
V = —
4!
Вычислите 5-матрицу для скаляр-скалярного рассеяния в по-
порядке д и с помощью этого результата найдите дифференци-
дифференциальное сечение. Рассчитайте поправочные слагаемые в S-мат-
рице для скаляр-скалярного рассеяния в порядке д2, взяв все
интегралы по ж и выразив результат в виде интеграла по
единственному 4-импульсу.
4. Каков вклад в фейнмановские диаграммы от свертки производ-
производной дираковского поля д^щ(х) с сопряженным полем Ц
Список литературы 385
5. С помощью теоремы из раздела 6.4 найдите выражения для
средних по вакууму от гейзенберговских операторов (Ч?0,Ф(х)Ч?0)
и (Ч'о,Т{Ф(х),Ф{у)}Ч'о) в теории, рассмотренной в задаче 1, в
порядках д и д2, соответственно.
Список литературы
1. Dyson, F.J., Phys. Rev., 75, 486, 1736 A949).
2. Формальное утверждение носит название теоремы Вика', см.:
Wick, G.C., Phys. Rev., 80, 268 A950).
3. Я не знаю, кто первым доказал эту теорему. Она была известна
в начале 50-х годов ряду теоретиков, включая М. Гелл-Манна и
Ф. Лоу.
4. Schwinger, J., Phys. Rev., 82, 914 A951).
Канонический формализм
С конца 1920-х годов, когда квантовая теория поля родилась в
работах Борна, Дирака, Ферми, Гейзенберга, Иордана и Паули,
ее развитие исторически было настолько тесно связано с канониче-
каноническим формализмом, что и в наши дни считается вполне естествен-
естественным начинать любое рассмотрение с постулирования лагранжиана
и применения к нему правил канонического квантования. Такой
подход используется в большинстве книг по квантовой теории поля.
Однако исторический прецедент — не самый убедительный довод в
пользу этого формализма. Если нам удастся построить квантовую
теорию поля, приводящую к физически удовлетворительной
5-матрице, то какое нам дело до того, что эту теорию нельзя,
может быть, получить квантованием какого-то лагранжиана?
Поставленный вопрос до некоторой степени спорный, так как в
разделе 7.1 мы увидим, что все самые известные квантовые теории
поля представляют собой канонические системы, которые легко
могут быть представлены в лагранжевой форме. Однако никто не
доказал, что любая приемлемая квантовая теория поля может быть
сформулирована таким образом. Но даже если это так, то сам этот
факт не объясняет, почему в качестве отправной точки при построе-
построении разных квантовых теорий поля следует предпочитать именно
лагранжев формализм.
Преимущество лагранжевого формализма заключается в том,
что он позволяет легко удовлетворить требованиям инвариантно-
инвариантности относительно преобразований Лоренца и других симметрии:
классическая теория с лоренц-инвариантным лагранжианом в ре-
результате канонического квантования приводит к лоренц-инвари-
антной квантовой теории. Иначе говоря, мы покажем ниже, что
7.1. Канонические переменные 387
такая теория позволяет построить подходящие квантово-механи-
ческие операторы, удовлетворяющие коммутационным соотноше-
соотношениям алгебры Пуанкаре и приводящие поэтому к лоренц-инвари-
антной 5-матрице.
Это далеко не тривиально. В предыдущей главе мы видели,
что в теориях со связью с производными или со спином j > 1
недостаточно записать гамильтониан взаимодействия в виде инте-
интеграла по пространству от скалярной плотности. Необходимо доба-
добавить к плотности гамильтониана взаимодействия нескалярные
слагаемые для компенсации нековарантных слагаемых в пропага-
торах. Канонический формализм со скалярной плотностью лагран-
лагранжиана автоматически приводит к нужным дополнительным сла-
слагаемым. Позднее, когда мы перейдем в т. II к обсуждению неабеле-
вых калибровочных теорий, это дополнительное удобство превра-
превратится в необходимость. Безнадежно пытаться угадать форму га-
гамильтониана в таких теориях, если не начать с лоренц-инвари-
антного и калибровочно инвариантного лагранжиана.
7.1. Канонические переменные
В этом разделе мы покажем, что различные построенные
нами до сих пор квантовые теории поля удовлетворяют коммута-
коммутационным соотношениям и уравнениям движения гамильтонова
формализма *. Для вычисления .^-матрицы (операторным методом
или с помощью функционального интеграла) нужен именно га-
мильтонов формализм, однако далеко не просто выбрать гамиль-
гамильтонианы, приводящие к лоренц-инвариантной 5-матрице. В ос-
остальной части этой главы мы будем рассматривать в качестве
отправной точки лагранжев формализм, и получим с его помощью
физически приемлемые гамильтонианы. Цель данного раздела —
* Мы используем русскую терминологию. Автор употребляет термин
Hamiltonian (Lagrangian) version of canonical formalizm, в дословном переводе:
гамилътонов (лагранжев) вариант канонического формализма. В русской
физической литературе используют термины лагранжев формализм и
гамилътонов, или канонический, формализм. Лагранжев и гамильтонов
формализмы однозначно связаны и эквивалентны; иногда говорят о
«гамильтонизации» лагранжевой теории. — Прим. ред.
388 Глава 7. Канонический формализм
определить канонические поля и им сопряженные в различных
теориях поля, показать, как выделять слагаемые в лагранжиане,
относящиеся к свободным полям, и, наконец, подтвердить, что
канонический формализм действительно применим к физически
реалистичным теориям.
Прежде всего, покажем, что построенные в гл. 5 свободные
поля автоматически образуют систему квантовых операторов
gn(x,t) и канонически сопряженных им импульсов pn(x,t), удовле-
удовлетворяющих известным каноническим соотношениям коммутации
или антикоммутации:
[qn(x,t),q^(y,t)]T=O, G.1.2)
[pn(x,t),p^(y,t)]+= 0, G.1.3)
где индекс + указывает, что если хотя бы один из двух операторов
рождает или уничтожает частицы, являющиеся бозонами, следует
брать коммутатор, а если оба оператора рождают или уничтожают
фермионы, то следует брать антикоммутатор. Например, в разде-
разделе 5.2 было показано, что действительное скалярное поле ф(х)
зарядово самосопряженной частицы нулевого спина подчиняется
коммутационному соотношению
[ф(ж),ф(у)]_ = Л(х-у),
где функция
^ k г ik-(x-y) -ik-(x-y)-,
— 5-е ю-е
J 2к°BжK
причем к0 = л/k2 + т2 . Заметим, что
А(х,0) = 0, А(х,0) = -г53(х).
(Точка означает производную по х°.) Легко показать, что поле ф и
его производная по времени ф удовлетворяют одновременным ком-
коммутационным соотношениям
7.1. Канонические переменные
389
[(p(x,t),(j)(y,t)]_=z53(x-y),
[(p(x,t),(p(y,t)]_=O,
[(j)(x,t),(j)(y,t)]_=O.
Поэтому можно определить канонические переменные
G.1.4)
G.1.5)
G.1.6)
G.1.7)
удовлетворяющие каноническим коммутационным соотношениям
G.1.1)-G.1.3).
В случае комплексного скалярного поля частицы спина нуль,
не совпадающей со своей античастицей, коммутационные соотно-
соотношения имеют вид
f ]_ = А(ж - у), [ф(ж), ф(у)]_ = 0.
Отсюда можно определить канонические переменные для свобод-
свободных частиц как комплексные операторы
g(x,t) = ф(х,?), G.1.8)
p(x,t) = <pt(x,t). G-1.9)
Эквивалентно, записав ф= (фх + Щ2)/-^2 с эрмитовыми ф^, к = 1,2,
получаем канонические переменные
G.1.10)
G.1.11)
удовлетворяющие коммутационным соотношениям G.1.1)—G.1.3).
Для действительного векторного поля частицы спина единица
коммутационные соотношения были выписаны в разделе 5.3:
[v»(x),vv(y)]_ =
т
А(х - у).
390 Глава 7. Канонический формализм
(Мы пишем v^ вместо V^, так как хотим сохранить заглавные буквы
для обозначения полей в гейзенберговском представлении.) В дан-
данном случае канонические переменные для свободных частиц можно
выбрать в виде:
g*(x,t) = u*(x,t), G.1.12)
dv°(x,t)
дхг
G.1.13)
где г = 1, 2, 3. Читатель может проверить, что величины G.1.12) и
G.1.13) удовлетворяют перестановочным соотношениям G.1.1)—G.1.3).
Полевые уравнения E.3.36) и E.3.38) вместе с формулой G.1.13)
позволяют выразить v° через другие переменные:
G.1.14)
поэтому г;0 не рассматривается в качестве независимой переменной
д. На случай комплексного векторного поля эти результаты обобща-
обобщаются точно так же, как и в случае комплексного скалярного поля.
Для дираковского поля немайорановских частиц спина 1/2 из
результатов раздела 5.6 следует, что антикоммутатор полей равен
Было бы непоследовательно выбрать \|/п и х^ в качестве независи-
независимых канонических переменных, так как их антикоммутатор не
обращается в нуль при равных временах. Вместо этого принято
определять
qn(x) = yn(x), G.1.15)
рп(х) = гУп(х). G.1.16)
Легко видеть, что G.1.15) и G.1.16) удовлетворяют каноническим
антикоммутационным соотношениям G.1.1)—G.1.3).
Для любой системы операторов, удовлетворяющих коммута-
коммутационным или антикоммутационным соотношениям типа G.1.1)—G.1.3),
7.1. Канонические переменные 391
можно определить квантово-механическую функциональную про-
производную. Именно, для произвольного бозонного функционала
F[q(t),p{t)] от операторов gn(x,t) и pn(x,t) при фиксированном време-
времени t мы определяем *
GJJ7)
5pn(x,t) v • •
Это определение мотивируется тем, что если записать F[q(t),p(t)]
так, что все g окажутся слева от всех р, то G.1.17) и G.1.18)
являются, соответственно, левыми и правыми производными по qn
и рп. Иначе говоря, для произвольной с-числовой ** вариации 5д и
5р операторов q и р имеем:
Для более общих функционалов следует дополнить определе-
определения G.1.17) и G.1.18) различными знаками и коммутаторами при
равных временах.
В частности, Яо является генератором трансляций по време-
времени, действующим на свободные частицы в следующем смысле:
gn(x, t) = ехр(Ш0?)дп(х,0) ехр(-Ш0?), G.1.19)
* Здесь используются обозначения, употребляемые далее по всей книге. Ес-
Если f(x,y) есть функция двух классов переменных, коллективно обозначенных
х и у, то F\f(y)] означает функционал, зависящий от значений f(x,y) при всех
х, но при фиксированном у. Бозонным мы называем такой функционал, в кото-
котором каждое слагаемое содержит только четное число фермионных полей.
** Если qn и рп — бозонные или фермионные операторы, то считается, что
dqn и дрп соответственно коммутируют или антикоммутируют со всеми фер-
мионными операторами и коммутируют со всеми бозонными операторами.
392 Глава 7. Канонический формализм
pn(x,t) = exp(zHot)pn(x,O)exp(-zHot), G.1.20)
так что операторы свободных частиц зависят от времени по закону:
йН
<j"(x,t) = i[H0,qn(x,t)] = ° G ! 21)
8pn(x,t) l ;
йН
pn(x,t) = z[H0,pn(x,t)] = ~s ° G.L 22)
Мы узнаем в этих выражениях всем известные динамические
уравнения гамильтонова формализма.
Гамильтониан свободных частиц задается, как всегда, выражением
a Ас а (к, о, п) а(к,о,'
G.1.23)
Его можно переписать через q и р, взятые в момент времени t.
Например, легко видеть, что для действительного скалярного поля
выражение G.1.23) с точностью до постоянного слагаемого равно
функционалу
j3h2\f^22\ G.1.24)
Более аккуратно, используя G.1.7) и фурье-разложение скалярного
поля ф, находим, что G.1.24) принимает вид
Яо = i JdW[a(k),af(k)]+ = J d3Wc0faf(k)a(k) + \ Й3(к - к)
G.1.25)
Это выражение совпадает с G.1.23), если не считать бесконечного
постоянного слагаемого. Подобные слагаемые влияют только на
выбор начала отсчета энергии, и в отсутствие гравитации не имеют
физического значения *.
* Однако изменения таких слагаемых, обусловленные изменением гра-
граничных условий на поля, как например, при квантовании полей не во всем
пространстве, а в пространстве между параллельными пластинами, не только
физически значимы, но и были измерены 1.
7.1. Канонические переменные 393
Явный вид Яо как функционала от переменных g и р для
других полей приведен в разделе 7.5.
В книгах по квантовой теории поля формула G.1.25) обычно
выводится из формулы G.1.24), которая, в свою очередь, выводит-
выводится из заданной плотности лагранжиана. С моей точки зрения, все
должно быть наоборот, так как формула G.1.25) обязана иметь
место. Если предполагаемый лагранжиан свободных частиц не при-
приводит к G.1.25) с точностью до постоянного слагаемого, можно сде-
сделать вывод, что этот лагранжиан неправильный. Вопрос следует
поставить иначе: какой лагранжиан свободных полей приводит к
формуле G.1.25) для бесспиновых частиц, или, в более общем
случае, к гамильтониану свободных частиц G.1.23). Ответ можно
получить с помощью хорошо известного преобразования Лежандра
от гамильтониана к лагранжиану. Для свободного поля лагранжиан
дается формулой:
q(t)] = ^^3х pn(x, t)g(x, t)-H0, G.1.26)
причем подразумевается, что pn везде заменяются своими выраже-
выражениями через qn и qn (и возможно, как будет видно ниже, через
некоторые вспомогательные поля). Например, исходя из гамильто-
гамильтониана G.1.24) и формулы G.1.7), можно вывести лагранжиан свобод-
свободного скалярного поля:
Lo =
G.1.27)
Каким бы не оказался лагранжиан скалярного поля, это сла-
слагаемое должно быть отделено от всех остальных и рассматриваться
как нулевое приближение теории возмущений. Аналогичное упра-
жение можно проделать для всех других канонических систем,
рассматриваемых в данном разделе. Однако с этого момента мы
сосредоточимся на угадывании формы лагранжиана свободных по-
полей, после чего будем проверять, что она приводит к правильному
гамильтониану свободных частиц.
Мы видели, что различные теории свободных полей можно
сформулировать в терминах канонических переменных. Нетрудно
394 Глава 7. Канонический формализм
продвинуться далее и показать, что это же верно для взаимодейст-
взаимодействующих полей. Можно ввести канонические переменные в так
называемом «гейзенберговском представлении», определяемом со-
соотношениями
Qn(x,t) = exp(zHi)qn(x,O)exp(-zHi), G.1.28)
Pn(x,t) = exp(zHt)pn(x,O)expHHt), G.1.29)
где Н — полный гамильтониан. Поскольку это пребразование подо-
подобия, коммутирующее с Н, то полный гамильтониан является таким
же функционалом от операторов в гейзенберговском представле-
представлении, каким он был как функционал от q и р:
H[Q,P] = eiHtH[q,p]e-iHt = H[q,p].
Кроме того, поскольку G.1.28)—G.1.29) определяют преобразование
подобия, операторы в гейзенберговском представлении вновь удов-
удовлетворяют каноническим коммутационным или антикоммутационным
соотношениям:
[Qw(x,t),P^(x,t)]T = г53(х-уM|, G.1.30)
[Qn(x,t),Q^(x,t)]_=0, G.1.31)
[Pn(x,t),P^(x,t)]_=0. G.1.32)
Однако зависимость от времени этих операторов имеет вид
Sir
<Ax,t) = t[H,Q»(x,t)] =
Pn(x,t) = i[H,Pn(x,t)] = -
Например, можно выбрать гамильтониан действительного скаляр-
скалярного поля в виде суммы гамильтониана G.1.24) свободных частиц
5Pn(x,
5Я
ROn (
t)'
,t) '
G.1.33)
G.1.34)
7. 2. Лагранжев формализм 395
и интеграла от скалярной плотности гамильтониана Ж, так что в
терминах гейзенберговского представления гамильтониан запишет-
запишется в виде:
Я = Jd3J|P2 +|(VQJ +|m2Q2 +.Ж(<2I G.1.35)
В этом случае канонически сопряженный к Q импульс дается той
же формулой, что и для свободных полей:
P = Q. G.1.36)
Однако далее мы увидим, что в общем случае соотношение
между канонически сопряженными импульсами Рп(х) и полевыми
переменными и их производными по времени не такое, как для
операторов свободных полей, а должно выводиться из уравнений
G.1.33) и G.1.34) *.
7.2. Лагранжев формализм
Как мы видели, многие реалистичные теории укладывают-
укладываются в рамки канонического формализма. Поэтому возникает во-
вопрос о выборе гамильтониана. В следующем разделе будет пока-
показано, что простейший способ обеспечить лоренц-инвариантность
и другие симметрии заключается в том, чтобы выбрать подходя-
подходящей лагранжиан и получить из него гамильтониана. При такой
процедуре не происходит потери общности. Имея реалистичный
гамильтониан, мы, как правило, можем реконструировать тот
лагранжиан, из которого данный гамильтониан выводится, обра-
обратив описанный ниже процесс перехода от лагранжиана к гамиль-
гамильтониану. (Вывод формулы G.1.26) — один из примеров такой
реконструкции.) Но хотя мы и можем переходить от гамильтони-
гамильтонианов к лагранжианам и наоборот, все же проще исследовать
физически удовлетворительные теории, перебирая не гамильто-
гамильтонианы, а возможные лагранжианы.
* Предполагается, что уравнения движения заданы в гамильтоновой фор-
форме. — Прим. ред.
396 Глава 7. Канонический формализм
В общем случае лагранжиан есть функционал * L[4f(t),4!(t)] от
множества произвольных полей 4?l(x,t) и их производных по време-
времени *j*(t). Сопряженные поля Пг(х,?) определяются как вариационные
производные **
Уравнения движения имеют вид
Полезно переформулировать эти полевые уравнения в форме ва-
вариационного принципа. Определим функционал от поля *Рг(ж) во
всем пространстве—времени, называемый действием:
= (
В результате произвольной вариации *Р(ж) изменение 1[Ч?] записы-
записывается в виде:
Ы[Ч>]= Г dt\d3x
* Напомним, что в используемых нами обозначениях функционал типа L,
в котором явно указывается переменная t, понимается как зависящий от
полей Ч*г(х,*:) и 4* (x,t), причем не выписанные переменные I и х пробегают
все возможные значения при фиксированном значении указанной перемен-
переменной t. Мы используем заглавные буквы "РиП, чтобы подчеркнуть, что это не
свободные, а взаимодействующие поля.
** Так как в общем случае Ч* и *Р не удовлетворяют простым соотношени-
соотношениям коммутации или антикоммутации, мы не можем дать простого определе-
определения возникающих здесь функциональных производных по аналогии с функ-
функциональными производными по Q и Р в предыдущем разделе. Вместо этого
договоримся, что вариационные производные таковы, какие они должны быть
для с-числовых переменных, с добавлением знаков «минус» и коммутаторов
или антикоммутаторов при равных временах, необходимых для того, чтобы
формулы стали квантово-механически корректными. Насколько я знаю, с
деталями этого вопроса не связано никаких особых проблем.
7. 2. Лагранжев формализм
397
Предполагая, что §4>1(х) обращается в нуль при t —» ±оо, можно
произвести интегрирование по частям и записать
- Л4,
5L
d 5L
(ж)
G.2.4)
Мы видим, что действие стационарно по отношению ко всем вариа-
вариациям 8Ч?1, исчезающим при t —> +°°, в том и только в том случае,
когда поля удовлетворяют уравнениям G.2.2)*.
Так как полевые уравнения определяются функционалом
1[^], то при попытках построить лоренц-инвариантную теорию
естественно считать этот функционал скаляром. В частности,
поскольку I[4f] равен интегралу по времени от L[*P(t),ti'(t)], мы
предполагаем, что L должен быть интегралом по пространствен-
пространственным переменным от обычной скалярной функции переменных
Ч?(х) и ЭЧ'/Эсс^, называемой плотностью лагранжиана 9Р,:
\^) G.2.5)
так что действие равно
ТО = J d4x 3>(Ч?(х), дЧЧх) I Ъх*). G.2.6)
Все теории поля, используемые в современных теориях элементар-
элементарных частиц, имеют лагранжианы указанного вида.
Варьируя *Рг(ж) на величину 6*Рг(а:) и интегрируя по частям,
находим для вариации лагранжиана:
5L = Jd2
х
ъя>
-у.
dSP
м
так что (опуская очевидные аргументы у функций)
* Строго говоря, излагаемая здесь формулировка вариационного принципа
предполагает, что искомые поля — решения полевых уравнений G.2.2) —
являются «стационарной точкой» действия G.2.3), т. е. входят в область
определения последнего (соответствующие интегралы G.2.5), G.2.6) сходят-
сходятся). — Прим. ред.
398 Глава 7. Канонический формализм
i^~i^~ '^' G'2-7)
5L Ш
В результате полевые уравнения G.2.1) принимают вид:
Э д9Р, д9Р,
дх^) дЧ<1 ' G'2'9)
Они называются уравнениями Эйлера-Лагранжа. Как и ожидалось,
если 9Р, — скаляр, то эти уравнения лоренц-инвариантны.
В дополнение к тому, что действие должно быть лоренц-
инвариантным, оно должно быть действительным. Это требова-
требование связано с тем, что мы хотим иметь ровно столько же полевых
уравнений, сколько имеется самих полей. Разбивая всякое ком-
комплексное поле на действительную и мнимую части, можно всегда
считать I функционалом только некоторого числа, скажем, N,
действительных полей. Если бы действие I было комплексным с
независимыми действительной и мнимой частями, то действи-
действительная и мнимая части условий стационарности I (уравнения
Эйлера—Лагранжа) приводили бы к 2JV уравнениям для N полей.
Это слишком много, за исключением специальных случаев. Кроме
того, в следующем разделе мы увидим, что действительность
действия обеспечивает эрмитовость генераторов различных пре-
преобразований симметрии.
Хотя лагранжев формализм позволяет легко строить тео-
теории, являющиеся инвариантными относительно преобразований
Лоренца и других симметрии, для вычисления .^-матрицы все же
нужна формула для гамильтониана взаимодействия. В общем слу-
случае гамильтониан определяется преобразованием Лежандра:
н = ? J а3хпг (х, t)i>1 (х, t) - L№)Mt)]. G.2.io)
Хотя формула G.2.1) в общем случае не позволяет однозначно выразить
Ч?1 через *Рг и Пг, легко видеть, что вариационные производные G.2.10)
по *Рг обращаются в нуль для любых Ч11, удовлетворяющих G.2.1).
7. 2. Лагранжев формализм
399
Поэтому функция Гамильтона является функционалом только от Ч*1 и
Пг. Ее вариационные производные по этим переменным равны *:
5Я
84*l(x,t)
п
5L
V ' 84"(x,t)
5L
84" (у, t)
5Я
8nl(x,t)
5L
(У, t)
V V ' 8nl(x,t)
84»'(У, *)
где нижние индексы указывают на те величины, которые считаются
постоянными при взятии вариационных производных. Используя
определение G.2.1) для Пг, можно упростить полученные выраже-
выражения:
ч>
5Я
8nl(x,t)
ч>
G.2.11)
G.2.12)
Тогда уравнения движения G.2.2) эквивалентны уравнению
5Я
S4'l(x,t)
G.2.13)
п
Возникает искушение отождествить исходные полевые пере-
переменные 4*г и сопряженные им импульсы Пг с каноническими пере-
переменными Q" и Рп таз предыдущего раздела и потребовать выполне-
выполнения тех же самых коммутационных соотношений G.1.30)—G.1.32).
При этом уравнения G.2.12) и G.2.13) совпадают с гамильтоновыми
* Строго говоря, нижеследующие формулы справедливы в предположении,
что Ц>1 однозначно выражаются через *Рг и Пг. — Прим. ред.
400 Глава 7. Канонический формализм
уравнениями движения G.1.33) и G.1.34). Именно так обстоит дело в
простом случае действительного скалярного поля Ф со связью без
производных. Рассмотрим плотность лагранжиана *
1 т2 „
9Р, = Э^ФЭ^Ф Ф2-.Ж(Ф), G.2.14)
Zu Zu
которую можно получить добавлением действительной функции -
.Ж(Ф) поля Ф к найденной в предыдущем разделе плотности лагран-
лагранжиана свободного поля. В данном случае уравнения Эйлера-Лагран-
жа имеют вид:
(П-т2)Ф = .^'(Ф), G.2.15)
Исходя из этой плотности лагранжиана, вычисляем канонически
сопряженный к полю Ф импульс:
дЬ ¦
П = ^ = Ф, G.2.16)
ЭФ
который совпадает с G.1.36), если отождествить Ф и П с канониче-
каноническими переменными Q и Р. Теперь согласно G.2.10) находим гамиль-
Н =
±т2Ф2
* Мы не включаем в слагаемое —гЭ^ФЭ^ произвольный множитель, по-
поскольку всякую такую положительную постоянную можно убрать в норми-
нормировку Ф. Если бы постоянная была отрицательной, то, как мы увидим, это
привело бы к неограниченному снизу гамильтониану. Постоянную т в этом
выражении называют голой массой. Наиболее общий лагранжиан, удовле-
удовлетворяющий принципу перенормируемости (см. гл.12), имеет указанный вид,
где Ж(Ф) — полином четвертой степени по Ф.
** Для интерпретации Я как энергии необходима ограниченность этой функции
снизу. Положительность двух первых слагаемых показывает, что мы правиль-
правильно угадали знак первого слагаемого в G.2.14). Остается условие, что комбина-
комбинация \т2Ф2 + М{Ф) должна быть ограничена снизу как функция Ф.
7. 2. Лагранжев формализм 401
что совпадает с гамильтонианом G.1.35). Это маленькое упражнение
следует рассматривать не как еще один вывод этого гамильто-
гамильтониана, а как оправдание пригодности лагранжиана G.2.14) * для
теории скалярных полей.
Однако не всегда дело обстоит так просто. Мы уже видели в
предыдущем разделе, что существуют полевые переменные типа
временной компоненты векторного поля или эрмитово сопряженно-
сопряженного дираковского поля, которые не являются каноническими поле-
полевыми переменными Qn и не имеют канонически сопряженных им
величин. Однако в силу лоренц-инвариантности эти переменные
обязаны содержаться в лагранжиане векторного и дираковского
полей.
С точки зрения лагранжевого формализма, особый характер
полевых переменных типа временной компоненты векторного поля
или эрмитово сопряженного дираковского поля возникает из-за
того, что сами они входят в лагранжиан, а их производные по
времени — нет. Обозначим через С те полевые переменные Ч?1, чьи
производные по времени не входят в лагранжиан. Остальные неза-
независимые полевые переменные являются каноническими перемен-
переменными Q". Для Q" канонически сопряженными импульсами будут
8L[Q(t),Q(t),C(t)]
РМ G218>
причем выполняются коммутационные соотношения G.1.30)—G.1.32).
Однако для С канонически сопряженных импульсов нет. Так как
8L / 8СГ =0, гамильтониан в общем случае имеет вид:
Н = Y,jd3xPnQn -L[Q(t),Q(t),C(t)], G219)
т
однако пользы от этого выражения мало, пока мы не выразим С и
Q через Q и Р. Уравнения движения для С содержат только поля и
их первые производные по времени:
* Здесь и иногда ниже автор употребляет один и тот же термин «лагранжиан»
как для собственно лагранжиана L, так и для плотности лагранжиана (? (см.
G.2.5)). Это смешение общепринято в современной литературе; содержание
термина обычно явно следует из контекста. — Прим. ред.
402 Глава 7. Канонический формализм
&L[Q(t),Q({),C(t)]
0=
В простейших случаях, рассматриваемых в этой главе, получен-
полученные уравнения вместе с уравнениями G.2.18) можно решить, и
найти С и Q как функции Q и Р. В разделе 7.6 показано, каким
образом можно на самом деле избежать реального решения уравне-
уравнений для Си Q.B калибровочных теориях типа электродинамики
следует использовать другие методы: либо выбирать конкретную
калибровку, как это сделано в гл. 8, либо применять обсуждаемые в
т. II более современные ковариантные методы.
Так как мы вывели выражение для гамильтониана как функ-
функционала от Q и Р в гейзенберговском представлении, то для исполь-
использования теории возмущений необходимо совершить переход к пред-
представлению взаимодействия. Гамильтониан не зависит от времени,
поэтому его можно записать через операторы Рп и Q" при t = 0,
которые совпадают с операторами рп и qn, взятыми в тот же момент
времени в представлении взаимодействия. Полученный таким обра-
образом гамильтониан можно выразить через q и р в представлении
взаимодействия и разбить на две части: должным образом выбран-
выбранный гамильтониан Яо для свободных частиц и оператор взаимодей-
взаимодействия V. Наконец, используются уравнения G.1.21) и G.1.22), уста-
устанавливающие зависимость от времени, и коммутационные или
антикоммутационные соотношения G.1.1)—G.1.2), чтобы выразить
q и р в V(t) в виде линейных комбинаций операторов уничтожения
и рождения.
Несколько примеров этой процедуры приведено в разделе
7.5. Сейчас ограничимся только одним простейшим примером —
скалярным полем с гамильтонианом G.2.17). Разбиваем Н на два
слагаемых — гамильтониан свободных частиц, и гамильтониан
взаимодействия:
Ho=J
H = H0+V,
d3x |П2+|(УФJ +
V =\в?хЖ{Ф).
G.2.21)
G.2.22)
G.2.23)
7. 2. Лагранжев формализм 403
Здесь Ф и П берутся в один момент времени t, a H не зависит от t,
хотя обычно это неверно для Яо и V.
Теперь переходим к представлению взаимодействия. Полагая
t = 0 в формулах G.2.22) и G.2.23), можно просто заменить Ф, П на
переменные в представлении взаимодействия ф, ж, так как соглас-
согласно G.1.28) и G.1.29) эти величины совпадают друг с другом при t = 0.
Чтобы получить оператор взаимодействия V(t) в представлении
взаимодействия, применим преобразование подобия C.5.5):
V(t) = exp(zHoi)V ехр(-гН0?) = J d3x .Ж(ф(х, t)). G.2.24)
Такое же преобразование, примененное к Но, оставляет его постоян-
постоянным:
Яо = exp(zHot)Ho exp(-zHot) = jd3xUjt2(x,t)+ -1(Уф(х,?)J . G.2.25)
Связь между лиф определяется формулой G.1.21)
Ф(х> *) = , , ° . = ^(х> *)¦ G.2.26)
8л(х t) *¦ ;
(Полученное соотношение совпало с G.2.16), но как будет видно
дальше, в общем случае это не так.) Кроме того, уравнение движе-
движения для ф определяется формулой G.1.22):
8Н
тс(х, t) = - °— = +У2ф(х, t) - ш2ф(х, t), G.2.27)
5ф(х,?)
что вместе с G.2.26) приводит к полевому уравнению
(?-т2)ф(х) = 0. G.2.28)
Общее действительное решение этого уравнения можно записать в
виде
Ф(ж) = Bjr)-3/2Jd3pBp°)-1/2[eipa;a(p)-e-ipa;af(p)], G.2.29)
404 Глава 7. Канонический формализм
V9 9
Р + "г , а а(р) - некоторая пока
что неизвестная операторная функция р. С помощью G.2.26)
получаем канонически сопряженный импульс
ж{х) = -zBjr)-3/2Jd3pBp°)-1/2[eipa;a(p)-e-ipa;af(p)]. G.2.30)
Чтобы получить желаемые коммутационные соотношения
[(p(x,t),Jt(y,t)]_ = z53(x-y), G.2.31)
[(p(x,t),(p(y,t)]_=O, G.2.32)
[7C(x,t)>7C(y,t)]_=0, G.2.33)
следует принять, что операторы а удовлетворяют известным ком-
коммутационным соотношениям
[a(p),aV)] = 53(p-p'), G-2.34)
= 0. G.2.35)
Кроме того, мы уже показали в предыдущем разделе, что с помо-
помощью этих выражений формула G.2.25) с точностью до неопределен-
неопределенной аддитивной константы переходит в обычную формулу D.2.11)
для гамильтониана свободных частиц. Как было отмечено, эти ре-
результаты не следует рассматривать как альтернативный вывод фор-
формул G.2.29), G.2.34) и G.2.35), полученных в гл. 5 из совершенно иных
соображений, а как проверку того, что первые два слагаемых в
G.2.14) являются правильным лагранжианом свободных частиц для
действительного скалярного поля. Теперь можно использовать тео-
теорию возмущений длля вычисления .^-матрицы, взяв за V(t) выраже-
выражение G.2.24), где поле ф(ж) дается формулой G.2.29).
Описанная здесь процедура будет рассмотрена в разделе 7.5
на более сложных и интересных примерах.
7.3. Глобальные симметрии 405
При изучении различных возможных плотностей лагранжиа-
лагранжианов физических теорий часто приходится применять интегрирова-
интегрирование по частям, рассматривая плотности лагранжианов, отличаю-
отличающиеся на полную дивергенцию d^F^, как эквивалентные. Очевидно,
что такие полные дивергенции не дают вклада в действие и поэтому
не влияют на полевые уравнения. Столь же очевидно, что слагае-
слагаемые с пространственной производной V-./в плотности лагранжиана
не дают вклада в лагранжиан и поэтому не влияют на определяе-
определяемую им квантовую теорию *. Менее очевидно и заслуживает упоми-
упоминания, что добавление производной по времени Эо,/° в лагранжиан
также не влияет на квантовую структуру теории. Чтобы увидеть
это, рассмотрим сначала результат добавления к лагранжиану
слагаемого более общего вида
AL(t) = Jd3xDnx[Q(t)]Q"(x,t), G.2.36)
где D — зависящий от п и х произвольный функционал от значений
Q в данный момент времени. Это приводит к следующей добавке к
сопряженным величинам P(t) как функционалам от Q(t) и Q{t);
w^jr <7-2-37)
Отсюда следует, что гамильтониан, записанный как функционал от
Q(t) и Q(t), не изменяется:
Jd3xAPn(x,t)Q"(x,t)-AL(t) = 0. G.2.38)
Поэтому гамильтониан как функционал старых канонических пере-
переменных Q" и Рп не изменяется, но как функционал новых канони-
канонических переменных Qn и Рп + АРп он имеет другой вид, а в
теории, описываемой новым лагранжианом (? + Д9?, каноническим
коммутационным соотношениям должны удовлетворять не Q" и Рп,
* Утверждение верно при обычном предположении, что поля исчезают на
бесконечности. При рассмотрении полей разной топологии (см. т. II) эти ре-
результаты не всегда применимы.
406 Глава 7. Канонический формализм
а новые канонические переменные Q" и Рп + АРп. Коммутаторы Q"
друг с другом и с Рт даются обычными каноническими соотноше-
соотношениями, но коммутаторы Рп друг с другом равны теперь
глр < ^ ар , Л1 -п,х№(^] .m,y[Q()] G-2-39)
+ APn x,t ,APm y,t = -г : + i - .
SQm(y,t) 5Q"(x,t)
В общем случае, это не равно нулю, однако если добавочное слагае-
слагаемое в лагранжиане является полной производной по времени,
AT f 7.4 'L-CV/J Г\П1 j-\
It = J Ж*™,„^ (X)); G-2-40)
то D в G.2.36) имеет специальный вид
^ _п _ 5G[Q(t)]
В этом случае коммутатор G.2.39) обращается в нуль, и перемен-
переменные Q" и Рп удовлетворяют обычным коммутационным соотноше-
соотношениям. Мы уже видели, что изменение лагранжиана вида G.2.36)
не изменяет формы гамильтониана как функционала от Q" и Рп.
Как только что было показано, коммутационные соотношения
для этих величин также не изменяются, поэтому добавление
слагаемого G.2.36) к лагранжиану не влияет на квантовую струк-
структуру теории. Таким образом, разные плотности лагранжианов,
получающиеся друг из друга интегрированием по частям, могут
рассматриваться как эквивалентные и в классической, и в кван-
квантовой теории поля.
7.3. Глобальные симметрии
Мы подошли к главному свойству лагранжева формализма: он
представляется наиболее естественным для квантово-механической
7.3. Глобальные симметрии 407
реализации принципов симметрии. Дело в том, что динамические
уравнения в лагранжевом формализме имеют форму, следующую
из вариационного принципа — принципа стационарности действия.
Рассмотрим любое бесконечно малое преобразование полей
4ll(x) + ie.Jl(x), G.3.1)
*.
оставляющее действие инвариантным
О = 51 = ге J d4a:
(Если ? - постоянная величина, такие симметрии называются гло-
глобальными. В общем случае -J1 зависит от полей и их производных в
точке х.) Конечно, соотношение G.3.2) автоматически выполняется
для всех бесконечно малых вариаций полей, если сами поля удов-
удовлетворяют динамическим уравнениям. Бесконечно малые преобра-
преобразования симметрии — это такие преобразования, которые оставля-
оставляют инвариантным действие даже тогда, когда динамические урав-
уравнения не удовлетворяются. Если теперь мы рассмотрим то же самое
преобразование, считая ? произвольной функцией точки простран-
пространства—времени,
Ч?1(х) —> Ч?1(х) + iz(x)ifl{x), G.3.3)
то в общем случае вариация действия не обратится в нуль. Однако
она должна иметь вид
G.3.4)
для того, чтобы быть равной нулю, когда е(х) действительно
постоянна. Если теперь принять, что поля в 1\Ч?] удовлетворяют
полевым уравнениям, тогда I будет стационарным по отношению к
* Нижеследующее рассмотрение (неявно) содержит два тонких пункта. Во-
первых, поля Ч*г(х) в G.3.1) должны включать решения динамических
уравнений, т. е. последние должны входить в область определения действия
2[Ч*] (см. примечание редактора на с. 397). Во-вторых, чтобы было верно G.3.2),
вариация симметрии iz$(x) должна быть допустимой (исчезать на
бесконечности),. — Прим. ред.
408 Глава 7. Канонический формализм
произвольным вариациям полей, обращающимся в нуль на боль-
больших пространственно-временных расстояниях, включая и варации
вида G.3.3), так что в этом случае G.3.4) должно обращаться в нуль.
Интегрируя по частям, видим, что J^(x) должен удовлетворять
закону сохранения
Отсюда немедленно следует, что
где
dF
0 = —, G.3.6)
dt
F=\d3xJ°. G.3.7)
Каждому независимому бесконечно малому преобразованию сим-
симметрии соответствует только один сохраняющийся ток J^ и один
интеграл движения F. Это общее свойство канонического формализ-
формализма, часто называемое теоремой Нетер: наличие симметрии влечет
существование законов сохранения *.
Многие преобразования симметрии оставляют инвариантным
не только действие, но и лагранжиан. Например, так обстоит дело в
случае пространственных трансляций и поворотов, а также изоспи-
новых преобразований и других преобразований внутренних сим-
симметрии, хотя для общих преобразований Лоренца это не выполня-
выполняется. Если лагранжиан инвариантен, можно продвинуться дальше и
написать явную формулу для сохраняющейся величины F. Рассмот-
Рассмотрим вариацию поля G.3.3), в которой е(х) зависит от t, но не от х. В
этом случае вариация действия равна
bLmt)Mt)]E{tyjl{xt)
i I \~ G-3-8)
e(t),/W)
dt
* Стандартно понимаемая теорема Нетер утверждает не только существование
законов сохранения, но и их конкретный вид, т. е. явный вид сохраняющегося
нетеровского тока J^ и интеграла движения F, отвечающих данному действию I и
данной симметрии G.3.1) (см ниже на с. 409). — Прим. ред.
7.3. Глобальные симметрии 409
Требование инвариантности лагранжиана под действием этого пре-
преобразования при постоянном ? приводит к равенству:
0 =
, 8ЦУ((),Ф(()] d ,
V ? / <-»- —,7 , . -¦ V ? /
G.3.9)
Поэтому для произвольных полей (удовлетворяющих или не удов-
удовлетворяющих полевым уравнениям) вариация действия равна
Сравнивая это с формулой G.3.4), получаем:
F = --,
G-3-и)
Используя условие симметрии G.3.9), читатель может легко убе-
убедиться, что полученная величина F действительно не зависит от
времени для любых полей, удовлетворяющих динамическим урав-
уравнениям G.2.2).
Другие преобразования симметрии, например, изоспиновые
вращения, оставляют инвариантными не только действие и лагран-
лагранжиан, но и плотность лагранжиана. В таких случаях можно продви-
продвинуться еще дальше и записать явную формулу для тока J^(x) *. Если
представить действие в виде интеграла от плотности лагранжиана,
как в G.2.6), то вариация действия при преобразовании G.3.3) с
произвольным бесконечно малым параметром ?(ж) имеет вид
* Явную формулу для тока J^{x) можно написать и в общем случае. В этом
и состоит конструктивное содержание теоремы Нетер. Именно, при общем
преобразовании симметрии G.3.1) плотность лагранжиана S{vf{x), Э\|/(х)/Эх^)
изменяется на полную дивергенцию, ЬЯ'= г'Э^(е2У(х)), откуда, при постоянном
8, следует явный вид сохраняющегося нетеровского тока:
*
— Прим. ред.
410 Глава 7. Канонический формализм
-ifl(x)e(x)
G.3.12)
dJifl(x)e(x))
Из инвариантности плотности лагранжиана при постоянном ? сле-
следует, что
Q — г1 :ж1(пгЛ _1_ ^
так что для произвольных полей эта вариация имеет вид
,,з.14,
Сравнение с G.3.4) показывает, что
if1.
С помощью условия симметрии G.3.13) нетрудно показать, что если
поля удовлетворяют уравнениям Эйлера-Лагранжа G.2.9), то вы-
выполняется равенство Э^11 = 0. Заметим также, что интеграл от
временной компоненты тока G.3.15) имеет ранее полученное значе-
значение G.3.11).
До сих пор все сказанное было применимо как для классиче-
классической, так и для квантово-механической теорий поля. Квантовые
свойства сохраняющихся величин F проще всего видны для симмет-
симметрии функции Лагранжа (не обязательно лагранжиана), преобра-
преобразующих канонические поля Qn(x,t) (т. е. те из полей Ч?1, производные
по времени от которых входят в функцию Лагранжа) в зависящие
* Ср. с выражением в примечании на с. 409 при ТI = 0. — Прим. ред.
7.3. Глобальные симметрии 411
от х функционалы от самих этих полей в тот же момент времени.
При таких преобразованиях
]. G.3.16)
Как мы увидим, бесконечно малые пространственные трансляции и
вращения, а также все бесконечно малые преобразования внутрен-
внутренних симметрии имеют вид G.3.1), G.3.16), где ,?п — линейный
функционал от Qm. Однако в данный момент не потребуется пред-
предположение, что симметрия линейна. Для всех подобных симметрии
оператор F не только сохраняется. В рамках квантовой механики он
также действует как генератор такой симметрии.
Чтобы увидеть это, прежде всего заметим, что в случае,
когда *Рг есть каноническое поле Q", функциональная производная
Ь^/ЬЧ11 равна канонически сопряженному импульсу Рп, тогда как
если Ч11 есть вспомогательное поле С, эта функциональная произ-
производная равна нулю. Поэтому можно переписать G.3.11) в виде:
F = -z
= -zJd3xJd3yPn(x,t),/"[Q(t);x]. G.3.17)
Чтобы вычислить коммутатор (но не антикоммутатор) F с
каноническим полем Qm(x,t) в произвольный момент времени t,
достаточно сослаться на закон сохранения G.3.6), согласно которому
в G.3.17) можно подставлять Q и Р в произвольный момент времени t,
а затем использовать канонические коммутационные соотношения
при равных временах G.1.30)—G.1.32). В результате получаем *:
[F,Qn(x,t)]_=-Jn(K,t). G.3.18)
Именно в этом смысле F является генератором преобразования
G.3.16). Из формулы G.3.17) и канонических коммутационных соот-
соотношений следует также, что
* Мы предполагаем, что для бозонных или фермионных Qn вариация .>"
также является, соответственно, бозонной или фермионной, так что F —
бозонный оператор. Единственным исключением являются так называемые
суперсимметрии, для которых F — фермионный оператор. Тогда, если
Qn — фермионный оператор, то в левой части G.3.18) стоит антикоммутатор.
412 Глава 7. Канонический формализм
(„19,
Если Fm линеен, то из G.3.19) вытекает, что Рп преобразуется
контраградиентно по отношению к Q".
В качестве первого примера преобразования симметрии рас-
рассмотрим пространственно-временные трансляции
4>1(х) ^4I{х + г) = 4>1(х) + е^Ч>1(х). G.3.20)
Оно имеет вид G.3.1) с четырьмя независимыми параметрами ?^ и
соответствующими четырьмя функциями преобразования
Как следствие имеем четыре независимых сохраняющихся тока,
которые принято объединять в тензор энергии-импульса T^v:
a^T^v = 0. G.3.22)
Отсюда можно вывести выражения для не зависящих от времени
величин, равных интегралам по пространству от временных компо-
компонент отвечающих трансляциям «токов» (не путать с канонически
сопряженными полевыми переменными Pn(x,t)):
Pv = jd3xT\, G.3.23)
d
— Pv=0. G.3.24)
dt
Лагранжиан инвариантен относительно пространственных
трансляций, так что в соответствии с изложенными выше общими
результатами можно сделать вывод, что пространственные компо-
компоненты Pv имеют вид
P = -Jd3xPn(x,t)VQ"(x,t). G.3.25)
7.3. Глобальные симметрии 413
Используя одновременные коммутационные соотношения G.1.30)—
G.1.32) находим коммутаторы этого оператора с каноническими
переменными — полями и сопряженными им импульсами:
(x,t), G.3.26)
n nx,t). G.3.27)
Отсюда следует, что для любой функции '§ от Q и Р, которая не
зависит явно от х, выполнено равенство
[P,<§(x)] = iV<§(x). G.3.28)
Эти результаты показывают, что Р действительно является опера-
оператором пространственных трансляций.
В противоположность этому, трансляции по времени не ос-
оставляют лагранжиан L(t) инвариантным. Однако мы уже знаем
вид генератора временных трансляций. Это гамильтониан Р° = Я,
который, как известно, удовлетворяет коммутационному соотно-
соотношению
[H,$(x,t)] = -i$(x,t). G.3.29)
для любой функции ^' от гейзенберговских операторов.
Если предположить далее, что лагранжиан равен интегралу
от плотности лагранжиана, то можно получить явную формулу для
тензора энергии-импульса T^v. Однако плотность лагранжиана (? (х)
неинвариантна относительно пространственно-временных трансля-
трансляций, так что в этом случае нельзя использовать формулу G.3.15).
Вместо этого заметим, что при трансляции, зависящей от про-
пространственно-временной точки,
4>1(х) ^4<1{х + е(ж)) = 4>1(х) + е^(х)д^Ч>1(х), G.3.30)
изменение действия имеет вид
414 Глава 7. Канонический формализм
В силу уравнений Эйлера-Лагранжа G.2.9) слагаемые, пропорцио-
пропорциональные ?, собираются в выражение * Е^д^Я?, так что
Интегрируя по частям, видим, что это соотношение принимает
форму G.3.4):
5 Jd4Vve^ G.3.33)
где «токи» имеют вид **:
В качестве проверки заметим, что пространственные компо-
компоненты интегралов движения G.3.23) совпадают с нашей прежней
формулой G.3.25) для Р, а для ц = 0 формула G.3.23) приводит к
обычному выражению для гамильтониана:
Ро =
G.3.35)
(Предупреждение: тензор T^v, полученный поднятием индекса в
G.3.34), в общем случае несимметричен, и поэтому не может
* Здесь, видимо, недоразумение: слагаемые, пропорциональные 8,
собираются в выражение 8^Э„^, где Э„ символизирует полную производную
Я'{х) как сложной функции х, безотносительно к уравнениям движения
G.2.9). Если же воспользоваться этими уравнениями с самого начала, то
подынтег-ральное выражение собирается в полную дивергенцию
и вариация 81 исчезает, как и положено. — Прим. ред.
** Этот вид нетеровских токов Т^ непосредственно следует из теоремы
Нетер в той формулировке, которая дана в прим. ред. на с. 409. Достаточно
заметить, что при трансляциях с постоянным е^ вариация '? имеет вид полной
дивергенции: Ь<Р = ецЭц^ = ЭДе^У) = Эу(ец8^|.— Прим. ред.
7.3. Глобальные симметрии 415
входить в правую часть полевых уравнений общей теории относи-
относительности. Правильный симметричный тензор энергии-импульса
®^v, который можно использовать как источник гравитационного
поля, вводится в следующем разделе.)
Во многих теориях имеется один или несколько дополнитель-
дополнительных принципов симметрии, утверждающих инвариантность дейст-
действия относительно некоторых линейных не зависящих от координат
преобразований как канонических полей
Qn(x)^Qn(x) + iEa(ta)nmQm(x), G.3.36)
так и любых вспомогательных полей С:
Cr(x) -> Cr(x) + iea(xa)rsCs(x). G.3.37)
Здесь tavi ia — наборы эрмитовых матриц, реализующих некоторые
представления алгебры Ли группы симметрии, и подразумевается
суммирование по повторяющимся групповым индексам а, Ъ, и т. д.
(Например, подобная симметрия существует в электродинамике,
когда единственная матрица tnm диагональна, причем на главной
диагонали стоят заряды соответствующего поля.) Каждая такая
симметрия порождает свой набор сохраняющихся токов J^:
Э^=0, G.3.38)
временные компоненты которых являются плотностями не завися-
зависящих от времени операторов
Та = jd3xJ^ . G.3.39)
Если не только действие, но и лагранжиан инвариантны относи-
относительно преобразований G.3.36), то из G.3.11) вытекает явная фор-
формула для Та:
Та =-z|d3xPn(x,t)(ta)"mQm(x,t). G.3.40)
Тогда из одновременных коммутационных соотношений следу-
следует, что
416 Глава 7. Канонический формализм
), G.3.41)
. G.3.42)
(В случае, когда оператор ta диагоналей, отсюда следует, что опера-
операторы Q" и Рп, соответственно, понижают и повышают значение Та на
величину, равную n-ому диагональному элементу ta.) Эти формулы
позволяют вычислить коммутаторы генераторов друг с другом:
[Ta,Tb]_ =ijd^-Pm(tarn(tb)\Qk+Pn(tb)\(ta)kmQm]. G.3.43)
Соответственно, если матрицы ta образуют алгебру Ли со структур-
структурными константами fabc,
[ta,tb]_ = ifabc tc , G.3.44)
это же верно и для квантовых операторов Та:
[Ta,Tb]_=ifabcTc. G.3.45)
Этот результат подтверждает правильную нормировку опера-
операторов G.3.40) как генераторов группы симметрии.
Если лагранжиан есть интеграл от плотности лагранжиана,
которая инвариантна относительно преобразований G.3.36) и G.3.37),
можно продвинуться дальше и получить с помощью G.3.15) явные
формулы для токов, соответствующихс этим глобальным симметриям:
J" s WWU"Qm 'э^Л)Г*С8 ¦ G-3-46)
В качестве иллюстрации предположим, что у нас имеется два
действительных скалярных поля равной массы с плотностью лаг-
лагранжиана
- \т2ф\ - \Э^Ф2Э^Ф2 - \т2Ф22 - Я(Ф^ +ф\).
G.3.47)
7.3. Глобальные симметрии 417
Она инвариантна относительно линейного преобразования вида
G.3.36):
5Ф1 = -еФ2, 8Ф2 = +гФ1,
так что существует сохраняющийся ток G.3.46)
Явную формулу G.3.46) для тока можно использовать для вывода
других полезных коммутационных соотношений. В частности, по-
поскольку плотность лагранжиана не содержит производных по вре-
времени от вспомогательных полей, имеем:
J°a=-iPn(tarmQm. G.3.48)
Поэтому можно получить одновременные коммутаторы каноничес-
канонических полей и сопряженных им импульсов не только с генераторами
симметрии Та, но и с плотностями J0:
"mQm(x,t), G.3.49)
[(m(y] (y(J"mPn(x,t). G.3.50)
Если вспомогательные поля построены как локальные функции от Р
и Q таким образом, что они преобразуются по представлению
алгебры симметрии с генераторами та, то для них
[J°(x, t), Cr(y, t)] = -53(x - у)(та)%С8(х, t). G.3.51)
Мы часто будем объединять G.3.49) и G.3.51) в одно коммутационное
соотношение
[J»(x, t),Ч1(у, t)] = -53(x - y)(tjv^'(x, t). G.3.52)
В гл. 10 коммутационные соотношения вида G.3.49)—G.3.51) будут
использованы для вывода соотношений, известных как тожде-
тождества Уорда, для матричных элементов операторов, включающих
ток J^.
418 Глава 7. Канонический формализм
7.4. Лоренцевская инвариантность
Мы собираемся теперь показать, что лоренц-инвариантность
плотности лагранжиана влечет за собой лоренц-инвариантность
5-матрицы. Рассмотрим бесконечно малое преобразование Лоренца
Л% = 5% + &Л, , G-4.1)
wnv = -^vn • G-4.2)
Согласно проведенному в предыдущем разделе анализу, инвари-
инвариантность действия относительно таких преобразований немедленно
влечет существование набора сохраняющихся «токов» .,М?^\
= 0, G.4.3)
G.4.4)
по одному току на каждую независимую компоненту со^. Интегра-
Интегралы от временных компонент этих «токов» дают набор не зависящих
от времени тензоров:
j G.4.5)
0. G.4.6)
dt
Окажется, что величины J^v являются генераторами однородной
группы Лоренца.
Хотелось бы получить явные формулы для тензора ЛР^,
однако преобразования Лоренца действуют на координаты и поэто-
поэтому не могут оставить инвариантной плотность лагранжиана*.
* Для сравнения укажем, что формулировка теоремы Нетер, приведенная
в прим. ред. на с. 409, немедленно приводит к результату. Достаточно заметить,
что вариация % отвечающая бесконечно малым преобразованиям Лоренца
= C0yXV, имеет вид полной дивергенции:
— Прим. ред.
7. 4. Лоренцевская инвариантность 419
Следовательно нельзя сразу же воспользоваться результатами
предыдущего раздела. Однако трансляционная инвариантность по-
позволяет сформулировать лоренцевскую инвариантность как сим-
симметрию плотности лагранжиана только относительно некоторых
преобразований полей и их производных *. Поля испытывают мат-
матричное преобразование
Ь^ = 1-^{$^тЧ™, G.4.7)
где Д^, - набор матриц, удовлетворяющих соотношениям алгебры
однородной группы Лоренца:
[/цу. /ра ] = #pvV " ^етЛцр - ^цаЛур + ^црЛуа ¦ G-4-8)
Например, для скалярного поля ф имеем 5ф = 0, так что j^v = 0, в
то время, как для неприводимого поля типа (А,В)
Зц = ?цк( 4 + %). Ао = -Я -4 - •%).
где -/ и .!# — спиновые матрицы для спина А и В, соответственно.
Специально отметим, что для ковариантного векторного поля
5VK = co^V^, так что
Производная поля, преобразующегося по закону G.4.7), сама преоб-
преобразуется как другое такое поле, но с лишним векторным индексом:
№ ¦ G.4.9)
Предполагается, что плотность лагранжиана инвариантна относи-
относительно совместных преобразований G.4.7) и G.4.9), так что
0 = 2 (JWm ^ ш'ч2 ('^y) m K
* He затрагивающих координат. — Прим. ред.
420
Глава 7. Канонический формализм
Полагая равным нулю коэффициент при @^v, находим:
м— (/ ? д чг»
2 дщ'
Э5Р
Используя уравнения Эйлера-Лагранжа G.2.9) и нашу формулу
G.3.34) для тензора энергии-импульса Т , можно записать послед-
последнюю формулу как
— — (Т —Т )
G.4.10)
Она немедленно подсказывает определение нового тензора энер-
энергии-импульса, известного как тензор Белинфанте 2:
_ г_ з
2
?1СР
G.4.11)
Величина в квадратных скобках явно антисимметрична по ц и к,
так что @^v удовлетворяет тому же закону сохранения, что и Т^у:
G.4.12)
По той же причине, когда мы полагаем ц = 0 в G.4.11), индекс к
принимает значения, отвечающие только пространственным ком-
компонентам, поэтому после интегрирования по всему пространству
слагаемые с производными выпадают:
G.4.13)
где Р° = Н. Таким образом, наряду с Т^у, тензор 0ЦУ также можно
рассматривать как тензор энергии-импульса. Однако из G.4.10)
7. 4. Лоренцевская инвариантность 421
следует, что тензор Белинфанте @^v, в отличие от тензора Т^у, не
только сохраняется, но и симметричен:
©цу = 0уц G.4.14)
Именно &™, а не T^v, выступает как источник гравитационного
поля.3 Как следствие симметрии 0^v, можно построить еще одну
сохраняющуюся тензорную плотность
_xv@?in_ G.4.15)
Она сохраняется в том смысле, что
= 0. G.4.16)
Таким образом, лоренцовская инвариантность позволяет опреде-
определить еще один не зависящий от времени тензор
xv@on)_ G.4.17)
Генератор вращений Jk = ?ijfcJlV2 не просто не зависит от времени,
но не имеет явной зависимости от времени, поэтому он коммутиру-
коммутирует с гамильтонианом:
[H,J] = 0. G.4.18)
Кроме того, применяя G.3.28) к функции 0% находим
—®ok -xk —
и поэтому
[Pj,Ji] = -ieijkPk. G.4.19)
С другой стороны, генератор «буста» Kk = Jk0 хотя и не зависит от
времени, но явно содержит временную координату:
422 Глава 7. Канонический формализм
Кк = Jd3x(xfc0oo-x°0ofc),
или подробнее
K = -tP + Jd3xx0oo(x,i). G.4.20)
Так как эта величина постоянна, имеем 0 = К = —Р + г[Н,К], откуда
[Н,К] = -гР. G.4.21)
Кроме того, еще раз применяя G.3.28), находим:
= -z5,fc[d3x000
J
дх]
и поэтому
G.4.22)
Для любой разумной плотности лагранжиана оператор G.4.20) бу-
будет «гладким» в смысле раздела 3.3, т. е. члены взаимодействия в
егЯ°*^3хх0оо(х,О)е~гЯ°* обращаются в нуль * при t —>±°°. (Заметим,
что члены взаимодействия в егЯ°*^3хх0оо(х,О)е~гЯ°* должны обра-
обращаться в нуль при t —> +°° для того, чтобы можно было ввести
понятия «ин» и «аут» состояний и 5-матрицы.) С учетом предполо-
предположения о гладкости и коммутационных соотношений G.4.21) можно
повторить аргументы раздела 3.3 и заключить, что .^-матрица
лоренц-инвариантна.
Те же аргументы были использованы в разделе 3.3, чтобы убедить-
убедиться, что остающиеся коммутационные соотношения группы Лоренца
для компонент J^v друг с другом имеют нужный вид. Это можно
* Когда говорят, что какой-то оператор в представлении взаимодействия об-
обращается в нуль при t —> ±ро, подразумевается, что в этом пределе обращаются
в нуль матричные элементы этого оператора между состояниями, являющими-
являющимися гладкими суперпозициями собственных состояний оператора энергии.
7.5. Переход к представлению взаимодействия. Примеры 423
проверить и непосредственно для коммутаторов генераторов вра-
вращений, которые имеют вид
Л = jd3x-^j(xidj4>1 -х^дг4>1 - i{Sij)lm^m)- G.4.23)
Так как плотность лагранжиана не зависит от производных по
времени вспомогательных полей, а генераторы вращений не сме-
смешивают канонические и вспомогательные поля, можно записать это
выражение как сумму только по каноническим полям:
J ", \ J ^ l ^ V7~ / re j \ i
Тогда из канонических коммутационных соотношений немедленно
вытекает, что
[ЛМп{х)]_ = -i(xidj-xjdi)Qn(x)-(r^)nn'Qn\x), G.4.25)
[Л,Рп{х)}_ = -i{xidj -х^{)Рп(х) + (с^)пп'Рп'(х), G.4.26)
Эти результаты можно использовать для вывода обычных
коммутационных соотношений J4 друг с другом и с остальными
генераторами *. Если нет никаких вспомогательных полей, те же
аргументы можно использовать и для генераторов «буста», завер-
завершив тем самым доказательство, что Р^ и J^y удовлетворяют комму-
коммутационным соотношениям неоднородной группы Лоренца. Однако
матрицы «буста» Ji0 в общем случае перемешивают канонические и
вспомогательные поля (так же, как в случае компонент V1 и V0
векторного поля), поэтому прямое доказательство коммутационных
соотношений Jl° друг с другом приходится проводить отдельно в
каждом случае. К счастью, это не требуется для приведенного в
разделе 3.3 доказательства лоренц-инвариантности .^-матрицы.
* Кроме того, поскольку операторы J4 коммутируют с Я и PnQn, они
коммутирует с У. Таким образом, коммутатор J4 со вспомогательными поля-
полями должен быть совместим с инвариантностью ^ относительно вращений.
424 Глава 7. Канонический формализм
7.5. Переход к представлению взаимодействия. Примеры
В конце раздела 7.2 мы показали, как можно использовать
лагранжиан простой теории скалярного поля для вывода структуры
взаимодействия и тех свободных полей, которые содержатся в нем
в представлении взаимодействия. Обратимся к более сложным и
поучительным примерам.
Скалярное поле. Связь с производной
Прежде всего, рассмотрим скалярное поле, но на этот раз с
взаимодействием с производными. Выберем лагранжиан в виде:
| Ф - .Ж(Ф), G.5.1)
где J^ — либо с-числовой внешний ток (не имеющий отношения к
введенным выше токам J^), либо функционал от некоторых других,
отличных от Ф, полей (в этом случае к G.5.1) следует добавить
слагаемые, содержащие эти поля). Канонически сопряженный к
полю Ф импульс имеет вид
ЪЗР,
П = э^ = Ф-/° , G.5.2)
а гамильтониан имеет вид
Н =
= J с*3хГп(П + J0) +1 (УФJ -1 (П + J0 )
122 J. УФ +J°(n °
2
Группируя слагаемые, можно записать его в виде
H = HQ+V, G.5.3)
G.5.4)
7.5. Переход к представлению взаимодействия. Примеры 425
V = jd3x\uj° + J • УФ + ^(J0J + .Ж(ФI. G.5.5)
Как объяснялось в разделе 7.2, переход к представлению взаимо-
взаимодействия осуществляется простой заменой П и Ф на ж и ф (аналогич-
(аналогично следует поступить и для всех полей , входящих в ток J*1, но мы
не будем это явно выписывать):
Яо = J d3x | ж2 (х, t) + | (Уф(х, t)J + | тп2ф2 (х, t)
V(t) = J d3x[jr(x, t)J° (x, t) + J(x, t) ¦ Уф(х, t)
G.5.7)
Гамильтониан свободных частиц совпадает с G.2.25) и приводит,
как и в разделе 7.2, к уравнениям G.2.26)-G.2.35). Какой бы ни был
полный гамильтониан, мы должны выделить в нем слагаемое G.5.6),
называемое гамильтонианом свободных частиц, а оставшуюся часть
считать взаимодействием, поскольку, как мы видели, именно эта
форма гамильтониана свободных частиц приводит к правильному
разложению G.2.29) скалярного поля по операторам рождения и
уничтожения, удовлетворяющим коммутационным соотношениям
G.2.34), G.2.35). Заключительный шаг состоит в замене л в гамильто-
гамильтониане взаимодействия на его значение ф в представлении взаимо-
взаимодействия (но не на его значение ф — J в гейзенберговском представ-
представлении):
V(t) =
G.5.8)
Как мы видели в разделе 6.2, дополнительное неинвариантное
слагаемое в G.5.8) необходимо для сокращения неинвариантного
слагаемого в пропагаторе поля Эф.
Векторное поле, спин единица
Аналогичные результаты получаются при каноническом кван-
квантовании векторного поля V^ для частицы спина единица. Не будем
426 Глава 7. Канонический формализм
вводить сначала никаких ограничений и запишем лагранжиан в
достаточно общей форме
G.5.9)
где ОС, C и т2 — пока что произвольные константы, а Р — либо
с-числовой внешний ток, либо оператор, зависящий от полей, отли-
отличных от У1 (в этом случае в 9?, следует добавить слагаемые, содержащие
эти поля). Полевые уравнения Эйлера-Лагранжа для Уц имеют вид
m2Vv = -Г .
После взятия дивергенции получаем
(а + &)ndxVx + m^V1 = -dxJx . G.5.10)
Это уравнение для обычного скалярного поля массой тп2/(а+C) с
источником Э^/(а+C). Мы хотим описать теорию, содержащую
только частицы спина единица, но не спина нуль. Поэтому, чтобы
избежать появления Э^У как независимо распространяющегося ска-
скалярного поля, нужно выбрать а = -C. Тогда Э^У^ можно выразить
через внешний ток или другие поля в виде —dyj/m2. Константу ОС
можно включить в нормировку поля Уц, так что положим а = -C=1.
В результате получим:
$ = -^F^-\m2V^-J^, G.5.11)
Fnv = 3nVv - 3vVn • G-5.12)
Производная лагранжиана по производной по времени векторного
поля имеет вид
Это выражение не равно нулю, если ц принимает пространствен-
пространственные значения г, так что Уг являются каноническими полями, а
сопряженные им импульсы имеют вид
7.5. Переход к представлению взаимодействия. Примеры 427
ГР =Fi0 =У*+Э.У°. G.5.14)
С другой стороны, F00 = О, так что уО не входит в лагранжиан.
Поэтому V0 является вспомогательным полем. Это не приводит к
особым трудностям: обращение в нуль Э^/ЭУ0 означает, что поле-
полевое уравнение для V0 не содержит вторых производных, и поэтому
может использоваться как связь, исключающая некоторую поле-
полевую переменную *. Конкретно, уравнение Эйлера-Лагранжа при
V = 0 имеет вид
Э -Fi0 = m2V° + J° , G.5.15)
так что с помощью G.5.14) находим
V°=^-(V-n-J°). G.5.16)
т
Вычислим теперь гамильтониан Н = \d3x(YI ¦ V - 9Р,) в этой тео-
теории. В силу уравнения G.5.14) можно записать V через П и J0:
V = -VV0 + П = П - Д- V(V • П - J0),
так что
Я = Jс*3х[П2 + m(V • П)(У • П - J°) - -|п2 + -|(V • VJ
+ k? -m(V • П - J0J + J • V - m-2J°(V • П - J
Вновь мы разбиваем это выражение на слагаемое Яо, отвечающее
свободным частицам, и взаимодействие V:
H = H0+V, G.5.17)
и переходим к представлению взаимодействия, заменяя величины
в гейзенберговском представлении V и Р на их аналоги в представ-
представлении взаимодействия v и р (так же следует поступить для всех
полей и сопряженных им импульсов, входящих в J^, хотя мы не
выписываем этого явно):
* В контексте лагранжева и гамильтонова формализма английскому термину
constraint соответствует русский термин связь. — Прим. пер.
428
Глава 7. Канонический формализм
- Глз
х
V= [d3J
J L
2m2
j -v-m-2J°V -n
2m2
G.5.18)
G.5.19)
Тогда v и п связаны соотношением
V =
^- = ж - m~2V(V • ж)
G.5.20)
а «полевые уравнения» имеют вид
5Я0(у,7г)
71 = --
5v
= +V2v - V(V • v) - m2v.
G.5.21)
Поскольку V0 не является независимой полевой переменной, она не
связана преобразованием подобия ни с каким объектом v° в пред-
представлении взаимодействия. Напротив, мы можем ввести величину
ь°=т~2^-ж. G.5.22)
Тогда с помощью формулы G.5.20) можно записать ж в виде
я = у + Уг;0. G.5.23)
Подставляя это выражение в G.5.22) и G.5.21), получаем полевые
уравнения:
VV +V -v-mV =0,
V2v - V(V • v) - v - Vt>° - m2v = 0.
Их можно записать в ковариантной форме
?г;^ - d^dyvy - m2v^ = 0. G.5.24)
После взятия дивергенции получаем:
= 0,
G.5.25)
7.5. Переход к представлению взаимодействия. Примеры 429
следовательно,
(П-т2)^=0. G.5.26)
Действительное векторное поле, удовлетворяющее уравнениям
G.5.25) и G.5.26), можно представить в виде фурье-разложения
G.5.27)
где р° = д/р2 +т2 > ?Ц(Р,<з) при a = +1, 0, -1 — три независимых
вектора, удовлетворяющих условию
^) = 0 G.5.28)
и нормированных так, что
(p,G)ev4(p,G) = тГ + PV / ™2 , G-5.29)
а a(p,a), a^p.a) - операторные коэффициенты. С помощью G.5.23),
G.5.27) и G.5.29) можно непостредственно убедиться, что v и %
удовлетворяют правильным коммутационным соотношениям:
G.5.30)
[Vх (х, t), v' (у, Щ = [%г (х, t), %i (у, t)] = 0,
если операторы a(p,a) и a^(p,a) удовлетворяют коммутационным
соотношениям вида
^CT, G.5.31)
[a(p,a),a(p/,a')] = 0. G.5.32)
Мы уже знаем, что векторное поле частиц спина единица должно
иметь вид G.5.27), так что представленный вывод этих результатов
430 Глава 7. Канонический формализм
служит лишь для проверки, что G.5.18) дает правильный гамильтониан
свободных массивных частиц спина единица. Легко проверить также,
что G.5.18) можно записать (с точностью до постоянного слагаемого) в
стандартной форме ?ст J d?p p°af (p, o)a(p, a) энергии свободных частиц.
Наконец, пользуясь G.5.22), можно записать выражение G.5.19) для
гамильтониана взаимодействия в представлении взаимодействия в виде
V(t)= \d3
x\j
2m
Дополнительное неинвариантное слагаемое в G.5.33) имеет как раз тот
вид, который, как мы установили в гл. 6, необходим для сокращения
неинвариантного слагаемого в пропагаторе векторного поля.
Дираковское поле, спин 1/2
Для дираковского поля частицы со спином 1/2 попробуем взять
лагранжиан в виде
SP. = -?(у^ + т)Ч> - Ж(Ч7, Ч>), G.5.34)
где Ж — действительная функция Ч* и Ч*. Такое выражение не
является действительным, однако действие удовлетворяет этому
требованию, так как
Таким образом, полевые уравнения, получаемые из требования
стационарности действия относительно вариаций *Р и *Р, являются
сопряженными друг к другу. Это и требуется, если мы не хотим
иметь слишком большое число уравнений поля. Импульс, канони-
канонически сопряженный к Ч?, есть
П = ^ = -Чу° , G.5.35)
поэтому мы не должны рассматривать *Р как поле наравне с Ч?,
а считать его пропорциональным импульсу, канонически сопря-
сопряженному к Ч?.
7.5. Переход к представлению взаимодействия. Примеры 431
Гамильтониан имеет вид
Я = J d3x[U4l -3>] = \ d3x [Пу° (у • V + т)Ч> + Ж].
Запишем это выражение в виде
H = H0+V, G.5.36)
где
Но= jd3xUy°(y-y + my?, G.5.35)
V = jd3xHD>,4>). G.5.38)
Переходим к представлению взаимодействия. Так как G.5.35) не
содержит времени, преобразование подобия G.1.28), G.1.29) немед-
немедленно приводит к соотношению:
% = -щ° . G.5.39)
Аналогично можно записать Но и V(t), заменив *РиПна\|/итсв
уравнениях G.5.37) и G.5.38). Отсюда приходим к уравнению движения *:
G.5.40)
071
или более компактно
^ + т)\[ = 0. G.5.41)
(Другое уравнение движения, тс = -5Я0/5\|/, просто совпадает с
сопряженным к уравнению G.5.41).) Всякое поле, удовлетворяющее
уравнению G.5.41), можно записать в виде фурье—разложения:
Щх) = Bтс)/2 J d3p ? {м(р, G)e^a(p, a) + и(р, а)е~^хЪ*(р, о)},
а
G.5.42)
* Следует иметь в виду, что производные по полю \|/ — левые, тогда как
производные по импульсу % — правые. — Прим. ред.
432 Глава 7. Канонический формализм
где р° = д/р2 + т2 > a(P»s) и b^p.s) - операторные коэффициенты, а
м(р,±г) и г;(р,±г) — два набора из двух независимых решений
уравнений
) = 0, G.5.43)
ц > с) = 0, G.5.44)
соответственно, нормированных так, что *
(-гуПр +тп)
Г1 ' G 5.45)
_ ¦„ + m)
i,o)v{p,o) = -' ' p . G.5.46)
Чтобы получить желаемые антикоммутаторы
= г(у°)ар53(х-у), G-5-47)
[\|/a(x,t),\|/p(y,t)]+=0, G.5.48)
следует принять антикоммутационные соотношения
[a(p,G),aV,c')]+ =[b(p,a),bt(p/,a/)]+ =53(p/-pMCT^, G.5.49)
o/)]+ =[b(p,a),b(p/,a/)]+ =
G 5 50)
[a(p,a),b(p/,a/)]+=[a(p,a),bV,a')]+=O.
* Матрица rfp^ имеет собственные значения ±т, так что ? ии и ^ ии долж-
должны быть пропорциональными проекционным матрицам {—i'f'p^ + га)/2га и
(гУр„ + m)/2m, соответственно. Коэффициент пропорцональности можно подоб-
подобрать с точностью до знака, включив его в определение uwv. Общий знак опре-
определяется условием, что Тг ?ип$ = Y.uTu иТг?ии|3 = ?и v положительны.
7.6. Связи и скобки Дирака 433
и им сопряженные. Эти соотношения согласуются с результатами
гл. 5, что подтверждает правильность выражения G.5.37) как га-
гамильтониана свободных частиц спина 1/2. Записанный через опера-
операторы а и Ь, гамильтониан имеет вид:
Яо =?jd3pp°(af(p,G)a(p,G)-b(p,G)bf(p,G)). G.5.51)
a
Полученное выражение отличается от общепринятого гамильтониа-
гамильтониана свободных частиц на бесконечное с-числовое слагаемое *:
Это с-числовое слагаемое в G.5.52) важно только тогда, когда
мы учитываем гравитационные явления. В противном случае, как и
для скалярного поля, можно отбросить это слагаемое, поскольку
оно влияет только на выбор начала отсчета энергии. После этого Яо
оказывается положительным оператором, как и для бозонов.
7.6. Связи и скобки Дирака
Главная проблема при выводе гамильтониана из лагранжиана
заключается в появлении связей. Стандартный анализ этой пробле-
проблемы принадлежит Дираку 5, и мы будем следовать его терминологии.
Анализ Дирака реально не требуется для обсуждаемых в этой главе
простых теорий, в которых нетрудно идентифицировать свободные
от связей канонические переменные. Для иллюстрации мы будем
использовать теорию действительного массивного поля, вернув-
вернувшись к дираковскому подходу в следующей главе, где он окажется
действительно полезным.
Первичные связи либо накладываются на систему (как напри-
например, в следующей главе, когда мы выберем калибровку электро-
* Заметим, что с-числовое слагаемое в данном случае имеет отрицатель-
отрицательный знак. Гипотетическая симметрия, известная под названием суперсим-
суперсимметрии 4, связывает между собой числа бозонных и фермионных полей та-
таким образом, что все с-числовые слагаемые в Яо взаимно сокращаются.
434 Глава 7. Канонический формализм
магнитного поля), либо возникают как следствие структуры самого
лагранжиана. В качестве примера такого рода рассмотрим лагран-
лагранжиан G.5.11) массивного векторного поля V^, взаимодействующего с
током J,,:
где
V^Vv-^V G.6.2)
Допустим, мы пытаемся рассматривать все четыре компоненты V^
как равноправные. Тогда мы должны определить канонически со-
сопряженные им импульсы
Пц ЕЕ
Отсюда немедленно получаем первичную связь вида
По = 0. G.6.4)
Вообще, мы сталкиваемся с первичными связями всякий раз,
когда уравнения Пг = 6Ь/6(Э0Ч'г) не могут быть разрешены отно-
относительно до4?1, т. е. не позволяют выразить все до4?1 через Пг и *Рг
(по крайней мере, локально). Такая ситуация возникает тогда
и только тогда, когда матрица 52L/5C0vPiMC0vPm) будет имеет
нулевой детерминант. Подобные лагранжианы называются нере-
нерегулярными.
Затем могут существовать вторичные связи, возникающие из
требования, совместности первичных связей с уравнениями движе-
движения. Для массивного вкторного поля такой связью является как раз
уравнение Эйлера-Лагранжа G.5.16) для V0:
Э,П, = m2V° + J°. G.6.5)
В данном случае этим все заканчивается, однако в других теориях
могут встретиться новые независимые связи, возникающие из тре-
требования совместности вторичных связей с полевыми уравнения-
7.6. Связи и скобки Дирака 435
ми и т. д. Разница между первичными связями, вторичными
связями и т. п. несущественна, мы будем рассматривать их все
одновременно *.
Но есть другое, более важное различие между определенны-
определенными типами связей. Те связи, которые мы нашли для массивного
векторного поля, относятся к так называемым связям второго
рода, для которых существуют универсальное предписание для
коммутационных соотношений. Чтобы пояснить разницу между
связями первого и второго рода, а также то предписание, которые
используется в случае связей второго рода, полезно сначала напом-
напомнить определение скобок Пуассона в классической механике.
Рассмотрим любой лагранжиан Ь(*Р, *Р), зависящий от набора
переменных *Pa(t) и их производных по времени *Ра(?). (Лагран-
(Лагранжианы квантовой теории поля относятся к специальному случаю,
когда индекс а пробегает все пары значений I и х.) Для всех этих
переменных можно определить канонические импульсы равенством
dL
П
Величины П и *Р в общем случае не независимы, и могут подчи-
подчиняться различными связям, как первичным, так и вторичным.
Скобка Пуассона определяется равенством
дА дВ дВ дА
где при вычислении производных по *Ра и Па связи не учитываются.
В частности, всегда [Ч"\ ПЬ]Р = 5аь (здесь и ниже все поля берутся в
один и тот же момент времени, а временной аргумент опущен).
Такие скобки имеют те же алгебраические свойства, что и комму-
коммутаторы:
[А,В]р=-[В,А]р, G.6.8)
[А, ВС]Р = [А, В]РС + В[А, С]Р , G.6.9)
* Строго говоря, здесь предполагается, что таким образом получаются все
связи. — Прим. ред.
436 Глава 7. Канонический формализм
включая тождество Якоби
[Д[В,С]Р]Р+[В,[С,А]Р]Р+[С,[ДВ]Р]Р=О. G.6.10)
Если можно было бы принять обычные коммутационные соотноше-
соотношения [4>а, Пь] = 5аь, [4>а, 4>ь] = [Па, Пь] = 0, то коммутатор любых
двух функций Ч1 и П был бы просто равен [А,В] = i[A,B]P. Однако
связи не всегда позволяют это сделать.
Связи в общем случае можно выразить в виде уравнений
XN = 0, где %N — набор функций от *Р и П. Поскольку мы включаем в
рассмотрение все связи, как первичные, так и вторичные, множе-
множество всех связей с необходимостью совместно с уравнениями дви-
движения А = [А, Я]р. Поэтому, при условии, что все
[XN,H]p=0, G.6.11)
уравнения связи %N = 0 удовлетворяются *. Некоторая связь **
называется связью первого рода, если ее скобка Пуассона со всеми
остальными связями обращается в нуль на поверхности связей
(после вычисления скобок Пуассона). Мы столкнемся в следующей
главе с простым примером такой связи при квантовании электро-
магнтитного поля, где связь первого рода возникает из симметрии
действия — электромагнитной калибровочной инвариантности. На
самом деле, множество связей первого рода cN = 0 всегда связано с
группой преобразований симметрии для произвольной величины А.
Бесконечно малое преобразование из этой группы имеет вид
* В современной терминологии для последнего условия используется также,
в частности, автором, термин «при наложении связей». Но наиболее
употребителен термин «на поверхности связей». Имеется в виду, что уравнения
связи %jv — 0 определяют в фазовом пространстве (Ч, Па) некоторую поверхность.
Ниже будет использоваться именно этот последний термин. Кроме того,
гамильтониан Я содержит дополнительные вспомогательные поля — лагранжевы
множители к связям. Уравнения G.6.11) могут определить некоторые из них
как функции 4е, Па. — Прим. ред.
** Согласно современной терминологии любая функция %N из набора,
определяющего поверхность связей %N — 0, называется функцией связи, или
коротко связью. Поэтому под связью в зависимости от контекста понимается
как уравнение связи %N - 0, так и сама функция связи %N. В данном контексте
термин связь понимается во втором смысле, как функция связи. — Прим. ред.
7.6. Связи и скобки Дирака 437
G.6.12)
(В теории поля такие преобразования локальны, поскольку индекс
N включает пространственно-временную координату.) Из формулы
G.6.11) следует, что такое преобразование оставляет гамильтониан
инвариантным **; инвариантной остается также поверхность свя-
связей. Теорию со связями первого рода можно рассматривать либо с
помощью выбора калибровки, либо калибровочно-инвариантными
методами, описанными в т. П.
Связи %n> дополнительные к связям первого рода, обладают
тем свойством, что никакая нетривиальная линейная комбинация
2^nun\.Xn'Xm'\p скобок Пуассона этих связей друг с другом не
обращается в нуль. Это означает, что матрица скобок Пуассона
оставшихся связей неособенная,
Det С Ф 0 , G.6.13)
где
С„М=[Х„,ХМ]Р. G.6.14)
Такие связи называются связями второго рода. Заметим, что
число связей второго рода всегда должно быть четным, поскольку
антисимметричная матрица нечетной размерности по необходимо-
необходимости имеет детерминант, равный нулю.
Как мы видели, в случае массивного действительного вектор-
векторного поля связи имеют вид
%ix=%2x=0, G-6.15)
где
%1Х=П0(х), %2х=Эдах)-т2У°(х)-Лх). G.6.16)
Скобка Пуассона этих связей равна
* Преобразования G.6.12) сопровождаются также определенными
преобразованиями лагранжевых множителей. — Прим. ред.
** На поверхности связей. — Прим. ред.
438 Глава 7. Канонический формализм
Cix,2y =-С2уДх =[%1х,%2у]Р =ш253(х-у) G.6.17)
и, конечно,
Cix,iy = C2x,2y=0. G.6.18)
Эта «матрица» очевидно неособенная, так что связи G.6.15) отно-
относятся ко второму роду.
Согласно Дираку, в случае, когда все связи являются связями
второго рода, коммутационные соотношения имеют вид:
[A,B] = i[A,B]B, G.6.19)
где [A, B]D - обобщение скобки Пуассона, известное как скобка
Дирака:
(Здесь N и М — составные индексы, включающие пространствен-
пространственную координату *, и принимающие в нашем примере векторного
поля значения типа 1,х и 2,х.) Дирак заметил, что дираковская
скобка, как и скобка Пуассона, удовлетворяет тем же алгебраиче-
алгебраическим соотношениям, что и коммутаторы:
[A,B]D=-[B,A]D, G.6.21)
[A,BC]D=[A,B]DC + B[A,C]D, G.6.22)
[А, [В, C]D ]D + [В, [С, A]D ]D + [С, [A, B]D ]D = 0,
G.6.23)
и, кроме того, соотношениям
[XN,B]B=0, G.6.24)
* Автор употребляет здесь термин compaund indices — составные
индексы, а ниже в Приложении общий термин compact notation —
компактные обозначения. В современной литературе более употреби-
употребителен общий термин condensed notation — конденсированные (сжатые)
обозначения. — Прим. ред.
7.6. Связи и скобки Дирака 439
благодаря которым коммутационные соотношения становятся со-
совместными со связями %N = 0. Кроме того, скобки Дирака не
изменяются, если заменить %N любыми другими функциями %'N,
для которых уравнения %'N = 0 и %N = 0 определяют одну и ту же
поверхность связей в фазовом пространстве. Однако все эти прият-
приятные свойства не доказывают, что коммутаторы действительно сле-
следует задавать формулой G.6.19), куда входят скобки Дирака.
Вопрос был, если и не разрешен до конца, то прояснен с
помощью мощной теоремы, доказанной Маскавой и Накаямой6.
Они показали, что для любого набора канонических переменных
Ч?а, Па, подчиняющихся связям второго рода, всегда можно
с помощью некоторого канонического преобразования * построить
два набора переменных Q", Зг и соответствующих им каноничес-
канонических импульсов Рп, ifr, так что уравнения связей будут иметь вид
'йг = ИРГ = 0. Используя эти координаты для вычисления скобок
Пуассона и переопределяя функции связей, так что %1г = 5Г,
%2г = Уг, получим
Cir,is = W,2s\p = 0, C2rj2s = [iPr,iPs]P =0,
а для любых функций А, В
* Напомним, что каноническим мы называем преобразование от одного
набора координат Ч, Па фазового пространствак другому набору Ч*а,Па,
причем [*а,Пь]Р = 5g и [Ча,Чъ]Р = [Па,Пь]Р = 0, где скобки Пуассона
вычисляются по Ч*а и Па. Отсюда следует, что скобки Пуассона любых функ-
функций А, В одинаковы, независимо от того, вычислены ли они по Ч и Па, или
по vfa и Па. Отсюда следует также, что если Ч и Па удовлетворяют га-
мильтоновым уравнениям движения, это же верно для ?°и Па с тем же
гамильтонианом **. При каноническом преобразовании лагранжиан изменя-
изменяется, но только на полную производную по времени, что не меняет величи-
величины действия.
** Конечно, в новых переменных гамильтониан, являющийся скаляр-
скалярной функцией, имеет другой вид. — Прим. ред.
440 Глава 7. Канонический формализм
[A] [А]
Выписанная С-матрица имеет обратную матрицу С = -С,
так что скобки Дирака G.6.20) имеют вид:
[A, B]D = [А, В]Р + [A, Xlr ]Р [%2г, В]Р - [А, х2г ]Р [%1г, В]Р
- ЭА ЭВ ЭВ ЭА - ЭА ЭВ - ЭВ ЭА G 6 25)
3Q" дРп 3Q"
Иными словами, дираковская скобка равна скобке Пуассона, вычис-
вычисленной с помощью редуцированного набора независимых канониче-
канонических переменных Qn, Pn.
Если предположить, что эти независимые переменные удов-
удовлетворяют каноническим коммутационным соотношениям, то ком-
коммутаторы произвольных операторов А, В выражаются через скобки
Дирака формулой G.6.19) *.
Вернемся к массивному векторному полю, чтобы показать,
как его можно проквантовать с помощью скобок Дирака. В этом
случае легко выразить зависимые переменные V0 и По через неза-
независимые переменные Vi и ITj**: имеем просто По = 0, а V0 задается
формулой G.6.5). Из G.6.15) и G.6.17) следует, что CNM имеет в
данном случае обратную матрицу вида:
* Все еще открытым остается вопрос, можно ли принять канонические
коммутационные соотношения для независимых переменных Qn, Pn, постро-
построенных с помощью канонического преобразования Маскавы—Накаямы. В ко-
конечном счете, проверкой таких коммутационных соотношений будет их со-
совместимость с выведенными в гл. 5 коммутационными соотношениями для
свободных полей, но чтобы воспользоваться этим тестом, нужно знать, чему
равны Qn и Рп. В Приложении к этой главе мы описываем два больших класса
теорий, в которых можно установить набор таких независимых величин Qn и
Рп, что дираковские коммутационные соотношения G.6.19) будут следовать
из обычных канонических коммутационных соотношений для Qn и Рп. Мы
покажем также, что в этих случаях гамильтониан, определенный через не-
независимые переменные Q и Р, может быть с тем же успехом записана и
через все переменные Ч'иП
** Это частный случай теорий, обсуждаемых в части А Приложения к этой
главе.
7.6. Связи и скобки Дирака 441
(С-1Iх,2у = _(С-1JуДх = _т-263(х _ у) > G.
(C-l)lx,ly = (С-1Jх,2у = 0 _ G.6.27)
Поэтому предписание Дирака G.6.19), G.6.20) приводит к одновре-
одновременным коммутаторам следующего вида:
[A,B] = i[A,B]F
+ im~2 J d3z([A, По (z)]P [Э-П ¦ (z) - т2V° (z) - J° (z), B]P - A <-» В).
G.6.28)
По определению, имеем:
[V^(x),nv(y)]P =53(x-yM^, [V^(x),Vv(y)]P =[П^(х),Пу(у)]Р =0.
G.6.29)
Отсюда получаем:
[У°(х),П3.(у)] = [У^(х),П0(у)] = 0,
Это в точности те коммутационные соотношения, которые мы
получили бы, предположив, что независимые переменные удов-
удовлетворяют обычным каноническим коммутационным соотноше-
соотношениям
[У* (х), П . (у)] = гб;.53(х - у), [У* (х), V* (у)] = [П ¦ (х), П . (у)] = 0,
и использовав связи для вычисления коммутаторов, содержащих
По и У0.
442 Глава 7. Канонический формализм
7.7. Переопределения полей и несущественные
константы взаимодействия *
В любое действие входят некоторые параметры взаимодействия,
от которых не зависят наблюдаемые, например, массы или мат-
матричные элементы ^-матрицы. Эти параметры называют несуще-
несущественными **. Такое имя они получили потому, что изменение этих
параметров можно устранить простым переопределением полевых
переменных.
Непрерывное переопределение полей, например, бесконечно ма-
малое локальное преобразование Ч!\х) —» Ч'1(х)+ гЕ1(Ч'(х),д11Ч'(х),...),
очевидно не может влиять на любую наблюдаемую в теории ***,
хотя, конечно, может изменить значения матричных элементов
самих полей.
Как узнать, может ли какое-то изменение параметров теории
быть скомпенсировано переопределением полей? Непрерывное ло-
локальное переопределение поля приводит к изменению действия
вида
Поэтому любое изменение 5д, параметров взаимодействия gt, для
которого изменение действия имеет вид:
G.7.2)
* Этот раздел лежит несколько в стороне от основной линии изложения
и может быть опущен при первом чтении.
** Автор употребляет здесь английский термин redundant, дословно —
излишний. — Прим. пер.
*** Например, теорема из раздела 10.2 показывает, что до тех пор, пока
мы умножаем на правильные константы перенормировки полей, элементы
^-матрицы могут быть получены из среднего по вакууму от хронологически
упорядоченного произведения любых операторов, имеющих неисчезающие
матричные элементы между вакуумом и одночастичными состояниями уча-
участвующих в реакции частиц.
7.7. Переопределения полей ... 443
может быть скомпенсировано переопределением полей
Ч>1 (ж) -» Ч>1 (ж) + E
—
dz
и, таким образом, не влияет ни на какую наблюдаемую. Иными
словами, параметр взаимодействия является несущественным,
если при вариации этого параметра изменение действия обраща-
обращается в нуль на уравнениях движения * Ы/ЬЧ11 = 0.
Например, предположим, что лагранжиан теории скалярного
поля имеет вид:
SP.=~ И(Э^ФЭ Ф + ш2Ф2) - -±г
Константа Z является лишней, поскольку
= J \аАхФ(ПФ-т2Ф-
и это выражение обращается в нуль на уравнениях движения
?Ф-ш2Ф = ^дгФ3.
Ь
С другой стороны, ни голая масса т, ни голая константа связи
д не являются несущественными, как и любая функция т и д.
В этом примере переопределение поля, требуемое для ком-
компенсации изменения Z, является простым изменением масштаба,
когда F просто пропорционально Ф. (По этой причине Z называют
константой перенормировки поля.) Это самое общее преобразование
поля, оставляющее инвариантным общую форму такого действия.
Однако для рассматриваемых в разделах 12.3 и 12.4 действий более
общего вида, содержащих произвольное число полей и их произ-
* Дословно автор пишет: «...когда мы пользуемся полевыми уравнениями»,
что в развернутой форме означает: «при условии, что поля в действии удов-
удовлетворяют полевым уравнениям». В современной русской терминологии для
этого условия общепринят термин «на уравнениях движения», который мы
используем здесь и ниже. — Прим. ред.
444 Глава 7. Канонический формализм
водных, нам придется рассматривать как линейные, так и нели-
нелинейные переопределения полей, и в результате несущественным
оказывается бесконечное подмножество параметров теории.
Приложение
Вывод скобок Дирака из канонических коммутаторов
В этом Приложении для теорий двух типов мы покажем, что
формула для коммутаторов в виде дираковских скобок, умножен-
умноженных на г, следует из обычных канонических коммутационных соот-
соотношений для редуцированного набора переменных.
А
Предположим (как это имеет место в случае массивного век-
векторного поля V^), что квантовые переменные Ч и Па, возникающие
из лагранжиана L, можно разделить на два класса *: один набор Q"
независимых канонических переменных (типа Vl(x)) с независимы-
независимыми канонически сопряженными импульсами Рп = dL/dQn, и другой
набор переменных ^(х) (типа V0), производные по времени которых
не входят в функцию Лагранжа. Первичные связи имеют вид
%1г = 0, где
— импульсы, канонически сопряженные к 5Г. Вторичные связи
возникают из уравнений движения 0 = dL/dif для if. Предполо-
Предположим, что эти связи могут быть «разрешены», т. е. их можно
записать в виде %2r = 0> где %2г имеет вид
* Мы вновь используем компактные обозначения, в которых метки а, те и
г включают пространственные координаты х, а также дискретные индексы.
По повторяющимся индексам проводится суммирование и интегрирование.
Считается, что все квантовые переменные вычисляются в один и тот же
момент времени, причем общий временной аргумент везде опущен. Величи-
Величины Qr тождественны введенным в разделе 7.2 величинам С.
Приложение 445
%2r = ^-r(Q,P). G.A.2)
(Примером может служить формула G.6.5), где V0 выражается
через независимые импульсы Р (в данном случае П,) и переменные
Q.) Предположим, что независимые канонические переменные Q и
Р удовлетворяют обычным каноническим коммутационным соот-
соотношениям:
[Qn,Pm] = ibl, [Qn,Qm] = [Рп,Рт] = 0. G.А.З)
Связь %2г = 0 приводит к следующим коммутаторам, включающим 3:
[^"] = -^'^'PJ = ^' G-A.4)
[3r,3s] = iTrs, G.А.5)
где Vs - скобка Пуассона
Г"=[Г,Г]Р, G-А.6)
а все коммутаторы, включающие ИРГ, естественно, равны нулю:
Щ,Q"] = Щ,Рп] = Щ, 3s] = [Щ.,%] = 0. G.А.7)
Сравним эти коммутаторы со скобками Дирака. Скобки Пуассона от
связей имеют вид:
Cir,iss[Xir.Xis]p=0, G.A.8)
s -C2Silr = [%ir,Z2s]p = -4 , G-A.9)
, >%2S]p =[fr(Q,P),f4Q,P)]P ^Г™. G.A.10)
(В примере с массивным векторным полем величины Vs обращают-
обращаются в нуль, но приведенная аргументация верна и для ненулевых
Гге.) Легко видеть, что матрица С имеет обратную:
(C-l)lr,lS=rrS> (СJ*-'28 =0,
(C-l)lr,2S = _(C-lJs,lr = 5r _ G.A.11)
446 Глава 7. Канонический формализм
Кроме того, скобки Пуассона любой функции А со связями имеют
вид
ЭА ЭА
[A, Xir ]р = ^Г, [А, %2г ]Р = - — - [A, fr(Q, Р)]Р •
Отсюда дираковская скобка имеет вид
ЭА ЭВ ЭВ ЭА
ЭА ЭВ ЭА ЭВ G.А.12)
г ?~[BJh~[AJh
Если А и В являются функциями только независимых канониче-
канонических переменных Q" и Рп, тогда ЭА/Э^ = дВ/д^ = 0, и скобка
Дирака равна скобке Пуассона. В частности,
Если А есть Зг, а В есть функция переменных Q и Р, то вклад дает
только пятое слагаемое в правой части G.А. 12). В частности,
G.A.14)
Если и. А, и. В суть переменные 5Г, остается только четвертое
слагаемое
[3r,3s]D =Trs. G.A.15)
Наконец, если А есть ;УГ, а В - любое, остаются только первое и
третье слагаемые, которые сокращаются:
ЭВ
№r,B]B=[0>r,B]P+—- = O. G.A.16)
эз
Сравнение формул G.А.13)-G.А.16) с G.А.З)-G.А.7) показывает, что
во всех случаях коммутаторы равны скобкам Дирака, умноженным на г.
Приложение 447
Этого и следовало ожидать, поскольку, как отмечалось в разделе 7.6, все
дираковские скобки, включающие функции связей, обращаются в нуль,
а дираковские скобки, включающие 5Г и/или ,J?S, можно вычислить,
используя уравнения связи для вьфажения 5 г и/или iPs через независи-
независимые переменные Q и Р.
В
Рассмотрим теперь случай, когда связи принимают вид ус-
условий %1г0Р) = 0 на Ч"\ которые можно разрешить, выразив все *Ра
через меньший набор независимых переменных Q", и такое же
число отдельных условий %2ДП) = 0 на Па, которые также можно
разрешить, выразив Па через меньший набор независимых
переменных Рп. (Соответствующий пример будет рассмотрен
в следующей главе, где связи на *Ра представляют собой условия,
фиксирующие калибровку, а связи на Па — вторичные связи,
возникающие из условия совместности связей первого рода
с полевыми уравнениями.) Предположим, что независимые пере-
переменные удовлетворяют обычным каноническим коммутационным
соотношениям [Qn,Pm] =i5nm, [Qn,Qm] = [Pn,PJ = 0. Зависимые
и независимые импульсы связаны соотношениями
дЬ дЬ дЧ
Отсюда следует, что
= [Ча,Рп] = г
[,ь][,п] г
или, иными словами,
{[^,nb]-z5g}^=0. G.A.18)
Связи %1г(Ч0 = 0 удовлетворяются для Ч = *Pa(Q) при всех Q, так что
0- GА-19)
448 Глава 7. Канонический формализм
Далее, векторы (Vr)b = д%1г/д4!ъ образуют полный набор векторов,
перпендикулярных ко всем векторам (Un)b = 3*Pb/3Qn, поскольку,
если бы существовал какой-то другой вектор Vb, удовлетворяю-
удовлетворяющий условию Vb(Un)b = 0 для всех п, то это означало бы наличие
дополнительных ограничений на хРа. Поэтому из G.А.18) вытека-
вытекает, что
^ G.A.20)
с некоторыми неизвестными коэффициентами саг. Чтобы опреде-
определить эти коэффициенты, используем другие связи, а именно, что
%2г(П) = 0. Из них следует, что
эпь
Используя G.А.20), получаем тогда
Э%2г(П)
GА-21)
Множитель при cas есть скобка Пуассона
ЭХ2г(П) _
[XX]
Кроме того, поскольку %ls зависит только от Ч1, a %2r ~ только от П, это
единственные отличные от нуля скобки Пуассона связей, тогда как
Таким образом, можно переписать G.А.21) в виде
-^ = -csCis,jv . G.А.22)
где N нумерует все связи. Для связей второго рода это уравнение
имеет единственное решение
Приложение
449
c,e=-
эп.
-(с
-1ч2г,Ь
G.А.23)
Подстановка его в G.А.20) показывает, что
а "%2г ,-/".-!-,2r,ls
ь"этГ(С }
Скобки Пуассона *Pa и Пь с функциями связей имеют вид
ггаа y 1 =0 [*Ра Y 1 = 2г
' 1гР ' зпа'
[%2г>Пь]Р=0,
G.А.24)
G.А.25)
так что величина в квадратных скобках в правой части формулы
G.А.24) есть скобка Дирака
[Ч?а,Пъ] = {[Ч>а,Пъ]Т), G.A.26)
что и требовалось показать. Кроме того, легко видеть, что посколь-
поскольку «диагональные» 11- и 22-компоненты матрицы С равны нулю,
остальные скобки Дирака имеют вид
[Ц>а^ъ]в=[Па,Пъ]в=0, G.A.27)
так что тривиальным образом получаем:
[4>a,4>b] = i[xPa,4?b]B, [Па,Пь] = г[Па,Пь]в. G.А.28)
В дополнение к правилам коммутации нам нужна явная формула
для гамильтониана. Согласно обычному каноническому формализму
гамильтониан следует взять в виде
= PnQn-L,
G.А.29)
450 Глава 7. Канонический формализм
где сумма берется по независимым каноническим переменным. В
теориях обоих типов, рассмотренных в этом Приложении, такой
гамильтониан можно записать через все переменные в виде
Н = ПаЧ<а-Ь. G.А.30)
Для теорий типа А это утверждение тривиально: сумма по а
берется по значениям п, для которых *РП = Qn и Пп = Рп —
независимые канонические переменные, а также по значениям г,
для которых Пг = ;УГ = 0. Для теорий типа В заметим, что из G.А.17)
следует
что вновь приводит к G.А.30).
Задачи
1. Рассмотрите теорию нескольких действительных скалярных
полей Фп с лагранжианом
где /пт(Ф) - произвольная действительная матричная функция
поля. (Такая теория называется нелинейной а-моделью.) Про-
Проведите каноническое квантование этой теории. Получите вид
взаимодействия V[(p(t), (j)(t) ] в представлении взаимодействия.
2. Рассмотрите теорию действительных скалярных полей Фп и
дираковских полей Ч11 с лагранжианом 9> = 5Р0 + 9>ь где 5Р0 -
обычный лагранжиан свободных полей, а (?х — взаимодействие,
содержащее поля Фп и Ч*', но не их производные. Получите
явное выражение для симметричного тензора энергии-импуль-
энергии-импульса 0^.
3. Пусть в теории, описанной в задаче 2, плотность лагранжиана
инвариантна относительно глобального инфинитезимального пре-
преобразования
Список литературы 451
5Ф" = ie? ?"тФт , 84|i = ге^. т^Ч" ¦
Получите явные выражения для сохраняющихся токов, свя-
связанных с этой симметрией.
4. Рассмотрите теорию комплексного скалярного поля Ф и дейст-
действительного векторного поля V^ с лагранжианом
СР — -СП ФI' №Ф — — F F^v -—m2V У^ -
J ~ У^\1^> ^ ^ 4 ^v 2 ^
где D^ = Эц — igV^ и F^v = ЭЦУУ - ЭУУЦ, а .Ж" - произвольная
функция. Проведите каноническое квантование этой теории.
Получите вид взаимодействия в представлении взаимодейст-
взаимодействия.
5. В теории, рассмотренной в задаче 4, получите выражения для
симметричного тензора энергии-импульса 0ЦУ и сохраняюще-
сохраняющегося тока, связанного с преобразованием симметрии, при кото-
котором 5Ф = геФ, 8W = 0.
6. Докажите, что скобки Дирака удовлетворяют тождеству Якоби
G.6.23).
7. Докажите, что скобки Дирака не зависят от выбора связи %N,
задающих данное подмногообразие фазового пространства.
Список литературы
1. Casimir,H.B.G., Proc. К. Ned. Akad.Wet., 51, 635A948); Spaarnay,
M.J., Nature, 180, 334 A957).
2. Belinfante, F., Physica, 6, 887 A939); см. также: Rosenfeld, L.,
Memoires de VAcademie Roy. Belgique, 6, 30 A930).
3. См., например: Weinberg, S., Gravitation and Cosmology (Wiley,
New York, 1972), ch. 12 (есть рус. пер.: С. Вейнберг. Гравитация
и космология. М.: Наука, 1972).
452 Глава 7. Канонический формализм
4. См., например: Wess, J. and Bagger, J., Supersymmetry and
Supergravity (Princeton University Press, Princeton, 1983)
и цитированные в этой книге оригинальные работы (есть рус.
пер.: Дж. Весе, Дж. Баггер. Суперсимметрия и супергравита-
супергравитация. М.: Мир, 1985).
5. Dirac, P.A.M., Lectures on Quantum Mechanics (Yeshiva Univer-
University, New York, 1964). См. также: Dirac, P.A.M., Canad. J. Math.,
2, 129 A950); Proc. Roy. Soc. London, ser. A, 246, 326 A958);
Bergmann, P.G., Helv. Phys. Acta Suppl. IV, 79 A956).
6. Maskawa, T. and Nakajima, H., Progr. Theor. Phys., 56, 1295
A976). Я благодарен Дж. Фейнбергу, обратившему мое внима-
внимание на эту ссылку.
8
Электродинамика
Первоначальный подход к квантовой электродинамике заклю-
заключался в том, чтобы принять как данное максвелловскую классиче-
классическую теорию электромагнетизма и проквантовать ее. Вероятно, чи-
читатель уже не удивится тому, что в этой книге мы пойдем другим
путем.
Сначала, анализируя специфические трудности, возникающие
при формулировке квантовой теории безмассовых частиц со спи-
спином, мы придем к необходимости принципа калибровочной инвари-
инвариантности, и затем выведем основные свойства электродинамики. Да-
Далее мы будем следовать более привычным современным путем, и
исходя из калибровочной инвариантности выведем существование
векторного потенциала, описывающего безмассовые частицы спина
единица.
Слишком рано говорить, какая из этих альтернатив отвечает
логическому порядку природы. Большинство теоретиков предпочи-
предпочитает брать за отправную точку калибровочную инвариантность, од-
однако в современных теориях струн1 аргументация иная: сначала
среди нормальных мод струны обнаруживается состояние нулевой
массы и спина единица, а затем из этого выводится калибровочная
инвариантность эффективной теории поля, описывающей такие час-
частицы.
Во всяком случае, как мы увидим, и тот, и другой подход
приводят к квантованной версии максвелловской теории, все еще
остающейся образцовым примером успешной квантовой теории по-
поля.
454 Глава 8. Электродинамика
8.1 Калибровочная инвариантность
Начнем с напоминания тех проблем, которые связаны с по-
построением ковариантных свободных полей для безмассовой части-
частицы спиральности +1. Мы видели в разделе 5.9, что для таких частиц
не составляет труда построить свободное антисимметричное тен-
тензорное поле /цу(ж). Это поле можно выразить через 4-потенциал ац(ж)
E.9.23) с помощью известного соотношения
/цу(ж) = Эцау(ж)-Эуац(ж)- (8.1.1)
Однако из формулы E.9.23) следует, что а^(х) преобразуется как
4-вектор только с точностью до калибровочного преобразования
U0(A)ail(x)Uu1(A) = Aily'av(Ax) + dilQ(x,A). (8.1.2)
На самом деле, нельзя построить истинный 4-вектор как линейную
комбинацию операторов рождения и уничтожения частицы спираль-
спиральности +1. Это объясняет наличие сингулярностей при т = 0 в про-
пагаторе массивного векторного поля
которые не позволяют рассматривать безмассовые частицы спираль-
спиральности ±1, просто переходя к пределу m -) 0 в теории массивных
частиц спина единица.
Можно обойти эти проблемы, потребовав, чтобы все взаимо-
взаимодействия включали не Ац(х), а только * ^цу(х) = ЭцАу(х) -ЭуАц(х) и
их производные, однако это и не самая общая возможность, и не
та, которая реализуется в природе. Вместо изгнания AJx) из дейст-
действия, потребуем, чтобы действие материи 1М, т. е. слагаемое в дейст-
действии, описывающее материю и ее взаимодействия с излучением,
было инвариантным относительно общего калибровочного преобра-
преобразования
* Мы теперь используем обозначения А„ и F^v для вектора электромагнит-
электромагнитного потенциала и тензора напряженности поля, так как это взаимодействую-
взаимодействующие поля.
8.1. Калибровочная инвариантность 455
А^(х) -> А^(ж) + Э^?(ж) (8.1.3)
(по крайней мере, если поля материи удовлетворяют полевым урав-
уравнениям), чтобы дополнительное слагаемое в правой части формулы
(8.1.2) не оказывало никакого влияния. Изменение действия для мате-
материи в результате преобразования (8.1.3) можно записать в виде
ЯГ Л4 ЩМ -
м ~ Ж sTT^4^" (8-1.4)
Поэтому из лоренцевской инвариантности 1М вытекает, что
Это тривиально верно, если 1М содержит наряду с полями материи
только F^x) и его производные. В этом случае
6/м _ озу б7м
Однако если в JM входит само поле А^(х), уравнение (8.1.5) становит-
становится нетривиальным ограничением на теорию.
Обсудим теперь, теории какого типа приводят к сохраняю-
сохраняющимся токам, с которыми может взаимодействовать поле А^(х). В
разделе 7.3 мы видели, что наличие непрерывных внутренних сим-
симметрии действия влечет за собой существование сохраняющихся
токов. В частности, если бесконечно малое преобразование *
ll{x) (8.1.6)
оставляет инвариантным действие материи при постоянном ?, то в
случае произвольной функции е(х) изменение действия материи
должно иметь вид
* Поскольку в данном случае матрица преобразования поля взята диаго-
диагональной, соглашение о суммирования для сумм по повторяющимся индексам
здесь неудобно, так что в формуле (8.1.6) нет суммирования по I.
456 Глава 8. Электродинамика
Ым = -J d4x ^(х)Э^?(х). (8.1.7)
Если поля материи удовлетворяют своим полевым уравнениям, дей-
действие материи стационарно по отношению к любым вариациям Ч11,
так что в этом случае правая часть формулы (8.1.7) должна обра-
обратиться в нуль, откуда
Э^=0. (8.1.8)
В частности, в разделе 7.3 мы видели, что если 1М есть интеграл от
функции У',ж, зависящей от Ч?1 и ЭцЧ^, то сохраняющийся ток дается
формулой *
г
и он порождает преобразования (8.1.6) в том смысле, что
[Q,4>l(x)] = -qi4>l(x), (8.1.9)
где Q — не зависящий от времени оператор заряда
= jd3xJ°. (8.1.10)
Поэтому можно построить лоренц-инвариантную теорию, где век-
векторное поле Ац взаимодействует с сохраняющимся током J^ в том
смысле, что вариационная производная 51м/5АI(х) пропорциональ-
пропорциональна «/^(х). Любая константа пропорциональности может быть погло-
поглощена переопределением общего масштаба зарядов qb так что мож-
можно просто приравнять эти величины друг другу:
(8.1.11)
* Здесь считается, что Ч*г пробегает множество всех независимых полей,
кроме АР. Мы используем заглавное Ч*, чтобы отметить, что это поля
в гейзенберговском представлении, зависимость от времени которых вклю-
включает эффекты взаимодействия. Конечно, эти Ч*г не следует путать с вектором
состояния или волновой функцией.
8.1. Калибровочная инвариантность 457
Сохранение электрического заряда позволяет зафиксировать зна-
значения всех зарядов, выразив их через значение любого из них. При-
Принято выбирать за основу значение заряда электрона, обозначаемое
—е. Именно формула (8.1.11) придает значению е определенный
смысл *.
Требование, выражаемое формулой (8.1.11), можно теперь
сформулировать как принцип инвариантности относительно совмест-
совместных преобразований вида
^ ^ (8.1.12)
=ie(x)ql4ll(x). (8.1.13)
Симметрия такого типа с произвольной функцией е(х) называется
локальной симметрией или калибровочной инвариантностью второ-
второго рода. Симметрия относительно преобразований с постоянным ? на-
называется глобальной симметрией или калибровочной инвариантно-
инвариантностью первого рода. В настоящее время известно несколько точных
локальных симметрии, однако чисто глобальные симметрии, по-
видимому, являются следствием других принципов (см. раздел 12.5).
Мы еще ничего не сказали о действии для самих фотонов. В качест-
качестве догадки можно попытаться взять его таким же, как и для мас-
массивных векторных полей, положив только т = 0:
(8.1.14)
Это действие совпадает с тем, которое используется в класси-
классической электродинамике, однако истинным оправданием выбора та-
такого действия является то, что оно (с точностью до константы) пред-
представляет единственный калибровочно-инвариантный функционал,
квадратичный по F^v и не содержащий высших производных. Кроме
того, как мы увидим в следующем разделе, оно приводит к
согласованной квантовой теории. Любые слагаемые в действии
более высокого порядка по производным и/или по F™, могут быть
* Конечно, (8.1.11) фиксирует определение е только после того, как опре-
определена нормировка Ац(х). Вопрос о нормировке электромагнитного поля обсу-
обсуждается в разделе 10.4.
458 Глава 8. Электродинамика
включены в то, что мы назвали действием материи. С учетом фор-
формул (8.1.11) и (8.1.14) уравнения электромагнитного поля имеют вид
5AV
Видно, что это обычные неоднородные уравнения Максвелла с то-
током Т1. Есть и другие, однородные, уравнения Максвелла
О = Э^уе + Эе^у + 3vFetl, (8.1.16)
которые непосредственно вытекают из определения F^v = д^Ау^
Выше мы исходили из существования безмассовых частиц спина
единица и были вынуждены потребовать инвариантности действия ма-
материи относительно локального калибровочного преобразования (8.1.12),
(8.1.13).
Обычно этот вывод производится в обратном направлении. Ины-
Иными словами, исходят из глобальной внутренней симметрии
8Ф1 = ЩЧ?1(х) (8.1.17)
и задают вопрос, что нужно сделать, чтобы расширить ее до ло-
локальной симметрии
SVl =i?{x)ql4ll{x). (8.1.18)
Если лагранжиан Я1, зависит только от полей Ч^х), но не от их
производных, то нет никакой разницы в том, постоянна величина ?
или нет. Инвариантность с постоянной ? влечет инвариантность и в
случае, когда ? есть функция пространственно-временных коорди-
координат. Однако все реалистические лагранжианы содержат производ-
производные, и мы сталкиваемся с проблемой, что производные полей пре-
преобразуются не так, как сами поля:
Ы^\х) = ie(x)qld[l4ll(x) + iql4ll(x)d[le(x). (8.1.19)
Чтобы второе слагаемое в этом выражении сократилось, мы
«руками» вводим векторное поле А^(х), преобразующееся по прави-
правилу
8.2. Связи и калибровочные условия 459
5А^(х) = Э^?(х), (8.1.20)
и требуем, чтобы лагранжиан зависел от Э„Ч*г и А„ только в
определенной комбинации
^ ^ г^г, (8.1.21)
которая преобразуется так же, как и поле Ч11:
bD^ix) = i?(x)qlD[l4ll(x). (8.1.22)
Если лагранжиан материи ,9?MD',D4'), построенный только из
Ч*г и DJ?l, инвариантен относительно преобразования с постоянной
величиной ?, то он будет инвариантным и относительно преобразо-
преобразований (8.1.18), (8.1.20) с произвольной функцией е(х). Для такого ла-
лагранжиана имеем
. , = _.
5А,
что совпадает с (8.1.11). (Можно было бы включить в 9Р,М также и F^v
и его производные.) С этой точки зрения, безмассовость частиц,
описываемых потенциалом А„, есть не предположение, а следствие
калибровочной инвариантности: слагаемое —2т2АА^ в лагранжиане
нарушало бы калибровочную инвариантность.
8.2. Связи и калибровочные условия
Электродинамика обладает рядом особенностей, препятствую-
препятствующих квантованию этой теории по типу рассмотренных в предыду-
предыдущей главе теорий массивных частиц. Как обычно, можно опреде-
определить канонический импульс для электромагнитного векторного по-
потенциала равенством
Квантование по обычным правилам приводило бы к формуле
460 Глава 8. Электродинамика
Но в данном случае это равенство невозможно, поскольку А„ и ГГ7
подчиняются ряду связей.
Первая из них следует из того факта, что лагранжиан не за-
зависит * от производной величины Ао по времени, и поэтому
П°(х) = 0. (8.2.2)
Это первичная связь, так как она следует непосредственно из струк-
структуры лагранжиана. Но здесь есть и вторичная связь, вытекающая из
уравнения поля для величины, фиксированной первичной связью **:
Э1ГЭ J°
так как слагаемое с производной по времени выпадает из-за равен-
равенства Foo = 0. Хотя лагранжиан материи может в общем случае зави-
зависеть от А0, плотность заряда зависит только от полей материи ***
Q" и канонически сопряженных им импульсов Рп:
J° = -iY Ш , qM = -гУ PnqnQn ¦ (о^лл
Следовательно (8.2.3) есть функциональное соотношение между ка-
каноническими переменными. Оба соотношения (8.2.2) и (8.2.3) несо-
несовместимы с обычными предположениями, что
* В случае Уу - -F^vF^v/4 имеем Э^/Э(ЭрАц) = -F0^, что равно нулю при
(Д, = 0, так как F^v — антисимметричный тензор. Для лагранжиана материи
Ум, включающего только Ч*гиОцЧ*г, предписание (8.1.21) утверждает, что Ум
не зависит от любых производных любых компонент Av. Даже если лагран-
лагранжиан материи зависит от F^v, производная Э.%/Э(ЭУА^) будет также антисим-
антисимметрична по ц и v и, следовательно, обратится в нуль при ц — v = 0.
** Как обычно, г, j, и т. д. принимают значения 1,2,3.
*** Ввиду истощения ресурсов алфавита, я вынужден использовать здесь
иные, чем в предыдущей главе, обозначения. Символы Qn и Рп сохранены для
обозначения полей материи и канонически сопряженных им импульсов, соот-
соответственно, а электромагнитные поля и сопряженные им канонические им-
импульсы обозначены соответственно через Ai и ГГ.
8.2. Связи и калибровочные условия
461
[Qn (x, t), nv (y, t)] = [Pn (x, t), nv (y, t)] = 0.
Мы сталкивались с аналогичной проблемой в теории массив-
массивного векторного поля. В том случае было предложены два эквива-
эквивалентных пути ее решения: либо методом скобок Дирака, либо более
непосредственно, принимая в качестве канонических переменных
только Aj и П' и разрешая аналог уравнения (8.2.3) относительно А0,
что позволяет выразить А0 через эти переменные. Ясно, что в дан-
данном случае нельзя использовать скобки Дирака. Функциями связей
X здесь являются П° и ЭД1, - J0 (вместо ЭД1, - т2А° -J0), и их
скобки Пуассона очевидно равны нулю. По терминологии Дирака,
связи (8.2.2) и (8.2.3) относятся к первому роду. Кроме того, мы не
можем устранить А0 как динамическую переменную, выразив ее
через другие переменные. Вместо того, чтобы определять А0 во все
моменты времени, уравнение (8.2.3) играет роль начального усло-
условия: если оно выполнено в один момент времени, то оно удовлетво-
удовлетворяется во все моменты, поскольку (в силу уравнений для других
полей А1)
Э,
¦-Jc
= -ЗА
-V0
и условие сохранения тока дает
= 0.
(8.2.5)
Не следует удивляться, что у нас имеются четыре компоненты
А^ и только три полевых уравнения. Дело в том, что эта теория обла-
обладает локальной калибровочной симметрией, что делает в принци-
принципе невозможным определить значения полей в произвольные мо-
моменты времени, зная их величину и скорость изменения в любой
определенный момент. Зная любое решение AJx,t) уравнений
462 Глава 8. Электродинамика
поля, всегда можно найти другое решение AI(x,t) + 3I?(x,t), имею-
имеющее те же значения поля и его производной по времени при t = О
(для этого нужно выбрать ? так, чтобы ее первая и вторая произ-
производные обращались в этот момент в нуль), но отличающееся от
А„(х,{) в последующие моменты времени.
Из-за такой частичной произвольности Ац(х,?) невозможно при-
применить процедуру канонического квантования непосредственно к А„
(или к А, как в случае конечной массы). Из множества подходов к
разрешению этой трудности особенно полезны два. Первый — со-
современный метод калибровочно-инвариантного квантования, кото-
который обсуждается в т. П. Второй, которому мы здесь последуем,
заключается в использовании калибровочной инвариантности тео-
теории для того, чтобы «выбрать калибровку». Именно, мы совершаем
конечное калибровочное преобразование
А (х) -> А (х) + Э Х(х), Ч<1 (х) -> ехр(щХ(х)У?1 (ж),
чтобы наложить на поле AJx) условие, позволяющее применить
методы канонического квантования. С точки зрения различных при-
приложений полезными оказываются различные калибровки, например *
калибровка Лоренца (или Ландау): д^А^ = 0;
кулоновская калибровка: V • А = 0;
временная калибровка: А0 = 0;
аксиальная калибровка: А3 = 0;
унитарная калибровка: поле Ф действительно.
Процедура канонического квантования легче всего реализует-
реализуется в аксиальной или кулоновской калибровках. Преимущество ку-
лоновской калибровки перед аксиальной состоит в том, что она со-
сохраняет явную инвариантность относительно вращений, поэтому
здесь мы предпочтем кулоновскую калибровку 2.
Чтобы убедиться, что она возможна, заметим, что если А^ не
удовлетворяет условию кулоновской калибровки, то калибровочно
* Здесь Ф — любое комплексное скалярное поле с q Ф 0. Такое калибровоч-
калибровочное условие используется в ситуации, когда калибровочная симметрия спон-
спонтанно нарушается за счет ненулевого вакуумного среднего поля Ф.
8.3. Квантование в кулоновской калибровке 463
преобразованное поле А^ + д^Х будет ему удовлетворять, если вы-
выбрать X таким, что V2X = — V • А. Начиная с этого момента, предпо-
предполагаем это преобразование выполненным, так что
V-A = 0. (8.2.6)
Далее удобно ограничиться теориями, в которых лагранжиан
материи 9Р,М зависит от полей материи и их производных
по времени, а также от поля А^, но не от его производных.
(Стандартные скалярная и спинорная электродинамики имеют ла-
лагранжианы именно этого типа.) Тогда единственным слагаемым
в лагранжиане, зависящим от F^, является кинетический член
-F)lvF|lv/4, так что уравнение связи (8.2.3) имеет вид:
-Э^° = J0 . (8.2.7)
В сочетании с условием кулоновской калибровки (8.2.6) получаем:
-V2A° = J° , (8.2.8)
решение которого имеет вид:
A°(x,t)= d3y -—. (8.2.9)
Оставшиеся степени свободы — поля A1, i = 1,2,3, подчиняющиеся
условию V • А.
Как отмечено выше, плотность заряда зависит только от полей
материи Qn и канонически сопряженных им импульсов Рп, так что
формула (8.2.9) дает явное решение для вспомогательного поля А0.
8.3. Квантование в кулоновской калибровке
Все же есть еще одно препятствие, мешающее каноническому
квантованию электродинамики в кулоновской калибровке. Даже по-
после использования формулы (8.2.9) для исключения А0 (и П°) из
списка канонических переменных, мы не можем использовать обыч-
обычные канонические коммутационные соотношения для Ai и ГТ^, так
464 Глава 8. Электродинамика
как остались еще две связи, наложенные на эти переменные *. Одна
из них — условие кулоновской калибровки:
Х1хееЭ^А*(х) = 0. (8.3.1)
Другая — вторичная связь (8.2.3), требующая, чтобы
Х2х = ЭДГ(х) + .70(х) = 0. (8.3.2)
Ни одна из этих связей не совместима с обычными коммутационны-
коммутационными соотношениями [АДх), П;(у)] = г5^-53(х - у), поскольку действие
производных д/дхг и Э/Эу-7 на правую часть дает ненулевой резуль-
результат.
Указанные связи относятся к типу, известному как связи вто-
второго рода. Для них существует универсальный рецепт построения
коммутационных соотношений, обсуждавшийся в разделе 7.6. За-
Заметим, что скобки Пуассона функций связи имеют вид:
Г --Г = Tv y I --V252(x-v)
Wx,2y ~ ^y,lx ~LAlx>X2yJP ~ v и *¦ У)>
С1х,1у =[%1х.%1у]р =0, (833)
С = \у v 1 — П
^гхДу — LXlx'XlyJp — и>
где подразумевается, что для любых функционалов 17 и V
517 5V 5V 517
[17,У]р =
5П.(х) 8А*(х) 5П.(х)
«Матрица» CNM неособенная, что как раз и отличает связи второго
рода. Кроме того, полевые переменные Аг можно выразить через
независимые канонические переменные, за которые можно взять,
например, Qlx = Ax(x), Q2x = A2(x), в то время, как А3 дается реше-
решением уравнения (8.3.1)
* В этом разделе i,j и т. д. пробегают значения 1,2,3. Мы продолжаем считать
все операторы взятыми в один момент времени и опускаем временной аргумент.
8.3. Квантование в кулоновской калибровке 465
Аналогично, с помощью уравнения связи (8.3.2) можно выра-
выразить импульсы Л,, канонически сопряженные полям Аг , через им-
импульсы Р1х и Р2х, канонически сопряженные переменным Qlx и Q2x.
В таких случаях, как показано в части В Приложения к предыду-
предыдущей главе, если независимые переменные Qlx, Q2x, Р1х и Р2х удов-
удовлетворяют обычным каноническим коммутационным соотношени-
соотношениям, то коммутаторы подчиняющихся связям канонических пере-
переменных даются (с точностью до множителя г) соответствующими
скобками Дирака G.6.20). Большое преимущество этого рецепта за-
заключается в том, что мы не должны использовать явные выраже-
выражения для зависимых переменных через независимые.
Чтобы вычислить скобки Дирака, заметим, что матрица С име-
имеет обратную:
BЯK
(8.3.4)
Кроме того, неисчезающие скобки Пуассона переменных А' и П, с
функциями связи имеют вид
7
ах
Отсюда, согласно G.6.19) и G.6.20), одновременные коммутаторы
имеют вид
~\9
Эх W I 4л
x-y
(8.3.5)
466 Глава 8. Электродинамика
Заметим, что эти выражения совместны с условиями кулоновской
калибровки (8.3.1) и (8.3.2), что и гарантируется общими свойствами
скобок Дирака.
Но что такое П в электродинамике? Для того класса теорий,
который обсуждался в предыдущем разделе, от Дв лагранжиане
зависит только кинетический член -ffixF^F^/i, варьирование
лагранжиана по А без учета связи V • А = 0 дает:
П= А'(х)
П9^
] 5А'(х
Однако, если А ограничено условием V • А = 0, то вариационные
производные по д, на самом деле, плохо определены. Если при
изменении А на 5А вариация L равна 5L = jd3x SP ¦ 5А, то, поскольку
V • 5А = 0, верно и равенство 5L = J d?x [SP + VF ] • 5А, где ,/(х) - лю-
любая скалярная функция. Поэтому все, что удается выяснить из ис-
исследования лагранжиана, сводится к тому, что П равно А(х) + VA°(x)
плюс градиент некоторого скаляра. Эта неоднозначность устраняет-
устраняется условием (8.3.2), требующим, чтобы V • П = -J° = V2A°. Так как
V-A = 0, приходим к выводу, что формула (8.3.6) действительно
дает правильное выражение для П,.
Хотя коммутационные соотношения (8.3.5) сравнительно про-
просты, мы сталкиваемся с той трудностью, что П не коммутирует с
полями материи и соответствующими им каноническими импульса-
импульсами. Если F — любой функционал этих степеней свободы материи, то
его скобка Дирака с А обращается в нуль, но скобка Дирака с П равна
[F,n(z)]D = - fd3xd3y[F,x2x]P —-^ [%1у,Щг)]р
J 4я| х - у|
= - Г d3xd3y[F, J°(x)]P 1 V53(y- z)
J 4л х - y|
= -Jd3y[F,A°(y)]PV53(y-z)
= [F,VA°(z)]P=[F,VA°(z)]D.
Чтобы упростить переход к представлению взаимодействия, мы за-
запишем гамильтониан не через переменные А и Р, а через переменные
А и П,, где П, — соленоидальная часть Р:
8.3. Квантование в кулоновской калибровке 467
± (8.3.7)
для которой [F, Iljjz)] = 0. Используя то, что Iljjx) коммутирует с
П(у) - П_|_(у) = VA°(y), и что Э,А°(х) коммутирует с Э^А°(у), легко
убедиться, что П_|_(х) удовлетворяет тем же коммутационным соот-
соотношениям (8.3.5), что и П(х), а также простому уравнению связи
У-П±=0. (8.3.8)
Теперь нужно построить гамильтониан. Согласно общим результа-
результатам Приложения к гл. 7, можно, не выписывая гамильтониан явно
через независимые переменные Q и Р, использовать обычное соот-
соотношение между гамильтонианом и лагранжианом, записанное че-
через подчиняющиеся связям переменные А и И±. В электродинамике
это приводит к формуле
Я = J й3х[ПиА{ + PnQn - SR], (8.3.9)
где, как упоминалось выше, Q" и Рп — поля материи и соответст-
соответствующие им канонические импульсы. (В формуле (8.3.9) можно ис-
использовать П± вместо П, так как V -А = 0.)
Для определенности, рассмотрим теорию с плотностью лагран-
лагранжиана
V^ + J^ + ^ (8.3.10)
где J,l — ток, не содержащий А*1, а ^материи — лагранжиан любых
других полей, входящих в J^, кроме их электромагнитного взаимо-
взаимодействия, которое задается в лагранжиане (8.3.10) явно слагаемым
J^A^- (Такой вид имеет лагранжиан электродинамики частиц спина
1/2, тогда как электродинамика частиц спина нуль более сложна.)
Заменяя везде А на П^, приходим к следующему виду гамильто-
гамильтониана (8.3.9):
Я = Г d3x\nl +1 (V х АJ -1 (П± + VA° J - J • А + J°A° 1 + Ям ,
где Ям — гамильтониан полей материи за вычетом их электромаг-
электромагнитного взаимодействия,
468 Глава 8. Электродинамика
Используя представление (8.2.9) для А0, находим
Н=
НМ. (8.3.11)
Слагаемое J°A°/2 выглядит несколько необычно, но это не что иное,
как знакомая кулоновская энергия
,8.3.12,
С помощью коммутационных соотношений (8.3.5) читатель может
проверить, что скорость изменения любой операторной функции F
от А и П дается, как и положено, формулой iF = [F,Я].
8.4. Электродинамика в представлении взаимодействия
Разобъем теперь гамильтониан (8.3.11) на слагаемое Яо, опи-
описывающее свободные частицы, и взаимодействие У:
Я = Я0+У, (8.4.1)
Яо = J d3a|iП2 +1(V х AJ J + Яматерии0, (8.4.2)
У = -J d3x J • А + Укулон + Уматерии . (8.4.3)
где Яматерии0 и Уматерии — входящие в Яматерии гамильтониан свобод-
свободных частиц материи и их взаимодеиствиея, а Укулон — кулоновское
взаимодействие (8.3.12). Полный гамильтониан (8.4.1) не зависит от
времени, поэтому выражения (8.4.2) и (8.4.3) могут быть вычислены
в любой желаемый момент времени (но один и тот же для обеих
слагаемых), в частности, при t = 0. Как и в гл. 7, переход к пред-
представлению взаимодействия производится с помощью преобразова-
преобразования подобия
8.4. Электродинамика в представлении взаимодействия
469
V(t) = exp(iHot)V[A,UL,Q,P]t=o exp(-zHot)
= V[a(t),n(t),q(t),y(t)],
(8.4.4)
где Р означает здесь импульсы, канонически сопряженные полям
материи Q, а любой оператор o(x,t) в представлении взаимодейст-
взаимодействия связан с оператором O(x,t) в гейзенберговском представлении
при t = 0 равенством
= exp(zH0i)O(x,0) exp(-zHoi),
(8.4.5)
так что
= [o(x,t),H0].
(8.4.6)
(Мы опустили индекс _L у к(х).) Так как (8.4.5) есть преобразование
подобия, коммутационные соотношения при равных временах име-
имеют тот же вид, что и в гейзенберговской картине:
5..53(x-y) + ^— —-i—
дхгдх] 4л|х -у
(8.4.7)
(8.4.8)
(8.4.9)
и аналогично для полей материи и соответствующих им канонических
импульсов. По тем же причинам остаются в силе уравнения связей
(8.2.6) и (8.3.8):
V-a = 0, (8.4.10)
V-Jt = O.
(8.4.11)
Чтобы установить соотношение между % и а, следует вычис-
вычислить а согласно формуле (8.4.6):
) = [a,(x,t),H0]
= z|d3y5i753l
дхгдх^ 4л| х - у
470
Глава 8. Электродинамика
Можно заменить Э/Эж-7 во втором слагаемом на ~д/ду\ проинтегриро-
проинтегрировать по частям и воспользоваться (8.4.11), что дает в результате
а = %,
(8.4.12)
как и в представлении Гейзенберга. Аналогично, полевое уравнение
определяется равенством
= -г d3y
5,,53(х-у)
дхгдх^ 4я| х - у
(VxVxa(y,t))r
которое после использования соотношений (8.4.10) и (8.4.12) прини-
принимает вид обычного волнового уравнения
?а = 0.
(8.4.13)
Поскольку А0 не является независимой полевой переменной в гей-
гейзенберговском представлении, а представляет собой функционал
(8.2.9) полей материи и соответствующих им импульсов, обращаю-
обращающийся в нуль в пределе нулевых зарядов, то в представлении взаи-
взаимодействия мы просто полагаем
а° = 0.
(8.4.14)
Наиболее общее действительное решение уравнений (8.4.10), (8.4.13)
и (8.4.14) можно записать в виде
= Bл)/2
/2р° а
(8.4.15)
где р° = |р|, ец(р,а) — два произвольных независимых «вектора по-
поляризации», удовлетворяющие условиям
р-е(р,а) = 0,
е°(р,а) = 0,
(8.4.16)
(8.4.17)
8.4. Электродинамика в представлении взаимодействия
471
а а(р,а) — пара операторных коэффициентов, отвечающих двум
значениям индекса а. Подобрав нормировку а(р,а), можно нормиро-
нормировать е|1(р,о) так, чтобы условие полноты имело вид
(8.4.18)
= 8tj -PiPj/Ы
Например, можно выбрать е(р,а) в таком же виде, как в разделе
5.9:
(8.4.19)
±i/j2
О
О
где К(р) — стандартное вращение, поворачивающее третью ось по
направлению р. Используя формулы (8.4.18) и (8.4.12), можно без
труда убедиться, что коммутационные соотношения (8.4.7)-(8.4.9) бу-
будут выполнены, если (и, на самом деле, только если) операторные
коэффициенты в (8.4.15) удовлетворяют коммутационным соот-
соотношениям
[а(р,а),а(р/,а')] =
(8.4.20)
(8.4.21)
Как отмечалось выше для случая массивных частиц, этот резуль-
результат следует рассматривать не столько как альтернативный вывод
соотношений (8.4.20) и (8.4.21), а как проверку, что (8.4.2) дает пра-
правильный гамильтониан свободных безмассовых частиц спирально-
сти ±1. Действуя в том же духе,можно подставить формулы (8.4.12)
и (8.4.15) в формулу (8.4.2) и вычислить гамильтониан свободных
фотонов
Яо = Jd3p?|p°[a(p,o),a+(p/,o/)]+
(8.4.22)
472 Глава 8. Электродинамика
который получается таким, какой и следовало ожидать (если не
считать несущественного бесконечного с-числового слагаемого).
Наконец, находим, что взаимодействие (8.4.4) в представле-
представлении взаимодействия имеет вид
V(t) = -jd3x ^ (x, t)aP (x, t) + Укулон (t) + Уматерии (t), (8.4.23)
где 7ц(ж) выражается через ток J в представлении взаимодействия:
jp (x, t) = exp(zHot) J^ (x,0) exp(-zHot), (8.4.24)
кулоновское слагаемое имеет вид
) = ехр(Ш0?)Укулон exp(-iHot)
J 4я| х - у
а Уматерии№ есть неэлектромагнитная часть взаимодействия полей
материи в представлении взаимодействия:
^матер„„Ш = ехр(Ш0?)Уматерии exp(-zHot). (8.4.26)
Заметим, что в выражении (8.4.23) написано j^ вместо j-a, однако
это одно и то же, поскольку мы определили 4-вектор а^ так, что
а0 = 0.
8.5. Пропагатор фотона
Согласно описанным в гл. 6 фейнмановским правилам, внутренняя
фотонная линия в диаграмме Фейнмана вносит в соответствующее
слагаемое в .^-матрице множитель, равный пропагатору
-гД^(х-у) = {ФуАС,Т{а[1{х),ау{у)}ФуАС), (8.5.1)
где Т, как обычно, обозначает хронологическое произведение. Под-
Подставляя формулу (8.4.15) для электромагнитного потенциала, находим:
8.5. Пропагатор фотона 473
-zAuv(x - у) = I d!P, Pm(v)[eipix-y)Q(x - у) + е*<У-хМу - х)],
где
-Рцу(р) = 52ец(Р)С)еУ(Р>аГ , (8.5.3)
ст=±1
а рц в показателях экспоненты берется с р° = |р|. Напомним, что
согласно формулам (8.4.17) и (8.4.18)
2 '
(8.5.4)
Как мы видели в гл. 6, тета-функции в (8.5.2) можно записать как
интегралы по независимой временной компоненте д° 4-вектора дц,
лежащего вне массовой поверхности, так что формулу (8.5.2) можно
переписать в виде
A^v (х - у) = Bл)-4 j d4g Pf^ е*<*-й , (8.5.5)
Таким образом, при использовании фейнмановских правил в им-
импульсном пространстве, вклад внутренней фотонной линии, несу-
несущей 4-импульс q и соединяющей две вершины, в которых фотон
рождается и уничтожается полями ац и аУ, дается выражением:
-г
BлL qz - ге
(8.5.6)
Очень полезно (хотя и кажется на первый взгляд извращением)
переписать (8.5.4) в виде
а°а п +а°а п -а а + а2п п
g guuv -rg gv иц gugv ^g "ii'lv
где пц = @,0,0,1) — фиксированный времениподобный вектор, q2
как обычно равно q2 - (g0J, но g° полностью произвольно. Мы
474 Глава 8. Электродинамика
выберем д° в представлении (8.5.7) так, чтобы эта компонента опре-
определялась законом сохранения 4-импульса: это есть разность
компонент р° импульсов частиц материи, входящих и выходящих
из той вершины, откуда исходит фотонная линия *. Поэтому сла-
слагаемые, пропорциональные дц и/или gv, не дают вклада в 5-матри-
цу, так как множители дц и gv действуют как производные Эц и 3V,
а фотонные поля а„ и пу связаны с токами j^ и f, которые удовле-
удовлетворяют условию сохранения д^ = 0 **. Слагаемое, пропорциональ-
пропорциональное ПуУЦ, содержит множитель д2, который сокращается с д2 в зна-
знаменателе пропагатора. В результате получается выражение, совпа-
совпадающее с тем, которое возникло бы от следующего слагаемого в
действии:
Здесь интеграл по g° дает дельта-функцию по времени, так что это
выражение эквивалентно следующей поправке к гамильтониану
взаимодействия V(t):
- у|
* В авторском тексте, если переводить дословно, говорится об отве-
отвечающих материи импульсах, «втекающих» и «вытекающих» из вершины.
В русскоязычных текстах более употребительна другая терминология, которой
мы здесь в основном придерживаемся. Именно, принято не только внешние
линии, отвечающие реальным частицам на массовой поверхности, но
и внутренние линии, отвечающие пропагатору некоторой частицы, отож-
отождествлять с самой частицей (называя ее виртуальной, т. е. лежащей вне
массовой поверхности). Соответственно говорят: частица входит и выходит
из вершины, импульс частицы и т. д. Говорят также (в частности, и автор
книги), что импульс соответствующей частицы входит в вершину или выходит
из вершины. — Прим. пер.
** Приведенные здесь аргументы не многим лучше простого размахива-
размахивания руками. Результат доказывается путем детального анализа фейнманов-
ских диаграмм,3 но простейший способ анализа проблемы связан с обсуж-
обсуждающимися в разделе 9.6 методами функционального интегрирования.
8.6. Правила Фейнмана для спинорной электродинамики 475
Она в точности сокращается со вкладом кулоновского взаимодейст-
взаимодействия (8.4.25). Таким образом, эффективно в качестве фотонного про-
пагатора можно взять ковариантное выражение:
- у) = Bл)-4 Гd^-^e^-rt , (8.5.8)
причем кулоновское взаимодействие выпадает. Мы видим, что ка-
кажущееся нарушение лоренц-инвариантности в мгновенном кулонов-
ском взаимодействии компенсируется другим кажущимся наруше-
нарушением лоренц-инвариантности, заключающимся, как отмечено в раз-
разделе 5.9, в том, что поля аЦх) не являются 4-векторами и поэтому
имеют нековариантный пропагатор. С практической точки зрения
важно то, что в правилах Фейнмана в импульсном пространстве
вклад внутренней фотонной линии дается выражением
а кулоновское взаимодействие отбрасывается.
8.6. Правила Фейнмана для спинорной электродинамики
Наконец мы можем сформулировать фейнмановские правила для
расчета 5-матрицы в квантовой электродинамике. Для опре-
определенности рассмотрим электродинамику одного сорта частиц со
спином 1/2, зарядом q = — е и массой т. Назовем эти фермионы
электронами, но тот же формализм применим и для мюонов и про-
прочих подобных частиц. Простейший калибровочно- и лоренц-инвари-
антный лагранжиан этой теории имеет вид *
+ mL. (8.6.1)
Тогда 4-вектор электрического тока дается простой формулой:
* В гл. 12 мы обсудим причины, по которым в лагранжиан не включаются
более сложные слагаемые.
476 Глава 8. Электродинамика
J» = — =-H
Взаимодействие (8.4.23) в представлении взаимодействия здесь имеет
вид:
V(t) = +iej d3x(^(x,t)y^(x,t)) а^х,*) + VKyjI0H(t). (8.6.3)
(В это выражение не входит Уматерии.) Как было показано, кулонов-
ское слагаемое VKyjI0H(t) нужно только для того, чтобы сократить не-
ковариантную и локальную по времени часть фотонного пропагатора.
Следуя общим результатам раздела 6.3, можно сформулиро-
сформулировать фейнмановские правила в импульсном пространстве для связ-
связной части .^-матрицы в такой теории.
1. Рисуются все фейнмановские диаграммы с числом вершин
вплоть до некоторого заданного. Диаграммы содержат электронные
линии со стрелками и фотонные линии без стрелок, которые
подсоединяются к вершинам, причем в каждой вершине есть одна
входящая и одна выходящая электронные линии и одна фотонная
линия. Каждой частице в начальном или конечном состоянии отвечает
внешняя линия, соответственно входящая в диаграмму снизу или
выходящая из диаграммы вверх. При этом электронам отвечают
внешние линии со стрелками, направленными вверх, соответственно,
в диаграмму или из диаграммы; позитронам отвечают внешние ли-
линии со стрелками, направленными вниз, соответственно, из диа-
диаграммы или в диаграмму. Кроме того, имеется столько внутренних
линий, сколько необходимо, чтобы к каждой вершине подсо-
подсоединялось нужное число линий. Каждой внутренней линии припи-
приписывается (и рисуется рядом с ней) 4-импульс вне массовой поверх-
поверхности *, определенным образом направленный вдоль линии (по
соглашению, импульс направлен вдоль стрелок на электронных ли-
линиях). Каждой внешней линии приписывается (и рисуется рядом с
ней) импульс частицы и z-компонента спина (для электрона) или
спиральность (для фотона) в начальном и конечном состояниях.
2. Элементам диаграммы сопоставляются определенные мно-
множители по следующим правилам.
* Говорят также, что линия несет на себе 4-импульс, который, как уже
отмечалось в прим. пер. на с. 474, отождествляют с 4-импульсом соответ-
соответствующей (виртуальной) частицы. — Прим. пер.
8.6. Правила Фейнмана для спинорной электродинамики 477
Вершины
Каждой вершине приписывается (и рисуется рядом с ней) че-
тырехкомпонентный дираковский индекс ОС около электронной ли-
линии со стрелкой, входящей в вершину, дираковский индекс C около
электронной линии со стрелкой, выходящей из вершины, и про-
пространственно-временной индекс ц около фотонной линии. Каждой
такой вершине сопоставляется множитель
BjcLe(Y%a84(fc-fc' + q), (8.6.4)
где к и к' — 4-импульсы электронов, входящие в вершину и выходя-
выходящие из вершины, ад — 4-импульс фотона, входящий в вершину (или
взятый с обратным знаком импульс фотона, выходящий из вершины).
Внешние линии
Каждой внешней линии приписывается (и рисуется рядом с
ней) 3-импульс р и z-компонента спина или спиральность о частицы
в начальном или конечном состоянии.
Каждой линии, отвечающей электрону в конечном состоянии
и выходящей из вершины с дираковским индексом C около этой
линии, сопоставляется множитель *
- (8-6.5)
Каждой линии, отвечающей позитрону в конечном состоянии
и входящей в вершину с дираковским индексом а около этой ли-
линии, сопоставляется множитель
Bл)
3/2
(8.6.6)
Каждой линии, отвечающей электрону в начальном состоянии
и входящей в вершину с дираковским индексом а около этой ли-
линии, сопоставляется множитель
ма(р,а)
Bл)
3/2
(8.6.7)
* Из выражения для взаимодействия (8.6.4) была предварительно выделена
матрица C, так что вместо uf и vf возникли и и v.
478 Глава 8. Электродинамика
Каждой линии, отвечающей позитрону в начальном состоя-
состоянии и выходящей из вершины с дираковским индексом C около этой
линии, сопоставляется множитель
5)
(8.6.8)
BлK/2
Здесь и и. v — четырехкомпонентные спиноры, свойства которых
обсуждались в разделе 5.5.
Каждой линии, отвечающей фотону в конечном состоянии и
подсоединенной к вершине с пространственно-временным индексом
ц около этой линии, сопоставляется множитель
(8.6.9)
Каждой линии, отвечающей фотону в начальном состоянии и
подсоединенной к вершине с пространственно-временным индексом
ц около этой линии, сопоставляется множитель
(8.6.10)
Здесь e^ — 4-вектор поляризации фотона, обсуждавшийся в пре-
предыдущем разделе.
Внутренние линии
Каждой внутренней электронной линии с 4-импульсом к,
идущей от вершины с дираковским индексом C к другой вершине с
дираковским индексом ОС, сопоставляется множитель
-i [-ilk + ш]ар
(Мы используем здесь очень удобное восходящее к Дираку «пере-
«перечеркивание»: для любого 4-вектора v^ символ t означает произве-
произведение YmU11.)
Каждой внутренней фотонной линии с 4-импульсом q и соеди-
соединяющей две вершины с пространственно-временными индексами ц
и V, следует сопоставить множитель
8.6. Правила Фейнмана для спинорной электродинамики 479
-г ЛцУ
7^7Т~ ~- (8.6.12)
BлL q1 - гг
3. Произведение всех указанных множителей интегрируется
по 4-импульсам всех внутренних линий и суммируется по всем ди-
раковским и пространственно-временным индексам.
4. Все результаты, полученные таким образом для каждой
фейнмановской диаграммы, складываются. Могут понадобиться до-
дополнительные комбинаторные множители и фермионные знаки, опи-
описанные в пп. 5 и 6 раздела 6.1.
Трудности при вычислении вкладов фейнмановских диаграмм
резко нарастают с ростом числа внутренних линий и вершин, по-
поэтому важно иметь представление о том, какие численные факторы
подавляют вклады более сложных диаграмм. Мы оценим эти чис-
численные факторы, учитывая не только степени электрического за-
заряда е, входящего в вершины, но и множители 2 и л от вершин,
пропагаторов и интегралов по импульсному пространству.
Рассмотрим связную фейнмановскую диаграмму с V вершина-
вершинами, I внутренними линиями, Е внешними линиями и L петлями.
Эти величины не являются независимыми, а связаны соотношения-
соотношениями, уже использованными в разделе 6.3:
L = I - V +1, 21 + Е = ЗУ.
От каждой вершины имеем множитель еBлL, от каждой внутрен-
внутренней линии — множитель Bл)~4, кроме того, каждой петле соответст-
соответствует интеграл по четырехмерному импульсному пространству. Эле-
Элемент объема в четырехмерном евклидовом пространстве, выражен-
выраженный через радиальный параметр к, равен л2к2<Лк2 *, так что каждая
петля вносит множитель л2. Таким образом, диаграмма содержит
множитель
* Предполагается, что выполнен так называемый евклидов (виковский)
поворот (см. ниже раздел 11.2), и интегрирование ведется по евклидову
импульсному пространству. Кроме того, предполагается, что результат
интегрирования не зависит от углов и по ним проведено усреднение (объем
единичной сферы равен 2л2). — Прим. ред.
480
Глава 8. Электродинамика
16л2
Число Е внешних линий в данном процессе фиксировано, по-
поэтому видно, что параметр разложения, определяющий подавле-
подавление вклада фейнмановских диаграмм с каждой дополнительной пет-
петлей, равен
а
4л
= 5,81x10
-4
К счастью, эта величина мала, так что можно добиться достаточ-
достаточной точности, рассчитав вклад фейнмановских диаграмм с неболь-
небольшим числом петель.
Следует добавить несколько слов о спиновых состояниях фо-
фотонов и электронов в реальных экспериментах, когда не каждая из
частиц в начальном и конечном состояниях обладает определенной
спиральностью или z-компонентой спина. Особенно это относится к
фотонам, которые на практике часто находятся не в состоянии с
определенной спиральностью, а в состоянии с поперечной или эл-
эллиптической поляризацией. Как показано в предыдущем разделе,
векторы поляризации фотонов со спиральностью +1 равны
е(р +1) = К(р)
где К(р) - стандартное вращение, переводящее ось z по направле-
направлению вектора р. Эти состояния фотонов не единственно возможные;
в общем случае состояние фотона есть линейная комбинация спи-
спиральных СОСТОЯНИЙ ^p+D
(8.6.13)
8.6. Правила Фейнмана для спинорной электродинамики
481
должным образом нормированная:
oc_|2 = l.
(8.6.14)
Чтобы вычислить матричный элемент поглощения или испускания
такого фотона, нужно просто заменить еI(р,±1) в фейнмановских
правилах на
_е^(р-1).
(8.6.15)
Векторы поляризации с определенной спиральностью удовлетворя-
удовлетворяют условию нормировки
и поэтому в общем случае
е*(р)е»Чр) = 1.
-ц
(8.6.16)
(8.6.17)
Предельными случаями являются круговая поляризация, для
которой ос_^= 0 или ос+ = 0, и линейная поляризация, для которой
ос+1 = |ос_| = l/V^- В последнем случае, подобрав общую фазу состоя-
состояния (8.6.13), можно сделать а+ и а_ комплексно сопряженными друг
другу, так что
ос+ = ехр(+гф) /
(8.6.18)
Тогда в правилах Фейнмана нужно использовать вектор поляриза-
поляризации
соэф
е(р) = К(р)
О
О
(8.6.19)
Здесь ф — азимутальный угол вектора поляризации фотона в плос-
плоскости, перпендикулярной вектору р. Заметим, что в данном случае
вектор поляризации фотона действителен, что возможно только
482 Глава 8. Электродинамика
для линейной поляризации. Между крайними случаями круговой и
линейной поляризаций находятся состояния эллиптической поля-
поляризации, для которых |а+| и |а_| не равны нулю и друг другу.
В более общем случае, начальный фотон может быть приготов-
приготовлен как статистическая смесь спиновых состояний. В самом общем
случае эта смесь может содержать любое число состояний
произвольных поляризаций е^(р), входящих с вероятностью Рг. Ве-
Вероятность поглощения такого фотона в данном процессе имеет вид
Kv^' (8.6.20)
г
где р — матрица плотности
п = V р (г)( \ (г)* ( \
Руц =2^rrev lPien IPJ- (8.6.21)
г
Поскольку очевидно, что р - эрмитова положительная матрица с
единичным следом (так как YjrPr = 1), причем pv0 = р0I = 0 и pV|1pv =
= Pv^p11 = 0, ее можно записать в виде
Руц = ^^sev(P;s)e^(p;s), (8622)
где eI(p;s) - два ортонормированных собственных вектора матрицы
р, для которых
о ^О, (8.6.23)
a Xs — соответствующие собственные значения, причем
s=l,2
Теперь можно записать вероятность процесса поглощения фотона
в следующем виде
Г=
s=l,2
(8.6.24)
8.6. Правила Фейнмана для спинорной электродинамики 483
Отсюда следует, что любая статистическая смесь начальных со-
состояний фотона всегда эквивалентна смеси всего двух ортонорми-
ортонормированных поляризацийм ev{p;s) с вероятностями Xs.
В частности, если мы совершенно ничего не знаем о поля-
поляризации начального фотона, то две вероятности Xs для векторов
ev(p;s) равны, так что Х1 = Х2 = 1/2, и матрица плотности (а отсю-
отсюда и вероятность поглощения) есть среднее значение по началь-
начальным поляризациям:
Pv = L е*(р; s)ei to s) = 2 FiJ ~ ВД) ¦ (8.6.25)
s=l,2
К счастью, этот результат не зависит от конкретной пары векторов
поляризации 6j(p;s), по которым мы проводим усреднение. Для не-
поляризованных фотонов можно усреднять вероятность поглоще-
поглощения по любой паре ортонормированных векторов поляризации. Ана-
Аналогично, если не делается попыток измерить поляризацию фотона
в конечном состоянии, тогда вероятность можно рассчитать путем
суммирования по любой паре ортонормированных векторов поляри-
поляризации конечного фотона.
Аналогичные замечания применимы к электронам и позитро-
позитронам. Если, как это обычно имеет место, не делается попыток приго-
приготовить электрон или позитрон так, чтобы одни спиновые состояния
были предпочтительнее других, тогда вероятность должна вычис-
вычисляться путем усреднения по любым двум ортонормированным на-
начальным спиновым состояниям, например, по состояниям с 2-ком-
понентами спина о = +1/2. Если не пытаются измерить спиновые
состояния конечных электрона или позитрона, то нужно суммиро-
суммировать вероятность по любым двум ортонормированным конечным
спиновым состояниям, например, по состояниям с z-компонентами
спина о = +1/2. Такие суммы можно вычислить с помощью соотно-
соотношений E.5.37) и E.5.38):
L
_ f—гр
Ца(р,о)Цр(р,о)=
484
Глава 8. Электродинамика
где р° = VP2 + m2 • Например, если начальное состояние содержит
электрон с импульсом р и z-компонентой спина а и позитрон с им-
импульсом р' и 2-компонентой спина а', то матричный элемент этого
процесса будет иметь вид ua(p',G')-#apWp(p,G). Поэтому, если не на-
наблюдаются спиновые состояния ни электрона, ни позитрона, веро-
вероятность будет пропорциональна
а ,ст
u
2p°
Техника вычисления таких следов описана в Приложении к этой
главе.
8.7. Комптоновское рассеяние
В качестве примера использования методов, изложенных в этой
главе, рассмотрим рассеяние фотона на электроне (или другой части-
частице со спином 1/2 и зарядом —е) в низшем порядке по е. Пусть началь-
начальные и конечные импульсы и векторы поляризации фотонов равны
соответственно
и
г', где к0 = |к|
и
к'0 = |к'
k,e
Р,
', е'
гО v
k,e
P',<f
"У
гО v
р, а
, e'
Рис. 8.1. Две фейнмановские диаграммы низшего порядка для комптоновского рас-
рассеяния. Сплошные линии — электроны, волнистые линии — фотоны
8.7. Комптоновское рассеяние
485
а начальные и конечные импульсы и z-компоненты спина электро-
электронов равны соответственно рц, а и p/fl, а', где р° = (р2 +т2)^2,
р'° = (р/2 + т2 )^2, тп — масса электрона. Фейнмановские диаграм-
диаграммы низшего порядка для этого процесса показаны на рис. 8.1. Ис-
Используя сформулированные в предыдущем разделе правила, нахо-
находим соответствующий матричный элемент рассеяния:
|, а + к, е -> р', а' + к', г') =
a'V е*' w(p,G)a
Bл)
3/2
BтгK/2
X
d4g
-г
BлL
-iq + m
q +т - гг
II" . II . "I
- (гл 'n' ut*\ I oi^y'tt\ Л/ t\ (/п п -4- 1/*\
[и U fv I tl^JU I R^t^ У И Ц > *W
\л ± JL put j
+[еBлLу^54(д - p' + /с)][еBлLу?а54(р - g - /с')]}.
(8.7.1)
Производя (тривиальное) интегрирование по д, собирая все множи-
множители i и 2л и переписывая результат в матричных обозначениях,
имеем более простое выражение:
S =
BлJл/2/с/02/с0
¦Щр'.о']
(ё'
/сJ
2 , ™2
(р-/с'J +ш
м(р,а).
(8.7.2)
(Здесь ^* означает не (^ )*, а е* уц. Кроме того, мы опускаем —ге, так
как знаменатели не обращаются в нуль.) Поскольку р2 = - т2 и /с2 =
/с'2 = 0, знаменатели можно упростить:
(p + kJ +m2 =2(p-fc),
(р-к'J +т2 =-2{р-к').
(8.7.3)
(8.7.4)
486 Глава 8. Электродинамика
Общее определение C.3.2) «фейнмановской амплитуды» М в данном
случае (поскольку предполагается, что какое-то рассеяние проис-
происходит) принимает вид
S = -2тпб4{р' + к'-р- к)М, (8.7.5)
так что
е2
е2
М = , Щтр',о')\е''[-г(р + t) + m]i/p-k
Ц2ж)Чк'°к°
(8.7.6)
-1[-г{р - W) + 7n\t'' / р • /с'}м(р,а).
Дифференциальное сечение определяется через М формулой C.4.15),
которая в данном случае имеет вид
da = BjrLM-1|M|254(p/ + /c/-p-/c)d3p/d3fc/. (8.7.7)
Так как одна из частиц имеет нулевую массу, из формулы C.4.17)
для относительной скорости находим:
M = |p-fc|/p°fc0. (8.7.8)
Чтобы продолжить вычисления, удобно перейти в специальную сис-
систему отсчета. Поскольку электроны в атомах являются нерелятиви-
нерелятивистскими, в опытах по рассеянию фотонов больших энергий (рентге-
(рентгеновских лучей или у-квантов) на электронах обычно (хотя и не все-
всегда) можно считать, что начальный электрон покоится. Примем здесь
именно эту систему отсчета, так что
р = 0, р°= т. (8.7.9)
Тогда скорость (8.7.8) равна просто
и = 1. (8.7.10)
Чтобы запись была компактнее, обозначим энергии фотонов через
e> = fc° =|k|=-p-fc/m, (8.7.11)
8.7. Комптоновское рассеяние 487
со' = /с/0 =|k/|=-p-/c//m. (8.7.12)
Наличие дельта-функции от 3-импульса в формуле (8.7.7) позволяет
проинтегрировать по р', полагая р' = к - к'. В результате остается
дельта-функция от энергии
5(р/0 + к'0 - р° - к0) = 5(V(k - к'J + т2 + со' - т - со). (8-7.13)
Этим фиксируется значение со', удовлетворяющее условию
со2 - 2СОСО' cos 0 + со'2 + т2 = со + т - со'.
где 0 - угол между к и к'. Возводя обе части в квадрат и сокращая
слагаемые со'2, получаем *
7ТЬ
со' = со
COA-COS0)
Дельта-функцию от энергии можно представить в виде
5(р/0+/с/0-р0-/с°) =
| Э[д/со2 - 2СОСО' cos 0 + со'2 + т2
+
(со'-соcos0)/ р'° +1| шсо
Кроме того, дифференциал в?к' можно записать как
* Эквивалентно эту формулу можно записать в виде, свидетельствующем
об увеличении длины волны при рассеянии:
1 1 1 - cos 6
ю ю т
Проверка этого соотношения А. Комптоном в 1922-23 годах в опытах по
рассеянию рентгеновских лучей на электронах сыграла ключевую роль в
подтверждении гипотезы Эйнштейна 1905 года о световых квантах, полу-
получивших вскоре после обнародования Комптоном результатов своих экспери-
экспериментов название фотонов.
488 Глава 8. Электродинамика
= (d'2do>'d?l, (8.7.16)
где dQ. — телесный угол, в который рассеивается конечный фотон.
Оставшаяся в (8.7.15) дельта-функция служит как раз для того, чтобы
исключить дифференциал dco" в (8.7.16), и мы приходим к диффе-
дифференциальному сечению
°со/3
mco
(8.7.17)
где р'° = т + со - со', и со' определяется формулой (8.7.14).
Обычно 2-компоненты спина начального или конечного электро-
электрона не измеряются. В таких случаях следует просуммировать по о' и
усреднить по о, или иными словами вычислить полусумму по о и о':
da(p + к,е —» р' + к',е) = — \\ do(p,a + к,е —» р', а' + к',е). ,n71m
ст',ст
Чтобы вычислить эту сумму, воспользуемся стандартной формулой
'°)= ZP2p«maP (8-7-19)
и аналогичной формулой для суммы по а'. Согласно этим формулам,
для произвольной 4x4 матрицы А имеем:
(8.7.20)
Напомним, что Ру^Р = -уц, тогда, подставляя А из формулы (8.7.6),
получаем:
8.7. Комптоновское рассеяние
489
а,а
хТг
64BлNсосо/р°р/0
,* [—г(р + %) + т]
[-i(p - Г) + т] ..
р ¦ к
р ¦ к'
\(-гр + га)
(8.7.21)
p- k
t'-t'
p-k'
\{-ip' + m)
(Вновь напомним, что i означает не (i)*, a e^'f-, и аналогично для
t' .) Мы проводим вычисления в «калибровке», в которой
е • р = г • р = г • р = г* • р = 0,
(8.7.22)
например, в кулоновской калибровке в лабораторной системе, где
е° = е'° = 0 и р = 0. * Тогда
[—гр + тЩ—ip + т] = t[—ip + т][—гр + т] =
= t(p2 +m2) = t(piipii +m2) = 0,
и аналогично для е' , t и ^'. Поэтому формулу (8.7.21) можно силь-
сильно упростить:
—е
64BлNсосо/р°р/0
-Tr
1 \(—ip + m)
p-k p-k')
- + ¦
р-к р-к'
{—ip' + m)
(8.7.23)
* Строго говоря, эта фраза становится понятной только после гл. 9, где пока-
показано, что при вычислении матричных элементов процессов с участием реаль-
реальных электронов и позитронов к вектору поляризации фотона е с 4-импульсом к
всегда можно добавить 4-вектор, пропорциональный к: ё1 —> ё1 + №. — Прим.
ред.
490 Глава 8. Электродинамика
След произведения любого нечетного числа у-матриц обращается в
нуль, так что последнее выражение разбивается на слагаемые ну-
нулевого и второго порядка по т:
М
? е4 f T, Т2
2 = — + +
++
а & 64BлN coco'pV° I, (р • кJ (р -к){р- к') (р -Щр- к')
+ ¦
Т4 m2^ m2t2 m2t3
(p.fc)(p.fc') (p.fc)(p.fc') (p-/c'JJ
(8.7.24)
где
{/**y} (8.7.25)
T2 =Tr{^/4ttp^/r^p/}, (8.7.26)
T3=Tr{rtW*^V}. (8.7.27)
T4 = TrfaY'pt'rty], (8.7.28)
{/**/} (8.7.29)
(8.7.30)
(8.7.31)
(8.7.32)
В Приложении к этой главе показано, как выразить любой
след Тг{&Ы<И...} через сумму произведений скалярных произведе-
произведений 4-векторов а, Ъ, с, d, ... В общем случае, вклады от произведе-
произведений 6 или 8 у-матриц типа tk или Тк будут даваться суммой
соответственно 15 или 105 слагаемых, но, к счастью, большинство
скалярных произведений равно нулю; в дополнение к соотношениям
(8.7.22) имеем к-к = к'-к' = 0. (Кроме того, е-е* = г-г* = 1.) Чтобы
упростить дальнейшие вычисления, ограничимся случаем линей-
линейной поляризации, когда ец и е^ действительны. Опуская звездочки
в (8.7.25), имеем:
Так как е^р^ = 0 и е^е^ = 1, получаем:
8.7. Комптоновское рассеяние 491
так что
7\ =
Кроме того, k^k^ = 0 и
ШрШ = -Шр + 2Ш(р ¦ к) = 2Ш(р ¦ к),
откуда
С помощью формулы (8.А.6) получаем:
Удобно совершить подстановки:
г ¦ р = г ¦ (р + к — к') = г ¦ к,
к-р' = -±(р-кJ-±т2 =-^(р-/с/J-1ш2 =р-к'.
так что
Тг = -16(р • к)(е ¦ кJ + 8(р -к)(р- к'). (8.7.33)
Аналогичное (хотя и более длинное) вычисление дает:
Т2=Т3= -8(е • к'J(р ¦ к) + 16(е • е'J(р • fc')(P • k) + 8(e • e'J(fc • k')m2
- 8(е • e')m2(k ¦ е')(к' ¦ е) + 8(е' • /сJ(р • к')
- 4(fc • рJ + 4(fc • fc')(p • р') ~ 4(fc • р')(р • fc'), (8.7.34)
Т4 = 16(р • fc')(e • fc'J + 8(p • fc)(p • к'), (8.7.35)
t1=t4=O, (8.7.36)
t2 = ц = -8(е • e')(fc • e')(fc' ¦ е) + 8(fc • fc')(e • e'J - 4(fc • k'). (8.7.37)
492
Глава 8. Электродинамика
Собирая все эти слагаемые в формуле (8.7.24), получаем:
IIM
2 _
64BлN coco'p0
'О
8(к-к'J
_(fc-p)(fc'-p)
32(е-е'J
• (8.7.38)
Это выражение верно в любой лоренцовской системе. В лаборатор-
лабораторной системе имеем:
k-k' = coco'(cos 0 - 1) = тпсосоч ,
vco со'у
р -к = -тсо, р -к' = -тсо'.
Комбинируя формулы (8.7.38) и (8.7.17), приходим к следующему
выражению для сечения в лабораторной системе:
a,a
64л2ш2со2 Ico' со
со
(8.7.39)
Это знаменитая формула, полученная О. Клейном и Й. Нишиной в
1929 году (с помощью старой теории возмущений).
Как обсуждалось в разделе 8.6, если налетающий фотон не
находится в состоянии с определенной поляризацией (как это обыч-
обычно и бывает), следует усреднить по двум ортонормированным зна-
значениям е. В результате такого усреднения имеем:
и соответственно дифференциальное сечение принимает вид:
1
4
64л2ш2со2 Leo' со
(8.7.40)
8.7. Комптоновское рассеяние 493
Видим, что рассеянный фотон преимущественно поляризован в на-
направлении, перпендикулярном направлению распространения как
начального, так и конечного фотонов, т. е. перпендикулярно плос-
плоскости рассеяния. Это хорошо известный результат, ответственный,
в частности, за поляризацию света от обращающихся друг около
друга двойных звезд *.
Чтобы рассчитать сечение для тех экспериментов, в которых
не измеряется поляризация конечного фотона, следует просумми-
просуммировать выражение (8.7.40) по е', используя формулу:
Тогда
I
е,е ,ст,с
е4со/2сШ Г со со' 2 (8-7.41)
— + 1 + cos2 0 ,
32л2т2со2 Leo' со
где 9 — угол между направлениями к и к'. В нерелятивистском слу-
случае со <^ т и формула (8.7.41) принимает вид:
(8-7-42)
Интеграл по телесному углу легко вычисляется:
2ти %
J A + cos2 0)сШ = J dcp J A + cos2 0) sin 0 d0 =
о о
16л
* Свет одной из звезд поляризуется при рассеянии на свободных электро-
электронах внешней атмосферы второй, более холодной звезды в то время, когда
обе находятся на одном луче зрения. Обычно такая поляризация не детекти-
детектируется, поскольку она исчезает, когда астрономы суммируют свет от всех
частей звездного диска. Но в те моменты времени, когда более холодная
звезда заслоняет свет только с одной стороны более горячей звезды, поляри-
поляризация света от двойных звездных систем наблюдалась.
494 Глава 8. Электродинамика
В результате полное сечение при со <х т имеет вид:
Часто эту формулу записывают в виде ат=8лг02/3, где
г0 = е2/Dлш) = 2,818-Ю3 см называется классическим радиусом
электрона. Формула (8.7.43) называется томсоновским сечением,
в честь Дж.Дж. Томсона, открывшего электрон. Формулы (8.7.42) и
(8.7.43) первоначально были получены в рамках классических ме-
механики и электродинамики при расчете переизлучения * света не-
нерелятивистским точечным зарядом в поле плоской электромагнит-
электромагнитной волны.
8.8. Обобщение: калибровочные поля как р-формы **
Антисимметричный тензор напряженности поля F™ в электромаг-
электромагнетизме представляет частный случай некоторого общего класса тензо-
тензоров, играющих важную роль в физике и математике. По определению,
р-форма есть антисимметричный ковариантный тензор ранга р. Имея
р-форму Vi,ti2.-,tV можно построить (р+1)-форму, которая носит назва-
название внешней производной *** dt, взяв производную и произведя анти-
антисимметризацию по всем индексам:
= Э[ц/ц2,ц3,-,Ир+1]
+ +(-1)рд
(8.8.1)
где квадратные скобки означают антисимметризацию по индексам
внутри скобок. Так как производные коммутируют, вторые внеш-
внешние производные обращаются в нуль:
* Мы сохранили дословно терминологию оригинала ввиду ее образно-
образности. — Прим. пер.
** Этот раздел лежит несколько в стороне от основной линии книги и
может быть опущен при первом чтении
*** Внешние производные и р-формы играют особую роль в общей теории
относительности, в частности, потому, что внешняя производная тензора
преобразуется как тензор, хотя она вычисляется с помощью обычных, а не
ковариантных производных 5.
8.8. Обобщения: калибровочные поля как р-формы 495
d(dt) = 0. (8.8.2)
Если внешняя производная р-формы обращается в нуль, то такая
р-форма называется замкнутой, а если р-форма сама есть внеш-
внешняя производная, она назывется точной. Из (8.8.2) следует, что вся-
всякая точная р-форма замкнута. Знаменитая теорема6 Пуанкаре ут-
утверждает, что в односвязной области всякая замкнутая р-форма
точна *. Например, однородные уравнения Максвелла (8.1.16) утвер-
утверждают, что 2-форма напряженности электромагнитного поля F™
замкнута. Из теоремы Пуанкаре следует тогда, что она точна, т. е.
может быть записана в виде внешней производной: F^ = Э„АУ — ЭУА„.
Вновь используя (8.8.2), убеждаемся, что 2-форма F^v не изменяет-
изменяется, если к А„ добавить внешнюю производную, т. е. совершить ка-
калибровочное преобразование ЬА^ = ЭЦ?Х
Имея формализм р-форм и внешних производных, естественно
рассмотреть возможность существования безмассовых частиц,
описываемых калибровочными полями **, являющимися р-формами ***
-^И1;...,ц , при условии инвариантности теории относительно калибровоч-
калибровочных преобразований
5А = dQ., (8.8.3)
* В многосвязных пространствах замкнутые формы не обязательно точны.
Хотя и можно локально представить замкнутую форму как внешнюю произ-
производную, в общем случае этого нельзя сделать гладким образом во всем про-
пространстве. Множество замкнутых р-форм, взятых по модулю точных р-форм,
образует так называемую р-ую группу когомологий де Рама данного простран-
пространства. Существует глубокая связь между группами когомологий де Рама данно-
данного пространства и его топологией.6 Подробнее это будет обсуждаться в т. П.
** Ниже такие поля мы называем просто р-формами и говорим о
калибровочных теориях р-форм. — Прим. пер.
*** Мы несколько неточно называем поле -^ц1;...,цр р-формой, так как для
того, чтобы F — dA был тензором, необходимо только, чтобы поле А было
тензором с точностью до калибровочного преобразования. На самом деле, мы
уже видели, что в случае четырех пространственно-временных измерений
невозможно построить 4-векторное поле из операторов рождения и уничто-
уничтожения физических безмассовых частиц спиральности ±1, поэтому мы долж-
должны иметь дело с полем АЦх), преобразующимся в соответствии с правилом
(8.1.2) как 4-вектор только с точностью до калибровочного преобразования.
496 Глава 8. Электродинамика
или подробнее
8Ащ,...^р =Э[ц1Пц2,..,цр]>
где ^ц1,...,цр_1 - произвольная (р-1)-форма. Из р-формы можно по-
построить калибровочно-инвариантный тензор напряженности поля
F = dA, (8.8.4)
или детальнее
(Альтернативно можно исходить из (р+1)-формы F, предположить
условие dF = 0 и отсюда вывести существование р-формы А, та-
такой, что F = dA.) По аналогии с электродинамикой можно ожидать,
что лагранжиан для А имеет вид
2(р + 1) ^'-'^+1 АИ.".,Цр' (8.8.6)
где J — антисимметричный тензорный ток (являющийся либо с-чис-
лом, либо функцией полей, отличных от А), который должен удов-
удовлетворять условию сохранения
a^j^i'-'^p =0. (8.8.7)
для того чтобы действие было калибровочно-инвариантным *. Урав-
Уравнения Эйлера-Лагранжа принимают вид
d^-Vp = -j»i--»p . (8.8.8)
р-Формы играют важную роль в калибровочных теориях с чис-
числом пространственно-временных измерений более четырех. Напри-
* Если ток J является функцией других полей, то он должен сохраняться
на уравнениях движения этих полей, а калибровочная инвариантность имеет
место для полного действия, включающего действие для других полей. —
Прим. ред.
8.8. Обобщения: калибровочные поля как р-формы 497
мер, в простейших теориях струн в 26 пространственно-временных
измерениях нормальная мода струны представляется при низких
энергиях 2-формой А„у. Однако в случае четырех измерений ис-
использование р-форм не открывает новых возможностей.
Чтобы показать это, заметим, во-первых, что в D простран-
пространственно-временных измерениях не существует антисимметричных
тензоров с более чем D индексами, поэтому в общем случае следу-
следует принять р + 1 < D. Как и любая другая (р+1)-форма с р + 1 < D,
напряженность поля F может быть выражена через дуальную
@-р-1)-форму i?:
Аналогично, р-форма тока J может быть записана через (О-р)-форму
тока /:
Уравнение поля (8.8.8) и условие сохранения (8.8.7) принимают тогда
простой вид
d,F = /, d/ = 0. (8.8.11)
Так как дуальный ток является замкнутой формой, его можно за-
записать через @-р-1)-форму if :
$ = &f. (8.8.12)
Из уравнений (8.8.11) и (8.8.12) следует, что разность ,/и //замкну-
//замкнута, поэтому в силу теоремы Пуанкаре
:7=<f + dty, (8.8.13)
где ф является @-р-2)-формой. Исключением является случай
р = D - 1, когда ,/и if оказываются 0-формами, т. е. скалярами, и
условие d,F = d.(f означает просто, что ,? и У отличаются на констан-
константу. В таком случае калибровочное поле не описывает вообще ника-
никаких степеней свободы. Поэтому можно ограничиться рассмотрением
случаев р < D - 2.
498 Глава 8. Электродинамика
При р < D - 2 однородные «уравнения Максвелла» dF = О
имеют вид
^-! =о, (8.8.14)
что совместно с формулой (8.8.13) приводит к уравнению поля для ф:
'^-^. (8.8.15)
Оно инвариантно относительно нового набора калибровочных пре-
преобразований ф —» ф + dco. Исключение — случай D - р - 2 = 0, когда
калибровочное преобразование, оставляющее F инвариантным, имеет
вид ф —> ф + с, где с — произвольная константа. Мы видим, что в
случае D пространственно-временных измерений калибровочная
теория р-формы А с током J эквивалентна калибровочной теории
(D — р — 2)-формы ф с током —дУ.
Теперь можно понять, почему калибровочные теории р-форм не
приводят к новым возможностям в четырех измерениях. Мы видели,
что нужно рассматривать только случаи р < D - 2, т. е. р = 0, 1, 2. 0-
формы являются скалярами S, для которых определение (8.8.5) при-
принимает вид F^ = d^S, а уравнения поля — вид OS = —J. В данном
случае калибровочная инвариантность означает инвариантность от-
относительно сдвига S —> S + с, где с — константа. Это теория без-
безмассового скалярного поля с взаимодействием с производными. 1-фор-
1-форма — это 4-вектор А^(х), взаимодействующий с сохраняющимся
4-вектором тока, т. е. электродинамика. Наконец, согласно приведен-
приведенному выше общему результату калибровочная теория 2-формы в че-
четырехмерном пространстве-времени эквивалентна калибровочной
теории 0-формы, а это, как мы видели, эквивалентно скалярному
полю с взаимодействием с производными.
Приложение. Следы
При вычислении матричных элементов ^-матрицы и вероят-
вероятностей переходов для процессов с участием частиц спина 1/2, часто
приходится вычислять следы от произведения у-матриц Дирака. По-
Поэтому полезно привести формулы для этих следов, которые ис-
используются во всех подобных вычислениях.
Приложение. Следы 499
Для произведения четного числа у-матриц след равен
Тг{Уц1'Уц2---'Уц2№ j = 4 2_! °Р 1 1 ^попарные ц • (8.А.1)
спаривания пары
Здесь сумма берется по всем различным способам спаривания ин-
индексов цъ...,ц2М. Спаривание можно рассматривать как перестановку
целых чисел 1,2,...,2JV в определенном порядке PI, P2, ..., PBN), в
которой мы спариваем индекс ЦР1 с ЦР2, ЦРЗ с ЦР4, и т. д. Перестанов-
Перестановка пар или перестановка m внутри пары приводит к такому же
спариванию, так что число различных спариваний равно
BJV)!/ N! 2N = BJV - 1)BJV - 3).. .1 = BJV - 1)!!. (8.А.2)
Можно избежать суммирования по эквивалентным спариваниям,
потребовав, чтобы
Р1 < Р2, РЗ < Р4,..., PBiV - 1) < PBiV), (8.A.3)
Р1<РЗ<Р5<... (8.А.4)
С учетом этих соглашений, множитель 5Р равен +1 или -1 в зависи-
зависимости от того, включает ли спаривание четную или нечетную пере-
перестановку индексов. Произведение в (8.АЛ) проводится по всем N
парам, причем n-ая пара вносит множитель г1цРB71_1)цРB71) • Например
(записывая ц, V, р, а, ... вместо ц1( Ц2> Цз> И^4> •••)> ПРИ N = 1, 2 и 3
имеем *
(8.A.5)
(8.А.6)
* Сейчас существуют компьютерные программы 7, с помощью которых про-
производится вычисление следов произведений большого числа матриц Дирака.
500 Глава 8. Электродинамика
(оУкУц\ = 4[ЛцуЛраЛкп - ЛцуЛркЛстп + ЛцуЛрт1Лсж
1црЛуСТЛкп + ЛцрЛукЛстп ~ ЛцрЛу^Лак + ЛцаЛурЛкп ~ ЛцСТЛукЛрт1
Для нечетного числа у-матриц результат намного проще:
= 0. (8.А.8)
Формула (8.А.1) доказывается по индукции. Заметим, прежде все-
всего, что
так что Тг{у„уу} = 4г1„у, в согласии с (8.А.1). Далее, предположим,
что (8.А.1) верна для N < М - 1. Тогда
-i J ~ TrU n2 • • • y^2M V J •
След любого коммутатора равен нулю, так что последнее вычитае-
вычитаемое выражение в правой части равно исходному выражению в ле-
левой части, и поэтому
(8 A 9)
- • • • + Лц^Т^^ • • • Yn_x j •
Приложение. Следы 501
Если предположить, что формула (8.А.1) правильна для следа любого
произведения 2JV-2 матриц Дирака, то формула (8.А.9) показывает,
что эта же формула (8.А.1) правильна для следа 2JV матриц.
Простейший способ убедиться в том, что след нечетного числа
дираковских матриц равен нулю, это заметить, что -у^ связана с у^
преобразованием подобия: -у^ = УэУ^УэГ1- Следы не меняются при та-
таком преобразовании, поэтому след нечетного числа дираковских мат-
матриц равен самому себе со знаком «минус» и следовательно равен нулю.
Мы сталкиваемся с еще одним типом следов вида
Такой след обращается в нуль при нечетных п по тем же при-
причинам, что и для следов без у5. Кроме того, этот след равен нулю
при п = 0 и п = 2:
Tr{y5} = 0, (8.A.10)
(Чтобы увидеть это, вспомним, что у5 = ^УоУгУгУз» и заметим, что
невозможно произвести спаривание индексов в Тг{у0у1у2у3} или
Тг^УоУ^УзУцУу} так> чтобы пространственно-временные индексы в ка-
каждой паре были одинаковы.) При п = 4 такое спаривание индексов
в ТМу^УзУзУцУуУрУс;} возможно, но только в том случае, если ц, V, р,
а являются какими-то перестановками 0, 1, 2, 3. Более того, этот
след должен быть нечетным относительно перестановок ц, V, р, о,
так как у-матрицы с разными индексами антикоммутируют. Следо-
Следовательно след ТМудУцУуУрУд} должен быть пропорционален полностью
антисимметричному тензору ецуро. Коэффициент пропорционально-
пропорциональности можно установить, положив ц, V, р, о равными 0, 1, 2, 3 и
вспомнив, что ?0123 = -1- Таким образом находим
(8.А.12)
След произведения у5 с шестью, восемью и более дираковскими
матрицами можно вычислить теми же методами, которые исполь-
использовались выше при доказательстве формулы (8.А.1).
502 Глава 8. Электродинамика
Задачи
L Вычислите дифференциальное и полное сечения процесса
е+ё~ —» Ц+Ц~ в низшем порядке по е. Считайте, что спины электрона и
мюона не регистрируются. Используйте для электронов и мюонов
простейший лагранжиан спинорной электродинамики.
2. Проведите каноническое квантование теории заряженного ска-
скалярного поля Ф и его взаимодействия с электромагнитным по-
полем, если лагранжиан равен:
ФJ F
Используйте кулоновскую калибровку. Выразите гамильтониан
через поля А, Ф и Ф^ и сопряженные им импульсы. Найдите
оператор взаимодействия V(t) в представлении взаимодействия
через поля в этом представлении и их производные.
3. Используя результаты задачи 2, вычислите в низшем порядке
по е дифференциальное и полное сечения рассеяния фотонов
на массивной скалярной заряженной частице.
4 Напишите калибровочно-инвариантный лагранжиан для теории
взаимодействия заряженного массивного векторного поля с элек-
электромагнитным полем.
5. Вычислите дифференциальное сечение электрон-электронного
рассеяния в низшем порядке по е. Считайте, что спины началь-
начальных и конечных частиц не регистрируются.
Список литературы
1. См., например, Green, M.B., Schwarz, J.H., and Witten, E. Super-
string Theory (Cambridge University Press, Cambridge, 1987), Section
2.2. (Есть рус. пер.: М. Грин, Дж. Шварц, Ю. Виттен. Теория
суперструн. Тт. 1, 2. М.: Мир, 1991)
Список литературы 503
la. Fock, V., Z. /. Phys., 39, 226 A927); Weyl, H., Z. Phys., 56, 330
A929). Термин «калибровочная инвариантность» возник по
аналогии с более ранними спекуляциями на тему о масштабной
инвариантности в книге: Weyl, H., Return, Zeit, Materie, 3rd ed.
(Springer Verlag, Berlin, 1920) (есть рус. пер.: Г. Вейль. Прост-
Пространство, время, материя. М., 1998). Историю вопроса расска-
рассказал Ч.Н. Янг в докладе в Сити-колледже (неопубликовано).
2. Использование кулоновской калибровки в электродинамике
активно поддерживал Швингер, во многом по тем же причинам,
что и в данной книге: нам не нужно вводить фотонов со спи-
ральностями, отличными от ± 1. См.: Schwinger, J., Phys. Rev.,
78, 1439 A948); 127, 324 A962); Nuovo Cimento, 30, 278 A963).
3. Feynman, R.P., Phys. Rev., 101, 769 A949), Section 8.
4. Klein, O. and Nishina, Y., Z. f. Phys., 52, 853A929); Nishina, Y.,
ibid., 869 A929); см. также: Tamm, I., Z. /. Phys., 62, 545 A930).
5. См., например: Weinberg, S., Gravitation and Cosmology (Wiley,
New York, 1972), Section 4.11 (есть рус. пер.: Вейнберг С. Гравитация
и космология. М.: Мир, 1976).
6. Доступное общее введение в геометрию и топологию р-форм мож-
можно найти в книге: Flanders, H., Differential Forms (Academic Press,
New York, 1963).
7. West, Т., Comput. Phys. Commun., 77, 286 A993).
9
Методы
функционального интегрирования *
В главах 7 и 8 мы применили операторный формализм канони-
канонического квантования для вывода фейнмановских правил в разных
теориях. Во многих случаях, например, для скалярного поля со вза-
взаимодействием с производными или для векторного поля с нулевой
или отличной от нуля массой, такая процедура оказалась хотя и
прямо ведущей к цели, но довольно сложной. Оказалось, что гамиль-
гамильтониан взаимодействия содержит как ковариантное слагаемое, рав-
равное взятому с обратным знаком члену взаимодействия в лагран-
лагранжиане, так и нековариантное слагаемое, необходимое для сокраще-
сокращения нековариантных членов в пропагаторе. В электродинамике такое
нековариантное слагаемое (кулоновская энергия) оказалось даже про-
пространственно нелокальным, хотя и локальным по времени. Оконча-
Окончательный результат достаточно прост: фейнмановские правила соот-
соответствуют тому, что мы имеем дело с ковариантными пропагатора-
* Начиная с этого момента мы последовательно переводим используемый
в англоязычной литературе термин path integral и его производные как
функциональный интеграл и производные от этого термина «функ-
«функциональная формулировка», «функциональный подход», «функциональный
формализм» и т. п., имея в виду, что буквальный перевод термина интеграл
по путям используется в русских пособиях и монографиях, когда речь идет
об альтернативной формулировке квантовой механики, а в применении к
квантовой теории поля и квантовой статистике используются более общие
термины. — Прим. пер.
Методы функционального интегрирования 505
ми, а для нахождения вкладов в вершины используем взятый со зна-
знаком «минус» член взаимодействия в лагранжиане. Сложность получе-
получения этих простых результатов, достаточно раздражающая в случае
теорий, рассмотренных в гл. 7 и 8, становится непереносимой в более
сложных теориях, типа обсуждаемых в т. II неабелевых калибровоч-
калибровочных теорий или общей теории относительности. Всякий предпочел
бы такой метод вычислений, который исходит непосредственно из
лагранжиана и приводит к фейнмановским правилам в их оконча-
окончательной лоренц-ковариантной форме.
К счастью, такой метод существует. Он связан с формули-
формулировкой квантовой механики на языке функциональных интегра-
интегралов. Впервые функциональный подход был изложен применитель-
применительно к нерелятивистской квантовой механике в диссертации Фейн-
мана 1, где было показано, как можно вместо гамильтониана рабо-
работать непосредственно с лагранжианом. В этом отношении работа
Фейнмана была инспирирована более ранней работой Дирака 2.
Позднее функциональный подход сыграл (наряду с вдохновенны-
вдохновенными догадками) важную роль при выводе Фейнманом правил диа-
диаграммной техники 3. Однако, хотя фейнмановские диаграммы ста-
стали общеупотребительными уже в 1950-е годы, большинство физи-
физиков (включая меня самого) предпочитали выводить правила для
них с помощью операторных методов Швингера и Томонаги, кото-
которые, как показал в 1949 году Дайсон, приводят к тем же правилам
диаграммной техники, что и полученные Фейнманом с помощью
его методов.
Функциональный подход возродился в конце 1960-х годов,
когда Фаддеев и Попов 4, а также Де Витт 5 показали, как приме-
применить его к неабелевым калибровочным теориям и общей теории
относительности. Для большинства теоретиков поворотным стал
1971 год, когда 'т Хофт 6 применил функциональный метод для
вывода фейнмановских правил в спонтанно нарушенных калибро-
калибровочных теориях (они обсуждаются в т. II), в частности, в теории
слабых и электромагнитных взаимодействий, использовав при этом
калибровку, в которой становится совершенно прозрачным пове-
поведение этих теорий при больших энергиях. Вскоре (об этом также
рассказывается в т. II) было обнаружено, что функциональный ме-
метод позволяет учесть вклады в .^-матрицу, которые существенно
сингулярны при нулевой константе связи и поэтому не могут быть
обнаружены в любом конечном порядке теории возмущений. С тех
506 Глава 9. Методы функционального интегрирования
пор описываемые ниже функциональные методы стали неотъем-
неотъемлемой частью вооружения всех физиков, использующих кванто-
квантовую теорию поля.
Читатель может в этом месте задать вопрос, почему же, раз
этот метод так удобен, мы мучились в гл. 7 с обоснованием канони-
канонического формализма. Похоже, и сам Фейнман поначалу полагал,
что его функциональный подход может стать заменой обычной ка-
канонической формулировки квантовой механики. Есть две причины
начинать с канонического формализма. Первая из них носит прин-
принципиальный характер: хотя функциональный формализм приводит
к явно лоренц-инвариантным правилам диаграммной техники, ос-
остается неясным, почему вычисленная таким способом 5-матрица
унитарна. Насколько мне известно, единственный способ доказать,
что функциональный формализм приводит к унитарной 5-матри-
це, заключается в том, чтобы использовать его для реконструкции
канонического формализма, в котором унитарность очевидна. В этом
вопросе срабатывает закон сохранения неприятностей: можно ис-
использовать канонический подход, в котором унитарность очевидна,
а лоренц-инвариантность спрятана, или функциональный подход,
который явно лоренц-инвариантен, но отнюдь не явно унитарен.
Так как ниже функциональный подход выводится из каноническо-
канонического подхода, мы уверены, что оба подхода приводят к одной S-
матрице, так что .^-матрица действительно должна быть как ло-
ренц-инвариантной, так и унитарной.
Вторая причина, по которой сначала рассматривается кано-
канонический формализм, более практического свойства: существуют
важные теории, где простейшая версия фейнмановского функци-
функционального метода, в которой пропагаторы и вершины взаимодей-
взаимодействия извлекаются непосредственно из лагранжиана, просто не-
неверна. Примером может служить нелинейная а-модель с плотнос-
плотностью лагранжиана 9> = -5ди(ф)Эцф/сЭ|1фг. В подобных теориях исполь-
использование наивных правил Фейнмана, выведенных непосредственно
из плотности лагранжиана, приводит к .^-матрице, которая не толь-
только неправильна, но даже не унитарна, да еще и зависит от спосо-
способа, которым мы определяем скалярное поле 7. В этой главе мы
выведем функциональный формализм из канонического формализ-
формализма и, таким образом, увидим, какие еще типы вершин необходи-
необходимы для того, чтобы дополнить простейшую версию фейнмановско-
фейнмановского функционального метода.
9.1. Общая формула для функционального интеграла 507
9.1. Общая формула для функционального интеграла
Начнем с рассмотрения произвольной квантово-механической
системы с эрмитовыми операторами «координат» Qa и сопряженных
им «импульсов» Ръ, удовлетворяющими каноническим коммутаци-
ЮаЛН^ь, (9.1.1)
[Qa,Qb] = [Pa,Pb] = 0. (9.1.2)
(В этом и трех следующих разделах ограничимся бозонными опера-
операторами, которые удовлетворяют коммутационным соотношениям. По-
Полученные результаты будут обобщены в разделе 9.5 на случай фер-
мионных операторов, удовлетворяющих антикоммутационным со-
соотношениям.)
В теории поля индекс а включает координату х и дискретные
индексы т, включающие лоренцовские индексы и сорта частиц, и
мы условимся о следующих обозначениях:
<Эх,т=<Эт(х), (9.1.3)
PXjm=Pm(x). (9.1.4)
Кроме того, кронекеровский дельта-символ в (9.1.1) понимает-
понимается в теории поля как
Sx,m;y,n=S3(x-yMmn. (9.1.5)
Однако сейчас будет удобно использовать более компактные обо-
обозначения, как в формулах (9.1.1) и (9.1.2). Операторы в этих фор-
формулах записаны в «шредингеровском представлении», т. е. взяты
* Здесь молчаливо предполагается, что все связи первого рода устранены
выбором калибровки, а все оставшиеся связи второго рода «разрешены»,
так что все степени свободы, на которые наложены связи, выражены че-
через независимые операторы Qa и Ра. Согласно разделу 7.6 непосредственное
использование функциональных методов к системам со связями описано
Фаддеевым 8.
508
Глава 9. Методы функционального интегрирования
в фиксированный момент времени (например, t = 0). Зависящие от
времени гейзенберговские операторы будут рассмотрены чуть позже.
Так как все Qa коммутируют, можно найти их общий одновре-
одновременный собственный вектор состояния \ф с собственными значениями
qa:Qa\q) = qa\q). (9.1.6)
(Мы используем строчные буквы q и р для обозначения собствен-
собственных значений, а не операторов в представлении взаимодействия,
как это мы делали в гл. 7, но поскольку представление взаимодей-
взаимодействия здесь не используется, никаких недоразумений не возник-
возникнет.) Собственные векторы можно считать ортонормированными,
(9.1.7)
(9.1.8)
Аналогично можно найти полный ортонормированный набор
собственных состояний Р.:
так что условие полноты имеет вид
1=
(9.1.9)
1 =
v)(v
(9.1.10)
(9.1.11)
Как обычно, из формулы (9.1.1) следует, что скалярное произ-
произведение состояний из этих двух полных наборов имеет вид *
* Доказательство проводится так же, как в квантовой механике точечных
частиц. Из формулы (9.1.1) видно, что Ръ действуют на волновые функции в q-
базисе как —id/dqb. Тогда правая часть формулы (9.1.12) есть волновая функ-
функция собственного состояния Р в этом базисе. Множитель П1/л/2л фиксиро-
фиксирован условием нормировки (9.1.10).
9.1. Общая формула для функционального интеграла
509
(Я I Р) =
аРа) •
(9.1.12)
В гейзенберговской картине операторы Q и Р обретают зависимость
от времени:
Qa(t) ее exp(zHt)Qa exp(-iHt),
(9.1.13)
Pa(t) ее exp(zHt)Pa exp(-iHt),
(9.1.14)
где Я — полный гамильтониан. Собственные состояния |g; t) и
|р; t) этих операторов
Qa(t)|g;t) = ga
определяются формулами
g; t) = exp(zHi)| g),
p; t) = exp(zHt)| p).
(9.1.15)
(9.1.16)
(9.1.17)
(9.1.18)
(Заметим, что \q;t) есть собственное состояние оператора Qa(t) с соб-
собственным значением да, а не результат эволюции состояния |д)
к моменту времени t. Именно поэтому зависимость от времени опре-
определяется множителем exp(zHt), а не ехр(-?Ш).) Эти состояния оче-
очевидно удовлетворяют условиям полноты и ортонормированности:
(g/;t|g;t) = 5(g/-g),
(p';t|p;t) = 5(p'-p),
jlldqa\q;t){q;t\=l,
p;t)(p;t\=l,
(9.1.19)
(9.1.20)
(9.1.21)
(9.1.22)
510 Глава 9. Методы функционального интегрирования
а также условию
F==e*V(iqaPa)- (9.1.23)
Если при измерении в момент времени t обнаруживается, что
система находится в определенном состоянии |g; t), то амплитуда
вероятности того, что при измерении в момент времени t' система
будет находиться в состоянии |g'; t'), равна скалярному произведе-
произведению (g'; t'\q; t). Главная задача динамики заключается в вычислении
этого скалярного произведения.
Это легко сделать, если t' и t бесконечно близки, скажем,
t' = х + dx и t = x. С помощью формулы (9.1.17) находим
(д'; х + dx | д; х) = (д'; т|ехр(-гШт)|д; х). (9.1.24)
Гамильтониан Н задается как функция H(P,Q), но поскольку
операторы (9.1.13) и (9.1.14) являются преобразованиями подобия, а
Н коммутирует сам с собой, можно записать гамильтониан как ту
же самую функцию операторов Q(t) и P(t):
Н ее H(Q, Р) = eiHtH(Q, P)e~iHt = H(Q(t), P(t)). (9.1.25)
Если менять порядок следования операторов Q и Р, исполь-
используя коммутационные соотношения (9.1.1) и (9.1.2), эту функцию
можно представить в разных формах, отличающихся постоянны-
постоянными коэффициентами. Здесь удобно выбрать стандартную форму
гамильтониана, когда все операторы Q находятся слева от всех
операторов Р. Например, если гамильтониан содержит слагаемое
вида PaQbPc, мы переписываем его следующим образом: PaQbPc =
QbPaPc - ibabPc. С учетом этого соглашения, операторы Qa(t) в га-
гамильтониане в формуле (9.1.24) можно заменить * на их собствен-
собственные значения q'a. Что касается P(t), то используя (9.1.23), можно
разложить состояние |g; t) по собственным состояниям |р; t) опера-
оператора Р, так что в результате
* Это возможно потому, что при бесконечно малых dx в разложении
ехр(—iHdx) можно ограничиться линейными по Я членами.
9.1. Общая формула для функционального интеграла
511
(g';x + dx|g;x) = | p^dpa(g';x|exp(-zH(Q(x),P(x))dx)|p;x)(p;x|g;x)
-iH{q, p)dx + iV {q'a - qa)pa
(9.1.26)
где по каждому pa проводится интегрирование от -°° до °о.
Вернемся к более общему случаю конечного интервала време-
времени. Чтобы вычислить матричный элемент (g'; t'\q; t) при t < t', разо-
бъем интервал времени от t до t' последовательными моментами
времени t, xv x2, ..., xN, t', где
х —х = dx = (t' — t) I (N + 1), (9.1.27)
на малые участки (t, x1), (x1( x2), ..., (xN, t')n просуммируем по пол-
полному набору состояний |g; xk) в каждый момент времени хк:
(q';t\q;t) = j dqv..dqN(q';t\qN;tN)(qN;tN\qN_1;tN_1)...(q1;t1\q;t).
(9.1.28)
После подстановки представления (9.1.26) получаем:
JV
1к,а
_к=1 а
N
пп
_к=0 а
2%
хехр
jv+1 Г
1 L L (qk,a ~ Як-1,а)Рк-1,а ~
fe=l I a
(9.1.29)
Qo = Ч , Ч jv+i = Ч
(9.1.30)
Полученной нами формуле (9.1.29) можно придать более эле-
элегантный вид. Определим гладкие интерполирующие функции д(х) и
р(х) так, что
= Чк,а . Va(Xk) = Vk,a
(9.1.31)
512
Глава 9. Методы функционального интегрирования
В пределе dx —> 0 (т. е. N —> °°) показатель экспоненты в форму-
формуле (9.1.29) превращается в интеграл по х:
JV+1
~ Як-1,а )Рк-1,а ~ Н^к > Pfe-1
k=l[ a
JV+lf
k=l[ a
(9.1.32)
Далее, можно определить интеграл по функциям д(х), р(х):
k,а
3.1.33)
Тогда формула (9.1.29) принимает вид
q;t) =
т,а
т,Ь
2л
х ехр
i\ dx ?да(х)ра(х)-Я(д(х),р(х))
L t
(9.1.34)
Правая часть формулы (9.1.34) называется также интегралом
по путям *, поскольку интегрирование проводится по всем путям
* Здесь мы частично сохранили авторскую терминологию — «интеграл по
путям». Этот исторически первый образный термин вполне уместен
применительно к квантовой механике с конечным числом степеней свободы,
поскольку здесь речь идет об интегралах по функциям одной переменной
(времени) (ср. прим. на с. 509). — Прим. пер.
9.1. Общая формула для функционального интеграла 513
д(х), идущим из точки g при х = t в точку q при х = t', а также по
всем р(х). Большое преимущество такой записи матричных элемен-
элементов заключается в том, что, как показано в разделе 9.3, функцио-
функциональные интегралы легко вычисляются, если разложить их по сте-
степеням константы связи в Я.
Формализм функциональных интегралов, или, коротко,
функциональный формализм, позволяет вычислять не только ам-
амплитуды вероятностей переходов типа (g'; t'\q; t), но также и мат-
матричные элементы хронологически упорядоченных произведений
произвольных операторов 0 [P(t),Q(t)] между состояниями (g'; t'\
и |д; 0 *.
Удобно определить эти операторы так, чтобы (в противопо-
противоположность Я) все операторы Р были слева, а все Q — справа. Тогда,
вставляя любой такой оператор O[P(x),Q(x)] в (9.1.26), получаем:
dx|qP(t),Q(t))|g;x) =
х (g'; х|ехр(-гЯ(<2(х), P(x))dx|p; x)(p; x|Q(P(t), Q(t))\q; x)
(9.1.35)
Qp,q).
Чтобы вычислить матричный элемент произведения опе-
операторов f)A{P{tA),Q{tA)) f)B(P(tB),Q(tB))..., где tA > tB > ..., можно
вставить ^-операторы между соответствующими состояниями в
правой части формулы (9.1.28) и воспользоваться формулой
(9.1.35). Например, если момент времени tA попадает между тк и
xfe+1, нужно вставить f)A(P(tA),Q(tA)) между (gfe+1;xfe+1| и |qk;xfe>. За-
Заметим, что каждая последующая сумма по состояниям в фор-
формуле (9.1.28) берется в более поздний момент времени, поэтому
указанная вставка является единственно возможной в силу на-
нашего предположения, что tA > tB > ... .
* Здесь случайным образом одной и той же буквой t обозначены временные
агрументы операторов P(t), Q(t), составляющих оператор С/, и состояния \q; t).
Вообще говоря, они не совпадают. Напротив, в нижеследующей формуле
(9.1.35) необходимо считать t = x, как в формуле (9.1.24), ведущей к формуле
(9.1.26). — Прим. ред.
514
Глава 9. Методы функционального интегрирования
Действуя как и выше, получаем общую формулу для функци-
функционального интеграла:
{q';t'\oA(P(tA),Q(tA))oB(P(tB),Q(tB))..\q;t)
(9.1.36)
Этот результат справедлив только при условии, что все мо-
моменты времени упорядочены и
t
t&
t
t .
(9.1.37)
Однако ничто в правой части формулы (9.1.36) не указывает на
порядок временных аргументов. Следовательно, если нам задан
функциональный интеграл того же вида, что и правая часть
формулы (9.1.36), но с tA, tB, ..., взятыми в произвольном порядке
(однако лежащими между t и t'', t < t'), то такой функциональный
интеграл будет равен матричному элементу типа того, который
стоит в левой части формулы (9.1.36), с операторами, расположен-
расположенными в порядке убывания моментов времени слева направо. Это
означает, что при расположении tA, tB, ... в произвольном порядке,
[q; t'\T{OA (P(tA), Q(tA ))f)B (P(tB), Q(tB)),... }|g; t)
(9.1.38)
9.1. Общая формула для функционального интеграла 515
где Т означает обычное хронологическое произведение.
Возможно, следует подчеркнуть, что с-числовые функции да(х),
ра(х) в (9.1.38) являются всего лишь переменными интегрирования
и, в частности, не подчиняются уравнениям движения классиче-
классической гамильтоновой динамики
ЭН(д(х),р())
^—w^' (9-L39)
. ч ЭЯ(д(х),р(х))
Р»{%)+ Эда(х)
(По этой причине гамильтониан Н(д(х),р(х)) в (9.1.38) не является
константой по х.) Тем не менее, в некотором ограниченном смысле
функциональнае интегралы «уважают» эти уравнения движения.
Предположим, что одна из функций в (9.1.38), например,
OA(P(tA),Q(tA)), совпадает с левой частью равенств (9.1.39) или (9.1.40).
Заметим, что (при t < tA < t')
где И — аргумент экспоненты в (9.1.38):
J t
До тех пор, пока tA не достигает t или t', интегрирования по
qa{tA) и pa(tA) ничем не ограничены, и при разумных предположени-
предположениях о сходимости интегралы от таких вариационных производных
должны обращаться в нуль. Следовательно функциональный инте-
интеграл (9.1.38) равен нулю, если f)A{p,q) взят равным левой части урав-
уравнений движения (9.1.39) или (9.1.40).
Это простое правило применимо только если переменные ин-
интегрирования qa(tA), pa(tA) не зависят от любой из переменных qa(tB),
516 Глава 9. Методы функционального интегрирования
pa{tB) и т. д., от которых зависят остальные функции 0в, 0с и т. д.
в формуле (9.1.38), и, следовательно, только если мы запретим tA
достигать значений tB, tc, ..., а также t и t'. Когда tA достигает,
скажем, tB, в функциональном интеграле возникает ненулевое сла-
слагаемое, пропорциональное &{tA — tB) или ее производным. Эти дель-
дельта-функции соответствуют тем дельта-функциям, которые возни-
возникают в рамках операторного формализма от производных по време-
времени ступенчатых функций, присутствующих в определении хроно-
хронологического произведения.
Для вычисления функциональных интегралов (9.1.34) и (9.1.38),
необходимо знать только классическую функцию Гамильтона, т. е.
с-числовую функцию H(q, р). Если мы хотим сформулировать тео-
теорию с помощью функциональных интегралов, естественно возни-
возникает вопрос, какая из многих возможных квантово-механических
функций Гамильтона H(Q, Р) (отличающихся порядком Q и Р) опи-
описывает квантовую теорию, соответствующую этим интегралам.
Предложенный вывод дает ответ на этот вопрос: в квантовой
функции Гамильтона все Q должны быть слева, все Р — справа.
Однако было бы ошибкой придавать этому рецепту слишком боль-
большое значение. Имеется множество способов интерпретировать ме-
меру I\dqa(t)Y[dpa(t) в интегралах типа (9.1.34) или (9.1.38). Наш ре-
рецепт расположения всех Q слева от всех Р годится только, если
мера определяется согласно формулам (9.1.31)—(9.1.33). Другие ме-
меры приводят к другим предписаниям по упорядочиванию операто-
операторов. Вопрос в целом не очень существен, так как разные рецепты
упорядочивания операторов в функции Гамильтона соответствуют
всего лишь разному выбору констант, входящих как коэффициен-
коэффициенты при разных слагаемых в этой функции, а мы всегда формули-
формулируем теории так, что эти константы рассматриваются как произ-
произвольные параметры.
Функциональный интеграл общего вида (9.1.38) трудно ис-
использовать для численных расчетов или для доказательства стро-
строгих теорем. Для этих целей лучше применять функциональный
метод для вычисления амплитуд в евклидовом пространстве, где
t заменено на мнимую величину —гж4, и показатель экспоненты в
формуле (9.1.38) — действительная отрицательная величина. То-
Тогда вместо быстрых осцилляции подынтегрального выражения в
результате малого дрожания путей все быстрые дрожания оказы-
оказываются экспоненциально подавлены.
9.2. Переход к S-матрице 517
Хотя мы не будем углубляться в этот вопрос, но квантовая
теория поля может быть с самого начала сформулирована в терми-
Ф« Яя
еинмановских амплитуд в евклидовом пространстве—времени .
При определенных разумных предположениях возможно реконст-
реконструировать фейнмановские амплитуды в пространстве Минковского,
зная их евклидовы аналоги 8б. Однако если использовать функцио-
функциональные интегралы для вычисления фейнмановских амплитуд по тео-
теории возмущений, то можно ограничиться их формулировкой в про-
пространстве Минковского.
9.2. Переход к ^-матрице
Как уже отмечалось, можно без труда переписать общие кван-
тово-механические результаты раздела 9.1 в обозначениях, пригод-
пригодных для квантовой теории поля, если принять, что индекс а прини-
принимает значения, отвечающие точкам х пространства и индексам т
спина и сорта частиц т, и заменить Qa(t) и Pa(t) на Qm(x, t) и Pm(x, t).
Тогда формула (9.1.38) принимает вид *:
(q, t'\T{OA [P(tA), Q(tA )],0B [P(tB), Q(tB)],.. \q, t)
X VA[p(tA),q(tA)]0B[p(tB),q(tB)]...
X exp i ^ di{j d3x qm (x, т)рт (x, x) - H[q(z), p(x)]} .
Однако формула (9.2.1) не совсем соответствует тому, что
хотелось бы иметь в теории поля. Экспериментаторы измеряют не
амплитуды вероятностей для переходов между собственными
* Мы записываем теперь аргументы операторов Я и О в квадратных ско-
скобках, чтобы напомнить, что H[q(t), p(t)] и fi[p(t), q(t)] являются функционалами
от qm(s.,t) и pm(s.,t) в фиксированный момент времени t.
518 Глава 9. Методы функционального интегрирования
состояниями (q',t'\ и \q,t), а элементы 5-матрицы, т. е. амплитуды
вероятностей для переходов между состояниями, которые при
t —> — °° или t —> +°° содержат определенное число частиц разных
сортов. Это так называемые «ин» и «аут» состояния |a,in) и |C,out),
где а и C обозначают наборы частиц определенных сортов с опреде-
определенными значениями импульсов, z-компонент спина (или спираль-
ностей).
Чтобы вычислить матричный элемент хронологически упоря-
упорядоченного произведения (возможно, и отсутствующего) между та-
такими состояниями, следует умножить (9.2.1) на «волновые функ-
функции» (C, out|g', f) и (g, t|ot, in) в любые фиксированные моменты вре-
времени t и t', которые для удобства взяты здесь равными -°° и +°о,
соответственно, а затем провести интегрирование по «аргументам»
gm(x) и g'm(x) этих волновых функций.
Однако вместо того, чтобы сначала выписать функциональ-
функциональный интеграл по gm(x,t) с условиями
gm(x,+oo) = g^(x), gm(x,-oo) = gm(x), (9.2.2)
а затем интегрировать по g'm(x) и gm(x), можно с тем же успехом
интегрировать по gm(x,t) без всяких условий (как и по pm(x,t)), пола-
полагая аргументы волновых функций равными тем значениям, кото-
которые даются формулой (9.2.2):
, out\T{f)A [P(tA), Q(tA )},f)B [P(tB), Q(tB)],.. \a, in)
= J П d(Ux>T) X\{dVm{*,x))l2%
T,x,m T,x,.m
XOA[p(tA),q(tA)VB[p(tB),q(tB)]...
Г г и , Л (9-2-3)
x exp iJ ^ dx|J d6x qm (x, x)pm (x, т) - Я[д(т),
X (P, OUt I q(+oo);+oo)(g(-oo);-oo | a, in) .
Кстати, этот результат немедленно приводит к формуле F.4.3),
т. е. к теореме, которую мы неоднократно использовали для того,
чтобы связать суммы фейнмановских диаграмм вне массовой по-
поверхности с матричными элементами операторов в гейзенберговском
9.2. Переход к S-матрице 519
представлении между собственными состояниями с определенной
энергией. *
Теперь необходимо установить, как вычислять волновые функ-
функции, являющиеся последними двумя множителями правой части
формулы (9.2.3). Рассмотрим сначала простейший и наиболее важ-
важный случай — вакуум. (В разделе 6.4 мы видели, что элементы
.^-матрицы легко вычисляются через средние по вакууму от хроно-
хронологических произведений.) Предположим, как обычно, что при
t —> +°° матричные элементы вычисляются так, как будто нет ника-
никакого взаимодействия.Таким образом, «ин»- и «аут»-вакуумы могут
быть определены условиями
ain(p,G,n)|VAC,in) = O,
aout(p,a,n)|VAC,out) = 0, {92А)
где операторы ain и aQUt являются коэффициентами при экспоненте
ехр(гр-х - iEt) в разложении оператора Qm(x,t) по плоским волнам при
t —> -°° и t —> +°°, соответственно. Например, в случае действительного
скалярного поля, отвечающего нейтральной бесспиновой частице, имеем
* Для доказательства необходимо лишь заметить, что если гамильтониан
имеет вид H[P(t), Q(t)] + LA Jd x ?A(x, t)OA(x, t), то б'-матрица определяется
согласно (9.2.3) следующим образом:
(p,outa,in)e= П dqm(x,z) П (dpm(x, т))/2я
т, х, т 1, х, .т
х expl i \di\ jd3xqm{x, х)рт(х, т) - Я[д(т),р(т)]
-L{d3X8A(x,t)OA(x,t)
A J
x (p, out | q(+°o);+°o)(q(-°o);-°° | a, in).
Левая часть формулы F.4.3) равна производной этого выражения по еа, еь и т.
д. при 8=0, что дает правую часть формулы (9.2.3). Вновь используя (9.2.3),
приходим к правой части формулы F.4.3).
520
Глава 9. Методы функционального интегрирования
Ф(х, t)
J
a
in
out
(9.2.5)
1/2
a
in
out
(9.2.6)
где p° = E = vp2 + m2 I здесь вместо Q и Р мы используем общепри-
общепринятые для скалярного поля обозначения Ф и П и опускаем ненуж-
ненужные индексы т, G, п. Обращая преобразование Фурье и беря ли-
линейные комбинации получившихся выражений, получаем, что
JEt
ain (p)= lim
"in
out
Bл)
3/2
(9.2.7)
Как отмечалось в разделе 9.1, «импульс» П(х,?) действует на волно-
волновые функции в ф-базисе * как вариационная производная -гб/5ф(х,?),
так что условия (9.2.4) в этом базисе принимают вид:
0 = d3xe~ipx
6ф(х)
Е(р)ф(х)
Ф(х);+°о
in \
VAC, . (9.2.8)
out/
Аналогичное обыкновенное дифференциальное уравнение име-
имеет хорошо известное гауссово решение, так что попробуем и здесь
воспользоваться гауссовской подстановкой:
* Дословный перевод англоязычного термина wave functions in <p-basis. В
русскоязычной литературе более употребителен термин волновые функци-
функционалы в (^-представлении (где оператор Ф(х) действует как оператор
умножения на функцию (р(х)). — Прим. ред.
9.2. Переход к S-матрице
521
VAC, \ = .Гехр --
в которой предстоит определить ядро S и константу ./!". Подставляя
правую часть формулы (9.2.9) в формулу (9.2.8), находим, что функ-
функциональное дифференциальное уравнение для вакуумного волново-
волнового функционала удовлетворяется, если при всех ф
О = Jd3xe-ip-x[Jd V(x,y)(p(y) -Е(р)ф(х)] (9.2.10)
или, другими словами, если
(9.2.11)
Решение легко находится обращением преобразования Фурье:
,у) = B7i)-3Jd3peip(x-y)E(p).
(9.2.12)
(Напомним, что Е(р) = Jp2 + т2 •) На самом деле, это самое полез-
полезное представление ядра й, но заметим попутно, что при х Ф у мож-
можно записать $ через функцию Ганкеля отрицательного порядка:
(9.2.13)
где г = |х — у|. Константа . !" формально определяется из условия
нормировки вакуумного состояния, но этот результат нам не пона-
понадобится.
Согласно формуле (9.2.9), при вычислении средних по вакууму
в теории скалярного поля произведение двух последних множите-
множителей в формуле (9.2.3) равно
|VAC, in)
(УАС,ои1|ф(оо);+оо)(ф(
_l .1-2
-оо);-оо
exp -^ f d3xd3yrS(x,y)^(x,-H>oMy,-H>o) + ф(х,-о°)ф(у ,-«>)]
,у)ф(х,х)ф(у,х)е-е|т
exp -
(9.2.14)
522
Глава 9. Методы функционального интегрирования
где ? — бесконечно малая положительная величина. При получении
окончательного выражения, мы воспользовались тем фактом, что
для любой достаточно гладкой функции /(х)
? fdx/(x)e~e|T
(9.2.15)
Подставляя представление (9.2.14) в формулу (9.2.3), получаем:
(vac, out\T{oA [n(tA), Ф(гА)], ов [n(tB), Ф(гв)],.. .| vac, in)
т,х
т,х
[/•ОО Г /•
г di\\ d3x ф(х, х)л(х, х)
(921б)
-Я[ф(х),
, х)ф(у, х)
В разделе 9.4 мы увидим, что совокупный эффект от последне-
последнего слагаемого в показателе экспоненты в правой части формулы (9.2.16)
заключается в появлении добавки —г? в знаменателе пропагатора ска-
скалярного поля в импульсном пространстве: [р2 + т2 — г?]-1. Мы не
будем вдаваться в детали соответствующих вычислений для полей
произвольного спина, а просто укажем, что в общем случае
(VAC, out\T{f)A[PA(tA),Q(tA)],f)B[PB(tB),Q(tB)],... | VAC, in)
=|./Г2
: OB[p(tB),q(tB)],... xexp
OA[p(tA),q(tA)]
dx Jd3x?qm(x,x)pm(x,x)
(9.2.17)
-Я[д(х), р(х)] + г? - слагаемые
9.3. Лагранжева форма функционального интеграла 523
Здесь <и?-слагаемые» приводят к появлению правильной добавки —г?
в знаменателях всех пропагаторов.
Сейчас уместно отметить, что не зависящие от полей множите-
множители в (9.2.17), типа константы |. Г |2, несущественны. Дело в том, что они
дают вклад и в матричный элемент перехода (VAC, out|VAC, in).
При вычислении связной части средних по вакууму от хронологи-
хронологических произведений (или .^-матрицы) мы избавляемся от вклада
несвязных поддиаграмм вакуумных флуктуации путем деления на
(VAC, out|VAC, in), так что все постоянные множители в вакуум-
вакуумных средних сокращаются.
Можно продвинуться дальше и вычислить матричные эле-
элементы между многочастичными состояниями, подставив соответ-
соответствующие «волновые функционалы» в формулу (9.2.3). Последние
можно вычислить, подействовав на вакуумное состояние сопря-
сопряженными операторами к операторам уничтожения вида (9.2.7).
Как и для гармонического осциллятора, такие волновые функ-
функционалы оказываются полиномами Эрмита по полям, умноженны-
умноженными на вакуумный гауссиан. Мы не будем развивать далее эти вы-
вычисления, поскольку, как показано в разделе 6.4, все, что нужно
для вычисления матричных элементов .^-матрицы, это знание сред-
средних по вакууму (9.2.17).
9.3. Лагранжева форма функционального интеграл
Подынтегральное выражение в показателе экспоненты в фор-
формулах (9.1.38) или (9.2.17) похоже на лагранжиан L для гамильто-
гамильтониана Я. Это сходство до некоторой степени вводит в заблужде-
заблуждение, так как «импульсы» pa(t) или pn(x,t) являются независимыми
переменными, еще не связанными с qa(t) или qn(x,t) или их произ-
производными.
Однако существует большой и важный класс теорий, в кото-
которых интеграл по «импульсам» может быть взят путем простой за-
замены их на те значения, которые диктуются каноническим фор-
формализмом. В этом случае подынтегральное выражение в показателе
экспоненты в интегралах по путям действительно совпадает с ла-
лагранжианом.
Гамильтониан таких теорий квадратичен по «импульсам»,
т. е. на языке теории поля
524 Глава 9. Методы функционального интегрирования
H[Q,P] = |? Jd3xd3yAxnjym[Q]Pn(x)Pm(y)
пт
(9-ЗЛ)
где «матрица» А — действительная, симметричная, положитель-
положительная и несингулярная.Тогда показатель в экспоненте в формуле (9.2.17)
квадратичен по р:
d-c
1
2
где
Q] = Ахп,уш [Q(-C)]8(T - т'), (9.3.3)
^ Вхп[д(т)]-д„(х,т), (9.3.4)
(9.3.5)
В общем случае интеграл от экспоненты, в показателе кото-
которой стоит квадратичное выражение типа (9.3.2), пропорционален
экспоненте, вычисленной в стационарной точке ее показателя.
В случае конечного числа действительных переменных Ъ, s эта фор-
формула имеет вид
_ г __ л (9.3.6)
(Det[zA/2jr])-1/2 exp -11? Asr^r - г^ Bs^s - гС ,
I sr s J
9.3. Лагранжева форма функционального интеграла 525
где ^ - стационарная точка,
r- (9.3.7)
г
(Доказательство формулы дано в Приложении к этой главе.)
Следовательно, если 0А, 0в и т. д. в (9.2.17) не зависят от р,
можно вычислить функциональный интеграл по импульсам р в фор-
формуле (9.2.17) в случае такого гамильтониана, взяв эти переменные в
стационарной точке квадратичного выражения в показателе экспо-
экспоненты. Однако вариационная производная этого квадратичного вы-
выражения равна
[ dx[ [ d3xqn(х, x)pn (x, x) - Я[д(х), р(х)] + г? - слагаемые}
()
(Слагаемые с г? зависят только от переменных д.) Таким образом,
стационарная «точка» pn(x, t), в которой эта производная обращает-
обращается в нуль, есть просто значение pn(x,t), задаваемое канонической
формулой
[8H[g(x),p(x)]
L Spn(x,x)
(9.3.8)
р=р
Если положить pn(x,t) равным этому значению, показатель экспо-
экспоненты в (9.2.17) превращается в обычный лагранжиан *
L[g(x),g(x)] =
и формулу (9.2.17) можно записать в виде
3.3.9)
* Точнее, в лагранжево действие. — Прим. ред.
526 Глава 9. Методы функционального интегрирования
(VAC, out\T{fJA[Q(tA)],0B[Q(tB)],... }|VAC, in)
— I2 | | | An (v Wno-fTOVir J\r,VC\~4" Г, \n(+ \Л Л \n(+ \Л
xexp
г (Лт{Ь[д(т), д(т)] + г? - слагаемые}
(9.3.10)
(Мы объединили множители 1/2л в интегралах по р с детерминан-
детерминантом из формулы (9.3.6).) Это и есть желаемая лагранжева форма
функционального интеграла.
При выводе (9.3.10) было необходимо предположить, что опера-
операторы 0А, 0в, ... не зависят от канонических «импульсов». Это условие
не такое жесткое, как может показаться. Например, в скалярной
теории поля, в которой канонически сопряженный полю Ф импульс
есть П = Ф, возможно вычислить матричный элемент хронологиче-
хронологически упорядоченного произведения операторов, один из которых есть
ф({), взяв разность матричных элементов, в которых этот оператор
заменен на Ф(т + dx) и Ф(т), поделив ее на dx и взяв предел dx —» 0.
Эквивалентно, до тех пор, пока t не совпадает ни с одним из осталь-
остальных временных аргументов оператора в формуле (9.3.10), можно просто
дифференцировать (9.3.10) по времени t
Единственное оставшееся серьезное осложнение в формуле
(9.3.10) связано с детерминантом -/[д]. Если -/[д] не зависит от по-
полей, то не возникает никаких проблем. Мы уже отмечали, что об-
общие константы не дают вклада в связные части ваккумных сред-
средних, так как при их вычислении производится деление на амплиту-
амплитуду перехода вакуум-вакуум, пропорциональную той же константе.
Именно так обстоит дело в теории нескольких взаимодействующих
друг с другом скалярных полей Фп без производных и/или взаимо-
взаимодействующих с производными, но с внешними токами Jn. Плотность
лагранжиана в этом случае имеет вид:
Очевидное обобщение результатов раздела 7.5, касающихся
взаимодействия с производными одного скалярного поля, на случай
9.3. Лагранжева форма функционального интеграла 527
нескольких скалярных полей приводит к гамильтониану
(Здесь скалярные поля Фп выбраны действительными скалярами,
однако можно включить в рассмотрение и комплексные скалярные
поля, разделив их на действительную и мнимую части.) В общем
случае возникает нетривиальное слагаемое, линейное по Пп, но ко-
коэффициент в квадратичном слагаемом есть константа, равная про-
просто единичной «матрице»
—1/2
В данном случае множитель (Det[2zJi.?/[g]]) в (9.3.10) есть
независящая от полей константа, не влияющая на результаты.
Однако не всегда все так просто. В качестве второго примера рас-
рассмотрим так называемую нелинейную а-модель, лагранжиан которой
[Ъпт + Unm (Ф)] - У(Ф).
Прямое вычисление приводит к гамильтониану
я =
Здесь 4 — зависящая от полей величина
В подобных случаях детерминант может быть записан в виде
вклада в эффективный лагранжиан, если воспользоваться соотно-
соотношением Det -А = exp Tr In А. Заменяя пространственно-временной
континуум дискретной решеткой точек посередине отдельных про-
пространственно-временных областей очень малого объема О., можно
интерпретировать дельта-функцию в Апхту следующим образом:
54(х - у) = ?Г1Ьху, так что
528 Глава 9. Методы функционального интегрирования
,у l!/ ЩФ(Х))) - 1 • 1П п]пт ,
где логарифм матрицы определяется своим разложением в ряд
U2 U3
ln(l + U) = U- — + — -...
Чтобы вычислить след, заметим, что Е^ - = ?1~ЦсРх ... . Тогда
детерминант равен
DetA ос expJ-П J d4x tr ln[l + ЩФ(х))]],
где символ «tr» означает след в обычном матричном смысле. Коэффи-
Коэффициент пропорциональности (возникающий из слагаемого -In Q) не
зависит от поля и поэтому не представляет интереса.
Можно рассматривать этот детерминант как поправку к эф-
эффективному лагранжиану
Ш = -\ йГЧг ln[l + ЩФ(а:))] •
Множитель ОТ1 можно представить в виде ультрафиолетово
расходящегося интеграла
Мы не будем этого показывать, но дополнительные слагаемые
в фейнмановских диаграммах для такой теории, связанные с поправ-
поправкой АУ, можно вывести и в рамках канонического формализма, учи-
учитывая слагаемые от одновременных коммутаторов в пропагаторе
производных по времени скалярного поля 7. Пренебрежение этой
поправкой приводит к ложной зависимости .^-матрицы от способа
определения скалярного поля, и, кроме того, несовместимо с лю-
любой симметрией лагранжиана относительно преобразований скаляр-
скалярного поля.
Даже в случае, когда множитель (Det -/)/2 в формуле (9.3.10)
для функционального интеграла не зависит от полей, лагранжиан в
этой формуле может отличаться исходного. Например, рассмотрим
теорию нескольких действительных векторных полей с плотностью
лагранжиана
9.3. Лагранжева форма функционального интеграла
529
где токи Jn^ являются либо внешними с-числовыми источниками,
либо зависят от других полей (в последнем случае в лагранжиан
следует добавить вклад других полей). Простое обобщение резуль-
результатов раздела 7.5 приводит к гамильтониану
Н=
А
>
В правую часть следует также добавить слагаемые от любых
других полей, входящих в Jn^ . Коэффициент при квадратичном
слагаемом здесь несколько сложнее, чем в первом примере, и ра-
равен
nix, mjy nm
но он не зависит от полей, так что множитель (Det -/) 1?2 несущест-
несуществен. С другой стороны, лагранжиан (9.3.9) отличается от исходного:
он выражается только через поля А и их производные по времени,
но не содержит вовсе временных компонент А0 *. По этой причине
лоренцовская инвариантность выражения (9.3.10) далеко не очевидна.
Чтобы исправить это положение, можно вновь ввести вспомо-
вспомогательное поле. Предположим, что мы добавили к гамильтониану
слагаемое
АН = ~ 2
* Это и неудивительно, поскольку мы имеем дело с теорией со связями
(второго рода), и приведенный гамильтониан получен в результате разрешения
этих связей, выражающих А0 через независимые поля А и сопряженные им
канонические импульсы. — Прим. ред.
530 Глава 9. Методы функционального интегрирования
и проинтегрировали по Ап°, а также по Ап и Пп. Результатом этого
может быть только появление не зависящего от полей общего мно-
множителя, поскольку АН квадратично по А0 (с независящим от полей
коэффициентом в слагаемом второго порядка по А0) и его стацио-
стационарное значение обращается в нуль. Однако предположим, что мы
интегрируем по Пд до интегрирования по Ап°. Гамильтониан в фун-
функциональном интеграле (9.2.17) заменяется на
Н + АН= fd3
Он все еще квадратичен по Пп с не зависящим от поля
(и даже более простым) коэффициентом при квадратичном слагаемом,
так что интеграл по всем Г^ можно взять, просто заменив Г^ на его
значение в стационарной точке функционала Еп|<Л3хП ¦ Ап—Н — АН:
Если Пп исключить именно таким способом, то Ejd3xn -А — Н — АН
есть в точности исходный лоренц-инвариантный лагранжиан.
Чтобы учесть возможную необходимость введения вспомога-
вспомогательных полей типа Ап°, будем с этого момента записывать форму-
формулу для функционального интеграла после исключения канонически
сопряженных импульсов в терминах полей щ, включающих как ка-
канонические поля qn, так и вспомогательные поля сг:
(VAC, out\T{fJA[4>A(tA)],fJB[4>B(tB)],...}\ VAC, in)
т,х,тг
(9.3.11)
xexp
\ dx{L[\|/(x), \\f(i)] + ie- слагаемые}
имея при этом в виду, что лагранжиан L может содержать слагае-
слагаемые, возникающие от зависящих от полей множителей вида
(Det ^Г1/2.
9.4. Вывод фейнмановских правил 531
9.4. Вывод фейнмановских правил
с помощью функциональных интегралов
Теперь мы готовы к тому, чтобы воспользоваться формализ-
формализмом функциональных интегралов для вывода фейнмановских пра-
правил для широкого класса теорий. Нас будут интересовать средние
по вакууму от хронологических произведений полевых операторов
(и сопряженных им операторов)
(V AC, out TJ^ (хА),^г (xB)...}|vAC,in)
MijbJvb-) = ± (vac, out | vie, in) • (9A1)
из которых (как показано в разделе 6.4) можно получить матричные
элементы .^-матрицы, отбрасывая пропагаторы внешних линий, свя-
связанные с каждым из этих полей, заменяя их на коэффициентные
функции, стоящие в качестве множителей перед операторами ро-
рождения и уничтожения в соответствующих выражениях для сво-
свободных полей, и суммируя по всем индексам этих коэффициентных
функций.
Для простейших теорий, гамильтониан которых квадратичен
по П, находим с помощью формулы (9.3.11):
ЩА1ВЛХАХВ---) - г > (Q л
где 1[\|/] - действие вида
), \j/(x)] + г? - слагаемые}, (9.4.3)
ДV] = J
причем L включает теперь любые возможные слагаемые, возника-
возникающие от зависящего от поля детерминанта в формуле (9.3.10).
Предположим далее, что лагранжиан равен интегралу от
плотности лагранжиана, содержащей квадратичное слагаемое 3?0,
532 Глава 9. Методы функционального интегрирования
остающееся и в отсутствие взаимодействий, и плотности лагран-
лагранжиана взаимодействия (?^\
= J d3x[s?0 (\|/(x, t), Э^у(х, t)) + ^(\|/(x, t), Э^у(х, т))] .(9.4.4)
Иными словами, действие (9.4.3) равно
Д?} = ^[?] + ^[?], (9-4.5)
^о [V] = J d4x^0 (\|/(х), Эц\|/(ж)) + г? - слагаемые, (9.4.6)
(9.4.7)
Так как 5Р0 и «г?-слагаемые» квадратичны по полям, можно всегда
записать 10 как обобщенную квадратичную форму
[V] = - ]-
Например, для действительного скалярного поля массой т невоз-
невозмущенный лагранжиан имеет вид
%0 = _1э^фЭ^ф-|ш2ф2 , (9.4.9)
а г?-слагаемые в 10 определяются формулой (9.2.16) в виде
— iF\rlt\rl^Trl^T'fi(Tc x'lmfx t)<n(Tc' t) (Q 4 1 ft)
* J J
так что
D^ x, = — Э-64(х - x') + m264(x - x') - z?E(x,x/N(t - t'). (9.4.11)
^~u Эх,',
(С этого момента мы опускаем множитель е ^ в г?-слагаемом, так
как от него возникают поправки более высокого порядка по ?.) Взаи-
Взаимодействия мы будем учитывать по теории возмущений, разлагая
экспоненту по степеням 1Ь
9.4. Вывод фейнмановских правил 533
°° iN n
^Ш^ /\/ 1 ^ ' уС/ шЛ.ш А. ?4 J
JV=O
а затем разлагая 1г по степеням полей. Интегралы, получающиеся в
числителе и знаменателе формулы (9.4.2), имеют следующий об-
общий вид:
¦ с \
(9.4.13)
где множители, содержащие поля ?;1(xi)?i2(x2), и т. д. возникают
из Ii[x|/] и/или из полевых множителей ?гл(жА), изначально при-
присутствующих в числителе (9.4.2). Если 10[\|/] имеет вид (9.4.8), инте-
интеграл (9.4.13) относится к тому же типу, что и интеграл, вычислен-
вычисленный в Приложении к данной главе, с той разницей, что дискретный
индекс s заменен парой индексов I, х. Поэтому можно воспользо-
воспользоваться формулами (9.А.12) и (9.А.15), что дает
юпаренные поля
по по
спариваниям парам
полей (9.4.14)
Это и есть ковариантные правила Фейнмана в координатном
пространстве для вычисления числителя в формуле (9.4.2). Мы про-
проводим разложение по взаимодействию 1Ь затем суммируем по все-
всевозможным спариваниям полей в множителях 1г друг с другом и с
полями \|/jA {xA) и т. д., причем каждое спаривание дает вклад в виде
интеграла по пространству—времени от произведения коэффициент-
коэффициентных функций полей в 11[\|/] и произведения «пропагаторов» — гД, где
Alili(x1,x2) = {c-f~l\Xl}iiXi ¦ (9.4.15)
(Множитель [Det(i(J)/2%)]—1/2 в формуле (9.4.14) представляет собой
вклад диаграмм с неограниченным числом одиночных петель, не
связанных с другими линиями, но в любом случае этот множитель
сокращается в отношении (9.4.2).)
Остается вычислить сами пропагаторы (9.4.15). Мы рассматри-
рассматриваем формулу (9.4.15) как интегральное уравнение
534 Глава 9. Методы функционального интегрирования
n
, А, , (жо,х,) = 54(x, -ХоM,7 . ,.,,,.
ilxl,l2x2 I2,i3\ и б> х 6 '1'з (9.4.16)
В отсутствие внешних полей в силу трансляционной инвари-
инвариантности величина (J) с необходимостью есть функция только разно-
разности Xi — x2 и может быть записана в виде интеграла Фурье:
*ре1рлх*-х*Ци1г(р). (9.4.17)
Решение уравнения (9.4.16) имеет тогда вид
At ~р ~р \ — (t)'Tr\~^ I г\ ^Tl p^V'\"c\~"c2'\~*)~^- (Tl\ tQ /I 1 Q Л
7 7 К**" 91 **" Ч) — l^'W I ^ H*~ *-^ \И)Ш [У.ТГ.1О)
li>l2 z ° J hfo
где (J~l — матрица, обратная к матрице Ч). Как будет показано, ге-
слагаемые приводят к тому, что такая обратная матрица хорошо
определена для всех действительных значений р. Таким образом,
задача вычисления пропагатора сведена к обращению конечномерной
матрицы.
Рассмотрим сначала массивное скалярное поле. В этом случае
A) имеет вид (9.4.11). Можно записать его в виде интеграла Фурье
«L,, = Bл)-4 fd4peip(a;-y)(p2 +m2 -
так что пропагатор равен
)
AXiV = Bл)-4 I d4peip(a;-y)(p2 +т2 - геЕ(р)) .
Видно, что это выражение совпадает со скалярным пропага-
тором, полученным ранее операторными методами. (Разница ме-
между ? и еЕ(р) несущественна, так как обе величины положитель-
положительны и бесконечно малы.)
В качестве второго примера рассмотрим действительное мас-
массивное векторное поле. Невозмущенный лагранжиан равен
L-l-.-v л —i л 1,-\11*л1 -\л» 1 II , -^-
I ri /1 у-1 /1
П — \ 11 ¦^^^V V
4
9.5. Функциональные интегралы для фермионов
535
Вновь можно записать 10[\|/] в форме (9.4.8) с ядром
px,oy
э2
э2
54(х — y) + ie — слагаемые
= Bл) \di/pelv'i-x~y)[r\рстр2 - РрРст + w2r( + ге - слагаемые].
Мы не будем тратить здесь время на то, чтобы показывать,
что «+г?-слагаемые» принимают простой вид — г?.Е(р)г|ро. Тогда про-
пагатор векторного поля получается простым обращением матрицы
4x4 в последнем подинтегральном выражении:
,ipix-y)
+mz - геЕ(р)
VpVa
т
(Слагаемые, пропорциональные ?, в числителе опущены. Они важны в
знаменателе, так как определяют, как следует рассматривать подын-
подынтегральное выражение вблизи массовой оболочки р2 = — т2.) Приве-
Приведенное выражение совпадает с полученным операторными методами,
если не считать того, что отсутствуют нековарантные слагаемые, про-
пропорциональные 5(х° — у0). Ранее эти нековариантные слагаемые были
нужны для того, чтобы сократить нековариантные добавки в гамиль-
гамильтониане взаимодействия. Теперь же вклады вершин в фейнмановских
правилах получаются непосредственно из ковариантного лагранжиана,
так что никакого сокращения не требуется.
Столь же просто рассматриваются теории с взаимодействием
с производными. Множитель, возникающий от спаривания произ-
производной поля д^лу^х) с любым другим полем \|/т(у) (которое само мо-
может быть производной), имеет вид
Э Mfl{x)Mfm{y)e
(9.4.19)
(Vl (Я) Vm (!/))¦
536 Глава 9. Методы функционального интегрирования
У таких пропагаторов отсутствуют нековариантные части. На-
Например, для действительного скалярного поля спаривание Эф
с Эуф приводит в результате к пропагатору в импульсном пред-
представлении kjcv/{k2 + т2 — г?). Кроме того, как мы видели в преды-
предыдущем разделе, вершины в теории скалярного поля, взаимодей-
взаимодействие которого с другими полями содержит производные, можно
непосредственно извлечь из лагранжиана, причем они по отдель-
отдельности ковариантны.
9.5. Функциональные интегралы для фермионов
Займемся теперь обобщением формализма функциональных
интегралов на теории, содержащие как бозоны, так и фермионы.
В принципе, нетрудно действовать чисто формально по аналогии с
бозонным случаем, и затем убедиться, что получились «правиль-
«правильные» фейнмановские правила. Мы предпочитаем вывести формализм
функциональных интегралов для фермионов непосредственно из
принципов квантовой механики, как это уже было сделано для бо-
бозонов 9.
Начнем с рассмотрения произвольной квантово-механической
системы, описываемой «координатами» Qa и канонически сопряжен-
сопряженными «импульсами» Ра, которые теперь удовлетворяют не коммута-
коммутационным, а антикоммутационным соотношениям
{Qa,Pb} = z6ab, (9.5.1)
{Qa,Qb} = {Ра,Рь} = 0. (9.5.2)
(Эти операторы берутся в шредингеровском представлении, или,
иначе говоря, в гейзенберговском представлении в момент времени
t = 0.) Позднее мы заменим дискретный индекс а на пространствен-
пространственную координату х и полевой индекс т.
Прежде всего, построим полный базис состояний, на которые дей-
действуют операторы Q и Р. Заметим, что при любом заданном а
Ql = Ра2 = 0. (9.5.3)
9.5. Функциональные интегралы для фермионов 537
Отсюда вытекает, что всегда существует «кет»-состояние 0), ко-
которое аннигилируется всеми операторами Qa:
QjO) = O, (9.5.4)
и «бра»-состояние @|, которое аннигилируется (справа) всеми опе-
операторами Ра:
@|Ра=0. (9.5.5)
Например, можно положить
где |/) и (д\ — любые кет- и бра-векторы, для которых эти выраже-
выражения не обращаются в нуль. (Построенные состояния не могут обра-
обращаться в нуль для всех |/) и (д\, если только не равны нулю опера-
операторы Па<Эа и Па-Ра, что по предположению не имеет места.) В силу
равенств (9.5.3) эти состояния удовлетворяют соотношениям (9.5.4) и
(9.5.5). В общем случае они не единственны, поскольку могут быть
дополнительные бозонные степени свободы, отличающие различ-
различные возможные состояния 0) и @ |. Для простоты, ограничимся рас-
рассмотрением случая, когда единственными степенями свободы явля-
являются те, которые описываются фермионными операторами Qa и Ра,
и предположим, что состояния, удовлетворяющие соотношениям
(9.5.4), (9.5.5), единственны с точностью до постоянного множителя,
который мы выберем так, чтобы
@|0) = 1. (9.5.6)
(Обратим внимание, что это условие нормировки не может быть
выполнено, если определить @ | как левое собственное состояние Qa
с собственным значением нуль, поскольку в этом случае @ |{Qa,Pa}| 0)
также обращалось бы в нуль, откуда с учетом (9.5.1) следовало бы,
что @ | 0) = 0.)
Как мы видели в разделе 7.5, в дираковской теории Qa неэр-
неэрмитовы, но имеют сопряженные операторы —iPa, и в этом случае @|
можно рассматривать просто как сопряженное состояние к |0).
538
Глава 9. Методы функционального интегрирования
Однако, существуют фермионные операторы (например, поля «ду-
«духов», которые мы введем в т. II), для которых Ра никак не связаны
с сопряженными к Qa операторами. В последующем нам не потребу-
потребуются никакие особые предположения об операторах, сопряженных
к Qa или Ра, а также о связи между @| и |0).
Полный базис в пространстве состояний этой системы состоит
из |0) и (антисимметричных по а, Ъ, ...) состояний
\а,Ъ,..) = РаРъ...\0)
(9.5.7)
с любым числом различных Р, действующих на |0). Это означает,
что результат действия на эти состояния любой операторной функ-
функции Р и Q можно записать как линейную комбинацию того же набо-
набора состояний. В частности, если индекс а не совпадает ни с одним из
индексов в \Ъ, с, ...), то
Qa|b,c,...} =
(9.5.8)
а О, <-,.../- a, U, С,.../.
(9.5.9)
С другой стороны, если а равно одному из индексов в после-
последовательности Ъ, с, ..., то всегда можно переписать это состояние
(возможно, изменив его знак) так, что а станет первым из этих
индексов, и тогда имеем:
Qa\a,b,c,...) = г\Ъ,с,...),
(9.5.10)
Pa|a,b,c,...) = 0.
(9.5.11)
Аналогично можно определить полный дуальный базис, со-
состоящий из @ и (антисимметричных по индексам) состояний
(9.5.12)
Используя соотношения (9.5.4)—(9.5.6) и антикоммутационные соот-
соотношения (9.5.1), видим, что скалярные произведения этих состоя-
состояний равны
9.5. Функциональные интегралы для фермионов 539
(c,d,...\a,b,..) = (O\...(-iQd)(-iQc)PaPb...\O)
_ ГО, если {c,d,...} Ф {а,Ъ,...}, (9.5.13)
[l, если с = a,d = Ъ,и т. д.,
где {...} означает набор индексов внутри скобок независимо от их
порядка.
При выводе фейнмановских правил хотелось бы переписать
суммы по промежуточным состояниям типа (9.5.7) как интегралы по
собственным состояниям Qa или Ра. Однако такие операторы не мо-
могут иметь (отличные от нуля) собственные значения в обычном смыс-
смысле. Допустим, мы пытаемся найти состояние |д), удовлетворяющее
(для всех а) уравнению
Qa\q) = qa\q). (9.5.14)
Из (9.5.2) следует, что
ЧаЧъ + QbQa = ° > (9.5.15)
что невозможно для обычных чисел. Однако ничто не может поме-
помешать нам ввести в рассмотрение алгебру «переменных» qa (их назы-
называют грассмановыми переменными), которые действуют как с-чис-
ла, если речь идет о физическом гильбертовом пространстве, но
которые все же удовлетворяют антикоммутационным соотношени-
соотношениям (9.5.15). Потребуем далее, чтобы
{Qa,Qb} = {Qa,Qb} = {Qa,Pb) = 0, (9.5.16)
где q и q обозначают любые два «значения» этих переменных. Теперь
можно построить состояния |д), удовлетворяющие уравнению (9.5.14):
д) = ехр -г?Рада |0), (9.5.17)
где экспонента определена как обычно своим разложением в ряд.
(Чтобы проверить , что уравнение (9.5.14) удовлетворяется, вос-
воспользуйтесь тем, что все Paqa коммутируют друг с другом и имеют
нулевой квадрат, так что
540
Глава 9. Методы функционального интегрирования
= [Qa - qa ][1 - гРада ] ехр -г ? Pbgb 10)
I )
Ъ*а
= [-i{Qa, Pa }qa - qa ] ехр -г ? Pbqb 10) = 0,
что и требуется доказать.) Аналогично можно определить левые соб-
собственные векторы состояния (q (не сопряженные к | д)) как
<Л =@ \[[Qa ехр +i?Paga , (9.5.i8)
где Па — символ произведения операторов в том порядке, который
принят за стандартный. По тем же соображениям, что и для уравне-
уравнения (9.5.14), видим, что
(g|Qa = (gk- (9-5.19)
Скалярное произведение таких собственных состояний имеет вид
]jQa ехр z
Переставляя теперь каждый оператор Qa направо (начиная с самого
крайнего справа), получаем множители i2(q'a — ga), которые мы вы-
выносим направо из-под знака скалярного произведения, и в резуль-
результате получаем:
(9.5.20)
9.5. Функциональные интегралы для фермионов
541
Мы увидим, что выражение (9.5.20) играет роль дельта-функции в
интегралах по д.
Аналогично можно построить правые и левые собственные со-
состояния операторов Ра:
(р\ра = (р|р0>
(9.5.21)
(9.5.22)
где ра являются, как и qa, антикоммутирующими с-числами (для
удобства считается, что они антикоммутируют не только друг
с другом, но и с qa и со всеми фермионными операторами):
р) = ехр -
o>.
(9.5.23)
(р| = @|ехр -г
(9.5.24)
со скалярным произведением (которое вычисляется перестановкой
всех Р налево)
(9.5.25)
Скалярные произведения двух разных типов собственных со-
состояний друг с другом имеют вид
(q|p) = (q|exp -
ПРа 1°) =
ПРа 1°)
так что
542 Глава 9. Методы функционального интегрирования
(Я IР) = Xw exp -i? ЧаРа = Xjv exp г^ Paqa , (9.5.26)
где Xjv — фаза, зависящая только от числа N операторов Qa:
Еще проще получается формула
Нетрудно видеть, что состояния \q) (как и состояния |р)) обра-
образуют в определенном смысле полный набор состояний. Из определе-
определений (9.5.17) следует, что состояние \а, Ъ, ...) из общего базиса есть
(с точностью до фазы) коэффициент при произведении qaqb... в раз-
разложении состояния \q) в сумму произведений грассмановских чисел
q. Поэтому всякое состояние |/) можно представить в виде
где / — численные коэффициенты, а нижние индексы аЪ ... при
символе \q) обозначают коэффициенты при произведении qaqb... в раз-
разложении состояния \q).
При суммировании по состояниям очень удобно ввести опре-
определенный способ интегрирования по фермионным переменным, из-
известный как интегрирование по Березину,10 который позволяет на-
находить коэффициенты при таких произведениях антикоммутирую-
щих с-чисел. Для любого набора этих переменных ?,п (состоящего из
величин р, q или и тех и других) самая общая функция /(^) может
быть представлена в виде
(9.5.28)
+ слагаемые, в которых множителей Ъ, меньше,
а интеграл по переменным Ъ, определяется как
9.5. Функциональные интегралы для фермионов 543
где тильда в формуле (9.5.29) соответствует удобному соглашению,
что дифференциалы записываются в порядке, противоположном по-
порядку произведения переменных интегрирования в (9.5.28). Так как
это произведение антисимметрично относительно перестановки лю-
любых двух ?,, то интеграл антисимметричен также относительно пе-
перестановки любых двух dt,, так что «дифференциалы» эффективно
антикомму тируют:
d§nd§m+d§md§n=O. (9.5.30)
Кроме того, коэффициент с может зависеть от других с-чис-
ловых переменных, по которым не проводится интегрирование,
и которые антикоммутриуют с теми ?,, по которым мы интегрируем.
В этом случае важно стандартизовать определение с, переместив
все Ъ, налево от с перед интегрированием по ним, как это и сделано
в формуле (9.5.28).
Например, самая общая функция от пары антикоммутирую-
щих с-чисел Ъ,х и Е,2 имеет вид
поскольку квадраты и все более высокие степени ^ и Е,2 обращаются
в нуль. Интегралы от этой функции равны
+C2>
Заметим, что многократный интеграл совпадает с повторным:
Этот результат можно легко распространить на интегралы
по любому числу фермионных переменных. (Именно для того, что-
чтобы получить указанную формулу без дополнительных знаковых
544
Глава 9. Методы функционального интегрирования
множителей, мы взяли произведение дифференциалов в (9.5.29) в
порядке, противоположном произведению переменных в (9.5.28).) Дей-
Действительно, можно было бы сначала определить интеграл по един-
единственному антикоммутирующему с-числу Ъ,ъ а затем обычным спо-
способом определить кратные интегралы путем итерации. Наиболее
общая функция антикоммутирующих с-чисел линейна по любому
из них:
(так как ^2 = 0), и ее интеграл по \х определяется как
Повторение этого процесса приводит к кратному интегралу,
совпадающему с интегралом, определенным формулами (9.5.28) и
(9.5.29).
Так определенный интеграл обладает еще рядом свойств, ана-
аналогичных свойствам многократных интегралов (от — оо до + °°) по
обычным действительным переменным. Однако есть и существен-
существенные отличия.
Очевидно, что интегрирование по Березину линейно в том смыс-
смысле, что
и, кроме того,
(9.5.32)
где а(?,') — любая функция (в том числе, константа) от любых анти-
антикоммутирующих с-чисел ^'т, по которым не производится интегри-
интегрирование. Однако линейность по отношению к левому умножению не
столь очевидна. Поскольку предполагается, что ^'т антикоммутриу-
ет со всеми Е,п, то при интегрировании по V переменным имеем
9.5. Функциональные интегралы для фермионов 545
так что
(9.5.33)
Поэтому очень удобно (хотя, строго говоря, и не обязательно)
считать, что дифференциалы dt,n антикоммутируют со всеми анти-
коммутирующими переменными (включая ?,п):
J^^J (9-5.34)
В этом случае (9.5.33) принимает более простой вид
j ] [ [ ) f& • (9.5.35)
Другое сходство с обычным интегрированием заключается в
том, что для произвольного антикоммутриующего с-числа ?,', не
зависящего от t,, выполнено равенство
(9.5.36)
так как сдвиг Ъ, на константу влияет только на слагаемые в / с
числом переменных t,, меньшим, чем их полное число.
С другой стороны, рассмотрим замену переменных
Sn ^ Sn b^TimSmi (9.5.37)
m
где У — произвольная несингулярная матрица из обычных чисел.
Произведение новых переменных равно
546 Глава 9. Методы функционального интегрирования
Однако J J ^>тп совпадает с произведением Ц Ъ,п (взятым в
первоначальном порядке), если не считать знакового множителя
?[т], равного +1 или -1 в зависимости от того, является ли пере-
перестановка п —> тп четной или нечетной перестановкой первоначаль-
первоначального порядка множителей:
Е П
Эта формула применима при любом порядке следования Ъ,п,
если только мы возьмем Е,'п в том же порядке. Отсюда следует, что
коэффициент при произведении Пп^'п в разложении любой функции
/(^) по ^' равен в точности коэффициенту при произведении Пп^п,
умноженному на (Det ff)~l. Мы записываем это утверждение как
/ = (Det .У) П &\п /. (9.5.38)
Это обычное правило замены переменных интегрирования, за ис-
исключением того, что (Det ff) входит в степени —1, а не +1. Далее мы
используем правило (9.5.38) и свойства линейности (9.5.31), (9.5.32) и
(9.5.35) для вычисления интегралов, встречающихся при выводе фей-
нмановских правил для теорий с фермионами.
Используя это определение интегрирования, можно записать
условие полноты как формулу для интеграла по собственным зна-
значениям. Как уже отмечалось, любое состояние |/) можно разложить
в ряд по состояниям |0), \а), \а,Ъ), и т. д., а сами эти состояния равны
(с точностью до фазы) коэффициентам при произведениях 1, qa,
gagb, и т. д. в разложении собственного состояняи \q) операторов Q.
Согласно определению интегрирования, можно извлечь коэффици-
коэффициент при любом произведении QbQcQd- B разложении состояния |q),
интегрируя произведение |q) со всеми qa, где а не равно Ъ, с, d, ...
Таким образом, выбирая функцию f(q) как подходящую сумму
9.5. Функциональные интегралы для фермионов
547
таких произведений разных q, можно записать любое состояние |/)
в виде интеграла
(9.5.39)
(Можно переставить \q) налево от дифференциалов без всяких из-
изменений знаков, поскольку в показателе экспоненты в формуле
(9.5.17), определяющей |д), содержится только четное число ферми-
онных переменных.) Чтобы найти функцию f(q) для заданного век-
вектора состояния |/), возьмем скалярное произведение вектора (9.5.39)
с некоторым бра-вектором (q'\ (где q' — любое фиксированное соб-
собственное значение операторов Q). В соответствии с формулами (9.5.35)
и (9.5.20) оно равно
№¦
Переставляя каждый множитель (qa — q'a) направо от каждого диф-
дифференциала dqb, получаем знаковый множитель (-)w2 = (—)w, где
теперь N равно полному числу переменных qa, так что
(q\f) = (-)
Hdqb\\l\(qa-qa)\f(q).
Можно переписать функцию f(q) как f(q +{q - q')) и разло-
разложить ее по степеням q — q. Все слагаемые, кроме слагаемого низше-
низшего порядка, обращаются в нуль при умножении на произведение
П(д0 - qa), и
(9.5.40)
что частично подтверждает наше предыдущее замечание, что для
интегралов по q выражение (9.5.20) играет роль дельта-функции.
548
Глава 9. Методы функционального интегрирования
С помощью (9.5.32) имеем
WI /) = (-)
Коэффициент при слагаемом в подынтегральном выражении,
пропорциональном Пда, равен f(q'), так что в согласии с нашим
определением интегрирования (q'\f) = (—)Nf(q')- Вновь подставляя это
выражение в формулу (9.5.39), получаем соотношение полноты в
виде
!/) = (-)" \\ч)
или в виде операторного равенства
i =
—dq (q .
(9.5.41)
Точно тем же способом можно показать, что
1 =
(9.5.42)
Наконец-то мы можем вычислить матричные элементы пере-
переходов. Как и ранее, определяем зависящие от времени операторы
Qa(t) ее exp(zHt)Qa exp(-zHt), (9.5.43)
Pa(t) = exp(iHt)Pa exp(-iHt), (9.5.44)
и их правые и левые собственные состояния
q; t) = exp(zHt) \q), \p;t) = exp(zHt) | p), (9.5.45)
(q;t\ = (q\exp(-iHt) , (p;t\ = (p\exp{-iHt). (9.5.46)
9.5. Функциональные интегралы для фермионов
549
Скалярное произведение собственных q-состояний, определен-
определенных в бесконечно близкие моменты времени, равно
{q;х + dx\q;х) = (q |ехр(-гШт)|q).
Вставим теперь единицу в форме (9.5.42) слева от оператора
ехр(—iHdx). Удобно представить гамильтониан H(P,Q) в форме, ког-
когда все операторы Р стоят слева от всех операторов Q, так что для
бесконечно малых dx
(р | ехр(-г'Я(Р, Q)dx)\ q) = (p q) ехр(-Ш(р, q)dx).
(Предполагается, что каждое слагаемое в гамильтониане со-
содержит четное число фермионных операторов, и поэтому можно
ставить с-число H(p,q) с любой стороны матричного элемента без
какого-либо изменения знака.) Имеем
(q';
q;x) =
dpa\ (p \ exp(-zHdi)| q)
Пользуясь формулами (9.5.26) и (9.5.27) и замечая, что произ-
произведения paqa и paq a коммутируют со всеми антикоммутирующими
с-числами, находим
dx \q;x) =
a exP
atea ~ Qo) ~ iH{p,q)dx
.(9.5.47)
Дальнейший вывод производится по той же схеме, что и в разделе
9.1. Для вычисления матричного элемента
(g; t
)...|g; t)
от произведения операторов (где t' > tA > tB > ... > t), разделим
временной интервал от t до t' на большое число очень малых шагов
550 Глава 9. Методы функционального интегрирования
по времени; на каждом шаге используем соотношение полноты
(9.5.41); используем формулу (9.5.47), чтобы вычислить получивши-
получившиеся матричные элементы (где это необходимо, вставляя 0А, 0в и т.
п.); передвинем все дифференциалы налево (это не вносит дополни-
дополнительных знаков, поскольку на каждом шаге имеется одинаковое
количество дифференциалов dp и dq); введем функции qa(t) и pa(t),
интерполирующие на каждом шаге значения qa и ра. В результате
находим
,... }\q;t)
XOA{p(tA),q(tA)),OB{p(tB),q(tB)),...
(9.5.48)
x exp
?ра(т)да(т)-Я(р(т),д(т))
Здесь символ Т означает обычное произведение, если момен-
моменты времени расположены в первоначально предполагавшемся по-
порядке: tA > tB > ... Однако правая часть равенства полностью сим-
симметрична по 0А, f)B, ... (если не считать отрицательных знаков, воз-
возникающих при перестановке антикоммутирующих с-чисел), так что
приведенная формула выполняется в произвольные моменты вре-
времени (между t и t'), при условии, что Т понимается как операция
хронологического упорядочивания с возможным общим отрицатель-
отрицательным знаком, если при таком упорядочивании приходится совер-
совершать нечетное число перестановок фермионных операторов.
До этого момента мы удерживали общий фазовый множитель
(—i)N%N. Однако в действительности эти фазы дают вклад только в амп-
амплитуды переходов вакуум-вакуум и не представляют для нас интереса.
Переход к квантовой теории поля производится по той же
схеме, как и для бозонных полей (см. раздел 9.2). Среднее по ваку-
вакууму от хронологически упорядоченного произведения операторов
дается формулой, похожей на (9.2.17):
9.5. Функциональные интегралы для фермионов
551
(VAC, out\T{flA{P(tA),Q(tA))Mp(tB)MtB)),...}\VAC, in)
OA[p(tA),q(tA)]
T,x,m
T,x,m
xOB[p(tB),q(tB)]...exip
-H[q(x), р(т)] + г? - слагаемые
(9.5.49)
где коэффициент пропорциональности одинаков для всех операто-
операторов 0А, С>в, и т. д., а г?-слагаемые возникают из волновой функции
вакуума. Как и ранее, мы заменили каждый дискретный индекс
типа а на пространственную координату х и индекс поля т. Мы
опустили также тильду над знаком произведения дифференциа-
дифференциалов, так как это влияет только на общую фазу в функциональном
интеграле.
Главное отличие фермионного случая от бозонного заключает-
заключается в том, что здесь не нужно интегрировать по р перед интегриро-
интегрированием по д. Действительно, в стандартной модели электрослабых
взаимодействий (и в других теориях, вроде старой теории Ферми
C-распада) канонические импульсы рт являются вспомогательными
полями, не связанными с qm, а лагранжиан линеен по qm, так что
величина Id3xEmpmgm - Я в формуле (9.5.49) и есть лагранжиан L.
Каждое слагаемое в гамильтониане для фермионного поля с нену-
ненулевым квантовым числом (например, поля электронов в квантовой
электродинамике) в общем случае содержит равное число перемен-
переменных р (пропорциональных qt) и д. В частности, слагаемое Яо в пол-
полном гамильтониане, отвечающее свободным частицам, билинейно
по р и д, так что
Г 1
di< d3x?pm(x,t)gm(x,T)-H0[g(T),p(T)] + z?- слагаемые^
(?mXtnyPm{x)qn{y)
(9.5.50)
552
Глава 9. Методы функционального интегрирования
где CJ) — некоторая числовая «матрица». Гамильтониан взаимодей-
взаимодействия V = Н — Но есть сумма произведений равного числа фермион-
фермионных полей q и р (с коэффициентами, которые могут зависеть от
бозонных полей). Поэтому при разложении матричного элемента
(9.5.49) по степеням V возникает сумма фермионных интегралов вида
Т,х,т
хехр -
d4xd4y
> X
N
т,х,т
(9.5.51)
причем каждое такое слагаемое приходится на каждую возможную
совокупность вершин в фейнмановской диаграмме, и каждая вер-
вершина дает вклад в общий коэффициент при каждом таком слагае-
слагаемом в виде множителя, который равен коэффициенту при произве-
произведении полей в соответствующем слагаемом в операторе взаимодей-
взаимодействия, умноженному на мнимую единицу г *.
Для вычисления подобного интеграла рассмотрим сначала про-
производящую функцию всех таких интегралов
х ехр -
)Чп(у)
d^ygn{y)qn{y) \,
(9.5.52)
* Необходимо также иметь в виду вершины от составных операторов О,
отвечающие им коэффициенты не содержат множителя г. — Прим. ред.
9.5. Функциональные интегралы для фермионов 553
где fm(x) и дп(у) — произвольные антикоммутирующие с-числовые
функции. Сделаем сдвиг в переменных интегрирования:
Рт(Х) = Рт(Х
Яп(У) = Яп(У)
Пользуясь условием трансляционной инвариантности (9.5.36),
находим
(9.5.53)
Интеграл есть константа, пропорциональная Det Ч) (т. е. не за-
зависит от функций / и д), что можно показать с помощью формулы
(9.5.38). Для нас более важен первый сомножитель. Разлагая его по
степеням произведения gf и сравнивая с прямым разложением вы-
выражения (9.5.52), видим, что
Snlmlnimi...nNmN (Ж1> У\> Х2 ' У2 ' ¦ ¦ ¦' XN> Уы)
ос V й TTc—ifyr1) CQ 5 541
J^ спаривания XX 'спаренные тх,пу (о.и.игг/
по спариваниям по парам
с коэффициентом пропорциональности, не зависящим от х, у, т
или п, а также от числа этих переменных. Сумма в выражении
(9.5.54) берется по всем способам спаривания peg, при этом спарива-
спаривания, отличающиеся только порядком пар, не считаются различны-
различными. Иными словами, мы суммируем по N] перестановкам либо р,
либо д. Знаковый множитель 8спаривания равен +1 или —1 в зависимос-
зависимости от четности или нечетности каждой перестановки.
554 Глава 9. Методы функционального интегрирования
Знаковый множитель и сумма по спариваниям совпадают с
теми, котрые были получены ранее при выводе фейнмановских пра-
правил, причем сумма по спариваниям соответствует сумме по спосо-
способам соединения линий, выходящих из вершин в диаграммах Фейн-
мана, а множители (®~1)тХ;Пу играют роль пропагаторов при спари-
спаривании qm(x) с рп(у)- В дираковском формализме для частиц спи-
спина 1/2 действие свободных частиц имеет вид
Vm (X> Х)Чт (X> X) ~ H0 [я№> P(^)]
(9.5.55)
в данном случае канонические переменные в обычных обозначени-
обозначениях имеют следующий вид:
qm(x) = \|/m(x), pm(x) = — [ty(x)y°]m = Щт{х), (9.5.56)
где т — дираковский индекс, принимающий четыре значения. Срав-
Сравнивая эти выражения с формулой (9.5.50), получаем
_Э_
(Хотя мы и опускаем детали, но слагаемое с г? возникает здесь во
многом аналогично случаю скалярного поля в разделе 9.2.) Тогда
пропагатор имеет вид
(9.5.58)
совпадающий с тем, что был найден в рамках операторного форма-
формализма. Дополнительный множитель -у0 возникает за счет того,
что этот пропагатор представляет собой вакуумное среднее от
{} а не от
Чтобы привести хотя бы один пример того, что функциональ-
функциональный метод иногда быстрее приводит к решению задачи, чем опера-
операторный метод, вычислим зависимость от поля амплитуды перехода
вакуум—>вакуум в случае дираковского поля, взаимодействующего
только с внешним полем. Возьмем лагранжиан в виде
^ + т + Г]\|/,
(9.5.59)
где Г(ж) — зависящая от х матрица, описывающая взаимодействие
фермиона с внешним полем. Согласно формуле (9.5.49), амплитуда
вероятности того, что вакуум останется вакуумом в присутствии
этого внешнего поля, есть
(VAC, out | VAC, in)r
x
-i dix
(9.5.60)
где коэффициент пропорциональности не зависит от Г(ж). Запишем
эту амплитуду в виде
VAC, out | VAC, in)r
(9.5.61)
где
Чтобы вычислить последнее выражение, заменим переменные ин-
интегрирования qn{x) на
(9.5.63)
556 Глава 9. Методы функционального интегрирования
Получившийся интеграл не зависит от Г, так что вся зависи-
зависимость от Г амплитуды вероятности вакууму остаться вакуумом со-
содержится в детерминанте, возникающем от замены переменных со-
согласно формуле (9.5.38):
(VAC, out | VAC, in)r~DetJr[r]. (9.5.64)
Чтобы воспроизвести результаты теории возмущений, пред-
представим .Х(Т) в виде
Г], (9.5.65)
пЬНх - У), (9.5.66)
и разложим правую часть формулы (9.5.64) в ряд по степеням ^'[Г]:
(VAC, out | VAC, in)r
= [Det2)]exp ? A) Tr {Vrl
\n=l П )
Это именно то, что следовало ожидать согласно фейнмановс-
ким правилам: вклады от внутренних линий и вершин в этой тео-
теории равны —i(/)~l и — i'ff [Г]; след от произведения п множителей — (/~
1(§[Г] соответствует петле с п вершинами, соединенными п внут-
внутренними линиями; 1/п — обычный комбинаторный множитель, свя-
связанный с такими петлями (см раздел 6.1); знаковый мнижитель ра-
равен (—l)n+1, а не (—1)", так как дополнительный знак «минус» связан
с фермионными петлями; наконец, сумма по п в показателе экспо-
экспоненты возникает потому, что в амплитуду вероятности вакууму
остаться вакуумом вносят вклад диаграммы с любым числом не-
несвязных петель. Не зависящий от Г множитель Det CJ) менее удобно
выводить из фейнмановских правил; он представляет собой вклад
произвольного числа фермионных петель без вершин.
Добавим, что формула типа (9.5.64) позволит получить непер-
турбативные результаты, используя топологические теоремы о соб-
собственных значениях ядер типа .Ж [Г]. Подробнее этот вопрос будет
рассмотрен в т. П.
9.6. Функциональная формулировка КЭД 557
9.6. Функциональная формулировка
квантовой электродинамики
Преимущества функционального подхода к квантовой теории
поля раскрываются в полной мере при его применении к калибро-
калибровочным теориям безмассовых частиц спина единица, подобных
квантовой электродинамике. Проделанный в предыдущей главе вы-
вывод фейнмановских правил для квантовой электродинамики со-
содержал немало аргументов на уровне «размахивания руками» при
доказательстве того, что слагаемые в фотонном пропагаторе A|lv(g),
пропорциональные q^ или gv, могут быть отброшены, а чисто вре-
мениподобные слагаемые в точности сокращают кулоновское сла-
слагаемое в гамильтониане, так что эффективный фотонный пропага-
тор можно взять в виде rj^/g2. Чтобы дать строгое обоснование
этого результата методами гл. 8, нам потребовался бы сложный
анализ фейнмановских диаграмм. Однако, как мы сейчас пока-
покажем, функциональный подход приводит к желаемой форме фо-
фотонного пропагатора автоматически, без какого-либо обращения к
деталям поведения фейнмановских диаграмм.
В главе 8 было показано, что в кулоновской калибровке га-
гамильтониан взаимодействия фотонов с заряженными частицами
имеет вид
Здесь А — векторный потенциал, подчиняющийся условию
кулоновской калибровки
V • А = 0, (9.6.2)
а П^ — вихревая часть отвечающего ему канонического импульса,
удовлетворяющая такому же ограничению
УхПх=0. (9.6.3)
Кроме того, Нм — гамильтониан материи *, a VKyjI — кулоновская
энергия
* Материей принято называть все поля, не являющиеся калибровочными
полями. Последние являются «переносчиками взаимодействия. — Прим. ред.
558
Глава 9. Методы функционального интегрирования
- у|
(9. 6. 4)
Как и для любой другой гамильтоновой системы, средние по
вакууму от хронологически упорядоченных произведений операто-
операторов можно вычислять как функциональные интегралы *:
[Т{0А0в..])
xexpjz
VAC
OA0B...
-г | dtV
где Х|/г(ж) — исходные поля материи. При записи формулы (9.6.5) в
термионах плотности лагранжиана материи мы предполагаем, что
Нм — локальный оператор, либо линейный по каноническим им-
импульсам материи (как в спинорной электродинамике), либо квадра-
квадратичный по ним с независящими от полей коэффициентами (как в
скалярной электродинамике). В формулу (9.6.5) включены дельта-
функции **, чтобы учесть связи (9.6.2) и (9.6.3).
* Заметим, что я(х) есть интерполирующее с-числовое поле для квантово-
квантового оператора П±, коммутационные соотношения компонент которого друг с
другом и с А те же, что и для П, но в отличие от П, этот оператор комму-
коммутирует со всеми каноническими переменными материи.
** Это не безупречно строгое утверждение. Если принять за канонические
переменные аь а2 и л1; Я2> и рассматривать а3 и л3 как функционалы от этих
переменных, определяемые уравнениями (9.6.2) и (9.6.3), то следует вставить
дельта-функцию
Э2л2(х))).
Однако она отличается от произведения дельта-функций в формуле (9.6.5)
лишь на множитель Det Э32, который, хотя и бесконечен, но не зависит от
полей и поэтому сокращается в отношениях типа (9.4.1).
9.6. Функциональная формулировка КЭД
559
Показатель экспоненты в (9.6.5) очевидно квадратичен по не-
независимым компонентам % (например, %1 и %2) с независимыми от
полей коэффициентами в слагаемых второго порядка по %. Таким
образом, в соответствии с формулой (9.А.9), можно взять инте-
интеграл по %, положив % равным значению в стационарной точке по-
показателя экспоненты % = а:
VAC
_х,г
хехр<|г | d4x|ja2 - j(VxaJ
—i \ d t УКул + ге - слагаемые
(9.6.6)
. X
Чтобы выявить фундаментальное свойство ковариантности этого ре-
результата, используем следующий прием. Введем новую перемен-
переменную интегрирования а°(х) и заменим кулоновское слагаемое в дей-
действии -\dt VKyjI на
(9.6.7)
Так как (9.6.7) квадратично по а0, можно взять интеграл по а0
(с точностью до постоянного множителя), положив а°(ж) равным зна-
значению в стационарной точке (9.6.7), т. е. в точке, отвечающей реше-
решению уравнения
-j°(x)-V2a°(x) = 0,
или, иными словами, в точке
a°(x,t)= d3y
4л|х-у
(9.6.8)
Подставляя это значение а0 в формулу (9.6.7), получаем как
раз кулоновское действие —\dt VKyjI. Следовательно, в формуле (9.6.6)
можно переписать показатель экспоненты в виде
560 Глава 9. Методы функционального интегрирования
= -¦j/mV/^v + anj^ + У-м +
полные производные,
где /цУ = Эцау — Эуац, и интегрировать по а0, по а и по полям материи.
Функциональный интеграл (9.6.6) примет тогда вид
VAC ndVa 7
Ж I I T1 /
-n- (9-6.9)
exp(i/[a,\|/])f[8(V.a(x)),
где I — исходное действие:
J[a,\|/] = d4x -| /^/^ + a^f + (?ш + г? - слагаемые. (9.6.10)
Теперь все выражения стали явно лоренц-инвариантны и ка-
калибровочно инвариантны, если не считать последнего произведения
дельта-функций, обеспечивающего выполнение условия кулоновской
калибровки *. Чтобы продвинуться дальше, применим простой вари-
вариант того приема 4>5, который в т. II будет использован в более слож-
сложном случае неабелевых калибровочных теорий. Для простоты будем
рассматривать ситуацию, когда операторы f)A[A,4?], f)B[A,4?], ..., а так-
также действие Да,\|/] и мера [Пс?а][ПсОД калибровочно инвариантны.
Во-первых, заменим везде в формуле (9.6.9) полевые перемен-
переменные интегрирования aJx) и Х|/(ж) на новые переменные
aiiA(x) = aii(x) + diiA(x), (9.6.11)
* Заметим, что теперь а\х) не равно значению (9.6.8), а является независи-
независимой переменной интегрирования. Мы не будем сразу же интегрировать по а°(х),
что вернет нас назад к (9.6.6), а рассмотрим эту переменную в тандеме с а(х).
9.6. Функциональная формулировка КЭД
561
(9.6.12)
с произвольной конечной функцией Л(ж). Этот шаг — такая же мате-
математическая тривиальность, как и запись интеграла j^ f(x)dx в ви-
Де П, f(y)dy, и не требует использования постулированной калиб-
калибровочной инвариантности теории. Далее, с учетом калибровочной
инвариантности заменим а„Л(х) и \|/гл(ж) в действии, мере и функци-
функциях 0 на первоначальные поля а^(х) и Щ(х), соответственно. Тогда
формула (9.6.9) примет вид
(T{fiA[A,4>l0B[A,4>],...})
VAC
OA[a,\\f],OB[a,\\f],...
(9.6.13)
x ехр(гДа,
• а(ж) + У2Л(ж)).
Далее, функция А(х) была выбрана произвольно, поэтому, не-
несмотря на то, что Л(ж) явно входит в правую часть формулы (9.6.13),
последняя не может зависеть от этой функции. Мы воспользуемся
этим фактом, чтобы представить функциональный интеграл в зна-
значительно более удобной форме. Домножим (9.6.13) на функционал
В[Л,а] = ехр -|га d4xCoa° - У2ЛJ
(9.6.14)
(где а - произвольная константа), и проинтегрируем по Л(ж). Сдвигая
переменную интегрирования Л(ж) и имея в виду реальную независи-
независимость выражения (9.6.13) от Л, видим, что все сводится к умножению
этого выражения на независящую от полей константу
exp \-\ia d4x(V2AJ
(9.6.15)
Этот множитель сокращается в связной части среднего по вакуу-
вакууму и поэтому не приводит к физическим следствиям. Однако (9.6.13) не
562
Глава 9. Методы функционального интегрирования
зависит от Л только после интегрирования по аЦх) и \|/(ж). С тем же
успехом можно проинтегрировать по А(х) перед интегрированием по
аЦх) и \|/(ж). В этом случае стоящий в правой части формулы (9.6.13)
множитель n^SfV • а(ж) + У2Л(ж)) заменяется на
exp\-\ia\ d4xCoa°-V2A) [Q5(V-а(ж) + У2Л(ж))
exp\-
(9.6.16)
где знак °< вновь означает пропорциональность с точностью до неза-
независящего от полей множителя. Опуская постоянные множители, при-
приводим представление (9.6.9) к виду
(т{оАов...у,
VAC
(9.6.17)
где
(9.6.18)
Это выражение явно лоренц-инвариантно.
Мы рассматриваем новое слагаемое в правой части формулы
(9.6.18) как вклад в невозмущенную часть действия, фотонная часть
которого принимает теперь следующий вид:
+ гг - слагаемые
(9.6.19)
9.6. Функциональная формулировка КЭД
563
D.
¦-A-ос)
54 (х - у) + ге - слагаемые
Теперь можно сразу же найти фотонный пропагатор, обращая 4x4
матрицу в подынтегральном выражении правой части формулы :
V A-a)
- ге ос (g2 - геJ
,iqix-y)
(9.6.21)
Мы вправе выбирать величину а из соображений удобства. Два
наиболее употребительных выбора — это ОС = 1, что приводит к
пропагатору в калибровке Фейнмана
= Bл) d4g
g2 - ге
eiq{x-y) _
(9.6.22)
или ОС = оо( тогда множитель (9.6.14) действует как дельта-функция,
и получается пропагатор в калибровке Ландау (часто называемой
также калибровкой Лоренца)
g - ie (g - ге)
7iq-(x-y)
(9.6.23)
При работе с такими явно лоренц-инвариантными оператора-
операторами взаимодействия и пропагаторами практические вычисления ста-
становятся намного удобнее.
9.7 Разные статистики *
Теперь можно вернуться к вопросу, поставленному в гл. 4:
какие существуют возможности для изменения векторов состояний
* Этот раздел лежит несколько в стороне от основной линии изложения и
может быть опущен при первом чтении.
564 Глава 9. Методы функционального интегрирования
при перестановке тождественных частиц? Для получения ответа
рассмотрим приготовление начального или конечного состояния в
некотором процессе рассеяния. Предположим, что в результате
воздействия каких-то медленно меняющихся внешних полей сово-
совокупность неразличимых частиц в каждом из этих состояний пере-
переводится из стандартной конфигурации с импульсами к1( к2 и т. д. в
конкретную конфигурацию с импульсами р1( р2 и т. д., причем
частицы остаются в этом процессе на достаточно больших рассто-
расстояниях друг от друга, что позволяет использовать нерелятивистс-
нерелятивистскую квантовую механику. (Спиновые индексы явно не выписаны;
подразумевается, что они включены в символы импульсов.) Для
вычисления амплитуды такого процесса можно использовать фун-
функциональный метод *, считая, что q и р из раздела 9.1. являются
не полями и им сопряженными импульсами, а координатами и
импульсами частиц. Эти величины всегда удовлетворяют канони-
каноническим соотношениям коммутации, а не антикоммутации, незави-
независимо от того, являются ли частицы бозонами, фермионами или
чем-то еще. Таким образом, здесь мы не связываем себя каким-то
определенным типом статистики. По формуле (9.1.34) для функци-
функционального интеграла амплитуда (р1; р2, ...| к1( к2, ...)Р записывается
как интеграл по траекториям (путям), вдоль которых импульс од-
одной частицы непрерывным образом меняется от значения кх до
значения р1( импульс другой тождественной частицы непрерыв-
непрерывным образом меняется от значения к2 до значения р2 и т. д. Индекс
Р указывает, что мы вычисляем амплитуду для различимых час-
частиц. В частности, такая амплитуда симметрична относительно пе-
перестановок импульсов р и одновременных перестановок импульсов
к, но не обладает определенной симметрией относительно пере-
перестановок р и к по отдельности. Однако если частицы действитель-
действительно неразличимы, то существуют другие топологически допусти-
* Здесь я следую рассуждениям Ладлоу и С. де Витт11, с той разницей, что
они применили функциональный метод ко всему процессу рассеяния, а не толь-
только к приготовлению начального или конечного состояния. В релятивистской
теории возможность рождения и уничтожения частиц делает необходимым при-
применение функционального метода к полям, а не к траекториям частиц. Для нас
это не составляет проблемы, так как мы ограничились вычислениями в доста-
достаточно ранние или достаточно поздние моменты времени, когда участвующие в
рассеянии частицы находятся достаточно далеко друг от друга.
9.7. Разные статистики
565
мые пути, приводящие к той же конечной конфигурации. В случае
пространства размерностью d > 3 единственными такими путями
являются те, которые переводят импульсы к1( к2, ... в некоторую
нетривиальную перестановку if импульсов р1( р2, ... *. Следователь-
Следовательно истинная амплитуда может быть записана как
1,k2,...) = ?Cp(pPl,pP2,...|k1,k2,...)D,
где сумма берется по всем JV! перестановкам N неразличимых час-
частиц в состоянии, а С f — совокупность комплексных констант. Эти
амплитуды должны удовлетворять следующему правилу компози-
композиции, справедливому для неразличимых частиц:
\Pl.P2.
h>k2>---) = ]^Jd39ld392---(Pl>P2>---|Cll>Cl2>---)
(9.7.2)
С учетом формулы (9.7.1), это требование принимает вид
?Cp(pPl,pp2,...|k1,k2,...}D =
'¦¦¦/D
Применяя перестановку $Р " одновременно к начальному и ко-
конечному состояниям в первой амплитуде справа, получим
* Формально это выражается утверждением, что первая гомотопическая
группа конфигурационного пространства в случае d > 3 есть группа переста-
перестановок 12. Под «конфигурационным пространством» для N неразличимых час-
частиц подразумевается пространство, точками которого являются N d-мерных
векторов, при этом исключаются конфигурации, когда некоторые d-векто-
ры совпадают (или находятся на расстоянии, не превышающем некоторого
заданного), а конфигурации, отличающиеся только перестановкой векторов,
отождествляются.
566
Глава 9. Методы функционального интегрирования
?Cp(pPl,pp2,...|k1,k2,...)D =—
р Л/!рр„
Однако амплитуды (р1; р2, ...| k1( к2, ...)D удовлетворяют пра-
правилу композиции для различимых частиц
4>k2>---)D = jd3q1d3q2...(v1,v2,...\n1,n2,...)D
(9.7.3)
,...)
так что правило композиции для физических амплитуд можно за-
записать как
^Cp(pPl,pP2,...|k1,k2,...)p =
i V .
РР'
х
\PP'P'1)PP'P'2>
что будет выполнено только и если только
с — с с
(9.7.4)
Таким образом, коэффициенты С f должны образовывать од-
одномерное представление группы перестановок. Однако эта группа
имеет только два таких представления: тождественное с Cf = +1
для всех перестановок, и знакопеременное представление с С f= +1
или Сf = —1 в зависимости от того, является ли Учетной или нечет-
нечетной перестановкой. Эти две возможности соответствуют статисти-
статистикам Бозе и Ферми *.
* В литературе многократно обсуждались возможности существования ста-
статистик, отличающихся от статистик Бозе и Ферми и объединяемых термином
парастатистики. Было показано п, что теории парастатистик в случае d> 3
пространственных измерений эквивалентны теориям, в которых все частицы
являются обычными фермионами или бозонами, но несущими дополнительное
квантовое число, так что волновые функции могут иметь необычные свойства
по отношению к перестановкам импульсов и спинов.
9.7. Разные статистики 567
Приятным свойством этого рассуждения является то, что оно
объясняет, почему случай двух пространственных измерений яв-
является исключением. В этом случае имеется значительно больше
различных топологически допустимых путей *. Например, путь, при
котором одна частица конечное число раз окружает другую, не мо-
может быть деформирован в путь, где этого не происходит. Как след-
следствие, в двух пространственных измерениях возможны анионы 15
— частицы с более общими свойствами перестановок, чем в ста-
статистиках Бозе или Ферми.
Приложение: Многократные гауссовы интегралы
Сначала вычислим многократный интеграл по конечному чис-
числу действительных переменных ?,г от экспоненты, показатель кото-
которой является произвольной квадратичной функцией Е,г:
Ц(%гехр{-0&)},
r§r + M. (9.A.2)
rs г
где Krs, Lr и М — произвольные константы, причем матрица К пред-
предполагается симметричной и несингулярной. С этой целью рассмот-
рассмотрим сначала случай, когда Krs, Lr и М все действительны, кроме
того, матрица К положительно определена. Общий результат мо-
может быть получен аналитическим продолжением.
Всякая действительная симметричная матрица может быть ди-
агонализована с помощью ортогональной матрицы. Это означает,
что существует матрица if , такая, что ее транспонированная со-
совпадает с обратной, У7 = У~г , и такая, что
. (9.A.3)
* Этот факт выражается утверждением, что первая гомотопическая группа
конфигурационного пространства в двух измерениях является не группой пе-
перестановок, а более широкой группой, известной как группа кос 14.
568 Глава 9. Методы функционального интегрирования
Поскольку предполагается, что К положительно определена и
неособенная, собственные значения 1^ положительны. С помощью
матрицы if можно совершить замену переменных
r&. (9.A.4)
Якобиан |Det У | этого преобразования равен единице, так что
многократный интеграл (9.А.1) переходит в произведение однократ-
однократных интегралов:
Но из формулы (9.А.З) следует:
Det К = Ц кг, К =
так что формулу (9.А.5) можно представить в виде
~м г (9А-6)
Формула (9.А.1) определяет функцию переменных Krs, Lr и М,
аналитическую по Krs в конечной области вокруг поверхности, на
которой матрица Krs действительна и положительно определена и
для которой интеграл сходится. Для таких Krs эта функция анали-
тична всюду по Lr и М. Поскольку выражение (9.А.6) равно выраже-
выражению (9.А.1) для действительных Krs, Lr и М, где матрица К положи-
положительно определена, то правая часть формулы (9.А.6) дает аналити-
аналитическое продолжение выражения (9.А.1) на всю комплексную плос-
плоскость с разрезом, определяемым квадратным корнем. Знак квад-
квадратного корня фиксируется этим аналитическим продолжением. В
теории поля матрица Krs на самом деле мнима, не считая малой
действительной части, обязанной «г?-слагаемому».
Приложение
569
Полезно записать выражение (9.А.6) через стационарную точку
-5Г ?_, TS S (9.А./)
S
функции (9.А.2),
= 0 при § = §,
в виде
= Det
К
2л
-1/2
ехр -
(9.А.8)
(9.А.9)
Этот результат стоит запомнить: гауссовские интегралы можно вы-
вычислить с точностью до множителя, содержащего детерминант,
положив переменную интегрирования равной значению в точке, где
показатель экспоненты стационарен.
Далее, мы хотим использовать полученный результат для
вычисления интегралов
. (9.А.1О)
(Подобные интегралы с нечетным числом множителей Е, очевидным
образом равны нулю.) Разложив в ряд ехр(—ErLr^r) в выражении
(9.А.1), получаем правило сумм
Е Е
JV=O 7V2...7-2JV
rl V r2N
-i: LЛr ~ \
Det
Det
К
2%
К
2л
-1/2
-1/2
—1
(9. A. 11)
570 Глава 9. Методы функционального интегрирования
Сравнивая коэффициенты при ^-'rJ-'ri---^-'riN с обеих сторон ра-
равенства, видим, что ^¦rlri...riN должно быть пропорционально сумме
произведений матричных элементов матрицы К, вид которой оп-
определяется требованием симметрии относительно перестановки ин-
индексов гъ г2, ..., r2W:
I =cm У TT(K~h
'ir2...r2jV N i-^ 1 1Л /спаренные индексы "
по спариваниям по парам (9.А.12)
rv..r2N
Здесь сумма берется по всем способам спаривания индексов rl...r2N,
причем два спаривания считаются одинаковыми, если они отлича-
отличаются порядком расположения пар или порядком индексов внутри
пары.
Для вычисления постоянного множителя cw заметим, что чис-
число Vw слагаемых в сумме по спариваниям в правой части формулы
(9.А.12) равно числу BJV)! перестановок индексов, деленному на число
N\ способов перестановки пар и на число 2N перестановок внутри
каждой пары :
BJV)!
(9.А.13)
" N!2N
Поэтому из формулы (9.А.12) следует, что
Lr1Lri—LrilfIr1ri...rilf=VNcN\Y<LrLsKr}\ ¦ (9.А.14)
Сравнивая это выражение с формулой (9.А.11), видим, что множи-
множители BJV)! и JV!2W сокращаются с vw, и в результате остается
с»=LDetl^JJ ¦ (9А-15)
Например,
Irr =L(K-1)rr , (9.A.16)
Irrrr =I0\(K-1)rr {K~l)rr +{К-1)ГГ{К~1)ГГ +{K~l)rr {K~l)rr 1 ,
rlr2r3r4 UL rlr2 r3r4 rlr3 r2r4 rlr4 r2r3 J
(9. A. 17)
Список литературы 571
и так далее, где 10 — интеграл без индексов:
1 г (к\}~1/2
тт / К с с > = Det —— . /о а 1 а\
rs J L V yj
Задачи
1. Рассмотрите нерелятивистскую частицу массой М, движущую-
движущуюся вдоль оси х в потенциальном поле V(x) = Мсо2ж2/2. Пользу-
Пользуясь методом функционального интеграла, найдите вероятность
того, что частица, находящаяся в точке х1 в момент времени
tb окажется в момент времени t между ж и х + dx.
2. Найдите волновой функционал (т. е. волновую функцию в ф-
базисе) состояния поля, сотвечающего одной бесспиновой час-
частице массы т Ф 0. Используя полученный результат, выведите
фейнмановские правила для испускания и поглощения такой
частицы.
3. Найдите вакуумный волновой функционал в теории нейтраль-
нейтрального векторного поля массы т Ф 0. Используя этот результат,
найдите вид г?-слагаемых в пропагаторе такого поля.
4. Плотность лагранжиана свободного поля Рариты—Швингера \\f^
спина 3/2 равна:
SP = -
С помощью функционального метода найдите пропагатор это-
этого поля.
Список литературы
1. Feynman, R.P. The Principle of Least Action in Quantum Mechanics
(Princeton University, 1942; University Microfilms Publication No.
2948, Ann Arbor). См. также: Feynman, R.P. and Hibbs, A.R.
Quantum Mechanics and Path Integrals (McGraw-Hill, New York,
572 Глава 9. Методы функционального интегрирования
1965) (есть рус. пер.: Фейнман Р., Хибс, А. Квантовая мезаника
и интегралы по траекториям. — М., Мир, 1968.) Общие ссыл-
ссылки см.: Glimm, J. and Jaffe, A. Functional Integral Point of View,
2-nd edn (Springer-Verlag, New York, 1987).
2. Dirac, P.A.M., Phys. Zeits. Sowjetunion, 3, 62 A933).
3. Feynman, R.P., Rev. Mod. Phys., 20, 367 A948); Phys. Rev., 74,
939, 1430 A948); 76, 749, 769 A949); 80, 440 A950).
4. Faddeev, L.D. and Popov, V.N., Phys. Lett., B25, 29 A967).
См. также: Feynman, R.P., Acta Phys. Pol, 24, 697 A963);
Mandelstam, S., Phys. Rev., 175, 1580, 1604 A968).
5. De Witt, В., Phys. Rev. Lett., 12, 742 A964).
6. Tt Hooft, G., Nucl. Phys., B35, 167 A971).
7. Gerstein, I.S., Jackiw, R., Lee, B.W. and Weinberg, S., Phys.
Rev., D3, 2486 A971).
8. Фаддеев, Л.Д., Теор. Мат. Физика, 1, 3 A969).
8a. Schwinger, J., Proc. Nat. Acad. Sci., 44, 956 A958).
8b. Osterwalder, K. and Schrader, R., Phys. Rev. Lett., 29, 1423 A972);
Commun. Math. Phys., 31, 83 A973); 42, 281 A975). Аксиомы
Остервальдера-Шрадера включают требования гладкости, ев-
евклидовой ковариантности, «положительности относительно от-
отражений», симметрии относительно перестановок и кластерно-
кластерного разложения.
9. Содержание этого раздела во многом определили дискуссии с
Дж. Польчинским.
10. Березин, Ф.А. Метод вторичного квантования. М., Наука, 1965.
11. Laidlaw, M.G.G. and de Witt, СМ., Phys. Rev., D3, 1375 A970).
12. Leinaas, J.M. and Myrheim, J., Nuovo Cimento, 37B, 1A977).
Список литературы 573
13. Ohnuki, Y. and Kamefuchi, S., Phys. Rev., 170, 1279 A968); Ann.
Phys., 51, 337 A969); Druhl, K., Haag, R., and Roberts, J.E.,
Commun. Math. Phys., 18, 204 A970).
14. Группа кос была введена Э. Артином. См. в сборнике: The
Collected Papers of E. Artin. Ed. by S. Lang and J.E. Tate (Addison-
Wesley, Reading, MA, 1965).
15. Wilczek, F., Phys. Rev. Lett., 49, 957 A982); Fredenhagen, K.,
Gaberdiel, R., and Ruger, S.M., Cambridge Preprint DAMPT-
94-90 A994). См. также [12].
10
Непертурбативные методы
Мы намерены теперь приступить к изучению вкладов высших
порядков теории возмущений в физические процессы, вкладов,
которые описываются фейнмановскими диаграммами с одной или
несколькими петлями. При этом было бы очень полезно иметь в
распоряжении метод, который позволяет получать результаты,
справедливые во всех порядках теории возмущений (а в некоторых
случаях и вне рамкок теории возмущений). Для этой цели мы будем
использовать в данной главе уравнения поля и коммутационные
соотношения для взаимодействующих полей в картине Гейзенберга.
Связь между гейзенберговской картиной и фейнмановскими диа-
диаграммами теории возмущений устанавливается теоремой, доказан-
доказанной в разделе 6.4: сумма всех диаграмм процесса а —» C с дополни-
дополнительными вставками, отвечающими операторам оа{х), оъ{у) и т. д.,
есть матричный элемент хронологически упорядоченного произве-
произведения соответствующих гейзенберговских операторов
В частном случае, когда операторы Оа{х), Оъ{х) и т. д. являются
полями элементарных частиц, этот матричный элемент равен сумме
вкладов всех фейнмановских диаграмм с входящими линиями на
массовой поверхности, отвечающими состоянию а, и выходящими
линиями на массовой поверхности, отвечающими состоянию C, соот-
соответственно, и линиями вне массовой поверхности (включая пропага-
торы), отвечающими операторам Оа{х), Оъ{х) и т. д. Изучив некото-
некоторые получающиеся таким образом непертурбативные результаты,
мы сможем приступить к вычислениям радиационных поправок.
10.1. Симметрии 575
10.1. Симметрии
Одним очевидным, но важным следствием упомянутой теоремы
является возможность использования принципов симметрии не только
применительно к матричным элементам ^-матрицы, когда 4-им-
пульсы всех внешних линий лежат на массовой поверхности, но и к
фейнмановским диаграммам, у которых некоторые или все внешние
линии находятся вне массовой поверхности.
Рассмотрим, например, симметрию относительно пространст-
пространственно-временных трансляций *. Следствием такой симметрии явля-
является существование эрмитова 4-векторного оператора Рц, обладаю-
обладающего тем свойством, что для любой локальной функции О(х) опера-
операторов поля и канонических импульсов
г i Э
\Р О(х)\ = г—-О(х) . A0.1.1)
L r J дх^
(См. формулы G.3.28) и G.3.29).) Кроме того, состояния а и C обычно
выбираются как собственные состояния 4-импульса:
Р»Х = рК , Р^р = р^р" . A0.1.2)
Отсюда вытекает, что для любого набора локальных функций
Оа(х), Оъ(х), ... полей и/или их производных справедлива формула
X ч A0Л-3>
--rp"'T{Oa(Xl)'°b(X2)'---K+)-
Это уравнение имеет решение:
(^-,Т{Оа(х:),Оь(х2),...}^а+)
/., . \_ , . A0.1.4)
= exp(z(pp-pa)-x)Fab (ж:-ж2,...),
Называемую также трансляционной инвариантностью. — Прим. ред.
576 Глава 10. Непертурбативные методы
где х — любое среднее пространственно-временных координат
х^ = схх^ +с2х%+..., сх+с2+...= 1, A0.1.5)
a F зависит только от разностей координат. (В частности, вакуумное
среднее может зависеть только от разностей координат.) Интегри-
Интегрируя отдельно по х^ и разностям координат, можно найти фурье-
образ выражения A0.1.4):
ч R4, , , (Ю.1.6)
х ехр(-г/с1 •х1-гк2- х2- ¦¦) <* о (рр-ра-к1-к2-¦¦¦)¦
В разделе 6.4 было показано, что выражение для матричного
элемента хронологического произведения определяется обычными
правилами Фейнмана в координатном представлении применитель-
применительно к сумме всех диаграмм с входящими частицами в состоянии ОС,
выходящими частицами в состоянии C, и внешними линиями,
которые оканчиваются в вершинах с координатами хъ х2, ... •
Соответственно, фурье-образ A0.1.6) определяется правилами Фейн-
Фейнмана в импульсном представлении для той же суммы диаграмм,
у которых внешние линии вне массовой поверхности имеют
4-импульсы къ к2, ... , направленные в диаграмму. Формула A0.1.6)
утверждает тогда, что эта сумма фейнмановских диаграмм сохра-
сохраняет 4-импульс. Такой результат очевиден в теории возмущений,
т. к. 4-импульс сохраняется в каждой вершине, поэтому неудиви-
неудивительно, что тот же результат можно получить, и не опираясь на
теорию возмущений.
Затратив несколько больше усилий, можно воспользоваться
свойствами гейзенберговских полей и ин- и аут-состояний (9.6.16)
по отношению к преобразованиям Лоренца, чтобы показать, что
сумма всех диаграмм с данным набором линий, находящихся как на
массовой поверхности, так и вне ее, обладает теми же свойствами
относительно лоренцовских преобразований, что и слагаемые низ-
низшего порядка.
Аналогичные аргументы применимы к сохранению внутрен-
внутренних квантовых чисел, таких как электрический заряд. Как показано
в разделе 7.3, поле или другой оператор Оа(х), уничтожающий
заряд qa (или рождающий заряд — qa), удовлетворяет уравнению
10.1. Симметрии
577
[Q,Oa(x)] = -qaOa(x)
как в гейзенберговском представлении, так и в представлении вза-
взаимодействия. Кроме того, если состояния свободных частиц а и C
имеют заряды qa и qn, то такие же заряды имеют соответствующие
ин- и аут-состояния. Тогда
= D>p,[Q,T{Oa(x),Ob(y),...}]4>+)
= -(qa+qb+...)(^,T{Oa(x),Ob(y),...}X)-
Следовательно, амплитуда yif^,Т{Оа(х),Оъ(у),...}Ч/^) обращается в
нуль, если только не выполнено условие сохранения заряда
Чъ
A0.1.7)
Несколько менее тривиальный пример — инвариантность относи-
относительно зарядового сопряжения. Как показано в гл. 5, существует
оператор С, преобразующий электронные операторы в позитрон-
ные и обратно:
Ca(p,G,e-)C-1=^a(p,G,e+),
Ca(p,a,e+)C =
где t, — фазовый множитель. Для свободного электронного поля Х|/(ж) это
означает, что
где (ЗС — матрица 4x4, имеющая (в используемом нами представле-
представлении дираковских матриц, где диагональна матрица у5) вид
0 0 0 1
0 0-10
0-100
10 0 0
578 Глава 10. Непертурбативные методы
Применительно к электрическому току свободных частиц в спинор-
ной электродинамике это означает:
Если потребовать сохранения оператора С в электродинамике, то
этот оператор должен антикоммутировать с полем свободных фотонов:
= -а» .
В теориях типа электродинамики, где С коммутирует как с Но, так и
с гамильтонианом взаимодействия, он коммутирует также и с опера-
оператором преобразования подобия ?2(t), связывающим гейзенберговское
представление с представлением взаимодействия. Поэтому С анти-
коммутирует с электрическим током взаимодействующих полей,
A0.1.8)
и электромагнитным полем в гейзенберговском представлении,
Отсюда вытекает, что среднее по вакууму от хронологическо-
хронологического произведения любого нечетного числа электромагнитных токов
и/или полей обращается в нуль. Поэтому равна нулю сумма всех
фейнмановских диаграмм с нечетным числом только фотонных
внешних линий (вне или на массовой оболочке).
Этот результат известен как теорема Фарри.1 Ее можно
доказать в рамках теории возмущений, заметив, что в диаграм-
диаграмме, состоящей из I электронных петель, к каждой из которых
подсоединяется щ фотонных линий, выполняется связь между
числом I внутренних и числом Е внешних фотонных линий,
аналогичная соотношению F.3.11):
21 + Е = У пх .
Отсюда следует, что если Е нечетно, то по крайней мере к одной из
петель должно быть подсоединено нечетное число фотонных линий.
10.2. Полология
579
Для каждой такой петли происходит сокращение диаграмм, отли-
отличающихся направлением обхода петли по стрелкам. Таким образом,
теорема Фарри представляет несколько менее тривиальное следст-
следствие принципа симметрии, чем трансляционная или лоренцовская
инвариантность: теорема верна не для отдельных диаграмм, а для
определенной их совокупности. Рис. 10.1 иллюстрирует применение
теоремы Фарри, которое оказалось исторически наиболее важным:
доказательство того, что при рассеянии фотона внешним электро-
электромагнитным полем отсутствуют вклады первого (или любого нечетно-
нечетного) порядка по внешнему полю.
Рис. 10.1. Диаграммы низшего порядка для рассеяния фотона электромаг-
электромагнитным полем. Прямые линии отвечают виртуальным электронам, волни-
волнистые линии — реальным или виртуальным фотонам, жирная линия
соответствует тяжелой частице типа атомного ядра, которая служит
источником электромагнитного поля. Вклады указанных двух диаграмм
сокращаются, как и требуется инвариантностью относительно зарядового
сопряжения
10.2. Полология
Одним из наиболее важных применений непертурбативных
методов, о которых идет речь в этой главе, является выяснение
полюсной структуры фейнмановских амплитуд как функций им-
импульсов внешних линий. Часто матричные элементы физического
процесса могут быть хорошо аппроксимированы вкладом одного
полюса. Кроме того, понимание полюсной структуры поможет
580 Глава 10. Непертурбативные методы
в дальнейшем разобраться с радиационными поправками к пропага-
торам частиц.
Рассмотрим амплитуду в импульсном представлении:
A0.2.1)
Здесь А — гейзенберговские операторы произвольного лоренцов-
ского типа, а (...H означает среднее по истинному вакууму Ч*о+= Ч*о~
= *Р0. Как обсуждалось в разделе 6.4, если Аъ ..., Ап — обычные поля,
входящие в лагранжиан, то A0.2.1) есть сумма вычисленных по
обычным фейнмановским правилам слагаемых, отвечающих всем
диаграммам с внешними линиями, соответствующими полям Аг, ...,
Ап, с 4-импульсами qx, ..., qn вне массовой поверхности, направлен-
направленными в диаграмму. Однако мы не будем ограничиваться этим случа-
случаем и допустим, что А^ могут быть произвольными локальными
функциями полей и их производных.
Нас интересуют полюсы диаграммы G при определенных зна-
значениях инвариантных квадратов суммарных 4-импульсов, отве-
отвечающих разным подмножествам внешних линий. Для определенно-
определенности рассмотрим G как функцию д2, где
g = g1+...+ gr=-gr+1-...-gn, A0.2.2)
и1<г<п— 1. Мы покажем, что G имеет полюс при д2 = —т2, где
т — масса любого одночастичного состояния, имеющего ненулевые
матричные элементы с состояниями А^ ... А/Ч'д и Аг+1 ... A^q, с
определенным вычетом:
B +
g + m — i?
A0.2.3)
где величины М определены следующим образом *:
*Напомним, что в отсутствие зависящих от времени внешних полей нет
разницы между одночастичными ин- и аут-состояниями, так что *РрО+ —
ш _ - ш
10.2. Полология
581
J d4^... d4xre"igi 'Xl ¦ ¦ ¦ e~iqr 'Xr {% ,П A (*i )• • • Ar (xr )}4<pa)
= BлL 54 (Ql +... + qr - p)M0|p;CT (g2... gr),
= BлL54(дг+1 +...+ qn + p)M |0(gr+2...gn)
A0 2 4)
A0.2.5)
(p° = д/р2 + m2 )> a сумма берется по всем спиновым (и другим)
состояниям частицы массой т.
Прежде, чем переходить к доказательству, полезно записать
выражение A0.2.3) в более развернутой форме, позволяющей луч-
лучше понять его важность
—г
BлL
/2
~ /с)BлK/2Bл/к2+ш2) М0|ка(д2...д
- гг
BтгL54(/с + дг+1 +... + д„)Bл/к2
1/2
A0.2.6)
М
ка|О(дг+2...д„) .
Это выражение как раз соответствует тому, что мы ожидаем от
вклада фейнмановской диаграммы с единственной внутренней лини-
линией, отвечающей частице массой т и соединяющей два блока диаг-
диаграммы (две поддиаграммы) с первыми г внешними линиями и после-
последними п — г внешними линиями соответственно *. Однако не являет-
является необходимым, чтобы частица массой т соответствовала полю,
входящему в лагранжиан теории. Формулы A0.2.3) и A0.2.6)
* См. рис. 10.2. Множители Bтг) ' [2(к + т )]' служат для устранения
кинематических множителей, связанных с внешней линией, отвечающей
частице массой т, в амплитудах М0|ко и Мко|0, а сумма по а произведения
этих двух матричных элементов, приводит к числителю пропагатора, отве-
отвечающего внутренней линии на рис. 10.2.
582
Глава 10. Непертурбативные методы
применимы даже в том случае, если эта частица является связанным
состоянием так называемых элементарных частиц, которым соот-
соответствуют поля, действительно входящие в лагранжиан. В этом
случае полюс возникает не от одной диаграммы, как на рис. 10.2, а от
бесконечной суммы диаграмм типа показанной на рис. 10.3. Здесь мы
впервые сталкиваемся с ситуацией, когда методы данной главы
приводят к результатам, выходящим за рамки тех, которые могут
быть выведены как свойства каждого порядка теории возмущений.
г+1
г+2
Рис. 10.2. Фейнмановская диаграмма с полюсной структурой A0.2.6). Здесь
линия с импульсом к представляет элементарную частицу, поле которой
входит в лагранжиан
г+1
г+2
п
Рис. 10.3. Одна из фейнмановских диаграмм, сумма которых имеет полюс-
полюсную структуру A0.2.6). Здесь полюс обусловлен составной частицей, кото-
которая является связанным состоянием двух элементарных частиц. Элемен-
Элементарные частицы, изображенные прямыми линиями, взаимодействуют
посредством обмена частицами, изображенными волнистыми линиями
10.2. Полология
583
Переходим к доказательству. Среди п! возможных упорядочи-
упорядочиваний моментов времени хД ..., хп° в формуле A0.2.1) существуют
n\/r\(n—r)\ таких, для которых все первые г моментов времени xt°
больше, чем последние (п—г). Выделяя вклад этой части объема
интегрирования в A0.2.1), получим
G(Qi • • • qn) = J d4xx... d4xne"igi ^... e~iq*'*«
Х0(тт[ж1°...ж°]-тах[ж°+1...ж°]) A0.2.7)
x(%,T{A1(x1)...Ar(xr)}T{Ar+1(xr+1)...An(xn)}%) + ДС ,
где «ДС» означает «другие слагаемые», отвечающие другим после-
последовательностям времен в аргументах операторов полей. Матричные
элементы в этом выражении вычисляются путем вставки между
хронологическими произведениями полного набора промежуточных
состояний. Среди этих состояний могут быть одночастичные состоя-
состояния Ч*р s определенного сорта частиц массой т. Выделяя вклад этих
одночастичных промежуточных состояний, имеем
G(Qi---qJ = ,
xe(min[x1°...x°]-max[x°+1...x°])?jd3p A0.2.8)
v Df Tl A It \ А (т \\Ч* VVU Tl А (т \ А (т \\Ч* \ 4- T\C
где теперь уже «ДС» означает другие слагаемые, возникающие не
только от других последовательностей моментов времени, но и от
других промежуточных состояний. Удобно осуществить сдвиг пере-
переменных интегрирования
Xj = Х^ + t/j , % = ^,о,... ,Т,
хг — хг+1 ^ Уг '' ~ ' ^ ^' •••'"¦'
Тогда, используя результаты предыдущего раздела, получим:
584 Глава 10. Непертурбативные методы
(Чр,а,Т{Аг+1(хг+1)...Ап(хп)}%)
Кроме того, аргумент тета-функции принимает вид:
min[x°...ж°] - тах[ж°+1 ...х°п]
= х° - x°r+1 + min[0y20...y°r]- тах[0уг°+1 ...у°п].
Подставим также фурье-представление F.2.15) ступенчатой функции:
2jk I со + ie
После этого интегралы по х1 и хг+1 приводят к дельта-функциям:
Х ~ 2лг/ ю^? exP(-4min[°!/2 • • • У г ] -
X
X
BлL53(р - qx -...- qrM(Vp2+m2+co - q? -...- q?)
1+...g0 +Л/р2+ш2+ю) +
Нас интересует только полюс, возникающий в результате
обращения в нуль знаменателя со + г?, так что можно положить
множитель ехр(—гсо(мин — макс)) равным единице. Интегралы по р и
со становятся тривиальными и дают:
G(qv..qn) -> гBлO54(д1 +...+ gj[g° - Л2 + т2 + ге] '
2---Qn) + ---. A0.2.12)
10.2. Полология 585
где теперь
q=q1+...qr = -qr+1-...-qn, A0.2.13)
х
(Ю.2.14)
(%,Т{А1@)А2(у2)...Аг(уг)}^а),
и заключительное многоточие в A0.2.12) обозначает слагаемые, не
содержащие данного полюса. («Другие слагаемые», возникающие от
других одночастичных состояний, приводят к полюсам по q в
других точках, а слагаемые, возникающие от многочастичных со-
состояний, приводят к появлению точек ветвления по д. Наконец,
слагаемые, возникающие от других последовательностей моментов
времени, приводят к полюсам и точкам ветвления по другим пере-
переменным.) С помощью формул A0.2.9) и A0.2.10) легко показать, что
полученные М в точности те же, что и определенные формулами
A0.2.4) и A0.2.5). Кроме того, вблизи полюса
m + гг
= >
q° - д/g2 + m + ie -(q° J
(Мы вновь переопределили ?, домножив на положительную величи-
НУ 2Jq2 + ттг2 > что допустимо, так как ? - произвольная положи-
положительная бесконечно малая величина.) Таким образом, выражение
A0.2.12) тождественно желаемому выражению A0.2.3).
Этот результат имеет классическое применение в теории ядер-
ядерных сил. Пусть Фа(ж) — любое действительное поле или комбинация
полей (например, пропорциональная кварк-антикварковому били-
билинейному коварианту qy^iaq), имеющие неисчезающий матричный
элемент между однопионным состоянием с изоспином а и вакуу-
вакуумом, нормированный условием:
//. A0.2.15)
586 Глава 10. Непертурбативные методы
Тогда матричный элемент Фа между однонуклонными состояниями
с 4-импульсами pup' имеет полюс при (р — р'J —> —шя2 с вычетом,
вид которого определяется изоспиновой и лоренцовской инвариант-
инвариантностью (включая инвариантность относительно пространственных
отражений) *:
где и и. и' — начальные и конечные нуклонные спинорные коэффи-
коэффициентные функции, зависящие также от изоспиновых перемен-ных
нуклонов, а та (а = 1, 2, 3) — 2x2 изоспиновые матрицы Паули.
Постоянная GK носит название пион—нуклонной константы связи.
Указанный полюс находится вне физической области матричного
элемента A0.2.16), в которой {р — р'J > 0, но его можно достичь с
помощью аналитического продолжения этого матричного элемента,
рассматривая, например, матричный элемент вне массовой поверх-
поверхности
Jd4x d Vе-ч^е'Р''*'(т{Фа@)N(x)N(x')})
VAC '
где N и N' — соответствующие компоненты оператора поля или
произведения полевых операторов с неисчезающими матричными
*Лоренцовская и изоспиновая инвариантности требуют, чтобы этот мат-
матричный элемент имел вид ( и'Тхаи), где Г — матрица 4x4, для которой били-
билинейная комбинация ( \|/ П|/) преобразуется как псевдоскаляр. Как всякая мат-
матрица 4x4, Г может быть разложена на сумму слагаемых, пропорциональных
дираковским матрицам 1, у^, [у^,уу], у5у^ и у5. Коэффициенты при них должны
быть соответственно псевдоскаляром, псевдовектором, псевдотензором, век-
вектором и скаляром. Из двух импульсов рир' невозможно построить псевдоска-
псевдоскаляры или псевдовекторы. В то же время, можно построить один псевдотензор,
пропорциональный ?^раррр'а, два независимых вектора, пропорциональных
р^ или p'v, и скаляр, пропорциональный единице, причем коэффициенты
пропорциональности при всех этих структурах являются функциями единст-
единственной независимой скалярной переменной (р — р'J. Используя уравнения Ди-
Дирака в импульсном пространстве для и и и, нетрудно показать, что тензорная
и псевдовекторная матрицы в Г дают вклад, пропорциональный у5.
10.2. Полология 587
элементами между однонуклонными состояниями и вакуумом. Со-
Согласно все той же теореме обмен пионом при рассеянии двух
нуклонов с начальными 4-импульсами р1 и р2 и конечными 4-
импульсами р\ и р'2 приводит к появлению в соответствующем
матричном элементе полюса при (рг - р\J = (р2 - р'2J —> -тж2:
^ (Pi + Р2 Pi P2) 772 2"
A0.2.17)
х{2ж)~3(ь
(Простейший способ определить фазы и численные множители в
подобных формулах заключается в использовании фейнмановских
диаграмм. Наша теорема утверждает, что полюсная структура
амплитуды совпадает с той, которая получилась бы в теории поля
с лагранжианом, включающим элементарное пионное поле.) Опять
же, этот пионный полюс находится вне физической области для
рассеяния нуклонов на массовой оболочке, в которой (р — р'J >
0, но достичь его можно путем аналитического продолжения мат-
матричного элемента /^-матрицы, рассматривая, например, матрич-
матричный элемент вне массовой оболочки
Г 4 4
Хотя пионный полюс и не попадает в физическую область нуклон—
нуклонного рассеяния, но масса пиона достаточно мала, так что
полюс лежит очень близко к физической области. При определен-
определенных условиях, например, при больших значениях I в разложении
по парциальным волнам, этот полюс может доминировать.
С точки зрения координатного пространства полюс указанного
типа при (рх - р\J = (р2 - р'2J —» -тж2 означает наличие силы
радиусом действия порядка 1/тж. Например, в первоначальной
теории ядерных сил Юкавы 2 обмен мезонами (в те времена счита-
считалось, что они скаляры, а не псевдоскаляры) порождал локальный
потенциал вида ехр(— тяг)/Dяг), и его фурье образ определял
^-матрицу нерелятивистского нуклон—нуклонного рассеяния в пер-
первом борновском приближении:
588 Глава 10. Непертурбативные методы
j d3xld3x2d3x[d3x2
ехр(-шя|х1-х2
[*r ¦¦ j. j. [*r ¦¦ ii ^j ^^ ¦¦ j. j. [*r ¦¦ ii ^
xl X2l
= -BлK53(р1+р2-р;-р2)
(Pi-PiJ+m
Множитель 1/[(P!—p/) + mjc ] представляет как раз нерелятивист-
нерелятивистский предел пропагатора l/[(Pi—р/J + 7?1я2] в формуле A0.2.17). (В
этом выражении передаваемая энергия р^ — р\° при |рг| <^ mN и
р/| <^ mN равна [рх2 - р1/2]/2тпи, что пренебрежимо мало по сравне-
сравнению с величиной передаваемого импульса |рг - р/|. Когда только
появилась теория Юкавы, считалось общепринятым, что подобный
тип зависимости нуклон-нуклонного рассеяния от импульсов возни-
возникает в теории из-за наличия мезонного поля. Лишь в 1950-е годы
стало понятным, что существование полюса при (р1 — р\J —> —fnK2
вытекает из существования частицы — пиона — и не имеет
никакого отношения к вопросу о том, является ли эта частица элемен-
элементарной, т. е. ей отвечает отдельное поле в лагранжиане.
10.3. Перенормировка поля и массы
Воспользуемся теперь частным случаем результата предыду-
предыдущего раздела, чтобы сделать более ясной интерпретацию радиаци-
радиационных поправок к внутренним и внешним линиям произвольного
процесса.
Интересующий нас частный случай — это случай, когда из
всех 4-импульсов внешних линий только один приближается к
массовой оболочке. (В обозначениях предыдущего раздела это соот-
соответствует г = 1.) Рассмотрим функцию:
и ч A0.3.1)
х (?0,Tfa to), А, (я2 ),...}?0),
10.3. Перенормировка поля и массы 589
где f'i(x) — гейзенберговский оператор, имеющий те же транс-
трансформационные свойства относительно лоренцовских преобразований,
что и некоторое свободное поле щ, принадлежащее неприводимому
представлению однородной группы Лоренца (для теорий, сохраняющих
четность,— группы Лоренца, включающей отражения), о чем свиде-
свидетельствует индекс I, а А2, А3, и т. д. — произвольные гейзенберговс-
гейзенберговские операторы. Предположим, что имеется одночастичное состояние
^q^cj, имеющее неисчезающие матричные элементы с состояниями
О ft?о и А2А%..У?ц. Тогда согласно доказанной в предыдущем разделе
теореме Gx имеет полюс при qx2 = -т2, причем
+т2
\
m - ге
A0.3.2)
x
Из лоренцовской инвариантности следует:
d1,cy), A0.3.3)
где Uj(q,o) равна (если не считать множителя Bя)~3/2) коэффициент-
коэффициентной функции * свободного поля \|/г с теми же трансформационными
свойствами относительно лоренцовских преобразований, что и опе-
оператор (\, а N — константа. (Именно для того, чтобы получить
формулу A0.3.3) с единственной свободной константой N, нам при-
пришлось предположить, что ()х преобразуется неприводимо.) Опреде-
Определим также «усеченный» матричный элемент Мг формулой
* Например, для стандартным образом нормированного свободного
,-1/2
скалярного поля U((q1;a) = I 2^/qj + m
590 Глава 10. Непертурбативные методы
Тогда формула A0.3.2) при qx2 —» —т2 принимает вид
-2iJ
q2 +
n.+Tn2T^^Wi'°^'i4i,o;"ir. (Ю.3.5)
Ui "T" lib it- ./
Согласно формулам F.2.2) и F.2.18), величина, входящая в
формулу A0.3.5) в виде множителя перед М{, равна матричному
пропагатору в импульсном пространстве — гД^^) для свободного
поля, имеющего те же трансформационные свойства относительно
лоренцовских преобразований, что и ()х (или, по крайней мере,
такими свойствами должен обладать предел при q2 —» —т2). Поэто-
Поэтому формула A0.3.5) позволяет отождествить Мг с суммой всех
диаграмм, внешние линии которых с импульсами q1( q2, ... отвечают
операторам С)ь А2, ..., причем пропагаторы, отвечающие линии (\,
отброшены. Тогда формула A0.3.4) является обычным предписанием
для вычисления матричного элемента испускания частицы в виде
суммы фейнмановских диаграмм: нужно отбросить пропагатор час-
частицы, заменив его сверткой с обычным множителем B%)~5//2и{ для
внешней линии. Единственным отличием от обычных фейнманов-
фейнмановских правил является множитель N.
Сформулированная выше теорема представляет собой знаме-
знаменитый результат Лемана, Симанчика и Циммермана3, известный
как редукционная формула. Мы доказали ее здесь несколько иным
способом, позволяющим легко обобщить результат на случай про-
произвольного спина. Важно отметить, что полученный результат при-
применим к любым операторам; оператор бг не обязан быть каким-то
полем, реально входящим в лагранжиан, а частица, рождаемая
этим полем, может быть связанным состоянием тех частиц, поля
которых действительно входят в лагранжиан. Этот результат позво-
позволяет извлечь важный урок и в том случае, когда (\ является одним
из полей Ч'1 из лагранжиана: если мы намерены использовать
обычные фейнмановские правила для вычисления матричных эле-
элементов ^-матрицы, необходимо сначала переопределить нормиров-
нормировку полей множителем 1/N, так что (с извинениями за многократное
использование символа Ч1 в разных смыслах)
!/2u,(q,G). A0.3.6)
10.3. Перенормировка поля и массы 591
Поле, нормированное так, как указано в формуле A0.3.6), носит
название перенормированного поля.
Константа перенормировки поля N возникает и в другом месте.
Предположим, что в формуле A0.3.1) на месте операторов А2, А3, ...
стоит только один оператор, сопряженный члену того же полевого
мультиплета, что и ()х. Тогда формула A0.3.2) принимает вид
т -ге
*~^ '
)BлL54
q( + т1 - гг ^
Мы получаем обычное поведение пропагатора (суммы всех диаг-
диаграмм с двумя внешними линиями) в окрестности его полюса, если
не считать множителя |iV|2. Согласно формуле A0.3.6), этот множи-
множитель исчезает в пропагаторе перенормированного поля Ч*г. Итак,
перенормированное поле — это такое поле, пропагатор которого
имеет такое же поведение в окрестности полюса, как и для
свободного поля, а перенормированная масса определяется положе-
положением полюса.
Чтобы увидеть, как это «работает» на практике, рассмотрим
теорию действительного самодействующего скалярного поля Фв
(индекс В добавлен здесь, чтобы напоминать, что пока что это
«голое» * (т. е. неперенормированное) поле. Лагранжиан, как обыч-
обычно, имеет вид
-УВ(ФВ). A0.3.7)
* Английский термин Ъаге в данном контексте обычно переводится как
голый или затравочный. — Прим. пер.
592 Глава 10. Непертурбативные методы
В общем случае нет оснований считать, что поле Фв будет удовлет-
удовлетворять условию A0.3.6), или что полюс по д2 будет находиться в
точке — тв2, поэтому введем перенормированные поле и массу:
В) (ю.3.8)
т2=т2в+Ът2, A0.3.9)
где Z выбирается так, что Ф удовлетворяет A0.3.6), а Ът2 подбира-
подбирается из условия, что полюс пропагатора находится в точке q2 = — т2.
(Использование символа Z в подобных случаях стало традицией;
каждому полю в функции Лагранжа соответствует свое Z.) Теперь
можно переписать лагранжиан A0.3.7) в виде
,$ = $0+$1, A0.3.10)
A0.3.11)
, (ю.3.12)
где
При вычислении поправок к точному * пропагатору в импуль-
импульсном пространстве для перенормированного скалярного поля, обыч-
обычно обозначаемому Д'(д), удобно рассмотреть отдельно одночастично
неприводимые API) диаграммы, т. е. такие связные диаграммы
(исключая диаграмму, состоящую из одной скалярной линии), ко-
которые нельзя сделать несвязными путем разрезания любой одной
внутренней скалярной линии. Пример показан на рис. 10.4. Принято,
опуская пропагаторные множители -гBл)(д2 + т2 — ге)-1 от двух
* Англоязычному термину complete propagator отвечают русскоязычные
термины полный пропагатор или точный пропагатор. Мы отдаем
предпочтение последнему. Встречающийся ниже термин bare propagator, так
же как и авторский термин uncorrected propagator мы переводим как свободный
пропагатор. — Прим. пер.
10.3. Перенормировка поля и массы
593
внешних линий, обозначать сумму всех таких диаграмм через
гBлLГТ(д2), звездочка напоминает, что в это выражение входят
одночастично неприводимые диаграммы. Тогда поправки к точному
пропагатору даются суммой цепочек из одной, двух, трех и более
этих одночастично неприводимых поддиаграмм, соединенных обыч-
обычными свободными пропагаторными множителями
BлL
—г
BлL q2 + т2 - г?
1
BлL q2+m2-i?
-г 1
BлL q2 + т2 - г?
х[гBлLГГ(д2)]
[гBлLГГ(д2)]
-г
BлL
—г
д2-
1
\-т2
1
-ге
BлL q2 + т2 - г?
A0.3.13)
-г
1
BлL ql + т1 - г?
или, в более простой записи,
A'(q) = [g2 + т2 - ге] + [д2 + т2 - ге] П*(д2)[д2 +т2 - ге]
+ [д2 + т2 - ге] П* (д2 )[д2 + т2 - Щ~1 П* (д2 )[д2 +т2 - ге] +...
A0.3.14)
Суммируя геометрическую прогрессию, получаем
.... Г 9 9 т—г* /9ч ¦ 1~1
A (q) = [q2+тп/-П (Q )-ге] .
A0.3.15)
При вычислении П мы учитываем древесные диаграммы, возни-
возникающие от однократной вставки вершин, отвечающих слагаемым
вида Э^ФЭ^Ф и Ф2 в A0.3.12) , а также слагаемое ГГШор> возникаю-
возникающее от петлевых диаграмм типа показанной на рис. 10.4а:
П*(g2) = -(Z - 1)[д2 + т2] + Zbm2 + Пшор(92)¦ (Ю-3.16)
594
Глава 10. Непертурбативные методы
Условие, что т2 является истинной массой частицы, сводится к
условию, что полюс пропагатора должен находиться при д2= — га2,
так что
П*(-т2) = 0.
A0.3.17)
Кроме того, условие, что полюс пропагатора при д2 = — т2 должен
иметь единичный вычет (как у свободного пропагатора), сводится к
условию
d
dq'
•nV)
= 0.
q2=-m2
A0.3.18)
Приведенные условия позволяют вычислить Z и бт2:
A0.3.19)
Z =
d
dq2
A0.3.20)
Отсюда вытекает, что Z5m2 и Z — 1 задаются рядами по степеням
константы связи без нулевых членов, что оправдывает рассмотре-
рассмотрение двух первых слагаемых в формуле A0.3.12) как части лагран-
лагранжиана взаимодействия 9?,^.
Рис. 10-4. Одночастично неприводимая диаграмма (а) и одночастично
приводимая диаграмма (Ь) в теории с четвертичным взаимодействием.
Примером такой теории является теория скалярного поля (р с взаимо-
взаимодействием, пропорциональным ф4
10.3. Перенормировка поля и массы 595
При проведении вычислений самое простое — это сказать, что
из петлевых слагаемых ГГшор^2) мы должны вычесть полином
первого порядка по q2 с коэффициентами, подобранными так, чтобы
разность удовлетворяла условиям A0.3.17) и A0.3.18). Как будет видно
далее, эта вычитательная процедура попутно сокращает бесконечно-
бесконечности, возникающие от интегралов в импульсном пространстве, опре-
определяющих ГГшор- Однако, как должно быть ясно, перенормировка
масс и полей непосредственно не имеет ничего общего с существова-
существованием бесконечностей и необходима даже в теории, в которой все
интегралы в импульсном пространстве сходятся.
Важным следствием условий A0.3.17) и A0.3.18) является ут-
утверждение, что не нужно включать радиационные поправки во
внешние линии на массовой оболочке, поскольку
+ш2 -ге] +П4(д2)[д2 +ш2 -ге]
^_m2 =0. A0-21)
Аналогичные замечания применимы к частицам произвольного спи-
спина. Например, лагранжиан «голого» дираковского поля имеет вид
Я = -Чв[д + твфв-Ув(Чв). (Ю.3.22)
Вводим перенормированные поля и массы:
2B A0.3.23)
т = тв+5т. A0.3.24)
(Индекс 2 у Z по традиции используется для обозначения константы
перенормировки фермионного поля.) Тогда лагранжиан можно пере-
переписать в виде:
(? = tf0 + $х, A0.3.25)
$0 =-Щд + т]Ч, A0.3.26)
У\ =-(Z2 -l)[?[d + mB]?] + Z28mW-VB(Z2W). A0.3.27)
596 Глава 10. Непертурбативные методы
Пусть гBлL Y,"(k)~ сумма всех связных диаграмм с одной
входящей фермионной линией с 4-импульсом к, и одной выходя-
выходящей линией с тем же 4-импульсом, которые нельзя сделать несвяз-
несвязными, раз-резав любую внутреннюю фермионную линию, причем
пропа-гаторное множители —гBрL и [ik + т — ге] для внешних ли-
линий опущены. (Здесь использована лоренцовская инвариантность,
согласно которой ХГ есть обычная функция скалярной матрицы
к = /с„у^.) Тогда полный фермионный пропагатор имеет вид
S'(k) = [ik + m- ге] + [ik + т - ге]Y?{k)[ik + т- ге]
+ [ik + т - ге] ?* (к)[гк + т - ге] ?* (к)[гк + т- ге] +...
= [№ + т-Ц{к)-Щ-1.
A0.3.28)
При вычислении Y,'{к) мы учитываем древесные диаграммы от
слагаемых в правой части A0.3.27), пропорциональных Ц'дЧ' и WW,
а также вклад петель:
m] + Z2bm + Iloop (*) • (Ю.3.29)
Условие, чтобы полный пропагатор имел полюс при к2 = —га2 с тем
же вычетом, что и свободный пропагатор, имеет вид:
1*(гт) = 0, A0.3.30)
дк
и поэтому
Z95m = -
jfe=tm
Как и для скалярных частиц, обращение в нуль [ik + m] E*№ B
пределе ^ —> гт показывает, что на массовой поверхности можно
пренебречь радиационными поправками к внешним фермионным
10.4. Перенормированный заряд и тождества У орда 597
линиям. Соответствующие результаты для фотонного пропагатора
будут получены в разделе 10.5.
10.4. Перенормированный заряд
и тождества Уорда
С помощью соотношений коммутации и законов сохранения
для гейзенберговских операторов можно установить связь между
зарядами (или аналогичными величинами) в плотности лагранжиа-
лагранжиана и свойствами физических состояний. Напомним, что инвариант-
инвариантность плотности лагранжиана относительно глобальных калибро-
калибровочных преобразований *Рг —» ехр(гдга)*1'г (с произвольной постоян-
постоянной фазой а) влечет за собой существование тока
удовлетворяющего условию сохранения
Э^=0. A0.4.2)
Отсюда вытекает, что пространственный интеграл от временной
компоненты J^ не зависит от времени:
г — Q = [Q,H] = 0, A0.4.3)
где
Q = jd3xJ°. A0.4.4)
(Очень важное возможное исключение связано с тем, что интеграл
A0.4.4) может не существовать, если в системе имеются дальнодей-
ствующие силы, обязанные безмассовым скалярам. Мы вернемся к
этому вопросу при рассмотрении нарушенных симметрии в т. П.)
Кроме того, поскольку Q является интегралом по пространству,
эта величина явно трансляционно-инвариантна:
[P,Q] = 0, A0.4.5)
598 Глава 10. Непертурбативные методы
а так как J^ — 4-вектор, Q инвариантен по отношению к однород-
однородным преобразованиям Лоренца:
г тцу ni - п П П 4 в)
Отсюда следует, что оператор Q, действуя на истинный вакуум *Р0,
дает другое лоренц-инвариантное состояние нулевой энергии и
импульса, которое (в предположении, что вакуум невырожден)
должно быть пропорционально самому Ч^. Но константа пропорцио-
пропорциональности должна обращаться в нуль, так как из лоренц-инвари-
антности следует, что (Ч^, Jm4\)) = 0- Отсюда получаем:
Q% =0. A0.4.7)
Кроме того, оператор Q, действуя на любое одночастичное состоя-
состояние Ч/роп, должен переводить его в другое состояние с теми же
энергией, импульсом и теми же трансформационными свойствами
относительно преобразований Лоренца, и следовательно (предпола-
(предполагая отсутствие вырождения одночастичных состояний), в состоя-
состояние, пропорциональное тому же одночастичному состоянию:
Лоренц-инвариантность Q гарантирует, что собственное значение
Q(n) не зависит от р и s, а зависит только от сорта частиц. Это
собственное значение известно как электрический заряд (или ка-
какое-то другое квантовое число, для которого J^ может быть током)
одночастичного состояния. Чтобы связать его с параметрами qx в
лагранжиане, заметим, что из канонических коммутационных со-
соотношений следует
^(x-y), A0.4.9)
или, после интегрирования по х,
A0.4.10)
То же верно и для любой локальной функции F(y) заданного числа
полей, их производных и сопряженных им величин:
10.4. Перенормированный заряд и тождества У орда 599
[Q,F(y)] = -qFF(y), A0.4.11)
где gF — сумма qx для всех полей и их производных в F(y) минус
сумма Q; для всех сопряженных полей и их производных. Беря
матричный элемент этого соотношения между одночастичным со-
состоянием и вакуумом и используя формулы A0.4.7) и A0.4.8),
получаем
(%,F(yL>pan)(qF-qin)) = 0. A0.4.12)
Следовательно, должно быть
Ч(п)=Чр, A0.4.13)
если только
(%,F(yLp>a>n)*0. A0.4.14)
Как мы видели в предыдущем разделе, при условии A0.4.14) функ-
функции Грина, включающие F, в импульсном пространстве имеют
полюсы, отвечающие одночастичному состоянию ?рап. Для одно-
частичного состояния, соответствующего одному из полей в ла-
лагранжиане, мы могли бы взять F = Ч?г, и в этом случае gF = qb
однако наши результаты применимы и к произвольным одночастич-
одночастичным состояниям, независимо от того, входят ли соответствующие
им поля в лагранжиан или нет.
Это почти полностью убеждает нас в том, что несмотря на все
мыслимые диаграммы высшего порядка, дающие вклад в амплиту-
амплитуды испускания и поглощения фотонов заряженными частицами,
физический электрический заряд строго равен параметру ql в функ-
функции Лагранжа (или сумме таких параметров типа gF). Уточне-
Уточнение, которое необходимо сделать, заключается в том, что требо-
требование инвариантности лагранжиана относительно преобразований
*Рг —> exp(zqj(XL'j никак не фиксирует общий масштаб величин дг.
Физические электрические заряды определяют отклик полей мате-
материи на заданное перенормированное электромагнитное поле А^.
Иными словами, масштаб величин qx фиксируется требованием,
чтобы перенормированное электромагнитное поле входило в ла-
лагранжиан материи 9Р,М в линейных комбинациях [Э„ — гдгА„]*1'г, так
что ток J^ имеет вид
600 Глава 10. Непертурбативные методы
г И М
J 6A~' A0.4.15)
Однако А^ и qx — не те же самые величины, что «голое электромаг-
электромагнитное поле» Ав^ и «голые заряды» qBX, входящие в лагранжиан,
записанный в простейшей форме *
A0.4.16)
Перенормированное электромагнитное поле (определенное так, чтобы
его точный пропагатор имел полюс при р2 = 0 с единичным вычетом)
принято записывать в терминах поля Авц в виде
А^ = Z~l/2A^ A0.4.17)
поэтому для того, чтобы заряд qx характеризовал отклик заряжен-
заряженных частиц на данное перенормированное электромагнитное поле,
нужно определить перенормированные заряды соотношением
A0.4.18)
Мы видим, что физический электрический заряд q любой частицы
просто пропорционален некоторому параметру дв, связанному с
теми параметрами, которые входят в лагранжиан, причем коэффи-
коэффициент пропорциональности Z3~1//2 одинаков для всех частиц. Это
позволяет понять, каким образом частица вроде протона, окружен-
окруженная облаком виртуальных мезонов и других сильновзаимодейст-
вующих частиц, может иметь тот же электрический заряд, что и
позитрон, все взаимодействия которого много слабее. Необходимо
всего лишь предположить, что по каким-то причинам заряды двг в
лагранжиане равны и противоположны по знаку для электрона и
совокупности тех частиц (двух м-кварков и одного d-кварка), из
которых составлен протон. Эффект поправок высшего порядка про-
проявится при этом только в появлении общего множителя Zg/2.
* Следует иметь в виду, что автор не выписывает слагаемые, фиксирующие
калибровку электромагнитного поля. — Прим. ред.
10.4. Перенормированный заряд и тождества У орда ° 01
Для того, чтобы перенормировка заряда возникала только от
радиационных поправок к фотонному пропагатору, должны про-
происходить сокращения большого числа других радиационных по-
поправок к пропагаторам и электромагнитным вершинам заряжен-
заряженных частиц. Можно чуть глубже проникнуть в природу этих
сокращений, если воспользоваться знаменитыми соотношениями
между пропагаторами заряженных частиц и вершинами, извест-
известными как тождества Уорда.
Рассмотрим, например, функцию Грина электрического тока
J^{x) совместно с гейзенберговским дираковским полем *Рп(у), имею-
имеющим заряд д, и ковариантно сопряженным ему полем 4fm(z). Опре-
Определим электромагнитную вершинную функцию Р1 заряженной час-
частицы формулой
A0.4.19)
= -iqS'nn,{k)Tln,{k,l)S'm,m{l)b4v + k-l),
где
-iS'nm(kMHk-l) = JdVMVK(y)^m(^oK*^+iK A0.4.20)
Согласно теореме раздела 6.4, формула A0.4.20) определяет сумму
всех фейнмановских диаграмм с одной входящей и одной выходящей
фермионной линиями,т. е. точный дираковский пропагатор. Кроме
того, формула A0.4.19) определяет сумму всех таких диаграмм, но с
дополнительной внешней фотонной линией, так что Р1 равна сумме
«вершинных» диаграмм с одной входящей и одной выходящей дира-
ковскими линиями и одной фотонной линией, но с отброшенными
точными пропагаторами дираковских внешних линий и свободным
пропагатором внешней фотонной линии. Чтобы окончательно выяс-
выяснить нормировку S' и Р1, заметим, что в пределе отсутствия взаимо-
взаимодействий эти функции принимают следующие значения:
S'(k) -> [iyxkX + т ~ ^Г1. Г^(к,1)->у^.
Однопетлевые диаграммы, дающие поправки к указанным пре-
предельным значениям, показаны на рис. 10.5.
602
Глава 10. Непертурбативные методы
Рис. 10.5. Диаграммы первых поправок к электронному пропагатору и
вершинной функции в квантовой электродинамике. Прямые линии отвечают
электронам, волнистые — фотонам
Можно вывести соотношение между Р1 и S', используя тожде-
тождество
5(х° -y°)T{[j°(xL>n(y)fVm(z)}
5(xo-zo)T{4>n(y)[j°(x),4m(zj\},
A0.4.21)
где дельта-функции возникают от дифференцирования ступенча-
ступенчатых функций. В силу закона сохранения A0.4.2) первое слагаемое
обращается в нуль. Второе и третье слагаемые можно вычислить с
помощью коммутационных соотношений A0.4.9), которые в данном
случае имеют вид
A0.4.22)
A0.4.23)
а для сопряженного коммутатора имеем:
Тогда формула A0.4.21) записывается в виде
= -g54(x -
q5Hx-z)T{4>n(yL>m(z)}.
A0.4.24)
10.5. Калибровочная инвариантность " " 3
Соответственно для преобразования Фурье получаем с учетом
соотношения A0.4.19)
или, иными словами,
,l) = iS'-\k) - iS'-\l). A0.4.25)
Это соотношение известно как обобщенное тождество Уорда, и
впервые получено (описанным методом) Такахаши 4. Первоначаль-
Первоначальное тождество, выведенное ранее Уордом 5 при анализе ряда тео-
теории возмущений, можно получить из A0.4.25), устремив I к к. В
этом пределе находим
) = -i^rS/~Hk). (ю.4.26)
Фермионный пропагатор связан формулой A0.3.28) с собственно-
энергетической вставкой * Y,'(k) в собственную энергию:
так что формулу A0.4.26) можно записать в виде
^(Ш). (ю.4.27)
Для перенормированного дираковского поля получаем из формул
A0.3.31) и A0.4.27), что на массовой оболочке
ик, (Ю.4.28)
где [гУцУ1 + т]ик = [i\№ + т]ик = 0. Таким образом, перенормировка
фермионного поля обеспечивает сокращение радиационных поправок
к вершинной функции Р1, когда фермион на массовой поверхности
* В русскоязычной литературе используется также термин массовый
оператор. — Прим. ред.
604 Глава 10. Непертурбативные методы
взаимодействует с электромагнитным полем с нулевой передачей
импульса, как это и имеет место в случае, когда мы измеряем
электрический заряд фермиона. Если бы мы использовали непере-
нормированное фермионное поле, то поправки к вершинной функ-
функции все равно сократились бы с радиационными поправками к
внешним фермионным линиям, оставив электрический заряд неиз-
неизменным.
10.5. Калибровочная инвариантность
Сохранение электрического заряда можно использовать для
доказательства полезных соотношений, которым удовлетворяют ве-
величины
В теориях типа спинорной электродинамики, где электромагнитное
взаимодействие линейно по полю А*1, это есть матричный элемент
произвольного перехода ОС —> C с испусканием (и/или поглощением)
фотонов, находящихся на или вне массовой поверхности, с 4-импуль-
сами q, q и т. д. (и/или —q, —q и т. д.), при этом коэффициентные
функции или пропагаторы внешних фотонных линий опущены *. Ут-
Утверждается, что выражение A0.5.1) обращается в нуль при свертке с
4-импульсом любого из фотонов:
ЧрМ$~(Ч,ч',-) = %>M$-(q,q',...) =...= 0. A0.5.2)
Так как амплитуда М определена симметрично по отношению к
фотонным линиям, достаточно показать обращение в нуль первой
из этих сверток.
Для этого заметим, что после интегрирования по частям
* Строго говоря, при вычислении матричного элемента нужно отбросить
все радиационные поправки к внешним линиям, либо взять корректное
выражение для тока. — Прим. ред.
10.5. Калибровочная инвариантность " " 5
d V... ^^щ'*'...
] A0-5-3)
Электрический ток J^{x) сохраняется, но отсюда сразу же не следу-
следует, что A0.5.3) обращается в нуль, так как следует учитывать еще
зависимость от ж0, содержащуюся в тета-функциях, которые вхо-
входят в определение хронологического произведения. Например, ог-
ограничиваясь двумя токами, имеем:
6(х° - y°)J»(x)Jy(y) + 6(у° - x°)J
так что, принимая во внимание сохранение «/^(х), получаем *
-y°)J0(x)Jv(y)-5(y0 -x°)J
A0.5.4)
= 5(x°-yo)[j°(x),Jv(y)].
Если токов более двух, мы получаем похожий одновременной ком-
коммутатор (внутри хронологического произведения) для каждого то-
тока, кроме самого J^(x). Чтобы вычислить такой коммутатор, напом-
напомним, что (как показано в предыдущем разделе), для любого произ-
произведения F операторов поля и сопряженных им величин и/или их
производных справедливо равенство
x, t), F(y, t)] = -QFF(x, tM3 (x - у),
где gF — сумма зарядов дг для полей и их производных, входящих в
F, минус сумма зарядов qx для сопряженных полей и их производ-
производных. Для электрического тока Qj равно нулю; •P'iy) сам есть электри-
электрически нейтральный оператор. Отсюда
* Приводимые здесь и ниже рассуждения носят наводящий характер из-за
сингулярного поведения произведений гейзенберговских операторов, которые
являются операторозначными обобщенными функциями по времени (об этом
ниже упоминает и автор). В частности, одновременные коммутаторы токов, и
даже полей, строго говоря, не существуют. — Прим. ред.
606 Глава 10. Непертурбативные методы
[j°(x,t),Jv(y,t)] = 0 A0.5.5)
и поэтому выражение A0.5.4) обращается в нуль, так что из A0.5.3)
находим
'(q,q',...) = 0, A0.5.6)
что и требовалось доказать.
В этом месте необходимо сделать важную оговорку. При
выводе соотношения A0.5.5) следует учитывать, что произведение
полей, взятых в одной пространственно-временной точке у, типа
оператора тока ¦P'iy), можно правильно определить только с помо-
помощью некоторой процедуры регуляризации содержащихся в таких
произведениях бесконечностей. Во многих случаях оказывается,
что существуют неисчезающие вклады в коммутатор J°(x,t) с
регуляризованным током J'(y,t), известные под названием швинге-
ровских членов 6. В случае, когда в токе содержатся слагаемые,
возникающие от заряженного скалярного поля Ф, имеются допол-
дополнительные не зависящие от регуляризации швингеровские члены,
содержащие Ф^Ф. Однако в многофотонных амплитудах все подоб-
подобные швингеровские члены сокращаются со вкладами квадратич-
квадратичных по электромагнитному полю дополнительных взаимодейст-
взаимодействий, которые возникают либо из процедуры регуляризации (при
условии калибровочной инвариантности), либо, если речь идет о
заряженных скалярах, содержатся в лагранжиане.
Мы будем главным образом иметь дело с заряженными спи-
норными полями и использовать процедуру регуляризации (раз-
(размерную регуляризацию), которая не приводит к появлению швин-
геровских членов, так что в последующем изложении мы будем
игнорировать это явление и продолжать пользоваться наивным
коммутационным соотношением A0.5.5).
Те же самые аргументы приводят к результату A0.5.2), когда
и другие частицы, помимо фотонов, находятся вне массовой по-
поверхности, но при условии, что все заряженные частицы берутся
на массовой поверхности, т. е. входят в состояниях *Рп~ и ^„^ В
противном случае левая часть A0.5.2) содержит ненулевые вклады
от одновременных коммутаторов, подобные тем, с которыми мы
встретились в предыдущем разделе при выводе тождества Уорда.
10.5. Калибровочная инвариантность " " ^
Одним из следствий формулы A0.5.2) является то, что мат-
матричные элементы ^-матрицы не изменяются, если заменить любой
фотонный пропагатор Лцу(д) на
Д^(д) -> Д^(д) + ос^ду + д^|Зу , A0.5.7)
или если заменить любой вектор поляризации на
ep(k,A,)->ep(k,A,) + cfcp, A0.5.8)
где к0 = |к|, а ац, CV и с — совершенно произвольные величины (не
обязательно постоянные и не обязательно одинаковые для всех
пропагаторов или векторов поляризации). Все это (несколько воль-
вольно) называется калибровочной инвариантностью /^-матрицы.
Чтобы доказать сделанное утверждение, необходимо всего
лишь явно выписать зависимость ^-матрицы от векторов поляриза-
поляризации фотонов и от пропагаторов:
л ер! \1%-1л'1)кр2\'%-2л'2)шшшКа1 \1%-1л'1)ко2 \л-2'^2>--- A0 5 9)
лдаЬа ^ g1; g2,...,g1,g2,..., «-i, к,2>---к'1> к2---> >
где Мра" — матричный элемент A0.5.1), вычисленный в отсутствие
электромагнитных взаимодействий *. Инвариантность A0.5.9) отно-
относительно «калибровочных преобразований» A0.5.7) и A0.5.8) немед-
немедленно следует из условий сохранения A0.5.2). (В разделе 9.6 мы
использовали формализм функциональных интегралов для доказа-
доказательства частного случая этой теоремы, именно, что средние по
вакууму от хронологических произведений калибровочно инвари-
инвариантных операторов не зависят от константы ос в пропагаторе (9.6.21).)
* Состояния а и Ъ совпадают с а и [3, если убрать все фотоны. Заметим,
что все аргументы М соответствуют входящим 4-импульсам. Именно по-
поэтому мы вынуждены вводить разные знаки в некоторые аргументы М в
выражение A0.5.9).
608 Глава 10. Непертурбативные методы
Этот результат не так тривиален, как кажется, так как он приме-
применим не к отдельным диаграммам, а только к суммам диаграмм,
в которых вершины токов вставлены во все возможные места.
Особенно важное применение формула A0.5.2) находит при
вычислении фотонного пропагатора. Точный фотонный пропагатор,
обозначаемый обычно A')lv(g), имеет вид
A;v(g) = Atlv(g) + Aw(g)MPa(g)Aav(g), A0.5.10)
где Мро пропорционален матричному элементу A0.5.1) с двумя
токами *, а и C — вакуумные состояния, и Ацу — свободный фотонный
пропагатор, который в общей лоренц-инвариантной калибровке
имеет вид
Из A0.5.2) имеем q^M^ = 0, так что
jf^ (Ю.5.12)
С другой стороны, по аналогии с тем, как это делалось для ска-
скалярного и спинорного полей в разделе 10.3, можно выразить точный
фотонный пропагатор через сумму П (д) диаграмм с двумя внешни-
внешними фотонными линиями, которые (в противоположность М) однофо-
тонно неприводимы:
А'(д) = А(д) + А(д) П* (д)А(д) + А(д) П* (д)А(д) П* (д)А(д) +...
или, иными словами,
* Напомним (см. начало раздела), что последнее утверждение верно
только для теорий типа спинорной электродинамики, где взаимодействие
линейно по А„. Однако важное для дальнейшего условие поперечности
A0.5.2) для MpC(q) верно для любой теории. — Прим. ред.
10.6. Электромагнитные формфакторы и магнитный момент 609
Для того, чтобы удовлетворить A0.5.2), необходимо выполнение
равенства
дрГГра(д) = О. (Ю.5.15)
Отсюда, совместно с лоренцовской инвариантностью, вытекает,
что поляризационный оператор П (д) должен иметь вид
= (д2Г|Рст-дРдст)л(д2). A0.5.16)
Тогда из представления A0.5.13) получаем следующий вид точного
пропагатора:
A;v(g) = '
[д^-гф-Жд^)] '"" '
где
] + л(д2). A0.5.18)
Далее, поскольку поляризационный оператор ГТ(д) содержит вкла-
вклады только от однофотонно неприводимых диаграмм, можно ожи-
ожидать, что эта величина не имеет полюса при д2 = 0. (Важным
исключением является случай нарушенной калибровочной симмет-
симметрии, обсуждаемый в томе П.) В частности, из отсутствия полюса
при д2 = 0 в слагаемом, пропорциональном дцду в ГТ(д) вытекает, что
у функции я(д2) также нет такого полюса, и в результате полюс в
точном пропагаторе A0.5.17) остается в точке д2 = 0. Это указывает
на то, что фотон не приобретает массы за счет радиационных
поправок.
Для перенормированного электромагнитного поля радиацион-
радиационные поправки также не изменяют калибровочно инвариантную
часть вычета в фотонном полюсе в A0.5.17), так что
л@) = 0. A0.5.19)
Это условие приводит к определению константы перенормировки
электромагнитного поля Z3. Напомним, что лагранжиан электроди-
610 Глава 10. Непертурбативные методы
намики, выраженный через перенормированное поле A0.4.17), име-
имеет вид
Тогда функция я(д2) в однофотонно неприводимой амплитуде имеет
вид
(Ю.5.20)
где JtLOOP определяет вклад петлевых диаграмм. Отсюда вытекает,
что
A0.5.21)
На практике, чтобы сделать л@) равным нулю, нужно просто
вычислить вклад петель и вычесть константу.
Наконец, формула A0.5.18) показывает, что при д2 Ф 0 калиб-
калибровочное слагаемое в фотонном пропагаторе изменяется за счет
радиационных поправок. Исключением является случай калибровки
Ландау, когда ^ = ^ = 1 для всех д2.
10.6. Электромагнитные формфакторы
и магнитный момент
Пусть мы хотим вычислить процесс рассеяния частицы на
внешнем электромагнитном поле (или электромагнитном поле другой
частицы) в первом порядке теории возмущений по этому полю, но во
всех порядках по всем другим взаимодействиям данной частицы
(включая электромагнитное). Для этого необходимо знать сумму вкла-
вкладов всех фейнмановских диаграмм с одной входящей и одной выхо-
выходящей линией частицы, каждая из которых находится на массовой
поверхности, и одной фотонной линией, которая может быть и на
массовой поверхности, и вне нее. Согласно теореме раздела 6.4, такая
сумма определяется одночастичным матричным элементом электро-
электромагнитного тока J^x). Посмотрим, что определяет общий вид этого
матричного элемента.
В силу трансляционной инвариантности одночастичный мат-
матричный элемент электромагнитного тока имеет вид
10.6. Электромагнитные формфакторы и магнитный момент
y?Pia) = ехр(г(р-р> x^^J^O)^). A0.6.1)
Условие сохранения тока d^J^ = 0 в этом случае означает, что
(р' - p)^pW, J40)%,a) = 0 • (Ю.6.2)
Кроме того, полагая ц = 0 и интегрируя по всем х, находим
Используя формулу A0.4.8), получаем
BжГ3ЧЬаа,, A0.6.3)
где q — заряд частицы.
В нашем распоряжении есть и ограничения на матричные эле-
элементы токов, накладываемые лоренц-инвариантностью. Чтобы по-
получить их, рассмотрим простейшие случаи: спин 0 и спин 1/2.
Представленный ниже анализ является примером полезной техни-
техники вычислений, используемой и для других токов, например, для
токов полулептонных слабых взаимодействий.
Спин нуль
В случае спина нуль требование лоренц-инвариантности приводит к
следующему общему виду одночастичного матричного элемента
тока:
() //р), A0.6.4)
где р° и р'° энергии на массовой поверхности (р° = Jp2 + т2 )> а
jtiv\р) — 4-вектор, являющийся функцией двух 4-векторов р/|Х и
р^. (Для удобства дальнейших выкладок мы выделили из J множи-
множитель, равный заряду частицы д.) Очевидно, что самый общий вид
такой функции — это линейная комбинация р/ц и р^ или, эквива-
эквивалентно, р/ц + рц и р'11 — р1, со скалярными коэффициентами. Однако
значения скаляров р2 и р'2 фиксированы: р2 = р'2 = — т2, так что
скалярные переменные, которые можно построить из р/ц и р^,
612 Глава 10. Непертурбативные методы
являются функциями единственной величины р-р' или, эквива-
эквивалентно, величины
к2 = (р- рJ = -2т2 - 2 р-р .
A0.6.5)
Следовательно функция ^Цр',р) должна иметь вид
г^(р,р) = (р + p)»F(k2) + i{p' - рТЩк2). A0.6.6)
Из того, что оператор J^ эрмитов , вытекает, что #^{р',р)" =
$Чр>р')> так что F(k2) и Н(к2) действительны. Далее, скалярное
произведение (р' — р)-{р' + р) обращается в нуль, а (р' — рJ = к2 в
общем случае не равно нулю, так что условие сохранения тока
принимает простой вид
Н(к2) = 0. A0.6.7)
Кроме того, полагая в формуле A0.6.4) р' = риц = 0и сравнивая с
формулой A0.6.3), находим, что
F@) = 1. A0.6.8)
Функция F(k2) называется электромагнитным формфактором час-
частицы.
Спин 1/2
В случае спина 1/2 требование лоренц-инвариантности приводит к
следующему общему виду одночастичного матричного элемента
тока:
() ^), A0.6.9)
где Р1 — 4-векторная 4x4 матричная функция величин pv, p'y и yv,
а и — обычная дираковская коэффициентная функция. Мы выдели-
выделили множитель iq, чтобы нормировка Р1 совпадала с приведенной в
предыдущем разделе.
10.6. Электромагнитные формфакторы и магнитный момент 613
Как и любую другую матрицу 4x4, можно разложить Р1 в
суперпозицию 16 ковариантных матриц 1, ур, [ур,уо], YsYp и Ys-
Поэтому наиболее общий 4-вектор Р1 можно представить в виде
линейной комбинации следующих величин:
YP: у^, р^р, р'^р, р V, P'V,
[YP, YcJ: tY", Pi №,Р'1 [Р, Р'№ЛР, Р']р'»\
YsYp : Y5Yp?№VCTPvPa>
y5: отсутствует,
причем коэффициенты при каждом слагаемом будут функциями
единственной скалярной величины A0.6.5). Полученное выражение
может быть сильно упрощено, если использовать уравнение Дира-
Дирака, которому удовлетворяют и ж и:
*Это утверждение очевидно для слагаемых р^р, р'^р, р^р' и р'^р', кото-
которые могут быть заменены, соответственно, на слагаемые гтр^, гтр'^,
impV-,imp'V-, совпадающие с уже имеющимися в нашем списке. Кроме
того,
что можно заменить на 2impil — 2р^, т. е. линейную комбинацию уже
имеющихся слагаемых. Это же относится к [у^,|>']. Далее,
[|>,|>'] = -2р'р + {р,р'} = -2р'р + 2р ¦ р',
что можно заменить на 2т2 + 2р-р' = —к2. Таким образом, слагаемые
[р,р']р^ и [р,р']р'^ также не дают ничего нового. Наконец, чтобы разо-
разобраться с последним слагаемым, следует воспользоваться соотношением
Y у gP^vo = — j(y^YvY° + Y°Y^YV + YVY°Y^ — YVY^Y° — Y^Y°YV — Y°YVY^1
Сворачивая его с pv и р'о и переставляя все множители р направо, а все р'
налево, видим, что это выражение опять сводится к линейной комбинации
р>\ pV и t-
614 Глава 10. Непертурбативные методы
1Г(р', a'){ip' + т) = 0, {ip + m)u(p, a) = 0.
Тогда можно отбросить* все слагаемые кроме трех первых, пропор-
пропорциональных р^, р'^ и у^. Мы приходим к выводу, что на массовой
оболочке для фермионов функцию Р1 можно выразить в виде
линейной комбинации у^, р^ и р'^. Выберем ее следующим образом:
п(р', а')Г^(р', р)м(р, а) = п(р', а')| Y^(fc2) ~т.— (Р + p')^G(/c2)
A0.6.10)
2m
Из эрмитовости J^{0) следует, что
р), A0.6.11)
так что F{k2), G{k2) и Н{к2) должны быть действительными функци-
функциями к2.
Закон сохранения A0.6.2) автоматически удовлетворяется для
первых двух слагаемых в A0.6.10), так как
(р' - р)„ у^ = -г[(гр' + т) — {ip + m)]
и
(р' - р) • (р' + р) = р'2 - р2 .
С другой стороны, (р' - рJ в общем случае не равно нулю, поэтому
сохранение тока требует, чтобы третье слагаемое отсутствовало:
Н{к2) = 0. A0.6.12)
Кроме того, устремляя р' —» р в формулах A0.6.9) и A0.6.10),
находим:
г 1
— p^G@) м(р,о).
m J
Используя тождество {yi1, гр + т} = 2ту^ + 2гр^, получаем также,
что
10.6. Электромагнитные формфакторы и магнитный момент 615
Напомним, что
M(p,o')w(p,o) = 5oo,m/p°
и поэтому
Сравнивая это выражение с A0.6.3), приходим к условию нормировки
F@) + G@) = l. A0.6.14)
Полезно отметить, что электромагнитная вершинная матрица Р1
обычно выражается через две другие матрицы в виде
Можно переписать матрицу, содержащуюся во втором слагаемом,
через те матрицы, которые использовались при определении F(k2) и
G(k2):
п(р', а') \ г[у^, yv ](р' - p)v w(p, a)
= п(р', а')[г(р^ + р^1) + 2mYtl]w(p, a).
Сравнивая A0.6.15) с A0.6.10), находим:
A0.6.17)
616 Глава 10. Непертурбативные методы
= -2mF2(k2). A0.6.18)
Условие нормировки A0.6.14) принимает теперь вид
Чтобы выразить магнитный момент частицы через ее формфакто-
ры, рассмотрим пространственную часть вершинной функции в
случае малых импульсов |р|, |р'| <^ т. Для этого удобно воспользо-
воспользоваться формулой A0.6.16) и переписать представление A0.6.10)
(с Я = 0) еще в одном виде:
L У №2) + G(k2)}
A0.6.19)
При нулевых импульсах матричные элементы коммутаторов дира-
ковских матриц определяются соотношениями E.4.19) и E.4.20):
Jk2 \ , и@,о')[у\у0]и@,о) = 0,
)
V
)а',а
где JB^ = г<5 — матрица углового момента для спина 1/2. Отсюда в
первом порядке по малым импульсам получаем
п(р',а')Г(р',рМр,<т) -> — [(р - р') х J(i)VffF@). A0.6.20)
ill/
Поэтому в случае очень слабого, не зависящего от времени внешне-
внешнего векторного потенциала А(х) матричный элемент гамильтониана
взаимодействия Я' = —J d3xJ(x) • А(х) между одночастичными со-
состояниями с малым импульсом равен
x^-P>xA(x) • [(р - р') X J(i)U
, (М A0.6.21)
t""'"(I WBW
10.6. Электромагнитные формфакторы и магнитный момент 617
где В = V х А — магнитное поле. В пределе медленно меняющегося
внешнего магнитного поля матричный элемент гамильтониана взаи-
взаимодействия принимает вид
• В53(р - р'). (Ю.6.22)
m
Магнитный момент ц произвольной частицы со спином j определя-
определяется утверждением, что матричный элемент оператора взаимодей-
взаимодействия частицы со слабым статическим медленно меняющимся маг-
магнитным полем имеет вид
A0.6.23)
Соответственно формула A0.6.22) дает следующее выражение для
магнитного момента частицы с зарядом q, массой т и спином 1/2:
A0-6-24)
Это выражение содержит как частный случай знаменитый резуль-
результат Дирака 7: для частицы спина 1/2 ц = q/2m без учета радиацион-
радиационных поправок.
Отметим без доказательства, что формфакторы F(k2) и G(k2)
протона можно измерить при к2 > 0 путем сравнения эксперимен-
экспериментальных данных по рассеянию электронов на протонах с формулой
Розенблюта 8 для дифференциального сечения рассеяния в лабора-
лабораторной системе:
618 Глава 10. Непертурбативные методы
где Ео — энергия начального электрона (считается, что Ео ^> те), 0 —
угол рассеяния, т — масса протона и
k2 =
sin2 @/2)
BEo/m)sin2@/2)'
10.7. Представление Чел лена—Лемана *
В разделе 10.2 мы видели, что наличие одночастичных про-
промежуточных состояний приводит к полюсам в фурье-образах мат-
матричных элементов хронологических произведений типа A0.2.1).
Многочастичные состояния приводят к более сложным особенно-
особенностям, которые трудно описать в общем случае. Однако в частном
случае средних по вакууму, содержащих только два оператора,
имеется удобное представление, явно демонстрирующее аналити-
аналитическую структуру фурье-образов. Такое представление существу-
существует, в частности, для пропагаторов, когда двумя операторами
являются поля, отвечающие элементарным частицам. В соедине-
соединении с квантово-механическими требованиями положительности **
такое представление приводит к интересным ограничениям на
асимптотическое поведение пропагаторов и величину констант
перенормировки.
Рассмотрим комплексный скалярный гейзенберговский опе-
оператор Ф(ж), который может как быть, так и не быть полем,
отвечающим элементарной частице. Среднее по вакууму от произ-
произведения Ф(х)фЦу) можно записать в виде
* Этот раздел лежит несколько в стороне от основной линии изложения
и может быть опущен при первом чтении.
** Имеется в виду требование положительной определенности метрики
гильбертова пространства состояний. — Прим. ред.
10.7. Представление Челлегт-Лемшш ° 19
где сумма берется по любому полному набору состояний. (Сумма по
п включает интегралы по непрерывным и суммы по дискретным
переменным.) Выбирая эти состояния как собственные состояния
4-вектора импульса Рц, на основании трансляционной инвариантно-
инвариантности получаем, что
<0| Ф(х)| п) = ехр(гр„ • х)<0| Ф@)| п),
(п\фЦу)\0) = ехр(-грп • у)(п\ФТ@)|0>
и поэтому
(я)фТ(у)) = ? ехр(гр„ • (х - у))\ <0| Ф(х)| п)\2 . {Ш73)
'о
п
Удобно переписать это выражение, введя спектральную функцию.
Заметим, что сумма ? 54(р-р )|@|Ф(х)|п)|2 есть скалярная функ-
функция 4-вектора рц и поэтому может зависеть только от р2 и (при р2 < 0)
от знака р°. На самом деле, для всех промежуточных состояний в
A0.7.3) р2 < 0 и р° > 0, так что сумма принимает вид
?54(р-рп)|<0|Ф@)|п)|2=B71)-3е(р°)р(-р2), A0.7.4)
п
где р(—р2) = 0 для р2 > 0. (Множитель Bл)~3 выделен из р для
удобства дальнейших выкладок.) Спектральная функция р(—р2) оче-
очевидно действительна и положительна. С учетом данного определе-
определения выражение A0.7.3) можно переписать в виде
(ф(х)Ф\у))о = Bл) J dAp ехр[гр • (х - у)]9(р° )р(-р2)
= Bл)-3 Jd4pjd|i2 ехр[гр • (х - у)]9(ро)р(ц2M(р2 + ц2). A0-7-5)
о
Меняя порядок интегрирования по рц и ц2, можно представить
последнее выражение в виде
620 Глава 10. Непертурбативные методы
со
= |ф2р(ц2)А+(х-у;ц2),
где А+ — знакомая нам функция
А+(х - у; ц2) = Bл) Jd4p ехр[гр • (х - у)]9(р°M(р2 + ц2). A0.7.7)
Совершенно аналогично можно показать, что
)) = |ф2р(ц2)Д+(у-х;ц2), A0 78)
/0 о
где вторая спектральная функция определена соотношением
A0.7.9)
п
Используем теперь требование причинности, заключающееся в
том, что коммутатор [Ф(х),фЦу)] обращается в нуль, если точки
х ж у разделены пространственноподобным интервалом. Среднее
по вакууму от коммутатора имеет вид
([Ф(х)фТ(у)]) =|с^ц2(р(ц2)А+(х-у;ц2)-р(ц2)А+(у-х;ц2)).(Ю.7.10)
о
Как указывалось в разделе 5.2, если интервал между х и у
пространственноподобен, функция А+(х — у) не обращается в нуль,
но является четной. Поэтому для того, чтобы выражение A0.7.10)
обратилось в нуль при произвольных пространственноподобных
интервалах, необходимо выполнение условия
Это частный случай СРТ-теоремы, доказанной здесь без обращения
к теории возмущений: для любых состояний с р2 = — JJ2, имеющих
квантовые числа оператора Ф, должны найтись соответствующие
состояния с р2 = — ц2, имеющие квантовые числа оператора Ф^.
10.7. Представление Челлегт-Лемшш ° 21
С помощью A0.7.11) среднее по вакууму от хронологического произ-
произведения запишется в виде
оо
(т{Ф(х)Ф\у)}H =-г|ф2ра12)ЛИх-у;ц2), A0.7.12)
где Ар(х — у; ц2) есть фейнмановский пропагатор для бесспиновой
частицы массой ц:
-iAF(x - у;ii2) = 9(х° - у°)Л+(х - у;ц2) - 9(у° - х°)А+(у - х; ц2).
A0.7.13)
Используя обозначения, введенные в разделе 10.3 для точных
пропагаторов, вводим в импульсном пространстве функцию
-гЛ'(р) ее Jd4xexp[-zp • (х - у)]{т{ф(х)Ф\у)}H. A0.7.14)
Напомним, что
Jd4xexp[-zp • (х - у)]Ар(х - у;ц2) = — ^——. (Ю.7.15)
Это приводит к искомому спектральному представлению 9:
*На самом деле, нет даже уверенности в том, что Л'(р) обращается в
нуль при |р2| —> оо, хотя, казалось бы, это следует из спектрального
представления. Проблема связана с изменением порядка интегрирования
по р^ и |дЯ Определенно можно утверждать (с помощью методов следующе-
следующего раздела), что Л'(р) есть аналитическая функция -р2 со скачком вдоль
положительной действительной оси —р2 = (д,2, равным лр((д,2). Отсюда следу-
следует, что для Л'(р) можно записать дисперсионное соотношение со спек-
спектральной функцией р(ц2) и возможными вычитаниями:
„
где п — положительное целое число, (А02 — произвольная положительная
константа, а Р{р2) - зависящий от ц02 полином по р2 порядка те-1,
отсутствующий при п — 0.
622 Глава 10. Непертурбативные методы
dii2
Д'(р) = I Р(Ц2)
vi + u — ге ^j-u.i.j-u;
о
Первым немедленным следствием этого результата в сочетании с
положительностью р(ц2) является то, что Л'(р) не может обращаться в
нуль при |р2| —» оо быстрее, чем свободный пропагатор 1/(р2+ т2 — ге) *.
Время от времени предлагают включить в невозмущенный лагран-
лагранжиан слагаемые с высшими производными, что привело бы к убыва-
убыванию пропагатора быстрее чем 1/р2 при |р2| —>°°. Однако спектральное
представление показывает, что это обязательно вступает в противоре-
противоречие с квантово-механическим постулатом положительности.
Спектральное представление вместе с одновременными ком-
коммутационными соотношениями можно использовать для вывода
интересного правила сумм для спектральной функции. Если Ф(х) —
обычным образом нормированный (но не перенормированный) кано-
канонический оператор поля, то
ГЭФ(М)
[ dt
Заметим, что
,Ф+(У,*) =-г63(х-у). A0.7.17)
Д+(ху4о=г/> г5(ху),
так что из спектрального представления A0.7.10) вместе с коммута-
коммутационными соотношениями A0.7.17) вытекает, что
|°°р(ц2)ф2 =1. A0.7.18)
Отсюда следует, что при |р2| —» °° пропагатор A0.7.16) неперенорми-
рованных полей в импульсном пространстве имеет асимптотическое
поведение, отвечающее свободному полю:
2
V
10.8. Дисперсионные соотгюиления 3
Такой результат имеет смысл только в рамках подходящей схемы
регуляризации ультрафиолетовых расходимостей. В рамках теории
возмущений неперенормированные поля имеют расходящиеся мат-
матричные элементы, так что их пропагаторы плохо определены.
Рассмотрим теперь возможность, что существует одночастич-
ное состояние |к) массой т, имеющее ненулевой матричный эле-
элемент с состоянием @|Ф@). Из лоренц-инвариантности вытекает, что
этот матричный элемент имеет вид
-1/2
= BлГ3/2Bл/к2 + m2) N, A0.7.19)
где N — константа. Согласно общим результатам раздела 10.3
пропагатор Л'(р) неперенормированных полей должен иметь полюс
при р2 —» —т2 с вычетом Z = |iV|2 > 0. Отсюда
, A0.7.20)
где о(ц2) > 0 — вклад многочастичных состояний. С учетом формулы
A0.7.18) получаем
1 = Z+ Го(ц2)ф2, A0.7.21)
Jo
так что
Z<1, A0.7.22)
причем равенство достигается только для свободной частицы, для
которой состояние @|Ф(х) не имеет ненулевых матричных элементов
с многочастичными состояниями.
Поскольку константа Z положительна, формулу A0.7.21) мож-
можно расматривать как устанавливающую верхнюю границу на силу
взаимодействия поля Ф с многочастичными состояниями:
< 1, A0.7.23)
* В физике конденсированных сред этот прием известен как «преобра-
«преобразование Хаббарда—Стратоновича» п. Оно будет использовано для введения
полей спаренных электронов при обсуждении сверхпроводимости в т. П.
624 Глава 10. Непертурбативные методы
причем равенство достигается при Z = 0. Предел Z = 0 имеет
интересную интерпретацию как условие того, что частица не
элементарна, а является составной 10. В данном контексте «состав-
«составная» частица понимается как такая частица, чье поле не входит в
лагранжиан. Рассмотрим такую частицу, например, нейтральную
частицу спина нуль, и предположим, что она уничтожается опе-
оператором FD?) с соответствующими квантовыми числами, постро-
построенным из других полей. Не составляет труда ввести поле Ф,
отвечающее такой частице, добавив в лагранжиан слагаемое вида*
Atf! = (Ф — F(*P)J, поскольку функциональный интеграл по Ф можно
взять, положив Ф равным значению в стационарной точке Ф =
F(*P), в которой KSP, = 0. Но предположим, что вместо этого мы
напишем KSP, =А9?0 + А9?ъ где A^o = -^Э^ФЭ^Ф - \т2Ф2 — обычный
лагранжиан свободного поля, и рассмотрим АХ1 = ASf! —Atf!0 как
взаимодействие. Слагаемое гЭ^ФЭ^Ф во взаимодействии не содер-
содержит ничего нового. Мы получали такое слагаемое, умноженное на
A — Z), в формуле A0.3.12). Единственная новость заключается в
том, что теперь Z = 0. Вместо того, чтобы подбирать константу Z
так, чтобы удовлетворить условию перенормировки поля в виде
ГГ'(О) = 0, мы должны рассматривать условие Z = 0 как условие на
константы связи составной частицы. К сожалению, применить
такую процедуру в квантовой теории поля не удается, поскольку,
как мы видели, условие Z = 0 означает, что частица взаимодей-
взаимодействует максимально сильно со своими конституентами *, а это
исключает применение теории возмущений. Условие Z = 0 оказы-
оказывается действительно полезным в нерелятивистской квантовой
механике. Например, оно фиксирует константу связи дейтрона с
нейтроном и протоном 12.
Хотя мы вывели спектральное представление только для бес-
бесспиновых полей, результаты легко обобщаются на другие поля.
Действительно, мы увидим в следующей главе, что в порядке е2
множитель Z для электромагнитного поля (обычно обозначаемый Z3)
дается формулой
* В русском языке закрепилась транслитерация английского термина
constituents, обозначающего элементарные частицы, составляющие дан-
данную составную частицу. — Прим. ред.
10.7. Представление Челлегт-Лемшш 5
Z, = 1 - ¦
12тг
(где Л » те — ультрафиолетовое обрезание) в согласии с ограниче-
ограничением A0.7.22).
10.8. Дисперсионные соотношения *
Провал первых попыток применить формализм теории возму-
возмущений в квантовой теории поля к слабым и сильным ядерным
взаимодействиям привел теоретиков в конце 1950-х годов к идее об
использовании аналитичности и унитарности амплитуд рассеяния
для вывода общих непертурбативных результатов, не зависящих
от конкретной теории поля. Это направление исследований началось
с возрождения интереса к дисперсионным соотношениям. В своем
первоначальном виде 13 дисперсионное соотношение представляло
собой формулу, выражающую действительную часть показателя
преломления в виде интеграла от его мнимой части. Формула была
получена как следствие свойства аналитичности показателя пре-
преломления как функции частоты, которое вытекало из условия, что
электромагнитные сигналы в среде не могут распространяться бы-
быстрее, чем в вакууме. Если выразить показатель преломления через
амплитуду рассеяния фотона вперед, то дисперсионное соотноше-
соотношение можно переписать как формулу, связывающую действитель-
действительную часть амплитуды рассеяния вперед с интегралом от ее мнимой
части, а следовательно, в силу условия унитарности, с интегралом
от полного сечения. Одним из вдохновляющих свойств такого соот-
соотношения было то, что оно представляло альтернативу обычной
теории возмущений: задавая амплитуду рассеяния в порядке е2,
можно было вычислить сечение и мнимую часть амплитуды рассея-
рассеяния в порядке е4, а затем с помощью дисперсионного соотношения
найти действительную часть амплитуды рассеяния вперед в этом
же порядке, не вычисляя при этом никаких петлевых диаграмм.
* Этот раздел лежит несколько в стороне от основной линии изложения
и может быть опущен при первом чтении.
626 Глава 10. Непертурбативные методы
Развитие современного подхода к дисперсионным соотношени-
соотношениям началось в 1954 году работой Гелл-Манна, Гольдбергера и
Тирринга 14. Вместо рассмотрения распространения света в среде,
они вывели свойство аналитичности амплитуды рассеяния непо-
непосредственно из условия микропричинности, утверждающего, что
коммутаторы операторов поля обращаются в нуль, когда точки, в
которых эти операторы заданы, разделены пространственноподоб-
ным интервалом. Вскоре такой подход позволил Гольдбергеру15
вывести очень полезное дисперсионное соотношение для пион—
нуклонной амплитуды рассеяния вперед.
Чтобы увидеть, как можно использовать принцип микропри-
микропричинности, рассмотрим в лабораторной системе рассеяние на угол
нуль безмассового бозона любого спина на произвольной мишени
а массой та > 0 и импульсом ра = 0. (Как обсуждается в т. II,
этот пример имеет важные приложения для рассеяния не только
фотонов, но и пионов в пределе тж = 0.) Двукратным применением
формулы A0.3.4) или теоремы Лемана—Симанчика-Циммермана 3
матричный элемент S-матрицы в этом случае представляется в
виде:
1
lim Iivy.
к'2
A0.8.1)
S = , lim, 2 „ lim, ,2
3VW||2 fc^° k
x
Здесь к и к' — начальный и конечный 4-импульсы бозона, причем со
— к0, со" = к'0; А(х) - произвольный гейзенберговский оператор с
неисчезающим матричным элементом
(VAC\A{x)\k) = {2%)-3/2{2@)-1/2Neik-x
между однобозонным состоянием \к) и вакуумом, а N — константа.
При рассеянии фотона оператор А(х) может быть одной из попереч-
поперечных компонент электромагнитного поля, а в случае рассеяния
безмассовых пионов - псевдоскалярной функцией адронных полей.
Дифференциальные операторы —№х и —№у вставлены для того,
чтобы появились множители ik'2 и гк2, необходимые для сокраще-
сокращения бозонных пропагаторов, отвечающих внешним линиям. Подей-
Подействовав этими операторами на АЦу) и А(х), получаем
10.8. Дисперсионные соотгюиления
7
x Jd4x Jd^ye-ik'yeikx<a|T{j\y), J(x)}\a) + OBK,
A0.8.2)
где J(x) = ?xA(x), а «ОВК» означает фурье-образ слагаемых от
одновременных коммутаторов, возникающих при действии произ-
производной на ступенчатую функцию в хронологическом произведении.
Коммутаторы операторов типа А(х) и АЦу) (или их производных)
при х° = у0 обращаются в нуль при х Ф у, так что слагаемое «ОВК»
есть фурье-образ дифференциального оператора, действующего на
54(х — у), и поэтому является полиномиальной функцией 4-импуль-
сов бозонов. Нас интересуют аналитические свойства матричного
элемента /^-матрицы, так что детальный вид этого полинома несу-
несуществен.
В силу трансляционной инвариантности матричный элемент
A0.8.2) ^-матрицы представляется в виде S = ~2%i5i(k/ — fc)M(co),
где
F(co) = J
4x e
i(alx
(a\
, J{x)}\ a) + OBK,
A0.8.4)
, где I — фиксированный 4-вектор,
при соглашении, что № =
такой, что 1Нц = 0 и 1° = 1.
Хронологическое произведение можно двумя способами пере-
переписать через коммутаторы:
f @), J(x)] + Jf @)J(x).
Соответственно,
F(co) = FA{(O) + F+(co) = FR(co) + F_(co),
A0.8.6)
где
628 Глава 10. Непертурбативные методы
FA{(?,) = jd^xQ{-x°)(a\[j\0),J{x)]\a)eMx +OBK, A0.8.7)
FR{(?>) = -j d^xQ{x°)(a\[j\0),J{x)]\a)eM-x +OBK, A0.8.8)
F+(co) ее Jd4x<oc| J(x)Jf@)|а)еШх, A0.8.9)
F_(co) ss Jd4x<a| Jf@)J(x)\a)eMx . A0.8.10)
Условие микропричинности утверждает, что подынтегральные выра-
выражения в формулах A0.8.7) и A0.8.8) обращаются в нуль, если только хц
не находится внутри светового конуса. Тогда наличие ступенчатых
функций приводит к тому, что хц в формуле A0.8.7) находится в
световом конусе прошлого, и х-1 > 0, а в формуле A0.8.8) — в
переднем световом конусе, и х-1 < 0. Отсюда следует, что FA((a)
аналитична при Im со > 0, a FR(co) аналитична при Im со < 0, так как
в обоих случаях множитель ега>1х обеспечивает сходимость интеграла
по х^. (Напомним, что слагаемое «ОВК» является полиномом и поэтому
аналитично во всех конечных точках.) Поэтому можно определить
функцию
\FA((O), Imco>0,
k? Imco<0, A0-8Л1>
аналитичную во всей комплексной плоскости со, за исключением
разреза вдоль действительной оси.
Выведем теперь дисперсионное соотношение. Согласно формуле
A0.8.6) скачок ./(со) на разрезе при любом действительном Е равен
,?{Е + is,) - ,F(E - г?) = FA{E) - FR{E) = F_{E) - F+{E). A0.8.12)
Если if (co)/con обращается в нуль при |со| —» °° как в верхней, так и в
нижней полуплоскости, то поделив эту функцию на любой полином
Р(со) порядка п, получаем функцию, которая обращается в нуль
при |со| —» °о и аналитична везде, за исключением разреза вдоль
действительной оси и полюсов в нулях соп полинома Р(со). (Если сама
./(со) обращается в нуль при |со| —» °о, можно взять Р(со) = 1.)
Согласно теореме о вычетах, имеем тогда
10.8. Дисперсионные соотгюиления 9
.У (со) у ,У(соу) = 1 Г .nz)dz
Р(со) ^(cov -co)P'(cov) 2%i J B - co)P(z)' (Ю.8.13)
где со — любая точка вне действительной оси, а С — контур,
состоящий их двух кусков: один проходит над действительной
осью от — °о + г? до +°° + г? и замыкается по большому полукругу в
верхней полуплоскости назад к — °° + г?, а другой проходит под
действительной осью от +°° — г? до — °° — г? и замыкается по
большому полукругу в нижней полуплоскости назад к +°° — г?.
Поскольку функция ;Цг)/Р(г) обращается в нуль при \z\ —> °°,
вкладом от больших полукругов можно пренебречь. С учетом
A0.8.12) формула A0.8.13) принимает вид:
Р(со) Г+°°F_(E) - FJE) 1
где Q(co) — полином (п — 1)-ой степени:
Говорят, что дисперсионное соотношение такого вида, где Р(со) и
Q(co) имеют соответственно порядок п и п — 1, имеет п вычитаний.
Если можно положить P=l, toQ = 0,h дисперсионное соотноше-
соотношение называется безвычитательным.
Если теперь устремить со к действительной оси сверху, то из
A0.8.14) получаем:
F (E)-F.(E)
Вспоминая формулы A0.8.6) и C.1.25), находим:
1 1 P((ii\ Г"*0 77* (]?\
F() F() ^j ^!
dE, A0.8.16)
где 1/(Е —со) понимается теперь в смысле главного значения
- со).
630 Глава 10. Непертурбативные методы
Этот результат полезен, поскольку функции F±(E) можно
выразить через измеряемые сечения. Суммируя в формулах A0.8.9)
и A0.8.10) по полному набору многочастичных промежуточных со-
состояний C (включая интегрирование по импульсам частиц в состоя-
состояниях C) и вновь используя трансляционную инвариантность, имеем:
F+(E) = BлL?| <р| J@)f | а)|2 54(-ра + El + Рр), A0.8.17)
Р
F_(E) = BлL? | <р| J@)| а)|2 54(ра + El - рр). (Ю.8.18)
Р
Однако матричные элементы поглощения безмассового скалярного
бозона В в реакции В + а —» C или его античастицы Вс в реакции Вс
+ ot —> C имеют соответственно вид
^<^°>fH- A0.8.19,
(ю.8.20,
Сравнивая с формулой C.4.15), видим, что функции F±(E) можно
выразить через полные сечения * при энергиях +Е:
F_(E) = Q(EJ^- Оа+В(Е). (Ю.8.22)
* В ряде случаев, когда правила отбора разрешают переходы
а—>а + Виа—> а + Вс, функции F±(E) содержат также слагаемые,
пропорциональные 5(Е), возникающие от вклада одночастичного состояния
а в сумме по промежуточным состояниям [3. Для поперечно поляризован-
поляризованных фотонов или псевдоскалярных пионов в пределе т% —> 0 подобная
ситуация не возникает.
10.8. Дисперсионные соотношения
631
Теперь при действительных со > 0 амплитуда рассеяния
М(со) =
-zQ(co) г
2co|iV|2 2BлK
Р(со)
coBjtL
>а+В
(Е)
о
¦ +
а+В'
(Е)
(Е - со)Р(Е) (Е + со)Р(-Е)
EdE.
A0.8.23)
Обычно принято записывать это дисперсионное соотношение через
амплитуду /(со) рассеяния вперед в лабораторной системе, которая
определена так, что дифференциальное сечение рассеяния вперед
в этой системе равно |/(со)|2. Эта амплитуда выражается через М(со)
следующим образом: /(со) = —4л2соМ(со) = 2jt2iF(co)/|iV|2, так что
A0.8.23) принимает вид:
гсо
/(со) = К(со) + — аа+в(со)
4л2
а
а+В^
а
¦ +
а+В'
.(?)
(Е - со)Р(Е) (Е + со)Р(-Е)
где К(со) = 2zJi2Q(co)/|iV|2. Оптическая теорема C.6.4) утверждает, что
второе слагаемое в правой части равно г1т/(со), так что это выраже-
выражение можно записать в более употребительной форме:
Re/(со) = К(со)+
Р(со)
4л2
'а+В
(Е)
а
а+Вс
(Е - со)Р(Е) (Е + со)Р(-Е)
EdE. (Ю.8.24)
В частности, видно, что если выбрать полином Р(со) действитель-
действительным, то полином i?(co) также действителен.
Амплитуда рассеяния вперед удовлетворяет также важному
условию симметрии. Меняя переменную интегрирования х в фор-
формулах A0.8.7) и A0.8.8) на — х и используя свойство трансляционной
инвариантности
<а| [ Jf @), J(-x)]\ а) = <а| [ Jf (x), j@)]| а),
632 Глава 10. Непертурбативные методы
видим, что при Im со < 0 функция FA(—со) совпадает с функцией
FR(co), если не считать перемены местами J и jt. Иными словами,
FA(-co) = F?(co) при Imco<0,
где верхний индекс с указывает, что амплитуда описывает рассеяние
античастицы Вс на мишени ОС. (Оставляем читателю показать, что это
соотношение не нарушается при учете слагаемых от одновременных
коммутаторов в A0.8.7) и A0.8.8).) Аналогично находим, что
FR(-co) = F|(co) при Imco>0,
и что для действительных со
F±(-co) = FTc(co).
Используя эти соотношения в формуле A0.8.6) и вспоминая, что /(со)
пропорциональна F(co), находим соотношение кросс-симметрии:
для действительных со
/(-со) =/с (о). A0.8.25)
Мы свободны в выборе Р(со) в виде любого полинома достаточно
высокого порядка, но тогда i?(co) зависит не только от Р(со), но и
от значений ,/(со) в нулях Р(со). Если Р(со) — действительный
полином n-ого порядка, единственными свободными параметра-
параметрами в A0.8.16) являются п действительных коэффициентов в дей-
действительном полиноме (п — 1)-ого порядка i?(co). Следовательно,
соотношение A0.8.16) содержит ровно п неизвестных действи-
действительных независимых констант, являющихся коэффициентами
полинома К(со) при заданном Р(со). По этой причине желательно
выбирать порядок п произвольного во всем остальном полинома
Р(со) как можно меньшим .
Можно попробовать взять Р(со) = 1, но это не сработает.
Анализ, проведенный в разделе 3.7, показывает, что амплитуда
рассеяния вперед должна расти как со или, возможно, как со 1п2со.
В этом случае, для того, чтобы /(со)/Р(со) обращалась в нуль при
со —> 0, достаточно взять Р(со) в виде полинома второго порядка,
10.8. Дисперсионные соотгюиления " 3 3
так что К(со) линеен по со. Выбирая для удобства Р(Е) = Е2,
представим соотношение A0.8.24) в виде
Re/(со) = а + Ьсо
(E - со) (Е + со)
dE
-|г. A0.8.26)
где а и Ь — неизвестные действительные константы. Из условия
кросс-симметрии A0.8.25) вытекает, что соответствующие констан-
константы в дисперсионном соотношении для амплитуды рассеяния анти-
античастиц /с(со) равны
ас=а, Ъс=-Ъ. A0.8.27)
Если предположить, например, что сечения Оа+В{Е) и Ga+Bc (E)
ведут себя при Е —» °° как разные константы, умноженные на (In
Е)г, то из A0.8.26) будет следовать, что
Re /(со) ~[оа+в(со) - оа+вс (со)] In со ~соAп соГ1, A0.8.28)
так что действительная часть амплитуды рассеяния будет расти в
In CO раз быстрее мнимой части. Это неприемлемо: мы видели в
разделе 3.7, что при со —» °° следует ожидать, что действительная
часть амплитуды рассеяния вперед много меньше мнимой части, и
это подтверждается экспериментом. Мы приходим к выводу, что
если оа+в(Е) и ®а+вс (Е) действительно ведут себя при Е —» °° как
константы, умноженные на (In E)r, то эти константы должны быть
равны. Поскольку мы рассматриваем предел высоких энергий, ре-
результат не зависит от предположения, что В — безмассовый бозон,
так что можно утверждать, что отношение сечений рассеяния
любой частицы и ее античастицы на фиксированной мишени
должно стремиться при высоких энергиях к единице. Этот резуль-
результат есть несколько обобщенный вариант так называемой теоремы
Померанчука 16. (Померанчук рассматривал только случай г = 0,
хотя из результатов раздела 3.7 и из наблюдаемого поведения
сечений следует, что значение г = 2 более предпочтительно.)
Хотя Померанчук получал свои оценки асимптотического
поведения амплитуд рассеяния на основании аргументов, близких
к изложенным в разделе 3.7, в наши дни поведение при высоких
634 Глава 10. Непертурбативные методы
энергиях обычно получают из теории полюсов Редже 17. Рассмот-
Рассмотрение деталей этого вопроса увело бы нас слишком далеко в
сторону. Достаточно сказать, что для адронных процессов асим-
асимптотическое поведение /(со) при со —> °° представляется суммой
слагаемых, пропорциональных а>а(-°\ где an(t) — множество «ред-
жевских траекторий», каждая из которых соответствует обмену
бесконечным семейством различных одноадронных состояний в
процессе рассеяния. Ведущей траекторией (на самом деле, ком-
комплексом из многих траекторий) является «померон», для которого
а@) близко к единице. Именно эта траектория дает сечения,
примерно постоянные при Е —> °°.
Согласно теореме Померанчука, померон одинаково связан с
любым адроном и его античастицей. Для низших реджевских траек-
траекторий можно оценить значения ОСП@), рассматривая спектр адронных
состояний. Необходимым, хотя и недостаточным условием 18 того,
что при значении массы т возникнет мезонный резонанс со спином j,
является равенство т2 тому значению t, при котором одна из траек-
траекторий CLn(t) равна j. Кроме померона, ведущей траекторией в пион-
нуклонном рассеянии является та, на которой мы находим при массе
т = 770 МэВ р-мезон с j = 1, при массе т = 1690 МэВ — g-мезон с
j = 3, и при массе т = 2350 МэВ — мезон с j = 5. Экстраполируя эти
значения (X(t) к t = 0, можно оценить, что для этой траектории
ос@) ~ 0,5. Связь такой траектории с %+ и %~ имеет разные знаки, так
что для пион-нуклонного рассеяния следует ожидать, что /(со) - /с(со)
ведет себя, грубо говоря, как со1/2.
В случае рассеяния фотонов нет разницы между В и Вс, так
что в этом случае из формулы A0.8.27) следует Ъ = 0, и соотношение
A0.8.26) принимает вид:
ю2 Г °(?) ^
1 -7". A0.8.29)
Е2 -со2
Это и есть по-существу первоначальное соотношение Крамерса—
Кронига 13. Как мы увидим в разделе 13.5, для мишени с зарядом е и
массой т константа а имеет известное значение Re /@) = —е2/т.
Задачи 635
Задачи
1. Рассмотрите нейтральное векторное поле v^{x). Какие условия
следует наложить на сумму П*цУ(&0 вкладов одночастично не-
неприводимых диаграмм с двумя внешними линиями векторного
поля, чтобы поле было правильно перенормировано и описыва-
описывало частицу с перенормированной массой т? Как следует для
этого разделить в лагранжиане слагаемые, отвечающие свобод-
свободному полю и взаимодействию?
2. Выведите обобщенное тождество Уорда, которому подчиняется
электромагнитная вершинная функция заряженного скалярно-
скалярного поля.
3. Какой вид имеет наиболее общая форма матричного элемента
(р2о21^|1(ж)|Р1с2) электромагнитного тока J^(x) между двумя од-
ночастичными состояниями спина 1/2, одинаковой четности и
разных масс т1 и т2? Как изменится результат, если четности
разные? (Предполагается сохранение четности.)
4. Выведите спектральное представление Челлена—Лемана для
среднего по вакууму (T{J|i(x) Jv(y)}H, где J^(x) - комплексный
сохраняющийся ток.
5. Выведите спектральное представление Челлена—Лемана для
среднего по вакууму (T{\\in(x) X|/m(y)}>0, где \|/(х) - дираковское
поле.
6. Не делая никаких предположений об асимптотическом поведе-
поведении амплитуды рассеяния или сечения, покажите, что ампли-
амплитуда рассеяния фотона на угол нуль не может удовлетворять
дисперсионному соотношению без вычитаний.
7. Выведите спектральное представление Челлена—Лемана для
комплексного скалярного поля, используя методы теории дис-
дисперсионных соотношений.
8. С помощью теории дисперсионных соотношений и результатов
раздела 8.7 вычислите в порядке е4 амплитуду рассеяния впе-
вперед фотонов на электронах в системе покоя электрона.
636 Глава 10. Непертурбативные методы
Список литературы
1. Furry, W.H., Phys. Rev., 51, 125 A937).
2. Yukawa, H., Proc. Phys.-Math. Soc. Japan, 17, 48 A935).
3. Lehmann, H., Symanzik, K., and Zimmerman, W., Nuovo
Cimento, 1, 205 A955).
4 Takahashi, Y., Nuovo Cimento, Ser. 10, 6, 370 A957).
5. Ward, J.C., Phys. Rev., 78, 182 A950).
6. Schwinger, J., Phys. Rev. Lett, 3, 296 A950).
7. Dirac, P.A.M., Proc. Roy. Soc. (London), A117, 610 A928).
8. Rosenbluth, M.N., Phys. Rev., 79, 615 A950).
9. Kallen, G., Helv. Phys. Ada, 25, 417 A952); Quantum Electro-
Electrodynamics (Springer-Verlag, Berlin, 1972); Lehmann, H., Nuovo
Cimento, 11, 342 A954).
10. Howard, J.C. and Jouvet, В., Nuovo Cimento, 18, 466 A960);
Vaughan, M.J., Aaron, R., and Amado, R.D., Phys. Rev., 125,
1258 A961); Weinberg, S., in: Proceedings of the 1962 High-
Energy Conference at CERN (CERN, Geneva, 1962), p. 683.
11. Stratonovich, R.I., Sov. Phys. Dokl, 2, 416 A957); Hubbard, J.,
Phys. Rev. Lett, 3, 77 A959).
12. Weinberg, S., Phys. Rev., 137, B672 A965).
13. Kramers, H.A., Atti Congr. Intern. Fisici, Como (Nicolo Zanichelli,
Bologna, 1927); reprinted in: Kramers, H.A., Collected Scientific
Papers (North-Holland, Amsterdam, 1956); Kronig, R., Ned.
Tyd. Nat. Kunde, 9, 402 A942); Physica, 12, 543 A946); Toll,
J.S., The Dispersion Relation for Light and its Application to
Problems Involving Electron Pairs (Princeton University Ph. D.
Спгюжлитературы 7
Thesis, 1952). Исторические обзоры см. в работах: Jackson, J.D.,
in Dispersion Relations, ed. by G.R.Screaton (Oliver and Boyd,
Edinburgh, 1961); Goldberger, M.L., in Dispersion Relations and
Elementary Particles, ed. by C. de Witt and R. Omnes (Hermann,
Paris, 1960).
14. Gell-Mann, M., Goldberger, M.L., and Thirring, W., Phys. Rev.,
95, 1612 A954). Непертурбативное происхождение этого резуль-
результата было показано в работе: Goldberger, M.L., Phys. Rev., 97,
508 A955).
15. Goldberger, M.L., Phys. Rev., 99, 979 A955).
16. Pomeranchuk, I.Ya., J. Expt. Theor. Phys. (USSR), 34, 725 A958).
Обобщение результатов этой работы см. в статье: Weinberg, S.,
Phys. Rev., 124, 2049 A961).
17. См., например, книгу: Collins, P.D.B., An Introduction to Regge
Theory and High Energy Physics (Cambridge University Press,
Cambridge, 1977) (есть рус. пер.: Дж. Коллинз. Введение в
теорию полюсов Редже. М.: Мир, 1980). Оригинальные работы:
Regge, Т., Nuovo Cimento, 14, 951 A959); 18, 947 A960).
18. График зависимости спина от квадрата массы называется диаг-
диаграммой Чу-Фраучи. См. работу: Chew, G.F. and Frautschi, S.C.,
Phys. Rev. Lett., 8, 41 A962).
11
Однопетлевые радиационные поправки
в квантовой электродинамике
В этой главе мы займемся некоторыми, ставшими уже клас-
классическими, однопетлевыми вычислениями в теории взаимодейст-
взаимодействия заряженных лептонов — массивных частиц спина 1/2 —
с электромагнитным полем. Известны три сорта лептонов, отли-
отличающихся своим «ароматом»: электрон, мюон и самый тяжелый срав-
сравнительно недавно открытый тауон. Для определенности будем все
заряженные частицы в наших расчетах называть электронами, хо-
хотя большая часть вычислений в равной степени применима к мюо-
нам и тауонам.
После ряда общих соображений в разделе 11.1, мы перейдем
к вычислению поляризации вакуума в разделе 11.2, аномального
магнитного момента электрона в разделе 11.3 и собственной энер-
энергии электрона в разделе 11.4. Попутно мы введем ряд математиче-
математических приемов, оказывающихся полезными при таких вычислени-
вычислениях, в том числе фейнмановскую параметризацию, виковский пово-
поворот, а также размерную регуляризацию 'т Хофта-Вельтмана и бо-
более ранний метод регуляризации Паули-Вилларса. Хотя при
расчетах и появятся бесконечности, мы увидим, что окончательные
результаты конечны, если их выразить через перенормированные
массу и заряд. В следующей главе мы распространим полученные
здесь результаты, касающиеся перенормировки, на случай общих
теорий в произвольных порядках теории возмущений.
11.1. Контрчлены 639
11.1. Контрчлены
Возьмем лагранжиан электронов и фотонов в виде *:
B , A1.1.1)
где А-? , xj/B и \|/в — голые (т. е. неперенормированные) поля фотона
и электрона, а —ев и тв — голые заряд и масса электрона. Согласно
предыдущей главе, можно ввести перенормированные поля, массу
и заряд соотношениями
A1.1.3)
в A1.1.5)
где константы Z2, Z3 и 8m подбираются так, чтобы пропагаторы
перенормированных полей имели полюсы в тех же точках и с теми
же вычетами, что и пропагаторы свободных полей в отсутствие взаи-
взаимодействий. Тогда лагранжиан можно записать через перенормиро-
перенормированные величины в виде
^ = ^0+^1+Ж,, A1.1.6)
где
^[}, A1.1.7)
A1.1.8)
* В этой главе нам не потребуется переходить от гейзенберговских опера-
операторов к операторам в представлении взаимодействия, поэтому мы вернемся к
общепринятым обозначениям, когда заглавная буква А и строчная буква \|/
используются для обозначения соответственно полей фотона и заряженной
частицы.
640 Глава 11. Однопетлевые радиационные поправки в КЭД
а $2 есть сумма «контрчленов»:
L2 = --(Z3 - 1)F^V - (Z2 - lJxj/Py^ + mki
_ _ A1.1.9)
Z28m\|A|/ - ze(Z 1)Aц
Оказывается, что все слагаемые в ^ — второго и более высоких
порядков по е, и их как раз хватает для того, чтобы сократить
ультрафиолетовые расходимости, возникающие от петлевых диа-
диаграмм.
11.2 Поляризация вакуума
Начнем наши вычисления петлевых радиационных поправок с
так называемого эффекта поляризации вакуума, т. е. с поправок к
пропагатору, отвечающему внутренней фотонной линии. Поляриза-
Поляризация вакуума приводит к измеряемым сдвигам энергетических уров-
уровней атома водорода и дает важный вклад в значения энергии связи
мюонов, находящихся на орбитах вокруг тяжелых ядер. Кроме то-
того, как мы увидим в т. II, вычисление поляризации вакуума явля-
является ключевым для определения поведения электродинамики и дру-
других калибровочных теорий при высоких энергиях.
Как и в разделе 10.5, определим гBлLП*ро(д) как сумму всех
связных диаграмм с двумя внешними фотонными линиями, несу-
несущими индексы поляризаций ц и V и 4-импульс д. В это выражение
не входят фотонные пропагаторы от двух внешних фотонных ли-
линий, а звездочка означает, что исключаются диаграммы, которые
становятся несвязными после разрезания некоторой внутренней фо-
фотонной линии. Точный фотонный пропагатор A/|lv(g) дается форму-
формулой A0.5.3):
А'= Д[1 - П* А], A1.2.1)
где A|lv(g) — пропагатор фотона без радиационных поправок. Наша
задача — вычислить главные вклады в П*ро(д)-
В низшем порядке имеется однопетлевой вклад в П*> отве-
отвечающий диаграмме рис. 11.1:
11.2. Поляризация вакуума
641
= - d4pTr<
—i(p — q)
—i -ip + m
BлL p2 + m2 - гг
BлL (p - qY +mz -ie
A1.2.2)
где первый знак минус справа отвечает наличию фермионной пет-
петли. В более простой записи:
-гг"
ip + m]yp[-i(p - q) + m]ya}
P (P2+m2-iE)((p-qJ+m2-iE)' AL2)
Первый шаг при вычислении этого интеграла заключается в
использовании приема, предложенного Фейнманом 1. Воспользу-
Воспользуемся элементарной формулой
dec
АВ
2 '
A1.2.4)
и запишем произведение скалярных пропагаторов в A1.2.3) сле-
следующим образом:
Рис. 11.1. Однопетлевая диаграмма поляризации вакуума в квантовой элек-
электродинамике. Волнистые линии отвечают фотонам, линии со стрелками —
электронам
642 Глава 11. Однопетлевые радиационные поправки в КЭД
(р2 + т2 - гг)((р - дJ + т2 - гг)
/•1 . __2
(р2 + т2 - гг)A - ее) + ((р - дJ + т2 - ггЫ dec
Г1 -2
= [р2 + т2 - гг - 2р • gee + д2ес1 dec
Г1 -2
= [(р - десJ + ш2 - гг + д2есA - ес)| dec.
(Это частный случай более общего класса интегралов, рассмотрен-
рассмотренных в Приложении к этой главе.) Теперь можно сдвинуть перемен-
переменную интегрирования в импульсном пространстве *:
р -» р + qx ,
так что выражение A1.2.3) принимает вид
г(р + qx) + m] yp [-г(р -q(l-x)) + m]ya}.
A1.2.5)
Используя результаты Приложения к гл. 8, можно без труда вы-
вычислить след в подынтегральном выражении:
Tr{[-i(p + qx) + m]yp[-i(p - q{\ - ее)) + m]ya}
= 4[-(p + gec)P(p - g(l - ec))° + (p + gee) • (p - g(l - ес))лра
-(p + gec)a(p-g(l-ec))P +m2ri
Следующий шаг носит название виковского поворота 2. До тех пор,
пока -д2 < 4т2, величина т2 + д2есA - ее) положительна при всех ее
* Строго говоря, этот шаг верен только для сходящихся интегралов. В
принципе, чтобы обосновать сдвиг переменных, следует ввести какую-то
схему регуляризации, делающую все интегралы сходящимися. Такой схемой
может быть, например, схема размерной регуляризации.
11.2. Поляризация вакуума
643
между 0 и 1, так что полюсы подынтегрального выражения в A1.2.5)
находятся в точках ро = ±д/р2 +т2 + q2x(l -x)-ie > т- е. чуть выше
отрицательной действительной оси и чуть ниже положительной дей-
действительной оси (см. рис. 11.2). Можно повернуть контур интегриро-
интегрирования по р° против часовой стрелки, не пересекая при этом ни од-
одного из полюсов, так что вместо интегрирования по р° вдоль дейст-
действительной оси от —оо до +°°, мы интегрируем вдоль мнимой оси от -
г°° до +г°°. Иными словами, можно написать р° = гр4, и теперь ин-
интегрировать по действительным значениям р4 от —оо до +°°. (Если бы
в знаменателе пропагатора входило г'? вместо —ге, следовало бы по-
положить р° = — гр4, причем р4 опять пробегало бы все действитель-
действительные значения от — °° до +°°. В результате просто изменился бы знак
(<?)•) Теперь формула A1.2.5) принимает вид:
-dec I -
(^Р)е[р
2 ^т2 +g2cc(l-cc)l
-2
X [-(p + qxfip - g(l - x))a + (p + qx) ¦ (p - g(l - х))ц?с
где
qxf(V-q(l-x)r
(d4p)E = dp1dp2dp3dp4
(n27)
Imp0
Rep0
Рис. 11.2. Виковский поворот контура интегрирования по р°. Маленькие кре-
крестики указывают положение полюсов в комплексной плоскости р°, стрелки
показывают направление поворота контура интегрирования от действи-
действительной к мнимой оси
644 Глава 11. Однопетлевые радиационные поправки в КЭД
и все скалярные произведения вычисляются с использованием евк-
евклидовой нормы
a-b = a1b1+a2b2+a3b3+aibi,
при соглашении, что q4 = — iq°. Кроме того, т\ра можно считать либо
кронекеровским дельта-символом с индексами, принимающими зна-
значения 1, 2, 3, 4, либо обычным тензором Минковского с индекса-
индексами, принимающими значения 1, 2, 3, 0 *.
Интеграл A1.2.7) сильно расходится. В конце концов все беско-
бесконечности сократятся, но чтобы увидеть это, необходимо использо-
использовать на промежуточных стадиях вычисления какой-то способ регу-
регуляризации, делающий интегралы сходящимися. Не годится просто
обрезать интегралы на некотором максимальном импульсе Л, интег-
интегрируя по рц только при р2 < Л2, поскольку это эквивалентно введе-
введению в электронный пропагатор ступенчатой функции 6(Л2 — р2),
а тождество Уорда A0.4.25) показывает, что для сохранения калиб-
калибровочной инвариантности любая модификация электронного пропа-
гатора должна сопровождаться модификацией электрон-фотонной
вершины. На самом деле, при обычном Л—обрезании радиационные
поправки будут индуцировать массу фотона, что явно нарушает
калибровочную инвариантность **.
Практика показала, что самым удобным способом регуляри-
регуляризации расходящихся интегралов, не нарушающим калибровочной
инвариантности, является техника размерной регуляризации, пред-
предложенная в 1972 году 'т Хофтом и Вельтманом 3 и основанная на
аналитическом продолжении по размерности пространства-времени
от четырех к произвольному числу d. Она состоит в усреднении по
* Первое соглашение относится к так называемому евклидовому
развороту (аналог виковского поворота). Именно, П*ШЕТЛ допускает
аналитическое продолжение по q° в евклидову область q° = iq4. По модулю
кинематических множителей (см. ниже формулу A1.2.16)) П*ШЕТЛ (точнее
функция %) является аналитической функцией —q2 в комплексной плоскости с
разрезом вдоль положительной полуоси —q2 > 4m2. В тексте рассматри-вается
область —q2 > 4m2. При —q2 > 4m2 физическому значению функции % отвечает
ее граничное значение сверху на этой полуоси. — Прим. ред.
** Именно, поперечность П*^у, имея в виду, что П^у не имеет полюсов
при q2 = 0 (см. гл. 10, раздел 5). — Прим. ред.
11.2. Поляризация вакуума 645
угловым переменным в интегралах типа A1.2.7), что сводится к от-
отбрасыванию всех слагаемых, нечетных по р, и замене слагаемых,
содержащих четное число множителей р, по правилу *
pV ^pVv /d, (П-2.8)
2). A1.2.9)
Далее, после того как подынтегральное выражение с помощью ука-
указанной процедуры запишется как функция только р2, следует
заменить элемент объема сРрЕ на D.dK^'1dK, где к = Jp% , a D.d —
площадь сферы единичного радиуса в d измерениях:
ud=2%d/2 /T(d/2). A1.2.10)
После этого интеграл A1.2.7) становится сходящимся в случае ком-
комплексной размерности пространства-времени d. Можно продолжить
интеграл от комплексных значений d к d = 4, и тогда бесконечности
проявятся как множители (d — 4).
Применяя метод размерной регуляризации к интегралу A1.2.7),
получаем:
nIPL°oop(Q) = 4б2% Г dx Г кЧ-Чк [к2 + m2 + q2x(l - х)\2
BлL Jo Jo L J
x
-2к
d
2
(к2 - g2cc(l - x))r\
\pc
Интегралы по к можно вычислить для любого комплексного d (или
для любого действительного d, не равного целому четному числу) **.
* Проще всего вывести эти формулы, заметив, что их вид диктуется ло-
ренц-инвариантностью и симметрией по индексам ц, v, p и т. д. Коэффициен-
Коэффициенты можно найти, требуя, чтобы правая и левая части давали одинаковый
результат после свертки с т|.
** Строго говоря, этот интеграл определен при 1 < Red < 4, а при прочих
d он определен аналитическим продолжением. — Прим. ред.
646
Глава 11. Однопетлевые радиационные поправки в КЭД
Воспользуемся хорошо известными формулами (в более общем ви-
виде они даны в Приложении к этой главе):
-2
r(d/2)rB-d/2), A1.2.11)
Kd+i |"K2 +y2j 2dK = -(v2J r(l + d/2)r(l-d/2), A1.2.12)
тогда
B7tL
dec
- 2 / d)rfc[m2 + g2cc(l - cc)J ГA + d/2)F(l - d/2)
i2 + g2cc(l-.
°cc(l - x) - д2
x r(d/2)FB - d/2)
Два слагаемых в подынтегральном выражении можно объединить,
если учесть соотношение
A - 2/d)F(l + d/2)F(l - d/2) = -F(d / 2)ГB - d/2).
В результате
- d/2)(gPg
Pg° -
Г1
с dxx(l-x)(m2+ q2x(l-x))d/2~2.
Jo
A1.2.13)
Очень важно то, что найденный вклад в П*ро удовлетворяет соотно-
соотношению
11.2. Поляризация вакуума 647
I) = 0, A1.2.14)
полученному в разделе 10.5 на основании сохранения и нейтрально-
нейтральности электрического тока. Именно ради достижения этого результата
мы и применили схему размерной регуляризации. Причина, по
которой размерная регуляризация приводит к такому результату,
заключается в независимости закона сохранения тока от размерно-
размерности пространства-времени.
Гамма-функция ГB - d/2) в A1.2.13) неограниченно растет
при d —> 4. К счастью, как мы видели в разделе 11.1, существует
другое слагаемое, возникающее от слагаемого —j(Z3 — tyF^F^ в ла-
лагранжиане взаимодействия, которое необходимо добавить к П*ро(д)-
Структура этого слагаемого аналогична A1.2.13):
П;р°(д) = -(Z3 - l)(q V° - qpqa), A1.2.15)
так что в порядке е2 суммарная величина ГТ имеет вид
, A1.2.16)
где
А
dxx(l-x)(m2+q2x(l-x)f/2-2-(Z3-l).
Jo
A1.2.17)
x " " "
'о
Как мы видели в разделе 10.5, определение перенормирован-
перенормированного электромагнитного поля требует, чтобы л@) = 0 (для того,
чтобы вычет в полюсе точного фотонного пропагатора при q2 = 0
был бы таким же, как и для голого пропагатора, если не считать
слагаемых, зависящих от калибровки). Поэтому в порядке е2
Bл)
так что в этом же порядке
- d I 2)(m')'i! X<1 ~x)dx> A1-2.18)
648 Глава 11. Однопетлевые радиационные поправки в КЭД
л(д2) = ——й. r(d/2)FB - d/2) f1 x(l - x) dx
BлL Jo
W2 , Я^_Я1 A1-2-19)
\(т2 +q2x(l-x)
Теперь можно снять регуляризацию, разрешив d принять его
физическое значение d = 4. Выше отмечено, что однопетлевой вклад
содержит бесконечность, возникающую из-за поведения гамма-
функции в этом пределе:
FB-d/2)-> у,
B-d/2)
где у = 0,5772157 — постоянная Эйлера. Бесконечная часть Z3 — 1
получается, если заменить ГB — d/2) на 1/B — d/2) и во всех ос-
остальных местах положить d = 4:
4е2 ¦ 27I2 1 е2 1
(Z1L
В т. II мы увидим, что этот результат можно использовать для
нахождения главного члена в уравнении ренормгруппы для заряда
электрона.
Очевидно, что полюсы при d = 4 в %(q2) сокращаются, так как
в этом случае выражения [т2 + q2x( l-cc)]d/2~2 и (m2)d/2~2 имеют одина-
одинаковый предел, равный единице. По этой же причине слагаемое —у в
ГB—d/2) сокращается в полном выражении для тг(д2), хотя оно и вно-
вносит конечный вклад в Z3 — 1. Есть и другие конечные вклады в Z3 — 1,
возникающие от произведения полюса в ГB—d/2) и линейных слагае-
слагаемых в разложении Q.dT(d/2) в окрестности d = 4, но и они сокраща-
сокращаются в полном %{q2). В действительности, проводя размерную регуля-
регуляризацию, можно было бы заменить Bл)~4 на B%)~d, a Tr 1 =4 —
на размерность 2d/2 гамма-матриц в пространстве-времени с произ-
произвольной четной размерностью d. Однако все это дало бы вклад только
в конечную часть Z3 — 1, но не в %{q2). Далее, нельзя считать
е2 независящим от d, поскольку из формулы A1.2.13) вытекает,
что квадрат заряда имеет зависящую от d размерность [Macca]4~d.
Если положить е2 <* fi4~d, где ц — некая величина размерности
11.2. Поляризация вакуума
649
массы, то в Z3 — 1 появятся дополнительные конечные слагаемые,
возникающие от произведения полюса в ГB - d/2) и слагаемого D—
d) In ц в разложении ji4~d по степеням D - d). Однако и они сокраща-
сокращаются с аналогичными слагаемыми в однопетлевом вкладе в тг(д2).
Единственные слагаемые, реально дающие вклад в %(q2) в пре-
пределе d —> 4, возникают от произведения полюса в FB-d/2) и линей-
линейных слагаемых в разложении [т2 + q2x(l-x)]d^2~2 и (m2)d^2~2 по степе-
степеням d — 4:
\d/2~2
(т2 + д2есA - ее)) - (т2 )й12'2 -» (d/2 - 2) In 1 + ¦
В результате приходим к выражению
27Г
Г1
есA -
J о
¦ ее) In 1 +
g2cc(l-cc)
dec .
т
A1.2.21)
A1.2.22)
Физический смысл поляризации вакуума раскрывается, если
рассмотреть влияние этого эффекта на рассеяние двух заряженных
частиц спина 1/2. Фейнмановские диаграммы на рис. 11.3 дают сле-
следующие вклады в матричный элемент рассеяния:
р2, - Pl
р2, - Р1 -
х
где ех и е2 — заряды рассеивающихся частиц, л(д2) вычисляется по
формуле A1.2.22), причем в качестве е следует взять заряд частицы,
которой отвечают линии, образующие петлю на рис. 11.3, q^ — пе-
передаваемый импульс, g = р1 — рг' = р2' — р2. С учетом закона сохра-
сохранения q^ui'^Ui = 0 обе диаграммы совместно приводят к выраже-
выражению для элемента /^-матрицы:
650
Глава 11. Однопетлевые радиационные поправки в КЭД
2'
У
2'
Рис. 11.3. Две диаграммы рассеяния заряженных частиц. Линии со стрелками
отвечают заряженным частицам, волнистые линии — фотонам. Диаграмма б
является поправкой низшего порядка, учитывающей эффект поляризации
вакуума, к древесной диаграмме а
Sa+b№ ~^ 1'2') ~ ~TT~
+p2, -Pl -p2)
A1.2.23)
В нерелятивистском пределе щу°щ — - ibo,o , а щу*щ — 0 (анало-
(аналогично для частицы 2). Кроме того, в этом пределе можно пренебречь
q° по сравнению с |q|. Тогда формула A1.2.23) принимает вид
Sa+b(l,2->l',2') =
Р2'
47t2q2
A1.2.24)
Это выражение можно сравнить с борновским приближением для
матричного элемента рассеяния на локальном, не зависящем от спина
центральном потенциале V(r):
Y +Е2, -Е, -Е2)ТБ A,2 ^ \',2'). A1.2.25)
-X2
х Bл)2/2 e"iPl' 'Xle
Полагая хг = х2 + г, получаем
A1.2.26)
+P2' "Pi -
AL2.27)
11.2. Поляризация вакуума 651
Сравнение этой формулы с формулой A1.2.23) показывает, что в
нерелятивистском пределе диаграммы рис. 11.3 приводят к такому
же матричному элементу рассеяния, что и потенциал V(r), такой,
что
1*2—^Г
или, обращая фурье-преобразование,
V(r) = еге2 Г d3g
q
2
A1.2.28)
В первом порядке по радиационным поправкам * выражение A1.2.28)
определяет ту же потенциальную энергию, что и энергия электро-
электростатического взаимодействия двух пространственных распределе-
распределений зарядов е1г)(х) и е2г|(у) на расстоянии г:
\ \^lrV (П.2.29)
где
() 53() + !fd3B)^r A1.2.30)
Заметим, что
J3 | l, A1.2.31)
так что полные заряды частиц 1 и 2, определяемые по (кулонов-
ской) асимптотике потенциала V(r) на больших расстояниях, — это
те же константы е1 и е2, которые определяют взаимодействия пере-
перенормированного электрического поля.
При г| Ф 0 интеграл A1.2.30) можно вычислить с помощью кон-
контурного интегрирования:
* Т. е. по параметру е2. — Прим. ред.
652
Глава 11. Однопетлевые радиационные поправки в КЭД
- x)dx
тг
- ее)
ехр
—тг
— х)
Это выражение везде отрицательно. Однако мы видели, что инте-
интеграл от Г|(г) по всем г равен +1. Поэтому функция Г|(г) должна со-
содержать слагаемое A+L)83(r), которое сингулярно при г = 0, a L
выбрано так, чтобы удовлетворить соотношению A1.2.31):
L =
— x)dx
1 +
mr
- x)
exp
—mr
AL2-32)
Соответственно полное выражение для плотности распределения
заряда имеет вид:
ЬM3(г)-
- x)dx
mr
— x)
exp
—mr
A1.2.33)
Физическая интерпретация этого результата заключается в том,
что голый точечный заряд притягивает из вакуума частицы с про-
противоположным зарядом и отталкивает на бесконечность соответст-
соответствующие античастицы, так что голый заряд частично экранируется.
В результате перенормированный заряд становится в 1/A+L) раз
меньше. В качестве проверки заметим, что если обрезать расходя-
расходящийся интеграл A1.2.32), полагая, что он берется только по области
г > а, то расходящаяся при а —> 0 часть интеграла равна
L =
12 л2
In a
-1
A1.2.34)
Следовательно, если отождествить обрезание Л в импульсном про-
пространстве * с а, то расходящаяся часть в L окажется связанной с
расходящейся частью Z3 — 1 соотношением
* Коротко его называют импульсом обрезания. — Прим. ред.
11.2. Поляризация вакуума 653
(Z3 - 1L = -2LX , A1.2.35)
поскольку в порядке е2 перенормированный заряд A0.4.18) дается
выражением
+ |(Z3-l)JeBi =A + L) 1eBl. A1.2.36)
Формула A1.2.35) подтверждается ниже.
Поляризация вакуума оказывает заметное влияние на энергети-
энергетические уровни мюонных атомов. Как будет показано в гл. 14, диа-
диаграмма рис. 11.3, б приводит к сдвигу энергии атомного состояния с
волновой функцией \|/(г) на величину
АЕ = Jd3rAV(r)|y(r)|2, A1.2.37)
где AV(r) — добавочное к кулоновскому слагаемое в потенциале
A1.2.28):
eie9
BлK
d3geiqr
7t(q2)
q
2
A1.2.38)
При г ^> т 1 эта добавка экспоненциально уменьшается. С другой
стороны, волновая функция электронов в обычных атомах в общем
случае сосредоточена в значительно большей области радиусом
а ^> т~1. Например, для орбит электронов вокруг ядра зарядом Ze
в водородоподобном атоме а = 137/(Zm) (здесь т = те). Поэтому сдвиг
энергетического уровня будет зависеть только от поведения волно-
волновой функции в области г <х а. Если орбитальный момент равен I,
волновая функция ведет себя как г1 при г <^ а, так что из A1.2.37)
находим, что АЕ пропорционально множителю (та)~Bг+31 Отсюда эф-
эффект поляризации вакуума для случая I = 0 много больше, чем для
более высоких угловых моментов. При 1 = 0 волновая функция при-
приблизительно постоянна и равна \|/@) для г, меньших или порядка
т~1, так что формула A1.2.37) принимает вид
AE=|V(O)|2 Jd3r AV(r). A1.2.39)
654 Глава 11. Однопетлевые радиационные поправки в КЭД
С учетом формул A1.2.38) и A1.2.22) интеграл от добавки к потен-
потенциалу (при е1е2 = —Ze2) имеет вид:
г 4Zoc
d3r AV(r) = -Ze V@) = 5-. A1.2.40)
J 1 R<m z
Кроме того, для состояний водородоподобного атома с I = 0 и глав-
главным квантовым числом п волновая функция в начале координат
принимает значение
2 C/2
Поэтому энергетический сдвиг A1.2.39) оказывается равным
4Z4a5m
АЕ = —. A1.2.42)
15лп3
Например, для 2s состояния атома водорода этот сдвиг равен
-1,222 • 10~7 эВ, что соответствует сдвигу частоты АЕ/2лЙ, равному
-37,13 МГц. Иногда этот эффект называют эффектом Юлинга 4. Как
обсуждалось в гл. 1, эти ничтожные сдвиги энергии оказалось
возможным измерить, поскольку в отсутствие разных радиационных
поправок чисто дираковская теория предсказывает полное вырож-
вырождение 2s и 2р состояний атома водорода. В гл. 14 будет показано, что
основная часть «лэмбовского сдвига» между 2s и 2р состояниями,
равная +1058 МГц, обусловлена другими радиационными поправ-
поправками, но согласие между теорией и экспериментом достаточно для
того, чтобы убедиться в наличии сдвига —37,13 МГц, обязанного
поляризации вакуума.
Хотя в обычных атомах поляризация вакуума определяет лишь
малую часть радиационных поправок, она становится определяю-
определяющей в радиационных поправках для мюонных атомов, в которых
вместо электрона на орбите находится мюон. Это происходит пото-
потому, что по размерным соображениям большинство радиационных
поправок приводит к энергетическим сдвигам уровней мюонных
атомов, которые пропорциональны т , в то время как суммарная
энергия поляризации вакуума jd3rAV за счет электронной петли
остается пропорциональной т ~2, как в формуле A1.2.40), что приво-
11.3. Аномальные магнитные моменты 655
дит к сдвигу энергетического уровня на величину т Зте~2 =B10Jт .
Однако в этом случае радиус мюонной орбиты ненамного больше
комптоновской длины волны электрона, так что приближенный ре-
результат A1.2.39) дает лишь порядок величины сдвига энергии за
счет поляризации вакуума.
Имея в виду сравнение с последующими вычислениями, заметим,
что если обрезать интеграл A1.2.7) на к = Л, то вместо A1.2.20) мы
придем к интегралу вида
где ц — эффективное инфракрасное обрезание порядка массы заря-
заряженной частицы в петле на рис. 11.1. (Простейший способ определе-
определения постоянного множителя в этом выражении состоит в требова-
требовании, чтобы его предел при d < 3 и Л —» °° совпадал с A1.2.20).) Введя
такое обрезание, можно перейти к пределу d —> 4, получая при
этом
2
(Z3-l)oo=--Tln(A/n). A1.2.43)
11.3 Аномальные магнитные моменты
и зарядовые радиусы
В качестве следующего примера вычислим изменение магнит-
магнитного момента и зарядового радиуса электрона или мюона за
счет радиационных поправок низшего порядка. Однопетлевые
диаграммы и диаграмма перенормировки фотон-лептонной вершины
показаны на рис. 11.4. Как обсуждалось в разделе 10.3, те из этих
диаграмм, которые содержат вставки во внешние входящие или
выходящие лептонные линии, обращаются в нуль, поскольку
лептон находится на массовой поверхности. Диаграмма, содержащая
вставку во внешнюю фотонную линию, описывает обсуждавшийся
656
Глава 11. Однопетлевые радиационные поправки в КЭД
в предыдущем разделе эффект поляризации вакуума. Таким обра-
образом, надлежит вычислить единственную однопетлевую диаграмму
(последнюю на рис. 11.4):
'>P) = J
—г
BлL (р' - kf + m2 - гг
И
х
—г
—г(р - Ik) + m
BлL
т2 -гг
-г
BлL kz - гг
A1.3.1)
где р'ир — 4-импульсы конечного и начального лептонов, соответ-
соответственно. (Вклад от вершины, связывающей внешнюю фотонную ли-
линию с внутренними электронными линиями, берется равным у1, т. к.
множитель еBлL был включен в определение Р1.)
Выписанный интеграл очевидно содержит ультрафиолетовую
расходимость типа Jd4fc/(/c2J. В отличие от поляризации вакуума,
здесь не нужно прибегать к специальным процедурам типа раз-
размерной регуляризации, чтобы сохранить требуемую калибровоч-
ЛАЛЛА
ЛЛЛАА
ЛАААА
а
Рис. 11.4. Однопетлевые диаграммы для фотон-лептонной вершинной
функции V1. Волнистые линии изображают фотоны, остальные линии —
электроны или мюоны. Диаграммы а и б сокращаются вкладом контрчленов
перенормировки лептонного поля, диаграмма в происходит от поляризации
вакуума, вычисленного в разделе 11.2, вклад диаграммы д вычисляется в
разделе 11.3
11.3. Аномальные магнитные моменты 657
ной инвариантностью структуру, поскольку фотон — нейтральная
частица. Поэтому интеграл можно сделать конечным подходящей
модификацией фотонного пропагатора (например, путем включе-
включения множителя М2/(к2 + М2) с большой регуляри-зующей массой
М), не вводя для сохранения калибровочной инвариантности ни-
никаких других изменений. Более того, мы увидим, что аномальный
магнитный момент и зарядовые радиусы можно вычислить, вооб-
вообще не учитывая ультрафиолетовые расходимости. В последующем
изложении оставим все интегралы для вершинной функции в их
расходящейся форме, понимая при этом, что при необходимости
любой расходящийся интеграл можно выразить через регуля-
ризующую массу М.
Начнем с объединения знаменателей, используя описанную в
Приложении к этой главе расширенную версию формулы Фейнмана:
^ = 2? dxj*dy [Ay + В(х - у) + СA - ее)] . A1.3.2)
Применяя ее к знаменателям в формуле A1.3.1), находим:
1 1 1
(р' - кJ + т2 - гг (р - кJ + т2 - гг к2 - гг
Г1 Сх
= 2 dec dy ]i{p' - кJ + т2 - гг)у + ((р - кJ + т2 - гг)(сс - у)
J 0 «^ О
+ (/с2 - гг)A - ее)]
= 2 da: dy \{k - р'у- р(х - у)J +т2х2 + q2y(x - у) - гг] ,
J о J о L J
A1.3.3)
где q = p — р' — переданный фотону импульс. После сдвига пере-
переменной интегрирования
к —> к + р'у + р(х — у)
интеграл A1.3.1) принимает вид
658 Глава 11. Однопетлевые радиационные поправки в КЭД
¦ 2 Г1 СХ
Г1Шор(Р'>Р) = -^Т dx dV
Bл) Jo Jo J [k2+m2x2+q2y{x-y)-ie]
x yp [-г(р'A -у)-Ik- p(x - у)) + m] y^1
x [-i(p(l - x + у) - ft - p'y) + m] yp . A1-3-4)
Следующий шаг — виковский поворот. Как объяснено в предыду-
предыдущем разделе, добавка — ге в знаменателе диктует необходимость
поворота контура интегрирования по к0 в сторону мнимой оси про-
против часовой стрелки, так что интеграл по к0 от — °° до +°° заменяется
интегралом по мнимым значениям от — г°° до +г°°, или, эквивалент-
эквивалентно, по действительным значениям величины /с4 = — гк° от — °° до +°°.
Воспользуемся также вращательной симметрией знаменателя в
A1.3.4), что позволяет отбросить в числителе слагаемые нечетной
степени по к, заменить к ка на т\ /с2/4 и заменить элемент объема
d4fc = zdfc1d/c2dfc3d/c4 на 2Mt2K3dK, где к — евклидова длина 4-векто-
ра к. После всех этих действий формула A1.3.4) принимает вид
—4тг2р2 Г1 Гх Г°° г
Т^г- (т\г т\\ — I r/'Y1 I rill I V Hv ] V Л/гЛ/ Л/г^Л/ Л/ / й.
1iloop(P>P)- BяL }Qdx j^yj^ KdKj кууууЛр/4
+ ур [-г(р'A - у) - р(сс - у) + ш)] у^[-г(рA - х + у) - p'y) + rn] yp \
[9 9 9 9 1~
кл+тх + ау(х-у)\
J A1.3.5)
Нас интересует только матричный элемент мТ^м вершинной функ-
функции между дираковскими спинорами, удовлетворяющими соотно-
соотношениям
п'[щ' + т] = 0 , [гр + т]и = 0 .
Поэтому можно упростить выражение A1.3.5), переместив с помо-
помощью соотношений антикоммутации дираковских матриц все мно-
множители р' налево и все множители р направо, и заменив их после
этого на гт. После прямого, но утомительного вычисления можно
привести выражение A1.3.5) к виду
11.3. Аномальные магнитные моменты 659
2е2 Г1 Гх Г
\ dx dy K3dK
dy K3
Jo Jo
\р) \ y
BлL Jo Jo Jo
-к2 + 2m2(x2 - 4x + 2) + 2q2(y(x - y) + 1 - x)]
+4zmp/tl(y - x + xy) + 4гтр^(х2 - xy - y)\u A1.3.6)
x [к2 + m2x2 + q2y{x -
Воспользуемся теперь симметрией последнего множителя в
подынтегральном выражении относительно отражения у —» х — у.
В результате такого отражения функции у — х + ху и х2 — ху — у, на
которые умножаются р/ц и р11 соответственно, меняются местами,
поэтому их можно заменить на среднее
!(у-х + ху) + 7г(ж2 -ху-у) = -jx(l-x).
Окончательно получаем
—4л2е2 Г1
dx
Jo Jo
4
BлL Jo
-4x +
- x)}m [k2 + m2x2 + g2y(x -
-K2 +2m2(x2 -4x + 2) + 2g2(y(x-y) + l-
Заметим, что теперь р^ и p/fl входят только в комбинации рУ- + р'^,
как и требуется сохранением тока.
Необходимо принять во внимание и другие диаграммы. Конеч-
Конечно, в Р1 есть вклад нулевого порядка ^ . Слагаемое, пропорцио-
пропорциональное (Z2 — 1), в контрчленах A1.1.9) дает в Р1 вклад
ГД =(Z2-1)Y^. A1.3.8)
Кроме того, поправка во внешний фотонный пропагатор дает
слагаемое
660 Глава 11. Однопетлевые радиационные поправки в КЭД
Г?оляриз. вак.(Р',Р) = —, ~2 -№v(p'-p)Yv • (Ц.3.9)
(р - р) -IE v '
Форма каждого из этих слагаемых находится в согласии с общим
результатом A0.6.10) (с Я(д2) = 0):
(ц.з.10)
В порядке е2 форм-факторы имеют вид:
4л2е2 Г1 Сх Г°°
F(g2) = Z2+Jt(g2) + —— dx dy \ кЧк
Bл) Jo Jo Jo
[к2 - 2m2(x2 - 4х + 2) - 2g2(у(х - у) + 1 - х)] (ц.3.Ц)
[к2 + m2x2 + g2y(x - у)]
^ 2ч -4л2е2 Г1 7 fx 7 Г 4m2x(l-x)K3dK
G(g ) = -г- dx dy -,, ,
BлL Jo Jo Jo [к2 + m2x2 + g2y(x - у)] AL3-12)
где Jt(g2) — функция поляризации вакуума A1.2.22).
Интеграл, определяющий форм-фактор G(g2), конечен и ра-
равен
е2т2 Г1 Гх
-е2т2 Г1 7 7 ()
dx d^ ^—г^ :¦ (п.3.13)
Jo Jo тЛхЛ + g y(x - у)
Это позволяет сразу вычислить аномальный магнитный момент. Как
отмечалось в разделе 10.6, в магнитный момент дает вклад только
слагаемое, пропорциональное У1, так что результатом радиацион-
радиационных поправок является умножение дираковского значения магнит-
магнитного момента е/2т на F@). Однако определение е как истинного
заряда лептона требует, чтобы
F@) + G@) = l, A1.3.14)
так что магнитный момент можно записать в виде
11.3. Аномальные магнитные моменты
661
A1.3.15)
Из A1.3.13) находим, что
-G@) = —- = 0,001161.
A1.3.16)
Это знаменитая поправка а/2%, впервые вычисленная Швингером 5.
Конечно, это лишь первая низшая радиационная поправка к
магнитному моменту. Уже в следующем, четвертом порядке по е
количество слагаемых столь велико, что вычисления становятся до-
довольно сложными. Однако из-за большой величины отношения масс
мюона и электрона, существует одна поправка четвертого порядка
к магнитному моменту мюона, которая несколько больше всех ос-
остальных. Она возникает от включения электронной петли в линию
виртуального фотона в диаграмме второго порядка (см. рис. 11.5).
Включение этой петли приводит к замене фотонного пропагатора
l/k2 в A1.3.1) на A +%е{к2))/к2, где %е{к2) дается формулой A1.2.22),
а масса т полагается равной массе электрона:
%е(к2) =
2%2
хA-хIп 1 +
к2хA-х)
\dx.
т„
УЧЛЛЛ
Рис. 11.5. Двухпетлевая диаграмма для магнитного момента мюона. Жирная
прямая линия изображает мюон, тонкая волнистая — фотон, остальные тонкие
линии — электроны. Эта диаграмма дает относительно большой вклад в
четвертом порядке в гиромагнитное отношение для мюона, пропорциональный
1п(тц/те).
662
Глава 11. Однопетлевые радиационные поправки в КЭД
Анализ выражения A1.3.12) показывает, что при вычислении мю-
онного магнитного момента эффективное обрезание импульса вир-
виртуального фотона к равно т . Отношение т /те столь велико, что
при к2 порядка т 2 можно приближенно записать
(ml
x(l — x)dx In
I т2е
¦In
т..
mt
A1.3.17)
где отброшенные слагаемые содержат вместо 1п(т 2/те2) коэффи-
коэффициенты порядка единицы. Полученное выражение есть константа,
поэтому изменение в — G@), обусловленное добавлением электрон-
электронной петли в виртуальную фотонную линию, определяется умноже-
умножением предыдущего результата A1.3.16) для — G@) на фактор A1.3.17),
так что
e2 e4
8л2 96л2
In
тг.
т2е
0A)
A1.3.18)
(В т. II мы увидим, что это рассуждение есть упрощенная версия
метода ренормруппы.) Формулу A1.3.18) можно сравнить с точным
результатом расчета до четвертого порядка включительно
6.
25
2тц 8л2 96л2
197 7Г
~24~ + T
In
т
т„
9CC)
- Зл2In 2 ¦
т..
A1.3.19)
Оказывается, что слагаемые порядка 0A) вносят величину —6,137 в
коэффициент при е4/96л2, что немногим меньше, чем ln(m 2/me2)
= 10,663, так что приближение A1.3.18) определяет вклад четвертого
порядка с точностью до множителя порядка 2. Точный результат чет-
четвертого порядка A1.3.19) приводит к значению ц = 1,00116546(е/2т ),
что можно сравнить с результатом расчета до второго порядка
включительно ц = 1,001161(е/2т ) и последним экспериментальным
результатом
= 1,001165923(е/2тц).
11.3. Аномальные магнитные моменты
663
Обратимся к другому форм-фактору. Интеграл в выражении
A1.3.11) для F(q2) содержит ультрафиолетовую расходимость. Одна-
Однако для того, чтобы удовлетворить условию неперенормировки за-
заряда A1.3.14), необходимо, чтобы константа Z2 имела значение
Z2=l
doc
8л2 BлL Jo Jo
¦х /-°°
dy к;
о Jo
X-
к2 -2m2(x2 -4х + 2)
A1.3.20)
[к2
¦ m x
(Напомним, что л@) = 0.) Это выражение также расходится, при-
причем расходящаяся часть имеет вид
„2
(Z2 - 1L = -
8JT
Г°° dx
J к '
A1.3.21)
Подставляя A1.3.20) обратно в A1.3.11), получаем
е2 4л2е2 Г1
8%z
г dx
Bжу Jo Jo
х С°°
dy K
o Jo
dK
x
[к2 - 2m2 (x2 - 4x + 2) - 2g2 (y(x - y) + 1 - x)]
[к2 + m2x2 + g2y(x -
[к2 -2m2(x2 -4x +
A1.3.22)
9 9
+ m x
Теперь интеграл по к сходится:
2л2е2 Г1
8л^
f-m2(x2 -
Bл)
2 Г1 Г^
г dx dy
4 Jo Jo
-In
m2x2 +g2y(x-y)
m2x2 + g2y(x - y)
I
- 4x + 2
x
9 9
m x
A1.3.23)
664 Глава 11. Однопетлевые радиационные поправки в КЭД
Однако интеграл по х и у логарифмически расходится при
х = 0иу = 0, т. к. знаменатели содержат только слагаемые второго
порядка по х и/или у, а в числителе есть слагаемые, содержащие
только дифференциалы dx и dy. Можно проследить, что эта
расходимость на самом деле возникает от обращения в нуль знаме-
знаменателя [к2 + т2х2 + q2y(x—y)]3 в A1.3.11) при х = 0, у = 0 и к = 0.
Поскольку она происходит от области малых, а не больших к, ее
называют не ультрафиолетовой, а инфракрасной расходимостью *.
Подробно инфракрасные расходимости будут рассмотрены в
гл. 13. Там будет показано, что инфракрасные расходимости в сече-
сечении процессов типа электрон—электронного рассеяния, вроде тех,
которые возникают из-за инфракрасной расходимости в электрон-
электронном форм-факторе F(q2), сокращаются, если наряду с упругим рас-
рассеянием рассматривать и испускание фотонов низкой энергии. Кро-
Кроме того, как будет показано в гл. 14, при расчете радиационных
поправок к энергетическим уровням атомов инфракрасная расходи-
расходимость в F(q2) обрезается за счет того, что связанный электрон не
находится строго на массовой поверхности свободной частицы. В дан-
данный момент продолжим вычисления, просто введя некоторую фик-
фиктивную массу фотона ц для того, чтобы обрезать инфракрасную
расходимость в F(q2), и оставим до гл. 14 обсуждение вопроса о том,
как использовать полученный результат.
Если масса фотона равна ц, то знаменатель к2 - ге в формуле
A1.3.1) следует заменить на к2 + ц2 - г?. В результате в выражениях,
стоящих в знаменателях формул A1.3.3)-A1.3.7), A1.3.11), A1.3.20)
и A1.3.22) под знаком третьей степени, добавится слагаемое ц2A-х).
Тогда формула A1.3.23) заменится на
2P2 ,1 ,x
dx dy
Jo
' 0 ->0
-m2(x2 -4x + 2)-g2[y(x-y) + l-x] m2[x2 -4x + 2]
-In
+ ¦
m2x2 + g2y(x - у) + ц2A - x) m2x2 + ц2A - x)
9 9 9 /
izxz +qzy{x-
2 2 2„ ч Г A1.3.24)
т2х2+ц2A-х) '
* В отличие от ультрафиолетовой расходимости эта расходимость есть
проявление особенности Гц(р, р) как функции р и р на массовой оболочке р2
= т2, р'2 = т2. — Прим. ред.
11.3. Аномальные магнитные моменты 665
Теперь интеграл полностью сходится. Его можно выразить через функ-
функции Спенса, но получающийся результат не слишком прозрачен. Для
целей гл. 14 будет достаточно вычислить поведение F(q2) при малых
д2. Как уже известно, из тождества Уорда следует, что F@) =
= 1 — G@) = 1 + е2/8л2, так что рассмотрим первую производную
F'(cf) в точке д2 = 0. Как следует из A1.3.24), эта производная имеет вид
2ж2р2 Г1 Гх
F'(O) = jt'(O) + —— dx dy
BлL Jo Jo
[ 2y(x -y) + l-x m2[x2 -4x + 2]y(x-y)| A1.3.25)
[ m2x2+fi2(l-x) [m2x2+fi2(l-x)]2 J
Вклад поляризации вакуума дается формулой A1.2.22) и равен
е2
Д @) = яп 2 2 • A1.3.26)
Опуская в A1.3.25) все слагаемые, пропорциональные степеням ц/т,
получаем *
г2
24л2т2
2 1
!5 + 4
A1.3.27)
где слагаемое 2/5 отвечает вкладу поляризации вакуума. С другой
стороны, из формулы A1.3.13) следует, что G(g2) имеет конечную
производную при д2 = 0
е2
2 2
(П.3.28)
Полученные результаты удобнее всего выразить через заря-
зарядовый форм-фактор Fx(g2), определенный в альтернативном пред-
представлении A0.6.15) вершинной функции:
* Интеграл по у тривиален. Интеграл по х проще всего вычисляется в
пределе (Д, <&. т путем разделения области интегрирования на две части: от
0 до s, где ц/т « s « 1, и от s до 1.
666
Глава 11. Однопетлевые радиационные поправки в КЭД
~ p)vF2(g2)ju(p,a).
Согласно формулам A.6.17) и A0.6.18)
F1(q2)=F(q2) +
При |g2| <ЗС m2 этот форм-фактор приближенно равен
2 3
Ъ+ 4
24л2 т2
m
A1.3.30)
A1.3.31)
Его можно выразить через зарядовый радиус а, определенный по-
поведением зарядового форм-фактора в пределе д2 —» 0:
^(д2)^1-д2а2/б . A1.3.32)
(Такое определение мотивируется тем, что среднее значение exp(iq-x)
по сферической оболочке радиуса а ведет себя при q2a2 <^ 1 как
1 — q2a2/6.) Зарядовый радиус электрона равен
а2=-
т
М 2 3
Н+5 + 4
A1.3.33)
В гл. 14 мы увидим, что для электронов в атомах роль массы фото-
фотона играет эффективное инфракрасное обрезание, много меньшее
т, так что логарифм в формуле A1.3.33) большой по величине и
отрицательный, и значение а2 положительно.
11.4. Собственная энергия электрона
Завершим эту главу вычислением собственно-энергетической
функции электрона. Само по себе это вычисление не имеет прямых
11.4. Собственная энергия электрона
667
экспериментальных приложений, однако некоторые результаты ока-
окажутся полезными в гл. 14 и т. II *.
Как и в разделе 10.3, определим гBяJ[Е*(р)]ра как сумму всех
диаграмм с одной входящей и одной выходящей электронной лини-
линией, несущими импульсы р и дираковские индексы ОС и C, соответст-
соответственно, причем звездочка указывает, что исключаются диаграммы,
которые становятся несвязными после разрезания какой-то одной
внутренней электронной линии, и отброшены пропагаторы, отве-
отвечающие двум внешним линиям. Тогда точный электронный пропа-
гатор дается суммой
где
r,2 + 2 _ •
A1.4.2)
Сумма тривиально вычисляется, и в результате получаем:
S'(p) = \ip + me -1* (р) - i
A1.4.3)
В низшем порядке в Y," дает вклад однопетлевая диаграмма,
изображенная на рис. 11.6. Этот вклад равен
х
—г
BлL к2 - г?
—i -ip + ilk + me
BлL (р - /сJ + т2 - г?
или в более простой записи
* Заметим, что эту функцию называют также собственно-энергетической
частью или массовым оператором электрона. — Прим. ред.
668
Глава 11. Однопетлевые радиационные поправки в КЭД
Рис. 11.6. Однопетлевая диаграмма для электронной собственно-энергети-
собственно-энергетической функции. Как обычно, сплошная линия изображает электрон, вол-
волнистая — фотон.
у*
ге
lLOOP^
к2 - ге
(р - кJ + т2 -ie
¦ A1.4.4)
(Это выражение записано в фейнмановской калибровке; амплитуды
с заряженными частицами, находящимися вне массовой поверхно-
поверхности, калибровочно неинвариантны.) Для последующих вычислений
лэмбовского сдвига удобно воспользоваться методом регуляризации,
предложенным Паули и Вилларсом 8. Заменим фотонный пропага-
тор (к2 — ге)—1 на
1
1
к1 -ге к1 + ц2 - ге '
так что электронная собственно-энергетическая функция станет рав-
равной
1
1
х
к2 -ге к2 + ц2 - ге
ур(-гр + г1 + те)ур
(р - кJ + т;^ - ге
A1.4.5)
Позднее можно будет отбросить регуляризующее слагаемое, уст-
устремив регуляризующую массу ц к бесконечности. В гл. 14 нас будет
также интересовать случай ц <х mg.
Используем прием Фейнмана для объединения знаменателей
и вспомним, что
= — 2ук, а Уу = 4. Тогда
11.4. Собственная энергия электрона
669
х dx
1
((fc - рхJ + р2A - х) + т2х + Ц2A - х) - г?)
((/с - рхJ + р2хA - х) + т2х + ц2A - х) - ге.у
х 4 g
Совершая сдвиг переменной интегрирования к —> к + рх и повора-
поворачивая контур интегрирования, получим
1
X
Г
B%у Jo
1
,2^ч2
(к2 + р2хA - х) + т2хJ (к2 + р2хA - х) + т2х + ц2 A - х)J
Интеграл по к тривиален:
-л2е2 Г1
BлL Jo
dx
BлL ^о
xln
р2хA - х) + m2x
A1.4.7)
A1.4.8)
Контрчлены A1.1.9) также вносят вклад в?*в виде перенормирующих
слагаемых —(Z2 - 1)(гр + те) + Z28me , где Z2 и 8те определяются ус-
условием, что точный пропагатор S'(p), рассматриваемый как функ-
функция гр, должен иметь полюс при гр = —те с единичным вычетом. (В
следующей главе мы увидим, что это условие делает Е* конечнымпри
(X —> оо во всех порядках по е.) В низшем порядке находим:
0те = ~Ь\ LOOP Hp=-me
т^2 f
BлL Jo
dx
т2х
670
Глава 11. Однопетлевые радиационные поправки в КЭД
Z2 - 1 = -i
'1LOOP
гр=-те
2%Ле
2 „2 Л
{2%f Jo
j-fdx (l-x)ln
ц2A-х) | 2ц2A-хJA
т2х
х(т2х + ц2A-х))
A1.4.10)
(В этом порядке нет разницы между 8те и Z28me.) Опуская слагае-
слагаемые, обращающиеся в нуль при ц2 ^°о, получаем из A1.4.8)—A1.4.10):
dx [2гA -x)p + 4me]ln —-
lp2
ц2A-х)
A1.4.11)
BлL Jo
dx 1 + х In
I
m2x2
A1.4.12)
Z2 - 1 = -
B%Г Jo
/:
dxj(l-x)ta|
X
A1-4.13)
Видно, что в точной собственно-энергетической функции слагае-
слагаемые с In jj2 сокращаются, и мы приходим к выражению
порядок е
_ -2л2е2
BЛL
~ (Z2 ~ ViW + ™е) +
dx \[i(l-x)p + 2m ]ln
m2(l-x)
p2x(l-x) + m2x
-m A + ж) In
1-х
x
- (гр + me
A - x) In
x
2(l-x2)
x
A1.4.14)
Приложение 671
Все еще остается расходимость в последнем слагаемом при х —> 0.
Можно проследить, что она связана с сингулярным поведением ин-
интеграла A1.4.5) по фотонному импульсу к при к2 = 0, когда при вы-
вычислении Z2 — 1 мы берем р2 в точке р2 = — т2. Детальное обсуждение
таких инфракрасных расходимостей дано в гл. 13. Сейчас для нас
самое главное, что сократились ультрафиолетовые расходимости.
Результат A1.4.9) для Ъте интересен сам по себе. Заметим, что bmj
те > 0, как и следовало ожидать для электромагнитной собствен-
собственной энергии, обязанной своим происхождением взаимодействию за-
заряда с собственным полем. Однако, в противоположность классиче-
классическим оценкам электромагнитной собственной энергии, выполнен-
выполненным Пуанкаре, Абрагамом и др.9, в формуле A1.4.9) содержится
только логарифмическая расходимость в пределе ц —» °°, когда сни-
снимается обрезание. В этом пределе
6т„%2е2 ( ц ^
5m^l^lrW AL4-15)
При вычислении лэмбовского сдвига в разделе 14.3 нас будет инте-
интересовать противоположный предел ц ^С те. В этом случае из A1.4.9)
получаем
Приложение. Некоторые инегралы
Чтобы объединить знаменатели N пропагаторов, необходимо заме-
заменить произведение типа D^1 D2-1... D^1 на интеграл от функции,
содержащей линейную комбинацию Dv D2, ..., DN. С этой целью
часто удобно воспользоваться формулой
672 Глава 11. Однопетлевые радиационные поправки в КЭД
1 ri ri fi
— = (iV-l)! dxJ dx2... dx^
2...DN Jo ^o z Jo JV L
(iVl)! dxJ dx2...
DXD2...DN Jo ^o z Jo
A1.A.1)
x[D1XjV_1 + D2 (xw_2 - хи_!)+.. .+DN A - xx)]
В этой главе мы использовали частные случаи этой формулы при
N = 2 и N = 3.
После объединения знаменателей, сдвига переменной интег-
интегрирования, виковского поворота и учета инвариантности относи-
относительно четырехмерных вращений, мы обычно приходим к интегра-
интегралам вида
d
(к* +v
2 \т
где (к2 + v2)m возникает от объединения знаменателей, а (/с2)" — от
числителей пропагаторов и импульсных множителей в вершинах.
Такие интегралы расходятся при 2п+4 > 2т, но их можно сделать
конечными, аналитически продолжая по размерности пространст-
пространства-времени от 4 к комплексному значению d. Для вычисления полу-
получающегося интеграла используем хорошо известную формулу
2)m
(K2+v2)
,.2т
ГA / 2)Г(т - I / 2)
(П.А.2)
где I = d + 2n. В разделе 11.2 использовались частные случаи этой
формулы при п = 0, т = 2ип= 1, т = 2.
Ультрафиолетовые расходимости проявляются в A1.А.2) как по-
полюсы в множителе Г(т—1/2) = Г(т—п—d/2) при d ЧВ4 и фиксирован-
фиксированном целом п. В случае 2 + п = т этот множитель ведет себя как
где у = 0,5772157... — постоянная Эйлера. Предельное поведение для
случая 2 + п > т можно найти из A1.А.З) и рекуррентных соотно-
соотношений для гамма-функций.
Список литературы 673
Задачи
1. Вычислите вклады в функцию поляризации вакуума тг(д2) и в
Z3 однопетлевых диаграмм, содержащих заряженные бесспи-
бесспиновые частицы массой ms. Какое влияние окажут эти поправки
на сдвиг уровней 2s состояния в атоме водорода, если
ms » Zame?
2. Пусть взаимодействие нейтрального скалярного поля ф массой
тф с полем электронов имеет вид дф \|А|/. Какое влияние окажет
это взаимодействие в однопетлевом приближении на магнит-
магнитный момент электрона и величину Z2?
3. Рассмотрите нейтральное скалярное поле ф массой тф и само-
самодействием дф3/6. Рассчитайте матричный элемент ^-матрицы
для скаляр-скалярного рассеяния в однопетлевом приближе-
приближении.
4. Рассчитайте в однопетлевом приближении влияние нейтраль-
нейтрального скалярного поля из задачи 2 на поправку Ъте к массе элек-
электрона.
Список литературы
1. Feynman, R.P., Phys. Rev., 76, 769 A949).
2. Wick, G.C., Phys., Rev., 80, 268 A950).
a 't Hooft, G. and Veltman, M., Nucl. Phys., B44, 189 A972).
Phys. Lett., 20, 682 A966); 21, 720 A966); Erickson, G.W. and
Liu, H.H.T., UCD-CNL-81 report A968).
4. Uehling, E.A., Phys. Rev., 48, 55 A935). Однопетлевая функция
л(д2) впервые была вычислена при д2 Ф 0 в работе: Schwinger,
J., Phys. Rev., 75, 651 A949).
5. Schwinger, J., Phys. Rev., 73, 416 A948).
674 Глава 11. Однопетлевые радиационные поправки в КЭД
6. Этот расчет (включая слагаемые, исчезающие в пределе
те <^ rriy) выполнен в работах: Suura, H. and Wichmann, E.,
Phys. Rev., 105, 1930 A957); Petermann, A., Phys. Rev., 105,
1931 A957); Elend, H.H., Phys. Lett, 20, 682 A966); 21, 720 A966);
Erickson, G.W. and Liu, H.H.T., UCD-CNL-81 report A968).
7. Bailey, J. et al. (CERN-Mainz-Daresbury Collaboration), Nucl. Phys.,
B150, 1 A979). Эти эксперименты были выполнены путем наблю-
наблюдения прецессии спина мюона в накопительном кольце.
8. Pauli, W. and Villars, F., Rev. Mod. Phys., 21, 434 A949). См.
также: Rayski, J., Phys. Rev., 75, 1961 A949).
9. См., например, в книге: Miller, A.I., Theory of Relativity —
Emergence A905) and Early Interpretation A905-1911) (Addison
Wesley, Reading, MA, 1981), Chapter 1.
12
Общая теория перенормировок
В предыдущей главе было показано, что вычисления в кван-
квантовой электродинамике, относящиеся к однопетлевым диа-
диаграммам, приводят к расходящимся интегралам в импульсном про-
пространстве, однако все расходимости сокращаются, если выразить
параметры теории через «перенормированные» величины вроде
реально измеряемых на опыте масс и зарядов. В 1949 году Дай-
сон 1 обрисовал доказательство того, что аналогичное сокращение
будет имет место во всех порядках теории возмущений в кванто-
квантовой электродинамике. Сразу же было очевидно (и это будет пока-
показано ниже в разделах 12.1 и 12.2), что аргументы Дайсона приме-
применимы к значительно более широкому классу теорий с конечным
числом сравнительно простых взаимодействий — к так называе-
называемым перенормируемым теориям. Квантовая электродинамика яв-
является лишь простейшим примером подобных теорий.
В течение ряда лет общепринятой была точка зрения, что
любая разумная физическая теория должна иметь форму пере-
перенормируемой квантовой теории поля. Требование перенормируе-
перенормируемости играло решающую роль при построении современной «стан-
«стандартной модели» слабых, электромагнитных и сильных взаимо-
взаимодействий. Однако, как мы увидим ниже, сокращение ультрафио-
ультрафиолетовых расходимостей реально не зависит от перенормируемо-
перенормируемости: до тех пор, пока мы включаем в теорию каждое из бесконеч-
бесконечного числа взаимодействий, разрешенных симметриями, так на-
называемые неперенормируемые теории становятся столь же пе-
перенормируемыми, как и перенормируемые теории.
В настоящее время общепризнано, что реалистические теории,
используемые для описания физики при доступных энергиях, отно-
676 Глава 12. Общая теория перенормировок
сятся к так называемым «эффективным теориям поля». Под этим
понимают низкоэнергетические приближения к более фундамен-
фундаментальной теории, которая может вообще не быть теорией поля (см.
раздел 12.3). Любая эффективная теория поля с необходимостью
включает бесконечное число неперенормируемых взаимодействий.
Тем не менее, как показано в разделах 12.3. и 12.4, мы полагаем,
что при достаточно низких энергиях все неперенормируемые взаи-
взаимодействия в этих теориях сильно подавлены. Таким образом, пе-
перенормируемые теории типа квантовой электродинамики или стан-
стандартной модели сохраняют свой особый статус в физике, хотя и по
причинам, несколько отличающимся от тех, которые первоначально
привели к предположению о перенормируемости этих теорий.
12.1. Индексы расходимости
Рассмотрим теорию весьма общего вида, содержащую взаи-
взаимодействия разных типов, помеченные индексом г. Каждое взаи-
взаимодействие можно охарактеризовать числом п^ полей каждого
типа / и числом йг производных, действующих на эти поля.
Начнем с вычисления индекса расходимости * D произволь-
произвольной связной одночастично неприводимой диаграммы Фейнмана в
такой теории. Он равен числу импульсных множителей в числите-
числителе минус число таких множителей в знаменателе подынтегрально-
подынтегрального выражения плюс четыре степени на каждый независимый 4-
импульс, по которому проводится интегрирование. Индекс расхо-
расходимости равен фактической степени расходимости, возникающей
при интегрировании по области импульсного пространства, в ко-
которой импульсы всех внутренних линий одновременно устремля-
устремляются к бесконечности. Именно, подвергнем все внутренние импульсы
однородному растяжению одним масштабным фактором к; тогда
* Автор использует принятый в англоязычной литературе термин
superficial degree of divergence. В переводе этого термина в опубликованных
книгах существует полный разнобой (условная степень расходимости,
кажущаяся степень расходимости, поверхностная степень расходимости и
т. п.). Мы решили использовать введенный в книге Н. Н. Боголюбова и
Д. В. Ширкова «Введение в теорию квантованных полей» термин индекс
расходимости. — Прим. ред.
12.1. Индексы расходимости 677
вклад в амплитуду от области больших импульсов, отвечающий
к —» °о, расходится при D > 0 как
Г
A2.4.1)
Точно так же, при индексе расходимости D = 0 интеграл
расходится логарифмически, а при D < 0 интеграл сходится, по
крайней мере, в рассматриваемой области импульсного простран-
пространства *. Позднее мы вернемся к проблеме, когда подинтегрирова-
ния ** ведут себя хуже, чем интеграл по всей области.
Для вычисления D потребуется следующая информация о
диаграмме:
Ir = число внутренних линий поля типа /;
Ег = число внешних линий поля типа /;
Ni = число вершин взаимодействия типа г.
Запишем асимптотическое поведение пропагатора Ai/с) по-
поля типа / в виде
А/(/с) - k~2+2sf . A2.1.2)
Заглянув в гл. 6, видим, что s, = 0 для скалярных, s, = 1/2 для
дираковских и s- = 1 для векторных полей. В более общем случае
можно показать, что для массивных полей типа (А,В) по отношению к
лоренцовским преобразованиям sf = А + В. Не очень точно можно
называть s, «спином». Однако, если отбросить те слагаемые, которые
не дают вклада в силу калибровочной инвариантности, то для эффек-
эффективного фотонного пропагатора Лму/^2 получаем s? = 0. Аналогичный
результат справедлив для массивного векторного поля, взаимодей-
взаимодействующего с сохраняющимся током, при условии, что ток не зависит
от векторного поля. Можно показать, что в том же смысле и для
гравитонного поля g пропагатор имеет s- = 0.
* Фактическая степень расходимости диаграммы может оказаться меньше ее
индекса расходимости. Конкретные примеры приведены ниже, в разделе 12.2. —
Прим. ред.
** Термин «подинтегрирование» означает интегрирование по части внут-
внутренних импульсов, тех, которые отвечают некоторой поддиаграмме данной
диаграммы (см. ниже). — Прим. ред.
678 Глава 12. Общая теория перенормировок
Согласно A2.1.2) полный вклад всех пропагаторов в D равен:
A2.1.3)
Кроме того, производные в каждом взаимодействии типа i
вносят <1г импульсных множителей под интегралом, что дает об-
общий вклад в D, равный
L*Nidi- A2.1.4)
г
Наконец, следует подсчитать полное число независимых
импульсных переменных интегрирования. Каждая внутренняя
линия несет 4-импульс, но не все они независимы, т. к. дельта-
функции, связанные с каждой вершиной, накладывают линейные
связи на внутренние импульсы, за вычетом одной общей дельта-
функции, выражающей закон сохранения внешних импульсов. Та-
Таким образом, элементы объема интегрирования в импульсном про-
пространстве вносят в D слагаемое
_ W
A2.1.5)
что, конечно, есть учетверенное число независимых петель в диа-
диаграмме. Складывая выражения A2.1.3), A2.1.4) и A2.1.5), находим, что
7 i A2-!-6)
В приведенном виде формула A2.1.6) не очень удобна, так
как значение D кажется зависящим от внутренних деталей дан-
данной диаграммы. К счастью, формулу можно упростить, восполь-
воспользовавшись топологическими тождествами
(Каждая внутренняя линия соединена с двумя вершинами, а ка-
каждая внешняя - только с одной.) Используя формулу A2.1.7) для
исключения L, видим, что A2.1.6) переходит в выражение вида
D = 42>(e + l)J>A, A2.L8)
12.1. Индексы расходимости 679
где Ai — параметр, характеризующий взаимодействия г-ого типа:
i/(s/+1)- A2.1.9)
Этот результат можно было бы получить путем простого раз-
размерного анализа, не прибегая к рассмотрению структуры фейнма-
новских диаграмм. Пропагатор поля есть четырехмерный фурье-
образ среднего по вакууму от хронологического произведения пары
свободных полей, так что обычным образом нормированное поле /,
(массовая) размерность * которого равна У)р имеет пропагатор раз-
размерности -4 + 2 У),. Поэтому, если пропагатор ведет себя как k Sf,
при к много большем массы, то поле должно иметь размерность
-4 + 2(/)= —2 + 2sр или У), = 1 + s~ Ваимодействие типа г, включа-
включающее nif таких полей и с^ производных, будет иметь размерность
dj + E/ij/(l + Sf)- Но действие должно быть безразмерно, поэтому
каждое слагаемое в плотности лагранжиана должно иметь размер-
размерность +4, чтобы сократить размерность -4 элемента объема d4x.
Отсюда следует, что константа связи данного взаимодействия должна
иметь размерность 4 - с^ - Еу>г^A + sf), что как раз равно парамет-
параметру Af Амплитуда в импульсном пространстве, отвечающая связной
диаграмме Фейнмана с Е, внешними линиями типа / есть фурье-
преобразование по 4Е#Е, координатам среднего по вакууму от
хронологического произведения полей с полной размерностью
Е#Е,A + sX так что она имеет размерность E#Ei-3 + sX В этом
выражении —4 приходится на размерности дельта-функции в им-
импульсном пространстве, a EjE^-2 + 2sf) — на размерность пропага-
торов внешних линий, так что суммарная размерность интеграла
по импульсному пространству вместе со всеми константами связи
равна
* В этой главе под словом «размерность» всегда подразумевается массовая
или импульсная размерность ** в степенях массы или импульса в системе еди-
единиц, где h — с — 1. Мы используем общепринятую нормировку полей, в том
смысле, что слагаемое в лагранжиане свободного поля с наибольшим числом про-
производных (определяющее асимптотическое поведение пропагатора) имеет безраз-
безразмерный коэффициент.
** Т. е. размерность такой же степени массы или импульса. Англоязычный
термин dimensionality in powers of momentum имеет устойчивый русско-
русскоязычный эквивалент массовая, или импульсная, размерность. — Прим. ред.
680 Глава 12. Общая теория перенормировок
;(-3 + sf) - (-4) - ?Е/(-2 + 2sf) = 4 -
Полная размерность всех констант связи для заданной фейнма-
новской диаграммы равна LjJVA так что размерность собственно
интеграла по импульсному пространству есть 4 - Y,fEJs, + 1) - Е/^Д-
Поскольку нас интересует область интегрирования, в которой все
импульсы совместно стремятся к бесконечности, индекс расходи-
расходимости интеграла по импульсам равен его размерности. Это и под-
подтверждает формулу A2.1.8).
Если для всех взаимодействий параметры Д^ > 0, формула
A2.1.8) дает верхнюю границу D, зависящую только от числа
внешних линий каждого типа, т. е. от физического процесса, ам-
амплитуда которого вычисляется:
Например, для простого варианта квантовой электродина-
электродинамики, рассмотренного в предыдущей главе, в табл. 12.1 приведе-
приведены типы слагаемых в лагранжиане. Для всех взаимодействий здесь
А^ > 0, и поэтому фейнмановская диаграмма с Е внешними фотон-
фотонными линиями и Ее внешними дираковскими линиями будет иметь
индекс расходимости, ограниченный условием A2.1.10):
D<4-|Ee-Ey. A2.1.11)
Таким образом, только конечное число типов диаграмм с оп-
определенными наборами внешних линий может оказаться расхо-
расходящимся. Все они будут перечислены в разделе 12.2. Мы собира-
собираемся показать, что в теориях, где размерности констант связи Ai
> 0 для всех взаимодействий и где число типов расходящихся
диаграмм ограничено, все расходимости автоматически устраня-
устраняются переопределением конечного числа физических констант и
перенормировкой полей. По этой причине такие теории называют
перенормируемыми. В разделе 12.3 мы перечислим все перенор-
перенормируемые теории и обсудим значение перенормируемости как кри-
критерия отбора физических теорий.
Термин «перенормируемое» применим также к отдельным
взаимодействиям. Перенормируемые взаимодействия — это те,
12.1. Индексы расходимости
681
у которых параметр Ai > 0, т. е. взаимодействия, константы связи
которых имеют неотрицательную размерность. Иногда различают
взаимодействия с Ai = 0, которые называют просто перенорми-
перенормируемыми, и с Д; > 0, которые называют суперперенормируемы-
ми. Поскольку добавление во взаимодействие дополнительных
полей или производных всегда уменьшает параметр Ар может
существовать лишь ограниченное число перенормируемых вза-
взаимодействий, содержащих поля любого данного типа. Мы виде-
видели, что в простейшем варианте квантовой электродинамики все
взаимодействия перенормируемы, а слагаемые с \|Л|/ суперпере-
нормируемы.
С другой стороны, если для какого-то взаимодействия Аг < О,
индекс диаграммы A2.1.8) неограниченнно возрастает по мере до-
добавления соответствующих вершин. Независимо от того, сколь
большими мы выберем разные Е,, в конце концов при достаточ-
достаточном количестве вершин типа г, для которых Аг < 0, выражение
A2.1.8) станет положительным (или нулем), и интеграл разойдет-
разойдется. Подобные взаимодействия, константы связи которых имеют
Таблица 12.1
Взаимодействие
—ie X|/gx|/
[-(Z2-l)m + Z2bm]
W
d,
0
2
1
0
1
2
0
0
2
0
2
2
4
4
4
4
A*
-1 -
- 2 -
- 1 -
- 3 =
3 =
[Si
3 =
1
0
0
0
Табл. 12.1. Слагаемые плотности лагранжиана квантовой электродинамики.
Здесь dt, тк, и пы — числа производных, полей фотонов и полей электронов,
соответственно в данном члене взаимодействия, a Ai — размерность соответ-
соответствующего коэффициента (напомним, что s = 0 и se — 1/2).
682 Глава 12. Общая теория перенормировок
отрицательную размерность, называются неперенормируемыми,*
так же, как и теории, включающие любые неперенормируемые
взаимодействия. Это не означает, что такие теории безнадежны;
мы увидим, что бесконечности в них также можно поглотить пе-
переопределением параметров теории, с той разницей, что необхо-
необходимо бесконечное число констант связи.
Следует иметь в виду, что вычисленный нами индекс диаг-
диаграммы определяет структуру расходимости фейнмановских ди-
диаграмм при интегрировании только по тем областям импульсного
пространства, в которых все внутренние 4-импульсы совместно
стремятся к бесконечности. Однако расходимости могут возникать
и от областей, в которых к бесконечности стремятся только
4-импульсы линий, принадлежащих некоторой поддиаграмме. На-
Например, для комптоновского рассеяния в квантовой электродина-
электродинамике (Ее = 2, Е = 2) из формулы A2.1.11) следует, что индекс
расходимости D < — 1, и, действительно, диаграммы типа пока-
показанной на рис. 12.1, а сходятся. Однако диаграммы рис. 12.1, б или
12.1, в логарифмически расходятся, т. к. они содержат поддиа-
поддиаграммы (выделенные пунктирными прямоугольниками) с D > 0.
Расходимости этих диаграмм объясняются аномально плохим асим-
асимптотическим поведением подынтегральных выражений в специ-
специальных (под)областях импульсного пространства. В этих облас-
областях восемь компонент двух независимых внутренних 4-импуль-
сов стремятся к бесконечности таким образом, что в действи-
действительности к бесконечности стремится толькот один 4-импульс —
тот, который циркулирует в петлях, вставленных либо во внут-
внутренние линии, либо в электрон-фотонную вершину *.
Было показано 2, что требование фактической сходимости ам-
амплитуды, соответствующей любой диаграмме, заключается в том, что-
чтобы подсчет степеней приводил к значению индекса расходимости D < 0
не только для всего многократного интеграла для полной амплитуды,
* В пертурбативной статистической механике неперенормируемые
взаимодействия носят название несущественных, так как они становятся
менее важными в пределе низких энергий. Перенормируемые или супер-
перенормируемые взаимодействия называются соответственно маргиналь-
маргинальными и существенными.
** Этот импульс можно взять в качестве независимого внутреннего
импульса. — Прим. ред.
12.1. Индексы расходимости
683
Рис. 12.1. Некоторые двухпетлевые диаграммы комптоновского рассеяния.
Здесь сплошные линии отвечают электронам, а волнистые — фотонам.
Интеграл по импульсному пространству для диаграммы а сходится, а для
диаграмм бив расходится из-за подинтегрирования, отвечающего
поддиаграммам в пунктирных рамках
но и для любого интеграла меньшей кратности, определяемого фикса-
фиксацией любых одной или более линейных комбинаций импульсов в пет-
петлях. (Диаграммы, приведенные на рис. 12.1, б и 12.1, в, не удовлетво-
удовлетворяют этому условию, поскольку для подинтегрирований по импульсам
в петлях внутри пунктирных прямоугольников D > 0.) Мы не будем
приводить здесь довольно длинное доказательство, поскольку оно хо-
хорошо изложено в имеющихся книгах3, да и сам метод доказательства
имеет мало отношения к тому, как реально делаются вычисления. В
следующем разделе мы опишем, как выполняется сформулированное
требование.
12.2. Сокращение расходимостей
Рассмотрим фейнмановскую диаграмму или ее часть с поло-
положительным индексом диаграммы D > 0. Та часть интеграла по им-
импульсному пространству, где все внутренние импульсы совместно
устремляются к бесконечности, будет расходиться как J°° fcD~1dfc.
Если продифференцировать D + 1 раз по любому внешнему им-
импульсу, то показатель степенной асимптотики подынтегрального
684 Глава 12. Общая теория перенормировок
выражения уменьшится на D + 1 *, что сделает интеграл по этой
части импульсного пространства сходящимся **. Правда, еще могут
оставаться расходимости, возникающие от поддиаграмм типа пока-
показанных на рис. 12.1, б и 12.1, в, но на некоторое время забудем об этой
возможности (мы вернемся к ее обсуждению в следующем разделе).
Поскольку (D + 1)-кратное дифференцирование делает интеграл конеч-
конечным, отсюда следует, что вклад такой диаграммы или поддиаграммы
может быть записан как полином порядка D по внешним импульсам с
расходящимися коэффициентами плюс конечный остаток.
Чтобы понять без лишних усложнений, как все это работает,
рассмотрим логарифмически расходящийся одномерный интеграл
с D = I — 1 = 0. После однократного дифференцирования
так что
${q) = - In q + с .
Постоянная с очевидно расходится, но остальная часть ин-
интеграла конечна. Точно так же можно оценить интеграл с D = 1
kdk
= а + bq + о m о
к + Ч
с расходящимися константами а и Ъ.
Далее, полином по внешним импульсам — это как раз то, что
возникает от добавления подходящих слагаемых в лагранжиан:
* Например, если внутренняя скалярная линия несет импульс к + р,
где р — линейная комбинация внешних 4-импульсов, а к — 4-импульс, по
которому проводится интегрирование, то производная пропагатора
[(к + рJ + т2] по р^ дает — 2(к + р ) [(к + рJ + т2], и этот множитель
ведет себя при к —> °° как к~3, а не как кг2.
** Говорят, что дифференцирование по внешним импульсам уменьшает
индекс диаграммы (на единицу при однократном дифференцировании). —
Прим. ред.
12. 2. Сокращение расходимостей 685
если диаграмма с Е, внешними линиями типа / имеет индекс рас-
расходимости D > О, то ультрафиолетово расходящийся полином сов-
совпадает с тем, который возник бы при добавлении различных взаи-
взаимодействий типа г, включающими nif = Ef полей типа / и <1г < D
производных. Если в лагранжиане уже имеются такие взаимодей-
взаимодействия, то ультрафиолетовые расходимости просто вносят поправ-
поправки к константам связи этих взаимодействий. Следовательно подоб-
подобные бесконечности могут быть сокращены путем включения
в константы связи подходящих бесконечных слагаемых. Все, что
мы когда-либо можем измерить, представляет собой сумму голой
константы связи и соответствующего коэффициента одного из рас-
расходящихся полиномов, так что если мы потребуем, чтобы эта сумма
равнялась измеряемому значению, которое предполагается конеч-
конечным, голая константа должна автоматически содержать бесконеч-
бесконечность, которая сокращает бесконечность от расходящегося инте-
интеграла по внутренним импульсам. (Одно уточнение: когда расхо-
расходимость возникает в диаграмме или поддиаграмме ровно с двумя
внешними линиями, возникающей как радиационная поправка к про-
пагатору частицы, мы должны требовать не равенства некоторой эф-
эффективной константы связи ее измеряемому значению, а того, чтобы
точный пропагатор имел полюс в том же месте и с тем же вычетом,
что и у пропагатора свободных частиц.) Таким образом, все бесконеч-
бесконечности поглощаются переопределением констант связи, масс и полей.
Чтобы такая программа перенормировок работала, сущест-
существенно, чтобы лагранжиан включал все взаимодействия, соответ-
соответствующие ультрафиолетово расходящимся частям фейнмановских
амплитуд. (Исключения из этого правила встречаются в супер-
суперсимметричных теориях 4.) Конечно, взаимодействия в лагранжиане
ограничены различными принципами симметрии вроде лоренц-
инвариантности, калибровочной инвариантности и т. п., но точно
так же ограничены этими требованиями и ультрафиолетовые рас-
расходимости. (Доказательство того, что неабелевые калибровочные
симметрии ограничивают бесконечности так же, как и взаимо-
взаимодействия, требует определенных усилий. Мы покажем это в т. П.)
В общем случае, нет никаких иных ограничений на ультрафиоле-
ультрафиолетовые расходимости, так что лагранжиан должен содержать все
возможные слагаемые, совместимые с принципами симметрии.
Однако существует важный класс теорий всего лишь с ко-
конечным числом взаимодействий, для которых также применима
686 Глава 12. Общая теория перенормировок
программа перенормировки. Это так называемые перенормируе-
перенормируемые теории, у которых для всех взаимодействий размерности
констант связи А. > 0. Из формулы A2.1.8) имеем:
поэтому расходящиеся полиномы возникают только в ограничен-
ограниченном числе типов фейнмановских диаграмм или поддиаграмм с дос-
достаточно небольшим числом внешних линий, так что D > 0. Вклад
таких расходящихся полиномов точно такой же, какой возник бы
после замены расходящейся диаграммы или поддиаграммы един-
единственной вершиной, возникающей от слагаемого в лагранжиане с
Ег полями типа / и 0,l,...,D производными. Однако, сравнивая с
формулой A2.1.9), видим, что это в точности то же самое, что
и взаимодействия, удовлетворяющие требованию перенормируе-
перенормируемости Аг > 0, или, иными словами,
Для того, чтобы в перенормируемой теории сократились все
расходимости, обычно необходимо, чтобы в лагранжиане содер-
содержались все перенормируемые взаимодействия, разрешенные тре-
требованиями симметрии *. Например, если есть скалярное (или псев-
псевдоскалярное) поле ф и фермионное поле \|/ со взаимодействия-
взаимодействиями Х|А|/ф (или \|/у5\|/ф), мы не можем исключить взаимодействие ф4,
в противном случае не нашлось бы контрчлена для сокращения
логарифмической расходимости от фермионных петель с четырь-
четырьмя прикрепленными скалярными или псевдоскалярными линиями.
* Кроме того, в лагранжиан могут входить взаимодействия и массовые
слагаемые, не разрешенные глобальными симметриями, при условии, что
они суперперенормируемы, т. е. имеют Ai > 0. Дело в том, что наличие
суперперенормируемого взаимодействия понижает степень расходимости,
так что нарушение симметрии не затрагивает те расходимости, которые
сокращаются строго перенормируемыми взаимодействиями с Ai = 0. Отме-
Отметим, что именно голые строго перенормируемые взаимодействия должны
удовлетворять требованиям данной симметрии; в перенормированных
взаимодействиях, определяемых через матричные элементы на массовой по-
поверхности, эффект нарушения симметрии в общем случае проявляется явно.
12. 2. Сокращение расходимостей 687
Рассмотрим более подробно, каким образом происходит со-
сокращение расходимостей в простейшей версии квантовой элек-
электродинамики. Из формулы A2.1.11) следует, что единственными
диаграммами или поддиаграммами, которые могут приводить к
расходящимся интегралам, являются следующие.
Ее = 2, Eg = 1
Это электрон—фотонная вершина Г®(р', р). (Верхний индекс
I указывает, что вершина включает только вклады от диаграмм с
петлями.) Для нее индекс расходимости D = 0, так что ее расхо-
расходящаяся часть не зависит от импульса. В силу лоренц—инвари-
лоренц—инвариантности расходящаяся константа может быть пропорциональна
только у , поэтому
A2.2.1)
где L — логарифмически расходящаяся константа, а Г*^ конечна.
Это еще не определяет константу L однозначно, так как всегда
можно перенести конечное слагаемое 8Ly из Г*^ в Ly . Чтобы
завершить определение, заметим, что, как показано в разделе
9.7, матричный элемент оператора Г (р,р), а следовательно и
Tf/\p,p), на массовой поверхности между дираковскими спинора-
спинорами свободных частиц пропорционален такому же матричному эле-
элементу оператора у^, поэтому можно определить L из требования
((p,a) = O. A2.2.2)
при р2 + те2 = 0.
Ее = 2, Eg = О
Это электронная собственно-энергетическая вставка 12 (р)-
Для нее D = 1, так что расходящаяся часть линейна по импульсу
р*1, который несут входящий или выходящий фермионы. Из ло-
лоренц—инвариантности (включая сохранение четности) следует, что
она может быть функцией только р, так что вклад петли можно
записать в виде
?(г)(р) = А - (гр + т)В + Е(/)(р), A2.2.3)
688 Глава 12. Общая теория перенормировок
где А и В — расходящиеся константы, a Y,^ конечна. Константы
А и В опять определены неоднозначно, т. к. всегда можно сдви-
сдвинуть Е(^ на конечный полином первого порядка по р. Определим
А и В предписанием
= 0 при i-p = -m. A2.2.4)
Эр
На самом деле, В не является новой расходящейся констан-
константой. До тех пор, пока мы используем процедуру регуляризации,
совместную с сохранением тока, Г и Е будут связаны тождест-
тождеством Уорда A0.4.27):
и поэтому
Lyil+rjf4p,p) = Byil + i ^ ^. A2.2.5)
Беря матричный элемент этого равенства между м(р,о') и
м(р,а) и используя формулы A2.2.2) и A2.2.4), находим:
L = В. A2.2.6)
Eg = 2, Ее = О
Это фотонная собственно-энергетическая вставка П* (д). Для
нее D = 2, так что расходящаяся часть есть полином второго
порядка по д. Из лоренц-инвариантности следует, что П* имеет
вид линейной комбинации т| и д gv с коэффициентами, завися-
зависящими только от д2, так что вклады петель имеют вид
n^(<3) = ci\y + С2%уЧ2 + Cgg^g,, + расходящиеся слагаемые,
где Cv C2 и С3 — расходящиеся константы. Поскольку мы исполь-
используем регуляризацию, не нарушающую сохранение тока, должно
выпоняться равенство
12. 2. Сокращение расходимостей 689
Это же должно быть верно и для расходящихся слагаемых,
так что C1gv + (С2 + C3)g2gv должно быть конечными для всех д.
Отсюда С1 и С2 + С3 должны быть конечными, так что их можно
внести в конечную часть П[^(д). Следовательно
^^( ), A2.2.7)
где я(д2) конечно, а С — единственная оставшаяся расходимость в
П . Чтобы зафиксировать определение С, можно включить в нее
любую конечную константу тс(О) *, так чтобы
л@) = 0. A2.2.8)
Eg = 4, Ее = О
Это амплитуда М рассеяния света на свете. Для нее D = 0,
так что, используя лоренц—инвариантность и требования бозе-
статистики, можно записать эту амплитуду (в нее не дают вклада
диаграммы без петель) в виде
+ ЛцрЛуо + ЛцоЛур) + конечные слагаемые,
где К — потенциально расходящаяся константа. Однако в силу
сохранения тока
= о,
так что комбинация K(qvr\ + q r\VG + доЛур) конечна. Чтобы это
равенство было верно при д Ф 0, константа К сама должна быть
конечной. Это хороший пример роли принципов симметрии в про-
программе перенормировок. Если бы К оказалась бесконечной, ее нель-
нельзя было бы устранить перенормировкой константы связи взаимо-
взаимодействия (А А^J, поскольку такое взаимодействие не допускает-
допускается калибровочной инвариантностью. Но константа К на самом де-
деле конечна благодаря условиям, вытекающим из сохранения то-
тока, которые накладываются калибровочной инвариантностью.
* Напомним, что для этого Jt(q2) как функция q2 не должна иметь особенности
(типа полюса) при q2 = 0. — Прим. ред.
690 Глава 12. Общая теория перенормировок
Eg = 1, Ее = 0 и Ее = 1, Eg = О, 1, 2
В этих случаях D = 3 и D = 5/2, 3/2, 1/2, соответственно,
однако все такие диаграммы обращаются в нуль в силу лоренц—
инвариантности *.
Еу = 3, Ее = О
В этом случае D = 1, но такие диаграммы обращаются в нуль
в силу инвариантности относительно зарядового сопряжения.
Читатель, возможно, уже обратил внимание на то, что не-
независимые расходящиеся константы А, В, С находятся в одно-
однозначном соответствии с независимыми параметрами Z2, Z3 и
5m контрчленов A1.1.9) в лагранжиане квантовой электродина-
электродинамики, которая содержит контрчлены. Эти контрчлены вносят не-
непосредственный вклад Z25m - (Z2 - 1)(гр + m) в Е*(р). Требование,
чтобы положение и вычет одночастичного полюса были бы таки-
такими же, как у свободного пропагатора, означает, что нужно вы-
выбрать Z2 и 5т таким образом, чтобы полная функция Е* удовле-
удовлетворяла условию A2.2.4), т.е.
Z25m = -A, A2.2.9)
Z2-l = -B, A2.2.10)
и полная электронная собственноэнергетическая вставка была бы
конечной функцией ТУКр)'-
A2.2.11)
Кроме того, контр члены i| вносят вклад в Г, равный (Z2 — 1)у .
Используя формулу A2.2.6), видим, что полная вершинная функ-
функция равна
A2.2.12)
* Точнее, обращаются в нуль функции Грина. В трех последних случаях
можно было бы сослаться также на глобальную калибровочную инвариантность
(сохранение электрического заряда). Но в этих случаях по указанной причине
не существует и самих диаграмм — их невозможно нарисовать. — Прим. ред.
12. 2. Сокращение расходимостей 691
Она не только конечна, но и удовлетворяет условию
п' гГ')У^(р,о), A2.2.13)
что можно иначе увидеть также из A0.6.13) и A0.6.14). Наконец, i^
вносит вклад -(Zg - l)(q2r|^v ~ g^gv) в П*цу(д). Для того, чтобы фо-
фотонный пропагатор имел полюс с тем же вычетом, что и для сво-
свободных полей, необходимо, чтобы коэффициент при (q2TLv ~ 9m9v)
в полном выражении для П (д) обращался в нуль, так что
Z3=l + C, 12.2.14)
и тогда фотонный пропагатор конечен:
22- A2.2.15)
До сих пор мы проверили, что расходимости, возникающие
от интегрирований по области импульсного пространства, в кото-
которой все внутренние имульсы велики (и имеют общие отношения),
являются полиномами по внешним импульсам, которые сокраща-
сокращаются при подходящем выборе контрчленов. Такие диаграммы бу-
будем называть расходящимися по индексу *. Прежде чем заключить,
что все ультрафиолетовые расходимости действительно можно уст-
устранить перенормировкой, следует рассмотреть расходимости, воз-
возникающие в диаграммах высших порядков при интегрировании по
областям импульсного пространства, где не все переменные интег-
интегрирования, а лишь их некоторое подмножество устремляется к
бесконечности. Например, в квантовой электродинамике расходи-
расходимости возникают от подинтегрирований, отвечающих расходящимся
* Появляющиеся здесь и ниже ключевые авторские термины superficially
divergent (convergent) diagrams (subdiagrams) и superficial divergence
(convergence) не имеют устойчивого русского эквивалента. Мы переводим их
здесь как «диаграммы (поддиаграммы), расходящися (сходящиеся) по индексу».
Расходимость (сходимость) диаграммы (поддиаграммы) по индексу означает,
что ее индекс расходимости неотрицателен (строго отрицателен) и опреде-
определяющий ее интеграл по внутренним импульсам расходится (сходится) в
области, где все внутренние импульсы однородным образом устремляются к
бесконечности. — Прим. ред.
692 Глава 12. Общая теория перенормировок
по индексам поддиаграммам, являющимся либо фотонными собст-
венноэнергетическими частями П*, либо электронными собствен-
ноэнергетическими частями ?*, либо электрон—электрон—фотонны-
электрон—электрон—фотонными вершинами Р1. Трудности рассмотрения этих расходимостей свя-
связаны с тем, что их нельзя устранить путем дифференцирования
по внешним импульсам: имеются слагаемые, в которых производ-
производные действуют только на внутренние линии в тех частях диаграм-
диаграммы, которые не входят в расходящиеся поддиаграммы, и тем са-
самым не уменьшают степень расходимости таких поддиаграмм. Как
отмечалось в предыдущем разделе, диаграмма или сумма диаграмм
действительно сходится тогда и только тогда, когда как она сама,
так и все ее поддиаграммы сходятся по индексу. Но где бы ни воз-
возникла такая расходящаяся поддиаграмма, она всегда сопровожда-
сопровождается бесконечным контрчленом. В электродинамике таковыми яв-
являются слагаемые в A1.1.9): -(Z3 - l)(g2TLv - q„gv) для каждого
U* (q), Z25m-(Z2 -l){ijp + m) для каждого L* и слагаемое (Z2- l)y-
для каждой вершины Р1. Как и для диаграммы в целом, эти контр-
контрчлены сокращают бесконечности в расходящихся поддиаграммах 1.
К сожалению, в такой простой аргументации есть пробел,
связанный с перекрывающимися расходимостями. Это означает, что
возможна ситуация, когда две расходящиеся поддиаграммы имеют
общую внутреннюю линию, так что нельзя рассматривать соответ-
соответствующие расходящиеся интегралы как независимые. В квантовой
электродинамике это случается только, если две электрон—элек-
электрон—электрон—фотонные вершины перекрываются внутри фотонной или элек-
электронной собственноэнергетической вставки* (см. рис. 12.2 и 12.3).
Полное рассмотрение проблемы перенормировки с учетом
перекрывающихся расходимостей должно включать рецепт уст-
* Если две собственноэнергетические вставки или такая вставка и вер-
вершинная часть будут иметь общую линию, то не хватит внешних линий,
чтобы прикрепить такую поддиаграмму к остальной части диаграммы. Ис-
Исторически тождество Уорда A0.4.26) использовалось для того, чтобы обой-
обойти проблему перекрывающихся расходимостей в собственной энергии элек-
электрона, выразив эту энергию через вершинную функцию, в которой пере-
перекрывающихся расходимостей не возникает. Мы не будем следовать таким
путем, поскольку в этом нет необходимости, кроме того, этот подход все
равно не решает проблемы собственной энергии фотона или других ней-
нейтральных частиц.
12. 2. Сокращение расходимостей
693
(Z2-D2
чЛЛЛЛЛ^ ЛлЛЛЛА
(Z2-lJ
ЛЛЛЛА)^ЛЛЛА
(^3 ~~ 1)перекрыв
Рис. 12.2 Некоторые диаграммы четвертого порядка для собственной энер-
энергии фотона в квантовой электродинамике, содержащие перекрывающиеся
расходимости. Линии со стрелками отвечают электронам, волнистые ли-
линии — фотонам. Крестиками отмечены вклады контрчленов
чЛЛАЛЛГ ЛлАЛЛА
Г
— 1)перекрыв
Рис. 12.3. Некоторые диаграммы четвертого порядка для собственной энер-
энергии электрона в квантовой электродинамике, содержащие перекрываю-
перекрывающиеся расходимости. Волнистые линии — фотоны, остальные линии —
электроны. Крестиками отмечены вклады контрчленов
ранения ультрафиолетовых расходимостей по индексу не только
для полной диаграммы, но и для всех ее поддиаграмм, а также
доказательство, что такой рецепт (по крайней мере формально)
осуществляется путем перенормировки масс, полей и констант
связи. Тогда теорема 2 утверждает, что все функции Грина пере-
перенормированных полей, выраженные через перенормированные
массы и константы связи, являются конечными. Первое доказа-
доказательство того, что перенормировка полей, масс и констант связи
делает как полную диаграмму, так и все ее поддиаграммы сходя-
сходящимися по индексу, было дано Саламом 5. Более детальный ре-
рецепт устранения ультрафиолетовых расходимостей был предло-
предложен Боголюбовым и Парасюком 6 и подправлен Хеппом 7, причем
694 Глава 12. Общая теория перенормировок
они показали эквивалентность своего рецепта перенормировке по-
полей, масс и констант связи. Наконец, Циммерман 8 доказал, что
этот рецепт действительно устраняет все расходимости по ин-
индексу как в полной диаграмме, так и во всех ее поддиаграммах,
и с помощью теоремы, доказанной в 2, пришел к выводу, что
перенормированные фейнмановские интегралы в импульсном про-
пространстве сходятся.
Коротко рецепт БПХЦ для устранения расходимостей по
индексу требует, чтобы мы рассмотрели все возможные способы
(их называют лесами) поместить полную диаграмму и/или ее под-
поддиаграммы в ящики, которые могут находиться один внутри дру-
другого, но не перекрываться. (Ниже приведен пример.) Для каждого
леса мы определяем вычитательное слагаемое, заменяя подын-
подынтегральное выражение для каждой поддиаграммы внутри ящика,
имеющей индекс расходимости D, (начиная с самых внутренних
ящиков и двигаясь наружу) на первые D + 1 слагаемых его раз-
разложения в ряд Тейлора по импульсам, входящим или выходя-
выходящим из этого ящика *. Фейнмановская амплитуда с вычитаниями
определяется исходными диаграммами минус все вычитательные
слагаемые, в том числе, и слагаемое для леса, состоящего из
единственного ящика, окружающего всю диаграмму.
Довольно легко показать, что вычисленная таким образом
фейнмановская амплитуда с вычитаниями совпадает с той, кото-
которую мы получили бы, заменив все поля, массы и константы связи
в исходном лагранжиане на их перенормированные аналоги. Разни-
Разница между этой процедурой и тем способом перенормировки, кото-
который был использован в гл. 11, заключается в том, что перенорми-
перенормированные поля, константы связи и массы определены через ам-
амплитуды, взятые в необычной точке нормировки **, в которой все
4-импульсы обращаются в нуль. (В этом смысле обсуждавшиеся
* В указанном виде рецепт применим как к неперенормируемым, так и
к перенормируемым теориям. Для последних этот рецепт означает, что не
следует делать никаких вычитаний, если только ящик не содержит одну
из конечного числа диаграмм, отвечающих перенормируемым слагаемым
в лагранжиане.
** Англоязычный термин renormalization point стандартно переводится
как точка нормировки (в этой точке перенормированная амплитуда при-
принимает заданные значения). — Прим. пер.
12. 2. Сокращение расходимостей 695
в начале данного раздела одномерные расходящиеся интегралы яв-
являются простейшим примером выделения расходящихся слагае-
слагаемых методом БПХЦ.) Однако в выборе такой точки нормировки нет
ничего особенного; если фейнмановская амплитуда становится ко-
конечной, будучи записанной в терминах необычным образом пере-
перенормированных величин, то ее можно записать и в терминах обыч-
обычным образом перенормированных полей, констант связи и масс, не
вводя при этом новых бесконечностей.
На практике нет необходимости пользоваться вычитатель-
ной процедурой БПХЦ. Замена полей, масс и констант связи их
перенормированными аналогами (определенными в любой удоб-
удобной точке нормировки) автоматически приводит к появлению
контрчленов, сокращающих все бесконечности. Вместо того, что-
чтобы доказывать, что вычитательная процедура БПХЦ действи-
действительно делает все интегралы сходящимися, рассмотрим один при-
пример, показывающий, как работает схема перенормировок даже
при наличии перекрывающихся расходимостей.
Рассмотрим вклад четвертого порядка в фотонную собствен-
ноэнергетическую вставку П*цу(д), показанную на рис. 12.2. (В этом
случае леса состоят из диаграмм, которым отвечают полный ин-
интеграл по р и р', подинтеграл только по р и подинтеграл только
по р' *.) С учетом соответствующих контрчленов для вершинных
частей и перенормировки поля фотона этот вклад имеет вид:
X Tr{S(p')yvS(p' + q)ypS(p
су
- 2(Z2 - 1J -^ Г d±p Tr{yvS(p + q)yilS(p)} A2-2-16)
- (Z3 - 1)nepeKp.(92'V - 9n9v)>
где S(p) = [-ip + m]/ [p2 + m2 - ie], (Z2-lJ - слагаемое второго по-
порядка по е в (Z2 - 1), (Zg - 1)перекр - логарифмически расходя-
расходящаяся константа четвертого порядка по е, сокращающая слагае-
слагаемые второго порядка по д^ в [П* (д)]п . Множитель 2 во втором
* В данном случае имеется пять лесов, но только три крестика. — Прим. ред.
696 Глава 12. Общая теория перенормировок
слагаемом возникает из-за того, что каждой из двух вершин в
диаграмме второго порядка собственной энергии фотона соответ-
соответствует перенормировочный контр член Z2 — 1. Заметим, что пер-
первое слагаемое можно понимать либо как результат вставки в фо-
фотонную собственноэнергетическую часть, даваемую интегралом по
р, вместо левой вершины поправки к ней, т. е. вершинной части
третьего порядка, которая дается интегралом по р', либо как ре-
результат вставки в фотонную собственноэнергетическую часть,
даваемую интегралом по р', вместо правой вершины поправки к
ней, даваемой интегралом по р. Однако нельзя рассматривать пер-
первое слагаемое как вставку двух независимых поправок к верши-
вершинам, т. к. в диаграмме есть только один фотонный пропагатор.
Чтобы понять, как обращаться с бесконечностями в A2.2.16),
заметим, что
[(z2 - D2 + ВД, = ^ J^T^ V(p')y^<pV ' A2-2Л7)
где R2 — конечный остаток. (В силу лоренц-инвариантности инте-
интеграл справа пропорционален у . Разность между этим интегралом
и (Z2 — 1 Jу равна полной перенормированной электрон—электрон-
фотонной вершине во втором порядке по е при нулевых значени-
значениях импульсов электрона и фотона, и поэтому конечна.) Это пово-
ляе переписать A2.16) в виде:
\2r
(р-р) -ге
72^
^ + q)ypS(p)y[lS(p)yp]
р* -ге
.¦_2
г4р Tr{yv^(p
ге2
- 1)перекр.(<? Лцу^Зц^у)- A2 2 18)
12. 2. Сокращение расходимостей 697
Рассмотрим сначала интегрирование только по р'. Каждое из
первых двух слагаемых логарифмически расходится, однако их раз-
разность конечна. Третье слагаемое также логарифмически расходится
(при калибровочно инвариантной регуляризации), но расходимость
в этом слагаемом (в противоположность двум первым) имеет вид
полинома второго порядка по g с конечным остатком. Эта остающая-
остающаяся расходимость сокращается со слагаемым -(Z3-l)(q2rfv - дцду),
которое уничтожает все слагаемые второго порядка в разложении
П* (д). Таким образом, подинтегрирование по р' приводит к конеч-
конечному результату. Из симметрии выражения A2.2.16) следует,
чтоточно таким же образом дает конечный результат подинтегри-
подинтегрирование по р. Общего вида подинтегрирования по р и р' при фикси-
фиксированном значении ар + Ър' (а и Ъ — произвольные ненулевые кон-
константы) явно сходятся, а результат совместного интегрирования по
р и р' приводится к конечному ответу с помощью включения контр-
контрчлена —{Zz—l){q2rf* — q^qv). Таким образом, интеграл A2.2.18) и лю-
любой его подинтеграл удовлетворяют требованиям сходимости по ин-
индексу, и поэтому согласно теореме 2, сформулированной в преды-
предыдущем разделе, все выражение действительно сходится.
В электродинамике существует естественное определение
перенормированных констант связи, масс и полей. Однако так бы-
бывает не всегда. Например, рассмотрим теорию одного действи-
действительного скалярного поля ф(ж) с лагранжианом
A2.2.19)
В однопетлевом приближении матричный элемент скаляр-
скалярного рассеяния согласно фейнмановским правилам имеет вид
S(qlq2
12
где
B%fA6E[E'2E1E2I/2
A2.2.20)
698
Глава 12. Общая теория перенормировок
1г п2Г -г 1
g1/g?)= -гBлLд + — Г-гBлLд1
х
+ /сJ + т2 - ге][(д2 - /сJ + т2 - ге]
—> —
A2.2.21)
и др д2, д'1, д'2 — входящие и выходящие 4-импульсы. Объединяя
знаменатели и обычным способом поворачивая контур интегриро-
интегрирования по к0, получаем:
F = 9"iS?
к3 dk dx \\k2 + m2 - sx{l - x)] 2
Jo L
[k2 +m2 -tx(l-x)]~2 +[k2 +m2 -ux(l-x)]~2}, A2.2.22)
где s, t и и — мандельстамовские переменные
связанные соотношением s + t + и = 4m2, a x — фейнмановский
параметр, вводимый при объединении знаменателей. Совершая
ультрафиолетовое обрезание при к = А, приходим к выражению
(при Л 3> т)
32л2
+ ln
'о
Л2
m - tx(l - x)
ym - sx(l - x)
Uf л:
т2-ихA-х)
Мы можем определить перенормированную константу gR как
значение F в любой точке s, t, и, при условии, что мы остаемся в
области, где F действительна. Например, предположим, что с
целью сохранить симметрию между скалярами, мы выбираем
12. 3. Нужна ли перенормируемость? 699
точку нормировки р2 = р| = р[2 = р?2 = Ц2, s = t = и = -4ц2 / 3 вне
массовой поверхности *. Определяя перенормированную констан-
константу gR как значение F в этой точке, имеем
3g2
32л2
i (A2) 1 (\ 1 f4x(l-x) , т2
1п|-т1-1-| dxln\ + ^^i 1-... A2.2.25)
Зависимость от обрезания в A2.2.24) сокращается в порядке
gR, и в результате остается конечная формула для F, выражен-
выраженная через gR.
( т + 4жA ж)ц / 3 | | т +4жAж)ц /3 |1
^ 2 2 \
A2.2.26)
Здесь ц2 можно считать любой действительной величиной,
большей — Зт2, и в этой области gR действительна. Явная зависи-
зависимость A2.2.26) от ц, конечно, сокращается с зависимостью от ц
перенормированной константы. Эта свобода изменять рецепт пере-
перенормировки (которая, конечно, существует и в электродинамике,
и в других реалистичных теориях) будет иметь большое значение,
когда мы перейдем к рассмотрению в т. II метода ренормгруппы.
12.3. Нужна ли перенормируемость?
В предыдущем разделе мы обнаружили специальный класс
теорий, в лагранжиане которых имеется лишь конечное чи-
число слагаемых, и к которым тем не менее применима программа
* Проследив еще раз вывод формулы A2.2.25), можно убедиться, что в
нем не использовались условия р^ = р^ = р'г2 = р'^ = -т2, так что форму-
формула A2.2.24) верна при любых значениях масс внешних линий.
700 Глава 12. Общая теория перенормировок
перенормировок. Это теории, в которых все взаимодействия удов-
удовлетворяют условию перенормируемости
где di и п^ — числа производных и полей типа / во взаимодейст-
взаимодействиях типа г, a s- есть (с некоторыми уточнениями) спин полей
типа /. Чтобы в таких теориях была осуществима перенормиров-
перенормировка, обычно еще необходимо, чтобы все разрешенные принципами
симметрии перенормируемые взаимодействия действительно со-
содержались в лагранжиане.
Важно, что существует лишь ограниченное число взаимо-
взаимодействий такого типа. Величина At становится отрицательной, ес-
если у нас слишком много полей или производных, или полей со
слишком большими значениями спина. Если нет специальных со-
сокращений, вообще не существует перенормируемых взаимодей-
взаимодействий, включающих поля спина s- > 1, поскольку единственное
возможное слагаемое в лагранжиане с А^ > 0, включающее такое
поле вместе с двумя или более другими полями, должно содер-
содержать одно поле с s- = 1 и два скаляра без всяких производных,
что противоречит лоренц-инвариантности. В т. II мы увидим, что
произвольные безмассовые калибровочные поля спина 1 в соот-
соответствующей калибровке эффективно имеют s-= 0 как у фотона,
кроме того, в т. II будет показано, что даже массивные калибро-
калибровочные поля могут эффективно иметь sf = 0 в зависимости от
того, каким образом они приобрели массу. Если не считать этих
особых случаев, в табл. 12.2 приведен список всех перенормируе-
перенормируемых слагаемых в лагранжиане, разрешенных лоренц-инвариант-
ностью и калибровочной инвариантностью и включающих скаля-
скаляры (s = 0), фотоны (s = 0) и фермионы спина 1/2 (s = 1/2).
Мы видим, что требование перенормируемости накладыва-
накладывает жесткие ограничения на возможные физические теории. По-
Подобные ограничения являются ценным ключом к пониманию струк-
структуры этих теорий. Например, лоренцовская и калибровочная
инвариантности сами по себе разрешают введение «паулиевского»
слагаемого, пропорционального X|/[yi,Yv]\|/FMV в лагранжиан кванто-
квантовой электродинамики, что сделало бы магнитный момент элек-
электрона настраиваемым параметром, но мы исключаем подобные
слагаемые, поскольку они неперенормируемы.
12. 3. Нужна ли перенормируемость?
701
Таблица 12.2
Скаляры
1
2
2
3
4
2
2
1
0
0
0
0
Фотоны
0
0
0
0
0
1
2
0
2
0
0
1
Спин 1/2
0
0
0
0
0
0
0
2
0
2
2
2
0
0
2
0
0
1
0
0
2
0
1
0
3
2
0
1
0
0
0
0
0
1
0
0
¦щ
ф
ф2
ЭцфЭ^ф
фЗ
Ф4
фЭцфА^
Ф2АЦА^
Ф W
W
Табл. 12.2. Допустимые перенормируемые слагаемые в лагранжиане,
содержащие скалярные поля (р, дираковские поля \|/ и поля фотонов А^.
Величины п^ и dj — число полей типа / и число производных во
взаимодействии типа i, \ — размерность соответствующего коэффициента
Успешные предсказания квантовой электродинамики вроде
описанного в разделе 11.3 вычисления магнитного момента электро-
электрона можно рассматривать как подтверждения принципа перенорми-
перенормируемости. Это же относится и к стандартной модели слабых, элек-
электромагнитных и сильных взаимодействий, обсуждаемой в т. П. Есть
множество слагаемых, которые можно было бы добавить в лагран-
лагранжиан этой теории, например, четырехфермионные взаимодействия
между кварками и лептонами, и которые полностью исказили
бы все предсказания стандартной модели, но такие слагаемые ис-
исключаются только на том основании, что они неперенормируемы.
Должны ли мы верить утверждению, что лагранжиан может
содержать только перенормируемые взаимодействия? Как мы ви-
702 Глава 12. Общая теория перенормировок
дели в предыдущем разделе, если включить в лагранжиан все бес-
бесконечное количество взаимодействий, разрешенных симметриями,
то для сокращения каждой ультрафиолетовой расходимости най-
найдется соответсвующий контрчлен. В этом смысле, как и утвержда-
утверждалось ранее, неперенормируемые теории так же перенормируемы,
как и перенормируемые теории, если только в лагранжиан вклю-
включены все возможные слагаемые.
В последние годы усиливается ощущение, что перенормируемость
не является фундаментальным физическим требованием, и что на са-
самом деле любая реалистичная квантовая теория поля должна содер-
содержать как перенормируемые, так и неперенормируемые слагаемые.
Такое изменение точки зрения можно отчасти проследить в продолжаю-
продолжающихся неудачных попытках построить перенормируемую теорию гра-
гравитации. В общем классе метрических теорий тяготения, подчиняю-
подчиняющихся эйнштейновскому принципу эквивалентности, вообще нет
перенормируемых взаимодействий: общековариантные взаимодействия
должны строиться из тензора кривизны и его общековариантных произ-
производных, и поэтому даже в «калибровке», в которой пропагатор гравито-
гравитона ведет себя как к~2, эти взаимодействия содержат слишком много про-
производных метрического тензора для того, чтобы быть перенормируемыми
В частности, неперенормируемость общей теории относительности сле-
следует из того известного факта, что константа гравитационного
взаимодействия 8jiGn = B,43 • 1018 ГэВ)~2 имеет отрицательную размер-
размерность. Даже если со всем остальным все в порядке, сокращение расходи-
мостей из-за виртуальных гравитонов будет требовать наличия в ла-
лагранжиане всех разрешенных симметриями взаимодействий, включающих
не только гравитоны, но и любые частицы.
Но если перенормируемость не является фундаментальным
физическим принципом, то как же объяснить успех перенорми-
перенормируемых теорий вроде квантовой электродинамики и стандартной
модели? Ответ можно получить с помощью простого размерного
анализа. Мы уже отмечали, что константа связи взаимодействия
типа i имеет размерность
[gJ~[Macca]AS A2.3.1)
где показатель Ai дается формулой A2.1.9). К неперенормируемым
относятся те взаимодействия, у которых константы связи имеют
отрицательную массовую размерность. Представляется разум-
12. 3. Нужна ли перенормируемость? 703
ным предположить на основании формулы A2.3.1), что константы
связи не только имеют размерности, определяемые значением At,
но имеют величину порядка
д. « МА< , A2.3.2)
где М — некоторая общая масса. (Именно так обстоит дело в слу-
случае эффективных теорий поля, которые рассмотрены ниже и,
более подробно, в т. П.) При расчете физических процессов, про-
происходящих на характерных масштабах к <^ М, включение непе-
ренормируемого взаимодействия типа i с At < 0 приводит к появ-
появлению множителя gfj ~ M { , который по размерным соображени-
соображениям должен сопровождаться множителем к i, так что в резуль-
результате такое взаимодействие подавляется * при к <^ М множителем
{к / M)~Ai <O- (Этот аргумент более аккуратно будет рассмотрен в
т. II с помощью метода ренормгруппы.) Успех перенормируемых
теорий электрослабых и сильных взаимодействий всего лишь по-
показывает, что М намного больше, чем тот масштаб энергий, на
котором эти взаимодействия проверены.
Например, ведущими неперенормируемыми поправками к
обычной электродинамике электронов или мюонов были бы те взаи-
взаимодействия размерностью 5, которые подавляются только одним
множителем 1/М. Лоренцовская, калибровочная и С Р—инвариант-
Р—инвариантность допускают единственное такое взаимодействие — паулиев-
ское слагаемое вида (ie/M) yh^YjyF^. Согласно A0.6.24), A0.6.17)
и A0.6.19), такое слагаемое вносит в магнитный момент электрона
* В этом месте существенно предположение, что ультрафиолетовые
расходимости были устранены с помощью перенормировки, так что от-
отсутствуют множители, содержащие ультрафиолетовое обрезание Л, ко-
которые могут помешать размерному анализу. В противном случае, из этого
анализа следует, что при Л —> °° каждая дополнительная неперенормиро-
ванная константа связи gi с Ai < 0 сопровождалась бы растущим множите-
множителем д~дг • Уже очень давно аргументы, основанные на размерных сообра-
соображениях, привели Гейзенберга к классификации взаимодействий в соот-
соответствии с размерностью их констант связи и к предположению10, что при
энергиях порядка gl!Ai должны возникать новые явления, например, при
энергии Gp ~ 300 ГэВ, где GF — четырехфермионная константа связи в
фермиевской теории бета-распада. После развития теории перенормиро-
перенормировок Саката и др. отметили11, что неперенормируемыми являются теории,
в которых константы связи имеют отрицательную размерность.
704 Глава 12. Общая теория перенормировок
или мюона вклад порядка 4е/М. Рассчитанное значение магнитно-
магнитного момента электрона согласуется с экспериментом с точностью
до слагаемых порядка 10~10(е/2те), так что М должна быть боль-
больше, чем 8 • 1010ше = 4 • 107 ГэВ.
Этот предел может быть ослаблен, если форму неперенор-
мируемых взаимодействий ограничивают другие симметрии. На-
Например, обычный лагранжиан квантовой электродинамики инва-
инвариантен относительно кирального преобразования \|/ —> YgV|/, если
не считать изменения знака у фермионного массового члена —т \|Л|/.
Если предположить, что полный лагранжиан инвариантен относи-
относительно формальной симметрии \|/ —> у5\|/, т —> —т, то паулиевское
слагаемое в лагранжиане должно было бы входить с дополнитель-
дополнительным множителем т/М, так что его вклад в магнитный момент был
бы только порядка 4ет/М2. Из-за появления лишнего множителя
т, самая значимая оценка на М извлекается из формул для мюо-
мюона, а не для электрона. Рассчитанное значение магнитного момента
мюона согласуется с экспериментом с точностью до слагаемых по-
рядка 10~8(е/2ше), так что М должна быть больше, чем -\/8-108гп„
~ 3 • 103 ГэВ. В любом случае, если М лежит где-то в области
значений 1018 ГэВ, мы с уверенностью пренебрегаем любыми не-
перенормируемыми взаимодействиями, которые могут возникать в
квантовой электродинамике.
Эти соображения позволяют разобраться с некоторыми про-
проблемами, связанными со слагаемыми с высшими производными в
лагранжиане. Например, в общей теории действительного ска-
скалярного поля ф можно ожидать появления в лагранжиане слагае-
слагаемых вида фПпф. Любое подобное слагаемое будет давать прямой
вклад в скалярную собственноэнергетическую функцию ГГ(д2), про-
пропорциональный (д2)". Если бы мы включили такой вклад во всех
порядках, но пренебрегли бы всеми другими эффектами непере-
нормируемых взаимодействий, то пропагатор скалярного поля
А'(д2) = 1 / (д2 + т2 — П (д2)) имел бы не один простой полюс по д2
при отрицательных д2, который можно ожидать на основании об-
общих соображений раздела 10.7, а п таких полюсов (некоторые из
которых могут совпадать), вообще говоря, при комплексных зна-
значениях д2. Но если неперенормируемое слагаемое фПпф содержит
коэффициент порядка М~2^п~1\ где М 3> т, тогда дополнительные
полюсы находятся при значениях д2 порядка М2, т. е. в области,
где неправомерно игнорировать бесконечное число других непе-
12. 3. Нужна ли перенормируемость? 705
ренормируемых взаимодействий, которые также должны появить-
появиться в лагранжиане. Итак, появление слагаемых с высшими произ-
производными в общем неперенормируемом лагранжиане не противо-
противоречит общим принципам квантовой теории поля, использован-
использованным в разделе 10.7. Однако по тем же соображениям нельзя ис-
использовать слагаемые с высшими производными, чтобы избежать
появления ультрафиолетовых расходимостей, как это неоднократ-
неоднократно предлагалось. Слагаемое ЛГ^^фП'Чр в лагранжиане обеспечи-
обеспечивает обрезание при импульсах q2 ~ М2, но при таких импульсах
нельзя игнорировать все другие неперенормируемые взаимодей-
взаимодействия, которые обязательно должны присутствовать.
Вклад неперенормируемых взаимодействий сильно подав-
подавлен, однако может быть обнаружен, если они приводят к эффек-
эффектам, запрещенным при отсутствии таких взаимодействий. Напри-
Например, мы увидим в разделе 12.5, что симметрии относительно за-
зарядового сопряжения и пространственной инверсии являются ав-
автоматическим следствием структуры электромагнитных взаимо-
взаимодействий, определяемой требованиями калибровочной и лорен-
цовской инвариантности и перенормируемости. Однако можно легко
вообразить неперенормируемые слагаемые, нарушающие эти сим-
симметрии, например, слагаемое с электрическим дипольным мо-
моментом электрона вида ?Y5[Ym>Yv]V^1m'v или фермиевское взаимодей-
взаимодействие Х|/у5Ум? WV Сейчас широко распространена точка зрения,
что сохранение барионного и лептонного чисел нарушается очень
слабыми эффектами сильно подавленных неперенормируемых
взаимодействий. Другим примером детектируемых неперенорми-
неперенормируемых взаимодействий является гравитация. Как отмечалось вы-
выше, у гравитонов вообще нет перенормируемых взаимодействий.
Но, естественно, мы наблюдаем гравитацию, потому что она об-
обладает особым свойством: гравитационные поля всех частиц в мак-
макроскопическом теле когерентно складываются.
Хотя неперенормируемые теории содержат бесконечное число
свободных параметров, они, тем не менее, сохраняют значительную
предсказательную силу 12: эти теории позволяют вычислить неанали-
неаналитические части фейнмановских амплитуд, типа слагаемых In q и q In q
в рассмотренных в начале предыдущего раздела одномерных приме-
примерах. Такие вычисления воспроизводят результаты, вытекающие из ак-
аксиом теории ^-матрицы, а именно, что .^-матрица обладает лишь те-
теми сингулярностями, которые требуются условием унитарности.
706 Глава 12. Общая теория перенормировок
Парадоксальным образом неперенормируемые квантовые тео-
теории поля оказываются наиболее полезными в случаях, когда прин-
принципы симметрии запрещают перенормируемые взаимодействия.
В таких случаях можно развить полезную теорию возмущений,
разлагая в ряд по степеням k/М. Такой подход был детально раз-
разработан для теории пионов низких энергий 12>13; которая будет
подробно обсуждаться в т. II, и в теории гравитонов низких энер-
энергий 14. Чтобы привести пример попроще, рассмотрим теорию дей-
действительного скалярного поля, удовлетворяющую принципу ин-
инвариантности относительно трансляций поля
ф(х) -» ф(х) + ? ,
где ? — произвольная константа. Эта симметрия запрещает любое
перенормируемое взаимодействие или массу скаляра, но допускает
бесконечное число неперенормируемых взаимодействий с производ-
производными
где д ~ М~4, а «...» означает слагаемые с большим числом произ-
производных или полей. (Для простоты здесь предполагается, что тео-
теория симметрична относительно отражения ф —> —ф.) Согласно про-
проделанному выше размерному анализу, диаграмма произвольной
реакции, в которой все энергии и импульсы порядка к <х М,
подавлена фактором (k/M)v, где
и пг, d^ — числа скалярных полей и их производных во взаимо-
взаимодействии типа i, а У. - число вершин таких взаимодействий в
диаграмме. При к <^ М главный вклад в любой процесс соответст-
соответствует наименьшему значению V. Формулу для V можно предста-
представить в более удобном виде, используя известные топологические
тождества для связных диаграмм:
12. 3. Нужна ли перенормируемость? 707
где I, E и L — числа внутренних линий, внешних линий и петель в
нашей диаграмме. Комбинируя эти выражения, получаем
Симметрия относительно трансляций полей требует, что-
чтобы каждое поле сопровождалось по меньшей мере одной произ-
производной, так что величина di — пг, а также L неотрицательны для
всех взаимодействий. Таким образом, для данного процесса (т. е.
при фиксированном числе внешних линий Е) главными будут
вклады от древесных диаграмм (с L = 0), отвечающим взаимо-
взаимодействиям с минимальным числом di = n{ производных. Иными
словами, в ведущем порядке можно считать, что лагранжиан
зависит только от первых производных поля. Поправки более
высокого порядка могут содержать петли и/или взаимодейст-
взаимодействия с большим числом производных от некоторых полей. Но в
любом данном порядке V по (к/М) нужно рассматривать только
конечное число диаграмм, для которых L < D — IE + v)/4, и только
конечное число типов взаимодействий.
Например, скаляр-скалярное рассеяние в ведущем порядке
определяется древесной диаграммой с одной вершиной, вклад ко-
которой можно найти, используя взаимодействие — д(д фЭ^фJ в пер-
первом порядке теории возмущений. Согласно нашей формуле для V,
главная поправка, подавленная при низких энергиях множите-
множителем (к/МJ, возникает от другой древесной диаграммы с одной
вершиной, порождаемой взаимодействием с двумя дополнитель-
дополнительными производными вида * Э ЭфЭ^фЭ^фЭЧр. Следующие поправ-
поправки, подавленные при низких энергиях двумя дополнительными
множителями к/М, возникают как от однопетлевой диаграммы
рис. 12.4 (с учетом перестановки внешних линий), вычисленной
только с учетом взаимодействия — д(д фЭ^фJ, так и от древесных
диаграмм с единственной вершиной, возникающей от четвертич-
четвертичного взаимодействия с восемью производными, константы кото-
* В согласии с замечанием в разделе 7.7, мы исключаем взаимодейст-
взаимодействия, содержащие dtp, поскольку с помощью уравнений поля для (р можно
выразить такие взаимодействия через другие.
708 Глава 12. Общая теория перенормировок
N
X
Рис. 12.4. Однопетлевая диаграмма скаляр-скалярного рассеяния в теории с
четвертичным взаимодействием с производными
рого содержат бесконечные вклады, сокращающие ультрафиоле-
ультрафиолетовые расходимости петлевой диаграммы *.
Петлевая диаграмма приводит также к конечным слагаемым
в амплитуде рассеяния, пропорциональным выражениям типа
s4 In s + t4 In t + м4 In и, s2t2 In и + t2u2 In s + u2s2 In t и т. д. с вычис-
вычисляемыми коэффициентами, пропорциональными д2. Указанные ко-
конечные слагаемые представляют поправки к амплитуде рассея-
рассеяния в низшем порядке, необходимые для обеспечения унитарности
5-матрицы, однако пока что самый простой способ их расчета —
пертурбативная квантовая теория поля.
Хотя неперенормируемые теории позволяют получить по-
полезные разложения по степеням энергии, они неизбежно теряют
всякую предсказательную силу при энергиях порядка характер-
характерной для всех констант общей шкалы масс М. Если буквально вос-
воспринимать такие разложения, то полученные для элементов
5-матрицы результаты будут противоречить при Е ^> М ограниче-
ограничениям, накладываемым условием унитарности. Похоже, что в отно-
отношении происходящего при таких энергиях существуют только две
возможности. Одна заключается в том, что растущий вклад эф-
эффектов неперенормируемых взаимодействий как-то насыщается,
так что никаких противоречий с унитарностью не возникает 15. Дру-
Другая связана с появлением на масштабах порядка М какой-то новой
физики. В этом случае неперенормируемые теории, описывающие
* Если использовать размерную регуляризацию, то это единственные
ультрафиолетовые расходимости, возникающие в однопетлевых диаграм-
диаграммах. В других методах регуляризации возникают также четвертичные и
квадратичные расходимости, которые сокращаются контрчленами в четы-
рехскалярных взаимодействиях с четырьмя или шестью производными.
12. 3. Нужна ли перенормируемость?
709
природу при энергиях Е <х М, являются не истинно фундамен-
фундаментальными, а просто эффективными теориями поля.
Вероятно, самым первым примером эффективной теории по-
поля была построенная в 1930-х годах Эйлером и др.16 теория низ-
низкоэнергетических фотон-фотонных взаимодействий (см. раздел 1.3).
По существу они вычислили вклад в фотон-фотонное рассеяние
фейнмановских диаграмм типа показанной на рис. 12.5, и обнару-
обнаружили, что при энергиях много меньших те рассеяние света на
света оказывается таким же, как если бы оно было вычислено с
помощью эффективного лагранжиана
°~2-[(Е2-В2J+7(Е-ВJ1
'-эфф
45mj
еЕ еВ
+ более высокие порядки по —- и
т„
т„
Эйлер и др. использовали этот эффективный лагранжиан толь-
только в древесном приближении, и вычислили ведущие слагаемые в
матричных элементах фотонного взаимодействия. Лишь намного
позднее такие лагранжианы, несмотря на их неперенормируемость,
стали использовать вне рамок древесного приближения 12>17.
Рис. 12.5. Диаграмма фотон-фотонного рассеяния. Ее вклад при низких энергиях
можно вычислить, исходя из эффективного лагранжиана Эйлера и др.16.
Прямые линии отвечают электронам, волнистые — фотонам
710 Глава 12. Общая теория перенормировок
На современном жаргоне мы говорим, что при получении
такого лагранжиана «по электронам было произведено интегри-
интегрирование», поскольку в однопетлевом приближении
ехр г «WE, В) d4x =
ехрЫ
Более общая процедура заключается в том, чтобы выписать
самый общий неперенормируемый эффективный лагранжиан, с
его помощью рассчитать различные амплитуды в виде разложе-
разложений в ряд по энергиям и импульсам, а затем выбрать константы в
эффективном лагранжиане, сравнив полученные результаты с те-
теми, которые выводятся с помощью лежащей в основе теории.
Мы еще вернемся к эффективным теориям поля, особенно
при рассмотрении нарушенных симметрии в т. П. Как будет пока-
показано, эффективные теории поля полезны, даже если их нельзя
вывести из лежащей в основе теории, либо потому, что эта тео-
теория неизвестна, либо потому, что взаимодействия в ней слишком
сильны, чтобы можно было использовать теорию возмущений. Дей-
Действительно, даже если мы ничего не знаем о свойствах заряжен-
заряженных частиц, рассеяние фотонов при достаточно низких энергиях
должно будет описываться эффективным лагранжианом, содер-
содержащим слагаемые (Е2 — В2J и (Е-ВJ, поскольку это единственные
четвертичные калибровочно и лоренц-инвариантные слагаемые,
не содержащие производных от Е и В. Слагаемые с такими произ-
производными должны быть подавлены при низких энергиях фотонов Е
дополнительными множителями Е/М, где М — некоторая типич-
типичная масса заряженных частиц, по которым было произведено
интегрирование. Можно продвинуться еще дальше: будет показа-
показано, что эффективные теории поля полезны даже в том случае,
когда описываемые ими легкие частицы вообще не присутствуют
в исходной теории, а состоят из тяжелых частиц, по которым
произведено интегрирование. Лежащая в основе теория может
вообще не быть теорией поля — трудности с включением грави-
гравитации привели многих теоретиков к убеждению, что такая тео-
теория есть на самом деле теория струн. Но откуда бы ни возникала
эффективная теория поля, она неизбежно должна быть непере-
нормируемой.
12. 4. Плавающее обрезание 711
12.4. Плавающее обрезание *
Прежде чем завершить эту главу, полезно сделать несколь-
несколько замечаний о связи общепринятой теории перенормировок с под-
подходом, впервые развитым Вильсоном 18. В методе Вильсона вво-
вводится «плавающее» конечное ультрафиолетовое обрезание (либо
резкое, либо сглаженное) при импульсах с компонентами порядка
Л, а затем вместо устремления Л —» °° требуется, чтобы голые
константы теории ** (входящие в лагранжиан) зависели от Л таким
образом, чтобы все наблюдаемые величины не зависели от Л.
Удобно работать с безразмерными параметрами. Если голая
константа связи или массовый параметр 5^(Л) имеют размерность
[масса]Аг', можно определить соответствующий безразмерный па-
параметр <$\ формулой
Л-А<д<(Л). A2.4.1)
На основании обычного размерного анализа получаем, что значе-
значение ^ при каком-то значении Л' параметра обрезания можно за-
записать как функцию значения <§г при другом значении параметра
Л и отношения Л'/Л:
A2.4.2)
В функции F не могут появиться никакие другие парамет-
параметры, кроме Л' и Л, поскольку в ней не может быть ультрафиоле-
ультрафиолетовых или инфракрасных расходимостей. Действительно, разни-
разница между константами при значениях Л и Л' возникает от диа-
диаграмм, у которых импульсы внутренних линий имеют значения
между Л и Л'. Дифференцируя A2.4.2) по Л' и полагая затем Л'
равным Л, приходим к дифференциальному уравнению для ^:
* Этот раздел лежит несколько в стороне от основной линии изложения
и может быть опущен при первом чтении.
** Имеются в виду параметры теории — как собственно константы
связи, так и массовые параметры. Ниже часто они все, для краткости,
называются константами связи (couplings). — Прим. ред.
712 Глава 12. Общая теория перенормировок
? A2.4.3)
dA
где РД5") = [3/92(Fi(^,2))]z=1. При малых константах связи функции
Р^(^) можно вычислить по теории возмущений. Это вильсоновский
вариант уравнения «ренормгруппы», которое мы в несколько иной
форме обсудим в т. П.
При любом конечном значении обрезания лагранжиан опре-
определяет эффективную теорию поля, в которой вместо интегриро-
интегрирования по «тяжелым» частицам вроде электрона в работе Эйлера
и др. (или в добавление к этому интегрированию) производится
интегрирование по всем частицам с импульсами больше Л. Даже
если в исходной теории есть конечное число параметров связи <fj®
при некотором значении обрезания Ло, при любом другом значе-
значении обрезания дифференциальное уравнение A2.4.3) приведет в
общем случае к ненулевым значениям всех констант связи, раз-
разрешенных принципами симметрии *.
Будем различать переномируемые и неперенормируемые кон-
константы связи, обозначив их, соответственно, ^а и ^п, где а нуме-
нумерует конечное число N констант связи (включая массы), для кото-
которых Аа > 0, a n нумерует бесконечное число констант связи с
размерностями Ап < 0. Мы хотим показать, что если константы
связи (§а(\) и (§п(\) при некотором начальном значении обреза-
обрезания Ло находятся на произвольной JV-мерной начальной поверх-
поверхности ,</q, тогда (с некоторыми уточнениями) при Л <х Ло они попа-
попадают на фиксированную поверхность У, не зависящую как от Ло,
так и от начальной поверхности **. Эта фиксированная поверх-
поверхность стабильна в том смысле, что порождаемая уравнением
A2.4.3) траектория, начинающаяся из любой точки поверхности,
остается на ней. Такая стабильная поверхность определяет мно-
* Единственными известными исключениями из этого правила являют-
являются теории, основанные на суперсимметрии 4.
** Эта теорема принадлежит Польчинскому 19. Ниже мы приводим со-
сокращенное и менее строгое ее доказательство. (В доказательстве Польчин-
ского начальная поверхность берется такой, что все неперенормируемые
константы связи равны нулю. Как мы увидим, константы связи достигают
одной и той же фиксированной поверхности при произвольной начальной
поверхности.)
12. 4. Плавающее обрезание 713
жество теорий с конечным числом параметров, физическое содер-
содержание которых не зависит от обрезания. Как пояснялось в преды-
предыдущем разделе, это есть существенное свойство перенормируе-
перенормируемых теорий. Далее, такая конструкция показывает, что исходная
теория, определенная при обрезании Ло, будет при Л « Ло выгля-
выглядеть как перенормируемая *.
Чтобы доказать приведенные утверждения, рассмотрим про-
произвольное малое возмущение Ъ'§г{А) значений %(Л), удовлетво-
удовлетворяющих уравнению A2.4.3). Оно удовлетворяет дифференциаль-
дифференциальному уравнению
где
М№ = Ш*№- A2.4.5)
Это уравнение связывает перенормируемые и неперенорми-
руемые константы связи, так что трудно увидеть разницу в их по-
поведении. Чтобы расцепить эту связь, введем линейную комбинацию
^n=8f5n-L^k^ 5%> A2.4.6)
аЪ бЭа \d(J Jab
где '§а° — значения перенормируемых констант связи при обреза-
обрезании Ло, которые мы будем использовать как координаты на на-
начальной поверхности, а ^п — значения неперенормируемых кон-
констант связи при обрезании Л, полученные из дифференциального
уравнения A2.4.3), причем начальные значения констант при об-
обрезании Ло отвечают точке на начальной поверхности с координа-
координатами 5а°. Чтобы вычислить производную ?,п по Л, заметим, что
производные Э^/Э^'0 удовлетворяют тому же дифференциаль-
дифференциальному уравнению A2.4.4), что и 6^. Доказательство того, что
* Конечно, симметрии некоторых теорий и их полевой состав таковы, что
невозможны никакие перенормируемые взаимодействия. К такому случаю
относятся теории, содержащие только поля фермионов, или только гравита-
гравитационное поле. При Л <?. AQ эти теории выглядят как теории свободных полей.
714 Глава 12. Общая теория перенормировок
^™> A2.4.7)
т
где
Nnm=Mnm-?-^\-^\ МЪт. A2.4.8)
аЪ дЬа \дЬ )аЪ
проводится элементарно. Теперь следует оценить матричные эле-
элементы матрицы Nnm. В теории свободных полей не требуется ни-
никаких обрезаний, поэтому при очень малых константах связи все
голые параметры становятся независящими от Л. Отсюда для ма-
малых констант безразмерные параметры ^ имеют масштаб Л ',
и матрица М-. имеет вид
Мц « -АД,- . A2.4.9)
Отсюда следует, что матрица iVnm приближенно равна —An5nm.
Определяющей характеристикой неперенормируемых констант
связи является условие Ап < 0. Из A2.4.7) следует, что, по край-
крайней мере для некоторой конечной области значений констант свя-
связи, где матрица iVnm положительно определена, величина Ъ,п ве-
ведет себя при Л « Ло как положительная степень Л/Ло. В этом
пределе возмущения связаны соотношением
] 85b- A2-4.10)
)аЪ
В частности, если немного изменить начальную поверхность
.9q и/или начальную точку на этой поверхности, и/или начальное
обрезание Ло, так что возмущения перенормируемых констант
связи 6^а обратятся в нуль при некотором обрезании Л <х Ло, то и
возмущения 6^' всех других констант также обратятся в нуль
при значении обрезания Л. Следовательно неперенормируемые кон-
константы ^П(Л) при Л « Ло могут зависеть только от перенормируе-
перенормируемых констант ^а(Л), а не от начальной поверхности, начальной
точки или начального обрезания Ло по отдельности. При Л « Afl
все константы достигают, таким образом, JV-мерной поверхно-
12. 4. Плавающее обрезание 715
сти У с координатами ^а(Л), которая не зависит ни от начальной
поверхности, ни от величины Ло.
Заметим, что неперенормируемые константы связи ^п на У
в общем случае не малы. Важно то, что они становятся функ-
функциями перенормируемых констант. Изменения Л при условии,
что Л много меньше Ло, изменяют константы, но они остаются
вблизи У (по крайней мере, до тех пор, пока константы связи не
станут настолько большими, что iVnm уже не будет положитель-
положительно определенной матрицей). Итак, У является стабильной по-
поверхностью, что и требовалось доказать.
Мы видели, что все физические величины можно выразить
через Л и '§п(А), причем физические величины от Л не зависят.
В частности, это верно для N обычных перенормированных кон-
констант связи и масс, вроде е и те в квантовой электродинамике. Но
теперь можно обратить это соотношение и выразить ^П(Л) через
обычные параметры и Л. Таким образом можно обосновать обыч-
обычную программу перенормировок: все физические величины выра-
выражаются независящим от обрезания способом через обычные пе-
перенормированные константы связи и массы.
Подход Вильсона имеет ряд практических преимуществ. Не
нужно беспокоиться о внутренних интегрированиях и перекры-
перекрывающихся расходимостях. Обрезание по импульсам применяется
ко всем внутренним линиям. Кроме того, ряд теорем о неперенор-
неперенормировке * для суперсимметричных теорий, утверждающих, что
некоторые константы не изменяются при учете радиационных по-
поправок, оказываются верными только для зависящих от обреза-
ния голых констант связи .
С другой стороны, у вильсоновского подхода есть и недостатки.
Приходится отказаться от ряда упрощений, возникающих при рабо-
работе с перенормируемыми теориями типа квантовой электродинамики.
Поскольку мы начинаем с того, что по частицам с импульсами, пре-
превышающими некоторый масштаб Л, производится интегрирование,
результирующая эффективная теория поля оказывается содержа-
содержащей все лоренц- и калибровочно-инвариантные взаимодействия с не
зависящими от Л константами. (Тем не менее, в физических процес-
процессах при энергиях ? « Л доминирующими будут все же перенорми-
* Англоязычный термин nonrenormalization theorem мы переводим как
теорема о неперенормировке. — Прим. пер.
716 Глава 12. Общая теория перенормировок
руемые константы связи.) Кроме того, обрезание в общем случае раз-
разрушает явную калибровочную инвариантность, а также либо явную
лоренц-инвариантность, либо унитарность. Ни одной из этих проблем
нет в физике конденсированных сред, для которых и был первона-
первоначально разработан метод Вильсона, поскольку никто не ожидает, что
реалистическая теория конденсированного вещества должна быть стро-
строго перенормируемой, и нет никаких фундаментальных физических
принципов, которые обязательно нарушаются обрезанием. На самом
деле, в кристаллах существует обрезание по импульсам фононов,
определяющееся периодом обратной решетки.
Если посмотреть глубже, разница между обычным и виль-
соновским подходами есть вопрос математического удобства, а не
физической интерпретации. Действительно, обычная перенорми-
перенормировка уже приводит к чему-то вроде настраиваемого обрезания:
когда мы выражаем наш ответ через константы связи, опреде-
определенные как значения физических амплитуд при некоторых им-
импульсах порядка ц (как для обсуждавшейся в предыдущем разде-
разделе скалярной теории поля), те сокращения, которые делают ин-
интегралы сходящимися, начинают действовать при виртуальных
импульсах порядка ц. Наоборот, зависящие от Л константы связи
в подходе Вильсона должны в конечном счете быть выражены
через наблюдаемые массы и заряды, и когда это сделано, резуль-
результаты совпадают с теми, которые получены обычными способами.
12.5. Случайные симметрии *
Как показано в разделе 12.3, есть хорошие основания счи-
считать, что перенормируемые теории поля приближенно описыва-
описывают природу при достаточно низких энергиях. Часто требование
перенормируемости оказывается настолько жестким, что эффек-
эффективный лагранжиан автоматически подчиняется одной или более
симметриям, которые не являются симметриями исходной тео-
теории и могут поэтому нарушаться подавленными неперенормируе-
мыми слагаемыми в эффективном лагранжиане. Действительно,
большинство экспериментально обнаруженных симметрии в фи-
* Этот раздел лежит несколько в стороне от основной линии изложения
и может быть опущен при первом чтении.
12. 5. Случайные симметрии 717
зике элементарных частиц являются «случайными симметриями»
указанного типа.
Классическими примерами могут служить инверсии и со-
сохранение аромата в электродинамике заряженных лептонов. Наи-
Наиболее общий перенормируемый лоренц-инвариантный и калиб-
ровочно инвариантный лагранжиан фотонов и полей \|/г спина 1/2
и заряда —е имеет вид
i[5 + j
A2.5.1)
где сумма по г, j является суммой по трем лептонным ароматам
(е, ц, т), XfLi и \|/Ri — левые и правые компоненты поля \|Л, опреде-
определенные согласно формулам
a ZL, ZR и М — числовые матрицы. Мы не делаем никаких предпо-
предположений о сохранении лептонного аромата, так что матрицы
ZL.., ZR.. и М-. не обязаны быть диагональными. Кроме того, мы
ничего не предполагаем относительно инвариантности по отноше-
отношению к Р, С или Т, так что нет никаких обязательных связей меж-
между ZL и ZR или между М и М^. Единственные ограничения на эти
матрицы вытекают из действительности лагранжиана, требую-
требующей, чтобы ZLi- и ZRi- были эрмитовыми, и из канонических соот-
соотношений антикоммутации, требующих, чтобы Zu. и ZR{. были по-
положительно определены.
Предположим теперь, что мы заменяем лептонные поля \|/L,
\|/R новыми полями \|/'L, i\f'R, определенными согласно формулам
где SLR — несингулярные матрицы, которые можно выбирать по
желанию. Лагранжиан, выраженные через новые поля, принима-
принимает тот же вид, что и A2.5.1), но с новыми матрицами
718 Глава 12. Общая теория перенормировок
Z'b = SfLZLSL , ZR = SRZRSR , M' = SfLMSR . A2.5.4)
Можно выбрать SL и SR так, что Z'L = Z'R = 1. (Достаточно
взять SLR = ULRDLR, где ULR — унитарные матрицы, диагонали-
зующие положительно определенные эрмитовые матрицы ZLR a
DLR — диагональные матрицы, диагональные элементы которых
равны обратным квадратным корням из собственных значений ZL R.)
Совершим теперь еще одно преобразование — от лептон-
ных полей \|/'г к полям \|/'г:
Vl = S'lVl . ?r = S'rVr ¦ A2.5.5)
Если выразить лагранжиан через новые поля, он вновь при-
принимает ту же форму с новыми матрицами
Z'l = S?S'L , Z? = S$S'R , М" = S?M'S'R . A2.5.6)
На этот раз выберем S'LR унитарными, так что опять Z'L =
Z'R = 1. Эти унитарные матрицы выбираются так, чтобы матрица
М" была действительной и диагональной. (Согласно полярному
разложения, М', как и любая квадратная матрица, может быть
представлена в виде М' = VH, где V — унитарная, а Я — эрмито-
эрмитова матрицы. Возьмем S'L = S'R^V^ и выберем в качестве S'R уни-
унитарную матрицу, диагонализующую Я.) Опуская штрихи, полу-
получаем, что лагранжиан принимает вид:
Я> — — — 7, F
A2.5.7)
где тг — действительные числа, равные собственным значениям
эрмитовой матрицы Я. Окончательно это выражение можно пред-
представить в более знакомой форме:
A2.5.8)
12. 5. Случайные симметрии 719
Если лагранжиан имеет такой вид, совершенно ясно, что любой
перенормируемый лагранжиан электродинамики лептонов автомати-
автоматически сохраняет Р, С и Т, а также числа лептонов (минус числа анти-
лептонов) каждого аромата: электронного, мюонного и тау-лептонно-
го *. В частности, несмотря на выражение A2.5.1), такая теория запре-
запрещает процессы типа ц —» е + у. Читатель может высказать опасение,
правильно ли идентифицировать лептонные поля с функциями щ (ко-
(которые ранее обозначались \|/'г) в лагранжиане A2.5.8), явно сохраняю-
сохраняющими лептонный заряд, а не с \|/г из лагранжиана A2.5.1), который
вроде бы допускает процессы типа ц —> е + у. Эти опасения можно
отбросить: как подчеркивалось в разделе 10.3, нет такого поля, кото-
которое можно идентифицировать с истинным полем мюона или электро-
электрона. На самом деле, лагранжиан A2.5.1) приводит к отличным от нуля
матричным элементами радиационного распада лептона 1 в лептон 2
вне массовой поверхности. Однако, беря импульсы лептонов на массо-
массовой поверхности, мы находим, что б'-матрица всех таких процессов,
даже вычисленных с помощью лагранжиана A2.5.1), обращается в нуль.
При получении этих результатов было существенно, что как
левые, так и правые компоненты лептонных полей, входящих в
A2.5.1), имели один и тот же электрический заряд или, иными сло-
словами, левые и правые компоненты лептонных полей преобразуют-
преобразуются одинаково под действием электромагнитных калибровочных пре-
преобразований. Как мы увидим в т. II, по схожим причинам современ-
современная перенормируемая теория сильных взаимодействий, известная
под названием квантовой хромодинамики, автоматически сохраня-
сохраняет С и (если не считать ряда непертурбативных эффектов) Р, Т, а
также числа кварков (минус числа антикварков) каждого кваркового
аромата. Мы также увидим в т. II, что по причинам, аналогичным
изложенным здесь для электродинамики, простейшая версия пере-
перенормируемой стандартной модели слабых и электромагнитных взаи-
взаимодействий автоматически сохраняет лептонный аромат (хотя и не
С и Р). Открытой остается возможность, что эффекты неперенор-
мируемых взаимодействий, идущие от больших масштабов масс,
могут нарушать любой из упомянутых законов сохранения.
* Впервые это было показано Фейнбергом, Кабиром и мной 21. Ранее Фей-
нберг22 отмечал, что эффекты слабых взаимодействий в теории с единствен-
единственным типом нейтрино приводят к наблюдаемой вероятности процесса (Д, —> е + у.
Эта проблема разрешилась только после открытия второго типа нейтрино.
720 Глава 12. Общая теория перенормировок
Задачи
1. В случае размерности пространства-времени, равной 2, 3 и 6,
перечислите все перенормируемые (или суперперенормируемые)
лоренц-инвариантные слагаемые в лагранжиане одного скаляр-
скалярного поля.
2. Покажите, каким образом в квантовой электродинамике со-
сокращаются перекрывающиеся расходимости в собственной
энергии электрона.
3. Рассмотрите теорию скалярного поля ф и спинорного поля \|/
с гамильтонианом взаимодействия дф \|Л|/. Запишите однопет-
левой вклад в собственноэнергетическую функцию скалярно-
скалярного поля П (д) как сумму расходящегося полинома по р^ и явно
сходящиегося интеграла.
4. Пусть квантовая электродинамика электронов и фотонов яв-
является на самом деле эффективной теорией поля, получен-
полученной из теории, где произведено интегрирование по неизвест-
неизвестным частицам массой М 3> те. Предположите калибровочную
и лоренц-инвариантность, однако не требуйте инвариантно-
инвариантности относительно С, Р и Т. Каковы неперенормируемые сла-
слагаемые в лагранжиане в ведущем порядке по 1/М? Как вы-
выглядят эти слагаемые в следующем порядке?
Список литературы
1. Dyson, F.J., Phys. Rev., 75, 486, 1736 A949). История вопроса
изложена в книге: Renormalization, ed. by L.M.Brown (Springer
Verlag, New York, 1993). Подробное современное изложение
см. в книге: Collins, J. Renormalization (Cambridge University
Press, Cambridge, 1984) (есть рус. пер.: Дж. Коллинз. Пере-
Перенормировка. М.: Мир, 1988).
2. Weinberg, S., Phys. Rev., 118, 838 A959). Это доказательство
опирается только на общие асимптотические свойства подын-
подынтегральных выражений в фейнмановских интегралах в евк-
Список литературы 721
лидовом импульсном пространстве, полученных виковским
поворотом всех контуров интегрирования. Доказательство было
упрощено за счет более детального анализа подынтегрально-
подынтегрального выражения в работе: Hahn, Y. and Zimmerman, W., Commun.
Math. Phys., 10, 330 A968), а затем распространено на интег-
интегралы в импульсном пространстве Минковского в работе: Zim-
Zimmerman, W., Commun. Math. Phys., 11, 1 A968).
3. Bjorken, J.D. and Drell, S.D., Relativistic Quantum Fields
(McGrow Hill, New York, 1965), sections 19.10, 19.11 (есть
рус. пер.: Дж.Д. Бьеркен, С. Дрелл. Релятивистская кван-
квантовая теория. Тт. 1, 2. М. : Наука, 1978.)
4. См., например, в книге: Wess, J. and Bagger, J.,Supersymmetry
and Swpergravity (Princeton University Press, Princeton, 1983)
и ссылки на литературу в ней (есть рус. пер.: Ю. Весе, Дж.
Беггер. Суперсимметрия и супергравитация. М.: Мир, 1986.
5. Salam, A., Phys. Rev., 82, 217 A951); Phys. Rev., 84, 426 A951);
Matthews, P.T. and Salam, A., Phys. Rev., 94, 185 A957).
6. Bogoliubov, N.N. and Parasiuk, O., Ada Math., 97, 227 A957).
7. Hepp, K., Commun. Math. Phys., 2, 301 A966). Хепп замеча-
замечает, что «трудно найти двух теоретиков с изоморфным пони-
пониманием основных шагов в доказательстве Боголюбова и Па-
расюка», но и работа самого Хеппа читается нелегко.
8. Zimmerman, W., Commun. Math. Phys., 15, 208 A969). См. так-
также статью В. Циммермана в сб.: Lectures on Elementary Particles
and Quantum Field Theory. Brandeis University Summer Institute
in Theoretical Physics (M.I.T. Press, Cambridge, 1970).
9. Heisenberg, W., Z. Physik, 110, 251 A938).
10. Heisenberg, W., Ref. [9] and Z. Physik, 113, 61 A939).
11. Sakata, S., Umezawa, H., and Kamefuchi, S., Prog. Theor.
Phys., 7, 327 A952).
722 Глава 12. Общая теория перенормировок
12. Weinberg, S., Physica, 96А, 327 A979).
13. Gasser, J. and Leutwyler, H., Ann. Phys. (NY), 158, 142 A984);
Nucl. Phys., B250, 465 A985).
14. Donoghue, J.F., Phys. Rev., D 50, 3874 A994).
15. Один из возможных способов того, чтобы это случилось, связан
с явлением «асимптотической безопасности». См.: Weinberg, S.,
in General Relativity — An Einstein Centenary Survey, ed. by S.W.
Hawking and W. Israel (Cambridge University Press, Cambridge,
1979), Section 16.3 (есть рус. пер.: Обгцая теория относитель-
относительности. Под ред. С. Хокинга и В. Израеля. М.: Мир, 1983).
16. Euler, H. and Kockel, В., Naturwiss, 23, 246 A935);
Heisenberg, W. and Euler, H., Z. Physik, 98, 714 A936).
17. Эффективный лагранжиан Эйлера и др. был использован в
однопетлевых вычислениях в работе: Halter, J., Phys. Lett.,
В 316, 155 A971).
18. Wilson, K.G., Phys. Rev., B4, 3174, 3184 A971); Rev. Mod.
Phys., 47, 773 A975).
19. Polchinski, J., Nucl. Phys., B231, 269 A984); lecture in Recent
Directions in Particle Theory — Proc. of the 1992 TASI Conf.,
ed. by J. Harvey and J. Polchinski (World Scientific, Singapore,
1993), p. 235.
20. Novikov, V., Shifman, M.A., Vainshtein, A.I., and Zakharov,
VI., Nucl Phys., B229, 381 A983); Shifman, M.A. and Vainshtein,
A.I., Nucl. Phys., B277, 456 A986) и ссылки в этих работах. См.
также Shifman, M.A. and Vainshtein, A.I., Nucl. Phys., B359,
571 A991).
21. Feinberg, G., Kabir, P., and Weinberg, S., Phys. Rev. Lett.,
3, 527 A959).
22. Feinberg, G., Phys. Rev., 110, 1482 A958).
13
Инфракрасные эффекты
При изучении радиационных поправок особую роль играют
те из них, которые обязаны своим происхождением "мягким" фо-
фотонам, т. е. фотонам, импульс и энергия которых много меньше
характерных масс и энергий изучаемого процесса. Дело не только
в том, что эти поправки часто бывают настолько большими, что
нужно учитывать их во всех порядках теории возмущений, но и в
том, что такое суммирование без труда осуществляется. Вклад фо-
фотонов бесконечно больших длин волн принимает форму расходя-
расходящихся интегралов, но, как мы увидим, все эти «инфракрасные
расходимости» сокращаются Ч
В большей части данной главы мы будем иметь дело с фото-
фотонами, взаимодействующими с заряженными частицами произволь-
произвольного типа и спина, включая атомные ядра, способные не только к
электромагнитным, но и сильным взаимодействиям. Однако не-
нетрудно приспособить представленные ниже вычисления к инфра-
инфракрасным эффектам, связанным с другими безмассовыми частица-
частицами вроде глюонов в квантовой хромодинамике. В разделе 13.4 мы
явно рассмотрим весьма широкий класс теорий безмассовых час-
частиц и докажем в общем виде сокращение инфракрасных расходи-
мостей.
После таких обобщений мы вернемся к изучению фотонов и
рассмотрим два практически важных вопроса:
рассеяние мягких фотонов заряженными частицами с произ-
произвольными неэлектромагнитными взаимодействиями, обладающими
произвольным спином;
представление тяжелых заряженных частиц типа атомных
ядер в виде источников внешнего электромагнитного поля.
724
Глава 13. Инфракрасные эффекты
13.1. Амплитуды испускания мягких фотонов
В этом разделе мы выведем универсальную формулу для ам-
амплитуды испускания произвольного числа фотонов очень малой энер-
энергии в процессе ОС —> В с участием произвольного числа более энергич-
энергичных заряженных частиц любого типа.
Начнем с амплитуды испускания одного мягкого фотона. Если
подсоединить линию мягкого выходящего фотона с импульсом q и
индексом поляризации ц к линии заряженной частицы, выходящей
из какой-то связной фейнмановской диаграммы процесса а —» В (рис.
13.1, а), то матричный элемент этого процесса следует умножить на
дополнительный пропагатор заряженной частицы с импульсом
р + q, который имела заряженная частица перед испусканием фо-
фотона, и на множитель, отвечающий вкладу возникшей новой вер-
вершины «заряженная частица—фотон». Если спин заряженных частиц
равен нулю, масса т и заряд +е, эти множители имеют вид
—г
_BлL
hqJ
1
+
т2
Р
А
-г?_
Рис. 13.1. Ведущие диаграммы испускания мягких фотонов в произвольном
процессе а —> C. Прямые линии изображают частицы в состояниях а и [3 (включая
возможные жесткие фотоны), волнистые линии — мягкие фотоны
13.1. Амплитуды испускания мягких фотонов 725
что в пределе g —> 0 сводится к множителю
p-q-гг
A3.1.1)
(Мы вправе переопределять величину положительной бесконечно
малой добавки ?, заботясь только о сохранении ее знака.) Получен-
Полученный результат на самом деле верен для заряженных частиц любого
спина. Например, для частицы спина 1/2 и заряда +е нужно заме-
заменить коэффициентную функцию м(р, а) для выходящей заряжен-
заряженной частицы на
-г
BлL (р + gJ +т2 -г?
В пределе q —> 0 числитель пропагатора равен сумме диад:
-гр + т = 2р°
так что получается сумма матричных элементов оператора у*1 между
спинорами с одинаковыми импульсами, имеющими вид
м(р, о)у^м(р, а') = -гЬаа>р^ / р°.
И в этом случае эффект сводится к умножению матричного элемен-
элемента процесса а —» C на множитель A3.1.1). Вообще, для заряженных
частиц любого спина 4-импульс р + g на новой внутренней линии в
пределе g —» 0 стремится к массовой поверхности, так что числи-
числитель пропагатора стремится к сумме диад коэффициентных функ-
функций, превращающей новую вершинную матрицу в множитель, про-
пропорциональный р^, и единичную матрицу по спиральным индексам.
В результате вновь приходим к A3.1.1). Далее, как мы видели в
гл. 10, поправки более высоких порядков не влияют на вычеты по-
полюсов пропагаторов на массовой поверхности, а также на матрич-
матричный элемент электрического тока между состояниями одной и той
же частицы при одинаковых импульсах, так что A3.1.1) определя-
определяет правильный во всех порядках теории возмущений множитель,
726 Глава 13. Инфракрасные эффекты
связанный с испусканием мягкого фотона с линии выходящей заря-
заряженной частицы.
Те же аргументы применимы к фотону, испускаемому в про-
процессе а —» В с линии входящей заряженной частицы, с той разни-
разницей, что после того, как входящая частица испустит фотон с 4-им-
пульсом д, линия заряженной частицы приобретает импульс р — д, и
вместо A3.1.1) получается множитель
р • g - гг
A3.1.2)
Фотон может, конечно, испускаться и с внутренней линии диа-
диаграммы процесса ос —> В, но в этом случае не возникает множителя,
ведущего себя как (р-g) при g —» 0. Таким образом, амплитуда Mga
(матричный элемент без дельта-функции закона сохранения энер-
энергии-импульса) испускания одного мягкого фотона с 4-импульсом g
и поляризационным индексом ц в процессе ОС —> C определяется сум-
суммой слагаемых типа A3.1.1) и A3.1.2), по одному на каждую выходя-
выходящую или входящую заряженную частицу:
где рп и +еп — 4-импульс и заряд n-й частицы в начальном или
конечном состоянии, а Г|п — знаковый множитель, равный +1 для
частиц в конечном состоянии В и —1 для частиц в начальном состоя-
состоянии а.
Прежде чем переходить к рассмотрению испускания несколь-
нескольких мягких фотонов, нелишне напомнить важное свойство 2 форму-
формулы A3.1.1). Чтобы вычислить амплитуду испускания фотона
определенной спиральности, нужно свернуть это выражение с соот-
соответствующим вектором поляризации eA(q,+). Однако мы видели в
разделе 5.9, что eJq,+) не является 4-вектором: под действием пре-
преобразований Лоренца Л*\, вектор поляризации преобразуется в
A|ivev(q,±) плюс слагаемое, пропорциональное дц. Для того, чтобы это
дополнительное слагаемое не разрушило лоренц-инвариантность,
необходимо, чтобы свертка Mga(g) с дц обращалась в нуль. Однако
при g —» 0 из A3.1.3) имеем
13.1. Амплитуды испускания мягких фотонов 727
Коэффициент при Мра в правой части равен полному заряду в ко-
конечном состоянии минус полный заряд в начальном состоянии, так
что условие обращения в нуль эквивалентно условия сохранения
заряда. Итак, без всяких дополнительных предположений о калиб-
калибровочной инвариантности, мы получаем, что для частиц со спином
единица и массой нуль из лоренц-инвариантности вытекает со-
сохранение любой константы связи типа электрического заряда, оп-
определяющей взаимодействие этих частиц при низких энергиях.
Между прочим, амплитуда испускания мягкого гравитона с 4-им-
пульсом q и тензорными индексами ц, V в процессе ot —> C дается
формулой3, аналогичной A3.1.3):
где /п — константа связи мягкого гравитона с частицами типа п. Из
лоренц-инвариантности вытекает, что свертка амплитуды с дц об-
обращается в нуль. Но
A3.1.6)
так что сумма ?/„р^ сохраняется. Однако единственная линейная
комбинация 4-импульсов, которая может сохраняться, не приводя к
запретам на все нетривиальные процессы рассеяния, это полный 4-
импульс, так что для сохранения A3.1.6) все /п должны быть равны.
(Общее значение /п можно считать равным ^SjiGjy , где GN— ньюто-
ньютоновская постоянная тяготения.) Таким образом, из лоренц-инвари-
лоренц-инвариантности вытекает, что низкоэнергетические безмассовые частицы
спина 2 одинаково взаимодействуют со всеми формами энергии и
импульса. Это первый шаг на долгом пути к доказательству, что прин-
принцип эквивалентности Эйнштейна является необходимым следствием
лоренц-инвариантности в применении к безмассовым частицам спи-
спина 2. Аналогично, амплитуда испускания мягкой безмассовой части-
частицы со спином j > 3 в процессе a —» C имеет вид
728
Глава 13. Инфракрасные эффекты
Требование лоренц-инвариантности приводит к тому, что сумма
Lgnynyn--- должна сохраняться. Но ни одна такая величина не мо-
может сохраняться без запрета на все нетривиальные процессы рас-
рассеяния, так что все gn должны обращаться в нуль. Безмассовые
частицы со спином j > 3 могут существовать, но их константы связи
должны обращаться в нуль в пределе низких энергий, в частности,
такие частицы не могут быть переносчиками сил, убывающих об-
обратно пропорционально квадрату расстояния.
Рассмотрим теперь испускание двух мягких фотонов. Вклад в
матричный элемент от диаграммы, в которой два фотона испуска-
испускаются с разных внешних линий процесса a —» C, определяется умно-
умножением матричного элемента ос —> C на произведение множителей
вида A3.1.1) или A3.1.2). Может быть, несколько удивительно, что
тот же результат верен, если два фотона испускаются со одной и
той же линии. Например, если фотон 1 испускается с внешней ли-
линии частицы с зарядом +е и 4-импульсом р после фотона 2, получа-
получаем множитель
r\epv
р • q1 - гцг
г|ери
если же фотон 2 испускается после фотона 1, этот множитель при-
принимает вид
г|ер
М-2
р • д2 - гг|?
r\epv
(См. рис. 13.2. Фактор Г| по-прежнему равен +1 или —1 в зависимости
от того, является линия заряженной частицы выходящей или вхо-
входящей.) Сложение двух множителей приводит к выражению
М-2
р • д2 - гг|?
р • q1 - щг
/ \ / \
13.1. Амплитуды испускания мягких фотонов
729
Рис. 13.2. Диаграммы испускания двух мягких фотонов одной и той же входя-
входящей заряженной частицей. Прямые линии — жесткие частицы, волнистые
линии — мягкие фотоны
равному произведению множителей, возникающих при испускании
одного фотона.
В общем случае при испускании произвольного числа фотонов
с одной и той же внешней линии, получаем сумму вида*
* Это тождество можно доказать методом математической индукции. Уже
показано, что оно верно для двух фотонов. Пусть оно верно для N — 1
фотонов. Для N фотонов следует написать сумму по перестановкам как
сумму по выбору первого излучаемого фотона и сумму по перестановкам
остающихся фотонов:
'1 [р • (qi + q2) "
\
x[p ¦ (Qi + Ч2 + •••+ 9лг) ~ гт18] •••+ перестановки
п-i
ЛГ
= 1
г=1
N
= 1
г=1
р •
ЛГ
vs=l
vs=l
-iTie
-1
[pqr- ще] : =
s=l
что и требовалось доказать.
730 Глава 13. Инфракрасные эффекты
+ перестановки
A3.1.7)
Отсюда следует, что амплитуда МЛ" N (qi-..qN) испускания N очень
мягких фотонов с поляризационными индексами ц1( ..., \iN и 4-им-
пульсами q1( ..., qN в процессе а —> C дается в пределе g —» 0 умноже-
умножением матричного элемента М$а для процесса а —» C на произведение
множителей типа A3.1.3), по одному на каждый фотон:
A3.1.8,
13.2. Виртуальные мягкие фотоны
Используем результаты предыдущего раздела, чтобы вычис-
вычислить во всех порядках вклад радиационных поправок за счет обме-
обмена виртуальными мягкими фотонами между линиями заряженных
частиц в процессе ОС—> C (рис. 13.3). Под «мягким» мы подразумеваем
фотон, имеющий импульс, меньший чем Л, где Л — некоторый
удобный разделительный импульс *, выбираемый достаточно ма-
малым, чтобы были справедливы сделанные в предыдущем разделе
приближения. Мы увидим, что рассматриваемые мягкие фотоны при-
приводят к инфракрасным расходимостям, так что в качестве времен-
временной меры мы будем вынуждены ввести также и нижний предел X
импульсов фотонов.
Важно понять разницу между этими двумя обрезаниями фо-
фотонных имульсов. Верхнее обрезание Л служит просто для опреде-
определения того, что мы понимаем под «мягкими» фотонами. Зависимость
от Л радиационных поправок за счет мягких фотонов сокращается с
зависимостью от Л остальной части амплитуды, которая вычисля-
* В русскоязычной литературе величину Л называют разрешающей
способностью прибора. — Прим. ред.
13..2. Виртуальные мягкие фотоны 731
Рис. 13.3. Типичная диаграмма для матричного элемента процесса а —> Ъ
с учетом ведущих радиационных поправок, обусловленных мягкими
виртуальными фотонами. Прямые линии отвечают частицам в состояниях а
и Ъ (включая жесткие фотоны), волнистые — мягким фотонам
ется с учетом только виртуальных фотонов с импульсами больше
чем Л. С другой стороны, нижнее обрезание X должно быть в конце
концов устранено переходом к пределу X —> 0. Мы увидим, что ин-
инфракрасные расходимости в этом пределе сократятся при учете ис-
испускания реальных мягких фотонов.
Каждому виртуальному мягкому фотону следует сопоставить
пропагатор
-г Лии'
ТГТ^— -> A3.2.1)
затем умножить амплитуду A3.1.8) на произведение таких пропага-
торов, свернуть по поляризационным индексам и проинтегрировать
по 4-импульсам фотонов. Кроме того, для N виртуальных фотонов
следует разделить результат на 2NNl, т. к. сумма по всем точкам,
к которым можно присоединить оба конца линии мягкого фотона,
включает фиктивные суммы по N1 перестановкам фотонных ли-
линий и по взаимным перестановкам двух концов этих линий. Вклад
732
Глава 13. Инфракрасные эффекты
радиационных поправок за счет N мягких фотонов сводится к умно-
умножению матричного элемента Мра процесса без таких поправок на
множитель
JV!2
JV
Bл)
\4 / -
N
A3.2.2)
d4g
„ • Ч ~ *1„е][-рт ¦ Я ~
,• A3.2.3)
Заметим, что мы изменили знак pm-q в знаменателе выражения
A3.2.3), т.к. если определить q как импульс, испускаемый с линии
п, то импульс, испускаемый с линии т, есть -д.
Суммируя по N, заключаем, что матричный элемент процес-
процесса, включающий радиационные поправки за счет любого числа мяг-
мягких фотонов с импульсами |q| > X, имеет вид
ехр
1
2BлL
A3.2.4)
где Mg^a — амплитуда, содержащая только виртуальные фотоны с
импульсами, большими Л.
Интеграл по д° в A3.2.3) можно взять методом вычетов. По-
Подынтегральное выражение аналитично по д°, не считая четырех по-
полюсов в точках
q°=\q\-iz,
g°=-|q
=vn-q-zr|n?, g° = vm -
zr|m?,
где vn = pn/pn°, vm определяется аналогично. Если частица п выхо-
выходящая, а частица т входящая, то г|п = +1, х\т = — 1, так что если
д°
замкнуть контур по g
ках д° = \п • q - Щпг или д° = v
гично, если п
в верхней полуплоскости, то полюса в точ-
т ¦ q + гг|т? не дают вклада. Анало-
входящая, а т — выходящая частицы, то эти
13..2. Виртуальные мягкие фотоны 733
полюсы не дают вклада при замыкании контура в нижней полу-
полуплоскости. В обоих случаях вклад дает один из полюсов в точках
q° = ±(|q| - ге), и в результате получается чисто действительный
интеграл:
V 77 Ч. * г?? /\-^ТП Ч. * Pm / /1 Q О R4
. ^1 o.Z.O j
(при Г1„ = -r|m = ±1).
С другой стороны, если частицы пит обе выходящие , или обе
входящие, то полюсы в точках q = vn • q - гг|п? и g° = vm • q + гг|т?
лежат по разные стороны действительной оси д°, так что один из
них обязательно дает вклад, как бы мы не замыкали контур:
d3g
Jnm =-
nm
ЛЬ:|Ч|Ь:/\ ' *¦ v '(¦ ¦¦¦¦¦¦ ft ' \ //t *¦ *¦ IIL '
Ш3 . (А) , .,. A3-2.6)
„ lnU- (при Т1„ =Лт =±1),
где Cnm — относительная скорость частиц п и т в системе покоя
одной из них:
J9 9
тгтг
1 - ,2 • A3.2.7)
Мнимая часть выражения A3.2.6) приводит к появлению в выражении
A3.2.4) инфракрасно расходящегося фазового множителя 4, который
выпадает, когда при вычислении вероятности процесса ot —> C бе-
берется модуль матричного элемента. (Этот бесконечный фазовый мно-
множитель есть релятивистский аналог хорошо известной особенно-
особенности нерелятивистского кулоновского рассеяния: та часть шредин-
геровской волновой функции, которая описывает расходящуюся
сферическую волну, зависит от радиальной координаты не как
ехр(грг)/г, а как ехр(г рг — ivln г)/г, где V — произведение зарядов,
деленное на относительную скорость 5.) На вероятность реакции ока-
оказывает влияние только действительная часть Jnm, которая при всех
г\п и г\т имеет вид
734 Глава 13. Инфракрасные эффекты
= -п(рп ¦ рт)\ —^—
J 1*11 (^«lP
После элементарного вычисления находим:
A3.2.9)
Подставляя это выражение в квадрат модуля амплитуды A3.2.4),
находим окончательно, что влияние мягких виртуальных фотонов
на вероятность процесса Гра определяется формулой:
ГрХа = [д J ГрЛа . A3.2.10)
где Гра^- и Грал — вероятности процесса а^|3 с учетом радиацион-
радиационных поправок за счет мягких фотонов с импульсами, большими X и
Л соответственно, а показатель степени А имеет вид
епетХ\п'Х\т л ( 1 + P
в 1В
2^ в 1-В " A3.2.11)
8я"
nm
Заметим, что полученный ответ является совершенно разумным,
поскольку поправочный множитель (Х/А)А оказался равным отноше-
отношению функции от X к такой же функции от Л, т. к. две вероятности в
формуле A3.2.10) могут зависеть, соответственно, только от Хили от Л.
Показатель степени А всегда положителен. Например, при рас-
рассеянии одной заряженной частицы на нейтральной частице или внеш-
внешнем потенциале, следует добавить в правую часть A3.2.11) слагае-
слагаемые, в которых частицы пит являются одновременно либо на-
начальной, либо конечной заряженной частицей (тогда r|nr|m = +1 и
Pnm = 0), или п есть начальная или конечная заряженная частица,
тогда т — другая частица (в этом случае rinrim = —1 и (Зпт = C,
причем 1 > C > 0). В результате
8тгЧ Р U-P
13..2. Виртуальные мягкие фотоны 735
и это выражение положительно для всех 1 > C > 0. Поскольку А
положительно, эффект инфракрасных расходимостей от мягких вир-
виртуальных фотонов сводится после суммирования во всех порядках
к тому, что вероятность любого данного процесса с заряженными
частицами а —»C обращается в нуль в пределе^ —» 0.
Прежде чем показать, каким образом испускание реальных
мягких фотонов сокращает эти инфракрасные расходимости, пре-
прервем ненадолго изложение и рассмотрим одну техническую деталь
приведенных выше расчетов, которая, насколько я знаю, всегда
игнорировалась в литературе. При расчете радиационных поправок
наряду с диаграммами, в которых виртуальный фотон испускается
и поглощается разными линиями заряженных частиц, мы включа-
включали и диаграммы, в которых виртуальный фотон испускается и по-
поглощается на одной и той же внешней линии. Но как было показано
в гл. 10, при расчете .^-матрицы не требуется включать радиацион-
радиационные поправки, возникающие от вставок собственноэнергетических
поддиаграмм на внешних линиях. Отсюда может показаться, что в
формуле A3.2.11) следует отбросить слагаемые с п = т , однако как
будет видно в следующем разделе, сокращение инфракрасных рас-
хоимостей будет при этом неполным.
Решение этой проблемы вытекает из наблюдения, что мягкие
виртуальные фотоны порождают инфракрасные расходимости не толь-
только непосредственно, но и через константы перенормировки Zn полей
заряженных частиц. (Константа перенормировки Zn в теориях типа
квантовой электродинамики с одним заряженным полем спина 1/2
называется Z2.) Эффекты радиационных поправок на внешних
линиях сокращаются контрчленами, пропорциональными (Zn — 1). Кон-
Конкретнее, перенормированное поле заряженной частицы типа п равно
произведению неперенормированного поля на Zn~1//2, так что когда
мы вычисляем .^-матрицу, используя перенормированные поля (что
соответствует опусканию радиационных поправок к внешним лини-
линиям), мы вводим дополнительный множитель Y\nZ^1^2, где произве-
произведение берется по всем заряженным частицам в начале и конце.
(Конечно, существуют и множители Zn-1^2 для нейтральных частиц,
но они не содержат инфракрасных расходимостей.) В несколько иных
обозначениях, указанный множитель равен
736 Глава 13. Инфракрасные эффекты
f
где Zj: — константа перенормировки полей типа /, Ef — число внеш-
внешних линий типа /, а произведение теперь берется по всем типам
заряженных полей. Однако эти константы перенормировки полей
появляются также внутри диаграмм. Если выразить взаимодейст-
взаимодействие типа г, содержащее N^ полей заряженных частиц типа /, че-
через перенормированные поля, возникнет инфракрасно расходящийся
множитель
(Например, контрчлен -ге^2-1)А„ \|//Ч|/ в A1.1.9) вместе с обычным
электромагнитным взаимодействием —ге \|//Ч|/ приводит к суммар-
суммарному взаимодействию —ieZ2 х^х/. За инфракрасную расходимость,
возникающую от второго слагаемого в скобках в A1.3.23) и в послед-
последнем слагаемом в A1.4.14), ответственна инфракрасная расходимость
множителя Z2.) Кроме того, такая расходимость имеется в пропага-
торах перенормированных полей: если выразить пропагатор пере-
перенормированного заряженного поля типа / через пропагатор непе-
ренормированного поля, то возникает множитель Zf~l.
Собирая все это вместе, находим, что общее число множите-
множителей Zs для каждого заряженного поля типа /, возникающих от контр-
контрчленов к взаимодействиям и от радиационных поправок ко внут-
внутренним и внешним линиям, равно
где If и. Ef — числа внутренних и внешних линий типа /, a V; —
число вершин взаимодействий типа г. Уже отмечалось в разделе
6.3, что эта величина равна нулю для каждого /. Таким образом,
контрчлены, сокращающие радиационные поправки ко внешним ли-
линиям, сами сокращаются множителями Zf, возникающими от внут-
внутренних линий и вершин. Поэтому формула A3.2.11) правильна в том
виде, как она написана, включая слагаемые с п = т.
13.3. Реальные мягкие фотоны. Сокращение расходимостей 737
13.3. Реальные мягкие фотоны. Сокращение расходимостей
Разрешение описанной в предыдущем разделе проблемы ин-
инфракрасной расходимости заключается в наблюдении, что реально
невозможно измерить вероятность Гпа реакции ОС —> C с участием
определенного числа фотонов и заряженных частиц, поскольку фо-
фотоны очень малой энергии всегда могут ускользнуть от регистрации.
Реально можно измерить вероятность Г^а(Е,ЕТ) такой реакции, в
которой регистрируются фотоны с энергией больше какой-то малой
величины Е, а нерегистрируемые мягкие фотоны, число которых
может быть произвольным, уносят общую энергию, не превы-
превышающую некоторую малую величину Ет. (Конечно, Е < Ет. В экспе-
эксперименте без детекторов мягких фотонов при определении преде-
предельной полной энергии Ет, уносимой этими фотонами, естественно
основываться на измерениях энергий «жестких» частиц в состояни-
состояниях а и C. В таком случае мы просто полагаем Е = Ет.) Обратимся к
вычислению такой вероятности.
Матричный элемент процесса а —» C с испусканием N реаль-
реальных мягких фотонов получается сворачиванием каждого из N индек-
индексов поляризации ц1( Ц2> - в амплитуде A3.1.8) с соответствующей
коэффициентной функцией
где q — импульс фотона, h = ±1 — его спиральность, а ?ц — соот-
соответствующий «вектор» поляризации фотона *. Тогда матричный эле-
элемент испускания фотонов (матричный элемент 5-матрицы без дельта-
функции) можно записать в виде
r=l п Рп'Чг
* Мы используем обозначение е^ вместо е^ для вектора поляризации
фотона, чтобы избежать путаницы с обозначением еп для электрических
зарядов.
738 Глава 13. Инфракрасные эффекты
(Верхний индекс X напоминает о том, что эти амплитуды должны
вычисляться при заданном инфракрасном обрезании X импульсов
виртуальных фотонов. В конце концов мы перейдем к пределу X —> 0.
Присутствие мягких виртуальных фотонов не противоречит ре-
результату A3.3.1) из-за обсуждавшейся в разделе 13.1 факториза-
факторизации.) Дифференциальная вероятность испускания N мягких фото-
фотонов в элемент объема импульсного пространства Пгй3дг задается квад-
квадратом этого матричного элемента, просуммированным по спираль-
ностям и умноженным на Пг<Л3дг. Напомним, что согласно формуле
(8.5.7) сумма по спиральностям при д2 = 0 принимает вид:
h=±l
где с = —q/2|q|2, a c° = l/2|q|. Условие сохранения заряда ЕпЛпеп = О
позволяет отбросить в A3.3.2) слагаемые, содержащие дц или gv, и
получить в результате дифференциальную вероятность *
{Vn.qr){Vm.qr) ¦ Aз.з.з)
Чтобы вычислить дифференциальную вероятность испускания
N мягких фотонов с определенными энергиями cor = |qr|, следует про-
проинтегрировать A3.3.3) по направлениям испульсов фотонов qr. Эти
интегралы уже встречались нам при вычислении интегралов A3.2.8):
_q.p1(? -q-p )|
У'-'п Ч Рп'У т 4 Vm> Vnm
Интегрируя A3.3.3) по направлениям фотонов, получаем диффе-
дифференциальную вероятность процесса с испусканием фотонов с энер-
энергией со1; ..., с%:
* В случае N = 1 выражение |q|d.rpot(q)/rpot соответствует классическому
распределению энергии, излучаемой скачком меняющейся 4-векторной
плотностью тока, имеющей вид: J^(x) = ?п'''с?3(х — vnt)pnJleri/?ri, причем при
t < 0 сумма берется только по частицам в начальном состоянии, а при
t > 0 — по частицам в конечном состоянии.
13.3. Реальные мягкие фотоны. Сокращение расходимостей 739
л л _ N dco, dcow
alp"(X((O1,...,(OjV) = lpaA(a —> p) -... —, A3.3.5)
где A(a —> C) — та же, что и в предыдущем разделе, константа:
Из выражения A3.3.5) следует, что неограниченный снизу ин-
интеграл по энергиям испущенных фотонов приведет к новым инфра-
инфракрасным расходимостям. Однако из условия унитарности вытекает,
что если было введено инфракрасное обрезание по импульсам вир-
виртуальных фотонов (на что указывает верхний индекс X), следует
проделать такое же инфракрасное обрезание импульсов реальных
фотонов. Для вычисления вероятности Г\а(Е,ЕТ) реакции a —» C, в
которой любой нерегистрируемый фотон уносит энергию не боль-
больше Е, а любое число нерегистрируемых фотонов уносит энергию не
более Ет (величины Е и Ет выбраны достаточно малыми, чтобы не
противоречить использованным при выводе формулы A3.3.1) при-
приближениям), следует проинтегрировать A3.3.5) по энергиям всех фо-
фотонов, при условии, что Е > сог > А. и Егсог < Ет, затем разделить на
N1, поскольку этот интеграл содержит конфигурации, отличающиеся
только перестановкой N мягких фотонов, и наконец просуммиро-
просуммировать по N. В результате получаем
A3.3.6)
7U_ Q f гл-^,.-» -^ 1 X „ ^ гл „ _ 1 ^*
Этот интеграл мог бы быть представлен как произведение N инте-
интегралов по отдельным сог, если бы не ограничение Ег<йг < Ет. Его
можно учесть, если включить в подынтегральное выражение в каче-
качестве множителя ступенчатую функцию
r
Q(ET - l^(Or) = - j ^du exp\iul^(Or |. A3_3_7)
Тогда формула A3.3.6) принимает вид
740 Глава 13. Инфракрасные эффекты
A3.3.8)
Интеграл в экспоненте можно взять в пределе X <^ Ет, записав его
как сумму интеграла от {е1№и — 1)/со, в котором можно положить
X = 0, и интеграла от 1/со, который тривиален. Делая масштабное
преобразование переменных и и со, получаем при X <^ Ет:
A3.3.9)
V/v J
где
,/(x; A) = i I du SU^ expf A J ^ (егЮм - 1)
p
и П J о со
г ^ ( х
x
CO
Если Е та Ет одного порядка и А « 1, множитель &(Е/ЕТ,А) в A3.3.9)
близок к единице. Например,
Так как A(a -^ C) > 0, множитель (Е/Х)А{а^^ в A3.3.9) стремится к
бесконечности в пределе X —> 0. Однако из формулы A3.3.10) видно,
что в этом пределе вероятность Г\а обращается в нуль:
Подставляя это выражение в A3.3.9), получаем, что в пределе
X <ЗС Ет инфракрасное обрезание X выпадает из ответа:
ГрЛа. A3.3.11)
13.4. Произвольные инфракрасные расходимости 741
Напомним, что энергия Л есть всего лишь удобная раздели-
разделительная точка между «мягкими» фотонами, вклад которых явно уч-
учтен в A3.3.11), и «жесткими» фотонами, вклад которых содержится
в ГЛра. Правая часть выражения A3.3.11) не зависит от Л, так как
ГЛпа <х ЛА. Однако в теориях с малой константой связи типа кванто-
квантовой электродинамики часто выгодно взять величину Л достаточно
малой по сравнению с типичными энергиями W в данном соударе-
соударении, так чтобы использованные приближения были верны для энер-
энергии фотонов, меньше Л, и в то же время достаточно большой, что-
чтобы выполнялось неравенство А(а —> C) ln(W/A) € 1. В этом случае
хорошим приближением может оказаться вычисление ГЛпа в низ-
низшем порядке теории возмущений, причем главные радиационные
поправки при ? « Л будут определяться множителем (Е/А)А в
выражении A3.3.11).
Такое же сокращение инфракрасных расходимостей происходит и
для мягких гравитонов 3. Вероятность любого процесса ОС —> C, в ко-
котором мягкие гравитоны уносят энергию, не превышающую Е, ока-
оказывается пропорциональной Ев, где
A3.3.12)
13.4. Произвольные инфракрасные расходимости
Рассмотренная до сих пор инфракрасная расходимость, обя-
обязанная своим происхождением мягким фотонам, есть лишь один из
множества примеров инфракрасных расходимостей, возникающих
в различных физических теориях. Другим примером является кван-
квантовая электродинамика безмассовых заряженных частиц. В этом слу-
случае, даже после сокращения инфракрасных расходимостей за счет
мягких фотонов, обнаруживается логарифмическая расходимость в
показателе степени А в A3.3.11). Согласно формулам A3.2.11) и A3.2.7),
для процесса, в котором все заряженные частицы — электроны,
показатель степени в пределе те —> 0 ведет себя как
742 Глава 13. Инфракрасные эффекты
2|р
4л „ 4л „^т [ те ) 2%
(На последнем шаге было использовано условие сохранения заряда
Enenr|n = 0.) Инфракрасная расходимость в этой формуле возникает
от мягких фотонов, испускаемых в направлении, параллельном им-
импульсу одного из «жестких» электронов в начальном или конечном
состоянии. Однако расходимость появляется и тогда, когда и фо-
фотон, и электрон не мягкие, т. к. знаменатель пропагатора (pn ± gJ
обращается в нуль при pn2 = g2 = 0, если рп параллелен q. Более
подробно, при pn2 = g2 = 0 интеграл от этого множителя * по направ-
направлениям фотонов принимает вид
qp±q =^TJ i q'
p q Jo 1 ~ cos0
где 0 — угол между импульсами фотона и заряженной частицы.
Интеграл логарифмически расходится при 0 = 0.
Конечно, в реальном мире нет безмассовых электрически заря-
заряженных частиц, однако в реакциях, где типичное значение Е2 ска-
скалярных произведений |pn-pm| много больше та2, представляет
интерес установить место возникновения большого множителя
ln(me/E). Часто в этом случае ведущая радиационная поправка опре-
определяется слагаемым -1п(ше/Е)Епеп2/2л2 в А. Еще важнее то. что в кван-
квантовой хромодинамике существуют безмассовые частицы глюоны, не-
несущие сохраняющееся квантовое число, называемое цветом и анало-
аналогичное электрическому заряду. В этом случае инфракрасные расхо-
расходимости возникают в результате испускания параллельных жестких
глюонов жесткими же глюонами или другими имеющими цвет жест-
жесткими частицами в начальном или конечном состояниях.
В общем случае такие инфракрасные расходимости не устра-
устраняются суммированием по подходящим наборам конечных состоя-
состояний. Однако Ли и Науенберг 6 заметили, что можно сократить
* Этот множитель не квадрируется, т. к. расходимость появляется толь-
только от интерференции этого слагаемого в матричном элементе S- матрицы
со слагаемыми, в которых фотон испускается с линии другой заряженной
частицы т Ф п. При т = п интеграл A3.2.8) пропорционален тп2.
13.4. Произвольные инфракрасные расходимости 743
инфракрасные расходимости, если суммировать не только по под-
подходящим конечным состояниям, но и предположить некоторое ве-
вероятностное распределение начальных состояний. Ниже приводит-
приводится модифицированная версия рассуждений Ли и Науенберга, из
которой станет сразу же ясно, почему в электродинамике с массив-
массивными электронами достаточно суммировать только по конечным со-
состояниям.
С этой целью удобно вернуться к «старой» теории возмущений,
в которой 5-матрица задается выражениями C.2.7) и C.5.3) в виде:
Sba = 8(Ь - а) - 2гжЬ(Еа - Еь)ТЬа , A3.4.1)
где
у, у V
{Ea-ECi+ie)...(Ea-ECv+ie)
(Интегрирование по с1( ..., сп подразумевает суммирование по спи-
спинам и типам частиц в этих состояниях, а также интегралы по 3-
импульсам частиц.) Инфракрасные расходимости могут возникать
из-за обращения в нуль одного или более энергетичеких знаменате-
знаменателей в этом выражении (и только по этой причине).
Однако не все обращающиеся в нуль знаменатели приводят к
инфракрасным расходимостям. Произвольное промежуточное состоя-
состояние с может иметь Ес = Еа, но обычно это всего лишь одна точка
внутри области интегрирования, так что интеграл по этой области
можно сделать сходящимся с помощью предписания, заключенного
в добавке г? в знаменателе. Промежуточное состояние с порождает
инфракрасную расходимость только в случае, когда энергия Ес = Еа
на границе области интегрирования. Такое случается, например,
если первое промежуточное состояние с± в A3.4.2) отличается от
начального состояния а только тем, что некоторая, любая, безмас-
безмассовая частица в этом состоянии заменена на струю, состоящую из
произвольного числа почти параллельно летящих безмасовых
частиц с полным импульсом, равным импульсу замененной на
струю частицы. В этом случае граничная точка, в которой
Ес1 = Еа, соответствует точке в импульсном пространстве, когда
все безмассовые частицы в каждой струе параллельны. В более об-
общем случае, можно заменить любое число безмассовых частиц
744 Глава 13. Инфракрасные эффекты
в состоянии а на струи почти параллельных безмассовых частиц и
произвольное число дополнительных мягких безмассовых частиц. Бу-
Будем называть множество всех таких состояний D(a). (Аккуратнее
следует ввести малый угол 0 и малую энергию Л, чтобы опреде-
определить, что понимается под «почти параллельными» и «мягкими» час-
частицами. Мы не станем заниматься выяснением зависимости D(a) от
0 и Л.) Состояния в D(a) «опасны» в том смысле, что обращение в
нуль энергетического знаменателя Еа — Ес1 в граничной точке может
привести к инфракрасной расходимости. Та граничная точка, в ко-
которой Ес1 = Еа, отвечает ситуации, когда все безмассовые частицы
в каждой струе параллельны, а все мягкие безмассовые частицы
имеют нулевую энергию.
Далее, если каждое из состояний с1( ..., сп принадлежит мно-
множеству D(a), то промежуточное состояние сп+1 также опасно в ука-
указанном смысле. С другой стороны, если какое-то промежуточное
состояние ст не принадлежит D(a), то последующее состояние ск с
к> т уже не будет опасным, даже если оно принадлежит D(a), т. к.
конфигурация жестких частиц или струй с 3-импульсами, равными
импульсам частиц в состоянии а, будет обычной точкой внутри об-
области интегрирования. Совершенно аналогично можно определить
множество состояний D(b), в которых одна или более безмассовых
частиц в состоянии Ь заменены на струи почти параллельных без-
безмассовых частиц, полный 3-импульс каждой из которых равен 3-
импульсу частицы, замененной на струю, и дополнительно испус-
испускается произвольное число безмассовых частиц. Промежуточное со-
состояние ст опасно, если оно принадлежит множеству D(b) и если
последующие состояния ск с к > т также все принадлежат D(b).
Чтобы изолировать вклады опасных состояний, перепишем
A3.4.2) в виде:
~\У
v=l\
_1_ Ор _1_ Ор
-V
Еа-Н0+ гг
A3.4.3)
'Ьа
где i'?a, ,УЪ и ;^йа5 — проекционные операторы на D(a), D(b) и все
остальные состояния соответственно. (Здесь предполагается, что ни
одна из заряженных частиц в Ь не имеет импульса, близкого
к импульсу какой-то заряженной частицы в а, так что множества
D(a) и D(b) не перекрываются.) Далее, при Л^ 0 и0^ 0 опасные
промежуточные состояния занимают столь малую область фазового
13.4. Произвольные инфракрасные расходимости
745
пространства, что ими можно пренебречь везде, где они не приво-
приводят к инфракрасным расходимостям. Поэтому степенной ряд A3.4.3)
принимает вид:
оо оо оо
= 111
r=0s=0v=0
V
V-
Еа - Но + гг
¦V
V
Еа-Н0+ гг
-V
Еа-Н0+ гг
A3.4.4)
Это равенство было бы точным, если бы все проекционные операто-
операторы &t a ь между крайними левыми и крайними правыми множителя-
множителями можно было заменить на 0Ра + Щ, + ИР?аъ, а 0Ра и &ь слева и справа
были бы заменены на ??а + ??ъ. Однако, как отмечалось выше, при
достаточно малых Л и 0 влияние такой замены на окончательный
результат было бы пренебрежимо мало.
Формулу A3.4.4) можно переписать в более компактном виде:
b S a'ba
где используемые в дальнейшем операторы ?1а+ и ?
извольных состояний ОС и В определяются формулами:
A3.4.5)
для про-
(°tL-E
of
'Са ^0{LEa-H0+K
A3.4.6)
db
Еъ - Но + гг
V
A3.4.7)
а «безопасный» оператор Ts — формулой *
* В формуле для (?1Ъ )db использовано то, что Ты вычисляется при Еъ -
Еа, а при вычислении (Ts)dc учтено, что действие проекционных операто-
операторов /Уа обращает (?1а+)са в нуль, кроме случая, когда Ес очень близко к Еа.
Кроме того, благодаря множителям ?lb~f и ?1а+ в A3.4.5) ./€cd = .
746 Глава 13. Инфракрасные эффекты
- ?
V
v=OV
<y<2c,d
Ес-Н0+ гг
V
A3.4.8)
>dc
Все инфракрасные расходимости изолированы теперь в двух опе-
операторных множителях О.а+ и Пп—.
Чтобы устранить эти инфракрасные расходимости, достаточ-
достаточно лишь заметить, что если бы не проекционные операторы на опас-
опасные состояния, операторы Q.a~ и Q.a+ были бы просто унитарными
операторами, преобразующими согласно формуле A3.1.16) состоя-
состояния свободных частиц соответственно в «ин» и «аут» состояния. Если
ограничить действие этих операторов подпространствами D(C) и D(oc)
состояний, которые являются опасными для данного конечного со-
состояния C и данного начального состояния а соответственно, то та-
такие операторы являются унитарными. Это означает, что для произ-
произвольных состояний C и ОС
ЩЯ>* Hgf = % A3.4.9)
Таким образом, вероятность перехода свободна от инфракрасных
расходимостей, если произведено суммирование по подпростран-
подпространствам состояний, которые являются опасными для любых задан-
заданных начального и конечного состояний C и ос:
аеО(а)
= Tr{^Wj}= ? ? \(Ts)bf
aeD(a) beD(p)
Чтобы окончательно удостовериться, что это утверждение ре-
решает проблему инфракрасных расходимостей в произвольном случае,
необходимо показать, что только суммы типа содержащихся в A3.4.11)
являются экспериментально измеримыми. Весьма правдоподобно, что
следует просуммировать по опасным конечным состояниям, чтобы по-
получить измеримую вероятность перехода, поскольку эксперименталь-
экспериментально невозможно отличить выходящую заряженную (цветную) безмас-
13.4. Произвольные инфракрасные расходимости 747
совую частицу от струи безмассовых частиц с почти параллельными
импульсами и той же полной энергией 7, сопровождаемую произволь-
произвольным числом очень мягких квантов с тем же полным зарядом (или цве-
цветом). Суммирование по начальным состояниям вызывает больше во-
вопросов. Вероятно, можно привести аргументы, что истинно безмассо-
безмассовые частицы всегда рождаются как струи, сопровождаемые ансамб-
ансамблем мягких квантов, однородно распределенных по некоторому объе-
объему импульсного пространства. Однако, насколько мне известно, никто
еще не сумел дать полное доказательство того, что экспериментально
измеримыми являются только суммы вероятностей переходов, сво-
свободные от инфракрасных расходимостей.
Эта проблема не возникает в квантовой электродинамике (с
массивными заряженными частицами), где, как мы видели, для
устранения инфракрасных расходимостей необходимо суммировать
только по конечным состояниям. Причина такой разницы заключа-
заключается в том, что в электродинамике состояния а, Ъ, с,... являются
прямыми произведениями состояний (отмеченных греческими бук-
буквами) с фиксированным числом заряженных частиц и жестких фо-
фотонов и состояний, содержащих только мягкие фотоны с энергией
меньшей некоторой малой величины Л. Тогда для реакции с образо-
образованием некоторого количества мягких фотонов /, рождаемых
в реакции а —» C между заряженными частицами и жесткими фото-
фотонами, формула A3.4.5) упрощается:
Тр/>а = (П-(Р)^+(а))/0(Т5)ра , A3.4.12)
где индекс 0 означает вакуум мягких фотонов, a Or вычисляются как
и выше, но в усеченном гильбертовом пространстве состояний толь-
только мягких фотонов, причем считается, что взаимодействие этих фо-
фотонов описывается гамильтонианом взаимодействия со всеми заря-
заряженными частицами в фиксированных состояниях, отмеченных ар-
аргументами C или а. Как и ранее, такие операторы унитарны в «опас-
«опасном» гильбертовом пространстве CJ) мягких фотонов, так что *
* Причина, по которой не появляется никакого множителя вида (Е/А)А,
как в формуле A3.3.11), заключается в том, что здесь мы приравниваем
максимальную энергию Е состояний реальных мягких фотонов, по которым
нужно суммировать, максимальной энергии Л «опасных» состояний мягких
фотонов, по которым производится суммирование при вычислении Or.
748 Глава 13. Инфракрасные эффекты
00
.„ A3.4.13)
= l(^)Pa|2-
без всякого суммирования по начальным состояниям.
13.5. Рассеяние мягких фотонов *
Исследуя в этой главе взаимодействия мягких фотонов, мы
рассматривали до сих пор только процессы, в которых мягкие фо-
фотоны испускаются или поглощаются в процессе ОС —> C, который про-
происходит и сам по себе. Однако можно высказать ряд полезных об-
общих утверждений относительно ситуаций, когда процесс ОС —> C три-
тривиален, а мягкие фотоны играют существенную роль в реализации
интересующей нас реакции. Рассмотрим простейший и наиболее
важный пример такого рода: рассеяние мягкого фотона на массив-
массивной частице произвольного типа и спина, когда а и C — одночастич-
ные состояния. Сложность здесь в том, что главное слагаемое в ам-
амплитуде рассеяния мягкого фотона возникает не от полюсных, а от
неполюсных слагаемых, связанных с полюсными слагаемыми через
условие сохранения тока.
Матричный элемент рассеяния фотонов может быть представ-
представлен в виде
?(дД;р,а->д'Д';р',а') = гBлL84(д + р - q - р')
где q и q' — начальный и конечный 4-импульсы фотона, р и р' —
начальный и конечный 4-импульсы мишени, X и X' — начальная и
конечная спиральности фотона, ?y(q',X') и e^q,^,) — соответствую-
соответствующие векторы поляризации фотонов, а и а' — z-компоненты спинов
* Этот раздел лежит несколько в стороне от основной линии изложения
и может быть опущен при первом чтении
13.5. Рассеяние мягких фотонов 749
начальной и конечной частиц—мишеней. Согласно теореме из разде-
раздела 6.4, амплитуду NP1^ можно записать в виде
) ... A3.5.2)
где J^(x) — электромагнитный ток, а точки указывают на возмож-
возможные слагаемые, изображаемые диаграммой типа «чайка», типа тех,
которые возникают в теории заряженных скалярных полей, когда
два фотона взаимодействуют не с отдельными токами, а в одной
вершине. Повторим теперь стандартные аргументы полологии,
изложенные в гл. 10 и уже использовавшиеся в разделе 13.1. Встав-
Вставляя полный набор промежуточных состояний между операторами
токов в правой части A3.5.2), интегрируя по ж и выделяя одночас-
тичные промежуточные состояния, получим:
q) - Е(р) - ди - г?
где G^ — одночастичный матричный элемент тока,
A3.5.4)
a iV^ представляет вклад всех других состояний кроме одночастич-
ных и любых слагаемых, изображаемых диаграммами типа «чайка».
(Формулу A3.5.3) следует понимать в смысле матричного умноже-
умножения, с не выписанными явно спиновыми индексами.) Относительно
JV^ мы знаем очень мало, не считая того, что эта величина не со-
содержит сингулярности при q^ —> 0, явно представленной первыми
двумя слагаемыми, и поэтому может быть разложена в ряд по сте-
степеням q^.
Используем теперь условие сохранения тока (или калибровоч-
калибровочную инвариантность):
^',р) = 0, A3.5.5)
q G(p + q,p) = [E(p + q) - ?(p)]G°(p + q,p), A3.5.6)
750 Глава 13. Инфракрасные эффекты
q • G(p', р - q) = [Е(р') - Е(р' - q)]G°(p', р - q). A3.5.7)
В применении к A3.5.3) эти условия приводят к желаемому условию
на №
q^N*1 (g; р', p) = -Gv (р', р' + q)G° (p + q, p) + G° (р', р' - q)Gv(р' - q, p).
A3.5.8)
Заметим также, что NP1^ удовлетворяет условию «кросс-симметрии»:
p-g;p',p), A3.5.9)
и так как полюсные слагаемые в A3.5.3) очевидно ему удовлетворя-
удовлетворяют, это же верно и для N4*1:
p-g;p',p). A3.5.10)
Мы воспользуемся этими соотношениями для нахождения первых
членов в разложении JV^ по степеням импульсов.
Прежде всего, следует что-то сказать о разложении одночас-
тичных матричных элементов тока G^p^p) по степеням импульсов
р и р'. Инвариантность относительно пространственного отражения
(если, конечно, она имеет место) требует, чтобы разложение G0 и
Gi (г = 1,2,3) содержало слагаемые соответственно только четного
или нечетного порядка по импульсам. Согласно формуле A0.6.3),
слагаемое нулевого порядка по импульсам в Goa'j(J равно e5a'a, где
е — заряд частицы. Тогда из условия сохранения тока вытекает, что
во втором порядке по импульсам
Следовательно, слагаемые в G первого порядка по импульсам име-
имеют вид е(р' + р)8о/;О/2т плюс возможное слагаемое первого поряд-
порядка, ортогональное к (р' - р). Из инвариантности относительно вра-
вращений вытекает, что это слагаемое должно быть пропорционально
(р' ~ Р) х Jo'o> гДе J ~ знакомая спиновая матрица заряженной час-
частицы. Суммируя все результаты, имеем следующее разложение:
G0(p',p) = el + квадратичные слагаемые, A3.5.11)
13.5. Рассеяние мягких фотонов 751
el iu.
G(p',p) = — (P' + P) + —Jx(p'-p)+ кубичные слагаемые, A3.5.12)
где «1» — единичная спиновая матрица, а слова «квадратичные» и
«кубичные» означают порядок отброшенных слагаемых по степеням
малых импульсов р и р'. Коэффициент ц/j в A3.5.2) действителен, т.
к. ток эрмитов. Если коэффициенты записаны в указанном виде (j —
спин заряженной частицы), то ц - величина, известная как магнит-
магнитный момент частицы.
Обратимся теперь к iV^ и рассмотрим разложение равенства
A3.5.8) по степеням малых импульсов ср, р и р'. Полагая п = 0 в
A3.5.8), видим, что qJVQ|1 по крайней мере квадратично по этим ма-
малым величинам. Не существует постоянного вектора, ортогонально-
ортогонального дц, так что iV0*1 должно быть по крайней мере первого порядка по
малым импульсам. Тогда из условия кросс—симметрии A3.5.10) вы-
вытекает, что N10 также должно быть по крайней мере первого поряд-
порядка по малым импульсам. Полагая ц = г в A3.5.8) и учитывая A3.3.12),
получаем:
к eV ,
1- квадратичные слагаемые,
m
откуда
e2
Ыг = 8ifc + линейные слагаемые. A3.5.13)
т
Так как Gi — по меньшей мере первого порядка по малым им-
импульсам, то так же ведут себя полюсные слагаемые в формуле A3.5.3)
для G*' Таким образом, в нулевом порядке остается единственное
неполюсное слагаемое Nlk:
Mik@;0,0) = Nik@;0,0) = - —8Л . A3.5.14)
lib
С помощью этого выражения можно вычислить сечение рассеяния
мягких фотонов. Но нет нужды реально проводить это вычисление.
Ведь теперь мы знаем, что амплитуда рассеяния фотонов в пределе
нулевого импульса зависит только от массы и заряда частицы-ми-
частицы-мишени и квадратична по заряду. Поэтому мы можем немедленно ис-
использовать результаты любого расчета сечения рассеяния фотонов
на частицах любого спина во втором порядке теории возмущений,
752 Глава 13. Инфракрасные эффекты
например, результат (8.7.42) для дифференциального сечения рас-
рассеяния фотонов в квантовой электродинамике:
-J7T = —^-^"A + cos20)- A3.5.15)
d& 32ж2т2
Теперь видно, что эта формула универсальна и верна в низкоэнер-
низкоэнергетическом пределе для частиц-мишеней массой т и зарядом е про-
произвольного типа и спина, даже если эти частицы составные и силь-
новзаимодействующие, например, атомные ядра. Гелл-Манн, Гольд-
бергер и Лоу8 показали, что эти результаты можно расширить и
получить следующее за главным слагаемое в разложении амплиту-
амплитуды рассеяния мягких фотонов, выразив его через массу, заряд и
магнитный момент частицы-мишени.
13.6. Приближение внешнего поля*
Интуитивно очевидно, что тяжелая заряженная частица вро-
вроде ядра атома приближенно может рассматриваться как источник
классического внешнего поля. В этом разделе мы покажем, как обос-
обосновать такое приближение, и выскажем соображения о границах
его применимости.
Рассмотрим фейнмановскую диаграмму или ту ее часть, где с
проходящей через всю диаграмму от начального до конечного со-
состояний линии тяжелой заряженной частицы испускаются N лежа-
лежащих вне массовой поверхности фотонов с 4-импульсами q1( q2, ..., qN
и поляризационными индексами ц1( ц2, •••> И-jv- Сумма всех таких
диаграмм или поддиаграмм (без N фотонных пропагаторов) приво-
приводит к амплитуде
Г 4 4 4 -' -' -'
¦Т° Х" "' ' A3.6.1)
* Этот раздел лежит несколько в стороне от основной линии изложения
и может быть опущен при первом чтении
13.6. Приближение внешнего поля 753
где матричный элемент вычислен с учетом всех взаимодействий, в
которых может принимать участие тяжелая частица, включая силь-
сильные ядерные взаимодействия. Такая амплитуда имеет кратный по-
полюс при q1( q2, ..., qN —> 0, возникающий от слагаемых в матричных
элементах произведения токов, в которых промежуточные состоя-
состояния содержат точно такую же тяжелую частицу, как начальное и
конечное состояния. Когда все компоненты qb q2, ..., qN малы по срав-
сравнению со всеми энергиями и импульсами, связанными с динамикой
(возможно, составной) тяжелой частицы, этот кратный полюс доми-
доминирует в A3.6.1). С помощью методов раздела 10.2 находим *:
xBJTL84(p/ + q1+q2+...+qJV - p)
a1>a2,...,aJV_1
"* (V)-.(^N „(p) A3-6.2)
X-
[2p • qx - г?][2р • (q1 + q2) - г?]...
+ перестановки,
где
= (р,а'\^@)\р,а), A3.6.3)
a "+ перестановки" означают, что производится суммирование по
всем перестановкам N фотонов. Для применений к атомным систе-
системам важно заметить, что A3.6.1) годится для частиц произвольного
спина, имеющих, как атомные ядра, и сильные, и электромагнит-
электромагнитные взаимодействия.
* В теории возмущений знаменатели происходят от знаменателей про-
пропагаторов:
(р +q1+...+qrf +т2 - ге -> 2р ¦ {ql+...+qr) - ге -» 2p-{ql+...+qr)-тя,
в то время как числители пропагаторов содержат множители ?гш+, приво-
приводящие вместе с матрицами в вершинах испускания фотонов к матричным
элементам A3.6.3). Матрица '§^ отличается от матрицы G^ из предыдущего
раздела множителем 2р°.
754 Глава 13. Инфракрасные эффекты
Отметим также, что для частиц произвольного спина и заряда Ze
матричные элементы электрического тока между состояниями с оди-
одинаковыми 4-импульсами имеют вид *
= JB%f ' A3-6-4)
так что
Важно, что все матрицы A3.6.5) коммутируют, так что их произве-
произведение может быть вынесено за скобки в сумме по перестановкам:
Ъа>2'' w(qi>Q2>--->Qjv;p)"^
-BлL84(р' + q1 + g2+...+gw - рMоЪ
1
[2р • Чг - Щ[2р ¦ (q, + q2) - ie]...[2p • (q^.-.+q^) - Щ
+ перестановки
В старшем порядке по q дельта-функцию можно записать в виде:
g2+...+gw - р) =
/ -I Q /У Г7 \
p/ + q1+...+qJV-p)8(p-(g1+g2+...+gJV)).
К счастью, оказывается, что результат суммирования в этом
случае значительно проще чем отдельные слагаемые. При
P'(Qi "*" 4.2 "*" - "*" Qjv) = 0 находим:
* Легче всего это доказывается следующим образом. Во-первых, в той
системе отсчета, где частица покоится, из требования инвариантности от-
относительно вращений следует, что пространственные компоненты матрич-
матричных элементов тока обращаются в нуль, а временная компонента пропор-
пропорциональна 5О'О, и более никуда зависимость от а' и а не входит. Во-вто-
Во-вторых, константа пропорциональности находится из A0.6.3), после чего пре-
преобразование Лоренца приводит к A3.6.4).
13.6. Приближение внешнего поля 755
!
+ перестановки = A3 6 8)
Bzjr)w-15(p-g1M(p-g2)...5(p-gw_1).
Например, при N = 2 имеем:
[р • Qi - г?] [р • д2 - г?] [р • q1 - ге] [-р • q1 - ie]
Общая формула A3.6.8) может быть легче всего получена как фу-
рье-преобразование тождества
0(х1 - х2 N(х2 - х3 )• • • 6(XjV_1 - xw) + перестановки = 1.
Подставляя A3.6.8) в A3.6.6), приходим к окончательному выраже-
выражению для амплитуды A3.6.1):
A3.6.9)
х S-^p' + q! +q2+...+qw - р)8(р • gx)8(p • g2)...8(p • qN).
Этот результат применим как к релятивистским, так и к медленно
движущимся тяжелым частицам, и может быть использован при
выводе приближенной формулы Вейцзеккера—Вильямса9 для рас-
рассеяния заряженных частиц. В частном случае нерелятивистской
тяжелой заряженной частицы с |р| ^С р° формула A3.6.9) дополни-
дополнительно упрощается:
х 53(р' + qx + q2+...+qw - pM(g1°M(g2°)...5(g0fM
A3.6.10)
СТ СТ '
где п — единичный времениподобный вектор,
п° = 1, п = 0.
756 Глава 13. Инфракрасные эффекты
Предположим теперь, что в начальном и конечном состояниях
присутствует одна тяжелая нерелятивистская частица * зарядом Ze
и нормированной волновой функцией в импульсном представлении
%о(р). Используя фурье—представление дельта-функции в A3.6.9),
находим, что матричный элемент ((j для такого состояния имеет вид
2jrZen5(g)e) A3.6.11)
r=l
где \|/(Х) — волновая функция в координатном представлении:
\|/а(Х) ее Bл)/2|с*3рхст(р)е^х. A3.6.12)
Поэтому, в силу факторизации правой части выражения A3.6.11),
результат добавления тяжелой заряженной частицы в данном со-
состоянии с точки зрения фейнмановских правил в импульсном про-
пространстве эквивалентен добавлению любого числа вершин нового
типа. В этих вершинах легкие дираковские частицы зарядом —е,
например, электроны, взаимодействуют с внешним полем, причем
каждая такая вершина вносит в полную амплитуду множитель **
(теперь уже учтены как фотонный пропагатор, так и электрон-
фотонная вершина)
BлL g2 -г?
A3.6.13)
где к и к' — начальный и конечный 4-импульсы электрона. Полная
амплитуда рассеяния должна быть усреднена по координате тяжелой
* Имеется в виду — помимо легких частиц. — Прим. ред.
** Первый множитель здесь — обычный множитель г, сопровождающий
по фейнмановским правилам константы в лагранжиане взаимодействия тя-
тяжелой заряженной частицы.
13.6. Приближение внешнего поля 757
частицы X с весовой функцией EJ\|/O(X)|2. Множитель A3.6.13) экви-
эквивалентен тому, который возник бы из-за нового слагаемого в ла-
лагранжиане взаимодействия:
3>ext(x) = J^x)Jf(x), A3.6.14)
где j^ = -texj/y^xi/ — электрический ток электронов, 4^ — вектор-
векторный потенциал внешнего поля:
A3.6.15)
BлL
-гг
Естественно, это сводится к обычному кулоновскому потенциалу:
Ze
^°(Ж)л|х-Х|' ^(X)-U- A3-6.16)
Если тяжелых заряженных частиц несколько (как в случае молеку-
молекулы), следует выразить 4^{х) как сумму слагаемых типа A3.6.16),
каждое со своим зарядом Ze и координатой X.
Полезно представлять, какие диаграммы суммируются при ис-
использовании приближения внешнего поля. Рассмотрим взаимодейст-
взаимодействие отдельного электрона (неважно, релятивистского или нет) с от-
отдельной тяжелой заряженной частицей, например, протоном или
дейтроном. Если пренебречь всеми другими взаимодействиями, то
фейнмановские диаграммы рассеяния электрона за счет взаимодей-
взаимодействия с внешним полем содержат произвольное число вставок вер-
вершин внешнее поле—электрон A3.6.14) в электронную линию (рис. 13.4).
Но, как следует из суммы по перестановками в формуле A3.6.2),
такие диаграммы в приближении внешнего поля возникают из диа-
диаграмм лежащей в основе этого приближения теории, где фотонные
линии, подсоединенные к электронной линии, подсоединяются к ли-
линии тяжелой частицы всеми возможными способами (рис. 13.5). «Не-
«Непересекающиеся лестничные диаграммы» (обозначенные буквой L) на
рис. 13.5 не являются доминирующими в этой сумме, если только
электрон и тяжелая заряженная частица не являются нерелятивист-
нерелятивистскими. (Такие диаграммы на языке старой теории возмущений содер-
содержат вклады от промежуточных состояний, в которых присутствуют
758
Глава 13. Инфракрасные эффекты
+
ЧЛАЛАЛЛХ
ЧЛАЛАЛЛХ
www\X
чллллллХ
Рис. 13.4. Диаграммы рассеяния электрона внешним электромагнитным полем.
Прямая линия изображает электрон; волнистые линии, оканчивающиеся
крестиками, изображают его взаимодействие с внешним полем
^ЛЛЛЛЛЛЛ
L
\лллллл/\
^ЛЛЛЛАЛА
L
Рис. 13.5. Диаграммы рассеяния электрона тяжелой заряженной частицей-
мишенью, которые в пределе большой массы мишени приводят к тому же
результату, что и диаграммы рис. 13.4. Одиночная прямая линия изображает
электрон, двойная прямая линия — тяжелую частицу-мишень, а волнистые
линии — виртуальные фотоны. Диаграммы, помеченные буквой L, называются
непересекающимися лестничными диаграммами; их вклад является
доминирующим, когда и электрон, и частица-мишень нереля-тивистские
Задачи 759
те же частицы, что и в начальном и в конечноь состояниях, а это
приводит к малым энергетическим знаменателям при условии, что
электрон и тяжелая заряженная частица — нерелятивистские. В то
же время, все другие диаграммы рис. 13.5 соответствуют промежу-
промежуточным состояниям, в которых присутствуют либо лишние фотоны,
либо электрон-позитронные пары и даже пары тяжелая частица и ее
античастица, вклад которых подавлен большими энергетическими
знаменателями.) Непересекающиеся лестничные диаграммы можно
отсуммировать, решив интегральное уравнение, известное как урав-
уравнение Бете—Солпитера 10, но нет никакого смысла в отборе именно
этого подмножества диаграмм, если только обе частицы не являются
нерелятивистскими, а в этом случае уравнение Бете-Солпитера просто
сводится к обычному нерелятивистскому уравнению Шредингера и
релятивистским поправкам, связанным со спин-орбитальным взаи-
взаимодействием, которые можно рассматривать как малое возмущение.
Следует сказать, что до сих пор теория релятивистских эффектов и
радиационных поправок в связанных состояниях не является полно-
полностью удовлетворительной.
При выводе формул A3.6.16) для внешнего поля мы учитывали
взаимодействие тяжелой заряженной частицы с электромагнитным
полем только в главном порядке по импульсу фотона. Существуют
поправки более высокого порядка по импульсу фотона, возникаю-
возникающие от учета магнитного момента тяжелой частицы, ее квадру-
польного электрического момента и т. д. Кроме того, конечно, суще-
существуют и радиационные поправки, возникающие от диаграмм кро-
кроме показанных на рис. 13.4, например, таких, где фотоны испуска-
испускаются и поглощаются на электронной линии, или со вставками элек-
электронных петель в фотонные линии. В следующей главе будет пока-
показано, что для связанных состояний диаграммы рис. 13.4 необходимо
учесть во всех порядках теории возмущений, а все другие поправ-
поправки более высокого порядка по импульсам фотонов или по е можно
включать как малые возмущения к этим диаграммам.
Задачи
1. Рассмотрите процесс е+ + е~ —» %+ + ТС в с. ц. м. при энергии
1 ГэВ и угле рассеяния 90°. Предположим, что при измерении
энергии конечных пионов мы обнаруживаем, что энергия, не
760 Глава 13. Инфракрасные эффекты
превышающая значения ЕТ <х 1 ГэВ, излучается в виде мягких
фотонов. Как зависит вероятность реакции от Ет?
2. Рассмотрите безмассовые бесспиновые частицы, описываемые
скалярным полем ф, лагранжиан взаимодействия которого имеет
вид (p(x)J(x), где J(x) включает только поля массивных частиц.
Выведите формулу для вероятности испускания произвольного
числа мягких скалярных частиц в процессе а —» C, если полная
энергия этих мягких скаляров меньше некоторой малой вели-
величины Ет. Учтите радиационные поправки за счет мягких скаля-
скаляров с энергией, меньшей некоторой малой величины Л.
3. Выведите формулу для следующего за A3.5.14) члена разложе-
разложения амплитуды рассеяния фотонов на произвольной мишени
при малых энергиях.
4. Пусть частица спина 1 и очень малой массой m описывается
векторным полем V^(x), взаимодействующим только со много
более тяжелым фермионом, описываемым дираковским полем
\|/(ж), причем лагранжиан взаимодействия имеет вид gVutyJ^ty ¦
Предположим, что тяжелый фермион обычно распадается на
другие частицы, не взаимодействующие с V^, и в таком распа-
распаде высвобождается энергия W 3> т. Рассмотрите такой процесс
распада, в котором дополнительно испускаются частицы V^,
причем энергия векторной частицы ограничена сверху значе-
значением Е, и W 3> Е ^> т. Как зависит от Е и т вероятность
процесса? Радиационными поправками пренебречь.
5. Докажите, что формула A3.6.8) верна при условии, что
p-(q1 + ... + qN) = 0.
Список литературы
1. Bloch, F. and Nordsieck, F., Phys. Rev., 37, 54 A937); Yennie,
D.R., Frautschi, S.C., and Suura, H., Ann. Phys. (NY), 13, 379
A961). См. также: Mahantappa, K.T., диссертация (Гарвардский
университет, 1961), неопубликовано.
Список литературы 761
2. Weinberg, S., Phys. Rev. Lett, 9, 357 A964); Phys. Rev., 135,
B1049 A964).
3. Weinberg, S., Phys. Rev., 140, B515 A965).
4. Эта фаза была учтена в ряде теории возмущений для нереляти-
нерелятивистского кулоновского рассеяния в работе: Dalitz, R.H., Proc.
Roy. Soc, London, 206, 509 A951).
5. См., например, в книге: Schiff, L.I. Quantum Mechanics (McGrow-
Hill, New York, 1949), Section 20 (есть рус. пер.: Л. Шифф.
Квантовая механика. М., ИЛ, 1958.)
6. Lee, T.D. and Nauenberg, M., Phys. Rev., 133, B1549 A964);
Kinoshita, Т., J. Math. Phys., 3, 650 A962); Sterman, G. and Wein-
Weinberg, S., Phys. Rev. Lett., 39, 1416 A977).
7. Sterman, G. and Weinberg, S., [6].
8. Low, F.E., Phys. Rev., 96, 1428 A954); Gell-Mann, M. and Gold-
berger, M.L., Phys. Rev., 96, 1433 A954). См. также: Weinberg,
S., in: Lectures on Elementary Particles and Quantum Field Theory
— 1970 Brandeis Summer Institute in Theoretical Physics, ed. by
S. Deser, M. Grisaru, and H. Pendleton (MIT Press, Cambridge,
MA, 1970).
9. Williams, E.J., Kgl. Dan. Vid. Sel. Mat.-Fys. Medd., XIII, No. 4
A935).
10. Bethe, H.A. and Salpeter, E.E., Phys. Rev., 82, 309 A951); 84,
1232 A951).
14
Связанные состояния во внешних полях
В гл. 11 при вычислении радиационных поправок мы сделали
всего лишь один шаг за рамки низшего порядка теории возмуще-
возмущений. Однако существует весьма важный класс задач, в которых да-
даже простейшие вычисления требуют с самого начала рассмотрения
совокупностей фейнмановских диаграмм произвольно высокого по-
порядка по константе связи типа е. Это те задачи, в которых участву-
участвуют связанные состояния, например, в электродинамике — обыч-
обычные атомы и молекулы, либо такие экзотические атомы как пози-
позитроний или мюоний.
Легко видеть, что попытка применения обычной теории воз-
возмущений в подобных задачах обязательно терпит крах. Рассмот-
Рассмотрим, например, амплитуду электрон-протонного рассеяния как
функцию энергии Е в с. ц. и. Как показано в разделе 10.3, существо-
существование связанного состояния типа основного состояния атома
водорода требует существования полюса у этой амплитуды при
Е = тр + те — 13,6 эВ. Однако ни один взятый в отдельности член
ряда теории возмущений для электрон—протонного рассеяния не со-
содержит такого полюса. Поэтому он может возникнуть лишь из-за
расходимости суммы всех диаграмм при энергиях в с. ц. и. вблизи
значения тр + те.
Причину такой расходимости ряда теории возмущений также
легко понять, особенно, если на время вместо фейнмановских диа-
диаграмм рассмотреть хронологически упорядоченные диаграммы ста-
старой теории возмущений. Пусть электрон и протон имеют в с. ц. и.
импульсы порядка q <x те. Рассмотрим промежуточное состояние, в
котором импульсы электрона и протона различаются, но остаются
порядка д. Каждое такое состояние вносит мультипликативным
14.1. Уравнение Дирака 763
образом вклад, равный произведению энергетического знаменате-
знаменателя порядка [д2/^] на матричный элемент кулоновского взаимо-
взаимодействия порядка e2/q2 (фурье-образ е2/г), а соответствующее ин-
интегрирование по импульсам внесет еще множитель порядка д3. Учи-
Учитывая все эти факторы, видим, что фактическим параметром раз-
разложения по степеням кулоновского взаимодействия является вели-
величина порядка
[g2/me]-V/g2][g3] = e2mjq.
Таким образом, теория возмущений терпит крах, если g мень-
меньше или порядка е2те, иными словами, если кинетическая и потен-
потенциальная энергии, равные по порядку величины q2/me, не превы-
превышают значения е4те, что, конечно, совпадает по порядку с энерги-
энергией связи атома водорода.
Наша цель заключается в том, чтобы научиться использовать
теорию возмущений для вычисления радиационных поправок в за-
задачах о связанных состояниях, суммируя во всех порядках те диа-
диаграммы, которые нужно, и ограничиваясь лишь конечным числом
тех, которые суммировать не следует.
14.1. Уравнение Дирака
Ограничимся в этой главе рассмотрением задач, в которых связан-
связанные состояния возникают из-за кулоновского взаимодействия элек-
электронов (или мюонов) с тяжелыми заряженными частицами типа атом-
атомных ядер. Как показано в разделе 13.6, такое взаимодействие мож-
можно учесть, добавив в лагранжиан взаимодействия слагаемое *, опи-
описывающее взаимодействие с с-числовым внешним векторным по-
потенциалом 4Цх):
4 -±(Z3 -1)(Э^ 4^ - 3V ^)(Э^ 4W -3V ^)
_ A4.1.1)
-ie{Z2-1L^4
* В этой главе мы вновь используем заглавную букву Ч* для обозначения
поля электронов в представлении Гейзенберга, а строчную букву \|/ исполь-
используем для обозначения дираковского поля, зависимость которого от времени
определяется только с-числовым внешним полем . -/^(х).
764 Глава 14. Связанные состояния во внешних полях
Оно получается заменой квантового векторного потенциала А^ на
сумму А^ +.:.</^ в отвечающем взаимодействию слагаемом в A1.1.6).
Например, для отдельной тяжелой частицы зарядом Ze, помещен-
помещенной в начале координат,
Именно взаимодействие A4.1.1) должно быть учтено во всех поряд-
порядках теории возмущений. В этом разделе мы рассмотрим теорию,
включающую только такое взаимодействие, оставив рассмотрение
радиационных поправок на последующие разделы.
Еще в детском саду физики узнают, что решение подобных
задач сводится к решению дираковского волнового уравнения в при-
присутствии внешнего поля. Вывод здесь этого уравнения может пока-
показаться лишней тратой времени, но, как подчеркивалось в гл. 1,
данное Дираком исходное его обоснование как разновидности реля-
релятивистского уравнения Шредингера не выдерживает критики.
Кроме того, в процессе вывода мы получим условия нормировки,
которые следует наложить на решения уравнения Дирака и кото-
которые в оригинальной работе Дирака кажутся взятыми несколько
«с потолка» . Обсуждаемые здесь решения дираковского уравнения
будут существенно использованы в следующем разделе при анали-
анализе радиационных поправок.
Мы проведем рассмотрение, используя вариант гейзенбергов-
гейзенберговского представления, в котором зависимость операторов от време-
времени определяется гамильтонианом, включающем только взаимодей-
взаимодействие A4.1.1) с внешним полем, но не другие взаимодействия. Поле
электронов Х|/(ж) в этом представлении удовлетворяет полевому урав-
уравнению
Г . Д , 1
:0. A4.1.3)
дхх
Это не уравнение Дирака в исходном понимании самого Дирака \
поскольку здесь \|/(ж) — не с-числовая волновая функция, а кванто-
квантовый оператор. Являющиеся с-числами дираковские волновые функ-
функции определяются равенствами:
), A4.1.4)
14.1. Уравнение Дирака 765
vN(x) = (<l>NMx)%), A4.1.5)
где Фдг — полный ортонормированный набор векторов состояний,
Фо — состояние вакуума. Из A4.1.3) немедленно вытекает, что эти
функции удовлетворяют однородному уравнению Дирака
X
д
дхх
uN(x) =
vN(x) = 0.
A4.1.6)
Кроме того, используя антикоммутаторы при равных време-
временах для дираковского поля, можно вывести условие нормировки.
Взаимодействие A4.1.1) не влияет на антикоммутаторы, поэтому они
имеют тот же вид, что и для свободных полей:
{\|/(х, t),Щу, t)} = гу°63(х - у). A4.1.7)
Беря среднее по вакууму и вставляя сумму по состояниям Ф№
находим:
Y,uN(x,t)Un(y,t)+Y,vN(x.,t)Vn(y,t) = 53(x-y). Ц4 18)
JV JV
Суммирование по N подразумевает интегрирование по состояниям
непрерывного спектра и суммирование по всем дискретным связан-
связанным состояниям.
Нас главным образом интересует случай не зависящего от вре-
времени внешнего поля типа A4.1.2). В подобных случаях состояния Фи
могут быть взяты как собственные состояния гамильтониана (вклю-
(включающего взаимодействие A4.1.1)) с энергиями EN. Из инвариантно-
инвариантности относительно временных трансляций следует, что зависимость
функций uN(x) и vN(x) от времени имеет вид
ww(x,t) = e-^4tw(x), vN(*,t) = e+iE"tvN(*). A4.1.9)
Тогда однородные уравнения Дирака запишутся как
• V + т + геух 4(х)]м„(х) = Ewww(x), A4.1.10)
766 Глава 14. Связанные состояния во внешних полях
• V + т + геух 4(х)]г;„(х) = -ENvN(x). A4.1.11)
Знак «минус» в правой части A4.1.11) указывает на то, что vN явля-
являются знаменитыми дираковскими решениями с «отрицательными
энергиями». Как видно из A4.1.8), такие решения необходимы для
полноты системы волновых функций. Конечно, при умеренных внеш-
внешних полях в теории нет состояний с отрицательными энергиями,
так что все EN положительны. Однако все еще есть существенная
разница между состояниями с неисчезающими uN или vN: из опре-
определений A4.1.4) и A4.1.5) следует, что состояния могут иметь uN Ф О
или vN Ф 0 только, если они имеют, соответственно,заряд —е или +е.
Именно в этом смысле решения уравнения Дирака с отрицательны-
отрицательными энергиями имеют отношение к существованию античастиц. Од-
Однако это соображение никак не связано с деталями уравнения Ди-
Дирака и даже со значением спина электрона.
Из дираковских волновых уравнений A4.1.10) и A4.1.11) легко
получить *, что волновые функции с разными энергиями ортого-
ортогональны. Именно,
(Ем - Е'м)(и„им) = V • (uNifyuM),
так что, если |х|2 \uNiy°yuM) остается ограниченным при |х| —» 0 и
х —> °о, то
j3
jd3
x (м^(х)мм(х)) = 0, если EN Ф Е*м . A4.1.12)
При аналогичных граничных условиях для vN находим тем же пу-
путем:
l3x [vTN(x)vM(x)) = 0, если EN Ф Е'м , A4.1.13)
jd3
= 0, если EW *-Е^ • A4.1.14)
* Следующим ниже, вообще говоря, нестрогим рассуждениям мож-
можно придать строгий математический смысл, если исходить из того, что
дифференциальный оператор гу°|^уУ + т + геу^А^(х^ (гамильтониан Дирака
во внешнем поле) является самосопряженным оператором в гильбертовом
пространстве дираковских спиноров \|/(х) со скалярным произведением
(\|/1;\|/2) = Jdx\|/t(x)\|/2(x). — Прим. ред.
14.1. Уравнение Дирака 767
Полагая N = М, получаем из A4.1.12) и A4.1.13), что все энергии
действительны. Опуская в A4.1.12)—A4.1.14) знак комплексного со-
сопряжения над Ем, находим, что функции и с разными энергиями
ортогональны, функции v с разными энергиями ортогональны, и
(до тех пор пока потенциал недостаточно велик, чтобы порождать
состояния отрицательной энергии) все и ортогональны ко всем v.
Подбирая подходящим образом дискретные квантовые числа, ко-
которые наряду с энергией характеризуют состояния, можно всегда
сделать так, чтобы
Jd3x(u^(x)uM(x)) = 0, если N±M, A4.1.15)
= 0, если N±M, A4.1.16)
0. A4.1.17)
Умножая A4.1.8) справа на им(у) или vM(y), находим, что эти волно-
волновые функции должны удовлетворять условиям нормировки
6WM, A4.1.18)
где 5WM - произведение кронекеровских дельта-символов и дельта-
функций в импульсном пространстве, причем нормировка согласо-
согласована с той, которая использовалась при определении EN, так что
^jv^jvm = 1- Эти условия нормировки непосредственно не имеют отно-
отношения к любой вероятностной трактовке дираковских волновых функ-
функций, а являются следствиями антикоммутационных соотношений
A4.1.7) для полей.
Обратимся к конкретному случаю чисто электростатического
внешнего поля с А = 0. В принятом нами стандартном представле-
представлении матрицы Дирака имеют вид:
В этих формулах о — обычный 3-вектор, составленный из 2 X 2
матриц Паули, а 1 и 0 — единичная и нулевая матрицы 2x2. Вве-
Введем двухкомпонентные волновые функции fN и gN, полагая
768 Глава 14. Связанные состояния во внешних полях
A4.1.19)
Уравнение на собственные значения энергии A4.1.10) примет вид:
(а • V)/w = (EN + e-J° + m)gN, A4.1.20)
(а • V)gw = -(EN + e-J° - m)fN. A4.1.21)
В нерелятивистском случае, когда е-/°г ~ Za <^ 1, энергия
связи т - EN порядка Z2a2m, в то время как оператор градиента
порядка Zam, так что gN приблизительно в Za раз меньше fN. (Что-
(Чтобы найти волновые функции позитрона, заменяем везде EN на — EN,
так что в этом случае fN меньше gN во столько же раз.) В конце
раздела мы вернемся к нерелятивистскому случаю.
Физические состояния можно расклассифицировать на чет-
четные и нечетные по отношению к пространственной инверсии:
РФ„ = Г|„Ф„ , A4.1.22)
где r|w — знаковый множитель, равный +1. Напомним, что если
определить внутреннюю четность электрона равной +1, то дира-
ковское поле преобразуется по отношению к инверсии по закону
так что из уравнений A4.1.4) и A4.1.5) следует, что дираковские
волновые функции удовлетворяют условию четности:
„ ии(-х), A4.1.23)
или эквивалентно,
/w(x) = r|w/w(-x), gw(x) = -r|wgw(-x). A4.1.24)
Обратим внимание, что четность состояния совпадает с четностью
/w(x), но не gw(x).
Если потенциал -/° инвариантен относительно вращений, ре-
решения волновых уравнений можно охарактеризовать их полным
14.1. Уравнение Дирака
769
угловым моментом j и четностью Т|. При заданном j компоненты / и
д можно разложить по сферическим гармоникам с орбитальными
моментами I = j + 2 и I = j — 2, но при заданной четности
Г) = (_]У+г" из уравнений A4.1.24) вытекает, что / содержит только
гармонику с I = j + 2, a 9 ~ только гармонику с I = j + г- Из обычных
правил сложения угловых моментов вытекает, что для состояния с
полным моментом j, z-компонентой полного момента ц и четностью
(_]У ^ «большая» двухкомпонентная волновая функция / имеет вид
Fflxl
A4.1.25)
где С и Y — соответственно обычные коэффициенты Клебша—Горда-
на и сферические гармоники 2. Кроме того, если задана любая вол-
волновая функция с определенными полным угловым моментом и чет-
четностью, можно построить другую волновую функцию с теми же j и
ц, но противоположной четностью, подействовав оператором (о-х),
так что «малые» компоненты можно взять в виде:
д(х) = (а • х)
X .
A4.1.26)
Принято определять орбитальный момент I состояния как орбиталь-
орбитальный момент «больших» компонент fN:
I = j + L A4.1.27)
так что четность всегда равна (—1)'.
Подставляя A4.1.25) и A4.1.26) в A4.1.20) и A4.1.21), получаем
систему зацепляющихся дифференциальных уравнений:
dr
A4.1.28)
770
Глава 14. Связанные состояния во внешних полях
4^ - ^—^ F - (Е + еА° + m)G = 0,
dr r
A4.1.29)
где при четности т\ = (—1)
к = ±(j +|).
A4.1.30)
Сосредоточимся на случае простого кулоновского поля A4.1.2), ко-
когда е.:</° = Zoc/r. Исследование уравнения Дирака в этом случае хо-
хорошо известно3, так что мы для полноты изложения коротко сум-
суммируем результаты. Легко видеть, что вблизи начала координат
решения ведут себя как г8, где s2 = к2 — Z2a2. (Обратим внимание,
что к2 > 1, так что показатель степени s действителен при
Zoc < 1.) Решения с s < 0 следует отбросить как несовместимые с
условием нормировки A4.1.18). После этого требование, чтобы вол-
волновые функции не стремились к бесконечности при г —» °о, опреде-
определяет разрешенные собственные значения энергии *:
= m
1 +
Zoc
п — 1 — г ¦
-1/2
A4.1.31)
где п — «главное квантовое число» и
j + 5 < п.
A4.1.32)
Примечательно, что эти значения энергии не зависят от чет-
четности или I, а зависят только от п и j. Для каждого п и. j существуют
два решения, отвечающие двум знакам к или двум возможным чет-
ностям, за исключением случая п = j + 2, когда единственной воз-
возможностью является к > 0 и четность (-1)J~2, так что I = j — \-
С учетом неравенства A4.1.32) это сводится к знакомому нереляти-
нерелятивистскому ограничению I < п — 1.
Для легких атомов с Za ^C 1 выражение A4.1.31) можно пред-
представить в виде ряда
* Речь идет о дискретном спектре. — Прим. ред.
14.1. Уравнение Дирака 771
Е = т
1--
Z2a2 Z4a4
2п2
A4.1.33)
Естественно, что первое слагаемое есть энергия покоя, а вто-
второе — энергия связи, согласно нерелятивистскому уравнению Шре-
дингера. Первая релятивистская поправка, зависящая как от п, так
и от j, дается третьим слагаемым. При п = 1 возможно только одно
значение полного момента j = 2, и так как в этом случаем п = j + 2,
то и одно значение четности (-1)J~2 = +1, что соответствует I = 0.
Поэтому для состояний водородоподобных атомов с п = 1 довольно
трудно наблюдать эффекты, обусловленные релятивистскими по-
поправками к энергии связи, которые даются формулой A4.1.33), хо-
хотя, как будет видно в разделе 14.3, это недавно стало возможным. С
другой стороны, при п = 2 имеются состояния с j = 2 и обеими
четностями (т. е. состояния 2s1/2 и 2р1/2), а также состояние 2р3/2 с
j = | и отрицательной четностью. Из формулы A4.1.33) определяет-
определяется расщепление р-уровней водорода:
2
ЕBр3/2) - ЕBр1/2) = (X^L = 4,5283 X1СГ5 эВ. A4.1.34)
Подобное релятивистское расщепление уровней носит назва-
название тонкой структуры атомных уровней. С самого начала было
известно, что это предсказание находится в хорошем согласии с
наблюдаемой тонкой структурой. С другой стороны, из уравнения
Дирака вытекает отсутствие разницы в энергиях состояний 2s1^2 и
2Pi/2> так что именно здесь уместно поискать вклады других попра-
поправок, что и будет рассмотрено в разделе 14.3.
Прежде чем завершить этот раздел, рассмотрим приближен-
приближенные выражения для волновых функций и матричных элементов в
нерелятивистском случае для произвольного электростатического
потенциала -/°. (Для кулоновского потенциала это соответствует пре-
пределу Za « 1.) Так как EN + т — 2т 3> |е-/°|, «малые» компоненты
волновой функции электрона приближенно выражаются через «боль-
«большие» компоненты:
A4.1.35)
772
Глава 14. Связанные состояния во внешних полях
Тогда уравнение A4.1.21) превращается в нерелятивистское урав-
уравнение Шредингера
V2
2т„
-еА°
A4.1.36)
Поскольку теперь в уравнении для fN уже нет никакой связи меж-
между спиновыми и орбитальными степенями свободы, можно искать
полную систему решений этого уравнения в виде:
/jv =
где Xn — двухкомпонентный постоянный спинор, а Х|/д(х) — обыч-
обычное однокомпонентное решение уравнения Шредингера. Однако часто
мы используем состояния с определенными значениями полного мо-
момента j, для которых fN (при ненулевом орбитальном моменте) пред-
представляется суммой таких решений.
В нерелятивистском приближении четырехкомпонентная ди-
раковская волновая функция принимает вид:
uN ^
1
A + ш • V / 2т) f.
N
_(l-za-V/2m)/WJ
а формула A4.1.18) определяет условие нормировки
Jd x(fN,fM) 6NM 4(v )NM
A4.1.37)
A4.1.38)
где
(v\M =-
При установлении связи матричных элементов во внешнем поле
с матричными элементами для свободных частиц полезно заме-
заметить, что волновая функция в импульсном представлении, отве-
отвечающая собственному значению энергии N, может быть записана
в следующем виде:
L.39)
14.1. Уравнение Дирака
773
где дираковский спинор для свободной частицы
'Г
,0,
а /jv(p) ~ фурье-образ двухкомпонентной шредингеровской волно-
волновой функции:
/и(р) = BлГ3/2
В заключение с целью вычисления вкладов различных возмущений
приведем главные члены матричных элементов 16 независимых 4x4
матриц по электронным состояниям.
(uMuN) ^
i(uy°
!(%У%) ~
1
тп
A4.1.40)
A4.1.41)
A4.1.42)
, A4.1.43)
A4. 1.44)
A4.1.45)
A4.1.46)
A4. 1.47)
774 Глава 14. Связанные состояния во внешних полях
14.2. Радиационные поправки во внешних полях
Учтем теперь наряду с внешним полем тяжелых заряженных
частиц также и квантовое электромагнитное поле и рассмотрим ра-
радиационные поправки к результатам предыдущего раздела, обус-
обусловленные взаимодействием электронов с квантовым электромаг-
электромагнитным полем. Такие радиационные поправки можно вычислить с
помощью обычной фейнмановской диаграммной техники, причем
весь вклад внешнего поля будет заключаться в модификации про-
пагатора поля электронов в присутствии внешнего электромагнит-
электромагнитного поля (и в добавлении зависящих от внешнего поля перенорми-
перенормировочных контрчленов из формулы A4.1.1)). Конкретнее, вклад от
включения любого числа вершин, соответствующих первому сла-
слагаемому в операторе взаимодействия A4.1.1), во внутреннюю элек-
электронную линию любой диаграммы заключается в замене голого про-
пагатора в координатном представлении —iS{x — у) на пропагатор
во внешнем поле
-iS 4{х,у) ее -iS{x - у) + (-гJ\d\S{x - z)ey^ J[l(z1)S(z1 - у)
+(-гK J d\ J d%S{x - zx) et ^ (Zl)S(Zl - z2) еу%(z2 )S(z2 - y)
+ ..., A4.2.1)
где, как обычно,
(Следует записывать S,/ как функцию х и у, а не х — у, поскольку
внешнее поле нарушает трансляционную инвариантность.) Соглас-
Согласно доказанной в разделе 6.4 теореме, S ь определяемый формулой
A4.2.1), совпадает с выражением, определяемым формулой
-iS 4{х,у) = {Ф0,Т{Щх),Щу)}Ф0) 4 , A4.2.2)
где нижний индекс 4 справа означает, что вакуумное состояние Фо и
электронное поле Х|/(ж) должны быть определены в гейзенберговском
представлении, в котором учитывается только взаимодействие A4.1.1)
с внешним полем. Вставляя полный набор промежуточных состояний
14.2. Радиационные поправки во внешних полях 775
Фи в A4.2.2), приходим к выражению этого пропагатора через вве-
введенные в предыдущем разделе дираковские волновые функции:
-iS 4{х,у) = 0(ж° -у°)^ми(ж)пи(у)-0(у° -x°)YJVM{x)vM{y).
N М
A4.2.3)
Можно получить пропагатор A4.2.2) и как решение неоднород-
неоднородного уравнения Дирака
ух —-j- + m + ieyx Jx(x) \s 4{x,y) = 64(ж - у), A4.2.4)
которое следует из полевых уравнений A4.1.3) и соотношений анти-
антикоммутации A4.1.7), или формально из ряда теории возмущений
A4.2.1). Кроме того, из формулы A4.2.3) вытекает, что этот пропага-
пропагатор удовлетворяет следующим граничным условиям: его фурье-
разложение содержит при х° — у0 —> °° только «положительночастот-
ные слагаемые», пропорциональные exp(-iE(x° - у0)) с Е > 0, а при
х° — у0 —> — °° — только «отрицательночастотные слагаемые», про-
пропорциональные ехр(+Щх° - у0)) с Е > 0. Даже в случаях, когда
внешнее поле слишком сильно, и использование ряда теории воз-
возмущений A4.2.1) недопустимо, можно с помощью неоднородного урав-
уравнения Дирака с такими граничными условиями получить численное
решение 4 для пропагатора во внешнем поле. Если только пропага-
пропагатор найден, амплитуды рассеяния во внешнем поле можно вычис-
вычислить, используя обычные фейнмановские диаграммы, заменив при
этом S(x — у) на S i(x,y) (и включив, где необходимо, соответствую-
соответствующие зависящие от 4 перенормировочные контрчлены).
Посмотрим теперь, как использовать ряд теории возмущений
с пропагатором во внешнем поле для вычисления сдвигов уровней
энергии связанных состояний. Рассмотрим полный электронный про-
пропагатор S' / (ж,у), учитывающий взаимодействие электрона как с
квантовым электромагнитным полем, так и с внешним полем:
-iS'4{x,y) = (ао,Т{ВД,?(т/)}ао) 4 , A4.2.5)
где *Р(ж) — электронное поле в гейзенберговском представлении с
учетом всех взаимодействий, а О.0 — вакуумное состояние полного
776 Глава 14. Связанные состояния во внешних полях
гамильтониана. В случае независящего от времени внешнего потен-
потенциала можно найти полный ортонормированный набор собственных
состояний ?lN полного гамильтониана с энергиями E'N. Вставляя сумму
по этим состояниям в произведение операторов в A4.2.5), находим:
—iS'4{x,y) = 0(ж° -у°)<
JV
-u(il° - -rO\p-iEN(yO-x°)
N
где
= e-iE^l7w(x), A4.2.7)
N0 ее e+iE^Vw(x). A4.2.8)
(Сумма включает интегрирование по непрерывному спектру и сум-
суммирование по дискретным связанным состояниям. Как и ранее, UN
и Vw не равны нулю, только если заряд состояния ?lN равен —е или
+е, соответственно.) Можно переопределить этот пропагатор, за-
задав его как функцию энергии, а не времени:
° eiE^-y^S'4{x,y). A4.2.9)
(Из инвариантности относительно временных трансляций следует,
что S' ({х,у) есть функция х° — у0, но не х° или у0 по отдельности.)
Из формулы A4.2.6) следует, что
Е_ъЬЕ
N N N N
A4.2.10)
В частности, S' Дх,у;Е) имеет полюса в точках, отвечающих как
энергии любого связанного состояния электрона, так и взятой с об-
обратным знаком энергии связанного состояния позитрона. (Конечно,
у позитронов нет связанных состояний в кулоновском поле обычно-
обычного положительно заряженного ядра.)
Рассмотрим теперь радиационные поправки низшего порядка
к полному пропагатору. В соответствии с фейнмановскими правилами
14.2. Радиационные поправки во внешних полях 777
полный пропагатор в этом порядке равен S\,( = S,/ + bS4, где по-
поправка
5S ;(х,у) = jd3zjd3wS ;(x,z)I.*;(z,w)S ;(w,y), A4.2.11)
а величина г Е*./ есть сумма всех однопетлевых диаграмм с одной
входящей и одной выходящей электронной линией (исключая по-
последние электронные пропагаторы), вычисленная с использованием
пропагатора S4(x,y) вместо S(x — у) для внутренних электронных
линий, плюс перенормировочные контрчлены второго порядка. Ис-
Используя вместо временных энергетические переменные, имеем:
(w,y;E), A4.2.12)
- A4.2.13)
За счет радиационных поправок изменяются волновые функции:
UN = uN + buN, VN = vN + bvN, и энергии связанных состояний:
E'N = EN + bEN, так что полный пропагатор равен:
¦E
EN-E
N N
-Y
L
N EN+E A4.2.14)
vN(x)vN(y)?>EN
(EN+EY
N (EN~EY ^ (EN
(Мы опустили слагаемые г?, поскольку теперь рассматриваются те
значения Е, которые не принадлежат непрерывному спектру со-
состояний рассеяния.) Видно, что сдвиг bEN энергии связанного со-
состояния электрона определяется коэффициентом при слагаемых
-uN(x)uN(y) I (EN - Е) в полном пропагаторе. Чтобы найти этот ко-
коэффициент, заметим, что из A4.2.3) вытекает:
¦ +E-ie' A4.2.15)
JV N N
778 Глава 14. Связанные состояния во внешних полях
Подставляя это выражение в A4.2.12), находим:
ци(х)цм(у)
nm(En-E)(Em-E)
A4.2.16)
где точки соответствуют дополнительным слагаемым, включающим
хотя бы один полюс при отрицательном значении энергии. Сравни-
Сравнивая коэффициенты при (EN — E)~2 здесь и в A4.2.14), получаем:
5EN =-Jd3xJd3yww(x)r^(x,y;Ew)ww(y). A4.2.17)
Функции uN являются решениями однородного уравнения Ди-
Дирака, удовлетворяющими условию нормировки A4.1.8), так что все
это весьма похоже на обычную теорию возмущений первого поряд-
порядка, с заменой в гамильтониане оператора возмущения на —? •
В общем случае bEN оказывается комплексным. Это есть след-
следствие нестабильности атомных уровней энергии по отношению к
радиационным переходам на нижние уровни. В гл. 3 мы видели, что
нестабильное состояние с энергией Е и вероятностью распада Г при-
приводит к наличию полюсов в разных амплитудах при комплексных
значениях энергии Е - гГ/2. Мнимая часть A4.2.17) равна по этой
причине —Т/2, а действительная часть определяет сдвиг энергии.
Фейнмановские диаграммы для ? показаны на рис. 14.1. (Об-
(Обратим внимание на то, что здесь появились новые фотонные
диаграммы—головастики, поскольку присутствие внешнего поля
нарушает лоренц-инвариантность и инвариантность относительно
зарядового сопряжения, запрещающие подобные диаграммы в обыч-
обычных правилах Фейнмана.) С помощью фейнмановских правил в ко-
координатном представлении получаем вклад этих диаграмм в виде
г I*, (х, у) = [еу» ] [-iS 4 (х, у)] [еу^ ] [-Щх - у)]
- у)] Jd4z [-iD(x - z)] Tr{[-iS 4(z,
-i(Z2 - 1)(Y^ + mM4(x - y) + г6ш54(ж - у)
+z(Z3 - l)HV]64(x - y) Jd4z[-iD(x -
14.2. Радиационные поправки во внешних полях
779
Рис. 14.1. Фейнмановские диаграммы низшего порядка для электронной
собственноэнергетической функции L%(x, у) в присутствии внешнего поля.
Двойные прямые линии изображают пропагатор во внешнем поле SA;
одиночные прямые линии — входящие и выходящие электронные линии;
волнистые линии — виртуальные фотоны; крестиками изображены
перенормировочные контрчлены
где перенормировочные константы (Z2 - 1), (Z3 - 1) и 5m вычислены
во втором порядке по е. (Знак «минус» во втором слагаемом привыч-
привычно сопровождает вклад замкнутой фермионной петли.)
В случае сильных внешних полей с Zoc порядка единицы, необ-
необходимы численные расчеты электронного пропагатора S / в конфигу-
конфигурационном пространстве и интегралов в A4.2.17) и A4.2.18).4 Однако
для слабых полей можно подставить несколько первых слагаемых
ряда A4.2.1) в A4.2.18) и вычислить эти интегралы в замкнутом виде.
Удобнее работать в импульсном представлении, определив
A4.2.19)
780 Глава 14. Связанные состояния во внешних полях
Е*ЛР',Р), A4.2.20)
p), A4.2.21)
A4.2.22)
(Мы допускаем здесь некоторую некорректность, используя один и
тот же символ для функции и ее фурье-образа, полагая, что явное
указание аргумента позволяет разобраться, что есть что.) Выраже-
Выражения A4.2.1) и A4.2.18) принимают вид
с ,„'„ч_ -гр + т
р2 + т2 - ie
-ip' + m ., , ч -гр + т A4.2.23)
р + т — ге р + т — ге
- т) + Z25m]54(p' - р) - ie{Z2 - 1).М(р' - р)
1 Г 4
"~ J7^ ~ d Cjf Tr{o y'(Q,Q + P~P)Ym} П 4 9 94\
I L/ L/ ^ tC- ^ '
+ tgl L [(P - p'J U{v - p) - (p - p')(p - p') • 4{v - P)l •
(p - p ) - ге L J
Поскольку внешнее поле не зависит от времени, S ((х,у) и
Е ,{(х,у) могут зависеть от ж0 и у0 только через разность ж0 — у0,
так что S ,{(р',р) и Е/(р',р), а также -/ц(р' — р) должны быть про-
пропорциональны 5(р'° — р°):
' - р) = 8(р'° - р°):^(р' - р), A4.2.25)
14.3. Лэмбовский сдвиг в легких атомах 781
Сдвиг энергии определяется из A4.2.17) и A4.2.13) в виде:
3puw(p/)E^(p/,p;Ew)uw(p), A4.2.28)
где Ес,/(р',р; EN) дается формулами A4.2.23), A4.2.24) и A4.2.27). Это
рабочая формула, которую мы используем в следующем разделе
для расчета энергетических сдвигов в слабых внешних полях.
14.3 Лэмбовский сдвиг в легких атомах
Рассмотрим радиационные поправки к уровням энергии нере-
нерелятивистского электрона в произвольном электростатическом поле,
например, в кулоновском поле легкого ядра с Zoc <C 1. В этом преде-
пределе естественно рассматривать кулоновское поле как малое возму-
возмущение, но, как мы увидим, это приводит к инфракрасной расходи-
расходимости, связанной с той, которая обсуждалась в разделе 11.3. На
самом деле, инфракрасная расходимость фиктивна, поскольку 4-
импульсы p,Ew и j>',EN не лежат на массовой поверхности электро-
электрона, тем не менее, нам нужно быть внимательными.
Обычно задачу решают, разбив интеграл по энергиям вирту-
виртуального фотона на область низких энергий, где электроны можно
рассматривать нерелятивистски, но учитывать вклады всех поряд-
порядков по внешнему полю, и область высоких энергий, где следует
учитывать релятивистские эффекты, но ограничиться только вкла-
вкладом первого порядка по внешнему полю.
Мы поступим иначе и введем фиктивную массу фотона ц, вы-
выбрав ее много большей, чем типичные кинетические энергии элек-
электрона, но много меньшей типичных импульсов электрона. В случае
кулоновского поля это сводится к требованию:
(ZocJme « ц « Zame. A4.3.1)
782 Глава 14. Связанные состояния во внешних полях
Запишем фотонный пропагатор в первых двух слагаемых пра-
правой части формулы A4.2.24) (включая выражения для контрчленов
Z2 — 1 и Z25m) в виде:
1
к - гг
1
к1 + \у - гг
к -гг к + ц - гг
A4.3.2)
Сдвиг энергии является, соответственно, суммой двух слагаемых,
отвечающих «высоким энергиям» и «низким энергиям». Слагаемое,
отвечающее высоким энергиям, вычисляется путем подстановки пер-
первого слагаемого в фотонном пропагаторе A4.3.2) в три первых сла-
слагаемых правой части A4.2.24) и прибавления результата к двум по-
последним слагаемым в A4.2.24) (отвечающим поляризации вакуума),
которые в любом случае не содержат инфракрасной расходимости.
Слагаемое, отвечающее низким энергиям, вычисляется подстанов-
подстановкой второго слагаемого из A4.3.2) в три первых слагаемых в A4.2.24).
Одним из преимуществ такой процедуры является то, что удается
непосредствено воспользоваться результатами релятивистских вы-
вычислений из разделов 11.3 и 11.4, не занимаясь довольно запутан-
запутанным переходом от массы фотона к инфракрасному обрезанию по
энергии. Конечно, в конце вычислений мы должны убедиться, что
зависимость от массы фотона ц в слагаемых, отвечающих высоким
и низким энергиям, взаимно сокращается и полный сдвиг энергии
не зависит от ц.
А. Слагаемое, отвечающее высоким энергиям
Поскольку ц выбрано значительно большим, чем энергии свя-
связи в атоме, можно оставить только слагаемые низшего порядка по
внешнему полю. Однопетлевая радиационная поправка к атомным
уровням энергии в произвольном не зависящем от времени внеш-
внешнем вектор-потенциале -/ц(х) определяется в импульсном представ-
представлении выражением A4.2.28), где собственноэнергетическая вставка
Е,,/(р',р) дается формулами A4.2.24) и A4.2.23). Слагаемые нулевого
порядка по внешнему полю просто сокращаются: слагаемое, про-
пропорциональное 5т, сокращается с первым слагаемым при А = 0;
слагаемое, пропорциональное Z3 - 1, сокращается с третьим сла-
слагаемым при .:.</ = 0; наконец, слагаемые, пропорциональные Z2 - 1,
обращаются в нуль, поскольку и(р) удовлетворяет уравнению
14.3. Лэмбовский сдвиг в легких атомах
783
Дирака. Слагаемое первого порядка по 4^ в Е*,/(р',р) можно пред-
представить в виде:
A4.3.3)
,P) — te/i^^p РД 1 (P ,P),
ге
х
BjiL J /c2 + ц2 - г?
-г(р-
(р' - kJ +m2 -i
ге у 1
BлL (р-р'J-ге
(р'-рJ -ге
(р - /сJ + т2 - ге
+ (Z2-1)Y^
A4.3.4)
Сравнение двух первых слагаемых этого выражения с форму-
формулами A1.3.1) и A1.3.8), а двух последних — с формулами A1.3.9),
A1.2.3) и A1.2.15) показывает, что F^ip^p) является полной одно-
петлевой вершинной функцией, включающей поляризацию вакуу-
вакуума и все контрчлены, матричные элементы которой на массовой
оболочке уже были вычислены в разделе 11.3. Используя представ-
представления A4.2.26) и A4.2.25), соответствующий вклад в сдвиг энергии
A4.2.28)можно записать в виде
]
Лвысокие энергии
\5EN]
x (uN (pOrf (p', E'N, p, EN )uN (p)) \ (p' - p).
A4.3.5)
(Вид этой формулы можно было бы угадать, просто заменив у1 в
вершине взаимодействия электрона с внешним полем на Г^.) Как
обсуждалось в разделе 14.1, в силу неравенства Zoc <^ 1 можно ап-
аппроксимировать дираковскую волновую функцию uN в A4.3.5) выра-
выражением:
A4.3.6)
784
Глава 14. Связанные состояния во внешних полях
где /w есть нерелятивистская двухкомпонентная волновая функция
электрона во внешнем кулоновском поле, а и(р,о) — четырехкомпо-
нентное нормированное решение уравнения Дирака в импульсном
пространстве:
A4.3.7)
соответствующее z-компоненте спина а. Так как uN(j>) приближенно
удовлетворяет уравнению Дирака для свободной частицы, то об-
общая форма матричного элемента Г^ дается формулой A0.6.15):
A4.3.8)
где q = p' — р. Волновые функции uN(j>) очень быстро убывают при |р|
3> Zame, так что нужны только выражения для F^q2) и F2(q2) в
пределе д2 <^ те2. В этом пределе с помощью формул A1.3.31), A0.6.18)
и A1.3.16) имеем:
24л2
ml
In
5 4
A4.3.9)
F2(g2) -
16т„%
2 "
A4.3.10)
Рассмотрим сначала вклад слагаемого Fx в формуле A4.3.8),
поскольку именно оно приводит к самому большому вкладу в сдвиг
уровней энергии и, кроме того, при его вычислении возникают наи-
наиболее интересные проблемы. В случае чисто электростатического
поля, когда ,4 = 0, из формул A4.3.5), A4.3.8) и A4.3.9) получаем:
х
'\ d3p uN (
In
т\
5 4
' - p))y° (p' - pJ uN (p).
A4.3.11)
14.3. Лэмбовский сдвиг в легких атомах
785
Для вычисления этого вклада можно использовать главное слагаемое в
нерелятивистском матричном элементе A4.1.41), так что в результате
имеем
! (V2) 2 3
A4.3.12)
или в координатном представлении
24л2ш2
A4.3.13)
В частности, для кулоновского потенциала A4.1.2) имеем: eV2-/°(х)
= —Ze253(x), индекс N включает главное квантовое число п и кван-
квантовые числа углового момента j, m, I, а из формулы A1.2.41) имеем:
[/njmj(O)]a = 2(Zame/n3K/25;05om/V4jL Соответственно сдвиг энергии
A4.3.11) принимает вид:
In
mi
8г,о
A4.3.14)
(Отсутствие зависимости ЪЕ от 2-компоненты т полного углового
момента гарантируется инвариантностью относительно вращений.)
Слагаемое 2/5 в скобках в A4.3.12) и A4.3.13) возникает за счет по-
поляризации вакуума и дает ту же величину сдвига, которая была
вычислена в разделе 11.2 с помощью скорее эвристических сообра-
соображений.
Прежде чем переходить к вычислению магнитного и низко-
низкоэнергетического вкладов в сдвиг энергии, стоит заметить, что с
помощью уже найденного результата можно без всякой дальней-
дальнейшей работы получить хорошую оценку лэмбовского сдвига по по-
порядку величины. Можно ожидать, что низкоэнергетические слагае-
слагаемые будут содержать член, пропорциональный 1п(ц/В), с таким ко-
коэффициентом, чтобы сократить зависимость от ц в A4.3.12).
Константа В есть энергия, необходимая для обезразмеривания
786 Глава 14. Связанные состояния во внешних полях
аргумента логарифма. Поскольку инфракрасное обрезание в конце
концов определяется энергией связи электрона в атоме, можно пред-
предположить, что В равна типичной энергии связи, т. е. В — (ZaJme.
Таким образом, полный сдвиг энергии в состоянии N с главным
квантовым числом п и орбитальным моментом I равен:
If0 +0A)]. A4.3.15)
Для 2s состояния атома водорода одно только логарифмическое сла-
слагаемое дает
ОС 7YI
8E2S -- -nr^ln(a4) = 5,5 х 10 эВ = 1300 МГц х 2жП.
Как мы увидим, слагаемые 0A) уменьшают полный сдвиг энергии
примерно на 25 %.
Рассмотрим теперь вклад слагаемого F2 в матричный элемент
Г]^. Как мы видели в разделе 10.6, это слагаемое можно интерпре-
интерпретировать как радиационную поправку к магнитному моменту элек-
электрона. Подставляя формулы A4.3.10), A4.3.8) и A4.3.6) в A4.3.5), на-
находим, что это слагаемое приводит к сдвигу энергии:
[5EN] = -
6 Ше A4.3.16)
или в координатном представлении
|(и[]и)^у A4.3.17)
libр
где
,^v(x) ее Э^у(х) - Эу,^(х). A4.3.18)
В случае чисто электростатического поля, когда .-Л = 0, этот сдвиг
принимает вид
14.3. Лэмбовский сдвиг в легких атомах
787
[bEN] =
A4.3.19)
В нерелятивистском пределе Za ^C 1 можно использовать прибли-
приближенный результат A4.1.43), который в данном случае имеет вид:
(uN[y°,y]uN) - -Ч(У/? -aafN)
о • V/w)]
= — [V(/^/w) - OT^ x o)fN - ifN (о х V/w)].
A4.3.20)
Подставляя это представление в правую часть формулы A4.3.19) и
интегрируя по частям, находим, что этот вклад в сдвиг энергии
дается формулой
+ 2z/;(x)o-(V(eA0(x))xV/w(x)].
A4.3.21)
Собирая вместе выражения A4.3.12) и A4.3.21), получаем полный
отвечающий высоким энергиям вклад в сдвиг энергии в произволь-
произвольном электростатическом потенциале -/°:
J высокие энергии
„2
In
m
ге
16%*т
2
2^2
J d3x /^ (х) a • (V(eA° (x) х V/w (х)).
A4.3.22)
Б. Слагаемое, отвечающее низким энергиям
Низкоэнергетический вклад в сдвиг энергии получается из пер-
первых трех слагаемых в A4.2.24) после подстановки
1
1
1
k -ie к - г? к
- ге
A4.3.23)
788
Глава 14. Связанные состояния во внешних полях
в фотонном пропагаторе. Эта подстановка по существу служит для
обрезания интеграла по компонентам 4-импульса фотона к на вели-
величинах порядка ц, но это невозможно увидеть, пока аккуратно не
учтена перенормировка массы, так что до этого момента мы воз-
воздержимся от любых нерелятивистских приближений. Кроме того,
сейчас мы учитываем импульсы фотонов того же порядка или мень-
меньше, чем энергии связи атомных состояний, так что необходимо рас-
рассмотреть ответственные за эту связь электростатические силы во
всех порядках.
Вместо того, чтобы работать с формулой A4.2.24) импульсного
представления, удобно вернуться к формуле A4.2.18) конфигураци-
конфигурационного представления. В этом представлении низкоэнергетический
вклад в собственноэнергетическую функцию электрона дается фор-
формулой
A4.3.24)
[L 4\X, УЛнизкие энергии ге У о ^(Х,у)Уp±J(X у, Ц]
+ 6те(цN4(х - у) - (Z2(n) - 1)(у^[Эц + ге^] + ше)б4(х - у),
где D(x — у, ц) — модифицированный фотонный пропагатор,
D(x - у; Ц) =
BлL
dikeik{x-y)
1
1
-ie
-ге
A4.3.25)
а контрчлены Z2(fi.) — 1 и 6т(ц) вычислены с помощью этого моди-
модифицированного пропагатора. Переходя от временной переменной к
энергетической, находим, что низкоэнергетический вклад в функ-
функцию A4.2.13) есть
, У; ?)]
ге
X
низкие энергии
1 1
,гк-(х-у)
'-fc°)Yp
к2 - ге к2 + ц2 - ге
- (Z2 (ц) - 1)(у • V + гу°Е + геуу 4У + те) б3 (х - у)
+ 6те(ЦN3(х-у).
A4.3.26)
14.3. Лэмбовский сдвиг в легких атомах 789
Соответственно низкоэнергетический вклад в сдвиг энергии соглас-
согласно формуле A4.2.17) принимает вид
-ie
изкие энергии J ^ ^J ^ У ^Л/ЛХД2^ -Дх> У>-^ЛГ Янизк:
j-jd^j d3xj d3y uN (x) yPS 4 (x, у; Е - k° )ypuN (y)
1 1
kz -ie kz + Li2 - -ie
gik-(x-y)
A4.3.27)
Заметим, что слагаемые, пропорциональные Z2(fi) — 1, выпали, так
как дираковская волновая функция uN{x.) удовлетворяет уравнению
Дирака A4.1.10). Для нахождения электронного пропагатора в при-
присутствии кулоновского поля воспользуемся формулой A4.2.15):
M M
где суммы в первом и втором слагаемых берутся по всем одноэлек-
тронным и однопозитронным состояниям, соответственно. Интегра-
Интегралы по к0 легче всего взять, замкнув контур интегрирования боль-
большим полукругом в нижней полуплоскости для первого слагаемого,
и в верхней полуплоскости — для второго:
d/cc
гтг
+ ц2 ^EM+Ew+Vk2+|i2 -ге
и поступив аналогично, когда ц заменяется на нуль. Теперь сдвиг
энергии принимает вид
790
Глава 14. Связанные состояния во внешних полях
[5Е
JV -1низкие энергии
м
X
rpMJV(k)
k|(EM-Ew+|k|-z?)
A4.3.28)
Ик|(Ем+Е„+|к|-г?)
-6me(ji)Jd3x
3x u
(x),
где
A4.3.29)
A4.3.30)
(Конечно, «сумма» по М в A4.3.28) означает вклады только от элек-
электронных состояний в первое слагаемое и только от позитронных
состояний — во второе.)
Формулу A4.3.28) можно было бы вывести более непосредст-
непосредственно из старой теории возмущений: энергетические знаменатели
Ем — EN + со и Ем + EN + со возникают в результате вычитания
энергии EN начального состояния из энергии промежуточного со-
состояния, содержащего либо электрон с энергией Ем и фотон с энер-
энергией со, либо позитрон с энергией Ем, фотон с энергией со и как
конечный, так и начальный электроны (см. рис. 14.2).
Прежде чем делать какие-то приближения в A4.3.28), удобно
выразить временные компоненты матричных элементов FJLN и f P
через соответствующие пространственные компоненты, используя
14.3. Лэмбовский сдвиг в легких атомах
791
Рис. 14.2. Диаграммы старой теории возмущений для низкоэнергетической
части сдвига энергии электрона. Сплошные прямые линии изображают
электрон; волнистые динии — фотон; пунктирные линии пересекают ли-
линии частиц промежуточных состояний, соответствующих первым двум
слагаемым правой части формулы A4.3.28)
соотношения , следующие из закона сохранения электрического
тока:
Em)Tmn(k),
A4.3.31)
A4.3.32)
Более того, используя соотношение полноты A4.1.8), можно непо-
непосредственно показать, что
м
A4.3.33)
и
* Чтобы получить A4.3.31), заметим, что
ВД„(к) = -ijd3xe~ikx V • (uM(x)yuw(x
o0nu
Формула A4.3.32) выводится аналогично.
792
Глава 14. Связанные состояния во внешних полях
(Ем -
(Ем +EN)]
м
м
A4.3.34)
= -гк • j d?xuN (x) у uN (x) = 0,
причем последнее равенство вытекает из условия четности A4.1.23).
Таким образом, соотношение A4.3.28) можно переписать в виде
JV -1низкие энергии
2B%У
B%У
м
(|rMW(k)|2-|k-rMW(k)|2/k'
|k|(EM-Ew+|k|-z?)
Гми(к)|2-|к-Гм„(к)|2/(к2+ц2)
д/k2 + ц2 (Ем +EN+ д/k2 + ц2 - ге)
м
MW
2 л 2
(k)|2-|k-rMW(k)|Vk
|k|(EM+Ew+|k|-z?)
fMW(k)|2-|k-fMW(k)|2/(k2+^i2)
д/к2 + ц2 (EM + Ew + д/к2 + ц2 - ie)
м
A4.3.35)
При получении предпоследнего слагаемого был использован эле-
элементарный интеграл
d3k
1
к2+ц2
14.3. Лэмбовский сдвиг в легких атомах
793
До сих пор все преобразования были точным переписыванием
формулы A4.3.28). Теперь следует сделать ряд приближений. Преж-
Прежде всего рассмотрим перенормировку массы. В разделе 11.4 уже бы-
было вычислено значение 5те(ц) в порядке а. Оно равно:
A4-3-36)
Хотя в разделе 11.4 величина ц рассматривалась как регуляризую-
щая масса, которую следовало считать много большей чем те, вы-
выражение A4.3.36) можно с тем же успехом использовать для вычис-
вычисления значения 6те(ц) в интересующем нас сейчас случае ц <х те. В
этом пределе формула A4.3.36) приводит к выражению:
A4.3.37)
Напомним, что при Za ^C функция uN(x) определяется форму-
формулой A4.1.37):
o-v/2+ ...)/„ (х)_
A4.3.38)
где точки отмечают слагаемые более высокого порядка по Zoc,
v — нерелятивистский оператор скорости —iV/me, а /w(x) — двух-
компонентный спинор, являющийся решением нерелятивистского
уравнения Шредингера, нормированный соотношением A4.1.38):
A4.1.39)
Отсюда находим коэффициент при 5ше(ц) в правой части A4.3.35):
A4.3.40)
Мы сразу же видим, что главное слагаемое в члене 5me(ji){d3x uNuN
сокращает слагаемое осц/2 в правой части A4.3.35). На самом деле,
794
Глава 14. Связанные состояния во внешних полях
такое сокращение можно было предвидеть, поскольку это слагае-
слагаемое выживает в пределе Zoc —» 0, а определение те(ц) как перенор-
перенормированной массы электрона требует, чтобы в этом пределе не бы-
было никакого сдвига энергии.
С помощью тех же рассуждений можно предвидеть, что сла-
слагаемое порядка 0Ц12/те в 5те(ц) (которое больше, чем порядка
a(ZocLme, и поэтому им нельзя просто пренебречь) сокращает имею-
имеющие тот же порядок второе и третье слагаемые в правой части
A4.3.35) *. С другой стороны, произведение слагаемого щу2/те в Ъте
со вторым слагаемым в матричном элементе A4.3.40) имеет порядок
* Убедиться в этом сокращении можно следующим образом. Мы исхо-
исходим из того, что второе и третье слагаемые в правой части A4.3.35) доста-
достаточно малы, так что их можно оценить с помощью предельно нерелятиви-
нерелятивистского приближения |3г%(х) - г%(х) в уравнении Дирака, которому удов-
удовлетворяет uN(x). С другой стороны, хотя и можно пренебречь кулоновской
силой в позитронных волновых функциях им(х), сумма по М в третьем
слагаемом содержит существенный вклад от релятивистских позитронов,
так что мы используем приближение иро(х) — Bл)-/2и(р,а)егр-а:, где и(р,а)—
введенный в разделе 5.5 позитронный спинор, нормированный услови-
условием u(p,a')u(p,a) = 8О'О. Таким образом, суммы по М во втором и третьем
слагаемых в A4.3.35) даются следующими приближенными формулами:
м
м
т„
г+т2е
2
т„ -т„
2д/к
2+т„2
В главном порядке по \i/me для этих слагаемых имеем соответственно
2{2%y
d6k
2 C-к2/(к2+ц2))
2 ,2 , „2
k
i2 + m\ + me
m2
(продолжение сноски на с. 795)
14.3. Лэмбовский сдвиг в легких атомах 795
(ZaJOCfJ.2/me <3C a(ZaLme, и поэтому им можно пренебречь. Единст-
Единственный остающийся в порядке a(ZaLme вклад от перенормировки
массы — это произведение старшего слагаемого в 5те(ц) со слагае-
слагаемым порядка (ZaJ в id3x uNuN:
16л
^JVJV
(Это отмеченное в разделе 1.3 влияние перенормировки массы на ки-
кинетическую энергию электрона.)
Оказывается, что последнее выражение в точности равно взя-
взятому с обратным знаком первому слагаемому в A4.3.35), если в нем
пренебречь разницей между уровнями энергии. Чтобы убедиться в
этом, заметим, что интеграл в этом слагаемом эффективно обреза-
обрезается на значениях |k| ~ jx <^ Zame, поэтому можно вычислить мат-
матричный элемент Гми(к) в пределе к —> 0. В низшем порядке по Zoc из
соотношения A4.2.32) находим:
rMW@) = (v)MW, A4.3.41)
и, используя полноту решений fN нерелятивистского уравнения Шре-
дингера, имеем:
м(к) — {vv]) NN, A4.3.42)
м
так что в этом порядке
* (Соотношение A4.3.32) исключает возможность того, что релятивист-
релятивистская поправка к последнему выражению могла бы не быть подавленной
множителем k2/me2, возникающим в самом выражении при |к|2 <?. те2.)
Указанные два слагаемых сокращаются со слагаемым +3(А2/4лте в члене
-5me((A)|d3x uN{s.)uN{s.). Наконец заметим, что релятивистские поправки к
указанным выше приближенным оценкам сумм по состояниям позитронов
включали бы дополнительные множители порядка и2/с2 ~ (ZaJ, что дава-
давало бы вклады порядка a(ZaJ(A2/me2 <SJ a(ZaLme. Этим оправдывается ис-
использованное здесь нерелятивистское приближение.
796
Глава 14. Связанные состояния во внешних полях
2BлK
dc
м
2-lk-rMw(k)i2/k2;
к-Гм„(к)|2/(к2+ц2
2B%У
-'JVJV
к2+ц2
2 A-к2/3(к2+ц2
3k2
2+ц2
к2+ц
16л
JjVW
Следовательно после перенормировки массы у нас остается только
первое слагаемое в A4.3.35) минус такое же слагаемое с отброшен-
отброшенной разностью энергий EN — Ем:
[5Е
N -1низкие энергии
м
X
(|rMW(k)|2-|k-rMW(k)|2/k2)
k2(EM-Ew+|k|-z?)
rMW(k)|2-|k-rMW(k)|2/(k2+n2))
(k2 + ц2 )(EM -EN+ Vk2 + Ц2 - ie) _
A4.3.43)
Снова используя A4.3.41), находим:
2
]низкие энергии
2{2%У
' MN
м
х d3k
3k2(EM-Ew+|k|-z?)
l-k2/3(k2 +ц
(к2 + ц2)(Ем - E
м - EN
A4.3.44)
14.3. Лэмбовский сдвиг в легких атомах
797
Даже несмотря на то, что типичные значения импульса электрона
много больше типичных атомных разностей энергии, это неверно
для типичных значений |к| в данном интеграле, поскольку он был
бы инфракрасно расходящимся, если не удерживать разность
EN — Ем в знаменателях. В пределе ц 3> \ЕМ — EN\ ~ (ZocJme инте-
интеграл можно вычислить, разбив область интегрирования по к на два
сегмента: от нуля до X и от X до бесконечности, где в остальном
произвольное значение X выбрано так, чтобы Ем — EN
Таким образом,
« X « ц.
k2dk
3k2(EM-EN + k-ie)
1-к2/3(к2+ц2)
(k2 + ц2)(Ем - E
N
In
2EM-EN\J 6
- гг)
- + i%Q(EN-EM)
Мнимая часть этого выражения отражает возможность перехода
атома из состояния N в состояние М с меньшей энергией. Это сла-
слагаемое дает вклад в вероятность распада, равную мнимой части
сдвига энергии. Нас же интересует действительная часть сдвига энер-
энергии, так что в дальнейшем мы опустим мнимую часть. Тогда из
формулы A4.3.44) следует
[8Е
JV -1низкие энергии
6л2
' MN
м
In
2\EN-E
м
5
+ -
A4.3.45)
В. Полный сдвиг энергии
Необходимо установить связь между суммой в формуле A4.3.45)
и одним из матричных элементов в слагаемом A4.3.22), отвечающем
высоким энергиям. Для этого посмотрим, прежде всего, какое
798
Глава 14. Связанные состояния во внешних полях
значение имела бы сумма в A4.3.45), если бы мы могли отбросить
логарифм. Заметим, что (Ем — EN)vNM = [v,H]WM, так что
м
м
1
Единственное слагаемое в нерелятивистском гамильтониане Я, ко-
которое не коммутирует с оператором импульса, это потенциал
—е.:.</°(х), так что
' MN
2 _
м
2ml
A4.3.46)
Из выражений A4.3.45) и A4.3.22) следует, что пропорциональное
In ц слагаемое в выражении, отвечающем вкладу высоких энер-
энергий, сокращается с таким же слагаемым в выражении для вклада
низких энергий:
5EN=[5EN\
высокие энергии
0% М
JV J низкие энергии
In
-Ем\]+6 5
A4.3.47)
JVJV
До этого момента речь шла о произвольном электростатиче-
электростатическом поле -/°(х). Рассмотрим теперь частный случай чисто куло-
новского поля:
Ze
х
A4.3.48)
В этом случае формула A4.3.46) принимает вид:
-Ew)|v
w)|vMW
2 =
. A4.3.49)
14.3. Лэмбовский сдвиг в легких атомах
799
Это выражение не равно нулю только при 1 = 0. Кроме того, мат-
матричный элемент в последнем слагаемом в A4.3.47) равен:
'ЛОТ
=-Z«Ao-L
A4.3.50)
что не равно нулю только при I Ф 0. Поэтому в этом месте полезно
разделить рассмотрение на два случая: I = 0 и I Ф 0.
а) 1 = О
Удобно определить среднюю энергию возбуждения AEN:
~EN)ln\EM -EN\= lnAEw?|vMW|2(EM -EN)
м
м
Ze2
In AEW (/>)/» @))-
A4.3.51)
Для s-состояний атома водорода индекс N включает глав-
главное квантовое число п и z-компоненту спина т, а значение
/Vi^, так что
A4-3.52)
Подставляя равенство( 14.3.51) и A4.3.52) в A4.3.47), получаем сдвиг
энергии этих состояний:
4a(ZaLrn
19
30
A4.3.53)
6I Ф О
В случае неравного нулю орбитального момента сумма A4.3.49)
обращается в нуль, так что определение A4.3.51) не годится. Вместо
этого принято определять среднюю энергию возбуждения AEN
формулой
800
Глава 14. Связанные состояния во внешних полях
' MN
l(EM-EN)ln\EM-E
N
2(ZocLme
In
2АЕ
JV
м
n
Z2a2
A4.3.54)
(Поскольку выражение A4.3.49) обращается в нуль, не имеет значе-
значения, в каких единицах измеряется EN — Ем в A4.3.54).) Кроме того, в
состоянии с полным угловым моментом j и орбитальным моментом I
скалярное произведение 0-L равно знакомому выражению j(j+l) —
1A+1) — |, так что для главного квантового числа п среднее значение
оператора 1/г3 равно
Г ,з , 2/3 2Z3a3m3
Jd3r|/w|2/r3 =
пЧ{1 + \){21-
A4.3.55)
Подставляя все результаты в A4.3.47), находим, что при I Ф 0
4a(ZaLme г ^-^„г
Зжпс
a(ZaLm
2%пс
A4.3.56)
Осталось лишь воспользоваться полученными формулами, чтобы
найти значения сдвигов энергии. Средние энергии возбуждения сле-
следует находить численно. Используя нерелятивистские волновые
функции электрона в атоме водорода, можно получить 5:
AEls = 19,769266917F) Ry,
AE2s = 16,63934203A) Ry,
AE2p = 0,970429318C) Ry,
где lRy = mea2/2 = 13,6057 эВ. Тогда из A4.3.53) находим:
14.3. Лэмбовский сдвиг в легких атомах
801
/.
т„
l2AEls
= 2%hx8127,4 МГц,
19
30
= 3,3612 х!0эВ
A4.3.57)
2АЕ.
2s .
= 2%Пх 1039,31 МГц,
19
30
-6
= 4,2982x10"° эВ
A4.3.58)
[8Е]
а5т„
2Pl/2
In
2АЕ
2р
=-5,3267 х!0"йэВ
A4.3.59)
= 2л/гх (-12,88) МГц.
Классический лэмбовский сдвиг — это разность энергий 2s и 2р1/2
состояний атома водорода, которые были бы вырожденными в от-
отсутствии радиационных поправок. Наши вычисления приводят к ре-
результату
[8?]2s - [§ЯЬР1/2 = 4,35152хЮ эВ = 2%Пх 1052,19 МГц.
Это численно близко (хотя аналитически не тождественно) старому
результату Кролла и Лэмба6 и Френча и Вайскопфа7, который был
получен с помощью старой теории возмущений. Ранее в этой главе
мы грубо оценили сдвиг в 1300 МГц, рассмотрев только вклад высо-
высоких энергий в сдвиг энергии 2s состояния, причем инфракрасное
обрезание было наугад выбрано порядка (Х2те = 2 Ry. Теперь мы
видим, что оценка была завышенной, и произошло это главным
образом потому, что правильное значение эффективного инфра-
инфракрасного обрезания AE2s = 16,64 Ry значительно больше того, кото-
которое предполагалось. С другой стороны, как было рассказано в раз-
разделе 1.3, в 1947 году Ганс Бете8 сумел дать достаточно хорошую
оценку лэмбовского сдвига —1040 МГц, рассмотрев только вклад
низких энергий в сдвиг энергии 2s состояния, и выбрав ультрафио-
ультрафиолетовое обрезание равным те. (Бете сделал и первую оценку энер-
энергии возбуждения AE2s — 17,8 Ry.)
Описанное здесь вычисление лэмбовского сдвига было откор-
откорректировано за счет включения радиационных поправок более
802 Глава 14. Связанные состояния во внешних полях
высокого порядка, учета размеров ядра и эффектов отдачи. В на-
настоящее время самая большая неопределенность проистекает от не-
неуверенности в знании правильного значения среднеквадратичного
зарядового радиуса гр протона. Для значений гр = 0,862 X 10~13 см
или г = 0,805 X 10~13 см одни вычисления 9 дают либо 1057,87 МГц,
либо 1057,85 МГц, в то время как другие 10 дают 1057,883 МГц или
1057,865 МГц. С учетом неопределенности в радиусе про-
протона, согласие с современным экспериментальным значением п
1057,845(9) МГц является превосходным. Точность эксперименталь-
экспериментальных данных ограничена главным образом естественной шириной ли-
линии 2р-уровня атома водорода, составляющей ~ 100 МГц, так что
дальнейшее увеличение точности является трудной задачей.
В последние несколько лет произошло важно продвижение
вперед в измерениях сдвига энергии самого Is состояния путем
прямого сравнения частоты Is—2s резонанса с учетверенными час-
частотами 2s-4s и 2s-4d двухфотонных резонансов. Эти s и d состоя-
состояния много уже 2р состояния, так что подобные разности частот
можно измерить более точно, чем классический лэмбовский сдвиг.
Некоторое время казалось, что здесь возникло противоречие меж-
между теорией и экспериментом. Расчеты 12>13 показывали, что при
радиусе протона гр = 0,862A1) X 103 см или 0,805A1) X 103 см
учет размеров протона и другие поправки увеличивают теорети-
теоретическое значение сдвига энергии Is состояния от приведенной вы-
выше величины 8127,4 МГц до 8173,12F) МГц или 8172,94(9) МГц,
соответственно. Так как считалось, что значение протонного ра-
радиуса гр = 0,862A1) X 10~13 см предпочтительнее, этот результат
несколько расходился с измеренным13 значением 8172,86E) МГц.
Однако последующие вычисления 14, в которых использовалось
именно это значение радиуса и были учтены поправки порядка
OC2(ZaM, привели к значениям сдвигов энергии Is, 2s и 4s состоя-
состояний, которые согласуются с экспериментом. Повидимому, кванто-
квантовая электродинамика вновь одержала победу.
Задачи
1. Рассмотрите заряженную скалярную частицу массой т Ф 0, опи-
описываемую полем ф(ж), которое взаимодействует только с внеш-
внешним независящим от времени электромагнитным полем АЦх).
Список литературы 803
Пусть Фи — полный набор нормированных однобозонных и
одноантибозонных состояний с энергиями EN. Определим
и„(х)е-^=(Ф0,ф(х,{)Ф„) и г;и(х)е^=(Фи,ф(х,?)Ф0), где
Фо — вакуумное состояние. Покажите, что uN и vN образуют
вместе полный набор состояний, и получите формулы для коэф-
коэффициентов при uN и vN в разложении произвольной функции
/(х).
2. Пусть мы включили в теорию, описанную в задаче 1, радиаци-
радиационные поправки. Пусть гП*(х,у) — сумма всех диаграмм с од-
одной входящей и одной выходящей линией скалярной частицы
(исключая конечные скалярные пропагаторы) в порядке а. По-
Получите формулу для сдвига энергий EN однобозонных состоя-
состояний за счет этих радиационных поправок, выразив результат
через ми(х) и ГГ(ж,у).
3. Используя результаты раздела 14.3, рассчитайте вероятность
радиационного распада 2р состояния атома водорода.
4. Пусть взаимодействие электрона с легким скалярным полем ф
имеет вид дф\|7е\|/е. Предположим, что масса скалярной части-
частицы тф имеет значение в интервале (ZaJme <ЗС тф <ЗС Zame. Рас-
Рассчитайте изменение энергии Is состояния водородоподобного ато-
атома за счет такого взаимодействия.
5. Проведите вычисления задачи 4 для случая тф = 0.
Список литературы
1. Dirac, P.A.M., Proc. Roy. Soc. (London), A117, 610 A928).
2. См., например: Edmonds, A.R. Angular Momentum in Quantum
Mechanics (Princeton University Press, Princeton, 1957) (есть рус.
пер.: Эдмондс А. Угловые моменты в квантовой механике. М.,
ИЛ, 1968); Rose, M.E. Elementary Theory of Angular Momentum
(John Wiley & Sons, New York, 1957).
804 Глава 14. Связанные состояния во внешних полях
3. См., например: Schiff, L.I. Quantum Mechanics (McGrow-НШ,
New York, 1949), Section 43 (есть рус. пер.: Шифф Л. Кванто-
Квантовая механика. М., ИЛ, 1959). Оригинальные работы: Darwin,
C.G., Proc. Roy. Soc. (London), A118, 654 A928); ibid., A120, 621
A928); Gordon, W., Z. /. Phys., 48, 11 A928).
4. Brown, G.E., Langer, J.S., and Schaefer, G.W., Proc. Roy. Soc.
(London), A251, 92 A959); Brown, G.E. and Mayers, D.F., Proc.
Roy. Soc. (London), A251, 105 A959); Desiderio, A.N. and Johnson,
W.R., Phys. Rev., A3, 1267 A971).
5. Huff, R.W., Phys. Rev., 186, 1367 A969).
6. Kroll, N.M. and Lamb, W.E., Phys. Rev., 75, 388 A949).
7. French, J.B. and Weisskopf, V.F., Phys. Rev., 75, 1240 A949).
8. Bethe, H.A., Phys. Rev., 72, 339 A947).
9. Sapirstein, J.R. and Yennie, D.R., in: Quantum Electrodynamics,
ed. by T. Kinoshita (World Scientific, Singapore, 1990), p. 575.
10. Grotch, H., Foundations of Physics, 24, 249 A994).
11. Lundeen, S.R. and Pipkin, F.M., Phys. Rev. Lett, 46, 232A981);
Metrologia, 22, 9 A986). Обзор проблемы см.: Pipkin, F.M., in:
Quantum Electrodynamics, ed. by T. Kinoshita (World Scientific,
Singapore, 1990), p. 697.
12. Weitz, M., Huber, A., Schmidt-Kaler, F., Leibfried, D., and
Hansch, T.W., Phys. Rev. Lett., 72, 328 A994).
13. Weitz, M., Huber, A., Schmidt-Kaler, F., and Hansch, T.W.,
Phys. Rev. Lett, 68, 1120 A992) и ссылка [12].
14. Pachucki, К., Phys. Rev. Lett., 72, 3154 A994).
Именной указатель
Aaron, R. 636
Aharony, A. 223
Aitken, A.C. 141
Amado, R.D. 636
Anderson, CD. 56, 58
Aramaki, S. 51
Argyres, P.C. 343
Artin E. 573
Bagger, J. 452, 721
Bailey, J. 674
Bakamijan, B. 253
Bargmann, V. 141
Belinfante, F. 451
Bethe, H. 58
Bethe, H.A. 61, 761, 804
Beyer, R.T. 51
Bhabha, H.J. 58
Bjorken, J.D. 721
Bloch, F. 59, 760
Bogoliubov, N.N. 721
Bohr, N. 55, 57, 223, 342
Born, M. 53, 55, 60, 221
Breit, G. 61, 222, 224
Brown, G.E. 804
Brown, L.M. 51, 58
Butler, C.C. 59, 222
Cao, T.Y. 51
Carlson, J.F. 58
Cartan, E. 342
Casimir,H.B.G. 451
Cassen, B. 222
Chadwick, J. 58
Chew, G.F. 60, 637
Chinowsky, W. 222
Christenson, J.H. 141, 223
Collins, J. 720
Collins, P.D.B. 637
Compton, A.H. 54
Condon, E.U. 222
Conversi, M. 58
Crichton, J.H. 253
Cronin, J.W. 141, 223
Curie-Joliot, I. 58
Dalitz, R.H. 223, 761
Dancoff, S.M. 59
Darwin, C.G. 55, 804
Davisson, С J. 53
de Broglie, L. 53
De Witt, B. 572
de Witt, CM. 572
Desiderio, A.N. 804
Dirac, P.A.M.
51, 53, 54, 55, 56, 57, 58, 59,
60, 140, 342, 452, 572, 635, 803
Donoghue, J.F. 722
Drell, S.D. 721
Drinkwater, J.W. 61
Druhl, K. 573
Dyson, F.J.
62, 141, 223, 343, 385, 720
Eckart, С 224
Edmonds A.R.
141, 222, 224, 342, 803
806
Квантовая теория поля. Т. 1
Ehrenfest, P. 56, 58
Einstein, A. 56
Elend, H.H. 674
Elsasser, W. 53
Epstein, S. 60
Erickson, G.W. 673, 674
Euler, H. 59, 722
Fabri, E. 223
Faddeev, L.D. 253, 572
Feenberg, E. 222, 223
Feinberg, G. 222, 722
Fermi, E. 51, 55, 57
Ferretti, B. 222
Feynman, R.P.
60, 61, 62, 503, 571, 572, 673
Fierz, M. 57, 59, 342
Fitch, V.L. 141, 223
Flanders, H. 141, 503
Fock, V.A. 57, 503
Foley, H.M. 61
Frautschi, S.C. 637, 760
Fredenhagen, K. 573
French, J.B. 61, 804
Friedman, J.I. 223
Friedman, J.J 141
Frohlich, H. 62
Froissart, M. 224
Fukuda, H. 61
Furry, W.H. 57, 635
Gaberdiel, R. 573
Gamov, G.A. 51, 55
Garwin, R. 141, 222
Gasser, J. 722
Gell-Mann, M. 222, 223, 636, 761
Georgi, H. 342
Germer, L. H. 53
Gerstein, IS. 572
Goldberger, M.L. 221, 636, 761
Goldstone, G. 253
Gordon, W. 53, 55, 804
Goudsmit, S. 54
Green, M.B. 502
Grotch, H. 804
Haag, R. 573
Hafstad, L.R. 222
Hahn, Y. 721
Halter, J. 722
Hansch, T.W. 804
Heisenberg , W. 54
Heisenberg, W.
53, 55, 57, 58, 59, 60, 221,
721, 722
Heitler, W. 58, 62
Hepp, K. 721
Herzberg, G. 58
Heydenberg, N. 222
Hibbs, A.R. 571
Hocking, J.C. 141
Hoddeson, L. 51
Houston, W.V. 61
Howard, J.C. 636
Hubbard, J. 636
Huber, A. 804
Huff, R.W. 804
Hugenholtz, N.M. 253
Infeld, L. 60
Inoue, T. 59
Inonu, E. 140
Ito, D. 62
Jackiw, R. 572
Jackson, J.D. 636
Jammer, M. 51
Jauch, J.M. 342
Johnson, W.R. 804
Joliot, F. 58
Joos, H. 343
Jordan, P. 53, 54, 57
Jost, R. 343
Jouvet, B. 636
Авторский указатель
807
Julian, R.S. 61
Kabir, P. 722
Kahn, B. 62
Kamefuchi, S. 573, 721
Kanesawa, S. 62
Kemmer, N. 59
Kinoshita, T. 761
Klein, O. 53, 57, 58, 503
Koba, Z. 60, 62
Kockel, B. 59, 722
Kollath, R. 224
Kramers, H. 141
Kramers, H.A. 61, 223, 636
Kroll, M. 61
Kroll, N.M. 804
Kronig, R. 636
Kubo, R. 253
Kush, P. 61
Kallen, G. 636
Laidlaw, M.G.G. 572
Lamb, W.E. 61, 62, 804
Lande, A. 54
Langer, J.S. 804
Lattes, C.M.G. 59
Lederman, L. 141, 222
Lee, B.W. 572
Lee, T.D. 141, 222, 253, 342, 761
Lehmann, H. 635
Leibfried, D. 804
Leinaas, J.M. 572
Leutwyler, H. 722
Lewis, H.W. 60
Lippman, B. 221
Liu, H.H.T., 673, 674
Low, F.E. 761
Lundeen, S.R. 804
Luders, G. 343
Mackey, G.W. 140
Maskawa, T. 452
Matthews, P.T. 721
Mayers, D.F. 804
Mehra, J. 51, 55
Miller, A.I. 52, 674
Miyamoto, Y. 61
Myrheim, J. 572
Moller, С 58, 60, 202
Nafe, J.E. 61
Nagel, D.E. 61
Nakajima, H. 452
Nappi, C.R. 343
Nash, С 141
Nauenberg, M. 761
Neddermeyer, S.H. 58
Ne'eman, Y. 222
Nelson, E.B. 61
Newton, R.G. 221
Nishina, Y. 58, 503
Nordheim, L. 58
Nordsieck, A. 59
Nordsieck, F. 760
Novikov, V. 722
Occhialini, G.P.S. 59
Ohnuki, Y. 573
Oppenheimer, J.R. 56, 57, 58, 59
Osterwalder, K. 572
Pachucki, K. 804
Pais, A. 52, 223
Pancini, E. 58
Parasiuk, O. 721
Pashen, F. 54
Pastern ack, S. 61
Pauli, W. 53, 55, 56, 57, 58, 59,
60, 342, 343, 674
Peierls, R.E. 57, 223
Petermann, A. 674
Piccioni, O. 58, 223
Pipkin, F.M. 804
Placzek, G. 223
808
Квантовая теория поля. Т. 1
Podolsky, В. 57
Polchinski, J. 722
Pomeranchuk, I.Ya. 636
Popov, V.N. 572
Present, R.S. 222
Rabi, LI. 61
Racah, G. 58
Rarita, W. 342
Rayski, J. 674
Rechenberg, H. 58
Regge, T. 637
Retherford, R.C. 61
Richardson, O. 61
Rindani, S.D. 343
Roberts, J.E. 573
Rochester, G.D. 59, 222
Rorlich, F. 342
Rose, M.E. 141, 222, 224, 343, 803
Rosenbluth, M.N. 636
Rosenfeld, L. 57, 342, 451
Ruger, S.M. 573
Sakata, S. 59, 721
Salam, A. 721
Salpeter, E.E. 761
Sapirstein, J.R. 804
Schaefer, G.W. 804
Schiff, L.I. 54, 56, 223, 761, 804
Schmidt-Kaler, F. 804
Schrader, R. 572
Schroer, B. 343
Schrodinger, E. 53
Schubert, K.R. 223
Schur, I. 342
Schwarz, J.H. 502
Schweber, S.S. 51, 52
Schwinger, J.
52, 56, 60, 61, 221, 342, 385,
503, 572, 635, 673
Seiler, R. 343
Sen, S. 141
Shifman, M.A. 722
Sivakumar, M. 343
Slater, J.C. 55
Sommerfeld, A. 54
Spaarnay, M.J. 451
Steinberger, J. 222
Sterman, G. 761
Stevenson, E.C. 58
Stoner, E.C. 55
Stratonovich, R.I. 636
Streater, R.F. 343
Street, J.C. 58
Suura, H. 674, 760
Swieca, A. 343
Symanzik, K. 635
't Hooft, G. 572, 673
Takahashi, Y. 635
Tamm, I. 503
Tati, T. 62
Telegdi, V.L. 223
Telegdi, V.V. 141
Thirring, W. 636
Thomas, L.H. 54, 253
Titchmarsh, E.C. 253
Toll, J.S. 636
Tomonaga, S.-I. 52, 60, 61, 62
Tung., Wu-Ki 141
Turlay, R. 141, 223
Turnbull, H.W. 141
Tuve, M.A. 222
Uehling, E.A. 61, 673
Uhlenbeck, G.E. 54
Umezawa, H. 721
Vainshtein, A.I. 722
Van der Waerden, B.L. 342
Vaughan, M.J. 636
Velo, G. 343
Veltman, M. 673
Villars, F. 674
Авторский указатель
809
Waller, I. 59
Ward, J.C. 635
Watson, K.M. 221, 223
Webb, N. 58
Weinberg, S.
52, 54, 60, 140, 222, 224,
253, 341, 342, 451, 503,
572, 636, 720, 722, 761
Weinrich, M. 141, 222
Weisskopf, V.F.
52, 56, 58, 59, 60, 61, 804
Weitz, M. 804
Wentzel, G. 52, 55, 60
Wess, J. 452, 721
West, T. 503
Weyl, H. 56, 503
Wheeler, J.A. 60, 221
Whittaker, E. A. 53
Wichmann, E.H. 253, 674
Wick, G.C. 140, 385, 673
Wightman, A.S. 140, 343
Wigner, E.P. 56, 57, 140, 141, 224
Wilczek, F. 573
Williams, E.J. 761
Williams, R.C. 61
Williams, W.E. 61
Wilson, K.G. 722
Witten, E. 343, 502
Wu, C.S. 141, 222
Yang, C.N. 221, 222, 253, 342
Yennie, D.R. 760, 804
Young, G.S. 141
Yukawa, H. 58, 635
Zacharias, J.R. 61
Zakharov, V.I. 722
Zimmerman, W. 635, 721
Zumino, B. 343
Zwanziger, D. 343
Предметный указатель
а-распад 212
Р-распад 30, 38, 169, 173, 194, 304, 703
А барион 219
А+ функция 268
AF функция 366
J/\|/-Me30H 299
р-мезоны 219, 299, 302, 634
со-мезон 302
Абелевы группы 71
Аксиальная калибровка 462
Аксиомы Остервальдера-Шрадера
517, 572
Алгебра Клиффорда 285
Амплитуда рассеяния 196, 204-205
Анионы 567
Аномальный эффект Зеемана 7-8, 31-32
Антиунитарные и антилинейные
операторы 66, 76
Античастицы 17
Ароматы (лептонов) 717
Барионное число 164
Бесконечности, см. ультрафиолетовые
расходимости, инфракрасные расходимо-
расходимости
Борновское приближение 153
Борновское приближение искаженных
волн 193
Бусты 79
Вакуумное состояние 32, 35
Вероятности в квантовой механике 9, 36-
37, 43, 65
Вероятности распадов, общая формула
181-182
Вершинная функция (Г^) 601, 655-661,
687,783
Внешние поля 354, 379-380, 555-556, 752-
759, 774-781
Внешние производные 494
Внутренние симметрии 161-162
Волновая функция 519-521
Волновые пакеты 144-146
Вращение Вигнера 88-91
Временная калибровка 462
Вспомогательные поля 401-402
Вырождение Крамерса 107
Вычитания в дисперсионных соотношени-
соотношениях 629
Галилеева инвариантность 81
Гамильтониан
- комплексного скалярного поля 29
- для уравнения Дирака 10
- в электродинамике 467-468
- для свободных частиц 234
- взаимодействующего дираковского
поля 431
- взаимодействующих скалярных по-
полей 262, 402
- взаимодействующего векторного
поля 427
- одномерного скалярного поля 20-22
Гауссовы интегралы 567
Гейзенберговское представление 145, 381,
394, 574
Генераторы симметрии 408-418
Гильбертово пространство, определение
63
Гиперзаряд 164
Гипероны, открытие 163
Главное значение 150
Глобальные симметрии, определение
407-417
Глюоны 742
Предметный указатель
811
Гомотопические группы и классы 118-
119, 127-133
- определение 132
Гравитон 97, 706, 727, 737, 742
Грассмановы переменные, определение
539
Группа SLB,C) 115
Группа Spin(d) 120
Группа SUB) 117
Группа Z2 116
Группа кос 567
Группы Ли 69
Группы, определение 67-71; см. также:
абелевы группы, гомотопические группы,
группы Ли, малые группы, представле-
представления, полупростые группы
Два-коциклы, определение 109
Двойные звезды 493
Действие 396, 407
Диаграмма Чу-фраучи 637
Диаграммы Фейнмана 48-49, 344-384
- в электродинамике 475-484
Дираковское представление однородной
группы Лоренца 283-292
Дисперсионные соотношения 624-634
Дифракционное рассеяние 197, 211
Дифференциальные формы, см. р-формы
Длина рассеяния 209
Древесные диаграммы 374, 694-695
Дуальность 308, 497
Евклидов функциональный интеграл 516
Законы сохранения
- углового момента 157
- заряда 163, 264, 577
- тока 281, 408, 647, 791
- энергии и импульса 156-157
- ограничения 337, 727-728
Замкнутые р-формы 495
Заряд см. Электрический заряд
Зарядовое сопряжение (С)
- случайная симметрия 705, 719
- определение 161, 174-175
- для фотонов 578
- внутренние фазы 175
- несохранение 176
- преобразование операторов рождения
236
- преобразование дираковских полей
301-302
- преобразование фермионных били-
билинейных ковариантов 304
- преобразование произвольных непри-
неприводимых полей 322-323
- преобразование скалярных полей 274
- преобразование векторных полей 283
Изоспин (изотопический спин) 163
Ин- и аут-состояния 143-149, 154
Инвариантные подгруппы и подалгебры
71, 116
Индекс расходимости 676-683, 691
Индуцированное испускание фотонов 23
Индуцированные представления 85
Интегрирование по Березину 542
Инфракрасные расходимости 43-44, 664,
671, 730-748
Калибровка Лоренца (Ландау) 462, 563
Калибровка Фейнмана 462, 563
Калибровочные преобразования 334-335,
454-459, 461, 495
Канонические коммутационные и антиком-
антикоммутационные соотношения 21, 26-29
Квантовая механика 63-64
Квантовая хромодинамика 164, 720, 743
Квантовая электродинамика 38, 40-50,
453-484, 557-563, 638-671,681,687-699, 716-
720, 762-802; см. также: квантовые поля,
электрон, фотон, калибровочная инвари-
инвариантность, ультрафиолетовые расходимо-
расходимости, инфракрасные расходимости
Квантовые поля
- дираковское поле 30-32, 292-305
- ранняя теория 19-40
- свободные поля 254-266
- произвольные квантовые поля 310
- безмассовых частиц 328-337
- переопределение 442
- скалярные 27-29, 32-36, 266-274
- единственность неприводимыъ полей
317
812
Квантовая теория поля. Ч. 1
- векторные 275-283
Кварки 302, 720
Кинетическая теория 199
Киральное преобразование 704
К-мезоны 163, 176
- открытие 38
Когерентные состояния 252
Когомология де Рама 495
Компактные и некомпактные группы 307
Комптоновское рассеяние 484-494
Контракция Иноню-Вигнера 81
Контрчлены в квантовой электродина-
электродинамике 639-640
Конференция в Шелтер Айленде 45047
Космические лучи 38, 164
Коэффициенты Клебша-Гордана 165,
202, 204, 205, 320
Кросс-симметрия 358, 632, 750
Круговая поляризация 481
Кулоновская калибровка 334, 463-468, 489
Кулоновская энергия 468, 472, 465-476,
757
Кумулянты 238
Лагранжианы 27, 393-406
- комплексного скалярного поля 27
- взаимодействующего скалярного
поля 400
- интегрирование по частям 405-406
- нерегулярные 434
Лептонное число 163, 719
Лептоны 638
Леса 694
Линейная поляризация 481
Локальные симметрии
- определение 84
-для разных импульсов 85-86
- для безмассовых частиц 330
Лучи, определение 63
Лэмбовский сдвиг 45-47, 665, 781-801
Магнитные моменты частиц спина 1/2
616-617, 655-666, 705, 751-752
Майорановские фермионы 300, 323
Малая группа 84-88
- т Ф 0 88
- т = 0 91-96
Мандельстамовские переменные 698
Маргинальные связи 682
Матрица у5 289-291
Матрица плотности 483
Матрицы вращений 89
Матрицы Дирака 11-12
- перечеркнутое обозначение, определе-
определение 478
- следы 498
Матрицы Паули, определение 288
Матричная механика 4-5
Меллеровское рассеяние 38
Метод ренормировки Вильсона 711-716
М-матрица, определение 155
Многовременной формализм 29
Множители от фазового пространства 184-
188
Молекулярный спектр N14 38
Мюон 50
- открытие 39
- магнитный момент 661-662, 705
Мюонные атомы 653-654
Мягкие фотоны 724-730, 748-752
Нарушенная симметрия 597, 609
Нейтрон 38
- нейтрон-протонное рассеяние 210
- рассеяние нейтронов на сложном
ядре 209, 213
Некомпактные группы, см. Компактные и
некомпактные группы
Нелинейная о-модель 450, 505, 527-528
Неприводимые представления, определе-
определение 83
Несохранение РТ 173
Несущественные связи 442
Нормальное упорядочение 234, 266, 348
Н-теорема Больцмана 201
Обращение времени (Т)
- следствия для 5-матрицы 170-173
- определение 76
- несохранение 178
- преобразование операторов рождения
236
- преобразование вырожденных муль-
типлетов 134-139
Предметный указатель
813
- преобразование дираковских полей
302-303
- преобразование произвольных непри-
неприводимых полей 323-324
- преобразование J^v и Р^ 99-100
- преобразование одночастичных состо-
состояний 102
- преобразование скалярных полей 274
- преобразование векторных полей 283
Общая теория относительности 340, 415,
421, 494, 701-703, 706
Ограничение Фруассара 211
Односвязные пространства, определе-
определение 111
Одночастично неприводимые диаграммы,
определение 592
Опасные состояния 744-747
Оператор импульса 80, 412-413
Операторы уничтожения и рождения 21,
26-27, 30-31, 34-37, 230-236
Оптическая теорема 197
Парастатистика 566
Паулиевское слагаемое 18
Перекрывающиеся расходимости 692-695
Перенормировка
- массы 588
- поля 588
Перенормируемость 44-50, 683-699
Петли 249, 358, 374, 479, 557
Пион-нуклонная константа связи 586
Пионы 18, 50, 587-588, 706
- распад я* 169
- распад п° 175
- внутренная фаза зарядового сопряже-
сопряжения для л° 175
- внутреннаяя четность 169
- предсказание и открытие 39
- рассеяние на нуклонах 625, 633-634
Плавающее обрезание 711-716
Плоскость Далица 188
Поворот Вика 642
Поглощение фотонов 23
Позитрон 17-18, 750, 766
Позитроний 301-302
Поле Рариты-Швингера 309, 571
Полевые уравнения 265, 281, 318
Положительность энергии 100, 400
Полупростые группы и алгебры Ли опре-
определение 93
Полюсы амплитуды рассеяния 579-588,
749
Поля, см. квантовые поля
Поляризация вакуума 42, 44, 640-655,
785
Поляризация
- массивной частицы спина 278, 282
- безмассовых частиц 458-459
- фотона 97-98
Пороговое поведение 209-210
Постоянная тонкой структуры 36
Постоянная Эйлера 648, 672
Правила суперотбора 69, 119-120
Представление взаимодействия 189, 380
- для связей с производными 424
- для дираковского поля 430
- для электродинамики 468-472
- для взаимодействующего скалярного
поля 402-404
- для векторного поля 425
Представление Челлена-Лемана 618-624
Представления групп, определение 68
- однородной группы Лоренца 305-310
Преобразование Хаббарда-Стратоно-
вича 623
Преобразования Лежандра 393, 398
Преобразования Лоренца
- действие на операторы рождения 236
- действие на произвольные состоя-
состояния 74
- действие на одночастичные состоя-
состояния 82-98
- определение 72-75
- однородная группа Лоренца, опреде-
определение 75
- общие представления 305-310
- в каноническом формализме 418-424
- матричных элементов вне массовой
оболочки 576-577
- в теории возмущений 191, 367-368
- сечений и вероятностей 184
- S-матрицы 154-160
- алгебра Пуанкаре 76
- группа Пуанкаре 74
814
Квантовая теория поля. Ч. 1
- собственная ортохронная группа Ло-
Лоренца 75
Принцип действия Швингера 381
Принцип запрета 15
Принцип кластерного разложения 2256
236-243
Принцип эквивалентности 727
Причинность 1926 2636 625
Проблема т-6 168
Проективные представления 68, 108
Пропагаторы 348, 363-371
Пространственная инверсия см. четность и
пространственная инверсия (Р)
Протон
- заряд 603
- зарядовый радиус 50, 802
- формфакторы 617
- как дырка 15
- в ядре 38
Пунктирные и непунктирные индексы 307
Радиационные поправки, см.: перенорми-
перенормировка, квантовая электродинамика, ульт-
ультрафиолетовые расходимости, инфракрас-
инфракрасные расходимости, собственноэнергетичес-
кие функции, вершинная функция, поля-
поляризация вакуума, мягкие фотоны
Разложение по парциальным волнам 201
Размерная регуляризация 606, 644-648,
671
Размерность полей и констант связи 679,
703, 711
Распад Со60 169, 173
Рассеяние Баба 38
Регулятор Паули-Вилларса 657, 668
Редукционная формула 590
Резонансы 211-219
Релятивистские волновые уравнения 1-19
Ренормализационная группа 662, 699, 712
Рецепт БПХЦ 693-694
Ридберг (единица энергии), определение
800
Рождение пар 38
р-формы 494-499
Ряд Дайсона 191
^-матрица 5, 42
- С, СР, СРТ 174-178
- определение 150
- внутренние симметрии 161
- лоренц-инвариантность 154-160
- четность 165-169
- РТ 173-174
- S-оператор 151
- обращение времени 170-173
- унитарность 150-151
см. также: Т-матрица, М-матрица
Связанные состояния см. составные час-
частицы
Связи 433-441
- в электродинамике 459
Связи второго рода, см. связи
Связи первого рода, см. связи
Связные амплитуды 237-243
Связь спина со статистикой 317
Сепарабельные взаимодействия 220
Сечения
- определение 182-185
- предел высоких энергий
- разложение по парциальным волнам
204-207
Сильные взаимодействия 39
3j-символы Вигнера 314
Симметрии 65-72, 120-127, 406-418, 575
см. также: законы сохранения, группы,
лоренц-инвариантность, четность, заря-
зарядовое сопряжение, обращение времени,
внутренние симметрии, изоспин, ?Т7C)
Симметрия 6Т7C) 164
Система центра масс 184
Скобки Дирака в электродинамике 438-
450
Скобки Пуассона, определение 435
Следы 498-501
Случайные симметрии 716-719
Собственноэнергетические функции
(П*, ?*) 593, 640-649, 666-671, 688-689,
692-697
Соотношение Крамерса-Кронига 634
Составные частицы 146, 623-624
Состояния стоячих волн 221
«Состояния» с отрицательной энергией
14-19, 30-36, 766
Спектральные функции, см. Представле-
Представление Челлена~Лемана
Предметный указатель
815
Спиновые матрицы, определение 307
Спиральность
- определение 94
- ограничения для безмассовых полей
частиц 337-339
- ограничения на целые и полуцелые
значения 119
Спонтанное испускание фотонов 23-24,
797
СР-инвариантность
- для вырожденных мультиплетов 138
- несохранение в распаде КР 176
СРТ-инвариантность 326
Старая теория возмущений, см. Теория
возмущений
Статистика Бозе-Эйнштейна 15, 226-
230, 563-567
Статистика Ферми-Дирака 15, 226-230,
355-360, 563-567,
Странность и странные частицы 163
Струи 742, 744
Структурные константы, определение 70
Суммирование по спинам 279, 298, 315-
316, 335, 483-484, 488, 738
Суперперенормируемые взаимодейст-
взаимодействия 681, 686
Суперсимметрия 433, 686, 712
Существенные связи 682
Сферические гармоники 203, 769
Тензор Белинфанте 420
Тензор энергии-импульса 412-414
Теорема Ватсона 173
Теорема Вигнера-Эккарта 204
Теорема Вика 385
Теорема Ли-Науенберга 741-748
Теорема ЛСЦ, см. редукционная форму-
формула
Теорема Нетер 408
Теорема о подсчете степеней 682
Теорема о полярном разложении 116,
718
Теорема Польчинского 712
Теорема Померанчука 633
Теорема Пуанкаре 495
Теорема Римана-Лебега 241
Теорема Фарри 578, 690
Теория возмущений
- старая 189-192
- зависящая от времени 189
Теория дырок 16, 38, 40
Теория струн 1, 19, 326, 497, 710
Т-матрица 148, 154, 188, 202, 744
Тождества Уорда и Уорда-Такахаши 603
Тождество Якоби 110
Томсоновское рассеяние 494
Тонкая структура 6-8, 771
Топология группы Лоренца и группы вра-
вращений 114; см. также: гомотопические
группы, односвязные пространства, ко-
гомология де Рама
Тормозное излучение 38
Точные р-формы 495
Траектории Редже 633-634
Трансляционно-инвариантная теория ска-
скалярного поля
Ультрафиолетовые расходимости 40-50,
644-645, 652-653, 663, 668-671, 676-683
Универсальная накрывающая группа 119
Унитарная калибровка 462
Унитарность ^-матрицы 150-154, 172,
195-201, 206, 214, 705
Уравнение Бете~Солпитера 759
Уравнение Дирака 1, 8-19
Уравнение Клейна-Гордона-Шредингера
1, 17, 27, 265
Уравнение Липпмана-Швингера 148
Уравнения Максвелла 1, 335, 453, 458,
495
Уравнения Фаддеева 251
Уравнения Эйлера-Лагранжа 398
Фазовые сдвиги 172-173, 206
Фейнмановские параметры 641, 657, 671
Формула Брейта~Вигнера 216
Формула Розенблюта 657
Формфакторы 610-617, 655-666, 784-786
Фотон
- фаза при зарядовом сопряжении 305
- спиральность и поляризация 97-98,
334, 480-492
- безмассовость 463, 609, 644
816 Квантовая теория поля. Ч. 1
- фотон-фотонное рассеяние 42, 689, - преобразование произвольных непри-
708-710 водимых полей 319-321
- пропагатор 472-475 - преобразование J^v и Р^99-100
Функционалы, обозначения 396 - преобразование одночастичных состо-
Функциональные интегралы яний 101-105, 137
-вывод 507-517 - преобразование скалярных полей 272
- для скаляров со связью с производ- - преобразование векторных полей 283
ной 526
- для фермионов 536-556 Швингеровские члены 606
- для безмассовых векторных полей 529 Шредингеровское представление 145
- для нелинейной о-модели 527
- для квантовой электродинамики 557- Электрические дипольные моменты
563 108,705
- для S -матрицы 517-523 Электрический заряд 456
- лагранжева версия 523-530 - сохранение 163, 727
- использование для вывода фейнманов- - перенормировка 457, 597-604, 639,
ских правил 531 649-653
Электрический зарядовый радиус 666
Хронологически упорядоченные произведе- Электрон
ния, определение 190 - зарядовый радиус 666
- классическая теория 40, 494, 671
Цвет 742 - магнитный момент 7, 13, 18, 47, 617,
Центральные заряды ПО 703
- спин 8-10
Частица Z0 212 Эллиптическая поляризация 482
Частицы W* 212 Энергетические сдвиги атомных уровней
Четность и пространственная инверсия (Р) 41-43, 775-781
- случайная симметрия 705, 719 - сдвиг Is -уровня 802
- определение 76 Энергия вакуума 326 35
- внутренние четности 165-169 Энергия возбуждения в атоме водорода
- несохранение в слабых взаимодействи- 799-801
ях 169 Энтропия 200
- связанных состояний электронов 768, Эффект Казимира 392
792 Эффект Рамзауэра-Таунсенда 220
- преобразование операторов рождения Эффект Юлинга 45, 654, 785
236 Эффективные теории поля 676, 709
- преобразование дираковских полей
294, 299-300 Ядерные силы 585-588