Проблемы принятия решений при нечеткой исходной информации - Орловский С.А.

Автор: Орловский С.А.
Теги: вычислительная математика численный анализ
Год: 1981
Похожие
Проблемы комбинаторного анализа
Численные методы в примерах и задачах
Проблемы дарвинизма
Методы решения экстремальных задач и их применение в системах оптимизации
Текст
                    Проблемы
ПРИНЯТИЯ РЕШЕНИЙ
ПРИ НЕЧЕТКОЙ
исходной
ИНФОРМАЦИИ


ОПТИМИЗАЦИЯ
И ИССЛЕДОВАНИЕ
ОПЕРАЦИЙ
Редактор серии
Н. Н. МОИСЕЕВ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1981
С. А. ОРЛОВСКИЙ
ПРОБЛЕМЫ
ПРИНЯТИЯ РЕШЕНИЙ
ПРИ НЕЧЕТКОЙ
ИСХОДНОЙ
ИНФОРМАЦИИ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1981
22.18
0-66
УДК 519.6
С. А. Орловский. Проблемы принятия решении при
нечеткой исходной информации. — М.: Наука. Главная редакция
физико-математической литературы, 1981, 208 с.
В книге излагаются способы математического описания и
анализа разнообразных задач принятия решений на основе
нового подхода, опирающегося на введенное Л. А. Заде понятие
нечеткого множества. Нечеткие множества используются для
математической формализации исходной информации об иссле-
дуемой реальной ситуации или процесса принятия решений,
которая может носить субъективный и потому нечеткий харак-
тер. В рамках предлагаемого в книге единого подхода анализи-
руются задачи математического программирования с нечетко
описанными множествами допустимых выборов и функциями
целн, некоторые типы игр в нечетко определенной обстановке,
а также задачи принятия решений с одним и несколькими отно-
шениями предпочтения на множестве альтернатив.
Книга рассчитана на широкий круг читателей, включающий
в себя специалистов по прикладной математике, инженеров,
а также лиц, интересующихся вопросами математической эко-
номики, теории систем и общими вопросами принятия решений.
Библ. 43. Илл. 14.
20204—067
053(02)-81
КБ-2-33—81. 1702070000
g) Издательство «Наука».
Главная редакция
физико- математической
литературы, 1981
ОГЛАВЛЕНИЕ
Предисловие редактора серии...................... 8
Предисловие автора .................................. 15
Глава 1. Нечеткие множества и нечеткие отношения	19
1.1.	Нечеткие множества......................... 19
1.1.1.	Определение нечеткого множества и термино-
логия ........................................... 19
1.1.2.	Операции над нечеткими множествами	...	23
1.1.3.	Множества уровня и декомпозиция нечеткого
множества ....................................... 28
1.1.4.	Нечеткие топологические пространства ...	30
1.2.	Нечеткие отношения......................... 36
1.2.1.	Свойства обычных отношений и операции над
ними ............................................ 37
1.2.2.	Определение нечеткого отношения ......... 40
1.2.3.	Операции над нечеткими отношениями ....	44
1.2.4.	Свойства нечетких отношений.......... 49
1.3.	Отображения нечетких множеств.............. 52
1.3.1.	Принцип обобщения.................... 52
1.3.2.	Прообраз нечеткого множества......... 56
1.4.	Соотношение двух подходов к определению нечетких
множеств и отношений............................ 58
1.4.1.	Нечеткие множества................... 58
1.4.2.	Нечеткие отношения................... 63
Глава 2. Задачи математического программирования
и игры при нечетких исходных условиях	.	.	67
2.1.	Введение ....................................... 67
2.2.	Задача достижения нечетко определенной цели (под-
ход Веллмана—Заде) .................................. 69
2.2.1.	Формулировка и определение решения	задачи	69
2.2.2.	Многоэтапные процессы принятия решений
при нечетких исходных условиях.............. 75
6	ОГЛАВЛЕНИЕ!
2.3.	Классификация задач нечеткого математического
программирования..................................... 81
2.4.	Задача математического программирования при не-
четком множестве ограничений......................... 85
2.4.1.	Решение 1, опирающееся на множества уровня
нечеткого множества ограничений................... 86
2.4.2.	Решение 2 и эквивалентность решений обоих
типов............................................. 92
2.5.	Игры в нечетко определенной обстановке...... 96
2.5.1.	Введение .................................. 96
2.5.2.	Описание игры ............................. 99
2.5.3.	Максимальные гарантированные	выигрыши	101
2.5.4.	Игры с противоположными интересами игроков	104
2.5.5.	Нечеткое равновесное решение игры.... 110
Глава 3. Принятие решений при нечетком отношении
предпочтения на множестве альтернатив . .	115
3.1.	Введение ....................................... 115
3.2.	Нечеткие отношения предпочтения................. 119
3.2.1.	Нечеткие отношения безразличия, квазиэкви-
валентности и строгого предпочтения.............. 119
3.2.2.	Линейность нечетких отношений............. 125
3.2.3.	Нечеткое подмножество недоминируемых аль-
тернатив ........................................ 128
3.2.4.	Четко не доминируемые альтернативы и их
свойства ......................................   132
3.2.5.	Условия существования четко недоминируе-
мых альтернатив.................................. 137
3.2.6.	Смешанное расширение задачи принятия ре-
шений ........................................... 141
3.3.	Несколько отношений предпочтения на множестве
альтернатив......................................... 144
3.4.	Отношение предпочтения на нечетком множестве
альтернатив......................................... 151
Глава 4. Общая задача нечеткого математического
программирования.................................... 153
4.1.	Введение ....................................... 153
4.2.	Обобщение нечеткого отношения на класс нечетких
множеств ........................................... 155
4.2.1.	Построение обобщенного отношения ....	155
* ОГЛАВЛЕНИЕ
7
4.2.2.	Некоторые свойства индуцированного отноше-
ния предпочтения............................... 158
4.3.	Недоминируемые альтернативы в общей задаче не-
четкого математического программирования ....	164
4.3.1.	Нечеткое множество недоминируемых альтер-
натив ......................................... 164
4.3.2.	Выбор альтернатив в случае числовых оценок
альтернатив.................................... 168
4.4.	Задачи математического программирования с не-
четко описанными параметрами....................... 170
4.4.1.	Введение ............................... 170
4.4.2.	Формулировка исходной задачи и сведение
ее к общей задаче нечеткого математического про-
граммирования ................................. 174
4.4.3.	Недоминируемые альтернативы в задаче с не-
четко описанными параметрами................... 177
4.5.	Задачи упорядочения при нечеткой исходной инфор-
мации ............................................. 188
4.5.1.	Введение ............................... 188
4.5.2.	Рациональный выбор альтернатив с учетом
набора признаков............................... 189
4.5.3.	Упорядочение	объектов по набору признаков 194
Литература ........................................ 200
Предметный указатель	........... 203
Список обозначений и сокращений.................... 205
ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
Проблема принятия решений или проблема выбора
альтернатив — это, может быть, самый распространен-
ный класс задач, с которыми сталкивается не только ис-
следователь, но и инженер-конструктор, хозяйствен-
ный руководитель и т. п. И математика, вооруженная
современными средствами вычислительной техники,
в анализе этих проблем может сыграть выдающуюся
роль, но лишь в том случае, если применять ее «пра-
вильно», т. е. использовать математические средства
соответственно их возможностям, не переоценивая и не
умаляя роли математики и математика в процессе при-
нятия решений.
Внедрение математики, расширение круга вопросов
человеческой практики, в которых математика оказы-
вается эффективной, часто тормозятся рядом иллюзий.
Люди, не владеющие профессионально математическими
методами, иногда думают, что любая проблема может
быть переведена на язык математики и, следовательно,
решена ее средствами. Часто высказывается и в точ-
ности противоположная точка зрения. Действитель-
ность гораздо сложнее таких крайних утверждений.
Любые ситуации, требующие принятия решений,
содержат, как правило, большое количество неопре-
деленностей. Их принято разделять на три класса.
Прежде всего это — «неопределенности природы» —
факторы нам просто не известные. Затем — «неопре-
деленность противника». Человек всегда существует
в условиях, при которых результаты его решений не
строго однозначны, они зависят от действий других
лиц (партнеров, противников и т. п.), действия которых
он не может полностью учесть или предсказать. И на-
конец, существуют так называемые «неопределенности
желаний» или целей. В самом деле, перед исследова-
телем всегда стоит несколько целей. Описать их одним
ПРЁДИСЛОВЙЁ РЁДАКТОРА СЕРИИ
9
показателем (критерием) невозможно. Конструктору
самолета, например, необходимо обеспечить не только
безопасность пассажиров, но и минимальную стоимость
перелета. Экономисту нужно построить такой план,
чтобы с «минимумом затрат добиться максимума вы-
пуска продукции» и т. п., причем эти требования, как
мы видим, часто противоречат друг другу.
Легко понять, что свести подобные задачи с неопре-
деленностями к точно поставленным математическим
задачам нельзя в принципе — для этого надо тем
или иным образом «снять» неопределенности, т. е. вве-
сти какие-либо гипотезы. Но формирование гипотез —
это уже прерогатива содержательного анализа, это
формализация неформальных ситуаций.
Таким образом, анализ задач принятия решений
в условиях неопределенности не может быть завершен
силами одних математиков. И всегда умение «эксперта»,
т. е. профессионала в данной конкретной области, бы-
вает необходимым, а подчас и решающим.
Но это вовсе не умаляет значения математики и ма-
тематических исследований. Прежде всего, ситуация
с проблемами принятия решений типична для любых
научных проблем. Сначала идет формирование гипо-
тез — акт неформальный в принципе, опирающийся
на опыт. Так обстоит дело и в физике, да и в самой ма-
тематике — вспомним аргументы Пойа в его превосход-
ной книге «Правдоподобные рассуждения».
Но вот гипотезы сформулированы, и математическая
модель готова. И здесь, если задачи, которые решаются
с ее помощью, достаточно сложные, без математики
уже обойтись не удается. По существу, любая постав-
ленная задача, отвечающая тем или иным гипотезам,
представляет собой закодированную информацию о свой-
ствах изучаемого явления, о результатах принятия
того или иного решения. И извлечь эту информацию,
раскодировать ее, представить ее оперирующей стороне
в том виде, который ей доступен, помочь избежать
ошибок и преодолеть неопределенности может только
математик. Таков афористичный смысл этой формы
деятельности математика: проблема принятия решений
в условиях неопределенности не является математи-
кой, но только математик может изучить все много-


10	ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
образие особенностей этой проблемы и создать системы
процедур, которые приведут оперирующую сторону
к варианту тех решений, в которых она действительно
нуждается.
t Вот почему в последние два десятилетия эта пробле-
матика привлекает к себе усилия многих математиков
как у нас в стране, так и за рубежом. Ю. Б. Гермейер,
Р. Беллман, Л. Заде — это лишь наиболее яркие имена
из того длинного перечня лиц, работы которых внесли
и новые идеи, и новые методы и результаты в теорию
принятия решений.
Если решение принимается в условиях неопределен-
ности, если, например, мы не знаем точно своей цели и
результат операции оценивается многими критериями,
то и само решение бессмысленно точно фиксировать.
Можно говорить о классе «подходящих» решений — не
более! Этот факт отчетливо понимается специалистами,
и, по существу, он уже давно используется при анализе
альтернатив возможных решений. Первым его доста-
точно четко сформулировал итальянский экономист
Парето еще в 1904 году в форме так называемого прин-
ципа Парето. Согласно Парето, возможные решения
следует искать лишь среди неулучшаемых альтерна-
тив, т. е. альтернатив, улучшение которых по одним
критериям приводит к их ухудшению по другим кри-
териям. Принцип этот достаточно очевидный и очень
важный с чисто прикладной точки зрения: он позволяет,
во-первых, сжать множество альтернатив, во-вторых,
он демонстрирует те потери, которые имеет оперирую-
щая сторона по тем или иным показателям, стремясь
улучшить какой-то определенный показатель. Умелая
работа с множеством Парето позволяет сделать нагляд-
ными многие особенности изучаемой операции.
Позднее появился еще целый ряд подходов, позво-
ляющих отбраковывать заведомо неприемлемые аль-
тернативы, сузить множество анализируемых вариан-
тов. Многие из этих подходов, таких, например, как
принцип равновесия Нэша, являются сейчас важными
инструментами анализа прикладных задач.
Покойный Ю. Б. Гермейер всегда подчеркивал, что
в проблемах принятия решений в условиях неопределен-
ности может быть лишь один строгий математический
ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
11
результат — это оценка, полученная на основе прин-
ципа максимина. Гарантированный результат — это
единственная опорная точка. Дальше лежат гипотезы
и риск. Это утверждение совершенно не означает, что
выбирать нужно именно ту альтернативу, ту стратегию,
которая реализует этот гарантированный результат.
Он может быть и очень хорошим, и совершенно непри-
емлемым — это всего лишь репер, информация, которая
полезна субъекту (оперирующей стороне). В конечном
счете никогда никакой математический анализ не может
дать строгого точного результата выбора альтернатив
в условиях неопределенности.
Именно с этих позиций надо оценивать и попытку
одного из известных современных специалистов в при-
кладной математике Л. Заде, который предложил от-
казаться от какого-либо четкого описания в задачах
принятия решений.
В основе теории Л. Заде лежит тоже достаточно
очевидный факт — субъективные представления о цели
всегда нечетки. Но он делает и следующий шаг — он
полагает, что и все оценки субъекта и ограничения,
с которыми он работает, также, как правило, нечетки,
а иногда и вообще лишены в своем начальном виде
количественных характеристик. Так он приходит к по-
нятию лингвистической переменной — красное, не очень
красное, совсем не красное и т. п. — а затем вводит
некоторую функцию принадлежности как способ фор-
мализации субъективного смысла этих качественных
показателей. Тот же прием позволяет охарактеризовать
принадлежность какому-либо множеству. Характери-
стической функцией множества оказывается тогда не
разрывная функция
1 — на множестве, 0 — вне его,
а некоторое распределение, напоминающее интуитив-
ные -вероятностные распределения. Заде развивает
технику использования подобных оценок и определен-
ный формализм, дающий новое описание моделей при-
нятия решений в условиях нечеткой информации. Как
мне кажется, основная цель подобных исследований —
научиться извлекать из этого нечеткого описания
правило выбора альтернатив, причем это правило также
12
ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
должно носить нечеткий характер. Оно также должно
формулироваться в терминах функций принадлежности.
Идеи эффективных компромиссов Парето, гаран-
тированных оценок Ю. Б. Гермейера, идеи выбора
решений на основе нечеткого описания Л. Заде — все
они относятся, по существу, к одному кругу идей —
развить принципы и создать аппарат, позволяющий по
возможности сузить множество допустимых альтерна-
тив. Математика не может дать окончательного крите-
рия отбора, если на самом деле их несколько! Если
такова природа конфликта! Но отбросить неконкуренто-
способные ,iвыделить наиболее перспективные множества
вариантов — это уже задача математики и математиков.
И все эти идеи следуют тому естественному ходу че-
ловеческой мысли, который свойствен человеку, анали-
зирующему более или менее сложную ситуацию. Эти
идеи восходят еще к А. А. Маркову, положившему
начало формализации процесса последовательного ана-
лиза. Это направление, трансформируясь через работы
Вальда и Айзекса, привело к появлению динамического
программирования Р. Веллмана и к методу ветвей и
границ. В Советском Союзе В. С. Михалевичем была
дана на сегодняшний день, вероятно, наиболее общая
схема формализованного описания последовательного
анализа, включающая в себя и схему динамического
программирования, и метод ветвей и границ.
Центральная процедура этого общего подхода к про-
блеме выбора альтернатив опирается на различные
принципы отбраковки. И в этом контексте принципы
Парето, гарантированного результата, формализм Заде
занимают свое вполне определенное место. Я думаю,
например, что развитие процедур типа ветвей и границ
на основе нечетких алгоритмов в смысле Заде будет
весьма серьезным развитием методов последователь-
ного анализа.
Очень важное место в проблемах принятия решений
занимает анализ ситуаций, в которых определяющими
являются не количественные, а качественныеТхарак-
теристики — холодный, не очень холодный, теплый
или красный, темно-красный, почти красный и т. д.
Конечно, в каждом конкретном случае для «качествен-
ных показателей» можно ввести определенную количе-
ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
13
ственную шкалу — уровень тепла характеризовать гра-
дусами, а цвет — длиной волны линий поглощения.
Но подобная «метризация» далеко не всегда помогает
делу, ибо, во-первых, она вообще не всегда возможна,
а во-вторых, не дает достаточно адекватного представ-
ления исходной информации. Начав еще в шестидеся-
тых годах заниматься проблемами нечетких множеств
и нечетких описаний, Л. Заде обратил внимание на
тот факт, что этот способ описания особенно удобен
при анализе ситуаций с величинами, оцениваемыми
качественными характеристиками. Так возникла его
теория лингвистических переменных, теория, которая
существенно расширяет область традиционных опера-
ционалистских исследований.
До работ Л. Заде подобная качественная информа-
ция, по существу, просто терялась — было непонятно,
как ее использовать в формальных схемах анализа
альтернатив. Поэтому шаг, который сделал Л. Заде,
носит действительно принципиальный характер. Но
в связи с этим я хотел бы еще раз подчеркнуть, что
техника, развиваемая Л. Заде, основывается на исполь-
зовании функций принадлежности. Эти функции явля-
ются, всегда являются, гипотезами! Они дают субъектив-
ное представление эксперта (исследователя) об особен-
ностях исследуемой операции, о характере ограничений и
целей исследования. Это всего лишь новая форма утвер-
ждения гипотез, но она открывает и новые возможности.
Имея в своем распоряжении функции принадлежности,
исследователь получает в свои руки и определенный ап-
парат, позволяющий строить оценки для альтернатив.
Итак, в схемах анализа, развиваемых Л. Заде,
так же как и в традиционных методах исследования
операций, строится некоторая система гипотез, только
теперь они формулируются в терминах «субъек-
тивной» принадлежности. Далее, в результате анализа,
так же как и в обычных задачах с неопределенностями,
мы получаем результат снова в нечеткой форме —
в форме функции принадлежности некоторому мно-
жеству. ЗнйЧит, техника Заде, подобно принципам
Парето или принципу максимального гарантирован-
ного результата, позволяет сжать множество возможных
альтернатив.
14
ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
Будущее покажет, насколько подобный подход сде-
лается полезным для решения прикладных задач. Под-
черкнем только, что вопрос о будущности всего этого
направления решается не столько математическим
совершенством развиваемой теории, сколько удобством,
которое обеспечивается оперирующей стороне при ана-
лизе и выборе альтернатив.
Теория Л. Заде еще не получила достаточно широ-
кой известности в нашей стране, и публикации на рус-
ском языке ограничиваются пока в основном только
переводами двух книг. Поэтому появление первой оте-
чественной монографии, посвященной изложению ос-
новных положений теории Л. Заде и ее развитию, пред-
ставляется не только полезным и важным, но и своевре-
менным. Книга С. А. Орловского отнюдь не пересказ
схемы Л. Заде. В ней сделана попытка еще одного шага
в данном направлении. Л. Заде показал, каким образом
нечеткую, качественного характера информацию можно
использовать в формализованных процедурах анализа.
По существу, он предложил такое расширение языка
математики, которое позволяет учитывать нечеткость
исходной информации в математических моделях.
Следующий шаг — это проблема математической
обработки той нечеткой информации, которая введена
в модель, и прежде всего — проблема сужения мно-
жества альтернатив на основе этой информации. Пер-
вый шаг на этом пути — последовательная перефор-
мулировка всех задач математического программиро-
вания. Эта проблема далеко не тривиальна, когда целе-
вые функции и ограничения записаны нечетким обра-
зом. Еще сложнее проблемы теории игр, когда субъект
пытается выбрать стратегию при нечеткой информации
о поведении других субъектов (других игроков), да
еще в условиях, когда множество собственных страте-
гий определено нечетко.
Предлагаемая книга как раз и посвящена обсужде-
нию подобных вопросов и предлагает определенные
приемы обработки нечеткой информации, заданной
в форме нечетких множеств, которые приводят к новым
формулировкам оптимизационных и игровых задач.
1979
Н. Н. Моисеев
ПРЕДИСЛОВИЕ АВТОРА
Для настоящего времени характерно стремление
ко все более широкому применению математических
методов для описания и анализа сложных экономиче-
ских, социальных, экологических и других систем.-
Отличительная особенность многих из этих систем
в том, что помимо объективных законов в их функцио-
нировании существенную роль играют субъективные
представления, суждения и даже эмоции людей.
Анализируя конкретную систему, мы фактически
рассматриваем выделенную нами часть более полной
сложной системы. Само это выделение мы производим,
поскольку не в состоянии охватить и достаточно ком-
пактно математически описать и исследовать все много-
образие свойств полной системы. То, какую часть бо-
лее полной системы мы выделяем, определяется целями
исследования и нашими представлениями о полной
системе.
Выделяя подсистему, мы фактически вводим гра-
ницы, которых на самом деле не существует. Полная
система не есть дискретная совокупность подсистем,
а скорее своего рода «континуум», в котором подсистемы
в некотором смысле «проникают» друг в друга. Переход от
подсистемы к подсистеме происходит не скачкообразно
через четкую границу, а плавно, непрерывно. Поэтому и
границ в обычном смысле между ними установить нельзя.
Анализируя выделенную подсистему, мы не можем
игнорировать ее связи с остальной частью более пол-
ной системы. Не имея возможности и средств точно
описать все эти связи, мы используем либо свои соб-
ственные представления об этих связях, либо обра-
щаемся за помощью к экспертам, которые этими пред-
ставлениями обладают. Важно то, что эти представле-
ния или, иными словами, информация о границах
анализируемой подсистемы чаще всего бывает выражена
16
ПРЕДИСЛОВИЕ АВТОРА
в понятиях, которые имеют нечеткий смысл сеточки
зрения классической математики.
Вместе с тем человек, моделируя реальность в таких
Понятиях, часто находит пусть не наилучшее, но при-
емлемое для него поведение в сложнейших с точки зре-
ния возможности математического описания реальных
ситуациях. В связи с этим можно говорить о том, что
язык традиционной математики, опирающейся на тео-
рию множеств и двузначную логику, недостаточно ги-
бак для моделирования реальных сложных систем,
поскольку в нем нет средств достаточно адекватного
описания понятий, которыми ^пользуется человек и
которые имеют неопределенный смысл.
Простейший пример — классификация объектов по
цвету. Пусть цели исследования таковы, что достаточно
различать лишь красные, желтые и зеленые объекты.
В традиционной математике классификация — это раз-
биение заданной совокупности объектов на три непере-
секающихся подмножества, т. е. введение четких гра-
ниц, отделяющих объекты одного цвета от объектов
другого цвета. Однако подобная классификация мало
соответствует нашему представлению о цвете объектов.
На самом деле мы не в состоянии обоснованно провести
четкую границу между классами, например, красных
и желтых объектов. В нашем понимании переход от
красного к желтому непрерывен. Мы допускаем, что
некоторые объекты могут в той или иной степени отно-
ситься к различным классам одновременно, т. е. что
границы между этими классами нечеткие.
Одна из основных целей построения математических
моделей реальных систем — найти способ обработки
имеющейся информации для выбора рациональных
вариантов управления системой. Очень часто, и осо-
бенно при доследовании экономических, социальных
и других систем, в функционировании которых уча-
ствует человек, значительное количество информации
о системе может быть получено от людей, имеющих
опыт работы с данной системой и знающих ее особен-
ности, от людей, имеющих представление о целях
функционирования системы и т. п. Эта информация
носит субъективный характер, и ее представление в есте-
ственном языке, как правило, содержит большое число
ПРЕДИСЛОВИЕ АВТОРА
17
неопределенностей типа «много», «мало», «сильно уве-
личить», «высокий», «очень эффективный» и т. п., ко-
торые не имеют аналогов в языке традиционной мате-
матики. Поэтому и описание подобной информации на
языке традиционной математики обедняет математиче-
скую модель исследуемой реальной системы и делает
ее слишком грубой. Вместе с тем наличие математи-
ческих средств отражения нечеткости исходной инфор-
мации позволило бы, по-видимому, построить модель,
£олее адекватную реальности.
Таким образом, для дальнейшего успешного при-
менения математических методов в качестве мощного
инструмента для анализа все более сложных систем
необходимо, по-видимому, создание средств более точ-
ного учета нечетких представлений и суждений людей
о реальном мире в математических моделях.
Одним из начальных шагов на этом пути можно
считать новое направление в прикладной математике,
связанное с именем видного американского математика
Л. А. Заде и получившее название теории нечетких
множеств. Лежащее в основе этой теории понятие не-
четкого множества предлагается в качестве средства
математического моделирования неопределенных поня-
тий, которыми оперирует человек при описании своих
представлений о реальной системе, своих желаний,
целей и т. п. Нечеткое множество — это математиче-
ская модель класса с нечеткими или, иначе, размытыми
границами. В этом понятии учитывается возможность
постепенного перехода от принадлежности к непри-
надлежности элемента множеству. Иными словами,
элемент может, вообще говоря, иметь степень принад-
лежности множеству, промежуточную между полной
принадлежностью и полной непринадлежностью.
Основополагающая работа Л. А. Заде «Fuzzy
Sets» [1] была опубликована в 1965 году. К настоящему
времени работы, посвященные многообразным аспек-
там этой теории и ее приложений, исчисляются сот-
нями. Свидетельством растущего интереса к этому на-
правлению в прикладной математике может служить
и организация в 1978 году специального Международ-
ного журнала «Int. Journal of Fuzzy Sets and Systems».
Применению языка и методологии нечетких множеств
2 С. А. Орловский
IS
ПРЕДИСЛОВИЕ ABtOt>A
в моделировании и анализе сложных систем были по-
священы многочисленные семинары и конференции
в различных странах, в том числе и в СССР.
Данная книга посвящена одному из важных направ-
лений применения нового подхода — проблеме приня-
тия решений при нечеткой исходной информации.
По сути дела, в ней анализируются различные классы
математических задач принятия решений, в которых
исходная информация описана в терминах нечетких
множеств и отношений в смысле Л. А. Заде. В нашем
понимании математический анализ задачи или ситуа-
ции принятия решений заключается в «отбраковке»
нерациональных альтернатив или вариантов, т. е.
в том, чтобы, использовав математические средства для
обработки всей имеющейся информации, сузить мно-
жество возможных вариантов или альтернатив, отбро-
сив те из них, для которых имеются заведомо более
приемлемые варианты или альтернативы. Этот подход
используется во всех моделях, рассмотренных в книге.
Основная цель книги — стимулировать интерес к но-
вому направлению в области математического модели-
рования и анализа сложных реальных систем. Быть
может, даже излишне отмечать здесь, что изложенные
в книге постановки задач и подходы к их анализу —
лишь один из возможных путей использования матема-
тических средств для обработки нечеткой исходной
информации. Но вместе с тем столь же излишне, по
нашему мнению, доказывать необходимость поисков
и исследований в этом направлении.
В своей работе в этой области, а также в работе
над книгой я постоянно пользовался вниманием и
поддержкой Н. Н. Моисеева. За все это я приношу
ему свою искреннюю благодарность.
Наконец, я хотел бы выразить свою надежду на
критику всего изложенного в этой книге. Появление
критики свидетельствовало бы о выполнении одной
из основных задач, стоявших передо мной при ее на-
писании.
t979
С. А. Орловский
ГЛАВА 1
НЕЧЕТКИЕ МНОЖЕСТВА
И НЕЧЕТКИЕ, ОТНОШЕНИЯ
Прежде чем приступить к описанию и анализу
различных моделей принятия решений с учетом нечет-
кой исходной информации, мы изложим в этой главе
основы математического аппарата теории нечетких
множеств и отношений, опираясь главным образом на
работы Л. А. Заде [1—5]. Вводимые здесь определения,
операции над нечеткими множествами, отображения
нечетких множеств и их свойства составляют матема-
тическую основу рассматривающихся ниже способов
построения таких моделей и обработки нечеткой исход-
ной информации.
Отметим, что в эту главу включены главным образом
лишь те сведения, которые потребуются в дальнейшем
при формулировке и анализе задач принятия решений.
Более полное представление о теперешнем состоянии
теории нечетких множеств и отношений можно получить,
ознакомившись с цитируемой ниже литературой.
1.1. Нечеткие множества
1.1.1. Определение нечеткого множества и термино-
логия. В традиционной прикладной математике мно-
жество понимается как совокупность элементов (объек-
тов), обладающих некоторым общим свойством. На-
пример, множество чисел, не меньших заданного числа,
множество векторов, сумма компонент каждого из ко-
торых не превосходит единицы, и т. п. Для любого
элемента при этом рассматриваются лишь две возмож-
ности: либо этот элемент принадлежит данному мно-
жеству (т. е. обладает данным свойством), либо не
принадлежит данному множеству (т. е. не обладает
данным свойством). Таким образом, в описании мно-
жества в обычном смысле должен содержаться четкий
критерий, позволяющий судить о принадлежности или
2*
20
НЕЧЕТКИЕ МНОЖЕСТВА
1
непринадлежности любого элемента данному множе-
ству.
Однако, как уже говорилось во введении, при по-
пытках математического описания сложных систем
язык обычных множеств может оказаться недостаточно
гибким. Имеющаяся информация о системе может быть
сформулированной на языке нечетких понятий, кото-
рые невозможно математически формализовать с по-
мощью обычных множеств.
Понятие нечеткого множества — попытка матема-
тической формализации нечеткой информации с целью
ее использования при построении математических мо-
делей сложных систем. В основе этого понятия лежит
представление о том, что составляющие данное множе-
ство элементы, обладающие общим свойством, могут
обладать этим свойством в различной степени и, сле-
довательно, принадлежать данному множеству с раз-
личной степенью. При таком подходе высказывания
типа «элемент х принадлежит данному множеству»
теряют смысл, поскольку необходимо указать «насколько
сильно» или с какой степенью данный элемент принад-
лежит данному множеству.
Один из простейших способов математического опи-
сания нечеткого множества — характеризация степени
принадлежности элемента множеству числом, например,
из интервала [0, 1]. Пусть X — некоторое множество
(в обычном смысле) элементов. В дальнейшем мы будем
рассматривать подмножества этого множества.
Определение 1.1.1. Нечетким множеством С
в X называется совокупность пар вида (х,	(я)), где
х £ X, а — функция X -> [0, 1], называемая функ-
цией принадлежности нечеткого множества С. Значе-
ние рс (х) этой функции для конкретного х называется
степенью принадлежности этого элемента нечеткому
множеству С.
Как видно из этого определения, нечеткое множе-
ство ’вполне описывается своей функцией принадлеж-
ности, поэтому ниже мы часто будем использовать эту
функцию как обозначение нечеткого множества.
«Можно определить нечеткие ^множества и более
общего вида. Так, например, в^книге [5] JL АЛЗаде
НЕЧЕТКИЕ МНОЖЕСТВА
21
1.11
вводит в рассмотрение нечеткие множества с функциями
принадлежности, значениями которых являются не-
четкие подмножества интервала [0, 1], и называет их
нечеткими множествами типа 2. Обычные нечеткие
множества, соответствующие определению 1.1.1, на-
зываются при этом нечеткими множествами типа 1.
Продолжая это обобщение, Л. А. Заде приходит к сле-
дующему определению.
Определение 1.1.2. Нечеткое множество есть
множество типа п, п=1, 2, 3, . . ., если значениями его
функции принадлежности являются нечеткие множе-
ства типа п—1. Функция принадлежности нечеткого
множества типа 1 принимает значения из интервала
[О, 11.
В работах Дж. Гогена [6, 7] рассматриваются не-
четкие множества, функции принадлежности которых
представляют собой отображения X -> L, где L —
произвольная структура типа решетки.
Всюду в этой книге рассматриваются нечеткие мно-
жества, соответствующие определению 1.1.1, т. е. по
терминологии Л. А. Заде нечеткие множества типа 1.
Обычные множества составляют подкласс класса
нечетких множеств. Действительно, функцией принад-
лежности обычного множества В сХ является его
характеристическая функция
{1, если х£В,
О, если X 5 В,
и в соответствии с определением 1.1.1 обычное мно-
жество В можно также определить как совокупность
пар вида (х,	(х)). Таким образом, нечеткое множе-
ство представляет собой болеэ широкое понятие, чем
обычное множество, в том смь*еле, чго функция при-
надлежности нечеткого'мно1 естча может быть, вообще
говоря^произвольной функцией^или даже произволь-
ным отображением.
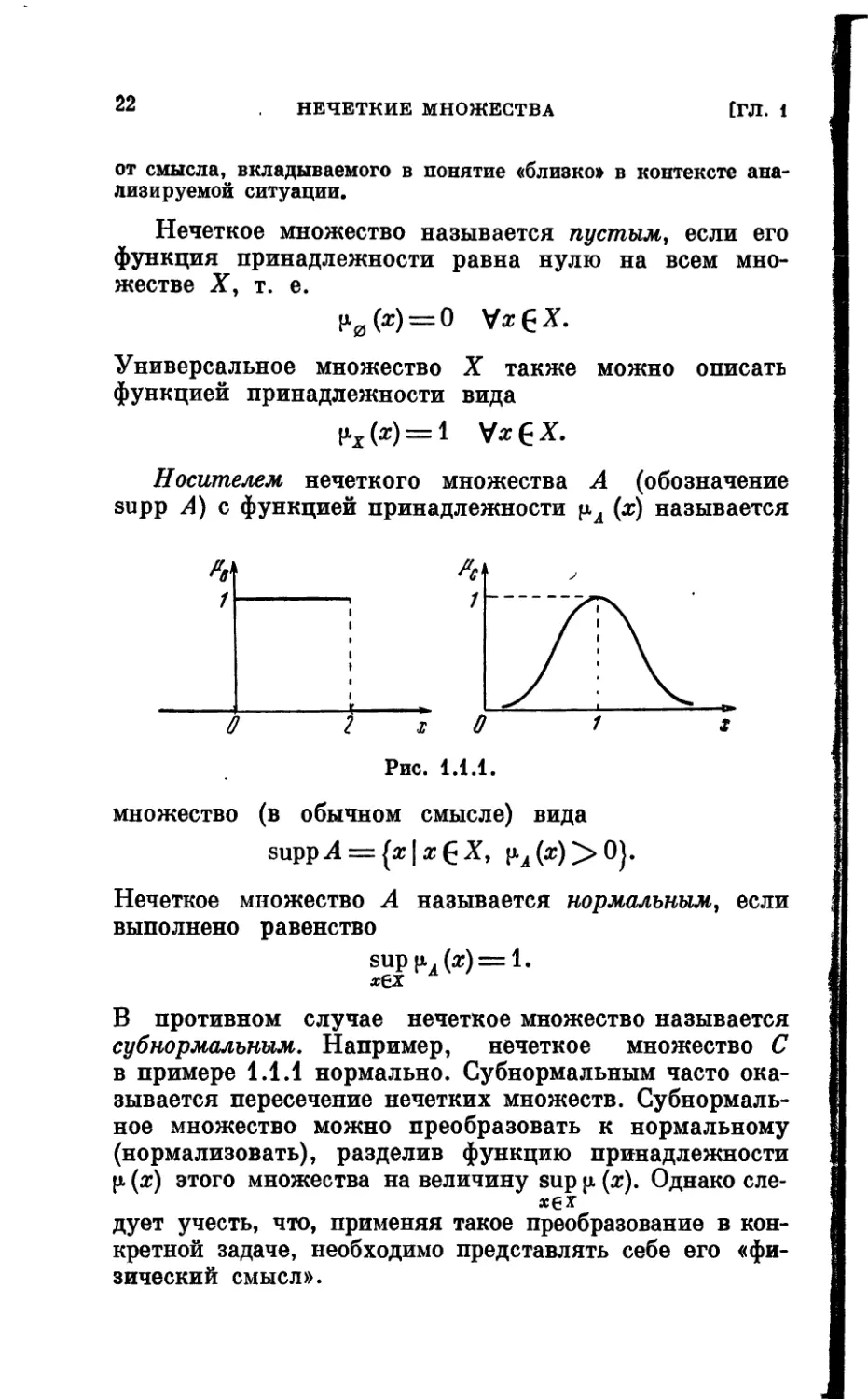
Пример 1.1.1. Для сравнения рассмотрим обычное
множество чисел (s|0 С х 2} и нечеткое множество чисел
С~{х\ «значение х близко к 1»}. Функции принадлежности
этих множеств представлены на рис. 1.1.1. Заметим, что вид
функции принадлежности |лс нечеткого множества С зависит
22
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
от смысла, вкладываемого в понятие «близко» в контексте ана-
лизируемой ситуации.
Нечеткое множество называется пустым, если его
функция принадлежности равна нулю на всем мно-
жестве X, т. е.
F0(*) = ° VxEX.
Универсальное множество X также можно описать
функцией принадлежности вида
Носителем нечеткого множества А (обозначение
supp А) с функцией принадлежности (х) называется
&
1
Рис. 1.1.1.
множество (в обычном смысле) вида
supp Л = {я| х£Х,
Нечеткое множество А называется нормальным, если
выполнено равенство
sup р. (я) = 1.
*ех
В противном случае нечеткое множество называется
субнормальным. Например, нечеткое множество С
в примере 1.1.1 нормально. Субнормальным часто ока-
зывается пересечение нечетких множеств. Субнормаль-
ное множество можно преобразовать к нормальному
(нормализовать), разделив функцию принадлежности
р (х) этого множества на величину sup у. (х). Однако сле-
дует учесть, что, применяя такое преобразование в кон-
кретной задаче, необходимо представлять себе его «фи-
зический смысл».
1.1 J
НЕЧЕТКИЙ МНОЖЕСТВА
23
Пусть А и В — нечеткие множества в X, а р-л(х) и
(х) — их Функции принадлежности соответственно.
Говорят, что А включает в себя В (т. е. В С А), если
для любого х£Х выполнено неравенство (х)	(х).
Множества А и В совпадают (эквивалентны), если
(ж) ~ Нд (ж) ПРИ любом х £ X. Если нечеткие мно-
жества Л и В таковы, что В С А, то и
supp В С supp А.
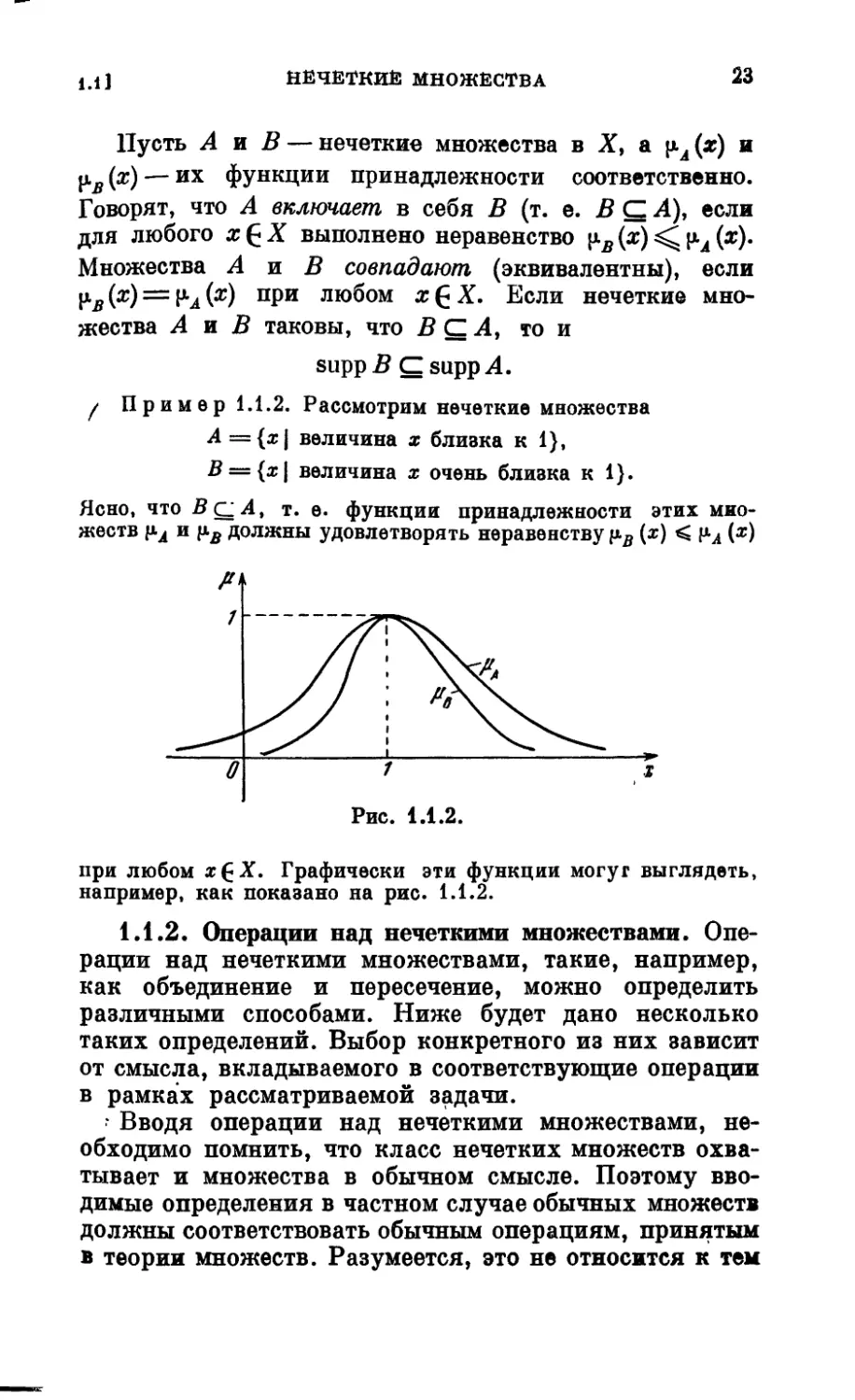
f Пример 1.1.2. Рассмотрим нечеткие множества
Л ={х| величина х близка к 1},
В — {х\ величина х очень близка к 1).
Ясно, что BqA, т. е. функции принадлежности этих мно-
жеств и рв должны удовлетворять неравенству {х) <	(х)
при любом х£Х. Графически эти функции могут выглядеть,
например, как показано на рис. 1.1.2.
1.1.2. Операции над нечеткими множествами. Опе-
рации над нечеткими множествами, такие, например,
как объединение и пересечение, можно определить
различными способами. Ниже будет дано несколько
таких определений. Выбор конкретного из них зависит
от смысла, вкладываемого в соответствующие операции
в рамках рассматриваемой задачи.
 Вводя операции над нечеткими множествами, не-
обходимо помнить, что класс нечетких множеств охва-
тывает и множества в обычном смысле. Поэтому вво-
димые определения в частном случае обычных множеств
должны соответствовать обычным операциям, принятым
в теории множеств. Разумеется, это не относится к тем
24
ЙЁЧЁТКИЁ МНОЖЕСТВА
[гл. 1
из вводимых ниже операций, которые для обычных
множеств не имеют смысла, например, к операциям
концентрирования, растяжения и выпуклой комби-
нации.
Определение 1.1.3. Объединением нечетких
множеств А и В в X называется нечеткое множество
A U В с функцией принадлежности вида
^ил(ж) = тах{М®)» М®)}’ Х^х-
Если [Ау) — конечное или бесконечное семейство
нечетких множеств с функциями принадлежности
Рис. 1.1.3.
Ра (ж> !/)> гДе У € Y — параметр семейства, то объедине-
нием С = U Av множеств этого семейства является не-
y v
четкое множество с функцией принадлежности вида
M®) = sup{v,(®> у)- ®€*-
Определение 1.1.3а. Объединение нечетких мно-
жеств А и В в X можно определить и через алгебраи-
ческую сумму их функций принадлежности:
1 при РА(«) + рв(а:)>1,
Илия (®)	(#) _|_	(#) в противном случае.
Пример 1.1.3. Пусть нечеткие множества А и В в число-
вой оси описываются функциями принадлежности, показанными
на рис. 1.1.3. Жирной линией на рис. 1.1.3 показана функция
принадлежности объединения этих множеств по определению
1.1.3.
1.1]
НЕЧЕТКИЕ МНОЖЕСТВА
25
Определение 1.1.4. Пересечением нечетких мно-
жеств А и В в X называется нечеткое множество
4f|B с функцией принадлежности вида
—	М*)}> Х£Х'
Если {4у} — бесконечное или конечное семейство
нечетких множеств с функциями принадлежности
(*> У)» гДе У € ¥ — параметр семейства, то пересече-
нием С = П Ад множеств этого семейства является
нечеткое множество с функцией принадлежности вида
^(a^inffi, (ж, ^), х£Х.
Определение 1.1.4а. Еще один способ опреде-
ления пересечения нечетких множеств А и В — исполь-
зование алгебраического произведения их функций при-
надлежности:
—	Х^Х.
Пожалуй, в наибольшей степени отличие этих
определений друг от друга проявляется в случае не-
четких множеств А и В таких, что В С А, т. е.
Ня (х) С (ж) при любом х £ X. По первому из этих
определений
т. е. функция принадлежности множества А фактиче-
ски «не участвует» в этом определении в результирую-
щей функции принадлежности, тогда как по определе-
нию 1.1.4а функция принадлежности всегда содержит
функции принадлежности обоих множеств.
Полезным может оказаться следующее свойство
носителей нечетких множеств:
supp (4 (J В) = (supp 4) U (supp В),
supp (4 П В) = (supp 4) П (supp В).
Легко проверить, что эти равенства справедливы для
любого из приведенных выше определений объедине-
ния и пересечения»
26
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
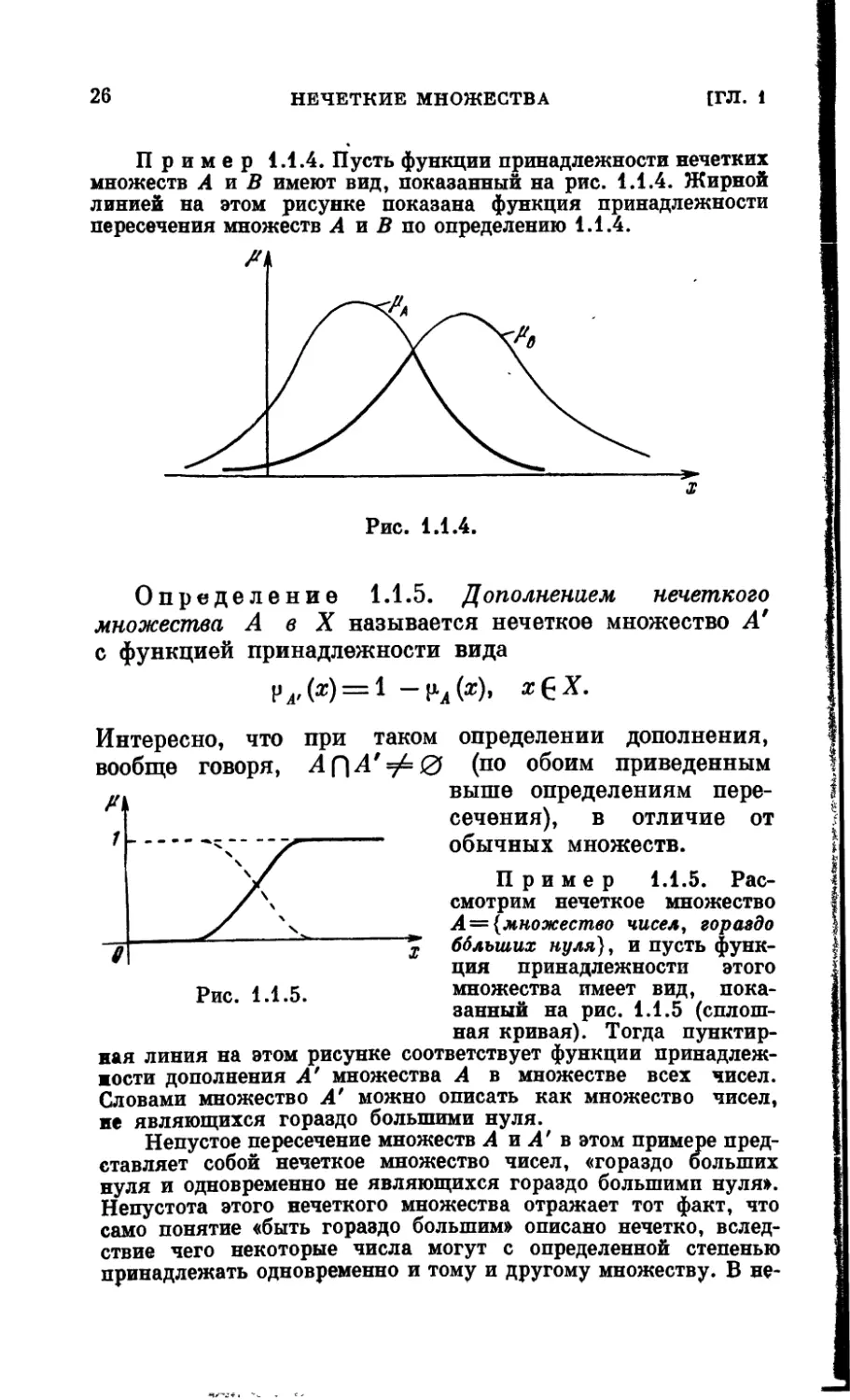
Пример 1.1.4. Пусть функции принадлежности нечетких
множеств А и В имеют вид, показанный на рис. 1.1.4. Жирной
линией на этом рисунке показана функция принадлежности
пересечения множеств А и В по определению 1.1.4.
Определение 1.1.5. Дополнением нечеткого
множества А в X называется нечеткое множество А'
с функцией принадлежности вида
рл,(ж) = 1 -М®)’ х£Х-
Интересно, что при таком определении дополнения,
вообще говоря, А(уА'^=0 (по обоим приведенным
выше определениям пере-
сечения), в отличие от
обычных множеств.
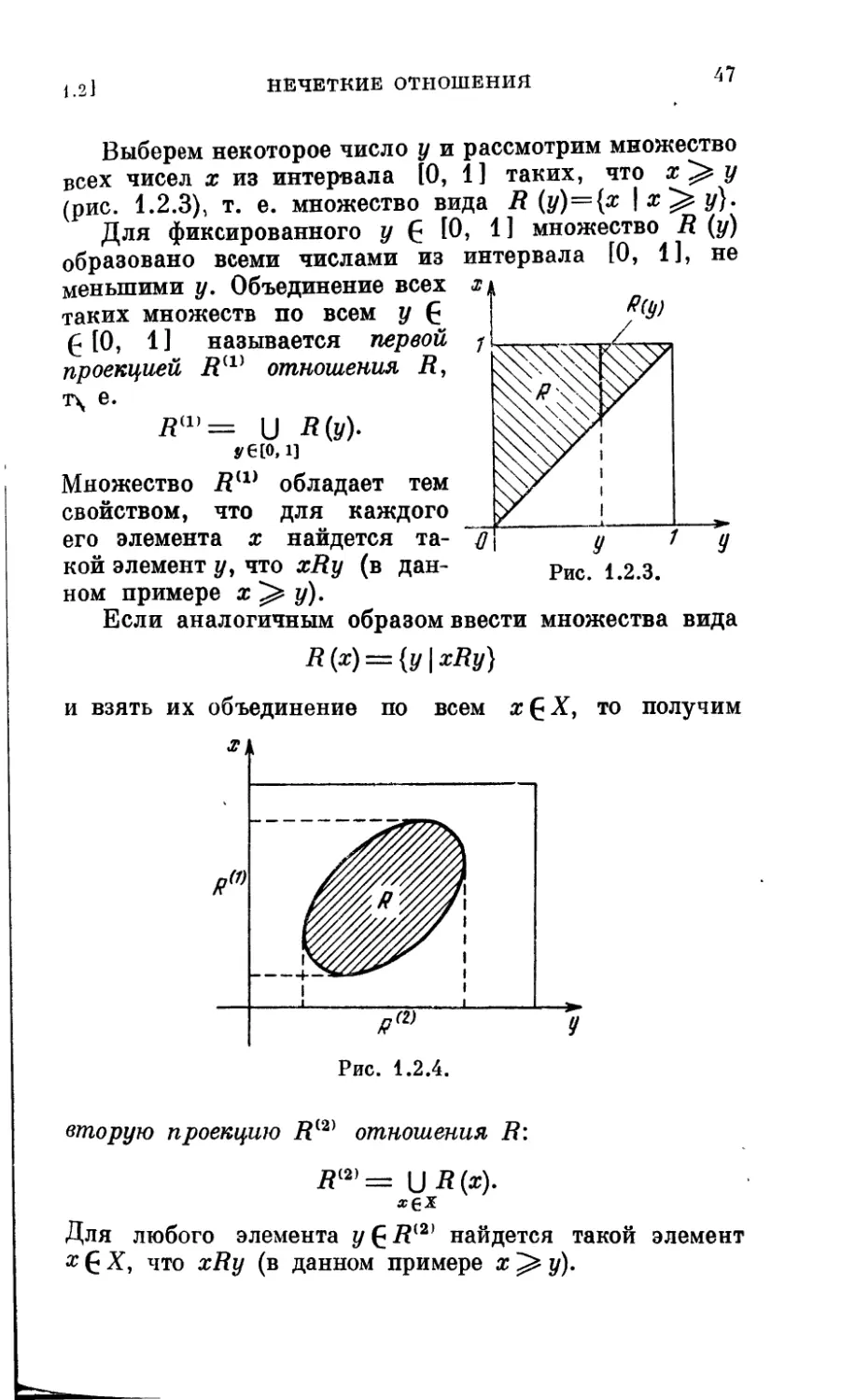
Пример 1.1.5. Рас-
смотрим нечеткое множество
А = {множество чисел, гораздо
больших нуля}, и пусть функ-
ция принадлежности этого
множества имеет вид, пока-
занный на рис. 1.1.5 (сплош-
ная кривая). Тогда пунктир-
ная линия на этом рисунке соответствует функции принадлеж-
ности дополнения Л' множества А в множестве всех чисел.
Словами множество Л' можно описать как множество чисел,
не являющихся гораздо большими нуля.
Непустое пересечение множеств Л и Л' в этом примере пред-
ставляет собой нечеткое множество чисел, «гораздо больших
нуля и одновременно не являющихся гораздо большими нуля».
Непустота этого нечеткого множества отражает тот факт, что
само понятие «быть гораздо большим» описано нечетко, вслед-
ствие чего некоторые числа могут с определенной степенью
принадлежать одновременно и тому и другому множеству. В не-
1,11
НЕЧЕТКИЕ МНОЖЕСТВА
27
котором смысле это пересечение можно рассматривать как нечет-
кую «границу» между множествами А и А'.
Определение 1.1.6. Разность множеств А и В
в X определяется как нечеткое множество с функ-
цией принадлежности вида
, . / Рл (я) — Ив (х) при	(ж) > Ив (я).
“ I
х I 0 в противном случае.
Отметим, что приведенное выше определение допол-
нения нечеткого множества вытекает из данного опре-
деления 1.1.6.
Определение 1.1.7. Декартово произведение
ЛхХ • • • X Ап нечетких множеств в i — 1, 2,..., n,
определяется как нечеткое множество А в декартовом
произведении X = ХгХ • • • ХХп с функцией принад-
лежности вида
Рл (х) = min (p.4i (жх),	(*»)}.
х — (xlt..., xn) X.
Определение 1.1.8. Выпуклой комбинацией не-
четких множеств Av...,An в X называется нечеткое
множество А с функцией принадлежности вида
рл(®)=5^ (®).
*=1
гДв Х<>0, i = l, 2,..и, =
<=1
Выпуклые комбинации нечетких множеств могут
найти применение, например, в задачах принятия реше-
ний с несколькими нечеткими ограничениями. Заме-
тим, что для обычных множеств эта операция не имеет
смысла.
Определение 1.1.9. Операции концентриро-
вания (CON) и растяжения (DIL) нечеткого множе-
ства А определяются следующим образом:
CON А = Л2, О1ЬЛ=ЛЧ
гДе Р-Ла(^) = Ил(а:)’	а>°-
28
НЕЧЕТКИЕ МНОЖЕСТВА
(ГЛ. 1
Применение операции концентрирования к задан-
ному нечеткому множеству означает, по сути дела,
уменьшение «нечеткости» этого множества. В реальной
задаче это может означать поступление новой инфор-
мации, позволяющей более точно (более четко) описать
данное нечеткое множество. Аналогичным образом,
операция растяжения может применяться для модели-
рования ситуации, связанной с потерей информации.
В книге Л. А. Заде [5] обсуждается применение этих
операций для представления лингвистических неопре-
деленностей.
1.1.3. Множества уровня и декомпозиция нечеткого
множества. Множеством уровня а нечеткого множе-
ства А в X называется множество в обычном смысле,
составленное из элементов х £ X, степени принадлеж-
ности которых нечеткому множеству А не меньше
числа а. Таким образом, если Ал — множество уровня
а нечеткого множества А, то
Аа={х\х£Х, |i1(x)>a}.
Как будет видно ниже, множествами уровня удобно
пользоваться при формулировке и анализе некоторых
задач принятия решений.
Пусть (A (J В)л и (A Q В)л — множества уровня а
объединения и пересечения нечетких множеств А и В
соответственно. Рассмотрим связь этих множеств
с множествами уровня Ав и Ва. Если для опера-
ций объединения и пересечения принять определения
1.1.4 и 1.1.3, то, как нетрудно видеть, эта связь такова:
(4UB)«=AU*«, (ЛЛЯ)«=АП*..
В случае же определений 1.1.3а и 1.1.4а имеем лишь
(Л и В), D Лви В„ (Л Л в)л С Л. Л вя.
Заметим, что в правых частях всех этих четырех со-
отношений используются обычные операции объедине-
ния и пересечения множеств, каждую из которых
можно рассматривать и как частный случай операции
по любому из соответствующих определений, приве-
денных в п. 1.1.2.
Если (ЛхХ • • • ХЛв)а — множество уровня а декартова
произведения нечетких множеств Лх,..., Л„, то из опре-
i.D
НЕЧЕТКИЕ МНОЖЕСТВА
29
деления 1.1.7 декартова произведения легко видеть, что
(Лхх... х А)в=(л^х... х(ля)а,
т. е. множество уровня а декартова произведения пред-
ставляет собой декартово произведение множеств уровня
а рассматриваемых нечетких множеств.
Множество (Л^ уровня а любой выпуклой комбина-
ции нечетких множеств (п. 1.1.2) А1,...}Ап содержит
пересечение множеств уровня а всех этих множеств, т. е.
f	П(А)«с4«.
»=1
В некоторых случаях (см., например, работу [8])
удобно пользоваться разложением нечеткого множества
по его множествам уровня, т. е. представлением этого
множества в виде
Л = (J аЛв,
а
где (х) =	(х), а объединение нечетких мно-
жеств аЛа берется в соответствии с определением по
всем а от 0 до 1.
Пример 1.1.6. Пусть Х=={1, 2,..., 6), а функция при-
надлежности нечеткого множества А в X задана таблицей
х 0	1	2	3	4	5	6
(х)	0 0,1 0,3 0,5 0,7 0,9	1
Тогда для А можно выписать следующие множества уровня:
Ло>1 = {1, 2,..., 6}, Ло>8 = {2, 3, 4, 5, 6},
Л0,б={3, 4, 5, 6), Лол = {4, 5, 6),
Ло в = {5, 6), Л1>0 = {6}
и представить нечеткое множество А в виде
А =0,1 <1, 2, 3, 4, 5, 6) U 0,3 {2, 3, 4, 5, 6}U0,5{3, 4, 5, 6}U
U 0,7 {4, 5, 6} U 0,8 {5, 6}(J46}.
Смысл произведений типа аЛм поясняется выше.
В книге [5] разложение по множествам уровня
используется для обобщения различных понятий тео-
рии обычных множеств на нечеткие множества.
30
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
1.1.4. Нечеткие топологические пространства. По-
явление нового понятия нечеткого множества стиму-
лировало рассмотрение так называемых нечетких то-
пологических пространств (н. т. п.), элементы топологий
которых суть нечеткие множества. Имеется уже до-
вольно значительное число работ на эту тему (см., на-
пример, работы [9—17], из которых видно, что н. т. п.
обладают многими своеобразными свойствами, которых
нет в обычных топологических пространствах. Тео-
рия н. т. п. в ее настоящем виде представляет интерес
лишь с чисто математической стороны, поскольку пока
еще нет примеров использования ее аппарата для ре-
шения конкретных задач.
Одной из интересных особенностей н. т. п. является
то, что понятие точки в них не является столь тривиаль-
ным, как в обычных топологических пространствах.
Обычное множество всегда можно представить в виде
объединения составляющих его одноточечных мно-
жеств. В случае же нечеткого множества подобные
одноточечные множества, вообще говоря, являются
нечеткими и требуют особого определения. В некотором
смысле роль «нечетких точек» в н. т. п. могут играть
вводимые ниже элементарные нечеткие множества.
Понятие точки в н. т. п. обсуждается и в работе
К. Уонга [13].
В этом разделе излагаются лишь некоторые сведе-
ния из теории н. т. п., с тем чтобы дать читателю пред-
ставление об этом интересном направлении развития
теории нечетких множеств.
Определение 1.1.10. Семейство Т нечетких
множеств в универсальном множестве X называется
нечеткой топологией, если
1.	Х£Т, 0£Т.
2.	U Ау (< Т любого семейства {Ау} нечетких
у
множеств в X такого, что {Лу} С Т.
3-	П Ау £ Т для любого конечного семейства {Ау}
у
нечетких множеств в X такого, что {Ау} сТ.
Множество X с введенной в нем нечеткой тополо-
* гией Т называется нечетким топологическим простран-
ством (н. т. п.) (обозначение {X, Т)). Элементы семей-
1.1]
НЕЧЕТКИЕ МНОЖЕСТВА
31
ства Т называются открытыми нечеткими множе-
ствами. Нечеткое множество, являющееся дополнением
в X (см. определение в п. 1.1.2) к открытому нечеткому
множеству, называется замкнутым.
Приведенное определение топологии аналогично
обычному определению, отметим лишь, что операции
объединения и пересечения нечетких множеств пони-
маются здесь в соответствии с определениями 1.1.3 и 1.1.4,
принятыми в п. 1.1.2 данной книги.
> Замыканием А нечеткого множества А в н. т. п.
(л, Т) назовем «наименьшее» замкнутое нечеткое мно-
жество, содержащее А. Пусть {Вл} — семейство всех
замкнутых нечетких множеств таких, что А С Вл, т. е.
Рл (я) Ив (ж) ПРИ любом х £ X, тогда А = Q Ва или
а	а
{х1(ж) = Ы(х„ (х), х£Х.
а. ®
Ясно, что для любого нечеткого множества А его
замыкание А замкнуто.
Свойства операции замыкания.
1.	А С А.
2.	Если В замкнуто, то В = В.
Эти два свойства с очевидностью следуют из при*
веденных выше определений.
3.	Аг CZ А^ АС А%.
Доказательство. По определению
[X, (ж) = inf |ЛВ (х),	(ж) = inf (ж),
1 веВ1
В< = {5||хв(ж)>Ид<(ж) Уж 6*}, f = l, 2.
Далее, С А => рД1 (ж)	(ж), поэтому В2 С Вх и,
следовательно,	(®) Уж£Х, т. е.
4.	J1U^a = AU А-	______
Доказательство, а) Покажем, что
C^U^a- Допустим противное, т. е. что найдется
££Х, для которого

32
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
т. е.
inf р.л (f) > max {inf р.Б (5), inf^(f)},
В	Bi	в2
B. = (B|^(x)>filf(a:) VxCX), i = l, 2,
В = (Я I («) > max {(1Л1 (ж),	(«)}}.
Тогда найдутся В' £ Вх и Вп £ В2 такие, что для
любого В£В выполняются Ил (я) Ид/(я) и Р*л(я)?>
Отсюда следует, что найдется такое В(* В,
что при любом В £ В выполнено невозможное неравенство
б) Покажем, что -dxLMa ^iU^2- Допустим про-
тивное, т. е. что найдется х£Х, для которого
Отсюда заключаем, что найдется В такое, что для
любого В^Вг (или В^В2) выполняется р-д (ж) > р.5 (х).
Но В £В, и потому последнее неравенство невозможно.
Из а) и б) заключаем, что yl1U^2 = ^iU^2-
Элементарные нечеткие множества. Эле-
ментарным нечетким множеством Ех (для фиксиро-
ванного х £ X) назовем пересечение всех замкнутых
нечетких множеств ВЛ таких, что р.Б (х) > 0. Рассмот-
рим некоторые свойства элементарных нечетких множеств.
1 • Р'л’д. (*^1)	С Ех.
Доказательство. По определению для любого
х£Х выполнено равенство
^(®) = 1пГНв(^)» в = {5|^(®)>0}-
В
Далее,
И- (*i) =inf 1*в (ж1) > 0 => 1*в (ж1) > ° VB 6 В,
В
т. е. (В | р5 (ях) > 0} С В и, следовательно, для любого
х £ X выполняется неравенство (х) <	(я), что и
означает EXi с Ех.
2. Любое элементарное множество Ех замкнуто как
пересечение замкнутых нечетких множеств,
1.1]
НЕЧЕТКИЕ МНОЖЕСТВА
33
Последовательности нечетких мно-
жеств. Пусть {Ла) — последовательность нечетких
множеств в н. т. п. Рассмотрим совокупность всевоз-
можных подпоследовательностей {4а)3 этой последова-
тельности, каждая из которых получена выбрасыванием
из {Ла} некоторого конечного числа членов. Пусть
lMap — замыкание объединения всех членов под-
последовательности {Ла}р. Нечеткое множество Во =
= назовем пределом последовательности (Ла).
3
/Компактность. Система {Ла} нечетких множеств
в н. т. п. (X, Т) называется покрытием нечеткого
множества А, если ЛсиЛа или
цл(я)< supper) Ух£Х.
Нечеткое множество называется компактным, если
из любого открытого покрытия этого множества можно
выделить его конечное подпокрытие.
Для компактных н. т. п. справедливо утверждение,
аналогичное соответствующему утверждению для обыч-
ных топологических пространств.
Теорема 1.1.1 [10]. Для того чтобы н. т. п.
было компактным, необходимо и достаточно, чтобы
оно удовлетворяло условию', каждая центрированная
система его замкнутых нечетких множеств имеет
непустое пересечение.
Теорема 1.1.2. Если н. т. п. компактно, то
любая последовательность его нечетких подмножеств
имеет непустой предел.
Этот факт легко следует из определения предела и
теоремы 1.1.1.
Теорема 1.1.3. В компактном н. т. п. любое эле-
ментарное нечетное множество Ех непусто (т. е.
0 для любого х£Х).
Доказательство. Система замкнутых нечетких
множеств (В* |	(х) > 0} является центрированной
для любого х£Х. Следовательно, в силу компактности
н. т. п. она имеет непустое пересечение (теорема 1.1.1), т. е.
Vx£X.
a
3 С. А. Орловский
34
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
Назовем н. т. п. отделимым, если для любых х^Х
и у£Х найдется такое замкнутое нечеткое множество
В, что
а) М*)>° и б) Ре(У) = °-
Теорема 1.1.4. В отделимом н. т. п. любое эле-
ментарное нечеткое множество либо пусто, либо
обладает свойством:
{*>0 при х' = х,
п
=0 в противном случае.
Этот факт с очевидностью следует из определений
отделимости и элементарного нечеткого множества.
Теорема 1.1.5. Если В — замкнутое нечеткое
подмножество отделимого н. т. п., то для любого
непустого Ех выполнено одно из условий: ЕхсВ или
Exf]B=0.
Доказательство. Пусть ЕХ(£В, т. е. (я)>
>	(х). При этом не может быть (х) > 0, так как
в этом случае В являлось бы членом семейства замкну-
тых нечетких множеств, пересечением которых является
Ех, неравенство рЕ (х)	(х) было бы невозможно.
Отсюда в силу отделимости н. т. п. и теоремы 1.1.4
получаем ЕХ("\В = 0.
К. Чанг [10] ввел следующее определение окрест-
ности нечеткого множества в н. т. п.
Определение 1.1.11. Нечеткое множество U
в н. т. п. (X, Т) называется окрестностью нечеткого
множества А, если существует такое открытое нечет-
кое множество А, что ЛсЛсС/.
Теорема 1.1.6 [10]. Нечеткое множество А
открыто тогда и только тогда, когда оно является
окрестностью любого своего нечеткого подмножества.
Пусть А и В — два нечетких множества н. т. п.
(X, Т), и пусть A ZD В. Тогда В называется внутрен-
ним подмножеством А, если А есть окрестность В.
Объединение всех внутренних подмножеств нечеткого
множества А называется внутренностью А и обозна-
чается Л °.
Теорема 1.1.7 [10]. Пусть А — множество
в н. т. п. (X, Т). Тогда нечеткое множество А° открыто
НЕЧЕТКИЕ МНОЖЕСТВА
35
и есть наибольшее открытое подмножество множе-
ства А. Нечеткое множество А открыто тогда и только
тогда, когда А=А°.
Доказательство. Поскольку А° — внут-
реннее нечеткое подмножество Л, то по определению
найдется такое открытое множество А, что А ° Q А с Л.
Но А С Л °, и, следовательно, Л—Л °. Поэтому Л ° —
наибольшее открытое подмножество множества Л.
Если Л открыто, то Л с Л°, поскольку в этом случае
Л — внутреннее открытое подмножество Л. Отсюда
Л Л °. Обратное утверждение очевидно. Теорема до-
казана.
К. Уонг [13] ввел определение нечеткой точки и
исследовал с его помощью локальные свойства н. т. п.
Нечеткой точкой р в множестве X он назвал нечеткое
множество с функцией принадлежности вида
( у при Ж=:яго,
(ж)	| о ПрИ х
где О <С У <С 1 • Элемент xQ g X называется носителем
нечеткой точки р.
Пусть р — нечеткая точка в X. Тогда говорят [13],
что р принадлежит нечеткому множеству Л (р £ Л), если
(х) Рл (х) Для любого х£ X.
Теорема 1.1.8 [13]. Если А = иЛ., г^е I — про-
извольное множество индексов, то р(< А тогда и только
тогда, когда найдется индекс iQI такой, что р£А..
Доказательство. 1. Ясно, что если p£Ai, то
р£Л.
2. Обратно, пусть р £ Л и пусть х$ — носитель не-
четкой точки р. Тогда (х0) = впр (я0).
♦ б-?
Возможны два случая:
а)	либо 3 i £ I, для которого выполнено
Нл^ (*^о)------Р'л (жо)>
б)	либо	Для любого iQI.
3*
36
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
В случае а) имеем	т. е. утверждение тео-
ремы. В случае б) из того, что р£А> получаем
(^о) < Р’л (®o)i — SUP V-A{ (жо)>
и, следовательно, найдется iQQI, для которого
M®o)<IV (xol
т. е. р£А{0. Теорема доказана.
Опираясь на введенное определение нечеткой точки,
К. Уонг [13] предлагает следующее понятие сходи-
мости в н. т. п. Пусть ря, п=1, 2, . . ., — последователь-
ность нечетких точек в н. т. п. (X, Т) с носителями
х„, п==1, 2 . . . Пусть р — нечеткая точка с носителем
х=£хп для всех п п0, где п0 — некоторое натуральное
число. Тогда говорят, что рп сходится к р, или рп -> р,
если для любого открытого множества А такого, что
р £ А, найдется натуральное число ш такое, что
рп £ А при всех п ш.
С помощью введенных определений К. Уонг [13]
исследовал такие свойства н. т. п., как наличие счетной
базы, сепарабельность, локальная компактность и др.
Во многих работах, посвященных н. т. п., исследу-
ются также топологические свойства отображений,
изучаются произведения и. т. п. и другие их особен-
ности, которые зачастую не имеют прямых аналогов
в обычных топологических пространствах.
1.2. Нечеткие отношения
Как будет видно из последующих глав этой книги,
нечеткое отношение представляет собой важное мате-
матическое понятие, позволяющее формулировать и
анализировать математические модели реальных задач
принятия решений. Отношение на множестве альтер-
натив, объектов и т. п. в таких задачах выявляется
обычно путем консультаций с лицом, принимающим
решения (л. п. р.), или с экспертами, которые зачастую
не имеют вполне четкого суждения об этом отношении.
В подобных случаях нечеткое отношение может служить
удобной и более адекватной реальности'формой пред-
1.21
НЁЧЕТКИЁ ОТНОШЕНЙЯ
37
ставления исходной информации, чем обычное отно-
шение.
В данном разделе нечеткое отношение выступает
как чисто математический объект. Описываемые здесь
свойства и особенности нечетких отношений исполь-
зуются в дальнейшем при анализе различных моделей
принятия решений.
Мы начнем изложение с краткого ознакомления
со свойствами обычных отношений. Обычное отноше-
ние — более привычный математический объект, и нам
т^азалось, что свойства нечетких отношений (или, ско-
рее, свойства отражаемых ими реальных отношений)
легче понять, используя их аналогию со свойствами
обычных отношений.
Исходя из потребностей задач, анализируемых в по-
следующих главах, мы ограничимся рассмотрением
лишь бинарных обычных и нечетких отношений, т. е.
отношений, связывающих друг с другом два объекта,
элемента и т. п.' Поэтому всюду ниже бинарное от-
ношение мы называем просто отношением. Пе-
рейдем теперь к точному определению этого поня-
тия.
1.2.1. Свойства обычных отношений и операции над
ними. Отношением R на множестве X называется
подмножество декартова произведения X X X.
В соответствии с этим определением задать отноше-
ние на множестве X означает указать все пары элемен-
тов, х, у £ X такие, что х и у связаны отношением R.
Для обозначения того, что элементы х и у связаны от-
ношением R, мы будем пользоваться двумя эквивалент-
ными записями: xRy или (х, у) £ R.
Простым примером отношения может служить отно-
шение «неменьше» на интервале [0,1]. На приведенном
здесь рис. 1.2.1 это отношение (т. е. все пары х, у £
£[0,1], связанные этим отношением) представлено за-
штрихованной областью. Нетрудно видеть, что от-
ношению «равно» в этом примере соответствует по-
казанная на рис. 1.2.1 диагональ единичного квад-
рата.
Если множество X, на котором задано отношение /?,
конечно, то это отношение удобно описывать матри-
цей ||го-1|, представляющей собой характеристическую
38
НЁЧЕТКИЁ МНОЖЕСТВА
[ГЛ. 1
функцию множества R С X X X. Элементы этой матрицы
определяются следующим образом:
{1, если (жР	(или x.Rxj),
О в противном случае.
Отношение в конечном множестве X можно описать
и ориентированным графом, вершины которого соответ-
ствуют элементам множества X, а дуга от вершины
к вершине х}. проводится в том
и только в том случае, если
xfixj (или (х., Xj)f*R).
Пусть на одном и том же
множестве X заданы два отно-
шения А и В, т. е. в декар-
товом произведении X X X за-
даны два подмножества А и
В. Множества С = А U В и
D = А П В называются соответ-
ственно объединением и пере-
сечением отношений А и В.
Нетрудно показать, что если
с=К4	и 4 =
= ||а^||, В = ||&о|| — матрицы этих отношений в случае
конечного множества X, то
cfy = max{ao., btJ}, d{J —min {aiJt b^}.
Говорят, что отношение В включает в себя отноше-
ние А, если для соответствующих множеств AClXxX
и В С X X X выполнено 4 С В. Так, например, если
Л = «) и В — {^ — отношения на одном и том же
множестве чисел, то А С В. Заметим, что из Л СВ
и хАу всегда следует хВу.
Если А — отношение на множестве X, то обратным
к А отношением называется отношение А"1 на X такое,
что хА~гу тогда и только тогда, когда уАх. Если А —
= |||| и Л-1 = ||Q..J|| — матрицы этих отношений (в слу-
чае конечного множества X), то элементы этих матриц
связаны соотношением = т. е. матрица Л”1 полу-
чается путем транспонирования матрицы Л.
1.2]
НЕЧЕТКИЕ ОТНОШЕНИЯ
39
Дополнением отношения R на множестве X назы-
вается множество, являющееся дополнением множе-
ства R в декартовом произведении ХхХ. Матрица
дополнения отношения R получается из матрицы от-
ношения R путем замены нулевых элементов единич-
ными, а единичных — нулевыми.
Произведение (или композиция) АоВ отношений
А и В на множестве X определяется следующим обра-
зом: хАоВу тогда и только тогда, когда найдется эле-
мент z (< X, для которого выполнены отношения
rfAz и zBy. Элементы матриц отношений С~АоВ, А
и В связаны соотношением
С,7 = max min (а.к, bkj},
к
т. е. матрица отношения С равна максминному про-
изведению*) матриц отношений А и В.
Перейдем к описанию основных свойств отношений.
Отношение R на множестве X называется рефлек-
сивным, если (я, х) £ R (или xRx) для любого х £ X.
В матрице рефлексивного отношения все элементы
главной диагонали равны единице. Примером рефлек-
сивного отношения может служить отношение R Q>)
на множестве чисел;
Отношение R на X называется антирефлексивным,
если йз того, что xRy, следует х=£у. Все элементы глав-
ной диагонали матрицы такого отношения равны нулю.
Отношение R на X называется симметричным,
если из того, что xRy, следует yRx. Матрица симметрич-
ного отношения—симметричная, т. е.	Граф
такого отношения — неориентированный.
Отношение R на X называется антисимметричным,
если из того, что xRy и yRx, следует х~у. Матрица
такого отношения обладает следующим свойством:
если i^k, то uikaki—Q,
Отношение R на X называется [транзитивным,
если из того, что xRz и zRy, следует xRy. Используя
определение произведения отношений, нетрудно про-
*) В максминном произведении матриц вместо арифмети-
ческих операций сложения и умножения используются опера-
ции max и min соответственно.
40
НЕЧЕТКИЕ МНОЖЕСТВА
(ГЛ. 1
верить, что транзитивность отношения R эквивалентна
условию RoR С R или R2 С R.
Транзитивным замыканием R отношения R на X
называется отношение, полученное из R следующим
образом:
Я^йилаия8и ...и ...
Транзитивное замыкание можно неформально опреде-
лить как «наименьшее» транзитивное отношение нажХ,
включающее в себя отношение R. Математически строго
этот факт можно выразить так: для любого отношения
R его транзитивное замыкание равно пересечению
всех транзитивных отношений, содержащих R.
Можно показать (см., например, [18]), что R —
транзитивное отношение тогда и только тогда, когда
оно совпадает со своим транзитивным замыканием,
т. е. когда R = R.
Этим мы завершаем краткий обзор свойств обычных
отношений и переходим к нечетким отношениям. Чи-
тателю, желающему глубже разобраться в свойствах
обычных отношений и познакомиться с отношениями
различных видов, мы рекомендуем обратиться к книге
Ю. А. Шрейдера [18].
1.2.2. Определение нечеткого отношения. В данном
и”двух последующих разделах описываются лишь об-
щие свойства нечетких отношений и операции над ними.
При формулировке задач принятия решений в гл. 3
мы’будем опираться на нечеткие отношения предпочте-
ния. К этим отношениям применимы все вводимые здесь
операции, и они обладают описываемыми здесь свой-
ствами. Вместе с тем, составляя отдельный класс,
нечеткие отношения характеризуются рядом особен-
ностей, которые делают их удобным инструментом для
анализа задач принятия решений. Представляется
более целесообразным описывать характерные свой-
ства нечетких отношений предпочтения в ""контексте
задач принятия решений, и поэтому мы отложили их
рассмотрение до гл. 3.
Изложение мы будем вести примерно в том же
порядке, что и выше в разделе, посвященном обычным
отношениям, но несколько подробнее. При этом легче
сопоставлять друг с другом свойства тех и других от-
1.2]	НЕЧЕТКИЕ ОТНОШЕНИЯ	41
ношений и легче понять смысл операции над нечеткими
отношениями.
Если вспомнить, что обычное отношение определя-
ется как подмножество декартова произведения, то
становится ясным, что переход (обобщение) от обычного
отношения к нечеткому в принципе тот же, что и пере-
ход от обычного множества к нечеткому. Описание не-
четкого отношения должно включать в себя не только
указание всех пар элементов исходного множества,
связанных этим отношением, но и числа из интервала
[0, 1], отражающие степени выполнения нечеткого
отношения для этих пар. Для описания отношения
необходимо указывать и множество, на котором оно
определено. Само это множество может быть нечетким
(описано нечетко), причем в нечетком множестве может
быть определено и обычное отношение. В данном и
двух последующих разделах мы ограничимся рассмот-
рением нечетких отношений в обычном множестве.
Определение 1.2.1. Нечетким отношением
R на множестве X называется нечеткое подмножество
декартова произведения X X X, характеризующееся
функцией принадлежности ХхХ->[0, 1]*. Зна-
чение pR (х, у) этой функции понимается как субъек-
тивная мера или степень выполнения отношения xRy.
Обычное отношение можно рассматривать как ча-
стный случай нечеткого отношения, функция принад-
лежности которого принимает лишь значения 0 или 1.
Здесь представляется уместным привести пример,
иллюстрирующий принципиальное различие обычных
и нечетких отношений. Для этого лучше всего рассмот-
реть два «похожих» отношения на одном и том же
интервале [0, 1], причем одно из этих отношений обыч-
ное (четкое), а другое нечеткое. В качестве обычного
отношения возьмем отношение R (L>), а в качестве
нечеткого отношения возьмем отношение R (»
(«много больше»).
На приведенном здесь рис. 1.2.2, а пары (я, у) из
интервала [0, 1], связанные отношением R (т. е. я, у —
такие, что х у), образуют множество, показанное
*) Нечеткое отношение может описываться и функцией при-
надлежности более общего вида. По этому поводу см. п. 1.1.1.
42
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
штриховкой. Диагональ единичного квадрата является
границей этого множества: все пары (#, у), находя-
щиеся за этой диагональю (вне штрихованной области),
не связаны данным отношением.
В случае же отношения R ситуация сложнее
из-за того, что понятие «много больше» является нечет-
ким. Пытаясь построить соответствующее отношению
R подмножество единичного квадрата, мы обнаружим,
что в этом квадрате есть пары (х, у), которые мы опре-
деленно относим к подмножеству R (т. е. считаем пары
(#, у) связанными отношением R), и пары, которые мы
считаем определенно не входящими в это подмножество
(т. е. считаем не связанными отношением R). Так, на-
пример, можно считать, что #х=0,9 определенно много
больше ух—0,001, т. е. #х >> ух. С другой стороны,
ясно, что для я2=0,8 и y2~0,Q можно столь же опре-
деленно записать х2 у2. Однако подобной определен-
ности нет в отношении, скажем, пары #3=0,9, у3=0,2.
Вместе с тем, если сравнить пару #3=0,9, i/3=0,2 с парой
#4=0,9, у4=0,3, то можно сказать, что отношение (>>)
в большей степенй приложимо к паре (#3, у3), чем к паре
Таким образом, существует некоторая промежуточ-
ная область перехода от пар, для которых отношение
(>>) определенно выполняется, к парам, для которых это
отношение определенно не выполняется, причем парам
(#, у) из этой области можно приписать степени выпол-
нения данного отношения или субъективные оценки,
зависящие от смысла, вкладываемого в понятие «много
больше» в контексте той или иной ситуации.
1.2J
НЕЧЕТКИЕ ОТНОШЕНИЯ
43
На рис. 1.2.2, б отсутствие четкой границы множества
Д показано изменением плотности штриховки.
Если множество X, на котором задано нечеткое от-
ношение R, конечно, то функция принадлежности pR
этого отношения представляет собой квадратную мат-
рицу. По смыслу эта матрицы аналогична матрице
обычного отношения, но элементами ее могут быть
не только числа 0 или 1, но и произвольные числа из
интервала [0, 1]. Если элемент этой матрицы
равен а, то это означает, что степень выполнения от-
вюшения XiRxj равна а.
По аналогии с обычным отношением нечеткое от-
ношение можно описать и ориентированным графом
(нечетким графом), каждой дуге которого приписано
число из интервала [0, 1]. С некоторыми свойствами
нечетких графов можно ознакомиться по книге А. Коф-
мана [19].
Носителем нечеткого отношения R на множестве X
называется подмножество декартова произведения
X X X вида
suppfl = {(a;, у)|(ж, у)£ХхХ, ?R(x, у)>0).
Носитель нечеткого отношения можно понимать как
обычное отношение на множестве X, связывающее
все пары (х, у), для которых степень выполнения дан-
ного нечеткого отношения не равна нулю. В случае
конечного множества X матрицу носителя можно полу-
чить, заменив в матрице исходного нечеткого отноше-
ния единицами все ненулевые элементы.
При анализе задач принятия решений с нечеткими
отношениями удобно пользоваться множествами уровня
нечеткого отношения. Поскольку нечеткое отношение
определяется как нечеткое множество, то и его множе-
ства уровня определяются как в п. 1.1.2, т. е.
#« = {(*> У) |(«. у)£ХхХ, р.д(х, у)>а).
Нетрудно видеть, что множество уровня а нечеткого
отношения R на X представляет собой обычное отно-
шение на X, связывающее все пары (х, у), для которых
степень выполнения отношения R не меньше а. Матрицу
множества уровня а можно получить, заменив в мат-
44
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
рице нечеткого отношения R единицами все элементы,
не меньшие числа а, и нулями — все остальные эле-
менты.
Разложение нечеткого отношения по множествам
уровня определяется так же, как разложение нечет-
кого множества (п. 1.1.3).
Пример 1.2.1. Пусть матрица нечеткого отношения R
на множестве Х={х1, ж2, х3, х±} имеет вид
	*1	х2	Х3	*4
*1	1	0,5	0	0,2
	0,3	1	1	0,4
*3	0	0,6	0,5	0,1
*4	1	0,7	0,3	0
Тогда матрица обычного отношения, являющегося множеством
уровня 0,5 этого нечеткого отношения, выглядит так:
Х2 #з #4
Хг	1
х3	0
Д?4	1
1	о	о
1	1	о
1	1	0
1	0	0
1.2.3. Операции над нечеткими отношениями.
Перейдем теперь к рассмотрению операций над нечет-
кими отношениями. Некоторые из этих операций яв-
ляются аналогами соответствующих операций для обыч-
ных отношений, однако, как и в случае нечетких мно-
жеств, существуют операции, характерные лишь для
нечетких отношений. Заметим, что так же, как и
в случае нечетких множеств, операции объединения и
пересечения нечетких отношений (и операцию произ-
ведения) можно определить различными способами.
Пусть на множестве^ заданы два нечетких отноше-
ния А и В, т. е. в декартовом произведении ХхХ за-
даны два нечетких множества А и В. Нечеткие мно-
жества С=А (J В и D=A П В называются соответ-
ственно объединением и пересечением нечетких отноше-
ний А и В на множестве X. Если воспользоваться
1.2]
НЕЧЕТКИЕ ОТНОШЕНИЯ
45
первыми из приведенных в п. 1.1.2 определений объеди-
нения и пересечения нечетких множеств, то для функ-
ций принадлежности отношений С и D получаем
у) = тж{?А(х, у),	i/)},
М*. y) = min (Мж> М®» У)}-
Говорят, что нечеткое отношение В включает в себя
нечеткое отношение А, если для нечетких множеств А
и В выполнено Л С В. Для функций принадлежности
этйх множеств неравенство рЛ(х, у)^.^в(х, у) выпол-
няется при любых х, у £ X. В рассмотренном выше при-
мере отношений (^>) и (>>) нечеткое отношение R содер-
жится в отношении R, т. е. должно быть рд(ж, у)^
у) для любых чисел ж, у из интервала [0, 1],
Если R — нечеткое отношение на множестве X, то
нечеткое отношение R, характеризующееся функцией
принадлежности
iv (ж> y)=i —	у)> х> у£х>
называется дополнением в X отношения R. Дополне-
ние имеет смысл отрицания исходного отношения.
Например, для нечеткого отношения R=(лучше) его
дополнение R' (не лучше).
Обратное к R нечеткое отношение R"1 на множестве
X определяется следующим образом:
xR~ry о yRx ух, У$х,
или с помощью функций принадлежности:
Нй-|(я> = ж) Vx, у£Х-
Важное значение в прикладных задачах имеет про-
изведение или композиция нечетких отношений. В от-
личие от обычных отношений, произведение нечетких
отношений можно определить различными способами.
Здесь мы приведем некоторые из возможных определе-
ний этой операции.
Определение 1.2.2. Максминное произве-
дение АоВ нечетких отношений А и В на множестве X
характеризуется функцией принадлежности вида
Р-Л.в(х’ y) = supmm(fj.4(x, z), ps(z, у)).
46
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
В случае конечного множества X матрица нечет-
кого отношения АоВ равнамаксминномупроизведению
матриц отношений А и 5, т. е. получается с помощью
тех же операций, что и матрица произведения обычных
отношений (см. п. 1.2.1).
Определение 1.2.2а. Минмаксное произве-
дение нечетких отношений А и В на X определяется
функцией принадлежности вида
Р-Л.в(^> y) = infmax{|ia(x, z), ji£(z, у)}.
z С X
Отметим, что интересное сравнение свойств нечет-
ких автоматов, основанных на максминном и минмак-
сном произведениях нечетких отношений, имеется в ра-
боте У. Уи и К. Фу [20].
Определение 1.2.26. Максщ^лътипликатив-
ное произведение нечетких отношений А и В определя-
ется функцией принадлежности вида
Pj.B («» У) = sup {рх (ж, z) X HB(z, у)}.
z$X
Для сравнения друг с другом введенных операций
произведения приведем простой пример произведения
отношений А и В на конечном множестве X, состоящем
из двух элементов.
Пример 1.2.2.
А	В
0,2 0,64/0,5 0,7\
0,5 0,8/ \0,3 1 )
А.В
<0,3	0,6\	। Максминное
<0,3	0,5>	' произведение
'0,5	0,7\	Минимаксное
<0,5	0,7/	произведение
'0,18	0»6\	Максмультиплика-
.0,25	0,8/	тивное произведение
Проекции нечетких отношений [5].
Проекции нечеткого отношения играют важную роль
в определении решений задач, рассматриваемых в гл. 4
данной книги. Для того чтобы лучше пояснить смысл
этого понятия, вновь обратимся к рассмотрен-
ному выше примеру обычного отношения R Q»
(см. рис. 1.2.2, а).
1.2]
НЕЧЕТКИЕ ОТНОШЕНИЯ
47
Выберем некоторое число у и рассмотрим множество
всех чисел х из интервала [О, 1] таких, что х у
(рис. 1.2.3), т. е. множество вида R (у)={х \х^у}-
Для фиксированного у Е Ю, 1 ] множество^ R (у)
образовано всеми числами из
меньшими у. Объединение всех
таких множеств по всем у (<
£ [0, 1] называется первой
проекцией R{1} отношения R,
т\ е.
интервала [0, 1], не
«27 А

Rm = U R(y)>
У б [0,1]
Множество Я(1) обладает тем
свойством, что для каждого
его элемента х найдется та-
кой элемент у, что xRy (в дан-
ном примере х у).
Если аналогичным образом ввести
Рис. 1.2.3.
множества вида
R = {у I xRy}
и взять их объединение по всем х£Х, то получим
вторую проекцию Я<2) отношения В:
Bl2' = \JB(x).
Для любого элемента yQR{2) найдется такой элемент
х 6 X, что xRy (в данном примере х у).
48
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
В приведенном примере первая и вторая проекции
отношения R совпадают со всем интервалом [0, 1],
т. е. /?а) = Я(2)=[0? 1]. Более общий случай иллюстри-
руется рис. 1.2.4.
Легко проверить, что декартово произведение
Ди) ХЯ(2) представляет собой наименьшее прямоуголь-
ное множество, содержащее R.
Вернемся к нечетким отношениям. Пусть R — не-
четкое отношение на множестве X с функцией принад-
лежности (ж, у). Для произвольного у £ X нечет-
кое множество R (у) представляет собой нечеткое мно-
жество элементов х множества X, связанных с выбран-
ным у отношением R. Функция принадлежности этого
множества имеет вид (х, у), где у — фиксированный
элемент множества X.
Например, для нечеткого отношения R= (близко к),
заданного на числовой оси, множество R (у) можно
понимать как нечеткое множество чисел, близких к вы-
бранному числу у.
Объединение нечетких множеств R (у) по всем
у £ X называется первой проекцией 7?(1) нечеткого
отношения R.
Согласно определению (первому) операции объеди-
нения нечетких множеств функция принадлежности ржп
имеет вид
Нв(.)(^) = 8ир|1д(ж) у), х£Х.
Вторая проекция R(2) нечеткого отношения R опре-
деляется аналогичным образом:
Fb(3>(J/) = suPHb(®. */)> у£х-
.г £Х
Если R — Я(1) X R™ — декартово произведение пер-
вой и второй проекций нечеткого отношения Я, то R С
С Й. Этот факт следует из определения функции при-
надлежности декартова произведения нечетких мно-
жеств (п. 1.1.2):
р-я (ж» У) = min {su₽ Ив (ж> у')’ SUP Ив (ж'. у)}-
[1.^2]
НЕЧЕТКИЕ ОТНОШЕНИЯ
49
Пример 1.2.3. Пусть матрица нечеткого отношения R
на множестве Х—{х1, х2, х3, х±} имеет вид
	*1	х3		*4
*1	0,3	0,2	0,1	0,6
х2	0	0,5	0,4	0,1
	0,5	0,4	0,6	0,2
*4	0,3	0,7	0,5	ОД
ч Тогда функции принадлежности первой и второй проекций этого
'отношения таковы:
X	*1		Х3	*4
Рй(1) (*)	0,6	0,5	0,6	0,7
Рд(2) (*)	0,5	0,7	0,6	0,6
1.2.4. Свойства нечетких отношений.
Рефлексивность. Нечеткое отношение R
па множестве X называется рефлексивным, если для
любого х £ X выполнено равенство
РтА ж) = 1.
В случае конечного множества X главная диагональ
матрицы рефлексивного нечеткого отношения R со-
стоит целиком из единиц. Примером рефлексивного
нечеткого отношения может служить отношение «при-
мерно равны» в множестве чисел.
Антирефлексивность. Функция при-
надлежности антирефлексивного нечеткого отношения
обладает свойством
х) = 0
при любом х £ X. Антирефлексивно, например, отно-
шение «много больше» в множестве чисел. Ясно, что
дополнение рефлексивного отношения антирефлексивно.
Симметричность. Нечеткое отношение R
на множестве X называется симметричным, если для
любых х, у £ X выполнено равенство
. М*’ у)=р-в(У’ х).
Матрица симметричного нечеткого отношения, задан-
ного в конечном множестве, симметричная. Пример
4 С. А. Орловский
50
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
симметричного нечеткого отношения — отношение
«сильно различаться по величине».
Антисимметричность. Функция при-
надлежности антисимметричного нечеткого отношения
обладает следующим свойством:
у)>°=>рд(у> «)=о.
Это свойство можно описать и следующими двумя экви-
валентными способами:
Рд (®» у) х рд (у, х) = 0	ух, у е X,
!/)> Рв(?6 *)} = 0 ух, у£Х.
Антисимметричным, например, является нечеткое отно-
шение «много больше».
Заметим, что не всякое нерефлексивное (несимме-
тричное) отношение является антирефлексивным (анти-
симметричным).
Транзитивность. Нечеткое отношение R на мно-
жестве X называется транзитивным, если
Из этого определения видно, что свойство транзи-
тивности нечеткого отношения зависит от способа опре-
деления произведения нечетких отношений. Если обо-
значить через Rj, R* и максминное, минмаксное
и максмультипликативное произведения отношения R
само на себя (см. п. 1.2.3), то нетрудно убедиться в том,
что С Rl С Действительно, при любых х, у, z £ X
выполняются неравенства
max (цв(а;, z), ^(z, у)} >min {y.R(x, z), pR(z, у)) >
•	z)XpB(z, у),
из которых и вытекают соответствующие включения.
Если к слову транзитивность приписывать назва-
ние соответствующей операции произведения нечетких
отношений, то получаем: (минмаксная транзитив-
ность R) => (максминная транзитивность R) => (ма-
ксмультипликативная транзитивность R). Иными сло-
вами, нечеткое отношение, обладающее свойством мин-
максной транзитивности, обладает транзитивностью и
двух других типов, а отношение, обладающее максмуль-
1.2]
Н Е ЧЕТКИЕ ОТНОШЕН И Я
51
типликативной транзитивностью, может, вообще го-
воря, и не быть транзитивным в двух других смыслах.
Для обычного отношения, т. е. в случае, когда функ-
ция pR принимает лишь значения 0 и 1, максминная и
максмультипликативная транзитивности эквивалентны
обычной транзитивности отношения.
Всюду ниже под транзитивностью нечеткого отно-
шения мы будем понимать максминную транзитивность,
т. е. считать, что при любых х, у £ X функция при-
надлежности транзитивного нечеткого отношения R
на множестве X удовлетворяет неравенству
у) > sup min {|ХЯ(х, z), PR(Z, у)}.
Транзитивным, например, является рассматривав-
шееся выше нечеткое отношение /?(>>).
В качестве упражнения можно проверить транзитив-
ность нечеткого отношения с матрицей вида
0,2	1	0,4	0,4’
0	0,6	0,3	0
0	1	0,3	0
>0,1	1	1	ОД
Транзитивное замыкание R нечет-
кого отношения R определяется по аналогии с обыч-
ными отношениями:

Вводя транзитивное замыкание, необходимо, как и
выше, указать способ определения операции произ-
ведения печетких отношений.
Нетрудно проверить, что транзитивное замыкание
представляет собой транзитивное нечеткое отношение
и что транзитивное нечеткоеу отношение совпадает со
своим транзитивным замыканием.
Вычисление транзитивного замыкания нечеткого
отношения —- довольно утомительное дело, даже если
множество X состоит из небольшого числа элементов.
Примеры таких вычислений можно найти в книге
А. Кофмана [19].
4*
52
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
1.3. Отображения нечетких множеств
1.3.1. Принцип обобщения. Во многих задачах
принятия решений возникает необходимость расши-
рить область определения X заданного отображения
или отношения, включив в нее наряду с элементами
множества X произвольные нечеткие подмножества
этого множества.
Пусть, например, на множестве управлений U за-
дано отображение /: U -* У, описывающее функцио-
нирование управляемой системы. Образ v=f (и) управ-
ления и £ U есть реакция данной системы на выбор
этого управления. Если выбранное управление описано
нечетко, например, в форме нечеткого подмножества
р. (и) множества управлений U, то для нахождения
реакции системы на такое управление необходимо опре-
делить образ р> (и) при отображении /. Иными словами,
необходимо расширить область определения этого ото-
бражения на класс всех нечетких подмножеств мно-
жества U,
Как будет видно из дальнейшего, аналогичная про-
блема расширения области определения нечеткого от-
ношения возникает в анализе общей задачи нечеткого
математического программирования.
Способ расширения области определения отображе-
ний на класс нечетких множеств и называется ниже
принципом обобщения. Важное значение принципа
обобщения еще и в том, что он позволяет обобщить опе-
рации, введенные для нечетких множеств типа 1, на
нечеткие множества типа 2, 3 и т. д. (см. определение
в п. 1.1.1).
Л. А. Заде [5] предложил следующий принцип обоб-
щения, в основе которого лежит определение образа
нечеткого множества при обычном (четко описанном)
отображении. Пусть ср: X Y — заданное отображе-
ние, и пусть А — некоторое нечеткое подмножество
множества X с функцией принадлежности (х).
В соответствии с принципом обобщения Л. А. Заде
образ А при отображении ср определяется как нечеткое
подмножество множества У, представляющее собой
совокупность пар вида
(У, Ив (у)) = (? (ж)> Pj (я)), ® е х,
1.3]
ОТОБРАЖЕНИЯ НЕЧЕТКИХ МНОЖЕСТВ
53
где	У -> [0, 1] — функция принадлежности образа.
Нетрудно понять, что функцию принадлежности
можно записать в виде
Mi/) = sup рл(ж), y£Y, (1.3.1)
хе ср”1 (у)
где множество ср“х (у) для любого фиксированного
у £ Y имеет вид
\	<?(х) = у},
т. е. представляет собой множество всех элементов
х £ X, образом каждого из которых при отображении
ср является элемент у. В работе [5] демонстрируются
разнообразные примеры использования принципа обоб-
щения в форме (1.3.1).
Применим теперь принцип обобщения в форме
(1.3.1) для расширения области определения нечеткого
отображения. Необходимость в рассмотрении нечетких
отображений может возникать, например, при анализе
задач принятия решений, в которых результат выбора
конкретного элемента из множества альтернатив изве-
стен нечетко, т. е., например, описан нечетким множе-
ством в универсальном множестве исходов. В задаче
управления этому соответствует случай, когда нечетко
описано функционирование управляемой системы.
Нечеткое отображение можно описать как отобра-
жение, при котором элементу х £ X ставится в соот-
ветствие не конкретный элемент множества У, а, во-
обще говоря, нечеткое подмножество множества У.
Описывается нечеткое отображение функцией вида
у. XxY [0, 1] так, что функция (я0, у) (при фик-
сированном х=х0) есть функция принадлежности нечет-
кого множества в У, представляющего собой нечеткий
образ элемента xQ при данном отображении.
Например, в случае управляемой системы нечеткое
множество (х0, у) можно понимать как нечеткое
описание реакции этой системы на воздействие (управ-
ление) х0.
Итак, пусть р : ХхУ-> [0, 1] — заданное нечет-
кое отображение, и пусть (х) — заданное нечеткое
множество в X. Если применить принцип обобщения
НЕЧЕТКИЕ МНОЖЕСТВА
(ГЛ. 1
в форме (1.3.1) для нахождения образа этого нечеткого
множества при отображении р , то получим совокуп-
ность пар вида
У), Рл(*)),	।
где р (х, у) при каждом фиксированном х 6 X (т. е.
в каждой такой паре) представляет собой нечеткое
подмножество множества Y. В результате получаем,
что образ нечеткого множества рл в данном случае
представляет собой весьма сложный объект: нечеткий
подкласс класса всех нечетких подмножеств множества
Y. Ясно, что использование подобных объектов в ана-
лизе реальных систем весьма затруднительно.
Имея это в виду, мы введем здесь принцип обобще-
ния в другой форме, положив в его основу определение
образа нечеткого множества при, вообще говоря, не-
четком отображении.
Определение 1.3.1. Образом В нечеткого мно-
жества А в X при нечетком отображении р?: X X Y
[0, 1] называется нечеткое множество с функцией
принадлежности вида
= sup min (х),	(х, у)}.	(1.3.2)
Заметим, что если понимать рл как нечеткое унар-
ное отношение на множестве X, то легко видеть, что
в основе этого определения образа лежит введенное
выше (п. 1.2.3) максминное произведение (композиция)
нечетких отношений рл и р .
Нетрудно проверить, что в частном случае, когда
р — обычное отображение вида <?: X-+Y (т. е. р?(х, у) —
= 1 при у — (х) и рт (х, у) — 0 для остальных пар х, у),
определение 1.3.1 дает
М?) = sup Рх(®).
что соответствует приведенному выше определению об-
раза при обычном отображении, лежащему в основе
принципа обобщения Л. А. Заде.
Во многих случаях заданное нечеткое отображение р
может зависеть от п переменных, т. е. иметь вид рф:
1.3 j
ОТОБРАЖЕНИЯ НЕЧЕТКИХ МНОЖЕСТВ
55
X X У —> [0,1 ], где X	... X Хп — декартово про-
изведение соответствующих множеств. Пусть в мно-
жестве X задано нечеткое подмножество В общем
случае функция принадлежности этого подмножества
имеет вид
(*i> • • •> *„) = min {И1 (хх), ..(*я (x„), v (хр ..хп)},
(1.3.3)
где р- (Z = l, .... и), и v — заданные нечеткие подмно-
жества соответствующих множеств X- (i — 1,. .п) и X.
Запись (1.3.3) означает, по сути дела, что множество
есть «совокупность» всех наборов xv .... хп таких, что
х. «принадлежит» нечеткому множеству (i = 1,..., п)
и (ягх, . . жя) «принадлежит» нечеткому множеству v.
Применяя в этом случае принцип обобщения в форме
(1.3.2), получим следующее выражение для функции
принадлежности образа нечеткого множества р.л:
(*/) = sup min {Pi (xr), .. .,	(x„),
(Л1> .. .	6-^
v(Xp ..хя), ^(Хр ..., хп, у)}.	(1.3.4)
Приведем пример применения принципа обобщения
в форме (1.3.4) для расширения области определения
арифметической операции сложения на класс «нечетких
чисел», т. е. на класс нечетких подмножеств числовой
оси.
Операция сложения в множестве чисел R1 представ-
ляет собой отображение ср: R1 X	<р(гх, г2) = г —
= гх4*г2. Пусть р.р р.2: .Я1->[0, 1] — два «нечетких
числа». Суммой р.в = р.14-р.а назовем образ пары (р^, |л2)
при отображении ср. G помощью равенства (1.3.4) полу-
чаем
Мг) = sup min^fo), 1*2(r3)}.	(1.3.5)
rt, r2£Rl
r^r2=r
В частности, если р.х и р.2 представляют собой интер-
валы [ах, и [а2, Ь2]» то из (1*3.5) получаем
[ар М + [а2, &2] = [«1 + «2, 61+ М-
56
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
В п. 3.3.2 подробно обсуждается обобщение на класс
нечетких множеств заданного нечеткого отношения пред-
почтения.
1.3.2. Прообраз нечеткого множества. Введем теперь
определение прообраза нечеткого множества при нечет-
ком отображении, а затем, используя принцип обобще-
ния (1.3.2), найдем явное выражение для его функции
принадлежности.
Определение 1.3.2 [21]. Прообразом А нечет-
кого множества В в Y при нечетком отображении р :
X X У->[0, 1] называется объединение всех нечетких
множеств, образы которых при этом отображении при-
надлежат (являются подмножествами) нечеткому мно-
жеству В.
Если образ нечеткого множества а при отображе-
нии р? обозначать как аор?, то в соответствии с опре-
делением 1.3.2 прообразом нечеткого множества В
является объединение всех множеств а, удовлетворяю-
щих условию
аоп С В
Г<р -
или, согласно принципу обобщения (1.3.2), условию
sup min {р.й (х), р. (х, у)Хрв(г/) V?/€y- (1-3.6)
х£Х
Явное выражение для функции принадлежности про-
образа определяется приведенной ниже теоремой 1.3.1.
Введем множества
N = {(x, г/)|(я, у)£Хх Y, у)>рв(у)},
Nx={y\y£Y, (х, y)£N},
Nv = {x\x£X> (х, y)£N},
Х0 = {х\х£Х, Nx=£0}.
Теорема 1.3.1. Во введенных выше обозначениях
нечеткое множество А (прообраз множества В) описы-
вается функцией принадлежности

inf рБ(у) при я£Х°,
1	при яг^Х\Х°.
1.3]	ОТОБРАЖЕНИЯ НЕЧЕТКИХ МНОЖЕСТВ	57
Доказательство 1. Покажем сначала, что не-
четкое множество А, определенное в утверждении тео-
ремы, удовлетворяет условию Ло^СВ, т. е. что нера-
венство (1.3.6) выполняется при любом y£Y.
а)	Пусть элемент у £ Y таков, что Ng=£ 0. Допустим,
что найдется элемент x^Ng такой, что
min{ inf	у))>нв(у)-	(I-3-?)
У ^x
Поскольку х £ Ng, то и у £ N%, и следовательно, не-
равенство
inf Му)>Му)
невозможно, т. е. невозможно неравенство (1.3.7).
б)	Для х и у таких, что Ng=£0 и x$*Ng, неравен-
ство (1.3.7) также невозможно, поскольку при этом
(я, у) N и, следовательно (см. определение множе-
ства N),
#ХМу)-
в)	Если у £ Y таково, что Ng = 0, то для любого
х £ X выполнено (х, y)^N, и вновь, как и в п. б),
неравенство (1.3.7) не выполняется ни при каком х £Х.
Таким образом, получаем, что
Мж> у)}<Му)
для всех пар (х, у)£Х X Y, откуда следует, что нера-
венство (1.3.6) выполняется при любом yf*Y.
2. Покажем, что А — объединение всех нечетких мно-
жеств а, удовлетворяющих неравенству (1.3.6). Пусть
Р — некоторое нечеткое множество в X такое, что Рс£Л.
Это означает, что найдется элемент х £ Х°, для которого
выполняется неравенство
[tp (х) > (г).	(1.3.8)
При этом из определения 1.3.2 следует, что множество
Nx^ 0 и что неравенство (1.3.8) можно записать в виде
p.p(f)>inf («/)•
58
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
Следовательно, при некотором выполнено
М*)>Му)-	(1.3.9)
Далее, поскольку у £ то (я, у) £ 2V, откуда
!\(*, »)>рв(у)-	(1.3.10)
Из (1.3.9) и (1.3.10) вытекает, что
min {цр (ж),	(ж, у)} >	$)
и, следовательно, неравенство
sup min (fip (ж), рт(ж, £)}<рл$)
невозможно, т. е. Ро^^В. Теорема доказана.
Нетрудно проверить, что если отображение — чет-
кое, т. е. |хт(ж, у) = 1 при У = <?(х) и ^(ж, у) = 0для
всех остальных пар ж, у £ X, где <р — отображение (обыч-
ное) X -> Y, то
МЖ) = Н? (?(*))	V«6X.
Введенное здесь определение прообраза при нечетком
отображении используется ниже в анализе задачи вы-
полнения нечетко определенной цели (п. 2.2.1).
1.4.	Соотношение двух подходов
к определению нечетких множеств и отношений
До сих пор мы опирались на определение нечеткого
множества как функции р.: Х->[0, 1]. Используя это
определение, мы ввели операции над нечеткими мно-
жествами и отношениями. В данном разделе мы обра-
тимся к другому определению нечеткого множества и
покажем, что это определение в определенном смысле
эквивалентно предыдущему.
1.4.1.	Нечеткие множества. Пусть X — некоторое
множество в обычном смысле, и пусть 2х — класс всех
обычных подмножеств X. Пусть Ф — класс функций
вида р: X -> [0, 1], т. е. класс всех нечетких подмно-
жеств X по определению 1.1.1. Наконец, обозначим Ф*
класс отображений [0, 1 ]-> 2х. Любой элемент этого
1.4]
СООТНОШЕНИЕ ДВУХ ОПРЕДЕЛЕНИЙ
59
класса ставит в соответствие любому числу а (ДО, 1]
некоторое подмножество множества X. Будем полагать,
кроме того, что любой элемент |** класса Ф* обладает
следующими свойствами:
а1> а2(И°> Н а1 > а2 => Р* (а1) С и* (а2)-
2.	j**(O) = X.
В данном разделе мы введем операции в классе Ф*,
соответствующие уже введенным выше операциям
в классе Ф, и покажем что эти классы изоморфны отно-
сительно этих операций. Фактически это будет означать,
что определения нечетких множеств как элементов
класса Ф и как элементов класса Ф* равноправны, т. е.
при формализации нечетких понятий в математических
моделях в принципе можно пользоваться любым из этих
определений.
Рассмотрим отображение /: Ф Ф* вида
I (р) = {Р* IР* е Ф*. Р*(а) = {* IS е X, Р (я) > «}> « € [0. 1]}
и покажем, что это отображение взаимно однозначно.
Действительно, однозначность прямого отображения оче-
видна и достаточно показать однозначность соответ-
ствующего обратного отображения, т. е. отображения
Л1: Ф* -> Ф вида
Z"1 (р*) = {р IР € ф> Z(p) = p‘).
Допустим противное, т. е. что найдутся такие р.х, р2 €
что и ьСГЦр*), |*2£Г1 ([**). Иными словами,
мы допустили, что I (p-J = I ([*2) — т- е- что множества
А* = {х | х £ X, (х)	а},
{х\х£Х, р2(я)>а)
эквивалентны при любом а £|0, 1].
Поскольку p.i=H=i*2> то существует такой, что
|*х (ж°) =^= р,2 (х°). Положим для определенности, что
l*i (я0) > р2 (я0), и обозначим (х1(ж°) = р1, р-2 (ж0) = р2, т. е.
Pi > ₽2* Отсюда получаем, что	т. е. мно-
жества ЛР», А%' не эквивалентны, что противоречит сде-
ланному выше допущению, и, следовательно, J — взаимно
однозначное отображение.
60
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ.11
Легко видеть, что отображение I каждой функции
принадлежности нечеткого множества (т. е. каждому
элементу класса Ф) ставит во взаимно однозначное со-
ответствие совокупность множеств уровня этого нечет-
кого множества (т. е. элемент класса Ф*). Далее для
каждой из введенных в Ф операций мы определим соот-
ветствующую операцию в Ф*, причем так, чтобы ото-
бражение 1 было изоморфизмом относительно каждой
такой пары операции.
ПуСТЬ |ЛХ,	И Рр р££Ф*, ПРИчем = и
p* = J(p2). Будем последовательно рассматривать введен-
ные ранее операции над нечеткими множествами и вво-
дить соответствующие им операции в классе Ф*.
1.	Отношение вложенности.
Hi С р2 Л (а) С (а) Va G [0, 1],
где рхСр2 означает, что (х) рь2 (я) Vx(<X. Доказа-
тельство этого факта не представляет труда и здесь не
приводится.
2.	Операция пересечения (по определению 1.1.4).
Пусть рьзСФ такова, что
р3 (х) = min {рх (ж), р2(ж)} Vx£X.
Введем р*: [0, 1]->2г следующим образом:
p;(«)=p»ni4(«) v«eio, и
Нетрудно показать, что
а)	т. е- удовлетворяет свойствам 1 и 2
в определении класса Ф*;
б)	Ь = 7(Нз).
3.	Операция пересечения (по определению 1.1.4а).
Пусть р3£Ф такова, что
Р-з (ж) = р-1 (a;)	(ж) Vx£X.
Введем р*: [0, 1]->2х вида
p;(a)= и МЖИ Va€[0, 1].
fee [0,1]
а)	Покажем, что р* (0) = X. Действительно, так как
р*, р^Ф*, то
и p;(wnp:(₽2)=tf(0)ni*:(0)=x.
1.41
СООТНОШЕНИЕ ДВУХ ОПРЕДЕЛЕНИЙ
61
б)	Покажем, что р£ (аг) С pj (а2) для любых 04, а2 £
£[0, 1],	Действительно, если а2 = 0, то из а)
и того, что р.*, р.* £ Ф*, следует р.* (aj С р-* (а2). Если
а2>0, то
№<)= U н(Р)П^(аМ / = 1,2.
₽6(0,1]
Тогда при любом |3 £ (0, 1J получаем
н:(Р)пр;(а1/₽)С|»:(?)пр:(аа/₽),
следовательно, и в этом случае	Таким
образом, мы показали, что р.*£Ф*. Покажем теперь, что
Нз = 7(Рз)> т. е. что
[x;(a) = {a:|a;tX, [л3(ж)>а)	V«€f°. !]•
Пусть х' £ (л* (а), т. е. х' £ U ;л* (,8j) ("] И* (₽2). Это озна-
0102^“
чает, что найдутся рр 02 € [0> 1], Р1Р2 a такие, что
т. е.
ж'€Р1(?1) или
х' € Р-2 (Рг) или (Л2 (ж') > р2.
Но тогда pi (ж') р2 (ж') > PjP2 > а, т. е. р3(ж')>а.
Обратно, пусть х' £ [х | х £ X, р.3 (х) а}, т. е.
р-з(я')^а. Покажем, что	Пусть р.1(я:') = ₽1 и
Н2(ж') = ₽2> так что Pi₽2>a- Но тогда я'Ен(Р1)> и
х СН2Ф2) и ₽1?2^а» следовательно, ^'бРз(а).
Таким образом, р* = 7(р.3).
4.	Операция объединения (по определению 1.1.3).
Пусть |л3СФ такова, что
р.3 (х) = max {р.х (х), р.2(х)} Ух£Х.
Введем р£ [0, 1] -> 2х вида р.* (a) = р.* (a) |J p.J (а). Не-
трудно показать, что
а) ^ЕФ* и б) р*з = /(р3).
5.	Операция объединения (по определению 1.1.3а).
Пусть р.3£ Ф такова, что
{т (х) = p,r (х)	Р-2 (я), если
Л
1	в противном случае.
62
НЕЧЕТКИЕ МНОЖЕСТВ
[ГЛ. 1
Введём рф [0, 1]->2х вида
и	v« е to, ij.
₽,. з2его, и
а)	Легко видеть, что р,*(О) = Х.
б)	Покажем, что р.* (04) CZ р.* (а2) для любых ар а26
£ [0, 1], ах>а2. Действительно, как нетрудно видеть,
i4(«2) = h;(«i)U( U 1Ш1Ш
т. е. р* (ах) С р* (а2). Таким образом, р*^Фч.
Покажем теперь, что р* = /(р3), т. е. что
Р-з (а) = {х I х € Х> Нз(а:)>а}	Va£[0> Ч-
Пусть х' ^pi*(a), т. е. найдутся р2 £ [0, 1], 8L р2 а
такие, что
*'€р!(₽1) или ц, (*')>₽!
и
или и2(И>₽2-
Отсюда, из определения р3 и того, что Pi~]-p2^a, сле"
дует, что р3 (xf) а.
Обратно, пусть р3 (#') а. Покажем, что х' £ р* (а):
Обозначим р^Дя') — рх и р2 (х') = р2. Тогда х' £ р* (Рх) и
х' £ р* (Р2) и, кроме того, Pi Р2 а> следовательно,
х' €р-з(а)- Таким образом, р* = /(р3).
6.	Дополнение множества. Пусть р3£ Ф такова, что
Рз (х) = 1 — рх (х) Ух £ X.
Введем р3: [О, 1]->2Хх* вида
p;(a) = X\ и ^(1-₽) VaE(0, и,
PG [0, а)
Н*з(0) = Х.
а)	Покажем, что р-3 (aj С р.3 (а2) для любых an a2g
£[0, 1], ах>а2. Действительно, если а2 = 0, то р3(ах)С
С р-* (а2) = X. Пусть а2 > 0, тогда
U п(1-Р) = ( и ^(l-pnu(ft и H(1-P)V
зе [о, а,)	\Ре[о,а2]	)	\ре[«2,«>1	/
1.4]
СООТНОШЕНИЕ ДВУХ ОПРЕДЕЛЕНИЙ
63
Отсюда и из определения ц3 следует, что С ц*(а2).
Таким образом, р*£Ф*.
б)	Покажем теперь, что — т. е. что
^(a) = {^|xGX,	VaG[0, 1].
Пусть а > 0 и х' G JJ-* (а), т. е.
*'6*\ и н(1-₽)-
Ре [о,«)
Это означает, что х' £ р.* (1 — Р) ни при каком р £ [0, а],
т. е. при любом Р£[0, а] выполнено
Pi (я'Х1— ₽ или ! —
Допустим, что 1 —	(х') а. Тогда найдется такое
Р' < а, что 1 — р4 (#') < р', а это невозможно. Следова-
тельно, 1 — pij (#') а, т. е. р.3 (х') а.
Обратно, пусть
xf	p-3(#)^a}> а^>0,
т. е. р.3(х')^а или (х')	1—а, но тогда при любом
р G [0, а) выполнено 14 (xf) < 1 — р, т. е.
*'G П Х\|4(1-Р)=Х\ и tf(l-P)=|x*3(a).
Зб[0, «)	Рб[в,«)
Если же а = 0 и х' £ {х I х £ X, [х3 (х) а} = X, то
Ж'е^(О)=х.
Таким образом, мы показали, что р.* = /(р.3).
1.4.2Ь Нечеткие отношения. Символом Фл будем
обозначать класс функций v: Хх^-*[0, 1], а симво-
лом Фд — класс отображений v*: [0, 1]->2ХхХ со свой-
ствами, аналогичными свойствам элементов введенного
выше класса Ф*.
Аналогично предыдущему введем взаимно однознач-
ное отображение I: Фд->Фя вида
/(v) = {v*|v*G®X, v*(a) =
= {(ar, J0|(a?, y)£XxX, v(x, y)>a), «£[0, 1]}.
Выше в п. 1.2.3 мы определили операцию компози-
ции нечетких отношений как операцию в классе Фд.
64
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
Введем теперь соответствующую операцию в классе Фя
и покажем, что I — изоморфизм относительно этих опе-
раций.
Итак, пусть vx, v2 £ Ф« и v*, v* € причем v* = I (vj,
v2 = I (v2). Пусть v3 (< Фд такова, что v3 (ж, у) =
= sup min {vx(ж, z), v2(z, у)} Vx, y£X. Для любого
отображения v*: [0, 1]->2ХхХ введем следующие обозна-
чения:
v^(a) = {x|a:GX, (ж, y)ev‘(a)}	V«6[0, 1],
*?(«)={УIг/6*. (*, г/)6Л«» Vaeto. 1].
Рассмотрим отображение [0, 1] -> 2ХхХ вида
>;(«)= A U («)Ху?,(₽»	Уа€(0, 1],
Рб[0, «)^6Х
vJ(0) = XxX.
Покажем, что Vg (ax) С v* (a2) для любых ax, ,a2 £[0, 1],
ax ctj. В случае = 0 этот факт достаточно очевиден.
Пусть а2 0. Тогда, как нетрудно видеть,
А U<|(P)X
Рб[О,«,)
*£(₽)=
= ( A U v’
\Рб[«2, «1)
'2 (?) j A v3 (“а)
и, следовательно, v3(ax) С v*(a2). Отсюда заключаем, что
Покажем, что v* = 7(v3), т. е. что
(а) = {(*- У) I (*, У) 6 X X X, v8 (х, у) > a} Va 6 [0, 1 ]•
В случае а = 0 этот факт с очевидностью следует из
определения v3 и v3. Пусть а>0, и пусть (ж', 2/z)6vs(a)»
т. е. для любого ₽ (^ [0, а) найдется при котором

z'Ev2>(P) ИЛИ V2(z,
Отсюда получаем, что при любом р £ [0, а)
sup min {vx (яг', z), v2(z, /)}>р,
z^X
а это означает, что у')^и<
1.4]
СООТНОШЕНИЕ ДВУХ ОПРЕДЕЛЕНИЙ
65
Обратно, пусть v3(rr',	т. е.
sup min z), v2(z,
Это означает, что для любого р (< [0, а) найдется z (< X,
при котором
z)J>p ИЛИ я'Е7*ИР),
*2(z, или у' €v8(P)-
Но тогда при любом р £ [0, а)
« /)€ U v*J(₽)x42(₽)
z£X
и, следовательно, (х', r/')£v*(a).
Таким образом, мы показали, что v* = 7(v3), а это и
означает изоморфность классов Фд и Фд относительно
введенных в них операций композиции.
Пользуясь этим изоморфизмом и определением свой-
ства транзитивности нечеткого отношения (т. е.
в классе Фд), можно следующим образом определить
свойство транзитивности в Фд: элемент у*£Фд назы-
вается транзитивным, если
П U (Р) X >:2 (Р) с v* (a) Va е [0, 1].
Рею, а)^ех
В заключение этого раздела выпишем пары соответ-
ствующих друг другу операций в классах Ф и Ф*, от-
носительно которых эти классы изоморфны при изо-
морфизме I.
КЛАСС Ф
КЛАСС Ф*
1.	Отношение вложенности
Pi (*) < Р«2 (*)	I р* (a)	p£(<z) V<zf[O, 1]
2.	Пересечение множеств
а)	Р-з (^) = min{p1 (ж), р2(я)}
б)	р3 (х) = Pj (х) р2 (х) 5
Р** (а) = Р'Т («) ПР-2 (а)
р£ (a)==U GOlWSO
5 С. А. Орловский
66
НЕЧЕТКИЕ МНОЖЕСТВА
[ГЛ. 1
3.	Объединение множеств
a) fis (х) = max {(11 (х), р.2 (х)}
б) =
m(x)=(ii(x) + (i2(x),
— -	т (х) < 1
1, т (х) > 1
Р-з (а) = («)1М (а)
^(«) = и
0,+02>«
4.	Дополнение множества
ц (х) == 1 — (1 (х)
р*(а)=Х\ U ^*(1—₽).
₽е[о,«)
аС(О, 1], р.*(0) = Х
5.	Композиция отношений
V»(®. у) =
= sup min {v] (х, z),	(z, у)}
v$(«)= П U*T1(₽)X
06(0,«)
Xvg(0). «>0. >?(0) = X
ГЛАВА 2
ЗАДАЧИ
МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
И ИГРЫ ПРИ НЕЧЕТКИХ
ИСХОДНЫХ УСЛОВИЯХ
2.1.	Введение
Во многих случаях задача принятия решений в об-
щем виде математически может быть описана множе-
ством допустимых выборов (альтернатив) и заданным
на этом множестве отношением предпочтения, которое
отражает интересы лица, принимающего решения
(л. п. р.). Как правило, это отношение бинарное, т. е.
позволяет сравнивать друг с другом лишь две альтер-
нативы, хотя возможны постановки задач и с тернар-
ными отношениями. Собственно задача принятия реше-
ний заключается при этом в выборе допустимой аль-
тернативы, которая лучше или не хуже всех остальных
альтернатив в смысле заданного отношения предпочте-
ния.
Бинарное отношение предпочтения на множестве
альтернатив может быть описано двумя способами:
в виде подмножества декартова произведения множества
альтернатив само на себя (т. е. как отношение в п. 1.2.1)
или в форме так называемой функции полезности.
Функция полезности обычно имеет вид отображения
множества альтернатив в числовую ось. Иными сло-
вами, каждой альтернативе эта функция ставит в соот-
ветствие число (оценку альтернативы), причем так,
что эквивалентным альтернативам соответствуют оди-
наковые числа (значения функции полезности), а из
каждых двух неэквивалентных альтернатив лучшей
приписывается большее число.
Следует отметить, что не всякое отношение пред-
почтения и не на всяком множестве альтернатив можно
описать функцией полезности. В некоторых случаях
отношение удается описать не одной, а лишь конечным
набором функций полезности, причем соответствую-
щие задачи принятия решений обычно называют много-
5*
68
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
критериальными. Вопросам описания отношений пред-
почтения функциями полезности посвящен специаль-
ный раздел прикладной математики — теория полез-
ности. Основные результаты этой теории достаточно
полно изложены, например, в книге П. Фиш-
борна [22].
Задачи принятия решений, в которых отношение
предпочтения описано в форме функции полезности,
называют задачами математического программирова-
ния. Рациональным решением в таких задачах явля-
ется выбор допустимой альтернативы, на которой
функция полезности принимает по возможности боль-
шее значение.
Нечеткость в постановке задачи математического
программирования может содержаться как в описании
множества альтернатив, так и в описании функции
полезности. В данной главе обсуждаются задачи, в ко-
торых нечетко описано множество альтернатив и
четко — функция полезности. Такие задачи мы назы-
ваем ниже задачами нечеткого математического про-
граммирования (н.м.п.). Анализ более общих задач
с нечетко описанной функцией полезности опирается
на аппарат нечетких отношений предпочтения, и мы
отложили их рассмотрение до гл. 3.
Анализируя задачи н.м.п. в данной главе, мы будем
опираться на два подхода к определению решения за-
дачи. По первому из этих подходов задача н.м.п. фор-
мулируется как задача выполнения нечетко определен-
ной цели, причем решением задачи считается пересече-
ние нечетких множеств цели и ограничений (допусти-
мых альтернатив). Работа Р. Веллмана и Л. Заде [23],
в которой был изложен этот подход, замечательна еще
й тем, что в ней была впервые сформулирована задача
принятия решений на языке нечетких множеств.
В ней же впервые анализировались многоэтапные (ди-
намические) задачи принятия решений при нечетких
исходных условиях методом динамического програм-
мирования. В данной книге этот подход достаточно под-
робно излагается в пп. 2.2.1 и 2.2.2. В п. 2.2.1 обсужда-
ется и некоторое обобщение этого подхода на задачи
управления системами, функционирование которых
описано нечетко.
2.21
НЕЧЕТКО ОПРЕДЕЛЕННАЯ ЦЕЛЬ
69
Интересным и практически важным представляется
применение подхода Веллмана—Заде к анализу и ре-
шению задач нечеткого линейного программирования.
Эти задачи впервые анализировались в работах
К. Негойты и сотр. [8, 24, 25], а также Г. Циммер-
манна и сотр. [26, 27]. Им посвящен § 2.3.
В другом излагаемом здесь подходе к задачам н.м.п.
предполагается, что решения должны выбираться
подобно тому, как это делается в задачах многокрите-
риальной оптимизации. При этом считается, что в ре-
шении исходной задачи должны присутствовать все те
и только те альтернативы (не сравнимые между собой
в рамках данной задачи), которые не доминируются
строго никакими другими альтернативами. При подоб-
ном понимании решения л.п.р. имеет возможность
в большей мере использовать свои субъективные пред-
ставления о реальной ситуации, которые не были
формализованы в математической постановке исход-
ной задачи. Подробнее этот подход излагается в § 2.4
данной главы.
Особый класс задач принятия решений составляют
так называемые игровые задачи, в которых результат
принятия решений определяется не только выборами
самого л.п.р., но и выборами его разумных партнеров.
Математическая формулировка подобной задачи опре-
деляется в первую очередь заложенным в ней принци-
пом принятия решений. Ниже в § 2.5 рассматриваются
постановки игровых задач при нечетких исходных ус-
ловиях, соответствующие двум упомянутым выше под-
ходам к решению задач н.м.п. Анализируются два ос-
новных теоретико-игровых принципа: принцип наилуч-
шего гарантированного результата с учетом информи-
рованности игроков и принцип равновесия Нэша.
2.2.	Задача достижения нечетко определенной цели
(подход Веллмана—Заде)
2.2.1.	Формулировка и определение решения за-
дачи. Основным в данном подходе к решению рас-
сматриваемой задачи является то, что цели принятия
решений и множество альтернатив рассматриваются
как равноправные нечеткие подмножества некоторого
70
МАТЕМАТИЧЕСКОЕ ПРОГРАММЙРОВАНИЕ
(ГЛ. 2
универсального множества альтернатив. Это позволяет
определить решение задачи в относительно простой
форме.
Пусть X — универсальное множество альтернатив,
т. е. универсальная совокупность всевозможных вы-
боров лица, принимающего решения (л. п.р.). Нечеткой
целью в X является нечеткое подмножество X, которое
мы будем обозначать G. Описывается нечеткая цель
функцией принадлежности : X -> [0, 1].
Допустим, например, что X — числовая ось. Тогда
нечеткой целью принятия решений может быть нечет-
кое множество типа «величина х должна быть примерно
равна 5» или «желательно, чтобы величина х была
значительно больше 10» и т. п. Будем полагать, что
присутствующие в подобных описаниях нечеткие поня-
тия вроде выделенных курсивом в предыдущих при-
мерах вполне точно описаны функциями принадлеж-
ности соответствующих нечетких множеств.
Чем больше степень принадлежности альтернативы
х нечеткому множеству цели pG, т. е. чем больше зна-
чение pG (х), тем больше степень достижения этой цели
при выборе альтернативы х в качестве решения. В этом
смысле нечетким описанием цели в рамках данного
подхода можно считать и функцию полезности в задаче
н.м.п., если нормировать к единице значения этой
функции (см., например, [25]).
Нечеткие ограничения или множества допустимых
альтернатив также описываются нечеткими подмноже-
ствами множества X. В приведенном выше примере
с Х=Я1 нечеткие ограничения могут иметь, например,
такой вид: «х должно быть не слишком большим», «х не
должно быть гораздо большим 30» и т. п. Как и прежде,
здесь полагается, что выделенные курсивом понятия
описаны функциями принадлежности соответствую-
щих нечетких множеств, которые мы будем обозна-
чать р-р.
Более общей является постановка задачи, в которой
нечеткие цели и ограничения представляют собой под-
множества различных универсальных множеств. Пусть,
как и выше, X — универсальное множество альтер-
натив, и пусть задано однозначное отображение
2.2]
НЕЧЕТКО ОПРЕДЕЛЕННАЯ ЦЕЛЬ
71
ср: X -> У, значения которого (элементы множества У)
можно понимать как реакции некоторой системы на
входные воздействия х£Х или как некоторые оценки
(эффекты) выборов соответствующих альтернатив.
Нечеткая цель при этом задается в виде нечеткого
подмножества универсального множества реакций
(оценок) У, т. е. в виде функции У -> [0, 1].
Задача при этом сводится к прежней постановке
(т. е. к случаю, когда цель — нечеткое подмножество
X) следующим приемом. Определим нечеткое множество
альтернатив обеспечивающих достижение заданной
цели pG. Это множество представляет собой прообраз
нечеткого множества pG при отображении ср, т. е. (см.
определение прообраза в § 1.3)
Ре (?(*))’
После этого исходная задача рассматривается как за-
дача достижения нечеткой цели при заданных нечет-
ких ограничениях.
Перейдем теперь к определению решения задачи
достижения нечеткой цели. Грубо говоря, решить за-
дачу означает достигнуть цели и удовлетворить огра-
ничениям, причем в данной нечеткой постановке сле-
дует говорить не просто о достижении цели, а о ее до-
стижении с той или иной степенью, причем следует
учитывать и степень выполнения ограничений. В под-
ходе Веллмана—Заде оба этих фактора учитываются
следующим образом. Пусть, например, некоторая аль-
тернатива х обеспечивает достижение цели (или соот-
ветствует цели) со степенью (х), удовлетворяет огра-
ничениям (или является допустимой) со степенью
(х). Тогда полагается, что степень принадлежности
этой альтернативы решению задачи равна минималь-
ному из этих чисел. Иными словами, альтернатива, до-
пустимая со степенью, например, 0,3, с той же сте-
пенью принадлежит нечеткому решению, несмотря на
то, что она обеспечивает достижение цели со степенью,
равной, например, 0,8.
Таким образом, нечетким решением задачи дости-
жения нечеткой цели называется пересечение нечетких
72
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
множеств цели и ограничений, т. е. функция принад-
лежности решений имеет вид
Их (x) = min (рв (х),	(х)).	(2.2.1)
При наличии нескольких целей и нескольких ограни-
чений нечеткое решение описывается функцией при-
надлежности
Ь (®) =	(ж)> • • •> Рс„ (®). РС1 (*)>• ^ст (*)}•
Если различные- цели и ограничения различаются по
важности и заданы соответствующие коэффициенты
относительной важности целей \ и ограничений Уу,
то функция принадлежности решения задачи опреде-
ляется выражением
= min (Х1Р.в| (х)..Хв|хСя (х), vltxCi (х),..., ^Ст (х)}.
В отмеченном выше случае, когда задано отображе-
ние ср множества альтернатив X в множество реакций
или оценок У, а нечеткая цель задана в множестве У,
нам понадобится и следующее эквивалентное приведен-
ному выше определение нечеткого решения.
Пусть G и С — нечеткие множества цели (в Y) и
ограничений (в X). Нечетким решением задачи дости-
жения цели G при ограничениях С называется макси-
мальное по отношению вложенности нечеткое множе-
ство JD, обладающее свойствами:
1. DQC (допустимость решения).
2. ср (D) С G (достижение нечеткой цели), где <р (D) —
образ D при отображении ср.
Пример 2.2.1. Рассмотрим очень простой пример, в ко-
тором X—{i, 2, . . ., 10}, а нечеткие цель G и два ограниче-
ния Ct и С2 заданы таблицей
X	1	2	3	4	5	6	7	8	9	10
1*0 (*)	0	0,1	0,4	0,8	1.0	0,7	0,4	0,2	0	0
Рх, (х)	0,3	0,6	0,9	1,0	0,8	0,7	0,5	0,3	0,2	0
V-ct (ж)	0,2	0,4	0,6	0,7	0,9	1,0	0,8	0,6	0,4	0,2
2.2]
НЕЧЕТКО ОПРЕДЕЛЕННАЯ ЦЕЛЬ
73
Тогда для решения D получаем
х i 23456789	10
pD(x) 0	0,1 0,4 0,7 0,8 0,7 0,4 0,2 0	0
Словами цель и ограничения можно выразить, например, так:
G=«x должен быть близким к 5»,
Су=^х должен быть близким к 4»,
С2—«х должен быть близким к 6».
Тогда решение
D = «x должен быть близким к 5».
Определенное таким образом решение можно рас-
сматривать как нечетко сформулированную инструк-
цию, исполнение которой обеспечивает достижение
нечетко поставленной цели. Нечеткость полученного
решения еть следствие нечеткости самой исходной
задачи. При таком представлении решения остается
неопределенность, связанная со способом исполнения
подобной нечеткой инструкции, т. е. с тем, какую аль-
тернативу выбрать. Различные способы разрешения
этой неопределенности предполагаются, например, в ра-
боте Л. Заде [28].
Один из наиболее распространенных в литературе
способов состоит в выборе альтернативы, имеющей
максимальную степень принадлежности нечеткому ре-
шению, т. е. альтернативы, реализующей
max (х) = max min ((х),	(я)).
х£Х	х£Х 1	}
Такие альтернативы называют максимизирующими
решениями. Отметим, что вопрос о выборе конкретных
альтернатив при решении задачи н.м.п. заслуживает
отдельного обсуждения, и мы вернемся к нему в § 2.4.
В заключение данного раздела мы обсудим приме-
нение подхода Веллмана—Заде к задачам н.м.п. с за-
данным нечетким отображением из множества альтер-
натив в множество реакций или оценок [21]. При этом
мы будем опираться на введенное в п. 1.1.6 определе-
ние прообраза нечеткого множества при нечетком
отображении.
74
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
Пусть X — универсальное множество альтернатив,
Y — универсальное множество реакций или оценок,
и пусть задано нечеткое отображение из X в У, описы-
ваемое функцией р : XxY -> [0, 1] (см. § 1.3). Каж-
дой альтернативе это отображение ставит в соответ-
ствие ее нечеткую оценку.
По аналогии с приведенным выше определением реше-
нием такой задачи достижения нечеткой цели G будем
считать максимальное по отношению вложенности нечет-
кое множество D, обладающее свойствами:
1. D С С (допустимость решения).
2. 2)ор (достижение нечеткой цели), где Dop?—
образ D при нечетком отображении р?.
Выше в § 1.3 максимальное по отношению вложен-
ности нечеткое множество D такое, что iiop^CG, было
определено как прообраз множества G при отображе-
нии р . Для того чтобы выписать функцию принадлеж-
ности множества D, введем множества (см. § 1.3)
N = {(я, у) | (х, у) 6 X X У, (х, у) >	(у)},
Мя={у\у£У, (x,y)£N}, Х°={х\х£Х, Nx^0}.
Во введенных обозначениях эта функция принадлеж-
ности имеет вид
inf р.д(у) при xQX°,
1	при
Далее, в соответствии с определением получаем, что
нечеткое решение рассматриваемой задачи имеет вид
}i2)(a:) = min{}iJ5(a:)) ре(х)},
т. е.
' min (я), inf ре(я)) при
}	(2.2.2)
?с(х)	при ж^Х\Х°.
Нетрудно проверить, что если рф — обычное (четкое) ото-
бражение, т. е.
{1 при у = ср (х),
О при у 7^= ср (х),
2.2]
НЕЧЕТКО ОПРЕДЕЛЕННАЯ ЦЕЛЬ
75
где <р — однозначное отображение X -> У, то решение
(2.2.2) принимает обычный вид (2.2.1). Действительно,
в этом случае (х) = (ср (я)) и, следовательно,
[1л(а:) = тт{|хв(а:), ^ (<?(*))}.
При необходимости выбора конкретной альтерна-
тивы в качестве решения задачи можно, например,
выбрать ту, которая с максимальной степенью при-
надлежит нечеткому решению т. е. альтернативу,
реализующую величину шах (ж). Однако, как уже
я» е х
отмечалось выше, такой способ выбора нельзя считать
достаточно обоснованным. Ниже в гл. 3 мы вернемся
к анализу этой задачи как частного случая более общей
задачи принятия решений при нечетком отношении
предпочтения и укажем другой способ выбора альтер-
натив, который представляется нам’более обоснованным.
2.2.2. Многоэтапные процессы принятия решений
при нечетких исходных условиях. В этом разделе мы
изложим постановку и анализ многоэтапной задачи
принятия решений, описанный Р. Веллманом и Л. Заде
в работе [23].
Рассмотрим задачу управления динамической си-
стемой. Пусть X — конечное множество возможных со-
стояний этой системы и U — конечное множество воз-
можных значений управляющего параметра. Состоя-
ния системы и значение управления в момент времени
t, t=0, 1, . . ., N—1, будем обозначать и ut соответ-
ственно. Функционирование системы, т. е. ее переходы
из состояния в состояние, описывается системой урав-
нений состояния
=	t = 0, 1....АГ-1.	(2.2.3)
Тип системы определяется типом заданного отобра-
жения /. Если / — однозначное отображение X X U -*
-> X, т. е. состояние системы в момент времени
^4-1 однозначно определяется ее состоянием и значе-
нием управления в момент t, то мы имеем дело с детер-
минированной системой. Если / — отображение X X СЛ-*
где — класс нечетких подмножеств множества
X, то мы имеем дело с системой, функционирование ко-
76
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
торой описано нечетко, т. е. нечетко описана реакция
системы на управление ut. Если же / — отображение
X X U -> Р, где Р ~ класс распределений вероят-
ности на множестве X, то система называется стоха-
стической.
Ниже мы рассматриваем лишь детерминированные
системы, т. е. системы, для которых отображение /
имеет вид XxU X. Нас будет интересовать задача
управления такой системой при нечетких исходных
условиях. Будем считать, что в любой момент времени
t значение управления ut должно подчиняться задан-
ному нечеткому ограничению Ct, которое описывается
нечетким подмножеством множества U с функцией
принадлежности (ut). Выше в п. 2.2.1 уже говори-
лось о возможных интерпретациях нечетких ограни-
чений.
Рассмотрим управление этой системой на интервале
времени от 0 до N—1. Пусть задана нечеткая цель уп-
равления в виде нечеткого подмножества Gn множества
X, представляющая собой нечеткое ограничение на
состояние системы xN в последний момент времени N.
Задача, таким образом, заключается в том, чтобы выб-
рать последовательность управлений u0,	. . ., un-i,
которая «удовлетворяет» нечетким ограничениям и
«обеспечивает» достижение нечеткой цели Gn. Началь-
ное состояние системы х0 полагаем заданным.
Заметим, что нечеткую цель Gn можно считать не-
четким подмножеством множества U X • • • X С7, поскольку
N
состояние Xn можно выразить в виде xn(x^ u0, . .
путем решения системы уравнений состояния (2.2.3) для
£ = 0, 1,. .., N — 1. После этого в соответствии с под-
ходом Беллмана—Заде нечеткое решение задачи можно
представить в виде
Нр (и0, ..., и^) = min {|ЛО (и0),...,	(и^), [iejv
т. е* в виде нечеткого подмножества множества U X • • •
Будем искать максимизирующее решение задачи,
Т. е. Последовательность управлений й0, ..., Яу-i, имею-
2.2]
НЕЧЕТКО ОПРЕДЕЛЕННАЯ ЦЕЛЬ
77
щую максимальную степень принадлежности нечеткому
решению Z), т. е.
р-Я (й0’ * ’ ’ ‘ Й^1) =
= max	Цс (^)}. (2.2.4)
«0,
Воспользуемся для этого обычной процедурой динамиче-
ского программирования. Запишем (2.2.4) в следующей
форме:
Ид (Яо,. . .,	J = max max min (fx0 (u0), ...
«0, ...» uN_2
• • •’ Jhr-iPGN(f(xN-i,	(2.2.5)
Имеет место следующее просто проверяемое равенство.
Пусть у — величина, не зависящая от u^-i, и g (u^-i) —
произвольная функция Тогда
max min {у, g (u^-i)} =min {у, maxg^-O}.
uN-l	UN—1
С помощью этого равенства запишем (2.2.5) в следую-
щей форме:
|ХЛ(ЙО, . .^_L)= max min Ь0(я0),..., l\v_2(^_2),
«0, ...,«V_2 I
max min (u^ ? (f w^))}!
UN—1	J
и введем обозначение
«ЛГ-1
Функция (^i) представляет собой функцию
принадлежности нечеткой цели для задачи управления
на интервале времени от 0 до N — 2, соответствующую
заданной цели Gn управления на интервале от 0 до
N — 1. Смысл этой функции можно пояснить следую-
щим образом. Допустим, что в результате выбора каких-
либо управлений и0, .... uN^ система перейдет из состоя-
ния х0 в состояние xN-ly определяемое системой урав-
нений (2.2.3). Тогда, как нетрудно понять, выбором
управления можно добиться максимальной степени
достижения заданной цели, равной (я^). Таким
78
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
образом, Д^-i) есть максимальная/степень достиже-
ния цели Gn в случае, когда на N — 2 шаге система
оказалась в состоянии xn-i-
Далее, поскольку	ия-ъ), то ясно, что
величина х(/(^_2, ^v-2)) есть максимальная степень
достижения цели Gn в случае, когда система оказалась
(после N — 2 шагов управления) в состоянии #у_2 и на
N — 1 шаге было выбрано управление un_2- Нетрудно
понять, что выбор Un-2 на N — 1 шаге следует сделать
так, чтобы обеспечить (с учетом нечеткого ограничения
на Un-2) по возможности большее значение величины
min(!^-2(Uy-2). ^.//(^-2, ^-2))}.
Введем соответствующее обозначение
(^-2) = т'П 0^-2 CW >4-1 V (^-2> “*-2))}-
«У-2
Величина (лу 2) — максимальная степень достиже-
ния заданной цели Gn в случае, когда на N — 2 шаге
система оказалась в состоянии яу_2.
Продолжая эти рассуждения для t = N — 3, . .О,
получим систему рекуррентных соотношений
fS-, = maX min	._,+1 (XA'-V+1)},
=	(2.2.6)
С помощью этих соотношений мы получаем последова-
тельно (начиная с v = l) функции йя-i (xy-i), ^n-2X
X (^л-2), • • •, йо(жо)’ а затем по заданному начальному
состоянию и пользуясь уравнениями состояния системы
(2.2.3), вычисляем в обратном порядке максимизирую-
щие решения
ЙО (*0)> Й1	(/ (*0> Йо)), Й2 = Я2 (/ (/ (*0> ®о)> ®1))> • • •
Для иллюстрации описанной процедуры решения приведем
пример из работы [23]. Рассмотрим трехэтапный процесс управ-
ления, т. е. примем, что #=2. В любой момент времени управля-
емая система может находиться в одном из трех состояний ах,
аа, <3g, а параметр управления uf может принимать лишь два
2.2]
НЕЧЕТКО ОПРЕДЕЛЕННАЯ ЦЕЛЬ
79
значения ах и а2. Нечеткая цель управления (ограничение на х2)
описывается таблицей
х2	о2 а8
0,3	1	0,8
Нечеткие ограничения на управления в моменты t—0 is t=l
имеют вид
“о / = 0: 		«1	«2	«1 	t f =			«1	а2
ft) («в)	0.7	1,0	(tlj)	1,0	0,8
Переходы системы иэ состояния в состояние описываются матри-
цей (отображение /):
Применим теперь рекуррентные соотношения (2.2.6) для ре-
шения задачи. Для t—1 получаем
	Oj	°2	оз
ft?, (®1)	0,6	0,8	0,6
а соответствующая максимизирующая функция имеет вид
*1	01	о2	Оз
»1 («1)	«2	«1	а2
80
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
Далее, на следующем шаге /=0 получаем
	<51	<32	
P'Gq (хо)	0,8	0,6	0,6
а соответствующая максимизирующая функция имеет вид
хо	<31	<32	<з3
Йо (*о)	«2	или а2	(Х-J или а2
Допустим теперь, что начальное состояние системы (т. е. состоя-
ние при t=0) #o=ai- Тогда соответствующее максимизирующее
решение исходной задачи имеет вид й0=а2, »i=ai, причем это
решение обеспечивает выполнение цели G2 со степенью 0,8.
В работе [23] описанный подход применяется также к ана-
лизу задач управления стохастической системой с фиксирован-
ным конечным моментом времени N и детерминированной систе-
мой с заданным множеством допустимых конечных состояний
системы.
Подход Веллмана—Заде опирается на возмож-
ность симметричного описания множеств цели и огра-
ничений в виде нечетких подмножеств одного и того же
универсального множества альтернатив. Это позволяет
определить решение задачи в довольно ^простой форме,
как описано выше. Однако в дальнейшем мы увидим,
что не всякую задачу принятия решений удается сфор-
мулировать в виде задачи достижения нечетко опреде-
ленной цели, описанной в форме нечеткого множества,
в связи с чем ниже рассматриваются и другие подходы
и постановки задач принятия решений.
В последующих разделах этой главы мы рассмотрим
задачи, которые можно классифицировать как задачи
нечеткого математического программирования. Некото-
рые из этих задач удается рассмотреть в рамках подхода
Веллмана—Заде, другие — свести к задачам в более
широкой постановке, рассматриваемым в гл. 4 этой
книги.
2.3]
КЛАССИФИКАЦИЯ ЗАДАЧ
81
Прежде чем перейти к рассмотрению различных
задач нечеткого математического программирования,
мы приведем в следующем разделе их краткую класси-
фикацию.
2.3. Классификация задач
нечеткого математического программирования
Стандартная задача математического программи-
рования формулируется обычно как задача максими-
зации (или минимизации) заданной функции на задан-
ном множестве допустимых альтернатив, которое опи-
сывается системой равенств или неравенств. Например,
/(ж)-» max,	j =
где X — заданное множество альтернатив, /: X -> R1 и <р:
X -> R1 — заданные функции.
При моделировании в такой форме реальных задач
принятия решений в распоряжении исследователя-ма-
тематика могут оказаться лишь нечеткие описания
функций / и ср, параметров, от которых зависят эти
функции, да и самого множества X. Подобное нечеткое
описание ситуации принятия решений может, например,
отражать недостаточность информации об этой ситуа-
ции или служить формой приближенного описания си-
туации, достаточного для решения поставленной задачи.
Более того, в некоторых случаях точно описанное мно-
жество ограничений (допустимых альтернатив) может
оказаться лишь приближением реальности в том смысле,
что в реальной задаче, лежащей в основе математиче-
ской модели, альтернативы вне множества ограничений
могут быть не допустимыми, а лишь в той или иной сте-
пени менее желательными для лица, принимающего
решения, чем альтернативы внутри этого множества.
В качестве примера можно рассмотреть ситуацию,
в которой множество допустимых альтернатив пред-
ставляет собой совокупность всевозможных способов
распределения ресурсов, которые л. п. р. собирается
вложить в данную операцию. В этом случае, по-види-
мому, нецелесообразно заранее вводить четкую гра-
ницу множества допустимых альтернатив (распределе-
ний), поскольку может случиться так, что распределе-
6 С. А. Орловский
82
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
ния ресурсов, лежащие за этой границей {т. е. вне огра-
ничений), дадут эффект, «перевешивающий» меньшую
желательность этих распределений для л.п.р. Таким
образом, нечеткое описание может оказаться более
адекватным реальности, чем в определенном смысле
произвольно принятое четкое описание.
Формы нечеткого описания исходной информации
в задачах принятия решений могут быть различными;
отсюда и различия в математических формулировках
соответствующих задач нечеткого математического про-
граммирования (н. м. п.).
Перечислим некоторые из таких постановок.
Задача I. «Максимизация» заданной обычной
функции f : X -> R1 на заданном нечетком множестве
допустимых альтернатив : X -> [0, 1].
Для решения подобной задачи К. Негойта и Д. Ра-
леску [25] предлагают рассматривать функцию / (х) =
= / (x)l sup f(x) (нормировка к 1) как функцию при-
suppi^
надлежности нечеткого множества цели л.п.р. Значе-
ние / (ж) этой функции рассматривается как степень
выполнения цели при выборе альтернативы х£Х. Это
позволяет непосредственно применить к решению этой
задачи подход Веллмана-—Заде. Рациональным
в книге [25] предлагается считать выбор альтернативы,
имеющей максимальную степень принадлежности не-
четкому решению, т. е. альтернативу, реализующую
величину
max min (ж), / (#)j.
Нетрудно проверить, что задачу отыскания такой аль-
тернативы можно сформулировать следующим образом:
k-^max,	х£Х.
Ниже предлагается иной подход к решению этой
задачи. Он излагается в § 2.4.
Задача II. Нечеткий вариант стандартной
задачи математического программирования.
Пусть определена следующая задача математиче-
ского программирования:
/(#)-> шах, ср(х)	0, х£Х.
2.31
КЛАССИФИКАЦИЯ ЗАДАЧ
яз
Нечеткий вариант этой задачи получается, если «смяг-
чить» ограничения, т. е. допустить возможность их
нарушения с той или иной степенью. Кроме того,
вместо максимизации функции f (х) можно стремиться
к достижению некоторого заданного значения этой
функции, причем различным отклонениям значения
/ (х) от этой величины приписывать различные сте-
пени допустимости (например, чем больше отклонение,
тем меньше степень его допустимости). Задачу при этом
можно записать так:
/(x)>z0, СР (х) < 0, х£Х,
где волнистая линия свидетельствует о нечеткости соот-
ветствующих неравенств.
Один из возможных подходов к формализации по-
добных нечетко сформулированных задач анализиру-
ется в работах [26, 27]. Заключается он в следующем.
Пусть Zq — заданная величина функции цели f (ж),
достижение которой считается достаточным для выпол-
нения цели принятия решений, и пусть имеются (за-
даны л. п. р.) два пороговых уровня а и Ь такие, что
неравенства / (х) < z0—а и ср (х) > Ъ означают сильное
нарушение соответствующих неравенств / (х) z0 и
ср (х)	0. Можно следующим образом ввести нечеткие
множества цели и ограничений:
(.г) =
0,	если	/(#)<^z0 —	а,
р.(я, а), если z0 —а </(#)< z0,
1,	если	/ (х)	z0,
0,	если	ср (х) Ь,
v (.г, 6), если	0 < <р (х) <	Ь,
1, если ср (х)	0,
где р. и v — некоторые функции X [0, 1], описы-
вающие степени выполнения соответствующих’ нера-
венств с точки зрения л.п.р.
В результате исходная задача оказывается сформу-
лированной в форме задачи выполнения нечетко опреде-
ленной цели, к которой применим подход Веллмана—
Заде.
84
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
В работах [26, 27] описанным здесь способом анали-
зируются задачи нечеткого линейного программирова-
ния, причем работа [27] интересна тем, что в ней фор-
мулируется соответствующая двойственная задача и
с ее помощью проводится анализ чувствительности ре-
шения исходной задачи по отношению к вариациям
пороговых уровней и параметров линейных функций
р. (х, а) и v (х, Ь).
Задача III. Нечетко описана «максимизируемая»
функция, т. е. задано отображение р, iXxT?1-»
-> [0, 1], где X — универсальное множество альтерна-
тив, R1 — числовая ось.
В этом случае функция р (я0, г) при каждом фикси-
рованном представляет собой нечеткое описание
оценки результата выбора альтернативы ж0 (нечеткую
оценку альтернативы х$) или нечетко известную реак-
цию управляемой системы на управление xQ. Задано
также нечеткое множество допустимых альтернатив
[0, 1].
Как будет видно из дальнейшего (гл. 3), к такой по-
становке сводится широкий класс задач н. м. п. Проб-
лема рационального выбора альтернатив при данном спо-
собе описания нечеткой исходной информации обсуж-
дается в § 4.3.
Задача IV. Заданы обычная максимизи руемая
функция f: X-+R1 и система ограничений вида (я)<^
i = l, ..., т, причем параметры в описаниях
функций ср. (х) заданы нечетко в форме нечетких мно-
жеств.
Например, в линейном случае (X — Rn) функции ср^ (х)
имеют вид
п
S i — l,.. ,т,
j=*
а каждый параметр и Ъ. описаны соответствующими
нечеткими множествами	Об интерпрета-
ции такого способа задания параметров говорится ниже
в § 4.3.
Один из подходов к решению задач нечеткого линей-
ного программирования описан в работе С. Негойты и
М. Сулариа [24]. Ниже в § 4.3 предлагаем другой более
2.41
НЕЧЕТКОЕ МНОЖЕСТВО ОГРАНИЧЕНИЙ
85
общий подход, который заключается в сведении этой
задачи к постановке задачи типа I, описанной в дан-
ном разделе.
3 а д а ч а V. Нечетко описаны как параметры функ-
ций, определяющих ограничения задачи, так и самой мак-
симизируемой функции.
Ниже в § 2.6 предлагается способ сведения этой
задачи к задаче III, описанной в данном разделе.
В последующих разделах данной книги мы рассмо-
трим перечисленные выше постановки задач н. м. п. и
предложим способы их решения.
2.4. Задача математического программирования
при нечетком множестве ограничений
Пусть X — универсальное множество альтернатив,
и пусть ср — функция X -> R1, значениями которой
оцениваются результаты выбора альтернатив из мно-
жества X. В множестве X задано нечеткое подмножество
: X -> [0, 1], которое мы называем нечетким множе-
ством допустимых альтернатив. Задача заключается
в «максимизации» в некотором смысле функции ср
на нечетком множестве р.6,.
Последнее общее предложение можно понимать
двояко. Под «максимизацией» можно понимать выбор
нечеткого подмножества множества (нечеткого ре-
шения), которому соответствует в некотором смысле
наилучшее нечеткое значение функции ср. Разумеется,
представление решения в форме нечеткого множества
имеет смысл, когда такая форма содержательно понятна
лицу, принимающему решения (т. е. когда л. п. р. поня-
тен язык нечеткого описания). Как бы то ни было,
подобное нечеткое описание столь же информативно,
как и нечеткое описание исходного множества допусти-
мых альтернатив.
Если же л. п. р. не приемлет нечеткого описания
решения задачи, то под «максимизацией» функции ср
следует понимать рациональный выбор конкретной
альтернативы или множества альтернатив. Рациональ-
ность при этом понимается в том смысле, что при выборе
конкретной альтернативы л. п. р. должно исходить из
86
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
необходимости компромисса между желанием получить
по возможности большее значение функции ср и жела-
нием выбрать по возможности более допустимую
альтернативу (т. е. желанием получить по возможности
большее значение функции принадлежности нечеткого
множества допустимых альтернатив).
В данном разделе рассматриваются два подхода
к решению этой задачи н. м. п. Один из них опирается
на разложение нечеткого множества ограничении по
множествам уровня, а в другом явно учитывается не-
обходимость указанного выше компромисса. Оба этих
подхода описаны в работе [30].
2.4.1. Решение 1, опирающееся на множества уровня
нечеткого множества ограничений. Рассматриваемый
здесь подход, по сути дела, состоит в том, что исходная
задача н.м.п. представляется в виде совокупности
обычных задач максимизации функции ср на всевозмож-
ных множествах уровня множества допустимых аль-
тернатив. Если альтернатива х^Х есть решение за-
дачи ср (х)'-* max на множестве уровня X, то, грубо
говоря, мы считаем, что число X есть степень принад-
лежности альтернативы я0 нечеткому множеству реше-
ний исходной задачи н. м. п. Перебрав таким образом
всевозможные значения X, мы получим функцию при-
надлежности нечеткого решения.
Перейдем к более подробному описанию и анализу
этого подхода. Будем обозначать множество уровня
X нечеткого множества допустимых альтернатив
Таким образом (см. п. 1.1.3),
Cx = {x\xQX, |\,(ж)>Х}.
Для любого Х^О такого, что^Сх^0, введем мно-
жество
N (X) = (х I х £ X, ср (х) — sup <р(х')},
представляющее собой множество решений обычной
задачи максимизации функции ср на множестве тех
альтернатив, которые со степенью не менее X считаются
допустимыми в исходной задаче н. м. п.
Для построения функции принадлежности нечет-
кого множества решений необходимо каждой альтер-
2.4] НЕЧЕТКОЕ МНОЖЕСТВО ОГРАНИЧЕНИЙ
87
нативе х £ X приписать степень принадлежности этому
множеству. Сделаем это следующим образом. Степенью
принадлежности альтернативы х0 нечеткому множеству
решений будем считать максимальное (точнее, верхнюю
грань) из чисел X, для которых (X). Более строго
это выражается следующим определением.
Определение 2.4.1. Решением 1 задачи н. м. п.
называется нечеткое подмножество множества р.с, опи-
сываемое функцией принадлежности вида
рх(я:) = sup X.
Следующее предложение дает возможность выразить
решение 1 в более простой форме.
Предложение 2.4.1. Если х £ suppр1 (х), то
Доказательство, а) Если х g supp р1 (х) и р1^)
> Рс (я), то sup X > р.с (х) и, следовательно, найдется
X: х£N (X)
такое число X, что	р*с (^) и #(<2V(X). Но по опреде-
лению 2.4.1	и поэтому Рс(я)^Х, т. е. неравен-
ство \>рс(х) невозможно.
б) Если х (< supp р1 (х) и р1 (х) < рс (х) или
sup X <р, (z) = v,
х: лелг(Х)
(2.4.1)
то для любого числа X такого, что xf< 2V(X), выполнено
я£С\сСх. Кроме того, x$2V(X), так как в противном
случае из (2.4.1) следовало бы невозможное неравенство
v<S. Отсюда
ср (х) < sup ср (ж') sup ср (#') = <р (ж).
л'бС'Х
Это противоречие и завершает доказательство предложе-
ния 2.4.1.
*) Напомним, что множество supp р (х) определяется так:
supp р (х) == {х | х С X, р (х) > 0).
88
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
Из предложения 2.4.1 и определения 2.4.1 нетрудно
заключить, что решение 1 представимо в виде
[	(х) при xd (J N (X),
р,1 (ж) = <	х>0
I 0 в остальных случаях,
и, таким образом, supp рА (х) = U N (X).
Х>0
Будем говорить, что решение 1 существует, если
рЛ(я)=^0 на множестве X. Из определения 2.4.1 полу-
чаем, что решение 1 рассматриваемой задачи н. м. п.
существует тогда и только тогда, когда найдется такое
число X > 0, что N (X) =/= 0.
Нечеткому решению 1 соответствует нечеткое «мак-
симальное» значение р.?(г) функции <?(#), представляю-
щее собой образ нечеткого множества р.1^) при отобра-
жении ср. Согласно определению образа (§1.3) получаем
р. (r)= sup р.1 (#):=: sup SUp X, (2.4.2)
где ср"1 (г) = {х | х £ X, ср(я) = г).
Если в задаче н.м.п. решения 1 не существует, то
можно воспользоваться е-оптимальным нечетким реше-
нием, которое для заданного е^>0 можно определить
следующим образом:
рЛ(я)= sup X,
X:	X)
N (в, X) = {х | х £ X, <р (х) sup ср (х') — в).
Соответствующее нечеткое значение функции ср описы-
вается функцией принадлежности рЛ(я)= sup рЛ(я).
т *е<р-1(г)
Предел р.® при е -> 0 можно понимать как верхнюю
нечеткую грань функции ср на нечетком множестве р^.
Заметим, что понятие е-оптимального решения полезно
не только в случае, когда р1 (ж) = О при любом х£Х,
но и в тех случаях, когда N (X) = 0 при некоторых X
из интервала [0, 1].
Далее устанавливаются некоторые свойства решения 1,
которые позволяют дать этому решению наглядную интер-
2.4]
НЕЧЕТКОЕ МНОЖЕСТВО ОГРАНИЧЕНИЙ
89
претацию. Мы сформулируем эти свойства в форме сле-
дующих трех предложений.
Предложение 2.4.2.
r0 е supp у. => и N (к) П ср-1 (г0)	0.	(2.4.3)
Иными словами, для любого г0 такого, что [Ар(го)>0,
найдется такая альтернатива х^Х, что <р(£) = г0
и xf<N(k) при некотором Х>0.
Доказательство. Согласно определению р? (см.
(2.4.2)) и множества supp р из левой части (2.4.3) полу-
чаем
sup sup к > О,
*е(*о) ^eJV(X)
т. е. найдется такая альтернатива х' £ <р-1 (г0), для кото-
рой
sup К > О,
х: л?'е^(Х)
а это в свою очередь означает, что найдется такое число
X > 0, что х' С N (X). Отсюда получаем х' С ср-1 (r0) р N (X),
что и доказывает (2.4.3).
Предложение 2.4.3.
r06suppy => sup {?(*)= sup ^(ж).
^е?-1 (г0)	хе?-1 (г0)
Доказательство. Поскольку из определения 2.4.1
следует, что р1 (х) р^ (х) при любом х£Х, то
sup р1^)^ sup р0(я).	(2.4.4)
Допустим, что при некотором r0£suppp? в (2.4.4)
выполнено строгое неравенство. Тогда для некоторого
неравенство
(2.4.5)
выполняется при любом х £ <р 1 (г0).
Далее, поскольку r0^supppT, то согласно предложе-
нию 2.4.2 найдутся такие х' и Х^>0, что х' £
6 ?-1 (г0) A N (X). Из того, что х' £ N (X) и X > 0, следует
согласно определению 2.4.1, что р1 (#') = р^ (#') X и,
90
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
следовательно, из (2.4.5) получаем, что
т. е. xq£(\.
Из того, что x'£N(k) и	т- е- —
получаем
? (И = sup ср (ж) = Го = ср (х0),
*б^х
так как xQ £ ср-1 (г0). Отсюда xQf<N(\) и, согласно опре-
делению 2.4.1, р1 (я0) = рс (я0), что противоречит (2.4.5).
Это противоречие завершает доказательство предложе-
ния 2.4.3.
Предложение 2.4.4. Функция рт(г) монотонно
убывает на множестве supp рф.
Доказательство. Достаточно показать, что pT(rJ
О<р(г2) Для любых гр r^supp^ таких, что г1'^>г2.
Допустим противное, т. е. что для некоторых гх>г2
из множества supp р? выполнено неравенство р (гх) >
>^(7*2). Тогда, согласно предложению 2.4.3, получаем
sup р-с(®)> sup ^(ж),
(п)	(г2)
т. е. найдется жх^ср г(гх) такой, что неравенство
Но (^1) > Н<7 (ж)	(2.4.6)
выполняется при любом х£Х.
Далее, поскольку r2 f< supp р , то из предложения 2.4.2
заключаем, что найдутся такие х2 £	и Х^>0,
что я2€^(к), т. е. г2 —ср(ж2)= sup ср(ж).
^е^х
Кроме того, отсюда и из (2.4.6) заключаем, что
следовательно,
Г2 =F= ? («2) = sup ?(*)>? (Xi) = Гр
или г2 гх, а это противоречит допущению о том, что
> г2. Полученное противоречие завершает доказа-
тельство предложения 2.4.4.
Обсудим теперь несколько подробнее свойства ре-
шения 1, которое установлено в предложении 2.4.4.
Нетрудно видеть, что функция р (г) определена таким
образом, что ее значение для данного r^R1 есть макси-
2.41
НЕЧЕТКОЕ МНОЖЕСТВО ОГРАНИЧЕНИЙ
91
мальная степень принадлежности множеству (х)
альтернативы х, на которой функция ср (х) принимает
значение г. Согласно предложению 2.4.4 функция
(г) монотонно убывает на множестве supp р.?. Это
означает, в частности, что в множестве X нет такой аль-
тернативы, для которой одновременно выполнялись бы
неравенства (х) >	(г) > 0 и ср (х) > г, т. е. нет
такого элемента х£Х, который имел бы большую, чем
(г), степень принадлежности множеству и давал
бы большее, чем г, значение максимизируемой
функции.
Если л. п. р. предпочитает выбрать в качестве реше-
ния конкретную альтернативу х(*Х, то его выбор дол-
жен опираться не только на степень принадлежности
этой альтернативы нечеткому множеству (ж), но и на
соответствующее значение функции ср (х). Как следует
из предложения 2.4.4, чем больше значение г0, тем
меньше степень принадлежности рс (х) той альтерна-
тивы, которая дает значение ср (ж)=г0. Поэтому л. п. р.
должно сначала обратиться к нечеткому «максималь-
ному» значению р.? (г) функции ср (х) и выбрать пару
(г0, Р’у (го))» которая согласуется с его желанием полу-
чить по возможности большее значение г0 и в то же
время по возможности большую степень принадлеж-
ности выбранного г0 множеству р^ (г). После выбора
такой пары имеет смысл выбрать такую альтернативу
я0£ср (г0), которая имеет наибольшую степень при-
надлежности множеству (х) (или альтернативу, ко-
торая в некотором смысле близка к х0).
Изложенный здесь подход к определению решения
задачи н. м. п. неудобен в двух отношениях. Во-первых,
в полученном решении недостаточно явно учитывается
необходимость при выборе альтернатив компромисса
между значениями максимизируемдй функции и зна-
чениями степени допустимости альтернатив. Во-вто-
рых, это решение неудобно для вычислений. В следую-
щем разделе вводится другое определение решения,
которое не обладает указанными недостатками и в то же
время эквивалентно решению 1 в том смысле, что дает
92
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
то же самое нечеткое значение максимизируемой функ-
ции ср.
2.4.2. Решение 2 и эквивалентность решении обоих
типов. В излагаемом здесь подходе к определению ре-
шения задачи н. м. п. явно с самого начала учитывается
то, что при выбре альтернатив л. п. р. должно руковод-
ствоваться желанием получить возможно большие зна-
чения как максимизируемой функции, так и функции
принадлежности нечеткого множества допустимых аль-
тернатив. Для этого в определение решения включа-
ются лишь те альтернативы, которые в задачах много-
критериальной оптимизации называются эффективными
или максимальными по Парето.
Альтернатива xQ £ X называется эффективной при
двух функциях ср (я:) и (х), если для любой другой
альтернативы xr £ X из неравенств (х')^>ср (х0) и (ж')
>	(ж0) следуют равенства <р (х')=<р (ж0) и р.6, (х') = рс (ж0).
Иными словами, если xQ — эффективная альтернатива
для функций <р(х), рс(х) на множестве X, то выбором
любой другой альтернативы из X невозможно увели-
чить (по сравнению с ср(я0) или ^(Яо)) значение одной
функции, не уменьшив при этом значения другой.
В задачах принятия решений с несколькими крите-
риями множество эффективных альтернатив предлага-
ется л. п. р. в качестве множества его возможных ра-
циональных выборов. (О задачах принятия решений
при нескольких критериях см., например, книгу [31].)
Итак, пусть Р — множество всех эффективных аль-
тернатив для рассматриваемых в задаче н. м. п. функ-
ций ср (х) и (х).
Определение 2.4.2. Решением 2 задачи н. м. п.
называется нечеткое множество с функцией принадлеж-
ности вида
, , . I (*) при * б Р,
Р- (*) = п
( 0 в остальных случаях.
В этом определении явно предполагается, что л. п. р.
должно использовать в своем решении лишь те альтер-
нативы универсального множества X, которые дают
одновременно неулучшаемые значения функций ср и рс.
2.41
НЕЧЕТКОЕ МНОЖЕСТВО ОГРАНИЧЕНИЙ
93
Соответствующее решению 2 нечеткое значение
функции ср записывается в виде
Р2ЛГ)= SUP rQR1.
х6<р-1 (г)
Покажем теперь, что при некоторых предположениях
решения 1 и 2 дают одно и то же нечеткое значение
функции ср.
Теорема 2.4.1. Если множество X компактно,
функция ср непрерывна на X, а функция (р^ полуне-
прерывна сверху на X, то при любом выпол-
няется равенство
Доказательство. Заметим сначала, что в усло-
виях теоремы множество ср-1 (г) замкнуто в X при лю-
бом r^R1 и, следовательно, для любого r^R1 най-
дется £06?-1(г) такое, что
sup (X1 (я:) = и1 (ж0).	(2.4.7)
Допустим, что найдется r^R1, для которого р^(г0)>
>^(г0) или
sup р.1^)^ sup р.2(я).	(2.4.8)
Чго)	л?е?-г(го)
В силу (2.4.7) и в условиях теоремы выражение (2.4.8)
можно записать в следующей форме:
ре(а:о)= max pc(s)= sup p1(a;)> sup ^(х),
ябр-ЧЛ))	явр-Чго)	!(ГО)
(2.4.9)
откуда следует, что
рс (жо) > Iх2 (х) Для любого	(2.4.10)
а)	Если р? (х) > 0 для некоторого х £ ср”1 (г0), то
р.2 (х) —	(ж) и получаем
<Р (*о) = <?(*) = П» Нс (*о) > Рс (4
Но это противоречит тому, что х — эффективная аль-
тернатива для функций ср и р.с.
94
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
б)	Если [12(ж) = 0 для любого ябТ^Оо)» то любая
альтернатива х б ср”1 (г0) не является эффективной, т. е.
для любого х' б<р”1 (г0) найдется #6^ такой, что
<р(ж)><р(ж') = г0, ^ (*) > Мж').	(2.4.11)
ИЛИ
Ф(х)><р(я:') = г0, ?с(х)	(ж').	(2.4.12)
Но если х' б f”1 (г0) П N (К) для некоторого К > 0 (см.
предложение 2.4.1), то из (2.4.12) получаем, что
и, следовательно,
<р(ж)<г0 = <р(ж'),
что противоречит неравенствам (2.4.12).
Что касается неравенств (2.4.11), то они не выпол-
няются для х' = х0, поскольку ябт’Ч7*©) и
рс(ж0)= юах М4
хбф-Чго)
Отсюда получаем, что рЛ (г) = р2 (г) Угб#1* Теорема
доказана.
Итак, принятие решений по первому и второму из
описанных подходов приводит к одному и тому же
результату.
Согласно определению 2.4.2 нахождение решения
2 сводится к определению множества Р эффективных
альтернатив для функций ср и рс. Однако это множество
содержит, вообще говоря, бесконечное число элемен-
тов, причем нет эффективного способа его описания.
Вместе с тем для получения решения 2 в конкретной
задаче практически достаточно указания конечного
числа эффективных альтернатив, достаточно равномерно
выбранных из множества Р.
Для нахождения таких альтернатив можно вос-
пользоваться следующим почти очевидным фактом.
Если для некоторых чисел vx > О, v2 > О альтернатива
х0 доставляет максимум функции
Z (ж) = vx<p (ж)(ж)
на множестве X, то эта альтернатива является эффек-
тивной для функций ср и р.с. Действительно, из
2.4]
НЕЧЕТКОЕ МНОЖЕСТВО ОГРАНИЧЕНИЙ
95
допущения о том, что упомянутая выше альтернатива
не является эффективной, вытекает существование
альтернативы х'(*Х, для которой выполняются либо
неравенства
либо
?(«')>? («о). ^(«')>Нс(а:о)>
противоречащие тому, что х0 доставляет максимум функ-
ции L (х).
Таким образом, придавая различные положитель-
ные веса функциям и и максимизируя соответ-
ствующие функции L (х), можно определить любое тре-
бующееся число эффективных альтернатив.
Полученные при этом альтернативы вместе с соот-
ветствующими им значениями функций ср и пред-
ставляются л.п.р., которое и делает окончательный
выбор из них, исходя из своих субъективных представ-
лений (или пользуясь информацией, не учтенной в дан-
ной математической модели) об относительной важности
значения функции ср и степени допустимости альтер-
натив.
В заключение этого раздела^ мы кратко обсудим
подход к задачам н. м. п., предложенный в книге К. Не-
гойты и Д. Ра леску [25].
Суть этого подхода заключается в том, что задача
«максимизации» функции на нечетком множестве фор-
мулируется как задача достижения нечетко определен-
ной цели типа рассмотренной в предыдущем разделе.
Заданная функция ср (х) (нормированная к 1) пони-
мается при этом как функция принадлежности нечет-
кого множества цели, а решение задачи определяется
как пересечение нечетких множеств цели и допустимых
альтернатив. Иными словами, решение имеет вид
|1(ж)==тт{<р(х), ^(ж)}.
При необходимости выбора конкретной альтерна-
тивы предлагается выбирать ту, которая имеет макси-
мальную степень принадлежности этому решению, т. е.
доставляет максимум функции р. (х).
96
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
Сравним теперь эту рекомендацию с тем, как опре-
деляется решение задачи н. м. п. по описанному в этом
разделе второму подходу (решение 2). Нетрудно убе-
диться в том, что альтернатива, максимизирующая
функцию р- (х), является одной из эффективных аль-
тернатив для функций ср и на множестве X. В рам-
ках же анализируемой математической модели эффек-
тивные альтернативы не сравнимы друг с другом, так
как в модели нет информации, пользуясь которой
можно было бы судить о том, что одна эффективная
альтернатива лучше (или не хуже) какой-либо другой
эффективной альтернативы. Это означает, что выбор
среди эффективных альтернатив может сделать лишь
л. п. р., обладающее какой-либо информацией (или сооб-
ражениями), внешней по отношению к данной матема-
тической модели.
Таким образом, решение рассматриваемой матема-
тической задачи должно включать в себя все множество
эффективных альтернатив или по крайней мере доста-
точно большую выборку из этого множества. Выбор же
конкретной альтернативы из этого множества следует
оставить на усмотрение л.п.р.
2.5. Игры в нечетко определенной обстановке
2.5.1. Введение. До сих пор мы рассматривали
задачи принятия решений, в которых результат (значе-
ние функции ср) однозначно определялся действиями
л. п. р. Такие задачи широко распространены в прак-
тике.
Вместе с тем в экономике, военном деле и многих
других областях человеческой деятельности часто
встречаются ситуации, в которых выполнение цели
или результаты принятия решений одним лицом (или
группой лиц) зависят не только от действий этого лица,
но и от действий (решений) другого лица или группы
лиц, преследующих свои собственные цели.
В связи с этим при анализе подобных ситуаций
с целью определить рациональный способ поведения
необходимо учитывать и возможные действия партне-
ров. В военном деле, например, успех проведения
операции невозможен без учета возможных действий
2.5] ИГРЫ В НЕЧЕТКО ОПРЕДЕЛЕННОЙ ОБСТАНОВКЕ
97
противника. При управлении экономической системой
необходимо учитывать, что поведение подсистем (на-
пример, отдельных предприятий) определяется
не только физическими или иными объективными за-
кономерностями, но и интересами участвующих в этих
подсистемах людей, которые могут не совпадать с ин-
тересами управляющего органа. Ясно, что подобных
примеров можно привести очень много.
Ситуации этого типа принято называть игровыми
(играми). Математические модели таких ситуаций изу-
чает теория игр — довольно обширный отдел приклад-
ной математики. (См., например, книги [32—35].) Ос-
новное направление в теории игр связано с выработ-
кой и анализом принципов рационального поведения
игроков в различных условиях.
Пожалуй, наибольшее внимание исследователей
в теории игр привлекают два теоретико-игровых прин-
ципа рациональности: принцип наилучшего гаранти-
рованного результата и принцип, опирающийся на по-
нятие равновесия. Оба этих принципа используются
ниже в анализе игр в нечетко определенной обстановке.
Здесь мы кратко обсудим эти принципы, считая для
простоты, что в игре участвуют лишь два партнера.
В соответствии с принципом наилучшего гаранти-
рованного результата игровая ситуация рассматри-
вается как задача принятия решений одним из игро-
ков (для определенности назовем его игроком 1). Вы-
боры другого игрока (игрока 2) считаются неопре-
деленными факторами. Эта неопределенность может
заключаться, например, в том, что игроку 1 в момент
принятия решения известна не конкретная реакция
(выбор) игрока 2, а лишь некоторое множество его
возможных реакций. Чем" больше известно игроку 1
об интересах и ограничениях игрока 2, тем «уже» это
множество, т."е.*тем меньше неопределенность в его
поведении с точки зрения игрока 1.
В основе принципа наилучшего гарантированного
результата лежит положение о том, что рациональным
является такой способ оценки игроком 1 своих выбо-
ров, при котором он рассчитывает на наихудшую для
него реакцию игрока 2 из множества возможных реак-
ций последнего. Наилучшей при этом естественно счи-
7 С. А. Орловский
98
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
тать ту из стратегий (выборов) игрока 1, которой соот-
ветствует наилучшая оценка.
Важным в применении этого принципа является
точный учет всей информации об игроке 2, которую
игрок 1 будет иметь в момент принятия решения, по-
скольку именно эта информация позволяет этому
игроку судить о возможных реакциях партнера на его
выборы.
Столь гибко понимаемый принцип наилучшего
гарантированного результата был впервые сформули-
рован Ю. Б. Гермейером. Подробное обсуждение этого
принципа, а также анализ принятия решений на его
основе в разнообразных ситуациях, имеется в книгах
Ю. Б. Гермейера [33, 34].
Еще один принцип рациональности, который ис-
пользуется ниже в анализе игр с противоположными
интересами (целями) игроков, опирается на понятие
ситуации равновесия по Нэшу. Он применим в тех
случаях, когда игроки имеют возможность договари-
ваться друг с другом с целью выработки совместного
в некотором смысле взаимовыгодного поведения.
В соответствии с этим принципом рациональным
считается выбор игроками некоторой пары стратегий
у0 (по одной каждым игроком), обладающей устой-
чивостью в следующем смысле: одностороннее наруше-
ние договоренности не выгодно ни одному из игроков.
Иными словами, если например, игрок 1 выберет
стратегию х вместо xQ, а игрок 2 останется «верен»
стратегии у0, то выигрыш игрока 1 в лучшем случае
не изменится. Обладающая такой устойчивостью пара
стратегий (т0, у0) называется ситуацией равновесия
по Нэшу.
При всей своей привлекальности этот принцип имеет
два немаловажных недостатка. Во-первых, ситуации
равновесия, как правило, неустойчивы по отношению
к изменению стратегий обоими игроками одновременно
(например, оба игрока могут получить бблыпие выиг-
рыши в какой-либо другой, вообще говоря, неравно-
весной ситуации). Во-вторых, в игре обычно имеется
широкое множество ситуаций равновесия, причем од-
ному из игроков могут быть предпочтительны одни
из этих ситуаций, а другому — другие. Это препятст-
2.5]	ЙЁРЫ В НЕЧЕТКО ОПРЁДЁЛЕНЙОЙ ОБСТАНОВКЕ
вует достижению договоренности между игроками
о выборе конкретной ситуации равновесия. Подроб-
нее о ситуациях равновесия можно прочесть в цити-
рованных выше книгах по теории игр.
Наиболее «удачны» ситуации (игры двух лиц),
в которых имеются стратегии игроков, рациональные
одновременно по обоим описанным выше принципам.
Таким свойством обладают многие игры двух лиц
с нулевой суммой (антагонистические игры). Ниже мы
покажем, что в определенной степени это свойство при-
суще и некоторым играм с противоположными целями
в нечетко определенной обстановке.
В данном разделе описываются игры в нечетко опре-
деленной обстановке [30, 36], т. е. игры, в которых
цели и допустимые выборы (стратегии) участников
описаны в форме нечетких множеств. При анализе
таких игр мы будем пользоваться подходами к задачам
н. м. п., описанными в двух предыдущих разделах.
Изложение ограничивается лишь играми двух лиц,
однако многие из приведенных ниже результатов не-
трудно распространить и на случай большего числа
участников.
2.5.2.	Описание игры. Пусть X и Y — универсаль-
ные множества стратегий, которые в принципе могут
выбирать игроки 1 и 2 соответственно. Допустимые
стратегии игроков описываются нечеткими множест-
вами р,1: X -> [0, 1] и р2: X -> [0, 1]. Выше в § 2.2
уже говорилось о возможных интерпретациях этих
нечетких множеств. Заданы функции /1? /2: XxY -> R1,
причем значение Д (х, у), i=l, 2, интерпретируется
как оценка игроком i ситуации (х, у). Множество 7?'
(числовая ось) интерпретируется при этом как универ-
сальное множество оценок.
Каждый из игроков стремится к достижению своей
нечетко описанной цели. Будем считать, что цель
игрока I описывается нечетким множеством G. в уни-
версальном множестве оценок R1 с функцией принад-
лежности рЬ: 7?1->[0, 1]. Об интерпретации такой цели
говорилось в § 2.2. Заметим лишь, что цель, постав-
ленная перед игроком, может оказаться плохо или во-
обще несовместимой с его возможностями, т. е. напри-
мер, с множеством его допустимых стратегий или с имею-
7*
100
МАТЕМАТИЧЕСКОЙ ПРОГРАММИРОВАНИЕ
ГЛ. 2
щейся у него информацией об интересах и ограниче-
ниях другого игрока. Подробнее этот вопрос рассмат-
ривается ниже.
Для анализа поведения игроков в сформулирован-
ной игре мы воспользуемся подходом, описанным
в § 2.2. В соответствии с этим подходом цель игрока г
мы будем описывать нечетким подмножеством множе-
ства ситуаций вида
Й (х, у) — у.'а (j( (х, у)), (х, y)£XxY.
Нетрудно видеть, что заданное нечеткое множество
таково, что его образом в R1 при отображении Д яв-
ляется заданное в R1 нечеткое множество цели G-
(см. § 1.3).
Если бы, например, цель игрока i была четко опре-
деленной, т. е. описывалась бы функцией принадлеж-
ности, принимающей лишь значения 0 и 1, то игрок i
стремился бы к реализации в игре какой-либо ситуа-
ции (Ж, у), ДЛЯ КОТОРОЙ р& (х, у) — 1.
Введем теперь нечеткие множества D± и D2 в X X Y
следующим образом:
рл (ж> у)=min (и1 (ж)> рЬ (®> у)}>
Рд (*> У) = min (р2 (у), (4 (х, У)}'
Иначе говоря, нечеткие множества D., 1=1, 2, суть
пересечения соответствующих нечеткого множества до-
пустимых стратегий и нечеткого множества цели.
Смысл множеств D± и D2 можно пояснить следую-
щим образом. Если, например, игроку 1, известен
конкретный выбор у £ Y игроком 2, то перед ним (игро-
ком 1) стоит описанная в п. 2.2.1 задача достижения
нечеткой цели р| (х, у) при множестве допустимых
альтернатив рА (ж). В соответствии с используемым
здесь подходом Веллмана—-Заде решение Dr такой
задачи определяется как пересечение нечетких множеств
р.1 и p.J(x, у),
Рд (*• у) = min (Р1 (х)’ Ре (*> уЯ-
Таким образом, нечеткое множество р.^ (ж, у) можно
рассматривать как семейство (по параметру у) решений
2.51 ЙГРЁ1 В ЙЁЧЕТКО ОПРЕДЕЛЕННОЙ ОЁСГАНОВКЕ
задач достижения нечетких цепей $ (х, у). Аналогич-
ный смысл можно придать и множеству
Для дальнейшего анализа игры необходимо уточ-
нить, какие выборы игроков считать допустимыми.
При наиболее общей постановке допустимыми нужно
считать выборы игроками произвольных нечетких под-
множеств множеств их допустимых стратегий и вести
анализ игры в классах подобных нечетких стратегий.
Мы же остановимся здесь на более узкой (и более про-
стой) постановке задачи, в которой выборами игроков
могут быть лишь стратегии-элементы соответствующих
универсальных множеств X и Y. При этом будем счи-
тать, что при каждом фиксированном выборе одного
игрока второй выбирает стратегию, которая максими-
зирует соответствующую ему функцию (х, у), т. е.
стратегию, которая имеет максимальную степень при-
надлежности нечеткому множеству D..
Имея это в виду, можно более точно сформулировать
цели игроков в рассматриваемой игре. Можно пола-
гать, что игрок i (г=1, 2) стремится к достижению
по возможности большего значения функции	у).
Рассматриваемая игровая ситуация формулируется при
этом следующим (четким) образом: X и Y — множества
стратегий игроков 1 и 2, и —их функции вы-
игрышей.
2.5.3.	Максимальные гарантированные выигрыши.
Если игрок целиком полагается лишь на свои возмож-
ности, то естественной представляется его ориента-
ция на получение наибольшего гарантированного выиг-
рыша. При этом, как уже говорилось выше, важную
роль играет имеющаяся в его распоряжении информа-
ция об интересах и ограничениях другого игрока.
От этой информации существенно зависит величина
выигрыша, который игрок может себе гарантировать.
Вопросы информированности и связанные с ней раз-
личные постановки задач принятия решений в условиях
неопределенности (и игровых задач в частности) под-
робно описаны Ю. Б. Гермейером [33, 34].
Пусть, например, игрок 1 имеет возможность пер-
вым выбрать свою стратегию и сообщить ее игроку 2.
102
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
Тогда наибольший гарантированный выигрыш игрока 1
равен
Af1 = max min	(х, у) = max min {р.1 (х), min рв(х,у)}.
у6Г(л?)	1	убУ(дг)
(Для простоты изложения будем считать, что всюду
ниже, где используются операции max и min, соответст-
вующие максимальные и минимальные значения до-
стигаются на указанных множествах.)
Присутствующее в этом выражении множество Y (х),
зависящее от х (и известное игроку 1), есть множество
возможных реакций (ответов) игрока 2 на сообщенный
ему игроком 1 выбор х. В этом смысле зависимость
Y (х) отражает степень информированности игрока 1
об интересах и ограничениях игрока 2.
Если игроку 1 известно об игроке 2 лишь множе-
ство У, то его нечеткое множество выборов имеет вид
ЁЧ (х) = min {Fi (®)> min pl (х, у)}.
ует
Конкретным выбором игрока 1 будет при этом страте-
гия, максимизирующая эту функцию на множестве X.
Если игрок 1 имеет больше информации о своем
партнере (т. е. в случае У (х) С У), то нечеткое мно-
жество его выборов имеет вид
р.; (ж) = min {н (ж), min (ж, у)}.
убГ(ж)
Нетрудно видеть, что при этом р/' (х)	р,' (х) для
любого х £ X, т. е. при большей информированности
игрока 1 его нечеткое множество выборов оказыва-
ется более широким. В этом смысле можно говорить
о том, что, имея больше информации о партнере,
игрок 1 имеет больше возможностей гарантировать
достижение своей цели.
Если величина М± слишком мала, то это значит,
что цель, к достижению которой стремится игрок 1,
слишком завышена (с учетом его возможностей). В этой
связи естественным образом возникает следующая за-
дача. Пусть сформулирована нечеткая цель игрока 1
в виде нечеткого множества $ в Д1. Каково должно
быть нечеткое множество его стратегий, которое гаран-
тировало бы ему (при заданной информированности
2.5] ИГРЫ В НЕЧЕТКО ОПРЕДЕЛЕННОЙ ОБСТАНОВКЕ ЮЗ
об игроке 2) достижение цели со степенью, не меньшей
некоторого заданного числа а? Иными словами, какова
должна быть функция (х), описывающая нечеткое
множество стратегий игрока 1, чтобы выполнялось
неравенство
Мг = max min (х), min (ж, у)} а?
Для решения этой задачи введем множество
Ха = (х I min р-е (х, у)У>а} с X.
yen*)
Если Ха=0, то, как легко видеть, М1<^а, и следова-
тельно, игрок 1 не может гарантировать достижение
своей цели со степенью большей или равной а незави-
симо от того, какое множество стратегий находится
в его распоряжении (например, в силу недостаточной
информированности об интересах и ограничениях
игрока 2, которая определяется характером отображе-
ния Y (х)).
Пусть , тогда нетрудно заключить, что гаран-
тировать достижение цели со степенью не менее а
можно тогда и только тогда, когда (х) а при не-
котором х 6 За-
имеет смысл и обратная задача: имеется нечеткое
множество допустимых стратегий игрока 1	(х).
Какие цели игрок 1 может гарантированно достигнуть
со степенью не менее а?
Для решения этой задачи введем множество
(*)>«}•
Ясно, что для достижения цели со степенью не менее а
необходимо и достаточно, чтобы нашлась такая стра-
тегия х£Х'а, для которой выполнялось неравенство
min (х, у)^а
или
V-a(x, у)'^а Vy£Y(x).
(2.5.1)
Пусть pi: R1 -* [0, 1] — некоторая функция цели игрока 1.
Введем множество
га = М^(2)>«}ся1.
104
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
Тогда, опираясь на (2.5.1), заключаем, что для дости-
жения цели [iff игроком 1 со степенью не менее а не-
обходимо и достаточно, чтобы нашлась такая страте-
гия х £ X', что f (х, у) £ Za при всех у £ Y (х), где
/ (#, У) функция оценки, введенная выше.
2.5.4.	Игры с противоположными интересами игро-
ков. Различие в интересах игроков означает, что раз-
личны отношения предпочтения этих игроков на мно-
жестве ситуаций игры. Напомним, что ситуацией игры
называется любой элемент множества XxY, где X
и У — множества стратегий. Таким образом, любая
ситуация игры имеет вид s=(x, у), где х — стратегия
игрока 1, а у —- игрока 2. Если для игрока i ситуация
$х не хуже (не менее предпочтительна) ситуации $2,
i
то мы будем писать $х $2.
Несовпадение интересов игроков может означать,
йапример, что для каких-либо ситуаций $х, $2, $з> $4
выполнены предпочтения
1	2	12
$1	$2’	$1	52» 53	$4’ $4	53>
т. е. предпочтения игроков могут быть одинаковыми
для одних пар ситуаций (sx и $2) и противоположными
для других пар ($3 и $4).
Если же предпочтения игроков противоположны
для всех пар ситуаций игры, то игра называется игрой
с противоположными интересами игроков. Иными сло-
вами, противоположность интересов игроков 1 и 2
означает, что для любой пары ситуаций s, q справед-
ливо утверждение:
1	2
либо s q, и тогда q s,
1	2
либо q 5, и тогда s q.
Если, например, игроки 1 и 2 сравнивают ситуации
игры по значениям своих функций выигрышей <рх (х,
у) и ср2 У)» причем срх (х, у)-НРг (я, у)=0 при любых
(х, У) € ХхУ, то интересы этих игроков противопо-
ложны. Игру в этом случае называют игрой с нулевой
суммой или антагонистической. Компактное изложе-
2.5] ИГРЫ В НЕЧЕТКО ОПРЕДЕЛЕННОЙ ОБСТАНОВКЕ 105
ние теории антагонистических игр имеется, например,
в книге Т. Партхасаратхи и Т. Рагхавана [35].
Игрой с противоположными интересами в нечетко
определенной обстановке мы будем называть игру,
в которой функции принадлежности й& (z) и функции
fi У), описывающие цели игроков, таковы, что
PG (zj > Йо (z2) о Йе (21) < йе (z2)-,	(2.5.2)
£в (Zx) = P-g (32) о-йв (zx) —	(z2),	(2.5.3)
А (*. У) = /г (*, У) V (*, у) е X X У.	(2.5.4)
В этом определении предполагается, что игроки одина-
ково оценивают ситуации игры (равенство (2.5.4)),
но цели их противоположны. Действительно, из не-
равенств (2.5.2) следует, что если при выигрыше
(оценке) z± степень достижения цели игрока 1 больше,
чем при выигрыше z2 (т. е. zx предпочтительнее для иг-
рока 1 в смысле достижения его цели), то степень до-
стижения цели игрока 2 при выигрыше z± меньше,
чем при ^выигрыше z2 (т. е. для игрока 2 выигрыш z2
предпочтительнее выигрыша zx).
Если воспользоваться подходом Веллмана—Заде
(§ 2.2), то нечеткую цель игрока i следует записать
в виде
У)=^(1АХ> У))>
т. е. как нечеткое подмножество множества всех ситуа-
ций игры	Цель в этом случае зависит как от
вида функции й&, так и от вида функции Имея
это в виду, противоположность интересов игроков можно
сформулировать в следующем более общем виде: инте-
ресы игроков противоположны, если функции йя и
i = l, 2, таковы, что для любых (xlt г/х), (х2, у2) из
множества X\Y выполнено одно из условий
Нс(ж1. У1)>Р-с(х2, У^оу-l^,	У^
У1) = P-G (*2, г/2)онс(жр J/i) = He(a:2. Уз)-
Так же, как и в предыдущем разделе, мы сформу-
лируем рассматриваемую игру в форме игры с функ-
циями выигрышей вида
4 (*> у) = min {th (*)» Р-G (х, у)},
4 (*, У) = min {р.2 (х),	(х, у)}
106
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
и множествами стратегий X и Y. Напомним, что
функции и р.2 описывают нечеткие множества стра-
тегий игроков 1 и 2 в исходной игре.
Пара стратегий (xQ, у0) называется ситуацией равно-
весия такой игры, если для любых х £ X и у (< Y вы-
полняются неравенства
Рд, (жо> Уо) > Рд, (я, Уо)>	(2.5.5)
Рд, («о» Уо) > Ид, (*0, У)-	(2.5.6)
Ниже рассматриваются некоторые свойства ситуаций
равновесия с учетом того, что интересы игроков про-
тивоположны в описанном выше смысле. Введем мно-
жества
<\ = {(х, у) I (х, y)£XxY, ^(х^рЦх, у)},
cz = {(ж» У) I (*» У) € ХХ Y> Р2 (У)	Ре (*. У)}-
Пусть, например, ситуация равновесия (х^ у^)£С2.
Это означает, что множество
<^2х0 = {у I У 6 Y, (х0, у) £ С2)
непусто. Из определения множества С2 следует, что
р,2 (г/) = (я0» У) ПРИ любом у £ С2х0 и, следовательно,
при любом у^С2х0 выполняются равенства
min{[i2(i/), р2с(х0, у)} = у.2а(х0, у).
Но тогда из (2.5.5) вытекает, что при любом у(< С2Хо
выполнено неравенство $ (xQi у0) ра (я0, у).
Отсюда, в силу противоположности интересов игро-
ков, получаем, что рс(^о> Уо)^?о(х& У) ПРИ любом
У € С2гСо и, следовательно,
min (ж0), &(х9, г/0)} < min (^ (ж0), ^(х0, у)},
т. е. Ид/яо» Уо) < Рд, (жо, У)-
Кроме того, (2.5.5) можно записать в виде
Рд(^0. Уо)>Рд,(ж, Уо)	^2у0,
где С2уа = {х | х £ X, (х, Уо)^^}- В результате мы по-
лучили неравенства
P-Р, (ж0, Уо) > Рр,	У о) Vх €
Рр, (^0» Уо) Рр, (Хо> у) У У € ^2х0*
2.5] ИГРЫ В НЕЧЕТКО ОПРЕДЕЛЕННОЙ ОБСТАНОВКЕ
107
Как нетрудно видеть, эти неравенства означают,
что рассматриваемая ситуация равновесия исходной
игры (Xq, Уо)£С2 представляет собой ситуацию равно-
весия некоторой игры игроков 1 и 2 с нулевой суммой
(р^ — функция выигрышей игрока 1, —	— игрока 2,
рD (—рр) — 0), в которой допустимыми считаются не
все ситуации множества	а лишь ситуации, со-
ставляющие подмножество этого множества С2сХхУ*).
Аналогичным образом можно исследовать и случай,
когда ситуация равновесия (ж0, у0) £ Сг.
Выше уже говорилось о том, что обычные игры
с противоположными интересами характерны тем,
что в них в любой ситуации равновесия игроки полу-
чают свои максимальные гарантированные выигрыши,
соответствующие их информированности лишь о мно-
жествах стратегий партнера. Имея это в виду, интересно
рассмотреть связь между наибольшими гарантирован-
ными выигрышами игроков и их выигрышами в ситуа-
циях равновесия в играх в нечетко определенной об-
становке.
При вычислении наибольших гарантированных вы-
игрышей будем полагать, что каждому из игроков из-
вестен лишь носитель нечеткого множества стратегий
партнера. Нетрудно видеть, что при этом наибольшие
гарантированные выигрыши записываются в виде
Af1 = maxminpn (х, у),
хбХ убУ 1
М2 = max min (х, у).
yer *ех *
Представим величину Мг в следующей форме:
= max {max рх (х), max min z/)}, (2.5.7)
где
Х0=--.{х\х£Х, С1х^0), Х' = Х\Х0,
I у е у, joeq,
а множество Сг введено выше.
*) Игры на произвольном подмножестве множества всех си-
туаций игры называются играми с запрещенными ситуациями.
Об особенностях таких игр см.» например, работы [34, 37, 38].
108
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
Будем рассматривать случай, когда Сх — С2 — С.
Пусть (х0, у0)— ситуация равновесия игры, причем
(•£о> £/о) € С*
1. Покажем, что	(я0, z/0). Действительно,
для любых (я, у) выполнено неравенство
min р.д (яг,	(аг, у)
1	1
> и, в частности, min р.~ (х, у') р^ (ж, г/0)- Отсюда
у'ек 1	1
Мг = max min р (х, у) < max рл (х, у0) = р„ (ж0, у0),
уег 1	хех 1	1
т. е.
Уо)-	(2-5.8)
2. Покажем теперь, что'	(я0, z/0). Действи-
тельно, для любого у £ Cx<t= g Y, (х0, у) £ С} (Ся,^0,
так как по предположению (а:0, yQ) £ С) выполнено нера-
венство рс(^0, Уо)^ Р'К^о» У)- Отсюда, в силу противо-
положности интересов игроков (см. выше), получаем,
что для любого у £ СХо справедливо неравенство ре (^0> У о)
Не (жо> У) и> следовательно,
mm{pi(x0), р^(ж0, y0))<min{pi(a:o), рс(ж0, г/)},
т. е. у.» (ж0, y0) = minp„ (ж0, г/) = тшр^(ж0, у).
Далее, легко видеть, что
max min (ж, у) min р.д (аг0, у) = р. (х0, у0)«
хех0 1 уе^0 1
Отсюда и из (2.5.7) получаем
(2.5.9)
Из (2.5.8) и (2.5.9) заключаем, что	(х0, yQ).
Аналогичным образом можно показать, что и М2 —
==:	(^о» Уо)*
Таким образом, мы пришли к выводу о том, что
в сформулированной здесь игре с противоположными
интересами выигрыши игроков в ситуации равновесия
из множества С являются их максимальными гаранта-
2.5] ИГРЫ В НЕЧЕТКО ОПРЕДЕЛЕННОЙ ОБСТАНОВКЕ Ю9
рованными выигрышами (при заданной выше инфор-
мированности игроков). Это значит, в частности, что
все ситуации равновесия из множества С эквивалентны
ДРУГ другу, поскольку во всех них игроки получают
одни и те же выигрыши. Заметим, что этот случай
типичен для обычных игр с противоположными инте-
ресами игроков.
Обратимся теперь к случаю, когда ситуация равно-
весия не принадлежит множеству С, т. е.
где С = (X X У)\С. Как следует из определения мно-
жества, при этом выполняются равенства
Р-л», (*о> Уо) = min (pj (ж0), р^ (х0, у0)} = рх (х0), (2.5.10)
Ид, (*0> Уо) = min {f*2 0/о)> Но (®о» Уо)} — Иг (Уо)- (2.5.11)
Кроме того, по определению ситуации равновесия
имеет место равенство
^,(*0, у0) = тахрв(ж, Уо)' (2.5.12)
Поскольку CVo\jCVo = X, то (2.5.12) можно записать
в виде (см. (2.5.10))
Ь,(*о» y0) = max{sup у. (х, у0), sup ps(x, у0)} =
хес»о
= max { sup рх (х), sup рЬ (х, у0)} = рх (ж0). (2.5.13)
x&y„ x^Va
Допустим, что
sup Pi (ж) < sup рА (ж, у0).
Тогда из (2.5.10) и (2.5.13) получаем
sup Р1(ж)<р1(ж0),
что невозможно, поскольку по предположению (ж0, у0) £ С
и, следовательно, жо^ГУо. Отсюда и из (2.5.13) сле-
дует, что
Hi (®о) = max р! (ж).
Аналогичным образом получаем
ра (у0) = max ра (у).
110
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
В данном случае, как и в случае (ж0, yQ)f* С, выпол-
нены неравенства
Ml < Рд, (жо- Уо), М2 С (х0, у0).
Однако обратные неравенства, вообще говоря, не имеют
места. Учитывая это и результат, полученный для
(х0, Уо) € С можно утверждать, что для обоих игроков
ситуация равновесия из множества С не хуже любой
ситуации равновесия из множества С, которая обеспе-
чивает игрокам получение лишь их максимальных
гарантированных выигрышей Мг и М2.
В заключение этого раздела отметим, что форму-
лировка рассмотренных выше игр опиралась на под-
ход Веллмана—Заде к задачам принятия решений
при нечетких условиях. Мы полагали при этом, что
на основе этого подхода игроки принимают решения
о выборе своих стратегий. Это позволило сформулиро-
вать игру в нечетко определенной обстановке в форме
обычной игры с четко описанными функциями выиг-
рышей и и множествами стратегий X и Y.
Для анализа таким образом сформулированных
игр в нечетко определенной обстановке применим ап-
парат теории игр. Было бы интересным, в частности,
исследовать вопрос о существовании и способах на-
хождения ситуаций равновесия в таких играх и свя-
занный с этим вопрос о возможности (и смысле) исполь-
зования игроками смешанных стратегий, т. е. распре-
делений вероятности на множествах X и У. Интересным
и практически важным представляется также исследо-
вание влияния различных способов обмена информа-
цией между игроками на величины их максимальных
гар антир ов анных выигрышей.
2.5.5. Нечеткое равновесное решение игры. Как
уже говорилось выше, формулировка и анализ игры
в нечетко определенной обстановке зависят от того,
по какому принципу игроки принимают решения о вы-
боре своих стратегий. Подход Веллмана—Заде при-
водит к формулировкам, описанным в двух предыду-
щих разделах. В данном разделе мы остановимся еще
на одной формулировке, опирающейся на принцип
принятия решений, описанный в § 2.4. Для упроще-
2.5] ИГРЫ В НЕЧЕТКО ОПРЕДЕЛЕННОЙ ОБСТАНОВКЕ
111
ния изложения мы, как и прежде, будем рассматри-
вать лишь игры двух лиц; распространение приведен-
ных выше рассуждений на случай большего числа
участников не представляет труда.
Итак, пусть X и Y — универсальные множества
стратегий игроков 1, 2, а X [0, 1] и р.2:	Ю,
1] — их нечеткие множества допустимых стратегий.
Функции выигрышей игроков будем, как и выше, обо-
значать Д (х, у) и Д (х, у). В отличие от предыдущего,
будем считать, что каждый из игроков стремится по-
лучить по возможности большее значение своей функ-
ции выигрышей.
Ниже мы попытаемся ввести некоторое понятие
нечеткого равновесного решения игры, которое может
служить основой для достижения договоренности
между игроками о выборе их совместного поведения
в игре.
Заметим, что при любой фиксированной (и извест-
ной игроку 1) стратегии у (< Y игрока 2 перед игроком 1
стоит рассмотренная в § 2.4 задача принятия реше-
ния о «максимизации» его функции выигрышей на не-
четком множестве его допустимых стратегий. В соот-
ветствии с описанным в § 2.4 подходом решением такой
задачи считается нечеткое множество вида
(*» у) =
Ь.С*’ У) при х£ и N (X, у),
1	Х>0
О в остальных случаях,
где
y) = {x\fi(x, у)= sup f^x', у)},
С{ = {х\х£Х, р1(ж)>Х).
Зависимость множества от у отражает тот факт, что
это множество является нечетким ответом игрока 1 на
выбор игроком 2 стратегии у.
Аналогичным образом, ответом игрока 1 на выбор
игроком 2 стратегии х £ X следует считать нечеткое
множество вида
( Р-2 (у) при у £ и м (р, х),
Рт>г(^ у) = \	р>0
I 0 в остальных случаях,
112
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
[ГЛ. 2
где
^(р, *)={у\М*>	/2(*> /)},
у'е<7р2
C* = {y\y£Y, Му)>р}.
Смысл, вкладываемый в так определенные решения,
обсуждался в § 2.4, и поэтому здесь мы на этом во-
просе не останавливаемся.
Введем теперь формальное определение нечеткого
равновесного решения рассматриваемой игры, а затем
установим некоторые его\ свойства, которые прояс-
няют его смысл.
Определение 2.5.1. Нечетким равновесным
решением рассматриваемой игры двух лиц называется
нечеткое подмножество множества ХхУ вида
y) = min(PJ>1(a:» У)>	»)}.
Иными словами, нечеткое равновесное решение
определяется как пересечение нечетких множеств
и D2.
Покажем теперь, что множество рЛ обладает следую-
щими важными свойствами:
1. Если (я0, y0)£suppp/, т- е- i/o) > °» то
найдутся такие числа Х° > 0 и р° > 0, что xQ £ N (Х°, у0)
и у0 6 М (р°, я0). Как нетрудно видеть (см. определение
ситуации равновесия в п. 2.5.1), последнее означает,
что пара стратегий (я0, у0) представляет собой ситуацию
равновесия исходной игры, в которой множествами до-
пустимых стратегий являются обычные множества (мно-
жества уровня) С{о и Сро. Действительно, из того, что
*oW, Уо) и УоЕ^(р°> *о), и из определения мно-
жеств /V (X, у) и М (р, х) следует
/1(^0»	Уо)	Ух £€!{<,,
fa(*o, УоУ>М*о’ У)	Vi/CCp2».
Такая ситуация равновесия соответствует тому слу-
чаю, когда игрок 1 считает допустимыми в одинаковой
степени все стратегии, принадлежащие нечеткому мно-
жеству р4 со степенью, не меньшей Х°, а игрок 2 —
стратегии, принадлежащие нечеткому множеству р.2 со
степенью, не меньшей р°.
2.5] ИГРЫ В НЕЧЕТКО ОПРЕДЕЛЕННОЙ ОБСТАНОВКЕ ИЗ
Из свойства 1 вытекает, что любая пара (х, у) из
носителя нечеткого множества р* является ситуацией
равновесия подобной игры при некоторых пороговых
уровнях Кир. Справедливо и обратное утверждение.
2. Если при некоторых Х°>0, р°>0 пара (я0, у0)
есть ситуация равновесия в игре с функциями выиг-
рышей /х, /2 и множеством ситуаций х С?°9 то
(*о> Уо) € supp р.’, Т. е. р.’(т0, у0)>0.
Действительно, если (xQ1 у0) — ситуация равновесия
в множестве ситуаций С {о X Сро, то
Уо) = sup Л(х, у0),
/2(^0, Уо) — sup /2(*о> у)-
Это в свою очередь означает, что я0€^(Х°, у0), у0£
£ М (р°, ж0) и, следовательно,
^(*0, Уо)>°»	2/о)>°,
откуда рЛ(х0, уо)>0, т- е. (я0, у0) G supp рЛ
Из свойств 1 и 2 вытекает, что носитель нечеткого
равновесного решения рЛ содержит все такие и только
такие пары {х, у), каждая из которых является ситуа-
цией равновесия игры на некоторых множествах уровня
нечетких множеств стратегий игроков.
Нечеткому равновесному решению соответствуют
следующие нечеткие выигрыши игроков:
рл(г)= sup р'(х, у)
Gw) ел1 (г)
Ру2(г) = sup_ рЛ(х, у)
где
/71(П = {(^ У)\(х> y)£XxY, f.(x9 y) = r}, i = l, 2
(при этом полагается, что sup по пустому множеству
равен нулю).
Нечеткое равновесное решение может служить ос-
новой для достижения договоренности между игроками
о выборе конкретной пары (я0, у0) в исходной нечетко
определенной игре. Заметим, что ситуация здесь ана-
8 С. А. Орловский
114	МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ [ГЛ. 2
логична ситуации, типичной для задач принятия реше-
ний по нескольким критериям, в которых лицу, при-
нимающему решения, предлагается набор не сравни-
мых между собой недоминируемых решений (вместе
со значениями критериев) для осуществления оконча-
тельного выбора. В данном случае, например, игроки
могут выбрать ситуацию вида
(*о> {/о)=агётах !*'(*> «/)>
хх г
т. е. ситуацию, имеющую максимальную степень при-
надлежности равновесному решению. Разумеется, это
не единственно возможный способ выбора компромис-
сного решения.
В этой главе мы имели дело с задачами принятия
решений, в которых нечетко были описаны лишь мно-
жества альтернатив. Для анализа более сложных
задач нам потребуется аппарат нечетких отношений
предпочтения, с изложения которого мы и начнем сле-
дующую главу.
ГЛАВА 3
ПРИНЯТИЕ РЕШЕНИЙ
ПРИ НЕЧЕТКОМ ОТНОШЕНИИ
ПРЕДПОЧТЕНИЯ
НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ
3.1.	Введение
При исследовании реальной ситуации или процесса
с целью принятия рационального решения естественно
начать с выявления множества всех допустимых реше-
ний или альтернатив. В зависимости от имеющейся
информации это множество удается описать с той или
иной степенью четкости. Пусть, например, X — не-
которое универсальное множество альтернатив и
(ж) — нечеткое описание его подмножества допусти-
мых альтернатив. Значения функции рс описывают
степени допустимости соответствующих альтернатив
в данной задаче.
Если кроме этой функции нет другой информации
об исследуемой реальной ситуации, то рациональным
остается считать выбор любой альтернативы из мно-
жества
Х» = (х\х£Х, !Xc(«) = supfxe(y)},
т. е. любой альтернативы, имеющей максимальную
степень допустимости, поскольку нет оснований пред-
почесть какую-либо из этих альтернатив остальным.
При введении в модель дополнительной информа-
ции рациональным может оказаться выбор альтерна-
тив из более узкого подмножества множества Хр или
каких-либо альтернатив, не принадлежащих этому
множеству. Эта информация может оказаться такой,
в частности, что на ее основе удастся выявить единст-
венную наилучшую из всех альтернативу, как, напри-
мер, при выборе альтернативы, максимизирующей
функцию, достигающую максимума в одной точке.
Информация о реальной ситуации или процессе
принятия решений, на основе которой одни альтерна-
8*
116 ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
тивы можно предпочесть другим, может быть задана
различными способами. В гл. 2 мы рассмотрели задачи,
в которых эта информация представлялась в форме
функций полезности, по значениям которых альтерна-
тивы сравнивались друг с другом. Но, как уже отме-
чалось выше, такой способ описания реальной информа-
ции возможен не всегда. Более универсальным явля-
ется описание информации в форме отношения пред-
почтения в множестве альтернатив.
Один из способов выявления отношения предпоч-
тения в множестве альтернатив при построении матема-
тической модели реальной ситуации или процесса при-
нятия решений — консультации с л. п. р. или с экспер-
тами. При этом имеется в виду, что л. п. р. или эксперты
обладают знаниями или представлениями об исследуе-
мом объекте, которые не были формализованы в мо-
дели в силу чрезмерной сложности такой формализа-
ции или по другим причинам.
Допустим, что с помощью л. п. р. или экспертов
выявлено четкое отношение нестрогого предпочтения *)
R в множестве допустимых альтернатив X. Это
значит, что относительно любой пары альтернатив
х, у £ X высказано одно из следующих утверждений:
1.	«х не хуже у», т. е. х^у или (х, y)£R.
2.	«у не хуже ж», т. е. у > х или (у, x)(<R.
3.	«х и у не сравнимы между собой», т. е. (х9 y)^R
и {у, x)^R.
Информация в такой форме позволяет сузить класс ра-
циональных выборов, включив в него лишь те альтер-
нативы; которые не доминируются ни одной альтерна-
тивой множества X.
Для того чтобы пояснить, какие альтернативы
считаются недоминируемыми, выделим соответствую-
щие отношению предпочтения R отношение строгого
предпочтения R9 и отношение безразличия R1. Будем
говорить, что альтернатива х строго лучше альтерна-
тивы у, если одновременно х у и у х, т. е. (х, у) £ R
и (у,: x)$R. Совокупность всех таких пар (х, у) и на-
♦) Напомним, что определения и некоторые свойства четких
и нечетких отношений рассматривались в § 1.2 (см. также [39]).
3.1]
ВВЕДЕНИЕ
117
зовем отношением строгого предпочтения R* на мно-
жестве X.
Для более компактной записи определения отноше-
ния R* воспользуемся определением отношения /?“х,
обратного к R (см. § 1.2):
(х, у) £ Я"1 эквивалентно (у, х) £ Я,
или
(ж, y)^R~1o{y, x)QR.
Отношение строгого предпочтения R8 можно записать
теперь в следующей форме:
Я® = Я\Я“Х.
Соответствующее Я отношение безразличия R1 в X
определяется следующим образом. Пара (я, у) £ RJ
тогда и только тогда, когда либо не выполнено ни пред-
почтение х у, ни предпочтение у > х, либо оба эти
предпочтения выполнены одновременно. Иными сло-
вами, (я, у) £ Я7, когда имеющаяся информация в форме
отношения предпочтения недостаточна для того,
чтобы сделать выбор между альтернативами х и у.
Нетрудно проверить, что отношение Я7 можно записать
в виде
Я7 = ((X X X) \ (Я и Я"1)) и (Я П Я'1).
Если (х, у) ЕЯ®, то будем говорить, что альтерна-
тива х доминирует альтернативу у{х^-у). Альтерна-
тиву х^Х назовем недоминируемой в множестве (X,
Я), если (у, я) ЕЯ® для любой альтернативы у Е X.
Иными словами, если х — недоминируемая альтерна-
тива, то в множестве X нет ни одной альтернативы,
которая бы доминировала х. Недоминируемые альтер-
нативы являются в определенном смысле неулучшае-
мыми в множестве (X, Я), и их выбор в задаче приня-
тия решений естественно считать рациональным в пре-
делах имеющейся информации.
Таким образом, информация в форме отношения
предпочтения Я позволяет сузить класс рациональ-
ных выборов в X до множества недоминируемых
(н. д.) альтернатив вида
хн-д- = {ж|хех, (у, ^еяхя-1 VyЕ*)-
118 ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
Ясно, что чем больше имеется информации о реальной
ситуации или процессе, тем уже отношение безразли-
чия (как подмножество декартова произведения ХхХ),
уже множество и, следовательно, меньше неопре-
деленность в рациональном выборе альтернатив.
При моделировании реальных систем могут встре-
титься такие ситуации (являющиеся, скорее, прави-
лом, чем исключением), когда у л. п. р. или у экспер-
тов нет четкого представления о предпочтениях между
всеми или некоторыми из альтернатив. В таких случаях
л. п. р. или эксперты затрудняются с полной опреде-
ленностью утверждать, что, например, альтернатива
х не хуже альтернативы у (т. е. что х у). Если же экс-
перт поставлен перед необходимостью высказывать
четкие суждения о предпочтениях, то при этом он будет
вынужден в некотором смысле «огрублять» имеющиеся
у него знания и представления, а математическая
модель окажется менее адекватной реальной ситуа-
ции. >
Более гибким способом формализации имеющихся
у экспертов знаний о реальной ситуации представля-
ется такой, при котором они имеют возможность опи-
сывать степень своей убежденности в предпочтениях
между альтернативами числа из интервала [0, 1].
В результате с помощью экспертов выявляется, вообще
говоря, нечеткое отношение предпочтения в множестве
альтернатив, в котором каждой паре альтернатив
(ж, у) соответствует число, описывающее степень вы-
полнения предпочтения х у.
Этот способ описания отношения позволяет в более
полной мере ввести в математическую модель знания и
представления экспертов и тем самым сделать модель
в определенном смысле более адекватной реальности.
Задача при этом заключается в том, как использовать
информацию в такой форме для рационального выбора
альтернатив. Таким задачам и посвящена данная глава.
Изложение материала главы мы начнем с обсужде-
ния и анализа свойств нечетких отношений предпочте-
ния, на которые опираются рассматриваемые ниже
подходы к решению соответствующих задач принятия
решений. При этом мы будем ссылаться на общие свой-
ства нечетких отношений, изложенные выше в § 1.2.
3.2]
НЕЧЕТКИЕ ОТНОШЕНИЯ ПРЕДПОЧТЕНИЙ
119
3.2.	Нечеткие отношения предпочтения
Пусть X — заданное множество альтернатив. Не-
четким отношением нестрогого предпочтения (н. о. п.)
на X буррм. называть любое заданное на этом множестве
рефлексивное нечеткое отношение. Как уже говори-
лось в § 1.2, нечеткое отношение можно понимать как
нечеткое подмножество декартова произведения X X X.
Имея это в виду, нечеткое отношение предпочтения
R на множестве X будем описывать функцией принад-
лежности вида ХхХ -> [0, 1], обладающей свой-
ством рефлексивности, т. е. pR (х, х)=1 при любом
х£Х.
Если — н. о. п. на множестве альтернатив X,
то для любой пары альтернатив х, у (*Х значение
у) понимается как степень выполнения предпоч-
тения «ж не хуже у» или х^у. Равенство рй(х, у) = 0
может означать либо то, что с положительной степенью
выполнено обратное предпочтение у х, т. е. что
Ртг (?» х) > либо то, что альтернативы х и у не
сравнимы между собой ни с какой положительной
степенью, т. е. что и pR(y> я) = 0.
Рефлексивность н. о. п. отражает тот естественный
факт, что любая альтернатива х £ X не хуже самой себя.
3.2.1.	Нечеткие отношения безразличия, квази-
эквивалентности и строгого предпочтения. По задан-
ному на множестве X н. о. п. R можно однозначно
определить три соответствующих ему нечетких отно-
шения: безразличия RT (&r), квазиэквивалентности
Re (р.д) и строгого предпочтения R8(pr), которые исполь-
зуются в дальнейшем для определения и анализа свойств
множества недоминируемых альтернатив в задачах при-
нятия решений [39].
По аналогии с обычными отношениями предпочтения
эти три отношения можно определить следующим
образом:
R1 = (X X X \ R U Д'1) U (Д П Д’1),
Re = Д П Д’1,	Д' = Д \ Д'1,
120 ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
где R"1— обратное к R отношение, описываемое функ-
цией принадлежности (см. § 1.2)
Нг- (ж> У) = Ив (У> х) V (ж, у) £ X X X.
Используя определения пересечения, объединения
и разности нечетких множеств (п. 1.2.2), получаем
следующие выражения для функции принадлежности
этих отношений:
1.	Нечеткое отношение безразличия:
У) = “ах{1— max(рв(х, у), ?в(у, ж)),
пнп{рв(ж, у), ?в(у, ж)}} =
= max {min {1 — Ив (ж, у), 1 — р-в (у, ж)},
тт{Рв(ж, у), р.в(у, ж)}}.
2.	Нечеткое отношение квазиэквивалентности *):
Р-Н*. р) = тт{рв(ж, у), у.в(у, ж)}.
3.	Нечеткое отношение строгого предпочтения:
Р-Н*. У) =
f у) — р-н(у> х) при у)>рй(г/> *).
{	0	при рв(ж, у)<рв(г/, ж).
Для иллюстрации этих определений рассмотрим
простой пример обычного (четкого) отношения, описан-
ного набором функций полезности.
Пример 3.2.1. На множестве альтернатив X заданы п
функций X-+R\ i = l, ..., п. Определим в X отношение
предпочтения R следующим образом:
xRy<=>f<(x)	V/ = l, ..., п.
Нетрудно видеть, что функция принадлежности (характери-
стическая функция) отношения R имеет вид
fl при fi (х) > fi (y)t i =
Цд (я, У) = { л
(0 в остальных случаях.
♦) По сути дела, это отношение описывает нечеткую экви-
валентность на множестве X, но мы оставляем термин «отноше-
ние эквивалентности» для нечетких отношений, которые явля-
ются рефлексивными, симметричными и транзитивными.
3.2]
НЕЧЕТКИЕ ОТНОШЕНИЯ ПРЕДПОЧТЕНИЙ
121
Заметим, что при таком отношении предпочтения в мно-
жестве X могут быть не сравнимые между собой альтернативы
(т. е., вообще говоря, R (J Л"*1 =£ X X X), т. е. такие альтерна-
тивы х, А, для которых выполнено (х,	напри-
мер, альтернативы х, у, для которых А (х) > А (у) Vi Ф i0 и
Ло (*)</,•„ (у)-
С помощью введенных выше определений получаем
/1 при /,(□:) = /; (у) Vi = l..п,
рЛ (х> У) = {
(0 в остальных случаях,
J1 при Л («)>/< (у). « = 1...3i0:	/,• (ж)>/< (у),
y) = U	°	’
(О в остальных случаях.
Отметим, что альтернативы, недоминируемые при описанном
здесь отношении предпочтения, называют эффективными или
оптимальными по Парето для набора функций А (х), 1=1,. . ., п.
Рассмотрим теперь некоторые свойства введенных
нечетких отношений peR и р.д.
Нетрудно убедиться в том, что нечеткие отношения
и рефлексивны и симметричны (см. определение
этих свойств в п. 1.2.4). Действительно,
1-	x) = Pr(x> х)~	^) = 1, поскольку
исходное н. о. п. рефлексивно по определению.
2.	Симметричность обоих отношений следует из самих
их определений.
Столь же просто показать, что н. о. п. рд антирефлек-
сивно и антисимметрично. Действительно,
1. p*r(x, гс) = О, так как исходное н. о. п. р.й реф-
лексивно, т. е. (х, х)1 при любом х £ X.
2. Пусть ^(ж, у)>0, т. е. рд(ж, у)—рй(у, ж)>0.
Тогда pr (у, х) = 0, а это и означает антисимметрич-
ность этого отношения.
Покажем теперь, что если исходное н. о. п. на
множестве X транзитивно, то тем же свойствОхМ обладают
соответствующие нечеткие отношения р% и pR.
Теорема 3.2.1. Если н. о. п. на X транзитивно, то
транзитивно и соответствующее нечеткое отношение р%.
Заметим, что из этой теоремы и из рассмотренных
выше свойств отношения pr вытекает, что в условиях
теоремы peR представляет собой нечеткое отношение эквива-
лентности (рефлективное, симметричное и транзитивное).
122 ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
Доказательство. Допустим, что в условиях
теоремы отношение не является транзитивным. По
определению транзитивности (п. 1.2.4) это допущение
означает, что найдутся такие х, у, zf*X, для которых
выполнено неравенство
Ня(«, у) < min {^(ж, z), p£(z, у)}.	(3.2.1)
Допустим теперь, что рд(я,	х) (в против-
ном случае доказательство совершенно аналогично).
Тогда из определения рЪ получаем, что	у) —
= pR(y, х). Пользуясь этим равенством, запишем неравен-
ство (3.2.1) в виде
Итг(£Л *) < min (х, z), p.'E(z, у)}.	(3.2.2)
Поскольку ря симметрично, то из (3.2.2) получаем
НЙ(У» X)<min {^(у. z),	х)}.	(3.2.3)
Далее, из определения рЪ следует, что
Р-Ш гХнй(г/, г), [Ifc(z, z)<ns(z, х),
т. е.
min{^(y, z),	х)} < min (р.й(у, z), p.fi(z, ж)}.
(3.2.4)
Из неравенств (3.2.3) и (3.2.4) заключаем, что
НЙ(У» ^)<min(}iB(i/) z), fiB(z, ж)}.
Последнее неравенство противоречит условию транзитив-
ности исходного н. о. п. Этим противоречием завер-
шается доказательство теоремы.
Теорема 3.2.2. Если н. о. п. на X транзи-
тивно, то транзитивно и соответствующее нечеткое от-
ношение, строгого предпочтения ^r.
Доказательство. Допустим, что в условиях
теоремы отношение рл не является транзитивным. Это
означает, что найдутся х, у, z £ X, для которых выпол-
нено неравенство
У) < min {р-в (ж, z), p.‘R(z, у)}.	(3.2.5)
3.21 НЕЧЕТКИЕ ОТНОШЕНИЯ ПРЕДПОЧТЕНИЙ ^23
Поскольку у)^0 при любых х, у(*Х, то, поль-
зуясь определением получаем из (3.2.5)
НИ*. z) = pR(x, 2)—flB(2, ж)>0,	(3.2.6)
pMz> y) = Mz> У) —РЯ(У» z)>°-	(3.2.7)
а) Допустим, что pR(x,	&)• Тогда, учиты-
вая транзитивность |1Д, можно записать неравенство
МУ’ ж)>Нв(®» у) > min {jib (ж, г), цв(2, у)}. (3.2.8)
Из транзитивности и неравенства (3.2.6) следует, что
z)>Mz> *)>mm{|xK(z, у), ?R(y, ж)}. (3.2.9)
Из (3.2.8) и (3.2.9) получаем
РВ(Ж,	2)>min{[iB(2, у),	y.R(x,	г)},	(3.2.10)
М®’ Z)>MZ-	У)>	(3.2.11)
и, следовательно, из (3.2.8) можно заключить, что
У)>М2’	У)-	(3.2.12)
Далее, поскольку транзитивно, то
(iB(y, 2)>тт{Ив(у, х), |1в(ж, г)).
Отсюда, учитывая неравенство (3.2.11) и принятое выше
допущение о том, что pR(x, У)^^К(У^ я), получаем
МУ’ г) > min {МУ> ж)> P-b(z> У)}>
>min([iB(x) у), (iB(2, у)}.
Из последнего неравенства и неравенства (3.2.12) сле-
дует неравенство р.л(у, z)^^R(z, у), которое противо-
речит (3.2.7).
Таким образом, мы показали, что из (3.2.5) следует
невозможность неравенства pR(x, у)<^р«д(у, х).
б) Допустим, что рл(я, у)>^д(у, х). Тогда
ня(^> у) = рй(я;. у) — Му> ж)>°
124 прМпочтенйя на множестве АЛЬТЕРНАТИВ [ГЛ. i
и нёравёнство (3.2.5) можно записать в виде
У) —	х)<
<тт([(1в(х, z) — р.й(г, ж)],
[Mz> *)]}.	(3-2-13)
Допустим, что pR(y, z)^p.R(y, х). Тогда в (3.2.13)
величину рй(у, z) можно заменить на величину (хд(у, ж):
У) —	z)~ Mz> ®)],
[Mz> У> — У-ц(У> *)]}•	(3.2.14)
Прибавив pR(y, x) к обеим частям этого неравенства,
получим
М®» к)<ш’п{[ня(®» z) +
+ (ня(у> ®) —Ря(г> ж))], HB(Z’ г/)}-	(3.2.15)
Здесь следует рассмотреть две возможности:
1. Если р.д(у, х)— pR(z, я)<^0, то из (3.2.15) по-
лучаем неравенство
М®»	z), {iB(z, у)},
которое противоречит транзитивности р.й,
2. Если р.й (у, х) —	(z, х) > 0, то, учитывая тран-
зитивность р.й> можно записать
Ря(У’ *)>MZ> *)>тт{цв(г, У)> ?я(У> *)},
откуда сразу следует неравенство pR(y, x)>pR(z, у),
которое противоречит допущению о том, что р.й (у, z)
^^R(yy х), и неравенству (3.2.7).
Таким образом, мы показали, что при условии
У)>Рц(У> х) из неравенств (3.2.6) и (3.2.7) вы-
текает неравенство
Ия(г/>	*)•
(3.2.16)
3.21 НЕЧЕТКИЕ ОТНОШЕНИЯ ПРЕДПОЧТЕНИЙ 1^5
Рассуждая аналогичным образом, можно показать,
что при условии рв(х, у)>рй(у, х) из (3.2.6) и (3.2.7)
вытекает неравенство
Mz> «ХМ?- х).	(3.2.17)
Далее, пользуясь неравенствами
РД(У> z)>min{{iB(y, х), ря(х, z)]t
Pb(z> *)>min{Mz> У)>	х)},
из (3.2.16) и (3.2.17) получаем неравенства
Р-В(У> Z»?AX’ z)> ?-r(z’ xY>Vr(z’ у)>
которые, как нетрудно видеть, противоречат неравен-
ствам (3.2.6) и (3.2.7). Этим противоречием завершается
доказательство теоремы 3.2.2.
Напомним, что обычное рефлексивное и транзитив-
ное отношение на множестве X называется квазипоряд-
ком на X, а антирефлективное, антисимметричное и
транзитивное отношение называется строгим порядком
на X (см. книгу [18]). Пользуясь этой терминологией
и проводя аналогию с обычными отношениями, теоремы
3.2.1 и 3.2.2 можно сформулировать следующим образом.
Теорема 3.2.3. Если — нечеткий квазипорядок
на множестве X, то peR— соответствующее нечеткое
отношение эквивалентности, a ph— соответствующий
нечеткий строгий порядок на X.
3.2.2. Линейность нечетких отношений. Важным
свойством заданного на множестве X' отношения пред-
почтения является его линейность. Отношение R на
X называется линейным, если этим отношением или
обратным к нему отношением связаны любые две аль-
тернативы данного множества. Иными словами, при
линейном отношении на множестве X нет не сравни-
мых между собой по предпочтению альтернатив.
Нетрудно понять, что линейность обычного отно-
шения эквивалентна условию
AU *XX,
12Й ПРЕДПОЧТЁНЙЙ ЙА ЙЙОЙСЁСТВЕ АЛЬТЕРНАЦИЙ ЬгЯ. $
где Я”1 — обратное к R отношение. Иначе это условие
можно записать в следующем виде:
xRy => yRx,
где R — дополнение R в X X X, или с помощью харак-
теристических функций
М*’ У) = °=>М^ *) = 1.
В случае нечеткого отношения однозначно можно
определить лишь полное отсутствие линейности: не-
четкое отношение pR не является линейным тогда и
только тогда, когда найдутся такие альтернативы
х, у(*Х, для которых выполнено равенство
Нй(®» y) = ?R(y, я) = 0,
где р.д(я, у) — функция принадлежности данного нечет-
кого отношения.
Свойство же линейности нечеткого отношения можно
понимать более широко, чем в случае обычного отноше-
ния, в силу того, что функция принадлежности такого
отношения может принимать кроме 0 и 1 любые про-
межуточные значения. Пользуясь этим, можно ввести
понятие степени линейности отношения.
Определение 3.2.1 [39]. Пусть X — некоторое
число из интервала [0, 1]. Нечеткое отношение pR
называется к-линейным, если его функция принадлеж-
ности удовлетворяет условию
тах{|хд(;г, у), ?в(у, ®)}>Х
при любых X, у(<Х.
Таким образом, если н. о. п. является, например,
0,7-линейным, то из каждых двух альтернатив по край-
ней мере одна не хуже другой со степенью, большей 0,7.
Рассмотрим еще один вид линейности нечеткого
отношения, которым будем пользоваться в дальнейшем.
Определение 3.2.2 [39]. Нечеткое отношение
называется сильно линейным, если его функция при-
надлежности удовлетворяет условию
тах{р.д(а;, у), pR(y, x)} = i
при любых X, у(*Х.
3.2]
НЕЧЕТКИЕ ОТНОШЕНИЯ ПРЕДПОЧТЕНИЙ
127
Иначе свойство сильной линейности можно опреде-
лить следующим образом:
Ьг У> > Рв (У> х) => Ив (ж> У) =1	(3.2.18)
при любых X, У^Х.
Чтобы пояснить смысл свойства сильной линейности,
покажем, что оно эквивалентно условию
М®’ у) — 1 — Р-Ш ж)	(3.2.19)
где pi* — соответствующее нечеткое отношение строгого
предпочтения. Действительно, если выполнено (3.2.18),
то по определению р.* получаем р,* (у, х) = 0, т. е. усло-
вие (3.2.19) также выполнено. Обратно, если выполнено
(3.2.19) и [хй(®, г/)>рй(у, х), то ^R(y, х) — 0 и
рд(я, у) = 1, т. е. выполнено (3.2.18).
Обратимся теперь к условию сильной линейности
в форме (3.2.19). Нетрудно понять, что его можно запи-
сать в виде
Д“1 = (ХхХ)\Л\	(3.2.20)
где R"1 — обратное к R нечеткое отношение, a R9 — соот-
ветствующее R нечеткое отношение строгого предпо-
чтения.
Смысл же (3.2.20) можно пояснить следующим обра-
зом. Если, например, альтернативы хну таковы, что х
строго лучше (предпочтительнее) у (х$-у) со степенью 1,
то (у, х) $ /Г1, т. е. у х ни с какой положительной
степенью. Если же х^у, то (у, x)f*R~\ т. е. у^х
со степенью 1. Если, наконец, х^—у со степенью а, то
со степенью 1 — а выполнено предпочтение у х. Таким
образом, по своему смыслу сильная линейность в наи-
большей степени аналогична свойству линейности обыч-
ного отношения.
Легко видеть, что из определения сильной линей-
ности следует, что при сильно линейном нечетком отно-
шении R на множестве X для любых двух альтерна-
тив х^ х2 выполнено по крайней мере одно из равенств
р.д (хх, я2) = 1,	(х2, Х^ — 1.
Еще одно свойство сильно линейного нечеткого отно-
шения состоит в том, что соответствующие ему нечет-
128 ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
кие отношения R1 и Re совпадают. Действительно,
допустим, что для некоторой пары (х, у)£Х выпол-
нено	#)• Тогда из определения 3.2.2
следует, что pR(x, z/) = l, а из определения полу-
чаем y) — pR(y, х). В силу симметричности р.*
в случае ?R(x, y)^R(y, х) имеем ^(х, y) = l>.R(x, у)
и, следовательно,
y) = min(|xB(a:, У)>	«)} = !хя(^ У)-
В дальнейшем мы будем пользоваться двумя типами
линейности нечеткого отношения: 0-линейностью, ко-
торую будем называть слабой, и сильной линейностью.
Как следует из определения 3.2.1, слабую линейность
можно определить и следующим образом: н. о. п. pR
на X называется слабо линейным, если оно обладает
свойством
М®* !/)=°=>!хв(г/> ж)>°
при любых Ж, у£Х.
В заключение данного раздела приведем для иллю-
страции простые примеры нечетких отношений, обла-
дающих линейностью различных типов. Будем считать,
что множество X состоит из четырех элементов.
1. 0,5-линейное нечеткое отношение:*
(1
О
0,2
0*8
0,55	0,6	0	\
1	0,3	1	I
0,6	1	0,4	I
1	0,7	1	/
2. Сильно линейное отношение:
(1	0,2	1	0	\
11	1 0,5 |
0	0,8	1	1	I-
1	1	0,3	1	/
3.2.3. Нечеткое подмножество недоминируемых аль-
тернатив. Обратимся теперь к задаче рационального
выбора альтернатив из множества X, на котором задано
нечеткое отношение предпочтения рч: ХхХ -> [0, 1].
Как уже говорилось во введении к данной главе, в слу-
чае, когда информация о ситуации принятия решений
3.2]
НЕЧЕТКИЕ ОТНОШЕНИЯ ПРЕДПОЧТЕНИЙ
129
описана в форме обычного отношения предпочтения,
рациональным естественно считать выбор недоминируе-
мых альтернатив. Математически такая задача сво-
дится к выделению в заданном множестве X подмно-
жества недоминируемых альтернатив.
В этом разделе мы сделаем попытку применить по-
добный подход к задаче принятия решений при нечетко
описанном отношении предпочтения на множестве аль-
тернатив. При этом мы рассмотрим сначала задачи,
в которых само множество альтернатив описано четко,
т. е. как обычное множество, а затем обратимся к более
общему случаю с нечетким множеством альтернатив.
Итак, пусть X — обычное (четко описанное) мно-
жество альтернатив и — заданное на нем нечеткое
отношение нестрогого предпочтения. Пусть, кроме
того, р-* — соответствующее нечеткое отношение
строгого предпочтения, введенное в п. 3.2.1. Попытаемся
определить подмножество недоминируемых альтерна-
тив множества (X, Заметим, что поскольку исход-
ное отношение предпочтения — нечеткое, то естественно
ожидать, что и соответствующее подмножество недо-
минируемых альтернатив окажется нечетким.
Предполагаемое ниже определение подмножества
недоминируемых альтернатив опирается на следую-
щие рассуждения. Согласно определению отношения
для любых альтернатив х, у £Х величина р* (ж, у)
есть степень, с которой альтернатива у доминируется
альтернативой х. Следовательно, при фиксированном
у £ X определенную на X функцию p*R (у, х) можно рас-
сматривать как функцию принадлежности нечеткого
множества «всех» альтернатив х, которые строго доми-
нируются альтернативой у. Пусть, например, степень
принадлежности альтернативы xQ этому множеству
(соответствующему некоторому фиксированному у)
равна 0,3. Это означает, что xQ доминируется альтерна-
тивой у со степенью 0,3.
Нетрудно понять, что множество «всех» альтерна-
тив х, которые не доминируются альтернативой у, пред-
ставляет собой дополнение в X введенного множества
р* (у, х). Согласно определению дополнения (п. 1.1.2)
Э С. А. Орловский
130
ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
получаем, что это новое нечеткое множество описыва-
ется функцией принадлежности вида
Х£х-	(3.2.21)
Если, например, р’(у, х) = 0,3, то со степенью 0,7
альтернатива х не доминируется альтернативой у.
Теперь ясно, что для выделения в X подмножества
«всех» альтернатив, каждая из которых не доминиру-
ется ни одной альтернативой из X, нужно взять пере-
сечение нечетких множеств вида (3.2.21) по всем у£Х.
Это пересечение мы и назовем нечетким подмножеством
недоминируемых альтернатив и обозначим его р."-*-.
Согласно определению пересечения нечетких мно-
жеств (п. 1.1.2) получаем следующее выражение для
функции принадлежности этого множества:
pH- д. (ж) = inf [1 — р’ (у, ж)], X е X,
ИЛИ
liH-A.(®) = l-supf*’(y, х), х£Х. (3.2.22)
Определение 3.2.3 [39]. Пусть X — множество
альтернатив и рл — заданное на нем нечеткое отношение
предпочтения. Нечеткое подмножество недоминируемых
альтернатив множества (X, рд) описывается функцией
принадлежности (3.2.22).
Значение р®-д- (х) представляет собой степень, с кото-
рой альтернатива х не доминируется ни одной из альтер-
натив множества X. Пусть ри-д-(ж0) = а для некоторой
альтернативы ж0. Тогда ж0 может доминироваться дру-
гими альтернативами, но со степенью не выше 1 — а.
Действительно, при этом
sup	Жо) = 1—а
и, следовательно, (у, xQ) 1 — а для любой альтерна-
тивы у(*Х.
Пользуясь определением нечеткого отношения р.*,
нетрудно показать, что
sup (у, X) = sup [ря (у, х) — |ХЙ (х, у)]	(3.2.23)
9.21
НЁЧЁТКИЁ ОТНОШЕНИЯ ПРЕДПОЧТЕНИЙ
131
при любом xQXt Действительно, пусть х £ X — произ-
вольно выбранная альтернатива. Введем множества
У1(ж) = {у|у^Х, рй(у, аг)>|*к(а;* у)}>
у2(ж)={у|у6-Х'. v-R(y> *)<Мг> у));
Пользуясь тем, что У1 (х) U У2 (х) — X при любом х £ Х^
запишем (3.2.23) в следующей форме:
supp* (у, ж) =
= max { sup р» (у, ж), sup р* (у, х)}. (3.2.24)
yer’w	yen*)
Далее, опираясь на определение рй, получаем из
(3.2.24)
supply, х) =
= max{ sup [ря(у, ж) — рй(ж, у)], 0} =
= max{ sup [рй(у, ж) —рй(ж, у)],
sup [РВ(У, *) —РЕ(ж, у)]} =
= suP[PB(y> ж) — Рл(ж> к)].
Уб*
Равенство (3.2.23) позволяет описать подмножество
недоминируемых альтернатив функцией принадлеж-
ности вида
рн-д-(ж) = 1—sup[pB(y, ж) — рй(ж, у)], (3.2.25)
где р.д — исходное н. о. п. на множестве X. Выражение
(3.2.25) можно рассматривать как способ обработки исход-
ной нечеткой информации, заданной в форме н. о. п.
для выделения в X подмножества недоминируемых
альтернатив.
Поскольку величина р«д,д,(^) есть степень «недомини-
руемости» альтернативы х, то рациональным при задан*
ной нечеткой информации естественно считать выбор
альтернатив, имеющих по возможности большую сте-
пень принадлежности нечеткому множеству т. е. тех
9*
132 ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
альтернатив, которые дают значение функции н1д' (х),
по возможности более близкое к величине
SUP Hr- Д- (®) = 1 — inf sup [рв (у, х) — |ЛЙ (х, у)].
Альтернативы, дающие в точности эту величину,
т. е. элементы множества
Хн-д- = (х | X £ X,	д- (х) = sup р.н-д- (z)},
мы будем называть максимальными недоминируемыми
альтернативами множества (X, рй).
Пример 3.2.1. Пусть в конечном множестве Х={ж1,
z2, х8, Xj} задано н. о. и. вида
		Xi	х2		*4
	*1	1	0,2	0,3	0,1
Pfl	Xj) —	*з	0,5 0,1	1 0,6	0,2 1	0,6 0,3
	*4	0,6	о,1	0,5	1
Пользуясь введенными	выше	определениями,			получаем
	*1	*2	ж3	*4
	0	0	0,2	0
№<> *,) = *2	0,3 0	0 0,4	0 0	0,5 0
	0,5	0	0,2	0
И				
	я2	х8		*4
Hr ”• (*<) =°.5	0,6	0,8		0,5
Отсюда видно, что наибольшую степень недоминируемости,
равную 0,8, имеет альтернатива z3, поэтому выбор ее в качестве
решения следует считать рациональным в рамках рассматри-
ваемого подхода.
3.2.4. Четко недоминируемые альтернативы и их
свойства. В этом разделе мы рассмотрим задачи ра-
ционального выбора альтернатив, в которых множе-
3.21 НЁЧЕ*ГКЙЕ ОТНОШЕНИЙ ПРЕДПОЧТЕНИЙ
ство недоминируемых альтернатив представляет собой
нормальное нечеткое подмножество множества X, т. е.
функция принадлежности этого подмножества обладает
свойством
sup р“ д- (х) = 1.
В этом случае для любой альтернативы х из множе-
ства Хн-Д- максимальных недоминируемых альтернатив
выполнено (х) — 1, т. е. степень недоминируемости
любой такой альтернативы равна 1. Иными словами,
для любой	и любой альтернативы у(*Х при
этом выполнено равенство р* (г/, х) — 0, т. е. ни одна
Альтернатива не доминирует с положительной степенью
данную альтернативу х.
Имея это в виду, такие альтернативы мы будем
называть четко недоминируемыми (т. е. со степенью 1
недоминируемыми) или, сокращенно, ч. н. д. альтерна-
тивами, а множество ч. н. д. альтернатив будем обозна-
чать Хч н-Д-. Таким образом,
ХЧ.Н.Д. —	(х) — 1).
Отметим, что ч. н. д. альтернативы представляют осо-
бый интерес в анализируемых здесь задачах рациональ-
ного выбора, поскольку множество	можно рас-
сматривать как в некотором смысле четкое решение
нечетко поставленной задачи. Разумеется, не всякая
задача имеет такое решение; некоторые достаточные
условия его существования будут сформулированы
в следующем разделе. Здесь же мы изучим некоторые
полезные свойства ч. н. д. альтернатив.
Рассмотрим сначала вопрос об эквивалентности
ч. н. д. альтернатив. Отметим прежде всего, что этот
вопрос весьма важен в задаче рационального выбора.
Как следует из приведенного ниже равенства (3.2.26),
ч. н. д. альтернативы могут быть сравнимыми лишь
по отношению квазиэквивалентности. Если они не экви-
валентны друг другу, то для обоснованного выбора
конкретной альтернативы необходимо привлекать до-
полнительную информацию, внешнюю по отношению
к изучаемой математической модели.
134 ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРЙАТЙЙ [ГЛ. 3
С другой стороны, если нее ч. и* д. альтернативы
эквивалентны друг другу со степенью 1, то такой ин-
формации не требуется и обоснованным (рациональ-
ным) является выбор любой из них. В действитель-
ности этот случай означает, что в рассматриваемой
модели уже имеется информация, достаточная для
рационального выбора конкретной альтернативы.
Эквивалентность ч. н. д. альтернатив с положитель-
ной степенью, меньшей 1, — промежуточная ситуа-
ция, в которой для обоснованного выбора конкретной
альтернативы требуется привлекать меньше дополни-
тельной информации по сравнению со случаем полной
неэквивалентности ч. н. д. альтернатив. Заметим, что
в этом смысле минимальную степень эквивалентности
ч. н. д. альтернатив можно рассматривать как некоторую
меру количества имеющейся в задаче информации, не-
обходимой для рационального выбора конкретной
альтернативы.
Как следует из определений множеств Хч-Н-Д- и д\
для любой ч. н. д. альтернативы (любого я£Хч-н д )
выполняется равенство
supp-^ (у, я) = 0,	(3.2.26)
Уб*
в котором р.*—соответствующее р-й нечеткое отношение
строгого предпочтения. Отсюда можно заключить, что
для любых xv я2£Хч,н*д* выполнено
р-д (яр х2) = р-д (я2, х^) -= 0.	(3.2.27)
Из определения р* следует, что равенство (3.2.27)
эквивалентно равенству
р-д {х^ х2) — р-д жх),
но тогда
p-'fo, z2) = max(l —p^fo, я2), р-д (ягр я2))>0,5,
т. е. любые две ч. н. д. альтернативы связаны отноше-
нием безразличия со степенью, не меньшей 0,5.
По определению нечеткого отношения р.* получаем
Р'я (ж1> жг)= P-r (xi> хъ)= P-r (ж2» ж1)	(3.2.28)
для любых xv я2£Хч-н-д-.
3.2]
НЕЧЕТКИЕ ОТНОШЕНИЯ ПРЕДПОЧТЕНИЙ
135
При произвольном н. о. п. р.д может оказаться, что
Р^(#р я2) = 0 при я2(«Хч-н-д-, т. е. ч. н. д. альтер-
нативы могут не быть эквивалентными ни с какой поло-
жительной степенью. Заметим, что в этом случае
pj(^v ж2) = 1, т- е- и х2 определенно не сравнимы
друг с другом. Однако это не так, если обладает
свойством линейности (см. п. 3.2.2). Рассмотрим два
типа линейности н. о. п., введенные в п. 3.2.2.
1. А-линейное н. о. п. рьд. Если р.д Х-линейно
и я2£Хч-н-д-, то из определения X-линейности и из
равенства (3.2.28) следует, что
Ид (*^1» жг) >
Иными словами, при Х-линейном н. о. п. р.д любые две
ч. н. д. альтернативы эквивалентны со степенью, боль-
шей X. В частности, при слабо линейном н. о. п. р.д любые
две ч. н. д. альтернативы эквивалентны с положительной
степенью.
Как уже отмечалось выше, величину
1= inf ^(^р х2)
^,х2е^ч-н-д-
можно рассматривать как меру количества имеющейся
в задаче информации, необходимой для однозначного
выбора альтернатив. Заметим, что эту же величину
можно считать и мерой линейности н. о. п. рд, поскольку,
как будет видно ниже, для сильно линейного у.д она
равна 1, т. е. своему максимальному значению.
2. С и л ь н о л и н е й ное н. о. п. |1д. Если н. о. п. рьд
сильно линейно и хг, я2£Хч н-д-, то из определения
сильной линейности и из равенства (3.2.28) следует, что
№r(XV ^2) —
т. е. любые две ч. н. д. альтернативы эквивалентны со
степенью 1 (т. е. определенно эквивалентны). Это озна-
чает, что выбор любой из них является обоснованным
в данной задаче.
Таким образом, сильно линейное н. о. п. р.д такое,
что в множестве (X, р.д) имеются ч. н. д. альтернативы,
136
ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
содержит в себе всю информацию, достаточную для
рационального выбора конкретной альтернативы.
Ч. н. д. альтернативы, соответствующие сильно ли-
нейному н. о. п. р.д, обладают еще и следующими важ-
ными свойствами.
Теорема 3.2.4. Если р.й— сильно линейное н. о. п.
на множестве X, то для любой альтернативы я0 £ Хч-Н,д-
равенство рл(ж0, х) = 1 выполняется для любой альтер-
нативы х£Х.
Доказательство. Допустим, что при некотором
х' £ X выполнено неравенство
Р'я (^0» Х ) < 1 •
Тогда из определения сильной линейности (п. 3.2.2)
получаем, что pR(x', xQ) = i. Из этих двух неравенств
заключаем, что pR(x', я0)>0, а это невозможно, по-
скольку я0£Хч-н-д-.
Теорема 3.2.5. Если pR— сильно линейное тран-
зитивное н. о. п. на множестве X и у (£Хч-н-д-, то
р.*(я, &ля любой альтернативы х.
Доказательство. Если у^Хч-Н-Д-, то р^-д-(у)<1.
Отсюда, пользуясь определением р.^-д-, можно заклю-
чить, что найдется такая альтернатива z £ X, для которой
^(z, у)>0.	(3.2.29)
Допустим, что для некоторого я£Хч*н-д* выполнено
равенство
у) = 0.	(3.2.30)
Кроме того, по определению ч. н. д. альтернативы имеет
место равенство р.’(у, я) = 0. Из этих двух равенств,
из определения отношения р.* и при условии сильной
линейности заключаем, что
PrOo ж) = 1*н(а;’ у) = 1-	(3.2.31)
Поскольку р.д транзитивно по условию теоремы, то
отношение р.^ тоже транзитивно (теорема 3.2.2). Отсюда,
3.2]
НЕЧЕТКИЕ ОТНОШЕНИЯ ПРЕДПОЧТЕНИЙ
137
пользуясь допущением (3.2.30) и неравенством (3.2.29),
получаем
0>тт{[х»(а;, z), р-* (z, у)} yz£Xt
т. е. У) — ® ПРИ ЛИ)бом zQX, а это противоречит
(3.2.29).
По сути дела, теорема 3.2.5 утверждает, что при
сильно линейном транзитивном н. о. п. любая ч. н. д.
альтернатива строго с положительной степенью домини-
рует любую альтернативу, не входящую в множе-
ство Хч-Н-Д*.
Следствие из теоремы 3.2.5. Если, н. о. п.
сильно линейно и транзитивно, х0^Хч-н-д- и для неко-
торой альтернативы х^Х выполняется условие
р.‘(я, ж0) = 1, то я£Хч-н-д*.
Доказательство. Из того, что peR(x, ж0) = 1,
вытекает, что р*(я0, х) = 0. Отсюда получаем, что
х £ X4'н-д-, поскольку в противном случае из теоремы 3.2.5
следовало бы р.^(а:0, я)>0.
Это следствие и теорема 3.2.5 позволяют утверждать,
что при сильно линейном транзитивном н. о. п. pR на
множестве X ч.н.д. альтернативы составляют класс
эквивалентности со степенью 1, причем любой эле-
мент этого класса доминирует с положительной сте-
пенью любую альтернативу, не входящую в этот
класс.
3.2.5. Условия существования четко недоминируе-
мых альтернатив. Мы сформулируем здесь условия
существования ч. н. д. альтернатив двух типов. В усло-
виях первого типа заданное н. о. п. не предполагается
транзитивным, однако на функцию принадлежности
этого н. о. п. и на само множество альтернатив X накла-
дываются некоторые топологические условия и требо-
вания выпуклости. Условия второго типа будут сфор-
мулированы лишь для конечного множества X и тран-
зитивного н. о. п. р.й.
Прежде чем переходить к обсуждению условий
первого типа, введем некоторые вспомогательные опре-
деления.
138
ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
Пара (ж0, у0) £ X называется седловой точкой функ-
ции ср (х, у) (максимум по х, минимум по у), если при
любых х, у £Х выполнены следующие неравенства:
У0) ><?(*, У0)-	(3.2.32)
Если (ж0, у0) и (ж1, у1) — две седловые точки функ-
ции ср (я, у), то (ж0, у1) и (х1, у0) — тоже седловые точки
этой функции и, кроме того,
?(*“> У1) = ?(а;0> г/°) = <р(а;1>	=	У°). (3.2.33)
Это равенство непосредственно вытекает из определе-
ния седловой точки.
Функцию <р(я, у) будем называть антисимметричной,
если при любых х, у (<Х выполняется равенство
<р(а:, у) = — <?(у, х).
Ниже мы будем опираться на следующие свойства
антисимметричной функции.
Если (ж°, у0) — седловая точка антисимметричной
функции <$(х, у), то (х°, ж0) и (у0, у0) — тоже седловые
точки этой функции. Действительно, по определению
седловой точки имеют место неравенства
Ж°)><р(а:0, у°)^<?(у°, У°).	(3.2.34)
С другой стороны, используя это определение и анти-
симметричность функции <р(я, у), можно записать
?(я°, я°Хср(у0, я°)<ср(у°, у0).	(3.2.35)
Из (3.2.34) и (3.2.35) следует, что
ср (я0, ж°) = ^(ж°, у°) = ср(у°, у0),
т. е. (ж0, ж0) и (у0, у0) — седловые точки функции ср (х, у).
Наконец, поскольку функция ср (х, у) принимает одно
и то же значение во всех своих седловых точках,
получаем
ср (ж0, х°) = —<р(я°, я°) = 0,
т. е. в любой седловой точке значение антисимметрич-
ной функции равно нулю.
Обратимся теперь к условиям существования ч. н. д.
альтернатив в множестве X с заданным в нем н. о. п.
3.21 НЕЧЕТКИЕ ОТНОШЕНИЯ ПРЕДПОЧТЕНИЙ	139
Пусть х f X — ч. и. д. альтернатива в множестве (X,
Согласно определению это означает, что
рв-д-(а:) = 1 — sup[pB(p, х) — цв(ж, у)] = 1,
Уб*
т. е.
sup[pB(y, х) — ^{х, у)] = О = рЕ(а: — х) — рв(х, х).
У6Х
Отсюда получаем
Р-В(.У, «) — Р-ц(х, у)<0	(3.2.36)
при любом у £ X. Поскольку [р.д (у, х) — рв (х, Z/)] —
антисимметричная функция, то из (3.2.36) можно заклю-
чить, что пара (х, х) — седловая точка этой функции
(максимум по у, минимум по х).
Верно и легко проверяемое обратное утверждение:
если пара (х, х) — седловая точка функции [р.д(г/, х)—
—	(я, z/)] на множестве X X X, то х — ч. н. д. альтер-
натива в множестве (X, р.д).
Таким образом, справедлива следующая
Теорема 3.2.6. Если р.д: ХхХ->[0, 1] — н. о. п.
на множестве альтернатив X, то xQ £ X — ч. н. д.
альтернатива в множестве (X, р.д) тогда и только
тогда, когда пара (я0, ж0) — седловая точка функции
[Рт? (х> У) — Р*я (2/, ж)] (максимум по х, минимум по у).
Из этой теоремы и Отмеченных выше свойств анти-
симметричной функции непосредственно вытекает сле-
дующее
Следствие. Элементы х0, yQ^X являются ч. н. д.
альтернативами в множестве (X, р.д) тогда и только
тогда, когда пара (ж0, z/0)— седловая точка функции
[Ря (х> У) — Р*я ж)] (максимум по х, минимум по у)
в множестве X X X.
Из теоремы 3.2.6 следует, что любые условия, доста-
точные для существования седловой точки функции
[Р'я (ж» У) — Рт? (У» ж)] на множестве X X X, достаточны
и для существования ч. н. д. альтернатив в множестве
(X, р.д). Различные достаточные условия существования
седловой точки излагаются во многих монографиях по

140 ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ (ГЛ. 3
теории игр (см., например, [35]). Для иллюстрации при-
ведем здесь следующие относительно простые условия.
Теорема 3.2.7. Если множество X выпукло и ком-
пактно, функция pR(x, у) непрерывна на тихоновском
произведении XXX, квазивогнута по х при любом у £ X
и квазивыпукла по у при любом xQX, то эта функция
имеет по крайней мере одну седловую точку в множе-
стве ХхХ и, следовательно, в множестве (X,
имеется по крайней мере одна ч. н. д. альтернатива.
Напомним, что функция <? (х) называется квазивогну-
той, если множество {х | х £ X, ср(я)^к} выпукло в X
при любом К > 0, и квазивыпуклой, если множество
{я'| х £ X, <р(яХ^Х) выпукло при любом Х>0.
В заключение этого раздела сформулируем простое
достаточное условие существования ч. н. д. альтернатив
в множестве X с заданным на нем транзитивным н. о. п.
(условия второго типа). Для этого введем в мно-
жестве X обычное отношение вида
8 = {(х, у)\х, у£Х, р.*(а:, г/)>0}.
Легко убедиться в том, что если н. о. п. транзи-
тивно, то S антирефлексивно и транзитивно и, следо-
вательно, конечное множество (X, S) содержит альтер-
нативу х0, обладающую свойством (у, xQ) S при любом
уех.
Для этой альтернативы получаем
Ня(У> ®о) = °
при любом у(*Х, и поэтому £0£Хч,п,д<. Таким образом,
мы получили следующее достаточное условие.
Теорема 3.2.8. В конечном множестве X с задан-
ным на нем транзитивным н. о. п. имеется по край-
ней мере одна ч. н. д. альтернатива.
Заметим, что из этой теоремы и из теоремы 3.2.6
следует, что транзитивность н. о. п. — достаточное
условие существования седловой точки функции
(х, у) — pR(y, я)] в конечном множестве X X X.
Приведем иллюстративный пример транзитивного
н. о. п. в конечном множестве X.
3.2]
НЕЧЕТКИЕ ОТНОШЕНИЯ ПРЕДПОЧТЕНИЙ
141
Пример 3.2.2. Пусть множество альтернатив X состоит
из пяти элементов:	х2, х3, х4> хь. Матрица и. о. п.
имеет вид
(1	0,7	0,8	0,5	0,5\
0	0	0,3	0	0,2 \
0	0,7	1	0’	0,2 I
0,6	1	0,9	1	0,6 Г
0	0	0	0	1 /
Построим матрицу соответствующего нечеткого отношения
строгого предпочтения:
(0	0,7	0,8	0	0,5’
0	0	0	0	0,2
О	0,4	0	0	0,2
0,1	1	0,9	0	0,6
О	0	0	0	0 ,
Функция принадлежности нечеткого множества недомини-
руемых альтернатив имеет вид
^1 х2 х3 х4 х6
д. (ж) =0,9	0	0,1	1	0,4
Таким образом, в рассматриваемом множестве (X, рьд) имеется
единственная ч. н. д. альтернатива х4 д* (х4) = 1). Заметим,
что эта альтернатива доминирует с положительной степенью
все остальные альтернативы, т. е. Pr(x4, жу)>0, / = 1, 2, 3, 5.
3.2.6. Смешанное расширение задачи принятия ре-
шений. Если требующиеся в теореме 3.2.7 условия
вогнутости-выпуклости функции (я, у) не выполнены,
то в множестве (X, может, вообще говоря, не быть
ни одной ч. н. д. альтернативы или, что эквивалентно
предыдущему, функция [рд(я, у) — pR(y, я)] может
не иметь ни одной седловой точки.
В этих случаях в теории игр используется следую-
щий прием. Вместо множества X рассматривается его
расширение («выпуклая оболочка»): множество X все-
142 ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
возможных распределений вероятности (смешанных стра-
тегий) на X, а вместо заданной функции ср (х, у) —
функция
Ф(Л 0= $$?(*, y)dP(x)dQ(y),
XX
определенная на множестве %ХХ.
Значение ф (Р, Q) новой функции при фиксирован-
ных распределениях Р (х) и Q (у) представляет собой
математическое ожидание значений функции ср (х, у).
Интерпретировать такое расширение можно, например,
следующим образом: величина ф (Р, Q) представляет
собой средний «выигрыш», получаемый при многократ-
ных выборах стратегий с вероятностями, соответствую-
щими распределениям Р и Q.
«Математический выигрыш» от такого расширения
заключается в том, что функция ф (Р, Q) билинейна на
множестве £хХ и, следовательно, вогнуто-выпукла
и в том случае, когда исходная функция ср (х, у) не
является таковой, и множество X выпукло. Поэтому
для существования седловой точки расширенной
функции ф (Р, Q) на исходное множество X и исход-
ную функцию ср (я, у) достаточно наложить лишь то-
пологические требования типа приведенных в теоре-
ме 3.2.7.
Мы воспользуемся здесь этим приемом в задаче
выбора альтернатив. Пусть X — множество всевоз-
можных распределений вероятности (смешанных альтер-
натив), определенных на исходном множестве альтер-
натив X, Выбор распределения PQX мы будем ин-
терпретировать как процесс многократного выбора
альтернатив из множества X с соответствующими ве-
роятностями. ~
Если Р, Q£X, то будем считать, что «в «среднем»
предпочтение Р Q выполнено со степенью
ЙВ(Р, Q)=	y)dP(x)dQ(y).
XX
Функция представляет собой расширение исходного
н. о^ п. на множество смешанных альтернатив X.
3.21 НЕЧЕТКИЕ ОТНОШЕНИЯ ПРЕДПОЧТЕНИЙ	143
Пользуясь теми же рассуждениями, что и в п. 3.2.3,
нетрудно получить, что нечеткое множество недомини-
руемых смешанных альтернатив описывается функцией
принадлежности вида
рв.Д. (Р) = 1 _ sup j j	(у, X) — fiB(х, у)jdP(х)dQ(у).
QG%xx
Так же, как и в п. 3.2.3, определим множество ч. н. д.
альтернатив в множестве (X, £д):
Хч.н.д. = {Р|Р££( |1Н.Д.(Р) = 1|
Теорему 3.2.7 для подобной расширенной задачи
можно выразить в следующей форме.
Теорема 3.2.9. Если множество X компактно,
функция р.д(я, у) непрерывна на тихоновском произве-
дении X X X, то в множестве (X, {1Д) имеется по край-
ней мере одна ч. н. д. альтернатива.
По отношению к исходной задаче смысл подобной
смешанной ч. н. д. альтернативы можно пояснить сле-
дующим образом. Из определения ч. н. д. альтернативы
нетрудно заключить, что
5 ([Мгл ®) —М*» у)]ЛР°(х)=о
XX
при любых у£Х и Р°£ХЧ-Н,Д-. Это означает, что ни-
какая альтернатива у £ X не доминирует с положитель-
ной степенью смешанную ч. н. д. альтернативу. Иными
словами, в многошаговом (формально бесконечношаго-
вом) процессе выбора альтернативы из множества X
в соответствии с распределением Р° (х) «средняя» (ма-
тематическое ожидание) степень доминирования выби-
раемых альтернатив альтернативой у£Х равна нулю.
Следствие из теоремы 3.2.9. В конечном
множестве альтернатив X с заданным на нем н. о. п.
XX -> [0, 1] (нетранзитивным, вообще говоря)
имеется по крайней мере одна смешанная ч. н. д. альтер-
натива.
144
ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
3.3. Несколько отношений предпочтения
на множестве альтернатив
Рассмотрим теперь следующую задачу. Пусть за-
дано множество альтернатив X и каждая альтернатива
характеризуется несколькими признаками с номерами
/=1, . . ., т. Информация о попарном сравнении аль-
тернатив по каждому из признаков / представлена
в форме отношения предпочтения Rj, Таким образом,
имеется т отношений предпочтения Rj на множестве X.
Задача заключается в том, чтобы по данной информации
сделать рациональный выбор альтернатив из множества
(X, Rlt . . Rm).
Обратимся сначала к простейшей ситуации, когда
отношения Rj описываются заданными функциями
полезности X -> 7?1, где R1 — числовая ось. Зна-
чение функции fj (х) можно понимать как числовую оценку
альтернативы х по признаку /. Альтернатива с боль-
шей оценкой fj (х) полагается более предпочтительной
по признаку /. Задача заключается в том, чтобы выбрать
альтернативу, имеющую по возможности бблыпие
оценки по всем признакам.
Рациональным в этом случае естественно считать
выбор альтернативы я0£Х, обладающей свойством
(у) > fjW» ; = 1.	=>//(г/)=Л (®о)’
7 = 1, ..., тп.	(3.3.1)
Такие альтернативы обычно называют эффективными;
решением же данной задачи выбора является множе-
ство всех эффективных альтернатив.
Нетрудно понять, что каждая из функций fj описы-
вает обычное отношение предпочтения на X следую-
щего вида:
R,.= {(x, у)\х,у£Х, f^x^f^y)}.
т
Пусть Qi — П R;- Покажем, что множество всех эффек-
>=i
тивных (недоминируемых) альтернатив в множестве (X, QJ
совпадает с множеством эффективных альтернатив для
набора функций /у, 7 = 1,..., т.
3.3]
НЕСКОЛЬКО ОТНОШЕНИЙ ПРЕДПОЧТЕНИЯ
145
Пусть — недоминируемая альтернатива в мно-
жестве (X, Qr). Это означает (см. п. 3.2.3), что для
любого у(*Х выполнено
(у, *о)€<21,	(3.3.2)
где Qf — соответствующее Q± отношение строгого пред-
почтения, имеющее вид (см. п. 3.2.1)
Qi = {{x,y)\x, у£Х,	7 = 1,...,тп,
t^>f^
Отсюда и из (3.3.2) заключаем, что
7=1, . . ., 7П,
т. е. xQ — эффективная альтернатива для функций /у,
7 = 1, ..., щ.
Столь же просто показать и обратное, т. е. то, что
любая эффективная альтернатива для функций /у (а),
7 = 1, ..., тп, является недоминируемой в множестве
(X,
Таким образом, для нахождения множества эффек-
тивных альтернатив можно вместо набора отношений Ду,
7 = 1, ..тп, взять пересечение этих отношений
и найти множество недоминируемых альтернатив в мно-
жестве (X, (?1).
Представим теперь пересечение отношений Ду в не-
сколько иной форме. Пусть
I 1 при (х, y)£Rf,
У) | о при &
— функция принадлежности отношения Ду. Тогда пере-
сечению этих отношений соответствует функция при-
надлежности
Ре, (®> у) = min (р-1 & у)> • • • - Нт (ж, у)}, (3.3.4)
аналогичная свертке критериев fj вида
F(x)= min k,/y,
у=1, т
Ю С. А. Орловский
146
ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
применяемой в многокритериальных задачах принятия
решений (см., например, книги [31, 33, 341). Числа
Ху в этой свертке играют роль коэффициентов относи-
тельной важности рассматриваемых функций. В свертке
отношений (3.3.4) Ху=1, /=1, . . ., т; это соответствует
тому, что все заданные отношения одинаково важно
учитывать при выборе альтернатив.
Если заданные отношения Rj различаются по важ-
ности, т. е. различаются по важности соответствующие
признаки, по которым нужно сравнивать альтернативы,
то в свертке (3.3.4) можно, вообще говоря, использовать
различные по величине коэффициенты Ху. Однако при
этом рассматриваемые в исходной задаче отношения
предпочтения необходимо погрузить в более широкий
класс нечетких отношений. Иными словами, в опреде-
лении функций принадлежности (3.3.3) числа 0 и 1
следует понимать не как значения булевой перемен-
ной, сигнализирующей о принадлежности или непри-
надлежности элемента множеству 7?у, а как крайние
точки единичного интервала возможных значений сте-
пени принадлежности.
В результате свертки исходных отношений /?у
т
с коэффициентами Ху такими, что 2
/=1
/ = 1, ..., тп, получаем функцию принадлежности вида
(®. у) = min (*. у), • • •> Vm (х, у)}, (3.3.5)
т. е. функцию принадлежности нечеткого отношения
предпочтения. Нетрудно видеть, что это отношение
предпочтения (3.3.5), вообще говоря, не рефлексивно,
т. е. не является отношением предпочтения в смысле
определения в п. 3.2.1. Поэтому свертка (3.3.5) неудобна
при необходимости учета различий в относительной
важности заданных отношений.
Введем теперь свертку исходных отношений дру-
гого вида:
т
(•*> у)=S V/ (*> у) <3-3-6)
У=1
3.3]
НЕСКОЛЬКО ОТНОШЕНИЙ ПРЕДПОЧТЕНИЯ
147
и обсудим ее роль в сформулированной задаче рацио-
нального выбора альтернатив. Заметим, что результирую-
щее нечеткое отношение р.^ , полученное в результате
свертки исходных обычных отношений /?у, рефлексивно,
так как рефлексивны исходные отношения Rj.
Пусть, как и прежде, все исходные отношения пред-
почтения одинаковы по важности. В (3.3.6) это соответ-
ствует тому, что Ху = 1/тп, у = 1,..т. Построим нечет-
кое подмножество недоминируемых альтернатив мно-
жества (X, р^)? пользуясь определениями, введенными
в п. 3.2.3:
т
р";д' (*) =1	sup 2 [Р/ ’ х>>~~ (х> х х-
(3.3.7)
Обозначим Ху н д- подмножество ч. н. д. альтернатив
множества (X, р.^) (т. е. Х? н д- — множество эффектив-
ных альтернатив для набора функций fj(x), j — l,...,™)
и Х^н-Д-— соответствующее множество в (X, р.^). Пока-
жем, что Х’-н-д- С Ху-Н-Д’.
Действительно, пусть гс0^Х^-н-д-. Согласно определе-
нию ч. н. д. альтернативы (п. 3.2.4) и (3.3.7) это озна-
чает, что
т
sup s [р,(у, а?о> — Ну (^0« 5')] = °
или
т
5 [р,- (У> ^о) — Р/ (х0’ У)] < 0	(3-3-5 * * 8)
/=1
при любом у(*Х.
Допустим, что z0(j< Хч н д*. Тогда, согласно (3.3.1)
и (3.3.3), получаем, что найдется у С*Х такой, что
р-у (у, х) = 1, у = 1,. .., т, и при некотором / = 70 выпол-
нено (s0, jd = O- Но тогда при этом у не выпол-
няется неравенство (3.3.8). Отсюда заключаем, что
жо€^1,н,д‘> т. е. Х™д-САрА
Заметим, что, вообще говоря, множество Х’ н д- не
охватывает все эффективные альтернативы для функ-
10*
148 ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
ций /у,	т, т. е. не совпадает с множе-
ством Ху-Н-Д-. Однако можно показать, что любая эффек-
тивная альтернатива, т. е. любой элемент
принадлежит множеству р“-д- с положительной степенью,
т. е. что
уч. н.д. Q supp [1^‘д\
Действительно, если для некоторой альтернативы х £ X
выполнено (х) = 0, то из (3.3.7) получаем, что най-
дется у^Х, для которого
*) —М*’ =	/ = !,.•-,«1,
т. е. p-у (/Л я) = 1 и fiy(я:, у) = 0 при всех ;== 1,. .., тп.
Это означает, что альтернатива у доминирует альтерна-
тиву х, т. е. f f 7 = 1, • ••, и, следова-
тельно, x не может быть эффективной альтернативой
для набора функций /у.
Обсудим теперь свойства альтернатив из множества
supp [ip*д*, т. е. альтернатив х С X, для которых д- (х) >0.
Нетрудно видеть, что функция р-^д,(я) принимает лишь
значения вида к/m, где к — натуральное число, и к^jn.
Пусть для некоторой альтернативы х' £ supp р,1®-д
рн.д. (ж') = ]фп. Согласно (3.3.7) это означает, что
sup S IK (У> х') — V-j (К у)\ = т — к (3.3.9)
yGX /=1
или
т
5	«') —у)]^т — к (3.3.10)
/=1
при любом у£Х.
Поскольку члены суммы в (3.3.10) принимают лишь
значения 0 и* +1, из (3.3.10) следует, что разность
между числом членов этой суммы, равных -|-1> и числом
членов равных —1, не превышает 1 — к при любом у £ X.
Иначе этот факт можно пояснить следующим образом.
Пусть р(у, х) — число функций/у из заданного набора,
по каждой из которых альтернатива у строго лучше xt
з.з]
НЕСКОЛЬКО ОТНОШЕНИЙ ПРЕДПОЧТЕНИЯ
149
и q (у, х) — число функций, по которым х строго лучше у.
Тогда, если р”-Д- (х') = к/m, то
р(у, x') — q(y, х')^т — к
при любом у(*Х.
Таким образом, функция р.“ д- упорядочивает альтер-
нативы по степени их недоминируемости. Например,
если рн-д‘(х0) = 3/4 (т. е. т — к=1) и некоторая альтер-
натива у £ X строго лучше альтернативы ж0 по каким-
либо двум критериям (признакам), то не менее чем по
одному из остальных признаков альтернатива ж0 строго
лучше альтернативы у.
Если взять пересечение множеств Ху-Н-Д- и р.“‘д*,
то получим соответствующее упорядочение на множестве
эффективных альтернатив, пользуясь которым можно
осуществить выбор среди них.
Если же в свертке (3.3.6) веса X. неодинаковы, то
каждая из введенных выше характеристик р (у, х') и
q (у, х') будет представлять собой не число соответ-
ствующих признаков, а их суммарный относительный
вес (важность).
Итак, применение свертки (3.3.6) исходных обыч-
ных отношений предпочтения в задаче принятия реше-
ний по набору функций позволяет получить дополни-
тельную информацию об относительной степени недоми-
нируемости эффективных альтернатив и тем самым
сузить класс рациональных выборов до множества
^ч.н.д. = (х\х рЛ-д-(я) = sup Р-п’Д* (#')).
В общей задаче, когда на множестве альтернатив
заданы т нечетких отношений предпочтения Rj,
j=i, . . ., т,и заданы коэффициенты Ху относительной
важности этих отношений, мол но поступать аналогия
ным образом.
1.	Строим нечеткое отношение (пересечение исход-
ных отношений):
У') — min {th (*’ у)’ ' • М®» у)}
150 ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ (ГЛ. 3
и определяем нечеткое подмножество недоминируемых
альтернатив в множестве (X,	):
^н.д.^)^! — sup[^(,,	—	г/)].
2.	Строим нечеткое отношение Q2 (свертка отношений
типа (3.3.6)):
у)= S xA/(*> у)
/=1
и определяем
альтернатив в
нечеткое подмножество недоминируемых
множестве (X, р.^):
д- (*) = ! — sup [рл (у, х) — р?2 (х, у)].
у 6Х
3.	Находим пересечение множеств р.^д- и ^‘д‘:
(1Н. Д. (х) — min (ин.д. (а.); ин.д. (Х)j
4.	Рациональными считаем выборы альтернатив из
множества
Хн- «• — {х | х £ X, р.н- Д- (х) = sup р.н-д- (ж')}.
х' ех
Здесь следует отметить, что в зависимости от типа задачи
рациональными могут считаться выборы не только альтер-
натив из множества Хн*д-, но и в том или ином смысле
слабо доминируемых альтернатив (или не очень сильно
недоминируемых), т. е. альтернатив, которые принадле-
жат множеству р,н-Д- со степенью не ниже некоторой
заданной.
П рим е р 3.3.1. Пусть X ~	х2, х3} и на X заданы
три одинаково важных отношения предпочтения:
3.41 НЕЧЕТКОЕ МНОЖЕСТВО АЛЬТЕРНАТИВ	151
1.	Строим отношение QT — 7?х р /?2 Q R3:
/1 1 0\
*/)= О 1 О
\о о 1 у
и находим подмножество не доминируемых альтернатив в мно-
жестве (X,
ж2 х3
?Q\ А- (Xi) =1	0	1
1
2.	Строим отношение Qz = у (н (х^ xj) + F4 (ж»» xj) +
+ Р*з (xi>
xL	х2	х3
Х1	1	1	1/3
Xj)= х2	2/3	1	2/3
1/3	0	1
и находим подмножество не доминируемых альтернатив в мно-
жестве (X,
хг	х2	х3
1	2/3	1/3
3.	Результирующее множество недоминируемых альтернатив
есть пересечение множеств р.^Дф и р-р‘д’-’
х^ ж2 х3
ри. д. (х.) = 1	0	1/3
Отсюда заключаем, что в данном примере рациональным
следует считать выбор альтернативы xlt имеющей максималь-
ную степень недоминируемости.
3.4. Отношение предпочтения
на нечетком множестве альтернатив
До сих пор в этой главе мы обсуждали задачи рацио-
нального выбора альтернатив, в которых множество
X допустимых альтернатив было описано четко, т. е.
в виде множества в обычном смысле. Однако нечеткость
исходной информации в задаче может относиться и
152 ПРЕДПОЧТЕНИЯ НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ [ГЛ. 3
к описанию самого множества X в том смысле, что аль-
тернативы могут различаться по степени допустимости
(или желательности их использования лицом, прини-
мающим решения). В данном разделе мы обсудим под-
ход к подобным задачам принятия решений.
Итак, пусть X — универсальное множество альтер«
натив. В X задано нечеткое подмножество допустимых
альтернатив v: X [0,1 ]. Смысл функции v (х) тот же,
например, что и в обсуждавшихся в § 2.4 задачах не-
четкого математического программирования. Заданное
на X нечеткое отношение предпочтения будем по-преж-
нему обозначать (ж, у).
Отличие этой задачи от рассматривавшихся выше
состоит в следующем. В задачах с обычным множеством
допустимых альтернатив рациональный выбор опреде-
лялся лишь заданными на множестве X нечеткими от-
ношениями предпочтения. Теперь же в данной задаче,
кроме предпочтений между альтернативами, описывае-
мыми отношением р.д, нужно учитывать еще и различия
в степени допустимости этих альтернатив. Более пред-
почтительными, кроме всего прочего, естественно счи-
тать альтернативы, имеющие по возможности бблыпую
степень допустимости, т. е. альтернативы, которым
соответствует по возможности большее значение функ-
ции v (х).
Иными словами, если говорить о рациональном
выборе альтернатив в данной задаче, то необходимо
учитывать еще и следующее отношение предпочтения,
индуцируемое на X функцией v:
1 при v(#)^>v(y),
О в остальных случаях.
Введением этого дополнительного отношения предпоч-
тения данная задача с нечетко описанным множеством
допустимых альтернатив сводится к постановке, кото-
рая обсуждалась в предыдущем разделе, и для ее ре-
шения можно использовать описанную там процедуру.
у)=
ГЛАВА 4
ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО
МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
4.1.	Введение
Задачи математического программирования состав-
ляют практически важный подкласс задач рациональ-
ного выбора альтернатив. Как уже отмечалось в гл. 2,
характерным для этих задач является то, что отноше-
ние предпочтения в них описано с помощью некоторой
функции (полезности), заданной на множестве альтер-
натив так, что более предпочтительным альтернативам
соответствуют большие значения этой функции. Факти-
чески с помощью такой функции исходная задача вы-
бора альтернатив сводится к, вообще говоря, более
простой задаче выбора чисел из некоторого подмноже-
ства естественно упорядоченной числовой оси.
Функция полезности или, как ее часто называют,
функция цели обычно составляет основу математиче-
ской модели реальной системы. Значения этой функции
описывают эффект от выбора того или иного способа
действий (альтернативы). В экономических задачах,
например, эти значения могут отражать величину при-
были, получаемой при тех или иных способах органи-
зации производства, в модели регулирования речного
стока — выработку электроэнергии при различных ре-
жимах пропуска воды через турбины гидроэлектростан-
ций и т. п. По сути дела, адекватность такой модели
реальности в большой мере определяется тем, на-
сколько правильно отражены в этой функции взаимо-
связи различных факторов реального процесса или
системы.
При математическом моделировании сложной си-
стемы невозможно учесть достаточно большое число
реальных факторов, поскольку это привело бы к чрез-
мерному усложнению модели. Поэтому в модель при-
ходится вводить лишь ограниченное число таких фак-
154
ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
торов, которые по тем или иным соображениям счи-
таются наиболее существенными. При этом возможны
два подхода. Неучтенные в описании модели факторы
можно считать абсолютно несущественными и полностью
их игнорировать при принятии решений с использова-
нием этой модели. С другой стороны, при втором под-
ходе можно явно не вводить «несущественные факторы»
в математическую модель, но учитывать их влияние,
допустив, что отклик модели на то или иное воздей-
ствие (выбор альтернативы) может быть известным
лишь приближенно, нечетко.
Для описания нечеткого отклика можно прибегнуть
к помощи экспертов, которые представляют собой влия-
ние на функционирование системы неучтенных в мо-
дели факторов. Разумеется, степень нечеткости описа-
ния откликов системы на воздействия тем меньше, чем
большее число факторов явно участвует в описании
математической модели.
Таким образом, при втором подходе сложная си-
стема описывается некоторой нечеткой функцией цели,
которая каждой альтернативе (воздействию на си-
стему) ставит в соответствие некоторый нечеткий отклик
системы на выбор этой альтернативы.
Если, например, отклики системы описываются
в форме нечетких подмножеств универсального мно-
жества откликов У, то отражающая функционирование
системы нечеткая функция цели имеет вид ср: X X У -►
-> ГО, 1], где X — множество альтернатив. Если xQ —
альтернатива, то определенная на У функция ср (х°, у)
представляет собой функцию принадлежности соответ-
ствующего нечеткого отклика системы на выбор xQ.
В задаче рационального выбора альтернатив при
подобном нечетком описании системы (функции цели)
альтернативы требуется сравнивать друг с другом по
соответствующим им нечетким значениям функции
цели: более «предпочтительным» нечетким откликам
соответствуют более предпочтительные альтернативы.
Таким образом, необходимым этапом в анализе подоб-
ной задачи выбора является построение отношения пред-
почтения в классе нечетких откликов. Этому вопросу и
посвящен следующий параграф.
4.2]
ОЕОБЩЕЯИЕ НЕЧЕТКОГО ОТНОШЕНИЯ
155
4.2.	Обобщение нечеткого отношения
на класс нечетких множеств
4.2.1.	Построение обобщенного отношения. Рас-
сматриваемую в этом разделе основную задачу можно
сформулировать следующим образом. На универсаль-
ном множестве Y задано н.о.п. R с функцией принадлеж-
ности р.д: YxY -> [0, 1]. Пусть у — класс всех не-
четких подмножеств множества У, т. е. класс всех
функций вида v: Y -> [0, 1]. Какое нечеткое отноше-
ние предпочтения индуцирует на класс у исходное
н.о.п.
Для решения этой задачи мы воспользуемся прин-
ципом обобщения, введенным в § 1.3 (см. также [40]).
Нетрудно понять, что заданное на множестве У
н.о.п. R можно рассматривать как нечеткое отобра-
жение У -> у. Образ любого элемента у0 £ У при этом
отображении есть нечеткое подмножество множества
У с функцией принадлежности (у0, у). По сути дела,
функция р-д (у0, у) описывает нечеткое множество
R (у0) элементов У, связанных с у0 отношением 2?,
т. е. таких у^У, что У^ВУ-
Пусть v: У -> [0, 1] — некоторое нечеткое подмноже-
ство множества У. Тогда согласно принципу обобщения
образ v при нечетком отображении есть нечеткое под-
множество У с функцией принадлежности вида
Ш y) = sup min{v(z), у)}.	(4.2.1)
Построенная таким образом функция т) описывает
нечеткое отображение у -^у и представляет собой обоб-
щение исходного нечеткого отображения р.д: У -> у.
Нетрудно понять и то, что эта функция описывает обоб-
щение R.' исходного н. о. п. R на множество у X У.
Иными словами, для фиксированного функция
fj(v0, у) описывает нечеткое множество элементов У,
связанных с >0 обобщенным отношением R,\ т. е. таких
у С У, что vQR'y. Величина (v0, у), таким образом, есть
степень, с которой нечеткое множество v0 предпочти-
тельнее элемента у.
156 ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
Рассуждая аналогичным образом, получаем, что вели-
чина
v0) = suP min(v(2)’ Му» z)}	(4.2.2)
z&f 1	7
есть степень обратного предпочтения у v0.
Рассмотрим простой иллюстративный пример.
Пример 4.2.1. Пусть Y — числовая ось и н. о. п. —
естественный порядок (>) на У. Тогда, как нетрудно видеть,
равенства (4.2.1) и (4.2.2) запишутся в виде
5j(v, у)= supv(z),	(4.2.3)
-г, УбГ
5j(y, v)= sup v(z).	(4.2.4)
Пусть нечеткое множество v имеет вид, показанный на
рис. 4.2.1.
Пользуясь (4.2.3) и (4.2.4), получаем
У1) = Ъ(Уг> v) = l, ^(v, у2) = ^(!/ь v) = 0,7.
Заметим, что из определений, приведенных в п. 3.2.1, полу-
чаем, в частности,
у эквивалентно у! со степенью 0,7,
v строго лучше у! со степенью 0,3,
v эквивалентно у2 со степенью 0,7,
у2 строго лучше v со степенью 0,3.
Продолжим процесс обобщения исходного н. о. п. R.
Будем рассматривать полученную функцию (4.2.1) как
нечеткое отображение Y -> где у — класс всех нечет-
ких подклассов класса у, т. е. всех функций вида
У~>[Р, 1], и пусть v0 — произвольный элемент Со-
4.21
ОБОБЩЕНИЕ НЕЧЕТКОГО ОТНОШЕНИЯ
157
гласно принципу обобщения образом v0 при нечетком
отображении vj является нечеткий подкласс класса у
с функцией принадлежности У У'-
v0) = sup min{v0(z/), ^(v, г/)},	(4.2.5)
yer
причем его можно понимать как подкласс нечетких под-
множеств v таких, что v v0. Иными словами, функ-
ция т] описывает обобщение н. о. п. В.' на множество
У Ху, & следовательно, и соответствующее обобщение
исходного н. о. п. В. Величина т] (ур v2) есть степень
выполнения предпочтения v2.
Из (4.2.1) и (4.2.5) получаем следующее выражение
для функции принадлежности обобщенного отношения
предпочтения:
чЬр v^supmin^Q/), sup min {v2 (z), p (y,z)}} =
y£Y	z&Y
= sup min bl (y)> v2(z), V-Лу, z)}.	(4.2.6)
z, у e г	4
Аналогичным образом можно прийти к выводу о том,
что обратное предпочтение (v2 vj выполняется со сте-
пенью, равной величине
vj = sup min {V1 (у), v2(z), |is(z, у)}.	(4.2.7)
z, у e z
Пример 4.2.2. Пусть, как и в примере 4.2.1, Y — число-
вая ось и £ — естественный порядок (>) на У. Рассмотрим
два нечетких подмножества У: и v2, показанные на рис. 4.2.2.
Пользуясь выражениями (4.2.6) и (4.2.7), получаем tj (vx, v2)=0,6
и т) (v2, vx)=l, т. e.
Vi эквивалентно v2 co степенью 0,6,
v2 строго лучше vj co степенью 0,4.
158 ОБЩАЯ ЗАДАЧА ЙЁЧЕТЁОГО П^ОГРАММЙРОЁАЙЙЯ [ГД. 4
4.2.2.	Некоторые свойства индуцированного отно-
шения предпочтения. Исследуем теперь некоторые свой-
ства введенного н. о. п. т], которые определяются свой-
ствами исходного н. о. п. и классом нечетких мно-
жеств, на котором рассматривается индуцированное н. о. п.
Теорема 4.2.1. Если н. о. п> р.д на Y рефлексивно,
то и индуцируемое им н. о. п. ц рефлексивно на классе
всех нормальных нечетких подмножеств множества У.
Доказательство. Если у£у нормально, т. е.
supv(z/) = l, то из (4.2.6) получаем
уег
(у, v) = sup min {v (у), у (z), pR (у, z)}
z, У^
sup min {v (у), V (у)} = sup V (у) = 1.
Поскольку 7] (у, у)< 1 при любом у £ у, то из этого
неравенства заключаем, что т](у, у) = 1 при любом v£ у,
что и означает рефлексивность т].
В следующих двух теоремах изучается вопрос о ли-
нейности н. о. п.
Теорема 4.2.2. Если н.о.п. p.R на Y сильно ли-
нейно, то и индуцируемое им н. о. п. сильно линейно
на классе всех нормальных нечетких подмножеств Y.
Доказательство. Поскольку по условиям тео-
ремы н. о. п. |лд сильно линейно, то, как следует из
определения сильной линейности, достаточно показать,
что для любых двух нормальных нечетких подмножеств
множества У выполнено по крайней мере одно из
равенств
va) = 1»	ъ) = 1’
Допустим противное, т. е. что для некоторых нор-
мальных ух и у2 одновременно выполнены неравенства
(vi> va) = sup min (vx (z), v2 (у), p.B (z, y)} = ax < 1, (4.2.8)
(v2. vi) = sup min {vx (z), v2 (г/),	(y, z)) == a2 < 1. (4.2.9)
4.2]
ОБОБЩЕНИЕ НЕЧЕТКОГО ОТНОШЕНИЯ
159
Выберем произвольно число е из интервала 0 < е <
< min ((1 — aj, (1 — а2)} и введем множества
Y‘t = {y\y£Y, v.(у)supv,(z) — s —1 — е}, i = l, 2.
z£Y
Поскольку сильно линейно, то для любых двух эле-
ментов z/i 6 У* и у2 Е Уе выполнено одно из равенств:
а) нЛ(г/1» у2)=1; б) pR(y2, у2)=1.
В случае а) получаем
7l(vi> v2) = supmin{v1(z), v2(p), pB(z, !/)}>
у,
> min bi (г/i), va (Уа),	(*/i> Уа)} > 1 — е > ar
Аналогичным образом в случае б) получаем т] (v2, >1)>а2-
Отсюда заключаем, что неравенства (4.2.8) и (4.2.9)
не могут выполняться одновременно и, следовательно,
н. о. п. т] сильно линейно.
Теорема 4.2.3. Если н. о. п. на У ^-линейно
(Х^О), то и индуцируемое им н. о. п. т] \-линейно на
классе всех нечетких подмножеств множества У, обла-
дающих свойством sup v (у) > X.
У£Т
Доказательство. Пусть vx и v2 — два нечетких
подмножества, удовлетворяющие условиям теоремы.
Введем множества
У* = {у\у^У, ^(у)>\}, i = l, 2.
Выберем произвольно ух £ У1 и у2 £ У2. Из Х-линейности
заключаем, что выполнено одно из неравенств:
а) Ня(»1> Уа)>х «ли б) ря(уа, ^)>Х.
В случае а) получаем
*2) > min (>i (У1), *2(у2), рй(^1, 1/2)}>Х.
Аналогично, в случае б) получаем т] (v2, vj > X.
Из двух последних неравенств заключаем, что
max {т) (vv v2), т] (v2, vj} >
т. e. что н. o. n. 7] Х-линейно.
160 ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
Таким образом, свойство линейности исходного
н. о. п. р-д переносится на индуцируемое им н. о. п. т] на
классе соответствующих нечетких подмножеств мно-
жества Y. Однако из транзитивности н. о. п. р-д, вообще
говоря, не вытекает транзитивность индуцированного
н. о. п. 1). Этот факт иллюстрируется, в частности, при-
мером, приведенным в конце данного раздела.
Обратимся теперь к случаю, когда исходное н. о. п.
Р-д на Y представляет собой обычное отношение пред-
почтения R, т. е. описывается функцией принадлеж-
ности, принимающей лишь значения 0 и 1. Из приве-
денного выше выражения (4.2.6) получаем, что отно-
шение R индуцирует н. о. п. т] следующего вида:
iq(vi, v2)= sup min {vp (z), v2(t/)}.	(4.2<6a)
yer
zRy
Нетрудно убедиться в том, что обычное линейное
отношение R (см. п.1.2.1) является сильно линейным
в смысле определения, данного в п. 3.2.2. Отсюда и из
теоремы 4.2.2 вытекает следующая.
Теорема 4.2.4. Н. о. п. tj, индуцируемое задан-
ным на Y обычным линейным отношением предпочтения
R, сильно линейно на классе всех нормальных нечетких
подмножеств множества Y.
С другой стороны, как было показано вп. 3.2.1, для
сильно линейного н. о. п. tj выполняются равенства
(Vl> v2) = 1 — (V2> Vl) Vvp V2 G У,
где — соответствующее т] нечеткое отношение стро-
гого предпочтения. Отсюда и из приведенных выше рас-
суждений получаем, что для любого и. о. п. т], индуци-
рованного обычным линейным отношением предпоч-
тения R для любых нормальных нечетких подмножеств
vx, v2 множества У, выполняется равенство
т]’ (vp v2) = 1 — sup min (p), v2 (z)}.
(y, z)£R
Если Y — числовая ось и R — естественный поря-
док (J>) на У, то н.о.п. т] описывается в более простой
форме, правда, на несколько более узком классе нечет-
ких подмножеств У. Введем следующее
4.2]
ОБОБЩЕНИЕ НЕЧЕТКОГО ОТНОШЕНИЯ
161
Определение 4.2.1. Нечеткое подмножество
v множества Y называется выпуклым, если любое мно-
жество вида
Ya = {y\y£Y, ^(у)>Л}, 0<а<1,
выпукло в У*).
Докажем теперь следующую теорему.
Теорема 4.2.5. Естественный порядок (^) на
числовой оси Y индуцирует н.о.п. щ на классе всех нечет-
ких подмножеств У, обладающее следующим свой-
ством: для любых двух нормальных выпуклых нечет-
ких множеств v1? v2 выполнено одно из равенств
1 Ov v2) = 1 - *101»	— sup min (vx (у), v2 (у)}.
убг
Доказательство. Введем обозначение
А 01, v2) = sup min (vj (у), v2 (у)}.
Поскольку (у, у) £ R, то для любых vv v2 выполнено
Ч (ъ Ъ) > A (VV V2),	(V2> Vl) > (VV va).
Отсюда, опираясь на теорему (4.2.4), можно заключить,
что для доказательства теоремы 4.2.5 достаточно пока-
зать, что для любых vx и va неравенства
Ч 01. va) > А 01» va)« 1 О2» vi) > А 01» va)
не могут выполняться одновременно.
Допустим противное, т. е. что для некоторых vx,
va£^/ одновременно выполнены неравенства
sup min (vx (z), v2 (у)} > Л (vx, v2),
sup min (vx (z), V2 (y)} > A (vx, v2).
Это означает, что найдутся такие z®, у®, z', у' £ Y, для
которых
a)	г°>г/°, г'</;
б)	vx (z®) > А К, v2), v2 (у°) > А (vx,
vi О') > Л 01, V2), v2 (г/') > A (vx, v2).
♦) При этом предполагается, что множество У замкнуто
относительно определенных в нем операций сложения и умно-
жения на число.
И С. А. Орловский
162 ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
Нетрудно проверить, что из условия а) вытекает непу-
стота множества
I = Con (20, z') П Con (y°, /),
где Con (xp x2) — отрезок, заключенный между точками
хг и х2. Далее, поскольку и v2 выпуклы по условию
теоремы, то из условия б) следует, что для любого
выполняются неравенства
vi (у) > A (Vj, v2), v2 (у) > A (vx, v2),
min {vx (у), v2 (у)} > A (vp v2) = sup min {vx (p), v2 (y)}.
Утверждение теоремы 4.2.5 вытекает из невозможности
последнего неравенства.
Если нечеткие множества и v2 невыпуклы, то
теорема 4.2.5 неверна. Покажем это на следующем
простом примере.
Пример 4.2.3. Пусть нечеткие множества и v2 имеют
вид, показанный на рис. 4.2.3 (У — числовая ось). Легко про-
верить, что в этом примере т] (vb v2)= (v2, v1)=l, но A (vn v2) <
< 1.
В заключение данного раздела мы сделаем несколько
замечаний о некоторых свойствах введенного н.о.п.
т] на классе нечетких множеств. Рассмотрим три нечет-
ких множества vn v2, v3 числовой оси (рис. 4.2.4).
С помощью приведенных выше определений получаем
*Г (vv va) = (v2. vs) =1,	(vi> vs) = °.	(v3. *1) =1 •
Таким образом, множества vx h v2 эквивалентны co сте-
пенью 1 (т. e. определенно эквивалентны). Этот факт
4.2]
ОБОБЩЕНИЕ НЕЧЕТКОГО ОТНОШЕНИЯ
163
может показаться несколько странным, поскольку мно-
жество v2 расположено на числовой оси правее множе-
ства vj, т. е. «смещено» относительно vx в сторону боль-
ших значений у.
Однако дадим vx, v2h v3 следующую интерпретацию.
Пусть точки оси У представляют собой значения длины,
а множество vt. (i/), Z=l, 2, 3, представляет собой ре-
зультат измерения длины некоторого стержня г, при-
чем «ширина» (ар множества v. (у) отражает точ-
ность этого измерения. Нетрудно понять» что при задан-
ной здесь точности (см. рис. 4.2.4) нет оснований утвер-
ждать о том, что стержень 2 длиннее стержня 1 (и тем
более утверждать обратное). Таким образом, при дан-
ной здесь точности стержни 1 и 2 неразличимы по
длине, и именно этот факт отражается равенством
*)'(*!» ^) = 1.
С другой стороны, данной здесь точности достаточно
для утверждения о том, что стержень 3 длиннее стержня
1, чему и соответствует равенство rf (v3, vx)==l.
Из данного примера видно также, что из транзитив-
ности исходного отношения (J» на Y не следует тран-
зитивность индуцированного отношения т]. Действи-
тельно, поскольку rf (vx, v3)=0, то из if (vx, v2)=l и
if (v2> уз)=1 не вытекает if (vx, v3)=l, как это должно
было бы быть при транзитивном н.о.п. iq (см. п. 1.2.4).
В следующем разделе мы применим полученные
здесь результаты для анализа общей задачи нечеткого
математического программирования.
11*
164 ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
4.3. Недоминируемые альтернативы
в общей задаче нечеткого
математического программирования
4.3.1. Нечеткое множество недоминируемых альтер-
натив. Обратимся теперь непосредственно к задаче,
которая обсуждалась в § 4.1. Пользуясь аппаратом, раз-
витым в предыдущем разделе, мы сведем ее* к рассмотрен-
ной в § 3.2 задаче принятия решений при нечетком от-
ношении предпочтения на множестве альтернатив.
Формально общая задача нечеткого математического
программирования описывается следующим образом.
Пусть X — универсальное множество альтернатив и
X -> [0, 1 ] — заданное нечеткое подмножество
допустимых альтернатив. Пусть Y — универсальное
множество оценок результатов выборов альтернатив из
множества X и YxY -► [0, 11 — заданное на
множестве Y нечеткое отношение предпочтения. Выборы
альтернатив оцениваются нечеткими значениями задан-
ной нечеткой функции цели ср: XxY [0, 11 (смысл
этой функции обсуждался в § 4.1). Задача заключается
в рациональном выборе альтернатив на основе инфор-
мации, заданной в описанной выше форме.
При анализе этой задачи в данном разделе мы будем
считать для простоты изложения, что множество допу-
стимых альтернатив описано четко, и будем обозначать
это множество тем же символом X, что и введенное выше
универсальное множество ~ альтернатив. В конце раз-
дела мы кратко остановимся и на задачах с нечетким
множеством допустимых альтернатив.
Для решения поставленной задачи мы построим на
множестве альтернатив X нечеткое отношение предпоч-
тения, индуцированное исходным н.о.п. pR и нечеткой
функцией цели ср, а затем выделим в X нечеткое под-
множество недоминируемых альтернатив.
Любой альтернативе xQ заданная функция ср ставит
в соответствие нечеткую оценку этой альтернативы
в форме нечеткого подмножества ср (х°, у) множества
оценок У. Пусть нечеткое отношение предпочте-
ния, индуцированное н.о.п. на классе у всех нечет-
ких подмножеств множества Y (§ 4.2). Пользуясь этим
4.3]
НЕДОМИНИРУЕМЫЕ АЛЬТЕРНАТИВЫ
165
отношением, можно сравнивать друг с другом по пред-
почтению нечеткие оценки альтернатив, а следова-
тельно, и сами альтернативы. Иными словами, степенью
предпочтения альтернативы Е X альтернативе Е X
мы будем считать степень предпочтения нечеткой
оценки ср (xj, у) нечеткой оценке ср (х2, у), т. е. положим
"Ч (*i. *2) = Ъ (? (*v У). ? («а. У)).
где ср (я*, у) и ср (х2, у) — соответствующие хг и х2 не-
четкие подмножества (оценки) множества У.
Таким образом, используя определение н. о. п. т,
(п. 4.2.1), мы получаем н. о. п. на множестве альтер-
натив X следующего вида:
Ч(*1» ж2) = sup min {<?(«!, z), <р(ж2, у), ?R(z, у)}. (4.3.1)
я, у€Г
Заметим, что в аналогичной задаче с четко описан-
ной функцией цели /: X -> Y (У — числовая ось) опре-
деление (4.3.1) сводится к обычному:
х1>а:2о/(а;1)>/(х2).
Действительно, в этом случае
( 1 при f(x) = y,
<р(х9	= < л
I 0 в остальных случаях,
и
[1ПРИ2></,
u (z, у) — \ л
"	( U в остальных случаях,
а равенство (4.3.1) принимает вид
J 1 при /(х1)>У(х2),
lite, Я2)—1 л
( 0 в остальных случаях.
После того как и в множестве альтернатив введено
н. о. п. т|, исходная задача сводится к задаче, рассмо-
тренной в § 3.2: имеется множество альтернатив X
с заданным на нем н. о. п. ц. Нетрудно убедиться
в том, что если функция ср обладает свойством
supcp(z, у) = 1
уег
166 ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
т. е. если оценка любой альтернативы — нормальное
нечеткое множество, то н. о. п. т] рефлексивно, т. е.
х) = 1 при любом
Выделим теперь в множестве (X, т]) нечеткое под-
множество недоминируемых альтернатив. Согласно опре-
делению (§ 3.2) оно имеет вид
т]н д- (я) == 1 — sup [iq (х'> х) — (х, ж')]. (4.3.2)
Отсюда и из (4.3.1) получаем
т/1*- (ж) = 1 — sup [ sup min {ср (х', z), <р (х, у),	(z, у)} —
х'бХ г, y£Y
— sup min {ср (я', z), ср (ж, у), ?R(y, z)}]. (4.3.3)
y&i
Необходимо отметить, что если функция ср (х, у)
такова, что для некоторой альтернативы ж0 выполнено
sup<p(a:0, у) = а<1,
убг
то значение т}4**’ (я0) может не отражать фактической
степени недоминируемости этой альтернативы. Для
иллюстрации рассмотрим крайний случай, когда а=0.
В исходной задаче это соответствует тому, что оценка
альтернативы ж0 неизвестна или не определена (или не-
известна реакция управляемой системы на управле-
ние я0). В то же время, как нетрудно убедиться по вы-
ражениям (4.3.1) и (4.3.2), для этой альтернативы
(ж0, я0) = 0 и ^и,д- (я0) = 1,
т. е. альтернатива х° оказывается определенно недоми-
нируемой, причем исключительно ввиду отсутствия
информации о ней. Поэтому величину (я0) необхо-
димо скорректировать, с тем чтобы исключить такие
«патологические» случаи.
В терминах нечетких множеств равенство
sup ср (я0, у) = 0
убУ
означает, что множество оценок (или реакций), соот-
ветствующее альтернативе я0, пусто. Если величина
а > О, но мала, то это множество можно понимать
как «почти пустое» и т. п. в соответствии с величиной
4.3]
НЕДОМИНИРУЕМЫЕ АЛЬТЕРНАТИВЫ
167
л, которая, таким образом, характеризует степень на-
личия информации об альтернативе xQ. Учитывая, что
малые значения а могут приводить к искусственно за-
вышенным значениям функции для соответствую-
щих альтернатив, для корректировки этой функции ее
значения нужно сопоставлять с соответствующими зна-
чениями а.
Опираясь на эти рассуждения, решением исходной
задачи будем считать не функцию принадлежности
а скорректированную функцию вида
(х) = min (тр**- (я), sup ср (х, у)}.	(4.3.2а)
убк
Нетрудно показать, что для любого х выполнено ра-
венство
sup? (ж, у) — ц (ж, ж),
убг
где т] — индуцированное отношение (4.3.1). Тогда вы-
ражение (4.3.2а) можно записать в виде
т|и д- (z) = min {^н д- (х), (х, ж)}.	(4.3.26)
Если отношение рефлексивно, т. е. т\(х, х) = 1 при
любом то, как следует из (4.3.26), функции
и совпадают друг с другом.
Для рассмотренного выше крайнего случая получаем
^и.д. (д.0) —О,
т. е. альтернатива ж0 исключается из решения задачи.
По сути дела, выражения (4.3.3) и (4.3.2а) описы-
вают способ обработки исходной информации для полу-
чения нечеткого множества недоминируемых альтер-
натив. Рациональным в данной задаче естественно счи-
тать выбор альтернатив, для которых функция тдн*д-
(скорректированная) принимает по возможности боль-
шие значения.
Если в общей задаче нечеткого математического
программирования множество допустимых альтернатив
описано нечетко, то выбор альтернатив следует осуще-
ствлять с учетом двух отношений предпочтения: по-
лученного выше индуцированного н.о.п. у и отношения
168 ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
предпочтения, отражающего степени допустимости аль-
тернатив. Более подробно этот вопрос обсуждается
выше в § 3.3., где была предложена возможная про-
цедура решения подобной задачи.
4.3.2. Выбор альтернатив в случае числовых оце-
нок альтернатив. Обратимся к более простой, но тем
не менее практически важной задаче, когда множество
оценок Y — числовая ось. В этом случае выражение
(4.3.1) принимает вид
TlGri, х2) = sup тш{ср(жх, z), ср(ж2, у)},	(4.3.4)
а решением соответствующей задачи нечеткого мате-
матического программирования является нечеткое под-
множество недоминируемых альтернатив вида
т|в-д- (х) = min {rf-*- (ж), iq (ж, я)},
где
if-*’ (х) = 1 — sup [sup min {ср (х'9 z), ср (ж, у)} —
— sup min {<р (я, z), ср (я', у)}]. (4.3.5)
Как уже говорилось в § 3.2, величина 7|в,д- (х) есть
степень недоминируемости альтернативы х. Если
т|в*д’ (х) а, то в множестве X нет ни одной альтерна-
тивы, которая доминировала бы альтернативу х со
степенью, большей, чем 1 — а.
Покажем, что для нахождения альтернативы, недо-
минируемой со степенью, не меньшей а, достаточно
решить следующую задачу математического програм-
мирования:
у -» max, ср (ж, у) а, х £ X, у £ Y. (4.3.6)
Теорема 4.3.1. Пусть нечеткая функция цели <р:
ХхУ->[0, 1] такова, что sup<p(x, у)^>а при любом
убг
xQX, и пусть т] — н.о.п. на X, индуцированное
естественным порядком Q>) на числовой оси оценок Y
и функцией <р. Если (ж0, у0) — решение задачи (4.3.6),
4.3]
НЕДОМИНИРУЕМЫЕ АЛЬТЕРНАТИВЫ
169
то 71в,д- (я0) а, где if (х) — нечеткое множество не-
доминируемых альтернатив в множестве (X, ц).
Доказательство. Пусть пара (х°, у0)£XXY —
решение задачи (4.3.6). Тогда, как следует из (4.3.5), для
доказательства теоремы достаточно показать, что
sup [sup min (ср {xf. z). ср (ж0, у)} —
— sup min {<р (ж0, z), <р(х',	—а.
Допустим противное, т. е. что найдутся х£Х и
е > 0, для которых
sup min {ср (ж, z). ср (х°. у)} — sup min {ср (я:0, z),
*>У
? (ж> У)} >1 — “ + 8- (4.3.7)
Выберем у £ Y, так, что ср (ж, у) а — в (существование
такого у следует из предположений о функции <р
в условиях теоремы). Поскольку пара (я0, у0) — решение
задачи (4.3.6), то у°^>у и, кроме того, ср (ж0, у°)^>а.
Отсюда получаем
sup min {ср (я0, z), ср (ж, у)}	а — в,
но тогда неравенство (4.3.7) невозможно, поскольку
левое слагаемое в его левой части не превышает 1.
Из доказанной теоремы вытекает, что любые усло-
вия, достаточные для существования решения задачи
(4.3.6), достаточны и для существования соответствующих
недоминируемых альтернатив в множестве (X, ij).
В частности, справедлива следующая.
Теорема 4.3.2. Если множества X и Y компактны,
причем Y — подмножество числовой оси, функция
ХХК->[0, 1] полунепрерывна сверху на тихоновском
произведении XX У, sup <р (я, у) а при любом х£Х и
y£Y
— н.о.п. на X. индуцированное естественным по-
рядком на Y и функцией ср, то в множестве (X, т|)
имеется по крайней мере одна альтернатива, для
которой if (х) а.
170 ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ.4
4.4. Задачи математического программирования
с нечетко описанными параметрами
4.4.1. Введение. В данном разделе обсуждаются
задачи нечеткого математического программирования,
которые описываются постановками IV и V в § 2.3.
Обратимся для примера к следующей упрощенной
модели распределения воды для орошения сельско-
хозяйственных культур. Допустим, что на землях общей
площадью X требуется разместить посевы т культур.
Урожайность /-й культуры обозначим так, что если
под культуру / отведена площадь посевов х^ то полный
урожай этой культуры будет равен с^х^ Для обеспече-
ния урожайности Су земли, отведенные под культуру /,
необходимо орошать. Пусть для орошения.единицы пло-
щади земли, занятой под культуру /, требуется еди-
ниц объема воды (за весь период роста культуры). Та-
ким образом, для орошения замель площадью х$ тре-
буется ^j-Xj единиц объема воды. Величину Wj назы-
вают нормой полива. Полное количество воды, которое
можно использовать для орошения всех т культур,
обозначим W. Наконец, пусть Ру, /=1, ...» иг, —
доход от реализации на рынке единицы урожая куль-
туры /.
Задача заключается в том, чтобы определить распре-
деление земель общей площадью X под т культур,
обеспечивающее по возможности больший доход от реа-
лизации урожая на рынке. При этом необходимо учи-
тывать ограниченное количество имеющейся воды для
орошения. Математически эта задача описывается как
стандартная задача линейного программирования.
т
Задача I. Максимизироватъ величину 2 Pjcjxj
при ограничениях
%х^Х, #у^>0.
J—l
Рассмотрим теперь более внимательно параметры
этой задачи Су и Wj. Нетрудно понять, что величины этих
параметров зависят от многих факторов реального про-
4.4]
НЕЧЕТКО ОПИСАННЫЕ ПАРАМЕТРЫ
171
цесса, не учтенных в приведенной здесь модели. Уро-
жайность, например, зависит, и довольно сложным
образом, от таких факторов, как наличие в почве тех
или иных питательных веществ, сроков и технологии
обработки почвы и внесения удобрений, солнечной
активности и многих других. То же самое относится и
к параметру w..
Если, желая сделать модель более адекватной реаль-
ности, внести в нее эти зависимости, то это приведет
к значительному ее усложнению и повысит размер-
ность задачи. Кроме того, может оказаться — при-
чем часто на это не обращают должного внимания —
что уточнение модели таким путем на практике сведется
на нет из-за невозможности измерить или измерить с до-
статочной точностью величины введенных в модель
факторов.
С другой стороны, модель с фиксированными зна-
чениями параметров (например, Cj и в данной мо-
дели) может оказаться слишком «грубой», поскольку
часто эти значения выбираются весьма произволь-
ным-образом. На самом деле следует, по-видимому,
учитывать по крайней мере тот факт, что известными
бывают не сами значения параметров, а множества их
возможных значений. Модель, в которой параметрам
приписаны не конкретные числа, а, например, интер-
валы возможных значений, более точно соответствует
реальности.
На этом пути мы от задачи I приходит к следующему
ее уточненному варианту.
Задача II. Требуется определить рациональное
распределение земель общей площадью X под посевы т
культуру если доход от распределения £=(#!, . . ., ят)
описывается в виде
т
S pfjxj
73=1
и должны выполняться ограничения
т
/=1
т
у=1
172 ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
Здесь Су, / = 1, ...,т,— множество возможных значе-
ний урожайности культуры /; j = 1,. .., тп, —
множество возможных значений норм полива; W — мно-
жество значений имеющегося полного количества воды
для орошения культур.
Задачу такого типа можно назвать задачей линей-
ного программирования с множественно-значными коэф-
фициентами. Ясно, что в рамках этой задачи не имеет
смысла говорить о максимизации функции цели (до-
хода), поскольку значения этой функции — не числа,
а множества чисел. В этом случае необходимо выяснить,
какое отношение предпочтения в множестве альтерна-
тив (т. е. в множестве возможных распределений пло-
щади земель) порождает эта функция, а затем исследо-
вать вопрос о том, какие выборы считать рациональ-
ными в смысле этого отношения предпочтения. Задачи
такого типа анализируются ниже.
Более простая задача этого типа с обычным макси-
мизируемым линейным критерием и с множественно-
значными параметрами в ограничениях рассматрива-
ется в работе А. Сойстера [41]. Эта задача описывается
следующим образом:
т
(4.4.1)
где x£Rm, a Kj, j = i,.. .,т, a K = {y\yQRn,
у g) — заданные выпуклые подмножества простран-
ства R\ Сумма произведений в (4.4.1) понимается при
этом следующим образом:
2	= (уI*/€#"»	a^K^R”,
где Xjdj — обычное произведение вектора a^R* на
число Ху. В работе [41] показано, что эта задача сво-
дится к следующей задаче линейного программирования:
Ьх -> max, Ах g, х О,
4-41
НЕЧЕТКО ОПИСАННЫЕ ПАРАМЕТРЫ
173
в которой матрица А определяется по заданным мно-
жествам Kj и К:
Л =||do.||, ^у = supa., i = l, ../ = 1,. . .,т,
абГу
at — компонента вектора а.
Следующим шагом на пути уточнения рассматривае-
мой здесь модели является описание параметров задачи
в форме нечетких множеств. При этом, кроме задания
множеств возможных значений параметров, в модель
вводится дополнительная информация в виде функций
принадлежности этих нечетких множеств. Эти функ-
ции можно рассматривать как способ приближенного
отражения экспертом в агрегированном виде имею-
щегося у него неформализованного представления
о реальной величине данного параметра. Значения функ-
ции принадлежности суть весовые коэффициенты, кото-
рые эксперт приписывает различным возможным зна-
чениям этого параметра.
Несомненно, что учет подобной дополнительной
информации усложняет исходную математическую
модель, но тем не менее она может оказаться проще
(и вместе с тем приемлемо точной) модели, учитываю-
щей многообразие дополнительных факторов, о которой
говорилось выше.
Итак, мы пришли к постановке задачи нечеткого
математического программирования, описанной в задаче
V § 2.3.
Задана «максимизируемая» линейная форма вида
т
2 ajxp
/=1
в которой значения коэффициентов описаны нечетко
в форме нечетких подмножеств соответствующих уни-
версальных множеств, т. е. заданы функции принад-
лежности Ху (ау), 7=1, . . ., т. Кроме того, заданы огра-
ничения (для простоты изложения одно)
т
174
ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
причем значения коэффициентов Cj и Ь описаны также
в форме нечетких подмножеств Vy (cj) и т] (Ь) соответ-
ствующих универсальных множеств. Требуется осуще-
ствить рациональный выбор вектора x£Rm, который
в некотором смысле «максимизирует» заданную не-
четко линейную форму.
Анализу задач принятия решений такого типа и шъ
священы последующие разделы.
4.4.2. Формулировка исходной задачи и сведение
ее к общей задаче нечеткого математического про-
граммирования. В данном разделе мы сформулируем
задачу математического программирования с нечетко
описанными параметрами и сведем ее к общей задаче
нечеткого математического программирования, с тем
чтобы воспользоваться результатами, полученными
в § 4.3, для построения множества недоминируемых
альтернатив.
Пусть X — заданное универсальное множество
альтернатив. Подмножество допустимых альтернатив
описывается неравенствами вида
7 = 1,..., п, (4.4.2)
где фу — заданные функции XxRp R1; bip f =
7 = 1,..., n, — числовые параметры, значения которых
описаны нечетко в форме нечетких подмножеств число-
вой оси; пусть (Ь^у), i = 1, • -., р; j = 1,..тп, —
заданные функции принадлежности этих нечетких мно-
жеств соответственно.
Выборы альтернатив оцениваются значениями за-
данной функции /: XxRq -> R1 вида
f(x,	(4.4.3)
в которой a., i=l, . . ., q, — числовые параметры,
значения которых также описаны нечетко в форме не-
четких подмножеств числовой оси; пусть (aj,
i=l, . . gr, — заданные функции принадлежности этих
нечетких множеств. Заметим, что в силу нечеткости опи-
сания параметров а. оценка любой альтернативы х £ X
(т. е. значение функции /) представляет собой нечеткое
подмножество числовой оси.
4.4]
НЕЧЕТКО ОПИСАННЫЕ ПАРАМЕТРЫ
175
Для завершения формулировки задачи необходимо
описать отношение предпочтения в универсальном мно-
жестве оценок альтернатив (иными словами, в универ-
сальном множестве значений функции /). В данном
случае это универсальное множество представляет со-
бой числовую ось R1 и мы будем считать, что исходное
отношение предпочтения совпадает с естественным
порядком (^) на R1.
Приведенную формулировку задачи следует рас-
сматривать как описание исходной информации, на
основе которой должен осуществляться выбор альтер-
натив из универсального множества X.
Далее мы сформулируем эту задачу в форме общей
задачи нечеткого математического программирования
(§§ 4.2, 4.3). Это позволит построить в множестве X не-
четкое отношение предпочтения, соответствующее ис-
ходной нечеткой информации. Затем, пользуясь ре-
зультатами, полученными в предыдущих разделах, мы
сможем выделить в множестве X подмножество недоми-
нируемых альтернатив, которое и будет служить осно-
вой для рационального выбора альтернатив.
Для формулировки соответствующей общей задачи
можно непосредственно применить принцип обобще-
ния (§ 1.3) для определения нечетких значений (образов}
функций фу и /, соответствующих нечетким значениям
входящих в них параметров. Мы же воспользуемся здесь
другим приемом, который представляется нам более
наглядным.
Обратимся сначала к нечетким ограничениям (4.4.2}
и построим соответствующее им нечеткое подмножество
допустимых альтернатив, функцию принадлежности
которого будем обозначать (х). При этом мы будем
опираться на следующие рассуждения.
Пусть 6Qy, i =	— некоторые
конкретные числовые значения соответствующих пара-
метров в ограничениях (4.4.2); степени их принадлеж-
ности заданным нечетким множествам равны соответ-
ственно (Ь?у), i = 1,..р; у — 1,..., п. Обозначим
р.0 минимальное из этих чисел, т. е.
F°=._min (&$/)•
176 ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
Если некоторая альтернатива х^Х удовлетворяет
неравенствам
<Ы*’ Ь?у,...,Ь®у)<0, / =
то естественно считать, что эта альтернатива принад-
лежит множеству допустимых альтернатив (т. е. допу-
стима) со степенью, не меньшей р.0, т. е. считать, что
Р'с (£)	И°- Этим, собственно говоря, уже и опреде-
ляется нечеткое множество допустимых альтернатив.
Для удобства записи его функции принадлежности
введем следующие обозначения:
V (В) = mill (&„), В = || by ||,
P(a:) = {B = |&<J, i = l,
7 = 1,... ,п|<|»у(ж, by, • ..,bp/X0, / = l,...,n).
В этих обозначениях получаем
?с(х) = SUP v(5)-	(ЬАА)
Ябф)
Каждой альтернативе функция ставит в соответ-
ствие степень допустимости этой альтернативы с уче-
том исходной нечеткой информации о параметрах огра-
ничений.
Обратимся теперь к заданной нечетко «максимизи-
руемой» функции (4.4.3) и представим ее в виде нечет-
кой функции цели вида ср:	1]. Рассуж-
дения здесь во многом аналогичны предыдущим.
Пусть aj, i — 1,..g, — некоторые конкретные чи-
словые значения параметров функции (4.4.3); степени
их принадлежности заданным нечетким множествам
равны соответственно (aj), i = l,...,g. Пусть —
минимальное из этих чисел, т. е.
<р° = mjn хДа®).
Пусть, наконец, х £ X — некоторая альтернатива, а число
r®=/(f, а®......................а®)
представляет собой соответствующее альтернативе £ и
значениям параметров а°( значение функции (4.4.3).
4.4]	НЕЧЕТКО ОПИСАННЫЕ ПАРАМЕТРЫ	177
Естественно считать, что это значение (число г0) при-
надлежит нечеткой оценке альтернативы х со степенью,
не меньшей ср0. Отсюда мы получаем, что искомая не-
четкая функция цели ср (х, г) имеет вид
ср (ж, г) = sup х (а),
г)
где
х(а)= min к. (aj, a — (av . . ., а?),
1=1, ...» q
Q(x,r) = {a\a^Rg, f (х, av ..aq) = r}.
Окончательно получаем, что исходная задача с не-
четко описанными параметрами формулируется в форме
следующей общей задачи нечеткого математического
программирования: «максимизировать» нечеткую функ-
цию цели
<?(х,г)= sup х(а)	(4.4.5)
г)
на нечетком	множестве допустимых альтернатив вида
Мж) = SU₽ V(5)-	С4-4-6)
Следующий	этап — нахождение	недоминируемых
альтернатив для сформулированной общей задачи.
4.4.3. Недоминируемые альтернативы в задаче с не-
четко описанными параметрами. Рассмотрим сначала
более простую задачу с нечеткой функцией цели (4.4.5)
и обычным (четко описанным) множеством допустимых
альтернатив, заданным неравенствами
П,
с точно известными значениями параметров.
Функция ср (я, г) и естественный порядок (?>) на
числовой оси (универсальном множестве значений функ-
ции f) индуцируют (§ 4.2) на множестве X нечеткое
отношение предпочтения вида
ж2) = sup minfcp^p z), <f(x2, y)} =
— sup min { sup x(a), sup x(a)}.
*>У	y)
12 с. А. Орловский
178 ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
Пусть т]в д (х) — соответствующее нечеткое множество
недоминируемых альтернатив в множестве (X, т]). Вы-
берем некоторое число а из интервала 0<а^1 и
рассмотрим задачу нахождения альтернативы, сте-
пень недоминируемости которой не меньше а, или
Будем предполагать, что все исходные нечеткие
множества к. [a.), i = 1, . . .. q, таковы, что sup х, (а.) а.

Покажем, что в этом случае функция (4.4.5) обладает
свойством
sup ср (гс, г) а
r£Rl
при любом х (< X, Допустим, что найдется х £ X, для
которого
sup ср (х, r) = d<^a.
r£Rl
(4.4.7)
Это означает (см. (4.4.5)), что при любом r^R1 и любом
г) выполняется неравенство
х (а) d а.
(4.4.8)
Выберем произвольно число е из интервала 0^е<^
а — d, и пусть av i = q, таковы, что
х< (5<) > 1 — е
(существование таких dl следует из предположений
о функциях xj. В результате получаем
х (а) = min х. (а{) >1 — е.
*=i,...»?
Вместе с тем для r = f(x, av . .aq) выполнено
а £(>(£, г). Однако в силу выбора е неравенство (4.4.8)
не выполняется для г f R1 и а £ Q (х, Г) и, следова-
тельно, не выполняется неравенство (4.4.7).
Итак, если все заданные нечеткие множества х. имеют
высоту, не меньшую а, то выполнены все условия тео-
ремы 4.3.1 и поэтому для нахождения альтернатив,
степень недоминируемости которых не меньше а, в рцс-
4.4Г
НЕЧЕТКО ОПИСАННЫЕ ПАРАМЕТРЫ
сматриваемом случае достаточно решить следующую
задачу математического программирования:
г -> max,
ср (ж, г)>а,
фДж, bv,..., Ь,у)<0, ; = !,..., п, (4.4.9)
r£Rl, х£Х.
Предположим для простоты, что множество X ком-
пактно, все функции x,(aj, i = l,..., g, непрерывны
на Я1, а функция f(x, av . .aq) непрерывна на тихо-
новском произведении X X R9* Нетрудно показать, что
в этих условиях задача (4.4.9) эквивалентна следующей
задаче:
f(x, av . .., ag)-^max
при ограничениях
*<(<*,)> а,	$ = 1,..., д,
, , /	•	4	(4.4.10)
фу(х, bv,..., bpJ)<0, J =
Действительно, пусть пара (х°, г°) £ X X R1 — реше-
ние задачи (4.4.9). В принятых выше предположениях
функция* х (а) непрерывна на Rq, а множество Q(x, г)
замкнуто в R1. Пусть вектор aQ(*Q(x, г) — такой, что
х(а°)^>а. Тогда по определению множества Q(x, г) по-
лучаем /(я0, av ..., aq) — rQ.
Допустим, что (я0, а0) не является решением задачи
(4.4.10), т. е. найдутся х1, а1, удовлетворяющие огра-
ничениям задачи (4.4.10), такие, что /(х1, а},..., а^) =
= г1 > г°. Это означает, что а1 £ Q (ж1, г1) и <? (ж1, г1) а,
т. е. пара (х1, г1) удовлетворяет ограничениям за-
дачи (4.4.9). Но тогда не может быть г1 > г°, поскольку
(xQ, г°) — тоже решение задачи (4.4.9).
Столь же просто показать, что любое решение за-
дачи (4.4.10) есть решение задачи (4.4.9).
Рассмотрим теперь задачу, в которой четко описаны
параметры a., i = l,..., g, максимизируемой функции
и нечетко — параметры 6^., i = 1,. .р; j = 1,. .., п,
ограничений (4.4.2).
12*
180 ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
В этом случае нечеткое множество допустимых аль-
тернатив описывается функцией принадлежности вида
(4.4.4):
М®) = sup v(B),
В6Р(®)
где
5 = 11М> A’ j =
Чв)= min
*=1,...»p
j=l,...» и
P(z) = {£=IIM> i = l,..., p;
7 = 1...../ = !>•••> n}.
Таким образом, данная задача представляет собой
задачу «максимизации» обычной функции f : X R1
на нечетком множестве (см. § 2.4). Выборы альтер-
натив в такой задаче оцениваются значениями двух
функций (критериев): /-«эффективностью» альтерна-
тивы и р^-степеныо ее допустимости, причем рацио-
нально так выбирать альтернативы, чтобы значения
обеих функций были по возможности большими. Иными
словами, данная задача свелась к задаче принятия
решений по двум критериям: / и
Нетрудно проверить, что ч. н. д. альтернативами
в рассматриваемом случае являются паретомаксималь-
ные альтернативы для пары функций / и Для на-
хождения таких альтернатив достаточно, например,
найти максимум следующей свертки этих функций:
L(я) =	(х, ач) +	(х),
где 0, Х2 0, Xj -р Х2 = 1.
Пользуясь выражением (4.4.4) для функции рс(х) и
сделанными выше предположениями, запишем функцию
Их) в виде
L (х) — max min {kJ(х, an ..а ) + k2v(b{,)},
БеР(ж)	р
..., п
где
В = р.у||, i = l, р-
4.4]
НЕЧЕТКО ОПИСАННЫЕ ПАРАМЕТРЫ
181
В результате задачу максимизации функции L (х)
можно сформулировать следующим образом (см. также
определение множества Р (х)):
с -> max,
Ы®’ Ъу,....
i = i. ..р; / = 1, • • •, п,
Kf (х, at) 4- x2vfy (6<y) > c,
1 = 1, . . p; j = 1, . . n,
x £ X.
Любое решение xQ £ X этой задачи — ч.н.д. альтер-
натива в исходной задаче.
Любая допустимая альтернатива, доставляющая
максимум функции L (#) на множестве X, является
паретомаксимальной для функций / и р<6,, а потому и
ч.н.д. альтернативой для исходной задачи. Выбирая
различные коэффициенты свертки > 0 и Х2 > О,
можно получить достаточное многообразие ч. н. д.
альтернатив.
Каждая из ч. н. д. альтернатив ж0 характеризуется
двумя числами: соответствующим ей значением функ-
ции / (х?) и степенью допустимости этой альтернативы
(ж0). При выборе конкретной альтернативы л.п.р.
должно исходить из компромисса между желанием вы-
брать по возможности более допустимую альтернативу
и желанием получить по возможности большее значе-
ние функции /. (Подробнее об этом см. в п. 2.4.2).
Общая задача. Обратимся, наконец, к об-
щей задаче, в которой нечетко описаны как параметры
а. функции /, так и параметры b.j ограничений (4.4.2).
Как показано выше, эту задачу можно сформулировать
в виде общей задачи (4.4.5) — (4.4.6).
Заметим прежде всего, что в данной задаче выбор
альтернатив должен осуществляться с учетом двух
отношений предпочтения на множестве альтернатив
X : нечеткого, индуцированного функцией ср (х, г)
(4.4.5), и четкого, индуцированного функцией рс и
естественным порядком на R1.
182
ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
Как было показано в § 4.2, функция ср (х, г) и есте-
ственный порядок (J» на R1 индуцируют на X нечет-
кое отношение предпочтения вида
х2) = sup min{<f>(xn у), <р(х2) z)}. (4.4.11)
У,
У^х
Второе отношение предпочтения на X определяется
тем, что более предпочтительны альтернативы, имею-
щие большую степень допустимости, т. е. те, которым
соответствуют большие значения функции Таким
образом,
х^ =
1 при
п . ..	. .	(4.4.12)
О при
Задачи такого типа (с несколькими отношениями
предпочтения) обсуждались выше в § 3.3, где была пред-
ложена процедура построения нечеткого подмножества
недоминируемых альтернатив. В соответствии с этой
процедурой требуется построить две свертки исходных
и. о. п. т]1 и т]2 : их пересечение и взвешенную сумму.
Пересечение т]1 и имеет вид
х2) — min {т]1 (хг, х2),	я2)}, (4.4.13)
а взвешенная сумма при условии одинаковых коэффи-
циентов важности исходных н. о. п. т]1 и т]2 имеет вид
1
Wp x2)=-2-h1(o;1,	+	®2)]. (4.4.14)
Пусть т)1н-д- и т)2н-д- — нечеткие подмножества недо-
минируемых альтернатив множеств (X, т)1) и (X, т}2)
соответственно. Тогда, согласно процедуре § 3.3, резуль-
тирующее подмножество недоминируемых альтернатив
имеет вид
т]н-д- (х) = min д- (я), т]2н-д- (х)}. (4.4.15)
Функция принадлежности ^н,д- служит основой для
выбора конкретных альтернатив в исходной общей за-
даче нечеткого математического программирования.
Как и прежде, в данной задаче представляет инте-
рес вопрос о нахождении альтернатив я£Х, для кото-
4.4]
НЕЧЕТКО ОПИСАННЫЕ ПАРАМЕТРЫ
183
рых (х) а, где а — некоторое заданное число
из интервала [0, 1], т. е. альтернатив, степень недоми-
нируемости которых не меньше а. Однако для упроще-
ния изложения ниже мы рассмотрим задачу нахожде-
ния ч. н. д. альтернатив, т. е. таких я: X, что т]н,д* (х)=1
(случай а=1). Рассуждения для более общего случая
а < 1 во многом аналогичны приведенным ниже.
Итак, рассмотрим задачу определения альтернативы
х^Х, для которой т]н-д (ж) = 1. Из (4.4.15) получаем,
что для этого необходимо и достаточно выполнения
условий
7)1н.д-(х) = 1, Т]2Н- д- (х) = 1,
т. е. чтобы х была ч. н. д. альтернативой одновременно
в множествах (X, т)1) и (X, т]2).
Выясним сначала условия, при которых х есть ч. н. д.
альтернатива в множестве (X, ^), т. е. ^1и д (ж) = 1.
Для этого обсудим прежде всего вопрос о линейности
н. о. п. TJ1.
Если исходные нечеткие множества \ (а.), 1 =
— 1,..., q, нормальны, т. е. sup xt.(aj = l, f =	...
.... q, то, как показано выше (a=l), функция
ср (я:, г) (4.4.5) обладает свойством
sup ср (яг, г) — 1
тек1
при любом х£Х. Отсюда и из теоремы 4.2.2 следует,
что н. о. п. т]1 — сильно линейное отношение.
Нетрудно видеть, что т]2— тоже сильно линейное
отношение. Однако пересечение (4.4.13) этих отно-
шений этим свойством, вообще говоря, не обладает.
Пусть, например, т]1 (яг2, х±) = 1,	х2) = a (0 < a< 1),
т]2(яг2, ^) = 0, rf(xv ж2) = 1. В этом случае ^1(я:1, х2) =
= а<1 и т)1^, я:1) = 0, т. е. rf(xv x2)>tf(x2, х^
но ^(^i,
Поскольку н. о. п. т;1 не является сильно линейным,
то для нахождения ч. н. д. альтернатив в множестве
(X, т)1) мы не можем воспользоваться теоремой 4.3.1
при a —1.
Пусть X?-н-д- — подмножество всех ч. н. д. альтер-
натив множества (X, т]2), т. е. множество всех xQ £ X,
для которых равенство rf (я:0, ж) = 1 выполняется при
184
ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
любом х £ X. Покажем, что ч. н. д. альтернативы мно-
жества (X, fi1) (т. е. ч. н. д. альтернативы по н. о. п. т]1)
достаточно искать среди элементов множества Х^н-Д-.
Пусть f]18 — нечеткое отношение строго предпочте-
ния, соответствующее н. о. п. т)1 (см. определение
в п. 3.2.1), и пусть ж°£Х£-нд-. Покажем, что
(х, xQ) — 0 при любом х (£ Xf н-д*. Допустим противное,
т. е. что найдется альтернатива	для кото-
рой т)1* (ж1, ж°)>0, т. е. (см. определение т)1 (4.4.13) и
fl18 (п. 3.2.1))
min {т]1 (ж1, ж0), т]2 (xv ж0)) —
— min {т]1 (ж0, ж1), т]2 (ж0, ж1)} > 0.	(4.4.16)
Но поскольку ж^Х^-и-Д-, я°£Х5’н-д- и ж2)^0
при любых xv ж2£Х, то 7]2(ж\ xq) — 0 и неравенство
(4.4.16) невозможно, т. е. выполнено ^(жр ж°) = 0.
Таким образом, ни одна альтернатива х XJ-н-д- не до-
минирует строго с положительной степенью альтерна-
тивы из множества Х^-н-д-.
Покажем теперь, что если х1 — ч. н. д. альтернатива
в множестве (Х^-н-д-, т]1), то она является таковой
и в множестве (X, т)1). Действительно, как показано
выше, при этом т]1’ (ж, х1) = 0 для любого х (£ Хч- “• д- С X.
Пусть ж£Х^-н-д-, тогда из того, что х1 — ч. н. д. аль-
тернатива в множестве (Х^-н-д-, т]1) и т]1 — сильно ли-
нейное н. о. п., получаем (теорема 3.2.4), что?]1 (ж1, х) = 1.
Кроме того, ^(я1, ж) = 1, поскольку	Отсюда
заключаем, что неравенство
if (ж, х1) = min {т]1 (х, х1), т]2 (х, ж1)} —
— min {т]1 (ж1, ж), т]2 (ж1, ж)} > 0
невозможно.
Итак, мы показали, что если ж1 выбрано описанным
выше способом, то равенство т]1в(ж, жх) = 0 выполняется
при любом ж g X, т. е. что ж1 — ч. н. д. альтернатива
в множестве (X, if).
Таким образом, для нахождения ч. н. д. альтерна-
тивы в множестве (X, т)1) достаточно найти ч. н. д.
альтернативу в множестве (Х^- н-д-, т]1). Пусть исходные
нечеткие множества ^(6^), Z = l,. .р; /=1,. . п,
таковы, что существуют 6^., для которых	=
4.4]
НЕЧЕТКО ОПИСАННЫЕ ПАРАМЕТРЕ!
185
Как нетрудно видеть, при этом множество Х^-н-д- со-
ставляют альтернативы х X, удовлетворяющие условиям
Ьру)<0,	] = п,
=	i = р; ] = п.
Задача нахождения ч. н. д. альтернативы в мно-
жестве (X, у1) аналогична задаче, рассмотренной в на-
чале данного раздела. Если выполнены все введенные
в той задаче предположения о множестве X и функции
/, то получаем следующую задачу для нахождения
ч. н. д. альтернативы в множестве (X, т}1):
f(x, av ..ag)->max	(4.4.17)
при ограничениях
ъ1р..., bPJf)<o, ь^ея1,
vv(M = 1’	* =	7 = 1. •••>«. (4.4.18)
xi(aj = l, a.^R1, j = l,..., g,
x£X.
Любое решение xQ£X задачи (4.4.17) — (4.4.18) есть
ч. н. д. альтернатива в множестве (X, т)1) и в то же
время ч. н. д. — альтернатива в множествах (X, т]1) и
(X, ^).
Покажем теперь, что любое решение этой задачи —
ч. н. д. альтернатива и в множестве (X, т/2). Действи-
тельно, нечеткое подмножество недоминируемых альтер-
натив множества (X, т)2) имеет вид (см. (4.4.14))
Т|2п-Д'(ж) = 1 — 4 sup К1»!1 (у. «) —у)) +
+ С»12(г/, ж) —т)2(ж, у))]. (4.4.19)
Пусть Xй — решение задачи (4.4.17) — (4.4.18). Тогда,
поскольку ж0 — ч. н. д. альтернатива в (X, к]1), то при
любом у£Х выполнено
7)U(y, Ж°) = 0
или
иЦу, «*) —цЧ®0» у)<0.
186
ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
Кроме того, х° — ч. н. д. альтернатива в множестве
(X, т]2), и, следовательно, при любом у £ X выполнено
?12'(У» я°) = 0 или Tja(y, а0) — т]2(я0, у)<0.
Из двух последних неравенств следует, что в (4.4.19)
sup [О)1 (у» я0) — ?]1 (я0, у)) 4- (т]а (у, Ж0) — 7]2(ж°, J/))] = 0,
Уб*
т. е.
^2н. Д. (£0)=1.
Итак, любое решение задачи (4.4.17) — (4.4.18) удов-
летворяет условиям
^ж-*-(ягО) = 1, т]2и-*-(я0) = 1,
и поэтому (см. (4.4.15))
д- (яг°) = 1,
т. е. -х°— ч. н. д. альтернатива для исходной общей
задачи.
Наличие в полученных выше задачах математиче-
ского программирования ограничений вида vt.y(bt.y) = l
и х^ (aj — 1 говорит о том, что для нахождения ч. н. д.
альтернатив в исходной задаче достаточно учитывать
лишь те значения параметров, которые заведомо, т. е. со
степенью 1, принадлежат соответствующим нечетким
множествам значений параметров. Поэтому, если инте-
ресоваться лишь ч. н. д. альтернативами, то при форму-
лировке исходной задачи можно не требовать полного
описания нечетких множеств значений параметров,
ограничиться лишь указанием интервалов их значений,
со степенью 1 принадлежащих этим множествам. За-
дача при этом аналогична той, в которой в виде интер-
валов заданы результаты измерений {значений пара-
метров с определенной степенью точности.
Аналогичными рассуждениями можно прийти^к вы-
воду о том, что для нахождения альтернативы, имею-
щей степень недоминируемости, не меньшую заданного
числа?а (тдн>х- (х)	а), достаточно решить следующую
задачу математического программирования:
/ (ж,	..., aq) -> max	(4.4.20)
4.4]
НЕЧЕТКО ОПИСАННЫЕ ПАРАМЕТРЫ
187
при ограничениях
Ш Ьц........6„)<О,
'=».....к /=1..........».	4421
zgX.
Нужно отметить, что формулировка получаемой
задачи для нахождения ч. н. д. альтернативы зависит
от принятого способа свертки (типа (4.4.14)) нечетких
отношений т]1 и т)2 (см. выше). При рассмотренном
здесь способе свертки с одинаковыми коэффициентами
важности этих отношений для нахождения ч.н.д.
альтернатив достаточно учитывать лишь значения па-
раметров, входящие в соответствующие нечеткие мно-
жества со степенью, не меньшей а (в задаче (4.4.20)—
(4.4.21)). При других способах свертки (с различными
коэффициентами важности) может потребоваться пол-
ное описание этих нечетких множеств, что можно видеть,
например, в описанной выше задаче с четкими значе-
ниями параметров а.. Выбор конкретного способа
свертки рассматриваемых нечетких отношений дол-
жен быть сделан с учетом особенностей рассматрива-
емой задачи принятия решений.
Решение задачи типа (4.4.20)—(4.4.21) позволяет
определить лишь некоторые из недоминируемых аль-
тернатив (с соответствующей степенью а) для исходной
общей задачи. Можно показать, что еще один способ
нахождения недоминируемых со степенью а альтерна-
тив заключается в решении следующей задачи:
min / (х, av . .., ад) шах
Лр •••> Qq
при ограничениях
i = р; ] = п,
х£Х.
Заметим, что получаемое в последней задаче зна-
чение функции / представляет собой наиболее осторож-
188
ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
ную («пессимистическую») оценку альтернатив, недо-
минируемых со степенью, не меньшей а, а соответствую-
щее значение / в задаче (4.4.20)—(4.4.21) — наименее
осторожную («оптимистическую») оценку. Заключен-
ный между этими оценками интервал позволяет судить
о возможных значениях функции / при выборе альтер-
натив, недоминируемых со степенью а.
Этим мы завершаем обсуждение задач нечеткого
математического программирования. Все сказанное
выше, несомненно, нуждается в конкретизации и
развитии, причем описанные выше подходы следует
рассматривать лишь как один из возможных путей фор-
мализации и использования нечеткой информации при
постановке и анализе реальных задач принятия решений.
4.5.	Задачи упорядочения при нечеткой
исходной информации
4.5.1.	Введение. По сути дела, в данном разделе
описываются подходы к решению задач принятия ре-
шений при нескольких отношениях предпочтения на
множестве альтернатив. Подобные задачи уже рассма-
тривались в § 3.3 данной книги. Там предполагалось,
что информация об относительной важности отношений
предпочтения задана в форме соответствующих коэф-
фициентов важности. Это позволяло выбирать альтер-
нативы, опираясь на свертку исходных отношений
в виде взвешенной суммы их функций принадлеж-
ности.
Здесь же нас будут интересовать ситуации, в которых
относительная важность заданных отношений пред-
почтения (признаков) описывается не коэффициен-
тами важности, как в § 3.3, а, вообще говоря, нечет-
ким отношением типа «не менее важно» на множестве
признаков.
Заметим, что известные коэффициенты важности
признаков однозначно определяй» отношение «не менее
важно» на множестве признаков. Поэтому описываемый
ниже подход применим и к решению задач, рассмотрен-
ных в § 3.3. Однако набор коэффициентов относитель-
ной важности содержит в себе больше информации, чем
соответствующее ему отношение «не менее важно», и
4.5]
ЗАДАЧИ УПОРЯДОЧЕНИЯ
189
поэтому для решения задач с заданными коэффициен-
тами более подходит процедура, описанная в § 3.3.
Нужно отметить еще и тот факт, что в реальных
ситуациях относительную важность отношений пред-
почтения (или признаков, по которым оцениваются аль-
тернативы) не всегда можно адекватно описать соот-
ветствующими коэффициентами. (Иными словами, не
всякое отношение можно описать функцией полезности).
Это особенно относится к случаю, когда информация об
относительной важности отношений предпочтения
имеет нечеткий характер. Поэтому рассматриваемые
ниже задачи, вообще говоря, не сводятся к зада-
чам § 3.3.
4.5.2.	Рациональный выбор альтернатив с учетом
набора признаков. Пусть задано множество альтернатив
(или объектов) X и задано множество признаков (или
экспертов) Р. Каждой альтернативе х£Х в той или
иной степени присущ каждый из признаков множества
Р. Для каждого фиксированного признака р£Р из-
вестно нечеткое отношение предпочтения ср на множе-
стве альтернатив X или, иными словами, известна
функция принадлежности ср : ХхХхР -> [О, 1], зна-
чение ср (х1У я2, р) которой понимается как степень
предпочтительности альтернативы хг альтернативе хг по
признаку р. Если Р — множество экспертов, то
ср («!, х2, р) — отношение предпочтения на множестве
альтернатив, предлагаемое экспертом р. Таким образом,
функция ср описывает семейство нечетких отношений
предпочтения на множестве X по параметру р.
Элементы множества Р, вообще говоря, различны по
важности. Пусть pi: Р><Р -> [0, 1] — заданное не-
четкое отношение важности признаков (экспертов);
величина рь (рх, р2) понимается как степень, с которой
признак Pi считается не менее важным, чем при-
знак р2.
Задача заключается в рациональном выборе аль-
тернатив из множества X с учетом описанной выше
информации. Ниже мы кратко очертим один из воз-
можных вариантов применения к решению этой задачи
развитого выше ^подхода, опирающегося на понятие
нечеткого множества недоминируемых альтерна-
тив.
190 ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
Пусть <рв- *• (х, р) — нечеткое подмножество недо-
минируемых альтернатив, соответствующее н. о. п.
ср (xj, х2, р) при фиксированномpQP, т. е. (см. п. 3.2.3)
?’•*•(*, р) = 1 — sup [ср (у, х, р) —ср(а:, у, р)].
У 6^
Если бы выбор альтернатив осуществлялся лишь с уче-
том одного признака р, то рациональным следовало бы
считать выбор альтернатив, доставляющих по возмож-
ности большее значение функции принадлежности
срн-д- (х, р) (степени недоминируемости) на множестве X.
В данном же случае требуется осуществить выбор с уче-
том совокупности признаков, различающихся по важ-
ности.
Нетрудно понять, что при фиксированном яг°^Х
функция ср1- *• (я0, р) описывает нечеткое подмножество
признаков, по которым альтернатива ж0 является недо-
минируемой. Ясно, что если для двух альтернатив
хг и х2 нечеткое множество признаков срн,д- (хх, р) «не
менее важно», чем нечеткое множество признаков
срн д-(х2, р), то и альтернативу хг следует считать не
менее предпочтительной, чем альтернатива х2. Таким
образом, ситуация в данном случае аналогична той,
которая рассматривалась в п. 4.3.1 при анализе общей
задачи нечеткого математического программирования.
Итак, в данном случае нужно обобщить заданное
нечеткое отношение р (рп р2) на множестве признаков
Р на класс нечетких подмножеств множества Р и счи-
тать полученное нечеткое отношение результирующим
н. о. п. на множестве альтернатив X.
Пользуясь рассуждениями и результатами, приве-
денными в пп. 4.2.1 и 4.3.1, получаем следующее н. о.[п.
на множестве X, индуцированное функцией срн-х- (ж, р)
и нечетким отношением р:
чя(ж1( х2) =
— sup	Pi),	Ра), Р2)}-
Pi,
Это н. о. п. можно рассматривать как!результат «свертки»
семейства нечетких отношений ср (хх, я2, р) в единое
результирующее н. о. п. с учетом информации об отно-
4.51
ЗАДАЧИ УПОРЯДОЧЕНИЯ
191
сительной важности признаков, заданной в форме не-
четкого отношения.
Построением н.о.п. цисходная задача выбора све-
дена к задаче выбора с единственным отношением пред-
почтения. Для ее решения достаточно определить соот-
ветствующее отношение т), скорректированное нечет-
кое множество недоминируемых альтернатив (см.
п. 4.3.1) ^выбрать альтернативы, доставляющие макси-
мум функции т]н-д- (ж).
Для иллюстрации описанного подхода рассмотрим
два простых примера. J
Пример 4.5.1 (четкие отношения). Пусть X={xj, х2»
я8, *<) — заданное множество альтернатив. Альтернативы срав-
ниваются друг с другом по трем признакам А, В, С. Пусть ре-
зультаты сравнения альтернатив по каждому из признаков
в отдельности описываются следующими матрицами отношения
нестрогого предпочтения:
по признаку А:
Д?2	*^4

Xi 1
х2 1
х2 О
1
по признаку В:
О	1	1
1	1	1
О	1	о
О	1	1
^2 Х9
	1	1	0	1
*2	0	1	1	0
Х3	0	0	1	0
Х1	0	1	1	1
по признаку С:	xi	х2	хз	*4
хх	1	0	1	1
х2	0	1	0	1
х9	1	0	1	1
х*	0	0	0	1
192
ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
Отношение относительной важности признаков описывается
матрицей
| Л В С
1
1
1
из Которой следует, что признаки А и В эквивалентны друг
ДРУГУ (одинаково важны) и каждый из них важнее признака С.
В соответствии с описанным выше подходом определим
множество недоминируемых альтернатив по каждому из призна-
ков. В результате получаем
Х1	х2		
<рн* А*(^, Л) = 0	1	0	0,
Х1	х2	я3	
^«•Д-(хй В)— 1	0	0	0,
«1	д?2	#3	
Д« (xit С) = 1	1	1	0.
Иными словами, недоминируемыми являются альтернативы:
а) по признаку А — альтернатива х2;
б)	по признаку В — альтернатива хг\
в)	по признаку С — альтернативы ж2, ж8.
Далее, используя выражение (4.3.1), получаем матрицу
индуцированного отношения предпочтения на множестве аль-
тернатив:
	Х1	х2	ж8	ж4
xi	1	1	1	0
7]^, Х,) =	1	1	1	0
	0	0	1	0
*4	0	0	0	0
а по выражению (4.3.2) — соответствующее (нескорректирован-
ное) множество недоминируемых альтернатив:
хх х2	х3	х4
д. ==	1	1	0	1	.
Наконец, по	формуле	(п.	4.3.1)
if- Д- (а;,) = min {т)и- «• (г,), i) (x<t х,)}
4.5]
ЗАДАЧИ УПОРЯДОЧЕНИЙ
193
находим скорректированное нечеткое множество недоминируе-
мых альтернатив:
Д- (х J =1	1 О О
Таким образом, приходим к выводу о том, что рациональным
в данной задаче следует считать выбор альтернатив или х2.
Заметим, что эти альтернативы не доминируемые по призна-
кам А и 3, которые являются наиболее (одинаково) важными.
Пример 4.5.2. (нечеткие отношения). Обратимся теперь
к следующей ситуации. Некто (л. п. р.) должен остановить свой
выбор на одной из четырех моделей мужского костюма А, Б, В
или Г. Не полагаясь целиком на свой вкус, он пригласил четы-
рех советчиков (экспертов) 31, 32, 33 и 34, причем к мнениям
различных советчиков л. п. р. относится (ценит) по-разному:
к мнению одного советчика прислушивается в некоторой сте-
пени больше, чем к мнению другого. Пусть относительные важ-
ности мнений советчиков л. п. р. описывает с помощью матрицы
нечеткого отношения «не менее важно» (н. о. п. р.) следующего
вида:
	31	32	33	34
31	1	0,4	0,6	0
32	1	1	0,8	1
33	0,2	1	1	1
34	0,8	0	1	1
По мнению советчиков, нечеткие отношения предпочтения
между моделями костюма описываются следующими матрицами:
31:	32:
	А	Б	в	Г
А	1	0,8	1	0
Б	0	1	0,2	1
В	0	0,8	1	0
Г	0	0	0	1
	А	Б	В	г
А	1	0	0,8	0
Б	0	1	0	0
В	0,1	0	1	0,4
Г	1	1	1	1
13 С. А. Орловский
		А	Б	в	Г
А		1	0,1	0,5	0,3
Б		0,8	1	0,8	0,8
В		0,5	0,3	1	0
Г		0,8	0	0	1
	А		Б	В	Г
А	1		1	0,9	О
Б	0		1	1	1
В	0,4		0	1	0
Г	0		0	0	1
194
ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
Пользуясь приведенным в п. 3.2.3 определением, найдем соот-
ветствующие нечеткие множества недоминируемых альтернатив:
	А	Б	в	Г
уП.Д. (., 31)	1	0,2	0	0
Э2)	0,3	1	0,5	0,2
33)	0	0	0,3	1
Э4)	1	0	0	0
Далее находим н. о. п. индуцированное на множестве функ- циями Д* и нечетким отношением р:				
	А	Б	В	Г
А	1	0,4	0,4	1
Б	1	1	0,5	0,8
В	0,5	0,5	0,5	0,5
Г	1	1	0,5	1
Наконец, находим соответствующее отношению 7) нечеткое подмножество недоминируемых альтернатив (моделей костюма):				
А Б В Г
т)«-д.= 1	0,4	0,9	0,8
н корректируем его в учетом выражения (4.3.26):
А	Б В	Г
Д*== 1	0,4	0,5	0,8
Наибольшую степень принадлежности этому нечеткому
множеству (т. е. наибольшую степень недоминируемости) имеет
модель А, поэтому, в соответствии с предлагаемым подходом,
выбор этой модели и следует считать рациональным.
Если наибольшую степень недоминируемости имеет не одна,
а несколько альтернатив, то л. п. р. может либо сам выбрать
одну из них, исходя из каких-либо дополнительных своих со-
ображений, либо расширить круг своих советчиков и вновь
найти множество т)н,д-, как это описано выше.
4.5.3.	Упорядочение объектов по набору признаков.
Основным элементом излагаемого здесь подхода можно
считать способ решения задачи упорядочения объектов
по важности (весам) при заданной матрице отношений
весов этих объектов, поскольку именно на этот способ
4.5]
ЗАДАЧИ УПОРЯДОЧЕНИЯ
195
опирается предложенный в работе [42] метод решения
задачи упорядочения по набору признаков.
В основе этого способа лежат следующие сообра-
жения. Пусть имеется п объектов Лх, . . ., Ап, и пусть
со=(о)1, . . ., %) — вектор относительных весов этих
п
объектов, причем S % = 1. Предполагается, что резуль-
1
таты попарного сравнения объектов по весам описыва-
ются отношениями весов этих объектов. В этом слу-
чае результаты такого попарного сравнения объектов
можно представить в форме следующей матрицы раз-
мером пХп:
А2 ... Ап
Ai <»i/wi
А 2 <^1^1 W2/W2 • • • w2/ww
Ая (Од/О)!	О)я/О)2 ...
Нетрудно убедиться в том, что матрица А обладает
свойством
или
(Л — n.Z)<D = 0,	(4.5.1)
где I — единичная матрица, а (о — вектор относитель-
ных весов рассматриваемых объектов.
Допустим теперь, что вектор весов ш неизвестен,
а известна лишь матрица Л. Тогда, как нетрудно видеть,
для нахождения вектора весов w по матрице Л доста-
точно решить уравнение (4.5.1). Поскольку ранг ма-
трицы Л равен 1, то п — единственное собственное
число этой матрицы и, следовательно, уравнение
(4.5.1) имеет ненулевое решение. Более того, оно имеет
п
единственное решение, обладающее свойством 2 — 1 •
1
Это решение и есть искомый вектор относительных ве-
сов объектов.
Допустим теперь, что элементы матрицы Л пред-
ставляют собой не точные значения отношений весов
объектов, а их оценки, предложенные экспертами, при-
13*
196 ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
чем по-прежнему выполнено af7=l/ayi. Ясно, что для
такой матрицы оценок, вообще говоря, не выполнено
свойство	необходимое для существования
нетривиального решения уравнения (4.5.1). Вместо
этого уравнения следует рассматривать более общее
уравнение вида
(Л -Хю„/)«>=0,	(4.5.2)
где Хтах — максимальное собственное число матрицы
(\пах ^).
Опираясь на приведенные выше рассуждения, не-
трудно понять, что слишком сильное отличие Хтах от
п сигнализирует о некоторой внутренней несогласован-
ности оценок экспертом значений элементов матрицы
Лио необходимости их пересмотра, уточнения. С дру-
гой стороны, если значение Хтах достаточно близко к п,
то нормированный к 1 вектор — решение уравнения
(4.5.2) — можно принять в качестве приемлемой оценки
относительных весов рассматриваемых объектов, вос-
становленных по матрице оценок Л.
Опишем теперь предложенный в работе [42] способ
упорядочения объектов по набору признаков. Восполь-
зуемся для этого одним из примеров, приведенных в ра-
боте [42].
Человеку необходимо остановить свой выбор на од-
ном из предлагаемых ему мест работы Л, В и С. Каж-
дое из них он оценивает по шести признакам: возмож-
ность научной работы (н. р.), возможности роста (в. р.),
материальные выгоды (м.в.), коллектив (к.), местополо-
жение (м.), репутация (р.), причем эти признаки разли-
чаются по важности. Пусть результаты попарного срав-
нения признаков друг с другом по важности (матрица
отношений весов признаков) имеет вид
	н. р.	в. р.	м. в.	к.	м.	р-
н. р.	1	1	1	4	1	1/2
в. р.	1	1	2	4	1	1/2
А. л == м. в.	1	1/2	1	5	3	1/2
к.	1/4	1/4	1/5	1	1/3	1/3
м.	1	1	1/3	3	1	1
р-	2	2	2	3	3	1
4.5]
ЗАДАЧИ УПОРЯДОЧЕНИЯ
197
а результаты попарного сравнения по важности мест
работы А, В и С по каждому из признаков в отдельности
описываются следующими матрицами (матрицы отно-
шений весов мест работы):
	А	В	С
А	1	1/4	1/2
В	4	1	3
С	2	1/3	1
	А	В	С
А	1	1/3	5
В	3	1	7
С	1/5	1/7	1
	АВС
А В С	1	1/4	1/5 4	1	1/2 5	2	1 АВС
А В С	1	1	7 1	1	7 1/7 1/7 1
	А	В	С
А	1	3	1/3
В	1/3	1	1
С	3	1	1
	А	в	с
А	1	7	9
В	1/7	1	5
С	1/9	1/5	1
Первый этап решения задачи упорядочения мест
работы — восстановление относительных весов (важ-
ностей) признаков по заданной матрице Лп, т. е. на-
хождение нормированного к 1 собственного вектора
этой матрицы, соответствующего максимальному соб-
ственному числу, путем решения уравнения типа (4.5.2).
В результате получаем
н. р. в. р. м. в. к. м. р.
а)п=0,16	0,19	0,19 0,05 0,12 0,30
Затем аналогичным образом находим относительные
веса мест работы по каждому признаку в отдельности:
	н. р.	в. р.	м. в.	к.	м.	Р-
А	0,14	0,10	0,32	0,28	0,47	0,77
В	0,63	0,33	0,22	0,65	0,47	0,17
С	0,24	0,57	0,46	0,07	0,07	0,05
В каждом столбце этой матрицы указаны относитель-
ные веса, приписываемые соответствующему месту ра-
боты по соответствующему признаку.
Поскольку место работы, обладающее большим ве-
сом, считается более предпочтительным, то распределе-
ние весов мест работы для данного признака (столбец
198
ОБЩАЯ ЗАДАЧА НЕЧЕТКОГО ПРОГРАММИРОВАНИЯ [ГЛ. 4
матрицы В) можно рассматривать как функцию цели,
соответствующую этому признаку. £ Таким образом,
на данном этапе исходная задача формулируется как
задача выбора альтернатив (мест работы) с учетом шести
функций цели, причем заданы коэффициенты относи-
тельной важности этих функций.
Для решения такой задачи в работе [42] предлага-
ется обычный прием: строится взвешенная сумма за-
данных функций цели с заданными коэффициентами
важности и выбирается та альтернатива, которой
соответствует наибольшее значение построенной взвеси.
Иными словами, для получения результирующего на-
бора весов мест работы А, В и С достаточно умножить
матрицу В на вектор-столбец соп. В результате полу-
чаем следующие относительные веса мест работы:
АВС
0,4	0,34	0,26
Наибольшим весом обладает место работы Л, и потому
его выбор следует считать рациональным.
Сравним теперь описанную здесь задачу с задачами
принятия решений, рассмотренными вышеТв § 3.3.
Заметим прежде всего, что информация в форме ма-
трицы А отношений весов альтернатив содержит в себе
четкое описание отношения предпочтения на множестве
альтернатив. Действительно, если некоторый элемент
а.^ этой матрицы больше или равен 1, то это означает,
что вес альтернативы i не меньше веса альтернативы
/, т. е. что альтернатива i определенно (со степенью 1)
не менее важна, чем альтернатива /. Таким образом,
матрица А однозначно определяет матрицу соответ-
ствующего четкого отношения предпочтения. Поэтому
описанная здесь задача относится к классу задач при-
нятия решений при нескольких четких отношениях
предпочтения.
Помимо этого, в матрице А содержится и дополни-
тельная количественная информация о величинах отно-
шений весов альтернатив, которая позволяет одно-
значно восстановить вектор весов. Иными словами,
матрица А представляет собой описание в определен-
ЗАДАЧИ УПОРЯДОЧЕНИЯ
199
ной форме функции полезности на множестве альтер-
натив, по которому эту функцию можно восстановить,
решив уравнение типа (4.5.2). При этом полагается,
что при решении практических задач экспертам легче
более адекватно отразить свои представления об отно-
сительной важности альтернатив в форме матрицы А,
чем путем непосредственного задания величин этих
весов.
ЛИТЕРАТУРА
1.	Z a d е h L. A. Fuzzy sets. — Inf. Contr., 1965, 8, p. 338—353.
2.	Zadeh L. A. Fuzzy orderings. — Inf. Sci., 1971, 3, p. 177—
200.
3.	Z a d e h L. A. Shadows of fuzzy sets. — Prob, in Trans,
of Informat., 1966, 2, p. 37—44.
4.	3 а д e Л. А. Основы нового подхода к анализу сложных
систем и процессов принятия решений. — В сб. «Матема-
тика сегодня». — М.: Знание, 1974, с. 5—49.
5.	3 а д е Л. А. Понятие лингвистической переменной и его
применение к принятию приближенных решений. — М.:
Мир, 1976.
6.	Goguen J. А. Л-fuzzy sets. — J. Math. Anal. Appl.,
1967, 18, p. 145-174.
7.	Goguen J. A. The fuzzy Tychonoff theorem. — J. Math.
Anal. Appl., 1973, 43, p. 734—742.
8.	Negoita С. V., Minou S., Stan E. On considering
imprecision in dynamic linear programming. — ECEESR,
1976, 3, p. 83-95.
9.	Brown J. G. A note on fuzzy sets. — Inf. Contr., 18,
p. 32-39.
10.	C h a n g C. L. Fuzzy topological spaces. — J. Math. Anal.
Appl., 1968, 24, p. 182-190.
11.	Wong С. K. Covering properties of fuzzy topological spa-
ces. — J. Math. Anal. Appl., 1974, 46, p. 697—704.
12.	Wong С. K. Fuzzy topology: product and quotient theo-
rems. — J. Math. Anal. Appl., 1974, 45, p. 512—521.
13.	Wong С. K. Fuzzy points and local properties of fuzzy to-
pology. — J. Math. Anal., Appl., 1974, 46, p. 316—328.
14.	L owen R. A comparison of different compactness notions
in fuzzy topological spaces. — J. Math. Anal. Appl., 1978,
64, p. 446—454.
15.	Weiss M. D. Fixed points, separation and induced topolo-
gies for fuzzy sets. — J. Math. Anal. Appl., 1975, 50, p. 142—
150.
16.	Michalek J. Fuzzy topologies. — Kybernetika, 1975,
11, № 5, p. 345-354.
17.	Kramosil I., Michalek J. Fuzzy metrics and sta-
tistical metric spaces. — Kybernetika, 1975, 11, № 5, p. 336—
345.
18.	in p e й д e p Ю. А. Равенство, сходство, порядок. — M.:
Наука, 1971.
ЛИТЕРАТУРА
201
19.	Kaufman A. Introduction to the theory of fuzzy subsets.™
N. Y.: Acad. Press, 1975. — v. 1.
20.	W e e W. G., F u K. S. A formulation of fuzzy automata
and its application as a model of learning systems. — IEEE
Trans., 1969, SSC-6, p. 215—223.
21.	О p л о в с к и й С. А. Об одной задаче принятия решений
в нечетко определенной обстановке. — В сб.: «Проблемы
прикладной математики». — Иркутск, 1976.
22.	Фишборн П. Теория полезности для принятия реше-
ний. — М.: Наука, 1978.
23.	Z a d е h L. A., Bellman R. Е. Decision-making in
a fuzzy environment. — Managem. Sci., 1970, 17, p. 141—164.
24.	N e g о i t a G. V., S u 1 a r i a M. On fuzzy mathematical
programming and tolerances in planning. — ECEESR, 1,
1976, p. 3—14.
25.	N e g о i t а С. V., R a 1 e s c u D. A. Application of fuzzy
sets to systems analysis. — Basel: Birkhauser Verlag,
1975.
26.	Zimmermann H.-J. Fuzzy programming with several
objective functions. — Fuzzy Sets and Systems, 1978, 1,
p. 46—55.
27.	Hamacher H., Leberling H., Zimmer-
mann H.-J. Sensititivy analysis in fuzzy linear program-
ming. — Fuzzy Sets and Systems, 1978, 1, p. 269—281.
28.	Zadeh L. A. Fuzzy algorithms. — Inf. Gontr., 1968, 12,
p. 94-102.
29.	Веллман P., Г л иксберг И., Гросс О. Неко-
торые вопросы теории процессов управления. — М.: ИЛ,
1962.
30.	О г 1 о v s к у S. A. On programming with fuzzy constraint
sets. — Kybernetes, 1977, 1, p. 197—201.
31.	Multiple Criteria Decision-making. — Leet. Notes Econ.
Math. Syst., 1976, 130.
32.	M а к - К и н с и Дж. Введение в теорию игр. — М.: Физ-
матгиз, 1960.
33.	Гермейер Ю. Б. Введение в теорию исследования
операций. — М.: Наука, 1971.
34.	Гермейер Ю. Б. Игры с непротивоположными интере-
сами. — М.: Наука, 1978.
35.	Партхасаратхи Т., Рагхаван Т. Некоторые
вопросы теории игр двух лиц. — М.: Мир, 1974.
36.	Орловский С. А. Игры в нечетко определенной обста-
новке. — Ж. вычисл. матем. и матем. физ., 1976, № 16,
с. 1427-1435.
37.	Орловский С. А. Бесконечные игры двух лиц с запре-
щенными ситуациями. — Ж. вычисл. матем. и матем. физ.,
1973, № 13, с. 775—781.
38.	О р л о в с к и й С. А. Ситуации равновесия в бескоали-
ционных играх с ограничениями. — Ж. вычисл. матем.
и матем. физ., 1975, № 15, с. 1597—1601.
39.	О г 1 о v s к у S. A. Decision-making with a fuzzy preference
relation. — Fuzzy Sets and Systems, 1978, 1, 3, p. 155—167.
202	ЛИТЕРАТУРА
40.	О г 1 о v s к у S. A. On formalization of a general fuzzy
mathematical programming problem. — Fuzzy Sets and Sy-
stems, 1980, 3, 3, p. 311—321.
41.	S о у s t e г A. L. Convex programming with set inclusive
constraints and applications to inexact linear programming. —
Operat. Res., 1973, 21, p. 1154-1157.
42.	S a a t у T. L. Exploring the interface between hierarchies,
multiple objectives and fuzzy sets. — Fuzzy Sets and Systems,
1978, 1, p. 57—68.
43.	T a m u r a S., Higuchi S., Tanaka K. Pattern
classification based on fuzzy relations. — IEEE Trans.,
1971, SMC-1, p. 61—66.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Альтернатива максимальная
не доминируемая 132
— максимизирующая 73
— четко недоминируемая 133
— эффективная 92
Выбор по набору признаков
189
Выпуклая комбинация нечет-
ких множеств 27
Граф нечеткого отношения 38
Декартово произведение нечет-
ких множеств 27
Декомпозиция нечеткого мно-
жества 28
Динамическое программирова-
ние 77
Дополнение нечеткого мно-
жества 26
—	— отношения 45
Замыкание нечеткого мно-
жества 31
Игра в нечеткой обстановке 96
— — — — антагонистичес-
кая 104
—	— — — с запрещенными
ситуациями 107
—	— — — с противополож-
ными интересами 105
Изоморфизм классов нечетких
множеств 59
—	— нечетких отношений 63
Композиция отношений 39
—	— нечетких 45
Концентрирование нечеткого
множества 27
Максимизирующее решение 75
Матрица отношения 37
— — нечеткого 43
Множество 19
— альтернатив недоминируе-
мых 128
—	— — четко 132
—	нечеткое 20
—	— выпуклое 161
—	— замкнутое 31
—	— компактное 33
—	— нормальное 22
--- открытое 31
—	— пустое 22
—	— решений 72
—	— субнормальное 22
—	— типа 1 21
—	— типа п 21
—	— универсальное 22
—	— элементарное 32
—	уровня декартова произве-
дения 28
—	- — нечеткого множества 28
Нечеткая граница множеств 27
—	топология 30
—	цель 70
Нечетко описанные параметры
170
Нечеткое максимальное зна-
чение 88
—	математическое программи-
рование 81
—	множество 20
—	— альтернатив 82
—	— ограничений 86
—	решение 72
—	— равновесное 112
—	топологическое простран-
ство 30
—	— — компактное 33
—	— — отделимое 34
204
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Носитель нечеткого множества
22
—	— отношения 43
Образ нечеткого множества 54
Окрестность нечеткого мно-
жества 34
Отношение 37
—	нечеткое 41
—	— антирефлексивное 49
—	— антисимметричное 50
—	— безразличия 119
—	— квазиэквивалентности
119
—	— обратное 45
—	— предпочтения 119
—	— — индуцированное 158
—	— — нестрогого 119
—	— — сильно линейное 126
—	— — слабо линейное 128
—	— — строгого 119
—	— рефлексивное 49
—	— симметричное 49
—	— транзитивное 50
—	— — Х-линейное 126
—	обычное 37
—	— антирефлексивное 39
—	— антисимметричное 39
—	— безразличия 117
—	— линейное 125
—	— обратное 38
—	— предпочтения 116
—	— — нестрогого 116
—	— — строгого 116
—	— рефлексивное 39
—	— симметричное 39
—	— транзитивное 39
—	— эквивалентности 117
Отображение нечеткого мно-
жества 52
Пересечение нечетких мно-
жеств 26
—	— отношений 44
Последовательность нечетких
множеств 33
Проекция отношения 46
Произведение нечетких отно-
шений 45
—-------максминное 45
Произведение нечетких отно-
шений максмультипликатив-
ное 46
—	— — минмаксное 46
Прообраз нечеткого множества
56
Разность нечетких множеств
27
Растяжение нечеткого мно-
жества 27
Решение задачи нечеткого про-
граммирования 87
Свертка отношений 146
Седловая точка 138
Ситуация равновесия 98
Степень недоминируемости 131
—	принадлежности 20
Теорема о компактности 20
—	о линейности индуцирован-
ного отношения 158
—	о нахождении недомини-
руемых альтернатив 168
—	о прообразе нечеткого мно-
жества 56
—	о рефлексивности индуци-
рованного отношения 158
—	о седловой точке 140
—	о смешанном расширении
143
—	о существовании недомини-
руемых альтернатив 140
—	о транзитивности нечеткого
отношения 121
—	об эквивалентности реше-
ний 93
Транзитивное замыкание 40
—	— нечеткого отношения 51
—	— обычного отношения 40
Упорядочение объектов 194
Функция антисимметричная
138
—	выигрышей 104
—	принадлежности 20
—	— нечеткого множества 20
—	— — отношения 41
—	цели 172
СПИСОК ОБОЗНАЧЕНИЙ И СОКРАЩЕНИЙ
5- =>	— лучше — не хуже — влечет
<=> 0 V 3 х£Х х X АаВ	— эквивалентно — пустое множество — для всех — существует — элемент х принадлежит множеству X — элемент х не принадлежит множеству X — множество А — собственное подмножество мно- жества В
А^В и п	— множество А — подмножество множества В — объединение множеств — пересечение множеств
\	— разность множеств
ЛхХ... X Ап — декартово произведение множеств
supp А CON А DIL А Л ^А А' А	— носитель нечеткого множества А — концентрирование нечеткого множества А — растяжение нечеткого множества А — множество уровня а нечеткого множества А — функция принадлежности нечеткого множества А — дополнение множества — замыкание множества
11-11 R-1 R1o Rt 7?'2> Rs R1 R'	— сумма по i от 1 до п — матрица — обратное к R отношение — композиция отношений — вторая проекция отношения — отношение строгого предпочтения — отношение безразличия — отношение эквивалентности
206	СПИСОК ОБОЗНАЧЕНИЙ И СОКРАЩЕНИЙ
Рв	— функция принадлежности нечеткого отношения
Нв	строгого предпочтения — функция предпочтения нечеткого отношения без-
Ив	различия — функция принадлежности нечеткого отношения квазиэквивалентности
и. д. ч. н. д. „и. д. ^в	— недоминируемый — четко недоминируемый — функция принадлежности нечеткого множества недоминируемых альтернатив
P-G 4(D) (X, Т) И. 0. п. н. т. п. V V	— функция принадлежности нечеткой цели — образ множества D при отображении <? — множество X с топологией Т — нечеткое отношение предпочтения — нечеткое топологическое пространство — класс нечетких подмножеств — нечеткий подкласс класса нечетких подмножеств
Сергей Алексеевич Орловский
Проблемы принятия решений
при нечеткой исходной информации
(Серия: «Оптимизация и исследование операций»)
М., 1981 г., 208 стр. с илл.
Редактор М. М. Горячая
Техн, редактор Л. В. Лихачева
Корректор Л. Н. Воровина
ИБ № 11645
Сдано в набор 20.06.80. Подписано к печати 11.03.81.
Т-05723. Бумага 84Х1081/»» тип. № 1.
Обыкновенная гарнитура. Высокая печать.
Условн. печ. л. 10,92. Уч.-изд. л. 10,42. Тираж 7600 экз.
Заказ № 1626. Цена книги 1 р. 20 к.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени
Первая типография издательства «Наука»
199034, Ленинград, В-34, 9 линия, 12
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
117071, Москва, В-71, Ленинский проспект, 15
ВЫХОДИТ ИЗ ПЕЧАТИ:
ЕВТУШЕНКО Ю. Г. Методы решения экстремаль-
ных задач и их применения в системах оптимизации
(Серия «Оптимизация и исследование операций»).
Книга посвящена созданию диалоговых человеко-
машинных систем оптимизации. Основное внимание уде-
ляется систематическому описанию алгоритмов решения
задач нелинейного программирования и оптимального
управления. На модельных примерах проводится сравни-
тельный анализ алгоритмов. Показано, что наиболее
высокую эффективность использования методов оптими-
зации можно получить путем последовательного приме-
нения разных алгоритмов. Обсуждаются вопросы органи-
зации человеко-машинного процесса расчетов, даны при-
меры реализации диалоговых систем оптимизации.
Для специалистов в области математического про-
граммирования, теории оптимального управления и ши-
рокого круга инженеров, студентов старших курсов,
аспирантов, применяющих и развивающих методы опти-
мизации.
ЗБТ
0~666
с. А. ОРЛОВСКИЙ