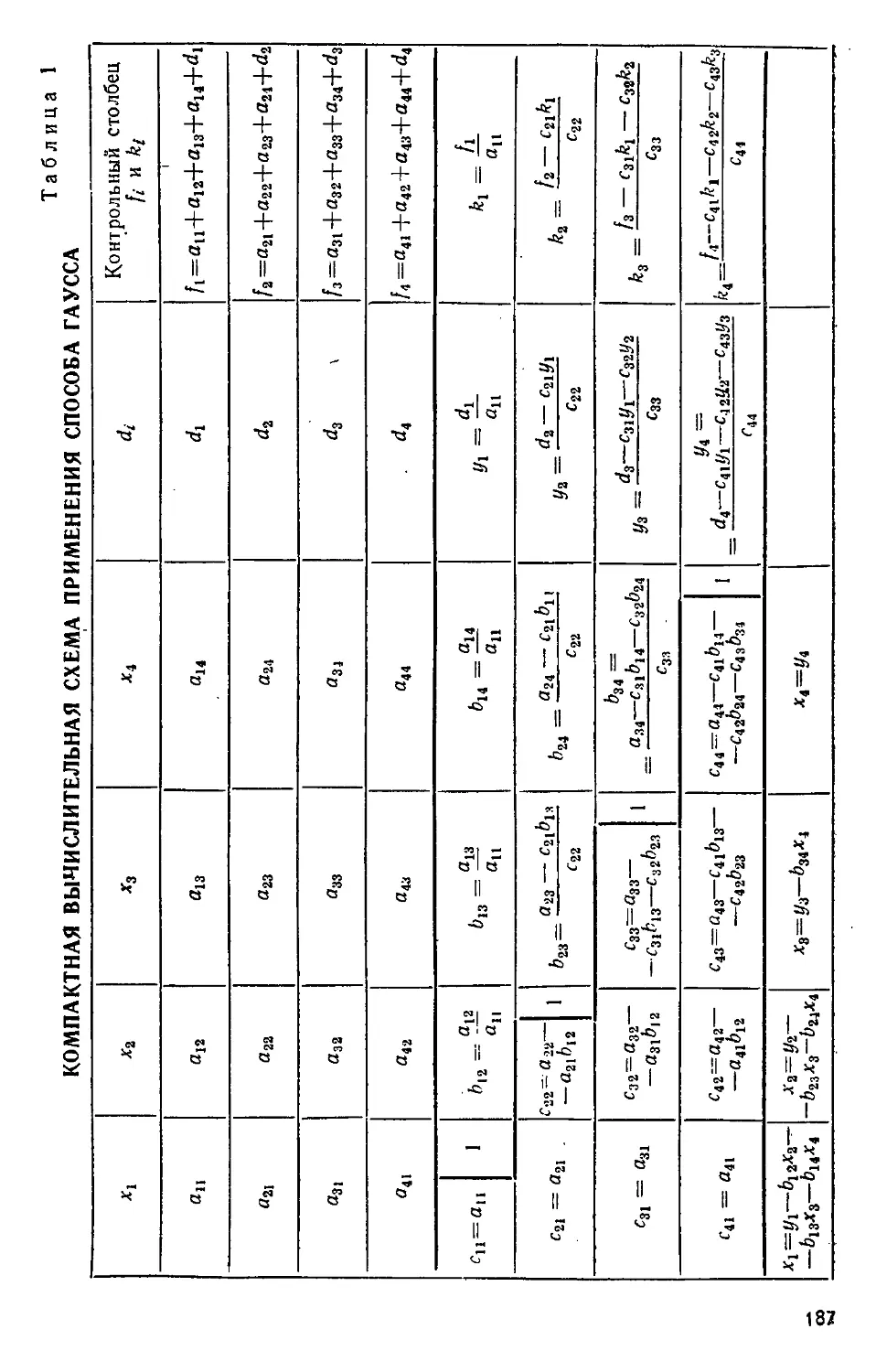
Похожие
Текст
И А. КАПЛАН
ПРАНТИЧЕСНИЕ ЗАНЯТИЯ
ПО ВЫСШЕЙ МАТЕМАТИНЕ
ЧАСТЬ V
(Численное решение алгебраических и трансцендентных уравне-
уравнений, матричное исчисление, векторный анализ и интегрирование
линейных дифференциальных уравнений первого порядка
с частными производными)
Издание второе, стереотипное
ИЗДАТЕЛЬСТВО
ХАРЬКОВСКОГО УНИВЕРСИТЕТА
Харьков 1972
617
K20
Книга содержит подробный разбор и решение
типовых задач по таким разделам высшей матема-
математики: векторный анализ, алгебра матриц и их
приложений к решению задач линейной алгебры,
линейные дифференциальные уравнения с част-
частными производными первого порядка, решение
алгебраических и трансцендентных уравнений.
Книга рассчитана на студентов высших тех-
технических учебных заведений и может быть по-
полезной также преподавателям, ведущим практи-
практические занятия.
Илья Абрамович Каплей
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Часть V
Редактор Р. М. Деревянкенко
Обложка художника И. Ф. Криворучко
Техредактор Г. П. Александрова
Корректор Л. П. Пипенко
Сдано в набор 28/VI 1968 г. Подписано к печати 20/Х 1968 г. БЦ 68807.
Формат 60x90Vi«. Объем: 25,75 физ. печ. л., 25,75 усл. печ. л., 22,3 уч.-нзд. л.
Зак. 2-177. Тираж 75000. Цена 92 коп. Св. ТП 197£ г. поз. 31.
Отпечатано с матриц Книжной фабрики им. М. В. Фрунзе Комитета по печати
при Совете Министров УССР, Харьков, Донец-Захаржевская, 6/8 на Тнпооф-
сетной фабрике «Коммунист» Комитета по печати при Совете Министров
УССР, Харьков, Энгельса, 11.
ПРЕДИСЛОВИЕ
Эта книга, как и ее предыдущие четыре части, предназначена
в основном для студентов, которые обучаются по вечерней си-
системе и заочно.
В книгу вошли упражнения по векторному анализу, исчисле-
исчислению матриц и их приложению к решению систем линейных алге-
алгебраических уравнений и приведению квадратичной формы к сумме
квадратов, а также упражнения по итерационным методам реше-
решения алгебраических и трансцендентных уравнений, решение линей-
линейных дифференциальных уравнений с частными производными пер-
первого порядка.
Цель книги — помочь студенту научиться с наименьшей затратой
времени самостоятельно решать задачи по этим разделам курса
высшей математики.
Весь учебный материал разделен на отдельные практические
занятия. Как и в предыдущих четырех частях, перед каждым из
занятий помещены основные сведения из теории, а также относя-
относящиеся к нему формулы, теоремы и определения.
К упражнениям по теории матриц сведения из теории приве-
приведены полнее, чем к практическим занятиям по другим разделам
курса. Это связано с тем, что в учебной литературе теории мат-
матриц и их приложений уделяется недостаточное внимание, несмотря
на их широкое применение в технике и вычислительной практике.
Важное место занимает определение собственных значений и соб-
собственных векторов матрицы методами акад. А. Н. Крылова и
Леверье.
Каждое практическое занятие содержит подробное решение
типовых задач различной степени трудности с полным анализом
решения. Многие задачи решаются различными способами, а целе-
целесообразность этих способов сравнивается.
Кроме этих решенных и разобранных задач, каждое практи-
практическое занятие включает большое число задач для самостоятель-
самостоятельного решения. Все они снабжены ответами, а многие из них —
промежуточными результатами и методическими указаниями. Такое
построение книги предоставляет студентам широкие возможности
для активной самостоятельной работы.
Студенты, пользующиеся этрй книгой, перед каждым практи-
практическим занятием должны выучить относящийся к нему раздел
теории, разобрать решенные задачи с выполнением всех действий
на бумаге н только после этого приступать к задачам, предложен-
предложенным для самостоятельного решения.
Книга написана так, что она допускает не только последо-
последовательное проведение всех практических занятий, но и использо-
использование их в выборочном порядке. Например, упражнения по век-
векторному анализу (практические занятия №.№ И, 12, 13 и т. д.)
и упражнения по теории матриц (практические занятия №№ 4,
5, б, 7, 8, 9) можно выполнять независимо друр от друга. Это
относится и к упражнениям по решению алгебраических и транс-
трансцендентных уравнений, а также дифференциальных уравнений
с частными производными.
Автор приносит глубокую благодарность рецензенту этой книги
доктору физико-математических наук, профессору Г. М. Баженову
и ее ответственному редактору кандидату физико-математических
наук, доценту Р. В. Солодовникову, а также кандидату техни-
технических наук А. А. Егоршину за ценные советы и замечания,
которые способствовали улучшению книги.
ПЕРВОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Численное решение алгебраических уравнений
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Алгебраическое уравнение степени п с действительными коэф-
коэффициентами
f(x) = аох" + а^-1 + а2х»-* +•■■+ ап_гх + ап = 0 A,1)
имеет п корней, среди которых могут быть действительные раз-
различные корни, действительные кратные корни, а также комп-
комплексные корни, попарно сопряженные. Если корнями уравнения
являются числа ли а2, ... , а„, то левая часть уравнения может
быть представлена в виде
f(x)=^ao(x~a1)(x — ai)(x—a3)... (* — «„). A,2)
Если а—корень уравнения, то левая часть уравнения делится
без остатка на х — а.
Прежде всего следует найти все действительные корни урав'
нения, а потом уже его комплексные, корни.
1. ОПРЕДЕЛЕНИЕ ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ
АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
При решении алгебраических уравнений степени выше второй
мы будем отыскивать действительные корни методами последова-
последовательных приближений с использованием схемы Горнера для деле-
деления левой части уравнения на х — а, где а — действительный
корень уравнения.
В методах последовательных приближений, применяемых при
решении уравнений, отыскивается последовательность чисел хи
х2, .... х„, которая имеет своим пределом число а, являющееся
корнем уравнения. Мы будем считать хп хорошим приближением
к корню а, если остаток от деления левой части уравнения на
х — хп достаточно мал.
Схема Горнера для деления многочлена на двучлен х — а, а
также схема для деления многочлена на квадратный трехчлен
х1 + рх + q, которая понадобится при определении комплексных
корней уравнения, даны ниже.
Сейчас же укажем правило Декарта, согласно которому можно
сделать заключение о числе положительных и отрицательных
корней алгебраического уравнения.
Правило Декарта
Если в уравнении A,1) у двух соседних коэффициентов разные
знаки, то говорят, что имеет место перемена знака; если же у
двух соседних коэффициентов одинаковые знаки, то говорят, что
имеет место сохранение знака. При этом учитываются только
коэффициенты, отличные от нуля.
Пример. В уравнении
имеют место две перемены знака (у членов первого и второго,
третьего и четвертого и одно постоянство знака у второго и
третьего членов).
Если в уравнении A,1) нет коэффициентов, равных нулю, то
оно называется «полным».
Для определения числа положительных и отрицательных кор-
корней алгебраического уравнения существует правило Декарта,
которое гласит:
Число положительных корней алгебраического уравнения равно
числу перемен знака в ряде коэффициентов этого уравнения или
на четное число меньше его, причем, равные нулю коэффициенты
просто не считаются.
Число отрицательных корней уравнения равно числу перемен
внака в ряде коэффициентов уравнения f( — х) — О или на четное
число меньше его.
Если уравнение иполное», то число его положительных корней
равно числу перемен знака или на четное число меньше его,
а число его отрицательных корней-равно числу постоянств знака
в ряде коэффициентов или меньше его на четное число.
Это правило мы неоднократно будем применять при решении
задач.
Отделение корней. Отделением корня уравнения f(x) — Q
называется нахождение отрезка [а, Ь], на концах которого функ-
функция принимает значения разных знаков и внутри которого на-
находится только один корень. Отделив корень, мы получаем воз-
возможность в качестве его приближенного значения принять любое
число из отрезка [а, Ь). Отделение действительных корней урав-
уравнения f (х) = 0 очень удобно производить графически. Значения
действительных корней уравнения ^ (дс) = 0 являются абсциссами
точек пересечения графика функции у = f (x) с осью Ох. Чтобы
указать отрезки, заключающие только по одному корню уравне-
уравнения,, не требуется особой точности.
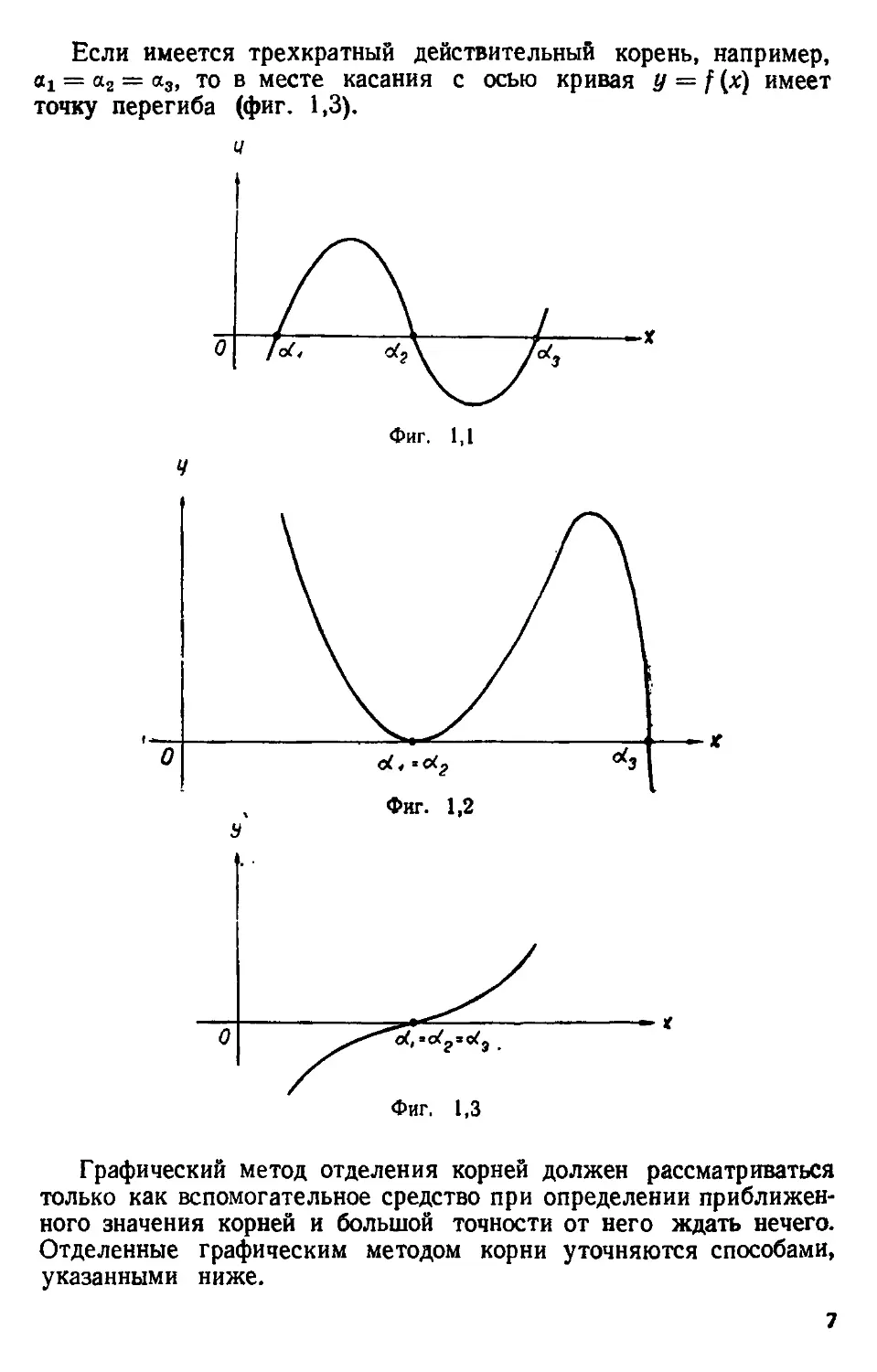
Пример. Если график функции имеет вид, указанный на фиг. 1,1 то
уравнение имеет три простых корня. Если какой-либо действи-
действительный корень является двукратным, например, о^ = а2 то кривая
y=zf{x) касается оси Ох в точке, где х = ах (фиг. 1,2).
Если имеется трехкратный действительный корень, например,
at = а2 = а3, то в месте касания с осью кривая у = f{x) имеет
точку перегиба (фиг. 1,3).
Фиг. 1,1
Фиг.
Графический метод отделения корней должен рассматриваться
только как вспомогательное средство при определении приближен-
приближенного значения корней и большой точности от него ждать нечего.
Отделенные графическим методом корни уточняются способами,
указанными ниже.
Способ № 1
(Способ Ньютона и его видоизменение *).
В этом способе приближенное значение действительного корня а
улучшается по формуле
f ()
(см. В. И. Смирнов. Курс высшей математики, т. I, гл. 6, § 2),
где через хп и хп+1 обозначены соответственно я-ое и (я+1)-ое
приближения корня. Эта формула дает возможность по известному
л-му приближению корня найти его (п -f l)-oe приближение.
Чтобы сократить вычисления по формуле A,3), можно для
всех приближений корня удовольствоваться одним и тем же зна-
значением производной, стоящей в знаменателе дроби в этой формуле,
вычислив ее значение только для первого приближения корня.
Способ Ньютона с этим упрощением мы будем называть видоиз-
видоизмененным (модифицированным) способом Ньютона.
Когда применяется способ Ньютона, корень необходимо отде-
отделить, т. е. определить отрезок [а, Ь], в котором находится един-
единственный действительный корень.
За первое приближение корня следует взять значение того
конца этого отрезка, на котором знак функции совпадает со зна-
знаком ее второй производной.
Способ № 2
(Способ линейной интерполяции и его видоизменение **)
В этом способе для вычисления (п+ 1)-го приближения корня
пользуются формулой
xn+l = xn~f (хп) f(x")-f{xt) A >4)
(см. например, В. И. Смирнов. Курс высшей математики, т. 1,
гл. 6, § 2), причем хп и xt — значения, между которыми нахо-
находится искомый корень. Формула A,4) дает возможность по най-
найденному n-му приближению корня найти его (n-f 1)-ое прибли-
приближение. В этом способе за первое приближение корня можно
принять значение любого из концов отрезка, на котором находится
отделенный корень.
Замечание. Значительную экономию вычислительной работы
можно получить при помощи этого способа, если значение дроби
* Этот способ называется также способом касательных.
** Этот способ называется также способом хорд.
в формуле A,4) брать одним и тем же для всех приближений
корня.
Способ, в котором будет применено это упрощение, мы будем
называть видоизмененным (модифицированным) способом линейной
интерполяции. Часто бывает выгодно одновременно применять
способ Ньютона и способ линейной интерполяции.
Способ №3
для определения приближенного значения наибольшего и наи~
меньшего по абсолютной величине корня алгебраического урав-
уравнения.
Если дано уравнение
/ (х) =хп + а,*"-« + а,*4-* + • ■ • + «„_,* + ап = 0, A,5)
то его простой, наибольший по абсолютной величине корень можно
приближенно найти из уравнения
x + at=0 Xz-Gf A,6)
или из уравнения
х2 + агх + а2 = 0, A,7)
взяв его больший по абсолютной величине корень.
Укажем, что найденные таким образом приближенные значе-
значения окажутся достаточно точными, если наибольший по абсолют-
абсолютной величине корень уравнения A,5) значительно превосходит
остальные корни этого уравнения.
Приближенное значение наименьшего по абсолютной величине
корня можно найти из уравнения
ап-гх + ап = 0 A.8)
или из уравнения
«ч-^2 + «я-,* + «я = 0. A.9)
взяв его наименьший по абсолютной величине корень. Улучшение
корня, найденного по этому способу, можно провести по способу
№ 1 и № 2 или видоизменениям этих способов, указанным выше,
определив отрезок, в котором находится найденный корень.
Способ №4
В уравнении
f{x) =xn + alXn-1 + а2хп-2 +■-•+ ап_^ + ап_гх + ап = О
отбираем три последних члена и решаем квадратное уравнение
«„-*** + «„-!* + °П = 0. A,Ю)
9
1. Если корни этого уравнения действительны, то поступаем
так: решаем уравнение
и за первое приближение корня берем
х = — -22- A 12)
°п—1
Левую часть уравнения A,5) делим на х — Х\. Деление про-
проводим по схеме Горнера (см. ниже) до тех пор, пока не останется
двучлен вида
Ьп-гХ + ап, A,13)
который не делится без остатка на л; — xv Приравниваем нулю
двучлен A,13) и из уравнения
V-.X + ап = О
находим второе приближение корня
*2 = -г^. A,14)
н—1
Теперь левую часть уравнения A,14) делим на х — х2 по схеме
Горнера и получаем остаток в виде
с^х + а» A,15)
с которым мы поступаем, как с предыдущим: приравниваем его
нулю
cn_lX + aa = 0. A,16)
Определяем третье приближение
** = --?- A.17)
п—1
и снова по схеме Горнера делим левую часть уравнения на х—х3.
Обычно этот процесс приводит к ряду значений xlt х2, х3, ... ,
приближающихся к искомому корню.
После того как мы остановились на некотором приближении
корня хп и приняли его за искомое значение корня, разделим
левую часть уравнения A,5) на х — хп. Получится многочлен
степени на единицу меньшей, чем левая часть данного уравнения.
Приравниваем этот многочлен нулю и с полученным новым урав-
уравнением поступаем, как было описано выше.
Замечание. При использовании этого способа может слу-
случиться, что последовательность чисел хи х2, х3, ... не прибли-
приближается к искомому корню, т. е. имеет место так называемый
to
расходящийся процесс. Приведем две рекомендации для улучше-
улучшения вычислений в тех случаях, когда приближение к искомому
корню происходит медленно шли «колебательно», т. е. не моно-
монотонно.
А. Если при определении вещественных корней уравнения A,5)
последовательные значения
xi — —z;—» -*г z—J *3 —; ... 1Ы°)
п—г n—i п—г
меняются не монотонно, а «колебательно», то следует брать новое
приближенное значение корня для следующего деления равным
полусумме предыдущего значения и того, которое получается из
остатка выполненного деления, т. е. брать в этом случае, напри-
например, третье приближение равным
) (U9)
г
fl—-1
Б. Если же при определении вещественных корней значения
A,18) меняются, хотя и не монотонно, но очень медленно, надо
следующее, например, третье приближение корня, брать в этом
случае в виде
где тх и г2 — остатки от деления левой части уравнения A,5)
соответственно на х — xlt и на х—х2.
2. Если окажется, что корни уравнения A,10) комплексны, то
для вычисления пары комплексных сопряженных корней посту-
поступаем так: представляем его левую часть в виде трехчлена
* + %=** + ^- (A)
Я—2 я—4
Этот трехчлен будем считать первым приближением к тому
трехчлену, из которого мы впоследствии определим пару корней.
На этот трехчлен делим левую часть уравнения A,5), пока не
останется трехчлен вида
который уже целиком не делится на (А). В качестве второго
приближения выделяемого трехчлена принимаем трехчлен
*+*£** + ■£*■ (В)
Я—2 п—2
и на него снова делим левую часть уравнения до тех пор, пока
не получится остаток вида
п
За третье приближение выделяемого трехчлена принимаем трех-
трехчлен
" '■ ' (С)
П—* л—2
По коэффициентам трехчленов (А), (В) и (С) судим о том, схо-
сходится ли этот процесс. Останавливаемся иа каком-либо прибли-
приближении, коэффициенты которого мало отличаются от коэффициен-
коэффициентов предыдущего. Если это будет трехчлен
то решение уравнения
х2 + Ьх + с = О
даст два корня исходного уравнения. На странице 17 указана
удобная схема для деления многочлена на квадратный трехчлен,
которая значительно облегчит процесс деления. Подробное изло-
изложение указанных выше способов можно найти, например, в книге:
И. С. Бе резин и Н. П. Жидков. Методы вычислений, Физ-
матгиз, 1959.
Схема Горнера
Чтобы не отсылать студента к учебникам, где изложен способ
Горнера для деления целой рациональной функции
f (х) = аохп + а^"-1 + а2хп-2 + • • • + а^х + ап
на линейный двучлен х — х0, приведем этот вывод здесь.
При делении многочлена
аохГ + aj*»-' + а,,*4-2 -| + aa_lX + ап на х — х0
получится в частном многочлен степени (я — 1)
to1-1 + ьхх»-*
и остаток т — число, так что
+ fli*" + Of*""8 H + an_lX + an =
+ Ьхх?-2 + Ьгх"~3 -\ h 6»-2j«: + 6«-)
A,21)
Определению подлежат коэффициенты b0, bx, b2t .... й„_,
частного и остаток от деления г.
12
Сравнивая коэффициенты при одинаковых степенях буквы к
в левой и правой частях равенства A, 21), получим:
= — b0x0
аг = —
Решая эти равенства относительно b0, bit b%, ..., &„_, и г,
найдем:
Ъх = а0х0
b2 = 6iJf0
Эти равенства показывают, что каждый последующий коэффи-
коэффициент Ье получается умножением предыдущего bi-\ на х0 и при-
прибавлением соответствующего коэффициента at. Остаток г из 6n_i
находится также. Вычисления удобно располагать по схеме, в ко-
которой принято а0 = 1.
Схема Горнера для деления многочлена
хп + агх"-1 + а^х"-2 + • • • + а„_|* + ап на двучлен х — х0
«к
в2
th
<»з
Me
в!
...
...
Ьп-2хо
а„
г
В первую строку вписываем коэффициенты делимого. Из схемы
видно, что коэффициенты частного получаются в третьей строке
от сложения чисел, стоящих над ними в первой и второй строках.
Приведем пример использования схемы Горнера. Разделим много-
многочлен
f (х) = х* + 5х* + 4х* — Ъх + 2
на х — 3. У нас ха = 3.
3
1
1
5
3-1 = 3
8
4
3 • 8 = 24
28
—3
3 • 28 = 84
81
2
3 • 81 = 243
245
Коэффициенты частного равны 1; 8; 28; 81; в частном полу-
получаем х3 4- 8*2 + 28* + 81, а остаток г = 245. Схемой Горнера удобно
пользоваться также для вычисления значений многочлена
f (х) = аох" + агх«-х + а,*"-2 + • ■ • + а„_,* + а„
при х = х0, т. е. значения f(x0). Вычисление f(x0) требуется при
нахождении корней по способу Ньютона, способу линейной интер-
интерполяции и при использовании способа № 4. Следует помнить, что
f{x0) равно остатку от деления многочлена / (х) на х — х0. Так,
в приведенном примере значение f (х) при х — 3 будет / C) = 245,
т. е. равно остатку от деления f (х) на х—3.
Случай кратных действительных корней уравнения
Известно, что если многочлен f(x) последовательно п раз де-
делить на х—а, то в остатках будем получать: после первого де-
деления f{a), после второго f (а), после третьего ^г Г (а) ••• , после
я-го. деления (/г_}) i Г (я)-
Если ах — корень кратности k уравнения A,1), то не только
/ (а,) = 0, но и Г (а,) = 0; Г Ы = 0 ... ; f(*-« (ах) = 0.
Пример. Рассмотрим уравнение
f (х) = х* — 9хг + 24*— 16 = 0.
Разделим f (х) на х—4 по схеме Горнера:
(остаток от деления; 0
есть значение функции
при х = 4).
Первое деление
4
Второе деление
А
1
1
1
—9
4
—5
4
— ]
24
—20
4
— 16
+ 16
0 = / D)
4
0
= Г С)
14
Поскольку не только f D) = 0, но и f' D) = 0, то х = 4 есть
двукратный корень нашего уравнения. Частное от деления f(x)
на (х—4)а равно х—1, а его коэффициенты 1 и—1 находятся
на последней строке. Поэтому третий корень уравнения получим
из уравнения
х— 1=0; х= 1.
Случай, когда уравнение имеет два близких корня
В способе № 1 (способ Ньютона) употребляется формула A,3)
X f(Xn)
Если уравнение имеет два близких по величине корня, то зна-
знаменатель дроби в формуле A,3) будет мало отличаться от нуля,
что повлечет за собой резкое изменение правой части этой формулы
при изменении х. В этом случае следует решить уравнение /' {х) = 0,
иайти его корень а и разложить / (х) по степеням х — а, сохраняя
в разложении только члены с х — аи (х — af, т. е. разложение
функции / (*) представить в виде
f {a) (x-a)
и рассмотреть уравнение f (х) — 0, или
Так как а есть корень уравнения f (х) — 0, то /' (а) = 0 и послед-
последнее уравнение запишется в виде
а отсюда
V 4-п*)
■krw
A,22)
Этими соображениями мы будем пользоваться всякий раз, когда
понадобится определить два близких между собой корня.
15
2. ОПРЕДЕЛЕНИЕ КОМПЛЕКСНЫХ КОРНЕЙ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
После того как определены все действительные кории алгебраи-
алгебраического уравнения, следует приступить к определению его комп-
комплексных корней.
Пусть найденные действительные корни уравнения A,5) есть
числа аъ а2, а3, ... , ak(k< п, если k — п, то решение закончено).
Разделим левую часть f (х) уравнения A,5) га произведение
(х — ах) {х — а2) (*— а3) ... (х— ак).
'ЧИТСЯ
В частном получится многочлен ср (х) степени п — k
fix)
{х — oj (x — о2) (х — о3) ... (х — а*) '
Деление следует проводить по схеме Горнера, разделив сначала
f(x) на х—аи затем полученное частное—иа х—а2 и т. д.
Так как все вещественные корни уже найдены, то уравнение
<? (*) = О
вещественных корней не имеет, а потому степень п — k многочлена
с? (х) будет обязательно четной. Пусть п — k = 21, а многочлен
<р(х) записывается так:
9 (х) = х21 + cdx2'-1 + d2x2l~2 H (- cB/-2a;2 -f dn-\x + dv = 0.
A,22a)
Для определения пары комплексных корней о (х) следует вы-
выделить квадратный трехчлен, являющийся делителем <?(х). Этот
делитель в первом приближении принимаем равным
/-2 а21-2
и делим на него многочлен <? (дг) до тех пор, пока не останется
трехчлен вида
ex' + fx + k,, A,24)
не делящийся на трехчлен A,23).
Трехчлен
полученный из предыдущего делением всех его членов на е, при-
принимаем за второе приближение выделяемого трехчлена. Теперь
16
делим <s (x) на A,25) до тех пор, пока не получится трехчлен
вида
егх2 + hx + К
уже не делящийся целиком на A,25).
Из этого трехчлена делением всех членов на et получаем трехчлен
который принимаем за третье приближение выделяемого трехчлена.
Обычно уже на третьем, четвертом шаге мы получим хорошее
приближение в виде трехчлена
Х +е!Х^еГ
приравниваем его нулю и находим пару комплексных корней-
Мы остановимся на том приближении, коэффициенты которого
мало отличаются от предыдущего. Разделив <в(х) на A,26) (соб-
(собственно, частное уже получено в последнем делении), получим
многочлен степени на 2 меньшей, чем о> (лс), и с ним поступаем
точно так же, как и с <? {х).
Замечание. Если вычисления при определении комплекс-
комплексных корней сходятся плохо, надо многочлен A,22а) преобразовать
заменой х — — в многочлен
<? (у) = ?i (г) = рг + &\ рщ + <*арга Н 1- dn-i — -г dm
или
?i (г) «= ju A + dtz + d2z2 +■■■+ cf2/-iz2'-' + d2lz2!)
и рассмотреть уравнение
?i(z) = 0. A,27)
Корни уравнения ср (д;) = 0 будут обратными величинами кор-
корней последнего уравнения A,27).
Схема для деления многочлена на квадратный трехчлен
Укажем теперь удобную схему для деления многочлена на трех-
трехчлен вида х2 + рх + q. Пусть
/ (х) = аох" + d*"-1 + аох"-2 Н Ь ап^х + ап =
- {х2 + px + q) (b0xn~2 + М"-3 + Ь2хп~* Н 1- Ьп-Зх + Ьп-2) +
+ bn-ix + 6„.
Коэффициенты Ьо, Ьи Ь2, ... , 6Л_2, &n-i, &„ находят по схеме,
которая легко получится, если, как и в схеме Горнера, сравнить
коэффициенты при одинаковых степенях х в левой и в правой час-
частях предыдущего равенства.
17
Схема имеет такой вид:
—р
—я
а*
Ьо
«1
—Pbo
К
—pbi
—qb0
bi
«3
—Ph
—яь,.
bs
at
—рЬз
—цЬг
bt
...
...
...
...
e«-2
—Pbn-3
an-\
~Pbn-2
-Фп-Ъ
K-\
«я
-Фп-2
В первую строку записываются коэффициенты многочлена f (х).
Коэффициент частного&о — о0. Образование чисел второй и третьей
строки ясно из схемы. Искомые коэффициенты получаются как
сумма чисел, стоящих в одном и том же столбце.
Так как в описываемом способе мы делим до тех пор, пока
не останется многочлен вида
ех% + fx + k,
то с помощью этой схемы коэффициенты е, f и k можно получить так:
коэффициент е — это йл_2 в третьем столбце схемы, считая
справа;
коэффициент f получится в предпоследнем столбце, если не
вписывать в него произведение — pbn-i,
коэффициент k равен аа — свободному члену уравнения. Иначе
говоря, е = 6n_2. f я ba_t + pbn_2, k = fln<
Приводим пример деления по этой схеме многочлена
f (х) = 5х* + Зх* — х* + 5х3 — Зд:2+4д: + 8 на хг
1
—7
—8
Со
5
5
3
-35
-32
j
224
—40
183
Ьг
«3
5
—1281
+256
—1020
ь*
—3
7140
—1464
5673
4
—39711
8160
—31547
Ь*
а»
8
—45384
—45376
18
Итак, чагтное от деления равно Ьх* — 32а? + 183а:2 — 1020 х +
+ 5673, а остаток равен—31547а:—45376.
Если же производить деление до получения в остатке интере-
интересующего нас квадратного трехчлена вида ех2 + fx + k, то он ока-
окажется равным 5673а:2 + 8164а: + 8, причем 8164 == 8160 + 4 (8160 —
выделено жирным шрифтом), а 8 — свободный член (мы сознательно
привели несколько громоздкий пример).
Проверка решения
Проверку всех найденных корней следует произвести, пользуясь
известными свойствами корней алгебраического уравнения (формулы
Виета).
Сумма всех корней алгебраического уравнения A,1)
III | — ^_^ "I /I oQ\
"Т" а2 I аЗ "Г" * * * I ал —' — ^Г~ » \'>^°)
а их произведение
п п п п •— ( 1 \п —5 /1 ОО\
После этих указаний приступим к решению задач. Рекоменду-
Рекомендуется пользоваться при этом арифмометром или любой клавишной
вычислительной машиной.
Задача 1,1. Решить уравнение
f(x) = x3 — 5a:2 + 4а: + 0,092
(с точностью 0,001).
Решение. Используя правило Декарта (стр. 6), заключаем,
что положительных корней будет два или ни одного, так как у нас
две перемены знака (Н \- +), отрицательный же корень только
один, поскольку уравнение «полное» (коэффициентов, равных нулю,
в уравнении нет), а число сохранении знака одно в последних двух
коэффициентах: + + (см. стр. 6). Будем пользоваться указаниями
способа № 3 для определения наибольшего по абсолютной вели-
величине корня.
Составляем квадратное уравнение вида A,7). У нас ах = —5;
а2 = 4 и это уравнение имеет вид
Решая его, находим
25
Принимаем хх = 4 за первое приближение наибольшего корня,
Теперь мы должны отделить корень (см. стр. 6). Делим f(x)
на х—4 по схеме Горнера (стр. 13V
19
1 —5 4 0,092
4—4 0
1 —1 0 0.092 = /D)
(остаток от деления 0,092 есть
значение левой части уравне-
уравнения при дг=4)
У нас / D) = 0,092 > 0. Возьмем х = 3,9. Разделив теперь f (х)
на х— 3,9, получим
1 —5 4 0,092
3.9
3.9 —4.29 —1.131
1 —1.1 —0.29 —1.039 = /C.9)
(остаток от деления —1,039 есть
значение левой части уравне-
уравнения при х = 3.9)
и f C,9) = — 1,039 <0.
Значит, /C,9)<0, a fD)>0 и корень содержится между 3,9
и 4. Из рассмотрения остатков деления 0,092 и —1,039 заключаем,
что искомый корень ближе к 4, чем к 3,9. Уточним корень ли-
линейной интерполяцией (способ № 2).
Второе приближение корня получим по формуле A,4), которая
для нашего случая запишется так:
Здесь хг и х, — концы отрезка [3,9; 4], в котором находится
корень. В формулу A,4) подставим
хх = 4; xt — 3,9;
/ (*i) = f D) = 0,092; a f (x£) = f C,9) = -1,039;
0,092 D -3.9).
*а 0.092— (—1.039)*
— 4 0-0092.
** 1,131 '
л:2 = 4 —0,008 = 3,992.
Значит, вторым приближением корня будет *2 = 3,992.
20
Разделим теперь f{x) на х—3,992 по схеме Горнера:
1 -5 4 0,092
-(А)
3,992
3.992 —4.024 —0,095
1 —1,008 —0.024 —0,003 = /C,992)
Остаток от деления получился значительно меньшим (г = —0,003
вместо —1,039 в предыдущем делении). Испробуем значение х —
= 3,993. Разделим f(x) нал;—3,993:
3,993
1
1
—5
3.993
— 1,007
4
—4.021
—0,021
0,092
—0.083
0,009 = / C,993)
От деления получился положительный остаток г = 0,009. Зна-
Значит, f C,993) > 0, a f C,992) < 0. Отсюда заключаем, что значение
искомого корня уравнения промежуточное — между 3,992 и 3,993.
Ограничиваясь тремя знаками, принимаем х = 3,992.
Считая, что х находится на отрезке [3,992; 3,993], мы допускаем
погрешность, меньшую 0,001.
В схеме (А) уже имеются коэффициенты частного от деления
f(x) на х —3,992. Эти коэффициенты равны 1; —1,008 и —0,024,
а само частное равно х2— 1,008* — 0,024. Приравнивая его нулю
и решая квадратное уравнение
х2— 1,008л;—0,024 = 0,
получим (при решении пользуйтесь таблицами для извлечения
квадратных корней)
х = 0,504 ± /0,254 + 0,024;
х = 0,504 ± К07278;
( 1,031;
х = 0,504 + 0,527 =
1—0,023.
Итак, корни уравнения равны
Xl = —0,023; х2 = 1,031; х3 = 3,992.
Количество полученных отрицательных и положительных кор-
корней уравнения соответствуют тому, которое было определено на
21
основании правила Декарта (см. начало решения). После того
как корни найдены, их следует располагать в порядке возрастания.
Проверка. х1 + х2 + х3 = —0,023 + 1,031 + 3,992 = 5,
и должно быть на основании формулы A,28), так как у нас
— ~ = 5 (а0 = 1; аг = —5).
На основании формулы A,29)
л = 3; ап = 0,092 и должно получиться, что хх • х2 • х3 = —0,092.
Фактически же мы получаем Xi • х2 • х3 — —0,096, что следует
признать достаточно хорошим приближением. Мы получили х2 —
= 1,031. Точным значением корня является х2 = 1,03.
Значение наименьшего по абсолютной величине корня х = — 0,023
можно было бы найти сразу, решив уравнение вида A,11)
а„ = 0.
В нашем случае это уравнение запишется так:
Ах + 0,092 = 0.
Отсюда х = т- 0,023.
Проверим этот .корень делением левой части уравнения на
х + 0,023:
-0.023
1
1
—5
—0.023
—5.023
4
+0.116
4,116
0,092
—0.094
—0.002 = /(—0.023)
(остаток от деления)
Поскольку остаток от деления мал, заключаем, что это хоро-
хорошее приближение.
Задача 1,2. Найти с точностью до 0,001 корни уравнения
f(x) = x9 — 4x2 — 7х+ 13 = 0.
Решение. По правилу Декарта заключаем, что положитель-
положительных корней два или их вовсе нет, так как в ряде коэффициентов-
уравнения две перемены знака. Отрицательный же корень один,
поскольку число сохранения знака в ряде коэффициентов равно 1,
Начнем с определения наибольшего по абсолютной величине
корня (способ № 3, прочтите его!). Для этого составляем квадрат-
квадратное уравнение A,7), в котором ах = —4, а2 = —7.
Уравнение A,7) принимает вид
22
Отсюда х = 2 ± Vi + 7;
(+
_ 1-1,317,
так как "|Л1 = 3,317.
Поскольку нас интересует больший по абсолютной величине
корень, берем л: = 5,317 и будем считать 5,317 первым прибли-
приближенным значением корня. Теперь определим отрезок, на котором
находится корень, т. е. отделим корень. Разделив по схеме Гор-
нера левую часть данного уравнения на х— 5,317, получим
I 1 -4 -7 13
5,317
5,317 7,002 0,011
I 1 1.317 0.002 13.011 =/E.317)
' (остаток от деления)
Остаток от деления 13,011 и есть значение левой части урав-
уравнения при х = 5,317. Возьмем теперь значение меньшее, чем 5,317,
например, х = 5, и для определения / E) разделим левую часть
уравнения на х — 5. Пользуясь схемой Горнера, получим
| 1 —4 —7 13
~5 j 13 5 —10
1 1—2 3=/E)
(остаток от деления)
Теперь остаток от деления равен 3 и/E) = 3. Возьмем значе-
значение меньшее, чем 5, например х = 4,8, и разделим / (х) на х — 4,8;
II —4 —7 13
4.8 I 4,8 3,84 —15,168
1 0.8 —3,16 —2,168 = /D,8)
(остаток отделения
Остаток от деления равен —2,168. Остаток поменял знак. Зна-
Значение левой части уравнения при х = 4,8 будет /D,8) = —2,168.
Поскольку /E) = 3>0, а / D,8) = —2,168 < 0, т. е. значения
левой части данного уравнения на концах отрезка [4,8; 5] имеют
различные знаки, искомый корень находится именно на этом
отрезке. Уточним значение корня по способу № 2 линейной интер-
интерполяции. Это удобно сделать именно этим способом, так как
все величины, входящие в формулу A,4), уже вычислены. Прини-
Принимаем за первое приближение корня х1 = 4,8. У нас xt = 5; хх =
= 4,8; f(xl) = 3; }(хг) = —2,168, и мы получаем второе прибли-
приближение корня по формуле A,4)
23
или, подставляя числа, будем иметь
хг = 4,8 — (—2,168) • _2&№-3•
Значение дроби
4,8 — 5 —0,2
-2.168-3 ~ =5Л68 -
и х2 = 4,8 + B,168) • (+0,039) = 4,8 + 0,084 = 4,884. Итак, второе
приближение корня х2 = 4,884.
Вычислим теперь значение левой части нашего уравнения при
х = 4,884. Вычисление производим по способу Горнера, путем деле-
деления левой части уравнения на х — 4,884:
4.884
1
1
—4
4,884
0,884
—7
4.317
-2.863
13
— 13.104
—0.104 = /D.884)
(остаток от деления)
Остаток от деления г = —0,104, а потому значение левой части
уравнения при х = 4,884 будет f D,884) = —0,104. Теперь отрезок,
на котором находится корень, сузился. Этот отрезок [4,884; 5],
и мы имеем f D,884) = —0,104 < 0, а Д5) = 3 > 0. Тем же спосо-
способом найдем и третье приближение по (рормуле A,4)
Здесь у нас х2 — 4,884; по-прежнему ' xt = 5;
f (x2) = f D,884) = -0,104; f (xt) = f E) = 3.
Подставляя эти значения в последнюю формулу, будем иметь
х3 = 4,884 - (-0,104) • ^40~23 •
Значение дроби
4.884-5 -0,П6 = 0>037 (В)
—0.104 — 3 ——3,104
(при вычислении хг — второго приближения аналогичная дробь была
равна 0,039); х3 = 4,884 — (—0,104). @,037); х3 = 4,884 + 0,004;
х3 = 4,888, т. е. третье приближение корня будет х3 = 4,888.
Вычислим теперь значение левой части уравнения при х = 4,888.
Воспользуемся снова схемой Горнера. Разделив левую часть урав-
уравнения на. х — 4,888, получим
24
I 1 —4 -7 13
4.888 4,888 4,340 —13.002 (С)
I 1 0888 —2.660 —0.002=/D,888)
I " (остаток от деления)
Теперь остаток от деления изменился с —0,104 в предыдущем
делении до —0,002, и значение левой части данного уравнения при
х = 4,888 будет f D,888) = —0,002.
Так как остаток от деления мал, испытаем значение на 0,001
большее, чем третье приближение, т. е. х = 4,889. Если окажется,
что левая часть уравнения при х = 4,889 будет положительной,
то искомый корень лежит на отрезке [4,888; 4,889]. Выполняем
деление левой части уравнения на х — 4,889:
| 1 -4 -7 13
4,889 j 4.889 4,346 —12,975
Г~1 0,889 —2,654 0.025 = / D,889)
Мы получили f D,889) = 0,025 > 0, а так как f D,888) =—0,002 < 0,
то искомый корень действительно находится на отрезке [4,888;
4,889], и мы достигли требуемой точности, так как длина этого
отрезка равна 0,001. Принимаем х = 4,888.
Вычисления можно было бы сократить, если бы при опреде-
определении третьего приближения вместо значения дроби (В), равного
0,037, мы взяли значение дроби (А), равное 0,039, которое уже
было вычислено при определении второго приближения (см. заме-
замечание к способу № 2). Тогда мы сразу получили бых3 = хг — f (х2) х
X 0,039, т. е. х3 = 4,884 — (— 0.Ю4) . 0,039 = 4,884 + 0,004; х3 =
= 4,888, как и прежде, но вычислительная работа сократилась бы
значительно.
Теперь покажем, как тот же корень можно определить по спо-
способу касательных (способ № 1 Ньютона).
Было установлено, что корень находится на отрезке [4,8; 5].
У нас f(x) = xa— 4x2 — 7х+ 13. Значит, f (х) = Ъхг — 8х—7,
a f"{x) = 6x— 8.
В способе Ньютона за первое приближение корня принимается
значение того конца отрезка, заключающего корень, на котором
'знак функции такой же, как и знак ее второй производной. Вто-
Вторая производная f" (х) положительна на всем отрезке [4,8; 5],
а функция f (x) положительна на правом конце этого отрезка
(/ E) > 0), и за первое приближение корня следует взять х = 5.
По формуле A,3)
Хг ~ * Г (*,)'
У нас ху — 5: уже было найдено, что f (хх) = f E) = 3, а /' (хг) =
= р E) = 3 • 52 — 8 • 5 — 7 = 75 — 40 — 7 = 28; f (x,) = 28 (ввиду
простоты вычислений схемой Горнера мы не пользовались).
25
Итак,
х2 = 5 — А = 5 — 0,107 = 4,893.
Для следующего применения формулы A,3) надо вычислить
значение левой части уравнения при х — 4,893. Пользуясь схемой
Горнера, разделим левую часть уравнения на х—4,893:
—4 —7 13
4.893
4.893 +4,369 —12,873
1 0.893 —2,631 0,127=/D.893)
' (остаток от деления)
Так как остаток от деления равен 0,127, то / D,893) = 0,127.
Вычислим теперь /' D,893). Для этого разделим f (х) = 3хг — 8х — 7
на х —4,893. Остаток от деления даст f'D,893):
| 3 —8 —7
4.893 | 14.679 +32,680
|3 +6.679 +25.680 = /'D.893)
и так как остаток от деления равен +25,680, то /' D,893) = 25,680.
По формуле A,3)
х3 = 4,893 — +°^0 = 4,893 - 0,005 = 4,888.
Мы получили то же, что и раньше. Можно было бы восполь-
воспользоваться указанием на возможную модификацию способа № 1
(стр. 8) и принять при вычислении третьего приближения знаме-
знаменатель дроби в формуле A,3) f (хг) таким же, каким он был при
вычислении второго приближения, т. е. равным f (xj = 28.
Приводим вычисления дробей j~^- и
I \2) I \X
В первом случае Ii|j = ^ = 0,00494.
Во втором случае ^j = Ц~ == 0,00454.
Если округлить полученные дроби до трех знаков после запя-
запятой, то в обоих случаях получим 0,005. При решении этого при-
примера мы убедились в выгодности применения модификаций способа
Ньютона и способа линейной интерполяции. Повторяем, что, при-
применяя способ Ньютона с целью сокращения вычислений в формуле
A,3), значение знаменателя /' (ял) можно принимать одним и тем
же при вычислении всех приближенных значений корня, а, поль-
пользуясь способом линейной интерполяции, можно при вычислении
26
всех приближенных значений корня в формуле A,4) принимать
одним и тем же значение дроби
Теперь уже определим остальные два корня нашего уравнения.
Из таблицы (С) видно, что частное от деления левой части урав-
уравнения на х— 4,888 имеет коэффициенты 1; 0,888 и —2,660 (в таб-
таблице (С) они подчеркнуты). Поэтому искомое частное будет равно
х* + 0,888х—2,660. Приравниваем его нулю и решаем квадратное
уравнение
Х2 + 0,888л:— 2,660 = 0;
х = —0,444 ± КО, 197 + 2,660;
х = —0,444 ± У2Щ;
*=-0,444 ±1,690 =
жд = — 2,134 и х2= 1,246.
Итак, *! = —2,134; х2= 1,246 и *3 = 4,888. Здесь снова под-
подчеркнем, что количество положительных и отрицательных корней,
полученных при решении, соответствует тому, которое следует из
правила Декарта.
Проверка.
*1 + Х2 + Х3 = 4,
что и должно быть в соответствии с формулой A,28), так как у нас
fli = —4; а0 = 1.
Вычислив затем произведение корней, получим хх • х2 • х3 =
= —12,997 вместо —13, что также следует признать хорошим
результатом — см. формулу A,29): п = 3; ап — 13; а0 = 1.
Это же уравнение
13 = 0
решим по способу № 4.
1. Составляем квадратное уравнение вида A,10). У нас а„_2=
= —4; an_2 = —7; ап = 13, и это уравнение запишется так:
—4*2 — 7х + 13 = 0,
или
4хг + 7х— 13= 0.
2. Корни этого уравнения действительны, а потому решаем
уравнение вида A,11), в котором ап-1 = —7; ап= 13, само урав-
уравнение имеет вид —7х + 13 = 0, а х — 1,857.
27
Это значение х примем за первое приближение к искомому корню
и обозначим его через хг. Делим левую часть уравнения на
л—1,857, пользуясь схемой Горнера, и получаем
1,857
1
1
—4
1.857
—2.143
—7
—3.980
—10,980
Ьп-1
13
13
Составляем уравнение вида A,13),.в котором Ьп_1 = —10,980
и по-прежнему ап = 13. Получаем —10,980* + 13 = 0, откуда
вторым приближением искомого корня будет jc = 1,184. Делим
теперь левую часть уравнения на х— 1,184, пользуясь опять-таки
схемой Горнера:
1.184
1
1
—4
1,184
—2.816
—7
—3,334
—10,334
13
13
Составляем теперь уравнение вида A,16), в котором будет
с„_! = —10,334 и по-прежнему ап — 13. Получаем —10,334* +
+ 13 = 0; х = 1,257. Это и будет третьим приближением корня.
Делим теперь левую часть уравнения на х— 1,257;
—7
13
1.257
1.257
—3.448
-2.743
13
Уравнение для определения следующего приближения имеет
вид —10,448л; + 13 = 0 и четвертое приближение корня *4 = 1,244.
Разделим левую часть уравнения на х— 1,244:
1
—7
13
1.244
1.244
—3,428
—2,756
—10,428
и уравнение для получения следующего приближения запишется
так:
—10,428* +13 = 0; xt= 1,246.
28
На следующем шаге мы найдем — то же значение х (проверьте!),
а потом на найденном значении и остановимся. Этот же корень
был получен и раньше. Способ № 4, которым мы только что поль-
пользовались, очень прост и доступен.
Задача 13. Найти корни уравнения f(x) = x?—10*2 + 44jc +
+ 29 = 0 с точностью до 0,0001.
Решение. Используя правило Декарта, заключаем, что урав-
уравнение имеет точно один отрицательный корень, так как в ряде
коэффициентов уравнения, ни один из которых не равен нулю,
число сохранений знака равно единице (у двух последних коэф-
коэффициентов).
Желая определить приближенное значение наименьшего по
абсолютной величине корня, решим, согласно способу № 3, уравне-
уравнение A,8). У нас а„_! = 44; а„ = 29 и уравнение A,8) запишется
в виде
44*+ 29 = 0,
х = —0,66.
Теперь определим интервал, в котором находится искомый
корень. Разделим левую часть уравнения на х -f- 0,66 и опреде-
определим остаток от деления:
1
—Ю
44
29
—0.66
—0.66
7.04
-33.69
(А)
1 —10,66 51,04 —4.69= / (—0.66)
(остаток от деления)
Отсюда заключаем, что значение левой части уравнения при
л: =—0,66 будет равно —4,69, т. е. / (—0,66) =—4,69.
Возьмем х — —0,56 и вычислим значение f {—0,56). Делим/(л;)
на х+ 0,56, снова применяя схему Горнера:
(В)
—0,56
1
1
-10
—0,56
-10.56
44
5,91
49.91
29
-27.95
1.05=/(—0,56)
(остаток от деления)
Теперь, сравнивая / (—0,66) = —4,69 и f (—0,56) = 1,05, заме-
замечаем, что значения левой части уравнения на концах отрезка
I—0,66; —0,56) имеют противоположные знаки. Следовательно,
искомый корень находится на этом отрезке. Значение корня уточ-
29
ним по способу № 2 линейной интерполяции. Первым приближе-
приближением корня будем считать х = —0,56 и воспользуемся формулой
A,4):
У нас Xi = —0,56; значение f (хг) уже подсчитано. Это оста-
остаток от деления в таблице (В): f{xi)= 1,05; */ = —0,66, a f(x,) =
= —4,69 — остаток от деления в таблице (А).
Подставляя эти значения в предыдущую формулу, имеем
п ее 1 пе —0.56 — (—0,66)
х,--0,56-1.0S 105_(Ц69/,
п ее 1 ле °-10
х2 = —0,56 — 1,05 гут.
Значение дроби
1^=0,0174. (С)
Этим значением нам придется пользоваться при вычислении сле-
следующих приближений, так как мы намерены применить способ
№ 2 в его модифицированном виде.
Итак,
х2 = —0,56 — 1,05 • @,0174) = —0,56 — 0,0183; х2 = —0,5783.
Разделим теперь левую часть уравнения на х + 0,5783 и опреде-
определим остаток от деления. Пользуясь схемой Горнера, получаем
—0.5783
1
1
—10
—0.5783
— 10.5783
44
6,1174
50,1174
29
—28,9829
0,0171 =* / @.5783)
(остаток от деления)
Остаток от деления 0,0171 достаточно мал. Значит, мы уже близко
подошли к искомому корню.
Так как мы ищем корень с точностью до 0,0001, то прежде
чем переходить к следующему, приближению, полезно испробовать
х = —0,5784, отличающееся от предыдущего на —0,0001. Разде-
Разделим левую часть уравнения на х + 0,5784 и определим остаток
от деления. Если он окажется противоположным по знаку преды-
предыдущему остатку, то цель достигнута.
I 1 —10 44 29
—0.5784
—0,5784 6,1185 —28,9895 (D)
1 —10,5784 50,1185 0.0115 =/(—0,5784)
i
30
Наши ожидания не оправдались, так как остаток не поменял
знака. Но очевидно, что значение х — —0,5784 является лучшим
приближением, чем значение х = —0,5783, поскольку остаток
уменьшился. Вычисление следующего приближения по формуле
A,4) приведет нас к
—0.5786
1
1
— 10
—0.5786
—10.5786
44
6,1208
50.1208
29
—28.9999
0.0001 = / (—0.5786)
(остаток от деления)
но значение дроби в правой части возьмем равным дроби (Q, т. е.
0,0174. У нас х2 = —0,5784; f (х2) есть остаток от деления f(x)
на х + 0,5784. В таблице (D) он уже вычислен и равен +0,0115
и /(-0,5784) = +0,0115.
Для х3 получаем
х3 = —0,5784 — 0,0115 • 0,0174,
х3 = —0,5784 — 0,0002; *3 = —0,5786.
Разделим теперь левую часть уравнения на х + 0,5786 и опре-
определим остаток от деления:
(Е)
Итак, /(—0,5786) = 0,0001 > 0. Вычислите самостоятельно оста-
остаток от деления левой части уравнения на х + 0,5787. У вас полу-
получится —0,0055, т. е. /(—0,5787) = —0,0055 < 0, на концах отрезка
[—0,5787; —0,5786] функция f(x) имеет разные знаки. Так как
величина —0,5786 отличается от —0,5787 на 0,0001, то требуе-
требуемая точность достигнута. Принимаем х = —0,5786.
Применим теперь для отыскания того же корня способ Нью-
Ньютона (способ № 1) в модифицированном виде, т.е. в формуле A,3)
знаменатель дроби /' (*„) будем считать одним и тем же для всех
приближений.
Корень у нас уже отделен, и мы знаем, что он находится на
отрезке [—0,66; —0,56]. В способе Ньютона, как указывалось, за
первое приближение корня следует принять тот конец этого отрезка,
на котором знак функции и знак второй производной одинаковы.
Находим вторую производную от левой части уравнения.
/ (х) = х3 — Юхг + 44* + 29.
Первая производная
/'(*) = 3*2 — 20*+ 44,
31
a /"(*) = 6a: — 20. На отрезке [—0,66; — 0,56] /" (л:) всюду отри-
отрицательна. Функция же f(x) отрицательна на левом конце этого
отрезка. Следовательно, совпадение знака функции со знаком второй
производной происходит на левом конце отрезка, а потому за пер-
первое приближение к искомому корню принимаем хг = —0,66.
В таблице (А) уже вычислено значение / (л^) = /(—0,66) = —4,69.
Теперь следует найти /'(д^) = /'(—0,66) и сохранить его значение
для всех последующих приближений, так как мы используем спо-
способ Ньютона в модифицированном виде. Делением f'(x) на х +
+ 0,66 найдем значение /'(—0,66). По схеме Горнера получаем
3 —20 44
—0,66 j —1,92 +14.4672
I 3 —21,92 58.4672=/'(—0.66)
I (остаток от деления)
Итак, сохраняя два знака после запятой, /'(—0,66) = 58,47. Это
значение производной будем брать и в последующих приближе-
приближениях.
Используем формулу A,3) и, полагая в ней п — 1, получаем
Xi ~ Xl f (*i) '
У нас х, = -0,66; / (хх) = -4,69; /' (хг) = 58,47;
х2 = -0,66 - =^ = -0,66 +. 0,0802;
х2 = —0,5798.
Для третьего приближения следует вычислить /'(—0,5798).
Делением / (л:) на х + 0,5798 получим
I 1 —10 44 29
—0,5798 I —0.5798 6.1342 —29.0678
I 1 —10,5798 50.1342 —0.0678=/(—0,5798)
Полагая в формуле A,3) п = 2, найдем
Но мы условились, что знаменатель дроби в правой части фор*
мулы A,3) будем брать одним и тем же во всех приближениях»
а потому возьмем его равным /' (*) = 58,47. Тогда х2 = —0,5798,
/ (л;,) = —0,0678, а
х3 = —0,5798 - =g^ = -0,5798 + 0,0012; х3 = -0,5786.
32
Это тот же корень, который был найден по способу № 2.
Закончим теперь решение этой задачи. У нас х = —0,5786.
В таблице (Е) уже проведено деление f {х) на х + 0,5786,
и коэффициенты частного от деления равны 1, —10,5786 и 50,1208,
а само частное будет л:2— 10,5786л: + 50,1208. Приравниваем его
нулю и решаем квадратное уравнение
х2 — 10,5786л: + 50,1208 = 0;
х = 5,2893 ± 1/27,9767 — 50,1208;
х = 5,2893 ± 1/22,1441/;
х = 5,2893 ± / • 4,7058.
Итак,
Xl = —0,5786;
х2 = 5,2893 + 4,7058/;
л:3 = 5,2893 — 4,7058/.
И здесь отметим, что уравнение в соответствии с правилом
Декарта действительно имеет только один отрицательный корень.
Проверка.
x-i+ х2 + х3 = Ю (верно!), так как сумма корней по A,28) должна
быть равна—^-, а у нас
<*! = —10; ао = 1 и — jjj = 10.
Найдем произведение корней: xi • х2 • х3 = —0,5786 • E,2893 +
+ 4,7058/) • E,2893 — 4,7058/)= —0,5786 х 50,1212 =—29,0001,
а должно быть —29, так как произведение корней по A,29) равно
(—lL^2. У нас показатель степени п = 3; ап = 29, а„ = 1 и
(—1)«Jj = —29.
Таким образом, проверка дала хорошие результаты.
Решим теперь этот же пример по способу № 4 (см. стр. 9).
1. Составляем квадратное уравнение вида A,10)
Это уравнение приобретает вид
— Юл;2 + 44л: + 29 = 0.
Умножая обе его части на —1, получим
Юл:2 — 44л: — 29 = 0.
2. Легко убедиться, что корни этого уравнения действительны.
Теперь решаем уравнение вида A,11), в котором у ап_г + 44;
ап = + 29, а само уравнение имеет вид
44л: + 29 = 0.
2 И. А. Каплан 33
Корень этого уравнения, « = —0,6592 принимаем за первое при-
приближение искомого корня Левую часть уравнения делим по спо-
способу Горнера на х + 0,6592 и получаем
—0.6592
1
1
—10
—0.6592
—10.6592
44
7.0265
51.0265
29
—
29
Составляем уравнение вида A,13), в котором Ьа_1 = 51,0265,
а„ = 29. Это уравнение имеет вид
51,0265*+ 29 = 0
Отсюда получаем второе приближение искомого корня
х2 = —0,5683
Теперь делим левую часть уравнения на х + 0,5683 по схеме
Горнера:
—0.5683
1 —10
44
29
—0.5683 6.0060 —
I —10.5683 50.0060 29
Затем составляем уравнение A,16), которое приобретает вид
50,0060а: + 29 - 0,
и находим, что третье приближение искомого корня будет
ха = —0,5799
Продолжая деление, на следующем шаге получаем
1 —10 44 29
0.5799
-0,5799 6,1353
1 —10.5799 50.1353 29
и составляем уравнение
50,1353а:+ 29 = 0.
34
Отсюда четвертое приближение
xt = —0,5784.
Снова деля, получим
—0,5784
1
1
—10
—0.5784
—10.5084
44
61185
50,1185
29
—
29
и для определения следующего приближения будем иметь урав-
уравнение
50, 1185а:+ 29 = 0;
*5 = —0,5786
Следующее приближение снова даст хв = —0,5786 (проверьте
самостоятельно) На этом значении мы и остановимся
Итак, х = —0,5786 Это то же значение, что и полученное
раньше Однако вычислительная работа была значительно мень-
меньшей и чрезвычайно простой Здесь способ № 4 быстро привел
к цели Он очень прост в применении
ВТОРОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Численное решение алгебраических уравнений
Задача 2,1. Найти с точностью до 0,00001 корни уравнения
Решение. Решим эту задачу по способу № 4. Составим
квадратное уравнение вида A,10)
— З*2— 17*+32 = 0.
Корни этого уравнения, как нетрудно видеть, действительны,
а потому решаем уравнение A,11), которое дает —17*+ 22 = 0,
откуда Xi = 1,294118 (вычисления будем вести с одним запасным
знаком). По схеме Горнера делим левую часть уравнения на
*—1,294118 и получаем
1.294118
1 —3
-17
22
1.294118 —2.207613
-24.856918
1 —1,705882 —19,207613 — 2,856918
Составляем уравнение вида A,13). У нас &„_, =—19,207613,
а свободный член уравнения ап = 22 и для определения второго
приближения имеем —19,207613* + 22 = 0; второе приближение
х2= 1,145379.
Делим левую часть уравнения по схеме Горнера на х — х2,
" 1145 379
т. е. на х —
1,145379
i.i^o a
1
1
/У.
—3
1,145379
—1.854621
—17
— 2,124244
—19,124244
са—х
22
—21,904507
+0.095493
36
(обратите внимание на то, что остаток уменьшился по абсолют-
абсолютной величине и изменил знак, однако он еще велик).
Теперь составляем уравнение A,16) в котором сл-1 = —
—19,124244 и по-прежнему ап = 22. Получаем
— 19,124244л: + 22 = О,
а третье приближение х3 = 1,150372.
Делим }(х) на х— 1,150372 по схеме Горнера:
1.150372
1
1
з
1,150372
—1.849628
—17
2,127660
—19,127660
22
—22,003924
— 0.003924
(остаток от
деления)
Решаем уравнение A,16) которое теперь принимает вид
• 19,127660а: + 22 = 0. Отсюда *4 = 1,150167.
Новое деление по схеме Горнера f(x) на х— 1,150167 дает
(А)
1,150167
1
1
—3
1.150167
—1,849833
—17
— 2.127617
—19.127617
22
—21.999954
+ 0.000046
(остаток от
деления)
Остаток от деления изменил знак по сравнению с предыдущим
и оказался теперь достаточно малым. Мы брали четвертое при-
приближение равным Хц = 1,150167. Округлим его до пяти знаков
и возьмем х = 1,15017. Произведем два деления: 1) f(x) на х —
— 1,15017 и 2) f(x) нах- 1,15016.
Первое деление дает
(А)
1.15017
1
1
—3
1.15017
—1.84983
(коэффициенты
—17
— 2.12762
—19.12762
частного)
-22
—22.00001
— 0.00001
(остаток от
деления)
и остаток от деления отрицателен.
Деление f(x) на х — 1,15016 дает
1.15016
1
1
-3
1,15016
—1.84984
-17
—2,12761
—19,12761
22
—21,99981
0,00019
(остаток от
деления)
и остаток от деления положителен.
Таким образом, в качестве искомого корня можно взять х =
= 1,15016 или х= 1,15017. Берем х = 1,15017. Разделим теперь
f(x) на х—1,15017. В таблице (А) уже найдены коэффициенты
частного, а само частное равно
х2— 1,84983л:— 19,12762.
Приравняем его нулю и решим уравнение
х2— l,84983x— 19,12762 = 0:
х = 0,92492 ± 1/0,85548+ 19,12762;
г Г +5,39516
х = 0,92492 ± /19,98310 = 0,92492 ± 4,47024 =
Таким образом, мы получили следующие корни: хх = —3,54532;
х2= 1,15017; *3 = 5,39516.
Проверка:
Сумма корней
*i+ *» + *» = +3,00001,
т. е. на одну стотысячную больше того, что должно было полу-
получиться. Произведение же корней
х1-х2-х3 = — 21,99995
вместо —2£, что также следует признать хорошим результатом.
Задача 2,2. Найти корни уравнения
f (х) = х3 — 10,91л:2 + 38,52л: — 44,36 = 0.
Решение. По правилу Декарта заключаем, что отрицатель-
отрицательных корней уравнение не имеет, так как нет ни одного сохра-
сохранения знака в ряде коэффициентов (-\ 1 ). Положительных
корней будет три или один, так как число перемен знака равно
трем. Испытаем в качестве корней числа 2 и 3, а / B) и / C)
38
найдем как остатки от деления f (х) соответственно на х — 2 и на
х — 3. Делим по схеме Горнера:
2
1
1
—10,91
2
8.91
38.52
—17,82
20.70
—44.36
41,40
—2.60 = /B)
(остаток от деления]
Итак, /B)==—2,60
3
1
1
—10.91
3
—7.91
38.52
—23,73
14,79
—44.36
44.37
+ 0.01 = /C)
(остаток от деления)
и /C) = -т-0,01. Поскольку /B) и /C) имеют различные знаки,
в отрезке [2; 3] имеется корень, причем, так как остаток от деле-
деления {(х) на х— 3 значительно меньше по абсолютной величине,
чем остаток от деления на х — 2, мы заключаем, что корень
имеет значение, близкое к 3.
Полезно исследовать, не будет ли уравнение иметь два близ-
близких корня. Используя указания на стр. 15, разделим /' (х) на
* —3. У нас /'(*) = 3*2 — 21,82* + 38,52. Деление дает
-21.82
38,52
-38.46
—12,82
0.06 = ГC)
Поскольку остаток от деления мал, делаем заключение, что
число, близкое к 3, является корнем и производной /'(*)■ Это
говорит о том, что уравнение имеет два близких корня.
Находим корень уравнения /' (х) = 0, т. е. уравнения
<Р (х) = З*2 — 21 ,82л; + 38,52 = 0.
Решение будем проводить по способу Ньютона. Первым прибли-
приближением корня будем считать х = 3. Двукратным последователь-
последовательным делением левой части последнего уравнения на х — 3 найдем
остаток от деления, причем первый остаток даст числитель,
39
а второй — знаменатель дроби в формуле A,3). Деление произво-
производим на одной таблице:
3
3
3
3
—21,82
9
-12,82
9
38,52
—38,46
+0,06 = <р C)
3,82 = ср'(З)
Считая в формуле A,3) первым приближением число 3, най-
найдем, что корень уравнения f {х) = 0, который обозначим буквой а,
равен
0,06
" - " _382 '
а = 3,0157.
Теперь воспользуемся формулой A,22, стр. 15), чтобы полу-
получить два близких между собою корня уравнения. Для того чтЪбы
воспользоваться этой формулой, нам следует найти
Да) и |ГИ-
Разделим f (х) на х — а три раза последовательно. Остаток от
яервого деления даст Да), а остаток от третьего деления
-=-/" (а). Деление по схеме Горнера произведем на одной таблице:
3,0157
3,0157
3.0157
1
1
1
1
— 10.91
3,0157
—7.8943
3,0157
4.8786
3,0157
— 1,8629 =
38,52
—23,8068
14.7132
—14.7124
| 0.0008 =
—44.36
44.3706
| 0,0106=/(о)
Г (а)
40
Теперь находим корни уравнения по формуле A,22). У нас
/ (о) = 0,0106; у Г (а) = -1,8629; а = 3,0157;
О П1С7 , l/— 0,0106
*,,2 = 3,0157+ у _18629;
jt,.2 = 3,0157 ± /0,0057 ;
jc,,2 = 3,0157 ±0,0747;
jcx = 3,0904;
х2 = 2,9410
Сохраняя после запятой только два десятичных знака, полу-
получаем jc, = 3,09; *2 = 2,94. Точные значения корней данного урав-
уравнения 2,92 и 3,12. Разделим f (х) на произведение (х— 2,94) К,
х(х — 3,09). По схеме Горнера сначала разделим на х— 2,94,
а потом на х — 3,09, причем деление выполним на одной таблице:
1 —10.91 38,52 —44,36
2,94 2,94 —23,43 +44,36
1 7,97 15,09 0 = /B,94)
3.09 3,09 —15,11
1 —4,89 — 0,02
Частное от деления равно х—4,89. Приравнивая его нулю, полу-
получаем уравнение для определения третьего корня
х— 4,89 = 0
откуда х — 4,89.
Итак, корни уравнения: хх = 2,94; х2 = 3,09; х3 — 4,89.
Проверка. Сумма корней дает хх + х% + х3 = 10,92 вместо
10,91, а произведение корней хх • х2 • хг = 44,40 вместо 44,36.
Полученные приближенные значения корней следует признать
хорошими.
Задача 2,3. f(x) = x*— 2х* — 3,74л:2 + 8,18л:— 3,48 = 0.
Решение. По правилу Декарта заключаем, что будет один
отрицательный корень, так как в ряде коэффициентов только одно
сохранение знака, положительных корней —один или три, по-
поскольку число перемен знака равно трем.
Для отыскания наибольшего по абсолютной величине корня
решим уравнение вида A,6), где в нашем случае Ci = —2.
Решаем уравнение
х— 2 = 0,
откуда х = 2.
Для определения значения левой части уравнения при х = 2
разделим f (х) на х — 2 по схеме Горнера:
4J
1 —2 —3.74 8.18 —3.48
—7.48
1.40
1 о -3.74 0.70 |-2,08= f B)
Теперь решим квадратное уравнение вида A,7). У нас ах ==
=—2; а2 — —3,74, и A,7) запишется в виде
jc2- 2х — 3,74 = 0;
x=\±V\ +3,74; х = 1 + ]/4J4; jc=1±2,17.
Выбираем jc= 1 + 2,17 или л: = 3,17, так как мы ищем при-
приближенное значение наибольшего по абсолютной величине корня.
Найдем теперь /C,17). Пользуясь схемой Горнера, получим
3.17
1
1
—2
3.17
1.17
—3.74
3.71
—0.03
8.18
—0,10
8.08
—3,48
25.61
22.13 =
Итак, Д2)<0, а Д3.17) >0 и, значит, искомый корень на-
находится на отрезке [2; 3,17], причем он ближе к 2, чем к 3,17,
так как остаток от деления на х — 2 меньше по абсолютной вели-
величине остатка от деления на х—3,17. Попробуем сузить отрезок,
на котором находится корень. Возьмем среднее арифметическое
2 4-3 17
абсцисс концов отрезка 2' — 2,58 и рассмотрим /42,58).
из
Применяя схему Горнера, получим
2,58
1 —2
—3.74 8.18 —3.48
2.58 1.50 —5,80 +6,14
(А)
1 0,58 —2,24 2.38 [2,66 = /B.58)
Поскольку / B,58) = 2,66, а / B) = —2,08, корень находится
в отрезке 12; 2,58]. Этот отрезок по сравнению с предыдущим
значительно сужен. Для решения задачи применим способ Нью-
Ньютона.
42
Определим f"(x), чтобы решить вопрос, какой из концов этого
отрезка принять за первое приближение корня.
/' (jc) = 4*3 — 6jc2 - 7,48л: + 8,18;
f(x) = 12л:2— 12л:— 7,48.
Найдем значение второй производной при х = 2 и при х =
= 2,58. Снова применяя схему Горнера, получим
2
2.58
12
12
12
12
—12
24
12
—12
30.96
18.96
— 7.48
*
24
| 16.52 = Г B)
— 7.48
48.92
[41.44 =/"B.58)
Легко проверить, что f (jc) внутри отрезка [2; 2,58] в нуль не
обращается. Таким образом, на всем этом отрезке /" (х) сохра-
сохраняет знак, оставаясь положительной. А так как функция / (л:)
положительна на правом конце отрезка [2; 2,58], то значение х
на правом конце этого отрезка, т. е. х = 2,58, и следует принять
за первое приближение искомого корня.
Нами уже найдено /B,58) = 2,66 (табл. А), определим /'B,58),
так как f'(xn) входит в формулу A,3) в способе Ньютона.
Для определения /'B,58) разделим /'(jc) на jc — 2,58 по схеме
Горнера (/' (х) было получено раньше):
2.58
4 — 6
- 7.48
8.18
10.32 11.14 9,44
4.32
3.66 17.62 = /' B.58)
(остаток от деления)
Итак, /' B,58) = 17,62.
43
По формуле A,3), в которой ^ = 2,58, /(*,.) = 2,66, /'(*)
= 17,62,
26
х2 = 2,58 - ygg = 2,58 — 0,15 = 2,43j
хг = 2,43 (второе приближение корня).
Вычислим теперь f (х2) и /' (х2) делением /(*) и f'(x) на х-
— 2,43, причем деление выполним на одной таблице:
2.43
2.43
1
1
1
—2
2,43
0,43
2,43
2,86
3,74
1,04
—2,70
6.94
4.24
8.18
—6.56
1,62
10.30
11.92 =
(остаток от
—3.48
3,93
0.45 =
(остаток от
/'B,43)
деления)
/B.43)
деления;
Итак, /B,43) =0,45, а /'B,43)= 11,92.
Формула A,3) дает третье приближение
х3
°'45-
ха = 2,43 — 0,0377; ха = 2,3923.
Найдем еще одно приближение. Получаем f(x3) и f'{x3).
По схеме Горнера
2,3923
1
1
—2
2,3923
0.3923
-3.74
0.9385
—2.8015
8.18
—6.7020
1.4780
—3.48
3.5358
0.0558 =
(остаток от
/B.3923)
деления)
2,3923
2.3923 6,6616 9,2345
2,7846 3.S601 10,7125 = /'B.3923)
(остаток от деления)
44
Четвертое приближение корня по формуле A,3) даст
*4 = 2,3923 - Г^Ц = 2,3923 - 0,0052;
дг4 = 2,3871.
Знаки /B,3871) и /B,3870) противоположны (проверьте), по-
поэтому мы можем утверждать, что * = 2,3871 с точностью до
одной десятитысячной дает искомый корень.
Разделим теперь / (х) на х— 2,3871 и частное приравняем нулю.
Выполним деление по схеме Горнера:
2,3871
1
1
—2
2.3871
0.3871
-3,74
0.9240
—2.8160
8,18
—6.7221
1,4579
—3,48
3,4801
0,0001
(остаток
= Д2.3871)
от деления'
Частное от деления равно
<р (х) = Xs + 0.3871*8 — 2,8160* + 1,4579. (В)
Округлим его коэффициенты до двух десятичных знаков, прирав-
приравняем нулю и решим уравнение
/i(jc) = х3 + 0,39л:2 — 2,82*2 + 1,46 = 0.
Находим приближенное значение наименьшего по абсолютной
величине корня этого уравнения. Решаем уравнение вида A,8).
У нас ап_1 = —2,82; ап = 1,46, и это уравнение принимает вид
— 2,82л: + 1,46 = 0,
откуда получаем приближенное значение корня х — 0,52.
Найдем теперь отрезок, на котором находится корень. Разде-
Разделим левую часть уравнения /j(jc) на х — 0,52, чтобы определить
h @,52),
0,52
0,39 —2,82
1,46
0,52
0,47 —1.22
1 0,91 —2,35 +0,24 = ^@.52)
(остаток от деления)
Предположим, что вторым концом отрезка будет х = 1. Оста-
Остаток от деления fi(x) на *— 1 даст значение /t(l)
4S
1
1
1
0.39
1
1.3?
—2.82
1.39
-1.43
1.46
—1.43
+0.03 = ^A)
(остаток от деления)
Остаток от деления сохранил знак, но значительно уменьшился.
Возьмем х= 1,1. Разделим ft(x) на х— 1,1;
1 о,39 , —2.82 1.46
1.1
1.1
1.64 —1.30
1 1,49 —1.18 + 0,16 =/хA.1)
Мы нашли, что Л A,1) больше, чем Ml), т- е- мы уходим от
корня, а не приближаемся к нему. Исследуем л: = 0,9. Деление
по схеме Горнера даст
0.9
1 0,39 —2.82
1.46
0.9
1.16
-1.49
1 1.29 —1.66 —0,03 = ^@.9)
(остаток от деления)
Таким образом, ft @,52) = 0,24, a fi @,9) = —6,03 и корень на-
находится на отрезке [0,52; 0,90], причем, так как МО,9) значи-
значительно меньше по абсолютной величине, чем /@,52), то заклю-
заключаем, что корень находится ближе к 0,9, чем к 0,52. Кстати, из
того, что fi @,9) < 0, а ДA) = +0,03 >0, можно сделать заклю-
заключение, что на отрезке [0,9; 1] имеется еще один корень уравне-
уравнения. Все это заставляет прийти к выводу, что есть два близких
корня на отрезке [0,52; 1], поэтому следует поступать в соот-
соответствии с указаниями, данными на стр. 15.
Решаем уравнение f[ (х) = 0, т. е. уравнение
3*а +0,78* —2,82 = 0,
и определяем его корни х = —1,10 и jc = 0,84. Выбираем 0,84,
так как это значение лежит на отрезке, на котором находится
корень. Полученное значение х = 0,84 и есть величина а в фор-
формуле A,22).
Теперь воспользуемся формулами A,22) и для этого вычислим
/\ @,84) и -j/i @.84). Величина -у /Г @,84) будет остатком от трех-
трехкратного деления fx(x) на х — 0,84:
0.84
0.84
0.84
1
1
1
1
0.39
0,84
1.23
0.84
2.07
0.84
2,91 =
1
2
—2.82
1.03
—1.79
1.74
1—0.05 = ;
Г@,84)
1.46
—1.50
|—0,04 = /, @,84)
ri @.84)
Итак, fj, @,84) = —0,04; -i-f @,84) = 2,91, и из формулы A,22)
(стр. 15) с учетом, что а = 0,84, получим
jc,,2 = 0,84 ± У 0,0137; хи2 = 0,84 ±0,11;
хх = 0,73 и х2 = 0,95.
Эти два корня попробуем улучшить, чтобы получить их с точ-
точностью до 0,0001. Начнем с корня jc1 = 0,73. Вычислим ^@,73)
и ^@,72) делением fx (х) сначала на х — 0,73, а потом на х — 0,72
0,73
0,72
1
1
1
1
0,39
0,73
1.12
0.39
0.72
1,11
—2.82
0,81
—2,01
—2,82
0.7992
—2.0208
1,46
— 1,4673
|—0,0073 = ^@,73) < 0
1.46
—1.4550
(+0,0050=/! @.72) >0
47
Таким образом, корень находится на отрезке [0,72; 0,73].
Если бы нас удовлетворяла точность в 0,01, мы бы на этом оста-
остановились.
Сузим отрезок [0,72; 0,73], взяв в качестве его левого конца
среднее арифметическое из значений 0,72 и 0,73, т. е. 0,725.
Определим знак функции на этом конце отрезка, но операции
будем производить не с многочленом fa (х), у которого коэффи-
коэффициенты округлены, а с многочленом (В).
Найдем значение многочлена (В), который у нас обозначен че-
через <р (х), и его производной при х = 0,725. Двухкратное деление
по схеме Горнера дает
0,725
0.725
1
1
1
0,3871
0,725
0,1121
0.725
1,8371
—2.8160
0.8063
—2.0097
1,3319
1—0.6778 =
1.4579
—1.4570
D-0,0009 = ср @,725)
Ч>' @,725)
Таким образом, корень находится на отрезке [0,725; 0,7301.
Уточним корень по способу Ньютона. Легко усмотреть, что <р" (х)
на отрезке [0,725; 0,730] сохраняет положительное значение,
поэтому за приближенное значение корня принимаем его значение
на левом конце интервала, т. е. 0,725, так как на этом конце
интервала и функция положительна: <р @,725) = +0,0009.
Пользуясь формулой A,3), в которой надо взять xt = 0,725;
) = +0,0009; /' (х{) = —0,6778, получим
х2 = 0,725 -
= 0,725 + 0,0013;
х2 = 0,7263.
Для выяснения знака <?(х) при х = 0,7263 разделим у[х) на
х — 0,7263:
0.7263
1
1
0.3871
0.7263
1.1134
—2.8160
0.8087
—2.0073
1.4579
1.4579
0 = <р @,7263)
48
x = 0,7263 является корнем уравнения. На этом заканчиваем
уточнение корня х — 0,73.
После того как найдем корень х = 0,7263, можно разделить
<?{х) на х—0,7263. Мы получили бы л:2 + 1,1134л:— 2,0073, а при-
приравняв нулю и решив квадратное уравнение хг + 1,1134* — 2,0073 =
= 0, нашли бы корни х = —2,0789 и х = 0,9655. Но для упраж-
упражнения в применении способа Ньютона уточним полученное зна-
значение корня * = 0,95.
На стр. 46 было выяснено, что корень находится на отрезке
@,9; 1]. На правом конце этого отрезка фA) >0; ф"(*) на этом
отрезке имеет положительное значение, а потому за приближен-
приближенное значение корня принимаем х = I, так как при х=\ и ф (х)
и ф" (х) совпадают по знаку. Вычислим значение ф (х) и <р' (х) при
х = 1 двукратным делением ф (х) на х—1.
1
1
1
1
1
0.3871
1
1.3871
1
2.3871
—2,8160
1.3871
—1.4289
2.3871
@.9582 = 9'
1.4579
—1.4289
0.0290 = 9@
A)
0.0290
и по формуле A,3) найдем х2 = 1 — jjggs!' Хг~ 1 — 0,0303; х2 =
= 0,9697.
Чтобы получить следующее приближение, определим у @,9697)
и ф'@,9697) двукратным делением ф (х) на х — 0,9697
0,9697
1,9697
1
1
1
0.3871
0.9697
1,3568
0.9697
2.3265
—2.8160
1.3157
—1,5093
2.2560
|0,7557 =
1,4579
—1.4548
|0,0031 = ср @.9697)
<р' @,9697)
4?
Теперь по формуле A,3)
х3 = 0,9697 — ^^; х3 = 0,9697 — 0,004!;
х3 = 0,9656.
Вычислим 9@,9656):
0.9656
1
1
0,3871
0,9656
1.3527
—2,8160
1.3062
—1.5098
1.4579
1.4579
|0 = <f @.9656)
Таким образом, х = 0,^656 является корнем уравнения. Три
корня заданного уравнения найдены: хх — 0,7263; х2 = 0,9656;
лг3 = 2,3871.
Деление f(x) на х—2,3871 было уже произведено, и частным
является многочлен (В). Разделив (В) на х — 0,7263, а новое част-
частное на х — 0,9656, получим уравнение wy. определения послед-
последнего, четвертого корня. Деление у(х) на х — 0,7263 выполнено
в таблице (D). Берем найденные в этой таблице коэффициенты
частного и делим его на х — 0,9656:
0,9656
1
1
1.1134
0.9656
2,0790
—2,0073
2.0075
+0,0002
Коэффициенты частного будут 1 и 2,0790, а само частное х +
4- 2,0790.
Решая уравнение х + 2,0790 = 0, найдем последний корень
Xt = —2,0790.
Корнями уравнения будут числа xt = 0,7263; х2— 0,9656; х3 =
-2,3871; х4 = — 2,0790.
Проверка. лг2 + х2 + х3 + х4 = 2, как и должно быть, а л^ х
X хг • х3 • х4 = —3,4804 (должно быть —3,48), что указывает на
хорошие результаты вычислений.
Это же уравнение можно решить проще, минуя довольно уто-
утомительное нахождение двух близких корней уравнения. Приме-
Применим способ № 4 для отыскания одного корня.
В нашем уравнении
х* — 2х* — 3,74л2 + 8,18лг — 3,48 = 0
50
выделим квадратный трехчлен вида A,10)
—3,74** +8,18*— 3,48.
Его корни действительны, поэтому берем уравнение вида A,11),.
т. е. 8,18* — 3,48 = 0, откуда получаем первое приближение корня
х = 0,4254.
Делим левую часть уравнения на х — 0,4254, пользуясь схе-
схемой Горнера:
0.4254
1 —2
-3.74
8.18
—3.48
0.4254 —0.6698 —1,8759
2.6818
1 —1.5746 —4.4098
Решаем уравнение A,13), в котором
= —3,48, т. е. уравнение
6.3041 —0.7982
Ьп-Х
&„.-! = 6,3041, а ап
6,3041 х—&48 = 0,
и находим второе приближение
х2 = 0,5520.
Делим левую часть уравнения на х—0,5520:
0.5520
1
1
—2
0.5520
—1,4480
—3.74
-0.7993
—4.5393
8,18
—2.5057
5.6743
—3.48
3,1322
—0.3478
Остаток от деления —0,3478 по сравнению с предыдущим
—0,7982 уменьшился по абсолютной величине, но все еще оста-
остается большим, поэтому для ускорения сходимости применим фор-
фулу A,20), в которой х2 = 0,5520, хх = 0,4254, гх = —0,7982,
г2 = —0,3478, и найдем третье приближение первого корня
_ 0,5520 (—0,7982) — 0,4254 • (—0,3478),
Хз ~ —0,7982 — (—0,3478) '
_ —0,2926, _
5t
Делим теперь левую часть уравнения на х — 0,6496:
0.6496
1
1
—2
0.6496
—1.3504
—3.74
—0.8772
—4,6172
8.18
—2.9993
5,1807
—а48
3,3654
—0,1146
Снова применяя формулу A,20) получим
_ 0,6496 (—0,3478) — 0,5520 (—0,1146).
—0,3478 —(—0,1146) '
—0,1627
Ч =
х, =
0,6977.
4 —0.2332' ■
Делим левую часть уравнения на х — 0,6977:
0.6977
1
1
—2
—0,6977
—1.3023
-3.74
—0,9086
—4.6486
8.18
—3.2433
4.9367
—3.48
а4443
—0.0357
Получаем следующее приближение по формуле A.20):
0,6977 (—0,1146) — 0,6496 (—0.0357).
Х%~ —0.1146—(—0,0357) ♦
_ —0,0568 _ n 7]QQ
** ~ —0.0789' Х% ~ '
Разделим теперь левую часть уравнения на х—0,7199:
0.7199
1
1
—2
0.7199
—1.2801
-3,74
—0.9215
—4,6615
8,18
—3,3558
4,8242
—3.48
3.4729
—0,0071
Поступая, как и раньше, найдем следующее приближение:
_ 0,7199 (—0,0357) —0,6977 • (—0,0071) _ —0.0207.
—0,0357 — (—0,0071)
ха = 0,7238.
—0,0286'
52
Делим теперь левую часть уравнения на х—0,7238:
0,7238
1
1
—2
0.7238
—1.2762
-3,74
—0.92-37
—4.6637
8.18
—3.3756
4,8044
-3.48
3.4774
—0,0026
Следующее приближение находим тем же путем:
_ 0,7238 . (—0.0071) — 0.7199 (—0,0026).
*? — —0,0071 — (—0,0026) '
Х7 = 0,7260.
Разделим левую часть уравнения на х — 0,7260:
0.7260
1
1
—2
0,7260
—1,2740
—3,74
0.9249
—4.6649
8,18
—3,3867
4.7933
—3.48
3.4799
—0.0001
Остаток от деления оказался очень малым, а потому на этом
приближении можно остановиться.
Корень 0,7260 отличается от значения 0,7263, найденного раньше,
только на 0,0003 (несмотря на то, что для улучшения сходимости
была использована формула A,20), изменение корня происходило
медленно, хотя применение этой формулы и ускорило сходи-
сходимость).
Задача 2,4. Решить уравнение
/ (х) = х*~ Юх3 + 48, 16аг2 + 108,08* + 70,76 = 0.
Решение (рекомендуется сначала прочесть на стр. 16 «Опре-
«Определение комплексных корней алгебраических уравнений»). Прежде
всего замечаем, что последние три члена соответствуют квадрат-
квадратному уравнению с комплексными корнями. В качестве первого
приближения выделяемого из f(x) трехчлена берем трехчлен
48,16*2 -f 108,08a; -f 70,76
и делением его на коэффициент при х2 получаем трехчлен
*а +2,24*+ 1,47, (А)
который принимаем за первое приближение выделяемого трех-
трехчлена.
Делим левую часть уравнения на трехчлен (А) по схеме деле-
деления, указанной на стр. 18, до получения в остатке квадратного
трехчлена, который уже не делится на делитель (А).
53
—2.24
1.47
1
—
—
1
—10
—2.24
—
-12.24
48.16
27,42
—1.47
74.11
108.08
—
17.99
126,07
70.76
70.76
Остаток от деления равен
74,11**+ 126,07* + 70,76.
Делением на коэффициент при хг получаем
*2 + 1,70* +0,95.
Делим левую часть данного уравнения на трехчлен (В)
-1,70
—0.95
1
—
—
1
—10
— 1.70
—
—11,70
48,16 ,
19,89
—0.95
67.10
108,08
—
+11.12
119.20
70.76
70.76
Остаток от деления равен
67,10*2+ 119,20*+ 70,76.
Делением его на коэффициент при *2 получаем
** + 1,78*+ 1,05.
, Если разделить левую часть уравнения на трехчлен (С),
чается:
—1.78
— 1,05
1
—
—
1
—10
—1.78
—
—11,78
48,16
20.96
—1.05
68.07
108.08
—
12,37
120.45
70.76
70.76
54
Коэффициенты остатка от деления подчеркнуты, а остаток от
деления будет равен
68,07** +120,45* + 70,76.
Деление на коэффициент при х2 приводит к трехчлену
** + 1,77*+ 1,03, (D)
который незначительно отличается от трехчлена (Q. Процесс очень
быстро сходился и можно было ограничиться только тремя деле-
делениями. Приравнивая трехчлен (D) нулю, решим квадратное урав-
уравнение
**+ 1,77*+1,03 = 0;
ЛП.2 = —0,88 ± 1/0,77—1,03;
х,,2 = —0,88 ± /—0,26
и окончательно
xi,2 = — 0,88 ± 0,5Н.
Для определения остальных двух корней надо разделить левую
часть данного уравнения на трехчлен (D). Коэффициенты част-
частного уже известны из последней таблицы. Это 1; —11,78 и 68,07.
Таким образом, частное равно х2—11,78* + 68,07. Приравниваем
его нулю и решаем квадратное уравнение
х2 — 11,78* + 68,07 = 0;
*з,4 = 5,89 ± /34,69—68,07;
*з,4 = 5,89 ± У —33,38;
*з,4 = 5,89 ± 5.78».
Итак, корнями являются числа *i2 = —0,88±0,5Н, *3 4 =
= 5,89 ± 5,78t.
Проверка.
xi + *2 + хя + *4 = 10,02 вместо 10;
хх • *2 • *3 • *4 = 70,14 вместо 70,76.
Задача 2,5. Решить уравнение
f(x) = ** — З*3 + 20*2 + 44* + 54 = 0.
Решение. Применим тот же способ, что и в предыдущей
задаче. Последние три члена в уравнении приводят к квадратному
уравнению с комплексными корнями — см. уравнение A,22а)
20*2 + 44* + 54 = 0.
После деления на коэффициент при *2 получаем первое прибли-
приближение выделяемого из /(*) трехчлена
** + 2,2* + 2,7. (А)
55
Делим теперь f(x) на трехчлен (А):
—2.2
—2.7
1
—
—
1
—3
—2.2
—
—5,2
20
11.44
—2.70
28.74
44
—
14.04
58.04
54
—
—
54
Коэффициенты остатка от деления подчеркнуты, а
ток равен
28,74*2 + 58,04* + 54.
После деления на коэффициент при х2 получаем
хг + 2,02х + 1,88
и делим левую часть уравнения / (х) на трехчлен (В):
—2.02
—1.88
1
—
—
1
—3
—2.02
—
—5,02
20
10,14
—1.88
28.26
44
—
9.44
53.44
54
—
—
54
Подчеркнутые числа являются коэффициентами ос
имеет вид
28,26л:2 + 53,44* + 54.
После деления на 28,26 этот остаток запишется так:
х*+ 1,89*+1,91.
Проделаем еще одно приближение:
—1,89
—1.91
1
—
—
1
—3
—1.89
—
—4.89
20
9,24
—1.91
27,33
44
—
9.33
53.33
54
—
—
54
56
Коэффициенты остатка подчеркнуты, а сам остаток равен
27,33л;2 + 53,33* + 54.
После деления на коэффициент при хг он принимает вид
л:г + 1,95л:+ 1,98. (D)
По сравнению с трехчленом (С) мы получили незначительные
изменения коэффициентов. Останавливаемся на этом приближении.
Приравниваем трехчлен (D) нулю и решаем квадратное урав-
уравнение
*2 + 1,95* + 1,98 = 0;
*, 2 = —0,975 ± /0,951— 1,980;
*,,2 = —0,975 + V—1.029;
Хи2 = -0,975+
Из последней таблицы уже известны коэффициенты частного
от деления левой части данного уравнения на трехчлен (С). Это
числа 1; —4,89; 27,33; само же частное имеет вид
*2 - 4,89* + 27,33.
Приравниваем его нулю и решаем уравнение
х* - 4,89* + 27,33 = 0.
*з,4 = 2,445 ± У 5,978—27,33;
*3i4 = 2,445 ± 4,620(.
Проверка.
xi + *2 + хз + *4 = 2,94 вместо 3;
*х • *2 • *3 • Xi — 54,1 вместо 54.
При той небольшой точности, с которой велся расчет, результаты
можно считать довольно хорошими.
Задача 2,6. Решить уравнение
/ (*) = *4 _f- 24.26*3 + 274.3*2 + 132,8* + 231 = 0.
Решение. Решение проведем по итерационному методу Фрид-
Фридмана, сущность которого поясним на примере.
Выделяем трехчлен вида A,21) для определения комплексных
корней с наименьшим модулем. Таким трехчленом будет 274.3*2 -j-
+ 132,8* + 231, который после деления на коэффициент при *2
запишется так: *2 +0,484* + 0,842.
1-й шаг. Расположим сначала делимое и делитель по убываю-
убывающим степеням буквы * и проведем деление по схеме деления
многочлена на квадратный трехчлен:
57
—0,484
—0.842
1
—
—
1
24.26
—0,484
—
23,77
274.3
-11.5
—0,842
261,9
(остальные столбцы не вычисляем, так как остатком от деления
мы не интересуемся).
Итак, частное равно *2 + 23,77* + 261,9. Разделим его на сво-
свободный член 261,9 и получим, располагая трехчлен по возрастаю-
возрастающим степеням буквы *,
1 + 0,09* + 0.004*2.
(А)
2-й шаг. Расположив левую часть данного уравнения по возра-
возрастающим степеням буквы *, найдем
231 + 132,8* + 274.3*2 + 24.26*3 + **.
(В)
Разделим теперь многочлен (В) на трехчлен (А). Деление выпол-
выполняем по той же схеме:
—0.09
—0,004
231
—
—
231
132.8
—20.79
—
112,01
274,3
—10,08
—0,92
263,30
Таким образом, частное равно 231 + 112,01* + 263.30*2. Разде-
Разделим этот трехчлен на коэффициент при *2 и получим
** + 0,425* + 0,877.
Повторим деление сначала так, как указано в 1-м шаге, а потом,
как указано во 2-м шаге. Выполняем его по той же схеме на
одной таблице:
58
—0,425
—0,877
После
деления
на 263,293
1
—
—
1
0,004
24.26
—0.425
—
23,835
0.9
274,3
—10,13
—0,877
♦263.293
1
274.3
— 10,08
—0,924
*263,296
132.8
-20,79
—
112.01
231
—
—
231
—0.09
—0.004
—
Частное от первого деления равно
хъ + 23,835* + 263,293.
(Q
Коэффициенты этЪго трехчлена делим на свободный член. Полу-
Полученные от деления коэффициенты помещены в последнем столбце
таблицы, а частное от второго деления (правая часть таблицы)
равно
263,296*8 + 112,01*+ 231.
Близость чисел, отмеченных звездочками, говорит о том, что
итерацию можно прекратить и считать, что левая часть уравне-
уравнения разлагается на множители
х2 + 0,425* + 0,877 и хг + 23,835* + 263,293,
из которых первый был найден раньше, а второй есть трехчлен (С).
Приравнивая каждый из этих множителей нулю, получим два'
квадратных уравнения:
х% + 0,425* + 0,877 = 0;
*2 + 23,835* + 263,293 = 0,
решая которые, найдем корни х\ 2 = — 0,213 ± 0,912i; *3 4 =
= — 11,92 ± 11,0».
Проверка.
Xi + x2+x3 + x4 = 24,266 вместо 24,26;
*! • *2 • *3 • *4 = 230,9 вместо 231.
Эти результаты можно признать достаточно хорошими.
Задача 2,7 (для самостоятельного решения). Решить уравнение
х3 — 5* + 1 = 0 по способу Ньютона с точностью до 0,001, а потом —
применяя способ Ньютона в модифицированном виде.
Ответ. * = 0,202.
59
Задача 2,8 (для самостоятельного решения). Решить уравне-
уравнение jc4 + 2jc2 — 6* -f 2 = 0, применяя способ линейной интерпо-
интерполяции, а потом тот же способ в модифицированном виде. Точ-
Точность 0,00001.
Ответ. х = 0,38687.
Задача 2,9_(для самостоятельного решения). Решить уравнение
х5 + 5л: +1 = 0 по способу № 4 с точностью до 0,00001.
Ответ. х = — 0,19994.
Задача 2,9а (для самостоятельного решения). Определить с точ-
точностью до 10~3 все корни уравнения
хв + 25,0С*8 + 282.3*4 + 337.5*3 + 338.4*2 + 179,9л: + 7,360 = 0
по способу № 4.
Ответ. xl = — 0,046; х2 = —0,698; хъл = —0,213^0,912i;
хв.б = —ll,92±ll,0H.
Задача 2,10 (для самостоятельного решения). Определить с точ-
точностью до 10~2 корни уравнения
х3 + 6,32лг2 + 27,5* + 31,6 = 0.
Ответ, х = —1,57.
ТРЕТЬЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Решение трансцендентных уравнений
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Графическое решение. Приближенное значение корней урав-
уравнения
/(*) = 0 C,1)
можнб получить, если тщательно вычертить на миллиметровке
кривую у = f(x) и определить абсциссы точек пересечения этой
кривой с осью Ох. Для уточнения корней, найденных графи-
графически, можно воспользоваться способом Ньютона или способом
хорд, которые описаны в первом практическом занятии, а также
указанными там же модификациями этих методов.
Вместо построения кривой у = f(x), которое может быть затруд-
затруднительным, часто полезно представить уравнение f(x) = 0 в виде
или
<?(*) = И*). C,2)
после чего построить кривые
*/ = ?(*) и у = ф(х), C,3)
причем, если удачно представить функцию f(x) в виде разности
<Р (л:) — ф(дг), то построить кривые C,3) будет значительно легче,
чем кривую у = f (x).
Если уравнение. f(x) = 0 заменено уравнением C,2), то реше-
решениями исходного уравнения будут абсциссы точек пересечения
кривых C,3). Приведем пример.
Пусть требуется решить уравнение
cos*.e*—1=0. (А)
Представим его в виде
cos х • е* = 1
или
s cs* e~"*. (В)
Построим кривые у = cos x и у = е~х.
61
Абсциссы точек пересечения этих кривых и будут искомыми
корнями данного уравнения. Очевидно, что построить кривые (В)
значительно проще, чем кривую y = cosx-ex—1 (см. фиг. 3,0).
Фиг. 3,0
Кроме метода Ньютона и метода хорд, которые известны из
предыдущих занятий, укажем еще один распространенный метод
итерации, хотя методы хорд и касательных также являются
■частным случаем итерационных методов.
Фиг. 3.1
2. Метод итерации. После того,, как уравнение f(x) = 0 пере-
переписано в виде <р (х) = t|> (дг), как уже было указано, даже грубое
изображение этих кривых позюлит найти приближенное значение
корней уравнения / (х) = 0. Пусть таким приближенным значением
одного корня будет х = х0. Проведем прямую х = х0. Она встре-
встретит рассматриваемые кривые в двух точках: фиг. 3,1 или фиг. 3,2.
62
Из этих двух точек следует выбрать ту, для которой угловой
коэффициент касательной к кривой в точке х0 имеет меньшую
абсолютную величину. Положим, например, что
На фиг. 3,1 и 3,2 такой является точка Ао на кривой у = <?(х).
В этой точке | <р' (*о) I < I ¥ (*о) I- По найденному значению х = хй
определяем ординату уо — 9 (*о) точки пересечения прямой д; = х0
с кривой у = <? (х). Через точку Ао [х0, ? (дгоI проводим прямую,
pi
[,
' 1
1
7* 1
'! !
1
1 1
1
1 1
1 1
*4 *3
Фиг. 3,2
параллельную оси Ох, до пересечения в точке В1 с кривой у —
= ф (д;). Ордината точки 5Х такая же, как и ордината точки Ао.
Подставляя в уравнение у = ф (х) вместо у значение у^ = <р (д:0)
и решая уравнение
находим значение дг! — второе приближение корня. Найденное xt
является абсциссой точки Bi и, следовательно, абсциссой точки Av
По известной абсциссе точки А1 находим ее ординату ylt которая,
равна значению функции ср (д;) при х = хъ т. е. г/i = f (*i).
Из точки Ах проводим прямую, параллельную оси Ох, до пере-
пересечения в точке В2 с кривой у = ф (дт). Ордината точки В2 такая же,
как и ордината точки лх. Подставляя в уравнение у = ф (д:) вместо у
значение gt = 9 (д^) и решая уравнение
ф (д:) = ср (*!),
находим д;2 — третье приближение корня, которое является одно-
одновременно абсциссой точек В2 и Аг.
63
Дальше поступаем так же. Зная аОсциссу точки А2 из урав-
уравнения у = 9 (дг), заменяя в нем х на х2, находим у2 = у (х2) —
ординату точки Аг. Из точки Аг проводим прямую, параллельную
оси Ох, до пересечения ее в точке В3 с кривой у = ф (я). Точка В3
имеет такую же ординату, как и точка А2. Зная ординату точки В3,
равную уг = 9 (хг), и подставляя это значение вместо у в уравне-
уравнение у — <[> (*), решаем уравнение
Ф (*) = ? (•««)
и определяем абсциссу х3 точки Bs. Значение х3 является четвер-
четвертым приближением искомого корня.
Следующие приближения находим так же.
Если угловые коэффициенты касательных к кривым у = 9 (*)
и у — *]>(х) вблизи точки пересечения имеют один и тот же знак,
то последовательные приближения дг0, хъ хъ ... стремятся к корню
с одной стороны (фиг. 3,1). а если эти угловые коэффициенты
имеют противоположные знаки, то приближения х0, xlt x2 стре-
стремятся к корню, принимая попеременно значения, то меньшие, то
большие корня (фиг. 3,2).
Но предложенный метод, который будем называть первым, не
является единственным. Все выкладки значительно упрощаются,
если заданное уравнение / (jc) = 0 представить в виде
* = ?(*). C,4)
а этого можно достигнуть всегда.
Действительно, если f (х) — 0, то и \f(x) = 0, где X—вели-
X—величина постоянная. Прибавляем л; к обеим частям последнего
уравнения:
л; + X/ (дг) = л;.
Обозначая теперь
x + \f(x) = 9{x), C,5)
получаем уравнение C,4).
Таким образом, показано, что уравнение / (л:) = 0 можно пре-
преобразовать к виду х = <?(х), но параметр X.остался свободным.
О выборе его будет сказано ниже (см. стрбб). После того как
заданное уравнение f {х) = 0 представлено в виде C,4)
х = 9 W.
поступают так: графически или методом проб находят первое при-
приближение корня л; = дгй. Для получения следующего приближе-
приближения в правую часть уравнения C^4) подставляют л;0 и тогда вто-
вторым приближением корня будет
Xi = 9 (■*<>)•
64
Подставляя в правую часть уравнения C,4) хх вместо х. находим
третье приближение хг корня
Таким образом, последовательные приближения получаются по
следующей схеме:
хг = <р (л;!);
C,6)
Определение последовательных приближений по этой схеме будем
называть вторым итерационным методом.
Могут встретиться два случая:
1) последовательность х0, хи х2, ..., хп, ... сходится, т. е.
имеет предел, и тогда этот предел будет корнем уравнения
/W = 0;
2) последовательность л;0, xi, хг, ... хп, ... расходится, пре-
предела не имеет.
Укажем теорему, выражающую условие, при котором итера-
итерационный процесс сходится.
Теорема. Пусть на отрезке [а, Ь] имеется единственный
корень уравнения х= <?(х) и во всех точках этого отрезка про-
производная <р' (х) удовлетворяет неравенству
\9'{х)\<М<\. C,7)
Если при этом выполняется и условие
а<<?(х)<Ь, C,8)
то итерационный процесс сходится, а за нулевое приближение х0
можно взять любое число из отрезка [а, Ь\.
Условие C,8) означает, что все приближения *0, хи хг,... ,
хп, ..., вычисленные по схеме C,6), находятся тоже на отрезке
[а, Ь]. Сходимость итерационного процесса будет тем лучше, чем
меньше | <р' (л:) |.
Чтобы закончить пояснения, относящиеся к теории итерацион-
итерационного метода, укажем, как определить точность вычисленных зна-
значений корня. Если а — точное значение корня уравнения х = <р (х),
а число М определяется из соотношения C,7), то справедливо
следующее соотношение:
а — х,
М ■ C,9)
1— м
Хп хп—1
3 И. А. Каплан 65
Из этого неравенства следует, что если поставлено условие,
чтобы приближение корня хп отличалось от его точного значения
меньше на заданное число е, то приближения х0, хъ хъ ... надо
вычислять до тех пор, пока правая часть неравенства C,9) не
станет меньше этого числа е или равной ему, т. е.
М ' -хп_,\<г C,10)
ИЛИ
м
C,11)
(Об условиях сходимости итерационных процессов и доказательство
относящихся сюда теорем см.: Б. П. Демидович и И. А. Ма-
Марон. Основы вычислительной математики, гл. IV. Физматгиз, 1960).
Заметим, что уравнение f {х) = 0 можно различными способами
привести к виду х = <р (дг). Из этих видов нужно выбрать тот,
в котором выполняется условие C,7) указанной теоремы.
Что касается числа X в формуле C,5), то его следует подо-
подобрать так, чтобы значение производной в левой части этой фор-
формулы было по абсолютной величине меньше единицы, т. е. чтобы
|
Из неравенства
|1 + Х
следует, что X должно удовлетворять неравенству
Такой выбор X гарантирует сходимость итерационного процесса
При решении задач этого практического занятия рекомендуется
пользоваться такими таблицами:
1. Б. И. С era л и К. А. Семендяев. Пятизначные математические
таблицы.
2. Л. Дж. Ко мри. Шестизначные математические таблицы Чемберса.
Вычисления следует вести при помощи настольной клавишной
машины или арифмометра, а также в нужных случаях пользо-
пользоваться логарифмической линейкой.
Геометрическая интерпретация итерационного процесса, при-
применяемого к уравнению х = <?(х) с учетом использования указан-
указанной теоремы, выглядит так, как показано на фиг. 3,3, где
изображен сходящийся итерационный процесс. Здесь кривая пере-
пересекает биссектрису в точке с абсциссой а и при х > а лежит под
биссектрисой, а у'(х) удовлетворяет условию 0<<?'(х)< 1. Ите-
Итерационный процесс сходится, а последовательные приближения
монотонно убывают.
66
На фиг. 3,4 производная (р' (х) < О» но по абсолютной вели-
величине меньше единицы: |ср'(дг)|<1. Итерационный процесс схо-
сходится, но приближения колеблются около точного значения корня.
На фиг. 3,5 показан расходящийся итерационный процесс.
Здесь щ'(д;)> 1. Кривая пересекает биссектрису у = х в точке а
и при х > а лежит над биссектрисой.
На фиг. 3,6 также изображен расходящийся процесс: |<р' (л:)| > 1.
На чертеже видно, как последовательные «приближения» уда-
удаляются от точного значения корня.
Теперь приступим к решению задач.
Задача 3,1. Решить уравнение
Решение. Перепишем уравнение в виде C,2)
и определим графически приближенное значение отрицательного
корня (положительного корня уравнение не имеет, так как при^
х>0ек>х2). Приближенное значение отрицательного корня'
примем
_ 1
Решим задачу сначала тем итерационным методом, который мы
назвали первым, а потом — вторым.
Решение первым методом. Прямая л: = —0,5 пересекает кри-
кривые 6 (дг) = х2 и <р (л:) — ех в двух точках. Нам следует выбрать
ту из них, в которой угловой коэффициент касательной меньший
3*
67
О У а" х0 X, хг х3
Фир. 3,5
У,
\
/
j_L
\
<^Ь
Фиг. 3,6
Хо
68
по абсолютной величине, т. е. точку, в которой абсолютное зна-
значение производной при л; = —0,5 является меньшим. У нас
ф (х) = х2; ф' {х) = 2х; ф' (-0,5) = 2 . (—0,5) = -1;
| ф' (д) | = | ф' @,5) | = 1;
<? (х) = ех; <?' (х) = е*; <?' (—0,5) = в-5 = 0,60653;
| «р' @,5) | = 0,60653.
Значит,
и точку следует выбрать на кривой ср (дг) = е*. Так как угловые
коэффициенты касательных, проведенных в точку пересечения
кривых ср (х) = ех и ср (д) = хг, у
противоположны по знаку, то
надо ожидать, что последова-
последовательные приближения будут
стремиться к корню, принимая
значения то больше его, то
меньше.
Чтобы найти второе прибли-
приближение, необходимо определить \ /
х из уравнения
0
т. е. из уравнения к задаче Зд
х2 = (*■> = е-0-5 = 0,60653.
Отсюда второе приближение
xx = — У 0,60653 = —0,77880.
(перед радикалом взят знак минус, так как корень уравнения
имеет только отрицательное значение).
Чтобы найти третье приближение корня, надо решить уравнение
т. е.
х* =
е-о.7788 = 0,45895;
х2 = — ]Л),45895 = —0,67746.
Четвертое приближение корня получим из уравнения
Ф (х) = <р (х2),
г* = g* = е-о.67746 = 0,50791;
т. е.
3 = — ]Л),5Л91 = —0,71268.
Пятое приближение кория вычислим, решив уравнение
ф (X) =
т. е. уравнение
х* = ех'= е-о.71268 = 0,49033;
дг4 = — j/0,49033 = —0,70023.
Шестое приближение корня ищем из уравнения
т. е. уравнения
хг = ех, = ^-0,70023 = 0,49647;
х% = —1/0,49647 = —0,70460.
Для определения седьмого приближения решаем уравнение
Ф (*) = ? (**)•
т. е.
л? = g* = е-о.7О4бо = 0,49431;
л;в - —1/0,49431 = —0,70307.
Решив уравнение
т. е.
л;* = е^. = е-о.7озо7 _ 0,49506,
найдем восьмое приближение корня
х7 = — 1/0,49506 = —0,70365.
Для девятого приближения
х* = <*' = е-о.70365 = 0,49477;
л;8 = —1/0,49477 = —0,70339.
Десятое приближение получим из уравнения
ф (л;) = <р (л;8),
т. е.
л;4 = е-0-70339 = 0,49490;
л:9 = —1/0,49490 = —0,70349.
Одиннадцатое приближение вычислим, решив уравнение
ф (л:) =
70
т. е.
х* = е*9 = е-о.70349 = 0,49485;
х10 = — У 0,49485 = —0,70346.
Двенадцатое приближение даст
ха = — j/0,49487 = —0,70347.
Таким образом, с точностью до 0,00001 искомый корень
х = —0,70346.
Из проведенного расчета видно, что итерационный процесс шел
очень медленно (сходимость была плохой). Как мы и ожидали,
последовательные приближения колебались около корня. Они были
то больше, то меньше. Составим таблицу приближений:
В этой таблице справа от зна-
значения приближений корня стоят
разности между этими значе-
значениями. Знаки разностей чере-
чередуются (+, —, +, —, ...), а
сами они по абсолютной величи-
величине убывают. Медленная сходи-
сходимость процесса объясняется
тем, что нулевое приближение
х0 было определено слишком
грубо. Если бы мы определили
интервал, на котором находится
корень, и подошли бы более
критично к выбору нулевого
приближения, то процесс сходи-
сходимости ускорился бы.
Чтобы убедиться в этом, най-
найдем интервал, на котором нахо-
находится корень. Для этого нужно
определить так называемую «вил-
«вилку», т. е. найти такие два значе-
значения х, при которых f(x) имеет
противоположные знаки. Эти
два значения х и определят ис-
искомый интервал, причем его надо сделать как можно меньшим
и следить за тем, чтобы на нем был единственный корень урав-
уравнения. В нашем случае имеется единственный отрицательный
корень. Методом проб определим «вилку». У нас f(x) = ex — х2.
Начнем со значения х = —0,6.
/(_0,6) = 0,54881 — 0,36 = 0,18881 > 0;
/(-0,7) = 0,49659 — 0,49 = 0,00659 > 0;
/ (—0,8) = 0,44933 — 0,64 = — 0,19067 < 0.
№ при-
приближений
0
1
2
3
4
5
6
7
8
9
10
11
Приближенное значение
корня
—0,50000
—0,78880
—0,67746
—0,71268
—0,70023
—0.70460
—0,70307
—0.70365
—0,70339
—0,70349
—0,70346
—0.70347
—0.28880
+0.11134
—0.03522
+0.01245
—0.00437
+0,00153
—0,00058
+0.00026
—0.00010
+0.00003
—0,00001
71
Таким образом, на концах интервала (—0,8;—0,7) функция f(x)
имеет различные знаки, причем, поскольку \f(—0,7)|<|/(—0,8)|,
то корень находится ближе к —0,7, чем к —0,8.
Попытаемся сузить интервал. Праный его конец оставим без
изменения, левый сдвинем направо
/ (—0,75) = 0,49237 — 0,49 < 0,
а поскольку /(—0,7) > 0, то корень находится на интервале
(-0,75; -0,7).
Попытаемся сузить и этот интервал, сдвигая его левый конец
вправо
/(—0,725) = 0,48432 — 0,52562 = —0,04130 < 0.
Так как /(—0,725) < 0, а /(—0,7) >0, то корень находится на
интервале (—0,725; —0,7). В качестве нулевого приближения
можно взять любой из концов этого интервала, а также любую
точку внутри его.
Мы возьмем за х0 правый конец интервала, т. е. х0 = —0,7.
Следующее второе приближение найдем из уравнения
У нас <р (х) — л:2, <р (х) = е*. Поэтому надо определить х из урав-
уравнения
*г = g*. в g-o.7 = 0,49659; X! = — 0,70469.
Третье приближение найдем из уравнения
т. е. из уравнения
х* = е*. = е-°-7от = 0,49494;
х2 = — К0.49494 = —0,70352.
Четвертое приближение
ф {х) = ср (х2);
х2 = g-o.7O352 = 0,49484;
х3 = — 1/0,49484 = —0,70345.
Этот корень, найденный в четвертом приближении, отличается от
полученного раньше в двенадцатом приближении только на 0,00002.
Пятое приближение
Ф (*) = «Р (*>)',
х* = ег> = е-о.70345 = 0,49488.
Таким образом, на пятом приближении мы имеем теперь то,
что раньше на двенадцатом. Отсюда видно, насколько важно
выбрать удачно нулевое приближение.
Всю предыдущую работу мы выполнили исключительно в мето-
методических целях: 1) на большом числе упражнений читатель
освоился с решением уравнения вида $(х)=*?(х) и 2) было по-
показано, что выбор нулевого приближения не может быть про-
произвольным, а его удачный выбор скорее ведет к цели.
Теперь для решения того же уравнения используем метод,
который мы назвали вторым: преобразуем заданное уравнение к
виду C,4)
и применим схему C,6) для его решения..
Из уравнения е* — х2 — 0 следует, что хг = ех, а х — — J/V
(перед радикалом удержан знак минус потому, что корень, как
мы знаем, отрицателен).
В виде C,4) уравнение запишется так:
д: = —е7.
Теперь проверим, выполнено ли условие C,7), т. е. выполняется
ли во всех точках интервала (—0,725; —0,7) неравенство
С этого всегда надо начинать решение уравнения вида C,4). У нас
|ср' (—0,725) | = 0,34727; | <?' (—0,7) | = 0,35230,
число М в формуле C,7) возьмем равным 0,36. Так как | <р' (х) | < 1,
то процесс будет сходиться. Мы хотим вычислить корень с точ-
точностью 0,00001, т. е. е = 0,00001. Надо остановиться на каком-то
приближении. Для этого определим по формуле C,11), какой по
абсолютной величине должна быть разность между двумя после-
последовательными приближениями, чтобы считать, что требуемая точ-
точность достигнута. Должно выполняться на основании C,11) не-
неравенство
I у t У I <^ ' ,
I лп лп-11 ^ до
Так как М = 0,36; е = 0,00001, то
0,00001 -A-0,36)
\Хп— *„_!
Таким образом, мы будем считать, что требуемая точность
достигнута, если абсолютная величина разности двух последова-
последовательных приближений не больше 0,00002.
73
За нулевое приближение принимаем по-прежнему х0 — —0,7.
Так как у нас у(х) = — е2 , то, применяя схему C,6) к уравнению
X
—0.7
—0.70460
—0,70307
—0.70360
—0,70342
—0,70348
—0,70346
X
~2
—О.ЗЬ
—0.35230
—0.35154
—0.35180
—0,35171
—0.35174
-еТ
—0.70460
—0,70307
—0,70360
—0,70342
—0,70348
—0.70346
х = —0,70346
и помещая вычисления в таб-
таблицу, получаем
Абсолютная величина разности
между хА — шестым приближен-
приближенным и хв — седьмым прибли-
приближенным равна 0,00002. Поэтому
на основании сделанного по фор-
формуле C,11) вычисления можно
считать, что требуемая точность
достигнута и за искомый ко-
корень принять любое из этих чи-
чисел, т. е.
или х — —0,70348.
От найденного первым методом х = —0,70347 эти значения отли-
отличаются только на 0,00001.
Читатель, по-видимому, заметил, что решение этим методом
оказалось проще, поскольку вычисления велись без извлечения
корня, как при решении первым методом, и все свелось только к вы-
вычислению степеней числа е. Быстрая сходимость здесь объяснялась
тем, что число М было ближе к нулю, чем к единице. На этом
примере мы подробно разобрали первый и второй методы. Сделаем
такое указание. Первый метод следует применять только тогда,
когда преобразование уравнения / (х) = 0 к виду х = ср (х) пред-
представляет большие трудности. Во всех других случаях надо
стремиться к тбму, чтобы заданное уравнение было преобразовано
к виду х = ср (х). Такое преобразование часто можно осуществить,
как уже указывалось, не единственным способом, причем выбрать
тот из видов, в котором число М было бы возможно меньшим,
так как при этом последовательность приближений будет быстрее
сходиться к корню заданного уравнения.
Повторим еще раз, что решение необходимо начинать с про-
проверки выполнения неравенства C,7)
во всех точках того интервала, на котором находится корень.
Задача 3,2. Решить уравнение
f (х) - cosх— х -f 4 = 0
с точностью до 0,00001.
74
Решение. Преобразуем уравнение к виду C,4) х — <р (х).
Получится
х = cos х + 4.
Значит,
<Р (*) = cos х + 4 (А)
Теперь, чтобы легче было графически определить приближенное
значение корня (см. рисунок), запишем уравнение в виде: cos x =
— х — 4. Абсцисса точки пересечения кривых приближенно равна 3.
Проверим, что корень находится на интервале C, тс):
/ C) = cos 3 — 3 + 4 = —0,98999 + 1 = 0,01001 > 0;
f(iz) = cos тс — тс + 4 = — 1 — 3,14159 + 4 = — 0,14159 < 0.
if
К задаче 3,2
Таким образом, «вилка» найдена. За нулевое приближение
корня надо взять число 3 — левый конец интервала, так как на
этом конце |/C)|< |/(тс)|. Теперь установим, будет ли сходиться
итерационный процесс, т. е. выполняется ли неравенство C,7)
во всех точках интервала C, тс). Из (А) следует, что
<Р (х) — cos х + 4; <?' (х) = —sin x;
|tp'(*)|=sin;t; |cp'C)|= sin 3 = 0,14122;
|ср'(тс)| = sin тс =0.
Во всех точках интервала C, тс) 19' (х) | < 1 и тем самым нера-
неравенство C,7) выполняется, процесс будет сходящимся, причем в
75
качестве числа М необходимо взять 0,15, так как и sin3 и sin u
меньше, чем 0,15. Итак, М = 0,15. Теперь определим, какой должна
быть абсолютная величина разности между двумя последователь-
последовательными приближениями хп и xn_lt чтобы обеспечить требуемую
точность в 0,00001.
У нас е = 0,00001, М = 0,15, а потому по формуле C,11)
Iv r \<r e('-^> - 0.00001-0-ОД5) _ 0,00001 . 0,85 _
\х„— *n_J < —355— оЛЗ Oil -
!*„-*„_! |< 0,00006. (А)
Таким образом, если между двумя последовательными при-
приближениями разность не будет превышать 0,00006, то итерацион-
итерационный процесс надо остановить и считать, что требуемая точность
достигнута.
После этих выкладок приступаем к решению задачи, поль-
пользуясь схемой C,6). У нас нулевое приближение
х0 — 3.
Применим схему C,6);
Xl=*<p (х0) = cos 3 + 4 « —0,98999 + 4 = 3,01001;
хг = ср (Xi) = cos 3,01001 + 4 = —0,99135 + 4 = 3,00865;
дз = ср (х2) = cos 3,00865 + 4 = —0,99117 -f 4 = 3,00883;
Ki = <р (л:3) = cos 3,00883 + 4 = —0,99120 + 4 = 3,00880.
На этом можно остановиться, так как
|*4-*з К 0,00006,
т. е. требование (А) выполнено.
Такая быстрая сходимость обусловлена здесь малостью числа
М и удачным выбором нулевого приближения.
Итак, искомый корень
х = 3,00880.
Задача 3,3. Решить уравнение
2х — 31п* — 3 = 0
с точностью до 0,00001.
Решение. Преобразуем прежде всего заданное уравнение к
такому виду, который позволит легче графически установить при-
приближенное значение корня. Запишем уравнение в виде
76
Построим кривые у = \их и у = j х—1 (см. рисунок). Из чер-
чертежа видно, что имеется два положительных корня. Определим
интервалы, в которых они содержатся.
Меньший корень *A) находится на интервале @,5; 0,6). Дей-
Действительно,
/@,5) =2 -0,5 —31п0,5 —3 = 1—3 • (—0,69315) — 3 =
= 0,07945 > 0;
f @,6) = 2 -0,6 —3 In 0,6 —3 = 1,2 —3 •(—0,51083) —3 =
= —0,26751 < 0.
0
У
f
1
1
1
гУ /
К задаче 3,3
Таким образом, первый корень находится на интервале @,5;
0,6), причем ближе к левому его концу, так как |/@,5)| < |/@,6)|.
Поэтому за нулевое приближение меньшего корня следует принять
*»ц-0.5.
Теперь преобразуем заданное уравнение к виду х = <? (х):
л: = 0,5C In л:+ 3). (А)
Вслед за этим определим, будет ли сходящимся итерационный
процесс. Для этого проверим выполнение для f' (x) неравенства
C,7): |<р'|(*I<1 во всех точках интервала @,5; 0,6). У нас
Очевидно, что на интервале @,5; 0,6) изоляции корня ?'(*)
7?
и, значит, условие C,7) не выполнено. Поэтому представим урав-
уравнение в другом виде. Из заданного уравнения
2х — 31их — 3 = 0
следует, что
Теперь уже
In х — -j х — 1,
(В)
2 ~*-i
-> з
' @,5)
- 4
Т*@.6) - |
Т * °<51342 " °'34228:
= |е-0'6 . 1 . 0,54881 = 0,36587.
Таким образом, на интервале @,5; 0,6) условие | «р' (*) | < 1
выполнено и итерационный процесс будет сходящимся. Возьмем
М =0,37. У нас е = 0,00001. Определим по формуле C,11), какой
должна быть разность между двумя последовательными приближе-
приближениями, чтобы мы имели право считать, что заданная точность до-
достигнута.
I _ I ^ *0—М) _ 0.00001 • A — 0,37) _
0.00001 • 0.63 _
0,37 :
: 0,00002.
Если абсолютная величина этой разности будет меньше или
равна 0,00002, то процесс итерации следует прекратить и считать,
что заданная точность достигнута.
За нулевое приближение меньшего корня возьмем, как мы ус-
условились, xq^ = 0,5, Применим итерационную схему C,6) к урав-
уравнению (В).
Вычисления удобно вести с помощью такой таблицы:
X
0.5
0.51342
0.51803
0.51963
0,52018
0,52037
0,52044
0,52046
2
их
0.33333
0.34228
0.34536
0.34642
0.34679
0.34692
0.34696
0,34698
т—
—0,66667
—0,65772
—0.65464
—0.65358
—0,65321
—0,65308
—0.65304
—0,65302
.*-
0,51342
0.51803
0.51963
0,52018
0 52037
0.52044
0,52046
0.52047
78
На этом процесс итерации можно остановить и считать, что
*<i> = 0,52047.
Приступим к определению большего положительного корня. Прежде
всего, определим интервал, в котором он находится. Из чертежа
к этой задаче видно, что второй корень *B>^3.
Рассмотрим интервал C,2; 3,3). У нас
f C,2) = 2 • 3,2 — 3 In 3,2 — 3 = 6,4 — 3,48549 — 3 = —0,08549 < 0;
/ C,3) = 2 • 3,3 — 3 In 3,3 — 3 = 6,6 — 3,58177 — 3 = 0,01823 > 0.
Корень ближе к правому концу интервала его изоляции, так как
|/C,3)|< |/C,2)|, поэтому за нулевое приближение большего кор-
корня *<2> возьмем х{о] = 3,3.
Исследуем теперь, будет ли сходящимся процесс, если поль-
пользоваться уравнением (А):
л: = 0,5C In *+3).
Здесь
?' C,2) = i| = 0,47; <р' C,3) = ^ = 0,45.
Возьмем М = 0,48. Таким образом, итерационный процесс будет
сходящимся.
Теперь определим, какой должна быть абсолютная величина
разности между двумя последовательными приближениями, чтобы
считать достигнутой заданную точность. У нас М = 0,48; е =
= 0,00001. По формуле C,11) должно быть
. . ^ е A — М) 0.00001 • A — 0,48)
\лп лп-1\^ м 0.48 ~~
0.00001-0,52 _
Как только разность между двумя последовательными приближе-
приближениями станет не больше 0,00001, мы процесс остановим. Все вы-
вычисления поместим в таблицу. Итак,, решается уравнение
х? = 3,3.
7?
X
3,3
3,29088
3,28724
8,28508
3,28408
3,28364
3,28342
3.28335
3.28329
3,28326
3.28324
3.28324
In x
1.19392
1.19116
1.19005
.18939
,18909
1,18895
1,18889
1,18886
1.18884
.18883
1.18883
1,18883
31n*
3.58176
3,57448
3,57015
3.56817
3,56727
3.56685
3.56670
3.56658
3.56652
3.56649
3,56649
3.56649
31n x + 3
6.58176
6,57448
6,57015
6,56817
6,56727
6,56685
6,56670
6,56658
6.56652
6,56649
6,56649
6.56649
0.5C1n;e4-3)
3.29088
3,28724
3,28508
3,28408
3,28364
3,28342
3.28335
3,28329
3,28326
3,28324
3.28324
3.28324
Больший корень
= 3,28324.
И здесь итерационный процесс шел очень медленно, так как М
было достаточно велико.
Задача 3,4. Решить уравнение
Точность 0,0001.
— 2 = 0.
■ж
К задаче 3,4
решение. Из решения предыдущих задач читатель уяснил
общую схему, которой мы придерживались. Она состоит в сле-
следующем:
1. Заданное уравнение следует привести к виду
х = ч> (х).
2. Чтобы графически отделить корень, функцию / {х) надо пред-
представить в виде
80
Так можно определить приближенное значение корня. Отделить
корень следует методом проб.
3. Необходимо проверить, удовлетворяет ли функция <р (х)
из п. 1 условию C,7)
во всех точках интервала изоляции корня.
4. Определить число М для использования неравенства C,11),
т. е. для того чтобы узнать, при какой абсолютной величине раз-
разности между двумя последовательными приближениями будет до-
достигнута требуемая точность.
5. Решение задачи провести по схеме C,6).
Придерживаясь этой схемы, решим предложенное уравнение.
1. Перепишем уравнение в виде
х2 = 2 — sin2 х = 1 + cos2 x,
откуда
х = ±1^1 + cos2 x. (А)
2. Для того чтобы упростить построение графика функции у =
= f(x), перепишем уравнение
sin2* = 2 — хг.
Из чертежа видно, что корни расположены симметрично относи-
относительно начала координат. Отделение корня дает
/ A) = р + sin21 — 2=1 + 0,70728 — 2 = — 0,29272 < 0;
f(l,l)= 1,1" + sin2 1,1 — 2= 1,21 +0,79388 —2 = 0,00388 >0.
Значение корня будет ближе к 1,1, чем к 1, так как
1/A,1)К I/O)!.
Таким образом, интервал изоляции корня определен.
3. Проверка условия C,7). Из (А) следует, что
, , . . . sin x cos x
I? (*) I = i/.-rrfj^
Вычислим 19'AI и I?'A,1) |, причем большая точность при этом
не требуется:
it'0I= 0.40; |т'A,1) 1 = 0,38.
Процесс будет сходиться, так как
1Ч>'(*)|<1
во всех точках интервала изоляции корня.
81
4. Число М возьмем равным 0,41. Теперь определим по фор-
формуле C,11), какой должна быть абсолютная величина разности
между двумя последовательными приближениями, чтобы считать
требуемую точность достигнутой.
\Xn~Xn-
п-г\
i 0,0001 . A — 0.41) _ 0.0001 • 0,59 л ллт
Тй = 041 511 ~и.иии1-
Таким образом, когда разность между двумя последовательными
приближениями будет равна 0,0001, итерационный процесс следует
остановить.
5. Воспользуемся схемой C,6) для вычисления корня уравнения.
Исходное уравнение имеет вид
Все вычисления поместим в таблицу:
X
1.1
1.09806
1,00878
1.09851
1,09861
COSX
0.45360
0.45532
0.45468
0.45492
cos2*
0.20575
0.20732
0.20673
0.20695
l + cos**
1,20575
1.20732
1,20673
1.20695
У 1 + cos* x
1,09806
1,09878
1.09851
1.09861
Округляя до четырех десятичных знаков, получаем два соседних
приближения
х3= 1,0985; *4= 1,0986.
Быстрота сходимости объясняется здесь удачным выбором нулевого
приближения, сравнительно небольшим значением числа М и не-
небольшой заданной точностью. Итак, уравнение имеет два решения
лгA) = —1,0985; х<2> = 1,0985.
ния
Задача 3,5. Найти наименьший положительный корень уравне-
уравнеtgx — х = 0
с точностью до 0,0001.
Решение. 1) Представим уравнение в виде
В нашем случае оно будет таким:
X = tg X.
С2
4
in
CO
83
2) Построим графики функций у — х и у = tg к (см. чертеж
к этой задаче). Легко усмотреть, что за нулевое приближение можно
принять xo = -jn- Таким образом корень находится на интервале
3) Проверяем выполнение условия C,7):
<р (*) = tg х-, ?' (х) = sec2 х.
Внутри интервала изоляции корня Ы, -j^n ?'(x)\ > 1, поэтому ус-
условие C,7) нарушено. Непосредственно видно, что если бы мы
вели решение по уравнению
и взяли х0 — -к it, то уже второе приближение не могло бы быть
найдено. Действительно,
_ з
Поэтому уравнение перепишем в другом виде, а именно
х = arctg х + it; xo = jtz = 4,71237.
Вычисления помещаем в таблицу. Следует иметь в виду, что к
значениям arctg*, которые находятся из таблиц (например, Чем-
берса) следует прибавлять число it, так как прямая у = х пересе-
пересекает ту ветвь кривой у — arc tg x, которая удовлетворяет условию
£ < arctg х < -5- г,
т. е. фактически
X
4.71237
4,50328
4,49386
4,49344
4,49341
х = arct
arcfg x
1.36169
1,35227
1.35185
1,35182
1,35182
gx -fir.
л
3,14159
3,14159
3,14159
3.14159
3.14159
arc f g x + я
4.50328
4,48386
4,49344
4.49341
4,49341
Таким образом, искомым корнем с четырьмя верными знаками яв-
является
х = 4,49341.
Ниже помещены задачи для самостоятельного решения.
64
Задача 3,6. Методом итерации найти корень уравнения
х7 — 2*" — 10л? + 1 = 0
с пятью верными десятичными знаками.
Указание. Уравнение переписать в виде
Ответ. х = 0,31529.
Задача 3,7. Вычислить с четырьмя верными десятичными зна-
знаками действительный корень уравнения
Ответ. х = — 0,9338.
Задача 3,8. Определить с шестью верными знаками корень урав-
уравнения
Зх — cosx— 1 = 0.
Ответ. х = 0,607104.
Задача 3,9. Найти корень уравнения
2х—
с точностью до 0,0001.
Ответ. х = 3,7893.
ЧЕТВЕРТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Основные определения теории матриц
I. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТРИЦ
1. Матрица и ее элементы
Матрицей называется система элементов (в частном случае
чисел), расположенных в определенном порядке и образующих
таблицу. Если в этой таблице т строк и п столбцов, а ее эле-
элементы обозначены через ац, где i — номер строки, а / — номер
столбца, на пересечении которых находится этот элемент, то
матрица записывается в следующем виде:
А =
а21
а
13
«22
D,1)
Короче эта матрица может быть записана так:
Л = [ац]*, (t= 1, 2, 3 т; /= 1, 2, 3 п) D,2)
Каждый элемент матрицы называется также ее компонентой.
Матрица D,1) имеет размер т х п.
Если число строк матрицы т не равно числу ее столбцов п,
то матрица называется прямоугольной.
2. Различные виды матриц
Матрица-столбец. Если в матрице только цдин столбец, т. е.
если п = 1, то она называется матрицей-столбцом и имеет такой
вид:
А =
D,3)
Матрица-столбец называется также вектором-столбцом.
* Матрицы в дальнейшем обозначаются знаком [ ], а определители квад-
квадратных матриц — знаком | |.
86
Матрица-строка. Если в матрице только одна строка,
называется матрицей-строкой и имеет такой вид:
А = [аи ап а13 . . • а1п].
Матрица-строка называется также вектором-строкой.
Примеры.
Матрица 1
2
3
5
7
то она
D,4)
есть матрица-столбец,
вектор-столбец.
Матрица
Ее размер 5x1. Иначе, это пятимерный
А = [2 0 4 3 7 2]
есть матрица-строка. Ее размер 1 х 6. Иначе, это шестимерный
вектор-строка. Когда это не может вызвать недоразумений, вектор-
столбец и вектор-строку мы будем называть просто вектором.
Транспонированная матрица. Если в матрице А поменять местами
строки и столбцы, то получится новая матрица, которая по сравне-
сравнению с матрицей А называется транспонированной. Транспониро-
Транспонированную матрицу будем обозначать через А'.
Примеры.
1) Если матрица
аг1
а31
агз a2i I,
то транспонированная матрица запишется так:
аи ап а31
г13 а23
hi «24
Матрица А имеет размер 3x4,
А' — размер 4x3.
[2 1 3 5]
2) А-[г 1 2 4J*
Транспонированная матрица
йзз
а транспонированная матрица
А' =
2
1
3
5
87
Транспонирование матрицы-столбца дает матрицу-строку и на-
наоборот.
Квадратная матрица. Если в матрице столько же строк, сколько
и столбцов, т. е. m = п, то матрица называется квадратной.
Чп
D,5)
Матрица D,5) имеет размер п х п. Однако в случае квадратной
матрицы вместо термина размер употребляется термин порядок.
Матрица D,5) — матрица n-го порядка. В квадратной матрице об
элементах ап, а22, аяз, ... , апп говорят, что они образуют главную
диагональ, или что они стоят на главной диагонали. Об элемен-
элементах, стоящих на линиях, параллельных главной диагонали, гово-
говорят, что они образуют побочную диагональ. В матрице порядка п
имеется п—1 побочная диагональ, расположенная выше главной,
ил— 1 побочная диагональ, расположенная ниже ее.
Пример.
Матрица
1
3
1
5
4
2
4
—7
—2
0
2
2
5
— 1
0
1
— квадратная матрица четвертого порядка. В ней число строк т=
= 4 и число столбцов п = 4.
Нулевая матрица. Матрица, все элементы которой равны нулю,
называется нулевой и обозначается символом 0.
т строк D,6)
0
0
0
0
0
0
0
0
0
0
0
0
о . •.
о .. •
0 • • •
0 •'• •
о
0
о !
0_
п столбцов
Диагональная матрица. Квадратная матрица, у которой все
элементы, расположенные вне главной диагонали, равны нулю,
88
называется диагональной.
А =
ах
0
0
Эта
i 0
а22
0
матрица
0
0 . . .
а»---
и
0
0
0
имеет следующий вид:
D,7)
ООО
Таким образом, в диагональной матрице все элементы с неравными
индексами равны нулю.
Скалярная матрица. Диагональная матрица, все элементы кото-
которой, стоящие на главной диагонали, равны между собой, назы-
называется скалярной матрицей. Скалярная матрица имеет такой вид:
5 =
~аа 0 0 • • • О
О аи 0 ••• О
О О ап • • • О
0 0 0
а.
D,8)
Единичная матрица. Диагональная матрица, у которой все эле-
элементы, стоящие на главной диагонали, равны 1, называется еди-
единичной. Единичная матрица обозначается символом Е и имеет
такой вид:
0 0 0
0 1
0 0 1
0 0 0
0 0
0
1
о"
о
о
о
0 0 0 0
1
D,9)
Индекс п в символе Е показывает порядок единичной матрицы.
В матричном исчислении единичная матрица играет роль, в извест-
известной мере аналогичную той, которую в арифметике играет единица.
Верхняя треугольная матрица. Квадратная матрица, в которой
все элементы, расположенные ниже главной диагонали, равны нулю,
называется верхней треугольной матрицей. Она имеет вид
ап а и а13 •
О О ам .
0 0 0-
D,10)
89
Нижняя треугольная матрица. Квадратная матрица, в которой
все элементы, расположенные выше главной диагонали, равны нулю,
называется нижней треугольной матрицей. Эта матрица имеет такой
вид:
~ап О 0 0 ... О
ап ап О .0. . • • 0
А =
«32 «33 0
о
«пЗ ап4
D,П)
Симметричная матрица. Симметричной матрицей называется
квадратная матрица, в которой все элементы, расположенные сим-
симметрично относительно главной диагонали, равны между собой.
Для симметричной матрицы имеет место равенство
CLlj = пц.
Пример квадратной симметричной матрицы:
- 4 21
4 3 6. D,12)
2 6 5J
Блочная матрица. Если в матрице провести горизонтальные и
вертикальные «перегородки», то матрица окажете^ разбитой на
прямоугольные или квадратные клетки, или блоки. Такая матрица
называется блочной. Вот пример такой матрицы:
A =
«П «12 «13 | «14 «18 «16
«21
«31
«41
«22
«32
«42
«52
«23
«33
«43
«83
«24,
«34
«44
«2»
«3»
a4S
«ss
«26
«36
«46
«ее
Элементы в каждом блоке образуют следующие матрицы:
Г«п «12 «is га а а Л
Ап = а21 а22 агз ; А21 = " 4г 43 ;
л n n L«si «»2 «S3J
I «31 «32 «33 J
Г«14
*12 = «24
«23
*32 «33J
Й1В Й16
«28 «£6
L«34 «38 «36.
д _Г«44 «45 «4в1
22 [а5, аьь аЪ6\'
90
Матрицу А можно представить в виде матрицы, элементами кото-
которой являются матрицы Ац.
[Ац
A2i
3. Определитель матрицы. Ранг матрицы
Определителем квадратной матрицы называется определитель,
составленный из элементов матрицы, расположенных так же, как
и в матрице. Определитель матрицы А обозначается символом | А \
или D(A).
Если определитель | А | матрицы не равен нулю, то матрица на-
называется неособенной (иначе, невырожденной). Если же определитель
| А | матрицы равен нулю, то матрица называется особенной (иначе,
вырожденной или сингулярной).
Ранг матрицы. В прямоугольной матрице можно вычеркнуть
несколько строк и несколько столбцов так, чтобы элементы, кото-
которые остались невычеркнутыми, образовали квадратную матрицу
порядка k. Определитель такой матрицы называется минором дан-
данной матрицы. Если, например (стр. 92) взять матрицу размером
3 х 4, то вычеркиванием одного какого-либо столбца можно полу-
получить четыре квадратных матрицы третьего порядка, вычеркиванием
двух столбцов и одной строки можно получить 18 матриц второго
порядка, а вычеркиванием трех столбцов и двух строк можно полу-
получить 12 матриц первого порядка.
Число матриц порядка к (k < min (s, r)), которое можно получить
из матрицы размером s x г, подсчитывается по формуле
где С* и С* есть соответственно число сочетаний из s элементов
по & в каждом и из г элементов по & в каждом, причем число
сочетаний из п элементов по т вычисляется по формуле
С" = т\{п~т)\ (" > т>-
Поскольку в указанной выше матрице s = 3, г = 4, число мино-
миноров порядка k — 3
„ ^з гз 3) 4! .
П = Сз • U = з!C-3)| ' 31D-3)! = 4
(надо учесть, что принимается 0! = 1).
Число миноров порядка k = 2
„ _ о2 ri _ 31 41 о о _ io
П - Сз • Ь4 - 21 C — 2I ' 21D-2)! ~ б'° ~ 1б>
Число миноров порядка k = 1
ri ni 3! 4! олю
" = Сз • С4 = 1[C_1)| • 1,D-1)! = 3 • 4 = 12.
91
Рассмотрим определители всех таких квадратных матриц.
Наибольший порядок г минора матрицы, не равного нулю, на~
зывается рангом матрицы. Так, если в матрице размером 3x4
определители всех матриц третьего порядка равны нулю, а хотя
бы один из определителей матриц второго порядка в этой таб-
таблице не равен нулю, то ранг заданной матрицы г равен двум
(г = 2).
Таким образом, чтобы определить ранг матрицы, надо из ее
элементов составить всевозможные квадратные матрицы вычерки-
вычеркиванием строк и столбцов и найти определители этих матриц. Ранг
заданной матрицы равен наивысшему порядку того из этих опре-
определителей, который не равен нулю.
Ранг нулевой матрицы равен нулю. Ранг диагональной квадратной
матрицы равен ее порядку, конечно, при условии, что ни один
из ее диагональных элементов не равен нулю.
Заданная матрица
1ап а12
■•33 4J
Матрицы 3-го порядка, полученные из заданной вычеркиванием
одного
столбца:
1
023 О24
ОЗЗ fl84J
Номер
2
Г°ц ои
вычеркнутого
"ё
столбца
3
022 024
ДзЗ ^34 J
III
4
ol8
Ога
Д|3 1
023
O33J
Матрицы 2-го порядка, полученные из заданной вычеркиванием
двух столбцов и одной строки:
Номер
вычеркнутой
строки
1
2
3
Номера вычеркнутых столбцов
1 и 2
Гааз о24]
1о3з o31j
[0|3 Oul
Га13 Oi4|
|^ о^з Оа^ J
1 и 3
Гагг о24]
[^12 0,4]
[«12 Оц\
[а-п a^i
1 и 4 2 и 3
Го22 ага]
1аза азз]
1аза азз]
1 0^2 ^23
1 |
lt 4 J
fou a14]
lo3i 034J
2 и 4
[Oji О43
[О31 О33
[eu ol3
1%I O33
[оц au
3 и 4
1 ^2| 2 1
L 81 ^*yij
|[SSI
[Оц а,г|
92
Матрицы 1-го порядка, полученные из заданной матрицы вычер-
вычеркиванием трех столбцов и двух строк:
Номера
вычеркну-
вычеркнутых строк
2 и 3
3 и 1
1 и 2
2, 3 и
"и
а21
аи
Номера
4
3,
вычеркнутых
4 и 1
а12
аы
аз,
4, 1
а
а
а
столбцов
и 2
13
!3
S3
1,
2 и 3
"и
аи
4L
4. Алгебраическое дополнение элемента матрицы.
Союзная матрица
Если из определителя квадратной матрицы порядка п вычерк-
вычеркнуть i-ую строку и /-ый столбец, на пересечении которых стоит
элемент ailt и составить из оставшихся элементов определитель
порядка п—1, умножив его на (—1)'+/, где i-\-j — сумма номе-
номеров вычеркнутой строки и столбца, то полученное произведение
называется алгебраическим дополнением элемента сщ матрицы
и обозначается символом Ац.
Союзная матрица. Если из алгебраических дополнений всех
элементов матрицы Л составить новую матрицу и транспониро-
транспонировать ее, то полученная так матрица называется союзной по отно-
отношению к данной. Союзная матрица обозначается символом А
и записывается так:
1 1 • • • "д1
Л12 Л2а А32 . . . Ап2
"За Азп' ' • "пп
Ы
DЛЗ)
Союзная матрица Л называется также присоединенной.
5. Формула для вычисления определителей
С вычислением определителей приходится встречаться во мно-
многих случаях. Укажем весьма удобную формулу для вычисления
определителя п-го порядка:
93
an al2 a13.
Й21 fl22 a23 •
a3i o32 a33.
. fl|. л—I 0\
■ 02.Л-1 Cs
. аз,я_1 а.
*m
гп9
. a
n- /i—1
all Ol2J |ЙЦ Й13
^21 ^221 1^21 ^23
an an\ \an a13
О31 О33
I flu
a3. n-i\
в*.
ЯЛ1 0Л2
n-l
u
D,14)
Предполагается, что au =?fc 0. Если ап = 0, то перестановкой
строк и столбцов всегда можно из данного определителя полу-
получить такой, в котором аи ф 0. Эта формула очень проста в упо-
употреблении и позволяет вычисление определителя порядка п свести
к вычислению определителя порядка п— 1.
II. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ НАД МАТРИЦАМИ
1. Равенство матриц. Две матрицы А и В называются рав-
равными, если: 1) обе они имеют один и тот же размер, т. е. если
число строк матрицы А равно числу строк матрицы В, а число
столбцов матрицы А равно числу столбцов матрицы В, и 2) соот-
соответственные элементы этих матриц равны между собой, причем
под соответственными элементами понимаются элементы с одними
и теми же индексами.
Таким образом, если матрица
«11 «12
. а
. а.
ат\
. . . О.
а матрица
bu 6ia . . . bJn
Ьо1 602 . . . &■
2/1
"m2 • • • "mn _
и ац = Ьц (t = 1, 2, ..., т\ / = 1, 2, ..., п), то А = В.
94
2. Линейное преобразование. Пусть п величин хи х2, х3, ...,
связаны с т
Ух =
Уг =
Ут =
величинами yt
= enx, + а12х2
= amlxx + am2x2
> Уг> Уз>
+ a13x3
+ a23x3
+ am3X3
+ ■
+ ■
• • +
• • +
• • +
•аким:
a\nxn
a2rixn
D,15)
По этим формулам величины уи у2, ... , ут выражаются линейно
и однородно через п других величин хи х2, х3 х„. Преобра-
Преобразование величин хи х2, ... , хп при помощи формул D,15) в вели-
величины уи у2 ут называется линейным преобразованием.
Формулы D,15) сокращенно можно записать так:
yt = E aaxi (*' = Ь 2> 3, .... т).
D,16)
Коэффициенты линейного преобразования D,15) величин х, (/ =
= 1, 2, ... , п) в величины yt{i = \, 2, ... , т) могут быть запи-
записаны в виде матрицы
" Си с,2. . . а,„ ~
а21 а22 . . . а2
А =
а2п
"mn _
которая называется матрицей линейного преобразования D,15)
величин Xj(j = 1, 2, ... , п) в величины yi(i = 1,2, ..., т).
Правила алгебраических преобразований над матрицами стано-
становятся наиболее понятными, если пользоваться введенным понятием
линейного преобразования одних величин в другие.
3. Сложение и вычитание матриц. Пусть имеется линейное
преобразование
Ух = 011*1 + ^1-2*2 + • • • + &ХПХП
. + а22*2 + • • • + а2пхп
Ут =
ат2х2
величин Xj(j = 1, 2, ... , п) в величины у,(у =1,2 т).
Матрица этого преобразования
. а
. а,
D,18)
. а„
9S
Пусть имеется другое линейное преобразование величин
1, 2 п) в величины f« (t = 1, 2, ... , т) по формулам
г2 =
b22x2
blnxni
Ьгпхп\
D,19)
ЬтпХа.
Матрица этого преобразования
п __
~bn Ь12
Кп ha
ьт1ьп
■ b
D,20)
Составим теперь линейное преобразование величин *,(/ =
= 1, 2, ... , п) в величины щA = 1, 2 т), являющиеся суммой
величин i/i и 2/. Для этого сложим линейные преобразования
D,17) и D,19) и получим
+ (а1л + Ь1п) хп,
+ (а2я + а2я) д:л;
(ап + bn) *i + {ап + Ьи
(а21 + 62J) Xi + (аа2 + Ь22) х2+
(а
т2
(ат
D,21)
Линейное преобразование D,21) представляет собой сумму линей-
линейных преобразований D,17) и D,19).
Матрицу этого преобразования
С =
~ап
a2l
bu
al2 -f b12
a22 + 622 .
. аы
. a2n
bln
b2n
Kl am2
• amn + К
D,22)
и следует рассматривать как сумму матриц линейных преобразо-
преобразований D,17) и D,19), т. е. как сумму матриц D,18) и D,19), т. е.
как А + В. Таким образом,
А + В = С. D,23)
Итак, суммой двух прямоугольных матриц А и В равных раз-
размеров (т х п) называется матрица С того же размера, элементы
которой ец равны сумме соответствующих элементов матриа
А и В.
96
если
D,24)
(f = 1, 2 m; /= 1, 2, .... n), т. е.
flu
flu
aaa . .
am2- •
" йц + &i
fl« + b2
_aml+bn
• «in
• a2n
+
Oil &12 .
ftn Ь„. . . b2n
"ml ^m2 " • ' "mn _
i fli2 + bi2- • ■ аы + Ьы
i Й22 + ^22- • • a2n + 62ft
%\ um2 < "mi • • • "«w т^ "mn _
Сц C12 . . . Cln
C21 Cg2 • • • C-in
Cm2
. .Cmn
D,25)
Сумму следует понимать в алгебраическом смысле. Это зна-
значит, что разность А — В матриц А и В одного и того же порядка
есть матрица D того же порядка, элементы которой равны раз-
разности соответствующих элементов матриц А и В, т. е.
d{/ — ац — Ьц.
Понятие суммы матриц распространяется на любое число
матриц. Сумма матриц подчиняется таким законам:
а) перемест ительному
А + В = В
б) сочетательному
Пример.
Г2 3 5 71 П —3 4 0
[1 4 2 3j + [2 13 —
_Г2+1 3 + (—3) 5 + 4
-[1 + 2 4+1 2 + 3 3
4 И. А, Каплан
7 + 0 I _ ГЗ 0
+ (—2)J ~[3 5
9 7
5 l
97
4. Умножение матрицы на число. Если умножить обе части
каждой из формул линейного преобразования D,17) на число а,
то получим
«i = «г/i = апо.Х! + а12лх2 + • • • + аиахп
v2 = cu/2 = a2laXl + а22ах2 + • • • + а2па.хп
ат2ах2
<**»««
D,26)
Формулы D,26) определяют линейное преобразование величин
X/(/ = 1, 2, ... , п) в величины vt(i — 1, 2, ... , т). Матрица коэф-
коэффициентов этого преобразования
-аап аа12 . . . ааь
01Q21 аа22 . . • а#2/
аа„
аа„
~тп_
D,27)
естественно, может рассматриваться как произведение матрицы А
преобразования D,17) на число а.
Таким образом, возникает правило умножения матрицы на
число: чтобы умножить матрицу А на число а, надо на это
число умножить каждый элемент матрицы А.
Пример.
2
1
2
3
2
1
4
—3
1
5"
0
3
0
5
Ю
15
10
5
20
— Г5
5
25
0
15
Имеют место следующие равенства:
(а + р) А = аА + $А 1
а(А + В) = аА + аВ)' ^'28)
5. Умножение матриц. Возьмем линейное преобразование вели-
величин Xj(j — 1,2,... , п) в величины #(/=1,2,..., т), опреде-
определяемое формулами
D,29)
у2 = а21хг + а22х2
агпхп
Ут = °W*1 + flffl2*2 H
с матрицей преобразования
~ап а12
ап а22,
атя ■ • • а„
D,30)
98
Рассмотрим еще одно линейное преобразование, которое пре-
преобразует величины t/,(i = 1, 2,..., т) в величины гг(г = 1,2,...
..., s) по формулам
22
D,31)
с матрицей преобразования
п
. . .6,
Jlm
'2m
_ЬЛ 6Й . . . bsm _
D,32)
Отметим уже в этом месте, что число строк в матрице А первого
линейного преобразования равно числу столбцов в матрице В
второго преобразования.
Поставим перед собой задачу выразить величины г, (г = 1,2,...
..., s) через величины х/(/=1, 2, , п). Для этого заменим
в формулах D,31$ величиня ^(i = 1, 2,... , nt) их значениями из
формуян D,29)г
alnxn)
02**2
+ <h«xn)+ ••«
1 (Oll*4 + Ol2*2
' Каждую из этих формул преобразуем, собирая члены с общими
множителями X/ и вынося эти множители за скобки:
2j= (ЬцЯц+612^21 + • • • + &i«aw) *i + ФиОи + Ь&аы + • • • +
4- blnamt) x2+ .- 4- (pu<hn 4- Ь^гп 4- • •• + bimamn) *я
г2 = F21au 4- ^214- • • • 4- &2maml) *i 4- (Ьг}«1г +
4- b22a22 4- • • • 4- hnflmz) *2 4- • • • 4- ф21а1ж + b22a2n +
+ • • • 4- ksmOW) *„
4-
1) *! 4-
4- 652
4-
H h
4- • • • 4-
4- ••• +bsrrflmn)xn.
Мы получили формулы линейного преобразования величин
x/(j = 1, 2, .... л) в величины гЛ(г= 1, 2,..., s), минуя проме-
С =
жуточное преобразование D,31). Матрица этого окончательного
линейного преобразования
(bnan + bi2a21 + • • • + bmaml)... (Ьца1п +
+ b12a2n + • • • + Ьшатп)
(b2lan + b22a21 + ... -f b2maml)... {b2ialn +
+ b22a2n +
bsmaml) ... (bslaln
D,33)
Матрица С называется произведением матрицы В на матрицу А.
= ВА.
Размер ее равен s x п.
b2l
bl2
bz%
• blm~
•b2m
ап
U22
bSi b^.. . . bs,
Элемент сц матрицы С, стоящий в i-ой строке и j-ом
столбце, равен сумме произведений элементвв i-ой строки мат-
матрицы В на соответствующие элементы j-го столбца матрицы
А, т. е.
bimaml =
Например,
£
D,34)
с23 =
Ь22а23
+ b2mat
mS'
Формула D,33) и определяет произведение матрицы В на матрицу А.
Свойства произведения двух матриц, а) Не всякие две мат-
матрицы можно перемножить. Произведение В А двух матриц в ука-
указанном порядке возможно в том и только в том случае, если
число ствлбцов матрицы В равно числу строк матрицы А. Если
размер матрицы В равен s x т, а размер матрицы А равен
т х п7 то матрица ВА имеет размер s x п. Символически это
можно записать так:
(s х т) • (т х п) — s х п.
D,35)
Значит, в матрице, являющейся произведением двух матриц,
число строк равно числу строк левого сомножителя, а число
столбцов—числу столбцов правого сомножителя.
б) Произведение двух матриц в общем случае не обладает
свойством переместительности (иначе говорят, что оно не обла-
обладает свойством коммутативности), т. е.
ВАфАВ.
100
Значит, в общем случае менять местами матрицы-сомножители
нельзя, не изменив их произведения. В этом состоит одно из от-
отличий законов алгебры матриц от законов элементарной алгебры.
Если изменить порядок сомножителей, может оказаться, что
вообще умножить матрицы невозможно.
В произведении ВА двух матриц В и А мы будем говорить,
что матрица А умножается слева на матрицу В, или что матрица В
умножается справа на матрицу А.
Если размер матрицы А равен (р X л), а матрицы В — (пх р),
то можно составить как произведение АВ, так и произведение ВА.
При этом размер матрицы АВ равен (р х р), а матрицы В А —
(п х «).
Укажем, что для двух квадратных матриц одного и того же
порядка это условие выполняется, но подчеркнем, что и в этом
случае, как правило, ВА ф АВ.
Две матрицы А и В называются перестановочными (иначе
коммутативными), если имеет место равенство В А = АВ. Приме-
Примером перестановочных матриц являются квадратная и единичная
матрицы одного и того же порядка.
Ниже дано большое число упражнений на произведение ма-
матриц. Здесь же для иллюстрации сделанного вывода выполним
подробно только один пример умножения двух матриц и покажем,
как применяется формула D>34) образования элемента матрицы-
произведения.
Пример.
5
1
2
4
•3
•3
• 3
•3
+
+
+
+
5 1-
11-
2 1-
_4- Ц
3-34
(-1)-
1 • 34
(-2)-
5
1 —
2
3 —2
1 0
1 3
4—2 2
f 3-24
Ь(—1) •
Ы-2 +
h (-2) •
-2)-
3 + 0 •
-3-3
3+2 •
-(-2)
2 + 0
3- 4
2 + 2
3 5
3 1
2
3 4
3
1
16
8
• 4
4
4
•5
•5
•5
•5
9
1
11
10
1
2
4
4-
+
+
+
2
1
2
5 •
1 •
2 •
4-
3-
3
5
3 —2
3 -4
2 + 3- 1 + (
2 + (-1)- 1
24-1-1+2
2 + (-2) - 1
(-2)+(-2)
(—1) - (—2) + 0
1 •
(—2) + 3 • '(—
(-2)-(-2)+ 2
15
0
18
12
27
7
—4
16
•
—2) 2
+ 0-2
S -2
+ 2 -2
-(-4)
•(-4)
-4)
•(-4) _
Здесь умножение было возможно, так как число столбцов в
первом сомножителе равно числу строк во втором. Первый сомно-
101
житель был размером 4x3, второй 3x4, а матрица-произве-
матрица-произведение имеет размер 4x4, как это следует из D,35).
6. Произведение нескольких матриц. Если перемножить две
матрицы Л и В, то мы получим в общем случае матрицу С =
АВ, которую можно умножить, если умножение допустимо, на
матрицу D, т. е. составить произведение трех матриц ABD.
Произведение трех матриц ABD следует понимать так: матри-
матрица А умножается справа на матрицу В, а полученная матрица
умножается справа на матрицу D. Количество перемножаемых
матриц может быть любым, лишь бы можно было перемножить
каждые две рядом стоящие матрицы.
7. Законы умножения матриц.
а) Если можно перемножить матрицы А и В и произведение
АВ этих матриц можно умножить на матрицу С, то допустимо
составить и произведения (АВ)С и Л (ВС). В таком случае полу-
получается равенство, выражающее ассоциативный (сочетательный) за-
закон произведения матриц.
А{ВС) = (АВ)С. D,36)
Имеют место также:
б) сочетательный закон относительно скалярного сомножителя
а(ЛВ)=»(аЛ)В«Л(аВ)
и два дистрибутивных закона:
в) (Л + В) ■ С = А ■ С + В ■ С;
г) С ■ (А + В) = С ■ А + С ■ В.
D,37)
D,38)
D,39)
8. Возведение матрицы в степень. Если Л — квадратная матри-
матрица, а п — целое положительное число, то
Ап =А- А- А- А
А
а множителей
Матрица А" называется и-ой степенью матрицы А. При этом
Аг = А- Л;
А» = А- Л2 = Л* • Л;
и т. д.
Матрица Л2 называется квадратом матрицы Л, а матрица А3 —
ее кубом.
Теперь приступим к решению задач.
Задача 4,1. Произведите указанные действия над векторами-
столбцами:
U =
' 3 '
1
2
• V =
-5 '
6
0
; W =
1 '
1
1
102
1) W\ 2) —V; 3) U + AV; 4)
6) W — 2V + AW; 7) 2У —'/ + 3W.
Решение.
1) На основании формулы D,27)
W; 5) U-
2) По формуле D,27)
у —
3) Матрица
9
3
6
=
Гз 1
1 +
.2 1
"—20 '
24
0
По формуле D,25), согласно которой для сложения двух матриц
равннх размеров надо сложить их соответствующие эяеюенты,
получаем
— 17
А = 25
2
4) Пользуясь формулой D,25) для сложения двух матриц, а
также сочетательным законом сложения, находим
U+V
j. V) + W =
"—2"
7
2
+
"
1
1
ГЗ
1
L2
=
Г
+
L
8
3
-5
6
0
1
1
1
m
5) Применяя сочетательный закон сложения матриц и правила
вычитания и сложения матриц, получаем
U—V
_ V) + W =
HI*
■f
1
1
1
2
=
—
—5
+6
0
-■]■
+
Г
l
l
103
6) На основании правила умножения матрицы на число, пра-
правила сложения и вычитания матриц и сочетательного закона для
сложения имеем
Гз
31/-2V + 4V-3|J
9
3
6
—
"—l(f
12
0
+
"
4
4
=
—2
M
6+4
OJ
9—(—10)+ 4'
3— 12+4
6 —
0 +4_
1
1
.1.
=
23"
— 5
10.
7) 2U —
= 2
6 + 5 + 3
2 — 6 + 3
4 — 0 + 3
+ 3
1
4
3
_2_
• V —
0
0
1
_2_
; W =
1
4
—2
_—1_
; Г-
— 1
—2
—3
4_
W — T\ 2)U—V + W — T\ 3)
4W + Т; 5) 3t/ + 2V + 4Г — 5Г.
Задача 4,2 (для самостоятельного решения). Произведите
указанные действия над матрицами-столбцами
£/ =
4) 2U — 3V
Ответ.
1)
Задача 4,3. Над векторами-строками U = [2, —1, 2]; V =
— [—1, 0, 5]; W=[l, 4, 3] провести указанные действия: 1) 2U)
2) —3V; 3) U + V—W; 4) 2U + V — 3W; 5) U + 2V + 3W.
Решение.
1) Пользуясь формулой D,27) умножения матриц на число, имеем
Я/= 2 [2, -1, 2] = [4, -2, 4].
3
10
5
_- 1_
; 2)
3
10
3
5
; 3)
1
6
—1
7
; 4)
5
22
— 8
2
; 5)
12
38
18
— 18
2) На основании той же формулы
— ЗУ = — 3[—1, 0, 5] = [3, 0,
■15].
104
3) Пользуясь формулой D,25) сложения матриц и свойством
сочетательности сложения, получаем
U + V — W = [2, —1, 2] + [—1, 0, 5] —[1, 4, 3] =
= [2 + (—1)—1, —1+0—4, 2 + 5 — 3] = [0, —5, 4].
4) 2U + V — № = 2[2, —1, 2] + [—1, 0, 5] —[1, 4, 3] =
= [4, -2, 4] + [-1, 0, 5]-[1, 4, 3] =
= [4 + (-1)-1, -2 + 0-4, 4 + 5-3] = [2, -6, 6].
5) U + 2V + Ш = [2, —1, 2] + 2[—1, 0, 5] + 3[1, 4, 3] =
= [2,-1, -2]+ [-2, 0, 10]+ [3, 12, 9] =
= [2 + (—2) + 3, —1+0+12, —2 + 10 + 9] =■ [3, 11, 17].
Задача 4,4 (для самостоятельного решения). Докажите, что
сумма вектора-столбца
U=
с нулевым вектором-столбцом
_ип_
о
6
- _
того же размера равна U, т. е. что
U + 0 = U.
D,40)
Докажите также, что равенство D,40) остается верным для
случая, когда U — вектор-строка, а 0 — нулевой вектор-строка
того же размера, что и U.
Задача 4,5 (для самостоятельного решения). Докажите, что
нулевой вектор-столбец или нулевой вектор-строка не изменяется
от умножения его на любое число.
Задача 4,6 (для самостоятельного решения). Докажите, что
если U и V — два вектора (оба векторы-столбцы или оба векторы-
строки) с одинаковым числом компонент, то
U + 0V = U;
0U + V = V.
Задача 4,7. Какое соотношение связывает компоненты векто-
векторов U и V, если имеет место равенство
105
Решение. Под 0 следует понимать нулевой вектор тех же
размеров, что и векторы U и V, размеры которых равны между
собой. Элементами вектора 3£/ — 2V являются числа 3Ut—2Уг.
Две матрицы равны, если равны их размеры и соответствующие
элементы (стр. 94).
Значит, должно выполняться равенство
а отсюда следует, что между компонентами матриц существует
зависимость
Задача 4,8 (для самостоятельного решения). Если векторы U,
К и 0 имеют один и тот же размер, то какое соотношение свя-
связывает компоненты векторов U и V при наличии следующих
равенств:
1) 2U + V— 5U + 4V = 0;
2) IOV — 3U + 3V + 4U = O;
3) U + V — 2U — 2К = 0.
Ответ. 1) Ut = ™'t 2) {/, = -131^; 3) Ut=*—V,.
Задача 4,9. Найти указанные суммы, а в случаях, когда это
невозможно сделать, объясните причину:
; 2) [5, 7, —4] + 0 . [5, 4, 2];
3) [7, 8, —
; 4) 2
1
+ 3
Задача 4,10. Найдите аи а2 и а3, если
«Л Г 21 Г 7
аЛ+ 3 = 8
OsJ L-U L-3
Решение. Складывая первую и вторую матрицы в левой
части равенства и приравнивая сумму правой части, получаем
"d + 2"
О.2 + 3
а8— 1.
=
7"
8
з
106
Используем теперь определение равенства двух матриц:
ах + 2 = 7; аа + 3 = 8; а3— 1 = — 3,
откуда
d = 5; а2 = 5; а3 = —2.
Задача 4,11 (для самостоятельного решения). Найдите
ненты bu ba и Ь3 вектора-столбца Ь, если
[1
2 X
Г
tx--C.6)
■Zx*(-6.-i2) /
Фиг. 4,1
Ответ. &i = y? fta = 0; bs = — -j.
Задача 4,12 (для самостоятельного решения). Чему
компоненты w{i ws\ w3 вектора-столбца w, если
0
0
0
-(-
Ю2
=
"
0
0
Ответ. wx = w2 = w3 = 0.
Задача 4,13 (для самостоятельного решения). Что можно сказать
о компонентах ац а8; а3 и а4 вектора а, если
a2
a3
=
0
0
0
Ответ. аь а2, а3 н а4 — любые числа.
Умножению вектора на число можно дать геометрическую
интерпретацию. Рассмотрим прямоугольную систему координат
У
Фиг. 4,2
на плоскости. Двумерный вектор-строку [а, Ь] можно рассматри-
рассматривать как точку этой плоскости, абсцисса которой — а, а ордината Ь.
Точки, определяемые произведением числа С на вектор [а, Ь],
т. е. точки С • [а, Ь) лежат на одной прямой, проходящей через
начало координат и точку [а, Ь]. На фиг. 4,1 показаны точки,
соответствующие вектору х = [3, 6) и векторам 2х, —х, —2х,
Сумме и разности векторов-строк можно также дать геометри-
геометрическое истолкование. Если х = [а, Ь], у = [с, d]. Составим век-
векторы х -\- у, х — у, у — х и —х — у. Эти векторы будут точками,
показанными на фиг. 4,2, для случая, когда х = [2, 3} и у = [7, 2].
Задача 4,14. Построить точки, соответствующие векторам дс =
= [2, 3] и у = [—3, 8].
108
Найти и построить точки, отвечающие векторам: 1) у х + у У,
2) лг + г/; 3) 2х — Зу; 4) 3* + 2у; 5) г/— 2л:.
Задача 4,15. Сложить матрицы
2 3
4 5
-1 2
О 5
1
2
—4
—7
-2 3
0 4
-3 5
1 1
—5
7
1
2
Решение. По формуле D,25) для матриц получаем
О 6
4 9
-4 7
—4
9
—3
1 6 —I
Задача 4,16. Вычислить матрицу
5 2
3 7
-4 5
Решение. Используя формулу D,27) для умножения матрицы
на число и формулу D,25) вычитания матриц находим последо-
последовательно
Г 10 41 Г
= 6 14 -
L- s ioj L
-12
3
6
15
3
0
22 —11
3 И
— 14 10
Задача 4,17 (для самостоятельного решения). Выполнить действия
2 5 4
1 0
2 4 5 -3
0 -3
Ответ.
Г—48 0 15 33
[—33 6 9 27
Задача 4,18. Матрицу
А =
0
0
0
5
0
0"
0
5
представить в виде произведения числа на единичную матрицу.
109
Решение.
Задача 4,19. Сложить матрицы
0
0
0
1
0
0
0
1.
7 0 4"|
0 7 2 и В =
-5 2 llj
2 0 3
0 2—1
4 5—7
Решение. Матрица А может быть записана в виде блочной
матрицы
2
0
_4
7
0
5~
0
7
~2~
0
2
_
5
4
2
TL
3
—1
—7_
=
=
_5
~2£
_4
7£
"г"
2
5
2
1
J
1
—
4
2
3~
1
7_
Так как матрицы
[J ?
то сумма
[о °] =
7Я2
_—5"~
2
4
2
+
2
_4~
9
0
£
5"
0
9
2 !
3
1-1
"!—7_
71
1
=
•
Е2 7
! 1
ПЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Умножения матриц. Формулы для проверки Умножение
матриц. Обратная матрица и способы ее получения.
А. ЗАДАЧИ НА ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Задача 5,1. Найти произведение вектора-строки
А = [alt a2, а3, .... а„]
на вектор-столбец
5=
Прежде чем умножать матрицы, надо убедиться, что такое
умножение имеет смысл.
Решение. В данном случае получить произведение возможно,
так как размер матрицы А равен 1 х п, а матрицы В— л х 1,
т. е. число столбцов матрицы А равно числу строк матрицы В (фор-
(формула D,35), стр. 100). В произведении будем иметь матрицу раз-
размером A х л) • (л х 1) = 1 х 1, т. е. некоторое число.
Действительно, на основании формулы D,34)
а2, а3 а„]
Ъг
Сумма этих произведений есть число. Еще раз подчеркнем, что
произведение вектора-строки (первый сомножитель) на вектор-
столбец (второй сомножитель) есть число (можно сказать, что
такое произведение является скаляром).
Задача 5,2. Найти произведение векторов
А = [2, 4, 5, 7] и В =
2"
— 3
— 1
4
ill
Решение. ЛЯ = 2.2 + 4- (—3) + 5 . (—1) + 7 • 4 =
= 4—12 — 5 + 28= 15.
Задача 5,3. Если а — вектор-строка, b — вектор-столбец с одним
и тем же числом элементов, а а — число, то доказать, что
а (а • Ь) = (аа) • b = а • (ab).
Доказательство. 1) Пусть
а = [аъ а2, а3 ап]; b =,
"V
-К-
Тогда по формуле умножения матриц
а • b — [alt а8, а3, ... , ап]
Jn-
= axbx + афг + a3b3 + ... + anbn;
a(a-b) = aa^! + aa2b2 + aa3b3 + ... + a anbn) (A)
2) a.a = a[alt a2, a3, ... , а„] = [aalt ааг, aa3, ... , aan)
по формуле D,25) умножения матриц (см. также предыдущую
задачу) _
V
Ъ = [аа1( аа2', аа3, .... аап] 2
аафх -f- <ш2Ь2 + aa3b3 + ... + «я.-А)- (В)
Сравнивая выражения (А) и (В), приходим к выводу, что
а (а • Ь) = (а • а) Ь.
Самостоятельно докажите, что каждое из этих выражений равно
а • {ab).
Задача 5,4 (для самостоятельного решения). Доказать, что
если а — трехмерный вектор-строка, b и с — трехмерные векторы-
столбцы и а — некоторое число, то имеют место равенства
а • (ab) = а (а - Ь);
а • (Ь + с) = а • b + a • с.
112
Задача 5,5. Пусть А = [х, у] и векторы-столбцы а и Ъ равны
соответственно
•-В1- 41-
Определить х, и г/, если известно, что А • а = х, а А • В = у*
Решение. По условию А • а = х, а А • b = у, т. е.
[х, у]
= *; l*.
Отсюда для определения х и у получится система уравнений
Зх + Ъу = х;
6х + 8у = у
или
Ах -j- oy = и,
Так как определитель этой системы
2 5
D= 6 ? = и —30 = —16^0,
то она допускает только нулевое решение: х = у = 0.
Задача 5,6 (для самостоятельного решения). Пусть х = [хи х2],
а векторы а и b равны соответственно
-ОД -U1-
Определить хг и дг2) если х • а = 4; х • b = —1„
Ответ: a;1=-5-; x2 = -j.
Задача 5,7. Найти произведение а • Ь, если
Г
а= 2 ; & = [2, 3, -1).
3
.—5.
Решение. По формуле D, 33) получаем
Г
а • b —
3
—5
[2, 3,-1]
1 -2
2-2
3-2
—5-2
1 -3
2-3
3-3
—5-3
1
2
3
—5
• (—1)
• (—1)
• (—1)
2
4
б
— 10
3
6
9
— 15
j
—2
—3
5
113
Обратим внимание на то, что произведение вектора-столбца справа
на вектор-строку представляет собой матрицу, а не число, как
в том случае, когда вектор-столбец умножался слева на вектор-
строку.
Размер полученной матрицы определяется по известной формуле
D,35), которая в нашем случае запишется так:
D х 1) • A X 3) = D х 3).
Действительно, получилась матрица с четырьмя строками и тремя
столбцами. Таким образом, произведение цектора-столбца справа
на вектор-строку есть матрица, у которой элементы любой ее строки
(столбца) пропорциональны соответствующим элементам другой ее
строки (столбца).
Задача 5,8 (для самостоятельного решения). Найти произведения
5"
[1, 2, -2, 3, 4]; 2)
7
-3
2
1
2
—3
[4, 5].
5
7
3
2
10
14
— 6
4
— 10
— 14
6
— 4
15
21
— 9
6
20
28
— 12
8
2)
4
8
— 12
5
10
—15
1)
Ответ.
1)
<В. ЗАДАЧИ НА ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И МАТРИЦ
Задача 5,9. Найти произведение АВ вектора А = [5, 7, —2]
,на матрицу
Г 2 3 1
5= 1 4 2
_2 3 —1
Решение. Убедимся прежде всего в том, что умножение имеет
смысл: число столбцов матрицы А равно трем, а в матрице В
столько же строк. Поэтому произвести умножение можно:
2 3 Г
1 4 2
-2 3 —1
= [5-2 + 7- 1 + (-2)-(-2); 5 • 3 + 7 ■ 4 + (-2) ■ 3;
5 ■ 1 + 7 • 2 + (—2) • (—1I = [21, 37, 21]. Получился вектор-строка
с тремя элементами, как и должно быть по правилу D,35):
A х 3) C х 3) = A х 3).
1 \*ГПЧ I1|/VII^UVV1 II
Г 2
3, 7, -21 • 1
L-5
.114
Задача 5,10 (для самостоятельного решения). Найти произведе-
произведение АВ, если
3 Г
Л=[1, 0, —1]; 5=2 3
1_2 8_
Ответ. A, —7).
Задача 5,11. Найти произведение АВ, если
■-В1
Решение. Умножение возможно, так как число столбцов,
матрицы А равно числу строк матрицы В.
По правилу D,34) умножения матриц получаем
о_[5-3 + 7-2 + (—4) • (—1I _ ГЗЗ]
_\ — L2-3 + 5-2+1- (—1) J-[l5_|-
Размер этой матрицы B х 1), как и должно быть по правилу
D,35):
B х 3) • C х 1) = B х 1).
Задача 5,12. (для самостоятельного решения). Найти произве-
произведение АВ матриц Л и В, если
-— Г
о
г2 —1 —3 0 41
Л= 7 2 5 5 2; В=
|_3 4 1—7 —lj
1
2
3
0_
гЗ
3
1
.2
7
1
4
0
2-1
3
2
5.
2) А =
3) А = [5, 7, -2, -3]; В =
Ответ.
1) f 2о|;
L-18J
2)
23п
14
15
L17J
Г2
3
5
L7
1
2
—4
2J
[0,21].
Задача 5,13. Подрядчик-строитель заключил договор на возве-
возведение таких строений: 3 жилых домов, 5 детских садов и 9 домов
отдыха. Материалами для строительства являются сталь, лес, стекло,
краска. Количество сырья, а также рабочей силы на каждый вид
115
•строения выражено в некоторых условных единицах и дается та-
такой матрицей
Сталь Лес Стекло Краска
Жилой дом ПО 17 8 5
Детский сад А = 7 12 4 3
Дом отдыха I 5 15 10 4
Рабочая сила
8 '
9
Единица стали стоит 12 рублей, единица леса — 7 рублей, еди-
единица стекла — 5 рублей, единица краски — 4 рубля, единица ра-
рабочей силы — 10 рублей.
Определить: 1) общее количество потребных материалов и ра-
рабочей силы; 2) стоимость материалов и рабочей силы для каждого
вида строений; 3) общую стоимость материалов и рабочей силы.
(Все цифры, входящие в задачу, условны и не соответствуют действи-
действительным данным).
Решение. Договор, заключенный подрядчиком на возведение
-строений, представим вектором-строкой В = [3, 5, 9]. Чтобы узнать
количество необходимых материалов, надо перемножить матрицы
В и Л и найти произведение В А в указанном порядке, т. е. матрицу
В умножить справа на матрицу Л. Это произведение имеет смысл,
так как в матрице В трн столбца, а в матрице А столько же строк.
В результате получится матрица, размер которой по формуле D,35)
равен A х 5), так как
A X 3) • C х 5) = A х 5),
т. е. получится вектор-строка с пятью элементами. Итак, общее
количество материалов, необходимых на все строения, в очень ком-
компактной записи равно
10 17 8 5 11
ВА = [3,5,9]- 7 12 4 3 8
5 15 10 4 9
= [3 • 10+5 • 7+9 -5; 3 • 17+5 -12 + 9-15; 3 -8+5 • 4+9 • 10;
3 -5 + 5 -3 + 9-4; г*3- 11+5 • 8+9 ■ 9] = [ПО, 246, 134, 66, 154]
(применено правило D,34) умножения матриц).
Таким образом, подрядчик должен приобрести: стали ПО еди-
единиц, леса 246 единиц, стекла 134 единицы, краски 66 единиц и
154 единицы рабочей силы.
Чтобы узнать стоимость материалов и рабочей силы для каж-
каждого вида строений, поступим так: расположим цены материалов
2"
в вектор-столбец и получим С =
7
5
4
10
Умножим теперь справа
.116
матрицу А на вектор-столбец С по правилу D,34) умножения
матриц и получим вектор-столбец с тремя элементами, так как
размер матрицы АС равен
C х 5) • E х 1) = C х 1).
10 17 8
ЛС= 7 12 4
5 15 10
10 • 12 + 17 • 7 + 8-5
7 ■ 12+ 12- 7+ 4-5
5- 12+ 15-7+ 10-5
5
3
4
5
3
4
11"
•4
• 4
•4
8
+
+
+
11
8
S
2"
7
5
4
• 10
• 10
• 10
409
280
321
(Умножение этих матриц в другом порядке С А не имеет смысла.
Почему?)
Итак, стоимость материалов и рабочей силы для жилого дома —
409 рублей, для детского сада—280 рублей, для дома отдыха —
321 рубль. Чтобы ответить на третий вопрос задачи, составим
произведение матриц
ВАС = {ВА) ■ С =
246, 134, 66, 154).
2"
7
5
4
= 5516.
Это же число можно получить и иначе:
09"
ВАС
= 13, 5, 9].
280
321
= 5516.
Итак, общая стоимость всех строений 5516 рублей (условных,
конечно).
Задача 5,14 (для самостоятельного решения). Произвести ука-
указанные действия:
3)
1
5
2
—3
—2
4
2
5
1
3
2
0
0"
4
2
— 1
3
5
2
1
— 1
117
5) [2, 0, -4]
7)
9)
ад
s
2 1
0 E
; 8)
>
"l
0
0
5
2
2
0
1
0
—2
4
1 —3
4 7
0'
0
1
fl
x2
x3
7'
5
3
>
6) [х, у)
[w t
m2 u3]
1
0
0
0
1
0
Г
0
1
4)
' 4"
11
3
—2
—5
3_
|; 5) [2, — Ш, 2, —20, —20, :
Ответ. 1) I ; 2) [—18, 14]; 3)
1 О I
I- J
6) [xu + yw, xv + yt\, 7) a^ ."8 ;
Xi
8) \x2
_*3j
; 9)
Задача 5,15 (для самостоятельного решения). Найти дг и д
из уравнения
Указание. Использовать определение равенства двух матриц
(стр. 100).
Ответ. * = ^; ? = {|.
Задача 5,16 (для самостоятельного решения). Из произведения
найти матрицу
[с
Г*
Указание. Использовать определение равенства матриц.
Ответ. [J у
118
Задача 5,17. Найти вектор а из уравнения
Решение. Система
ai —#2 = 13
= —4
противоречива. Величины at и а2 определить невозможно.
Задача 5,18. .Найти вектор и из уравнения
Решение. Произведя умножение в левой части равенства,
получим
Г-5М1 + ЗиЛ Г 7]
[ 10М1-6ы2] L-14J'
откуда, пользуясь определением равенства двух матриц, находим
систему уравнений
\0ui — 6м2 = —14 J'
Легко усмотреи», что второе уравнение является следствием
первого. Оно получается из первого умножением обеих его частей
на —2. Поэтому фактически мы имеем одно уравнение с двумя
неизвестными
—5«j + Змг = 7,
откуда
5«! = Зм2 — 7.
Обозначим и2 через k. Тогда
= Ik — --
1 ~~ 5 5 '
а искомый вектор
-РЛ
где k — любое число.
Таким образом, предложенное уравнение имеет бесконечное
множество решений.
119
Задача 5,19. Найти вектор и, если
Г2 3] ГиЛ „к!
Решение. Выполнив в левой части равенства умножение
матриц, а в правой умножение числа на матрицу, получим
Г11 мЛ
[П и2}'
Но если две матрицы равны, то их соответствующие элементы
равны, потому получаем систему уравнений:
2«! + 3«2 = 1 1«1 )
6«х + 9и2 = 11м2 /
или
6мх — 2и3 = 0 у
Получилась система из двух линейных однородных уравнений
с двумя неизвестными. Так как определитель этой системы
—9 3
6 —2
то система допускает решения, отличные от нулевого. Легко усмот-
усмотреть, что второе уравнение есть следствие первого. Оно получается из
2
первого умножением его на — у. Таким образом, мы имеем одно
уравнение с двумя неизвестными, и решений будет бесконечное
множество. Из второго уравнения следует, что
и2 = Зих.
Если обозначить их = k, то u2 — 3k и вектор
где k — любое число.
Задача 5,20 (для самостоятельного решения). Найти х и у из
уравнений:
-К
Ответ. 1) х = 3ft; у = 2k; 2) x = 4k; y = bk, где k — любое
число.
120
С. УМНОЖЕНИЕ МАТРИЦ
Задача 5,21. Даны матрицы
л_[ 2 5 7 41
L—1 2 0 —3|
5
2
3
1
7
3
0
г
1
0
1
2
2
2
1
—2
1
2
1
1
2
0
1
2
; 0 =
2
3
5
1
— 1
0
—2
—3
1 О
О 1
4 1
О 2
Найти: 1) компоненту матрицы АВ, стоящую во второй строке
и третьем столбце;
2) компоненту, стоящую в третьей строке и втором столбце
матрицы BD;
3) компоненту, стоящую в последней строке и последнем столбце
матрицы AD;
4) компоненту, стоящую в третьей строке и первом столбце
матрицы CD.
Решение. Искомую компоненту будем обозначать во всех
четырех случаях через Сц, причем первый индекс i означает номер
строки, а второй индекс /—номер столбца, в которых находится
эта компонента.
1) Умножим вторую строку матрицы А на третий столбец
матрицы В:
1-23
[-1, 2, 0, -3]
= 1—1-1 + 2.0
(—3) -21 =
2) Умножим третью строку матрицы В на второй столбец
матрицы D:
= 1-3, 0, 1, И
—3
= — 3 • (— 1) + 0 . О + 1 • (—2) + 1 • (—3) = —2.
3) Матрица AD по правилу D,35) имеет размер
B х 4) • D х 2) = B х 2).
Поэтому в ней две строки и два столбца. Значит, ее последней
121
строкой является вторая и последним столбцом — второй. Искомая
компонента
: = [-!, 2, 0, -3]
О
—3
= 4 • 2 + 1 • 3 + 1 • 5 4- Ы =
Задача 5,22. В условии предыдущей задачи определить размеры
матрицы; 1) АС; 2) DA; 3) AD; 4) ВС; 5) СВ\ 6) ВАС; 7) BCD А.
Решение. 1) Размер матрицы АС B х 4) • D х 4) = B х 4).
Она имеет две строки и четыре столбна.
2) Размер матрицы DA определится из формулы
D х 2) • B х 4) = D х 4).
Значит, матриад DA — квадратная с четырьмя строками и четырьмя
столбцами.
3) Размер жмриця AD B х 4J • D х 2) =* B х 2). Это тоже
квадратная матрица с двумя строками и двумя столбцами.
4) Размер матрицы ВС D х 4) • D х 4) = D х 4).
5) Размер матрицы СВ D х 4).
6) Матрица DAC можно получить в таком порядке: a) DA,
б) (DA) С или составить сначала произведение АС, а потом умно-
умножить его слева на D : D • (АС). Размер DA определен в пункте
2. Он равен D X 4). Если матрицу А размером 4x4 умножить на
матрицу С размером 4x4, то получим матрицу DAC размером
D х 4) • D х 4) = D х 4).
Если же взять DAC = D • (АС), то, зная, что размер АС равен
B х 4), и учитывая, что размер D равен Dx2), а также, что
матрица АС умножается на матрицу D слева, находим
D х 2) х B х 4) = D х 4).
7) Размер произведения четырех матриц BCDA можно опреде-
определить так, если учесть сочетательное свойство произведения:
а) BCD А = (ВС) ■ (DA);
б) BCD А = В • (CD А);
в) BCD A = (BCD) • А.
Для упражнения определим размер матрицы BCDA во всех этих
трех случаях:
122
а) Размер матрицы ВС равен D х 4) (см. пункт 4). Размер
матрицы DA тоже равен D х 4). Поэтому размер матрицы BCDA
равен D х 4) • D х 4) = D х 4).
б) Определим сначала размер матрицы CD А. Матрица CD A =
= С • (DA). Но размер матрицы С равен D х 4), а размер матрицы
DA уже определен в п. 2 и тоже равен D х 4). Поэтому матрица
CD А имеет размер D х 4) • D х 4) = D х 4). Умножая эту мат-
матрицу слева на матрицу В, размер которой равен D х 4), найдем,
что матрица BCD А имеет размер
D X 4) • D X 4) = D X 4).
Как и следовало ожидать, мы получили тот же результат.
в) Вычисления надо выполнить самостоятельно. Результат, ко-
конечно, должен получиться тот же самый. Правило умножения
матриц дается формулой D,34). На первый взгляд, оно может по-
показаться громоздким и сложным. Однако те, кому приходится часто
и много работать с матрицами, очень быстро привыкают безоши-
безошибочно это правило применять и оно представляется им исключи-
исключительно простым; палец левой руки должен скользить слева направо
вдоль строк первой матрицы, а палец правой руки должен при этом
скользить по столбцам второй матрицы.сверху вниз. Проделав не-
несколько упражнений, правило умножения матриц можно легко осво-
освоить.
Здесь мы приведем три способа проверки правильности проде-
проделанного умножения. Эти способы указана Л. К- Нарадои и мы по-
покажем их на примерах.
А =
способ проверки. Пусть
Г7 4 21
1.6 —3 5J'
С = АВ = Г
2
—1
5
A)
27
17
20
40
Для проверки умножения составляем две матрицы-столбца D
и F: в первой матрице D элементы равны сумме элементов в соот-
соответствующей строке матрицы В
D =
1 +2
3 + (
4 + 5
B)
а во второй матрице F элементы равны сумме элементов в соот-
соответствующей строке матрицы произведения С
[27 + 201 Г47]
1.17 +40 J [57j"
C)
123
Произведение матрицы А и D должно равняться матрице F (AD = F)
\7 4
-3 5
б-3 —
5-9
57
11 способ проверки. Составляем две матрицы-строки G и Н:
в первой матрице G элементами являются суммы элементов в каж-
каждом столбце в первом сомножителе (матрица А)
4-3, 2+ 5] = [13, 1, 7],
E)
а во второй матрице Н элементами являются суммы элементов
в каждом столбце матрицы произведения С
Н = [27 + 17, 20 -(- 401 = [44, 60]. F)
Произведение матриц О и В должно равняться матрице Н (GB = Я).
GB = [13, 1, 7]
1 2
3 —1
= [13- 1 + 1 -3 + 7-4;
L4 5
13 • 2 + 1 • (—1) + 7 • 5] = [44, 60) = Н.
G)
III способ проверки. Составляем матрицу-строку G, элементы
которой равны сумме элементов в соответствующих столбцах пер-
первого сомножителя G = [13, 1, 7]. Составляем матрицу-столбец D
так, что ее элементы ргвны сумме элементов в соответствующих
строках второго сомножителя
Гз"
D
Произведение GD должно быть равно сумме всех элементов
матрицы С
GD = [13, 1, 7].
L
= 13-3+1 .2 + 7-9=104 =
= 27 + 17 + 20 + 40.
Задача 5,23. Перемножить матрицы
А =
2
1
3
3
0
2
— 1
5
0
2
— 1
1
4"
2
—4
; В =
~ 2
1
4
—2
— 1
3
2
—5
—3
4
124
Решение (столбцы I, II отделены пунктирной линией)
Г2.2 + 3.1 + (-1)-4 + 2-(-2) + 4-(-1)
[-2 + 0- 1 + 5-4 + (-1)-(—2) + 2 - (—1)
$.2 + 2- 1 +0-4+1 (-2) + (-4). (-1)
2 • 3 + 3 • 2 + (—1) - (—5) + 2 - (—3) + 2 - 4
1-3 + 0.2 + 5- (—5) + (-1) • (—3) . + 4 • 4
3 • 3 + 2 - 2 + 0 • (—5) + 1 - (—3) + (—4) • 4
~—5 27
22 —11
10 —6
-t- v •
Получилась матрица размером 3x2, как и должно быть:
C х 5) • E х 2) = C х 2).
Правильность выполненного умножения установите первым спо-
способом проверки.
Задача 1
1
aJ
1
>,24.
Г2
4
12
Найти
3
3
4
П
~2
1
произведение матриц
| 1
и В = \
Г-2
1
-3
4
2
1
5
4
2
8
j
5
1
0
3
4
3
Решение (столбцы I—IV отделены пунктирными линиями)
4 • (-2) + 3
2 • (-2) + 4
1 + 1 • (-3)
1+(-2)-(-3)
• 1 + 1 • (-3)
2-5 + 3-4+ 1 .2
4.5 + 3-4 + (—2) • 2
2-5 + 4- 4+ 1 .2
2.4 + 3-2+b'l
4-4+3-2 + (—2)
2-4 + 4-2+ Ь 1
J2.8 + 3 -(—1)+ 1 -5
14-8 + 3- (—1L-1—2). 5
]2 . 8 + 4 • (- 1) + 1 - 5
2-1+3-0+1.4
4 - 1 + 3 - 0 + (—2) - •
.2.1 + 4-0+1-4
—4 15
1 20
j 2-3 + 3-4+1-3
14-3 + 3-4 + (—2) • 3
24
28
18
19
2-3 + 4
6 21"
—4 18
4+1 -3
—3 17 28 17 6 25
Получилась матрица размером 3x6, как и должно быть по пра-
правилу D,35), так как размер матрицы Л равен Cx3), матрицы В C X 6),
а размер матрицы АВ (произведения матриц Аи В) равен C х 3) х
х C ч 6) = C х 6).
Правильность умножения самостоятельно установите вторым спо-
способом проверки.
125
Задача 5,25 (для самостоятельного решения). Найти произведе-
произведение матриц:
2 3 01
1 '< I Л I
1) А
2) А =
3) А =
4) Л =
Правильность умножения проверьте по одному из указанны* спо-
способов.
3
5
Ответ. 1)
— 19 15]
— 12 26 ;
— 15 19J
О
10
13
1
3].
J'
3)
10 -1
4
6
4)
—3
6
3 —8
7 —19
9 —26
L—10 27
6 11
O 17
8
22
44
—30
14 11
21 18
Г
6
25
—7
29'
Задача 5,26. Доказать, что произведение АВ матриц
d\
есть нулевая матрица
Доказательство.
0 = L _ .
Го о] Го о]
[с d\~[o 0\~
Эта задача показывает, что произведение двух матриц
может быть нулевой матрицей и тогда, когда ни одна
из матриц сомножителей не является нулевой.
Задача 5,27 (для самостоятельного решения). Доказать, что
если
Го о] D Г
то
[о о!
= [о о\
126
и придумайте пример, когда произведение двух квадратных матриц
третьего порядка является нулевой матрицей, а ни одна из пере-
перемножаемых матриц не является нулевой.
Задача 5,28. Доказать, что произведение двух диагональных
матриц одного и того же порядка есть диагональная матрица того
же порядка.
Доказательство. Пусть даны диагональные матрицы Л и В:
А =
«„ О О
О а22 О
0 0 0
.. 0
.. 0
в =
о ьг.
0 ... 0 1
о ... о
Lo о о ...
Тогда
о
.0
Ьп
о о ... о
«22^22 0 ... О
о ' о .'. .'«„;
что и доказывает требуемое.
Отметим, что произведение двух диагональных матриц одного
и того же порядка коммутативно: для этих матриц АБ — В А.
Задача 5,29. Доказать, что произведение АЕи = А, если А —
квадратная матрица порядка я, а Ея — единичная матрица того же
порядка. Убедиться, что АЕ„ = ЕпА, т. е. матрицы А и £ — ком-
коммутативны, если они одного и того же порядка.
Доказательство. Пусть
А =
«11 «12 °13
Й21 «22 «23
-10 0 ... О
О 1 0 ... О
Lo о о
i.
По правилу умножения матриц получаем
гап а12 ап ... а1П
АЕп =
«12 Ol3
«22 «23
Этот пример показывает, что в матричной алгебре единичная
матрица играет такую же роль, какую в обычной алгебре играет 1.
Задача 5,29а (для самостоятельного решения). Убедиться, что
матрицы Л и В не коммутативны.
Г5 2 П ГЗ 2 11
Л=4 3 8; Я=2 4—2.
Ll 5 2J Ll 2 3J
127
BA =
Задача 5,30. Даны матрицы
24
24
16
С =
17
6
23
Г 1
-2
21
30
23.
3
4
Убедиться, что выполняются следующие алгебраические законы:
1) (А+В)С = АС+ ВС;
2) А{В-\-С) = АВ + ВС;
3) А (ВС) = (ЛБ) • С.
Задача 5,31. Проверить ассоциативный закон умножения мат-
матриц на примере матриц
Г-2 3 5] Г-1 7 2] Г-1 2]
- I — 4 2 3J} В = 3 14; С = 30.
L 0 5 7j L 0 5J
Задача 5,32 (для самостоятельного решения). На примере квад-
квадратной и диагональной матриц третьего порядка убедиться в спра-
справедливости таких утверждений:
1) умножение квадратной матрицы слева на диагональную мат-
матрицу сводится к умножению на постоянную величину всех эле-
элементов каждой строки этой матрицы;
2) умножение квадратной матрицы справа на диагональную
матрицу сводится к умножению на постоянную величину всех
элементов каждого столбца этой матрицы.
О. СТЕПЕНИ КВАДРАТНОЙ МАТРИЦЫ
Если А — квадратная матрица, то Л* • А1 = Ak+l; (AkY = Akl.
Задача 5,33. Матрица
Найти Л2, А3, А* и Л8.
Решение.
«_лл-Р ЧЛ2 П-Г7
л -лл-[3 4j |3 4J-[l8 1
Лз_ЛМ_[ 7 61 Г2 1]_[32 ]
А -А л_|18 19j j^3 4J ~[93 94J
л«_/лм_Г 7 61 Г 7 6 _П57 156].
л -(A) _^l8 igj j18 19J — [468 469J'
лв_/лм_C2 31] [32 311 _ Г 3907 39061
л -\А) -[93 94J " [93 94j"~[U718 11719J*
128
Задача 5,34 (для самостоятельного решения). Матрица
Найти
От
Л3
ве
и
т.
А3
Л5.
= 1
1,
120
л [1,000
н ~ [0,200
0,6081.
о,
1,
А6-.
2001
oooj-
ЛИ
Задача 5,35 (для самостоятельного решения). Показать, что
все степени матрицы
А
Г0 1 0]
= 0 0 1,
Ll 1 Oj
начиная с пятой, не содержат элементов, равных нулю, а степени
меньше пятой этим свойством не обладают.
Задача 5,36 (для самостоятельного решения). Доказать, что
любая целая степень п единичной матрицы Е есть та же единич-
единичная матрица, т. е.
£" = £.
Е. ОБРАТНАЯ МАТРИЦА И СПОСОБЫ ЕЕ ПОЛУЧЕНИЯ
Если две матрицы А и В—квадратные одного и того же порядка,
а их произведение АВ есть единичная матрица
ЛБ = £,
то матрица В называется матрицей обратнэй к Л и обозначается
символом А~х
AA~i = E. E,1)
Следует иметь в виду, что квадратная матрица Л и ей обрат-
обратная Л коммутативны, т. е. Л • Л = А~1 ■ Л = Е.
Для того, чтобы квадратная матрица А имела обратную,
необходимо и достаточно, чтобы определитель \ А \ матрицы А
не был равен нулю, т. е. матрица Л не должна быть особенной
(вырожденной).
Формула для вычисления обратной матрицы
Если Л — союзная матрица для матрицы Л (формула D,13),
стр. 93), то обратная матрица для Л
т. е., чтобы найти матрицу, обратную матрице Л, надо составить
для Л союзную матрицу Л, найти определитель | Л | матрицы А
5 И. А. Каплан 129
и разделить Л на \А\. Следует иметь в виду, что если порядок
матрицы А большой, то получение обратной матрицы по этой
формуле требует сложной вычислительной работы. Кроме того,
существуют другие способы нахождения обратной матрицы. Мы
укажем их после нескольких упражнений на применение фор-
формулы E,2).
Операция определения обратной матрицы Л" имеет исклю-
исключительно важное значение для решения системы линейных алгеб-
алгебраических уравнений.
Задача 5,37. Доказать, что матрица
является обратной для матрицы
Г4 О
Л= 0 1
1.3 О
Г 4 0 -51
^ —18 1 24
L —3 О 4J
51
-6
4J
0 —51
1 24 =
О 4J
0 + 0. 1 + 5-0
О + 1 • 1 + (-6)
0 + 0- 1+4-0
4 • (—5) + 0-24 + 5 • 4 1 Г1 0 01
О • (—5) + 1 . 24 + (—6) -4 = 0 1 0 « £.
3-(— 5)+ 0-24+ 4-4 J LO О 1J
Легко проверить, что и произведение Л на Л в обратном
порядке, т. е. А~х • А тоже есть единичная матрица. Действительно,
4 0 —5] Г4 О 51 Г1 О О
= 1—18 1 24-0 1—6 = 0 1 0
-3 0 4j L3 0 4] Lo 0 1
-5] Г4 0 51 N
24-0 1 —6 = С
4j L3 0 4] LC
юзную матрицу д
ГЗ 1 -21
= 4 2 1 .
L3 -1 5J
= Е
Задача 5,38. Найти союзную матрицу для матрицы
:з 1 — т
А= |4 2
.3 -1 5J
A)
Решение. Напомним (см. стр. 93), что для составления
союзной матрицы Л надо найти алгебраические дополнения Ац
элементов матрицы Л, из этих элементов составить матрицу
■11 Л12 Л13
l2i Л22 Л23 B)
130
и транспонировать ее, т. е. поменять местами строки и столбцы,
сохраняя их порядок. Полученная матрица А и будет союзной
для матрицы А
" ==
А1
_А13
2
А23
А31
2
Аза_
В нашем случае
Л,1 = (— 1
~^
составляем матрицу B)
11
—з
5
— 17 —10
21 6
— 11 2
Транспонируем ее и получим союзную матрицу
C)
Задача 5,39. Найти матрицу Л, обратную матрице А преды-
предыдущей задачи.
Решение. Чтобы воспользоваться формулой E,2), надо знать
союзную матрицу А для матриц А и определитель матрицы А.
В предыдущей задаче союзная матрица А найдена. Это матрица
C). Осталось найти |Л|, Воспользуемся правилом Сарруса
= 3-2-5 + 4(— !)•(—2)+ 1 - 1 - 3 —
3 1 —2"
\А\= 4 2 1
3 —1 5_
— (— 2)-2.3 — (— 1). 1 • 3 — 4- 1-5 = 30 + 8 + 3
+ 12 + 3 — 20 = 36.
131
Подставляя значения А и j A | в формулу E,2), получаем
11
— 17
— 10
—3
21
6
5'
— 11
2
11
36
17
36
1^
12
7
12
1
т
5
36
11
36
J^
18
Проверка:
А • Л"» =
-2|
1 .
5J
U
36
17
6
5
8
1
12
7
12
6
5^
36
11
'36
J^
18
1
0
0
0
1
0
0"
0
1
Задача 5.40 (для самостоятельного решения). Найти обратную
матрицу А~1 для матрицы
Г2 1 Г
10 2
3 1 2
и показать, что АА~г = А~1А = Е.
Ответ.
—2 —1 2
4 1 —3
1
1
1
Задача 5,41 (для самостоятельного решения). Найти матрицу
Л, обратную матрице
и проверить, что А
Ответ.
А =
. Л =
А~1 =
2
3
1
л-1.
* 2
1
4
1
2
2
Л =
2
— 1
—3
1
1
0_
>
Е.
—Г
1
1_
132
Задача 5,42. Матрица
2
3
1
2
1
2
2
0
1
1
0
2
0
3
2
i
Найти для нее обратную матрицу Л и проверить, что АА~Х =
Указание. Определитель Л удобно вычислить по формуле
D,14). Применение этой формулы приведет к вычислению опре-
определителя
1 —1
-1 41 = 7.
2
Ответ
Задача 5,43. Для матриц
А =
найти обратные.
Ответ.
Го 1 01
0 0 1 и
Li о oj
_
7_
1 0 0
0 0 1
0 10
о
о
1
о
о
1
Выше было указано, что процесс определения обратной матрицы
очень трудоемкий, когда порядок матрицы п большой. Уже для
случая и=4 определение обратной матрицы в задаче 5,42 потре-
потребовало достаточно много времени. Мы укажем прием для вычис-
вычисления обратной матрицы, который не вызывает столь значительных
трудностей.
Пусть требуется найти матрицу, обратную квадратной матрице
А порядка п. Разобьем эту матрицу на блоки и представим ее
в виде
|а11 «121
L<X2l
_ Га
E,3)
133
где <ха и <х22 — квадратные матрицы, а матрицы <х12 и <х21 могут
быть как квадратными, так и прямоугольными. Пусть
-1
= а22 — а21аиАа12. E,4)
Тогда Л, обратная матрица для матрицы А, находится по формуле
._,
Ki1 + «П1*"?*^^ —«П1аиР1
-сеч
E>5)
Непосредственным умножением А на Л легко усмотреть, что
Л/Г1 = £.
Будем обозначать через Л2, Л3, Л4, ... квадратные матрицы
порядков, соответственно равных 2, 3, 4, ... (т. е. индекс при
названии матрицы указывает ее порядок).
Если обозначить
7 = Г^и. E.6)
то формула E,5) примет более простой вид:
,_, IV + V«uTV -Ve"P~ll
А I -tV Г1 J-
E,7)
Этой формулой мы и будем пользоваться на практике. Она удобна
тем, что содержит только две обратные матрицы: a^j1 и (J—1. Вы-
Выполним несколько упражнений на применение этой фррмулы. В даль-
дальнейшем операцию нахождения обратной матрицы Для данной бу-
будем называть обращением матрицы.
Задача 5,44. Для матрицы
Л =
найти обратную.
В задаче 5,42 обратная матрица для заданной была уже най-
найдена самостоятельно. Здесь мы определим обратную матрицу по
формуле E,7).
Решение. Матрицу Л разобьем на блоки и представим ее в
таком виде:
~2 1 | 1 0-
_3 2_|j_ 3_
1 2 10 2
2
3
1
2
1
2
2
0
1
1
0
2
0
3
2
1
2 10
2 0 ! 2 1
= ["«11 «12J
La2i a22J
134
У нас
2 11 Г1 01 П 21 ГО 2
11
2J!
OJ:
Чтобы найти р,' надо знать матрицу ап1, обратную матрице <хп.
Найти а очень просто по формуле E,2), которую мы здесь пе-
перепишем в виде
I аи I
Для матрицы,аи союзная матрица
а" = [-3 2J •
а определитель матрицы <хи равен
Поэтому по предыдущей формуле
-1 Г 2 —11
а" =[-3 2\'
Определяем р по формуле E,4). Для этого вычислим произве-
произведение трех матриц
Г1 21 Г 2 -11 Г1 01 Г—4 31 ^
[2 0J L-3 2j ll 3j = [ 4 -2JX
п 01 _ Г—1 91
xLi 3J L 2 -6j;
m 21 f—1 91 Г1 —
a12 =
71
7J.
Чтобы использовать формулу E,7), надо вычислить матрицу В,
обратную матрице р. Для этого применим формулу E,2). Союзная
для 8 матрица
й \7 71
Р"Ь- lJ'
а | р | = 7. Поэтому
р-1 = |.[7 ^
135
Теперь переходим к вычислению элементов матрицы E,7).
Начнем с ее элемента а + ^л1ЛаТ^- Прежде всего определим
f по формуле E,6):
* \7 71 Г1 21 » Г21 141
ТЪ l] [2 J [ j
-1
_х Г 2 -11 Г1 01 Г 1 -31
па"=[_3 2J Ll SJ^L-I 6j;
_f 1 —3 . J_[21 14] 1 f 15 141
r L—1 6 * 7 [ 2 oj~ 7 4—9 — 14Г
_ 1 Г 15 141 Г 2 — П i Г—12 131
"T'[-9 -14J L-3 2\-T'l 24 -191 ~
2 —1
—3 2
12 13'
T T
24 19
7 7 J
Первый элемент первой строки в матрице E,7) равен
[2
—3
2
3 2
12
"Т
24
7
13"
T
19
7
7
3
.7
6"
7
5
7-
Второй элемент первой строки
-i R-i Г 2 -1! Г1
Первый элемент второй строки в формуле E,7)
±.[7 7|
7 [0 11
_, -2.
14] Г
oJ'L-
2 —1
3 2
° —
Второй элемент второй строки
Подставляя найденные элементы матрицы E,7), получаем окон-
окончательно _
2 1.1"
7 7
2. А
7 7
0 -1
1
1
О
7
1
У
1
1
т
136
К решению задачи можно подойти и иначе. Разобьем матрицу
А на блоки так:
'2 1 110
2
3
1
2
1
.2
2
0
1
1
0
2
2
_2_
О
1
2~
3
2
"Г"
Теперь уже
2
3
1
1
2
2
1
1
0
; <*i2 =
0
3
2
а21=[2 0 21; а22 = 1.
Для применения формулы E,7) надо найти матрицу а, обрат-
обратную матрице <хи. Это можно сделать так: рассмотреть матрицу
1 Г
Л3= 3 2 1
1 2 0_
и найти ей обратную по той же формуле, разбив ее на блоки
следующим образом:
1 I Г
Здесь
I 3 2_| 1 j
и
= А =
1
и
2 j О
[ j JJ a2i = [l, 21; а22 = 0.
Матрицу, обратную Аг = L Л, надо найти непосредственно по
формуле E,2).
Если провести все вычисления, то окажется, что
"—2 2 —Г
.4—3 1.
Остальные вычисления следует провести самостоятельно.
Задача 5,45. Найти обратную матрицу для матрицы
765
7 10 8 7
6 8 10 9
5 7 9 10
137
Решение. Разобьем матрицу А на блоки
■41
6
_5
•41
10
8
1
■41
6 1
8 I
10 1
9
5~
■41
9
10_
—
_5
3
7 9
5
■41
9
10
Здесь
а.п— А3
5 7 6"
7 10 8 ; а12 =
6 8 10_
= [5. 7, 91; а22 = 10.
Для применения формулы E,7) надо найти матрицу а, обрат-
обратную матрице ап = А3, т. е. найти сначала Л. Сделаем это также
по формуле E,7).
Представим А3 в виде блочной матрицы
5
6
7 1
10 |
8 1
8
ю_
_6
8
6"
8
10
А3 =
Полагаем, что здесь
7 10J' Kia = [ 8 J: ап = [6> 8]; а22 = 10-
Чтобы использовать формулу E,7) для вычисления Л, надо найти
а = А~\ Это следует сделать непосредственно по формуле E,2).
Окажется, что
Ь-1 - А-г _ [ 10 -71
аи ~Л2 -[_7 5J'
При вычислении А31 получим р = 2,
18
— 11
2
— 11
7
1
—2
1
138
При вычислении А~* найдем, что Р = у,
[50 —30 -15 1
—30 18 9 ;
— 15 9 4,5 J
с
«u
50 —30 —15
30 18 9
15 9
68 -41 -17
—41 25 10
— 17 10 5
Окончательно
Г 10 1
-fa = [10, -6, -3J.
68 —41 —17 10"
—41 25 10 —б
— 17 10 5 —3
Ю —6 —3 2
Задача 5,46 (для самостоятельного решения) Найти матрицы,
обратные данным:
3) Л4 =
Ответ.
1) V =
[
2
1
3
А
_1
1
1
) +
1
1
0 2
1 2_
3
0
1
_0
2"
—3
— 1
i-i
1
0
J
2
; 2)
—2
2
—2
1
2)
1
1
_1
1
А3
0
2
—3
2
—2
0
3
—6
1
4
2
— Г
1
—2
1_
=
— -
—4""
— 1
6
— 10
2
5
8
•
5"
8
5
!2
5
*
3
6
9_
•
"I
"
"5 ~1
139
Обращение матрицы является весьма существенным при реше-
решении систем линейных алгебраических уравнений.
На этом занятии мы выполнили упражнения, которые знакомят
с принципиальной стороной этого вопроса, с основной формулой
для получения обратной матрицы [формула E,2)] и ее примене-
применением, а также упражнения по формуле E,7), которая не требует
столь громоздких вычислений, как формула E,2).
С другими численными методами получения обратной матрицы
читатель может познакомиться по книге Р. Фрезер, В. Дункан
и А. К о л л а р. «Теория матриц и ее приложения к дифференциаль-
дифференциальным уравнениям и динамике» (Изд-во «Иностранная литература»,
Москва, 1950).
ШЕСТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Обращение треугольной матрицы (верхней и нижней).
Разложение квадратной матрицы на произведение двух треугольных. Вычис-
Вычисление обратной матрицы при помощи представления ее в виде произведения
двух треугольных матриц.
I. ОБРАЩЕНИЕ ВЕРХНЕЙ ТРЕУГОЛЬНОЙ МАТРИЦЫ
Краткие сведения из теории
Сущность метода обращения верхней треугольной матрицы
разберем на матрицах четвертого порядка, а формулы для обра-
обращения верхней треугольной матрицы любого порядка приведем
без вывода. (Заметим еще раз, что обращение матриц имеет исклю-
исключительно большое значение для решения систем линейных алгебра-
алгебраических уравнений, которыми, мы будем заниматься на следующем
практическом занятии)
Пусть А — верхняя треугольная матрица четвертого порядка
А =
ап
О
О
0
а12
а22
0
0
а13
а23
а33
0
а21
аи
а44_
а искомая обратная ей матрица, элементы которой aw подлежат
определению, запишется в виде
all
«21
«31
12
3
*23
4
;42 a43 a44.
По определению обратной матрицы должно выполняться равенство
Д-М = Е,
т. е.
л21
-«41
«12
«22
a32
«42
«13
«23
a33
«43
«14
«24
a34
«44.
«11
0
0
.0
au
«22
0
0
«13
«23
a33
0
24
1
0
0
0
0
1
0
0
0
0
1
0
0"
0
0
1
141
Используя правило умножения матриц, перемножим матрицы
в левой части равенства
а13сЗЗ
аззсзз
«41а12
allOl4 +
a2ia14 +
+ а13С34 +
+ a23aS4 +
+ Оз3а34 4-
+ 043034 + «44^4.
0 0 0
10 0
0 10
0 0 0 _
Исходя из определения равенства двух матриц, для отыскания
неизвестных величин получаем уравнения, сравнив соответствую-
соответствующие элементы первых строк,
яцОц = 1;
anai2 + a12a22 = 0;
«цО13 + а^Огз + »1зОзз = 0;
а, 1014 + a12a<j4 + ai3a34 + амО44 = 0.
A)
B)
C)
D)
Из этих уравнений следует:
из A) <хп = ~;
из B) а12 =
из C) au=*-2u£«L±
из D) a14 = —
°12а23
<*зз
E)
F)
G)
(8)
Проделав аналогичную работу для второй, третьей и четвер-
четвертой строк, получим для второй строки
a21au = 0; (9)
a21a12 + аис22 = 1; A0)
a21ai3 + a22a23 -f a23a33 ==0; A1)
«2iC14 4" «22024 4" <*23О34 4" «24О44 = 0 A2)
из (9) а,, = 0. A3)
142
С учетом, что а21 = 0, получаем:
из A0) «22=^; A4)
из (И) а23 = — = —-—а22а23; По)
3 аЗЗ
3
На П91 г, — а21°14 + а22°24 + а23°34 ' V^ _ п (\р\
из (U) а24 = — = —— 2^ <*-2kakf По)
Для третьей строки
аз1аи = 0; A7)
а31а12 + а32а22 = 0; A8)
«31а13 Ч" «32а23 ~Ь «ЗЗаЗЗ == 1» A9)
«31а14 + «32^24 + <*ЗЗа34 + «34а44 = 0. B0)
Из этих уравнений следует:
из A7) asl = 0. B1)
Учитывая, что <х31 = 0, из A8) получаем
«32 = 0, B2)
а учитывая, что и а31 = 0, и а32 = 0, находим:
из A9) «зз = ~; B3)
из B0) я34 = -^ = -~ «33^34- B4)
И наконец, для четвертой строки имеем
«41011 = 0; B5)
«41^12.+ «42^22 = О? B6)
«4ia'l3 + «42^23 + «43^33 = 0', B7)
а41а14 + а42а24 + «4зС34 + «44«44 = Ь B8)
Из B5), B6) и B7) следует, что
а41 = 0; B9)
а42 = 0; C0)
«43 = 0, C1)
а с учетом этого из B8) получаем
«44=™- C2)
Равенства (9), B1), B2), B9), C0) и C1) показывают, что
равны нулю те элементы обратной матрицы А, у которых пер-
первый индекс i больше второго индекса /, т. е. если i > j, то
«,7 = 0. F,1)
143
Из равенств E), A4), B3) и C2) диагональные элементы обратной
матрицы А'1, у которых первый и второй индексы равны (i = j),
определяются так:
1111
aii=^—; а22 = ^—; «зз = х—; «44 = г—»
а11 а22 "88 а44
что можно объединить одной записью: если i = /, то
а" = ^' F,2)
По формулам F), G), (8), A5), A6), B4) и C2) определяются
те элементы обратной матрицы для верхней треугольной, у кото-
которых первый индекс i меньше второго индекса / (£ < /), т.е. эле-
элементы, стоящие над главной диагональю. Полученная по этим
формулам обращенная матрица будет также верхней треугольной.
Когда верхняя треугольная матрица имеет порядок п, эле-
элементы обратной ей матрицы находятся по аналогичным формулам,
которые имеют следующий вид:
если i = /, то аи = —; F,3)
если i > /, то aij = 0; F,4)
/-1
если i < /, то «// = — ^- Jj a'*c*/- F>5)
Например, по формуле F,5) элемент обратной матрицы
4
+ Оцв4«)- F,6)
Замечания. Применяя формулу F,5), надо иметь в виду,
что будут равны нулю те произведения, в которых первый индекс
элемента а больше второго индекса. Можно указать простое пра-
правило для определения элементов обращенной верхней треугольной
матрицы.
1. Определить диагональные элементы обращенной матрицы
пэ формуле F,3).
2. После этого матрицы подписать одну под другой.
3. На места элементов, стоящих ниже главной, вписать нули.
4. Чтобы определить элемент, стоящий над главной диагональю
обратной матрицы, надо составить алгебраическую сумму произ-
произведений элементов, стоящих в обращенной матрице Л, левее
определяемого, на соответствующие элементы того столбца мат-
матрицы А (т. е. той матрицы, для которой ищется обратная), в ко-
144
тором стоит определяемый элемент. Эту алгебраическую сумму
надо разделить на диагональный элемент матрицы Л, стоящий
в том же столбце, что и определяемый элемент. Определяемый
элемент равен этому частному, взятому с обратным знаком.
По этому правилу выражение в скобках в F,6) получается
так: искомый элемент als матрицы А~х находится в первой строке
и пятом столбце. Перед ним в первой строке обратной матрицы
Л стоят элементы аш а12, а13, и а14, а в пятом столбце матрицы
Л — элементы a1S) a23, Язв и аи- Составляется алгебраическая
сумма произведений первого элемента в первой строке матрицы
Л на первый элемент в пятом столбце матрицы А, второго
элемента в первой строке матрицы Л на второй элемент в пятом
столбце матрицы Лит. д. Для уяснения этого правила решим
несколько задач.
Задача 6,1. Найти обратную матрицу для матрицы
Л =
3 1 2 Г
0 8 3 2
0 0 6 4
0 0 0 4
Решение, п. 1. Находим диагональные элементы аш а22, а33
и а44 обращенной матрицы по формуле F,3)
пп. 2 и 3. Подписываем матрицы одну под другой и вписываем
нули на места элементов, стоящих под главной диагональю
•3 1 2 Г
0
0
0
1
3
0
0
0
8
0
0
\
\
1
8
0
0
3
6
0
\
\
ll
т
0
2
4
4_
\
1
4
п. 4. Определяем элементы а,,-, стоящие над главной диагональю
(t < /), по формуле F,5), пользуясь указанным в п. 4 правилом.
145
1
3
0
0
0
1
3
■ 1
8
1
8
0
0
1
0-
0-
1
24
(-1)
'+!■
+ 0-
4
-1
0
0
0
1
3
0
■•+(
4
2 + (-
4
1
4
1
24
1
8
0
0
■+(-
6
•2 + 1
6
1
6
0
144/
13
144
1
— T6
6" "
0
A)-
• 3
4
n
1
b
1~
36
0
1
"".
l
4
3
1
36
-13
144
1
16
Для проверки перемножьте матрицы А и Л" и убедитесь,
что получится единичная матрица
~1 0 0 0~
0 10 0
0 0 10
_0 0 0 1.
При решении этой задачи все элементы обратной матрицы
были представлены в виде простых дробей. Мы так поступили
для облегчения контроля. На практике же все вычисления ведутся
в десятичных дробях.
Отметим, что вычисление $] а/*а*/ по формуле F,5) с помощью
настольных клавишных счетных машин или на арифмометре не
требует никаких промежуточных записей, так как эти машины
позволяют производить накопление произведений.
146
Задача 6,2 (для самостоятельного решения). Найти матрицы,
обратные верхним треугольным:
2 5 4 3"
0 3 4 2
0 0 3 1
0 0 0 4
2) А =
3) А =
—3 2
0 2
0 0
0 0
О О
О О
1 2
О —1
О О
О 0
О О
0 5 4 6
■4 0 2—1
1—3 2 7
6 3 0 1
0 0 4 2
0 0 0 3
-1 3
2 1
5 —2
0 1
о о
и проверить ответ умножением А на А~1 (произведение должно
быть единичной матрицей).
Ответ. 1)
Д-1 _
+4
5"
72
1
18
1
Т2
\_
4
2)
0 —1
о о
о о
о о
3)
о
о
о
о
5
о
о
-1 -1
3 3
Т 2
0 1
о о
о о
31
5
2
т
10
т
7
20
о -4-
и
9
2
1
г
о
4_
~2"
5_
' 4
J_
2
0 -^
71"
27
\3,
3
_7_
Т
1
9"
4
0
Ю*
147
«I. ОБРАЩЕНИЕ НИЖНЕЙ ТРЕУГОЛЬНОЙ МАТРИЦЫ
Поступая так же, как и для обращения верхней треугольной
матрицы, получаем формулы для определения элементов матрицы,
которая обратна нижней треугольной матрице
~Ьи 0 0 0... 0'
ь22
о
0...
0...
Р21
Рм
bn2 Ьп3 bn
О 0 0... 0"
р22 о . о... о
Рзг Рзз 0... 0
S 3 9 й
til гя2 гиЗ гп4"' ггы
При i < / 8,,- = 0 F,7)
(т. е. все элементы, находящиеся над главной диагональю, равны
нулю).
При i = j Pa =5-.
По этой формуле находятся диагональные элементы.
При I > / fa = — -
F,8)
F,9)
По этой формуле определяются элементы, находящиеся ниже
главной диагонали. Из приведенных формул видно, что обратная
матрица для нижней треугольной является также нижней треуголь-
треугольной.
Пример применения формулы F,9). Пусть требуется определить
Р53 =
В скобки заключена алгебраическая сумма произведений элемен-
элементов, начиная с первого, того столбца, в котором находится опре-
определяемый элемент, на соответствующие элементы той строки мат-
матрицы В (той матрицы, для которой ищется обратная), в которой
стоит определяемый элемент. Среди произведений, стоящих в скобке,
могут быть и равные нулю. Это будут, те произведения, у которых
множитель р имеет первый индекс меньше второго.
148
Задача 6,3. Найти матрицу, обратную нижней треугольной
матрице
'1 О О СГ
0 2 0 0
2—3 4 0
3 2—13
Решение. Прежде всего по формуле F,8) определяем диаго-
диагональные элементы: £ц = -г- = т = 1; р22 = г- = -н-; Рзз = Л =
Вписываем эти элементы в главную диагональ и вписываем
нули на места над ней. Теперь следует определить элементы р21;
31» Р32> Р41> Р42. Р43-
Эти элементы вычислим по формуле F,9). Для удобства по-
помещаем матрицу В под матрицей В.
1
0
2
3
0
2
—3
2
1
~~ 2
0
0
4
— 1
1
•(!•
0
0
0
3
0) =
—L Г1 . 2 + 0 • (—3) ] =
— -g- I столбец
0
\_
2
_ 1 [о • 2 + у • (-3)] = ~ II столбец
о
о
1
т
III и IV
столбцы
149
1
0
1
2
7
"б""
0
1
7
3
8
5
24
0
0
1
4
1
12
0
0
0
1
3
Задача 6,4 (для самостоятельного решения). Найти
обратные следующим:
1
2
3
0
3
1
0
0
4
3)
' 2)
2 0
1 2
2 2
1 3
В =
0 "
0
3
—2
" 1
—2
4
2
0 0"
0 0
0 0
4 0.
0
1
5
1
0
0
3
1
(У
0
0
2
_3 —2—12 5
и вычисления проверить умножением В на В К
Ответ.
2)
1)
1 __
■
е
1
~т
—6
~48
7
40
1
2
3
7
~Т2 "
1 0
> 1
} ~т
1
т
0
1
7
~т
~24
20
0
1
3
1
2
0
0
т
1
6-
0
0"
0
1
т_
0
0
т
1
"
__
1
0"
0
0
1
7_
0
э
1
4
1
0 '
»
0
0
0
0
1
5
150
III. РАЗЛОЖЕНИЕ КВАДРАТНОЙ МАТРИЦЫ НА ПРОИЗВЕДЕНИЕ
ДВУХ ТРЕУГОЛЬНЫХ
Основные сведения из теории
Многие методы решения системы линейных алгебраических
уравнений основаны на представлении квадратной матрицы (не треу-
треугольной) в виде произведения двух треугольных матриц, из кото-
которых одна нижняя, а другая верхняя. Для любой квадратной мат-
матрицы
~ап о12 • • • а1п
О><£1 CI22 * " * ^2"
ап2
такое представление является возможным и единственным при соб-
соблюдении следующих условий:
1) диагональные элементы одной из треугольных матриц от-
отличны от нуля;
2) главные диагональные миноры отличны от нуля (так назы-
называются миноры определителя матрицы, у которых на главных диа-
диагоналях стоят диагональные элементы матрицы).
Такими минорами, например, будут:
а21
2
«22
1
ап
а21
aai
2
(hi
а13
Сад
а-зз
а также и сам определитель матрицы | А |.
Рассмотрим такое представление на примере квадратной мат-
матрицы четвертого порядка (п = 4). Пусть требуется матрицу
Й22 а23
о42 Щ3
представить как произведение двух треугольных матриц (нижней
и верхней)
С =
Cll
c21
C31
0
C22
c3i
0
0
C33
0
0
0
С42
И В =
Ь13
Ьы
0
0
0
&22
0
0
O23
^33
0
ist
т. е. предполагается, что имеет место равенство
о21
а3}
а41
а12
а22
а32
«42
а13
о23
Язз
ai3
аи
о24
«34
О44
Сц 0
с21 с
C3i С
Си С
0
22 0
32 С33
42 ^43
о -
0
0
С44
*
~Ьц
0
0
0
ь12
Ьц
0
0
ь13
Ьгз
Ь3з
0
^34
F,10)
Задача заключается в определении элементов сц (i > /) и Ьц (i < /).
Таких неизвестных элементов у нас 20, так как пг + п = 16 +
+ 4 = 20. Это следует из формулы для суммы членов арифмети-
арифметической прогрессии.
Перемножим матрицы в правой части равенства F,10) по пра-
правилу умножения матриц и, пользуясь равенством
приравняем элементы матрицы СВ соответствующим элементам
матрицы А.
Получим такие равенства:
-О)
B)
СцЬ13 = о13;
= а14;
— о21;
c21bu + c22fc24 = о24;
с31Ьц = а31;
= а32;
С41ЬП = о4ь;
c43b
3i
C)
D)
E)
(8)
(9)
Щ
F,11)
A3)
Мы получили 16 уравнений для определения 20 неизвестных.
Поэтому четырем неизвестным можно приписать любые значения,
причем для этого имеется бесконечное множество возможностей.
Пользуясь произвольностью выбора значений четырех неизвест-
неизвестных, положим, что каждый из четырех диагональных элементов
в первой матрице правой части F,10) равен единице:.
сХ1 = 1; с2з = 1; c3S = 1; С44 = !•
152
Тогда первые четыре уравнения в F,11) позволят определить
неизвестные элементы bu, b12, bla, bu, и окажется, что
Ьц = пц; Ь1г = ап; Ь13 = а13; Ьи = ан. F,12)
Из уравнений E), (9) и A3) с учетом, что bu =au, получаем:
Зная, что с22 = 1, из уравнений F), G) и (8) находим
1
&22 — ^22 С21^12 == а22 — Zj С2£^А2>
й= 1
1
&24 = fl24 *
ft = l
1
Здесь символ суммирования ^ , собственно, ничего нового не
дает. Мы его ввели для последующих обобщений — см. формулы
F,19) и F,20).
Замечание. Как покажут дальнейшие вычисления, сумми-
суммирование производится по индексу k, который изменяется от 1 до
i — 1, где i — первый индекс у определяемого элемента. В дан-
данном случае у определяемых элементов b22, b23 и b2i первый индекс
1 = 2.
Из уравнений A0) и A4) находим сзг и с42:
r °82 C31^12
С32 Г —
_ а4г — c4lblt k=i
С42 т — т .
°22 °22 )
1 ,
В символе 5j индекс суммирования k изменяется от 1 до 1,
*=i
т. е. фактически принимает только одно значение, равное 1, при-
причем 1, стоящая сверху, есть 2—1, т. е. /—1, где /' — второй
индекс у определяемых элементов с32 и с42. Как уже было заме-
замечено выше, введение такого символа в этом месте ничего нового
не дает, но необходимо для ссылок при последующем обобщении
этих формул.
153
Из уравнений A1) и A2) определим элементы Ьи и Ь33 (учи-
(учитывая, что с33 — !)•"
2
= 2j
кк 1
2
F,16)
2
В этих формулах индекс суммирования k в символе Y изме-
няется от 1 до 2, а стоящее сверху этого символа число 2 = 3— 1,
т. е. i — 1, где i — первый индекс у определяемых элементов Ь33
И Ьм.
Теперь из уравнения A5) найдем
г
2
В символе 2 индекс суммирования k изменяется от 1 до 2,
k=i
причем число 2, стоящее сверху, есть/— 1, где / — второй индекс
у определяемого элемента с48.
Наконец, из уравнения A6), учитывая, что с44 = 1, получаем
з
Ьи == аи — c41feL — с42&24 — c43fe34 = вм — Е eikbki. F,18)
3
Обратим опять внимание на то, что в символе £ индекс сумми-
рования & изменяется от 1 до 3, причем число 3, стоящее сверху,
есть 4—1, т. е. i—1, где i — первый индекс у определяемого
элемента fc44.
Заметим, что определение элементов Ьц и Сц чередуется: по
формулам F,12) определяются элементы bu(j=>.\, 2, 3, 4) затем
по формулам F,13) — элементы оа (i = 2, 3, 4). После этого опять
определяются элементы by (/ = 2, 3, 4) по формулам F,14), а вслед
за этим по формулам F,15) — элементы ci2 (i = 3, 4), потом — опять
элементы Ь3/(/=3, 4) по формулам F,16), а за ними — элементы
С43 по формуле F,17) и, наконец, определяется элемент bti по фор-
формуле F,18).
Если объединить формулы F,14), F,16) и F,18) в одну, то
окажется, что
Ьц = а„ - Л clkby- (I < I) F,19)
(i = 2, 3, 4; I = 2, 3, 4),
154
а объединение формул F,15) и F,17) дает
c// = -^—; («>/) F,20)
(i = 3,У/4; / = 2, 3).
Формулы F,19) и F,20) остаются верными для представле-
представления квадратных матриц любого порядка п в виде произведения
двух треугольных матриц.
Легко показать схематически последовательность, в которой
определяются элементы Ьц и cit: сначала заполняются строки, а по-
потом— столбцы (см. табл. 1)
Таблица 1
ап а12 а13 аы~
-а41
Озз
а43
1 0 0
с21 1 0
с31 с32 1
Lc41 С42 С43
0~| Г6П 612
0 II 0 622
Of 0 0
iJ Lo 0
68S 634
о ^
"и
с21
&22
^32 1
!
ь33
624
b3i
— первый шаг
— второй шаг
— третий шаг
— четвертый шаг
/-1
Представление квадратной матрицы в виде произведения ниж-
нижней и верхней треугольных матриц производится так: для удобства
вычислений записывается данная матрица А, а под ней — матрицы
С и В, как указано в табл. 2, на стр. 156, причем вместо диаго-
диагональных элементов матрицы С вписываются единицы.
Первая строка матрицы В и первый столбец матрицы С за-
заполняются так, как указано в табл. 2:
1. На основании формул F,12) в первую строку вписываются
соответствующие элементы матрицы А, а элементы первого столбца
матрицы С равны соответствующим элементам первого столбца
матрицы А, разделенным на его первый элемент — формулы F,13).
2. Элементы, стоящие над ступенчатой линией, находятся по
формуле F,19) так: берется соответствующий элемент матрицы А
и из него вычитаются произведения элементов, стоящих в той же
строке левее и в том же столбце выше, что и вычисляемый эле-
элемент, причем первый элемент строки умножается на первый элемент
столбца, второй элемент строки — на второй элемент столбца и т. д.
155
Таблица 2
аг1
«81
а*
а12
а&
«32
а,
ai3
«33
3
6l2=a12
1
*»-
«14
024
4
«44
= «13
^23
Саз = 1
^43
3
Ьи
»24
^34
С44=1
4
3. При вычислении же элементов, расположенных под ступен-
ступенчатой линией, поступают так же, как в п. 2, но полученный ре-
результат делят на диагональный элемент ЬA(\ = 2, 3), стоящий в том
же столбце (формула F,20), что и определяемый элемент. При вы-
вычислениях с помощью арифмометра или настольных клавишных
машин никаких записей вне таблицы производить не придется.
Этот алгоритм вычисления элементов двух треугольных мат-
матриц— нижней и верхней, на которые разлагается матрица Л, легко
распространяется на квадратные матрицы любого порядка, что
будет показано на ряде примеров, помещенных ниже.
Задача 6,5.
Матрицу
А =
- 1
—1
2
„ 4
2
2
4
3
3
4
5
2
4"
з
—2
1.
представить в виде произведения нижней и верхней треугольных
матриц.
Решение. Используем только что указанный порядок дейст-
действий и расположим действия, как в табл. 2, причем приведем
подробно все выкладки в каждой клетке и будем придерживаться
порядка заполнения клеток, указанного в табл. 1:
156
1
—1
2
4
2
2
4
3
3
4
5
2
4
-3
—2
1
•1'
-т—
2
1
2-<-1)х
Х2=4
4-2-2 _Q
4
3 — 4-2 5
4 ~ 4
3
4_(_1).3 = 7
1
5—2.3—Ох
Х7 = -1
2-4.3-И).7 5
—1 4
4
—3 — (—1) .4 = 1
—2—2-4 — 0-1 = —10
1
■-«-(-4)-
Итак, нижняя треугольная матрица
' 1 0 0 0"
— 1 10 0
2 0 10
4 4
а верхняя треугольная матрица
ь
Легко проверить,
Сделайте это.
} =
что
1
0
0
0
2
4
0
0
СВ
3
7
— 1
0
-А
4
1
— 10
5
4
157
2
1
5
—4
3
1
2
1
2
5
2
3
2
2
—3
3
2
2
— 1
—3
1
9
~~ 2
2_y.(_3) ]9
9 9
2
9
2
8
~~ 9
-i--|-(-3)
9
2
7
~ 9
4
—2
—1
0
1
4
1
1 2 ' 4
23
~ 9
23
9
40
~ 23
,_1.4_I.(_4)
23
9
17
~23
5
2
3
—5
2
5
ЙД
i
_5 _ (~2)x
~{~!h
233
-~~23"
2 3 5 7_
Xl 2} 23X
/ 233\ 26
4 23/ 233
—I
4
2
0
4
—1
2
0-
-
1
-|.«-o-
J9 _9 5
- (-2)-(-!)-
154
~ 23
♦-4 •<-!>-
7 9 17
9 2 23х
/ 154\ 1153
X\ 23/ 233
158
Решение было проведено в простых, а не десятичных дробях,
как это обыкновенно делается на практике, для облегчения после-
последующей проверки.
Проведем вторично подробное решение еще одной аналогичной
задачи для матрицы пятого порядка.
Задача 6,6.
Матрицу
2
1
5
—4
3
—3
3
2
2
j
4
2
— 1
0
1
5
2
3
—5
2
— 1
4
2
0
4
представить в виде произведения нижней и верхней треугольных
матриц.
Решение. Поступаем так же, как и в предыдущей задаче:
искомые матрицы подпишем под матрицей А, неизвестные эле-
элементы определяем в порядке, указанном в табл. 1, а их число-
числовые значения — по приведенному алгоритму (см. пояснения, дан-
данные к табл. 2). Решение проведено на стр. 158.
Таким образом, данная матрица равна произведению двух тре-
треугольных матриц:
О
1
О
О
О 1» .
9 ° ч"
19
9
40
23
_7_ 17
9 23
0 0
0 0
0 0
1 0
Л 1
233 \
2 —3
о 4
0 0
о о
о о
4
-4
23
' 9
о
о
5
1
2
76
9
233
23
о
— 1
9
2
—5
154
3"
1153
233
Задача 6,7 (для самостоятельного решения). Представить ма-
матрицы
1)
2 3
5 2.
4 5
1 2
— 1 4
—2 3
—7 4
3 4
4 0
2
2)
3)
—2
—5
3
1
5
—4
4
4 —2
3 4
О -7
2 3
-2 1
2 0
-1 2
0 5
1 3
3
—2
2
— 1
4
4
3
2
—2
159
в виде произведения нижней и верхней треугольных матриц,
лученные ответы проверить умножением.
Ответ.
По-
2)
1
0
2,5 1
2 0,1818
0,5 —0,9909
1 0
5 1
—4 —0,7272
—4 —0,8182
3)
X
-1
0,5
1,25
1.0
_0,5
~4
0
0
1
—0,6964
0
0
1
0,7183
0
1
0,5
2,5
-1,5
0
0 —2
0
0
0
0
0
0
4
1
-5
0
0
0
0
0
'J
0"
0
0
0
0
1
0,8185
0,4545
5
2 —3
0 -
0
0
-5
0
0
2
0 —11
0
.0
>
—'
—2
5
—7
— 1,7726
0
0
0
0
0
0
1
— 1
0,5
—5,0909
0
0
2
6,4544
0
0"
0
0
0
M542 1
3
-3,5
0
—4,7500
31.2324
4
у
—2,7274
—0,5357_
4 "
— 17
5,6376
—3,9589_
X
Задача 6,8. При определении неизвестных элементов сц и Ъц
мы приняли, что Си = 1 (t = 1, 2, 3, 4). Показать, что если
взять bu= I (i = 1. 2, 3, 4), то неизвестные элементы Ьц и сц
матриц, стоящих в правой части формулы F,10), определятся
по следующим формулам:
Ьп = Ьг% = &33 = Ьи = 1
O/i —
, если i < j
пц
cikbkl, если i > /
F,21)
160
Указание. В этом случае матрица А представляется в виде
произведения таких двух треугольных матриц (нижней и верхней):
an
a3l
am
Ol2
a22
aS2
а„2
Ol3 • • •
a23 ...
033 • • •
on3 • • •
X
aln"
агп
a3n
ann-
~1 t
0
0 (
'l2
bv
) 1 *
_0 0 0
cu
C21
C31
• • *
• •
0
c22
C32
К
1
С
)
0
сзз
с„з
1
•
... 0
... 0
... 0
... с
X
Последовательность определения элементов с и (i > f) и Ь// (t</)
указывается такой схемой:
Сц = .
II
с41 = 41 |
С22 ^2з
III IV-
С32
С42
С31
V
С43|
-»■
VI—4
[ и т.
->-
Д.
(Римские цифры над стрелками указывают последовательность,
в которой должны определяться элементы).
Задача 6,9. Пользуясь формулами F,21), представить матрицу
А =
- 2 4 6 21
4 2 2 1
12 11
—3112
в виде произведения двух треугольных матриц нижней и верхней.
Решение. Поступим так же, как и в предыдущем случае.
Напишем матрицу А, а под ней матрицы С и В — см. формулу
F,10), причем вместо диагональных элементов матрицы В впи-
впишем 1. В нижней таблице подробно выполнены все вычисления по
формулам F,21).
6 И, А. Каплан
161
2
4
1
—3
2
1
4
1
—3
4
2
2
1
2
2—4-2 =
= —6
2—1-2=0
1 — (—3) - 2 =
= 7
2
1-
1 —
6
2
1
1
3
— 4-3
—6 '
-1.3 =
(-3) • 3
5
3
-3
1
— 7x
5
~T
2
1
1
2
1
1 — 4-1
—6
1 — 1-1 —
2
2-(-3-1)
0-
3
2
1
2
1
2 0
7X
1
Таким образом, матрица А представлена в виде произведения
2
4
1
—3
.0
—6
0
7
0
0
2
5
"""IF
0~
0
0
3
•
~1
о
0
0
2
1
0
0
3
5
3
1
0
1
1
2
0
1
На стр. 156 было указано правило преобразования матрицы
в произведение двух треугольных для случая, когда с,7^= 1. Вы-
Выведите аналогичное правило для рассматриваемого случая, когда
в матрице В диагональные элементы Ьн— 1.
Задача 6,10. Полагая, что в формуле F,10) элементы Ьи= 1,
представить указанные матрицы в виде произведения двух тре-
треугольных матриц:
1)
1
0
3
1
4
5
—4
0
5
1
5
1
7~
—2
1
2
3
2
2
1
6
3
4
1
9
0
— 1
2
—3
1
2
— 1
162
Ответ:
1)
0
3
1
-з
2
2
1
0
5
— 16
—4
0
— 1
0
—1
0
0
— _
5
16
т
0
0
—7
5
о-
0
0
99
0~
0
0
~т
•
•
0
0
_0
0
0
0
4
1
0
0
2
1
0
0
5
1
т
1
0
3
6
1
0
7
2
5
66
Т7
1
— 1
—3
4
1
2)
Замечание. Во всех предыдущих вычислениях мы пред-
представляли матрицу в виде произведения двух треугольных: пер-
первый сомножитель был нижней, а второй — верхней треугольной
матрицей. Однако такой порядок сомножителей не является обя-
обязательным и матрицу можно разложить на произведение двух
треугольных матриц так, чтобы первый сомножитель был верх-
верхней, а второй — нижней треугольной матрицей. Относящиеся
к этому случаю формулы мы указывать не будем.
IV. ОПРЕДЕЛЕНИЕ ОБРАТНОЙ МАТРИЦЫ ПРИ ПОМОЩИ
ПРЕДСТАВЛЕНИЯ ЕЕ В ВИДЕ ПРОИЗВЕДЕНИЯ ДВУХ
ТРЕУГОЛЬНЫХ МАТРИЦ
Задача 6,П. Доказать, что если матрица А представлена в виде
произведения двух матриц С и В, т. е.
А = СВ, A)
то матрица А~г, обратная матрице А, определяется по формуле
Доказательство. Обе части равенства A) умножим слева
на матрицу С, обратную матрице С
= С~1СВ,
B)
по произведение С~ХС есть единичная матрица Е, т. е. С~1С = Е,
а потому равенство B) перепишется так:
-М = £5 =
C)
так как произведение матрицы на единичную матрицу в любом
порядке оставляет эту матрицу без изменения. Теперь обе части
163
равенства C) умножим слева на матрицу В, обратную матрице В,
и получим
S-iC-M = В'1В = Е.
Таким образом, произведение матриц
Б-iC-M = Е. D)
Перепишем D) в виде
Усматривая, что произведение матриц (В^С) и А есть еди-
единичная матрица Е, заключаем, что матрица В~1С~1 является
обратной для матрицы А, т. е. матрица В~1С~1 есть А~1. Итак,
А'1 = В-Ч:-\ F,22)
что и требовалось доказать.
Заключение. Матрица, обратная произведению двух матриц,
равна произведению обратных матриц сомножителей, взятых в об-
обратном порядке.
Можно доказать, что и вообще, если матрица А равна произ-
произведению п матриц
А = А1 ' А2 • А3 ... Ап,
то
А'1 = А~1 ... Л-M-'V
(доказательство проведите самостоятельно).
Читателю уже известно, что любая матрица А, удовлетворяю-
удовлетворяющая условиям, указанным на стр. 151, может быть представлена
в виде произведения двух треугольных матриц С и В, а обраще-
обращение треугольной матрицы, как видно из предыдущего, не пред-
представляет больших затруднений (задачи 6,1—6,4).
Таким образом, для обращения матрицы А надо: 1) предста-
представить ее в виде произведения двух треугольных матриц С и В
(нижней и верхней, или верхней и нижней), 2) определить ма-
матрицы, обратные этим треугольным, и 3) полученные в п. 2 матрицы
перемножить в обратном порядке, т. е. если
А = СВ,
то
А-1 = В-'С. F,22)
Формула F,22) дает еще один способ получения обратной матрицы.
Итак, задачу определения обратной матрицы при помощи ис-
использования двух треугольных можно считать решенной. Однако
можно найти матрицу, обратную данной, минуя определение
матриц, обратных полученным треугольным.
164
V. ОПРЕДЕЛЕНИЕ ОБРАТНОЙ МАТРИЦЫ ДЛЯ ДАННОЙ
БЕЗ ОПРЕДЕЛЕНИЯ МАТРИЦ, ОБРАТНЫХ ТРЕУГОЛЬНЫМ
Покажем, что обращение матрицы можно произвести и без ис-
использования формулы F,22), т. е. минуя определение матриц В~г
и С, обратных тем треугольным, на которые разложена ма-
матрица А.
Из формулы F,22) умножением ее обеих частей сначала слева
на матрицу В, а потом справа на матрицу С получаем
В А-1 = ВВ^С-К
Но произведение ВВ~1 матрицы В на обратную ей матрицу В~х
есть единичная матрица Е, потому
ВЛ-1 = ЕС~\ F,23)
а произведение ЕС~* единичной матрицы Е на матрицу С остав-
оставляет эту последнюю без изменений: ЕС~г = С~К Поэтому F,23)
перепишется так:
ВА-1 = С. F.24)
Аналогично легко показать, что
А~Ю = В-1. F,25)
Введем такие обозначения:
1) элементы матрицы А будем обозначать через ац, а элементы
ей обратной матрицы — через atj\
2) элементы треугольных матриц В и С обозначим через Ьц
и сц соответственно, а элементы, им обратных матриц — через §ц
и Т//-
В развернутом виде формула F,24) запишется так, причем мы
рассмотрим только тот случай, когда диагональные элементы ма-
матрицы В равны 1 (см. задачу 6,8 и указание к ней);
ВА~1 = С
1
0
0
0
bu
1
0
0
bis
b2s
1
0
\B
...ь1п
... bw
b3i ■■■ b3n
0 ... 1 _
=
~*Tu 0
T21 T22
T31 T32
-Tnl Tn2
•
«1
«2
0
0
Тзз
Тиз
iC
1
L
I
0
0
0
a12
«22
«32
««2
..
••
&X3 • . . Otj/i
OtoQ ... Oto/1
«33 • • • Язи
«ЛЗ • . • «nrj
. 0~
. 0
. 0
• Tnn—
165
Из этой формулы легко определятся те элементы aih которые
стоят в треугольнике над главной диагональю (для них первый
индекс i меньше второго индекса /: i < j). Для этого надо исполь-
использовать правило умножения матриц и условие равенства двух матриц.
Например, умножая элементы первой строки матрицы В на соот-
соответствующие элементы второго столбца матрицы А~1к приравни-
приравнивая сумму произведений нулю — элементу 712 в матрице С, полу-
получим
«12 + &12«22 + Ь13а32 + &14<*42 + . . • + ЬщО.пг = О
или
«1
2+ Е Ьц,ак2 = О,
откуда
Здесь нижний индекс суммирования k = 2 есть первый индекс 1
определяемого элемента а12, сложенный с 1, т. е. 2=1 + 1. Легко
установить и общую формулу для определения элементов al7 при
о// = — 2] Ь1ка.ы. (i < /).
«=/'+1
F,26)
Для определения диагональных элементов а.и и элементов а^,
стоящих под главной диагональю (i > j), воспользуемся формулой
F,25)
А~1С = В'1.
~си О О ... О
С%\ ^22 *-* • • • v
Сз1 С32 С33 ... О
1
О
О
о
■р»
. 1
О
О
1
Pl3
Р23
1
О
В~1\
0
• • • Р1п
... ?2П
... Рз»
... 1
Определяемые из этой формулы элементы стоят в треугольнике
первого сомножителя. Напомним, что если диагональные элементы
треугольной матрицы равны 1, то в обратной для нее матрице
диагональные элементы также равны 1 — см. формулу F,8).
166
Например, элемент а^, определится из произведения элементов
последней строки первого сомножителя на соответствующие эле-
элементы последнего столбца второго, если сумму этих произведений
приравнять на основании условия равенства двух матриц элементу
р„„ матрицы В*1:
«ях • 0 + <х„2 • 0 + • • • + <хп„ • ст = $т = 1;
Рассмотрим вычисление какого-либо другого диагонального
элемента, например <х33;
аз1 % 0 + а32 - 0+ а3з • с3з +■ аз4 • ci3 +
<*зз = -— A — («34^43 + «ssCss Н + азлс„з)];
=^г 1! ~~ 2Кз
(здесь нижний индекс суммирования 4 = 3+1, т. е. он равен
индексу t определяемого элемента плюс 1) и вообще
F>27)
а элемент а{/, стоящий под главной диагональю (i > /), находят,
как легко проверить, по формуле
(i >/) F,28)
Из формул F,26) и F,27) видно, что элементы ait обратной
матрицы Л выражаются через элементы Ьц и Сц тех треуголь-
треугольных матриц, в виде произведения которых представлена данная
матрица А, а элементы матриц, обратных треугольным, определять
нет надобности. Для удобства выпишем формулы F,26), F,27) и
F,28), по которым определяются элементы обратной матрицы:
167
В заключение укажем последовательность, в которой следует
вести вычисление элементов alh так как между ними существует
зависимость, определяемая формулами F,26) —F,27), причем эту
последовательность укажем применительно к матрице пятого
порядка
VIII
IX au
VII а
21
V а
3,
III а
41
а42
*81
«52
VI
a23
a33
IV
«14 t
Л24
а34
<*43
II
Из этой схемы видно, что сначала следует определить элемен-
элементы последней строки, начиная с последнего a6S, a затем элементы
последнего столбца, начиная тоже с последнего, затем — элементы
предпоследней строки и предпоследнего столбца, опять-таки начи-
начиная с последнего и т. д. Стрелки и римские цифры, проставлен-
проставленные на этой схеме, указывают необходимую последовательность.
На практике обратную матрицу получают, пользуясь такой
схемой:
1. Выписывают данную матрицу.
2. Под ней образуют две треугольные матрицы, произведение
которых равно данной (см. предыдущие задачи).
3. Под этими матрицами по формулам F,26) — F,28) получают
обратную матрицу данной, соблюдая последовательность опреде-
определения элементов по указанной схеме.
Этот способ обращения матриц достаточно компактен и при
использовании клавишных вычислительных машин не требует про-
промежуточных записей вне таблиц, так как эти машины позволяют
вести «умножение с накоплением». Ниже эта схема применяется
при решении ряда примеров.
Задача 6,12. Обратить матрицу
CSI
5
3
6
7
CSI
4
8
1
0
CSI
4
4
j
1
3
168
Решение
2
5
3
6
2
I
5
3
6
1
12
5
24
7
~24
0
7
2
4
8
7
Т
31
2
1
13
2
—13
5
24
1
~48
13
-8
0
1
0
2
4
1
2"
5
31
48
ЗТ
1
96
31
23
24
67
48
7 '
48
—2
4
—1
1
3
2
22
31
1
Т
1
1
1
2
3
4
1
т
1
[Ь„]
Ниже приведены подробные вычисления элементов а.п обрат-
обратной матрицы.
1 ' оТ
«44С43 _ 31 _ о
48
31
а42 = —
g44c42
169
-»(-¥)*■■-» в_„
2
4
.. - ,. -■ .' g4aC31 + g44c4
tt41 = __== _
Q.'5-K—2)-3+l »6_n.
— 2 U'
<. /Mil
= —634 - «44 = — (— -4-J • 1 = T;
«34
4
tt24 = 2j '
ft=3
_ /5 ±j_^ A- ii_ 3.
C1 " 4 ~*~ 31 / 124 ~ 4 '
I Г. V4 1_ ' /i ! Ж\ 7
^"l 21 a34C«J- 48 " 1 T * 3T/ ~ 48'
J 48 " 1 T * 3T/ ~ 48
4
£ «Sft ' Cki
32 c22 сгг
_ *=£ g32C2l + Д3.4С31 + 4C41 _
5 + ^3 + 6
_
24'
4
a23 = — 2^ b2ka.k3 = —
_ Г5 7 22 9_
[31 ' 48 "^ ЗГ <- ^^ J -48
4
ai3 = — 2j blkak3 = — F12а
/7 67 1 7 «Л 23.
= "" (~2 • 48 + T * 48 + 2(-2>J = — 24'
170
4
— ! 1 — 2j «
22 й=з
1 I i 67
ЗЦ 1~48"
"~2J { Т){~16>\~
±
48'
1
'48"
_ g22C21 + gi3C31 + g24C41 __
S-3+/--$6 5
= 24'
ou
= — j 1 —
1 1 П 1
j = — [1 — 0C12C21 — a13c.,i — a14c4i] =
Итак, обратная матрица
A
Проверка.
i
48
—4
10
— 14
0
1
-45
1
~ 48"
1
~~Т2
5
24 •
7
~~24
0
~— 4
10
— 14
0
5
23
24 24
I 67
48 48
13 7
~48 48
0 —2
10 —46
- 1 67
-13 7
0 —96
Должно быть А~л ■ А =
1С
—
) —46
67
— 13 7
<
~48
0
0
_ 0
Э —96
0 0
48 0
0 48
0 0
24
-36
12
48_
0"
0
0
48
—
2
5
3
_6
~1
0
0
_0
1
2"
з
— т
1
т
1 _
24~
—36
12
48_
•
Е. Действительно,
7 1
2 0
4 2
8 4
0 0
1 0
0 1
0 0
0
о
0
1
4
— 1
1
3_
—
Г~1
= п.
171
Повторяем, что все вычисления были выполнены в простых
дробях для более простой проверки произведенных действий. На
практике вычисления обыкновенно ведутся в десятичных дробях,
но вносимые округления влекут за собой неизбежные погрешности.
Задача 6,13 (для самостоятельного решения). Пользуясь фор-
формулами F,26) — F,28) и указанной схемой получения обратной
матрицы, обратить следующие матрицы:
2 3
1 О
4 2
3 4
4
5
1
—2
—2
—3
1
5
; 2)
А =
0,888 1,059 0,6671
1,059 1,512 1,031 .
.0,667 1,031 0,837 I
Вычисления производить в десятичных дробях с помощью ариф-
арифмометра или клавишной вычислительной машины. Полученные
результаты проверить: произведение А~г ■ А должно быть равно
единичной матрице
А-1 ■ А = Е.
Ответ. 1) Для контроля
С =
2)
2 0 0 0
1 —1,5 0 0
4 —4 —15 0
_3 —0,5 —9 2,4667_
1,5 2 -1
0 1 —2 1,3333
0 0 1 —0,6889
0 0 0 1
—0,0538 —0,1168 +0,4414 —0,1804"
+0,4052 —0,2884 —0,1441 0,0181
—0,2163 +0,5314 —0,2342 0,2793
_—0,3784 +0,5134 —0,2432 0,4054.
8,08977 —7,93495 3,32745"
Л = |—7,93495 11,91472 —8,35304
3,32745 —8,35304 8,83220
172
СЕДЬМОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Матричная запись системы линейных алгебраических урав-
уравнений. Численное решение линейных алгебраических уравнений способом
исключения.
СВЕДЕНИЯ ИЗ ТЕОРИИ
Система п линейных алгебраических уравнений с п неизвест-
неизвестными имеет такой вид:
а11Х1 ~Ь
-f-
"f"
азгхг + а33х3
G,1)
a x, 4- n x A- a x -!-••• 4-я г = Л
Мы будем рассматривать только такие системы линейных алге-
алгебраических уравнений, у которых число уравнений равно числу
неизвестных. В системе уравнений G,1) неизвестными являются
хъ х2, х3, ... хп, а коэффициенты alt (i, j = 1, 2, 3, ... п) при
неизвестных и свободные члены dt (i = 1,2, 3, ... п) — действи-
действительные числа.
Составим матрицу А из коэффициентов аЛ- при неизвестных
А =
U21
а13
а23
■*иЗ
матрицу-столбец дс из неизвестных
X =
х3
и матрицу-столбец d из свободных членов
d =
Jn.
173
Учитывая правило умножения матриц и условие равенства
дпух матриц, систему G,1) можно записать в виде
an
ai2 а2а ... a2n
o32 a3S... aSn
X\
хг
x3
~d~
do
d3
G,2)
или, учитывая введенные обозначения, всю систему уравнений G,2)
можно записать компактно в виде одного матричного уравнения
Ах = d. G,3)
Такая запись большого числа линейных уравнений в виде
одного уравнения является одним из достоинств матричных обо-
обозначений.
На предыдущем практическом занятии мы уделили большое
внимание вычислению обратной матрицы. Покажем теперь
применение этой операции для решения системы линейных алгеб-
алгебраических уравнений.
Если матрица А — неособенная, то она имеет обратную мат-
матрицу Л". Умножим слева обе части уравнения G,3) на Л и,
заметив, что А~х • А = Е—единичная матрица, получим столбец
неизвестных х иа равенства
x = A-*d. G,4)
В этой формуле х может быть не только матрицей-столбцом, но
~й матрицей размера яхт. В этом случае и матрица d состав-
составленная из свободных членов, должна тоже иметь размер п х т.
Такой случай имеет место, например, в задаче G,3).
Таким образом, нам стоит только определить элементы а,/
(i, / = 1, 2 п) обратной матрицы Л~й, и задачу определения
неизвестных систем G,1) можно считать решенной. Несколько
таких упражнений мы выполним в начале этого практического
занятия.
Но здесь же следует заметить, что в случае большого числа
п неизвестных вычисление элементов обратной матрицы становится
громоздким и затруднительным. Поэтому формула G,4) имеет
больше теоретическое значение, чем практическое, так как по
сравнению с формулами Крамера для решения системы линейных
алгебраических уравнений она никаких преимуществ в вычисле-
вычислениях не дает.
Эта формула оказывается безусловно полезной тогда, когда
рассматриваются такие системы уравнений, у которых матрица
коэффициентов при неизвестных одна и та же (такие системы
уравнений встречаются, например, в строительной механике). Вы-
174
числение обратной матрицы в таком случае приносит большую
экономию в вычислительной работе (см., например, задачу G,3).
Это практическое занятие проведем в таком порядке: сначала
будем решать системы уравнений с небольшим числом неизвестных
(два, три) по формуле G,4) (задачи 7,1—7,7), а потом укажем
удобную компактную схему решения системы G,1) методом исклю-
исключения (алгоритм Гаусса), которому дадим матричную трактовку.
Теория этого метода, формулы, сюда относящиеся и схема его
применения указаны после задачи 7,7.
Задача 7,1. Записать систему уравнений
2*1 + Зх2 = 9;
Зхх— 4jc2 = 5
в виде одного матричного уравнения и решить ее по формуле G,4).
Решение. Систему представим в виде
Р.-М-Й-
Здесь матрица
Найдем обратную ей матрицу по формуле E,2), которая в
развернутом виде выглядит так:
"Л
Л,
II
21
"з!
2
^33
га
"■In "-Z
G,5)
где \А\ — определитель матрицы Л, а элементы Ац — алгебраиче-
алгебраические дополнения ее элементов ац, причем матрица в правой части
формулы G,5) есть союзная матрица А для А. Но здесь еще раз
подчеркнем, что когда п > 3, то формулой G,5) для обращения
матрицы обыкновенно не пользуются, а применяют методы, рас-
рассмотренные на пятом и шестом практических занятиях.
Воспользуемся формулой E,2) для определения обратной матрицы
2 3
3 —4
= -17;
Ап = (-l)i+i . (_4) = _4; Ап = {-\у+* • 3 - -3;
Аг1 = (-1Р1 • 3 = - 3; А2г = (-1J+2 • B) = 2.
175
Составим матрицу, союзную матрице А
[А АЛ Г 4 3"!
А = [а1 а1\-[-Ъ 2\
и поэтому по формуле E,2)
-17 [_3
Теперь по формуле G,4)
17 17
.17 17
х^А-Ч.
з
17 17
3_ —2
Ll7
Ш_ 17 17 [91
кг 1 i=h L5J
м
51
17
17
LT7J
v _51_Q. r -IZ-1
Xl ~ 17 "" °' Л2 — I7 — i.
Задача 7,2 (для самостоятельного решения). Записать систему
уравнений
в виде одного матричного уравнения и решить ее по формуле G,4)
Указание. Обратная матрица по формуле E,2)
--If3 Ч
-1б[1 —5J-
л 29 33
Ответ. *1 = те; *2 = -f6.
Задача 7,3. Решить системы уравнений:
1) 3*!— 2х2 = 2; J 2) 3*з— 2х4 = 3;
3) 3*-2х, = 5;
4д;5 — х6 = 7.
4 = 3; 1
= 4; J
Решение. Матрица А коэффициентов при неизвестных во
всех трех системах одна и та же:
-Р -]•
176
Это тот случай, когда применение формулы G,4) является выгод-
выгодным, т. е. выгодно решить все три системы путем отыскания обрат-
обратной матрицы А~1 для матрицы А. Запищем все три системы в
виде одного матричного уравнения
Г2 3
хь\-[\ 4
р р
ГЗ —2] Где, ха х,1 Г2 3 51
[4 -l]'|*2 х, хь\-[\ 4 7J
(отметим, что матрица, составленная из неизвестных, должна иметь
тот же размер, что и матрица, составленная из свободных членов).
Легко видеть, что для матрицы А обратная матрица
— 1
—4
3 =
а потому по формуле G,4)
[
I
~~ 5
4
-~ 5
2"
5
3
Т-
Г*
[х2
1уле {i,y
_ Г 1 2"
х3 хь\_\~Т Т
Хц ЛГ61 I 4 3
Выполняя умножения в правой части равенства, получим
О 1 -1
\Xl
[х2
х3
-1 ° h
откуда
= 0;
= и
9
*2
х*
= —
= 0.
]
Решение этих трех систем уравнений по формуле G,4) путем
отыскания обратной матрицы потребовало значительно меньше
труда, чем решение их по известным читателю формулам Крамера.
Задача 7,4 (для самостоятельного решения). Решить системы
уравнений:
1) 2хг + Зх2 = 7; | 2) 2х3 + Здг4 = 1
3) 2х5 + Зхв = 9; - j 4) 2х7 + Зд:8 = 1;
О *» О *# _ .. Q» I О и О v i Q
Указание. В матричной записи все четыре системы запишут-
запишутся так (проверьте, используя правило умножения матриц и условие
их равенства):
Г2 3] Г*! х3 хъ хЛ\1 1 9 1]
13 — 2\" [х2 х4 хв xs\ ~[l 0 3 3j'
177
Для матрицы
обратная матрица
Л =
13 —3
—2 —3
2_
13
13
_3_"
13
2
Отве
Задача
пользуясь
Реше
нения
т.
*i =
Хз =
хъ
х7-
_ >7.
х2-
_ 2 .
13' *4 =
_27.
= 13 ' Х* ~~
_ 11.
" 13' *8
7,5. Решить систему уравнений
формулой
2х
Ъх
2х
G,4).
+ (/ — 2г = 5;)
— 2(/ + Зг = 4;[
— 3(/ + 5г= 1J
19
"" 13'
3
з;
21
~Тз;
3
~ Тз*
н и е. Запишем систему в виде одного матричног
3
2
1
—2
з
—2"
3
5
•
X
' у
г
—
" 5 "
4
1
Здесь матрица коэффициентов
2 1 —2
3—2 3
2—3 5
а неизвестные х, у и г найдутся из формулы
г
Обратим матрицу Л, для чего применим формулу E,7)
1 1-2
Л = _3_—2 j__3_
2 —3 | 5
178
Здесь
1) Оц1 находим непосредственно
if -2 -11
a"=~L-3 2j-
2) р = a22 — о^а^Ча = 5 — [2; —3J •
«22=5.
2
7
3
7
I
7
2
7
У 1
3 5
7 7
*
)
—2
3
Итак, р = у; р-1=»7.
3) T = p-ia21 = 7[2; —31 = [14; —21].
4) a'V^-ja =
=
" 1"
7
12
7
1
7 7
3 2
-7 7
[14; —21].
C\ t ^™ ^
01 ^м i "|" ^11 12 ill ™**
•[
7
3
L7
Г5
7
60
.7
2
f
3
6) — 7a = — [14; -211 •
7) — ацоцр-» = —
z
У
3
7
1
У
2
' 1
-2
3
.
1"
7
2
7
8~'
7
96
7
1 "
У
2
+
7
3
-7
•[1
■
14; —21] •
f — 2 3]
L 24 Зб] '
у
У ~~У
60 96
7 7
I '
У
2
7_
= -1-5;
1.7 — —
1
У
12
7
2 I
7 7
3 2
7 7
1"
7 7
3 2
[_7 7_
1 -11
Э — 14J
8] - [5;
Теперь все элементы обратной матрицы известны и по
муле E,7)
Л =
1
9
5
— 1
— 14
-8
12
-
1
=
=
-81;
фор-
179
Заметим, что вычисление по формуле E,2) оказалось бы менее
громоздким. Следовало бы вычислить 9 определителей второго,
один определитель третьего порядка и образовать союзную ма-
матрицу Л.
Подставляя матрицу А~1 в формулу (а), получим
5
4
1
откуда
т. е. х = 2; у = 1; г = 0.
Задача 7,6. Решить системы уравнений
1) 4*х + 5*я = 7;
*2 —6*з= 11;
2)
— 6*в = 2;
+ 4*6=ll;J
3) 4*7 + 5*9 = 0;
*8 — 6*9 = 5;
3*, + 4*9= 1..
Решение. Запишем все три системы в виде одного матрич-
матричного уравнения
*!
х-
*8
*4
*5
_*3 Хв
Из этого следует, что матрица неизвестных
*! *4 *7 7 10
*2 *5 *8 = А~г 11 2 5
*3 *в х9] [—2 11 1
где Л —обратная матрица для матрицы коэффициентов
4 0 5'
0
(а)
Л =
—6
4
Найдем для этой матрицы обратную. В данном случае, учи-
учитывая характер этой матрицы, удобнее воспользоваться обшей
формулой E,2) для определения обратной матрицы. Определитель
матрицы Л
[Л|1
180
Алгебраические дополнения
Ai = 4; Л, = —18;
Al3 = -3;
Дп = —5; А32 = 24; Аи = 4.
Составляем матрицу из алгебраических дополнений
4—18 —3"
О 1 О
—5 24 4
транспонируем ее, чтобы получить союзную матрицу А и делим
на \А\ = 1. Учитывая, что на основании формулы E,2)"
А_
получаем
4 0 —5
— 18 1 24
—3 0 4.
Из равенства (а) следует, что
х2
х.
Xi
хв
Хь
4
-18
—3
0
1
0
—5
24
4
7 1 0
11 2 5
-2 11 1
Отсюда, выполняя умножение матриц в правой части, полу-
получаем
а-ь
38 —51
= 1—163 248
—29 41
-5
29
4
1 Хц Х1
Х-1 Xi Х$
3 . Х$ Х9_
Учитывая условия равенства матриц, находим
Xi = 38; х% = —163; х3 = —29;
х, — 51 • х, — 248- х =41-
X-j == ~~О\ Х^ ==z J>u\ Х$ ^= 4»
Отметим безусловную выгоду, которую мы извлекли, приме-
применяя в данном случае определение обратной матрицы и используя
формулу G,4). Если бы эти системы решать по формулам Кра-
Крамера, то пришлось бы вычислять 10 определителей третьего
порядка. Однако подчеркнем, что экономия в вычислениях полу-
получилась вследствие того, что матрица коэффициентов во всех трех
системах была одной и той же.
1Я1
Задача 7,7 (для самостоятельного решения). Решить системы
уравнений, применяя метод, указанный в предыдущей задаче:
1J*,+ #i+ г! =11;] 2) 2*2 + у2 + г2 = 2;
Xl + 2г,= 15; ) х2 + 2г2 = 1;
3*i +У1 + 2г, = 14; J 3*2 + у2 + 2г2 = —4;
3) 2хл + у3 + г., = -3; | 4) 2ж4 + yt + г4 = 0;
Л j —J~ £*&.'£ -— 1 , I Л^ ~у~ £ti^ —— у ^
Ov 1 ,. | О— С. I Ov _j_ f/ | О7 IO
Указание. Все четыре системы представить в виде одного
матричного уравнения
2 1 1
1 0 2
3 1 2
J L
Для контроля
Ответ.
*, =
*2 =
X • =
*4 =
Задача 7,8
уравнений
-9;
-13;
15;
25;
(для
г
«.
)
*1 Х2
х3 х
Ух Уг У* 1
2! 22 г3 2
Л =
2
4
1
У\ =
Уг —
Уа =
У* =
'4
/4
=
— 1
1
1
17;
21;
-26;
-37;
11
15
.14 ■
2
—3
__ 1
2
1
-4
г2
23
Zx
самостоятельного решения).
5*1 — 2л;2
2*2 + 2д
С! — 2*2 — 3*з
-*4
■>3+Х1
-2х>
*2 + 2л;3 + х^
=--1;
__ 1,
= 1.
—3 0
1 —1
5 12,
= 12;
= 7;
= '\
= -13;.
Решить систему
Указание. Обратная матрица коэффициентов
1—2 —4"
0 1 0: —1
—1—13 6
2 1 —6 — Ю_
Ответ. Xi — —4; х2 = 0; *3 = 7; xt = —13.
Теперь приступим ко второй части упражнений этого практи-
практического занятия.
182
СВЕДЕНИЯ ИЗ ТЕОРИИ
Из большого числа известных методов решения систем линей-
линейных алгебраических уравнений мы будем пользоваться только
одним из наиболее распространенных методов—методом исключе-
исключения, который обычно называется методом Гаусса (с другими мето-
методами читатель может ознакомиться по книге: Д. К. Фаддеев
и В. Н. Фаддее в а. Вычислительные методы линейной алгебры,
Физматгиз, 1960).
Метод Гаусса в матричном виде позволяет указать удобную для
практики компактную схему решения, которая сводится к пред-
представлению матрицы коэффициентов в виде произведения двух тре-
треугольных матриц, а эту задачу мы уже подробно разобрали на
предыдущем практическом занятии.
В матричном виде система линейных алгебраических G,1) за-
записывается так G,3):
Ах = d,
где А — матрица коэффициентов системы G,1).
Представим матрицу А в виде произведения нижней треуголь-
треугольной матрицы С на верхнюю треугольную матрицу В, причем ин-
интересующие нас формулы выведем применительно к случаю, когда
диагональные элементы матрицы В равны 1.
Тогда уравнение G,3) запишется в виде
СВх = d. G,6)
Произведение Вх матрицы В на х — матрицу-столбец неизвест-
неизвестных, — будет матрицей-столбцом, который мы обозначим через у
Вх = у. G,7)
Уравнение G,6) перепишется в виде
Су = d. G,8)
После того как из уравнения G,8) будет определена матрица-
столбец у, из уравнения G,7), в котором, таким образом, правая
часть окажется известной, можно определить матрицу-столбец х,
чем и закончится решение задачи.
Распишем подробно уравнение G,8), учитывая, что С — нижняя
треугольная матрица:
'си О
-Cnl Cn2
О
о
^пЭ
О
о
о
С«4
0~
0
0
спп-
У\
У2
Уз
-Уп-
~d{~
d2
ds
Jn-
G,9)
183
Здесь элементы сц (i, / = 1,2, ... , п) иззестны, так как матрица
А коэффициентов при неизвестных считается уже разложенной на
произведение двух треугольных матриц С к В.
Перемножив матрицы в левой части G,9) с учетом условия
равенства двух матриц, получаем такие уравнения для определе-
определения неизвестных уи уг уп:
СЪ\У\ Ч~ СиУч. = i
сг\У\ + СзгУг + с3зу3 = d3;
G,10)
1У1
cm9i + с*гУ2 + спзУз + • • • + Сппуп = dn.
Из этой системы уравнений, начиная с' первого, получаем зна-
значения неизвестных ус:
= — ;
из 1-го уравнения Ух = — ;
сп
из 2-го уравнения у2 =
из 3-го уравнения у3 =
С33
из &-го уравнения
— c^j/д — скгуг — ck3y3 — • ♦ Ck. к~\Ук~\
_
и, наконец, из n-ого уравнения
^П СщУ1 СпчУч - СдзУз — * » ■ —- Сп, п iyn—i
Все эти формулы можно объединить в одну
G.П)
После того как все yt (i = 1, 2, ... , п) определены по фор-
формуле G,11), их надо подставить в уравнение G,7), в котором все
элементы Ьц (t, / = 1, 2, ... , п) верхней треугольной матрицы В
уже известны, так как, повторяем еще раз, что матрица А пред-
представлена как произведение двух треугольных матриц.
184
В развернутом виде уравнение G,7) запишется так:
[ Ь,2 Ь,л ... Ь,,
О 1 Ь23
О 0 1
-"In
0 0 0 ... 1 Ъп_ип
0 0 0 ... О 1
Х\
*2
ж3
-** _
Уу
Уч.
Уг
Уп-1
_ Уп-
G,12)
Все диагональные элементы матрицы В равны 1. Умножив матрицы
в левой части уравнения, получим матрицу-столбец, а учитывая
условие равенства двух матриц, будем иметь такую систему урав-
уравнений
ху + Ь12х2 + Ь^хл + • • • + Ь1пх„ = tfi,
•■■ + Ь2пхп = у2;
ч+ ••• + ь3пхп = у»
Хп-\ "Г "п—1 > пХп — Уп-V
хп = Уп-
G,13)
Начиная решение этой системы уравнений с последнего, по-
получим
Хп—1 = Уп—1 "п—1> пхп>
Х3 === Уз ^34*^4 ^~ "з5**5 ' * * * ЗпХп*
Xi = У\"— bl2x2 — Ь1ах3 — • • • — Ь1пхп.
Общая формула для определения х, (i = 1, 2 п) запишется
так:
п
% G,14)
п
= у,— % bikxk.
«(+1
Для удобства напишем рядом формулы G,11) и G,14)
си
п
185
По формуле G,11) элементы gt находятся так же, как и эле-
элементы b(i (i < /) верхней треугольной матрицы по формулам F,21).
Ниже приводится так называемая компактная вычислительная
схема для применения метода Гаусса решения линейных систем
алгебраических уравнений (табл. 1).
Таблица 1 указывает компактную схему решения системы ли-
линейных алгебраических уравнений. Приведенный аппарат формул
для решения системы линейных алгебраических уравнений по спо-
способу Гаусса приводит к такому простому правилу:
1. Заготавливаются схемы, аналогичные схеме на стр. 187.
2. Вычисления ведутся в такой же последовательности, как
и в схеме на стр.155: сначала определяются элементы столбцов,
а потом элементы строк, т. е. элементы первого столбца, элементы
первой строки; элементы второго столбца, а потом элементы вто-
второй строки; элементы третьего столбца, а потом элементы третьей
строки и т. д.
3. Чтобы получить элементы, расположенные на главной диа-
диагонали или ниже ее, берется соответствующий элемент матрицы
А и из него вычитается сумма произведений элементов, располо-
расположенных в той же строке и в том же столбце, что и вычисляемый
элемент, причем произведения берутся так, что умножается первый
элемент в строке на первый элемент в столбце, второй в строке —
на второй в столбце и т. д.
4. Чтобы получить'элемент, стоящий над главной диагональю,
поступают так же, как указано в п. 3, но полученное от вычитания
число надо еще разделить на диагональный элемент той же строки,
в которой стоит вычисляемый элемент.
5. Искомые неизвестные вычисляются в таком порядке:
Х^, Х3, Х-2, Х\,
т. е. так называемым «обратным ходом» по формуле G,14)
Если вычисления ведутся с помощью арифмометра или клавиш-
клавишной машины, то элементы в табл. 1 получаются без каких бы то
ни было промежуточных записей.
Все вычисления должны быть проконтролированы. Контроль
осуществляется так: для него отводится последний столбец и по-
последняя строка вычислительной схемы. Последний столбец делится
на две части: верхнюю и нижнюю (см. табл. 1). Элемент верхнего
столбца, который мы обозначим через ft, равен сумме элементов,
стоящих с ним в одной и той же строке,
h •= t a'i + di-
186
КОМПАКТНАЯ ВЫЧИСЛИТЕЛЬНАЯ СХЕМА ПРИМЕНЕНИЯ СПОСОБА ГАУССА
Таблица 1
*1
аи
021
а3|
«41
fn = a,i
1
с2] — а2, .
^31 — а31
f41 — а41
—613^3—^14^4
Ч
ап
аг%
аэ%
а*г
h - а'2
f 22—а 22—
—аг\Ь\г
1
С32~ Яз2—
031*12
С42 Я42
—а4А2
Хг=Уг~
~Ьггк3—Ь^х^
*з
^13
^23
Озз
ап
и ai3 — c2i*la
f'22
сзз—°зз
■C3i*i3 Сзг^гз
1
С43=°43—С41*13—
С42*23
Хй=Уз— *34*4
*4
014
«24
°31
а44
, а24 —C2i*i
°24 ' .
С22
1
*34 =
а34—С31*14—С32*24
^33
С44 = а44 С41*14
—^42*84—С43*34
1
*4=г/4
di
di
d2
d3 \
■ dt
1 an
d% — cuyx
У-i r
C22
я"з—сз\У\—СзгУъ
У" c33
«/4 =
—С41У1— С.12Й2— СлзУз
Контрольный столбец
U и kt
!i=all+al2+al3+ali+dl
/а=а21+а22+а23 + О24+^2
/3=031+032+033+034+^3
А =а41+«42 + 043+044+^4
k k
1 а„
и /2 — f2i*i
"а ■ ■
С22
и /з — Г31^1 — C3ik2
сзз
и /■!" С41Л1— С42*2—^43*3
С41
Элементы же нижнего контрольного, которые мы обозначим через
k,, получаются, как и элементы верхней треугольной матрицы, т. е.
по формуле
*,-=
'=1
Контроль состоит в том, что элементы контрольного столбца
должны быть равны сумме элементов, стоящих в той же строке
над главной диагональю. Например, в схеме элементы контроль-
контрольного столбца должны быть равны:
&2 = 1 + Ь23 + Ьм -f- Уъ
h = 1 + b3i + Уз,
kt = yt.
Контроль должен осуществляться после вычисления каждой строки.
Таблица 2
н
3
1
1
2
3
1
1
1
2
1
х.
2
1
— 1
—3
coj S3
1
3
1
5
13
3
2
х.
—1
— 1
1
—1
1
~ 3
_2
—2
1
—9
5
х.
5
1
2
3
5
"
—2
+4
+4
1
—2
—8
-4
0
—15
8
3
—4
2
—2
t
У/
ft и ft/
1
—2
3
—14
1
3
—7
9
2
—1
t
188
Задача 7,9. Решить по способу Гаусса систему уравнений
Х\ -у- Х<% ~~ Х$ ~т" Х% = "~~4j
Х\ — Х2 + *з + 2-^4 = 0;
£*А,\ ^^ *->А>2 ~^ Лд (" «J^4 ~^ i*J»
Решение. Используя указанный аппарат формул G,11) и G,14),
с также схему, приведенную в табл. 1 на стр. 187, располагаем
все вычисления, как указано в табл. 2, стр. 188. (Вычисления про-
проведены в простых дробях для упрощения проверки по ходу реше-
решения. Дальнейшие задачи решаются в десятичных дробях).
Задача 7,10. Решить по способу Гаусса систему уравнений
2*, + *2 — 3*з + 5*4 = 18,9012;
Xi — *2 + *з — 3*4 = 14,0800;
3*! + х2 — *3 + 2*4 = —2,2954;
5*i + 2*2 — 3*з + *4 = —6,3764.
Таблица 3
2
1
3
5
2
1
3
5
3,5359
t
1
—1
1
2
0.5000
—1,5000 1
—0.5000
—0.5000
—26.4498
t
х3
-3
1
—1
—3
— 1.5000
— 1,6667
2,6667 1
3,6667
-8.8281
t
Ч
5
—3
2
1
2.5000
3,6667
—1.3750
—4,6251 1
2.3590
t
*
18,9012
14.0800
—2.2954
—6.3764
9.4506
—3.0863
—12,0717
2,3590
t
fi и ki
23.9012
12.0800
2,7046
—1,3764
fit
11,9506
-0.0863
—12.4467
3.3590
t
х.
VI
kt
189
Решение. Для решения используем компактную схему, при-
приведенную на стр. 187, в которой как уже указывалось, использо-
использованы формулы G,11) и G,14). Последний столбец отведен для
контроля. Читатель должен проделать все вычисления с помощью
арифмометра или настольной клавишной вычислительной машины.
Все вычисления помещены в табл. 3. на стр. 189.
Задача 7,11 (для самостоятельного решения). Решить систему
уравнений
0,8320*! + 0,4670л:2 + 0 + 0 + 0,0155л:5 = 0;
0,4670*!+1,5160*, +0,0467*3+ 0 + 0,0294*5 =—0,302; .
0,0155*, + 0,0294*2 + 0,0561*3 + 0,0561*4 + 0,0283*5 = —0,634;
0 + 0,4670*2 + 1,7850*з + 0,5120*4 + 0,0561*5 = — 1,163;
0 + 0 +0,5120*з+1,4720*4 + 0,0561*5 = —1,977.
Ответ. *, = 0,378; *2 = 0,0485; *3=0,184; *4 = —0,580; хъ =
= -21,7.
Задача 7,12 (для самостоятельного решения). Решить систему
уравнений
*i + *2 + хз+ xi-r *5 = 3;
*х + 2*2 + 2*з + 3*4 + 4*5 = 9;
2*, + *2 — 2*з + 2*4 + 3*5 = —16;
3*! + 2*2 — 3*3 + 4*4 + *5 = 2;
—*i + х2 — 4*3 + 4*4 + 2*6 = —12.
Ответ. *, = 1: *2 = — 1; х3 = 2; *4 = —2; *5 = 3.
Задача 7,13 (для самостоятельного решения). Решить систему
уравнений
10*!+ хг— 2*з+ *4+ 2*6 = —20;
2*!+ 20*2+ 3*з— *4+ 3*5= 15;
3*!— 2*2 + 25*з+ *4— 2*5 = —20;
—*,— 2*2+ *з— 10*4+ 2*5 = —40;
2*j+ 2*2+ 3*з— 4*4 + 50*6 = —75.
Ответ. *, = — 2,411; *2= 1,439; *3 = —0,633: *4 = 3,664;
х» = —1J30.
Задача 7,14 (для самостоятельного решения). Решить систему
уравнений
0,5*,+ 0 + *3+ 1,023*4 = 4,725;
1,5*!+ *2+ 0 +3,702*4 = 3,402;
1,273*!— 2,752*2 + 3,208*з~ 1,305*4 = 2,709;
2*i + *2 + *з + 4,007*4 = 1,231.
Ответ. *! = —14,980; *2 = —9,682; *3 = 2,390; *4 = 9,604.
190
ВОСЬМОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Характеристическое уравнение матрицы. След матрицы.
Характеристические числа и собственные векторы матрицы. Нормирование век-
вектора. Скалярное произведение двух векторов. Ортогональные векторы. Орто-
Ортогональные матрицы. Преобразование характеристического уравнения методом
Леверье.
СВЕДЕНИЯ ИЗ ТЕОРИИ
Характеристическое уравнение. Пусть матрица
• ai
• а,
А =
Й22 Й23
«32 а33
а
an
(8,1)
а вектор-столбец
х =
х3
(8,2)
Умножим матрицу А на вектор х. Произведение будет векто-
вектором-столбцом, элементы которого обозначим через yi (i=}, 2,
3 п). Если окажется, что элементы yt этого вектора-столбца
пропорциональны соответствующим элементам вектора-столбца х
с коэффициентом пропорциональности X, т. е. если
yi = ha (i = 1, 2 ... , л),
то вектор-столбец х называется собственным вектором матрицы А,
а коэффициент пропорциональности X характеристическим числом
матрицы А, или ее собственным значением.
191
Таким образом, вектор х называется собственным вектором
матрицы А, а число X — ее характеристическим числом, или
ее собственным значением, если выполняется равенство
Ах = he. .
Перепишем это уравнение в виде
Ах— Х* =
или
{А — Щх = О,
(8,3)
(8,4)
где Е—единичная матрица, порядок которой равен порядку мат-
матрицы А, а 0 — нулевой вектор-столбец, т. е. столбец, все элемен-
элементы которого равны нулю. Без множителя Е при X уравнение
(8,4) не имело бы смысла.
При условии, что вектор х ф 0, равенство (8,4) возможно
только тогда, когда определитель его левой части равен нулю, т. е.
И— Щ =
(8,5)
Уравнение (8,5) называется характеристическим уравнением
матрицы А, а его левая часть Л — Х£—характеристическим много-
многочленом. Получим уравнение (8,5) в развернутом виде. Произведение
Х£= X
1
0
0
0
1
0
0
0
1
0 ...
0 ...
0 ...
0 0 0 0
0"
0
0
1
=
X
0
0
0
X
0
0
0
X
0 ...
0 ...
0 ...
0
0
0
0 0 0 0
Поэтому уравнение (8,5) на основании правила вычитания мат-
матриц с учетом равенства (8,1) в развернутом виде запишется так:
аи —
а21
а31
х а12
Й22 *
«32
аП2
а13
«23
азз-Х
и
. . . й\п
• • • 02п
••• а3п
... длп — Х_
= 0
(8,6)
Уравнение (8,6) и есть характеристическое уравнение (8,5).
Оно называется также вековым уравнением и очень часто встре-
встречается в теории колебаний, теоретической и строительной меха-
механике, в аэродинамике, в небесной механике и играет большую
роль в алгебре матриц. Вековым это уравнение называется пото-
потому, что к нему приводит в небесной механике задача исследова-
исследования вековых возмущений планет.
Характеристические числа или собственные значения матрицы.
Если раскрыть определитель в левой части уравнения (8,6), то полу-
192
чится уравнение относительно X, степень которого равна порядку
матрицы А (в данном случае степень этого многочлена равна п).
Характеристическое уравнение (8,6) запишется так:
(— 1)" ~
Ап = О,
(8,7)
где
Ai — сумма всех диагональных миноров 1-го порядка;
Аг—сумма всех диагональных миноров 2-го порядка;
Ап— сумма всех диагональных миноров /1-го порядка.
Неизвестная величина X, определяемая из этого уравнения,
имеет п значений
*i» Xj, Х3, ... , Хп,
среди которых могут быть равные.
Таким образом, квадратная матрица А порядка п имеет п
характеристических .чисел.
Собственный вектор. Каждому характеристическому числу 1{
(i=l, 2, 3, ... , п) характеристического (векового) уравнения
(8,7) соответствует на основании уравнения (8,3) собственный век-
вектор.
Собственным вектором матрицы А, принадлежащим собствен-
собственному значению X,., называется ненулевой вектор, для которого
столбец х, составленный из его элементов, удовлетворяет матрич-
матричному уравнению (8,3)
Ах — \х.
Будем собственный вектор, соответствующий корню Хг харак-
характеристического уравнения, обозначать через bt, а его элементы —
через bu, b2i, b3i bni, т. е.
Jnl-
(i = l,2 n)
(элементы вектора называются также его координатами, а иногда
компонентами).
7 И. А. Каплан
193
Для определения координат собственного вектора, соответству-
соответствующего характеристическому числу X,., перепишем уравнение (8,4)
в развернутом виде.
«11 —
«21
«31
a«i
«12
Й22 X
«32
an2
0K
Й23
йзз-
n
3/1
. . . aln
... a2n
••• аз„
... йл„-Хг
•
Ьц
bSi
0
0
0
Выполнив умножение матриц в левой части этого уравнения,
учитывая условие равенства двух матриц, получим систему одно-
однородных уравнений для определения координат bu, b2i, Ьы ... ,
Ьп1 собственного вектора Ь{
(«и — hV>u + aiAi + al3b3l H h fliAi = °;
u + («28 — ^i) b2l + a^bg, -£ • • • + aznbnl — 0;
u + a32b2l + (a33 — \{)ba[ + ♦ • • -f- a3nbnl — 0; (8,8)
0.
= 1, 2, 3 /i)
Определитель системы равен нулю, так как из этого условия
были определены собственные значения X, матрицы Л (следовательно,
эти уравнения не являются независимыми). На примерах будет
показано, как определяются неизвестные bai (i, a — 1, 2, .... п).
Таким образом, будут определены все элементы собственного
вектора bt.
Следует иметь в виду, что собственный вектор можно опреде-
определить с точностью до постоянного множителя.
Подставляя в (8,8) поочередно Х„ Х2, ..., Х„, получим п соб-
собственных векторов.
Нормированный вектор. Вектор называется нормированным,
если сумма квадратов его элементов (компонент, координат)
равна 1. Так, если вектор
то он будет нормированным при выполнении условия
2 2,2
V1 + Х>г + V з +
+ Vn = i.
194
Чтобы нормировать вектор, надо все его элементы умножить на
число
У Vl + vl + • • • +
Пример. Нормировать вектор
101
15 |.
.—6
Находим, что
N 1. _| _1_
~ |/l0a+ 15*^ (—6)» ~~ |/ЗбГ ~~ 19
и поэтому нормированный вектор
- 10-
19
15
19
6
_ 9
Действительно,
,A5\' / 6\«
Скалярное произведение двух векторов. Скалярным произве-
произведением двух векторов называется сумма произведений соответ-
соответствующих элементов. Так, если
Щ
то их скалярное произведение
VW = VyWi + v2w2
v3w
3w3
+ vnwn.
Взаимно-ортогональные векторы. Два вектора называются вза-
взаимно-ортогональными, если их скалярное произведение равно нулю.
Ортогональные матрицы. Матрица называется ортогональной,
если ее столбцы попарно ортогональны.
Ортонормированные матрицы. Матрица называется ортонорми-
рованной, если каждый ее столбец есть нормированный вектор,
а все столбцы попарно ортогональны.
7*
195
-1
2
1
т
1
2
1
2
0
1
~т
1-
2
1
2
1
2
Легко проверить, что, например, матрица
V =
является ортогональной.
Раскрытие определителя в формуле (8,6). Раскрытие опреде-
определителя в левой части векового уравнения (8,6) представляет собой
очень громоздкую задачу, причем вычислительная работа стано-
становиться особенно трудоемкой при больших значениях п.
Вопросу о раскрытии этого определителя, т. е. преобразовании
его в многочлен, и тем самым преобразовании (8,6) в алгебраи-
алгебраическое уравнение, посвящено большое число работ. Существует
много методов этого преобразования, среди которых наиболее
распространенными и эффективными являются: метод А. К. Кры-
Крылова, метод Данилевского, метод Микеладзе, метод Леверье, метод,
основанный на решении системы п линейных алгебраических урав-
уравнений. Каждый из этих методов имеет как свои преимущества, так и
недостатки. Мы выполним на этом практическом занятии упражнения
по определению собственных значений матрицы и ее собственных
векторов методом Леверье, а на следующем практическом заня-
занятии — методом академика А. Н. Крылова. Заметим, что метод
Леверье в последнее время нашел большое применение в связи
с использованием счетных машин, для которых определение сте-
степеней матрицы (на чем основан этот метод) является очень прос-
простой задачей.
Метод Леверье. Следом матрицы называется сумма ее диаго-
диагональных элементов. След матрицы А обозначается символом SpA.
Для матрицы А в (8,1)
SpA =
it.
Чтобы упростить последующие формулы, введем такие обозна-
обозначения для следа степеней матрицы Л:
след матрицы А : SpA = Sx;
след матрицы Л2: SpA2 = 52;
след матрицы Л3: SpA3 = S3.
Вообще след SpAk k-oh степени матрицы Л будем обозначать
через Sk
SpAk = Sk.
Коэффициенты At (i — 1, 2, .... n) уравнения (8,7)
+ (_ 1)«-зл,х»-з + ... + (_ i) An_iX + An = 0
196
определяются по таким рекурентным формулам:
А1 = Ао • Si,
А3 = у D,S, —
(8,9)
— A2Sz -f-
Коэффициент А1 есть сумма диагональных элементов матрицы А,
т. е. след матрицы А. С другой стороны, на основании теоремы
Вьета сумма корней характеристического уравнения равна Л,.
Таким образом, сумма корней характеристического уравнения
матрицы равна ее следу.
Коэффициент Ап в уравнении (8,7) численно равен определи-
определителю | А | матрицы, а потому последняя из формул (8,9) позволяет
найти величину определителя матрицы А.
Применение этого аппарата формул связано с определением
степеней матрицы А. Решим ряд задач на применение метода
Леверье.
Задача 8,1. Определить собственные значения и собственные
векторы матрицы
1 4"
3 3 2
6 2 10.
Решение. Характеристическое уравнение (8,6) имеет вид
т. е.
5 —I 1 4
3 3-Х 2
6 2 10—X
= 0.
После раскрытия определителя в левой части этого уравнения
получится
+ А3 = 0; (8,10)
197
а коэффициенты At, A2 и Аа определятся по формулам (8,9).
Находим степени матрицы А и следы полученных матриц:
A2 =
=
5
3
6
2
36
96
5
3
6
1
3
2
1
3
2
4"
2
1°.
16
16
32
4
2
10
.
52
62
38
128
j
5
3
6
+
S
1
3
2
16
3
6
+
1
3
2
= 5 +
41
2 U
10J
128 =
4"
2
10.
3 + 10 =
Г52 16
= 36 16
[96 32
= 196;
80
•
18;
62'
38
128_
>
160
1728.
S3 = 680 + 160 + 1728 = 2568.
Очевидно, что в наивысшей из вычисляемых степеней матрицы А
следует определить только диагональные элементы, ибо она больше
в умножении не участвует, а нас интересует только ее след, т. е.
сумма диагональных элементов.
Применяем формулы (8,9):
Аг = if
Л, = 18;
A - A0S2) - 1 A8 • 18 - 1 • 196) = 64;
у = у F4 • 18 — 18 • 196 + 2568) = 64
(проверьте, что определитель матрицы А равен А3 = 64). Подстав-
Подставляем эти значения в уравнение (8,10):
Хз _ 18Х4 + 64Х — 64 = 0.
Очевидным корнем этого уравнения является \1 = 2. Разделив левую
часть уравнения на -X—2 по схеме Горнера, получаем
1 —18 64 —64
2 —32 64
~~\1 —Ш 32 Т
Подчеркнутые числа — коэффициенты того квадратного уравнения,
из которого найдем остальные два корня
Х*_ 16Х + 32 = 0;
X = 8 ± /32;
Итак, X, = 2; Х2 = 4 B + /2); Х3 = 4 B —1/2).
198
Проверьте, равно ли произведение корней характеристического
уравнения определителю матрицы А.
Теперь приступим к определению собственных векторов. Си-
Систему (8,8) для нашей задачи, учитывая, что
ап = 5; а12 = 1; а13 == 4;
а21 = 3; а22 = 3; а23 = 2;
а31 = 6; а32 = 2; а33 = Ю,
перепишем так:
ЪЬи + C — X,) 62i + 2b3l = 0;
6bu + 2b2i + A0 — у b3l = 0.
(8,11)
Определение первого собственного вектора (i = 1). Для
Xj = 2 получаем
З&ц + Ьп + 4&31 = 0;
66ц + 2621 + 8&31 = 0.
Определитель этой системы, конечно, равен нулю (почему?).
Третье уравнение является следствием первого: если первое урав-
уравнение умножить на два, то получится третье. Отбросим третье
уравнение и решим систему двух линейных однородных уравнений
с тремя неизвестными:
36ц + Ьи + 4631 = 0j
3&u + 6,i + 2&3i = 0.
Напомним решение таких систем. Если имеется система уравне-
уравнений вида
= 0;
«23*3 = 0,
ТО
021*1
ж,=
Й12
«22
*13
il
«23
аи а12
Й21 «22
Здесь k имеет произвольное значение, а определители полу-
получаются из матрицы коэффициентов
1 О-и а13
I «22 О
вычеркиванием из нее столбца коэффициентов при определяемом
неизвестном.
199
В нашем случае матрица коэффициентов имеет вид
Ьц=*
1 4
1 2
Р
|з
ft; b21 =
1
4 3
2 3
**» иа\
13 1
3 1
ft;
Первый собственный вектор
2
6
О
Определение второго собственного вектора (£ = 2). Подставляя в
систему (8,11) второе собственное значение матрицы >.г = 4B + /2),
получаем систему уравнений
E—8—4У2)Ьи
— 8-41/2) Ь„ + 26зз
гг +A0 —8 —
=0;
= 0;
или
(-3 — 4 J/2) 6„ + 622
3&12 + (—5 — 4
6Ь12 + 2Ь2г
+
26
зг
= 0;
= 0;
+ B-4/2)Ь32 = 0.
Определитель этой системы также равен нулю. Отбросим третье
уравнение и решим систему уравнений
(-3 -4 /2) Ьа + Ь22 + 4Ь32 = 0;
Ы12 + (-5 - 4 /2) Ьгг + 2Ь32 - 0.
Матрица коэффициентов записывается так:
Г_з -4/2 1 41
[ 3 —5—4/2 2J-
а неизвестные равны
6.2 =
1 4
—5—4/2 2
ft;
J22 :
О.Ч2 =
—3—4/2
4 -3-4/2
2 3
1
ft;
—5—4/2
ft,
т. е.
612-B2+16/2)ft; 622 = A8+ 8/2N; 632 = D4 + 32/2)ft.
200
Второй собственный вектор
22 + 161/2
18+ 8J/2
.44 +
Определение третьего собственного вектора (/=3). Для Х3 —
= 4B — /2) из системы (8,11) получаем
E-8+4 V2) bls + b2S
З613 +C-8
46
3S
= 0;
=0;
41/2N33 = 0
млн
- C- 4/2) bu + 6
2S
+ 4Ь
зз
= 0;
=0;
33 =0.
Ясно, что определитель н этой системы уравнений равен нулю.
Отбрасываем первое уравнение и решаем систему уравнений
i3 + (-5 + 41/2) 623 + 2Ьзз = 0;
6i3 + 2623 + B + 41/2) 633 = 0.
Получаем
&зз = Cб — 24/2) ft.
Таким образом, третий собственный вектор
18—12 ]/^2
6—121/2
.36 — 241/2
Учитывая, что собственные векторы определяются с точностью
до постоянного множителя, можно, полагая k— 1, матрицу соб-
собственных векторов записать в таком виде:
[—2 22 + 161/2 18—121/2
6 18+ 8/2 6— 121/2
О 44 + 32/2 36 —24/2_
Замечание. Очевидно, что, давая множителю k различные
значения, этой матрице можно придать бесконечное множество
видов. Данное замечание относится и к следующим задачам, в
которых, определяются собственные векторы и их матрица.
201
Задача 8,2. Для матрицы
" 11 —6
А = — 6 10 —4
2 —4
найти ее собственные значения и собственные векторы.
Решение.
Заданная матрица — симметричная.
Эти матрицы обладают такими важными свойствами:
1. Матрица, составленная из собственных векторов симмет-
симметричной матрицы, ортогональна.
2. Матрица, составленная из собственных нормированных
векторов симметричной матрицы, также ортогональна.
3. Если матрица b — ортонормированная, то матрица, транспо-
транспонированная по отношению к ней, является для нее и обратной,
т. е.
Ь • Ь' = £,
а это значит, что
V = Ь~К
Следует также иметь в виду, что если b—симметричная
матрица, то транспонированная по отношению к ней матрица Ь'
совпадает с матрицей Ь.
4. Если 6— матрица, составленная из собственных нормиро-
нормированных векторов, то произведение
А
х,
Ь •А •Ь=
т. е. это произведение равно диагональной матрице, диагональные
элементы которой равны собственным значениям матрицы.
5. Собственные значения симметричной матрицы — вещественные
числа.
Характеристическое уравнение (8,6) в нашем случае запишется
так:
11—X —6 2
—6 10—X —4 =0. (8,12)
2 _4 6—X
Если раскрыть определитель в левой части, то получится на
основании (8,7) уравнение
(_1)зХз + (-ljMiA* + (-1)Л2Х + А3 = 0
или
X" — AiV + Ati — Л3 = 0. (8,13)
202
Определяем вторую и третью степени матрицы А:
11 + 10 + 6 = 27;
— 134
152 -
— 76
S2= 161 + 152 + 56 =369;
4
Л" = Л, • Л =
I-
161 —134 58
134 152 —76
58 —76
'2691
581
-76
66j
2628
756
11
—6
2
—6 2
10 —4
—4 6
S3 = 2691 + 2628 + 756 = 6075.
Мы заметили, что данная матрица А — симметричная. Ее квад-
квадрат Л2 — также симметричная матрица.
Теперь определяем коэффициенты Аи А3 и А3 характеристи-
характеристического уравнения по формулам (8,9)
Л2 = ^-<
л с i 97 97.
A — S2) = i- B7 • 27 — 369) = 180;
+ S3) = 1 A,80 • 27 — 27 • 369 + 6075) = 324
(проверьте что определитель матрицы А равен А3 = 324).
Таким образом, уравнение (8,13) запишется в виде
\з _ 27Х2 + 180Х — 324 = 0.
Одним корнем уравнения является Хх = 3, в чем легко убе-
убедиться непосредственной проверкой. Разделим левую часть урав-
уравнения на X — 3 по схеме Горнера:
1 —27 180 —324
3 —72 324
1 —24
108
0
203
Коэффициенты частного подчеркнуты. Квадратное уравнение
для определения остальных двух корней запишется так: "
Х*_ 24Х+ 108 = 0;
X = 12 ± К144—108;
Х2 = 6; Х3 = 18.
Итак, корни характеристического уравнения
Xj = 3; Х4 = 6; Х3 = 18
(проверьте, равна ли сумма корней следу матрицы, а их произ-
произведение—ее определителю).
Система уравнений (8,8) для определения координат собствен-
собственных векторов в нашем случае запишется так:
(И — \)Ъи— 662, + 263, = 0;
—66ц + (Ю - \) Ьи — 4b3i = 0;
(8,14)
Подставим в нее поочередно Хь Х2 и Х3.
Определение первого собственного вектора (/= I). Подставляем
в систему (8,14) Ха = 3 и получаем
Ь3, = 0;
2Ьп—
Ясно, что определитель этой системы равен нулю. Здесь неза-
независимы только два уравнения (действительно, если сложить второе
уравнение с третьим и сумму умножить на —2, то получится пер-
первое уравнение). Рассмотрим систему, состоящую из первого и вто-
второго уравнений
Матрица коэффициентов
Г 8 -6 21
[-6 7 -4|'
Ьп = 10fe; b21 — 20fc; bsl
а первый собственный вектор
b\ — k
10
20
20
204
Определение второго собственного вектора (/ = 2). Подставляем
в систему (8,14) Х2 = 6 и получаем для определения координат
второго собственного вектора систему уравнений
5Ь12 — 6Ь22 + 2Ь32 = 0;
C.U I Ли Ли Л.
2Ь12 — 4622 = 0,
определитель которой равен нулю. Независимых уравнений в этой
системе только два (если второе уравнение разделить на —2 и сло-
сложить с третьим, то получится первое).
Решим систему, состоящую из второго и третьего уравнений.
Матрица коэффициентов
г_б 4 —41
2 -4
Ь12 = —16й;
а второй собственный вектор
= —8k; b3i = l&k,
— 16
—8
16
Определение третьего собственного вектора (/ = 3). Система
(8,14) для Х3 = 18 примет такой вид:
—7Ь13 —
8Ь23 — 4Ь33 =
Определитель этой системы равен нулю. Здесь опять-таки только
два уравнения независимы (если первое уравнение умножить на
—2, а второе на 2 и сложить их, то получится третье уравнение).
Матрица коэффициентов первых двух уравнений
b13 =
Г-7 -6 2].
[_6 —8 —4J'
г; Ь23 = — 40/г; b33 = 20k,
а третий собственный вектор
b. = k ■
Так как собственные векторы определяются с точностью до по-
постоянного множителя, то можно взять k =■ 1 для blt Ья и Ь3.
205
Матрица Ь собственных векторов матрицы А при k — 1 запи-
запишется так:
"Ю —16 40"
b = 20 — 8 —40
20 16 20_
Матрица b по свойству 1 симметрических матриц (стр. 202), как
легко проверить, действительно ортогональна:
Ьх. Ь2 = 10 • (—16) + 20 • (—8) + 20 • 16 = 0;
6, . Ь3 = 10 • 40 + 20 . (—40) + 20 • 20 = 0;
Ь2. Ь3 = —16 • 40 + (—8) • (—40) + 16 • 20 = 0.
Пронормируем, каждый из собственных векторов blt b2 и b3 и со-
составим матрицу из нормированных собственных векторов.
Для первого собственного вектора 6Х нормирующий множитель
(см. стр. 194).
Для второго собственного вектора Ь2 нормирующий множитель
N 1 1_
2 ~~ —/(—16)» + (—8)г+ 1бг ~" ^4'
Знак минус перед корнем выбран для того, чтобы матрица пре-
преобразования Ъ была симметричной.
Для третьего собственного вектора Ь3 нормирующий множитель
1 1
60"
3 /40* _j_ (_40)г + 20а
Нормированные собственные векторы обозначим соответственно
через bv b2, b3:
~ 1 ~
~ъ
2
3
2
3_
•
i
2~
1
3
2
_ 3_
h
) "з =
- 2~
Т
2
3
1
3_
и составим из них матрицу
ь =
Ьг
~1
3
2
3
2
_3
ь2
2
3
1
3
2
3
ь3
2-
3
2
— т
1
3
(8,15)
206
Проверим выполнение свойства 2 симметричных матриц (стр. 202).
Составим скалярные произведения Ъх • Ь2, 6Х • Ь3 и Ъ2 • Ь3. Легко
убедиться, что каждое из них равно нулю.
(8,16)
Таким образом, векторы Ьи Ь2 и Ь3 попарно ортогональны,
матрица (8,15) — ортогональная матрица, а так как векторы bv
b2 и b3 нормированы, то матрица (8,15) ортонормирована.
Заметив, что матрица (8,15) ортонормированная, проверим выпол-
выполнение третьего свойства.
Составим произведение b • В' и убедимся, что получится еди-
единичная матрица. Это будет означать, что матрица В' обратна
матрице Ъ:
-\
3
2
У
2
_3
2
3
1
3
2
~У
2
3
2
1
3_
-1
3
2
3
2
_У
2
3
1
3
2
3
2~
3
2
3
1
3_
1
0
0
0
1
0
0"
0
1_
Поскольку b • b' — Е, то Ъ' есть матрица, обратная Ь.
Теперь проверим выполнение свойства 4. Составим произведе-
произведение b • А • Ь:
X
ь
1
3
2
3
2
• А • Ь-1 =
2 5
з :
1
У ~1
2
~У 1
-1
3
2
3
2 1
У У
2 2
_3 3
—
Г
1
4
12
2~
3
2
3
1
з_
2
•
11
—6
2
2
2 —4
— 12
6
•
~1
3
2
3
со| to
—6
10
—4
—
2
4
coj to
1
3
coj to
6
—
><
2
3
2
3
1
3
3
0
0
0
6
0
0
0
18
(8,17)
207
Действительно, получилась диагональная матрица с диагональ-
диагональными элементами, равными X, = 3, Х2 = 6 и Х3 = 18.
Отметим также выполнение свойства 5: все собственные числа
симметричной матрицы — действительные числа. Этим мы и за-
закончим решение данной задачи.
Задача 8,3. Найти собственные значения и собственные век-
векторы симметричной матрицы
Гб 3 2
А = 3 6 2
2 2 1_
и проверить свойства 1 и 2 симметричных матриц, указанные в
предыдущей задаче.
Решение. Характеристическое уравнение запишется так:
6—X 3 2
3 6—X 2
2 2 1-Х
0.
Если раскрыть определитель в его левой части, то получится
уравнение такое же, как и (8,13).
\3 А \2 _|_ А \ А (\ (Я \Я\
л л^л -j- Л2Л — /*13 — «• \°»ltJ/
Чтобы найти коэффициенты Alt А2 и Л3, найдем Л2 — вторую
степень матрицы А и диагональные элементы матрицы А3.
= А- А =
6 3 2
3 6 2
2 2 1
6 3 2
3 6 2
2 2 1
6 3 2
3 6 2
2 2 1
i = 13;
49 40 20
40 49 20
20 20 9
; S2 = 107.
49
40
20
40
49
20
20"
20
9
3
2
3
6
2
2"
2
1
454
454
89
Ss = 997.
А, = 5, = 13?
3. 13— 107) = 31;
= у C1 • 13— 13
208
С этими значениями коэффициентов уравнение (8,18) запишет-
запишется так:
—3 = 0.
Его корнем, как легко проверить, будет Xj = 3. Разделим левую
часть этого уравнения на X—3 по схеме Горнера;
1_13 31 —3
3 —30 3
I —12 1 °
Коэффициенты частного от деления подчеркнуты, а квадрат-
квадратное уравнение для определения остальных двух корней будет
таким:
Х3 = 5 —2Кб.
Таким образом, собственные значения матрицы найдены
Хх = 3; Х2 = 5 + 2J/6; Х3 = 5 — 2уЪ.
Система уравнений (8,9) для определения собственных векто-
векторов с найденными собственными значениями матрицы А запишет-
запишется так:
F — \)bu+3b2i+2b3l = 0
3*„ + F - X.) *2. + 2b3l = 0 (8,19)
2bu + 2b.2i + (l — Х,.)*3, = 0
Для определения собственных векторов подставляем в эту си-
систему поочередно X,, Х2 и Х3.
Определение первого собственного вектора (* = 1). При X х = 3
система (8,19) примет вид
3*ц+3*2,+2*,i = 0;
ЗЬп + ЪЬ21 + 2Ьа1 = 0;
2*ц + 2*21 — 2&31 = 0.
Определитель этой системы равен, конечно, нулю. Здесь вто-
второе уравнение совпадает с первым. Независимых уравнений в си-
системе два.
Решим систему уравнений из второго и третьего уравнений
2*ц +2*2i — 2*3i = 0.
209
Матрица коэффициентов записывается так:
[3 3 2]
[2 2 —2J'
bn = — 10fe; bn = 10/г; b31 = О,
а первый собственный вектор
Определение второго собственного вектора (/ = 2). Для Х2 =
= 5 + 2/6 система (8,19) запишется так:
F — 5 — 2/6N12 + 36г2 +2Ь32 =0;
3&12 + F-5-2/6)&22 + 2632 _ =0;
2Ь12 + 2Ь22 +A — 5—2/6N32 = 0
или _
A — 2КбN12 + 3b22 +2b32 =0;
ЗЬ12 + A - 21^6) Ь22 + 2Ь32 - 0;
2Ь1г + 2ЬИ + (-4 - 21/6) Ь32 = 0.
Определитель этой системы равен нулю, в ней только два неза-
независимых уравнения.
Решим систему из первого и второго уравнений
ЗЬ12 + A — 2 /6) b22 + 2fc32 = 0.
Матрица коэффициентов этой системы имеет вид
П —2/6 3 _ 2]
[ 3 1 — 2/6 2J*
Неизвестные определяются формулами
Второй собственный вектор
4 + 4/6
4 + 4/6
.16—4/6
210
Определение третьего собственного вектора (/ = 3). При Х3 =
= 5 — 2/бГ система (8,19) примет следующий вид:
F-5 + 2/б)Ь13 + ЗЬ23 _ +2Ь3з =0;
3fci3 + F - 5 + 2 /6) b23 + 2b33 = 0;
2ft,, + 2Ь2а + A-5 + 2/б)Ь3з = 0
или
(l + 2/6N13 + 3fc2, _ +2ft,, =0:
3&13 + A + 2 Кб) 623 + 2&33 _ =0;
2b13 + 2fc23 + (-4 + 2 /6) b33 = 0.
Опять-таки определитель этой системы равен нулю, независимых
уравнений в ней два. Решая систему из первого и второго урав-
уравнений, находим, что
633 = A6 + 4/6)fc,
а третий собственный вектор
[4 —4/бЛ
4-4/6 .
16 + 4/eJ
Так как собственные векторы определяются с точностью до постоян-
постоянного множителя, то, полагая k = 1 в выражениях для Ьи Ьг и Ь3,
получаем матрицу собственных векторов
Ь\ Ьг Ь3
■ Ю 4 + 4/6 4 —4/б
10 4 + 4/6 4—4/6
0 16 — 4/6 16 + 4/6
(8,20)
Убедимся в выполнении первого свойства симметричных матриц:
составим скалярные произведения собственных векторов
Ьф2 = —Ю • D/6 + 4) + 10D/6 + 4) + 0 • A6 — 4/6) = 0;
Ьф3 = —10D—4/6)+ 10D—4/6)+ 0A6 +4/6) = 0;
Ьф3 = D/6 + 4) D— 4 /6) + D/6 + 4) D— 4/6^ +
+ A6 — 4/6) A6+ 4/6) = 0.
Таким образом, матрица (8,20), составленная из собственных
векторов симметричной матрицы А, является ортогональной.
Теперь пронормируем собственные векторы bu b2 и Ь3 и убе-
убедимся в выполнении второго свойства симметрических матриц,
указанного в предыдущей задаче.
211
Для первого собственного вектора нормирующий множитель
N = = _
1 /(—10)*+10* 10 /2~'
а сам этот вектор в нормированном виде
1
/?
о
Для второго собственного вектора нормирующий множитель
д, 1 I
/V2 = _ - _ -^ — ,
УD + 4 /бJ + D + 4 /бJ + A6 — 4 /бJ 8 К9 — /б
а сам этот вектор в нормированном виде
1
У 6 + 2 /<Г_
Наконец, для третьего собственного вектора нормирующий мно-
множитель
^ ==_ 1 1
]/D _ 4/бJ + D — 4 /б)» + A6 + 4 /6J 8J/9+ /б'
а в нормированном виде
Матрица 6 нормированных собственных векторов имеет вид
&1
1
/2
/2
0
02
1
2]/з-/б
1
2 Уз — /6
1
Кб+ 2/6
ь3
1 ~
2 У 3 + /6
1
2 У 3 + /б
1
]/ 6 — 2 /6 _
212
Легко проверить, что и эта матрица ортогональна, так как
&!•*, = 0; &!•&, = 0; Ьг - Ь3 = 0;
Тем самым выполнено и свойство 2.
Теперь легко проверить, что
3 0 _ О
О 5 + 2/6 О
О 0 5—2/6
т. е. выполняется и четвертое свойство ортогональных матриц.
Выполняется и свойство 5: все собственные значения задан-
заданной симметрической матрицы — действительные числа.
Задача 8,4 (для самостоятельного решения). Найти собственные
значения и собственные векторы матрицы
3
2
1
2
4
'2
1
2
3
Промежуточные результаты:
1. Характеристическое уравнение
Хз — 10Х8 + 24Х — 16 = 0.
2. Собственные значения матрицы
Х1 = 2; Х2 = 4 + 2/2; Х3 = 4—2/2.
3. Система уравнений для определения собственных векторов
+Ь„
=0;
=0;
Первый собственный вектор (/ = 1)
Г
О
— 1
Второй собственный вектор
Ьа = k •
[
4 + 2/2
4 + 4/2
4 + 2/2
213
Третий собственный вектор
4 — 2/2
4 — 4/2
4—2/2
Матрица собственных векторов
1 4 + 2|/2 4—2/2
О 4 + 4 /2 4 — 4 /2
— 1 4 + 2/2 4—2/2
Проверить, что имеют место равенства
[2 0 0
b -b' = Е и b ■ A'b' = о 4+2/2 0
О 0 4—2/2
Задача 8,5 (для самостоятельного решения). Найти
ные значения матрицы
1 3 2
А =
2 а 1 3
4 2 4 6
3 13 4
Промежуточные результаты:
1. Характеристическое уравнение
5—X 1 3 2
2 3-Х 1 3
4 2 4-Х 6
3 1 3 4—)
2. Степени матрицы А:
5 16 34 39
= 0.
А2 =
29 16 22 31
58 24 48 62
41 16 34 43
'45
29
16 34 39"
16 22 31
13 2"
2 3
4 2
58 24 48 62
_41 16 34 43
10 200 404 498
358 152 284 362
716 288 576 724
502 200 404 506
_3 1 3 4_
214
10 200 404 498 5 13 2
358 151 284 362 2 3 13
716 288 576 724 4 2 4 6
502 200 404 506_ _3 1 3 4.
6060
1744 •
• 6912
• • 6052
3. Следы матрицы
51 = 16—след матрицы А;
52 = 152 — след матрицы А2;
S3= 1744—след матрицы А3;
S4 = 20768—след матрицы А*.
4. По формулам (8,9) определяются коэффициенты характеристи-
характеристического уравнения:
A1 = S1= 16;
^ = {ИА- S2) = -iA6> 16—152) = 52;
A, =
Sa) = -i E2 • 16— 16 ■ 152 + 1744) = 48;
^ ^s— S4)=^-D8- 16 — 52- 152 + 16 x
X 1744—20768) = 0.
5. Характеристическое уравнение
Ответ. Собственные значения матрицы А:
A.j = 0; л2 = 2; А3 = 12; л4 = 2;
bi + ^+^ + ^Sx.
Убедиться, что определитель матрицы
|Л| = 0,
т. е. матрица особенная (иначе — вырожденная).
215
ДЕВЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Преобразование характеристического уравнения методом
академика А. Н. Крылова, Теорема Кэли — Гамильтона.
1. МЕТОД АКАДЕМИКА А. Н. КРЫЛОВА ДЛЯ РАСКРЫТИЯ
ОПРЕДЕЛИТЕЛЯ В ВЕКОВОМ УРАВНЕНИИ
Академик А. Н. Крылов указал удобный метод раскрытия опре-
определителя в левой части уравнения (8,6). Сущность этого метода
заключается в том, что определитель путем алгебраических преоб-
преобразований приводится к такому виду, который позволяет его легко
вычислить.
Трудность раскрытия определителя состоит в том, что неиз-
неизвестная величина X входит только в диагональные элементы. Мето-
Методом А. Н. Крылова определитель в левой части (8,6) преобразу-
преобразуется так, что неизвестные величины X. оказываются не диагональ-
диагональными его элементами, а элементами столбца. Это дает возмож-
возможность на основании известных свойств определителей разложить
его по элементам этого столбца, довольно просто представить
определитель в уравнении (8,6) в виде многочлена и получить
алгебраическое уравнение с неизвестным X.
Ознакомиться с теорией этого вопроса можно по таким источ-
источникам:
1. А. Н. Крылов. О численном решении уравнения, которым в техни-
технических вопросах определяются частоты малых колебаний материальных систем
(«Известия Академии наук СССР», 1931).
2. Н. Н. Лузин. О методе академика Крылова составления векового
уравнения («Известия Академии наук СССР», 1931).
3. А. К. Сушкевич. Основы высшей алгебры, глава IX, § 171 (Изда-
(Издательство ОНТИ, 1937).
Здесь же, не вдаваясь в теоретические подробности, мы изло-
изложим метод академика А. Н. Крылова и покажем на примерах его
применение.
Левая часть векового уравнения (8,6) записывается так:
\А— Щ.
Для применения метода Крылова надо выполнить следующее:
1. Составить первые строки последовательных степеней матрицы
Л, т. е. первые строки матриц Л2, Л8, Л4, ... , Л".
216
Если обозначить через а$ элементы первой строки к-ой сте-
степени матрицы А, то их просто можно определить по формуле при-
приведения
5>
(9,1)
где верхний индекс (&) — указатель степени матрицы, причем k =
= 2, 3, 4, .... л; /'=1,2 л, а'}' = ац. Эта формула по-
позволяет по известным элементам первой строки матрицы Ак~1
и элементам матрицы А найти элементы первой строки матрицы Л*.
Таким образом, должны быть составлены матрицы
-B)"
hn
"_<з) _(з) л'з)
аи а12 ... а1п
D) д<4> QD)
«п «12 • • • ат
а12 ... ам
2. После того как первые строки степеней матрицы А найдены,
составить определитель такого вида:
D(\) =
1
X
X2 а
1 О
О
О
и
,B)
11
,C)
«13
„A)
«1л
X» а» а!
«12
«
II1
II
а
ш
„(я)
«12
(9,2>
в котором степени неизвестной величины X уже расположены в пер-
первом столбце, а строки степеней матрицы А являются строками
минора элемента, стоящего в левом верхнем углу в (9,2).
217
Этот определитель тождествен определителю левой части урав-
уравнения (8,6), а раскрыть его значительно проще: его надо только
разложить по элементам первого столбца. Получится уравнение
степени л относительно X. Решение его и даст собственные значения
исходной матрицы. Определитель (9,2) называется определителем
Крылова. Преобразованием определителя \А — \Е\ в уравнении
(8,6) к виду (9,2) обойдены все большие трудности, связанные с его
раскрытием.
3. Надо с помощью тождественных преобразований определи-
определителя (9,2) внести дальнейшие упрощения в разложение этого опре-
определителя по элементам первого столбца.
Предполагая, что элементы второй строки в (9,2) а^, о["
1 не равны нулю, разделим элементы столбцов, начиная с третьего,
что равносильно вынесению
а,Ч' .. ai\\ После этого
я{
{д
соответственно на
за знак определителя произведения а£
деления получится.определитель вида
13
1
и
«
0 О
1 1
... о
... 1
а1
(9,3)
Обозначим дроби — через b^k, где k
2, 3, 4, ... п; / = 2, 3,
4,
п, т. е.
и определитель (9,3) примет вид
1
X
X2
Хз
1
"и
ап
ап
0
1
1,B)
иЬ)
2
0
1
1,B)
&13
U(S)
°1S
... 0
... 1
1,B)
• • • °ln
••• ЬЫ
«11
tin) и
^12 °
13
(9,4)
21В
Вычтем теперь из элементов четвертого и следующего за ним
столбцов определителя (9,4) соответствующие элементы третьего
столбца и получим определитель
где
1 1
X2 а
11
,B)
И
О
1
«,B)
2
О
О
сB)
„C)
In «W
О
О
„(8)
cm
(9,5)
: = 3, 4, ... л; / = 2, 3, 4, ... л)
c[2J неравны
С определителем (9,5) поступаем так же, как и с определителем
(9,2), но начиная уже- с четвертого столбца.
Предполагая, что элементы третьей строки с^', [J р
нулю, разделим все элементы столбцов, начиная с четвертого со-
соответственно на с[з*. ... , с|*\ т. е. на верхний, не равный нулю
элемент этого столбца.
Такое деление равносильно вынесению за знак определителя
B)
произведения с^
с[„. Получится определитель вида
1 1
х 1!
О
1
°12
О
О
1
.. о
.. о
.. 1
Лп) иЫ An)
II 1J It)
г1п
i
hi
(9,6)
где
=~wAk> / = 3, 4. ... л);
После этого вычтем из элементов пятого и следующего за ним
столбцов соответствующие элементы четвертого столбца, отчего
величина определителя не изменится.
219
Определитель примет вид
1 1 О
X aiV 1
Ь
О
О
X»
«и
B)
12
/3)
12
•*13
..О|
.. О
...О
(з)
• • • С1л
«11
где
е1к
1) j(rt) (я)
2 3 • • • Ё1П
d<n — dl/)
alk 3
я); k = 4, 5,
(9J)
(/ = 3, 4 л); * = 4, 5 л).
Поступая так же с элементами пятого и следующих столбцов,
получим в конце концов определитель такого вида:
1
X
Xs
а
"и
"и
„C)
«11
О
1
и(г)
и\г
и(з)
"и
°п
13
is
О
О
О
о
1
SpA
(9,8)
Следует помнить, что в правом нижнем углу определителя дол-
должен получиться след SpA матрицы А. Заметим, что чем выше
порядок матрицы А, собственные значения которой отыскиваются,
тем эффективнее описанный метод, предложенный академиком Кры-
Крыловым.
Переходя к уравнению (8,6), мы видим, что в его левой части
находится определитель (9,8), множителями перед которым будут
указанные выше произведения
/л(п п<и a(l)WcB) . cB) ci2)\ (9 9^
(ai2 а1з • • • ат) lcis cu • • • С1Я J • • • » \у>у)
а в правой части — нуль.
Эти множители можно отбросить, что равносильно сокращению
уравнения на все произведение (9,9). После описанных преобразо-
преобразований вместо уравнения (8,6) получится уравнение
11 0 0 0 ... 0
к
X3
X"
"и
«11
я(з)
«11
«11
1
иB)
2
и(з)
2
и
1
С
0 ...
0 ...
1 ...
р'п)
С|4 . . .
0
0
0
1
= 0.
(9,Ю)
220
Если среди элементов, на которые требовалось производить де-
деление, окажутся равные нулю, то надо сразу раскрывать опреде-
определитель (9,2), не прибегая к дальнейшим его преобразованиям, или
переставить строки так, чтобы избежать этой неприятности. Теперь
применим описанный метод к нескольким матрицам, выполняя все
указанные операции последовательно. В качестве матриц возьмем
те, которые нам уже встретились в задачах 8,1 — 8,5.
Задача 9, 1. По методу академика А. Н. Крылова найти ха-
характеристическое уравнение матрицы
1 4"
3 3 2
6 2 10
Решение. 1. С этой матрицей мы уже встречались в задаче
8,1. Находим первые строки последовательных степеней матрицы А
по формуле приведения (9, 1)
52 16 62
680 224 860
Первые строки матриц Аг и А3 можно получить проще, не при-
прибегая к формуле (9,1): на отдельном листке бумаги написать мат-
матрицу А и этот листок приставлять поочередно к матрице Л и Л2,
составляя сумму произведений элементов первой строки этих мат-
матриц на соответствующие столбцы «приставной» матрицы.
2. Составляем определитель вида (9,2)
D(X) =
1
X
X2
Х«
1
5
52
680
0
1
16
224
0
4
62
860
(первая строка за-
заданной матрицы)
3. Теперь разделим элементы каждого столбца, начиная с треть-
третьего, на верхние их элементы, находящиеся во второй строке:
D(X) =
221
1
X
X2
Xs
1
5
52
680
0
1
16
224
0
1
62
4
860
4
= 4
1
X
X2
X3
1
5
52
680
0
1
16
224
0
1
31
2
215
Вычтем из элементов четвертого столбца соответствующие эле-
элементы третьего. Получится определитель
D(X) =
1
5
О
1
О
1—1
X
X* 52
X3 680
1
X
X»
X3
16 у —16
224 215 — 224
1
5
0
1
0
0
52 16 —y
680 224 —9
Теперь разделим все элементы четвертого столбца на — -=•:
1
X
X*
X3
1
5
52
680
О
1
16
224
О
О
1
18
Еще раз напомним: последний элемент последнего столбца равен
следу заданной матрицы, т. е. сумме ее диагональных элементов,
а предпоследний элемент должен быть равен 1. Раскроем этот опре-
определитель по элементам первого столбца, начиная с его последнего
элемента.
( L)
\ 2/
X
1
52
680
—X3
0
16
224
1
г
52
0
1
18
0
, 1
» 16
+ 1 •
0
0
1
+ Ха
5 1
52 If
680 22<
1
5
680
0
> 1
1 18
0 0
1 1
224 18
1
1. Определитель при X3 равен
1 0 0
5 1 0
52 16 1
1 0
16 1
= 1.
(Напомним, что если все элементы какого-либо ряда определителя,
кроме одного, равны нулю, то определитель равен произведению
этого, не равного нулю элемента, на его алгебраическое дополне-
дополнение).
222
2. Определитель при Ха
1
5
680
0
1
224
3. Определитель при X
1 0
52 16
680 224
4. Свободный член
0
О
18
О
1
18
1
224
16
224
О
18
= 18.
18
= 64
5
52
680 2
1 0
16 1
224 18
—28
—440
=
1
18
О 1
—28 16
—440 224
О
1
18
_ = _ (—64) = 64.
Таким образом,
D (X) = 4 • (-1) (-ХЗ + 18Х« + 64Х + 64).
Характеристическое уравнение запишется так:
D(X) = 0
или
~ т) (~хз
64) =
Сокращая на множитель 4 • (— -Л и умножая обе части уравне-
уравнения на —1, получим окончательно
X3 — 18Хг — 64Х — 64 = 0.
Это же уравнение было найдено в задаче 8,1.
Задача 9,2. Найти методом академика А. Н. Крылова харак-
характеристическое уравнение матрицы
11—6 2"|
— 6 10—4
_ 2 -4 6J'
Решение. Эта матрица нам уже встречалась в задаче 8,2.
1. Находим первые строки ее степеней А2 и Л3, пользуясь фор-
223
мулой (9,1) или приставной табличкой (это в данном случае, пожа-
пожалуй, проще)
61 —134 58
691 —2538 1208"
2. Составляем определитель вида (9,2)
110 0
X 11 —6 2
X2 161 —134 58
X3 2691 —2538 1206
£>(Х)
первая строка
матрицы А
3. Разделим элементы третьего столбца на элемент — 6, а эле-
элементы четвертого столбца на 2, в результате чего определитель
D (к) = — 6 ■ 2
Вычтем из элементов четвертого столбца соответствующие эле-
элементы третьего столбца. Тогда
110 0
I 11 1 0
1
X
X*
X3
1
11
161
2691
0
1
67
Т
423
0
1
29
603
D (X) = — 6 • 2
= —6-2
0
0
20
3
180
20
Разделим элементы четвертого столбца на у:
X2
Xs
1
X
X2
X3
161
2691
1
11
161
2691
з у з
423 603 — 423
0
1
67
3
423
20
1
X
X2
X3
1 0
11 1
16, I
2691 423
0
0
1
27
224
Контроль: Последний элемент в последнем столбце равен следу
матрицы А.
Разлагаем этот определитель по элементам первого столбца,,
начиная с его последнего элемента
20
D (к) = -6 • 2 . у I
— X3
1
11
0
1
161 z 1
1
11
2691
0 0
1 0
423 27
— X
1 О О
161 Е 1
2691 423 27
Определитель при X3
11 1 О
161 § 1
2691 423 27
1
11
О
1
■61 Ц
Определитель при" X4
1 О
11 1
1 О
Е 1
3 1
= 1.
2691 423 27
Определитель при X
1
161
2691
Свободный член
11
2691
1 О
423—27
= 27.
0
67
3
423
0
1
27
=
67
У
423
1
27
= 180.
1
?
423
0
1
27
254
1
67
—1962 423
О
1
27
(к элементам первого столбца прибавлены элементы второго
столбца, умноженные на —11)
254
—г *
1962 27
= _ (—324) = 324.
8 И. А. Каплан
225
Таким образом, приравнивал D (X), нулю, получаем характери-
характеристическое уравнение для матрицы А
D (X) = — 6 • 2 • ~ (—X» + 27X2 — 180Х + 324) = О,
или окончательно
).з_27Х2 + 180). — 324 = 0.
Такое же уравнение найдено и в решении задачи 8,2.
Задача 9,3. Методом академика Крылова найти характеристи-
характеристическое уравнение матрицы
[6 3 2'
3 6 2
2 2 1_
Решение. С этой матрицей мы встречались в задаче 8,3.
1. Определим первые строки ее степеней Аг и А3, пользуясь
формулой приведения (9,1) или «приставной» матрицей
49 40 20
454 427 198
2. Составляем определитель вида (9,2)
1
X
Хг
Xs
1
6
49
454
0
3
40
427
0
2
20
198
>- первая строка
матрицы А
3. Разделим все элементы третьего столбца на 3 (верхний эле-
элемент этого столбца в его второй строке), а элементы четвертого
на 2 (верхний элемент во второй строке этого столбца):
D (X) » 3 • 2
1
X
X2
Xs
1
6
49
454
0
1
40
3
427
3
0
1
10
99
226
Теперь из элементов четвертого столбца вычтем соответствую-
соответствующие элементы третьего столбца
110 0
X 6 1 0
D (X) = 3 • 2 •
49 ^ -^
™ 3 3
Лг. 427 130
454 -д- --3-
ю
Разделим все элементы четвертого столбца на элемент —я- и по-
получим
D (X) = 3 • 2 • (-
1
X
X*
Xs
1
6
49
454
0
1
40
~3~
0
0
1
13
Разлагаем этот определитель по элементам первого столбца,
начиная с его последнего-элемента,
—Xs
1
6
49
0
1
"з"
0
0
1
+ х«
1
6
О
1
454 Щ- 13
Определитель при X3
1
49
454
0
40
3
427
0
1
13
+
1
6
49
454
1
40
3
427
0
1
13
1
6
У
0
1
40
3"
0
0
1
1
40
Т
0
= 1.
Определитель при Ха
1 О
6
454
1
427
0
0
13
1
427
3
0
13
13.
227
Определитель при X
1
49
454 -о-
0
40
3
427
3
0
1
13
40
3
427
3
1
13
= 31.
Свободный член
6
49
454
1
40
Т
427
0
1
13
0
—31
—400
1
40
3
427
3
0
1
13
(элементы второго столбца умножены на —6 и прибавлены
к элементам первого столбца)
—31 1
-400 13
-(-3) = 3.
Подставляя эти значения определителей в D (X) и приравни-
приравнивая нулю полученное выражение, находим характеристическое
уравнение
= 0
и окончательно
_ 13Х8
—3 = 0.
Это же уравнение было получено в задаче 8,3.
Задача 9,4 (для самостоятельного решения). Методом академика
Крылова найти характеристическое уравнение матрицы
А =
3 2 1
2 4 2
1 2 3
Ответ. Xs — ЮХ2 + 24Х — 16 = 0 (см. задачу 8,4).
Задача 9,5 (для самостоятельного решения). Найти методом
академика Крылова характеристическое уравнение матрицы
13 2-
2 3 13
4 2 4 6
3 13 4
228
Промежуточные результаты:
45 16 34 39
510 200 404 498'
6060 2416 4840 6036
2. Определитель (9,2) имеет вид
D(X) =
Ответ. Х« — 16Х3 + 52Х2 — 48Х = 0.
Задача 9,6 (для самостоятельного решения). Найти методом
академика Крылова характеристическое уравнение матрицы
432 Г
4 8 6
1
X
X*
X3
х«
1
5
45
510
6060
0
1
16
200
2416
0
3
34
404
4840
0
2
39
498
6036
А =
4 2
3 6 9 6 3
2 4 6 8 4
12 3 4 5
и ее собственные значения.
Промежуточные результаты:
Первая строка в матрице А2
55 80 81 64 35.
Первая строка в матрице As
1001 1672 1863 1568 889.
Первая строка в матрице Л4
21307 36608 41877 35968 20651.
Первая строка в матрице А6
471185 814528 938223 810656 467281.
229
Определитель
D(X) = ,
1
X
X2
Xs
(9,2)
1
5
55
100 i
0
4
80
1672
0
3
81
1863
0
2
64
1568
0
1
35
889
X* 21307 36608, 41877 35968 20651
X5 471185 814528 938223 810656 467281
После преобразования по указанной схеме получится характе-
характеристическое уравнение
0
0
0
0 =0.
1
X5 471185 203632 15587 814 35
После разложения этого определителя по элементам первого
.столбца и вычисления определителей при степенях X это уравне-
уравнение примет вид
Хб _ 35Х« + 336Х3 — 1296Х3 + 2160Х — 1296 = 0.
Его корни — собственные значения матрицы А
1
X
X2
Xs
X*
1
5
55
1001
21307
0
1
20
418
9152
0
0
1
29
4807
7
0
0
0
1
230
7
Х1==2; Х2 = 3; Х3 - 6;
12
Xs=12 —
Задача 9,7 (для самостоятельного решения) Методом Крылова
найти характеристическое уравнение матрицы
0
0
—6
1
0
—1
0
1
4
и ее собственные значения
Ответ. X3 — 4Х* -j— X -f- 6 = 0;
Xj = — 1; Х2 = 2; к3 = 3.
Задача 9,8. Методом Крылова найти характеристическое урав-
уравнение матрицы
0
0
0
48
1
0
0
—28
0
1
0
о
0
0
1
7
и ее собственные значения.
230
Ответ. Х« — 7Х» + 8Х2+28Х — 48 = 0;
Лх = —2; Х2 = 2; Х3 = 3; Х4 = 4.
II. ТЕОРЕМА КЭЛИ-ГАМИЛЬТОНА.
Теорема Кэли-Гамильтона в матричном исчислении является
одной из важнейших. Вот ее формулировка:
Каждая квадратная матрица удовлетворяет своему характе-
характеристическому уравнению, которое следует понимать в матрич-
матричном смысле.
Объясним это.
Если для матрицы А характеристическое уравнение имеет вид
(8J)
(— 1)" Xя + (— I)" А}\«-1 + (— iy-2 Л2Х"-2 + • • • +
+ (—1) Л„_, X + Л„ = 0,
то получается матричное равенство
(9,11)
где Е — единичная матрица того же порядка, что и А, а 0 —
нулевая матрица.
Определение обратной матрицы при помощи
теоремы Кэли-Гамильтона
Если А — невырожденная матрица, то равенство (9,11) позво-
позволяет найти А~1 — матрицу, обратную А.
Умножим (9,11) слева на А~1:
(— 1)"Л«-1 + (— I)"-1 ЛИ" + ... + (— 1)Л„_,Л-М + Л„Л~1£'=0
Отсюда, учитывая, что А~1А = Е, получим
Л-1 = - '[(_1)«Л"-2+(-1)"-1Л1Л'-2+ ... +(_1)Л„_,£1. (9,12).
Эта формула дает удобный практический метод вычисления
обратной матрицы, так как определить коэффициенты Alt A2
А3, . ■ ■, А„ характеристического уравнения можно по формулам
(8,9).
Задача 9,9. Доказать, что матрица
231
удовлетворяет своему характеристическому уравнению
X8 — 18Х2 + 64а. — 64 = О
(см. задачу 9,1).
Решение. Заменим в левой части характеристического, урав-
уравнения А. на матрицу А:
A* —ISA2 +64Л — 64£ (9,13)
или
5 1
3 3
6 2
4
2
10
II-
18.
5 1
3 3
6 2
5 1
3 3
6 2
10
— 64
Убедимся, что это выражение равно нулевой матрице.
Найдем сначала квадрат, а потом куб матрицы А
А2 =
5 1
3 3
6 2
4
2
10
а Г5 '
= 3 3
[б 2
Г5
3
ь
;
5
3
6
1
3
2
4
2
10
52 16 62
36 16 38
96 32 128^
52 16 62] |~5 1 4
36 16 38 • 3 3 2
.96 32 128 J L6 2 10.
[680 224 860"
456 160 556
1344 448 1728
Подставляем полученные степени матрицы А в выражение (9,13)
и убедимся, что оно обратится в нулевую матрицу
[680 224 860] [52 16 62
456 160 556 —18. 36 16 38
1344 448 1728 J [96 32 128^
14] П 0 0"
-64-
64.
3 3
4
2
6 2 Ю
680 224 860
456 160 556
1344 448 1728
320 64 256
192 192 128
384 128 640
1-
64
0
0
0 1 0
О 0 1
936 288 1116
648 288 684
1728 576 2304
О О
64 О
О 64
О 0 0]
0 0 0.
О 0 Oj
232
Задача 9,10. Найти матрицу, обратную матрице А предыдущей
задачи.
Решение. Характеристическим уравнением матрицы А явля-
является уравнение
Х8_18Х4 + 64Х — 64 = 0
(см. задачу 8,1).
На основании теоремы Кэли-Гамильтона матрица А удовлет-
удовлетворяет этому характеристическому уравнению. Поэтому
А* — 18Л2 + 64/4 — 64£ = 0.
Умножая, как это делалось при выводе формулы (9,12), обе
части этого уравнения на А~1, получим
откуда
а
Матрица А2 уже была найдена в предыдущей задаче
2 16 62^
l-i. /43— 18/4-1. Аг + 64Л-1 . А — 64/4-1 • Е = О,
Л» — 18/4 + 645 = 64Л-1,
1
/4* =
36 16 38
96 32 128
Поэтому обратная к А матрица
52 16
36 16
62
38
1
:64
96 • 32 128
52 16
36 16
96 32 128
1
64
5 1 4
— 18 . | 3 3 2
.6 2 10
90 18 72
54 54 36
108 36 180
26 —2 —10
— 18 26 2
— 12 —4 12
+ 64
+
1 0 0
О 1 О
О 0 1
64 О О
О 64 О
О 0 64
Таким образом, обратная матрица
26 —2
/4-1
1
64'
А-1~а-
— 18 26
— 12 —4
13 —1
—9 13
—6 —2
— 10
2
12
—5"
1
233
Проверка:
1
3
—9
.—6
=
1
0
0
—1
13
2
0
1
0
0"
0
1
-5"
1
6
5 1
3 3
6 2
4
2
10
Заметим, что формула Кэли-Гамильтона позволяет, зная
(п— 1)-ую степень матрицы А, найти ее я-ую степень, учитывая,
что коэффициенты характеристического уравнения легко вычисля-
вычисляются по формулам (8,9).
Так, из характеристического уравнения задачи 9,9
Хз_ 18X2+ 64Х —64 = 0
на основании теоремы Кэли-Гамильтона следует
Л»—18/4а + 64Л — 64£ = 0,
А3 = 18Лг—64Л + 64Я.
откуда
Действительно, легко проверить, что найденное раньше значе-
значение (см. задачу 9,9)
18
52 16
36 16
96 32
62
38
128
-64-
10
+ 64
0 01
о 1 о Г
0 0 1J
Убедитесь, что это выражение равно матрице
680 224
456 160
1344 448
860
556
1728
:]■
Задача 9,11 (для самостоятельного решения). Доказать, что
матрица
11 —6 2
—6 10 —4
2 —4 6.
удовлетворяет своему характеристическому уравнению
ХЗ_27Ха + 180Х —324 = 0
и найти матрицу А~1, обратную матрице А.
234
Ответ.
Задача 9,12 (для самостоятельного решения). Для матрицы
[6 3 2'
А =
характеристнческим уравнением является
Xs — 13Ха + 13Х — 3 = 0.
Найти л3 и А~К
Указание. На основании теоремы Кэли-Гамильтона мат-
матрица А удовлетворяет своему характеристическому уравнению,
т. е. имеет место равенство
А3 —\ЗА2+31А — 3£ = 0.
Отсюда
/43 = 13/42 — 31/4+ 3£,
а на основании формулы (9,12)
А~1 = 1 (Л2 — 13Л
Ответ.
Г454 427 198"
Л3 =427 454 198,
198 198 89
31Е).
1 Г 2 1 -б"!
; Л- = 1- 1 2 -61
,J |__6 -6 27 J
Задача 9,13 (для самостоятельного решения). Для матрицы
А
ГЗ 2 П
.-2 4 2
L1 2 3J
характеристическим является уравнение
X3 — 10Х* + 24Х —16 = 0.
Убедиться, что эта матрица удовлетворяет этому характери-
характеристическому уравнению. Определить обратную матрицу А~х и
найти А3.
Ответ.
l-i = i (Л2—ЮЛ
ID x
—
16
24£);
8 —4 О'
4 8 —4
0—4 8
235
Л8 =
48
= ЮЛг-
=
' 84
112
76
■24Л
112
160
112
+ 1б£;
76'
112
84
Задача 9,14 (для самостоятельного решения). Найти характе-
характеристическое уравнение матрицы
2 2"
2 1
2 —2
2
1
ее собственные значения и, пользуясь теоремой Кэли-Гамильтона,
обратную ей матрицу А~*
Ответ. 1) X3 — ЗХ2 — 9Х + 27 = 0;
2)
3)
— 3; Х2 = 3; Х3 — —3;
_ j
[—3 —6 -I
-6 -3 I
—6 6 —
-6"
6
3
ДЕСЯТОЕ ПРАКТИЧЕСКОЕ ЗАДАНИЕ
Содержание. Применение матриц к приведению квадратичной формы
двух переменных к сумме квадратов (к каноническому виду). Упрощение урав-
уравнений кривых второго, порядка.
СВЕДЕНИЯ ИЗ ТЕОРИИ
Упрощениями уравнений кривых второго порядка мы уже за-
занимались в первой части этой книги на четырнадцатом практи-
практическом занятии. Сейчас возвратимся к этому вопросу и покажем,
что привлечение матричного исчисления к решению этой задачи
значительно облегчит его.
Прежде всего кратко изложим теорию приведения квадратич-
квадратичной формы двух переменных к сумме квадратов, к так называе-
называемому каноническому виду, и полученные выводы применим к уп-
упрощению общего уравнения кривой второго порядка.
КВАДРАТИЧНАЯ ФОРМА ДВУХ ПЕРЕМЕННЫХ
И ПРИВЕДЕНИЕ ЕЕ К СУММЕ КВАДРАТОВ
(К КАНОНИЧЕСКОМУ ВИДУ).
Квадратичной формой двух переменных называется выражение
вида
2 2
F(*u *2>= S Еа//**/. A0,1)
В развернутом виде оно записывается так:
2
F (*1, х2) = 2 iflxixix, + a2ix2Xf) =
Окончательно
t, x2) = aux\ + al2xyx2 + а^х^хг + ai2x\. A0,2)
Если окажется, что коэффициенты а12 и а21 при произведении
равны между собой, т. е. а21 = а12, то формула A0,2) при-
примет вид
F (хи х2) = ац*2, + 2а12х1Хг + <hix\. A0,20
237
С таким видом квадратичной формы мы будем встречаться
при решении задач. Легко проверить, что выражение A0,2) может
быть записано в виде произведения трех матриц
F{xux2)=[xux2]-\a» !"]-[*х|. (Ю.З)
L1 2J l-*2J
Введем такие обозначения:
аП "] (Ю'4)
А — матрица коэффициентов квадратичной формы.
Если квадратичная форма имеет вид A0,2), то матрица ее
коэффициентов будет симметричной и запишется так:
A = Ia»
a 12
Ч
ам1
Таким образом, элементы, стоящие на второй диагонали, равны
между собой и каждый из них равен половине коэффициента при
произведении xtx2 в квадратичной форме A0,2i). Именно в таком
виде A0 А) мы и будем применять матрицу А коэффициентов квад-
квадратичной формы при решении задач. Обозначим
(ю'5)
X' = [*i х2] A0,6)
(матрица X' является транспонированной матрицей X).
Выражение A0,3) с этими обозначениями запишется так:
F(xlt x2) = X'AX. A0,7)
Задача состоит в том, чтобы выражение A0,2!) или, что то
же, выражение A0,7) представить в виде суммы квадратов. В этом
виде оно не должно содержать члена с произведением переменных
Xi и х2. Преобразуем это выражение к новым переменным х\ и х'г
так, чтобы оно приняло вид
F (*'„ х'2) = X,*;* + \гх'2\ A0,8)
причем может оказаться, что один из коэффициентов \у или Х2
будет равен нулю. Это выражение, как легко проверить, можно
представить в виде произведения трех матриц
о1
23В
или, введя обозначения
'* = {х[ х'г);
получим
L-[o У
F(x'v x'2) = X'*LX*.
(Ю,Ю)
A0,11)
A0,12)
A0,13)
Таким образом, задача сводится к определению коэффициентов
и Ха в выражении A0,8).
М
Фиг. 10,1
Перейдем к геометрическому истолкованию этого преобразо-
преобразования. Будем рассматривать переменные д^ и х2 как координаты
точки М на плоскости в системе прямоугольных координат (xlt
х2): ось Охг — ось абсцисс, а ось Охг — ось ординат. Сохраняя
без изменений начало координат, повернем систему координат
хг0х2 на некоторый угол а. Мы получим новую систему коор-
координат, которую обозначим х[0х'2, а координаты точки М в новой
системе координат — через х\ и х2 (фиг. 10,1).
Единичные векторы осей первоначальной системы координат
назовем t и /, а новой системы координат — соответственно tx и /V
Обозначим
cos(i, ij) =s cos a = /n; cos(t, ji) = cos (90° -f а) = —sin а = /12;
cos(/, Гх) = cos(90° — a)=sina = /21; cosiQ', /1)=cosa=i22. A0,14)
239
Радиус-вектор точки М (хи х2) в первоначальной системе коор-
координат
г = Xii -{- xzj*
а в новой системе координат
7 — у'7 1 *.'?
поэтому
„ У I "; »Т | ' J МЛ 1КЧ
* "Т" Х%] — *1 l~ j1# V^^-'i^^'/
Умножая обе части этого равенства сначала на Г, а потом на
/, учитывая также, что скалярное произведение двух векторов
равно произведению их модулей на косинус угла между ними,
принимая во внимание обозначения A0,14) и то, что модуль орта
равен единице, зная, что для скалярных произведений ортов осей
прямоугольной системы координат имеют место равенства
), если k ф р
1, если k = р,
получаем
х2 = х[1г1 + х'21г2. A0,16)
Эти формулы выражают первоначальные координаты дсх и хг
точки через ее новые координаты х[ и х'2. В матричном виде эти
формулы выглядят так:
Учитывая уже введенные обозначения A0,5) и A0,10) и вводя
обозначение
S= " и , A0,18)
Ihi hi*
формулы A0,17) перепишем в виде
X = SX*. A0,19)
Матрица S называется матрицей преобразования. Заметим, что,
как это следует на основании A0,14), она ортонормирована. Дей-
Действительно,
/и/» + '21*22 = 0; /*, + 1\х = 1;
Из этого вытекает, что транспонированная к ней матрица
5' =
240
является для нее и обратной, т. е.
S' = S A0,20)
(убедитесь, что SS' = Е).
Умножив обе части формулы A0,19) слева на S~1, получим
или, читая справа налево,
X* = S^X. A0,21)
Для перехода от новых координат х[ и х'2 точки М к ее пер-
первоначальным координатам надо уравнения A0,16) решить относи-
относительно х[ и х'2. Это легко сделать, умножив скалярно обе части
равенства A0,15) сначала на ilt а потом на jx. Учитывая замеча-
замечание относительно скалярного произведения ортов осей прямоуголь-
прямоугольной системы координат (стр. 240) и прочитывая полученные равенства
справа налево, получим
Jfj = Х^и -f- Jf2*21>
4 = Xiht + *A* A0,22)
Эти формулы выражают новые координаты х\ и х'г точки М через
ее первоначальные координаты.
В матричном виде они запишутся так:
Но матрица
Г/и 1И1
L'i2 '22J
по отношению к матрице S A0,18) является транспонированной,
а поэтому она равна S', а на основании A0,20) она равна S.
Поэтому формула A0,23) совпадает с ранее полученной форму-
формулой A0,21)
X* = S-W.
Легко проверить, что наряду с A0,21) имеет место и равенство
X'* = X'S, A0,24)
а с равенством A0,19) — равенство
X' = X'*S-K A0,25)
Теперь уже мы можем от старых переменных перейти к новым,
для чего заменим в A0,7) X' по формуле A0,25), а X—по формуле
A0,19). В новых переменных х[ и х'2 функция F{xi, x2) запишет-
запишется так:
F (*;, х'2) = X'*S-]ASX*. A0,26)
241
Если обозначить
S-iAS = A*, A0,27)
то
F (х[, х'2) = Х'*А*Х*.
Сравнивая это выражение с выражением A0,13), приходим к вы-
выводу, что
A* = L,
т. е. на основании A0,27)
= L.
Если это равенство умножить слева на S, то
ИЛИ
AS=SL. A0,28)
Из этого матричного уравнения должны быть определены эле-
элементы матрицы L, т. е. величины \t и Х2, а также элементы
матрицы S, т. е. величины /п, /12, /21 и /22.
Выполним умножение в левой и правой частях A0,28), учиты-
учитывая A0,4), A0,12) и A0,18),
01
t22j L0 X2J
Отсюда следует:
(flll'll "Ь ^12*21 flll'l2 "f" al2'22| f'll^l '12X2I
a2i'n ~\~ а22'г1 fl2i *12 "f" fl22^22' ^21^-1 ^ггХг'
На основании условия о равенстве двух матриц получаем
1111 ~1 12 23 *~"~ * 11 1* 1 11 12 ~1— 12 22 ^~ 12 2' I
2l'll- ~Т~ 22 21 — 21 1* 21 ^1' ~1— «22^22 == 22 2" *
Эти две системы уравнений перепишем:
{аи — Xj) ln + fli2Z2i = 0; (йц — Х2) 112 -\- я12/22 = 0;
Ш21 ^22-" Lt2i Z22J lZ2i /22J L
(«22 — Xl) ^21 = О! Я21*12+ («22 Х)/ = 0
Запишем их и в виде одной системы уравнений
(flu - К) hi + aJn = 0
в которой индекс i может принимать значения 1 и 2.
Эта система является системой двух линейных однородных
уравнений. Для того чтобы она имела не тривиальное решение, не-
242
обходимо и достаточно, чтобы ее определитель был равен нулю,
т. е. чтобы
Х °12_J = 0 A0,31)
(индекс i у X мы опустили).
Нетрудно видеть, что уравнение A0,31) есть характеристичес-
характеристическое уравнение матрицы А. Раскрыв определитель A0,31), полупим
квадратное уравнение, решив которое, определим Xj и Х2, т. е.
собственные значения матрицы А. Подставляя поочередно эти
значения X в систему A0,30), найдем элементы /ш /21, /12, /22
матрицы преобразования S. После того как определены X! и Х2,
преобразование квадратичной формы к каноническому виду можно
считать законченным. Элементы матрицы S необходимы для того,.
чтобы по формулам A0,16) выразить первоначальные координаты
X] и хг через новые координаты х[ и х'г.
Заметим, что, решая квадратное уравнение относительно X,
можно встретиться с тремя случаями: 1) X, и Х2 различны; 2) Xt=
= Х2; 3) какое-нибудь из этих значений равно нулю.
Задача 10,1. Преобразовать к каноническому виду уравнение
5*f—4*!*г + 2*2 = 24.
Решение. Матрица коэффициентов А в формуле A0,4) в дан-
данном случае имеет вид
5 —21
А~\-2 2
а характеристическое уравнение A0,31) запишется так:
5 — X —2
-2 2-Х ~и*
Отсюда
E-Х)B-Х)-4 = 0,
т. е.
Х2 _ 7Х + 6 = 0
Х,= 1, Х2 = 6.
Возникает вопрос— какому из найденных значений X приписать
значение Хь а какому Хг? Условимся так нумеровать значения X,
чтобы угол поворота а координатных осей хх0хъ был острым, т. е.
так, чтобы выполнялось неравенство tga>0. В матрицу S фор-
формулы A0,18) входят элементы /и, /2] и /12, Z22. На основании
формул A0,14)
/n = cos a; l12 = —sin a
/21 = sin a; /22 = cos a,
243
а потому
:=js, или tga = -^s. A0,32)
«U '2»
j
Пользуясь системами A0,29), надо так пронумеровать X, чтобы
отношения
и га
были положительными.
Примем сначала Xt = 1.
В первую систему A0,29) подставим Xt = 1. Учитывая, что
aii=5; «12 = — 2; а21 = — 2; (а12 = а21); а^2 = 2,
получим
5)/2
и + ()/иа
Отсюда
4/ц —2/„ = 0;
—Яп + /и = 0.
Очевидно, что второе уравнение является следствием первого. От-
Отбрасывая второе уравнение, имеем
откуда
— = 2
т. е. на основании A0,32) tga = 2>0.
На этом положительном значении tga мы и остановимся и будем
считать, что Хх = 1, а значит, Х2 = 6. В дальнейшем нет надоб-
надобности рассматривать два уравнения в каждой из систем A0,29),
так как второе уравнение в них является следствием первого.
Если бы мы в качестве X приняли Xt = 6, то с учетом зна-
значений ап, а12, а22 получили бы
E —6)/u —2/tl = 0j
-/11-2/2! = 0,
откуда
т. е. на основании A0,32) tg a = — -^. Заметьте, что произведение
найденных тангенсов равно —1. Так как при Хх = 1 мы получили
tg a > 0, а при Xt = 6 оказалось, что tg a < 0, надо оставить
именно эту нумерацию и взять
Хх =1; Х2 = 6.
244
В преобразованном виде заданное уравнение запишется так (фор-
(формула 10,8):
v'2 4- fir'2 94
Оно определяет эллипс
24" ^~Т =
с полуосями
а = 2/6; 6 = 2.
Из условия, что tga=2, мы определим и угол поворота.
К задаче 10,1
Задача 10,2 (для самостоятельного решения). Преобразовать
к каноническому виду уравнение
5/- —78 = 0.
Указание. В отличие от предыдущей задачи переменные
здесь обозначены через х и у, а не через xt и дг2.
Корнями X! и Х2 характеристического уравнения являются
числа 3 и 13. Чтобы выполнялось неравенство tg a > 0, надо за-
занумеровать X
Хх = 13; Х2 = 3.
Окажется, что
2 '
Если бы взять Xt = 3, то
tga = -2.
Заметьте, что произведение найденных тангенсов равно —1.
245
Ответ. Преобразованное уравнение имеет вид
13*2 + Ъу\ — 78 = U
или
Кривая — эллипс с полуосями а = \^&\ Ъ = >/26.
Задача 10,3 (для самостоятельного решения). Упростить урав-
уравнение линии
13х2 + бху + 5г/2 — 56 = 0.
Указание. Характеристическое уравнение имеет вид
13-Х 3
3 5-Х ~и'
Его корнями являются числа 4 и 14. Если принять, что Xj = 4,
то
Если же \ = 14, то tga = -j. Это значение tg a определится из
уравнения
-1п + 3/21 = 0.
Ответ. В каноническом виде заданное уравнение запишется
так:
14*? + 4у* — 56 = 0
или
г г
?
г г
? + £-■■
Кривая — эллипс с полуосями а = 2; Ь = ]/~14.
Теперь решим несколько задач на упрощение общего уравнения
кривой второго порядка.
Задача 10,4. Привести к простейшему виду уравнение линии
2x1 + 9*i + 12*2-2 = 0.
Решение. Матрица коэффициентов квадратичной формы 2х\ +
+ lOjqjta + 2x\, входящей в левую часть уравнения, запишется так:
А _ \2 51
Лб 2\'
а характеристическое уравнение этой матрицы
[2~Х 5 1 = 0
L 5 2-XJ и>
246
Его корнями являются числа — 3 и 7. Выясним, какое из них
принять за Хь а какое — за Х2. Для этого воспользуемся первым
уравнением первой системы A0,29), полагая в нем ап = 2; а12 =
= а21 — 5; а22 = 2, ^ = —3.
12 - (-3)} /„ + 5/и = 0; Ып + 5/21 = 0;
tg а = ^ = — 1
Таким образом, если X, = —3, то tg а < 0. Положим теперь, что
Хх = 7. Тогда из того же уравнения
B — 7) 1и + 5/21 = 0; —5/„ + 5Z21 = 0; ltl = ln;
tgen=jfi=l. A0,33)
На этом значении мы и остановимся, приняв, таким образом, что
Xj = /J /.2 г= О.
Квадратичная форма 2x1 + Ю*1*г + %Х1 приобретет вид
1х'\—Ъх'\. A0,34)
Чтобы определить все элементы матрицы преобразования S, нам
осталось найти соотношение, связывающее /12 и /22. Для этого
воспользуемся первым уравнением второй системы в A0,29):
(«а — Х2) /12 + a12Z22 = 0
или
B — (—3)] 1и + 5/22 = 0; 5/w + 5/22 = 0;
'12 1. / I
J- — 1, *22 '12-
»22
Так как на основании A0,32)
ТО
tga=l.
Таким образом, получилось прежнее значение для tga — см. A0,33).
С учетом найденных зависимостей между 1-п и 1п и между /22
и /12 матрица преобразования
S = [!n H-f!» H. A0,35)
U2i hii L/n — 112J
Но следует иметь в виду, что в формуле A0,18) матрица S яв-.
ляется ортонормированной, как это было подчеркнуто на стр. 240
и использовано в последующем выводе. Поэтому и, полученную
при решении этой задачи матрицу S в формуле A0,35) надо при-
привести к такому же виду, чтобы она стала матрицей преобразования.
24?
Нормирующий множитель для элементов первого столбца
1 1 1 1
нормирующий множитель для элементов второго столбца
"•"±/2/,,*
Теперь возникает вопрос, какой знак перед корнем в выраже-
выражениях нормирующих множителей пх и п2 должен быть выбран. Так
как мы условились угол поворота о брать в первой четверти, то
tgo>0, sina>0 и cosa>0. Поэтому в матрице преобразования
S элементы первого столбца /и = cos a и /21 = sin a должны быть
положительными: 1и > 0; /21 > 0. Во втором столбце элемент /12 =
= — sin a, а потому этот элемент должен быть отрицательным,
ибо, если —sin a < 0, то sina>0 и второй элемент этого столбца
/22 = cosa и должен быть положительным. В связи с этим после
нормирования матрицы S в формуле A0,35) следует взять у /tj. пе-
перед корнем знак плюс, а у п2 — знак минус:
1 1
• I «2 =
После этого мы можем преобразовать к новым осям и линейную
часть заданного уравнения 9xt + 12*2 — 2. На основании формулы
A0,19)
т. е. с учетом матрицы SH0Pm
L*,J~
V2
1
1 -
J
ИЛИ
Отсюда
-V2
1 ■ 1
\i\
1
1
/Г1
9
12"
2 - 21 г'
Учитывая, что квадратичная форма в составе заданного уравнения
приобрела вид A0,34), запишем его так:
1х'\-
,, . 21/2 .
С 2 "I 9 Л1
248
Выделим полные квадраты в левой его части, переписав уравнение:
или
К задаче 10,4
Теперь сделаем параллельный перенос координатных осей. Поло-
Положим, что
. , 3/2
= *i + -J- »
• /2
i — Л2 4 *
249
Из этих формул видно, что новое начало координат Ot в системе
31/2
координат хг0х2 имеет абсциссу, равную — , и ординату, рав-
i/2 / з /2 /2\
ную ~, т. е. 0J ^-, ~-J (см. формулу A2,12) преобразо-
преобразования координат' при параллельном переносе координат в двенад-
двенадцатом практическом занятии первой части этой книги). Уравнение
A0,35) принимает вид
или
f[x Н 1
19 19 **
14
Кривая — гипербола с полуосями
Первоначальная система координат xfix2 была повернута на угол
а, тангенс которого на основании A0,33) равен 1, а сам угол а = ^-.
В этой повернутой системе координат центр гиперболы находится
в точке
/ 3/2 /2\
I f • Т/-
Задача 10,5. Упростить уравнение линии
12л;2 — 4ху —15у2 — 48х— 168у + 400 = 0.
Решение. Матрица коэффициентов квадратичной формы 12*2 —
— 4ху -f 15y2, входящей в уравнение,
12 ~21
-2 15J*
Характеристическое уравнение этой матрицы
имеет корни 11 и 16.
Определим матрицу преобразования S. Из системы A0,29) при
I = 11 получаем
'и—2/2i=0 и — 4/и — 2Z22 = 0.
250
Отсюда из первого уравнения
а из второго
/22 = 2/12.
Угол поворота координатных осей определится из равенства
Так как при X = 11 оказалось, что tg а > 0, мы припишем. X пер-
первый номер. Итак,
Х1 = 11; Х2= 16.
Квадратичная форма 12л:2 — Аху + \5уг, входящая в уравнение, при-
приобретает после поворота осей вид
Пх]+\6у\. A0,37)
Матрицу преобразования S, учитывая, что 1п = у /и, а /22 = — 2/12,
запишем так:
Нормирующий множитель первого столбца
t 2
A0,38)
п, =•
±Vlin
Нормирующий множитель второго столбца
1 1
«2 =
На основании разъяснений относительно выбора знака у корня в
выражении для пх и я2 (стр. 248) выбираем у пх знак плюс, а у
пг — минус
Внося эти множители в матрицу A0,38), получаем
' 2 1_-
VI VI
251
Обратимся к преобразованию линейной части —48* — 168г/ + 400
заданного уравнения.
По формуле A0,19) выразим х и у через новые координаты лсг и у^.
X = SX*;
2\
y
_
/5 ~V
_L _L
/5 /5J
(здесь Xi заменен на х, а х2 на у).
2 1
A0,39)
С помощью этих формул линейная часть заданного уравнения
-48* - 16% + 400 = - Щ хг - Щ Vl + 400.
С учетом того, что квадратичная часть заданного уравнения на
основании A0,37) преобразовалась в \\х\ + 16i/J, все заданное урав-
уравнение перепишется так:
Теперь нам осталось выделить полные квадраты
-^*|)+ 400-0;
Й-^Л)+400-0;
11^-^L 16(^-^-576
Сделаем параллельный перенос координатной системы
дем замену
12 _ 9
*г — хх — —jtl ; уг — Ух — гу= .
У 5 V о
252
A0,40)
^. вве-
ввеЭтим преобразованием начало повернутой системы координат пере-
A2 9 \
-тг, -tz\ (учесть, что это координаты нового
начала в системе координат fiy^)
В системе координат хг0хуг уравнение A0,40) запишется так:
11**+ 16г/|= 176
или
1
ж
К задаче 10,5
Кривая — эллипс. Его полуоси: а = 4; 6 = 1/11. Координаты но
12 9
вого начала 0г в системе координат xiOyx равны -= и —=.;
1/5 1/5
12 9
Докажите, что координаты нового начала 0х в первоначальной
системе координат равны C; 6), а фокусы находятся в точках с
координатами A; 5); E; 7).
Задача 10,6 (для самостоятельного решения). Упростить урав-
уравнение линии
Зле2 — 8ху + Зу* + 8х + 8у — 39 = 0
и определить координаты ее центра и фокусов в первоначальной си-
системе координат.
253
Указания и промежуточные результаты
1. Матрица коэффициентов
1
]-
2. Характеристическое уравнение
X" _ 6Х — 7 = 0.
3. За Х2 принять Х = —1, а Х2 = 7.
К задаче 10,6
4. Квадратичная форма уравнения Зх2 — 8ху + Зуг
зуется к виду
-х\ + 7у\.
5. Угол поворота определится из условия tg а = 1
6. Нормирующие множители
254
7. Нормированная матрица преобразования
"J_ _ J_~
V2 Уг
\_ j_
У"% Уг_
Линейная часть заданного уравнения 8* + 8г/ — 39 преобразуется
к виду y~xi— 39.
Ответ. Кривая — гипербола. Ее каноническое уравнение
У\
х\
В первоначальной системе координат ее центр находится в точке
D; 4), а фокусы —в точке B; 6) и F; 2).
Задача 10,7 (для самостоятельного решения). Упростить урав-
уравнение линии
144л:2 — №ху -f 2Ъу2 — 1090л: — 2616г/ + 24961 = 0.
Указания и промежуточные результаты
1. Матрица коэффициентов
Г 144 -601
[-60 25Г
2. Характеристическое уравнение
X2 — 169Х = 0.
Принять, что Хх = 0; Х2 = 169. Квадратичная форма 144л;2 — \2Qxy +
+ 25г/2 преобразуется в 169г/|.
Л"
3. tg a = -jT-;
= у 1п; 122 = — -^
4. Нормирозанная матрица преобразования
13
12
13
5
5. Линейная часть уравнения
— 1090* + 2616г/ + 24961
преобразуется к виду —2834л:! + 24961.
255
Ответ. Кривая — парабола, определяемая уравнением 13г/| =
= 218*2. В системе координат хг0у1г вершина параболы находится
в точке ( -^g- 5 OJ.
Задача 10,8. Упростить уравнение линии
8хг + Аху + Ъуг + 48а; — 24г/ + 108 = 0
и определить координаты ее фокусов в первоначальной системе
координат.
Промежуточные результаты
1. Характеристическое уравнение
X* _ 13Х + 36 = 0.
2. Матрица преобразования
•Jhoom —
'норм
1
4. В повернутой системе координат xiOyx заданное уравнение
приобретет вид
5. После выделения полных квадратов это уравнение запишется
так:
Ответ.
4 + 9
Координаты фокусов в первоначальной системе координат:
1-5; 6); (-3, 2),
256
ОДИННАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Поверхности уровня, производная по направлению, градиент
функции.
Это и шесть следующих практических занятий посвящаются
векторному анализу.
Прежде чем решать задачи из этого практического занятия,
рекомендуется повторить основы векторной алгебры, в особенности
такие понятия, как скалярное и векторное произведения, векторно-
скалярное произведение, двойное векторное произведение, а также
основы теории проекций.
Ниже для справок помещены основные понятия и формулы век-
векторной алгебры.
1. Вектор и его координаты. В прямоугольной системе коорди-
координат каждому вектору а ставятся в соответствие три числа — его
проекции ах, ау и аг на координатные оси Ox, Оу, Oz. Эти числа
называются координатами вектора, а вектор записывается в виде
а{ах, ау, аг]. Если точка А (хх, ylt zx)—начало вектора, а точка
В (хг, у2, z2) — его конец, то его проекции на оси прямоугольной
системы координат равны разностям между одноименными коорди-
координатами его конца и начала
Учитывая эти формулы, вектор а можно записать и в таком виде:
а{х2 — хи Уг — Уи Zi — Zi).
2. Длина вектора. Длина вектора а, или (что то же) его мо-
модуль, обозначается одним из символов | а | или а и определяется
по формуле
а = Уах + а\ + аг =
= V(x2~ Xly + (у2 - уtf + (z2 - z,)*.
3. Равенство векторов. Два вектора одинаковой длины, лежа-
лежащие на параллельных прямых и одинаково направленные, назы-
называются равными.
4. Произведение вектора на скаляр. Произведением вектора
а на скаляр т называется вектор, модуль которого равен та —
произведению числа т на модуль вектора а. Этот новый вектор
направлен так же, как.и вектор а, если т>0, и противоположно
9 И. А. Каплая 257
ему, если т < 0. Вектор —5 называется противоположным век-
вектору а.
5. Единичный вектор. Орт. Вектор, по направлению совпадаю-
совпадающий с данным вектором и по модулю (длине) равный единице,
называется единичным вектором данного вектора, или ортом.
Единичный вектор обозначается той же буквой, что и данный, но
с ноликом в виде показателя степени. Таким образом, единичный
вектор вектора а обозначается й°
а = аа°.
6. Направляющие косинусы вектора. Косинусы углов, которые
-вектор составляет с положительными направлениями координатных
осей, называются направляющими косинусами вектора. Углы, состав-
составляемые вектором с координатными осями Ох, Оу и Oz, обознача-
обозначаются в дальнейшем соответственно через а, р и у.
Между направляющими косинусами вектора существует соот-
соотношение
cos2 a + cos2 р + cos2 т = 1.
7. Проекция вектора на ось. Проекция вектора а на ось есть
скалярная величина, равная произведению модуля вектора на ко-
косинус угла между направлением оси и направлением вектора:
at = npj5 = a cos G, а).
Проекции вектора а на оси Ох, Оу и Oz прямоугольной си-
системы координат обозначаются соответственно через ах, ау и аг и
определяются по формулам
ах =' a cos a; cos а = —;
ау = acosfr, cosC = —;
аг — a cos y; cos y = —
(обозначение углов вектора с координатными осями дано в преды-
предыдущем пункте). Если а0 — единичный вектор, то на основании этих
формул (учитывая, что в этом случае его модуль равен 1) его
проекции на оси Ох, Оу, Oz равны его направляющим косинусам
(а0).,. = cos а; (а°)у — cos Р; (а°)г = cosy,
8. Разложение вектора по трем координатным осям прямо-
прямоугольной системы координат. Если ах, ау и аг — проекции век-
вектора а на оси Ох, Од и Oz прямоугольной системы координат, a i, j
и k — единичные векторы этих осей, то имеет место формула
а = a~i + aj+ a~k.
258
9. Радиус-вектор точки. Радиусом-вектором точки М (х, у, г)
называется вектор, обозначаемый обыкновенно через 7, имеющий
начало в начале координат, а конец — в этой точке. Проекции
радиуса-вектора 7 на оси Ох, Оу, Ог равны соответственным ко-
координатам его :;онца
тх = х; гу = у, -гг = г,
поэтому
10. Скалярное произведение двух векторов. Скалярным произ-
произведением двух векторов а и Ь, которое обозначается символом
а • Ь, называется произведение их модулей на косинус угла между
ними. Если угол между векторами обозначить буквой <р, то согласно
этому определению скалярное произведение а • b векторов а и Ь
находят по формуле
а • b = ab cos 9.
Скалярное произведение двух векторов есть число. Так как
fecostp = пр^б, a a cos 9 = пр^а,
скалярное произведение
a t b = а пр-6 = b пр^а.
СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
I. Если векторы с и Ь перпендикулярны: a j_ b; то их скаляр-
скалярное произведение
а • Ь = 0.
11. Скалярное произведение двух равных векторов (иначе, ска-
скалярный квадрат) равно квадрату модуля
а 'й — а?.
III. Скалярное произведение векторов подчиняется законам, ана-
аналогичным законам произведения чисел:
а) а • b = b • а переместительный (коммутативный) закон;
б) (а + Щ • с = а • с + Ь • с закон распределительности (дистри-
(дистрибутивности) по отношению к сложению;
в) (/ад) • Ъ = п(а'- Ъ) сочетательный (ассоциативный) закон по
отношению к умножению на число.
IV. Выражение скалярного произведения а • Ь через проекции
этих векторов на оси прямоугольной системы координат.
Если _
а{ах, ау, аг], а Ь{ЬХ, Ьу, Ьг},
то
а •~Ь = ахЬх + а(ру + агЬг.
о*
а 259
Если векторы а и b перпендикулярны, то
aj>x + ajby + арг = 0.
V. Косинус угла между двумя векторами.
Если <? — угол между векторами а и Ь, то
coscp
ab
ИЛИ
axbx + а^у + о А
Если вектор а с координатными осями Ох, О у и Ог составляет
углы, соответственно равные а, р и к, а вектор!» с теми же осями
составляет углы а1( pi и 71. то косинус угла ср между этими век-
векторами определяется по формуле
cos <? = cos a cos a.x + cos р cos px + cos у cos т1#
11. Векторное произведение двух векторов. Векторным произ-
произведением двух векторов а и ft, которое обозначается символом
а х 6 (читается «а крест ft»), называется вектор, модуль которого
равен произведению модулей перемножаемых векторов на синус
угла между ними. Вектор а у. b направлен по перпендикуляру к
плоскости, определяемой перемножаемыми векторами а и Ь в такую
сторону, что наблюдателю, смотрящему с конца вектора с х Ь на
перемножаемые векторы а и Ь, кажется, что для совмещения пер-
первого множителя а со вторым множителем Ь по кратчайшему пути
первый множитель нужно вращать против движения часовой стрелки.
Свойства векторного произведения двух векторов
I. По определению векторного произведения
\Ъ X b\ = afesina.
II. а х Ь = —b х а,
т. е. изменение порядка сомножителей в векторном произведении
влечет за собой изменение его знака: векторное произведение не
подчиняется переместительному закону.
III. Векторное произведение подчиняется распределительному
закону по отношению к сложению
(а+Ъ) хс = а Хс + Ьхс.
IV. Векторное произведение подчиняется сочетательному закону
относительно умножения на число
(па) хЪ = п{а xb).
260
V. Если известны проекции векторов а и Ь на оси прямоугольной
системы координат
а{ах, ау, az); b~{bx, Ьу, Ьг),
то их векторное произведение определяется по формуле
а х Ъ = (aj)z — а\ЬиI + (a'zbx — аАO +*(аА —
где i, j и k — орты координатных осей.
Отсюда видно, что проекции векторного произведения на коор-
координатные оси равны
(ахЬ~)х = ajbz — агЬу] (а X Ь)у = aj)x — aj);,
Векторное произведение axb двух векторов а{ах, аи, аг) н
Ъ{ЬХ, Ьу, &г) может быть записано в виде определителя
5x6
Г? 7 ь
= \ах ау аг
VK Ьу Ьг.
VI. Условие параллельности двух векторов. Необходимым и
достаточным условием параллельности двух векторов а{ах, ау, аг}
и Ъ\ЬХ, by, bz} является равенство нулю их векторного произве-
произведения, т. е. необходимым и достаточным условием_параллельности
двух векторов является выполнение условия а хЪ = 0, или, что
равносильно, пропорциональности их одноименных проекций
ах Оу Ог
Ъх by Ьг '
12. Векторно-скалярное произведение трех векторов. Так на-
называется произведение трех векторов типа (а х Ъ) • с. Здесь сна-
сначала выполняется векторное произведение а х Ь, а затем оно ска-
лярно умножается на вектор с. Через проекции сомножителей на
оси прямоугольной системы координат векторно-скалярное произ-
произведение
Су С,
E х Ь) • с =
ау аг
Ьу Ь,
Свойства векторно-скалярного произведения
I. Если в векторно-скалярном произведении два каких-либо
множителя коллинеарны, то это произведение равно нулю.
II. В векторно-скалярном произведении допустима циклическая
перестановка множителей.
261
13. Векторно-векторное произведение трех векторов. Так назы-
называется произведение трех векторов, имеющее вид
а х (& х с).
Иногда вектбрно-векторное произведение называетсядвойным вектор-
векторным произведением.
Векторно-векторное произведение а х (b X с) трех векторов вы-
вычисляется, по формуле
ах E х с) «= b (а • с) — с (а • Ь).
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Физическое поле. Физическим полем называется часть прост-
пространства или все пространство, в котором происходит физическое
явление.
2. Скалярное поле. Физическое поле называется скалярным,
если физическое явление, его образующее, характеризуется функцией
f — f(x, у, г), зависящей только от координат точек про-
пространства, в котором это явление происходит. Скалярное поле пол-
полностью определено заданием одной функции / {х, у, г) трех незави-
независимых переменных. Эта функция, независимо от ее физического
смысла, называется потенциалом поля.
Если физическое явление образовало скалярное поле, то каждой
точке Р(х1у Уи Z\j пространства, в котором происходит это явле-
явление, ставится в соответствие определенное число, характеризующее
данное явление в рассматриваемой точке. Это число есть частное
значение функции f (х, у, z), вычисленное в точке Р (примерами
скалярного поля являются; поле электростатического потенциала,
давление в атмосфере).
3. Поверхность уровня. Если однозначная функция соответствует
скалярному полю, образованному физическим явлением, то поверх-
поверхностью уровня (или эквипотенциальной поверхностью) этого поля
называется поверхность, во всех точках которой функция / {х, у, Z)
сохраняет одно и то же значение.
Поверхности уровня определяются уравнением
f{x, у, г) = С, A1,1)
где С—постоянная величина.
Придавая постоянной С различные числовые значения, получим
семейство поверхностей уровня. Через каждую точку пространства
проходит одна поверхность уровня. Во всех точках поверхности
уровня физическое явление протекает одинаково.
Уравнение поверхности уровня, проходящей через точку
Р(хи уи Zi), имеет вид
f{x, у, z) = f(xlt ylt z,). A1,2)
262
4. Производная по направлению. Производная от функции
<р (х, у, г) по направлению (Г) характеризует скорость изменения
функции <р (х, у, z) по этому направлению, вычисленную в точке
с координатами х, у, г. Эта производная вычисляется по формуле
J = gcosG, x) + %cos(l, у) +gcosG, z). A1,3)
Величина производной по направлению зависит рт выбора точки Р,
в которой она вычисляется, и от выбора направления, по которому
она вычисляется. Направляющие косинусы направления 7 входят
множителями в формулу A1,3), а координаты точки Р являются
аргументами частных производных, входящих в эту. формулу.
5. Градиент функции. Градиентом скалярной функции <р (х, у, г)
называется вектор, проекции которого на координатные оси 0*.
Оу и Ог соответственно равны ^, —^ н ^, т. е.
На основании этого определения проекции вектора grad<p на
координатные оси запишутся так:
(grad f)x = %; (grad т)„ = |; (grad ?), = | A1,5)
(предполагается при этом, что 9 (х, у, г) — однозначная непрерывная
функция, имеющая непрерывные частные производные).
Модуль вектора grad<p вычисляется по формуле
Если Г — единичный вектор направления /
7° = cos G, х) i + cos G, у) j + cos (/, г) k,
то правая часть формулы A1,3) есть скалярное произведение век-
вектора grad tp на этот единичный вектор 7°
| = gradT-7°. A1,7)
Так как | Р | = 1, то скалярное произведение
grad <р • Г == | grad <р | • 1 • cos (grad <p, 7°) = | grad cp | -cos (grad <p, 7°),
поэтому наибольшее значение скалярного произведения grad<р • Т
равно модулю gradtp, т. е. |grady|. Это будет иметь место тогда»
263
когда направление / совпадет с направлением вектора grad <p, так
как в этом случае cos (grad <?, /°) = 1.
Поскольку производная функции <р по направлению характери-
характеризует скорость изменения функции 9 по этому направлению, то можно
сказать, что вектор grad <p есть вектор, в направлении которого ско-
скорость изменения функции <р является наибольшей и эта наибольшая
скорость [д\ по модулю равна | grad ер |, т. е.
= 1 grad ср | A1,7а)
или
Вектор grad <р в каждой точке направлен по нормали
к поверхности уровня, проходящей через точку, в сто-
сторону возрастания функции. Модуль этого вектора равен ско-
скорости изменения функции <р (х, у, г) по этому направлению нор-
нормали. Скорость изменения скалярной функции 9 (х, у, z) по неко-
некоторому направлению G) равна проекции вектора grad «p на это
направление, т. е.
g A1,8)
В этом состоит основное свойство градиента функции: производ-
производная функции ср no направлению 1 равна проекции вектора гради-
градиента ср «а направление 7.
Величина и направление градиента не зависят от выбора коорди-
координатной системы.
Задача 11,1 (для самостоятельного решения). Найти поверх-
поверхности уровня потенциала ср = у- электростатического поля точеч-
точечного заряда, где г — расстояние точки М поля от точки, в которой
находится электрический заряд.
Решение. Поместим начало координат в точку, в которой
находится заряд. По формуле A1,1)
Если координаты точки М есть х, у и г, то
г =
264
ё1
Уравнение хг + У2 + z* = ga" определяет семейство концентриче-
концентрических сфер с центром в точке, в которой помещен заряд.
Задача 11,2. Найти градиент потенциала <р=у- электростати-
электростатического поля, | grad 91 и его направляющие косинусы, где г =
= Ух* + уг + г2—расстояние точки А(х, у, г) поля от начала
координат, в котором находится заряд е.
Решение. Чтобы воспользоваться формулой A1,4) для опре-
определения grad <р, надо найтн ^, ^ и ■£■. У нас <р = -р-, а потому
проекция градиента этой функции на ось Ох
Поэтому
дг_ _ 2х х х_
дх ~ 2 ух* + у* + г* ~~ V*3 + У1 + г2 ~ г '
Значит,
Аналогично
ду г" ' dz г" *
Подставив значения найденных частных производных ^, ^
и ^в формулу A1,4), получим
х и - z ~
или
grad у = — J U? + yj + 2^).
Но вектор « + г// + zk равен радиусу-вектору г точки А (х, у, г)
поля: xi -f у/ + z^ = г, поэтому grad <р = §' г • Учитывая, что
— = г°, получим окончательно
265
По закону Кулона напряженность Е в точке- электростатического
поля точечного заряда определяется вектором -jr". Последнюю
формулу поэтому можно переписать в виде
grad <р = — Ё
или
-gradf = £.
Из формулы A1,6)
Направляющие косинусы вектора grad— найдем по формулам
-ЯЛ
(grad f, х)
cos^gradf, 5) = — f 5 cos(grady, *) = — 7-.
Задача 11,3. Найти градиент функции <р(г), где г — расстояние
точки А (*, у, г) поля до начала координат (г = У х? + уг + г1).
Решение. Чтобы воспользоваться формулой A1,4), определим
дг 2х
дх 2yx*+yi + ,
дг и дг г
и аналогично ^- = -^ \ ^ = —.
Получаем
dtp 3j 3r ,,. х_
дх ~~ дг ' дх ~~ У V>~
ду~ дг ' ду~ t v ) ' 7"
Отсюда следует
266
так как xl + y'j + zk = ~r, a r° — орт вектора г • (r° = у].
Итак,
grad<p(r) = <р'(г) -г». A1,9)
Рассмотрим важные частные случаи:
1) (р (г) = г; 9' (г) — ^J
Тогда
gradr = r° = -£-! A1,10)
Окончательно
gradl = --l. A1,11)
Если С—постоянная величина, то
^ = _^.7. A1,12)
Укажем на одно из применений только что полученного ре-
результата.
По закону Ньютона материальная точка О массы т притяги-
притягивает материальную точку А (х, у, г) массы 1 с силой F, модуль
которой F = k -^-, где г = У хг + у2 + z2, a k — постоянная при-
притяжения.
Эта сила направлена от Л к О.
Поместим в точку О начало координат. Обозначим через г ра-
радиус-вектор О А точки А, а соответствующий ему единичный век-
вектор — через ?>(?> = —I.
Тогда — г° будет единичным вектором для вектора АО, противо-
противоположного вектору г = О А. Сила F будет равна ее численной ве-
величине F, умноженной на — г,° и
т. е.
I *~~ К a * Г*
267
На основании формул A1,И) и A1,12)
■р 1 km
F = grad —.
Легко проверить, что проекции силы притяжения Fx, Fy и Fz
являются частными производными функции V = — соответственно
по координатам *, у и г. Действительно, из F = — k -^ • г сле-
следует, что
Р km _ р km _ р km
Если же взять частные производные от функции V = —$, учи-
учитывая, что г — У х* + уг -f z2, получим
3V fon Зг ftm х_ km
и аналогично
й1/_ fen dV _ km
•щ r* У' дг ^ г,
т. е. проекции силы притяжения равны
Таким образом, сила притяжения F = — -^- • г, о которой шла
речь, является градиентом функции V = — , т. е.
а ее проекции на оси прямоугольной системы координат равны
частным производным от функции V = —, которая называется по-
потенциалом силы притяжения (это свойство потенциала силы при-
притяжения было замечено Лагранжем). Поэтому для определения силы
притяжения между двумя точками надо только найти ее потенциал,
отыскать его частные производные по координатам х, у и г, кото-
которые равны проекциям силы притяжения, а ее модуль найдется
по формуле
268
Если на точку А действует не только точка О, но и неподвиж-
неподвижные точки Аи А2, ... , А„ с массами, соответственно равными тъ
т2> ... , тп, то потенциал точки А
V = — 4-— 4- — 4- ••• -+• — *
ИЛИ
»•—1
где г( есть расстояние ААЬ причем предполагается что г, Ф 0.
Если масса непрерывно заполняет дугу кривой, поверхность или
тело, то потенциал этой массы относительно точки А вычисляется
по следующим формулам:
для случая кривой
; A1,15)
для случая поверхности
(s)
для тела
ДО
(V)
В этих формулах dm—элемент массы.
Если точка А находится вне притягивающих масс, то все вхо-
входящие в эти формулы интегралы собственные.
В случае, когда точка А находится внутри притягивающей
массы, г становится равным нулю, подынтегральные функции не-
неограниченно возрастают, а интегралы делаются несобственными.
Однако эти интегралы существуют и проекции силы и в данном
случае определяют также по формулам A1,13). Доказательство
этого положения можно найти, например, в учебнике Г. М. Фихтен-
гольца «Курс дифференциального и интегрального исчисления»,
т. III, § 638.
Задача 11,4. Вычислить потенциал однородного призматического
стержня длиной 2/ относительно материальной точки М с массой,
равной 1, лежащей на продолжении его оси. При этом учесть,
что поперечное сечение s стержня настолько мало, что стержень
можно рассматривать как отрезок прямой линии (см. чертеж).
* В этой и следующих формулах принято, что постоянная притяжения
k = 1. Это означает, что за единицу силы притяжения принята сила, с кото-
которой притягиваются друг к другу две материальные точки с массами, равными 1,
находящиеся одна от другой на расстоянии, равном единице.
269
Решение. Поместим начало координат в середину стержня./
Расстояние точки М от начала координат обозначим через х. При
решении задачи будем считать стержень отрезком прямой, поэтому
воспользуемся формулой A1,15). Если бы в условии задачи не было
этой оговорки, интегрирование следовало бы производить по объему
стержня при помощи формулы A1,17).
Входящий в числитель подынтегрального выражения A1,15)
элемент массы мы найдем как произведение объема элемента стержня
на его плотность
dm = ?s dr,
где у—постоянная плотность стержня (постоянная потому, что
стержень однороден), dr —элемент длины стержня.
М
-е о е х
К задаче 11,4
В формуле A1,15) г—расстояние точки М до любой точки N
стержня, причем это расстояние на стержне при условии, что
х > I, изменяется от х—l до * + /. По формуле A1,15) находим
х+1
J
X—I
Если бы точка Р находилась на продолжении оси стержня слева
от него (х < — /), то пределы интегрирования были бы х + 1
и х — /. В этом случае
Итак, относительно точки М потенциал стержня
V — -rs In i-ii , если х > I
или
V = ys In X^-r^i, если х < — I.
Зная потенциал V, вычислим величину силы, с которой стер-
стержень притягивает точку М (формула A1,14). Если х> I, то
р dV
Если же х < — /, то
с dV 21
270
Учитывая, что масса т стержня равна его объему, умножен-
умноженному на плотность (стержень однороден), имеем
т = 2tsi
н тогда
т
Где верхний знак соответствует случаю х < — /, а нижний — слу-
случаю х> I. Если бы в точке М была помещена не единица массы,
а масса тъ то сила притяжения была бы равна
mm'
(-е.о)
К задаче 11,5
Задача 11,5.. Вычислить потенциал однородного стержня дли-
длиной 2/ относительно точки М массы т=\, если точка находится
в любом месте плоскости (но только не внутри стержня и не на
его поверхности). Стержень рассматривать как отрезок прямой.
Решение. Обозначим координаты точки М через х и у. Ее
расстояние до переменной точки ЛГ(и, О) стержня вычисляется
по формуле.
Если поперечное сечение стержня равно s, а его плотность 7.
то элемент стержня длиной du имеет массу
dm = 7s du.
По формуле A1,15) потенциал стержня
= Г tsdu
где х и у следует рассматривать как величины постоянные, а пере-
271
меннои интегрирования является и. Выполняя интегрирование, по-
получим
= Ts [in (/ -х + V(l -xf + у2) - In(- / - x + Vd + xf + ?)].
Окончательно
Таким образом, потенциал V является функцией х и у.
Теперь, зная потенциал, определим силу, с которой стержень
притягивает точку М. Выполним дифференцирование функции V
по х к у:
F -^ = ТЛ ' , / -*'
xf+y2
' . / l + x _ А]
+y* — l-x \V(l + xf + у» }\
или
F _
x
F
x
- xf + у»
l+x-Y(l+xf+ у*
xf + y* - I - *) V(l + xf +
Отсюда
11
„ _
x ~
x
Замечая, что знаменатель первой дроби есть расстояние точки М
до левого конца стержня В(—/, О), т. е. ВМ, а знаменатель вто-
второй дроби есть расстояние точки М до правого конца стержня
А{1, О), т. е. AM, получаем
F* = ^s [Ш ~ М}'
9V = Г
= 9V = s
у ду '
ду
В первых дробях каждого из произведений в квадратной скобке
последнего выражения уничтожим иррациональность в знаменателе:
У(( + х*) + у* +
Vu—xr + f
272
I + х \
t J
или
= V /i *
У \ УA-
и окончательно
Fy = _ 2l1 '~и — 4-
Учитывая, что 1-х —AC; l + x = BC
УA — xf + уг = AM, a ]/"(/ + xf -f у1 = BM,
получим
1 у - ~ у {am т- вм\-
Преобразуем теперь выражения, найденные для Fx и Fy. Из чер-
чертежа видно, что
cos p cos а ЛЛа Вт. •
поэтому Fx и Fj, могут быть записаны в виде
у У
Модуль силы притяжения
и тогда
F = y i-i- (cos p — cos a)a + 14-(sina + sinPJ =
= — ]/cos2 p — 2cos a cos p + cos2 a -f sin2 a + 2sin a sin p + sin2 p =
= H|/2 —2(cosacos? —sinasinp) =
F-2J1 Sin 1+1 (\)
Из'чертежа видно, что, если провести дугу окружности с цент-
центром в точке М радиусом равным ординате точке М, то длина
хорды ED, которая стягивает дугу этой окружности, заключен-
заключенную между отрезками, соединяющими точку М с концами стержня,
будет равна
273
Умножая в (Л) числитель и знаменатель дроби на у и замечая,
что масса т хорды ED (если считать ее плотность и поперечное
сечение такими же, как и у стержня АВ) будет равна
получим
длина хорды
г» т
т. е. величина силы притяжения стержнем точки М равна силе,
с которой эту точку притягивала бы масса т, сосредоточенная
в середине дуги ED, построенной, как указано выше. .
Задача 11,6. Определить потен-
потенциал круглого однородного диска от-
относительно точки М единичной мас-
массы, находящейся на перпендикуляре
к диску, восстановленном из его цент-
центра. Расстояние точки М от. диска рав-
равно г, плотность диска f, его радиус R,
толщину диска h во внимание не
принимать. Определить также силу
притяжения диском указанной точки.
Решение. Поскольку, как ука-
указано в условии задачи, толщину дис-
диска не следует принимать во внимание,
диск можно рассматривать как круг,
а поэтому при вычислении потен-
потенциала ■ будем пользоваться формулой
A1,16). Если бы этого указания не
было, вычислять лотенциал следовало бы по формуле A1,17).
Введем на плоскости диска полярные координаты р и ср, по-
поместив полюс полярной системы координат в центр диска. В поляр-
полярной системе координат элемент площади равен р dp d<f>. Элемент
объема диска
Лр dp dtp,
а масса этого элемента
dm = 7/2 pd pdcp.
В формуле A1,16) расстояние г точки М до элемента диска
равно
К задаче 11,6
и тогда потенциал
V =
2*
U)
274
Модуль силы притяжения найдем по формуле A1,14). Так как
точка М симметрична по отношению к диску, то проекции Fx и
¥'и силы притяжения на оси Ох и Оу равны нулю: Fx = Fy — 0.
Остается найти Fz = j-
Если учесть, что масса диска т — icR2fh, то fh = -^-2 и поэтому
г. =2т г —
г R*' V
Задача 11,7. Определить потенциал и силу притяжения по-
полого шара (шарового слоя) относительно точки М единичной
массы, лежащей: 1) вне шара; 2) внутри полого пространства
3) внутри массы слоя.
Радиусы шаровых поверхностей, ограничивающих слой для
внутренней и внешней поверхности, равны соответственно а и R
(a<R), плотность у является известной функцией р — расстояния
точки слоя от центра шара: f = Ф (р).
Решение. Обозначим расстояние точки М от центра шара через
г и расположим координатные оси так,, чтобы положительное на-
направление оси Oz проходило через точку М. На чертеже ОС = а;
OD = R; ОМ — z; ON = р. Применим сферические координаты.
Известно, что в сферической системе координат элемент объема
Поскольку плотность 7 = <|>(р), находим, что масса элемента
слоя
dm = ф (р) р2 sin б dp d<pd6.
Так как мы имеем дело с телом, то для решения задачи надо
воспользоваться формулой A1,17). Входящая в нее величина
Г = |/22 + р2 —2p2COS0
равна расстоянию MN точки М до элемента объема и тогда по-
потенциал
1/_ ГГГ Ф(р) Р2sin 6dp d<p d6
JJJ V*г+ P2 — 2pzcost)
y= Г. /^ » j_ П. Г sinBde
a 0 0
275
Начнем с вычисления внутреннего интеграла
sin в dfl 1 , /—5
Vz2
Г
= \
J
0
—2pzcos«
5 п п
2 — 2p2cos9
о
уг (Vz* + P2 + 2Pz — Vz* + p2 - 2Pz).
При вычислении интеграла была использована формула \~dx =
J К«
= 2 Vu + с. Производная подкоренного выражения по переменной
О равна 2рг sin 0. Следует учесть, что
2 — р,) если г > р (т. е. если точка М лежит вне шарового слоя)
~ р — г, j если 2< р (т. е. если точка М лежит внутри полого простран-
пространства).
Случай 1 (фиг. 11,1)- Когда точка М лежит вне шарового слоя,
то 2>р, У'(г—рJ = 2—р, а
2к
Тогда, учитывая, что \ dcp = 2%, получаем
о
или иначе
!dP. A1,18)
а
Выражение Ar.p2dp есть объем бесконечно тонкого шарового
слоя, а так как <1> (р) — плотность, то 4wJ>(p)p2dp есть масса бес-
бесконечно тонкого шарового слоя, поэтому \ 4wJ» (p) p2 dp равен всей
а
массе т рассматриваемого шарового слоя.
Окончательно относительно внешней точки потенциал шарового
слоя
У = ^-. A1,19)
Случай 2. Если точка М лежит внутри полого пространства
шара, то 2<р, V^(z — рJ = р — 2, а интеграл
276
и тогда относительно точки, лежащей внутри полого пространства,
2
с учетом того, что \ dcp = 2х,
о
V = 4* J «J. (p) pdp.
A1,20)
Из этой формулы следует, что внутри полого пространства потен-
потенциал шарового слоя не зависит от z, т. е. он одинаков во всех
точках.
Нам осталось рассмотреть случай, когда точка М лежит внутри
шарового слоя.
г
Фиг. 11,1
Фиг. 11,2
Случай 3 (фиг. 11,2). Проведем две концентрических шаровых по-
поверхности: одну — радиусом z — £, другую — радиусом z + e. Эти две
поверхности разделят шаровой слой на три части: Ти То и Т2.
Точка М лежит в слое То. По отношению к слою 7\ она является
внешней. Поэтому потенциал этого слоя, который мы обозначим через
Vlt следует вычислять по формуле A1,18), а интеграл, входящий
в эту формулу, надо вычислять в пределах от а до z — е, после
чего вычислить предел полученного выражения при е -> 0. Таким
образом,
г—е
I/ 4л..
По отношению же к слою Т2 точку М нужно рассматривать
как лежащую внутри полого пространства. Поэтому потенциал
277
этого слоя, который мы обозначим через V2, следует вычислять
по формуле A1,20), интеграл в ней взят в пределах от г + е до R,
а в полученном выражении перейти к пределу, устремляя е к нулю.
Таким образом,
н
= 4*Hm Г
z+e
Потенциал V всего шарового слоя рассмотрим как сумму потен-
потенциалов слоев Тг и Т2.
V — У, 4- Уо
т. е.
Z—5 Л
1^ = — lim I ф (р) р2 dp-j-4ic lim I ij>(p)pdp. (U>21)
a z+i
Если плотность <ji (p) слоя есть величина постоянная, равная у,
ф (р) =. const = 7,
то
z— • Л
4лт ,. р8
* 1 ■ m г
4iclim Г
Z е-»
а г+t
+ 4ict Hti4- = -y^ lim [B—е^-^а3] + 2irj lim [/?2— (г + еJ].
Вычисляя входящие в эту формулу пределы, можно сделать
вывод, что если шаровой слой однороден, то его потенциал на вну-
внутреннюю точку
V = 4-^{& — а3)+ 2*ч (Я2 — г2). A1,22)
При а = 0 в шаре не будет полого пространства (полный шар)
и тогда при постоянной плотности -у относительно внешней точки
потенциал шара на основании A1,19)
где М — масса шара.
В случае же, если точка находится внутри полного шара, а —
= 0 из A1,22) потенциал
V z2
или
У = 2*ТЯ2—|«Тг2. A1,23)
278
Если точка лежит на поверхности шара, то г = R и из A1,23)-
следует, что потенциал однородного шара относительно точки, ле-
лежащей на его поверхности,
или
Теперь перейдем к вычислению силы, с которой точка притяги-
притягивается шаровым слоем.
Случай 1 (точка лежит вне шарового слоя). Потенциал V вы-
вычисляется по формуле A1,19). Проекция Fz силы притяжения на
ось Ог
F - dV — т /II 9Л\
Очевидно, что проекции Fx и Fy силы притяжения на оси Ох
и Оу ввиду симметрии точки М относительно шара равны нулю:
На основании A1,24) мы заключаем, что шаровой слой притя-
притягивает точку, находящуюся вне его, с такой же силой, как если
бы вся его масса шара была сосредоточена в его центре.
Случай 2 (точка лежит внутри полого пространства шара). По-
Потенциал подсчитывается по формуле A1,20), от г он не зависит.
Поэтому проекция силы притяжения на ось Ог
Случай 3 (точка находится внутри однородного шарового слоя).
На основании формулы A1,22)
A1,25)
Но масса слоя Тх, которую мы обозначим через тх, равна
-g- %i (г3 — а3), поэтому
Таким образом, получается, что сила притяжения шаровым,
слоем точки, находящейся внутри его, такая же, как если бы вся
масса этого шарового слоя находилась в его центре. Можно по-
показать, что это заключение остается верным и для неоднородного
шарового слоя.
279
Укажем, что формулы A1,24) и A1,26) верны и тогда, когда
вместо шарового слоя берется полный шар. Тогда в этих форму-
формулах т — масса полного шара, а тх масса шара радиуса z(z< R).
Из формулы A1,23) заключаем, что притяжение полным шаром
постоянной плотности внутренней точки
dv
т. е. притяжение пропорционально расстоянию точки от центра
шара.
Замечание, Если в точке М помещена не единичная масса, а мас-
масса т0, то при вычислении потенциала и притяжения в соответствую-
соответствующих формулах этой задачи правые части следует умножить на т0.
2 «Л
Задача 11,8. Дано скалярное поле ср = -f-. В каком направле-
направлении функция <р будет возрастать быстрее всего, если исходить из
точки А A, 2, —1)?
Решение. Известно, что направление, в котором функция
растет с наибольшей скоростью, указывается градиентом этой
функции. Поэтому прежде всего найдем градиент заданной функ-
функции в произвольной точке. У нас
* ~ г* ' дх г* 5 ду ~ г2 ' дг ~
Подставляя значения этих производных в формулу A1,4), опреде-
определяющую градиент функции, получаем
Теперь найдем grad<p в точке ЛA, 2, —1), заменив в этой
формуле х, у и г их значениями в точке А:
x=h у = 2; г = —1.
Вектор (grad с?)л = 16t -f- 12/ + 16& и указывает направление, в ко-
котором заданная функция растет скорее всего, если исходить из
точки А.
Задача 11,9 (для самостоятельного решения). Докажите, что
функция V = — (г — |/*2 + г/2 + гЛ удовлетворяет уравнению Лап-
Лапласа
Указание. Используйте найденные в задаче 11,4 значения
dV dV^ dV_
дх ' ду' дг'
280
ОСНОВНЫЕ ФОРМУЛЫ ТЕОРИИ ГРАДИЕНТА
Задача 11,10. Доказать, что:
1) grad (ср + Ф) = grad ср + grad ф; A1,27)
2) grad (ср • ф) = ? grad ф +. ф grad cp; A1,28)
3) grad F (ср) = F' (?) grad <p, A1,29)
где со = ср (х, у, г); $ = ф (х, у, г).
Решение. 1. Формула A1,27) следует прямо из формулы A1,4).
Действительно,
grad (ср + ф) = §-х (cf + *) i +1 (? + ф) / +1 Op + 1») Л,
поэтому
= grad cp -j- grad <!>
и формула A1,27) доказана. Несмотря на свою простоту она очень
важна, так как с ее помощью решается вопрос о построении сум-
суммы векторных полей.
Частный случай. Если ф = С, то, поскольку в этом случае
частные производные
$ф dty $ф Л
дх ду~дг~ '
имеем
grad (ср + С) = grad ср.
2. Докажем теперь формулу A1,28)
Легко получаем:
Умножая обе части каждого из этих равенств соответственно
на Г, f и Ъ и почленно складывая, имеем
grad (срф) = ф grad «р + ср grad «j».
281
Частные случаи: а) если ср = ф, то
grad сра = 2<р grad <pj
б) если ф = С, то
grad С ср = С grad у.
3. Формулу A1,29) докажите самостоятельно.
Задача 11,11. Доказать, что, если г — радиус-вектор точки
А (х, у, г), а <р = с?(х, у, г) —функция трех независимых перемен-
лых, то
d<f=tdr • gradcp
(dr • grad <p—скалярное произведение векторов dr и grad 9).
Решение. Если функция <р = ср(х, у, г), то ее полный диф-
дифференциал
Радиус-вектор точки Л(дг, у, 2)
7 = xi + yj + zk,
а его дифференциал
dr •= dx • t + dy ' j+dz • к
Так как вектор
то скалярное произведение
Сравнивая это выражение с выражением (А) для полного диффе-
дифференциала функции 9. получаем требуемое равенство:
dcp = dr ■ grad tp.
Отсюда можно сделать заключение, что, если
d<? = Ir.~a, A1,30)
то вектор с необходимо является градиентом некоторой функции
■? = ?(*, У, г):
a = grad<p. A1,31)
.282
Задача 11,12 (для самостоятельного решения). Найти
Задача 11,13 (для самостоятельного решения). Найти
grad (л? + у2 + г%
Ответ. 2л
Задача 11,14 (для самостоятельного решения). Найти градиент
скалярного произведения г • а, где а — постоянный вектор, а г —
радиус-вектор точки _А (х,_у, г) (г == xl + yj+ zk).
Ответ, grad (r • а) = а.
Полученный результат указывает на то, что вектор grad (r • а)
во всех точках поля сохраняет постоянное направление, совпадаю-
совпадающее с направлением вектора а.
Кроме общего способа, основанного на применении формулы
A1,4) к функции ср = г • а — ах • х + ау • у +' аг • г, можно также
воспользоваться.результатом задачи A1,И)- У нас функция ср =
= г • а (а — постоянный вектор)
dtp == d (r • а) = а • dr.
Следовательно, на основании формулы A1,31)
а = grad ср = grad (r • а).
Читая это равенство справа налево, получаем требуемое
grad (r • а) = а.
Задача 11,15. Определить grad ср(ы, v), где и=*и(х, у, z), v —
= v(x, у, г).
Решение. Чтобы воспользоваться формулой A1,4), опреде-
определим частные производные -^, j- и ^ по формуле дифференци-
дифференцирования сложных функций
д<р дер ди . д<р да #
дх ди дх, до дх'
д<? ду ди . д<? до ф
ду ~ ди ду' до ду'
ду _ д<? ди . (Эср до
Т~дйдг + дгШ'
283
Умножая обе части каждого из этих равенств соответственно на
i, j и k и почленно складывая их, получим
grad 9 (", v) = д| grad и + ^
Задача 11,16. 1. Найти производную функции и — и(х, у, г) в
направлении градиента функции v — v (х, у, г). 2. При каком усло-
условии эта производная равна нулю?
Решение. На основании формулы A1,4)
до-. . dv- , dv-r
Проекция вектора grad у на оси прямоугольной системы координат
Направляющие косинусы вектора с находят, как известно, по фор-
формулам
Направляющие косинусы вектора grad у определим по формулам
dv
i л ^ \ (grad v)x дх
cos (grad Ol до =jLJj;
cos (grad Л) =
Производную функции ы = и (х, у, г) по направлению вектора
7 = grad v, характеризуемому только что определенными косинусами,
найдем по формуле A1,3)
dv dv dv
du du дх ди ду . du dz
dl дх | grad v\ ' dy ' \ grad v\ ' dz ' | grad v |
ИЛИ
du dv du fo , du dv
du дхд~х^"д~уду~т~Щ dz
dl ~~ | grad у| '
284
а так как
g = (grad и),; щ = (grad о)„; g = (grad v)z>
то числитель последней дроби равен скалярному произведению
векторов grad и и grad v ц тогда окончательно
ди grad и • grad v
Ж ~ | grad v | *
Теперь переходим ко второму вопросу задачи.
Найденная производная щ будет равна нулю, если числитель
последней дроби равен нулю, т. е. если
grad и • grad v = 0.
Из этого следует, что производная функции и = и {х, у, г) по
направлению градиента функции v — v (x, у, г) равна нулю, если
векторы gradu и grad у перпендикулярны.
ДВЕНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Векторное поле. Потенциальные векторы. Потенциал век-
векторного поля. Циркуляция вектора. Линейный интеграл. Вихрь вектора.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Векторное поле. Физическое.поле называется векторным, если
образующее его физическое явление характеризуется вектором
(например, поле силы тяжести, поле скоростей).
В случае векторного поля каждой точке Р пространства, в кото-
котором происходит образовавшее его физическое явление, ставится
в соответствие определенный вектор а{Р), являющийся функцией
координат точки, т. е. а = а(х, у, г).
Вектор а (х, у, г) можно представить в виде
а (х, у*, г) = ах (х, у, z) i + ау(х, у, z) / + аг (х, У, г) Ъ.
Из этого следует, что для полного определения векторного поля
требуются три Скалярные функции трех независимых переменных
х, у и г:
ах(х, У, г); ау(х, у, г); аг(х, у, г)~
— проекции вектора о (дг, у, г) на оси прямоугольной системы коор-
координат (во всех последующих формулах предполагается, что эти
функции непрерывны, однозначны и имеют непрерывные частные
производные).
1. Потенциальный вектор. Вектор а называется потенциаль-
потенциальным, если он является градиентом некоторой скалярной функции
<f (х, у, z)(a = grad <р). Поле потенциального вектора а — grad <p на-
называется потенциальным, а скалярная функция <р — потенциалом.
этого поля. В дальнейшем предполагается, что функция <р и ее
частные производные до второго порядка включительно непрерывны.
Необходимым и достаточным условием потенциальности вектора
а является выполнение равенств:
дау _
дах да
г
да,,
286
Пример. Потенциальным векторным полем является поле силы
Т = -у г тяготения, вызываемого материальной точкой массы пг,
помещенной в цачале координат. Здесь г = Ух2 + у2 + z2— рас-
расстояние произвольной точки пространства А (х, у, г) с массой тх=
= 1 до начала координат (г ф 0). Потенциалом этого поля является
функция v = — (см. задачу 11,3).
2. Циркуляция вектора и линейный интеграл. Циркуляцией fL
вектора а = а {х, у, z) по замкнутой линии L называется интеграл
вида
Г1 = у ах dx + ау dy + аг dz, A2,2)
причем, обход замкнутого контура L в правой системе координат
должен происходить против движения часовой стрелки.
Если L — незамкнутая кривая, то интеграл в формуле A2,2)
называется линейным интегралом вектора а и обозначается буквой и
и= .) ахdx + aydy + агdz A2,3)
или в векторной форме
и= J 'a-d'r, A2,4)
(АВ)
где dr — дифференциал радиуса-вектора точки, движущейся по кри-
кривой АВ
dr = dx • i + dy ' j + dz • Ъ.
Если вектор а — сила, то формула A2,3) определяет работу
этой силы при перемещении точки по дуге АВ.
3. Векторная линия. Векторной линией векторного поля вектора
а называется кривая, в каждой точке которой касательная совпа-
совпадает с направлением вектора а. Через каждую точку Р векторного
поля вектора а проходит по одной векторной линии.
Дифференциальные уравнения векторных линий записываются
так:
% = %==%- A2,5)
4. Вихрь вектора. Вихрем вектора, или ротором вектора а =
= а (х, у, г), обозначаемым rota, называется вектор, определяе-
определяемый формулой
— Ida, **"i/\ т !дпг дп,\ -, (даи с
rot a = I - — —-11 -j- I —— д-^ I / -f-1 —-
287
Проекции этого вектора на координатные оси равны
, - дах daz
" ог ох
_.! ~ _ даи дах
A2,7)
Модуль вектора rot а определяется формулой
Формулу A2,6) можно записать в виде, удобном для запоми-
запоминания
7 / I
rota =
1 i. £
d* di/ дг
ах ау аг
A2,9)
При этом произведения символов ^, j- и ^- на ах, ау, аг
следует понимать так:
д ^ау. д дах
дх ' йу ~ ~дх ' ду ' а* ~ ~ду ' '
И т. Д.
Задача 12,1. Известно, что безвихревым движением жидкости
называется движение, при котором в каждой точке жидкости вы-
выполняется условие
rot v = О,
где вектор v = v (x, у, г) — скорость жидкости в рассматриваемой
точке.
Доказать, что при безвихревом движении жидкости и сущест-
существовании однозначного потенциала скорости v циркуляция скорости
v, взятая по лйбой замкнутой кривой, равна нулю.
Решение. Обозначим проекции скорости v на оси прямо-
прямоугольной системы координат через vxt vy, vz. Равенство rot v=0 на
основании формулы A2,6) можно переписать в виде
Из этого следует, что
ду
dvy _
~дТ ~
dv,
дг
дх
у
дх '
dvx
288
Выполнение этих равенств является необходимым и достаточ-
достаточным условием для того, чтобы вектор v был потенциальным —
см. определение на стр. 286 и формулы A2,1).
Поскольку вектор v потенциальный, то существует такая ска-
скалярная функция ср = у (дг, у; г) — потенциал скорости, что
v = grad «р
(см. определение на стр. 263).
Отсюда
т. е. если скоростью — потенциальный вектор, а функция с» =
=9(х,у, г) — потенциал скорости, то проекция скорости на коор-
координатную ось прямоугольной системы координат равна частной
производной от потенциала скорости по соответствующей этой оси
координате.
Из (А) следует
о, dx + vydy + vzdz = %dx + |d«/ -f %dz - df.
Линейный интеграл A2,3) по кривой АВ от выражения vxdx+
+ vydy + vz dz
J vxdx + vydy + vzdz=
I/4S)
это значит, что он не зависит от вида кривой, а только от коор-
координат ее концов А и В, так как у (Л) и ср (В) — значение потенциала
ср в точках Л и В (предполагается однозначность потенциала ско-
скорости — функции ср).
Таким образом, линейный интеграл по кривой АВ от потен-
потенциального вектора равен разности значений потенциала ср в кон-
концах кривой, вдоль которой ведется интегрирование.
Если кривая АВ — замкнутая, то линейный интеграл в равен-
равенстве (В) есть циркуляция скорости, а <р(В) — ср (А) = 0, так как
точки А и В в случае замкнутости кривой АВ совпадут.
Отсюда следует вывод, что циркуляция скорости по любой
замкнутой кривой при наличии однозначного потенциала равна
нулю, т. е., если o = gradcp и у — однозначная функция, то
f
'vx dx + oydy + vzdz = 0.
(Предположение об однозначности функции ср является весьма суще-
существенным. Если ср — неоднозначная функция, то сделанный вывод
не всегда верен).
10 И. А. Каплая 289
Замечание. Следует иметь в виду, что теорема о равенстве
нулю криволинейного интеграла от потенциального вектора по замк-
замкнутому контуру верна только тогда, когда пространство односвязно.
Задача 12,2. Доказать, что если v — потенциальный вектор (у =
= grad<p), то вихрь этого вектора равен нулю, т. е. что
rot (grad ер) = 0.
Решение. В предыдущей задаче было показано, что из равен-
равенства rota = 0 следует, что v есть вектор потенциальный, т. е.
v — grad ср. Теперь решаем обратную задачу, т. е. хотим доказать,
что' если вектор v потенциальный, то его вихрь равен нулю.
Итак, дано, что v = grad ср. Отсюда
>х~ ду дг ~ ду \дг) дг \ду) ~ дг ду ду дг '
Поскольку при ограничениях, наложенных на функцию у, изме-
изменение порядка дифференцирования не изменяет величины ее вто-
второй смешанной частной производной, то т^" = д~х» поэтому
(rot v)x = 0. Аналогично найдем, что (rot v)y = 0 и (rot v)z = 0, а
отсюда
rot v = 0.
Так как v = gradср, то rot (grad?) = 0.
Заключение. Вихрь потенциального вектора равен нулю.
Задача 12,3. Проекции 'ускорения частицы жидкости на оси
прямоугольной системы координат даются формулами
диг dvz , dv2 , диг
Доказать, что при существовании потенциала скорости уско-
ускорение W также является потенциальным вектором.
Решение. По условию y = gradcp, где <р — потенциал ско-
скорости. Отсюда
:-%'■«.-%< >.-%•'
290
Дифференцирование обеих частей каждого из этих равенств по
х, у, г и t дает
dvx _ д\ ff£
d ~ ddt' dt
dt ~ dxdt' dt ~ dydt' dt ~ дг dt
dvx d2? dvx д\ ( dvxd*y
~дх"~дх*1 Ъ~у ~ ЫсЪ~у' Тг ~
дх ~ дудх' ду ~ ду*1 дг
dvz d2tp # dvz d2tp dvz й^р
57 ~~ дгдх' dy ~~ дгду' ^F ~" дг8 '
Подставляя эти значения в выражения для Wx, Wy, Wz из ус-
условия задачи, получим
* ~ дх Л "•" дх» ' дх """ дхду ' ду^~ дхдг' дг ~
у~ dydt^ дудх дх^ду* ду^ дудг дг
гго __ ^у д\
г~~дГЫ ~дТЫс
Замечая, что
предыдущие равенства перепишем в виде
и, таким образом, проекции ускорения частиц жидкости являются
частными производными по координатам одной и той же функции
Т °а ~1~ * » а 0ТСК>Да на основании определения градиента функции
заключаем, что
10* 29J
Итак, вектор W есть градиент некоторой функции. Это значит, что
он вектор потенциальный.
Задача 12,4. Дифференциальное уравнение неразрывности для
несжимаемой жидкости имеет вид
Доказать, что при потенциальном движении жидкости потен-
потенциал скорости — функция <р удовлетворяет уравнению Лапласа
SJfl + а? + 5? ~ 0>
Решение. Если предположить, что движение жидкости потен-
потенциальное, то скорость v = v (х, у, г) жидкости является градиен-
градиентом некоторой функции ср:
й = grad<p,
а отсюда проекции скорости на оси прямоугольной системы коор-
координат равны частным производным потенциала скорости <р по соот-
соответствующим этим осям координатам, т. е.
dtp dtp dv
^ = Е; ^ = р; v = T
- Дифференцируя обе части первого равенства по х, второго —•
по**/, третьего — по г, получим
дх дхл * ду ду2' дг дг2 '
Складываем эти равенства почленно:
Их ~5у ' дг дх2 ' ду2 ' дг2" *
По условию задачи левая часть этого равенства есть нуль, сле-
следовательно, и правая его часть равна нулю, т. е.
дх2 ду2 dz2 ' V'*,1'-'/
Заключение. Потенциал скорости несжимаемой жидкости
удовлетворяет уравнению Лапласа A2,10).
Обычно левая часть этого уравнения обозначается сокращенно
через Д<р, поэтому A2,10) записывается так:
Д<р = 0. A2,11)
292
Функция <р, удовлетворяющая этому уравнению,
называется гармонической. В случае плоского потенциаль-
потенциального движения несжимаемой жидкости уравнение Лапласа A2,11)
имеет вид
д^ + д$ = 0- A2,12)
Задача 12,5 (для самостоятельного решения). Доказать, что функ-
функция у = In г удовлетворяет уравнению Лапласа A2,12) (г =
Задача 12,6. Дано поле вектора
а = 2х • i — у • j + z • k
Найти уравнение векторных линий.
Решение. Дифференциальные уравнения векторных линий
имеют вид A2,5). В нашем случае
а, = 2х\ ау = —у, аг = г
и система дифференциальных уравнений (!2,5) запишется так:
dx dy_ da
или
,v dx dy, o\£f_^£
' 2x у ' ' 2x г
Интегрируя, получаем семейства векторных линий
1) -у In х = -
и
2) -i-1п л; = In z + In C2,
а отсюда уже
1) \п(У~ху) = In С; Уху = С; ху2 = С2; уг = ^, где Сг = С2.
2) In Ух = In Сгг\ Ух = Сгг\ х = С\гг или z2 = С3х, где
Итак, имеем следующие уравнения семейства векторных линий:
у2 = £i и г2 = С3д;.
Надо иметь в виду, что начало координат является здесь особой
точкой: если х-»-0, то г/->оо при СхФО.
293
Задача 12,7. Движение жидкости задано проекциями скорости
где k — постоянная величина. Требуется найти линии тока и направ-
направление движения.
Решение. Если в уравнениях A2,5) ах, ау, аг — проекции
скорости частицы жидкости, то эти уравнения при установившемся
движении жидкости называются дифференциальными уравнениями ли-
линий тока. В каждый данный момент времени каждая частица жидкости,
находящаяся на линии тока, имеет скорость, совпадающую по на-
направлению с касательной к этой линии (движение жидкости назы-
называется установившимся, если проекция скорости частицы жидкости
не зависит от времени).
В нашем случае эти дифференциальные уравнения A2,5) запи-
запишутся так:
dx _ dy
-ky~ kx'
Отсюда
kx dx = —ky dy.
Сокращая на & и интегрируя, получаем
ИЛИ
*• + у2 = С
— линии тока—семейство концентрических окружностей с цент-
центром в начале координат.
Теперь определим направление движения. У нас Vx = —ky\
Vy = kx, поэтому
V=
cos (F, „ - *, , ^^ cos
Из
равенства cos (V, x) = — , ^ следует, что если х > О
и у > 0, то cos (P, х) < 0 и скорость V с положительным направ-
направлением оси Ох образует тупой угол. Это говорит о том, что дви-
движение происходит против хода часовой стрелки
Задача 12,7а. Движение жидкости задано проекциями скорости
294
Определить:
1. Уравнение семейства линий тока, а также линию тока, про-
ходящую через точку А (—2, —3) в момент времени t = 0.
2. Траекторию частицы жидкости, которая в момент времени
^ = 0 находилась в точке А(—2, —3).
Решение. 1. Дифференциальное уравнение семейства линий
тока на основании A2,5) имеет вид
Ах _ dp
Считая t — фиксированным и интегрируя, получим
— In (-л:+ 0 = In [у + 0 — 1пС,
откуда
t) = C. (A)
Линиями тока в каждый момент времени является семейство
гипербол. При t = 0 это семейство имеет уравнение
—ху = С.
Подставляя сюда на основании условия задачи координаты точки
А (—2, —3), получим С = —6. Искомым уравнением линии тока,
соответствующим условию задачи, будет
2. Чтобы ответить на второй вопрос задачи, надо знать следу-
следующее:
1. Движение жидкости называется неустановившимся, если
проекции скорости Vx, Vy и Vz являются функциями не только
координат, но и времени, т. е. если
Vx = Vx(x, У, 2, t); Vu = Vy(x, у, г, (); V2 = Vz(x, у, г, t).
2. Дифференциальные уравнения траекторий жидкой частицы
в этом случае имеют вид
dg их
Vx (х, у, г, t) Vy (х, у, г, t) Vг (х. у, г, t)
,,
Тогда, чтобы получить траекторию частицы жидкости, надо про-
проинтегрировать такую систему уравнений:
% = УУ(х, у, г, о;
зг = у г (*> у» 2, 0-
295
В нашем случае уравнения этой системы запишутся так
dT
= ~х
Каждое из них — линейное неоднородное уравнение первого по-
порядка с постоянными коэффициентами.
Перепишем их в виде
— 4- х - t
dy
Интегрируем эти уравнения по правилам интегрирования ли-
линейных дифференциальных уравнений:
*-1. (В)
Подставляем в эти уравнения t — О, х — —2, у = 3. Получится,
что Cj = —1, С2 = —2 и уравнения траектории примут вид
у = -~ 2е< — t— 1.
Замечание. Сравнивая уравнения (А) и (В), видим, что при
неустановившемся движении жидкости линии тока не совпадают
с траекториями жидкой частицы (при установившемся движении
жидкости линии тока являются одновременно и траекториями
частиц).
Задача 12,8. (для самостоятельного решения). Поле скоростей
жидкости задано следующим образом:
у =1
* 4it 2
V = £
г2)
У
//2 +г2
4- у2 + г2) Ух2 +
где Q — постоянная величина.
Определить линии тока.
Ответ.
у — Сгх (семейство плоскостей, проходящих через ось Ог)\
z = СоХ (семейство плоскостей, проходящих через ось Оу).
Линии пересечения плоскостей одного семейства с плоскостями
другого семейства — прямые, проходящие через начало координат.
296
Задача 12,9. (для самостоятельного решения). Напряженность
электростатического поля определяется вектором-^г°, где е — по-
положительный электрический заряд, г—расстояние точки поля до
заряда, г° — единичный вектор вектора г, соединяющего точку
поля с зарядом.
Определить векторные линии поля.
OTBej. Лучи, выходящие из заряда.
Задача 12,10. Твердое тело вращается с постоянной угловой
скоростью to вокруг некоторой оси. Известно, что во вращательном
движении линейная скорость v точек тела определяется по формуле
v = Z X г,
где г — радиус-вектор точки А (х, у, г) тела. Найти rot v.
Решение. Направим вектор ш по оси вращения, которую
примем за ось Ог, в сторону, откуда вращение представляется про-
происходящим против движения часовой стрелки. Проекции векторов
<и и г на координатные оси равны:
шх = 0; % — 0; шг = ш;
/■„ =
= х; гу = у; гг = г.
(А)
Так как вектор v равен векторному произведению векторов <о и
г, то
I j k
V = ш X г =
Подставляя значения проекций векторов в иг из равенства (А),
получаем
1 ] I
v= 0 0 (о
х у г
откуда следует, что проекции вектора Ъ равны:
vx = — шу, vy = <одг; vz = 0.
Чтобы воспользоваться формулой A2,6) для определения ротора
вектора, найдем входящие в эту формулу частные производные
от проекций вектора v:
dvx до.. av
dvu
дх ~ ду
дг
дг'
297
Подставляем эти значения в формулу A2,6):
(dv dv \ - -
djf- ф/k = [о)- {-")]'k = 2о)&-
Итак,
rot v = 2сй&.
В связи с тем что вектор ш = u>k, приходим к заключению:
rotu = 2сй,
а отсюда следует: ротор линейной скорости точек вращающегося
твердого тела имеет постоянное значение во всех точках тела
и равен удвоенной угловой скорости его вращения.
Задача 12,11 (для самостоятельного решения). Найти векторные
линии поля вектора
а — —Щ1 + ч>х] -f- hk,
где о) и Л — величины постоянные.
Указания.
1. Уравнения векторных линий запишутся так:
dx _ dy _ rfz _ ..
—v>y ~ ч>х~ h ~
или
2. Из первых двух уравнений получаем, дифференцируя обе
части каждого из них по t,
3. Общими решениями этих линейных однородных уравнений с
постоянными коэффициентами будут:
х = Ах cos со^ + Вх si n Ы; (В)
t/ = А2 cos о)^ + В2 sin wf.
4. Учесть уравнения (А) и показать, что между произвольными
постоянными существуют соотношения
5Х = — А2; В2 = Аг
298
и тогда уравнения (В) перепишутся так:
х = Ах cos Ы — А2 sin Ы)
у = А2 cos <nt + Ах sin u>t.
(С)
5. Если А1 = R cos а, а Л2
■■-jr, то уравнения (С) запишутся так:
sin а, т. e. R = VA\ + A\, tg a=
= R cos (Ы + a);
Третье уравнение системы (А) дает
z = ht + A3.
Таким образом, введены только три про-
произвольные R, a и А3, как и должно
быть.
Уравнения (D) и (Е) определяют
винтовые линии, расположенные на ци-
цилиндре радиуса R, ось которого совпа-
совпадает с осью Ог.
Задача 12,12. Найти линейный ин-
интеграл вектора а = хН -•» г/4/ вдоль пер-
первой четверти окружности
х = R cos t; i/ = Я sin *.
(D)
(E)
К задаче 12,12
Решение. Чтобы найти значение вектора а на заданной ок-
окружности, заменим в его выражении х на Rcost, ay — на Rsint.
Тогда
а — #4 cos41 • i — R* sin4 //'.
Отсюда
a, = #4cos4 ау = — R* sin41. (A)
Чтобы воспользоваться формулой A2,3), найдем dx и dy из
уравнения окружности
* = R cos <;
у = Я sin f.
Отсюда
dy = R cos tdt. * ^В)
Подставляя значения (А) и (В) в формулу A2,3), получаем, учи-
299
тывая, что при движении по дуге L параметр t изменяется от О
= ^ R4 cos* t(—Rs\nt) dt~
0
— R* sin4 tR cos t dt = R5 j [cos41 • (—sin t) — stn41 cos t) dt
К задаче 12,14
Задача 12,13 (для самостоятельного
решения). Найти линейный интеграл
вектора а = Л' — г/3/ вдоль первой чет-
четверти окружности х = R cost; у = /? sin г.
Ответ, и = — у Я4.
Задача 12,14. Найти циркуляцию
вектора а = ли' — #/ вдоль замкнутой
кривой, образованной осями координат
и первой четвертью астроиды х =
= fll cos3 /; у = a, sin3 L
Решение. Линия L в формуле A2,2) состоит из дуги АВ
астроиды и отрезков АО и ОВ координатных осей. Поэтому
J aKdx + aydy
АО
АО
\axdx + aydy.
OB
Каждый из этих интегралов вычислим отдельно: при вычислении
первого интеграла по дуге астроиды АВ следует учесть, что так как
а = x~i — yj, то ах = х; ау = —у.
На астроиде х = ад cos31; у = at sin31, поэтому
ax — x = ax cos3 ?; ay = —i/ = —ax sin3 /.
Из уравнений астроиды определим dx и ф
d* = —Зах cos* t sin f d^; dy = Зах sin8 / cos / dt.
300
На дуге астроиды ВА при движении от В к А параметр t изме-
изменяется от 0 до y • поэтому
к
т
ах dx + aydy = [ ax cos31 (—3at cos2 ts\nf)dt —
i о
— at sin31 Cat sin2 f cos t) dt —
1С
T
— Ъа2\ \ (—cos51 si n t—si n51 cos /) dt =
1С
e«/ sin»Л Й o_a/ 1 1
На отрезке АО оси Ог/ имеем: ^ = 0; dx — 0; вектор a = —у/;аж
==0; ар = —у, а г/ изменяется от ах до 0
о
АО at '
На отрезке OS оси Ох у — 0; dy — 0; вектор a = xi; ax
J
ов
Таким образом,
a, a,
о =T
Задача 12,15 (для самостоятельного решения). Найти циркуля-
циркуляцию вектора а = y*t по замкнутой кривой, составленной из верх-
верхней половины эллипса
х = acost; у — bsint
и отрезка оси Ох.
Указание. На верхней половине эллипса параметр t при
движении против хода часовой стрелки изменяется от 0 до те.
Промежуточный результат: I s\n3 tdt = —-j.
Ответ, -к- ab2.
О
301
Задача 12,16. Найти rota, если вектор
а = {Зх*уЧ + 3**) i + 2x*yzj
Решение. Проекции вектора а
г; а, «= ж3у* + Зг8.
Применяя формулы A2,7) найдем, что rot a = О
Задача 12,17 (для самостоятельного решения). Доказать, что
поле сил тяготения точечной притягивающей массы, помещенной
в начале координат
является безвихревым, т. е. что rotF = 0.
Указание.
ТРИНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Поток векторного поля. Дивергенция вектора. Формула
Остроградского.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Поверхностные интегралы. Пусть 5 — гладкая или кусочно
гладкая поверхность, ограниченная определенным контуром, кото-
который будем считать ее краем. На такой пЬверхности будем разли-
различать две стороны, понимая под этим следующее: движущаяся по
поверхности точка может с одной стороны поверхности перейти
на другую не иначе, как пересекая край поверхности.
Одну из этих сторон поверхности назовем внешней (верхней),
другую — внутренней (нижней). Внешней стороной считается та,
которая соответствует положительному направлению оси Oz, a
внутренняя сторона соответствует отрицательному направлению
оси Oz. На нормали к поверхности 5 можно рассматривать два
возможных направления: одно, идущее в сторону возрастающих,
другое — в сторону убывающих z-ов. Если на нормали выбрано
направление в сторону возрастающих z-ов, то она называется
внешней и связывается с внешней стороной поверхности. Нормаль,
направленная в сторону убывающих г-ов, называется внутренней
и связана с внутренней стороной поверхности 5.
ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ ПЕРВОГО ТИПА
(поверхностный интеграл по площади поверхности)
Пусть в каждой точке поверхности S задана функция f{x, у, г).
Поверхность 5 разобьем на п частей, площади которых обозначим
через А5Ь AS2, ... ASn. На каждой такой площадке &Sk выберем
произвольную точку Ak{xk, yk, гк), вычислим в ней значение за-
заданной функции f{x, у, г), т. е. найдем число f(xk, yk, zk) и
составим сумму произведений (интегральную сумму)
Уъ Zi) ASi + f (*2, «/2, z2) AS2-] +/ (*„, уп, гп) ASn
Если функция f {x, у, г) непрерывна во всех точках поверхности S,
то предел этой интегральной суммы при условии, что максималь-
зоз
ный диаметр частей ASk стремится к нулю, существует и не зав(и-
сит от способа разбиения поверхности 5 на части и выбора точки
Ак на каждой из этих частей. Этот предел называется поверх-
поверхностным интегралом первого типа от f (х, у, z)dS, распространен-
распространенным на поверхность 5, и обозначается символом
Ш(*> У, z)ds.
Таким образом,
max дТ^О £/(**• ук, Zk)bSk= JJ f(x, у, Z) dS.
Пч-сс fc=l E)
Формула для вычисления поверхностного
интеграла первого рода
Если поверхность S определяется уравнением г = <? {х, у), а —
ее проекция на плоскость хОу, a f — угол между внешней нор-
нормалью к поверхности S и положительным направлением оси Ог,
то имеет место формула
(x, у, z)dS=Nf[x, у, 9(х, у)]^. A3,1)
(о)
Косинус угла т между внешней нормалью к поверхности, опре-
определяемой уравнением г — у(х, у), и осью Ог вычисляется по
формуле
Формула A3,1) с этим значением cost перепишется так:
JJ(*. у, z)dS = ^f[x, у, Т(х, r,
iS) (о)
Косинусы углов аир между внешней нормалью к поверхности
г = ср {х, у) и осями Ох и Оу соответственно равны:
cos а = - _дх A3,3)
У7ШШ
дг
* A3,4)
304
Если S — замкнутая поверхность, то поверхностный интеграл пер-
первого рода обозначается символом IJ f {x, у, г) ds.
IS)
ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ ВТОРОГО ТИПА
(поверхностный интеграл по координатам)
Пусть / {х, у, г) ■— функция, заданная в каждой точке поверх-
поверхности S. Разобьем поверхность 5 на п частей с площадями ASb
AS2 ASn.
На каждой из этих частей выберем произвольную точку
Ak(xk, yk, zk) и вычислим в ней функцию f (х, у, г), т. е. найдем
число f(xk, yk, zk). Спроектируем все площади ASk, на которые
разбита поверхность S, на плоскость хОу и обозначим площади
этих проекций соответственно через Да1( Ло2, ... , Дзп. Если была
выбрана внешняя сторона поверхности S, то эти проекции будем
брать со знаком плюс. Если же выбрана нижняя сторона поверх-
поверхности S, то возьмем знак минус. Составим интегральную сумму
Если функция f {х, у, г) непрерывна в каждой точке поверх-
поверхности S, то ее предел при условии, что max AS4 -*• 0 существует,
называется поверхностным интегралом второго типа от / {х, у, г) da,
распространенным на выбранную сторону поверхности (S), и обоз-
обозначается символом
£j/(x, д, г)da или Ufix, yt z)dxdy.
(Si (S)
Таким образом,
г "
maxAS^-0 ]£/(*fc, t/k, Zk)= \,)f(x, у, z)dxdy.
{ПЧ-») k=\ (S)
При замене выбранной стороны поверхности S противоположной
ее стороной знак интеграла поменяется на противоположный, а его
абсолютная величина сохранится прежней.
Если элементы, на которые разбита поверхность 5, проекти-
проектировать на плоскость Юг и yOz, то получаются соответственно два
интеграла
ЦД*. у, z)dxdz и j J7(*. у, z)dydz.
IS) (S)
Если Р(х, у, г), Q{x, у, г) и R {х, у, г) — функции, определен-
определенные во всех точках поверхности 5, то под составным поверхност-
поверхностным интегралом второго типа понимается интеграл вида
Я
, Р(х, у, z)dydz + Q(x, д, z)dzdx + R{x, у, z)dxdy.
iS\
305
Подчеркиваем еще раз, что поверхность 5 является двусторонней*
а интеграл распространяется на ее определенную сторону, причем
указание этой стороны следует всякий раз оговаривать.
Поверхностный интеграл второго типа вычисляют по формуле
JJ(x, у, z)dxdy = JJ/[x, у, <р(х, y)]dxdy, A3,5)
(S) <»)
в которой z = ср (х, у) — уравнение поверхности S, а (о) — проекция
поверхности S на плоскость хОу.
Если S — часть цилиндрической поверхности с образующими,
параллельными осями Ог, то все ее элементы имеют проекции на
плоскость хОу, равные нулю, поэтому
a
f(x, у, z)dxdy = 0. A3,6)
Общая формула, по которой поверхностный интеграл второго
типа сводится к поверхностному интегралу первого типа запи-
записывается так:
ЙРdydz + Qdzdx + Rdxdy = \\ [Pcosa -f-Qcos p 4. Rcos7] dS,
(S)
A3,7)
где Р, Q и # —ограниченные функции, определенные во всех
точках поверхности 5, а cos a, cosf3, cos -j- — направляющие коси-
косинусы нормали, направление которой соответствует выбранной сто-
стороне поверхности.
2. Поток вектора. Потоком вектора а через поверхность S на-
называется скаляр, определяемый формулой
nds, A3,8)
где ап — проекция вектора а на нормаль к поверхности S, причем
нормаль берется определенная — внешняя или внутренняя.
Проекцию вектора а на нормаль к поверхности находят по
формуле
an = axcos(n, х) + аиcos(n, y) + a2cos(h, 2). A3,9)
где cos (n, х), cos(n, у), cos (п, г) — направляющие косинусы нор-
нормали к поверхности S, поэтому A3,8) можно записать в виде
П = J j [а, cos (n, x) + ay cos (h~> у) + аг cos (n, z)] ds. A3,10)
(S)
306
Учитывая, что
cos (n, x) ds = dy dz\ cos (h, y) ds ■= dz dx\ cos (n, z) ds = dx dy,
A3,100
формулу A3,10) запишем так:
П=\[ах dy dz + ay dz dx + аг dx dy. A3,11)
E)
В векторной форме A3,10) запишется в виде
A3,12)
JJ
(S)
где h — единичный вектор нормали, направленной от отрицатель-
отрицательной стороны поверхности к положительной (поверхность обыкно-
обыкновенно ориентируют так, что ее внешнюю сторону считают поло-
положительной, а внутреннюю — отрицательной). В случае замкнутой
поверхности вектор п — единичный вектор внешней нормали.
3. Дивергенция. Дивергенцией (расхождением) поля вектора
а = а(х, у, z), обозначаемой diva, называется скалярная величина,
определяемая формулой
За да да
а
7
Из этого определения видно, что дивергенция вектора а — ве-
величина скалярная и ее определение связано с выбором координат-
координатной системы. Ниже в связи с формулой Остроградского дается
другое определение дивергенции вектора а, которое устраняет этот
недостаток.
Термин «поток вектора» имеет физическое происхождение. Ука-
Укажем примеры физических величин, которые вычисляются при по-
помощи формулы A3,11):
а) Если векторное поле рассматривать как поле скоростей
движущейся жидкости, то поток ее П через поверхность 5 равен
количеству жидкости, протекающей через поверхность 5 в единицу
времени в направлении от отрицательной к положительной стороне
поверхности. Если поток через замкнутую поверхность S положи-
положителен, то это значит, что из части пространства, ограниченной
поверхностью 5, вытекает больше жидкости, чем втекает в нее.
Это объясняется тем, что внутри S имеются источники, выде-
выделяющие жидкость.
Если поток отрицателен, то внутрь поверхности S втекает
больше жидкости, чем вытекает из нее. Это означает, что внутри
S имеются стоки, поглощающие жидкость.
307
б) Поток тепла имеет направление и является векторной вели-
величиной. Обозначим вектор потока тепла через а. Его длина изме-
измеряет количество тепла, протекшего сквозь единицу площади в
единицу времени. Полный тепловой поток наружу через поверх-
поверхность 5 определяется также по формуле A3,11).
4. Формула Остроградского. Формулой Остроградского назы-
называется формула
ССПдР , dQ dR\
Т, + Т, + Т> =
(») (Id, 14)
[P cos (n, x) + Q cos (n, y) + R cos (n, г)) ds.
Здесь: cos(n, x), cos (л, у), cos (л, г) — направляющие косинусы
внешней нормали к поверхности s, ограничивающей объем v; Р,
Q, и R — сокращенное обозначение функций Р — Р(х, у, г); Q =
= Q {х> У> 2); R = R (х, у, г), которые предполагаются определен-
определенными в объеме v и непрерывными вместе с их частными произ-
производными первого порядка.
Формула A3,14) позволяет преобразовать интеграл, распрост-
распространенный на некоторый объем у, в интеграл по поверхности s,
которая ограничивает этот объем.
В другом виде с учетом A3,10t) формула Остроградского за-
записывается так:
+ % + ш)dv = Я р ty^ + Qdzdx + RdxйУ- (I3'I5)
М _ (s)
Если а = а(х, у, г)— вектор, проекции которого на координат-
координатные оси равны ах, ау, аг и ах = Р(х, у, г); ау = Q{x, у, г); аг =
= R {х, у, г), тоформула A3,7) запишется так:
Ш^)Я™*>+ „„а,
+ ау cos (n, у) + аг cos (n, г)] ds.
Формула Остроградского A3,14) в векторной форме (если ее
прочесть справа налево):
JJJ A3,17)
(S) (D)
т. е. поток вектора а, являющегося непрерывной функцией точки,
через произвольную замкнутую поверхность равен интегралу от
дивергенции этого вектора по объему, ограниченному этой поверх-
поверхностью. Формула A3,17) выражает поток вектора через замкну-
замкнутую поверхность через значения дивергенции этого вектора в точ-
точках, лежащих внутри поверхности.
зоа
В теории векторного поля формулы A3,16) и A3,17) имеют
исключительно важное значение.
Левая часть формулы A3,17) определяет поток вектора а через
замкнутую поверхность 5 — см. формулу A3,8).
Отсюда следует, что поток вектора а через замкнутую поверх-
поверхность 5 равен интегралу от дивергенции вектора, взятому по
объему, ограниченному поверхностью S.
Теперь мы можем дать определение дивергенции вектора в
точке М объема V, независящее от выбора координатной системы.
Поток векторного поля через замкнутую поверхность S назы-
называют также производительностью той части пространства V, кото-
которая ограничена поверхностью S. Если найти отношение потока П
через поверхность S к величине объема V, ограниченного этой
поверхностью, то мы получим среднюю производительность во
всей области V. Чтобы оценить производительность в точке М
объема V, необходимо вычислить среднюю производительность во
все меньших и меньших областях, окружающих точку М. Переходя
к пределу, стягивая объем такой малой области в точку, мы получим
число, характеризующее производительность векторного поля в
окрестности точки М. Это число и называется дивергенцией век-
векторного поля в точке М.
Дивергенцией векторного поля вектора а в точке М назы-
называется предел, к которому стремится отношение потока через
замкнутую поверхность, окружающую точку М, к объему обла-
области, органиченной этой поверхностью. Этот предел вычисляется
при стягивании объема V в точку М.
Таким образом,
II
(а • n)ds
div5 = lim ^—г A3,18)
V-M V
В этой форме определение дивергенции не зависит от выбора
координатной системы. Те точки векторного поля, в которых
дивергенция положительна, называются источниками, а те, в кото-
которых она отрицательна, — стоками. Эти термины объясняются
гидродинамическим истолкованием векторного поля. Если около
точки, являющейся источником, описать достаточно малую поверх-
поверхность, то поток через эту поверхность окажется положительным
и жидкость будет вытекать наружу.
Задача 13,1. Вычислить интеграл / = j j {x2 + У2) zds, raeS —
(s)
верхняя половина сферы радиуса R с центром в начале коорди-
координат.
Решение. Заданный интеграл принадлежит к поверхностным
интегралам первого типа. Его следует вичислить по формуле A3,2).
Поверхность 5 определяется уравнением х2 + У1 + г2 = #а
-х'^у* (А)
309
(перед корнем удержан знак плюс потому, что рассматривается
верхняя часть поверхности сферы).
Теперь вычислим 1/ 1+/^) + (§7Г) ' вх°Дяи*.ий в формулу A3,2).
Из (А) следует, что
дг х дг
Искомый интеграл после подстановки г = У R1 — хг—у2 перепи-
перепишется по формуле A3,2) так:
(в
Перейдем к полярным координатам. В них
х2 -f- у2 = р2, a da = р dp d<p.
Поэтому
/ = J j р8 • р dp dip.
(")
Так как а — проекция S на плоскость хОу, то о — круг радиуса
R, ограниченный окружностью х2 + у2 = R2- Переменные р и?
изменяются в таких пределах: р от 0 до/?, срот0до2т:
О < р < R;
О < ? < 2«.
Поэтому
2я Л
Задача 13,2. Вычислить поверхностный интеграл
где S — часть параболоида z = хг -\- у*, ограниченная плоскостью
(
Решение. Заданный интеграл — поверхностный интеграл пер-
первого типа. Применим для его вычисления формулу A3,2). Из уравнения
310
поверхностиг =х*+угнайдем|i , ^ивычислим у 1+№
входящий в эту формулу:
дг
Подставляя это значение корня и заменяя г на х2 -\- у2 в A3,2)г
получим
С)
где о — проекция поверхности S на поскость хОу. Эта проекция —
круг радиуса а. Его ограничивает окружность хг + у2 = а2.
И здесь выгодно перейти к полярным координатам, в которых
х2 + #2 = р2; do =
Поэтому
2ic a
(о) О О
Внутренний интеграл
а
J1/TT4? dp = -I (^-vT+lfl5 + 4"ln 12
о
J
о
Указание.
[f-^L^p,
?d?
а i у г взять по частям, полагая и = р; dv = тл===
V Г " J "Р К * " J
4р*
Ответ. / e«
Задача \%,Ь (для самостоятельного решения). Вычислить поверх-
поверхностный интеграл первого типа
/-JJ/д« + у» +*•</*,
311
где S — поверхность конуса z2 = х* + у2, ограниченного сверху
плоскостью z — h.
Указание. Воспользоваться формулой A3,2). После замены
под корнем г2 на х2 + у2 и вычисления 1/ ] _|_ (Л\ -j-(j-) (учесть,
что г = )/jc2 + у1) должно получиться
Перейти к полярным координатам.
Ответ. / =—о—.
О
Задача 13,4. Найти поверхностный интеграл первого типа
где S — полная поверхность тетраэдра, отсекаемого от первого
октанта плоскостью х + у + г = 1.
Решение. Здесь поверхность S составлена из четырех частей.
Значение величины ds в формуле A3,2) ниже указано для каж-
каждой из этих частей:
Sx — треугольник в плоскости хОу: 2 = 0; ds = dx dy. Он
ограничен осями Ох, Оу и прямой х + у — 1.
52 — треугольник в плоскости хОг: у — 0; dz = dx dz. Он ог-
ограничен осями Ox, Oz и прямой х-\-z = 1; г= 1—х.
53 — треугольник в плоскости yOz: х = 0; ds = dy dz. Он огра-
ограничен координатными осями Оу, Oz и прямой y + z=l; z =
1
19.
S4 — заданная плоскостью, на которой z = 1 — х — у; ds =
§
так как £-§--,, а /1 + (|)' + (|)° =- /5,
поэтому
niJnJJJJ
(S) (S,) (S2) (S.) (S.)
Учитывая значение ds на каждой из частей и заменяя в пос-
последнем интеграле z на 1 — х — у, a ds на -/lidxdy и вычисляя
отдельно каждый из четырех этих интегралов, получаем:
1) jJ22ds = JJo -dxdy =0;
(S.) ft,)
312
2) \\z2ds=\\z2dxdz=\dx\ z2dz = ~ \A — xfdx = -^;
(S,) (S.) 0 0 0
1 \-y I
3) \\z2ds—\\z2dydz=\dy \ z2dz = ~\{l~yfdy =-^;
(S,) S, 0 0 0
4) JJ^ds-
Окончательно
Задача 13,5. Вычислить поверхностный интеграл второго типа
И
(S)
по верхней стороне нижней половины сферы радиуса а.
Решение. Уравнение сферы х2 + у1 + гг = а2. На нижней
половине сферы г = —yfa2 — х2—у2. Проекция этой сферы
на плоскость хОу есть круг радиуса а, ограниченный окруж-
окружностью х2 + уг = а2. Применяя формулу A3,5) и заменяя под
знаком интеграла z на —j/ а2 — хг — г/2, получаем
где о — проекция сферы на плоскость хОу. Перейдем в полярные
координаты: a:=pcos<p; </=psincp, элементы же площади dxdy
надо заменить на pdpdcp/Гогда
>_p3
2к а
/ = — ]sin2(pj ,^__ dp.
313
Внутренний интеграл вычисляем по частям
о
dp
+
2p dp
Поэтому
2л
2*
-fa»
Задача 13,6. Вычислить поверхностный интеграл второго типа
=jj'-?
где S — поверхность конуса г2 = хг + уг, ограниченная плос-
плоскостью 2 = Л.
Решение. Применяя формулу A3,5) и заменяя г* наж8 + </8,
получаем
Ь
где о — круг, являющейся проекцией поверхности S на плоскость
хОу, ограниченный окружностью ж2-f-г/2 = Л2. После перехода
к полярным координатам
(р cos уJ • (р sin
5^
Я
С)
р dp dcp ■
2it
ИГ Г
sin8 cp • cos2 cp ■ р3 dp dcp = i sin8 cp cos2cp dcp I p8 dp.
V J
(о) О О
Интеграл
2* 2* 2*
I sin2 cp • cos2 cp dcp = I f-I sin 2cpj dcp = -j-1 sin2 2cp dcp =
2*
l-
Ответ: /
«ft*
IF"
314
ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ ПОТОКА ВЕКТОРА
Задача 13,7. Определить поток вектора г — радиуса-вектора
точки через полную поверхность прямого кругового цилиндра,
если нижнее основание цилиндра лежит в плоскости Юу, его
центр находится в начале координат, радиус основания цилиндра
равен R, высота его Н.
Решение. При решении задачи воспользуемся формулой
A3,8). Через полную поверхность цилиндра попок
= "бок. лов. Н~ " нижн. осв. ~Г ":
верхи, осн.
(А)
К задаче 13,7
1. При вычислении потока черев боковую поверхность цилиндра
следует учесть, что внешняя нормаль к этой поверхности в любой
ее точке перпендикулярна оси Oz, а потому проекция га радиуса-
вектора г на нормаль к боковой поверхности цилиндра равна
радиусу цилиндра, т. е. rn = R и тогда
Ябок. пов. = J J rn ds = j j Rds = R' J j ds = R. 2-kRH,
(бок. (бок. (бок.
пов.) пов.) пов.)
с с
так как ] J ds равен боковой поверхности цилиндра. Окончательно
(бок.
пов.)
ЯбоК. ПОВ. = 2izR2H.
2. На нижнем основании цилиндра вектор г перпендикулярен
вектору п — внешней нормали нижнего основания, а потому про-
315
екция вектора г на внешнюю нормаль п равна нулю, т. е. гп — О
и
(инжн.
оси.)
3. На верхнем основании внешняя нормаль к нему параллельна
оси Oz и имеет то же направление, что и ось Ог, поэтому проек-
проекция радиуса-вектора г точек верхнего основания цилиндра на
внешнюю нормаль равна высоте цилиндра Н и
JJ rnds= j j j{
(нерхн. (верхи. (верха,
осн.) осн.) осн.)
так как j j ds равен площади верхнего основания, т. е. nR2.
(всрхн,
осн.)
Подставляя найденные значения потоков через боковую поверх-
поверхность цилиндра, его нижнее и верхнее основание в (А), получим
поток через полную поверхность цилиндра
П = 3*Д2Я.
Задача 13,8. Определить поток радиуса-вектора ? точки через
прямой круговой конус, основание которого лежит в плоскости
хОу, ось совпадает с осью Ог, радиус основания равен R, вы-
высота ~Н.
Решение. Через полную поверхность конуса поток
"полк. пов. кон. == "бок. пов. ков. ~Г '^осн. кон.>
Очевидно, что поток вектора 7 через основание конуса равен
нулю, так как на основании конуса вектор г перпендикулярен
к нормали основания.
Проекцию радиуса-вектора 7 на нормаль к боковой поверх-
поверхности найдем по формуле A3,9). У нас
г =xl + yj + zk,
поэтому
rn = х cos (я, х) + у cos (я, у) + z cos (n, z)
и по формуле A3,10)
Ябок. пов. кон = 11 [X COS (Й, X) + у COS (n, у) + Z COS (Й, Z)\ ds =
xdydz + ydzdx + zdx dy.
316
(бок.
пов.
кон.)
(бок.
пов.
кон)
Остается вычислить интегралы:
xdydz:
ydzdx:
(бок.
пов.
кон)
(бок.
пов.
кон)
2 dx dy.
(A)
(бок.
пов.
кон)
Найдем уравнение поверхности конуса. Если на конусе взять
произвольную точку А(х, у, 2), то из подобия треугольников ВОС
и ABD следует, что
-£- = j£ , но AD =
\ BD=H~z
К задаче 13,8
и тогда
R
Я - Н-г '
Отсюда уравнение поверхности конуса:
(В)
Последний из интегралов в (А), если в него подставить г из
уравнения (В), приведется к виду
(бок.
пов.
КОВ)
(осн.
кон)
317
причем dxdy есть проекция элемента ds поверхности конуса на
плоскость хОу и интегрирование будет вестись по проекции по-
поверхности конуса на эту плоскость, т. е. по основанию конуса.
Если перейти к полярным координатам, то, учитывая, что-
в них у^х2 -j- у2 = р, а элемент площади ds= pdpdcp, получим
(осн. (оси
кон) кон.)
2* Я 2*
Два других интеграла (А) вычислить самостоятельно.
При вычислении jj xdydz учесть, что областью интегриро-
(бок.
пов.
кон)
вания явится проекция боковой поверхности конуса на плоскость
yOz, т, е. треугольник BEF. Множитель х, входящий в подынтег-
подынтегральное выражение, определить из уравнения (В) поверхности
конуса.
Уравнения сторон BE и BF треугольника BEF получаются из
уравнения (В) поверхности конуса как уравнения линий пересече-
пересечения поверхности конуса с плоскостью уОг (уравнение этой плос-
плоскости х = 0).
В выражении (С) для х возьмем знак плюс перед корнем. Желая
вычислить \\ xdydz по всей боковой поверхности конуса и счи-
(бок.
пов.
кон)
тая х
318
= -j-1/ R2 (l — ^f — уг, мы должны будем вследствие сим-
метрии поверхности конуса относительно плоскости уОг получен-
полученный результат удвоить, т. е.
jj xdydz = 2 Jj xdydz =
(бок. лов. iBEF
кок)
При вычислении внутреннего интеграла использована формула
J /3TZу* Л = J. /W^P + у arc sin -i + С,
причем принято, что а2 = R2 A — ^-] . Вычисление последнего
интеграла тем же путем даст
(бок.
пов.
кон.)
и тогда окончательно поток
н. пов. кон.
т. е.
"полн. пов. кон. == ЛА " •
Мы решили эту задачу, не прибегая к формуле Остроград-
Остроградского. Используем ее и убедимся, что это значительно сэкономит
вычисления. Поток вектора через замкнутую поверхность S нйхо-
дят по формуле Остроградского A3,17).
Применим эту формулу для случая, когда вектором является
радиус-вектор точки r = xi + yj + zk. На основании A3,13)
а потому
319
Ho rx = xi ry — y\ гг = z, поэтому
it*- i, £bc_ i. ^._i
Значит, для радиуса-вектора г1 divr = 3.
Интересующий нас поток радиуса-вектора г через замкнутую
поверхность будет равен на основании формулы A3,17)
ЦЩЩЩ-Зо, A3,19)
(S) (о) (о) (»)
т. е. поток радиуса-вектора точки через замкнутую поверхность
S равен утроенному объему, ограниченному этой поверхностью.
Для потока-через-полную поверхность конуса, рассматриваемого
в этой задаче, имеем, учитывая, что объем конуса о = -^-kR^H,
П
пот. пов. кон.
Получен тот же результат, что и раньше, но со значительно
меньшей затратой труда, притом получен и дополнительный ре-
результат.
В задаче 13,1 поток радиуса-вектора точки через полную по-
поверхность прямого кругового цилиндра П = 3kR2H, т. е- поток
радиуса-вектора точки через полную поверхность прямого круго-
кругового цилиндра равен утроенному объему цилиндра, как это сле-
следует и из формулы A3,19).
Формулу A3,19) можно истолковать так: если в установив-
установившемся потоке несжимаемой жидкости скорость любой частицы
равна ее радиусу-вектору, то количество жидкости, вытекающее
из какого-либо тела за единицу времени, равно утроенному объ-
объему этого тела.
Задача 13,9. Доказать, что если во всех точках некоторого
объема v, ограниченного поверхностью S, дивергенция вектора а
равна нулю, то поток вектора а через поверхность S равен нулю.
Решение. По формуле A3,10) поток вектора
(о) (»)
Вектор а, для которого дивергенция равна нулю, называется
соленоидальнын.
Задача 13,10. Доказать, что если во всех точках некоторого
объема V, кроме одной точки А, дивергенция вектора равна нулю,
то поток этого вектора через замкнутую поверхность, окружающую
точку А, не зависит от формы этой поверхности.
320
Решение. Пусть_ во всех точках объема V, кроме точки А,
дивергенция вектора а равна нулю: diva = 0. Окружим точку А
поверхностью {Sj) (см. чертеж). Тогда по условию задачи всюду
в объеме, заключенном между поверхностями S и Su diva = 0, а
поток вектора а через поверхность S + Si равен нулю на основа-
основании результата предыдущей задачи, т. е.
или иначе
а„ ds + ]) а„, ds = 0. (Л)
(S.)
К задаче 13,10
В этой формуле я„ — проекция вектора а на внешнюю нор-
нормаль п к поверхности S, а а„, — проекция вектора а на внешнюю
нормаль пх к поверхности Sx. Внешняя нормаль к поверхности Sx
направлена внутрь (противоположно направлению внешней нормали
на поверхности S). Учитывая, что изменение направления нормали
на противоположное изменяет знак интеграла, получим
nds. (В)
Заменяем в (А) второе слагаемое в левой части равенства его
значением из (В):
и окончательно
что и требовалось доказать. Решим задачу на применение этого
результата.
II И. А. Каплая 321
(S) " (S,)
(S)
Задача 13,11. Напряженность Е поля точечного электричес-
электрического заряда е на расстоянии г от этого заряда
£«=£?, (А)
где 7 — радиус-вектор, проведенный из заряда в рассматриваемую
точку поля А. _
Определить поток вектора Е через любую замкнутую поверх-
поверхность в двух случаях:
1) когда эта поверхность не охватывает заряда е и
2) когда заряд е расположен внутри замкнутой поверхности.
Решение. 1. Для ответа на первый вопрос воспользуемся
формулой A3,17). Поток вектора через замкнутую поверхность S
Будем считать, что заряд е помещен в начале координат, а
точка А имеет координаты _х, у и г. Тогда радиус-вектор г =
= xi + yj + zk, а его модуль г — У хг + уг + гг
Поэтому равенство (А) перепишется так'.
т т » dEv дЕп дЕ ?
Найдем теперь -^, -^ и -^.
оЕх
г*
дг 4.x
1 Ух*+у» + г*
х
Поэтому
г* 3г*Х' г г* — З
Аналогично
дЕу __ г2 — Зуа t дЕг _ г2 — Зга
~ дх ' ду "•" дг *
322
поэтому
(г*-3г») _ 3r«- 3(л« + y* + г*).
e j^ —
Но так как х* -f уг + z* = г2, то числитель последней дроби равен
нулю и в рассматриваемом случае div Е = 0.
Поскольку знаменатель последней дроби г6, то это заключение
является верным только тогда, когда г ф 0, т. е. всюду, кроме
начала координат. В рассматриваемом случае, когда поверхность S
не охватывает заряда е, радиус-вектор г не может быть равен
нулю, поэтому поток вектора £
Заключение. Поток П вектора Е — напряженности элект-
электрического поля точечного заряда — через всякую замкнутую по-
поверхность равен нулю, если эта поверхность не охватывает заряда е.
2. Когда заряд е расположен внутри замкнутой поверхности,
т. е. когда начало координат находится внутри замкнутой по-
поверхности сделанное выше заключение оказывается неверным, так
как в этом случае радиус-вектор г в начале координат равен нулю.
Для ответа на второй вопрос задачи воспользуемся резуль-
результатами задачи A3,10).
Поскольку в рассматриваемом случае во всех точках объема
V, ограниченного поверхностью S, кроме начала координат,
div E =± 0, то* поток вектора Я не зависит от формы поверхности
S, в связи с чем за поверхность S примем сферу радиуса R с цен-
центром в начале координат.
Так как внешняя нормаль в любой точке сферы совпадает с
направлением радиуса-вектора 7 этой точки, то вектор Е имеет
то же направление, что и внешняя нормаль к сфере, поэтому
проекция Еп вектора Е на внешнюю нормаль равна его модулю.
Так как £ = ^-г = ^-£, а у есть единичный вектор г0 ради-
радиуса-вектора г точки, то Ё— -^ • г0, а его модуль Е = -^. Поэтому
Е — —
Модуль радиуса-вектора точек сферы равен радиусу R сферы,
поэтому г = R и тогда Еп = 4-г, а поток вектора Е
п=lKЯ MJ
(S) (S) (S)
так как j I ds равен поверхности сферы, т. е. 4я#2.
(S)
II* 323
Заключение. Если точечный заряд е расположен внутри
замкнутой поверхности, то поток вектора Е — напряженности ноля
данного заряда — через эту поверхность равен 4ке.
Задача 13,12. Найти поток вектора а — хЧ + уЦ-\-z2k через
положительный октант сферы х? + у2 + z2 = R2 (х > 0, у > О,
г>0).
Решение. Воспользуемся формулой A3,11), в которой надо
взять ах = х2; ау = уг\ аг = г'2. Тогда поток вектора
(A)
где под S понимается поверхность сферы, расположенная в пер-
ьом октанте.
Представим интеграл в формуле (А) в виде суммы трех интег-
интегралов. Областями интегрирования при вычислении этих интегралов
будут проекции поверхности S соответственно на координатные
плоскости yOz, xOz и хОу. Это видно из наличия в первом ин-
интеграле произведения dydz, во втором dxdz, в третьем dxdy
zidxdy.
При вычислении интеграла It выразим х2 через уг и z2. Из урав-
уравнения сферы лс2 + у2 + г2 = R* следует, что хг = R2 — (у2 + г2).
Перейдем к полярным координатам, в которых у1 -j- гг = р2; г
=/?2 — р2, a dt;dz надо заменить на dd
Поэтому
С Я* Я4 я *Я4
J 4 т 4 2 8
о
Вычисляя /2 и /3, найдем, что каждый из этих интегралов
также равен ^g-, а потому поток
324
Задача 13,13 (для самостоятельного решения). Найти поток
вектора а = хЧ + уЦ -j- ггк через поверхность сферы х2 + уг +
+ г2 = Я2.
Указание. Воспользоваться формулой A3,11). Удобно начать
с вычисления ]] г2 dxdy. Из уравнения сферы х2 + уг + г2 = Яг
sx0y
найти г2 = R2 — \хг + у2). Перейти к полярным координатам.
Ответ. Я =|-*#4.
Задача 13,14. Найти поток вектора а = yi-\-zj-\-xk через
часть плоскости х + у + z = а, расположенную в первом октанте
(х > 0, у > 0, г > 0).
Решение. Воспользуемся фор-
формулой A3,8), по которой
П
a.ds,
и вычислим проекцию ап вектора
а на внешнюю нормаль к плоскости
х + у + г = а по формуле A3,9)
а„ = ах cos (и, х) + ау cos (n, у) +
+ a2cos(n,z).
Так как эта нормаль образует
с осью Oz острый угол, в формуле
для cos (и, г) возьмем знак плюс,
а направляющие косинусы нормали
найдем по формулам A3,3) и A3,4).
-
COS (П, 2) =
где
Уравнение плоскости х + у + г — а разрешим относительно г
и получим г = а — х — у, откуда
Т
cos (n, у) = ^=; cos (й, г) = ^=.
325
Из условия задачи ах — у, ау — г; аг — х. Поток П вектора о
будет равен на основании A3,10)
(S)
где интеграл S распространен на часть плоскости х + у + г = а,
расположенную в первом октанте. Но в последнем интеграле по-
подынтегральную функцию х + у + г можно заменить из уравнения
поверхности на а, так как на поверхности S х-\- у + г = а,
7JJ
(S)
Треугольник ABC равносторонний (АВ = АС — ВС), значит,
каждый его угол равен 60°. Из равнобедренного прямоугольного
треугольника АОС следует, что АС = Va1 + a2 = a Y%. Высота
BD - АС . sin60° = АС • ^ = а/2 . ^ = 1р , а потому
и окончательно
п о О2/3 а8
Задача 13,15 (для самостоятельного решения). Определить по-
поток вектора ~а = yl + zj + x~k из предыдущей задачи через полную
поверхность пирамиды, ограниченной плоскостью х + y-\-z=*a и
координатными плоскостями (см. чертеж к предыдущей задаче).
Указание. Искомый поток рассмотреть как сумму потоков
через грани пирамиды АОВ, ВОС, АОС и ABC, причем использо-
использовать результат предыдущей задачи: через грань ABC поток вектора
а Я = у. При вычислении потока этого вектора, например через
грань АОВ, учесть, что на этой грани cos (n, x) =cos(n, 2) = 0,
a cos (л, у) = —1 и вычисление потока через эту грань приведет
к интегралу — i \ г ds, в котором элемент ds площади треуголь-
АОВ
ника АОВ должен быть заменен на dxdz. Уравнение прямой АВ:
x-\-z = a. Отсюда Паов = — ^- •
Поток через полную поверхность рассматриваемой пирамиды
равен нулю.
Ответ. Я = 0.
Задача 13,16 (для самостоятельного решения). Найти поток
вектора а = хЧ -f уг\ -f z2k через сферу {х — аJ -+- (у — ЬJ +
+ (г —сJ = /?4.
326
Указания. Искомый поток вычисляется по формуле A3,11).
1. Удобно перейти к сферическим координатам. Положим
х — а — R cos <p sin в;
у — 6 = R sin <р sin 6;
г — c lAJ
Проверьте, действительно ли (x — aJ -f- (y — bJ -|- (z — cJ = R2.
2. При вычислении, например \j\zzdxdy, рассмотреть его как
сумму двух интегралов
§[z*dxdy + JJ z2djtdt/,
<sB) <sH)
где SB — верхняя сторона верхней половины сферы, а
SH — нижняя сторона нижней половины сферы.
Тогда
J ( г2 djc dy = J f г2 cos (л, г)в ds + J [ г2 cos (n, г)„ ds,
(S) SB (*H)
где cos (я, г)в и cos(n, г)я — косинусы угла между внешней нор-
нормалью и осью Oz соответственно на верхней стороне верхней поло-
половины и на нижней стороне нижней половины сферы.
3. Разрешить уравнение поверхности относительно г — с
с=± V R2 — (x — af — {y~
г = с ± YR*-(x~aY — (y-b)\ (В)
где знак плюс надо взять для верхней половины сферы, а знак
минус — для нижней.
На верхней стороне верхней половины сферы cos (n, г) > О
cos (и, г) = —■■■ ' , (С)
а на нижней стороне нижней половины сферы cos (й, г) < О
cos (п, г) = — •
Вычисляя ~ и ~ из уравнений (В) и подставляй в (С) и {D), полу-
получим в двух случаях для cos (п, г) одно и то же выражение cos (h, z) =
327
= ^-н- • Тогда, если учесть, что в сферических координатах эле-
элемент поверхности
ds = R2 sin 6 db df
(см. В. Смирнов. Курс высшей математики, т. II, стр. 190),
11 г2 cos (h, г)ъ ds+ г1 cos (h г)„ ds =
<SB) <SH)
= Г [ г2 • г-~ • Я2 sin 6 d8 d? = # J J г8 (г — с) sin 6 db do.
(S) (S)
Так как cos(n, z) имеет одно и то же выражение на поверх-
поверхностях EП) и (SH), мы от интегралов по этим поверхностям пере-
перешли к интегралу по всей поверхности сферы. Вычислить последний
интеграл несложно. В нем на основании равенства (А) следует
взять
г — с = Я cos 6,
пределы интегрирования по 6 будут 0 и i, a no f они равны 0
и 2%.
После вычислений получим
Я о
z2 dxdy — -j r.cR3.
(S)
Аналогично вычисляются и два других интеграла:
] ] хг dydz и J ] уг dx dz.
"(S) (S)
Ответ. П = -j тс^3 (а + & -f с).
Задача 13,17 (для самостоятельного решения). Найти поток
вектора а — хЧ + g*j + 22fe через верхнюю сторону верхней поло-
половины сферы
(х — af + (# — ЬJ + (г — сJ = /?2.
Ответ. Я = 2*Я
Задача 13,18 (для самостоятельного решения). Вычислить поток
вектора
а = (х + уI + (у — х) / + zk
через поверхность шара единичного радиуса с центром в начале
координат.
Указание. Вычислить дивергенцию вектора а. Окажется, что
diva = 3,
и применить формулу Остроградского.
Ответ. /7 = 4^.
328
ЧЕТЫРНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Свойства дивергенции. Упражнения, связанные с форму-
формулами Остроградского и Стокса.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Формула Стокса. Эта формула связывает криволинейный ин-
интеграл по замкнутому контуру L с интегралом по поверхности,
ограниченной данным контуром. Она записывается так:
%-%)<»*•■ *»+(£-%)«*■• •»+
Здесь L—замкнутый контур, ограничивающий поверхность S. На-
Направление нормали к поверхности S выбирается так: для наблю-
наблюдателя, стоящего на поверхности и смотрящего на нее с конца
нормали, обход контура L в правой системе координат должен
происходить против движения "часовой стрелки.
Формула A4,1) на основании формул A2,7) может быть запи-
записана так:
ф ах dx + ay dy + a2dz = j ] [rot, a cos (л, х) +
L (S)
+ Totyacos(n, у) -f rot2acos(n, z)\ds. A4,2)
2. Формула Стокса в векторной форме. Учитывая, что выра-
выражение в квадратных скобках под интегралом в A4,2) есть проек-
проекция вектора rota на нормаль к поверхности, т. е. (rota)n, формула
A4,2) в векторной форме запишется так:
§ а- Ш = JJ (rot a)nds, A4,3)
L (S)
где dl — элемент дуги кривой L, рассматриваемый как малый век-
вектор, проекции которого на координатные оси равны dx, dy и dz.
Из формулы Стокса A4,2) заключаем, что циркуляция произ-
произвольного вектора по замкнутому контуру равна потоку ротора
329
этого вектора через любу» поверхность, опирающуюся на этот
контур (направление обхода контура L и направление нормали к
поверхности 5 должны быть согласованы одно с другим).
Свойства дивергенции
Задача 14,1. Доказать что
div (a+ 6) = div a + div Б,
где
а = а{х, у, z), b = b(x, у, г).
Решение. Векторы 5 и 5 определяются равенствами
a = aj + aj + ajt\
b=*bxl + b~j + b'k;
Согласно формуле A3,13)
diva = £*
ox
Поэтому
дау даг\ jdbx дЬ
Выражение, стоящее в первой скобке, есть diva, а выражение,
стоящее во второй скобке, есть divb.
Итак,
div (a -f- b) = div a -f div b.
Задача 14,2 (для самостоятельного решения). Доказать, что
div (t/a) ="a • grad U, где а — постоянный вектор, U — U (х, у, г),
a a 'gradf/ — скалярное произведение векторов а и grad 11.
Задача 14,3. Доказать, что, если а = а{х,.у, z)\ а функция
U = £/ (х, у, г), то
div (Ua) = Udiva + a- gradU *
* В отличие от предыдущей задачи здесь а — переменный вектор.
330
Решение. Вектор а = aj+ а~\ + аг&;
Ua=(Uax)~i + (Uay)~i + (U
div (С/а) - £ (£/а,) +£ (£4) +
a • drad U
+ Up + d^ + ^)^Udiva+agradU.
diva
(Сумма, стоящая в первой скобке, есть а • grad С/, так как проекции
вектора grad U на координатные оси Ох, Оу и Ог равны соответ-
dU dU dU -
ственно -j-, -j- и -jr, а проекции вектора а иа те же оси соот-
соответственно равны ах, а у и а2).
Задача 14,4. Найти div (grad U), где U = U(x, у, z\.
Решение, div (grad U) =
= ^ (grad U)x + ~ (grad U)y + | (grad Uz) =
_ /^ 3L _i_ ^ j. ^
дг { дг) дд-2 + ф»" дг*
— tsU (Л — оператор Лапласа).
Задача 14,5 (для самостоятельного решения). Доказать, что
если г = */х* + уг + г%, то
Указание. Учесть, что
дх и ^r'J ~" dr дх~ dr r '
Задачи на формулу Остроградского
Задача 14,6. Применяя формулу Остроградского, преобразовать
поверхностный интеграл
f f л8 dy dz + у3 dx dz + г8 dx dy,
(I
если 5 —гладкая поверхность, ограничивающая объем V.
331
Решение. На основании формулы A3,8), полагая в ней Р = х3;
Q = у3; R = г8, получаем
j j x?dydz + у3 dx dz + z*dxdy =
ffi [й И + Ту <Л + Ш И] dv = Щ (Зх- + W + W) dv =
W (V)
(V)
Задача 14,7. Применяя формулу Остроградского, преобразовать
/ = [ \ Ух2 + у2 + г2 (cos a + cos р + cos 7) ds,
E
E)
где S — гладкая поверхность, ограничивающая объем V,
cos a, cospHcos-j- — направляющие косинусы внешней нормали к
поверхности S.
Решение. Полагая в формуле A3,7) Р = Q = R =Yx2+y2+z2,
получаем
(V)
= ггг/ г *2 г+ уг г+ 2 гг Ьл =
^ х у х у г у г
(V)
Задача 14,8 (для самостоятельного решения). Преобразовать по
формуле Остроградского
33
х cos а + у cos р + г cos 7
сохраняя обозначения предыдущей задачи.
ОТвет. 9 ГГГ dv
(V)
Задача 14,9 (для самостоятельного решения). Доказать, что
J j
xdydz + ydxdz + zdxdy
равен утроенному объему тела, ограниченного поверхностью S.
332
Задача 14.10 (для самостоятельного решения). Применяя фор-
формулу Остроградского, преобразовать поверхностный интеграл
где S — гладкая поверхность, ограничивающая объем V, cos a,
cosp, cos7 — направляющие косинусы внешней нормали к поверх-
поверхности S.
Ответ.
(V)
или в другой записи
Щ Au • do,
(V)
где Ли = -Л + -g^ + ^f есть лапласиан функции и.
Задача 14,11 (для самостоятельного решения). Доказать, что
если S — замкнутая простая поверхность, / — любое постоянное
направление, а п внешняя нормаль к поверхности S, то
cos (и, l)ds = 0.
(S)
Указание. Заменить cos(n, /) по формуле
. cos (п, I) = cos (п, х) cos G, х) + cos (п, у) cos (I, у) +
+ cos(n, z)cosG, z).
Задача 14,12. С помощью формулы Остроградского доказать,
что поток вихря вектора а через замкнутую поверхность равен нулю.
Решение. Вихрь вектора а определяется формулой A2,6).
Поток вектора rota через замкнутую поверхность S вычисляется
по формуле A3,8)
П =
Нам следует найти проекцию вектора rot d на нормаль к поверх-
поверхности. Пользуясь формулами A2,7) и A3,9), определим
^ = (t - If)
cos <«.*> + (%-1)cos
333
поэтому искомый поток
п -1] Ш - *)см <я- >*
Теперь применим формулу Остроградского A3,15), полагая
в ней
р _ &h даи. Л _ da* йвг. р _ f?5* *!«.
r ~" ay dy ' v ~ дг djc ' d* ф '
д [да2 даЛ ■ д (дах даг\ д (дау дах
д д)
дг дх) ^ \дг ду дх ду) ^ \дх дг ду дг
Легко убедиться, что выражение, стоящее в квадратной скобке,
равно нулю:
/7 = 0.
Задача 14,13. С помощью формулы Остроградского вычислить
/ = И х* dy dz + и3 dx dz + г3 dx dy,
где S — внешняя сторона сферы хг + у2 + z2 = а2.
Решение. В задаче 14,6 этот интеграл был преобразован
к виду
С Р С
(х2 +у2 + z2) dv.
Наличие под знаком интеграла суммы квадратов координат ука-
указывает на целесообразность перехода к сферическим координатам,
в которых
/ = 3 $$ J р2 • Рг sin 8 dp db d<? = 3 l\l P4sin6 dp d8 d<?,
где V—объем шара, ограниченного поверхностью S.
2it n R
334
так как
Я it 2*
0
sin9d9 = — cos9
2;
Задача 14,14 (для самостоятельного решения). С помощью фор-
формулы Остроградского вычислить
j J х2 dy dz + у2 dx dz + z2 dx dy.
где S — внешняя сторона куба 0 < x < с; 0 < у < a; 0< z < а.
Ответ. -|а4'
Указание. При вычислении тройного интеграла JJJU +
+ у + г) do имеет смысл представить его в виде суммы трех
интегралов
а*
причем каждый из них окажется равным -^.
i — проекция поверхности S на плоскость yOz.
Задача 14,15 (для самостоятельного решения). Пользуясь фор-
формулой Остроградского, вычислить
JJ*cos(n, x)ds,
xi y2 Z2
где S—поверхность эллипсоида -j + р- + ^ — 1.
Ответ. -g%abc.
Задача 14,16. Вычислить по формуле Остроградского
] j [y2z cos (n, z) — yz2 cos (n, y)] ds,
E)
x2 и2 г2
где S — поверхность эллипсоида -5 + ^ + -^ = 1.
Решение. Полагаем в формуле A3,15) Р = 0; Q = — yz*i
j J [t/2zcos (n, г) — yz* cos (n, y)\ ds = J J J (y2 — z2) dv,
(S) (V)
где V — объем эллипсоида.
335
Тройной интеграл вычислим по формуле C,46), которую мы
уже применяли на третьем практическом занятии в четвертой
части этой книги.
$$$Дх, у, z)dv = [dz JJ f{x, у, z)dxdy, A4,4)
(V) 20 ЕхОу
где Ему — проекция на плоскость хОу фигуры, получающейся
в сечении объема V, плоскостью, параллельной плоскости хОу,
которая соответствует фиксированному значению г. При этом z0 <
< z < ги a z = z0 и z = zx — уравнения плоскостей, между которыми
содержится объем V тела, причем фигура, получающаяся в сече-
сечении, проектируется без искажения. Применим эту формулу для
вычисления интересующего нас тройного интеграла. Представим
его в таком виде:
I j J (У2 -z*)dv= J J $ f dx dy dz - И J г2 dx dy dz =
=- J #г <fc И dxdz-\ z* dz № dx dy.
Здесь: 1) Е„ог — проекция из плоскость xOz сечения эллипсоида
плоскостью, параллельной плоскости xOz, при фиксированном зна-
значении у\ J j dx dz равен площади этой проекции. Уравнение кон-
ЕхОг
тура проекции получим из уравнения поверхности эллипсоида
xi ф гг
— +|г +^г= 1, считая, что в этом уравнении у — величина фик-
фиксированная.
Уравнение этого контура будет иметь вид
ИЛИ
Полуосями этого эллипса будут
а его площадь равна тм^, т. е.
Е*ог = юге (l-f!)
336
и тогда в правой части (Л) интеграл.
]] y
ЕхОг
ь
Ь ЕхОг -Ь
2. Точно так же вычислим в правой части (А) интеграл )) dx dy,
ЕхОу
учитывая, что Еюу есть проекция на плоскость хОу сечения эллип-
эллипсоида плоскостью, параллельной плоскости хОу.
Уравнение контура этого сечения получим из уравнения поверх-
поверхности эллипсоида, считая, что z имеет в этом уравнении фикси-
фиксированное значение.
Уравнение контура Е„оу будет
a1
а площадь эллипса
■(-Й *(-Й '
В правой части (А) второй интеграл
ЕхОу
поэтому окончательно искомый интеграл
zi)dv = ~ ■касЬ3 — j| ъаЬс3 = ~каЬс (Ьа — с2).
(V)
Задача 14,17. Вычислить интеграл Гаусса
где S — простая замкнутая гладкая поверхность, ограничивающая
объем х; п — внешняя нормаль к поверхности S в ее точке
Л(л:, у, z); r — радиус-вектор, соединяющий фиксированную точку
В (а, Ь, с) с переменной точкой А(х, у, z) поверхности.
Рассмотреть два случая:
1) когда поверхность S не окружает точку В и не проходит
через нее;
337
2) когда поверхность S окружает точку В.
Решение. Косинус угла между нормалью п и радиусом-век-
радиусом-вектором г определяется по формуле
cos (п, ?) = cos (п, х) cos (г, х) + cos (п, у) cos (л, у) +
+ cos (п/г) cos (г, г) (А)
(обозначения не требуют пояснений).
Модуль радиуса-вектора г
г = V (x-af + (y-by + {г-с)\ (В)
Косинусы углов между радиусом-вектором и координатными осями
равны '
COs(r, x) = x~=^', cos(r, y) = y-~; cos(r, г) = г-~. (С)
Подставляя эти значения в формулу (А), имеем
cos(n, r) = ^cos(n, A:) + ^cos(n, y) + i=-ccos(n, г)-
Теперь вычисляемый интеграл G перепишется так:
G = jf [^ cos Сп, х) + ^cos (n, у) + ^cos (h, z)) ds. (D)
Для вычисления этого интеграла применим формулу Остроградского
A3,7), в которой надо считать, что Р = ^^; Q = ^pf-; /? = -^5-'
Л дР дО dR
Определим -, - и ^.
Но из формулы (В) следует, что
дг х — а х — а
&< ~ Vix-a)*+{y-b)* + (z-cf ~ '
Поэтому
г» Ч <*-аJ г8
<!£ _ ~~Г~'Г _ г«-3<* — аJг»
д* ~ г» г'
6Р гг — 3(^ — а)8
338
и аналогично
(V)
или
Так как (х —
dQ
ду
L
■5
г*-3(у— Ь)\
3.
{У — Ь)г + (г-
dR
дг
— 3(у-
J+ @
г1*
-сJ =
Г2_3(г-с)».
= Г2, ТО
г-*
Uv.
При этом существенно следующее: применять формулу Остро-
градского надо так, чтобы была соблюдена непрерывность функ-
функций Р, Q и R и их производных з-. я^ и зг • Их непрерывность
будет соблюдена, когда г =£ 0, т. е. когда точка В (а, Ь, с) нахо-
находится вне поверхности S.
Итак, отвечая на первый вопрос задачи, можно сказать, что
когда фиксированная точка В находится вне поверхности S, ин-
интеграл Гаусса C = 0.
Теперь рассмотрим случай, когда поверхность S окружает
точку В (а, Ь, с). Преобразуя по формуле Остроградского A3,14)
двойной интеграл по поверхности S к тройному интегралу, рас-
распространенному на объем V, ограниченный этой поверхностью,
надо иметь в виду, что г — радиус-вектор, соединяющий точку
В (а, Ь, с) о любой точкой А (х, у, z) уже не поверхности S,
а области (К). Поэтому в самой точке В он равен нулю, а функ-
функции Р, Q и R и их частные производные, в которых г находится
в знаменателе, перестают быть непрерывными в этой единственной
точке области V (во всех остальных точках этой области они
непрерывны), и формулу Остроградского для преобразования ин-
интеграла Гаусса применить во всем объеме V нельзя (интеграл
Гаусса в данном случае становится несобственным).
Изолируем точку В и тем самым получим возможность во всем
оставшемся объеме применить к интегралу Гаусса формулу OGTpo-
градского.
Образуем вокруг точки В (а, Ь, с) сферу 5Р такого радиуса р,
чтобы она целиком содержалась внутри объема X. Тогда для
объема Vu заключенного между поверхностью S и поверхностью
339
сферы Sf, формула Остроградского применима и поэтому по фор-
формулам (D) и (Е) получаем
^cos ^' ^+У~^cos *л> ^+г~^cos ^* z^Jds ~~
Отсюда вычисляемый интеграл
0 ~ Я ^) ds = J J [fzif cos {n,x)
(Sp)
7cos (л, zy.dv.
На сфере Sp рассматривается внешняя нормаль.
На поверхности сферы S? г = р, нормаль к сфере п направлена
по ее радиусу, а потому направляющие косинусы cos (n, x), cos («, у),
и cos (я, г) нормали п равны направляющим косинусам радиуса-
вектора р, которые получаются из формул (С) заменой в них г
на р.
Таким образом, последнее равенство перепишется так:
~* I
Р
(Sp)
1
Здесь величина -j , как постоянная, вынесена за знак двойного
интеграла, а двойной интеграл )) ds по поверхности (Sp) равен
(sp)
площади этой поверхности, т. е. 4яр2.
Итак, на второй вопрос задачи следует ответить так: если
поверхность S окружает фиксированную точку В {а, Ь, с), то ин-
интеграл Гаусса G = 4т:.
Укажем для справки, что, когда поверхность S проходит через
точку В, то интеграл Гаусса G = 2~. Доказывать этого мы не будем.
340
Задача 14,18. Доказать, что. вихрь суммы векторных полей
равен сумме вихрей этих полей
rot (а + 6) - rot а + rot Ъ.
Решение. Из определения вихря вектора следует
а (ах + Ьх) д (аг
Тг
A4,5)
Тх
\д(ау+Ьу) д (ах + Ьх)] т _
l Т + Г \к-
l Тх
+
Гу
(дЬ2 дЪу\- 1дЪх дЬЛ- (дЬу
дьЛ-г
Первые три слагаемые есть rot а, а вторые три — rot b. Этим до-
доказано требуемое:
rot (а + Ъ) = rot а + rot Ъ.
Задача 14,19. (вычисление вихря произведения скалярной функ-
функции на вектор). Доказать, что
rot («a) = grad и х а + « rot a,
A4,6)
где и — скалярная функция от х, у, г.
Решение. Докажем, что проекции векторов, стоящих в левой
и правой частях доказываемого равенства, равны между собой
ди
даг ди
да и
(А)
Векторное произведение векторов grad и и а равно:
, - аи ои аи
grad и х а = ~- д- з-
Отсюда следует, что
i
ди
дх
ах
/
ди
ду
пУ
k
ди
дг
аг
341
В равенстве (А) первые два слагаемых есть (grad и ф а)х, а выра-
выражение в круглых скобках есть проекция rota на ось Ох. Таким
образом,
(rot ш)Л_== (grad и х а)х + и (rot а)х. (А)
Аналогично
(rot иа)у = (grad и Ха)у+ и (rot а)у (В)
(rot иа)г = (grad и X а)г + и (rot а)^ (С)
Умножая (А), (В) и (С) соответственно на?, / и ~ки почленно скла-
складывая, получим требуемую формулу.
Задача 14,20 (градиент скалярного произведения). Доказать,
что
grad(a • b) = a x rot b + Ъ х rota -f ^ + *. A4,7)
do da
Решение. В правой части доказываемого равенства послед-
последние два слагаемых являются производными одного вектора по дру-
другому вектору. Начнем с определения того, что называется произ-
производной вектора по другому вектору.
Определение. Производной вектора а по вектору Ъ называется
вектор
da да , , да , , да ,
Ь+Ь + Ь
Найдем проекции этого вектора на координатные оси:
да
дх
да
ду
да
дг
дах- , да „7
дх * дх '
= д-ё1+дЦ1-
дах т . да у ~.
дг дг '
^Жк
г ду
Умножая каждое из этих равенств соответственно на Ьх, Ьуи. Ьг
и почленно складывая, найдем, что вектор
da да, .да, , да, (дах , ,дах, \da*h
S = d-xb*+Tyby+Tzb* = [-dx-b*+-dJby+-dT4
i даи h х доо и \ :• , (даг и ,da2h ,da
342
da
Отсюда следует, что проекции вектора -= на координатные оси
do
равны:
da\ дах , , дах
sir1* х+1%
dbly дх
da) даг.
аау и (
даг
A4,8)
Спроектируем левую и правую части доказываемой формулы A4,7)
на координатные оси (очевидно, что каждая из частей этой фор-
формулы есть вектор). Учитывая, что
а • Ъ = aj>x + ajby + арг,
grad (a • Ь) =§-x{axbx + ayby + a
получим
+ щ (а А + а spy + aj>z) i + Ш ^х + atPy + a£*> k-
Продифференцировав первое слагаемое правой части, найдем,
что проекция grad (а • Ъ) на ось Ох равна
. _ дЬи . да, , . db.
дЬ
или в более удобной записи,
[grad(о • Ь)]х = -£Ьх +-^Ьу + -§1Ьг + -££ ^
A4,9)
Теперь спроектируем на ось Ох вектор, - стоящий в правой части
формулы A4,7),
(а х rot Ъ)х = ау (rot Ь)г — а2 (rot Ь)у =
Точно так же, меняя местами а и 6, получаем:
E х
(В)
343
Легко заметить, что^ от почленного сложения (А), (В), (С) и (D)
получим Igrad (а • Ь)]х. Точно так же мы прийдем к заключению,
что и проекции левой и правой части A4,7) на оси Оу и Oz равны
между собой. Но если проекции двух векторов соответственно
равны, то и сами векторы равны. Значит, требуемое доказано.
Задача 14,21 (дивергенция векторного произведения). Доказать,
что
div (а х Ъ) = Ъ iot а — а rot Ъ
(вектор а = axi -f- ayj + ajz; вектор b — bxi -f bj + bjk, причем
проекции векторов есть функции х, у и г).
Решение. Расписываем дивергенцию вектора по формуле
A3,6):
div (a xi)=|(ax b)x + §-y(a x6)s + ^(ax Ь)г;
div(ax6)=^(aj>,- aj}y) + ^(aj>x-aj>2) +
, д . , • \ дпи • , db, da,. db
{выражения в скобках в первой строке есть проекции вектора rot a
соответственно на оси Ох, Оу, Oz, а во второй строке выражения
в скобках являются проекциями на те же оси вектора rot b. Таким
образом, правая часть есть разность скалярных произведений
Ъ • rota — а • rotЪ
и, следовательно, требуемое доказано.
Задача 14,22 (дивергенция градиента). Доказать, что
div (grad f) = bf,
где
(Л/ называется лапласианом функции f).
Решение. Известно, что
344
По A3,6)
_ d2f 4- d2l . ?V _ Af
~ а** + a^+ a*2~~ ' ■
что и требовалось.
Задача 14,23 (дивергенция вихря). Доказать, что дивергенция
вихря равна нулю, т. е.
div(rota) = 0. D,11).
Решение. По формуле A3,6)
div(rot a) =
Ho
■ ~ да, да и
rot, a — -— д^;
* dy dz'
, — дах да,
ro V - "af - aP
, ~ dau dar
rot^ = "alf—w-
поэтому
>
да у dax\ d2az d2ay , д*ах d%az d2ay
\dx dy )г dx dy dz dx ~~*~ dz dy dx dy ' dx dz
Задача 14,24 (дивергенция лапласиана). Доказать формулу
-A (diva). A4,12)-
Решение. Выше в формуле A4,10) уже употреблялся термин
«лапласиан». Возвратимся к этому весьма важному понятию. Опе-
Оператором Лапласа называется выражение вида
Если его применить к скалярной функции /, то
al ~ dx* ' ду* ~*~ dz2 ■
Применяя оператор Лапласа к вектору а, имеем
._ d2a , d2~a d2a ... 1ОЧ
Аа = а^ + а? + а72- A4'13>
Так как
a = aj + aj + ajk,
345
то, применяя к вектору а оператор Лапласа, получаем
Да = £ (aj + aj + агЪ) + g2 (aj + aj +
+ M) + jp Ш + aj + azk) =
Отсюда, применяя оператор Лапласа к вектору а, найдем
Да = ках • i + Aflj, • / + &аг • k.
Используя формулу (А), докажем требуемое
/а»вг а^ а2а
\дх* + ауа + аг*
Выполняем в каждой скобке дифференцирование и почленно скла-
складываем:
а» /аая aaj, ааг\ а» /ао^ , ft»» , даг
W ~ + ~ + ~? + ? + +
Выражение в круглых скобках (оно во всех слагаемых одно
и то же) есть дивергенция вектора а, а потому из последней фор-
формулы заключаем, что требуемое доказано.
Задача 14,25 — для самостоятельного решения (вихрь гради-
градиента). Доказать, что вихрь градиента равен нулю, т. е. что
rot (grad f) = 0. A4,14)
Задача 14,26 (для самостоятельного решения) (ротор- вектор-
векторного произведения). Доказать, что
rotEx 6)=adivb — Ъд\\Ъ+-.— *. A4,15)
db da
Указание. Использовать формулу A4,8) для определения
проекций вектора — на координатные оси и найти проекции левой
db
и правой части доказываемой формулы на координатные оси. Ока-
Окажется, что проекция левой части этой формулы на ось Ох
rot, (a X b) = | (axby - aybx) -1 (a& - aj)z). (A)
346
Проекция же на ось Ох правой части
(дЬх дЬу дЬЛ , 1дак дау , даг) ,
,дах, ,дах. ,дах, dbs дЬх дЬх
+ ЖЬ*+ЦЬУ + -дГЬ*—дх-а*—дёа!'--дГаг'
Продифференцировав выражение (А), найдем, что оно равно выра-
выражению (В).
Задача 14,27 (вихрь вихря). Доказать, что
rot (rot a) = grad (div о) — До. A4,16)
Решение. Обозначим
rot a — Ъ. (А)
Тогда
rot (rot a) = rot b.
Проекция rot (rot а) на ось Ох
[rot (roto)J, = rot.b = Py-j*. (В)
Но из (А) следует, что
h __ ££ж d<h.
у~ дг дх'
Подставляя эти значения в формулу (В), получим
д (дЦМ даА д (да*
= дхду~ ~df ~дЖ + дх~дг'
Прибавим и отнимем в правой части этого равенства -^. Тогда
д*ах
Аналогично докажем, что проекции вектора rot (rot 5) на оси Оу
и Ог равны
[rot (rot 5)J, <■ щ (div о) - Да,; (D)
trot (rot 5)]2-^ (diva)-Да, (Е)
Умножая обе части равенств (С), (D) и (Е) соответственно на I, j
и ft и почленно складывая, получим требуемое.
347
ПЯТНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Гармонические функции. Формулы Грина.
Гармоническая функция. Функция U = U(x, у, г), имеющая
непрерывные частные производные по переменным х, у и г до
второго порядка включительно, называется гармонической, если
она удовлетворяет уравнению Лапласа
д*и дЧ/ дЮ _ „
ал-2 + ду* + дг* - и'
Левая часть этого уравнения обозначается символом Ш и на-
называется лапласианом функции U.
Задача 15,1. Показать, что из формулы Остроградского A3, 17)
следует
(о) (s)
причем я — внешняя нормаль к поверхности s, a MJ — лапласиан
функции U.
Решение. На основании формулы A3, 17), прочитывая ее
справа налево, найдем
jj Jands. (A)
(о) (s)
Если вектор а является градиентом скалярной функции U —
= U {х, у, г), то
ах = (gradU)x = §; ay = (gradU)v = %l
az=(grad U).= §.
,r ,. — дпг , да» , да.
Учитывая, что div a = -^ + ^ + у^, получим
divgrad f/ = ^)+|-(^)+|fa
ь адг \дх I ~ ду\ду ) ~ dz\dz
ИЛИ
,. ... a2t/ , d»U . дЮ ...
d.vgrad [/ = ЙГ+д-г+д? = Д[/
(эта формула уже была выведена в задаче 14,22).
348
Известно, что проекция ап вектора а — grad U на нормаль п
равна °^ — см. формулу A1,8).
Теперь, полагая в (А) вектор а = grad U, получаем требуемую
формулу
(У)
Задача 15,2. (для самостоятельного решения). Основываясь на
результатах предыдущей задачи, доказать, что если U = U (х, у, г)—
гармоническая функция во всех точках области v, ограниченной
поверхностью s, то
II
(s)
д- ds = О,
т. е. поток градиента гармонической функции через любую
замкнутую поверхность равен нулю.
Задача 15,3 (для самостоятельного решения). Доказать, что
функция U = — (г = У^х2 + уг + z2) — гармоническая функция во
всех точках, где она и ее частные производные до второго по-
порядка включительно непрерывны.
Задача 15,4 (для самостоятельного решения). Доказать, что
если функция ср (х, у, г) — гармоническая, то и функция ^ также
гармоническая.
Указание. Продифференцировать по х уравнение Лапласа
<?? j- a2<? _l ^ — п
дх* + Эр + Эга ~~ и*
Задача 15,5 (для самостоятельного решения). Доказать, что
если U (х, у, г) — гармоническая функция, то и выражение
dU , dU , dU
х+у + г
есть также функция гармоническая.
Указание. Учесть, что, например,
где А оператор Лапласа
л_ * _и # -и *
а - ет + эр + Эг* •
а если £/ — гармоническая функция, то AU = 0.
349
Задача 15,6 (для самостоятельного решения). Доказать, что
если U = U(x, у, z) — гармоническая функция, то выражение
г и\г * г ' г)'
где г = Ухг + У* + г8, —также гармоническая функция.
Задача 15.7. Доказать, применяя формулу Остроградского, что
dU dV , dU aV , dU dV\ , CC., dV
(S)
где x — объем, S — ограничивающая его поверхность,
dV_
дп
dV
-х производная функции V по внешней нормали, а
Решение. Рассмотрим вектор U grad V, где функция U ■-
= U {х, у, z), и найдем его дивергенцию
div {U grad V) = ~ (U grad V)x +f(U grad V)y + ^{U grad V)z.
Учитывая, что
получаем
av ,,,M , /at/ av , „ачл /at/ av
aai/ e*i/ aav
Раскрывая скобки и учитывая, что ^ + -^ + aF — д^> находим
зи 3V , at/аи . at/ av
(A)
Проекция на нормаль к поверхности S вектора V grad V равна
(UgradV)n = U^. (В)
*
Полагая теперь в формуле A3, 17)
а = grad V,
получаем
350
f J J div {U grad V) d% = J J (t/ grad У)„
(т) (S)
а используя равенства (А) и (В), имеем доказываемое равенство
(?) (S)
Учитывая, что вектор
... dU - . dU -. . dU т
gTadU = -wi+-Sy-] + -wk,
а вектор
для их скалярного произведения получаем
dU dV dU dV dU dV
Поэтому формула (С) может быть записана так:
ШU^Vd'c+ fff (gradU • gradV)dz= [[u^ds.
(t) (x) (S)
Задача 15,8 (для самостоятельного решения). Основываясь на
результате, полученном в предыдущей задаче, доказать, что
Указание. В формуле (С) предыдущей задачи взять V = U.
Задача 15,9 (для самостоятельного решения). Из формулы пре-
предыдущей задачи, считая, что U — гармоническая функция, полу-
получить формулу
(в гидродинамике эта формула используется при вычислении кине-
кинетической энергии в безвихревом движении жидкости).
Задача 15, 10. Исходя из результата задачи A5, 7), вывести
первую формулу Грина
(t) (S)
( dU dV
(производные -j- и -^- вычисляются по внешней нормали к по-
поверхности SJ •
351
Решение. В указанной задаче былаг получена формула
jjj UAV dz + jjj (grad U . grad V) d* = j'j t/ -J ds. (A)
(t) (t) (S)
Поменяем в этой формуле местами функции U и V:
+ Щ (grad К • grad £/) dx = f f l/ Щ- ds. (B)
"(Si
Вычтем из равенства (А) равенство (В), учитывая, что скаляр-
скалярное произведение
gradL/ • grad V = grad V - gradL/,
и получим первую формулу Грина:
(т)
Подчеркиваем, что эта формула имеет место для функций U
и V, непрерывных вместе с их производными первого и второго
порядка в области т. ограниченной поверхностью S. Стоящие
„ , •? dU dV
в правой части формулы производные— и -^—берутся по направ-
направлению внешней нормали к поверхности S. Формулу Грина можно
записать в удобном для запоминания виде:
*i£L ds.
Ш
V
AV
* if
JJ
(S)
аи
дп
V
dV
дп
Задача 15, 11. Применить первую формулу Грина
(т)
(S)
к функции U = —, где г — расстояние от постоянной точки
А (а, Ь, с) области т до переменной в этой области точки P(x,y,z).
Решение. Расстояние
г = V(x — сJ + (у - bf + B — сJ.
Функция U будет непрерывной функцией со своими частными про-
производными во всех точках области т за исключением точки А,
где г = 0. В этой точке сама функция U = — и ее производные
претерпевают разрыв непрерывности.
352
Известно, что функция — — гармоническая функция всюду, где
она непрерывна, вместе со своими частными производными до
второго порядка включительно. Значит, в нашем случае эта функ-
функция будет гармонической во всей области t за исключением
точки А.
Выделим из объема т сферу о, описанную из точки А радиу-
радиусом р, таким, что о и х не имеют общих точек. Часть области т,
полученную после этого выделения, назовем ть причем в области
■tj функция U = — будет гармонической, а потому в ней Ш =
= Д( —1 = 0. По формуле Грина A5,1) для тройного интеграла,
распространенного на область tl> учитывая, что U = — и в обла-
области ti Ш = 0, будем иметь
(о)
3V
причем во втором интеграле правой части производные -^— и
di—) берутся по внутренней нормали к поверхности о.
дщ
Рассмотрим предельное значение равенства (А), когда радиус р
сферы о стремится к нулю. В этом случае область х, будет стре-
стремиться к области т и тройной интеграл левой части равенства (А)
будет стремиться к тройному интегралу, распространенному на
область х
Ш
(т)
Первый интеграл в правой части равенства (А) распространен на
поверхность S, от р не зависит, поэтому при р -*■ 0 сохранит зна-
значение, которое имеет в равенстве (А). Остается рассмотреть пре-
предел второго интеграла правой части равенства (А) при р -> 0.
I dV уд{т))
(В)
12 И. А. Каплав --,
Определим сначала первый предел в правой части этого равен-
равенства. На поверхности сферы о г = р, поэтому у =ч — . Обозначим
через (-fa-) значение производной -^- в некоторой точке Q на
сфере о. Тогда, используя теорему о среднем, получаем
l
{() (^) limp-О
(учтено, что j j do = 4«р2, т. е. равен площади поверхности сфе-
ры о).
Что касается второго предела в правой части равенства (В), то
прежде чем его вычислять, учтем, что нормаль к сфере о и ее
радиус совпадают, но направление нормали противоположно на-
направлению радиуса-вектора р точек поверхности сферы. Поэтому
вычисление производной по нормали пх можно заменить вычисле-
вычислением производной по р, но тогда
v '
Если теперь обозначить через A/)q, значение функции V в не-
некоторой точке Qj сферы о и учесть (С), то для рассматриваемого
предела найдем
p-»0
: — lim (V)Ql . -4"' 4«p* = — 4u . lim (V)Ql = — Am {V)A,
так как при р -*■ О тогда Qx поверхности схеры о будет стремиться
к точке А.
Таким образом,
354
и равенство (А) дает
ГG... Щ
' ds — 4я
Ч V \Г ОП ОП I
E)
Отсюда окончательно
Замечание. Проведенные рассуждения понадобились нам
в связи с тем, что точка А находилась внутри области т, поэтому
функция U = — в этой точке претерпевала разрыв непрерывности.
Если бы точка А находилась вне области х, то функция -- , как
функция точки P(x,y,z), была бы непрерывной и тогда, учиты-
учитывая, что эта функция гармоническая, т, е. что Л (—] = 0, мы из
первой формулы Грина сразу бы получили
дп
Эта формула называется второй формулой Грина.
Если функция V = V(x, у, г) —гармоническая в области х, то
АК = 0 и тогда формула (D) запишется так:
Эта формула дает выражение гармонической функции внутри об-
области через значения, принимаемые данной функцией и ее произ-
производной по нормали на границе этой области.
Задача 15, 12. Доказать, что если функция V = V (х, у, z) —
гармоническая функция в некоторой области, a S — сфера радиуса
R с центром в точке А{а,Ь,с), лежащая со своими внутренними
точками в этой области, то
(S)
Решение. Формулу A5,2), полученную в предыдущей задаче,
применим к случаю, когда S — сфера радиуса R.
3/4 12*
355
Вычисляя первый интеграл этой формулы, следует т заменить
его значением на поверхности сферы, *. е. на R, а величину -к-,
как постоянную, вынести за знак интеграла
(S) (S)
так как V — гармоническая функция, а поэтому 11 -s— ds = 0. (см.
&г
задачу 15,2).
Во втором интеграле производная от функции —, вычисленная
по внешней нормали, будет равна производной от этой функции
по R, так как нормаль к сфере совпадает с ее радиусом, причем
направление внешней нормали совпадает с направлением радиуса
вектора R точек сферы. Значение этой производной должно быть
вычислено на поверхности сферы, т. е. при г = R. Итак,
!Ш 1Ш JL
дп ~ dR Л8 '
Учитывая эти рассуждения, получаем. для значения функции
V в центре сферы А
что и требовалось доказать.
Это равенство выражает теорему Гаусса: значение гармониче-
гармонической функции в центре сферы есть среднее арифметическое из
ее значений на поверхности сферы.
Если V — потенциал скорости жидкости, то эта формула выра-
выражает среднее значение потенциала скорости жидкости на любой
сферической поверхности, которой ограничивается объем, целиком
лежащий в жидкости, и показывает, что это среднее значение
равно значению потенциала скорости в центре сферы.
ШЕСТНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Оператор Гамильтона
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Студентам рекомендуется изучать этот вопрос по книге Н. Е. Ко-
чина «Векторное исчисление и начало тензорного исчисления».
Под оператором Гамильтона понимается символический диф-
дифференциальный оператор, обозначаемый знаком у (набла) и опре-
определяемый в декартовой системе координат равенством
где i, /, k — единичные векторы координатных осей Ох, Оу, Ог.
Этот оператор в дальнейшем называется «Оператор у».
Основная цель введения оператора у состоит в упрощении
таких операций над векторами и скалярами, как получение градиента
скалярной функции, образование дивергенции и ротора вектора,
образование оператора Лапласа.
Следует запомнить, что оператор у является символическим
вектором.
Оператор у .часто встречается в приложениях векторного ана-
анализа и усвоение правил обращения с ним значительно облегчает
изучение, например, такого предмета, как электротехника.
Хотя вектор у является символическим вектором, а не реаль-
реальным, мы будем формально считать, что он обладает свойствами
реального вектора, и рассматривать его произведение на скаляр-
скалярную функцию, скалярное и векторное произведение его на век-
векторы, а также и другие операции с ним.
Это не должно смущать читателя, так как из дальнейшего
видно, что в результате воздействия оператора у на скаляры
и векторы получаются величины, имеющие не символический,
а вполне реальный определенный смысл. (Однако укажем, что
недопустимо употреблять, например, такие термины: «вектор у
параллелен вектору а» или «вектор у перпендикулярен вектору а».
Бессмысленно также, например, говорить, что «вектор у равен
вектору а», так как символический вектор у не может быть ра-
равен реальному вектору а, как он не может быть ему параллелен
или перпендикулярен).
357
В дальнейшем приняты такие обозначения:
1. Для численного произведения вектора а на функцию »(х, у, г)
О? (X, у, 2).
2. Для скалярного произведения векторов а и b
а'В.
3. Для векторного произведения двух векторов а и Ъ
ахЪ.
4. Из A6,1) видно, что проекции оператора у на оси прямоугольной
•системы координат равны
_ д _ д __ д
V* ~ ~Ш; Чу - -gjfl V,- - -37 •
Сводка правил обращения с оператором
!. Оператор у действует на величины, стоящие за ним, и не
действует на величины, которые стоят перед ним. Так, в записи
(а • у) ср оператор у действует на ср и не действует на а.
Иногда для того, чтобы указать величину, на которую не рас-
распространяется действие оператора у, у этой величины ставится
индекс, показывающий, что данная величина рассматривается как
постоянная Например, в записи (у • а,) ср следует считать, что у
на аГ не действует, а на ср действует.
Выражение такого вида надо, если это возможно, преобразо-
преобразовать так, чтобы величины с индексом с стали впереди у. Как
только это будет достигнуто, индекс с можно опустить, поскольку
оператор у на величины, стоящие перед ним, не действует.
2. Численное произведение оператора у на сумму двух функ-
функций вычисляется по формуле
V (9 + Ф) = V <Р + У Ф- A6,2)
3. Скалярное произведение оператора у на сумму двух векто-
векторов вычисляется по формуле
v . E + 5) = v • 5 + у . В. A6,3)
4. Векторное произведение оператора у на сумму двух векто-
векторов вычисляется по формуле
yX(a+6) = yXa-fyxb. A6,4)
358
5. Произведение yep оператора у на скалярную функцию
равно градиенту функции <р, так как
д т , д -
1+ l
- , д -Л
При вычислении, например j- (icp), постоянный вектор ? выне-
вынесен за знак производной. Так же было сделано и при вычислении
щ (к) " §-г (%)•
6. Скалярное произведение оператора у на вектор
a U, у, г) = аЛ(х, г/, г) i + а^Д*. у, z)~j + аг (х, у, г) Ъ
равно дивергенции вектора а.
д д д
Действительно, так как у* = gj 5 V» = gp' V? — <5г» то ска'
лярное произведение у •а. равное алгебраической сумме произве-
произведений одноименных проекций, можно записать в виде
Если теперь условиться под произведением ^ ах понимать част-
дах
ную производную от ак по к, т. е. -g-, и аналогично считать,
д day д даг
ТО
V * ^ == T7 "Ь 77 "Ь "ТгГ =
у. а = diva A6,6)
7. Векторное произведение оператора у на вектор
а (х, у, г) = ах (х, у, г) I + ау (х, у, zfj + аг {х, у, г) £,
равно ротору вектора а.
12 И. А. Каплаи 359
Действительно, так как векторное произведение двух векторов
а и ft вычисляется по формуле
г / ъ
b ха = Ьх Ьу Ьг
a (t а?
то, заменяя здесь вектор о оператором V=g^l + <j-/ + a? и
учитывая, что проекции оператора у на координатные оси
д д д
будем иметь
V х а =
1 j k
д д д
дх ду Ш
V х о = rot a
A6,7)
8. Оператор у применяется к скалярному и векторному произ-
произведению двух множителей так, как к ним применяется производ-
производная, т. е. для того чтобы применить оператор к произведению
двух множителей, надо образовать сумму двух слагаемых, в каж-
каждом из которых оператор действует только на один из сомножите-
сомножителей, в то время как другой остается постоянным. Например,
Ьс)
Ь)
A6,8)
причем наличие у вектора индекса с, как указывалось выше, озна-
означает, что на этот вектор оператор у не действует.
Выражения, полученные от воздействия оператора у на произ-
произведение двух сомножителей, надо преобразовать так, чтобы посто-
постоянные сомножители были поставлены перед оператором у..
Дифференциальные операции первого порядка
Задача 16,1. Найти градиент произведения двух функций ft
и h-
Решение. По правилу 8 из сводки правил, применяя фор-
формулу A6,5), имеем
grad (Ш = у (/i/2) = у i}uh) + у (Л/*).
360
В первом слагаемом правой части равенства оператор у не
действует на постоянный множитель /1г, а во втором — на постоян-
постоянный множитель f2r Поэтому эти множители в каждом слагаемом
правой части могут быть вынесены за знак оператора н мы полу-
получаем
Применяя теперь в правой части этого равенства формулу A6,5)
и опуская индекс с за ненадобностью, получаем окончательно
grad (/y2) = ftff2 + f2yft A6,9)
Задача 16,2. Найти дивергенцию произведения <ра, где <р—функ-
<р—функция.
Решение. По формуле A6,6)
div (ера) = у
В правой части этого равенства оператор у применяется к чис-
численному произведению функции на вектор, поэтому на основании
правила 8 из сводки правил
= V ' (<Р<я) + V • (<Я) = фг (V • а) + агу ?.
Запись второго слагаемого правой части в виде Ъс • (у?) была
бы неверной, так как под (у • ср) следует понимать скалярное про-
произведение вектора-оператора у на функцию «р. чего быть не может,
поскольку понятие скалярного произведения относится к произ-
произведению двух векторов.
Замечая на основании A6,6), что у • a — diva,'a на основании
A6,5) yf = grad <p и опуская индекс с, получаем окончательно
div (?а) = «р div а -f ~а • grad <p A6,10)
Эта формула была уже получена в задаче 14,2.
Задача 16,3 (для самостоятельного решения). Найти диверген-
ци ю поля «р (г) г, где г — радиус-вектор.
Указание. Использовать формулу A6,10) и учесть, что если
г = xi + yj + zk, то divr = 3, а на основании результата задачи
11,3 gradcpH =<p'(r)r°. где r°—единичный вектор вектора г.
Ответ, div [? (г) г] = 3? (г) +"°<р'@-
Задача 16,4. Найти ротор произведения <рй.
Решение. На основании формулы A6,7) и правила 8 из
сводки правил
rot («р а) = у х (<f 5) = у х (f, а) + у х (срас) =
= ?г (у х а) — ае х (у?).
12* 36»
Изменение между слагаемыми плюса на минус объясняется тем,
что в случае векторного произведения перестановка сомножителей
влечет за собой изменение знака векторного произведения.
Замечая, что на основании формулы A6,7) у х а = rota, а по
формуле A6,5) y<p = grad?, получаем окончательно, опуская ин-
индексы в последнем равенстве
I rot (сро) = <р rot а — ах grad у A6,11)
Эта формула также была получена в задаче 14,19.
Задача 16,5 (для самостоятельного решения). Вычислить ротор
поля у (г) • г, где г — радиус-вектор.
Указание. Использовать формулу A6,11) и учесть, что век-
векторы г и grad <р (г) — коллинеарны, так как grad <р (г) = <р' (г)г°, г"—
для вектора г является единичным вектором, а также то, что
векторное произведение двух коллинеарных векторов равно нулю.
Установить, что ротор радиуса вектора г равен нулю (rot г = 0).
Ответ.
rot I» (г) ■ г] = 0
A6,12)
Задача 16,6. Найти div(ox5).
Решение. На основании формулы A6,6) и правила 8 из
сводки правил
div (а х 5) = у • (а х В) — у • (ас х 5) + у • (а х Ъс). (А)
Дальнейшее преобразование сводится к тому, чтобы постоянные
множители в каждом из слагаемых правой части оказались перед
оператором у. В данном случае следует использовать свойство
цикличности смешанного произведения трех векторов, согласно
которому
а • ф х с) == b • (с х а) — с • (а хЪ)
A6,13)
Преобразуем отдельно на основании этой формулы каждое сла-
слагаемое правой части равенства (А;
у • (Or х В) = ас • ф х у).
Tertepjj в векторном произведении b x у переставим местами век-
векторы Ъ и у и так как от такой перестановки знак векторного про-
произведения изменяется на обратный, то
6ху = — ух 5.
362
Замечая, что по A6,7) — у xt? =—rotF и опуская индекс с
у ас, получим окончательно для первого слагаемого
у • (аг х Ь) = —а • rot&.
Используя снова формулу A6.13), преобразуем второе слагаемое
в равенстве (А)
V • (а х Ьс) = Ьс • (у х а) =ЬГ ■ rot a = b rot a,
так как у х а = rota, а индекс с у Ьс может быть опущен.
Итак, окончательно
div (а у b) = b • rot a — <Г • rot 6
A6,14)
Эта формула также была получена выше, в задаче 14,21.
При решении следующих задач придется пользоваться форму-
формулой для вычисления двойного векторного произведения*.
Ах(В хС) = В (А- С) — С(А -Ъ), A6,15)
согласно которой двойное векторное произведение А х (В х С) равно
произведению среднего вектора В на скалярное произведение двух
других минус правый крайний вектор С, умноженный на скаляр-
скалярное произведение двух других.
Формула A6,15) может быть записана в удобном для запоми-
запоминания виде и так: _
5 С A6,16)
т. е. двойное векторное произведение равно определителю второго
порядка, в первой строке которого элементами являются векторы,
стоящие во внутренней скобке, написанные в том же порядке, а
во второй строке элементами являются скалярные произведения
этих векторов на первый вектор.
Задача 16,7. Определить rot (a x Ъ).
Решение. На основании правила 8 из сводки правил и фор-
формулы A6,7)
rot [а х Ь) = у х (а х 5) = у х (ас х Ъ) + у х (а х Ьс).
Каждое слагаемое в правой части представляет собой двойное
векторное произведение, которое вычислим по формуле A6,16) и
* Вывод формулы A6,15) можно найти, например, в учебнике И. И. При-
Привалова «Аналитическая геометрия».
363
преобразуем так, чтобы постоянные множители стояли перед
знаком у:
у X (ас х Ъ)
V •
V *
ас b
ас • у div Ъ
Очевидно, что у • ас — ас • у, так как скалярное произведение
двух векторов не зависит от их порядка, а постоянный множитель
должен стоять перед знаком у, скалярное же произведение у • b
на основании A6,6) равно div Б.
Раскрывая последний определитель и опуская теперь за нена-
ненадобностью индекс с, получаем
уХ (ас X Ъ) = a div Ъ — {а • у) Ъ.
Точно так же
у х (а х Ъс) =
а _ Ьс_
у . а у • Ьс
а Ъс
у • а Ьс • у
= ф • у) а — b div о.
(индекс с опущен, у • а = diva).
Складывая полученные результаты, окончательно имеем
rot (a X b)=~ad\vb— bdiva + (b ■ у)а —(а .у)Б. A6,17)
Дополнительные сведения из теории
Выясним теперь смысл выражений вида а • у, встретившихся
в формуле A6,17), т. е. смысл скалярного произведения вектора а
на оператор у, стоящий справа от него, (следует отличать выраже-
выражение а • у от выражения у • а)
Так как
а =
ayj+ агк; у = £Г-f |/
то
A6,18)
Проекции аЛ, ар) аг вектора а определяются ло формулам
ax = a cos (a, л:); a^ = a cos (а, у);
аг = a cos (a, г),
поэтому по формуле A6,18)
a, х) т + a cos (a, t/W
A6,19)
364
Выполним теперь операцию а • у над функцией <р:
(а• у) <Р = a cos (сСх) ^ + a cos (а"Гу) ^ + а cos (а^г) ^ =
= а Ц? cos (аГ*) + ру
cos
+ ^ cos
Выражение, стоящее в квадратных скобках на основании A1,3)
равно производной р от функции <р по направлению вектора а,
поэтому
A6,20)
т. е. результат применения операции а • у к функции <р
произведению длины вектора а на производную от функции <р по
направлению вектора а.
На основании A6,20) операция а • у может быть записана в
виде
A6,21)
Выполнение операции а ■ у над вектором Ъ на основании A6,18)
приводи! к вектору
a^x + ayfy + a2§, A6,22)
откуда следует, если учесть равенство (В),
(а • у)£= а cos (аГ*)^ + а cos (а, у) щ + a cos (afz) ^
= а [|cosE, ^) + |cos(a, у) + %со5(аГг)]. A6,23)
Выражение, стоящее в квадратных скобках, есть производная
вектора Ь по направлению вектора а, т. е. ^. Получаем оконча-
окончательно
A6,24)
Задача 16,8. Определить grad (a • Ъ).
Решение. На основании A6,5) и правила 8 из сводки правил
имеем
grad (а • Ъ) = у (а ■ б) = у & • Ц + V (а • *,). A6,25)
365
Перепишем A6,15) в виде
С (А В) = В (Л • С) —Л X (В X С). A6,26)
Для вычисления у (а, -б) положим в A6,26), что
С = у; 3 = аг; Ъ—Ъ.
Тогда
V [ае • 6) — Ъ (Ее • V) — ас X (Ь х у);
V(Oc • Ь) = (£ • VN — ас х (б х у)- A6,27)
Так как в случае векторного произведения перестановка сомножи-
сомножителей изменяет знак векторного произведения, то в последнем
равенстве
— Ос х (В х у) = ас х (у X 5).
Но на основании A6,7)
у х b = rot 5,
а потому
— ас х F х у) = а> х rot Ъ. (А)
Окончательно из A6,27)
V (flc • В) = (ас • V) ^ + 5с х rot Ъ.
Теперь преобразуем второе слагаемое A6,25) с помощью A6,26),
полагая там
С = у; 3 = £с; S = а:
у (а • 5с) = Q Eс • у) — \ х (а х у) =
= (& • V)^ + 5с х (у х а) = E, • у)а + 5с х rota. (В)
Складывая полученные результаты (А) и (В) и опуская за не-
ненадобностью индекс с, окончательно имеем
grad(а • 5) = (а • уM + E • у)а + а х rotM- b x rota. A6,28)
Задача 16.9 (для самостоятельного решения). Доказать, что для
всякого постоянного вектора а имеет место соотношение
V(a • Ь) = (а • у)Ь + а х rotЪ.
Задача 16,10 (для самостоятельного решения). Доказать, что
из A6,28) при а = Ь следует
■g- grad а" = (а • v) a + а х rot а. A6.29)
366
Дифференциальные операции второго порядка
Задача 16,11. Рассмотреть у2— квадрат оператора у, понимая
под этим скалярное произведение вектора у на самого себя.
Решение. Помня, что скалярное произведение двух векторов
равно алгебраической сумме произведений одноименных проекций
и что проекции оператора у на оси прямоугольной системы коор-
координат равны ^-х, щ, ^, получаем
^-г,.г,-1.1+1. 1 + 1.1-
V - V V ~ дх дх^ду ду^дг дг'
Но так как ^ + ^-2 + jp — оператор Лапласа Д, то
у* = Д, A6,31)
т. е. квадрат оператора у равен оператору Лапласа. Поэтому
уравнение Лапласа Д<р = 0 может быть записано в виде у2о = 0.
Задача 16,12 (для самостоятельного решения). Доказать, что
Задача 16,13. С помощью оператора у найти
div gradf.
Решение. На основании A6,5) grad<p = V?> а на основании
A6,6) div а = у • а. Поэтому
div grad cp = у • уср
Из результата задачи A6,11) у у = у2 н поэтому
div grad <p = у2?. A6,32)
Учитывая A6,30), получаем
A6,33)
Задача 16.14. Найти вихрь градиента скалярного поля, т. е.
rot grad *.
Решение. На основании A6,7) rot grad ^ = у х grad ?, а так
как по A6,5) grad ср = у«р, то
rot grad f = у х у?-
367
Скалярный множитель <р можно вынести за знак векторного про-
произведения, поэтому
V х V<P = (V х V)<P-
Но векторное произведение двух равных векторов равно нулю, а
потому ух v = 0 и окончательно
rot grad <p = О
A6,34)
т. е. вихрь градиента любого скалярного поля равен нулю.
Задача 16,15. Найти grad diva, где а = а(х, у, г).
Решение. На основании A6,5) и A6,6)
да да
Было бы ошибкой считать, что у (V • а) — Vafl> так как и ПРИ
ствиях с обыкновенными векторами умножение вектора Ъ на ска-
скалярное произведение Ъ • с, т. е. Ъ ■ ф • с) Ф Ьг • в.
(Выражение уга есть вектор, имеющий такой смысл: у2а =
д*Ь дга &*-а -
gji + ал + -07» • ^е слеАУет смешивать у2а с (yaf, как нельзя сме-
смешивать у2<р с (у«рJ)
Задача 16,16. Определить divrota, гдеа = а(дс, у, г).
Решение. По формулам A6,6) и A6,7)
div rot a = у • (v x a)-
Здесь мы имеем дело с векторно-скалярным произведением трех
векторов. Из векторной алгебры известно, что это произведение
обращается в нуль, если в него входят два равных вектора.
Таким образом
div rot a — О
A6,35)
Более сложным путем получен этот_ результат в задаче A4,23).
Задача 16,17. Определить rot rot а, гдеа = а(х, у, г).
Решение. На основании A6,7) rot rot о = у х (v X fl). Ис-
Используя теперь формулу A6,16) для двойного векторного произве-
произведения, получаем
V с
V X (у X а) =
V • V у» а
= V(V • а) —(V ' V)o-
368
Но на основании A6,6) \?-a = diva, а по A6,5) v(diva) =
= grad diva. На основании задачи 16,11 у • у = ys, поэтому окон-
окончательно
V х (у X а) = grad diva — у2а
A6,36)
В задаче 14,27 эта формула была получена значительно более
сложными выкладками.
СЕМНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Криволинейные координаты. Ортогональные криволинейные
координаты. Запись в ортогональных криволинейных координатах основных
дифференциальных операций теории поля: градиента, дивергенции, ротора
и оператора Лапласа. Выражения градиента, дивергенции, ротора и оператора
Лапласа в цилиндрической и сферической системах координат.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
На предыдущих практических занятиях мы пользовались такими
пространственными системами координат: прямоугольной, цилиндри-
цилиндрической и сферической. В каждой из этих систем положение точки
в пространстве определяется тройкой чисел (и, v, w), причем раз-
различным точкам однозначно соответствуют различные тройки чисел
по определенному закону, присущему данной системе координат.
В прямоугольной системе координат такой тройкой чисел являются
(х, у, г)—абсцисса, ордината и аппликата точки.
В цилиндрической системе координат положение точки в про-
пространстве однозначно определяется тройкой чисел (г, ?, г), которые
называются цилиндрическими координатами точки. Здесь г и ср —
полярные координаты проекции точки на плоскость хОу
@<ср<2*); @<г<+со),
ъ. г — ее аппликата (—со<г<+со).
Между прямоугольными и цилиндрическими координатами точки
существует зависимость, определяемая формулами
х = г cos ». i/ — rs\n<?, z = г. A7,1)
В сферической системе координат положение точки в простран-
пространстве однозначно определяется тройкой чисел (р, 0, ср), которые назы-
называются сферическими координатами точки. Здесь р — расстояние
точки от начала координат @ < р< + °°), 6 — угол между радиу-
радиусом-вектором точки и положительным направлением оси Ог@<
<6<т:I ср — угол между положительным направлением оси Ох
и проекцией радиуса-вектора точки на плоскость хОу @ < ср < 2т:).
Зависимость между прямоугольными и сферическими координатами
дается формулами
х = р sin 6 cos cpi
у = р sin 8 sin cpj A7,2)
г = р cos 6.
370
Координатная поверхность. Координатной называется поверх-
поверхность, на которой одна из координат точки остается постоянной.
Координатными поверхностями в прямоугольной системе координат
являются плоскости, параллельные координатным плоскостям хОу,
хОг и уОг (фиг. 17,1). На каждой из этих плоскостей одна ко-
координата сохраняет постоянное значение.
Координатными поверхностями в цилиндрической системе ко-
ординат являются: 1) плоскости, параллельные плоскости хОу,
т. е. поверхности, на которых координата г остается постоянной:
2) поверхности прямых круговых цилиндров, общей осью которых
является ось Ог; на этих поверхностях постоянное значение имеет
COI?St
Фиг. 17,1
Фиг. 17,2
координата г; 3)полуплоскости, проходящие через ось Ог и огра-
ограниченные ею; на них координата <р сохраняет постоянное значение
(фиг. 17,2).
Координатными поверхностями в сферической системе коЬрдинат
являются: 1) сферы с центром в начале координат; на них коорди-
координата р сохраняет постоянное значение; 2) полуплоскости, прохо-
проходящие через ось Ог и ограниченные ею; на этих кооодинатных по-
поверхностях постоянное значение сохраняет координата ср и 3) кру-
круговые конусы, общей осью которых является ось Ог; на каждой
из этих координатных поверхностей координата 8 сохраняет посто-
постоянное значение (фиг. 17,3).
Координатные линии. Координатными называются такие линии,
вдоль которых изменяется только одна координата, а две другие
сохраняют постоянное значение. Каждые две координатные поверх»
ности при пересечении образуют координатную линию.
В прямоугольной системе координат такими линиями являются
прямые, параллельные координатным осям. Например, координат-
координатная д;-линия параллельна оси Ох (фиг. 17,4).
371
Координатными линиями в цилиндрической системе координат
являются: г-линия — прямая, параллельная оси Ог, <р-линия — ок-
const
9-tonst
P'Const
~ У
Фиг. 17,3
ружность, лежащая в горизонтальной плоскости с центром на оси
Ог, г-линия — луч, выходящий из произвольной точки оси Ог, парал-
параллельный плоскости хОу (фиг. 17,5).
z-линая
2-линии
Фш> 17,4
Фиг. 17,5
Координатными линиями в сферической системе координат яв-
являются: р-линия — луч, выходящий из начала координат, 9-линия —
полуокружность с центром в начале координат, соединяющая две
372
точки на оси Ог, и «р-линия— окружность с центром на оси Ог,
лежащая в плоскости, параллельной плоскости Юу (фиг. 17,6).
Криволинейная ортогональная система координат. Криволиней-
Криволинейная система координат называется ортогональной, если в любой
точке касательные к координатным линиям, проходящим через эту
точку, пересекаются под прямым углом. Например, цилиндрическая
и сферическая системы координат являются ортогональными криво-
криволинейными системами координат. Кроме этих координатных систем,
которые являются криволинейными ортогональными, существуют
и другие.
Рассмотрим в общем виде систему ортогональных криволиней-
криволинейных координат (фиг. 17,7).
Из формул A7,1) и A7,2) видно, что
прямоугольные координаты х, у, иг точки
являются в цилиндрической системе коор-
координат функциями г, ср и г, т. е.
х=х(г, ?);
у = у(г, <р); (А)
2 = 2,
а в сферической системе координат х, у
и 2 является функциями р, 8 и ср, т. е.
х = х(р, 8, <р);
у = у(р, 8, <р); (В)
2 = 2(р, 8).
Пусть в общем случае в трехмерном *
пространстве кроме прямоугольной системы Фиг. 17.6
координат введена также криволинейная
система координат (и, v, w) и между ними и прямоугольными коорди-
координатами х, у и г установлено взаимно однозначное соответствие, ко-
которое описывается формулами, аналогичными формулам (А) и (В):
х— x(u, v, w);
у = у (u, v, w)\
г = г {и, v, w).
A7,3)
Каждая пара координатных поверхностей, проходящих через фик-
фиксированную точку М, образует в пересечении координатную линию.
В фиксированной точке М проведем касательные к координатным
линиям Ми, Mv и Mw. Будем рассматривать только ортогональ-
ортогональные системы криволинейных координат. Это означает, что векторы
L1( 12, L3, лежащие на этих касательных, будут попарно пер-
перпендикулярны.
373
выражения для элементов длины, площади объема
в ортогональных криволинейных координатах
Элемент длины в ортогональных криволинейных координатах.
Рассмотрим бесконечно малый криволинейный параллелепипед, вы-
вырезаемый тремя парами координатных поверхностей, соответствую-
соответствующими значениям координат и, v, w и и -f- Аи, v + До, w -f- Дю.
Точка М имеет координаты и, v, w:M(u, v, w). «Гранями» этого
параллелепипеда являются координатные поверхности:
,Мг. ЛШ,М5Л17; ЛШ,М4Л17;
Фиг. 17,7
Его «ребрами» являются координатные линии, которые получаются
в пересечении указанных «граней».
Квадрат элемента длины в прямоугольной системе координат
dsl = йхг + dtf + dz1. (.17,4)
Из формул A7,3) следует, что
A7,5)
*=&du
374
Возведем каждое из этих равенств в квадрат, почленно их сложим
и подставим в A7,4). Тогда
Рассмотрим три вектора Lb L2, и Is, лежащие на касатель-
касательных, проведенных из точки М к координатным линиям ММи ММа
и ММЯ соответственно:
■7 дх т . ду - . дг т
где -*, Л, j—проекции вектора 1Ь на оси Ох, Оу,Ог;
аи ' df' Т — пр^кции вектора 12 на те же оси;
Й % £ вект°Ра 1з на те же о011:
a i, /', и Ъ — орты этих осей.
Так как векторы Lb L2, и L3 попарно перпендикулярны, то их
скалярные произведения Lx • L2) L2 • L3 и Lx • Ls равны нулю. Но
на основании A7,6)
7 7 дх дх . ду ду дг дг Л
^•^^аГ^ + й'^ + й'а^01
7 7 — дх дх >дУ дУ _l дг дг — п-
Ll " Ьз ~ да * to + й * Л» + да ' Ли ~ и>
7 7 — ajc а-* j_ ^ ^ j_ йг дг — п
L2 • Ls - gj • s + gj; • ^ + gjj • я - 0,
поэтому в формуле для ds2 три последние слагаемые равны нулю
и тогда оказывается, что в случае ортогональных криволинейных
375
координат квадрат элемента длины содержит только квадраты диф-
дифференциалов du?, db2 и dw, a
Выражения, стоящие здесь в квадратных скобках, есть квадраты
длин векторов Lb la и 1^, определенных формулами A7,6), т. е.
эти выражения равны
поэтому
, На основании формулы A7,8) длины «ребер» рассматриваемого
бесконечно малого параллелепипеда следует принять.равными:
Щи
= L2dv; A7,9)
Эти формулы и выражают элементы длины в ортогональных
криволинейных координатах.
Множители Llt L2, L3l которые входят в эти формулы, есть
длины векторов Llt L2 и L3, введенных формулами A7,6), равные
Величины tb L2, i-з называются коэффициентами Ляме, отвечаю-
отвечающими точке с координатами и, v и ш. От точки к точке коэф-
коэффициенты Ляме будут изменяться, поэтому они являются функция-
функциями координат точки. Вследствие этого коэффициенты Ляме назы-
называют также единицами локальной (местной) длины.
376
Элемент площади в ортогональных криволинейных координатах.
Так как рассматриваемая система криволинейных координат орто-
ортогональна, то площадь «грани» ММхМаМг, которую с точностью
до бесконечно малых высшего порядка будем считать прямоуголь-
прямоугольником,
(do)m = {ds)u • Що = (Ljdu) • (L,dv);
A7,11)
Аналогично площади двух других граней MM2MtMi и
равны соответственно
Щи* = Що • (ds)w = L2L3dv dm, A7,12)
(do)uw = (ds)u • (ds)w = L,L3d« dw. A7,13)
Формулы A7,11), A7,12) и A7,13) и определяют элемент площади
в ортогональных криволинейных координатах.
Элемент объема в ортогональных криволинейных координатах.
Чтобы определить элемент объема в ортогональных криволинейных
координатах, найдем объем рассматриваемого бесконечно малого
криволинейного параллелепипеда. Считая с точностью до бесконеч-
бесконечно малых высшего порядка этот параллелепипед прямоугольным,
определим, что его объем
dv = (ds)u ■ (ds)v ■ (ds)w\
dv — (Lxdu) ■ (L2dv) • (L3dw).
Окончательно элемент объема в ортогональных криволинейных ко-
координатах
dv = LxL2Lbdu dvdw. A7,14)
Выражение проекций вектора А на касательные к координат-
координатным линиям Ми, М,о Mw, проведенным в точке М (х, у, г}
через его проекции на оси прямоугольной системы координат.
Проекции вектора А на оси прямоугольной системы координат
обозначим через Ах, Ау, Аг, а на касательные к линиям Ми, Mv и
Mw — через Аи, Av и Аш.
Тогда по известным формулам векторной алгебры имеем
Аи — Axcos(x, u)+Aucos(y, u) + Azcos(z, и);
Ао = Axcos{x, v) -f Al)cos(y, v) + A2cos(z, v)\ A7,15)
Aw = /^cos (x, w) + Aycos {y, w) + Azcos(г, w).
Входящие сюда девять косинусов легко определятся из формул
A7,6). Косинус угла между вектором а и осью Ъ равен проекции
вектора на эту ось, разделенной на модуль вектора, т. е.
- aL
cos (a, L) = —.
377
Так как косинус угла между касательной к линии Ми и осью Ох
равен косинусу того угла, который вектор Lx составляет с осью
Ох, то, учитывая, что Llx = ^ , имеем
дх
, . ди 1 дх
cos(*. u) = I-i = 1-i-d-u.
Аналогично получаем и значения остальных косинусов. Таким об-
образом,
, . \ дх . . 1 ди . . 1 дг
cosU, и) = ^-й; cos (у, u)=Ti-fu\ cosB) и) = ^-й;
1 дх . . 1 ди , . \ дг
; cos(y, v)=j-.tv; cosB, о) = 5-55;
. . 1 дх
cos(*, а») = ц'й;
1 ди
\ дг
В дальнейшем рассматриваются только Ортогональные криво-
криволинейные координаты, которые для сокращения записей мы будем
называть просто криволинейными, опуская слово «ортогональные».
Вывод формул для вычисления градиента, дивергенции, ротора
и оператора Лапласа в криволинейных координатах
Задача 17,1. Найти коэффициенты Ляме Llt L2 и L3 для цилин-
цилиндрических координат.
Решение. В цилиндрических координатах криволинейные ко-
координаты и, v, w имеют значения и = г, v = <p, w = г, а по фор-
формулам A7,1)
дх дх
г- = т — cos 9;
дх_дх
dv ду
-г sin cp;
ду ду
a-u = ^
ду ду
дУ _ дУ _ л.
ЪЪ - Ш ~ Ul
г = г.
дг
ди~2
дЪ-Тг^"'
По формулам A7,10) получим
Ц = l/cos2 to + sin2 <в = 1;
5г __ <3г _ Л
л^ — л~. — и>
аг
аш'
1.
= г;
A7,16)
Итак, в цилиндрических координатах
378 Li=l; L2 = r, L3=l.
A7,17)
Задача 17,2. Найти коэффициенты Ляме для сферических ко-
координат.
Решение. В сферических координатах криволинейные коор-
координаты и, v и w имеют значения и = р; v = 6; w — <р.
По формулам A7,2)
х= psin9costp;
у= р sin 6 sin cp;
2 = р cos 6;
дх дх
ОН UQ
дх = дх
дх дх
ду
дЬ
Psincpcos8;
Ж = Ё=
дг дг
иг uz . Q
aU-=ae=-Psin9;
L, = l/(cos<psin8J + (sintpsin8)a + (cos8J = 1;
Li = V (p cos cp cos 8J -f (p sin tp cos 8J -f (—p sin 8J = p;
La = V(—psintpsin8J -f (pcostp sin6J = psin8.
Итак, в сферических координатах
U= 1; L2 = p; L3= psin8.
A7,18)
Задача 17,3. Определить градиент функции V = V(x, у, г) в
криволинейных координатах, причем
х=х{и, v, w); у=у{ц, v, w); г = г(и, v, w).
Решение. Известно, что
,,i dV~ . dV~ . dV 1
grad V = -^-i + s-t +-V-R.
ь дх ' ду' ' дг
По формулам A7,15) проекция graduV на направление касательной
в точке М к дуге ММХ (фиг. 17,7) равна
прц grad V = прЛ grad V • cos (д;, и) + пр^ grad V • cos (у, и) +
+ np^grad V - cos B, «). (А)
Учитывая, что
8V. ..- .,9V .,, 9V
а на основании формул A7,16)
cos I*, «>-£•£; cos(i,,«) = ^|; cos
37»
переписываем (А) в виде
... dV 1 дх . dV 1 ду . dV 1 дг
ПО ^ГЗи V ^ — * -~* • г* — * ~~* * *т^ Ч * ~~~ • ^~
и to дх L\ ди ду L,\ ди oz L\ ou
1 IdV дх . dV ду dV
_± dV дх dV ду dV_ дг\
Ц\дх да ' ду ' ди дг ди) '
Выражение в скобках есть нечто иное, как производная по и от
сложной функции V U, у, г), где
х=х(и, V, w); у=у(ц, v, w); z = z(«, v, w),
dV
т. е. "з- .
ди
Поэтому
npugradK = l fu. A7,19)
Точно так же найдем проекции градиента функции V на касатель-
касательные, проведенные в точке М к дугам ММ2 и ММ3:
l^; A7,20)
Поэтому grad V в криволинейных координатах
где еи, е0, еш — орты осей Ои, Ov и Ow соответственно.
Задача 17. Найти выражение дивергенции вектора А в криво-
криволинейных координатах.
Решение. Известно, что дивергенцией векторного поля век-
вектора А в точке М называется предел, к которому стремится отно-
отношение потока этого вектора через замкнутую поверхность S, окру-
окружающую точку М, к объему V области, ограниченной этой поверх-
поверхностью, при условии, что объем V стягивается в точку М, т. е.
A7,23)
Поэтому мы можем дивергенцию вектора А в точке М вычислить,
применяя формулу A7,23) к элементарному объему в криволиней-
криволинейных координатах, т. е. применяя ее к нашему бесконечно малому
криволинейному параллелепипеду. Вектор А в криволинейных коор-
380
динатах запишется через его проекции на касательные в точке М
к координатным линиям так:
А = Аиеи + Л Я + Awew. A7,24)
Вычислим поток вектора А через все шесть граней этого парал-
параллелепипеда.
Рассмотрим сначала две «грани», перпендикулярные к коорди-
координатной линии ММХ (напоминаем, что мы рассматриваем ортогональ-
ортогональные криволинейные координаты), т. е. «грани» ММ2МьМ3 и
MiM^M^Mi. Так как внешние нормали к этим граням имеют
противоположные направления, то проекции вектора А на них бу-
будут отличаться только знаком. Единичные векторы ^тих нормалей
будут — еи на левой грани и еи на правой, так как еи направлен в
сторону возрастающих_значений координаты и. Из A7,24) следует,
что проекция вектора А на нормаль к левой грани будет равна — Аи,
а на нормаль правой грани эта проекция равна Аи.
Поток через «грань» ММ2МьМ3 равен площади этой грани fai =*
= LJLidudw, умноженной на — Аи, т. е.
Пмм,м,м, = ~AuLiL2dvdw.
Поток через противоположную «ц>ань» МхМ3МйМ4 от только чта
определенного отличается на величину частного дифференциала по
переменной и от величины AuLiL2, т. е. на величину
так как на этой грани криволинейная координата равна не и, а
и -f du, а две другие координаты v и w имеют то же значение,
что и на левой «грани». Таким образом, поток вектора А череа
правую грань
Пм,м3м,м. = [.4UL1L2 -f ~ (AuLiLz) d«j dv dw.
Складывая найденные потоки через две рассматриваемые грани,
найдем, что поток через эти две грани равен
^ {AULXL2) duj dvdw + [—
= ^ (AuLiLz) du dv dw.
Аналогично поток через две грани MM^MtMa и М3М^МЬМ2 равен
13 И А. Каплан
38t
а через две грани ММ1М3М2 и
Поток через весь объем бесконечно малого криволинейного парал-
параллелепипеда равен сумме этих потоков, т. е.
[§-и (AuL2La) +1 (AJ^L,) + ± (AJ.^)] du dv dw.
Разделив это выражение на объем параллелепипеда, равный на осно-
основании формулы A7,14) LxLiLadudv'dw, найдем" по A7,23), что в
точке М
[ ^L^ + ^Л^^) + £ (AJ.^)] . A7,25)
Задача 17,5 (для самостоятельного решения). Найти: 1) divett;
2) d\\eu и 3) divew.
О т в е т. 1) div ;„ = ццц ¥и (LtL3)\
Задача 17,6. Найти выражение для вихря вектора А в ортого-
ортогональных криволинейных координатах.
Решение. Положим в формуле A7,22) V = u. Так как част-
частные производные от и по v и w равны нулю, потому что и не за-
зависит от v и w, получим
= r-iu. A7,26)
Вычислим вихрь от обеих частей этого равенства
rot grad и = rot L- eu).
Но на основании A6,34) rotgrad« = 0, а потому
rot(leu) = 0. A7,27)
По формуле A6,11)
rot/a = grad/ x с + /rota.
На основании этого и учитывая A7,27), получаем
382
Вычислим grad (j-j no формуле A7,22)
Выполняем дифференцирование в каждом слагаемом:
ff \Ч ~ L\ U. <>u e" L\ U dv e" £ Ls dw
Отсюда следует
Выражение, стоящее в скобках правой части последнего ра-
равенства, на основании формулы A7,22) равно gradLb поэтому
окончательно
grad(') = — -j
Тогда из A7,28) получаем
rot e
tt = £- grad Lx x eu.
Вычислим теперь векторное произведение j- grad Lx x eu:
A7,29)
7-gradZ-! xett = r
(grad /.!)„(grad L^(grad,
1 0 0
Заменяя элементы второй строки этого определителя по фор-
формулам A7.19), A7,20) и A7.21), получим
by
5U ev ew
Lt du L% dv Ls dw
1 0 0
Lj Us <?k> e& л2 ay
а отсюда уже окончательно получаем из A7,29)
. - 1 dLi _ 1 dLi я
13*
383
Точно так же определим
После того как найдены вихри единичных векторов
можно определить и вихрь вектора А
А = Лиёи -р "bCt т
где Аи, Ао, Aw — проекции векторов А по осям и, v и
rot Л = rot (Д,5И) + rot (AveD) + rot (Л^еа,)
Пользуясь тем, что на основании A6,11)
rot/6 = grad/ х a + frots,
получим
rot A = grad Аи х ёи + grad Avxev + grad Aw xew
+ Au rot ёи + Ao rot ev + Aw rot se, =
L, да Lt dv L3 du
0 1 0
до.
С
1
п
\a
~d
0
1 - -ц
Li du Lt
1
и Lt do
0
e0
dv Lt
0
i ajL
Ц dw
1
1 * '0
ew
-d£
0
+
/
1 ■**li 1 1
\i
Г2 "&Г
; "^ё—цц ^
(цц ajёю ~"
1 «л, 1 дАо , aL3 1
Ц1ь "~ Ц а» + Z^T ш ЕГ ~ ES
1^~ГЖ + 7^ЦЛГ
384
i ди Ц dv "•" Z.2Z., a~uT
r l рЧл/,)
dw
И окончательно для вихря вектора А в криволинейных ортогональ-
ортогональных координатах
Задача A7,7). Найти выражение оператора Лапласа AV в орто-
ортогональных криволинейных координатах.
Решение. Из формулы A6,32) известно, что
ДУ = div grad V.
Проекции grad V вычисляются по формулам A7,19), A7,20), A7,21)
Заменяем в формуле A7,25) проекции вектора А проекциями grad V
д_ /Lji, dV\ д_ (L^ dV\]
dv[ U до)~*~ dw\ Ls dwj\'
Значит, в ортогональных криволинейных координатах оператор
Лапласа
AV = ЦЦц [дй (тг аг)+ Tv 1~ЕГ ^г) + a5i (~tf a»/J *
385
Определение градиента, дивергенции, ротора и оператора
Лапласа в цилиндрических и сферических координатах
Задача 17,8. Найти выражение градиента, дивергенции, ротора
и оператора Лапласа в цилиндрических координатах.
Решение. Из задач A7,1) и A7,2) известны значения коэф-
коэффициентов Ляме в цилиндрических и сферических координатах.
В цилиндрических координатах
Li = 1, L2 — Г, L3 = 1.
1. Внося эти значения и в формулу A7,22), получим выраже-
выражение градиента в цилиндрических координатах
dV „ , 1 dV „ , dV я
2. Из формулы A7,25)
Окончательно
3. Внося значения A7,32) в формулу A7,30), находим вираже-
ние ротора в цилиндрических координатах
1
Выполняя дифференцирование, получаем окончательно в цилиндри-
цилиндрических координатах
4. Выражение оператора Лапласа в цилиндрических координа-
координатах находим, внося значения A7,32) в формулу A7,31)
д I I dV\ . д
Выполняем дифференцирование:
1 ev . e»v . 1 ЭгУ . dW
7 Tr + Si* + Ww + a?
386
оператор Лапласа в цилиндрических координатах
л__|_а д* 1 ?!!_ I а2
А ~ г дг~г дг* + г* df* + дг*'
В полярных координатах на плоскости выражение оператора Лап-
Лапласа получим, опуская в нем последнее слагаемое, так как в этом
случае функция V зависит только от г и (р. Таким образом, в по-
полярных координатах оператор Лапласа
л-±1. + *_ + ±д±.
г дг^~ дг*'1' г2 д?2 *
Задача 17,9 (для самостоятельного решения). Определить гра-
градиент, дивергенцию, ротор и оператор Лапласа в сферических
координатах.
Указание. Воспользоваться результатами задачи A7,2), в ко-
которой было найдено
Z.J = 1; L2 = р; L3 = р sin 8; и = р; v = 0; да = ср.
Ответ.
3) rot?4 = ^p4,, + j-gf
p sin
^ р <Эр "^ ар2 +
387
ВОСЕМНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Интегрирование линейных дифференциальных уравнений с
частными производными первого порядка.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Чтобы выяснить происхождение линейных уравнений с частны-
частными производными первого порядка, прежде всего найдем уравне-
уравнения поверхностей цилиндрических, конических и поверхностей
вращения, а потом покажем, что найденные уравнения эквивален-
эквивалентны некоторым уравнениям с частными производными первого
порядка.
1. Цилиндрические поверхности.
Найдем уравнение цилиндрической поверхности в том случае,
когда образующая ие параллельна ни одной из координатных осей,
а ее направляющей является линия, определяемая уравнениями
F(x, у, г) = 0;
причем вовсе не обязательно, чтобы эта линия лежала в одной из
координатных плоскостей.
Цилиндрическая поверхность, или цилиндр, — поверхность, опи-
описываемая прямой, которая движется, оставаясь параллельной
данной прямой, пересекая при этом данную кривую, называемую
направляющей.
Уравнение образующей, если предположить, что она пересе-
пересекает плоскость хОу и проходит через точку (а, Ь, 0), имеет вид
где а и b — переменные параметры, а т, п и р — постоянные ве-
величины, так как по определению образующая сохраняет достоян-
достоянное направление в пространстве.
Из A8,2)
х — а _ г ш у — Ь г_
т р ' п р
Из этого следует, что уравнение образующей может быть за-
записано в виде
383
где
ь — — • / — —
Так как прямая A8,2) пересекает направляющую A8,1), то,
подставляя в A8,1) значения х и у из A8,3), получаем
F (kz + а, lz + b, z) = О
Если из этой системы исключить г, то получится соотношение
вида
<р(а, &) = 0, A8,4)
которое связывает переменные а и Ь.
Из системы A8,3) следует, что
а = х — kz;
b =y — lz
и потому соотношение A8,4) перепишется в виде
<p(x — kz, y — lz) = O. A8,5)
Этому уравнению будут удовлетворять координаты любой точ-
точки образующей цилиндрической поверхности.
Замечание. Если образующая не пересекает плоскость хОу
(т. е. параллельна ей), то вместо точки (а, Ь, 0) надо взять точку
пересечения ее с другой координатной плоскостью.
Пример. Найти уравнение цилиндрической поверхности, для
которой направляющей служит окружность
х* + у* = 25; \
2 = 4, J
а направление, образующей дано отношениями т:я:р = 2:3: 1.
Решение. Выполним решение рассмотренным способом.
1. Уравнение образующей запишется в виде
х — а у — Ь г— О
2. Выразим х к у из этого уравнения через z
* — а — ~. У — Ь — г /д\
откуда
3. Эти значения х к у подставим в уравнение направляющей
и получим уравнения вида
Г:?)
(В)
389
4. Теперь из этой системы уравнений исключим г и будем иметь
соотношение вида A8,4), связывающее а и Ь.
В первое уравнение системы (В) подставим из второго 2 = 4.
(8 + af + A2 + bf = 25. (С)
5. Из (А) определим а и b
а = х — 2г; b = у —Зг.
Подставляя эти значения в (С), получим уравнение искомой
поверхности в виде
(8 + х — 2гJ + A2 +у — Зг)г = 25
или, раскрывая скобки, найдем
х2 + у2 + 13г2 — \хг — буг + \6х + 2\у — 88г + 183 = 0.
2. Конические поверхности.
Конической поверхностью, или конусом, называется поверхность,
описываемая непрерывным движением прямой (образующей), ко-
которая проходит через неподвижную точку А (а, Ь, с) — вершину
конуса и пересекает данную линию (направляющую).
Пусть точка А(а, Ь, с) — вершина конуса, а уравнения направ-
направляющей
F(x,y,z) = 0;\
F^x, у, г) = 0.|
(А)
Уравнения образующей конуса, как уравнения прямой, прохо-
проходящей через точку А (а, Ь, с), запишутся в виде
х — а _ У — Ь г —с Rv
Переменные параметры m, n и р в этих уравнениях связаны
требованием, чтобы образующая пересекала направляющую. Урав-
Уравнения (В) решим относительно х и у:
x=k(z~c) + a; y = l(z-c) + b, (С)
где
Ь — — • 1 — —
р р
Так как образующая конической поверхности пересекает на-
направляющую, то эти значения х и у должны удовлетворять урав-
уравнениям (А). Подставляя эти значения х и у в каждое из уравне-
уравнений направляющей (А), мы получим систему двух уравнений, из
390
которых можно исключить переменную г. В результате будет
уравнение вида
/(*,/>=-О, (D)
связывающее переменные параметры k н /.
Из уравнений (С) следует
k ^x~a- i -J~b
z — c' г —с '
Заменяя в уравнении (D) k и / этими их значениями, полу-
получим уравнение вида
которому будут удовлетворять координаты любой точки образую-
образующей во все время ее движения; таким образом, уравнение A8,6)
и будет уравнением конической поверхности.
Решим задачу, связанную с определением уравнения кони-
конической поверхности.
Пример. Найти уравнение конуса с вершиной в начале коорди-
координат и направляющей
о5" ' W ~
z = с
(эллипс, лежащий в плоскости z = с).
Решение. Выполним решение в соответствии с указанным
способом. Образующая, как прямая, проходящая через начало
координат, будет иметь уравнения
х — 0_ у — о_ г —о
от я р
или
х_ у z_
т п р '
Определим из последних уравнений х и у через г
x = kz;y = lz (ft-^l-i) (E)
и, подставив эти значения в уравнения направляющей, получим
Z =С.
Теперь из этих двух уравнений исключим г. Этого легко достичь,
подставляя в первое уравнение системы г — с. Получаем уравнение
/-2 А
k* — 4- Z2 — — 1
а8 ' Ь2~ '
39»
т. е. уравнение вида A8, 6). Из соотношений (Е) следует
*-£'-{■•
Подставляем эти значения k и I в последнее уравнение:
Преобразуем его к более удобному виду. Обе части уравнения
Z2
умножим на -2:
Q2 ~ ftl — C3
ИЛИ
~.9 \^ W>. -9 yj*
Полученное уравнение есть уравнение конуса. Заметим, что
оно не содержит свободного члена, а все текущие координаты вхо-
входят в одной и той же степени — второй.
3. Уравнение поверхностей вращения.
Эти поверхности образуются при вращении кривой АВ, назы-
называемой образующей, около неподвижной прямой OR.
Поместим начало координат на неподвижной прямой О#, назы-
называемой осью вращения. Каждая точка М образующей АВ описы-
описывает окружность, центр которой находится на 0#, а плоскость,
в которой она лежит, перпендикулярна OR: образованную так
поверхность можно рассматривать как геометрическое место этих
окружностей.
Пусть
будут уравнения оси OR. Тогда уравнение плоскости, перпенди-
перпендикулярной к ней,
ах + by + сг = а.
Поэтому уравнения переменного круга
ах + by + сг = а; х2 + у* + г* = р. (В)
так как круг можно рассматривать как пересечение плоскости,
перпендикулярной к OR, со сферой, имеющей центр в точке О.
Для того чтобы выразить, что этот круг пересекает кривую
АВ, нужно исключить х, у и г из уравнений (В) и уравнений
кривой АВ, а это приводит к соотношению
( Р 0
392
откуда
«=Ф(Э). (С)
Уравнение поверхности вращения получим, исключив а и ,3
из (В) и (С), заменив в (С) а на ах + by + сг, а р — на х2 +
+ У2 + г8
ах + by + сг = Ф {х% + у1 + г2). A8,7)
Это и есть общее уравнение поверхностей вращения вокруг
прямой — = -т- = — при произвольной функции Ф.
Найдем те дифференциальные уравнения с частными производ-
производными, которые эквивалентны полученным уравнениям цилиндри-
цилиндрической и конической поверхностей и поверхности вращения.
Введем обозначения
а) Из уравнения A8,5) цилиндрической поверхности следует
у — Ьг = Ф(х — аг). A8,8)
Это уравнение определяет при произвольной функции Ф цилин-
цилиндрическую поверхность, образующие которой параллельны данной
прямой A8,2), какова бы ни была направляющая.
Продифференцируем обе части A8,8) сначала по х, а потом
по у и получим с учетом введенных обозначений
— Ьр = Ф' (х — аг) • A — ар);
1 — bq = Ф' {х — аг) • (— ад).
Исключая из этих уравнений Ф\ найдем
ap + bq = l A8,9)
(ИЛИ 0^ + ^=1).
Это уравнение уже не содержит произвольной функции и имеет
такую же степень общности, как и уравнение A8,8). Оно являете»
дифференциальным уравнением в частных производных цилиндри-
цилиндрических поверхностей.
б) Теперь' обратимся к определению дифференциального урав-
уравнения конических поверхностей. Из A8,6) следует, что
Это уравнение при произвольной функции Ф определяет кониче-
коническую поверхность с вершиной в точке (а, Ь, с). Продифференци-
Продифференцируем обе части этого уравнения по х и по у, рассматривая г как
39*
функцию независимых переменных хну. Получаем при диффе-
дифференцировании по х
При дифференцировании по у
z — c — q(y — b) ф, (х — а\ (х — а)д
* \г-с) ' (г-с)*'
ф (
B-е)* * \г-с) ' (г-с)*
Исключаем из этих двух соотношений Ф':
z-c, A8,11)
иначе: (х — а)рх + (у — Ь) fy = г — с.
Это уравнение не содержит произвольных функций. Оно является
дифференциальным уравнением конических поверхностей.
в) Нам следует теперь определить дифференциальное уравнение
поверхностей вращения. Дифференцируя обе части уравнения A8,7)
сначала по х, а потом по у, получим
а + ср = Ф' (*г + уг + 22) • Bдс +2гр);
Ь + cq =. Ф' (х* + у* + г2) • Bу + 2zq).
Исключаем из этих двух уравнений Ф':
(cy — bz)p + (az — cx)q = bx — ay, A8,12)
иначе: (су — Ьг) ~ + (аг — сх) ру = Ьх— ау.
Уравнение A8,12) и есть уравнение с частными производными
поверхностей вращения. Выпишем полученные уравнения:
уравнение цилиндрических поверхностей
уравнение конических поверхностей
(х — а) р + (у — Ъ) q = г —с;
уравнение поверхностей вращения
(су — bz)p + (az -~cx)q = bx— ay.
ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ В ЧАСТНЫХ
ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА
Линейное однородное уравнение с частными производными пер-
первого порядка имеет такой вид:
394
Здесь г—искомая функция от п независимых переменных хи х2 х„,
а Хх, Х2, ..., Хп — коэффициенты, которые являются функциями
тех же я независимых переменных, причем ни в один из коэффи-
коэффициентов искомая функция не входит.
Задачу интегрирования этого уравнения сводят к задаче интег-
интегрирования системы обыкновенных дифференциальных уравнений.
Уравнение A8,13) заменяют такой системой обыкновенных диффе-
дифференциальных уравнений:
р = р=... = р. A8,14)
Если проинтегрировать эту систему уравнений, то получим ее
(п—1) решений, которые содержат (п—1) различных произволь-
произвольных постоянных d, C2, .... Сп_х. Разрешив эти решения отно-
относительно произвольных постоянных, найдем выражения вида
Ul (Х1г Х2г • • • J -О = ^й
u2(xlt *2 хп) = С2; A8,15)
ия—i(xlt х2, ..., хп) — Сп_1,
где функции иъ и2, ..., ип_х есть известные функции независимых
переменных *ь х2, ... , хп, причем все эти функции различны и
соотношения между ними не существует.
Укажем следующие теоремы:
Теорема 1. Всякий интеграл системы A8,14) есгь интеграл
уравнения A8,13) и наоборот: всякий интеграл уравнения A8,13)
есть интеграл системы A8,14).
Теорема 2. Уравнение A8,13) или система A8,14) допускают
п — 1 различных интегралов иъ иг, ..., ua_lt все остальные ин-
интегралы заключены в формуле
где <р — произвольная функция.
На основании этих теорем заключают,, что всякое выражение
вида
<р(иь и2, ... , ип),
какова бы ни была функция <р, будет интегралом системы A8,14),
а потому и уравнения A8,13).
Общий интеграл уравнения A8,13) имеет вид
г = «р(иь и2, ..., ип). A8,16)
Из всего этого следует такое правило интегрирования линей-
линейного однородного уравнения первого порядка с частными произ-
производными:
39S
Правило. Чтобы проинтегрировать уравнение A8,13), надо со-
составить систему обыкновенных дифференциальных уравнений вида
A8,14) и проинтегрировать ее. Полученные п—1 соотношения раз-
разрешить относительно произвольных постоянных. Полученные функ-
функции ии и2, ••• , "„-1 будут интегралами уравнения A8,13), а его
общий интеграл следует записать в виде A8,16)
2 = ср(Иь И2, ... , Un),
где ф — произвольная функция.
Подчеркнем, что общие решения обыкновенных дифференциаль-
дифференциальных уравнений содержат произвольные постоянные, а общие реше-
решения, дифференциальных уравнений с частными производными — про-
произвольные функции.
Примечание. Это правило сохраняется и тогда, когда коэф-
коэффициенты Х{ в уравнении A8,13) содержат, кроме независимых
переменных хи х2, ..., х„, также и искомую функцию z.
К решению A8,16) следует присоединить и самоочевидное (три-
(тривиальное) решение уравнения A8,13)
z = Cn. A8,17)
Задача Коши. Эту задачу для уравнения A8,13) рассмотрим
только для того случая, когда искомая функция z является функ-
функцией двух независимых переменных, которые обозначим через х
и у. Уравнение A8,13) запишется в виде
й %0' <18ЛЗ'>
а система A8,14) запишется в виде одного обыкновенного диффе-
дифференциального уравнения
A814)
Разрешая его интеграл относительно произвольной постоянной, по-
получим
иЛх, У) = СХ, A8,15')
а общий интеграл уравнения A8,13') запишется так:
2 = TW- A8,160
К этому общему интегралу следует присоединить и самоочевидное
решение A8,17)
г = С2. A8,17')
Общий интеграл A8,16') уравнения A8,13') определяет семейство
поверхностей, которые называются интегральными поверхностями
этого уравнения.
396
Задача Коши состоит в том, что требуется найти в этом
семействе такую поверхность, которая проходит через заданную
кривую, определяемую уравнениями
/(ЛМ=п 1 08,18)
Для того чтобы эту поверхность найти, поступают так: из урав-
уравнений A8,15'), A8,17') и A8,18) исключают х, у и z и получают
уравнение, связывающее С, и С2; после этого Сг заменяют на ии
а С2 на 2. Полученное уравнение и определит ту интегральную
поверхность из семейства A8,16'), которая проходит через кри-
кривую A8,18).
Выделенную таким путём из общего интеграла A8,16') интег-
интегральную поверхность будем называть частным решением уравнения
A8,13').
Задача 18,1. Найти общий интеграл уравнения
дг дг п
УХ 0
и его частные решения, предполагая, что определяемая этим урав-
уравнением поверхность проходит через:
1) окружность у2 + 22 = R2; х = 0; (А)
2) эллипс jj + з = 1; х = 0; (В)
U2 22
3) гиперболу р — ^-= 1; х = 0; (С)
4) параболу г/2 = 2pz; x = 0. (D)
Решение. Заданное уравнение есть линейное однородное урав-
уравнение с частными производными первого порядка.
Составляем уравнение A8,14')
йдг dg
Интегрируя его, получим
х2 + t/a = d. (E)
Присоединяем к этому решению самоочевидное решение A8,17')
2 = C2. (F)
Общий интеграл в виде A8,16') запишется так:
2 = <р (х* + у2).
Это уравнение определяет поверхности вращения — см. формулу
A8,7).
Теперь найдем частные решения.
1. Исключив х, у и г из уравнений (А), (Е) и (F), получим
уравнение, связывающее CL и С2;
С + С\ = R\
397
Заменяя Ct и С2 их значениями из (Е) и (F), получим
х2 + уг + гг = RK
Таким образом, искомой поверхностью является сфера.
2. Исключив х, у и г из уравнений (В), (Е) и (F), найдем
уравнение, связывающее Сх и С2:
Заменяем Сх и С2 их значениями из (Е) и (F)
б2 "*"са ~ '*
т. е. эллипсоид вращения. Поступаем так же в третьем и четвер-
четвертом случаях: в третьем случае
Ьг са ~~ ''
отсюда
т. е. искомой поверхностью является двухполостный гиперболоид
вращения. В четвертом случае искомой поверхностью является па-
параболоид вращения
2рг = х* + у\
Задача 18,2. Найти общий интеграл уравнения
и его частные решения, предполагая, что определяемая им поверх-
поверхность проходит через такие линии:
1) окружность у2 + г2 =* /?2; х — а; (А)
2) эллипс -^ + — = 1} х = а; (В)
3) гиперболу £ — ^- = 1{ д; = а; (С)
4) параболу у2 = 2рг; * = с. (D)
Решение. Предложенное уравнение — также линейное одно-
однородное уравнение с частными производными первого порядка. На
основании A8,14') ему соответствует уравнение
<Ц _dy
* ~ у'
Интегрируем его:
In х = In у— In Съ или х = gr,
398
откуда, разрешая последнее равенство относительно С,, имеем
— = Li- (E)
Присоединяем к этому интегралу самоочевидное решение
г=С2, (F)
и получаем общее решение в виде A8,16')
Исключив х, у и 2 из уравнений (А), (Е) и (F), имеем уравне-
уравнение, связывающее С2 и С2
а подставляя сюда значения Сх и С2 из (Е) и (F), находим частное
решение
aV + *У = R2x2 = 0.
Приводим ответы на второй, третий и четвертый вопросы задачи:
2) а2с2г/2 + b*xh2 — 6Vx2 = 0;
3) а*с*у* — b2x2z2 — Ь2с2х* =» 0;
^ 1
Задача 18,3. Найти общий интеграл уравнения
Это уравнение — уравнение с частными производными первого по-
порядка.
Решение. Составляем прежде всего обыкновенное уравнение
вида A8,14'), которое соответствует данному
(А)
Решение данного уравнения г = Сь которое является самоочевид-
самоочевидным, мы сразу же используем для интегрирования уравнения (А),
подставив в него Сх вместо г. Получим
dx
х y—~VR*—Cl
откуда
ydx-
или
xdy ~ydx = — VR* -~ C\ dx.
399
Разделим обе части на х2:
хйу— ydx 1/"ds Л* d*
—^— — — УК —bi-s
или, учитывая, что х у~^у = d [~\, а -^ = d (— —), интегрируя,
получим
или
X
Заменим теперь Сх на г:
— У Я2 —г3
Значит, общий интеграл на основании A8,16') будет таким:
Задача 18,4. Найти общий интеграл уравнения
Решение. Это линейное уравнение с частными производными
первого порядка, искомой функцией ср от независимых переменных
х, у, z и и. Составляем систему A8,14) обыкновенных дифферен-
дифференциальных уравнений, соответствующую заданному
dir __ dy dz da
x_~ \ — уг~ а — уг~ b — уи*
У
или, умножая все знаменатели на у, будем иметь
dx dy d£ du .д.
7 - у A - у*) — у(а - уг) ~ у(Ь - уиУ *А>
Отсюда выделяем такие три уравнения
,,dx_ dy
V х ~ у{\-у*У
<Л dy = dz
> У(\-У2) У{<*-угУ
«, d£ du
й> х ~ уф-уиУ
400
Интегрируем первое из них:
d£ dy С dx _ С dy
х ~ у(\-у*У J "Г" J </A-Л!)-
Вычислим интеграл в правой части
Г dy р-уг + yi , (> Г yrfy
J yd —у2) J г/A-г/2) ^ J у ~rhi-y2)~
Отсюда для первого уравнения
J
2
ln* = In t/ — 4"In A — l/2) + InQ
и, потенцируя, имеем
ху\ТГу~г
у
Теперь приступаем к интегрированию второго уравнения, при-
присоединив к его правой части дробь — из системы (А)
dy dz ш zdy ydz dx ш
уA-уг)~ у(а-уг)' угA-у*)~ уЦа-уг)~~х'
ydz — zdy dx m ydz — zdy dx #
ay2 — y3z — yz+ y3z~~ x ' ay2 — уг ~ х '
ydz — zdy /_z\ /z\
г ~ x ' г ~ x ' z x '
a a a
У У У
Интегрирование этого уравнения дает:
откуда
х (z — ay) r
= О 2.
У
Подобным же образом для третьего уравнения получим
х(и— by)
у~Сз
и общий интеграл напишется так:
УТ=7 x(z-ay) х(и-Ьу)]
У ' У ' У Г
401
Правило для интегрирования линейных уравнений
общего вида с частными производными первого порядка
Это уравнение имеет вид
£ &...+Хя*.я-г. A8,19)
где г — неизвестная функция от xlt xit ..., хп, а Хи X , Хп,
Z — данные функции от хи х2, ..., хп, г. От уравнения A8,13)
оно отличается тем, что его правая часть не нуль, а функция не-
независимых переменных и искомой функции г.
Правила интегрирования. Для интегрирования уравнения A8,19)
следует написать соответствующую ему систему обыкновенных урав-
уравнений
dxl _dx2 _dxn_dz л Я 9m
АГ = хГ= ••■ -35Г-Г- A8>20)
Проинтегрировав эту систему и разрешив ее интегралы отно-
относительно произвольных постоянных, получаем п различных интег-
интегралов
Ut(xu xit ... , хп, г) = С,(< = I, 2, 3, ... , п). A8,21)
Общий интеграл уравнения A8,19) есть неявная функция г и запи-
записывается так:
V(UuU2,...,Un) = 0 A8,22)
где V — произвольная функция.
Произвольную функцию, входящую в общее решение, можно
найти, если известно, что определяемая ею поверхность проходит
через заданную линию A8,18). Эту поверхность находят описанным
выше способом.
Задача 18,5. Проинтегрировать уравнение
дг , . дг ,
асГХ + Ь1Гу=1
и найти произвольную функцию из условия, что интегральная по-
поверхность проходит через эллипс
S + S-'S-Л (А)
Решение. Система A8,20) обыкновенных уравнений, соответ-
соответствующая этому уравнению, будет выглядеть так:
dx _ dy _ d£
~а ~ Ь ~ 1 *
Выделяем уравнения — = -~ и -у = у • Интегрируя, получаем
dx = adz; ■ х = аг + Сх; х — аг = Сх; (В)
dy = bdz; у = Ьг+Сг; у — Ьг = Сг. (С)
402
Согласно изложенной теории на основании A8,21) общее реше-
решение имеет вид
V (х — аг, y—bz) = 0.
Сличая с формулой A8,5), заключаем, что полученное общее ре-
решение есть уравнение цилиндрических поверхностей.
Разрешим общее решение относительно искомой функции г
Теперь найдем вид произвольной функции /, исходя из условий
задачи. Исключая для этого х, у и z из уравнений (А), (В) и (Q
и найдем соотношение между Сг и С2
г2 г!
Я1« ^ П« Ly
заменяя С1 и С2 их значениями из (В) и (С), получаем
(x-azY (y-bz)* _ .
Это уравнение определяет эллиптический цилиндр.
Задача 18,6. Найти общее решение уравнения
ди , иди ди
аЛЪС
Решение. Система обыкновенных уравнений, соответствующая
данному, запишется так:
dx _ dy dz du
a b с хуг '
Выделим из этой системы три таких уравнения:
dx __dy. dx __ ~dz # dx du_
a ~~ b ' а с ' а хуг '
Первые два из них дают возможность найти два первых интеграла
ady — bdx,
или
ady — bdx = 0.
После интегрирования получим
ау—Ьх = Си
или
„_С1±Ьх
403
Точно так же второе уравнение после интегрирования даст
аг — сх = С2,
или
а •
Подставим полученные значения у и г в третье уравнение
dx du_
а хуг'
что даст
dx a*du
а ~ (Cl + bx)(Ci+cx)x*
ИЛИ
cPdu = х (Cj, + bx) (С, + ex) dx,
откуда, интегрируя, получаем
а*и = САу + (ЬС2 + 00^ + Ьс^ + С3,
а, заменяя Сх и С2 их значениями, будем иметь
а'и = (ау — bx) (аг — сх) у + [Ь(аг —
+ Ьс-^ + С3,
или после упрощений
а'и = а2уг ^-аFг + су) £ ^
откуда
t*u — a*yz!j + a(bz + су)^ -Ьс^ = С3.
Общий интеграл запишется так:
v(a*u— a*yzj + афг + сд)~ — Ьс^, ау — Ьх, аг —
или
а*и — а*уг£ + а(Ьг + су)~ — Ьс~ = <?(ау-Ьх, аг — сх).
Задача 18,7. Проинтегрировать уравнение
Решение. Составляем систему A8,20) обыкновенных диффе-
дифференциальных уравнений, соответствующую заданному
dx dy dz
~ip ~ х~у~ ахг'
„ dx dy dy dz
Выделяем уравнения ^ = fy и fy = —.
404
Преобразовывая их, получим
xdx — ydy = 0
и
dy dz
у ~ аг'
а интегрируя, находим первые интегралы
2 2 ~~ 2
ИЛИ
*•-*• = С,
и
In£/r=lln2 In C2,
v a a "
откуда
In г/ = - In J.
ИЛИ
fT я г г _ п
с;; у - с;; ^ ~ Сг<
Общий интеграл будет выглядеть так:
откуда
ИЛИ
Задача 18,7. Найти общий интеграл уравнения
дг , дг 1
Решение. Предложенное уравнение является линейным. Соот-
Соответствующая ему система A8,20) обыкновенных уравнений
dx dy dz
T = f "I
ИЛИ
Умножая на ху, запишем нашу систему в виде
ydx = xdy = x2y2dz;
405
а так как
ydx 4- xdy = d (xy),
можем переписать,
ИЛИ
±. £(**!>-
2 ()i -
±
2
Таким образом, мы получили два уравнения:
dx
Интегрируем первое из них:
1п*= \пу — 1пСь
или
— = X
т. е.
X *'
Интегрирование второго дает
а общий интеграл его имеет вид
или
и окончательно
Задача 18,8. Найти общий интеграл уравнения
дг дг ,
Решение. Предложенное уравнение является
стема A8,20) обыкновенных уравнений, которая ему
запишется так:
d£ _ dy dz
~U ~x ~ x + y'
406
и мы получим два уравнения
У
или
Интегрируем первое
т. е.
откуда
т. е.
х х+ у х+ у
dx — dy = dz.
из них:
— xdx = ydy,
xdx + ydy = 0,
*,»*_ с,
~2 "^ ~2 — ~2 '
x* + y* = Cv
Интегрируя же второе, будем иметь
dx
или
Общий интеграл
\
откуда
т. е.
а полагая
— dy = dz; d (л: — r/) = dz;
x — у — z = C2.
2 = *— t/ — f(x* + уг),
общее решение получим в виде
2=x-y + f(x* + y*);
Задача 18,9. Найти общий интеграл уравнения
| g =1.
Решение. Это уравнение также является линейным неодно-
неоднородным уравнением, и система A8,20) обыкновенных уравнений,
ему соответствующая, будет такой:
dx dy dz
sin x cos x 1 '
,. dx dy cos x . , «. dx dz
откуда 1) -:— =—— или -:— dx = dy и 2) -— = -p.
J ' sin x cos x sin x a ' sin x 1
407
Интегрируем первое из них:
In sin* = у— Сх
или
у — In sin х = Cj.
Интегрирование же второго уравнения дает
или
г — In tg у = С2.
общий интеграл
V\z — In tg ^, y~\nsinxJ=Q,
т. е.
г — In tg-| = <р (г/ — In sin *),
или
г = In tg у + 9 (г/ — In sin *).
Задача 18,10 (для самостоятельного решения). Найти общий
интеграл уравнения
ox v ду
Ответ.
1 1
ч *""', ху) = 0;
Задача 18,11 (для самостоятельного решения). Найти общий
интеграл уравнения
_у_ дг , х дг
Т* дх + ёУ Ту * ХУ2'
Ответ. Общий интеграл уравнения
V[е^-*)'х -г, (х— 1)ех — (у— 1)ev] = 0,
откуда
еР-*) *хг = <? [(х — 1) ех — (у — 1) еу\
или
г = е'*-1) '~х • 9 [(* — 1) е* — (г/ — 1) е").
Задача 18,12. Найти общий интеграл уравнения
408
Ответ.
X ' Z X'
1
или, решая относительно ие*. имеем
5/1 1 1
Задача 18,13. Определить общий интеграл уравнения
дг , дг
х + У
Решение. Система A8,20) обыкновенных уравнений, соответ-
соответствующая этому линейному неоднородному уравнению, будет запи-
записана так:
dx dy dz
х ~ У ~ Ух* + у*'
Из нее выделим два уравнения
dx dy dx dz
~*~ У x ~ yx* + ys'
Интегрируем первое,
In x = In у — In Cx
или
■* ~ c~ • T* e> ~x ~ ^v
С помощью полученного решения проинтегрируем второе урав-
уравнение
dx dz
которое преобразуем так:
dx_ dx
х
Заменим в нем ~ на С\.
Сокращаем еще на —:
dz
dx =
T+cf
409
и, интегрируя, получим
х г \ г
— 11 » т '
У\ + с]
или, подставляя Сх = —, найдем
с
X —
а отсюда
хг р
Теперь общий интеграл запишется так:
или
* У х* + у* -хг = Ух* + f 9 (-2.
Обозначая
имеем окончательно
Задача 18,14 (для самостоятельного решения). Найти общие
интегралы уравнений
+ *
Ответ.
1) г =
2) г =
3) г = ^(*2
4) г =
5) г =
410
Задача 18,15 (для самостоятельного решения). Найти общие
интегралы уравнений и их частные решения, предполагая, что по-
поверхность, определяемая уравнением, проходит через заданную
кривую
Кривая
2 = 0; ху — а2\
Кривая
х + у + г = 0; х2 + у2 + z2 = R\
Ответ.
1) ху + г2 = а2;
2) (х2 + у2 + г2J = 2R2 (х2 + у2 + ху).
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1. Ф. Р. Рант махе р. Теория матриц. Изд-во «Наука», М., 1967.
2. С. В. Фролов, Р. Я. Шостак. Курс высшей математики. Изд-во
«Высшая школа», М., 1966.
3. Р. Фрезер, В. Дункан, А. Коллар. Теория матриц н ее прило-
приложения к дифференциальным уравнениям и динамике. Изд-во иностр. литературы,
М., 1950.
4. А. П. Фили и. Некоторые элементарные сведения из линейной алгебры.
Изд-во «Судпромгнз», 1961.
5. Б. В. Булгаков. Колебания. Гос. изд-во техн.-теорет. лит-ры, М., 1954.
6. К. Л а н ц о ш. Практические методы прикладного анализа. Гос. изд-во
фнз.-матем. лит-ры, М., 1961.
7. М. Дж. Сальвадор и. Численные методы в технике. Изд-во иностр.
лит-ры, М., 1955.
8. Б. П. Д е м н д о в и ч и И. А. Марон. Основы вычислительной матема-
математики. Физматгиз, М., 1960.
9. А. С. X а у с х о л д е р. Основы численного анализа. Изд-во иностр. ли-
литературы, М., 1956.
10. И. П. Мы со вс к их. Лекции по методам вычислений. Физматриз, М.,
1962.
11. И. С. Бе резин и Н. П. Жндков. Методы вычислений, Физматгнз,
М., 1959.
СОДЕРЖАНИЕ
Стр.
Первое практическое занятие. Численное решение алгебраических урап-
нений 5
Второе практическое занятие. Численное решение алгебраических урав-
уравнений (продолжение) • 36
Третье практическое занятие. Решение трансцендентных уравнений . . 61
Четвертое практическое занятие. Основные определения теории матриц 86
Пятое практическое занятие. Умножение матриц. Формулы для про-
проверки умножения матриц. Обратная матрица и способы ее получения ... 111
Шестое практическое занятие. Обращение треугольной матрицы. Разложе-
Разложение квадратной матрицы на произведение двух треугольных. Вычисление
обратной матрицы при помощи представления ее в виде двух треугольных
матриц 141
Седьмое практическое занятие. Матричная запись системы линейных
алгебраических уравнений. Численное решение линейных алгрбраических
уравнений способом исключения 173
Восьмое практическое занятие. Характеристическое уравнение матрицы.
След матрицы. Характеристические числа и собственные векторы матрицы.
Нормирование вектора. Скалярное произведение двух векторов. Ортого-
Ортогональные матрицы. Преобразование характеристического уравнения методом
Леверье 191
Девятое практическое занятие. Преобразование характеристического
уравнения методом академика А. Н. Крылова. Теорема Кэли—Гамильтона 216
Десятое практическое занятие. Применение матриц к приведению
квадратичной формы двух переменных к сумме квадратов (к каноническому
виду). Упрощение уравнений кривых второго порядка 237
Одиннадцатое практическое занятие. Поверхности уровня. Производ-
Производная по направлению. Градиент функции 257
Двенадцатое практическое занятие. Векторное поле. Потенциальные
векторы. Потенциал векторного поля. Циркуляция вектора. Линейный ин-
интеграл. Вихрь вектора 286
Тринадцатое практическое занятие. Поток векторного поля. Дивер-
Дивергенция вектора. Формула Остроградского 303
Четырнадцатое практическое занятие. Свойства дивергенции. Упраж-
Упражнения, связанные с формулами Остроградского и Стокса 329
Пятнадцатое практическое занятие. Гармонические фунции. Формулы
Грина 348
Шестнадцатое практическое занятие. Оператор Гамильтона 357
Семнадцатое практическое занятие. Криволинейные координаты. Орто-
Ортогональные криволинейные координаты. Запись в ортогональных криволиней-
криволинейных координатах основных дифференциальных операций теории поля: гра-
градиента, дивергенции, ротора и оператора Лапласа. Выражения градиента,
дивергенции, ротора и оператора Лапласа в цилиндрической и сферической
системах координат 370
Восемнадцатое практическое занятие. Интегрирование линейных диф-
дифференциальных уравнений с частными производными первого порядка . . . 388
412