И.К. Волков, СМ. Зуев, Г.М. Цветкова
СЛУЧАЙНЫЕ
ПРОЦЕССЫ
Под редакцией
д-ра техн. наук., профессора B.C. Зарубина
и Д-ра физ.-мат. наук, профессора А.П. Крищенко
Рекомендовано Министерством общего
и профессионального образования
Российской Федерации
в качестве учебника для студентов
высших технических учебных заведений
Москва
Издательство МГТУ им. Н. Э. Баумана
1999

УДК 517.1
ББК 22.171
В67
Рецензенты: проф. В.Н. Новосельцев, проф. И.Б. Погожев
В67 Волков И.К., Зуев СМ., Цветкова Г.М. Случайные
процессы: Учеб. для вузов / Под ред. B.C. Зарубина, А.П. Кри-
щенко. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1999. -448 с.
(Сер. Математика в техническом университете; Вып. XVIII).
ISBN 5-7038-1267-4 (Вып. XVIII)
ISBN 5-7038-1270-4
Книга является восемнадцатым выпуском учебного комплекса „Мате-
„Математика в техническом университете", состоящего из двадцати выпусков,
и знакомит читателя с основными понятиями теории случайных процес-
процессов и некоторыми из ее многочисленных приложении. По замыслу авто-
авторов, данный учебник должен явиться связующим звеном между строгими
математическими исследованиями, с одной стороны, и практическими за-
задачами — с другой. Он должен помочь читателю овладеть прикладными
методами теории случайных процессов.
Содержание учебника соответствует курсу лекций, который авторы
читают в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов. Может быть полезен
преподавателям и аспирантам.
Ил. 34. Библиогр. 30 назв.
Выпуск книги финансировал
Московский государственный технический
университет им. Н.Э. Баумана
УДК 517.1
ББК 22.171
© И.К. Волков, СМ. Зуев,
Г.М. Цветкова, 1999
@ Московский государственный
технический университет
ISBN 5-7038-1267-4 (Вып. XVIII) им' НЭ' ВаУмана-1999
ISBN 5-7038-1270-4 © Издательство МГТУ
им. Н.Э. Баумана, 1999

ПРЕДИСЛОВИЕ
Теория случайных процессов — интенсивно развивающийся
раздел теории вероятностей, имеющий многочисленные при-
приложения в физике, технике, биологии, медицине, экономике и
других областях знаний. Для овладения методами этой тео-
теории нужны знания не только в объеме базового курса высшей
математики и традиционных разделов курсов теории вероят-
вероятностей и математической статистики, но и ряда специальных
курсов. В частности, мы предполагаем, что читатель может
оперировать основными понятиями теории дифференциальных
уравнений математической физики, а также владеет методами
теории интегральных преобразований.
Ориентируясь на студентов технических вузов, инженеров
и научных сотрудников прикладных специальностей, мы ста-
старались вести изложение на доступном уровне, отступая иногда
от строгого математического стиля. В основном, этот подход
использован при анализе различных задач прикладного харак-
характера, если содержательный смысл их решений интуитивно ясен.
Естественно, что в одной книге невозможно охватить все
основные разделы теории случайных процессов и, тем более,
все ее приложения. По замыслу авторов, данный учебник
должен помочь читателю овладеть прикладными методами
теории случайных процессов и явиться связующим звеном
между строгими математическими исследованиями, с одной
стороны, и практическими задачами — с другой.
Надеемся, что книга будет полезна студентам, аспирантам,
научным сотрудникам и не только технических специально-
специальностей.
В начале книги (после предисловия и введения) помещен
список основных обозначений, содержащих расшифровку часто
встречающихся в тексте символов. В большинстве математи-

6 Предисловие
ческих символов использованы буквы латинского и греческого
алфавитов, написание и произношение которых представлены
после списка основных обозначений.
В конце книги приведен список рекомендуемой литерату-
литературы и предметный указатель, в который входят в алфавитном
порядке (по существительному в именительном падеже) все вы-
выделенные в тексте полужирным курсивом термины. Для
каждого термина указан номер страницы книги, на которой
он определен и выделен полужирным курсивом, или номер вы-
выпуска, в котором дано его объяснение. Выделение термина
светлым курсивом означает, что в данном параграфе он явля-
является одним из ключевых слов и читателю должно быть знакомо
значение этого термина. Читатель может уточнить это зна-
значение, найдя при помощи предметного указателя необходимую
страницу. Ссылки на другие источники даны либо путем указа-
указания номера выпуска, либо путем упоминания фамилий авторов,
по которым можно определить полные данные этих источников,
обратившись к списку рекомендуемой литературы.
Ссылки в тексте на номера формул и рисунков набраны
обычным шрифтом (например, A0.4) — четвертая формула в
десятой главе, (П2.9) — девятая формула во втором приложе-
приложении, (рис. 9.2) — второй рисунок в девятой главе).
Прежде чем приступать к изучению теории случайных про-
процессов, мы предлагаем читателю ответить на вопросы для
самопроверки и убедиться в том, что он готов к усвоению
излагаемого материала. В конце каждого вопроса римскими
цифрами обозначен содержащий соответствующий материал
номер выпуска комплекса учебников „Математика в техниче-
техническом университете".
Задания для самопроверки
1. Что понимают под множеством? Какие множества на-
называют: а) конечными; б) счетными; в) несчетными? Что
называют диаметром множества в метрическом простран-

стве? Что называют: а) объединением множеств; б) пере-
пересечением множеств; в) разностью множеств; г) допол-
дополнением множества? [I]
2. Дайте определение отображения (функции). Что
называют: а) образом множества X при отображении /;
б) прообразом множества при отображении /? [I]
3. Какие функции называют: а) четными; б) нечетными;
в) периодическими; г) тригонометрическими? Запишите
формулы Эйлера и докажите основные свойства тригономе-
тригонометрических функций. [I], [IX]
4. Что называют: а) скалярной функцией векторного
аргумента; б) вектор-функцией; в) векторной функци-
функцией векторного аргумента; г) координатной функцией;
д) бесконечно малой функцией? Как сравнивают бесконеч-
бесконечно малые функции? [I], [II], [V]
5. Дайте определение предела: а) последовательности;
б) функции. Сформулируйте признаки существования преде-
предела. Перечислите свойства функций, имеющих конечный пре-
предел. [I], [V]
6. Какую функцию называют непрерывной: а) в точке;
б) на множестве? Перечислите основные свойства функций,
непрерывных: а) в точке; б) на множестве. [I], [V]
7. Дайте определение дифференцируемой функции:
а) в точке; б) в области. Что называют частной производ-
производной от скалярной функции векторного аргумента? Приведите
формулировку теоремы о равенстве смешанных производ-
ных. [II], [V]
8. Для скалярной функции векторного аргумента запишите
формулу Тейлора и сформулируйте условия ее применимо-
применимости. [V]
9. Дайте определение локального экстремума (макси-
(максимума и минимума) скалярной функции векторного ар-
аргумента. Сформулируйте необходимые и достаточные усло-
условия его существования. [V]

Предисловие
10. Дайте определение касательной плоскости к по-
поверхности в заданной точке. При каких условиях касательная
плоскость существует? [V]
11. Что называют определенным интегралом и какой
геометрический смысл он имеет? Запишите формулу ин-
интегрирования по частям. Дайте определение те-кратного
интеграла. [VI], [VII]
12. Что называют матрицей и что понимают под разме-
размером матрицы? Какую матрицу называют: а) квадратной;
б) единичной; в) нулевой или нуль-матрицей; г) симме-
симметрической; д) диагональной; е) трехдиагональной; ж) не-
невырожденной; з) блочной; и) положительно определен-
определенной; к) неотрицательно определенной; л) ортогональ-
ортогональной? [III], [IV]
13. Сформулируйте основные свойства следующих опера-
операций над матрицами: а) сложение матриц; б) умножение
матрицы на число; в) умножение матриц; г) транспони-
транспонирование матрицы. Дайте определение обратной матрицы
и укажите ее основные свойства. Какие матрицы называют
коммутирующими (перестановочными)? [III]
14. Что понимают под следом SpA матрицы А1 Докажи-
Докажите следующие равенства, полагая, что все указанные матрицы
квадратные одного порядка, а матрица D невырожденная
симметрическая и имеет собственные числа Ajt (k=l,n):
a) Sp(A + B) = Sp{A) +Sp(B); б) Sp{AC) = Sp(CM); в) Sp{Dm) =
= t A?, m e N; r) Sp(D~l) = ? A;1. [Ill], [IV]
k=\ k=\
15. Дайте определение системы линейных алгебраиче-
алгебраических уравнений. Какую систему линейных алгебраических
уравнений называют совместной? Сформулируйте условия
существования и единственности решения системы линей-
линейных алгебраических уравнений. [III]
16. Дайте определение линейного пространства. Что
называют: а) линейной оболочкой системы векторов ли-
линейного пространства; б) линейно (не)зависимой системой

векторов линейного пространства; в) базисом линейного
пространства; г) размерностью линейного простран-
пространства? [IV]
17. Что понимают под скалярным произведением в
линейном пространстве и что называют евклидовым про-
пространством? Можно ли утверждать, что любое линейное
пространство со скалярным произведением является нор-
нормированным пространством? Дайте определение орто-
нормированного базиса евклидова пространства и запишите
формулу для скалярного произведения в этом базисе. [IV]
18. Запишите неравенство Коши — Буняковского. В
каких случаях это неравенство обращается в равенство? [IV]
19. Что называют квадратичной формой? В каких слу-
случаях квадратичную форму называют: а) положительно
определенной; б) отрицательно определенной; в) неполо-
неположительно определенной; г) неотрицательно определен-
определенной? Изложите принципиальную схему приведения квадратич-
квадратичной формы к каноническому виду с помощью ортогональ-
ортогонального преобразования. [IV]
20. Дайте определение линейного оператора. Какая
связь существует между линейными операторами и матрица-
матрицами? Дайте определение собственного вектора и собствен-
собственного значения линейного оператора. Изложите общую
схему их нахождения. [IV]
21. Что называют линейным дифференциальным опе-
оператором и обыкновенным линейным дифференциаль-
дифференциальным уравнением? Дайте определение фундаментальной
системы решений обыкновенного линейного дифференциаль-
дифференциального уравнения. [VIII]
22. Сформулируйте задачу Коши для: а) обыкно-
обыкновенного дифференциального уравнения те-го порядка;
б) системы обыкновенных дифференциальных уравне-
уравнений первого порядка; в) системы уравнений в част-
частных производных параболического типа. Сформулируй-

10 Предисловие
те теоремы существования и единственности решения этих за-
дач. [VIII], [XII]
23. Что называют дифференциальным уравнением в
частных производных: а) параболического типа; б) эл-
эллиптического типа; в) гиперболического типа? [XII]
24. Что понимают под смешанной задачей для урав-
уравнения в частных производных параболического типа?
Изложите идею метода Фурье разделения переменных для ре-
решения смешанных задач. Сформулируйте задачу Штурма —
Лиувилля. [XI], [XII]
25. Дайте определение устойчивости и асимптотиче-
асимптотической устойчивости решения задачи Коши для системы
обыкновенных дифференциальных уравнений первого
порядка. [VIII]
26. Что называют: а) интегральным преобразованием;
б) оригиналом интегрального преобразования и его изо-
изображением; в) интегральным преобразованием Фурье;
г) интегральным преобразованием Лапласа; д) сверткой
оригиналов? Сформулируйте условия представимости функ-
функции интегралом Фурье. [XI], [IX]
27. Дайте определение числового ряда. Какой числовой
ряд называют: а) знакоположительным; б) знакочереду-
знакочередующимся; в) знакопеременным; г) сходящимся; д) сходя-
сходящимся абсолютно; е) сходящимся условно? [IX]
28. Дайте определение функционального ряда. Какой
функциональный ряд называют: а) сходящимся; б) абсо-
абсолютно сходящимся; в) равномерно сходящимся? Перечи-
Перечислите основные свойства функциональных рядов, сходящихся:
а) абсолютно; б) равномерно. [IX]
29. Что называют рядом Фурье функции f(x) в L2[o,6]?
Сформулируйте условия Дирихле поточечной сходимости
тригонометрического ряда Фурье. Что называют: ор-
тонормированной тригонометрической системой функ-
функций? [IX]

и
30. Что понимают под: а) аппроксимацией; б) абсолют-
абсолютной погрешностью аппроксимации; в) относительной
погрешностью аппроксимации? [XIII]
31. Запишите: а) формулу полной вероятности; б) фор-
формулу Байеса. Дайте определение полной группы собы-
событий. [XVI]
32. Какую случайную величину называют случайной
величиной, распределенной по: а) нормальному зако-
закону; б) закону Пуассона; в) экспоненциальному закону;
г) равномерному закону; д) логарифмически нормаль-
нормальному закону; е) закону „хи-квадрат"; ж) закону Стью-
дента? [XVI], [XVII]
33. Приведите определения начальных и центральных
моментов случайной величины. Для моментов первого
и второго порядков приведите содержательную интерпрета-
интерпретацию. [XVI]
34. Дайте определение сходимости последовательности
случайных величин: а) по вероятности; б) почти навер-
наверное (или сильно); в) в среднем квадратичном. [XVI]
35. Что понимают под: а) случайными и систематиче-
систематическими ошибками измерений (наблюдений); б) реализа-
реализацией случайной величины; в) выборочной статистикой?
Как определяется: а) выборочное среднее; б) выбороч-
выборочная дисперсия; в) исправленная выборочная дисперсия;
г) выборочная ковариация? [XVII]
36. Дайте определение оценки числовой характеристи-
характеристики случайной величины, полученной по данным случайной
выборки. Как можно оценить ее качество? [XVII]
37. Что называют статистической гипотезой? Изло-
Изложите общую схему проверки любой статистической гипоте-
гипотезы. [XVII]

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
¦4 и > — начало и окончание доказательства
# — окончание примера, замечания
Е — множество действительных чисел 1-1.3
С — множество комплексных чисел 1-4.3
N — множество натуральных чисел 1-1.3
Z — множество целых чисел 1-1.3
Е" — (декартово) произведение п множеств действитель-
действительных чисел 1-2.5
Mnm(R) — множество матриц типа п х т с элементами из Е
III
М„(Е) — множество квадратных матриц порядка п с элемен-
элементами из Е III
/„, Е — единичная матрица в Мп(Ш) III
О — нуль-вектор в Е" IV
9т, в — нулевая матрица в Мпт(Ш) III
а ? А — элемент о принадлежит множеству А 1-1.1
а ? В — элемент о не принадлежит множеству В 1-1.1
iat}iLi — множество из элементов oi, 02, ..., адг 1-1.1
А — {х: ...} — множество А состоит из элементов х, обладаю-
обладающих свойством, указанным после двоеточия 1-1.1
Ad В — множество А является подмножеством множества В
(А включается в В) 1-1.2
— разность множеств А и В 1-1.4
— объединение множеств А\, А2, ..., А^ 1-1.4
л\
N
м
N
п
а =
В
Ах
^C
пересечение множеств А\, А2, ..., А^ 1-1.4
из высказывания а следует C (если а, то /3) 1-1.5

a <—> ft — высказывания а и (З равносильны (а тогда и только
тогда, когда/3) 1-1.5
V и Л — символы дизъюнкции (а V /3 читается: а или 0) и
конъюнкции (аЛ/3 читается: а и /3) 1-1.5
—>ot — отрицание высказывания а (не а) 1-1.5
Vz — для любого х 1-1.5
Зх : ... — существует такое х, что ... 1-1-5
$х : ... — не существует такое х, что ... 1-1.5
= — равно по определению 1.1
/: X —> Y — отображение / множества X в (на) множест-
множество Y 1-2.1
U(xo,e) — ^-окрестность точки xq I-5.2
N
J2 ак — сумма слагаемых alt a2, ..., aw 1-2.6
N
Yl o-k — произведение ./V сомножителей aj, a2, ..., aw 1-2.6
k=i
k=l,N — число к принимает последовательно все значения
из множества натуральных чисел от 1 до N включи-
включительно 1-2.6
х —>• a — переменное х стремится к a I-2.7
(a, 6) — скалярное произведение элементов а и 6 в евклидо-
евклидовом пространстве IV
||а|| — евклидова норма элемента а в евклидовом простран-
пространстве IV
o(h) — величина, более высокого порядка малости, чем h
1-10.1
argmax/(x) — значение аргумента функции f(x), при кото-
ром достигается тах/(х), или решение уравнения
f(y) = тах/(х) относительно у ? В 9.6
хеВ
S(x) — (J-функция Дирака XII
J(x) — единичная функция (функция Хевисайда) XI

14 Основные обозначения
А — матрица, транспонированная к матрице А III
А — матрица, обратная к матрице А III
RgA — ранг матрицы А III
detA, |Л| — определитель матрицы А III
diag(ai, ..., оп) — диагональная матрица с диагональными
элементами oi, ..., оп III
SpA — след матрицы А IV
а* — число, комплексно сопряженное к числу о 1-4.3
(?1,А,Р) — вероятностное пространство XVI, П1
Q — пространство элементарных событий XVI, П1
и — элементарное событие (исход) XVI, П1
Р[а] — вероятность события а XVI, П1
(Х,В) — измеримое пространство П1
?(и>) — случайная величина XVI, П1
F^(x) — функция распределения вероятностей случайной ве-
величины ?(и) XVI, П1
fo(x) - плотность распределения (вероятностей) случайной
величины f (w) XVI, III
)] — математическое ожидание случайной величины
f (w) XVI, П1
] — дисперсия скалярной случайной величины f(w) XVI,
П1
cov[?(lj);t](u>)] — ковариация скалярных случайных величин
?(w) и т}(ш) XVI, П1
р[€iw)'irl(UJ)] ~ коэффициент корреляции скалярных случай-
случайных величин f (w) и r}{u) XVI, П1
?f, cov[^(ol>)] — ковариационная матрица случайного вектора
f (ш) XVI, П1
Fe(x\y) = Fe(x\T)(u}) = у) — условная функция распределения
(вероятностей) случайной величины ?(<*>) при усло-
условии ф) = у, где е(ш) ± (fT(w) r)T(u))T XVI, П1

15
fe(x\y) = f?(x\ri(u>) = у) — условная плотность распределения
(вероятностей) случайной величины ?(w) при усло-
условии т}(ш) = у, где е(ш) = (fT(w) ^иГ XVI, П1
M[f(w)|y)] = М[?(и>)\г}(и>) = у] — значение условного матема-
математического ожидания случайной величины ?(w) при
условии rj(u>) = у XVI, П1
M[?(cj)|;7(cj)] — условное математическое ожидание случайной
величины ?(ш) при условии г}{ш) XVI, П1
D[?(w)|y)] = D[?(w)|;7(w) = у] — значение условной дисперсии
случайной величины ?(w) при условии т)(ш) = у
XVI, П1
D[?(cj)|;7(cj)] — условная дисперсия случайной величины ?(w)
при условии т)(и) XVI, Ш
?(t,uj), t € Т, — случайная функция 1.1
?(t,u), t Е Т = [а, 6], — случайный процесс 1.1
?(t,u), t е Т — N, {^k(^)}^Li — случайная последовательность
1.1
i^(a;|t) — одномерная функция распределения случайного про-
процесса ?(t,и), teT 1.1
f((x\t) — одномерная функция плотности вероятностей слу-
случайного процесса ?(?,и), t G Т 1.1
...,a;(jy)|ti,...,fjv) — /V-мерная функция распределения
случайного процесса f(?,u>), t e T 1.1
:B(N)l*ii'"i*Jv) — /V-мерная функция плотности ве-
вероятностей случайного процесса ?(t,w), t ? Т 1.1
— математическое ожидание случайного процесса
Z(t,uj),teT 1.2
— ковариационная матрица случайного процесса ?(i,tj),
teT 1.2
— дисперсия случайного процесса f (?,w), teT 1.2
) — ковариационная функция случайного процесса
?(t,w), *еГ 1.2

16 Основные обозначения
\,t2) — взаимная ковариационная функция случайных
процессов ?(i,o>), t ? Т, и r)(t,Lj), t ?T 1.2
>)||с/< — СК-нормаслучайного процесса ?(i,o>), t?T 3.1
lim ?(t,ij) — предел (в смысле СК-сходимости) случайного
'~**° процесса f(i,w), te Т, при i->• ?0 (*о е Т) 3.1
lim ?/то>(?,^) — предел (в смысле СК-сходимости) последова-
тельности случайных процессов {?(m)(?,^),? GTjJ^Li
3.1
?(t,Lj),t G 7о С Т — производная случайного процесса ?(i,o>),
* е т, в г0 с т з.з
f (p(t,t')?(t',u})dt' — интеграл от случайного процесса ?(t,u)),
т t G Т, с весовой функцией </>(?,?') по Т 3.4
?<[?(?,а>)] — результат воздействия линейного оператора Lt на
случайный процесс ?(i,o>), i G T 3.5
^(^) — спектральная плотность стационарного скалярного
случайного процесса ?(t,u), t ?T = [0,оо) 4.2
{Sfc}?=1 — множество возможных состояний марковского про-
процесса с дискретными состояниями 5.1
sJk — случайное событие, состоящее в том, что после j
этапов исходная система 5 находится в состоянии
5* 5.1
Pk(j) — вероятность того, что после j этапов исходная
система S находится в состоянии S^ 5.2
— условная вероятность реализации случайного собы-
события sJk при условии sJm 5.2
— матрица переходных вероятностей 5.2
р@) — вектор начальных вероятностей состоянии 5.2
Pk{i) — вероятность реализации случайного события s^., со-
состоящего в том, что в момент времени t G Т система
S находится в состоянии Sfc 5.3
Ajj(i) — плотность вероятности перехода системы из состо-
состояния S, в состояние S3 в момент времени t 5.3

17
p(t) — вектор вероятностей состояний системы в момент
времени t 5.3
Ф{и>) — частотная характеристика линейной динамической
системы 4.4
Г — матрица спектральных интенсивностей белого шу-
шума 7.1
о
?(t,Lo), t&T — центрированный случайный процесс 4.1
t
/ 4l(w(T,uj),T)dw(T,u>) — стохастический интеграл Ито функ-
s ции Ф по винеровскому процессу w(t,uj), tET —
t =[0,oo) 7.3
ty(w(T,u),T)d+w(T,ijj) — стохастический интеграл Стратоно-
вича функции Ф по винеровскому процессу w(t,(j),
teT = [0,оо) 7.3
ft(t,X,T,Y) — условная функция плотности вероятностей мар-
марковского процесса ?(t,u), t ? Т 8.1
U, Um, Umn — множества реализаций случайного процесса
Z{t,u>),teT 9.1
&к (w) — оценка вектора неизвестных параметров /3 Е В С KL,
полученная на основе случайной выборки объема К
из генеральной совокупности случайного процесса
?(t,u), teT, зависящего от 0 9.3
f(y\0) — функция плотности вероятностей случайной выбор-
выборки из генеральной совокупности случайного процес-
процесса ?(t,u>), t ET, зависящего от вектора неизвестных
параметров /3 G В с KL 9.1
A(j3) — информационная матрица Фишера 9.4
L(a\U*) — функция правдоподобия, f/* в {U,Um,UMN} 9.6
Ф(а|{/*) - критерии метода наименьших квадратов 9.7
L(a\U*) — функция квазиправдоподобия 9.6

18
Основные обозначения
Буквы латинского алфавита
Начертание
А
В
С
D
Е
F
G
Н
I
J
К
L
М 1
а
Ь
с
d
е
f
g
h
i
j
k
1
n
A a
В b
С с
D d
E e
F f
G 9
H h
I г
J j
К к
L I
M m
Произно-
Произношение
a
бэ
цэ
ДЭ
e
эф
же
аш
и
йот
ка
эль
эм
Начертание
N п
0 о
Р р
Q q
R г
S s
Т t
U u
V v
W w
X х
Y У
Z z
N п
0 о
Р р
Q ч
R г
S s
Т t
U u
V v
W w
X х
У у
Z z
Произно-
Произношение
эн
о
пэ
ку
эр
эс
тэ
У
вэ
дубль-вэ
икс
игрек
зэт
Представлен наиболее употребительный (но не единствен-
единственный) вариант произношения (в частности, вместо „йот" иногда
говорят „жи").
Буквы греческого алфавита
Начер-
Начертание
А
В
Г
Д
Е
Z
Н
G
a
C
7
S
Е
С
V
Произно-
Произношение
альфа
бета
гамма
дельта
эпсилон
дзета
эта
тэта
Начер-
Начертание
I
К
Л
м
N
[I]
0
п
ь
К
А
М
V
Z
0
IT
Произно-
Произношение
йота
каппа
ламбда
ми
ни
кси
омикрон
пи
Начер-
Начертание
Р
?
Т
т
ф
X
ф
п
р
a
т
V
X
Ф
ю
Произно-
Произношение
ро
сигма
тау
ипсилон
фи
хи
пси
омега
Наряду с указанным произношением также говорят „лямб-
„лямбда'
,мю и „ню

ВВЕДЕНИЕ
Содержание выпуска относится к одному из специальных
курсов высшей математики, который является составной ча-
частью теории вероятностей. В процессе развития теории веро-
вероятностей как науки можно условно выделить три этапа, первый
из которых связан с понятием случайного события, второй —
с понятием случайной величины, а третий — с понятием слу-
случайной функции. При этом начало первого этапа относится к
середине XVII в., второго — к середине XIX в., а третьего —
к 20-30 гг. XX в., и начало каждого следующего этапа, в прин-
принципе, не связано с завершением предыдущего.
Теория случайных процессов возникла вследствие практиче-
практической необходимости математического моделирования реальных
процессов различной природы, состояние каждого из которых в
любой фиксированный момент времени представляет собой слу-
случайный вектор соответствующей размерности. Примером слу-
случайного процесса является процесс изменения во времени про-
пространственных координат частицы, совершающей броуновское
движение. Другими примерами случайных процессов являют-
являются: процесс стабилизации полета самолета в реальных условиях,
когда он находится под постоянным воздействием случайных
изменений вектора скорости ветра и других параметров тур-
турбулентной атмосферы; процесс развития неоднородной популя-
популяции с несколькими типами индивидуумов; процессы спроса и
предложения на рынке товаров и т.д.
Фактически теория случайных процессов занимается изуче-
изучением различных семейств случайных величин, эволюционирую-
эволюционирующих во времени. При этом логически корректное определение
основных понятий теории случайных процессов в рамках акси-
аксиоматики теории вероятностей создавало и создает много труд-
трудностей теоретико-множественного характера. Они связаны,

20 Введение
например, с определениями непрерывности, дифференцируемо-
сти, интегрируемости и других свойств случайных процессов.
Именно поэтому в монографиях по теории случайных процес-
процессов значительное место занимает анализ развития теоретико-
множественных конструкций. Они написаны на высоком те-
теоретическом уровне и, как правило, сложны для понимания
специалистов, занимающихся прикладными проблемами в раз-
различных областях человеческой деятельности, решение которых
предполагает широкое использование методов теории случай-
случайных процессов. А так как литература по прикладным аспектам
теории случайных процессов, доступная для понимания ши-
широкому кругу студентов, аспирантов и научных работников,
имеющих математическую подготовку в объеме стандартного
курса высшей математики, весьма немногочисленна, то возни-
возникла необходимость в написании этой книги.
Основной целью написания предлагаемого учебника яви-
явилось систематическое изложение элементов теории случайных
процессов, усвоение которых должно способствовать активно-
активному овладению ее прикладными методами при решении прак-
практических задач. Различный уровень общей математической
подготовки читателей и разнообразие их запросов авторы по-
попытались учесть компоновкой материала по разделам с воз-
возрастающими уровнями сложности. Все основные понятия и
методы иллюстрированы примерами, а в конце каждой главы
приведены контрольные вопросы и упражнения.
Отметим, что учебник не содержит библиографии по тео-
теории случайных процессов и ее приложениям. В списке рекомен-
рекомендуемой литературы указаны лишь те источники, обращение к
которым поможет читателю получить более полные сведения по
отдельным вопросам теории случайных процессов и в смежных
разделах высшей математики.
Содержание первых четырех глав соответствует базовому
курсу теории случайных процессов. Мы предполагаем, что
читатель может оперировать основными понятиями высшей
математики (элементы линейной алгебры, дифференциальное

21
и интегральное исчисление, тригонометрические ряды Фурье
и интеграл Фурье, обыкновенные линейные дифференциальные
уравнения) и теории вероятностей в объеме втузовского курса.
При этом, для удобства читателей и во избежание разночтения
в соответствующих определениях теории случайных процессов,
авторы сочли целесообразным привести основные определения
базового курса теории вероятностей в приложении 1.
В первой главе введены и обсуждаются основные поня-
понятия теории случайных процессов: случайная функция; случай-
случайный процесс; случайная последовательность; сечение случайной
функции; реализация случайной функции; конечномерный за-
закон распределения случайной функции. Обсуждается вопрос
о корректности задания случайного процесса посредством его
конечномерных законов распределения. Дается определение
стохастически эквивалентных случайных процессов, анализи-
анализируются их свойства и возможные приложения. Вводятся по-
понятия математического ожидания, ковариационной матрицы,
ковариационной функции и связанных с ними числовых харак-
характеристик случайного процесса с последующим изучением их
основных свойств.
Во второй главе рассмотрены важнейшие типы случайных
процессов, представляющих особый интерес для приложений
(стационарные, гауссовские, с независимыми приращениями,
винеровские, марковские, пуассоновские). При этом отмеча-
отмечается особое место винеровских процессов как в теоретических,
так и в прикладных исследованиях.
Третья глава посвящена изложению элементов стохастиче-
стохастического анализа (предел, непрерывность, дифференцируемость
и интегрируемость случайных процессов) с использованием по-
понятия сходимости в смысле среднего квадратичного как наибо-
наиболее приемлемого для практических приложений. В теории слу-
случайных процессов используют и другие виды сходимости и, как
следствие, другие виды непрерывности, дифференцируемости
и интегрируемости — эту информацию читатель может найти
в специальной литературе, например в книге А.Д. Вентцеля.

22 Введение
При рассмотрении технических приложений, в частности при
решении задач о реакции линейных динамических систем на
„шумы" входных сигналов, в данной и последующих главах со-
соответствующие стохастические дифференциальные уравнения
следует воспринимать формально, так как их теория изложе-
изложена лишь в седьмой главе. В последнем разделе третьей главы
введены основные понятия эргодических случайных процессов
и изучены их свойства.
В четвертой главе рассмотрены основные положения спек-
спектральной теории стационарных (в широком смысле) случайных
процессов: представимость стационарных случайных процес-
процессов в виде конечных или счетных сумм гармоник с различными
частотами и случайными амплитудами; интегральное предста-
представление стационарного случайного процесса. Следует отметить,
что в данном учебнике изложена лишь принципиальная схема
обоснования возможности интегрального представления стаци-
стационарного случайного процесса, так как строгое доказательство
является достаточно сложным, в чем читатель может убедить-
убедиться сам, ознакомившись, например, с соответствующим разде-
разделом книги А.Д. Вентцеля. В процессе анализа достаточных
условий существования интегрального представления стацио-
стационарного случайного процесса введено понятие спектральной
плотности как изображения экспоненциального интегрального
преобразования Фурье его ковариационной функции. Приве-
Приведены содержательные интерпретации спектральной плотности
и рассмотрены ее основные свойства. Далее дано определение
„белого шума" как стационарного (в широком смысле) случай-
случайного процесса, обладающего постоянной спектральной плотно-
плотностью, изучены его свойства и возможности использования при
решении практических задач. В качестве одного из возможных
приложений спектральной теории рассмотрены задачи, связан-
связанные с преобразованиями стационарных случайных процессов
при их прохождении через линейные динамические системы.
Следующие две главы посвящены изучению теоретических и
прикладных аспектов теории марковских процессов с дискрет-

23
ными множествами состояний. Заметим, что многие реальные
физические системы имеют не более, чем счетное множество
возможных состояний, а их поведение адекватно моделируется
посредством марковских процессов. Поэтому аппарат теории
марковских процессов с дискретными состояниями широко ис-
используется в теории систем, в исследовании операций и других
прикладных дисциплинах.
В пятой главе, после введения основных понятий теории
марковских процессов с дискретными состояниями и их обсу-
обсуждения, основное внимание уделяется обоснованию и анализу
системы уравнений Колмогорова для вероятностей состояний.
Детально изучаются свойства решения задачи Коши для си-
системы уравнений Колмогорова, для чего использовано пред-
представление соответствующей нормированной фундаментальной
системы решений в виде матричной экспоненты, основные све-
сведения о которой читатель может найти в приложении 2. Для
иллюстрации основных положений теории марковских процес-
процессов с дискретными состояниями даны определения процесса
„гибели — размножения" и циклического процесса, проанали-
проанализированы их свойства и предельные (t~? +oo) характеристики.
В шестой главе изложена элементарная теория массового
обслуживания, которая опирается на методы исследования мар-
марковских процессов с дискретными состояниями. Материал этой
главы предназначен для первого знакомства с теорией массо-
массового обслуживания и ее возможными приложениями, а также
для подготовки читателя к освоению специальной литературы
по этому разделу.
Для усвоения материала седьмой и восьмой глав, в которых
содержатся основные положения теории марковских процес-
процессов с непрерывными состояниями и некоторые ее приложения,
читатель должен быть знаком с элементами теории дифферен-
дифференциальных уравнений математической физики, иметь предста-
представление о постановках задач для дифференциальных уравнений
с частными производными параболического типа и методах их
Решения.

24 Введение
В седьмой главе сформулирован основной принцип постро-
построения детерминированной модели состояния динамической си-
системы, обоснована необходимость введения в нее случайных
возмущений. Доказано, что процесс случайных возмущений
является „белым шумом", и выписана стохастическая модель
состояния, представляющая собой задачу Коши для системы
стохастических дифференциальных уравнений. Далее изучены
свойства решения задачи Коши для системы линейных стоха-
стохастических дифференциальных уравнений и доказано, что этим
решением является нормальный марковский процесс, матема-
математическое ожидание и ковариационная матрица которого явля-
являются решениями соответствующих детерминированных задач
Коши. Кроме того, определены условия, при выполнении кото-
которых этот случайный процесс является стационарным или может
считаться стационарным. В этой же главе введены понятия
стохастических интегралов и дифференциалов, рассмотрены их
свойства и возможности применения при изучении нелинейных
стохастических моделей состояния.
В восьмой главе рассмотрены общие свойства марковских
процессов с непрерывными состояниями, обосновано уравне-
уравнение Маркова — Смолуховского — Чепмена — Колмогорова,
на базе которого выведены первое и второе уравнения Кол-
Колмогорова для условных вероятностей. Значительное внимание
уделено анализу возможных постановок задач для уравнений
Колмогорова и методам их решения. Доказано, что любая
стохастическая модель состояния определяет некоторый мар-
марковский процесс и любой марковский процесс удовлетворяет
некоторой стохастической модели состояния. В качестве ил-
иллюстраций рассмотрены: задача об определении вероятности
пребывания значений марковского процесса в заданной обла-
области; задача об определении закона распределения времени пре-
пребывания значений марковского процесса в заданной области;
задача об определении среднего числа выбросов значений мар-
марковского процесса за данный уровень.

25
Последние две главы посвящены задаче оценивания неиз-
неизвестных параметров случайного процесса по дискретным зна-
значениям его выборочных реализаций. Эта задача занимает
особое место в статистике случайных процессов в связи с ее
прикладной значимостью. Мы предполагаем, что читатель мо-
может оперировать основными понятиями математической ста-
статистики в объеме базового курса.
В девятой главе, после анализа различных возможных ва-
вариантов наблюдений и статистических моментов случайного
процесса, сформулированы задача оценивания его неизвестных
параметров и требования, предъявляемые к ее решению. Для
изучения свойств оценок и методов их определения рассмотре-
рассмотрены случайные выборки, соответствующие различным возмож-
возможным вариантам данных наблюдений, и их совместные функции
плотности вероятностей. Дано определение эффективной оцен-
оценки вектора неизвестных параметров случайного процесса и
проведен анализ неравенства Рао — Крамера. Сформулирова-
Сформулирована и доказана теорема о единственности решения задачи оце-
оценивания. Рассмотрены методы максимального правдоподобия
и наименьших квадратов для нахождения оценок неизвестных
параметров случайного процесса по данным наблюдений и про-
проанализированы их свойства.
Результаты, полученные в девятой главе, использованы в
следующей десятой главе для решения задачи оценивания не-
неизвестных параметров стохастической модели состояния по
данным наблюдений. Установлены условия единственности ре-
решения этой задачи и рассмотрен случай, когда данные наблюде-
наблюдений содержат случайную ошибку измерений. Последнее сделало
уместным рассмотрение основ теории фильтрации, а именно,
фильтра Калмана.

1. ИСХОДНЫЕ ПОНЯТИЯ
И ОПРЕДЕЛЕНИЯ
Теория случайных функций является разделом теории веро-
вероятностей и, как следствие, относится к классической математи-
математике, которая строится дедуктивно, исходя из некоторой системы
аксиом. Основой теории случайных функций являются фун-
фундаментальные понятия и результаты базовых разделов теории
вероятностей.
1.1. Случайная функция, случайный
процесс и случайная последовательность
Пусть (?1,А, Р) — вероятностное пространство; (Кп,В) —
измеримое пространство; t — параметр, совокупность значе-
значений которого Т в общем случае является произвольным множе-
множеством; и G fi — элементарное событие.
Определение 1.1. Случайной функцией f (t,w), t e T,
называют измеримое отображение ?: Q —>¦ Е" пространства
элементарных событий Q в Rn, зависящее от параметра t.
Если Т = [а, 6] — отрезок числовой оси, а параметр t ин-
интерпретируют как время, то вместо термина „случайная функ-
функция" используют термин „случайный процесс". При п= 1
случайный процесс f (?,w), t Е Т, называют скалярным слу-
случайным процессом, а при п J> 2 его называют векторным
случайным процессом или п-мерным случайным процес-
процессом. Векторный (n-мерный) случайный процесс ?(i,o>), t ? Т,
Т
можно записать в виде ?(t,Li>) = (?i(t,uj) ... ^n(^^)) • При этом
скалярные случайные процессы ?t(t,u)), t E.T, называют его ко-
координатными случайными процессами.

1.1. Случайная функция, процесс и последовательность
27
Если T — N, то вместо случайной функции ?(t,u), t ? Т,
говорят о случайной последовательности, которую обо-
обозначают также {^(^)}ь=1-
При любом фиксированном значении параметра t ? Т слу-
случайная функция ?(t,w), t ? Т, является случайным вектором,
называемым сечением этого случайного процесса.
Если зафиксировать элементарное событие ш ? Q, то в этом
случае ?(t,u) является (неслучайной) функцией параметра t,
которую называют траекторией случайного процесса
?(t,u), t ? Т, или его реализацией.
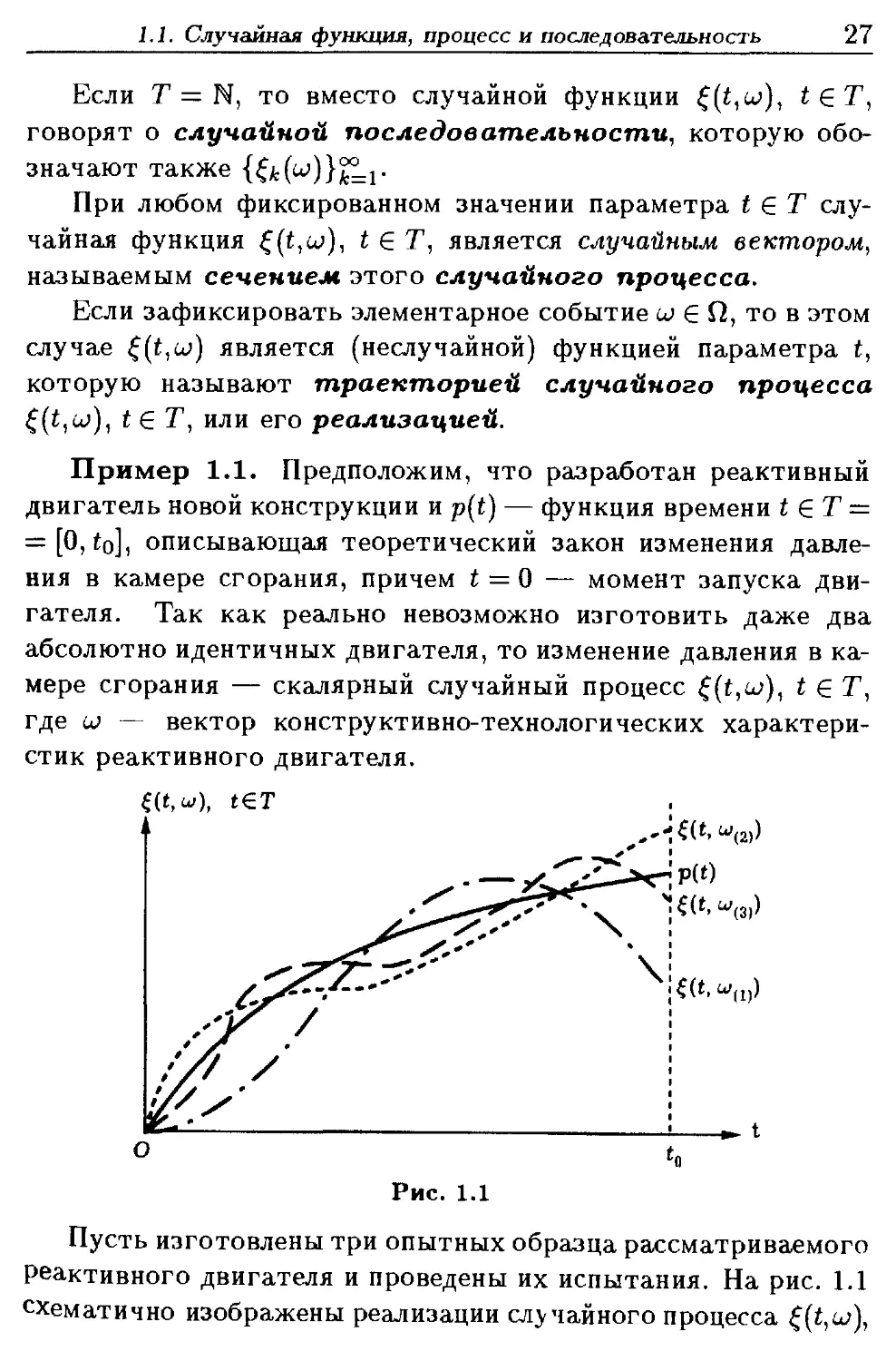
Пример 1.1. Предположим, что разработан реактивный
двигатель новой конструкции и p{t) — функция времени t ? Т —
= [0, to], описывающая теоретический закон изменения давле-
давления в камере сгорания, причем t = 0 — момент запуска дви-
двигателя. Так как реально невозможно изготовить даже два
абсолютно идентичных двигателя, то изменение давления в ка-
камере сгорания — скалярный случайный процесс ^(t,o>), t ? Т,
где и — вектор конструктивно-технологических характери-
характеристик реактивного двигателя.
t€T
(«)
Рис. 1.1
Пусть изготовлены три опытных образца рассматриваемого
реактивного двигателя и проведены их испытания. На рис. 1.1
схематично изображены реализации случайного процесса ?(t,u>),

28 I. ИСХОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
t ЕТ = [0, to]- При этом W(fc) — вектор конструктивно-техно-
конструктивно-технологических характеристик А:-го образца; ?(?,W(fc)) — изменение
давления в камере сгорания Аг-го образца реактивного двигате-
двигателя; t0 — момент окончания фиксации давления. #
Если для случайного процесса ?(t,u>), t ? Т, зафиксировать
произвольное значение параметра t, то получим n-мерный слу-
случайный вектор ?(?,о>), являющийся сечением случайного про-
процесса. Закон распределения вероятностей этого случайного
вектора называют одномерным законом распределения
случайного процесса ?(t,u), t ? Т. Функцию распределения
(вероятностей) случайного вектора ?(t,uj)
X
Ft(x\t)±P[t(t,u,)<x]= J f((y\t)dy,
— оо
где
X Х\ Хп
Jft(y\t)dy = J...Jft(yi,...,yn\t)dyi...dyn,
— оо —оо
называют одномерной функцией распределения случай-
случайного процесса ?(t,tj), t gT, a f((x\t) — одномерной функ-
функцией плотности вероятностей случайного процесса
?(t,u)y t Е Т, которая может быть и обобщенной (см. П1).
Если зафиксировать значения t^ параметра t E T, k — 1, п, то
приходим к совокупности из N случайных n-мерных векторов
^)}^-1 с функцией распределения (вероятностей)
F({x{1),...,x{N)\tu...,tN)±P[{{tk,U) < x(k), k=TJ?} =
= ] ¦¦¦] fdy(i),--4y(N)\h,---,tN)dy{1)...dy{N),
— оо —оо

1.1. Случайная функция, процесс и последовательность 29
называемой конечномерной (N-мерной) функцией рас-
распределения случайного процесса (j{t,Li>), t ? Т. В этом слу-
случае Д(?(!),...,Z(jv)|*i)- -.,?n) — конечнолсернал (JV-лсернал)
функция плотности вероятностей случайного про-
процесса ?(t,u>), t ? Т, (возможно обобщенная). Функции
задают конечномерный (N-мерный) закон распределения
случайного процесса ?(t,a>), t ?Т.
Не следует путать конечномерные функции плотности веро-
вероятностей (функции распределения) случайного процесса и ко-
конечномерные функции плотности вероятностей (функции рас-
распределения) его сечений. В зависимости от контекста мо-
может идти речь об /V-мерной функции плотности вероятностей
(функции распределения) скалярного случайного процесса и об
одномерной функции плотности вероятностей (функции рас-
распределения) векторного случайного процесса.
Фактически случайный процесс ?(?,w), t ? Т, можно рассма-
рассматривать как совокупность всех его возможных сечений. Таким
образом, в общем случае случайный процесс ?(t,u), t ? Т, не
может быть полностью определенным, так как он представим
несчетной совокупностью своих сечений и невозможно постро-
построить совместный закон распределения всех его сечений. Поэтому
любой случайный процесс ?(t,uj), t ? Т = [а, Ь], в общем случае
не является полностью определенным и при решении различ-
различных задач, как теоретического, так и прикладного характера,
исследователь вынужден ограничиваться использованием ко-
конечномерных законов распределений.
Определение 1.2. Случайные процессы f (t,w), t ? Т, и
^(^w), t ? Т, определенные на одном и том же множестве Т, в
одном и том же вероятностном пространстве (Q,A,P) и прини-
принимающие значения в одном и том же измеримом пространстве
(К71,/?), называют стохастически эквивалентными, если
Р [?{t,u) ф r](t,u)] = 0 для любого t ? Т.

30 1. ИСХОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Таким образом, стохастически эквивалентные случайные про-
процессы ?(t,u)), t Е.Т, и ri(t,uj), t GT, могут отличаться друг от
друга лишь на подмножестве Qq множества Q, имеющем нуле-
нулевую вероятность.
Если случайные процессы ?(?,w), t Е Т, и r}{t,u)), t ? Т,
являются стохастически эквивалентными, то их конечномерные
функции распределения совпадают, т.е.
для любого N ^ 1 и для любых tk € Т, к = 1, N.
Реализации стохастически эквивалентных случайных про-
процессов могут быть совершенно различными.
Пример 1.2. Пусть Т = [0,1] и случайная величина г(ш)
распределена равномерно на множестве Т. Рассмотрим два
случайных процесса:
[о, гфт{ы),
Эти скалярные случайные процессы являются стохастиче-
стохастически эквивалентными. Действительно, при любом t E T имеем
P[S(t,u>)fr(t,u,)] = P[t=T(u)] =0,
n(t, ш), t€T так как в случае непрерывной ска-
скалярной случайной величины веро-
вероятность попадания в точку равна
нулю. Любая реализация случай-
случайного процесса ?(i,w), t е Т, — то-
тождественный нуль, а реализация
случайного процесса ri(t,Lj), t 6 Т,
имеет разрыв в случайной точке
Рис. 1.2 t = r{u)) (рис. 1.2). #
При решении различных задач теоретического и прикладно-
прикладного характера в ряде случаев бывает удобной замена исходного

1 2. Математическое ожидание и ковариационная функция 31
случайного процесса стохастически эквивалентным. Тогда по-
получаемые выводы с точностью до случайных событий, облада-
обладающих нулевой вероятностью реализации, могут быть отнесены
к исходной задаче.
1.2. Математическое ожидание
и ковариационная функция случайного процесса
Совокупность всех конечномерных законов распределения
случайного процесса является полной его характеристикой. Но
при решении многих прикладных задач по разным причинам
ограничиваются использованием одно- и двумерных законов
распределений случайных процессов и связанных с ними мо-
моментов первого и второго порядков, существование которых
предполагается. Отметим, что моментами k-го порядка
случайного процесса называют соответствующие моменты
его сечений.
Определение 1.3. Математическим ожиданием век-
векторного случайного процесса ^(t,uj), t g X1, называют неслу-
неслучайную вектор-функцию m^(t), значение которой при каждом
фиксированном t g T равно математическому ожиданию слу-
случайного вектора ?(t,u>), являющегося сечением исходного слу-
случайного процесса, соответствующего рассматриваемому значе-
значению t.
Если f^(x\t) — одномерная функция плотности вероятно-
вероятностей n-мерного случайного процесса ?(t,u>), t g X1, т.е. плот-
плотность распределения (вероятностей) его сечения (возможно
обобщенная), соответствующего рассматриваемому значению
t G X1, то, согласно определению П1.13 математического ожида-
ожидания случайного вектора, имеем
me (t) =
= J xft(x\t)dx,

32
1 ИСХОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
где f{(x\t) = f((xi,.. ,xn\t), dx-dxidx2...dxr
и для любого фиксированного к = 1, п имеем
где f?k(x).\t) — плотность распределения (вероятностей) к-й
компоненты сечения исходного случайного процесса в момент
времени t ? Т. Таким образом
mk{t)= / xkft(x\t)dx =
К"
— oo \R"-1
и окончательно
teT.
Математическое ожидание m^(t) случайного процесса ?(t,u),
t G Т, можно интерпретировать как его усредненную траекто-
траекторию.
Если / : X —> Y, где X — некоторое множество и У с
С Mmn(R), то при дальнейших рассуждениях будем говорить,
что определена матричная функция типа mXnc областью
определения X и областью значений Y С Mmn{R)

I 2 Математическое ожидание и ковариационная функция 33
Определение 1.4. Ковариационной матрицей (мат-
(матрицей ковариаций) n-мерного случайного процесса ?(t,uj),
t ? Т, называют неслучайную матричную функцию T>t(t) типа
п X п, которая при каждом фиксированном t ? Т представля-
представляет собой ковариационную матрицу случайного вектора ?(?,и),
являющегося сечением исходного случайного процесса, соот-
соответствующего рассматриваемому значению t.
Если f({x\t) — одномерная функция плотности вероятно-
вероятностей в-мерного случайного процесса ?(t,u>), t ? Т, то
= J(x -
x -
где
1
mn(t) J \xn
eMn(R),
и поэтому ковариационная матрица n-мерного случайного про-
процесса f (?,w), t G Т, является симметрической. Ее диагональные
элементы имеют вид
2)] = <rl(t), A = 17^.
Таким образом, при каждом фиксированном i ? Т значение
равно дисперсии скалярной случайной величины, являю-
Щеися k-ii компонентой сечения исходного случайного процесса,

34 1. ИСХОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
соответствующего рассматриваемому значению t. При i ф j по-
получаем, что
т.е. при каждом фиксированном t G Т значение StJ(i), гф j, рав-
равно ковариации двух скалярных случайных величин, являющихся
г-й и j-й компонентами сечения исходного случайного процесса,
соответствующего рассматриваемому значению t.
При решении прикладных задач используют понятие дис-
дисперсии сг?@ n-мерного случайного процесса ?(?,w), t ? Т.
По определению полагают, что
т.е. она равна следу SpS^(t) ковариационной матрицы этого
векторного случайного процесса. При этом очевидно, что
a\{t) = M[{t(t,U) - m^(t))T^(t,u) - т&))].
Определение 1.5. Ковариационной функцией п-мер-
ного случайного процесса ?(?,w), t E T, называют матричную
функцию Kz(ti,t2) типа пхп двух скалярных переменных t\
и ^2) значение которой при фиксированных ti,t2 ё Т равно
ковариации двух случайных векторов ?(t\,u) и
определяемой следующим образом:
=J /
R
(*1(A:) ••• *n(fe)) S Rn И
ная функция плотности вероятностей (возможно обобщенная)
исходного случайного процесса.

1.2. Математическое ожидание и ковариационная функция 35
Согласно определению 1.5, на пересечении г-й строки и j-ro
столбца ковариационной функции K^(ti,t2) га-мерного случай-
случайного процесса ?(t,w), t ?T, находится скалярная функция
KUj{tut2) = M[tf,(tbw) - m,(ti))(f,(t2,w) - m}{t2))]
двух скалярных переменных t\ и t2. Ее значение при фиксиро-
фиксированных t\, ti G Т равно ковариации двух скалярных случайных
величин ?,(t\,u) и ?j(?2)^)j обладающих математическими ожи-
ожиданиями mt(ti), m^t-i) и являющихся г-й и j-й компонентами
и-мерных случайных векторов ?(t\,uj) и ?{t2,u>) соответствен-
соответственно, т.е.
Пример 1.3. Пусть а(и) и /3(и) — скалярные случай-
случайные величины с числовыми характеристиками: М[а(ш)] = та;
ЪЛ[/3{ы)] = тр- D[o(w)] = а2а; D[/3(w)] = <r|; cav[a{u)tfi(u)] = x.
Определим математическое ожидание и ковариационную функ-
функцию скалярного случайного процесса
?(t,w) = а{ш)cos{(pt) + C{uj)s\n{ipt), t e T = [0, ос),
где <р ? R — постоянная. Имеем
= macos(ipt)
Пусть далее
Тогда
0 о °
= a(u)cos(<pt)+f3{u)sln(<pt).

36 1 ИСХОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
В этом случае
[i(t,,w)i(t2,w)] = M[(aHJ]cosM
cos((pt2)}
s\n(<pt2) = <TaCas(<pt
+t2)] + (Tps\n(<ptx) sin (<pt2).
В частности, если случайные величины a(a>), /3(a>) являются
некоррелированными {х— 0) и сг^ = сг2 = сг^, то
Теорема 1.1. Пусть ?(i,a>), t ?Т, — n-мерный случайный
процесс, для которого существует ковариационная функция
Kz(ti,t2). Тогда
3) евклидова норма ковариационной функции, т.е. корень
квадратный из суммы квадратов ее элементов, удовлетворяет
неравенству Коши — Буняковского
4) если (p(t) — неслучайная n-мерная вектор-функция ска-
скалярного аргумента t 6 Т, A{i) — матричная неслучайная функ-
функция типа п X п, определенная на Т, и
teT,
то в этом случае
5) если ковариационная функция K^(ti,t2) непрерывна в
точках диагонали tx = t2 квадрата Т х Т, то она непрерывна
в любой другой точке этого квадрата;

1 2 Математическое ожидание и ковариационная функция 37
6) для любого тI и для любого множества {^IJiLj S Т
точек отсчета квадратичная форма
nm переменных z,k, г = 1, n, к = 1, m, является неотрицательно
определенной.
•4 Первое утверждение следует непосредственно из определения
ковариационной функции и свойств операции транспонирова-
транспонирования матриц, так как
Второе утверждение следует непосредственно из определе-
определения 1.4 ковариационной матрицы и определения 1.5 ковариаци-
ковариационной функции случайного процесса, так как
Третье утверждение следует из неравенства Шварца для
математического ожидания
в котором
a(w) = (o!H ... on(w))T,
если считать, что
Для доказательства неравенства Шварца предположим, что
А € К — неслучайный параметр. Тогда для любого А
О <С М[(а(ш) + \р(и))Т(а{и) + Щи))] =

38 1. ИСХОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
и поэтому дискриминант этого квадратного трехчлена неотри-
неотрицателен. Это дает неравенство
В случае скалярных случайных величин а(ш) — Q:;(u)), /3(ш) =
= /3j(w) это неравенство превращается для них в неравенство
Шварца
Используя его в векторном случае, получаем
i=\ j=\ i=\
что и завершает доказательство неравенства Шварца.
Чтобы доказать четвертое утверждение, достаточно вос-
воспользоваться очевидными равенствами:
J7(t,w) - mv{t) = A{t){t{t,u>) - me(t)), t e T,
и определением 1.5 ковариационной функции. Действительно,
Для доказательства пятого утверждения положим

1.2. Математическое ожидание и ковариационная функция 39
и рассмотрим
+
где использованы неравенство треугольника [IV] и неравенство
Шварца. А так как
Л,« + Л) - ff{(M + Л) - ||
и по условию
lim Kf{t + h,t + h)= lim AV(t + h,t) = lim ^(t,t + Л) = Kt(t,t)
Л+0 v /i>0 V ' /i>0 V tV '
Для любого t € Г, то утверждение 5 доказано полностью.
Для доказательства шестого утверждения теоремы 1.1 рас-
рассмотрим выражение

40 1. ИСХОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
А так как в левой части записано математическое ожидание
неотрицательной случайной величины, то оно неотрицательно,
и утверждение 6 доказано. >
Замечание 1.1. По аналогии с коэффициентом корреля-
корреляции двух скалярных случайных величин в теории случайных
процессов используют понятие корреляционной функции
Замечание 1.2. Если случайный процесс ?(t,u), t e T,
принимает значение в измеримом пространстве X С С, то его
называют комплексным случайным процессом. Для него
где символ ,,*" означает операцию комплексного сопряжения.
Таким образом, если ?(i,tj), t ? Т, — комплексный случайный
процесс, то
где f(t,w) A ^(t,uj) + tft(«,w), * G T, a €i(t,w), t G T, и
t ?T, — скалярные случайные процессы.
Пример 1.4. Пусть A(uj) = o(u) + ib(u) — комплексная
случайная величина с нулевым математическим ожиданием,
(р ? К — неслучайный скалярный параметр и комплексный
случайный процесс ?(i,w), t ?T, имеет вид
b(u)s\n(<pt)) +
+ i F(w) cos(y>i) + o(w) sin(^)), t G Г = [0, oo).

1.2. Математическое ожидание и ковариационная функция 41
Тогда
(uf)etvt] = M[A(u)]etvt = G;
= M[A*(uj)A(u)]exp[iip(t2 -h)] =
= M[a2{u) + 62(cj)]cos(v>(t2 -ti)) +
+ iM[a2(w) + b2{u)]sm(<p[t2 -
Определение 1.6. Взаимной ковариационной функ-
функцией двух n-мерных случайных процессов ?(t,u), t ? Т, и
r)(t,u>), t ? Т, определенных на одном и том же множестве
TcR и на одном и том же вероятностном пространстве
(Q,A,P), принимающих значения в одном и том же измери-
измеримом пространстве X с Кп, называют неслучайную матричную
функцию K^v(ti,t2) типа пхп двух скалярных аргументов t\
и t2, значение которой при фиксированных t\tt2 S Т равно ко-
вариации случайных векторов f(?i,w) и r](t2,u), определяемой
следующим образом:
Ktn{h,t2) —
Г Г
;-mc(ti)) (y-mv(t2)) f(n{x,y\tut2)dxdy,
где ftr){x,y\ti,t2) — функция плотности вероятностей Bп)-
Мерного случайного вектора (^ (ti,u) T}T(t2,uj)) .
Согласно определению 1.6, на пересечении г'-й строки и j-ro
столбца взаимной ковариационной функции /^(ti,^) находит-
находится скалярная функция

42 I. ИСХОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Взаимная ковариационная функция обладает следующими
свойствами:
a) ^
в) если (pi(t), <fi2{t) — неслучайные n-мерные вектор-функ-
вектор-функции, A\(t), Лг@ — неслучайные матричные функции типа
п X п, определенные наТсК, и при к = 1,2
* б Г,
где ^(i)(t,w) и fB)(?,w) — n-мерные случайные процессы, опре-
определенные на одном и том же множестве TcR, одном и том
же вероятностном пространстве (Q,A,P) и принимающие зна-
значения в одном и том же измеримом пространстве X С Кп, то
Вопросы и задачи
1.1. Почему любое сечение n-мерного векторного случайно-
случайного процесса является n-мерным случайным вектором?
1.2. Существует ли связь между /V-мерным и (N — ^-мер-
^-мерным законами распределения случайного процесса, где N ^ 2?
Если эта связь существует, то укажите ее с использованием:
а) функций распределения; б) функций плотности вероятно-
вероятностей.
1.3. Возможно ли в общем случае адекватное описание слу-
случайного процесса с помощью конечномерных законов распреде-
распределения?
1.4. Можно ли определить математическое ожидание слу-
случайного процесса, если известна его: а) одномерная функция
распределения; б) двумерная функция плотности вероятностей?
1.5. Как связаны между собой дисперсия и ковариационная
матрица случайного процесса?

Вопросы и задачи 43
1.6. В чем заключается принципиальное отличие ковариа-
ковариационной функции случайного процесса от его ковариационной
матрицы?
1.7. Можно ли ввести корреляционную функцию для скаляр-
скалярного случайного процесса? В случае положительного ответа,
сформулируйте ее основные свойства.
1.8. Постройте семейство реализаций (траекторий) скаляр-
скалярного случайного процесса
где и(ш) — скалярная случайная величина, распределенная по
закону Пуассона с параметром ц = 0,5.
Ответ: A + t2)~ln; n = 0, 1, 2,...
1.9. Докажите, что конечномерные распределения стохасти-
стохастически эквивалентных случайных процессов совпадают.
1.10. Являются ли стохастически эквивалентными скаляр-
скалярные случайные процессы ?(t,u), t ?Т, и ri(t,u>), t ? Т, если
Г = [а,Ь]и:
а) ф,ы) 4 ${t,u){J(t - a) - J[t - (a + 6)/2]};
б) r}(t,u)=?(t,u){l-S[t-(a + b)/2]}, где J(t) — единичная
функция, a S(t) — ^-функция Дирака.
Ответ: а) нет; б) да.
1.11. Пусть а(и) и /3(tj) — неотрицательные скалярные
случайные величины с известным совместным законом распре-
распределения, а скалярная случайная величина j{u>) не зависит от
них и равномерно распределена на отрезке [0, 2тг]. Докажите,
Что любое конечномерное распределение скалярного случайно-
случайного процесса
(u>)t + 7(w)], t G T С R,
не зависит от сдвига по времени, т.е. для любых N ^ 1, ?* € Г,
к= 1, N, и h € R, такого, что f* -f h e T, к ?= 1, iV, имеет место

44 1. ИСХОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
тождество
1.12. Для случайного процесса из задачи 1.8 определите
математическое ожидание и дисперсию.
Ответ: m{(t) = 1/2A -И2); a*(t) = 1/2A -И2J-
1.13. Определите математическое ожидание, дисперсию и
ковариационную функцию скалярного случайного процесса
?(i, w) = 2tt(w)ein(irt) + 3u(u)i2 + 5, t e Г,
где v — известный неслучайный параметр, а и(и) и u(w) — ска-
скалярные случайные величины с известными числовыми характе-
характеристиками: М[и(и>)] = 1; M[v(u)] = 2; D[u(u)] - 0,1; D[u(w)] =
= 0(9;/)(ti(w);»(w)) = -0,3.
Ответ:
m^(i) = 2sin(i^) + 6t2 + 5;
aj(t) = 0,4sin2(i/f) +8,It4 - l,08?2sin(i/f);
t2) =0,4sin(i/ti)sin(i/t2) |
1.14. Пусть известны числовые характеристики двумерного
случайного вектора и(и) = (ui(lj)
Найдите математическое ожидание, дисперсию и ковариацион-
ковариационную функцию скалярного случайного процесса
?(?,ш) = ui(uj)cost + U2(ti>)smt + t, t eT.
Ответ:
^{t) = -0,5 cost + siat +1;
2 2 2,9sin2t-2sin2f;
- 2sin(ii

Вопросы и задачи 45
1.15. Найдите математическое ожидание, ковариационную
функцию, дисперсию и одномерный закон распределения ска-
скалярного случайного процесса
где а(ш) и j3(u;) — независимые скалярные случайные величины,
распределенные по нормальному закону с нулевым математиче-
математическим ожиданием и дисперсией о1 — 0,25.
Ответ:
f2) = 0,25^2
o\{t) = 0,25?2(l+?2); Д(яг|*) =
1.16. Найдите ковариационную функцию и дисперсию ска-
скалярного случайного процесса
fc(w)ras(i/*t) +/3*Hsm(i/Af)], (eTcE,
если i/к, /с = 1,п, — известные неслучайные параметры, не-
некоррелированные скалярные случайные величины <*/ь(и;), /3k(u),
/с=1,п, имеют нулевые математические ожидания и равные
дисперсии D[aifc(a>)] = D[/3fc(a>)] = о\,к = Т~п.
Ответ:
KdhM) = f^clco&kih - t,)]; o\(t) =
1.17. Найдите взаимную ковариационную функцию скаляр-
скалярных случайных процессов
?{t,u) = а(ш) sin(i/t) + /3(и) cos(ut), t e Г С R,
77(t,o>) = a(w)sin(i/t) +7(w)cos(i/t), t ? T с R,

46 1. ИСХОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
если v — известный неслучайный параметр, а скалярные слу-
случайные величины л(и»), /3(ш), т(и>) являются попарно некорре-
некоррелированными.
Ответ: K^fafy) = sin(i/?i)sin(i/?2)D[a(u>)].
1.18. Пусть ?i(t,w), t € Т, и ?2(t,^), teT, — два скаляр-
скалярных случайных процесса, для которых известны ковариацион-
ковариационные функции K^(ti,t2), KB(t\,t2) и взаимная ковариационная
функция K^2(ti,t2). Найдите ковариационную функцию ком-
комплексного случайного процесса
если a(i), 6(i), c(t), d(t) — известные неслучайные функции,
определенные при t ? Т.
Ответ:

2. НЕКОТОРЫЕ ТИПЫ
СЛУЧАЙНЫХ ПРОЦЕССОВ
Для построения конструктивной теории, позволяющей ре-
решать различные задачи как теоретического, так и прикладного
характера, необходимо конкретизировать общее определение
случайного процесса (см. 1). Рассмотрим важнейшие типы слу-
случайных процессов, представляющих особый интерес для прило-
приложений.
2.1. Стационарные случайные процессы
Определение 2.1. Случайный процесс €(t,u), t G T = [а, 6],
называют стационарным в узком смысле, если для любых
N^l,tk?T, k = T77V, и h € К, такого, что tk + h ? Т, k = 1,7V,
имеет место тождество
или, что то же самое,
, • • • ,tN) = /e(z(i),... ,Z(N)Ni + h,...,tN + h).
Если стационарный в узком смысле случайный процесс
?(t,tj), t?T — [a,b], имеет моменты первого и второго по-
порядков, то его математическое ожидание M[?(t,tj)] = m^ —
постоянный вектор, а ковариационная функция зависит лишь
от разности аргументов, т.е.
Действительно, полагая h = a — t, получаем
*,ш)]= I xfi{x\t)dx= I xfi(x\a)dx =
R" Rn

48 2. НЕКОТОРЫЕ ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ
Совершенно аналогично, полагая h = a — t\, приходим ко второ-
второму тождеству:
= / I
R"R"
/ (x(i
R"R"
Определение 2.2. Случайный процесс ?(t,u>), t ?T, назы-
называют стационарным в "широком смысле, если его матема-
математическое ожидание — постоянный вектор, а ковариационная
функция зависит от разности аргументов, т.е.
Mfc(t.w)] = mi = const, K((tut2) = Kt{t2 - tj).
Таким образом, из стационарности в узком смысле следует
стационарность в широком смысле.
В той мере, в какой теория случайных процессов отражает
явления реального мира, понятие стационарности случайного
процесса отражает идею неизменности (стационарности) усло-
условий, в которых он протекает.
Заметим, что случайный процесс, рассмотренный в примере
1.3, является стационарным в широком смысле, если случайные
величины a(u>), /3(w) являются некоррелированными, имеют
нулевые математические ожидания и одинаковые дисперсии.
Пример 2.1. Пусть скалярные случайные величины а(о>),
/3(w), у(ш) обладают следующими свойствами:
а) a(w) и /3(и>) положительный /«/3B:1,2:2) — плотность рас-
распределения (вероятностей) случайного вектора (<*(uj) /3(w)) ;
б) у(ш) не зависит от а(ш) и /3(w) и распределена по равно-
равномерному закону на отрезке [0, тг].

2.1. Стационарные случайные процессы
49
Докажем, что случайный процесс
, teT=[a,b],
является стационарным в узком смысле, начав с определения
его одномерного закона распределения.
Фиксируем значение t ? Т. В этом случае сечением рассма-
рассматриваемого случайного процесса является случайная величина
представляющая собой функцию случайных величин a(w), /3(ш),
7(w). Функция плотности вероятностей случайного вектора
(а(и>) /3(ш) у(ш)) имеет вид
/а/З-у {Х\ , Х2, Х3) = fa
(Х3).
Из равенства
следует, что
О,
Поэтому, согласно теории построения законов распределения
функций случайных величин, находим [XVI]
оо оо
где
,-1

50 2. НЕКОТОРЫЕ ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ
и не зависит от значения t. Кроме того, по условию случайная
величина у(и>) распределена равномерно на отрезке [0,7г], т.е.
функция плотности вероятностей /«у инвариантна относительно
сдвига аргумента. Таким образом,
Для N > 1 нужно определить закон распределения N-мерно-
го случайного вектора с компонентами
и доказать, что
Л (У1, - - •, УЛГ | *i, • • -,*лг) = Л (yi, - ¦ ¦, !/jv | «1 + Л,..., *tv + Л).
Далее принципиальная схема рассуждений аналогична ис-
использованной в одномерном случае и потому не приводится.
2.2. Нормальные процессы
Определение 2.3. Случайный процесс ?(t,w), t G T =
= [a, b], называют нормальным, или гауссовым процессом,
если любые его конечномерные законы распределения являются
нормальными.
Пусть ?(t,uj), t ЕГ, — n-мерный нормальный процесс с ма-
математическим ожиданием m^(t) и ковариационной функцией
К{A,т). В этом случае для любого JV^l и для любых ?& G Т
известны значения его математического ожидания
W)]) k=l,N,
и ковариационной функции

2.2. Нормальные процессы
51
Введем в рассмотрение блочные матрицы-столбцы, которые
при дальнейших рассуждениях будем называть блочными
векторами:
те(и\ \
и блочную матрицу
... K€{tutN)
,t2) ... K^(tfi,tN)
Не останавливаясь на анализе особых случаев, связанных с
возможной линейной зависимостью сечений рассматриваемого
случайного процесса, будем считать, что |V}v| ф 0.
Блочный вектор г}^(ш) является (пЛ^)-мерным случайным
вектором с математическим ожиданием т^ и ковариационной
матрицей V)y. А так как ?(t,w), t GT,
чайный процесс, то случайный вектор
нормальному закону и
нормальный слу-
слу) распределен по
ш =
1
I ехр
Г 2 ^У ~
является iV-мерной функцией плотности вероятностей для
случайного процесса ?(t,uj), t ?T.
Таким образом, любой конечномерный закон распределения
нормального случайного процесса полностью определяется его
математическим ожиданием и ковариационной функцией.
Если ?(t,u>), t G T, — n-мерный стационарный нормаль-
нормальный случайный процесс, то его математическое ожидание —
постоянный п-мерный вектор, а аргументом ковариационной
функции является параметр г = *2 ~h-

52 2. НЕКОТОРЫЕ ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ
В силу центральной предельной теоремы [XVI] нормальные
случайные процессы в ряде случаев оказываются предельными
для сумм возрастающего числа случайных процессов.
2.3. Процессы с независимыми приращениями
Определение 2.4. Случайный процесс?(?,w), t ? Т С R, на-
называют процессом с независимыми приращениями, если
для любых N > 1 и tk ? Т, к — 1, N, таких, что t\ < ti < ... < tyy,
случайные величины
являются мезависильи«и.
В практике научных исследований встречаются случайные
процессы, родственные (в определенном смысле) случайным
процессам с независимыми приращениями. Отметим некото-
некоторые из них.
1. Если n-мерные случайные векторы ^(^,0;), ?(?2,w) -
-f(*bw)i •••, ?(?n,w) - ?(?n-1iw) являются, вообще говоря,
зависимыми, но некоррелированными, то n-мерный случайный
процесс ?(?,w), t G Т, называют процессом с некоррелиро-
некоррелированными (ортогональными) приращениями.
2. Если для любых N > 1 и tk ? Т, к = 1, N, закон распреде-
распределения приращения ?(?fc+1,w) — ?(?/t,w) зависит лишь от t^+i — t^,
k= 1, TV—1, то случайный процесс f(?,w), ? е Т, с независимы-
независимыми приращениями называют процессом со стационарными
независимыми приращениями.
Случайный процесс f (?,u>), t G Т С К, с независимыми при-
приращениями полностью определен одномерным законом распре-
распределения Д(х|?), характеризующим случайный вектор ?(?i,w), и
двумерным законом распределения /{(*(iIa;B)Uii*2), характе-
характеризующим приращения ?(?jt+ilW) — ?(?*,«), &= 1,-W—1.

2.3. Процессы с независимыми приращениями 53
Пример 2.2. Пусть ?(t,u), teTcR, — случайный процесс
с ортогональными приращениями и требуется определить его
ковариационную функцию.
Полагая t2 > ^1, имеем
= cov
cov [
где последние равенства следуют из свойств ковариации и
некоррелированности случайных величин ?(t\,u)) и ?(?2,w) —
Рассуждая аналогично, при t\ > t2 получаем
Таким образом, с учетом связи ковариационной функции слу-
случайного процесса и его ковариационной матрицы, имеем
О*;
s^t. #
Отметим, что процесс с независимыми приращениями явля-
является процессом с ортогональными приращениями. Поэтому
результат, полученный при рассмотрении примера 2.2, имеет
место для любого процесса с независимыми приращениями.
Пример 2.3. Пусть ?(t,u>), teTcR, — процесс с ортого-
ортогональными приращениями. Для t, s ?T, s <t, положим
Так как исходный случайный процесс является процессом с
ортогональными приращениями и s < t, то
-?fe,w)l=0.

54 2 НЕКОТОРЫЕ ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ
Таким образом,
-s) = covR;(*,w) -?(e,w); ?(t,w)] =
т.е. ковариационная матрица приращения ?(?,w) — ^(s,uj) равна
разности ковариационных матриц соответствующих сечений
?(t,u>) и ?(s,u) исходного случайного процесса. #
Если воспользоваться формальным определением функции
— s), приведенным в примере 2.3, то при s < f и s, t>0
Но в этом случае
flc(*-e) = cov
- K(«,w) - ?@,w)); Й(«,w) - f@,w)) - (f(e,w) -
А так как
(e,w); (f (t,w) - ^(e,w)) + (f (e,w) -
то приходим к равенству

2.4. Винеровскнй процесс 55
которое имеет место для любых t,s?T, удовлетворяющих нера-
неравенству s < t. Можно показать, что если R((t) — непрерывная
функция, то
= At.
Кроме того, для процесса с ортогональными приращениями
?(t,uj), t ?T, такого, что
имеют место равенства
Значит, ковариационная функция равна
или
Kz{s,t) = Amin{t;s}.
2.4. Винеровский процесс
Определение 2.5. Если ?(t,w), t?T= [0,со), — п-мерный
случайный процесс, то его называют винеровским процес-
процессом, выходящим из О, если выполнены три условия:
2) для любых N > 1 и tk e T, k = 1, N, таких, что 0 < t\ <
2 < ... <tN, случайные векторы ^(ti,u), ^(t2,uj) -^(ti,u), ...,
,uj) —?(tN-\,uj) являются независимыми;
3) для любых tltt2 е Т, таких, что 0 ^ tx < t2, случайный
вектор ?(?г,^) -?(ti,u>) распределен по нормальному закону с
нулевым математическим ожиданием и ковариационной ма-
матрицей (*2 - t\)a2ln, где /„ € Mn(R) — единичная матрица.
Винеровский процесс, или процесс броуновского движения,
имел большое значение при разработке теории случайных про-
процессов. Многие распределения, используемые в теории упра-

56 2 НЕКОТОРЫЕ ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ
вления, можно моделировать процессами, порождаемыми вине-
ровскими процессами.
В 1827 г. английский ботаник Р. Броун заметил, что
маленькие частицы диаметром около микрона, погруженные
в жидкость, находятся в постоянном хаотическом движении.
В 1905 г. А. Эйнштейн объяснил это движение как результат
столкновения частиц с молекулами жидкости. Он разработал
математическую модель броуновского движения и определил
число Авогадро, равное числу молекул в объеме, занятом молем
газа.
Строгий математический анализ броуновского движения
дал Н. Винер в 1923 г. Эвристически броуновское движение
можно объяснить следующим образом. Рассмотрим отдельную
частицу, погруженную в жидкость, обозначив через ?i(?), ?г@>
?з@ ее координаты в момент времени t > 0. Будем считать, что
в начальный момент времени t = 0 она находится в начале ко-
координат, т.е. &@) = 0, к = 1,2,3. Движение частицы на любом
конечном временном интервале является результатом измене-
изменения импульса (количества движения) вследствие практически
бесконечно большого числа независимых друг от друга соуда-
соударений с молекулами жидкости. Поэтому естественно считать,
что применима центральная предельная теорема [XVI]. Кроме
того, можно допустить, что:
а) смещения частицы в ортогональных направлениях проис-
происходят независимо;
б) ?k{t), к = 1,2,3, распределены по нормальному закону с
нулевым математическим ожиданием и дисперсией <r^(t);
в) смещение частицы в каждом к-ои ортогональном напра-
направлении на различных непересекающихся временных интервалах
0 < t\ < ... < ttf представляется независимыми случайными ве-
величинами €k(h), &(<2)-&(*i), •••> &(fN)-6:(fN-i);
г) смещение частицы в каждом к-ом ортогональном напра-
направлении на временном интервале (t, t + h), равное ?k{t + h) —
имеет ту же функцию распределения, что и смещение

2.4. Винеровский процесс 57
Отметим также, что дисперсия o2{t) = D[?/t(?)] обладает
любопытным свойством:
где постоянную а2 интерпретируют как коэффициент диф-
диффузии. Действительно, согласно допущению в), случайные
величины ?/t@ и ?/t(? + /i) — ?k{t) являются независимыми. По-
Поэтому
или
c2(t + h) = (T2(t
А так как, согласно допущению г),
D[&(t + Л)-
то
откуда и следует отмеченное свойство (см. пример 2.3). Заме-
Заметим, что этот результат является следствием из рассмотренных
свойств процессов с ортогональными приращениями.
Замечание 2.1. Если в определении винеровского процесса
условие ?@,w) = 0 заменить условием ?@,w) = х, где х ? X С Кп,
то получим определение винеровского процесса, выходящего из
точки х.
Замечание 2.2. Если ?(?,w), t ? Т, — винеровский про-
процесс с коэффициентом диффузии а2, то случайный процесс
?(?,u))/vcr2, t ? Т, называют стандартным винеровским
процессом. Для любых t\, t2 ? Т, таких, что 0 < h < t2, случай-
случайный вектор ?{t2,u>)Va2~ — ?(tl,u))V<T2~ распределен по нормально-
нормальному закону с нулевым математическим ожиданием и ковариаци-
ковариационной матрицей (t2 — h)In. #

58 2. НЕКОТОРЫЕ ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ
Следует также отметить два характерных свойства вине-
ровских процессов.
1. Винеровский процесс является процессом со стационар-
стационарными приращениями.
2. Если ?(t,w), t G T, — винеровский процесс и а2 — его
коэффициент диффузии, то для любых ti,t2 ? Т, таких, что
О ^ t\ < t2, ковариационная функция равна
так как винеровский процесс является процессом с независи-
независимыми приращениями.
Пример 2.4. Докажем, что винеровский процесс является
нормальным процессом.
Для упрощения дальнейших рассуждений ограничимся рас-
рассмотрением скалярного винеровского процесса ?{t,u>), t € Т =
= [0,со), предполагая, что он является стандартным. Докажем,
что для любых N ^ 1 я {tk}%=l G Т, таких, что 0 < ti < ti < ... <
< tN, случайный вектор
распределен по нормальному закону.
Пусть далее
*о = 0;
Согласно определению 2.5 винеровского процесса, плотность
распределения [вероятностей) случайного вектора 1}[ш) явля-
является плотностью iV-мерного нормального распределения [XVI],
которая в данном случае имеет вид
= JI /, f ехр[-оГ, Х\ ч]'
к=\ V к ~ к~1 ' "~ к~х'

2.5. Марковские процессы
59
Если ввести в рассмотрение матрицу
/ 1 0 0 ... О 0\
-1 1 0 ... 0 0
А =
0 -1 1
о о
\ 0 0 0 ... -1 \)
eMN(R),
то, согласно общей теории построения законов распределения
функций случайных величин [XVI], с учетом очевидных ра-
равенств
имеем
Л(У1,У2,.-мУЛг) = Л(у) =
= /ч(У1. У2 ~ У1, •••, VN - VN-i)-
Таким образом, если уо = 0, то iV-мерная плотность распреде-
распределения (вероятностей)
Щк-tk-x
f
является плотностью iV-мерного нормального распределения,
что и требовалось доказать.
2.5. Марковские процессы
В теоретических и прикладных исследованиях, связанных с
марковскими процессами, для их конечномерных (iV-мерных)
функций плотности вероятностей f^(x^,...,x^\tu...,tN) ис-
используют сокращенные обозначения /(хн\,х^),--

60 2. НЕКОТОРЫЕ ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ
Определение 2.6. Пусть ?A,ш), t ? Т С R, —n-мерный слу-
случайный процесс, конечномерные функции плотности вероят-
вероятностей которого (возможно обобщенные) /(a^i),^),---,
заданы для любых N ^ 1 и tj ? Т, к = 1, N, таких, что t\ <
< ti < ... < tjy. Если при этом условная функция плотности
вероятностей имеет вид
f{x{N)\x(N-l),---ixl) = f{x{N)\x{N-\)),
то ?(?,w), t G Т, называют ^иартеовски^и процессом.
В связи с тем, что марковские процессы занимают особое
положение в теории случайных процессов и ее приложениях, они
будут рассмотрены отдельно. На данном этапе отметим лишь,
"что любой конечномерный закон распределения марковского
процесса выражается через его двумерный закон распределе-
распределения, так как
= f(x{N) I S(jv-l), • • •, х(\)) f{x{\), ¦ ¦ ¦. x(N-\)) =
= f(x(N) I x{N-\)) /(^AI • • 4«(JV-1)) = • • • -
= f(x(N) I X(N-1)) f(x(N-\) I x(N-2)) ¦ ¦¦f{xB) I x(\)) f(x(l))-
Пример 2.5. Пусть ?(t,w), t G Г, — винеровский ска-
скалярный процесс, выходящий из нуля. Для винеровского ска-
скалярного процесса iV-мерная функция плотности вероятностей
ft(xi,...,xN\ti,...,tN) равна (см. пример 2.4)

2.6. Пуассоновский процесс 61
Поэтому
_ f{xi,X2,...,XN)
°Г
/
y/2n(tN-tN-i)
(xN-xN-
1 V =
/-U
и, согласно определению 2.6, винеровский процесс является
марковским процессом.
2.6. Пуассоновский процесс
Определение 2.7. Пуассоновским процессом с пара-
параметром А > 0 называют скалярный случайный процесс ?(t,w),
t ЕТ = [0, со), обладающий следующими свойствами:
2) для любых N > 1 и tk G T, k = 1, N, таких, что 0 =
< t\< ... < tjq случайные величины f(?fc,u>) — ^(tfc_i,w), к — 1, N,
являются независимыми;
3) для любых ti,ti G Т, таких, что 0 < tx < t2, случайная
величина ?(?г,<*0 — ^(ti,w) распределена по закону Пуассона с
параметром A(t2 — ti), т.е.
= e()t ,
Замечание 2.3. Пуассоновский процесс играет важную
роль в различных приложениях теории случайных процессов,
в частности, в теории массового обслуживания.

62 2. НЕКОТОРЫЕ ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ
Вопросы и задачи
2.1. Докажите, что из стационарности в узком смысле
следует стационарность в широком смысле, но не наоборот.
2.2. Является ли винеровский процесс: а) гауссовским
процессом; б) марковским процессом?
2.3. Определите N-мерный закон распределения пуассонов-
ского процесса.
2.4. Какими общими свойствами обладают винеровские и
пуассоновские процессы?
2.5. Докажите, что пуассоновскии процесс является марков-
марковским.
2.6. Пусть v — неслучайный параметр, а а(ш) и /?(w) — не-
некоррелированные скалярные случайные величины с нулевыми
математическими ожиданиями и одинаковой дисперсией, рав-
равной а1. Является ли скалярный случайный процесс
?(t,u) = o(w)sin(i/t) +/3(w)cos(i/t), teTcR:
а) стационарным в широком смысле; б) стационарным в узком
смысле?
Ответ: а) да, так как для такого процесса m^[t) = 0 и
= (T2cos[i/(t2 — ti)]; б) в общем случае нет, так как
-1">-\*т[иA2-1г)]\
sm[u{t2-ti)] '
2.7. Решите задачу 2.6, если известна совместная функция
плотности вероятностей случайных величин а(ш) и 0(ш):
{24-2 2 .2 |,.2<1.
2 2,
0, 1221

Вопросы и задачи 63
Ответ: а) да, так как для такого случайного процесса
= 0 и K{(tx,t2) = C/8)cos[v(t2-ti)]; б) нет, так как
\x\ca§,(ut{) — a;2cos(i/<2)]
2.8. Является ли случайный процесс
i?(t,wL?(t>w) + ti(w), teTcR,
стационарным в широком смысле, если ?(t,w), t G T, — стаци-
стационарный случайный процесс и: а) для любого фиксированного
t G Т случайные векторы ?{t,w) и и(ш) являются независимыми;
б) и(и)±?Aо,и;),где1оеТ.
Ответ: а) да; б) нет.
2.9. Пусть ?(t,u)), t G T, — скалярный нормальный стаци-
стационарный в узком смысле случайный процесс. Найдите одно-
одномерную и двумерную функции плотности вероятностей этого
случайного процесса.
Ответ:
fr(v\t\ — _ ,___
fe(xi,x2\ti,t2) =
где
Z =

64 2. НЕКОТОРЫЕ ТИПЫ СЛУЧАЙНЫХ ПРОЦЕССОВ
2.10. Ковариационная функция К#{т) угла крена корабля
#(?,u>), t € Т, имеет вид
Определите вероятность того, что в момент времени t<i =
= h + т угол крена будет больше 15°, если #(?,w), t ?Т, —
скалярный нормальный стационарный случайный процесс с
нулевым математическим ожиданием и i?(?i,w) = 5°, т — 2с,
а = 30 град2, 0 = 0,02 1/с, v = 0,75 1/с.
Ответ: P[ti{h + r,w) > 15°|ti{h,u>) = 5°] = 0,0037.
Указание: использовать результаты решения задачи 2.9.
2.11. Использование эхолота с корабля, испытывающего
бортовую качку, возможно, если угол крена корабля #(?,и>),
t ?Т, удовлетворяет условию: |#(?,о>)| ^ #о- Определите веро-
вероятность того, что второе измерение возможно через го секунд
после удачного первого измерения, если угол крена корабля —
скалярный нормальный стационарный случайный процесс с ну-
нулевым математическим ожиданием и известной ковариацион-
ковариационной функцией К#(т).
Ответ:
-КЦто)} J
Указание: использовать результаты решения задачи 2.9.
2.12. Пусть ?(t,uj), t G T, — гауссовский стационарный ска-
скалярный случайный процесс с нулевым математическим ожида-
ожиданием и известной ковариационной функцией К^{т). Определите

Вопросы и задачи 65
математическое ожидание случайного процесса
считая г параметром.
Ответ: M[r){t,uj)] = ж~1 arccos[-A>(r) К~1Щ.
2.13. Пусть ?{t,oj), t 6 Т = [0, 6], — винеровскии скалярный
процесс, выходящий из нуля и имеющий единичный коэффици-
коэффициентом диффузии. Докажите, что
о] = ]/^
а] =

3. ЭЛЕМЕНТЫ
СТОХАСТИЧЕСКОГО АНАЛИЗА
Стохастический анализ — это раздел математики, в
котором случайные функции и их обобщения изучают метода-
методами математического анализа. Термин „стохастический анализ"
часто употребляют для наименования лишь основ стохасти-
стохастического анализа, объединяющих теорию пределов, дифферен-
дифференциальное и интегральное исчисление и их непосредственные
приложения.
Понятие сходимости является основополагающим не только
в классическом математическом, но и в стохастическом анали-
анализе. В теории случайных процессов рассматривают различные
виды сходимости и, как следствие, различные виды непрерыв-
непрерывности, дифференцируемости и т.д. Напомним, что в теории
вероятностей используют следующие виды сходимости. Го-
Говорят, что последовательность случайных величин {?/fc(w)}?Lj
сходится к случайной величине ?(w):
1) по вероятности, если для любого е > 0 существует
2) сильно, или почти наверное, если
3) в среднем квадратичном, если
Далее используем лишь одно понятие сходимости — сходи-
сходимость в смысле среднего квадратичного, или СК-сходимость.
Это связано с тем, что понятие СК-сходимости является наи-
наиболее приемлемым с точки зрения приложений. В соответствии

3.1. Сходимость в смысле среднего квадратичного 67
с этим авторы сочли возможным сохранить стандартные обо-
обозначения математического анализа и в дальнейшем изложении
опускать пояснения типа „в смысле средней квадратичной схо-
сходимости", если это не может вызвать недоразумений.
Следует также отметить, что при использовании СК-сходи-
мости изучение векторных случайных процессов в значитель-
значительной степени сводится к изучению их координатных случайных
процессов, а анализ существования предела, непрерывности,
дифференцируемости и интегрируемости скалярных случай-
случайных процессов — к изучению соответствующих свойств их
математических ожиданий и ковариационных функций.
3.1. Сходимость в смысле среднего
квадратичного (СК-сходимость)
Определение 3.1. Пределом n-мерного случайного про-
процесса ?(t,w) = (&(t,w) ••• ?*(*,w))T, t?T CR, при t->t0€T
в смысле СК-сходимости называют случайный вектор Т)(ш) =
— [tj\(uj) ... г}п(ш)) и обозначают
если существует предел
li
I—Ко
где
•) чу и I — *
евклидова норма n-мерного случайного процесса ?(t,u>) — т^{ш),
Приняв за основу понятие СК-сходимости, мы тем самым
определили выбор нормы [IV] для анализа случайных процес-

68 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
сов:
\
xTxft(x\t)dx.
В соответствии с этим, в данной книге ограничимся рас-
рассмотрением только таких случайных процессов, для которых
указанная СК-норма является конечной. Случайные процес-
процессы, удовлетворяющие этому условию, называют случайными
процессами второго порядка.
Таким образом, видим, что в основе понятия сходимости
в смысле среднего квадратичного лежит понятие СК-нормы,
которую мы ввели как неотрицательную скалярную функцию
параметра t € Т. Убедимся в том, что при любом фиксиро-
фиксированном t € Т эта функция действительно определяет норму.
Для этого рассмотрим множество НТ(Ж) n-мерных случайных
процессов второго порядка, определенных на Т С R, и будем
считать, что случайные процессы?(f ,w), t ?Т, и r)(t,uj), t ?T,
из этого множества равны, если
)-»7(*,w)||ck = 0) t?T.
В этом случае множество НТ(Щ со стандартными операциями
сложения своих элементов и их умножения на число являет-
является линейным пространством, а n-мерный случайный процесс
второго порядка ?(?,а>), t G Г, является нулевым, т.е. является
нейтральным элементом линейного пространства Нт(&), если
Пусть теперь для любых двух элементов ?(t,uj), t ? Т,
и r}(t,Lj), t ? Т, линейного пространства #T(R) определена
скалярная функция параметра t ?Т:
J J

3.1. Сходимость в смысле среднего квадратичного 69
где fE(x,y\t) — одномерная функция плотности вероятностей
Bте)-мерного случайного процесса
Непосредственной проверкой читатель может убедиться в
том, что при каждом фиксированном t G Т скалярная функция
("> ")ск Удовлетворяет аксиомам скалярного умножения:
1) для любого ?{t,u)) e H^(R) имеет место неравенство
причем равенство (?(t,u)),?(t,uj))CK = 0 выполняется тогда и
только тогда, когда ?(t,uj) = 0;
2) для любых ?(t,u)),n(t,uj) G Я?(К) и t G Т имеет место
равенство
3) для любых Z(t,w),r}(t,w) е Нт{Щ, A G R и t e T имеет
место равенство
4) для любых €(t,Lj),n(t,uj),a(t,Lj) ? НТ(Ш) и t ? Т имеет
место равенство
//ск
, W), *(t,u;))CK.
Так как линейное пространство НТ(Ж) с введенным скаляр-
скалярным произведением является евклидовым пространством, то
при любом фиксированном t ? Т норма может быть введена
стандартным способом [IV]:

70 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
и при этом автоматически удовлетворяются все аксиомы нор-
нормы:
1) для любого ?(t,u)) G Hj(R) имеет место неравенство
причем ||f(?,u))||CK = 0, t G Т, тогда и только тогда, когда
?(t,w) = O;
2) для любых ?(t,uj) € Ht(R), t G Т и A G R имеет место
равенство
)||CK> teT;
3) для любых ?(t,uj), r)(t,u>) G Hj(R) и t € T имеет место
неравенство треугольника
,w)
Заметим, что СК-норма и порождающее ее скалярное произ-
произведение, введенное на линейном пространстве п-мерных случай-
случайных процессов HT(R), обладают известными свойствами [IV].
В частности, для любых ?(t,w), r}(t,uj) G Hj(R) выполняется не-
неравенство Коши — Буняковского
), r,(t,u))CK | < \№,и)\\ск \\т,A,Ш)\\ск, t G Т.
Теорема 3.1. п-мерный случайный вектор
является пределом n-мерного случайного процесса
, «ег,

3.1. Сходимость в смысле среднего квадратичного 71
при t —t to ? Т тогда и только тогда, когда для любого к =
= 1, п случайная величина т?/ь(и)) является пределом при t -t to
скалярного случайного процесса ?k{t,u)), t ?T.
^ Необходимость. Обозначим через
4
V(to,8) 4 {t е Т С R: 0 < \t - to\ < 8}
проколотую ^-окрестность точки to € Т. Пусть существует
т.е. для любого е > 0 существует 6(е) > 0, такое, что
w)-!7(w)||2]<e, teV(to,8).
А так как для любого к= 1, п имеет место неравенство
m=l
то очевидно, что
Таким образом, из существования предела
lirn ?(t,u) = i7(w)
следует существование пределов
Достаточность. Пусть для к = 1,п существует предел
т.е. для любых е > 0 я к=1,п существует 8ь(?) > 0, такое, что
t,w) - %(^)|2] < ^, t € V(toA).

72 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
Если
6(е)±тт_{6к(е)},
к1
о
то при t е V(tQ,S)
M[\\t(t,u)-r,(u>)\\2] =
к=1
Таким образом, из существования пределов
[
k=l
п
t,u) = r}k(w), к=1,п,
следует существование предела
и теорема доказана. >
Определение 3.2. n-мерный случайный процесс ?(t,u)),
(GTcK, называют пределом последовательности п-мер-
п-мерных случайных процессов {?(m)(t,u>), t G Т С K}m=i и обозна-
обозначают
если существует предел
Jim^MlH^Ct.w) -?(t,w)||2] =0, t е Г,
где

3.1. Сходимость в смысле среднего квадратичного 73
Теорема 3.2. n-мерный случайный процесс ?(t,w), t ? Т,
является пределом последовательности n-мерных случайных
процессов {?(m)(t,u), t e T}™=1 тогда и только тогда, когда для
любого к= 1,п скалярный случайный процесс ?fc(?,w), t e Т,
является пределом последовательности скалярных случайных
процессов {?(ТО)* (i,w), t e Г}?=1.
^ Доказательство аналогично доказательству теоремы 3.1. >
Как следует из теорем 3.1, 3.2, сходимость векторного слу-
случайного процесса и сходимость последовательности векторных
случайных процессов эквивалентны сходимости координатных
скалярных случайных процессов и их последовательностей. По-
Поэтому далее основное внимание уделено скалярным случайным
процессам.
Пример 3.1. Пусть ?(t,w), tGT = [0,oo), — винеровский
скалярный процесс, выходящий из нуля и имеющий единичный
коэффициент диффузии. Пусть [а, 6] С Т и а = ?о < *i < • • • < ?лг =
= 6. Покажем, что в смысле СК-сходимости существует предел
N
Согласно определению винеровского процесса, случайные
величины ?(tk,u>) -?(tk-\,w), k = 1, N, являются независимыми,
имеют нулевые математические ожидания и дисперсии
А так как
N
N N

74 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
то очевидно, что
lim Ml
N
Кроме того, случайная величина
распределена по нормальному закону с нулевым математиче-
математическим ожиданием и единичной дисперсией, а случайная величина
гЦ(ш) распределена по закону х?- Поэтому [XVII] Dfoj^w)] = 2
и
Таким образом,
N
i /.
lim M
i \
к=1
N
= 2 lim
lim
= 2F-a) lim raaxftj - tk-i) = 0,
ах(<<)Ю /г
что и требовалось доказать.

3.1. Сходимость в смысле среднего квадратичного
75
Теорема 3.3. Если существует предел скалярного случай-
случайного процесса ?{t,u>), t ? Т, второго порядка при t -)• t0 G T,
равный случайной величине т)(ш), то существует и предел ска-
скалярной функции M[f (?,w)] при t —> t0 G Т, равный М[т?(ш)].
< Предварительно отметим два неравенства. Во-первых, верно
неравенство
так как
оо оо
|MK(t,w)]|= J xft(x\t)dx $ J
—оо —оо
Во-вторых, верно неравенство Шварца
которое можно рассматривать как неравенство Коши — Буня-
ковского для скалярных случайных процессов второго порядка
t,w)|, t е Т, и |i7(t,w)|, t e T, так как
Для доказательства теоремы запишем неравенства
По условию при t -4 t0 ? Т случайный процесс ?(t,u>), t eT,
сходится к случайной величине т)(ш). Следовательно, при t -4
-4 to G Т правая часть неравенства, а как следствие, и его левая

76 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
часть стремятся к нулю. Таким образом,
t—«О
откуда
Замечание 3.1. Можно показать, что для последователь-
последовательности {f(/t)(?,^), t ? Т1}^! скалярных случайных процессов вто-
второго порядка из существования предела
limf(/t)(f,u>)=f(?,u>), teT,
следует существование предела
lim M[t(k){t,u>)] = M[t{t,u>)].
Теорема 3.4. Если f (?,w), teT, — скалярный случайный
процесс второго порядка и существует предел
Iimf(t,w) = j7(w), toeT,
t—Ио
то существует и предел
lim M[te(t,w)-?(r>W)|2]=0.
(t,T)-+(tO,tO)
¦4 Пусть выполнены условия теоремы, т.е. существует предел
Согласно очевидному неравенству 2|о| \Ь\ ^ о2 + Ь2, получаем
2|f (f,W) - т}(и)\2 + 2|f (r,w) - ^И|2.

3.1. Сходимость в смысле среднего квадратичного 77
Воспользовавшись свойствами математического ожидания (см.
П1, свойства а) и Ь) математического ожидания), приходим к
неравенству
из которого и следует утверждение теоремы. >
Замечание 3.2. Воспользовавшись определением 3.2 пре-
предела последовательности случайных процессов и техникой до-
доказательства теоремы 3.4, можно доказать, что для последова-
последовательности {?(*.)(?, w), f eT}g.,, случайных процессов второго
порядка из существования предела
lim ?(*)(*,w) = ?(t,w)
следует существование предела
lim M[\t{k)(t,u)-t{m)(t,u>)\2\=0, teT. #
Условия, сформулированные в теореме 3.4 и в замечании 3.2,
являются не только необходимыми, но и достаточными услови-
условиями существования соответствующих пределов. Это следует из
теоремы Фишера — Рисса*, однако обсуждение этих вопросов
выходит за рамки данного учебника. Они известны как сто-
стохастические критерии Коши для случайных процессов и
для последовательностей случайных процессов.
Теорема 3.5. Пусть ?(t,w), t ?T, — скалярный случайный
процесс второго порядка. Предел ?A,ш), t GT, при t -4 to G T
существует тогда и только тогда, когда существует конечный
предел скалярной функции M[?(?,w)?(r,u))] двух переменных t
и т при (t,r) -4 (?о,*о)-
'См.: Острем К.Ю.

78 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
¦4 Доказательство опирается на очевидное равенство
Пусть существует и конечен предел
lim
тогда существует и конечен предел
w)|2] = lim M
Следовательно, существует и предел
Таким образом (см. стохастический критерий Коши), суще-
существует предел lim ?(t,u>).
Докажем обратное утверждение. Если существует предел
lim ?(t,u>), то, согласно стохастическому критерию Коши, су-
ществует предел
Следовательно, существует предел
*,u,)|2] +М[\?(т,и;)\2} -2Mfc(t,«)€(r,«)]} =0.
Отсюда следует существование конечного предела
так как ?(t,w), teT, — случайный процесс второго порядка. >

3.2. Непрерывность случайного процесса 79
Следствие 3.1. Для скалярного случайного процесса
второго порядка ?(t,u), teT, предел
t.w), toeT,
существует тогда и только тогда, когда существуют и конечны
пределы
lim M[Z(t,w)] = m0, lim КМ,т) = Ko.
t-Wo tT+*
¦4 Для доказательства утверждения достаточно воспользовать-
воспользоваться очевидным равенством
и обратиться к теоремам 3-3 и 3.5. >
3.2. Непрерывность случайного процесса
Определение 3.3. Скалярный случайный процесс второго
порядка ?(t,u>), t?T, называют непрерывным в точкет6Т,
если существует предел
или, что то же самое,
Определение 3.4. Если скалярный случайный процесс вто-
второго порядка ?(t,w), t G Т, является непрерывным в каждой
точке t G Т, то его называют непрерывным на множе-
множестве Т.
Пример 3.2. Пусть ?{t,u), t еТ = [0,оо), — скалярный
винеровский процесс. Тогда для любых t,r G T, t > г, имеет
место равенство

80 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
Таким образом, скалярный винеровский процесс является не-
непрерывным на Т, так как
2 =
= lim(?-rW2 =
t*T
Теорема 3.6. Скалярный случайный процесс второго
порядка ?(t,u>), t еТ, непрерывен на Т тогда и только тогда,
когда на Т непрерывно его математическое ожидание
а на Т х Т непрерывна его ковариационная функция
¦4 При доказательстве воспользуемся соотношениями
вытекающими из свойств математического ожидания и кова-
риации (см. П1).
Необходимость. Для непрерывного на Т скалярного
случайного процесса ?(t,u), t ?T, при t,r &T имеем
= |М[t(t,u>) - f(r,w)] |Ч М[^(t,w) -
Таким образом, из существования предела
следует существование предела
|
т.е. функция m^(t) непрерывна на Т. Для доказательства не-
непрерывности ковариационной функции наТхТ воспользуемся

3.2. Непрерывность случайного процесса 81
отмеченным свойством ковариации и неравенством Шварца.
Имеем
\Ktitun) - Kt(t,r)\ =
Итак, из существования предела
lim
HO^H - mc(ti)m{(ri)| = 0
следует существование предела
т.е. AT{(t,r) непрерывна на Т х Г.
Достаточность. Полагаем, что m^(t) и /<Q(?,r) непре-
непрерывны на Г и на Г х Г соответственно. В этом случае
- me(r)J -

82 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
Таким образом, существует предел
что и требовалось доказать. >
Пример 3.3. Случайный процесс
t{t,u>) = a{u)coe(<pt) + /?(u>) einfo*), t e T = [О, оо),
из примера 1.3, имеющий параметры М[а(и>)] = та, M[/?(w)] =
= тр, Л[а(ш)] = <г1, D[/3(u))] = tr|, cov[a(u));/3(u))] =x, является
непрерывным на Т, так как функция
t,u>)] = macos(<pt)
непрерывна на Т, а функция
непрерывна наГхГ.
3.3. Дифференцируемость случайного процесса
Определение 3.5. Скалярный случайный процесс второ-
второго порядка ?(t,u)), t G 7\ называют дифференцируемым в
точке to G Т, если существует случайная величина ?Aо,ш), для
которой
||(^|^Г], (зл)
Определение 3.6. Если скалярный случайный процесс
второго порядка ?(?,w), t ? Т, является дифференцируемым
в точке ?о G Т, то случайную величину ?(to,u)) называют его
производной в этой точке.

3.3. Диффереицируемость случайного процесса
83
Определение 3.7. Если скалярный случайный процесс
второго порядка ?{t,u)), t€T, является дифференцируемым в
каждой точке открытого множества Го С Т, то его называют
дифференцируемым на множестве То, а случайный про-
процесс ?(t,w), t G To, — производной случайного процесса
?{t,u)), t€T, на множестве То-
Теорема 3.7. Для того чтобы скалярный случайный про-
процесс второго порядка ?(t,w), t G Г, был дифференцируем в
точке to ?Т, а для случайной величины f (to,w) существовали
математическое ожидание и дисперсия, необходимо и доста-
достаточно, чтобы в этой точке была дифференцируема функция
m^(t) и существовала вторая смешанная производная функции
K^(ti,t2) при t\=t2 = tQ.
¦4 Необходимость. Пусть скалярный случайный процесс
второго порядка ?(t,u>), t?T, дифференцируем в точке to € Т,
для случайной величины ?(to,u>) имеет место равенство C.1), а
также существуют M[?(?0,w)] и D[?(to,u>)].
Воспользовавшись свойствами математического ожидания
и ковариационной функции (см. доказательство теоремы 3.6),
приходим к неравенствам
М
t-t0
А так как выполняется равенство C.1), то существует предел
ЛТ 2
lim
t-to
Отсюда следует существование предела
те (to) = lim
= 0.
t-t0

84
3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
и выполнение равенства
i=to
C.2)
Чтобы доказать существование второй смешанной произ-
производной от ковариационной функции K^tify) в точке (to,to),
рассмотрим неотрицательную функцию
[I h-to
С учетом неравенства Шварца получаем
h-t0
t2-i
+ М
xM
-10
]}

3.3. Дифференцируемость случайного процесса
85
А так как имеет место равенство C.1), то существует предел
lim <p{to,ti,t2) = 0. C.3)
Далее, опять используя неравенство Шварца, получаем
h-to
хМ
>
({h'TT'u) ¦
I, "• ^1 — ^о
А так как
-to
и имеют место равенства C.1), C.3), то существует предел
)-№,ш)л _
-'to -I
(*i,*a)-+(*o,*o)
— *0

86 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
или, что то же самое,
/tf{(M2)tf{(M2)tf{(*l,*0) + tf{(*0,*0) ,
lim < ; rr г Ь
И() < {tt)(tt)
— to t<i — tg
Таким образом, существует предел
(*1,*з)-+(*о,*о) (*1
= B[?(to,u;)]. C.4)
Кроме того, с учетом C.3) имеем
0= lim <p(to,h,t2) =
(*ь*2Н(*о,*о) П h-to t2-to
n
1
В фигурных скобках в правой части последнего равенства
записана линейная комбинация разностных аппроксимаций вто-
вторых смешанных производных для ковариационной функции
K^(ti,t2) в точке (to,to). Поэтому существование для нее ну-
нулевого предела при ti,t2 —> to с учетом равенства C.4) означает

3.3. Дифференцируемость случайного процесса
87
существование вторых смешанных производных для
точке (to,to) и выполнение следующих равенств:
C.6)
Достаточность. Предполагаем, что условия C.2), C.6)
выполняются. В этом случае для доказательства равенства 3.1
достаточно проверить стохастический критерий Коши:
lim M
t\ — to
= 0.
Это может быть реализовано повторением в обратном порядке
цепочки равенств, приводящих к равенству C.5). Действитель-
Действительно, если C.2) и C.5) выполняются и
A(to,tut>)={
то существуют пределы
lim
ti,t2-+t0
Но тогда имеем
0= lim
{ti-to)(t2-to)
lim B(to,ti,t2)=0.
ti,t2-*t0

88 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
Таким образом, существует случайная величина ?(to,u), такая,
что верно равенство C.1). >
Следствие 3.2. Для дифференцируемого на множестве Т
скалярного случайного процесса второго порядка ?(t,u), t?T,c
математическим ожиданием m^(t) и ковариационной функцией
K^(h,t2) определен скалярный случайный процесс ?(t,(jj), teT.
При этом, если r)(t,cj) = ?(t,u), teT, — случайный процесс
второго порядка, то
Следствие 3.3. Если ?(t,uj), t ?T, — дифференцируемый в
Т стационарный скалярный случайный процесс второго поряд-
порядка с математическим ожиданием т^ = const и ковариационной
функцией К^(т), T = t2 — t\, &r)(t,w) —?{t,u), teT — случайный
процесс второго порядка, то
Пример 3.4. Рассмотрим скалярный случайный процесс
?(i,w) = a(w)cos(<pt) + /3(ш)влп{<р?), t е Т = [0, со),
где a(ut) и /3(ш) — независимые случайные величины с матема-
математическими ожиданиями та и тр соответственно, одинаковыми
дисперсиями, равными а2, а <р 6 R — известная постоянная. В
этом случае (см. пример 1.3)
= macos((pt) + mpsm((pt),
t2) = <r2cos[<p(t2 — ti)].
А так как существуют производные
dmeii) r . ,
—-у^^ = ipympcosyipt)-таът{ч>Щ, teT,
dt
d2Ki{h,t2) _ 02/Q(tbt3) _ 2 2

3.3. Дифферешщруемость слученного процесса 89
то исходный случайный процесс является дифференцируемым
на множестве Т. При этом, если r)(t,u>) =?(t,w), t € Т, то
= <p[mpcos(<pt) — masin(ipt)],
и можно утверждать, что скалярный случайный процесс r}(t,w),
t?T, также является дифференцируемым на множестве Т, т.е.
определен скалярный случайный процесс ?(t,u)), t G Т и т.д.
Пример 3.5. Пусть ?(t,u>), t ?T, — стационарный скаляр-
скалярный случайный процесс с ковариационной функцией
/Q(r) = <r2exp(-a2|r|), r = t2-t1.
На первый взгляд этот случайный процесс не является диффе-
дифференцируемым, так как при г = 0 функция К^(т) не имеет даже
первой производной. Но при более внимательном рассмотрении
с учетом существования и равенства пределов
lim K'J(t) = <rV = lim K'J(t)
убеждаемся в ошибочности этого вывода.
Пример 3.6. Пусть ?(t,w), t G Г = [0, со), — пуассонов-
ский процесс с параметром А > 0. В этом случае, согласно
определению 2.7, для любых t\,t,t2 G T, t\ < t < t2, случайные
величины f(ti,u>) — ?{t,w) и ?(t,u>) - ?(*2,w) являются незави-
независимыми и распределены по закону Пуассона с параметрами
X(t — t\) и X(t2 — t) соответственно. Рассматриваемый случай-
случайный процесс не является дифференцируемым ни в одной точке
t G Г. Это объясняется тем, что не удовлетворяется стохасти-
стохастический критерий Коши:
Цт
t2-t tx-t
\ _
_

90 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
так как из независимости случайных величин ?(?i,w)
?(t,u)) -?(t2,u)) следуют равенства
lim
= lim
'1 .
и для к = 1, 2
= A(tfc - t) + *2(tk - tJ.
3.4. Интегрируемость случайного процесса
Определение 3.8. Скалярный случайный процесс второ-
второго порядка ?(t,uj), t е Т — [а,Ь], называют интегрируемым
на множестве Т с весом <p(t,t'), где <p(t,t') — неслучайная
функция, определенная на Т х Г, если существует скалярный
случайный процесс ij(t,u}), t G Г, такой, что независимо от вы-
выбора разбиения П = П(а, 6) = {tk}nk=0 U {С>^=о С Т, а = tQ $ t'o $
< h ^ t[ ^ t2 ^ ... ^ ^_х ^ tn = 6, с параметром d(l"l) = max Д^ =
= max(?fc+i — <jt) существует предел
; т. (з.7)
к=О
По поводу интегрируемых случайных процессов второго
порядка отметим следующее.
1. Если скалярный случайный процесс ?{t,<J), t G Г = [а, Ь],
является интегрируемым на Г с весом <p(t,t'), то скалярный
случайный процесс i](t,uj), t G Т, обозначают как интеграл:
ь
p{t,t')Z(t',u)dt', teT.
f

3.4. Интегрируемость случайного процесса 91
2. Если <p{t,t') = А = const, то для интегрируемого на Т
случайного процесса f (?,w), t G Г,
случайная величина.
3. Если
;>;:¦
единичная функция, то
t
,t')Z{t',u)dt' = J Z{t\u>)dt' -
скалярный случайный процесс, который называют интегра-
интегралом с переменным верхним пределом от скалярного ин-
интегрируемого случайного процесса.
Теорема 3.8. Скалярный случайный процесс второго по-
порядка ?(?,w), t G T = [а, 6], является интегрируемым на множе-
множестве Т с весом <p(t,t') тогда и только тогда, когда на Т с весом
у>(?,?') интегрируемо его математическое ожидание инаТхТ
с весом (p{t,ti)(p{t,t2) интегрируема его ковариационная функ-
функция.
^ Доказательство данной теоремы имеет много общего с
доказательством теоремы 3.7. Поэтому известные свойства и
оценки будем использовать без дополнительных пояснений.
Необходимость. При доказательстве необходимости
предполагаем интегрируемость скалярного случайного процес-
процесса f (?,w), t e T = [а, 6], на множестве Т с весом <p(t,t'). В этом
случае для любого разбиения П(а,6) имеет место тождество

92
3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
C.7). Таким образом,
0= lim M
lim
= lim
n-l
откуда и следует интегрируемость математического ожидания,
т.е. существует
J
т т
Далее, кроме произвольного разбиения П(а,Ь) множества Г,
выберем произвольным образом еще одно разбиение П*(а,Ь) =
= Of }?о и {^^"о1 с т, а = tj < ^ < «К 'Г < '5 < • • • < С-1 <
^ tfn = b, с параметром d(n*) = max Д^* = max(t*+1 -1*) и введем
функции разбиений
n—I
m—1
it=o i=o
= lim М[и(П)-Л(гГ)|21
С учетом тождества C.7) имеем
О ^ 6@ = lim М[|(Л(П) - r,(t,u)) -
а(П)—Ю
(
lim
u f П) ~^О
М
+ 2у/м[\А(П)-г,A,и)\1]М[\А(П*)-г,A,ы)\1]} = 0.

3.4. Интегрируемость случайного процесса 93
Таким образом,
О = b(t) = lim (М [ А (П) Л(ПI -
<*(п)-ю V. L J
d(n*)-fO
-2М[Л(П)Л(П*)]+Л
откуда следует интегрируемость ковариационной функции, так
как, например,
[n-lm-1
Jt=O j=0
n-lm-1
= E E
Jt=O j=0
а условие интегрируемости математического ожидания выпол-
выполняется.
Достаточность. Пусть теперь выполнены условия C.5).
С учетом обозначений, введенных при доказательстве необхо-
необходимости и существования интеграла, имеем
т т
n-lm-1
*= lim
а(П)—fO
Совершенно аналогично можно доказать равенства

94 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
Таким образом,
0= lim {М[Л(П)Л(П)]-2М[Д(П)Л(ГГ)] +
(
М[А(П*)А(П*)]}=
откуда, согласно стохастическому критерию Коши, и следует
достаточность в утверждении теоремы. >
Следствие 3.4. Если ?(t,w), t е Г = [о, 6], — интегриру-
интегрируемый на множестве Т с весом <p{t,t') скалярный случайный
процесс второго порядка и
t,t')?{t',bj)dt', teT,
f
то
= j<p{t,t')mz{t')dt',
т
v(h,t2) = J j
T T
T T
Следствие 3.5. Если ?(?,w), t eT = [a,b], — скалярный
случайный процесс второго порядка, интегрируемый на мно-
множестве Т с весом <p(t,t') = J(t — t'), где J(t — t') — единичная
функция, то скалярный случайный процесс
Т
является дифференцируемым на множестве Т и ?(t,u)) = f}(t,u)),

- 3.4. Интегрируемость случайного процесса 95
Действительно, в рассматриваемом случае из равенств
* *1 «2
J f j
1 2
')dt', Kr,(tut2) = f jKt(t',t")dt'dt"
в точках непрерывности подынтегральных функций следуют
равенства [VI], [VII]
и осталось воспользоваться теоремой 3.7. >
Следствие 3.6. Если скалярный случайный процесс второ-
второго порядка ?(t,cj), t G jT, интегрируем на множестве Т с весом
<p{t,t) и
т
то
Kir,{ti,t2) =
= J<p(t2,t')Kz(t1,t')dt'.
Пример 3.7. Пусть €{t,uj), t € T = [0, со) — скалярный
винеровский процесс, выходящий из нуля. Докажем, что он
является интегрируемым на Т с весом <p(t,t') = J(t — t').
В рассматриваемом случае имеем

96 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
где
Е (tl h) E
\ti ?2 /
Таким образом,
1
( f2
h(t2-h) \-h
Но в этом случае существует
оо
rj(t,L})= ff(t,t')
0
причем
mv(t
и существует
t t
D[rt(t,u)]= 1 jK^h
0 0
t
0
it' = fi{
0
i{(r)rfr =
,t2)dtidt2 ^
t ti
= fdh jt2dt2
0 0
t',Lj)dt',
0,
t
+ Jhdtl
0
X.
te
t
h
¦(
'i'2
")•
t3
Пример 3.8. Пусть ?{t,u), teT, a r}(t,u), teT, — скаляр-
скалярные случайные процессы, определенные в примере 3.7. Найдем
их совместный закон распределения при каждом фиксиро-
фиксированном t ^ 0, т.е. одномерный закон распределения векторного
случайного процесса
е(*>ы) = \{«Ы)\ *ег=[о,оо).
\v(tb>)J

3.4. Интегрируемость случайного процесса 97
Предварительно отметим, что в смысле СК-сходимости опе-
операции интегрирования и дифференцирования случайных про-
процессов сводятся к суммированию с весами их сечений и последу-
последующему предельному переходу. А из курса теории вероятностей
[XVI] известно, что линейная комбинация конечного числа слу-
случайных величин, распределенных по нормальному закону, —
случайная величина, распределенная по нормальному закону.
Таким образом, можно утверждать, что, как при интегриро-
интегрировании, так и при дифференцировании нормальных процессов,
являющихся соответственно интегрируемыми или дифференци-
дифференцируемыми, получаем нормальные процессы.
В рассматриваемом случае ?(t,u)), t G [0,oo), — скаляр-
скалярный винеровский процесс, выходящий из нуля. Он является
нормальным скалярным процессом с нулевым математическим
ожиданием и дисперсией D[?(?,w)] = ? (см. пример 2.4). А так
как
t
f ter,
то и T)(t,bS), t ? Т, — нормальный скалярный процесс с мате-
математическим ожиданием mn{t) = 0 и дисперсией D[rf(t,uj)] =
(см. пример 3.7). При этом, согласно следствию 3.6,
t
Kir){t,t) = J
=^, teT.
Поэтому при любом фиксированном t ^ 0 можно считать, что
двумерный случайный вектор e(t,u>) распределен по нормаль-
нормальному закону с нулевым математическим ожиданием и ковариа-
ковариационной матрицей
72 C/ЗГ l-6/t2

98 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
Таким образом, одномерная функция плотности вероятностей
двумерного векторного случайного процесса s(t,u), t G [0, сю),
имеет вид
* , .ч л/12 / 2х\
Mxlx2\t) = ^eXp{-1±
3.5. Действие линейного
оператора на случайный процесс
Пусть скалярный случайный процесс
ri{t,u)±Lt[t{t,u)], teTGR, C.8)
есть результат воздействия линейного оператора Lt на исход-
исходный скалярный случайный процесс ?(t,u)), t G Г, обладающий
необходимыми свойствами (дифференцируемость, интегрируе-
интегрируемость и т.д.). Если Lt — это оператор умножения на неслучай-
неслучайную функцию, определенную на множестве Т, либо оператор
дифференцирования, интегрирования или их композиция, то с
учетом результатов, изложенных в 1.2, 3.3, 3.4, приходим к
следующим равенствам:
го, @ = Lt[m((t)], K^tuh) = Lt.L^K^h^)]. C.9)
При этом следует отметить, что равенства C.9) могут быть
получены непосредственно из определения математического
ожидания и определения линейного оператора, которым также
является и оператор математического ожидания.
Равенства C.8), C.9) являются весьма полезными при реше-
решении многих прикладных задач.
Пример 3.9. Пусть ?(t,uj), t G T = [0, оо), — дифференци-
дифференцируемый скалярный случайный процесс с известными математи-
математическим ожиданием m^(t) и ковариационной функцией

3.5. Действие линейного оператора на случайный процесс 99
Найдем математическое ожидание и ковариационную функцию
скалярного случайного процесса
T, t G T,
где a(t), C(t), j(t) — неслучайные скалярные функции, опреде-
определенные при t ^ 0.
В рассматриваемом случае оператор
о
является линейным и для решения исходной задачи можно
воспользоваться равенствами C.9). Таким образом,
t
mn(t) = Lt[mt(t)] = a(t)mt(t) + 0(t)^^ + 7(t) J e-T
о
А так как
0
J
о о
«1 «2
rln+r*)[.]dndT2,
о о
«1 *2

100 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
то искомая ковариационная функция равна
V
иъ2
h
h t2
\ffe-^^Ki{rl,T2)dndT2. #
о о
Следует отметить, что если случайные процессы ?(t,u),
t G T — [0, со), и r)(t,u>), t€T, определены и связаны равенством
C.8), а линейный оператор Lt является обратимым, то обрат-
обратный оператор LJ1 также является линейным оператором и в
этом случае имеют место равенства, аналогичные равенствам
C.9). Во многих технических дисциплинах* широко исполь-
используют понятие линейного динамического звена п-го поряд-
порядка, под которым понимают подсистему любой динамической
системы, состояние которой y(t) адекватно описывает мате-
математическая модель, представляющая собой задачу Коши для
*См.: Директор С, Рорер Р.

3.5. Действие линейного оператора на случайный процесс 101
линейного неоднородного дифференциального уравнения п-го
порядка:
У(О) = Уо, У(Л)@) = Уо*. * = 1, та—1,
где ak(t), к=1,п, — известные неслучайные функции, опре-
определенные при t > 0, a f(t) — известная неслучайная функция
(входной сигнал). Если у0 = 0 = уо/ь fc = 1, п - 1, то линейное
динамическое звено называют невозмущенным и функцию
y(t) — его реакцией на входной сигнал. Бели на вход линей-
линейного динамического звена поступает случайный процесс ?(t,u)),
t G Т, то реакция линейного динамического звена — случайный
процесс r)(t,u>), t G Т, и мы приходим к равенству
LMt,u)] = t(t,u>), teT,
которое фактически является стохастическим дифферен-
дифференциальным уравнением, линейным относительно случайного
процесса r}(t,u>), teT.
Теория стохастических дифференциальных уравнений бу-
будет рассмотрена в гл. 7. А так как реакция линейного ди-
динамического звена на входной сигнал — удобный объект для
иллюстраций, то в дайной и последующих главах под стохасти-
стохастическим дифференциальным уравнением будем понимать равен-
равенство двух случайных процессов ?(t,w), t G Т, и Lt[r](t,u))], t G T,
которое будем использовать для определения связей между их
характеристиками.
Пример 3.10. Рассмотрим задачу Коши
которую можно записать в операторном виде

102 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
и интерпретировать как задачу о нахождении реакции невозму-
невозмущенного (по начальному состоянию) линейного динамического
звена первого порядка с параметром a(t) (а(?) — непрерывная
неслучайная функция при t > 0) на входной сигнал ?(t,u), t>0,
который представляет собой скалярный случайный процесс с
математическим ожиданием m^(t) и ковариационной функци-
функцией K{(ti,t2)- Определим математическое ожидание и кова-
ковариационную функцию скалярного случайного процесса rj(t,u),
teT = [0,со).
В рассматриваемом случае [VIII]
ri{t,u) = LTl№,")] = J'exp(- Ja(
О т
Таким образом,
*i H *i h
= I I exp(- I a(s)ds- j a(s)ds)^(r1,r2)dr1dr2. #
0 0 Ti T2
Из теории обыкновенных дифференциальных уравнений
[VIII] известно, что если {yjt@J=i — фундаментальная систе-
система решений однородного линейного дифференциального урав-
уравнения
где ack{t), k=l,n, — неслучайные непрерывные при ? > О
функции, то решение задачи Коши
о

3.5. Действие линейного оператора на случайный процесс 103
или в операторном виде
Lt[y(t)] = f(t),
может быть представлено следующим образом [VIII]:
где
R(t,r) =
уп(т)
У'п[т)
(n-2), \ (n-2)/ \
Ух V) ¦¦¦ Уп '(т)
Уп(т)
y'n{r)
-1
Если теперь рассмотреть задачу о реакции ri(t,w), t ^ 0,
невозмущенного (по начальному состоянию) линейного дина-
динамического звена n-го порядка, параметрами ajt(<), k = l,n,
которого являются неслучайные непрерывные при t > 0 функ-
функции, на входной сигнал ?(t,w), t ^ 0, с характеристиками
t2), то приходим к задаче Коши
= 0,
которую можно записать в операторном виде
Таким образом,
t
rf(t,u) = LJ [?(?>w)] = / R(t,
, t > 0;

104 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
*i t2
= I f
R{tun)R{t2,T2)Ki{TUT2)dTldT2.
о о
Как следует из проведенных рассуждений, исходная задача
фактически сведена к нахождению функции R(t,r), зачастую
называемой передаточной функцией линейного динамиче-
динамического звена. Если а*(?) = a* = const, k — l,n, то для нахо-
нахождения функции R(t,r) можно воспользоваться интегральным
преобразованием Лапласа с параметром s. Действительно, в
изображениях интегрального преобразования Лапласа
о
оо
О
задача Коши (ЗЛО) принимает вид
Таким образом,
Если при этом
<г+«'оо

3.5. Действие линейного оператора на случайный процесс 105
то для получения окончательного результата достаточно вос-
воспользоваться теоремой о свертке [XI]:
В рассматриваемом случае R(t,r) = R(t — т).
Пример 3.11. Найдем математическое ожидание mv(t)
и дисперсию Dv(t) реакции невозмущенного (по начальному
состоянию) линейного динамического звена второго порядка:
\
f Lafo(«, w)] = rj(t,u) + 2hfi(t,u) + k2V(t,u;) = k2?(t, w),
17@,0;) = 0, ?)@,w) = 0, k>h>Q,
на входной сигнал №?(t,w), где f (t,u), t € T = [0,00), — скаляр-
скалярный стационарный случайный процесс со следующими харак-
характеристиками:
т&) = 0, Щт) = <r2e-"
где «г2, а, /3 — известные постоянные, а г = t2 —1\.
Следует отметить, что сформулированная задача может
иметь различную интерпретацию. В частности, к подобной
задаче сводится задача определения вероятностных характе-
характеристик бортовой качки корабля при волнении (угловые накло-
наклонения на правый и левый борт судна). В этом случае T)(t,u) —
угол наклона палубы корабля в момент времени t > 0, а ?(t,u) —
угол наклона касательной плоскости к поверхности моря в дан-
данной точке в момент времени t > 0 относительно линии горизон-
горизонта, ортогональной направлению киля корабля.
В рассматриваемом примере
L2[s] = s2 + 2hs + к2 = (s + hJ + (к2 - h2).

106 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
Воспользовавшись соответствующими теоремами и таблицами
интегрального преобразования Лапласа [XI], находим
Таким образом,
к*
о
и можно записать решение исходной задачи:
,«) ± L^m»)] = - J е-^-т)> япДО - т)Щт,и) dr, t > 0,
Dv(t) = Kv(t,t) = LtlLt2[Kt(h,t2)]\tl=t2=t =
^еЛ(т1+75-20 sm[<p(t-ri)] sm[<p(t-T2
о о
Дальнейшие вычисления уже не вызывают трудностей, и мы их
опускаем.
3.6. Эргодические случайные процессы
При решении прикладных задач, когда по наблюдаемым
значениям изучаемого случайного процесса требуется оценить
его моменты, большое значение приобретает информативность
выборочных реализаций. Это особенно важно в тех случаях,
когда условия, в которых проводят наблюдения, позволяют
получить лишь одну реализацию.
В связи с этим возникает естественный вопрос — можно
ли по одной реализации случайного процесса делать какие-либо
заключения о его свойствах? Оказывается, что можно, но

3.6. Эргодическяе случайные процессы 107
не для всех случайных процессов, а лишь для тех, которые
удовлетворяют определенным условиям.
Определение 3.9. Скалярный случайный процесс ?(t,w),
t € Т = [0, /], интегрируемый на множестве Т с весом <p(t,t') =
= l/l, t, t' € Т, и обладающий постоянным математическим
ожиданием т^, называют эрг одическим по отношению к
математическому ожиданию т^, если существует предел
f
1 Г
или, что тоже самое,
ГМ Г |2l
limM 7 t(t,u)dt-mA \= 0.
¦-ЮО [I ( У I J
/-+OO
О
Теорема 3.9. Пусть ?{t,w), t € Т = [0, /], — скалярный
случайный процесс второго порядка, интегрируемый на мно-
множестве Т с весом p(t), где p(t) — некоторая произвольная
неслучайная интегрируемая на Т функция. Предел
iv^JpWltfru)-'
lim
/-+OO
0
существует тогда и только тогда, когда существует предел
UmJ f
о
о о
¦4 Из условий теоремы следует существование случайной вели-
величины
±J C.11)

108 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
с математическим ожиданием
тп А М[»?И] = Jp(t) mt(t)dt C.12)
и дисперсией
Dv±I>[ri(u)] = J J
C.13)
т т
Если воспользоваться определением дисперсии скалярной слу-
случайной величины, то с учетом C.11), C.12) получаем
D, = М[\г,(и) -
Сопоставив этот результат с C.13), приходим к равенству
т т т
Из определения предела следует, что
lim p(t)[t(t,i
I—+ОО /
тогда и только тогда, когда
dt =
0 = lhn M
dt
/ i
= jm^ffp{t1)p{t2)Ki{h,t2)dtldt2
о о
Значит, теорема доказана. >

3.6. Эргодические случайные процессы 109
Следствие 3.7. Если в условиях теоремы 3.9 p(t) = 1/1,
teT = [0,l], то
о
тогда и только тогда, когда
lim h f I
/-Kx> PJJ
0 0
Следствие 3.8. Если скалярный случайный процесс вто-
второго порядка ?{t,u), t € Т = [О, I], интегрируем на множестве Т
с весом p(t) = 1/1 и m^(t) = m^ — const, то условие
lim i / [щгиЬ2)Л1Л2 = 0 C.14)
О О
является необходимым и достаточным для эргодичности этого
случайного процесса по отношению к математическому ожида-
ожиданию.
Следствие 3.8 — отражение общей эргодической теоре-
теоремы, утверждающей следующее. Для скалярного случайного
процесса ?{t,u)), t € Т = [0, /], с постоянным математическим
ожиданием условие, что среднее значение этого случайного
процесса по области Т в пределе при / —f ос равно его математи-
математическому ожиданию, равносильно условию, что среднее значение
по области ТхТ ковариационной функции при / -> сю стремится
к нулю.
Практическая проверка реализуемости необходимого и до-
достаточного условия C.14) эргодичности случайного процес-
процесса относительно его математического ожидания может быть
связана с преодолением значительных трудностей. Поэтому

110
3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
зачастую, особенно в случае стационарных случайных процес-
процессов, целесообразно использовать достаточные условия эргодич-
эргодичности.
Теорема 3.10. Пусть скалярный случайный процесс вто-
второго порядка ?(t,w), t G Т = [О, I], интегрируемый на множестве
Т с весом 1/1, имеет постоянное математическое ожидание
тп{. Тогда для его эргодичности относительно математическо-
математического ожидания достаточно существования предела
Kt(ti,t2) = 0. C.15)
4 Пусть выполнены условия те-
теоремы. Тогда для любого е >
> 0 существует такое /о > 0, что
при |*2 — *i| > /о верно неравенство
< ?. Обозначим См =
Рис. 3.1
{A,з)|12|0}
G2 = TxT\Gi (рис. 3.1). Если
N = maxD[?(i,w)] = maxK(t,t),
а тп(См), m(G2) — площади областей Gi и G2 соответственно,
то
i J J
о о
= UJJKt(t1,t2)dt1dt2 + jj
G
<?i
em(G1)+Nm(G2)
/2
,

3.6. Эргодические случайные процессы 111
так как имеют место неравенства (см. рис. 3.1)
m{Gi) < I2, m(G2) < 2ll0.
Таким образом, из C.15) следует C.14), что и требовалось
доказать. >
Пример 3.12. Скалярный стационарный случайный про-
процесс €(t,u), t G Т = [0, оо), с характеристиками
], a > О,
(см. пример 3.11) является эргодическим относительно матема-
математического ожидания. Действительно:
а) по условию М[?(?,и;)] = 0, t ? Г, т.е. случайный процесс
?(t,w), t € Г, имеет постоянное математическое ожидание;
б) он является интегрируемым на любом отрезке [0, /] С Г,
/ > 0, с весом 1/1, так как существуют интегралы
}//
о о
в) выполняется достаточное условие C.15), которое при г =
= ti — t\ означает существование предела
lim
It 1-й»
Замечание 3.3. Для эргодического по отношению к мате-
математическому ожиданию скалярного случайного процесса ?(?,и),
t G Т = [0, /], с известной реализацией x(t) в качестве оценки его
математического ожидания можно использовать величину

112 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
При этом, как известно из курса математической статистики
[XVII], качество этой оценки возрастает с ростом /.
Замечание 3.4. Возможность получения оценки математи-
математического ожидания эргодического случайного процесса по одной
его реализации, т.е. по результатам одного эксперимента, зача-
зачастую избавляет исследователей от проведения многочисленных
экспериментов, связанных с затратами материальных и вре-
временных ресурсов.
Замечание 3.5. Если ?(t,w), t G Т С R, — скалярный ста-
стационарный случайный процесс, то
гп? = M[?(?,w)] = const; D^ = D[?(?,w)] = const.
Скалярный случайный процесс (?(?,w) — m^) , t G T, имеет по-
постоянное математическое ожидание D$ и при выполнении со-
соответствующих условий является эргодическим по отношению
к математическому ожиданию. Таким образом, можно вести
речь о том, что исходный случайный процесс ?(t,u), t G T,
является эргодическим по отношению к дисперсии и рас-
рассматривать возможность построения качественной оценки для
его дисперсии по одной реализации.
Определение 3.10. Скалярный стационарный случайный
процесс второго порядка ?(t,w), t G T= [0,1], интегрируемый
на Т с весом 1/1, называют эргодическим по отношению к
дисперсии D{, если существует предел
о
или, что тоже самое,
=0.

Вопросы и задачи 113
В заключение отметим, что если скалярный случайный про-
процесс ?(t,u)), t ? T — [а, /], эргодический по отношению к диспе-
дисперсии D^, то скалярный случайный процесс ri(t,u)) = (^(t,u;) —
m^j , t G Г, согласно определению 3.6, эргодический относи-
относительно математического ожидания M.[r)(t,w)] = D$ = const. Та-
Таким образом, условие
lim i / f Kv
[-+ОО I* J J
lim
/-ЮО I
О О
необходимо и достаточно, а условие
lim Kv{tut2) =
|**|W°
достаточно для эргодичности исходного скалярного стационар-
стационарного случайного процесса ?(t,u), t G Г, относительно диспе-
дисперсии.
Вопросы и задачи
3.1. Являются ли: а) стохастически эквивалентные слу-
случайные процессы равными в смысле СК-нормы; б) случайные
процессы, равные в смысле СК-нормы, стохастически эквива-
эквивалентными?
3.2. Можно ли утверждать, что предел случайного процесса
обладает обычными свойствами предела неслучайной функции?
3.3. Можно ли утверждать, что предел последовательности
случайных процессов обладает обычными свойствами предела
последовательности?
3.4. Докажите теорему 3.2.
3.5. Докажите утверждение из замечания 3.1.
3.6. Определение 3.3 непрерывности случайного процесса
в точке является аналогом первого из двух эквивалентных

114 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
определений непрерывности функции в точке. Сформулируй-
Сформулируйте определение непрерывности случайного процесса в точке,
аналогичное второму определению непрерывности функции в
точке.
3.7. Пусть {(t>w) = (fc(*,«) 6(*,^))Т, * € T = [0, оо), — дву-
двумерный винеровский процесс, выходящий из 0. Пусть [а, 6] С Т
и о = t0 < t\ < ... <tn=b. Докажите, что существует предел
п-1
"iiirf
где
3.8. Докажите следствие 3.1 из теоремы 3.5.
3.9. Докажите, что линейная комбинация и произведение
непрерывных на Т скалярных случайных процессов — непре-
непрерывные на Т скалярные случайные процессы.
3.10. Пусть ?fc(w), k= 1,оо, — некоррелированные случай-
случайные величины и
Докажите, что последовательность случайных величин {rin(u)}
сходится тогда и только тогда, когда одновременно сходятся
числовые ряды
3.11. Пусть Z(t,u), Z(k)(t,u),k = l,oo, v(t,u), tiln)(t,u), n =
= 1, оо, — скалярные случайные процессы, t ? Т С R, причем
fau) = ri(t,u).

Вопросы и задачи 115
Докажите, что
Urn M[Z{k)(ttu)ri(n)(ttu)] = M[{{t,u)ri(t,u)].
3.12. Докажите следствия 3.2, 3.3.
3.13. Докажите, что скалярный случайный процесс
?(t,u;) = e-2*ein[t + ?>(u;)], t € Т,
где <р{ш) — случайная величина, распределенная по равномер-
равномерному закону на отрезке [0, 2тг], дифференцируем на Т.
Указание: воспользоваться критерием дифференцируе-
мости случайного процесса.
3.14. Пусть <р(ш) — случайная величина, распределенная по
равномерному закону на [0,2тг] и
{(t,w) = |sint| ein[2t +v(w)], t € T = [0,oo).
Является ли: а) случайный процесс ?(t,w), t G Г, дифферен-
дифференцируемым? б) произвольная реализация случайного процесса
?(t,u;), ? G Т, дифференцируемой?
Ответ: а) случайный процесс ?(?,u;), t G Г, является
дифференцируемым при любом t ?Т; б) любая реализация не
имеет производных в точках t = ктг, к — 0, оо.
3.15. Найдите математическое ожидание, дисперсию и ко-
ковариационную функцию случайного процесса
ri(t,u)±?{t,u), teT CR,
если известно, что
где a(w) и /3(ш) — некоррелированные случайные величины с
нулевыми математическими ожиданиями и одинаковыми дис-
дисперсиями, равными 0,1.
Ответ: m^t) = 1; tf{t) = 0,4i2 + 0,9i4; Kn{tut2) = 0,4hh +

116 3. ЭЛЕМЕНТЫ СТОХА СТИЧЕСКОГО АНАЛИЗА
3.16. Найдите математическое ожидание и ковариационную
функцию скалярного случайного процесса
i7(t,«) =?(*,«), t€Tt
если известно, что
Ответ: ro,(t) = 2sin2@,5?); Kv(tltt2) = 2 + cost2 + costi +
3.17. Дифференцируемый случайный процесс ?(t,w), t 6 T,
имеет математическое ожидание m^(t) и ковариационную фун-
функцию Kt(ti,t2). Найдите математическое ожидание и ковариа-
ковариационную функцию случайного процесса
Ответ: mv(t) = m^t) + m'^t); Kv(tut2) = K(.{tut2) +
dK((ti,t2) , дК((Ь,Ь) .
dh dhdtt '
3.18. Является ли дифференцируемым винеровский про-
процесс?
Ответ: нет.
3.19. Пусть ?(t,w), t € Т, — стационарный в широком
смысле случайный процесс, дифференцируемый на Т. Является
ли стационарным в широком смысле случайный процесс ^(t,w),
iGT?
Ответ: да.
3.20. Докажите, что производная от гауссовского процес-
процесса — гауссовский процесс.

Вопросы и задачи 117
3.21. Найдите вероятность того, что производная от гаус-
совского стационарного случайного процесса ?(t,w), t G Т, бу-
будет иметь значения большие, чем с1 = у/5м/с, если М[?(?,ш)] =
= 10м,
Ответ: 0,3085.
3.22. Пусть ?(t,w), t G Т, — стационарный в широком
смысле случайный процесс с ковариационной функцией
Сколько раз он дифференцируем?
Ответ: два раза.
3.23. Найдите одномерный закон распределения векторного
случайного процесса T)(t,w) = (?(t,w) ?(t,w)) ,t?T, earn?(t,u>),
t G T, — нормальный скалярный стационарный в широком смы-
смысле случайный процесс с нулевым математическим ожиданием
и ковариационной функцией К^(т) = A +Г2).
3.24. Докажите следствие 3.6.
3.25. Найдите дисперсию случайного процесса rf(t,u), teT,
при t = 10 с, если
t
5 [t, и) at, t G 1,
о
a ?(t,w), t бГ= [0, со), — интегрируемый на Т скалярный
случайный процесс и К^(т) = о2{\ +а|г|е~а1т1), а2 = 10 (см/сJ,
а = 0,5с.
Ответ: 1366 см2.
3.26. Найдите математическое ожидание, ковариационную
функцию и дисперсию случайного процесса:
t

118 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
= 0,2cos2(W), K^ti,^) =0,4cos(i/ti)cos(i/t2) и v —
известная постоянная;
6)Z(t,u)=:t + a(u))cost+f3(w)smt,teT, гдеа(и),0(и) — не-
независимые случайные величины с нулевыми математическими
ожиданиями и D[a(w)] = 0,1, D[/?(w)] = 0,2.
Ответ: а) m^t) = 0,l[i + {2v)~l sm{2vt) ], Kn{tut2) =
2 <?\ - 0,4^~2sin2(i/t); 6) mn{t) = 0,5t2,
4() ()[()][()]^(
= 0,1 sin2 (i)+0,8 sin2 @,5t).
3.27. Пусть r}(t,w), t € T = [0,oo), — скалярный стационар-
стационарный в широком смысле дифференцируемый на Т случайный
процесс. Выясните, является ли стационарным в широком смы-
смысле случайный процесс
ter.
Ответ: да.
3.28. Пусть ?(t,u), t G Т = [0,оо), — интегрируемый на
Т скалярный случайный процесс с известной ковариационной
функцией K^(ti,t2). Найдите взаимную ковариационную функ-
функцию K^(ti,tt), если
teT.
J
о
Ответ:
3.29. Пусть ?(?,w), t G Т = [0,оо), — винеровский скалярный
процесс, выходящий из нуля. Докажите, что случайный про-

Вопросы и задачи 119
цесс
оо
4
V(t,u,) 4 |(е'-'' - 2е2«-*'>) ?(*» < t € Т,
t
является стационарным в широком смысле случайным процес-
процессом; найдите его математическое ожидание и ковариационную
функцию.
О т вет: т, = 0, Кп(т) = б^е-М - tt^e-'M.
3.30. Найдите дисперсию случайного процесса ?(t,u), t e
GT = [0,oo), если tXt,u) + v2{{t,u) = e{t,u), t е Т, a e(t,w),
t G Т, — скалярный нормальный процесс с нулевым мате-
математическим ожиданием и ковариационной функцией Ке(т) =
= <т2е~а\т\, v, а, а2 — неслучайные параметры, а > 0.
Ответ:
о, . <т2 / 3f2-Q2 а а
3.31. Является скалярный случайный процесс ?(t,w), t G
Т= [0,оо), эргодическим по отношению к математическому
ожиданию, если
= 0,
о(^) — случайная величина, распределенная по нормально-
нормальному закону с нулевым математическим ожиданием и дисперси-
дисперсией <т2?
Ответ: нет.
3.32. Выясните, является ли двумерный случайный процесс
?(?,u;), t G Т = [0, оо), эргодическим по отношению к математи-
математическому ожиданию, если

120 3. ЭЛЕМЕНТЫ СТОХАСТИЧЕСКОГО АНАЛИЗА
где ?о(и) — двумерный случайный вектор, распределенный по
нормальному закону с нулевым математическим ожиданием и
ковариационной матрицей Е,
E =
Ответ: нет.
3.33. Рассмотрим дифференцируемый на Т скалярный слу-
случайный процесс ?(t,w), t € Т, имеющий постоянное матема-
математическое ожидание и ковариационную функцию Kz(t\,ti) =
- а2е-а(ь-н)* Пусть а > о и ф,ш) = ?(t,u), t e Т. Найдите
Kv(t\,t2) и определите ее наибольшее значение. Докажите эр-
эргодичность случайного процесса r}(t,w), teT, относительно его
математического ожидания.
Ответ: ff4(*i,*3) = 2acr2exp[-a(t2 -hJ] [l-2a(t2-t1J];
ti,t2) — 2acr2.

4. СПЕКТРАЛЬНАЯ
ТЕОРИЯ СТАЦИОНАРНЫХ
СЛУЧАЙНЫХ ПРОЦЕССОВ
В классическом математическом анализе теории рядов и
интегралов Фурье объединяет гармонический анализ. Сво-
Своим названием он обязан простейшей периодической функции
/(?) = .4sin(wt + tp), t ? R, которую в приложениях называют
гармоникой. Константы А, и и <р представляют собой соот-
соответственно амплитуду, частоту и начальную фазу гармони-
гармоники. Одной из задач гармонического анализа является задача
о представимости функции в виде суммы гармоник, каждая
из которых соответствует определенной частоте. Множество
этих частот образует спектр функции, который играет су-
существенную роль для решения широкого класса прикладных
задач, поскольку, располагая спектром, всегда можно восста-
восстановить исходную функцию с наперед заданной точностью.
При изучении случайных процессов гармонический анализ
приобретает особо важное значение. В самом деле, ни одна
из реализаций случайного процесса не может быть известна за-
заранее. Однако заранее можно установить, как распределяется
дисперсия случайного процесса по частотам составляющих его
гармоник. Такая информация не уступает по значимости спек-
спектру детерминированной, т.е. неслучайной функции. Ис-
Использование этой информации при изучении стационарных (в
широком смысле) случайных процессов составляет существо их
спектральной теории.
Напомним, что скалярный случайный процесс (веществен-
(вещественный или комплексный) ?{t,w), t G Г С R, является стационарным
(в широком смысле), если он обладает двумя свойствами:
= ro?= const, teT;
))] ), tut2 e T,

122 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
где символ * означает переход к комплексно сопряженному
выражению в случае комплексного случайного процесса, а
г = <2 — *1- При этом из общих свойств ковариационных функ-
функций (см. 1.2) следует, что если ?(t,w), t € Т С R, — скалярный
стационарный случайный процесс, то
Спектральная теория позволяет заменить исследование ис-
исходного стационарного случайного процесса исследованием его
изображения при интегральном преобразовании Фурье, являю-
являющегося случайной функцией некоторого вспомогательного пе-
переменного, которое во многих приложениях имеет размерность
частоты. А так как применение интегрального преобразования
Фурье зачастую существенно упрощает выкладки, то оно по-
получило широкое распространение как в теоретических, так и в
прикладных исследованиях.
4.1. Стационарные случайные
процессы с дискретным спектром
В этом разделе, говоря о стационарных случайных процес-
процессах, будем иметь в виду стационарные случайные процессы в
широком смысле.
Одним из основных вопросов является представимость ста-
стационарных случайных процессов в виде конечных или бесконеч-
бесконечных сумм гармоник с различными частотами и случайными
амплитудами.
Определение 4.1. Случайный процесс ?(t,w) = a(u))<p(t),
t € Т С R, где q(w) — случайная величина, a <p(t) — неслучайная
функция, определенная на множестве Т, называют элемен-
элементарным случайным процессом.
Пример 4.1. Рассмотрим скалярный случайный процесс
¦[0,1], D.1)

4.1. Стационарные случайные процессы с дискретным спектром 123
представляющий собой конечную сумму элементарных случай-
случайных процессов. Предполагая, что
M[5n(t,w)] = 0, teT, D.2)
найдем условия стационарности случайного процесса 5n(t,w),
teT.
Из определения 4.1 элементарного случайного процесса
Sn(t,u), teT, и свойств математического ожидания (см. П.1)
имеем
Поскольку тригонометрические функции из этой суммы линей-
линейно независимы на отрезке [0, /] [IX], то условие D.2) выполнено
тогда и только тогда, когда
)] = M[/?fc(u,)] = O, k = l,n. D.3)
Далее, в соответствии с определением ковариационной функции,
свойствами математического ожидания (см. П.1) и равенства-
равенствами D.2), D.3), имеем
ut2) = M[Sn(ti,u)Sn(t2,u)] =
КИа™И]соз—-— cos
Ыга=1
+ М [/?fc(w)/3m(w)]Sln
sin—y~^
M[/?fc(w)am(w)Jsin—— cos——.

124 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
Преобразуя произведения тригонометрических функций в их
суммы или разности, получаем, что ковариационная функция
будет зависеть лишь от г = ti —t\, т.е.
тогда и только тогда, когда
cov[ak(u);am(u)] = cov[#t(w);/?m(w)] = 0, k,m = T~n, k ф m;
Следовательно, случайный процесс Sn{t,u), t^T, вида D.1),
удовлетворяющий условию D.2), является стационарным тогда
и только тогда, когда ак(ы), 0к(ш), к = 1, п, являются некор-
некоррелированными случайными величинами с нулевыми математи-
математическими ожиданиями и дисперсией D[afc(w)] = Т)\рк(ш)] = сг\,
к = Т~п.
Заметим, что в этом случае
^, B[Sn(t,u;)] = KSn@) = X>f'
k=i k=i
rf
где <у\ — дисперсии случайных амплитуд ак(ш) и /Зк(и), соот-
ветствующих частоте —г-- #
Пусть скалярный стационарный случайный процесс ?(t,u),
t & Т = [0,1], имеет нулевое математическое ожидание и ко-
ковариационную функцию К^{т) — /Q(?2 - *i), которая является
непрерывной на отрезке [—/, /] и удовлетворяет на этом отрезке
условиям Дирихле. Принимая во внимание четность ковариа-
ковариационной функции К{(т), имеем
, тгкт о 2 / „ , . пкт
1 '
2 Г пкт
= - / K{(r)cos—— йг; к = 0, со.

4.1. Стационарные случайные процессы с дискретным спектром' 125
Далее предполагаем, что в этих разложениях отсутствуют
нечетные гармоники, т.е.
Jfc=O
2 f
2жкт
D-4)
_
= 0,сю.
В соответствии с принятыми допущениями ряды Фурье D.4)
сходятся равномерно, а рассматриваемый скалярный случайный
процесс ?(t,w), t G Т, является интегрируемым на множестве Т
cos—— }k=Q и {sin —}Ь1, что следует из теоремы
3.4, так как при любых значениях k, m ^ 0 в силу непрерыв-
непрерывности подынтегральных функций существуют и ограничены
интегралы
l i
о о
/ 1
cos—-—dtidt2,
2nmt2 , ,
cos —-— dti dt2,
о о
Таким образом, на множестве Т определен скалярный слу-
случайный процесс
, teT, D.5)
Jfc=l

126 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
где
Если случайный процесс Si(t,u>), t € Т, является стационарным
и сходится к исходному случайному процессу ?(t,w), t G Т, то
можно говорить о дискретном спектре {27rfc//}?l0 частот ста-
стационарного случайного процесса ?(t,w), t G Т. Корректность
данной гипотезы подтверждается следующими теоремами.
Теорема 4.1. Если ковариационная функция К^(т) скаляр-
скалярного стационарного случайного процесса ?(t,w), t G Г = [0,1],
с нулевым математическим ожиданием является непрерывной
на отрезке [-/,f], удовлетворяет на нем условиям Дирихле и
представима в виде D.4), то случайный процесс 5„(?,ш), t ? Т,
определяемый согласно D.5), является стационарным.
-4 Так как по условию М[?(?,ш)] = 0, t G Т, то в соответствии с
D.5)
2 Г 2я"]Ь?
м [<**(«)] = у у м [?(*,«)] «ж -у- а = о,
lirkt

4.1. Стационарные случайные процессы с дискретным спектром 127
Далее, с учетом равномерной сходимости рядов Фурье D.4) и
ортонормированности на отрезке [0, /] системы тригонометри-
тригонометрических функций
2" 2кЫ [2 . 2nkt
JV V7COS
имеем
о о
2*qt2
-cos-
о о
4 » ^ 1 I I f 2ттkt\ 2wkt2 . 2ккЬ\ . 2Trkt2\
= 7Г У ak I I (cos —;— cos sm sm )
12& Ч J \ I I I I J
x cos —-—cos —-— dtidt2 =
x
fc=o 0 0
I COS ; COS ; «fti / COS COS ; dt2 —
fc=O
- / sin —-— cos —-— dti J sin —— cos —7~^ *2 ) =
oo
p#g.

128
4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
Совершенно аналогично можно доказать равенства
cov /?,(w);/??(w)J = { cov[ap(u);f3q(u)]=0.
[о, рФч,
Таким образом, можно утверждать (см. пример 4.1), что
Si(t,w), t еТ = [0,1], — стационарный скалярный случайный
процесс. >
Следствие 4.1. Если выполнены условия теоремы 4.1, то
имеют место равенства:
D
= D
= crl * =
jfc=O
Теорема 4.2. Если ковариационная функция К^(т) стаци-
стационарного скалярного случайного процесса ?(?,w), t е Г = [0, /], с
нулевым математическим ожиданием является непрерывной на
отрезке [—/, /], удовлетворяет на нем условиям Дирихле и пред-
ставима в виде D.4), то при п -*¦ сю случайный процесс Si(t,u),
t G Т, определяемый согласно D.5), сходится к исходному слу-
случайному процессу:
i4)), teT,
или, что то же самое, существует предел
)\*\ = 0, teT.

4.1. Стационарные случайные процессы с дискретным спектром 129
4 Воспользовавшись видом D.5) скалярного случайного про-
процесса Si(t,u), t ? Т = [0, /], получаем
fc=i
При этом из D.5) и равномерной сходимости ряда Фурье D.4)
следует, что
Г / ч2 f г, ч 2nks j 1 2nkt
= М\?{t,w)-? / ?(s,w)cos —-—ds\ cos— h
0
/
t,u)- /^(s,w)sin—-—ds sin—;— =
I J I J I
¦cos-
. 2nkt 27Г/Ы , 2 f T. . . 2irk(t - s) ,
+ Sin —;— Sin ; US = - I Ke(t — S) COS US =
' ' J ' J '
•/¦
Совершенно аналогично можно доказать равенство
2 V^ 2 /" 2тгт(г - s) 2тгАг(? - s) ,
= у2° / cos 1 cos i ds =
cos cos -
m=0

130 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
Таким образом, с учетом D.6), получаем
^u;)]- D-7)
fc=0
Для завершения доказательства теоремы рассмотрим тожде-
тождество
- 2М [{(t,U)SZ(t,U)
Из условия
и равенств D.6), D.7) следует, что
u)\>] =D[t(t,u)]-2D[Si(ttu)]
a\ -
k=n+l
п-к остаток сходящегося знакоположительного числового ряда
с общим членом {&\}. Таким образом, существует предел
что и требовалось доказать. >
Следствие 4.2. Если ?(t,w), t ?Т = [0,1], — стационарный
скалярный случайный процесс с математическим ожиданием
гп?, а его ковариационная функция К^(т) непрерывна на отрез-
отрезке [—/, /], удовлетворяет на нем условиям Дирихле и представи-
ма в виде D.4), то центрированный случайный процесс
(t,w)-m6 teT,

4.1. Стационарные случайные процессы с дискретным спектром 131
может быть представлен суммой ряда Фурье:
fc=l
где равенство следует понимать в смысле СК-нормы и
2 Г °
-y / ?(t,
2wkt
——dt =
i
2 /\. . 2nkt , .
= yK(t,u)cos —Л, fc = 0,oo;
, ч . 2wkt ,
(t,w)sin—:—at —
9 /* Owht
= - / f(i,u)sin-y— dt, fc=l,oo.
Следствие 4.З. Некоррелированные амплитуды гармоник
имеют нулевые математические ожидания, а их дисперсии
являются коэффициентами ряда Фурье для ковариационной
функции исходного случайного продесса при соответствующих
частотах.
^ Это утверждение вытекает из результатов примера 4.1, а
также теорем 4.1 и 4.2. >
Пример 4.2. Пусть ?(?,w), t ?T = [0,1], — стационарный
скалярный случайный процесс с нулевым математическим ожи-
ожиданием и ковариационной функцией
где a > 0 — известная постоянная (рис. 4.1). Убедимся в том,
что этот случайный процесс может быть представлен суммой
ряда Фурье.

132
4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
-I
Действительно, ковариационная функция К^(т) непрерывна
и на отрезке [—/, /] удовлетворяет условиям Дирихле, т.е. она
может быть представлена суммой ряда Фурье:
k=0
где для к = 0, оо
жкт
2 f
-JJ Kt(T
о
1/2 I
2 f _aT жкт 2 f _ап_т) жкт
= - I e cos —— ат + - I e v ' cos —r- ат
Отсюда видно, что при m = 0, оо
4а/
2 _
2 _

4.2. Стационарные случайные процессы с непрерывным спектром 133
Таким образом, для ковариационной функции К^{т) имеет
место представление D.4):
и, согласно следствию 4.2, случайный процесс ?(t,w), t G Г,
может быть представлен суммой ряда Фурье. #
В заключение заметим, что ограничения, накладываемые
на ковариационную функцию К^(т) стационарного скалярного
случайного процесса ?(?,w), t G T = [0, /] (в том числе и требо-
требование четности гармоник), являются излишне жесткими. Они
необходимы лишь для получения более или менее простых и
наглядных доказательств соответствующих утверждений. Это
тем более очевидно, что мы понимаем равенство случайных
процессов в смысле СК-нормы.
Из теории рядов Фурье известно [IX], что тригонометри-
тригонометрическая система функций полна на Г и что любая функция
К^(т), интегрируемая на Г с квадратом, может быть предста-
представлена рядом Фурье по тригонометрической системе. При этом
рассматривают сходимость по норме в классе функций, инте-
интегрируемых с квадратом на Г, являющейся аналогом СК-нормы.
Именно поэтому возможно разложение в ряд Фурье даже обоб-
обобщенных функций, представителем которых является 8-функция
Дирака*, что и использовано далее без дополнительных разъяс-
разъяснений.
4.2. Стационарные случайные
процессы с непрерывным спектром
В этом разделе, как и выше, под стационарным случайным
процессом будем понимать стационарные случайные процессы
в широком смысле.
*См. также Пугачев B.C.

134
4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
Пусть ?(t,w), t G Т = [О, I], — стационарный скалярный слу-
случайный процесс с нулевым математическим ожиданием и ко-
ковариационной функцией К^(т), которая является непрерывной
на отрезке [—1,1], удовлетворяет на нем условиям Дирихле и
представима в виде D.4). В этом случае, согласно теореме 4.2,
рассматриваемый случайный процесс представим суммой ряда
Фурье:
где
k=l
2 f
= у /
2nkt
dt, Л = 0,oo,
При этом амплитуды гармоник ctfc(w) и /8fc(w) (k = 1, oo) явля-
являются некоррелированными случайными величинами, имеют ну-
нулевые математические ожидания и дисперсии
где а\ — коэффициенты ряда Фурье для ковариационной
функции К{(т):
к=0
Если воспользоваться формулами Эйлера и ввести случай-
случайные величины

4.2. Стационарные случайные процессы с непрерывным спектром 135
то приходим к следующему представлению исходного скаляр-
скалярного случайного процесса:
^ , , 2nkt
()
_.2jrfct
-e ' /
^22l
2vkt
\ _
Ф*Мехр(г—J, tGT.
fc=—oo
Нетрудно показать, что комплексные случайные величины
), k G Z, являются некоррелированными, имеют нулевые
математические ожидания и дисперсии
2
Кроме того, их можно представить в виде
Ф*М = уУ?(*,
о
При этом
ik=-oo
Если ffc = — частота fc-й гарлом«к«, то при / -? +сю
приходим к случаю непрерывного изменения частот и пере-
переходим от ряда Фурье к интегралу Фурье. При выполнении

136 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
определенных условий этот переход приводит к интегральному
представлению ковариационной функции К^(т), и становится
естественной задача об аналогичном представлении стационар-
стационарного скалярного случайного процесса ?(t,u), t € Т = [О, оо).
Определение 4.2. Бели ковариационная функция
стационарного скалярного случайного процесса ?(t,w), t G T =
[О,оо), является оригиналом интегрального преобразования
Фурье, т.е. на любом конечном интервале [—/, /] она удовлетво-
удовлетворяет условиям Дирихле и является абсолютно интегрируемой в
R, то ее изображение
dr
называют спектральной плотностью этого случайного
процесса.
Приведем некоторые свойства спектральной плотности.
Свойство 4.1. Бели ковариационная функция К^(т) стаци-
стационарного скалярного случайного процесса ?(t,w), t G Т = [0, оо),
является оригиналом интегрального преобразования Фурье и
Ч {") — его спектральная плотность, то
оо
= f
Свойство 4.2. Бели исходный случайный процесс является
вещественным, то:
а) s€(i/)>0;
б) «?(-!/) = «?(!/);

4.2. Стационарные случайные процессы с непрерывным спектром 137
о
оо
д) Ке(т) = 2 [Si(v)cos(vT)dT;
Из свойства 4.2 е) следует, что спектральная плотность
s^(v) представляет собой плотность распределения дисперсии
случайного процесса по частотам его гармоник.
Спектральная плотность s^(u) стационарного скалярного
случайного процесса ?(t,w), t€.T — [0, сю), является аналогом
последовательности {В[Ф(.(ш)]}, т.е. является аналогом после-
последовательности {&\} дисперсий некоррелированных случайных
амплитуд гармоник исходного случайного процесса.
Пример 4.3. Пусть стационарный скалярный случайный
процесс ?{t,u), t G Т — [0, сю), имеет ковариационную функцию
где а > 0 и а2 = К^(О) = D[?(?,w)]. В этом случае спектральная
плотность случайного процесса равна
ОО ОО
1
h
—оо
—оо О
_ <т2 / 1 1 \ _ аа2

138
4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
При увеличении параметра а вне ^-окрестности нуля зна-
значения ковариационной функции К^(т) уменьшаются, а график
спектральной плотности s^(i/) становится все более пологим
(рис. 4.2). При этом
00 оо
f , ч , ст2 f a , a2 v
1 Sf^dv = — / dv = —arctg-
т.е. площадь криволинейной трапеции, ограниченной графиком
спектральной плотности и осью Ov, численно равна дисперсии
исходного стационарного скалярного случайного процесса (см.
свойство 4.2 спектральной плотности). #
2a
За
«- v
Рис. 4.2
В различных приложениях теории случайных процессов ве-
величину iiQ(O) = D[f(?,w)] зачастую интерпретируют как энер-
энергию стационарного скалярного случайного процесса, а величи-
величину st(v) — как плотность энергии на единицу частоты. Термин
„энергия стационарного случайного процесса" обязан своим по-
появлением реализациям стационарных случайных процессов в
электротехнике (напряжение или сила электрического тока). В
этом случае величина s^{v)dv пропорциональна энергии, прихо-
приходящейся в среднем на гармоническое колебание частоты i>, так
как энергия электрического тока пропорциональна квадрату
амплитуды соответствующей гармоники.

4.2. Стационарные случайные процессы с непрерывным спектром 139
Перейдем к рассмотрению вопроса о существовании инте-
интегрального представления стационарного скалярного случайно-
случайного процесса ?(t,w), t G T = [0,оо), с нулевым математическим
ожиданием и ковариационной функцией К^(т), являющейся
оригиналом интегрального преобразования Фурье. При этом в
соответствии с проведенными рассуждениями нетрудно пока-
показать, что для любого конечного / > 0 имеют место равенства:
fc=-oo
2пк
—r-',
М[Ф*(и;)] = 0;
2тг
D.8)
;ФпИ] = 0, к ф j;
fc=-oo
Если ввести в рассмотрение случайную функцию
1
то, согласно D.8), имеем
(ш) = i>(i/k,u,l)Ai/k, к € Z;
fc=-oo
t€T.
Если / -+ +оо, то Aj/fc -+ 0 и значения частот ик заполняют
всю числовую прямую, т.е. реализуется переход от дискретного
спектра к непрерывному. Так как ковариационная функция

1404. СПЕКТРАЛЬНАЯ ТЕОРИЯ
), согласно принятому допущению, является оригиналом
интегрального преобразования Фурье, то можно доказать, что
существует предел
оо
1 f
" ' ' Я" J
О
fc=-oo
7
J ф(»,и
при / -юо. Таким образом, для стационарного скалярного слу-
случайного процесса ?(t,u>), t G T = [0, оо), получаем интегральное
представление
оо
t[t,u>)= J ф(и,и)еы^, teT, D.10)
где фA/,и) — изображение интегрального преобразования Фу-
Фурье для этого случайного процесса.
Следует отметить, что случайная функция ф{и,ш), vgR,
связана с последовательностью {$&(<*>)}?1_оо и в определенном
смысле является аналогом последовательности случайных ком-
комплексных амплитуд гармоник при переходе к непрерывному
спектру частот. Определим математическое ожидание и ко-
ковариационную функцию случайной функции ф{и,и).
В соответствии с D.9) имеем
о
= - [M[Z{t,u)]e-il/fdt = 0, v e R,
т J

4.2. Стационарные случайные процессы с непрерывным спектром 141
так как
MK(t,w)] = O, t€T.
Если воспользоваться интегральным представлением 8-функ-
ции Дирака
оо оо
6(х) = ~ J eiXxd\, J S(x)e-iXxdx = l, D.11)
—оо —оо
то, полагая г = t2 - h, приходим к следующему представлению
ковариационной функции (
[оо оо
^ f f {{tuuiKforfexpiiitt! -ivit2)dtxdt2\ =
о о
о о
оо оо
о о
оо оо
= -j / /
о о
Из проведенных рассуждений вытекает следующая теорема.
Теорема 4.3. Если ковариационная функция К^(т) стацио-
стационарного скалярного случайного процесса ?(?,w), t g T = [0, cxd),
обладающего нулевым математическим ожиданием, является

142 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
оригиналом интегрального преобразования Фурье (т.е. удовле-
удовлетворяет условиям Дирихле на любом конечном интервале [—/, /]
и абсолютно интегрируема в R), то существует скалярная слу-
случайная функция ф{и,и), vGR, такая, что
»,и)] = 0, i/GR; КФ{v,их) =
оо
С позиций теории интегральных преобразований Фурье ин-
интегральное представление D.10) стационарного скалярного слу-
случайного процесса ?(?,w), t €. Т, удовлетворяющего условиям
теоремы 4.3, указывает на то, что он является оригиналом экс-
экспоненциального интегрального преобразования Фурье. Но в
этом случае случайная функция ф(и,ш), i/GR, — его изображе-
изображение и должно иметь место равенство D.9):
Если тп? ф 0, а все остальные условия теоремы 4.3 выпол-
выполняются, то интегральное представление случайного процесса
?(t,w), t € Т, принимает вид
оо
I
,и)е^<1и, t € Т.
В условиях теоремы 4.2 имеет место равенство
со со оо
/ s^{u)du= I I K^{v,

4.3. Белый шум 143
Действительно,
оо
и, кроме того,
оо ор
/ / K${v,v\)dvdv\= I I sz(vi)S(v-v\)dv\dv =
—оо —оо
оо оо
= / S((v\)dvi / &(v-vi)dv= /
Полученный результат можно интерпретировать следую-
следующим образом. „Средняя энергия" стационарного скалярного
случайного процесса может быть получена путем „суммирова-
„суммирования" квадратов модулей амплитуд гармоник, соответствующих
всем частотам.
4.3. Белый шум
Определение 4.3. Скалярный случайный процесс ?(t,u;),
? € Т = [0, оо), называют белым шумом, если он является
стационарным (в широком смысле) и обладает постоянной
спектральной плотностью с, называемой интенсивностью
белого шума.
Рассмотрим свойства белого шума.
Свойство 4.3. Ковариационная функция К^(т) для белого
шума имеет вид
. D.12)

144 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
< Если скалярный случайный процесс €(t,u>), t G Т = [О, оо),
является белым шумом, то для любого действительного v
s^{y) — с — const. D-13)
Таким образом, из свойств спектральной плотности и ин-
интегрального представления 8-функции Дирака D.11) следует
D.12). >
Свойство 4.4. Бели ковариационная функция стационар-
стационарного скалярного случайного процесса ?(t,u>), t G Т = [О, оо),
имеет вид D.12), то этот случайный процесс является белым
шумом.
4 Это свойство непосредственно следует из определения 4.2 и
равенства D.12). >
Пример 4.4. Пусть ?{t,w), ? € Т = [0, оо), — скалярный
винеровский процесс с коэффициентом диффузии а1. Он имеет
ковариационную функцию
, h,t2eT.
Таким образом,
[2 h<t2;
и смешанная вторая производная не существует, т.е. (см. теоре-
теорему 3.7) рассматриваемый случайный процесс недифференциру-
недифференцируем ни в одной точке в Т. Но переходя к обобщенным функциям,
к которым относится и (У-функция Дирака, формально полу-
получаем
т.е. в классе обобщенных функций производная винеровского
процесса есть белый шум с интенсивностью с— <72/2я\

4.3. Белый шум 145
Свойство 4.5. Случайные величины, являющиеся сечения-
сечениями белого шума, некоррелированы.
4 Это следует из D.12), так как для любых tx,t2 € Т = [О, оо),
h ф t2, имеем т = t2 - tx ф 0 и Кк(т) - 2жс8(т) - 0. >
Свойство 4.6. Белый шум обладает бесконечной диспер-
дисперсией.
¦4 Это вытекает из равенства
выполняющегося в силу D.12). >
Появление термина „белый шум" объясняется следующим.
Слово „белый" указывает на сходство с белым светом, у кото-
которого спектральный состав примерно однороден, а слово „шум"
говорит о том, что подобные процессы впервые привлекли к
себе внимание в радиотехнике, где их наличие приводит к воз-
возникновению шумов в линиях радиопередач.
Белый шум обладает бесконечной дисперсией и практиче-
практически не может быть реализован. Но из физических соображений
ясно, что любая динамическая система является инерционной и
очень высокие частоты не могут оказывать значимого влияния
на ее поведение. Это открывает возможность моделирования с
помощью белого шума реальных случайных процессов. Напри-
Например, белый шум часто используют для моделирования случай-
случайных процессов, имеющих постоянную (или почти постоянную)
спектральную плотность в определенной полосе частот, прене-
пренебрегая поведением спектральной плотности вне этой полосы.
Подобные ситуации возникают при изучении многих физиче-
физических явлений, связанных с воздействием отдельных молекул или
электронов на макроскопические системы (например, во всех
явлениях, родственных броуновскому движению). Подобные

146 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
случайные процессы мы также будем называть „белым шумом",
отмечая кавычками условность такого подхода.
Пример 4.5. Пусть скалярный случайный процесс ?(t,w),
t € Т = [0,оо), является стационарным и его спектральная
плотность равна
/с, H<JV;
() |
Рассматриваемый случайный процесс имеет ковариацион-
ковариационную функцию
N
= f ceil/Tdv = — sin(JVr). D.14)
-N
Чтобы он обладал свойствами „белого шума", значение пара-
параметра N должно быть достаточно большим, но в этом случае
достаточно большой будет и дисперсия
А так как
то можно получить сколь угодно малое абсолютное значение
коэффициента корреляции для любых двух сечений ?(t\,ut) и
?(?2,w) при достаточно большом значении \т\ = |?2 - h\. При
фиксированном значении N абсолютное значение коэффициен-
коэффициента корреляции сечений ?(?i,u>) и ?(?2,и;) значимо, когда величи-
величина |*2 ~ Ы достаточно мала.
Чтобы найти предел ковариационной функции D.14) при
iV —>¦ +оо, введем функцию
Nt
= 2с I ^Ш d\
= 2с J *±t

4.3. Белый шум 147
Так как
О оо
/sin х [ sin x ж
ах = I ах = —,
х J х 2'
о
то нетрудно убедиться, что существует предел
lim КЛг)
ЛГ-Н-оо
{О, г < 0;
же, т = 0;
2тгс, г > 0.
Формально дифференцируя полученную функцию, приходим к
6-функции Дирака:
lim К{{т) = 2жс6{т).
Рассмотренный случайный процесс является одной из возмож-
возможных моделей „белого шума". #
Помимо ограниченного в некоторой полосе частот (см.
пример 4.5), часто используют скалярный случайный процесс
(см. пример 4.3) с ковариационной функцией
а^, а>0,
и спектральной плотностью
Q2
4V ' Q2 + l/2
В этом случае
lim se{v) = l и lim К*(т) = 2ж5(т).
Некоррелированность случайных величин, являющихся се-
сечениями белого шума в различные моменты времени — одна

148 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
из основных причин его широкого применения. При исполь-
использовании ограниченного по полосе шума мы все же получаем
значимое абсолютное значение коэффициента корреляции для
случайных величин, являющихся сечениями случайного процес-
процесса при близких значениях t\ и ?г, что зачастую существенно
затрудняет анализ полученных результатов. Использование бе-
белого шума в теории случайных процессов во многом аналогично
использованию ^-функции Дирака в теории линейных систем и
математической физике.
4.4. Преобразование стационарного
случайного процесса при его прохождении
через линейную динамическую систему
В 3.5 уже рассмотрена задача о преобразовании случайного
процесса при его прохождении через линейную динамическую
систему и отмечались трудности, возникающие при ее реше-
решении. Спектральная теория стационарных (в широком смысле)
случайных процессов открывает новые возможности исследова-
исследования подобных задач. Они аналогичны возможностям теории
интегральных преобразований применительно к решению за-
задач математической физики и задач Коши для обыкновенных
линейных дифференциальных уравнений и систем таких урав-
уравнений.
В этом разделе под стационарным случайным процессом
будем понимать стационарные случайные процессы в широком
смысле.
Теорема 4.4. Пусть Т = [0,оо), a ?(?,w), t € Т, и ф,ы),
t G Т, — стационарные скалярные случайные процессы со спек-
спектральными плотностями s^{u) и s^iy) соответственно. Пусть
случайный процесс ?(t,u), t ? Т, является п раз дифференциру-
дифференцируемым на множестве Т. Если
ter,

4.4. Преобразование стационарного случайного процесса ... 149
то имеет место равенство
< Для доказательства теоремы достаточно воспользоваться
свойствами 4.1, 4.2 д)-е) ковариационной функции, определе-
определением спектральной плотности и ее свойствами 4.2 а)-г). Дей-
Действительно, если
,М4
то имеет место равенство (см. следствие 3.3)
или, что тоже самое,
оо оо
= (-l)n A(ij/JV"Ts4(j/)dj/= f
откуда и вытекает нужный результат. Законность дифферен-
дифференцирования под знаком интеграла следует из существования п-й
производной для исходного случайного процесса, что эквива-
эквивалентно сходимости несобственного интеграла [VI]
оо
f
v2nSi(v)dv.
Теорема 4.5. Если ?{t,u), t ? Т = [0, оо), — стационарный
п раз дифференцируемый на Т скалярный случайный процесс

150 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
со спектральной плотностью s^ (i>) и
=
fc=O
где bk, к = 0, п — известные постоянные, то »?(?,w), t е Т, —
стационарный скалярный случайный процесс со спектральной
плотностью
fc=O
-4 Так как ?(t,u), teT, — стационарный случайный процесс,
то его математическое ожидание т^ является величиной
постоянной и
"fc=o ~"
" Дп-к
= 2_Л ~dfi=kM№(t>u}fi = ft«m«= const-
fc=0
Согласно теореме 4.3,
oo
?(t,w) = mt+ J i>{v,u)eividv, t e T.
—oo
А так как случайный процесс ?(t,u), teT, является п раз диф-
дифференцируемым на Т, то, как и при доказательстве теоремы
4.3, приходим к равенству
со
.,w) d^, fc = M,
—оо
и, как следствие, получаем
оо
[

4.4. Преобразование стационарного случайного процесса ... 151
Таким образом, с учетом равенства M[rf(t,uj)] = bnm^ и
теоремы 4.3 имеем
—оо к=0
со
х (
-со
со со
= f
-оо-оо
п
к=0
со оо
= f f
J J
-co-co
n
откуда и следует искомый результат. >
На практике встречаются весьма разнообразные варианты
преобразований стационарного случайного процесса при его
прохождении через линейную динамическую систему. Рассмо-
Рассмотрим достаточно общий случай. Пусть ?(t,w), t € Г = [0, сю), —
стационарный m раз дифференцируемый на Г скалярный слу-
случайный процесс с математическим ожиданием тп^ и спектраль-
спектральной плотностью s^(y), а скалярный случайный процесс r/(t,u}),
t?T, является п раз дифференцируемым на Г и удовлетворяет

152 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
уравнению
SdF^e(''w)' *>0' DЛ5)
к=0
в котором at (А; = 0, п) и &_, (j = 0, m) — известные постоянные.
Случайный процесс rj(t,u), t € Г, можно рассматривать как
стационарный скалярный случайный процесс с математиче-
математическим ожиданием mv и спектральной плотностью sv(y) лишь при
достаточно больших значениях времени t, т.е. лишь после за-
затухания переходных процессов. В этом случае имеем
k=0 j
откуда
m^^im4i вчМ = |ФИ|2в{М, D-16)
где функцию
!D-17)
Ё ak{iu)n-k
к=о
называют частотной характеристикой
системы, которая описывается дифференциальным уравнени-
уравнением D.15).
Для иллюстрации полученных результатов рассмотрим два
примера.
Пример 4.6. Рассмотрим задачу прохождения белого шу-
j<a^(t,w), t € Т = [0, ос), через линейную динамическую систему
первого порядка, описываемую обыкновенным дифференциаль-
дифференциальным уравнением
r)(t,u) + ari(t,u)=((t,u),
где a ? R — известный параметр, а случайный процесс ?(t,u>),
t € Т = [0, ос), имеет постоянную спектральную плотность.

4.4. Преобразование стационарного случайного процесса ... 153
Согласно равенствам D.15), D.16) и D.17),
1 , . с
v2 '
Реально скалярный случайный процесс ?(t,uj), t ? Т, не явля-
является белым шумом, но его можно аппроксимировать „белым
шумом" со спектральной плотностью (см. пример 4.5)
(с, \v\<N;
^И=[0, W\>N
В этом случае при определении дисперсии D[r}{t,u>)] случайного
процесса т}A,ш), t > О,
возникает погрешность Д. Оценим ее:
оо TV оо
|Д|< Г Cdv Г Cdv -2cf dv -
-N
N
2c v
= — arctg —
a a
1с (ж N
= — I a.rrt.cr —
N
arctg — ).
Относительная погрешность для дисперсии
вается следующим образом:
2 7V
< 1 arctg—.
7Г а
оцени-
оцениD[v(t,u)]
Пример 4.7. Пусть функционирование линейной дина-
динамической системы описывается линейным дифференциальным
уравнением первого порядка

154 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
где ао, fli, bo, b\ — известные параметры, a ?(t,u>), t?T =
= [0, оо), — стационарный скалярный случайный процесс с
математическим ожиданием т?<и ковариационной функцией
К^{т) = <т2ехр(—Q2|r|). Найдем математическое ожидание mr) и
дисперсию <т2 реакции системы на входной сигнал ?(?,w), t G T,
если его производная рассматривается в классе обобщенных
функций (см. пример 4.5).
Согласно равенствам D.15), D.16) и D.17),
о
т„ = —
а0
i (iu)
А так как (см. пример 4.3)
то спектральная плотность реакции изучаемой динамической
системы равна
Воспользовавшись свойством 4.2 е) спектральной плотности,
находим
со со
ОО
?о-2
_2о?о-2 П Л М ч
тг /V+a4 e^ + aj/
о
2aV/A А /г oifxl00
= ( —arctg —Н arctg ) =
ж \az а2 алпп an / L
а*

Вопросы и задачи 155
где использованы обозначения
А =
2  ) г* л О 9
Ч "о а а1 а0
Окончательный результат можно представить в следующем
виде:
2_ 2
Вопросы и задачи
4.1. Можно ли в условиях теоремы 4.2 считать, что ковари-
ковариационная функция удовлетворяет условию К^(т) G L2[—l,l], но
не удовлетворяет условиям теоремы Дирихле?
4.2. Определена ли спектральная плотность стационарного
случайного процесса, ковариационная функция которого удо-
удовлетворяет условию К{(т) G L2[-oo,+oo]?
4.3. Пусть для стационарных случайных процессов ?(t,w),
t G T = [0, оо), и ri(t,w), t G Г, выполнены условия теоремы 4.3,
т.е. существуют интегральные представления
оо
= J
Пусть случайные функции ф{1>,ш) и *p(v,u/) обладают свойством
(функцию «^(f) называют взаимной спектральной плот-
плотностью исходных случайных процессов). Докажите, что в
этом случае:

156 4 СПЕКТРАЛЬНАЯ ТЕОРИЯ
6)Кф)=
-оо
оо
г) если исходные случайные процессы являются комплекс-
комплексными, то s*ir){v) = 8^{и);
д) если исходные случайные процессы являются веществен-
вещественными, то s^v(—v) — sv^(v).
4.4. Найдите ковариационную функцию К^(т) стационар-
стационарного случайного процесса ?(t,ui), t eT — [0, оо), если его спек-
спектральная плотность равна
1с
Ответ: К^(т) = — [si
4.5. Пусть ?(t,uj), t G T = [0, оо), — дифференцируемый ста-
стационарный скалярный случайный процесс и Tj(t,uj) = ?(t,uj),
t G Т. Определите D\j]{t,uj)\, если известна спектральная плот-
плотность
где а2 и а2 — известные величины.
Ответ: D,, = D[ri{t,u)] = О.
Указание: предварительно докажите равенство
4.6. Определите ковариационную функцию К^(т) стацио-
стационарного случайного процесса ?(?,a;), t ? Т = [0, оо), если извест-

Вопросы и задачи
157
на его спектральная плотность
ак
где ajt, ajt (Аг = 1, п)
Ответ:
известные величины.
п
4.7. Определите спектральную плотность стационарного
скалярного случайного процесса ?A,ш), t G Т = [0, оо), если
известна его дисперсия а2 и корреляционная функция
A--, |т| < -г0;
К[17 1 — \
I 0, |г| ^ г0,
где Го — известная величина.
п < л 2°2 ¦
итвет: stlis) = —=-sin
пиг 2
4.8. Найдите спектральную
плотность стационарного скаляр- Рис. 4.3
ного случайного процесса ?(t,w),
t ? Т — [0, оо), ковариационная функция которого:
а) равна К^(т) = <72A + &|г|)ехр(-а|г|), где а2, а — извест-
известные величины;
б) задана графически (рис. 4.3).
. . . 2<т2а3 . t ч 4.3!/.!/
4.9. Пусть ^(i,w), i G T = [0, оо), — нормальный стационар-
стационарный скалярный случайный процесс с нулевым математическим
ожиданием и ковариационной функцией К^(т). Пусть r](t,w) =
?2(t,w), t eT. Докажите, что
оо
(i/) = 2 /

158 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
Указание: последовательно докажите следующие утвер-
утверждения:
1) Kv{t) =
2) MK2(tbw)f2(t2,w)] = 2КЦт) + К2@);
оо оо
3) *,(*>) = ^ f 2К\{т)<Г™dr = 2 J
4.10. Пусть ?(t,w), t G T — [0, сю), — нормальный стационар-
стационарный скалярный случайный процесс с нулевым математическим
ожиданием и ковариационной функцией
= cr2[cos(/3r) + -^si
где а2, а, /3 — известные положительные величины. Определи-
Определите спектральную плотность случайного процесса
Указание: используя равенство [у2(ж)]' = 2у'(х)у(х), ре-
результаты задачи 4.9 и свойства спектральной плотности, Дока-
Докажите, что
оо
,2
V1 Г
4.11. Пусть f (t,w), t G T = [0, оо), и rf{t,u), teT, — нормаль-
нормальные стационарные скалярные случайные процессы с нулевыми
математическими ожиданиями и a(t,u) = ?(t,u)ri(t,u}), t?T.

Вопросы и задачи 159
Докажите, что
оо
/
оо
где S?,,(i>) и sv?(i>) — взаимные спектральные плотности.
4.12. Два стационарных скалярных случайных процесса
?(t,u>), t G T = [О, оо), и T)(t,u>), t € Т, связаны равенством
;), teT.
Определите математическое ожидание и дисперсию случайного
процесса т}(Ь,ш), t € Т, если тп^ = О и К^(т) = 2е~а1т1, где а —
известная положительная величина.
Ответ: т,, = 9; а^ = 0,4— —.
Указание: используйте свойства спектральной плотно-
плотности.
4.13. Работу дифференцирующей ДС-цепочки (рис. 4.4)
описывает уравнение
RCr}(t,u) + n{t,u) = RC?(t,u), t e T = [0, oo).
Найдите математическое ожида-
ожидание и дисперсию случайного про-
процесса T](t,u>), teT, если m^ — 0 и
K{(t) = <72cos(/?r), где <т2 и /3 —
известные величины. р
Ответ: тп = 0; а2 =

160 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
4.14. Функционирование интегрирующего устройства мо-
моделируется уравнением
^k(t>w)> *ет=[0) °°)i
где С, /?, Ri — известные положительные величины, a ?(t,u),
t?T, — белый шум с интенсивностью No/4k. Определите спек-
спектральную плотность и ковариационную функцию случайного
процесса t)(t,u), t ?T.
2
твет:
N0R(R + 2Rl) / |r|
4.15. Ошибка e(t,u>) измерения ускорения самолета акселе-
акселерометром определяется уравнением
e(t,u) + 2M(t,u) + n2e(t,u) = дп2ф,и), t ? Т = [0, оо),
где h, n, g — известные постоянные, а случайный процесс
T](t,u>), t?T, характеризующий случайные возмущения, испы-
испытываемые чувствительным элементом акселерометра, является
белым шумом с интенсивностью с2. Найдите дисперсию скоро-
скорости самолета, определяемой путем интегрирования показаний
акселерометра в течение времени t, если при интегрировании не
возникает дополнительных ошибок, а время переходного про-
процесса много меньше t.
Ответ:
t t t
«(t,w)] = Г IKe(t2 - tx)dtidt2 и It IКе(т) dr = 2irg2c2t.
0 0 0
Указание: ошибка в определении скорости самолета
равна
= I
t?T.

Вопросы и задачи 161
4.16. Пусть дана система дифференциальных уравнений с
постоянными коэффициентами ац, l,j= I, n, соответствующая
устойчивой динамической системе
f}k{t,u) +J2<ikjT}j(t,u) =?k(t,u), t€T = [0,oo), к =
где ?t(?,w), ? € T, A; = 1, те, — стационарные скалярные случай-
случайные процессы с известными ковариационными и взаимными
ковариационными функциями. Пусть время t велико. Дока-
Докажите, что T)k(t,u>), t € Т, к — 1, те, — стационарные случайные
процессы, спектральные и взаимные спектральные плотности
которых определяются равенствами:
где Д(г/) — определитель матрицы (a,jk) + wE (E — единичная
матрица); Ajk(v), j,k = l,n, — алгебраические дополнения
соответствующих элементов определителя A(v);
оо
оо
—оо
взаимная спектральная плотность, а
ts и * \ А.
взаимная ковариационная функция стационарных случайных
процессов ?i(t,w), t € Т, и ?,-(*,<*;), t € Т.
4.17. Пусть ?i(t,w), t€T=[0,oo), и 6(*,w), t € Т, —
стационарные скалярные случайные процессы с известными

162 4. СПЕКТРАЛЬНАЯ ТЕОРИЯ
спектральными плотностями
и взаимной спектральной плотностью
где of, crl, a — известные величины. При больших значениях
времени t ? Т определите sm (*/), sm(v), smm(v), если при t ? Т
rn(ttu) +4rn(t,u) = fi(t,w) - %(*.w),
Ответ:
7T(*/2+4) (*/
1
t/2 - 4J + 4t/2] V tt{u2 + 1) +
2a[v2-9(v2-2J\\
(^-2L + ^ У
iv-9) 1a\
+
/ a(i
v* - 4) + 2w]{v2 + 81) V {v* - 2J + iv + n{v2 + 4)

5. МАРКОВСКИЕ ПРОЦЕССЫ
С ДИСКРЕТНЫМИ СОСТОЯНИЯМИ
И ЦЕПИ МАРКОВА
Аппарат теории марковских процессов с дискретными со-
состояниями и цепей Маркова широко используют в теории си-
систем, в исследовании операций и других прикладных дисци-
дисциплинах. Это обусловлено многими причинами, среди которых
отметим следующие:
1) многие реальные технические системы имеют конечные
множества возможных состояний, а их поведение в процессе
функционирования адекватно моделируется марковскими про-
процессами;
2) теория марковских процессов с дискретными состояния-
состояниями и цепей Маркова разработана настолько глубоко, что позво-
позволяет решать широкий класс прикладных задач.
Именно поэтому основной материал главы связан с изу-
изучением прикладных аспектов теории марковских процессов с
дискретными состояниями и цепей Маркова.
5.1. Основные понятия
Определение 5.1. Марковский скалярный процесс ?(t,uj),
t G Т = [а, Ь] называют марковским процессом с дискрет-
дискретными состояниями, если для любого фиксированного момен-
момента времени t G Т случайная величина ?(t,uj) является дискрет-
дискретной.
Пусть 5 — некоторая физическая система с возможными
дискретными состояниями {Sfc}?=1, которая случайным обра-
образом время от времени скачком (мгновенно) переходит из со-

164 5. МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
стояния в состояние. Если этот процесс является марковским,
то имеем марковский случайный процесс с дискретными состо-
состояниями.
При анализе марковских процессов с дискретными состоя-
состояниями удобно пользоваться геометрической схемой — графом
состояний, который изображает возможные состояния систе-
системы и возможные переходы этой системы из одного состояния в
другое, указываемые стрелками.
Пример 5.1. Техническая система 5 состоит из двух узлов
с номерами 1 и 2, каждый из которых в процессе функциониро-
функционирования системы может выйти из строя. Возможные состояния
системы:
Si — оба узла работают;
5г — первый узел отказал, а второй
работает;
53 — первый узел работает, а второй
отказал;
54 — оба узла отказали.
рис. 5.1 На рис. 5.1 изображен граф состояний
рассматриваемой системы S в предположе-
предположении, что ремонт узлов в процессе ее функционирования не
производится.
Определение 5.2. Случайную последовательность {&(<*>)}
называют цепью Маркова, если для любого натурального
числа п > 1 имеет место тождество
где/(жп|а;п_1;а;п_2;...;а;1) и f{xn\xn_x) — условные плотности
распределения случайного вектора (?i(w) ?г(^) ¦•• ?n(w)) •
Пусть некоторая физическая система 5 может находить-
находиться лишь в одном из возможных состояний {Sk}1^-1, a ?(t,u>),
t € Т, — соответствующий марковский процесс с дискретны-
дискретными состояниями. Если для системы 5 переход из состояния в

5.1. Основные понятия 165
состояние возможен лишь в фиксированные моменты времени
tj} j = 1,2,..., где t\ < t2 <¦¦¦< tj <..., то эти моменты вре-
времени принято называть шагами или этапами марковского
процесса ?(?,w), t G Т. А так как в данном случае Т = {tj}^
и ?j(u>) =?(?j,w), то имеем дело со случайной последовательно-
последовательностью, которая является цепью Маркова, если для каждого шага
вероятность перехода системы 5 из любого состояния Sk в лю-
любое состояние Sm не зависит от того, когда и как она попала в
состояние Sk-
Во многих прикладных дисциплинах зачастую вместо тер-
термина „случайная последовательность" употребляют термин
случайный процесс с дискретным временем.
Если ввести случайное событие s^, состоящее в том, что
после j этапов исходная система S находится в состоянии Sk,
то для каждого фиксированного j' ^ 1 имеем полную группу
событий {^}?=1, т.е.
Пример 5.2. Цель (самолет) обстреляна из зенитного
автомата очередью в четыре снаряда. Если At — интервал
между последовательными выстрелами, a ?i — время первого
выстрела, то t2 = ?i + Д?, ?з = ^1 + 2Д?, t4 — t\ + ЗД?.
Возможные состояния цели (системы 5):
S\ — цель невредима;
5г — цель получила незначительные повреждения;
53 — цель получила существенные
повреждения, но еще может функциони-
функционировать;
54 — цель поражена, т.е. не может
функционировать (самолет сбит).
Если в начальный момент времени
t — to система 5" находилась в состоянии
Si, то граф ее состояний изображен на
рис. 5.2. Рис. 5.2

166 5. МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
5.2. Цепи Маркова
Для формализованного описания цепи Маркова удобно ис-
использовать понятия вероятностей состояний и переходных ве-
вероятностей. Поэтому введем следующие обозначения.
Пусть {Sk}%=1 — множество возможных состояний системы
5. Вероятность реализации случайного события s-J., состояще-
состоящего в том, что после j этапов система находится в состоянии 5*,
обозначают Pk(j) — Р[«*] и называют вероятностью состо-
состояния. Вектор вероятностей состояний системы 5 после
j этапов обозначим
j) = (PlU) P2(j) -..
а вектор вероятностей начальных состояний
p@)^(pi@) р2@) ... Рп@))Т.
Если ввести матрицу-строку
то равенство
k=l k=l
можно представить в виде
Если {Sk}%=J — множество возможных состояний системы
S, a sj — случайное событие, состоящее в том, что после
j этапов система находится в состоянии 5*, то условную
вероятность события s^ при условии s^T1 обозначают
и называют переходной вероятностью.

5.2. Цепи Маркова 167
Определение 5.3. Матрицу Р^ = (р3^) G Mn(R) для ка-
каждого фиксированного j' ^ 1 называют матрицей переход-
переходных вероятностей.
Определение 5.4. Цепь Маркова называют однородной,
если матрица Р переходных вероятностей системы не зависит
от номера этапа j, j ^ 1. В противном случае цепь Маркова
называют неоднородной.
Рассмотрим некоторые свойства матриц переходных веро-
вероятностей.
Свойство 5.1. Сумма элементов любой строки матрицы
переходных вероятностей равна 1, т.е. /т = рУ)/т, j ^ 1.
< Действительно, {^.}^=1 — полная группа событий для любо-
любого j ^ 1. Следовательно,
k=i k=\
Свойство 5.2. Вектор вероятностей состояний после j
этапов равен произведению транспонированной матрицы пере-
переходных вероятностей P(J') на вектор вероятностей состояний
после (j — 1) этапов, т.е. p(j) = (P^^)Tp{j - 1), j' ~? 1-
4 Так как {s^.}^_j — полная группа событий при любом
натуральном j, то по формуле полной вероятности имеем
m=l
или, что то же самое,
п
m=l
Свойство 5.3. Вектор вероятностей состояний p(j) после
j этапов однозначно определяется матрицами переходных ве-
вероятностей Р^1), ..., Pf-7' и вектором вероятностей начального

168
5. МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
состояния р@): p(j) = (Р(*)рB) ...Р^)тр@). При этом, если
цепь Маркова является однородной, то Р^ = Р, j ^ 1 и
где Р7 — j'-я степень матрицы Р.
^ С учетом свойства 5.2 имеем
U - 2) =
Замечание 5.1. При рассмотрении однородных цепей
Маркова зачастую бывает удобно пользоваться графом состо-
состояний, на котором у стрелок выписаны соответствующие пере-
переходные вероятности. Такой граф принято называть разме-
размеченным графом состояний.
Пример 5.3. Определим вероятно-
вероятности состояний цели из примера 5.2 после
обстрела, если в начальный момент вре-
времени она находилась в состоянии S\, a
размеченный граф состояний изображен
на рис. 5.3.
Из графа состояний имеем
Рис. 5.3
Pi2 = 0,
Р21 - О,
Рз1 = О,
Р41 = О,
= 0,2,
Р32 = О,
Р42 = О,
Pl4 = 0,1,
Р24 = 0,2,
Рз4 = 0,7,
Р43 = 0,
Рп = 0,3,
Р22 = 0,4,
Рзз = 0,3,
где вероятности р„ найдены из соотношений ^2 Pik = 1, i = 1, 4.
Таким образом, матрица переходных вероятностей имеет вид
Р =
@,3
0
0
^ о
0,4
0,4
0
0
0,2
0,4
0,3
0
0,1
0,2
0,7
1

5.2. Цепи Маркова
169
@,3
0,4
0,2
^ 0,1
0
0,4
0,4
0,2
0
0
0,3
0,7
0\
0
0
1/
4
/
V
1\
0
0
o/
/0,0081
0,0700
0,1288
U,7931
А так как по условию р@) = A000), то, согласно свойству
5.3 матрицы переходных вероятностей, находим
рD) = (РТ) V0) =
Таким образом, найдены вероятности всех исходов обстрела
цели одной очередью из четырех выстрелов:
цель не повреждена: piD) = 0,0081;
цель получила незначительные повреждения: />гD) = 0,07;
цель получила значительные повреждения: рзD) =0,1288;
цель поражена: Р4D) = 0,7931.
Пример 5.4. Цель (самолет) обстреляна из зенитного
орудия тремя выстрелами с корректировкой наводки после
каждого из них. Цель может находиться в одном из четырех
состояний, определенных в примере 5-2, а матрицы переходных
вероятностей равны:
0,3
0
0
0
0,4
0,4
0
0
P
JT
0,2
0,4
0,3
0
0,1 \
0,2
0,7
1 /
/0,0J
I
1
°
V о
r
0,3
0,1
0
0
0,4
0,6
0,1
0
/0,1
0
0
V о
0,25 \
0,3
0,9
1 /
0,4
0,2
0
0
*
0,3
0,5
0,2
0
0,2
0,3
0,8
1
Определим вероятности состояний цели после каждого выстре-
выстрела, если в начальный момент цель находилась в состоянии S\,
т.е. р@) = A00 0)Т.

170 5. МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
Согласно свойству 5.2, имеем
рA) = (Р^)'1р@) = @,г 0,4 0,2 0,1)Т,
рB) = (Р<2))трA) = @,03 0,20 0,33 0,44)т,
рC) = (рC>)трB) = @,002 0,029 0,165 0,804)Т.
5.3. Уравнения Колмогорова
для вероятностей состояний
При рассмотрении цепей Маркова (с конечным числом воз-
возможных состояний) с использованием матриц переходных ве-
вероятностей и вектора вероятностей начальных состояний
удается эффективно определять вектор вероятностей состо-
состояний исходной системы после любого числа этапов. Также
решается и аналогичная задача для марковских процессов с дис-
дискретными состояниями и непрерывным временем, при анализе
которых широко используются графы состояний.
Рассмотрим марковский процесс с дискретными состояни-
состояниями, описывающий поведение системы 5 с множеством воз-
возможных состояний {Sk}^=l. Обозначим через sjj. случайное
событие, состоящее в том, что в момент времени t G Т = [а,Ь]
система S находится в состоянии S*, а вероятность реализации
этого события обозначим
В этом случае вектор вероятностей состояний
p(t) = (pl(t) P2(t) ... pn(t))T
определяет вероятности состояний системы S в момент време-
времени t e Т. А так как в любой фиксированный момент времени t
совокупность случайных событий {sJUjLj — полная группа, то
> 1, *ег, E.1)
i
где/=A ... l)€Mln(R).

5.3. Уравнения Колмогорова для вероятностей состояний 171
Определение 5.5. Пусть S — некоторая система с воз-
возможными дискретными состояниями {Sk}^=l. Под плотно-
плотностью вероятности перехода этой системы из состояния
Si в состояние Sj в момент времени t понимают число
А,-,-@=
д*-ц-о
At
где Pij(t; At) — вероятность того, что система S, находившаяся
в момент времени t в состоянии 5,, за время At > 0 перейдет в
состояние Sj.
Заметим, что в определении 5.5 Pij(t;At) — P[s*-+A*|.s*].
Таким образом, с точностью o(At) имеет место равенство
т.е. плотности вероятностей перехода системы из одного воз-
возможного состояния в другое обладают обычными свойствами
условных вероятностей и, в частности, являются неотрицатель-
неотрицательными.
Определение 5.6. Скалярный марковский процесс с дис-
дискретными состояниями, описывающий поведение системы S,
называют однородным, если для любых г, j = 1, п
Xij (t) = Xi:l - const, t € Т.
В противном случае его называют неоднородным.
Если для всех пар состояний Si и Sj из
множества возможных состояний системы S
известны плотности вероятностей перехода
{Xij(t)}, то граф состояний системы S мож-
можно превратить в размеченный граф состоя-
состояний, проставив у стрелок не переходные веро-
вероятности, а плотности вероятностей перехода
(рис. 5.4).
Рис. 5.4

172 5. МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
Теорема 5.1. Пусть система 5 имеет множество возмож-
возможных состояний {Sfclfc-j, а процесс изменения состояний этой
системы представляет собой случайный процесс, причем для
всех пар возможных состояний 5,- и Sj определены плотности
вероятностей переходов Kj(t) и А_,,(?). Тогда вероятности со-
состояний системы pk(t) удовлетворяют системе уравнений
Колмогоров а:
t'=l
E.2)
4 Так как процесс изменения состояний системы S предста-
представляет собой марковский процесс и {«?}?_! — полная группа
событий, то по формуле полной вероятности имеем
= Е
Из определения 5.5 следует, что с точностью o(At)
Если i = к, то, переходя к противоположному событию, находим
с точностью o(At)
Таким образом, с точностью o(At) равенство E.3) может быть
преобразовано к следующему:
хфк \фк

5.3. Уравнения Колмогорова для вероятностен состояний 173
или, что то же самое,
Pk(t + At)-pk(t) =
i^k хфк
и для завершения доказательства достаточно перейти к преде-
пределу при At —> +0. >
Система уравнений Колмогорова E.2) не является линейно
независимой, т.е. она является избыточной, что следует из
равенства E.1).
Если I — A ... 1) € Min(R), а компонентами вектора
являются плотности вероятностей переходов системы S из
состояния Sk во все иные возможные состояния, то
E.4)
хфк
суммарная плотность вероятности перехода системы из состо-
состояния Sk, взятая со знаком „минус". При этом, если ввести
матрицу
A@ = (M0)€Afn(R), E-5)
диагональные элементы которой определены согласно E.4), то
E.2) переходит в матричное уравнение Колмогорова
p'(t) = \(t)p(t), teT=[a,b], E.6)
где p(t) — вектор вероятностей состояния системы S в момент
времени t.
Если определен вектор вероятностей ра начальных состоя-
состояний системы S в момент t = а и определена матрица А(?), то с
учетом E.6) приходим к задаче Коши для матричного уравне-

174
5. МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
ния Колмогорова:
, t>a;
E.7)
Если X(t) непрерывна при t > а, то задача Коши E.7) имеет
единственное решение и, следовательно, вектор вероятностей
состояний исходной системы 5 определен однозначно в любой
t
момент времени t > а. Если при этом матрицы X(t) и jA(r)dr
а
коммутируют при каждом фиксированном t ? Т = [a, ft], то ре-
решение задачи Коши E.7) с использованием матричной экспо-
экспоненты можно записать в явном виде (см. П2):
t?T.
E.8)
Согласно E.5), k-u столбцом матрицы X(t) является вектор
), у которого k-я компонента заменена, согласно E.4), на
Xkk(t) = — I\1(t), а все остальные — соответствующие плотно-
плотности вероятностей переходов из состояния 5*. Эту информа-
информацию проставляют на размеченном графе состояний системы на
стрелках, п выходящих из состояния 5^" (при их отсутствии со-
соответствующая компонента равна нулю). При этом
IX(t) = О.
E.9)
Пример 5.5. Размеченный граф со-
состояний системы S, процесс изменения
состояния которой представляет собой
однородный марковский процесс с дис-
дискретными состояниями, изображен на
рис. 5.5. Сформулируем задачу Коши
для системы уравнений Колмогорова, ес-
если Т = [0, оо) и в начальный момент времени t — 0 система
находится в состоянии 5].

5.3. Уравнения Колмогорова для вероятностей состояний 175
Согласно заданному размеченному графу состояний, имеем
2 - Ai3
А12
А13
0
0
0
0
0
0
0
0
Азг
— Азг — А34
А34
0
0
0
0
— А45
А45
0 >
0
А53
0
-*53 )
р@) = A 0 0 0 0).
Таким образом, вектор p(t) вероятностей состояний изучаемой
системы 5 является решением следующей задачи Коши:
- (A
32
- A53P5W,
#
Если решение задачи Коши E.7) представимо в виде E.8),
то оно удовлетворяет равенству E.1).
Действительно, имеет место тождество E.9): /А(?) = О, где
/= A ... 1) G Min(R)). Кроме того, Ip(a) — 1. Таким образом,
из E.8), свойств матричной экспоненты (см. П2) и тождества
E.9) следует, что
p(a) =
к—0
k=l
p(a) = 1 + 0=1.

176 5. МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
По своему смыслу компоненты Pk{t) вектора вероятностей
состояний системы S не могут быть отрицательными, т.е.
0, k=l,n, t<ET = [a,b]. E.10)
Условия E.10) накладывают вполне определенные ограничения
на компоненты матрицы А(?), т.е. на плотности вероятностей
переходов системы S из одного состояния в другое. Эти огра-
ограничения имеют важное значение при изучении так называемых
предельных режимов однородных марковских случайных про-
процессов с дискретными состояниями, играющих существенную
роль в различных приложениях.
Теорема 5.2. Решение задачи Коши E.7) для матрично-
матричного уравнения Колмогорова при любом векторе вероятностей
начальных состояний системы S имеет неотрицательные ком-
компоненты.
< Для упрощения дальнейших рассуждений будем считать, что
решение задачи Коши E.7) может быть представлено в виде
E.8). А так как компоненты вектора вероятностей начальных
состояний ра изучаемой системы являются неотрицательными,
то достаточно доказать неотрицательность элементов матрич-
матричной функции
ехр( / \{т)йт I, teT.
а
Из определения плотности вероятности перехода системы S
из состояния 5, в состояние Sj, где г' ф j, следует, что A,j(?) ^ 0
при любых t G Т. Таким образом,
C{t)= f^ J\tj(r)dr^0, teT,

5.3. Уравнения Колмогорова для вероятностей состояний 177
и, согласно E.4), E.5), все элементы матричной функции
t
/¦
a
являются неотрицательными. Но в этом случае (см. П.2) нео-
неотрицательными являются и все элементы матричной функции
t
a
коммутирующей с матричной функцией
А так как е~с^ > 0 при t ? Т и
t t
а а
то теорема доказана (произведение матриц с неотрицательны-
неотрицательными элементами является матрицей с неотрицательными элемен-
элементами). >
Следствие 5.1. Если решение задачи Коши E.7) предста-
вимо в виде E.8), то для выполнения неравенств
Pk(t)>0, к = 1,п, te(a,b],
необходимо и достаточно, чтобы
t
\ц (г) dr > 0, i,j = Т7п, гфз, te (a, 6].
/¦
< Сформулированное утверждение вытекает из доказатель-
доказательства теоремы 5.2. >
Следствие 5.2. Если процесс изменения состояния систе-
системы S представляет собой однородный марковский процесс с

178 5 МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
дискретными состояниями, то неравенства
Pk(t)>0, *=l,n, te(a,b],
выполняются тогда и только тогда, когда
Утверждение следствия 5.2 означает следующее. Вероятно-
Вероятности состояний ненулевые в любой момент времени t > а тогда
и только тогда, когда по графу состояний можно перейти из
любого состояния 5, в любое состояние S3 за конечное число
шагов.
Определение 5.7. Пусть {5'jt}^_1 — множество возможных
состояний системы 5, а процесс ее перехода из одного воз-
возможного состояния в другое представляет собой однородный
марковский процесс с дискретными состояниями, определен-
определенный на множестве Т = [а, сю). Если p(t) = (pi(t) ... pn(t)) —
вектор вероятностей состояний системы 5 в момент времени
t G Т и существует предел
Jim p(t),
то вектор р называют вектором предельных вероятно-
вероятностей состояний системы.
Существование вектора предельных вероятностей состоя-
состояний означает, что с течением времени в системе 5 наступает не-
некоторый стационарный режим. Он состоит в том, что система
случайным образом меняет свои состояния, но вероятность ка-
каждого из них уже не зависит от времени. Каждое из состояний
реализуется с некоторой постоянной вероятностью, интерпре-
интерпретация которой может быть связана со средним относительным
временем пребывания системы 5 в данном состоянии.
Равенство E.8), полученное без учета каких бы то ни было
ограничений на область Т = [a, ft], для однородного марковско-
марковского случайного процесса позволяет сформулировать следующее
утверждение: для существования вектора предельных вероят-

5.3 Уравнения Колмогорова для вероятностей состояний 179
ностей состояний системы 5 необходимо и достаточно суще-
существование предела
lim ехр{А(? - a)}pa.
t—foo
Если p(t) — вектор вероятностей состояний системы 5 и
/=A ... 1), то для любого* еТ = [0, сю) решение задачи Коши
для матричного уравнения Колмогорова
P(O) = Po
удовлетворяет равенству Ip(t) = 1.
Таким образом, вектор р предельных вероятностей состо-
состояний системы 5 представляет собой асимптотически устойчи-
устойчивую точку покоя для нормальной однородной системы обыкно-
обыкновенных дифференциальных уравнений с постоянными коэффи-
коэффициентами p'(t) = Xp(t), имеющую неотрицательные координаты
и расположенную на гиперплоскости р\ + ... + рп — 1. Как след-
следствие, вектор р удовлетворяет матричной системе
{?-"' (Ы1)
Следующий пример поясняет проведенные рассуждения.
Пример 5.6. Размеченный граф состояний системы 5, для
которой процесс изменения состояния представляет собой од-
однородный марковский процесс, изображен на рис. 5.6. Необхо-
Необходимо найти предельные вероятности
состояний системы 5.
Согласно заданному графу состо-
состояний, имеем
А =
А.,=2
-5
2
3
0
0
-1
0
1
1
2
-3
0
0
0
2

180
5. МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
и, согласно E.11), приходим к системе
-Ърх + Орг + 1рз + 0р4 = О,
решение которой нетрудно найти:
_1_ _ 1
Pl~24' P2~2' Рз
5 1
5.4. Процесс гибели — размножения
и циклический процесс
Определение 5.8. Марковский процесс с дискретными
состояниями {Sfc}2=1 называют процессом гибели — раз-
размножения, если он имеет размеченный граф состояний, изо-
изображенный на рис. 5.7.
•^п-2,п-1
\i-l,n-2 ^n.n-1
Рис. 5.7
Для процесса гибели — размножения граф состояний можно
вытянуть в цепочку, в которой каждое из состояний Sk прямой
и обратной связью связано с каждым из соседних состояний
(крайние состояния Si и 5г имеют лишь одно соседнее состоя-
состояние).
Название „процесс гибели — размножения" имеет своими
истоками биологические задачи, в которых такими процессами
описывают изменение численности особей в популяциях.
Пример 5.7. Техническое устройство состоит из трех оди-
одинаковых узлов, каждый из которых может выходить из строя.

5.4. Процесс гибели — размножения и циклический процесс 181
При этом отказавший узел немедленно начинает восстанавли-
восстанавливаться. Возможные состояния системы:
50 — все три узла исправны;
51 — один узел отказал и восстанавливается, а два исправ-
исправны;
5г — два узла отказали и восстанавливаются, а один
исправен;
5з — все три узла отказали и восстанавливаются.
Необходимо найти вектор предельных вероятностей со-
состояний исходной системы, 2 13
имеющей размеченный граф (?")¦ \??Л \?^Л 'ч?у
состояний, который изобра-
изображен на рис. 5.8. Рис> 5-8
Согласно заданному графу состояний, имеем
А =
-2 3 0 0\
2-420
0 1-52
0 0 3 -2
и, согласно E.11), приходим к системе
0ро+ Pi-
P2+ Р3=
имеющей решение
6 4
15' Р2~Т5'
=15- *
Если процесс гибели — размножения представляет собой
однородный марковский процесс с дискретными состояниями,

182
5. МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
то его называют однородным процессом гибели — раз-
размножения. Для такого процесса, согласно виду размеченного
графа состояний (см. рис. 5.7), имеем трехдиагоиальиую ма-
матрицу
А =
О
О
О
-(А32+А34)
О
О
О
О
\
О
О
о
о
о
о
• •• АП)П_]
порядка п, которой соответствует однородная система линей-
линейных алгебраических уравнений относительно вектора предель-
предельных вероятностей состояний:
= О,
= О,
п-2,п-1Рп-2 - (^n-l,n-2 + An_i>n)pn_i + An>n_i/>n
n-l,nPn-l - An,n_iPn = 0.
Из первого уравнения записанной системы имеем
= О,
Значит, второе уравнение может быть представлено в виде
Продолжив аналогичные выкладки, приходим к следующим
соотношениям:
Afc,fc+iPfc = Afc+1)fcpfc+1, к = 1, п-1,

5.4. Процесс гибели — размножения и циклический процесс 183
или, что то же самое,
Таким образом,
l2
Pi — \—Pi i
л21
Агз АхгАгз
Рз = т—Vi = 1—l—Pi I
Л32 А21Л32
E.12)
_
Рп —
_
Рп-1 —
Pi 1
и для окончательного решения исходной задачи, т.е. для на-
нахождения вектора предельных вероятностей состояний, доста-
достаточно соотношения E.12) подставить в E.1). В результате
находим
-1
»=
Подставляя E.13) в E.12), получаем
Pi+i =
E.13)
= М^Т. E.14)
Определение 5.9. Марковский процесс с дискретными
состояниями {5fc}2=1, называют циклическим процессом,
если он имеет размеченный граф состояний, изображенный
на рис. 5.9. При этом, если такой процесс является к тому
же однородным, то его называют однородным циклическим
процессом.

184
5. МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
¦41
Рис. 5.9
Характерным признаком циклических процессов является
кольцевая (циклическая) связь возможных состояний с одно-
односторонними переходами (см. рис. 5.9).
Согласно виду размеченного графа состояний однородного
циклического процесса, матрица А плотностей вероятностей
переходов системы 5 из одного состояния в другое имеет вид
А =
Г-А12
A12
0
0
^ 0
0
-A23 •
Агз
0
0
0
0
0
.. -An_iitl
• • An_x„
Ani
0
0
0
— Anl
По известной матрице А можно записать однородную систе-
систему линейных алгебраических уравнений относительно вектора
предельных вероятностей состояний:
А12Р1 ~ АгзРг = О,
- А34Рз = О,
An-2,n-lPn-2 - Ап_1)Пр„_1 = О,
An-i,nPn-i - Anlpn = 0,
А12Р1 - Anipn = О,
из которой следует, что
А»
fc=l,n-l;
Рк =
= п.

5.4. Процесс гибели — размножения и циклический процесс 185
Таким образом, с учетом условия E.1) имеем
Pk =
3=1
1 /n~x 1 1 \-1
E.15)
k — n.
В соответствии с формулами E.15) и определением 5.7
можно показать*, что для однородного циклического процесса
среднее время пребывания системы в состоянии Sk равно
E.16)
Но в этом случае, согласно E.15), E.16), получаем
_ tk
E.17)
Пример 5.8. ЭВМ может находиться в одном из следую-
следующих состояний:
S\ — исправна, работает;
5г — неисправна (остановлена) и идет поиск неисправности;
5з — неисправность обнаружена и идет ремонт;
•!>4 — ремонт закончен и идет подготовка к пуску.
Необходимо определить предельные вероятности состояний
рассматриваемой системы, если известно следующее: среднее
время безотказной работы ЭВМ равно 12 часам; для ремонта
ее приходится останавливать в среднем на 6 часов; поиск
неисправностей длится в среднем 0,5 часа; подготовка к пуску
занимает 1 час.
'См.: Вентцель Е.С.

186
5 МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
Рис. 5.10
Рассматриваемая система
имеет граф состояний, изо-
изображенный на рис. 5.10, так
как по условию среднее вре-
время (в сутках) ее пребывания
в каждом из возможных состояний равно: t\ — 1/2, ?2 = 1/48,
t-} = 1/4, ?4 = 1/24. Для определения предельных вероятностей
достаточно воспользоваться формулами E.17):
24 1 12 2
т>\ = —. Vi= —. 7>ч = —. Рл == —.
4Q 40 4Q 4Q
tJI/ tJI/ %Уч7 %У*7
Вопросы и задачи
5.1. В чем состоит принципиальное отличие марковского
процесса с дискретными состояниями от цепи Маркова?
5.2. Чем неоднородная цепь Маркова отличается от одно-
однородной?
5.3. Как с помощью матрицы переходных вероятностей
для цепи Маркова можно определить вероятности состояний
после j шагов, если цепь Маркова является: а) однородной;
б) неоднородной?
5.4. Запишите систему уравнений Колмогорова для марков-
марковского процесса с множеством возможных состояний {5*}?_1.
Почему эта система является избыточной? В каких случаях
вероятности состояний определяются однозначно?
5.5. Всегда ли задача Коши для системы уравнений Колмо-
Колмогорова имеет неотрицательное решение?
5.6. Пусть система S — это автомашина, которая может
находиться в одном из следующих состояний: Si — исправна,
работает; 5г — неисправна, ожидает осмотра; 5з — осматрива-
осматривается; 54 — ремонтируется; Ss — списана. Как выглядит граф
состояний системы 5?
Ответ: граф состояний системы представлен на рис. 5.11.

Вопросы и задачи
187
Рис. 5.11
5.7. Постройте граф состояний системы S из примера 5.1,
если отказавший узел немедленно начинает восстанавливаться.
Ответ: граф состояний системы представлен на рис. 5.12,
при этом использованы обозначения:
S\ — оба узла работают;
5г — первый узел работает, а второй
восстанавливается;
53 — второй узел работает, а первый
восстанавливается;
54 — оба узла восстанавливаются. рис 5Л2
5.8. Из таблицы, содержащей все целые положительные чи-
числа от 1 до т включительно, наудачу последовательно выби-
выбирают числа. Система находится в состоянии 5-,, если число
j является наибольшим из выбранных. Найдите вероятность
того, что после выбора из таблицы п чисел наибольшее число
будет равно к, если перед этим наибольшим было число »'.
О, i > к;
Ответ: р"к —
5.9. Для однородной цепи Маркова заданы матрица пе-
переходных вероятностей и вектор вероятностей состояний на
нулевом шаге:
О 1 О
Р= | 0,6 0 0,4
0,3 0,5 0,2
р@) =

188
5. МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
Найдите векторы вероятностей состояний после первого и
второго шагов.
Ответ: рA) = (О 1 0)Т; рB) = @,6 0 0,4)Т.
5.10. Известна матрица Р переходных вероятностей од-
однородной цепи Маркова. Определите: а) число возможных
состояний этой цепи; б) вероятности состояний после двух ша-
шагов, если на нулевом шаге вероятности состояний одинаковы, а
/1 1 1 \
Р =
3
I
3
6
I
6
1
б/
Ответ: а) 3; б) рB) = A/2 1/3 1/6) .
5.11. Матрица переходных вероятностей однородной цепи
Маркова имеет вид
/О 0
0,3 0,7
0 1
0 0
Р =
1
0
0
,6
о >
0
0
0,4 У
Определите: а) состояния, из которых достигается состояние
Sk, к = 1,4; б) состояния, которые достигаются из состояния
5„* = 1Л
Ответ: а) состояния 5*., к= 1,2,3, достигаются из любого
состояния, а состояние 54 не достигается ни из одного состоя-
состояния; б) из состояний 5*., к = 1,2,3, достигаются все состояния,
кроме 54, а из состояния 54 достигаются все состояния.
5.12. Пусть в начальный момент времени t = 0 система с
равной вероятностью находится в одном из возможных состо-
состояний, изображаемых точкой на оси Ох: х = — 1 — состояние Si;
х = 0 — состояние 5г; х = 1 — состояние 5з; х = 2 — состояние
54. В зависимости от случая точка может перемещаться впра-
вправо или влево на единичное расстояние: вправо с вероятностью

Вопросы и задачи
189
1/6, влево с вероятностью 5/6. Из состояний S\ и 54 перемеще-
перемещения невозможны. Найдите матрицу переходных вероятностей и
векторы вероятностей состояний на нулевом, первом и втором
шагах.
Ответ:
1 О О
5
6
о
РA)=
о
ь
5 Q
6
о о
1].
24
_5_
24
1
24
2_
\24/
i О
РB) =
91
144
5
144
5
144
43
\ 144
4
1
4
1
4
1_
\4/
\
5.13. Граф состояний системы представлен на рис. 5.13.
Запишите систему линейных алгебраических уравнений для
предельных вероятностей состояний. /^^ А12
Ответ:
- Л21Р2 - ^31Рз = 0,
24)Р2 = 0,
+ А23Р2 - А31Р3 + А43Р4 = 0,
= 0,
Рис. 5.13
5.14. Размеченный граф состояний системы представлен на
рис. 5.14. Определите: а) тип ^_^ 2 ^_^ 1 ^^ 3
процесса; б) предельные веро-
вероятности состояний, если они
существуют. Рис* 5*14

190
5. МАРКОВСКИЕ ПРОЦЕССЫ И ЦЕПИ
Ответ: а) процесс гибели — размножения; б) р\ =6/15,
р2 = 4/15, рз = 2/15, рА = 3/15.
5.15. Граф состояний системы представлен на рис. 5.15.
Определите предельные вероятности ее
состояний.
Л„/ \А3, Ответ:
1 Aj2 Aj2
Рис. 5.15 -г _ Ai2 Ai2
АгЗ А31
5.16. Вычислительный комплекс может находиться в следу-
следующих состояниях: S\ — исправен, работает; 5г — неисправен,
остановлен и ведется поиск неисправности; 5з — неисправность
оказалась незначительной и устраняется местными средства-
средствами; S\ — неисправность оказалась значительной и устраняется
специалистами; 5s — подготовка к пуску. Процесс перехода
комплекса из одного состояния в другое марковский. Среднее
время непрерывной работы комплекса Т[, среднее время поиска
неисправностей tj, среднее время ремонта местными средства-
средствами ?3> среднее время ремонта специалистами I4, среднее время
подготовки к пуску ts- Неисправность может быть устранена
местными средствами с вероятностью Рис вероятностью 1 — Р
требует вызова специалистов.
Определите предельные веро-
вероятности состояний, если они
существуют.
Указание: воспользуй-
воспользуйтесь графом состояний, кото-
который изображен на рис. 5.16.
рз = Р<з~Д, р4 = A - Р)ЦА,
Рис. 5.16
Ответ: pi =
= ?5 Д, Д = [I
p2 =

6. ЭЛЕМЕНТЫ ТЕОРИИ
МАССОВОГО ОБСЛУЖИВАНИЯ
6.1. Процессы массового
обслуживания (основные понятия)
При решении многих прикладных задач исследователи стал-
сталкиваются с процессами, для которых характерна следующая
общая структура (рис. 6.1): в определенную совокупность пунк-
пунктов, называемую системой обслуживания, через некоторые
промежутки времени поступают объекты (входной поток),
которые подвергаются там соответствующим операциям (об-
(обслуживанию) и затем покидают систему (выходной поток),
освобождая место для следующих объектов. Промежутки вре-
времени, через которые поступают объекты, и время их обслужи-
обслуживания, как правило, имеют случайный характер. Поэтому при
массовом поступлении объектов в системе обслуживания могут
возникнуть очереди.
Входной
Очереди
Система
обслуживания
Выходной
поток
Рис. 6.1
Процессы, объединенные общей структурой, изображенной
на рис. 6.1, называют процессами массового обслужива-
обслуживания. Они типичны для связи (телефон, телеграф, почта),
транспорта (воздушные, наземные и морские перевозки), куль-
культурно-бытовых предприятий (театры, магазины, поликлини-
поликлиники), производственных процессов (сборочные линии, ремонт и
обслуживание оборудования) и так далее.

192 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Вне зависимости от конкретной природы и характера объ-
объектов, поступающих в систему обслуживания, их называют
заявками, или требованиями. Входной поток заявок рас-
рассматривают как последовательность случайных событий, сле-
следующих через какие-то промежутки времени (например, вызо-
вызовы на станции скорой помощи, выход из строя станков и так
далее). Закон распределения входного потока в значительной
степени обуславливает и характер процесса массового обслу-
обслуживания.
Структура очередей и поступление из них заявок на об-
обслуживание определяются как свойствами и возможностями
систем обслуживания, так и установленными правилами про-
прохождения заявок через эти системы (дисциплина очереди).
Заявки могут выполняться в порядке поступления (операции
на конвейере), с приоритетом (внеочередное право получения
билета), в случайном порядке (отбор образцов для статистиче-
статистического анализа), в порядке первого очередного поступления при
освободившемся канале обслуживания (прием вызова телефон-
телефонной станцией) и так далее.
Очереди могут ограничиваться по длине, т.е. по числу на-
находящихся в ней заявок, и по времени ожидания обслуживания.
Эти ограничения обусловлены либо возможностями самой си-
системы массового обслуживания (число мест в театре, объем
оперативной памяти ЭВМ), либо поведением объектов обслу-
обслуживания (отказ от обслуживания из-за неприемлемости длины
очереди или времени ожидания в ней, регламентация поряд-
порядка обслуживания, т.е. дисциплина очереди, и так далее). В
конечном счете основной характеристикой очереди является
время ожидания обслуживания. Система обслуживания со-
состоит из определенного числа обслуживающих единиц, называ-
называемых каналами обслуживания, и может иметь различную
организацию: с последовательными, параллельными и комби-
комбинированными каналами, некоторые из которых могут быть
специализированными. При этом в зависимости от поступле-
поступления заявок и образования очередей эта система может обладать

6 2 Простейший поток 193
способностями к изменению своей организации. В свою оче-
очередь, изменение организации системы обслуживания влияет на
структуру очереди и на отношение к ней объектов обслужива-
обслуживания. Так, при занятости всех каналов обслуживания поступаю-
поступающие заявки могут получить отказ (системы обслуживания
с отказом) или становится в очередь (системы обслужи-
обслуживания с очередями, которые называют также системами
обслуживания с ожиданием).
Изучение процессов массового обслуживания составляет
предмет теории массового обслуживания. Она являет-
является весьма развитой математической дисциплиной с обширными
приложениями в различных областях знаний. Математиче-
Математические модели теории массового обслуживания используют и в
различных задачах принятия решений, связанных с рациональ-
рациональной организацией систем массового обслуживания или выбора
оптимального варианта из некоторой их совокупности.
6.2. Простейший поток
Определение 6.1. Входной поток называют простей-
простейшим, если:
1) вероятность появления того или иного числа заявок на
бременном интервале зависит лишь от его длительности и не
зависит от его расположения на временной оси (стационар-
(стационарность входного потока), причем заявки поступают пооди-
поодиночке (ординарность входного потока) и независимо друг
от друга (отсутствие последействия во входном по-
потоке);
2) вероятность реализации отдельного случайного события
(появление заявки) на временном интервале малой длительно-
длительности At пропорциональна At с точностью до бесконечно малой
более высокого порядка малости по сравнению с At, т.е. равна
А>0.

194 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
3) вероятность реализации двух и более случайных событий
(появление двух или более заявок) на временном интервале
малой длительности At есть величина o(At).
Отсутствие последействия в определении простейшего вход-
входного потока означает, что для любых непересекающихся вре-
временных интервалов число заявок, поступающих на одном из
этих интервалов, не зависит от числа заявок, поступающих на
других интервалах.
Несмотря на то, что входные и выходные потоки многих
реальных систем обслуживания не удовлетворяют полностью
определению простейшего потока, понятие простейшего по-
потока широко используют в теории массового обслуживания*.
Это обстоятельство связано не только с тем, что простейшие
потоки достаточно часто встречаются на практике, но и с
тем, что сумма неограниченного числа стационарных ординар-
ординарных потоков с практически любым последействием является
простейшим потоком. В связи с этим рассмотрим основные
свойства простейшего потока.
Теорема 6.1. Дискретная случайная величина г](и>), при-
принимающая значения 0, 1, 2, ... и характеризующая при про-
простейшем входном потоке число заявок, поступающих в систему
обслуживания на временном интервале длительности t, распре-
распределена по закону Пуассона с параметром \t.
¦4 Рассмотрим скалярный случайный процесс ?(t,u>), t G T =
= [0, оо), с дискретными состояниями {5^}^.о (т.е. для любо-
любого фиксированного момента времени t ? Т его сечение ?(t,u>)
является дискретной случайной величиной с множеством воз-
возможных значений {5^}). Пусть его пребывание в состоянии
5*; означает наличие в системе обслуживания к заявок. В со-
соответствии с условиями теоремы и определением простейшего
потока случайный процесс ?(t,u), t ? Т, является марковским
однородным процессом с дискретными состояниями, причем
'См.: Ивченко Г.И., Каштанов В.А., Коваленко И.Н.

6.2. Простейший поток 195
для любых целых неотрицательных i и j плотность вероятно-
вероятностей перехода системы обслуживания из состояния 5, в состо-
состояние Sj в любой момент времени t ^ 0 определяется равенством
Поэтому в данном случае система уравнений Колмогорова
имеет следующий вид:
где Pk(t) — вероятность того, что на временном интервале
длительности t в изучаемую систему обслуживания поступит
к заявок. А так как из определения 6.1 простейшего потока
заявок следует, что
то приходим к задачам Коши относительно функции Po(t):
и функций Pk(t), к G N:
рк + pk-i t), F^
Последовательно решая задачи Коши F.3), F.4), в случае
простейшего входного потока находим вероятность Р[т](ш) = п]
того, что число заявок i](u>) на временном интервале длитель-
длительности t будет равно п, п— 1, 2,...:
F-5)

196 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Соотношения F.5) означают, что случайная величина г](ш)
распределена по закону Пуассона с параметром Xt. >
Следствие 6.1. Если входной поток является простейшим,
то среднее число заявок, поступающих в систему обслуживания
на временном интервале длительности t, равно Xt.
А Чтобы определить среднее число заявок, нужно найти ма-
математическое ожидание случайной величины rj(u>). А так как,
согласно F.5), она распределена по закону Пуассона с параме-
параметром Xt, то [XVI]
Mfo(w)] = At. > F.6)
Согласно доказанному следствию, параметр А представляет
собой среднее число заявок, поступающих в единицу времени.
Поэтому его называют интенсивностью, или плотностью
простейшего потока.
Следствие 6.2. Если входной поток заявок является про-
простейшим, то дисперсия скалярной случайной величины rj(u>),
характеризующая рассеивание числа заявок, поступающих в
систему массового обслуживания на временном интервале дли-
длительности t, относительно их среднего значения, равно Xt.
4 Если входной поток простейший, то, согласно F.5), случай-
случайная величина г}(и>) распределена по закону Пуассона с параме-
параметром Xt. Следовательно,
Dfo(w)] = At. > F.7)
Обратим внимание на то, что, согласно F.6) и F.7), у
случайной величины, распределенной по закону Пуассона, ма-
математическое ожидание и дисперсия совпадают.
Пример 6.1. В бюро обслуживания в среднем поступает 12
заказов в час. Считая поток заказов простейшим, определим
вероятность того, что: а) за 1 минуту не поступит ни одного
заказа; б) за 10 минут поступит не более трех заказов.

6.2. Простейший поток 197
Так как поток заказов является простейшим и интенсив-
интенсивность А = 12(заказов/час) = 0,2(заказа/мин), то, согласно F.5),
имеем:
a) Pfo(w) = 011= 1] = в-2 и 0,819;
к=0 к=0
Л=0,2
1=10
. # F.8)
В соответствии с определением 6.1 простейшего потока,
длительность г временного интервала между двумя последова-
последовательно поступающими заявками является случайной величиной
т(ш). Для построения математических моделей систем об-
обслуживания необходимо знание функции распределения FT{T) =
= P[r(w) < Т] случайной величины т(и>) или ее плотности рас-
распределения (вероятностей) /Т(Т).
Теорема 6.2. В случае простейшего входного потока с
интенсивностью А длительность т(ш) временного интервала
между двумя последовательными заявками имеет экспоненци-
экспоненциальное распределение с параметром А.
4 Вероятность реализации случайного события {т(ш) ^ Т},
означающего, что длительность временного интервала между
поступлениями двух заявок будет больше некоторой величины
Г, равна вероятности отсутствия заявок в этом интервале.
Поэтому
С учетом F.5) при Т > 0 имеем
Р[тИ < Т] = 1 - Р[тИ ? Т] = 1 - ро(Т) = 1 - е"АТ.

198 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Очевидно, что Р[т(и>) < Т] = 0 при Т ^ 0. Согласно определению
функции распределения случайных величин (см. П1),
Г1е, Т>0;
= P{t(u;)<T} = {
т.е. случайная величина т(и>) распределена по экспоненциально-
экспоненциальному закону с параметром Л. >
Следствие 6.3. В случае простейшего входного потока
с интенсивностью Л длительность т(и>) временного интервала
между двумя последовательно поступающими заявками являет-
является случайной величиной с плотностью распределения (вероят-
(вероятностей)
/(т)-{Ле"АТ' т>0;
М >~\ 0, 74 0,
математическое ожидание и дисперсия которой определяются
равенствами
M[r(u)]=j, F.9)
D[rM]=i F.10)
Согласно следствию 6.3,
P[t(u)>T + s\t(l;)>s] =
= Р[(г(ь;) > Т + 8) Л (т(и) > s)) = Р[т(и)
=
Р[т(ш) > s) P[r(w) > в]
e-A(T+s)
"АТ р№)
]- (б-")
Таким образом, вероятность появления очередной заявки по
прошествии времени Т при простейшем потоке не зависит от
момента появления предшествующей, что является следствием
отсутствия последействия в простейшем входном потоке.

6.3. Время ожидания и время обслуживания 199
6.3. Время ожидания и время обслуживания
В теории массового обслуживания время обслуживания,
т.е. время пребывания одной заявки в канале обслуживания
считают случайной величиной, распределенной, как правило,
по экспоненциальному закону с плотностью распределения
(вероятностей)
[це-^\ t>0;
g(t) = { F-12)
и (о, ко. ;
Это обусловлено многими причинами, среди которых следует
отметить: 1) отсутствие последействия; 2) достаточно кор-
корректное отражение свойств многих реальных систем обслужи-
обслуживания; 3) простоту и удобство аналитических выражений.
Согласно F.12), среднее время обслуживания заявки равно
\j\i (ср. F.9)). Величину \х называют интенсивностью об-
обслуживания. Функция распределения времени обслуживания
заявки равна
G(t)= / g(x)dx=l F.13)
W J K ' I О, КО. V '
v
Ее значение равно вероятности того, что к моменту времени t
обслуживание заявки будет завершено, т.е. освободится канал
обслуживания.
Время ожидания (время пребывания заявки в очереди, если
последняя существует) также считают случайной величиной,
распределенной, как правило, по экспоненциальному закону с
плотностью распределения (вероятностей)
Щ = {"'• <>0; F.14)

200 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
и функцией распределения
t ,
H(t)= I' h{x)dx=\l~e"/t) t>0> F.15)
У> J ^ ' •] 0, КО, K '
где v — величина, обратная среднему времени ожидания, а
значение H(t) равно вероятности того, что в момент t начнется
обслуживание заявки.
6.4. Основные принципы построения
марковских моделей массового обслуживания
1. Процессы массового обслуживания представляют собой
случайные процессы с дискретными состояниями. Переход из
одного возможного состояния в другое происходит скачком в
момент, когда реализуется какое-то случайное событие (по-
(поступление новой заявки, начало или окончание обслуживания,
уход заявки из очереди и т.п.), вызывающее такой переход.
2. Для процессов массового обслуживания с простейшим
входным потоком и экспоненциальным законом распределения
времени обслуживания характерно отсутствие последействия.
Таким образом, будущее развитие рассматриваемых процессов
зависит лишь от их текущих состояний и не зависит от того,
как происходило их развитие в прошлом. А это означает,
что процессы массового обслуживания с простейшим входным
потоком заявок и экспоненциальным законом распределения
времени обслуживания являются марковскими процессами с
дискретными состояниями.
3. Предположим, что в систему обслуживания с т иден-
идентичными параллельными каналами обслуживания поступает
простейший входной поток. При наличии хотя бы одного сво-
свободного канала немедленно начинается обслуживание заявки, а
если все каналы заняты, то заявка становится в очередь (в си-
системах обслуживания с отказами заявка покидает систему; в

6.4 Построение марковских моделей массового обслуживания 201
системах обслуживания с ограниченной длиной очере-
очереди заявка становится в очередь, если там есть свободное место,
и покидает систему в противном случае).
Пусть 5, — возможное состояние рассматриваемой системы
обслуживания, характеризуемое тем, что в ней занято ровно i
каналов обслуживания, i = 0, m, а возможное состояние системы
Sm+r характеризуется тем, что все т каналов обслуживания
заняты и очередь состоит из г заявок, где г ^ 1. Если
на длину очереди не накладывают ограничений, то г может
быть сколь угодно большим и система может иметь счетное
множество состояний. Системы обслуживания с отказами и с
ограничениями на длину очереди могут иметь лишь конечные
множества возможных состояний.
4. За бесконечно малый промежуток времени At система
обслуживания с простейшим входным потоком заявок и экс-
экспоненциальным законом распределения времени обслуживания
либо остается в прежнем состоянии E,), либо переходит в со-
соседнее (S,+i или 5,_i при i ^ I, S\ при i = 0).
Таким образом, в любой момент времени t система обслужи
вания с т идентичными параллельными каналами обслужива-
обслуживания находится в одном из своих возможных состояний {5,}"_0,
п? N или п = оо. При этом:
если i = 0, т, то занято г каналов и очереди нет;
если i — т-\- 1,п, то заняты все т каналов и в очереди
находится (п — т) заявок;
если п = т, то рассматривают систему обслуживания с
отказами;
если т < п < оо, то рассматривают систему обслуживания
с ограниченной длиной очереди;
если п = оо, то рассматривают систему обслуживания с
ожиданием без ограничений на длину очереди.
5. Пусть {S'tJJl.Q — множество возможных состояний рас-
рассматриваемой системы обслуживания. Для i = 0, п введем
случайное событие а,, заключающееся в том, что в момент

202 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
времени t ^ 0 система находится в состоянии St, и обозначим
вероятность его реализации через p,(t): р,(?) = Р[а,]. В лю-
любой момент времени исходная система может находиться лишь
в одном из возможных состояний, поэтому {а,}"=1 — полная
группа событий и, как следствие,
г=0
Одна из задач теории массового обслуживания сводится к
определению вероятностей p,(t), i = 0, п, как функций времени.
6. Из приведенных выше рассуждений и определения 5.8
марковского процесса с дискретными состояниями следует, что
рассматриваемые процессы массового обслуживания являются
процессами гибели — размножения. К изложенному в 5.4
добавим следующее:
а) элемент размеченного графа состояний системы S, со-
соответствующий возможному состоянию Sk, будем называть
к-й вершиной графа; стрелки, указывающие возможные пе-
переходы системы S из состояния в состояние, с записанными
переходными вероятностями, — нагруженными дугами, а
переходные вероятности — весами;
б) при составлении системы уравнений Колмогорова можно
использовать следующее правило: производная от вероятности
пребывания системы в состоянии 5, в момент времени t рав-
равна сумме произведений весов дуг, инцидентных г-й вершине
размеченного графа состояний, на вероятности состояний, к
которым они направлены; при этом вес дуги берется со знаком
„плюс", если дуга направлена к г-й вершине, соответствующей
состоянию S,, и со знаком „минус" в противном случае;
в) плотности вероятностей переходов {Xt}}, а следова-
следовательно, и переходные вероятности могут зависеть от струк-
структуры системы, характеристик входного потока и параметров
законов распределения времени ожидания и времени обслужи-
обслуживания.

6.4. Построение марковских моделей массового обслуживания 203
Пример 6.2. Рассмотрим простейшую задачу теории мас-
массового обслуживания — задачу о функционировании однока-
нальной системы обслуживания с отказами, на вход которой
поступает простейший поток заявок с интенсивностью А (за-
(заявка, заставшая канал занятым, покидает систему), а время
обслуживания заявки — случайная величина, распределенная
по экспоненциальному закону с параметром fi = const.
В данном случае система имеет лишь
два возможных состояния: So — канал сво- /tn 2L_w^T\
[ о о I (о 1 1
боден; S\ — канал занят. Ее размеченный ч~' \ v-y
граф состояний изображен на рис. 6.2.
Далее (см. 6.5) мы докажем, что Aoi = А ис. .
и Аю = ц. Если считать, что в начальный момент времени
t = 0 система находилась в состоянии So, то математическая
модель изучаемого процесса массового обслуживания имеет
следующий вид:
= l, pi@) = 0.
При этом, учитывая, что, согласно F.16),
математическую модель можно упростить:
Решив полученную задачу Коши, находим (рис. 6.3)
Х+ц

204 6 ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
1 с
Рис. 6.3
Важнейшими характеристиками системы обслуживания с
отказами являются:
а) абсолютная пропускная способность — среднее
число заявок, которое может обслужить система в единицу
времени;
б) относительная пропускная способность — отно-
отношение среднего числа заявок, обслуживаемых системой в едини-
единицу времени, к среднему числу поступивших за это время заявок.
Нетрудно убедиться в том, что в примере 6.2 функцию
Po(t) можно интерпретировать как относительную пропускную
способность системы. Действительно, po(t) есть вероятность
того, что в момент t канал обслуживания свободен, т.е. что
заявка, поступившая в момент t, будет обслужена. А это
означает, что po(t) есть отношение числа обслуженных заявок
к их общему числу, или относительная пропускная способность
системы.
При стационарном (установившемся) режиме функци-
функционирования имеем
«о = lim Po(t) —
t-foo
Поэтому в рассматриваемом случае относительная пропуск-
пропускная способность системы обслуживания равна ц/(Х + ц)- Мож-
Можно показать, что абсолютная пропускная способность равна
= A1?

6 4 Построение марковских моделей массового обслуживания 205
величине обратной сумме среднего времени ожидания заявки
и среднего времени ее обслуживания:
1 Xfi
Л ц
Пример 6.3. Одноканальная система обслуживания пред-
представляет собой телефонную линию. Заявка-вызов, поступив-
поступившая в момент, когда линия занята, получает отказ. Интен-
Интенсивность потока заявок 0,8 (вызовов в минуту). Средняя
продолжительность разговора 1,5 минуты. Считая поток за-
заявок простейшим, а время обслуживания распределенным по
экспоненциальному закону, определим в стационарном режиме
функционирования:
1) абсолютную пропускную способность канала связи Q;
2) относительную пропускную способность канала связи q;
3) вероятность отказа рот.
Имеем
А = 0'8< ^ = 175 = 1-
Таким образом,
Относительная пропускная способность канала связи
А
есть вероятность того, что заявка будет обслужена, не получив
отказа. Поэтому
Рот = 1 - q = т-— « 0,5454.
Отметим, что номинальная пропускная способность рассма-
рассматриваемого канала связи QHOM, являясь величиной обратной по

206 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
отношению к средней продолжительности времени разговора
(Qhom = М — 2/3 и 0,66), почти вдвое больше его пропускной
способности Q, определенной с учетом случайного характера
потока заявок и времени обслуживания.
6.5. Системы массового
обслуживания с ожиданием
При рассмотрении примера 6.2 мы уже столкнулись с необ-
необходимостью определения плотностей вероятностей переходов
при разметке графа состояний простейшей одноканальной си-
системы обслуживания. В дальнейших рассуждениях в качестве
объекта исследований будем использовать систему обслужива-
обслуживания с ожиданием, имеющую т идентичных каналов обслужи-
обслуживания и простейший поток с интенсивностью А, предполагая
что время обслуживания и время ожидания — случайные вели-
величины, распределенные по экспоненциальному закону с параме-
параметрами fi к v соответственно.
Предположим, что в момент времени t рассматриваемая
система находилась в состоянии 5,. Вероятность того, что
за временной интервал бесконечно малой длительности At она
из состояния 5, перейдет в „старшее" состояние S,+i, зависит
лишь от потока заявок, каждая из которых либо поступает в
канал обслуживания, либо становится в очередь. А так как
поток заявок является простейшим с интенсивностью А, то
вероятность P,)t+i(?; Д?) того, что за время At поступит одна
заявка (вероятность перехода из состояния 5, в состояние S,+i),
согласно определению 6.1, равна
Ptii+l{t;At) =
Следовательно,
-

6.5. Системы массового обслуживания с ожиданием 207
Переход из состояния 5, в „младшее" состояние 5,_i зави-
зависит лишь от освобождения каналов обслуживания. Если ц —
интенсивность обслуживания, то функция распределения вре-
времени обслуживания определяется по формуле F.13). Поэтому
Piti-i (t; At) = G{At) = 1 - е~дА* = fiAt + o(At)
и, следовательно,
Таким образом, при наличии лишь одного канала обслуживания
плотность вероятности перехода в „младшее" состояние равна'
[I. Если занято i каналов и i ^ т (т — число каналов
обслуживания), то в силу независимости их функционирования
интенсивность обслуживания возрастает в г раз, т.е. Л, ,_i = ifi.
При возникновении очереди каждое состояние рассматрива-
рассматриваемой системы обслуживания характеризуется занятостью ка-
каналов обслуживания. Поэтому интенсивность освобождения
каналов становится постоянной и равной тц. Как только ка-
канал обслуживания освобождается, он немедленно приступает к
обслуживанию следующей заявки из очереди и система перехо-
переходит в „младшее" состояние. Такой переход может быть вызван
также уходом из очереди одной заявки, если время ожидания
превышает допустимое.
Закон распределения времени ожидания определяется «к-
тенсивностъю v ухода из очереди при наличии в ней одной
заявки (см. равенства F.14), F.15)). В силу независимости по-
поступления заявок (см. определение 6.1 для очереди длины г ^ 1)
интенсивность, с которой заявки отказываются от обслужива-
обслуживания и уходят из очереди, равна rv. Таким образом, плотность
вероятности перехода системы из состояния Sm+r в состояние
5m+r_1 равна сумме интенсивностей освобождения каналов об-
обслуживания и отказа от обслуживания:
Am+r,m+r-l =

208 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Проведенные рассуждения позволяют построить размечен-
размеченный граф состояний рассматриваемой системы обслуживания
(рис. 6.4).
Л х—^ Л у—>. Л
(m-l)jj N—-/ тц
тц+(г-\)и
is,
Рис. 6.4
Воспользовавшись этим графом и правилом построения
системы уравнений Колмогорова, получаем
ri/)pm+r(t)
-l, F.17)
Если на длину очереди, т.е. на возможные значения г, не
накладывают ограничений, то линейная система обыкновенных
дифференциальных уравнений F.17) является бесконечной.
Если в начальный момент времени t = 0 рассматриваемая си-
система обслуживания находилась в одном из своих возможных
состояний Sj, то начальные условия для нее выглядят следую-
следующим образом:
{ ww. <6Л8>
Пример 6.4. Построим математическую модель однока-
нальной (т — 1) системы обслуживания с ожиданием, на вход
которой поступает простейший поток заявок с интенсивностью
А = const, если интенсивность обслуживания ц = const, коли-
количество мест в очереди ограничено числом ./V < оо, т.е. заявка,

6 6 Стационарный режим системы обслуживания
209
поступившая в момент, когда в очереди уже находится ./V за-
заявок, покидает систему.
В рассматриваемом случае система обслуживания имеет
следующие возможные состояния:
So — канал свободен;
S\ — канал занят, но очереди нет;
Si+j — канал занят и в очереди находится j заявок, 1 ^ j ^.N.
При этом единственной причиной отказа от обслуживания
является отсутствие места в очереди, и, значит, интенсивность
ухода из очереди равна v = 0.
Размеченный граф состояний исходной системы обслужи-
обслуживания, изображенный на рис. 6.5, позволяет записать систему
уравнений Колмогорова на интервале t > 0, если считать t = 0
моментом начала функционирования системы
.РЛГ+I (*) = ^PN(t) ~ (iPN+l{t).
Для завершения построения математической модели доста-
достаточно задать начальные условия согласно F.18).
6.6. Стационарный режим функционирования
системы обслуживания
(основные понятия и соотношения)
В теории массового обслуживания и ее приложениях основ-
основное внимание уделяется анализу стационарных режимов функ-
функционирования систем обслуживания. Математическая модель

210 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
стационарного режима функционирования любой системы об-
обслуживания, в предположении его существования, формально
является предельным {t —> оо) случаем ее общей математиче-
математической модели. При стандартных предположениях относительно
исходного процесса массового обслуживания эта модель пред-
представляет собой задачу Коши для соответствующей системы
уравнений Колмогорова и является частным случаем матема-
математической модели процессов гибели — размножения.
Базируясь на результатах анализа стационарных режимов
процессов гибели — размножения (см. 5.4), проведем анализ
стационарного режима функционирования системы обслужи-
обслуживания с ожиданием как наиболее общей. Согласно F.16), F.17),
для стационарного режима функционирования имеем
Аро + HPi = 0,
,_1 - (А + ip)pt + {i + l)npi+i = 0, i = l,ro-l,
0 ^o
I k=o
В стационарном режиме функционирования изучаемая система
также меняет свое состояние случайным образом, но вероятно-
вероятности состояний уже не зависят от текущего времени. Каждая
из них, являясь постоянной величиной, характеризует относи-
относительное время пребывания системы в данном состоянии.
Из первого уравнения системы F.19) находим
где величина
«=? F-20)
определяет среднее число требований, поступающих в систему
обслуживания за среднее время обслуживания одной заявки,

6.6. Стационарный режим системы обслуживания 211
так как интенсивность А простейшего потока определяет
среднее число заявок, поступающих в систему обслуживания
в единицу времени, а величина l/fi, обратная интенсивности
обслуживания ц, численно равна среднему времени обслужи-
обслуживания одной заявки. Эту величину называют приведенной
плотностью потока заявок.
Последовательно разрешив каждое из уравнений системы
F.19) относительно p,+i и подставив в полученные равенства
выражения р, = р,(ро) и р,_х = р^_х(ро), находим
F.21)
¦рт, г>1, F.22)
/?=-, F-23)
равную отношению среднего времени обслуживания одной за-
заявки A//х) к среднему времени ожидания, называют приве-
приведенной плотностью потока ухода заявок из очереди.
Подставив F.21), F.22) в последнее уравнение системы F.19),
находим
<«.«>
Среднюю длину очереди г определяют как математическое
ожидание числа заявок, находящихся в очереди. Из F.22),
F.24) находим
оо °° г
T-— Ро- F-25)
Точно так же
Pm+r ml '
где величину
г
п
а'
Pi = — Ро,
Ро
(го + Щ
i
г
п
= 1
а
(го
, го.
+ kC)
k=\

212 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
А так как некоторые требования, не дождавшись обслужива-
обслуживания, уходят из очереди с интенсивностью v, то без обслужи-
обслуживания систему покидает в среднем vr заявок в единицу време-
времени. Значит, из Л поступивших заявок будет обслужено лишь
(Л — vr). Можно найти относительную пропускную способ-
способность системы _ _
А ^~vr _ _ YL (Р, or)
и среднее число занятых каналов обслуживания, которое с
учетом F.20) и F.23) можно записать в виде
щ±Ь^* = а-Рг. F.27)
Величина q определяемая равенством F.26), характеризует
вероятность того, что заявка, поступившая в систему обслужи-
обслуживания, будет обслужена. При отсутствии очереди г = 0и </=1,
т.е. все заявки обслуживаются.
Величина т, определяемая равенством F.27), есть мате-
математическое ожидание числа занятых каналов обслуживания.
Воспользовавшись тождеством F.16) при п = оо и тем обстоя-
обстоятельством, что в состояниях {Sm+r}r^o все каналы обслужива-
обслуживания заняты, находим
т —1 оо т —1 тп —1
г=0 r=0 j=0 «=0
ИЛИ
¦)•
тп-1
тп = т — тпро — / {тп — i)pt, F.28)
«=о
где тп — число одинаковых параллельных каналов обслужива-
обслуживания в исходной системе, а вероятности pk, к = 0, тп— 1, находят
по формулам F.21), F.24).
Значение т, определяемое равенством F.28), вычислить
много проще, чем значение г, определяемое формулой F.25).

6.7. Стационарные режимы некоторых систем 213
Поэтому, учитывая F.26), F.27), находим
_ а — т А — fifn
Г~~Р~~ L _ F.29)
и А — fim fi то
q = 1 — — • = —тп = .
A v A a
Отметим, что, согласно F.29), относительная пропускная
способность q системы обслуживания равна отношению сред-
среднего числа занятых каналов к приведенной плотности потока
заявок.
6.7. Стационарные режимы функционирования
некоторых вариантов систем обслуживания
Из результатов достаточно общего характера (см. 6.6) мож-
можно сделать весьма интересные для практических приложений
выводы. Исследуем стационарные режимы функционирования
некоторых вариантов систем обслуживания при сделанных вы-
выше (см. 6.2-6.4) предположениях относительно входного по-
потока, структуры системы и законов распределения времени
обслуживания и времени ожидания. Другие варианты систем
обслуживания анализируются аналогично, а результаты анали-
анализа подробно описаны в специальной литературе*.
Чистые системы обслуживания с ожиданием. Чи-
Чистой системой обслуживания с ожиданием называют
такую систему, в которой заявки не покидают очереди. Отме-
Отметим особенности таких систем.
1. Эти системы имеют неограниченное время ожидания.
2. Интенсивность ухода заявок из очереди нулевая: v — О,
и, согласно F.23), /? = 0. Из F.24) следует, что
F-30)
'См.: Ивченко Г.И., Каштанов В.А., Коваленко И.Н.

214 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
3. Если приведенная плотность потока заявок а не меньше
числа каналов обслуживания т (а ^ т), то ряд с общим членом
(а/тп)г будет расходящимся. Значит, согласно F.30), ро = 0, а
из F.21), F.22) получаем, что рк =0, к ^ 0, и тождество F.16)
нарушается, т.е. стационарного режима нет.
В рассматриваемом случае среднее число требований, при-
приходящееся на среднее время обслуживания одной заявки, не
меньше числа каналов обслуживания. Поэтому длина очереди
неограниченно возрастает.
4. Если приведенная плотность потока заявок а меньше
числа каналов обслуживания тп (а < т), то ряд в F.30) с
общим членом (a/m)r сходится, его сумму легко найти (это
геометрическая прогрессия) и равенство F.30) равносильно
следующему:
Средняя длина очереди г может быть найдена из F.25) при
0 = 0:
а \г ат а
Пример 6.5. На железнодорожную сортировочную горку
прибывают составы с интенсивностью 2 состава в час. Среднее
время обработки состава равно 0,4 часа. Составы, прибывшие
в момент, когда сортировочная горка занята, становятся в
очередь в парке ожидания с тремя путями, каждый из которых
предназначен для одного состава. Если все пути в парке
ожидания заняты, то прибывший состав ожидает свою очередь
на внешней ветке. При отмеченных выше предположениях
необходимо найти:
1) среднее число составов, ожидающих обработки;
2) среднее время пребывания состава в парке ожидания;

6.7. Стационарные режимы некоторых систем 215
3) среднее время пребывания состава на внешней ветке;
4) среднее время пребывания состава на сортировочной
горке, включая время ожидания и время обслуживания;
5) вероятность того, что прибывший состав займет место
на внешней ветке.
Имеем интенсивность входного потока А = 2, интенсивность
обслуживания ц — 1/0,4 = 2,5, приведенную плотность потока
заявок a = X/fi = 0,8. В системе один канал обслуживания
(сортировочная горка), поэтому т = 1. А так как a — 0,8 < 1 =
= m, то система справляется с обслуживанием входного потока
и, согласно F.31) при т = 1, ро = 1 — а. По формуле F.32)
вычисляем среднюю длину очереди ( в составах):
F 3l2.
1 - а 1-0,8
Вероятность того, что прибывший состав займет место
на внешней ветке, находим из F.22) при m = 1, р0 = 1 — а и
/3 = 0, так как имеем дело с чистой системой обслуживания с
ожиданием, для которой v — 0 и, согласно F.23), C = 0. Искомая
вероятность равна вероятности того, что длина очереди будет
больше трех:
оо оо оо
Рьь = ]Г> = ]Г>+' = 5^а"+1A - а) = а4 = 0,4096.
k=4 r—3 r=3
Среднее время ожидания на внешней ветке (в часах) равно
г+1)-3.
г=3 *~ k=l
ч,4
а — =0,8192.

216 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Среднее время ожидания (в часах) в парке с тремя путями,
на каждом из которых может находиться лишь один состав,
равно
1 2 3 °°
tno — —Pi + —Р2 + -
Ц \1 (I
\-а/
= - (аро + 2а2р0 + 3 ]П afcp0) =
/ о а3 \ аA — а3)
(а + 2а2 + 3- ) = -у f = О,
V 1 - а/ /хA-а)
7808.
Таким образом, среднее время ожидания обслуживания в
рассматриваемой системе ( в часах) равно
too = tno + tbb = 1,6,
а среднее время пребывания состава на сортировочной горке
составляет
t = to0 + - = 2. #
Системы обслуживания с отказами. Эти системы
имеют следующие особенности.
1. Заявка, поступающая в такую систему в момент, когда
все каналы обслуживания заняты, покидает систему. Это
означает, что в рассматриваемом случае очередь отсутствует
и система имеет конечное множество состояний {Sk}™=0, где
тп — число каналов обслуживания.
2. В соответствии с F.16) — F.18) математическая модель
системы обслуживания с отказами имеет следующий вид:
() i(tI t>0, i = 0,m,
sO, pm+i(t) = O,
т
«=0

6.7. Стационарные режимы некоторых систем 217
3. При изучении стационарных режимов функционирования
систем обслуживания с отказами можно использовать резуль-
результаты из 6.6, учитывая, что в данном случае интенсивность
ухода из очереди равна v = оо. Согласно F.23), из v = oo сле-
следует /3 — оо, поэтому из F.21), F.24) получаем
a'
Po ~
При этом, полагая
m
^e-a i 0~^i R{m;a)
^, , R{m;a) = ^Р(г», F.33)
t=0
приходим к формулам
Р'= R(m-a) ' г = °'т- F-34^
Формулы F.33), F.34), известные как формулы Эрланга,
названы по имени датского инженера А.К. Эрланга, который
в 20-х гг. XX в. впервые исследовал систему обслуживания с
отказами применительно к телефонной связи.
4. Формулами Эрланга F.33), F.34) удобно пользоваться
при больших значениях г, так как в этом случае
X
Где Ф(х) = —= / е~* /2dt — функция Лапласа.
л/2тг J
о
5. Полагая г = m в формулах F.33), F.34) (все каналы
заняты), находим вероятность отказа
Ро,к=рт = 1-Щ™-\а). F.35)

218 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Все заявки, не получившие отказа, должны быть обслужены.
Поэтому вероятность того, что заявка, поступившая в систему,
будет обслужена, есть не что иное как относительная пропуск-
пропускная способность q изучаемой системы. Итак,
F.36)
6. Согласно определению математического ожиданья для
дискретной случайной величины, среднее число занятых кана-
каналов в исходной системе обслуживания равно
к .
В вычислительном аспекте величину Кср удобнее определять
как отношение абсолютной производительности системы (сред-
(среднее число заявок, обслуженных в единицу времени) к интенсив-
интенсивности обслуживания д (среднее число заявок, обслуживаемых
в единицу времени одним каналом):
г, АA-ротк) Д(го-!;<*)
Кср= — '- = aq-a—)- -А F.37)
ц Щт;а)
Пример 6.6, Автоматическая телефонная станция обес-
обеспечивает не более 120 переговоров одновременно. Средняя
продолжительность разговора 60 секунд, а вызовы поступают
в среднем через 0,5 секунды. Рассматривая такую станцию как
многоканальную систему обслуживания с отказами и простей-
простейшим входным потоком, определим:
1) среднее число занятых каналов Кср;
2) относительную пропускную способность q;
3) среднее время tcp пребывания вызова на станции с учетом
того, что разговор может и не состояться.

6.7. Стационарные режимы некоторых систем 219
Рассматриваемая система представляет собой систему об-
обслуживания с отказами, находящуюся в стационарном режиме
функционирования. Она обладает следующими характеристи-
характеристиками: число каналов обслуживания m = 120 велико; интен-
интенсивность входного потока А = 1/0,5 = 2; интенсивность обслу-
обслуживания fi — 1/60; приведенная плотность потока заявок а —
Учитывая F.37) и используя таблицы функции Лапласа
[XVI], получаем
19;
ДA20;120)
так как
V120
I + Ф(-0,046) = 0,5 - Ф@,046) и 0,482,
- + Ф(-0,046)и 0,518.
Далее, согласно F.37), находим
0,931.
а
А так как А есть интенсивность входного потока (число заявок
в единицу времени), то Xtcp — Кср и

220 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Системы обслуживания с ограниченной длиной оче-
очереди. Отметим особенности стационарных режимов функци-
функционирования таких систем.
1. Для m-канальной системы обслуживания, длина очереди
которой ограничена числом N < оо, интенсивность и ухода
заявок из очереди зависит от ее возможного состояния 5,:
ГО, 0iiim + N;
у оо, г > т + N.
При стандартных предположениях относительно входного по-
потока и законов распределений времени обслуживания и времени
ожидания (см. 6.2, 6.3) математическая модель исходной систе-
системы в соответствии с F.16)-F.18) имеет следующий вид:
1(t), t = 0,ro-l,
р_г(О=О, t>0,
p'm+r{t) = bpm+r-i{t) - (X + mn)pm+r(t) +
+ mfipm+r+l (t), r = 0, N-1, t > 0,
m+N
k=0
ч
0,
где k = I, m+N и j — некоторый фиксированный элемент
множества {0, 1, ..., m + N}.
2. При изучении стационарных режимов функционирования
систем обслуживания с ограниченной длиной очереди можно
использовать результаты из 6.6, учитывая, что в данном случае
множество возможных состояний системы {Sk}™^* конечно,
а интенсивность ухода заявок из системы нулевая {и — 0) и,

6.7. Стационарные режимы некоторых систем 221
согласно F.23), /3 = 0. Из F.21), F.22), F.24) с учетом F.38),
F.23) находим вероятности состояний:
¦
Pi=— Po, г=1,т,
Вероятность отказа равна ротк = pm+N, а относительную про-
пропускную способность системы вычисляем через вероятность
отказа: q = 1 — рОТк-
Пример 6.7. Два рабочих обслуживают шесть однотипных
станков. Остановка каждого работающего станка происходит
в среднем каждые полчаса, а процесс наладки занимает в
среднем 10 минут. Необходимо определить:
1) среднюю занятость рабочих;
2) среднее количество неисправных станков;
3) абсолютную пропускную способность рабочей бригады.
В данном случае интенсивность входного потока А = 1/0,5 =
= 2, интенсивность обслуживания ^ = 6, число каналов обслу-
обслуживания т = 2 (два рабочих с одинаковой квалификацией).
Возможны следующие состояния системы:
50 — все станки работают и рабочие свободны;
51 — один станок остановился и один рабочий занят, а
второй свободен;
5г — два станка остановились и оба рабочих заняты;
S2+r — остановились 2 + г станков, г =1,4, оба рабочих
заняты и г станков ждут обслуживания.
На рис. 6.6 изображен размеченный граф состояний рассма-
рассматриваемой системы обслуживания — типичного представителя
так называемых замкнутых систем обслуживания. В

222 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Рис. 6.6
этих системах интенсивность потока заявок зависит от состоя-
состояния самой системы обслуживания. Данная специфика не позво-
позволяет непосредственно использовать результаты, приведенные
выше.
Для построения системы линейных алгебраических урав-
уравнений относительно стационарных вероятностей pk (к = 0,6)
пребывания системы в возможных состояниях Sk воспользуемся
размеченным графом состояний и результатами анализа стаци-
стационарных режимов процессов гибели — размножения (см. 5.4).
На основании этих результатов получим
=0.
6Лро - EА + ц)рг + 2№ = 0,
5Ар, - DА + 2ц)р2 + 2цр3 = 0,
4Ар2 - (ЗА + 2м)р3 + 2цр* = 0,
ЗАр3 - BА + 2ц)р4 + 2цр5 = 0,
Ар5
= 0.
Решая эту систему линейных алгебраических уравнений при
А = 2 и ^ = 6, находим
5 10
Pl = Zpo, Р2 — ~РО, РЗ — ~Р0, Pi
Тождество F.16) принимает вид
5
;=—Ро, Рб=7^>Р°-
К 1о2
Отсюда находим вероятность пребывания исходной системы в
состоянии Sq:
162
Ро = ТобТ-

Вопросы и задачи 223
Среднее число неисправных станков есть математическое
ожидание числа станков, связанных с процессом обслуживания
(ремонтируются или ждут обслуживания):
к-1
9 27 162
Среднюю занятость рабочих р находим как математическое
ожидание числа налаживаемых станков:
= Pi + 2A - ро - Pi) = 2A - 2р0) и 1,389.
При интенсивности обслуживания ц — 6 станков в час
абсолютная пропускная способность рабочей бригады равна
цр- 8,336.
Вопросы и задачи
6.1. Сформулируйте определение простейшего входного
потока. Какие вероятностные характеристики простейшего
потока Вы знаете?
6.2. Какую простейшую процедуру проверки статистиче-
статистической гипотезы о соответствии реального входного потока про-
простейшему потоку Вы можете предложить?
6.3. Какие законы распределения обычно используют в те-
теории массового обслуживания при анализе времени обслужи-
обслуживания и времени ожидания? Каким образом интерпретируют
параметры этих законов?
6.4. При каких допущениях процессы массового обслужива-
обслуживания являются марковскими случайными процессами?

224 6 ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
6.5. Докажите тождественность правых частей равенств
F.25), F.29) для определения среднего числа занятых каналов
обслуживания.
6.6. Что можно сказать о существовании стационарных
режимов функционирования чистых систем обслуживания с
ожиданием?
6.7. Чем чистая система с ожиданием отличается от обыч-
обычной системы обслуживания с ожиданием?
6.8. В чем заключается принципиальное отличие замкнутых
систем обслуживания от следующих систем: а) чистой системы
с ожиданием; б) системы с отказами; в) системы с ограничен-
ограниченной длиной очереди?
6.9. Выясните, можно ли использовать расчетные формулы
F.20)-F.24) для определения предельных вероятностей следу-
следующих типов систем обслуживания: а) чистых систем с ожида-
ожиданием; б) систем с отказами; в) систем с ограниченной длиной
очереди; г) замкнутых систем. Дайте обоснование ответа.
6.10. В систему обслуживания поступает в среднем две
заявки в час. Считая входной поток простейшим, определите:
а) среднее число заявок, поступающих в систему обслуживания
за 8 часов; б) вероятность того, что в течение одного часа
поступит по крайней мере одна заявка.
Ответ: а) 16; б) 0,865.
6.11. В ресторан прибывает в среднем 20 посетителей в час.
Считая поток посетителей простейшим и зная, что ресторан
открывается в 11.00, определите:
а) вероятность того, что в 11.12 в ресторан придет 20
посетителей при условии, что в 11.07 их было 18;
б) вероятность того, что между 11.28 и 11.30 в ресторане
окажется новый посетитель, если известно, что предшествую-
предшествующий посетитель прибыл в 11.25.
Ответ: а) 0,262; б) 0,487.

Вопросы и задачи 225
6.12- Система обслуживания представляет собой автома-
автоматическую телефонную станцию, которая может обеспечить не
более трех переговоров одновременно. Заявка-вызов, поступив-
поступившая в тот момент, когда все каналы заняты, получает отказ и
покидает систему. В среднем на станцию поступает 0,8 вызо-
вызовов в минуту, а средняя продолжительность одних переговоров
равна 1,5 минуты. Для стационарного режима функционирова-
функционирования системы необходимо определить: а) вероятности состояний
системы; б) абсолютную и относительную пропускные способ-
способности; в) вероятность отказа; г) среднее число занятых кана-
каналов.
Ответ: а) р0 « 0,312, рх « 0,374, р2 к 0,224, р3 т 0,090;
б) 0,728, 0,910; в) 0,090; г) 1,09.
6.13. Автозаправочная станция имеет одну бензоколонку с
площадкой, допускающей пребывание в очереди на заправку не
более трех автомашин одновременно. Если в очереди на заправ-
заправку уже находятся три автомашины, то очередная автомашина,
прибывшая на станцию, проезжает мимо. В среднем на за-
заправку прибывает одна автомашина в минуту, а сам процесс
заправки в среднем длится 1,25 минуты. Для стационарного ре-
режима функционирования автозаправочной станции необходимо
определить: а) вероятность отказа; б) относительную и абсо-
абсолютную пропускные способности; в) среднее число автомашин
в очереди на заправку; г) среднее число автомашин, находящих-
находящихся на автозаправочной станции; д) среднее время ожидания в
очереди; е) среднее время пребывания автомобиля на автоза-
автозаправочной станции.
Ответ: а) 0,297; б) 0,703, 0,703; в) 1,56; г) 2,44; д) 1,56;
е) 2,44.
6.14. Найдите решение задачи 6.13, если в ее условия вне-
внесены следующие изменения: автозаправочная станция распо-
располагает двумя бензоколонками; в среднем на автозаправочную

226 6. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
станцию прибывает две автомашины в минуту; в среднем время
обслуживания — две автомашины в минуту.
Ответ: а) 0,502; б) 0,488, 0,496; в) 2,18; г) 4,14; д) 1,09;
е) 2,07.
6.15. Рабочий обслуживает три однотипных станка. Ка-
Каждый станок останавливается в среднем два раза в час, а
процедура наладки занимает в среднем 10 минут. В стацио-
стационарном режиме функционирования системы нужно определить:
а) вероятность занятости рабочего; б) абсолютную пропуск-
пропускную способность рабочего; в) среднее количество неисправных
станков; г) среднюю относительную потерю производительно-
производительности обслуживаемых станков за счет неисправностей.
Ответ: а) 0,654; б) 3,94; в) 1,04; г) 0,347.

7. СТОХАСТИЧЕСКИЕ
МОДЕЛИ СОСТОЯНИЯ
Решение практически важных задач, будь то расчет подъ-
подъемной силы крыла самолета или прогнозирование динамики
распространения инфекции в определенном регионе, предпо-
предполагает наличие математических моделей изучаемых явлений,
позволяющих применять количественные методы исследования.
Напомним, что под математической моделью понимают при-
приближенное описание какого-либо класса явлений реального ми-
мира, выраженное с помощью математической символики. На
данном этапе мы не будем заниматься разработкой матема-
математических моделей конкретных явлений, тем более, что, со-
согласно высказываниям многих видных специалистов в области
математического моделирования, искусство построения мате-
математической модели есть именно искусство и опыт в этом деле
приобретается постепенно.
В данной главе рассматриваются математические модели,
представляющие собой системы обыкновенных стохастиче-
стохастических дифференциальных уравнений, дополненные соответству-
соответствующими начальными условиями. Эти модели описывают обшир-
обширный класс явлений реального мира.
7.1. Случайные возмущения
в динамической системе
Рассмотрим математическую модель, описывающую эво-
эволюцию изучаемого объекта на отрезке времени Т = [0, ?„]:
,{), „<*«<„ A)

228 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
где X(t) — n-мерная вектор-функция, которую называют век-
тором состояния; а € Rm — вектор параметров, не завися-
зависящий от времени t; А — n-мерная векторная функция п-\-т + 1
переменного, удовлетворяющая условиям теоремы существо-
существования и единственности решения задачи Коши G.1); Хо —
начальное значение вектора состояния X(t). Из G.1) следу-
следует, что скорость изменения состояния в любой момент времени
t > О определена его текущим состоянием в этот момент вре-
времени и вектором параметров а. Математическая модель G.1),
которую называют детерминированной (неслучайной) мо-
моделью состояния, является достаточно общей и может быть
использована для описания обширного класса динамических си-
систем. Поясним сказанное примером.
Пример 7.1. Рассмотрим математическую модель про-
простейшей следящей системы:
где хо G R — начальное значение состояния системы x(t) € R,
А > 0 — параметр системы; ?*(?) — скалярная функция време-
времени, заданная на отрезке Т — [О, ?»].
Система функционирует таким образом, что отклонение от
заданного состояния x*(t) уменьшается со скоростью, пропор-
пропорциональной текущей величине отклонения. Причем реакция
системы на изменение состояния тем быстрее, чем больше зна-
значение параметра А > 0.
Математическая модель позволяет заранее рассчитывать
изменение состояния изучаемой системы на отрезке Т путем
решения задачи Коши G.2). Если же требуемые значения со-
состояния ?»(?) в моменты времени t € Т заранее неизвестны,
например, вследствие их зависимости от множества непро-
непрогнозируемых факторов, то x*(t) следует рассматривать как
случайный процесс г»(?,и>); t ?Т, математическое ожидание

7.1. Случайные возмущения в динамической системе 229
которого m(t) = M[a:,(t,w)], как правило, известно. В этом
случае случайный процесс xm(t,u>), t ? Т, можно представить
в следующем виде:
а математическую модель G.2) записать так:
' x(t) = -X[x(t) - m(t)
)
G-3)
u), teT.
При этом состояние x(t) следящей системы уже не является
детерминированной функцией, а представляет собой случайный
процесс x(t,u>), t € Т.
Таким образом, математическая модель G.3) может рассма-
рассматриваться как результат случайных возмущений детерминиро-
детерминированной модели G.2). В этом случае невозможно заранее рас-
рассчитать изменения состояния следящей системы на Т, а можно
лишь анализировать вероятностные характеристики случайно-
случайного процесса x(t,u), t ? Т. #
Используя аналогию с рассмотренным примером, перейдем
к анализу общего случая. Ограничимся математической моде-
моделью G.1) и установим условия, которым должен удовлетворять
процесс случайных возмущений.
В правую часть нормальной системы обыкновенных диффе-
дифференциальных уравнений (ОДУ) G.1) добавим в-мерный случай-
случайный процесс r)(t,oj), t ? Т, который будем называть процессом
случайных возмущений. При этом отметим, что в общем
случае этот случайный процесс может зависеть и от текущего
состояния, и от вектора параметров а, т.е. г) — r)(X,a,t,u) —
n-мерная случайная функция. Но для упрощения дальнейших
рассуждений будем считать, что процесс случайных возмуще-
возмущений является линейным относительно некоторого п-мерного

230 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
случайного процесса ?(t,us), t G T:
где В* — матричная функция п-\-т-\-1 переменного типа пхп.
При добавлении г)(Х,а, t,u) в правую часть нормальной систе-
системы обыкновенных дифференциальных уравнений, входящих в
математическую модель G.1), ее вектор состояния будет п-мер-
п-мерным случайным процессом X(t,w), t G Т. Поэтому и начальное
состояние в общем случае следует считать n-мерным случайным
вектором Хо(ы)- Если же по смыслу решаемой задачи началь-
начальное состояние изучаемой системы задано, т.е. Х@,ш) = Хо, то
Х@,ш) всегда можно рассматривать как п-мерный случайный
вектор, который с вероятностью 1 принимает значение Хо € R".
Таким образом, приходим к так называемой стохастиче-
стохастической модели состояния
(X(t,u) = A(X,a,t)+B.(X,a,t)t(t,u), 0<t^.>
{ G-4)
)
где ?(t,u>), t eT — [0,г*] — в-мерный случайный процесс, без
конкретизации свойств которого дальнейший анализ не пред-
представляется возможным.
Для процесса случайных возмущений естественно требо-
требовать выполнение следующих условий.
1. Не теряя общности дальнейших рассуждений, можно
считать, что
Действительно, если m(t) = М[?(?,а>)]^ 0 на Г, то достаточно
ввести центрированный случайный процесс
i(t,u)±t(t,u)-m(t), teT,

7.1. Случайные возмущения в динамической системе 231
с нулевым математическим ожиданием, а затем стохастиче-
стохастическую модель состояния G.4) преобразовать к виду
X(t,u) = A.(X,a,t) + B.(X,a,t)t(t,W), 0< t ^ t.,
2. Чтобы сохранить основное свойство исходной математи-
математической модели G.1), состоящее в том, что скорость изменения
состояния определяется текущим состоянием и не зависит от
его предыстории, следует потребовать, чтобы любые два сече-
сечения процесса случайных возмущений были независимы, т.е.
чтобы для любых различных t\, t2 € Т были независимы случай-
случайные векторы ?(tx,w) и ?(?2)W).
3. Для сохранения непрерывности производной случайно-
случайного процесса X(t,w), t € Г, следует потребовать непрерывности
процесса случайных возмущений ?(t,u), t G Т. Это требование
сводится к существованию ограниченной дисперсии (см. тео-
теорему 3.6). Таким образом, в предположении, что случайный
процесс ?(t,u>), t 6T, центрирован, имеем
M[f(t,u)Z(t,u)]<C<oc, teT.
Рассмотрим процесс случайных возмущений ?(t,u>), t ? Т,
удовлетворяющий требованиям 1-3, и попытаемся понять, что
он из себя представляет. Ответ на этот вопрос дает следующая
теорема.
Теорема 7.1. Пусть n-мерный случайный процесс ?(t,u),
t ? Т = [0, *„,], удовлетворяет условиям:
2) для любых различных tx, t2 € Т сечения ?(ti,u) и
яются
з)мк
Тогда
являются независимыми случайными векторами;
3) M[?(t,u)?(t,u)] < С < оо, t € Т.

232 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
4 В соответствии с принятыми допущениями определен п-мер-
ный случайный процесс (см. 3.4)
(T,u)dr, teT,
0
и с учетом условия 1 теоремы
= /
Кроме того, из существования случайного процесса e(t,u),
t ?Т, и условия 2 теоремы вытекает, что для любых ?, € Т,
г = 0, iV, таких, что 0 = ?о < ti < • • • < ?дг == t ^ I*, имеет место
равенство
)fe
«=0 j=0
ЛГ-1
где
Ati — tt+i-ti, d=m&x{Ati}.
Пусть
Q
AU^j-, Q = const > 0.
Тогда с учетом условия 3 теоремы имеем
M[eT{t,u)?(t,u)] < CBm ]?(Д*,J < C^lirn Njj^ = 0.
о °°

7.1. Случайные возмущения в динамической системе 233
Таким образом, при t € Т
Mf(lim ^' + ^)-^',"))T ,im s(« +Л,*)-г(«,Ч]
M[\e'T{t,u)E{t+A,u)\] +Mils'* (t+h,u)e{t,u)\]
так как в силу неравенства Шварца
(t2)«)e(tj,W)] s 0. >
Следствие 7.1. Если случайный процесс ^(^,w), t ? Т,
удовлетворяет условиям теоремы 7.1, то в смысле среднего
квадратичного (см. 3.1)
или, что то же самое,
Следствие 7.2. Если X(t) — решение задачи Коши G.1),
a X(t,u), t G T, — решение стохастической задачи Коши
G.4), в которой процесс случайных возмущений ?(t,u), t € Т,
удовлетворяет условиям теоремы 7.1 и Х0(и) = Хо, то в смысле
среднего квадратичного

234 .7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
или, что то же самое,
M[\\x(t,u)-x(t)\\2] = o, teT,
так как случайная величина с нулевой дисперсией является
детерминированной [XVI].
Следствие 7.3. Не существует ненулевых случайных про-
процессов с независимыми сечениями и ограниченной дисперсией.
Итак, стохастическая модель G.4) не дает никакой новой
информации по сравнению с исходной детерминированной мо-
моделью G.1). Нетрудно догадаться, что этот результат является
следствием слишком жестких требований, предъявляемых к
процессу случайных возмущений. Проанализируем эти требо-
требования с точки зрения их возможного ослабления или устране-
устранения.
Первое требование не является принципиальным, что уже
было отмечено, а второе отражает основной принцип постро-
построения математической модели, согласно которому скорость из-
изменения состояния объекта определяется его текущим состоя-
состоянием. Таким образом, мы можем отказаться лишь от третьего
требования, предъявляемого к процессу случайных возмуще-
возмущений. Этот шаг является естественным, так как в силу не-
независимости сечений случайного процесса ?(t,u), t ? Т, его
ковариационная функция имеет следующий вид:
K((t1,t2) = 2nrS(t2-t1), h,t2eT, G.5)
где S(t) — 6-функция Дирака, а Г € Мп(Ж) — постоянная ма-
матрица. Таким образом, случайный процесс ?(t,w), t б Т, с
независимыми сечениями является белым шумом. Его спек-
спектральная плотность
постоянна и не зависит от частоты v. Матрицу Г называют
матрицей спектральных интенсивностей.

7.1. Случайные возмущения в динамической системе 235
Отказ от требования ограниченности дисперсии процесса
случайных возмущений является основополагающим при по-
построении стохастических моделей состояния. Действительно,
при проведении гармонического анализа в детерминированной
модели состояния G.1) каждой компоненте Xk(t) вектора состо-
состояния X(t) соответствует вполне определенный ограниченный
спектр частот. Пусть относительно процесса случайных воз-
возмущений ?(t,u), t G Т, приняты самые общие допущения, но
полоса спектра каждой его компоненты ?fc(?,u>), t € Т, содер-
содержит весь спектр частот компоненты Xk{t) вектора состояния
X{t). В этом случае для каждого к = \,п спектр случайного
процесса ?k(t,w), t G Т, можно считать постоянным в пределах
ограниченного спектра к-а компоненты вектора состояния. А
это означает, что для вектора состояния X(t) детерминирован-
детерминированной модели состояния G.1) процесс случайных возмущений —
белый шум.
При проведении дальнейших рассуждений воспользуемся по-
положительной определенностью и симметричностью матрицы Г
спектральных интенсивностеи случайного процесса?(?,u>), t?T,
обладающего нулевым математическим ожиданием и ковариа-
ковариационной функцией G.5). Из теории матриц известно [IV], что
существует квадратная невырожденная матрица /3 ? Mn(R), та-
такая, что
Г = CCТ.
Введем в рассмотрение n-мерный случайный процесс
который также является белым шумом. Действительно,
= 2nS(t2 - t1)p-lr{p-l)T = 2nS(t2 - t,)/ni tu t2 6 T.

236 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
Полагая t* = оо (т.е. Т — [О, оо)), заключаем, что случай-
случайный процесс e(t,u), t € [0, оо), в классе обобщенных функций
(см. пример 4.4) можно рассматривать как производную п-мер-
ного винеровского процесса w(t,u), t € Т, с коэффициентом
диффузии а1 = 1. Таким образом,
= [0,ос).
Полагая в G.4), что
приходим к следующей стохастической модели состояния:
= ад„,()+8№м|
Выше доказано (см. пример 4.4), что винеровский процесс
не является дифференцируемым в смысле сходимости в сред-
среднем квадратичном. Поэтому для корректности представления
стохастической модели состояния G.6) используем следующую
форму записи:
,t)dt + B(X,a,t)dw(t,u),
(?7)
поскольку винеровский процесс имеет непрерывные траекто-
траектории в смысле среднего квадратичного*.
Заметим, что при изложении элементов стохастического
анализа мы не ввели понятия стохастического дифференциала
и восполним этот пробел лишь в 7.3. А здесь будем считать,
что дифференциал случайного процесса — главная линей-
линейная часть его приращения в смысле среднего квадратичного, и
от дальнейших комментариев воздержимся.
*См.: Вентцель А.Д., а также Пугачев B.C., Синицын И.И.

7.2. Линейные стохастические дифференциальные уравнения 237
Стохастические модели состояния G.6), G.7) представляют
собой задачи Коши для стохастических дифференциальных
уравнений, простейшими представителями которых являются
линейные стохастические дифференциальные уравнения.
7.2. Линейные стохастические
дифференциальные уравнения
Исследование нелинейных стохастических моделей состоя-
состояния G.6), G.7) в общем случае связано со значительными труд-
трудностями принципиального характера. Однако оно существенно
упрощается, если возможна линеаризация исходной математи-
математической модели, т.е. замена нелинейной стохастической модели
состояния некоторым ее линейным приближением.
Определение 7.1. Стохастической задачей Кохии
(задачей Коши для системы линейных стохастических диффе-
дифференциальных уравнений) называют систему уравнений
,u) = a{a,t)X(t,u)dt + b(a,t)dw(t,u),
G-8)
) Х()
где a(a,t) и b(a,t) — известные матричные функции типа
пх п, зависящие от переменного t € Т = [О, оо) и от т-мерного
вектора а параметров; w(t,u), t ?Т, — n-мерный винеровский
процесс, выходящий из 0 и имеющий коэффициент диффузии
<т2 = 1; Xq(u) — n-мерный случайный вектор с известным
законом распределения, характеризующий начальное состояние
неизвестного n-мерного случайного процесса X{t,u), t ? Т.
При дальнейших рассуждениях будем предполагать, что
матричные функции a(a,t) и b(a,t) являются непрерывными в
промежутке Т = [0, оо).
Для любого фиксированного иЕЙ стохастическая задача
Коши G.8) переходит в задачу Коши для системы обыкновен-
обыкновенных линейных дифференциальных уравнений. А так как при

238 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
этом выполнены условия теоремы существования и единствен-
единственности ее решения, то при любом фиксированном ш € Q задача
Коши G.8) однозначно определяет соответствующую реализа-
реализацию случайного процесса X{t,w), t € Т.
Пусть X(t) — фундаментальная матрица решений для нор-
нормальной системы обыкновенных дифференциальных уравнений
x'(t) — a(a,t)x(t). Для любого фиксированного ш ? Q решение
задачи Коши G.8) можно записать в следующем виде [VIII]:
t
,u) = R{t,0)Xo{u) + f R(t,s)b{a,s)dw{s,u), t^O, G.9)
о
где R(t,s) = X~1(s)X(t) — нормированная фундаментальная
матрица решений, или резольвента. Резольвента удовлетво-
удовлетворяет матричному уравнению
R't(t,s) = a{a,t)R{t,s)
и начальному условию
R{s,s) = In.
t
При этом, если матричные функции a(a,t) и fa(a,s)ds комму-
о
тативны относительно умножения, то (см. П2)
t
G.10)
Стохастическая задача Коши G.8) определяет всю сово-
совокупность возможных реализаций рассматриваемого случайного
процесса X(t,uj), t € Т. О решении этой задачи можно судить
лишь по вероятностным характеристикам n-мерного случайно-
случайного процесса X(t,uj), t € Т.
Теорема 7.2. Если a(a,t) и b(a,t) — матричные функ-
функции типа в X в, непрерывные на промежутке Т= [0, оо), w(t,u),

7.2. Линейные стохастические дифференциальные уравнения 239
t ? Т, — n-мерный винеровский процесс с коэффициентом диф-
диффузии а2 — 1, выходящий из 0, a Xq{u) — n-мерный случайный
вектор, распределенный по нормальному закону с математи-
математическим ожиданием то и ковариационной матрицей Ео, то ре-
решение задачи Коши G.8) является n-мерным нормальным мар-
марковским процессом.
4 Воспользовавшись разностной аппроксимацией задачи Коши
G.8), в соответствии с определением винеровского процесса,
выходящего из 0, при t = О имеем
-b(a,Q)w{At,u))=O, G.11)
а при t > О
lim ~(x{t + At,u)~ \In + a(a,t)At]X{t,u)-
At-f+O At V
-b{a,t)[w(t + At,u)-w{t,u)]\ -0. G.12)
А так как в соответствии с определением винеровского процес-
процесса для любого N > 1 и для любых tk ? Т, таких, что 0 < tx < ti <
<...<tiy, случайные векторы w(ti,u), w{t,2,u) — w(ti,u), ...,
w(t]y,u) — u;(tjv_i,w) являются независимыми, то состояние
X(t + At,u) определяется текущим состоянием X(t,u) и значе-
значением n-мерного случайного вектора b(a,t)[w(t + At,и) — w(t,w)].
При этом значение указанного вектора не зависит от предыду-
предыдущих состояний X(t — At,u>), X(t — 2At,u) и т.д. Таким образом,
если iV > 1, t-\-kAt g T, k = 2—N, 1, и ./V-мерная функция плотно-
плотности вероятностей n-мерного случайного процесса X(t,u>), t G T,
имеет вид

240 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
то его условная функция плотности вероятностей обладает
свойством
f(x(N)\x(l),---,x(N-l)) — f{x(N)\x(N-l)),
т.е. в-мерный случайный процесс ЛГ(?,и>), t € Т, является мар-
марковским процессом. При этом, согласно условиям теоремы и
определению винеровского процесса, в-мерные случайные век-
векторы Xq(u), w(At,u), w(t + At,w) — w(t,w) распределены по
нормальному закону. Поэтому из G.11) и G.12) следует, что все
условные и одномерные законы распределения случайного про-
процесса X(t,u), t € Т, являются нормальными. А так как X(t,u),
t € Т, — марковский процесс, то его iV-мерная функция плот-
плотности вероятностей имеет вид
ЛГ_1) | 2(ЛГ-2)) • • • f(XB) I г
а все его конечномерные законы распределения являются нор-
нормальными законами распределения, что и требовалось дока-
доказать. >
Если проанализировать доказательство теоремы 7.2, то
нетрудно убедиться в том, что в условиях, относящихся к
ЛТо(и>), можно добавить: „или ЛГо(^) = ЛГо — детерминиро-
детерминированный (неслучайный) в-мерный вектор". В этом случае
плотность распределения начального состояния является обоб-
обобщенной (см. П1) и ее можно рассматривать как предельный
случай для fx0 плотности распределения случайного вектора
Х0(ш), когда его ковариационная матрица Ео —> G.
Следствие 7.4. Решение X(t,u), t ? Т, стохастической
задачи Коши G.8) полностью определяется своим математиче-
математическим ожиданием и ковариационной функцией.
¦4 Действительно, решение X(t,uj), t € Г, является в-мерным
нормальным марковским процессом. >

7.2. Линейные стохастические дифференциальные уравнения 241
Теорема 7.3. Если выполнены условия теоремы 7.2 и слу-
случайный процесс X(t,w), t € Т, является решением стохастиче-
стохастической задачи Коши G.8), то его математическое ожидание m(t)
и ковариационная функция K(ti,t2) удовлетворяют соотноше-
соотношениям
m(t) = R(t,0)mo, t?T; G.13)
<>> ^f P.14)
{S(t,)R(t2,t,), <i«<2,
где R(t,s) — резольвента нормальной системы линейных диф-
дифференциальных уравнений rh(t) = a(a,t)m(t), mo = М[Хо(ш)],
ti,t2 ?T = [0, оо), а ковариационная матрица T,(t) случайного
процесса X(t,u), t ? Т, является решением следующей задачи
Коши:
(«, t) + b(a, t) br(a, t),
4 Решение стохастической задачи Коши G.8) при каждом фик-
фиксированном ш ? Q может быть представлено в виде G.9). При
этом, как известно из теории линейных дифференциальных
уравнений, для любого фиксированного т ^ 0 решение задачи
Коши G.8) с использованием резольвенты при t ^ r может быть
записано так [VIII]:
t
I
R(t,s)b(a,s)dw(s,u).
В общем случае интеграл в правой части равенства G.9)
представляет собой интеграл от детерминированной функции
R(t,s)b(a,s) по винеровскому процессу w(s,u>), sG [0,t]. Так

242 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
как стохастические интегралы по винеровскому процессу рас-
рассматриваются в 7.3, то на данном этапе ограничимся лишь их
формальной записью.
Определяя математическое ожидание левой и правой ча-
частей G.9), получаем G.13), поскольку можно показать, что
b/L[dw(s, и)] = 0 при s ^ 0.
Доказывал равенство G.14), можем считать, что то = О, так
как в силу линейности стохастической задачи Коши G.8) всегда
можно перейти к центрированному случайному процессу
X(t,u)±X(t,u)-m(t), t>0,
имеющему нулевое математическое ожидание при t ^ 0. Для
ti^^c учетом предположения о центрированности случайного
процесса X(t,w), t ^ 0, имеем
R(t2,s)b(a,S)dw(s,u)f] =
= M[X(t1,u)XT(t1,u)} RT
f
В последней сумме второе слагаемое равно нуль-матрице, по-
поскольку w(s,u), sg [0,i], не зависит от X(ti,u) для любых s ^ t\,
а математические ожидания сомножителей в квадратных скоб-
скобках равны нулю. Поэтому
Аналогично можно доказать, что при t\ ^ t2

7.2. Линейные стохастические дифференциальные уравнения 243
Чтобы получить уравнение, которому удовлетворяет кова-
ковариационная матрица ?(?), рассмотрим разность
Л)-?(*) =
h,u) -X{t,u)) (X(t + h,u)- X(t,u))T +
+ X(t,u) (X(t + h,u) - X(t,uj))T +
+ {X(t + h,u)- X{t,u))XT(t,u)].
Пусть 0 < h <c 1. Согласно G.8), при dt — h с точностью o(h)
имеем
h,u)- X(t,u) = a(a,t)X(t,u)h + b(a,t) Aw(h,u),
= w(t + h,u) -w(t,u).
Поэтому
h)-E(t) = MUa(a,t)X(t,u>)h + b(a,t)Aw(h,u)) X
X (a(a,t) X(t,w)h + b(a,t) Aw(h,w))T +
+ X(t,u)(a(a,t)X(t,u;)h + b(a,
+ {a(a,t)X{t,u)h + b{a,t)Aw(h,u))XT(t,u;)\.
А так как Aw(h,u) не зависит от X(t,u) и M[Aw;(/i,w)] = О, то
Z(t) = a(a,t)M[X(t,u)XT(t,u)]aT(a,t)h2 +
+ b(a,t)M[Aw(h,u) (Aw{h,u))T]bT (a,t) +
и для получения окончательного результата достаточно раз-
разделить правую и левую части полученного равенства на h и
перейти к пределу при h -4 +0 с учетом того, что
M[Aw(h,u)(Aw(h,u)f] = hln, M[X(t,u)XT{t,u)] = Щ). >

244
7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
Пример 7.2. Пусть в стохастической задаче Коши G.8)
п = 2 и
В этом случае резольвенту R(t,r) можно найти в виде G.10):
/sh(t-r) ch(t-r)\
и, согласно G.13), математическое ожидание решения стоха-
стохастической задачи Коши G.8) определено равенством
t>0.
В рассматриваемом примере начальное состояние является
детерминированным, поэтому So = в 6 Мг(К) и задача Коши
G.15) для определения ковариационной матрицы T,(t) = (?,_,-(?))
с учетом ее симметричности может быть представлена в следу-
следующем виде:
Решение этой задачи Коши можно найти стандартными мето-
методами [VIII], П2, и оно имеет вид
sh{2t)
shBt)
Для завершения рассмотрения примера достаточно подставить
полученные результаты в правую часть G.14). #

7.2. Линейные стохастические дифференциальные уравнения 245
Из теорем 7.2, 7.3 можно сделать следующие выводы.
1. Так как решение X(t,oj), t G T = [0, оо), стохастической
задачи Коши G.8) является n-мерным нормальным марковским
процессом, то его одномерная функция плотности вероятно-
вероятностей является плотностью n-мерного нормального распределе-
распределения [XVI] и имеет следующий вид:
fix 11) = . l expf-i \x - m(t)]' fE(Ol ~* f* - m(
где a; — n-мерный вектор-столбец, математическое ожидание
m(t) определяют согласно G.13), а ковариационная матрица
?(?) является решением задачи Коши G.15).
2. Поскольку X(t,<j), t eT, — марковский процесс, то его
./V-мерная функция плотности вероятностей f(x^,x^,...,xiN\)
может быть представлена в следующем виде (см. 2.5):
f(X@), «A), • • •, Z(N)) = /(Z(o)) Y[ f(X(k) I *(fc-l)),
k=l
где условная функция плотности вероятностей
G.16)
является условной плотностью распределения n-мерного слу-
случайного вектора Х{рк,ш) при условии, что n-мерный случайный
вектор X(tk-i,u) принял некоторое фиксированное значение
Z(fc-i) € R", а Bп)-мерный случайный вектор
X(tk,u)
имеет нормальное распределение. При этом можно показать,
что условное математическое ожидание m(tk\tk~i) и ковари-
ковариационная матрица S(^Ufc-i) являются решениями следующих

246 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
задач Коши:
dm(t\tk..i)
_1), tk-\ < t < tk,
k-i \tk-i) — «(fc-i),
b{a,t)bT(a,t), tk-!<t^tk, GЛ8)
3. Условную функцию плотности вероятностей для нормаль-
нормального процесса можно получить и не прибегая к условным ма-
математическим ожиданиям и ковариационным матрицам. Дей-
Действительно, пусть 0 < 11 < ?2 < оо и X(ti,u), X{ti,ui) — два сече-
сечения п-мерного нормального марковского процесса X(t,u), t € Т,
являющегося решением стохастической задачи Коши G.8). Его
условная функция плотности вероятностей может быть пред-
представлена в виде
G.19)
где математическое ожидание m(t), ковариационная функция
K(t\,t2) и ковариационная матрица ?(?) случайного процесса
ХA,ш), t ?T, рпределены равенствами G.13), G.14) и G.15)
соответственно, а
- K{tut2)
Vi2 = [K(t2,h) - E(t2)
V21 = [K(tut2) - Eft
yl K{tut2)}-\

7.2. Линейные стохастические дифференциальные уравнения 247
Чтобы доказать равенство G.19), рассмотрим Bп)-мерный
случайный вектор у(ш), для которого
и который имеет Bп)-мерное нормальное распределение. В
этом случае его плотность распределения равна
Х1\) ^B)) 6 ^2"- При этом из условия T,V
получаем систему матричных уравнений
Выразив из второго уравнения Vjn = — [Efa)]'1 K(t2,ti)Vn и
подставив в первое уравнение, приходим к равенству
из которого и определяем матрицу Уц. Совершенно аналогично
находим матрицы V\2, V21, V22 и устанавливаем равенство
,-1

248
7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
Блочная матрица V = S г является симметрической, т.е. Vn =
= Vii, V22 = ^22) Vyz — ^2i) TaI< как симметрической является
ковариационная матрица S Bп)-мерного случайного вектора
7(w). Для вычисления определителя матрицы V используем ос-
основное свойство блочных матриц, согласно которому операции
над блочными матрицами выполняются по тем же правилам,
что и операции над числовыми матрицами [III]. Таким образом,
\z-1\ = \v\ =
Vu V12
v21 v22
V21
0
V22
А так как непосредственной проверкой можно убедиться в
справедливости равенств
(Y-m)TV(Y-m) =
= (x{1)-m{t1)\T /Vn V12\
\XB)-m(t2)) \V2i V22J
= [«B) ~ ™(Ы + V2'21Vi2(x{l
X У22 [x{2) - m{t2) + Vjj1 V21 (
x{2)-m(t2)
то плотность распределения Bп)-мерного случайного вектора
у(ш) можно представить в следующем виде:
x —
V22[x{2) - m(t2) + V2~21V2i(xA) -
1
[(^)]

7.2. Линейные стохастические дифференциальные уравнения 249
где множитель
есть не что иное, как плотность распределения случайного
вектора X(ti,u). Но тогда условная плотность распределе-
распределения в-мерного случайного вектора X(t2,w) при условии, что
в-мерный случайный вектор X(ti,u) принял некоторое фик-
фиксированное значение хщ ? R", действительно задается равен-
равенством G.19), так как
4. Если в стохастической задаче Коши G.8) a(a,t) = a,
b(a,t) = Ь при любых t ?Т, где a,b € Mn(R) — постоянные ма-
матрицы, причем действительные части всех собственных чисел
матрицы а отрицательны, то при больших значениях времени
t решение X(t,u), t € Т, можно считать стационарным (в ши-
широком смысле) нормальным марковским случайным процессом.
В самом деле, m(t) является решением задачи Коши для нор-
нормальной системы линейных обыкновенных дифференциальных
уравнений (ОДУ)
(m{t) = am(t),
\т@) — т0,
которая в силу отрицательности вещественных частей соб-
собственных чисел матрицы а является асимптотически устой-
устойчивой, т.е.
lim m(t) = 0.
t-ЮО V '
Поэтому для любого сколь угодно малого е > 0 существует
такое ?*, что для любых t ^ t* имеет место неравенство
\\m(t)\\<e,

250 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
т.е. можно считать, что m(t) т 0 для всех t ^ t*. Теперь
осталось показать, что при больших значениях fг, t2 ? Т, где
t\ <t2, имеет место приближенное равенство
Для упрощения дальнейших рассуждений ограничимся ска-
скалярным случаем стохастической задачи Коши G.8), в которой
a(a,t) = —d2, b(a,t) = b при любых t ? Т, где Ь и d — дей-
действительные числа, т.е. рассмотрим скалярную стохастическую
задачу Коши:
jdy(t,u) = -d2y(t,u)dt + bdw(t,u),
где u(t,u), t > 0, — скалярный винеровский процесс, выходящий
из 0 и имеющий коэффициент диффузии а2 — 1.
В сформулированной стохастической задаче Коши началь-
начальное условие является детерминированным, а резольвента R(t,r)
соответствующего обыкновенного дифференциального уравне-
уравнения u'(t) — —d2u(t) имеет следующий вид:
Согласно G.15), ковариационная матрица ?(?) — дисперсия
скалярного случайного процесса y(t,u), t > 0, — в данном
случае является решением задачи Коши
которое можно найти стандартными методами [VIII]:

7.2. Линейные стохастические дифференциальные уравнения 251
Чтобы показать, что при больших значениях t\, t% € T значение
ковариационной функции K(tl,t2) определяется в основном раз-
разностью t2 — ti, достаточно воспользоваться равенством G.14)
при t\ <t2- Действительно, в данном случае
^(
= ^(exp[-d2(t2-tl)]-exp[-d2(tl+t2)]')
что и требовалось доказать.
Замечание 7.1. Марковский процесс с течением времени
„забывает" свое исходное состояние. Покажем это в частном
случае. Пусть в стохастической задаче Коши G.8) a(a,t) — а,
b(a,t) = Ь при любых t ?Т, где а и Ь — постоянные квадрат-
квадратные матрицы порядка п, причем действительные части всех
собственных чисел матрицы а отрицательны. Выберем про-
произвольный момент времени s ? Т, обозначим его через tk-i
и зафиксируем значение случайного процесса X(t,u), t ? Т,
т.е. полагаем X(s,u) = x(s). При сделанных предположениях
из G.17) следует, что условное математическое ожидание удо-
удовлетворяет соотношению m(t\s) —»• rrioo = 0 при t —> oo. Кроме
того, можно показать, что ?(? | s) —t Т,^ при t —t oo, где матрица
?ос ? Мп(Щ удовлетворяет матричному уравнению
aSoo + SooaT + bbT = О
и, согласно теории матриц*, может быть представлена в следу-
следующем виде:
— /
*См.: Беллман Р.

252 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
Поэтому f{x(()\x(a))-^f{X(t)) при t-юо, где f{x{t)) — функ-
функция плотности вероятностей n-мерного случайного вектора,
распределенного по нормальному закону с нулевым математи-
математическим ожиданием и ковариационной матрицей Eoq.
Замечание 7.2. Если выполняются предположения из заме-
замечания 7.1, то ковариационную матрицу Е(?) можно представить
в виде
где u(t) — некоторая матричная функция. Эта функция, со-
согласно G.15), является решением задачи Коши
ju(t) = au(t) + u(t)aT,
Так как решение этой задачи известно:
u{t) = exp(ai) (Eo - Е*,) exp(aTi),
то ковариационная функция Е(?) имеет следующий вид:
E(t) = exp(ot) (Ео - Еоо) exp(aTi) + Ето.
В рассматриваемом случае математическое ожидание m(t) ре-
решения стохастической задачи Коши G.8) удовлетворяет нор-
нормальной системе обыкновенных дифференциальных уравнений
m(t) = am[t), резольвента которой (см. П2)
R{ti,t2) = exp(a(i2 - h)) = R{t2 - ti).
Поэтому, если в стохастической задаче Коши G.8) вектор на-
начального состояния Xq(u) обладает нулевым математическим
ожиданием и ковариационной матрицей Е0 = Еоо, то ее реше-
решением является стационарный (в широком смысле) случайный
процесс, что следует из G.13), G.14), тождества Е(?) = Е,» и
вида резольвенты

7.3. Стохастические интегралы и дифференциалы 253
Замечание 7.3. Пусть в стохастической задаче Коши G.8)
Xq(u) =.xq? R", a(a,t) = a a b(a, t) = b при любых t^O, где a и
6 — постоянные квадратные матрицы порядка п и действитель-
действительные части собственных чисел матрицы а отрицательны. Если
эту стохастическую задачу Коши интерпретировать как мате-
математическую модель линейной динамической системы с невозму-
невозмущенным начальным состоянием, на вход которой поступает бе-
белый шум, то ее реакцию можно рассматривать как стационар-
стационарный (в широком смысле) нормальный марковский случайный
процесс лишь при больших значениях текущего времени t, так
как в рассматриваемом случае So = в ф Soo (см. замечания 7.1
и 7.2). При больших значениях текущего времени в любой ди-
динамической системе, обладающей свойством асимптотической
устойчивости (решение соответствующей нормальной системы
обыкновенных дифференциальных уравнений является асимп-
асимптотически устойчивым), происходит фактическое затухание
переходных процессов. На этот факт мы уже обращали вни-
внимание, анализируя преобразование стационарного случайного
процесса при его прохождении через линейную динамическую
систему.
7.3. Стохастические интегралы и дифференциалы
Изучение нелинейных стохастических моделей состояния
вида G.7)
представляет собой сложную задачу, успех решения которой
в значительной степени зависит от конкретного вида правой
части матричного нелинейного стохастического дифференци-
дифференциального уравнения. Но общие принципы и особенности иссле-
исследования таких моделей можно установить. Именно этому и

254 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
посвящен данный параграф. Предполагается, что для любо-
любого фиксированного ш ?il соответствующая детерминированная
задача Коши удовлетворяет условиям теоремы существования и
единственности решения. Это означает, что матричные функ-
функции А(Х,а,i) и В(Х,а,t) удовлетворяют определенным услови-
условиям гладкости, а исходная математическая модель может быть
представлена в виде интегрального уравнения
t
X(t,u) = X0(u) + f А{Х(т,и),а,т)ёт +
о
t
+ IB{X(T,u),a,r)dw(T,u), t^O. G.20)
о
Первый интеграл в правой части уравнения G.20) пред-
представляет собой интеграл от случайной функции по времени,
а второй — интеграл от случайной функции по винеровскому
процессу. Понятие стохастического интеграла по винеровско-
винеровскому процессу и его свойства требуют обстоятельного изучения.
Изучение таких интегралов начнем с простого примера.
Пример 7.3. Пусть w(t,u), t?T—[0, со), — скалярный
винеровский процесс с коэффициентом диффузии а2 = 1. Рас-
Рассмотрим интеграл I(t,s) от винеровского процесса по этому же
винеровскому процессу:
t
I(t,s)=
oo.
Отметим сразу, что если w(t,u) = w(t) — непрерывно диффе-
дифференцируемая неслучайная функция, то
I(t,s)=l-(w2(t)-w2(s)).

7.3. Стохастические интегралы и дифференциалы 255
Для любых t, s 6 Т, t > s, интеграл I(t,s) определяют сле-
следующим образом. Пусть у € [О, 1] — параметр, At = (t — s)/N,
tkAs+(k- 1)At, fc = l,iV+l. Тогда
7(t,s) 4 jim
~* fc=i
X [w;(tA+i,w)-w;(tA,w)] = lim ( - V [w2{tk+i,u) - w2{tk,u)]
N
+ (t " г) S [
fc=l
1
+ G ~ 2) i
А так как u>(?,u>), t?T, — винеровский процесс, то w(tk+i,w) —
— w{tk,u), k = I, N, — независимые случайные величины, рас-
распределенные по нормальному закону с нулевым математиче-
математическим ожиданием и дисперсией, равной At. Таким образом,
случайная величина
/ \ д {w(tk+i,u) — w(tk,w)\
e(u) = I —* j=—i 1
распределена по закону х2 с одной степенью свободы и, значит
[XVII],
М[е(и)]=1, D[e(w)] = 2.
Поэтому
M[(w(tk+i,u) - w(tk,u)J] =B[w(tk+i,u) - w(tk,u)] = At,
T>[(w{tk+l,u)-w(tk,u)J] =
= M[{(w(tk+1,u) - w{tk,u)J - AtJ] = 2(AtJ.

256 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
Введем случайные величины
щ{и) A [w{tk+i,u) - w(tk,u)Y- At, k = \,N.
Они являются независимыми как функции от независимых
случайных величин и
Но тогда
*к+1,ы) ~ w{tk,u)]2= Yi
k=l k=l
N
— lim (NAt)+ lim У)щ(и) = t- s,
так как NAt = t- s,
N N
k=i
]
при At —> 0, а любая случайная величина с нулевым матема-
математическим ожиданием и нулевой дисперсией есть нуль. Таким
образом,
I{t,s) = I^{t,s) = 0,5[w2(t,u) - w2(s,u)} - G - 0,5)(t - s),
и мы имеем однопараметрическое семейство интегралов с па-
параметром 7 € [0, 1].
Замечание 7.4. В практике научных исследований исполь-
используют два типа стохастических интегралов из множества 7^(^,s):
I0{t,s) = 0,5(w2(t,u) - w2(s,u)) - 0,5(t - s),
IOjs(t,s) = 0,5(w2(t,u) - w2(s,u)).

7.3. Стохастические интегралы и дифференциалы 257
Интеграл Io,b{t,s) внешне совпадает с интегралом от неслучай-
неслучайной функции w(t). На первый взгляд, следовало бы именно его
использовать при анализе стохастических моделей состояния.
Но далее убедимся, что интеграл /o(?,s) имеет ряд преимуществ
при решении задач о нахождении математического ожидания
случайного процесса.
Рассмотрим интеграл по случайному процессу от неслучай-
неслучайной функции:
t
= Jip(r)dv(r,u),
где (p(t), t GT, — непрерывная неслучайная скалярная функция,
a v(t,u), t ? Т, — дифференцируемый скалярный случайный
процесс с ортогональными приращениями, причем для любых
t
mv(t)AM[v(t,u)}=mv{s)+fm'v{T)dT,
s
t
Dv(t) = M[(v(t,u) - mv(t)J] = Dv(s) + fD'v(T)dr.
Определение 7.2. Стохастическим интегралом от
неслучайной скалярной функции <p(t), t ? Т, по дифферен-
дифференцируемому скалярному случайному процессу со стационар-
стационарными независимыми приращениями v(t,u), t ? Т, в пределах от
s ? Т до t ? Т называют случайную величину
t
I(t,s)±J<p(T)dv(T,u),

258 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
определяемую равенством
N
I(t,s) = Jim S2<p(tk)[v(tk+1,w) - v(tk,u)],
N —foo
k-1
t, k=l,N+l, At=(t-s)/N.
Покажем, что при сделанных предположениях относительно
неслучайной функции <p(t) и случайного процесса v(t,u>), t G T,
t
<р(т) тпу[т) ат, {'-^l)
s
t
<p2(T)D'v(r)dT. G.22)
Действительно, согласно определению 7.2, из свойств ска-
скалярного случайного процесса v(t,u), t 6 Т, следует, что
N
М[/(М)]= H
N
lim
N-юо
где в соответствии с принятыми допущениями использовано
свойство дифференцируемости функции. Таким образом, ра-
равенство G.21) доказано.
Для доказательства равенства G.22) рассмотрим центриро-
центрированный случайный процесс

7.3. Стохастические интегралы и дифференциалы 259
и напомним (см. пример 2.3), что для случайного процесса с
ортогональными приращениями
cov[v(t,u>) - v(s,u);v(t,u>) - v(s,u)] = Dv(t) - Dv(s).
С учетом этого рассмотрим разность
N
,s)} = lim J2<p{tk) [v(tk+1,u) - v{thu)] -
N
^<p{tk)[mv(tk+i,w) - mv(tk,u>)] -
N
Таким образом,
N N
k=\ j=l
N
,,u))] = Jim
= Yim ^2<p2(tk) [D'v(tk)At + o(At)] = / v2(t)D'v(r)dr,
где в соответствии с принятыми допущениями использовано
определение дифференцируемости функции. Таким образом,
равенство G.22) также доказано полностью.

260 7 СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
Теперь перейдем к рассмотрению важного случая, когда
подынтегральная функция зависит от винеровского процесса.
Определение 7.3. Пусть w(t,u), t ? Т = [0, оо) — в-мер-
ный винеровский процесс, выходящий из 0, и 4>(w(t,u);t) —
матричная функция типа п х п, определенная для всех t ? Т.
Если для любых s,t ?Т, таких, что s > t, и для любого у ? [0, 1]
существует предел
lirn У'
N -к» ^—'
х (w(tk+uu)-w(tk,u)),
где At = (t — s)/N, tk = s+(k — 1)At, k = 1, iV+1, то его называ-
называют стохастическим интегралом функции Ф по винеров-
винеровскому процессу w(t,и), t ? Т, и обозначают I^(t,s). При этом,
если 7 — 0, то его называют стохастическим интегра-
интегралом Ито, а при у = 0,5 — стохастическим интегралом
Стратоновича.
Замечание 7.5. Прежде, чем приступать к изучению
свойств стохастического интеграла по винеровскому процессу,
отметим три важных момента, относящихся к дальнейшим
рассуждениям.
Во-первых, будем далее предполагать, что матричная функ-
функция Ф(а:,?) удовлетворяет определенным условиям гладкости, в
частности, имеет непрерывные первые и вторые частные про-
производные по х для всех t.
Во-вторых, чтобы избежать недоразумений и не путать
стохастические интегралы Ито и Стратоновича, интеграл Ито
будем записывать как и выше:

7 3 Стохастические интегралы и дифференциалы 261
а в интеграле Стратоновича будем ставить „звездочку" при
дифференциале:
t
/o,s(M) = [
В-третьих, для упрощения выкладок при доказательстве
свойств стохастических интегралов Ито и Стратоновича, будем
рассматривать случай скалярной функции Ф(я;?) и скалярного
винеровского процесса. Обобщение результатов на случай ма-
матричной функции Ф(я;?) и векторного винеровского процесса
связано лишь с техническими трудностями.
Теорема 7.4. Интеграл Ито Io(t,s) имеет нулевое матема-
математическое ожидание и
w(T,u);T)]dT. G.23)
По определению интеграла Ито имеем
k=\
N
^ЩУЫ^,и)^к)]М^Aк+1,и) - w(tk,u)] =0,
так как математическое ожидание винеровского процесса рав-
равно нулю и для любых т\,Т2 ? Т, п < Т2, случайные величины
u>(ri,u>) и w(t2,u) — w(ti,u) независимы.
Равенство G.23) можно доказать аналогично. Следует лишь
учесть, что в соответствии с определением 2.6 винеровского
процесса с коэффициентом диффузии <т2 = 1 при t > s (?, s ? Т)
M[(w(t,u) - w(s,u)J] =t-s.

262 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
Действительно,
N
N N
fc=l .7=1
X (u;(
N
N «
= Jimo^M[*2(u;(ifc,a;);ifc)]Ai= / М[ф2(ш(г,а;);г)] rfr. >
fc=i e
Для того чтобы определить математическое ожидание и
дисперсию для интеграла Стратоновича, установим связь меж-
между I0{t,s) И /0,5 (*,»)•
Теорема 7.5. Интегралы Ито и Стратоновича связаны
следующим равенством:
dr. G.24)
x=w(t,w)
По определению 7.3 интеграла Стратоновича имеем
ад*,.) = j
fc=i
x(w(tk+i,u>)-w{tk,u>)). G.25)

7.3. Стохастические интегралы и дифференциалы
263
Используя формулу Тейлора в окрестности точки (w(tk,u);tk)
и ограничиваясь линейными членами, получаем
) + w{tk,u) tk+1+tk
+
где приближенное равенство понимают в смысле среднего ква-
квадратичного 3.1. Подставляя это выражение в правую часть
G.25), находим
N
Io,s(t,s) = h
w(tk+1,u) - w(tk,u>))
+
_ x=w(tk,u)
Первое слагаемое в правой части этого равенства по опреде-
определению 7.3 является интегралом Ито. Второе слагаемое тожде-
тождественно равно нулю, так как элементы суммы в смысле среднего
квадратичного имеют порядок (AtI'5. Действительно (см. при-
пример 7.3, также 3.1),
M[(w(tk+Uu) - w(tk,u)J] = At,
\\At(w(tk+1,u)-w(tk,u))\\CK-At\\w{tk+uu)-w(tk,u)\\CK-=
= Aty/M[(w{tk+1,u) - w(tk,u)J] = (AtI'5.

264
7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
Можно также показать, что третье слагаемое равно
дЩх,т)
х=ш(т,ш)
s
и доказательство завершено. >
Из теорем 7.4, 7.5 следуют равенства
dr
M[/O2,5(t,s)] =
. G.27)
Если Ф(ж,^) — матричная функция типапх п, a w(t,u), t?T,
n-мерный винеровский процесс, то
dr, G.28)
OXj x=w(t,uj)
где ^j(x,t) — j-й столбец матричной функции Ф(я,?);
M[/0(t,s)] = O, G.29)
t
M[Io{t,s)Io(t,s)]= f
. G.30)
Эти результаты, равно как и выражения для математического
ожидания и ковариационной функции для интеграла Страто-

7.3. Стохастические интегралы и дифференциалы 265
новича, можно получить*, используя технику доказательства
теорем 7.4, 7.5.
Теперь вернемся к исходной нелинейной стохастической мо-
модели состояния G.7) в интегральном представлении G.20). Воз-
Возникает естественный вопрос: какой стохастический интеграл
по винеровскому процессу записан в правой части этого урав-
уравнения — Ито или Стратоновича?
Можно показать**, что в интегральном представлении G.20)
исходной стохастической модели состояния G.7), полученной
как результат введения процесса случайных возмущений в де-
детерминированную модель, стохастический интеграл по вине-
винеровскому процессу представляет собой интеграл Стратонови-
Стратоновича. Таким образом, в соответствии с замечанием 7.5 исходная
нелинейная стохастическая модель состояния в интегральном
представлении имеет следующий вид:
t
ХЦ,ш) = Х0{и)+ jA(X(T,u),a,T)dr +
о
t
+ IB(X(T,u),a,r)d*w{T,u), t^O. G.31)
о
Ее называют стохастической моделью состояния в фор-
форме Стратоновича. При этом, чтобы подчеркнуть, что
именно она соответствует рассматриваемой стохастической
модели состояния G.7), при записи последней вместо dw(t,u)
пишут d*w(t,u). Соответственно и исходную стохастическую
модель состояния представляют в виде
B(X{t,u),a,t)d.w{t,u), t>0, G.32)
*См.: Пугачев B.C., Синицын И.Н.
"См. там же.

266 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
Если в-мерный случайный процесс X(t,u), t ^ О, задан сто-
стохастической моделью состояния G.32) или стохастической мо-
моделью состояния в форме Стратоновича G.31), то он зависит
от винеровского процесса w(t,u>), t^ 0. Поэтому в рассуждени-
рассуждениях случайный процесс X(t,u), t ^ 0, более удобно и корректно
обозначать как X(t,w(t,u)), t ^ 0. Используя это обозначе-
обозначение и равенство G.28), связывающее интеграл Стратоновича
с интегралом Ито, можно показать, что стохастическая модель
состояния в форме Стратоновича G.31) может быть преобра-
преобразована к следующему виду:
t
X(t,u) = X0{u)+f(A{X(T,u),a,T)
ди
t
B{X(T,u),a,r)dw(T,u), t^O, G.33)
о
где bk(X(t,u),a,t) представляет собой к-й столбец матричной
функции B(X(t,u),a,t). Интегральное представление G.33)
исходной стохастической модели состояния G.32) называют
стохастической моделью состояния в форме Ито.
Определение 7.4. Пусть случайный процесс X(t,u), t ?
? Т = [0,оо), удовлетворяет уравнению G.31). В этом случае
выражение
называют стохастическим дифференциалом случайного
процесса X(t,u), t ? Т, в форме Стратоновича.

7.3. Стохастические интегралы и дифференциалы 267
Стохастический дифференциал в форме Ито для
исходной стохастической модели состояния имеет вид
4^
+ B(X(r,u),a,t)dw(t,u), G.34)
что следует из G.33).
Обратим внимание на то, что в случае B(X(t,Lj),a,t) =
= B(a,t), t ?T, вид соответствующих представлений исходной
стохастической модели состояния в форме Ито и Стратоновича
G.34) и G.32), G.33) и G.31) совпадает с точностью до обозна-
обозначений соответствующих интегралов.
В этой книге даны лишь минимальные сведения из диффе-
дифференциального исчисления Ито и Стратоновича, необходимые
для усвоения основного материала. Более полную информацию
по этому вопросу можно получить из специальной литературы3.
Отметим, что основные правила дифференциального и инте-
интегрального исчислений Стратоновича аналогичны обычным пра-
правилам дифференцирования и интегрирования функций одного
и многих переменных [II], [V], [VI], [VII]. Сказанное не от-
относится к дифференциальному и интегральному исчислениям
Ито.
Пример 7.4, Рассмотрим скалярную стохастическую мо-
модель состояния в форме Ито:
(dx(t,u) - a(x(t,u),t) dt + b(x(t,u),t) dw(t,u),
3Cm., например: Евланов Л.Г., Константинов В.М., а также Пугачев
B.C., Синицын И.И.

268 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
и найдем дифференциал скалярной функции y(x(t,u>),t), пред-
предполагая, что она удовлетворяет необходимым условиям гладко-
гладкости.
Воспользовавшись разложением в ряд Тейлора и ограничив-
ограничившись в нем членами второго порядка, получаем
Поскольку в смысле среднего квадратичного элементы в правой
части равенства, заключенные в квадратные скобки, имеют по-
порядки малости O(dt2), O(dt1>5), O(dt1<5) соответственно, то при
дальнейшем анализе ими можно пренебречь. Таким образом, с
учетом исходной стохастической модели состояния имеем
2a(x,t)b(x,t)dtdw(t,u)
с=хA,ш)
В правой части этого равенства во второй квадратной скобке
лишь третье слагаемое имеет порядок малости O(dt), поскольку
M[(dw(t,uJ] =D[dw(t,u)] =dt.

7.3. Стохастические интегралы и дифференциалы 269
Таким образом,
dy(x{t,u),t) =
. # G.35)
х=хA,ш)
Равенство G.35) известно как правило дифференцирова-
дифференцирования Ито. В общем случае, когда x(t,w), t G T, — n-мерный
Т
случайный процесс, a(x,t) = (aj(x,i) ... an(x,t)) —n-мерная
векторная функция, а b(x,t) = (b{j(x,t)) — матричная функция
типа п х п, правило дифференцирования Ито имеет вид
T
)
где х = (xi ... хп) , a (b(x,t)dw(t,u}))^ — i-й элемент вектора
b(x,t)dw(t,u).
Отметим, что в обычном дифференциальном исчислении, в
отличие от дифференциального исчисления Ито,
p-(dxJ\ _ =O(dt2).
Пример 7.5. Рассмотрим скалярную стохастическую мо-
модель состояния

270 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
где ?(t,u), t G T = [0,оо), — белый шум с нулевым математиче-
математическим ожиданием и спектральной интенсивностью Ь2, а А > 0 —
параметр.
Представив процесс случайных возмущений как производ-
производную от винеровского процесса, запишем исходную стохастиче-
стохастическую модель состояния в форме Стратоновича G.32):
{dx(t,u) = — \x(t,w) + bx(t,u)d*w(ttu),
х{0,и)=1
с последующим переходом к форме Ито G.34):
(dx(t,u) = @,5b2 - \)x(t,u) dt + bx(t,u) dw(t,u),
z@,u>) = l.
GЛв)
Применив к стохастической задаче Коши G.36) оператор ма-
математического ожидания с учетом того, что m(t) = M[a;(t,w)],
получаем
Гт(г) = @,5Ь2-Л)т(г),
\m@) = l.
Таким образом, математическое ожидание состояния равно
, t?T.
Для нахождения дисперсии D(t) состояния введем функцию
y{x{t,u)tt) = x{ttu)-m{t), t?T.
Тогда
dy(x(t,u),t) = dx(t,u) - dm(t) -
= @,5Ь2 - A) y(x(t,u),t) + bx{t,u) dw(t,u),
= M[y2(x(t,u),t)], M[y(x(t,u),t)}=0.

7.3. Стохастические интегралы и дифференциалы 271
По правилу дифференцирования Ито G.35) находим
Jy2(x(t,u),t) = [(Ь2 - 2А)y2(x(t,u),t) + b2x2(t,u)] dt +
+ 2by{x(t,u),t)x{t,u)dw(t,u).
А так как
M[x2(t,u)]=D(t)-m2(t),
то приходим к задаче Коши для D(t):
решив которую, находим
Для определения типа закона распределения случайного
процесса x(t,u), t G Т, введем функцию
z{x(t,u),t)Mnx(t,u), teT,
и воспользуемся правилом дифференцирования Ито G.35). По-
После преобразований получаем
dlnx(t,u) = -Xdt + bdw(t,u), t>0. G.37)
А так как уравнение G.37) является линейным относительно
функции lnx(t,u), то этот случайный процесс имеет нормаль-
нормальное распределение, а случайный процесс x(t,u), t G T, — лога-
логарифмически нормальное распределение.
Отметим, что уравнение G.37) непосредственно вытекает
из исходной математической модели, представленной в форме
Стратоновича. Но при использовании дифференциала Страто-
новича нам не удалось бы так просто получить уравнения для
определения математического ожидания и дисперсии случайно-
случайного процесса x(t,u), t G Т. #

272 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
В заключение отметим следующие моменты.
1. Совершенно очевидно, что в общем случае установить
даже одномерный закон распределения случайного процесса
X(t,u), t ? Т, удовлетворяющего нелинейной стохастической
задаче Коши G.7), не так-то просто.
2. Практически полностью повторив доказательство тео-
теоремы 7.2 для нелинейной стохастической задачи Коши G.7) в
предположении, что для каждого фиксированного wEfi вы-
выполнены условия теоремы существования и единственности ее
решения, приходим к выводу, что случайный процесс X(t,u>),
t ? Т, является n-мерным марковским процессом. Поэтому
дальнейшая перспектива в изучении нелинейных стохастиче-
стохастических моделей состояния связана с изучением специфических
свойств марковских процессов, чему и посвящена следующая
глава.
Вопросы и задачи
7.1. Сформулируйте основной принцип построения матема-
математической модели G.1).
7.2. Чем обусловлена необходимость введения случайных
возмущений в математическую модель состояния G.1)?
7.3. Сформулируйте и обоснуйте основные свойства про-
процесса случайных возмущений.
7.4. Случайный процесс ЛТ(?,и>), ? ? Т = [0, оо), задан ли-
линейной стохастической моделью состояния при стандартных
допущениях. Какими свойствами обладает этот случайный
процесс?
7.5. Почему решение стохастической задачи Коши G.8)
может быть представлено в виде G.9)?
7.6. В каких случаях решение линейной стохастической
задачи Коши G.8):
а) можно считать стационарным (в широком смысле) нор-
нормальным марковским случайным процессом;

Вопросы и задачи 273
б) является стационарным (в широком смысле) нормальным
марковским случайным процессом?
7.7. Докажите равенства G.26)-G.30).
7.8. Докажите правило дифференцирования Ито для общего
случая.
Указание: см. пример 7.4 и комментарии к этому при-
примеру.
7.9. Докажите, что решение нелинейной стохастической
задачи Коши G.7) является марковским процессом.
Указание: предполагая, что для каждого фиксирован-
фиксированного uGfi выполнены условия теоремы существования и един-
единственности решения задачи Коши G.7), воспользуйтесь логикой
доказательства теоремы 7.2.
7.10. Пусть в стохастической задаче Коши G.8) в = 2,
b(a,t) = I2,
Определите ковариационную матрицу и математическое ожи-
ожидание ее решения.
Ответ:
"*>
=(_!)«-". -~=h(l i)
Указание: воспользуйтесь замечанием 7.5.

274
7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
7.11. Пусть в стохастической задаче Коши G.8) п = 2,
о = бB? I)"
Определите математическое ожидание, ковариационную мат-
матрицу и ковариационную функцию ее решения.
Ответ:
Г 1/30 б\ (,_
-8 1\-з(«-.)
6 1,-8 je '
7.12. Пусть скалярный случайный процесс x(t,u), t G T =
= [0, оо), является решением стохастической задачи Коши
f dx(t,w) = \x(t,u)dt + bdw(t,u),
\х@,и) = 0,
где А и b — неслучайные параметры. Можно ли этот процесс
по прошествии некоторого времени считать стационарным (в
широком смысле)?
Если процесс x(t,u), t ? Г, можно считать стационарным (в
широком смысле), то чему равна его спектральная плотность?
Ответ: можно при всех А < 0. В этом случае

Вопросы и задачи 275
7-13. Найдите математическое ожидание и дисперсию сто-
стохастического интеграла
оо
1(ы)= f e-atdw(t,u)
о
по винеровскому процессу с <т2 = 1, где a — положительный
неслучайный параметр.
Ответ: M[/(w)] = 0, D[/(w)] = 1/2а.
7.14. Найдите математическое ожидание и дисперсию ин-
интеграла Ито
/o(t,0)= I e-aw^
Ответ: M[/o(t,0)] = 0, D[/o(t,0)]= [expBa2t) - l]/Ba2).
7.15. Найдите дисперсию стохастического интеграла Ито
t
/o(t,0)= fx{T,u)dw(r,u),
о
где x(t,u), t G T1 = [0,oo) — скалярный случайный процесс;
mx(t)=-ct; Kx(t,s) = exp[a(t + s) -/3\t - s\]; c, a, /3 — неслу-
неслучайные параметры.
^ „rr , ,, сЧ3
Ответ: D[/o(t,0)]= — +
7.16. Докажите равенство
(
,с))" dr = I ((tP(^I)W+1 - / Иг,a,))" ^(r,a,)).
о о
7.17. Докажите, что случайный процесс x(t,u>) = [^(^w)]"
t gT, имеет стохастический дифференциал в форме Ито:
) = a;3(i,w)di - x2(t,u)dw(t,u).

276 7. СТОХАСТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ
7.18. Докажите, что стохастическое дифференциальное
уравнение
dx(t,u) = 0,25dt + y/x(t,u)dw(t,u)
имеет решение
удовлетворяющее начальному условию х@,и) = 1.
7.19. Докажите, что стохастическая задача Коши
' dx(t,u) = —0,5x(t,и) + y(t,u>) dw(t,u),
dy(t,u) = -0,5y(t,w) - x(t,u) dw(t,u),
имеет решение
x(t,u) =sm(w(t,u>)), y(t,u) = cos(w(t,w)).
7.20. Пусть случайный процесс x(t,u), t?T, удовлетворяет
стохастическому дифференциальному уравнению
dx(t,u) = -Xx(t,u) dt + bx(t,u) dw(t,u), t € T.
Докажите, что его условная функция плотности вероятностей
равна
где Л и Ь — неслучайные параметры.

8. МАРКОВСКИЕ ПРОЦЕССЫ С
НЕПРЕРЫВНЫМИ СОСТОЯНИЯМИ
В соответствии с определением 2.6 марковского процесса и
результатами исследований стохастических моделей состоя-
состояния, в основе понятия марковского процесса лежит представле-
представление об эволюционирующей во времени системе 5, обладающей
свойством отсутствия последействия — отсутствием „памяти".
Иными словами, для марковского процесса будущее состояние
определяется настоящим и не зависит от прошлого.
Пример 8.1. Пусть 5 — техническая система, которая уже
эксплуатировалась определенное время и пришла в некоторое
состояние, характеризуемое определенной степенью изношен-
изношенности. Нас интересует, как она будет работать в будущем.
Ясно, что по крайней мере в первом приближении характе-
характеристики функционирования системы S в будущем зависят от
состояния этой системы в настоящий момент и не зависят от
того, когда и как она достигла своего настоящего состояния.
При этом, если учесть результаты исследований стохастиче-
стохастических моделей состояния, то становится понятным, что состоя-
состояние изучаемой системы должно являться марковским процессом
и, вообще говоря, удовлетворять некоторой стохастической
модели состояния в форме Ито
U) = 6>(w). #
Характерной особенностью марковских процессов является
возможность выражения любых конечномерных законов рас-
распределения через двумерные законы распределения (см. 2.5).
В данной главе мы рассмотрим .марковские процессы с
непрерывными состояниями, в которых сечения являются
n-мерными непрерывными случайными векторами.

278 8. МАРКОВСКИЕ ПРОЦЕССЫ
8.1. Общие свойства марковских процессов
Пусть ?(?,u>), t G Т = [а,Ь], — n-мерный марковский процесс
с непрерывными состояниями и t,r G T, t < г, — два фикси-
фиксированных момента времени. Введем обозначения для одномер-
одномерных, двумерных и условных функций плотности вероятностей
случайного процесса:
Л 00 = /<№)> f81)
f(t,X,r,Y)±f<:(Y\X),
где X € К", У € К". Если случайный процесс ?(t,w), t € Т,
является скалярным (п = 1), то вместо ЛГ и Y используют
обозначения хну соответственно. Напомним (см. 2.5), что
любая конечномерная функция плотности вероятностей мар-
марковского процесса ?(?,u>), t ? Т, может быть выражена че-
через его двумерную функцию плотности вероятностей /2(ЛГ,У).
Отметим, что условную функцию плотности вероятностей
Д(У|ЛГ) =/г(ЛГ,У)//х(ЛГ) в теории марковских процессов рас-
рассматривают как функцию четырех аргументов t, X, т, У, что
и отражено в обозначениях (8.1). Условная функция плотно-
плотности вероятностей любого случайного процесса представляет
собой условную плотность распределения одного из его сече-
сечений при условии, что другое его сечение приняло некоторое
фиксированное значение. Поэтому, исходя из свойств услов-
условной плотности распределения и определения J-функции Дирака
[XII], можно показать, что условная функция плотности веро-
вероятностей f(t,X,T,Y) имеет следующие свойства:
f(t,X,r,Y) > 0, f(t,X,r,Y)\t=T = 8(Х - Y),
Jf(t,X,r,Y)dY = l, f2(X,Y) = f(t,Xr,Y)f1(X),
= ff(t,X,r,Y)MX)dX.
R»

8.1. Общие свойства марковских процессов 279
Теорема 8.1. Если ?(t,u), t € Т1 = [а, Ь], — n-мерный мар-
марковский процесс и t, т € Т (t < т) — любые два фиксированных
момента времени, то для любого значения t' G {t,r) имеет место
равенство
f(t,X,r,Y) = Jf(t,X,t',Z)f(t',Z,r,Y)dZ. (8.2)
М Для упрощения и наглядности проводимых рассуждений
ограничимся скалярным случаем, т.е. полагаем п = 1. Пусть
t,t',r ?T, t <t' < г — любые три фиксированных момента вре-
времени и /2B;, у) — двумерная функция плотности вероятностей
изучаемого случайного процесса ?(?, u>), t 6 Т, соответствующая
моментам времени t и г, а /з(ж,-г,у) — его трехмерная функция
плотности вероятностей, соответствующая моментам времени
t, t', т. При этом
оо
= J f3{x,z,y)dz. (8.3)
А так как случайный процесс ?{t,u), t € 71, является марков-
марковским, то
и равенство (8.3) преобразуется к следующему:
оо
= f
Для завершения доказательства достаточно перейти к обозна-
обозначениям (8.1). >
Равенство (8.2) известно как уравнение Маркова —
Смолуховского — Чепмена — Колмогорова. В конце
XIX в. русский математик А.А. Марков получил аналог урав-
уравнения (8.2) для марковских процессов с дискретным временем
(цепи Маркова), польский физик-теоретик М.Ф. Смолуховский

280 8. МАРКОВСКИЕ ПРОЦЕССЫ
в начале XX в. использовал уравнение (8.2) при изучении бро-
броуновского движения, английский геофизик С. Чепмен в 30-х гг.
XX в. использовал уравнение (8.2) для решения кинетического
уравнения Больцмана, а русский математик А.Н. Колмогоров
в 40-х гг. XX в. разработал общую аналитическую теорию мар-
марковских процессов.
8.2. Уравнения Колмогорова
Основная особенность марковских процессов связана с тем,
что их условные функции плотности вероятностей f(t,X,T,Y)
удовлетворяют дифференциальным уравнениям в частных про-
производных параболического типа. Это не только существенно
упрощает процедуру нахождения f(t,X,r,У), но и позволяет
найти решения многих задач прикладного характера.
Условная функция плотности вероятностей f(t, X, г, У) п-мер-
ного марковского процесса ?(?, u>), t?T = [a,b], с непрерывными
состояниями, рассматриваемая как функция параметров на-
начального состояния t ? Т и X = (xi ... хп) , удовлетворяет
уравнению
в котором векторная функция векторного аргумента
:HmM€(r'w) *№Ш>Ы)-Х (8.5)
.ая(дг,о;
характеризует скорость изменения значений исходного случай-
случайного процесса. Матричная функция векторного аргумента
= hm — , (8.6)

8.2. Уравнения Колмогорова 281
принимающая значения в множестве Mn(R),характеризует ско-
скорость изменения условной дисперсии этого случайного процес-
процесса. В литературе a(X,t) и b(X,t) часто называют вектором
сноса и матрицей диффузии соответственно. Из неотри-
неотрицательной определенности любой ковариационной матрицы и
тождества (8.6) следует неотрицательная неопределенность ма-
матрицы диффузии.
Условная функция плотности вероятностей f(t,X,r,Y), рас-
рассматриваемая как функция параметров конечного состояния
Т
т € Т и У = (j/i ... уп) , удовлетворяет уравнению
-kttjS^i^Or.r)/)^ (8.7)
Уравнения (8.4) и (8.7) называют первым и вторым
уравнениями Колмогорова соответственно. Уравнение (8.7)
называют также уравнением Колмогорова — Фоккера —
Планка, поскольку оно встречалось в работах М.К. Планка,
А.Д. Фоккера и других физиков еще до того, как его обосновал
А.Н. Колмогоров.
Вывод уравнений Колмогорова (8.4), (8.7), приведенный ни-
ниже, весьма схематичен и реализован для скалярного марковско-
марковского процесса (в = 1) при излишне жестких ограничениях. Но он
позволяет уяснить как содержательный смысл самих уравне-
уравнений, так и входящих в них параметров.
Вывод первого уравнения Колмогорова. Пусть ?(t,u>),
t?T= [a,b], — скалярный марковский случайный процесс и
f(t,x,T,y) — его условная функция плотности вероятностей. В
уравнении Маркова — Смолуховского — Чепмена — Колмо-
Колмогорова (8.2) при п — 1 полагаем t' = t + Д, где 0 < Д < г -t, и

282 8. МАРКОВСКИЕ ПРОЦЕССЫ
записываем его в следующем виде:
оо
= J f(t,x,t + A,z)f(t + A,z,r,y)dz. (8.8)
Предположим, что условная функция плотности вероятно-
вероятностей f(t + A,z,t,у), как функция скалярного аргумента 2, в
окрестности точки z = х может быть разложена по формуле
Тейлора:
A,x,r,y) ld2f(t + A,x,r,y) 2
Эх [Z ) + 2 Эх* ( Х}
(
где |е| ^ 1. Тогда, согласно (8.8), получим
f(t,x,t + A,z)dz +
j
—оо
оо
A,s,r,2/)
дх
—оо
f (z-x)f(t,x,t + A,

8.2. Уравнения Колмогорова 283
Учитывая, что в силу свойств условной функции плотности
вероятностей f(t,x,T,y)
оо
/
A,z)dz=l,
переносим первое слагаемое в правой части (8.9) в левую часть,
делим обе части полученного равенства на А и переходим к
пределу при А —>¦ +0. Этот предельный переход возможен, если
существует предел
lim (j- f
Эх3
x{z-xKf(t,x,t + A,z)dz)=O. (8.10)
В результате получаем первое уравнение Колмогорова (8.4) при
п= 1, в котором функции a(x,t) и b(x,t) заданы соотношениями
(8.5) и (8.6) соответственно.
Предположение (8.10) в сущности означает, что вероят-
вероятность больших отклонений |?(?',u>) — ?(?,u>)| снижается при
уменьшении А = t' — t, причем все моменты случайной величины
\?(t',w) — ?(t,(jj)\, начиная с третьего, имеют порядок малости
о(А).
В предельном переходе к уравнению (8.4) для функций a(x,t)
и b(x,t) получаем соотношения
оо
а(г,0 = д1ш1од / (z-x)f{t,x,t + A,z)dz,
— оо
оо
b(x,t) = Jim+^ J {z-xJf(t,x,t + A,z)dz,
которые эквивалентны представлениям (8.5), (8.6), если в них
положить т = t + A.

284 8. МАРКОВСКИЕ ПРОЦЕССЫ
Вывод второго уравнения Колмогорова. Второе урав-
уравнение Колмогорова (8.7) является сопряженным* по отношению
к первому уравнению Колмогорова (8.4). Поэтому его вывод
осуществляется несколько более искусственным способом, чем
вывод (8.4).
Пусть аи/? — границы интервала изменения значений ска-
скалярного марковского процесса ?(t,u), t ? Т = [а, Ь], с условной
функцией плотности вероятностей f(t,x,r,y), a R(y) — любая
дважды непрерывно дифференцируемая на этом интервале не-
неслучайная функция, удовлетворяющая условиям
Я(а) = Д'(а) = R(/3) = R'(/3) = 0. (8.11)
Тогда
0
^.'Г'У R(y)dy =
= AlimQ^ J{f(t,x,r + А,у) - f(t,x,r,y)) R(y)dy, (8.12)
I
так как в правой части равенства возможен предельный пере-
переход под знаком интеграла [VII]. Согласно уравнению Марко-
Маркова — Смолуховского — Чепмена — Колмогорова (8.2),
0
/(*,*, г+ Д,у)= f(t,x,T,z)f(T,
а
Поэтому
0 0 0
t,x,T + A,y)R(y)dy=JJf(t,x,T,z)f{T,z, )
а а а
Если в двойном интеграле справа изменить обозначения пе-
переменных интегрирования, заменив z на у и у на z, то с его
•См.: Марчук Г.И.

8.2. Уравнения Колмогорова 285
помощью равенство (8.12) приводится к следующему:
0
A,z)R(z)dz-R(y)\dy\. (8.13)
Согласно принятому допущению, функция R{z) дважды
непрерывно дифференцируема на интервале интегрирования.
Поэтому ее можно представить в виде
С учетом обозначений (8.5), (8.6) и в силу принятого допуще-
допущения (8.10) о вероятности больших отклонений
получим
+ l-R"(y)(z-yJ + o(\z-y\2))dz-
1
2
Подставив этот результат в (8.13), приходим к равенству
0
0
f df(t,x,r,y) р,
j —^i R{y)dy =

286 8. МАРКОВСКИЕ ПРОЦЕССЫ
которое интегрированием по частям [VI] с учетом условий
(8.11) преобразуется к виду
Полученное уравнение в силу произвольности функции Щу)
приводит ко второму уравнению Колмогорова (8.7).
Пример 8.2. Рассмотрим n-мерный случайный процесс
?(t,w), t G T — [О, оо), удовлетворяющий стохастической моде-
модели состояния в форме Ито:
где w(t,uj), t?T, — n-мерный винеровский процесс, выходящий
из О. Пусть при каждом фиксированном и € П и X = ?(t,u)
векторная функция 4>(X,t) и матричная функция G(X,t) удо-
удовлетворяют условиям теоремы существования и единственно-
единственности решения задачи Коши (8.14) и являются непрерывными
по t на промежутке Т. В этом случае, как уже отмечалось
в 7.2, стохастинеская модель состояния (8.14) задает марков-
марковский процесс ?(t,w), t G Г, и его условная функция плотности
вероятностей должна удовлетворять уравнениям Колмогорова
(8.4), (8.7). Определим коэффициенты этих уравнений, для чего
воспользуемся интегральным представлением стохастической
модели состояния (8.14). Имеем
,u)-t{t,u) - J Ф(^,г)йг+ J G(?,T)dw(T,u). (8.15)

8.2. Уравнения Колмогорова 287
Второй интеграл в правой части (8.15) является стохастиче-
стохастическим интегралом Ито. Повторив рассуждения, проведенные в
7.3 (см. доказательство теоремы 7.4), получим
t+д
\ (8.16)
t+A t+A
t
t+A
М [( J
t t
= f G(X,t)Gt{X,t)cIt. (8.17)
t
А так как Ф(ЛТ,?) непрерывна по t, то из (8.15), согласно (8.16)
и теореме о среднем [VI], имеем
t+д
где t ^ r» ^ i + Д. Подставив полученный результат в (8.5) и
перейдя к пределу при А —> +0, находим
а(Х,0 = Ф(Х,0- (8.18)
А так как
t+A t+A
/)(
t t
то, согласно (8.6), (8.15)-(8.17),
t+д
b(X,t)= lim I- f G(X,T)GT(X,r)dT = G(X,t)GT{X,t). (8.19)

288 8. МАРКОВСКИЕ ПРОЦЕССЫ
8.3. Стохастические модели состояния
и уравнения Колмогорова
Равенства (8.18), (8.19) устанавливают связь между стоха-
стохастической моделью состояния в форме Ито (8.14) и уравнения-
уравнениями Колмогорова при довольно жестких ограничениях. Поэтому
возникает естественное желание ослабить эти ограничения и
получить уравнения Колмогорова непосредственно исходя из
стохастической модели состояния.
Пусть ?(t,uj), t G T, — n-мерный случайный процесс, удовле-
удовлетворяющий стохастической модели состояния (8.14) в форме
Ито, a f^(X\t) — его одномерная функция плотности вероят-
вероятностей. Определим характеристическую функцию изуча-
изучаемого случайного процесса ?(t,u), t G T:
g(\, t)±M [eixW^] = j eiXXff: (X11) dX,
где A= (Ai ... An), и рассмотрим разность
g(\,t + At) -g{\,t) = M[
Нас будет интересовать предел
,t + ?it)-g(\,t)
A<-f+O At
Поэтому в дальнейших рассуждениях с целью упрощения вы-
выкладок будем пренебрегать слагаемыми порядка малости o(At)
и писать:
At,u) - ?(t,u) =
,Lj) = W(t+ At,Lj) —

8.3. Стохастические модели состояния и уравнения Колмогорова 289
Таким образом, при f = ?(t,u), t?T,
= M [(е"СУ(«,*)Д«/(е1-А*(«,«)Д' _ ^ + e,\G(t,t)Aw _
, t)
Фиксируем t ?T. Обозначим через /»(AT,Z|i) плотность
распределения случайного вектора (?T(t,u) Aw (t,u>)} , а че-
через fw(Z\t) — плотность распределения случайного вектора
Aw(t,u). Тогда в силу независимости сечений Aw(t,u) от
?(t,u>) имеем
Таким образом,
g(\,t + At) - g(\,t) = J f(i\9{X,t) Atei
= f(i\9(X,t)bt JetXG(x>t)zfw(Z\t)dZ +
R"
/\
ex\G(X,t)Zf• (z\t)dZ- 1 )eixxMX\t)dX.
R»
R»
А так как w(t,u), t ? [0, oo), — n-мерный винеровский процесс и
М [Aw{t,и)} = О, М [Aw(t,w) (Aw(t,u))T] = InAt,

290 8. МАРКОВСКИЕ ПРОЦЕССЫ
то плотность распределения fw(Z\t) для случайного вектора
Aw(t,u>) есть плотность n-мерного нормального распределения
[XVI] с нулевым математическим ожиданием и ковариационной
матрицей ? = InAt и определяется равенством
Следовательно,
x
R"
так как функция
1
является n-мерной плотностью нормального распределения и,
следовательно,
Jf(Z)dZ=l.
R»
Используя полученный результат, заменяя экспоненту первыми
двумя членами ее разложения по формуле Тейлора и отбрасывая

8.3. Стохастические модели состояния и уравнения Колмогорова 291
слагаемые порядка малости o(At), получаем
g(X,t + At) - g(X,t) = J(iX9(X,t) д^-
= f (iXV(X,t)At(l- 0,5XG(X,t)GT{X,t) \TAt) -
R"
-Q,b\G{X,t)GT{X,t)\cAt)eixxfi{X\t)dX =
= [(iX9(X,t) At - 0,5XG{X,t)GT(X,t) X1
Разделив правую и левую части полученного равенства на
и перейдя к пределу при Д? —>• 0, найдем
R"
Для перехода от характеристической функции к функции
плотности вероятностей достаточно воспользоваться формулой
обращения экспоненциального интегрального преобразования
Фурье: (
R"
В результате [XI] приходим к следующему уравнению относи-
относительно функции ft(Y\t):
(8.20)

292 8. МАРКОВСКИЕ ПРОЦЕССЫ
Прежде чем приступать к анализу полученного уравне-
уравнения (8.20), приведем без доказательства некоторые свойства
5-функции Дирака*:
1)еслиА=(А1 ... Ап) и X = (х\ ... хп) , то
R» k=1 -оо
2) если функция ip{X) непрерывна в Rn, то для любого
/<р(ХN(Х-Y)dX= f(p(X)S(Y -X)dX =
R"
3) если функции ip(X) и ip'Xk(X) непрерывны в R", то для
любого УеГ
f
J
J dxk
R» R"
x)dx-
4) если функции tp(X) и (p"iX (X) непрерывны в Rn, то для
любого У G Rn
OXiOXj X=Y
R" R"
5) в интегралах, содержащих ^-функцию Дирака и ее про-
производные, можно выполнить дифференцирование по параметру
под знаком интеграла сколько угодно раз;
6) для частных производных ^-функции Дирака имеют
место интегральные представления
- B7Г)" 7 *Afce dA) dxidxj - B*)» J A'V
R R"
дхк () j ()
R" R"
*Cm.: [XII], а также Пугачев B.C.

8.3. Стохастические модели состояния и уравнения Колмогорова 293
Обратимся теперь к уравнению (8.20). Если
k-я координатная функция для векторной функции 4>(X,t), a
Gij(X,t) — скалярная функция, расположенная на пересечении
г'-й строки и j-ro столбца матричной функции G(X,t)G (X,t),
то (8.20) может быть представлено в следующем виде:
Rn
Таким образом, согласно свойствам ^-функции Дирака,
R"
R"
R" R"
R"
и мы приходим ко второму уравнению Колмогорова (8.7) при
замене t на г:

294 8. МАРКОВСКИЕ ПРОЦЕССЫ
Если вспомнить, что Ф;ь — к-я координатная функция век-
векторной функции Ф, a Gt] — скалярная функция, расположенная
на пересечении г'-й строки и j-ro столбца матричной функции
G(X,t)G (X,t), то из сопоставления полученного уравнения с
(8.7) можно получить (8.18) и (8.19). Заметим также, что при
выводе второго уравнения Колмогорова в данном случае не ис-
использовалось ограничение (8.10), а равенства (8.18) и (8.19) вер-
верны и при отсутствии непрерывности функций Ф(ЛГ,?), G(X,t)
note Т.
Равенства (8.18), (8.19) позволяют реализовать переход от
стохастической модели состояния (8.14) к уравнениям Колмо-
Колмогорова (8.4), (8.7), которым удовлетворяет условная функция
плотности вероятностей f(t,X,T,Y) марковского процесса
?(?,u>), t 6 Т, определяемого стохастической моделью состояния
(8.14). А так как уравнения Колмогорова (8.4), (8.7) полностью
определяются матричной функцией b(X,t) и векторной функци-
функцией a(X,t), то равенства (8.18), (8.19) позволяют реализовать и
обратный переход от уравнений Колмогорова к стохастиче-
стохастическому дифференциальному уравнению.
Пример 8.3. Пусть второе уравнение Колмогорова для
условной функции плотности вероятностей f(t,x,T,y) скалярно-
скалярного марковского процесса?(t,uj), t ?T = [0,оо), имеет следующий
вид:
Согласно (8.7), имеем
a(x,t) — — х2, b(x,t)— 2sin(tx).
Так как (см. 8.2) матрица диффузии неотрицательно определе-
определена, то уравнение Колмогорова определено лишь для значений т
и у, удовлетворяющих неравенству sin(rj/) ^ 0. Таким образом,
из соотношений (8.18), (8.19) следует, что
G(x,t) = y/28in{tx),

8.3. Стохастические модели состояния и уравнения Колмогорова 295
т.е. скалярный марковский процесс ?(?,u>), t ? Т, удовлетворяет
стохастическому дифференциальному уравнению в форме Ито:
= -t2{t,u>)dt+y/2Bin(tZ(t,u>))div(t,u>),
где w(t,uj), t € Г, — скалярный винеровский процесс, выхо-
выходящий из О. Знак перед радикалом в выражении для G(x,t)
не играет роли в силу свойств случайного процесса w(t,oj),
0 0. #
Если векторная функция a(X,t) известна, то векторную
функцию Ф(ЛГ,?), входящую в стохастическую модель состо-
состояния (8.14), можно однозначно определить из (8.18). Пусть
известна матричная функция b(X,t). Рассмотрим (8.19) как
нелинейную систему алгебраических уравнений относительно
элементов gtJ (X, t) матричной функции G(X,t). Нелинейная си-
система (8.19) вследствие симметричности матричной функции
b(X,t) (это следует из равенства (8.6)) имеет лишь п(п+ 1)/2
линейно независимых уравнений и п2 неизвестных gtJ{X,t). A
так как при п > 1 имеет место очевидное неравенство п2 >
> п(п+ 1)/2, то в общем случае система (8.19) имеет беско-
бесконечное множество решений.
Итак, в общем случае переход от уравнений Колмогорова
к стохастическим моделям состояния, определяющим исходные
марковские процессы, не является однозначным. Более того,
эта неоднозначность возможна и в скалярном случае, т.е. при
п = 1 (см. задачу 8.11, пример 8.3).
В практике научных исследований для матричной функции
G(X, t) вводят, как правило, дополнительное ограничение
позволяющее преобразовать матричное уравнение (8.19) к стан-
стандартному виду

296 8. МАРКОВСКИЕ ПРОЦЕССЫ
Тогда можно достаточно просто найти решение этого уравне-
уравнения с помощью квадратного корня из квадратной сим-
симметрической матрицы*, который определяется с точно-
точностью до знака:
G(X,t)=y/b(X,t). (8.21)
Пример 8.4. Определим систему стохастических диффе-
дифференциальных уравнений, которой удовлетворяет двумерный
марковский процесс
если условная функция плотности вероятностей этого случай-
случайного процесса f(t,x\,X2,T,yi,y2) удовлетворяет первому урав-
уравнению Колмогорова с известными параметрами к, и2, h:
Согласно (8.4), имеем
ai(X,t) = х2, a2(X,t) = -(k2xt + 2hx2),
bu{X,t) = b12{X,t) = b2i(X,t) = 0, b22(X,t) = a2.
Таким образом, матричная функция b(X,t) является симметри-
симметрической и для завершения решения исходной задачи достаточно
воспользоваться равенствами (8.18), (8.21):
и выписать систему стохастических дифференциальных урав-
уравнений, входящих в стохастическую модель состояния (8.14):
'См.: Директор С, Рорер Р.

8.3. Стохастические модели состояния и уравнения Колмогорова 297
где w(t,u), t ?T, — скалярный винеровский процесс, выходя-
выходящий из нуля. #
В заключение отметим следующее.
1. При любых фиксированных значениях X и t матрица
диффузии b(X,t) является симметрической и неотрицательно
определенной. Поэтому с помощью ортогонального преобразо-
преобразования ее можно привести к диагональному виду, т.е. существу-
существует такая ортогональная матрица T(X,t), что
При этом для определенности полагаем
V^(^ = diag(!&(*,01, -> I/W
А так как равенство
G2(X,t) = b(X,t)
эквивалентно равенству
(TT(X,t)G(X,t)T(X,t)J = TT(X,t)b(X,t)T(X,t)
то
Пример 8.5. Чтобы вычислить квадратный корень из не-
неотрицательно определенной симметрической матрицы
Д ( 2'5 ~1Л
находим ее собственные числа/3^ = 1, /3| = 4 и соответствующие
им единичные собственные векторы, которые образуют орто-
нормированную систему. Затем записываем матрицу
Т =

298 8. МАРКОВСКИЕ ПРОЦЕССЫ
Таким образом,
1 (I \\(\ 0\/1 1\_/ 1,
2^1 -1Д0 2Д1 -\) 1,-0,
,5 -0,5
,5 1,5
2. Переход от уравнений Колмогорова к соответствую-
соответствующим системам стохастических дифференциальных уравнений
в общем случае не является однозначным, но представляет ин-
интерес, так как эти системы определяют марковские случайные
процессы, эквивалентные по своим вероятностным свойствам
процессам, для которых заданы соответствующие уравнения
Колмогорова.
3. Случайные процессы ?(?,u>), t ? Т, и t)(t,u), t ?T, назы-
называют независимыми случайными процессами (некорре-
(некоррелированными случайными процессами), если для любых
t, г € Т случайные величины ?(t,u) и r}(t,u) независимые (не-
коррелированные).
8.4. Постановки задач
для нахождения условной функции
плотности вероятностей
Уравнения Колмогорова (8.4), (8.7) являются уравнениями в
частных производных параболического типа. Для того чтобы
их решение определялось однозначно, необходимо задать на-
начальные и граничные условия.
Начальное условие определяет зависимость искомой функ-
функции f(t,X,r,Y) от „пространственных координат", предста-
представленных та-мерным вектором X для первого уравнения Колмо-
Колмогорова и n-мерным вектором Y для второго уравнения Кол-
Колмогорова, в заданный (начальный) момент времени, определя-
определяемый значением переменного t или т соответственно.

8.4. Постановки задач 299
Начальные условия для уравнений Колмогорова, как прави-
правило, устанавливают из смысла решаемой задачи. Для второго
уравнения Колмогорова (8.7) естественно считать начальным
значением временной переменной г настоящий момент време-
времени t. Если начальное значение исходного марковского процесса
?(?,u>), t G Т, предполагается заданным, то условная функция
плотности вероятностей f(t,X,r,Y) в начальный момент вре-
времени г = t обращается в 8-функцию Дирака. Таким образом, в
данной ситуации начальное условие имеет вид
f(t,X,r,Y) =S(X-Y). (8.22)
r—t
Если начальное состояние изучаемого случайного процесса не
известно, оно должно рассматриваться как случайный вектор
с плотностью распределения /о(У), а начальное условие при-
принимает следующий вид:
f(t,X,r,Y)\ =/0(У). (8.23)
Начальное условие для первого уравнения Колмогорова вводят
аналогично начальным условиям (8.22), (8.23) для второго.
Уравнения Колмогорова (8.4), (8.7) можно интерпретиро-
интерпретировать с позиций математической физики [XII] как уравнения
массопереноса. При таком подходе функции а и Ь, определяе-
определяемые равенствами (8.5), (8.6), будут характеризовать конвектив-
конвективные и диффузионные составляющие процесса массопереноса.
Поэтому их элементы зачастую называют коэффициентами
сноса и диффузии соответственно.
Граничные условия для каждого из уравнений Колмогоро-
Колмогорова фактически являются условиями изолированности области
G С R" изменения рассматриваемого n-мерного марковского
процесса ?(t,u), t ?T = [a,b]. В рамках рассматриваемой ин-
интерпретации этих уравнений условия изолированности области
G С R" означают, что соответствующие суммарные потоки

300 8. МАРКОВСКИЕ ПРОЦЕССЫ
обращаются в нуль на границе области Го- С учетом этого
граничные условия (8.7) можно задать следующим образом:
для второго уравнения Колмогорова
= 0, к = 1,п, (8.24)
для первого уравнения Колмогорова (8.4)
m=l
= 0, k = l,n. (8.25)
Если G = R™, то граничные условия (8.24), (8.25) можно
упростить:
для первого уравнения Колмогорова
lim /(*,А-,г,У) = 0, (8.26)
\\Х\\-*оо
для второго уравнения Колмогорова
lim f(t,X,r,Y) = 0. (8.27)
ЦУЦ-+00 V ; y '
Решения уравнений Колмогорова (8.4), (8.7) для началь-
начальных и граничных условиях вида (8.14)-(8.19) должны удовле-
удовлетворять стандартным требованиям, предъявляемым к любой
условной функции плотности вероятностей:
f(t,X,T,Y)}0, Jf(t,X,r,Y)dY = l.
R»
Пример 8.6. Рассмотрим скалярный случайный процесс
?(?,u>), t € Т = [0, оо), который является решением стохастиче-
стохастической задачи Кохии:

8.4. Постановки задач
301
где а, га, х0 — неслучайные величины, a r](t,u>), t € Т, — белый
шум с единичной интенсивностью.
Исходная стохастическая модель состояния может быть
записана в форме Стратоновича:
t,u) dt + md*w(t,u),
В данном случае га не зависит от состояния ?(t,u), t ? Т.
Следовательно, стохастическая модель состояния в форме
Ито имеет тот же вид. Таким образом, ?(?,u>), t € Т1, является
марковским процессом и его стохастическую модель состояния
характеризуют функции
= -ах,
G(x,t) =
и детерминированное начальное состояние xq.
Для определения коэффициентов сноса и диффузии доста-
достаточно воспользоваться равенствами (8.18) и (8.19):
a(x,t) =
= -ax,
b(x,t) = G2(x,t) = га2.
А так как начальное состояние является детерминированным,
то, согласно (8.7), (8.22), (8.27), можно сформулировать задачу
для нахождения условной функции плотности вероятностей
f(t,x,T,y) случайного процесса ?(t,u), t ? Т — [0, оо):
(8.28)
решение которой может быть получено с помощью интеграль-
интегральных преобразований [XI].
f(t,x,r,y) =6(x-y),
T = t

302
8. МАРКОВСКИЕ ПРОЦЕССЫ
Полагая р = т — t, к задаче (8.28) применяем экспоненциаль-
экспоненциальное интегральное преобразование Фурье по переменному у. В
этом случае изображением экспоненциального интегрального
преобразования Фурье условной функции плотности вероятно-
вероятностей f(t,x,r,y) является характеристическая функция случай-
случайного процесса ?(t,u>), t 6 Т:
оо
д{\,р,х)= J etXyf{t,x,T,y)dy,
которая, в силу (8.28) и свойств экспоненциального преобразо-
преобразования Фурье [XI], является решением следующей задачи:
тп
9д
р=О
или, что то же самое,
ding n
dp i
lng(X,p,x)
ding
ЭХ '
р>0,
= i\x.
Применив интегральное преобразование Лапласа по перемен-
переменному р, приходим к обыкновенному дифференциальному урав-
уравнению первого порядка относительно изображения по Лапласу
E(X,s,x) функции \пд(Х,р,х):
ХЭЕ „ т2Х2 ., х „
«А-——sb = гХх, X € К,
оХ 2s
которое можно решить стандартными методами [VIII]. Из
свойств условной функции плотности вероятностей f(t,x,r,y)

8.4. Постановки задач 303
(см. 8.1) и связи между характеристической функцией д(А,р,х)
и функцией f(t,z,T,y) следует, что
оо
д@,р,х) = / f(t,x,T,y)dy=l.
—оо
Поэтому
,/э,а;) = О, E@,s,x) = 0
..,2
m* 2 ix
2ф-2а) s-a
По изображению Е находим оригинал Ing:
\2 2
МА.р.я;) = гАаге-0" - ^?-A - е~2а").
Теперь достаточно записать выражение для характеристи-
характеристической функции д(Х,р,х) и при помощи обратного экспонен-
экспоненциального преобразования Фурье перейти к условной функции
плотности вероятностей f(t,x,r,y). Но обратим внимание на
то, что в правой части полученного равенства записан нату-
натуральный логарифм характеристической функции для нормаль-
нормального распределения [XVI] с математическим ожиданием хе~ар
и дисперсией (m2/2a)(l — е~2ар). Поэтому с учетом обозначе-
обозначения р = т — t получаем
где
m(x,T-t) = хе~а(т~1\ о2(т-Ь) — —-(l ->

304 8. МАРКОВСКИЕ ПРОЦЕССЫ
8.5. Три характерные задачи теории
марковских случайных процессов
с непрерывными состояниями
В практике прикладных исследований встречаются задачи,
для корректного решения которых аппарат корреляционной те-
теории случайных процессов недостаточен. К подобным задачам
в первую очередь относятся задачи определения вероятности
выброса значений случайного процесса за пределы заданной
области и задачи определения закона распределения времени
этого выброса. Решение этих задач для случайных процес-
процессов произвольного типа связано с преодолением значительных
трудностей принципиального характера*. Но если случайный
процесс является марковским, то решения удается получить от-
относительно просто.
Вероятность пребывания марковского случайного
процесса в заданной области. Простейшей задачей данного
класса является вычисление вероятности того, что скалярный
случайный процесс ?(?,u>), t € Т = [a,b], в течение интервала
времени (t, t + to) С Т удовлетворяет неравенству
ui<f(t,w)<ua, (8.29)
где ui и и2 заданы.
Определение вероятности пребывания значений случайного
процесса в заданной области необходимо при решении многих
прикладных задач. В частности, к ним относятся задачи тео-
теории надежности, в которых для нормального функционирова-
функционирования изучаемой системы нужно, чтобы параметры, характери-
характеризующие систему во время ее работы, не выходили за некоторые
допустимые пределы.
Рассмотрим решение подобных задач для скалярного мар-
марковского процесса ?(t,u), t € Т. Пусть значения изучаемого
'См.: Фомин Я.А., а также Свешников А.А.

8.5. Три задачи теории марковских процессов 305
случайного процесса в интервале времени (t,r) С Г ни разу не
вышли за границы области, определенной неравенствами (8.29),
а вероятность того, что в момент времени т ? Т его значе-
значения будут находиться в интервале (у, у + dy), с точностью до
o(dy) равна W(r,y)dy. Очевидно, что W(r,y) — это услов-
условная функция плотности вероятностей, а искомая вероятность
Р{т) того, что граница области к моменту времени г = t + to не
будет достигнута, определяется равенством
«2
Р(т) = Jw(T,y)dy. (8.30)
Если условие (8.29) выполнено, то функция W(r,y), будучи
условной функцией плотности вероятностей скалярного мар-
марковского процесса ?(t,u), t ? Т, удовлетворяет второму урав-
уравнению Колмогорова, т.е.
)^()^O (8.31)
при щ < у < и2. Нарушение условия (8.29) связано с моментом,
когда значение случайного процесса достигнет („коснется")
границы, т.е. при у = щ или у — и2. В этом случае попадание
значений случайного процесса в интервгил (y,y-\-dy) без дости-
достижения границ становится невозможным и для любого г ? Т
условная функция плотности вероятностей равна W{r,y) = 0,
т.е. имеют место граничные условия
и2)=0, t>L (8.32)
Если начальные условия для W(r,y) заданы равенствами (8.22)
или (8.23), то исходная задача может быть сведена к смешанной
задаче для уравнения Колмогорова (8.31) с граничными усло-
условиями (8.32) и начальными условиями (8.22) или (8.23).
Пример 8.7. Пусть ?(t,u), t ET, — скалярный марковский
процесс, определенный в примере 8.6. Найдем вероятность

306 8. МАРКОВСКИЕ ПРОЦЕССЫ
того, что в течение времени г значения рассматриваемого
случайного процесса не выйдут за пределы ±/i, если ?@,о>) =0.
В соответствии с результатами, полученными в примере
8.6, приходим к смешанной задаче (8.31), (8.32), (8.22) для
уравнения Колмогорова, решением которой является функция
плотности вероятностей W(r,y):
dW{r,y) т2д2\У(т,у) d(yW(r,y))
ду2 +а ду 'r>O'l2>l<ft'
(8-33)
Для решения задачи (8.33) можно воспользоваться методом
Фурье разделения переменных [XII]. В этом случае
W(T,y)=A(r)B(y),
где функция В(у) является решением задачи Штурма — Лиу-
вилля [XI]:
( В"(у) + 2ат-2[уВ(у)]' + Х2В(у) = О, \у\ < h,
{ (8.34)
[В(-/г) = "
а функция А(т) удовлетворяет линейному дифференциальному
уравнению первого порядка
A'(r) + ^m2A2A(r) = 0, г>0. (8.35)
Как известно [XII], ортонормированная система решений за-
задачи Штурма — Лиувилля (8.34) может быть представлена в
виде
Вк(у) = с*ехр ( - -^у2)DVk (^У), к = 1, 2,...,

8.5. Три задачи теории марковских процессов 307
где Dl/(z) — функция параболического цилиндра (функция
Вебера — Эрмита [XII]); Vk = m2\\/ot — порядок функции
параболического цилиндра, определяемый из уравнения
Ck — нормирующий множитель, который можно вычислить по
формуле
-1/2
Используя свойство ортонормированности системы функций
{Вк(у)} с весом р(у) — ехр(агп~2у2) и равенства А/*@) = 1,
получим разложение
оо
к=1
где
h
-h
Таким образом, если А2 = А? = avk/m2, то решение уравнения
(8.35) имеет вид Afc(r) = с^ехр(—0,5си/^г) и можно записать
разложение для условной функции плотности вероятностей
fc=l k=l
Для получения окончательного результата достаточно восполь-
воспользоваться (8.30) при щ = -h и u2 — h:
-h

308 8. МАРКОВСКИЕ ПРОЦЕССЫ
где Vk, к — 1, 2, ... — корни уравнения Dl/{-^2ah/m) = 0;
-h
Если ?(t,u), t?T, — n-мерный марковский процесс, то мож-
можно рассматривать различные постановки задач о вероятности
пребывания его значений в заданной области G С Кп. Эти раз-
различия главным образом связаны с видом области G, а основная
идея решения исходной задачи практически та же, что и в ска-
скалярном случае.
Действительно, пусть к моменту времени г ? Т значение
та-мерного марковского процесса ?(t,u), t ? Т, ни разу не
пересекало границы Го области G С Кп, а вероятность того,
что в момент времени г значение случайного процесса попадает
в га-мерный интервал (Y, Y-\-dY), т.е. для любого к=1,п его
к-я компонента попадает в интервал {yk, Ук+dyk), с точностью
o(||dF||) равна W(r,Y)dY. Тогда, рассуждая так же, как и в
скалярном случае, приходим к выводу, что функция W(t,Y)
удовлетворяет второму уравнению Колмогорова, граничным
условиям
W(t,Y)
verG
= 0,
одному из начальных условий (8.22) или (8.23), а искомая
вероятность Р(г) того, что граница области не достигнута,
равна
Р(т)= fw{r,Y)dY.
G
Закон распределения времени пребывания марков-
марковского процесса в заданной области. Пусть fp(z) — функ-
функция плотности вероятностей времени пребывания скалярного
марковского процесса ?(t,u), t ? Т, в заданной области, опре-

8.5. Три задачи теории марковских процессов 309
деленной неравенствами (8.29). Если к моменту времени т
значения рассматриваемого случайного процесса еще ни разу
не достигали границ области, то время р их пребывания в до-
допустимой области будет не менее, чем (г — t). Вероятность
реализации этого события равна
оо
/
fp(z)dz.
т-t
С другой стороны, эта же вероятность определена равенством
(8.30), т.е.
/
«2
r-t
Таким образом,
«2
(8.36)
T=t+z
r=t+z
1. Если за начальный момент времени взят момент пере-
пересечения значениями случайного процесса границы допустимой
области, то функция fp(z), определяемая равенством (8.36),
устанавливает закон распределения времени пребывания зна-
значений этого случайного процесса в допустимой области от
момента входа в нее и до момента выхода.
2. Если и2 = +оо, то функция fp(z) устанавливает закон
распределения времени выброса значений рассматриваемого
случайного процесса за уровень щ „снизу вверх".
3. Если функция fp(z) плотности вероятностей времени
пребывания значений скалярного марковского процесса ?(?,ы) в
допустимой области определена, то математическое ожидание
этого времени пребывания равно
(8.37)

310 8. МАРКОВСКИЕ ПРОЦЕССЫ
Выражение в правой части (8.37) отвечает определению мате-
математического ожидания, если для функции плотности вероятно-
вероятностей fp{z) воспользоваться представлением (8.36) с последую-
последующим интегрированием по частям.
4. Если в уравнениях Колмогорова, соответствующих рас-
рассматриваемому скалярному марковскому процессу ?(t,u>), t?T,
коэффициенты сноса и диффузии не зависят от времени, т.е.
a(x,t) = a(x), b(x,t) = b(x),
то математическое ожидание р можно определить, не используя
(8.37). Действительно, в этом случае (см. пример 8.6) условная
функция плотности вероятностей W(r,y) будет зависеть не от
t и г, а от разности т — t. Поэтому
dW dW
dt ~~ дт'
До того момента, когда значения случайного процесса ?(t,u),
t?T, достигают границы допустимой области, функция W(t,x)
является решением первого уравнения Колмогорова:
dW . ,dW 1., ,d2W n
Заменив в этом уравнении W( на -W'T и проинтегрировав его
по переменному у в пределах от ui до U2, с учетом равенства
(8.30) приходим к дифференциальному уравнению в частных
производных относительно Р(т):
др эр 1 в2р
Так как, согласно определению вероятности Р(т), имеют место
равенства
P(t) = l, P(oo)=0,

8.5. Три задачи теории марковских процессов 311
то после интегрирования этого уравнения по г в пределах от t
до +оо в соответствии с равенством (8.37) приходим к обыкно-
обыкновенному дифференциальному уравнению второго порядка от-
относительно ~р = ~р{х):
hb{x)p"{x) + a(xtf{x) + 1 = 0, их < х < u2, (8.38)
дополняемому очевидными краевыми условиями
p(ui)=FM = 0. (8.39)
Пример 8.8. В условиях примера 8.7 примем коэффициент
диффузии равным Ь(х) = т2, а коэффициент сноса а(х) = —ах.
Тогда краевая задача (8.38), (8.39) относительно ~р{х) примет
следующий вид:
-т2р"{х) - axp'ix) + 1 = 0, \х\ < h,
Понизив порядок уравнения, без особых трудностей находим
значение математического ожидания времени пребывания зна-
значений исходного случайного процесса в пределах ±/г в зависи-
зависимости от его начального значения х:
J/м^у2-
-h -h-h
Отметим, что (8.36), (8.37) справедливы и для векторных
марковских процессов.
Среднее число выбросов значений марковского про-
процесса за данный уровень. Задача определения среднего
числа выбросов значений марковского процесса за данный уро-

312 8. МАРКОВСКИЕ ПРОЦЕССЫ
вень в единицу времени, для каждого из которых время пре-
пребывания вне допустимой области больше заданного значения
ро, сводится к решению соответствующих задач для уравне-
уравнений Колмогорова. При этом логика решения исходной задачи
аналогична логике решения задачи об определении вероятности
пребывания значений марковского процесса в заданной обла-
области.
Рассмотрим временной интервал (t, t + A)cT,B течение ко-
которого значения марковского скалярного процесса ? {t,u>), t?T,
пересекли уровень у = и2. При этом условии вероятность того,
что к моменту времени *т € Т значения изучаемого случайно-
случайного процесса принадлежат интервалу (г/, y + dy) и ни разу за
промежуток времени (t,r) не опускаются ниже уровня у = и2,
представим в виде произведения v(r,y)A. Это представление
верно с точностью о(Д). А так как длина Д временного интер-
интервала (?,? + Д) не зависит ни от г, ни от у, то функция v(t,у)
должна удовлетворять второму уравнению Колмогорова:
^ (a(ytT)v(T,y))(b(yiT)v(T,y)) = Q. (8.40)
Начальное и граничные условия для уравнения (8.40) долж-
должны отражать два обстоятельства:
1) для моментов времени, предшествующих t, значения слу-
случайного процесса ?(t,u), t ?T, находятся ниже уровня у = и2;
2) в некоторый момент времени из интервала (?, t + Д)
значения случайного процесса ?(t,u), t?T, пересекают уровень
у = и2.
Из первого условия следует, что
v{r,y) =0, (8.41)
так как для моментов времени, предшествующих t, значения
случайного процесса ?(t,u), t ? Т, не могут быть больше,
чем и2, ни разу не опускаясь ниже этого уровня, поскольку
предполагается наличие выброса в окрестности значения t.

8.5. Три задачи теории марковских процессов 313
Так как время выброса точно не известно, а известно лишь,
что выброс произошел в интервале времени (?, t-\- Д), то второе
условие означает, что интеграл от и(г,у)Д по переменному
т в пределах от t до t + Д при у — и2 должен определять
вероятность попадания значений случайного процесса ?(t,u),
t € Т, в окрестность значения и2. Таким образом,
и окончательно
v{T,u2) = 6(T-t)f(t,u2), (8.42)
где f(t,x) — функция плотности вероятностей случайной вели-
величины ?(t,u) в заданный момент времени t. Условия (8.41), (8.42)
полностью определяют частное решение уравнения (8.40).
Число выбросов п(и2,/>о)Д) длительность которых не мень-
меньше заданной величины ро и которые происходят в среднем в
течение интервала времени (t,t-\-A), равно вероятности того,
что выброс, начавшийся в интервале (?, t-\- Д), не закончится к
моменту T — t-\-A. А так как условная вероятность реализа-
реализации этого случайного события в принятых обозначениях равна
оо
i / v(po,y)dy,
«2
то окончательное решение исходной задачи имеет вид
оо
п{и2,ро)= v(po,y)dy. (8.43)
В заключение отметим следующее.
1. Введем в рассмотрение функцию и(т,у), определяемую
равенством

314 8. МАРКОВСКИЕ ПРОЦЕССЫ
Тогда из (8.40)-(8.43) следует, что
оо
{и2,ро) = f(t,u2) I u(po,y)dy,
у) д 1 д2 (8-44)
дт~~+ду~(а{У'Т)и{ТуУ)> ~ 2Ъу^^У'Т)и(т'У)> =0>
и2<у<оо, и(т,у) = 0, и(т,и2) =S(T-t).
На практике при определении среднего числа выбросов мар-
марковского процесса за заданный уровень удобно представлять
исходную задачи в виде (8.44), так как в таком виде легче обес-
обеспечить численное решение.
2. Если исходный случайный процесс является стационар-
стационарным в широком смысле, то
f(r,y) = f(y), a(r,y) = a(y), b(r,y) = b(y) (8.45)
и функция f(y) должна удовлетворять второму уравнению
Колмогорова, которое в данном случае имеет вид
= 0, (8.46)
иу i uy-
стандартному свойству функции плотности вероятностей
сю
/
f(y)dy=l
и граничным условиям (8.24) в виде
(^(%)/Ы)-«Ы/Ы)| =0, (8.47)
где То — {а, 0} — множество граничных точек области G
изменения значений рассматриваемого случайного процесса,

8.5. Три задачи теории марковских процессов
315
Представляющей собой конечный или бесконечный интервал
(а, C). Интегрируя правую и левую части уравнения (8.48) по
у в пределах ота= —оо до у € G с учетом граничного условия
(8.47) при у — а, приходим к следующей задаче относительно
функции f(y):
(8.48)
3. Пусть исходный случайный процесс является стационар-
стационарным в широком смысле и
оо
,y) = J e-s(T-^u{T,
U(s
изображение по Лапласу для оригинала и(т,у). В соответствии
с (8.44) и (8.45) функция U(s,y) является решением следующей
задачи:
jjji№ U(s,y)) - 2^И</) U(s,y)) - 2sU(s,y) = О,
u2<y<oc, U(s,u2) = l, U(s,oo) = 0,
где условие U(s, сю) = 0 соответствует граничному условию
(8.27). Кроме того, если
оо
J
О
То из первого уравнения (8.44) следует, что
оо
i,s) = f(u2)Ju(s,y)dy.
u2

316 8. МАРКОВСКИЕ ПРОЦЕССЫ
Интегрируя уравнение (8.49) по у в пределах от и2 до +оо,
получаем
'У)
U(8,y)dy= (-a(y) - ±--?-(b(y)U(s,y)))
так как по условию U(s, оо) = 0. Таким образом,
и для того, чтобы найти среднее число выбросов значений мар-
марковского процесса за уровень у = и2 в единицу времени, каждый
из которых имеет длительность более заданного значения ро,
достаточно обратить интегральное преобразование Лапласа.
Пример 8.9. Для случайного процесса ?(t,u), t € Г, опре-
определенного в примере 8.6, определим среднее число выбросов
п@,ро) за нулевой уровень, длительность которых превосхо-
превосходит ро,
В рассматриваемом случае
а[у,т) = —ау, Ь(у,т) = гп .
Согласно (8.48),
оо
m2f'{y)+2ayf(y) = 0, Jf{y)dy=l.
—оо
Следовательно,
является функцией плотности вероятностей нормального за-
закона распределения с нулевым математическим ожиданием и
дисперсией а2 — тп2/Bа). А так как по условию и2 = 0, то

Вопросы и задачи 317
В соответствии с (8.49) изображение по Лапласу U(s,y)
функции и(т, у) является решением следующей задачи:
т2
оу2 т2 оу
,0) = l, I7(s,oo) = 0.
Таким образом [XII],
Подставив полученные результаты в (8.50), с учетом свойств
функции параболического цилиндра найдем
откуда
n@,/90) = —
- e~2aT
¦ #
Т=Р0
4. Все полученные результаты могут быть обобщены и на
случай m-мерного марковского процесса.
Вопросы и задачи
8.1. Напишите уравнение Маркова — Смолуховского —
Чепмена — Колмогорова. Почему оно справедливо лишь для
марковских процессов?
8.2. Докажите теорему 8.1 при п > 1.
8.3. Перечислите типовые постановки задач для определе-
определения условной функции плотности вероятностей f(t,X, r, Y).
8.4. Можно ли утверждать, что:
а) каждая стохастическая модель состояния однозначно
определяет марковский процесс;

318 8. МАРКОВСКИЕ ПРОЦЕССЫ
б) каждый марковский процесс порожден стохастической
моделью состояния;
в) каждый марковский процесс однозначно определяет сто-
стохастическую модель состояния?
8.5. Как связаны между собой параметры уравнений Колмо-
Колмогорова и соответствующей стохастической модели состояния?
8.6. Изложите основную идею решения задачи определения
вероятности пребывания значений марковского процесса в за-
заданной области.
8.7. Изложите основную идею решения задачи определения
закона распределения времени пребывания значений марков-
марковского процесса в заданной области.
8.8. Возможно ли обобщение краевой задачи (8.38), (8.39)
для определения математического ожидания времени пребы-
пребывания значений скалярного марковского процесса в заданной
области на случай векторного марковского процесса?
8.9. Почему при постановке задачи определения среднего
числа выбросов значений марковского процесса за заданный
уровень накладывается ограничение на время пребывания зна-
значений случайного процесса вне допустимой области?
8.10. Изложите основную идею решения задачи определения
среднего числа выбросов значений марковского процесса за
заданный уровень.
8.11. Пусть u»i(t,w), *еГ = [0,оо), и to2(t,w), t € T, —
независимые винеровские скалярные процессы, а скалярный
случайный процесс r)(t,w), t 6 Т, определен стохастическим
дифференциальным уравнением
dr)(t,u>) + rJ(t,uj)dt= y/2&in(tr)(t,u)) — c2dtVi(t,u) +cdw2(t,u),
где с — произвольная постоянная. Докажите, что r)(t,u}),
t ?Т, — марковский процесс, которому соответствует урав-
уравнение Колмогорова, приведенное в примере 8.3.

Вопросы и задачи 319
8.12. Предположим, что условная функция плотности ве-
вероятностей f(t,X,T, Y) n-мерного марковского процесса удо-
удовлетворяет второму уравнению Колмогорова (8.7), в котором
коэффициенты сноса заданы равенствами
т=1
а коэффициенты диффузии Ькт(У,т), к,тп= 1, п, равно как и
параметры otkm, flk, k,m=l, n, являются известными постоян-
постоянными. Воспользовавшись начальным условием (8.22), обобщите
результат, полученный при рассмотрении примера 8.6, и дока-
докажите, что исходный случайный процесс является гауссовским.
8.13. Пусть ?(t,u>), t G T — [О, оо), — скалярный гауссовский
стационарный (в широком смысле) случайный процесс, спек-
спектральная плотность которого равна
где а, /3, с — известные постоянные. Докажите, что ?(t,u),
t € Г, можно рассматривать как компоненту векторного мар-
марковского процесса r)(t,u), t ? Т. Определите размерность тако-
такого случайного процесса и коэффициенты уравнений Колмого-
Колмогорова для него.
Ответ: ?(?,w), t ? Т, — первая компонента двумерного
Марковского процесса. При этом ai(X,t) — х2, a2(X,t) =
= -(a2 + {32)Xl - 2az2, bn(X,t) = с2, bi2(X,t) = b21(X,t) =
-2<*c2, b22(X,t) = 4a2c2.
8.14. Получите систему стохастических дифференциальных
Уравнений, определяющих двумерный марковский процесс, ес-
если его условная функция плотности вероятностей удовлетворя-
удовлетворяет уравнению Колмогорова
9/ 1/ df , .df\ 1 /d2(y2f) x
ду2) ц2\ ду\ 2 ду

320 8. МАРКОВСКИЕ ПРОЦЕССЫ
где ц и х — известные постоянные, а <р — известная неслучай-
неслучайная скалярная функция.
Ответ:
Т
где w(t,u)) = (w\(t,oj) w2(t,u)) , t 6T, — двумерный винеров-
ский процесс, выходящий из 0.
8.15. Закон отклонения руля высоты самолета, которое со-
сообщается автопилотом для ликвидации воздействия пульсаций
ветра, характеризуемых случайным процессом ?(t,u), t ? Г,
можно приближенно описать стохастическим дифференциаль-
дифференциальным уравнением
T0ri(t,u)+Ti(t,Lj)=loe(t,u>), t?T,
где Го, /о — известные постоянные. Определите условную
функцию плотности вероятностей f(t,x,r,y) для случайно-
случайного процесса r)(t,u), t € Т, если известно, что М[?(?,ы)] = 0,
t2) = ^S(t2 - h) и t)(t,ui) = х при т — t.
Ответ:
а/ 1 d(yf) ifajd2/
дт Го ду 2Г02 9у2 и'
S(t'x'T>y)= ^Цг-г)'*< 2,.(г-.) )¦
8.16. Пусть r)(t,u), t?T, — ш-мерный марковский процесс.
Определите вероятность того, что в момент времени г € Г

Вопросы и задачи 321
значение его первой компоненты будет находиться в интервале
Р сю ею
Ответ: Р\{т)= / /•••/ W(r,y1,y2,.. ,ym)dyidy2...dym.
а —сю —оо
8.17. Угловые отклонения щ и 7/2 оси гироскопического
маятника от вертикали в первом приближении удовлетворяют
системе стохастических уравнений
где X-i 9 — известные постоянные, a ?\(t,u), t € T = [0,сю),
и ?2(?,^), *6Г, — горизонтальные ускорения точки подвеса
маятника, которые можно считать независимыми случайными
процессами, обладающими свойствами белого шума:
Определите вероятность того, что в течение интервала вре-
времени Т ось маятника ни разу не выйдет за пределы конуса,
образующая которого составляет угол j с вертикалью, если в
начальный момент времени ось маятника вертикальна.
Ответ:
Р(Т)= Л W(T,yi,y2)dyidy2,
где W(T,yi,y2) — решение задачи
x2c2(d2W d2W\
=0'
dW 8W dW x2c2(d2W d2W\
j— xgyi- т~\^~т + ^~т) =
дт ' ™»'дУ1 ™»ldy2 2 \ду\ ' 5у|
= 0.

322 8. МАРКОВСКИЕ ПРОЦЕССЫ
Решение смешанной задачи может быть получено методом Фу-
Фурье разделения переменных [ХИ]в полярной системе координат
и имеет вид
угТч 2
Р(Т) = ХХ*)
к—1 q
где /ifc — корни уравнения /o(/i) = 0, a /i(x) и /о(х) — функции
Бесселя [XI].
8.18. Пусть r}(t,L)), t ?T, — двумерный марковский процесс
с известными коэффициентами сноса и диффузии. Изложи-
Изложите общую схему решения задачи определения среднего числа
выбросов его ординаты за уровень, определяемый уравнением
+ ^22/2 = d, в направлении вектора нормали (о^ а2) •

9. ЭЛЕМЕНТЫ СТАТИСТИКИ
СЛУЧАЙНЫХ ПРОЦЕССОВ
Подобно тому, как результаты теории вероятностей нахо-
находят свое практическое применение в методах математической
статистики, так и результаты, содержащиеся в предыдущих
главах, являются теоретической основой для построения мето-
методов статистики случайных процессов.
Из всего многообразия задач статистики случайных про-
процессов рассмотрим лишь задачу оценивания параметров слу-
случайного процесса по дискретным значениям его выборочных
реализаций. Это оправдано, во-первых, тем, что ее постановка
является типичной для весьма обширного класса прикладных
задач, а во-вторых, тем, что ее решать можно различными
методами. Применение таких методов показано в этой гла-
главе. Более полное изложение статистики случайных процессов
читатель может найти в специальной литературе*.
Приступая к обсуждению задачи оценивания параметров
случайных процессов по дискретным значениям их выбороч-
выборочных реализаций, введем некоторые обозначения и рассмотрим
типовые варианты данных наблюдений.
9.1. Данные наблюдений
Напомним, что если ?(и) — n-мерный случайный вектор
с множеством возможных значений X С Кп и плотностью
распределения вероятностей f^{x\/3) = Д(?1,...,?п|/3ъ--чAl),
где E ? KL — вектор параметров, то случайной выборкой
*См.: Липцер Р.Ш., Ширяев А.Н.

324 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
объема N для ?(и) называют блочный случайный вектор
?A)(ш)
?B) И
с множеством возможных значений Y = XN С KnN и функцией
плотности вероятностей
N
к=1
который составлен из независимых n-мерных случайных век-
векторов ?(?)(ы), k= I, N, имеющих тот же закон распределения,
что и n-мерный случайный вектор ?(и>). Конкретное значение
случайного вектора Qn[?(u)*)] называют реализацией слу-
случайной выборки.
Пусть теперь ?(t,u), t?T = [a,b], — n-мерный случайный
процесс, характеризующий состояние изучаемого объекта, а
€ fi, является его k-n реализацией, k= 1, т. Будем
предполагать, что при проведении к-го испытания в результате
наблюдений за состоянием изучаемого объекта в дискретные
моменты времени ^, j = 1, N(k), a ^ ifcl < tk2 < ... < tkN^ ^ b,
определена выборочная реализация
: t € Г(Ч} , Т(к) 4 {^}fj*>, (9.1)
(к)
являющаяся совокупностью 7V(Ar) значений случайного процесса
?(t,u), t ? Т, в дискретные моменты времени, составляющие
множество Tif.), при фиксированном значении w = oj,k\ ? fi.
Совокупность m таких выборочных реализаций обозначим как
множество
Um ^ {аТ(к),и{к))}Т=1, (9.2)
а при m = 1 вместо U\ будем просто писать ?7.

9.1. Данные наблюдении
325
Предполагая, что случайные процессы
)i t ? Т, к =
= 1, т, независимы и имеют те же конечномерные законы рас-
распределения, что и исходный случайный процесс ?(t,u), t € Т,
можем считать ?(T(j.),(j(j.)) выборочной реализацией случай-
случайного процесса ^k)(t,u), t ? Т, и в этом смысле говорить о
независимости выборочных реализаций, представленных
множеством Um.
Далее мы предполагаем, что для всех к = 1, т значения
^(tkj,^(k))j j = 1) ^(^)i случайного процесса ?(t,u>), t ?T, опре-
определены точно путем прямых измерений значений компонент
вектора состояния изучаемого объекта. Таким образом, счи-
считаем, что выборочные реализации не содержат ни системати-
систематических, ни случайных ошибок измерений.
В практических задачах встречаются самые разнообразные
варианты данных наблюдений в зависимости от возможностей
их получения. Например, множества Т^,Т^2),• • • ,Т^т) могут
не содержать общих элементов (рис. 9.1), но может иметь
место ситуация, когда Т^ц = ГB) = ... = Т(т), т.е. значения
выборочных реализаций измерены в одни и те же моменты
времени t3, j = l,N, где для всех k=\,m имеем N(k)=N
и tkj=tj, j = I, N (рис. 9.2). На рис. 9.1 и 9.2 элементы
множества Um для скалярного случайного процесса ?(t,u>),
t € Т, представлены в виде точек, расположенных на его
траекториях.
Щ2) = 8
*j ' !
f* • I
0 a txl j tn
1
.,.,. -"—^
Г ' . ' i
* 1 'I
,-*¦
{*" "г *Ч-*"^
1 '
1
1 J
1 J
J 1
('*
r-r «
1
'
J
J
tie
§(«
b t
hi
Рис. 9.1

326 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Довольно часто встречается случай, когда одно испытание
позволяет произвести лишь одно измерение вектора состояния
(например, если в результате измерения или после него объект
разрушается). В этом случае для получения данных о динами-
динамике вектора состояния используют N практически одинаковых
объектов, испытания которых начинают одновременно, но из-
измерение состояния j-ro объекта производят в момент времени
tj € Т. При этом tj+i >tj,j = l,N — l,& j-я выборочная реали-
реализация состоит из одного значения вектора состояния:
и) Д {^}f=1 С Т. (9.3)
Множество f/jv таких выборочных реализаций обозначим через
Uin, тем самым указывая, что оно представляет собой как бы
одну выборочную реализацию, но состоящую из N независи-
независимых значений рассматриваемого случайного процесса, где
независимость понимают в смысле независимости выборочных
реализаций. Этот вариант является частным случаем более
сложного испытания, когда в момент времени t = а одновремен-
одновременно начинают испытания М практически одинаковых объектов.
В моменты времени tj, j = 1, N, a <J t± < t2 < ... < t^j <J b, произ-
производят измерения состояния соответственно у mi, тп2, ..., тдг
объектов. После измерения состояния объект выбывает из рас-
рассмотрения. Поэтому после измерений в момент времени t = t\

9.1. Данные наблюдений
327
будет получено т.\ значений вектора состояния и останется
М — тп\ действующих объектов. После измерений в момент вре-
времени t = ?2 будет получено еще Ш2 значений вектора состояния
и останется М — (mi + га2) действующих объектов и т.д. При
этом М = т\ + 7712 + • • • + mN¦ Таким образом, в момент време-
времени tj имеется тп, независимых значений случайного процесса
Множество таких реализаций обозначим через
(9.4)
(рис. 9.3).
Заметим, что если т} — 1 для всех j = 1, iV, то приходим к
предыдущему варианту испытаний.
Конечно, существуют выборки и других видов, но мы огра-
ограничимся данным рассмотрением, которого вполне достаточно
Для иллюстрации применения основных методов статистики
случайных процессов. В заключение отметим лишь, что при
Правильном планировании проводимых исследований не вид
выборки определяет выбор метода ее анализа, а наоборот — ис-
исходная задача и выбранный метод ее решения должны являться

328 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
основой для планирования необходимых измерений. К сожале-
сожалению, это не всегда удается. Зачастую исследователь вынужден
искать компромисс между этими крайностями, что требует
определенного искусства и стимулирует его к созданию новых
методов решения прикладных задач. В этой главе, рассматри-
рассматривая тот или иной метод статистики случайных процессов, мы
будем использовать соответствующую этому методу выборку.
9.2. Статистические моменты
случайного процесса
Рассмотрим случай, когда полностью отсутствует какая-
либо априорная информация о закономерностях поведения изу-
изучаемого объекта и в результате испытаний получено множе-
множество независимых выборочных реализаций Um, определяемое
соотношениями (9.2), (9.1) при
Т(к) = Г@) = Oj}j=i С Т, к=1,тп. (9.5)
При каждом фиксированном t € Т/0\ исследователь располага-
располагает реализацией случайной выборки объема m для п-мерного
случайного вектора ^(t,и). Эта реализация представляется ма-
матрицей
где
к=
Оценки основных моментов рассматриваемого случай-
случайного процесса, т.е. оценки его математического ожидания,
ковариационной матрицы и ковариационной функции, могут

9.2. Статистические моменты случайного процесса 329
быть найдены с использованием известных формул математи-
математической статистики [XVII]. Так, для оценки математического
ожидания имеем
1 m 1
771 *—** 771
k=l
т
где / = A ••• 1) ? Mmi(K) — единичная матрица-столбец.
Оценку ковариационной матрицы можно определить следую-
следующим образом:
/t=i
~|Т, teT@). (9.7)
Диагональными элементами матрицы ?^(?) являются исправ-
исправленные выборочные дисперсии компонент вектора состояния
изучаемого объекта в момент времени t G Т/Оу Совершенно
аналогично вычисляют оценку ковариационной функции:
zrr-%M/T)T. *,rer@). (9.8)
fit— J.
Заметим, что множество Um выбрано с условием (9.5) далеко
неслучайно. Во-первых, указанное условие позволяет усред-
усреднять значения выборочных реализаций для каждого t G Т@),
а в противном случае пришлось бы проводить интерполяцию
реализаций. Во-вторых, при нарушении условия (9.5) исполь-
использование множества Umn для оценки ковариационной функции
некорректно, поскольку в этом случае оно представляет собой
(по условиям испытаний) множество независимых значений слу-
случайного процесса.

330 9 ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Пример 9.1. Пусть ?(t,u), t eT, — двумерный случайный
процесс, Т@) = {^i, t2} CT, а результаты испытаний предста-
представлены в следующей таблице.
6(<,w(fe))
6(<,W(fc))
< = <2
4l(',w(fc))
^2(',W(fc))
W(l)
1,2
3,3
W(l)
0,7
2,1
u>B)
0,9
2,9
WB)
0,9
2,3
U)
1
3
w
1
2
C)
,1
,1
C)
,1
,0
и
0
2
w
0
1
D)
,5
4)
,6
,9
и
1
3
w
1
1
E)
,o
,2
5)
,2
,7
В данном случае m — 5 и п = 2. Согласно (9.6),
Поэтому
П 1 П 1 ft 9 ft
-0,1 0,1 -0,5 0,2
0 0,2 -0,3 0,3
0,3 0 -0,1 -0,3
и для нахождения оценок ковариационной матрицы и ковари-
ковариационной функции достаточно воспользоваться равенствами
(9.7) и (9.8):
0,045 ОДОО
v и \- ( О-065 "О'
' ^^-^-0,020 0,
0,0100 0,0025^
0,0425 -0,0025;- #
"О'020
050
Если заранее известно, что процесс изменения состояния
изучаемого объекта является эргодическим по отношению к
рассматриваемому моменту, то для решения задачи оценивания
этого момента можно обойтись одной реализацией
U =

9.2. Статистические моменты случайного процесса
331
Действительно, если изучаемый случайный процесс является
эргодическим по отношению к математическому ожиданию и
Г = [0,оо), то
\ J
о
и для оценки математического ожидания имеем
t
1
о
где интеграл в правой части равенства находят численно с ис-
использованием выборочной реализации. В частности (рис. 9.4),
если ti — 0,5Д? и At = tJ+i -t3)j = l, N-l, то
т.е. оценкой математического ожидания в рассматриваемом
случае является среднее арифметическое выборочной реализа-
реализации.
At

332 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Аналогично, если стационарный (в широком смысле) слу-
случайный процесс ?(t,u)), t ? Т = [0, оо), является эргодическим
относительно ковариационной функции (обобщение понятия
эргодичности скалярного случайного процесса относительно
дисперсии), то
t-т
1 Г
- T J
О
и оценка ковариационной функции при t — г > 0 имеет вид
t-т
1 /"
где интеграл в правой части равенства находят численно,
используя выборочную реализацию. В частности (см. рис. 9.4),
если наблюдения являются равноотстоящими, то оценку fh^
получают согласно (9.9), а оценку ковариационной функции —
по формуле
1 N-m
m k=l
где N — m > 1, ^+m = tk + mAt. При m = 0 из (9.10) получаем
Пример 9.2. В условиях горизонтального полета самолета
произведена запись вертикальной перегрузки, действующей на
самолет. Перегрузка регистрировалась с интервалом в 2 с в
течение 200 с. Результаты измерений приведены в следующей
таблице.

9.2. Статистические моменты случайного процесса
333
t
0
2
4
б
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
x(t)
1,0
1,3
1,1
0,7
0,7
1,1
1,3
0,8
0,8
0,4
0,3
0,3
0,6
0,3
0,5
0,5
0,7
0,«
0,6
1,0
t
40
42
44
46
48
50
52
54
56
58
60
62
64
66
68
70
72
74
76
78
x(t)
0,5
1,0
0,9
1,4
1,4
1,0
1,1
1,5
1,0
0,8
1,1
1,1
1,2
1,0
0,8
0,8
1,2
0,7
0,7
1,1
t
80
82
84
86
88
90
92
94
96
98
100
102
104
106
108
ПО
112
114
116
118
x(t)
1,5
1,0
0,6
0,9
0,8
0,8
0,9
0,9
0,6
0,4
1,2
1,4
0,8
0,9
1,0
0,8
0,8
1,4
1,6
1,7
t
120
122
124
126
128
130
132
134
136
138
140
142
144
146
148
150
152
154
156
158
x(t)
1,3
1,6
0,8
1,2
0,6
1,0
0,6
0,8
0,7
0,9
1,3
1,5
1,1
0,7
1,0
0,8
0,6
0,9
1,2
1,3
t
160
162
164
166
168
170
172
174
176
178
180
182
184
186
188
190
192
194
196
198
x(t)
0,9
1,3
1,5
1,2
1,4
1,4
0,8
0,8
1,3
1,0
0,7
1,1
0,9
0,9
1,1
1,2
1,3
1,3
1,6
1,5
Необходимо определить оценку корреляционной функции
изучаемого случайного процесса, если известно, что он явля-
является эргодическим по отношению к ковариационной функции.
В данном примере x(t) =?(?,W(i)), где €(t,u), t eT, — ска-
скалярный случайный процесс значений вертикальной перегрузки,
действующей на самолет в горизонтальном полете. Имеем
N — 100 и в соответствии с формулами (9.9), (9.11) находим
- 0,98,
= % = 0,1045.
Так как At = 2 и
То для завершения анализа достаточно воспользоваться фор-
формулой (9.10) и учесть связь ковариационной и корреляционной

334 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
функций:
= 0,505,
= 0,276,
= 0,277,
) = 0,231,
3tf A0) = -0,015,
^ = 0,014,
= 0,071,
Функция к^(т) изображена на рис. 9.5 набором точек, через
которые проведена непрерывная кривая. Не совсем гладкий
вид этой кривой объясняется недостаточным объемом экспе-
экспериментальных данных.^ На рисунке также приведен вариант
аппроксимации оценки к^(т) гладкой функцией, ф
при решении реальных задач математического моделиро-
моделирования наличие априорной информации об изучаемом процессе
позволяет существенно сократить необходимый объем данных
наблюдений, получение которых, как правило, связано со зна-
значительными затратами материальных и временных ресурсов.
Априорная информация об изучаемом процессе может быть
самой разнообразной, но в том или ином виде она всегда имеет-
имеется в распоряжении исследователя. Поэтому далее рассмотрим
методы, предполагающие определенные априорные знания об
изучаемых случайных процессах.

9.3. Оценивание параметров случайного процесса 335
9.3. Постановка задачи оценивания
параметров случайного процесса
Задача, о которой пойдет речь, состоит в том, чтобы по
данным выборочных реализаций случайного процесса ?(t,u>),
t € X1, построить оценки неизвестных параметров, составляю-
составляющих вектор /3. Эту задачу, известную как задача оценивания
параметров случайного процесса по данным его выбороч-
выборочных реализаций, будем рассматривать в предположении, что:
1) динамика состояния изучаемого объекта представляет
собой n-мерный случайный процесс ?(t,oj), t ? Т;
2) состояние изучаемого объекта от значений ряда параме-
параметров объекта, представленных вектором /3 = [j3\ ... j3i) ;
3) невозможно прямое определение параметров изучаемого
объекта, представленных вектором /3.
Рассматривая сделанные предположения как априорную ин-
информацию относительно случайного процесса ?(t,u), t ? Т, при-
приходим к выводу, что все его конечномерные законы распреде-
распределения зависят от вектора параметров /3. Таким образом,
ft(x\t)=ft(x\t;/)),
..,X(N)\ti,...,tN;f3), N > 1.
Из этого следует зависимость от вектора параметров /3 момен-
моментов изучаемого случайного процесса. В частности,
Пример 9.3. Пусть скалярный случайный процесс описы-
описывается стохастической моделью состояния:
eit^^xoexpi-fat + fawfau)), teT = [0,oo), (9.12)
где w(t,u>), t G T, — скалярный винеровский процесс, вьйсо-
дящий из 0, с коэффициентом диффузии а2 — 1; хо > 0 —
Известное детерминированное значение начального состояния;
/3 = (/?! /?2) — вектор неизвестных параметров.

336 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Из (9.12) следует, что
so
Таким образом, при любом фиксированном t ? Т случай-
случайная величина ln(?(?,w)/z0) распределена по нормальному за-
закону с математическим ожиданием —flit и дисперсией {i\t. A
это значит, что одномерная функция плотности вероятностей
изучаемого случайного процесса является плотностью логариф-
логарифмически нормального распределения и зависит от вектора па-
параметров /3, т.е. fz(x\t) = ft(x\t;/3). #
По результатам качественного анализа изучаемого случай-
случайного процесса ?(t,u), t ? Т, с учетом содержательной интер-
интерпретации неизвестных параметров, составляющих вектор /3,
может быть выдвинуто предположение о том, что вектор /3
принадлежит некоторому открытому выпуклому множеству
В С M-L. Если ограничения на значения вектора параметров /3
отсутствуют, то полагают В = KL. Именно этот случай и ис-
исследуется далее.
Итак, мы приходим к следующей задаче: по известным
значениям n-мерного случайного процесса ?(t,u>), t G Г, пред-
представленным множеством {/*, где {/* —любое из рассмотренных
в 9.1 множеств данных наблюдений, необходимо построить
качественную оценку /3 = C(U+) € В вектора неизвестных па-
параметров /3.
Для уяснения понятия „качественная оценка" рассмотрим
случайную выборку объема К для случайного процесса ?(t,u>),
t ?T, зависящего от вектора неизвестных параметров /3:
I \
е[и>)= I *v"'x J , (9.13)
) /
где случайные векторы ^^(и), к=1,К, являющиеся функци-
функциями сечений случайного процесса ?(t,u), t ?T, независимы и
имеют один и тот же закон распределения.

9.3 Оценивание параметров случайного процесса 337
Каждая случайная выборка объема К для случайного про-
процесса ?(t,u), t ? Т, связана с конкретным видом функциональ-
функциональной зависимости случайных векторов ?(fc)(tj), k=l, К, от сече-
сечений случайного процесса ?(t,u), t ?T. Поэтому при решении
практических задач способы формирования случайной выбор-
выборки е(и) определяются схемой испытаний, которые проводятся с
целью получения данных наблюдений, представленных множе-
множеством U*. Значит, {/* — реализация случайной выборки е(и).
Конкретные способы формирования случайной выборки
е(и), соответствующие данным наблюдений, которые предста-
представлены множествами Um, Uin, Umn, рассмотрены в 9.4.
Пусть /Зд (и) — оценка вектора неизвестных параметров /3,
полученная на основе случайной выборки е{и), определенной
в (9.13), т.е. выборочная статистика. В этом случае оценка
/3([/») является реализацией случайного вектора 0к{и) и каче-
качество оценки /3A/*) определяется требованиями, предъявляемы-
предъявляемыми к вероятностным свойствам случайного вектора {Зк (^) • Эти
требования хорошо известны из курса математической стати-
статистики [XVII].
Во-первых, это требование, чтобы оценка была несмещен-
несмещенной:
Во-вторых, это требование, чтобы оценка была состоя-
состоятельной, т.е. для любого числа е > О
Jim Р{|&И-/3||>е} = 0.
Это требование означает, что при неограниченном увеличении
объема случайной выборки оценка /Зк{и) сходится по вероят-
вероятности к истинному значению вектора параметров /3. Заметим,
Что оценка /Зд'(^) является состоятельной, если
&ltficifj) - /?)T(/3a-H - 0)] = 0.
Наконец, в-третьих, это требование, чтобы оценка была
эффективной, т.е. чтобы эта оценка как L-мерный случайный

338 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
вектор, имела минимальный разброс относительно истинного
значения вектора параметров /3, или минимальную дисперсию.
Если первые два требования понятны, то понятие эффек-
эффективности оценки требует разъяснений.
9.4. Эффективные оценки.
Неравенство Рао — Крамера
При изучении свойств оценок и методов их определения
будем использовать функцию плотности вероятностей слу-
случайной выборки объема К для n-мерного случайного процесса
€(t,u>), t € Т, зависящего от L-мерного вектора неизвестных па-
параметров /3 € В. В соответствии с (9.13) эту случайную выбор-
выборку обозначим через ?{ь>), а ее функцию плотности вероятностей
через f(y\fl). Выясним, что представляют собой случайные вы-
выборки и их функции плотности вероятностей, соответствующие
рассмотренным вариантам данных наблюдений.
Пусть fz(X(k)\/3) — fc-мерная функция плотности вероят-
вероятностей случайного процесса ?A,ш), t?T:
~~ ft(x(i\ ••• x{k\\t\ •¦¦ tk'0) (9-14)
где X (к) G Rnk. Будем предполагать существование и ограни-
ограниченность частной производной
дЫХШр) п „ г
Рассмотрим множество реализаций изучаемого случайного
процесса, определенных в (9.2), (9.1):
Вследствие независимости этих реализаций данным наблюде-
наблюдений соответствует случайная выборка е{ш) объема К = т, к-я

9.4. Эффективные оценки. Неравенство Рао — Крамера 339
блок которой
представляет собой случайный вектор размерности nN(k) с
функцией плотности вероятностей ft(X(N(k))\p). При этом
Щк)№,и), t € Т, к = 1,т — независимые п-мерные случайные
процессы, имеющие те же конечномерные законы распределе-
распределения, что и исходный случайный процесс. Поэтому функция
плотности вероятностей рассматриваемой случайной выборки
объема тп имеет вид
m
Если данные наблюдений представляют собой множество
U\n, определяемое согласно (9.3):
l
w) A {((ttUU)Y-1 € T(J)), TW 4 {tj},
то К = N и в силу независимости значений случайного про-
процесса в этом множестве ему соответствует случайная выборка
объема N с функцией плотности вероятностей
N
(9.17)
Для множества независимых значений Umn, определяемого
равенствами (9.4):
(Л' ^
,3-1

340 9 ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
функция плотности вероятностей соответствующей случайной
выборки объема
N
имеет вид
N
П
(9Л8)
Пусть теперь /Зк(и)) — оценка вектора неизвестных пара-
параметров /3, полученная на основе случайной выборки е(и>) объема
К для n-мерного случайного процесса ?(t,u), t G Г, зависяще-
зависящего от L-мерного вектора /3. Обозначим через Ьд"(/3) смещение
оценки (Зк(и)):
М[рк(и>)-(}]= J@K(y)-(})f(y\P)dy, (9.19)
где в правой части равенства находится nA'-кратный интеграл,
а область интегрирования имеет вид
Y={y€RnK:f(y\f))>0}.
Смещение оценки зависит от вектора параметров /3, поскольку
оценка /?a-(w) определена по данным случайной выборки с
функцией плотности вероятностей f(y\/3).
Известно, что неравенство
(9.20)
называемое неравенством Рао — Крамера, определяет ниж-
нижнюю границу для дисперсии оценок вектора параметров. Это
матричное неравенство понимают как поэлементное неравен-
неравенство. Здесь Ъ'к{C) ? Ml(K) — производная смещения оценки

9.4. Эффективные оценки. Неравенство Рао — Крамера 341
по вектору параметров /3; //, € Ml(R) — единичная ма-
матрица; А(/3) — информационная матрица Фишера:
е{и) — случайная выборка объема К для n-мерного случайного
процесса ?(t,u>), t € Г, зависящего от L-мерного вектора /3.
Случайная выборка e(uj) определена равенством (9.13) и
имеет функцию плотности вероятностей f(y\C). Согласно
(9.14)-(9.18), информационная матрица Фишера определена
для любого /3 G В.
Если неравенство Рао — Крамера переходит в равенство,
то оценка 0к{и) является эффективной оценкой вектора пара-
параметров /3.
Для уяснения смысла неравенства Рао — Крамера огра-
ограничимся анализом скалярного случая, когда /3 € R и L = 1, а
неравенство (9.20) имеет вид
D [&И] = М[(&И - fiJ} > A+у, (9.22)
где
Величина А(/3) служит мерой информации, содержащейся в
случайной выборке, и ее называют количеством информации
по Фишеру. Согласно неравенству (9.22), чем больше Д(/3),
тем меньше дисперсия. Вопрос лишь в том, удается ли
использовать эту информацию полностью, чтобы получить
оценку с минимально возможной дисперсией.

342 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Определим количество информация по Фишеру, содержа-
содержащееся в случайной выборке, соответствующей множеству Um,
для чего воспользуемся равенством (9.16):
Учитывая независимость реализаций и (9.23), находим
Так как количество информации по Фишеру, содержащееся в
к'к выборочной реализации, равно
то общее количество информации, содержащееся в случайной
выборке, соответствующей множеству Um, равно
(9.25)
В частности, если ГA) = ГB) = ... = Г(т), то
(9.26)
Таким образом, учитывая (9.22)-(9.26), заключаем, что для
случайной выборки, соответствующей данным наблюдений,
представленным множеством Um, неравенство Рао — Крамера
имеет вид
Е-4Д/3)

9 4 Эффективные оценки Неравенство Рао — Крамера 343
В частности, при Т^ц = ГB) = ... = Г(т) имеем
где Ьк{&) — смещение оценки /?k-(w), определенное в (9.19), и
К = тп.
Для случайной выборки, соответствующей данным наблю-
наблюдений, представленным множеством Umn, с учетом (9.17) по-
получаем аналогичное соотношение:
Таким образом, если
(9.27,
то количество информации в момент времени t =.t3 равно
тп^Щ и
,а,(/?). (9.28)
В соответствии с (9.22), (9.23), (9.27), (9.28) имеем
Полученные неравенства наглядно показывают, что с увели-
увеличением объема выборки теоретически можно строить оценки

344 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
неизвестного параметра /3 со сколь угодно малой дисперси-
дисперсией. При этом, однако, следует учитывать, что мы имеем дело
не с выборочными значениями случайной величины, а с выбо-
выборочными реализациями случайного процесса. Специфическая
особенность последних состоит в том, что задача оценивания
параметров случайного процесса требует исследования един-
единственности ее решения.
9.5. Единственность решения задачи
оценивания параметров случайного процесса
Анализ единственности решения задачи оценивания пара-
параметров случайного процесса по данным наблюдений начнем с
примера.
Пример 9.4. Рассмотрим скалярный случайный процесс
где T](t,u>), t G Г, — стационарный гауссовский случайный про-
процесс с нулевым математическим ожиданием и ковариационной
функцией Кп{т) = е~а I7"', а — известный параметр, a ft, ft, ft,
ft — неизвестные положительные параметры.
В данном случае вектор в неизвестных параметров образо-
л Т
ван четырьмя компонентами /3,-: /3 = (ft ft ft ft) • При t ?T
имеем
а случайный процесс ?(t,u>), t G Т, представляет собой скаляр-
скалярный гауссовский процесс.
Предположим, что для оценивания вектора /3 € Е4 мы рас-
располагаем данными наблюдений, представленными множеством
Umn, где N = 2, т.е. наблюдения проводились лишь в моменты
времени t — t\ и t = ?2 из Т.
Поскольку изучаемый случайный процесс является гауссов-
ским, то его одномерные функции плотности вероятностей

9.5. Единственность решения задачи оценивания параметров 345
f^(x\ti;/3) и fz(x\t2;f3) полностью определены его математиче-
математическим ожиданием и дисперсией, которые по условиям испытаний
можно оценить с использованием стандартных формул (9.6),
(9.7) с учетом того, что М = m\ +m2, mx > 1, т2 > 1. Таким
образом,
Tflf
1 м
1=1
= ^rj+i
Оценку параметра 04 можно строить на двух очевидных равен-
равенствах:
В качестве реализации такой оценки используем функцию
[XVII]
Для построения оценок оставшихся неизвестных параме-
параметров мы не располагаем никакими данными, кроме оценок
математического ожидания fh^(t\) и fh^(t2), используя которые
можно записать систему нелинейных алгебраических уравне-
уравнений относительно оценок /3\, /32, /Зз неизвестных параметров
/?ъ /?2) 0з соответственно:
Piexp{-p2tk) + fo = mt{tk), к = 1,2. (9.29)
Эта система состоит из двух уравнений и содержит три неиз-
неизвестных параметра, т.е. имеет бесчисленное множество реше-
решений.

346 * ЭЛЕМЕНТЫ СТА ТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Таким образом, по данным наблюдений, представленным
множеством Umn с N — 2, задача оценивания неизвестных па-
параметров изучаемого случайного процесса ?(t,u;), t € Т, реша-
решается неоднозначно не зависимо от того, сколько произведено
измерений в моменты времени t\ и ?г-
Если N > 2 и система (9.29) имеет решение, удовлетворяю-
удовлетворяющее условиям положительности своих компонент, то это реше-
решение единственно.
Заметим, что рассматриваемый скалярный случайный про-
процесс при t —> +oo становится стационарным случайным процес-
процессом с математическим ожиданием 0з и дисперсией /?4- Пусть
тетерь Т = [0,ос) и to 6 Т — момент времени, начиная с кото-
которого исходный случайный процесс ?(t.u;), t ?T, можно считать
стационарным. Если t0 6 Т принять за начало наблюдений, то
параметры /3\ и 02 оценить невозможно, как бы мы ни выби-
выбирали моменты измерений t, > t0, и сколько бы измерений ни
проводилось в эти моменты времени, поскольку стационарные
изменения состояния не зависят от значений параметров /?i, /?2
),t>to. #
Для того чтобы сформулировать условие единственности
руления задачи оценивания неизвестных параметров случай-
случайного процесса по данным наблюдений, напомним, что любой
случайный процесс в общем случае не является полностью опре-
определенным и при решении различных задач как теоретического,
ток и прикладного характера исследователь вынужден огра-
ограничиваться использованием конечномерных законов распреде-
распределений. Совокупность конечномерных закоиов распределений
является более или менее полной характеристикой случайно-
случайного процесса. При этом, если ?(t,u), t ?Т= [a,b], — n-мерный
случайный процесс, зависящий от L-мерного вектора неизвест-
неизвестных параметров /3, а Т^щ = {^}?Li С Г, то N-мерная функция
плотности вероятностей

9.5. Единственность решения задачи оценивания параметров 347
содержит исчерпывающую информацию об исходном случай-
случайном процессе на множестве T^n)-
Определение 9-1. Пусть ?(t,u), t € Т = [а,6], — п-мерный
случайный процесс, зависящий от L-мерного вектора неизвест-
неизвестных параметров /?. Говорят, что JV-мерная функция плотности
вероятностей f^(X(N) \0) определяет на Т^) исходный случай-
случайный процесс единственным образом, если равенство
верно тогда и только тогда, когда а = /?.
Интуитивно понятно, что если по данным наблюдений уда-
удается определить такую ЛГ-мерную функцию плотности веро-
вероятностей, которая на некотором множестве Г(дг) С Т задает
изучаемый случайный процесс единственным образом, то су-
существует и единственное решение задачи оценивания вектора
его неизвестных параметров. Для того чтобы практически ре-
реализовать эту идею, будем считать, что /? € В — истинное
значение вектора неизвестных параметров случайного процес-
процесса ?(*,ш), t € Т, и введем скалярную функцию векторного аргу-
аргумента
/(а) = М[1пД(»?(а»)|о)] = I (\nfz(y\a)) f((y\(i)dy, (9.30)
Y
где а е В, Y^ {ye RnN: /4{y\a) > 0}, a
блочный случайный вектор размерности пЛГ. Нас интересует
экстремум этой функции. В связи с этим напомним, что
функцию <р(х) называют выпуклой («низ) на множестве X,

348 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
если для любых х, у ? X и для любого А € [0, 1] имеет место
неравенство
V?(Ax + A - Х)у) <$ \tp(x) + A - \)<р(у).
Известно [V], что для выпуклой (дифференцируемой) функ-
функции <р(х) справедливо неравенство
ip(x) ^ <р(хо) + <р'(хо)(х-хо), х,хо?Х.
Пусть х = х(и)) — случайный вектор и хо — ЪЛ[х(и))}. В этом
случае
Определив математические ожидания правой и левой частей
этого неравенства, приходим к неравенству Иенсена для
выпуклой функции:
Теперь можно сформулировать и доказать теорему един-
единственности решения задачи оценивания неизвестных параме-
параметров случайного процесса по данным наблюдений.
Теорема 9.1. Пусть iV-мерная функция плотности ве-
вероятностей случайного процесса ?(t,u), t ? Т, зависящего от
вектора неизвестных параметров /3 ? В, определяет его на мно-
множестве Т(дг) единственным образом. Тогда задача оценивания
вектора неизвестных параметров этого случайного процесса по
данным наблюдений имеет единственное решение /3, определя-
определяемое условием
тах/(а) =
где функция 1{а) определена равенством (9.30).
А Поскольку —In(а) — выпуклая функция, то по неравенству
Иенсена имеем
м[ I

9.5. Единственность решения задачи оценивания параметров 349
или, что то же самое,
Y Y
где Y = {у G RnN: f^{y\a) > 0, a G В}. А так как для любого
Y Y
то последнее неравенство принимает вид
[
J
Y fdvlft
(9.31)
Это неравенство превращается в равенство тогда и только
тогда, когда
Поэтому из неравенства (9.31) и условия теоремы получаем, что
для любых а € В\ {/3}
f"(ln/«fol/?)) fdv\ftdy> I\\пШа)) Ш/3)<1у,
или, что то же самое,
Таким образом, функция 1(а) имеет на В единственный макси-
максимум в точке а = /3, что и требовалось доказать. >
Доказанную теорему можно использовать для решения прак-
практических задач даже в тех случаях, когда вид iV-мерной функ-
функции плотности вероятностей изучаемого случайного процесса

350 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
неизвестен, а на множестве 7W\ определены лишь его мате-
математическое ожидание и ковариационная матрица как функции
неизвестных параметров.
Рассмотрим этот случай, поскольку он чаще других встре-
встречается в приложениях. Будем считать, что m(t\a) и ?(?|а)
при t € Т(лг) содержат все интересующие нас параметры. Это
означает, что вся интересующая нас информация об изучаемом
случайном процессе представлена в совокупности его одно-
одномерных функций плотности вероятностей {f^(x\t;^): t € Т^}.
Отсюда следует, что для решения задачи оценивания его не-
неизвестных параметров вполне подходит случайная выборка,
соответствующая множеству Umn, функция плотности веро-
вероятностей которой определена равенством (9.18):
П П
C
Для того чтобы выяснить достаточность этих данных для
однозначного оценивания неизвестных параметров, рассмо-
рассмотрим следующую функцию плотности вероятностей
3-Х
н введем множества
G={y: /(у|/3) > 0}, G, = {х: Д(х|«,;/?) > 0}, j = IjV.
При выполнении условий теоремы 9.1 при любых аф(} имеем
f{infW))f{y\0)dy>jQnf(y\a))fW)dy,
G

9 5 Единственность решения задачи оценивания параметров 351
т.е. с учетом определения функции /
N
? I{\nft{x\t3;0))U{x\t,M$)dx>
N
или
N N
3 = 1 J=l
Однако по условию задачи вид функции плотности вероятно-
вероятностей fz(x\t;C) неизвестен. Тем не менее, задачу можно решить,
если в качестве f^(x\t;/3) использовать плотность нормального
закона распределения и наложить на функции m(t\a) и Е(?|а)
дополнительные ограничения.
Определение 9.2. Будем говорить, что функции m(t\a)
и Е(? | а) разделяют точки множества В на множестве
^(ЛГ) = {^}jLi с Т, если для любых а, у G В, а ф у, существует
хотя бы одно значение tay ? T^n)j такое, что
m{tai | а) ф m(tay 17), E(tay \ а) ф S(ia717).
Теорема 9.2. Пусть математическое ожидание m(t\a) и
ковариационная матрица Е(?|ек) n-мерного случайного процесса
€(t,u)), t 6 Т, зависящего от L-мерного вектора неизвестных
параметров /3 € В, разделяют точки множества В на множестве
T(N) С Т. Тогда задача оценивания неизвестного вектора
параметров /3 G В имеет единственное решение, определяемое
условием

352 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
где
N
N
'=4
| m(?|a),E(?|a)) — плотность нормального распределения:
1
fH(x\m(t\a),E(t\a)) = -
a f^{x\t]f3) — неизвестная истинная одномерная функция плот-
плотности вероятностей случайного процесса.
Доказательство теоремы 9.2 опирается на следующее утвер-
утверждение.
Лемма 9.1. Пусть г)(и) — n-мерный случайный вектор с
функцией плотности вероятностей fv(%), математическим ожи-
ожиданием mv и ковариационной матрицей ?,,, a /#(:r|m,?) —
плотность распределения вероятностей n-мерного случайного
вектора, распределенного по нормальному закону с математи-
математическим ожиданием m и ковариационной матрицей Е. Тогда для
любых m ? Rn и Ее Мп(Щ, таких, что m ф mv нЕ^ T,v, верно
неравенство
-4 Докажем, что
maxM [In /я{г,{и) \ то, Щ = М [in fH{V{lj) \ тч, Е„)].

9.5. Единственность решения задачи оценивания параметров 353
Действительно,
п/я(т?(^) |т,Е)] = max(-0,5nlnB7r) -
- 0,51n(detE) - O,5M[(f7(w) - m^E {tj{oj) - m)]) =
= -0,5nlnB7r)-0,5minZ(m,E),
где
Z(m, S) = In (det S) + M [(ij(w) - m)T E (fj(w) - m)].
Поскольку М[т7(ы)] — mv, то Z'm(m,S) = 0in тогда и только то-
тогда, когда M[(t7(w) — т)т?-1] = 8in. Таким образом, функция
Z(m,E) достигает минимума при m = mv. А так как, соглас-
согласно свойствам следа для произведения согласованных матриц*,
верно представление
Z(m,E) = ln(detE) +SP(E-1M[(t?(w) - m) {tj(oj) - m)T]),
то очевидны равенства
Z(m4lE) = ln(detE) + Sp(E-1ET;), Z(mv,Zv) = ln(detE4) + n.
При этом Zj^m^E) = 8nn тогда и только тогда, когда Е —
- (Е~1JЕТ, = 8ПП. Таким образом,
minZ(m,E) = Z(m,,E4) = ln(detE4) + n,
771,E
т.е. при любых m / mv иЕ/Е^ имеем
М[1п/д(|7(ы)|тч,Еч)] >М[1п/я(т?И|т,Е)]. >
Теперь вернемся к доказательству теоремы 9.2.
М Функция
~ N
^[и)\а)] (9.32)
*См.: Беллман Р.

354 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
при а = /3 достигает максимума, так как при j = 1, N
M[(Z(tj,u,)-m(tj\f3))(Z(tj,u>)-m(tj\l3))T]='E(tj\l3)
и в соответствии с леммой 9.1 каждое слагаемое в правой части
(9.32) достигает максимума, поскольку /н{х\1;а) — функция
плотности вероятностей нормального закона распределения.
Этот максимум является единственным, т.е. для любого
a ? В, такого, что а ф /3, имеем
N
3 = 1
N
и)|а)]=*(а), (9.33)
3 = 1
так как функции m(t,oi) и ?(?|а) определены на множестве
Т{м)= {tj}jLi единственным образом и при а ф /3 всегда най-
найдется хотя бы один момент времени ta$ ? Г(дл, такой, что
а значит, для соответствующих ему слагаемых в суммах нера-
неравенства (9.33) будем иметь
M[\nfH{Z(ta0,u>)\l3)]>M[lnfH(Z(ta0,u>)\a)\.
Поэтому для любого a G В, такого, что а ф /3, имеем
а следовательно,
тах7(а)=7@). >
Итак, в ряде случаев, нередко встречающихся в приложе-
приложениях, единственность решения задачи оценивания неизвестных

9.6. Метод максимального правдоподобия 355
параметров изучаемого случайного процесса по данным наблю-
наблюдений можно проверить непосредственно на основании получен-
полученных теоретических результатов.
Из теоремы 9.2 вытекает весьма важное следствие, состо-
состоящее в том, что в тех случаях, когда конечномерные функции
плотности вероятностей исходного случайного процесса неиз-
неизвестны, для решения задачи оценивания можно использовать
функции плотности вероятностей нормального закона распре-
распределения.
Вопрос о том, как повлияет замена неизвестного конечно-
конечномерного закона распределения изучаемого случайного процесса
соответствующим нормальным законом распределения на каче-
качество оценок неизвестных параметров, пока оставим открытым
и вернемся к нему при рассмотрении квазиправдоподобных оце-
оценок.
Прежде чем перейти к анализу методов оценивания неиз-
неизвестных параметров изучаемых случайных процессов, отме-
отметим, что пример 9.4 наглядно иллюстрирует идею метода мо-
моментов [XVII]. Эта идея состоит в том, что для нахождения
оценок неизвестных параметров исходного случайного процес-
процесса составляют систему уравнений путем приравнивания те-
теоретических моментов, являющихся функциями неизвестных
параметров, к соответствующим статистическим моментам,
которые являются функциями данных наблюдений. Метод мо-
моментов далее мы рассматривать не будем.
9.6. Метод максимального правдоподобия
Метод, о котором пойдет речь, получил, пожалуй, наи-
наибольшее распространение в практике научных исследований.
Он является весьма эффективным средством решения зада-
задачи оценивания параметров случайного процесса по данным
наблюдений при известном виде законов распределения соот-
соответствующих случайных выборок, зависящих от оцениваемых
параметров.

356 9 ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
На первый взгляд может показаться, что необходимость
знания вида этих законов распределения является слишком
жестким ограничением для практического применения рассма-
рассматриваемого метода. Однако, как станет ясно из дальнейших
рассуждений, этот метод позволяет получать состоятельные,
асимптотически несмещенные и асимптотически нормальные
оценки неизвестных параметров даже в тех случаях, когда те-
теоретический и фактический законы распределения случайных
выборок изучаемого случайного процесса не совпадают.
Идея этого метода состоит в следующем. Пусть iV-мерная
функция плотности вероятностей
ftW) = fdxV.),-,x(N)\h,..;tN;P), y = X(N)
изучаемого n-мерного случайного процесса ?(t,u), t ?T, зави-
зависящего от L-мерного вектора неизвестных параметров /3 € В,
определяет этот процесс на множестве 7W) = {tk}^=1 С Т един-
единственным образом. Если воспользоваться функцией 1(ос), опре-
определяемой равенством (9.30), то из теоремы 9.1 можно за-
заключить, что в рассматриваемом случае для любого а ? В \ {/3}
выполняется неравенство
откуда
Для практического использования этого результата в по-
последнем равенстве заменим математическое ожидание его
оценкой, определяемой по данным наблюдений, представлен-
представленным множеством Um. Тогда с учетом (9.1), (9.2), (9.14), (9.16)
получим
, т 1 m
к=\ к=1
где /Зт — оценка вектора неизвестных параметров /3.

9.6. Метод максимального правдоподобия 357
Такой метод оценивания, известный как метод максималь-
максимального правдоподобия, был предложен К. Гауссом. Оценку (Зт
вектора неизвестных параметров /3 называют оценкой мак-
максимального правдоподобия (или максимально правдоподобной
оценкой), а функцию
m
L{a\Um)±-Y,\nf({((T(k),u,(k))\a) - (9.34)
Ш *=i
функцией максимального правдоподобия. В рассматриваемом
случае оценку максимального правдоподобия /Зт вектора неиз-
неизвестных параметров /3 определяют из уравнения
и записывают так:
/?m = argmaxL(a|[/m). (9.35)
а?В
Если данные наблюдений представлены множеством Umn,
то с учетом (9.4) и (9.18) функцию максимального правдоподо-
правдоподобия можно записать следующим образом:
N 1
3
А так как в рассматриваемом случае множество Umn является
реализацией соответствующей случайной выборки объема М
для изучаемого случайного процесса ?(t,u), t G Г, зависящего
от вектора неизвестных параметров /3 ? В, то с учетом (9.36)
оценка максимального правдоподобия равна
/?M = argmaxL(a|[/M;v). (9.37)
Из (9.34), (9.36) и (9.35), (9.37) видно, что влияние специфи-
специфики данных наблюдений на формальную процедуру определения
оценок максимального правдоподобия для вектора неизвестных
параметров не является принципиально значимым для дальней-
дальнейшего изложения. Поэтому, исходя исключительно из сообра-

358 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
жений компактности и> наглядности представления материала,
ограничимся данными наблюдений, представленными множе-
множеством Um.
В литературе по математической статистике функцией
максимального правдоподобия принято называть совместную
функцию плотности вероятностей случайной выборки [XVII].
А так как при решении теоретических и практических за-
задач, как правило, используют не саму функцию максимального
правдоподобия, а ее натуральный логарифм, то сочтем возмож-
возможным назвать функцией максимального правдоподобия функ-
функцию L{ot\U*). По этой же причине при рассмотрении теории
квазиправдоподобных оценок функция L(a\U*) названа функ-
функцией квазиправдоподобия.
Оценку называют асимптотически несмещенной, ес-
если при неограниченном возрастании объема случайной выборки
она становится несмещенной. Аналогично определяются поня-
понятия асимптотически эффективной и асимптотически
нормальной оценки. Оценку называют нормальной оцен-
оценкой, если она получена по данным случайной выборки, распре-
распределенной по нормальному закону.
Теорема 9.3. Пусть iV-мерная функция плотности вероят-
вероятностей
n-мерного случайного процесса ?(t,u), t G Т, зависящего от
L-мерного вектора неизвестных параметров /3 € В, разделяет
точки В на множестве Т(дг) = {tk}^-1 С Т. Пусть для функ-
функции f^(y\a) при любом а € В существуют и ограничены все
частные производные по компонентам вектора а до третьего
порядка включительно. Тогда, если данные наблюдений пред-
представлены множеством Um, то оценка максимального правдо-
правдоподобия /Зт, определяемая равенствами (9.35), (9.34), является
состоятельной, асимптотически несмещенной, асимптотически
эффективной и асимптотически нормальной.

9.6. Метод максимального правдоподобия 359
Доказательство сформулированной теоремы при сделанных
предположениях практически ничем не отличается от доказа-
доказательства соответствующей теоремы о свойствах максимально
правдоподобной оценки параметра распределения случайной
величины, которое можно найти в литературе по математиче-
математической статистике*. Не останавливаясь на доказательстве теоре-
теоремы 9.3, проиллюстрируем метод максимального правдоподобия
на примере скалярного случайного процесса (9.12) (см. пример
9.3).
Пример 9.5. Рассмотрим скалярный случайный процесс,
определенный стохастической моделью состояния в форме
Ито:
,u>) dw(t,u),
где w(t,u>), ieT = [0,oo), — скалярный винеровский процесс
с единичным коэффициентом диффузии; х0 > О — известное
начальное состояние, а 0 — ф\ fa) — вектор неизвестных
параметров с положительными компонентами.
Для того чтобы записать TV-мерную функцию плотности ве-
вероятностей рассматриваемого случайного процесса, полагаем
Как показано в примере 7.5, скалярный случайный процесс
T](t,u>), t G Т, определен следующей стохастической моделью
состояния:
(9.OOJ
где уо = \пхо. Поэтому он является гауссовским скалярным
процессом. Кроме того, непосредственно из стохастической мо-
модели состояния (9.38) вытекает, что математическое ожидание
"См.: Крамер Г., Мудрое В.И., Кушко В.Л.

360 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
ttj-tj(i J /3) является решением задачи Коши:
и (9-39)
Чтобы определить дисперсию Dv{t\f3), рассмотрим случайный
процесс
который, согласно (9.38), (9.39), удовлетворяет стохастической
модели состояния
и имеет нулевое математическое ожидание. Так как в этом
случае Dv(t\/3) = M[z2(t,u)], то
\Д,(О|/З) = о. (9-40)
Для того чтобы определить выражения для условного ма-
математического ожидания
mv(ti+1\ti;C) =
и условной дисперсии
математические модели (9.39), (9.40) следует рассматривать
на временном интервале (t,-,t,-+i]:
Dri(ti\ti;/3) = 0.

9.6. Метод максимального правдоподобия 361
Решая задачи Коши (9.41), (9.42), получаем
mr,(tt+1\ti;t3) = y(ti)-f3l(ti+1-ti), Dn{ti+l \tt;f3) = CJ(ti+1 -«,-).
Теперь можно записать условную функцию плотности вероят-
вероятностей:
. (9.43)
Поскольку рассматриваемый случайный процесс r)(t,u), ? ? Т,
является марковским процессом, его iV-мерная функция плот-
плотности вероятностей имеет вид
ЛГ-1
Ш0)= YlfMU+i)\v(tiY,0)- (9-44)
Приступим к решению задачи оценивая неизвестных пара-
параметров /3i и /З2, составляющих вектор /3, методом максималь-
максимального правдоподобия. Предположим, что данные наблюдений
представлены множеством Um и определены согласно (9.1),
(9.2). Для упрощения записи введем обозначение:
) =
х) = Wkj^ik)), j = l,N(k), k = T^n~.
Тогда, согласно (9.34), (9.44) и равенству
функцию максимального правдоподобия L(j3\Um) можно запи-
записать в виде
m
k-\ j=

362 9. ЭЛЕМЕНТЫ СТА ТИСТИКИ СЛУ ЧА ИНЫХ ПРОЦЕССОВ
С учетом представления (9.43) получаем
m)=C-~
2тп ^—' ^—'
fc=i j=i
где
m m N{k)-1
/ у Orr> f У f У
k=\ k=\ J = l
Отметим, что С не зависит от /3. Нетрудно убедиться в том,
что функция максимального правдоподобия имеет единствен-
единственный максимум в точке /3 с координатами:
m N{k)-1
к=\ j=i
Л 1 m
где
суммарное время наблюдений. Координаты Ci и /3i удовлетво-
удовлетворяют системе алгебраических уравнений
дЩ\Цт) _^ дЩ\Цт) _Q #
Сделаем одно важное замечание, касающееся применения
как метода максимального правдоподобия, так и других мето-
методов. Дело в том, что мы считаем известным вид функции плот-
плотности вероятностей f^(y\a), которая при а — C представляет

9 6 Метод максимального правдоподобия 363
собой iV-мерную функцию плотности вероятностей изучаемого
случайного процесса. Ослабим это условие и предположим, что
iV-мерная функция плотности вероятностей рассматриваемого
случайного процесса ?{t,u>), t ?T, задана функцией f*(y\ot), в
то время как в действительности она представляет собой функ-
функцию fz{y\a)- В этом случае полагают
Y
и рассматривают функцию квазиправдоподобия
В качестве оценки вектора /3 неизвестных параметров берут
квазиправдоподобную оценку
/3m = arg max L (a \ Um) ¦
Это мы уже рассматривали в 9.5: в теореме 9.2 было показа-
показано, что при известных предположениях относительно функции
плотности вероятностей нормального закона распределения за-
задача оценивания вектора неизвестных параметров C имеет
единственное решение. В общем случае следует потребовать
выполнения неравенства
Т@)>Т(а), ае
Так как выборочное среднее является состоятельной оценкой
для математического ожидания, то
и с учетом предыдущего неравенства можно доказать состоя-
состоятельность квазиправдоподобной оценки /Зт вектора неизвест-
неизвестных параметров /3.
Пусть

364 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
гдеаеВп у € Y = {у € RnN: Му\а)МУ\а) > °Ь Предполо-
Предположим, что выполнены следующие условия.
1. При каждом а ? В и у ? Y существуют все частные
производные для функции Ф(у\а) по компонентам вектора а
до третьего порядка включительно и
2. При любых а ? В и у
д3Ф(у\а)
причем
I h(y) ft(y\a)dy < М < <х(М > 0).
Y
3. При каждом а € В
I
A(y\a)f(:(y\a)dy =
Y
4. При каждом а ? В существуют матрицы
Г(а)±-JB(y\a)fz(y\a)dy,
Y
{*)± JAT(y\a)A(y\a)ft(y\a)dy,
Y
причем матрица Г(а) положительно определена.
Теорема 9.4. Если выполнены условия 1-4, то квазиправ-
квазиправдоподобная оценка (Зт сходится по вероятности к истинному
значению неизвестного вектора параметров и является асимп-
асимптотически несмещенной и асимптотически нормальной оценкой
с ковариационной матрицей

9.6. Метод максимального правдоподобия 365
Доказательство этой теоремы также можно найти в литера-
литературе по математической статистике*. Не приводя его, поясним
теорему на конкретном примере.
Пример 9.6. Рассмотрим скалярный случайный процесс
?(t,u>), t ? Т — [О, оо), определяемый стохастической моделью
состояния в форме Ито
= @з-@1-О,502К(г,о;))сЙ +
>)dw(t,u), (9.45)
где w(t,u), t €T, — скалярный винеровский процесс с коэф-
коэффициентом диффузии <т2 = 1; io > 0 — известное начальное
Т
состояние, а /3 = @i 02 0з) — вектор неизвестных параметров
с положительными компонентами.
При 0з = 0 получаем стохастическую модель состояния, рас-
рассмотренную в примере 9.5. Однако при 0з > 0 записать iV-мер-
ную функцию плотности вероятностей изучаемого случайного
процесса, как это было сделано в примере 9.5, не удается. Дей-
Действительно, пусть
В этом случае по правилу дифференцирования Ито получаем
'dT){t,U>) = (-^~ -
где T](t,ui), t € Г, — исходный случайный процесс.
Поскольку мы не можем определить iV-мерную функцию
плотности вероятностей случайного процесса r)(t,u), t ? Т, то
для решения задачи оценивания неизвестных параметров мо-
модели (9.45) по данным наблюдений мы не можем использовать
*См.: Мудрое В.И., Кушко В.Л.

366 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
метод максимального правдоподобия. Для определенности бу-
будем считать, что располагаем данными наблюдений, предста-
представленными множеством Umn- Получим квазиправдоподобные
оценки неизвестных параметров модели (9.45), представленные
вектором /3.
Так как в рассматриваемом случае данные наблюдений
представлены множеством Umn и определены согласно (9.4),
то функция квазиправдоподобия имеет вид
N 1
WUmn) = Y,—
Если для упрощения записи ввести обозначение
x)±t(tJtu,(i)), j = l,N, ieIU) = <
k=i
и подставить выражение для функции плотности вероятностей
нормального закона распределения, то получим
1 N
| = -0,5ЛГ1пB7г)--5>О(^|/3)-
3 = 1
И--(',Wf (946)
,
В соответствии с результатами, приведенными в 7.2, функции
m(t\/3) и D{t\K) являются решениями следующих задач Коши:
(М7)
(9>48)

9.7. Метод наименьших квадратов 367
Нетрудно убедиться в том, что при N > 3 функции т(у\E)
и D(y\/3) разделяют точки области изменения параметров на
множестве Г(дг) = {^}^=i- Поэтому задача оценивания имеет
— л* —— X
единственное решение /3= (/?i /Зг 0з) , представляющее собой
квазиправдоподобную оценку вектора неизвестных параметров
/3. Эта оценка обладает всеми свойствами, перечисленными в
теореме 9.4, поскольку выбранная для решения задачи гауссова
функция плотности вероятностей удовлетворяет условиям дан-
данной теоремы.
Заметим, что решения задач Коши (9.47), (9.48) можно
записать в явном виде и подставить в правую часть (9.46).
Однако сложность получаемых зависимостей не позволяет в яв-
явном виде записать координаты точки максимума для функции
L{P\Umn), как это было сделано в примере 9.5. Поэтому в дан-
данном случае квазиправдоподобную оценку находят с помощью
численных методов решения экстремальных задач [XIV].
9.7. Метод наименьших квадратов
Рассмотрим случай, когда данные наблюдений представле-
представлены множеством Umn, а математическое ожидание m(t\a) и
ковариационная матрица ?(?|ог) изучаемого n-мерного случай-
случайного процесса ?(t,u), t € Г, зависящего от L-мерного вектора
неизвестных параметров /3 € В, разделяют точки В на мно-
множестве T(jv) = {^j}^Li С Т. Будем считать, что отсутству-
отсутствует априорная информация относительно одномерной функции
плотности вероятностей f^(x\t;/3). В этом случае, согласно
теореме 9.2, при решении задачи оценивания вектора неизвест-
неизвестных параметров C ? В случайного процесса ?(t,u), t?T, можно
использовать плотность нормального распределения.
Действительно, согласно теореме 9.2,
(9.49)

368 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
где
N
Заменив математическое ожидание его оценкой, приходим к
функции, аналогичной функции максимального правдоподобия
(9.36):
Так как
то точки максимума функции L(a| ?/д/Лг) совпадают с точками
минимума функции
C{a\UMN)±-2L(a\UMN)-nNln{2ic) =
N N
Согласно теореме 9.2 и результатам, приведенным в 9.6,
квазиправдоподобная оценка вектора неизвестных параметров
/3 € В равна
Если ковариационная матрица изучаемого случайного про-
процесса известна и не зависит от вектора неизвестных параме-
параметров, т.е. S(i|et) = S(?) при а ? В и t ? Т^, то в этом случае

9.7. Метод наименьших квадратов 369
сумма
N
не зависит от а и для решения исходной задачи оценивания
можно использовать функцию
-E^E№'u(.))-m(M«))Tx
,o>(i))-m(*»), (9.50)
где ?(?j), j = 1,ЛГ, — известные квадратные матрицы поряд-
порядка п.
Функцию Ф(а|{/млг) называют критерием метода наи-
наименьших квадратов, оценку
/Зм = а^ттФ(о!|С/млг) — (9.51)
оценкой наименьших квадратов для вектора /3, а рассмо-
рассмотренный метод решения задачи оценивания — методом наи-
наименьших квадратов. Известные матрицы ?(?j), j = l,N,
называют весовыми матрицами критерия.
Поскольку (9.51) в данном случае эквивалентно (9.37), то
оценка наименьших квадратов обладает всеми свойствами ква-
квазиправдоподобной оценки, т.е. она является состоятельной,
асимптотически несмещенной и асимптотически нормальной.
Заметим также, что в случае, когда изучаемый случайный
процесс является гауссовым, она представляет собой оценку
максимального правдоподобия и, как следствие, является еще
и асимптотически эффективной.
Отметим, что метод наименьших квадратов позволяет оце-
оценивать только те параметры изучаемого случайного процесса,
от которых зависит его математическое ожидание, и лишь при
условии, что оно определено на множестве Х^дп единственным

3 70 9. ЭЛЕМЕНТЫ СТА ТИСТИКИ СЛУЧА ИНЫХ ПРОЦЕССОВ
образом. Во многих практических задачах весовые матрицы
S(?) при различных значениях t ? Т(дг) неизвестны. В этих слу-
случаях „веса" назначают исходя из каких-либо дополнительных
соображений, а если таковые отсутствуют, то чаще всего про-
просто полагают
?(*) = /„, t € T[N). (9.52)
Для пояснения сказанного обратимся еще раз к скалярному
случайному процессу, рассмотренному в примере 9.3:
ftf.wj^xoexpf-frf + ftu^.w)), *еГ=[0,оо),
где w(t,u>), t ? Т, — скалярный винеровский процесс с коэф-
коэффициентом диффузии а2 = 1, хо > 0 — известное детерминиро-
детерминированное значение начального состояния, а /3 = {j3\ fa) — вектор
неизвестных параметров. Как мы уже знаем,
Предположим, что мы располагаем данными наблюдений, пред-
представленными множеством Umn и определяемыми согласно (9.4).
Очевидно, что в этом случае функция m(t\/3) не разделяет точ-
точки В на множестве 77дг), поскольку она однозначно зависит
лишь от параметра
А> = -01 + 0,5/32.
Следовательно, методом наименьших квадратов можно оценить
лишь параметр Cq. Для этого составим сумму квадратов
отклонений (9.50). Предполагая, что дисперсия случайного
процесса нам неизвестна, введем „веса" в соответствии с (9.52)
и в результате получим
В соответствии с проведенными рассуждениями оценка параме-
параметра /Зо определяется как точка минимума функции Ф(Cо \

Вопросы и задачи 371
В заключение сделаем замечание, касающееся рассмотрен-
рассмотренных методов оценивания неизвестных параметров.
Замечание 9.1. Условие единственности решения задачи
оценивания получены нами как условие единственности экстре-
экстремума функции
= J {In ft(y\(}))f((y\(})dy.
Y
При решении конкретных задач, располагая случайными вы-
выборками ограниченного объема, мы заменяем математическое
ожидание его оценкой. Получаемая при этом функция (функ-
(функция правдоподобия или функция Ф в методе наименьших ква-
квадратов) на самом деле может иметь несколько экстремумов.
Полученные условия гарантируют единственность экстремума
лишь при неограниченном увеличении объема выборочных реа-
реализаций.
Вопросы и задачи
9.1. Что Вы знаете о данных наблюдений, представленных
множествами Um и UmnI В чем заключается их принципиаль-
принципиальное отличие?
9.2. Сформулируйте задачу оценивания параметров случай-
случайного процесса по данным наблюдений.
9.3. Что представляют собой случайные выборки, реали-
реализациям которых соответствуют данные наблюдений, предста-
представленные множествами Um и Umn^
9.4. Какой вид и почему имеют функции плотности вероят-
вероятностей случайных выборок, соответствующих данным наблю-
наблюдений, представленным множествами Um и Umn1-
9.5. Определите количество информации по Фишеру, со-
содержащееся в случайных выборках, соответствующих данным
наблюдений, представленным множествами Um и

372 9 ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
9.6. При каких условиях iV-мерная функция плотности
вероятностей f^{y\C) определяет исходный случайный процесс
на множестве Т^дг) С Т единственным образом?
9.7. В каких случаях функции m(t\a) и ?(*|а) определены
на множестве Т^ с Т единственным образом?
9.8. Сформулируйте теорему единственности решения за-
задачи оценивания вектора неизвестных параметров случайного
процесса в случае, когда вид функции плотности вероятностей
для этого случайного процесса неизвестен.
9.9. В чем состоит основная идея метода максимального
правдоподобия?
9.10. При выполнении каких условий оценка максималь-
максимального правдоподобия является состоятельной, асимптотически
несмещенной, асимптотически эффективной и асимптотически
нормальной?
9.11. Какую оценку вектора неизвестных параметров изу-
изучаемого случайного процесса называют квазиправдоподобной?
В чем принципиальное отличие оценки максимального правдо-
правдоподобия от квазиправдоподобной оценки?
9.12. В чем состоит основная идея метода наименьших
квадратов?
9.13. Связаны ли между собой оценка наименьших квадра-
квадратов, оценка максимального правдоподобия и квазиправдопо-
квазиправдоподобная оценка? Если между перечисленными оценками суще-
существует связь, то какова она?
9.14. Пусть выполнены условия единственности решения за-
задачи оценивания неизвестных параметров случайного процесса
по данным наблюдений. Допустим, что решение задачи оце-
оценивания возможно одним из известных методов. Возможна
ли ситуация, когда применение различных численных методов
приводит к различным результатам решения задачи оценива-
оценивания?

Вопросы и задачи 373
9.15. Пусть ?(t,u), t € Г, — скалярный случайный процесс,
данные наблюдений представлены множеством Um, a t^ = ?,,
к = 1,т, j = 1, N. Докажите, что оценка
mlt) =
является эффективной оценкой математического ожидания m(t)
рассматриваемого случайного процесса.
9.16. Пусть ?(t,u>), t (E T, — скалярный стационарный гаус-
совский случайный процесс с математическим ожиданием /З1/3
и дисперсией 1, а данные наблюдений представлены множе-
множеством Uin- Докажите, что:
а) оценка
N з
)
является асимптотически несмещенной оценкой параметра /3 и
имеет смещение 6jv(/3) = SN'1^1^3 +/3;
б) оценка
N
является несмещенной оценкой параметра /3.
9.17. В условиях задачи 9.16 докажите, что оценка
является смещенной и асимптотически смещенной.
Указание: убедитесь, что смещение оценки /Здг имеет вид
/

374 9. ЭЛЕМЕНТЫ СТАТИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
9.18. Покажите, что для оценки /Здг в задаче 9.16 неравен-
неравенство Рао — Крамера имеет вид ffg ^ 9N~l04/3.
9.19. Докажите, что в примере 9.5 оценка 0\ является несме-
несмещенной, а оценка 0\ — смещенной. Определите несмещенную
оценку для параметра 0\.
Ответ: $ = N/(N-1).
9.20. Убедитесь в том, что в примере 9.5 функция правдо-
правдоподобия имеет единственный экстремум.
9.21. Докажите, что в примере 9.6 математическое ожи-
ожидание m(t\0) и дисперсия D(t\0) при N > 3 разделяют точки
области изменения параметров В на множестве Ti^y
9.22. Докажите, что в примере 9.5 случайные величины
fa-fa JN-lm
~W и ~~a—\~~n~ '
где 0i a 02 — неизвестные истинные значения параметров,
имеют соответственно распределения х2 и Стьюдента с числом
степени свободы N — 1.

10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
СТОХАСТИЧЕСКИХ
МОДЕЛЕЙ СОСТОЯНИЯ
В этой главе продолжим изучение методов статистики слу-
случайных процессов, но от общих теоретических положений и
иллюстративных примеров, приведенных в предыдущей гла-
главе, перейдем к задаче параметрической идентификации
стохастических моделей состояния. Другими словами,
будем рассматривать задачу оценивания неизвестных параме-
параметров, входящих в стохастическую модель состояния, по дис-
дискретным значениям его выборочных реализаций.
10.1. Еще раз о стохастической модели состояния
В 7.1 стохастическая модель состояния, представляющая
собой задачу Коши для системы стохастических дифферен-
дифференциальных уравнений и описывающая изменения состояния изу-
изучаемого объекта во времени, была получена как результат
возмущения исходной детерминированной модели. Разумеет-
Разумеется, существуют и другие пути, приводящие к стохастическим
моделям. Однако в рамках этой книги мы не будем на них оста-
останавливаться и продолжим обсуждение, начатое в 7, поскольку
именно этот подход чаще всего используют в технических при-
приложениях.
Пусть спроектирован некий объект и для описания изме-
изменений его состояния во времени разработана математическая
модель, представляющая собой задачу Коши для системы обык-
обыкновенных дифференциальных уравнений
(X'{t) = F(X,a),
{ W K ' 10.1)

376 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
где X(t) — n-мерный вектор состояния объекта в момент вре-
времени t, Xq — его начальное состояние, а а ? KL — вектор
параметров объекта. В процессе эксплуатации объекта эти
параметры 7)шумят", т.е. по тем или иным непрогнозируемым
причинам отклоняются от своих номинальных значений. Так,
например, для электронного устройства компонентами вектора
параметров а могут являться значения емкостей, индуктивно-
стей, сопротивлений и других характеристик его элементов,
которые, например, могут зависеть от температуры, влажно-
влажности и других внешних воздействий. Поэтому, повторив рассу-
рассуждения, приведенные в 7.1, приходим к выводу, что реально
наблюдаемые изменения состояния рассматриваемого объекта
должны удовлетворять стохастической модели состояния
где ?(t,u), t?T= [0, оо), — m-мерный белый шум с единичной
матрицей спектральных интенсивностей, а П ? MLm(K) — в
общем случае неизвестная матрица.
Далее будем говорить, что детерминированная модель
состояния A0.1) устойчива к возмущениям П?(?,ы), t ?T =
= [0, сю), вектора параметров а, если для любого е > 0 суще-
существует такое t* ? Т, что ||Х(?,ы) — Х(?)||ск < е при t ^ t*, где
случайный процесс X(t,u), t?T, задан стохастической моде-
моделью состояния A0.2).
Следует отметить, что введение в детерминированную мо-
модель состояния изучаемого объекта случайных возмущений в
виде белого шума может привести к нарушению ее устойчиво-
устойчивости. Поясним сказанное на следующем примере.
Пример 10.1. Рассмотрим простейшую детерминирован-
детерминированную модель состояния
(x'(t) = -ax(t),
Ь@) = 1,

10.1. Еще раз о стохастической модели состояния 377
в которой a > 0. В этой модели состояние изучаемого объекта
x{t) = e~at, t^ 0, стремится к нулю при t -t +oo.
Предположим, что случайным возмущениям подвержен па-
параметр а. Тогда стохастическая модель состояния, соответ-
соответствующая исходной детерминированной модели, имеет вид
= -ax[t,U)
at
шх@,ч>) = 1,
где 72 — известная постоянная величина, называемая спек-
спектральной интенсивностью процесса случайных возму-
возмущений, &€(t,u>), t еГ = [0,оо), — белый шум с интенсивностью
с—\. Воспользовавшись результатами, изложенными в 7.3, за-
запишем стохастическую модель состояния в форме Ито:
fdx(t,oj) = ~(a- 0,5f2)x(t,u>) dt + fx(t,w) dw(t,w),
где w(t,u)), t ?T, — скалярный винеровский процесс с коэф-
коэффициентом диффузии а2 = 1. В примере 7.5 мы показали, что
математическое ожидание состояния x(t,u), t J> 0, в рассма-
рассматриваемом случае равно
((a-0,572)*), * ? 0,
а его дисперсия равна
B(t) = y2texp(-2(a-j2)t), t^O.
Таким образом, если а < -у2, то математическое ожидание
m(t) изучаемого случайного процесса x(t,u), t E T, неограни-
неограниченно возрастает при t —» +оо. То же самое происходит и с
его дисперсией. А так как при а < 72 динамика состояния де-
детерминированной модели принципиально отлична от динамики
математического ожидания m(t) состояния ее стохастического
аналога, то в этом случае исходная дехерминированная модель
состояния не обладает устойчивостью к возмущениям входя-
входящих в нее параметров.

378 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Заканчивая анализ, заметим, что рассмотренная стохасти-
стохастическая модель состояния сохраняет устойчивость при у2 < а,
т.е. при малых случайных возмущениях. #
Заметим, что детерминированная модель состояния, рас-
рассмотренная в примере 10.1, будет обладать устойчивостью к
возмущениям входящих в нее параметров, если процесс случай-
случайных возмущений ввести аддитивно:
Но в этом случае интерпретация этих возмущений будет уже
иной и может быть связана не с зависимостью значения пара-
параметра а от случайных внешних воздействий, а с их непосред-
непосредственным влиянием на скорость изменения состояния. В общем
случае мы должны учитывать возможность как аддитивных,
так и мультипликативных возмущений. Применительно к усло-
условиям примера 10.1 это означает необходимость рассмотрения
следующей стохастической модели состояния:
= (a + 7i&(*w)M*w) +-»6(*,">), * > 0,
где ?i(?,w), t ?T, — мультипликативное, a %2(t,u), t G T, —
аддитивное возмущения.
Детерминированные модели состояния, которые не облада-
обладают устойчивостью к возмущениям входящих в нее параметров,
требуют специального рассмотрения, выходящего за рамки
книги. Для упрощения дальнейших рассуждений ограничим-
ограничимся детерминированной моделью состояния A0.1), обладающей
устойчивостью к малым возмущениям вектора параметров а.
Термин „малые возмущения" указывает на необходимость вве-
введения малого параметра [XIII] в стохастическую модель со-
состояния, а точнее — в „механизм" случайных возмущений

10.1. Еще раз о стохастической модели состояния 379
исходной детерминированной модели состояния A0.1). В соот-
соответствии с этим приходим к следующей стохастической модели
состояния:
dX(t,oj) _
dt
где ?(t,u), t GT = [0, сю), — m-мерный белый шум с единич-
единичной матрицей спектральных интенсивностей, П G M^m(R) —
неизвестная матрица, а ? — малый положительный параметр.
Естественно, что в каждом конкретном случае возмущения
могут быть введены в исходную детерминированной модель
состояния A0.1) различными способами. С этим мы уже столк-
столкнулись при обсуждении примера ЮЛ. Поэтому остановимся на
рассмотрении достаточно общего случая, когда детерминиро-
детерминированной модели состояния A0.1) соответствует стохастическая
модель состояния вида
A0„
где w(t,u), t G T, — m-мерный винеровский процесс с коэф-
коэффициентом диффузии <т2 = 1, е — малый положительный пара-
параметр, Г G Мгт(Щ — неизвестная матрица.
Теорема 10.1. Пусть F{X,a) = (Fi(X,a) ... Fn(X,a)f
и a(X,a) = (<7tJ(X,a)) G Mnr(R). Если для любых г — 1,п и
j=l,r скалярные функции Ft(X,a) и atJ(X,a) в некоторой
окрестности точки (X, a) G Kn+L имеют ограниченные част-
частные производные до второго порядка включительно по всем
Т
компонентам вектора X = {х\ ... хп) , то решение стохасти-
стохастической задачи Коши A0.3) может быть представлено в виде
X(t,oj) = XqW+eX^u) + R{t,u), t ;> 0,
где
^[\\{)\\i]^C?2 @<C<oo),
teT

380 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
вектор-функция Xo(t) определена исходной детерминированной
моделью состояния A0.1):
а n-мерный случайный процесс Xi(t,u>), ? ^ 0, является решени-
решением стохастической задачи Коши
гДеВ(Х,а)±(дЪ(Х,а)/дх;).
Доказательство этой теоремы приведено в книге А.Д. Вент-
целя и М.И. Фрейндлина, которую мы рекомендуем для изуче-
изучения не только в связи с рассматриваемой задачей. Заметим
лишь, что с точностью до величин порядка е2 решение стоха-
стохастической задачи Коши A0.3) можно аппроксимировать гаус-
совским процессом
X0(t)+eXi(t,u), *€Г = [0,оо).
Если X(t,u>), t?T, — решение стохастической задачи Коши
A0.3), a X0(t) удовлетворяет исходной детерминированной
модели состояния A0.1), то в соответствии с теоремой 10.1
процесс случайных отклонений
SX[t,u)=X{t,u)-X0{t), t?T, A0.4)
с точностью до величин порядка ё1 должен удовлетворять
стохастической модели состояния
'd8X{t,u) = B{X0(t),aNX{t,u)dt +
+ a{X0(t),a)Qdw{t,u>), t > 0, A0.5)
где Q = еГ.

10.1. Еще раз о стохастической модели состояния 381
В этой модели
M[6X(t,u)] = 0, A0.6)
так как, согласно формулировке A0.5), свойствам винеровского
процесса и математического ожидания, имеем
Таким образом, из A0.4) и A0.6) следует, что с точностью до
величин порядка е2 имеет место равенство
Заметим, что задача Коши для определения математиче-
математического ожидания случайного процесса, удовлетворяющего сто-
стохастической модели состояния A0.5), была получена в 7.2. Там
же доказано, что ковариационная матрица T,(t \ a,G) этого про-
процесса является решением следующей задачи Коши с G = QQ :
cT(Xo(t),a)Gcr'I(Xo(t),a), t>0,
Таким образом, процесс случайных отклонений 8X(t,u),
t G Г, с точностью е2 полностью определен, поскольку в соот-
соответствии с результатами исследований стохастической модели
состояния A0.5), приведенными в 7.2, он является гауссовским
марковским процессом.
Процесс случайных отклонений зависит от L-мерного век-
вектора параметров а и матрицы G = QQT = ?2ГГТ, которые будем
считать неизвестными и предполагать, что для их оценивания
мы располагаем данными наблюдений, отражающими измене-
изменения состояния изучаемого объекта.

382 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
10.2. Единственность решения задачи
параметрической идентификации
стохастической модели состояния
Стохастическая модель состояния A0.5) определяет п-мер-
ный процесс случайных отклонений 8X(t,u), t ? Т = [0, сю). А
так как он является гауссовским и марковским процессом, то
его iV-мерная функция плотности вероятностей имеет вид
N
,G)'[[f(X(i)\X{i.1)la,G), A0.8)
t=2
где условная функция плотности вероятностей равна
f(X(i\\X,i_n,a,G)=
() ( '
X exp(--(X{i) - m(ti\ti-i,a) + X0(*,-i))T X
). (Ю.9)
При этом, согласно A0.4)-A0.7) и в соответствии с выводами
из теорем 7.2 и 7.3 (см. 7.2), условное математическое ожи-
ожидание
является решением задачи Коши
а условная ковариационная матрица

10.2. Единственность решения задачи идентификации 383
является решением задачи Коши
at
+ Z(t\tt-1,a,G)BT(Xo(t),a)+ A0Л0)
+ a(Xo{t),a)Ga'I(Xo{t),a), tt^ <t^tt,
Для этой матрицы в дальнейшем будем использовать обозначе-
обозначения
E(«i|tt-_lla,G) = Et-(alG). A0.11)
Поскольку ковариационные матрицы {Е(?, |?,_i,a,G)} не за-
зависят от {^(j)}, то представление iV-мерной функции плотно-
плотности вероятностей в виде A0.8), A0.9) означает, что п-мерные
случайные векторы {X(ti,u>) — m(^|?,_i,a)} являются независи-
независимыми и
М[X(tutj) - m{ti| t,-_i,a)] = ЛГо(^), г = 1, iV.
Теперь установим условия, при выполнении которых iV-мер-
ная функция плотности вероятностей A0.8), A0.9) разделяет
точки области изменения параметров изучаемого случайного
процесса на множестве
Начнем с математического ожидания Xo{t) изучаемого
случайного процесса X(t,cj) = X0{t) + 8X(t,u), t G T = [0, сю),
который удовлетворяет исходной детерминированной модели
состояния A0.1):

384 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
и зависит от вектора параметров а. Рассмотрим случай, когда
эта модель является линейной по параметрам, т.е.
F(Xo(t),a) = 4f{Xo{t))a, A0.12)
где Ф(Ло@) — матричная функция, принимающая значения в
Mul(R). Таким образом, согласно A0.1) и A0.12) будем исполь-
использовать следующую детерминированную модель состояния:
dXo(i) ,
Согласно определению 9.2, функция X0(t) = X0(t,a), t?T,
разделяет точки множества D = KL возможных значений
вектора параметров на множестве Т(дг) С Т, если для любых
а ф 0 из D существует значение t = tap ? Г(дг\, такое, что
Xo(tap,oi) ф Xo(tap,C). В соответствии с этим определением
вначале установим необходимые условия существования tap.
Теорема 10.2. Пусть для любых а ? D и t ? Т — [0, оо)
dt { о\Ч)аТ®
и существует хотя бы один момент времени s ? Т, в который
матрица
X=X0{s)
является невырожденной для любых а ? KL\ {О}. Тогда равен-
равенство Xo(t,a) = Xo(t,/3) выполнено для всех t ? Т только в том
случае, когда а = C.
М Пусть выполнены условия теоремы и
в), t ? Г,

10.2. Единственность решения задачи идентификации 385
при некоторых а, /3 G ?>, а ф /3. Тогда имеем
0=
Таким образом, для любых t ? Т
А так как а^/Зи(к-/ЗЕ M.L \ {О}, то при t = s верно равенство
dY(t)
= 0,
t=s
dt
которое противоречит первому условию данной теоремы. >
Заметим, что теорема 10.2 может быть доказана и при
менее жестких ограничениях на матрицу* Ф{Х). Из теоремы
10.2 и непрерывности функции Xo(t) следует, что при а ф /3
всегда существует окрестность S С Т, такал, что для любых
т ? S имеет место неравенство
Х0(т,а)фХ0(т,/3).
Следовательно, в условиях теоремы 10.2 всегда можно выбрать
множество Т(дг) = {A}?Li С Т так, что математическое ожида-
ожидание Xo(t) изучаемого случайного процесса, являющееся реше-
решением задачи Коши A0.13), будет разделять точки множества D
возможных значений вектора параметров на множестве Ti^y
В частности, можно показать, что для этого достаточно вы-
выбрать N ^ L.
Заметим также, что исследуемый случайный процесс не
должен быть стационарным. Это следует непосредственно из
первого условия теоремы 10.2 и согласуется с результатами
примера 9.4 и его обсуждением.
*См.: Зуев СМ.

386 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Теперь с учетом тождества A0.12) перейдем к рассмотре-
рассмотрению ковариационных матриц ?,(a,G), г— l,N, для чего выбе-
выберем два набора неизвестных параметров: {eti;Gi} и {et2;G2}.
Предположим, что а = at = а2 и G\ ф G2. Пусть
AEt(a,GuG2) ± EiKGO - ?,(a,G2).
С учетом A0.10) и A0.11) приходим к выводу, что матричная
функция
является решением задачи Коши
' dAE{t\a,GuG2)
— —
or
(у (Л
О задаче A0.14) известно (см. 7.2), что она имеет нулевое
решение тогда и только тогда, когда является однородной —
в рассматриваемом случае при G\ — G%. Таким образом, при
а\ = а% и G\ ф G% случайные векторы X(ti,w) — m(?,|?,-i,et)
имеют одинаковые математические ожидания, но различные
ковариационные матрицы, а при оц ф а2 всегда найдутся два
случайных вектора из указанной совокупности с различными
математическими ожиданиями. Поэтому две iV-мерные функ-
функции плотности вероятностей A0.8), A0.9) равны тогда и только
тогда, когда а^ = а2 и Gi = G2.
Отметим, что фактически мы получили условия единствен-
единственности решения задачи параметрической идентификации не-
нелинейной стохастической модели состояния A0.3), если рас-
рассмотренная линейная модель A0.5) содержит все неизвестные
параметры исходной нелинейной модели A0.3). Поэтому при

10.3. Выбор наблюдаемых переменных 387
выполнении условий единственности решения задачи параме-
параметрической идентификации линейной модели мы можем оценить
все параметры исходной нелинейной стохастистической модели
состояния. Но при этом следует помнить, что сделанный вы-
вывод касается только условий единственности решения задачи
параметрической идентификации, но не качества получаемых
оценок. По вполне понятным причинам они будут смещенны-
смещенными, причем смещение будет стремиться к нулю при увеличении
числа наблюдений, если е -4 0.
10.3. Выбор наблюдаемых переменных
Рассмотрим еще одну особенность задачи оценивания пара-
параметров случайного процесса
по данным наблюдений, определяемого детерминированной
моделью состояния A0.1):
и стохастической моделью состояния A0.5):
{8Х{0,и) = 0.
Эта особенность заключается в том, что в практических ис-
исследованиях нередкой является ситуация, когда в процессе на-
наблюдений за изменениями состояния изучаемого объекта могут
быть измерены значения не всех компонент его вектора состо-
состояния. Если в результате наблюдений за изменениями состояния
изучаемого объекта могут быть измерены значения фиксиро-
фиксированной компоненты его вектора состояния, то эту компоненту

388 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
называют наблюдаемым переменным состояния. В про-
противном случае компоненту вектора состояния называют нена-
ненаблюдаемым переменным состояния.
Изучение указанной особенности задачи параметрической
идентификации стохастической модели состояния A0.5) на-
начнем с рассмотрения примера.
Пример 10.2- Пусть двумерный случайный процесс X(t,u),
t ? Т = [0, оо), задан стохастической моделью состояния A0.3),
которой соответствует детерминированная модель состояния
A0.1) следующего вида:
( dx\
j—
at
A0.15)
где С\ и C2 — известные положительные константы, ха-
характеризующие начальное состояние изучаемого объекта, а
ai,Q!2,ft3 — неизвестные положительные параметры.
Выше было показано (см. ЮЛ), что решение задачи Коши
A0.15)
в линейном приближении представляет собой математическое
ожидание случайного процесса X(t,u), t G Г = [0, ос). Предпо-
Предположим, что N = 3, т.е. Т^щ = {ti, ti, ?3} и выполнены условия
теоремы 10.1, а измерения проведены лишь для второй компо-
компоненты вектора состояния, причем так, что известны матема-
математические ожидания b/l[x2(t},u))], j = 1, 3.
Решая задачу Коши A0.15), получаем
Xi(t) = Ciexp(-a2* - а1а3С2(е-аз' - 1)), x2{t) = С2е~аз*.

10.3. Выбор наблюдаемых переменных 389
В результате для определения оценки а<зз параметра аз мы
располагаем системой уравнений
, j = 1, 3.
У нас нет никаких данных для нахождения оценок aOi и а02
параметров ац и а\. Таким образом, в рассматриваемом случае
задача оценивания вектора неизвестных параметров а имеет
бесчисленное множество решений.
Наоборот, если известны b/l[xi(t3,u)], j = 1, 3, то для опре-
Т
деления оценки ощ = (otoi (*02 <*оз) вектора неизвестных пара-
параметров а мы располагаем системой уравнений
Если эта система совместна, то она позволяет найти оценки
всех неизвестных параметров.
Таким образом, для решения задачи параметрической иден-
идентификации детерминированной модели состояния A0.15) в ка-
качестве наблюдаемого переменного состояния следует выбрать
xi(t) и провести измерения ее значений, как минимум, в три
момента времени, ф
В общем случае решение вопроса о выборе наблюдаемых
переменных состояния связано с анализом функций чувстви-
чувствительности, которые представляют собой частные производ-
производные компонент вектора состояния
исходной детерминированной модели A0.1) по параметрам «i,
ct2, ..., Oil, которые являются компонентами вектора а €
? D С К^. При этом, если ввести матричную функцию
чувствительности

390 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
детерминированной модели состояния A0.1), то эта матрица
при выполнении некоторых условий является решением задачи
Кош и
при записи которой использованы матрицы Якоби [V]
ШХа)
В(Х,а)-
Можно показать, что если существует строка матрицы S(t)
с номером к, элементы которой не обращаются в нуль ни при
каких значениях (H и вектора параметров а ? D, то для
решения задачи параметрической идентификации детермини-
детерминированной модели состояния A0.1) достаточно иметь данные
измерений значений компоненты Xk{t) вектора состояния X(t)
в дискретные моменты времени tj, j = 1,N, где N ^ L. Ес-
Если же такой строки нет, то из строк матрицы S(t) следует
сформировать такую матрицу S*(?), каждый столбец которой
содержит хотя бы один элемент, отличный от нуля для всех
t ^ 0 и а ? D. Номера строк матрицы S(t), составляющих
матрицу S«(?), и являются номерами тех компонент вектора
состояния, значения которых следует измерять в дискретные
моменты времени, чтобы обеспечить выполнение необходимо-
необходимого условия единственности решения рассматриваемой задачи.
Если матрица S*(t) совпадает со всей матрицей S(t), то
следует измерять все компоненты вектора состояния. Если
из матрицы S(t) можно выделить несколько матриц S*(t),
то мы имеем несколько вариантов для набора наблюдаемых
переменных и можно использовать любой из них. Конкретный
выбор диктуется возможностью измерения входящих в нее
переменных.

10.3. Выбор наблюдаемых переменных 391
Пусть мы располагаем данными измерений значений к A <С
<С к < п) наблюдаемых компонент n-мерного вектора состояния
исходной детерминированной модели A0.1) в дискретные мо-
моменты времени tj, j = 1, N. Тогда при N ^ L можно найти един-
единственную оценку вектора параметров а. Однако при переходе
к стохастической модели состояния A0.3) с ее последующим
преобразованием к стохастической модели состояния A0.5) не-
необходимо оценить еще и элементы матрицы G € Mr(R). При
этом, согласно A0.7) и A0.5), матрица G = QQ =?2ГТ являет-
является симметрической, т.е. неизвестными параметрами являются
г(г + 1)/2 ее элементов.
Пусть E(t) — ковариационная матрица n-мерного векто-
вектора состояния X(t,u), t > 0, стохастической модели A0.3). Так
как наблюдают к компонент вектора состояния, естественно
считать известными (к + 1)к/2 элементов матрицы ?(?). При-
Приравнивая соответствующие элементы матрицы Y,(t\a,G), опре-
определяемой согласно A0.11), элементам матрицы S(?) в каждый
момент времени t3, j = l,N, получим к(к+ 1)/2 уравнений,
содержащих г(г+1)/2 неизвестных. А так как число оцени-
оцениваемых параметров не должно быть больше числа уравнений
связи, то должно быть выполнено неравенство
Nk(k + l) ^
2^2'
При этом мы должны учесть ограничение N ^ L, полученное
при исследовании задачи оценивания вектора параметров а.
Таким образом, число N моментов времени для измерения
значений наблюдаемых компонент вектора состояния следует
выбирать так, чтобы выполнялось условие
где к — число наблюдаемых компонент n-мерного вектора со-
состояния, г — порядок симметрической матрицы G, a L — раз-
размерность вектора параметров а. Заметим, что если наблюдают

392 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
все компоненты вектора состояния (к = п), а число оценивае-
оцениваемых параметров равно размеру вектора состояния (L = п), то
полученное условие принимает вид N ^ п.
Отметим, что при выполнении условия A0.16) изучаемый
случайный процесс X(t,u), t ? Т = [0, оо), однозначно определен
на множестве Т^ = {tj}jLi своей iV-мерной функцией плотно-
плотности вероятностей A0.8), A0.9) и для оценивания входящих в
нее неизвестных параметров можно использовать методы, рас-
рассмотренные в предыдущей главе.
10.4. Специфика задачи оценивания
при наличии ошибок измерений
До сих пор мы предполагали, что измерения значений ком-
компонент вектора состояния осуществляют точно, т.е. отсут-
отсутствует случайная ошибка измерений. Это было удобно для
выяснения тех вопросов, которые были рассмотрены в 10.1-
10.3. Чтобы приблизить постановку задачи параметрической
идентификации стохастической модели состояния к реаль-
реальным условиям, откажемся от этого предположения и будем
считать, что данные наблюдений могут быть представлены в
виде
Y(t,oj)=CX(t,oj) + v(t,oj), t?T{N)cT, A0.17)
где Т(дг) = {tj}f=1; X(t,u), t ? Т"(дг), — ненаблюдаемое значение
п-мерного вектора состояния; Y(t,u), t ? ^(jv)) — наблюдаемое
значение указанной функции вектора состояния; С ? М^„(Е) —
известная матрица ранга к, причем 1 ^ к ^ п; r){tj,u), j =
l,iV — независимые как по отношению друг к другу, так
и по отношению к вектору состояния, случайные векторы,
распределенные по fc-мерному нормальному закону с нулевым
математическим ожиданием и ковариационной матрицей Еч.
Как правило, X(t,u), t ? Т"(дг), интерпретируют как сигнал,
задачи Коши A0.1), A0.5) — как модель сигнала, гауссовский

10.4. Специфика задачи оценивания при ошибках измерений 393
белый шум r)(t,u),te Г(дг), с дискретным временем, имитирую-
имитирующий ошибки измерений, — как помеху, а уравнение A0.17) —
как модель канала связи. В этой терминологии наша зада-
задача формулируется как задача оценивания параметров сигнала.
Для ее решения мы располагаем моделью канала связи A0.17)
и моделью сигнала A0.1), A0.5).
Отметим, что существуют два основных типа моделей ка-
канала связи, первый из которых соответствует прямым изме-
измерениям значений наблюдаемых компонент вектора состояния,
а второй — косвенным измерениям. В первом случае дан-
данные наблюдений содержат сумму помехи и истинного значения
соответствующей компоненты вектора состояния сигнала, а во
втором — сумму помехи и линейной комбинации истинных зна-
значений компонент вектора состояния сигнала. В первом случае
любая строка матрицы С, входящей в модель канала связи
A0.17), состоит из одной единицы и нулей, а во втором слу-
случае эта матрица может иметь любую другую структуру, но при
этом должна иметь максимальный ранг: RgC = k. Конкретный
вид матрицы С определяется как специфическими особенно-
особенностями изучаемого случайного процесса, так и возможностями
эксперимента.
Рассмотрим первый случай, предполагая, что расположение
единиц в матрице С обеспечивает выбор наблюдаемых пере-
переменных состояния в соответствии с исследованием функции
чувствительности, приведенным в 10.3. Поскольку измерения
производят в дискретные моменты времени t ? Т^щ, то реше-
решение линейной по отношению к процессу случайных отклонений
стохастической задачи Коши A0.5) может быть представлено
в виде
I.
/
R{ti,s) a(X0(s),a)Qdw(s,u>),

394 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
где R(t,s) — резольвента. В данном случае резольвента
является решением задачи Коши
= B(X0(t),a)R(t,s), U-1 4s<t<tu
Обозначим
± f R(ti,8)<r(Xo{8),a)Qdu>(8,u>)
и заметим, что n-мерные случайные векторы W,-(w), i— l,n,
являются независимыми и имеют нулевые математические ожи-
ожидания (см. 7.3).
С учетом введенных обозначений, включая и A0.4), модель,
описывающая данные наблюдений, принимает вид
A0.18)
где rj(ti,oj), i = l,N, — независимые как по отношению друг
к ДРУГУ, так и по отношению к Wi(u), i — l,N, случайные
векторы, распределенные по fc-мерному нормальному закону с
нулевым математическим ожиданием и ковариационной матри-
матрицей Еч, a Xo{t) — решение задачи Коши A0.1).
Чтобы решить задачу оценивания неизвестных параметров
изучаемого случайного процесса, необходимо записать функ-
функцию плотности вероятностей блочного случайного вектора
(YT(tuu>) Y T
которую обозначим через

10.4. Специфика задачи оценивания при ошибках измерении 395
При этом, согласно A0.18), для всех г = 1, ЛГ
r)(ti,u) = Y{ti,u)-CX0(tt)-C6X(ti,u),
где 6X(t,u>), t € T = [0, сю), — наблюдаемый процесс случайных
отклонений. Поэтому, если воспользоваться независимостью
случайных векторов r)(t{,u)), г = 1, N, и Wi(u), i = 1, ЛГ, то с уче-
учетом A0.18) можно сделать вывод, что функция плотности веро-
вероятностей f(Y | а, (?,?,,) зависит от ненаблюдаемой переменной
и не может быть использована для решения задачи оценивания
параметров изучаемого случайного процесса.
Учитывая соображения, высказанные в 10.2, представим
функцию плотности вероятностей f(Y | а, <?,?,,) в виде A0.8):
i=2
А поскольку каждый сомножитель в правой части этого равен-
равенства является функцией плотности вероятностей нормального
закона распределения, то fc-мерные случайные векторы
Z2(u,) = Y(t2,u>)-M[Y(t2,u>)\Y{l)],
Z3(u) = Y(t3,u>) - M[Y(t3,u) | YA
tZN(u>)=Y(tN,u>)-M[Y(tN,u,)\Yll),Ym,...,YlN.1)]
независимы, имеют нулевые математические ожидания и кова-
ковариационные матрицы V,, к = 1, ЛГ. Таким образом, для решения
задачи оценивания неизвестных параметров изучаемого слу-
случайного процесса необходимо определить величины
= 2, ЛГ, и Vt, i=

396 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
В соответствии с A0.18) найдем условное математическое
ожидание
M[Y(ti,u)\Yll),...,Y[i_1)]=M[CX0(ti)+C6X(ti,u>) +
+ r](tuu)\Y{1),...,Y{i_1)]=CX0(ti)+C6X{i),
где i — 2, N и
оценка сигнала для момента времени t = t\ по наблюдаемым
значениям Y^, Y^2), ..., V(,_i). Таким образом, при наличии
ошибок измерений приходим к необходимости оценивания не-
ненаблюдаемого состояния системы
по данным наблюдений Yn\, FB)> •••? ^(«'-i)> содержащим линей-
линейные комбинации компонент неизвестного вектора состояния и
ошибки измерения. Эта задача имеет самостоятельный инте-
интерес. Ей посвящен обширный раздел теории случайных процес-
процессов — теория фильтрации и упреждения. В связи с этим
отвлечемся от рассматриваемой задачи параметрической иден-
идентификации, к которой вернемся позже.
10.5. Фильтр Калмана
Рассмотрим задачу оценивания вектора состояния объекта
по данным наблюдений, содержащим случайные ошибки изме-
измерений, в ее простейшей стандартной постановке:
где X(t,u>), t G Г(дг\ = {yi}?Li, — n-мерный вектор состояния
изучаемого объекта; Y(t,u), t ? Г(дг\, — р-мерный вектор на-
наблюдаемых переменных состояния; Ф ? Мп(Щ и Q ? Мрп(Ш.) —

10.5. Фильтр Калмана 397
известные матрицы; Si(u>), i = l,T, — независимые случайные
векторы, распределенные по n-мерному нормальному закону с
нулевым математическим ожиданием и ковариационной ма-
матрицей ??; r)i(u>), i=l,N, — независимые случайные векторы,
распределенные по р-мерному нормальному закону с нулевым
математическим ожиданием и положительно определенной ко-
ковариационной матрицей ?,,.
Предположим, что случайные векторы €k(t,u)), k=l,N, и
r)k(t,u), k= 1, N, независимы, а начальное состояние изучаемо-
изучаемого объекта представляет собой независимый по отношению к
ним n-мерный случайный вектор, распределенный по нормаль-
нормальному закону с математическим ожиданием то и ковариацион-
ковариационной матрицей ?о- Отметим, что в общем случае матрицы Ф,
Q, ?e, T,v могут зависеть от времени t.
Дальнейшее рассмотрение опирается на следующие теоре-
теоремы, касающиеся свойств многомерного нормального распреде-
распределения.
Теорема 10.3. Пусть случайный вектор а,(ы), i = 1, 2,
имеет размерность п(г), математическое ожидание ттг, и ко-
ковариационную матрицу ?,-. Если случайный вектор 0(и>) =
= (a^(w) «2@;)) распределен поп-мерному нормальному зако-
X
ну, п = n(l)+nB), с математическим ожиданием m = (тп[ тп^)
и ковариационной матрицей
то случайные векторы tti(w) - M[ai(w) \a2(u>) — Y2] и
являются независимыми.
Ч Доказательство этой теоремы фактически содержится в
обосновании вывода 3 из теорем 7.2, 7.3. Действительно,
V V? = (Si - ЕпЕ^ЕзО (Е21 -

398 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
А так как плотность распределения вероятностей случайного
вектора /3(и>) может быть представлена в виде
где
\Y2) = JJ^j ехр(-^(Г! - m, + V^V2\{Y2 - m2))T x
X Vn (П - mi + V^(Гз - m2))),
то теорема доказана полностью. >
Замечание 10.1. Если выполнены условия теоремы 10.3,
то непосредственно из вида условной плотности распределения
ffi(Yi \Y2) следует равенство [XVI]
так как V^V^ = J
Теорема 10.4. Если закон распределения блочного случай-
у Т Т ^Г ч Т
ного вектора (а (и>) /3 (и>) у (w)j нормальный и /3(и>), у(ш)
независимы, то
= М[а(ы) | ^(w) = F] + М[а(ы) | у (и) = Z] + M[a(w)].
•< Пусть случайные векторы сх(ш), 0(и>), у(и>) имеют мате-
математические ожидания ma, mp, пг1 и ковариационные матри-
матрицы Sa, S^g, S7 соответственно. Рассмотрим случайный век-
X
тор $(ш) = (/Зт(и>) у (и>)) с математическим ожиданием тп$ =
X
= (т^ тп^) . Так как по условию случайные векторы /3(w) и

10.5. Фильтр Калмама 399
7(w) независимы, для ковариационной матрицы случайного век-
вектора 8(и) имеем
E* =
e ?7Г а Vе S71
Введя обозначения
Еа0 А М [(«И - та)
EQ7 Д М[(<*И - та) G(w) - m7)T],
нетрудно убедиться, что
± М [(а{ш) - та) F {и) - msf] =
= M
Следовательно,
/3(и) \ I me \ \ \ ,^
= ISgS
J.
Для завершения доказательства достаточно воспользоваться
теоремой 10.3 и замечанием 10.1. Действительно,
= ma + EQ/3 Е-1 (У - т0) + EQ7 E;1 (Z - m7) =
3{) Y]M[()\() Z] >
Обратимся теперь к математической модели A0.20). Пусть
(Yt(u) A (Y(tu<j), Y(t2,u,), ..., Y(U,b>)),
)}

400 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Из теоремы 10.3 следует, что Yi^i(u) и
Yx{u) A Y(titu>) -M[Y(ti,u) | У--1И] =
= Y(ti,u) -M[QX(ti,u) + т(и) | Ъ-^и)] = Y(tt,u) -
-QX(i\i-l)=Q(X{titu>)-X{i\i-l))+rn(u>) A0.22)
независимы. Величину Yj(u) называют невязкой оценива-
оценивания. При этом
Yi(u>) = QXi(u>) + rH(u>), Xi(u>)±X(titu>)-X{i\i-l). A0.23)
В соответствии с исходными допущениями относительно
математической модели A0.20) случайные векторы X(ti+i,u>),
Y(ti-i,u), Y(ti,u) имеют нормальные законы распределения.
При этом, согласно A0.21),
А так как из A0.22) следует равенство
то с учетом определения и свойств условного математического
ожидания имеем
+ M[X(tt+uoj)\Yi,(oj)]+M[X(ti+1,oj)]. A0.24)
Согласно A0.20), A0.21), получаем
i\i-l). A0.25)

10.5. Фильтр Калмана 401
Для определения условного математического ожидания вектора
X(ti+i,u>) относительно Yi(u>) воспользуемся теоремой 10.3 и
замечанием 10.1:
M[X(ti+l,u>)\Yi(u>)]=M[X(ti+l,u>)] +
+ Ех9 Еу1 (Y(U,u>) - M[Y(ti,u>) | Yi-i (w)]) -
1)У)] + Е^Е^И, A0.26)
где, согласно A0.20), A0.22), A0.23), для ковариационной
матрицы Е ~ имеем
так как X(i\i— 1) и Х{(и) независимы. Аналогично с учетом
независимости 7?,(w) и Xi(u>) находим
w) + !k(w)) X
х (gx,(w) + w(w))T] = QM[ii(W) xtT(w)] gT
Таким образом,если
A0.27)
то, подставляя A0.25) —A0.27) в A0.24), приходим к рекуррент-
рекуррентным соотношениям
A0.28)

402 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
с начальным условием
t=i
В A0.28) входит матрица K(i), которая, согласно A0.27),
определена через ковариационную матрицу P(i). Эту матрицу
нам и нужно найти для завершения процедуры оценивания. Для
достижения этой цели из первого уравнения A0.20) вычтем
первое уравнение A0.28) и с учетом A0.23) получим
М - K(i) Щи>).
Но, согласно A0.23), имеем
Поэтому
Xi+l(oj) = (Ф -
и в соответствии с A0.27) для ковариационной матрицы Р(г)
находим
Р(г + 1) = М[((Ф - K
= (Ф - /JT(i)Q) P(»)(Ф - ^
где /("(г) определено равенством A0.27) и P(l) =E0.
Таким образом, если Yj, j = 1, N, — измеренные значения
состояния р-мерного случайного процесса с дискретным вре-
временем Y(t,u), t ? Г(л?) = {tj}f=l, то для оценки состояния

10.5. Фильтр Калмана
403
окончательно получаем для i = I, N
= (Ф -
i) (Ф - K(i)Q)
A0.29)
Совокупность рекуррентных соотношений A0.29) для оцен-
оценки состояния объекта по данным наблюдений, содержащим
случайные ошибки измерений, известны в литературе* как те-
теорема Калмана или фильтр Калмана.
Пример 10.3. Пусть в задаче оценивания A0.20)
Ф=
1 1
0 1
*? °Д «.= (""
0 <гк I \т20
710
О
Q = A, 0), Ev = 1, {Vi}^! — экспериментальные данные. Пола-
Полагая i= 1 в фильтре Калмана A0.29), вычисляем
1 1
0 1
'20,
О
0)
'10
Г20.
О
-1
Ч
"Чо
'См.: Острем К.Ю.

404 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
и находим оценку
Полагая г = 2 в фильтре Калмана A0.29), вычисляем
4
)
_2 ¦ _2 _2 , 2
и 1 Т 0 0 Т 0
+ ^10 1 + ^0
^
и находим оценку
ХC|2) = ФХB|1) + АГB)(У2-дХB|1)) = ... #
Из проведенных рассуждений следует, что рекуррентные
соотношения A0.29), определяющие фильтр Калмана, остаются
справедливыми и в случае, когда матрицы Ф, Q, Ее, ?,, зависят
от времени, т.е. при Ф = Ф(<,), Q = Q(ti), Ee = Ee(f,), ?„ = ?„(?,-),
i = TJf.
В заключение отметим, что мы рассмотрели лишь основы
теории фильтрации. Для более серьезного изучения этой
теории необходимо обратиться к специальной литературе*.
"См.: Балакришнан А.В., также Ярлыков М.С., Миронов М.А. и
Пугачев B.C., Синицын И.Н.

10.6. Оценивание параметров при наличии ошибок измерений 405
10.6. Оценивание параметров
при наличии ошибок измерений
Вернемся к математической модели A0.18), в которой не-
неизвестные параметры представлены вектором а Е D С &L, ма-
матрицей G € Mll(R) и ковариационной матрицей Т,п € Mfc^(R),
где к — число наблюдаемых переменных состояния X(t,oj),
t € Т(дп = {?«}?Lii т>е> размерность вектора Y(t,w), t € Tin)-
Итак, рассмотрим математическую модель
Y(titu) = CX0(ti) +C5X{ti,u;) + r)(t,,u;), i = 1, N,
A0.30)
где Xo(t) — n-мерная вектор-функция, удовлетворяющая исход-
исходной детерминированной модели состояния A0.1); C€M^n(R) —
известная матрица ранга к, причем 1 ^ к ^ n; R(t,s) — ре-
резольвента линейной задачи Коши A0.5); {^{и,^)}^ — не-
независимые случайные векторы, распределенные по fc-мерному
нормальному закону с нулевым математическим ожиданием и
ковариационной матрицей Еч;
Wi(u)= f R(t,,8)tr(Xo(8),a)Qdw(8,Lj).
t.-i
Предполагаем, что п-мерные случайные векторы \У{(ш), г =
= 1, N, независимы, имеют нулевые математические ожидания,
а их ковариационные матрицы определены непосредственно с
использованием свойств винеровского процесса:
E(t,,t,_1,G,a)= J R(ti,t)<T(X0(t),a)G(TT{X0(t),a)Rrr(ti,t)dt,
где G = QQT.

406 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Поскольку случайные векторы Zi(cj), г = 1, N, определяемые
равенствами A0.19), могут быть представлены в виде
Zi{u>) = Y(ti,u>) - CX0(ti) - CSX{i), i = 1, N,
являются независимыми и распределены по нормальному зако-
закону, то
N
где
/я (Z(i) | a, G, Е„) = 1 х
Матрицы ?(ij,?j_i,G,cv) и ^^(t) вычисляют с использованием
фильтра Калмана A0.29), который в данном случае принимает
вид
= Xq, 5X{0) = 0,
В соответствии с методом максимального правдоподобия оцен-
оценки a, G, S4 неизвестных параметров, представленные вектором
а и матрицами G, ?,,, находят из условия
max ln/(y|a,G,E4) =

10.6. Оценивание параметров при наличии ошибок измерений 407
Задача оценивания параметров изучаемого случайного про-
процесса имеет единственное решение, если выполнены условия,
сформулированные в 10.2, 10.3.
В заключение сделаем следующие замечания.
Замечание 10.2. Рассматривая решение задачи оцени-
оценивания параметров случайного процесса при наличии ошибок
измерений, мы умышленно выбрали Um в качестве данных на-
наблюдений, чтобы прийти к фильтру Калмана. Если бы мы
располагали данными наблюдений, представленными множе-
множеством Uin, то для решения основной задачи не было бы не-
необходимости использовать фильтр Калмана, чтобы оценить
ненаблюдаемые состояния. Это связано со спецификой дан-
данных наблюдений, представленных множеством U\n (cm. 9.1).
Действительно, в этом случае для любого i = 2, N справедливо
равенство
W) | УA),. ..,?(,¦_!)] = M[Y (i,-|W)].
Случайные векторы Z,(w), i~ 1, /V, определяемые по формулам
A0.19), независимы и распределены по нормальному закону с
нулевым математическим ожиданием и ковариационной матри-
матрицей ?(?|cv,G) -f- Sjj. Это позволяет сразу записать их совмест-
совместную функцию плотности вероятностей.
Замечание 10.3. В случаях, когда наблюдения зависимы,
можно также обойтись без оценки ненаблюдаемых переменных
состояния. Действительно, независимые случайные векторы
Zi(w), г = 1,7V, определяемые по формулам A0.19), использу-
используются лишь для того, чтобы записать их совместную функцию
плотности вероятностей в виде произведения функций плотно-
плотности вероятностей нормального закона распределения, завися-
зависящих от неизвестных параметров. Но независимые случайные
векторы для этой цели можно получить и другим способом*.
'См.: Volkov I.K., Zuyev S.M. 1994, 1995

408 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Рассмотрим задачу оценивания A0.30) в предположении,
что N — 2N*. Ее можно переформулировать так, что при
этом функция правдоподобия не изменится. Из модели A0.18)
получаем
, A0.31)
u) - CX0(t2i) = CR(t2i,t2i^) SX(t2i-i,u;) +
,-(w), (Ю.32)
где i=l,N*. Из A0.31) имеем
ОЛ [t2i — \)Ш) — О I I yl2i — \jUJj — L/Aq| ^2i — \\) — ^ Tj\*'2i— I j^J •
Подставляя это выражение в A0.32), для i = 1, Л^» находим
¦Г(«2,-,ы)-СХо(*й)-
М-^С'1 {Y(t2i-i,b>)-CX0(t2i-i)), A0.33)
Случайные векторы ?»(<*>), »' = 1, ЛГФ независимы, распределены
по нормальному закону с математическим ожиданием
,, M,) №*-1,и)] = в
и ковариационными матрицами

Вопросы и задачи 409
Таким образом, можно записать совместную функцию плот-
плотности вероятностей случайных векторов ?»(ь-0, i = l,N*, и с
учетом равенств A0.33) избежать оценивания ненаблюдаемо-
ненаблюдаемого состояния при решении основной задачи. Тем не менее, мы
отказались от такого подхода с тем, чтобы сделать уместным
изложение фильтра Калмана.
Мы закончили изучение методов статистики случайных
процессов. Отметим, что вычислительные аспекты решения
рассмотренных задач остались за рамками книги. Однако
изложенного материала вполне достаточно для того, чтобы
читатель мог самостоятельно применять конкретные вычисли-
вычислительные методы, изучив их в обширной литературе по вычи-
вычислительной математике.
Вопросы и задачи
10.1. Чем вызвана необходимость введения малого параме-
параметра в стохастическую модель состояния?
10.2. Пусть SX(t,cj) = X(t,cj) - X0(t), t eT, — процесс
случайных отклонений для стохастической модели состояния
A0.3).
1. Какой стохастической модели состояния удовлетворяет
случайный процесс 6X(t,u), t б Т?
2. Чему равно математическое ожидание процесса случай-
случайных отклонений SX(t,cj), t б Г?
3. Какой математической модели удовлетворяет ковариаци-
ковариационная матрица процесса случайных отклонений 6X(t,w), ? б Г?
4. Почему процесс случайных отклонений 8X{t,u), t € Г,
является гауссовским марковским процессом?
10.3. Пусть случайный процесс X(t,u) = X0(t) + SX(t,oj), t €
Г, и вектор-функция X0(t), t 6 Г, удовлетворяют задаче Коши
A0.1), а случайный процесс SX(t,u;), t € Г, — стохастической
задаче Коши A0.5). В каких случаях его математическое

410 10. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
ожидание определено на множестве Т(щ единственным образом
и может ли он в этих случаях быть стационарным?
10.4. Сформулируйте условия единственности решения за-
задачи параметрической идентификации стохастической модели
состояния, линейной по оцениваемым параметрам. Что можно
сказать об условиях единственности решения задачи параме-
параметрической идентификации стохастической модели состояния,
нелинейной по оцениваемым параметрам?
10.5. Изложите принципиальную схему выбора наблюдае-
наблюдаемых переменных при решении задачи параметрической иденти-
идентификации стохастической модели состояния по данным наблю-
наблюдений.
10.6. Предположим, что решается задача параметрической
идентификации стохастической модели состояния A0.1), A0.5)
по данным измерений значений к наблюдаемых компонент
n-мерного вектора состояния в N дискретных моментов вре-
времени. Какое ограничение должно быть наложено на N, если
вектор параметров а не выходит за пределы области D С RLt
10.7. Какие типы моделей канала связи Вы знаете? В чем
их принципиальное отличие?
10.8. В чем заключается специфика задачи оценивания
неизвестных параметров стохастической модели состояния при
наличии случайных ошибок измерений?
10.9. Что называют фильтром Калмана? Опишите принци-
принципиальную схему реализации фильтра Калмана.
10.10. Опишите принципиальную схему решения задачи па-
параметрической идентификации стохастической модели состоя-
состояния при наличии ошибок измерений.
10.11. Пусть y(oj) — ненаблюдаемая случайная величина,
которая зависит от наблюдаемого случайного вектора х(и).
Обозначим через <р(Х) оценку случайной величины у(ш), по-
полученную по данным наблюдений случайного вектора х(из),

Вопросы и задачи 411
представленным матрицей X. Докажите, что в смысле мето-
метода наименьших квадратов наилучшей оценкой является оценка
<р(Х) = М[у(и)\Х].
10.12. Случайный вектор х(и) распределен по п-мерному
нормальному закону с математическим ожиданием тх и кова-
ковариационной матрицей Ех. Пусть у — выборочное среднее на-
наблюдаемого m-мерного случайного вектора y(oj) = Сх(ш) +е(ш),
где С € Мтп(К) — известная матрица, а ошибка измерения е(ш)
не зависит от х(ш), распределена по m-мерному нормальному
закону с нулевым математическим ожиданием и ковариацион-
ковариационной матрицей Ее. Докажите, что наилучшая в смысле метода
наименьших квадратов оценка х для случайного вектора x(oj),
полученная на основе измерений значений случайного вектора
у(о;), имеет вид
х = тх + (СЕ*)Т (СЕ*СТ + Е,)-1 (у - Стх).
10.13. Пусть х(ш) и у(ы) — случайные векторы, распре-
распределенные по n-мерному и m-мерному нормальным законам со-
соответственно. Докажите, что всегда можно найти матрицу
С € Mmn(R) и m-мерный случайный вектор е(ш), распределен-
распределенный по нормальному закону с нулевым математическим ожи-
ожиданием, такие, что
где е(ш) не зависит от х(ш). (Этот результат позволяет свести
ряд практических задач к задаче 10.12).
10.14. Для математической модели
X(tt+\,tj) — ФХ(Ь{,ш) 4- ru(ti) +Ei(u)), i = 1, N,
u})=QX(ti,u) + rfr(u), i = l,N,
полагая, что функция u(t), t € T, известна, докажите, что

412 Ю. ОЦЕНИВАНИЕ ПАРАМЕТРОВ
где Y{ti) — реализация случайного вектора У(?,-,о;), а матрица
К (и) определена в 10.6.
Указание: обратите внимание на то, что каждое из ма-
матричных уравнений, входящих в рассматриваемую математиче-
математическую модель, при стандартных предположениях относительно
случайных векторов с компонентами Е{{ш) и гц{ш) практически
идентично соответствующему матричному уравнению в задаче
10.12.
10.15. Пусть математическая модель в задаче 10.12 имеет
следующий вид:
{(ш), i=l,2N,
i = l,2N,
где скалярные случайные величины fi(w) и тц(ш) независимы
как по отношению к скалярным случайным величинам Х{(ш),
так и между собой, распределены по нормальным законам с
нулевыми математическими ожиданиями и дисперсиями <г2,
ст2 соответственно. Полагая, что параметры а, <т2 и <г2
неизвестны, докажите, что их оценки по данным наблюдений
Y2n = {У|}{^1 могут быть определены как координаты точки
максимума функции
Ца, ol,o\ | Y2N) = Nln (<rl + (
Указание: воспользуйтесь схемой рассуждений из заме-
замечания 10.3.

Приложение 1. ОСНОВНЫЕ ПОНЯТИЯ
ТЕОРИИ ВЕРОЯТНОСТЕЙ
Применение теории вероятностей базируется на понятии
случайного испытания, т.е. такого эксперимента или опы-
опыта, результаты которого нельзя предсказать исходя из условий
его проведения. Отказываясь от прогнозирования результа-
результатов конкретного испытания, теория вероятностей выявляет
и исследует закономерности, возникающие при многократном
проведении случайного испытания. Отметим, что во многих
практических ситуациях оценка серий испытаний куда более
важна, нежели оценка одиночного испытания. Из сказанного
следует, что при построении вероятностной модели исследова-
исследователь всегда предполагает, что условия проведения одиночного
испытания могут быть воспроизведены сколь угодно раз.
Конкретные результаты проведенного случайного испыта-
испытания называют его исходом. Эти результаты на практике
могут, например, выражаться определенным сочетанием ка-
качественных факторов или значением измеряемых параметров.
Важнейший принцип теории вероятностей состоит в стати-
статистической устойчивости частот возможных исходов ис-
испытаний. Под этим понимают то, что при неограниченном
возрастании количества случайных испытаний доля испыта-
испытаний, приведших к заданному исходу, в ряду всех проведенных
испытаний стабилизируется около некоторого предельного чи-
числа.
При построении вероятностной модели выделяют такой на-
набор исходов данного случайного испытания, который удовле-
удовлетворяет двум условиям. Во-первых, при проведении случайного
испытания должен наступить один из исходов в выбранном на-
наборе исходов. Во-вторых, все исходы в наборе являются взаим-

414 ПРИЛОЖЕНИЕ 1. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
но исключающими, т.е. случайное испытание не должно завер-
завершаться одновременно двумя исходами. Исходы в таком наборе
называют элементарными исходами или элементарны-
элементарными событиями, а всю их совокупность — пространством
элементарных исходов* (пространством элементар-
элементарных событий). Пространство элементарных событий при-
принято обозначать через Q, а элементарные исходы — через и
(возможно, с дополнительными индексами).
Часто об элементарных событиях говорят как о неделимых,
подразумевая под этим следующее. Если в результате проведе-
проведения случайного испытания могут наступить исход А и исход В,
то в качестве исходов можно рассмотреть следующие: АВ (оба
исхода наступили одновременно), АВ (наступил исход В, а ис-
исход А не наступил) и т.д. В результате множество возможных
исходов дробится, делится. Когда мы охватим все мыслимые
варианты завершения случайного испытания и эти варианты
не делятся в указанном выше смысле, то мы получим простран-
пространство элементарных исходов.
Важнейшим в теории вероятностей является понятие со-
события, которое отождествляют с некоторым подмножеством
пространства элементарных событий. Наступление события в
результате проведения случайного испытания равнозначно то-
тому, что это испытание завершилось одним из элементарных
исходов, входящим в указанное множество. Здесь событие —
это совокупность возможных вариантов завершения случай-
случайного испытания, значимых с точки зрения исследователя. В
некоторых случаях термину „событие" придают более содер-
содержательный смысл, связывал его с конкретными особенностя-
особенностями проводимых случайных испытаний. Тогда его отличают
от соответствующего множества в пространстве элементарных
исходов, которое в таком случае называют характеристиче-
характеристическим множеством события.
'Иногда термином „исход" обозначают не вообще любой возможный
вариант завершения испытания, а именно элементарный исход, т.е. один
из взаимоисключающих вариантов.

415
Поскольку события — это подмножества пространства эле-
элементарных событий, с ними можно выполнять операции теории
множеств, однако в теории вероятностей эти операции назы-
называются по-другому. Пересечение множеств превращается в
произведение событий, объединение множеств — в сумму со-
событий, дополнение множества в пространстве элементарных
событий — это противоположное событие, пустое множество
обозначает невозможное событие, а все пространство элемен-
элементарных событий есть достоверное событие.
Уместен вопрос, всякое ли подмножество пространства
элементарных событий можно рассматривать как событие.
Это можно принять, если пространство элементарных событий
конечно (т.е. содержит конечное число элементов). Однако
в общем случае такой подход оказывается слишком общим
и не приводит к содержательной теории. Значит, нужны
понятия и условия, описывающие те подмножества, которые
могут рассматриваться как события.
Современная теория вероятностей строится, как и многие
другие математические дисциплины, на системе аксиом. Впер-
Впервые аксиоматическое построение теории вероятностей предло-
предложил А.Н. Колмогоров*. Изложим кратко суть современного
подхода в изложении теории вероятностей.
Определение П1.1. Пусть П — некоторое множество. Не-
Некоторое семейство А подмножеств из ?2 называют а-алгеброй,
если:
а) оно содержит множество П, т.е. Г2 € А;
б) если В € А, то и его дополнение В принадлежит А;
в) если Bk € А, к € N, то
оо оо
U вк <= А и (~)вкеА.
k=l
*А.Н. Колмогоров A903-1987) — выдающийся советский математик,
имеющий фундаментальные результаты в теории функций, теории веро-
вероятностей и ряде других областей современной математики.

416 ПРИЛОЖЕНИЕ 1. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Кратко можно сказать, что сг-алгебра— это некоторое мно-
множество А подмножеств Г2, замкнутое относительно теоретико-
множественных операций, в том числе относительно счетного
объединения и счетного пересечения.
Определение П1.2. Пару (Г2, А) из множества Г2 и сг-алге-
бры А подмножеств из п называют измеримым простран-
пространством.
Определение П1.3. Вероятностью (вероятностной
мерой) на измеримом пространстве ($1,А) называют скаляр-
скалярную функцию Р: А —? R, определенную на cr-алгебре А, которая
удовлетворяет трем условиям:
а) Р[А] > О, А в А;
б)Р[П] = 1;
в) для любых попарно не пересекающихся множеств Вк € А,
к ? N, имеет место равенство
Эти определения вводят основные понятия теории вероят-
вероятностей. Множество Г2, на котором задана cr-алгебра А, — это
пространство элементарных исходов, элементы cr-алгебры А —
это события, а вероятностная мера Р — это функция, задаю-
задающая вероятности всевозможных событий.
Определение П1.4. Тройку (п,А,Р) из непустого множе-
множества Г2, заданной на ?2 ст-алгебры А и определенной на ст-алгебре
А вероятностной меры Р называют вероятностным про-
пространством.
Определение П1.5. Пусть (п,А,Р) — вероятностное
пространство и А\, А2 € А — события, причем Р[А{\ > 0. Под
условной вероятностью события Л2 относительно события
А\ понимают число
. . д Р[Л,ПЛ2]

417
Определение Ш.6. Пусть (п,А,Р) — вероятностное про-
пространство. События А, В е А, для которых Р[Д] > 0 и Р[В] > О,
называют независимыми, если выполнены равенства
Р[А\В] = Р[А] и Р[В\А] = Р[В].
В противном случае события А и В называют зависимыми.
Определение П1.7. Отображение ?: Г2 -> X измеримого
пространства (?1,А) в измеримое пространство (Х,В) называ-
называют измеримой функцией, если для любого В € В прообраз
множества В, т.е. множество ?~l(B) = {oj € Г2: ?(ь;) € 5}, при-
принадлежит Л.
В теории вероятностей измеримое пространство ($1,А) вхо-
входит в состав вероятностного пространства (Q,A,P) (т.е. до-
дополнительно задана вероятностная мера). В этом случае изме-
измеримая функция ?(ш), и; ? п, преобразует вероятностную меру
Р на (Sl,A) в вероятностную меру Р^, определяемую равен-
равенством Р$[В] = P[^-1(fl)] и тем самым превращает измеримое
пространство {Х,В) в вероятностное пространство (Х,В,Р().
Таким способом можно заменить вероятностное пространство
„данное от природы", на более удобное и простое.
Особую роль играет случай, когда X — R, а В — борелее-
скал а-алгебра, т.е. минимальная ст-алгебра, содержащая все
промежутки (открытые, замкнутые, полуоткрытые) на число-
числовой оси. В этом случае измеримую функцию можно определить
как функцию ?(oj), oj ? Г2, для которой прообраз любого множе-
множества В вида В = {х ? К: х < а} принадлежит ст-алгебре А, или,
иначе, является событием. Такую измеримую функцию в тео-
теории вероятностей называют случайной величиной.
На множестве Кп можно задать ст-алгебру, отталкиваясь от
множеств вида
где Т, — промежутки числовой оси (такие множества мож-
можно было бы условно назвать n-мерными параллелепипедами).

418 ПРИЛОЖЕНИЕ I. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Борелевская ст-алгебра 05 в К" — это наименьшая ст-алге-
бра, содержащая указанные множества. Измеримая функция,
отображающая Г2 в К", представляет собой, по-существу, со-
совокупность п случайных величин — ее координатных функ-
функций. Такую функцию называют n-мерным случайным век-
вектором. Случайный вектор можно рассматривать как много-
многомерное обобщение понятия случайной величины. Поэтому далее
мы будем иногда трактовать случайную величину как п-мер-
ный случайный вектор с п — 1.
Случайный вектор можно определить как n-мерную век-
векторную функцию €(oj), oj € Г2, для которой при любом х ? Кп
множество
Ах ^ {и 6 U: ?(ш) < х}
принадлежит А (является событием). В данном случае
и неравенство ?(и) < х означает, что ?k(u) < Xk, к = 1, п.
Изучение случайной величины ?(о;), и; ?$1, сводится к анали-
анализу вероятностной меры Р^, которая порождается этой функци-
функцией на борелевской «т-алгебре. При этом исходное вероятност-
вероятностное пространство (Г2,.Д,Р) перестает играть роль. Отметим,
что в силу свойств вероятности вероятностная мера Р^ полно-
полностью определяется по своим значениями на промежутках вида
(—оо, а), так как, комбинируя такие промежутки и используя
свойства аддитивности и счетной аддитивности вероятности,
можно найти значение вероятности на любом множестве боре-
борелевской сг-алгебры.
Определение П1.8. Пусть ?(ш), и; е п, — случайная вели-
величина (случайный вектор). Скалярную функцию F^(x) = Р^[АХ],
где х е R (х € R") и Ах = {и 6 п: ?(и) < х}, называют функци-
функцией распределения (вероятностей) случайной величины
(случайного вектора) ?(ь;), о; 6 Q.

419
Случайные величины ?,(lj), и € Г2, i— 1, га, можно рассматри-
рассматривать как координаты n-мерного случайного вектора и ввести
для этого вектора функцию распределения. Это объясняет,
почему иногда функцию распределения случайного вектора на-
называют совместной функцией распределения.
Для функции распределения n-мерного случайного вектора
часто используют сокращенные формы записи, например:
[] ,...,xn) = P[tk{u>) <xk, k = TH].
Определение П1.9. Случайную величину (случайный век-
вектор), принимающую не более чем счетное множество значений,
называют дискретной случайной величиной (дискрет-
(дискретным случайным вектором).
Для дискретного случайного вектора?(о;), и ?$1, множество
значений можно записать в виде конечной или бесконечной
последовательности {хщ}к=1 С Кп, где N ^ оо, а функция
распределения имеет вид
Определение П1.10. Непрерывным случайным век-
вектором называют п-мерный случайный вектор ?(о;), функцию
распределения которого можно представить в виде
где х = (х\ ... хп) ,{/=A/! ... уп) , или, что то же самое,
XI Х„
1,...,хп)= ... Myi,...,yn)dyi...dyn.
—оо —оо

420 ПРИЛОЖЕНИЕ 1. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Функцию f{(x) = f^(xi,...,xn) называют плотностью рас-
распределения (вероятностей). В частном случае при п — 1
непрерывный случайный вектор €(ш) называют непрерывной
случайной величиной.
Плотность распределения f((x) n-мерного непрерывного
случайного вектора ?(ш) имеет следующие свойства:
а) Д(г)^0, х?Кп;
б) вероятность Р [?(lj)€G] попадания в произвольную п-мер-
ную область G может быть представлена n-мерным интегра-
интегралом: Р[?(^) € G] = f f{(x)dx; в частности, J f^(x)dx = 1; веро-
G R"
ятность попадания значения случайного вектора в множество
нулевой площади в Кп (в том числе, в фиксированную точку)
всегда равна нулю;
в) при соответствующей гладкости функции распределения
F^(x) плотность распределения f((x) в своих точках непрерыв-
непрерывности совпадает с n-й смешанной производной
г) если ^(lj) = (t)T(lj) eT(u;)) , где ?(lj) — n-мерный, t)(oj) —
m-мерный @ < тп < п), а е(ш) — (п — т)-мерный непрерывные
случайные векторы с плотностями распределения Д(ж), friiv))
Л (г), то
ЫУ)=
Rn-m
•ешт, zeRn~m,x~(yT zT) екп.
Для дискретного случайного вектора ?(и)) с множеством
возможных значений {xik)}^-i С Rn> N §С сх>, можно ввести

421
обобщенную плотность распределения (вероятнос-
(вероятностей)*
ft(x)=
где 8(х) = 8(х\)8(х2) ¦ ..8(хп) — 6-функция Дирака. Это позволя-
позволяет упростить изложение, в котором дискретные и непрерывные
случайные векторы обсуждаются с единых позиций.
Функцию распределения и плотность распределения случай-
случайного вектора ?(w) = (?i(w) ... ?п(^)) называют также сов-
совместной функцией распределения и совместной плот-
плотностью распределения случайных величин ?i(^), ..., ?п(^)-
Если задана функция распределения или плотность распреде-
распределения случайного вектора ?(о;), то говорят, что для этого
случайного вектора задан закон распределения случайного
вектора (случайной величины при п = 1). Закон распреде-
ления случайного вектора ?(lj) = (?1@;) ... ?п(^)) называют
также совместным законом распределения случайных ве-
величин ?i(w), ..., ?n(w).
Определение П1.11. Случайные векторы ?jfe(w), k = l,N,
заданные на одном и том же вероятностном пространстве
(?2,.4,Р), называют независимыми в совокупности, если
функция распределения F^(xi,...,xn) блочного случайного век-
вектора ?(ш) - (fi(w)T ... ?„(о;)т) имеет вид
N
где F^k(xk), k = l,N, — функции распределения случайных
векторов ?jt(w). Если ^ife(w), k — 1, iV, — случайные величины,
то говорят о независимых случайных величинах.
*См.: Пугачев B.C.

422 ПРИЛОЖЕНИЕ 1. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Определение П1.12. Пусть г}(ш) — n-мерный, е(ш) —
m-мерный, ?(w) = G7 (ш) е (о;)) — (тг-(-т)-мерный случайные
векторы с плотностями распределения (возможно, обобщенны-
обобщенными) fv(x), fe(y), f{(x,y). Условной плотностью распре-
распределения (условным законом распределения) случайного
вектора т}(ш) при условии, что случайный вектор е(ш) принял
некоторое фиксированное значение у 6 Rn, называют функцию
п m Му) '
Пусть на вероятностном пространстве (П, А,Р) задан п-мер-
п-мерный случайный вектор, множество возможных значений кото-
которого включается в множество S С Rn. Если <р: S -> Rm — изме-
измеримая (относительно борелевской алгебры 03 в R") векторная
функция, то определена композиция функций r)(w) = <р(?(ш)),
которая является измеримой функцией на измеримом простран-
пространстве (Г2,.Д) и, следовательно, представляет собой т-мерный
случайный вектор. Этот случайный вектор называют вектор-
векторной (скалярной при т = 1) функцией случайного векто-
вектора (случайной величины при п = 1) ?(w). Отметим, что в
качестве измеримой функции <р(х) можно взять любую непре-
непрерывную или кусочно непрерывную векторную функцию. Изме-
Измеримыми также являются интегрируемые функции.
Определение П1.13. Математическим ожиданием
n-мерного случайного вектора?(lj) = (?i(w) ... ^пО^)) с функ-
функцией плотности вероятностей f$(x) = f^(x\,...,xn) называют
n-мерный вектор
компонентами которого являются числа
R"

423
Числа M[?t(o;)], ° которых говорится в определении, пред-
представляют собой математические ожидания координатных слу-
случайных функций ?*(<*>)• Отметим, что все или часть матема-
математических ожиданий M[?fc(o;)] будут не определены, если пред-
представляющий их несобственный интеграл расходится. Тогда и
математическое ожидание случайного вектора не определено.
Так как математическое ожидание случайного вектора соста-
составляется из математических ожиданий координатных случай-
случайных функций, свойства математического ожидания достаточно
описать лишь в одномерном случае.
Пусть ?(о;), г)(ш) — случайные величины, имеющие мате-
математические ожидания, а а, /3 € К — произвольные постоянные.
Тогда:
а) если ?(oj) ^ 0 (т.е. принимает только неотрицательные
значения), то M[?(lj)] ^ 0;
б)
г) если ?(о;), г}(и) — независимые случайные величины, то
д)
Понятие математического ожидания является одним из
основополагающих в теории вероятностей. Рассматривая ма-
математическое ожидание части компонент случайного вектора
с использованием их условной плотности распределения веро-
вероятностей относительно других компонент, приходим к поня-
понятию условного математического ожидания. Например,
пусть г)(ш) — n-мерный, е(и;) — m-мерный случайные векторы
и f(x I У) — условная плотность распределения г){ш) при усло-
условии, что е(ш) принял значение у. Тогда значением М[г)(и}) \у]
условного математическим ожидания случайного век-
вектора г}(ш) при условии е(и) = у называют m-мерный вектор
M[V(u;)\y]±Jxf(x\y)dx.
R"

424 ПРИЛОЖЕНИЕ 1. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Значение условного математического ожиданияМ[77(ь->) \у] явля-
является некоторой функцией <р(у) переменного у, меняющегося в
области значений случайного вектора е(и). Функцию <р(е(ш)) =
a M[t](oj) \e(u;)] от случайного вектора е(и) называют услов-
условным математическим ожиданием случайного вектора
г}(и;) при условии e(uj).
Определение П1.14. Дисперсией D[?(o;)] скалярной слу-
случайной величины ?(oj) называют математическое ожидание
случайной величины (?(ь;) — M[?(lj)]) , т.е. число
Для случайной величины ?(ш) с плотностью распределения
f((x) (возможно, обобщенной) дисперсия может быть вычисле-
вычислена интегрированием:
Непосредственно из определения и свойств математическо-
математического ожидания получаем свойства дисперсии:
г) если случайные величины ?(lj) и г}(и;) независимые, то
д) D[cv] = 0, т.е. дисперсия случайной величины, имеющей
постоянное значение (детерминированной величины), равна
нулю;
Определение П1.15. Ковариацией двух случайных
величин ?(и) и г}{ш) называют число
cov

425
Если для случайных величин ?Н и t)(gj) задана совместная
плотность распределения f^v(x,y), то ковариация этих случай-
случайных величин может быть вычислена интегрированием:
= JJ
JJ(x - MK(W)])(y- M[r,(u,)])ftn(x,y)dxdy.
R2
Ковариация имеет следующие свойства:
a)
в) если случайные величины ?Н и tj(cj) независимые, то
г)
д)
Определение III.16. Коэффициентом корреляции
скалярных случайных величин ?(ш) и ?/(ы) называют число
Две случайные величины ^(о;) и t)(lj) называют некоррели-
некоррелированными, если />[?Н,?7Н] = ^' или' что то же самое>
Коэффициент корреляции двух скалярных случайных вели-
величин обладает двумя основными свойствами:
а) р[?(ы),г)(и})] ^ 1;
б) ^[?Н,т?Н] = 1 тогда и только тогда, когда г)(ш) =
= а?Н +/3, где а, /3 € К, причем а > 0 при р[€{и),г)(и)] —la
а < 0 при ^>[?Н, т?Н] = — 1.
Определение П1.17. Ковариационной матрицей слу-
случайного вектора ?Н = (^i(o;) ... ^п(<^)) называют мат-
матрицу
covff (w)l =

426 ПРИЛОЖЕНИЕ 1. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Итак, ковариационная матрица n-мерного случайного век-
вектора представляет собой квадратную матрицу порядка п из
ковариаций пар координатных случайных функций. Из свойств
ковариации двух случайных функций вытекают свойства кова-
ковариационной матрицы:
а) cov[?(lj)] — симметрическая неотрицательно определен-
определенная квадратная матрица порядка п;
б) если т)(и) = А?(и;) +6, где А € Mmn(K) — фиксированная
матрица, 6 € К — фиксированный вектор, то cov[t)(u)] =
= Acov[?(u;]AT.
Определение П1.18. Характеристической функцией
n-мерного случайного вектора ? называют функцию
где А ? Кп, а г — мнимая единица.
Для случайного вектора ?(lj) с плотностью распределения
f((x) (возможно, обобщенной) характеристическая функция
может быть представлена интегралом:
= I exp(i\rx)fi(x)dx,
т.е. характеристическая функция является изображением экс-
экспоненциального интегрального преобразования Фурье. Значит,
в классе функций, интегрируемых с квадратом, существует
взаимно однозначное соответствие между характеристически-
характеристическими функциями и плотностями распределения.
Отметим некоторые свойства характеристической функ-
функции:
в) <pz(-\) = v|(A), т.е. при изменении знака аргумента зна-
значение характеристической функции меняется на комплексно
сопряженное;

427
д) если т}(ш) — A?(gj) + b, где матрица А € Mmn(R) и вектор
Ь е Rm фиксированы, то <pv{fj) = exp(i/iTT
е) если случайные величины ?fc(w), k= 1,7V, независимы в
N
совокупности, T)(u) = Zi(w) + ... + Zn(w), то <рт,(\)= I
fc
т
где Л= (Ai ... An) .

Приложение 2. МАТРИЧНАЯ
ЭКСПОНЕНТА
Рассмотрим линейное пространство Mn(R) квадратных ма-
матриц порядка п, в котором выбрана некоторая кольцевая норма
|| • ||, т.е. такая норма, что для любых матриц А, В € М„(К)
выполняется неравенство ||Л5|| ^ ||Л||||5||. В качестве такой
нормы можно взять евклидову норму, определяемую для матри-
матрицы А = (dij) равенством
Введение нормы позволяет в линейном пространстве МП(К)
ввести сходимость последовательностей и рядов. Последова-
Последовательность матриц {Ап} С Mn(R) сходится по норме || • || к ма-
матрице А € Mn(R), если числовая последовательность ||ЛП — А||
является бесконечно малой, т.е. lim ||ЛП — А|| = 0. Аналогично
п-Юо
вводится понятие сходимости матричного ряда (определения и
основные свойства последовательностей и рядов в нормирован-
нормированных пространствах изложены в [IX]). Отметим, что сходимость
последовательностей и рядов в конечномерном нормированном
пространстве на самом деле не зависит от выбора конкретной
нормы. При любом выборе нормы последовательность {Ап}
матриц Ап = {a\V) сходится к матрице А= (aij) тогда и толь-
только тогда, когда при любых фиксированных i,j = 1, п числовая
последовательность {а)"'} сходится к а^ при п->оо. Удачный
выбор нормы позволяет упростить анализ последовательностей
и рядов — и только. В частности, именно этим объясняется
требование, чтобы норма была кольцевой.

429
Для любой матрицы А € Mn(R) можно рассмотреть ряд
п=0
который сходится по норме при любом выборе А, причем
абсолютно [IX], так как
оо
п=0
Ап
п
п=0
п!
< ОО.
Определение П2.1. Матричной экспонентой матри-
матрицы А называют матрицу еА, равную сумме матричного ряда
(П2.2).
B 1\
Пример П2.1. Пусть Л = I I. Непосредственной
проверкой можно убедиться в том, что
Поэтому
)-\о
еА±
Матричная экспонента позволяет определить матричную
функцию eAt, которая действительному числу t G К сопоста-
сопоставляет матричную экспоненту матрицы At = tA. Отметим, что
часто именно эту матричную функцию и определяют как ма-
матричную экспоненту, так как с ней связаны наиболее важные
приложения матричной экспоненты.
Рассмотрим свойства матричной экспоненты.
Свойство П2.1. Если матрицы А, В е Mn(R) являются
коммутирующими, то
еА+в=еАев.

430 ПРИЛОЖЕНИЕ 2. МАТРИЧНАЯ ЭКСПОНЕНТА
< Используя определение матричной экспоненты, можем запи-
записать:
... , N ТП\ ) *-~<^ к\т\
k=Q ' xm=0 ' Ь0т=0
Изменим порядок суммирования с помощью замены р = к + тп,
q = к. Из этих соотношений получаем к = q и тп = р — q, откуда
с учетом неравенств к ^ 0, тп ^ 0 получаем g ^ 0, р - g ^ 0.
Значит, двойное суммирование должно идти по таким парам
(р, q), для которых верны указанные два неравенства, т.е. мы
можем записать
ЬОтгО pq
У"^У Р . (П2.3)
Так как матрицы А и В коммутирующие, то и их любые
степени Ар и В4 являются коммутирующими. Поэтому
^h)i- (П2-4)
Сопоставляя (П2.3) с (П2.4), заключаем, что
Свойство П2.2. Для любой матрицы А 6 МП(К) ее матрич-
матричная экспонента еА является невырожденной, причем обратная
матрица равна е~А, т.е. {еА)~х = е~А.
< Матрицы А и —А являются коммутирующими. Поэтому,
согласно свойству П2.1,

431
где 0 — нулевая матрица. Легко проверить непосредственно по
определению матричной экспоненты, что е0 = I — единичная
матрица. Поэтому еАе~А = J. Но точно так же е~АеА = J.
Значит, согласно определению обратной матрицы, еА и е~А
являются обратными друг к другу. В заключение отметим,
что матрица, имеющая обратную, невырождена. >
Свойство П2.3. Для любой матрицы А € Мп
le = Ae = eA.
at
Согласно определению матричной экспоненты, имеем
Aktk
Iм
-Е-
В силу равномерной (по t) сходимости этого ряда на любом
отрезке числовой оси имеем
d At_df, АН* ^ АН ^ (Д0 м
Аналогично получаем равенство —eAi — eAtA. >
at
Свойство П2.4. Для любой матрицы А € МП(К) решение
однородной задачи Коши
(ХA» = Ха k '
имеет вид
X[t) = eAtX0, t^O, (П2.6)
т.е. матрица eAt является резольвентой, или нормированной
фундаментальной матрицей этой задачи Коши.

432 ПРИЛОЖЕНИЕ 2. МАТРИЧНАЯ ЭКСПОНЕНТА
4 Ясно, что Х@) = е3Xq = IXq = Xq. Согласно свойству П2.3,
Таким образом, eAtX0 является решением задачи (П2.5), что и
требовалось доказать. >
Свойство П2.5. Для любой матрицы А€ Мп(К) и п-мер-
ной непрерывной на @, оо) вектор-функции B(t) решение неод-
неоднородной задачи Коши
может быть представлено в виде
t
X{t) = eAtX0+ j eA^-^B{r)dr, t^O. (П2.9)
о
< Представление (П2.9) вытекает из метода вариации посто-
постоянных для системы обыкновенных дифференциальных урав-
уравнений. Поэтому доказательство сформулированного свойства
можно было бы провести с помощью этого метода. Однако
в данном случае проще проверить, что правая часть в (П2.9)
удовлетворяет задаче Коши. Действительно, начальное усло-
условие выполнено и
t
dt
о
t
= AeAtX0 + (jteAt) J е~АтВ(т) dr + ем^]е~АгВ{т) dr =
о о
t
[eA(t-T'>
= AeAtX0 + A
о

433
Свойство П2.6. Пусть X(t) является решением задачи Ко-
ши (П2.5) с матрицей А = (atJ) € Мп(Ш) и вектором начальных
условий Xq с неотрицательными компонентами. Тогда для того
чтобы все компоненты функции X(t) были неотрицательными
при любом t ^ 0, необходимо и достаточно, чтобы все недиа-
недиагональные элементы cijj матрицы А были неотрицательными,
т.е.
a.j^O, i,j = T~n, гф]. (П2.10)
-4 Обозначим R{t) = {Rij{t)) = eA\ X(t) = (Xl(t) ... xn(t))T',
т
Xo — (iio ... xno) и воспользуемся представлением решения
задачи Коши (П2.5) в виде (П2.6). Тогда
Х><(г) = XI Rkm(t)xm0, к = Т~П.
т=1
А так как zmo, тп — 1, п, — произвольные неотрицательные
числа, то очевидно, что функции Zk(t), /г = 1,п, являются
неотрицательными при t ^ 0 тогда и только тогда, когда при
t ^ 0 являются неотрицательными функции .Rfcm(i), к, тп = 1, п.
Выберем произвольное е € @, 1) и столь малое положитель-
положительное число ?i, что
max|a,-j|?i ^ -.
ij Tl
Тогда для любых неотрицательных t ^ t\ с учетом определения
евклидовой нормы матриц имеем оценку
| = |«НИ1Ю
и с точностью о(е) получаем
dint
anlt an2t ... l + annt)

434 ПРИЛОЖЕНИЕ 2. МАТРИЧНАЯ ЭКСПОНЕНТА
Следовательно, при малых неотрицательных значениях t усло-
условие (П2.10) является необходимым и достаточным условием
неотрицательности компонент матричной экспоненты eAt.
Если t не является малым, то выбираем целое положитель-
положительное число N столь большим, что t\ = t/N будет удовлетворять
условию (П2.11). Но тогда при выполнении условия (П2.10)
матричная экспонента eAi^ имеет лишь неотрицательные эле-
элементы. Следовательно, и матричная экспонента
eAt = (eAt/N)N
имеет лишь неотрицательные элементы, так как является про-
произведением конечного числа матриц с неотрицательными эле-
элементами. >
Отметим, что матричная экспонента, как резольвента со-
соответствующей задачи Коши, может быть найдена с помощью
любых методов решения задач Коши, в том числе с помощью
операционного исчисления [XI].
Переходим к рассмотрению линейных нестационарных мо-
моделей состояния. Пусть X(t) и B(t) — n-мерные вектор-функ-
вектор-функции, a A(t) — матричная функция порядка п скалярного аргу-
аргумента t. При анализе задачи Коши
(П2.12)
по аналогии со скалярным случаем возникает естественное
предположение относительно ее резольвенты:
t
= ехр( I А{т)<1т\ (П2.13)
S
так как в скалярном случае фундаментальная матрица может
быть записана в виде
t

435
а резольвента есть нормированная фундаментальная матрица,
т.е.
При этом верны равенства
Д@,0) = ехр(вп) = /n, R(t,0) = A(t)R(t,0).
Заметим, что
1
Д(*,0)=Нт-
— lim —
h
t+h t
exp( f A{T)dT J -exp( f А(тLт\
t t+h t
exp( f A(r)dr+ f A(t)dA - exp( f А(т) dr\
При /i«0 можно считать, что
t+h
Кроме того, если при t > 0 имеет место равенство
t t
A[t)jA{r)dr= (У' A(r)dAjA{t), (П2.14)
о о
то, воспользовавшись свойством П2.1, получаем
R(t,0)= lim ^
t
( f
= A(t)R(t,0).

436 ПРИЛОЖЕНИЕ 2. МАТРИЧНАЯ ЭКСПОНЕНТА
Таким образом, если выполняется условие (П2.14), то ре-
резольвента задачи Коши (П2.12) определена равенством (П2.13),
а ее решение может быть представлено в виде
t
X(t) = R{t,0)Xo+ fR{t,r)B(r)dT. (П2.15)
о
На практике условия (П2.14), как правило, выполнены, но
их проверкой не стоит пренебрегать.
Пример П2.2. Рассмотрим задачу Коши (П2.12) при п = 2,
B(t) = О и A(t) = П ^ J. В этом случае
При этом
и равенство (П2.14) не выполняется.
Действительно, непосредственной проверкой легко убедить-
убедиться в том, что в данном случае
Введя матрицу

437
получим
#
Здесь приведены лишь минимально необходимые сведения
о матричной экспоненте и ее приложениях. Более подробную
информацию можно найти в специальной литературе*.
'См.: Беллман Р., а также Директор С, Рорер Р.

СПИСОК РЕКОМЕНДУЕМОЙ
ЛИТЕРАТУРЫ
Учебники и учебные пособия
Вентцель А.Д. Курс теории случайных процессов: Учеб. пособие для
вузов. М.: Наука, 1975. 320 с.
Вентцель Е.С. Теория вероятностей: Учеб. для втузов. М.: Наука,
1969. 576 с.
Гихман И.И., Скороход А.В. Введение в теорию случайных процессов:
Учеб. пособие для вузов. М.: Наука, 1977. 568 с.
Ивченко Г.И., Каштанов В.А.У Коваленко И.Н. Теория массового
обслуживания: Учеб. пособие для вузов. М.: Высш. школа, 1982. 256 с.
Марчук Г. И. Методы вычислительной математики: Учеб. пособие для
вузов. М.: Наука, 1989. 608 с.
Пугачев B.C. Теория вероятностей и математическая статистика:
Учеб. пособие для втузов. М.: Наука, 1979. 496 с.
Пугачев B.C., Синицын И.Н. Стохастические дифференциальные си-
системы: Учеб. пособие для втузов. М.: Наука, 1985. 560 с.
Случайные функции: Учеб. пособие / Тескин О.И., Цветпкова P.M.,
Козлов Н.Е., Пашовкин Е.М. М.: Изд-во МГТУ, 1994. 80 с.
Задачники
Емельянов Г.В., Скитпович В.П. Задачник по теории вероятностей и
математической статистике. Л.: Изд-во ЛГУ, 1967. 330 с.
Прохоров А.В., Ушаков В.Г., Ушаков Н.Г. Задачи по теории вероят-
вероятностей. М.: Наука, 1986. 328 с.
Сборник задач по математике для втузов / Под ред. А.В. Ефимова. В
3 т. Т.З. М.: Наука, 1984. 608 с.
Сборник задач по теории вероятностей, математической статистике и
теории случайных функций / Под ред. А.А. Свешникова. М.: Наука, 1965.
632 с.
Монографии
Балакришнан А.В. Теория фильтрации Калмана / Пер. с англ. Под
ред. А.А. Новикова. М.: Мир, 1988. 168 с.

439
Беллман Р. Введение в теорию матриц / Пер. с англ. Под ред.
В.Б. Лидского. М.: Наука, 1969. 368 с.
Вентцель А.Д., Фрейдлин М.И, Флуктуации в динамических системах
под действием малых случайных возмущений. М.: Наука, 1979. 424 с.
Директор С, Рорер Р. Введение в теорию систем / Пер. с англ. Под
ред. Н.П. Бусленко. М.: Мир, 1974. 464 с.
Евланов Л.Г., Константинов В.М. Системы со случайными параме-
параметрами. М.: Наука, 1976. 568 с.
Зуев СМ. Статистическое оценивание параметров математических
моделей заболеваний. М.: Наука, 1988. 176 с.
Карлин С Основы теории случайных процессов / Пер. с англ. Под ред.
И.Н. Коваленко. М.: Мир, 1971. 536 с.
Крамер Г. Математические методы статистики / Пер. с англ. Под ред.
А.Н. Колмогорова. М.: Мир, 1975. 648 с.
Леей П. Стохастические процессы и броуновское движение / Пер. с
франц. Под ред. Н.Н. Ченцова. М.: Наука, 1972. 375 с.
Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов. М.:
Наука, 1974. 696 с.
Мудрое В.И., Кушко В.Л. Методы обработки измерений. М.: Радио и
связь, 1983. 303 с.
Острем К.Ю. Введение в стохастическую теорию управления / Пер. с
англ. Под ред. Н.С Райбмана. М.: Мир, 1973. 319 с.
Свешников А.А. Прикладные методы теории случайных функций. М.:
Наука, 1968. 464 с.
Фомин Я.А. Теория выбросов случайных процессов. М.: Связь, 1980.
216 с.
Шварц Л. Анализ / Пер. с франц. Под ред. С.Г. Крейна. В 2 т. Т. 1.
М.: Мир, 1972. 824 с.
Ярлыков М.С., Миронов М.А. Марковская теория оценивания случай-
случайных процесов. М.: Радио и связь, 1993. 464 с.
Периодическая литература
Volkov I.K., Zuyev S.M. On identifiability of mathematical models of
evolutionary processes from data of discrete Measurements of state vector //
Russ. J. Numer. Anal. Math. Modelling, 1994. V. 9, N 4. 395-404 p.
Volkov I.K., Zuyev S.M. Conditions for identifiability of mathematical
models of evolutionary processes with partially determined initial states. //
Russ. J. Numer. Anal. Math. Modelling, 1995. V. 10, N 2. 149-157 p.

предметный указатель
Аксиомы нормы IV, 70
- скалярного умножения IV, 69
Амплитуда гармоники IX, 121
Анализ гармонический 121
- стохастический 66
ХЭектор блочный 51
- вероятностей состояний 166
начальных 166
предельных 178
- детерминированный 240
- случайный 418
- дискретный 419
-- непрерывный 419
- сноса 281
- состояния 228
Векторы случайные независимые в
совокупности 421
Величина случайная 417
- дискретная 419
- непрерывная 420
Величины случайные независимые
421
- некоррелированные 425
Вероятность 416
- переходная 166
- состояния 166
- условная 416
Вершина графа 202
Вес 202
Время обслуживания 199
- ожидания 192
Выборка случайная 323
1 армоника IX, 121
Граф состояний 164
-- размеченный 168
Дисперсия 424
— случайного процесса 34
Дисциплина очереди 192
Дифференциал случайного
процесса 236
— стохастический в форме Ито 267
Стратоновича 266
Дополнение алгебраическое III
Дуга нагруженная 202
«Задача Коши стохастическая 237
— оценивания параметров
случайного процесса 335
— параметрической идентификации
стохастических моделей
состояния 375
Закон распределения случайного
вектора 421
процесса конечномерный
(TV-мерный) 29
одномерный 28
— случайной величины 421
— случайных процессов
совместный 96
— совместный 421
— условный 422
Заявка 192
Звено линейное динамическое 100
невозмущенное 101

441
Значение условного
математического ожидания 423
Значения процесса случайного
независимые 326
Измерение косвенное 393
- прямое 393
Изображение XI
Интеграл с переменным верхним
пределом от случайного процесса
91
- стохастический Ито 260
- от функции неслучайной по
случайному процессу 257
- по вииеровскому процессу 260
- Стратоновича 260
Интенсивность белого шума 143
- обслуживания 199
- простейшего потока 196
- спектральная процесса
случайных возмущений 377
- ухода из очереди 207
Испытание случайное 413
Исход элементарный 414
.Канал обслуживания 192
Ковариация 424
- двух случайных векторов 34
Количество информации по
Фишеру XVII, 341
Кореиь квадратный из квадратиой
симметрической матрицы 296
Коэффициент диффузии 57, 299
- корреляции 425
- сиоса 299
Критерий Коши стохастический 77
- метода наименьших квадратов
369
Матрица весовая 369
- диффузии 281
- коваривциоииая случайного
вектора 425
процесса 33
- переходных вероятностей 167
- спектральных иитеисивиостей
234
- Фишера информационная XVII,
341
- фундаментальная VIII-147, 431
Мера вероятностная 416
Метод вариации постоянных VIII
- максимального правдоподобия
XVII, 557
- наименьших квадратов 369
Множество возможных значений
случайного вектора XVI
- выпуклое V
- открытое 1-181
- характеристическое события 414
Модель канала связи 393
- математическая II
- сигнала 392
- состояния детерминированная
228
устойчивая 376
-- стохастическая 230
в форме Ито 266
Стратоиовича 265
Момеиты процесса случайного 328
Момент к-го порядке случайного
процесса 31
Невязка оценивания 400
НерввеиствоИеисеиа 348
- Рао — Крамера XVII, 340
- Шварцв 37

442
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Норма евклидова IV, 428
- кольцевая IV, 428
- СК 68
Ожидание математическое 422
- случайного процесса 31
-- условное 423, 424
Ординарность входного потока 193
Оригинал XI
Отсутствие последействия во
входном потоке 193
Оценка асимптотически
несмещенная 358
- нормальная 358
- эффективная 358
- квазнправдоподобная 363
- максимального правдоподобия
XVII, 557
- наименьших квадратов 369
- несмещенная XVII, 557
- нормальная 358
- состоятельная XVII, 557
- эффективная XVII, 557
Очередь 191
Переменное состояния
наблюдаемое 388
- ненаблюдаемое 388
Плотность вероятности перехода
171
- потока заявок приведенная 211
- ухода заявок нз очереди
приведенная 211
- простейшего потока 196
- распределения (вероятностен) 420
обобщенная 421
- совместная 421
- условная 422
- спектральная 136
'— взаимная 155
Помеха 393
Последовательность случайная 27
Поток входной 191
- простейший 193
- выходной 191
Правило дифференцирования Ито
269
Предел последовательности
случайных процессов 72
- случайного процесса 67
Преобразование интегральное
Лапласа XI
- Фурье экспоненциальное XI
Производная случайного процесса в
точке 82
на множестве 83
Пространство вероятностное 416
- измеримое 416
- элементарных исходов 414
- событий 414
Процесс вннеровский 55
- стандартный 57
- гауссов 50
- гибели — размножения 180
однородный 182
- марковский 60
-- с дискретными состояниями 163
неоднородный 171
однородный 171
непрерывными состояниями
277
- массового обслуживания 191
- нормальный 50
- пуассоновскнй 61
- случайный 26
- векторный 26
-- второго порядка 68
- дифференцируемый в точке 82
на множестве 83
-- интегрируемый с весом 90

443
Процесс случайный комплексный 40
— координатный 26
-- непрерывный в точке 79
на множестве 79
— с дискретным временем 165
— скалярный 26
— стационарный в узком смысле
47
широком смысле 48
— центрированный 130
— элементарный 122
— эргодический по отношению к
дисперсии 112
математическому
ожиданию 107
— п-мерный 26
— случайных возмущений 229
-- отклонений 380
— с приращениями независимыми
52
стационарными 52
некоррелированными
(ортогональными) 52
— циклический 183
— однородный 183
Процессы случайные независимые
298
— некоррелированные 298
-- равные 68
— стохастически эквивалентные
29
Реакция на входной сигнал 101
Реализации выборочные
независимые 325
Реализация выборочная 324
— случайного процесса 27
— случайной выборки 324
Режим функционирования
стационарный 204
Резольвента 238
- задачи Коши 431
Стечение случайного процесса 27
Сечения независимые 231
Сигнал 392
- входной 101
Система линейных ОДУ
нормальная асимптотически
устойчивая VIII, 2?9
- обслуживания 191
- замкнутая 221
- с ограниченной длиной очереди
201
ожиданием 193
чистая 213
отказом 193
очередью 193
- ОДУ нормальная VIII
- уравнений Колмогорова 172
Смещение оценки 340
Событие элементарное 414
События зависимые 417
- независимые 417
Спектр функции IX, 1Z1
Способность пропускная
абсолютная 204
- относительная 204
Стационарность входного потока
193
X еорема Калмаиа 403
- эргодическая 109
Теория массового обслуживания
193
- спектральная 121
- фильтрации и упреждения 396
Траектория случайного процесса 27
Требование 192

444
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Уравнение Колмогорова второе
281
-- матричное 173
- первое 281
- Колмогорова — Фоккера —
Планка 281
- Маркова — Смолуховского —
Чепмена — Колмогорова 279
- стохастическое
дифференциальное линейное 101
Условия граничные XII
- начальные XII
Устойчивость частоты
статистическая 413
Фаза начальная гармоники IX, 121
Фильтр Калмаиа 403
Формулы Эрлаига 217
Функция выпуклая (вниз) II, SJ,1
- детерминированная 121
- измеримая 417
- интегрируемая с квадратом XI
- квазиправдоподобия 363
- ковариационная 34
- взаимная 41
- корреляционная 40
- Лапласа XVI, 217
- максимального правдоподобия
XVII, 557
- матричная 32
- обобщенная XII
- передаточная 104
- плотности вероятностей
случайного процесса
конечномерная (TV-мерная) 29
одномерная 28
- разделяющая точки множества
351
Функция распределения
(вероятностей) случайного
вектора 418
случайной величины 418
- случайного процесса
конечномерная (jV-мериая) 29
одномерная 28
- совместная 419, 421
- случайная 26
- случайного вектора векторная
422
скалярная 422
- случайной величины векторная
422
скалярная 422
- характеристическая случайного
вектора 426
процесса 288
- чувствительности 389
- матричная 389
Характеристика частотная
динамической системы 152
Цепь Маркова 164
-- неоднородная 167
-- однородная 167
Частота гармоники IX, 121
Шаг марковского процесса 165
Шум белый 143
«Зкспонеита матричная 429
Этап марковского процесса 165
{-функция Дирака XII
<т-алгебра 415
- борелевская 417

ОГЛАВЛЕНИЕ
Предисловие 5
Основные обозначения 12
Введение 19
1. Исходные понятия и определения 26
1.1. Случайная функция, случайный процесс и случайная
последовательность 26
1.2. Математическое ожидание и ковариационная функция
случайного процесса 31
Вопросы и задачи 42
2. Некоторые типы случайных процессов 47
2.1. Стационарные случайные процессы 47
2.2. Нормальные процессы 50
2.3. Процессы с независимыми приращениями 52
2.4. Винеровский процесс 55
2.5. Марковские процессы 59
2.6. Пуассоновский процесс 61
Вопросы и задачи 62
3. Элементы стохастического анализа 66
3.1. Сходимость в смысле среднего квадратичного (СК-схо-
димость) 67
3.2. Непрерывность случайного процесса 79
3.3. Дифференцируемость случайного процесса 82
3.4. Интегрируемость случайного процесса 90
3.5. Действие линейного оператора на случайный процесс 98
3.6. Эргодические случайные процессы 106
Вопросы и задачи 113
4. Спектральная теория стационарных случайных про-
процессов 121
4.1. Стационарные случайные процессы с дискретным спек-
спектром 122
4.2. Стационарные случайные процессы с непрерывным
спектром 133

446 ОГЛАВЛЕНИЕ
4.3. Белый шум 143
4.4. Преобразование стационарного случайного процесса
при его прохождении через линейную динамическую
систему 148
Вопросы и задачи 155
5. Марковские процессы с дискретными состояниями
и цепи Маркова 163
5.1. Основные понятия 163
5.2. Цепи Маркова 166
5.3. Уравнения Колмогорова для вероятностей состояний 170
5.4. Процесс гибели — размножения и циклический процесс 180
Вопросы и задачи 186
6. Элементы теории массового обслуживания 191
6-1. Процессы массового обслуживания (основные понятия) 191
6.2. Простейший поток 193
6.3. Время ожидания и время обслуживания 199
6.4. Основные принципы построения марковских моделей
массового обслуживания 200
6.5. Системы массового обслуживания с ожиданием . . . 206
6-6. Стационарный режим функционирования системы об-
обслуживания (основные понятия и соотношения) . . . 209
6.7. Стационарные режимы функционирования некоторых
вариантов систем обслуживания 213
Вопросы и задачи 223
7. Стохастические модели состояния 227
7.1. Случайные возмущения в динамической системе . . . 227
7.2. Линейные стохастические дифференциальные уравне-
уравнения 237
7.3. Стохастические интегралы и дифференциалы .... 253
Вопросы и задачи 272
8. Марковские процессы с непрерывными состояния-
состояниями 277
8.1. Общие свойства марковских процессов 278
8.2. Уравнения Колмогорова 280
8.3. Стохастические модели состояния и уравнения Колмо-
Колмогорова 288
8.4. Постановки задач для нахождения условной функции
плотности вероятностей 298

447
8.5. Три характерные задачи теории марковских случай-
случайных процессов с непрерывными состояниями 304
Вопросы и задачи 317
9. Элементы статистики случайных процессов 323
9.1. Данные наблюдений 323
9.2. Статистические моменты случайного процесса . . . 328
9.3. Постановка задачи оценивания параметров случайного
процесса 335
9.4. Эффективные оценки. Неравенство Рао — Крамера 338
9.5. Единственность решения задачи оценивания парамет-
параметров случайного процесса 344
9.6. Метод максимального правдоподобия 355
9.7. Метод наименьших квадратов 367
Вопросы и задачи 371
10. Оценивание параметров стохастических моделей со-
состояния 375
10.1. Еще раз о стохастической модели состояния 375
10.2. Единственность решения задачи параметрической иден-
идентификации стохастической модели состояния .... 382
10.3. Выбор наблюдаемых переменных 387
10.4. Специфика задачи оценивания при наличии ошибок
измерений 392
10.5. Фильтр Калмана 396
10.6. Оценивание параметров при наличии ошибок измере-
измерений 405
Вопросы и задачи 409
Приложение 1. Основные понятия теории вероятностей 413
Приложение 2. Матричная экспонента 428
Список рекомендуемой литературы 438
Предметный указатель 440

Учебное издание
Математика в техническом университете
Выпуск XVIII
Волков Игорь Куприянович
Зуев Сергей Михайлович
Цветкова Галина Михайловна
СЛУЧАЙНЫЕ ПРОЦЕССЫ
Редактор В.И. Трефилое
Художник С. С. Водчиц
Корректор О.В. Калашникова
Оригииал-макет подготовлен
в Издательстве МГТУ им. Н.Э. Баумана
под руководством АН. Канатнике* ва
Изд. лиц. № 020523 от 25.04.97
Подписано в печать 07.06.98 Формат 60x88 1/16.
Печать офсетная. Бумага офсетная № 1.
Усл. печ. л. 28. Уч.-изд. л. 27,82.
Тираж 1000 экз. Изд. № 121. Заказ №1986
Издательство МГТУ им. Н.Э. Баумана.
107005, Москва, 2-я Бауманская, 5.
Отпечатано в Производственно-издательском комбинате ВИНИТИ,
140010, Люберцы, Московской обл., Октябрьский пр-т, 403.
Тел. 554-21-86