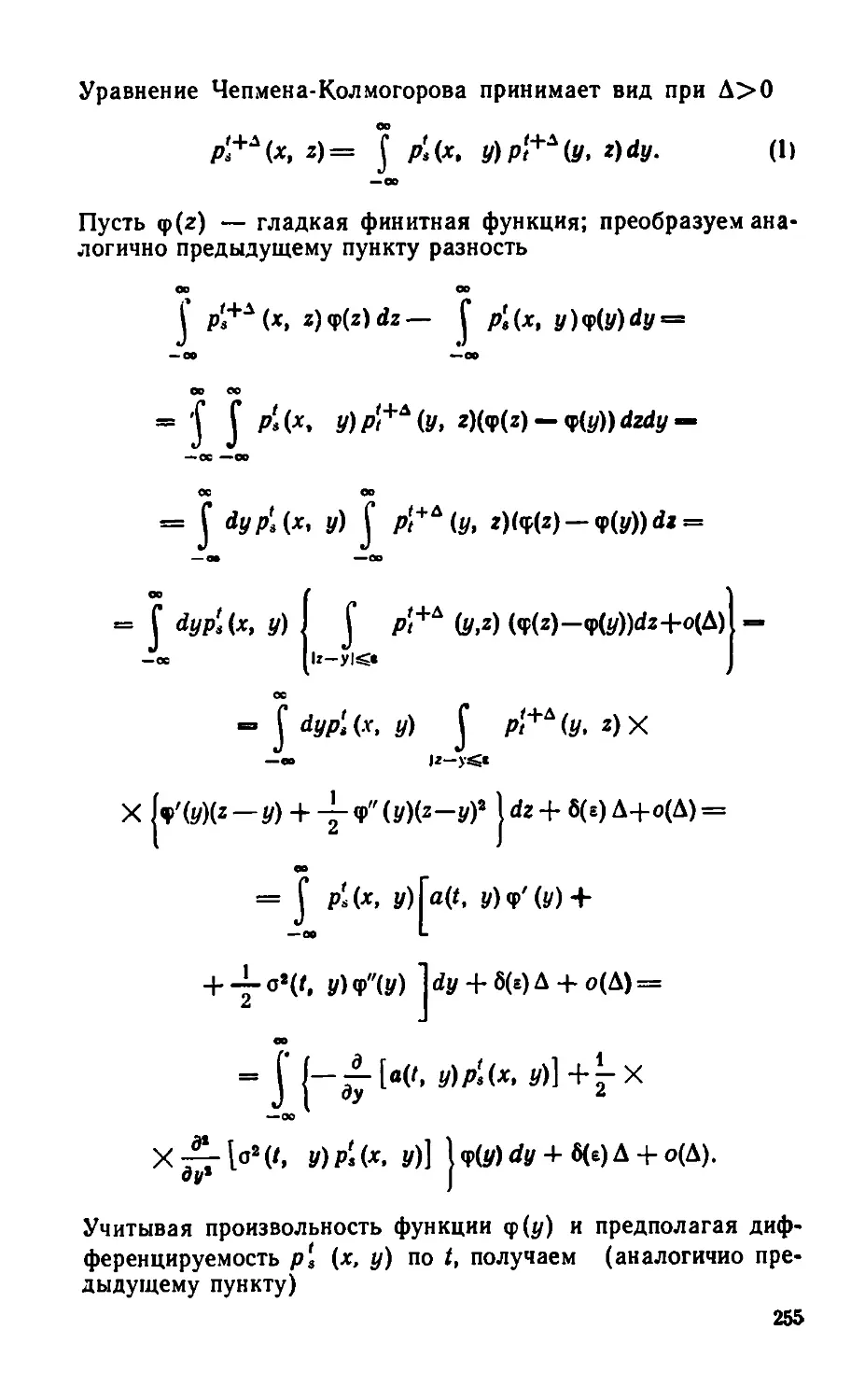Теория вероятностей и случайных процессов - Тутубалин В.Н.

Автор: Тутубалин В.Н.

Теги: теория вероятностей и математическая статистика теория вероятностей математическая статистика комбинаторный анализ теория графов математика математическая физика высшая школа учебное пособие для студентов издательство мгу

ISBN: 5-211-02264-5

Год: 1992

Похожие

Теория случайных процессов в примерах и задачах

Теория вероятностей, случайные процессы и математическая статистика

Прикладной анализ случайных данных

Конспект лекций по теории вероятностей, математической статистике и случайным процессам

Текст

В.Н.Тутубалин
ТЕОРИЯ
ВЕРОЯТНОСТЕЙ
И СЛУЧАЙНЫХ
ПРОЦЕССОВ
В. Н. Тутубалин
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И СЛУЧАЙНЫХ ПРОЦЕССОВ.
ОСНОВЫ
МАТЕМАТИЧЕСКОГО
АППАРАТА
И ПРИКЛАДНЫЕ
АСПЕКТЫ
Допущено Государственным комитетом СССР по
народному образованию в качестве учебного
пособия для студентов физико-математических и
физико-технических специальностей вузов
ИЗДАТЕЛЬСТВО
МОСКОВСКОГО
УНИВЕРСИТЕТА
4992
ББК 22.171
Т 91
УДК 519.21
Рецензенты:
кафедра высшей математики МФТИ,
доктор фнз.-мат. наук Ю. Н. Тюрин
Тутубалин В. Н.
Т 91 Теория вероятностей и случайных процессов: Учеб,
пособие. — М.: Изд-во МГУ, 1992. — 400 с.
ISBN 5-211-02264-5
В учебном пособии рассматриваются основы теории вероятнос-
тей н понятия статистической проверки гипотез. Обсуждаются теория
стационарных случайных процессов, теория марковских цепей п про-
цессов, включая центральную предельную теорему для цепей Мар-
кова и предельный переход от динамической системы к диффузион-
ному процессу. Обобщен опыт различных конкретных применений
теории вероятностей. Рассмотрены вопросы приложений теории слу-
чайных процессов, включающие, в частности, проблему прогноза с
использованием вероятностных моделей и методов.
Для студентов физико-математических и физико-технических
специальностей высших учебных заведений.
1602090000(4309000000)—025
Т 077(02)—92 83—92
ББК 22.177
ISBN 5-211-02264-5
© Издательство Московского
университета, 1992
ОГЛАВЛЕНИЕ
Предисловие................................................ 6
Часть первая
ОСНОВЫ МАТЕМАТИЧЕСКОГО АППАРАТА
Глава 1. Дискретное пространство элементарных событий .... 9
§ 1. Основные понятия................................. 9
§ 2. Исчисление вероятностей......................... 14
§ 3. Условная вероятность............................ 17
$ 4. Независимость................................... 22
§ 5. Случайные величины...............................30
§ 6. Системы случайных величин........................36
§ 7. Проверка статистических гипотез..................45
Глава 2. Аксиоматика Колмогорова...........................52
§ 1. Введение.........................................52
§ 2. Основные понятия теории вероятностей по Колмогорову 58
§ 3. Основные формулы исчисления вероятностей .... 68
§ 4. Примеры применения основных понятий и формул . . 77
Глава 3. Суммы независимых случайных величин...............89
§ 1. Постановка задачи и основы математического аппарата 89
§ 2. Слабая сходимость. Теорема Хинчина. Центральная пре-
дельная теорема ..................................... 98
§ 3. Статистические приемы, связанные с центральной пре-
дельной теоремой и нормальным распределением ... ПО
Глава 4. Подходы к изучению зависимости...................132
$ 1. Общая теория условных математических ожиданий ... 133
§ 2. Корреляционная теория случайных величин.........146
§ 3. Теорема Колмогорова о продолжении меры..........158
Глава 5. Корреляционная теория случайных процессов........168
$ 1. Средиеквадратическая теория.....................169
§ 2. Обыкновенные и обобщенные стационарные случайные
процессы.............................................175
§ 3. Спектральное разложение корреляционного функционала 181
§ 4. Спектральное разложение обобщенного стационарного
случайного процесса..................................187
§ 5. Применения спектральной теории..................191
Глава 6. Марковские процессы..............................211
$ 1. Основные понятия................................211
§ 2. Конечные марковские цепи........................223
$ 3. Примеры марковских цепей и некоторые дополнения . 237
§ 4. Марковские диффузионные процессы................247
Часть вторая
ПРИКЛАДНЫЕ АСПЕКТЫ ТЕОРИИ ВЕРОЯТНОСТЕН
II ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Предисловие ко второй части книги ............ 267
Глава 1. Элементарные применения элементарной теории вероятно-
стей .................................................... 269
3
§ 1. Нужно ли заземлять крест?....................269
§ 2. Вероятностный дьявол.........................272
§ 3. Наука или натурфилософия?....................284
Глава 2. Применения центральной предельной теоремы.....291
§ 1. Электрические сети зданий....................291
§ 2. Отопление....................................301
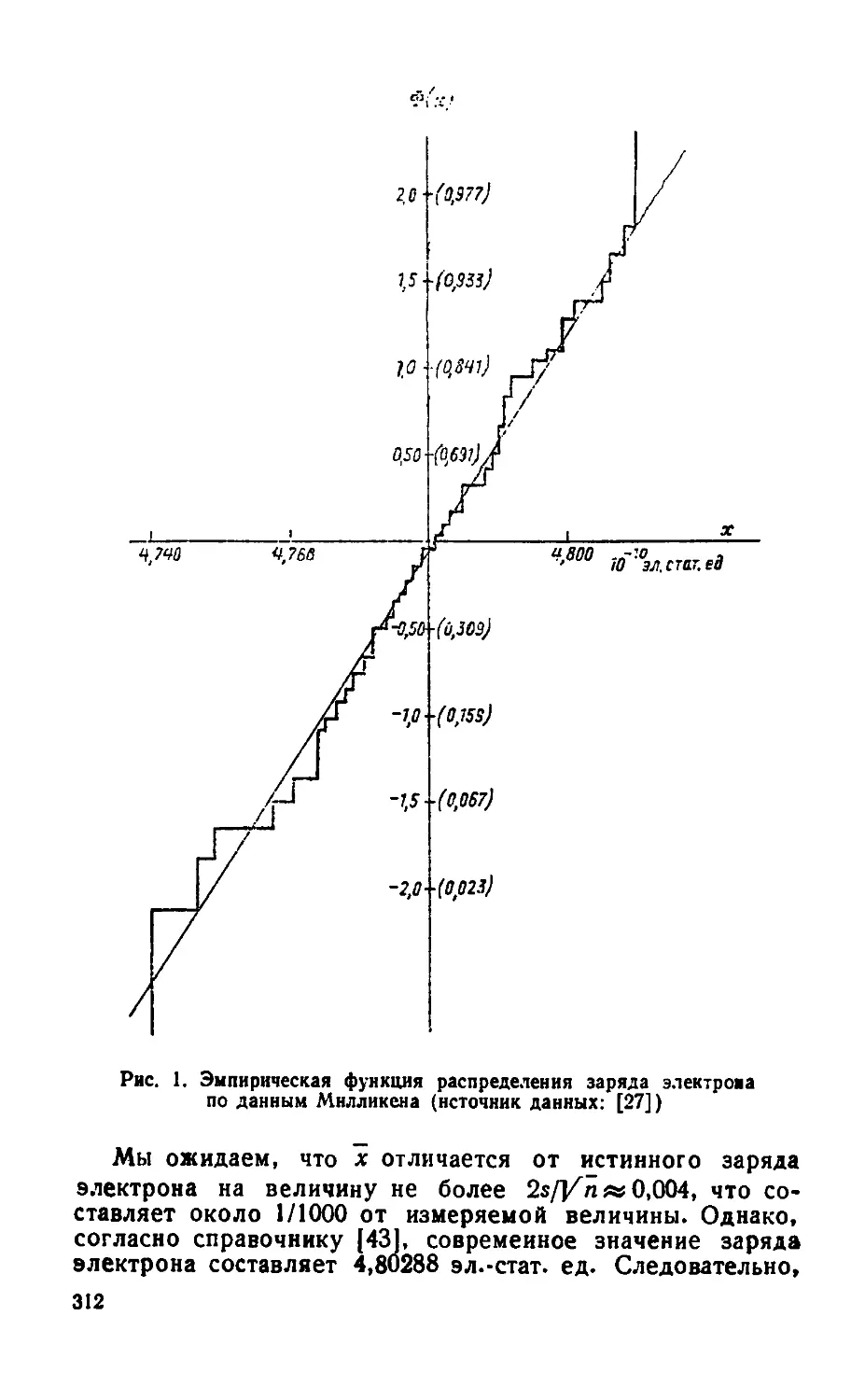
§ 3. Обработка измерений (наблюдений) ............308
Глава 3. Примеры применения математической статистики . . . .316
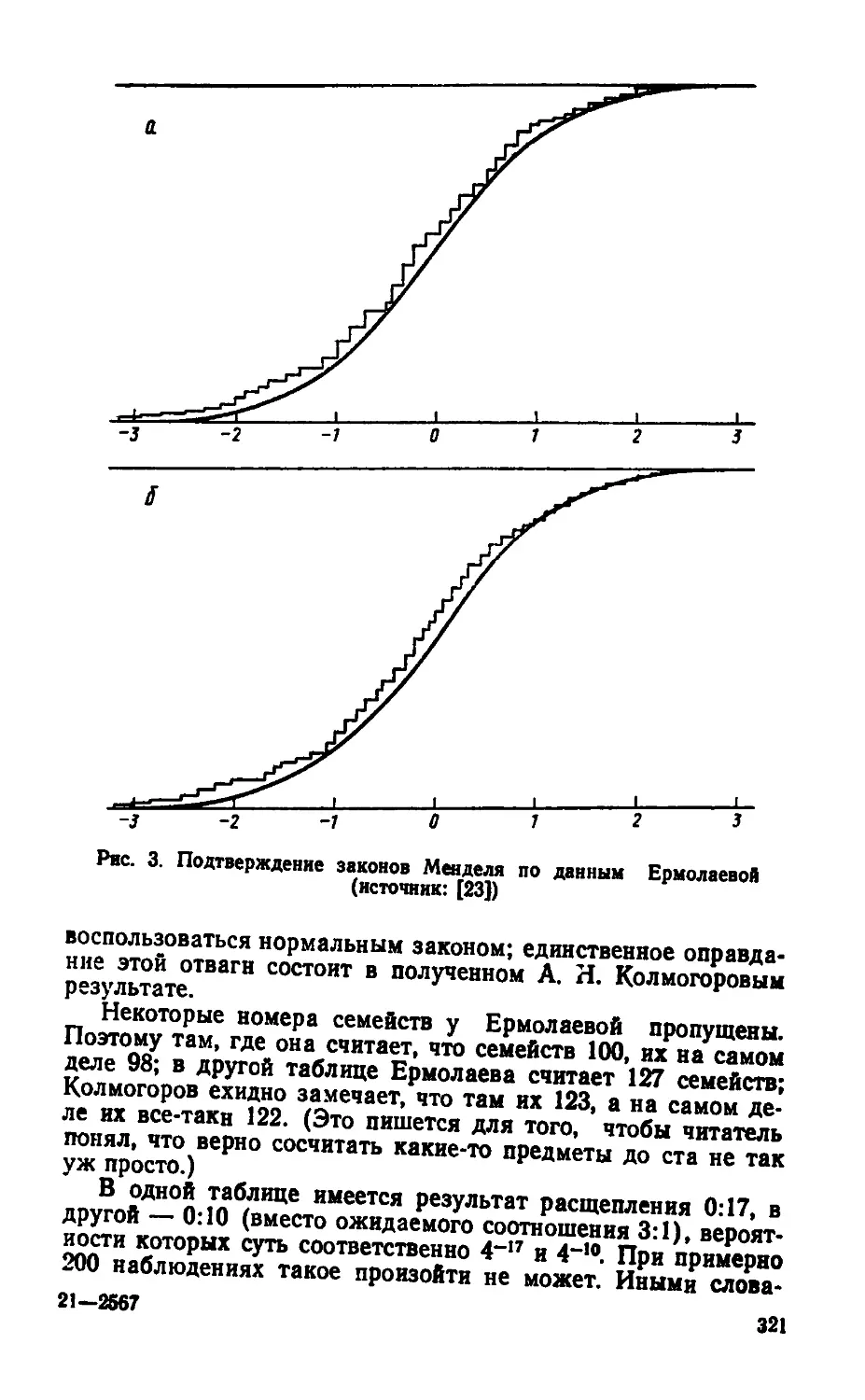
$ 1. Критерий Колмогорова.........................317
$ 2. Дискриминантный анализ.......................326
$ 3. Метод наименьших квадратов...................332
Глава 4. Примеры применения теории случайных процессов . . . .341
11. Ранние применения теории случайных процессов . . . 342
2. Стационарные приращения......................353
3. Проблема прогноза случайных процессов........367
4. Колебания уровня Каспийского моря............372
5. Металлический волновод.......................382
Литература ................... . . 393
Наверное, это нескромно с моей стороны, но я
посвящаю эту несовершенную книгу памяти Андрея
Николаевича Колмогорова. Поразительно, что эле-
ментарный студенческий курс, призванный отразить
наиболее простые и существенные итоги развития
теории вероятностей и случайных процессов, более
чем наполовину состоит из результатов, лично при-
надлежащих этому великому ученому. Лишь эле-
ментарное введение в теорию вероятностей, включая
центральную предельную теорему, представляет со-
бой создание классиков XIX в.; что же касается зна-
чительной части включенных в книгу приемов мате-
матической статистики и почти всего материала по
математической теории случайных процессов, то все
это создал А. Н. Колмогоров.
Еще более важную роль играют для нас общий
подход и конкретные результаты А. Н. Колмогоро-
ва в приложениях вероятностно-статистических ме-
тодов. Без его работ, личного влияния и примера мы
вообще не понимали бы, что такое эффективное ес-
тественнонаучное приложение теории случайных
процессов и в каких областях науки такие прило-
жения возможны. Собственно говоря, в данной
книге проводится та мысль, что приложения такого
уровня глубины и эффективности, как, например,
колмогоровская теория локального строения тур-
булентности, доступны лишь Андрею Николаевичу,
в то время как другие исследователи должны удов-
летвориться более скромным уровнем согласия с
действительностью, следовательно, и более скром-
ными выводами. Тем более мы должны быть бла-
годарны А. Н. Колмогорову за установление дей-
ствительно яркого идеала научного достижения.
АВТОР.
ПРЕДИСЛОВИЕ
Эта книга возникла из курса лекций, который автор читал
студентам специальности «Механика» на механико-математи-
ческом факультете МГУ, и анализа разнообразных работ в об-
ласти приложений теории вероятностей. Она, однако, предла-
гается в качестве одного из возможных учебных пособий по
теории вероятностей также для студентов физических специ-
альностей и для студентов вузов с расширенной математичес-
кой подготовкой.
Этот тезис следует защитить. Дело в том, что широко из-
вестно, например, мнение Л. Д. Ландау, состоящее в том, что
теорию вероятностей студентам-физикам должен преподавать
не математик, а физик, потому что при изучении квантовой
механики студенты легко и удобно усваивают основные зако-
ны теории вероятностей. Это мнение, действительно, весьма
серьезно, потому что замена физика математиком означает
дальнейшую узкую специализацию преподавания, отрицатель-
ные стороны чего вполне очевидны. Математику остается от-
ветить лишь одно: доказать, что за счет лучшего знания ма-
тематики он может сообщить студентам нечто ценное, чего
физик, меньше знающий математику, сообщить не может. Тог-
да речь может пойти о допущении математика к преподава-
нию для физиков — конечно, не в качестве единственно пра-
вильного толкователя единственно правильного учения, а в
рамках лозунга «пусть расцветают сто цветов».
Но кого же выбрать в качестве представителя тех физи-
ков, которые из-за недостаточного знания математики кое-чего
важного ие сообщают своим студентам? Хорошо бы выбрать
человека великого.
Наверное, такой замечательный физик и преподаватель
физики, как Р. Фейнман, любимейший автор очень многих (в
том числе и автора данной книги), является здесь неплохим
эталоном. Так вот, отношение Р. Фейнмана к математике та-
ково: математики отправляются от аксиом, строго рассужда-
ют и у них все хорошо выходит, только, может быть, не имеет
отношения к реальности. А в данной книге студенту показыва-
ется, что математика имеет свои трудности, которые стано-
вятся очевидными при трактовке случайных процессов сред-
ствами теории меры и как-то упираются в математическую
модель континуума. Общий дух произведений Р. Фейнмана
таков, что он бы непременно отметил это обстоятельство, если
бы достаточно четко представлял его себе: об этом ие мешает
6
знать не только физику-теоретику, но и любому человеку,
имеющему дело с математикой.
Вторым аспектом, в котором математик пользуется некото-
рым преимуществом в сравнении с физиком, является более
широкое (хотя и менее глубокое) представление о приложени-
ях. Не все же физики после завершения образования будут
заниматься микромиром, для которого законы, имеющие веро-
ятностную форму, допустим, единственно правильны. Судьбу
вероятностных представлений при столкновении их с различ-
ными областями применений лучше сумеет проследить мате-
матик, чем специалист по квантовой механике, у которого
других представлений и не бывает. Вообще, когда, например,
Р. Фейнман говорит о роли физических идей в технике, он, по-
жалуй, проявляет излишний оптимизм. Тут, конечно, дело не
в незнании: не мог Р. Фейнман не знать, что до применения в
технике физические идеи должны пробить себе путь через та-
инственную кухню, называемую «материаловедением»: из ка-
кой стали, например, нужно делать магнитопроводы электри-
ческих машин — горячекатаной или холоднокатаной? Но все
же как-то дать понятие о реальных возможностях теории ве-
роятностей (скажем, регрессионного анализа) в том же мате-
риаловедении удобнее математику.
Предисловие получилось бы слишком пространным, если
бы в нем описывать, что есть н чего нет в данной книге. Поэто-
му подробные указания такого рода перенесены в конкретные
разделы. Скажем кратко, что первая часть книги примерно
охватывает стандартные основы теории вероятностей и содер-
жит некие избранные главы теории случайных процессов. Она
адресована читателю, владеющему математическим анализом,
линейной алгеброй н основами функционального анализа и
теории меры. Теория меры существенна; при необходимости
ознакомиться с нею можно, например, частично прочитав, а
частично просмотрев 26 страниц приложений 1—3 к книге
А. А. Боровкова [3]. Многие вопросы теории случайных про-
цессов, не рассмотренные в данной книге, можно найти в кни-
гах Ю. А. Розанова [30—33], рассчитанных примерно на ту же
категорию читателей.
Вторая часть книги, посвященная примерам приложений
теории вероятностей, в основном совершенно элементарна, но
в самом конце все-таки требует знаний на уровне первой части
книги. Двадцать лет назад вышла книга автора [39], в кото-
рой тоже кое-что говорилось о приложениях. Данная книга ие
является вторым изданием книги [39] как в части математи-
ческой (хотя, естественно, кое-что по существу сохранилось),
так в особенности в части прикладной. Дело в том, что в [39]
было допущено много схоластики, раздражавшей наиболее
квалифицированных читателей, вроде, например, такого рас-
суждения: как мы можем быть уверены, что нам дан статис-
7
тический ансамбль экспериментов, проводимых в одинако-
вых условиях? Если мы контролируем все условия экспери-
мента, то и исход будет всегда один (ничего случайного), а
если не все, то как мы можем быть уверены, что то, чего мы
не контролируем, остается одинаковым? Научную нелепость
такого софизма автор понимал и в 1972 г., но включил его в
книгу [39J по методическим соображениям: чтобы удивить
студента, который еще никогда не задумывался над сложной
диалектикой применения понятий любой науки к действитель-
ности.
В данной книге (как надеется автор) схоластика убрана, а
изложение второй части основывается на фактических приме-
рах, значительная часть которых имеет широкий интерес.
Каждый пример имеет целью проследить в конкретных усло-
виях судьбу тех или иных вероятностных понятий и методов
при их столкновении с реальностью. Более подробно содержа-
ние второй части книги описывается в предисловии к этой
части.
В заключение предисловия несколько слов благодарности.
Возможностью заниматься разнообразными приложениями,
на основе чего и написана данная книга, автор в значительной
мере обязан свободной и доброжелательной атмосфере, соз-
данной Б. В. Гнеденко на кафедре теории вероятностей меха-
нико-математического факультета МГУ, которой он в течение
многих лет заведует. Б. В. Гнеденко прочитал рукопись дан-
ной книги и сделал ряд ценных замечаний. Пониманием мно-
гих вещей автор обязан В. В. Налимову, который в течение
ряда лет был заместителем заведующего лабораторией ста-
тистических методов (заведовал же ею А. Н. Колмогоров). Ав-
тор благодарит внимательных и доброжелательных рецензен-
тов данной книги — С. В. Резниченко (Московский физико-
технический институт), Ю. Н. Тюрина (Московский универси-
тет) и М. Г. Шура (Московский институт электронного маши-
ностроения) — за многочисленные замечания, позволившие
улучшить текст книги. Наконец, автор благодарен коллективу
кафедры высшей математики Московского физико-техничес-
кого института и ее заведующему Г. Н. Яковлеву за полез-
ное обсуждение этой книги.
ЧАСТЬ ПЕРВАЯ
ОСНОВЫ МАТЕМАТИЧЕСКОГО АППАРАТА
ГЛАВА 1
ДИСКРЕТНОЕ ПРОСТРАНСТВО ЭЛЕМЕНТАРНЫХ СОБЫТИЙ"
§ 1. Основные понятия
Мы будем заниматься теорией вероятностей в основном*
как одной из математических наук. Наука вообще, а матема-
тическая наука в особенности есть вещь сравнительно ясная,
которая строится и излагается так, чтобы ее вполне сложив-
шиеся части нетрудно было полностью понять. Но причины,
по которым та или иная наука существует, преподается и раз-
вивается, коренятся в малодоступных анализу глубинах ин-
дивидуальной и общественной психологии. Из многих источ-
ников хорошо известно, что с давних пор внимание человека
привлекали «эксперименты» (как мы говорим сейчас), исход
которых не вполне однозначен: эксперимент может кончиться
одним из исходов, полный список которых обозначим
={<01, <02,....<оп}. Например*, в греческой и римской цивили-
зациях важным элементом общественной жизни было гадание
(в частности, по внутренностям жертвенных животных);
впрочем, сомнительно, чтобы существовал полный список воз-
можных исходов такого «эксперимента». Различные вариан-
ты средневекового «божьего суда», например судебный по-
единок, а в наше время жеребьевка для решения тех или иных
спорных вопросов; наконец, азартные игры всех видов — все
* В данной книге мы неоднократно будем обращаться к тем пли иным
историческим сведениям, в особенности, к истории теории вероятностей.
Однако систематического характера эти сведения не носят. Причина их
фрагментарности состоит главным образом в том, что на общепринятые
исторические взгляды нельзя полагаться без их фундаментальной провер-
ки. Ярким примером такого рода является, например, знаменитая форму-
ла Лейбница—Ньютона, которая, как оказывается, была настолько хоро-
шо известна до Лейбница и Ньютона, что эти два великих ученых никог-
да из-за нее и не спорили, хотя, как кажется, не упустили ни одной воз-
можности для приоритетных споров, нелепый характер которых служит
вечным назиданием потомству. Автор данной книги не занимался необхо-
димой переоценкой исторических взглядов, следовательно, и не мог
браться за систематическое изложение истории теории вероятностей. Чи-
тателю, заинтересованному в подобном систематическом изложении, горя-
чо рекомендуется обратиться к историческому очерку в учебнике Б. В. Гне-
денко (шестое издание 1986 г.), который содержит много интересного.
»
это примеры «экспериментов» с неопределенным исходом.
Например, при бросании монеты она может упасть вверх гер*
бом (что мы будем изображать единицей) или цифрой (что
мы будем изображать нулем). Не следует непочтительно от-
носиться к бросанию монеты: из многих бросаний можно
сконструировать достаточно интересные эксперименты, а из
•счетного числа — даже бросание случайной точки на конти-
нуум [0, 1]. Для этого нужно на нули и единицы, возникаю-
щие при бросании монеты, посмотреть как на знаки двоичной
дроби, определяющей вещественное число.
Понятия теории вероятностей применимы не ко всем экспе-
риментам с неопределенным исходом. Давно было замечено,
что эксперименты, производимые с помощью достаточно акку-
ратно сделанных «аппаратов», как, например, монета, иг-
ральная кость, рулетка или колода игральных карт, обладают
двумя свойствами: 1) непредсказуемостью (в смысле невоз-
можности заранее предсказать исход такого эксперимента);
2) статистической устойчивостью: при большом числе повто-
рений эксперимента частота осуществления того или иного ис-
хода оказывается близкой к некоторому числу, которое и на-
зывают вероятностью данного исхода. (Частотой называется
отношение числа наступлений данного исхода к числу всех
экспериментов).
Иногда вероятности исходов можно угадать из соображе-
ний симметрии. Так, для монеты вероятность выпадения гер-
ба, очевидно, должна быть такой же, как н для выпадения
цифры, т. е. равняться *7г- Опыты с реальными монетами это
подтверждают. Аналогично для игральной кости (кубик с
шестью гранями, на которых нанесены точки числом от 1 до 6)
вероятность выпадения каждой грани должна равняться '/6.
Но опыты это не всегда подтверждают. Впрочем, эти (вообще
говоря, ие равные между собой) вероятности все-таки оказы-
ваются близкими к ’/в. так что в учебных задачах с хорошим
приближением считается, что мы имеем дело с идеальной
костью с вероятностями выпадения отдельных граней, равны-
ми 76-
Анализ классических монографий и учебников по теории
вероятностей (начиная от Лапласа, Пуассона, Чебышева и
до наших дней) показывает, что все они начинаются с одной
и той же математической модели случайного эксперимента, в
которой считается заданным множество Q элементарных исхо-
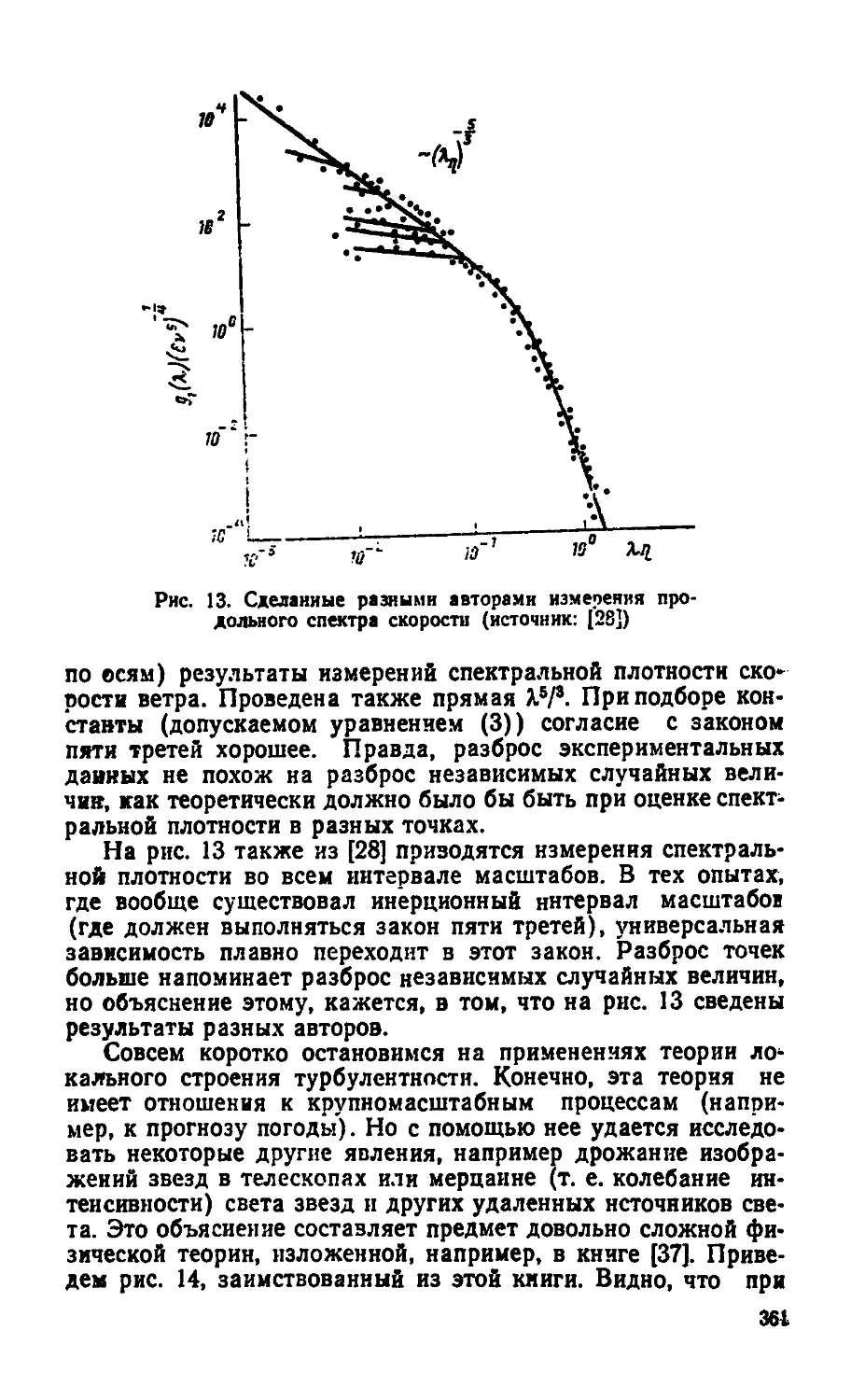
дов эксперимента и вероятности Р (со) каждого элементарно-
го исхода соей. В классических учебниках Q конечно, а в
современных (по ряду разумных причин) счетно.
Определение 1. Вероятностным пространством назы-
вается не более чем счетное множество й={ю), каждому эле-
менту и которого поставлено в соответствие число Р((о)>0,
называемое вероятностью <о.
10
При этом должна выполняться единственная
Аксиома.
2Р(ш)=1
<|»ВД
(сумма вероятностей всех элементарных исходов равна едини-
це).
Кроме элементарных исходов эксперимента (синоним: эле-
ментарные события) в теории вероятностей выделяются со-
бытия, которые в классических учебниках задавались словес-
ным описанием, например событие, состоящее в том, что при
бросании кости выпадает четное число очков. Постепенно бы-
ло осознано, что событие лучше всего определить как произ-
вольное подмножество множества Q.
Определение 2. Событием А называется произвольное
подмножество AsQ. Вероятность Р(А) события А определя-
ется формулой
PM) = SP(«.)
(вероятность события есть сумма вероятностей входящих в
него элементарных исходов).
Совокупность определений 1 и 2 и единственной аксиомы
дает полное описание элементарной модели теории вероятнос-
тей. В принципе эта модель достаточна для решения всех за-
дач, связанных со случаями, когда множество элементарных
событий дискретно (т. е. конечно или счетно), но перед изу-
чающим теорию вероятностей стоит (вообще говоря, нелегкая)
задача перевода формулировок ситуаций, заданных в терми-
нах обычного языка, на язык вероятностного пространства,
т. е. й и Р(ю). Если взглянуть на проблему изучения теории
вероятностей шире — изучение с целью применения к реаль-
ным явлениям, — то вырисовывается еще более сложная кар-
тина.
Дело в том, что любая математическая наука (теория ве-
роятностей в том числе) не несет в самой себе никаких указа-
ний на возможные области и способы применений. Например,
при изучении математического анализа функций нескольких
переменных, векторных (и тензорных) полей совершенно ни-
откуда не следует, что этот аппарат находит применение в
электродинамике. А скажем, уравнение струны в уравнениях
математической физики изучают никак не ради скрипичной
струны. Задачник по теории вероятностей суммирует (на-
сколько сумеет) накопленный веками опыт применения этой
науки к реальным явлениям. Поэтому ситуации задачника не
могут и не должны формулироваться в чисто математических
терминах. В реальной научной деятельности предполагается
Двухэтапный перевод: реальной ситуации в ситуацию задач-
11
ника, затем ситуации задачника в ситуацию Q, Р (со). В учеб-
ном процессе изучается в основном лишь второй этап.
Надо отметить, что описание множества Q обычно не пред-
ставляет трудностей: это просто множество всех возможных
исходов эксперимента. Но задача определения Р(о>) часто яв-
ляется трудной. Существует классический прием, так назы-
ваемая «классическая вероятность», когда множество Q ко-
нечно, а все Р (<о) равны между собой (в этом случае Р (о» > =
= 1/7V, где W=W(Q) — число элементов в множестве Q). Для
любого события А в этом случае имеем
Р(Л) = УР(ш) = -^1,
c»gA N(Q)
где N(A) — число элементов в множестве А.
На классическом языке все шеЛ называются элементар-
ными исходами, благоприятными для события А, и получаем
классическое «заклинание»: вероятность события равна отно-
шению числа исходов, благоприятных для данного события,
к числу всех возможных исходов.
Следует отметить, что классики теории вероятностей, ска-
жем Лаплас, прекрасно понимали, что элементарные исходы
могут быть и не одинаково вероятными. Но «классическая ве-
роятность» закрепилась в науке как прием, позволяющий
быстро и легко (хотя, быть может, и неверно) решить задачу
об определении Р(ю). Это решение обычно мотивируется теми
или иными соображениями о «симметрии», т. е. соображения-
ми теоретико-групповыми.
Рассмотрим пример древней процедуры жеребьевки, кото-
рая возобновляется и в наши дни при каждой сдаче экзамена
группой студентов. Пусть имеется W экзаменационных биле-
тов, из которых п «счастливых» (в том смысле, что все студен-
ты их знают), a N—п «несчастливых» (т. с. ни один из студен-
тов их не знает), причем для простоты обозначений всех сту-
дентов тоже N. Жеребьевка (т. е. раздача билетов) происхо-
дит по очереди: сначала берет билет первый в очереди сту-
дент, затем второй и т. д. Понятно, что для первого студента
вероятность вытащить счастливый билет равна nfN, но как
быть со вторым? Если первый студент вытащит счастливый
билет, то шансы второго составят (п—l)f(N—1), т.е.умень-
шатся, а если первый студент вытащит несчастливый билет, то
шансы второго будут n/(N—\)>n/N. Для третьего студента
нужно рассмотреть еще более сложный набор ситуаций и т.д.
Пусть Л/ — событие, состоящее в том, что /-й в очереди сту-
дент вытащит счастливый билет. Попытаемся найти Р(Л()>
введя множество Q элементарных событий так, чтобы они бы-
ли равновероятными.
12
Предлагается под отдельным элементарным событием <>
понимать тот список, который окажется в руках у экзаменато-
ра после окончания раздачи билетов:
/I 2 ... / . . . N\
ю = ( ' )
\ й G ••• О • • • W
(в первой строке — номера студентов, во второй строке — но-
мера билетов). Если угодно, это подстановка из W чисел. Но-
мера билетов й, 1'2» ...» hr как-то зависят от того порядка, в ко-
тором их разложил на столе экзаменатор. Можно предполо-
жить, что экзаменатор положил сверху счастливые билеты, а
несчастливые засунул под них. Тогда первым студентам в оче-
реди будет лучше (если они не будут хитрить, а возьмут по-
просту те билеты, которые лежат сверху). Можно предполо-
жить, что экзаменатор сделал наоборот. Оба этих случая не
приведут к задаче на классическую вероятность. Но если
предположить, что экзаменатор подобными пустяками не за-
нимается, то тогда задача инвариантна относительно любых
перестановок номеров билетов. Но перестановка номеров h и
I/ эквивалентна перестановке первого и /-го студентов, так что
ясно, что должно быть Р(Л/)=Р(Л1)=П/У.
Можно сосчитать эти вероятности и из классической фор-
мулы. Очевидно, что Af(Q)=W! Для подсчета М(Л/) заме-
тим, что для оеЛ/ номер I/ может принимать п различных
значений; й — все значения, кроме «/, т. е. N—1 значений,
?2 — все значения, кроме I/ и й» т. е. N—2 значений и т. д.
Поэтому N(Aj)=n(N— 1)! и Р(Л>) =У(Л,)^(Й) =n/N.
Таким образом, вероятность вытащить счастливый билет
не зависит от места в очереди: не нужно ни приходить порань-
ше, чтобы занять очередь, ни стараться оказаться в конце
очереди. Этот вывод целиком зависит от предполагаемой рав-
новероятности элементарных событий. Каким образом можно
было бы обосновать это допущение?
Имея в виду связь между вероятностью и частотой, можно
было бы представить себе экспериментальную проверку: в
длинном ряде экспериментов определяются частоты наступ-
ления различных элементарных событий; если эти частоты
оказываются близкими, то мы заключаем, что соответствую-
щие вероятности в самом деле равны. Однако элементарных
событий у нас NI; чтобы частоты их наступления сделались
похожи иа вероятности, необходимо провести столько экспе-
риментов, чтобы каждое элементарное событие произошло
хотя бы несколько раз, т. е., скажем, 1ОАГ! или 1ООАП экспе-
риментов. Ясно, что это совершенно невозможно уже при уме-
ренном N. Следовательно, мысль об экспериментальной про-
верке равновероятности должна быть оставлена.
Теоретические соображения о равновероятности сводились
У нас к тому, что экзаменатор не станет заниматься такими
13
пустяками, как создание заведомо неравновероятной ситуации.
Это совсем не означает, что автоматически создается равнове-
роятность: например, опыты с игральными картами показали,
что колоду карт нужно очень долго тасовать, чтобы достаточ-
но хорошо разрушить какой-то первоначальный порядок. С
экзаменационными билетами этого никто не делает.
Поэтому правильнее будет сказать, что если различные
элементарные события неравиовероятны, то ни экзаменатор,
ни студенты совершенно не знают, какие из этих событий име-
ют большие вероятности, а какие — меньшие. Это незнание
мы и моделируем в математической модели с равновероятны-
ми элементарными событиями. Если угодно, наша равноверо-
ятность в этой задаче субъективная; несмотря на все попытки
изгнать субъективизм из науки, что-нибудь от него всегда ос-
тается.
§ 2. Исчисление вероятностей
В предыдущем параграфе был приведен пример практи-
ческого вывода, который можно извлечь из подсчета вероят-
ностей: очередь за экзаменационными билетами занимать
смысла не имеет. Какие выводы можно вообще извлечь из
знания вероятностей, пока сказать не можем: это станет яс-
ным лишь после изучения основных законов теории вероят-
ностей. Пока что наша задача — облегчить подсчет вероят-
ностей. Дело в том, что прямой подсчет с помощью определе-
ния 2 § 1, конечно, часто бывает трудным. Следует вывести
ряд простых формул, вытекающих из определения 2, которые
будем называть формулами исчисления вероятностей.
Под исчислением вообще понимаются какие-то способы пи-
сать формулы и выводить из одних формул другие. Огром-
ную нагрузку несут в современной культуре дифференциаль-
ное и интегральное исчисления. Роль исчисления вероятнос-
тей не столь фундаментальна, но все же велика. Кроме облег-
чения подсчетов вероятностей, можно отметить два аспекта
работы того небольшого исчисления, которое сейчас разовьем.
1. Выведенные для дискретного Q формулы исчисления
сохраняют свой вид для произвольного сложного Q, облегчая
понимание общей аксиоматики.
2. Лишь в учебниках теории вероятностей действует схема,
согласно которой для реального явления нужно сначала по-
строить модель из Q и Р(ш) и воспользоваться определени-
ем 2 § 1. Фактически вероятности одних событий находятся
по вероятностям других событий без полного описания (иног-
да) Q и (как правило) Р(со), а прямо путем обращения к
формулам исчисления.
Итак, рассмотрим операции над событиями и свойства ве-
роятностей. Поскольку события трактуются как подмноже-
14
ства Q, то операции над ними — это обычные теоретико-мно-
жественные операции, но следует иметь в виду, что в теории
вероятностей сохранилась старая терминология, употребляв-
шаяся еще до возникновения теории множеств (в этом есть*
свой смысл, так как в применениях теории вероятностей собы-
тие есть, конечно, подмножество Q, но, как правило, не любое,
а задающееся достаточно простым высказыванием).
Дополнение (или отрицание, или противоположное собы-
тие). С каждым событием А связано событие Л=Й\Л, кото-
рое состоит из тех и только тех элементарных событий юей,
которые не входят в А. Это событие А называется дополнени-
ем к событию А, либо отрицанием события А, либо событием,.
противоположным для события А. Из определения 2 § 1 вы-
текает, что
Р(Л)+Р(Л) = 1,
так как
р (Л) + р( л) = S Р(«“) + 3 Р(Ч=3 Р(«0 = 1 •
и'фА u'GQ
Поупражняемся немного в классической терминологии
теории вероятностей. Будем говорить, что событие Л насту-
пило в опыте, если опыт закончился таким элементарным со-
бытием to, что <оеЛ. Тогда сможем заявить, что противопо-
ложное событие Л наступает тогда, когда событие Л не нас-
тупает: во всяком опыте наступает Л или А, но никогда оба
вместе.
Объединение, или сумма. Суммой событий Лназывает-
ся теоретико-множественное объединение соответствующих
подмножеств Л и В.
Пересечение, или произведение. Произведением А(\В=АВ
называется теоретико-множественное пересечение подмно-
жеств Л и В.
Очевидно, что сумма событий наступает тогда, когда нас-
тупает хотя бы одно из них, а произведение — тогда, когда
наступают оба вместе. Имеет место формула
Р(Л1|В) = Р(Л)+Р(В)— Р(ЛВ).
Действительно, в сумме Р(Л)4-Р(В) вероятности элементар-
ных событий, входящих и в Л и в В, будут сосчитаны дважды;
но если теперь вычесть Р(ЛВ), то остается сумма вероятнос-
тей элементарных событий, входящих в Л и В, в которой каж-
дое элементарное событие сосчитано ровно один раз. А это и
есть Р(ЛиВ).
В этой книге мы резервируем знак «плюс» для обозначения
суммы непересекающихся множеств: будем писать вместо
ЛОВ сумму Л + В, если известно, что пересечение АВ пусто:
ЛВ=0. В таком случае Р(ЛВ)=0 и получаем
Р(Л4-В)=Р(Л) + Р(В).
15
В элементарном случае (когда й не более чем счетно) эта
формула является простенькой теоремой; она сохраняется и
для общего случая, но уже в качестве аксиомы.
Свойств операций над событиями можно отметить великое
множество, например дополнение к сумме событий равно пе-
ресечению их дополнений; дополнение же к пересечению
есть, наоборот, сумма дополнений. Свойствам операций отве-
чают и какие-то свойства вероятностей. Однако основные фор*
мулы исчисления, которые исчерпывают значительную часть
того, что обычно требуется в выкладках, уже приведены.
Рассмотрим теперь следующую задачу. Некто написал п
писем, предназначенных п различным адресатам; затем на
конвертах написал п адресов и случайно разложил письма по
конвертам. Какова вероятность того, что хотя бы одно пись-
мо попало в свой конверт?
Элементарные события здесь, очевидно, подстановки; сло-
ва «случайно разложил» обозначают, что эти подстановки рав-
новероятны. Спрашивается, сколько таких подстановок, в ко-
торых хотя бы один символ переходит в себя. Этот подсчет
может показаться затруднительным. Воспользуемся форму-
лами исчисления. Пусть событие At означает, что i-e письмо
попало в свой конверт: очевидно, что Р(ЛЛ = 1/л. Нас спра-
шивают о вероятности суммы Ail)A2U... UAn- Оказывается, что
имеет место формула
Р(Л U A, U • • • U Ап)- 2 Р(Л<) - 2 Р(Д,Л/) +
i /</
4- 2 Р(А,4/А»)-. . .±Р(АА,. . . Лп).
/<7<»
Докажем эту формулу. Для этого нужно доказать, что в
сумме, стоящей в правой части, вероятность Р(ш) каждого
(i)e4iUA2U - UAn учтется ровно один раз. Пусть для опреде-
ленности, (1)еД1Д2—Ал, но <о^Д*+1,.... (о^Лп. Тогда в пра-
вую часть Р (<о) войдет следующее число раз:
Cl — Сл + &- . . . ±С{=1,
так как
o=(i. ±С*.
Формула доказана.
Заметим теперь, что
Р(М.- . =
так как событие Л1Л2...Л* означает, что первые & писем попали
в свои конверты, а остальные п—k переставились как угодно,
Учитывая это, находим, что
16
₽(AUAU • • • U^) = C*^-J>L
- — + -— . . . ± —,
2! 31 n!
в чем нетрудно узнать отрезок ряда для 1-е~1»2/3.
Таким образом, при большом п вероятность каждому от-
дельному письму попасть в свой конверт весьма мала, но из
большего числа маловероятных событий хотя бы одно прои-
зойти вполне может. Этот вывод мы будем развивать неод-
нократно.
§ 3. Условная вероятность
Малоинтересно рассматривать одно случайное событие: у
такого события закон один — может наступить или не насту-
пить. Сколько-нибудь содержательная наука начинается тог-
да, когда в рассмотрение вводится много событий. В математи-
ческой схеме все они являются подмножествами одного Q (оп-
ределение 1 § 1), но в реальной жизни нужно уметь выбрать
Q и определить Р(<о) для юей. Если мы ввели в рассмотре-
ние какие-то события Ль Л2, ...,ЛП, то должны иметь право
рассматривать и их комбинации (т. е. то, что получится из них
операциями дополнения, суммы и пересечения). Отсюда выте-
кает, что наименьшее Q, пригодное для описания п событий Ль
Л;...Лп, состоит из элементарных событий вида BiB2...,Bn,
где каждое В,- может принимать два значения Л; и Ai. (Иными
словами, если мы ввели в рассмотрение события Ль Л2,.... Лп,
то мы ввели в рассмотрение все ситуации, когда некоторые из
этих событий происходят, а некоторые — не происходят). Сле-
довательно, нужно уметь определить вероятности P(BtB2...
Bn).
Как для этой цели, так и для ряда других применяется по-
нятие условной вероятности. Математический термин часто не
имеет ничего общего с общеязыковым смыслом соответствую-
щего слова (вспомните, например, алгебраические «кольца»,
«поля», «идеалы»). Но в случае термина «условная вероят-
ность» это, к счастью, не так — математический термин точно
соответствует общеязыковому смыслу высказывания: «вероят-
ность того, что событие В произойдет, если известно, что со-
бытие Л произошло».
Вдумаемся, действительно, сначала в общеязыковый смысл
слов «условная частота события В при условии, что событие Л
произошло». Нужно представить себе длинный ряд из п опы-
2-2567 17
тов, в котором событие А произошло пл раз, а событие В — пв
раз. Тогда частота события А равна пл/п, а частота события В
равна пв/п. Что же такое условная частота события В при ус-
ловии, что А произошло? Очевидно, из всех п опытов нужно
рассмотреть лишь те Пд опытов, в которых А произошло, и вы-
числить частоту наступления В в этих опытах. Но число нас-
туплений события В в этих опытах есть, очевидно, число нас-
туплений события АВ во всех опытах, и его естественно обоз-
начить Пав. Итак, условная частота события В при условии»
что А произошло, есть
Пдв/Пл=(Пдв/л) / (Лд/п).
Но если число л всех опытов достаточно велико, то частоты
должны быть близки к вероятностям: пав/п^Р(АВ) и па(п^
~Р(А). Примем поэтому математическое определение услов-
ной вероятности Р(В/А) события В при условии, что событие
А произошло, в следующем виде:
Р(ВМ) = ?^1
РМ)
(«вероятность совместного наступления, деленная на вероят-
ность условия»). Предполагается, конечно, что Р(Л)#=0.
Учебники (особенно старые) из этого определения считают
нужным вывести «теорему умножения вероятностей» в виде
Р(ЛВ) = Р(Л) Р(В/Л),
сопровождая ее «заклинанием» следующего вида: «вероят-
ность совместного наступления двух событий равна вероят-
ности одного из них, умноженной на условную вероятность
второго при условии, что первое наступило».
Не следует видеть в этом лишь пристрастие к многократно-
му переписыванию тривиальностей. Это тривиальности, если
мы каким-то образом ввели безусловные вероятности, но на
практике введение безусловных вероятностей обычно трудно.
Разберем, например, знаменитую ошибку прекрасного уче-
ного Д’Аламбера. Речь идет об одновременном бросании двух
монет. В результате этого опыта либо: 1) обе монеты выпада-
ют гербом вверх (ГГ); 2) обе монеты выпадают цифрой вверх
(ЦЦ), наконец, 3) монеты выпадают разными сторонами квер-
ху. Д’Аламбер считал, что эти результаты опыта равноверо-
ятны (следовательно, вероятность каждого равна */3). Между
тем и до Д’Аламбера, и после Д’Аламбера существовал пра-
вильный взгляд на вещи, который состоит в том, что мысленно
следует сделать монеты (а также кости и т. п.) различимыми;
тогда исход 3) представится как объединение исходов
ГЦиЦТ; четыре исхода ГГ, ЦЦ, ГЦ, ЦГ нужно считать рав-
новероятными; в частности, исход 3) имеет вероятность V2-
18
Следовало бы обосновать, почему не прав Д’Аламбер. На-
сколько понимает автор данной книги, сделать это чисто логи-
ческим путем невозможно: придется в конце концов промям-
лить что-нибудь вроде того, что мнение Д’Аламбера не согла-
суется с опытом. Действительно, в физике микромира бывают
ситуации, в которых скорее прав Д’Аламбер. Но надо хорошо
представлять себе, к какому именно опыту мы апеллируем;
нам ведь слишком скучно бросать монеты, чтобы речь могла
идти о личном опыте. Речь идет о некотором исторически на-
копленном опыте игроков в орлянку или кости (вроде знаме-
нитого шевалье де Мере), которым почти бессознательно поль-
зуемся.
Смысл теоремы умножения вероятностей состоит в том,
что она часто облегчает введение безусловных вероятностей,
если они сразу не очевидны. Приведем соответствующий при-
мер.
Рассмотрим опять задачу о раздаче экзаменационных би-
летов из § 1. Предположим, что номера экзаменационных би-
летов, доставшихся студентам, для нас ненаблюдаемы, а на-
блюдаемо лишь выражение лица — счастливое или несчаст-
ное. Допустим, что мы верим в принцип, согласно которому
ненаблюдаемые веши не следует вводить в модель. Тогда для
ситуации с первыми двумя студентами у нас будут 4 элемен-
тарных события: 1с 2с (первый счастливый, второй счастли-
вый), 1с 2н (первый счастливый, второй несчастный) и ана-
логично 1н 2с, 1н 2н. Как найти вероятность Р(1с 2с)? Запи-
шем теорему умножения вероятностей
Р(1с2с) - Р(1с) Р(2с/1с)
и с удовольствием убедимся, что входящие в правую часть
вероятности нам совершенно ясны:
P(lc) = -£, P(2c/lc)=
Поскольку 2с = lc2cU 1 н2с, аналогично получаем
Р(2с)»Р(1с2с) + Р(1н2с) = у - -1^- +
N — п п п
+ W ’ N-l
т. е. шансы первого и второго одинаковы.
Конечно, математически аккуратное решение этой задачи
должно включать определение безусловных вероятностей всех
четырех элементарных событий и проверку единственной ак-
сиомы (сумма вероятностей элементарных событий равна 1).
Не мешает убедиться и в том, что условные вероятности, най-
денные из безусловных с помощью математического опреде-
ления, совпадают с теми и без того ясными условными веро-
ятностями, которые послужили опорой нашей интуиции. За
математическую строгость надо платить, совершая иногда
лишние действия (лишние — с точки зрения здравого смыс-
ла). Другим важным неудобством предложенного сейчас ре-
шения является его крайняя громоздкость для случая более
чем двух студентов. Таким образом, введение только мысли-
мых, но ненаблюдаемых событий, сводящее всю задачу к част-
ному случаю групповой инвариантности (перестановка сту-
дентов в очереди эквивалентна перестановке билетов в куче,
разложенной на столе; однако все порядки билетов в куче
равновероятны), является предпочтительным.
С условными вероятностями связаны две формулы исчис-
ления, с которыми необходимо познакомиться.
Формула полной вероятности. Пусть множество элемен-
тарных событий й разбито на п не пересекающихся подмно-
жеств Hi,..., Нп:
Q в Hi+H2+...+Hn.
Пусть B^Q. Тогда имеем B=BHi+BH2+... +ВНп\
Р(В) - Р(ВН1 + . . . + ВНп) - 3 Р(ВЯ,) =
/-1
- 3 Р(я1)Р(в/яа.
Эта формула называется формулой полной вероятности*. Под-
множества Яь Я2.... Яп называются гипотезами. Получен-
ная формула в виде «заклинания» выглядит так: «вероят-
ность какого-нибудь события равна сумме вероятностей гипо-
тез, умноженных на условную вероятность события при дан-
ной гипотезе».
Формула Байеса. Произведем выкладку
Р(Я IB} = *Н,В) . Р(Я|)Р(Д/Н{)
' ‘ 1 Р(Я) »
з р(я()Р(в/яо
i-l
Полученная формула называется формулой Байеса. В этой
формуле вероятности гипотез Р (Я/) называются априорными,
а условные вероятности Р(Я,/В) — апостериорными. Эти
названия связаны со следующей схемой научного исследова-
ния.
О природе некоторого явления имеется п гипотез Яь Я2,
..., Яп, в которые мы верим с вероятностями Р(Hi), Р(Н2),
* Формула полной вероятности, очевидно, справедлива в случае не
только конечного, но н счетного разбпения й=Я1-|-Я2+....
20
Р(Нп). Чтобы узнать, какая из гипотез верна, производим
эксперимент, в результате которого может наступить или не
наступить событие В. Пусть известны условные вероятности
наступления В при каждой из гипотез. Допустим,
что в результате эксперимента событие В наступило. Тогда мы
можем с помощью вычисления вероятностей Р(Я(/В) переоце-
нить нашу степень доверия к каждой из гипотез на основании
исхода эксперимента. Вместо априорных (доопытных) веро-
ятностей Р Р(Н2), .... Р(Нп) получаем апостериорные
(послеопытные) вероятности P(Hi/B), Р(Н2/В), ..., Р(Нп[В).
Вообще говоря, такая схема слишком наивна, чтобы в са-
мом деле моделировать процесс научного познания (откуда
взять вероятности P(Ht) и Р(В/Н()?), но даже рассмотрение
проблемы с грубыми значениями этих вероятностей может
иной раз пролить новый свет на некую практическую ситуацию
в целом.
Рассмотрим в качестве примера проблему массовых диаг-
ностических обследований, ориентируясь на данные, пример-
но характеризующие флюорографические обследования. По-
ликлиника не будет вас обслуживать, если вы не пройдете раз
в год флюорографию. Это обследование нацелено на выяв-
ление грубых повреждений легких типа туберкулезного про-
цесса, которые в течение некоторого времени могут проходить
бессимптомно, так что больной о них не знает. Вероятность
возникновения такой болезни в течение года у ранее здорово-
го человека Р (Б) составляет величину порядка 0,001. После
выявления болезни больные получают специализированное
лечение (скажем, в туберкулезном диспансере) и флюорогра-
фия им больше не нужна, но поскольку доля больных среди
населения невелика, можно грубо сказать, что флюорографи-
ей охватывается все население страны (порядка 200 млн чело-
век). Доля Р(3) здоровых (в смысле патологии, выявляемой
флюорографией) среди населения составляет примерно 0,999 =
= 1—0,001. Здоровому (в указанном смысле) человеку флю-
орография также не нужна: для него это некоторая повин-
ность, наложенная государством ради своевременного выяв-
ления заболевших. Рассмотрим с помощью выведенных фор-
мул один из аспектов этой повинности..
Флюорографический снимок бывает довольно мелким и во-
обще не слишком высокого качества. Способ его обработки
должен быть достаточно простым, поскольку речь идет о весь-
ма массовом обследовании. Пусть событие П обозначает
трактовку снимка как положительную в медицинском смысле,
т. е. как заключение о наличии болезни. При этом возможны
и ошибки. Допустим, что удалось подобрать такой хороший
способ обработки, при котором Р(П/Б)=0,9 (т. е. обнаружи-
ваются 90% всех больных), но Р(П/3)=0,01, т. е. 1% здоро-
21
вых ошибочно зачисляются в больные. К чему это приведет?
По формуле полной вероятности
Р(П)=Р(Б) Р(П/Б) +Р(3) Р(П/3) =
=0,001 0,9+0,999-0,01 =0,0108.
Это означает, что около 1 % людей будут, кроме флюорогра-
фии, вызваны на дополнительное обследование (в масштабе
страны порядка 2 млн человек ежегодно). Далее по формуле
Байеса
Р(Б/П)=_________Р-<Б>Р<П/Б>_____=
Р(Б)Р(П/Б) + Р(3)Р(П/3)
__ 0,001-0,9 _ 1
“ 0,001-0,9 4-0,999-0,01 Ю’
Это означает, что из 10 человек, вызванных на дополнитель-
ное обследование, 9 являются здоровыми, а беспокоили их
напрасно (беспокойство состояло не только в трате времени на
дополнительное обследование, но и в возможном внушении
мысли о наличии серьезного заболевания).
Таковы неизбежные издержки массовых диагностических
обследований. Их можно примерно оценить с помощью эле-
ментарных формул исчисления вероятностей.
В наших оценках все цифры грубо прикидочные. На осно-
ве реальной статистики их можно заменить более точными
(попросту узнать реальную долю больных среди вызванных
на дополнительное обследование). Но мы все равно не сумеем
однозначно оценить, желательно или нежелательно массовое
диагностическое обследование, поскольку слишком разные ве-
щи положены на чашки весов: издержки на обследование са-
мого разного рода, включая напрасное беспокойство здоро-
вых людей, против обнаружения случаев болезни, о которых
не знали сами больные (еще вопрос, в какой мере удастся по-
мочь этим больным). Социальные проблемы сложны и не
сводятся к оценкам вероятностей, но иметь в виду эти оценки
все же нужно, хотя бы ради осознания сложности проблемы.
§ 4. Независимость
4.1. Определение независимости. Сравнение условных и
безусловных вероятностей представляет собой некоторый спо-
соб оценки влияния наступления одних событий на наступле-
ние других, т. е. в каком-то смысле измеряет зависимость со-
бытий. Но по массовости и сравнительной простоте приложе-
ний особую роль играет случай, когда никакой зависимости
нет: условная вероятность равна безусловной. Это означает
что
22
Р(В) = Р(в/Л) = -^2-,
или
Р(ЛВ)=Р(Л) Р(В_),
т. е. вероятность совместного наступления двух событий рав-
на произведению вероятностен». Это свойство и является ма-
тематическим определением независимости.
Сложнее обстоит дело с независимостью нескольких собы-
тий. Не вдаваясь в обсуждение возможных определений, за-
метим, что наиболее важным является так называемое поня-
тие независимости в совокупности.
Определение. События Ль Л2...... Лп называются не-
зависимыми в совокупности, если для любых из них вы-
полняется соотношение
Р(ЛЧЛ;, . . . ЛЦ) = Р(ЛОР(ЛЙ). . . Р(Л1к).
Заметим без полного доказательства, что для событий, не-
зависимых в совокупности, вереи следующий факт: любая
комбинация (в смысле теоретико-множественных операций)
одной группы этих событий не зависит от любой комбинации
другой группы этих событий.
Примеры.
1. Р(Л1Л2Лз) = P(AiA2)-P(AiA2A3)=P(AlA2) —
-Р (Л,Л2) Р(Лз)-.Р(Л!Л2) (1—Р(Л3)) = Р(Л1Л2) Р(Лз) =
= РМ,) Р(Л2) Р(Л3).
2. Р((Л,иЛ2)Л3) = РМ.ЛзЦЛгЛз) = Р(Л!Лз)+Р(Л2Лз) -
-РГЛ.ЛгЛз) = (РМО+РИ^-РИИз)) Р(Л3) =
= Р(Л(иЛ2)Р(Лз).
Определение независимости представляется на первый
взгляд экзотическим: с чего бы двум событиям Л и В лежать в
Q так. чтобы вероятность Р (ЛВ) их общей части равнялась
Р(Л) Р(В)? Такие случаи действительно бывают. Например,
при бросании игральной кости события, состоящие в выпаде-
нии четного числа очков и выпадении числа очков, кратного
трем, независимы. Но настоящая сфера применимости поня-
тия независимости относится к опытам, независимым друг от
друга по здравому смыслу: если в одной комнате бросается
монета, а в другой — игральная кость, то результаты бросаний
независимы.
Нам предстоит понять естественность соответствующей ве-
роятностной модели. Пусть один опыт описывается вероятност-
ным пространством (Q(1>, Р(‘>}, второй — вероятностным про-
странством {й(2), Р(2)). Спрашивается, как описать сложный
23
опыт, состоящий из двух опытов, с соблюдением всякого рода
независимостей?
Ясно, что пространством элементарных событий будет пря-
мое произведение
Q=Q('>XQ<2)={(ос», Ш(2)):Ш(”е Q(*>, ffl(»eQ(2)}.
Вторая мысль состоит в том, что события, связанные с исхо-
дом только первого (или только второго) опыта, можно с удоб-
ством описывать в рамках более сложного пространства эле-
ментарных событий: Q=Q(,)XQ(2). Действительно, пусть
Рассмотрим
Л(1)=Д(1)Хй<2’={((о(1), со<2>) : со<’> еДО,
Так вот, сказать ли, что наступило Д(1) (т. е. первый опыт за-
кончился исходом ©МеЛ^)), или сказать, что наступило Д(1)
(т. е. первый опыт закончился исходом а второй
опыт — каким угодно исходом и^ей12’), совершенно все
равно.
Третья мысль: для достижения независимости введем на
множестве й={((о(|>, cot2)} вероятность Р по формуле
Р{ (0(2)} = Р(')(ш(1)) р(2) (e)(2)).
При этом переход от к Л(1> не меняет вероятности:
р(Л(1»)- 2 Р((ш<п, ш<2’)}=
<.‘2’)бл0’
3
.’VW*
Р(1’(ш(1)) P'V’’)-

2 р(2,(ш<2)) =
-<w>
(здесь использована аксиома 2 P(2,(u)<2’) = 1\
u'2»en(2> )
Наконец, последняя мысль: независимыми в смысле умноже-
ния вероятностей оказываются не только элементарные собы-
тия, но и любые события Л(1> и А&\ из которых первое связа-
но лишь с исходом первого опыта, а второе — с исходом вто-
рого опыта. Действительно,
Р(л“>Л<2,) = 2 р|(<Л о/2’)} =
м
3 P<“(w<,,)P,V2,)==
= 3 P(V’)- 3 р(2,(ш(2)) =
J'W1’ ЛЯ
= Р«’(Л(,)) P<2,U,2)) = P(A(n) Р(Л(2)).
Совокупность этих соображений показывает, что в прямом
произведении вероятностных пространств пары независимых
событий возникают совершенно естественно. Для получения п
независимых в совокупности событий естественно взять пря-
мое произведение п вероятностных пространств. Выкладки,
основанные на разложении суммы произведений вероятностей
в произведение сумм, при этом не изменяются.
Поскольку содержательные законы теории вероятностей
относятся к большому числу событий, а наиболее простой спо-
соб комбинации событий — предположение их независимости,
то простейшая часть этой науки развертывается в прямом про-
изведении пространств, когда число сомножителей стремится
к бесконечности. Следует хорошо понять эту ситуацию.
4.2. Испытания Бернулли. Приведем важнейший (по ши-
роте употребления) частный пример — испытания Бернулли.
Одно испытание Бернулли — это опыт с двумя исходами,
допустим 0 и 1, причем Р(1)=р, P(0)=p, p+q=\. Единица
(допустим) называется успехом, нуль — неудачей. Примером
является бросание правильной (тогда р=у=х1г} или искрив,
ленной монеты (тогда p^q). Интерес представляют не одно,
а и независимых испытаний Бернулли. Итак, «испытания Бер-
нулли — это независимые испытания с двумя исходами и с ве-
роятностью успеха, не меняющейся от испытания к испыта-
нию:». Это — определение на уровне здравого смысла, а на
математическом уровне определение выглядит так:
2 = (О, 1)Х(0. 1)Х • • - X (0, 1>»
п раз
<о — последовательность нулей и единиц длины п,
P((1))=pi‘(»)fl,n-|i(»)>
где ц(<о) — число единиц в последовательности со, которое
можно назвать числом успехов в п испытаниях.
Функция от элементарного события в теории вероятностей
называется случайной величиной: в данном случае ц(со) за-
висит от случайного исхода п испытаний Бернулли. Возмож-
ными значениями величины р(со) являются числа 0, 1, 2, ...,
п- Подсчитаем вероятность события {p=zn}={co:p(co) =т}.
По определению вероятности события (определение 2 § 1)’
25
имеем
Р(|л = т}= 3 P(u») = C”pV~M (О
ш:|А(и>)мт
(так как число элементов со, таких, что р(со)=/п, равно С™ )•
Набор вероятностей различных значений случайной величи-
ны называется распределением вероятностей (или просто
распределением). В частности, формула (1) задает так назы-
ваемое биномиальное распределение (название связано с тем,
что правая часть (1) есть член разложения бинома (p+q)n).
Простая формула (1) является удивительно содержатель-
ной. Чисто математическое исследование поведения правой
части (1) при больших п и различных тир (возможно, зави-
сящих от п) нетривиально настолько, что в данный момент мы
нм заниматься не будем, заметив лишь, что оно приводит к
весьма интересным результатам. С другой стороны, модель
испытаний Бернулли часто с той или иной точностью сопостав-
ляется с реальными явлениями.
Пусть, например, завод собирается выпустить п изделий,
причем вероятность выпустить бракованное изделие равна р
(известна по прошлым данным). Каково распределение веро-
ятностей для числа ц ожидаемых рекламаций? Оценка этого
распределения с помощью формулы (1) будет более или ме-
нее грубой (в смысле соответствия фактическим данным) в за-
висимости от того, насколько точно выполняются предполо-
жения модели, т. е. независимость брака для разных изделий
и постоянство доли брака р. В связи с возможными колеба-
ниями уровня технологии и качества сырья могут возникнуть
отклонения от модели испытаний Бернулли, которые можно
интерпретировать как нарушение независимости брака для
разных изделий (при сохранении доли брака р), либо как
колебания вероятности р (при сохранении независимости),
либо как оба явления вместе. Но на практике обычно нет све-
дений, количественно оценивающих отклонения от модели ис-
пытаний Бернулли, известна (да и то по прошлым данным)
лишь доля брака р в готовой продукции, и ничего, кроме фор-
мулы (1), для практического применения не остается.
Иногда модель испытаний Бернулли является весьма точ-
ной (бросания монеты и другие более сложные азартные иг-
ры).
Но значительное число применений модели испытаний Бер-
нулли связано не столько с тем, что она хорошо или приемле-
мо описывает некие явления, сколько с тем, что бывает важно
выяснить, что эта модель изучаемого явления не описывает.
Испытания Бернулли — это простейшая модель полной слу-
чайности. Если полной случайности нет, скажем, число бра-
кованных изделий колеблется не так, как полагалось бы по
биномиальному закону, то это может быть важной информа-
цией для совершенствования производства.
26
Словом, на примере модели испытаний Бернулли целесооб-
разно познакомиться с проблемой проверки статистических
гипотез. Статистическая гипотеза — это утверждение о веро-
ятностях тех или иных событий; проверкой гипотезы называет-
ся то или иное сопоставление ее с рядом экспериментов.
Пусть, например, двое играют в орлянку, причем монету
бросает все время первый игрок (если монета выпадает гер-
бом, то первый игрок получает с второго копейку, в противном
случае отдает второму копейку). Второму игроку инте-
ресно знать, честно ли бросает монету первый игрок, потому
что, возможно, бывают такие специалисты, которые по своему
желанию могут выбросить монету любой наперед заданной
стороной, хотя на вид монета бросается честно. Пусть для на-
чала монета бросается п=100 раз, после чего второй игрок
имеет возможность решить, продолжать дальше игру или нет,
на основании изучения результатов 100 бросаний. Как ему
поступить?
Для понимания реальных возможностей вероятностных ме-
тодов нужно прежде всего понять, что так поставленный воп-
рос ответа не имеет. Дело в том, что любой результат 100 бро-
саний монеты, например последовательность из 100 гербов
либо последовательность из 100 цифр, либо, наконец, последо-
вательность ГЦГЦ..., в которой герб и цифра строго череду-
ются, имеет одну и ту же (при р=’/2) вероятность 2-100. Ни
одна из последовательностей, которые могут получиться в
опыте, не лучше и не хуже, чем другая. Ни одна научная ги-
потеза (в данном случае — гипотеза испытаний Бернулли)
не может быть проверена, если не указать альтернативных ги-
потез, т. е. каких-то сведений о том, как именно проверяемая
гипотеза может нарушаться: гипотеза всегда проверяется
против каких-то альтернатив.
В нашем примере простейшая альтернативная гипотеза мо-
жет состоять в том, что первый игрок, стремясь выиграть по-
больше, будет выбрасывать герб не с вероятностью ’/г, а чаше
(возможно, не случайно). Тогда число выпадений герба ц бу-
дет принимать в каком-то смысле большие значения, чем было
бы при вероятности р= */2- Пусть, скажем, в 100 бросаниях
оказалось ц=60 выпадений герба. Мы можем вычислить с по-
мощью таблиц Р(ц^60} при гипотезе р=Чг (это будет число
порядка 2%). Речь должна идти именно о вероятности
Р'ц>о0), но не о вероятности P{j.i=60}: кажется подозритель-
ным не то, что число успехов именно 60, а то, что их значи-
тельно больше 50. Дальше рассуждаем так: возможно, что
первый игрок бросал монету честно, но произошло выгодное
для него случайное событие (позволившее ему выиграть 20 ко-
пеек), вероятность которого около 2%; возможно, что первый
игрок бросал монету нечестно, следует прекратить игру.
Второй игрок должен принять какое-то решение.
27
Рассмотрим последствия различных решений второго иг-
рока. В азартные игры играют не ради наживы (теоретические
соображения, в том числе довольно сложные, в которые мы
сейчас не будем вдаваться, показывают, что в азартных играх
с равноправными игроками типа орлянки наживы быть не мо-
жет), а ради получаемого от игры удовольствия. Если же
партнер оказался шулером, то об удовольствии речи быть не
может. Таким образом, если второй игрок будет прекращать
игру в том случае, если в первых 100 бросаниях его партнер
выбросит герб 60 раз или более, то лишь примерно в 2% встреч
с честными игроками он напрасно бросит игру (т. е., так ска-
зать, лишится 2% удовольствия).
Иначе можно сказать, что вероятность напрасно обидеть
честного партнера составляет около 2%. Различные логичес-
кие видоизменения этого утверждения типа: «если р.<60, то
с вероятностью 0,98 партнер — не шулер» либо «если ц>60,
то с вероятностью 0,98 партнер — шулер» — будут неверными;
несостоятельными в данной постановке задачи будут и вероят-
ностные оценки надежности избавления от шулеров, которая
достигается ценой потери 2% удовольствия. Дело в том, что
шулер никак не описан: в сущности, о нем сказано лишь то,
что он обладает непостижимыми для обычного человека (вто-
рого игрока) способностями. Не сказано и какова доля шу-
леров среди возможных партнеров: например, если их нет
вовсе, то партнер — не шулер с вероятностью 1, а не 0,98 или
0,02. Если же шулера имеются н используют свои сверхчело-
веческие способности для того, чтобы не попадать под дей-
ствие критерия {ц>60), имитируя при первых 100 бросаниях
полную случайность, то применение этого критерия абсолют-
но ничего не дает в смысле избавления от шулеров,
Мы встретимся в данной книге с ситуацией, когда альтер-
нативная гипотеза описывается не в крайне неопределенной
форме «партнер—шулер», а также в виде вероятностной ги-
потезы, которая приписывает наблюдаемым событиям вероят-
ности, не совпадающие с теми, которые приписывает им про-
веряемая гипотеза. В этом случае рассмотрение проверки ги-
потез можно углубить, дав, в частности, вероятностную оцен-
ку гарантий, связанных с применением того или иного ста-
тистического критерия.
4.3. Распределение Пуассона. Мы видели, что, в частности,
задача проверки гипотезы полной случайности потребовала
вычисления вероятностей вида Р{ц>а). Конечно,
P{j*>a)= S P{!A = w), (2)
т>а
где вероятности Р{ц=т) даются формулой (1). Громоздкость
вычислений при больших значениях тип побудила ряд ма-
тематиков искать для вероятностей (1) и (2) какие-то простые
28
приближенные выражения. Оказывается, что асимптотический
анализ этих вероятностей приводит к двум наиболее универ-
сальным законам распределения, значение которых выходит
далеко за рамки сравнительно убогой модели испытаний Бер-
нулли. Это нормальное распределение (или распределение
Гаусса—Лапласа) и распределение Пуассона. Нормальным
распределением займемся позже, а сейчас рассмотрим рас-
пределение Пуассона.
Это распределение возникает из формулы (1) при пре-
дельном переходе, когда п—►*, р—►О, но так, чтобы пр-*).,
где Х>0 — фиксированное число. Так как в пределах одной
последовательности испытаний Бернулли р постоянно (и сле-
довательно, не может быть так. чтобы р-*-0), нужно рассмот-
реть несколько более сложную схему: последовательность се-
рий испытаний Бернулли.
В первой серии пусть будет л=1 испытание с вероятностью
успеха рь во второй серии п—2 испытания с вероятностью ус-
пеха р2 и т. д., наконец, в n-й серин рассмотрим п испытаний
с вероятностью успеха рп каждое, причем прп-»-?.. Пусть
}i.(n) — число успехов в n-й серии; т — фиксированное целое
неотрицательное число.
Теорема Пуассона. При п-+<х> выполняется предель-
ное соотношение
Доказательство. В точном выражении
Р{н(п)-т) = О:(1-рп)’^я
перейдем к пределу при л—►«>, pns=X/n+o(l/n), m фик-
сированном. Поскольку
Р{и(л)-m} = х
то при этом предельном переходе главный член скобки
(X/n +o(l/n))m будет (X/n)m (так как другие члены разло-
жения этого бинома содержат о(1/л) в некоторой степени
и ограниченные — зависящие лишь от т — коэффициенты).
Скобка (1 —Х/л —о(1/л))п-т имеет пределом е . Учитывая,
что п(п—1). . . (п — т + 1)(Х/л)'”-*Хт1 получаем утверж-
дение теоремы-
29
В этой теореме числа рт = \те 1т\ выступают как пре-
дельные значения биноминальных вероятностей. Можно
ввести случайную величину, для которой вероятности
Рт будут точными вероятностями различных значений.
Действительно, положим Q = {0, 1,. . . , т, . . . учи-
оо
тывая, что У рт=1, введем вероятности элементарных
Я!— О
событий формулой Р{/п) = рт и введем, наконец, случай-
ную величину £ как функцию на множестве й, заданную
формулой £(m)=m. Тогда, очевидно,
ут х
P{g = m} = A-e-\ (3>
т!
Такое распределение вероятностей называется распределени-
ем Пуассона.
Распределение Пуассона очень часто находится в разум-
ном согласии с экспериментом — от числа частиц, зареги-
стрированных счетчиком радиоактивного излучения за какой-
то промежуток времени, до числа вызовов, поступивших на
телефонную станцию, либо числа отказов какого-то оборудо-
вания. Оно необычайно удобно для иллюстрации основных
вероятностно-статистических понятий, так как формула (3),
зависящая от двух параметров т и X, несравненно легче под-
дается табулированию, чем формула (1), зависящая от трех
параметров т, п, р. Но для наибольшего удобства обраще-
ния с распределением Пуассона нам необходимо понять веро-
ятностный смысл параметра X, что лучше сделать в рамках
общих понятий, связанных со случайными величинами.
§ 5. Случайные величины
Случайной величиной (как уже говорилось в предыдущем
параграфе) называется функция £=g(ci)), определенная на
множестве элементарных событий й={ш}. Пока множество
Q не более чем счетно, функция g (со) совершенно произволь-
на. Значениями случайной величины могут быть веществен-
ные или комплексные числа, а также кватернионы, матрицы,
операторы и т. д. Но для определенности будем говорить о
случайных величинах с вещественными значениями.
Точка зрения, с которой функции £=£((о) рассматрива-
ются в теории вероятностей, не совсем похожа на точку зре-
ния математического анализа. На первый план выступают
множества уровня функции g(co): пусть ah а2, ..., ап,... —
различные значения случайной величины £•; рассмотрим
множества вида {co^fco) =а,}, сокращенно обозначаемые
{£=а,}. и их вероятности
зо
Pie P{£ “ ai} =• S ₽(“)•
a ।
Табличка вида
/вд в2 . . . ап . . . \ {ц
\Р1 Р» ... Рп • • • /
называется распределением вероятностей (или просто рас-
пределением) случайной величины £.
Понятно, что р<>0 и Sp,= l. С другой стороны, для любо-
го распределения вида (1), такого, что р,->0 и Sp(=l, най-
дется случайная величина с этим распределением. Действи-
тельно, достаточно положить Q = (ai, a2> —. ап,...), P(at)=pi
и ^(аг)=а,-. (Это тривиальное замечание впоследствии
разовьется в так называемую «теорему Колмогорова», опре-
деляющую вероятностную меру в функциональном прост-
ранстве).
Почему в теории вероятностей центральную роль играют
множества уровня случайных величин и распределения веро-
ятностей? Дело в том, что даже счетное Q может быть весь-
ма сложным (прямое произведение большого числа про-
странств). Задание вероятностной меры в таком Q, особенно
если не предполагается независимости, может быть затрудни-
тельным. Но случайная величина может принимать одно и то
же значение а, на многих а, и тогда определение вероятнос-
тей pi=P(^=a,) — из опыта на основании частоты наступле-
ния события {£=а,} или как-нибудь иначе — может быть
делом более простым, чем определение вероятностей Р(а).
Однако при большом числе различных значений а(- даже оп-
ределение вероятностей pt может быть сложным. Поэтому
распределение вероятностей на практике пытаются характе-
ризовать каким-то небольшим набором чисел, которые назы-
ваются параметрами. Важнейшим таким параметром являет-
ся математическое ожидание.
Определение. Математическим ожиданием М* слу-
чайной величины £=£(со) называется сумма
М5= £l(a>)P(a>) (2)
(в предположении, что S |£(Ш)Р(Ш) < °°¥
Если предположение абсолютной сходимости не выполне-
но, то говорят, что случайная величина £ не имеет математи-
ческого ожидания.
Из формулы (2) очевидным образом вытекают следующие
правила исчисления:
М(с£) =сМ£, если с — константа;
М(£-|-т]) =М£+Мт], если М£ и Мт) существуют
31
(второе из этих правил вытекает из того, что абсолютно схо-
дящиеся ряды можно складывать почленно). В этих правилах
подразумевается, конечно, что — это случайная величина,
определяемая соотношением (с|) (ci))=c£(co), а сумма
5+т] — это случайная величина, определяемая соотношением
(£+<о) (ш) =5(ш)(ш)- При этом случайные величины £ и
1) должны быть определены на одном и том же пространстве
элементарных событий (это всегда подразумевается).
Лемма. Для любой функции f(x) вещественного пере-
менного
М^) = £/(а<)Р|
ei
(3)
где р1=Р{£=а,}, a f (£) (со) =f [5(со)].
Доказательство. Лемма, конечно, верна только в том
случае, если ряд в правой части (3) сходится абсолютно.
Рассмотрим следующие преобразования:
МЯЭ=2Л5(®))Р(»)-
»€Я
= 2 Г 2 /G(<*>))P(<*>)1 = 2 [ 2 f(«i)P(«»)l =
= 2Г/(а<) 2 Р{«>)1 = 2Ка1)Ри = аЛ =
at «:5(«)=а| I а(
= 2/(а<)А-
а1
Очевидно, что все ряды, участвующие в этих преобразовани-
ях, одновременно сходятся или не сходятся абсолютно. В
предположении же абсолютной сходимости существует неко-
торое конечное число членов ряда, сумма которых не более
чем на заданное е>0 отличается от суммы ряда, в то время
как сумма модулей остальных членов не более е. Поэтому
всевозможные группировки членов ряда сводятся к группи-
ровкам слагаемых в конечной сумме и тем самым законны.
Следовательно, произведенные преобразования верны, что и
доказывает лемму.
В частности, полагая f(x)=x, получаем
(4)
что в виде словесного «заклинания> выглядит так: математи-
ческое ожидание случайной величины равно сумме ее значе-
ний, умноженных на вероятности этих значений. Таким обра-
зом, математическое ожидание однозначно определяется рас-
пределением случайной величины.
32
Замечание. Но если (4) принять за определение мате-
матического ожидания, то будет неудобно доказывать, что
М (£+»]) = Mg + Mrp
Математическое ожидание имеет точную и прозрачную ме-
ханическую аналогию. Если распределение случайной вели-
чины (1) изобразить в виде одномерной механической систе-
мы, поместив в точку с абсциссой as массу pt, то, в силу ус-
ловия 2р, = 1, получим, что Mg есть абсцисса центра масс
такой системы. Механикам, правда, обычно не приходит в го-
лову особо оговаривать, что S|a(|p,<oo, ибо размеры меха-
нических систем конечны. Но в теории вероятностей вместе со
случайной величиной £ часто приходится рассматривать, на-
пример. 1/g, Ing или tgg, так что условие абсолютной сходи-
мости существенно, ибо без него правила исчисления (ска-
жем, М(£ + т])=М£-|-Мт]) просто неверны.
Если математическое ожидание есть некий центр, вокруг
которого группируются возможные значения случайной вели-
чины, то, наверное, должен существовать и параметр распре-
деления, характеризующий величину возможного разброса
значений случайной величины вокруг их центра. Мы его не-
медленно получаем из механической аналогии: в механике
это — момент инерции, а в теории вероятностей — дисперсия.
Определение. Дисперсией Dg случайной величины £
называется число, определяемое формулой
Dg ° M(g - М&)1 = 2 (at - Мg)« pt (5)
°*
(предполагается, конечно, что ряд в правой части сходится).
Проделаем следующую небольшую выкладку:
Dg=M(g-Mg)2=M(g2-2Mg-g+(Mg)2) =
= Mg2—M(2Mg • g) +M(Mg)2=
= Mg2—2 (Mg)2+ (Mg)2=Mg2- (Mg)2.
»'Для понимания этой выкладки следует иметь в виду, что в
ней Mg выступает в одних местах как число, а в других —как
случайная величина, принимающая единственное значение:
например, M(Mg)2= (Mg)2. Так в математическом анализе в
выражении sinx-f-l единица выступает то как число, то как
функция, тождественно равная 1.)
Таким образом, Dg выражается через Mg и Mg2. Посколь-
ку Dg>0, то получаем, что Mg2>(Mg)2. Заметим, что выра-
жение Mgft называется моментом k-го порядка случайной ве-
личины g. Моменты — это тоже параметры распределения.
После этих общих определений рассмотрим пример
распределения Пуассона. Пусть случайная величина при-
нимает значения Q, 1, 2, . . . , причем P(g = m} = — е-х.
3-2567
33
•» во ут
Вычислим М£: М£= 3 mP{t=m}= S /__ п> е“х—Хе~хХ
т»0 m-i' '
ОО 5ff|—1
Небольшое вычисление показывает, что Dg также равняется
X. Поскольку Dg=M(£—Mg)2, то типичное значение l£—Mgl
имеет порядок величины Vi. Если X велико, то X^VX, так что
отклонение возможных значений величины £ от М£=Х мало
по сравнению с X; в этом смысле |«Х по порядку величины.
Попытаемся теперь практически применить распределе-
ние Пуассона, в частности понять роль, которую могут иг-
рать в жизни общества маловероятные события. В математи-
ческой теории случайная величина — это функция от элемен-
тарного события; в приложениях это число, характеризующее
исход случайного эксперимента. Поэтому, говоря о случайных
величинах в приложениях, мы должны как-то представлять
себе ансамбль возможных случайных экспериментов.
Пусть нам сообщили такое «статистическое данное»: ве-
роятность аварии самолета равна 10-6 за один час полета
(это не реальное, а некоторое произвольное число). Преиму-
щество чисел такого рода состоит в том, что ясно, по крайней
мере, как они получаются: нужно взять (за определенный про-
межуток времени для определенной группы самолетов) общее
число аварий и разделить его на общее число летных часов.
Недостаток же этих чисел состоит в том, что при ближайшем
анализе становится затруднительным сказать, вероятность ка-
кого именно события они характеризуют: слишком различны
самолеты и условия полета, чтобы можно было все промежут-
ки полета длительностью в 1 ч считать ансамблем статисти-
чески однородных экспериментов. Поэтому к выводам, полу-
чаемым из таких данных, нужно относиться не как к имею-
щим точный количественный смысл, а как к некоторым каче-
ственным рассуждениям.
Как в этой качественной модели применить закон Пуассо-
на? Поскольку речь идет о редких событиях, будем предпо-
лагать, что число аварий в какой-то совокупности полетов
есть случайная величина, распределенная по закону Пуассо-
на. Для подсчета параметра X заметим, что математические
ожидания суммируются: будем разбивать рассматриваемую
группу полетов на полеты длительностью в 1 ч и суммировать
соответствующее число раз 10-в. Тут есть некоторое противо-
речие: если речь идет о полетах одного человека, то наша мо-
дель выглядит так, что после гибели этого лица в одной ава-
рии оно воскресает и намеченное число полетов выполняет.
Это огрубление несущественно, поскольку вероятность отдель-
ной аварии в наших расчетах будет довольно малой.
34
Сначала рассмотрим вопрос об опасности полетов на са-
молете с точки зрения отдельного лица: пусть некто в тече-
ние 20 ч в год летает в служебные командировки и продол-
жает это дело в течение 30 лет до выхода на пенсию. Общее
число часов полета 600, пуассоновский параметр
Х=10-6-600=6 10-4,
а вероятность гибели равна
1—Р{^=0}=1—е-х«Х=610-4.
Эта вероятность пренебрежимо мала в сравнении с вероятно-
стью смерти от других причин (о продолжительности челове-
ческой жизни см. ниже в этой книге).
Теперь рассмотрим тот же вопрос с точки зрения общества
в целом. Пусть в служебные командировки (по 20 летных ча-
сов в год) летает 106 человек. Математическое ожидание для
числа погибших £ (за 30 лет) будет
М£ = 106Х= 10е • 6 • 10-4=600.
Не следует думать, что число погибших тоже будет под-
чиняться закону Пуассона. (Если £ — пуассоновская случай-
ная величина, то kl-, k=2, 3,..., уже не подчиняется закону
Пуассона. Это означает, что если маловероятные события мо-
гут возникать целыми группами — а так и бывает в авиаци-
онных авариях: при аварии гибнет группа людей, — то рас-
пределения Пуассона не будет.) Дисперсия Щ числа погиб-
ших будет в несколько раз больше, чем Mg, но все-таки
можно ориентироваться по порядку величины колебаний на
TMg, поскольку VMg<CMg. Итак, то, что пренебрежимо мало
с точки зрения отдельного лица, никак не мало с точки зре-
ния общества в целом.
Теперь рассмотрим ту же задачу с точки зрения члена лет-
ного экипажа. Продолжительность рабочей недели у нас
(грубо) 40 ч, т. е. 2000 ч за год. Таким образом, если бы все
рабочие часы были летными (на самом деле это не так), то,
допустим, за 20 лет работы член экипажа находился бы в
воздухе 4 I04 ч. Пуассоновский параметр
Х=4104Ю-в=0,04,
что не так уже мало.
Наконец, рассмотрим ту же задачу с точки зрения боль-
шого аэропорта, в котором имеется 1000 экипажей. За год пу-
ассоновский параметр числа аварий будет
Х=2000 1000 10-в=2,
т. е. в среднем две аварии в год, и лишь с вероятностью е_к=
=е-2й1/7 год проходит без аварий. Так как в пределах од-
3* 35
ного аэропорта работники немедленно узнают об авариях (а
то и принимают участие в ликвидации последствий), то две
аварии в год создают чрезвычайно напряженную обстановку.
Малая вероятность аварии какого-то технического средства
(10~е) при его массовом применении оказывается слишком
большой: ее необходимо снижать. За счет каких-то техничес-
ких п организационных усилий общество может ее снизить —
допустим, вдвое или в несколько раз. Но довести до нуля —
вряд лп.
Остановимся еще на часто встречающемся заблуждении.
Если Х=2, то фактическое число аварий за год может при-
нимать любые значения О, I, 2.Обычно если в одном году
была одна авария, а в следующем происходит, скажем, 4, то
считают, что аварийность возросла, и начинают искать вино-
ватых. На самом деле это может быть и чисто случайном ко-
лебанием: при Х=2 Р{£<1}=0,41, Р{£>4}=0,14 и в ряду лет
то и другое событие могут встретиться совершенно случайно.
§ 6. Системы случайных величин
6.1. Введение. Система случайных величин, т . е. вектор
1=(?ь 62» Вп)> компоненты которого являются случайными
величинами, в сущности, не требует нового определения, так
как введенные в § 5 случайные величины могут принимать н
векторные значения. Значением векторной случайной величи-
ны ; является, естественно, вектор а=(аь ..ап), т. е. со-
бытие {В=а} можно записать в следующем виде:
{£=в}= П {?<в = {5i=ai» = 5л=ая)-
Для вероятности получаем
Р{В=а}=Р{ё1=Ль S2=fl2.....Ъп=ап}.
Набор вероятностей Р{£=а}, отвечающий всем возможным
различным значениям вектора а (их не более чем счетное
число, поскольку Q, на котором определено £=|((о) не более
чем счетно), называется распределением вектора £ либо сов-
местным распределением его компонент —> Вп- Из сов-
местного распределения нетрудно получить распределения
отдельных компонент (так называемые маргинальные распре-
деления):
P{6l в " S Р{?1 в ?1 — 6явЛп).
а...............
Л
В двумерном случае (п=2) вероятности
62=0/}
36
записывают в таблицу наподобие матрицы (но матричные
операции не используются). В многомерном случае непонят-
но, какой способ записи многомерного массива Р{£=а} мо-
жет быть лучше.
Уже поэтому ясно, что с многомерными распределениями
произвольного вида трудно что-либо сделать. Упрощения
идут по двум линиям: 1) на первый план выдвигаются те или
иные параметры распределения (в частности, так называемые
ковариации и корреляции случайных величин, что приводит к
корреляционному анализу); 2) рассматриваются частные ви-
ды распределений (в частности, независимые случайные вели-
чины). Комбинация этих видов упрощения ведет к установле-
нию простой (по нынешним временам), но важной теоремы,
называемой законом больших чисел, которой мы и завершим
данный параграф.
6.2. Корреляционный анализ. Основным понятием корреля-
ционного анализа является ковариация.
Определение. Ковариацией двух одномерных случай-
ных величин е и т) называется следующее выражение:
covG, П)=М(В-М6)(П-МП) (1)
(в формуле (1) сначала делается умножение (£—М£)Х
Х(т)—Мт]), а математическое ожидание берется от произведе-
ния). Коэффициентом корреляции величин £ и т) называется
следующее выражение:
cov(5, ц) ,2.
«» — (4)
Коэффициент корреляции есть величина безразмерная (т. е.
не меняющаяся при линейной замене £—► т)—► ат)4-Ь).
Из неравенства Коши — Буняковского следует, что
—
причем в случае г{л=±1 величины £ и т) линейно зависимы:
i]=c£+d, end — числа.
Можно считать, что D£=cov(£, £). Важнейшее значение
имеет следующая
Лемма 1. Для суммы £i+fc2+—+£n случайных величин
Вь £2. .... Вп справедливы формулы
+ . . . + U =Дt cov(L I,) =
= S D& + 3 covfo, у - 3 + 2 3 cov(eb £j). (3)
i—1 it I i=l i</
Доказательство. В силу определения дисперсии
имеем
37
-M(g»+g,+ . . .+и|»=м 2
D(£i4-S.+ . • .+U = M[(li + b+. . .+W-
(g,-Mg,)J-
=м £ x (g, - M£( )(g> - Mg,)] - S t M(g, - Mg/) x
X0i-M6/)-i^jcov(lo tj).
Позже (после изучения общей аксиоматики) мы разовьем
корреляционный анализ несколько дальше. Сейчас же пере-
ходим к понятию независимости.
6.3. Независимые случайные величины. Случайные величи-
ны ^2...... gn называются независимыми в совокупности,
если для любых числовых множеств Ai, Аг, ..., Ап события
(giedi), ...» {gns^n} (4)
независимы в совокупности.
Из независимости в совокупности вытекает, что совмест-
ное распределение случайных величин gi, g2, .... gn является
прямым произведением одномерных распределений величин
gi, ег. ...» gn- Это означает, что
Р{5 = в) = P{gi = alt gs = at, . . . , gn = an} =
= nPVi = «J (5)
i-1
(для доказательства достаточно положить в определении (4)
Л1={а1), Аг={а2}, ...,Ап—{ап}). Наоборот, из (5) вытекает
независимость в совокупности событий (4). Действительно,
например, для двух событий имеем
Р{£1 е Alt g. е Л,} = 2 Р(gx = alt В, = а,) =
в|€Х(> авбЛв
= Р^1 = Р{ь« = =
- S P{£i-eJ • S P(gi = e,)-P{gieA} P{S,ex1}.
o,€Ai aiEA,
Ta же самая выкладка справедлива для любого числа собы-
тий (4).
Наиболее простой способ построить независимые случай-
ные величины состоит в том, чтобы построить й как произве-
дение Й=£У*>ХЙ(2)Х — Х£Уп) вероятностных пространств и
для точки (1)=|((|)<1>, со(2\.... а>(п)) определить случайные величи-
ны gi, g2, .... gn как такие функции от со, что gi зависит лишь
38
от g2 — лишь от ы(2), gn — лишь от <о(п). Выкладка,
проведенная в § 4 для случая п=2, без труда обобщается на
произвольное п и показывает, что так определенные случай-
ные величины будут независимы в совокупности.
Лемма 2. Если случайные величины g и т) независимы и
существуют Mg и Мт), то существует Mgr) и MgT)=MgMr)
(.математическое ожидание произведения независимых вели-
чин равно произведению их математических ожиданий).
Доказательство. Полагая в соотношении (3) § 5
f(x, у)—ху, получаем
Mgiq —2«bP{g = = Р(£=«)Р{’1=И и
а.Ь а» Ь
= £ар(£ва} . £6P{geft}-Ml • Mt),
а Ь
причем выкладка справедлива, если ряды 2flPU=a) и
vbP{g = b} сходятся абсолютно. Лемма доказана.
ь
Лемма 3. Функции от независимых случайных величин
суть независимые случайные величины.
Эта лемма означает, что если fi, f2, fn — произвольные
функции вещественного переменного, a gi, g2. gn — неза-
висимые случайные величины, то случайные величины т]1=
= МЫ. T]2=f2(B2). гь^Мбп) также независимы. Дей-
ствительно, для любых числовых множеств At, А2, .... Ап по-
ложим (Ai), B2=f~2(A2), .... Вп—1п*(Ап), где под
знаком f~l понимается взятие полного прообраза. Тогда собы-
тия т)1еЛь т]2еЛ2, .... т]п^Лп, совпадающие с событиями
gie/r1^1)=Bi, g2efr’ (А2)—В2, .... gnef7‘ (Ая)=Вп,неза-
висимы в силу независимости случайных величин gi, gz,
..., gn.
Лемма 4. Ковариация двух независимых случайных ве-
личин g, 1] равна нулю.
Действительно, в силу лемм 2 и 3
cov(g, n)=M(g-Mg) (т)-Мл)= M(g-Mg) M(n-MT])=0.
Лемма 5. Дисперсия суммы независимых случайных
величин равна сумме дисперсий слагаемых. (Лемма 5 выте-
кает из лемм 1 и 4.)
Теоремы о свойствах математического ожидания и дис-
персии дают средства, иногда позволяющие избежать слож-
ных вычислений. Подсчитаем для примера математическое
ожидание и дисперсию биномиального распределения. Пред-
ставим число успехов ц в п испытаниях Бернулли в виде
Ц = |А1 + |А2 + ... + Цп.
39
где случайная величина ц,- связана с исходом лишь i-ro испы-
тания: ц< = 1, если в t-м испытании был успех, и ц>=0 — в
противном случае (если угодно, рДсо), где со — набор нулей
и единиц, равна i-fi координате набора со). Случайные вели-
чины р.1, цг.. Мп независимы (как функции от различных
координат точки прямого произведения вероятностных прост-
ранств); легко видеть, что Мр,=р, Dp,=Mp;2— (Мц.)-' =
=р—p-=pq. Поэтому Mj.i = np, D^=npq. Отправляясь от
определения биномиального закона, мы получили бы
М«х= SmCpV™, Ц* - £ (« — NW*C'nP':,qn~m,
т—0 in—О
и сразу не ясно, что такие суммы редуцируются к очень про-
стым выражениям.
С другой стороны, свойства математических ожиданий и
дисперсий позволяют получить весьма общий факт, называе-
мый законом больших чисел.
6.4. Закон больших чисел. Статистиков XVII в. поражал
тот факт, что средние арифметические из большого количест-
ва каких-то величин обнаруживали гораздо меньшие колеба-
ния, чем сами слагаемые. Это означает, что если взять, на-
пример, среднюю за ряд лет урожайность чего-либо н срав-
нить ее со средней урожайностью того же самого за другой
ряд лет, то разница между средними будет обычно гораздо
меньше, чем колебания урожайности от года к году. Иными
словами, малая урожайность в какие-то годы компенсируется
большей урожайностью в другие годы, а в целом получаются
колебания около среднего. Чтобы понять, что здесь удиви-
тельного, надо иметь в виду, что могло бы быть совсем не так:
в случае систематического изменения погодных условий (или,
например, в XX в. — растущего применения удобрений) сред-
ние за два ряда лет урожайности могли бы отличаться силь-
нее, чем урожайность в близкие годы. В дальнейшем устой-
чивость средних была проверена на другом материале, на-
пример на измерениях тех или иных физических величин. Воз-
ник вопрос о теоретическом объяснении факта устойчивости
средних. В XIX в. это объяснение видели в законе больших
чисел теории вероятностей. С точки зрения XX в. оно состоит
из двух частей: 1) представления о наблюдаемых значениях
как о значениях неких случайных величин (в классической
теории вероятностей эти величины независимы, в современ-
ной — могут быть и зависимы); 2) математической теоремы,
устанавливающей факт устойчивости средних для сумм слу-
чайных величин.
Если первая часть (модель случайных величин) в настоя-
щее время уточняется (нужно сказать, в каком ансамбле эк-
спериментов рассматриваются случайные величины), оспари-
40
вается, а иногда и отвергается, то вторая (математическая)
часть есть твердо установленный факт. Первоначально (Ла-
плас, Пуассон) закон больших чисел выводился из более'
сложной центральной предельной теоремы теории вероятнос-
тей. Впоследствии П. Л. Чебышев нашел элементарное и бо-
лее общее доказательство, с которым мы и познакомимся.
(В оригинальном изложении Чебышева также присутствуют’
длинные вычисления, с нашей точки зрения совершенно не-
нужные. Следует иметь в виду, что когда в учебнике сказано,
что излагаются результаты того или иного ученого, на самом
деле речь всегда идет о некоторой коллективной переработ-
ке оригинального изложения, делающей его несравненно бо-
лее удобопонятным. Можно сравнить, например, изложение
электродинамики в трактате Максвелла или лекциях Больц-
мана с современными нам учебниками.)
Неравенство Чебышева. Мы говорили, что дисперсия слу-
чайной величины | измеряет в каком-то смысле возможные'
отклонения | от М|. Этот смысл уточняется неравенством Че-
бышева.
Лемма 6. Пусть существует D£ и дано число е>0. Тог-
да
Р{Ц-M|l>e}<D|/e2.
Доказательство. Запишем цепочку равенств и нера-^-
венств:
m - Mg - М£)« = у (at - Ml)1 Р (| = а,} >
> S (аг-М|)«Р(| = а,)>
М£|>1
> »’ S Рй = а{} - Р {|* - MUI >8).
Отсюда вытекает утверждение леммы.
Определение. Говорят, что последовательность слу-
чайных величин |ь |2, .... - сходится к нулю по вероятно-
сти, если для любого е>0
P{l|nl>e}—►О (п—>оо).
Из неравенства Чебышева (лемма 6) вытекает, что для схо-
димости к нулю по вероятности последовательности (|п—
—М|п} достаточно, чтобы D£n—»-0.
Теорема (закон больших чисел в форме Чебышева).
Пусть случайные величины £2,..., £п,... попарно независи-
мы, причем D£i<C<oo. Тогда
41
р || Е1+Е. + - • -Мл _мЕ1+ме»+-+ мбл|>е1 _>о
II п п | |
три п —► оо для любого е>0.
Доказательство. Достаточно установить, что
JD{(I1+I2+—+|п)/п)-Ю. Имеем (в силу леммы 5)
D /*» +к+щ±Л\ = -L D(4 -н, + . • .+5»)-
\ Л / rtB
п* п* п
4=1
Замечание. Для доказательства закона больших чи-
сел мы применили несложный (но и не тривиальный, посколь-
ку Лаплас и Пуассон его не видели) аппарат, состоящий из
неравенства Чебышева и способа вычислять дисперсию суммы
li+12+...+ln. Этот аппарат пригоден и для зависимых слу-
чайных величин, если, например, предположить, что
cov(|,-, |/)—►О при 11—/I—»-оо каким-нибудь таким обра-
зом, что D(|i + £2+... + U)/n2—►О.
Комментарий. Таким образом, среднее арифметичес-
кое (I1 + I2+ — + %п)/п из большого числа п случайных вели-
чин с вероятностью, сколь угодно близкой к 1, ие отличается
более, чем на в от неслучайной величины (MI1 + MI2+....
... + М|п)/п. Допустим, что |1, |2, .... |п — результаты измере-
ний некоторой физической величины в ансамбле однотипных
опытов. Тогда естественно предположить, что все величины
|ь I2. In имеют одно и то же распределение вероятностей,
в частности,
М|,=М|2=... =М|„=а, (6)
и получаем, что Р{1 (I1 + I2+ - +|n)/«—al <е) -И при
п—»-оо, т. е. постоянная величина а может быть найдена как
среднее арифметическое из результатов наблюдений как
угодно точно, лишь бы п было велико. Классики аргументиро-
вали, что а и есть истинное значение измеряемой величины.
(Их аргументация сводится к тому, что одинаково вероятно
наблюдению |,- отклониться от истины на данную величину
в положительную и отрицательную сторону, а тогда М|,=а
и есть истина). Получается 'парадоксальный вывод, что
можно узнать некую длину с точностью до микрона, пользу-
ясь в качестве измерительного прибора масштабной линейкой.
Элементарная ошибка здесь очевидна: измеряя длину 50,1-мм
масштабной линейкой, всегда будем получать 50 мм;
возникает систематическая ошибка. Более подробное обсуж-
42
дение вопросов обработки измерений см. во второй части
книги.
6.5. Элементарная задача из теории игр. Вероятностная
постановка задачи приводит к некоторому однозначному ана-
лизу ситуации, возникающей в играх двух игроков. Считает-
ся. что каждый из игроков имеет конечный набор стратегий,
занумерованных числами 1, 2../ для первого игрока и чис-
лами 1, 2....................J для второго игрока. Пусть прн выборе первым
игроком t-й стратегии и при выборе вторым игроком /-й стра-
тегии выигрыш первого игрока составляет а,/ (числа посчи-
таются известными). Спросив себя, как надо играть (допустим,
первому игроку), видим, что не можем ответить иа этот воп-
рос, так как стратегии первого игрока, которые хороши про-
тив одних стратегий второго игрока, могут оказаться плохими
против других стратегий, и начинается обсуждение психоло-
гических колебаний между разными выборами стратегий в
последовательных играх, не ведущее к научному решению
вопроса.
Вероятностный подход позволяет в каком-то смысле раз-
рубить этот гордиев узел. Предлагается рандомизировать си-
туацию, т. е. при каждом повторении игры выбирать страте-
гию случайно (в зависимости от исхода случайного экспери-
мента, производимого тайно от противника). Разгадать вы-
бор стратегии противник принципиально не может. Что же
здесь нужно максимизировать?
Поскольку случайный эксперимент вводится в игру, то
выигрыш первого игрока есть случайная величина (в азарт-
ных играх это всегда имеет место; речь идет о рандомиза-
ции игр, которые сами по себе не являются азартными).
Обозначим через &....... £п выигрыши первого игрока в п
последовательных повторениях игры; тогда интерес представ-
ляет суммарный выигрыш Sn=|i + ^2+ — + |n. т. е. сумма
одинаково распределенных случайных величин. Но поведение
суммы Sn в основных чертах описывается законом больших
чисел. Полагая a=Mli и повторяя выкладки из доказатель-
ства закона больших чисел, получим, что
Sn=na+8n,
где есть величина порядка Т/п (точно это означает, напри-
мер, следующее: для всякого е>0 найдется число Се, такое,
что лри каждом п
Р{1бп1<СеУп}>1—е).
Таким образом, при а>0 первый игрок обогащается, при
в<0 разоряется. (Случай а=0 теми элементарными метода-
ми, которыми мы пока владеем, исследован быть не может.)
Итак, если согласиться на асимптотический анализ проб-
43
лемы, первый игрок должен максимизировать а (за счет вы-
бора вероятностей своих стратегий), а второй — минимизи-
ровать а. Оказывается, что существует такое значение а*
(«цена игры»), которое является минимаксным в следующем
смысле: первый игрок может обеспечить М£»=а*, какие бы
стратегии (случайно или не случайно) ни выбрал второй иг-
рок; с другой стороны, второй игрок может выбрать такие ве-
роятности своих стратегий, что МЬ- а* при любой игре пер-
вого игрока.
Приведем пример нахождения а* для так называемой иг-
ры в 10 и 20 коп. Первый игрок прячет одну из двух монет —
10 или 20 коп., а второй угадывает, какая монета спрятана.
Если он угадал правильно, то он получает эту монету; если
ошибся — платит первому 15 коп. На первый взгляд условия
игры совершенно симметричны для обоих игроков, но анализ
показывает, что у первого игрока есть преимущество.
Итак, пусть первый игрок прячет 10 коп. с вероятностью:
р, 20 коп. — с вероятностью 1—р. Подсчитаем математичес-
кое ожидание а его выигрыша в двух случаях: 1) когда вто-
рой игрок называет 10 коп.; 2) когда второй игрок называет
20 коп.
1) случай: с вероятностью р первый игрок проигрывает
10 коп.; с вероятностью 1—р выигрывает 15 коп.,
а=—10р+15(1—р) = 15—25р;
2) случай: аналогично а=15р—20(1—р)=35р—20.
При любом поведении второго игрока математическое ожида-
ние выигрыша первого ие менее чем
min(15—25р, 35р—20).
Максимум минимума достигается при 15—25р=35р—20, т.е.
при р=7/12 и равен +5/12 коп. Поэтому, чтобы ни делал
второй игрок, его проигрыш будет составлять в среднем 5/12
копейки, если первый игрок будет пользоваться рандомизи-
рованной стратегией. Не составляет труда подсчитать, что
если второй игрок будет пользоваться рандомизированной
стратегией, то его проигрыш составит в среднем 5/12 коп.
независимо от поведения первого игрока. Итак, а*=5/12 коп.;
игра выгодна для первого игрока.
К сказанному нужно прибавить два комментария.
Во-первых, реализация случайного эксперимента с вероят-
ностью одного из исходов р=7/12 достаточно трудна. Если
же окажется, что на самом деле р=1/2, то преимущество
первого игрока будет полностью потеряно (а=0). Лучше вос-
пользоваться заготовленной заранее (например, с помощью
ЭВМ) таблицей случайных чисел. Однако в этом случае про-
тивник может разгадать алгоритм, с помощью которого полу-
44
1!еиа вся последовательность («случайные» числа ЭВМ на са-
мом деле — псевдослучайные, получаемые с помощью некото-
рых чрезмерно простых алгоритмов; мы еще встретимся с
этой проблемой).
Во-вторых, мы произвели лишь асимптотический анализ за-
дачи (при очень больших п). Для каких реальных п приго-
ден наш анализ, например сколько раз нужно повторить иг-
ру, чтобы с близкой к 1 вероятностью можно было выиграть
рубль, мы пока сказать не можем. Из неравенства Чебыше-
. ва такие оценки вытекают, но они слишком грубы. Ниже мы
увидим, что приносит для этой задачи центральная предель-
ная теорема.
§ 7. Проверка статистических гипотез
Этим параграфом мы заканчиваем элементарное введение
в теорию вероятностей, из которого (кроме элементов матема-
тического аппарата) должно быть, в общем, можно понять,
каков круг одновременно наиболее простых и наиболее мас-
совых применений теории вероятностей. Целесообразно про-
верку статистических гипотез рассмотреть с точки зрения ка-
кой-нибудь актуальной общественной проблемы: какую роль
могут играть в решении этой проблемы вероятностно-стати-
стические методы? Имеется целый ряд таких проблем; мы бо-
лее пли менее произвольно выбираем проблему качества про-
дукции.
Надо прежде всего понять, что оценка качества продук-
ции на основании предъявленного единичного готового изде-
лия есть дело практически безнадежное. Допустим, что мы
купили в магазине настольную лампу, которая эстетически
достаточно хороша, но должна, конечно, еще и гореть. В на-
стольной лампе имеется порядка десятка винтов электричес-
ких контактов, которые все должны быть плотно завинчены.
Если какие-то из них завинчены неплотно, то лампа может
гореть в магазине, некоторое время дома у покупателя, но
вскоре контакты обгорят и лампа погаснет (в данном контек-
сте мы не рассматриваем возможность развития дефекта в
сварено). Чтобы проверить затяжку контактных винтов, су-
ществует лишь один способ — разобрать лампу и завинтить
все винты самому. (Измерение электрических сопротивлений
на новой лампе ничего не даст.) Пожалуй, ни отдел техни-
ческого контроля завода, выпускающего лампы, ни (как пра-
вило) покупатель на этот способ не согласится.
В лампе есть еще шнур, в котором может нарушиться це-
лостность токоведущих жил. Правильно ли свиты проводнич-
ки в этих жилах — под изоляцией не видно ни покупателю,
ли ОТК- За шнур несет ответственность не тот завод, кото-
рый выпускает настольные лампы, а тот, который делает
45
шнуры. Есть еще выключатель и одна-две лампочки накали-
вания, которые делают совсем другие заводы. В общем, даже
для простейшего изделия возникает целая система коллек-
тивной ответственности, которая с точки зрения покупателя
оказывается полной безответственностью. Как же быть, если
мы покупаем не настольную лампу, а более сложное изделие»
например автомобиль?
Ни один автомобиль не мог бы никогда тронуться с места»
если бы общество не создавало (худо или хорошо) целой сис-
темы контроля, исключающей (на деле — хотя бы ограничи-
вающей до разумных пределов) выпуск непригодных деталей
и узлов еще задолго до того, как они будут собраны в гото-
вое изделие. Роль вероятностных методов (в частности, про-
верки статистических гипотез) в этой системе может состоять,
в том, чтобы с большей чувствительностью или большей обос-
нованностью выявлять тех, кто работает хуже других (каса-
ется ли это людей, сырья или технологического оборудова-
ния и т. д.). Рассмотрим логическую схему проверки гипотез
и простой пример способа выделения худших ситуаций.
Фольклор естествознания говорит, что природа в ответ на
наши вопросы отвечает «нет» громко, а «да» тихо. Проверка
любой научной гипотезы обычно устроена следующим обра-
зом. Известно, что если гипотеза Н верна, то некое явление
S произойти в опыте не может. Предположим, что в опыте
явление S произошло. Тогда (громкое «нет») мы отвергаем
гипотезу Н. Если же явление S не произошло, то иногда мы
с радостью говорим, что гипотеза Н подтвердилась, но исто-
рический опыт учит нас, что это неправомерно: следует
скромно сказать, что гипотеза Н не отвергается (тихое «да»).
Проверка статистических гипотез следует той же логичес-
кой схеме (напомним, что статистической гипотезой называет-
ся нечто такое, что позволяет вычислять вероятности собы-
тий, которые могут наблюдаться в опыте). Только событие S
должно быть не совсем невозможным, а маловероятным. Ор-
тодоксальная логическая схема требует, чтобы до опыта было
указано событие S (критерий, или критическое множество),
удовлетворяющее условию
P(xeS/tf}<a, (1)
где a — некоторое число, называемое уровнем значимости.
Поясним обозначения формулы (1). Как всегда, мыслит-
ся, что существует некоторое пространство элементарных со-
бытий, может быть, очень сложное. В опыте наблюдается не-
кий результат х, являющийся функцией от элементарного со-
бытия (разным элементарным событиям может соответство-
вать одно и то же х). Все возможные х 'образуют выборочное1
пространство Х={х}; S есть некоторое подмножество X. Рас-
46
пределенне вероятностей на множестве элементарных собы-
тий (следовательно, и порождаемое им распределение вероят-
ностей на X) теперь не одно: оно определяется принятой для
рассмотрения гипотезой Н. Вероятность того, что результат
опыта х попадает в некоторое Л=Х, отвечающая гипотезе
Н, записывается в форме Р{хеЛ/Я), совпадающей с формой
записи условной вероятности, но не обязательно по сути явля-
ется условной вероятностью (самим гипотезам Н вероятности,
вообще говоря, не приписываются). Словесная форма чтения
выражения Р{хеЛ/Я) следующая: «вероятность того, что
хеЛ, если на самом деле верна гипотеза Я».
Проверка гипотезы Н состоит в следующем. До опыта
указывается критическое множество S; затем производится
опыт. Если результат опыта x&S, то, грубо говоря, гипотеза
Н не отвергается, а более точно — говорится, что «отклоне-
ния от гипотезы Н, значимого на уровне а, не наблюдено».
Если xeS, то гипотеза, грубо говоря, отвергается, а более
точно — говорится, что «гипотеза отвергается на уровне а»
либо «наблюдается значимое на уровне а отклонение от гипо-
тезы Я».
Смысл уровня значимости состоит в том, что это число
ограничивает сверху вероятность отвергнуть гипотезу Я в тех
случаях, когда оиа на самом деле верна. Уровень значимости
обычно выбирается из ряда значений
0,001; 0,01; 0,05; 0,10,
но возможны и любые другие значения.
В § 4 мы уже рассматривали проверку гипотезы об испы-
таниях Бернулли и выяснили наглядный смысл уровня значи-
мости (вероятность напрасно обидеть честного партнера в иг-
ре в орлянку). Мы отметили невозможность ответа на ряд во-
просов при той постановке задачи, которой придерживались
в § 4. Здесь введем дополнительное предположение, состоя-
щее в том. что возможными альтернативами к проверяемой
гипотезе Я являются также вероятностные гипотезы (это оз-
начает, что если гипотеза Я неверна, то верна какая-то дру-
гая гипотеза, также позволяющая вычислять вероятности то-
го, что хеЛ=Х). Пусть имеющиеся гипотезы параметризова-
ны некоторым параметром а: имеются гипотезы На, причем
некоторое значение а, например а=О, играет особую роль.
Говорим тогда о проверке гипотезы Яо по отношению к аль-
тернативам На, а^0. Критерий S характеризуется функцией
M(a)=P{x<=S/Ha}, (2)
равной вероятности отвергнуть гипотезу Яо, если на самом
деле верна гипотеза На. Функция М(а) называется функци-
ей мощности статистического критерия S.
При а=0
М(0)=Р{хе5/Я0)
47
есть вероятность напрасно отвергнуть справедливую гипоте-
зу Яо; она называется еще вероятностью ошибки 1-го рода.
При а#=0 имеем
1— М(а) = 1—P{xf=S/Ha}=P{x<£S/Ha},
т. е. величина £(а) = 1— М(а) равна вероятности ошибочно
не отвергнуть гипотезу Яо. когда на самом деле верна гипоте-
за На\ она называется вероятностью ошибки 2-го рода.
Хотелось бы вероятности ошибок 1-го и 2-го рода сделать
(за счет выбора критерия S) маленькими, в идеале — равны-
ми нулю. В практически важных случаях это невозможно,
причем если выбирать уровень значимости а (напомним, что
Л1(0) = Р{хе5/Яо}^а) поменьше, то и при а#=0 обычно
М(а) делается меньше: критерий теряет чувствительность к
отклонениям а от 0, или, что то же, растет р(а) = 1—М(а).
Если же стараться сделать больше М(а) при а=£0, то увели-
чивается и Л1(0), т. е. вероятность ошибки 1-го рода. При
оценке практических качеств той или иной проверки гипотез
и нужно следить за балансом возможных ошибок 1-го и 2-го
рода.
Рассмотрим пример. Пусть некий хлебозавод выпус-
кает сладкие булочки с изюмом, причем по государственному
стандарту на 1000 булочек полагается 10000 изюмин. Подо-
зреваем, что изюм могут украсть (скорее частично, чем пол-
ностью), и хотим это проверить. Для контроля можем купить
одну (или несколько) булочку и сосчитать, сколько там изю-
мин (т. е. речь идет о контроле по готовому изделию). Что в
такой задаче могут дать статистические методы?
1. Формулировка статистических гипотез. Есть разные спо-
собы перемешивать тесто. Например, можно засыпать изюм
в одно место, а помешать в другом (когда же начальство от-
вернется — выгрести обратно неразмешанный изюм). Мы не
сможем охватить такие ситуации и предположим, что пере-
мешивание изюма в тесте происходит равномерно. Выделим в
тесте объем, отвечающий купленной нами булочке (он будет
составлять 1/1000 от всего объема теста). Организуем теперь
схему испытаний: испытаний всего будет п=10000 (по числу
изюмин); каждое испытание будет состоять в том, что мы
посмотрим (мысленно), попала ли данная изюминка в нашу
булочку (успех) или не попала (неудача). Тогда при рав-
номерном перемешивании теста вероятность успеха р= 1/1000.
Испытания не вполне независимы: если первые две тысячи
испытаний все кончатся успехом, то, пожалуй, в объеме на-
шей булочки уже не останется места для новых изюмин, так
что остальные испытания кончатся неудачами. Но ясно, что
такая ситуация практически (при равномерном перемешива-
нии) невозможна. Приближенная независимость испытаний
имеется. Поэтому принимаем приближение Пуассона, причем
-48
К=пр= 10
есть среднее число изюмин на одну булочку.
Если же предположить, что доля a, O^a^l, всего изюма
украдена, то
>.=7.(а) = 10(1— а).
Итак, имеется гипотеза Но (т. е. а=0), состоящая в том, что
ничего не украдено. Эту гипотезу естественно объявить основ-
ной. Альтернативные гипотезы имеют вид На. Число изюмин
в купленной нами булочке подчиняется (при верной гипотезе
На) закону Пуассона с параметром Х(а) = 10(1—а).
2. Возможные стратегии правоохранительных органов.
Предположим, что хлебозаводов много, т. е. правоохранитель-
ные органы сталкиваются со статистической ситуацией. Их
задача состоит в том, чтобы нарушителей закона выявить и
изъять, ни в коем случае не тронув честных лиц и не остано-
вив производства булочек с изюмом.
Первичным материалом являются жалобы покупателей
на то, что в булочках нет (или мало) изюма. Можно попы-
таться встать на крайнюю позицию: как только поступила
(допустим, достоверная) жалоба на отсутствие изюма — са-
жать пекаря. Посмотрим, что из этого получится.
Если никакого воровства нет, то вероятность того, что в
наудачу взятой булочке не окажется изюма (х=0), дается
формулой
Р{х=О/Яо}=е-Х(О)=е-,о«О,51О-4.
Вероятность того, что хотя бы в одной из 1000 булочек не
окажется изюма, нужно подсчитывать как вероятность суммы
событий, т. е. суммировать вероятности событий, вычитать
вероятности попарных пересечений и т. д. Оценки показыва-
ют, что пересечениями можно пренебречь и принять прибли-
женно сумму вероятностей:
1000 0,5-10-4=0,05.
Таким образом, если предположить, что каждый из 1000 по-
купателей, купив булочку без изюма, тут же пишет жалобу,
то вероятность того, что хоть одна жалоба будет, есть 0,05.
Поэтому вероятность честному пекарю остаться на свободе
есть 0,95. Но булки пекутся каждый день, так что вероят-
ность в течение года остаться на свободе равна
(0,95)385« ехр{—0,05 -365} ~ е-'»,
что весьма близко к нулю. Через год ни одного пекаря не ос-
танется на свободе, а производство прекратится.
4-2567 49
Итак, при массовом производстве какое-то количество яв-
ного брака всегда неизбежно и не обязательно говорит о не-
добросовестности .
3. Проверка статистических гипотез. Каким должно быть
критическое множество для гипотезы Но? Без долгих раз-
мышлений заключаем, что против гипотезы Но может свиде-
тельствовать лишь малое число изюмин х в купленной для ис-
следования булочке, но никак не большое. Критическая об-
ласть, следовательно, должна иметь вид S={x; x^k], где k
предстоит выбирать из соображений уровня значимости (или
функции мощности). Уровень значимости а в нашем слу-
чае — гарантия честного работника от ложного подозрения;
а надо брать малым. Попробуем два значения: ai=0.01 и
а2=0,001. Из таблиц закона Пуассона получаем:
для «1 значение k=k\=3 (Р{х^3///о)«*0,010),
для аг значение Л=Л2=1 (Р{х^1/Я0}«0,0005).
Приведем отдельные значения функции мощности. Для
а=0,1 (украдена 1/10 изюма)
Р{х<3/Я0,1}«0,020, Р(х<1/Яо.1}~О,ОО11.
Наша моральная шкала и шкала качества готового изделия
резко не совпадают: по моральной шкале случаи а=0 и
а=0,1 резко различны, но в случае а=0,1 среднее число
изюмин в булочке снижается лишь на 10%. Соответственно
если невиновному человеку предоставить гарантию: вероят-
ность ложного обвинения не выше 0,01, то того, кто украл
1/10 изюма, мы обвиняем лишь с вероятностью 0,02 (а если
гарантия: не выше 0,001, а фактически 0,0005, то при краже
1/10 изюма вероятность обвинения 0,0011). Для а=0,5 (ук-
радена половина изюма)
Р(х<3/Н0,5} « 0,26, Р{х< 1 /Н0,5) «0,040.
Второе из этих чисел крайне мало, что связано с малостью
«2=0,001.
Таким образом, проверка статистических гипотез не поз-
воляет создать достаточно резкого различия между ситуаци-
ей Яо и На при а=#0, что связано с неэффективностью конт-
роля по единичному изделию. Действительно, для отличения
гипотез Но и Ны нужно отличить значения пуассоновского
параметра Л=10 и Х=9. Поскольку отклонение значения
случайной величины от ее математического ожидания X со-
ставляет (для закона Пуассона) величину порядка У?., ясно,
что значения Х=10 и Х=9 различить трудно. Выход может
состоять в том, чтобы взять для исследования не одну бу-
лочку, а, скажем1100. Тогда нужно будет отличить 51=1000
от Х=900 при УЛ«30, что гораздо легче. Впрочем, подсчет
50
числа изюмин в 100 булочках выглядит непривлекательно с
точки зрения трудовых затрат на такой подсчет.
Гипотезы Но и Я0.5 отличаются гораздо более заметно:
вероятность обвинения, если украдена половина изюма, во
много раз больше вероятности обвинения честного человека.
Очевидно, на этом и нужно сыграть, если стремиться исполь-
зовать статистические методы.
4. Какая польза может быть от статистических методов?
Вышеприведенные расчеты ясно показывают, что для окон-
чательного решения вопроса о наличии правонарушения ста-
тистические методы непригодны (они могут составлять лишь
часть доказательств). Должны применяться более прямые
методы, но их применение трудоемко. Между тем, если пред-
положить, что, скажем, 80% всех работников честны и лишь
20% нечестны, то в 80% случаев усилия будут потрачены
впустую. Рассмотрим применение статистической проверки
гипотез лишь для предварительного отбора объектов: по-
английски это называется screening, т. е. просеивание. Бу-
дем проверять гипотезу Но не на малом, а на большом уров-
не значимости, скажем, на уровне а=аз=0,15, делая вывод
не о наличии или отсутствии правонарушения, но лишь о же-
лательности или нежелательности более непосредственной
проверки. В этом случае k=k3=6, причем Р{х<6/Яо)=О,13.
Это означает, что если вместо чисто случайного выбора
объекта для проверки принять чуть более сложную процеду-
ру — сначала случайно выбирается хлебозавод, потом из
его продукции берется одна булочка и проверка производит-
ся лишь в том случае, когда число изюмин в ней х<6, — то
проверка будет напрасной лишь с вероятностью 0,8-0.13=
=0,104. Иначе говоря, лишь 10% усилий будут потрачены
впустую.
Этот оптимистический вывод нужно правильно понять.
Речь идет о сравнении двух следующих ситуаций: 1) в нача-
ле рабочего дня случайно выбирается хлебозавод, на кото-
рый сотрудники едут с проверкой; 80% рабочих дней в этом
случае будет потеряно впустую; 2) в начале рабочего дня
случайно выбирается хлебозавод, берется булочка из его
продукции, и если число изюмин в ней х<6, то сотрудники
едут на этот завод, а если х>6, то занимаются другим по-
лезным делом (в этом случае день не потерян); тогда поте-
рянных впустую дней будет 10% от всех рабочих. Общее
число проверок хлебозаводов во второй ситуации сильно со-
кратится, за счет чего и произойдет в основном сокращение
числа потерянных впустую дней. Если возникает какая-либо
третья ситуация: в начале рабочего дня случайно выбирают-
ся один за другим хлебозаводы, берутся булочки из их про-
дукции до получения результата х<6, а тогда уже следует
проверка, то эффективность такого метода будет, конечно,
4* 51
не 90%, а гораздо ниже (ее нельзя подсчитать количествен-
но, не задаваясь распределением вероятностей параметра а).
Сокращая напрасные потери времени, наш скрининг не-
значительно уменьшает вероятность обнаружения того, кто
украл половину (или более) изюма. Таблицы закона Пуас-
сона показывают, что P{xc6///o.s}~O,76. Это означает, что
при повторении процедуры случай а=0,5 ловится довольно
быстро. Случай же а=0,1, конечно, ловится плохо: в нашей
задаче числа подобраны так, чтобы была ясна необходи-
мость исследования возможностей статистического метода.
На самом деле, при длительном статистическом исследо-
вании прекрасно можно отличить гипотезу Но от гипотезы
Яо,1 и гипотезу Яо,1 от гипотезы Н0,2 и т. д., если, конечно,
предположить, что доля а стабильна во времени. Можно оце-
нить и объем необходимого для этого статистического мате-
риала. Вообще, при массовых и (или) продолжительных ста-
тистических исследованиях поведения в эксплуатации той
или иной продукции могут быть обнаружены очень тонкие на
первый взгляд эффекты, которые вызовут изумление непос-
вященного. Но для подобных статистических обработок нуж-
но знать теорию вероятностей примерно на уровне централь-
ной предельной теоремы, которой мы еще не изучали.
ГЛАВА 2
АКСИОМАТИКА КОЛМОГОРОВА
§ 1. Введение
Крайне элементарная в математическом отношении пер-
вая глава настоящей книги имела целью дать общее поня-
тие о предмете теории вероятностей и о возможностях ее
приложений. На самом деле с дискретной моделью связаны
глубокие и интересные аналитические задачи (см., например,
первый том книги В. Феллера [40]), совершенно не отражен-
ные в первой главе. Но укоренившееся в физико-математи-
ческих науках представление о числовом (пространствен-
ном) континууме делает нежелательным такой учебник тео-
рии вероятностей, который слишком долго не желает заме-
чать этого представления. Действительно, конечное число п
испытаний Бернулли требует конечного множества элемен-
тарных событий вида <о= (ei,....еп), где е(-=0 или 1, но как
только мы поставим вопрос типа: «какова вероятность того,
что в последовательности испытаний Бернулли нечто когда-
нибудь случится» (например, произойдет подряд 100 успе-
хов, за которыми последует ровно 100 неудач), нам потребу-
ется уже счетное число испытаний Бернулли. Множество
52
счетных последовательностей <о= (et,.... е„,...) имеет мощ-
ность континуума, и дискретная модель вероятностного
пространства здесь бессильна.
Любопытно, что если вероятность успеха в испытаниях
Бернулли принять равной р = ‘/2 и точке <о= (ei, ...,е„,...) по-
ставить в соответствие точку x=S8^2_, отрезка [0, 1], то все
точки отрезка окажутся равновероятными (поскольку все
наборы (ei...е„,...) равновероятны, но только в каком
смысле?). Это будет случайное бросание точки х на отрезок
[О, 1].
Представление о случайном бросании точки & на числовой
континуум (—оо, оо) естественно возникает н в связи с во-
просом о математической модели для физического измере-
ния, подверженного случайным ошибкам; для случайных
моментов времени, когда происходят физические события
(типа момента распада ядра атома и т. п.), подобные ситуа-
ции весьма разнообразны.
Элементарную ситуацию, рассмотренную в первой главе,
можно назвать ситуацией случайного выбора элемента дан-
ного конечного или счетного множества. Сейчас мы видим,
что нужно уметь охватить математической моделью ситуа-
цию случайного выбора точки из множества, имеющего мощ-
ность континуума. Но и это не предел: в экспериментах,
когда записывается некоторая функция (допустим, функция
времени), при наличии случайности получается случайная
функция. Иначе говоря, речь идет о выборе наудачу такой
функции из заданного множества функций. Как известно,
множество функций аргумента, пробегающего множество
мощности континуума, имеет (вообще говоря) мощность
большую, чем континуум.
В современной теории вероятностей математической мо-
делью случайного выбора является мера, заданная на соот-
ветствующем множестве элементарных событий. Эта концеп-
ция сформулирована 60—70 лет тому назад в виде так назы-
ваемой «аксиоматики Колмогорова:». В разработке ее участ-
вовали кроме А. Н. Колмогорова ряд выдающихся ученых
(упомянем французского математика Э. Бореля, работавше-
го в этой области несколько раньше А. Н. Колмогорова, и аме-
риканского математика Дж. Л. Дуба, работавшего несколь-
ко позже, а также советского математика А. Я. Хинчина, ра-
ботавшего одновременно с А. Н. Колмогоровым). Тот, кто
начинает изучение теории вероятностей, должен понимать,
что эта концепция не обладает такой простотой, ясностью и
законченностью, как классическая концепция дискретного
пространства элементарных событий; более того, кроме ряда
значительных преимуществ она имеет и недостатки. Класси-
ческая концепция производит впечатление чего-то столь же
вечного, сколь вечна элементарная арифметика; при знаком-
53
стве с общей аксиоматикой все время возникает желание
что-то изменить. Нужно понимать, что первоклассные уче-
ные, создавшие эту аксиоматику, в свое время тщательно
продумали, вероятно, все возможные варианты. Попытки из-
менения будут, следовательно, беспочвенными, если исходить
из тех же знаний (имеются в виду прежде всего представле-
ния о строении континуума), которыми располагали созда-
тели аксиоматики. Наоборот, при изменении представлений о
природе континуума (если бы, например, была построена со-
стоятельная физико-математическая теория дискретного
пространства), возможно, уместно было бы поставить воп-
рос о новой аксиоматике теории вероятностей.
Теория меры (в том виде, как она излагается, например,
в учебнике А. Н. Колмогорова и С. В. Фомина [23]) предпо-
лагается в данной книге известной. Но некоторые принципи-
альные моменты будут по ходу изложения напоминаться. Ос-
новным фактом является существование счетно-аддитивной
меры Р на подмножествах пространства й элементарных со-
бытий, где й может быть весьма общим (отрезок, прямая R1,
евклидово пространство Rn и т. д. и даже пространство функ-
ций). Рассмотрим подробнее смысл этого «существования».
В современной философии науки выработалось понятие
«парадигмы» данной научной области: это греческое слово,
обозначающее «пример» или «образец», употребляется для
обозначения коллективных взглядов ученых, работающих в
данной области, на то, что «научно» или «ненаучно», т. е.
правильно или неправильно. Интересное наблюдение филосо-
фов состоит в том, что парадигма существует, конечно, в лю-
бой области науки, но никогда не выражается в виде полной
системы правил. Например, всякая физическая теория долж-
на, вне всякого сомнения, подтверждаться экспериментом, но
что в точности означают эти слова? Ведь и в эксперименте
неизбежны ошибки, так что согласие между теорией и экспе-
риментом не бывает полным. До какой же степени оно мо-
жет быть неполным? На этот вопрос общего ответа нет и,
очевидно, быть не может.
Парадигма математики состоит в том, что истинным счи-
тается то, что выведено из аксиом и уже известного путем
строгого математического доказательства. Математики
(включая студентов, изучающих математику) обычно прек-
расно могут сказать, является ли данное рассуждение стро-
гим математическим доказательством чего-то или нет. Но
попытка сформулировать систему правил, определяющих ма-
тематическую строгость, всегда будет неполной. Получается
некоторая система запретов типа: «никогда не надо путать
определение, аксиому и теорему», «стыдно не уметь отличить
прямую теорему от обратной», «просто позорно, когда в рас-
суждениях получается логическое противоречие» и, наконец,
«не смей никогда думать и, тем более, говорить о множест-
ве всех множеств». Нет, однако, никаких гарантий, что к лю-
бому списку подобных запретов не придется добавить еще и
еще; да и сами запреты, если в них вдумываться, достаточ-
но точного смысла не имеют. Язык математики хотя и стро-
же, чем обычный разговорный язык, но все-таки несет черты
обычного языка. Как разговорному языку, так и языку ма-
тематики мы учимся, не имея полной системы правил. Кста-
ти, тот язык, на котором сейчас говорит большая часть ма-
тематики, называется «языком наивной теории множеств».
Античная математика (насколько известно автору данной
книги) сравнительно мало страдала от логических противо-
речий. В новое время — с расширением предмета математи-
ки — противоречия становятся настоящим бичом. В XVIII в.
лишь люди высокого ума, как Эйлер или Д’Аламбер, могли
без больших ошибок обращаться с понятиями и формулами
математического анализа. (Рассказывают, что когда ученики
стали жаловаться Д’Аламберу на то, что из-за недостаточной
строгости они теряют всякую уверенность в новой матема-
тике, он отвечал им так: «Идите вперед, уверенность появит-
ся».) Лишь теория пределов Коши сделала математический
анализ доступным для массового изучения, в том числе в
технических вузах. (Люди высокого ума тоже выиграли: им
не нужно думать об элементарном анализе и можно обра-
тить свой ум к более достойным предметам.) С возникнове-
нием в XIX в. теории множеств возникли и новые противо-
речия.
Попытки изгнать эти противоречия, ограничив (но ие
чрезмерно) предмет или методы рассуждений математики, к
удовлетворительному успеху не привели. В математике удер-
жался язык наивной теории множеств, дополненный некото-
рыми запретами типа запрещения говорить о множестве всех
множеств либо о «множестве, для задания которого требует-
ся не более 100 слов русского языка». Непротиворечивость
допущенных в математику рассуждений является не более,
чем экспериментальным фактом. В сомнительных случаях
понятие математически приемлемого основано иа том, что
многие весьма остроумные люди, нарочно пытаясь скомпро-
метировать те или иные объекты или методы, приведя их к
противоречию, так и ие преуспели в этом занятии.
Высказанное выше утверждение о существовании счетно-
аддитивной меры Р надо, например в случае Q=[0, 1], пони-
мать следующим образом. Конечно, поскольку отрезок [0, 1]
есть теоретико-множественное объединение его отдельных то-
чек, было бы хорошо, если бы его мера (в частном случае —
длина), а также мера его подмножеств складывались бы из
мер отдельных точек. Однако мысленные опыты показывают,
55
что это совершенно невозможно. Поэтому будем понимать
длину отрезка [0, 1] и меньших отрезков так, как ее пони-
мал Архимед. При этом множества, являющиеся конечными
объединениями отрезков (или интервалов), также получают
длину (как было совершенно ясно и Архимеду), и длина
оказывается конечно-аддитивной функцией таких множеств.
Оказывается, что, отправляясь от древнего понятия длины
отрезка, можно путем математически строгой процедуры
(строгой в смысле вышеописанного экспериментального по-
нятия строгости) определить длину гораздо более сложных
множеств. Эта длина (называемая мерой Лебега) будет
счетно-аддитивной функцией множества.
Конечно, математики должны были как-то поисследовать
понятие меры Лебега: например, все ли множества имеют
меру (измеримы). Оказывается, что можно привести пример
неизмеримого множества (удобнее это делать не на отрезке
[О, 1], а на окружности длины 1). Рассмотрим этот пример,
чтобы понять, какими способами рассуждений нужно здесь
воспользоваться. Разобьем единичную окружность на классы
рациональности Fa: две точки х и у входят в один класс Fa,
если длина (любой) дуги, соединяющей точки х и у, рацио-
нальна. Возьмем из каждого Fa ровно по одной точке и со-
ставим из них множество М. Утверждение: множество М не-
измеримо по Лебегу. Действительно, поскольку мера Лебега
строится с помощью некоторых длин покрытий, мера любого
множества должна быть инвариантной относительно поворо-
тов окружности Qt на любой угол (измеряемый дугой г). При
рациональном z=r множества М и 0ГЛ4 ие пересекаются, так
как иначе в множестве М нашлись бы две точки, отличаю-
щиеся на рациональное число, т. е. взятые из одного и того
же класса Fa. Объединение 0ГЛ! по всем рациональным г
дает всю окружность (так как каждая точка окружности
входит в некоторый класс Fa и, следовательно, отличается
на рациональное число от той единственной точки Fa, кото-
рая входит в М). Таким образом, мера ие мо-
жет ии равняться нулю (тогда множества 6ГМ не могли бы в
сумме дать окружность), ии отличаться от нуля (тогда
объединение QrM имело бы бесконечную меру). Остается
принять, что множество М неизмеримо.
В этом рассуждении мы воспользовались так называемой
аксиомой произвольного выбора, состоящей в том, что если
дана некая система множеств Fa, то позволительно думать
и говорить о множестве, составленном из элементов, взятых
по одному из каждого множества Fa. Эта аксиома была
предметом пристального внимания ряда остроумных мате-
матиков. Не то чтобы они привели ее к явному противоре-
чию, но все-таки удалось получить (из аксиомы произволь-
ного выбора) ряд чрезмерно удивительных следствий. На-
56
пример, шар можно разбить на четыре подмножества (ко-
нечно, неизмеримых по Лебегу), таких, что два из них, буду-
чи передвинуты евклидовыми движениями, дадут в сумме
первоначальный шар, а два других — другой шар того же
радиуса. Аналогично из частей одного шара, передвинутых
евклидовыми движениями, можно, оказывается, сложить
шар большего радиуса. Возникает представление некоторого
неблагополучия (по крайней мере — крайней нефизичнос-
ти), связанного то ли с аксиомой произвольного выбора, то
ли с представлениями о континууме. Понятно, конечно, что
при эмпирическом подходе к математической строгости меж-
ду вещами безусловно разрешенными и безусловно запре-
щенными должны существовать и сомнительные. Видим, что
некоторые сомнительные вещи непосредственно соприкаса-
ются с простейшими вопросами теории меры.
Не приходится поэтому особенно удивляться тому, что ак-
сиоматика, основанная на теории меры, разрешает одни воп-
росы теории вероятностей весьма просто и изящно, другие
же — менее просто и менее изящно. В нашем курсе ие бу-
дем пытаться чрезмерно углублять вопросы, связанные с ме-
рой и понятием континуума.
Остановимся еще на вопросе об использовании счетно-ад-
дитивных или конечно-аддитивных мер для аксиоматизации
теории вероятностей. Математическую модель случайного
бросания точки на отрезок [0, 1] (либо на окружность еди-
ничной длины) можно построить разными способами. Мож-
но сказать, что элементарные события — все вещественные
числа этого отрезка, события — измеримые по Лебегу мно-
жества, а вероятность совпадает с мерой Лебега. При этом
получим тот вывод, что мера множества рациональных чисел
равна нулю, а мера множества иррациональных чисел равна
единице. Пожелаем ли мы интерпретировать этот вывод так,
что наудачу брошенная на отрезок точка с вероятностью 1
оказывается иррациональной? Понятно, что в таком выводе
нет физического смысла. Следовательно, наша модель име-
ет тот недостаток, что ие все математически верные для нее
теоремы допускают физическую интерпретацию. Если же-
лать иметь дело со счетно-аддитивной мерой, то с таким не-
достатком придется мириться.
С другой стороны, можно сказать, что элементарными со-
бытиями являются рациональные числа (поскольку резуль-
тат физического эксперимента — бросания малого предмета
на отрезок — может быть записан лишь с конечным числом
Десятичных знаков либо в виде дроби т/п). Под вероят-
ностью попадания точки на малый отрезок можно все равно
понимать длину отрезка (а событием будет множество ра-
циональных точек, лежащих на этом отрезке). Тогда мера
будет лишь коиечио-аддитивной (вероятность попадания в
57
отдельную рациональную точку равна нулю, а в одну из ра-
циональных точек отрезка [0, 1] — единице). Парадокс е ир-
рациональностью наудачу брошенной точки исчезает, но мы
попадаем в положение древних греков, для которых иррацио-
нальные числа казались таинственными.
На уровне постановки задачи превосходства модели со
счетно-аддитивной мерой над моделью с конечно-аддитивной
мерой не видно; однако при развитии теории модель со счет-
но-аддитивной мерой ведет к гораздо более интересной и ана-
литически удобной математике (в частности, к построению
интеграла Лебега). (К этому утверждению следует отно-
ситься как к экспериментальному факту.) Следы обдумыва-
ния возможностей модели с конечно-аддитивной мерой мож-
но найти в работе А. Н. Колмогорова «Общая теория меры
и исчисление вероятностей» [22, с. 48—58]. В более поздней
работе [21] сказано лишь, что почти невозможно разъяснить
эмпирическое значение счетной аддитивности и что (для бес-
конечных множеств элементарных событий) мы «произволь-
но ограничиваемся» счетно-аддитивным случаем. Вероятно,
все это свидетельствует о том, что конечно-аддитивный ва-
риант был обдуман и отвергнут.
Резюмируем смысл сказанного во введении. Читатель дол-
жен представлять себе, что за кадром замкнутого в себе ма-
тематического изложения аксиоматики (оно сейчас последу-
ет) существуют некоторые серьезные проблемы, которые, мо-
жет быть, не легче для нас, чем проблема иррациональных
чисел для древних греков. Возможно, что с этим как-то свя-
заны те недостатки аксиоматики, которые (как мы увидим)
особенно заметны в теории случайных процессов.
§ 2. Основные понятия теории вероятностей по Колмогорову
2.1. Вероятностным пространством называется тройка
{Q, ®, Р). Греческая буква Q (омега) обозначает здесь мно-
жество элементарных событий, которое может быть конеч-
ным или счетным множеством, подмножеством евклидова
пространства /?" (возможно, совпадающим с Rn, возможно —
нет, например, поверхностью единичной сферы в /?п), некото-
рым множеством функций (целочисленного, вещественного
или более сложного аргумента); словом, для общности, Q —
произвольное множество. Это множество интерпретируется
как множество всевозможных исходов некоторого случайно-
го эксперимента, хотя, конечно, в словах «результатом экс-
перимента является функция времени» присутствует очень
большая идеализация: нет ведь такого носителя информации,
на котором можно было бы записать континуум значений бо-
лее или менее произвольной функции, чтобы задать соответ-
ствие между значениями аргумента и функции.
58
Готическая буква 95 обозначает некоторую о-алгебру
подмножеств множества й. Напомним, что о-алгеброй на-
зывается совокупность подмножеств О, обладающая следую-
щими свойствами: 1) 0е95, Йе95; 2) с каждым подмно-
жеством Лей его дополнение Л = й\Ле95; 3) если дана
счетная система подмножеств Ль Л2.Л„,... е95, то
U Л| е95, П At е 95.
i«l i=l
Элементы о-алгебры 95 называются событиями; они идеали-
зируют события, реально наблюдаемые в опыте. Например,
при бросании точки на отрезок [0, 1] множество элементар-
ны?: событий й={0, 1], а в качестве элементов 95 могут быть
взяты подмножества отрезка [0, 1], измеримые по Лебегу.
Этих подмножеств с большим избытком достаточно для опи-
сания всего того, что можно попытаться наблюдать в физи-
ческом опыте. Естественно даже попытаться уменьшить их
запас.
Заметим, однако, что такое уменьшение не может пойти
особенно далеко. Действительно, отказаться от возможности
наблюдать событие, состоящее в том, что случайная точка <в
попадает на некоторый отрезок [а, 0], Оса<0^1, было бы
нелепо. Но 95 — о-алгебра, т. е. если положим, что [а, р]е 95,
то мы должны включить в 95 все множества, которые полу-
чаются из отрезков счетными операциями суммы и пересе-
чения; следовательно, включить в 95 и те множества, кото-
рые получаются счетными операциями над тем, что получа-
ется счетными операциями, из отрезков, и т. д. Дальше мож-
но продолжить по индукции, но не по обычной математичес-
кой индукции по членам натурального ряда, а по индукции,
трансфинитной по счетным вполне упорядоченным множест-
вам. Ясно, что хорошо бы иметь более простое описание эле-
ментов той о-алгебры, которая возникает из отрезков.
Такое описание состоит в следующем. Заметим, что пере-
сечение любого множества о-алгебр 95а (все о-алгебры со-
стоят из подмножеств одного и того же множества Й) есть
опять о-алгебра. Назовем наименьшей о-алгеброй, содержа-
щей данную систему подмножеств Л₽, пересечение всех
о-алгебр, каждая из которых содержит систему Лр. (Хотя
бы одна такая о-алгебра заведомо существует — это о-алгеб-
ра всех подмножеств й.) Говорят еще, что наименьшая о-ал-
тебра порождается системой Лц.
Определение. Наименьшая о-алгебра, содержащая
все интервалы [а, р]=(0, 1], называется о-алгеброй борелевс-
ких подмножеств отрезка [0, 1]. Аналогично о-алгеброй боре-
левских подмножеств прямой R1 называется наименьшая
59
о-алгебра, содержащая все интервалы [а, (в п-мерном
пространстве — все параллелепипеды).
Таким образом, для задачи бросания точки на отрезок
наименьшая возможная а-алгебра — это о-алгебра борелевс-
ких подмножеств (борелевская о-алгебра). Она несколько
уже, чем о-алгебра измеримых по Лебегу подмножеств, но>
это различие не имеет существенного значения.
Замечание 1. Обратите внимание на то, что в наив-
ной теории множеств думать о «множестве всех множеств»
нельзя, а о «множестве всех о-алгебр, состоящих из подмно-
жеств данного множества Q>, — можно. Мы даже сумеем
кое-что доказать, опираясь на данное определение борелевс-
кой о-алгебры.
Наконец, латинская буква Р в обозначении вероятностно-
го пространства обозначает счетно-аддитивную меру, опреде-
ленную на а-алгебре ®, подчиненную дополнительному усло-
вию
Р(Я) = 1.
Это означает, что если множества Ль Аг,..., А„,... е® не пе-
ресекаются между собой, то, во-первых, определены значе-
ния Р(Л,), 0<Р(Л,)<1, как и значение Р(Л1+Л2+ ... +
+Л„+ ...), и
Р(Л1 + Л,+ ... +л„+ .. )= з Р(Л,). (1)
1—1
В дискретной модели (1) является простенькой теоремой; в
общей теории это аксиома, выражающая свойство вероят-
ностной меры Р.
Замечание 2. Аксиоматикой Колмогорова называется
перечисление (в любой форме) свойств объектов (Q, ®, Р).
Мы предпочитаем говорить об основных понятиях теории ве-
роятностей по Колмогорову, включая в их число еще опреде-
ление случайной величины и математического ожидания.
2.2. Случайные величины. Предстоит идеализировать поня-
тие результата измерения или какой-то другой физической ве-
личины, зависящей от вмешательства случая. Будем твердо
держаться той концепции, что случайная величина £ есть
функция £=£(<>) от элементарного события ioeQ, но теперь
это будет не произвольная (как в дискретной модели), а
измеримая функция.
Понятие измеримой функции зависит от двух а-алгебрг
одна о-алгебра составлена из подмножеств того пространства,,
где принимает значения аргумент; вторая — из подмножеств
того пространства, где принимает значения функция. По-
скольку Q в нашей аксиоматике — произвольное множество»
ничего содержательного нельзя сказать о о-алгебре ® под-
60
множеств Q. Разберемся немного с а-алгебрами в области
значений функции, которые обычно называются борелевскими
о-алгебрами (или а-алгебрами борелевских подмножеств).
Говоря о а-алгебрах борелевских множеств, можем широ-
ко варьировать системы множеств, которыми эти а-алгебры
порождаются. Так, в случае /?’ можно начинать с замкнутых
интервалов [а,₽]=/?’, но можно и с открытых интервалов (а,
р) (поскольку замкнутый интервал есть счетное пересечение
открытых, а открытый — сумма счетного числа замкнутых).
Можно начинать с полубесконечных интервалов (—оо, а),
поскольку из их дополнений и пересечений легко создать ко-
нечные интервалы.
В случае R" можно начинать с параллелепипедов, или с
шаров (параллелепипед — открытый — есть счетная сумма
шаров и наоборот), или с углов вида
{*= (*i..хп) :х1<а1,...,хп<ап}.
Если потребуются борелевские множества на сфере, можно
начинать со сферических треугольников (многоугольников)
либо с кругов на сфере н т. д.
Измеримым пространством, вообще, называется некоторое
множество, на котором задана некоторая а-алгебра его под-
множеств (меры не предполагается).
Измеримым отображением называется такое отображение
одного измеримого пространства в другое, при котором про-
образы измеримых множеств измеримы (в смысле соответст-
вующих а-алгебр). Функцией называется однозначное (но не
обязательно взаимно однозначное) отображение. Понятие
случайной величины связано с измеримой функцией, отобра-
жающей пространство (Q, ®) в какое-нибудь другое измери-
мое пространство. Дадим определение случайной величины,
принимающей вещественные значения, т. е. отображающей
(Й. ®) в R1 с о-алгеброй борелевских подмножеств.
Определение. Случайной величиной называется изме-
римая функция £=£(w) со значениями в R1.
Измеримость означает, что для любого борелевского
B^R1 его полный прообраз измерим, т. е.
?-,(В)={(й:5((»)еВ}е®.
Лемма 1. Для любой функции £=£(w) со значениями в
R1 множество таких подмножеств B^R1, что £“* (Д)е ®, об-
разует с-алгебру.
Доказательство. Полный прообраз R' есть Q; полный
прообраз пустого множества 0 есть пустое множество, т. е.
Я* и 0 обладают тем свойством, что их полные прообразы
принадлежат ®. Далее, операция взятия полного прообраза
61
перестановочна с теоретико-множественными операциями
дополнения, суммы и пересечения:
-й\е*(В), 5-1 (U в.) = у s-' (вд
(здесь а пробегает любое, не обязательно счетное, множе-
ство). Если же а пробегает счетное множество и ^-‘(Bje®,
то и U£-1 (Ва)е® (и аналогично для пересечения), так как
а
83 —о-алгебра. Это и доказывает лемму.
Следствие. Для того чтобы функция g была измери-
мой, достаточно, чтобы £-1 (В) е 85 для такого набора множеств
В, что наименьшая о-алгебра, содержащая набор множеств Вг
содержит о-алгебру борелевских подмножеств R1.
Таким образом, достаточно, например, потребовать, чтобы
для любого а,— оо<а<оо, множество
Г* {(-оо, а)} = {«> :{(«)< а} е®.
Кроме случайных величин, принимающих вещественные
значения, бывают случайные величины с комплексными зна-
чениями, случайные точки многообразий, случайные кватер-
нионы, матрицы, функционалы, операторы и т. д. Все они в
рамках основных понятий теории вероятностей по Колмого-
рову определяются единообразно, как только в множестве
значений соответствующего неслучайного объекта введена ка-
кая-нибудь о-алгебра. Если на этом множестве имеется какая-
то топология (т. е. система открытых подмножеств; открытые
подмножества — кроме экзотических случаев — не образуют
о-алгебры), то обычно берется о-алгебра, порождаемая откры-
тыми подмножествами. Она называется борелевской о-алгеб-
рой.
Таким образом, описание самых разнообразных случайных
объектов выглядит весьма естественно в системе основных по-
нятий по Колмогорову.
Рассмотрим понятие функции от случайной величины.
В теории вероятностей вместе со случайной величиной | час-
то приходится рассматривать различные функции, вроде
sin g, 1п£ и т. д. Это понятие также находит весьма естест-
венное место в системе основных понятий.
Определение. Функция f(x) из R' в R1 называется
измеримой по Борелю, если для любого борелевского B^R'
полный прообраз f-I(B)=(x:f(x)eB} есть также борелев-
ское множество.
Лемма 2. Измеримая функция от случайной величины
есть снова случайная величина.
62
Действительно, пусть f—измеримая по Борелю функция.
Образуем /(£)(<>) =f [£(<“)]• Имеем для борелевского В
{со ; /К(«)]еВ)={Ы : В(®)еГ‘(В)}еВ,
поскольку f-1 (В) — борелевское множество.
Замечание. Совершенно ясно, что не обязательно брать
функцию f такую, что f: Rl-*-Rl, а можно брать любую функ-
цию, отображающую одно измеримое пространство в другое
(и являющуюся измеримой).
Предполагается, что из курса теории меры читателю из-
вестно, что запас измеримых функций весьма широк, в част-
ности обычные функции анализа являются измеримыми. Та-
ким образом, возможность образовывать функции f(£), где
f(x) — измеримая функция (может быть одной, а может
быть и нескольких вещественных или комплексных перемен-
ных), заведомо обеспечивает потребности любых приложе-
ний. Широта запаса измеримых функций связана с тем об-
стоятельством, что предельный переход сохраняет свойство
измеримости; если f(x) — llmfn(x) в каждой точке х,.
где fn — измеримые функции, то f(x) также измеримая функ-
ция (никакой равномерной сходимости не требуется). В част-
ности, все непрерывные функции измеримы как пределы мно-
гочленов. (Измеримость же многочлена устанавливается как
измеримость суммы одночленов; измеримость одночлена ус-
танавливается непосредственно из определения.) Можно на-
чинать не с многочленов, а, наоборот, со ступенчатых функ-
ций ^а^А^х), где А, — измеримые множества, 1Л/— инди-
каторы этих множеств, — все равно после предельного пе-
рехода получим тот же запас измеримых функций.
Наконец, в рамках основных понятий по Колмогорову
естественно разрешается вопрос о распределении вероятнос-
тей случайной величины.
Определение. Пусть £=£(ы) —случайная величина
(со значениями, для разнообразия, в Rn). Положим для бо-
релевского B^Rn
щ (В) = Р{(в : | (Ш) еВ)=Р{£-1 (В)}.
Тогда щ — мера, определенная на борелевской о-алгебре в
Rn. Эта мера называется распределением вероятностей (или
просто распределением) случайной величины g.
Замечание. Свойство
+ • • • ) = 3 Щ(£/)
i»l
вытекает из того, что S“’(BI+Bl+ ...)=^_|(В1)+^_<(В1)+...
63
(свойство полного прообраза), и счетной аддитивности веро-
ятностной меры Р.
2.3. Интеграл Лебега. В этой книге было бы трудно на-
поминать в деталях теорию меры. Впрочем, использование
теории меры сводится лишь к тому, чтобы заметить, что (в
силу теоремы о продолжении меры) во многих интересных
случаях на множестве й элементарных событий можно, в са-
мом деле, определить счетно-аддитивную вероятностную меру
Р (используется лишь существование меры, но не сама кон-
струкция продолжения). Что же касается интеграла Лебега,
то его конструкция необычайно проста (проще, чем для ин-
теграла Римана) и к тому же будет использоваться в данной
книге при построении интеграла по случайной мере. Поэтому
напомним эту конструкцию.
Пусть, для начала, 5 (и) — элементарная случайная вели-
чина, т. е. случайная величина, принимающая не более чем
счетное число значений оь а2,....ап..... Это означает, что
£(<в) можно записать в виде
^ = ^1^), (1)
где At — измеримые (в силу измеримости 5) подмножества Q.
Договоримся считать, что числа а, в (1) не обязательно раз-
личны между собой, но множества Л,- между собой не пере-
секаются, причем
Л1-|- ... +ЛП + ... =Q.
(Если угодно, принимаем (1) с указанными свойствами а, и
At за определение элементарной случайной величины.)
Определим значение интеграла Лебега следующей форму-
лой:
^(<o)P(du>) = ^a1P(Ai), (2)
предполагая, что ряд в правой части абсолютно сходится; в
противном случае считаем, что интеграла Лебега от £ не су-
ществует.
(Часто вместо P(dw) пишут dP(<o); мы, однако, исполь-
зуем обозначения А. Н. Колмогорова, поскольку в случае об-
щего Онио каком дифференциале dP(w) речь не идет.)
Определение (2) формально противоречиво. Дело в том,
что представление функции £(“)» в виде (1) неодно-
значно: в формуле (1) сказано то и только то, что имеется
разбиение Й на части Ль Л2,..., причем на каждой части At
функция £ (ш) принимает постоянное значение а,. Если части
At подразделить на более мелкие (либо объединить такие Л, и
А/, что а,-=а/), получится другое разбиение Й на части,
-64
удовлетворяющее тому же самому условию: окажется, что
Цш) = (3)
(числа Ь,в (3) — те же, что числа а, в (1), но занумерован-
ные, вообще говоря, в другом порядке). Тогда в правой час-
ти (2) возникнет сумма ^bjP(Bj), и необходимо дока-
зать, что она равна 2а«Р(Л<). Между прочим, лишь в этом
доказательстве используется тот факт, что Р есть мера, так
как (2) можно было бы написать и не предполагая, что Р
есть (счетно-) аддитивная функция множества.
Это доказательство и составляет единственную (неболь-
шую) трудность, которую нужно преодолеть для построения
интеграла Лебега.
Преодолевается она следующим образом. Пусть
?(<»)-^а/л/(«) = ^Мв/(ш).
Положим Dij=AiBj (возможно, некоторые D,/ пусты); на
каждом Da величина £(<о) принимает постоянное значение
(если оно не пусто). Следовательно,
$(«)••= ^/^(и) (4)
(причем в правую часть (4) можно без ущерба включить и
пустые Da с любыми dq). Рассмотрим преобразования:
P(Dq) = (24/Р(Ло)) - 2 ^a^D,^ -
= S(a^P(DV)) = S(<»<P (5)
Эти преобразования основаны на том, что при фиксиро-
ванном I имеем: D^^At, следовательно, dtl — а{ — j(®)
при ш€Л(, и на том, что ^А/ = (Л)- Преобразования
рядов (5) законны* если хотя бы один ряд, входящий в
формулы (5), сходится абсолютно (а это мы предполо*
жили). Таким образом, сумма ^dyPtPy). может быть
преобразована к виду ^а«Р(А<). Переставляя порядок
суммирования, получим, что та же сумма может быть
преобразована к виду ^bjP(Bj). Итак,
£а{Р(Л) = руР(ВД
что и требовалось доказать.
Теперь немедленно получим, что для элементарных слу-
чайных величин £ и л имеем
5—2567 65
GM + -J £(и)Р(Л)+^«)p (du). (6)
Действительно, если
6(“) = 3 <ЫА.(<»), т((ш) = biIAl(<o)
(т. е. £(ы) и т](<о) являются линейными комбинациями инди-
каторов одних и тех же множеств Лг), то (6) автоматически
получается нз определения (2) (в предположении, конечно,
абсолютной сходимости). Если же это не так:
(7>
£(<•>) = ajX1(u>), >)(«>) = bjIBj(u) ,
то образуем систему множеств Dij=AiBl и запишем £(со) и
т](ы) как линейные комбинации индикаторов множеств Оц.
Для предельного перехода от элементарных случайных ве-
личин к произвольным отметим оценку
[p(<0)P(d<D)| < SUp |*(<0)|,
непосредственно вытекающую из (2) в силу того, что-
^Р(Л0=1.
Пусть теперь £(<в) — произвольная (только лишь изме-
римая) функция, £п(ю) — последовательность элементарных
функций, равномерно сходящаяся к £(<в):
sup !$(«*>) — gn(a>)| -» О (п -> оо). (8)
и 60
Покажем, что последовательность gn(w) P(da>) фунда-
ментальна. Действительно, пусть при т, n>N
|В(®)—Ь(®»)1<в, G(w)— £п(ш)|<е.
Тогда, в силу (6), (7) и того, что |£т(<о)—£п(ю)К2е,
LGm(w)P(d«>) -J U«)P(d«)| = |}(U®)-U®)P(*»)I<2«,
что и требовалось доказать.
Итак, если выполнено (8), мы можем положить
££(<>) Р (dw) -1 im J £л((в) ?(d<a),
и П—«в П
(9>
причем уже доказано, что предел в правой части (9) не за-
висит от выбора последовательности £п(<о). равномерно схо-
дящейся к £(ы). Осталось показать, что для каждой измери-
мой В(ы) существует хотя бы одна последовательность
£п(со) элементарных функций, равномерно сходящаяся к
Построим такую последовательность следующим обра-
зом. Пусть п — натуральное, k — целое.
вб
Положим
4Л) = (и : < £(<») < ^±], £>) = у — Z {Й)(Ш).
I п п I /I ЛЬ
I /ж
Это означает, что для таких ш, что kin <{(«>)<(&+!)//?,
функция £„(*") принимает значение к!п (множества Л»1 из-
меримых в силу измеримости функции £(<»)). Очевидно,
что — £я(ш)|< Мп. Таким образом, можно записать,
что
|№)P(<M-limfWP(<fa) =
о *—«о
= ПтУ— Р (®: (Ю)
П-ое * » I П П J
Суммы, входящие в правую часть (10), называются интег-
ральными суммами Лебега. Легко видеть, что если при каком-
нибудь п существует (в смысле абсолютной сходимости ря-
да по k) такая сумма, то существуют и все остальные.
(В противном случае говорим, что интеграла Лебега от ;(ы)
не существует.)
Определение. Математическим ожиданием М= слу-
чайной величины £ называется значение интеграла Лебега:
М|=^«)Р(<Ь)
(в предположении, что этот интеграл существует).
Замечание. Простота построения интеграла Лебега
основана на возможности думать (непротиворечивым об-
разом) о мере Р{Л/л<В<(Л+l)/n}= P{w:fc/n<g(w)<
<(£ + 1)/п). Даже если Q —отрезок [0, 1], а В(о>) — глад-
кая функция вещественной переменной ™g[0, 1], мно-
жества {ш:kin<g((o)<(k + 1)/п) могут быть достаточно
сложными (вспомним о поведении функции £(ш) — <oNsin(l/a>)
в окрестности точки ш — 0; путем сдвига точки ш=0н
суммирования подобных функций с быстроубывающими
коэффициентами особенности такого рода можно нагро-
моздить по всему отрезку [0, 1], не теряя гладкости
функции). Поэтому добраться до возможности измерять
длину множеств {<о:Л/л<££(ш)<(£ + 1)п), отправляясь от
архимедова понятия длины, достаточно сложно. Этот
путь и пройден теорией меры.
С другой стороны, интеграл Лебега имеет тот недостаток,
что его непонятно как вычислить (в общих пространствах й
отсутствует какой-либо аналог формулы Ньютона — Лейбни-
ца). Тем более интересно будет увидеть в следующем пара-
графе, что одна лишь возможность думать об интеграле Лебе-
га ведет к некоторым формулам исчисления, которые, по-ви-
5* 67
димому, невозможно (либо крайне антиэстетично) получать
другим путем.
§ 3. Основные формулы исчисления вероятностей
Безнадежно, пожалуй, пытаться свести все вычисления ве-
роятностей, математических ожиданий и т. д., которые встре-
чаются в математических и прикладных вопросах, к неболь-
шому количеству основных формул. Но если ие все, то очень
многие вычисления сводятся к двум основным формулам,
первая из которых относится к вычислению математических
ожиданий, а вторая — к преобразованию совместной плот-
ности распределения нескольких случайных величин при за-
мене переменных.
3.1. Вычисление математических ожиданий. Пусть | —
случайная величина, принимающая значения в некотором из-
меримом пространстве (для простоты рассмотрим случай
£(<в)е/?п). Напомним, что распределением случайной вели-
чины § называется мера щ, определяемая соотношением
щ(В) = Р(|еВ), В — борелевское подмножество Rn. Пусть
на Rn задана функция f(x), x^Rn, принимающая значения в
R'. Выразим сейчас математическое ожидание случайной ве-
личины f(s) через распределение ц«.
Теорема 1. Имеет место равенство
М/(?) f«)P(da>) = fnf(x)|i5(d.v), (!)
причем оба интеграла Лебега в (1) существуют одновремен-
но.
Доказательство. Покажем, что лебеговы интеграль-
ные суммы у обоих интегралов (1) одинаковы. Действитель-
но, преобразуем интегральную сумму для левого интеграла
следующим образом:
д
п
п
ю:/(£((в))е
k А + 1
п ’ п
«8
г'([т-‘-Я)}=
причем в этих формулах f~l обозначает полный прообраз;
f~'([kln, (Л 4-л))—борелевское множество (в силу изме-
римости функции f). Последняя сумма в этих формулах
есть лебегова сумма для правого из интегралов (1). Тео-
рема доказана.
Даваемое формулой (1) выражение для Mf(£) в виде ин-
теграла по Rn, вообще говоря, проще, чем его выражение в
виде интеграла по й, поскольку евклидово пространство Rn
может быть гораздо проще, чем произвольное множество й
(например, множество функций). Однако интеграл Лебега
общего вида по Rn все равно вычислен быть не может. Пре-
образовать правую часть (1) к чему-то более явному можно в
двух случаях: 1) когда распределение щ дискретно; 2) когда
распределение щ абсолютно непрерывно (а также когда щ
есть линейная комбинация дискретного и абсолютно непре-
рывного распределения).
Распределение щ называется дискретным, если мера
щ сосредоточена на некотором не более чем счетном мно-
жестве К = |аь ..., ап,...). (Это означает, что
Рх(К) = 1) В этом случае Rn = К U (Я*\К)» причем
МЯП\К) “ 0. Поэтому интеграл по Я" сводится к интег-
ралу по К, а последний распадается в счетную сумму:
f flx^dx) = f /(*)|i?(rfx) = 3 /(а»)Р{5 = <*/) (2)
л" к «|6К
(мы воспользовались известным из теории меры и интегра-
ла фактом, состоящим в том, что интеграл Лебега по мно-
жеству Л=Л1+Лг+ ... равен счетной сумме интегралов по
множествам Ль Аг,...: счетной аддитивностью интеграла Ле-
бега как функции от области интегрирования). Мы узнаем в
формуле (2) обобщение способа вычисления математическо-
го ожидания для случая дискретного й: здесь Й —произволь-
ное, но случайная величина £ принимает лишь счетное число
различных значений ait аг,....
Распределение щ называется абсолютно непрерывным
(относительно меры Лебега в Rn, элемент которой обознача-
ется dx), если существует измеримая (по Борелю) функция
Рг(х), такая, что для любого борелевского B^Rn выполняет-
ся соотношение
69
р {£ е в} = !А,(В) = у Pi(x)dx. (3)
в
Функция Pi(x) называется плотностью распределения случай-
ной величины £ (также плотностью случайной величины
плотностью вероятности случайной величины £). Смысл тер-
мина прозрачен: если плотность массы есть такая функция,
что интеграл от нее по некоторому объему равен массе ве-
щества в этом объеме, то плотность вероятности — это то,
интеграл от чего равен вероятности (попадания значения слу-
чайной величины £ в область интегрирования В). Очевидно,
что р.(х)^>0 (для всех х, кроме, быть может, множества ле-
беговой меры нуль) и что
fp5(x)da;epgeBn}- 1.
я"
Обратно, неотрицательная измеримая по Борелю функция
р(х), интеграл от которой по Rn равен 1, является плот-
ностью распределения некоторой случайной величины.
Действительно, положим Q=Rn, ® — о-алгебра боре-
левских множеств в Rn и для Be 93
P(B)-^x)dx. (4)
Тогда (в силу только что отмеченной счетной аддитивности
интеграла Лебега) Р — счетно-адднтивная мера на ® и {Rn,
93, Р) — вероятностное пространство. Положим, наконец,
для <ое/?п |(<в)=(». Тогда £ — случайная величина, такая,
что Pi(x)=p(x).
Теорема 2. Для любой измеримой (по Борелю) функ-
ции f(x) имеем в случае абсолютно непрерывного распреде-
ления ц.
I ~ f f(x)pi(x)dx (5)
я" я"
(оба интеграла существуют одновременно).
Действительно, если /(х)=/в(х), борелевское, то
Г 1в(х)^1х) - |*е(В) = f pt(x)dx = f lB{x)pi(x)dx.
яа R*
Если f(x) — линейная комбинация счетного числа индикато-
ров непересекающихся множеств, то (5) также справедливо
(если существует хотя бы один нз интегралов, входящих в
(5)). Произвольная же измеримая функция f(x) может быть
аппроксимирована (равномерно) счетными линейными ком-
бинациями индикаторов, и доказательство теоремы заверша-
ется предельным переходом.
Таким образом, для абсолютно непрерывного распределе-
ния получаем формулу
70
МД£) = J /(*)ps(x)dx, (6)
Rn
которая вместе с формулой (2) н исчерпывает большую часть
случаев, когда математическое ожидание возможно подсчи-
тать. (Возможна, конечно, и линейная комбинация этих двух
случаев.)
У читателя, ориентированного на приложения, естествен-
но должен возникнуть вопрос: зачем, собственно, начинать с
общего понятия интеграла Лебега? Не проще ли определить
математическое ожидание формулой (6)? (При этом если
позволить себе включить в плотность р«(х) некоторую линей-
ную комбинацию б-функций Дирака, то формула (2) вклю-
чится в формулу (6).) Оказывается, однако, что так посту-
пить совершенно невозможно.
Дело в том, что, например, для получаем
СО
М£= J xp^x)dx, (7)
—СО
а для какой-нибудь функции /(g), например f(g)=sing, хо-
тим иметь возможность воспользоваться формулой
Msin£ = f slnxp5(x)dx. (8)
—СО
Но sing есть опять случайная величина: i]=sing, и в силу
(7) должна быть справедлива формула
М sin g=Mtj = [ xflpfl(x)dx« [ xp,lnl(x)dx. (9)
—СО —со
Мы должны быть в состоянии доказать, что интегралы (8) и
(9) равны между собой, т. е. что знак sin можно снять из
индекса у плотности и перенести на переменную интегриро-
вания. Такой удивительной теоремы не бывает в курсах ма-
тематического анализа, базирующихся на интеграле Рима-
на. так как в терминах римановского интеграла ее доказы-
вать крайне неудобно (при монотонной функции f(x) это лег-
ко, а при f(x)=sinx уже неприятно).
Понятие интеграла Лебега ( в виде доказательства теоре-
мы 1) существенно в данном элементарном вопросе. Это оз-
начает, что если когда-нибудь будет пересмотрена теория ме-
ры, понятие интеграла Лебега должно сохраниться.
Что касается включения в р«(х) обобщенных функций, то
такое возможно, но при условии, что в таком выражении чи-
татель сумеет правильно сделать замену переменной х на
другую, связанную с х гладким обратимым преобразоваин-
71
ем. На другом языке то же самое можно сказать, отметив,
что величина р*(х) — размерная (если случайная величина
5 измеряется в сантиметрах то Pi(x) — в обратных сантимет-
рах и т. д.: чтобы выражение pt(x)dx было безразмерным).
Математические учебники не хотят замечать этого обстоя-
тельства: никогда не встречается записи типа
р.(х) = — е~^ — ;
г У&. см
наименование всегда опускается. Опускать наименование пра-
вильно либо в том случае, когда £ безразмерна, либо когда
в записи типа
р (X) =« —- в-(«-а)»/2в«
6 ’ ' У&
указание на размерность обеспечивается наличием в формуле
размерного параметра о. Но если вместо о (и параметра а)
подставляются числа, то нужно писать и размерность. Таким
образом, понимать под Pi(x) обобщенную функцию можно,
если при знаке 6-функции Дирака мы сумели правильно ука-
зать н размерность. Поскольку дискретные распределения
имеют дело непосредственно с вероятностями (которые без-
размерны), проще не связываться в данном случае с обоб-
щенными функциями.
3.2. Понятие функции распределения. Для одномерной
случайной величины большую роль (особенно в мате-
матической статистике) играет понятие функции распределе-
ния. По определению, функцией распределения случайной ве-
личины £ называется функция Ft(x), задаваемая равенством
А(*)=РЦ<Я=т((-~,х)). (О
Из (1) следует, что при а<Ь
Pi([a, 6)) = Р(а<£<М=Р{£<М-Р{£<а)=Л(Ь)-Л(а). (2)
Это означает, что заданием функции распределения однознач-
но определяются значения щ((а, 6)). Но из теории меры из-
вестно, что мера на прямой (в частности, вероятностная ме-
ра цЕ) однозначно определяется своими значениями на интер-
валах [а, 6). Таким образом, более сложный объект — мера
щ, определенная на борелевских подмножествах прямой, од-
нозначно определяется более простым объектом — функцией
Ft(x), определенной на хе/?1.
Функция Ft(x), очевидно, монотонна: при xi<x2 Ft(xi)c
СЛ(*г). Небольшое размышление показывает, что она не-
прерывна слева. Действительно, интервал (—оо, х) является
объединением интервалов (—оо, xn), хп|х. Но для любой
72
счетно-аддитивной меры ц справедливо следующее утвержде-
ние:
если
А1 г At г . . . . и Л [J At, то
<»*t
Пгп|*(Лп) = |*(Д).
Л-*ОО
Следовательно,
хп\) = F5(^)-*F.(x) = |*5((—оо, х)).
Функция F^(x), вообще говоря, может иметь разрывы'
(но не более счетного числа, как всякая монотонная’
функция). Величина скачка Л(х4-0)—F5(x) = lim(F5(x+»)—
«10
—Fz(x) равна, очевидно, limP{x<£<* + «) *»Р[5-х) (так
• 10
как пересечение событий {х<5<х+в| при всех »>0 сов*
падает с событием {В—х)). Таким образом, разрывы функ-
ции Fr(x) возможны лишь в таких точках х, что Р{£=х}>
>0. (Конечно, таких точек х имеется не более чем счет-
ное число.)
Возможно построение интеграла
J f(x)dF,(x) (3)
—00
как интеграла Римана—Стильтьеса. Нам нет нужды этим
заниматься: просто будем понимать интеграл (3) как дру-
о»
гое обозначение для интеграла Лебега J /(x)n5(dx). Итак»
— оо
по определению
J /(x)dF5(x)« JB/(x)|*c(dx).
—00 —00
Можно доказать, что любая монотонная и непрерывная*
слева функция Г(х), такая, что
lim F(x) “ 0, lim F(x) = 1,
Ж-»—во x-^f-00
является функцией распределения некоторой случайной вели-
чины, но мы пока не будем этим заниматься (см. обсужде-
ние теоремы Колмогорова о продолжении меры).
Остановимся на связи между понятиями функции распре-
деления и плотности распределения.
В силу определения плотности для абсолютно непрерыв-
ного распределения щ имеем
73
^5U) = I\((—oo, *)) = J p£y)dy. (4)
— 00
Если x — точка непрерывности функции ps(x), то из (4) сле-
дует, что

df5(x)
dx
(5)
В точках разрыва функции Pt(x) равенство (5) неверно.
Ошибкой было бы считать (5) определением плотности
распределения, пригодным для прикладных целей. В прило-
жениях нельзя ограничиться непрерывными плотностями рас-
пределения: вскоре увидим, что такие практически важные
распределения, как равномерное, показательное и т. д., имеют
разрывные плотности. Поэтому потребовать выполнения (5)
для всех точек х нельзя. Если же потребовать выполнения
(5) не для всех точек х, то обычно хочется сказать, что «для
всех х, кроме множества лебеговой меры нуль». Такое опре-
деление плотности оказывается неверным: математики при-
думали примеры таких монотонных и непрерывных функций
F(x), что dF(x)/dx=O для всех точек х, кроме множест-
ва лебеговой меры нуль, но функция F(x) благополучно из-
меняется от 0 до 1.
Определением плотности распределения может быть (4).
Определение функции распределения существует и для
многомерной случайной величины £=(£i, •••. %n)^Rn-
Так называется функция Frfx), задаваемая соотношением
^?(х) = Fs, . . (Xi, . . • , Хп) = P{?l<TXj, . . . , £n<Xn).
Вероятность попадания случайного вектора § в прямоуголь-
ный параллелепипед (часть границы которого включается,
часть — нет), может быть (при некотором терпении) выра-
жена через Ft(x). Это означает, что распределение щ опре-
деляется по Fi(x) однозначно. Однако роль понятия много-
мерной функции распределения невелика. Дело в том, что в
одномерном случае существует единственная система коорди-
нат на прямой, с точностью до монотонной замены перемен-
ной. При монотонной замене переменной закон преобразова-
ния одномерной функции распределения ясен. В многомер-
ном же пространстве возможны весьма многие системы коор-
динат. Уже при повороте пространства параллелепипеды с
гранями, параллельными координатным плоскостям, непос-
редственно связанные с многомерной функцией распределе-
ния, перейдут в некие прямоугольные, но «косо» расположен-
ные параллелепипеды, непонятно как связанные с функцией
распределения. Фактически нет иного средства для того, что-
74
бы установить связь между функциями распределения в раз-
ных системах координат, как только по функции распределе-
ния восстановить соответствующую ей меру.
В частности, одним из великих благ аксиоматики Колмо-
горова является то, что в ней не надо строить интеграла Ри-
ман а—Стильтьеса
ОО во
J ... [ /(<1. . . . , ЯпМ’ЛС*!....хп)
-ОО —во
в многомерном случае. (Достаточно интеграла Лебега по ме-
ре щ, совершенно безразличного к размерности.)
Короче говоря, в многомерном случае работать нужно не
с функцией распределения, а с плотностью распределения.
Закон преобразования плотности распределения достаточно
ясен, к этому вопросу мы и переходим.
3.3. Преобразование плотности распределения при замене
переменных. Пусть £= (£ь £2, .... £п) — случайная величи-
на, принимающая значения в Rn (либо в некоторой области
/?”); y=f(x) — гладкое взаимно однозначное отображение
Rn на Rn (либо указанной области на некоторую область);
это означает, что в координатах отображение y=f(x) записы-
вается в виде
У1 = ft (xi, ..., хп), i=l....п;
причем якобиан — определитель матрицы ||df</dx/||, <*. /=1.-,
п, отличен от нуля.
Пусть случайная величина $ имеет плотность распределе-
ния Рх(х). Нашей задачей является вычисление плотности
Рп(у) случайной величины
т. е случайного вектора r]=(iii, .... t]n) с компонентами
.....5п), 1=1.....п.
Заметим, что интегральное определение плотности распре-
деления случайной величины определяет эту функцию с точ-
ностью, как говорят, до множества меры нуль, т. е. если
значения плотности распределения изменить на множестве
(лебеговой) меры нуль, то интегральное свойство плотности
не нарушится. Это означает, что если речь идет об определе-
нии плотности распределения, то вполне достаточно найти
эту функцию для всех точек пространства R'1, кроме множе-
ства меры нуль.
В нашем определении плотность распределения является
лишь измеримой функцией. Такая общность в приложениях,
как правило, не нужна: обычно плотность распределения яв-
ляется кусочно-непрерывной функцией (т. е. разрывы этой
функции лежат на каких-то поверхностях меньшей раамерно-
75
сти). Поэтому вполне достаточно определить плотность Рп(У)
в точках у, являющихся точками непрерывности этой функ-
ции. Но в точке непрерывности у имеем, используя интег-
ральное определение плотности,
Р,(И = Ит
л О(»Ц у
р{т,ео(у)}
V(O(y))
(1>
где О(у) обозначает окрестность точки у, предельный пере-
ход О(у)\у означает, что диаметр (наибольший размер) О(у)
стремится к нулю, a V(O(y)) обозначает объем О(у). Про-
изведем следующую выкладку:
Р(чеО(у)1 Р(де)ео(у)) _
V(O(id) V(O(y))
_ Ptteog-M) У{О(Г*(У))} (2)
V(O(v)) V{O(r‘(v))} ’ V(O(V))
Замену }~'(О(у)) на O(f-'(y)) надо понимать в том смысле,
что при (однозначном) обратном отображении f~' окрест-
ность О (у) переходит в некоторую окрестность O(f~l(y))
точки f~'(y), причем если 0{у)1у, то и O(f~l(y))
Известно, что при этом
V(O(v))
(3)

где через Df~'(y) обозначено значение якобиана отображе-
ния )-1 в точке у. Поэтому, переходя в (2) к пределу ври
О(у)^у, получим
рДу)-р^-Чу№~Чу)\ (4)
Мы получили следующую лемму.
Лемма. Значение плотности рп (У) случайной величины
дается формулой (4).
На самом деле, формула (4) верна и для произвольных
измеримых плотностей распределений. Она, собственно, пред-
ставляет собой частный случай формулы замены переменной
в кратном интеграле.
Поскольку f(f~'(.y))=y, Df(f~'(y)) Df-'(y) = l-, исполь-
зуя обозначение f-l(y)—x, получим, что
D/-«(y)= l/Df(x), (5>
если y=f(x) (или, что то же, х—[~1(у)). Иногда формула (5)
полезна при вычислениях.
7в
§ 4. Примеры применения основных понятий
и формул
Имеется очень большое количество конкретных вероятно-
стных моделей, в которых найденные из тех или иных наво-
дящих соображений распределения вероятностей более или
менее точно моделируют свойства изучаемого явления. При-
ведем сравнительно небольшое число таких примеров (за не-
возможностью объять необъятное). Но начнем с некоторых
общих понятий, чтобы увидеть, насколько легко н естественно
переносится то, что мы ранее изучали в дискретном случае,
на случай произвольного й.
4.1. Общее понятие независимости. Двум (или несколь-
ким) независимым опытам соответствует прямое произведе-
ние вероятностных пространств. Фактически это понятие изуча-
ется в теории меры; нам остается лишь его напомнить.
Пусть {QCJ, ®<п, Р(1>) и {й<2;,®(2), Р(2))—два вероятностных
пространства. Образуем новое й как прямое произведение
Й=Й(1,ХЙ(2>. Что касается о-алгебры событий в й, то ее
формирование протекает в два этапа; сначала рассматрива-
ются подмножества Лей, имеющие вид Л=Л(1)ХЛ(2\ где
Л"'е 1=1,2. Вероятностная мера Р на этих подмножест-
вах определяется по формуле Р(Л) = Р(|> (Д1’>) Р(2) (Л(2>)- За-
тем (по теореме о продолжении меры) мера Р продолжается
на некоторую о-алгебру S5 измеримых подмножеств й (кото-
рая несколько шире, чем наименьшая о-алгебра, порождае-
мая «прямоугольниками» Л(1> X Л<2>).
Независимыми случайными величинами называются такие
величины gt, g2, •. • , £п, что для любых борелевских подмно-
жеств В|, В2, ... , Вп события
{ 51 sBl { ?2 е В2 }, . . . , ( gn
независимы в совокупности. Так же, как и в дискретном слу-
чае, доказывается, что любые (измеримые) функции от неза-
висимых случайных величин являются независимыми.
Плотность распределения случайного вектора g= (gi,
. . . , gn) в Rn называется еще плотностью совместного
распределения случайных величин gi, gz, ... , gn. Если вели-
чины gi, gz, .... gn независимы и существуют плотности рас-
пределения pt каждой случайной величины gf (так называе-
мые одномерные плотности распределения), то существует и
плотность совместного распределения p=pif причем в некото-
ром специальном смысле есть произведение одномерных
плотностей. Точно это означает, что
p(xh х2, ... , хп) = Pi(xi)pi(xi) ... рп{хп). (1)
Докажем формулу (1). Для этого нужно проверить интег-
ральное определение плотности
77
P{6=(5i, 5», . . • , 5n)eB}« J p(xit .... xJdXi... dxn.
в
(2>
Заметим, что левая н правая части (2) определяют (как
функции от В) счетно-аддитивные меры. Для доказательства
совпадения двух счетно-аддитивных мер на всех борелевских
B^Rn достаточно показать, что они совпадают на любой сис-
теме множеств которая порождает борелевскую 0-ал-
гебру. Рассмотрим множества В, имеющие вид B = £?iX
XBjX ... ХВ„, гдеВ,-— одномерные борелевские множества.
Для таких В, в силу независимости случайных величин
61, ^2...5л, имеем
р{5 е в} = р{^ е BJP& ев,}... р{5„ е вп}« (3>
вП f f • • • ^Pi(xMxi)...Pn(xl,)dxldxt...dxn,
z-i в, Ах... хвя
поскольку предполагается, что существуют одномерные плот-
ности (последний переход представляет собой применение тео-
ремы Фубини, если речь идет об измеримых pi(xt), либо из-
вестное свойство кратных римановских интегралов, если речь,
идет лишь о кусочно-непрерывных р, (х,) и достаточно простых
В\, В2, ... , Вп). Равенство (3) означает, что если взять в
качестве совместной плотности р(хьх2,....хп) =pi(*i)р2(х2) ...
— Рп(хп), то интегральное определение плотности распре-
деления удовлетворяется.
Если для произвольных (не обязательно независимых) слу-
чайных величин gi, ... , 5п существует совместная плотность
распределения, то существуют и одномерные плотности. Дей-
ствительно, например,
во во
Рь(*1)= J • • • f U1. *!»• •• ,*n)dxt... dxn. (4)
— ОО
В самом деле, нужно проверить, что функция, задаваемая
правой частью (4), удовлетворяет соотношению
Р&еВЛ - [ p^dx^ (5>
в.
Но
P{5ieB1}-P(5ieBl, , -оо<|п<оо}=
со во
- I У • • • У • • • ц х............. x^dxidx» ’ • •
*1€В1 — ов —ОО
Известно, однако, что интеграл, стоящий в правой части (6)»
можно взять сначала по переменным х2, ... , хп (в пределах
78
от —оо до оо), а затем от того, что получится (а получится
именно правая часть (4)), взять интеграл по jneBi. Это и
доказывает (5).
Таким образом, в случае существования плотностей рас-
пределения (одномерных или совместной) равенство (1) мож-
но принять за определение независимости случайных величин
£i> &....
Если плотностей не существует, а существуют лишь
меры (|*5(В) = Р{& = (6.......U е В), В с Яп) и in,
(l*^ (Bt) = P(g, s Bt}, то определением независи-
мости является следующее:
= XX . . . (7)
(в правой части (7) стоит прямое произведение мер).
Замечание. Счетная система независимых случай-
ных величин . • , L, • • (либо счетное произведе-
ние мер X X . • . X X ...) не может быть в дан-
ный момент определена. Для введения этих объектов
требуется теорема Колмогорова о продолжении меры.
4.2. Общие свойства математических ожиданий и диспер-
сий. Из определения математического ожидания
~(Ч((о)Р(<Ь)
h
вытекает его линейность: М(а£+Ьт|) =oMg+bMi], где а нЬ—
числа, £ и 1] — случайные величины, имеющие математичес-
кое ожидание.
Дисперсию D£ случайной величины £ заново определять не
нужно: как и в дискретном случае
Щ=ЛШ-М£)2.
Аналогично дискретному случаю
D(£i + ?.+ .••+ U - J DB, + J cov (Ь, Ij).
i-i W
где cov (Ь, £/)=М(£,—Mg,) (gz-Mg/).
Для независимых случайных величин & и т], имеющих
(каждая) математическое ожидание, верно равенство
Mg4=MgMri, (1)
а следовательно, в случае независимости
D(6» + S>+... + U) = 2^.. (2>
i-1
79
Для доказательства (1) можно использовать соотношение
Mbl- J J xy^z(dx)^(dy)
— 09 —OP
и теорему Фубини. Можно использовать дискретную форму
(1) и предельный переход:
5п-»5» 1п-»1’
где £п = Л/л, если Л/л <£(<•>)< (Л + 1)/л (и аналогично для
i)n). Тогда £п и тдп независимы (как функции от незави*
симых случайных величин £ и ->]). Покажем, что так же,
как и в случае дискретного пространства элементарных
событий, справедливо равенство М£п1л = МЕлМт1я. Дейст-
вительно, разбивая множество Q в сумму непересекаю-
щихся множеств Ак[ вида
А/в { ш : £п(ш) = —» ’1п(<в)“— I» Л, /=0±1, ±2,...,
I п п I
мы получим, что интеграл Лебега по множеству Q от произ-
ведения £пт]п разобьется в (счетную) сумму интегралов по
множествам Ан- Но
f UeKWW-i- -PfU--|P(ln--|.
I J I J
что п означает, что M^n1n = MgnMr)n. Имеем далее
151 — Snlnl — |5l — Sin + Sin — 5п1л| =
= 15(1 - 1л) + (5 - Dini <1151 + 4 linl.
n n
Следовательно (поскольку существует Mlfcl, Mh]', а стало
быть, н Mlrinl <Mlnl + 1/л),
= lim M £nT]n — lim Mg„ • lim Мцп — MSMtj.
П-*оо /Woo Л—*eo
В общем, вывод (1) требует незначительных усилий.
Неравенство Чебышева в общем случае доказывается так
же, как и в дискретном.
Но комбинация (2) и неравенства Чебышева автоматиче-
ски приводят к доказательству закона больших чисел. Таким
образом, фактически одно лишь правильное понимание не-
зависимости случайных величин в общем случае (совместное
распределение есть прямое произведение одномерных) сразу
позволяет обобщить (с дискретного случая на общий) закон
больших чисел.
Перейдем к конкретным примерам распределений.
ЯО
4.3. Равномерное распределение. Пусть результат некото-
рого измерения записывается с округлением до ближайшего
целого числа (при соответствующем выборе единицы измере-
ния); б—ошибка округления. Тогда величина б принимает
значения на интервале [—0,5; +0,5] и любые возможные зна-
чения б равновероятны (в интуитивном смысле, предполагаю-
щем некую изначальную случайность ряда результатов мно-
гих измерений: результату измерения все равно, в какую точ-
ку попасть между ближайшими целыми числами). Формали-
зуем эту интуитивную вероятность, сказав, что плотность рав-
на нулю вне отрезка [—0,5; +0,5], а на этом отрезке прини-
мает постоянное значение. В выбранных единицах, очевидно,
вс 0,5
Pt(x) = 1, поскольку ДОЛЖНО быть 1 = f p6(x)dx= Р pb(x)dx,
-о -0.5
откуда р«(х) = 1 (размерность 1/ед. длины).
Очевидно, что
MS = 0,
0,5
D6 = М о2 = j’ х’д8(х)йх = -у
-0.5
0.5
-0.5
= -^~ (кв. единиц).
Сделаем линейное преобразование, при котором отрезок
[—0,5; 0,5] переходит в отрезок [а, б]. Случайная величина б
перейдет при этом в случайную величину j с плотностью рас-
пределения рг(х) = \/Ь—а, хе[а, б]; pt(x) = 0. хё[а, б]. Та-
кое распределение называется равномерным на отрезке [а, б].
Легко видеть, что
Dg = l(6-a)«.
4.4. Нормальное распределение. Существует большое коли-
чество способов прийти к знаменитому в теории вероятнос-
тей нормальному распределению. Лаплас пришел к нему с по-
мощью центральной предельной теоремы (в простейшем слу-
чае к нему можно прийти с помощью анализа распределения
числа успехов в п испытаниях Бернулли при л-*сю); Гаусс —
путем исследования разумных оснований того, что при боль-
шом числе наблюдений за наилучшее приближение к истине
мы берем среднее арифметическое. Можно прийти к нор-
мальному распределению, поисследовав, какие распределения
воспроизводят сами себя при суммировании независимых
случайных величин; можно — постулировав статфизическое
распределение Гиббса. Но никакой из этих способов не дает
«-2567 8t
полной гарантии того, что некоторая конкретная задача при-
водится к нормальному распределению — попросту потому,
что не существует гарантий статистической однородности, т.е.
того, что конкретная задача вообще приводится к каким-то
распределениям вероятностей. Поэтому введем нормальное
распределение чисто математическим определением.
Говорят, что случайная величина £ имеет стандартное нор-
мальное распределение (иначе— распределение N(0, 1), т. е.
нормальное распределение с параметрами (0, 1)), если ее
плотность pt выражается формулой
А(<) ~ ~ — оо <х< оо.
(Числовой множитель 1/У2л подобран так, чтобы интеграл от
Pi(x) равнялся 1.)
Очевидно, М£=0; простой подсчет показывает, что D£=l.
Нормальным распределением N (а, о) с параметрами а и
о (а—вещественное число, а>0) называется распределение
случайной величины
т] = о£ + а.
Переход от £ к т] можно интерпретировать как переход к но-
вому началу отсчета и новой единице измерения. Согласно
лемме п. 3.3, получим
'>,9)=^ехрН^}'
Очевидно, что Мт) = а, Dt) = o2; о есть, таким образом, средне-
квадратическое уклонение для t).
Нормальное распределение является любимой моделью
при статистической обработке наблюдений (мы позже позна-
комимся с этой ситуацией). Вообще, при создании каких-то
вероятностно-статистических моделей думают прежде всего о
нормальном распределении и лишь при явной необходимости
прибегают к более сложным. По мнению автора данной кни-
ги, часто лучше удовлетвориться умеренным согласием нор-
мального закона с фактическими данными, чем искать хорошо'
согласующийся более сложный закон: попытки достичь луч-
шего согласия за счет более сложной модели обычно лишь
скрывают отсутствие статистической однородности.
С нормальным законом связано так называемое распреде-
ление хи-квадрат. Так называется распределение суммы квад-
ратов
f-m »1 ' =2 I • • • ' ®т>
где §|, ... ,1m — независимые между собой случайные ве-
личины, каждая из которых имеет стандартное нормальное
82
распределение N(0, 1). Число слагаемых т в этой сумме на-
зывается числом степеней свободы; само же распределение
величины Хм называется распределением хи-квадрат с т
степенями свободы. Это название связано с физическим смыс-
лом распределения хи-квадрат.
Именно, в максвелловской модели идеального газа проек-
ции скорости молекулы v?, v3 на оси координат считаются
независимыми случайными величинами, имеющими (каждая)
нормальное распределение ЛЦО, о) (при этом о2=Ми‘/ тако-
во, что выполняется соотношение ma2—kT, т—масса молеку-
лы, k—постоянная Больцмана, Т—абсолютная температура).
Тогда кинетическая энергия молекулы есть
у (*? + о» + vl),
&
что с точностью до числового множителя совпадает с распре-
делением Хз- Материальная же точка имеет три степени сво-
боды.
4.5. Показательное и обобщенное показательное распреде-
ления. Пусть некий прибор начинает работать в момент /=0
и работает до случайного момента отказа т. Попытаемся по-
нять, каким может быть распределение вероятностей случай-
ной величины т. Для этого составим дифференциальное урав-
нение для функции
Q(t) = P{T>rt.
Сделаем следующее предположение: если прибор исправ-
но проработал до момента времени t, то условная вероят-
ность того, что он проработает еще немного времени, т. е. до
момента t+Ы, есть единица минус величина, пропорциональ-
ная А/ (т. е. вероятность отказа на интервале времени (t, t+
+ А/] равна k(t) Af+o(Af)« Имеем
Q(f+ АО = Р{т>/ + АО = Р{т>«Р{т>/+
+ А//т>/} = Q(t) (1—Х(ОА/ + ofAO).
Отсюда получаем дифференциальное уравнение
Q'(t) = -W) Q(t),
решение которого (учитывающее начальное условие Q(0) = l)
дается формулой
Q(t) « exp — J k(s)ds
(1)
Особое внимание привлекает случай Х’(0 =X=const (что ин-
терпретируется как отсутствие старения прибора», действи-
тельно, тогда вероятность того, что прибор откажет за время
от t до /+Д/, не зависит от t: прибор, проработавший время
t, по надежности такой же, как новый). В этом случае
t
Fx(t) = р{т < 0 = 1 - Q{t) = 1 — = J ).e-Xsds, (2)
а распределение случайной величины с функцией распреде-
ления (2) называется показательным распределением с пара-
метром X. Плотность показательного распределения px(t) да-
ется формулой
px(t) = her*-1 при />0; pt(/)=0 при /<0.
Небольшое вычисление показывает, что
Mt = l, Dt-1. (3)
Для эффективного применения распределения (1), кото-
рое будем называть обобщенным показательным распределе-
нием, необходимо знание функции 'k(t), которая называется
интенсивностью отказов. Интенсивность отказов может быть
оценена по статистическим данным об испытаниях большого
количества приборов (вероятность отказа k(t)^t в достаточно
малом интервале времени (t, /+Д/] может быть оценена по
частоте отказов для определенного набора интервалов време-
ни). Обычно считается, что при t, близких к нулю, 1(1) не-
сколько выше (приработочный период), затем снижается и
довольно долгое время остается постоянной (как если бы мы
имели дело с простейшим показательным законом (2)), а за-
тем увеличивается (эффект старения).
Обобщенный показательный закон тесно связан с законом
Пуассона. Модель этой связи состоит в следующем. У каж-
дого прибора есть своя «судьба», состоящая в том, что ему
«предопределены» отказы в случайные моменты ti, т2, ... ,
тп, ... (после отказа прибор ремонтируется, время ремонта
не учитывается). Предполагается, что моменты отказов обра-
зуют пуассоновский поток. Это означает, что число отказов за
интервал времени [s, /] (т. е. величин л, т2, ... , тп, ... . по-
падающих в интервал [s, fl) подчиняется закону Пуассона с
параметром
Л(а, fl = ( )(т)Л. (4)
«
Числа отказов, отвечающие непересекающимся интервалам
времени, считаются статистически независимыми.
Из такой модели вытекает закон (1). Действительно, мо-
мент первого отказа r=min (л, т2, ... , тп, ...) обладает сле-
дующим свойством: событие (т>/) состоит в том, что на ин-
84
тервал времени [0, /] «судьба» не предназначила ни одного
отказа. Вероятность того, что пуассоновская случайная ве-
личина с параметром А принимает значение 0, есть
exp (—А); поэтому, полагая в (4) s=0, получаем из (4) за-
кон (1).
Посмотрим, какие качественные выводы вытекают из поня-
тия показательного закона. Пусть некоторый радиоэлектрон-
ный прибор («телевизор») состоит из п (для простоты обоз-
начений — одинаковых) приборов («электронных ламп»).
Пусть «телевизор» работает только в том случае, когда все п
«ламп» исправны; моменты же отказов «ламп» t\, tz, ... , tn
статистически независимы и подчиняются показательному за-
кону с параметром X. Тогда момент t отказа «телевизора» за-
дается формулой f=min(7i, t2, ... , tn), а закон его распре-
деления Q(l)=P(t^l) выглядит следующим образом:
Q(Z) = р{/>/)=Р(л>г, tn>i)= п Р(«<>0 =
/=1
Пусть теперь на «телевизор» установлен гарантийный срок 1
год. Мы хотели бы, чтобы гарантийному ремонту подверга-
лась небольшая часть (допустим, около 10%) всех телевизо-
ров. Это означает, что Q(l)>0,9, что будет обеспечено, если
лХ«0,1, т. е.
1=10л.
п X
Поскольку 1/Х есть математическое ожидание случайной ве-
личины, то, скажем, при л=20 получаем следующий вывод:
чтобы «телевизор» мог более или менее надежно проработать
год, нужно, чтобы «электронные лампы» работали в среднем
200 лет. (Не нужно понимать этот вывод совершенно бук-
вально: лишь на протяжении немногих лет электронная лам-
па может работать без старения. Но если мы по испытаниям
электронных ламп в течение года будем определять закон
продолжительности их жизни, считая его показательным, то
отказы должны быть столь редки, что для 1/Х получается зна-
чение 200 лет.)
Требования к надежности отдельных элементов сложных
приборов очень высоки. Такие сложные приборы, как ЭВМ,
могут вообще работать только за счет резервирования их эле-
ментов (и систем, обеспечивающих постоянную проверку ра-
ботоспособности и ввод резерва).
Продолжительность человеческой жизни. Еще примерно
лет полтораста назад продолжительность человеческой жизни
85
было предложено описывать с помощью интенсивности отка-
зов, имеющей вид
l(t) = А + /?ехр (at). (5)
Это так называемый закон Гомперца—Мейкема. В последнее
время в рамках этого классического подхода были получены
новые интересные результаты, которые частично излагаются
здесь по книге Л. А. Гаврилова и Н. С. Гавриловой [11].
Формула (5) пригодна для описания закона распределе-
ния продолжительности жизни взрослых людей (детская
смертность этой формулой не охватывается). Фактические
данные, иа которых основываются экспериментальная про-
верка формулы (5) и подбор значений ее параметров, публи-
куются в весьма архаической форме (но других нет). Речь
идет о так называемых таблицах смертности.
Составление таблиц смертности, как и прочие вопросы
изучения динамики населения, относится к особой науке —
демографии. Наука эта — по-видимому, во всем мире — ар-
хаична и собирает (по традиции, сложившейся в прошлом
веке) данные о народонаселении с такой точностью, какая до-
статочна лишь для того, чтобы страховые компании не оста-
лись в убытке, но совершенно не достаточна для более тонких
статистических обработок. При регистрации смерти возраст
покойника учитывается с точностью до одного года. Возраст
живых людей учитывается (по весьма приблизительным дан-
ным переписей) тоже с точностью до одного года. Так или
иначе, статистика приносит (каждый календарный год) чис-
ленности Dx умерших в данном году в возрасте х и числен-
ности Рх живых людей (в том же году), имеющих возраст х.
Учитывая, что умерший в данном году человек все-таки в
среднем полгода прожил, вероятность смерти qx (в возрасте
х) рассчитывается по формуле
II " /
Далее берется число /0= 100000 (как бы родившихся в дан-
ном году) и рассчитывается по формуле
— ?х)» 1» 2, . . . ,
численности 1Х людей из этих 100000, доживающих до возрас-
та х (если вероятности смерти остаются такими, какими они
вычислены из статистических данных, относящихся к данно-
му календарному году).
Число лет, прожитых всеми людьми из 100000 родившихся
в этой модели, делится на 100000, в результате чего получа-
86
ется важнейший демографический показатель — средняя про-
должительность жизни. Следует понимать, что определяемый
таким образом показатель средней продолжительности жизни
не совпадает со средним возрастом покойника, который мож-
но узнать, собрав статистику по надгробным памятникам на
кладбище (либо — более научно — собрав лишь сведения о
возрасте покойников, умерших в данном году по данным ре-
гистрации смертей), так как в показателе средней продолжи-
тельности жизни замешана и возрастная структура населе-
ния. Демография мыслит в терминах условной вероятности
смерти в возрасте от х до х+1 лет (при условии дожития до
х лет), т. е. в терминах, аналогичных терминам теории на-
дежности, что, в общем, правильно; ио в наш век следовало
бы прямо использовать непрерывную модель теории надежно-
сти, поскольку использование ЭВМ для всяческих статисти-
ческих обработок делает это вполне возможным.
Один из интереснейших наблюдаемых в демографии фак-
тов состоит в том, что в первой половине XX в. продолжи-
тельность человеческой жизни (в частности, средняя продол-
жительность жизни) возрастала, а примерно в 60-х годах это
возрастание прекратилось.
По таблицам смертности (т. е. по наборам 1Х) можно про-
изводить оценку параметров модели (5). Эти параметры силь-
но колеблются в зависимости от страны, но общая тенденция
состоит в следующем.
В развитых странах в течение XX в. значения параметра
А снизились примерно в десять раз и в настоящее время на-
столько малы, что в формуле (5) несущественны (в старших
возрастах). Авторы [11] интерпретируют параметр А как не-
кую «фоновую», или «случайную», смертность, которую мож-
но снять за счет повышения уровня жизни и медицинского
обслуживания. Наоборот, значения параметров R и а в (5)
изменились мало. Авторы интерпретируют член R ехр(а/) как
показатель «естественной» или «возрастной» смертности, су-
щественно повлиять на которую ие удается. Примерные зна-
чения параметров
Я = 3 • 10~* год-’, а — 0,1 ГОД*1.
Для возраста f=40 лет вероятность «возрастной» смерти в
течение года есть примерно
Яехр (at) - 3 10-» • е* « 160 • 10-5 « 0,0016.
Вклад члена А сильно колеблется от страны к стране, но по
порядку величины составляет 0,001.
Таким образом, для возраста 40 лет возрастная и фоновая
смертность составляют величины одного порядка; при увели-
чении же возраста за счет быстрого роста члена /?ехр (at)
возрастная смертность преобладает над фоновой. Снижение
87
смертности в XX в. шло за счет фоновой компоненты смерт-
ности, которая в развитых странах приблизилась к нулю. По-
сле этого дальнейшее снижение смертности (в частности, воз-
растание средней продолжительности жизни) прекратилось.
Ограничимся изложением лишь этого вывода из книги [’.I],
которая содержит также ряд других, не менее изящных ин-
терпретаций статистических фактов. Чтобы у читателя не
создавалось чрезмерных иллюзий относительно возможностей
чисто статистического подхода к описанию продолжительно-
сти человеческой жизни, обратим внимание на один, на пер-
вый взгляд технический, вопрос.
При определении параметров A, R и а модели на основании
таблиц смертности согласие между условными вероятностями
смерти, даваемыми формулами (1) и (5), и фактическими
данными демографии получается неплохим, но при огромных
объемах выборок, с которыми имеет дело демография, это
согласие должно быть, вероятно, еще лучшим. Точнее говоря,
оно, возможно, должно было быть лучшим, если бы на смерт-
ность людей можно было смотреть как на чисто статистичес-
кое явление. (Эти слова означают, что вероятность смерти от-
дельного человека дается формулами (1) и (5), в то время
как смерти различных людей являются статистически незави-
симыми событиями.) В следующей главе увидим, как подсчи-
тать, насколько фактически частоты смерти могут (при чисто
статистической модели) отклоняться от вероятностей. К со-
жалению, данные демографии слишком грубы, чтобы однознач-
но провести это сравнение, но прикидки показывают, что точ-
ность выполнения закона Гомперца—Мейкема должна была
быть гораздо большей, чем это реально наблюдается. Населе-
ние любой страны неоднородно по многим признакам: социаль-
ному, профессиональному, территориальному, генетическому
и т. д. Эти различия сказываются в том, что одни группы на-
селения могут иметь большую смертность, другие — мень-
шую. В масштабе всей страны получаем довольно точное спи-
сание смертности законом Гомперца—Мейкема. Это некото-
рое статистическое чудо, связанное с нивелировкой групповых
различий в очень большой совокупности. Для отдельных групп
населения закон, параметры которого определены по данным
для всей страны, может давать гораздо худшее согласие (так
именно и выделяются группы повышенного или пониженного
риска). Наличие таких неоднородностей проявляется в том,
что в масштабе целой страны закон Гомперца—Мейкема дей-
ствует с меньшей точностью, чем наблюдалось бы в условиях
идеальной статистической однородности. Наконец, для инди-
видуального прогноза продолжительности жизни (данного
конкретного человека), как это, вероятно, совершенно ясно
читателю, статистическое описание в виде закона Гомперца—
Мейкема почти бессодержательно.
88
Г Л А В A 3
СУММЫ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
§ 1. Постановка задачи и основы математического аппарата
1.1. Введение. Если какие-либо измерения либо статисти-
ческие данные (либо что-нибудь иное) мы идеализируем в ма-
тематической модели как значения случайных величин |ь£2,...
то достаточно часто нас будут интересовать значения
каких-то функций f(gt, £2, .... |п). Простейшей возможной
функцией является сумма S„=£i+ &?+••• +£п, с одной сторо-
ны, суммы случайных величин встречаются достаточно часто
(при любой статистической обработке); с другой — в общем-то
среди всех возможных функций f лишь для сумм (и сводящих-
ся к суммам функций) существуют достаточно эффективные
математические методы исследования получающихся распре-
делений вероятностей.
1.2. Распределение суммы независимых случайных величин.
Пусть случайные величины || и g2 независимы, имеют плот-
ности распределения Pi(x) и р2(х), хе/?1; спрашивается, как
найти плотность распределения их суммы £i+£2? Сумма есть
значение функции f(xit x2)=xi+x2 от пары £2. В принципе
задачи о распределениях вероятностей различных функций от
случайных величин решаются единообразно: сначала дополним
интересующую нас функцию несколькими другими, чтобы по-
лучить взаимно однозначное (гладкое) соответствие. В инте-
ресующем нас случае суммы положим
yi=fi(xi, x2)=xi+x2, У2=1г(х1, х2)=х2. (1)
Соответственно рассмотрим случайные величины
Л1 *= 51 + &г, Л2=52.
По лемме п. 3.3 главы 2 найдем плотность распределения слу-
чайного вектора n=(ni, т)2), а из этой плотности интегрирова-
нием по второму аргументу получим интересующую нас плот-
ность случайной величины тр. Конкретно имеем: в силу неза-
висимости случайных величин |i и |2
РД*) = *i) = Р^Р^М - Pi(*i)Pt(*»)«
Если/ — это отображение (1), то обратное отображение f-1
имеет вид
Х1=У1— у2, х2=у2-,
(2)
якобиан отображений (1) и (2) равен 1. Поэтому
Р^У) - Рг.^,(У1' Уг) = Р^У—УМУгЬ
89
а следовательно,
Ри(Уд = P5l+-., (У i) = J Pi(yi—yJpMMh- (3)
-оо
Операция (3), дающая по плотностям pt и р2 плотность суммы
Рш (01)» называется композицией (или сверткой) плотностей
Pi и р2.
На первый взгляд формула (3) означает следующее. Бе-
рется любое возможное значение у2 случайной величины |2;
если то для того, чтобы сумма fci + Ь равнялась у\,
нужно, чтобы |i =01—02- Вроде бы в формуле (3) Р<1»=02}
умножается на P{£i=0i—у2} и все такие произведения сумми-
руются в интеграле (3). Это, однако, совершенно ложный
взгляд на вещи: ие следует путать плотность вероятности (ве-
личину размерную, зависящую от выбора единицы измерения
случайных величин) с вероятностью попадания случайной ве-
личины в точку (равной нулю в случае существования плот-
ности распределения и в любом случае — безразмерной).
Формула (3) получает вышеуказанный вид только потому, что
якобиан отображений (1) и (2) равен 1; если бы мы имели
дело не с суммой 1i!+|2. а, допустим, с произведением 1i£2
или частным £1/£г, то в аналогичную формулу вошло бы зна-
чение якобиана соответствующего отображения.
В силу коммутативности (и ассоциативности) сложения
вещественных чисел для получения плотности суммы п неза-
висимых случайных 'величин нужно взять (в любом порядке)
последовательные композиции их плотностей. Например, для
двух равномерных законов распределения на отрезке [0, 1]
получаем после композиции так называемый треугольный за-
кон распределения: плотность Ри+к,(У) равна у при О<0^1
и равна 2—у при 1<0^2 (и равна, разумеется, нулю при
0<О и 0>2, так как складываются величины £i и £2, прини-
мающие значения между 0 и 1).
Можно выписать и плотность распределения суммы п не-
зависимых случайных величин, каждая из которых имеет
равномерное распределение иа отрезке [0, 1]. Впервые эту
формулу получил, по-видимому, Н. И. Лобачевский, который
занимался этим вопросом в связи с обработкой наблюдений
для проверки гипотезы о том, что сумма углов треугольника,
возможно, меньше двух прямых. (Впрочем, в эксперименталь-
ной проверке своей геометрии Н. И. Лобачевский успеха ие
имел.) Но получающаяся формула неудобна для исследова-
ния.
Спрашивается, а как же исследовать композицию п более
или меиее произвольных законов распределения при п—►оо?
Ясно, что последовательное вычисление интегралов вида (3)
90
вряд ли приведет к какому-нибудь успеху. Общий метод ис-
следования сумм независимых случайных величин, действи-
тельно, существует. Он основан иа преобразовании Фурье.
В результате применения этого метода получим так называе-
мую центральную предельную теорему, которая состоит при-
близительно в том, что распределение вероятностей суммы S.
при достаточно большом п близко к нормальному распреде-
лению. Поскольку нормальное распределение определяется
своими параметрами — математическим ожиданием и диспер-
сией, — то распределение S„ также приблизительно характе-
ризуется этими параметрами: MS„=Mgi + Mg2+... +Mg„ и
DSn=Dgt + Dg2+... + Dgn. Иными словами, чтобы охарак-
теризовать распределение S„, не нужно знать в деталях рас-
пределения вероятностей gIt g2.g„: достаточно знать Mg, и
Dg, i= 1,...,п, которые, вообще говоря, можно определить по
экспериментальным данным (позднее увидим, как именно).
Это замечательный результат (впервые для одинаково распре-
деленных независимых случайных величин он был установлен
Лапласом, хотя и без полного математического доказатель-
ства). Он производил большое впечатление на современников;
ведь из него, в частности, вытекает следующая привлекатель-
ная возможность. Пусть gi, g2,.... g„ — наблюдения некото-
рой физической величины а; можно на основании только лишь
чисел si, g2.. g„ (ничего не зная нн о физике явления, ни о
способе наблюдения) определить с некоторой точностью Mg,
и Dg/ (предполагается, что точное значение Mg, совпадает с
я), описать поведение суммы gi+g2+— +gn и, в частности,
решить вопрос о том, насколько среднее арифметическое из
наблюдений (gi +... +g„)/n может отличаться от истинной
величины а. (Впрочем, во второй части данной книги мы уви-
дим, что в точном количественном смысле эта надежда не под-
тверждается.) Так или иначе, но весь XIX в. теория вероят-
ностей вращалась вокруг центральной предельной теоремы.
Возникавшие в конце XIX в. представления о зависимых слу-
чайных величинах использовали вместо дисперсии ковариа-
цию (близкую по замыслу к дисперсии) и незначительно от
нее отличающийся коэффициент корреляции.
Это направление мыслей сохраняется и до настоящего вре-
мени. В частности, в данной книге увидим, что иногда потреб-
ности практики, если даже они лежат в области описания по-
ведения динамической системы, находящейся под воздействи-
ем случайных процессов, можно удовлетворить, не выходя
за пределы математических ожиданий, дисперсий и ковариа-
ций (соответствующий аппарат называется теорией марков-
ских диффузионных процессов).
Что же касается произвольных функций от случайных ве-
личин, то для них столь далеко идущие упрощения, сводящие
распределение вероятностей функции f(gi, g2, ..., g„) к немно-

гим параметрам распределений случайных величин gi, £»,
.... gn, вообще говоря, невозможны.
1.3. Преобразование Фурье. В теории вероятностей преоб-
разование Фурье называется характеристической функцией.
Определение. Характеристической функцией случай-
ной величины £ называется функция ft (О вещественной пере-
менной t, задаваемая соотношением
f.(0 = Me1'?.
Записывая математическое ожидание через интеграл по
распределению вероятностей щ, получим
/.(!)= p'-'Mdx), (П
—00
а в случае существования плотности р5
f5(0 = f e,txpjx)dx. (2)
— 30
Таким образом, ft(/) есть преобразование Фурье меры щ ли-
бо плотности Р\.
Замечание. Интегралы Лебега от функций с комплекс-
ными значениями (в данном случае от eltx либо от e<tx) ес-
тественно понимаются в смысле интегрирования вещественной
и мнимой частей. Мнимая единица i в показателе нужна для
того, чтобы интегрировать ограниченные функции (тем самым
интегралы существуют для любых случайных величин).
Основное свойство характеристических функций состоит в
том, что для независимых случайных величин и
f-v+5,(o - W0- (3)
Действительно,
Me"«*+&> = М еи«} = Me"?* Ме“ъ=
(использованы независимость величин и е‘7?*, вытекаю-
щая из независимости и ?2« й свойство математического
ожидания произведения независимых случайных величин).
В частности, если существуют плотности р. и то
(3) означает, что преобразование Фурье свертки (компози-
ции) плотностей р^ и р^ равно произведению их преобразо-
ваний Фурье.
Таким образом, характеристическая функция суммы £„.=
e5i+^2+ — + ^n независимых случайных величин равна по-
просту произведению характеристических функций слагаемых.
Вопрос заключается в том, чтобы заключить отсюда нечто (а
именно — центральную предельную теорему) о самих распре-
92
делениях вероятностей. Способы перехода от характеристи-
ческих функций к распределениям вероятностей разнообразны
и отличаются большей или меньшей трудностью (и соответ-
ственно меньшей или большей аналитической глубиной). Вы-
бираем самый легкий (и самый неглубокий) способ, основан-
ный на элементарных понятиях теории обобщенных функций.
Ситуацию можно пояснить с помощью следующего примера.
Пусть 2п(х) — сумма п членов ряда Фурье (никакая не
случайная величина) некоторой периодической функции
/(х), хе[-я, л]. Можно указать по крайней мере два способа
понимать соотношение Sn(x)-*f(x) при п->оо. Первый способ
(более глубокий аналитически, но и более трудный для дока-
зательства) состоит в исследовании сходимости 2„(х)—►/(х)
в каждой точке х. Доказательство состоит в выражении сум-
мы Zn(x) через интеграл от /(х) с некоторым ядром и в ис-
следовании этого ядра при п—>-сю (нужно проследить, как при
п—►оо ядро становится похожим на б-функцию, сосредоточен-
ную в точке х). Другой способ состоит в исследовании схо-
димости Sn-*f, например, в пространстве L2 (функций, сум-
мируемых с.квадратом). Тригонометрические функции орто-
гональны в гильбертовом пространстве L2; нужно установить
лишь их полноту (а она вытекает из того, что тригонометри-
ческим полиномом можно приблизить непрерывную функцию;
полином не должен быть отрезком ряда этой функции). Этот
способ проще аналитически, но ничего не говорит о сходимос-
ти в каждой отдельной точке х. Если угодно, первый способ
есть способ классического анализа, второй — функциональ-
ного анализа.
В теории вероятностей имеется большое количество теорем
как первого, так и второго рода. Было выяснено, что теоремы
первого рода (так называемые локальные предельные теоре-
мы) не дают наиболее коротко формулирующихся результа-
тов. Теоремы второго рода (называемые интегральными пре-
дельными теоремами) более просты по формулировкам, не
говоря уж о доказательствах. В данной книге, ориентирован-
ной на приложения теории вероятностей, мы останавливаемся
на более простых интегральных предельных теоремах, так как
лишь очень редко может встретиться такая практическая си-
туация, в которой играет какую-то роль различие между ин-
тегральными и локальными теоремами.
Изучение интегральных теорем основано на понятиях пре-
образования Фурье и слабой сходимости. Напомним сейчас
простейшие свойства преобразования Фурье, которые будут
еще раз использованы в данной книге при построении спект-
рального разложения (обобщенного) стационарного случай-
ного процесса.
1.4. Обобщенные функции и преобразования Фурье. От-
правляемся от известных из анализа определений и формул.
93
Пусть f(x)—некоторая функция от хе/?1, суммируемая на
всей прямой. Тогда функция
7(0- Je^/(x)dx (I)
—«•
называется преобразованием Фурье функции f (х).Если7(/)—
суммируемая функция (переменного t), то имеет место фор-
мула обращения:
оо
= f 7^- (2>
** I
“ОО
Надо иметь в виду, что условие: 7(0 — суммируемая
00
функция (т. е. j |7(f |i/< оо)— довольно ограничительно.
Например, если Дх)=1 при 0<х<1, f(x) = O при х<0 и
х>1, то /(г) —не суммируемая функция.
Поэтому ограничимся более узким классом функций f(x):
будем рассматривать лишь дважды непрерывно дифференцн*
руемые финитные (т. е. обращающиеся в нуль вне некоторого
конечного отрезка) функции. Такне функции будем называть
гладкими финитными.
Вычислим преобразование Фурье функции f'(x). Имеем
Z~(0 = J e,/v f'(x)dx--J ite^f(x)dx = (-it)J(t).
ОС “ со
Таким образом, дифференцированию функции отвечает в
преобразовании Фурье умножение на (—it). Следовательно,
функция (—t2) f(t) есть преобразование Фурье функции
Так как функция f"(x) непрерывна и финитна (вместе с функ-
цией f(x)), то преобразование Фурье функции f"(x) ограни-
чено. Следовательно, 7(01 ограничено при всех t. По-
скольку функция f(t) непрерывна, запишем неравенство
\f(t)\<C/(l + t2), (3)
где С — некоторая константа (неравенство (3) выражает тот
факт, что |7(0 | ограничен при ограниченных t и на бесконеч-
ности убывает не медленнее чем СИ2). Но тогда функция 7(0
суммируема. Получили следующую лемму.
Лемма. Преобразование Фурье гладкой финитной функ-
ции является суммируемой функцией.
Рассмотрим теперь (не обязательно гладкую) суммируе-
мую функцию F(x), вообще говоря, с комплексными значе-
ниями. Определим линейный функционал, который эта функ-
пня задает на гладких финитных функциях, обозначаемый
(Г, f) либо F(f).
94
Определение. (Г, /) = £(/) JF(x)f(x)dx.
Подставим в это определение выражение (2) функции
f(x) через ее преобразование Фурье. Получим, изменяя
порядок интегрирования,
оо / во \
(F, f)~ С F(xjl 4- f U =
e~ilJ F(x)dx\~f(t)dt= (4)
где F(t) есть преобразование Фурье функции F(x), определяе-
мое формулой
?(/)= J eiixF(x)dx,
GO
F — функционал (в пространстве функций от t), определяе-
мый функцией F(t). (Перемена порядка интегрирования за*
нонна, так как в силу суммируемости F(x) преобразование
Фурье F(t) ограничено; а тогда в силу суммируемости и ог-
раниченности f(t) любой из интегралов, входящих в (4), сво-
дится к интегралу в конечных пределах.)
Пусть теперь функция F(x) — не обязательно суммируе-
мая на всей прямой (но локально, т. е. на любом конечном
отрезке суммируемая, например, Г(х) = 1 или F(x)=x, |х|, х2
и т. д.). Из-за расходимости интегралов мы не знаем, как оп-
ределить преобразование Фурье функции Г(х). Запишем,
однако, начало и конец формулы (4):
(F, J) - 2к(£, /). (5)
Договоримся понимать преобразование Фурье функции F как
функционал F, действующий в пространстве преобразований
Фурье основных функций, по формуле (5). Такое определение
годится не только для неограничеииой функции F(x), ио и для
любого функционала F над гладкими финитными функциями.
Замечание. На самом деле в теории обобщенных функ-
ций речь идет не о любых функционалах F, а лишь о линей-
95
них непрерывных функционалах. Мы пока не уточнили, в ка-
ком смысле понимается сходимость гладких финитных функ-
ций (следовательно, не можем говорить и о непрерывности
функционалов). Но в дальнейшем это сделаем.
Приведем примеры вычисления преобразования Фурье.
ЕслиГ(х) = 1, то
(F. T) = 2*(F, f)-2K Jf(x)dx = 2*f(0).
Функционал, ставящий в соответствие функции f значение
/(0), называется 6-функцией Дирака б(/). Получаем, что
F = 2*6(0-
Функционал F в (5) можно называть обратным преобразо-
ванием Фурье от функционала F. Если обратное преобразова-
ние Фурье от Г=2л6(/) есть функция Г =1, то обратное пре-
образование Фурье от 6(0 есть 1/2л. Это согласуется и с
формулой
Прямое же преобразование Фурье от 6(х) есть, очевидно, 1.
Тогда обратное преобразование Фурье от 1 есть б(х).
Получается несколько экзотическая формула
00
-J- J e-“*dt = 6(x),
— ОО
точный смысл которой придается с помощью понятия обобщен-
ной функции.
Еще интереснее получаются преобразования Фурье от рас-
тущих (при х—»-оо) функций. С ними можно познакомиться,
например, по книге И. М. Гельфанда и Г. Е. Шилова [13].
Пусть щ — распределение вероятностей случайной величи-
ны £, ф—гладкая финитная функция. Имеем
Мф(£)= J <p(x)^(dx) = (|*5, ф), (6)
•“О©
где левая часть является определением функционала щ,
стоящего в правой части. Подставим в (6) выражение ф через
преобразование Фурье и сделаем перемену порядка интегри-
рования:
96
Мф® = Ф)
pe(<fr)=
e-u*p (dx) |ф(0Л= -(h, ф),
* I «к
где h — функционал, задаваемый характеристической функ-
цией:
/5(0 - Ме'^ - J e,/J>£(dx); f?(0 = J »-“x?z(dx).
«О* 9B
Следует отметить законность перестановки порядка инте-
грирования. Все наши выделения не всех функций <р(х), а
лишь гладких и ограниченных нужны лишь для обеспечения
законности этой выкладки (и ей подобных). Теорема Фубини
состоит в том, что для интегралов Лебега (при наличии абсо-
лютной сходимости) всегда можно менять порядок интегриро-
вания. Абсолютная сходимость обеспечивается конечностью
меры щ и интегрируемостью функции |<р(/)|^С| (1 +/)2.
Итак, если под щ понимать функционал, задаваемый ме-
рой щ, то его преобразование Фурье есть функционал, зада-
ваемый характеристической функцией:
Неe f ?•
Мы решили проблему однозначности соответствия между
распределениями вероятностей и характеристическими функ-
циями: по характеристической функции мера определяется
однозначно. Действительно, зная МО, получаем
К* Ф)= f Ф(*К(ЛО = £ (М ф)
* I w ел
для любой гладкой финитной функции <р. Но значениями
(jii, ф) мера цс определяется однозначно.
В самом деле, пусть [а, Ь) — полуоткрытый интервал. Рас-
смотрим гладкую функцию ф„, равную 1, на интервале [а,
Ь—1/л], а на интервале (а— l/п, а) и (b—1/n, Ь) принимаю-
щую значения, заключенные между нулем и единицей (и об-
ращающуюся в нуль вне интервала (а—1/л, Ь)). Значения
(щ, фп) определены однозначно. Но при л->оо
Фп(х) -* /|а,Ь)(х)
в каждой точке хе/?*. Следовательно, по теореме о предель-
ном переходе под знаком интеграла Лебега
7—25В7 97
(|\. Фп) = j ФпСФ?(<**) -* j /(а, Ь|(х)^х)==|»?{[а, Ь)}.
Таким образом, щ {[а, Ь)} определяется однозначно для любо-
го интервала [а, Ь). Следовательно, однозначно определена и
мера щ (по теореме о продолжении меры).
§ 2. Слабая сходимость. Теорема Хинчина.
Центральная предельная теорема
2.1. Слабая сходимость. Распределение суммы Sn=£i +
+&+...+5» не может быть очень похожим на нормальное.
Например, если слагаемые принимают только целочислен*
ные значения, то S„ также принимает только целые значения;
в то же время, с точки зрения нормального распределения»
множество целых чисел имеет вероятность нуль. Далее, в
теории вероятностей постепенно было понято, что удобно
рассматривать сходимость распределений вероятностей к не-
которому предельному распределению. Между тем последо-
вательность распределений сумм S„, как правило, ни к какому
предельному закону не сходится: для любого фиксированного
А при п->сю Р{ |S„| <Л}->0, в то время как любой закон рас-
пределения вероятностей у. обладает тем свойством, что для
е>0 найдется А, такое, что р,{х: |х| <Л)>1—е.
Мы обязаны Лапласу пониманием того, что нужно рассмат-
ривать не сами суммы S„, а так называемые «нормированные
суммы»:
s»=(Sn-MSn)//DS;.
Очевидно, что Ms*»0, Ds^—l, но совершенно не очевид-
но, что распределение вероятностей s' стремится к нор-
мальному закону АГ(О, 1) (это мы и должны доказать).
В каком же смысле может происходить это стремление?
Если S„ — целочисленная случайная величина, то значениям»
s' являются хоть и ие целые числа, ио все же элементы не-
которого счетного множества.
{хт‘.хт — (т— MSn)/VDSn, т — целое},
имеющего (в смысле нормального распределения) меру нуль.
Дело в том, что среди всех возможных математических
идеализаций понятия «множество возможных результатов
наблюдений» нет ни одной абсолютно удовлетворительной.
Сказать, что возможными результатами являются любые ве-
щественные числа, нехорошо, так как нет такого носителя ин-
формации, на котором можно было бы записать счетную пос-
ледовательность десятичных знаков. Сказать, что результа-
98
том является рациональное число, записанное конечным чис-
лом десятичных знаков, тоже нехорошо, так как мы тогда те-
ряем иррациональные числа (да и число */з. например, запи-
сывается конечным числом знаков в троичной системе счисле-
ния, но бесконечным — в десятичной). Поэтому правомерна
концепция, в которой точному знанию результата наблюдения
не приписывается особой роли. Прибор, который призван ре-
гистрировать, произошло или нет событие (£е[а, Ь]}, на самом
деле обладает некоторой неопределенностью: при очень
близком к одному из концов отрезка [а, Ы, он будет регистри-
ровать это событие с какими-то ошибками.
Идея слабой сходимости основана на том, чтобы ска-
зать' что указанный прибор при очень большом числе
испытаний будет измерять не вероятность Р(£е[а, 6]} =
=М/|в.ь](5), а М<р(Э, где ф(х)—некоторая гладкая функ-
ция, похожая на /[О,ь](*)- Обычно в учебниках теории
вероятностей рассматриваются непрерывные функции ф(х);
но ограничение гладкости, принятое здесь, сильно упро-
щает рассуждения (ничего не меняя по существу, так
как непрерывная функция может быть равномерно ап-
проксимирована гладкими).
Определение. Говорят, что последовательность веро-
ятностных мер ц„, п=1, 2, ..., слабо сходится к мере ц, если
для любой гладкой (дважды непрерывно дифференцируемой)
и финитной функции ф(х) справедливо предельное соотноше-
ние
* ••
Мф) - (и», ф) - J фММ^х) -* (и, ф) - J фМн(^)- (1)
Замечание. Конечно, выполнение (1) для любой глад-
кой финитной функции не претендует на особенную физич-
ность; слабая сходимость есть также не вполне совершенная
идеализация.
Теорема. Для слабой сходимости ц„—►р, необходима и
достаточна сходимость соответствующих характеристических
функций
fn(t)= Je%(dx). (2)
Замечание 1. Эта теорема называется теоремой о не-
прерывности соответствия между законами распределений ве-
роятностей и характеристическими функциями (взаимная од-
нозначность соответствия доказана в предыдущем парагра-
фе).
Замечание 2. Мы будем понимать сходимость в (2) как
поточечную сходимость при любом t. Но можно доказать, что
'* 99
эта сходимость может быть только равномерной в каждой ог*
раниченной области значений t.
Доказательство теоремы. Достаточность.
Пусть выполнено (2). Как показано в предыдущем параграфе,
|x(<p)=-J- f/(O$(0*.
«К J лК J
— оо —
00
Так как |/n(0|< 1, a J |ф(Ф* < оо, то н«(<Р) —> н(ф) по тео-
реме о предельном переходе под знаком интеграла Лебе-
га (подынтегральные выражения ограничены суммируе-
мой функцией).
Необходимость. Во-первых, если цв—►ц слабо, то
существует (для любого е>0) число Л„ такое, что
ц{х: |х| <А.}>1—е, ц„ (х: 1x1 <Л,)>1—е
для достаточно больших п. Действительно, существует число
В„ такое, что для предельной меры ц выполняется соотноше-
ние ц{х:|х|<В,}>1—в/2. Положим At=Bt+l и рассмотрим
гладкую функцию ф(х), которая заключена между 0 и 1, рав-
на 1 при |х|<В, нравна нулю при |х|>Л„ Тогда ц(ф)>1—е/2.
Однако Цп(ф)-*р(ф). следовательно, при достаточно большом
л Мп (ф)>1— 8.Но этого не может быть, если цп{х: |х| <Л,}<
<1—е, так как цв(ф)<цв{х:|х|<Ле), поскольку 0<ф(х)<1,
причем ф(х)=О при |х| >Ле.
Нам нужно доказать, что fn(t)—Функции f„(t) и
f(t) получаются интегрированием от (—оо) до оо ограничен-
ной функции t"x по мерам и ц. Мы уже показали, что срав-
нение интегралов в пределах от (—оо) до оо приводится к
сравнению интегралов в пределах от (—Ле) до А,. Заменим
функцию е<,х на функцию ф(х), совпадающую се"1 при
1x1<Л,, равную нулю при |х| >Л,+1 и гладкую. Значения
интегралов, определяющих f„(t) и f(t), при этом (для доста-
точно больших л) изменятся не более чем на е; но при л—►оо
они обязаны неограниченно сближаться. Этим доказано, что
для достаточно больших л имеем: |f„(/)— f(t) |<2е; в силу
произвольности е>0 теорема доказана.
2.2. Теорема Хинчииа. Поскольку рассматриваемые в тео-
рии вероятностей случайные величины сами могут быть функ-
циями от других случайных величин, притом неограниченны-
ми, интересно бывает освободиться от условия ограниченнос-
ти дисперсии, входящего в теорему Чебышева. Оказывается,
что для одинаково распределенных случайных величин не
требуется существования дисперсии.
Лемма. Пусть существует Mg. Тогда характеристическая
функция fi(t) имеет производную, причем
100
f'(O)-»Mg.
Доказательство. Продифференцируем под интегралом
выражение для характеристической функции; получим
«о
J ixe'^dx). (1)
—00
Полагая в (1) /=0, получим утверждение леммы; однако нуж-
но установить законность дифференцирования. Для этого дос-
таточно заметить, что полученный после дифференцирования
интеграл по х равномерно (по t) сходится, что вытекает из
оценки |txei/Jt| = 1x1 и существования Mg. Лемма доказана.
Замечание. Аналогично при существовании момента
/е-го порядка Mg* (k=2, 3,...) существует k-я производная
характеристической функции причем
f<*)(0) - (*М£*.
Пусть даны независимые одинаково распределенные слу-
чайные величины gt, g2,..., gn, ... (т. е. распределения щ„
ц?,, .... одинаковы; обозначим это распределение ц).
Пусть существует
Mg(= jxp(<fr) — а.
08
Теорема Хннчина. Последовательность
$п • • • +6и t а
п п
в смысле сходимости по вероятности (т. е. разность 5п/л—а->
—"-О по вероятности,.
Доказательство. Установим сначала слабую сходи-
мость. Поскольку
а— *»+*«+ -••+$» Я1_ (Si-«)+К1-“)+ • - • +(*»-«)
П П П
можно считать, что а=0. Рассмотрим характеристическую
функцию
fv(0 - М exp (it
п
101
где
/(O-Mexp(ftg(k)= Je“>(dx).
Поскольку [|*HdxXoo, существует f'(t)=ia*=O. Но тог-
да
f рЛТ*=1 l+f'(0)i + о f-Un=( l + o f-ЦГ—1 (n-oo).
I Л I I I л \ n /1 I \ n I I
Таким образом, Sn/n сходится к случайной величине, прини-
мающей значение 0 с вероятностью 1 в смысле слабой сходи-
мости (поскольку функция f(/) = 1 есть характеристическая
функция именно такой величины).
Выведем из слабой сходимости сходимость по вероятности.
Нужно доказать, что для любого в>0 вероятность Р{ |S„|л|>
>г)—*-0. Возьмем гладкую функцию <р(х), заключенную меж-
ду 0 и 1, равную 1 в точке х=0 и равную нулю при |х|>е.
Тогда
МФ(^-)— МФ(0)-1.
Но Мш (S„/n)< 1—P{|Sn/n|>e), откуда вытекает, что
P{|S„/n| >в)-Ч). Теорема доказана.
2.3. Центральная предельная теорема. Вычислим сначала
характеристическую функцию f(t) для стандартного нормаль-
ного закона N (0, 1). Имеем
f(ft “ f е“х —— е-ж’/2 dx = —— f cos txe-Wdx.
J rs J
Есть много способов вычисления такого интеграла. Например,
продифференцируем его по параметру t:
//(0=Г (“х) s*n tx е~^,гЛх =
J sin txe-^d
102
1
e-x’/2d(sinrx) = — t f(t).
Решая это дифференциальное уравнение (с условием f(0) =
= 1), получаем
ДО =
Для случайной величины т)=а£+а, имеющей нормальное
распределение N(а, о) с параметрами а и а, получаем
f (ОМе"” = Ме//(а'+°> = = eitae~a,t^2.
Пусть теперь имеются две независимые нормальные случай'
ные величины i;, и т)2 с параметрами соответственно (ai, oi)
и (й2, а2). Имеем
к+«.(0 = ЦО/JO
что соответствует нормальному распределению с парамет*
рами (at+at, + Таким образом, двухпараметри-
ческое семейство нормальных законов 4 = 0% +а перехо-
дит в себя при композициях. Можно доказать, что Дру-
гих таких семейств (при условии конечности дисперсии)
не существует (но это доказательство существенно выхо-
дит за рамки данной книги; см., например, книгу
Б. В. Гнеденко и А. Н. Колмогорова [16]).
Пусть теперь |2, ..., £П(- — одинаково распределенные
случайные величины с распределением ц и конечными мате-
матическим ожиданием н дисперсией:
8
а = J XR'(djt), а* =
Образуем Sn в 51 + Е» + • • - + L.
s*n = (Sn-MSn)//DST- (Sn-na)/(aV7i).
Центральная предельная теорема. При
п—»-оо распределение s*n стремится к стандартному нормаль-
ному распределению ЛЦО, 1) (в смысле слабой сходимости).
Доказательство. Представим s* в виде
( (х—a)’|*(dx).
103
где (£,;—а)/а. Очевидно, что Mvjy — O, Dtjj « l. Обозна-
чим через g(f) характеристическую функцию любой из
случайных величин Вычислим характеристическую
функцию а*:
Its* Г / t \1« Г t 1 i*
Me |-У = 1+я'(0)-7т- + -5-Г(0)7 +
L \ i'n / J L 'a £ n
। \ 1"
+ ° “1 •
l n j I
Перейдем к пределу при фиксированном t (либо при t, меня-
ющемся в ограниченных пределах: |/|^Л<оо), п—»-оо, учи-
тывая, что g'(0) =iMtv=0, g"(0)=—Dt)/=—I.
Получаем
if»* Г It*
Me "= 1---4-0Г-Н
I 2 n \п/ I
Теорема доказана.
Замечание 1. Величина o(t2/n), вообще говоря, комп-
лексная, но для комплексных чисел гп—*-0 (но таких, что
nzn—►») справедливо соотношение lim(l+zn)n=expw.
Замечание 2. Имея в виду применение таблиц нор*
мального закона (т. е. функции Лапласа Ф(л) *
« ।
= f ——e-y*^dy\ центральную предельную теорему обыч-
J У2к
но формулируют следующим образом:
W₽{«4-P(4 ("-«>). (’>
Из слабой сходимости нетрудно вывести сходимость функ-
ций распределения. Пусть действительно последовательность
распределений цп—слабо; обозначим через Fn(x) и F(x)
соответствующие функции распределения цп((—оо, х)} и
ц{(—о°, х)}.
Утверждение. Если х0 — точка непрерывности пре-
дельной функции F(x), то Fn(xo)—<~F(x0).
Доказательство. В §2 (при доказательстве теоремы
о непрерывности соответствия) мы заметили, что для каждо-
го 8>0 существует число Л„ такое, что ц(х:|х| <Л,}^1—е,
Цп{х:1х1 <Л,}>1—е (для достаточно больших п). Это озна-
чает, что прн 1x1 >А, функции распределения Fn(x) и F(x)
близки. Пусть 1х01<Л,. Введем две гладкие функции:
<р+(х; х0) и <р_(х; х0) следующим образом. Обе эти функции
заключены между 0 и 1, обращаются в нуль при х<—Л,—1;
при —Л,^х^х0—б функция <р_(х; хо) равна 1 и обращается
104
в нуль при х>д0; при —Ле^х^хо функция <f+(x; х0) равна 1
и обращается в нуль при х>х0+б (б>0 — произвольное).
Тогда значения Fn(x0) и F(x0) отличаются не более чем нае
от чисел, заключенных соответственно между цп(ф-) и
р„(ф+) и между ц(ф-) и ц(ф+). Так как х0 — точка непре-
рывности функции F(x), то (при малом б) величины ц(ф_)и
р(ф+) могут быть сделаны сколь угодно близкими. Но при
п —-оо Цп'(ф-)—-и(ф-), Цп(ф+)—-р(ф+). И таким образом,
доказано, что при достаточно большом п сколь угодно близ-
ки Fn(x0) и F(x0). Это и есть сходимость Fn(x0) —<~F(x0).
Для нормального закона любая точка х является точ-
кой непрерывности функции распределения Ф(х). Поэто-
му F4j(x) —> Ф(х) в любой точке х. Учитывая монотонность
Fsj(x) и Ф(х), легко видеть, что такая сходимость обяза-
тельно равномерна по х, —оо <Г х оо.
Итак, центральную предельную теорему можно сформули-
ровать в виде утверждения о равномерной сходимости в (1).
(Нетрудно показать, что из сходимости функций распреде-
ления, наоборот, вытекает слабая сходимость.)
Проблема практических применений. Мы изложили лишь
небольшую часть того, что в настоящее время известно на
чисто математическом уровне о центральной предельной тео-
реме. За кадром нашего изложения остался ряд интересных
и глубоких аналитических результатов; однако все эти ре-
зультаты не проливают достаточно света на то, как следует
(или как не следует) применять центральную предельную тео-
рему в различных практических ситуациях. На практике, ко-
нечно, нельзя дождаться, пока п будет стремиться к оо. Име-
ется ряд численных расчетов, которые показывают (на пра-
вах экспериментального результата), что при числе слагае-
мых п порядка нескольких десятков имеет полный смысл
заменить распределение суммы s‘ нормальным распределе-
нием на правах точного выражения. Однако нужно предупре-
дить об одной опасности, связанной с так называемыми
«хвостами распределений».
Довольно часто нас интересуют такие х, что вероятности
P{s*<x} или, наоборот, Р{$^>х) крайне малы — порядка
0,01 или еще меньше (такие вероятности называются «хвос-
тами» функции распределения). Фактически в этих выраже-
ниях х оказывается не постоянной величиной, а функцией от
п: мы так подбираем х=хп. чтобы сделать «хвосты» доста-
точно малыми. Существует, вообще говоря, проблема малове-
роятных событий, которая, в общем, состоит в том, что такие
события оказываются для нас плохо постижимыми как в чис-
то математическом, так и в любом практическом смысле: мы
не уверены как в том, что их вероятности вообще существу-
ют (в том, например, смысле, что нам дан в опыте ансамбль.
105.
статистически однородных экспериментов), так и в том, что
мы сколько-нибудь правильно нашли их (если они существу-
ют). Применительно к нормированной сумме s* чисто мате-
матическая проблема состоит в следующем.
Утверждается, что Р{«*<х]->Ф(х) равномерно по х; но
не утверждается, что отношение Р{з*<х)/Ф(х) (либо отно-
шение P(s* >х)/(1 — Ф(х)) сходится к единице равномерно
по х. (Утверждение об отношении математически невер-
но.) Следовательно, возможна, например, ситуация, когда
₽{<<*}-0,01, а Ф(х)=0,001: разность между этими чис-
лами мала, но их отношение равно 10. Если событие
(<<х) моделирует аварию единичного изделия, а мы со-
бираемся наладить массовый выпуск этих изделий, то мы
не должны ошибаться в 10 раз при оценке вероятности
аварии. Между тем при использовании центральной пре-
дельной теоремы это вполне возможно.
С этим затруднением наука борется. Нормальное распре-
деление в «хвостах» заменяется другими: это так называемые
«вероятности больших уклонений». С большими уклонениями
можно познакомиться, например, по книге В. Феллера [40].
Другой способ борьбы — это так называемые «вероятности
экстремальных значений», когда моделью является не сумма
независимых случайных величин, а большое число независи-
мых одинаково распределенных величин, из которых берется
максимальная или минимальная (об этом см. книгу Гумбеля
[17]). Но распределения, возникающие из этих двух моделей,
не обладают достаточной практической надежностью, чтобы
их можно было безоговорочно рекомендовать к употреблению.
Бывают удивительные совпадения, но это совсем не обяза-
тельно.
Практически оценки вероятностей любых событий, в осо-
бенности маловероятных, не должны обычно претендовать на
некую количественную правильность; роль их — чисто ориен-
тировочная. Если, например, стандарт требует обеспечить на-
дежность некоторого изделия «пять девяток», т. е. 1—10-s, то
мы ни-когда не можем быть уверены, что девяток именно
пять, а не три или семь, пока изделие находится на стадии
испытаний. Если изделие пойдет в массовую серию, то мы,
конечно, в конце концов узнаем, какова его надежность, но
будет уже поздно. По-видимому, нет научного способа для
избежания таких ситуаций.
2.4. Качественная картина, связанная с центральной пре-
дельной теоремой. Интересно переформулировать централь-
ную предельную теорему в случае, когда а#=0. Из таблиц
нормального закона узнаем, что для нормальной случайной
величины т)=о| + а с параметрами а, о верно, например, сле-
дующее:
106
P{lq—al >3o}=P{lgl >3}«0,3%,
т. e. практически достоверно, что |ц—a]<3o (правило «трех
сигма»). Применяя нормальное распределение на правах точ-
ного для «л, получим, что практически достоверно, что lsn 1^
<СЗ, т. е. что
|5n-MSJ<3/DS;.
Но fASn=na пропорционально п (если a#=0), VDSn=oVn
пропорционально }'п. Таким образом, Sn, вообще говоря, при
больших п ведет себя как па (как неслучайная величина), а
отклонения, связанные со случайностью, имеют меньший по-
ряде?; величины }'п: как говорили классики, детерминирован-
ная составляющая в конце концов (при большом п) возобла-
дает над случайной. Лаплас считал следствием из централь-
ной предельной теоремы такое утверждение: если за морем у
некоторого государства имеется колония, то она в конце кон-
цов освободится, потому что ее желание освободиться — де-
терминированное (не очень понятно, почему желание метро-
полии удержать в своей власти колонию Лаплас считал слу-
чайным). Так или иначе, получается красивая натурфилософ-
ская картинка: при малых п сумма Sn ведет себя в высшей
степени неопределенно; но с ростом п детерминированная
составляющая проявляется все отчетливее, пока, наконец,
совсем не возобладает.
Закончим, ориентируясь на эту картинку, исследование иг-
ры в 10 и 20 коп., начатое в первой главе (§6). В смысле
математического ожидания Mg выигрыша g при одном повто-
рении игры первому игроку выгодно прятать 10 коп. с веро-
ятностью 7/12 и 20 коп. с вероятностью 5/12. Тогда незави-
симо от действий второго игрока Mg = 5/12 коп. Для просто-
ты предположим, что второй игрок (от которого Mg не зави-
сит) называет любую монету с вероятностью 1/2. Небольшой
подсчет дает следующее распределение вероятностей для g:
-Ю +15 — 20 \
7/24 1/2 5/24)'
Подсчитаем дисперсию g:
Dg = Mg2—(Mg)2«Mg2=225.
При этом Mg=5/12 надо сравнивать с VDg = 15: при одном
повторении игры преобладает случайный разброс.
Сколько же раз нужно повторить игру, чтобы первый иг-
рок мог с хорошей вероятностью (например, равной 0,975)
выиграть хотя бы рубль? Для ответа на этот вопрос нужно
подобрать п из соотношения
107
p{Sn = b+.. .Ч-Ь1>100)«Р
5
100
/225л
₽0,975
Из таблиц нормального закона (применяя его на правах точ-
ного) получаем, что
/100--п /1/2257; = - 1,96.
( 12 I / г
Хотя это уравнение и квадратное относительно Vn, но лучше
его решать подбором; получаем п»«5150. Это означает, что
если игру повторять 10 раз в минуту, то придется играть
8,5 ч без отдыха, чтобы с гарантированной вероятностью вы-
играть рубль. Игроку очень трудно скопить начальный капи-
тал (лучше это сделать каким-нибудь иным способом).
Но ситуация профессионального игрока иная: обычно у
него начальный капитал уже есть. Тогда, играя по 10 раз в
минуту, он будет зарабатывать в среднем по 2,5 руб. в час,
что довольно прилично. Правда, имеется некоторая вероят-
ность разорения за счет случайных колебаний. Для ее вычис-
ления нужно знать распределение вероятностей min Sn(pa-
л-1, 2....
зорение произойдет, если minSn<—К, где К — начальный
капитал). Эта задача не была доступна классикам: она ре-
шена лишь в XX в. Она выходит и за пределы данной книги
(см. гл. XII второго тома книги В. Феллера [40]). В общем,
вероятность разорения быстро убывает с ростом К\ игра с
большой вероятностью продолжается неограниченное время»
принося в среднем 2,5 руб. в час первому игроку.
Видим, что вероятностные модели никак не исключают су-
ществования удачливых профессиональных игроков, и притом
не шулеров, если игра не чисто азартная (не все зависит от
случайного эксперимента), и за счет допускаемых правилами
игры приемов игрок в состоянии обеспечить себе положитель-
ное математическое ожидание выигрыша (см., например, из-
вестные воспоминания А. Я. Панаевой о Н. А. Некрасове).
2.5. Испытания Бернулли. Отметим особо важный част-
ный случай. Пусть р — число успехов в п испытаниях Бер-
нулли; положим
P = Pl + l*2+ - +1*П,
где р« есть нуль или единица в зависимости от того, неудача
была в t-м испытании или успех.
Поскольку а=Мн=р, нормированное чис-
ло успехов р* имеет вид: р*=(р—np)/Vnpq. Таким обра-
зом, центральная предельная теорема получает вид:
108
pM«»tz2£< ф(х).
I J
(l)
Эта теорема может быть выведена и без характеристических
функций: путем терпеливого преобразования вероятности
P{p=m}=C"pm(l—р)п~т с помощью формулы Стирлинга.
Результат (1) носит наименование теоремы Муавра — Лапла-
са; впрочем, как отмечалось, Лапласу были известны метод
характеристических функций и гораздо более общие резуль-
таты.
2.6. Различно распределенные слагаемые. Центральная
предельная теорема верна при довольно широких условиях н
сумм независимых различно распределенных величин.
Одним из известных условий такого рода является условие
Ляпунова. Оно состоит в том, что при некотором 6>0
п
" *11
где В3п — 2 D£*- Если, например, слагаемые 5..........
*«i
примерно одинаковы в том смысле, что
0<c<D^<C<oo, M(£k-M5k)2+»<D<oo,
то условие Ляпунова выполнено. Действительно, В3 име-
ет порядок величины п, следовательно, В2+8 —порядок
п
величины п,+8'2; сумма же 2 —М£м|2+* имеет поря*
*-i
док величины п.
Доказательство теоремы в условиях Ляпунова не пред-
ставляет для нас принципиального интереса, так как дело
сводится к оценке и суммированию логарифмов характеристи-
ческих функций. В предельных теоремах интересны не столь-
ко доказательства, сколько выработанные путем проб условия
теорем, в частности довольно хитрое условие Линдеберга,
непосредственно связанное с исследованием вопроса о том,
какие вообще предельные законы могут возникнуть из сумми-
рования независимых случайных величин (это также дости-
жение XX в.). Со всем этим можно познакомиться по книге
Б. В. Гнеденко [15].
109
§ 3. Статистические приемы, связанные с центральной
предельной теоремой и нормальным распределением
3.1. Модель выборки. Теория вероятностей имеет дело с
c-алгебрами и мерами; статистика — с конкретными числа-
ми, взятыми из наблюдений. В то время как мысль о конти-
нууме с заданной на нем мерой обычно не противна людям с
физико-математическим складом ума, мысль об обширной
таблице с числовыми данными, а тем более непосредственное
созерцание такой таблицы, погружает многих в тоску. Что-
бы можно было преодолеть эту тоску и приступить к какой-
то статистической обработке, необходимо иметь систему тео-
ретических ожиданий чего-то интересного, проявляющегося
путем обработки (не столь даже важно, чтобы эти ожидания
обязательно оправдались). Простейший способ создавать тео-
ретические ожидания связан с моделью выборки.
Та (часто единственная) совокупность результатов наблю-
дений х\, Х2, ..., хп, которая нам предъявлена, мыслится име-
ющей интерес не сама по себе, но как представитель статисти-
ческого ансамбля, который можно было бы иметь при много-
кратном повторении системы опытов, принесшей один раз ре-
зультаты Xi, х2, .... хп- Иначе говоря, набор х2, .... хг. объ-
является реализацией некоторого случайного вектора g;. |2. •••»
...,|п. Выборка, по определению, получается, если |2, ...»
.... £п — независимые одинаково распределенные случайные
величины. Итак, о том единственном, что у нас есть — наборе
чисел Xi, хг, .... хп мы думаем с помощью того, чего у нас
нет — набора случайных величин £2, .... £п, которые явля-
ются измеримыми функциями на некотором й (для моделиро-
вания независимости й можно считать прямым произведени-
ем вероятностных пространств). Следовало бы сами конкрет-
ные числа xi обозначить £t, .Sn, но мы сохраняем обще-
принятое обозначение Х2, .... хп.
Итак, Xi, х2, ..., хп — случайные величины. Нам неизвест-
но их распределение, но мы сейчас его приблизительно узна-
ем. Пусть F(x) — функция распределения: F(x) = P{xi<x},
xeR1.
Определение. Эмпирической (выборочной) функцией
распределения называется функция Fn(x), задаваемая соот-
ношением
£п(х)д™“° Xi<x .
п
Теорема 1. При п—+оо для любого х Fn(x) —► F(x)
в смысле сходимости по вероятности.
Доказательство. Заметим, что Fn(x) представимо в
виде
ПО
Fn(x) = lV Ш), (I)
n
где функция Ix(y) определяется следующим образом: Ix(y) =
=0 при у^х, L(y) = l при у<х.
Поскольку Xi — независимые случайные величины, слага-
емые /А(х,) — также независимые случайные величины. При
этом P{/x(x,) = l} = P{x,<x}=F(x), следовательно,
NlIx(Xi)=F(x), а дисперсия D/X(x,) ограничена (например,
единицей, поскольку 1/*(У)1^1, y^Rx). Применяя к (1) за-
кон больших чисел, получаем утверждение теоремы.
Таким образом, при достаточно большом п по эмпиричес-
кой функции распределения Fn(x) можно неплохо судить об
истинной (или теоретической) функции распределения F(x)
каждой из случайной величин х,.
Оказывается, что можно указать распределение вероятно-
стей для расстояния между теоретической и выборочной
функциями распределения, т. е. для случайной величины, оп-
ределяемой как sup|Fn(x)— F(x |. Причина того, почему это
X
вообще возможно, устанавливается следующей леммой 1;
технические же детали сложны, и мы сформулируем оконча-
тельный результат без доказательства.
Лемма 1. Пусть g=g(x) — непрерывная строго моно-
тонная функция (хе/?1, g(x)eR'). Пусть £ и т) — случайные
величины с функциями распределения Ft(x) и Fn(x). Пусть
П*=£(П)- Тогда
sup |F(x) — F (х)| = sup |F »(х) — F .(x)|.
X x 4
Доказательство. F.,(x) - Fr,(x) = P|g*<x}— P{tj*<
<x)=PU(6Kx)- PU(t;)<x} - P($<g-'(x)}- Ph<£ -'(x)) -
= F.(g~l(x)) — Fn(^“’(x)). Следовательно, если sup|F_(x) —
Ffl(x)| Достигается на последовательности точек
п» 1, 2......то такое же значение |F_.(x) — Fr»(x)| дости-
гается на последовательности точек x=g(x„), л«1, 2, . . . .
Лемма доказана.
Замечание. Пусть случайная величина & имеет строго
монотонную и непрерывную функцию распределения Ft(x).
Тогда случайная величина Ft(%) имеет равномерное распре-
деление на отрезке [0, 1]. В самом деле, при хе[0, 1] сущест-
вует F~l (х) и
P{F^)<x} - Р{5<^’(х) - F?(F-«(x)) = х.
но функция х на отрезке [0, 1] есть функция распределения
равномерного закона.
111
Пусть теперь теоретическая функция распределения F(x)
строго монотонна (может быть, на полупрямой или отрезке)
и непрерывна. Пусть ..., хп — выборка. Образуем выбор-
ку У\, .... Уп, где yi=F(xi), теоретический закон которой —
равномерное распределение на отрезке [0, 1]. Заметим, что
расстояние между теоретической и выборочной функцией
распределения для выборки Хь .... хп такое же, как для вы-
борки yi...уп с равномерным законом. (Чтобы свести это
утверждение к лемме 1, заметим, что на эмпирическую функ-
цию распределения можно смотреть как на функцию распре-
деления случайной величины, принимающей значения
хь Хг, .... хп с вероятностью 1/п каждое.) Таким образом,
wn = sup | Fn( <) — ri x | есть случайная величина, распре-
X
деление которой не зависит от F(x): можно считать, на-
пример, что теоретическое распределение — это равномерный
закон на отрезке [0, 1]. Поэтому для распределения а/п может
быть (при каждом п.) составлена таблица. Более или менее
полные таблицы такого рода имеются, например, в сборниках
таблиц Л. Н. Большева н С. В. Смирнова [2] и Я. Янко [49].
Оказывается, что при л->оо, величина шп по порядку
величины составляет \l\fn. При этом распределение вели-
чины ]/п'шп « Уп sup ^„(х)—F(x)\ стремится к некоторому
предельному распределению, которое называется распре-
делением Колмогорова (этот результат получен А. Н. Кол-
могоровым в 1933 г.). Таблица функции распределения
Колмогорова имеется в сборниках таблиц (а пример при-
менения см. во второй части данной книги). Асимптотика
неплохо действует, начиная с п порядка нескольких де-
сятков.
В том случае, когда ожидается какое-то определенное тео-
ретическое распределение, например, нормальное, эмпири-
ческую функцию распределения интересно нарисовать в так
называемом нормальном масштабе. Могут быть два случая:
1) параметры нормального закона заранее известны; это бы-
вает редко; 2) параметры нормального закона заранее неиз-
вестны (это бывает чаще). В обоих случаях теоретическая
функция распределения имеет вид Ф((х—а)/а), где Ф —
функция Лапласа.
Если мы выберем по оси ординат такой масштаб, в кото-
ром функция распределения нормального закона при каких-
то значениях параметров а=а0 и о=оо изображается пря-
мой линией, то и при других значениях параметров функция
Ф((х—а)/а) тоже будет изображаться какой-то другой пря-
мой линией (из-за линейности замены переменной х при пе-
реходе от одних значений параметров к другим). Такой мас-
штаб и называется нормальным. Эмпирическая функция рас-
112
пределения будет представлять собой ступенчатую функцию,
которую можно неплохо сгладить прямой линией с помощью
прозрачной линейки.
Изображение эмпирической функции распределения (осо-
бенно в нормальном масштабе) представляет собой испытан-
ное на практике средство для снятия чувства отвращения к
числовым данным. При этом производится самая важная гла-
зомерная проверка нормальности; могут быть определены
графически и приблизительные значения параметров нор-
мального закона. Действительно, пусть Ф(х) — результат
глазомерного сглаживания; тогда Ф(х)~Ф((х—а)/о), где
апо — истинные значения параметров. Найдем по чертежу
точку х0, в которой Ф(х0) = 1/2. Тогда и Ф((х0—а)/о)«1/2,
откуда х0—а~0, т. е. а«х0. Далее, найдем точку хь в кото-
рой Ф(Х1)=0,84. Тогда (xt—х0)/а»1 (ибо Ф(1)=0,84 сог-
ласно таблицам нормального закона), откуда o»Xi—х0. Для
более точной оценки о найдем точку х_ь в которой Ф(х-1) =
=0,16. Тогда oftsfxi—X-t)/2. Таким образом, обычное иссле-
дование наблюдений с помощью так называемой «теории
ошибок» может быть сведено к изображению эмпирической
функции распределения в нормальном масштабе.
Более подробное описание этой техники с практическими
рекомендациями можно найти в книге А. Хальда [41]. Заме-
тим, что функция распределения Колмогорова относится к
различию между Fn(x) и Г(х); в случае нормального закона
/•’(’х) —Ф ((х—а)/о), где ано — истинные значения парамет-
ров. Нельзя вместо Ф((х—а)/а) употреблять Ф(х), так как
Ф(х) есть функция, подобранная по данной Fn(x), которая
гораздо ближе к Fn(x), чем теоретический закон Ф((х—а)/о)
(иными словами, нельзя вместо а и а вставлять их оценки,
полученные по наблюдениям, и при этом пользоваться пре-
дельным распределением Колмогорова).
Есть иной способ графического представления выборочно-
го закона распределения — с помощью так называемой гис-
тограммы. Ось значений х делится на некоторое число интер-
валов, и над каждым интервалом строится ступенька, высота
которой равна доле наблюдений {х,}, попавших в данный ин-
тервал (частоте). Частота попадания в интервал аппроксими-
рует соответствующую вероятность, которая является интег-
ралом (по данному интервалу) от плотности распределения.
При достаточно малом интервале (однако не настолько ма-
лом, чтобы в него попадало слишком мало наблюдений) и
учете единиц измерения частота похожа на плотность рас-
пределения. Диалектика, стоящая в скобках в последней
фразе, осложняет применение гистограммы. Во всяком слу-
чае, построение гистограммы осмысленно при нескольких де-
8—2567 из
сятках или сотнях наблюдений. В то же время построение
эмпирической функции распределения имеет смысл уже при
нескольких наблюдениях. Поэтому функция распределения
предпочтительнее, хотя при большом числе наблюдений гис-
тограмма тоже вполне приемлема.
3.2. Оценка параметров по выборке. Применение к методу
Монте-Карло. Средствами центральной предельной теоремы
мы могли бы оценить возможное различие между Fn(x) и
F(x) в данной точке х. Практический интерес представляет
sup |Fn(x) — F(x)i, но принципиальные и технические слож-
X
ности заставили нас привести соответствующий результат
А. Н. Колмогорова без вывода. Однако имеется ряд ста-
тистических вопросов, которые непосредственно являются
частными случаями центральной предельной теоремы.
3.2.1. Оценка математического ожидания и дисперсии. Па-
раметры теоретического закона распределения часто пред-
ставляют собой какие-то математические ожидания или свя-
заны с ними. Для определения выборочных (или эмпиричес-
ких) аналогов теоретических параметров обычно употребляет-
ся следующее правило: представим себе случайную величину,
принимающую значения хь х2, .... хп с вероятностями 1/п
каждое, и напишем для нее соответствующее математическое
ожидание. Например, теоретическое математическое ожида-
ние (или теоретическое среднее) дается формулой
er
e= JxdF(x) = Mx( для любого i— 1, ..., п. Его эмпири-
ческий аналог получится в виде математического ожидания
случайной величины со значениями Х\, х2, .... хп, принимаемы-
ми каждое с вероятностью 1/л: это среднее выборочное
г=т2х- <•>
/=1
Аналогично дисперсия o2=Dx,=M(x1—М х,)2 имеет эмпири-
ческий аналог (называемый эмпирической дисперсией S2), оп-
ределяемый следующим образом:
л п
5*=т S to-*)* = 7 2 (2>
z=l Z—I
(последнее равенство в (2) есть следствие общего соотноше-
ния Щ=М|2—(М£)2). Некоторые соображения (с которыми
мы вскоре познакомимся) заставляют употреблять чуть из-
мененный выборочный аналог дисперснн
114
= -Ц- У (х4-х")« = -2— S*. (3)
/г—1 Ав л—1
Аналогично если Л-м (теоретическим) моментом каждой
из случайных величин xt называется ак—!Лх*, то его вы*
1 п
борочный аналог есть afc= — 2 х}; если Л-м центральным
(теоретическим) моментом называется М(х,— Мх()*, то
его выборочный аналог есть — 2 (х( — х)* и т. д.
Если мы не знаем каких-либо теоретических параметров,
то надеемся узнать их приближенно с помощью их выбороч-
ных аналогов. Иначе это выражают, говоря, что выборочные
характеристики являются оценками соответствующих теоре-
тических. Хорошие оценки получаются лишь при большом
объеме выборки; понятно, что это свойство в какой-то мере
проявляется в следующем математическом определении:
оценка называется состоятельной, если при п —► оо ее значе-
ния сходятся по вероятности к истинному (теоретическому)
значению параметра.
Например, х—►св силу закона больших чисел.
Для того чтобы установить, что S2—*-о2, воспользуемся
следующей леммой.
Лемма. Пусть функция f(x, у) двух переменных непре-
рывна в точке х—а, у=Ь; пусть последовательности случай-
ных величин |п и т)п, л = 1, 2.сходятся по вероятности со-
ответственно к числам а и Ь. Тогда последовательность
f(ln. л»») —b) (по вероятности).
Действительно, пусть при lx—а|<6 и |у—а|<6 выполне-
но неравенство: \f(x, y)—f(a, &)|<s. Нужно доказать, что
P{lfUn. 1)»)~f(a’ при любом 8>0. Но событие
{I/Un. Лп)—f(a> &)1^е} может произойти, если выполняется
хотя бы одно из событий: l|n—al >6 или |т)п—Ы>6. Однако
вероятность любого из последних двух событий стремится к
нулю по условию леммы. Но тогда и P{lfUn. т]п)—f(a> Ь)1>
—► 0, что и требовалось доказать.
Пусть теперь существует Мху. Тогда - но
теореме Хинчина, а в целом правая часть (2) есть функ-
— 2 х?, х I, если положить G(x, у)=х—у*. Функция
п /
8*
115
G(x, у} непрерывна во всех точках; поэтому —
— (Mxi)1 — а’ в силу леммы.
Конечно и «’-нт1 (нужно применить лемму к функции
Н(х, у) = ху, положить £я = —->|, Tin = S’).
/1—1
Можно доказать (предполагая, что №х\ существует)
сходимость aft->efc и т. д.
Разберем теперь, чем вызвано применение s2 вместо S2.
Полезным свойством оценки является несмещенность: оценка
называется несмещенной, если ее математическое ожидание
равно теоретическому значению параметра. (Если это свой-
ство выполнено, то, пользуясь оценкой много раз, мы не бу-
дем систематически завышать или занижать истинные значе-
ния параметра.) Вычислим (считая, очевидно, без ограниче-
ния общности, что №xt=a=0, следовательно, D.r,=Mx'=o2)
математическое ожидание MS2:
п
М$« = Мх? — М(х)’ = о« — - V Мх{х;=а’/1—
п* \ п I
I. /=.! \ /
(использовано соотношение: МХ|Х/=Мх,Мх;=0, если i^j>
в силу независимости Xi и X/ — такова ведь модель выборки).
Таким образом, переход от S2 к s2 связан с желанием
обеспечить несмещенность: Ms2=o2 для оценки дисперсии.
Замечание. Конечно, оценкой среднеквадратического
уклонения о будет VS2 либо Vs2. Обе эти оценки, вообще го-
вцря, смещенные, но их нельзя поправить, не зная закона
распределения F(x) = P{xi<.x}. Оценку же для о2 поправить
можно; это и используется в статистике. Смещение составля-
ет величину порядка 1/п; можно выяснить, что случайные от-
клонения S2 (или s2) от о2 имеют величину порядка 1/Vn, так
что поправка существенна лишь при совместной обработке
многих оценок дисперсии (когда детерминированное смеще-
ние может каким-то способом проявляться).
Замечание о вычислениях. Многие думают, что
арифметические вычисления S2 нужно производить по второй
из формул (2). Для ЭВМ это все равно; при ручных же вы-
числениях ни в коем случае: только по первой. Иначе нужно
удерживать слишком большое количество значащих цифр.
Такой замечательный вычислитель, как П. Л. Чебышев, при
обработке данных Г. Кавендиша о плотности Земли, произво-
дя вычисления по второй формуле («Опыт элементарного
анализа теории вероятностей», самый конец работы), удер-
жал-такн не вполне достаточное число значащих цифр в
Sx//n (при всего п=29 наблюдениях).
116
Посмотрим теперь, насколько х может отличаться от а
при не очень большом п (достаточном, однако, для действия
центральной предельной теоремы). Имеем
~ „ S*i — па ®»Z . — па
х —а ----------- — , s =-----------.
« /Й • /й
Следовательно,
Р||х-а|>е|-Р
/я
~2Ф f—— У
\ 9 /
Это соотношение, вытекающее из центральной предельной
теоремы, давало бы нам исчерпывающую характеристику воз-
можных отклонений х от а, если бы нам было известно а. Дей-
ствительно, из таблиц нормального закона можно узнать, на-
пример, что 2Ф(—1,96) =0,05. Если (при данном п)_ опреде-
лить 8 из соотношения eVn/o=l,96, т. е. s=l,96o/Vn, полу-
чим, что
Р{х —8<а<х 4-е) = 0,95. (4)
Таким образом, интервал [х—е, x+s] со случайными (за-
висящими от наблюдений) концами ловит неизвестное значе-
ние параметра а с вероятностью 0,95; такой интервал назы-
вается доверительным интервалом для параметра а с коэф-
фициентом доверия 0,95.
Можно, наоборот, заранее задать s и спросить, каким дол-
жно быть число наблюдений п, чтобы выполнялось (4) (от-
вет: таким, чтобы sVn/a=l,96).
Но на практике о, как правило, неизвестно. (Это странно:
если Xi — измерения, то, казалось бы, можно было бы из ана-
логичных измерений определить а и записать его в паспорт
прибора. Такие попытки не дают, однако, устойчивых значе-
ний а.) Сложилась концепция, согласно которой а определя-
ется из тех же наблюдений xi (путем любой из оценок Sus).
Если теперь поставить вопрос о точности, с которой опре-
делено о, то придется исследовать формулу (2); дисперсия
S2 выразится через четвертые моменты MxJ. При оценке чет-
вертых моментов точность их определения выразится через
шестые и восьмые и т. д. Нужно волевым образом оборвать
эту незамкнутую цепочку, и на практике вставляют вместо о
его оценку s на правах точного значения. Это, в общем, оп-
равдано следующими соображениями. Коэффициент доверия
0,95 в формуле (4) назначен достаточно произвольно. Если
117
вместо 0,95 назначить 0,99, то вместо 1,96 будет 2,58, т. е. 8
увеличится на 32%. Но уже при п порядка нескольких десят-
ков точность определения о по s будет заметно выше, чем
30%, т. е. ошибка, связанная с заменой а на s, малосущест-
венна.
О практических результатах, связанных с применением
понятия доверительного интервала, см. подробнее во второй
части данной книги.
3.2.2. Применение к методу Монте-Карло- Рассмотрим вы-
числение многомерного интеграла
1 1
/== J f .... xn)<*xt . . . dxn.
о о
Вычислять его с помощью каких-то приближенных квадра-
турных формул довольно безнадежно, так как каждой из пе-
ременных Xi, .... хп надо дать хотя бы десяток различных
значений, а тогда всего будет 10" различных точек сетки, что
при п порядка нескольких десятков исключает всякую воз-
можность счета. Предположим, что мы умеем моделировать
случайные числа, принимающие значения на [0, 1] с равно-
мерным распределением и независимые друг от друга (реше-
на проблема датчика случайных чисел). Если £=(ti....|п)—
набор п таких одномерных случайных чисел, то £ имеет рав-
номерное распределение на n-мерном единичном кубе. Но
тогда /=М/(|). Реализуя случайный вектор £ N раз:
£(1), ..., |(-V) и образуя выборку
х,=/(?<«).......
для чего нужно лишь уметь вычислять значения функции f,
получаем уже рассмотренную задачу оценки математического
ожидания по выборке.
На самом деле, проблема датчика случайных чисел не ре-
шена. Со случайными числами происходило всякое. Напри-
мер, долгое время во всем мире использовались такие «слу-
чайные» числа, что линейная комбинация любых последова-
тельных трех из них с небольшими целочисленными коэффи-
циентами равнялась нулю (и никто этого не замечал). Одна-
ко экспериментальная проверка действия статистической
оценки точности счета, изложенной в предыдущем пункте
(на интегралах с известным ответом), вроде бы приводит к
выводу, что она, в общем, действует; автор книги имел слу-
чай убедиться в этом на собственном опыте (правда, на срав-
нительно очень простых интегралах).
3.2.3. Оценка вероятности по частоте. Рассмотрим вопрос
о том, насколько может отклониться частота успеха в п ис-
пытаниях Бернулли от вероятности успеха р. Для числа успе-
хов дисперсия Dp=np<7; для частоты Л=ц/п тогда Dft=
118
—РЧ/п. Отклонение Л—р_составит величину порядка lpq/n,
причем отклонение „а 2УD/i маловероятно, а на ЗУВЛ почти
невозможно.
Теперь рассмотрим численный пример. Известно, что зна-
менитый американский статистик начала XX в. К- Пирсон
бросил монету «=24000раз, причем герб выпал р= 12012 раз.
Отклонение ц—п/2=12, среднеквадратическое отклонение
)бц=77,5.
Если бы 1ц—п/21 было существенно больше, чем 77,5, то
это можно было бы объяснить несовершенством формы мо-
неты, несовершенством метода ее бросания, на худой конец,
ошибками в подсчете гербов (каждый, кто бросит монету хо-
тя бы 20 раз, поймет, что подсчет результатов и есть един-
ственная трудность этого опыта). Но отклонение, много мень-
шее, чем теоретически ожидаемое, автоматически наводит на
мысль о подтасовке результатов опыта. Итак, в отношении
опыта К. Пирсона возникает нехорошее подозрение. Для про-
верки этого подозрения вычислим
< / t V I
= Ф(0,155) — Ф(—0.155)« 0,124 « 1 /8.
К. Пирсон реабилитирован: он не подделывал результаты.
Могло же повезти великому человеку настолько, что произо-
шло приятаое для него событие, вероятность которого 1/8.
Тем более что на самом деле было так: сначала Пирсон бро-
сил монету 6000 раз, но результат ему не понравился. Тогда
он бросил ее еще 6000 раз и опять не понравилось. Пришлось
бросить монету еще 12000 раз, и результат (всех бросаний)
оказался замечательным.
3.2.4. Проверка гипотез о математическом ожидании.
Центральная предельная теорема позволяет проверять гипо-
тезы о математическом ожидании по выборке. Пусть, напри-
мер, для измерения некоторой физической величины предло-
жено два метода. Первым методом получены наблюдения
Х\, х2, ..., хт, вторым методом — уь у2, ..., уп. Мы не можем
гарантировать чисто статистическими методами отсутствие
систематической ошибки: возможно, что Мх,-=/=а и Му/=#о,
где а — истинное значение измеряемой величины. Но мы мо-
жем проверить равенство Мх,=Му/, и если оно имеет место,
то будем склонны считать, что оба метода не дают система-
тической ошибки (так как с чего бы двум разным методам
давать одну и ту же систематическую ошибку?). Итак, пусть
гипотеза Н состоит в том, что Мх,=Му/.
Естественно, что критическая область должна иметь
вид {|х— у1->Л), и для выбора А по заданному уровню
119
значимости а нужно уметь вычислять вероятность попа-
дания в критическую область. Но х имеет нормальное
распределение с дисперсией о’//п, у —с дисперсией а2/п,
где о’ и о’— теоретические дисперсии двух выборок. Ес-
тественно предположить, что xv . . . , хт и yv . . . , уп не-
зависимы, тогда независимы и х и у. При верной гипоте-
зе И имеем Мх=Му. Следовательно, разность х — у
имеет нормальное распределение с нулевым средним и
дисперсией в’/л»4-о’/л. В таком случае статистика (статис-
тикой называется любая функция от выборочных значе-
ний)
(х — у}{а*1т 4-0у/п)_,/’
имеет распределение 2V(0, 1), из_чего и вытекает способ
вычисления вероятностей Р{|х— j/| > А}: нужно одновре-
менно |х — у\ н А умножить на число (вх/т + ау/п)~,'г и
воспользоваться стандартными таблицами нормального
закона.
На практике (при числе наблюдений в каждой выбор-
ке порядка нескольких десятков или более) заменяют не-
известные о’ и о’ выборочными аналогами s’ и s’.
Нетрудно прикинуть, какой величины должно быть раз-
личие между средними Мх, и !Лу/, чтобы его можно было об-
наружить, — порядка двух-трех величин
3.3. Метод наименьших квадратов. В данном пункте пред-
положим, что распределение каждой измеряемой величины в
точности нормальное. В этом предположении разберем так
называемую общую линейную модель, охватывающую боль-
шое количество частных случаев.
3.3.1. Общая линейная модель. Обобщим модель выборки
следующим образом. Пусть наблюдения х<, i=l,...,n, имеют
вид xi=ai+6i, где а, — некоторые (неизвестные, подлежа-
щие оценке) неслучайные величины — параметры модели;
б, — независимые случайные величины, имеющие каждая
распределение N(0, о), причем неизвестное о не зависит от
I. (Классический метод наименьших квадратов допускает
так называемые веса наблюдений; это означает, что Dd-=
=a2/wit где о’ неизвестно, a wt — известные числа, называе-
мые весами наблюдений. Веса наблюдений могут, например,
возникнуть в том случае, когда каждое х,- есть среднее иэ
wt наблюдений. Однако умножением наблюдений xi на
общий случай сводится к случаю равных весов tO|=o,';=...
... =и»п=1.)
Основное предположение состоит в том, что
120
a=(ah a2,an)(=L,
где L — некоторое известное линейное подпространство (слу-
чай, когда L — линейное многообразие, т. е. имеет вид L=
=Lq+oo, где Lq — подпространство, а0 — вектор, сводится к
случаю многообразия вычитанием из всех наблюдений компо-
нент вектора ао).
Разберем примеры общей линейной модели.
1. Пусть а,, аг, а, — углы плоского треугольника; xv
х2, хя — их измерения (допустим, не имеющие системати-
ческой ошибки). Тогда xi=al+6l, где —ошибка i-ro из-
мерения. Должно, однако, выполняться равенство at+at+
4- а, «= it. Вопрос состоит в том, чтобы использовать эту
информацию для некоторого улучшения наблюдений xlt
хг, х,: за приблизительные значения углов треугольника
нужно взять некоторые другие значения xj, х', х3, такие,
что х' 4 х' 4- х3 — я; хорошо бы, чтобы значения xj, х', х3
были (в каком-то среднем смысле) ближе к истинным
значениям av at, а3, чем первоначальные измерения хр
х2, хэ.
Такая задача называется задачей уравнивания измерений.
При триангуляциях в геодезии задача уравнивания относится
к целой сети треугольников, углы которых измеряются с
ошибками. Впрочем, применимость модели со случайными,
независимыми и одинаково распределенными ошибками на-
блюдений в геодезии достаточно сомнительна. Сомнительны,
следовательно, и узаконенные методы уравнивания.
2. Пусть имеются два груза at, а2, которые хотим точно
взвесить. Сначала кладем их на весы поодиночке и получаем
результаты х> и х2, а затем взвешиваем оба груза на одной
чашке весов (результат х3) н, наконец, кладем их на разные
чашки весов и уравновешиваем весом гирь х< Если а,=Мх/,
то, очевидно, должны выполняться линейные соотношения
Оз=О1 + О2, —О2.
Возникает некоторая задача уравнивания измерений.
3. Если xt. хп образуют выборку, at=^Xi, то выполня-
ются линейные соотношения
01=02=... =an=a=Mx;.
4. Пусть известно, что длина некоторого тела / линейно
(а возможно, что и квадратично) зависит от его температу-
ры t. Придадим в опыте t значения tb t2, ..., tn (некоторые
из которых могут быть равными между собой); пусть эти зна-
чения выдерживаются достаточно точно, но соответствующие
длины k измеряются с ошибками б,. Нужно найти темпера-
турный коэффициент расширения тела и проверить гипотезу
о линейной зависимости длины от температуры.
121
Математическая модель наблюдений выглядит так:
Xi - x(tt) — а9 + a^i + + 6f,
где б, — ошибка i-ro наблюдения длины (причем неизвестно,
отличен лн от нуля коэффициент аг).
Образуем векторы x = (xi« . . ., хп), Г° = (1, 1, .... 1),
Т1- (tvit.... tn), t2, ... , t2). Тогда вектор Их
математических ожиданий (считается, что М8(=0) компо-
нент вектора наблюдений х имеет вид
Мх = а0Г° + а1Г1 +
т. е. лежит в известном подпространстве L (линейной оболоч-
ке векторов Т°, Т', Т2). Мы вновь сталкиваемся с линейной
гипотезой. Данная задача называется задачей сглаживания
наблюдений х>, .... хп с помощью многочлена. Нужно найти
оценки неизвестных коэффициентов а0, at, а2 и решить, дос-
таточно ли велико значение а2, чтобы надо было признать,
что имеется квадратичная зависимость длины от температу-
ры.
5. Пусть поле разбито на делянки, каждая из которых за-
нумерована парой индексов (i, j), i=l, .... I, j=l, .... /, та-
ким же образом, как элементы прямоугольной матрицы.
Пусть на делянке (i, j) посеян i-й сорт некоторой культуры и
применен /-й вариант удобрения; хц — урожайность на
(i, /)-й делянке. Предполагается, что Мх,7=а,+Ь/, где а< —
средняя урожайность i-ro сорта, Ь, — средняя прибавка уро-
жая при /-м варианте удобрения (одинаковая для всех сор-
тов). Не исключается, что все Ь/=0 (удобрения неэффектив-
ны). Требуется проверить эту последнюю гипотезу. Эта зада-
ча называется задачей дисперсионного анализа. Здесь в ли-
нейном пространстве размерности II выделяется линейное
подпространство L размерности 1+J векторов {с,/} с коорди-
натами Сц вида Cij==ai+bj, в котором лежат Mr,,-. Предпо-
лагается, конечно, что Х1,=!Лхц+Ъц, где б,/ независимы и
имеют каждая распределение N(0, о). Вновь получаем част-
ный случай линейной модели.
После этих примеров наблюдений, которые могут быть
описаны линейной моделью, переходим к описанию общих
принципов обработки подобных наблюдений.
3.3.2. Метод максимума правдоподобия. Принцип (или
метод) максимума правдоподобия впервые сформулирован
Гауссом. Он заключается в следующем. Пусть распределение
вероятностей каких-то наблюдений Х|. х2, .... хп зависит от на-
бора параметров a=(at, а2, ..., ат). Иными словами, совмест-
ная плотность имеет вид
р(хь х2,..., хп; ах, а2. .... ат)—р(х, а).
(122
Замечание. Сложившаяся традиция обозначать наблю-
дения х\, х2. .... хп приводит к тому, что и случайные величи-
ны и переменные интегрирования в выражении для плотно-
сти распределения в математической статистике обозначают-
ся одинаково. Читатель должен учитывать возможность по-
добных загадок.
Пусть в опыте получены значения xit ..., хп и нужно оце-
нить а=(а\, .... ат). Рассмотрим р(х; а) при данных xit ...,хп
(полученных в опыте) как функцию от а. Такая функция на-
зывается функцией правдоподобия. Принцип Гаусса состоит
в том, чтобы за оценку а взять такой набор значений пара-
метров а=(аь .... а,п), который дает максимум функции прав-
доподобия.
Принцип максимума правдоподобия оказался удивительно
удачным. С его помощью найдено большое количество оценок
параметров в конкретных ситуациях. Доказан ряд его полез-
ных свойств (правда, не в столь общей ситуации, в какой мы
сформулировали этот принцип: в нашей формулировке нет,
например, никакой независимости наблюдений (xit .... хп) —
может быть, это всего одно наблюдение, повторенное п раз;
тогда, конечно, нет речи о хороших свойствах). Ограничимся
тем. что применим этот принцип к линейной модели.
Итак, пусть x1=aJ4-8i, 8(~jV(O, 6), a = (ap . . . , a„)Gi,
L — известное подпространство. В силу независимости х(
/ 1\
\ о)'2ж/

р(х; л) - П Р(х^ ад
i—l
ехр
= С еХр [~ 2* (А'“ Х“в)(
При известном x=(xv .... хп), очевидно, р(х; а) обра-
щается в максимум при таком а, при котором (х — а, х — а)
—»min. Иными словами, поскольку a&L,
a = projLx. (1)
Но x=a-|-8, где 8«(8lt . . . , 8П). Следовательно,
a=a+projL8. (2)
В общей форме применение метода максимума правдопо-
добия к линейной модели абсолютно просто: (1) дает реше-
ние задачи об оценках параметров, а (2) разницу между ис-
тинным значением а набора параметров и оценкой а: а—а=
= projL6. Этот ответ был бы совершенно достаточным, если
бы мы полностью знали распределение 6; однако мы его зна-
ем лишь с точностью до параметра o2=D6,. Нужно как-то
123
оценить параметр о2 и сделать определенные выводы о рас-
пределении вероятностей разности и—а. В полном объеме это
было сделано в начале XX в. Гаусс довольствовался прибли-
женным решением.
3.3.3. Статистическое исследование решения.
Лемма. Пусть U — ортогональное преобразование. Рас-
пределение вектора S'=U6 совпадает с распределением век-
тора 6 (иными словами, распределение б сферически инваров-
ант но).
Действительно, плотность распределения вектора б есть
Ръ(х) = ......хп) =
= П expl——Ц » /—!—ехр|----------— (х, х)1.
I 2o*J I 2o* I
Согласно формуле преобразования плотности распределе-
ния при замене переменных, плотность распределения 3'
получится, если взять р6(х) в точке x = Uy~l (но (Uy~l,
У)) и разделить ее на модуль соответствующего
якобиана (но он равен 1). Лемма доказана.
Следствие. Распределение projLб зависит лишь от
размерности dim£. Если LjiL,, то projL 3 и projL б —не-
зависимые случайные величины.
Действительно, в силу леммы можно считать, что 6
записывается в таком ортонормированием базисе, что
(для первой части следствия) первые dim L векторов это-
го базиса образуют базис в L; либо (для второй части
следствия), что первые dimLj+dimL» векторов базиса об-
разуют базис в LtQ Lt. В первом случае projL 3=(бь 68,...
..., 3din) L) полностью определяется dim L. Во втором слу-
чае projLi б — (Bj, Oj, . . . , Odim L,) И proj^ О = (Odim L,+b • • •
.. . , 6dimLn-dim l,) суть векторы, составленные из незави-
симых компонент; следовательно, независимые случайные
величины. Следствие доказано.
Теперь дадим оценку о2. Рассмотрим так называемый век-
тор кажущихся ошибок наблюдений
х — а = х—proji х = б — pro jL 3 = pro ji' б,
где L' — ортогональное дополнение к L. (Название обра-
зовалось вот как: х—а — вектор ошибок наблюдений; а
нам неизвестно, мы заменяем его на .кажущийся* вектор
параметров а; тогда естественно сказать, что компоненты
вектора х — а суть .кажущиеся* ошибки.) Рассмотрим
квадрат длины вектора ||х — а|р = ЦхЦ* — ||а||2 (теорема Пи-
124
фагора), причем ||х — а||* = ||proj’l-б||*. В силу следствия к
лемме распределение вероятностей последней величины
*
совпадает с распределением 2 гДе " d*m L' ~п ~~
»=t
—dimL. Но каждая величина 8, может быть представле-
на в виде 8( — 8£о где , £п — независимые нормаль-
ные М(0, 1) величины. Итак,
«—i
где у2— случайная величина, имеющая распределение
хи-квадрат с k степенями свободы.
Если k достаточно велико, то (в силу закона боль-
ft
тих чисел) есть примерно k— 2 (Нетрудно подсчи-
<=1
тать, что (М^)’=2.) Поэтому оценкой для о*
является величина
-J-Ik—«11*.
к
Этим результатом пользовался Гаусс. В XX в. были рассчи-
таны таблицы распределения хи-квадрат. С помощью них
легко для данного небольшого числа а найти такие числа а
а А, что
Р{х2<а}=х/^ И P(xJ>A}=a/2. Тогда P{a<x2<A}=l-а.
Подставим в последнее выражение величину ||х—аЦ2^2,
имеющую распределение у». Получим
Решая неравенство, стоящее под знаком вероятности,
относительно неизвестного параметра а*, получаем
Р{||х - а||2|А < о» < ||х - a||2|a} - 1 - a,
что дает доверительный интервал для о2.
При малом k этот интеграл получается широким; при
большом k — узким. Действительно, в силу центральной
предельной теоремы распределение х* при большом k
аппроксимируется нормальным N(k, y'Sk), так что числа
А и а, имея порядок величины k, отличаются друг от
125
друга на величину порядка Vk, т. е. отношение Л/а
близко к 1.
Теперь рассмотрим так называемую „стыодентпзацию
(прием, связанный с псевдонимом „Student* английского
статистика Госсета). Нас интересует случайная величина
a — a = projL8. Ее распределение известно нам с точнос-
тью до параметра о (который входит линейным множи-
телем в компоненты вектора 8). Если мы разделим
а—а на какую-нибудь случайную величину, в которую
тоже входит линейным множителем о, то а сократится
и получится случайная величина, распределение которой
не зависит от неизвестного параметра. В качестве знаме-
нателя удобно взять а =|И|х — а||*/Л — • Получим
выражение (а— а)/о, в котором числитель и знамена-
тель— независимые случайные величины (числитель есть
проекция S на L, а знаменатель есть функция от проек-
ции б на L', ортогональное к £'): распределение этого
отношения не зависит от о.
Последнее выражение рассматривают либо по компо-
нентам а(—а4 вектора а—а, либо в смысле квадрата дли-
ны ||а — а||2/оа.
Для рассмотрения по компонентам служит так называе-
мое «распределение Стьюдента».
Определение. Пусть £ — случайная величина с рас-
пределением Af(O, 1); — независимая от £ случайная ве-
личина, имеющая распределение хи-квадрат с k степенями
свободы. Распределением Стьюдента с k степенями свободы
называется распределение частного
Переходя к рассмотрению компонент а,—а,= (proji.6),-,
мы должны теперь сказать, какой выбран базнс в L. Проще
всего, если этот базис — ортонормированный. Тогда все
а,—at (при различных i) независимы, имеют распределение
N (0, о) и каждое отношение случайных величин (а,—а,)/о
имеет распределение (ft=dimZ/=n—dim L). Отсюда легко
написать доверительные интервалы для а,-.
Но в конкретной задаче ортонормированный базис может
оказаться нефизичным (ниже скажем об этом подробнее). В
любом случае а,-—а,- есть линейная комбинация величин
б|... 6п, а следовательно, имеет нормальное распределение
N(0, о,), где а> пропорционально о (гарантирована также неза-
висимость а,-—а, от о). Следует подсчитать в зависимости от
конкретного выбранного в L базиса, чему равняется о„ и до-
126
бавить такой постоянный множитель с„ чтобы дисперсия
с,(а,—а,) равнялась а. Тогда сДа/—а,)/о вновь имеет рас-
пределение Стьюдента. Однако при разных i получаем, вооб-
ще говоря, зависимые величины.
Теперь рассмотрим квадрат длины На—alP/o2.
Определение. Пусть хт и х « — две независимые слу-
чайные величины, имеющие каждая распределение хи-квад-
рат, соответственно с т и п степенями свободы. Распределе-
нием Фишера с (т, п) степенями свободы называется рас-
пределение частного
F 1 I у 2
* т. п — — I ““
т п
Рассмотрим (не зависящее от выбора базиса в L) выражение
1
dim L
Оно, очевидно, имеет распределение Фишера FatmL. n-dimr..
Отсюда легко написать доверительную область для а, имею-
щую вид шара, лежащего в L.
Продолжим теперь разбор некоторых примеров, связан-
ных с общей линейной моделью. Ограничимся случаем вы-
борки и сглаживания наблюдений.
3.3.4. Выборка. Соответствующее линейное пространство
L={(ab ..., an):ai= ... =ап}
одномерно; базис в нем состоит из одного вектора е=
= (1/Ул...... l/Ул). Проекция вектора наблюдений х—
= (х],.... хп) на L имеет вид
projL х = (х, е)е
- (*..........*).
т. е. оценкой математического ожидания а=Мх,- является х.
Далее,
Цх—projLx||3=Z(x/—х)2= (л—l)s8
не зависит от х и имеет распределение o’xn-t (°* “ Dx().
Вектор (а, а, . . . , а) имеет вид а\/~п (1/}/лГ,..., 1/р5Г) —
= а|/л~е. Поэтому распределение Стьюдента /л~1 будет
иметь отношение разности ^xiVn—aj/n = (х—а)
к s = а. Впрочем, и без соображений, связанных с проек»
<27
циями, ясно, что Уп (х — а) имеет нормальное распреде-
ление N(0, а). Итак,
/я_1 =-]/л (х — a)/s
имеет распределение Стьюдента с п—1 степенями свободы.
Отсюда обычным путем можно получить доверительный ин-
тервал для а.
Замечание. Стьюдентовская теория справедлива лишь
в том случае, когда распределение элементов выборки {х(}
нормальное. Оно действует при любом объеме выборки п^2.
Если не предполагать нормального распределения х,-# то воз-
можна лишь асимптотическая теория для больших п, осно-
ванная на центральной предельной теореме.
Любопытно, что стьюдентовский вариант сравнения мате-
матических ожиданий двух выборок xi,...,xm и у\..уп воз-
можен лишь в предположении Ох=оу=о. Он состоит в сле-
дующем. _ _
Если то разность х—у имеет (при независи-
мости _хь .... хт _н у\, уп) нормальное распределение;
М(х—у)=0, D(x—y)=c2(\/m+\/n). Оценки дисперсии sj
и s* независимы; следовательно, сумма
(т — 1)«ж + (п - 1)«у = — i)2 + S [tjj — £)2
имеет распределение a,Xm4-4_2. При этом совместное расп-
— — 2 1
ределение л, yt sXi sy есть распределение четырех незави-
симых случайных величин. Отсюда вытекает, что дробь
(х — у)/]/ l/m+1/n
2 = —
V [(« — +(«- 1 )«*]/(« + п -2)
имеет распределение Стьюдента с т + п—2 степенями свобо-
ды.
С помощью таблиц распределения Стьюдента обычным
путем назначается критическая область для проверки гипоте-
зы ТЛх1=Му/.
Если ах=/=ау, то стьюдентовского варианта сравнения ма-
тематических ожиданий не существует.
Сравнение таблиц распределения Стьюдента с таблицами
нормального закона показывает, что при малом числе степе-
ней свободы k распределение tk «шире» нормального (это оз-
начает, что если, например, для случайной величины В, под-
чиняющейся закону Af(O, 1), имеем: Р{|£|<Л)=р, то для ве-
личины tn обязательнр.Р{(/»|<Л}<р). Следовательно,довери-
тельные интервалы, построенные с помощью распределения
Стьюдента, будут шире, чем построенные с помощью нор-
428
мального распределения (так учитывается несовпадение оцен-
ки дисперсии s2 с истинной дисперсией о2). При k порядка30
и более различие делается ничтожным.
3.3.5. Сглаживание наблюдений. Общая линейная модель
может быть не вполне адекватной задаче сглаживания на-
блюдений многочленом. Так, в примере 4 п. 3.3.1 коэффици-
енты а0, аь а2 многочлена x(t) имеют четкий физический
смысл: а0 — длина тела при /=0, а( — коэффициент линей-
ного расширения, а2 — возможная поправка на нелинейность.
Между тем с точки зрения линейной модели все равно, ка-
кой базис выбрать в L (т. е. все равно, какие линейные ком-
бинации коэффициентов а0, at, а2 считать подлежащими оп-
ределению). Но мы рассмотрим задачу сглаживания наблю-
дений, считая, что интересен лишь результат сглаживания.
Для начала пусть известна степень k многочлена, которым
мы собираемся сгладить наблюдения. Итак, пусть
xi = X(G) e = а0 + aitj +...-}- akti +
где 6{ независимы и имеют нормальное распределение
N(Q, о). Вводя векторы х = (хр xlt..., хп), Г*=(1, 1,..., 1),
Г1 =» (fx, tt, ... , tn), . . . , Tk = (ti, t2, ... , tn) и считая, что
векторы Т°, Т1, . . . , Тк линейно независимы, сведем за-
дачу к проектированию х на линейную оболочку L век-
торов Т9, Т1, . . . , Тк. При этом оценки коэффициентов
а0, ai> • • • > ак определяются из условия
projLx=a0T° + a1T1 + . . . +а]сТк,
что эквивалентно условиям ортогональности разности
k
х — 3 aiT1 к любому Т1, /«=0, 1, ...» Л. Из условий
>-о
ортогональности получаем для определения а0, аи..„ а*
систему уравнений
k
3 £4(Т', Т') = (х, TJ), j = 0, 1, . . . , k.
i=l
Квадрат нормы
позволит описанным выше образом оценить дисперсию
наблюдений.
Остановимся теперь на вопросе о выборе степени k сгла-
живающего многочлена. Чем ниже степень многочлена, тем
больше результат сглаживания освобождается от случайных
ошибок. Поэтому стараются пробовать малые значения
6=0, 1, 2, .... переходя к каждому большему значению толь-
ко при явной необходимости. Сформулируем процедуру ста-
тистической проверки гипотезы, предназначенную для выяс-
9—2567 129
нения того, есть ли такая необходимость. Сначала мы берем
значение k—kt, затем значение k=k2 и смотрим, нужно ли
отказаться от k\ в пользу k2>kt.
Мы собираемся решить этот вопрос на основании сумм
квадратов кажущихся ошибок Д? н Д2, отвечающих значени-
ям kt и k2 (или линейным подпространствам соответственно
Li<zL2). Всегда будет Д?<Д1. Поставим вопрос о том, как
проверить гипотезу о статистически значимом уменьшении
До по сравнению с Д i.
Для преобразования распределения разности Д?—Д2 к ка-
кой-то величине с известным распределением нужно исклю-
чить неизвестную дисперсию наблюдений о2. Сделаем это с
помощью предположения, состоящего в том, что вектор
Мх= (Мхь .... Мхп) заведомо лежит в L2, т. е. что степень
k2 заведомо достаточна. Проверим при этом предположении
гипотезу Н: Мх^ЦаЦ.
Если М* е L±, то proji, х—projL, х = projt' x = projt<
где Li — ортогональное дополнение Lt в Lt. Следователь-
но,
Д2 - Д’ = llprojL. X — projt, x||’ = ||projL- 6||*
имеет распределение о2/?*,-*,) (так как k2—kt = dim£i). Эта
величина не зависит от о2 =—-—||х — projL,х||2. Таким об-
п — kt
разом, при верной гипотезе Н отношение
°2
имеет распределение Фишера с указанным числом степеней
свободы. Проверка гипотезы Н сводится к проверке того, не
является ли значение статистики (1) значимо большим с точ-
ки зрения указанного распределения Фишера.
Пример. Рассмотрим задачу сглаживания наблюдений
Xi, х2, хп прямой, т. е. модель
Xi=a0+aiti+6i.
Ортогонализуем систему векторов Т°=(1, .... 1) и Т* =
•••> tn)-
Получим систему и T=(t\—1, tn—i), где 7==
=SA/n, и модель вида
x=b0T°+ bi Т+6, bi=at- (2)
Очевидно, Ь0=х,
130
ь =»(Х,Г) — (x —хТ», г) _ — -~t)
1 = (Г,Г)“ (Г, Г)
Поставим вопрос о том, значимо ли отличается
от нуля (этот вопрос интерпретируется как вопрос
о наличии связи между значениями xt и если
можно принять bt = 0, то значения xt не зависят от ^).
В силу ортогональности Т° и Г из (2) получаем —
— (8, Т)/(Т, ТУ, следовательно, разность — Ь1 имеет нор-
мальное распределение, причем м(бх — bj = О, — bj =
= &КТ, Т).
Сумма квадратов кажущихся ошибок
Д’ = 2 fa - х — b^t] — t) )2
имеет распределение а2/п-2- Поэтому статистика
‘n-2 , — (’J/
/д«/(п- 2)
имеет распределение Стьюдента с п—2 степенями свободы.
Проверка гипотезы t»i=0 сводится к вычислению левой
части (3) при Ь]=0 и определению того, не является ли по-
лученное число значимо большим (по модулю) с точки зре-
ния распределения /п-2-
Для того чтобы сравнить полученный результат с резуль-
татом, который вытекает из другой статистической модели —
модели зависимых случайных величин (ее мы рассмотрим в
следующей главе), запишем его в других обозначениях. По-
ложим
= “ *,2; s'= dr S ~
stx = —Ц- V (*< - х)(*1 — t).
П — 1
Выборочным коэффициентом корреляции называется отно-
шение
г = stx / sxsi — St.J(sjcst)‘
В данных обозначениях bi=rsx/st, (Т, Т) = (п— 1)$?,
А* = 2 (х, - х)2 - Ьг1(Т, Т) = (п — l)[s* - г’&гМ =
= (л — 1)«х(1 — Г*).
9*
131
Поэтому при Ь|=0 дробь (3) превращается в выражение
Мы нашли преобразование, приводящее случайную величину
г к случайной величине tn-2 с известным распределением. От-
вергаем гипотезу об отсутствии связи между xt н Л, если зна-
чение величины (4) слишком велико по абсолютной величи-
не.
В точности такое же правило получается (как увидим в
следующей главе) при проверке наличия зависимости между
компонентами двумерного нормального распределенного век-
тора. Не следует, однако, смешивать эти модели: в модели
метода наименьших квадратов теснота связи между и ti
измеряется дисперсией случайной добавки D6“=o2. При на-
личии хоть какой-нибудь связи (,bi=#0, но сколь угодно мало)
высокий коэффициент корреляции г может быть получен за
счет произвольного расширения интервала, на котором бе-
рутся (по нашему выбору) значения независимой переменной
fi. ts. tn- Следовательно, близкое ±1 значение г может
быть следствием выбора очень широкого интервала для из-
менения t.
В модели с двумерной случайной величиной разброс зна-
чений каждой компоненты не в нашей власти: что уж прине-
сет случайный эксперимент. В этой модели близкое к ±1
значение г с большим основанием указывает на тесноту свя-
зи между компонентами.
Замечание. При проверке адекватности сглаживания
наблюдений многочленом (или какой-то другой функцией) не
ограничиваются, конечно, исследованием суммы квадратов
остатков. Сама последовательность остатков должна по своим
свойствам напоминать последовательность независимых слу-
чайных величин (а не какую-нибудь плавно изменяющуюся
функцию вроде синусоиды). Мы не имеем здесь возможности
останавливаться на соответствующих статистических крите-
риях.
ГЛАВА 4
ПОДХОДЫ К ИЗУЧЕНИЮ ЗАВИСИМОСТИ
В главе 2 мы занимались в основном общими понятиями,
а в главах 1 и 3 — независимыми событиями и случайными
величинами (дискретный случай — в главе 1, общий слу-
чай — в главе 3). Теория вероятностей в случае независимо-
сти имеет одно важное достоинство: она в известном смысле
132
самозамкнута, так как, в общем, умеет сказать, каким обра-
зом нужно извлекать из эксперимента необходимые для при-
ложений вероятности, математические ожидания или диспер-
сии. Есть у нее и важный недостаток: она не вполне правиль-
на, например, извлекаемые из нее доверительные интервалы
часто не удовлетворяют теоретическим ожиданиям (не со-
держат истинного значения измеряемой величины). Все же
общая качественная картина явлений, даваемая этой теори-
ей, очень часто заслуживает внимания; надо только правиль-
но к ней относиться.
Теория зависимых событий и случайных величин строится
не для того, чтобы быть более правильной: с точки зрения
приложений она может быть ориентирована лишь на еще бо-
лее приближенное соответствие, чем теория случая незави-
симости. Ее цель — охватить совсем другой круг явлений,
включая, например, поведение динамической системы под
действием случайных возмущений, когда напрямую о незави-
симости говорить нельзя. Исследование ситуаций зависимо-
сти является более фрагментарным, чем для случая незави-
симости, также н с теоретической точки зрения. Например,
если в теории мы представляем себе последовательность не-
зависимых одинаково распределенных величин, то заданием
распределения каждой из них однозначно задаются любые
вероятностные свойства всей последовательности в целом. В
случае же зависимых случайных величин чаще ограничива-
ются исследованием отдельных вероятностных свойств, не
претендуя на исчерпывающее описание.
Мы соединяем в данной главе два теоретических вопро-
са — общую теорию условных математических ожиданий и
теорему Колмогорова о продолжении меры и один (сравни-
тельно) прикладной — корреляционную теорию конечного
числа случайных величин.
§ 1. Общая теория условных математических ожиданий
1.1. Введение. Классическое определение условной вероят-
ности события В при условии, что событие А наступило:
Р('В|Л) = Р(ЛВ)|Р(Л) (1)
пригодно, если Р(Л)>0. Однако, оперируя с более или ме-
нее общим понятием случайной величины, мы, конечно (имея
в виду зависимость случайной величины tj от случайной ве-
личины £), хотим говорить о вероятности того, что, например,
{п>1} при условии, что {£=х}, хе/?1. Как правило,
PU=*}=0, так что классическое определение использовано
быть не может. Впрочем, если Р(Л)=0, то для любого В,
очевидно, Р(ЛВ)=0, так что в правой части (1) имеется не-
которая неопределенность, которую (по крайней мере, в ка-
133
kiix-to частных случаях) можно надеяться раскрыть. Чтобы
это сделать, надо придать определению условной вероятности
некоторую интегральную форму. Как всегда, удобней начать
с дискретного случая, вывести для этого случая ряд правил
исчисления, а затем, вдохновляясь ими, дать общие опреде-
ления (таким, однако, образом, чтобы правила исчисления
сохранились и в общем случае).
1.2. Дискретный случай. Пусть пространство элементар-
ных событий й={(о} конечно или счетно. Рассмотрим разбие-
ние 31={Д1, Л2, ...,ЛП,...} множества Q на (не более чем)
счетное множество частей Alt А2,...,Ап, ••• Й“Л1+Л2+...
+ЛП+ .... А(А}-0, Р(Л,)>0. i— 1, 2, ... (2)
(Ж — готическая буква «А»).
Для любого В^Й определены условные вероятности
PA,(B) = P(B/Ai) = P(AiB)/P(Ai), i=l, 2..
которые разумно рассмотреть совместно. Оказывается, это
совместное рассмотрение хорошо (с точки зрения вывода
простых формул исчисления) сделать некоторым хитрым об-
разом, объявив вероятности Рд (B)=P(B/At) значениями
некоторой случайной величины. Введем в рассмотрение ус-
ловную вероятность относительно разбиения 31, обозначае-
мую Ри(В), или Р(В/%.).
Определение 1. Положим
Рй(В)|« = 2 РаДЯ) 1а, И, S й, (3)
где РЯ(В)|« обозначает значение случайной величины РЯ(В)
на элементарном событии («ЕЙ, Pa4(B)= Р(В/Л{) — клас-
сическую условную вероятность.
Иными словами, на <оеЛ,- условная вероятность Р%(В)
принимает значение Р(В/А,).
Лемма 1. МРЯ (В) = Р(В) (4)
(математическое ожидание условной вероятности равно безус-
ловной вероятности).
Действительно,
мря(В) = 2 Р(В/ЛОР(Л() = Р(В)
(в силу формулы полной вероятности).
Иначе можно сказать, что формула полной вероятности
получила эквивалентную чуть более краткую формулировку
(4).
Введем теперь понятие условного математического ожи-
дания. Пусть дана случайная величина £=£(<о), приннмаю-
134
щая значения сь с2, .... сп>... на множествах Сг, .... Сп,...:
g«g(<o) = gc//C/(<o). (5)
Определение 2. Назовем условным математическим
ожиданием M(g/3t)=M«g случайной величины £ относи-
тельно разбиения 31 случайную величину, определяемую сле-
дующей формулой:
M(g|30 = M«gvc.p«(C,). (6)
Нужно, конечно, убедиться, что ряд в правой части
(6) сходится. Обычно определяют условное математичес-
кое ожидание M(g|3l) в предположении, что безусловное
математическое ожидание Mg существует, т. е. Sk/lP(c/X
<оо. Так как при по определению 1
Ри(С/)|<.= Р(С;Л)/Р(Л),
то (при (оеЛ,) правая часть (6) допускает оценку
2 l9|P«(Q)|<. = 3 |с,|Р(С/Л0/Р(Л,) <
со
/-1
Поэтому при каждом <о (каждое <oeQ принадлежит какому-
то Л О правая часть (6) определена корректно, если только
Mg существует.
Как ранее определение интеграла Лебега для элементар-
ной случайной величины, наше определение (6) формально
зависит не только от самой случайной величины g=g(<o)
(т. е. от соответствия <о—► g(<o)), но и от способа представ-
ления g (<о) суммой вида (5). Нам снова нужно доказать, что
если случайная величина g=g((o) представима в двух раз-
ных видах:
g - g(<0) = 5 cjlcp) - g dkID^} (7)
(где как множества {С/}, так и множества {D*} дают разбие-
ния Q на непересекающиеся части), то два соответствующих
выражения для условного математического ожидания дают
одну и ту же случайную величину.
С этой целью заметим, что классическая условная вероят-
ность Ра(В) = Р(В/А) как функция множества В есть счет-
но-аддитивная мера: Рд(В|+В2+...)=ZPa(Bi) (все дроби
135
^A(Bj)=P(ABj)/P(A) имеют общий знаменатель Р(.4).
Пусть теперь дано (7). Образуем множества Ejk=CjDk и за-
метим, что £=£ (со) можно представить в виде
£ = $(<») = 2 (8>
Запишем для шеЛ, значение М(£/Я1). вытекающее из (8),
и преобразуем полученную сумму:
e S e/kP(^j»Mi) =
= X S elkP(El1t\ А) = X с, [2 Р(£Л/Л0] =
= 2^р(С//ла
I
(использовано равенство е/л = |(w)|MgF/lk = Cj при фиксиро-
ванном j и равенство = Cj). Беря суммирование сна-
чала по у, а потом по k, мы из того же выражения полу-
чили бы Корректность определения (6) дока-
зана. Как и в случае интеграла Лебега (безусловного ма-
тематического ожидания), отсюда вытекает линейность.
Доказана
Лемма 2.
+ dr) — сМи? +
где cud — числа (и известно, что Mlgl-Coo, М|т]|<оо).
Лемма 2 представляет собой правило исчисления, анало-
гичное правилу для безусловных математических ожиданий.
Замечание 1. Условную вероятность Р« (В) можно
понимать как условное математическое ожидание: очевидно,
Ри(В) = Мя7в 1в — индикатор множества В.
Замечание 2. Из леммы 1 вытекает такое правило ис-
числения:
М«М$ - ли. (9)
Действительно, пользуясь определением (6), получаем
Нужно, однако, обосновать перестановку математичес-
кого ожидания и суммирования. Для этого проще всего
прибегнуть к явному виду М(М«[£):
м(мя£) = 2Р(А) - 2 (У Р(Л) =
138
-Зе)Р(СЛ)
i, /
и воспользоваться конечностью ^|су|Р (Су).
I
Выведем теперь одно новое правило исчисления, аналогич-
ного которому нет в безусловном случае. Окажется, что это
правило можно будет принять за определение условного ма-
тематического ожидания и применить для раскрытия неопре-
деленности в (1) в случае произвольного пространства эле-
ментарных событий.
Скажем, что случайная величина т) является 91 -измери-
мой, если на любом элементе разбиения At величина т) при-
нимает постоянное значение. С разбиением 91 = (Ль Л2, ...
..., Ап,...) связана о-алгебра, элементами которой являются
всевозможные (не более чем счетные) суммы элементов раз-
биения. Очевидно, что введенное понятие измеримости отно-
сительно разбиения эквивалентно измеримости функции т] от-
носительно описанной о-алгебры.
На дискретной модели (в которой все подмножества
й измеримы) не очень виден тот аспект понятия измери-
мости, в котором это понятие важно для использования
условных математических ожиданий. Поясним этот аспект.
В этой теории вероятностей строятся очень сложные про-
странства 2 (даже и в дискретном случае). Можно, нап-
ример, представить себе прямое произведение очень боль-
шого (но пока—конечного) числа пространств элементарных
событий, отвечающее п опытам. Допустим, что нас инте-
ресует не набор результатов всех п опытов, а какая-то
суммарная характеристика £ = £('«) (что-то вроде суммар-
ного числа успехов в п испытаниях Бернулли). Если все
возможные значения случайной величины £(ш) обозначить
av аг, . . . , а„, . . . т. е. £ (со) = £ .(о), то полу-
чим разбиение й =- Аг 4- Аа + . . . + 4П + . . . . Случай-
ная величина »}, измеримая относительно разбиения 9( (ко-
ротко: Ж-измеримая), обладает, очевидно, тем свойством,
что как только мы знаем, какое из событий At, Аа,..., Ап,...
произошло, мы знаем и значение, которое приняла »].
Иными словами, >} = g(£), где g = g(x) — некоторая функ-
ция (на множестве {а,, а>, . • . , ап . . . }): Ж-измеримые
случайные величины — это такие случайные величины, ко-
торые однозначно определяются суммарной характеристи-
кой £ для п опытов. Таким образом, вместо о-алгебры всех
событий в Й мы рассматриваем более простую, включаю-
щую не все события, а только некоторые, характеризуемые
некоторой суммарной характеристикой. В подобных упро-
щениях и заключен смысл использования понятия изме-
римости при вычислениях условных математических ожи-
даний.
137
Лемма 3. Мя(тгё) = iqMgg, если случайная величина яв-
ляется ^-измеримой (£— произвольная случайная величина,
М|£|<оо, М|^|<оо). Иными словами, ^-измеримую случайную
величину можно выносить из-под знака условного математи-
ческого ожидания Ми-
Доказательство. Лемма весьма прозрачна, так как
в силу определения (6) значение М(||$0 “ на каждом
элементе разбиения At получится, если взять значения
ct случайной величины & и взвесить их с весами, равны-
ми P(Cy|4i) = P{g = <44i). Если вместо величины g взять
произведение -qg, то, если произошло значение
будет отличаться от значения £ множителем
принимающим при постоянное значение. Взвешен-
ная сумма, следовательно, умножится на это самое чис-
ло. Формулами это записывается так: если -ц —
« = 5 сДсу(<“), ТО
Ми('’]5)|иеАт = 2 2 5 amc/P МлАМл) “
= ^jamc/P(Q^m) =
(использованы соотношения P(A(Cy|Am) = 0 при i + tn,
P(AmCJAm)-P(qAm)).
Замечание 3. В случае безусловного математического
ожидания существует вырожденный вариант леммы 3: возь-
мем разбиение Q, состоящее из единственного элемента Q;
тогда условное математическое ожидание совпадает с безус-
ловным; единственная измеримая функция есть константа с\
лемма 3 сводится к утверждению: М(с£)=сМ£.
Замечание 4. Пусть А = Xi, + 4i,+. . . есть объе-
динение каких-то элементов разбиения %. Тогда по лем-
ме 3
М«(7^) - /аМя5. (10)
Применяя к (10) правило (9), получим
ММя(7а£) = М1Л = М(/дМа£), (11)
или в терминах интеграла Лебега
. j gp(d«) = j /лМ^Р(Ло) - f М«;Р(dm). (12)
Утверждение. Условное математическое ожидание
Ми В однозначно определяется следующими двумя свойства-
ми:
1) Ми£ есть %-измеримая функция; (13)
2) (14)
А А
138
Действительно, беря в качестве А одно нз At, из (14) одно-
значно определим (по g) значение M»g на <оеЛ,-: левая часть
(14) определяется по £ однозначно, M«g=di при <оеЛ,- в си-
лу {[-измеримости M«g. Тогда из (14) получаем
di = fSP(d(O)|P(4i).
Ai
Вскоре увидим, что свойства (13) и (14) можно положить
в основу общего определения условного математического
ожидания. Но сначала рассмотрим пример применения пра-
вил исчисления.
1.3. Пример применения правил исчисления. В статистике
довольно широко употребляется такое заклинание: «диспер-
сия случайной величины равна математическому ожиданию
условной дисперсии плюс дисперсия условного математичес-
кого ожидания». Его смысл состоит в следующем.
Пусть даны случайная величина £ и разбиение %. Ус-
ловной дисперсией называется = Ма(5 — Мя;)*. Утвер-
ждается следующее равенство:
DS = MDag + DMaS. (1)
Действительно,
Dg = M(g - Mg)* = MM«(g - Mag + M«g - Mg)» =
= MM«((g - M«g)» + 2(g - M»g)(Mag - Mg) + (M«g -
— Mg)»] = MM«(g - M«S)» + M(M«g — Mg)« +
+ 2MM»(g - Mag) (Mag - MS).
Первые два члена дают правую часть (1), последний член
равен нулю: так как выражение M«g — MS является ^-из-
меримым, MM«(g - M«S)(MaS - MS) ° M((MaS-ME)Ma(5—MaS)},
Ma(S-MaE) = MaS —MaMaS = 0, ибо MaM.g=MaE (M«S
есть уже {[-измеримая функция и второй оператор Ма
ее не меняет). Итак, формула (1) доказана.
Применим ее к следующей практической задаче. Биоло-
гия в наше время настойчиво хочет быть количественной на-
укой и постоянно определяет количество особей разных видов.
Конкретно речь пойдет о фитопланктоне.
Количественный учет фитопланктона заключается в том,
что нз водоема берется проба — некоторое количество воды,
которая процеживается через мелкую сетку, задерживающую
фитопланктон (чтобы слить лишнюю воду). Потом сетка опо-
ласкивается небольшим количеством воды, и получается кон-
центрированная проба планктона объемом в несколько куби-
ческих сантиметров. Из этой пробы после перемешивания бе-
рется одна или несколько капель точно известного объема
0,05 см3 и под микроскопом (практически без ошибок) опре-
139
деляются все виды клеток фитопланктона и число клеток
каждого вида, которые находятся в этой капле. Потом про-
изводится пересчет на объем водоема (верхнего слоя, в ко-
тором живут фотосинтезирующие водоросли). Спрашивается,
с какой точностью оценивается число клеток в водоеме?
У этой проблемы есть два аспекта — трудный и простой.
Трудный аспект заключается в том, что в естественных усло-
виях планктон распределяется в водоеме крайне неравномер-
но. Можно лишь экспериментально (беря много параллель-
ных проб) оценить степень этой неравномерности (эту зада-
чу мы рассматривать не будем). Легкий же аспект относится
к точности определения числа клеток в пробе по данным об.
обработке нескольких капель по 0,05 см3. Если бы фитопланк-
тон плавал одиночными клетками, мы ориентировались бы
на закон Пуассона.
Именно если всего сосчитано ц клеток данного вида, то
оценкой математического ожидания Л числа клеток (в соот-
ветствующем числе капель) будет само р, а порядок величи-
ны возможного отклонения будет УК, который мы заменяем:
на Ур. Относительная ошибка будет примерно Ур/р. Напри-
мер, если сосчитано р=100 клеток, то с определенной гаран-
тией относительная ошибка не превосходит 2Ур/р=20%.
Но отдельные клетки фитопланктона объединяются в ко-
лонии. Живые колонии могут состоять из десятков клеток.
При хранении проб колонии разрушаются, но все-таки могут
иметь несколько клеток. Ясно, что из-за этого относительная
точность делается хуже, но нужно узнать, насколько именно.
Построим статистическую модель. Представим себе следую-
щую схему. В пипетке, которой отбирают 0,05см3, оказыва-
ется некоторое случайное число v колоний, допустим, подчи-
ненное закону Пуассона (опыты не совсем подтверждают за-
кон Пуассона, но дают довольно близкий результат). При ус-
ловии, что число колоний равно п, численности клеток в них
Pi. рз.. Цп представляют собой случайную выборку из тех
численностей колоний, которые вообще имеются в данном
объеме воды. (Закон распределения размеров колоний мо-
жет быть, следовательно, получен статистической обработкой.)
Общее число клеток есть
p=pi4-p24- - 4-Цм.
Нужно найти дисперсию Dp (точнее, отношение VDp/Mp, на-
зываемое коэффициентом вариации).
Для читателя, впервые знакомящегося с вероятностно-
статистическими методами, небезынтересно будет узнать, ка-
кое здесь пространство элементарных событий. Пусть N обоз-
начает натуральные числа 1, 2, ....
Число колоний v принимает значения n=0, 1, 2, ... .
140
Пространство Q есть объединение О, N, N2, .... Nn. Ис-
ход опыта характеризуется значением v=n и п натуральны-
ми числами — численностями п колоний. Распределение ве-
эоятностей для п — пуассоновское, а условное распределение
в соответствующем Nn — прямое произведение лХ ... Хп в
количестве п штук, где каждое л — распределение вероятно-
стей числа клеток в наудачу взятой колонии.
Подсчитаем Мр. и Dp. Имеем ( обозначая через Mv, D„ ус-
ловное математическое ожидание и дисперсию по разбиению
й в сумму 0+Л^+№+...):
Мр = 4- ... + р,) = M(v М [л.) = MvM.Uj = ХМ р,;
Dp = MD,p + DM,p = M(vDpt) + D(vMpi) =
Dpi • Mv + (Mp()s • D v = '(Dpt + (Mpz)s) = kMp2
(здесь X = Mv — параметр закона Пуассона; при этом Dv —
= Mv — a; Мр(, Dpt, Мр? — параметры, характеризующие
размеры колоний). Окончательно
УБ7 ________________L_./TM =
Mu хм.и( | Мн
— 1 1/
р МрГ у мн
При одиночных клетках коэффициент вариации соста-
вил бы 1//Мр. Он увеличивается в J^Mpf/Mps раз (прак-
тически Мр нужно заменить числом всех подсчитанных
клеток, а Мр/и М р? —определить по выборке). Напри-
мер, если число клеток в колонии может с равной ве-
роятностью (= 1/5) принимать значения 1, 2, 3, 4 и 5, то
Mpi = 3, Мр? = 11, а коэффициент вариации ухудшается
почти в два раза (при 100 подсчитанных клетках гаран-
тируется ошибка, не большая 40%). Чтобы вернуться к
точности 20 % (как для одиночных клеток), нужно под-
считывать не 100, а 400 клеток.
1.4. Условная вероятность по А. Н. Колмогорову. Пусть да-
но произвольноэ вероятностное пространство {Q, Р|, в
котором выделена еще некоторая о-алгебра, St С®. Наг-
лядный смысл о-алгебры St состоит в том, что это гораз-
до более простая, чем ®, о-алгебра, содержащая мень-
ше множеств.
Например, если й — квадрат, являющийся прямым про-
изведением отрезков [0, 1]Х[0, 1], то в качестве ® обычно бе-
рется борелевская о -алгебра на квадрате, содержащая, в
частности, разнообразные геометрические фигуры. В качестве
141
91 может выступать о-алгебра «полосок» вида А={(х. у):
хеВь ОСуСП, где Bi — борелевские подмножества отрезка
[О, 1]. Соответственно случайные величины — измеримые
функции двух переменных f(x, у). Случайные же величины,
измеримые относительно 91, — это функции, зависящие от
х (и не зависящие от у).
Пусть £ — случайная величина (измеримая относительно
Ж); пусть М|£|<оо.
Определение. Условным математическим ожида-
нием М(?|И) = М8!^ называется случайная величина, удов-
летворяющая следующим двум условиям:
1) она измерима относительно о-алгебры К;
2) для любого А ё=91 выполняется интегральное соот-
ношение
fgP(d®)-.fM«P(do>). (1>
А А
В примере с квадратом речь идет о том, чтобы так усред-
нить функцию £=f(x, у) от двух переменных по переменному
у, чтобы получилась функция g(x, у), зависящая от одного
переменного х, удовлетворяющая (1) для любой полоски А.
Если Р — мера Лебега (P(dx, dy)=dxdy), то результат
прост:
1
g(x, i/) = J7(x, y)dy.
О
Действительно, если Л=В1х[0, 1], то
И f(x> y)dxdy = ,f f f(x, y)dxdy = ,f (f f(x, y)dy\ dx =
А В, 0 B»\0 /
t
- И g(4, y)dxdy.
A,о
Существование условного математического ожидания в
общем случае вытекает из теоремы Радона — Никодима, изу-
чаемой в теории меры. Для интересующего иас случая веро-
ятностного пространства эта теорема состоит в следующем.
Пусть на некоторой о-алгебре 91 = ® определена счетно-ад-
дитивная функция множества Q(A) (это значит, что функция
множества Q(A) принимает произвольные — не обязательно
положительные — вещественные значения, причем Q(A\ +
+A2+...)=Q(At) + Q(A2) + ...). Пусть Q обладает свойством
абсолютной непрерывности: если Р('А)=0, то Q(A)= 0. В
таком случае существует измеримая относительно 91 функция
т) (ы), такая, что
QiA) = (2>
А
142
причем т)(со) определяется однозначно с точностью до мно-
жества вероятности нуль (см. книгу А. Н. Колмогорова и
С. В. Фомина [23]).
Выведем из этой теоремы существование условного мате-
матического ожидания. Если положим для данной случайной
величины £=£((!>)
Q(A) = .^HP(d<o), (3)
А
то случайная величина ^(ы), определяемая (2), может быть
взята в качестве Мя£.
Условной вероятностью Р(В|Я1)= РЯ(В) назовем Мя7д.
Проверим выполнение основных правил исчисления. Под-
ставив в качестве А все Q в (2) и (3), найдем, что
[M£P(da>) = ММЯ£ = J ВР(^) = М
Очевидно и свойство линейности:
Мя(а| + b-q) = аМя + ЬМ«, а, b — числа.
Что касается последней формулы исчисления — леммы
3 п. 1.2, 1 о нетрудно проверить, что она также верна.
Возьмем сначала т) = /Л>, АоеЭ1. Проверим, что ЛМ^) —
— т)МяЕ. Измеримость т)Мя£ очевидна. Подставим в
интегральное тождество:
J/AMagP(d<o)=: f M^P(d<»)= f £P(d<») =
A AAt AAt
= f /д,£Р(&0).
A
Итак, интегральное тождество выполнено.
Если, далее, т> — конечная линейная комбинация индика-
торов множеств из А, то для нее также верно, что
МЯ(Ь)) = 7)МЯ|.
Пусть т) — произвольная случайная величина, такая, что
М|л||<оо. Пусть т]п—где каждая т)п есть конечная ли-
нейная комбинация индикаторов:
k п
причем сумма берется по k, таким, что |Л| < п2. Тогда ин-
тегральное тождество выполняется для величин
Но и функции 7)пМя£ равномерно интегри-
руемы. (Это означает, что для всякого е>0 найдется
5>0, такое, что если Р(А)<3, то |(т)пМя£Р(da)|<г.
143
Действительно, |fт)лМя^Р(Ло)|=Ц&gnP(d<»)|<№l(hl +—^P(d<0).
но функции |Щ и ||| предполагаются интегрируемыми.
Как известно, из равномерной интегрируемости следует
возможность предельного перехода под знаком интегра-
ла, а следовательно, выполнение интегрального тождества
для т)МиЕ. Итак, свойство Ми(В^) = »)№«£, если М,£|< оо,
М|Ь)|<оо, случайная величина rf измерима относительно
31, доказано.
Замечание. Несмотря на успешное и легкое обобщение
основных правил исчисления на общий случай условных ма-
тематических ожиданий, невозможность определить это по-
нятие иначе, как с точностью до множества меры нуль, ве-
дет к существенным трудностям. Невозможно, например, без
дополнительных уточнений рассмотреть условную функцию
распределения
P{t<x|3l}
при всех хеЛ1, так как при каждом х возникает свое исклю-
чительное множество Ах' меры нуль; однако различных х
имеется континуум, так что объединение |_Их' может быть не-
X
измеримым (либо иметь меру, отличную от нуля). Мы не бу-
дем рассматривать эти трудности, ограничившись тем, что в
простейшем случае укажем способ вычисления условных ма-
тематических ожиданий. (По поводу трудностей такого ха-
рактера см. книгу А. Н. Ширяева [46].)
1.5. Условная плотность. Пусть £ —случайная величина.
Обозначим через 31 — 31Е наименьшую о-алгебру, относи-
тельно которой £ измерима, — множество всех прообра-
зов = {<в:5(ш)еД| борелевских подмножеств В пря-
мой R1. Будем обозначать через условное математи-
ческое ожидание М»..
Измеримые функции относительно ЗЦ имеют вид С =»
= g(£), где g(x) — измеримая по Борелю функция х (нам
понадобится лишь очевидное утверждение, что g(z) из-
меримо относительно 3ls).
Пусть В, т) — пара случайных величин, имеющих совмест-
ную плотность распределения р^(х, у). Введем понятие ус-
ловной плотности рп/5=х (у) распределения случайной вели-
чины т) при условии, что случайная величина | приняла зна-
чение х.
Определение. Положим
Pent*, у)
РЕ(х)
О

, если ре(х)=#=0
, если рЕ(х) — О,
144
Укажем способ вычисления где /(х) — измери-
мая по Борелю функция х. Окажется, что эта случайная
величина имеет вид g(B), где g — измеримая по Борелю
функция. Следовательно, на множестве {<» : |(ы) = х} зна-
чение M.fh) есть g(x). Обозначим значение g(x) =
= через ВДт))|£ = х).
Теорема. Значение условного математического ожида-
ния выражается формулой
M(f(7))|g = x) = g(x)= f f(z/)pnli.x(z/)d</. (1)
—ОО
Доказательство. Выражение, стоящее под знаком
интеграла в правой части (1), представляет собой результат
интегрирования по переменной!/ некоторого выражения, со-
ставленного из измеримых по Борелю функций; следователь-
но, в целом есть некоторая измеримая функция g(x). Остает-
ся проверить интегральное тождество. Каждое Ле 31. имеет
вид А = £-1(В), В В1. Следовательно, 7л(«) « ZB(^((o)).
Поэтому
J /(>j)P(<Zg>) = J Zb(»/(ti) Р(*») = М {1в$Ш}. (2)
А 41
Далее,
M№HW)PW = М(/в(^)). (3)
А П
Для вычисления математических ожиданий в (2) и (3), ра-
венство которых нам нужно доказать, воспользуемся выраже-
нием математического ожидания функции от случайной ве-
личины через интеграл от плотности распределения. Получим
f J’ IB(x)f(y)pZli(x, y)dxdy\ (4)
—OO —00
M(ZB(£)g(£)) = 7 le[x)g(x)p£x)dx =
— oo
oo f oo \
- J M*) f f(y)p^x(y)dy\p{x)dx =
—OO V — 00 J
= ? lB(x)
—00
f(y)
p^(x, У)
P^x)
p^x)dx =
= J Ie(x)f(y)PUx, y)dxdy. (5)
—oo
10-2567
145
ибо повторный интеграл Лебега (в случае абсолютной сходи-
мости, которая гарантирована тем, что МГ/(т])1<°°) можно
превращать в двойной. Но (4) совпадает с (5). Теорема дока-
зана.
Замечание 1. Нам понадобится тот факт, что для не-
зависимых случайных величин условное математическое ожи-
дание совпадает с безусловным. При наличии совместной
плотности распределения это вытекает из доказанной теоре-
мы. Но более правильно выводить этот факт прямо из опре-
деления условного математического ожидания. Пусть, в са-
мом деле, даны две о-алгебры 911 и Э12. независимые между
собой в том смысле, что для и А2^%12 имеем
Пусть случайная величина измерима относительно
о-алгебры Э1а. Тогда = Mtj.
Действительно, пусть сначала т; = 1А„ Л2€=Ш2, =
= Р(Л,). Проверим интегральное тождество:
f T)P(d(D)= у Р(Лв)= Р(ЛЛ,)= Р(Д,)Р(Л2) =
л, д,л,
= f P(4,)P(d<o).
л.
Дальнейшее доказывается переходом к линейным комбина-
циям и предельным переходом.
Замечание 2. Так же, как и в безусловном случае, сле-
дует отрицательно ответить на вопрос о возможности опреде-
ления условного математического ожидания формулой, запи-
санной в теореме. Именно при определении M(sinT]l£=.v) мы
не будем знать, воспользоваться лн совместной плотностью
pSn либо совместной плотностью Pi.sinn. и должны быть увере-
ны, что оба варианта приведут к одному результату. В безус-
ловном случае для доказательства аналогичного факта всего»
естественнее привлечь интеграл Лебега. В случае условного
математического ожидания столь же необходимым представ-
ляется использование общего понятия условного математи-
ческого ожидания по Колмогорову.
§ 2. Корреляционная теория случайных величин
Корреляционной теорией называется подход к' изуче-
нию совместного распределения случайных величин
• • •. £п» использующий лишь знание математических
ожиданий дисперсий DEi и ковариаций cov(^, t})=
= M(g,— — Mt>) (либо коэффициентов корреля-
ции г(|о £у) = соу(£о 5y)/KDEiD^ —безразмерных аналогов
ковариаций). Корреляционная теория самозамкнута в том
смысле, что включает способы определения этих пара-
146
метров по статистическим данным. Рассмотрим ее основ-
ные понятия.
2.1. Матрица ковариаций. Пусть дан случайный вектор
$=•(&. &... &.). Ковариации c//=cov(|.-, £/). Ь /—1. *»
записываются в матрицу Ct=llcf/ll, называемую матрицей ко-
вариаций случайного вектора £, так как обычные операции
над матрицами и векторами позволяют получить ряд полез-
п
ных формул. Напомним, что (х, у) = 3 xtyt означает скаляр-
ное произведение векторов x=(xt, .... хп) и у=(уь .... уп)-
Матрица ковариаций Ct, очевидно, симметрична, так что
(Ctx, у) = (х, С\у)\ при этом (С{х, х) есть некоторая квадра-
тичная форма. Вероятностный смысл этой формы устанавли-
вается следующей леммой.
Лемма 1. (С^х, х) = D(x, Е) (D обозначает дисперсию.
(х, = для любого неслучайного вектора х = (хь...,
Доказательство. D(x, 5) = D(^x^,-) = V xlxjcov(Ei,
Ъ) = (С,х, х).
Следствие 1. Поскольку D(x, |)^0, матрица С5 неот-
рицательно определенная (т. е. определяет неотрицательную
квадратичную форму).
Следствие 2. Если для некоторого вектора хое/?пиме-
ем: (С,х0, хо)=О, то случайный вектор £ с вероятностью 1
лежит в линейном многообразии вида (х0, £) =а, а — число.
(В самом деле, поскольку D(x0, £)=0, с вероятностью 1 слу-
чайная величина (х0, е) принимает постоянное значение а.)
Следствие 3. Если случайный вектор т) связан со слу-
чайным вектором £ линейным преобразованием: т)=Л|+&
(А — матрица, b — вектор), то справедливо соотношение
= АС,А'
(А' —транспонированная матрица А).
Действительно, D(x, t;) = D(x, 4B + 6) = D(x, Ag) = D(A'x,
В) = (C^A'x, A'x) = (ACcA'x, x) = (C^x, x).
Лемма 1 и следствия пз нее устанавливают простую связь
между понятиями корреляционной теории и квадратичными
формами. Все обычные преобразования квадратичных
форм — замену переменных, в частности приведение к глав-
ным осям; проектирование одних случайных величин на дру-
гие, определяемое скалярным произведением (&, |/) =
==cov(g,, I,), и т. п. — можно интерпретировать в вероятно-
стных терминах. Каждая такая интерпретация обычно носит
громкое имя «анализа»: «анализ главных компонент», «фак-
торный анализ», «регрессионный анализ», «дискриминантный
10* 147
анализ» и т. п. С частью этих «анализов» мы кратко позна-
комимся. Следует понимать, что — будучи достаточно прими-
тивными в чисто математическом смысле — эти «анализы»
обычно представляют большие практические трудности. Нуж-
но организовать сбор и обработку больших массивов стати-
стической информации (и притом проявить достаточно здра-
вого смысла, чтобы вероятностная модель реализаций значе-
ний случайных векторов как независимых одинаково распре-
деленных величин не была бессмысленной); определить по
статистическим данным матрицу ковариаций; получить в тер-
минах этой матрицы ответы на какие-то содержательные во-
просы и т. д. В общем, во многих случаях на практике не сле-
дует идти дальше простейших операций со скалярными про-
изведениями п квадратичными формами; да и этот аппарат
оказывается слишком сложным, едва ли достаточно обеспе-
ченным фактическими данными. По совокупности всех этих
обстоятельств имя «анализа» часто бывает вполне оправдан-
ным.
2.2. Регрессионный анализ. В математической модели речь
идет о возможно точном определении значения случайной
величины т] по наблюдаемым значениям случайных вели-
чии Ед, Е«,. . ., gn. Для простоты обозначений предполо-
жим, что ожидания всех случайных величин равны нулю
(т. е. вычтены). Вообще говоря, речь идет о разыскании
такой функции f от величин Ei> Еа,. . ., £п, чтобы значе-
ние Es,. . ., Ел) было возможно ближе к т). Разли-
чие между •>) и ДЕд, Еа,. . ., Ея) обычно измеряется в смыс-
ле Lq — гильбертова пространства случайных величин Е,
таких, что MIEI’<С°°> в котором скалярное произведение за-
дается формулой (В, 7)) = М£т) =: j£((o)7)(a>)P(d<e) (заметим, что
о
в случае величин с комплексными значениями (Е, т;) =
=МЕт;). Иными словами, расстояние между т) и ДЕд, gs,...,
Ея) равно, по определению, Mh — ДЕд, g...........gn))».
Оказывается, что в общих терминах функция f(gt, £а. ...»
.... Еп) может быть найдена очень легко. Действительно, мы
сейчас покажем, что следует положить
Ж 5........... Ел)=м=1...5я7), (I)
где Мг,...5л обозначает условное математическое ожида-
ние относительно a-алгебры событий, порожденной собы-
тиями вида {Ед е в1г Е, е в2.Еп е в„), где в1г. . ., вп-
одномерные борелевские множества. В самом деле, мно-
жество L случайных величин вида g(Ex.........Ел), где
g(xi......хп) — измеримая по Борелю функция, есть,
очевидно, линейное подпространство пространства Z-u. Не-
трудно доказать и его замкнутость (настоящими подпрост-
148
ранствами гильбертова пространства являются замкнутые ли-
нейные пространства). Искомой функцией .............Вп)
является проекция случайной величины tj на L. Покажем,
что этой проекцией является tj.
Действительно, Ms,-?»1! является функцией от Bi..Вп»
т. е. принадлежит L. Нужно лишь проверить, что раз-
ность •») — ортогональна L. Однако для g(Zu—> Bn)G
GEL имеем
= ММ51...;я{(71-М;1...^)^1,. . Вп)} =
- «МВХ,. . ., ВЛ,...^ - Мъ.Ляч) = 0,
что и требовалось доказать. (Сравните доказательство
формулы DB“MDaB+DMaB в п. 1.3 предыдущего пара-
графа.)
Для вычисления (1) нужно знать совместную плотность
распределения случайных величин т), , Вп- Опыт
приложений показывает, что такое требование обычно
неприемлемо. Поэтому на практике ограничиваются (обыч-
но) линейными функциями /(В»,. . . ,Bn) = Sa«Bi. Тогда
речь идет о подпространстве La всевозможных линейных
комбинаций 2а»В,- Линейная комбинация 2 а& будет рав-
на projt т), если разность у — %а&=6 ортогональна всем
Bi. Таким образом, для минимизации 1И(т) — 2нужно
определить а„ . . ., ап из системы линейных уравнений
h - S£;) = М(т) - V a(B,)Bj = О,
т. е. (так как MBi““. . . =МВл“Мт) = 0)
SC0V(Bi, Bj)<Xi = cov(t), В»), /— 1, 2,. . ., n. (2)
i
Соотношение
T)=Sa.Bi+6, (3)
в котором at найдены из системы уравнений (2), называется
уравнением регрессии случайной величины т) на величины
Вь .... Вп-
Коэффициент корреляции
Г = г(7), V = М(7) V а&) //dt)• D(s afc) (4)
называется множественным коэффициентом корреляции меж-
ду случайной величиной т) и случайными величинами Вь Вг.
...,Вп.
Так как случайные величины 2а,В> и 6 в (3) ортогональ-
ны, имеем:
149
M (T)2W =м (Sa,|,)2 = D (Sa,|,);
(5)
Dq=D(Sa,g1)4-D6= M(qSa,g,) + D6.
Сопоставляя (4) и (5), получаем
D(Sa,£,j =r2Dr), D«=(l-r2)Dr]. (6)
Соотношения (6) имеют следующий наглядный смысл. Мы
собираемся «объяснить» случайную величину т) с помощью
линейной комбинации Sa,-^,. Если множественный коэффици-
ент корреляции равен г, то общий разброс значений tj, изме-
ряемый дисперсией Dt], объясняется с помощью 2а,£, в доле
г2; остается необъясненным разброс значений величины 6, из-
меряемый дисперсией Do=(l—r2)Dr).
Например, при г=0,7 имеем г2«0,5; это означает, что
Sa,|; и б — одинаковые по величине разброса случайные ве-
личины; иначе говоря, т) представляется в виде суммы двух
равноправных некоррелированных слагаемых Sa& и 6: грубо
говоря, мы объяснили значения случайной величины т) при-
мерно наполовину.
Теперь кратко рассмотрим практическую сторону приме-
нения уравнения регрессии. Нужно иметь в виду какую-ни-
будь практическую задачу. Пусть, например, нам нужно най-
ти зависимость между химическим составом и каким-нибудь
свойством стали, скажем, прочностью при испытании иа раз-
рыв. Если химсостав характеризуется процентным содержа-
нием элементов ..., U а т] — интересующая нас прочность,
то уравнение (допустим, линейное) регрессии т)»2а&+6 и
есть искомая зависимость (особенно при близком к 1 значе-
нии г). Но вместо теоретических математических ожиданий
М£;, Мт) и ковариаций мы должны воспользоваться их выбо-
рочными аналогами. Предположим, что имеется N плавок
стали, для каждой из которых определены значения хР ,...,
...,х(п/> , /=1, —, N, независимых переменных (химсостава) и
значения прочности. За оценки математических ожиданий
берутся средние выборочные значения, за оценку ковариа-
ций — выражения вида
N
7=1
N
-2—
/=»
Фактически вместо проектирования в Lq случайной
величины т; на линейную оболочку Lt случайных величин
150
£lr •»5п Происходит проектирование вектора (t/(<> — у,...,
y(tf) — у) на линейную оболочку векторов (хР — ........
XiW) — Xi) в смысле обычного TV-мерного евклидова про-
странства. При N-*-eo оценки ковариаций сходятся к
их теоретическим значениям, т. е. находим близкие к
истинным значения коэффициентов линейной комбинации.
Легко понять, что при конечном п отличие выборочных
ковариаций от истинных составляет величину порядка
1/УN. Однако для решения системы (2) нужна не сама
матрица ковариаций, а обратная к ней. При большом чис-
ле независимых переменных выборочная матрица кова-
риаций оказывается близкой к вырожденной (так как,
например, при N <п векторы (х)1’,. . ., х(Л'), i=l,..., п,
будут обязательно линейно зависимыми, а следовательно,
матрица выборочных ковариаций — вырожденной). Поэто-
му для успеха всей процедуры (называемой регрессион-
ным анализом) нужно, чтобы число наблюдений N было
гораздо больше числа независимых переменных п (к со-
жалению, нельзя сказать —во сколько раз, так как ответ
на этот вопрос зависит от того, какова теоретическая
матрица ковариаций, не говоря уже о приложимости са-
мой модели независимых одинаково распределенных век-
торных величин).
Приходится, следовательно, считаться с нестабильностью
результатов регрессионного анализа. Так, связи между хим-
составом и свойствами стали получаются различными для
различных металлургических заводов. Метод регрессионного
анализа — это метод слабый (по незначительности глубины
и неконкретности положенных в его основу теоретических
предпосылок), но относительно простой и потому широко при-
меняемый. Его применение для выяснения связей между пе-
ременными обычно дает хоть небольшой успех. Например,
если он применяется для прогноза значений переменной т) по
значениям gi, ..., gn, то ошибка прогноза имеет среднеквадра-
тичное значение VI—г2 VDr) в сравнении с разбросом значе-
ний т), равным VDt). При единичном прогнозе множитель
VI—г2 (равный, скажем, 0,7 при г=0,7) маловажен, но при
многих прогнозах дает определенный выигрыш.
2.3. Многомерное нормальное распределение. Корреляци-
онная теория оказывается необходимой и достаточной в од-
ном частном случае — когда рассматриваемые случайные ве-
личины имеют так называемое многомерное нормальное рас-
пределение.
Определение 1. Говорят, что вектор £=(£ь £2,...,£п)
имеет стандартное нормальное распределение (или нормаль-
ное распределение с параметрами (0, Е)), если его компо-
151
ненты независимы и имеют каждая одномерное нормальное
распределение с параметрами (0, 1).
Таким образом, стандартная нормальная плотность имеет
вид
Р^х) = Х„) =
-^ГП
J/2* / »=1
е
= (—^VexpJ—х)|. (1>
I 2 I
Определение 2. Говорят, что вектор т] имеет много-
мерное нормальное распределение, если т) можно предста-
вить в виде т]=Л£ + а, где вектор £ имеет стандартное нор-
мальное распределение (Л — матрица, а — вектор).
Очевидно, что для стандартного нормального распределе-
ния М£=0, Ct=E (Cs — матрица ковариаций). Следова-
тельно, для произвольного нормального вектора i] имеем:
Мт)=а, СП=ЛЛ'.
Найдем (в случае невырожденной матрицы Л) плотность рас-
пределения вектора т). Имеем
Рг.(у) = - a)J |det Л-'| = (2к)-"й |det Л|-1 X
Хехр 1--~-(Л“’(у-а), А~\у — а))|= (2>
= (2тг)-п/2(detСч)-,/2ехр у -а), у- а)|.
Следовательно, р^(у) выражается, через вектор средних а и
матрицу ковариаций Сп. Никаких понятий, кроме понятий
корреляционной теории, не нужно.
Если матрица Л вырождена (следовательно, вырождена и
матрица СП=ЛЛ'), то возьмем такой ортогональный базис в
Rn, что в этом базисе матрица Сп диагональна. Часть ее диа-
гональных элементов равна нулю, часть — отлична от ну-
ля. Поэтому распределение случайного вектора т) сосредото-
чено в некоторой гиперплоскости; если случайный вектор т)
записать в базисе, векторы которого лежат в этой гипер-
плоскости и в ортогональном дополнении, то в гиперплоско-
сти получится невырожденное нормальное распределение (все
собственные значения матрицы ковариаций отличны от ну-
ля).
Пусть теперь даны два случайных вектора тц и т]2, такие,
что их компоненты не коррелированы (т. е. имеют нулевые
152
ковариации), а совместное распределение т)! и т)2 (в прямом
произведении евклидовых пространств) является многомер-
ным нормальным. Утверждение: векторы гц и т]2 независимы.
Действительно, пусть (для простоты обозначений) Mtii =
= Мт)2=0. В прямом произведении евклидовых пространств,
где принимает значения вектор (i)b 142). выберем такой ба-
зис, что в этом базисе компоненты вектора т|1 имеют невы-
рожденное нормальное распределение в гиперплоскости Ц (а
остальные компоненты равны нулю в силу Мт)1=0); анало-
гично компоненты вектора т)2 имеют невырожденное нормаль-
ное распределение в гиперплоскости Ьг (остальные компонен-
ты равны нулю). Тогда в прямом произведении L1XL2 век-
тор (т]1, т]г), записанный в указанном базисе, будет иметь не-
вырожденное нормальное распределение (с нулевыми кова-
риациями компонент, отвечающих rji и т)2- в новом базисе
эти компоненты суть линейные комбинации старых). Поэто-
му матрица ковариаций С, вектора t)i и т)2 получит клеточ-
ный вид; квадратичная форма (С, у, у) разобьется в сумму
квадратичных форм, а совместная плотность (по формуле
(2)) — в произведение плотностей. Это и доказывает незави-
симость.
Кратко доказанное свойство выражают так: в нормаль-
ном случае из некоррелированности следует независимость.
Пусть случайные величины т), gi, .... £п имеют (вместе)
многомерное нормальное распределение. Напишем уравнение
регрессии (для простоты обозначений Мт)=М£1 = ...=М5П =
=0):
т)=2 ад4+б- (3)
<=1
В этом уравнении случайная величина б не коррелирована с
величинами .... gn, следовательно (поскольку рассматри-
вается случай совместного нормального распределения), ине
зависит от величин ..., |п- Распределение б — нормальное,
Мб=0 и D6= (1—r2)Dr), где г — множественный коэффици-
ент корреляции.
Так как б не зависит от £(, .... |п. то условное распреде-
ление б при данных £|, .... gn совпадает с безусловным. Это
означает, что условное распределение т) при данных £i,....sn—
нормальное с математическим ожиданием Sa,£(- и дисперси-
ей D6=(l—r2)Di|.
В частности, условное математическое ожидание т) при из-
вестных ^i, ...Лп есть линейная функция от £1,..., |п. т. е. наи-
лучшая функция, дающая оценку значения т) при известных
si, .... U в случае многомерного нормального распределения
вектора (т), .... £п) совпадает с линейной.
153
В качестве следствия рассмотрим, например, вопрос о том,
как узнать по наблюдениям значений (хи yi), .... (хп, Уп)
случайного вектора (g, т]), имеющего (как предполагается)
некоторое двумерное нормальное распределение, зависимы
или независимы случайные величины £ и т). Проверяемой ги-
потезой является гипотеза независимости — теоретический
коэффициент корреляции r(g, т])=0; мы будем отвергать ги-
потезу независимости, если-выборочный коэффициент корре-
ляции r=(n—\)-lZ(x!—x)(yi—y)/(s3^y) (где Sx =
— (п—1)-Ч(х1—х)2, з2= (п—1)-Ч(у1—у)2) окажется слиш-
ком большим. Для определения критического значения гк₽
(такого, что Р{И>Гкр}=а, а — уровень значимости) нужно
знать распределение г. Получим его почти без вычислений.
Записывая уравнение регрессии
т|—Мт)=а (g—Mg) +6,
или
т)= (Мт)—aMg) +ag+6=c+ag+6, с=Мт]—aMg,
видим, что при фиксированном g распределение т) является
нормальным со средним с-bag и дисперсией o2=D6, не зави-
сящей от g (вопрос же о том, верно ли, что r(g, т))=0, экви-
валентен вопросу, верно ли, что а=0). Поэтому при любых
фиксированных значениях ..., хп случайной величины g
для значений уи.... уп действует модель
у,=с+ах;+б,-, б, —Л’(0, о),
уже рассмотренная нами в теории метода наименьших квад-
ратов. Поэтому при любых фиксированных xt, хп условное
распределение выборочного коэффициента корреляции (при
гипотезе а=0) приводится к распределению Стьюдента
/п-2 преобразованием
f„_2 = г —г8 .
Но тогда и безусловное распределение вероятностей для
rYn— 2/К1 — г* есть tn-2.
2,4. Центральная предельная теорема. Критерий хи-квад«
рат. Преобразование Фурье функций от п переменных
получится, если ехр (Их) заменить на exp {i (t, х)} =
(п )
t’S tjxi (• Таким образом, теория центральной пре*
/«I I
дельной теоремы переносится (по крайней мере, для одина-
ково распределенных слагаемых) на случай суммирова-
ния векторных величии совершенно автоматически. Сум-
му Sn = + . . . + £n независимых случайных векторов с
математическими ожиданиями Mg4 = a и матрицами ко-
<54
вариаций -С^ = С можно (также н при вырожденной мат-
рице С) преобразовать к виду
s’ = —($„ — па).
V»
Тогда получится слабая сходимость к многомерному нормаль-
ному распределению с нулевым средним и матрицей ковариа-
ций С.
Применим это утверждение к выводу так называемого
критерия хи-квадрат. Пусть имеются испытания, каждое из
которых может иметь один из m исходов с вероятностями
Р\, > Pm, pi+... +рт=1. Иначе говоря, результатом t'-ro ис-
пытания является случайный вектор е< размерности т, одна
из компонент которого равна 1, а остальные — нулю. Пусть
в результате п независимых испытаний первый исход наблю-
дался р1 раз, второй pa раз, ..., m-й исход Цт раз. Иначе гово-
ря,
81+ — +еп={|А1> ...» Цт}, Ц1 + ... Цт=П.
Спрашивается, совместимо ли это с гипотезой, что вероят-
ность i-ro исхода равна р,?
Ответ должен базироваться на сравнении частоты \ч/п
i-го исхода с вероятностью р,; оказывается, что расстояние
между векторами {щ/п, .... цт/п) и (pi, .... рт) можно изме-
рить в такой метрике, что распределение получающейся слу-
чайной величины будет (в пределе для достаточно больших
л) не зависящим от параметров р1( .... рт и совпадающим с
распределением хи-квадрат с (т—1) степенями свободы. Вы-
ведем этот знаменитый результат К- Пирсона.
Ориентируясь на центральную предельную теорему, вы-
числим сначала вектор математических ожиданий и корреля-
ционную матрицу для ел Получаем
Ntei = (Pi, .... Рт)-,
учитывая, что лишь одна компонента вектора е, может быть
отлична от нуля, находим
(А(1—А) — Р1Рг ... — PiPm \
~PtPi Рг^—Рг) ... -Ptfm |
- PmPl — PmPt рп{ l—Pm) /
Эта матрица вырождена, так как сумма компонент вектора
е, равна 1. Суть открытия К. Пирсона состоит в том, что сле-
дует рассмотреть вектор
- .г У к pi— Л/h Ит — nP*l
...:"Н г™ ........... г
Очевидно, что МС = (М£1,. . ., М£т) = 0. Вектор £ лежит
в гиперплоскости = 0; обозначим через L эту ги-
перплоскость. Посмотрим, чему равна матрица ковариа-
ций Ct вектора £, если ее рассматривать в этой гипер-
плоскости, т. е. для векторов z = (zi...zm), таких, что
Матрицу ковариаций можно понимать как мат-
рицу такого (симметричного) линейного оператора что
D(£, z) = (Cxz, г). Используя тот факт, что матрица запи-
санная в базисе всего m-мерного евклидова пространства»
имеет элементы > где С = ||с(/|| —матрица ковариа-
ций случайного вектора elt проведем следующее вычис-
ление:
D(C, z) = (Qz, z) = (1 — px)zi — VZj?2 — ... —
— VPJm 4zm + (— Vptfl + (1 — Pi)zi —
— Vp^ 2jZs - ... — + . .. + (—-
-ZmZ, - . . . + (1 — pm)Z^) - Z? + Z? + . . . +
+ Zm — ZX /pl (Z Zi Vpl ) - • • • — 2m (S Z, ) >7) =-
л о л
= 2j + 22 + . . . + Zm-
ТаКИМ образом, для zeL
(C^Z, 2) = z24-z2+. . . J-z’=(z, z).
Это означает, что нормальное распределение в плоскости L
с матрицей ковариаций С£ есть стандартное нормальное рас-
пределение в пространстве размерности (т— 1). Таким обра-
зом И£Ц2 при больших п имеет приблизительно распределение
хи-квадрат с (т—1) степенями свободы:
ц-ц,= у <*—*>
Т=1 "р‘
Такова метрика, в которой удобно рассматривать различия
между pi и Зная распределение статистики Н^Н2 мы без
труда назначаем критическую область для проверяемой гипо-
тезы. С другими вариантами применения критерия хи-квад-
рат (в том числе при неизвестных pi, зависящих от каких-то
параметров) можно познакомиться по книге Г. Крамера [24].
2.5. Дискриминантный анализ. Пусть имеется некоторая
совокупность объектов, которая состоит из объектов (для
156
простоты) двух классов: «здоровых» и «больных». У каждого
объекта можем измерить набор параметров |=(£ь .... £п).
Требуется на основании этих измерений отнести данный объ-
ект к одному из двух классов, т. е. сказать «здоров» он или
«болен».
В математической модели предполагается, что вектор 5
имеет многомерное нормальное распределение с различными
векторами средних at и а2 для двух классов объектов, но
(обычно) с одинаковой матрицей ковариаций о2. Практичес-
ки — на основании корреляционного анализа наблюдений
над объектами, класс которых известен, — сначала оценива-
ются параметры щ и а2 и матрица о2 (последняя путем взя-
тия средневзвешенных ковариаций между параметрами объ-
ектов двух классов). Затем для неизвестных объектов произ-
водится классификация.
Если предположить, что матрица о2 единичная, то для но-
вого объекта, характеризуемого набором х— (хь ...,хп), надо
выбрать тот класс (т. е. такое среднее или а2), до которо-
го меньше расстояние от точки х до центра распределения:
взять
min{llx—ajl2, Их—a2ll2}.
Таким образом, все пространство /?пэх разделится на два
подпространства гиперплоскостью, проходящей через середи-
ну отрезка [аь а2] и ортогональной к этому отрезку. Правда,
в зависимости от целей исследования, можем предпочесть, на-
пример, чаще ошибочно относить объекты второго класса в
первый, чтобы зато не терять объекты первого класса, оши-
бочно относя их во второй. Тогда можем предпочесть другую
гиперплоскость: будем относить объект к первому классу,
если
(а2—ah х) <с,
где константу с будем выбирать, исходя из получающихся
ошибок первого и второго рода.
Случай произвольной матрицы о2 сводится к случаю еди-
ничной матрицы преобразованием t/=o-1x. Математические
ожидания для объектов двух классов при этом преобразуют-
ся в о-’й! и о-1а2, а гиперплоскость вида (а2—аь х) в гипер-
плоскость
(а-,(а2 —а,), о-1 х) = (а-2(а2 — ах), х)<с.
Иными словами, речь идет о расстоянии в метрике, определя-
емой матрицей о-2, т. е. матрицей, обратной к матрице кова-
риаций (так называемое расстояние Махаланобиса). Таким
образом, можно кратко сказать, что задача отнесения объек-
та к одному из двух классов решается путем сравнения рас-
стояний вектора наблюдений х до двух центров распределе-
157
ний О] и аг, но только расстояние понимается в метрике Ма-
халанобиса. В этом и состоит в простейшем случае дискри-
минантный анализ, но только требуется определить по на-
блюдениям неизвестные параметры распределений.
Сделаем в заключение несколько замечаний о статистичес-
ких исследованиях, основанных на гипотезе многомерного
нормального закона. В то время как для одномерного нор-
мального закона возможна наглядная проверка нормальности
с помощью выборочной функции распределения, в многомер-
ном пространстве такие проверки затруднительны. Дело не
только в том, что против хорошо сформулированной альтер-
нативы в многомерном случае технически труднее провести
проверку нормальности; просто в многомерном пространстве
так много места, куда может спрятаться отклонение от нор-
мальности, что затруднительно предложить разумный круг
альтернатив. Поэтому для многомерных распределений про-
верка нормальности обычно не производится. Тем не менее
даже в случаях, когда нормальности заведомо не может быть
(например, потому что какие-то случайные переменные при-
нимают дискретные значения О, 1, 2, ...), применение методов,
якобы имеющих теоретическое обоснование в многомерной
нормальности, оказывается удивительно эффективным (см. во
второй части книги § 2 гл. 3). Очевидно, многомерное прост-
ранство так трудно осмыслить без математической обработ-
ки, что даже заведомо несовершенная обработка может до-
вольно часто принести полезный результат.
§ 3. Теорема Колмогорова о продолжении меры
3.1. Введение. Речь идет о том, чтобы с помощью теории
продолжения меры сделать то, чего никак нельзя сделать с
помощью древнего понятия длины, площади, объема, — ввес-
ти (вероятностную) меру в бесконечномерном пространстве.
Будем считать, что с мерами в конечномерном пространстве
мы уже достаточно освоились. Теоретически запас таких мер
у нас, действительно, достаточно велик: любая неотрицатель-
ная функция, интеграл от которой по всему пространству ра-
вен единице, может, например, выступать как плотность рас-
пределения вероятностей. Практически же мы знакомы с не-
большим запасом одномерных распределений различных
частных видов; с понятием независимости, позволяющим кон-
струировать многомерные распределения из одномерных пу-
тем прямого произведения, и с функциями, превращающими
независимые случайные величины в зависимые. Так построе-
но, например, многомерное нормальное распределение.
Но у нас пока нет средств для того, чтобы доказать, ска-
жем, что такой объект, как счетная последовательность слу-
чайных величин (определенных, естественно, на одном прост-
158
ранстве й элементарных событий), действительно существу-
ет. Например, в центральной предельной теореме, когда речь
шла о сумме Sn=£i4-- + £n независимых случайных величин
при п—>-оо, мы для каждого п можем построить систему из
п независимых случайных величин (считая, что й=/?п, ме-
ра — прямое произведение одномерных распределений), но,
строго говоря, эти й различны для различных п. Правда, по-
ка речь идет (как в центральной предельной теореме) лишь о
распределениях вероятностей, можно вероятность Р снабдить
индексом п: Pn{Sn<*}—► Ф(х), а по существу в аналитичес-
ком аппарате характеристических функций ничего не изме-
нится. Но вопросы, относящиеся к счетному числу случайных
величин (например, сходимость ряда ^1 + ^2+—+gn + -
и т. п.), мы рассматривать пока не можем.
Напомним в общих чертах теорию продолжения меры.
Конструкция счетно-аддитивной меры на о-алгебре 8 под-
множеств й начинается с того, что счетно-аддитивная мера
задается на более простой, чем о-алгебра, системе множеств.
Достаточно сделать это на полукольце множеств S, т. е. на
такой системе, что
1) если AeS и BeS, то Af|B=ABsS;
2) если AeS, Ai^S н AicA, то найдутся множества
А2, AneS (в конечном числе) такие, что А=А1+Аг+...
... +АП (знак 4- при объединении множеств означает, что
А(А/=0, £=#=/). Например, на прямой удобным полукольцом
является множество всех полузамкнутых интервалов вида
[а, Ь), а<Ь.
Теорема о продолжении меры утверждает, что счетно-
аддитивную меру, заданную на полукольце множеств, можно
продолжить на некоторую о-алгебру, содержащую это полу-
кольцо.
Но на полукольце S должна быть установлена именно
счетная аддитивность (конечной аддитивности мало). Как,
например, установить, что длина (по Архимеду) является
счетно-аддитивной мерой на полукольце интервалов? Если,
допустим, интервал [0, 1) разбит на сумму интервалов
[О, 1/2), [1/2, 3/4), [3/4, 7/8), .... то счетная аддитивность яс-
на: в этом случае лишь у точки 1 происходит накопление ин-
тервалов разбиения, а на любом отрезке [0, 1—е], е>0, до-
статочно воспользоваться конечной аддитивностью, которая
со времен Архимеда считается достаточно ясной. Таким обра-
зом, единичная длина отрезка [0, 1) представится в виде сум-
мы членов геометрической прогрессии 1/2, 1/4.Но интер-
валы разбиения могут накапливаться не обязательно к точке
1. а, скажем, также и к точке 1/2; далее, можно точки накоп-
ления интервалов разбиения заставить накапливаться к ка-
кой-то внутренней точке отрезка [0, 1); и точки накопления
точек накопления заставить накапливаться куда-нибудь и т. д.
159
Счетное множество — вещь необычайно сложная, и ясно, что
хорошо бы иметь простое и несомненное доказательство счет-
ной аддитивности длины на полукольце интервалов.
Такое доказательство состоит в следующем. Ясно, что
сумма длин любого конечного числа непересекающихся ин-
тервалов, лежащих на интервале [0, 1), не более 1 (эти ин-
тервалы покрывают [0, 1) не полностью, а с некоторыми дыр-
ками). Следовательно, и сумма длин счетного числа интерва-
лов не превосходит 1, а надо доказать, что она в точности
равна 1. Для этого достаточно доказать, что для любого е>0
найдется такое конечное число интервалов, что сумма их длин
не меньше чем 1—е. Поступим следующим образом.
Занумеруем наше счетное число интервалов разбиения:
получим интервалы [ап, Ьп), п = 1, 2,.... Интервалы [ап, Ьп)
покрывают интервал [0, 1), следовательно, и отрезок [0,1—
—е/2]. Рассмотрим чуть расширенные открытые интервалы
(ап—е/2п+‘, Ьп), которые также покрывают отрезок [0, 1—
—е/2]. Из этих открытых интервалов, покрывающих замкну-
тый отрезок, выберем конечное покрытие. Сумма длин от-
крытых интервалов этого покрытия не меньше, чем 1—е/2. Но
она превосходит сумму длин соответствующих полузамкнутых
интервалов не более чем на е/4 + е/8+е/16+ ...=е/2. Следо-
вательно, сумма длин этих полузамкнутых интервалов не ме-
нее 1—е/2—е/2=1—е, что и требовалось доказать.
Аналогичным путем рассмотрим следующий вопрос теории
вероятностей: пусть дана функция F(x), монотонная по х и
непрерывная слева, причем F(—оо)=0, F( + oo) = l. Как до-
казать, что эта функция определяет на прямой счетно-адди-
тивную вероятностную меру?
Положим для интервала [a, b), a<Zb,
р{[а, b)}—F(b)—F(a).
Тогда на полукольце интервалов S определится конечно-ад-
дитивная мера. Для доказательства счетной аддитивности
нужно заменить интервалы [ап, Ьп) на открытые интервалы
(ап—Еп, Ьп), такие, что \F(an—en)— F(an)\ = F(an)—
—F(an—en)^e/2n+1, что возможно в силу непрерывности
F(x) слева. Меру всей прямой нужно определить дополни-
тельно как
lim[r(x„)-F(-x„)] = 1. (1)
Таким образом, на интервалах определяется счетно-аддитив-
ная мера.
Теория продолжения меры утверждает, что с помощью не-
которой конструкции счетно-аддитивную меру, заданную на
S, можно продолжить на некоторое о-кольцо множеств. Если
речь идет о подмножествах множества Q, причем само Q
|60
измеримо (как в случае, когда действует определение (1)),
то указанное о-кольцо содержит Q, т. е. является о-алгеброй
(в случае длины это не так: длина всей прямой бесконечна).
Ссылаясь на теорию продолжения меры, видим, что моно-
тонная непрерывная слева функция задает меру на некоторой
о-алгебре подмножеств прямой, содержащей S (т. е. все ин-
тервалы). Следовательно, эта мера определена, в частности,
на наименьшей о-алгебре, содержащей S, т. е. на всех боре-
левских множествах.
Нечто аналогичное будем делать и в бесконечномерном
случае: доказывать счетную аддитивность меры на некоторой
алгебре множеств (конечно, всякая алгебра является полу-
кольцом) и использовать теорию продолжения меры.
3.2. Конечномерные распределения случайного процесса.
Случайным процессом называется функция g(f, <о) двух пере-
менных t, со. Часто переменная t понимается как время; в
этом случае множество T={t} значений переменной t есть
обычно интервал прямой либо вся прямая (либо множество
целых точек 0, ± 1, ±2,..., или только неотрицательных целых
точек 0, 1, 2,...; в этих случаях говорят, что время дискрет-
но). Но для последующих рассуждений природа множества
Т совершенно не важна. Может быть, например, что T=R3
есть евклидово пространство, причем |(f, <о) есть случайная
величина — давление среды в точке f; в этом случае говорят
о случайном поле давления. В качестве t может выступать
течка многообразия, скажем, сферы, и тогда говорят о слу-
чайном поле на сфере. В общем, Т — произвольное множест-
во, и лишь для наглядности будем говорить о нем, как о мно-
жестве моментов времени.
При каждом фиксированном t^T значение В (Л со) должно
(как функция от со) быть случайной величиной, т. е. функци-
ей соей, где Й — вероятностное пространство (наделенное,
как всегда, о-алгеброй S5 и вероятностной мерой Р). Суще-
ствование такого Q, на котором можно рассматривать конти-
нуум случайных величин |(/, w), /еТ, нам как раз и неясно
и устанавливается теоремой Колмогорова. Но пока предполо-
жим, что такое Й существует, и рассмотрим некоторые общие
понятия, которые при этом возникают.
Объявить, что точно наблюдаемой является функция
£(£, со) как функция t при каждом <о, мы не решимся. Но ска-
жем, что для каждого конечного набора Л. h, .... tn значений
t являются точно наблюдаемыми случайные величины
£(/ь со), .... l(tn, о). На математическом языке это означает,
что для любого борелевского можно говорить о веро-
ятности

11—2567
(1)
161
Вероятностная мера Pt,...rn определена на борелевских под-
множествах 2? с=Яп. Она называется конечномерным распре-
делением. случайного процесса £, = £(/» о) (отвечающим
набору моментов времени tit. . ., tn). Посмотрим, каким
условиям должны удовлетворять конечномерные распре-
деления по смыслу определения (1). Эти условия носят
название условий согласованности.
Пусть s — перестановка п символов. Эту перестановку
можно заставить действовать на n-мерных наборах t—
= (6, tn)‘ положим
s/=(7si, .... tm)>
где si... sn) — тот набор, в который перестановка s пере-
водит набор (1, п). Можно заставить s действовать и на
Rn, положив для х=(хь .... xn)^Rn
SX=(xsi, Х,п).
Событие, стоящее под знаком вероятности Р в (1), есть-
некоторое условие, наложенное на значения случайных
величин — £(*!, w),..., ltn = l(tn, ш). Например, в част-
ном случае В =* X . . . х Вп это событие можно пере-
писать в виде
...» lt„^Bn}.
Ничего не изменится, если моменты Л, .... tn и события
Bi, .... Вп в (2) переставим одной и той же перестановкой.
Но, очевидно,
s(BiX... X Вп) =Bal X... X Bsn.
Таким образом, совпадают события
{®:(?Zi,. . ., . .ХВп} =
= • . •, EBS1X...X Bsn}.
Следовательно, равны и их вероятности. Иными словами, дол-
жно выполняться следующее условие:
P7(fi)=Ps7(^)> (2)
где символом Ру(В) кратко обозначена конечномерная
вероятность (или конечномерное распределение), отвечаю-
щее набору Г=(<х........tn).
(Мы доказали (2) для случая В = В1Х . . . X Вп-, но ле-
вая и правая части (2) являются мерами в Вп, которые
однозначно определяются своими значениями на „парал-
лелепипедах" B = BiX- . X Вп.)
162
Далее, рассмотрим два набора моментов времени: (ti,... tn)
и более широкий набор (Л, ..., tn, 1/, tm')- Совпадают сле-
дующие события:
{«*»: (I,, >. . - . Ъя) е В} = {ш: Ьп,
I,',. . ., tt'}^BXRm].
1 m
Это означает, что должно выполняться следующее соотноше-
ние:
Р/..../я(В) (В х Д'"). (3)
" л 1 m
Условия (2) и (3) называются условиями согласованности.
Они обязаны выполняться для любого случайного процесса
£=£(/’, <o), iogQ.
3.3. Теорема Колмогорова. Мы убеждались, что для
любого заданного распределения вероятностей и в Rn су-
ществует случайная величина ё, имеющая и своим распре-
делением вероятностей (для этого надо положить Й = ЯП,
в качестве измеримых подмножеств взять борелевские,
положить Р(В) = ц(В) и, наконец, взять g(w) = u>, шей").
Теорема Колмогорова утверждает, что любому набору сог-
ласованных распределений (т. е. мер в пространствах Rn,
удовлетворяющих условиям (2) и (3) предыдущего пункта)
отвечает случайный процесс, для которого меры яв-
ляются конечномерными распределениями.
Пусть Т есть множество значений t. Возьмем в качест-
ве О пространство RT, т. е. множество функций
В число измеримых множеств, т. е. событий, включим для
начала так называемые цилиндры в Вт: каждому набору
моментов времени tv . . ., tn и каждому борелевскому
множеству B^Rn поставим в соответствие подмножество
(В) cz RT, определяемое формулой
Cti...tn(B) = {«> = <о(О:(«>(/!),...» (1)
которое и называется цилиндром, определяемым набором
(t\, .... tn) и основанием В. Иногда для цилиндра (1) приме-
няют следующую выразительную запись:
Cti..tn(B) = BXRT^h....Ч
которая явно показывает, что речь идет о прямом произведе-
нии основания В на такое количество прямых, сколько име-
ется точек в множестве T\(t\, .... tn).
11* 1СЗ
В дальнейшем мы, конечно, положим (вдохновляясь ана-
логией со случайной величиной)
(О)=Ш('О.
Поэтому мы должны положить
P(Ctl.../n(B)) = P/l...,n(B). (2)
Но запись цилиндра Ctt..jn(B) в форме (1) неоднозначна.
Можно переставить моменты tv . . ., tn и одновременно
переставить координаты точек В: получится тог же самый
цилиндр. Но первое условие согласованности (формула
(2) предыдущего пункта) говорит нам, что при этом пра-
вая часть (2) ие изменится.
Можно к моментам tv. . ., tn добавить некоторое число
моментов времени^,..., t'm, записав, что в моменты t'm
функция ш(0 принимает любые значения из R1. Опять по-
лучится тот же самый цилиндр, но второе условие сог-
ласованности (формула (3) предыдущего пункта) говорит
нам, что и в этом случае правая часть (2) будет опре-
делена без противоречия.
Описанная неоднозначность полностью исчерпывает неод-
нозначность записи цилиндра: если два цилиндра определе-
ны на одном и том же наборе моментов времени (ti, .... tm),
записанном в одном порядке, то они совпадают в том и толь-
ко в том случае, когда совпадают их основания. Итак, опре-
деление (2) корректно.
Цилиндры образуют алгебру: любое конечное число ци-
линдров можно определить на одном и том же наборе момен-
тов времени (взяв теоретико-множественное объединение на-
боров моментов времени для всех цилиндров и записав его в
каком-то определенном порядке). Тогда теоретико-множест-
венные операции над цилиндрами будут эквивалентны тем же
операциям над их основаниями. Мера Р, определенная соот-
ношением (2), рассмотренная для конечного числа цилинд-
ров будет эквивалентна мере в конечномерном пространстве;
следовательно, на алгебре цилиндров мера Р конечно-адди-
тивна.
Теорема Колмогорова. На алгебре цилиндров ме-
ра Р счетно-аддитивна.
Доказательство. Как известно, счетная аддитив-
ность на алгебре эквивалентна аддитивности и так назы-
ваемой непрерывности сверху: если имеется последова-
тельность измеримых множеств Л1 э А — ... э А„ = .... та-
п
кая, что Г1 Ai = 0, то должно выполняться соотношение
•!
Р(ДП)—>0. Следовательно, нужно доказать лишь непрерыв-
164
ность сверху меры Р. Это означает, что требует дока-
зательства следующее утверждение: если имеется вло-
женная последовательность цилиндров Схэ С2 э...= Сп =
= .... такая, что Р(СП) >е>0, то пересечение Г) С/ непусто.
i— 1
Без ограничения общности можно предположить, что ци-
линдры Сь С2,..., Сп... определяются все время расширяющи-
мися множествами моментов времени: при увеличении номе-
ра п на единицу к набору моментов времени, определяющему
цилиндр Сп, лишь добавляется какое-то конечное число точек
(возможно, равное нулю) для задания цилиндра Сп+ь
Пусть цилиндры Ci, С2, Сп, ... определяются основания-
ми Bi, В2, ..., Вп, •••, причем Р(Сп)>е>0. Конечномерные
вероятности обладают следующим свойством: для любого бо-
релевского Вп найдется компакт Кп^Вп, такой, что конечно-
мерная вероятность Кп не менее чем конечномерная вероят-
ность Вп минус в/2п. Рассмотрим цилиндры Dit D2, Dn....,
определяемые основаниями Кп (и теми же моментами време-
ни, что и цилиндры Сь С2, .... Сп,...). Тогда цилиндры
£i=Di, £2=Р!П£>2,..., £п=^1П-О2П-П^п, •••
1) являются вложенными: £i^£2^ ... ^>£п^>...;
2) имеют компактные основания;
3) их вероятности удовлетворяют неравенству Pf£n)^e/2.
Свойство 1) очевидно; докажем 2) н 3). Для того чтобы
пересечь цилиндры Dt, ..., Dn, надо взять наибольший набор
моментов времени, отвечающий цилиндру Dn; образовать ос-
нования (в соответствующем конечномерном пространстве)
K^XR"", ЬхГ',..-, Kn-i* /Г*’1, Кп,
mi>m2>... >tnn-i (3)
и пересечь множества (3). Но множества (3) замкнутые, мно-
жество Кп — ограниченное; следовательно, пересечение мно-
жеств (3) замкнуто и ограничено, т. е. компакт.
Далее, цилиндры Dn получаются из вложенных цилиндров
Сп выбрасыванием множеств вероятности не более е/2п. Поэ-
тому
Р(£п)>Р(Сп)-2 е/2«>е/2.
л—1
Поскольку Еп^Вп, то для доказательства того, что Г\Вп^=0,
достаточно доказать, что П£п содержит хотя бы одну точку.
Поскольку Р(£п)^е/2, каждое множество £п непусто. Возь-
мем в каждом множестве £п точку а>п=а>п(().
Проследим за «координатами» точки <оп, т. е. за значения-
ми функции шп(0 при таких t, которые входят в наборы мо-
ментов времени
165
... C/Wc...,
определяющие цилиндры Ct, Сг,. . ., Сп,. . . (следова-
тельно, и цилиндры Ev Е2,. . ., Еп,. . .). Конечномер-
ный вектор <un(0lz получаемый подстановкой вместо t
моментов из t<m* при т^п, принадлежит компактному
основанию цилиндра Ет (ибо Ет^Еп). Сейчас мы обра-
зуем предельным переходом от точек шп(0 точку, принад-
лежащую всем Еп. Для этого рассмотрим сначала после-
довательность векторов о>„(0| , _,(!>> принадлежащих основа-
нию Ev Выберем такую последовательность значений п, что
соответствующие точки ®n(i)| t сходятся, очевидно, к
точке, принадлежащей основанию Et в силу компактнос-
ти. Из полученной последовательности значений п выберем
такую подпоследовательность, чтобы сходились точки
wn(0!z ((2> к точке, принадлежащей основанию £2. Затем из
полученной подпоследовательности значений выберем та-
кую подпоследовательность, чтобы <*)„(*)! сходились к
точке, принадлежащей основанию £3, и т. д. Наконец, из
всех подпоследовательностей значений п выберем диаго-
нальную подпоследовательность. Если брать значения п из
диагональной подпоследовательности, то для любого т по-
следовательность <ол(01 будет сходиться к некоторой
точке wm, принадлежащей основанию Ет. Но тогда точка
©(/), такая, что u,(OI/_,(m> = “m принадлежит всем Ет, т. е.
пересечение Г) Ет непусто, что и завершает доказательств
во теоремы.
3.4. Борелевская о-алгебра в пространстве функций. Из
теоремы Колмогорова вытекает возможность продолжения
меры Р на некоторую о-алгебру, содержащую все цилиндры;
в частности, на наименьшую такую о-алгебру, которую есте-
ственно называть борелевской о-алгеброй в пространстве
функций. Любой сколько-нибудь физически осмысленный во-
прос. который относится к поведению значений процесса £<=
= 5(t ci))=ci)(7J на каком-то не более, чем счетном множест-
ве значений t, приводит к событию из этой о-алгебры. Кро-
ме того, в ней имеется большое число событий, не отвечаю-
щих физически осмысленным вопросам, например событие
{(о:£(Л со) рационально при t=t\, t2, .... tn,
В частности, если множество T={f} не более чем счетно, о-ал-
гебры борелевских множеств достаточно для описания сколь-
ко-нибудь интересных событий, связанных с поведением про-
цесса
166
К сожалению, это совершенно неверно для случая, ког-
да Т — {t} несчетно. Например, событие
(ш: sup £(t, со) < с) (1)
a^t<b
не входит в борелевскую о-алгебру (вообще говоря). Дока-
жем это с помощью простого примера.
Пусть Q=[0, 1], Р — мера Лебега, Т=(0, 1]. Рассмотрим
два случайных процесса: ©)=0 для всех t и со;
§2(г, (о) = 1, если и g2(f, w)=0, если t=a>. Конечномер-
ные вероятности для процессов и £2 одинаковы, так как
при каждом t (следовательно, и для конечного числа значе-
ний г), очевидно, £i (t, со)=^г(Л со) с вероятностью 1. Однако
sup gj(t, w) =0, sup g2(Z, о>)=1 для всех w. Поэтому вероят-
ность события (1) не определяется конечномерными веро-
ятностями, а следовательно, это событие не входит в боре-
левскую о-алгебру.
Именно это неудобство (с событием вида (1)) можно пре-
одолеть, отправляясь не от любых функций в качестве эле-
ментов пространства Q, а оттак называемых «сепарабельных»
(функция <х>(/) называется сепарабельной, если ее график,
т. е. плоское множество точек вида (f, w(0), лежит в замы-
кании графика той же функции, рассмотренной для значений
аргумента teZ, где Z — счетное всюду плотное подмножество
Т). Но с дальнейшим развитием теории случайных процессов
подобные «теоретико-множественные» трудности возникают
вновь и вновь. Если мы захотим, чтобы случайный процесс
Ц/, со) был измеримой функцией от пары (t, со), т. е. на про-
изведении QxT, опять придется подчищать множество эле-
ментарных событий. В теории марковских процессов обычного
марковского свойства оказывается недостаточно, и появляют-
ся строго марковские процессы. Наконец, если мы пожелаем
рассмотреть число пересечений траекторией процесса некото-
рого уровня, то сначала надо доказать, что это число с веро-
ятностью 1 конечно, а затем уже подсчитывать (совершенно
иным методом) его вероятностные характеристики, например
математическое ожидание.
Обилие этих теоретико-множественных трудностей при не-
возможности справиться с ними радикально заставляет при-
знать. что объект RT=Q при несчетном Т оказался довольно
диким и не полностью укротимым средствами теории меры.
Если при этом вспомнить, что абстракция точной наблюдае-
мости значений g(f, со) как при конечном числе значений t,
так и при всех feT является довольно условной, то становит-
ся ясным, что тому, кого теория вероятностей интересует с
точки зрения приложений, лучше держаться подальше от тео-
167
ретико-множественных трудностей, связанных с понятием
случайного процесса. В частности, в данной книге теорема
Колмогорова применяется на математически строгом уровне
лишь для счетного Т. Как известно, в математике все связано,
н из теоремы Колмогорова, относящейся к мерам в функцио-
нальном пространстве, получим, в частности, свойства собст-
венных значений некоторых самых обыкновенных конечных
матриц. Но в ряде случаев, когда Т несчетно, наше изложе-
ние будет не вполне математически строгим.
ГЛАВА 5
КОРРЕЛЯЦИОННАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
Введение. Основной целью настоящей книги в части тео-
рии случайных процессов является изложение простейших
методов исследования динамических систем, подверженных
действию случайных возмущений. Динамическую систему по-
нимаем узко — как систему, описываемую обыкновенными
дифференциальными уравнениями (не касаясь, следователь-
но, систем, описываемых уравнениями в частных производ-
ных). В систему обыкновенных дифференциальных уравне-
ний могут (в качестве правых частей, коэффициентов или
как-нибудь иначе) входить случайные процессы.
Читатель заметит, что определение случайного процесса у
нас все время несколько меняется в зависимости от рассмат-
риваемых конкретных вопросов. В корреляционной теории
случайный процесс — это непрерывная кривая в гильберто-
вом пространстве. Для решения линейных дифференциальных
уравнений с постоянными коэффициентами, в правую часть
которых входят случайные процессы, очень полезно преобра-
зование Фурье; но наибольшую естественность это понятие
имеет не в обычных, а в обобщенных функциях. Поэтому по-
являются обобщенные случайные процессы. Марковские це-
пи (в гл. 6) рассматриваются с помощью теоремы Колмогоро-
ва о продолжении меры (оказывается, что таким методом на-
иболее просто доказать некоторые свойства собственных век-
торов обычных матриц конечных размеров). В основу рас-
смотрения динамических систем со случайными воздействия-
ми положено понятие цепи Маркова, а диффузионные про-
цессы вообще рассматриваются на физическом уровне стро-
гости; к динамическим системам имеют прямое отношение
лишь их распределения вероятностей в рамках некоторой пре-
дельной теоремы. Не рассматриваются стохастические ин-
тегральные уравнения по весьма прозаической причине: курс
теории вероятностей и случайных процессов, на основе кото-
рого написана книга, оказался последним, математическим
168
курсом в учебном плане и был поэтому задуман как повторе*
ние основного математического материала, изучавшегося ра-
нее. Между тем стохастические уравнения потребовали бы
привлечения довольно сложного аппарата, который на уров-
не знаний студента следовало бы считать существенно новым
и ранее не изучавшимся. Включить же в книгу, предназначен-
ную прежде всего в качестве учебного пособия, материал, ра-
нее не прочитанный несколько раз в лекциях для студентов,
совершенно невозможно (как понимает каждый, кто когда-
либо писал учебник).
Таким образом, предлагаемая в данной книге трактовка
краткого курса теории случайных процессов может рассмат-
риваться лишь как один из многих возможных вариантов по-
строения этого курса для студентов естественнонаучных специ-
альностей с математическим образованием: отчасти эта трак-
товка отвечает хотя бы субъективным взглядам автора, сло-
жившимся на основе опыта каких-то приложений (по боль-
шому счету — опыта довольно случайного), а отчасти же оп-
ределяется вообще малосущественными обстоятельствами.
§ 1. Среднеквадратическая теория
1.1. Основные понятия. В корреляционной теории рассмат-
риваются такие случайные процессы со), что
Mlg(7)l2 конечно при любом t^T. Иными словами,
eLn, где La — гильбертово пространство случайных вели-
чин, суммируемых с квадратом (из сведений об La нам по-
надобится факт, состоящий в том, что La полно). Если пред-
положить, что l(t) непрерывно зависит от t как элемент La,
то получается, что случайный процесс есть непрерывная кри-
вая в гильбертовом пространстве. При этом о зависимости
i(t)=^(L со) от соей можно (в большинстве рассуждений)
попросту забыть.
Как и для конечного числа случайных величин, в корре-
ляционной теории случайных процессов вводятся в рассмот-
рение лишь «моменты первого и второго порядка», т. е. ма-
тематическое ожидание
№,(t)=m(t), teT, (1)
и так называемая корреляционная функция B(s, t) случай-
ного процесса g(f). По определению,
B(s, t)=Nl£(s)1-(t) при этом B(s, t) = B(t, s), (2)
где черта сверху обозначает комплексное сопряжение. (Мы в
конце концов собираемся решать дифференциальные уравне-
ния, в которые входят случайные процессы. Известно, что в
169
случае обычных детерминированных функций при решении
дифференциальных уравнений весьма полезно рассматривать
функции с вещественным аргументом t, но с комплексными
значениями. Соответственно и мы не можем ограничиться
случайными процессами лишь с вещественными значениями.)
Подчеркнем, что в определении (2) корреляционной функ-
ции входит именно N^,(s)£(t), а не ковариация M(£(s)—
—m(s)) X (S(0—«(0) и не коэффициент корреляции. Часто
в приложениях считается, что неслучайную функцию m(t) =
=Nl£(t) можно каким-то образом определить и вычесть, т. е.
положить Однако (например, при решении уравне-
ний движения) мы постоянно переходим от одних случайных
процессов к другим, в том числе различными нелинейными
преобразованиями. Если то, например, М[£(7)]2=#
=й=0, так что возможность ненулевого математического ожи-
дания случайного процесса нужно учитывать.
Замечание 1. Над чем ставить комплексное сопряже-
ние в (2) — над или над ^(t) — в принципе совершенно
все равно, но только нужно выбрать какой-то определенный
способ и всегда его держаться, иначе будет путаница в фор-
мулах.
Замечание 2. Если случайный процесс t(t) принима-
ет комплексные значения: %(t)=%i(t) + i%,2(t), то с точки
зрения корреляционной теории полной его характеристикой
(кроме математического ожидания) является система трех
функций: М||ОД|(0, М£2(Х)£2(0 и М£,(Х)£2(7). В понятие
корреляционной функции (2) входит некоторая комбинация
этих трех функций. Поэтому задание двух функций — веще-
ственной и мнимой части B(s, t) — не определяет полного
набора корреляционных характеристик случайного процесса
£(7). Мы будем рассматривать лишь такие вопросы, для ре-
шения которых достаточно знания B(s, t), но не нужно забы-
вать, что если бы мы, например, пожелали рассмотреть ком-
плексный гауссовский случайный процесс (т. е. такой, для ко-
торого все конечномерные распределения — нормальные), то
нам бы не хватило B(s, t) для задания распределений (ср. с
рассматриваемым ниже вещественным случаем).
Выведем одну простую формулу исчисления. Вычис*
лим квадрат нормы в Ln линейной комбинации J
где Сц — числа (вообще говоря, комплексные). Имеем
М
п
ck 50k)

470
= 2 ti)c^c‘- (3)
Таким образом, функция B(s, t) обладает тем свойством, что
при любых t\, .... tn эрмитова матрица k, /=!,..., п,
неотрицательно определена. Такая функция B(s, t) называ-
ется положительно определенной.
Так как B(s, t) есть скалярное произведение (£($), £(/))
в пространстве Ln, а зависимость %(t) от t предположена не-
прерывной (в смысле Ln), то функция B(s, t) непрерывна по
совокупности переменных s и t. Обратно, если B(s, t) =
= и функция B(s, t) непрерывна по совокупности
переменных s и t, то зависимость £(7) от * непрерывна. Дей-
ствительно, по формуле (3) получаем
М1^+Л0—UOI2=S^+ AL t + M)—B(t+bt, t)—
—B(t. t+bt) + B(t, t).
что стремится к нулю при Д£—►О.
Так как
| m(t + At) — m(t) | = |M|(t + ДО - М$(01 <
<м1£(« + Д0-5(01<V MI50 + AO-K0I1»
то и функция т(7) обязана быть непрерывной.
В вещественном случае матрица ковариаций случайных
величин %(tt), .... %(tn) при каких-то 0, .... 1п^Т имеет вид
...M = llcov(gf/,/ fc(7J)ll= nB(tltf)-m(ti)m(ti)«.
Если имеются непрерывные функции B(s, 0 и т(0> связан-
ные так, что при любых ft, .... tn^T матрица С(Л, .... tn) бы-
ла неотрицательно определенной, то каждому набору 0......
..../пеТ отвечает некоторое многомерное нормальное (гаус-
совское) распределение с вектором средних (m(ti)..m(tn))
и матрицей ковариаций C(ti, .... tn). Взяв эти распределения в
качестве конечномерных распределений случайного процесса
(они. очевидно, согласованы), получим, что функциям B(s,t)
и m(t) отвечает гауссовский случайный процесс с данными
конечномерными распределениями. Мы, таким образом, мо-
жем быть спокойны в том смысле, что объект корреляционной
теории — случайный процесс с данными m(t) и B(s, t) —
действительно существует. Гауссовский процесс (веществен-
ный) еще и однозначно определяется по m(t) и B(s, Г).
1.2. Аналитические операции. Рассмотрим дифференциро-
вание и интегрирование случайных процессов. Смысл введе-
171
ния этих операций заключается в следующем. Описывая ка-
кую-то динамическую систему дифференциальным уравнени-
ем, мы обычно не доказываем в рамках математического до-
казательства, что некое дифференциальное уравнение дейст-
вительно описывает процесс, а приводим какие-то правдопо-
добные соображения, из которых дифференциальное уравне-
ние возникает затем в статусе математического определения.
Эти правдоподобные соображения, как правило, не станут ху-
же, если предположить, что на рассматриваемую систему влия-
ют не детерминированные, а случайные процессы. Един-
ственное, о чем следует договориться, — это как понимать
производные (или интегралы) от случайных процессов. Мож-
но понимать дифференцирование (интегрирование) %(t) =
=fc(f, cd) как дифференцирование (интегрирование) по t при
фиксированном со. Но, испортив функции £(/, <о) при каждом
отдельном г с вероятностью 0 (что не влияет на конечномер-
ные распределения), можем превратить их на любом отрезке
значений t в недифференцируемые (а если очень постарать-
ся, то в неинтегрируемые). Поэтому ясно, что такое понима-
ние аналитических операций над случайными процессами
связано с теоретико-множественными затруднениями. Меж-
ду тем в среднеквадратичной теории возможен совершенно
элементарный подход, который мы и изложим.
Начнем с теоретически более простой операции —ин-
тегрирования. Пусть Т — конечный отрезок, g(t) — непре-
рывная кривая в Определим интеграл как пре-
дел римановых интегральных сумм
(4)
где ti, t2,.... tn — разбиение отрезка Т.
Нужно уметь доказать, что при измельчении разбие-
ния (max(t+I — суммы (4) сходятся к пределу в
Lq, иначе говоря [(в силу полноты 1%), получается фунда-
ментальная последовательность.
Как н для обычных интегралов Римана, ключевым момен-
том доказательства является оценка разности между суммой
(4) и такой же суммой, но отвечающей более мелкому разби-
ению. Это означает, что второе разбиение получается добав-
лением некоторых новых точек к разбиению ti, t2, .... tn. При
этом отдельное слагаемое l(ti)(Yl+l—ti) заменится суммой
S £(*/)( —*/)>
172
где t/ означают точки нового разбиения. Оценим раз-
ность между (t/+, — /,) и суммой (5):
— G) — 2 l( */)( ~ */)=
= 2 (£(**)— U о)( г/+‘ ~ */)• (6)
Поскольку
II ИМ - § (t'i) 1Г = в (t<, Л) - в(гь <) -
-B(th ц} + B(tf,
а функция B(s, t) равномерно непрерывна на ТхГ, то при
1Л-+,—/,|<6 выражение (6) оценивается как е(б)(Л+1—Л), а
разница между двумя суммами, отвечающими разбиению
U} и {MU{//}- — как е(6) I Т\, где |Т| — длина отрезка Т и
£ (б) —*-0 при б—►О.
Если теперь взять два произвольных разбиения отрезка
Т точками {s,} и точками {//}, то, объединяя точки {s,} и точ-
ки {?/}, получим разбиение, более мелкое как по отношению
к первому разбиению, так и по отношению ко второму раз-
биению. Если
то каждая из сумм, отвечающих {s,} и {//}, отличается не бо-
лее чем на е(б) |Г1 от суммы, отвечающей объединенному раз-
биению. Следовательно, друг от друга эти суммы отличаются
не более чем на 2е(б)ITI —►О при б —►О. Построение интег-
рала Римана закончено.
Аналогичные рассуждения доказывают существование ин-
теграла
Кф)= [Поф(О^. (7)
т
где <р (0 — непрерывная функция на Т. Подсчитаем квадрат
нормы выражения (7):
115 (ф) II2 = М1£(ф) I2 = Нт 2 М W/) X
ti-tj
X ф(6) Ф(М (/<+1 -*«)( ti+i - ti) =
=> f j1 B(s, t) q>(s) <p(7) ds dt =
TT
173
= Jf B(s, t)q>(s)<p (t)ds dt,
поскольку после замены M 5(G) 5(G) на B(t„ tj) = B(tjt t,)
двойная сумма no tt и tj превращается в интегральную
сумму для двойного интеграла от непрерывной функции
B(s, 0<р(з)ф(7) (либо для функции B(s, t) <p(s)<p(O).
Замечание. Если понимать5(0 = £(G ш) как измеримую
функцию от пары t, ш, то тот же результат может быть
получен проще с помощью теоремы Фубини. Действи-
тельно,
15(ч>) I1=5(Ф) • Йф) = j ЙО ф(0 dt • f 5(«) ф(Г) -
т т
- f [ 5(»)5tO«P(s) ф(0
т т
Применяя к последнему равенству операцию М вычисления-
математического ожидания (т. е. интегрирования по ueQ) и
переставляя интегрирование по ю с интегрированием по $ и
по t, получаем
м 15(ф)1’ = f f M5(s) ЙОФ(О ф(0 dsdt -
т'т
— ( J B(s, t) <f(s) <р(0 dsdt. (8)
тт
Видим, что общие представления (в данном случае — об из-
меримости g(f, со)) могут приводить к аналитическим форму-
лам (мы много раз это видели ранее). Но обоснование воз-
можности понимать 5 (Л со) как измеримую функцию на Гхй
выходит за пределы данной книги (с ним можно познако-
миться, например, по [19]).
Обратимся к дифференцированию. Мы хотим, чтобы
существовал предел lim(g(f+ А) —Н(/))/Л, конечно, в смыс-
*-о
ле Ln.
Рассмотрим скалярное произведение
ft(s+h)-5(s) \ _
\ А ’ * /
= ± М(5(» + h) - 5(s) (g(t+*)_5W)=
пл
_ J(B(s+h,t+k)—B(s,t+k) B(s+h,t)-B(s,t) ] /Q,
к ( h h ]' U
174
Предел выражения (9) при Л—►О, k—►О обязан существо-
вать, если существуют производные случайного процесса
в точках s и t (скалярное произведение есть непрерывная
функция). Но на предел выражения (9) можно смотреть как
на некоторую обобщенную вторую производную от корреля-
ционной функции, которая, конечно, совпадает с B5t (s, t), ес-
ли корреляционная функция дважды непрерывно дифферен-
цируема. В частности,
limM 6(‘+Л)-£('> ' =
*—О л
(10)
Установим обратное: если корреляционная функция дважды
непрерывно дифференцируема, то случайный процесс %(t)
имеет производную (в среднеквадратическом смысле). Для
этого нужно проверить фундаментальность отношения
при Л—►О. Имеем, используя (9) и (10),
_ $(t+*)-g(n I * =
Л Л | =
= 1|« +»)-£(<) «_
* I *
_ /6(t+M-at) w-H)-ao \ _
1л’ л I
_ w+h)-w) \
( k k )
0 + ^0. 0 — — t)=o
(предел берется при h—►О, k—►О; для исследования преде-
ла выражения (9) проще всего воспользоваться формулой
Тейлора для функции B(s, t)).
Таким образом, для существования какого-то числа про-
изводных у случайного процесса достаточно существования
двойного числа производных у корреляционной функции. От
кривых в гильбертовом пространстве мы перешли, изучая
возможность аналитических операций, к свойствам функций
обычного анализа.
§ 2. Обыкновенные и обобщенные стационарные
случайные процессы
2.1. Понятие стационарности. Чтобы быть в прикладном
смысле самозамкнутой, корреляционная теория должна обес-
печить возможность практического определения своих поня-
тий — моментов первого и второго порядка. В принципе лю-
175
бые математические ожидания определяются путем много-
кратной реализации случайного объекта (в данном случае —
многократного получения реализаций случайного процесса) и
усреднения по ансамблю реализаций тех функционалов, для
которых нужно получить математические ожидания. Но на
практике — в силу ли особенной неопределенности понятия
ансамбля для реализаций случайного процесса (пытаясь вос-
произвести много реализаций, мы рискуем нарушить стати-
стическую однородность экспериментов) либо практического
удобства — стараются заменить усреднение по ансамблю ус-
реднением по времени. Это возможно для процессов, вероят-
ностные характеристики которых не меняются во времени,
г. е. для так называемых стационарных процессов.
Существуют два основных математических определения
стационарности. Стационарностью в узком смысле называют
неизменность любых конечномерных распределений процесса
при сдвиге времени: для любого набора моментов времени
Л, ^2. tn и любого Л
Р»1 Ч- - .tn = Р/1+Л. t,+h.tn + h •
Стационарностью в широком смысле называют неизменность
при сдвиге времени математического ожидания: m(t)=Ni^(t)
не зависит от t, т. е. m(t)=a, где а — константа, и корреля-
ционной функции
B(s, t)=B(s+h, t+h)
для любых s, t и й, что означает, что B(s, t) зависит толь-
ко от разности s—t=u. Иначе говоря, функция двух перемен-
ных B(s, t) сводится к функции одного переменного, которую
мы будем обозначать той же буквой В: B(s, t)=B(s—1) =
=В(и). Делая замену s=t+u, получим
B(u)=B(t+u, t)=^(t + u)J(r)=l^(i)W + u) (1)
(обратите внимание на расстановку комплексного сопряжения,
например, при «>0 более раннее значение gff) входит в ком-
плексно-сопряженном виде, а более позднее %(t+u) без ком-
плексного сопряжения).
Конечно, справедливо соотношение В(—и) = В(и).
В практических вопросах, пока мы пользуемся корреляци-
онной теорией, фактически применяется стационарность в
широком смысле. Но мотивируется она обычно тем, что
«процесс во все моменты времени протекает одинаково», т. е.
стационарностью в узком смысле. (Конечно, в математике из
стационарности в узком смысле вытекает стационарность в
широком смысле лишь в предположении существования соот-
ветствующих математических ожиданий, которые выражают-
176
ся через конечномерные распределения.) Поскольку стацио-
нарный процесс определяется как инвариантный по отноше-
нию к сдвигу времени, область Т={/} значений временного
аргумента также должна быть инвариантной по отношению к
сдвигу; это возможно либо в случае Т= (—оо, оо), либо (для
дискретного времени) в случае T=Z, где Z — множест-
во целых чисел 0, ±1, ±2,... (тогда сдвиг времени h тоже
должен быть целым числом). Вообще говоря, t — не обяза-
тельно время. Стационарность возможна, если 7'={/} есть
некоторый объект, на котором определено действие группы
преобразований, например окружность, сфера, плоскость Ло-
бачевского и т. д. Но мы будем понимать t как время.
Выпишем аналог формулы (8) п. 1.2 предыдущего пара-
графа для стационарного случайного процесса. Рассмотрим
функцию <р(0, убывающую при t—►±оо достаточно быстро,
чтобы существовал (в смысле Lq) интеграл
СО
£(ф) = (Жф(0*»
о» СО
аналогичный интегралу (7) при Т=(—оо, оо). Подставляя в
(8) вместо B(s, t) функцию B(s—t)=B(u), получим (делая
замену s=f+u)
СО со
А*|£(<р)|,= J J B(s — t)ff(s)<f{t)dsdt =
—ОО —00
— м |£(ф)|* = J j B(s — t) <f(s) <p(£) dsdt =
= J B(u) J <p(s) <p(s—u) ds du =
= J B(u) <p* o(u)du,
—•30
где функция <р» ф есть свертка (композиция) функции
ф(0 с функцией ф(О = Ф(—0» задаваемая формулой
Ф*ф(и)= J ф($) ф (u — s)ds =
J ф(«)ф(5 — и) ds.
12—2567
177
Формула
М|5(ф)|,= J В(ы)ф* ф(ы)4и (2)
—со
будет положена в основу определения обобщенного стацио-
нарного случайного процесса.
2.2. Обобщенные стационарные случайные процессы. Сна-
чала напомним простейшие понятия теории обобщенных
функций. Обобщенная функция есть, по определению, не-
прерывный линейный функционал, определенный на некото-
ром пространстве основных функций. Интерес представляют
следующие два пространства основных функций.
Пространство К состоит из финитных бесконечно диффе-
ренцируемых функций <р; сходимость <рп—‘ф понимается сле-
дующим образом:
1) существует интервал, вне которого все <рп обращаются
в нуль;
2) функции фп вместе с любыми их производными ф *,
£=1, 2, ..., равномерно сходятся к функции ф или ее произ-
водным:
5ир|фп(0 —ф(01->-0, sup^*’(0 —
t t
— Ф<*>(01—»0, * = 1, 2, . . . . (1)
Пространство S состоит из бесконечно дифференцируемых
функций ф^), убывающих на бесконечности быстрее любой
степени вместе с их производными: для любого т^О
(1+ |/|"’)ф(*>(0—*0 (|/|—оо); k=0, 1....
Сходимость в S понимается как равномерная сходимость
функций и их производных, которая не исчезает при умноже-
нии на любую степень |f|: последовательность <pn(t) сходится
к в смысле сходимости в S, если для любого т>0
sup |(1 + КГ) (ф^ (П - Ф(*’ (0 ) | - 0, k = 0, 1. (2)
Функционалами на К являются прежде всего выражения
вида
F(T) = (F, ф)= J F(0<p(0dt, (3)
— СО
где F(t) — локально интегрируемая функция (это означает,
что интеграл от |F(f)| по любому конечному отрезку коне-
чен). Выражение (3) задает функционал на S, если предпо-
178
дожить дополнительно, что функция F(t) на бесконечности
медленно возрастает: это значит, что функция F(t) возраста-
ет не быстрее некоторой степени: существует такое иг>0
(некоторая степень t), что
sup|F(0(l + r|)-‘l<oo. (4)
t
Действительно, при выполнении (4) <peS интеграл (3), оче-
видно, сходится, и если <рп—► ф в S, то F(q>n) —►Е (ф). Если
(3) заменить на интеграл от некоторой производной ^k>(t),
то также получится непрерывный функционал. Например,
если F(t) = \ при /^0 и F(t)=O при t^O, то
ос О
f Л(<)ф'(0й/= [ ф'(*)Л = ф(0)
—СО — ОО
(так как ф(—оо)=0 для основных функций ф). Мы ранее
(п. 1.4 из § 1 гл. 3) рассматривали такой функционал под
названием б-функции Дирака. Познакомиться с общим ви-
дом функционалов в пространствах К и S можно по [14].
Не представляет труда определить обобщенный случай-
ный процесс над любым пространством основных функций.
Определение. Обобщенным случайным процессом
5=£(ф) будем называть непрерывное линейное отображение
£:ф—► Лп множества основных функций ф в множество слу-
чайных величин La
Если g(7) — обычный случайный процесс с корреляцион-
ной функцией B(s, t), то, в силу формул (7) и (8) (при Т=
= (—оо, оо)) п. 1.2 предыдущего параграфа, возникает и
отображение £—►£(<₽), т. е. обобщенный случайный процесс.
Вообще говоря, формулы (7) и (8) имеют смысл лишь для
финитных ф, т. е. мы получили обобщенный случайный про-
цесс над К, но если функция B(s, t) возрастает при |s| —►оо
или Ш—►оо не очень быстро, то соответствующие интегралы
сойдутся и для феЗ, т. е. получится обобщенный случайный
процесс и над 3.
Получить обобщенные случайные процессы, не сводящие-
ся к обыкновенным, можно, например, операцией дифферен-
цирования. Действительно, в предыдущем параграфе мы вы-
яснили, сколько раз можно (и можно ли хотя бы один раз)
дифференцировать обыкновенный случайный процесс. Обоб-
щенный же случайный процесс можно дифференцировать
сколько угодно раз, пользуясь определением
(V. ф)—а. ф'),
аналогичным определению производной обобщенной функ-
12* 179
ции. После того как обыкновенный процесс продифференци-
ровали столько раз, сколько позволяет гладкость корреляци-
онной функции, дальнейшие производные будут обобщенны-
ми процессами.
Аналогами понятий корреляционной теории будут:
1) математическое ожидание
т(ф)=М£(ф)
(это линейный, в силу линейности £(<p):£(<pi+<P2)=£(<pi) +
+ |(ф2) функционал);
2) корреляционный функционал
В(<р, ф)=М£(<р)£(ф)
(это билинейный эрмитов функционал: В(ф, ф)=В(ф, ф)).
Стационарный обобщенный случайный процесс (в ши-
роком смысле) нужно определить как процесс, инвариант-
ный относительно сдвигов. Именно положим <pA(O=q>(i—Л)
и потребуем, чтобы /п(фА) = /п(ф) и Я(фЛ, 6А) =• 5(ф, 4-).
Тогда сравнительно нетрудно показать, что т(ф) =
= т ( ф(/)Л» где аг — некоторое число, но гораздо труд-
— ОО
нее исследовать корреляционный функционал (см. [12]).
В данной книге принят упрощенный путь введения поня-
тия обобщенного стационарного процесса. Во-первых, мы
вводим его не над К., а над S; во-вторых, определяем корре-
ляционный функционал не через билинейный, а через линей-
ный функционал. (Это соответствует тому, что для обычного
стационарного случайного процесса корреляционная функция
есть функция не двух переменных, а одного.) Впервые такой
способ предложен японским математиком К- Ито в 1954 г.
Можно было бы подумать, что за счет расширения прост-
ранства основных функций (что должно вести к сужению
класса возможных функционалов) и ограничения вида корре-
ляционного функционала мы потеряли некоторые обобщенные
случайные процессы. Но оказывается, что для стационарных
обобщенных случайных процессов это не так: получается в
точности тот же класс процессов (см. [12]). С другой сторо-
ны, при нашем подходе теория стационарных обобщенных
процессов превращается в довольно простое упражнение, для
которого не нужно знать ничего, кроме основных определе-
ний (например, основная теорема о виде корреляционного
функционала доказывается проще, чем известная теорема
Бохнера — Хинчина для обыкновенных процессов: сравните
изложение в [15]) с последующим изложением).
Итак, дадим основное определение. Обобщенным стацио-
нарным случайным процессом (в широком смысле) называ-
ло
ется отображение £:<р—*-Lq пространства 5={<р} основных
функций в La, для которого
СО
М£(<р) = /п у <p(/)rft, т~ число;
—СО
м|Мф)|‘=(в, <р* <р),
где В — обобщенная функция над S, называемая корреляци-
онным функционалом.
В силу формулы (2) п. 2.1 данного параграфа это опреде-
ление обобщает понятие обыкновенного стационарного про-
цесса.
§ 3. Спектральное разложение корреляционного
функционала
Какие-либо примеры обыкновенных или обобщенных слу-
чайных процессов удобнее приводить после того, как будет
построена общая теория, состоящая в изучении преобразова-
ния Фурье. Начнем с преобразования Фурье корреляционного
функционала. Следует иметь в виду одну историческую осо-
бенность. Спектральное разложение стационарного случайно-
го процесса, эквивалентное его преобразованию Фурье, было
впервые выведено А. Н. Колмогоровым как частный случай
так называемой «теоремы Стоуна» о спектральном разложе-
нии однопараметрической группы унитарных операторов. При
этом прямое и обратное преобразования Фурье оказались пе-
реставленными. Чтобы не нарушать общепринятых обозначе-
ний, будем заниматься обратным преобразованием Фурье
корреляционного фукционала и самого стационарного про-
цесса. Сами эти объекты окажутся прямыми преобразования-
ми Фурье их обратных преобразований.
Напомним, что преобразованием Фурье функционала
F=iF(<p), определенного на некотором пространстве основ-
ных функций {<п}, называется функционал F, определенный на
пространстве {<р} преобразований Фурье основных функций
<р формулой
(Л $)-2k(F, <р).
Следовательно, обратным преобразованием Фурье функцио-
нала F называется функционал F, определяемый соотноше-
нием
(А ф) = Г" Ф)»
181
где ф — обратное преобразование Фурье функции ф.
В случае, когда {ф}=3, где 5 — множество гладких быст-
ро убывающих функций (переменного t), множества {ф} и
{ф} также состоят из гладких быстро убывающих функций
(другого переменного Л), так как при преобразовании Фурье
умножение на степень аргумента переходит в дифференциро-
вание и наоборот. Кратко это выражают формулой 3=3=3,
но надо не забывать о том, что функции из этих пространств
зависят от различных аргументов.
Нетрудно проверить непосредственно, исходя из определе-
ния свертки ф»ф двух основных функций, что
Ф* ф(Х) = 2« ф (X) ф (X).
Поскольку для функции фСО=ф(—t) имеем, очевидно,
ф(Х)=><р(Х) ,
имеем следующее важное для нас соотношение:
Ф» ф (Х)-2к|ф(Х)|«. (1)
Пусть F(A) — неотрицательная счетно-аддитивная функ-
ция множества (определенная на ограниченных подмножест-
вах А прямой (—оо, оо)), такая, что для некоторого
^-<оо.
(2)
Тогда F называется мерой степенного роста. Мера степенного
роста, очевидно, задает функционал на пространстве 3 по
формуле
ЛФ) = (^ Ф)- J ❖<X)F(dk).
Теорема. Пусть В — корреляционный функционал обоб-
щенного стационарного случайного процесса. Тогда
B=F,
где F — мера степенного роста.
Эта теорема называется теоремой о спектральном разло-
жении корреляционного функционала. Она означает, что
182
В($) = (В, ф) = 2к(В, ф) =
= 2к j i(X)F(rf).), (3)
— 00
00
где Ф(Х)= -J- (* е“ихф(«)Л.
2я I
Доказательство. Поскольку для любой функции
Фе$
О < М16(ф)|« = (в, ф » ф) - 2к (В, 2к |фГ) =
= 4^(5, |ф|2),
то получаем важное свойство положительности функцио-
нала В: (В, |ф|2) > 0. Отсюда и выведем, что В —не что
иное, как счетно-аддитивная мера (на ограниченных под-
множествах прямой), а затем оценим ее рост на беско-
нечности.
Прежде всего нужно доказать, что (В, <р)^0 для любой
финитной неотрицательной функции Конечно, ф=
= ()Ар) , но ]Ар не обязательно входит в S, так как в тех
точках Л, в которых ф(Х)=О, может при извлечении корня на-
рушиться гладкость. Поэтому для данной финитной ф(Х)^О
образуем последовательность функций
W= ^Ф(>-)+ 1/«а(Х), n= 1, 2...........
где a(X)eS, а(Х) равна 1 при тех Л, для которых <р(Х)=/=О и
а (Л) финитна. При этом
|фя(М1в« ( Ф(М+ —
\ п 1
в смысле сходимости в S. Но функционал В непрерывен на
S, а тогда В непрерывен на S и, следовательно,
(В, ф) = lim (В, |ф„ (к)|«) >0, ф>0. (4)
Теперь продолжим функционал В на непрерывные финитные
функции. Пусть последовательность фп(Х) функций из S рав-
номерно сходится к непрерывной финитной функции %(Х)^0.
Имеем для любого ®>0 при nit п^п—п^)
183

<5>
Пусть при IXl >a имеем: %(X)—0 и фп(Х)=О при всех п, а
функция a(X)eS финитна и равна 1 при IXl^a. Умножим
обе части неравенства (5) на а (Л); так как фя(Х)а(Х) =
=фп (X), получаем
— ('•) — К (М < £а(Л)-
Но в силу (4), применение функционала В сохраняет нера-
венства между функциями из S. Поэтому
- е (Й, a ) < (В, фЯ1) - (В, ф„.) < е(Й, а),
что и доказывает, что можно определить (В, %) как
lim (В, фп).
П“*00
Итак, функционал В можно продолжить (как линейный
непрерывный функционал) на непрерывные функции, обра-
щающиеся в нуль вне любого отрезка. Положительным функ-
циям будут соответствовать неотрицательные значения функ-
ционала. По теореме Рисса (см. [23]) такой функционал за-
дается функцией с ограниченным изменением; из неотрица-
тельности его значений на положительных функциях вытека-
ет, что он задается мерой F.
Остается оценить рост меры F на бесконечности, т. е. уста-
новить оценку (2). Допустим противное: при любом Л>0 ин-
теграл (2) расходится. Тогда укажем некоторую функцию
<peS, к которой нельзя применить функционал В, что будет
означать противоречие.
Действительно, если при любом Л=1, 2,... интеграл (2)
расходится, то существует последовательность чисел 0<mi<
..., такая, что, например, mk>k2,
расстояние mh+i—тк>2 и
J ' <6>
Возьмем функцию ₽(Х), равную на отрезках вида тк +
+ l/2<|XKmfc+1 — 1/2 функции 1/(1 + |Х|*), k= 1, 2,...,
...» и равную нулю между этими отрезками. В силу (6)
интеграл J p(X)F(dX) = оо. Функция 0(Х) убывает быстрее
• ••
любой степени X, но это еще не есть искомое противоре-
чие, поскольку Р(Х)—как разрывная функция —не входит
184
в S. Возьмем свертку ₽(Х)» d(X), где d(X) — гладкая функ-
ция, обращающаяся в нуль при |Х| > 1/2 и такая, что
f d(X)dX = 1. На отрезке /пк4- 1<|Х|<тд+1 — 1 функция
—ев
I —i
р(Х) • d(X) будет не менее, чем — U + W*) (так как при
в
I Х| > ть > k* отношение (1 4- |Х|*)| (1 4- (X 4- !)*)« f 14——)*
близко к 1), следовательно, интеграл J 0(Х)» d(X)F(dX)v
' —00
= оо в силу (6). Но — как свертка с гладкой финитной
функцией — эта функция гладкая, убывает быстрее лю-
бой степени вместе со своими производными (для диф-
ференцирования свертки р(Х)» d(X) достаточно дифферен-
цировать d(X) и потому входит в S. Теорема доказана.
Рассмотрим теперь случай обыкновенного процесса. В слу-
чае обыкновенного процесса корреляционная функция B(t)
удовлетворяет неравенству \B(t) 1^2?(0) (в силу положи-
тельной определенности). Покажем, что отсюда вытекает, что
мера F от всей прямой конечна. Действительно,
м 1£(ф)|2 = (5, Ф* ф) = J B(t) ф • ф (0 dt <
<В(0) [ ф*ф(Л dt.
Возьмем в качестве ф(/) плотность нормального зако-
на с параметрами (0, о): ф(<) = (о ехр { — t* 12 с1}.
Тогда
£ ф* <p(t)dt = 1,
Ф(Х)-J-exp {-О‘Х«|2}.
Мы получаем, что при любом а>0
(В, ф * ф) = 2к (в, |ф|“) -
= J ехр(—a*X*)f(dXX Д(0)-
— СО
185
Устремляя о-*0, получаем, что J F(dty<В(0).
—оо
На самом деле, В(0) = J F(dk)-, более того,
—ОО
В(0- J eu*F(dK) (7)
—ОО
(так называемая теорема Бохнера — Хинчина).
В самом деле для любой <peS
(В, <р)= J Bit)4(t)dt==2*(B, ф) =
—о»
= 2к f F(dk) . I— f е~"Хф(Х)Л ] =
J I 2“ J I
»oo \ —oo J
- J ( J (8)
—00 \ —00 /
поскольку в силу конечности J |ф(/) | dt и меры F|(— оо,
—•О
оо
оо)} = J F(dk) интегрирование можно производить в лю-
— 00
бом порядке. Из (8) получаем B(t)= J e~wxF(dX), что в
—00
силу вещественности (неотрицательности) F эквивалент-
но (7).
Легко проверить, что всякая функция вида (7) является
положительно определенной (следовательно, может быть кор-
реляционной функцией стационарного случайного процесса).
Мера F в теореме и соотношении (7) называется неслу-
чайной спектральной мерой стационарного случайного про-
цесса. Если мера имеет плотность
FM)=p(X)rfX,
то f(k) называется спектральной плотностью стационарного
случайного процесса (в следующем параграфе у нас появит-
ся случайная спектральная мера, входящая в спектральное
разложение самого случайного процесса; случайной же спек-
тральной плотности не бывает).
!86
§ 4. Спектральное разложение обобщенного
стационарного случайного процесса
Стационарный случайный процесс является преобразова-
нием Фурье от некоторого нового объекта — случайной меры
с ортогональными значениями (короче: ортогональной слу-
чайной меры). Рассмотрим сначала этот объект.
4.1. Ортогональные случайные меры. Пусть каждому ог-
раниченному борелевскому множеству Лс(—оо, оо) по-
ставлена в соответствие случайная величина Z(A)eL'(1,
причем выполняются свойства:
1)Z(Ai + At+ . ..) = 2 ДА) с вероятностью 1 (ряд
z=i
сходится в La, если множество Л14-Л1+ . . . ограни-
чено);
2) M(Z(A)Z(B))=0, если АВ = 0. Тогда Z(A) называет-
ся случайной мерой с ортогональными значениями. По-
ложим
F(A)=!A\Z(A)\2.
В силу свойств 1) и 2) имеем
F(4t + X,+ . . .) = M|Z(A+А1+ . - •)|,=
= м 12 Z(4)|’ = 2 MZ(A<) Z(A7) =
-2 M|Z(A<)|’= 2/W,
i i
t. e. F является мерой (с неслучайными значениями), оп-
ределенной на ограниченных борелевских множествах.
Введем интеграл Лебега |' <р(Х) Z(dk). Пусть сначала
—ОО
<Р(Мв2а<Л(М. где А, — непересекающиеся ограничен-
Ai
ные борелевские множества. Положим по определению
J <p(k)Z(dk) = 2>Z(A(). (1)
—••
Чтобы правая часть (1) существовала как элемент
La, должно выполняться соотношение
М12 «1 Z(At) 1 = М 2 at Z(Ai) Z(A}) =
187
= 2 № - j I<PW I’ =ll<p|l’ < °®.
/ — OO
где через ||ф||>> обозначен квадрат нормы функции ф(Х) в
пространстве L2F — пространстве функций, суммируемых
с квадратом по мере F. Предположим, что ||<р||’<оо. Про-
веденные выкладки доказывают, что
Конечно, необходимо проверить, что определение инте-
грала (1) не зависит от способа представления ф(Х) в виде
<р(Х) = 2а|7л (А). Это делается обычным приемом, когда от
двух представлений
фС0 = 2а</л.(М- %Ь,1В М
i II
переходим к третьему представлению с помощью индикато-
ров множеств AiBj. При этом используются счетная адди-
тивность меры Z и тот факт, что при суммировании каких-то
счетных выражений, составленных из ортогональных векто-
ров гильбертова пространства, можно выделить конечное чис-
ло членов так, чтобы норма суммы всех остальных была
сколь угодно мала (следовательно, допустим любой порядок
суммирования).
Поскольку отображение (1) оказывается в силу (2)
изометрическим линейным отображением Lp-+La, оно про-
должается предельным переходом на все Lp. Результат и
понимается как определение интеграла у ф(Х)2(<й) для
— 00
любого ф е I?F.
Замечание. Существование такого объекта, как орто-
гональная случайная мера, не очевидно. Вместо того чтобы
приводить сейчас примеры ортогональных случайных мер
построим в общем виде этот объект как (обратное) преобра-
зование Фурье стационарного случайного процесса.
4.2. Спектральное разложение обобщенного стационарного
случайного процесса.
Теорема. Обратное преобразование Фурье обобщенно-
го стационарного процесса есть случайная ортогональная ме-
ра Z, такая, что M|Z(4)|2= F(4), где F(A) — неслучайная
спектральная мера.
188
Это означает, что значение процесса £(ф) может быть за-
дано следующим образом:
£(Ф) (5, <Р) - 2к (Z, ф) = 2n J ф(Х) ЖГ (1)
—ОО
где Z — комплексно-сопряженная к Z мера.
Доказательство. Если формула (1) верна, то зна-
чение Z(A)= Z(Л) можно получить, применяя £ к такой
функции <р, что <р = /А/2к. Трудность, которую надо пре-
одолеть, заключается в том, что функция <р S, следова-
тельно, и возможность применения & к ф нужно
обосновать путем предельного перехода. В силу теоремы
о спектральном разложении корреляционного функциона-
ла для фе5 имеем
м |г(ф)|«=(в, ф * ф)=2z (f,|;|2| =
= 2z J |ф(k)PF(A). (2)
—00
Соотношение (2) означает, что ||£(ф)|я = 2к||ф||2.Следо-
вательно, еслиф„->ф в L2f, то |(фп) сходится в 1?а. По-
ложим §(ф)= Иш|(фп) и продолжим таким способом функ-
ционал | на все такие ф, что в частности на та-
кие ф, что ф — индикаторы 1А ограниченных борелевских
множеств. После этого положим
Z(A) = ^p), ф =/А/2к.
В силу справедливости соотношения (2) для норм выпол-
няется следующее соотношение для скалярных произведений:
М£(ф)|)ф) = 2к J
— 00
из которого следует, что если ф — 1А, ф = 1В, АВ^0,
то
MZ(A)Z(B) = MZ(AjZ(B) =0.
Свойство же ZfAtJ+Z(’A2^ + ... ^Z(Ai+A2+,..) есть просто
свойство линейности функционала £.
Осталось доказать формулу (1). Но левая и правая
части этой формулы линейны по ф и <р и (1) выполняется
189
(по определению Z(A)) для <р, таких, что ф = Za. Следо-
вательно, эта формула справедлива для ф = 2с<Ла/(*).
тогда предельным переходом получаем, что она верна
для любых <ре L~f, в частности для ф е S, т. е. для <p=S.
При атом имеем
M|Z(X)|«=M|g(<p)|« =
= 4к>||7а|2к||7. = ||/а|Г£ = Г(4).
Теорема доказана.
Рассмотрим случай обыкновенного процесса £(/). В этом
случае
ОО
£(ф)= J t(0<P(0^, Ф е S,
— 00
(3)
мера F((— оо, оо)) конечна, а следовательно, любые огра-
ниченные функции от ). (в частности, е'п ) входят в 1Л.
В силу (1) имеем для фе£
£(ф) = 2"
e“‘7XZ(dX) )ф(0Л
(перестановка порядка интегрирования обосновывается сна-
чала в конечных пределах по t и X путем приближения функ-
ции e-i,Ky(t) ступенчатыми функциями; затем используется
тот факт, что е_<<*ф(0е£2 относительно произведения меры
F на лебегову меру).
Сравнивая (3) и (4), находим, что
6(0- J ei/xZ(dX). (5)
— 00
Формула (1) для обобщенного процесса и формула (5) для
обыкновенного процесса называются спектральным разложе-
нием стационарного случайного процесса.
Замечание 1. В типичном случае существования спек-
тральной плотности имеем
M|Z(A)|« = F(4)= |7(а) dl.
А
190
Если А — отрезок длины Д, то MIZ(A)!1 по порядку
величины есть Д; тогда Z(A) имеет порядок величины
У&, так что никакая ,случайная спектральная плотность"
невозможна: Z(A)|A имеет величину 1|)/Д—>оо при Д-»0.
Иными словами, если рассмотреть, например, функцию
Z(X)=Z{[0, X)}, то эта функция (как функция от X) не будет
функцией ограниченной вариации. Возможность определения
интеграла по случайной мере связана не с ограниченностью
вариации, а с ортогональностью приращений функции Z(X).
Таким образом, записать интеграл типа (5) в каком-то виде,
напоминающем интеграл Римана (по мере dX), нельзя.
Замечание 2. Случай вещественного случайного про-
цесса £(<) » g(0 выделяется в формуле (5) условием
Z(A)= Z(— А),
в частности, Z({0}) вещественно. Можно превратить (5) в
вещественное выражение, связанное (вместо и Z(A)) с ко-
синусами, синусами и двумя взаимно некоррелированными
ортогональными мерами, но мы не будем этим заниматься.
В наших обозначениях корреляционная функция вещест-
венного процесса есть преобразование Фурье от спектраль-
ной плотности f(X), которая определена при —оо<Х<оо и
является четной функцией: f(X) =f(—X). Часто рассматрива-
ется спектральная плотность f+(X)=2f(X) для Х>0, не опре-
деляемая при Х<0. Для перехода к нашим обозначениям
нужно f+(X) разделить пополам и продолжить четным обра-
зом для Х<0. При этом, однако, f(O)=f+(O) (значение в точ-
ке нуль не удваивается), что обычно несущественно.
§ 5. Применения спектральной теории
5.1. Случайные колебания с дискретным спектром. Модели
случайных процессов, правдоподобно отражая одни черты
какого-то явления, часто являются бессмысленными в других
отношениях. Следует это понимать и не напрягать модель
выше пределов ее возможностей.
Рассмотрим для начала модель суммы случайных перио-
дических колебаний. Пусть, для наглядности, на некотором
перекрытии установлено несколько станков, вращающиеся
части которых создают периодические дисбалансы, а нас ин-
тересует суммарная нагрузка на перекрытие. Попробуем изо-
бразить ее моделью стационарного случайного процесса.
В спектральном разложении случайного процесса его ма-
тематическое ожидание a-tA^(t), очевидно, дает неслучай-
ный вклад в спектральную меру Z, равный аб(Х) (где б(Х) —
191
дельта-функция, т. е. мера, равная 1 и сосредоточенная в
точке Х=0). Отсюда вытекает, что мера Z'(A)=Z(A)—
—аб(А) не зависит от а. Иными словами, для любого А, не
содержащего точки Х=0, имеем
MZ(4)=0. (1)
Итак, постоянную во времени составляющую (в на-
шем примере суммарный вес всех станков) можно вклю-
чить в Z либо вычесть из £(<)• Будем для простоты обоз-
начений считать, что MJj(/) = O. Каждый станок создает
(в нашей модели) колебания на некоторых частотах (X у
нас — круговая частота). Объединение всех частот ко-
лебаний по всем станкам обозначим (Xj....Эти ча-
стоты будем считать неслучайными, а амплитуды колеба-
ний аь а,, . . , <х„ — случайными. В модели стационарного
случайного процесса возникает мера Z, причем в ком-
плексной записи мера Z помещается в точках Хь . . . ,
н в точках (— \)....(— Хп) так, чтобы Z(4) = Z(- А), а
мера Z была ортогональной: MZ (A)Z(B) = 0, АВ — 0.
Пусть Z(X/) = z? = rJ e*’’/, тогда Z(—Ху) = гу = гзв-/<1,/. Орто-
гональности меры Z проще всего добиться, считая Zj при
разных / независимыми, но в точке Ху и точке (—Ху) долж-
но соблюдаться соотношение
MZ(Xy)Z (- Ху) = M[Z(Xy)]« = Mr? eivi = 0. (2)
Кроме того,
MZ(Xy)eMrye^=O. (3)
Соотношения (2) и (3) проще всего удовлетворить, считая
г/ и ф/ независимыми, а величины ф/ — равномерно распре-
деленными на единичной окружности. В этих предположени-
ях есть разумный физический смысл — ведь фаза колебания
Ф/ связана с моментом включения /-го станка и ее естествен-
но считать равномерно распределенной на окружности (прав-
да, ф/ и фл при j^=k могут относиться в нашей модели к од-
ному станку, так что их независимость — а тем более неза-
висимость амплитуд г/ и гл — достаточно проблематична).
Получаем спектральное разложение вида
5(0= J eiMZ(&) = = J п (e1<V+’/) + e-i(x/'+’/)J =
—ОО /=1
192
= У 2 r} cos (X/ + фу) = 2 Ricos M + ФЛ RJ = 2rj- <4)
/-1 /=1
Итак, мы получили сумму гармонических колебаний со слу-
чайными амплитудами и фазами.
Нетрудно найти корреляционную функцию случайного
процесса (4). Действительно, F(A)=MlZ(A)l2 есть мера, со-
средоточенная в точках ±Л1, .... ±ХП. причем
Г( ± Ху) = М |Z( ± X,) |» = М rf = -J- М2?’.
Следовательно,
B(/)-Mg(s)g(« + 0 = J eiM F(dX) =
—00
h
COSX/t.
(5)
Иными словами, корреляционная функция есть сумма гар-
монических колебаний. Мы описали некоторую модель слу-
чайных вибраций.
Однако модель (4) имеет следующее парадоксальное свой-
ство. Реализации случайного процесса %(t) как функции t
являются аналитическими функциями. Поэтому, наблюдая
реализацию t,(t) в течение сколь угодно малого промежутка
времени, мы можем точно определить эти аналитические
функции для всех остальных значений t, в частности для
каждой реализации точно определить R;, к/, ф/. (Этому соот-
ветствует и тот факт, что при t—► <» корреляционная функ-
ция B(t) не стремится к нулю: между сколь угодно далекими
по времени значениями процесса присутствует связь.) Ясно,
что в практическом отношении такой вывод неразумен. Не
следует догматизировать абстракцию точной наблюдаемости
значений %(t).
5.2. Винеровский процесс и белый шум. Как известно, броу-
новским движением называется наблюдаемое под микроско-
пом движение мелких частиц (размером порядка 1 мкм и
несколько менее), взвешенных в жидкости. Построим его
математическую модель. Пусть w(t) — абсцисса движущей-
ся точки в момент t, f^Q- для простоты ш(0)=0. Броунов-
ская частица ведет себя столь нерегулярно, что для любых
значений Л<4< ... <tn приращения процесса w(t), т. е.
разности
13—2567 193
w(tl)—W(Q)=w(ti), w(t2)— w(tn)— W(tn-\), (1)
естественно считать независимыми случайными величинами.
Предположим дополнительно, что распределение любой из
разностей w(ti+l)—w(t,) нормально с нулевым математичес-
ким ожиданием и дисперсией o2(f<+i—к), где о — некоторый
параметр. Этим предположением задается совместное рас-
пределение разностей (1): как распределение независимых
случайных величин. Следовательно, задается и распределе-
ние величин
w(ti), w(t2), .... w(tn)
как функций от величин (1), т. е. конечномерное распреде-
ление процесса w(t) (очевидно, получаем набор согласован-
ных распределений). Случайный процесс с такими конечно-
мерными распределениями называется винеровским процес-
сом (по имени американского ученого Н. Винера). Конечно,
как модель физического броуновского движения он услове»
(позже познакомимся с более точной моделью) и действует
при не слишком малых разностях /,+|—tt. Принимая эту мо-
дель для любых разностей, мы должны быть готовы полу-
чить удивительные выводы.
Например, докажем теорему, состоящую в том, что
по наблюдениям w(t) на сколь угодно малом интервале
[О, Г] можно точно определить а1. Действительно, положим
т
ti = — i9 i«0, 1, ...» п и составим выражение
п
з’=2 (»(»('.))-' Р>
Z-0
В силу определения винеровского процесса
и*1--Мв°,г-
i-0
л—1
Подсчитаем DS2 = 2 В{(®(^+1) —НО))2}- Для нормаль-
ной случайной величины £ с параметрами М£ = 0 и D£ =
= а2 имеем D{£2} = M£*— (М|2)2 = 2о*. Поэтому
DS> = 3(<,+1
Z—1
= 2а4п- /—У — 2а*Т/п,
In I
194
что стремится к нулю при п—► <». Итак, в силу неравенства
Чебышева получаем, что при и —► оо S2 —► о2? по вероятно-
сти. Казалось бы, что для точного определения о2 нужно
только составлять выражение (2) для все больших п, но по-
нятно, что практически это не может иметь смысла как по
причине неточных наблюдений w(t), так и по причине непол-
ного соответствия модели винеровского процесса реальному
процессу броуновского движения.
Но как математический объект винеровский процесс
очень интересен. После некоторой борьбы с теоретико-мно-
жественными трудностями оказывается, что его реализации
непрерывны, но нигде не дифференцируемы. С его помощью
строятся так называемые стохастические уравнения (к со-
жалению, не вошедшие в данную книгу), которые являются
новым математическим средством, например, для изучения
задач уравнений с частными производными с помощью тео-
рии вероятностей (т. е. методами теории меры). Ограничим-
ся тем, что построим с помощью винеровского процесса (су-
ществующего в силу теоремы Колмогорова о продолжении
меры) случайную меру с ортогональными значениями.
Выпустим из точки ш(0)=0 две независимые реализации
винеровского процесса wt(t) и w2(t), На оси значений
X: —оо<Х<оо введем функцию Z(X) по следующему прави-
лу: Z(0) =0, для Л>0 положим Z(h)=wi(k), а для Л<0
положим Z(X)=—м>2(—Л) =—w2(IXl) (можно с тем же ус-
пехом положить и ^(Л)=к»2(1Л|)). Для отрезка [Ль Л2],
Xi <Л2, положим
-Z{[X1, M)=Z(X2)-Z(M
(для 0<Л1<Л2 случайная мера Z{[Xi, X2]}=u>i (Л2) — u>i (М);
для Л1<Л2^0 случайная мера Z{[Xi, Л2]}=—Щ2(|Л21) +
+ а>2(1Х11)=а/2(1Х11)—102(|Х2|), а если Л1<0<Л2, то мера
2{[Ль Л2]} равна сумме мер отрезков [Ль 0] и [0, Л2]). При
этом M|Z{[X|, Л2])12=о21Л|—Л21, MZ{[Xi, Л2В=0, а для непе-
ресекающихся отрезков [Ль Л2] и [Л/, Л/j значения меры Z
независимы, следовательно, и ортогональны.
Немного повозившись, можно продолжить меру Z на бо-
релевские подмножества А, получив, что
F(A) - М |Z (Л) |> - а> 1(A), /(к) = Л41 «
где 1(A) — лебегова мера (длина) А. Мера F(A) есть мера
степенного роста:
F(dX) = f аМХ
14-л« I 1+х»
13*
195
Следовательно, можно рассматривать обобщенный слу-
чайный процесс £ со спектральной мерой Z. Этот процесс
называется белым шумом интенсивности о3. Его корреляцион-
ный функционал В является преобразованием Фурье от ме-
ры а21(А), т. е. равен 2ло26(7). Следовательно,
М 1£(Ф)1* = (В, Ф * <р) = 2№ . J |ф(0|« dt =
—ОО
= 2то1||ф ||2, (3)
где ПфН2 понимается в смысле нормы в L3 по мере Лебега.
Если на всей прямой —оо</<оо определить винеров-
ский процесс w(t) (так же, как это было сделано для функ-
ции Z(X)) с параметром 2 ла2, то случайный процесс мож-
но понимать как обобщенную производную w(t). Действи-
тельно, для гладкой финитной функции ф=ф(/)
(а/, ф) =» — (®, ф') = — j ы>(/)ф' (t)dt =
—ОО
= - J w{t) йф (/) = — lim 2 w(ti) (<p(*i+i) — Ф('«)) =•
—ОО
= lim 2 Ф(4) («К**) — ))•
i
откуда
М|(щ', ф)|’=2ко3 lim 21Ф&) I’ (li — *«-i)в
I
==2ко8 J 1ф(0|‘Л, (4)
—ОО
М(о>', ф) = 0.
Равенства (4) означают, что (как обобщенный процесс в
широком смысле) w' =
Итак, белый шум есть производная от винеровского про-
цесса (которой в обычном смысле не существует). Посколь-
ку приращения винеровского процесса в различные момен-
ты времени независимы, говорят еще, что белый шум есть
процесс с независимыми значениями. Его спектральная плот-
ность равна константе.
Часто на практике случайный процесс, о котором мало
что известно, считают белым шумом. Мы сейчас увидим, что
при расчете прохождения процесса через различные филь-
196
тры это может быть достаточно разумно. В других случаях
пользуются белым шумом в полосе частот Л: считают, что
^(Х)=С при 1М<Л и f(X)=O при |Л1>Л. Нелишне заме-
тить, что белый шум в полосе частот — это обыкновенный
процесс, реализации которого являются аналитическими
функциями t. Поэтому не следует абсолютизировать эту мо-
дель (как и модель белого шума, значения которого при каж-
дом t бесконечны).
5.3. Дифференциальные уравнения со случайной правой
частью. Дифференцировать случайный процесс
5(0-J e‘x'Z(dk) (1)
— одно удовольствие:
£’*>(/)= J (iX)‘eix'Z(dk),
—00
и это имеет смысл в области обыкновенных процессов, пока
M|g<*>(0|,= J |(iX)‘e,xT F(dk) =
—СО
00
= f |k|2* F(dA) < oo,
— 00
а в области обобщенных процессов имеет смысл всегда, так
как если мера F является мерой степенного роста, то и при
любом k мера, элемент которой равен |A,l2ftF(dX), тоже есть
мера степенного роста.
Рассмотрим уравнение
р(±\ *(0=5(0.
\ al I
(2)
где Р — полином с постоянными коэффициентами, 5(0 —
случайный процесс, заданный спектральным разложением
(1). Достаточно найти какое-нибудь частное решение (2).
Поищем его в виде стационарного случайного процесса
х(0= J eiX'<p(X)Z(dk). (3)
197
Подставляя (3) в (2), получаем
ОО
eix'<p(X)P(tX)Z(d).) =
eix'Z(dX),
(4)
т. е. чтобы удовлетворить (4), достаточно положить
<р(к) =
____1_
Р(<к) •
(5)
Так положить будет хорошо, если при веще-
ственных А. Если же это не так, то нас не спасает ника-
кая теория обобщенных процессов: интеграл (3), вообще
говоря, не существует (он существует лишь в случае
«о I \
[ ф(А)!1 00 )• В частности, в следующем пункте мы
—оо /
исследуем уравнение
t
*'(/) = £(/), x(Oe p(s)ds,
которое не имеет решения, являющегося стационарным слу-
чайным процессом (в то время как формула (3) всегда зада-
ет стационарный процесс).
Решение (3) с практической точки зрения выглядит
странно: оно выражено через какой-то сложный объект —
случайную ортогональную меру Z. Но его практически важ-
ные характеристики легко подсчитываются, например,
М|х(Г)|‘= J |Ф(>.)1,Л^).
Mx(s)x(H-s)= j еш |<р(Х)|« (6)
— 00
Из (6) следует, что если f(k) — спектральная плотность про-
цесса %(t), то спектральная плотность решения (3) есть
1ф(*)12/(М.
Частное решение (3) уравнения (2) должно быть допол-
нено решением однородного уравнения. Если уравнение (2)
устойчиво (корни многочлена Р(А)=О имеют отрнцатель-
198
яые вещественные части), то решение однородного уравне-
ния при t—»-оо убывает, и остается лишь решение (3). Гово-
рят, что решение выходит на стационарный режим. Таким
образом, возмущение устойчивой системы стационарным
процессом £(t), стоящим в правой части (2), приводит к воз-
никновению стационарного режима. Это не мешает тому, что
решение (3) в какие-то моменты времени принимает боль-
шие по модулю значения, но при каждом данном t это ма-
ло вероятно (в силу неравенства Чебышева). Большие значе-
ния реализуются за очень большое время. Учет нелинейности
(или дополнительной диссипации энергии при больших x(t))
приводит к тому, что большие значения решения не реали-
зуются никогда.
При неустойчивом уравнении (2) рост решения будет оп-
ределяться главным образом растущим по экспоненте реше-
нием однородного уравнения. Добавка случайного процесса
(3) может оказаться практически несущественной.
Аналогично рассматривается система линейных диффе-
ренциальных уравнений с постоянными коэффициентами и со
случайными возмущениями в правых частях.
5.4. Статистические вопросы, связанные со стационарны-
ми случайными процессами.
5.4.1. Оценка среднего значения. Оценку среднего значе-
ния а = Мб(0 естественно производить с помощью вре-
! т
менного среднего £т= — Посмотрим, возможно
6
ли это.
Используя спектральное разложение процесса #1), по-
лучим

JxiKr—1 Г 1
L z(dk)=z(O)+ J—Lz(dx). (i)
• Ал I (Ал
1>|>« |Х|>0
Покажем, что второе слагаемое в (1) стремится к ну-
лю при Т-*-со в смысле Zn. Имеем
М
Г е‘хг-1
J
1Т\>0
|Х|>0
,iXT_. I»
ТГ-| '<*>•
(2)
199
Так как выражение
/хг-| *
созХГ—1
XT
IsinXf
X?
ат
ограничено при любых Л и Г и стремится к нулю при Т-*
—► <» для любого Л#=0, то (для обыкновенного процесса
\(t), для которого F{(—оо, оо)}<оо) в силу теоремы Лебега
о предельном переходе под знаком интеграла получаем, что
(2) стремится к нулю прн Т —► оо.
Таким образом, при Т—►оо имеем —►Z(O). Однако
спектральная мера Z(0)=a+6, где а=Й;, а б — возмож-
но, какая-то случайная величина, такая, что Мб=О. Значе-
ние %(t) случайного процесса представляется в виде %(0 =
=а+&+%*(1), где l*(t) такой случайный процесс, для кото-
рого Z (0) =0. Можно считать, что значение б прибавлено к
реализации процесса a+£*(?) в бесконечно далеком про-
шлом. Иначе говоря, если б#Ю, то бесконечно далекие про-
шлые значения процесса связаны с его значениями при
OcfcT.
Свойство независимости значений случайного процесса
lift) в момент t от его значений в далеком прошлом называ-
ется эргодичностью. Математические определения эргодич-
ности бывают различными. Например, можно понимать эр-
годичность в том смысле, что fr—► а в L». Мы видели, что
для такой эргодичности необходимо и достаточно, чтобы
Z(0)=a, т. е. 6=0. Практически спектральная мера, конеч-
но, не бывает известной, и вопрос об эргодичности понима-
ется как вопрос о независимости значений процесса в любой
данный момент времени от его значений в далеком прошлом.
Этот вопрос каким-то образом решается на уровне опыта и
интуиции.
Пусть процесс £(0 эргодичен. Оценим близость выра-
жения к Mg(f) = a (предполагая без ограничения общ-
ности, что в = 0). Существуют математические теоремы,
которые устанавливают, что при некоторых условиях,
усиливающих свойство эргодичности, распределение вы-
т
ражения —Jg(/)df при больших Т приблизительно нор-
мально. Следовательно, достаточно оценить дисперсию
этого выражения.
Аналогично формулам (1) и (2) имеем
D
----У- F(dk).
(3)
о
200
Пусть в точке Л=0 существует непрерывная спектральная
плотность f (X). Тогда, заменяя F(dX) на f (X)dX и делая за-
мену переменной ХТ—и, Ъ.=и/Т, из (3) получаем
= 2«||/|o.tl(O|Pf(O)-2Bf(O).
(В последней выкладке использованы нормы в L2 по мере
Лебега и равенство Парсеваля 11<рИ2=2л11<р112.)
Таким образом, при оценке МЦ1) с помощью мы
ориентируемся на нормальный закон и среднеквадратич-
ное уклонение вида У2п((0)/Т. К сожалению, последнее
выражение зависит от неизвестного (в большинстве прак-
тических ситуаций) значения f(0). Конечно, спектральная
плотность стационарного процесса может оцениваться по
наблюдениям, но именно оценка спектральной плотности
ДХ) в точке X = 0 представляет практические затрудне-
ния. Однако какое-то понятие о ДО) на основании наблю-
дений получить обычно можно.
5.4.2. Оценка корреляционной функции. Если случайный
процесс \(t) (пусть для простоты вещественный) нам интуи-
тивно представляется стационарным эргодическим (в смысле
независимости будущего от прошлого), то многие функции
от него,напримерт) Д, t+u) =l(t)£(t+u), тоже будут стацио-
нарными эргодическими процессами (и фиксировано, t ме-
няется). Следовательно, можно по реализации процесса
r}(t, t+u) оценивать математическое ожидание
МЛ(?, t+u)=Nb(t)W+u)=B(u),
где В (и) — корреляционная функция процесса %(t). Правда,
по наблюдениям процесса %(t) на отрезке мы смо-
жем (при м>0) составить значения процесса т|(С Г+ц) лишь
на отрезке О^Г^Т—и. Соответственно оценкой Вт(и) функ-
ции В (и) будет
Т-и
Вт(и) = ^±- (‘ l(t)W + u)dl.
о
(О
201
На какие теоретические функции В (и) мы ориентируемся?
Если, например, отправляться от белого шума, спектральная
плотность которого есть константа, и рассматривать соглас-
но п. 5.3 решения дифференциальных уравнений, в правую
часть которых входят сначала белый шум, а потом и другие
процессы, получаемые из белого шума, то мы придем к клас-
су процессов со спектральными плотностями вида
|P(iX)/Q(iX) |2, где Р и Q — многочлены с какими-то (посто-
янными) коэффициентами. Такие спектральные плотности
называются рациональными, хотя на самом деле они пред-
ставляют собой квадраты модулей рациональных выраже-
ний. Ввиду равенства
PW_I* = ( X_вещественно, (2)
I 0(Л)ё(-А)
где коэффициенты многочленов Р и Q комплексно сопряже-
ны соответственно коэффициентам многочленов Р и Q, эти
спектральные плотности, рассматриваемые на веществен-
ной оси 7тХ = 0, в самом деле являются значениями на этой
оси рациональных функций переменного X (теперь будем рас-
сматривать и комплексные значения X). Соответствующая
корреляционная функция
В(и) =
1
&
е
QM
— СО
может быть, в силу (2), вычислена с помощью вычетов,
г» 1и>ь
В результате получится сумма слагаемых вида аке я
(или чуть более сложных), т. е. корреляционная функция
В(и) будет суммой гармоник с убывающими при и -* оо
амплитудами (Xfc — комплексные).
Ожидаем, что оценка Вт(и) при достаточно большом Т
ведет себя похожим образом. Но существенное практическое
осложнение состоит в том, что при различных ui и и2 оценки
Bt(ui) я Вт(и^) зависимы (как случайные величины). В ре-
зультате на графике Вт(и) как функции и (этот график на-
зывается коррелограммой) видны обычно волны, но неиз-
вестно, с чем эти волны связаны: то ли с тем, что истинная
корреляционная функция В(и) ведет себя похожим образом,
то лн они являются артефактом, связанным с недостаточно
большим отрезком времени наблюдений Т. Конечно, вычис-
ление Вт(и) по другой реализации процесса позволило бы
это понять, но не всегда есть возможность наблюдать дру-
гую реализацию.
202
В общем, обманчивость коррелограмма настолько не нра-
вится статистикам, что обычно предпочитают оценивать не
корреляционную функцию, а спектральную плотность.
5.4.3. Оценка спектральной плотности. Математики оце-
нивают спектральную плотность, превращая наблюдаемый
процесс 1(f) в процесс с дискретным временем, т. е. беря
его в точках tk=kh, Л=0, ±1, ±2,..., где шаг дискретиза-
ции ft достаточно мал, и обрабатывая значения на ЭВМ
с помощью так называемого «быстрого преобразования
Фурье». Мы эту науку рассматривать не будем (с ней мож-
но познакомиться, например, по [4]). Физики и инженеры
оценивают спектры путем пропускания наблюдаемого про-
цесса z(t) через систему фильтров. Выведем формулу, поз-
воляющую оценить разброс получающихся оценок спек-
тральной плотности (при замене одной реализации процес-
са другой). Смысл этой формулы состоит в том, что она в
принципе позволяет понять, сопоставляя результаты опреде-
лений спектральной плотности по ряду реализаций одного и
того же процесса, — имеем ли мы дело, действительно, с
ансамблем реализаций стационарного процесса или с чем-то
более сложным.
Фильтром называется линейный оператор, превращаю-
щий одну функцию времени x(t) в другую y(t) (нелинейный
оператор называется нелинейным фильтром). Имея в виду
преобразование реализаций стационарного процесса с целью
оценки спектральной плотности, вполне достаточно ограни-
читься интегральными операторами с ядром K=K(t, s) =
= K(t—s), зависящим от разности t—s. Это означает, что
K(t-s)x(s)ds. (1)
—•о
Чтобы интеграл (1) сходился, нужно потребовать какого-ли-
бо убывания функции —s) при |/—s|->-oo и (или) как-
то ограничить функцию x(s). Например, если y(t) и x(t)
связаны дифференциальным уравнением
= <2>
I at I
где Р — многочлен с постоянными коэффициентами, причем
этот многочлен устойчив (корни имеют отрицательные ве-
щественные части), то, как известно, решение (2) y(t) мож-
но получить по формуле (1), причем K(t—s)=0 при s^t и
K(t—s) убывает экспоненциально быстро при t—s—»-оо.
(Такой фильтр, для которого K(t—s)=0 при s^t, т. е. ин-
теграл (1) превращается в интеграл в пределах от —оо до
203
t, называется физически осуществимым: значение y(t) не за-
висит от x(s) при будущих значениях Нам нет необхо-
димости ограничиваться физически осуществимыми филь-
трами: траекторию случайного процесса можно сначала за-
писать, а потом анализировать.) Понятно^ что практически
интеграл (1) заменяется интегралом в конечных пределах.
Применим (1) к реализации случайного процесса g(s)
(вместо x(s))-, получим вместо y(t) случайный процесс
т](0' задаваемый формулой
^(t)« J K(f-sK(s)ds= J K(t-s)X
e^sZ{ik)
ds= [ Z(dX) j eiX’K(/-s)ds =
— CO —CO
= J Z(dX) f eiX('+“’K(u)du =
—eo — во
= J eiXf<p(X)Z(rfX),
(3)
где <p(X) в J eiXujf(u)do есть преобразование Фурье функ-
—во
ции К = К(и). ^Сравните с п. 5.3: в случае, когда фильтр
состоит в подстановке процесса в правую часть урав-
нения 1 »ХО = ё(0. функция ф(Х) = 1/Р(/Х)
\ dt }
Из (3) следует, что
МI ч(0|’ = J MX) |« F(dX) = у |Ф(Х)|« /(X) dX. (4)
—СО —СО
В радиотехнике известно великое разнообразие фильт-
ров. В частности, можно подобрать фильтр так, чтобы
функция |ф(Х)|* была похожа на в(Х — X,,). Тогда правая
часть (4) даст примерно /(Хо), а левая часть может быть
, . т
оценена как средняя мощность йт|‘=Л процес-
са т](0 (если процесс tj(0 — ток или напряжение в неко-
тором месте радиотехнической схемы,, то И0|* есть, с
точностью до множителя, мощность) или можно подоб-
рать фильтр так, чтобы |<р(л)|2 =/|а ftJi (X). Тогда правая.
204
часть (4) даст интегральное среднее значение спектраль-
ной плотности в некоторой полосе частот [а, Ь], а левая
оценится точно так же, как средняя мощность. В этом
и состоит радиотехнический метод оценки спектральной
плотности с помощью фильтров. Реализация процесса 5(f)
подается на вход некоторой радиотехнической схемы, а
с нескольких выходов снимаются усредненные по време-
ни значения мощностей профильтрованных процессов
т]Л(/), ft=l, 2, ... , N. Получаются приближенные значе-
ния спектральной плотности в ряде точек. Исследуем
статистические свойства этих значений.
Процесс %(t), так же как и профильтрованные процессы
т)л(О- будем считать вещественным. (Для того чтобы функ-
ция фильтра К(и) была вещественной, его спектральная ха-
рактеристика <р(Л) должна удовлетворять соотношению
<р(—х)=<р(Л).) Если функцию <р(Х) брать достаточно «уз-
кой> (чтобы |ф(Л) I2 было похоже на б-функцию), то функ-
ция К(и) будет, наоборот, широкой. Поэтому разумно пред-
положить, что процесс i\(t), получающийся усреднением (с
весом К(1—s)) значений процесса для достаточно ши-
рокого интервала значений s, будет гауссовским процессом.
Если теперь есть два процесса и т|2(?), отвечающие
функциям ф1(Х) и фг(Х), связанным с различными интерва-
лами частот: ф1(Л)ф2(Л)=0, то значения тц(Л) и т]2 (6) не
коррелированы:
1101)- J eiW‘<Pi(MZ(dk), ^(/,)= J elx/‘91(X)Z(dX),
—во —00
00 Т12(^) = Мти (tt) =
= f е,Х('‘-/*’ф1(А)фа(Х)да)«О.
В гауссовском случае некоррелированность означает незави-
симость.
Получаем, таким образом, следующее весьма важное
свойство: оценки спектральной плотности в различных ин-
тервалах частот статистически независимы. Это свойство вы-
годно отличает оценки спектральной плотности от оценок
корреляционной функции. Для описания совокупных стати-
стических свойств оценок спектральной плотности в различ-
ных интервалах частот достаточно описать свойства одной
оценки.
Из формулы (4) ясно, что оценивается не f (Хо), а интег-
рал, задаваемый правой частью (4). Если в некотором ин-
205
тервале частот f (X) близко к f (Хо). то оценим и f (Хо); если
f(k) быстро колеблется с изменением X, то не сможем оце-
нить f (Хо) достаточно точно. Иными словами, какое-то систе-
матическое смещение у наших оценок будет, но трудно ска-
зать, какое именно, поскольку истинные значения спектраль-
ной плотности неизвестны.
При проверке статистической однородности главный во-
прос состоит в дисперсии оценки. Реально мы наблюдаем про-
цесс %(t) на некотором конечном интервале Значе-
ния процесса т)ГО имеет смысл брать на некотором меньшем
интервале —I", где f и t" выбираются, исходя из ско-
рости убывания функции К(и) при возрастании lul: это учет
так называемого времени установления фильтра. Для просто-
ты обозначений рассмотрим — [H(0|2dt Дисперсия тако-
го интеграла выразится через интеграл от математичес-
ких ожиданий произведений вида |tj(s)|2 • |ij(0|2. В гауссов-
ском случае они могут быть выражены через корреля-
ционную функцию (спектральную плотность) процесса
Этим выражением мы и займемся.
Лемма 1. Пусть тр= (%, ijt, •>],, т4)— гауссовский случайный
вектор с нулевым средним и с корреляционной матрицей С =
= RJ|, /=1. 2. 3, 4. Тогда
АН ъ Т|» ’)< = <44 + Си + С3< С1»-
Доказательство. Рассмотрим многомерную харак-
теристическую функцию Gi. G. *». Q =
=М ехр(»(/, •>])}. Поскольку т| = 4F, где % — стандартный нор-
мальный вектор, АА'=С, имеем:
ЦО-МЛ'0 = ехр(--1- (A't, A't)l =
= ехр |-у(СГ, oj. (5)
Очевидно,
Ml1 (6)
Для вычисления (6) разложим (5) в точке /=0 в ряд Тейло-
ра с учетом членов четвертой степени относительно ti. (Чле-
ны более высокой степени при вычислении четвертой произ-
водной в точке t=0 будут давать нуль.) Имеем
/,(0-1- 0>+... • (7)
А О
206
Четвертая производная от первых двух членов выражения
(7) в точке t=0 равна нулю; следовательно,
М 7J1 ?)9 1]9 7]4 = —------—------(Ct, /)2|. 0 =
1 № *’ “ 8 dtidt2dtadtt ' ’ “-°
= -Г 0 + (С'’ е')]'=о^
4 att ot3 ait
1 д3
2 dt2dtsdlt
(Ct, t)(Cei, <)|(»o =
\2(Cet, t)(Cet, t)+(Ct, ^Celt e2)],_0 =
-1-^-[2(Св1, e9)(Ce1, 0 + 2(Ce2> Г)(Сеь e9) +
+ 2(Cet, t)(Celt e2)],_9 = (Cet, et)(Celt e4) -|-
+ (Ce2, с*ХСсь es) + (Cet, et)(Celt e9) =
= ci<+ cm cis 4" Cm cu.
что и требовалось доказать (в этой выкладке ei—dtfdh —
i-й базисный вектор).
Лемма 2. Пусть — вещественный гауссовский про-
цесс со спектральной плотностью f (Л). Тогда
/ г
Dl — (
т
о
Доказательство. Заметим, что M |£(/)|’dt
= 5(0).
Вычислим (с помощью леммы 1) выражение
М f Ь J |«0l’dЛ = 1- М j* С (^(s))« (l(t)? dsdt =
= ± [ f (2B*(t - s) + B*(O))dsdt =
о о
= £Jp4f-s)<fc<W + <B«(0).
О *0
207
Следовательно,
D
Сделаем в двойном интеграле по квадрату [О, Т]Х[0, Г] за-
мену переменных t—s=u, s=w. Тогда и изменяется от
(—Т) до Т, а при данном и переменная s=w изменяется от
lul до Т— ltd. Поэтому
J + о(1)
>00
(последнее в силу равенства Парсеваля). Лемма доказа-
на.
Применим лемму 2 к процессу rj(t) со спектральной
плотностью |<р(А) |2/(к). Получим, что дисперсия о2 оценки
. г
т)]т = — f|Tj(i)|2di примерно дается формулой
00
а’ = у j l4>WI‘TO^.
— 00
(8)
Если функция 1<р(Х)|2 похожа на [S(X—k0)+S(—X—Х0)]/2
(при вещественной функции К(и) функция ф(Х) должна
удовлетворять соотношению ф(—Х)=ф(х) ), то из (8) полу-
чаем, что (в силу соотношения /(—Хо) = /(Хо))
/оо \ 1/2
= у р ю.) J 1ф(Х)Ы .
* \ —/
Таким образом, коэффициент вариации оценки спект-
ральной плотности (т. е. отношение среднеквадратично-
го уклонения к математическому ожиданию) равен
\1/2
|ф(Х)|4 dk ] . При сужении
|ф(Х)|2 к симметричной
208
6-функции коэффициент вариации возрастает, так как
растет интеграл от |ф(/.)]4. Если при этом выбрать Т по-
больше, то этот коэффициент все же будет мал. Целесо-
образно рассматривать логарифмы оценок спектральной
плотности: у них будет известен не коэффициент вариа-
ции, а дисперсия.
Действительно, если случайная величина £ представи-
ма в виде £ = а + б, где ]/D6/a (т. е. коэффициент ва-
риации £) невелик, то тогда для типичного 6 и отношение
(б|/а невелико. Следовательно,
log В — log(a + S) = log а + 1 og( 1 + б/а)«
log а + б/а,
причем дисперсия D(6/a)=D6/a2 равна квадрату коэффи-
циента вариации. Поэтому разброс эмпирических оценок
спектральной плотности обычно исследуют в логарифмичес-
ком масштабе.
В заключение рассмотрим пример. Пусть мы хотим оце-
нить спектральную плотность с помощью полосового филь-
тра с шириной полосы 1 герц=2л1/с=Д с коэффициентом
вариации оценки 5%. Спрашивается, какой (временной) дли-
ны нужна для этого реализация процесса?
Полосовой фильтр означает набор фильтров со спек-
тральными характеристиками фА(Л),_ устроенными следую-
щим образом. При Л=0 фо(Х) = 1/УД при 1Л|^Д/2, фо_(Л) =
=0 при 1Л|>Д/2; при k=£0, k=l, 2, ... фл(Х) = 1/ДУ2 прн
1Л—£Д1^Д/2 и при IЛ+ЛДI ^Д/2 (фй(Л)=0 прн остальных
/.).
Оценим сначала время установления. Имеем (при k=£Q;
случай k = 0 аналогичен):
ОС ЛЛ+Л/J
Кк(и) = }- f f cosZu—L-dX =
2r- J * J д/2
— ЛЛ-А/2 r
= 1 sin и(ДДЦ-Д/2)—sintt(&A—Д/2) _
cos uk& sin(ttA/2)
и
Наибольшее 2начение Кк1и достигается при и = 0 и
составляет 1 /—|/" 2. Если мы пожелаем отбросить такие и,
при которых Kft(u) составляет менее 0,01 от своего зна-
чения в нуле, то (заменяя косинус и синус единицей) по-
лучим достаточное условие:
14 - 2567
209
/2/кД|и|< 0,01/к/2,
т. е. |м|^200/Д=32 с.
Следовательно (так как функция Лй(ы) четная), отрезок,
на котором наблюдается 1(1), придется слева и справа со-
кратить на 32 с. Это даст очень хорошую точность установ-
ления, так как нас интересует ошибка |T]h(l)l2, которая бу-
дет порядка (0,01)2 = 10-4.
Подсчитаем (при Л#=0, случай Л=0 аналогичен)
ОО
J |ФЙ(М|‘^ = 2Д-
— оо
Таким образом, для коэффициента вариации 0,05 имеем ус-
ловие
/4^/Т". 1/ /Д = 0,05,
откуда Т = 400- 4-/Д = 800 с.
Здесь Т есть общее время наблюдения процесса т]А(Т),т. е.
всего нужно 800 с 4-64 с=864 с ( — 15 мин).
Время, которое нужно, чтобы различить значения спек-
тральной плотности с интервалом в 1 Гц и оценить их с хо-
рошей точностью, оказывается довольно большим.
Многие случайные процессы ведут себя так, что в окре-
стности нулевой частоты происходит резкий подъем спек-
тральной плотности. Понятно, что для изучения таких про-
цессов приходится различать очень близкие частоты, напри-
мер 0,01 Гц и 0,02 Гц. Ясно, что при этом время наблюде-
ния должно оказаться очень большим. Для многих важных
для радиотехники процессов шума («фликкер-шум>) так
толком и неизвестно, имеем ли мы дело со стационарным
процессом (тогда f(k) может иметь в точке Х=0 лишь ин-
тегрируемую по Л особенность) или модель стационарного про-
цесса должна быть вообще отвергнута; последнее означало
бы, что со временем происходит некое изменение свойств эле-
ментов радиотехнических схем (т. е. сопротивлений, конден-
саторов, транзисторов, электронных ламп и т. д.), которое
нет возможности описывать стационарным случайным про-
цессом.
ГЛАВА 6
МАРКОВСКИЕ ПРОЦЕССЫ
§ 1. Основные понятия
1.1. Статистический смысл цепей Маркова. В современной
науке не так уж часто бывает, чтобы некоторое важное поня-
тие или метод были, бесспорно, творением одного человека.
Однако именно так обстоит дело с понятием марковской за-
висимости: автором этого понятия — единогласно во всем ми-
ре — считается А. А. Марков (старший). Посмотрим сначала,
нз каких соображений исходил А. А. Марков.
Проверка пригодности тех или иных вероятностных моде-
лей для описания действительности облекается в форму ста-
тистической проверки гипотез и обставляется сложными на
первый взгляд понятиями вроде критической области, уровня
значимости и т. д. Может показаться, что и ответ, который
при этом получается, бывает более или менее неопределен-
ным: на одном уровне значимости гипотеза отклоняется, а на
другом — нет. Но на самом деле так может случиться лишь
при отдельно взятом акте проверки гипотезы; если гипотеза
проверяется многократно и на большом статистическом мате-
риале, то ответ часто оказывается вполне определенным.
Рассмотрим, в частности, гипотезу независимости некото-
рых испытаний (пусть, для простоты, каждое испытание име-
ет два исхода, т. е. мы проверяем гипотезу испытаний Бер-
нулли). Если в п испытаниях произошло т успехов, то мы бе-
рем за оценку неизвестной вероятности успеха в одном испы-
тании р частоту р=т!п и никакой независимости проверить
вообще не можем: всю информацию, данную нам в наблюде-
ниях, мы израсходовали на определение единственного неиз-
вестного параметра р.
(Если нам дано не только общее число успехов т, но и
полный список исходов отдельных испытаний, то проверка не-
зависимости вполне возможна, но пока отвлечемся от этой си-
туации.)
Но пусть серии из п испытаний Бернулли с (одной и той
же для всех серий) вероятностью успеха р реализуем k раз:
получаем ц. успехов в i-й серин из n-испытаний. При этом
= Dpi = npq, q=l—p,
причем за оценку р неизвестного параметра р возьмем, есте-
ственно,
р = (pi + ... , и*) /nk.
Теперь мы можем посмотреть на согласие отдельных значе-
ний с их ожидаемыми значениями пр, в частности на сог-
14* 211
ласие ожидаемой дисперсии пр (1—р) с эмпирической дис-
персией
2 *
S2 = ---
А-1
к к
Gi - Й)2 = У1. Gi - пр)2
i=l i=l
(поскольку |Л= (|М +.. . +Hk)/k=np).
Например, можно взять коэффициент дисперсии
s2/np (1— р)
и посмотреть, близок ли он к 1.
Статистики, изучавшие коэффициент дисперсии на разно-
образном фактическом материале, убедились в том, что иног-
да он действительно близок к 1, но чаще бывает либо неос-
поримо больше 1, либо неоспоримо меньше 1 (соответственно
дисперсия s2 называется нормальной, сверхнормальной либо
поднормальной). Например, А. А. Марков брал в качестве
последовательности испытаний последовательность букв тек-
ста «Евгения Онегина»; успехом испытания считал гласность
буквы (неудачей — согласность), а твердый н мягкий знаки
и «и краткое» выбрасывал. Набрав п= 10000 испытаний, он
разбил их на 100 серий по 100 последовательных букв в каж-
дой и подсчитал коэффициент дисперсии. Он оказался при-
мерно 0,2. Таким образом, число гласных средн 100 последо-
вательных букв русского текста оказалось гораздо более ста-
бильным, чем было бы в том случае, если бы А. С. Пушкин
просто выбирал буквы путем независимых случайных испы-
таний, соблюдая вероятности их появления, характерные для
русского текста.
Если взять, наоборот, число уличных травм за сутки в
большом городе, то при независимости травм для отдельных
жителей мы бы ориентировались (для общего числа травм £)
на распределение Пуассона с некоторым параметром М|=Х,
который мы могли бы определить по статистическим данным
«скорой помощи». С другой стороны, взяв наблюдения
?2> ••• . 5* за k каких-то суток, мы могли бы определить
к
s2 =. к 1 - 1)2- В случае закона Пуассона Щ=М|=Х,
т. е. коэффициент дисперсии s2/h примерно равен 1. Каким он
будет реально? Вне всякого сомнения, s2/X значительно боль-
ше 1 (интересно было бы это проверить по фактическим дан-
ным).
Как интерпретируются поднормальная и сверхнормальная
дисперсия ? В случае независимости испытаний в каждой се-
рии (нормальной дисперсии) дисперсия pi есть дисперсия сум-
212
мы независимых слагаемых. Если между этими слагаемыми
есть положительная (отрицательная) корреляция, то диспер-
сия суммы будет больше (меньше), чем в случае независимо-
сти. Таким образом, сверхнормальная (поднормальная) дис-
персия интерпретируется как указание на положительную (от-
рицательную) корреляцию между результатами испытаний.
Так, появление на каком-то месте в русском тексте глас-
ной буквы, очевидно, означает, что дальше скорее всего по-
следует согласная буква (отрицательная корреляция между
результатами соседних испытаний). Соответственно диспер-
сия поднормальная. Уличные же травмы могут учащаться под
влиянием общей для всех жителей причины (вроде гололе-
да). Соответственно дисперсия должна быть сверхнормаль-
ной.
В XIX в. было хорошо известно, что во многих случаях
дисперсия бывает поднормальной либо сверхнормальной, так
что о модели независимых испытаний говорить нельзя. Конеч-
но, дисперсия любой суммы случайных величин определяется
их ковариациями (либо коэффициентами корреляции), но оп-
ределять из эксперимента коэффициенты корреляции между
результатом i-ro и j-ro испытания на практике часто неудоб-
но из-за ограниченности экспериментального материала (воз-
никает слишком много параметров: корреляций, грубо гово-
ря столько, сколько пар (i, j)). Возник вопрос о модели за-
висимых испытаний, в которой участвовало бы лишь неболь-
шое число неизвстных параметров. Наиболее удачной оказа-
лась модель, которую А. А. Марков называл «моделью» испы-
таний, связанных в цепь», а мы называем «цепью Маркова».
Опишем эту модель. Пусть испытания занумерованы чис-
лами n = 0, 1, 2, ... , а каждое испытание имеет N возмож-
ных исходов, занумерованных числами 1, 2, ... , N. Можно
себе представить, что исходы 1, 2, ... , N изображены N точ-
ками, поставленными па чертеже; тогда последовательность
испытаний наглядно представляется блужданием точки х(п)
(х(л) — исход л-го испытания) по множеству исходов: в мо-
мент времени п—0 частица возникает в какой-то точке io =
=х(0); затем в момент времени л=1 эта частица перескаки-
вает в точку i’i=x(l), из этой точки в момент п = 2 перескаки-
вает в точку i2 = x(2) и т. д. Элементарными событиями, опи-
сывающими первые п испытаний, будут последовательности
{(io, й ... in), i*=l, 2, ... , N). Марковская цепь получается
при определенном способе введения вероятностей событий.
Опишем этот способ, используя соображения, относящиеся
к условным вероятностям. Именно, следуя А. А. Маркову,
предположим, что условная вероятность P{x(n)=j/x(n—
—1), ... , х(0)) (это условная вероятность события (х(п) =
=/} относительно разбиения, задаваемого значениями случай-
ных величин х(п— 1).......х(0)) зависит лишь от значения
213
х(п—1). Но тогда эта функция переменных х(п—1)......х(0)
окажется измеримой относительно разбиения, задаваемого
значениями случайной величины х(п—1). Следовательно (см.
утверждение замечания 4п. 1.1 из § 1 гл. 4), должно выпол-
няться соотношение
P{x(n)=j / х(п—1), ... , х(0)} = P{x(n)=j/x(n-l)}. (1)
Используем (1) как наводящее соображение для введения
безусловных вероятностей на уровне строгого математичес-
кого определения.
Именно, обозначим значение правой части (1) на элемен-
те разбиения {х(п— l)=i} = {(io, й ... , in) :in-t = i) через
Pij(n—1). (Эта величина называется вероятностью перехода
из состоянния i в состояние / на (п—1)-м шаге п ) Введем так-
же величины nj=P{x(0) =/}; набор л=(ль ... , лЛ) назы-
вается начальным распределением. Элементарное событие
(io, й •. • , in) будем понимать как пересечение событий
{х(0) = io) fl {х(Ч) = й> П ... П <x(n) = in }•
Заметим, что теорему умножения вероятностей можно по-
нять следующим образом: для любых k событий В\, В2, ... ,
В,
Р{В}В2 ... Вк) = Р{ (BiB2 ... Вк_})Вк} =
= P{Bft/BiB2 • • Bfc-i} P{BiB2 ... =
= P { Вк / B\B2 . . B*-i } P { Bk-\ I B\B2 ... Bk-2) ...
... P(B2IB,)P(BX).
Поэтому в силу марковского свойства (1) должно выпол-
няться соотношение
Р{(«., «1 • • • й,» - Р«0) = ЙЛРИ1) = hHO) = i0}...
...P{x(n) = in\x(n — 1) = i n =
= 4,Pi.i.(0)Pi,,(1). . . Pln_1(„(n - I)- (2)
В словесном выражении формула (2) означает следующее.
Для того чтобы блуждающая по состояниям {1, 2, ... , N)
точка за время от 0 до л прошла путь {io й • • • in}, нужно,
чтобы в нулевой момент времени п=0 она возникла в состо-
янии ig, в первый момент времени п=1 перескочила в состоя-
ние й, во второй момент времени п=2 перескочила из й в i2 и
т. д. В таком описании цепь Маркова напоминает описание
некоторого физического движения, и мы вскоре увидим, что в
современной науке так оно и есть.
Дадим теперь математическое определение цепи Маркова.
N
Пусть даны числа ~,>0, такие, что 3 «> = 1 и для каж-
/-1
дого п > 0 задана так называемая стохастическая матрица
214
Р(п) = ||p(/n)||, т. е. такая матрица, что ри(п) > 0ш
If
У, Рн(п)я> 1. Скажем, что испытания с номерами 0, 1,..., п
/-1
образуют цепь Маркова, если вероятности элементарных со*
бытий задаются формулой (2).
Не мешает, конечно, проверить, что, отправляясь от безус-
ловных вероятностей (2), получим те самые условные вероят-
ности, о которых шла речь выше. Эта проверка совершается
автоматически: например,
Р {x(n) - j\x(n — 1) = I, х(п — 2) = й_2,..., х(1) — it,
x(0) = fo) = Р [(ioh - in-2 i/)}|S P{(»o h- in-i i/)) -
/
_ - -2i(n — 2)Я/(ге — I) _ / _ n
Vit,tPV1(0)...Pin_2i(n-2)pi/(n — 1) РиП
так как 1) = 1.
Стохастические матрицы P(n) называются еще матрицами
перехода (точнее: матрицами переходных вероятностей). Ес-
ли матрица перехода Р(п) = Р не зависит от п, то соответст-
вующая марковская цепь называется однородной по времени.
Таким образом, если в случае независимых испытаний одно-
родная по времени ситуация характеризуется вероятностями
Р\, ... рх каждого из возможных N исходов, то в случае це-
пи Маркова имеются N начальных вероятностей nb ... , tin
и № элементов переходной матрицы (связанных N соотноше-
ниями 5 Рц = 1, » = 1,. . ., N ). С ростом числа испытаний
п количество параметров, определяющих вероятности элемен-
тарных событий, не изменяется. В принципе начальные веро-
ятности при довольно общих условиях в дальнейшем окажутся
несущественными (при больших п), а переходные вероятности
Ра могут быть определены по частотам тех случаев, когда за
состоянием i следовало состояние / (по отношению к общему
числу наблюдений состояния i среди п испытаний).
Концепция зависимости х(п) только от х(п—1) может по-
казаться слишком ограничительной: возможно, например, что
х(п) зависит от х(п—1) и х(п—2). Но в этом случае ничто не
мешает рассмотреть пары [х(0), х(1),] [х(1), х(2)], ... ,
fx(n—1), х(п)] как значения новой марковской цепи с фазо-
вым пространством (1, ... , х (’1, ... , N). Тогда паре
[х(п— 1), х(п)] предшествует пара [х(л—1), х(п—2)], и прн
фиксировании этой последней пары член х(п—1) «будущей>
пары [х(п— Г), х<п)] точно известен, а член х(п) отделен от
215
«прошлых» пар [х(п—3), х(п—2)], ... , [х(0), х(1)] не менее
чем двумя промежутками времени, т. е. в целом пара [х(п—
—1), х(п)] при известной паре [x(n—1, х(п—2)] не должна
зависеть от «прошлых» пар. За счет расширения фазового
пространства концепция цепи Маркова может быть сделана
довольно общей.
Заметим, что в данном рассуждении мы несколько пере-
формулировали концепцию (1) марковского свойства, сказав,
что это свойство состоит в том, что «при известном настоя-
щем будущее не зависит от прошлого». Точно понимать эту
формулировку нужно следующим образом: при любом нату-
ральном k<.n («настоящий момент») называем «прошлым»
всевозможные события, порождаемые величинами х(0), ...
... , x(k—1), а «будущим» — всевозможные события, по-
рождаемые величинами х(&+1), .... х(п); «настоящим» же
называем события, порождаемые случайной величиной x(k).
Утверждается, что условная вероятность события АВ, где А—
событие из прошлого, В — событие из будущего (относитель-
но разбиения, порождаемого настоящим, т. е. {x(k) = j,
/=1, ... , N}, равна произведению условных вероятностей.
Нетрудно проверить, что такая формулировка эквивалентна
заданию вероятностей элементарных событий в виде (2).
Какие достижения в описании реальных явлений связаны
с изложенным понятием цепи Маркова? Например, чередова-
ние гласных и согласных букв в тексте «Евгения Онегина»
отвечает случаю W = 2. Начальные вероятности здесь прини-
маются равными частотам гласных и согласных букв (причи-
на этого станет ясной ниже). Для описания модели простой
цепи Маркова нужно определить четыре элемента матрицы
llPi/ll, но условия 2 Р</=1, i=l. 2, показывают, что достаточ-
/=1
но определить лишь два числа, например частоту следования
гласной буквы за гласной и гласной буквы за согласной. Ока-
зывается, что из знания этих параметров однозначно вытека-
ет коэффициент дисперсии числа гласных букв в отрезке тек-
ста длиной 100 букв (как вытекает, это предмет излагаемой
далее теории). Он оказывается равным примерно 0,3 (при эм-
пирическом значении 0,2). Таким образом, полного согласия
с моделью простой цепи Маркова нет, но все же результат,
состоящий в том, что колебания числа гласных в длинном от-
резке текста можно довольно близко объяснить на основании
свойств локального взаимодействия (т. е. взаимодействия
близких, в данном случае — рядом стоящих букв), представ-
ляется замечательным. А. А. Марков замечает, что лучшего
результата, возможно, удалось бы достичь с помощью моде-
ли сложной цепи, т. е. с помощью усложнения фазового про-
странства, как описано выше.
216
В настоящее время известно много случаев, когда модель
цепи Маркова применяется для статистического описания раз-
личных явлений (вроде поведения крысы при обучении прео-
долению лабиринта). Как чередование букв в тексте, так и
поведение крысы в лабиринте представляют собой весьма
сложные явления, на поверхности которых наблюдаются слу-
чайные закономерности, неплохо следующие простым вероят-
ностным моделям (в данном случае — моделям цепей Марко-
ва). Для каких-то практических целей эти модели могут быть
и адекватными: если, например, мы не собираемся понимать
«Евгения Онегина», а хотим лишь передать текст поэмы по
телеграфу и решаем, как бы лучше выбрать кодирование (мо-
жет быть, лучше кодировать не отдельные буквы, а, скажем,
их пары и т. д.). Но предвидеть на основании статистических
применений концепции цепи Маркова, что эта концепция мо-
жет иметь важное физическое значение, пожалуй, невозмож-
но. Сам А. А. Марков (насколько можно судить на основа-
нии его частично опубликованной переписки) скептически от-
носился к физическим приложениям, в которых (как теперь
ясно) независимо от работ А. А. Маркова возникла эквива-
лентная концепция. (Дело в том, что А. А. Марков ограничи-
вал свои интересы достаточно строгими в математическом от-
ношении работами. Он уличал в математических ошибках
С. В. Ковалевскую, К. Пирсона и других; эти уличения фор-
мально справедливы, но не имеют тон важности, с которой к
ним относился А. А. Марков.)
Короче говоря, физическое значение цепей Маркова было
понято на несколько лет позже — в связи с работами ряда
физиков и математиков по теории броуновского движения и
диффузии. В настоящее время физический смысл марковских
цепей мыслится еще проще и шире, с чем мы и познако-
мимся.
1.2. Физический смысл цепей Маркова. Сначала посмот-
рим. как можно моделировать цепь Маркова методом Монте-
Карло. Пусть датчик случайных чисел выдает последователь-
ность Во. .......Вп • • • . которую мы считаем последова-
тельностью независимых случайных величин, каждая из ко-
торых равномерно распределена на отрезке [0, 1]. Для нача-
ла моделируем начальное распределение точки х(0) по сос-
тояниям 1, 2.....N. Для этого разделим отрезок [0, 1] на
п
отрезки At ... , Ay длиной ль ... , пн, 5 л>=1, и поло-
/-1
жим х(0)=/, если Во попадает в /-й маленький отрезок А/
длиной л> Если мы введем функцию f0(x) таким образом, что
f0(x) =ij, если xeAj, то можно положить, что х(О)=Д>(ъо)> и
тогда будет автоматически соблюдаться соотношение
**{х(0)=/} = яр / = 1,
217
Пусть переход из х(0) в х(1) управляется вероятностями
ру(0). Если x(0)=i, то х(1)=/ с вероятностью р>,(0); та-
ким образом, при каждом i этот переход можно моделиро-
вать, взяв функцию ft(i, $i), такую, что мера множества та-
ких точек, хе[0, 1], что fi(i, x)=j равна р«/(0). Иначе го-
воря, можно положить x(l)=fi(i, £1), причем автоматически
соблюдается соотношение
P{x(l)=//x(0)-0-ptf(0).
Аналогично можно положить
Х(п) = fn(x(n—l), U) (1)
так, чтобы соблюдалось соотношение
Р{х(п) = j / х(п—\) = i} — рц(п—1).
При фиксированных х(0), ... , х(п—1) соотношение (1) оп-
ределяет х(п) как функцию от х(п—1) и от новой случайной
величины £п, ранее (при меньших п) в рекуррентном соотно-
шении вида (1) не фигурировавшей; не зависящей, следова-
тельно, от х(0) ... , х(п—1) (так как функции от независи-
мых случайных величин независимы). Это значит, что при
фиксированном настоящем х(п— 1) прошлое х(0), х(1), ... ,
х(п—2) и будущее х(п) независимы.
Таким образом, эквивалентным определением марковской
цепи является следующее: марковская цепь есть последова-
тельность х(п), задаваемая формулой (1) при п>0 и фор-
мулой х(0) =А>(Ы. где go. Вь • •• . £п, ... есть последова-
тельность независимых случайных величин.
В физических приложениях марковские цепи возникают,
как правило, в виде (1). Конечно, фазовое пространство при
этом не бывает конечным (1, ... , N}, а представляет собой
фазовое пространство X некоторой динамической системы.
Пусть, для определенности, эта система имеет вид
х, £(/)), х(О)-х„ (2)
где 6 (О — некоторый случайный процесс.
Для концепции случайного процесса характерно, прежде
всего, представление о том, что значения процесса, разделен-
ные достаточно большим промежутком времени, представля-
ются нам никак не связанными. В математике отсутствие свя-
зи понимается как статистическая независимость; следова-
тельно, речь должна идти о каком-то стремлении к независи-
мости для событий, связанных с поведением реализаций про-
цесса l(t) на достаточно далеких интервалах времени. Мате-
матические формы такого «стремления к независимости» вы-
218
работаны (даже в слишком большом числе вариантов), но с
практической точки зрения они не вполне удачны. Например,
если *(t) — стационарный процесс с ограниченным спектром
(это означает, что спектральная плотность тождественно
равна нулю вне некоторого интервала частот), то реализации
процесса аналитичны; следовательно, по значениям реализа-
ции l(t) на любом (сколь угодно малом) интервале времени
мы можем точно определить ее значения на любом другом
(сколь угодно далеком) интервале времени. Поэтому о поте-
ре зависимости (в смысле любого математического определе-
ния ) не может быть речи. Настаивать же на том, что мы всег-
да имеем дело именно со стационарным процессом, но обяза-
тельно с неограниченным спектром частот, неудобно в связи с
представлением о частотных фильтрах: фильтр ведь срезает
те или иные частоты. Фактически речь идет, по-видимому, о
том, что на небольших интервалах времени £(f) — стационар-
ный процесс, а на больших интервалах времени происходят
некие дополнительные вмешательства, приводящие к исчез-
новению статистической зависимости.
Эта ситуация несколько грубовато охватывается следую-
щей моделью случайного процесса с обновлением. Будем счи-
тать. что имеются моменты времени 0=/0<Л< • • <6>< • •
(может быть, случайные), такие, что в эти моменты одна
реализация случайного процесса заменяется на другую, ста-
тистически независимую:
при (2)
где ••• —независимые реализации одного и того
же случайного процесса. Рассмотрим динамическую систему
(2).в моменты времени t0, tif ... , tn, ... : положим хп=
=x(in). Поскольку на интервале времени [/п-ь М система
уравнений (2) решается однозначно, получим
*П = -^Gn) = 1» ^п)» (3)
где через F"_t(xn-t, Ел) обозначено решение системы (2)
с начальным условием x(/n_f) = xn_i на отрезке (fn-i. /„)•
Правая часть (3) представляет собой некий функционал
от значений &, = Bn(f), Поскольку (3) совер-
шенно аналогично (2), то ясно, что последовательность
{«„, п = 0, 1,. . .} должна быть цепью Маркова, если, ко-
нечно, удастся создать концепцию цепи Маркова с произ-
вольным фазовым пространством (это вполне возможно).
Конечно, чтобы получить цепь Маркова, мы должны взять
моменты 0 = to < t\ < ... < t„ < ... достаточно редко (что-
бы интервалы между этими моментами были много больше,
чем «время корреляции», т. е. время, на котором еще замет-
на зависимость между значениями процесса £(/)). Это нас
не всегда устраивает. Но во многих случаях этого впол-
219
не достаточно. Например, если процесс 1,(0 представляет со-
бой малое возмущение, то в промежутках между моментами
to, t....tn, ... динамическая система почти точно описы-
вается невозмущенным уравнением, и вполне достаточно рас-
сматривать ее в редкие моменты времени.
С другой стороны, если процесс £(7) не мал, но коротко
коррелирован (сбелый шум»), то интервалы между момента-
ми to, t\...tn, ... можно делать малыми (они будут все
равно много больше времени корреляции процесса £,(/)), и
мы получим марковскую цепь с очень частыми скачками. Та-
кая цепь напоминает уже рассмотренный винеровский про-
цесс, и мы в дальнейшем рассмотрим соответствующую пре-
дельную теорему.
Рассмотрим математическую концепцию марковского про-
цесса, в котором время может принимать заданные значения
to, #i, ... , tn> ... либо произвольные (неотрицательные) зна-
чения, а фазовое пространство — достаточно произвольно.
Пусть X — произвольное измеримое пространство. (Это оз-
начает, что выделена некоторая о-алгебра подмножеств X; в
случае достаточно простого X— прямой, евклидова простран-
ства, какого-то многообразия в евклидовом пространстве —
она совпадает с о-алгеброй борелевских подмножеств). Пусть
л — некоторая мера на X (начальное распределение). Время
t пусть изменяется на полупрямой [0, оо]. Для любых момен-
тов s<Zt пусть задана так называемая переходная вероят-
ность (или переходная функция) Р' (х, Г), вероятностный
смысл которой состоит в следующем: это вероятность того,
что блуждающая частица, находясь в момент $ в точке х, по-
падает в момент />$ в множество ГеХ. Переходная вероят-
ность как функция х при фиксированном измеримом Г=Х
должна быть измеримой функцией; а при фиксированном
хеХ как функция ГеХ должна быть вероятностной мерой.
Замечание. Если речь идет о динамической системе,
задаваемой соотношениями (2) и (3), то переходную вероят-
ность надлежит подсчитать (зная вероятностные характери-
стики случайного процесса £(7)). Вообще говоря, это весьма
трудная задача, но в дальнейшем увидим, что во многих слу-
чаях достаточно ограничиться весьма грубым приближенным
подсчетом.
Вернемся к общей концепции. Предполагается, что выпол-
нено следующее равенство (называемое равенством Чепме-
на—Колмогорова): при s<Zt<Zu
Ри(х, Г) = f dy)p“(y> Г). (4)
х
Равенство (4) представляет собой интеграл Лебега от из-
меримой функции Pt(y, Г) как функции от у по мере, за-
220
даваемой переходной функцией Р$(х, Г) как функцией от
Г. Его вероятностный смысл состоит в том, что для то-
го, чтобы попасть за время от s до и в множество Г, на-
до за время $ до t<u попасть из точки х в какую-нибудь
точку уЕХ, а затем за время от t до и попасть из у в Г.
Определение марковского процесса х(0 на Т = [0, оо) с
начальным распределением -к и переходной вероятностью
Ps(x, Г) состоит в указании соответствующих конечномер-
ных распределений. Правило состоит в следующем: если
дан набор моментов времени, то сначала этот набор сле-
дует упорядочить и добавить к нему момент t = 0, если
этого момента не было в наборе. Далее, конечномерное
распределение, т. е. вероятность Р{(л(0),. . х(/п))еВ},
B^Rn, достаточно задать на „параллелепипедах** В =
=Д1Х . . . ХВп, BtczRi. Положим, по определению, для
набора 0 = 0 < tz < . . . < tn
Phtt...tn{Bt X Вг x-Х Вп) = Р{х(0) е Ви
x(tJ<=B..... <)е£„} = f J ... J dx2)...
Bi Bi Bn-1
... Р,я-‘(х,1_2, (Хл-i, Г). (5)
'п-2 'л-1
Входящие в (5) интегралы понимаются в следующем смыс-
ле. Сначала берется интеграл измеримой функции Р п (хя_ь
6i—1
Г) от Хя-jSSn-i по мере Рп~* (хя_2, •). Получается из-
tn—2
меримая функция от хя_». От нее берется следующий
интеграл и т. д.
Чтобы свойство (5) задавало конечномерные распределе-
ния, должны выполняться условия согласованности. Условие,
относящееся к перестановке моментов времени, выполняется
автоматически, так как моменты времени, по определению,
сначала упорядочиваются. Нужно проверить лишь условие,
относящееся к добавлению моментов времени. Достаточно ра-
зобрать случай добавления одного момента времени. Пусть к
моментам /1<...</„ добавлен момент f, tk<t’<tk+\. Тогда
в правой части (5) возникает сомножитель
P'tJXk, dx')Pt*+l(x\ dxk+i),
причем по переменному х' интегрирование будет по мно-
жеству В' =» X. При последовательном выполнении интег-
рирований в (5), как указано выше, на этот сомножитель
221
надвинется некая ограниченная измеримая функция g(x*+1),_
которая без добавления момента t' надвинулась бы на
сомножитель P*+i(xk, dx*+i). Иными словами, нужно до-
казать, что
f f р'./х,, dx')p'*+A (х', dz*+1)g(x*+1) =
в' e*+i
= 1 ^+,(ХА. dxk+i)g(xk+i). (6)
Bt+i k
Но если g(xA+i) — Ir(xk+i), то (6) есть уравнение Чепмена —
Колмогорова (5). Левая и правая части (6) суть линейные
функционалы от функции g. Следовательно, (6) верно и для
линейных комбинаций индикаторов, но тогда (в силу предель-
ного перехода) и для любой ограниченной измеримой g. Сог-
ласованность конечномерных распределений (5) доказана.
Мы не будем особенно вдаваться в формулировку марков-
ского свойства в терминах условных вероятностей (в качест-
ве варианта условной вероятности для Xt при условии, что
x(s)=x, s<J, можно, конечно, взять Р' (х, Г)). Нам потре-
буется лишь тот факт, что при s<t
M{f(x(0)|x(s) = х) Pj(x, dy)f(y). (7)
Докажем (7). Полагая g(x) = \ P's(x, dy)f(y), мы должны
x
проверить для функции g(x(sY) измеримость относительно
о-алгебры, порождаемой случайной величиной х($) (что
очевидно), и интегральное тождество
М(/л£(х($))) =М(Л,/(Х(0)), (8)
где А — подмножество в пространстве функций, выделяемое
условием
А = {x(t): x(s)eB), В<=Х.
Распределение вероятностей для x(s) есть, согласно (5),
мера jis, определяемая формулой
«,(Г) = f *(dx)PS(x, Г),
х
Следовательно,
M(IAg(x(s))) = M{fs(x(s))g(x(s))} = f g(x)-s(dx).
в
С другой стороны, согласно (5), совместное распределение
x(s) н x(t) задается формулой
222
Р{х(») е С, *(/) е D} = J -xdx)X(x, оу.
С
Поэтому
M(ZJ(z(/))) = M{/B(x(s))f(x(/))J = f f ^(dx)P'(x, dy)f(y) -
В X
= \ g(x)^s(dx),
в
что и доказывает (8).
§ 2. Конечные марковские цепи
2.1. Спектр матрицы переходных вероятностей. В этом па-
раграфе рассматриваем конечные однородные марковские це-
пи, т. е. цепи с конечным фазовым пространством Х=
..., Д'), временем п, принимающим целые неотрицательные
значения 0, 1, 2, .... и не зависящими от времени вероятно-
стями перехода
Ра = Р{х(п) = j /х(п—1) = I},
образующими переходную матрицу Р= II р,, II, i, j=l, ... , N.
Такие объекты можно нарисовать, изобразив на чертеже W
точек, попарно соединив их стрелочками и написав возле
стрелочки, ведущей из i в j переходную вероятность p-j (слу-
чай i=j не исключается). При попытке нарисовать такой
чертеж всякий поймет, что изучаемый объект является весьма
сложным. В направлении стрелочек возможны самые разно-
образные движения, вроде хождения по кругам, которое иног-
да прерывается перескоком с одних кругов в другие, и т. д.
Наука в состоянии изучить свойства этого объекта лишь час-
тично, ориентируясь на самые грубые характеристики движе-
ния, выявляемые при /г->оо.
Формула (2) п. 1.1 предыдущего параграфа (при p,j(k) =
=Pij, k=Q, 1, ... ) определяет вероятности элементарных
событий, описывающих блуждание до момента времени п
включительно. Она, очевидно, является частным случаем фор-
мулы (5) п. 1.2, а следовательно, задает систему согласован-
ных конечномерных распределений. Нам будет чрезвычайно
полезно (для решения некоторых чисто аналитических вопро-
сов) рассматривать марковскую цепь для бесконечного числа
моментов времени, что можно делать в силу теоремы Колмо-
горова о продолжении меры. События типа «частица когда-
нибудь попадет в заданное подмножество множества состоя-
ний», очевидно, входят в соответствующую о-алгебру (так
как являются счетным объединением по п событий «частица
попадает в заданное подмножество за время от 0 до п»).
223
Пусть n=n(O) = (jii, .... пн) — начальное распределе-
ние, т. е. распределение х(0). Найдем распределение л(п)
случайной величины х(п) — положения частицы в момент п.
По формуле (2) п. 1.1 имеем
1г/п) = Р{х(л) = /}= 2 Wi- • • '«-!/)} =
X..‘п -1
— 2 • • • Pin-11 ~ Ь'’
«.• ••• *и-1
где (лРп)/ обозначает /-ю компоненту вектора-строчки лР'\
Рп—п-я степень матрицы Р. Иначе говоря,
л(п) = лРп, л = 1, 2, ... . (1)
Соотношение (1) может быть интерпретировано и так: Рп
есть матрица вероятностей перехода за п шагов, т. е. (Pn)i}
есть вероятность перехода из состояния I в состояние j за п
шагов (чтобы в этом убедиться, положим л*=0 при k^i,
л, = 1). Таким образом, исследование поведения цепи за п
шагов требует изучения степеней Р“ матрицы Р.
Единственный общий способ рассматривать степени мат-
риц состоит в приведении их к жордановой форме.
Напомним, что жордановой клеткой называется матрица
вида ХЕ + В, где X — (комплексное) число, Е — единичная
матрица, В — матрица, все элементы которой равны нулю,
кроме элементов, равных единице, стоящих непосредственно
над главной диагональю. При возведении матрицы В в сте-
пень эта параллельная главной диагонали система единиц
сдвигается вправо и вверх: таким образом, Вт=0, где т —
порядок матриц. Следовательно,
(/£ 4- В)п = Х«£ + CiX"-' В + С’^2 В2 +
4-. . . 4-С_,Хя"га+1Бт-1. (2)
Жордановой формой А называется матрица, составленная,
из жордановых клеток и диагональных матриц. Всякую мат-
рицу А можно привести невырожденным преобразованием
к жордановой форме; это означает, что А можно пред-
ставить в виде А = С_|АС, где С—невырожденная матрица.
Тогда, очевидно, Ап = С~'ЛпС, причем отдельные клетки мат-
рицы А возводятся в степень, никак не взаимодействуя друг
с другом. Каждое X есть собственное значение матрицы А.
Совокупность собственных значений матрицы называется
ее спектром. Займемся изучением спектра стохастической
матрицы Р.
Распределение вероятностей л стохастической матрицей Р
преобразуется в распределение вероятностей пР. Обратно ес-
224
ли любое распределение вероятностей, т. е. вектор-строчка л=
= (ль , n,v), 2л3=1, матрицей P = llpi/ll преобразуется в
распределение вероятностей, то матрица Р—стохастическая,
т. е. Ри^О, ^Рц = 1", (для доказательства положим л3=0,
если j=/=i, л< = 1; тогда пР есть i-я строчка матрицы Р). Сле-
довательно, из (1) вытекает, что при любом п матрица Рп—
стохастическая.
Лемма 1. Собственные значения X стохастической мат-
рицы Р не превосходят по модулю 1. Если 1X1 = 1, то такому
Ь не может отвечать жорданова клетка.
Доказательство. Пусть Р=С~'ЛС, тогда Л= СРС~Х
и ЛП = СРПС_|. Поскольку Рп—стохастическая матрица, то
элементы матрицы Лп должны быть ограничены при п-»-оо. Но
если 1X1 >1, то согласно (2) диагональные элементы матрицы
(Х£ + В)п стремятся по модулю к оо. Если же I X I = 1, но
жордановая клетка нетривиальна (не сводится к диагональ-
ной матрице, т. е. В=/=0, т^2), то матрица СП-1 Xn-m+l Bm~l
состоит из единственного элемента (которому в сумме (2)
не с чем сократиться) порядка величины nm-1->-oo при /г-»-оо.
Полученное противоречие доказывает лемму.
Замечание. Поскольку |Х|п-*0 при п-*оо, если |Х|<1,
то при возведении в степень матрицы Р существенную роль
играют лишь точки спектра, равные по модулю 1.
Изучим точки спектра X, такие что IX 1 = 1. На распреде-
ления вероятностей я матрица Р действует, как на строчки
(путем умножения справа я-^лР). Рассмотрим действие той
же матрицы на столбцы.
Столбец f будем обозначать через f(x), х=1, ..., N, и
интуитивно понимать как функцию на пространстве состоя-
ний Аг={1, ... , N}. Рассмотрим оператор Т, определяемый
формулой
Tf(x) = M(f(x(l)) /х(0)=х) = M(f(x(zi)) /х(л-1)-х),
где М (• / х(0) =х) обозначает условное математическое ожи-
дание при условии, что в предыдущий момент времени части-
ца находилась в точке хеХ. По формуле (7) п. 1.2 предыду-
щего параграфа
т. е. действие оператора Т есть как раз умножение вектора-
столбца f на матрицу Р слева.
Полагая f(x)=l для всех хеХ, видим (в силу равен-
ства Spxy«"lj, что Х=1 является собственным значением
матрицы Р. Доказать, что существует собственная вектор-
строчка, являющаяся распределением вероятности, проще
всего с помощью теоремы Брауера о неподвижной точке: рас-
15-2567 225
пределеиия вероятностей образуют симплекс S = {«=(14,...
..: «у >0, 5nj = 1J, а преобразование к—>кР пе-
реводит 5 в себя и является непрерывным отображени-
ем. Следовательно, существует неподвижная точка -=р:
.рР=р.
Пусть теперь /—произвольный собственный вектор,
отвечающий собственному значению X = 1: Tf(x) = f(x).
Рассмотрим точки х0, такие, что |f(x0| = max |/(х)|; пусть
Хо = {*о}- Если х(0) = х0, то /(х0) = £о /(у); но так как
v
Vp =1, то это равенство возможно лишь в том слу-
v х,у
чае, когда /(у) = /(х0) для всех у, для которых рх_у>0.
Итак, из любой точки хв е Хо за один шаг можно пе-
рейти лишь в такую точку у, что у^Х0. Это значит, что
из множества Хо марковская цепь никогда не сможет
выйти (множество Хо называетсястохастически замкнутым).
Пересечение двух стохастически замкнутых множеств
также стохастически замкнуто. Поскольку общее число
состояний у нас конечно (следовательно, и все рассмат-
риваемые множества состоят из конечного числа элемен-
тов), то существуют наименьшие стохастически замкну-
тые множества (из которых нельзя выбросить хотя бы
одну точку так, чтобы осталось стохастически замкнутое
множество). Наименьшие стохастически замкнутые мно-
жества называются классами. Два класса либо не пересе-
каются, либо совпадают.
Мы доказали, что каждому f такому, что Tf = /, от-
вечает хотя бы один класс, являющийся частью множе-
ства X. = /х0 : И(х0)| = max |f(x)| I. Аналогично показывает-
I хбЛ J
ся, что множества
X+ , j х+: /(х+) = max /(*)), Х_ =
= :/(х_) = minf(x)l.
являются стохастически замкнутыми, следовательно, каж-
дое из них содержит класс. Если собственное значение
л = 1 является кратным, то существует отличная от по-
стоянной функция f, такая, что Tf=f. Для такой функции
Х+ и Х_ не пересекаются. Итак, если X = 1 кратное соб-
ственное значение, то классов более одного. Покажем,
что верно и обратное: если классов более одного, та
собственное значение X = 1 является кратным.
226
Лемма 2. Если К—класс, то существует такая функция
f, что Tf=f, 0<f (х) <1 и f (х) = 1 при хе/С
Доказательство. Пусть Р*(х) — вероятность того,
что траектория {x(n), п=0, 1. ... } цепи Маркова, выходя-
щая из точки х (т. е. при условии, что х(0)=х), когда-либо
достигает класса К (существует п0, такое, что х(по)еК). По
формуле полной вероятности
Рк (х) = 2 Р{х(1) - ylx(0) = xl Рк (у) = 2ржу Рк (у). (3)
У I У
Таким образом, 7Рк(х)=Рк(х), но очевидно, что Ос
<Рк(х)<1 и что Рк(х) = 1, если хе/С Лемма доказана.
Таким образом, если имеются два класса Кх и К2, то
имеются две функции РЯ1(х) и PKt(x), собственные для
оператора Т с собственным значением 1 и, очевидно, ли-
нейно независимые (для хеК, имеем: РК1(х) = 1, РК1(х) =
= 0; для xeKt имеем: РЯ1(х) = 0, Рк,(*)=1)- Значит,
X = 1 — кратное собственное значение.
Классы — это ловушки. Действительно, пусть S — объ-
единение всех классов. Для каждой точки х еХ\ 5 =S
вероятность Ps(x) когда-либо достигнуть S либо равна
нулю, либо больше нуля. Но такие точки х, что Ps (х) =
= 0, сами обязаны образовывать класс (в силу (3)). Сле-
довательно, Ps(x)>0 для любого xeS. Но тогда для
каждого х существует п(х), такое, что с положительной
вероятностью траектория, выходящая из х, достигает S
не более, чем за л(х) шагов. Полагая n—maxn(x), полу-
*ex\s
чаем, что за п шагов каждая траектория, выходящая из
xeS, достигает S с вероятностью а(х)>0. Если a=mina(x),
то а>0. Таким образом, вероятность частице не попасть
в S за первые п шагов не более 1 —а; вероятность не по-
пасть в S за 2п шагов не более (1—а)’ и т. д. В конце
концов частица попадает в S с вероятностью 1. При этом
она распределяется между классами, образующими S, с
теми или иными вероятностями.
Теперь рассмотрим собственное значение /. #= 1, но та-
кое, что Р-| = 1. Если Г/(х) =• Xf(x), то из точки х0, такой,
что |/(х0)| = max|f(x)|, можно попасть с положительной ве-
роятностью только в такие точки у, что f(y)«»Xf(x0); из
точки у только в такие точки г, что ((г) «= 't-f(y) = л2/(х0) и
т. д. Если среди чисел 1, К, X2, . . . нет одинаковых, то
15*
227
Х= |1.......N} разобьется на бесконечное число непере-
секающихся множеств, чего не может быть. Значит, су-
ществуют тип, такие, что л« = Х", т. е. Xm~n=l. Вывод:
/.— обязательно корень некоторой степени из 1. Пусть
k — наименьшее натуральное число такое, что Х* = 1. Тог-
да из множества точек vt для которых f(y) = k*~,/(х0)]ча-
стица попадает в множество то тек, где значение функции
f равно /(хв). Мы описали циклическое движение точки
по подмножествам
{х:/(х)==/(х0)|, {х:/(х) = ХДх0)}, . . .
... ,{х :/(%) =
Если в этих подмножествах выделить минимально возмож-
ные так, чтобы в целом осталось стохастически замкнутое
множество, то получится то, что называется системой под-
классов.
Вспомним теперь понятие эргодичности как независимо-
сти далекого будущего случайного процесса от прошлого. За-
метим, что наличие двух или более классов или хотя б<ы од-
ной системы подклассов исключает эргодичность. Действи-
тельно, помещение начального состояния цепи х(0) в один
из нескольких классов либо в данный конкретный подкласс
никогда не будет забыто. В случае класса траектория цепи
навсегда останется в этом классе; в случае же подкласса каж-
дые k шагов будет возвращаться в тот же подкласс.
2.2. Эргодические цепи. Определим эргодическую цепь как
такую, которая не имеет ни различных классов, ни подклас-
сов. Иначе можно сказать, что матрица Р для эргодической
цепи имеет однократное собственное значение Х=1, а собст-
венных значений, таких, что I Л I = 1, но Х^=1, не имеет.
Достаточным условием эргодичности является следующее
условие Маркова: существует такое п0, что ровно за п0 ша-
гов можно из любого состояния цепи перейти в любое:
Р/?’ >0 для любых I, /;= 1, . . . , N, где ру"' — элемент
матрицы Р"*. Действительно, условие Маркова исключа-
ет, очевидно, непересекающиеся классы и подклассы.
С другой стороны, условие Маркова не является необхо-
димым для эргодичности. Если имеется ровно один класс S,
то, выходя из состояния x^S, траектория цепи в конце концов
оказывается в 3. Состояния поэтому называются несу-
щественными. Несущественные состояния не мешают эрго-
дичности; при этом возможно, что нз одного несущественного
состояния никогда нельзя попасть в другое.
Переформулируем в удобном для нас виде теорему о при-
ведении матрицы к жордановой форме. Пусть для стохасти-
ческой матрицы Р, отвечающей эргодической цепи Маркова,
228
имеем Р=С~'ЛС, причем наибольшее по модулю собственное
число Х=Хо=1 стоит в левом верхнем углу матрицы Л. Соот-
ношения
С-'Л = PC-1, СР = ЛС
означают, что первый столбец е матрицы С-1 и первая строч-
ка р матрицы С являются собственными для матрицы Р с
собственными значениями Хо='1. Уговоримся выбрать посто-
янные множители, с точностью до которых определяются соб-
ственные векторы, так, чтобы выполнялись соотношения:
1) е есть единичный вектор (т. е. все его компоненты
ej равны 1);
2)pc = SP;^j=l (это следует из 1) и того, что
С“‘С = Е).
Если считать, что компоненты р, неотрицательны (со
ссылкой на теорему Брауера), то из 2) следует, что р — рас-
пределение вероятностей, такое, что рР=р, т. е. так называ-
емое стационарное распределение вероятностей. Однако из
дальнейшего будет следовать, что р^О, и без ссылки на тео-
рему Брауера.
Разложим матрицу А в сумму: А=Л1+Л2, где матрица
At имеет единственный элемент, отличный от нуля: (Л1)ц =
=Хо=1, а Л2=Л—Ар Все жордановы клетки, составляю-
щие матрицу Аг, отвечают собственным значениям, по моду-
лю меньшим 1; это значит, что AJ —>0 при п—► оо (всмыс-
ле любой разумной матричной нормы, например максимума
по строчкам сумм модулей элементов каждой строчки: это
норма матрицы как оператора в пространстве векторов-
столбцов f, если ||/|| = max|/(х)к Сходимость Л? к нулю
хех J
экспоненциально быстрая; ||Ail|<cexp (— ла), а>0, с —
константа.
Соответственно матрица Р разложится в сумму
P=Pi + P2, P^C-’AiC, Р2=С~1Л2С,
причем Рп=Р" + Р*, где ||Р»1| -*0 экспоненциально быст-
ро. При этом оператор Рх действует на столбец f следу-
ющим образом:
Pif = h>(pf)e, pf = Zpjfp Xo= 1; (3)
на строчку л оператор Pi действует следующим образом:
лР1 = Хо (ле) р, ле = = 2л/, Хо = 1. (4)
(Равенства (3) и (4) непосредственно следуют из рассмотре-
ния матрицы Р1 = С_,Л1С с учетом того, что лишь один эле-
мент матрицы Л1 отличен от нуля.)
229
Из изложенного вытекает, что для любого начального
распределения п имеем
кРп -* itPl = X0(ire) р = р,
т. е. для эргодической цепи распределение вероятностей сос-
тояний в момент п, т. е. я(п)=лРп стремится к стационар-
ному распределению вероятностей р экспоненциально быстро
(поскольку п(п) при любом п есть распределение вероятно-
стей, то отсюда вытекает, что р — также распределение веро-
ятностей). Факт экспоненциально быстрой сходимости
л(л)-»-р независимо от начального распределения л носит
название эргодической теоремы для цепей Маркова. Очевид-
но, что сходимость п(п)-*-р независимо от л есть необходи-
мое и достаточное условие эргодичности (т. е. отсутствия раз-
личных классов и подклассов).
2.3. Суммы случайных величин, связанных в цепь Маркова.
Пусть на пространстве состояний X = {1, ... , N} задана
некоторая функция f(x), а {х(п), n = 0, 1, ... } — марков-
ская цепь. Образуем сумму Sn вида
п
Sn= 2 (О
*-1
(сумма Sn есть сумма п слагаемых; хотя марковская цепь на-
чинается с Л = 0, сумма Sn начинается со слагаемого f(x(l)):
так сделано для того, чтобы последующие формулы получи-
ли наиболее простой вид). Сумма (1) носит название «сум-
мы случайных величин, связанных в цепь» — таково ориги-
нальное название А. А. Маркова. На самом деле цепью Мар-
кова являются, вообще говоря, не слагаемые f(x(k)), а зна-
чения аргумента х(Л); может быть, лучше было бы сказать
«сумма случайных величин, связанных с цепью» либо «свя-
занных через цепь». Важнейшим открытием Маркова явля-
ется выражение характеристической функции ТЛехр (itSn) в
компактном виде через некоторые матричные операции, кото-
рое позволяет в дальнейшем доказать закон больших чисел и
центральную предельную теорему для суммы Sn.
Введем матрицу P(t) с элементами Р/л(О. !> k=l,...,N,
задаваемыми формулой
Р/*(0 = Pjtexp (itf(k))
(это означает, что k-к столбец матрицы Р=||р/*|| умножа-
ется на exp (itf(k)), t—вещественное число; при t-*-0 матри-
ца P(t)-*-P). Введем также вектор-столбец е с компонента-
ми, равными 1; обозначим через л=л(0) начальное распре-
деление цепи Маркова х(п).
230
Лемма. Мехр (itSn) — пРп (t)e.
Доказательство. Будем вычислять Мexp(i/Sn), пе-
реходя к условным математическим ожиданиям, вынося из-
меримую случайную величину за знак условного математи-
ческого ожидания и используя марковское свойство:
М ехр (itS,) « М ехр
it 2 f(x(*))
*-1
“ ММж(0) х(1, . jr(n-l) ®ХР
it 2 Г(х(*))1»
*-i J
«= Мехр
n-t \
it 2 Мх(0)х(1)......х(я_0 ехр {itf х(п))}=
*=i J
= Мехр
«2 «*(*))
л—1
Мж<л-1) ехР iitf(x(n))}=
= Мехр
П-1 1 N
а 2 л*(*)> 2 е™' =
*=i j /-1
— Мехр
|7 2/(х(Л))
*-1

ММ х(0). х(1).....х<л-2) еХР
it
— Мехр
л—2
и 2
Л=1
М4(я_2) ехр {Hf 1))) X
XP(t)e(x(n-\))-
= Мехр |« 2 f(x(k)) 2 Px(n_,uX
I *—i j-t
X exp («/(/) | P(t)e(j)-
(Л— i
tf 2 /w*))
P\t)e{X(n~ 2)) =
— ММХ(О) х(ц>
х(л—i) expL't 2/M*))
I *—i
Р«(0е(х(П-2)) =
In—S
it 2
k—i
МЖ(л-3)
X exp{ftf (x(n — 2))) P*(t) e(x(n—2)) =
231
= M exp
«"s /и*))
P»(t)e(x(n-3)) =
= ... = Mexp {itf (x(l)))P'-1(0e(x(l)) =
- MMX(O) exp Рп-> (0 e(x(l)) =
N
= M 2 ₽x(0)./exp{«/(/)}Pn-1(0e(/)»
/-»
N
= МР"(0ф(О))= 2 =
/-i
Лемма доказана.
2.4. Закон больших чисел и центральная предельная тео-
рема. Закон больших чисел будет (как и в случае незави-
симых слагаемых) относиться к Sn/n, а центральная пре-
дельная теорема — к нормированной сумме. В обоих слу-
чаях нам достаточно будет изучать поведение характерис-
тической функции Mexp(tASn) при сколь угодно малых зна-
чениях t. Предположим, что марковская цепь х(п) эргодич-
на. Тогда при t=Q имеем Р(0)=Р и степени Рп(0) изучают-
ся путем выделения максимального собственного значения
1о=1 матрицы Р. Но так как в эргодическом случае собст-
венное значение 1о=1 однократно (это означает, что произ-
водная det(Р — ХЕ) не обращается в нуль в точке 1=1),
dX
то по теореме о неявной функции при t, достаточно близ-
ких к нулю, выделяется собственное значение 1=1(7) мат-
рицы P(t), которое будет по модулю больше всех остальных
собственных значений. Эти остальные собственные значения
при /=0 строго меньше 1, т. е. вне некоторого круга ради-
уса 1—в с центром в точке 1=0 и вне некоторого круга ра-
диуса в>0 с центром в точке 1=1 характеристический мно-
гочлен detfP^)—IE) не обращается в нуль. Тогда при до-
статочно малых t не обращается в нуль det(P(7)—IE) вне
круга радиуса 1—е/2 с центром в начале координат и вне
круга радиуса е/2 с центром в точке 1=1. Итак, при доста-
точно малых |/| спектр матрицы P(t) устроен следующим
образом: имеется одно собственное значение 1(0, близкое к
1 по модулю, а остальные собственные значения строго мень-
ше 1 по модулю.
Поэтому аналогично п. 2.2 оператор P(t) разлагается в
сумму Р(0=Р>(0+Р2(0 так, что Р"(0-Р? (0+PJ (0>
причем оператор Р?(0 действует на вектор-столбец f сле-
дующим образом:
232
= (1)
а оператор Pz(t) обладает тем свойством, что Pj(/)-*O при
п-*-оо.
(Здесь p(t) и е(/) — соответственно собственные строчка
и столбец матрицы P(t), отвечающие собственному значению
},(!).) Собственное значение k(t) гладко зависит от /; собст-
венный вектор-столбец e(t) :P(t)e(t) и собствен-
ная вектор-строчка p(t) также могут быть выбраны гладко
зависящими от t. Действительно, собственный столбец полу-
чается решением системы однородных линейных уравнений
ранга N—1, в которой при t=0 можно выбрать отличный от
нуля минор (допустим, при неизвестных eit ... , еы-i), а сво-
бодное неизвестное вы положить равным 1. Тогда этот же ми-
нор будет отличен от нуля и при малых t, и надо только сох-
ранить выбор свободного неизвестного ey(t) = l, чтобы обес-
печить непрерывность и гладкость e(t). В частности, е(0)=е.
Если гладкий вектор-столбец e(t) уже выбран, то для вы-
бора собственной вектор-строчки p(t) надо взять тот же от-
личный от нуля минор, а значение свободного неизвестного
выбрать из условия p{t) e(t) — \. Получится гладкая строчка
р(1). Наконец, оператор P2(t) = P(t)—P\(t) также будет глад-
ко зависеть от t, а оценку нормы II Рг (О I С сехр(—па)
можно будет дать с не зависящими от t константами с и а.
Следовательно, согласно лемме предыдущего пункта, при до-
статочно малых 1/1
М ex р (i/Sn)= ^Рп (0 е —
= >п (П(Р(0 е) (МО) + кРЗ (0 е, (2)
где р(/)е->1, ле(/)-»-1 при /-►0, а член QnfO = nPa (0е экс'
поненциально быстро стремится к нулю. Таким образом, ха-
рактеристическая функция Mexp(itSn) сводится к Хп(/),т. е.
к степени некоторой функции, как это было в случае харак-
теристической функции суммы независимых одинаково рас-
пределенных величин. Понятно, что отсюда должны вытекать-
теоремы, сходные с законом больших чисел и центральной
предельной теоремой. Мы сейчас увидим, что так оно и есть,
с точностью до некоторых деталей.
Теорема 1. (закон больших чисел). При п-»-оо Sn/n-+a
(в смысле сходимости по вероятности).
Замечание. Увидим, что константа а вычисляется сле-
дующим образом: a=Mf(x(k)), если распределение х(0)
(следовательно, и x(k) при любом Л^О) есть стационарное
распределение р.
Доказательство теоремы. Поскольку
233
M exp (itS„ln) = Mexp
n
причем f/n-*O при n-*-<x>, то предел Mexp(ifSn/«) совпадает
с пределом
lim X"
'j = limfx(O) 4-X'(0) — 4- о
\/l / л-»оо I П
-lim Г 1 + - X'(0)4- о
П—со I П
= exp (tX'(0)).
Как и при доказательстве теоремы Хинчина (гл. 3, п. 2.2),
получаем, что Sn/n сходится по вероятности к случайной ве-
личине^ принимающей постоянное значение X'(0)/i (здесь
i=l/— 1). Неплохо было бы доказать, что X'(0)/i веществен-
но, и заодно указать способ вычисления этой величины.
Принципиально X' (0) может быть найдено с помощью теоре-
мы о неявной функции, но этот путь несколько громоздкий,
и предпочтительнее следующие вероятностные рассуждения.
Предположим, что начальное распределение л совпадает
со стационарным распределением р. Тогда JASn=na, где а
определено в замечании к теореме. Хорошо бы установить,
что X' (0) =7а. Для этого продифференцируем (2) и положим
t=0:
~ Mexp(iTSn)-i«e =
= nXn-‘ (t) Х'(0) (p(t) е («e(O)Uo +
4-хп (*)£ Кр(О «)(«*(*)) 1U +
+ -^ЬРг(М/-о = лХ'(О) +
а*
+ £ ((Р(О е) (МО) IU 4- £ [кРЗ(0 е] |г_0 • (3)
Заметим, что член («Р" (0 е] стремится к нулю при
«-♦<» (и достаточно малых (t). Действительно, так как
Pt(t), вообще говоря, есть некоммутирующая с Pt(t)
234
матрица, то — [«/*5(0 в] является суммой вида VkP!(0X
dt *-о
X (-7-(0 е. Но в силу ограниченности — Pt(t) и
оценки ||?а (ОН < се~а“ вся эта сумма оценивается как
п • const • е-“* е_“(я-*+1) _ п . consf . е_“(я~о-»0 при л-н».
Величина [(р(/) е)(ке(/))| также ограничена. Следователь-
dt
но, разделив обе части (3) на и и устремляя п к беско-
нечности, получим, что
K(0) = ia, т. е. X'(0)/i = a,
что и требовалось доказать. Доказательство закона боль-
ших чисел закончено.
Для формулировки центральной предельной теоремы вве-
дем нормированную сумму s*n =(Sn—na) /Уп. несколько ина-
че, чем для суммы независимых одинаково распределенных
случайных величин. Для суммы независимых случайных ве-
личин нормировка включала деление на ol/n, где о2—диспер-
сия отдельного слагаемого. В случае величин, связанных в
цепь Маркова, дисперсия DSn не равна сумме дисперсий сла-
гаемых f(x(k)), потому что между этими слагаемыми могут
быть ненулевые ковариации. Легко понять, что ковариация
cov {f(x(k)), (f(x(m)))}= M{f(x(k)) —
- Mf(x(k)) } Щх(т)) - !Af(x(m)) }
стремится к нулю при Ik—m\-*-<x> экспоненциально быстро.
Действительно, выразим при k<Zm математическое ожида-
ние через условное математическое ожидание
ГЛ{Цх(к)) - JAf(x(k))}{f(x(m)) - Mf(x(m))} =
= !A!AxW{f(x(k)) - Mf(x(k))}{f(x(m)) - Mf(x(m))} =
= М{/(х(Л))-М/(х(Л))}Мх(*Л(х(т))-М/(х(т))}. (4)
В силу эргодичности при т—k-*-co условное распределение
х(т) при известном x(k) стремится к стационарному экспо-
ненциально быстро; следовательно, условное математическое
ожидание мало отличается от безусловного M{f(x(m))—
—JAf(x(m)) }=0. Поэтому при т—Л->-оо правая часть (4)
стремится к нулю экспоненциально быстро.
Но при близких hum ковариации Цх(к)) с f(x(m)) су-
щественны. За счет них дисперсия DSn может вести себя до-
вольно странно, например не стремиться к оо при п-*-со. По-
нятно, что так будет всегда в тривиальном случае f(x) =
= сопзЬ Но можно себе представить, например, что f (х) ¥=
235
T^const, но переходы в цепи Маркова устроены так, что за лю-
бым состоянием х, таким, что f(x) = l, следует состояние уг
такое, что f(y) =—1 (а в остальных точках f(x)=O). Тогда
на первый взгляд f (х) =#= const, но в сумме Sn одни слагаемые
с вероятностью 1 уничтожаются другими (цепь же вполне
может быть эргодической). Мы сейчас частично поисследуем,
какова может быть дисперсия суммы Sn.
Предположим, что из значении функции f(x) при всех
. . . , Л') вычтено значение а, т. е. а'(0) = 0. Про-
дифференцируем дважды по t выражение (2), пренебре-
гая (как и при доказательстве закона больших чисел>
членом яР2(0е:
Mexp(i7Sn) = £ р.п(0(Р(0е)(М0)) + о(1) =
= £ {л/."-1 (0 к' (О (АО е)(яе (0) +
+ а" (0 ~ [(P(OO(MO)l j + АП =
-пк"-1(0>"(П(А0е)(ке(0) +
+ п(п- 1)А"-2(0(к'(0)‘(р(0е)(М0) +
+ 2п а""1 (0 >/(<) [(АО е)М» 14-
al
+ >-п(0^-[(А0О(^(0)1 + о(1).
Теперь положим t = 0. Получим, учитывая, что Х(0)»15
к'(0) = 0, А0) = А е(О) = е,
= па" (0) + ± {(p(t)е)(ке(О)]|,_0+ о(1).
Полагая Х"(0) =—а2, видим, что а2 вещественно и неотрица-
тельно. Если а2>0, то DSn имеет порядок величины па2 ес-
ли же а2=0, то DSn ограничены при всех п. Вышеприведен-
ные рассуждения показывают, что случай о2=0 вполне воз-
можен. По-видимому, неизвестны достаточно общие и легко
проверяемые условия, при которых о2>0, хотя чаще всего
бывает именно этот случай.
236
Теорема 2 (центральная предельная теорема). При
,*i—>оо распределение нормированной суммы Sn=(Sn—
—па)/1п стремится к нормальному распределению Л/(0, о)
с нулевым средним и дисперсией с2 (в смысле слабой сходи-
мости).
Замечание. При о2>0 получается содержательная
предельная теорема; при о2=0 мы делим случайную величи-
ну Sn—па, дисперсия которой ограничена, на Уп-»-оо. Норми-
ровка оказывается слишком сильной, в пределе получается
вырожденное распределение (сосредоточенное в точке 0 с ве-
роятностью 1), и мы нс получаем информации о функции рас-
пределения ненормированной суммы, т. е. центральная пре-
дельная т,еорема малосодержательна (сводится к утвержде-
нию, что (Sn—па)/Ип-*Ъ по вероятности).
Доказательство теоремы 2. Не ограничивая
общности, предположим, что X'(0)=ia=0. Тогда (Sn—
—па)/Ц1Г= Sn/Уп и, применяя (2), получаем
Mexp (t7S„/Кл ) = U lVn](p (* V»”)®) X
X М* //«)) + о(1) = (ЦО) + Х'(0) t /Уп +
+ у Z"<°) + ° /И*)*])’X
X (p(t /Кп ) e)(ze(z /У»)) + о(1) =
=(1 — г аЧ^п+°</2//г> У Х
X (p(t!Vn)е)(«е(<lV"n)) + о(1)-*exp(— оМ/2),
что отвечает нормальному распределению N(Q, о). Теорема
доказана.
§ 3. Примеры марковских цепей и некоторые дополнения
3.1. Цепь с двумя состояниями. Пусть цепь имеет два сос-
тояния: Х={0, 1}, как, например, в случае гласных и соглас-
ных букв в русском тексте. Переходная матрица может быть
записана в виде
/ АюА1\ _ / Ри 1 Ро \_/Ро Я о \ 9в e 1 Ро>
\PuPnl ~ ‘ Pi l~pj~ \Pi <ИГ Я1= 1 - Pi,
где pw=po, P\o=Pi — соответственно вероятность следования
нуля за нулем и нуля за единицей.
Стационарное распределение (р, 1—р) находится из урав-
нения: рр0+ (\—p)Pi=p, откуда р=Р1/(1+р1—ро).
237
Для большей наглядности сравнения с испытаниями Бер-
нулли перепараметризуем переходную матрицу. При взгляде
на последовательность нулей и единиц, полученную из какого-
то опыта, мы прежде всего оцениваем доли нулей и единиц,
которые будут близки к стационарным вероятностям р и q =
= 1—р. Введем еще параметр б=ро—Pi- В терминах пара-
метров р, q, б имеем p0=p + dq, Pi=p—&р, 6=ро—Pi-
Займемся теперь числом нулей в п испытаниях. Полагая
Я
f(0) = l, f(l)=0, получим, что $п = f есть число
k=t
нулей в испытаниях с номерами 1, 2.. п. Для нахождения
асимптотики распределения Sn учтем, что при стационарном
начальном распределении MSn=np; что же касается дис-
персии DSn, то она (асимптотически при л-м») есть па2,
где о2 находится следующим способом.
Пусть Х(/) есть то собственное значение матрицы
р ((P + bq)^ 1 -p-6q \
’ \(Р — Ър)еи 1-р + 6р Г
которое при 1 = 0 обращается в единицу. Тогда
о2 = —X" (0) — р2.
Чтобы найти М0> нужно всего лишь решить квадратное урав~
нение det(P(7)—Х£)=0. Так как detP(O) = detP = d, то это
уравнение принимает довольно простой вид
X2 — (1 — р + бр + (р + бр)е") к + 6eit = 0. (1)
Все-таки решение уравнения (1) по школьной формуле не
приносит удовольствия, и как кажется, проще всего посту-
пить следующим образом. Напишем разложение
k(t) = 1 + X'(0)Z +4-V'(0)/2 + o(t2) (2)
и учтем, чтоХ' (0)=ip и что е“ = 1 +it—t2/z+o{t2).
Тогда, приравнивая в (1) нулю члены до второго порядка
по t, получим для неизвестного к" (0) некоторое уравнение,
из которого (после небольшого счета) найдем
-Х"(0) = р(1 — б + 2рб) / (1 — б)
и, наконец,
о» = рд(1+8)/1-б. (3>
Поскольку для испытаний Бернулли дисперсия числа успехов
есть npq, то коэффициент дисперсии получается равным
238
DSn _ 1+»
npq 1—В
Это и есть та формула, с помощью которой А. А. Марков
объяснял дисперсию числа гласных в 100 последовательных
буквах текста. Видим, что если б>0, т. е. Po=Poo=p+bq>p
(нуль после нуля более вероятен, чем в стационарном распре-
делении), то коэффициент дисперсии больше единицы. Инту-
итивный смысл этого состоит в следующем. Представим себе,
что нуль «тянет за собой» нуль, а единица — единицу так,
что если в нулевом испытании появился нуль, то и все ос-
тальные испытания (с близкой к 1 вероятностью) тоже да-
ют нули (а если в нулевом испытании единица, то все осталь-
ные тоже единицы). Тогда для числа нулей в п испытаниях
возможно либо очень большое значение порядка п, либо
очень маленькое — близкое к нудю (при этом можно взять
p = q=l/2, б«1, матрица Р будет близкой к диагональной).
Поэтому дисперсия числа нулей в п испытаниях будет боль-
шой.
Наоборот, если нуль с большей вероятностью «тянет» еди-
ницу (и наоборот), то в п испытаниях нулей и единиц будет
примерно по п/2, и дисперсия числа нулей окажется малой.
3.2. Движение по компасу. Представим, что путешествен-
ник хочет пройти полосу леса шириной 10 км в восточном на-
правлении (так как он знает, что на расстоянии L=10 км от
того места, где он стоит, через лес проходит шоссе с автобус-
ным сообщением, причем остановка автобуса находится как
раз в восточном направлении). У путешественника есть маг-
нитный компас, и он действует следующим образом. С по-
мощью компаса он намечает примерно на расстоянии 1=
= 100 м ориентир, достигает его, намечает следующий ориен-
тир и т. д. Сделав так примерно п=£//= 100 раз, он выходит
на шоссе, но только вопрос — в каком расстоянии от авто-
бусной остановки?
Направим ось абсцисс на восток (она проходит через авто-
бусную остановку), ось ординат — на север. Если y(k) — ор-
дината путешественника после k-ro перехода длины I, то оче-
видно
y(k + 1) = y(k) + y(k+\) — y(k) - y(k) + 6*+1,
6*+1 = y(k +1) — y(k), (1)
a y(n) — отклонение от автобусной остановки.
Сделаем теперь вероятностные гипотезы о 6|, 62, • • • • Иде-
ально было бы, если бы 61=62= ••• =0, но каждый пони-
мает, что при движении по компасу это невозможно. Ошибка,
связанная с движением по компасу, состоит в том, что ори-
ентиры замечаются неточно в восточном направлении (как
239
потому, что азимут измеряется неточно, так и потому, что
точно на востоке может не оказаться заметного ориентира).
Пусть ошибка в определении направления на Л-й ориентир
есть ф*; тогда 6л = /з1пф*«/фл, если углы измерять в радиа-
нах. Угловая ошибка имеет систематическую составляющую
(связанную с магнитным склонением), а в остальном — слу-
чайна.
Пусть магнитное склонение известно и на него введе-
на поправка. Тогда М<ЬЙ=О, следовательно, и МбА==0.
Оценим дисперсию D6fc. Примем, что среднеквадратичное
значение примерно есть цена деления шкалы ком-
паса, т. е. что-то около 6°=1/10 радиана. Тогда ]/D6a «
«Z/Ю.
Примем также упрощение, состоящее в том, что отдельные
случайные величины бь 62, • • • независимы. (Это, вообще го-
воря, необязательно, так как если на каком-то довольно
длинном участке пути есть густой подлесок и ориентиры за-
мечать трудно, то соседние б* будут принимать большие по
модулю значения; а скажем, на болоте, где идти трудно, но
видимость отличная, соседние б* будут, наоборот, малыми).
Тогда y(k) есть сумма k независимых случайных величин
(тем самым, конечно, и цепь Маркова, но это малоинтерес-
но), и мы ее немедленно исследуем о помощью центральной
предельной теоремы.
Действительно, _для у(п) среднеквадратическое значение
будет Vn-VD6* = Vn//10=100 м, т. е. на пути L=10 км
ошибка с близкой к 1 вероятностью не должна быть больше
200...300 м. Отсюда, между прочим, очевидно, что очень важ-
но учесть магнитное склонение (его величина тоже может
быть порядка 6°, т. е. связанная с ним ошибка составит
L/10=l км). Без знания теории вероятностей можно было
бы подумать, что раз магнитное склонение лежит на пределе
точности определения азимута, то можно его и не учитывать.
Но нет: при многократных измерениях систематическую со-
ставляющую ошибки весьма полезно вычесть.
Теперь заставим путешественника пользоваться инерци-
альным компасом. Система инерциальной навигации способ-
на все время указывать раз заданное направление (допустим,
на север), но, конечно, с некоторой ошибкой, зависящей от
динамики движения объекта (путешественник может, напри-
мер, упасть, и тогда система инерциальной навигации отра-
ботает угол поворота с некоторой ошибкой). Ошибка все вре-
мя накапливается: она является чем-то промежуточным меж-
ду систематической ошибкой и случайными ошибками при на-
хождении ориентиров.
Тем не менее всю систему «путник—инерциальный ком-
пас» можно представить цепью Маркова, усложнив фазовое
240
пространство. Выберем в качестве точки фазового простран-
ства пару чисел: отклонение y(k) системы от оси абсцисс и
угол ф(&) ухода инерциального компаса от направления на
север. Тогда в момент k следующий ориентир будет замечен
в направлении отклоняющемся от нужного, на угол ф(£)+ф*,
где ф* — случайная ошибка, а отклонение от оси абсцисс
y(k +1) получает вид
У (k + 1) = y(k) + /sin (ф(£) + фЛ) « y(k) +
+ I (Ф(£) + Ф4+1) • (2)
При этом за время от k до &+1 уход инерциального компаса
изменится на величину
ф(£+1) — = ал+ь (3)
зависящую лишь от динамики движения путешественника за
время от k до &+1. Предполагая случайные величины
ст, а2, ..., независимыми между собой и не зависящими от
величин фЬ фг, .... получим, что положение (y(k+l,
1)) всей системы есть функция от (y(k), ф(&)) и от но-
вых (независимых от всего прошлого движения) случайных
величин afc+i и ф*+1, т. е. соотношения (2) и (3) задают цепь
Маркова. Согласно правой части (2) уход инерциального ком-
паса ^(k) и ошибки в определении ориентира ф* дают в об-
щую ошибку такие вклады, которые попросту суммируются.
Можно считать, что ошибки в определении ориентира мы уже
изучили. Будем считать, что Ф1=ф2= ... =0, и изучим вклад
ухода компаса ф(&).
и
Полагая, что ф(0) = 0, получим <[>(£) = 2 “/• Тогда y(k+
/-1
i
-+-])= y(k) 4-Z 2 аь a следовательно,
/=i
= /(««! + (n—l)a2+ ... +<хл). (4)
Дисперсия выражения (4) дается формулой
DMl«+2» +
+ . . . +ns)«/«Daj. п’/З, (5)
(если считать, что Da1=Da2 = ... = Dan). Таким обра-
зом, среднеквадратическое уклонение УЫМя+Ш имеет
порядок величины п3/2 . Постепенно нарастающая случай-
ная ошибка хуже не нарастающей систематической, ко-
торая дает ошибку в окончательном положении системы
порядка п. (Если бы была линейно нарастающая система-
тическая ошибка, то она дала бы вклад порядка п*).
16—2567 241
Конечно, носимый в кармане инерциальный компас есть в
наше время объект пока еще фантастический. Но множитель
п3/2 показывает, как высоки должны быть требования к точ-
ности реальных систем инерциальной навигации.
Эргодическая теорема в применении к уходу инерциаль-
ного компаса мало интересна. В ней речь идет о столь дале-
кой асимптотике (т. е. о столь больших значениях п), когда
устанавливается стационарное распределение. Нетрудно ви-
деть, что для модели ухода инерциального компаса в виде сум-
мы независимых случайных величин такое распределение
лишь одно — равномерное распределение на окружности. Ко-
нечно, пользоваться инерциальным компасом без коррекции
столь долго, чтобы вместо севера он с равной вероятностью
показывал любое направление, неразумно.
Нашу схему можно усложнить; пусть путешественник кро-
ме инерциального компаса возьмет с собой и гирокомпас, что-
бы время от времени поправлять инерциальный компас. (Для
этого путешественник должен остановиться, включить мотор-
гирокомпаса и выждать несколько десятков минут, пока по
показаниям гирокомпаса можно будет с достаточной точно-
стью понять, где север). Возникнут противоречивые желания:
с одной стороны, нужно все-таки идти, а с другой стороны,
чтобы идти точно, нужно почаще поправлять инерциальный
компас. Предположим, что включение гирокомпаса происхо-
дит через каждые т переходов; тогда цепь Маркова, изобра-
жающая уход инерциального компаса, сделается неоднород-
ной по времени: в моменты времени т, 2т, ... вместо пере-
хода в новое состояние путем добавления нового угла ухода
будет происходить перескок ошибки компаса в состояние
нуль. Но можно уговориться, что путешественник при каждом
новом переходе будет посредством случайного эксперимента
решать, что ему делать — идти или поправлять инерциаль-
ный компас. Если вероятность того, что он поправляет ком-
пас, выбрать примерно \/т, то получится однородная марков-
ская цепь, близкая по свойствам к неоднородной. У нее будет
некоторое разумное стационарное распределение; ошибка по-
ложения путешественника будет величиной порядка Уп (так
как в этой постановке действует центральная предельная тео-
рема). Но конкретные расчеты здесь лучше проводить мето-
дом Монте-Карло (да и назвать реальные значения парамет-
ров задачи затруднительно).
3.3. Произведения случайных матриц. Вполне непрерыв-
ные интегральные операторы по своим спектральным свойст-
вам совершенно аналогичны матрицам, т. е. операторам, дей-
ствующим в конечномерном пространстве. Цепь Маркова с
дискретным временем n=0, 1, 2, ... на произвольном фазовом
пространстве задается переходной функцией P*+l (х, Г).
Пусть фазовое пространство X есть гладкое компактное мно-
242
гообразие с некоторой мерой dx на нем, а переходная веро-
ятность задается плотностью р (k, х, у):
Р*+‘(х, Г) = .|’р(Л, х, y)dy.
г
В однородном по времени случае p(k, х, у)=р(х, у) от k не
зависит.
Возникают операторы Т, действующие на функциях f(x),
х^Х по формуле
Tf(x) = $p(x, y)i{y)dy, (1)
Л'
и сопряженные им операторы Р, действующие на плотностях
распределения л на X по формуле
Pr-(y) = \ р(х, y)r(x)dx. (2)
х
Если предположить, что объем \ dx многообразия X конечен,.
х
а плотность р(х, у) непрерывна и ограничена (следователь-
но, интегрируема с квадратом на ХхХ), то применима тео-
рия Фредгольма. Оператор (1) можно рассматривать лишь
на непрерывных функциях f(x), и вся наука, касающаяся
классов, подклассов и эргодических свойств, может быть пе-
ренесена со случая конечного фазового пространства
Х={1, на случай многообразия. Переносятся также за-
кон больших чисел и центральная предельная теорема.
Не приводя подробностей этой теории, ограничимся тем,
что укажем ее связь с исследованием произведений случайных
матриц. Случайные матрицы возникают, например, при ис-
следовании линейных дифференциальных уравнений, коэф-
фициенты которых зависят от случайных процессов. В моде-
ли случайного процесса с обновлением возникает произведе-
ние фундаментальных матриц (матриц монодромии), кото-
рые являются статистически независимыми.
Рассмотрим общую схему. Пусть В(п) =BiB2... Вп — про-
изведение независимых одинаково распределенных случайных
матриц порядка пг. Рассмотрим действие еВ(п) матрицы
В(п) на вектор-строчку е. Положим е(0)=е, е(1) =е(0)Вь...,
...,е(п)=е(п—1)В„=е(0)В1...Вп. Конечно, е(0),е(1),...,е(п)
образуют марковскую цепь (новое состояние е (п) есть функ-
ция от старого е(п—1) и от независимой матрицы Вп). Но
фазовое пространство этой цепи Rm некомпактно, так что эр-
годическая теория применяться непосредственно не может.
Идея метода состоит во введении полярных координат.
Положим е(п)=г(п)и(п), где r(n) = ||e(n) ||, u(n) =
= e(n)/||e(n)|| — точка единичной сферы. Имеем
,6* 243
e(n) = e(n—l)B„ = r(n— \)u(n — l)Bn =
= r(n- l)||(u(n—l)fin||
u(n — 1)бя
Таким образом, можно положить
r(n)=r(n—l)||u(n—1)ВП||,
u(n)=u(n—l)B„l\\u(n—l)Bn\\.
Рассмотрим последовательность u(n). Равенства (1) показы-
вают, что и(п) есть функция от и(п—1) и Вп, т. е. {и(п),
n=0, 1,...} есть марковская цепь. При широких условиях
эта цепь эргодична, так как ее фазовое пространство (еди-
ничная сфера) компактно. Далее, рассмотрим пару (u(n),
Bn+i). Равенства (1) показывают,что (и(п), Bn+i) естьфунк-
ция от (u(n—1), Вп) и новой независимой случайной матри-
цы Bn+i. Интуитивно понятно, что добавление независимой
матрицы Bn+i не может изменить эргодические свойства, ко-
торыми обладает цепь {и(п), n=0, 1,...}. Но согласно перво-
вому из равенств (1)
lnr(n) =lnr(n—1) +1п||п (п—1)В„||,
т. е. In г(п) является суммой случайных величин, связанных в
цепь Маркова.
Таким образом, в полярных координатах (г(п), и(п))
вопрос о поведении вектора е(п) =е(0)В(п) достаточно ясен:
для 1пг(п) ожидается нормальное распределение, а для
и(п) — некоторое стационарное распределение на единичной
сфере. Некоторые соображения показывают, что совместное
распределение г(п) и и(п) приближается при п->-оо к рас-
пределению независимых случайных величин.
Рассмотрим пример. Возьмем дифференциальное уравне-
нение х+(1 + е^(0)х=О, где %(t) — случайный процесс с
обновлением в какие-то моменты, е. — малый параметр. Ос-
новной качественный вывод, который получим, состоит в том,
что при любом е>0 решение x(t) этого уравнения стремит-
ся к бесконечности экспоненциально быстро, т. е. |х(0|>
cexp(af), где а>0 (по порядку величины а есть е2). Таким
образом, случайные колебания упругости маятника без тре-
ния ведут к экспоненциальному росту решения. Так как до-
бавление трения ведет к экспоненциальному затуханию ре-
шения, то при коэффициенте трения, малом по сравнению с
е2, будет наблюдаться экспоненциальный рост.
Проведем соответствующие вычисления. Допустим, что мо-
менты обновления процесса £(0, обозначаемые
244
/о=О</1</2<
можно выбрать в следующем виде: /*+i—tk=a+6k, где а—
некоторое число (намного большее 2л), 6л — случайная вели-
чина, равномерно распределенная на отрезке [0, 2л]. Матри-
ца монодромии Вк на отрезке [/*—i, /*] будет .матрицей моно-
дромии на отрезке длины а, умноженной на матрицу моно-
дромии на отрезке случайной длины <2л. При малом г мож-
но считать, что последняя матрица есть примерно матрица
поворота на угол б*. Поэтому для любого вектора и единич-
ной окружности распределение вектора uB*/||uB*|| будет рав-
номерным на окружности. Это означает, что стационарное
распределение цепи Маркова и(п) будет равномерным.
Вычислим a=Mln||uBn|| (порядок роста 1пг(п) =
1п||еВ(п)|| есть как раз па). Заметим, что матрица Вп унп-
модулярна, а любую унимодулярную матрицу В можно при-
вести к виду
d__,, / X 1 0 \ „
\ О А /
где и v2 — ортогональные матрицы. При 8=0, очевидно,
Х=1; при 8=0 элемент X диагональной матрицы есть (для
матрицы монодромии) некоторый функционал от процесса
£(/), который нетрудно выписать методом последовательных
приближений с учетом членов порядка 8 и е2. Нам важно
лишь то, что для матрицы монодромии Х=14-6, где б — ве-
личина порядка 8.
При вычислении In ||uB|| ортогональные сомножители
Vi и v2 не влияют на ||иВ||. Следовательно, нужно лишь
вычислить М1п||иД||, где A = diag(X-1, X). Пусть и — (cosф,
в1пф), ф имеет равномерное распределение на отрезке
(0, 2те], а А фиксировано. Имеем
In ||«Д |( = 1/2 ln(X-2 cos2 ф + X* sin2 ф) =
= 1/21п|(1 + В)-2 cos2 ф 4- (1 4- В)2 sin2 ф] =
= 1/21п]со82ф4-з1п2ф4-((1 4- В)"2 — 1)со$2ф4-
4- (26 4- В2) sin2 ф] = 1 /2 ln( 1 4- (- 26 4- ЗВ2) cos2 ф 4-
4- (28 4-В2)sin2<р + . . .),
где многоточие заменяет члены порядка В2 и выше- Раз-
лагая In с учетом членов порядка 82, получаем
2 In ||uA || = (— 2В 4- ЗВ2) cos2 ф 4- (28 4- В2) sin2 ф —
— 1 /2(482 cos4 ф 4- 482 sin4 ф — 862 sin2 ф cos2 ф).
245
При равномерном распределении ф на отрезке (0, 2я]
М зш2ф — М cos2 ф = 1/2, М sin2 ф cos2 ф = 1/8,
М sin4 ф = М cos4 ф = 3/8.
Поэтому при фиксированном Л = diag [(1 + 3)_|, 1+8]
имеем
М In ||«Л || = 1 /232(2 - 2 • 3/4 + 1/2) = 1 /2о«.
При усреднении по матрице Л получим
а=1/2М32«са2, с>0, (2)
что и требовалось доказать. (Коэффициент с в (2) в принци-
пе может быть выражен через статистические характеристи-
ки случайного процесса 5(0 — математическое ожидание,
если оно отлично от нуля, и корреляционную функцию).
3.4. Пуассоновский процесс. Теперь рассмотрим простей-
ший марковский процесс с непрерывным временем. Построим
математическую модель для числа 5(0. Т) частиц, зарегист-
рированных счетчиком радиоактивного излучения за время
(О, Г). Если
0=Л</2<... <tn=T,
то
U0, Т) =g(0, Л)+£(6, /2)+...+g(Ub tn), (1)
причем естественно считать, что различные слагаемые в сум-
ме (1) статистически независимы. Сумма (1) не приводит
обязательно к нормальному закону, так как при измельче-
нии разбиения отдельные слагаемые в ней также изменяются
(при очень малых длинах интервалов (/,-, /,+1) большинство
слагаемых в сумме (1) вообще равно нулю). Между тем
центральная предельная теорема относится к сумме возрас-
тающего числа одинаково распределенных величин.
Увидим, что для суммы (1) получится распределение Пу-
ассона. Рассмотрим для n=0, 1, 2,... вероятности
Р„(Г) = Р{5(0, 7)=и).
Дадим Т небольшое приращение ДГ. Понятно, что за малое
время ДТ может прибавиться, самое большее, одна частица.
Если средняя интенсивность счета есть Л, то
Р{5(7; 7’+Д7’) = 1}=ЛД7+о(Д7’),
Р{£(7; Г+Д7)=0)=1—(ХДГ+о(ДГ)),
а вероятность
Р{5(Г, 7+ДГ)>1}=о(ДГ).
Поэтому
P = U(0, F+ДГ) =0} = Р(5(0, Г)=0) Р(5(7, Г+ДГ),=0) =
246
= Р{£(0, Т)=0}(1—{ЛДТ+о(ДТ)}).
Следовательно, для р0(Т) = Р{£(0, Т)=0} получаем уравне-
ние
----W). (2)
Для рп(Т) при п=#0 получаем
рп(Т+ ДГ) =р„(Г) (1-{ХДГ+о(ДГ)}) +
+Pn-i(T) (ЛДГ+о(Д7)),
откуда
4- ра(Т) = - крп(Т) + ХрЛ_,(Г). (3)
ат
Решая (2) с очевидным начальным условием ро(О) = 1, по-
лучаем
Ро(Л=ехр(-ХГ). (4)
Подставляя (4) в (3) при п=1 и т. д., получаем (если угод-
но — методом вариации постоянной)
Рп(Т) = -^ехр(-ХГ).
и!
Таким образом, распределение величины g(0, Т) есть распре-
деление Пуассона с параметром ЛГ.
Процесс £т=ь(0, Т) называется пуассоновским процес-
сом с параметром Л. Его конечномерные распределения оп-
ределяются условиями:
1) £о=§(О, 0)=0;
2) разности — Ц = 5(6-ь 6) — независимые пуассо-
новские случайные величины с параметрами /.(6— 6-1).
Реализация 5, процесса Пуассона есть кусочно-постоянная
функция, которая в случайные моменты времени прирас-
тает скачками, высота которых равна 1.
Рассматриваются также более общие пуассоновские про-
цессы, траектории которых прирастают скачками в те же мо-
менты, что и траектория процесса Пуассона, но величины
этих скачков случайны (независимы друг от друга) и имеют
заданное распределение вероятностей.
§ 4. Марковские диффузионные процессы
4.1. Основные понятия. Если не в физике, то в математи-
ке возможно такое движение, при котором абсцисса
247
x(t) движущейся точки за время Д/ изменяется на величину
порядка УД£ (см. в гл. 5 винеровский процесс). Такой способ
движения прямо противоположен рассмотренному случаю пу-
ассоновского процесса, когда траектория изменяется скачка-
ми. В то время как обобщенный пуассоновский процесс назы-
вается скачкообразным, процессы типа винеровского называ-
ются диффузионными. (Случай, когда x(t) за время &t изме-
няется на величину порядка Д/, в марковских процессах не-
возможен, если не заниматься тривиальным случаем детер-
минированного процесса.)
В рамках теории диффузионных процессов достигается не-
кая вершина развития корреляционной теории: для полного
описания распределений вероятностей оказывается достаточ-
ным знания лишь математического ожидания и дисперсии
приращения Дх(^) =х(/ + Д/)—x(t) для малых Д/ (если
процесс x(t) многомерный, то надо включить и ковариании
приращений отдельных компонент).
Рассмотрим (для простоты — в одномерном случае) со-
ответствующие определения. Пусть имеется марковский про-
цесс х(0, <>0, переходные вероятности которого обладают
следующими свойствами.
Г. Для любой точки х фазового пространства X=R'
P't+*(x, ад) = о(Д) (Д->0) (1)
для любого е>0, где Ос(х) означает е-окрестность точки
х: О,(х)={у: |у—х|<е}.
Свойство Г означает, что вероятность выхода
за время от t до «-+-Д из точки х за пределы любой
ее фиксированной окрестности есть о(Д), т. е. отноше-
ние Р<+Д(х, О,(х))/Д—>0 при Д—>0. Вероятность, задавае-
мая переходной функцией, может пониматься и как ус-
ловная вероятность при условии, что х(/) = л:
Р;+А(х, ад) = Р(х(* + Д)(Е О.(х)|х(0 = х}.
2е. Для любой точки хеЛ=Р’, полагая Дх(0«
=х(Л-Д)—x(t), имеем следующие соотношения:
M/.хМО = a(t, х)Д + о(Д), (2)
М/. х[Дх(/)]* = х)Д + о(Д). (3)
В этих выражениях знак Л4/,х означает следующее. Вообще-
то речь идет об условных математических ожиданиях Дх(0
при условии, что х(/)=х. Но из-за (маловероятных в силу
(1), но все-таки возможных) больших значений Дх(0 могут
не существовать условные математические ожидания
248
Mt,xAx(t) и, тем более Afr,*[Ax(/)F. Поэтому, выбрав некото-
рое 8>0, берем условные математические ожидания величин
Дх(/) =Дх(/), если Дх(/)<8, и Дх(?)=0, если |Дх(/)|>е.
Таким образом,
М,.хДл(П= МлхДф), М,.4Дх(/)]г=М<,4Дх(0]2. (4)
Выражения (4) зависят от 8, но в силу свойства Г зависи-
мость от 8 дает вклад порядка о(Д). Поэтому величины
а(/, х) и о2 (Г, х) определяются не зависящим от 8 способом,
и для краткости обозначений записываем в виде (2) и (3).
Замечание. Необходимость «урезания» приращений
Дх(/), т. е. перехода к Дх(/), связана с тем, что желательно,
чтобы функция от диффузионного процесса
x(t) также оказывалась диффузионным процессом; однако
функции f бывают и неограниченные. Если считать, что
Дх(0 имеет гауссовское распределение (как для винеров-
ского процесса), то при неограниченной f приращение
Sy(t) =f[x(t) + Дх(/)] — f(x(t)) может не иметь конечного
математического ожидания.
Величина a(t, х) называется коэффициентом сноса (в мо-
мент t в точке х), величина o2(t, х) — коэффициентом диф-
фузии. В записи через переходную вероятность имеем следу-
ющие выражения для этих коэффициентов:
a(t, х) Г (у — х)Р'(+л(х, dy), (5)
Д—в a J
I у—
о2(/, x) = lim —
Л—О Д
(Р-Х)2Р/+Д(Х, dy).
(6>
По указанной выше причине выражения (5) и (6) не зависят
от произвольно выбранного 8>0.
Таким образом, математические ожидания первой степени
и квадрата малого выражения Дх(О оказываются величина-
ми одного порядка. Это возможно потому, что положитель-
ные и отрицательные значения случайной величины Дх(?)
(которые сами по себе имеют порядок величины УД) комби-
нируются так, что дают величину порядка Д; значения же
[Лх(?)Р все неотрицательные. Если взять [Дх(/)]3, [Дх(0?,
..., то соответствующие математические ожидания (если они
существуют) либо математические ожидания «урезанных» ве-
личин [Дх(<)Р. [Дх(?)]4, ... при естественных условиях должны
иметь высший порядок малости по сравнению с Д.
249
Нужно привести какой-то пример диффузионного процес-
са. Воспользуемся для этого ранее рассмотренным винеров-
ским процессом, для которого Ax(f) =х(?+Д)—x(t) есть
гауссовская случайная величина с нулевым средним и дис-
персией б2Д. Проверим свойство Г:
Р{+Д(х, ОД?)) - Р{|Дх(01 > е|х(0 = х} (7)
есть вероятность_того, что величина Дх(/)/(бУД) превысит
значение г=е/бУД. Но величина Дл:(^)/(6УД) имеет стандар-
ное нормальное распределение Af(O, 1), для которого вероят-
ность выхода за интервал (—г, z) есть примерно ехр{—z2/2).
Следовательно, (7) оценивается величиной ехр{—е2/(2б2Д)) =
=о(Д) при любом е<0.
Очевидно, что для винеровского процесса a(t, х)=0 и
o2(t х)=о2.
Существование диффузионного процесса с более или ме-
нее произвольными коэффициентами a(t, х) и o2(f, х) вывес-
ти не так-то просто. Можно построить реализации такого
процесса, исходя из реализаций винеровского процесса (это
так называемый метод стохастических уравнений). Пусть,
действительно х(1) — винеровский процесс, y(t) — искомый
процесс, причем (для простоты) у(0)=0, а кусок реализации
процесса y(t) при удалось каким-то способом постро-
ить; при этом оказалось, что у(Т)=у. Положим у(Т+ЬТ) =
=у(Т)+&у(Т), где
Д«/(Т)=а(Г, у)&Т+с(Т, у)Ьх(Т).
Тогда, очевидно, М (&у(Т)) =а(Т, у)ЬТ,
М[Ьу(Т)]2=с2(Т, у)ЬТ+о(ДТ).
Так можно построить последовательность величин y(t) с дис-
кретным шагом по t. Но доказательство того, что при измель-
чении шага получится сходимость к некоторой функции непре-
рывного времени y(t), которую можно принять за реализа-
цию искомого процесса, технически весьма сложно. В данной
книге мы не будем заниматься этим вопросом (тем более что
нужно учитывать некоторую физическую нереальность траек-
торий винеровского процесса, о которой говорилось в гл.5).
Можно пойти по другому пути: вывести уравнения, кото-
рым должны удовлетворять переходные вероятности диффу-
зионного процесса. Если сослаться затем на общие результа-
ты теории уравнений математической физики, из которых вы-
текает существование (и единственность) решений, то мож-
но получить, что переходные вероятности существуют, удов-
летворяют уравнению Чепмена-Коломогорова, а стало быть,
определяют и некоторые марковские процессы. Из этой нау-
ки, в частности, следует, что переходные вероятности одноз-
250
начно определяются коэффициентами сноса и диффузии. Та-
кой путь вполне возможен, но входить в подробности его кон-
кретной реализации мы также не будем.
4.2. Дифференциальные уравнения для переходных веро-
ятностей. В данном пункте, не стесняя себя в смысле различ-
ных предположений дифференцируемости, выведем знамени-
тые уравнения Эйнштейна — Смолуновского — Фоккера —
Планка — Колмогорова — Феллера для переходных вероят-
ностей диффузионного процесса. Переходная вероятность
Pf (х, Г) имеет, так сказать, «два конца»: левый конец отно-
сится к моменту времени $ и точке х (начало траектории), а
правый конец — к моменту времени t и множеству Г (конец
траектории). Соответственно выводятся отдельные уравнения
на левом и правом концах.
4.2.1. Уравнения на левом конце. Рассмотрим вместо пе-
реходной вероятности Р^(х, Г) оператор Т\, действую-
щий по формуле
Ts/(x) = M(/(x(t))|x(s) = .v) J 1(у}Р[(Х, dy). (1)
—00
Фиксировав t, рассмотрим функции g(s, х) — Г1/(х). Со-
ставим для функции g(s, х) уравнение, действующее в об-
ласти s<t. Так как при s-И промежуток [s, укорачи-
вается до нуля, то естественно считать, что при этом
переходная вероятность Р1(х, Г) превращается в некото-
рое подобие 6-функции 6(у — х). Следовательно, должно
выполняться граничное условие, получающееся соответ-
ствующей подстановкой в (1):
lim g(s, х) = /(х). (2)
s—*t
Прямо наложить условия гладкости на переходную
функцию Р\(х, Г) нельзя из-за упомянутого превращения
ее в 6-функцию. Но при гладкой ограниченной /(х) есте-
ственными являются условия гладкости gis, х). Пусть эта
функция имеет непрерывные ограниченные производные
первого порядка по s и второго порядка по х. Составим
для нее дифференциальное уравнение.
Пусть Д>-0; тогда из равенства (1) и равенства Чеп-
мена-Колмогорова следует, что TV-д Г, =« 7^_д. Следо-
вательно,
g(s — Д, х) = Т!_д g(s, х);
g(s —Д, х) — g(s, х) = f g(s, у)Р/_&(х, dy) — g(s, x) =
251
= J (g(s, У) — g(s, x)) г:_д (x, dy) =
— 00
= f (g(s, y)—g(s, х))Р’_д(х, dy) +
+ f (g(s, y) —g(s, х))Р’_д(х, dy). (3)
|y-x|> t
Предположим, что Р^-д (x, 0,(x)) = о(Д) (это условие име-
ет тот же смысл, что и условие 1® предыдущего пункта,
хотя несколько отличается по математической форме);
тогда интеграл по у. \у — х|>е в (3) есть о(Д) в силу ог-
раниченности функции g (вытекающей из ограниченности
функции f). Разность g(s, у) — g(s, х) в первом интеграле
формулы (3) разложим по формуле Тейлора:
g(s. У) — g(s, х) = (у- х) g'x (s, х) +
+ у (У — x)*gxx(s, х) +
+ V (У — х)г [fxx (s, X + 0(у - х)) -gxx (s, х) I,
где О<0^1. Предполагая (аналогично соотношениям (2) и
(3) предыдущего пункта), что
j (У — х) Pj-д (х, dy) = a(s — b, х) Д 4- о(Д),
|у-ж|^е
J (У — *)* (х* dy) = °4S — А. х) Д + о(Д),.
|У -х/<«
учитывая, что при достаточно малом е>0, |у—х|се
|gxx(s, х4-0(0 — x)) — gxx(s, х)|<б = б(г),
получим, что сумма (3) преобразуется к виду
a(s — Д, x)^gx(s, х)4-
4- у о’(« — Д, х) gxx (s, х) Д 4 о(Д) 4- Т,
где |у|< -i- o2(s—Д, х) Д6(е), причем б(е)-*О прие-*О.
252
Деля g(s — A, x) — g(s, x) на А, предполагая непрерыв-
ность a(s, x) и o2(s, x) no s и устремляя затем e—>0, на-
ходим, что должно выполняться уравнение
«(,. х) + -L «(., х) , (4)
ds дх 2 дх*
зазываемое уравнением на левом конце. Его нужно решать
с условием (2) в полуплоскости Из-за того, что при
dgfds стоит знак минус, уравнение теплопроводности (4) кор-
ректно решается именно в этой полуплоскости.
Замечание 1. Если бы процесс x(t) ={xi (t), ...,xn(t)}
был процессом в Rn, то, полагая
a^s, х) = Ит 4- I (i
Д-*0 Д V
Пу—
= lim — М
д-о
Дх-*
Д 5-Д,х“*И
J* (Уг~х^Уг-Х{) Р‘з-ь (A dy) =
x) = lim —
А 11у-л||<е
= lim — lAs-д.х [Axj Дх,],
д-о А
совершенно аналогично получили бы уравнение
_«L_VeX,.x)
ds &xi
+ (5)
где g(s, x) определяется формулой (1) с заменой 7?’ на К*.
Набор a(s, x) = (ai(s, х),...,а„(х, х)) называется вектором
сноса, матрица l|oz/(s, х) II — матрицей диффузии. Следует
иметь в виду, что название «вектор» применительно к a(s, х)
не совсем правильное. Вектор есть не просто набор п чисел,
а набор, преобразующийся определенным образом при заме-
не координат. Между тем если мы возьмем замену координат
y=f(x), то из случайного процесса x(t) получим случайный
процесс: y(t) =f(x(t)). Математическое ожидание MAg(f) =
М (у (/+Д )—y(t)) надо вычислять, учитывая Axz(/) =
=х,(/ + Д)— xi(t) и также квадраты и попарные произведе-
ния этих величин, ибо
253
Л1Дх,(/), Nl{&Xi(t) Sxj(t)}
имеют один порядок величины Д. Например, для =
fi(xi(t),...,x„(t)) получим
AXi(0 +
ДУ1(0“У10 + А)-л(0
АхДОДх/О,
иными словами,
lim JLM, УЛУ1(О- *) +
Д-0 Д • у dXi
I
_i_ (t х)
2 j^dxtdx) 1
(6>
Первое слагаемое в (6) соответствует векторному закону пре-
образования, второе — нет.
Замечание 2. Как известно, уравнение теплопровод-
ности выводится из закона Фурье (количество тепла, проте-
кающего через единицу площади сечения, пропорционально
градиенту температуры); закон же Фурье может быть понят
только в рамках флогистонной теории теплоты. Несмотря на
ненависть, которую история науки на уровне средней школы
проявляет к флогистону, фактически это понятие продолжа-
ет жить. Конечно, уравнение теплопроводности (из которого,
в частности, следует, что скорость распространения теплоты
бесконечна) сейчас рассматривается лишь как грубое при-
ближение для реально происходящих процессов. Но в тео-
рии диффузионных процессов флогистон вновь оживает под
именем переходной вероятности, и уравнение теплопровод-
ности рассматривается как точное. Об отношении диффузи-
онных процессов к поведению распределений вероятностей
динамических систем см. ниже.
4.2.2. Уравнения на правом конце. Для вывода уравнений
на правом конце предположим, что существует гладкая пе-
реходная плотность р' (х, У):
Pj(x, Г)- J р'(х, y)dy.
254
Уравнение Чепмена-Колмогорова принимает вид при Д>0
р'+Л(х, 2)= J р\(х, у)р‘+л(у, z)dy. (1)
—оо
Пусть <p(z) — гладкая финитная функция; преобразуем ана-
логично предыдущему пункту разность
оо оо
j Рз+А(х, z)q>(z)dz — j* р',(х, y)q>(y)dy =
— оо — оо
оо оо
= 'J J Ps(xt у)^(У. z)(<p(z) — q>(y))dzdy —
—ос —со
ос оо
= j dyp[(x, у) J Pt+*(y, z)(<f(z) — T(y))dz =
J dyp'Ax, у)
—ОС
J Р/+Л (у,г) (ф(г)—<p(i/))dz+o(A)
1г-УК»
e J dyplfx, у) у р!+л(у, г)Х
—«О 1г—)К»
X (ф'(//)(г — у) + <р"(у)(з-у)* 1 dz + 6(e) Д+о(Д) =
I « I
рЛ*, у) alt, г/)ф'(у) +
+ 4-°г(г. у)ф"(у) Idy-f-6(e) Д + о(Д) =
I
= j {—дГ[e('* y)pts{Xt *)]+rx
—оо
Хт^-[ог(Л У)Р>(х, у)] lq>(y)Jy-l-6(e) Д + о(Д).
dy1 I
Учитывая произвольность функции <р(у) и предполагая диф-
ференцируемость pi (х, у) по t, получаем (аналогично пре-
дыдущему пункту)
255
аф£ = _ ±|а((, „)Х(х.!,)] +
dt ду
+ у^х>
2 dy*
(2)
Уравнение (2) есть снова уравнение теплопроводности. Оно
называется уравнением на правом конце. Его нужно решать
в полуплоскости />.$ с условием, что при t->~s решение пре-
вращается в б-функцию б (у—х) (такое решение называется
фундаментальным решением уравнения теплопроводности).
Оператор, входящий в правую часть (2), получается, если
заменить в операторе, стоящем в правой части уравнения (4)
предыдущего пункта, «левый конец» (s, х) на «правый ко-
нец» (t, у) и взять сопряженный оператор. Аналогично заме-
чанию 1 предыдущего пункта по этому же правилу пишется
уравнение на правом конце в случае диффузионного процес-
са в Rn.
В случае однородного по времени диффузионного процес-
са коэффициенты сноса и диффузии не зависят от времени/.
Получаются уравнения, к которым можно применять преоб-
разование Фурье (Лапласа) по переменному t. От этого за-
дача решения уравнения упрощается, но обычно остается до-
статочно сложной.
В частности, замечая, что функция
g(s, x)=JA{f(x(t))/x{s)=x}
зависит в однородном по времени случае от t—s: g(s, х) =
= g(t—s, x), и подставляя в уравнение на левом конце
dg/dt = —dglds, получаем для функции
h(t, x)=M{f(x(/)/x(s)=x},
рассматриваемой как функция t при фиксированном $, урав-
нение
<J/i , . dh . ... d-h
— = а(х)---------— о2(х) —
dt ' dx 2 v ' dx*
которое надо решить в полуплоскости />$, с граничным ус-
ловием h(s, x)=f(x). Обычно полагают $ = 0.
Из уравнения на правом конце можно (в стационарном
по времени случае) получить уравнение для стационарной
плотности распределения вероятностей. Именно, допустим, что
при фиксированном $ и t—>-оо плотность р» (х, у) стремится
к стационарной плотности р(у), а производная dpl/dt стре-
мится к нулю. Тогда получим
256
о — у- |л(у) ₽(</)] - -^—[оЧМу)],
dy 2 dy1
4.3. Динамические системы и диффузионные процессы.
Наши знания о случайных процессах, действующих на дина-
мические системы, обычно настолько скромны, что предполо-
жить обновление случайных процессов (т. е. их замену на
независимые) в какие-то моменты времени достаточно ес-
тественно. В этом случае получаем для системы общего вида
модель цепи Маркова. Замена же движения системы диффу-
зионным процессом есть, наоборот, довольно частный случай.
Даже в случае, когда собственного движения системы нет
(т. е. без случайных возмущений ничего не меняется), мы не
обязательно увидим диффузионный процесс. Например, пусть
положение системы в момент k есть сумма Sfc=£i + ga+ — +
+ независимых одинаково распределенных случайных ве-
личин. Допустим, что, собираясь наблюдать систему до
(большого) времени п, мы посмотрим на нее в перевернутый
бинокль, уменьшающий все размеры в п раз. Тогда увидим
$k=Skln, что есть ka/n, где а=М&, плюс случайная добавка
с дисперсией k<j2/n2, где o2=D^. Однако при k=l,...,n име-
ем £<j2/n2«j2//i->-0, т. е. в бинокль увидим детерминирован-
ное движение. Только если а=0, а бинокль взять с уменьше-
нием в In раз, увидим Skl1n, что напоминает винеровский
процесс х(1) с диффузией о2, если положить t=kjn, 1.
Если скорость невозмущенного движения системы доста-
точно велика (за то время, за которое теряется зависимость
между значениями случайного процесса, невозмущенная сис-
тема заметно сдвигается), то шансы на возможность аппрок-
симации диффузионным процессом падают. Рассмотрим, на-
пример, систему из одного уравнения
где а —константа, £(/) —случайный процесс. Ее решение
t
имеет вид x(t) = (ехр[а(/—$)] £(s)ds, что (в модели слу-
b
чайного процесса с обновлением) представится в виде
суммы независимых случайных величин:
fn h
J en</-s,E(s)ds = J e^^ds+
о 0
+ . . . + j (1)
'л-1
17-2567
257
Но слагаемые в сумме (i) резко неравноправны, так как
входят с экспоненциальным весом ехр[а(/—«)]• Рассчитывать
на применение центральной предельной теоремы, в частнос-
ти на то, что закон распределения суммы (1) определяется
лишь математическим ожиданием и дисперсией, не приходит-
ся. Исключением является лишь случай а=0. Между тем
диффузионный процесс определяется сносом и диффузией,
т. е. понятиями корреляционной теории; следовательно, нель-
зя рассчитывать на сведение данной простейшей динамичес-
кой системы к диффузионному процессу.
Качественно картина выглядит следующим образом. Если
роль случайных возмущений, действующих на каком-то от-
резке времени в дальнейшем возрастает (случай а>0« или
становится пренебрежимо малой (случай а<0), то нет ос-
нований думать о том, что удастся обойтись средствами кор-
реляционной теории (в частности, диффузионным приближе-
нием). К таким случаям относятся всякого рода полеты —
от артиллерийских снарядов до космических аппаратов, кото-
рые производятся без коррекции в процессе полета. Роль воз-
мущений на начальном участке в таких полетах исключи-
тельно велика. Например, нормальное распределение на плос-
кости точек падения артиллерийских снарядов есть, вероят-
но, фикция, которая, может быть, и наблюдается на полиго-
не в условиях тщательной стабилизации износа орудий, веса
снаряда, температуры заряда, условий наводки, метеофакто-
ров и т. д., но только не в реальной боевой обстановке.
Только если возмущения на различных участках как-то
равноправно взаимодействуют друг с другом (вроде суммы
примерно одинаково распределенных слагаемых), можно рас-
считывать на корреляционную теорию.
При наличии невозмущенного движения вопрос об аппро-
ксимации диффузионным процессом зависит от возможности
найти некую замену переменной, в результате которой марков-
ская цепь, описывающая движение системы, превращается в
движение некоторыми малыми скачками. Например, если по-
ложение системы, наблюдаемой в перевернутый бинокль,
есть Зл/п, то нужно из него вычесть детерминированное дви-
жение kaln = tASh/n, а на разность посмотреть в микроскоп,
увеличивающий в Уп раз. Если еще сделать замену времени,
то мы увидим движение, похожее на винеровский процесс.
Если невозмущенное движение есть вращение по окруж-
ности, а случайные возмущения медленно изменяют радиус
этой окружности, то нужно следить за возмущениями этого-
радиуса (превратив их в марковскую цепь). Если случайные
возмущения приводят к медленному уходу системы коорди-
нат, которую инерциальная система навигации должна под-
держивать параллельно заданной неподвижной системе, тс-
нужно, проследив за взаимодействием возмущений с состав-
258
ными элементами инерциальной системы (среди которых есть
быстро вращающиеся роторы гироскопов), получить корре-
ляционные характеристики соответствующей цепи Маркова
на группе вращений трехмерного пространства. Эта цепь бу-
дет изменяться малыми шагами, которые взаимодействуют
друг с другом не путем сложения, а путем умножения в ор-
тогональной группе, но это не мешает переходу к диффузион-
ному процессу, если, конечно, удастся выделить и убрать де-
терминированную составляющую движения.
Таким образом, имеется значительное количество случаев
(хотя и сравнительно частных), допускающих переход к диф-
фузионному процессу. Общим математическим средством для
этого является так называемая «теорема перехода» А. Н. Кол-
могорова, впервые опубликованная в 1931 г. со ссылкой на
то, что она представляет собой переработку доказательства
Линдеберга центральной предельной теоремы. Изложи:;! эту
теорему в других обозначениях.
Итак, марковская цепь как модель описания системы со
случайными возмущениями — если предположить всякого
рода статистические однородности, без которых вообще нель-
зя говорить о вероятностях, — есть модель сравнительно об-
щая. Речь идет о переходе от цепей Маркова (исследование
которых, вообще говоря, крайне затруднительно) к диффузи-
онным процессам (которые можно исследовать более удоб-
но, в частности средствами уравнений теплопроводности).
Пусть на некотором отрезке времени [0, 1] задан диффу-
зионный процесс с переходной функцией (х, Г), для кото-
рого функция
Tf, f (х) g (s, t, х) = М (f ix (t))!x (s) x)
при любой гладкой финитной функции f = f(x) является глад-
кой функцией с ограниченными производными. (Допустим,
например, что это известно из теории уравнения теплопровод-
ности).
Пусть на том же отрезке задана последовательность раз-
биений a={/o=O<fi< ... </п=1) и каждому а соответствует
марковская цепь с переходной функцией (х, Г), по своим
свойствам похожая на диффузионный процесс. Это означает,
что при |а|-*0, где |а| =max (/+i—/<) выполняются такие
предельные соотношения:
1°. «Р*+' (х, ОМ) = о ( - t,)' £ > 0;
2°. J (у — х) aPt( (х, dy)= a(tt, х)( — f<)-|-
+ о (f/+J — *i);
17»
259
.[ (У - x)\p';+l (x, dy) = o*(tlt *)x
ly-x|=St
Х(*/+1-Л) + о(,ж-Ч).
В этих соотношениях a(t„ х) и a2(t,-, х) — это коэффициен-
ты сноса и диффузии для диффузионного процесса; что же
касается выражений вида o(t1+i—t,j, то будем считать, что
их отношения к t,+i—ti равномерно стремятся к нулю при
|а|->0 относительно любых переменных, от которых выраже-
ния o(ti+l—t,) могут зависеть (a, t/, х). Коэффициенты
a(t,-, х) и o2(t,-, х) предположим равномерно ограниченными.
Введем оператор aQs формулой
a$/(*) = J dy)f(y).
—»оо
Теорема перехода А. Н. Колмогорова. При
sup|Tj/(x)-aQj/(x)|->O,
для любой ограниченной (со своими производными) функции
f=f(x).
Замечание. Эта теорема означает слабую сходимость
переходной функции аРо к переходной функции диффузионно-
го процесса. Поэтому при совпадении (или сходимости) на-
чальных распределений для цепей и для процесса сходятся
и их распределения вероятностей в момент /=1.
Доказательство теоремы. Имеем
То = T't\ Т',' . . . т’^,
«Qo = ЛЧ «Qh • • • J?'»-! •
Посмотрим, насколько увеличится разность Tt*—aQt" f
при переходе от tk к tfc_,. Напишем тождество
а q'; / - i т\: f -
=. о!.*-,. Ф - .<?;?- г;; /+X-1т'" < - ч t -
-.Л*., + (.<&-,) т'у-
Положим ||/|| = slip |/(х)|. Оператор, связанный с любой
X
переходной функцией, имеет тогда норму, равную 1.
Поэтому
260
II. t-r',1 .,|| <||. -Tty Ц+
Оценим норму второго слагаемого. Имеем, полагая
g(tk, х) = Т^1(х) и учитывая гладкость и ограниченность
производных функции g(tK, х) по х,
(.elL,J <w-
— •8
dy)]g(tk> у)=
= J [« р'*-1 (Л» dy) - pb-i <-х> аУ)\ X
X(g(tk, y)-g(tk, *)) =
= ( J + f 'j [а Р'Д-1 (*> -
\IV-X|>e |y-x|sSe /
— y)-g((k< *))•
Интеграл по области \y—xi>e оценивается (в силу свойства
1°) как o(tk—/д-i). В области lj/—х) =^е рассмотрим разность
g(h> У) - х) = (У- x)g^K> х> +
+ (у — X)2 gxx (tK, х) + 6(е)(у — х)2,
где 6(e)—>0 при е —>0.
Интеграл по области \у—хКе сведется к сумме интегра-
лов от (у—х) и от (у—х)2, которые (в силу 2°) отличаются
на o(f*—/д-i), плюс величина, не превосходящая
6(e) (/д — /д-i) с, с = sup о2 (tk, х).
Vх
Следовательно, при замене th на /д_< норма разности
eQj"/ — T^f увеличивается не более, чем на
6(0 С (/д-Гд.О+о^
Поэтому при переходе от /п=1 к 4=0 общее увеличение со-
ставит не более чем
6(е)с+о(1).
Устремляя е к нулю, заканчиваем доказательство теоремы.
261
Приведем два примера на использование этой теоремы.
1. Доказательство центральной предельной теоремы.
Пусть gi, £2,— независимые одинаково распределен-
ные случайные величины, для простоты обозначений Mg,=0,
Dg. = l.
Рассмотрим нормированную сумму s’, = (£1+...-г£п)/1/Г^
Введем марковскую цепь
х(0) = 0;
1 «
Коэффициент сноса для этой марковской цепи есть
коэффициент диффузии есть
Речь идет, следовательно, о сходимости к винеровскому
процессу с коэффициентом диффузии вг=1. Соответст-
dg 1 d*g *
вующее уравнение теплопроводности-------- =----- обла-
ds 2 дх*
дает всеми свойствами гладкости и ограниченности реше-
ния. Для применения теоремы перехода остается лишь
установить, что для любого е>0
>8
-Р{||*+1|>8 К«} = О
В самом деле,
Р{|Ь+>1>еL_ f
(е 1 п)2 J _ С*+‘ ’
|x|>el'n
ОО
так как |* — (*, Cx*u.(dx)= I, а следовательно, при
30
П —♦ оо J *,tx(dx) —> О, е > 0.
262
2. Более реалистическая модель броуновского движения.
Рассмотрим скорость v(t) броуновской частицы. На броу-
новскую частицу действуют, во-первых, стоксово трение (свя-
занное с вязкостью жидкости), а во-вторых, случайные толч-
ки со стороны молекул жидкости. Сила стоксова трения про-
порциональна Скорости о(0; что же касается добавки скоро-
сти из-за случайных толчков, то примем, что она не зависит
от v(r) (полагая, что эффект относительной скорости части-
цы в жидкости мы учли в стоксовом трении). Тогда при ма-
лом Ы
&v(t) » v (t + ДО — v(t) = —av (t) Д/ 4- g, М£ =0.
Следовательно,
М{Ду(0 / v(t) = v} = —avht,
М{[Дц(0Р / v(t) = v} = Mg2 + о(Д/).
Примем, что М£2=о2Д/; тогда коэффициенты сноса и диффу-
зии получаются следующие:
а (7, v) = —av, а2 (t, v) = а2.
Путь, проходимый в броуновском движении, — это интеграл
от скорости; его мы рассмотрим чуть позже.
Казалось бы, что, зная коэффициенты сноса и диффузии,
мы должны прямо приступить к решению уравнения для пе-
реходной плотности, чтобы полностью описать процесс v(t).
Но такое решение было бы не слишком приятным, и мы пред-
почтем обходной путь, который за счет комбинации уравне-
ний на правом и левом конце и некоторых других соображе-
ний позволит обойтись почти без вычислений.
Сначала найдем стационарное распределение для скоро-
сти. Имеем уравнение
° - - у (-awp(o)) + 4 Ti
do 2 do*
Интегрируя один раз, получим
—<wp(v) = p\v) 4- С.
&
По физическому смыслу скорость броуновской частицы в
стационарном режиме не должна принимать особенно
больших значений; это означает, что при v—► ±оо долж-
но быть vp(y)-*0 и р'(и)-+0. Но тогда С-О. Следова-
тельно,
р’(о) _
p(i>) а*
263
откуда p(v) « сехр J — — val, т. e. стационарное распреде-
I О* I
ление для v— нормальное с дисперсией а2/2а, откуда
с = [а ^к/а]
Поскольку для диффузионного процесса безразлично, ка-
ким принимать распределение вероятностей для £ (лишь бы
М£=0, М£2=о2Д0, примем это распределение нормальным.
Тогда условное распределение для скорости при любом на-
чальном условии v(0)=i> тоже нормальное (как для линей-
ного функционала от независимых гауссовских толчков).
Найдем его параметры.
Для однородного по времени марковского процесса
функция M(y(f)|a(0) = v} = g(t, v) удовлетворяет уравне-
Qg дс 1 л
НИЮ —= — CLV — 4- — о. С другой стороны, поскольку
случайные толчки £ не влияют на Мс^+Д/), можно пред-
положить, сохраняя только трение, что g(t, v)—ve~a'. Дей-
ствительно, эта функция удовлетворяет указанному урав-
нению.
Найдем теперь ковариацию N\v(0)v(t), считая распреде-
ление 1>(0) стационарным. Имеем
Mv(Q)v'J)= М M{r(O)f(0|v(O)}=Mt'(0)M|v(0|y(0))=
= Me(0)*p(0)e-a/ = е~ atNl [ i>(0)]2 = — e~al.
Если распределение о(0) стационарное, то распределение
v(t) также стационарное, и тогда коэффициент корреляции
г(0 = Гг(0), г(0 — €~at‘
Предположим теперь, что совместное распределение с(0)
и v(t) гауссовское (двумерное нормальное). Тогда условная
дисперсия v(t) при известном о(0) должна равняться
(l_r»(0)Da(t)=a2(l-e-2«')'.
Имеем соотношение
М (Ра(0|о (0) = v) = D(t-(0|v(0) = г) +
+ [ М(и(0Н0) = v)]a= ^(1-е-2»') -J- v2e~^‘.
264
Подставляя эту функцию в качестве g(t v) в уравнение, ви-
дим, что уравнение удовлетворяется. Так как удовлетворяет-
ся и граничное условие
M(ya(Z)|z/(0) = =
то мы нашли верное выражение для D{v(0 / v(0) = v}.
Но отсюда следует, что совместное распределение для
:’(0) и v(t) действительно гауссовское. В самом деле, совмест-
ное распределение однозначно определяется распределением
г'(0) и условным распределением v(t) при известном v(0). Но
эти распределения такие же, как у двумерного нормального
распределения.
Выпишем формулу для переходной плотности p(t, v, w):
это гауссовское распределение со средним ve~at и диспер-
сией — (1 — с--1'). Имеем формулу
2а
pit, v, w)=-----------------------ехр
а(и'—ие а<)*
С2(!_е-2^)
Видим, что даже подстановка такой плотности для про-
верки уравнения на правом конце представляет известные
трудности (чем н объясняется избранный нами обходной
путь).
Мы получили описание скорости броуновского движе-
ния в виде гауссовского стационарного процесса с кор-
О8
реляционной функцией — e~at, f>0. Соответствующая
2а
спектральная плотность /(>.) дается формулой
оо
/(}.)= 1 f е"х • - • e~aWdt = — (—— -+
' ’ 2r. J 2а 4«а а-»Х
—оо
1__\ _ а»
а + iX J г^а’+Х*)
Интеграл от скорости в пределах от 0 до Т имеет гауссов-
ское распределение примерно с дисперсией 2л/(0)Т=Го2/а2.
Поскольку стоксово трение а известно, по наблюдениям рас-
стояния, проходимого броуновской частицей за время Т, мож-
но узнать а2 — оценить интенсивность толчков, которые испы-
тывает броуновская частица со стороны молекул жидкости.
Замечание. В последнее время описанная модель броу-
новского движения подвергается сомнению с теоретической и
экспериментальной стороны. Утверждается, в частности, что
корреляция между значениями скорости броуновской части-
цы спадает медленнее, чем полагалось бы по: экспоненциаль-
265
ному закону exp (—at). Во всяком случае изложенное пред-
ставление о скорости броуновской частицы как о гауссовском
марковском стационарном процессе (так называемый про-
цесс Орнштейна—Уленбека) держалось в науке почти столь
же долго, как и представление о флогистоне. Насколько мог
выяснить автор данной книги, в настоящий момент речь идет
именно о сомнениях в модели процесса Орнштейна—Уленбе-
ка применительно к скорости реальной броуновской частицы,
но все-таки не о том, что эта модель окончательно отвергну-
та и заменена более правильной.
ЧАСТЬ ВТОРАЯ
-ПРИКЛАДНЫЕ АСПЕКТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
И ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
ПРЕДИСЛОВИЕ
ко второй части книги
Обе части книги в целом образуют единое учебное посо-
бие. так как нецелесообразно учиться теории вероятностей,
не составляя себе при этом какого-то представления о том,
как и зачем эта наука может применяться (и как не может).
Выделение прикладных аспектов в отдельную часть книги
связано прежде всего с тем, что здесь речь идет о некото-
ром более широком взгляде на роль и место теории вероят-
ностей в научном исследовании, в принятии тех или иных
технических решений, в общей системе культуры современно-
го общества и т. д.; словом, о некотором понимании предме-
та по существу. Математические методы теории вероятнос-
тей, рассматриваемые, в частности, в первой части данной
книги, составляют лишь некоторую необходимую, но не до-
статочную часть такого более широкого понимания.
Но это понимание теории вероятностей по существу (как,
впрочем, понимание по существу и любой другой теоретичес-
кой науки) — как вещь трудная, глубокая и тонкая — никак
не может быть подвергнуто архаической и варварской про-
цедуре экзамена, граничащей если не прямо с пытками инк-
визиции, то во всяком случае с допросом той же инквизиции;
процедуре, ориентирующей не на широкое понимание пред-
мета, а лишь на рабское повторение заученного путем наси-
лия над памятью. Нельзя, впрочем, отрицать, что результа-
ты. показываемые на экзаменах, находятся в тесной корре-
ляционной связи и с творческими способностями личности.
Кроме того, сложившиеся в обществе нормы социальной жиз-
ни (имеется в виду обычай подвергать студентов экзаменам)
не могут быть произвольно изменены. Но конечно, предметом
экзамена могут быть лишь технические навыки: «как из фор-
мулы А следует формула В»; на экзамене нельзя поставить
вопрос о том, как воспользоваться формулами А, В, С и т.д.
в их взаимосвязи для ответа на некоторый существенно но-
267
вый вопрос. Для удобства учащегося эти технические навы-
ки и выделены в первую часть книги.
Кроме того, если уж говорить о прикладных аспектах, то
любая теоретическая наука применяется как некоторая бо-
лее или менее целостная идеология, т. е. не мелкими частя-
ми в виде отдельных формул или теорем, но частями круп-
ными, например может использоваться все «учение» о незави-
симых случайных величинах, включающее центральную пре-
дельную теорему. С чисто математической стороной такого
учения — как с вещью сравнительно очень простой — весь-
ма целесообразно познакомиться отдельно и заранее.
Если форма изложения чисто математических вопросов
усилиями поколений преподавателей и авторов учебников в
достаточной степени выверена и различия между существую-
щими текстами сравнительно второстепенны, то вопрос о
том, в какой форме следует передавать учащемуся то более
широкое понимание, о котором шла речь выше, абсолютно
не разработан (настолько, что многие современные учебни-
ки теории вероятностей такой задачи перед собой и не ста-
вят). На тему применений математики вообще и теории ве-
роятностей в частности можно, конечно, теоретизировать; од-
нако, по крайней мере у автора настоящей книги, такие по-
пытки выходят скучными. Так и в средние века прихожане
во время проповедей, наполненных теологическими тонкостя-
ми, ужасно страдали от скуки; однако аудитория дружно про-
сыпалась, как только проповедник приводил какой-нибудь
«пример» о том, как черти таскали душу некоего грешника в
ад и что он там видел. Существовал особый жанр литерату-
ры — сборники примеров (exempla) для использования в
проповедях. В сущности говоря, в этом жанре и написана
вторая часть данной книги.
Точнее говоря, используется древняя форма нравоучитель-
ного сочинения: сначала сообщается некий факт, а затгм
формулируются (если нужно) общие выводы, в каком-то
смысле вытекающие из этого факта. Факты сообщаются, ко-
нечно, верные и документированные так, как это принято в
научной литературе нашего времени (не так, как это делали
авторы exempla, хотя можно предположить, что углубленный
психологический анализ, в частности, на уровне бессозна-
тельного выявил бы немало сходства между тем и другим
способом документирования). Но обобщение фактов как в
средние века, так и сейчас — дело, достаточно субъектив-
ное. (Уже поэтому содержание второй части данной книги
не может быть предметом экзамена). Обобщение опыта при-
менений теории вероятностей представляет собой вещь, быст-
ро и радикально изменяющуюся на протяжении истории нау-
ки (при удивительной стабильности математического аппа-
268
рата). Понятно, что в этом смысле и данная книга не претен-
дует на окончательную точку зрения.
ГЛАВА 1
ЭЛЕМЕНТАРНЫЕ ПРИМЕНЕНИЯ ЭЛЕМЕНТАРНОЙ
ТЕОРИИ ВЕРОЯТНОСТЕЙ
Элементарные применения интеллектуально малопривле-
кательны; нельзя отрицать, однако, что чем элементарнее ма-
тематическая (да и любая) наука, тем чаще и шире она ис-
пользуется обществом. Четыре действия арифметики нужны
всем; извлечение корней и логарифмы — уже сравнительно
немногим; формулой же интегрирования по частям вряд ли
владеет каждый инженер не потому, что у него не хватает
для этого ума (интегрировать по частям гораздо проще, чем,
скажем, закрыть наряды), а потому, что это ему не нужно.
В этой главе делается попытка рассказать о такой теории ве-
роятностей, которая нужна всем примерно как арифметика.
§ 1. Нужно ли заземлять крест?
В наше время реставрируются многие церкви; имеет мес-
то, очевидно, изменение в отношении общества к религии, и
в частности к культовым зданиям. Автору данной книги не
приходилось видеть, чтобы при реставрации церкви в сельс-
кой местности производилось заземление крестов и других
высокорасположенных частей здания с целью грозозащиты.
(Такое заземление представляет собой довольно толстую
проволоку, соединяющую молниеприемник, т. е. попросту
металлический стержень, установленный на крыше здания,
с контуром заземления, который закапывается в землю. Эту
проволоку проще всего прокладывать по наружным стенам
здания, а тогда она должна быть хорошо заметной.) Посмот-
рим, что говорят по поводу грозозащиты современные пра-
вила. Берем для этого брошюру В. Н. Черкасова [45].
Прежде всего число ударов молнии в год в незащищен-
ную колокольню есть, конечно, случайная величина, подчи-
ненная закону Пуассона, и вопрос состоит в том, чтобы оце-
нить его параметр — математическое ожидание, или среднее
значение. Изложение у Б. Н. Черкасова несколько запутано
и содержит опечатки, но смысл состоит в следующем. На ши-
роте Москвы среднее число ударов молнии в год на 1 км2
земной поверхности составляет от 3 до 9 (примем среднее
значение 6). Для оценки среднего числа ударов молнии в
здание нужно взять территорию, контур которой удален от
контура основания здания на три его высоты, и сосчитать
269
среднее число ударов молнии в эту площадь. Например, есл»
высота колокольни 33 м, то в круг радиусом /?=100 м =
=0,1 км в среднем приходится
л=л/?2 • 6=0,18
удара молнии в год, и это есть искомый параметр закона
Пуассона. Таковы принятые официальные правила.
С точки зрения количественного соответствия рассчитан-
ного параметра закона Пуассона и фактической опасности
поражения молнией результат получился совершенно фан-
тастический: 0,18 удара молнии в год означает, что вероят-
ность поражения колокольни за 6 лет составит
1—ехр(—0,18 • 6) «2/з,
т. е. 2/з колоколен должны простоять не более 6 лет. Очевид-
но, что поражения молнией фактически бывают несравнен-
но реже. Можно указать и вероятную причину несоответст-
вия: откуда взялось правило о том, что от контура здания
нужно отступить на три его высоты? По-видимому, из модель-
ных опытов с высоковольтными электрическими разрядами, в
которых было выяснено, что если в отсутствие здания точка
поражения молнией находится за пределами указанного кон-
тура, то при наличии здания его поражения никогда не про-
исходит. Словом, тройная высота дана, очевидно, с большим
запасом. Если тройную высоту заменить на одинарную, то
параметр закона Пуассона уменьшится в 9 раз, что уже бо-
лее реалистично.
(Крайне интересно было бы собрать архивные материалы
по ударам молнии в отдельно стоящие, в частности, церков-
ные здания и таким образом оценить реальную опасность
поражения.)
Но одно дело — расчет вероятности поражения молни-
ей, а другое дело — принятие технического решения: зазем-
лять или не заземлять крест. Какая вероятность поражения
молнией представляется нам настолько малой, что при этой
вероятности заземление креста излишне? Допустим, что офи-
циальные рекомендации на два порядка (т. е. в 100 раз) за-
вышают вероятность поражения, а фактически она составля-
ет 0,18 • 0,01 ~0,002, т. е. один раз в пятьсот лет. Следует ли
из этого, что крест заземлять не нужно?
Вряд ли, так как расходы на заземление, к счастью, край-
не незначительны в сравнении с общей стоимостью здания, в
то время как эти расходы должны быть сопоставлены с воз-
можностью гибели невоспроизводимых ценностей и даже лю-
дей, которые могут находиться в здании во время грозы.
Если уж положено заземлять силосные башни и водонапор-
270
ные вышки, то, наверное, следует таким же образом защи-
щать и церковные здания.
Любопытно посмотреть, с каким клубком проблем мы-
сталкиваемся при попытке решения, казалось бы, простого
техническрго вопроса. Официальная оценка опасности пора-
жения молнией очевидно и грубо неверна. Можем ли мы бо-
лее правильно оценить эту опасность? Более или менее на-
дежно установлены средние цифры — число ударов молнии
в год на 1 км2 земной поверхности. Если бы все точки этой
поверхности ничем не отличались друг от друга, то распре-
деление точек поражения молнией было бы равномерным по
площади. Но ведь церкви ставятся не в наудачу выбранных
точках: они стоят на красивых возвышенных местах, чтобы
быть видными издалека. На возвышенностях вероятность по-
ражения молнией должна быть выше, но на сколько имен-
но? В модельных опытах с высоковольтными разрядами до-
статочно трудно учесть уже рельеф местности. Но учета рель-
ефа местности мало: не мешает смоделировать также электри-
ческую проводимость почвы, которая различна в различных
местах и толком никому не известна. Опять-таки электричес-
кие поля в атмосфере зависят от пространственного распре-
деления зарядов в грозовых облаках, которое нет уже совсем
никакой возможности смоделировать сколько-нибудь пра-
вильно, особенно в его динамике. Короче говоря, сколько-ни-
будь точно оценить вероятность поражения молнией мы не в
состоянии.
С другой стороны, как только что было показано, если бы
мы точно знали эту вероятность, мы бы не знали, как ее ис-
пользовать, ибо речь идет о сопоставлении материальных
затрат с вещами, которые в виде затрат не выражаются.
Наконец, третья проблема состоит в том, что устройство
заземления — это не только материальные затраты. С ред-
кими событиями типа удара молнии связана масса предста-
влений, которые являются грубыми суевериями не только с
точки зрения той идеологии, которую мы называем наукой,
но и с точки зрения современной религии. Мысль о том, что
молния не станет поражать божий дом на равных правах с
водокачкой и силосной башней, нельзя и в наше время на-
звать полностью чуждой народному сознанию. Между тем
когда мы строим храм, мы ведь устраиваем над ним крышу,
так как совершенно не рассчитываем на то, что над храмом
не будет выпадать дождь или снег. Удар молнии — такое же
погодное явление, как дождь или снег, только редкое. Точка
полезного приложения идеологии теории вероятностей в дан-
ном вопросе как раз и состоит в преодолении суеверий, свя-
занных с редкостью события. Небезынтересно было бы и на-
звать более близкую к действительности (чем официальный
расчет) оценку вероятности поражения молнией. Вероятност-
271
ная идеология указывает и средство для достижения обеих
этих целей — статистическую обработку архивных данных о
поражении молнией. Такие обработки, конечно, проводились
в давние времена, когда решался вопрос о целесообразнос-
ти грозозащиты. Но при этом вряд ли обращалось достаточ-
ное внимание на проверку разного рода статистических од-
нородностей (либо исследование отклонений от однороднос-
ти). Верно ли, например, что вероятность поражения молни-
ей отдельно стоящего здания пропорциональна квадрату его
высоты? (Точнее говоря, той площади, о которой идет речь
в правилах грозозащиты). Может быть на местности имеют-
ся точки, «излюбленные» молниями и поражаемые сравни-
тельно часто, так что опасность поражения определяется не
столько размерами здания, сколько его положением на мест-
ности?
Статистическая обработка фактических данных, которая
ответила бы на подобные вопросы, вполне возможна, но она,
конечно, выходит за рамки массового применения теории ве-
роятностей на уровне четырех действий арифметики.
§ 2. Вероятностный дьявол
В старых учебниках физики рассказывается, что Уатт,
устанавливая единицу мощности паровой машины — лошади-
ную силу, на всякий случай ввел коэффициент 1,5, т. е. ло-
шадиная сила мощности паровой машины отвечает полутора
средним лошадям. Иными словами, в киловаттах (1 кВт=
= 1,4 л. с.) мощность лошади примерно 0,5 кВт, что при
массе лошади 500 кг (объем 0,5 м3) дает концентрацию мощ-
ности примерно 1 кВт в 1 м3. Уже такая концентрация мощ-
ности представляет определенную опасность для человека:
например, в задачнике Л. Д. Мешалкина [27, с. 127] можно
найти данные о числе военнослужащих, убитых ударом ко-
пыта в прусских армейских корпусах (эти данные прекрас-
но согласуются с законом Пуассона).
Элементарный подсчет показывает, что концентрация
мощности в костре в 1000 раз больше: примерно 1 кВт в 1 дм3.
Такова же концентрация мощности в электромоторе, в дви-
гателе внутреннего сгорания, в ядерном реакторе РБМК и
т. д.
Еще большие концентрации мощности создаются в спе-
циальных устройствах, применяемых не особенно широко.
Например, в электрической сварочной дуге (если учитывать
только дугу, но не сварочный трансформатор) выделяется
примерно 1 кВт в 1 см3; столько же выделяется и в свароч-
ном пламени кислородно-ацетиленовой горелки (если учиты-
вать только зону сварки, но не весь газовый факел).
272
Таким образом, основные технические устройства имеют
примерно такую же концентрацию мощности, как и древний
костер, и эта концентрация примерно в 1000 раз выше, чем
в живых существах. Понятно, что необходимы какие-то прис-
пособления, которые удерживали бы мощность такой степе-
ни концентрации в заданных границах. Древнейшим таким
устройством является очаг, обложенный по краям камнями.
Такой очаг согревал жилище наших древних предков. Кам-
ни— высокоэффективная защита от пожара, но, конечно, не
абсолютная. Могли загореться расположенные рядом с оча-
гом запасы топлива, одежды, утварь и т. д.
Каков вероятностный взгляд на возможность выхода энер-
гии из-под контроля? Пусть имеется п однотипных устройств,
для каждого из которых вероятность аварии за определен-
ный период времени есть р, и пусть эти устройства статис-
тически независимы. Тогда (при большом п и малом р) об-
щее количество аварий имеет распределение Пуассона с па-
раметром к=пр. С развитием техники энерговооруженность
растет, что в модели изображается соотношением п->-оо, если
при этом р>0 остается фиксированным, то Х->-оо, а так как
фактическое число аварий может отличаться от £воего мате-
матического ожидания X на величину порядка VX, то факти-
ческое число аварий обязано расти. Чтобы удержать его в
каких-то приемлемых границах, общество должно позабо-
титься о том, чтобы с ростом п уменьшалось р, но этого не
просто добиться.
Наши древние предки, конечно, считали пожар в своем
жилище делом злого духа. Более современная форма этого
суеверия состоит в вере во «вредительство», в «разгильдяйст-
во» и т. д. Но вот оказывается, что и без всякого злого умыс-
ла, без преступной небрежности (хотя все это, конечно, мо-
жет иметь место и чрезвычайно осложнить ситуацию), а по
чисто вероятностным соображениям аварии практически неиз-
бежны, если эксплуатируется очень большое число устройств,
каждое из которых не абсолютно надежно. Если угодно, это
вероятностный дьявол, потому что практически безразлично,
сказать ли, что в каждом электромоторе сидит черт, который
стремится вырваться наружу и натворить бед, или сказать,
что электромоторов много и каждый из них не абсолютно на-
дежен.
Если наши древние предки должны были отстаивать се-
бя от нападений хищных зверей, то эпоха развития техники
есть и эпоха технических катастроф, эпоха тяжелейшей борь-
бы с вероятностным дьяволом. О деталях этой борьбы не
очень принято говорить (как и о смерти, потому, что именно
об этом, в сущности, идет речь). Но при вероятностном
взгляде на вещи становится совершенно ясным, что массово-
го потребителя никто и ничто не может достаточно надежно
18—2567 273
защитить, кроме него самого. Поэтому представляется необ-
ходимым показать на конкретных примерах, каков на самом
деле накал борьбы в той области, которая скромно называ-
ется «техникой безопасности»; какой ценой достигается то
видимое благополучие, которым (почти всегда) пользуется
широкий потребитель и каким непрочным оно может ока-
заться. Хоть во многом знании и многая скорбь, но зато в
непредвиденной ситуации знающий может иметь огромное
преимущество перед незнающим.
Итак, рассмотрим вкратце вопросы электробезопасности.
Вопрос о технической осуществимости вполне безопасных
электрических машин должен быть после недолгого размыш-
ления снят. Например, обмотки электродвигателей, транс-
форматоров, реле и т. д. наматываются проводом, покрытым,
слоем эмали толщиной порядка 0,01 мм. Это так называе-
мая витковая изоляция. Между прикасающимися друг к дру-
гу витками обмотки напряжение очень мало, и такой изоля-
ции, вообще говоря, достаточно: лишь бы не было касания
металла с металлом. Существует еще главная изоляция, ко-
торая всю обмотку в целом отделяет от остальных частей
машины: эта изоляция гораздо толще, она и защищает, в
частности, потребителя. Витковая изоляция может быть лег-
ко повреждена (в частности, механически при намотке об-
мотки, под влиянием нагрева обмотки в работе и 7. д.).
Если металлический контакт двух соседних витков все-таки
образуется, то возникает так называемый короткозамкнутый
виток, представляющий собой колечко небольшой длины, а
следовательно, малого сопротивления. Переменное магнитное
поле машины создаст в этом колечке большой ток, который
течет только в короткозамкнутом витке: об этом токе ниче-
го не знает электрическая защита машины в целом. Виток
нагревается и либо расплавляется (тогда всего лишь маши-
на выходит из строя), либо, до расплавления, прожигает
главную изоляцию. В последнем случае на корпусе машины
появляется напряжение.
По-видимому, бывают случаи, когда пробой главной изо-
ляции может не обязательно начаться с виткового замыка-
ния, даже если эта изоляция не была дефектной после сбор-
ки машины. Короче говоря, выход напряжения на корпус
электрической машины есть вещь вполне реальная. Конеч-
но, теперь не бывает саблезубого тигра, но нечто похожее
может войти в наше жилище под видом пылесоса, стираль-
ной машины, электрического чайника и даже электробрит-
вы. Что будет дальше? Дадим краткое переложение учебни-
ка П. А. Долина [18].
Для человека опасно не непосредственно напряжение, под
которым он может оказаться, а проходящий через тело ток.
Для переменного тока 50 Гц опасный для жизни предел на-
274
ходится где-то в области от 0,05 до 0,1 А. Чтобы рассчитать
возможный ток, нужно разделить приложенное напряжение
(в нашем случае, скажем, 220 В) на сопротивление тела че-
ловека; последнее же широко варьирует. Наиболее тяжелое
обстоятельство состоит в том, что сопротивление тела чело-
века резко падает при возрастании приложенного напряже-
ния (происходит пробой основного диэлектрического барье-
ра — рогового слоя кожи), поэтому измерить его в диапазо-
не безопасных напряжений нельзя. Мало могут помочь и
опыты на животных, так как животные, в том числе круп-
ные, оказывается, гораздо легче поражаются электрическим
током, чем человек. (Интересно отметить, что на крупных
фермах — во избежание массовой гибели животных — офи-
циально предусматриваются столь сложные и дорогостоящие
меры электрической защиты, что они не применяются для
защиты людей ни в жилых, ни в промышленных зданиях.)
Опыты над трупами людей не вполне убедительны.
Короче говоря, американские ученые решились на ужас-
ную методику — измерения во время казней на электричес-
ком стуле (результаты опубликованы в 1922 г.). Цитируем
учебник П. А. Долина [18, с. 30]: «Так, во время одной каз-
ни при напряжении в несколько вольт сопротивление состав-
ляло 40 кОм, при НОВ — 10 кОм и, наконец, при 2000В —
200 Ом».
В нашей стране ориентировочное значение сопротивления
тела человека принято равным 1000 Ом. Конечно, при опре-
делении силы тока в расчет должно быть принято не толь-
ко сопротивление тела человека, но и сопротивление всей це-
пи, по которой проходит ток. Система энергоснабжения во
всем мире принята трехфазная, но для бытовых нужд ис-
пользуется почти исключительно однофазный ток. Это озна-
чает, что в каждую квартиру вводятся два совершенно оди-
наковых на вид, но принципиально различных по сути прово-
да — фазный и нулевой. Фазный провод соединен с одной из
фаз трехфазной системы, а нулевой провод (нейтраль) сое-
динен, во-первых, с нейтральной точкой трехфазного транс-
форматора, а во-вторых, многократно и возможно более на-
дежно — с землей. Прикосновение к нулевому проводу (при
нормальном режиме работы сети) безопасно, а при прикос-
новении к фазному проводу электрическая цепь замыкается
через обувь человека, опору, на которой стоит человек, на
землю, нулевой провод и, наконец, на нейтральную точку
трансформатора. Поэтому если человек стоит на сухом дере-
вянном полу (сопротивление которого составляет сотни мега-
ом), то прикосновение к фазному проводу тоже безопасно.
Одновременное прикосновение к фазному и нулевому про-
воду означает, что в расчет нужно принимать только сопро-
тивление тела человека. Такое прикосновение может вести к
18* 275
разным последствиям — от легкой встряски, если цепь замы-
кается через пальцы одной руки, до остановки сердца и/или
дыхания, если цепь замыкается через две руки или через ру-
ку и ногу.
Случай одновременного прикосновения к двум проводам в
науке об электробезопасности не рассматривается: считается,
что потребитель должен уберечь себя сам от такого прикос-
новения.
Итак, если фазное напряжение 220 В выходит на металли-
ческие части электробритвы, а человек, который ею в это вре-
мя бреется, стоит в жилой комнате на деревянном (или пок-
рытом линолеумом) полу, то не происходит ничего. Некото-
рые люди при этом имеют едва заметное ощущение вибрации,
другие не чувствуют ничего, следовательно, вообще не знают,
что оказались под напряжением. Положение резко меняется,
если бритье происходит в ванной комнате, а человек, допус-
тим, рукой взялся за водопроводный кран или присел на край
ванны (ванна соединена с водопроводом через специальную
проволоку — уравниватель электрических потенциалов). Цепь
замыкается через водопровод, имеющий практически нулевое
сопротивление, на землю и на нейтраль. Сопротивление цепи
сводится к сопротивлению тела человека. Ориентировочное
значение тока 220 В/1000 Ом = 0,2 А. Ситуация становится
смертельно опасной. А связано это с режимом нейтрали:
нейтраль могла бы быть изолированной от земли (это не оз-
начает дополнительных затрат, а, наоборот, некоторую не-
большую экономию за счет отсутствия заземляющих уст-
ройств). Почему же выбрано такое техническое решение, при
котором нейтраль заземляется? Ответ: по соображениям
борьбы с вероятностным дьяволом.
Дело в том, что в больших и разветвленных сетях с изо-
лированной нейтралью вполне возможно случайное соедине-
ние одной из фаз с водопроводом, металлическими конструк-
циями и т. д., вообще говоря, с землей. Электрические аппа-
раты защиты на такое соединение никак не реагируют, пото-
му что при изолированной нейтрали никаких токов через зем-
лю нет. В то же время потребители привыкают к мысли, что
прикосновение к любому (одному) проводу всегда безопасно.
Но если с землей соединилась одна фаза, а потребитель
(стоя на земле или на чем-то металлическом, соединенном с
землей) прикасается к другой фазе, то он оказывается под
напряжением и притом не фазным, а междуфазным (т. е. не
220 В, а 380 В). Поэтому в бытовых электрических сетях ней-
траль, как говорят, «глухо» (т. е. возможно более надежно)
заземляется, чтобы при соединении одной из фаз с землей
создался большой ток, который вызывает срабатывание элек-
трической защиты. Зато одновременное прикосновение к фаз-
ному проводу и каким-то металлическим конструкциям, сое-
276
диненным с землей, становится столь же опасным, как при-
косновение к двум проводам — фазному и нулевому. Выри-
совывается, конечно, вероятностная задача: что хуже (т. е.
изолированная нейтраль или заземленная)? К сожалению, в
этой задаче невозможны ни теоретические оценки соответст-
вующих вероятностей, ни сбор статистических данных (кто
же решится изменить однажды принятый режим нейтрали
ради сбора статистики?!). Интуитивно кажется, что заземле-
ние нейтрали —правильная мера, но, конечно, несущая свои
опасности.
Что делается для повышения электробезопасности? В от-
ношении бытовых сетей основные меры следующие: 1) двой-
ная изоляция; 2) зануление корпусов электрооборудования;
3) разделяющие трансформаторы и, наконец, в будущем —
4) защитное отключение.
Двойная изоляция применяется в основном для электро-
двигателей (обмотка которых в любой момент может про-
биться на корпус). Она состоит в том, что корпус двигателя
дополнительно изолируется от корпуса и рабочих частей ка-
кой-то бытовой машины достаточно толстыми изоляционны-
ми прокладками (тут уже никаких тонких эмалевых слоев
нет). Для характеристики этой меры приводится следующее
личное наблюдение автора.
Получено известие: «кусается» стиральная машина ЗВИ
(очень старого выпуска примерно 1960 г.; к более новым ма-
шинам ЗВИ все дальнейшее не относится: по крайней мере,
по внешнему виду монтажа они выполнены лучше). Посколь-
ку стирка происходит в ванной комнате, это грозный сигнал;
поэтому производится тщательное расследование. Оно как
обычно не приносит ничего, и приходится переходить к опы-
там. Включаю все, что можно включить в машине, и измеряю
вольтметром напряжение между корпусом и водопроводом.
На вольтметре нуль. Прикасаюсь одной рукой к корпусу ма-
шины и металлической оболочке душевого шланга — ничего.
Осмелев, пробую то же разными руками — опять ничего.
Переворачиваю машину вверх колесами и осматриваю мон-
таж. Двойная изоляция на месте: все моторы стоят на тол-
стых текстолитовых основаниях, но... все контакты выполнены
открытыми, как будто внутрь машины никогда не может по-
пасть вода. Однако никаких следов перекрытия изоляции не
вижу. Произношу по адресу разработчиков машины и всего
коллектива завода имени Владимира Ильича древнюю рус-
скую формулу, выражающую моральное осуждение, но по су-
ществу сделать ничего не могу. «Мастера» вызывать в таких
случаях вполне бесполезно: в таком монтаже перекрытие
изоляции от попадания воды могло быть где угодно, но его
не найдешь. Кроме того, испытываю принципиальное недове-
рие к «мастерам». Решаю заземлить корпус машины, т. е.
277
соединить его с водопроводной трубой. В случае чего эта ме-
ра либо вызовет срабатывание защиты на квартирном щит-
ке, либо по меньшей мере выровняет почти полностью элек-
трические потенциалы между водопроводом и корпусом ма-
шины. Для этого один конец провода завинчиваю под болт
на корпусе машины, а другой прижимаю латунным хомути-
ком к зачищенной трубе водопровода (паять трубу, запол-
ненную водой, бесполезно — ее не удастся нагреть настолько,
чтобы пристал припой). Объясняю домашним, что этот про-
вод обрывать ни в коем случае нельзя: на нем и только на нем
покоится единственная надежда на избавление от смерти.
Проверяю омметром сопротивление между различными точка-
ми машины и водопровода: омметр показывает значение, ра-
зумно близкое к нулю, и на том успокаиваюсь. После этого
много лет стираем без каких-либо происшествий. Наконец, со-
бытие: неизвестно где внутри машины проскочили искры и сра-
ботал автомат на квартирном щитке. После долгих поисков
нахожу: выгорел кусочек пластмассы на корпусе блокировоч-
ного выключателя крышки центрифуги (контактный винт рас-
положен слишком близко к корпусу машины). Предположи-
тельный диагноз: хроническое перекрытие изоляции из-за по-
падания воды с выходом напряжения на корпус. Оно долгое
время не давало знать о себе из-за уравнивания потенциалов
с водопроводом (без заземления корпуса оно было бы край-
не опасным). Наконец, из-за прохождения тока через корпус
машины и заземление пластмасса в месте перекрытия изоля-
ции обуглилась, и тогда возникла дуга, оставившая заметный
след, который потом удалось найти. В момент появления дуги
сработал автомат. Ну что же, выдираю с мясом блокировоч-
ный выключатель крышки центрифуги (его роль в том, чтобы
не дать включить центрифугу при открытой крышке, но без
этой блокировки вполне можно обойтись), а заземление кор-
пуса оставляю. Позже мы рассмотрим вероятностный смысл
подобной самодеятельности потребителя, вынуждаемого к
ней обстоятельствами. Пока же запомним, как выглядит на
практике такая теоретически превосходная защитная мера,
как двойная изоляция. (Разумеется, без этой меры стираль-
ная машина была бы столь опасной, что ее просто нельзя
было бы использовать; однако и с двойной изоляцией воз-
можны пренеприятные происшествия.)
Теперь рассмотрим разделяющий трансформатор. Двой-
ную изоляцию имеет и электробритва. Но, видимо, с бритва-
ми неоднократно происходили тяжелые аварии. Поэтому ре-
шено было обуздать именно электробритву. В новых квар-
тирах в ванной комнате устанавливается розетка, питающая-
ся от разделяющего трансформатора (этот прибор превраща-
ет заземленную нейтраль в изолированную, но только в пре-
делах ванной комнаты данной квартиры). Жильцы обычно
278
не знают, что в эту розетку можно включать только бритву
и ничего более: трансформатор установлен крайне маломощ-
ный, защищенный предохранителем примерно на 0,1 А. Как
только хозяйка включает в эту розетку стиральную машину,
предохранитель мгновенно перегорает, и далеко не все могут
его сменить. Интересно было бы провести статистическое ис-
следование (хоть в виде анкеты) — какая часть разделяю-
щих трансформаторов действительно используется?
Занулению корпуса подлежат бытовые приборы мощ-
ностью более 1,3 кВт, не имеющие двойной изоляции. Реаль-
но это электрические плиты. Зануление состоит в том, что
корпус прибора специальным проводом (в котором не долж-
но быть ни выключателей, ни предохранителей) соединяется
с нулевым проводом сети. (Это лучше, чем соединение корпу-
са с водопроводом). Но в быту применяется большое коли-
чество чайников, самоваров, кипятильников, утюгов и других
нагревательных приборов, которые не имеют ни зануления
корпуса, ни двойной изоляции. В некоторых электроплитах
даже сделана специальная розетка для подключения подоб-
ных приборов. Во всех этих приборах напряжение довольно
часто выходит на корпус. Создается опасная (и запрещенная
всеми правилами устройства электроустановок) ситуация,
когда в одном помещении (да и просто рядом) находятся
приборы с зануленными и незануленными корпусами. Теоре-
тически массовый потребитель в быту считается технически
безграмотным, ничего не понимающим в устройстве электри-
ческих сетей (кроме того, что нельзя одновременно браться
за два провода). Заботу о его безопасности (в теории) берут
на себя государственные организации. А на деле эти органи-
зации упорно не видят, что зануление корпуса электроплиты
создает в массовых масштабах потенциально опасную ситуа-
цию. Не видят они этого потому, что из этой ситуации нет
технически удобного выхода: с одной стороны, корпус элек-
троплиты нельзя оставить без зануления, а с другой стороны,
нельзя и запретить пользоваться в кухне (рядом с электро-
плитой) нагревательными приборами, не имеющими зануле-
ния корпуса. Каждый потребитель должен по меньшей мере
понимать опасность сложившейся ситуации.
Кроме того, зануление корпуса электроплиты устроено так,
что сначала замыкается зануляющий контакт, а потом —
рабочие. Плиту нельзя включить, не включив зануления кор-
пуса. Между тем, при всевозможных ремонтах часто бывает
нужно включить плиту при открытом монтаже. Если при этом
включить и зануление корпуса, то как потребитель, занима-
ющийся ремонтом самостоятельно, так и профессиональный
электрик будут рисковать во много раз больше. В общем-то
нужно иметь приспособление, позволяющее включать плиту,
279
не включая зануление корпуса; однако потребитель должен
понимать, как и когда пользоваться этим приспособлением.
Наконец, скажем несколько слов о защитном отключении.
Использование электроники позволяет контролировать элек-
трическую сеть по многим параметрам. Например, при нор-
мальной работе сети сумма токов в фазном и нулевом про-
воде равна нулю. Если же это правило нарушено, то возмож-
но, что человек одновременно прикоснулся к фазному прово-
ду и к земле (ток, минуя нулевой провод, проходит через зем-
лю). Нетрудно создать электронную схему, которая при воз-
никновении рассогласования между токами в фазном и нуле-
вом проводе выключала бы напряжение, в чем и состоит идея
защитного отключения (это одна из многих возможных схем).
Но тут дело в том, что все наши рассуждения с токами верны
для переменного тока лишь приближенно. На самом деле,
бытовые приборы имеют так называемые токи утечки (ток в
фазном и нулевом проводе может отличаться на единицы мил-
лиампер). Опасными для человека являются токи в десятки
миллиампер. Может быть, между нормальными токами утеч-
ки и токами, свидетельствующими об опасности для челове-
ка, и есть какой-нибудь интервал, в котором можно распо-
ложить пороги срабатывания средств защитного отключения,
но во всяком случае опасность ложных срабатываний велика.
А ложные срабатывания приведут к тому, что потребители
станут выводить из строя устройства защитного отключения
либо заниматься иной самодеятельностью, которую невоз-
можно предвидеть заранее. Перспективы применения защит-
ного отключения неясны.
Суммируем изложенные факты. Проблема электробезо-
пасности (даже в быту, не говоря о промышленности) пол-
ностью не решена. Предлагаемые массовые технические ре-
шения иногда находятся в нелепом логическом противоречии
между собой (как, например, разделяющий трансформатор
только лишь для электробритвы в ванной комнате и зануле-
ние корпуса электроплиты в кухне). Совершенно ясно, что
такая концепция электробезопасности, при которой потреби-
тель должен лишь пунктуально выполнять правила пользо-
вания электроприборами, не понимая их смысла, нежизнен-
на. Какое правило, например, спасет потребителя, у которо-
го рядом с электроплитой стоит чайник с пробитой изоляци-
ей? (Потребитель ведь не должен непрерывно измерять соп-
ротивление изоляции и узнает о том, что изоляция пробита,
лишь тогда, когда будет поздно).
Какова здесь может быть роль теории вероятностей? К
сожалению, в наиболее принципиальных вопросах (типа,
например, выбора режима нейтрали — заземленная или изо-
лированная) оценка вероятностных характеристик безопас-
ности невозможна из-за принципиальной недопустимости экс-
280
периментирования с целью сбора статистических данных. В
более частных вопросах статистические исследования вполне
возможны. Почему бы не узнать, например, какая доля элек-
трических чайников или утюгов, эксплуатируемых в быту,
имеет на самом деле выход напряжения на корпус. Если бу-
дут статистические данные, необходимо будет и использовать
теоремы теории вероятностей (в городе А доля Л] всех чайни-
ков имеет повреждение изоляции; в городе Б — доля Л2; про-
верить гипотезу о том, что соответствующие вероятности на
самом деле равны, а различие между h\ и h2 объясняется
чисто случайными причинами). Но проведение статистичес-
ких исследований требует, как всякая научная работа, созда-
ния организации, специализации и т. д. и не может иметь
столь массового характера, как использование элементарной
арифметики. Посмотрим, каким, например, может быть мас-
совое использование вышеприведенного «учения» о вероят-
ностном дьяволе, в котором из математической науки содер-
жится всего лишь теорема Пуассона: к=пр, и если мы хо-
тим, чтобы «-*«>, нужно позаботиться о том, чтобы р—0.
Представим себе, что мы обучаем электрика. Электрик дол-
жен, во-первых, уметь позаботиться о собственной безопас-
ности, а во-вторых, добросовестно делать свою работу, чтобы
не снижать чрезмерно безопасность других. И вот мы говорим
ему следующее: «Человеческая жизнь сейчас устроена так,
что мы ездим на черте, обогреваемся и освещаемся — чер-
том, еду себе готовим — на черте, вечером смотрим телеви-
зор — при помощи черта, наконец, бреемся и то чертом.
Черт чрезвычайно редко выходит из-под нашего контроля,
поэтому каждый отдельный человек с ним, может быть, ни
разу не столкнется за всю жизнь. Но электрик — это вроде
экзорциста в средние века (монаха, который занимался из-
гнанием чертей из одержимых). Ему все время приходится
иметь дело с чертями. Заметь, что конкретные проявления
черта в электричестве крайне разнообразны, каждое отдель-
ное из них мало вероятно, а с какими из них придется столк-
нуться данному конкретному электрику, заранее совершенно
неизвестно. Маловероятные события обладают тем свойст-
вом, что личный опыт каждого человека против них почти
бессилен. Только коллективный опыт общества в целом мо-
жет дать что-то существенное. Потому люби и чти прекрас-
ную книгу, которая называется «Основы техники безопаснос-
ти». В ней худо ли, хорошо ли, но этот коллективный опыт
суммирован. Изучай эту книгу: она научит тебя видеть и от-
ражать черта на дальних подступах, когда он еще только
чуть-чуть высунул свои рожки. А кроме того, когда ты при-
соединяешь провод зануления, не ленись как следует завора-
чивать гайки. Если ты поленишься сменить гайку, на которой,
как ты заметил, при заворачивании сорвалась резьба, то
281
никто этого и не узнает, потому что узнать это можно толь-
ко в том случае, если всю работу за тебя переделать зано-
во. Но к в законе Пуассона для числа несчастных случаев
при этом увеличится в несколько раз. Мы не знаем и скорее
всего никогда не узнаем, чему именно равно это X, но допус-
тим, для примера, что Х=1, а ты сделал Х=5. Погибнет пять
человек; одного из них убил черт, а четверых — ты своей
гайкой».
Между прочим действительно интересно отметить, сколь
велика и практически бесконтрольна власть над потребите-
лем того человека, который делает какую-то работу, ну хотя
бы заворачивает гайки. Нет технически удобных приемов
контроля этой работы. Можно только обращаться к совести
работающего. Но и здесь мотивация должна быть вероятнос-
тной: как правило, гайка с частично сорванной резьбой удов-
летворительно справляется со своей задачей, увеличивается
лишь вероятность какой-то аварии (допустим, с 10-6 до 10~5).
Но вероятности 10-6 и 10~5 неотличимы одна от другой с
точки зрения индивидуального опыта отдельного рабочего.
Только общество в целом придет в ужас, заметив по данным
статистики десятикратное увеличение количества аварий.
Если так можно сказать молодому человеку, который еще
только учится, то что можно сказать взрослому, способному
сознавать свою ответственность, чтобы он осознал эту ответ-
ственность еще лучше?
Выше мы показали на примерах, имеющих массовый ха-
рактер, что усилия того сравнительно узкого круга рабочих
и инженеров, которые занимаются электробезопасностью на
профессиональном уровне, не привели и не могут привести в
обозримом будущем к полному решению этой проблемы да-
же в бытовых условиях (не говоря уж о промышленных).
Думать, что эту проблему можно решить усилиями того же
круга специалистов, если только подбодрить их каким-нибудь
новым, очень страшным выговором — явная глупость. Каж-
дый человек должен сам подумать о безопасности — это оз-
начает знания, приборы, материалы, инструменты и т. д. Но
если все это есть, то возможности отдельного человека тво-
рить в области электротехники существенно расширяются.
С одной стороны, этой самодеятельности избегать не следу-
ет, так как фактический уровень безопасности весьма сильно
зависит от разума и осторожности потребителя. Но с другой
стороны, в технике безопасности нет ничего хуже полузнания.
Совсем безграмотный технически человек довольствуется тем,
что ему дано, и не пытается что-либо изменить. Человек же,
который что-то знает, начинает действовать, не всегда пред-
видя последствия своих действий. Вероятностная точка зре-
ния состоит в том, что в технике безопасности, имеющей де-
282
ло с маловероятными событиями, каждое конкретное из кото-
рых в личном опыте отдельного человека почти никогда и не
встречается, техническое полузнание практически неизбежно.
Мало может помочь и официальная наука техника безопас-
ности, так как вновь появляющаяся техническая самодея-
тельность будет создавать для этой науки новые проблемы,
которые она может осознать лишь с большим опозданием.
Не существует абсолютных мер предосторожности, кото-
рые, устраняя какую-то одну опасность, не создавали бы ка-
кой-то другой, хотя, допустим, и менее вероятной. Например,
мы создаем некое официально не предусмотренное заземле-
ние корпуса машины за водопровод. Если то событие, ради
которого мы создавали заземление, происходит во время
ремонта водопровода, когда система труб разорвана, то часть
водопроводной сети может оказаться под напряжением (это
создает для слесарей опасность, о которой они, может быть,
никогда прежде не думали). Со стиральной машиной такое
трудно представить (потому что без воды не постираешь), но
с другими электроприборами — возможно.
Далее, все электроизмерительные приборы имеют клем-
мнме устройства не столь безопасные, как в бытовых прибо-
рах. Нужно бывает подумать, в каком порядке втыкать про-
вода в прибор и в электрическую сеть, чтобы не попасть под
напряжение.
Наконец, возможно и не предвидимое заранее использо-
вание технических средств. Например, как все-таки узнать,
можно ли пользоваться чайником или утюгом (т. е. не про-
бита ли изоляция на корпус)?
Не у всякой домашней хозяйки есть омметр; кроме того,
обычное измерение сопротивления изоляции омметром, ра-
ботающим от батарейки, может оказаться недостаточно по-
казательным, так как пробой изоляции может выявляться
лишь при приложении достаточно высокого напряжения. Че-
ловеческий изобретательный разум решил эту проблему пу-
тем изобретения мегаомметра. Мегаомметр работает от руч-
ного генератора высокого напряжения, скажем, на 1000 В.
Конечно, на выводах генератора получается 1000 В, только
если сопротивление нагрузки очень велико; в противном слу-
чае напряжение на выводах будет значительно меньше: боль-
шой ток получить от ручного генератора нельзя. Но мы ведь
хотим проверять исправную изоляцию, и на ней мы получим
примерно 1000 В, так что если мегаомметр не показывает
неисправности изоляции, то на напряжение 220 В прибор
обычно включать можно. (Правда, постоянное напряжение
1000 В от мегаомметра не совсем то же самое, что 220 В пе-
ременного тока, и, главное, несколько встряхнув или повер-
нув чайник или утюг, мы можем иногда создать замыкание
за корпус, которого не было в момент испытания изоляции
283
мегаомметром). Таким образом, проблема создания безопас-
ного источника достаточно высокого испытательного напря-
жения решена.
Вторая проблема состоит в том, что при ручном приводе
испытательное напряжение сильно колеблется, что, казалось
бы, должно сделать точность измерений сопротивления весь-
ма плохой (а результаты — нестабильными, следовательно,
и недостоверными). Но человеческий гений изобрел так на-
зываемую логометрическую схему измерительного прибора,
при которой показание прибора зависит лишь от отношения
сил токов в двух его обмотках (следовательно, колебания
приложенного напряжения не имеют значения). Вместе гене-
ратор и прибор составляют мегаомметр, которым обычно и
проверяют изоляцию.
Что же, выдвинем лозунг «мегаомметр — каждой домаш-
ней хозяйке»? Автору по опыту известно, что мегаомметр —
предмет восторга детей, так как восхитительно щиплется В
то же время больших токов от ручного генератора получить
нельзя (а ведь опасно не напряжение, а ток). Ну что же.
пускай дети балуются и заодно изучают прибор.
Но что будет, если эти проклятые дети догадаются, ради
усиления эффекта пощипывания, зарядить от мегаомметра
хороший конденсатор, который весьма нетрудно найти на
свалке в старом радиоприемнике или телевизоре? Конечно,
конденсатор можно зарядить и от сети (эпидемии таких
«опытов» иногда вспыхивают в школах). Но наличие мегаом-
метра может, во-первых, стимулировать интерес к зарядке
конденсатора, а во-вторых, от сети можно получать не более,
чем амплитудное значение напряжения 220V2=309B, а от
мегаомметра — теоретически больше. Автору книги точно не-
известно, но теоретически сочетание мегаомметра с конденса-
тором смотрится как не вполне безопасное.
Но если что-нибудь не вполне безопасно, то при массовом
применении обязательно будет опасно. Видим, что несложная
на первый взгляд и, казалось бы, давно решенная проблема
контроля изоляции при необходимости дать ее массовое ре-
шение приобретает новые черты. Хорошая, конечно, вещь
технические знания, умения, приборы, машины и т. д., но по
разным поводам мы все чаще сталкиваемся с необходимо-
стью как-то разумно ограничить рост насыщения техникой
как у себя дома, так и в масштабе целого общества, потому
что мы все время обнаруживаем, что то, что сначала каза-
лось знанием, на деле оказывается полузнанием.
§ 3. Наука или натурфилософия?
Результаты борьбы за электробезопасность было бы инте
ресно и необходимо сопоставить со статистическими данными
284
э несчастных случаях; но таких данных нет в распоряжении
автора. В учебнике П. А. Долина указываются лишь относи-
тельные цифры: доля электротравм среди всех несчастных
случаев на производстве составляет 0,5—1%, а в электро-
энергетике, конечно, несколько выше, но всего лишь 3—3,5%.
Однако среди всех смертельных случаев на производстве
20—40% наступает в результате поражения электрическим
током (в энергетике до 60%), причем 75—80% смертельных
поражений током происходит в установках низкого напряже-
ния (т. е. до 1000 В), потому что их много. К сожалению, аб-
солютные цифры не приводятся. В этом смысле больше по-
везло с данными по пожарной опасности электроустановок:
в книге Г. И. Смелкова [36] приведена таблица, которую мы
и воспроизводим (имеется в виду количество пожаров на 1
млрд кВт. ч выработанной в СССР электроэнергии).
Годы 1971 1972 1973 1974 1975 1976 1977 1973 1979 1930
Кол-во пожаров на 1 млрд, квт/ч 26,6 27,1 23.3 23,3 24,0 22,1 22,4 21.7 22,7 22,2
Мы собираемся проанализировать эти данные на статис-
тическую однородность. Верно ли, что количество пожаров
есть случайная величина, распределенная по закону Пуассо-
на с параметром, пропорциональным выработке электроэнер-
гии? Если эта гипотеза верна, то различия (по годам) для
чисел, приведенных в таблице, объясняются лишь случайны-
ми отклонениями пуассоновской случайной величины от ее
математического ожидания. Действительно, на первый взгляд
колебания чисел таблицы невелики.
Для каких-то статистических обработок относительные по-
казатели обычно непригодны; к счастью, в данном случае их
нетрудно перевести в абсолютные, так как данные о выра-
ботке электроэнергии в СССР известны, Так, согласно книге
И. К. Тульчина и Г. И. Нудлера [38], в 1970 г. потребление
электроэнергии (включая собственные нужды энергосистем и
передачу электроэнергии) составляло 741 млрд квт. ч; в
1975 г. — 1039 млрд квт. ч; в 1980 г. — 1295 млрд. квт. ч.
Для наших целей достаточно принять грубо, что за весь пе-
риод, указанный в таблице, производство электроэнергии сос-
тавляло примерно 1000 млрд. квт. ч в год. Значит, для полу-
чения абсолютных цифр из относительных, указанных в таб-
лице, нужно эти последние умножить примерно на 1000. Итак,
число пожаров от электроустановок в год составляет величи-
285
ну порядка 20—25 тысяч. Таково по порядку значение пара-
метра Л, в соответствующем распределении Пуассона. Отно-
сительное отклонение пуассоновской случайной величины от
X может составлять величину порядка 2/VX или 311/}.. При
Х=2-104
З/УХ=0,021 =2,1 %.
Так как при пересчетах в относительные показатели относи-
тельные разбросы не меняются, то относительный разброс в
таблице должен был бы составлять величину порядка 2% от
самих этих чисел, т. е. величину порядка 0,4—0,5%. На са-
мом деле разброс значительно больше. Таким образом, не
прибегая ни к каким сколько-нибудь сложным критериям,
видим, что гипотезу о пуассоновском распределении числа по-
жаров в год следует отвергнуть: разброс относительных чи-
сел, данных в таблице, гораздо больше, чем полагается для
закона Пуассона со столь большим параметром. Интерпрета-
ция этого факта неоднозначна: можно говорить об отсутст-
вии пуассоновского распределения, в то время как нормаль-
ное якобы действует. На наш взгляд, честнее интерпретиро-
вать этот факт как отсутствие статистической однородности.
Если так, то само понятие вероятности возникновения пожа-
ра от электроустановок становится шатким: в 1971 г. эта
вероятность одна, в 1976 г. — другая.
Существует, конечно, достаточно много ситуаций в физике
и отчасти в технике, когда вероятностные модели дают коли-
чественное описание тех или иных явлений; количественное в
том смысле, что, например, частоты совпадают с вероятнос-
тями, вычисленными из модели, в тех пределах точности, в
которых частота (при данном числе опытов) вообще может
совпадать с вероятностью. (Эти пределы, несмотря на их ка-
жущуюся размытость, в большом числе случаев являются, на
самом деле, весьма узкими). Такая точность отвечает приня-
тым в наше время научным стандартам строгости, поэтому
условно такие применения теории вероятностей будем назы-
вать научными. В других случаях мы строим вероятностную
модель явления без надежды на количественное совпадение,
но рассчитывая извлечь какие-то качественные выводы, воз-
можно, вполне достаточные для принятия тех или иных (до-
пустим, технических) решений. В смысле научной строгости
такие модели представляют собой шаг назад; чтобы это под-
черкнуть, мы будем называть подобные применения натур-
философскими. Но основная мысль данной главы этой книги
состоит в том, что для массового потребителя натурфилософ-
ские применения теории вероятностей преобладают. Наобо-
рот, форсирование вероятностных моделей без достаточных
оснований до уровня количественного соответствия гибельно
с точки зрения массовых применений.
286
Как сказано в предисловии ко второй части книги, она
имеет форму правоучительного сочинения, в котором те или
иные общие выводы обосновываются примерами. Мы начали
главу с простого и очевидного вопроса о том, нужно ли зазем-
лять крест, и решили, что — да, конечно, нужно, хотя коли-
чественный расчет опасности поражения молнией, проведен-
ный по официальной методике, приводит к явно и фантасти-
чески завышенному результату. Во втором параграфе мы рас-
смотрели гораздо более важное и массовое решение — режим
нейтрали: изолированная или заземленная? — и даже без
всяких попыток количественного сравнения двух вариантов
поняли, что общепринятое решение (заземленная нейтраль)
является правильным. Таким образом, примеры успешных
натурфилософских применений вероятностных моделей даны:
нужно теперь обосновать вторую часть тезиса — о гибельнос-
ти форсирования количественного совпадения.
Автору крайне не хотелось бы, чтобы отрицательные при-
меры, которые при этом придется привести, были бы для ко-
го-то источником обиды: точка зрения автора по существу
иная и ни для кого не обидная. Но если прямо приступить к
делу, т. е. к приведению отрицательных примеров, то, напри-
мер, такой заведомо заслуживающий всяческого уважения
ученый, как уже немного цитировавшийся Г. И. Смелков,
неизбежно и односторонне будет представлен в нелепом виде.
Поэтому автор считает необходимым обратиться к историчес-
кой перспективе, чтобы более правильно оценить те «неле-
пости», которые могут быть связаны с именем почти любого
ученого.
Итак, осуждение Галилея. Не все знают, что осуждению
Галилея инквизицией предшествовала его научная дискус-
сия с палой римским, на определенном этапе которой науч-
но прав был папа. В вольном изложении эта дискуссия выг-
лядит так.
«Отец мой, — сказал Галилей, — я нашел неопровержи-
мое доказательство движения Земли. Известное явление мор-
ских приливов и отливов никак не может быть объяснено, ес-
ли считать, что земля покоится. Так и вода в покоящемся ко-
рыте неподвижна, но стоит начать возить корыто взад и впе-
ред, как вода будет приливать то к одному краю корыта, то
к другому».
«Сын мой, — ответил папа, — твои аргументы с корытом
меня не убеждают. Если мы не видим в настоящее время
причины, которой можно объяснить приливы и отливы, то,
может быть, богу угодно будет когда-нибудь открыть нам
эту причину: я большой любитель наук и верю в научный
прогресс. Но мне кажется, что ты пришел ко мне затем, что-
бы я снял запрещение публиковать в печати доказательства
движения Земли. Для твоего же блага, сын мой, воздержись
287
от таких публикаций, не то святая инквизиция, сам понима-
ешь...».
Галилей, будучи противником астрологии, не желал допус-
тить никакого вмешательства Луны в земные дела; он был
научно не прав, так как связь высоты прилива с положением
Луны («сизигий», т. е. новолуние или полнолуние, либо «квад-
ратура» — когда направления на Луну и Солнце образуют
примерно прямой угол) устанавливается элементарно: сизи-
гийные приливы гораздо выше. Инквизиция осудила Гали-
лея не за научное несогласие с папой римским, а за наруше-
ние формального запрета на публикацию.
Сказанное не имеет, конечно, целью оправдать неизъясни-
мо гнусную процедуру судебного процесса инквизиции. Инк-
визиция, может быть, и понимала если не разумом, то живо-
том, что происходит что-то не то (отсюда и относительная
мягкость приговора, вынесенного Галилею), но остановиться
не могла, достигнув некоего шизофренического состояния,
когда правая рука не знает, что делает левая, а голова не
знает, что делают руки.
Для нас важно, однако, подчеркнуть, что Галилей впадал
в научную ошибку, слишком расширительно толкуя свое пра-
вильное в общем убеждение, что светила не вмешиваются в
земные дела. Слишком расширительные толкования тех или
иных научных результатов нередко встречаются в истории
науки. Например, Лаплас в «Философском очерке теории ве-
роятностей» превращает в некое посмешище Лейбница, ко-
торый толковал двоичную систему счисления будто бы так:
«единица (т. е. бог) вытягивает из небытия (т. е. из нуля)
все (все числа)». Более того, Лейбниц пытался сообщить
эту идею китайскому императору в надежде, что, узнав та-
кое, тот немедленно обратится в христианство. Но когда мы
теперь читаем в «Философском очерке» мнение самого Лап-
ласа о том, что если за морем у какого-то государства имеет-
ся колония, то с течением времени она добьется свободы — и
это происходит в силу центральной предельной теоремы тео-
рии вероятностей, то мы, очевидно, тоже сталкиваемся с чрез-
мерно расширительным толкованием некоторого математи-
ческого результата. По-видимому, наука является предметом
коллективного творчества в гораздо большей мере, чем нам,
может быть, хочется признать: что верно и что неверно, что
возможно и что невозможно — узнается лишь в результате
коллективных усилий поколений ученых.
После этого исторического отступления, пожалуй, можно
(без риска нанести несправедливую личную обиду) обратить-
ся к тому, с чего начинается этот параграф, — к пожарной
опасности электропроводок.
Частично цитируем, а частично пересказываем [36, с.
115—116].
288
«Вероятностная оценка пожарной опасности электроизде-
лий и связанная с ней возможность нормирования их пожар-
ной безопасности представлялись весьма перспективными,
однако долгое время не могли быть использованы из-за от-
сутствия четких указаний по выбору уровня значимости, оп-
ределяющего допустимую величину безопасной вероятнос-
ти».
Речь идет о том, что мы не знаем, какая вероятность воз-
никновения пожара может считаться приемлемой (мысль о
полной безопасности как для автора данной книги, так и для
Г. И. Смелкова является прекраснодушным, но неисполни-
мым пожеланием). Но поскольку пожар потенциально связан
с невосполнимыми потерями, не поддающимися количествен-
ной оценке, ясно, что оценка этой вероятности может явить-
ся только в виде «четкого указания», а лучше сказать —
«откровения» откуда-то «свыше». И вот это откровение сни-
зошло в июле 1977 г., «когда вступил в действие разработан-
ный во ВНИИ пожарной охраны МВД СССР совместно с
рядом других организаций ГОСТ 12.1.004—76 «Пожарная бе-
зопасность. Общие требования». Было установлено, что веро-
ятность возникновения пожара от каждого пожароопасного
узла в год не должна превышать 10-6. Самое интересное
состоит в том, что при этом не было определено понятие по-
жароопасного узла и его пришлось устанавливать по статис-
тическим данным, считая, что уж наверно в детских садах и
школах требование ГОСТа 12.1.004—76 обеспечено. В дет-
ских садах и яслях (см. [36, с. 132]) длина электропроводки
на один пожароопасный узел составляет 5,1 м; в школах —
2,3 м, а вероятность возникновения пожара соответственно
3.1 10-6 и 7,8 10~8 на один узел в год. При этом каждый
находящийся в здании человек тоже считается за пожаро-
опасный узел электропроводки.
Из разнобоя данных по детским садам и школам, да и из
нелепости ситуации в целом (не определено понятие пожаро-
опасного узла), кажется, достаточно ясно, что попытка чис-
ленной оценки и нормирования вероятности возникновения
пожара является крайне неудачной: эта задача невыполни-
ма.
В заключение попытаемся осмыслить, что означает в наше
время постановка невыполнимой задачи перед какой-то на-
учной организацией или научным направлением. Есть страш-
ное психическое заболевание — шизофрения, при котором по
непонятным причинам происходит раскол, расщепление раз-
личных психических функций: странно деформируются эмо-
ции, органы чувств поставляют материал для нелепого бреда
и т. д.; по-видимому, это состояние имеет в виду древняя
формула «без царя в голове». Это заболевание встречается с
частотой порядка 1%, т. е., с точки зрения отдельного лица,
19-2567 289
редко (хотя с точки зрения общества — слишком часто). Ис-
ходом заболевания может явиться полный идиотизм.
В сколько-нибудь сложной коллективной деятельности —
научной или технической — расщепление функций задано с
самого начала: в работе неизбежно участвуют много специа-
листов в различных узких областях, которые с трудом пони-
мают друг друга. На самом деле, это весьма серьезная проб-
лема, создаваемая ограниченностью человеческих способнос-
тей, может быть, прежде всего памяти; так или иначе, с раз-
витием науки специальности все сужаются, а число их рас-
тет. Таким образом, для научного коллектива своеобразная
шизофрения задана изначально; между тем для успеха ра-
боты требуется почти столь же совершенное согласование
усилий различных специалистов, какое мы наблюдаем з нор-
мальной человеческой психике между ее различными функ-
циями. Вопрос для коллектива стоит не таким образом: «по-
чему нет царя в голове?», а таким образом: «откуда бы взять
царя?». Этим «царем» может быть ясная правильно постав-
ленная задача, незаурядная личность формального или не-
формального руководителя, исторически сложившаяся общ-
ность цели и т. д. Но нет лучшего способа довести коллектив*
до шизофренического состояния (с классическим исходом —в
идиотизм), чем постановка невыполнимой задачи. В этом
случае вместо решения задачи все усилия подчиняются дру-
гому: обоснованию того, что не мы, а кто-то другой виноват
в том, что поставленная задача не решается. А уж отдельные
специалисты занимаются чем угодно без всякого согласова-
ния функций. В таком шизофреническом состоянии заложена
и возможность превращения научной организации в подобие
того, чем была инквизиция во времена Галилея, которая ведь
тоже поставила себе невыполнимую задачу контроля над мыс-
лями. Реализуется или нет эта возможность — зависит от
более широких условий жизни общества в целом; но для под-
держки абсурда может явиться закон в виде ГОСТа. Другое
дело, что в эпоху, когда этот закон явился, он фактически
никого ни к чему не обязывал, так что превращение в инкви-
зицию на деле не состоялось.
Любопытно, что описанная попытка пропагандировать
вероятностные методы путем превращения их в ГОСТы яв-
ляется далеко не единственной (конечно, судьба всех этих по-
пыток одна и та же). Понимание того, что в технических
вопросах теория вероятностей может быть (чаще всего) лишь
натурфилософией, конечно, удержало бы от попыток ее прев-
ращения в закон.
290
Г Л А В A 2
ПРИМЕНЕНИЯ ЦЕНТРАЛЬНОЙ ПРЕДЕЛЬНОЙ ТЕОРЕМЫ
Было бы наивно думать, что одно лишь применение ве-
роятностных методов способов привести к решению научной
или технической проблемы — такие проблемы решаются
комплексно, путем разностороннего исследования имеющих-
ся возможностей (см. об этом, в частности, предыдущую гла-
ву данной книги). Одна из точек зрения в подобных комплек-
сных исследованиях — вероятностно-статистическая. Прове-
дение вероятностно-статистического исследования не есть уже
предмет общедоступного и массового применения теории ве-
роятностей — это дело специалистов и специальных научных
организаций. Но если теперь под «массой» или «массовым
потребителем» понимать этих специалистов, то соответствую-
щим теоретическим «ширпотребом» будет теория независи-
мых случайных величин, в определенном смысле завершаемая
центральной предельной теоремой. Применяется, естествен-
но, не центральная предельная теорема сама по себе, а не-
кая идеология — распределения вероятностей случайных ве-
личин, парметры распределений и их оценки, понятие неза-
висимости и т. д. Этот математический аппарат сложился
еще в IX в.; попытки работы с зависимыми случайными ве-
личинами начинаются в конце XIX в., в основном являются
предметом исследований XX в.
§ 1. Электрические сети зданий
Вопросов электробезопасности мы будем здесь касаться
только вскользь — не потому, что мы их исчерпали (это не-
возможно), а по другой причине. На уровне центральной
предельной теоремы теория вероятностей могла бы приме-
няться к этим вопросам в том случае, если бы речь шла о
каких-то выборочных статистических обследованиях. Однако
такие обследования толи не проводятся, то ли их результаты
просто неизвестны автору данной книги. Между тем вероят-
ностные методы властно вторгаются в техническую полити-
ку в области энергетики еще и с другой стороны: довольно
нелепо рассчитывать электрические сети (и конечно, станции)
на максимальную (суммарную) нагрузку всех подключенных
к ним электроприемников, так как хоть в жилых зданиях,
хоть в промышленности никогда не бывает так, чтобы все
электроприемники работали одновременно. Поэтому мы ищем
какие-то вероятностные модели для включения в работу элек-
троприемников, стремясь заведомо обеспечить реальные пот-
ребности, но не создавать ненужных резервов (которые, как
увидим, были бы многократными).
19* 291
Рассмотрим сначала на элементарном уровне вопрос о
резерве мощности различных устройств для производства
энергии.
Древняя отопительная печь в прежние времена никак не
рассчитывалась по теплопроизводительности. В настоящее
время такие приблизительные расчеты существуют: известно,
сколько примерно килокалорий тепла может выделить печь.
Расчет производится, исходя из одной или двух топок печи в
день, каждая примерно по 1,5 ч, т. е. суммарно 3 ч в день.
Но в случае необычно сильных холодов ничто не мешает то-
пить печь в течение 6 или даже 12 ч в день. Конечно, встав
на вероятностную точку зрения, мы не можем не подумать о
том, что при этом возрастет вероятность возникновения пожа-
ра. Действительно, в какой-то степени рост числа пожаров
при повышении интенсивности использования печей происхо-
дит, но это касается лишь печей, имеющих грубые дефекты.
Вообще говоря, нагреть поверхности кирпичной кладки до
опасных температур невозможно даже при непрерывной топ-
ке печи: кирпич, с одной стороны, материал выдерживающий
высокую температуру (в отличие, например, от железобето-
на), а с другой стороны, материал древний, резко неоднород-
ный по прочности и вынуждающий этим к кладке печей с
большим запасом толщины стен дымоходов. Поэтому пожа-
ры, связанные с интенсивной топкой печей в зимнее время,
представляют собой достаточно редкое и изолированное яв-
ление, во всяком случае не вырастающее до размеров массо-
вого бедствия для населения какого-то региона. Таким обра-
зом, можно согласиться с тем, что обычная отопительная печь
имеет, как правило, многократный запас по теплопроизводи-
тельности.
Иначе обстоит дело с более современными устройствами.
Современные электрические машины изготовляются по более
стабильной технологии, чем печи, и из гораздо более совер-
шенных материалов, чем кирпич. Зато — в погоне за эффек-
тивностью — мы и нагружаем эти машины до предела их воз-
можностей. Перегрузить вдвое генератор, трансформатор или
электромотор нечего и думать (разве лишь на немногие ми-
нуты): повысится температура машины и начнет гореть преж-
де всего изоляция. Чтобы этого не случилось, машины обору-
дуются защитой, которая отключает их, если нагрузка на
немногие проценты превышает номинальную. Если вспомнить
о вероятностном дьяволе, то становится ясно, что новый эле-
мент — защита — при массовом применении создает свои
проблемы (что может выражаться как в отказе срабатывания
в нужный момент, так и в срабатывании тогда, когда это не
нужно или, по крайней мере, лучше было бы без этого обой-
тись). Этих проблем слегка коснемся позже, а пока согла-
симся на том, что электрические устройства, в отличие отпе-
292
чей, резервов мощности практически не имеют: их номиналь-
ная мощность есть и их предельная мощность. Это же отно-
сится и к проводам электрических сетей, которые также име-
ют свою защиту.
Таким образом, с помощью теории вероятностей желатель-
но было бы так выбрать номинальную мощность, скажем,
электрических сетей здания, чтобы она была во много раз
меньше суммарной мощности установленных электроприем-
ников, но при этом обеспечивала бы реальные потребности.
Существенно превысить эту номинальную мощность ни при
каких обстоятельствах не удастся: это заложено в конструк-
ции, в частности в электрической защите.
Существо технической проблемы энергоснабжения жилого
(и общественного) здания не будет понятно, если не привес-
ти элементарные, но далеко не всем известные данные о не-
обходимых энергозатратах на те или иные нужды. Энергия в
квартире может использоваться в виде механической энергии,
в виде тепловой энергии и, так сказать, на «развлечения»
(радиоприемник, телевизор, магнитофон и т. д.). На «развле-
чения» используется небольшая мощность: телевизор имеет
мощность порядка 0,2 кВт; однако одновременное включение
и выключение миллионов телевизоров во время тех или иных
передач может создать проблему для электростанций энерго-
системы (но не для электрических сетей). Всевозможные ме-
ханические устройства (пылесос, стиральная машина, холо-
дильник, наконец, различный инструмент и т. д.) имеют мощ-
ность порядка 0,5 кВт или менее, используются недолго и не-
одновременно в различных квартирах. Они также не созда-
ют проблемы для сетей. Но положение резко меняется, если
рассматривать энергию в виде тепла.
Мощность одной конфорки газовой плиты составляет вели-
чину порядка 2 кВт; духовки, — грубо говоря, вдвое больше,
так что установленная мощность четырехконфорочной газо-
вой плиты составляет 12 кВт. Ее электрический эквивалент
— электроплита — имеет мощность порядка 5—8 кВт, но за
счет несколько лучшего коэффициента полезного действия
электроплита, допускающая одновременное использование
8 кВт, приближается по своим свойствам к газовой плите.
Наиболее эффективным средством для кипячения воды яв-
ляются погружаемые в воду нагревательные элементы (так
работают электрические чайники, кипятильники, самовары и
т. д.). Мощность каждого такого элемента находится в пре-
делах 1—1,5 кВт. Их использование наряду с электроплита-
ми широко распространено.
На отопление требуется, грубо говоря, 1—2 кВт на каж-
дую комнату квартиры, но зато круглосуточно.
На горячее водоснабжение требуется весьма различная
мощность в зависимости от того, как происходит нагрев во-
293
ды — заранее или в момент ее использования. Проточный
газовый водонагреватель (газовая колонка), который дает
сравнительно небольшую струю горячей воды, использует во
время работы мощность порядка 20 кВт.
Для электрического бытового прибора такая мощность
рассматривается как недоступная. Поэтому проточных элек-
трических нагревателей не бывает: бывают емкостные нагре-
ватели, в которых мощность 1—2 кВт должна использовать-
ся несколько часов (например, в ночные часы, когда нагруз-
ка энергосистемы резко снижается).
Сложилась ситуация, когда отопление и горячее водо-
снабжение в современном городском доме централизованы,
но общественное питание, на которое когда-то возлагались
надежды в смысле механизации и централизации приготовле-
ния пищи, фактически играет ничтожную роль. Поэтому ос-
новными потребителями энергии в современной квартире
являются кухонная плита и другие нагревательные приборы
мощностью порядка 10 кВт в сумме.
Существуют два основных энергоносителя — газ и элек-
тричество. Газ как энергоноситель, не зависящий от электри-
чества и от теплоснабжения, имеет большое преимущество в
смысле надежности энергоснабжения. Но прокладка газовой
сети требует затрат, а главное, этот энергоноситель взрыво-
опасен. Взрывоопасная концентрация метана в воздухе сос-
тавляет от 5 до 15%. Довольно типичная ситуация, когда
одна из конфорок газовой плиты заливается бегущей жид-
костью, а рядом продолжает гореть другая конфорка, вос-
принимается как крайне опасная. Правда, если установленная
нормами вентиляция кухни действительно соблюдается, а ме-
тан распределяется более или менее равномерно по всему
объему кухни, то элементарный расчет показывает, что взры-
воопасная концентрация метана не может быть достигнута.
Нередко, впрочем, происходят хлопки в духовке (т. е. взры-
вы газа в объеме духовки), которые обычно не имеют особо
тяжелых последствий.
Но если учесть, что нормы вентиляции могут быть нару-
шены (например, вентиляцию могут заклеить от тараканов);
учесть возможность наркотизации жильцов и т. п., то нельзя
исключить возможности взрыва газа в объеме кухни или це-
лой квартиры. Никто не может поручиться, что при этом не
будут вырваны из стен целые панели, а это может привести
к разрушению дома в целом. Конечно, при наличии газовой
сети небрежность жильцов — далеко не единственный источ-
ник опасности взрыва.
Таким образом, как по соображениям экономии на газо-
вой сети, так и по соображениям безопасности, для наиболее
многоэтажных жилых зданий принято электричество в ка-
честве единственного энергоносителя для бытовых нужд.
294
Корпуса мощных электроприемников (типа электрической
плиты) полагается занулять. Мы уже обсуждали обоюдоост-
рый характер этой меры. Но происшествия, связанные с элек-
тричеством, должны при каждом отдельном случае вовлекать
гораздо меньшее число людей, чем происшествия, связанные
с газом.
Теоретически, конечно, можно себе представить все что
угодно. Например, по какой-то небрежности электриков мо-
жет произойти перефазировка проводов, в результате кото-
рой нулевой защитный провод окажется под напряжением (а
с ним и все зануленные корпуса электроплит). Правда, это-
му препятствует глухое заземление нейтрали, но при обрыве
зануляющего провода такое, вообще говоря, возможно. Дру-
гой вариант — попадание высокого напряжения (скажем,
10 кВ (в сеть низкого напряжения 380/220 В, которое может
быть при неисправности изоляции трансформатора. Таким
образом, опасность массовых несчастных случаев и при заме-
не газа электричеством до конца не снимается, но тем не ме-
нее принятое техническое решение интуитивно представляет-
ся правильным.
Теперь о расчете электрических сетей. Рассмотрим книгу
[38, с. 40—49]. Сети рассчитываются на получасовой макси-
мум нагрузки. Это означает, что сутки разбиваются на пери-
оды продолжительностью в полчаса, по каждому пери-
оду производится усреднение нагрузки, и наибольшее из по-
лученных чисел и есть та нагрузка, на которую должна быть
рассчитана сеть. Вопрос состоит в том, как из теоретических
или экспериментальных соображений оценить нагрузку этого
наиболее тяжелого получаса.
Вводится понятие средней вероятности включения элек-
троприемников
P^S/SycT,
где S — средняя потребляемая мощность за период Т (он
имеет какое-то отношение к наиболее нагруженному получа-
су, но явно в книге об этом не сказано), SycT — суммарная
установленная мощность. Определение р, очевидно, ориенти-
рует на нахождение этой величины по показаниям счетчиков
электроэнергии. Интерпретация ее как вероятности включе-
ния вряд ли имеет смысл: например, у электроплиты не два
состояния: «включено», «выключено», а несколько десятков в
зависимости от различных положений различных переключа-
телей. Увидим, что в дальнейшем интерпретация р как веро-
ятности включения используется для цели, которая не может
быть достигнута. _
После определения р в книге следует (с. 41) нелепое ут-
верждение: «при включении группы электроприемников неза-
295
висимо друг от друга средние вероятности включения сум-
мируются», а приводимая формула выражает ту мысль, что
средние потребляемые мощности суммируются. Оказывается,
что понятие независимости электроприемников вводится для
того, чтобы как-то охватить ситуации вроде следующей: при
включении телевизора вряд ли включается утюг, пылесос или
стиральная машина. Но такие вопросы требуют детальных
социологических обследований, которые с помощью одних
лишь электросчетчиков провести невозможно: если бы соот-
ветствующий фактический материал был бы собран, то по-
нятие р стало бы неинтересным.
Далее упоминается биномиальный закон. Для биномиаль-
ного закона существует один параметр: вероятность успеха р
в одном испытании. Математическое ожидание числа успе-
хов в п испытаниях есть пр, а дисперсия равна пр(1—р). Ес-
ли теперь вероятность успеха р понимать как р, то, зная
только р, можно подсчитать дисперсию потребляемой мощнос-
ти и нет необходимости оценивать эту дисперсию из факти-
ческих данных. Вот эта надежда и является грубо ошибочной:
ситуация, например, с электроплитой не имеет ничего обще-
го с испытаниями Бернулли. Наконец, появляется централь-
ная предельная теорема; приводится гистограмма максиму-
мов нагрузки на вводе в квартиру (неизвестно, по какой вы-
борке полученная). Из гистограммы совершенно ясно, что
распределение не похоже на нормальное (вероятности боль-
ших нагрузок слишком велики; распределение имеет слиш-
ком длинный правый «хвост», и этот факт нельзя оставить
без внимания). Тем не менее авторы утверждают, что, «сое-
динив средние точки абсцисс, получим кривую нормального
закона распределения».
Далее на с. 44 авторы вроде бы оставляют биномиальный
закон и рассматривают статистические методы определения
среднего и дисперсии нагрузки, а на с. 45 биномиальный за-
кон без предупреждения возникает вновь. Следует заметить,
что при всякой статистической обработке нужно создать ан-
самбль каких-то наблюдений: что есть ансамбль — наблюде-
ния над одной квартирой в последовательные дни года или
наблюдения над разными квартирами и т. д. Эти вопросы об-
ходятся молчанием. Наконец, на с. 46 возникает корреляцион-
ный анализ, который каким-то образом позволяет определить
наибольшую нагрузку (на квартиру?!) в домах с электро-
плитами по формуле
Р max = 0,401 + 5,08Vn,
где Ртах в кВт, п — число присоединенных квартир. В таб-
лице на с. 52 указаны несколько иные данные, например, при
п=100 в домах с электроплитами расчетная нагрузка приня-
296
та 1,15 кВт на квартиру. По этому поводу хочется заметить,
что нагрузка вряд ли может рассчитываться на квартиру
(без учета того, что бывают однокомнатные, двухкомнатные
и т. д. квартиры): уж если создавать усредненный показа-
тель, то на квадратный метр (жилой или полезной) площади.
В целом изложение представляет собой пример отсутст-
вия достаточной ясности как в основных понятиях, так и в
математических деталях. Вероятностные методы привлека-
ются не затем, чтобы с их помощью узнать что-то определен-
ное, а лишь затем, чтобы избежать упрека в отсутствии ис-
пользования этих методов.
На самом деле явно имеет место трагическая ситуация,
связанная с постановкой невыполнимой задачи. От теории
вероятностей хотят ответа на вопрос, какова может быть наг-
рузка на электрическую сеть, если примерно известно, каки-
ми электроприборами и в каком количестве будут пользо-
ваться жильцы дома. Недостаток статистических данных пы-
таются возместить за счет использования вероятностных мо-
делей, в частности модели независимых испытаний, которые
явно не имеют отношения к фактическому положению дел.
Можно было бы, не ссылаясь на вероятностные методы,
просто отметить как экспериментальный факт, что при расче-
те сети, исходя примерно из 1 кВт мощности на квартиру,
жизнь в доме в большинстве случаев протекает нормально.
Посмотрим, нет ли факторов, которые могут нарушить эту
нормальную жизнь, но которые не описываются никакой ста-
тистической моделью и, как правило, не могут быть охваче-
ны статистическим исследованием.
Речь идет о двух вещах: 1) о сложном процессе взаимо-
действия людей с техническими устройствами в тех условиях,
в которые их ставит то или иное массовое техническое реше-
ние; 2) о сложном процессе развития аварии, если таковая
возникла. Во всех последующих рассуждениях собственно
вероятностная идея одна: если некоторое событие не являет-
ся совсем невозможным, то при массовом повторении соот-
ветствующих «испытаний» оно обязательно произойдет.
Итак, пусть для конкретности в доме 100 квартир, мощ-
ность одних электроплит 800 кВт, а сеть рассчитана на 100
кВт. Как правило, жизнь идет нормально. Но в жизни есть
такой фактор, как праздники (он вряд ли учтен в статисти-
ческих исследованиях, о которых выше шла речь). Накануне
праздников хозяйки начинают печь пироги, используя (более
или менее одновременно во всех квартирах), скажем, 4 кВт
мощности. Если число таких квартир достигнет 50 (т. е. мощ-
ность 200 кВт), то защита заведомо должна отключить сеть.
(Кроме того, на ту же сеть ложатся нагрузки от других при-
боров). Поскольку сеть для освещения и электроплит выпол-
нена общей, дом погружается во тьму (лифты и телефон про-
297
должают работать). Жильцы вызывают электрика, часть
электроплит, допустим, к его приходу уже отключена (пото-
му что хозяйки, отчаявшись, бросили выпечку пирогов), и
электрик благополучно включает автомат. Все опять в поряд-
ке.
Однако то же самое повторяется в следующий праздник.
Допустим, что в доме живет один-два, ну не графомана в ме-
дицинском смысле этого слова, а просто человека, которые
хотят постоять за свои права не путем разбора технической
стороны дела, а путем жалоб в инстанции. Итак, каждый
праздник — куча писем. Что остается делать электрику?
Электрик, допустим, работает хорошо и знает, в частности,
что от него лично ничего не зависит: так рассчитана сеть. Но
он должен как-то прекратить поток жалоб. Тут и начинается
непредвиденное взаимодействие человека и техники.
Лучшее, что может сделать электрик, — это поставить
автоматический выключатель, рассчитанный на больший ток,
худшее — вообще вывести из строя защиту, поставив, напри-
мер, перемычки на клеммы автомата.
Теперь все довольны. О том, что защиты нет, никто не
знает. Сеть, правда, иногда работает с перегрузкой, но это
еще не обязательно пожар. Подходит зима, приближается
Новый год, а на улице температура, допустим, —35°. Систе-
ма отопления (для условий, скажем, Москвы) рассчитана на
наружную температуру —25° и несколько не справляется с
нагрузкой (а резервов у нее нет: это не печь). Возникает
второй мощный фактор, обусловливающий одновременное
включение электроплит, — желание использовать их для до-
полнительного обогрева. Развитие ситуации в пожар элек-
тропроводки делается возможным, но это не самое худшее,
что может произойти.
Электросеть дома является частью системы электроснаб-
жения; иногда неблагополучие в части системы может раз-
виться в аварию, проникающую (до каких-то пределов) во
всю систему.
Итак, домовая сеть перегружена, а выключатель, который
должен был бы ее отключить, неработоспособен. Перегруз-
ка может быть, например, восьмикратной. В таком случае в
электрических сетях срабатывает следующий выключатель,
который выключает какой-то больший участок сети, чем это
было бы необходимо (это называется нарушением избира-
тельности действия защиты; интересно, что существующие
правила требуют обеспечить избирательность лишь «по воз-
можности»). В нашей ситуации, может быть, и была бы из-
бирательность, но она нарушена в результате того, что в
борьбе между жильцами и электриком защита выведена из
строя.
298
В этом большом участке сети, который теперь отключен,
вполне могут оказаться и циркуляционные насосы отопления.
Если ранее отопление лишь несколько не справлялось с
крайне низкой наружной температурой, то теперь его нет
совсем. Нет не только электроплит — нет даже аварийного
освещения. Не работают лифты. Телефон — по-разному, в
зависимости от принятой схемы его электроснабжения.
В результате население дома (а может быть, и микрорай-
она) может — вместо привычного комфорта и благополучия
— оказаться в тяжелейших условиях. Конечно, на место ава-
рии такого масштаба немедленно выезжает аварийная бри-
гада и пытается включить нужный выключатель, но он тут
же отключается вновь, так как восьмикратная перегрузка
сети ничем не лучше короткого замыкания. А бригада еще
должна разобраться, в чем дело: она ведь не знает, что за-
щита домовой сети выведена из строя. Считается, что в
сильный мороз допустима остановка отопления на 2 часа:
дальше возникает опасность замерзания воды в некоторых
участках системы отопления. Поэтому если ликвидация ава-
рии затягивается, то лучшее, что можно сделать, — это
слить воду из водопровода (холодного и горячего) и систе-
мы отопления. Тогда через несколько дней дом можно будет
снова привести в жилое состояние; если же замерзнет вода в
трубах, то на ремонт потребуется несколько месяцев. На это
время жильцов нужно будет куда-то поселить, но спраши-
вается — куда?
В нашем стремлении к эффективному использованию
электросети и прочего оборудования есть обратная сторона
— практическое отсутствие резервов. Это отсутствие резер-
вов ведет, вообще говоря, к социальной напряженности (в
нашем примере — к жалобам на электрика), а социальная
напряженность обычно исключает разумные в техническом
отношении действия. Начинается непредусмотренная техни-
ческим решением самодеятельность, вообще говоря, несущая
в себе зародыши общественного бедствия. Если такие заро-
дыши появляются в широких масштабах, то в конце концов
некоторые из них реализуются. Органы власти окажутся пе-
ред проблемами (в нашем случае — куда девать жильцов?),
к которым они не готовы и с которыми не смогут справить-
ся. В частности, необычно холодная зима представляет со-
бой страшное испытание не только для электросетей и энер-
госистем, но и для всей прочей техники, обеспечивающей
жизнь города: вся она рассчитана на эффективное исполь-
зование, а следовательно, больших резервов не имеет. Отка-
зы техники непредсказуемы и не даны нам даже в виде ста-
тистических данных: из-за редкости аварийных ситуаций и
крайнего их разнообразия такие данные, вообще говоря, не
могут быть собраны.
•299
Кратко остановимся на проблеме развития аварий. В
электрических системах возможны аварии любого масшта-
ба. Дело в том, что электрические машины оборудованы за-
щитой, которая отключает их, если какие-то параметры вы-
ходят за заданные пределы. В случае аварии какой-то, до-
пустим, сравнительно мелкой (с точки зрения энергосисте-
мы) машины обычно эта машина отключается, на чем ава-
рия и заканчивается. При этом потребители даже и не знают,
что произошла какая-то авария, так как вышедшая из строя
машина автоматически резервируется другими машинами си-
стемы. Но бывает так, что при отключении одной машины
на некоторые другие элементы системы падает (пусть крат-
ковременно) большая нагрузка. Если бы система защиты
знала, что это повышение нагрузки кратковременно, то она
бы не стала отключать эти элементы. Но релейная зашита
не думает. Лавина отключений нарастает, пока не отклю-
чатся все (исправные!) машины системы. Такая редкая, но
ужасная авария называется развалом энергосистемы.
В результате нее крупный город может на несколько часов
остаться без электроэнергии, последствия чего частью оче-
видны, а частью непредсказуемы.
Может ли развал энергосистемы начаться с того, что хо-
зяйка поставила на электроплиту чайник с пробитой изоля-
цией? По-видимому, при крайне безобразном отношении к
устройствам защиты на всех уровнях энергосистемы такое,
возможно.
Какова может быть роль теории вероятностей в рассмот-
ренной ситуации? Расчеты вероятностей аварий и того или
иного их развития вряд ли могут осуществляться с хорошим
приближением к действительности. Но в рядовых повседнев-
ных исследованиях роль теории вероятностей может быть
существенной. Мы не знаем, например, какая часть из мил-
лионов автоматических выключателей, установленных на
квартирных щитках, действительно работоспособна (если та-
кой выключатель исправен, то пробой изоляции чайника за-
ведомо не приведет к развалу энергосистемы). По личному
опыту автору известно, что если подать ток 60 А на выклю-
чатель с номинальным током 15А, то примерно половина
выключателей серии АБ-25 начинает горйеть, но при этом
не отключается. (Не следует относить это утверждение к
выключателям других серий). Но каких-либо широких ста-
тистических исследований такого рода, по-видимому, не су-
ществует. Если бы такие исследования проводились, то на-
шлись бы и разумные применения вероятностных методов.
Поскольку самые напряженные ситуации создать искус-
ственно либо нельзя (как сочетание особо сильного мороза с
новогодним праздником), либо во всяком случае недопусти-
мо, единственное, что нам остается, — это изучать ситуации
300
менее напряженные, как-то оценивая, что произойдет в бо-
лее напряженных. Можно рассматривать разные технические
решения, например, если, действительно, признавать электро-
плиты потенциально опасным потребителем, то, может быть,
стоит иметь для них отдельную сеть (чтобы выключение
этой сети защитой не приводило к погружению дома в
тьму). Но прежде всего нужны статистические данные о со-
стоянии аппаратов защиты, о числе и продолжительности
отключений и т. п.
Крайне необходимо было бы иметь и какие-то статисти-
ческие данные о взаимодействии людей с техникой в тех или
иных условиях. Если, например, создать отдельную сеть для
электроплит, то отключение только этой сети будет не столь
трагичным, как полное отключение сети в доме. Возможно,
что по этой причине оно и ликвидироваться будет не столь
быстро. Но тогда жильцы станут запасаться всякого рода
керосинками, примусами, портативными газовыми плитками
и т. д. и создавать запасы горючего для этих приборов, что
потенциально гораздо опаснее в смысле пожаро- и взрыво-
опасности, чем стационарно проложенная газовая сеть. (Хо-
тя бы потому, что при отсутствии в продаже керосина в при-
мусы пойдет бензин.) Спрашивается, при какой ненадежнос-
ти электроснабжения этот процесс принимает значительные
размеры? В принципе на подобные вопросы можно ответить
путем статистических исследований (хотя бы в форме ан-
кет) .
§ 2. Отопление
В современном городе отопление централизовано. Су-
ществуют, конечно, вопросы надежности и безопасности
отопительных сетей и приборов, но за отсутствием факти-
ческих данных мы их рассматривать не будем. Оказывает-
ся, что и в том случае, когда отопительная система работает
«согласно проекту», результаты ее работы во многих слу-
чаях требуют вероятностной оценки. Мы опираемся на фак-
тические данные, приведенные в книге [7].
По принятым нормам, температура воздуха внутри жи-
лого здания должна быть в пределах 18—22°, относитель-
ная влажность — в пределах 30—65%. А. П. Васьковский с
сотрудниками в течение многих лет исследовали фактичес-
кое положение дела для различных зданий, причем обнару-
жились значительные отклонения от указанных норм. Стати-
стическое описание этих отклонений представляется естест-
венным: если установленные нормы соблюдаются не всегда,
то с какой же вероятностью? Понимание вероятности в дан-
ном случае весьма неоднозначно. Это может быть доля вре-
мени (что соответствует случайному выбору момента време-
301
ни) или доля всех помещений (что соответствует случайно-
му выбору помещения); комбинация обоих этих способов,
случайного выбора. Можно выбирать момент времени не
случайно в течение всего года, а лишь в наиболее холодном
месяце и т. д. Можно привлечь к рассмотрению погодные
условия и получить вероятность соблюдения нормированных,
значений температуры и влажности при определенных погод-
ных условиях и т. д. Короче говоря, при подобных исследо-
ваниях должна быть точно описана методика сбора статис-
тических данных, чтобы было понятно, о каком ансамбле на-
блюдений идет речь при определении вероятностей и частот.
Это условие в основном соблюдается в обсуждаемой книге.
Остановимся сначала на общих закономерностях, отме-
ченных в книге А. П. Васьковского. Как в средних шпротах,
так в особенности и на Севере нужно считаться с ветром,
который в многоэтажном здании дует снизу вверх (из-за то-
го, что столб воздуха в пределах здания имеет меньшую
плотность, чем более холодный наружный воздух). На Севе-
ре, в условиях вечной мерзлоты недопустим прогрев под-
вальных помещений, так что помещения первого этажа под-
вергаются действию ветра, дующего снизу вверх, и низких
температур. Отопительные приборы, устанавливаемые на
стенах здания, иногда не могут обеспечить сколько-нибудь
приемлемую температуру. Так, в зрительном зале Дворца
культуры в г. Норильске температура на полу оркестровой
ямы составляла 2,5°С, а температура воздуха над ямой и
над сценой была 9,5° С. Наоборот, в помещениях верхних
этажей здания температура может быть выше нормируемой.
Учет влияния ветра, дующего снизу вверх, на этапе конст-
руирования системы отопления затруднен из-за того, что
этот ветер зависит от непредусматриваемых неплотностей в
перекрытиях. Кроме того, теплоизоляционные свойства ог-
раждающих конструкций могут не соответствовать данным,
заложенным в расчет; наконец, сами погодные условия, в
которых эксплуатируется здание, принимаются ориентиро-
вочно. Короче говоря, провести статистическое исследование
фактического температурного и влажностного режима край-
не желательно.
Приведем, следуя книге А. П. Васьковского [7], примеры
такого исследования и роли в нем вероятностно-статистичес-
ких методов.
Пример 1. Исследуются малоэтажные жилые дома в
г. Якутске, специально запроектированные для условий Се-
вера. Новшеством является принудительная приточно-вы-
тяжная вентиляция с увлажнением и подогревом приточно-
го воздуха, которая, впрочем, не работает из-за отсутствия
увлажнительных установок. Дома эксплуатируются как
302
обычные; предстоит оценить, соответствует ли нормам тем-
пературно-влажностный режим.
Сбор фактических данных заключается в том, что в четы-
рех выбранных домах в каждой жилой комнате замеряется
(на высоте 0,75 м от пола) температура и влажность. Не
указано, к сожалению, сколько замеров и с каким времен-
ным интервалом делалось в каждой комнате, но указывает-
ся, что в одних случаях температура наружного воздуха бы-
ла —35°С, а в других —46° С. Таким образом, на охват
представительной выборкой тех ситуаций, которые встреча-
ются в разные сезоны года, исследование не претендует.
Оказалось, что значения температуры колеблются от 13
до 26° С, влажности — от 8 до 70%. Таким образом, сани-
тарные нормы нарушены, и это ясно без какого-либо ис-
пользования теории вероятностей. Теперь следует поставить
вопрос о причинах этого положения, в частности о том, иг-
рает ли какую-либо роль ветер, дующий снизу вверх. Дела-
ется следующее: данные об измерениях температуры и
влажности в пределах каждого этажа рассматриваются как
выборка (совокупность независимых одинаково распределен-
ных случайных величин); привлекаются нормальный закон
распределения и статистические процедуры сравнения сред-
них и дисперсий. В результате оказывается, что средние и
дисперсии (по этажам одного и того же дома) отличаются
незначимо. Отсюда делается тот вывод, что конструкция и
выполнение междуэтажных перекрытий достаточно хороши
(для этих малоэтажных зданий), чтобы исключить перете-
кание воздуха снизу вверх.
Не оспаривая этот окончательный вывод, посмотрим, все
ли здесь ясно с вероятностной точки зрения. Прежде всего
модель выборки для температур и влажностей в различных
комнатах данного этажа довольно произвольна: причем
здесь независимые одинаково распределенные величины?
Комнаты имеют разную величину, по-разному расположены
(например, по отношению к тому ветру, который был вне
здания во время измерений); наконец, некоторые хозяева
квартир согласны терпеть температуру 13°С (соответствен-
но 26°), в то время как другие хозяева в такой ситуации
включают электроприборы (соответственно открывают фор-
точки). В колебаниях температуры, вызванных этими (или
другими) причинами, может потеряться тенденция измене-
ния температуры снизу вверх здания (если, конечно, эта
тенденция довольно слабая). Более корректно было бы об-
разовать разности температур в комнатах, находящихся
друг под другом (почти несомненно, что все этажи жилого
дома устроены одинаково); тогда проверке подлежала бы
гипотеза о том, что математическое ожидание таких разнос-
тей равно нулю. Но все равно для проверки этой гипотезы
зоз
пришлось привлечь бы статистическую технику работы с вы-
борками, т. е. не бесспорную статистическую модель. Про-
верять в такой ситуации гипотезу на каком-то строго фикси-
рованном уровне значимости (допустим, 0,05), пожалуй, бес-
смысленно.
Гипотеза нормальности с теоретической точки зрения вы-
глядит в данной ситуации довольно странно. Помимо учас-
тия этой гипотезы в статистических проверках, у нее имеет-
ся, пожалуй, гораздо более важная роль: редукция факти-
ческой информации к параметрам нормального закона. Дан-
ные по различным этажам каждого в отдельности из изу-
ченных четырех домов объединяются в одну выборку; рас-
пределения этих выборок аппроксимируются нормальной
плотностью, и приводится чертеж графиков этих плотностей,
из которого видно, например, что в доме № 4 холоднее и су-
ше, чем в доме № 1. Следует заметить, что такого же удоб-
ства в представлении данных можно добиться, не используя
никакой гипотезы о виде распределения, а рисуя графики
эмпирических функций распределения.
С помощью нормальных плотностей были оценены доли
комнат, в которых температура и влажность 1) ниже нор-
мы, 2) в пределах нормы и 3) выше нормы. Комнат, в кото-
рых один из этих показателей находится выше нормы, почти
нет; проблемой являются низкие значения температуры и
влажности. Доли комнат, в которых температура находится
в пределах нормы, составляют (для домов № 1—4) соответ-
ственно
0,68; 0,68; 0,34; 0,40;
аналогично по влажности
0,39; 0,53; 0,68; 0,22.
К сожалению, не приводятся (и не вытекают из приводимых
данных) доли комнат, в которых оба показателя одновре-
менно находятся в пределах нормы.
Пример 2. Аналогичное исследование проводилось для
зданий повышенной этажности (9-этажные кирпичные жи-
лые дома). На этот раз в течение недели производилась не-
прерывная запись температуры и влажности в различных
комнатах жилых домов. Из непрерывной записи путем ус-
реднения по непересекающимся интервалам времени длиной
2 ч формировалась последовательность дискретных наблю-
дений, которая считалась выборкой (72—84 наблюдения;
теоретически при сплошной записи в течение 7 дней должно
было бы во всех случаях быть 7 • 12=84 наблюдения; види-
мо, в некоторых случаях не учитывались выходные дни).
В данном случае весьма сложен вопрос о статистическом
ансамбле. Конечно, непрерывную запись температуры или
304
влажности хочется назвать реализацией случайного процес-
са. Но при этом нужно уметь сказать, каким образом полу-
чить статистически однородный ансамбль таких реализаций
(другими словами это называется — указать «генеральную
совокупность»).
Имеется в виду совокупность домов аналогичной конст-
рукции, помещенных в аналогичные погодные условия? По-
видимому, нет, так как выводы, которые дальше делаются,
вполне достаточно сделать для домов, охваченных исследо-
ванием, и примысливание ансамбля домов, которые не ис-
следовались, но в принципе могли бы исследоваться, не яв-
ляется необходимым.
С другой стороны, в книге А. П. Васьковского обсужда-
ется концепция стационарного случайного процесса. Это оз-
начало бы, что статистический ансамбль образуется путем
сдвигов времени наблюдений. Но из-за сезонного хода по-
годных условий концепция стационарного процесса также не
кажется приемлемой; во всяком случае нельзя говорить что
исследования, проведенные в течение недели, являются
сколько-нибудь представительными для существенно более
широких интервалов времени (сезон, год).
Таким образом, для усреднения по двухчасовым интерва-
лам времени значений параметров модель выборки стано-
вится весьма условной, в частности, применять статистичес-
кие критерии считая, что каждая исследованная комната
приносит 72—84 независимых наблюдения, нужно с большой
осторожностью. Но все это не обязательно ставит под сом-
нение полученные выводы.
Из этих выводов отметим явную зависимость температу-
ры от этажа здания: самая низкая температура на 1-м эта-
же; она повышается до 5-го этажа, а далее остается на од-
ном уровне, либо даже несколько снижается. В первый год
эксплуатации значения температуры на каждом этаже на
4—5° ниже, чем во второй год. Это связано с высыханием
конструкций здания. В целом температурно-влажностный
режим этих домов установленным нормам не удовлетворя-
ет. Принудительная вентиляция в домах (в тех случаях,
когда она работала) была неэффективной.
Попытаемся обобщить изложенные факты.
1. Научные статистические исследования фактической
эффективности работы тех или иных систем (в данном слу-
чае — системы отопления) имеют огромное значение, так
как (в отличие от жалоб жильцов) дают более или менее
объективную базу для оценки сложившегося положения и
принятия каких-то решений.
2. Сколько-нибудь сложные методы теории вероятностей
и математической статистики (в данном случае — статисти-
ческая проверка гипотез, основанная на центральной пре-
20—2567 305
дельной теореме) не являются вполне бесспорными из-за
спорности положенных в их основу вероятностных моделей
(в данном случае — модели выборки). Как некое средство
контроля получаемых выводов эти методы применять мож-
но, но не следует абсолютизировать результаты их приме-
нения до уровня научной истины. Обработав несколько по-
иному тот же фактический материал, иногда можно полу-
чить иные выводы. Например, не исключено, что при срав-
нении температур в расположенных друг над другом комна-
тах жилого здания (вместо того, чтобы сравнивать средние
значения температур по этажам) мы обнаружили бы в мало-
этажных зданиях ветер, дующий снизу вверх. Но и при та-
кой обработке, если фактический материал не допускает
вполне однозначных выводов, мы должны были бы обра-
титься к статистическим критериям, основанным на модели
выборки, которая продолжает оставаться спорной.
Обратимся, однако, к техническим выводам, которые
вполне бесспорно следуют из фактической информации,
представленной в исследованиях А. П. Васьковского.
Централизованная система отопления не всегда (а мо-
жет быть и никогда) может с достаточной точностью решить
поставленные перед ней задачи. В книге [7] говорится" об ав-
томатическом регулировании температуры, но из приведен-
ных результатов статистических исследований следует, что в
рамках централизованной системы отопления возможностей
для такого регулирования нет. Действительно, в нижних
этажах дома холодно, в верхних — жарко; что же будет де-
лать централизованная система регулирования — повышать
или понижать температуру воды, поступающей в отопитель-
ную систему? Независимо от всякой статистической модели
и применяемых методов проверки гипотез из описанных ис-
следований вытекает тот важный технический вывод, что ре-
гулирование должно быть местным: оно должно быть з ру-
ках потребителя. В настоящее время обсуждается вопрос о
смешанной системе отопления: централизованная система
водяного отопления обеспечивает некоторую базовую тем-
пературу, а кроме того, каждая квартира оборудована спе-
циальными «электродоводчиками», которые могут довести
температуру в данной квартире до той, которая нужна пот-
ребителю. (Фактически сейчас такая доводка осуществляется
— или не осуществляется — стихийно, путем покупки элек-
троотопительных приборов.) При централизованной установ-
ке доводчиков могут быть достигнуты большие выгоды, на-
пример использование электроэнергии тепло аккумулирую-
щими печами в ночные часы, на которые приходится мини-
мум нагрузки энергосистем, либо (в каких-то климатичес-
ких условиях) применение тепловых насосов. Но не следу-
ет забывать о вероятностной точке зрения, которая в дан-
306
ном случае состоит в том, что расширение использования
электроэнергии ляжет тяжелым грузом не только на мощ-
ности электростанций, но и на проблемы надежности (а мо-
жет быть и безопасности) электроснабжения. В принципе
все возможно, в том числе и электродоводчики отопления, но
при наличии соответствующих технических решений. Напри-
мер, может быть стоит вместо одной электрической сети зда-
ния для всех бытовых нужд иметь три различные сети: для
электроплит, для отопления и для прочих бытовых нужд, со
своими проводами и автоматами защиты. Тогда авария пли
перегрузка в одной сети не будет приводить к отключению
двух других, т. е. повысится надежность работы. С другой
стороны, прокладка трех сетей вместо одной, вероятно, ухуд-
шит (некоторым заранее непредсказуемым образом) условия
электробезопасности, не говоря уж о дополнительных затра-
тах.
Итак, что же мы можем сказать об инженерном обору-
довании современного городского жилого дома? Электри-
ческая сеть, по-видимому, не вполне надежна и не вполне
безопасна, но что и как в ней, следовало бы изменить —
абсолютно неизвестно, так как нет статистических исследова-
ний фактического положения дел (по крайней мере, так: е ис-
следования неизвестны автору данной книги). В отношении
отопления такое исследование есть, и его результаты опреде-
ленно показывают, что было бы желательно предоставить
жильцам дома какие-то возможности регулирования темпе-
ратуры помещений. Что же касается влажности воздуха, то
автору данной книги трудно судить о возможности ее регу-
лирования, но, судя по книге А. П. Васьковского, простыми
вещами вроде мокрых тряпок на батареях отопления здесь
обойтись нельзя, и нужно либо терпеть резко сниженную
влажность в зимний период, либо осуществлять достаточно
сложные системы вентиляции с увлажнением. Ясно, что в
ближайшем будущем следует ориентироваться на терпение.
Роль вероятностных методов в подобных статистических
исследованиях второстепенна (по сравнению с самим получе-
нием фактических данных). Не следует, конечно, забывать о
том, что сами по себе первичные данные обычно дают не-
приятную для глаза и ума картину полного беспорядка:
смысл и порядок в этой картине выявляются только после
усреднения, сглаживания и вообще какой-то обработки. Поэ-
тому вероятностные приемы (пусть простейшие) являются
необходимым вспомогательным средством. Но хотя бы не-
большое усложнение используемых приемов (например, до
уровня проверки простейших статистических гипотез) прино-
сит, вообще говоря, не бесспорные результаты из-за фунда-
ментальных сложностей, связанных с выбором вероятностной
модели.
20*
307
§ 3. Обработка измерений (наблюдений)
Чем проще теоретическая наука, тем шире область ее
применений, и, наоборот, чем сложнее наука, чем она глубже
и интеллектуально привлекательнее, тем уже (но, впрочем, и
интереснее) область применений. Эта мысль в данной книге
повторяется неоднократно. Дав на примерах некоторое по-
нятие о том, до какой степени сложности может дойти тео-
рия вероятностей, используемая в процессе принятия массо-
вых технических решений (или, если угодно, как реальная
техническая ситуация не допускает попыток слишком глубо-
кого использования теории вероятностей), мы, начиная с дан-
ного параграфа, обращаемся к более узким применениям те-
ории вероятностей, в рамках, так сказать, «чисто научных»,
непосредственно с техническими решениями не связанных.
(Вероятностное рассмотрение может быть одним из многих
мотивов технического решения.)
Для любой науки характерна задача той или иной обра-
ботки наблюдений. Применительно к астрономическим (гео-
дезическим) наблюдениям эта задача с вероятностной точки
зрения рассматривалась в начале XIX в. Лапласом и Гаус-
сом. В результате были вызваны к жизни нормальное рас-
пределение в качестве закона распределения вероятностей
для ошибок наблюдений, а также метод наименьших квадра-
тов. В начале XX в. К. Пирсоном, Стьюдентом и Фишером
были уточнены приемы Лапласа и Гаусса так, чтобы было
возможно охватить и случай выборок малого объема; при
этом были введены распределения хи-квадрат (Пирсона),
Стьюдента и Фишера (математические детали см. в первой
части книги). Здесь мы остановимся лишь на больших выбор-
ках, т. е. на приемах обработки наблюдений с помощью
центральной предельной теоремы в том виде, в каком такую
обработку предложили Лаплас и Гаусс.
Чтобы не создавать у читателя ложного впечатления, не-
обходимо заметить, что Лапласа и Гаусса интересовали
прежде всего так называемые косвенные измерения. Положе-
ние небесного тела в пространстве является, в силу законов
Ньютона, функцией от времени и некоторых параметров его
орбиты в солнечной системе. Мы же наблюдаем его положе-
ние на небесной сфере, определяемое некоторыми углами, ко-
торые оказываются, таким образом, функциями времени и
параметров орбиты. Нужно восстановить (возможно точнее)
параметры орбиты, учитывая, что наши наблюдения углов
подвержены случайным ошибкам. Таким образом, для астро-
нома вероятностная модель ошибок наблюдений является
чем-то промежуточным, что, собственно, его мало интересу-
ет. Обрабатывая методом наименьших квадратов измерения
положений светил, Лаплас и Гаусс узнали много бесспорно
308
верного и замечательного. Но нас в этой книге интересуют
не астрономические выводы, а сама вероятностная модель
ошибок наблюдений. Ограничимся поэтому исключительно
прямыми измерениями, когда в опыте измеряется непосред-
ственно та физическая величина, которая нас интересует.
Например, в наше время ни в одном медицинском журнале
нельзя опубликовать попросту среднее значение какой-то ве-
личины для определенной совокупности пациентов, а нужно
опубликовать Л1 ± т, где М — среднее значение, ат —
ошибка среднего значения, вычисляемая по таинственным для
большинства медиков правилам (а на самом деле — по пра-
вилам, установленным Лапласом). Действительно ли эта
ошибка т имеет тот смысл и значение, какой с давних пор
(фактически следуя Лапласу) придают ей учебники матема-
тической статистики?
Вероятностная модель ситуации прямых измерений состо-
ит в том, что
Xi = a + 6i, i=l,...,n, (I)
где Xt — результат i-ro измерения, б,- — ошибка i-ro измере-
ния, причем ошибки в разных измерениях 6», 62,. .. 6П — не-
зависимые случайные величины и Мб,=0.
Очень важно сказать, что такое а. Если M6f=0, то а —
= NiXi, т. е. современный статистик скромно говорит, что а —
это математическое ожидание отдельного наблюдателя. Но
классики и за ними и очень многие люди на протяжении XIX
и XX вв. полагали, что а — это истинное значение измеряе-
мой величины. Аргументация сводилась к тому, что ученый —
вообще человек честный, да и врать ему, сознательно пре-
увеличивая или преуменьшая, скажем, среднее расстояния от
Земли до Солнца, совершенно незачем. Поэтому ему одина-
ково вероятно при измерениях ошибиться на ( + е) и на
(—е), т. е. плотность распределения для результата наблю-
дения симметрична относительно точки а — истинного значе-
ния измеряемой величины, но тогда Мх,=а, следовательно,
Мб<=0 (т. е. нет систематической ошибки наблюдений).
В гл. 1 ч. I данной книги (при обсуждении закона больших
чисел) мы уже видели, что в точности так не может быть:
измеряя длину 50, 1 мм масштабной линейкой, самый чест-
ный человек всегда будет получать 50 мм, т. е. систематичес-
кая ошибка будет. Но не возбраняется думать, однако, что —
при современном разнообразии способов как угодно растя-
нуть шкалу измерительного средства — систематическая
ошибка будет намного меньше случайных ошибок. Это и оз-
начает, что в модели можно считать, что систематической
ошибки нет.
Целесообразно для начала привести пример ситуации,
когда систематической ошибки действительно нет.
309
Пример 1. Простейшим из известных автору приборов, в
показаниях которого в отдельных измерениях можно наблю-
дать разброс, является микрометр. Например, измерения
диаметра монеты с помощью масштабной линейки или штан-
генциркуля никакого разброса вообше не дают. Но микрометр
устроен хитрее: его измерительная шкала растянута за счет
того, что при измерении вращается винт, причем полный обо-
рот винта соответствует перемещению измерительного упора
на 0,5 мм. Разделив окружность головки винта на 50 частей,
получаем, что одно деление шкалы соответствует 0,01 мм.
При такой точности монета перестает быть правильным круг-
лым диском: результат измерения зависит от угла поворота
Ф монеты относительно системы координат, связанной с ми-
крометром. Иначе говоря, перестает существовать диаметр
монеты вообще, но существует диаметр а(ф) в данном на-
правлении ф: это то расстояние, на которое можно свести упо-
ры микрометра, если между ними находится монета, повер-
нутая на угол ф. (Усилие давления на измеряемый предмет
стабилизируется простеньким механизмом, называемым тре-
щоткой.) Факт существования диаметра а(ф) в данном на-
правлении есть факт экспериментальный: если относительное
положение монеты и микрометра не менять, то результаты
измерения стабилизируются в пределах одного деления.
Если мы все же хотим иметь понятие диаметра монеты,
не зависящего от угла ф, то мы должны ввести его определе-
ние, например определить его как среднее значение:
а - [ а(ф)*р. (2)
Если i-му измерению соответствует поворот ф(-, то
х,~ а (ф,) = а+а (ф1) — а=а+б,-,
где б;—а(ф;)—д. Можно себе представить программу из-
мерений для определения а вида: ф, == фй 4- iДф- В таких
измерениях нет ничего случайного. Можно, наоборот,
считать, что Ф1, . . . , фп — независимые случайные величи-
ны с равномерным распределением на окружности (каж-
дая). Тогда формула (2) означает, что M.v( = Мл(ф() = а,
т. е. систематической ошибки нет. Распределения вели-
чин xt (либо ошибок Bj-asXj — а), конечно, отличаются от
нормального. Но при нескольких десятках наблюдений
распределение величины х = — V xt уже должно быть
п
близким к нормальному; дисперсию а’оцениваем с по-
310
moilljo sa — j V (xi — x)2 и применяем центральную пре-
дельную теорему. В результате узнаем, насколько х мо-
жет отличаться от а.
Если мы сделали две серии измерений одним и тем же
микрометром, то две оценки значения а будут, скорее всего,
разумно близки (различие между этими оценками не долж-
но быть высоко статистически значимым с точки зрения обыч-
ной техники проверки гипотез, основанной на центральной
предельной теореме). Но если в двух сериях измерений ис-
пользовать два различных микрометра (у которых, например,
по-разному сбиты измерительные шкалы, либо по-разному от-
регулированы трещотки), то можно говорить о систематичес-
ком сдвиге показаний и т. д. Иначе говоря, уже в описанном
простом примере измерения возникают разнообразные проб-
лемы.
Но можно еще и диаметр определить по-другому, на-
пример положить а* = supа(ср). Тогда все наблюдения
ф
будут иметь систематическое смещение:
Mxj — а, а —а* —а — sup а(<р) < 0.
ф
Наконец, с точки зрения концепции допусков и посадок
диаметр почти круглого предмета естественно определить как
диаметр наименьшего идеально круглого отверстия, в кото-
рое можно этот предмет просунуть .(без натяга). Связь так
понимаемого диаметра с измерениями при помощи микромет-
ра вообще неоднозначна: здесь требуются иные средства из-
мерений.
Вывод заключается в том, что предположение отсутствия
систематической ошибки может выполняться или не выпол-
няться в зависимости от конкретной задачи измерения.
Пример 2. Обратимся теперь к реальному физическому
примеру. Рассмотрим известные измерения Милликена заря-
да электрона (задачник [27], задача 456). Имеются 58 наб-
людений, которые дают значения заряда от 4,740 до
4,810 • 10-10 эл.-стат. ед. На рис. 1 изображена в нормальном
масштабе эмпирическая функция распределения. По глазо-
мерной оценке, сходство этой ступенчатой функции с прямой
(изображающей в этом масштабе нормальный закон) на-
столько хорошее, насколько вообще может быть при объеме
выборки п = 58. После сглаживания получаем х~4,781,
0,0155. Арифметические вычисления дают х=4,7808, s=
=0,0153. Среднеквадратическая ошибка выборочного сред-
него значения составляет
з!У~п = 0,00202.
311
Рис. 1. Эмпирическая функция распределения заряда электрона
по данным Милликена (источник данных: [27])
Мы ожидаем, что х отличается от истинного заряда
электрона на величину не более 2s/]/n« 0,004, что со-
ставляет около 1/1000 от измеряемой величины. Однако,
согласно справочнику {431, современное значение заряда
электрона составляет 4,80288 эл.-стат. ед. Следовательно,
312
если принять значение справочника за точную истину,
имеем
(4,80288 - 4,7808)/(s/n> » 11
вместо числа порядка 2...3. Ввиду того что получилось яркое
противоречие выводу теории ошибок, не мешает документаль-
но подтвердить, что физики начала XX в. понимали теорию
ошибок именно так, как здесь изложено. Для этого восполь-
зуемся книгой [5] (переиздание книги, вышедшей в 1935 г.),
На с. 101 сказано: «Точность опытов Милликена такова, что
невероятно ожидать ошибки большей, чем тысячная доля из-
меряемой величины». Процитируем также [10, с. 195]: «... эта
теория, обоснованная и развитая Лапласом, позволяет, на-
пример, вычислить точность результата тех или иных подсче-
тов и наблюдений». Имеется в виду, конечно, оценка точнос-
ти, исходя из разброса результатов отдельных измерений.
Пример с доверительным интервалом для заряда электро-
на далеко не единствен. В «Философском очерке теории ве-
роятностей» Лаплас, определив отношение массы Юпитера к
массе Солнца, предлагает пари, что будущие поколения уче-
ных не изменят найденное им число более чем на 1% (веро-
ятность того, что это произойдет, согласно Лапласу, ничтож-
но мала). Но современное значение отличается от найденного
Лапласом примерно на 2%. Касательно расстояния от Земли
до Солнца можно заметить, что каждое новое, более точное оп-
ределение этой величины не укладывается в доверительный
интервал, построенный по старым наблюдениям. Наконец, с
введением радиолокационных наблюдений, число которых
можно делать как угодно большим, несостоятельность теории
ошибок в смысле модели (1) стала совершенно явной.
Шествие М±т по страницам медицинских или биологи-
ческих журналов следует вообще признать вредным. В слу-
чае физических измерений мы хотя бы не сомневаемся в том,
что сама измеряемая величина (как заряд электрона или
среднее расстояния от Земли до Солнца) существует (в том
смысле, что в наших масштабах времени не меняется). Но
что сказать о среднем значении систолического кровяного
давления? Оно относится к данной совокупности больных, в
данном их состоянии, и никакого теоретического постоянства
этой величины нет. Интересен весь диапазон изменения изу-
чаемой величины, который наблюдался в том или ином ис-
следовании, и его лучше привести, например, в виде эмпири-
ческой функции распределения (что и места занимает нем-
ного). Публикация же данных в виде М±т обычно влечет
за собой досаднейшую потерю информации.
Пример 3. Приведем, однако, и пример, когда доверитель-
ный интервал для физической величины, выведенный на ос-
новании разброса наблюдений, блестяще подтвержден после-
313
дующими поколениями. Обратимся к работе [44]. Это сочи-
нение представляет собой магистерскую (по-современному —
кандидатскую) диссертацию П. Л. Чебышева, опубликован-
ную в 1845 г. Задача диссертации состояла в том, чтобы дать
элементарные доказательства полезных для практики основ-
ных теорем теории вероятностей, которые могли бы понять
люди, знающие только алгебру. Поэтому работа подчиняет-
ся несколько странному для нас условию — запрещается
употреблять понятие и знак интеграла. Между тем она изо-
билует довольно сложными выкладками (например, вместо
нормального интеграла возникает сумма, содержащая 1013
слагаемых), которые гораздо сложнее понять, чем интегралы.
Практических приложений в работе два: доверительный ин-
тервал для вероятности рождения мальчика во Франции
(0,50715; 0,51615) с коэффициентом доверия 1 — 3 • 10-5 и об-
работка наблюдений плотности Земли, сделанных Г. Кавен-
дишем.
Рассмотрим последний пример. Эмпирическая функция
распределения для соответствующих п=29 наблюдений при-
ведена на рис. 2. Находимые по графику значения (в г/см3)
Т~5,49 н 0,205 опять близко совпадают с найденными
П. Л. Чебышевым х=5,48; s=0,202. Доверительный интер-
вал (по П. Л. Чебышеву) есть 5,48±0,1 (коэффициент до-
верия 0,99248). Современное нам значение плотности есть
5,52, что отличается от х=5,48 всего лишь на l,06s/Vn.
Как можно в целом оценить ситуацию с «теорией ошибок»
и иными вероятностными методами обработки наблюдений?
Попытка оценить величину возможного отклонения от истин-
ного значения лишь на основании разброса наблюдений есть,
как мы видели, не более чем красивая мечта (иногда это вы-
ходит, иногда нет, а сказать, что в каких случаях бывает, нет
возможности). Критика старых концепций обработки наблю-
дений содержится, например, в книге [48]. В этой книге мож-
но найти ряд очень красивых высказываний, как, например,
«...состоятельность статистических оценок можно с полным
основанием считать одним из «мифов XX века»» (см. 93). Но
позитивная программа этой книги остается не вполне понят-
ной. Конечно, можно несостоятельность оценки среднего
арифметического объяснить наличием хотя бы небольших кор-
реляций (порядка 0,1) между всеми слагаемыми (всего в
сумме п слагаемых будет почти п2 таких корреляций). Но
если речь идет в самом деле о радиолокационных наблюде-
ниях искусственных спутников, то ведь по большому числу
наблюдений параметры орбиты определяются довольно точ-
но. Пересчитав, где был спутник час назад, можно в явном
виде получить ошибки тех наблюдений, которые делались час
назад. Может быть, посмотрев на эти ошибки, мы и пришли
314
Рис. 2. Эмпирическая функция распределения плотности Зем-
ли по данным Кавендиша (источник данных: [44])
бы к выводу о том, что они хорошо описываются моделью
корреляций, но, однако, никаких фактических данных такого
рода в книге П. Е. Эльясберга нет. Читатель остается в не-
доумении: что модель корреляций основана на каких-то фак-
тах или является чисто умозрительной моделью, как и клас-
сическая модель с независимыми одинаково распределенными
ошибками?
Но если не претендовать на оценку отклонения от абсо-
лютной истины, то методы обработки наблюдений могут при-
нести известную пользу. Например, измерения одной и той же
физической величины одинаковыми методами (скажем, изме-
рения в последовательные дни на одной и той же аппарату-
ре) должны, конечно, согласоваться между собой в преде-
лах, определяемых теорией ошибок. Если такого согласия нет
(а возникает, допустим, корреляция между близкими во вре-
мени измерениями), то это есть важная информация о рабо-
те измерительной аппаратуры. В качестве другого примера
рассмотрим намеренную рандомизацию (т. е. придание слу-
чайности). В частности, случайный выбор объектов в экспе-
315
риментальную и контрольную группы весьма часто применя-
ется в медицинских и биологических исследованиях (посколь-
ку иным путем нельзя оценить, есть или нет действие у испы-
туемого препарата). Средние значения существенных пара-
метров объектов, составляющих экспериментальную и конт-
рольную группы, не должны статистически значимо отличать-
ся (правда, если параметров, по которым производится
сравнение, не один, а много, причем их значения не неза-
висимы, то тут возникают проблемы). В общем, теория оши-
бок на уровне центральной предельной теоремы должна
быть вероятно, известна если не каждому человеку, то каж-
дому научному работнику, собирающемуся ставить экспери-
менты и обрабатывать их результаты; при этом должна быть
известной и возможность неправильных выводов.
ГЛАВА 3
ПРИМЕРЫ ПРИМЕНЕНИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Постепенно переходим ко все более сложным применени-
ям вероятностно-статистических методов. В гл. 1 ч. II данной
книги речь шла о некоторой элементарной натурфилософии,
связанной с вероятностными представлениями, которая явля-
ется общедоступной. В гл. 2 («на уровне центральной пре-
дельной теоремы») теория вероятностей выступала как сред-
ство, общедоступное для научных работников, которые не
должны быть специалистами ни в теории вероятностей, ни в
математике вообще, но могут (худо или хорошо) использо-
вать в своих исследованиях сравнительно несложные и давно
освоенные вероятностные методы. Дальнейшее усложнение
этих методов требует, как правило, участия в исследовании
специалистов по теории вероятностей — просто потому, что
человеческие способности ограничены, и у того, кто желает
овладеть теорией вероятностей на более глубоком уровне, как
правило, не остается времени и сил, чтобы быть еще профес-
сиональным инженером или естествоиспытателем. Наоборот,
профессиональная специализация в какой-то технической или
научной области, как правило (т. е. за исключением людей
весьма выдающихся способностей), не оставит времени и сил
на профессиональное овладение математикой вообще и тео-
рией вероятностей в частности. Итак, данная глава посвя-
щена таким применениям теории вероятностей, которые (как
правило) требуют сотрудничества математиков и специалис-
тов в какой-то конкретной научной области. На вид в конк-
ретно применяемых приемах и методах нет ничего такого,
что не могло бы с легкостью быть постигнуто и без участия
математика; однако выбор из всего известного в математи-
ческой статистике каких-то приемов, более или менее адек-
ватных данной конкретной ситуации, обычно требует (в ка-
316
честве необходимого, хотя и не достаточного условия) учас-
тия специалиста-математика.
Данная глава обращена глазным образом к такому чита-
телю, который желает (или которому приходится) стать по-
добным специалистом. Рассматриваемые здесь конкретные
примеры приложений носят (каждый в отдельности) весьма
частный характер, так как создать сколько-нибудь общий спи-
сок ситуаций, с которыми приходится иметь дело в прило-
жениях математической статистики, не представляется воз-
можным. Но есть общая мысль (по-видимому, не вполне три-
виальная для студента), которая состоит в следующем.
Когда студент слушает лекции по математической статис-
тике (или читает учебник), перед ним предстает некоторая до-
вольно сложная, но логически и математически совершенно
корректная система постановок задач, понятий и теорем, ко-
торую ценой известного напряжения мысли вполне возможно
понять и усвоить. Учащийся может подумать, что и в прило-
жениях к тем или иным конкретным вопросам достаточно
только аккуратно и последовательно применить усвоенную
систему знаний, чтобы получить правильный ответ на прак-
тически интересный вопрос. Но это заблуждение, от которого
нужно освободиться. Никаких до конца аккуратных и после-
довательных применений математики, скажем, в физике, а
физики — в технике и т. д. не существует. В особенности это
относится к применениям вероятностных моделей прежде все-
го из-за принципиальной неясности понятия статистического
ансамбля. Конкретные применения математической статисти-
ки полны логических противоречий; самое большее, на что в
них можно претендовать, — некоторая «истинность» в «це-
лом», в «общем». Эта «истинность в общем» имеет место не
потому, что мы все делаем правильно; она устанавливается
путем коллективных усилий — в сопоставлении выводов, по-
лучаемых различными исследованиями.
§ 1. Критерий Колмогорова
1.1. Введение. Напомним, что в первой части данной
книги (§ 3, гл. 3) мы видели, что распределение статис-
тики sup|Fn(x) — F(x)| (где F(x) — теоретическая функция
распределения, Fn(x) — эмпирическая функция распреде-
ления, отвечающая выборке объема п) не зависит от F(x)
(если предположить, что F(x) — непрерывная функция).
Делом довольно сложной техники (не описываемой в
данной книге) является вычисление распределения веро-
ятностей этой статистики. В частности, при л->оо
Р Wn sup|Fn(x) - Г(х)Ю} К (у), (1)
317
где К(у) — так называемая функция Колмогорова; принтом
прикидки скорости сходимости в (1) показывают, что пре-
дельным соотношением (1) можно пользоваться на правах
точного выражения, начиная с п порядка нескольких десят-
ков.
Заметим, что использование статистических критериев,
основанных на (1) (либо на точном распределении
sup |F„(x) — F(x)| при данном п), требует знания теоретн-
X
ческой функции распределения Г(х). В приложениях чаще
встречается случай, когда теоретическая функция распре-
деления известна с точностью до параметров. Например,
мы довольно охотно пользуемся предположением о том,
что функция Г(х) = Ф((х—а)/о) отвечает нормальному за-
кону с параметрами а и в, где апо неизвестны. Если в
(1) в качестве функции F(x) брать Ф((х—а)/о), где а заме-
няется на х, а о—на $, причем хит получаются по той
же выборке, что и функция Fn(x), то утверждение (1)
становится неверным. (Вместо К(у) в правой части (1)
нужно брать другой закон, вообще говоря, зависящий от
предположения о виде распределения F(x); в настоящее
время эти законы известны, но нам не понадобятся.)
Все-таки встречаются и случаи точно известного F(x}. Два
таких случая мы и рассмотрим.
1.2. «Об одном новом подтверждении законов Менделя».
Так называется одна из работ Колмогорова, опубликованная
в 1940 г. в Докладах АН СССР (в отделе биологии); она пе-
реиздана в [23]. Речь идет о печально знаменитой дискуссии
по вопросам генетики. Рассматривается простейший случай
расщепления признака: существует доминантная форма А
и рецессивная форма а. Сначала получаются две чистые ли-
нии с генотипами АА и аа. Эти линии принудительно скрещи-
ваются н дают смешанную линию — потомство с генотипом
Аа. Потомки скрещиваются свободно и дают второе поколе-
ние, в котором возможны сочетания генотипов
АА, Аа, аА, аа.
В генотипе признак а проявляется только при геноткк.е аа,
т. е. с вероятностью 1/4.
Например, желтый цвет семян гороха А является доми-
нантным по отношению к зеленому а. В смешанной линии все
семена будут желтыми. Если теперь эти желтые семена вы-
сеять и дать растениям свободно опыляться, то среди потом-
ства желтых горошин будет примерно 1/4 зеленых, или отно-
шение числа желтых горошин к числу зеленых будет состав-
лять примерно 3:1. Так и получилось в опытах самого
Г. Менделя.
318
К 30-м годам нашего века менделевская теория наслед-
ственности стала общепризнанной; воевать с ней означало
воевать с ветряными мельницами. Но усилиями Т.Д. Лысенко
и его школы эта война состоялась. Следуя А. Н. Колмогоро-
ву, мы рассмотрим две работы: Н. И. Ермолаевой «Еще раз
о «гороховых законах» (Яровизация. 1939. № 2 (23)) и
Т. К. Енина «Результаты анализа расщепления гибридов то-
мата по отдельным семьям» (ДАН СССР. 1939. Т. 24, № 2).
Без сомнения, читатель уже понял по названиям работ и
журналов, кто воюет против менделевской теории и кто ее
защищает. Интересно, что статистический анализ результа-
тов работ переставляет роли: оказывается, что Ермолаева
подтвердила менделевский закон расщепления в отношении
3:1, а у Енина этот закон выполняется слишком точно, сле-
довательно, возбуждает подозрение.
Переходя к изложению работы А. Н. Колмогорова, нач-
нем, во избежание искажения исторической перспективы, с
се § 1 и начала § 2, хотя для дальнейшего изложения нам
этс.т материал не нужен. Здесь закон расщепления призна-
ков в отношении 3:1 выводится, исходя из предположения,
что особь, имеющая генотип Аа, производит равное число га-
мет с генотипом Лис генотипом а, причем любое сочетание
гамет, производимых различными особями, имеет одну и ту
же вероятность дать потомство. Указывается, что эта модель
(следовательно, н закон расщепления в отношении 3:1) мо-
жет нарушаться при неравной жизнеспособности гамет, нали-
чии селективного оплодотворения либо неравной жизнеспо-
собности потомства с различными генотипами. Точка зрения
менделизма, по Колмогорову, состоит в том, что модель рав-
новероятных сочетаний гамет является достаточно хорошим
первым приближением во многих случаях; школа же Т. Д.
Лысенко считает, что селективное оплодотворение и неравная
жизнеспособность играют всюду столь решающую роль, что
мендслевские законы для биологии бесплодны.
Таким образом, в уста Т. Д. Лысенко вкладывается апри-
ори разумная точка зрения. Для автора данной книги это
является загадкой: разве не верно, что школа Т. Д. Лысен-
ко вообще отвергала понятие гена, генотипа и т. д.? Остается
предположить, что «кристаллизация бреда» (это термин пси-
хиатрии) школы Т. Д. Лысенко произошла не к 1940 г., а
позже, скажем, к дискуссии 1948 г.
Опыты времен 30-х годов отличались от классических тем,
что материал рассматривался не целиком, а по отдельным
«семействам». Например, в опытах с томатами «семейством»
называются все растения второго поколения (того, в котором
должно произойти расщепление в отношении 3:1), выросшие
в одном ящике. Каждый ящик засеивается семенами, взяты-
ми из плодов ровно одного растения первого поколения (сме-
319
ванного генотипа Аа). Поскольку число растений з семействе
невелико, частота появления рецессивного признака во мно-
гих случаях весьма заметно отличается от вероятности.
Подход А. Н. Колмогорова состоит в том, чтобы для k се-
мейств численностью щ, п2, .... п*, в которых рецессивный
признак появился соответственно щ, р.2... р* раз, составить
значения
Vnipq
2
4 ’
1
р=7
9
имеющие приблизительно нормальное распределение с пара-
метрам:! (О, 1). Из работы Ермолаевой берутся две таблицы,
подходящие для такой обработки (надо сказать, что общий
стиль работы — гнусный, а оформление с профессионально-
статистической точки зрения — весьма небрежное). В резуль-
тате возникают два варианта эмпирической функции распре-
деления, показанные (вместе с функцией Лапласа на
рис. 3, а, б. (Слишком мелкий рисунок в оригинале не допус-
кает хорошего качества копирования.) Совершенно ясно,
что отклонения р., от npi в основном, прекрасно объясняется
схемой Бернулли и нормальным законом. Объективный спо-
соб оценки, например, вычисление статистики Колмогорова
К'' sup |Fn(x) — F(.r)|. Вероятность получить лучшее согласие
(т. е. меньшее, чем фактически полученное, значение этой
статистики) равно в случае а) 0,49, а в случае б) — 0,37.
Отсюда А. Н. Колмогоров делает вывод, что получилось подт-
верждение закона Менделя.
Конечно, в целом этот вывод совершенно правилен. Всерь-
ез говорить о том, что из данных Ермолаевой можно извлечь
какие-то выводы, не согласные с законами Менделя, нельзя.
Но с учебной целью мы сейчас поупражняемся в анализе
таблиц Ермолаевой так, как если бы к этому источнику мож-
но было относиться серьезно. Прежде всего на обоих
рис. За, б, показаны наблюдения —3. Вероятность попа-
дания каждого отдельного щ в эту область есть 0,0014. Но
поскольку на рис. а и б представлено примерно по сотне на-
блюдений (в случае а — 98, в случае б — 122 наблюдения),
то вероятность появления хотя бы одного ц i в этой области
примерно в 100 раз больше, т. е. 0,14. Но два случая из двух
имеют вероятность (0,14)2«0,02, что уже статистически зна-
чимо. Имея такое подозрение, целесообразно обратиться к
первоисточнику.
В первоисточнике мы видим прежде всего, что многие се-
мейства крайне малочисленны: единицы или первые десятки
наблюдений. Нормальная аппроксимация для числа успехов
должна быть очень грубой. Нужна некоторая отвага, чтобы
320
Рис. 3. Подтверждение законов Менделя по данным Ермолаевой
(источник: [23})
воспользоваться нормальным законом; единственное оправда-
ние этой отваги состоит в полученном А. Я. Колмогоровым
результате.
Некоторые номера семейств у Ермолаевой пропущены.
Поэтому там, где она считает, что семейств 100, их на самом
деле 98; в другой таблице Ермолаева считает 127 семейств;
Колмогоров ехидно замечает, что там их 123, а на самом де-
ле их все-таки 122. (Это пишется для того, чтобы читатель
понял, что верно сосчитать какие-то предметы до ста не так
уж просто.)
В одной таблице имеется результат расщепления 0:17, в
другой — 0:10 (вместо ожидаемого соотношения 3:1), вероят-
ности которых суть соответственно 4~17 и 4_,°. При примерно
200 наблюдениях такое произойти не может. Иными слова-
21-2567 321
ми, если бы таблицы Ермолаевой заслуживали доверия, то
на основании их, несомненно, должен был бы быть постав-
лен вопрос об отклонениях от закона Менделя.
Во всяком случае в начале своей работы А. Н. Колмогоров
весьма правильно оценил закон Менделя как некоторое ра-
зумное приближение.
В работе А. Н. Колмогорова подробно не анализируется
работа Т. К- Енина «Результаты анализа расщепления гибри-
дов томата по отдельным семьям» АН СССР. 1939. Т. 24,
№ 2, причина чего может состоять в том, что сравни-
тельно малое количество семейств Енина неудобно анализи-
ровать с помощью распределения Колмогорова, а может со-
стоять и в нежелании А. Н. Колмогорова компрометировать
верную точку зрения менделизма. С учебной целью приведем
этот анализ.
У Енина 2 серии наблюдений по срокам посева: в одной
11, в другой 14 семейств, но сами семейства имеют много
(сотни) наблюдений, так что здесь применимость нормально-
го закона вне сомнения. Бессмысленно было бы вычерчивать
гистограммы (для величин ц ) при таком числе наблюдений,
но эмпирические функции распределения (в нормальном мас-
штабе) выглядят достаточно интересно и приведены на рис. 4
(одно наблюдение из первой серии, равное (—2, 4) на ри-
сунке не поместилось). Теоретическая функция Ф(л') изобра-
жается биссектрисой координатного угла.
Для первого срока посева эмпирическая функция распре-
деления расположена левее и выше теоретической и неплохо
сглаживается на глаз прямой линией, параллельной Ф(х).
Речь, таким образом, идет о сдвиге функции распределения;
если же речь вдет о сдвиге, то нужно пользоваться статисти-
ческими критериями, основанными на выборочном среднем.
Оно равно (—0,64); близкое значение получается и по черте-
жу. Дисперсия выборочного среднего есть 1/V11=0,30, т. е.
отклонение (превосходящее по модулю «два сигма») является
высоко статистически значимым. Применяя же таблицу для
распределения статистики sup |Fn(x)—F(x)l прн n=l 1, нахо-
дим весьма умеренную значимость (>20%). Как всегда,
разные статистические критерии не вполне согласуются друг
с другом.
Насколько сильным должно быть отклонение от закона
Менделя, чтобы объяснить полученный результат? В нашем
понимании закон Менделя выглядит так: «испытания Бер-
нулли с вероятностью успеха р=1/4». Отклониться от этой
гипотезы можно весьма различными способами: сказать, что:
1) нет статистического ансамбля (тогда нечего говорить о те-
ории вероятностей) или 2) нет статистической независимости
отдельных испытаний (тогда мы не сумеем сказать, какова
322
Рис. 4. Неудачная попытка подтверждения законов Менделя (ис-
точник данных н объяснения см. в тексте)
должна быть зависимость) и т. д. Все эти способы бессодер-
жательны; мы поэтому остановимся на простейшем способе:
скажем, что 3) есть испытания Бернулли, но с вероятностью
успеха р=ро+Лр, где р0=1/4, Др — некоторая добавка. До-
статочно ли, чтобы Др составляло 1/10 от ро: Др=—1/40,
чтобы объяснить полученный в опыте результат?
Такое значение Др крайне мало меняет дисперсию на-
блюдений (1*- изменится лишь математическое ожидание
примерно на величину п^р/у ntpn(l—ре). Полагая, что п>
>200 (лишь в одном наблюдении первой серии п» 100,
а в остальных больше 200), найдем, что сдвиг математи-
ческого ожидания составит примерно ЗОДр, т. е. величи-
на Др=—1/40 вполне объясняет смещение (—0,64).
21е 323
В работе Енина есть н некоторое объяснение результатов
эксперимента: при первом посеве в теплице в феврале расте-
ния страдали ет недостатка тепла и света; часть семян по-
гибла. Возможно, что растения с рецессивным признаком
имели меньшую (всего лишь на 10%) вероятность выжива-
ния. (Чтобы это утверждение было убедительным, нужно бы-
ло бы проверить его в специальном эксперименте.) Таким
образом, данные первой серии можно рассматривать как не-
кое неполное подтверждение закона Менделя.
Обратимся теперь к данным по второму сроку посева.
Соответствующая эмпирическая функция распределения
проходит близко к началу координат, по-видимому, пло-
хо сглаживается прямой линией (это субъективное впе-
чатление автора), но во всяком случае имеет гораздо
больший наклон, чем функция Ф(х). Чтобы подтвердить
это глазомерно наблюдение статистическим критерием,
14
достаточно вычислить статистику S* = 2 (и-*)*» которая
Z-1
теоретически имеет распределение хи-квадрат с 14 степе-
нями свободы. Вычисление дает S’= 2,85, что почтя не-
возможно при указанном теоретическом распределении.
Значение статистики sup |Fn(x)—F(x)| равно 0,33, что
X
при .'1=14 значимо примерно на 5%-м уровне.
Комбинация незначимого смещения с большей близостью
к нулю значений щ, чем полагается по закону Менделя, на-
водит на мысль о подтасовке результатов. Истину теперь вы-
яснить невозможно, нс су^-сгвует предположение о том, что
в работе Енина приведены не все экспериментальные резуль-
таты. По-видимому, это предположение должно относиться
лишь ко второй серии опытов.
Резюмируем наше обсуждение. Статистические приемы (в
данном случае — критерий Колмогорова) являются тонким
средством анализа экспериментального материала (даже при
сравнительно небольшом числе наблюдений). В материале
открываются такие свойства, которые совершенно не соответ-
ствуют намерениям авторов этого материала. (Аналогично,
рассматривая, например, материалы аварийной статистики,
можно открыть чисто вероятностными средствами, что эти
материалы неполны или вообще недостоверны.) С другой
стороны, применение вероятностных методов имеет свои ус-
ловности; как и всякая наука, математическая статистика не
дает нам в готовом виде объективной истины, и результаты
применения ее методов должны интерпретироваться в согла-
сии со здравым смыслом.
1.3. Атомные массы химических элементов. Мы иллюст-
рируем с помощью эмпирической функции распределения
324
старую проблему атомных масс химических элементов. Ис-
точником для нас будет уже цитировавшаяся прекрасная по-
пулярная книга М. П. Бронштейна [5]. В ней (после изложе-
ния истории определения атомных масс) приводится совре-
менная таблица, по поводу которой автор замечает, что
очень многие атомные массы близки к целым числам. Мы по-
нимаем теперь, что та атомная масса, которую получают в
своих опытах химики, зависит от пропорции, в которой в при-
роде смешаны изотопы данного элемента. Казалось бы, для
дробных долей атомных масс должно было бы выполняться
равномерное распределение на отрезке [0, 1].
На рис. 5 приведена эмпирическая функция распределения
для выборки, полученной следующим образом. Из 104 хими-
ческих элементов мы исключили элементы с целочисленными
атомными весами, а также кислород, атомный вес которого
равен 15,9994 (близость этого числа к целому связана с вы-
бором единицы измерения атомного веса — углеродной еди-
ницы). Осталось л=86 элементов, дробные части атомных
весов которых мы и рассматривали как выборку. На рис. 5
приведена и теоретическая функция равномерного распреде-
ления. Значение статистики Колмогорова Vn sup |Гя(х)—F(x)|
X
равно 2,5. Это высокозначимое отклонение. Особенно много
325
дробных атомных весов имеют значения, близкие к единице.
Так, в интервале [0,9; 1] заключены 32 элемента выборки
(при ожидаемом числе 8,6). При проверке критерием хи-
квадрат соответствующий член суммы дает очень большое
значение 63,9. Таким образом, равномерного распределения
дробных долей атомных весов нет.
Как интерпретировать это наблюдение? Конечно, доволь-
но трудно представить себе статистический ансамбль экспе-
риментов, в каждом из которых возникает то или иное соот-
ношение изотопов данного химического элемента в земной ко-
ре (следовательно, и дробная доля атомной массы). Но на
поверхности многих весьма сложных явлений часто возни-
кает случайность. В данном случае это не так: простейшей
формы случайности в виде равномерного распределения дроб-
ных долей нет. Вероятностный метод всего лишь помогает
придать наукообразную форму замечанию автора книги [5] о
том, что многие атомные веса близки к целым числам. Поста-
новка вопроса о том, почему здесь нет чистой случайности,
делается более обоснованной. (Автору данной книги неизвест-
но, существует ли ответ на этот вопрос в какой-либо форме.)
§ 2. Дискриминантный анализ
Применения многомерного статистического анализа мы
иллюстрируем данными знаменитого Фрэмингемского иссле-
дования факторов риска ишемической болезни сердца
(ИБС). Фрэмингем (Framingham) — это небольшой город в
США, население которого удалось убедить принять участие
в некотором массовом и продолжительном медицинском об-
следовании. Цель обследования — прояснить факторы риска,
связанные с ИБС.
Согласно [55] к ИБС относились случаи инфаркта миокар-
да, коронарной недостаточности, грудной жабы и смерти от
нарушений коронарного кровообращения. Известно, что ИБС
является одной из основных причин смерти, а кроме того, час-
то поражает людей, еще находящихся (в других отношениях)
в расцвете жизненных сил.
Существуют определенные представления (качественно,
несомненно, верные, но в количественном отношении весьма
смутные) о роли факторов жизни современного индустриаль-
ного общества в развитии ИБС (малая физическая актив-
ность, нервно-эмоциональный стресс, употребление наркоти-
ков, в частности наиболее массовая наркомания — курение,
нерациональное питание и т. д.). Многие из этих факторов
количественно вообще не выражаются. Поэтому представля-
ют интерес другие факторы, хотя лишь косвенно связанные
с факторами современной жизни (в том, например, смысле,
что человеку, желающему снизить риск ИБС, не вполне по-
32в
нятно, как воздействовать на эти новые факторы), но зато
объективно измеряемые.
В конце концов авторы работы [55], о которой идет речь,
остановились на следующих семи факторах:
1) возраст (в годах), конечно, фактор первостепенной
важности;
2) содержание холестерина в сыворотке крови (мг/100мл);
3) систолическое кровяное давление (мм. рт. ст.);
4) относительный вес (т. е. вес тела, выраженный в про-
центах по отношению к среднему весу для соответст-
вующего пола и роста);
5) содержание гемоглобина в крови (г/100 мл);
t<) курение, кодируемое следующим образом:
О — для некурящих;
1 — для выкуривающих менее одной пачки сигарет в
день;
2 — одна пачка сигарет в день;
3 — более одной пачки сигарет в день;
7) электрокардиограмма (ЭКГ), кодируемая следующим
образом:
О — нормальная;
1 — с выраженными отклонениями (точно перечисляе-
мыми в работе [55]).
Фактический материал работы [55] охватывает 12-летние
наблюдения над лицами, которые в начале обследования име-
ли возраст в пределах 30—62 года и не были больны ИБС.
Таких оказалось 2187 мужчин и 2669 женщин. В течение
12 лет наблюдения ИБС обнаружилась у 258 мужчин (11,8%)
п у 129 женщин (4,8%). (Давно известно, что женщины бо-
леют ИБС значительно реже, чем мужчины.) Каждый чело-
век, охваченный обследованием, характеризуется вектором
x=(xit значений семи факторов в начале обследования
и фактом заболевания ИБС в течение последующих 12 лет.
Желательно выявить связь между значениями факторов
хи ...,х7 и вероятностью возникновения ИБС.
Понятно, что никаких методов, кроме чисто статистичес-
ких, для решения этой задачи не существует. Если бы речь
шла об одном факторе, то медики, в общем, удовлетворились
бы следующим подходом.
Разобьем область возможных значений фактора на три
части: «мало», «средне» и «много». Для каждой группы зна-
чений возьмем частоту возникновения ИБС; если при этом
окажется, что эти частоты статистически значимо возрастают
с повышением уровня фактора, то вопрос решен: фактор дей-
ствительно является фактором риска. Если факторов два, то
устраивают двумерную классификацию: составляют, напри-
мер, девять групп, комбинируя «мало», средне», «много»,
одного фактора с теми же вариантами для другого.
327
Но при увеличении числа факторов подобный подход гу-
бит любые усилия по сбору фактического материала. Напри-
мер, при 7 факторах получим 37=2187 групп, т. е. примерно
по одному наблюдению на группу и по 1/10 случая ИБС на
группу. Ни о какой оценке вероятности заболевания речи
быть не может.
Поэтому нри значительном числе факторов требуется
принципиально иной подход. В наиболее общей форме его
можно сформулировать следующим способом. Допустим, что
вероятность заболевания есть функция <р(у) от линейной
комбинации факторов у—Ъсш, где функция <р(у) монотонно
меняется от 0 до 1, когда у меняется от (—оо) до оо. Коэф-
фициенты at предстоит найти по фактическим данным так,
чтобы зависимость вероятности заболевания от линейной ком-
бинации была возможно более выраженной.
Последним словам нужно придать точный смысл, заодно и
указать способ нахождения а,-. Обе эти задачи авторы работы
[55] решают, привлекая для описания наблюдений модель
многомерного нормального распределения, которая, конечно,
не может выполняться точно хотя бы потому, что некоторые
факторы вообще принимают лишь целочисленные значения.
Точнее говоря, предполагается, что имеются два многомерных
нормальных распределения с одной и той же матрицей ко-
вариаций, но с различными векторами средних: одно соот-
ветствует совокупности «случаев», т. е. тех лиц, ко-
торые в последующие 12 лет заболеют ИБС; другое — сово-
купности «не-случаев» (т. е. тех лиц, которые не заболеют
ИБС). При этом векторы средних оцениваются, естественно,
как средние арифметические по группам «случаев» и «не-
случаев», а общая матрица ковариаций — как средневзве-
шенная выборочная матрица ковариаций по группам «слу-
чаев» и «не-случаев» (с весами, пропорциональными числу
наблюдений).
Посмотрим, к какой математике ведет эта модель. Пусть
вероятность «случая» есть р; тогда вероятность «не-случая»
есть 1—р, пусть при этом плотность распределения вероят-
ностей вектора факторов есть fi(xi, ...,х*) для «случаев» и
fo(xi, ...,хл) для «не-случаев». Тогда по формуле Байеса ве-
роятность того, что лицо с вектором факторов х=(хь—.*0
есть «случай», дается формулой
P(xv хк)----------------..........-------------=
.....х*)+(1-д)/о(Х1...**)
= 1 /\ 1 .................*»)1
/ [ Р М*1, •••.**)]'
328
Пусть теперь f0 и Л — нормальные плотности
1 exp I —(С '(х~а<0.
(2K)"/2KdetC I 2
-----L—_ expl-Cr1^). ^)1
(г^У det с 1 2 I
с одной и той же матрицей ковариаций С.
Тогда, очевидно,
1—
Р
х»)
X»)
= ехр
где а и р, понятным образом выражаются через р, оо, ai, С~1.
Таким образом,
Р(хр . .
,xft)=l
1 4- ехр
(1)
Выражение (1) как функция от переменных xi,...,Xk называ-
ется многомерной логистической функцией. Практически при-
ходится вместо р, а3, at, С-1 пользоваться их выборочными
оценками, т. е. в (1) войдут оцененные значения а, £ь
Теперь рассмотрим некоторые результаты работы [55].
Если вставить в (1) оцененные значения а и р, то для
каждого обследованного можно получить значение рИС-
ft
ка: у = a + 30Л- Упорядочим полученные значения у по ве-
Г"1
личине и разобьем их на 10 равных по численности групп,
называемых децилями: в первую группу войдет 10% лиц,
имеющих наименьшее значение риска, во вторую группу 10%
лиц, имеющих несколько большие значения риска, и т. д. Для
каждой группы можно подсчитать ожидаемое значение числа
«случаев» (суммируя для этой группы значения 1/(1+ег'»))
и сравнить его с фактическим. Результаты приведены в сле-
дующей табл. 1.
Несмотря на очевидное невыполнение предположения мно-
гомерной нормальности, согласие между ожидаемыми и фак-
тическими численностями «случаев» неплохое. Это объясня-
ется тем, что при группировке на основании риска (значения
329
Таблица 1
Ожидаемые и фактические численности случаен ИБС по децилям риска
2187 мужчин 2669 женщин
Леииль риска Ожилае- мое Фактическое Ожидаемое Фактическое
ЧИСЛО случаев % заболе- ваемости число случаев % заболе- ваемости
10 90,5 82 37.5 70.4 54 20,2
9 47,1 44 20.1 24,7 23 8.6
8 32,6 31 14.2 15.0 21 7.9
7 25,0 33 15.1 9,8 14 5.2
6 19,7 22 10,1 6.5 5 1.9
5 15,0 20 9.1 4.4 6 2.2
4 11,5 13 5.9 3.2 2 0.7
3 8,6 10 4.6 2.3 0 0
2 6,0 3 1.4 1.7 3 1.1
1 3,4 0 0 1.1 1 0.4
Всего 259,4 258 11,8 139,1 129 4.8
некоторой линейной комбинации факторов) для применения
логистической функции нужно лишь чтобы значения этой ли-
нейной комбинации давали нормальное распределение (с рав-
ной дисперсией по группам «случаев» и «не-случаев»). Ко-
нечно, линейной комбинации значений факторов легче иметь
нормальное распределение, чем отдельным факторам. Пора-
жает в табл. 1 чрезвычайно сильная зависимость вероятности
заболевания от риска: разница между группой наивысшего и
наинизшего риска — в десятки раз. Конечно, хорошо было бы
часть фактического материала использовать для оценки па-
раметров в формуле (1), а на другой части испытать возмож-
ности получающегося разделения на децили. Но и то, что
предъявлено в работе [55], производит глубокое впечатление.
Например, если мы пытаемся проводить какую-то профилак-
тику ИБС, нужно сосредоточить усилия на одной или не-
скольких группах наивысшего риска; риск же можно оценить
на основании простейших семи параметров.
Теперь посмотрим на сами оценки коэффициентов в фор-
муле (1). Эти данные нужно оценивать следующим образом.
Один год жизни дает увеличение риска для мужчин на
0,0708 (для женщин — очень близкое число). Факт курения
(1 балл, т. е. менее одной пачки сигарет в день) увеличивает
риск для мужчин на 0,3610, т. е., грубо говоря, ускоряет воз-
330
Оценки коэффициенте*
Таблица 2
Мужишы Женщины
Константа —10,8988 —12,5933
Возраст 0,0708 0.0765
Холестерин 0,0105 0,0061
Систолическое давление 0,0188 0,0221
Относительный вес 0,0138 0,0053
Гемоглобин — 0,0837 0,0355
Курение 0,3810 0,0766
ЭКГ 1,0459 1,4338
аикновение ИБС на 5 лет (для женщин лишь на 1 год —
трудно разобраться, есть ли эта разница лишь артефакт ста-
тистического обследования или она отражает существо проб-
лемы курения). Очевиден огромный вес ненормальности ЭКГ,
хотя это явление встречается довольно редко. По гемоглоби-
ну данные для мужчин и женщин противоречивы; по-видимо-
му, влияние этого фактора сомнительно. Для понимания
вклада холестерина, систолического давления н относитель-
ного веса нужно знать, насколько вообще могут колебаться
значения этих факторов. Опуская подробности, заметим, что
(согласно [55]) холестерин важен, систолическое давление
несколько менее, а относительный вес маловажен.
Такая же картина неплохого согласия ожидаемых числен-
ностей «случаев» с фактическими при очень сильной зависи-
мости вероятности заболевания от риска характерна для
различных разбиений фактического материала: по возраст-
ным группам и по уровням отдельных факторов риска. Та-
ким образом, дискриминантный анализ, основанный на гипо-
тезе многомерной нормальности, оказывается полезным ору-
дием для анализа факторов риска.
Отметим, однако, что все эти результаты не годятся для
целей индивидуального прогноза. Одно дело — совет врача:
«у Вас риск ИБС повышен; постарайтесь изменить свой об-
раз жизни»; другое дело — индивидуальный прогноз: будет
ли в ближайшие 12 лет ИБС у данного пациента или нет.
Даже в группе наивысшего риска табл. 1 частота возникно-
вения ИБС составляет 37,5%; поэтому, даз для пациентов
этой группы плохой прогноз, мы ошибемся в 62,5% случаев.
Для групп меньшего риска мы должны, очевидно, дать бла-
гоприятный прогноз; при этом 258—82=176 случаев, или
331
71%, произойдут тогда, когда обещали, что ИБС не будет.
Впрочем, и само собой понятно, что задача индивидуального
прогноза на такой срок, как 12 лет, далеко выходит за рамки
возможностей медицины, хотя бы и подкрепленной статисти-
ческими исследованиями.
§ 3. Метод наименьших квадратов
3.1. Введение. Метод наименьших квадратов мы иллюст-
рируем конкретным материалом по надежности электричес-
кой изоляции, в обработке которого автор книги принимал
непосредственное участие; не потому, чтобы метод наимень-
ших квадратов на этом материале применялся особенно изящ-
но с математической точки зрения (ои абсолютно не изящен),
а потому, что здесь автор лучше разбирается в особенностях
практических применений.
Речь идет о так называемой главной статорной изоляции
крупных генераторов (крупных — это значит мощностью от
10 до 1000 МВт). Современные крупные генераторы устрое-
ны так, что большие токи и высокие напряжения возникают
в них в обмотке статора. «Обмотка» эта делается не из вит-
ков проволоки, а из довольно толстых медных стержней,
каждый из которых набирается из отдельных («элементар-
ных») проводников. Элементарные проводники также изоли-
руются друг от друга специальной «изоляцией элементарных
проводников» (наподобие витковой изоляции малых машин),
а весь стержень в целом изолируется от стали статора глав-
ной изоляцией. Как и в малых машинах, пробой изоляции
может начаться с повреждения изоляции элементарных про-
водников, привести к их нагреву и далее к прожиганию глав-
ной изоляции. Комиссиям, расследующим причины аварий,
иногда удается это обнаружить; но никто не знает — всегда
ли. Для нас наблюдаемым фактом является повреждение
главной изоляции. На такое повреждение должна реагиро-
вать система зашиты, которая отключает генератор, останав-
ливает турбину (паровую или гидро-), стравливает в атмо-
сферу пар из котла и т.д. Возможно при этом и развитие ава-
рии (например, на атомных станциях нужно остановить и ре-
актор, но если ядерную реакцию можно остановить быстро,
то этого нельзя сделать с искусственной радиоактивностью, и
надо предусмотреть специальные системы, которые позволя-
ют куда-то деть тепло, выделяющееся за счет искусственной
радиоактивности, н т. д.). Проблем развития аварии мы не
рассматриваем.
Л. А. Белова собрала данные об авариях, сопровождав-
шихся повреждением изоляции, практически по всем круп-
ным генераторам Советского Союза, начиная примерно с
1928 г. В 1963 г. автор книги был приглашен ею для уч ас-
332
тия в статистической обработке (а автор в это время только
что кончил математическую аспирантуру и в практических
вопросах ничего не понимал). Но простейшая схема теории на-
дежности, когда показатели надежности рассчитываются на
одно изделие, т. е. в данном случае на один генератор, все-
таки показалась автору неприменимой. Крупные генераторы
(как, наверно, и любые крупные машины) слишком различны
по габаритам и мощности, чтобы считать их элементами од-
ного статистического ансамбля. Производство их является
мелкосерийным: если имеется несколько десятков идентичных
машин (одного конструктивного типа), то это уже очень мно-
го. Если вести раздельную обработку данных по конструктив-
ным типам, то всю совокупность аварий мы разделим на мел-
кие группы (от нескольких единиц до немногих десятков ава-
рий в группе) и богатый статистический материал не получит
единой обработки. Короче говоря, нужно было какое-то хоть
приближенно верное теоретическое представление (оно в дан-
ном случае называется статистической моделью), которое поз-
волило бы обработать совместно данные по всем авариям.
Возникла довольно легкомысленная статистическая мо-
дель, в которой количество аварий подчиняется закону Пуас-
сона, параметр которого X зависит лишь от площади изоля-
ции машины S и срока ее работы Т (учитывается лишь рабо-
чее время). Формулой это записывается так:
т
\ = S\h(t)dt, (1)
6
где S — площадь изоляции машины (удобная единица изме-
рения 100 м2 — это по порядку величины площадь изоляции
одной крупной машины), h(t) — известная в теории надеж-
ности функция, называемая интенсивностью отказов, Т —
время эксплуатации машины. Было еще предположено, что
количества аварий данной машины на непересекающихся про-
межутках времени — независимые случайные величины (в
терминах теории надежности это означает, что поток отказов
является простейшим пуассоновским потоком, возможно, с
переменной интенсивностью). Понятно, что если нужно опи-
сать распределение числа аварий по какой-то группе машин
(за какие-то интервалы времени, возможно, различные для
разных машин группы), то следует просто просуммировать
соответствующие пуассоновские параметры для отдельных
машин. Нужно только более или менее точно определить
функцию h(t) по статистическим данным (для этого и потре-
буется метод наименьших квадратов).
Против модели (1) можно выдвинуть ряд возражений,
которые лишь постепенно становились ясными ее авторам.
ззз
Однако, работая с этой моделью более 25 лет, мы не нашлв
ни нужным, ни возможным ее принципиально изменить
(принципиально — значит включить другие факторы, кроме
$ и Т). Между прочим поскольку энергетика развивается ес-
ли и не по экспоненте, то все же довольно быстро, за эти
25 лет фактический материал многократно возрос (по срав-
нению с имевшимся в 1963 г.). Поэтому возможность сохра-
нить модель (1) нельзя объяснить ничем другим, как тем,
что новичкам вообще везет. Однако все эти 25 лет происхо-
дила борьба за то, чтобы реальную статистически неоднород-
ную изоляцию можно было с пользой сравнивать с матема-
тической моделью, в которую закладывается предположение
статистической однородности (поскольку иным способом ду-
мать о случайных явлениях наука вообще не умеет).
Чтобы обрисовать общую ситуацию, объясним подробнее,
почему модель (1) является легкомысленной.
Начнем с того, что при работе генератора вовсе не вся
изоляция находится под номинальным напряжением. Напря-
жение равномерно распределяется по длине обмотки ст ну-
левого до номинального; причем же тут общая площадь изо-
ляции? Но на самом деле это не возражение, поскольку во
всех машинах под напряжением, составляющим данную до-
лю номинального, находится строго одинаковая часть изоля-
ции, и модель (1) сохраняется.
Пойдем чуть дальше: всякий стержень обмотки имеет па-
зовую часть (которая лежит в пазу активной стали) и лобо-
вую часть (которая находится в воздухе и служит лишь для
соединения стержней между собой; между прочим, именно
соединения стержней обмотки составляют единственную хит-
рую и сложную вещь в электрической машине). Изоляция
лобовых частей работает в гораздо более легких условиях,
чем изоляция пазовых частей; фактические данные показыва-
ют, что отношение площадей изоляции лобовых и пазовых
частей сильно колеблется для разных конструктивных типов
машин. Мы получили принципиальное возражение; ответ ста-
тистика на него состоит в том, что статистическую неоднород-
ность аварий изоляции разных машин никогда'не удавалось
объяснить различием в соотношении площадей пазовых и ло-
бовых частей.
Далее, условия эксплуатации различных машин различны.
Например, особое внимание привлекал вопрос о так называе-
мых профилактических испытаниях. Дело в том, что маши-
ны время от времени выводятся в ремонт (примерно раз в
3 года). Хорошо было бы выявить во время ремонта ослаб-
ленные места в изоляции, чтобы заменить соответствующие
стержни и не допустить аварий во время работы машины (в
частности, вполне бы отпала возможность развития аварии).
Никакой дефектоскопии иа этот счет нет, кроме следующей:
334
приложить к обмотке повышенное испытательное напряже-
ние. Точных норм на этот счет нет, н одни машины испыты-
ваются, скажем, напряжением 1,3 номинального, а другие —
напряжением 1,7 номинального. При повышении испытатель-
ного напряжения число пробиваемых стержней резко растет;
хотелось бы думать, что машины, испытанные более высоким
напряжением, будут надежнее в эксплуатации. Тогда и в мо-
дель (1) надо ввести (не очень понятно, как это сделать) ус-
ловия профилактических испытаний.
Но в действительности оказалось (насколько можно было
заметить), что по статистическим данным нет разницы меж-
ду аварийностью (в работе) машин, испытанных разным ис-
пытательным напряжением (при ремонте). Однако, по нашим
данным, если профилактическая роль испытаний незаметна,
то весьма заметна их диагностическая роль: те машины, ко-
торые больше повреждаются в работе (чем это полагается
для статистически однородной совокупности), больше повреж-
даются и при испытаниях. А поскольку пробоев при испыта-
ниях гораздо больше, чем аварий в работе, получаем ценный
источник информации о состоянии изоляции (к сожалению,
исследование этой проблемы не доведено до конца).
Короче говоря, модель (1) может быть лишь более или
менее грубым приближением к действительности, хотя те или
иные делаемые против нее возражения могут и не быть осо-
бенно весомыми при фактической проверке.
3.2. Применение метода наименьших квадратов. По ста-
тистической науке полагается дать какой-нибудь параметри-
ческий вид функции h(/), например *,й (/) =a+bt2 с неизвест-
ными параметрами а и 6; записать функцию правдоподобия,
т. е. плотность вероятности для результатов наблюдений (ре-
зультатами наблюдений являются моменты аварий на каждой
из рассматриваемых машин либо указание, что на данной ма-
шине аварий не было), и найти оценки а и b из условия мак-
симума функции правдоподобия. Можно прикинуть и распре-
деление оценок а, Ъ, в частности возможную величину разнос-
тей а—а, b—Ь. Но в 1963 г. возможностей выполнить такие
вычисления не было: позже же стало понятно, что ошибки
при определении а и b будут определяться не свойствами
оценок максимального правдоподобия, а степенью нарушения
статистической однородности изоляции (для тех машин, ко-
торые включены в расчет), т. е. вещью совершенно неизвест-
ной (можно вспомнить про доверительные интервалы, не за-
служивающие доверия, описанные в гл. 2).
* После некоторых пробных обработок материала стало ясно. vto он
не допускает определения более двух параметров в выражении для функ-
ции, поэтому брался многочлен второго порядка без линейного члена.
335
Поэтому мы остановились на грубо приблизительном ме-
тоде наименьших квадратов. Дискретизуем значения времени
t (удобный шаг />+1—f<=1044 рабочего времени, что соответ-
ствует примерно полутора календарным годам эксплуата-
ции). Будет неплохо, если мы будем знать величины
*z-i
которые практически (из-за малости величин р,) совпадают
с вероятностями аварии единицы площади изоляции при экс-
плуатации ее в интервале рабочего времени [/,-ь Л] (причем
/о=0).
Теперь организуем обработку фактических данных сле-
дующим образом: пусть в интервале [Z,-i, /,] прошли эксплуа-
тацию машины с общей площадью изоляции Si, причем прои-
зошло аварий. Тогда оценкой величины р,- является pi/Si—
частота аварий. Если будем считать, что р, гладко зависят
от I, то мы сумеем увеличить точность определения отдель-
ных значений pi за счет сглаживания частот p,i!Si методом
наименьших квадратов.
Изложим результат по работе [51] 1965 г. В этой работе
применена маленькая премудрость, вызванная страхом перед
неизвестностью весов (или дисперсий отдельных наблюде-
ний) в методе наименьших квадратов; действительно,
D(p,/S/= (D|a/)ZS2«P//S/ зависит от неизвестного pi. Следо-
вало попросту как-нибудь сгладить pi (хоть от руки), исполь-
зовать сглаженные значения для определения весов и про-
вести метод наименьших квадратов с этими весами. Вместо
этого применяется более сложный прием — преобразование,
выравнивающее дисперсии:
H/S( -»2 arcsin V^IS-, « 2
сглаживаются величины 2Vpi*-|Sz, имеющие примерно рав-
ные дисперсии, и производится обратное преобразование.
В конце концов возникает гладкая зависимость от i.
При замене переменной x=x/=i/22 (22 интервала по 104 ч
каждый дают максимальный срок эксплуатации 220000 ч)
окончательно получается следующий ответ:
а) для турбогенераторов напряжением 10,5 кВ
Pi • p(Xi) = 0,010 + 0,024x2 + 0,014л4;
б) для турбогенераторов напряжением 6,3 кВ
А = Р(х,) = 0,007 + 0,034x3 + 0,037х«;
336
в) для смешанной группы всех напряжений (6,3; 10,5;
13,8; 15,75; 18 кВ.)
Pi=р(х() = 0,010 + 0,019*2 + 0,010х*.
При этом в каждом случае а), б), в) методом наименьших
квадратов определялись два параметра (т. е. величины
2 j/S, сглаживались многочленом а+Ьх2 в случаях а) и
в) и многочленом а+Ьх3 в случае б): в случае б) этот мно-
гочлен подошел лучше, чем а+Ьх2). Четвертая и шестая сте-
пени для х получились после обратного преобразования. Кри-
вые для случаев а), б), в) достаточно близки, и в качестве
наиболее точной рекомендуется кривая в). Ей соответствуют
генераторы ссуммарной площадью изоляции Si=962x 100 м2,
$22=30,9 x100 м2, на которых произошло в обшей сложности
90 аварий. В общем, р(х) — это монотонно возрастающая
кривая, изменяющаяся от примерно 0,010 при х, близких к 0,
до примерно 0,040 при х=1. Оценены по порядку величины
и точность определения р(х): на начальном участке (при х,
близких к нулю) это примерно ±0,001, а на конечном участ-
ке (при х, близких к 1) это примерно ±0,02.
Рассмотренная задача отличается от общей задачи мето-
да налменьших квадратов тем, что дисперсия ошибки отдель-
ных наблюдений есть не просто некоторое неизвестное о2. На-
блюдения суть частоты, отвечающие вероятностям р,-; после
определения этих вероятностей дисперсии наблюдений ста-
новятся известными. Поэтому существует статистический кри-
терий для проверки всей концепции: определенным образом
преобразованные квадраты разностей nt/Si—р(х,) должны
дать в сумме случайную величину с известным распределени-
ем. После уточненных подсчетов получается, что фактичес-
кие значения этой величины примерно равны математическо-
му ожиданию этой случайной величины (полученному из тео-
ретических соображений). В целом представляется, что ста-
тистическая обработка вышла неплохо.
3.3. Проблема статистической однородности. С точки зре-
ния инженера, тот факт, что некоторые аварии идеально опи-
сываются такой-то статистической моделью, в сущности, ма-
лоинтересен. Наоборот, если статистическая однородность
нарушена, т. е. есть группы более аварийных и менее аварий-
ных (чем полагается по статистической модели) машин, то
это интересно: можно говорить о выяснении причин, об изме-
нении сложившегося положения и т. д. Рассмотрим вопрос
о статистической однородности изоляции генераторов по ра-
боте [52] 1967 г. В этой работе (после небольших уточнений
зависимости Pi=p(xt)) рассматривается сначала следующий
тест модели.
22—2567
337
Допустим, что зависимость pi=p(xi) определена точно-
Тогда для /-й машины некоторой рассматриваемой совокуп-
ности мы знаем пуассоновский параметр X/ для числа ава-
рий; следовательно, можем рассчитать вероятности Pj(k) то-
го, что на этой машине было ровно k аварий (расчет для
конкретных данных имеет смысл при Л=1, 2, 3, 4). При этом
вероятности Р/(Л) малы; следовательно, общее число машин,
имеющих k аварий (в рассматриваемой совокупности), име-
ет распределение Пуассона с параметром 2Р/(Л).
Если статистическая однородность нарушена таким обра-
зом, что некоторые машины более аварийны, а некоторые —
менее аварийны, то число машин с одной аварией будет мень-
ше (чем полагается по модели), а число машин с двумя, тре-
мя и т. д. авариями будет соответственно больше.
Конкретно в [52] рассматривается 285 турбогенераторов,
на номинальное напряжение 10,5 кВ. Фактические численнос-
ти машин с одной... четырьмя авариями равны
27; 10; 1; 1,
а соответствующие суммы . 4 равны
I
29,6; 5,7; 1,5; 0,44.
Сколько-нибудь значимым является лишь отклонение факти-
ческого значения 10 от математического ожидания 5.7; веро-
ятность такого отклонения есть 0,065. Но если посмотреть на’
это отклонение как на максимальное из 4 отклонений, то со-
ответствующий уровень значимости есть 1—(1—0,065)4«
«0,25, т. е. полученный результат статистически незначим.
Таким образом, достоверные нарушения статистической
однородности рассматриваемым критерием не обнаружены.
Но могут быть сравнительно малочисленные группы гене-
раторов, отклоняющиеся от статистической однородности, не
улавливаемые подобными глобальными критериями. Они не
могут быть выделены чисто статистическими приемами; нуж-
но иметь какой-то содержательный принцип классификации
для их выделения. Для изоляции генераторов таким принци-
пом оказался конструктивный тип.
Для каждого конструктивного типа можно общее числе
аварий для машин данного типа сравнить с его пуассоновс-
ким параметром. Из рассматриваемой совокупности выделя-
ются три типа с более высокой аварийностью:
1) число аварий 5; пуассоновский параметр 0,37;
2) число аварий 9; пуассоновский параметр 2,7;
3) число аварий 9; пуассоновский параметр 2,9.
Возникает, правда, некоторая проблема, связанная с тем, что
при большом числе групп некоторые из них будут иметь чис-
то случайным образом большие расхождения между факти-
338
ческим числом событий и его математическим ожиданием. Но
после подсчета уровней значимости выясняется, что выделен-
ные группы скорее всего реальны. В этих группах 32 маши-
ны (из 285), т. е. нарушение статистической однородности
рассматривается как довольно редкое исключение.
Следовательно, в работе [52] возникает концепция основ-
ной статистически однородной совокупности машин при на-
личии сравнительно немногочисленных исключений.
3.4. Дальнейшая судьба работы. Обратимся теперь к ра-
боте [53] 1979 г. В генераторостроении во второй половине
XX в. происходит если не революция, то во всяком случае су-
щественный прогресс. Вводится водородное и водяное ох-
лаждение вместо воздушного (водородное охлаждение озна-
чает, что герметически закрытый корпус генератора запол-
няется водородом, а водяное охлаждение — это элементар-
ные проводники делаются полыми и по ним циркулирует
охлаждающая вода). Кроме того, разрабатываются новые
виды изоляции: ранее это была микалента; теперь вводится
изоляция на термореактивных связующих. Микалента пред-
ставляет собой ткань, на которую наклеены листочки слюды,
перекрывающие друг друга. Ею оборачивают в несколько
слоев стержень, а потом пропитывают компаундом. Изоля-
ция на термореактивных связующих представляет собой по-
рошок слюды, перемешанный с массой, твердеющей при на-
гревании. Стержень, покрытый такой смесью, нагревают в
специальных формах, получая изолированный стержень.
Совершенствование охлаждения позволяет повысить мощ-
ность машин при тех же габаритах (откуда и берутся «мил-
лионники», т. е. машины мощностью 1000МВт =1000000 кВт).
Термореактивная изоляция в несколько раз надежнее мика-
лентной.
Работа [53] имеет дело с микалентной изоляцией. Если в
1965 г. было 684 генератора с общей площадью изоляции
962 • 100 м2, то теперь рассматривается 1919 генераторов с
площадью изоляции 3434 • 100 м2 (из них 1683 • 100 м2 в воз-
душной среде и 1751 • 100 м2 в водородной среде). Для воз-
душной среды кривые вероятностей по данным 1965 г. и по
данным 1979 г. весьма близки. Что касается водородной сре-
ды, то в ней, оказывается, нет старения изоляции: 0,007.
Эти результаты относятся, однако, к среднестатистическим
группам машин. Имеются еще группы лучших и худших кон-
структивных типов.
Количественно эти выделяющиеся группы немногочислен-
ны: по площади изоляции среднестатистическая группа со-
ставляет 77,6% для воздушных и 72,7% для водородных ма-
шин. Однако по числу аварий на среднестатистическую груп-
пу приходится лишь примерно половина (54,5% для воздуш-
ных и 48% для водородных машин). На худшую группу при-
22* 339
ходится 37,8% аварий для воздушных и 46,5% аварий для
водородных машин. При этом для худшей группы фактичес-
кое число аварий примерно вчетверо превосходит его мате-
матическое ожидание, вычисленное по кривым вероятностей
аварий для среднестатистической совокупности (для лучшей
группы соответственно в два-три раза меньше).
Сама среднестатистическая группа подвергается в работе
дальнейшему тестированию на однородность, которое позво-
ляет бросить определенную тень сомнения: скорее всего ее
однородность лишь приблизительная. Это не лишает опреде-
ленного смысла кривую вероятностей аварий, построенную по
материалу этой группы. Например, сравнивая количество
аварий с его математическим ожиданием, вычисленным по
этой кривой, нетрудно показать, что крайне неудачным явля-
ется сочетание водяного охлаждения и микалентной изоля-
ции: на холодном стержне микалентная изоляция ведет себя
плохо (этот факт, очевидно, трудно было предвидеть зара-
нее).
Но для общих концепций теории надежности отсюда по-
лучается тот вывод, что количественного смысла они скорее
всего иметь не могут. Изоляция, конечно, самый повреждае-
мый элемент генератора, но далеко не единственный. Други-
ми элементами мы не занимались, но в принципе представить
себе такие исследования возможно. Спрашивается, если бы
эти исследования были проведены, то могли бы мы количест-
венно описать вероятностной моделью поток аварий генера-
торов? Пример изоляции говорит, что нет: моделью пуассо-
новского потока с переменным параметром можно в лучшем
случае описать половину аварий изоляции, а другая полови-
на связана со статистической неоднородностью. Эта неодно-
родность неустойчива во времени. (Например, потому, что ма-
шины, плохо показавшие себя во время эксплуатации, рекон-
струируются с заменой обмотки и устранением неудачных
элементов конструкции.) С другой стороны, в процессе раз-
работки новых конструктивных типов машин некоторые де-
тали конструкции могут оказаться неудачными, о чем мож-
но будет узнать только по результатам эксплуатации. Таким
образом, электропромышленность, отнюдь того не желая, все
время рискует подбросить менее надежные конструктивные
типы. В такой динамической ситуации невозможно количест-
венное описание аварийности выделяющихся групп.
Мы вновь приходим к тому выводу, что вероятностные мо-
дели не описывают поведения реальных событий на уровне
количественного соответствия; практически важные выводы из
них должны быть достаточно простыми и грубыми, не боящи-
мися определенной неточности количественного описания
(например, «в водородных машинах нет старения изоляции»,
«недопустимо сочетание водяного охлаждения с микален-
340
той»). Более сложные расчеты характеристик надежности
функционирования электрических машин и систем, требую-
щие количественного описания потока аварий, рискуют ока-
заться необоснованными.
Г Л А В А 4
ПРИМЕРЫ ПРИМЕНЕНИЯ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Во второй части данной книги мы переходили от общедо-
ступных применений теории вероятностей к применениям, до-
ступным для научных сотрудников в тех или иных областях
либо для объединенных усилий математиков и специалистов
других областей. В данной главе мы добираемся, наконец, до
применений, строго говоря, не доступных никому, поскольку
они еще не вполне сложились в науке. Речь идет о зависи-
мых случайных величинах в большом числе, т. е. о случай-
ных процессах.
Теория случайных процессов и ее применения возникли
сравнительно недавно — уже в XX в., так что при изложе-
нии этих вопросов можно себе позволить немного историзма,
не слишком загромождая текст. Основная мысль главы со-
стоит в том, что сначала модели случайных процессов при-
менялись статистиками к изучению динамики тех или иных
экономических показателей. Но аппарат этот по отношению
к экономическим явлениям неадекватен (как, вероятно, и лю-
бой другой математический аппарат). Поэтому хоть офици-
ально и не объявлено, что от применений теории случайных
процессов в экономике ждать особенно нечего, но фактичес-
ки это так. Интерес приложений случайных процессов сме-
щается от экономики (и некоторых других наук) к физике
либо к технической физике, где теория вероятностей вообще
и теория случайных процессов в частности действительно на-
ходят себе разумное поле приложений — либо на научном
уровне, т. е. на уровне количественного соответствия, либо
на натурфилософском уровне, т. е. на уровне качественных
^моделей. Для физики любой из этих уровней по-своему по-
лезен.
Кое-что в этой главе рассмотрено на конкретном уровне,
а кое-что — на обзорном. В частности, на обзорном уровне
рассматриваются замечательная статистическая теория ло-
кального строения турбулентности Колмогорова — Обухова и
ее приложения к вопросам распространения света в атмо-
сфере. Здесь достигнуто определенное количественное соответ-
ствие между вероятностными моделями и действительностью,
341
но созданная наука сложна и представляет не очень широ-
кий интерес. Поэтому ее вряд ли стоит подробно излагать в
элементарном учебнике.
Вопросы прогноза случайных процессов приобрели с лег-
кой руки Н. Винера большую популярность. В данном случае
Н. Винер оказался не прав (а прав А. Н. Колмогоров, кото-
рый в своих работах по прогнозу случайных процессов ни
словом не обмолвился о том, что такой прогноз представля-
ет практическую ценность). По-видимому, ни в каком случае
(даже и для атмосферной турбулентности) прогноз случай-
ных процессов особой практической ценности не представля-
ет. В данной главе вопросы прогноза рассматриваются час-
тично обзорно, а частично конкретно, на примере (неудачно-
го) прогноза колебаний уровня Каспийского моря.
Завершается глава примером из технической физики, в
котором давно известная проблема неустойчивости периодо-
граммы как оценки спектральной плотности предстает в но-
вом обличье: как невозможность (без использования теории
случайных процессов) выполнить некоторые измерения, не-
обходимые для проектирования длинной волноводной линии.
§ 1. Ранние применения теории случайных процессов
1.1. Введение. Полученную в эксперименте запись зави-
симости одной величины от другой (вторую переменную мы
будем называть «временем») можно представлять себе в
двух вариантах: либо это запись самопишущего прибора, ко-
торая в каждой точке довольно неточна, а преобразуется ка-
кими-то аналоговыми средствами, например, фотографичес-
кими; либо это «ряд наблюдений», в котором записываются
пары значений времени и зависящей от времени переменной.
В дальнейшем такие записи преобразуются средствами обра-
ботки дискретной информации. Предполагается, что в этом
случае значения обеих переменных записаны достаточно точ-
но.
В настоящее время основным видом записи информации
является дискретный; даже результаты измерения аналого-
выми приборами преобразуются обычно к дискретному виду
(при выборе достаточно мелкого шага времени). Таким об-
разом, объектом исследования является (конечная, но, воз-
можно, достаточно длинная) последовательность
Xi,X2,...,Xt.................... (1)
где t — целочисленный параметр.
Сложилась не совеем удачная терминология. Обычно по-
следовательность (1) называется «временным рядом», но
этим же термином называется и случайный процесс с диск-
342
речным временем. Однако необязательно связывать любые
-наблюдения с какими-то моделями теории вероятностей. По-
этому самую общую последовательность вида (1) мы пред-
почитаем называть «рядом наблюдений».
Человек анализирует ряды наблюдений совсем не так,
как устройства для переработки дискретной информации.
Приведем для начала очень яркую цитату из работы
Е. Е. Слуцкого — одного из основателей теории случайных
процессов (см. [35, с. 99]).
«Почти все явления хозяйственной жизни, подобно мно-
гим другим процессам: социальным, метеорологическим и
т. д., — протекают во времени чередой подъемов и падений
подобно волнам, бегущим одна за другой. И как на море по-
следовательные волны не повторяют в точности друг друга,
так и здесь соседние циклы никогда не совпадают одни с
другим ни по продолжительности, ни по высоте подъема. И
однако же как там, так н здесь почти всегда сквозь все это
многообразие индивидуальных особенностей более или менее
явственно проступают черты известного единообразия и не-
которой приблизительной правильности. Глаз наблюдателя
совершенно инстинктивно открывает на волнах одного поряд-
ка другие, меньшие волны, так что идея гармонического ана-
лиза... кажется напрашивающейся сама собою».
Какие же существуют математические модели рядов на-
блюдений, позволяющие доказательным образом выявить
волны, которые глаз наблюдателя открывает инстинктивно?
Простейшая модель состоит в том, что в действительно-
сти явление описывается периодической функцией времени
«рСО, но мы наблюдаем эту функцию с ошибками. Тогда мо-
делью ряда наблюдений (1) будет следующая:
Х/«=Ф(0+6ь (2)
тде б/ — ошибка наблюдения в момент t (проще всего, если
{б,} — независимые при различных t и одинаково распреде-
ленные случайные величины).
Некоторая проблема может быть связана с тем, что ис-
тинный период Т функции <р(7) и произвольно выбранная
нами единица времени (шаг дискретизации по I) могут на-
ходиться в сложном отношении друг с другом (например,
быть несоизмеримыми). Но если Г»1, то существует мощ-
ный метод выделения периодической составляющей <р(7) из
наблюдений (2): нужно рассмотреть периодограмму
/().)
х^в™
(3)
343
как функцию от X. При частотах 1, таких, что им отвечают
гармоники е*х<, имеющие период Т (для этого нужно, чтобы
ХТ=2Лл, Л=1, 2,...), эти гармоники будут входить в резо-
нанс с функцией <р(7), н0 не со случайными ошибками бь
Поэтому при XT=2kn периодограмма /(X) будет (как функ-
ция от X) иметь локальные максимумы. Так периодические
составляющие (при достаточно большом числе наблюдений
п) могут быть выделены из столь зашумленных (ошибками
б<) наблюдений, что глаз наблюдателя без обработки ника-
ких периодов не видит. (Вместо функций eiKt могут быть
взяты и другие периодические функции.)
Но для выделения периодической компоненты нужно
прежде всего, чтобы эта компонента существовала. Это оз-
начает, что периоды колебания должны выдерживаться
столь точно, что при большом п за время от 1 до п не про-
исходит заметного сбоя фазы колебаний <р(/): иначе приме-
нение функций ем (либо других строго периодических функ-
ций), которые точно выдерживают фазу колебания, не имеет
смысла.
Классическим примером строго периодического процесса
являются, например, затменные переменные звезды (вокруг
одной звезды обращается другая). Мы не можем разрешить
эти звезды, т. е. увидеть их, как отдельные, а наблюдаем
как бы одну звезду переменной яркости. Но где же в явле-
ниях хозяйственной жизни либо в социальных, метеорологи-
ческих и т. д. найти механизмы, обусловливающие точную
периодичность во времени? (Под метеорологическими явле-
ниями подразумевается не то, что происходит в течение го-
да — тут был бы строго периодический процесс в виде дви-
жения Земли по орбите, а то, что происходит в течение мно-
гих лет.) Кроме того, модель (2) со случайными ошибками
6t, каждая из которых не влияет на дальнейший ход про-
цесса (является в чистом виде ошибкой наблюдений), во мно-
гих случаях уже при глазомерном анализе ряда наблюдений
(1) выглядит нереалистической: никакого независимого раз-
броса наблюдений вокруг некоторой гладкой линии не видно.
Поэтому попытки применения теории случайных процессов
начались с создания моделей, способных описывать волно-
образные колебания, не имеющие, однако, строго определен-
ного периода. Рассмотрим модели скользящего среднего и
авторегрессии.
1.2. Скользящее среднее. Модели случайных процессов
строятся тем или иным способом, исходя из модели незави-
симых случайных величин. Е. Е. Слуцкий [35, с. 99—132]
предложил следующую модель скользящего’ среднего:
rn—I
= 2 «S 6/-5Г (И
е—0
344
уел. ед.
Рис. 6. Индекс английской конъюнктуры (сплошная ли-
ния) и отрезок ряда скользящих средних (пунктир) (ис-
точник: [35])
где а» — некоторые (неслучайные) числа, {б/} — последо-
вательность независимых одинаково распределенных вели-
чин. Из рядов наблюдений обычно тем или иным способом
вычитают неслучайную составляющую; остаются, следова-
тельно, величины, колеблющиеся вокруг нуля. В математи-
ческой модели считаем, что
М|,=М6(=0. (2)
Интерпретировать модель (1) можно, например, так. Значе-
ние экономического показателя рассчитанного в году t,
есть сумма значений его «причин» б/, б<-ь .... б/-т-н за tn
лет, но причины эти берутся с весами а», вообще говоря,убы-
вающими с ростом s.
Используя случайные числа, полученные при розыгрыше
облигаций займов, Е. Е. Слуцкий моделировал несколько
рядов скользящих средних. Удалось даже подобрать отре-
зок такого ряда, похожий на отрезок значений индекса ан-
глийской конъюнктуры за 1855—1875 гг. (рис. 6). Таким
образом, по зрительному впечатлению модель скользящего
среднего может дать ряд наблюдений, похожий на ряд на-
блюдений некоторого экономического показателя. Никаких
более глубоких выводов Е. Е. Слуцкий не делает.
При какой-то статистической обработке конкретных дан-
ных с помощью модели скользящего среднего пришлось бы
определить параметры этой модели, т. е. порядок т, коэф-
фициенты а« и дисперсию величин б/. Идентификация пара-
метров, как оказывается, довольно неудобна, и потому широ-
ких попыток применения модели скользящего среднего нет.
Несколько более повезло в этом смысле следующей ниже
модели авторегрессии.
345
1.3. Авторегрессия. Модель авторегрессии предложена
Э. Юлом в работе [57], посвященной исследованию измене-
ния во времени числа солнечных пятен. Юл рассуждал при-
мерно следующим образом.
Весьма легко представить себе процессы, в которых слу-
чайное вмешательство в момент времени t включается в
дальнейший ход процесса. Предположим, например, что в
комнату, где качается (без трения) маятник, проникли
мальчишки и принялись стрелять в маятник горошинами.
Пусть мы регистрируем положение маятника в дискретные
моменты времени Г=1, 2,... и хотим по этим наблюдениям
найти важную физическую величину — период невозмущен-
ного колебания маятника.
Юл полагал, что моделью, описывающей подобные на-
блюдения, является следующая:
£«=ai5f—1 + ... + От5<-»п+6ь (1)
где {6J — последовательность независимых одинаково рас-
пределенных случайных величин, причем бе не зависит также
от gt-i, Уравнение (1) называется уравнением ре-
грессии; поскольку речь идет о регрессии значения процесса
на предыдущие значения £/-i, ^_г, ..., £е-т того же процес-
са, то модель (1) называется моделью авторегрессии.
В частности, для маятника (без трения), описываемого
моделью t/"+ai/=0, если мы его регистрируем в моменты
to+kh, k=0, 1, 2,..., Юл предлагал использовать модель
Д% + а2Л»хк = 6*+2, (2)
где xk — y(t0+kh), у(0— реализация возмущенного движе-
ния; {8к) — независимые случай-
ные величины. Разрешая (2) относительно xk+2, получаем
модель вида (1). Однако Юл ошибался. Анализируя
уравнение
У"+^УЧ(О
.при наиболее естественных предположениях (к мало по
сравнению с периодом 2 л/а, процесс f(t) за время h обнов-
ляется в смысле исчезновения статистической зависимости),
.приходим в конце концов к модели
&*хк+^хк^Ш(\+1-\), (3)
где {6а} — независимые случайные величины. (Малоинтерес-
ные выкладки здесь опущены.) Модель (3) есть некоторая
комбинация скользящего среднего и авторегрессии, а не про-
сто модель авторегрессии.
346
Да и вообще, колебания маятника без трения под воз-
действием случайных сил приводят к нестационарному слу-
чайному процессу: амплитуда колебаний возрастает. Между
тем. говоря о солнечных пятнах, мы подразумеваем стацио-
нарный процесс. Впрочем, и сами конкретные результаты
применения модели авторегрессии к солнечным пятнам в ра-
боте Э. Юла [57] нельзя признать особенно удачными.
Чтобы модель (1) приводила к стационарному процессу,
необходимо и достаточно, чтобы уравнение
= CZ15/-1 т... +
получающееся из (1) при б<“0, имело лишь затухающие ре-
шения, т. е. чтобы корни многочлена
zm=aizm-1-r... +a,n
были все по модулю меньше 1. Обычно рассматривается
именно этот случай, а под процессом авторегрессии понима-
ется стационарное решение уравнения (1). Посмотрим, как
можно определить параметры модели для случая /п=2 (ав-
торегрессия второго порядка):
5/=ai£r-i+a2b<-2+6<. (4)
Умножая (4) на и £г-2, беря математическое ожидание,
получаем с учетом независимости 6t от и £<-2 следующие
два уравнения:
B(l)=aiB(0)+a2B(l).
(5)
B(2)=aiB(/)+a2B(0).
где B(u)=Nl$fa+u — корреляционная функция случайного
процесса с,. Таким образом, узнав (приближенно) по реали-
зации случайного процесса величины В(0), В(1), В (2),
можем найти из системы линейных уравнений (5) ai, аг-
Умножая (4) на Ь при s<t—2 и полагая t—s=u, полу-
чаем (после взятия математического ожидания)
B(u)=aiB(u— 1)+агВ(и—2). (6)
Решение разностного уравнения (6) выражается известным
образом через корни уравнения
г2—aiz—«2=0.
Если корни этого квадратного уравнения комплексно сопря-
жены (и по модулю меньше 1),* то корреляционная функция
В (и) при изменении и от 0 до оо совершает колебания
уменьшающейся амплитуды. Полагая а=—си, b=—а2, по-
лучаем, что для этого должны выполняться соотношения:
347
а2<46, 0<Ь<1. Нетрудно получить для коррелограмма
= выРажение
г __В(й) у* sin (k fl-r|)
sin 4-
в котором
p = Vb, 0 = arccos , tg ф — ~ tg 0.
2yd I-6
Кроме того,
- (1 + 6X1 - 6)-4(l + 6)‘- a2}-» D6#
(см. книгу Кендалла н Стьюарта [20]), так. что D6< можно
узнать по Dgt и параметрам а и Ь.
Таким образом, параметры модели авторегрессии в прин-
ципе достаточно легко определяются по наблюдениям. Мо-
дель авторегрессии была применена ко многим рядам эконо-
мических показателей. Чаще эти применения оказались не
вполне удачными (в том смысле, что модель авторегрессии1
тем или иным статистическим критерием отвергалась); од-
нако в книге Кендалла и Стьюарта [20] приводится и впол-
не удачный пример для поголовья овец в Англии за 1867—
1939 гг.
Остановимся на критическом рассмотрении этой модели
и некоторых других вопросов, данных в книге Кендалла
[50].
1.4. Критика Кендалла. Книга [50] открывается интерес-
ным эпиграфом, который можно перевести примерно так:
«... основы наших убеждений должны сравниваться не столь-
ко с солидным фундаментом обычного здания, сколько с ку-
чами роттердамских домишек, которые неведомо как поко-
ятся на глубоком ложе из мягкой грязи». Для начала
М. Г. Кендалл задается вопросом: на чем основано наше
убеждение, что мы можем судить по коррелограмму, имеем
ли мы дело с авторегрессией? С этой целью моделируется
ряд наблюдений £/ согласно уравнению
&-г2= 1Л&+1 —0,5£/ + 8/+2»
£о=О, 51 = 15,5; б/ — моделированные с помощью таблиц
случайных чисел случайные величины, принимающие целые
значения от (—49) до (+49) с равной вероятностью. Всего
моделировано 480 членов ряда.
Поскольку в экономических рядах обычно не бывает
больше нескольких десятков наблюдений, 480 членов разде-
лены на 8 групп по 60 членов. Для этих групп были под-
348
Рис. 7. Графики первых 50 значений коррелограмма, рассчитан-
ные по 4 отрезкам а), б), в), г) ряда Кендалла длиной каждый
60 членов (источник: [50])
считаны коррелограммы прн /=!,...,50. Четыре из них при*
водятся на рис. 7. Эти коррелограммы абсолютно не похожи
друг на друга, хотя вычислены для различных реализаций
одного и того же процесса. Они не обнаруживают никакого
стремления затухать при больших t.
На рис. 8 приведен коррелограмм для всего ряда, т. е.
для 480 наблюдений. Он больше похож на теоретический, хо-
тя также не затухает при больших t. Кендалл указывает, что
при работе с временными рядами нужно ориентироваться не
на число наблюдений, а на число периодов 2л/0, которые
помещаются на отрезке наблюдения. Для авторегрессии
Рис. 8: а) 50 значений коррелограмма ряда Кендалла, рассчитанные
по всему ряду из 480 значений; б) теоретический коррелограмм ряда
Кендалла (источник: [50])
349
iM
D*t
10 20 30 40 50
T‘2x/X
Рис. 9. Периодограмма ряда Кендалла (источник: (50])
второго порядка 0=arccos (—a/2Vb), и в данном случае
2л/0=9,25.
Кендалл строит также периодограмму по 480 значениям
ряда. Она приведена на рис. 9. Пики этой периодограммы,
отвечающие периодам 20, 26 и 42, не имеют никакого отно-
шения к реальному периоду 9,25. Вывод Кендалла состоит в
том, что если мы имеем дело с авторегрессией, то примене-
ние периодограммы «...приводит к выводам почти настолько
ложным, насколько это вообще возможно». И тут неплохо
достается известному английскому экономисту У. Биверид-
жу, который анализировал с помощью периодограммы длин-
ные экономические ряды, в частности ряд значений цен на
пшеницу. Например, сам У. Биверидж насчитал в этом ряду
19 локальных максимумов, а М. Г. Кендалл — ровно вдвое
больше. Это означает, что У. Биверидж не озаботился да-
же о том, чтобы четко определить понятие локального мак-
симума, которым он лично пользовался, что весьма зазорно
для статистика.
1.5. Резюме. Модели случайных процессов применительно
к динамике экономических показателей уже потому не могут
дать особенно содержательных результатов, что обычно име-
ющееся количество наблюдений абсолютно недостаточно
(нужны ведь и какие-то гарантии того, что вероятностный
механизм одинаков в начале, конце и середине ряда). Лю-
бопытно напомнить, что Н. Винер в «Кибернетике» ([8,
с. 201—202]) весьма критически отозвался о потенциальных
возможностях изучения экономических явлений. Его аргу-
ментация сводится к тому, что эти явления интересуют нас
в слишком мелких подробностях, в то время как научная
350
Рис. 10. Спектральная плотность ряда Кендалла н различные спо-
собы ее оценки путем сглаживания периодограммы (источник дан-
ных: [42])
теория если и возможна, то лишь в более обобщенном мас-
штабе. Например, статистическая механика мало чего стоит
с точки зрения отдельной молекулы.
Посмотрим, в частности, на рис. 10, на котором даны
спектральная плотность ряда Кендалла (нормированная
множителем 2л/В(0)) н различные ее оценки по книге Хен-
нана [42]. Ни одна из оценок не позволяет понять, где нахо-
дится максимум истинной спектральной плотности (та су-
щественная частота колебаний процесса авторегрессии, ко-
торую предполагал искать Э. Юл).
351
Реальная область применения теории случайных процес-
сов — это широко понимаемая физика, где, по крайней ме-
ре, число наблюдений можно сделать сколь угодно большим.
Посмотрим, например, что пишут об оценке спектральной
плотности А. С. Монин и А. М. Яглом ([28, с. 14—15]).Спек-
тральная плотность обозначается £(ш).
«Пусть, например, процесс u(t) реализуется в виде флюк-
туирующего электрического напряжения (если u(t) — пуль-
сации скорости или температуры в точке турбулентного по-
тока, то их преобразование в пульсации напряжения обычно
автоматически осуществляется измерительными приборами).
Подадим напряжение u(t) на вход фильтра, пропускающего
лишь колебания с частотой, меньшей некоторого шо. н изме-
рим мощность тока на выходе фильтра с помощью ваттмет-
ра. Стрелка этого прибора покажет значение интеграла
ш,
E(w)da> (осреднение по времени... как правило, будет
о
осуществляться самим ваттметром, обладающим определен-
ной инерцией). Меняя значение соо и продифференцировав
полученную эмпирическую кривую, мы найдем и саму функ-
цию Е (ш) ...».
Для примера в книге [28] приводится график спектраль-
ной плотности, полученный еще в 1938 г. Симмонсом и Сол-
тером «... с помощью специальной системы электрических
фильтров». Часть данных с этого графика воспроизводится
на рис. 11 (точки, кружки и крестики соответствуют разным
скоростям потока в аэродинамической трубе). Опыт, веро-
ятно, имел целью показать наличие универсальной (т. е. не
зависящей от U) зависимости в координатах [/£(ш)/В(0) и
<a/2nU.
Рассматривая рис. 11, мы прежде всего констатируем, что
качество оценки спектральной плотности несравненно лучше,
чем для ряда Кендалла из 480 наблюдений. Очевидно, что с
помощью системы электрических фильтров спектральную
плотность измерить можно. Но, с точки зрения статистика, не
мешало бы выяснить, чем объясняется разброс точек отно-
сительно проведенной на рисунке гладкой линии. В теории
случайных процессов нет другого источника ошибок оценки
спектральной плотности, как только недостаточное время ус-
реднения мощности профильтрованного сигнала. Действи-
тельно ли этим объясняется разброс, по приводимым в [28]
данным выяснить невозможно.
Вообще, прекрасные графики измерений спектральных
плотностей, в большом числе приведенные в [28], по-видимо-
му, не анализировались с точки зрения небольших отклоне-
ний измерений от теории. Гипотеза автора настоящей книги
состоит в том, что эти отклонения (сами по себе небольшие)
352
все же значительно больше того, что вытекает нз чисто ве-
роятностной оценки ошибки, связанной с временем усредне-
ния. Но анализ этих отклонений вряд ли поведет к чему-ни-
будь интересному, так как, например, выяснится нестабиль-
ность во времени каких-нибудь условий опыта по измерению
спектральной плотности (т. е. время усреднения увеличить
нельзя). Описание подобной нестабильности, вероятно, вы-
ходит за рамки наших возможностей, а тогда их обнаруже-
ние не принесет научной пользы. Но вообще-то иметь в ви-
ду вероятностные оценки точности определения спектраль-
ной плотности и как-то сопоставлять их с наблюдаемым раз-
бросом все-таки следовало бы.
§ 2. Стационарные приращения
2.1. Введение. Сказать, что мы наблюдаем реализацию
случайного процесса fy, значит сказать довольно много. Дол-
жны быть какие-то мысли об ансамбле реализаций, т. е. о
том, что нужно (в принципе) сделать, чтобы получить еще
много реализаций того же самого процесса £« (совершенно
одинаковых по вероятностным свойствам). Например, если
производится опробование некоторого месторождения полез-
ного ископаемого, то может означать суммарное содержа-
ние полезного компонента в скважине с номером t, в то вре-
мя как скважины расположены с равным шагом на некото-
рой прямой (профиль опробования). Как взять другую реа-
лизацию £(? Можно взять другой профиль опробования, но
23—2567 353
ои пройдет уже в другом месте, и думать, что вероятностные
свойства содержаний полезного компонента будут тем* же
для другого профиля, нет оснований. (Например, если один
профиль проходит по самому богатому месту рудного тела,
а другой — по более бедному, то средние значения величин
It изменятся.)
Иными словами, изменчивость какого-либо свойства но-
сит смешанный характер — что-то меняется детерминиро-
ванным образом, а что-то, может быть, и случайным.
Надежда на применение вероятностных методов во мно-
гих областях науки связана с тем представлением, что из-
менчивость в разном масштабе ведет себя по-разному: в
крупном масштабе (т. е. на больших расстояниях) мы стал-
киваемся с некоторой сложной изменчивостью, а в мелком
масштабе (на малых расстояниях) — с вероятностной из-
менчивостью. Иначе говоря, если есть ряд наблюдений то
описание его в целом вероятностной моделью может быть
задачей безнадежной (или не нужной), но разности
для достаточно близких t и s описываются моделью случай-
ных величин. Кстати, если ряд дан нам в единственном эк-
земпляре (но достаточно длинный), то разностей &—мож-
но получить довольно большое число: из начала ряда, из се-
редины, из конца и т. д.; можно в какой-то мере проверить
и однородность статистических свойств этих разностей.
Так, если результаты опробования месторождения по раз-
ным профилям явно зависят от профиля, то, может быть,
статистические свойства разностей по отдельным (до-
статочно близким) скважинам в пределах одного профиля
уже и не будут зависеть от профиля. Взятием разности де-
терминированная (крупномасштабная) компонента изменчи-
вости приводится приблизительно к нулю, а мелкомасштаб-
ная (случайная) компонента даже несколько подчеркивает-
ся.
Изложенные соображения приводят к концепции процес-
са со стационарными приращениями. Если дан некоторый
ряд наблюдений то для всего ряда мы никакой вероятно-
стной модели не строим, но зато разности считаем
случайными величинами. Можно говорить о совместном рас-
пределении случайных величин: приращений
......(1)
Приращения (1) назовем стационарными, если совместное
распределение (1) не изменится при сдвиге времени: Л—*
—st—*-st+h (а в рамках корреляционной теории —
если математические ожидания и ковариации прираще-
ний (1) не меняются при сдвиге времени).
354
Понятие процесса со стационарными приращениями вве-
дено А. Н. Колмогоровым в связи с описанием локальной
структуры турбулентности. Изложим основы соответствую-
щего математического аппарата.
2.2. Основы математического аппарата. Будем рассмат-
ривать только процессы с вещественными значениями. В рам-
ках корреляционной теории нужно задать математические
ожидания и ковариации величин (1). Поскольку М(£г—5,)
должно зависеть лишь от разности t—s н при любых s<i<
<u выполняется соотношение
М(£а-^)= М
то математическое ожидание не может быть ничем другим,
как только линейной функцией
Чаще всего, впрочем, считают, что а=0, т. е. приравнивают
нулю математические ожидания приращений (1).
На первый взгляд математическое ожидание произведе-
ния
(L - *„)(*' ~ U
является функцией четырех переменных U, s,, tj, Sf (а с уче-
том постоянства при сдвиге времени — трех переменных).
Но на самом деле, за счет использования алгебраического
равенства
(a—b)(c-d)=l/2{(a-d)a+(6-c)a—(а-с)а-(6—d)8}
дело удается свести к М(£о—$-ч)2; с учетом же стацио-
нарности—к функции М(^ — &,)2.
Определение. Функция задаваемая формулой
Dt(O=M(^-g0)2.
называется структурной функцией процесса
Структурную функцию можно использовать вместо кор-
реляционной функции и для задания обычного стационарного
процесса. Действительно, если — стационарный процесс
с корреляционной функцией то имеем равенство
D£(0-Mg2+M^-2M^=2[56(0)-B.(/)],
откуда
В.(С-55(0)-1/2О^).
Обычно >-0 при *—►(); тогда получаем 2?_(0) =
= 1/2 lim так что корреляционная функция процесса
может быть выражена через структурную.
23* 355
Если процесс является процессом со стационарными
приращениями, то Dt(t) стремится к оо при t—►оо. Посколь-
ку (при целом t)
м(ЬЧ)*-м J (€<——5/-0
кг.
то стремление Dz(t) к оо при t->^o не может быть более
быстрым, чем с1я, с=>£.(1)— константа.
При непрерывном времени t процесс со стационар-
ными приращениями удобнее всего определить как такой
процесс, что его производная £' = -q, есть стационарный
процесс. Тогда получим
t
в
5/ -
Пользуясь спектральным разложением
Ъ - p,x“Z(dA),
““ОО
где Z — случайная ортогональная мера, найдем
С1Ы eiXs
а
Z{dK),
а тогда получим следующее спектральное разложение струк-
турной функции:
ев
Р£(0 - М(Ь - W - J |е<”-1|« -
““ОО
1-£2SWF(A) в2 у(1 _cosXf)G(dX)j
где F(A) = M|Z(4)|*, G(dX) — F(dk)A*. (Последний интеграл,
очевидно, сходится, если, например, — обыкновен-
ный случайный процесс, т. е. F{(—оо, оо)} конечно.)
Посмотрим теперь, что даст фильтрация процесса со ста-
ционарными приращениями.
Пусть спектральная характеристика фильтра ф(1) такова,
что ф(1)=0 при Ш<а, а — некоторое число. В частности,
356
это означает, что не зависящая от времени величина на вы-
ходе фильтра дает нуль, а поэтому безразлично, подавать л:<
на вход фильтра £(/) или £(7)—£ (0). Кроме того, предполо-
жим, что достаточно низкие частоты не влияют на выход
фильтра, и потому можно записать вход фильтра £(1)—£(0)
в виде интеграла лишь по частотам, таким, что |Х1>Ь (где
ад -5(0)= f -!^ £(<».)- f
,Х |Х,1 ь ,к р.|’о ,А
Второе слагаемое в последней формуле не зависит от вре-
мени t и потому (как предполагается) на выходе фильтра
даст нуль. В результате получаем, что выход фильтра t,(t)
записывается следующим спектральным разложением:
ад- -^-<р(а)2(Л),
Х|>Ь '
а следовательно,
ВДО!2- f |<F(X)|«G(d>).
р.Ьь
Делая функцию фильтра <fG) такой, чтобы квадрат |ф(л)|3
походил на 1/2i6(/—л0) 4-6(АЧ-)0)), сможем оценить спект-
ральную плотность g()) = G(d).)/d\ в точке Х=Х0. Учитывая
четность функции gp.) (предполггаем, что плотность ме-
ры G существует) и полагая g^i.) = 2g{'i~), получим сле-
дующую форму спектрального представления структур-
ной функции:
D,(t) = 2 f (1 — cos .
6
Таков список основных определений и формул, связанных с
понятием процесса со стационарными приращениями.
2.3. Теория локального строения турбулентности по Кол-
могорову— Обухову. Пусть v(x, t) — скорость потока в
точке хе/?3 в момент t в некотором большом турбулентном
потоке, например в свободной атмосфере или в океане. В
целом поле скоростей определяется крупномасштабными
процессами вроде некоторого среднего ветра в атмосфере
либо среднего течения в океане. Но предметом изучения яв-
ляются приращения
Дги(х, t)=v(x+r, t)—v(x, t),
357
которые предлагается описывать чисто статистически. (Мож-
но брать приращения и по времени.)
Представим себе измерительный прибор, описываемый
парой векторов г и а, который, будучи приложен в точке х
в момент t, измеряет проекцию вектора Дго(х, t) на направ-
ление а. Корреляционная теория должна иметь дело с кова-
риациями показаний двух таких приборов (ru aj и (гг, а2),
прикладываемых в разных точках пространства и в различ-
ные моменты времени. Но можно показать (см. книгу
А. С. Монина и А. М. Яглома [28, с. 94]), что достаточно ог-
раничиться ковариацией показаний приборов с одним и тем
же г=Г1=г2, приложенных в одной точке. (Разные моменты
времени могут быть приведены к одному моменту времени с
помощью некоторой весьма правдоподобной гипотезы «замо-
роженной турбулентности».) Таким образом, прибор, изме-
ряющий корреляционную характеристику, должен измерять
M(projoArv(x, t) - projfl ДХ*» 0}- (1)
Делается предположение локальной изотропности, которое
заключается в том, что показание прибора (1) не изменится,
если тройку векторов (г, ait аг) повернуть как целое одним
вращением пространства (а также точку x^R3 заменить на
х' и момент времени t заменить на t').
Понятно, конечно, что любые пары векторов et и а,
можно свести к случаю, когда векторы at и а2 совпа-
дают с ортами некоторой ортонормированной системы
координат. Выберем систему координат специфическим
образом: орт L направим вдоль вектора г = (rv rt, rs), а
два других орта Л\ и Nt направим произвольно (перпен-
дикулярно L и друг другу). Обозначим через uL проек-
цию приращения Д,и(*> 0 на орт L, через uNt и —про-
екции этого приращения на и Nz. Из предположения
изотропности легко следует, что uL не коррелировано с
иЛГ) и и^, а также, что uN> и иЛ ие коррелированы друг
с другом, причем М|илг>|г=М|п№|». Положим |г|=^г’+^4-г32,
M|uJ« - D£i(|r)|, M|uWi|« - М|«№|‘ ~ D„N(r).
Первая нз этих функций Ды.(|г|) называется продольной
структурной функцией, вторая Dww(|r|) — поперечной. Ока-
зывается, что несжимаемость среды, в которой рассматрива-
ется турбулентный поток, ведет к соотношению
ОЛ,ИИ)-ОЫ|Г|)+У^^.,
2 d|r|
358
так что корреляционная структура локально изотропной тур-
булентности однозначно определяется единственной функци-
ей £>£Ь(|г|) скалярного аргумента |г|.
(Читатель должен иметь в виду, что мы даем здесь упро-
щенное резюме некоторой алгебраической по методам теории,
изучающей корреляционный тензор локально-изотропного по-
ля.)
Но самое интересное состоит в том, что на основании тео-
рии размерности (если угодно, тоже алгебраической теории,
изучающей свойства, инвариантные относительно преобразо-
ваний подобия) можно пойти еще гораздо дальше в уточне-
нии вида функции (| г |).
Существует классическое понятие коэффициента кинема-
тической вязкости v некоторой среды; в частности, для воды
v=)0-2 см2/с, для воздуха v=15 • 10~2 см2/с. Кроме того, вво-
дится понятие средней диссипации (т. е. перехода в тепло)
энергии е в данном турбулентном потоке (за единицу време-
ни в единице массы среды):
«=д,
2 f?t\dxl дх*)
где черта сверху обозначает усреднение по ансамблю турбу-
лентных движений с фиксированными внешними условиями.
(В смысл последнего выражения лучше глубоко не вдаваться,
полагая, что усреднение можно понимать как усреднение по
времени в произвольной точке данного в единственном эк-
земпляре турбулентного потока.) В отличие от кинематичес-
кой вязкости, диссипация 8 в эксперименте бывает известной
очень грубо.
Из размерных параметров е и v можно единственным спо-
собом составить комбинации, которые имеют соответственно
размерности длины, скорости и времени:
— !/4, _ (w)t/4, т =vi/»e—1/2,
Величина -q называется колмогоровским масштабом турбу-
лентности.
Подход А. Н. Колмогорова заключается в том, что если
выразить длину, скорость потока н время в безразмерных ве-
личинах с помощью введенных единиц, то статистические ха-
рактеристики этих безразмерных величин будут уже совер-
шенно универсальными, не зависящими от конкретного пото-
ка. Точнее говоря, знаменитые «гипотезы подобия» А. Н. Кол-
могорова состоят в том, что 1) статистические характеристи-
ки приращений определяются параметрами е и v; 2) в облас-
ти инерционного интервала, т. е. достаточно больших масш-
табов (|r |>t]=v3/<8I/4), вязкость v не играет роли. Неболь-
359
Рис. 12. Измерения спектров: а) вертикальное и б) горизонтальное
скорости ветра на высоте 300 метров (источник: [28])
шая математическая обработка этих гипотез приводит к фор-
муле
Ах(И) - MlrR.
причем при х |г|Л] > 1
p;L(x)« Сх^,
где С — так называемая константа Колмогорова.
После элементарных преобразований получаем
D£L(|r|) ~ Сг=/’|г|Ч (2)
где |г | достаточно велико (ио много меньше, чем характер-
ный размер турбулентного потока).
Формула (2) называется «законом двух третей» Колмого-
рова. В терминах спектральной плотности gi.(X) ему соответ-
ствует закон
gx(>.)==C1S2/3A-5/3, С,~С/4, К (3)
называемый «законом пяти третей» Обухова.
Теоретические результаты теории турбулентности были
опубликованы в 1940—1941 гг. С физической точки зрения
они не вполне бесспорны (имеется возражение, принадлежа-
щее Л. Д. Ландау [28, с. 517]). Но в последующие двадцать
лет они получили полное экспериментальное подтверждение.
На рис. 12 из [28] приводятся (в логарифмическом масштабе
360
по осям) результаты измерений спектральной плотности ско-
рости ветра. Проведена также прямая Л5/®. При подборе кон-
станты (допускаемом уравнением (3)) согласие с законом
пяти третей хорошее. Правда, разброс экспериментальных
данных не похож на разброс независимых случайных вели-
чин, как теоретически должно было бы быть при оценке спект-
ральной плотности в разных точках.
На рис. 13 также из [28] приводятся измерения спектраль-
ной плотности во всем интервале масштабов. В тех опытах,
где вообще существовал инерционный интервал масштабов
(где должен выполняться закон пяти третей), универсальная
зависимость плавно переходит в этот закон. Разброс точек
больше напоминает разброс независимых случайных величин,
но объяснение этому, кажется, в том, что на рис. 13 сведены
результаты разных авторов.
Совсем коротко остановимся на применениях теории ло-
кального строения турбулентности. Конечно, эта теория не
имеет отношения к крупномасштабным процессам (напри-
мер, к прогнозу погоды). Но с помощью нее удается исследо-
вать некоторые другие явления, например дрожание изобра-
жений звезд в телескопах или мерцание (т. е. колебание ин-
тенсивности) света звезд и других удаленных источников све-
та. Это объяснение составляет предмет довольно сложной фи-
зической теории, изложенной, например, в книге [37]. Приве-
дем рис. 14, заимствованный из этой книги. Видно, что при
361
Рис. 14. Рассчитанные по метеорологическим измере-
ниям турбулентности (2о|)и наблюдавшиеся в опы-
те (2ох) значения среднеквадратичных флюктуаций
логарифма интенсивности света, вызванных атмос-
ферной турбулентностью. Пунктирная прямая —пер-
вое приближение. Сплошная кривая — более со-
вершенная теория В. И. Татарского (источник: [37])
малой интенсивности турбулентности согласие между раз-
бросом 261 логарифма интенсивности света, рассчитанным по
измерениям турбулентности (т. е. в конечном счете по метео-
рологическим измерениям) и измеренным в опыте 26х, хоро-
шее. При больших интенсивностях турбулентности согласие
более приблизительное, но все же впечатляющее. Заметим,
что при данном 261 имеется заметный разброс значений 2бх,
что, по-видимому, означает либо иеабсолютную точность из-
мерения параметров турбулентности, либо возможную неточ-
ность локально-изотропной модели.
В заключение несколько слов об измерении константы
Колмогорова С. Это универсальная физическая константа,
притом безразмерная (вроде числа л). Речь идет, так ска-
зать, об экспериментальном определении л человеком, не
имеющим ни одного правильного круглого предмета. Первое
определение С сделал А. Н. Колмогоров, получивший С=1,5.
Впоследствии было показно, что в тех экспериментах, на ко-
торых он основывался, вряд ли существовал инерционный
интервал масштабов (С определялось в предположении его
существования). Через многие годы было получено С=1,9±
±0,1 [28], что оказалось неожиданно близко к первой оценке
А. Н. Колмогорова.
Работы А. Н. Колмогорова по теории турбулентности пред-
ставляют один из редчайших примеров сочетания математи-
362
ческой новизны и естественнонаучной значимости. Обычно
в наше время математик, работающий в приложениях, поль-
зуется готовыми математическими результатами (либо ес-
тественнонаучный смысл не бесспорен). Однако вполне мож-
но представить себе неразумно жесткого рецензента научно-
го журнала, которые не допустил бы эти работы в печать за
отсутствием полного экспериментального подтверждения
(оно пришло примерно через двадцать лет).
2.4. Оценка запасов полезных ископаемых. Вернемся к
схеме, с которой начинается этот параграф. Пусть для опре-
деления количества полезного компонента некоторое рудное
тело разведано системой параллельных канав прямоугольно-
го сечения, расположенных на равном расстоянии друг от
друга. Пусть & — концентрация полезного компонента в ка-
наве с номером t (т. е. общее содержание полезного компо-
нента в грунте, вынутом нз t-ti канавы, деленное на объем
вынутого грунта). Тогда фактическое содержание полезного
компонента во всем рудном теле будет чем-то вроде интег-
рала S^tdt, а для оценки этого интеграла у нас имеются
а
наблюдения gi, ...,£п при целочисленных значениях t. Хоро-
шо при этом считать, что а=Чг, Ь=п+1/г, так как тогда не-
посредственно применяется формула прямоугольников, и мы
получаем
Ь п п
J St,
a i-1 t
поскольку в наших обозначениях шаг h равен единице. Воп-
рос состоит в оценке разности
Ь п п /+12
f (ь-wt. (i)
a i-l
Поскольку дело свелось к разностям S(—где t меняет-
ся в узких пределах от i—1/2 до *4-1/2, то очень хочет-
ся применить для статистического описания этих разнос-
тей концепцию процесса со стационарными приращения-
ми.
Первая такая попытка сделана в переведенной у нас кни-
ге Ж. Матерона [26], который, по-видимому, независимо от
работ А. Н. Колмогорова пришел к концепции процесса со
стационарными приращениями. Однако изложение в книге
[26] чрезвычайно запутано и малоубедительно. Советскому
читателю, интересующемуся задачей оценки запасов, естест-
венно обратиться к гораздо более совершенной книге А. М.
Шурыгина [47].
363
Мы дадим здесь краткое изложение этой книги в обзор-
ном порядке. Основной моделью структурной функции в ]47]
является степенная модель
£\(0 - М(Ь+/ -D* - 0< V< 2, (2)
зависящая от двух параметров со и у. Определять эти
параметры рекомендуется статистически —на основании
усреднения (по реализации процесса h) квадратов раз-
ностей ({•,+,—&) при разных з и t и сглаживания резуль-
татов усреднения. Первый момент М(^+г—U принимает-
ся равным нулю. (Автор настоящей книги ие берется су-
дить, встречается ли в геологических задачах такая си-
туация, когда из наблюдений сначала нужно вычесть
некоторую детерминированную функцию <$), а уж с раз-
ностями Е,—q.(z) поступать как с процессом со стационар-
ными приращениями. Умозрительно такая ситуация воз-
можна. Функцию <р(Л, конечно, пришлось бы подбирать
иа основании самих наблюдений g<.)
Вроде бы А. М. Шурыгин рассматривает и сами на-
блюдения как случайные величины и ставит задачу
вычисления условнсго математического ожидания от
ь
J Kfdt при известных £х, Е3, . . . , с„. В этом он видит су-
щественную идейную разницу с подходом Ж. Матерона
(см. [47, с. 129]). Автор данной книги с этим более чем
согласен: по мнению автора, вообще существует только
условное распределение %t, a^J^b, при данных . . ?п
(выраженное через распределение приращений), а безус-
ловного распределения Е, в модели стационарных при-
ращений не бывает.
Распределение вероятностей концентраций А. ЛА. Шуры-
гин принимает либо гауссовскими, либо гауссовскими счита-
ет распределения логарифмов концентраций. Если начать
ь
вычислять условное математическое ожидание Jпри
а
известных Ь,..., ^ в предположении, что гауссовские
распределения задаются струкгурной функцией вида (2),
то получится некоторая сложная линейная комбинация
значений Ev . .. , En. А. М. Шурыгин на это не идет (ве-
роятно, совершенно правильно), преобразуя постановку
задачи так, чтобы ответом была формула интегрирова-
ния методом прямоугольников. Основной вопрос — в Ha-
ft
писании доверительного интервала для %tdt на основании
364
наблюдений I»,..., sn: насколько может отличаться
р/Л ОТ 2
а /—<
В данной книге достаточно говорилось о том, что довери-
тельные интервалы для (якобы) независимых случайных из-
мерений не всегда заслуживают доверия. Поэтому ясно, что
в задаче оценки запасов рассчитывать на быстрый н легкий
успех ие приходится. Здесь важно накопление опыта.
Посмотрим сначала на эту проблему теоретически.
Мы, конечно, уповаем на нормальное распределение раз-
Ь я
ностн —2 Вопрос, следовательно, лишь в вы-
а /*>1
числении дисперсия. В силу (1) искомая дисперсия выра-
зится как сумма ковариаций
f/4-1/2 /4-1/2
М f J fa-Mdt
U-I/2 /—1/2
<+•1/2 /4-1/2
- j j м^-^хЧ-^)Л1Л..
/—1/2 /—1/2
Ковариация AI(cfi— —£>) выражается через структур-
ную функцию (пусть, скажем, вида (2)). Дело сводится,
следовательно, к некоторому нудному интегрированию и
суммированию, причем вполне вероятно, что для струк-
турной функции вида (2) возможны существенные упро-
щения.
На наш взгляд, этот путь был бы проще, чем довольно
трудные вычисления с условными распределениями, которые
применял А. М. Шурыгин для оценки дисперсии; впрочем,
эти оценки получены (см. [47]).
Теперь начинается самое интересное — нужно проверить,
годятся ли получаемые доверительные интервалы. При об-
суждении модели процесса с независимыми приращениями
(для самих ли величин или для их логарифмов) в книге [47]
приведен ряд конкретных геологических данных, в том чис-
ле и таких, которые не очень соответствуют модели стацио-
нарных приращений. Проверить экспериментально довери-
тельные интервалы для запасов означает сравнить их с ре-
зультатами разработки месторождения. Таких данных иет ни
у Ж. Матерона, ни у А. М. Шурыгина. Но у А. М. Шурыгина
приводится серия очень интересных экспериментов по опре-
делению площади географических объектов (таких как озе-
ро Байкал, Чехословакия иля остров Мадагаскар) на осно-
363
ваиии измерения ряда их поперечных сечений. Конкурируют
два метода вычисления ошибки — как ошибки численного
интегрирования и как ошибки в модели стационарных при-
ращений (третий метод — ошибка выборочного среднего
независимых случайных величин — во всех случаях дает не-
лепо завышенный результат). В большинстве случаев ошиб-
ка, вычисленная как ошибка численного интегрирования, ока-
зывается заниженной, а ошибка в модели стационарных при-
ращений — близкой к истинной ошибке. Следует особо отме-
тить, что автор книги [47] не скрыл и нескольких противопо-
ложных случаев.
В книге [47] рассмотрен еще целый ряд интересных воп-
росов (например, ситуация, когда концентрация является
экспонентой гауссовского процесса, приводящая к определен-
ным правилам взвешивания проб), но они не очень глубоко
сопоставляются с фактическими данными, и мы их здесь упо-
минать не будем.
В целом можно, пожалуй, высказать такое мнение. Если
в теории локального строения турбулентности мы имеем де-
ло с достаточно твердо установленным сходством статисти-
ческой концепции и опытных результатов, то в оценке запа-
сов концепция стационарных приращений полного количест-
венного соответствия с реальностью, видимо, не достигает.
Да и речь при оценке запасов идет не о примерном выпол-
нении закона двух третей или пяти третей, а о гораздо более
трудной вещи — доверительном интервале. Социальная важ-
ность проблемы оценки запасов, конечно, несравненно выше,
чем проблемы локального строения турбулентности. К сожа-
лению, научная судьба той или иной проблемы мало связана
со степенью важности социального заказа. Все-таки некото-
рые удачные оценки доверительных интервалов с помощью
модели стационарных приращений должны стимулировать
дальнейшие гораздо более широкие исследования в этом на-
правлении.
2.5. Несколько слов о случайных процессах в радиотехни-
ке и электронике. Существует мнение, что в радиоэлектрон-
ных устройствах происходят хорошо изученные случайные
процессы. Действительно, например, процессы дробового н
теплового шума имеют прозрачные физические модели и по-
нятные вероятностные свойства. Но ие эти процессы опреде-
ляют функционирование радиоэлектронных приборов, на-
пример, точность измерений, если это измерительный прибор
(какой-нибудь вольтметр, включающий и усилительную схе-
му). Свойства элементов радиоэлектронных приборов посто-
янно изменяются во времени. Например, для электронных
ламп характерен эффект мерцания (или фликкер-шум), свя-
занный с тем, что эмиссионная способность катода колеблет-
ся. Если попытаться анализировать этот шум как случайный
366
процесс, определяя экспериментально его спектральную
плотность, то обнаруживается пренеприятное свойство: чем
ниже частота Л, тем больше значение спектральной плотно-
сти f(X). Если мы пожелаем анализировать /(X) вблизи точ-
ки а,=0, то мы должны уметь разделить значения f(k\) и
/(Хг) в точках А.1 и Х2, близких к нулю, следовательно, и близ-
ких между собой. Применяемые фильтры должны быть очень
узкими. Но тогда время усреднения должно быть очень боль-
шим. И вот опыты длятся неделями и месяцами, а приносят
одно: вблизи нуля /(X) устроена как 1/Хп, где п вполне мо-
жет быть таким, что эта особенность неинтегрируема. Тогда
речь должна идти о нестационарном процессе; неясно, мож-
но ли говорить о стационарных приращениях. Чувствуется
настоятельная потребность в физической теории фликкер-
шума (чисто статистическими средствами здесь явно не рас-
путаться), но, насколько известно автору, такой теории нет.
Таким образом, имея несомненное значение для описания
простейших физических процессов (броуновское движение»
дробовой шум и т. д.), теория случайных процессов не мо-
жет в более сложных случаях заменить полноценную физи-
ческую теорию.
§ 3. Проблема прогноза случайных процессов
3.1. Введение. Математические основы теории прогноза
случайных процессов были созданы А. Н. Колмогоровым и
Н. Винером. В соответствующих работах А. Н. Колмогорова
нет каких-либо указаний на практическую значимость раз-
виваемых математических выводов. Иную позицию занимал
Н. Винер. Мы резюмируем ее по автобиографической книге
[9, гл. 12]. В этой главе идет речь о попытках Н. Винера с
начало.м второй мировой войны переключиться иа военную
тематику. Перечисляется ряд тем, работа над которыми по
тем или иным причинам ие состоялась, и, наконец, автор пе-
реходит к задачам управления огнем противовоздушной ар-
тиллерии. Центральной проблемой, конечно, оказывается,
проблема экстраполяции траектории самолета. Правильно
отмечается, что прибор для экстраполяции, построенный для
наилучшего слежения за гладкой кривой, будет непригоден
для экстраполяции нерегулярной, например ломаной, линии.
В качестве выхода предлагается статистический подход. Про-
цитируем с. 232 книги [9].
«Зиая статистическое распределение кривых, которые нам
надо экстраполировать, т. е., например, зная статистическое
распределение путей самолетов, по которым ведется стрель-
ба, можно искать такой метод прогнозирования, при кото-
ром некоторая величина, характеризующая ошибку, прини-
мает наименьшее значение».
ЗЯ7
Короче говоря, предлагается применить среднеквадрати-
ческое прогнозирование случайных процессов.
Далее говорится, что задача экстраполяции математичес-
ки аналогична задаче о выделении сигнала на фоне шума, и,
следовательно, параллельно удалось решить эту важную для
радиолокации задачу.
Затем рассказывается об опытах генерирования случай-
ных кривых с помощью устройства, в котором движение све-
тового зайчика на потолке сложным образом зависело от
поворота оператором некоторых рукояток. Утверждается
(с. 238), что «...мы нашли способ воспроизведения «сновных
черт нерегулярного движения самолета в полете».
Дальше обсуждаются вопросы работы систем с обратной
связью, и в свободном полете мысли автор касается некото-
рых проблем патологического тремора у человека. Но на
с. 242 говорится, что <...мы пришли к выводу, что можем уже
перейти от наших грубых экспериментальных установок к
созданию полной системы управления противовоздушным ог-
нем».
Впрочем, «...окончательно отработать конструкцию пред-
ложенной системы слежения нам не поручили; вместо того
меня попросили написать книгу, посвященную временным
рядам, экстраполяции и интерполяции».
Каков диагноз вышеописанной ситуации?
Бесспорно сильный математик Н. Винер от всей души хо-
чет сделать что-то полезное для спасения Англии от воздуш-
ных бомбардировок. У него рождается идея смотреть на
движение самолета как на случайный процесс, разумеется,
в рамках корреляционной теории. Он абсолютно не имел де-
ла со статистической стороной вопроса: как определить на
практике необходимые корреляционные функции и сущест-
вуют ли они вообще применительно к реальным условиям
полета бомбардировщиков? Несмотря на существующее бое-
вое применение радиолокаторов, которые в принципе отсле-
живают траектории полета самолетов, получить необходи-
мые фактические данные невозможно, потому что в боевых
условиях ие до того, чтобы записывать траекторию полета
самолета (а автоматические системы записи еще ие сущест-
вуют). Поэтому реальное движение самолета имитируется с
помощью некоторой (вероятнее всего нелепой) машины в
виде светового зайчика, но и движение зайчика, видимо, эк-
страполируется не очень здорово.
За словами «...окончательно отработать конструкцию...
нам не поручили» скрывается, по-виднмому, мнение каких-то
разумных практиков о том, что работа зашла в явный тупик.
Единственное, что может сделать Н. Винер, — это напи-
сать книгу о своих идеях, что какие-то разумные люди ему
и поручили.
308
Тем не менее Н. Винер уверен, что он решил (или почти
решил) задачу управления зенитным огнем. Например, в до-
кладе [56] на Международном математическом конгрессе
1950 г. он пишет, что его побуждала <...задача предсказания
будущего положения самолета иа основе общих статистичес-
ких сведений о способах его полета и более конкретного зна-
ния прошлой траектории:». Самооценка его такова: <Моя ра-
бота касается приборов, которые необходимы, чтобы реали-
зовать теорию предсказания в автоматическом аппарате для
стрельбы с упреждением по самолету...».
Мы имеем дело, конечно, с очень ярким примером пере-
оценки ученым возможностей созданной им теории, доходя-
щей в данном случае до очевидного абсурда. Действительно,
что именно следует трактовать как реализацию случайного
процесса? Неужели в чистом виде траекторию полета само-
лета? Такие траектории никакого статистического ансамбля
не образуют (поскольку очень зависят от конкретной такти-
ческой обстановки). Может быть, в противозенитном манев-
ре и есть какая-то статистическая составляющая, но прежде
всего нужно было бы сказать, как ее выделить.
Другое дело, что разработанные методы могли оказаться
полезными для решения других задач: каких-то фильтраций
сигнала. Всякого рода фильтры в настоящее время применя-
ются широко, и нет сомнений, что в идейном отношении их
истоки восходят, в частности, и к работам Н. Винера. Впро-
чем, если результаты фильтрации оказываются в практичес-
ком отношении вполне удовлетворительными, то это ие оз-
нзчает, что их качество вполне отвечает тем ожиданиям, ко-
торые вытекают из принятой вероятностной модели (срав-
нение этих охсиданий с фактически достигнутыми результа-
там;: обычно не проводится). Так, иикто не спорит с тем, что
среднее арифметическое из наблюдений — вещь полезная
(если во всех наблюдениях измеряемая величина постоян-
на), но доверительные интервалы представляют собой нере-
шенную проблему.
Было бы желательно рассмотреть с последовательно ве-
роятностной точки зрения конкретные примеры каких-либо
довольно сложных фильтраций, но автору данной книги та-
кая возможность не представилась.
Коротко рассмотрим ситуацию, сложившуюся с прогно-
зом случайных процессов.
3.2. Математические основы. В ширпотребе статистичес-
ких прогнозов, предназначенном для использования в прило-
жениях, ничего, кроме тех или иных вариантов корреляцион-
ной теории, не существует. Типичной является следующая
задача.
Пусть стационарный процесс %(t) (с нулевым математи-
ческим ожиданием) наблюдается при (т. е. известны
24—2567 369
значения %(t), t^O), а требуется возможно точнее предска-
зать £(т) при некотором т>0. Ответом является проекция
f элемента гильбертова пространства £(т) на подпростран-
ство, порожденное величинами {£(0* *С0).
Если бы речь шла о проекции £(т) иа линейную оболоч-
ку конечного числа случайных величин то для
проекции и для среднеквадратической ошибки прогноза по-
лучились бы громоздкие выражения через ковариации вели-
чин ..., K(tn)> Нт) между собой. Привлекательная сто-
рона задачи прогноза для случайных процессов, т. е. для
бесконечного числа моментов ?С0, состоит в том, что для
ошибки прогноза, а в некоторых случаях — и для самого
прогноза (т. е. соответствующей проекции) получаются прос-
тые явные формулы (см., например, книгу Ю. А. Розанова
[30] или справочник Ю. В. Прохорова и Ю. А. Розанова
29]).
Но при этом возникают некоторые математические ре-
зультаты, которые трудно признать соответствующими прак-
тической реальности. Например, оказывается, что значение
Нт) при т>0 может быть во многих случаях точно предска-
зано по значениям {Н0> при сколь угодно большом
т. (Такие процессы называются линейио-сингулярными.)
Практически естественно рассмотреть такой класс процессов,
для которых дисперсия ошибки прогноза стремится при
т-»-оо к дисперсии o2=Dg(x). Такие процессы называются
линейно-регулярными. Оказывается, что для того, чтобы про-
цесс был линейно-регулярным, необходимо и достаточно,
чтобы его неслучайная спектральная мера допускала спек-
тральную плотность f(X), причем сходились интегралы
a) f log /(X)<fA>—оо в случае дискретного времени;
б)
dk
14-Х»
>—оо в случае непрерывного времени.
В частности, обращение в нуль спектральной плотности
f(X) на любом множестве значений X положительной лебего-
вой меры делает процесс лннейно-сннгулярным.
В случае непрерывного времени довольно естественно бы-
вает предположить, что мы имеем дело с процессом £(7) с
ограниченным спектром частот: f(X)=O при 1X1 >А. Оказы-
вается, такое предположение ведет к возможности безоши-
бочного прогноза процесса lift). Иначе это можно объяснить
следующим образом. В спектральном разложении самого
процесса
370
[e™Z(dJ
—GO
можно считать, что интеграл берется лишь по области
{Л:1Х|<Л}. Тогда траектории процесса, очевидно, допускают
производные всех порядков, а небольшое уточнение показы-
вает, что реализации £(/) можно считать аналитическими
функциями t. Но аналитическая функция восстанавливается
однозначно по своим значениям на вещественной полуоси.
Вывод о возможности точного предсказания будущего
значения процесса с ограниченным спектром по его прошлым
значениям явно не имеет практического значения. С другой
стороны, для линейно-регулярных процессов интервалы вре-
мени, на которые возможно эффективное прогнозирование,
обычно оказываются (с практической точки зрения) слиш-
ком малыми.
Короче говоря, имеется существенный разрыв между точ-
но решаемой математической задачей и практической ситуа-
цией, в которой нужно еще определить корреляционную
функцию (либо спектральную плотность) процесса по стати-
стическим данным.
3.3. Практические результаты. На практике те корреля-
ционные связи, которыми пытаются воспользоваться для
прогноза случайного процесса, весьма далеки от возможно-
сти обеспечить точный прогноз (т. е. от теоретически ярко
вырисовывающегося сингулярного случая). Корреляционные
связи оказываются слишком слабыми (а также неустойчивы-
ми). В сравнительно недавнее время в книге Бокса и Джен-
кинса [1] была сделана попытка использовать для прогноза
модель стационарных приращений. Однако приводимый в
этой книге пример прогноза (некоторых экономических пока-
зателей) при ближайшем знакомстве оказывается неубеди-
тельным.
Казалось бы, прогноз на короткое время, скажем, неко-
торых технологических параметров (допустим, с целью уп-
равления) мог бы быть более перспективным: корреляцион-
ные связи хотя и слабы, но все же лучше, чем ничего. Но
здесь существует проблема выделения статистической ком-
поненты технологического процесса (возможно ли и нужно
ли такое выделение?). В общем, ии одного практически важ-
ного примера прогноза случайного процесса автор данной
книги не знает.
В следующем параграфе мы рассмотрим (также неудач-
ный) пример прогноза с использованием вероятностных ме-
тодов, в котором, впрочем, нет никакого прогноза случайных
пооцессов, а вероятностная модель используется лишь для
24* 371
построения доверительных интервалов (поистине злосчаст-
ный объект, как многократно показывается в данной книге).
§ 4. Колебания уровня Каспийского моря
4.1. Введение. Вопрос о прогнозе колебаний уровня Кас-
пийского моря тесно связан с более широким вопросом о
частичной переброске на юг стока северных рек. Автор дан-
ной книги не берется высказать сколько-нибудь обоснован-
ное мнение относительно целесообразности такой переброс-
ки. Возможно, что недостаток воды настолько схватит за
горло наших ближайших потомков, что они сочтут переброску
необходимой. С другой стороны, водопроводчики считают, что
установка водомеров в квартирах примерно вдвое снижает
расход воды на бытовые нужды. Это при существующей сим-
волической цене воды по 6 коп. за кубометр, которая явно не
ограничивает удовлетворения разумных нужд. Речь практи-
чески идет о том, что без учета воды жильцы ие устраняют
ненужные утечки, а если приходится платить хотя бы симво-
лическую цену, то значительное число утечек устраняется.
Что для нас проще — установить в десяти миллионах квар-
тир двадцать миллионов водомеров (по одному для холод-
ной и горячей воды) или перебросить сток северных рек, —
это тяжелый вопрос, который автор решать не берется.
Существует другой вопрос: достаточно ли у нас знаний о
природных процессах, чтобы отважиться на переделку при-
роды такого масштаба, как переброска стока? Этот вопрос
нужно ставить более конкретно, и мы займемся более част-
ным аспектом, именно, прогнозом уровня Каспийского моря.
Изложим сначала внешние факты.
Реально для прогноза уровня Каспийского моря исполь-
зовалась так называемая модель Крицкого — Менкеля, из-
ложенная, в частности, в книге [25]. Существует мнение, что
методику Крицкого — Менкеля одобрил (или хотя бы как-то
положительно оценил) А. Н. Колмогоров. Сделанные на ос-
новании этой методики варианты прогноза на перспективу
до 2000 г. были опубликованы в [25] и послужили одним из
основных аргументов в пользу переброски стока. Переброска
стока, как известно, осуществлена не была, но было осуще-
ствлено отделение залива Кара-Богаз-Гол, давшее совершен-
но нежелательные последствия (это отделение учитывалось
в прогнозе, так что здесь прогноз не нуждается в поправке).
А море повело себя странно: вместо того чтобы снижаться
согласно прогнозу, его уровень стал повышаться: достиг той
высоты, которая (по прогнозу) могла быть достигнута лишь
с ничтожной вероятностью (меньше 1%), и для народного хо-
зяйства причиной убытков стало не понижение, а повышение
372
уровня моря. Посмотрим, в какой мере нам удастся разо-
браться в причинах такого скандала с прогнозом.
4.2. Модель Крицкого — Менкеля. В предисловии к моно-
графии [25], состоящей из четырех глав, указывается, что
главы написаны разными авторами: первую и третью главы
написал Д. В. Кореннстов, вторую главу — С. Н. Крицкий,
четвертую главу — Д. Я. Раткович. Это мы упоминаем для
того, чтобы отметить, что специализация в данной области
зашла настолько далеко, что даже сравнительно частный во-
прос о прогнозе колебаний уровня не может охватить один
человек. Действительно, главы Д. В. Кореяистова (первая
и третья) посвящены конкретным числам, связанным с Кас-
пийским морем (в том числе н злополучному прогнозу —
глава третья); глава С. Н. Крицкого (вторая) посвящена
теоретическим выкладкам; лишь ее последний параграф, по-
священный моделированию методом Монте-Карло, содержит
числа, имеющие какое-то (но не вполне точное) отношение
к Каспийскому морю; наконец, четвертая глава Д. Я. Ратко-
вича представляет собой современное развитие модели Криц-
кого — Менкеля. Эта глава содержит очень интересную
формулировку модели (непонятно только, насколько верную
фактически) и также очень интересные результаты модели-
рования методом Монте-Карло. Несколько слов об этой гла-
ве мы скажем позже.
Начнем с теоретического описания модели Крицкого —
Менкеля. Изложение в гл. 2 монографии [25] имеет один эс-
тетический дефект. Он часто бывает присущ сочинениям, ко-
торые по жанру и содержанию являются математическими,
но написаны авторами, которые (по образованию либо по
складу мышления) не являются математиками: не выбирает-
ся кратчайший и наиболее ясный путь изложения, в котором
посылки однозначно увязаны с результатом, а математичес-
кие формулы наиболее коротки. Сначала рассматривается
постановка задачи в ненужной общности, от которой потом
приходится отказываться, несколько путаются обозначения
и т. д. Но проверка показывает, что на самом деле все верно.
Сформулируем поэтому модель, не вполне придерживаясь
текста первоисточника. Основные понятия модели — приток
воды в море Vi (за i-й календарный год), — испарение во-
ды в i-м году, Wi — объем воды в море в конце i-ro кален-
дарного года. Приток Vi и объем Wi измеряются попросту в
кубических километрах, а испарение ei (точнее, видимое ис-
парение, т. е. разность между количеством испаряющейся во-
ды с 1 км2 площади моря и количеством выпадающих на
этот 1 км2 осадков) измеряется толщиной слоя видимого ис-
парения, т. е. в миллиметрах. Еще в модели участвует пло-
щадь поверхности моря Л (на конец i-ro года), которая
предполагается линейно связанной с объемом Wi. Суммар-
373
ное испарение воды за i-й календарный год принимается
равным et(Fi-i+Fi)/2, поскольку средняя площадь моря в
t-м году есть (Г,-14-Л)/2.
Качественно структура модели состоит в следующем.
Приток воды Vi и испарение ei определяются метеорологи-
ческими условиями, и лучшее, что мы можем о них ска-
зать,— это считать их случайными процессами (по имею-
щимся данным — независимыми друг от друга). Если бы
мере представляло собой бассейн с вертикальными стенками,
то объем воды в море в л-м году был бы суммой случайных
величин (разностей между притоком и испарением за прош-
лые годы), т. е. уровень моря совершал бы возрастающие ко-
лебания, наподобие траектории броуновского движения.
Единственный известный иам механизм стабилизации этих
колебаний состоит в том, что при возрастании (убывании)
объема воды в море увеличивается (уменьшается) его по-
верхность, однозначно связанная с потерями воды на испа-
рение. (Другие потенциально мыслимые механизмы, напри-
мер. тектонические движения дна, малоизвестны и не рас-
сматриваются.) Посмотреть, насколько эффективным может
быть этот механизм стабилизации, есть дело, несомненно,
благое и интересное.
Гидрологи считают, что в последние несколько десятков
лет притоки Vi в Каспийское море определялись достаточно
точно. Есть, правда, подземный сток, который оценивается
довольно произвольно в 3 км3 в год, ио он незначителен (по-
рядка 1% общего притока). Таким образом, несколько десят-
ков наблюдений Vi имеется. Что касается наблюдений испа-
рения ei, то они производятся в основном балансовым мето-
дом: считается, что по уровню моря мы достаточно точно
оцениваем объем воды в нем, а тогда по известному прито-
ку мы определяем испарение. Есть, правда, другие методы
дающие не вполне согласующиеся результаты, но на этих
противоречиях мы остановимся позже.
Теперь выпишем математическую модель. Пусть е„=
= <е{> — среднее испарение, V.=<V/> — средний при-
ток. Если бы случайных колебаний притока и испарения ие
было (т. е. все Vi равнялись V,, а все е> равнялись то
уровень моря соответствовал бы такой его площади F,, что
V,=F,e..
По площади F. однозначно устанавливается объем моря
U’» и соответствующий уровень Z*, называемый уровнем тя-
готения. Для Каспийского моря в [25] этот уровень Z* при-
нимается равным —28,5 м (грубо говоря, по отношению к
уровню Балтийского моря). Если принять линейную связь
между объемом воды Wi и площадью моря
374
Fi=Fo+AWi
(где Fo и А известны по морфометрическим данным)
и учесть, что испарение е,- в i-й год разумнее относить к сред-
ней площади моря
l/2(F/-t +Fi)=F0+ \l2A(Wi_y +W,)~F, cp,
то получится следующее балансовое уравнение:
\W^W,-W^x^Vx-elFa-\l2eiA(Wi^^Wi). (I)
Из этого уравнения можно было бы выразить Wt как
функцию от случайных величин е,, V, и известных чи-
сел А и Го- Получилось бы вполне пригодное для исследо-
вания методом Монте-Карло уравнение (при условии, что
мы умеем моделировать последовательности {е,}, {V<}):
* “ 1 + 1/2е{Л 1-1 14- 1/2«М
(2)
Нетрудно понять (интегрируя уравнение (2)), что то обстоя-
тельство, что коэффициент, стоящий в правой части (2) при
W<-i, всегда меньше 1, делает это уравнение устойчивым. Но
аналитическое исследование уравнения (2) затруднительно,
и Крицкий и Менкель линеаризуют уравнение (1), считая,
что Wt мало отличаются от wt, Ft мало отличаются от Ft, е,
мало отличаются от е». Тогда связь между площадью и объе-
мом моря целесообразно записать в форме
Fi=F.+A(Wi—W.),
в качестве переменных модели ввести vt—
=Vt—etF,, после чего балансовое уравнение (1) примет
форму
До», = w, — - Wt — W/-i = V, — е,(Г, +
+ l/2(w,+»<_,)}-pt— l/2(e<—
Если в последнем члене этого уравнения мы пренебре-
жем произведением 1/2Л(е«—е*Хи,<+а,/-1)» сохранив лишь
произведение 1/2Леа(ш( -f- то и получим модель
Крицкого и Менкеля
-
!=JZ2Ae. J4
14-1/2Ле. 14-1/2Ле.
(3)
(это как раз уравнение (5) монографии [25, с. 67], если по-
править имеющуюся в [25] опечатку).
375
Уравнение (3) есть устойчивое разностное уравнение,
но число ф=(1—1/2Ле#)/( 1 + 1/2Лев) очень близко k J: для
Каспийского моря принимается <p=0,97U4 (25, с. 105]. Это
означает, что влияние случайных колебаний, задаваемых
последним членом (3), растягивается на долгий ряд лет.
В книге [25, гл. 3] уравнение (3) немного поправляется:
отдельно выделяется отток воды в Кара-Богаз-Гол, посколь-
ку было известно, что он будет сокращен путем строительст-
ва дамбы.
Прогноз заключается в том, что, во-первых, путем усред-
нения уравнения (3) находится уравнение для среднего зна-
чения При этом среднее значение <о/> находится
с учетом планируемого изменения оттока воды в Кара-Богаз-
Гол, некоторой модели линейного роста изъятий воды на
нужды хозяйства страны и некоторой модели переброски
стока. Отношения к теории вероятностей этот расчет (сред-
них) не имеет: это просто арифметика. Вероятностная часть
прогноза состоит в вычислении дисперсии случайных вели-
чии wt. Понятно, что эти дисперсии выражаются (с по-
мощью уравнения (3)) через ковариации случайных вели-
чин vi=Vi—т. е. в конечном счете через ковариации
величин притоков Vi и испарений е().
Вопрос упирается, следовательно, в статистическую мо-
дель для Vi и е,-. Как было сказано, эти случайные последо-
вательности считаются независимыми, следовательно, нужно
дать модель каждой из них.
Подход, использованный в книге [25], состоит в следую-
щем. Проще всего было бы объявить {Vi} независимыми
(при разных i) величинами, но это противоречит наблюдае-
мым «периодам», когда соседние значения Vi оказываются
одновременно слишком малыми или слишком большими.
Так, в 1933—1940 гг. притоки воды были малыми, что приве-
ло к падению уровня Каспийского моря (к 1941 г. на 1,9 м
по сравнению с 1929 г.). Предлагается охватить эти явления
моделью цепи Маркова: немного загадочно говорится, что
последовательность Vi — это цепь Маркова с коэффициентом
корреляции между соседними членами г=0,3. Фактически
используется следующее утверждение: коэффициент корре-
ляции между Vi и Vi+k равен гк, где г=0,3. Относительно
испарения а широких статистических исследований нет: ар-
гументация в [25] сводится к тому, что «логично допустить»,
что vt = Vi—e.F„ коррелированы между собой так же, как
К (с. 64).
В каком-то смысле это действительно логично, так как
эквивалентно допущению, что et коррелированы между со-
бой так же, как Vi. В самом деле, если коэффициенты корре-
ляции между случайными величинами и £?, а также между
376
случайными величинами гр и г)2 равны г (причем 0^=0^,
Di)i=Dr|2 — это предположение стационарности), то коэф-
фициент корреляции между линейными комбинациями
+ Об2+/>П2
также равен г (пара (^. £.) не зависит от пары Од, ^8)>
Дейс.вигельно, cov(et, Fg)=rDc,-, cgv/t](, rlt) = rDrlt но тог-
да cov(agi + d7]b ags-H’/kj —'(«’Dci-F fcjDr;,) = rD(a&]-Ьгъ), i —
= I, 2, t. e.
cov (a?j -I- Ьтл, a-|- bTa$D(ah + b"$ • D(a;3+brj—r.
Если же коэффициенты корреляции между о/ известны (а
дисперсии i'i одинаковы и тоже известны), то вопрос о дис-
персии а1, в модели (3) есть вопрос непосредственных вы-
числений, которые и выполнены в книге [25, гл. 2].
Мы полностью описали модель и методику прогноза по
Крицкому — Менкелю. Речь не идет о прогнозе на будущее
значений стока и испарения: это признается невозможным.
В модель закладываются те или иные мыслимые варианты
детерминированного изменения стока (забор воды на нужды
хозяйства, переброска стока северных рек), на основании
которых рассчитывается математическое ожидание объема
воды в море, однозначно связанное с его уровнем. Дисперсия
объема воды рассчитывается как дисперсия результата ли-
нейных операций над случайными величинами с известными
дисперсиями и корреляциями. Про вычисление доверитель-
ны?< интервалов в книге [25] толком как-то не сказано. Не-
видимому, применяется нормальное распределение.
4.3. Анализ причин неудачи прогноза. Прежде всего, что
именно одобрил А. Н. Колмогоров? Автор книги по личным
воспоминаниям может засвидетельствовать следующее. В
1957 г. А. Н. Колмогоров читал студентам нашего курса
теорию случайных процессов. Когда речь шла о гауссовском
марковском стационарном процессе (который в данной кни-
ге называется процессом Орнштейна — Уленбека для скоро-
сти броуновской частицы,см. конец первой части), А. Н. Кол-
могоров упомянул о колебаниях уровня Каспийского моря
примерно следующим образом. Видим, что в последнее вре-
мя уровень моря, в общем, снижается, но, может быть, это
всего лишь колебание стационарного случайного процесса
(подробно это в лекции не развивалось).
Поскольку (как видно из вышеизложенного) аналогия
между процессом Орнштейна — Уленбека и моделью Криц-
кого— Менкеля полная, то речь шла, конечно, именно о мо-
дели Крицкого — Менкеля. Следует ли из этого, что
А. Н. Колмогоров выдал авторам модели индульгенцию на
право количественного прогноза уровня Каспийского моря на
377
будущие времена с ручательством, что этот прогноз будет ко-
личественно оправдываться и может быть использован для
расчета того, что случится при переброске стока северных
рек?
Прежде всего ие в обычае Андрея Николаевича было да-
вать такие индульгенции. Ученые обычно склонны к пере-
оценке роли развиваемых ими методов, но если в истории
науки были вообще люди, свободные от этого недостатка, то
прежде всего к ним надо отнести А. Н. Колмогорова. В та-
ких делах он скорее бы проявил излишнюю осторожность, чем
недостаточную. Речь могла идти о качественной картине ко-
лебаний уровня Каспийского моря, которая вытекает из ма-
лой стабилизирующей способности испарения (близкое к 1
значение <р в модели (3)).
Форсировать до уровня количественного согласия те до-
верительные интервалы, которые вытекают из модели мар-
ковской цепи для стока и испарения, А. Н. Колмогоров ни-
как не мог: каждому специалисту по теории вероятностей
ясно, что само предположение стационарности погодных яв-
лений (как случайных процессов) вряд ли может рассматри-
ваться особенно серьезно: были же, например, ледниковые
эпохи.
Наконец, индульгеиция, о которой идет речь, ие могла су-
ществовать уже потому, что авторы книги [25] ею не поль-
зуются. Процитируем третью главу Д. В. Коренистова
(с. 108—109):
сИсследования будущего уровенного режима Каспийского
моря как предмет настоящей работы носили в основном ме-
тодический характер. Конкретные данные прогноза могут
поэтому служить только для общей ориентировки в тенден-
циях процесса. Уточнение исходных гидрометеорологических
характеристик, не исключаемое и в будущем, может привес-
ти к тому или иному изменению уровней моря, ожидаемых
к концу текущего столетия».
Таким образом, сама трактовка прогноза по модели
Крицкого — Менкеля как точного количественного прогноза
не принадлежит ни авторам книги [25], ии А. Н. Колмогоро-
ву. Такая трактовка представляет собой некоторую нелепую
обработку конкретных научных попыток, возникшую в про-
цессе общественной борьбы вокруг вопроса о переброске сто-
ка. Эту обработку, как нам кажется, лучше всего понять с
помощью представления о трудно избегаемой шизофрении
коллектива узких специалистов. (Не зря ведь главы книги
[25] написаны разными авторами.)
Другой вопрос: в чем конкретная причина неудачи прог-
ноза? Естественное мнение на этот счет специалиста по тео-
рии вероятностей заключается в том, что модель марковской
цепи для погодных явлений столь груба, что от нее и нельзя
378
ожидать ничего хорошего. Если годы 1933—1940 были мало-
водными в смысле притока, то достаточно, чтобы, скажем,
годы 1983—1990 были многоводными (в той степени, в какой
это не допускается моделью цепи Маркова), и тогда уровень
моря повысится за пределы всяких доверительных интерва-
лов. К сожалению, это простейшее объяснение, по-видимому,
не подтверждается в достаточной мере данными о притоке.
Для анализа причин неудачи прогноза приходится глуб-
же заглянуть в предпосылки модели. Мы представляем себе
простейший арифметический баланс между притоком и испа-
рением; такие балансы часто рассматриваются в различных
науках, ио иногда природа наказывает нас за излишнее уп-
рощение тем, что сами понятия, в которых строится наш ба-
ланс, фактически не имеют смысла.
Обратимся к первой главе книги [25]. В начале нее дают-
ся морфометрические характеристики Каспийского моря.т.е.
поверхность различных его частей (и всего моря без залива
Кара-Богаз-Гол) в зависимости от уровня моря. В табл. 1
(с. 9) есть опечатка (досаднейшая для того, кто впервые
знакомится с предметом): в заголовке последнего столбца
(объем моря над отметкой — 38,0 м) единицы измерения
указаны в виде тыс. км3; на самом же деле речь идет, по-ви-
димому, о км3. Если эту поправку принять, то изменению
уровня моря на 1 м соответствует примерно 370—400 км3 во-
ды, что чуть больше годового притока (около 300 км3 без
учета изъятий воды). Далее приводится сравнение уровней
моря в разных точках; выясняются, в частности, факт и ско-
рость опускания футштока в г. Баку. Приводится график
уровней Каспийского моря, начиная примерно с 1830 г., а
также данные о стоках рек, начиная с 1881 г. Все это хоро-
шо, по крайней мере, насколько может понять неспециалист.
Но вот мы обращаемся к данным об испарении (начиная
со с. 41). Один метод определения испарения — с помощью
водного баланса. Но существуют и другие методы, в кото-
рых осадки и испарение учитываются раздельно и ие по ба-
лансу. Средние многолетние величины, получаемые разны-
ми методами, неплохо согласуются. Но в отдельные годы
различия велики — до 100 мм и больше (в то время как
среднее многолетнее значение слоя испарения принято рав-
ным е.=730 мм). Такие расхождения отвечают 40—60 км3
воды. Но главный вопрос состоит в том, что оценки испаре-
ния в разных частях моря дают довольно сильно отличаю-
щиеся величины. На северных мелководьях вода сильно
прогревается, и средняя многолетняя оценка испарения сос-
тавляет 904 мм, в то время как для среднего района моря
имеем 740 мм, а для южного — 659 мм. При таких данных
становится весьма проблематичным, к какой площади нуж-
но относить среднегодовое испарение с единицы площади
379
моря: к полусумме (Fz-itF>)/2, где F,- — площадь моря на
конец i-ro года, пли к какой-либо иной; процесс испарения
зависит от годовой динамики зеркала моря и метеоусловий
(включающих температуру, скорость ветра, облачность
и т. д.). Возникает подозрение, что мы оперируем вообще
несуществующим понятием испарения с единицы площади
моря. В книге [25] нет удовлетворительного анализа этого
подозрения; нет, например, никакой попытки ответа на сле-
дующий вопрос: к какому уровню моря мы бы пришли в
1970 г., если бы, взяв за исходный фактически1’1 уровень
1940 г., рассчитали бы дальнейший ход уровня моря, под-
ставляя в модель Крицкого—Менкеля фактические прито-
ки последующих лет и значения испарения, полученные не из
балансовых данных? Если бы такой расчет был проведен,
мы, может быть, сразу поняли бы, почему получилась скан-
дальная неудача с прогнозом. Ведь 40—60 км3 расхождения
в отдельные годы вполне могут объяснить несогласное с
прогнозом поведение уровня моря (если эти расхождения
наблюдаются несколько лет подряд).
Есть в первой главе и данные, подвергающие сомнению
модель марковской цепи. На с. 51 указывается, что вероят-
ность столь малого среднего за 8 лет (1933—1940 гг.) прито-
ка составляет величину порядка 1/300—1/1000. Да к тому
же это маловодье коррелировано с увеличением видимого
испарения (вероятность столь большого среднего за 8 лет
значения составляет 3—6%). В модели же сток и испарение
принимаются независимыми.
Резюмируем наше обсуждение. Не только вероятностная
сторона модели Крицкого — Менкеля (стационарная марков-
ская цепь), но и основная балансовая арифметика возбуж-
дают определенные сомнения. Выяснить доказательным об-
разом конкретную причину расхождения прогноза и факти-
ческого поведения уровня Каспийского моря ни автору дан-
ной книги, ни, по-видимому, кому-либо другому не удалось.
Поэтому совершенно ясно, что в настоящее время "даже в
гидрологии, в области водных балансов мы не обладаем до-
статочно достоверными данными, позволяющими понять, что
выйдет из переброски стока северных рек — зло или благо.
Но переброска рек — это ие только гидрология, но и био-
логия. Например, сколько рыбы разных видов и размеров
будет к 2000 г. в Каспийском море, если осуществить пере-
броску стока в определенных объемах?
На такие вопросы пытаются отвечать, составляя и решая
разностные уравнения для численностей (либо биомасс) рас-
тений и животных разных трофических групп, которые раз-
множаются и едят друг друга и где-то на верхнем трофичес-
ком уровне сами служат кормом для рыбы. Но коэффициен-
ты этих уравнений (т. е. кто кого ест и в каком количестве
380
н насколько размножается, если съест определенное количе-
ство пищи) должны браться только из опыта. Для такого
опыта точность 20% — большое достижение. Рассмотрим
для примера простейшее разностное уравнение
Хп+'.=Ахп, Хз—1, п=0, 1, 2...
где коэффициент А определен с точностью до 20%, т. е. то ли
Д=0,8, то ли Л = 1, то ли /1 = 1, 2. Чему равно х20 (т. е. че-
рез 20 лет): то ли (0,8)20, то ли 1, то ли (1,2)20?
Идея дифференциального (разностного) уравнения, ко-
нечно, хороша: запишем, что делается с системой за неболь-
шое время (это гораздо проще, чем сказать, что происходит
за большое время), а дальше предоставим решение уравнений
математике (в лице ли аналитических формул или в лице
ЭВМ). Но при этом законы изменения системы за малое вре-
мя должны быть известны очень точно. Между тем, хоть в ма-
тематической биологии, хоть в экономике, хоть в гидрологии,
мы часто обнаруживаем, что сами понятия, с которыми мы
работаем, лишены достаточно точного смысла (например, ис-
парение с единицы площади моря достаточно сильно зависит
от того, где находится эта единица — в северных мелковод-
ных районах или в южных глубоководных).
По всему этому необходимо признать, что никаких науч-
ных способов расчета последствий преобразования природы
такого масштаба, как переброска стока северных рек, в на-
стоящее время нельзя себе и представить.
4.4. Смысл марковской модели метеорологических фак-
торов. В количественно точном смысле эта модель приме-
няться явно не может. Посмотрим, нельзя ли все-таки из-
влечь из нее какие-то достаточно разумные выводы. Обра-
титься к четвертой глазе книги [25], написаииой Д. Я. Рат-
ковмчем. Для начала делается некоторое очень сильное ут-
верждение. Оно высказано в терминологии, не совсем при-
вычной для математика, так что о смысле его приходится
догадываться, но вот, по-видимому, верная разгадка.
Для любой реки по данным многолетних наблюдений
можно установить функцию распределения годового стока
Г(х). Сделаем замену переменной: положим Pi=Frl(Xi),
(xi — сток в i-й год). Тогда величины pi имеют равномерное
распределение на отрезке [0, 1]. Утверждается, что по данным
многолетних наблюдений над 289 реками мира найдено, что
для кдждой реки последовательность {р,} представляет со-
бой цель Маркова с двумерной плотностью распределения
Кр.. P,+l) = 1 + 3reuv + |r*(3u«-lX3»«-l) +
4
+ — r?(5u*—3u)(5i/s — 3v) +
4
38!
+ - f4(35u‘- 30u»-r 3)(35o4-30i>«+3),
64
где u=2pt— 1, u=2pi+l—1, r0 — параметр (коэффициент
корреляции между р, и р>+\), который принимает значения
0,3; 0,4; 0,5 в зависимости от модуля стока водосборного бас-
сейна (т. е. стока на единицу площади). Такая же модель
принимается и для видимого испарения. Если сток и испаре-
ние описаны, то для Каспийского моря возникает балансо-
вая модель, которая и рассчитывается на 1000 лет вперед
путем моделирования двух (независимых) марковских цепей
для стока и испарения. (Заметим, что на получившемся гра-
фике нет ни одного такого случая, чтобы уровень моря упал
за 10 лет настолько — почти на 2м, — насколько он в реаль-
ности упал за время маловодья 1933—1940 гг.) На модели
уровень моря колеблется примерно в пределах от —24,5 до
—29 метров.
Рассматривается вариант переброски, когда при низком
уровне моря в год перебрасывается 20 или 40 км3 воды (в
зависимости от уровня). Тогда колебания уровня вниз среза-
ются (уровень не бывает ниже —27,5 м), но колебания вверх
остаются. В результате необходимая для хозяйства стабиль-
ность уровня все равно не обеспечивается. При этом периоды
времени, в течение которых производится переброска стока,
могут быть очень длительными (до 20—30 лет подряд и бо-
лее).
Рассматривается также проект отделения дамбой север-
ной части Каспийского моря с тем, чтобы осуществлять про-
пуск воды в южную часть только при достаточно высоком ее
уровне в северной. Тогда уровень в северной части стабили-
зируется лучше, но все еще не вполне, а колебания урозня
в южной части значительно увеличиваются.
Такие указания на недостижимость идеальной ситуации в
случае осуществления тех или иных проектов, полученные на
модели марковской цепи, как нам кажется, являются вполне
убедительным свидетельством того, что и в реальности эта
идеальная ситуация достигнута быть не может. Поскольку
затраты на подобные научные разработки совершенно нич-
тожны в сравнении с затратами на осуществление грандиоз-
ных технических проектов, общество почти даром получает
полезное предупреждение. Такова, как нам кажется, в дан-
ном случае польза вероятностных моделей.
§ 5. Металлический волновод
5.1. Введение: общее описание технической проблемы.
При обсуждении проблемы существования внеземных циви-
лизаций. между прочим, отмечают следующее обстоятельст-
382
во. Каким образом можно было бы узнать из достаточно
удаленной точки космоса, что на нашей Земле существует
разумная жизнь? Оказывается, что на частотах, отвечающих
диапазону радиовещания и, в особенности, телевидения,
Земля излучает сравнительно огромную мощность, никаки-
ми способами, кроме существования технически развитой
цивилизации, необъяснимую. Не то чтобы иас особенно бес-
покоили напрасные потери этой мощности (потому что она
весьма мала по сравнению с общими мощностями, которыми
мы располагаем); хуже то, что станции, ведущие радио- и
телепередачи, будут мешать друг другу, если их частотные
диапазоны не разнести достаточно далеко. Следовательно, в
свободном пространстве (атмосфере) может быть создано
лишь крайне ограниченное число каналов связи. Телефонные
каналы связи упрятаны в кабели и под землю, но так прямо
поступить с телевизионными нельзя, так как высокочастот-
ные электромагнитные колебания, требуемые для телевиде-
ния, в телефонных (и коаксиальных) кабелях распространя-
ются весьма плохо. Нужен, стало быть, какой-то тракт свя-
зи, в котором могли бы распространяться высокочастотные
колебания, практически не выходя за пределы этого тракта.
На примере этой проблемы интересно рассмотреть фак-
тическую роль фундаментальных наук (в данном случае —
физики). В противоречие со своим названием никакого проч-
ного фундамента под решение технических проблем эти нау-
ки не закладывают: их роль сводится к разведке, в каком
месте и зачем такой фундамент, вообще говоря, стоило бы
заложить. Конкретно среди многих предложений для высо-
кочастотного тракта связи рассматривалось и предложение
металлического волновода, который представляет собой ци-
линдр, обычно круговой, но, вообще говоря, произвольной
формы поперечного сечения (вроде водопроводной трубы).
Уравнения Максвелла сначала решались для волновода с
идеально проводящими стенками; как всегда в теории урав-
нений с частными производными, решение разлагается в ряд
по некоторым частным решениям, называемым модами вол-
новода. Затем научились учитывать конечную проводимость
стенок и при этом выяснился чрезвычайно удивительный
факт: для некоторых мод (в частности, для так называемой
моды //ci в круглом волноводе) потери энергии падают с воз-
растанием частоты колебаний. Поскольку малые потери и
большая частота — это как раз то, что и нужно для тракта
связи, в этом теоретическом факте стали видеть указание
на одно из возможных технических решений проблемы трак-
та. Такой тракт представлялся состоящим из участков вол-
новодов длиной порядка 15—20 км с ретрансляторами меж-
ду ними (при дискретной форме передачи сигнала, которая
допускает исправление формы импульса, лишь бы только
383
ретрансляционное устройство достаточно надежно отличало
импульс от паузы).
Практическая работа по реализации этой идеи началась
в конце 50-х — начале 60-х годов. В те годы во многих об-
ластях техники, в частности и в этой, не было и речи о тех-
нической отсталости нашей страны: работы по металлическим
волноводам велись одновременно в ряде стран; в нашей стра-
не — в Институте радиотехники и электроники АН СССР.
Проблема состояла в том, чтобы сказать, пригодны ли те
трубы, которые могла без чрезмерных затрат выпустить про-
мышленность, для создания тракта волноводной связи (ли-
бо форма их настолько далека от кругового цилиндра и
(или) дефекты внутреннего медного покрытия настолько ве-
лики, что расстояние между ретрансляторами для волновод-
ного тракта, собранного нз этих труб, должно быть чрезмер-
но малым).
Казалось бы, нужно просто измерить потери энергии ос-
новной моды Hqi и степень ее преобразования в другие моды
(распространяющиеся с другой групповой скоростью и пото-
му создающие искажения сигнала) в тех реальных трубах,
которые изготовила промышленность, и вопрос будет ясен.
Но измерения оказались крайне нестабильными: стоило чуть
изменить длину измеряемой трубы либо частоту, на которой
производились измерения, и результат менялся весьма су-
щественно. Поэтому никакой уверенности в результатах из-
мерений не было. Возникал вопрос, не окажется ли и длин-
ный волноводный тракт, собранный из подобных волновод-
ных труб, нестабильным по частоте, что привело бы к недо-
пустимым искажениям формы сигнала.
Прояснить проблему и создать надежную методику изме-
рений удалось, исследуя математическую модель явления ме-
тодами теории случайных процессов. Мы изложим в следую-
щем пункте полученные результаты по книге Р. В. Ваганова,
Р. Ф. Матвеева и В. В. Мериакри 16]. Сейчас скажем нес-
колько слов о дальнейшей судьбе этой проблемы. После по-
явления лазеров делались попытки организовать связь по
лазерному лучу, распространяющемуся в свободной атмос-
фере (от верхушки одной башни к другой). Но атмосферные
явления (дождь, туман, снег) начисто губили такой канал
связи, и стало ясно, что лазерный луч тоже нужно заключить
в какой-то тракт связи. Начало решения этого вопроса от-
носится к 1970 г., когда был разработан метод получения
весьма чистого стекла, заготовка из которого затем вытяги-
валась в стекловолокно диаметром порядка 0,1 мм. Такое
волокно отлично удерживает лазерный луч при весьма не-
значительных потерях (меньших, чем в металлическом вол-
новоде); частота же световых колебаний, естественно, гораз-
до выше, чем тех колебаний миллиметрового диапазона длин
384
золя, которые соответствуют металлическому волноводу.
Есть, правда, некоторые проблемы, связанные с тем, что све-
товодные волокна, как правило, многомодовые, что ограни-
чивает их пропускную способность. Но, грубо говоря, одно
волокно означает одни телевизионный канал, а изготовление
и прокладка волоконного кабеля, вполне заменяющего ме-
таллический волновод, обойдутся неизмеримо дешевле. Луч-
шее, как известно, враг хорошего.
В нашей стране работы по стекловолокну начались с
большим опозданием. Положение отсталой страны в принци-
пе не так плохо, как кажется на первый взгляд: тот, кто раз-
рабатывает новые подходы, несет огромный груз исследова-
тельских попыток в разных направлениях, лишь немногие из
которых оказываются эффективными. Отсталой стране не
нужно весь этот путь проходить заново: принципы эффектив-
ных разработок, вообще говоря, не держатся в секрете.
(Только поэтому некоторые отсталые страны могут превра-
щаться в передовые). Если бы попытаться засекретить науч-
ные разработки на уровне теоретических принципов, то, ве-
роятно, не удалось бы никогда понять, какие нз этих принци-
пов действительно могут рассчитывать на эффективные
практические применения: применения сравнительно далеки
от принципов, и чтобы пройти путь от принципов до приме-
нений, нужно, чтобы информация о принципах была широко-
доступной. Роль теоретиков в отсталой стране хоть и иная,
чем в передовой, но тоже важная: нужно сохранить хотя бы
общее понимание того, что происходит в мире в области ре-
шения тех или иных проблем. Таково современное положе-
ние в области науки о новых трактах связи; мы же обратим-
ся к деталям недавней истории — к исследованию металли-
ческих волноводов.
5.2. Математическая модель. При решении уравнений
Максвелла в регулярном (т. е- имеющем форму геометри-
чески правильного цилиндра) волноводе отыскивается
система мод, т. е. полная система решений, которые за-
висят от временя через множитель е*** (“> — частота ко-
лебаний), от продольной координаты z (направленной
вдоль оси волновода) через множитель e-^f, где /’ — но-
мер моды, (Л^=ЛДо>) зависит от со), а от поперечных коор-
динат в сечении волновода электрическое и магнитное
поля зависят некоторым сложным образом^ знать кото-
рый нам ие понадобится. В дальнейшем зависимость от
времени явно в обозначения не включается и мы гово-
рим, что поле, отвечающее распространению j-й моды в
сечении г волновода, получается, если амплитуду Л/z) =
=e-zy умножить иа некоторые функции от поперечных
координат. Можно сказать, что выполняется уравнение
25—2567 385
2.Лу(г) = -1ЛЛ(г). (1)
as
В случае идеальной проводимости стеиок волновода числа
hj вещественны; при неидеальной проводимости
Л/=₽/—ia/. —»Л/=»₽/—«;,
т. е. мода распространяется, уменьшаясь по амплитуде
умножением на множитель е_“Л
Физики утверждают, что они в состоянии вычислить
затухание а,, исходя из известной проводимости стенок
волновода (и структуры полей в поперечном сечении).
Для волноводов, рассматриваемых в книге [6], потери
основной моды Нп по расчету должны были составлять
1 дБ/км, в то время как по измерениям, описанным в [6],
упорно получается примерно вдвое больше (если читате-
лю нужно пояснить понятие децибела, то пояснение со-
стоит в следующем: при z=l км теория дает, что е~11!=
s=10“0-1, а измерения дают, что е~9а*г=10~°л, где номер
7=«1 отвечает волне Нп). Разница между теорией и экспе-
риментом списывается на дефекты медного слоя, покры-
вающего изнутри волноводные трубы. Во всяком случае
в отношении потерь основной моды в стенках волновода
получается если и не полное совпадение с теоретическим
расчетом, то близкое по порядку величины значение.
Если волновод нерегулярен, т. е. его форма отклоняется
от идеальной, то предлагается приближенно считать, что
электромагнитное поле в сечении z все равно может быть
разложено по модам идеального волновода, взятым с неко-
торыми амплитудами А/(г). В качестве модели предлагается
так называемая система уравнений связанных мод
(a. + + 2 с^)Л/(г), (2)
а*-----------------------------------------i+l
которая, в отличие от уравнения (1), включает преобразова-
ния мод друг в друга, т. е. коэффициенты сц(г). Система
(2), конечно, как-то основывается на уравнениях Максвелла,
но не надо преувеличивать непосредственность этой связи —
лучше дать системе (2) статус некоторого постулата (он
единодушно считается достаточно правильным). Коэффици-
енты связи образуют косоэрмитову матрицу:
М2)-—
Для металлических волноводов речь идет о системе (2) срав-
нительно небольшой размерности: кроме амплитуды Ai(z)
386
основной моды //oi нужно еще учесть амплитуды от одной
до пяти других мод, так называемых паразитных. Тут, прав-
да, есть одно не очень ясное место, поля учитываемых мод
(в смысле их зависимости от поперечных координат х и у)
не все обладают круговой симметрией, а тогда вместо одной
моды нужно рассматривать две, отличающиеся поворотом
на 90°, — синусную и косинусную. Между этими двумя мо-
дами может существовать эффективный переход (т. е. срав-
нительно большой коэффициент Сц(г), но, следуя [6], мы бу-
дем считать, что этого нет. Тогда все коэффициенты связи
Cji(z) в (2) можно считать малыми.
Модель (2) годится для расчета волноводов, имеющих
(достаточно малые) детерминированные нерегулярности: из-
гибы, переходы от одного радиуса к другому и т. д. В таких
случаях коэффициенты сц(г) могут быть рассчитаны явно.
Но когда речь идет об анализе партии волноводных труб,
теоретически прямолинейных и одинаковых, то ничего друго-
го не остается, как предположить Сц(г) стационарными слу-
чайными процессами. Это предположение и завершает опи-
сание модели.
5.3. Проблемы анализа модели. Напомним, что требова-
лось сделать. Имея некоторое число изготовленных промыш-
ленностью волноводных труб (длина одной трубы 2,5 м; дли-
на всех труб 500 м), требовалось по каким-то измерениям
решить, каким должно быть расстояние между ретранслято-
рами для длинной волноводной линии, изготовленной из
этих труб (если 20 км, то хорошо, а если 10 км, то плохо).
Основное требование на длину участка между ретранслято-
рами — не слишком большое затухание мощности (если
40 дБ, т. е. от начала к концу участка доходит 10-4 от по-
сланной мощности, то это очень хорошо, а уж если 60 дБ,
т. е. доходит 10-6 от посланной мощности, то это почти не-
приемлемо). Таким образом, речь шла о том, чтобы по изме-
рениям потерь мощности в коротких линиях — из одной пли
нескольких труб — довольно точно определить потери мощ-
ности в длинном волноводе.
Математической моделью явления является система (2)
п. 5.2, в которой а/ и 0/ можно узнать на основании теории
или достаточно простых измерений, но случайные процессы
Cji(z) прямо в наблюдении не даны. Вообще говоря, элек-
тродинамика позволяет сосчитать коэффициенты связи
Сц(г), если точно задать отклонения настоящей формы тру-
бы от идеального цилиндра. Казалось бы, проблема лишь
в достаточно точных механических измерениях, но небольшое
размышление показывает, что именно эта проблема и не мо-
жет быть разрешена: слишком много информации нужно со-
брать и переработать, чтобы описать истинную форму твер-
дого тела. И в самом деле, когда такие попытки были пред-
25* 38-
приняты, они дали для некоторых функционалов от процес-
сов Сц(г) значения, многократно заниженные по сравнению
с реальностью [6, с. 215—218]. Авторы же книги [6] с само-
го начала не пошли по этому пути. Речь могла идти лишь об
измерениях некоторых функционалов от процессов Сц(г)\
грубо говоря, об измерении мощностей мод, т. е. квадратов
iA,(z)l2 при некоторых значениях z, при условии, что на
вход волновода (точку z=0) подается основная волна еди-
ничной амплитуды, т. е. Ai(0) = l, А/(0)=0 при /#1. (Ре-
альная задача физических измерений гораздо сложнее пото-
му, что нужно измерять малое отличие IAi(z)l3 от 1 и малые
величины |A,(z) |2; но примерно ситуацию можно понимать
так, как это делается в настоящем тексте.)
Значит, нужно измерить такие функционалы, знание кото-
рых позволило бы исследовать скорость убывания решения
системы (2) при больших z. Как кратко описано в первой
части настоящей книги, система (2) со случайными коэффи-
циентами приводится к произведению случайных матриц, ко-
торое исследуется переходом к полярной системе координат.
В системе (2) малы числа а/ и случайные процессы сц(г), а
постоянные распространения различных мод, наоборот, ве-
лики (£Д/=2л, где к/ — длина волны j-й моды — величина
порядка нескольких миллиметров). Важно на самом деле,
чтобы и разности 1{1/—{VI были велики, но на этот счет при-
нимаются специальные меры (например, покрытие стенки
волновода изнутри диэлектриком). При этом условии не-
большое рассмотрение показывает, что марковская цепь на
сфере (к которой сводится исследование произведения слу-
чайных матриц) допускает диффузионное приближение, пол-
ностью определяемое значениями измеряемых функционалов,
т. е. мощностей различных мод.
Но в начале 1960-х годов науки о произведениях случай-
ных матриц еще не существовало. Р. Ф. Матвеев [6, гл. 4],
используя малость отношений lA/(z)l/lAi(z)f, применил за-
мену переменной
{Л,(г), Л,(2), ...» ЛАГ(г)}—>
и получил эквивалентный позже появившейся науке резуль-
тат плюс приближенные методы расчета асимптотики
loglAi(z)| в условиях малости IA/(z)l/IAi(z)l. Примерно в
то же время американский теоретик Роу (54], занимаясь
той же задачей, рассмотрел систему двух уравнений
Г, ,ч М»(«)
Л1(2)’ Uw’
anw Г
^1(г) )
W —Г.Ш + /ф)/4(2),
388
/J(z) = »c(z)Z0(z) - ГЛ(г),
в которой О<Го<Г1, т. е., в общем, ту же самую систему
уравнений связанных мод. Но Роу сделал следующую заме-
ну переменных:
/о(2) = е-г‘г0.(2), /1(2) “ е-^г),
и эта (казалось бы, вполне безобидная) замена погубила де-
ло. Причина этого в том, что при z—>-оо обе функции l0(z)
и Ц(г) имеют одинаковый порядок убывания
|/.(z)|~e-r‘, |/>(2)|
где ГоСГсГь так что при замене переменных, сделанной
Роу, |G0(z)|—►О, |Gi(z)|—>-оо и вся картина стационарно-
го процесса ll(z)/Jo(z) потеряна. Тем не менее Роу каким-
то образом угадал правильный ответ, эквивалентный ответу
Р. Ф. Матвеева, но счел нужным приписать в статье [54] за-
мечание, сводящееся к тому, что хотя многие в этот ответ
верят, но ни в работе [54], ни в других нет ничего, что этот
ответ обосновывает. Так, успех математического исследова-
ния может зависеть от как бы случайной удачи или неудачи,
например замены переменных.
Но решение математической задачи — ие то, что интере-
сует нас в первую очередь (потому мы и описываем матема-
тическую сторону весьма кратко). Перейдем к вопросу о со-
ответствии модели случайного процесса действительности.
5.4. Статистическая сторона. Общее правило для обраще-
ния с системами уравнений, включающими малые случайные
возмущения, состоит в том, чтобы решить систему с точно-
стью до членов второго порядка по возмущениям. Следуя
[6, с. 114], рассмотрим частный случай системы уравнений
связанных мод, когда длина волновода z настолько мала, что
(а/—ai)z<l. Тогда можно положить a/=0, j—1............ N, н
амплитуда /-й моды иа выходе линии Af(z) получит вид
A/(z) = e-^f 1
6
(и несколько более сложный вид для /=!), где 0л=₽/—
а начальное условие имеет вид
А(0) = 1, Л,(0)= .. . -Л„(0)=0.
Согласимся (несколько легкомысленно), что мы можем
измерить

389
где
4(*) = f qдt) cos Ы0 dt< A(z) e [ q/(0sin Ы0 dt-
о о
Если z, с одной стороны, достаточно мало, чтобы
(а—«1)г<;1, а с другой стороны, достаточно велико по
сравнению с радиусом корреляции случайного процесса
Cii(t), то 11(г) и Iz{z) имеют нормальные распределения с
нулевым средним и одинаковой дисперсией, причем ковариа-
ция между J\(z) и l2(z) намного меньше их дисперсии. Сле-
довательно, |Л/(г)|2 имеет распределение суммы квадратов
двух независимых нормальных величин, т. е. показательное
распределение. Посмотрим, что это означает практически.
Постоянные и Р/ являются функциями частоты колеба-
ний « (примерно пропорциональны частоте). Следовательно,
при изменении частоты измеряемая мощность IA/(z)la будет
вести себя аналогично периодограмме (рассматриваемой как
функция частоты): в среднем (по ансамблю волноводов) она
будет давать спектральную плотность процесса Сц(1) (на
частоте Рл=₽/1 (®)), но при этом обнаруживать большой
разброс. Поскольку |Л/(7)|2 есть мощность /-й моды, она ин-
терпретируется как потеря мощности основной (первой) мо-
ды на преобразование в /-ю моду. Если мы ее измеряем с
большим разбросом (а коэффициент вариации показательного
закона равен, как известно, единице), то те суммарные поте-
ри мощности в длинном волноводе, которые являются целью
исследования, определяются крайне неуверенно. Сходная си-
туация возникает и при изменении длины линии г.
Модель случайного процесса дает следующее. Конечно,
измерения на разных частотах следует усреднить, при этом
точность определения среднего может быть оценена, исходя
из модели случайного процесса. Для длинной волноводной
линии это среднее будет иметь гораздо больше смысла, чем
для короткой, так как затухание (в децибелах) в длинной
линии есть примерно сумма независимых случайных величии
(затуханий на отдельных участках). Иными словами, с объ-
яснением причины разброса измерений чисто вероятностны-
ми средствами получаем определенную уверенность в том,
что можно ориентироваться иа средние результаты измере-
ний при проектировании длинной линии.
Экспериментальная проверка модели случайного процес-
са состоит, в частности, в том, что проверяется показатель-
ное распределение потерь на преобразование в ансамбле
волноводных секций.
Кратко опишем экспериментальный материал. Промыш-
ленность имела две технологии изготовления волноводных
труб; после предварительных измерений была принята техно-
390
логия холодной обкатки на точных оправках. Отдельная сек-
ция имеет длину 2,5 м, внутренний диаметр 60±0,05 мм, мед-
ное покрытие изнутри толщиной 15 мкм, на которое наносит-
ся диэлектрическая пленка толщиной 90 мкм. Допуски на
точность изготовления учитывали ограничение периодических
неоднородностей с периодами, входящими в резонанс с
ехр(фиг). Общая длина изготовленных секций была более
500 м.
На этих секциях был проведен ряд электрических и ме-
ханических измерений, в результате чего были отоираиы
лучшие трубы общей длиной около 200 м. Этн трубы дали
линию с потерями 3,4 дБ/км. Если же из иих отобрать наи-
лучшую треть, т. е. 70 м, то получаются потери 2,6 дБ/км.
Основное требование при укладке — отсутствие изгибов со
стрелой прогиба более 10 см на 10 м.
Теперь о статистических свойствах. В 83 секциях, состав-
ленных каждая из двух 2,5-метровых труб, были измерены
потери на преобразование моды в моду Hi2. Теоретичес-
ки возможны два крайних случая. 1) Ось секции является
плоской кривой, т. е. мода Hi2 рассматривается в одном ва-
рианте. Тогда распределение потерь на преобразование дол-
жно быть показательным. 2) Ось секции изгибается в про-
странстве, причем ее проекции на любую пару взаимно пер-
пендикулярных плоскостей независимы и имеют одинаковые
статистические характеристики. Тогда мода Hi2 существует
в виде двух независимых мод — синусной и косинусной, и
теоретическое распределение потерь есть сумма двух показа-
тельно распределенных независимых случайных величин.
Эмпирическая функция распределения потерь превраща-
ется в прямую линию именно в показательном масштабе
(6, с. 214—215], т. е. для 5-метровых секций осуществляется
первая возможность.
Кроме этого, измерения проводились на трех линиях дли-
ной по 70 м. Значения потерь на преобразование, получен-
ные при разных частотах, приблизительно рассматривались
как выборка. Выборочная функция распределения превраща-
ется в прямую в масштабе, отвечающем сумме двух пока-
зательных распределений. Это находит свое объяснение в
том, что при большой длине линии ее ось превращается в
пространственную кривую [6, с. 219—220].
В книге [6] приводятся и результаты иных обработок. В
целом выводы из модели случайного процесса находятся в
неплохом согласии с экспериментальными данными. В рас-
сматриваемой задаче технической физики такое согласие не
разумеется само собой и даже довольно удивительно. Дей-
ствительно, статистический ансамбль волноводных труб по-
лучается путем отбраковки 60% всех имевшихся труб, т. е.
можно было бы ожидать каких-то урезанных распределений
391
вероятностей (для функционалов, т. е. мощностей мод, отве-
чающих оставшимся в эксперименте трубам). Но в действи-
тельности этого не наблюдается: наблюдаются примерно те
распределения, которые предсказываются теоретически. Раз-
брос измерений мощностей паразитных мод, в общем, объяс-
няется тем разбросом, который теоретически должна йметь
периодограмма, построенная по реализации случайного про-
цесса. Теоретическое объяснение разброса создает опреде-
ленную уверенность в усредненных результатах измерений,
которые без такого объяснения представлялись бы ненадеж-
ными.
ЛИТЕРАТУРА
книги
1. Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз-
и управление. Вып. 1—2. М.: Мир, 1974.
2. Большее Л. Н., Смирнов Н. В. Таблицы математической-
статистики. М.: Наука, 1983.
3. Боровков А. А. Теория вероятностей. М.: Наука, 1986.
4. Брнллинджер Д. Временные ряды. Обработка данных и тео-
рия. М.: Мир, 1980.
о. Бронштейн М. П. Атомы н электроны//Библиотечка «Квант»..
Вып. 1. М.: Наука, 1980.
6. В а г а н о в Р. Б., М а т в е е в Р. Ф., Мериакрн В. В. .Много-
волновые волноводы со случайными нерегулярностями. М.: Советское ра-
дио, 1972.
7. Васьковский А. П. Микроклимат и температурно-влажност-
ный режим ограждающих конструкций зданий на Севере. Л.: Стройиздат.
1986.
8. В ин е р Н. Кибернетика. М.: Советское радио. 1958.
9. В и и е р Н. Я- — математик. М.: Наука. 1964.
10. Воронцов-Вельяминов Б. А. Лаплас. М.: Наука, 1985.
11. Гаврилов Л. А., Гаврилова Н. С. Биология продолжитель-
ности жизни. М.: Наука, 1986.
12. Гельфанд И. М., Виленкин Н. Я- Некоторые применения
гармонического анализа. Оснащенные гильбертовы пространства // Обоб-
щенные функции. Вып. 4. М.: Физматгиз. 1961.
13. Гельфанд И. М., Шилов Г. Е. Обобщенные функции и дей-
ствия над ними //Обобщенные функции. Вып. 1. М.: Физматгиз, 1958.
14. Гельфанд И. М., Шилов Г. Е. Пространства основных и
обобщенных функций // Обобщенные функции. Вып. 2. М.: Физматгиз,
1958.
15. Гнеденко Б. В. Курс теории вероятностей. М.: Наука, 1988.
16. Гнеденко Б. В., Колмогоров А. Н. Предельные распреде-
ления для сумм независимых случайных величин. М.; Л.: Гостехиздат.
1949.
17. Гу м бель Э. Статистика экстремальных значений. М.: Мир,
1965.
18. Д о л и и П. А. Основы техники безопасности в электроустановках.
М.: Эиергоатомиздат, 1984.
19. Дуб Дж. Л. Вероятностные процессы. М.: ИЛ. 1956.
20. Кендалл М. Дж., Стьюарт А. Многомерный статистический
анализ и временные ряды. М.: Наука, 1976.
21. Колмогоров А. Н. Основные понятия теории вероятностей. М.:
Наука, 1974.
22. Колмогоров А. Н. Теория вероятностей и математическая ста-
тистика (сборник работ). М.: Наука, 1986.
23. К о л м о г о р о в А. Н., Ф о м и и С. В. Элементы теории функций
и функционального анализа. М.: Наука, 1981.
393
24. Крамер Г. Математические методы статистики. М.: Мир, 1975.
25. К р и ц к и й С. Н., К о р е и и с т о в Д. В., Р а т к о в и ч Д. Я. Ко-
лебания уровня Каспийского моря. М.: Наука. 1975.
26. Матерой Ж. Основы прикладной геостатистики. М.: Наука,
1968...
27. М е ш а л к и н Л. Д. Сборник задач по теории вероятностей. М.:
Изд-во МГУ, 1963.
28. М о н и н А. С., Я г л о м А. М. Статистическая гидромеханика. М.:
Наука, 1967.
29. Прохоров Ю. В., Розанов ГО. А. Теория вероятностей (Ос-
новные понятия. Предельные теоремы. Случайные процессы) // Справоч-
ная математическая библиотека. М.: Наука, 1973.
30. Розанов Ю. А. Стационарные случайные процессы. М.: Физмат-
гиз, 1963.
31. Розанов Ю. А. Введение в теорию случайных процессов. М.:
Наука, 1982.
32. Розанов Ю. А. Теория вероятностей, случайные процессы и ма-
тематическая статистика. М.: Наука, 1985.
33. Розанов ГО. А. Лекции по теории вероятностей. М.: Наука,
1986.
34. Севастьянов Б. А., Чистяков В. П„ Зубков А. М.
Сборник задач по теории вероятностей. М.: Наука, 1980.
35. Слуцкий Е. Е. Избранные труды. М.: Изд-во АН СССР, 1960.
36. См ел ков Г. И. Пожарная опасность электропроводок при ава-
рийных режимах. М.: Энергоатомиздат, 1984.
37. Татарский В. И. Распространение воли в турбулентной атмо-
сфере. М.: Наука, 1967.
38. Т у л ь ч и и И. К., Н у д л е р Г. И. Электрические сети жилых и
общественных зданий. М.: Энергоатомиздат. 1983.
39. Тутубалин В. Н. Теория вероятностей. М.: Изд-во МГУ, 1972.
40. Феллер В. Введение в теорию вероятностей и ее приложения.
Т. 1. М.: Мир, 1964; Т. 2. М.: Мир. 1967.
41. Хальд А.Математическая статистика с техническими приложе-
нии. М.: ИЛ, 1956.
42. X е н н а н Э. Анализ временных рядов. М.: Наука, 1964.
43. Чайлдс У. Физические постоянные. М.: Физматгиз, 1961.
44. Чебыщев П. Л. Полное собрание сочинений. Т. 5. М., Л.: Изд-
во АН СССР, 1951.
45. Черкасов В. Н. Молниезащита сооружений в сельской местно-
сти. М.: Россельхозиздат, 1983.
46. Ширяев А. Н. Вероятность. М.: Наука, 1989.
47. Шурыгин А. Н. Статистика при подсчете запасов месторожде-
ний. М.: Изд-во МГУ, 1978.
48. Э л ь я с б е р г П. Е. Измерительная информация: сколько ее нуж-
но? как ее обрабатывать? М.: Наука, 1983.
49. Я н к о Я- Математико-статистические таблицы. М.: Госстатнздат,
1961.
50. Kendall М. G. Contributions to the study of oscillatory time-
series. Cambridge, 1946.
СТАТЬИ
51. Белова Л. A., Ma и икон я нц Л. Г., Тутубалин В. Н. Ве-
роятность аварийного пробоя изоляции обмоток статоров турбогенерато-
ров в зависимости от длительности работы // Электричество. 1965. № 4.
С. 42—47.
52. Белова Л. А., МамиконянцЛ. Г., Тутубалин В. Н. О
статистической однородности корпусной изоляции статоров турбогенерато-
ров // Электричество. 1967. № 6. С. 40—46.
394
53. Белова Л. А., Мамиконянц Л. Гч Тутубалин В. Н.Ти-
повые кривые вероятности аварийных пробоев изоляции статоров гидро-
генераторов // Электричество. 1979. № 5. С. 54—58.
54. Rowe Н.‘ Е. Approximate solution for the coupled line equation Ц
Bell, system techn. burn. 1962. V. 41. N 3. P. 1011—1029.
55. Truett J., Cornfield J., Kannel W. A multivariate
analysis of the risk of coronary heart disease in Framingham // Joum. of
ohron. diseases. 1967. V. 20. P. 511-524.
56. Wiener N. Comprehensive view of prediction theory // Proc, of
intern, congr. of math. 1950. V. 2. P. 308—321.
Учебное издание
Тутубалин Валерий Николаевич'
теория вероятностей и случайных процессов
Зав. редакцией Н, М. Глазкова
Редактор Л. А. Николова
Художественный редактор А. Л. Прокошев
Технический редактор М. Б. Терентьева
Корректоры Л. А. Костылева, Л. А, Айдарбекоеа
ИБ № 4475
Сдано в набор 19.09.91. Подписано в печать 4.03.92
Формат 60X90‘/ie. Бумага тип. № 2. Гарнитура литературная.
Высокая печать. Усл. печ. л. 25,0. Уч.-изд. л. 24,55.
Тираж 5400 экз. Заказ 2567. Изд. № 1758.
Ордена «Знак Почета» издательство Московского
университета.
103009, Москва, ул. Герцена, 5/7.
Серпуховская типография Упрполиграфиздата
Мособлисполкома