3. ФЛЮГГЕ
Задачи
по квантовой
механике
том 1
Перевод с английского
кандидата физ.-мат. наук, доцента
Б. А. ЛЫСОВА
Под редакцией
доктора физ.-мат. наук, профессора
А. А. СОКОЛОВА
Издательство «Мир»
МОСКВА 1974

DIE GRUNDLEHREN DER
MATHEMATISCHEN WISSENSCHAFTEN
in Einzeldarstellungen
mit besonderer Berucksichtigung
der Anwendungsgebiete
Band 177
Practical
Quantum Mechanics I
by
SIEGFRIED FLOGGE
Physlkalisches Institut
der Unlversitat Freiburg
SPRINQER-VERLAQ
BERLIN - HEIDELBERG — NEW YORK
1971

УДК 530.145@75)
Книга Флюгге представляет собой своеобразное изложение
квантовой механики на базе анализа задач н примеров. Она охва-
охватывает почти все разделы квантовой механики, нашедшие большое
практическое применение. Внимательно читая книгу Флюгге,
можно не только изучить основы квантовой механики, но и на-
научиться применять ее к конкретным задачам.
Книга разделена на два тома. Первый том состоит из двух
глав. Первая глава посвящена основным принципам квантовой
механики, а вторая — анализу многочисленных задач, связанных
с движением одной бесспиновой нерелятивистской частицы. В за-
задачах, посвященных проблеме рассеяния, приводится расчет фазо-
фазовых сдвигов для парциальных волн, рассматриваются уравнение
Калоджеро и полксы Редже. Есе это впервые излагается в учеб-
учебной литературе.
Книга полезна студентам и преподавателям, а также широ-
широкому кругу физиков-экспериментаторов, не обладающих достаточ-
достаточным опытом выполнения конкретных квантовомеханических
расчетов.
Редакция литературы по физике
20402—068
Ф ¦* ——68—74 © Перевод на русский язык, «Мир», 1974

Предисловие редактора перевода
Книга „Задачи по квантовой механике", перевод которой пред-
предлагается вниманию советского читателя, написана немецким фи-
физиком-теоретиком старшего поколения Зигфридом Флюгге. Он
начал работать еще в 30-е годы с Максом Борном, а в настоящее
время уделяет большое внимание издательской деятельности,
в частности как редактор широко известной многотомной „Физи-
„Физической энциклопедии" (Handbuch der Physik).
Квантовую механику, как и любой другой раздел теоретиче-
теоретической физики, невозможно изучить, ограничиваясь только рас-
рассмотрением теоретических положений. Поэтому нет ни одного
курса по квантовой механике как советских, так и иностранных
авторов, в котором с помощью волновых уравнений не рассматри-
рассматривались хотя бы основные квантовые задачи: гармонический осцил-
осциллятор, ротатор, водородоподобный атом, эффект Зеемана, учет
релятивистских и спиновых эффектов, атом гелия, простейшие
молекулы и т. д. Более того, на базе решения этих конкретных
задач и сравнения теоретических выводов с экспериментальными
данными возникла сама квантовая механика; вначале она была
нерелятивистской (матричная механика Гейзенберга, волновое
уравнение Шредингера), а затем пришлось построить такое вол-
волновое уравнение, которое объясняло бы не только спиновые
(уравнение Паули), но и релятивистские эффекты (уравнение
Дирака). К сожалению, далеко не все задачи решаются точно
с помощью волновых уравнений Шредингера или Дирака и т. д.
Поэтому необходимо было создать еще и приближенные методы,
например метод Вентцеля — Крамерса — Бриллюэна (ВКБ), тео-
теорию возмущений и т. д. С помощью волновых уравнений кван-
квантовой механики находятся, как правило, так называемые стацио-
стационарные состояния (без учета излучения).
Для последовательного разрешения квантовой проблемы
электромагнитного излучения пришлось развить теорию вторич-
вторичного квантования и применить ее к решению конкретных вопро-
вопросов. В частности, на основе метода возмущений была развита
квантовая теория спонтанного и вынужденного излучений, кото-
которая вначале была построена Эйнштейном с помощью принципа
соответствия полуклассической боровской теории.

Предисловие редактора перевода
Чтобы изучить, а главное овладеть методами квантовой меха-
механики, явно недостаточно ограничиться волновыми уравнениями
и решением с их помощью некоторых основных задач. Поэтому
не удивительно, что в учебном плане университетского курса
квантовой механики наряду с лекциями предусмотрены еще прак-
практические занятия, где студентов учат решать с помощью кванто-
квантовой механики самые разнообразные задачи.
Если в литературе имеется достаточное количество учебников
по квантовой теории, написанных советскими [1—6] и иностран-
иностранными [7—10]г) авторами, то задачников по квантовой механике
весьма мало. Один из первых задачников был написан Зигфридом
Флюгге на немецком языке еще в 1947 г. [11]. Это пособие
стало классическим задачником, которым пользовались не только
иностранные, но и советские специалисты, несмотря на то, что
он не был переведен на русский язык. В советской литературе
имеется лишь несколько сборников задач по курсу квантовой
механики, наиболее известными из которых являются задачники
[12, 13]2). К сожалению, они относятся к 1956—1§57 гг. и не-
несколько устарели, не говоря о том, что в них рассматриваются,
как правило, только нерелятивистские задачи. Поэтому не уди-
удивительно, что появление в 1971 г. задачника по квантовой меха-
механике Флюгге всячески приветствовалось. Книга Флюгге — по
существу заново переработанное и дополненное издание его за-
задачника 1947 г. [11]. Автор вынужден был разбить новое изда-
издание на два тома, поскольку 219 задач с подробными решениями
и комментариями оказалось неудобно поместить в один том.
В книге Флюгге 1971 г. собрано не только значительно больше
задач, чем в издании 1947 г., но, что не менее важно, помещены
задачи из новых разделов квантовой механики (например, реля-
релятивистской квантовой механики и теории излучения), которые
фактически отсутствовали в изданных до настоящего времени
задачниках.
Глава I посвящена основным принципам квантовой механики,
включая вопросы, связанные с интерпретацией математического
аппарата. Здесь же рассмотрены связь между шредингеровским
и гейзенберговским представлениями и переход к импульсному
представлению.
Наибольший интерес в первом томе представляет гл. II,
в которой собрано большое число задач, связанных с движением
бесспиновой частицы в полях различного вида. В этой главе
11 Наш список учебников по квантовой механике, изданных на русском
языке, является далеко не полным. Мы не приводим и соответствующую лите-
литературу, не переведенную на русский язык.
2> Существует ряд задачников по теоретической физике вообще, в которых
лишь весьма небольшой раздел отведен некоторым специальным задачам кван-
квантовой механики [14—16].

Предисловие редактора перевода
наряду с задачами, помещенными во многие пособия (прямо-
(прямоугольная потенциальная яма, гармонический и ангармонический
осциллятор, момент количества движения в сферических коорди-
координатах, проблема Кеплера и др.), имеется довольно много задач,
связанных с использованием приближения ВКБ. Это вполне
естественно ввиду возрастающей роли приближения ВКБ при
изучении многих проблем квантовой механики. В конце главы
разобраны задачи о движении заряженной частицы в магнитном
поле.
Весьма интересна, как нам кажется, серия задач этой главы,
посвященная упругому рассеянию на сферически симметричном
потенциале. Автор использовал здесь результаты ряда оригиналь-
оригинальных научных статей, сравнительно недавно появившиеся в науч-
научной периодике и не вошедшие еще в учебную литературу. Мы
имеем в виду прежде всего расчет фаз рассеяния для парциаль-
парциальных волн методом последовательных приближений, уравнение
Калоджеро, полюсы Редже, вариационный принцип Швингера
и т. д.
Второй том начинается с гл. III, посвященной движению
нерелятивистских частиц со спином 1/%. Вся глава разбита на
две части: в части А рассматриваются одночастичные задачи,
в части Б—двух- и трехчастичные задачи.
Глава IV также разбита на две части, включающие соответ-
соответственно задачи со сравнительно небольшим (часть А) и с очень
большим числом частиц (часть Б). В части А рассматриваются
задачи о возбужденном состоянии атома гелия, об основном со-
состоянии лития с обменными поправками и т. д. В части Б пред-
представлены задачи, при решении которых используются методы
квантовой статистики (влектронный газ в металле, модель атома
Томаса — Ферми и т. д.).
Глава V посвящена в основном нестационарным задачам,
включая дираковскую теорию возмущения.
В гл. VI собраны задачи, связанные с релятивистским урав-
уравнением Дирака. Здесь весьма подробно разбираются проблема
Кеплера с учетом релятивистских и спиновых эффектов, теория
дираковских спиноров, переход к нерелятивистскому уравнению
Паули и т. д.
В последней, гл. VII излагаются элементы теории вторичного
квантования как нерелятивистского уравнения Шредингера, так
и уравнения Максвелла—Лоренца. На основе вторичного кван-
квантования разбираются задачи, касающиеся вероятности излучения,
интенсивности линий лаймановской серии в атоме водорода,
эффекта Комптона и тормозного излучения.
Для удобства читателя в конце книги помещено математиче-
математическое приложение справочного характера. В нем в компактном
виде изложены вопросы, связанные с применением различных

Предисловие редактора перевода
систем координат: сферической, параболической, цилиндрической,
эллипсоидальной. Здесь же даны определения и приведены основ-
основные формулы для ряда специальных функций, наиболее часто
встречающихся в квантовой механике (гипергеометрическая функ-
функция, Г-функция, функции Бесселя, Эйри, Лежандра и т. д.).
Подробный предметный указатель, который помещен во вто-
втором томе, позволяет быстро находить номера задач, интересующих
читателя. Это особенно важно, поскольку физически родственные
задачи по тем или иным методическим соображениям могут быть
помещены в различные разделы.
В заключение отметим некоторые особенности книги Флюгге.
Ее нельзя рассматривать как стандартный задачник, в котором
лишь формулируется та или иная задача, а затем дается ответ или
приводятся указания к ее решению. В книге во многих задачах
развиваются соответствующие теоретические положения квантовой
механики, причем сами задачи снабжены весьма подробными ре-
решениями, а результаты проиллюстрированы числовыми приме-
примерами и графиками, что несомненно облегчает их понимание.
Теория, развиваемая при решении задач, практически охватывает
курс квантовой механики (примерно в объеме университет-
университетской программы), включая ее принципиальные законы. Поэтому,
внимательно читая книгу Флюгге, можно не только изучить
квантовую механику, но и научиться применять ее к конкретным
задачам. Потребность в руководствах такого рода в последние
годы стала особенно ощутимой, поскольку квантовая механика
находит применение во все более широких областях физики,
а контингент лиц, изучающих ее, быстро возрастает. Поэтому
мы надеемся, что выпускаемая на русском языке книга Флюгге
будет полезна не только студентам различных вузов, изучающим
теоретическую физику, а также преподавателям, ведущим
занятия по квантовой механике, но и широкому кругу физиков-
экспериментаторов, не обладающих достаточным опытом при вы-
выполнении конкретных квантовомеханических расчетов.
Мы сочли возможным внести в текст некоторых задач неболь-
небольшие изменения с целью устранить замеченные в процессе перевода
неточности и опечатки. Кроме того, там, где автор цитирует
малоизвестные у нас монографии, пришлось дать дополнительные
ссылки на доступные советскому читателю книги, в которых
разбираются соответствующие вопросы.
Конечно, книгу Флюгге можно было бы дополнить более
сложными задачами, связанными, например, с ролью симметрии
в квантовой механике, или задачами, решение которых опирается
на теорию абстрактного гильбертова пространства. Однако это
значительно увеличило бы объем, тем более что многие близкие
вопросы изложены в специальной литературе, носящей характер
задачников (см., например, [17]). Во всяком случае, еще раз

	Предисловие редактора перевода	9
повторяем, что книга Флюгге будет полезна всем физикам, кото-
которые не только хотят изучить принципиальные вопросы квантовой
механики, но и желают научиться применять их к решению кон-
конкретных задач.
А. А. Соколов
Москва, июнь 1973 г.
Литература
1.	Блохинцев Д. И., Основы квантовой механики, изд-во „Высшая школа",
1963.
2.	Ландау Л. Д., Лифшиц Е. М., Квантовая механика, Физматгиз, 1963.
3.	Соколов А. А., Лоскутов Ю. М., Тернов И. М., Квантовая механика,
изд-во „Просвещение", 1965.
4.	Соколов А. А., Тернов И. М., Квантовая механика и атомная физика,
изд-во „Просвещение", 1970.
5.	Матвеев А. Н., Квантовая механика и строение атома, изд-во „Высшая
школа", 1965.
6.	Давыдов А. С, Квантовая механика, изд. 2-е, перераб., изд-во „Наука",
1973.
7.	Ферми Э., Квантовая механика, изд-во „Мир", 1968.
8.	Зоммерфельд А., Строение атома и спектры, т. 1 и 2, Гостехиздат, 1956.
9.	Шифф Л., Квантовая механика, ИЛ, 1959.
10.	Морс Ф., Фешбах Г., Методы теоретической физики, т. 1 и 2, ИЛ,
1958, 1960.
11.	Fliigge S., Rechenmethoden der Quantentheorie dargestellt in Aufgaben und
Losungen, Springer, Berlin, 1947. x>
12.	Гольдман И. И., Кривченков В. Д., Сборник задач по квантовой механике,
Гостехиздат, 1957.
13.	Коган В. И., Галицкий В. М., Сборник задач по квантовой механике,
Гостехиздат, 1956.
14.	Иродов И. Е., Сборник задач по атомной и ядерной физике, Атомиздат,
1971.
15.	Скачков С. В. и др., Сборник задач по ядерной физике, Физматгиз, 1963.
16.	Фейнмановские лекции по физике (Задачи и упражнения с ответами и
решениями), изд-во „Мир", 1969.
17.	Халмош П., Гильбертово пространство в задачах, изд-во „Мир", 1970.
11 Второе A952 г.) и третье A965 г.) издания написаны 3. Флюгге сов-
совместно с Г. Маршаллом.

Предисловие автора
Впервые эта книга под названием Rechenmethoden der Quan-
tentheorie1' была издана в 1947 г. в Германии. Она была предна-
предназначена студентам, только еще приступающим к изучению кван-
квантовой механики, и тем специалистам-экспериментаторам, которые
ранее никогда не пользовались ею в качестве рабочего аппарата.
Книга имела цель помочь тем и другим научиться применять
общую теорию к практическим задачам атомной физики. С тех
давних пор было написано много прекрасных книг, служащих
введением в общую теорию и необходимых для более глубокого
понимания предмета. Однако нам кажется, что при этом чисто
практическая сторона дела в какой-то мере была упущена из
виду, если, конечно, не говорить о тех многочисленных моно-
монографиях, где со всеми подробностями освещаются отдельные
специальные вопросы. Иными словами, мы до сих пор все еще,
по-видимому, не имеем всестороннего практического руководства
по квантовой механике, и такое пособие могло бы оказаться
полезным.
Надеясь заполнить указанный пробел, автор пошел навстречу
желанию издателей, предложивших модернизировать старое не-
немецкое издание и написать новый вариант книги на английском
языке с тем, чтобы сделать ее более доступной широким кругам
студенческой и научной общественности.
С самого начала не могло быть никаких сомнений в том, что
объем книги должен значительно возрасти. Нужно было добавить
новые приближенные методы и другие новейшие достижения, в
особенности относящиеся к проблеме рассеяния. Кроме того, нам
казалось необходимым включить в книгу релятивистскую кван-
квантовую механику и хотя бы бегло затронуть теорию излучений,
как пример квантования волновых полей. Наконец, сам подбор
задач, бывший ранее в известной мере случайным, нуждался
теперь в тщательном пересмотре.
В итоге число задач по сравнению с последним немецким из-
изданием возросло почти вдвое. Ни одна из них не является про-
простым переводом первоначальной задачи, и примерно лишь 50 задач
11 Методы решения задач по квантовой механике.— Прим. ред.

12	Предисловие автора
возникло в результате переработки первоначального текста. Таким
образом, подавляющее большинство задач публикуется здесь
впервые. Тем не менее общий характер книги остался прежним,
но теперь тенденция иметь в конце каждой задачи пригодные
для обсуждения буквенные результаты и числовые значения, как
нам кажется, выражена отчетливее.
Мы не стали исключать более элементарные задачи, такие,
как задача о частице в прямоугольной яме, но несколько сокра-
сократили их объем. Общее введение к немецкому изданию, что-то
около 20 страниц, посвященных основным уравнениям и их интер-
интерпретации, в этом издании опущено. Любой студент, пользующийся
задачником, достаточно знаком с предметом, поэтому такой шаг
вполне оправдан. Однако нам казалось, что читателям принесет
пользу математическое приложение, где собраны и ластично вы-
выведены формулы, относящиеся к специальным функциям, которые
широко используются на протяжении всей книги.
Не без колебаний согласился автор с практическими доводами
издателей, пожелавших иметь настоящее издание книги в виде
двух отдельных томов, надеясь, что этот шаг не нанесет серьез-
серьезного ущерба ее внутренней структуре и единству.
Хинтерцартен, март 1971

Содержание
Предисловие редактора перевода 		5
Предисловие автора 		11
I. Общие принципы
-1. Закон сохранения вероятности		17
2.	Вариационный принцип Шредингера		18
3.	Классическая механика для пространственных средних ....	21
4.	Классические законы для момента количества движения ....	22
5.	Закон сохранения энергии	' . . .	23
6.	Эрмитово сопряжение		24
7.	Построение эрмитова оператора		25
8.	Дифференцирование оператора		28
9.	Изменение средних значений со временем		29
10.	Картина Шредингера и картина Гейзенберга		30
11.	Гамильтониан, зависящий от времени		32
12.	Повторное измерение 		33
13.	Криволинейные координаты		35
14.	Волновые функции в импульсном представлении		36
15.	Пространство импульсов. Периодические и непериодические вол-
волновые функции		38
II. Одночастичные задачи без учета спина
А. Одномерные задачи		40
16.	Фундаментальные решения в случае свободного движения ...	40
17.	Волновой пакет в случае свободного движения		43
18.	Стоячие волны 		46
19.	Полупроницаемая перегородка		49
20.	Полупроницаемая перегородка в виде б-образного потенциаль-
потенциальною барьера		53
21.	Рассеяние на б-образном потенциальном барьере		55
22! Рассеяние на симметричном потенциальном барьере		56
23.	Отражение от прямоугольного барьера		58
24.	Инверсия отражения		60
25.	Прямоугольная потенциальная яма		62
26.	Прямоугольная потенциальная яма между двумя бесконечными
стенками		66
27.	Виртуальные уровни		70
28.	Периодический потенциал		75
29.	Дираковская потенциальная гребенка		78

14	Содержание
30.	Гармонический осциллятор		81
31.	Осциллятор в абстрактном гильбертовом пространстве (осцилля-
(осциллятор в представлении Фока)		84
32.	Использование лестничных операторов для нахождения собст-
собственных функций осциллятора 		87
33.	Гармонический осциллятор в матричном представлении ....	89
34.	Волновые функции осциллятора в пространстве импульсов . .	92
35.	Ангармонический осциллятор		93
36.	Приближенные волновые функции		97
37.	Потенциальная ступенька		99
38.	Потенциальная яма Пешля —Теллера		102
39.	Модифицированная потенциальная яма Пешля — Теллера . . .	106
40.	Свободное падение вблизи земной поверхности		112
41.	Ускоряющее электрическое поле		116
Б. Задачи с двумя или тремя степенями свободы без сфери-
сферической симметрии		118
42.	Круговой осциллятор		118
43.	Эффект Штарка для двумерного ротатора		121
44.	Ион молекулы водорода		123
45.	Наклонное падение плоской волны		128
46.	Симметричный волчок		131
В. Момент количества движения		135
47.	Бесконечно малые вращения		135
48.	Момент количества движения в сферических координатах . . .	137
49.	Момент количества движения и оператор Лапласа		139
50.	Преобразования в гильбертовом пространстве 		140
51.	Коммутаторы в координатном представлении		142
52.	Частица со спином 1		143
53.	Перестановочные соотношения компонент тензора		144
54.	Тензор квадрупольного момента. Сферические гармоники . . .	146
55.	Преобразование сферических гармоник		148
56.	Построение собственных векторов оператора Lz в абстрактном
гильбертовом пространстве		151
57.	Ортогональность сферических гармоник		153
Г. Сферически симметричные потенциалы		154
а. Связанные состояния		154
58.	Средние значения компонент момента количества движения . .	156
59.	Радиальная компонента оператора импульса		159
60.	Решения, близкие к собственным функциям		161
61.	Квадрупольный момент		163
62.	Частица внутри непроницаемой сферы		165
63.	Сферически симметричная прямоугольная яма конечной глубины,	168
64.	Потенциал Вуда—Саксона		171
65.	Изотропный осциллятор		175
66.	Вырожденные состояния изотропного осциллятора		177
67.	Проблема Кеплера		180
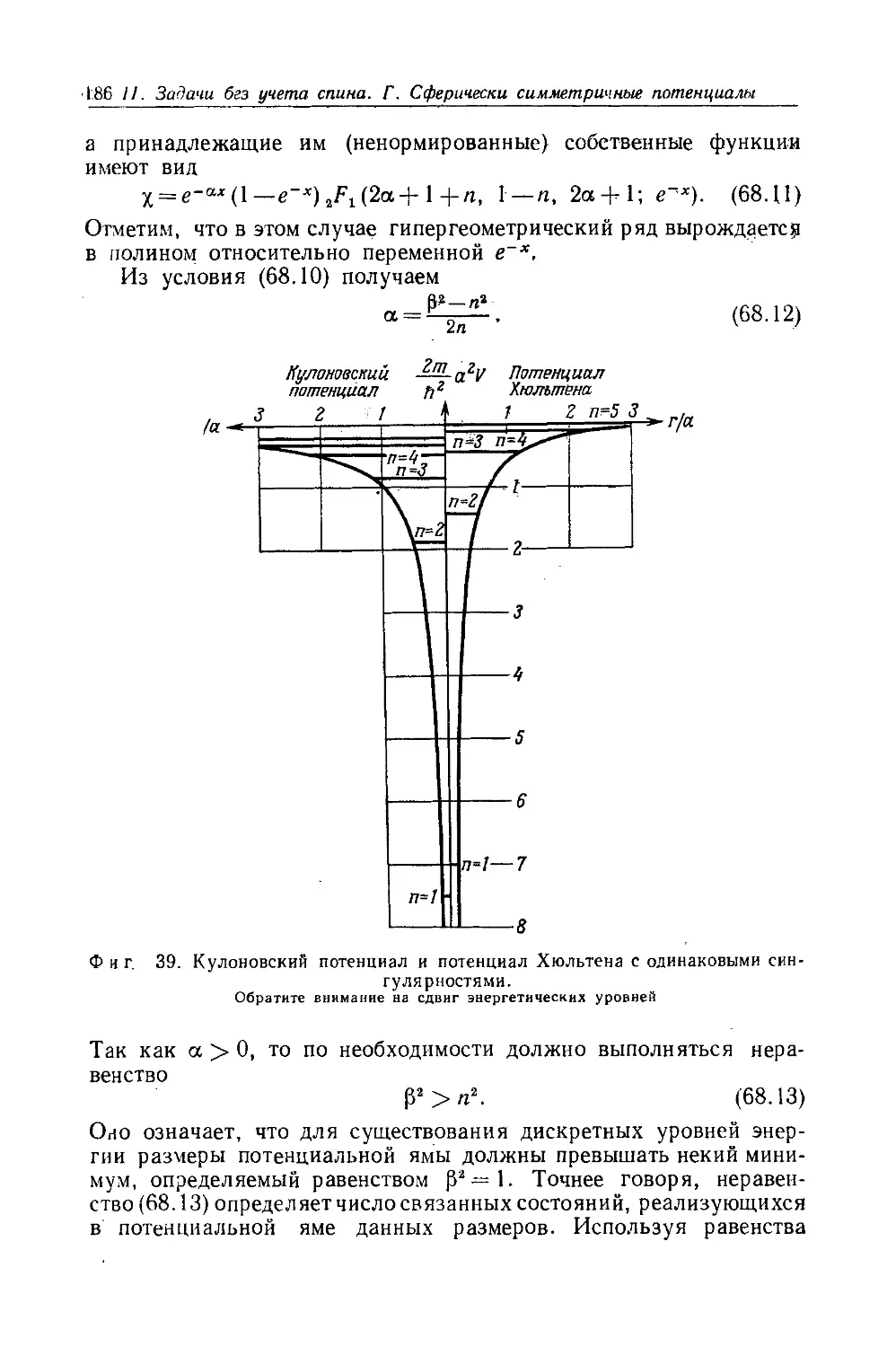
68.	Потенциал Хюльтена	,	184
69.	Молекулярный потенциал Кратцера		187
70.	Потенциал Морса		191
71.	Ротационные поправки к формуле Морса		196
72.	Потенциал Юкавы		198

Содержание	15
73.	Изотопический сдвиг границы рентгеновского излучения ....	200
74.	Основное состояние мезоатома		202
75.	Модель дейтрона с центральным взаимодействием		205
76.	Импульсное представление для волновых функций в поле цент-
центральных сил		210
77.	Уравнение Шредингера в импульсном представлении в поле
центральных сил		212
78.	Водородные волновые функции в импульсном пространстве . .	214
79.	Штарк-эффект у пространственного ротатора		215
б. Упругое рассеяние		217
80.	Интерференция падающей и рассеянной волн		217
81.	Разложение плоской волны по парциальным волнам		220
82.	Разложение амплитуды рассеяния по парциальным волнам . . .	223
83.	Рассеяние при низких энергиях		225
84.	Рассеяние на сферически симметричном прямоугольном потен-
потенциальном барьере		227
85.	Аномальное рассеяние		232
86.	Рассеяние на резонансных уровнях		235
87.	Вклад состояний с высшими значениями момента количества
движения		239
88.	Приближение, не зависящее от формы потенциала		241
89.	Низкоэнергетическое рассеяние на сферически симметричной
прямоугольной яме		245
90.	Низкоэнергетическое рассеяние и связанные состояния ....	247
91.	Дейтронный потенциал с жесткой сердцевиной и без нее . . .	249
92.	Низкоэнергетическое рассеяние при наличии жесткой сердце-
сердцевины и без нее		252
93.	Низкоэнергетическое рассеяние на модифицированном потенциале
Пешля — Теллера		253
94.	Радиальное интегральное уравнение		256
95.	Вариационный принцип Швингера	, .	260
96.	Последовательные приближения для фазы рассеяния		263
97.	Уравнение Калоджеро		266
98.	Линеаризация уравнения Калоджеро		268
99.	Длина рассеяния потенциала, имеющего вид степенной функции
100.	Второе приближение к уравнению Калоджеро		269
101.	Длина рассеяния для сферически симметричной прямоугольной	272
потенциальной ямы		225
102.	Длина рассеяния потенциала Юкавы 		277
103.	Улучшение сходимости рядов сферических гармоник		280
104.	Интеграл по прицельному расстоянию 		282
105.	Борновское рассеяние. Последовательные приближения ....	284
106.	Рассеяние на потенциале Юкавы 		287
107.	Рассеяние на экспоненциальном потенциале 		290
108.	Борновское приближение для рассеяния на сферически симмет-
симметричном распределении заряда 		294
109.	Высокоэнергетическое рассеяние на жесткой сфере		298
ПО. Формула Резерфорда 		300
111.	Разложение кулоновской функции по парциальным волнам . .	303
112.	Аномальное рассеяние 		307
113.	Преобразование Зоммерфельда — Ватсона		308
114.	Полюс Редже 		310
Д. Приближение Вентцеля — Крамерса — Бриллюэна (ВКБ)	313
115.	Разложение эйконала		313
116.	Применение метода ВКБ к радиальному уравнению 		315

16	Содержание
117.	Граничное ВКБ-условие Лангера		316
118.	Гармонический осциллятор в приближении ВКБ		321
119.	Уровни ВКБ в однородном поле		322
120.	Проблема Кеплера в приближении ВКБ		324
121.	Фазы ВКБ для свободного движения		326
122.	Вычисление фаз ВКБ		327
123.	Расчет кулоновских фаз методом ВКБ .		328
124.	Квазипотенциал		331
Е. Магнитное поле		332
125.	Введение магнитного поля		332
126.	Плотность тока в присутствии магнитного поля		334
127.	Нормальный эффект Зеемана		336
128.	Парамагнитная и диамагнитная восприимчивости без учета
спина		338

I. Общие принципы
Задача 1. Закон сохранения вероятности
Вероятностная интерпретация условия нормировки
=1,	A.1)
при которой выражение i|)*»j)d3x отождествляется с вероятностью
обнаружить рассматриваемую частицу в элементе объема d3x,
с необходимостью приводит к закону сохранения. Найдите этот
закон и обсудите возможную интерпретацию полученного резуль-
результата с точки зрения классических представлений.
Решение. Искомый закон сохранения должен иметь вид урав-
уравнения непрерывности
|f	O,	A.2)
где
р = 1П>	A.3)
— плотность вероятности,	a s—плотность тока вероятности.
Поскольку р — билинейная	форма относительно г|> и г|Л уравне-
уравнение A.2) можно получить	лишь в результате комбинации двух
уравнений Шредингера
с одним и тем же гамильтонианом
H = -^V + V(r)	A.5)
в обоих случаях. Таким образом, получаем
Согласно A.2), левая часть этого соотношения должна записы-
записываться в виде дивергенции. Действительно,
^	4>V V) = —^ div M>*Vi|>—
поэтому можно для вектора s написать
s=ш №w

18	/. Общие принципы
К классической интерпретации полученного результата можно
прийти, рассуждая следующим образом. Если умножить обе вели-
величины р и s на массу частицы т, то в результате у нас получатся
плотность массы рга и плотность импульса g":
Р» = '"Р» g=ms,	A.7)
тогда уравнение непрерывности естественно интерпретировать как
закон сохранения массы. Точно так же, умножив на заряд частицы е,
придем к плотности заряда рг и к плотности электрического тока J:
Р* = Ф> У=«г,	A.8)
а уравнение A.2) станет законом сохранения заряда.
Примечательно, что закон сохранения массы и закон сохра-
сохранения заряда по существу идентичны, так как оба они обуслов-
обусловлены конвекционным током одной и той же часТицы.
Выражение для полного импульса шредингеровского поля,
полученное из соотношений A.6) и A.7),
р | gd3x J
gd3x = -J. j (ц*щ—W) dsx,
с помощью интегрирования по частям второго слагаемого можно
привести к виду
A.9)
-Wf
что находится в согласии с определением (см. задачу 3) среднего
значения оператора импульса (%/i) V в квантовом состоянии г|).
Задача 2. Вариационный принцип Шредингера
Заменить уравнение Шредингера
-^Ч2У + У(г)У=ЕЦ	B.1)
вариационным принципом для энергии.
Решение. Всякое решение г|> дифференциального уравнения B.1)
удовлетворяет уравнению связи "
=1,	B.2)
поэтому выражение для энергии получается путем умножения
уравнения B.1) на г|>* и последующего интегрирования по всему
пространству:
^[^	]	B.3)
11 Это утверждение верно лишь для состояний дискретного спектра.—
Прим. ред.

	2. Вариационный принцип Шредингера	Н>
Интегрирование по частям первого члена с учетом формулы
Грина дает
\ i))*Vs^8x = § г|>*Vtydf— \ {Щ*) ¦ (Vi|)) d*x.	B.4)
Далее нормировочный интеграл B.2) существует лишь в случае*
если решение г|> на больших расстояниях г убывает не медлен-
медленнее, чем
г|>~ г-'/»-*, е>0.
Но при этом условии поверхностный интеграл в B.4), взятый no-
поверхности бесконечно удаленной сферы, исчезает, поэтому вы-
выражение B.3) можно записать в виде
(г)^]с13х.	B.5)-
Это равенство совершенно симметрично по отношению к функциям
г|> и if* точно так же, как и условие нормировки B.2), и мы
с таким же успехом могли бы получить его, исходя из уравнения
И *• = ?*••	B.1а>
комплексно сопряженного уравнению B.1).
Было бы нетрудно показать, что уравнения B.1) и B.1а)
представляют собой уравнения Эйлера для вариационной задачи
об экстремуме интеграла B.5) при наличии связи B.2). Мы, од-
однако, не будем пользоваться аппаратом вариационного исчисле-
исчисления, предпочтя ему прямое доказательство.
Пусть г|>а, — решение дифференциального уравнения B.1), при-
принадлежащее собственному значению ?х- Оно дает для интег-
интеграла B.5) значение Е%. Заменим теперь % на близкую функцию
% + 6г|), где 6т|)—малая, но произвольная вариация, если не
считать условия B.2), которому функция \р\ + 6Ч|) должна удов-
удовлетворять в той же мере, что и %:
и, следовательно,
J (г|^6г|)» + 4>x8i|>) dH + J (8i|>*8i|>) d»x = 0.	B.6>
После подстановки г|?^ -j— 6\Jj в интеграл B.5) получаем для энер-
энергии выражение Е\-\-8Ех, где
))]^)} ffix
сРх. B.7)
В первой строке здесь собраны члены первого, а во второй—вто-
второй—второго порядка малости. С помощью интегрирования по частям^

20	I-Общие принципы
обратного выполненному ранее, мы можем в первой строке вер-
вернуться к выражениям 8r|>V*^ и 6t|)*V2%u а затем воспользоваться
уравнениями B.1) и B.1а) для того, чтобы избавиться от про-
производных. В результате мы, например, получаем
поэтому первая строка в соотношении B.7), если учесть равен-
равенство B.6), будет также давать вклад второго порядка малости:
3x- B-8)
Так как у нас не осталось членов, линейных по 6т|э или 6г|>*, то
энергия Е%, очевидно, будет иметь либо максимум, либо минимум
при 6г|) = 0, т. е. для тех чря., которые являются решениями урав-
уравнения Шредингера. Ответ на вопрос о том, что_ представляет
собой экстремум—максимум или минимум,—зависит от знака
выражения B.8).
Чтобы несколько глубже разобраться в этом последнем вопросе,
мы воспользуемся совокупностью решений {%} уравнения B.1)
и построим из них ортогональную систему функций:
^6^-	B.9)
Теперь разложим по этой системе функций вариацию 6г|>:
4=2MV	B.10)
V
Тогда равенство B.8) примет вид
U V
и v	J L
или с учетом B.9) и B.1)
2|c,i№-?x).	B-11)
Если Еь относится к основному состоянию, то для всех состоя-
состояний г|)ц имеем Ец^Ех и вариационный принцип, таким образом,
дает для Е%. минимум, так как сумма B.11) положительна. Для
возбужденных состояний нельзя установить такого общего пра-
правила, так как в сумме B.11) в этом случае содержатся как
положительные, так и отрицательные слагаемые.

3. Классическая механика для пространственных средних	21
Задача 3. Классическая механика для пространственных средних
Показать, что основное уравнение классической ньютоновской
динамики
dp
¦i = F,	C.1)
где р—импульс, a F—сила, действующая на частицу, для про-
пространственных средних (математических ожиданий) имеет место и
в квантовой механике.
Решение. Пусть сила F выражена через потенциал, F= — \V,
а импульс р заменен оператором (fl/i)V- Интересующие нас сред-
средние определяются равенствами
^	C.2)
^(y	C.3)
Наша задача — показать, что интегралы C.2) и C.3) удовлетво-
удовлетворяют уравнению C.1), если функции г|> и г|)* удовлетворяют
уравнениям Шредингера
C-4)
Доказательство мы начнем с того, что продифференцируем
равенство C.2) по времени:
р A C(ij)*v»|)f^*V^)d3x
Выше мы учли, что вклад от поверхностного интеграла, появ-
появляющегося при интегрировании по частям второго слагаемого,
равен нулю и его можно опустить. Избавляясь здесь от г|)* и ф
с помощью уравнений C.4), получаем
] d5x + $irVv^ + Kw*> d"x-
C.5)
Интегрирование по частям
(V V)	J
показывает, что оба слагаемых в первом интеграле из C.5) вза-
взаимно сокращаются. Применяя далее интегрирование по частям
к последнему из оставшихся в C.5) слагаемому, получаем
— V (Vty)] d'6x.

82	/¦ Общие принципы
Воспользовавшись в заключение формулой
приходим к уравнению
р = _ J ц,« (vF) ц d*x = F,
в справедливости которого требовалось убедиться.
Задача 4. Классические законы для момента количества движения
Показать, что для пространственных средних классическая
связь между моментом количества движения L = гхр и моментом
силы T—rxF (здесь р означает импульс, a F—силу)
имеет место и в квантовой механике.
Решение. Как и в предыдущей задаче, начнем с определения
пространственных средних:
j,	D-2)
Т = — l^{rxVV)^dsx.	D.3)
Снова предполагается, что волновые функции 1|) и т|з* удовлетво-
удовлетворяют уравнениям Шредингера C.4).
Наше доказательство мы начнем с дифференцирования по
времени равенства D.2):
L = ~ J [Г (г х V4>) + Г (г X VW] d*x.
Преобразуем второе слагаемое с помощью тождества
и учтем, что к первому члену правой части этого тождества в
дальнейшем можно применить общую формулу векторного анализа
D.4)
где / = т|Л{>. Это дает
/, = — \ гх(ф*\7'<|'—'фУ'ф*) dax.
Избавляясь теперь от т|з* и ij) с помощью уравнений C.4), полу-
получаем
= - %п 1гх №*Г) (П) (^) C4K +
d3x.	D.5)

	5. Закон сохранения энергии	23
Так как
то выражение, стоящее в скобках под знаком первого интеграла,
является градиентом скалярной функции / = (V>|>*)t(V'>|>)» поэтому
этот интеграл, согласно D.4), исчезает. Выражение, стоящее
в скобках под знаком второго интеграла, равно V (ty*ty)- Используя
далее тождество
7V (г|>*ф) = V
и снова прибегая к помощи формулы D.4), где / — Ут|Л|з, окон-
окончательно преобразуем второй интеграл к виду
г X [Vy (г|Л|>)] dax = — ^ г X (i|3*i|3V^) d3x,
что совпадает, как это и требовалось доказать, с выражением
D.3) для среднего значения момента силы.
Задача 5. Закон сохранения энергии
Пусть энергия шредингеровского волнового поля описывается
интегралом B.5) из задачи 2, в этом случае закон сохранения
энергии должен иметь вид
^ + divS-0,	F.1)
где W — плотность энергии, a S—плотность потока энергии. Тре-
Требуется вывести указанный закон сохранения, сконструировав
подходящий вектор Умова — Пойнтинга S.
Решение. Как было найдено, согласно B.5)
E=^Wd*x,	E.2)
где
^	m.	E.3)
Здесь первый член — плотность кинетической, а второй—плот-
второй—плотность потенциальной энергий. В соответствии с уравнением E.1)
нам нужна производная
Й	E.4)
Так как
и
(W) (V^) = v
то мы можем преобразовать ту часть выражения E.4), которая

24	/. Общие принципы
обусловлена кинетической энергией, и написать
E.5)
Уравнения Шредингера C.4) позволяют нам в последних слагае-
слагаемых заменить пространственные производные и потенциал произ-
производными по времени. Результирующие члены в точности сокра-
сокращаются друг с другом:
так что уравнение E.5) действительно совпадает по форме
с уравнением E.1), а искомый вектор Умова — Пойнтинга S равен
^	E-6)
Задача 6. Эрмитово сопряжение
Оператор Q+, эрмитово сопряженный с оператором Q, опреде-
определяется равенством
^	^	F.1а)
которое с помощью символики функционального анализа можно
записать в виде
<Щ) | ф> = <1|> | Q+<p>.	F.16)
Здесь 1|) и ф — произвольные функции, подчиняющиеся условию
нормировки:
<1|)|г|5> = 1, <ф|Ф>=1.	F.2)
Сформулируйте данное определение на языке матричного пред-
представления. Что вы можете сказать о собственных значениях
эрмитова оператора, определенного равенством Q = Q1?
Решение. Матричное представление оператора определяется
выбором полного набора ортонормированных функций {uv\:
6ЦЛ,.	F.3)
Для произвольных нормированных функций 1|) и ф имеют место
разложения:
i|) = 2av"v. ф = 2Ьцыи-	F-4)
V	Ц
Подставляя рааложения F.4) в определение F.1), получаем
ц v

7. Построение эрмитова оператора	25
Предполагается, что это равенство справедливо для любой пары
функций i|) и ф, поэтому оно должно выполняться для каждого
слагаемого в отдельности:
<fiuv | Ыц> = <«v | й+ | "ц>-	F.5)
Используем теперь полный набор {uv} для определения матрицы
оператора Ш, переписав правую часть равенства F.5) в виде
Что касается левой части, то ее можно преобразовать следующим
образом:
ый> = ^ (Quv)*ulldx = QuJ(Quv)dx]'= <ым | й | uv>*= й*у.
Следовательно, матричные элементы матриц Q и й+, согласно
F.5), должны быть связаны соотношением
(QV = QvM.	F.6)
Иначе говоря, элементы эрмитово сопряженной матрицы й+ по-
получаются из элементов матрицы Q с помощью операций транспо-
транспонирования (fi^v) и комплексного сопряжения.
Стоит отметить, что из соотношения F.6) мы сразу же полу-
получаем Qtt = Q.
Для эрмитовой (самосопряженной) матрицы й, когда по опре-
определению й = й+, мы согласно F.6) имеем
Q(iV== ^VJLl.	F.7)
Диагональные матричные элементы fi = v действительны. Послед-
Последнее утверждение справедливо для любого ортонормированного
набора функций (т. е. при любом выборе координатной системы
в гильбертовом пространстве). В частности, это справедливо и
для такого набора {uv}> с помощью которого матрица ЙЙУ при-
приводится к диагональному виду:
^nv = «u6wv.	F.8)
Так как выше (оц суть собственные значения матрицы й, то
отсюда следует, что собственные значения эрмитовой матрицы
действительны.
Замечание. Именно в силу этого последнего результата операторы всех
физических величин (наблюдаемые) эрмитовы.
Задача 7. Построение эрмитова оператора
Найти квантовомеханический оператор, сопоставляемый клас-
классическому произведению хрх.

26	/. Общие принципы
Решение
а. Так как операторы х и рх некоммутативны и удовлетво-
удовлетворяют перестановочному соотношению
т,	G.1)
которое легко проверяется в координатном представлении, где
'-«ТЖ.	<7'2>
то следует ожидать, что классическому произведению хрх будет
соответствовать каждый оператор вида
Q = (l-a)xpx + aPxx.	G.3)
Предположим сначала, что постоянная а действительна. Эту
постоянную мы должны подобрать таким образом, чтобы для
всякого квантового состояния ij> среднее значение Q было дейст-
действительным:
<й> = \ i|)*Qi|)dsx = Действительная величина.	G.4)
Пользуясь выражением G.2) для оператора рх, перепишем ра-
равенство G.4) в развернутом виде
Отделяя теперь действительную часть i|> от мнимой:
получаем
Второй интеграл в правой части этого равенства действителен.
Что же касается первого интеграла, то он чисто мнимый и
в силу G.4) должен исчезнуть. Так как, кроме того,
= 1,
то это условие можно записать в виде равенства
которое после интегрирования по частям дает
а = |.	G.5)

7, Построение эрмитова оператора	27
Таким образом, правильной является симметричная комбинация
±	G.6)
обеспечивающая эрмитовость оператора Q.
Если перейти к комплексным а, то годным будет любое а
вида
где р — произвольное действительное число. В самом деле, в этом
случае
—хрх),	G.8)
и мы только что показали, что среднее значение первого слагае-
слагаемого действительно, второе же слагаемое благодаря перестано-
перестановочному соотношению G.1) дает при усреднении постоянный
вклад |ш независимо от выбора квантового состояния. Следова-
Следовательно, это слагаемое не имеет физического смысла и его можно
опустить.
б. Условие эрмитовости оператора с равным успехом можно
определить соотношением
<« | Qv> = <пи | v>	G.9а)
или подробнее
$ и*пvd3x=^(?luyv dax.	G.96)
Здесь и и v—произвольные комплексные функции, выбор кото-
которых ограничивается лишь требованием существования интегралов.
Для оператора G.3) при действительном а это дает
^	^ od,Xt
или
Изменяя здесь порядок слагаемых, получаем
J х -^ (u*v) d*x = —2а Г u*v d3x.
Взяв теперь интеграл, стоящий слева, по частям, находим
— J u*v dax = —2а ^ u'w d*x.
Это, разумеется, дает наш старый результат G.5), т. е. а =

28		/. Общие принципы
Задача 8. Дифференцирование оператора
Пусть f(p, х)— целая функция операторов pk, хк. Показать,
что из коммутационных правил следуют соотношения
где в целях сокращения введено обозначение
[/. g]=j(fg-gf).
Решение. Канонические коммутационные правила задаются
формулами
[рк, Л]=О, [хк, х,] = 0, [рк,х,] = 6ы.	(8.3)
Доказательство справедливости соотношений (8.1) и (8.2) распа-
распадается на четыре последовательные стадии.
1.	Пусть f = pt, тогда df/dxk = 0 и df/dpk — 6к{. Следовательно,
соотношения (8.1) и (8.2) принимают вид
[/>*. Pi] = С [Pi, хк] = б«
и, таким образом, согласуются с формулами (8.3). Аналогично
устанавливается их справедливость и в случае, когда f = xt,
bfldxk = bkl< df/dpk = O.
2.	Пусть соотношения (8.1) и (8.2) справедливы для функций
/ и g, но тогда в силу линейности они будут справедливы и для
всякой линейной комбинации cJ-\-c^ с произвольными комп-
комплексными числами сг и с2.
3.	Будучи справедливыми для функций fug, эти соотноше-
соотношения справедливы и для их произведения fg. В случае (8.1) это
легко проверить непосредственными вычислениями
— \ {fgPk—fpkg+fpkg—Pkfg) = — [fg,
Аналогичные выкладки нетрудно провести и в случае соотноше-
соотношения (8.2).
4. Из предыдущего следует, что рассматриваемые соотношения
справедливы для произвольной линейной комбинации произведе-
произведений, содержащих любое число сомножителей рк и хк. Но тем
самым они справедливы для любой целой функции переменных
рк и хк, что и требовалось доказать.

9. Изменение средних значений со временем	29
Задача 9. Изменение средних значений со временем
Пусть <Л>—среднее значение не зависящего явно от времени
оператора А в состоянии^, которое меняется с течением времени.
Выясните, как меняется <Л> со временем. Чю вы можете сказать
об изменении средних значений <_хк> и
Решение. Скорость изменения среднего значения
<A> = <$\A№ = lv(t)Ay(,t)dT	(9.1)
равна
!^	^	(9.2)
Производные волновых функций if и гр* по времени подчиняются
уравнениям Шредингера
-Аф = ЯЧ>, т-ф* = Я+Ч>*,	(9.3)
где гамильтониан Н эрмитов, так что # = #+. Подставляя (9.3)
в равенство (9.2), получаем
или в обозначениях функционального анализа
±	(9.4)
Преобразовав первое слагаемое в (9.4) с помощью тождества [см.
F.16)]
имеем
поэтому равенство (9.4) принимает вид
-?f<A> = j<r!p\HA — AH\ty>,	(9.5)
или короче
-|-<Л> = <[//, А]>.	(9.6)
Применим соотношение (9.6) в частных случаях А = хктл А = рк.
С учетом соотношений (8.1) и (8.2) это дает
Таким образом, средние значения подчиняются каноническим
уравнениям классической механики п.
и Во избежание недоразумений следует отметить, что в общем случае
— Прим. ред.

30	/. Общие принципы
Задача 10. Картина Шредингера и картина Гейзенберга
Когда при выборе системы координат в гильбертовом прост-
пространстве мы пользуемся так называемой картиной Шредингера,
операторы pk и qk не зависят от времени, а вектор состояния т|з
меняется с течением времени согласно уравнению Шредингера
-\$=Н%	A0.1)
где Н (pk, qk) — гамильтониан рассматриваемой системы. Пусть
гамильтониан Н не зависит явно от времени. Покажите, что пе-
переход к „вращающейся" в гильбертовом пространстве системе
координат, в которой вектор состояния т|з остается неподвижным
{картина Гейзенберга), осуществляется с помощью унитарного
преобразования U (/) и что в этой системе операторы pk и qk
меняются с течением времени согласно каноническим уравнениям
Решение. Будем писать у всех не зависящих от времени опе-
операторов индекс 0 вверху. Пусть далее в момент времени / = 0
обе системы координат, „неподвижная" и „вращающаяся", совпа-
совпадают, тогда любой гейзенберговский оператор й (/) при добу-
добудет совпадать с соответствующим шредингеровским оператором
Q @) = й°.
Шредингеровский и гейзенберговский векторы состояний т|з (t)
и а|>0 связаны между собой соотношением
Следует заметить, что на выбор начального состояния ip @) = чр°,
если не считать условия нормировки, не налагается никаких огра-
ограничений. В силу условий нормировки
=1 и <фвЦ>в>=1,	A0.4)
оператор U должен быть унитарным, т. е. должно выполняться
соотношение
WU=\.	A0.5)
Действительно, легко видеть, что
но последнее выражение совпадает с <т|з° |т|з°> в том и только в том
случае, когда выполняется соотношение A0.5).
Оператор U можно получить, подставляя A0.3) в уравнение
A0.1):
— ~0^П°и,	A0.6)

	10. Картина Шредингера и картина Гейзенберга	31
где теперь мы предусмотрительно написали Я0 вместо Я, поскольку
в картине Шредингера в уравнении A0.1) используется оператор,
не зависящий от времени. Дифференциальное уравнение A0.6)
с начальным условием U @) = 1 имеет решение
U{t) = e % ,	A0.7)
где под экспонентой следует понимать соответствующий ей сте-
степенной ряд.
Среднее значение любого оператора в любом состоянии т|з должно
быть одним и тем же, пользуемся ли мы картиной Шредингера
или же картиной Гейзенберга:
<t @1 Q" Ц> @> = <Г | Q @ | Ч>°>.	(Ю.8)
Так как
<г|51 Q" | г|» =
то равенство A0.8) будет выполняться для тех и только для тех
Q (t), которые определяются соотношением
Q(t) = U*(t)Q°U(t).	A0.9)
Нелишне отметить, что оператор Н°, согласно A0.7), ком-
коммутирует с оператором U, так что
Я (t) = UWU = UWH0 = Я0,
поэтому он инвариантен по отношению к рассматриваемому пре-
преобразованию. Таким образом, нет необходимости вводить различ-
различные операторы Н° и Я, что апостериори оправдывает обозначе-
обозначения, принятые нами в уравнении A0.1).
Чтобы удостовериться в справедливости канонических урав-
уравнений A0.2), рассмотрим производную по времени от оператора
A0.9):
п = #+Й°?/ + U*Q°U.	A0.10)
Из уравнения, сопряженного с уравнением A0.1),
-f А^ = ^я	A0.1а)
(здесь учтено, что оператор Я эрмитов, # = Я+) мы по аналогии
с A0.6) получаем
+ у #+»•«?/+	A0.6а)
и, таким образом, можем избавиться от производных в равенстве
A0.10):
U	=jlHQ — QH). A0.11)
Мы получили важное правило: производная по времени от опе-
оператора й, который сам не зависит явно от времени, равна его

32	/. Общие принципы
квантовым скобкам Пуассона с гамильтонианом Н:
A0.12)
[H,Q]=4-
л
Правило A0.12), примененное к операторам pk и qk, сразу же
дает
Р*=[Н,рк], qk = [H,qk].	A0.13)
Этим алгебраическим соотношениям можно придать иную форму,
если воспользоваться полученными с помощью основных комму-
коммутационных правил формулами задачи 8:
[я.л] = --з?.[я,?*]=|й;,	A0Л4)
что непосредственно приводит к каноническим уравнениям A0.2).
Замечание. Выше предполагалось, что в картине Шредингера операторы Н
и Q не зависят от времени. Если же такая зависимость имеется, то это при-
приводит к появлению дополнительной частной производной по времени. Кроме
того, весь формализм становится значительно сложнее, так, например, опера-
оператор U (t) уже не будет простой экспонентой из-за появления в ее степенном
разложении операторов Я, относящихся к различным моментам времени.
Задача П. Гамильтониан, зависящий от времени
Пусть оператор Н из предыдущей задачи зависит явно от
времени (например, вследствие действия на систему переменного
электрического поля). Требуется найти унитарный оператор U (t)
ь этом более общем случае.
Решение. В случае гамильтониана Н (pk, qk\ t) в нашем рас-
распоряжении все еще имеется уравнение Шредингера
Переход к картине Гейзенберга осуществляется теперь с помощью
унитарного оператора U (t)
q(t) = U(t)r,	(Не-
U(t)r,	(Некоторый подчиняется дифференциальному уравнению
-\O(t) = H(t)U(t)	(ц.з)
с начальным условием
t/@)=l.	A1.4)
Положим для простоты
—? = х,	A1.5)

12. Повторное измерение	33
тогда решением уравнения
с начальным условием A1.4) будет бесконечный ряд
U(t)= l+x lH(t')dt' + n^H(t')dt' J H(t")dt"-\-
0	0	0
t	/¦	Г
+ и3 \ Н (Г) dt' \ Н {?) dt" [ Н (t'") dt'" +... . A1.6)
0	0	0
В этом легко удостовериться, почленно дифференцируя ряд A1.6):
U(t) = xH (t) + и2Я (/) J Н (Г) dt" +
о
/	t"
+ х3Я (/) J Н (Г) dt" J H (t'") dt'" + ...=
о
о
= xH(t)\ 1 + x ) H(t")dt" + x2) H(t")dt"\ H(t'")dt'" + .
L	0	0	0	J
Следует заметить, что в этих интегралах />?'>/"> ... > 0,
так что сомножители Н, взятые в различные моменты времени,
образуют упорядоченное во времени произведение, причем сомно-
сомножители, относящиеся к более поздним моментам времени, всегда
стоят перед сомножителями, относящимися к более ранним мо-
моментам времени.
Задача 12. Повторное измерение
Гамильтониан системы Н не зависит от времени, а его собст-
собственные векторы | v> принадлежат невырожденным собственным
значениям fmv :
Н | v> = Л-cov | v>.	A2.1)
В том же самом гильбертовом пространстве состояний определен
оператор А, также обладающий невырожденными собственными
значениями."
А\п> = ап\п>.	A2.2)
Вначале система находится в состоянии | v>, затем в этой системе
производят измерение наблюдаемой А. Чему равно математиче-
математическое ожидание наблюдаемой А и какова вероятность обнаружить
в результате этого измерения значение наблюдаемой А, равное ат7
Пусть в результате измерения наблюдаемой А получено значе-
значение ат. Чему равна вероятность обнаружить это же значение ат,
2 № 1050

34	/. Общие принципы
если спустя время / произвести повторное измерение наблюдае-
наблюдаемой А?
Решение. В начальном состоянии математическое ожидание
наблюдаемой А равно <v|j4|v>. Подставляя сюда разложения
получаем
<v | А | v> = 2 <v 1 /г'> </г' 1 Л | пу
п, п'
Так как
то последнее выражение упрощается:
<v | Л | v> = S «„! <v | л> |2.	A2.3)
п
Поэтому вероятность обнаружить в результате первого измере-
измерения значение а,п равна
Pra = |<m|v>|2.	A2.4)
Сразу же после измерения система вместо исходного состоя-
состояния |v> оказывается в состоянии \ту. Дальнейшая эволюция
системы определяется уравнением Шредингера
ih-?f\ty = H\ty	A2.5)
и начальным условием
|0
Здесь и далее \ty означает вектор состояния в момент времени t.
Так как гамильтониан Н не зависит от времени, то
|г> = е-(«/Ь>"|т>.	A2.6)
Если воспользоваться разложением вектора | ту по собствен-
собственным векторам гамильтониана Н,
и учесть, что
то выражение A2.6) нетрудно привести к виду
|<> = 2e~'Vlli><Hm>.	A2.7)
м-
Аргументация, которая ранее привела нас к соотношению A2.4),
позволяет теперь заключить, что вероятность вновь обнаружить
значение ат при повторном измерении в момент времени t равна
P'm=\<m\t>\a,	A2.8)

13. Криволинейные координаты	35
причем
<m\t> = 2le-""»i\<m\\»\2.	A2.9)
д
Задача 13. Криволинейные координаты
В уравнении Шредингера для системы точечных масс сделать
переход к обобщенным криволинейным координатам.
Решение. Самое главное в этой задаче — преобразовать опера-
оператор кинетической энергии
7 = -lfrY—-21	A3.1)
2 Zu m дхя
где /лд имеет одно и то же значение для каждой тройки слага-
слагаемых, соответствующих одной частице. Выражение A3.1) пред-
представляет собой квантовомеханическии аналог классического вы-
выражения
4
Введем вместо координат х^ координаты
?д=К^*д,	A3.3)
тогда
4&.	A3.4)
Произведя теперь в ^-пространстве с элементом длины
замену координат SM на обобщенные координаты qk и учитывая,
что в новых координатах
ds» = SSft*^'^*.	A3-6)
t k
получаем
i k
Вернемся к квантовой механике. Выражение A3.1) эквива-
эквивалентно выражению
Далее из дифференциальной геометрии известно, что при замене
координат Ij, координатами q' оператор Лапласа преобразуется

36	/. Общие принципы
к виду
A3.9)
где g—определитель метрического тензора gik, a g'k—его кон-
контр авар иантные компоненты. Последние можно найти из соотно-
соотношения
*'* = ^.	A3-10)
в котором Gik означает алгебраическое дополнение элемента glk
в определителе g. Равенством A3.9) полностью исчерпывается
решение нашей задачи, так как теперь оператор кинетической
энергии, соответствующий классическому выражению A3.7),
можно записать в виде
Вычисление потенциальной энергии, разумеется, тривиально.
Замечание. Этот метод применим и к тем задачам, в которых не фигури-
фигурируют прямоугольные координаты точечных масс. В этом случае он просто
связывает классическое выражение A3.7) с оператором A3.11). Однако указан-
указанную связь ни в коем случае нельзя считать тривиальной (см. замечания
к теории симметричного волчка в задаче 46).
Задача 14. Волновые функции в импульсном представлении
Фурье-образ/(й) волновой функции г|з(г) характеризует распре-
распределение импульсов в квантовом состоянии т)з. Требуется вывести
интегральное уравнение для /(?) с фурье-образом потенциала
в качестве ядра.
Решение. Между функциями г|з (г) и / (к) имеются два взаимно
обратных соотношения1)
г|> (г) = BяГ'/г ^ е'*г / (к) d3k,	A4.1)
/ (й) = Bя)" '/г J <?-'*'г|> (г) d3x-	A4.2)
Положим далее
V (г) = J ёЬг W(k) dak,	A4.3)
11 Если соотношение A4.1) использовать в качестве определения f (к) и
применить к нему операцию \ е~ rd?x, то с учетом определения 3-мерной
6-функции,
в результате, как нетрудно убедиться, получится обратное соотношение A4.2).
Аналогичные соображения использованы ниже при выводе соотношения A4.8).

14, Волновые функции в импульсном представлении	37
тогда для фурье-образа потенциала будем иметь
W (k) = Bя)-* $ е- ik-rV(r) d*x.	A4.4)
Предполагается, что волновая функция 1|>(г) удовлетворяет
уравнению Шредингера
-^V\ + V(r)* = Ey.	A4.5)
Подставляя сюда вместо о|> и V соответственно выражения A4.1)
и A4.3), получаем
[~ С eikrk2f (к) d3k + j d3k
В двойном интеграле перейдем от интегрирования по переменной
k к интегрированию по переменной k" = k-\-k', а затем эту новую
переменную вновь обозначим посредством k. Интеграл по k
обращается в нуль при любом значении г лишь в том случае,
когда само подынтегральное выражение равно нулю, но тогда
f (k) = - j W (k-k1) f (k1) dW.	A4.6)
Это и есть искомое интегральное уравнение с фурье-образом
потенциала W (k—k') в качестве ядра.
Конечно, интегральное уравнение A4.6) можно получить
только при условии, что фурье-образ потенциала A4.4) существует;
для этого, например, потенциал V (г) должен убывать на боль-
больших расстояниях по меньшей мере как г~1~Е, где е > 0.
Необходимо отметить, что из условия нормировки
J | г|5 (г) |2 d3x = 1	A4.7)
следует равенство
J»Jfe=l.	A4.8)
Это можно показать, подставив в A4.7) выражение A4.1) для
функции т|з:
$ |Ч> (г) I2d3x = Bя)~3 J d3x J dsk J е<<*-*о-'/ (k) f* (kr)d3k'.
Если здесь сначала выполнить интегрирование по d3x, то мы без
труда получим соотношение A4.8)х>.
11 См. в этой связи замечание в конце следующей задачи.

38	/. Общие принципы
Задача 15. Пространство импульсов.
Периодические и непериодические волновые функции
Рассмотрите вопрос о вероятностной интерпретации волновой
функции в импульсном пространстве. Начните с периодической
волновой функции t|>(r) в конфигурационном пространстве и
исследуйте предельный переход к кубу периодичности с беско-
бесконечно большим ребром.
Решение. Обозначим через L длину периодичности в каждом
из направлений х, у, z конфигурационного пространства. Тогда
ряд Фурье
будет содержать лишь такие члены, для которых компоненты
каждого из векторов k определяются соотношением
Л, = -^л„ л, = 0, ±1, ±2, ... .	A5.2)
Это означает, что в Л-пространстве при больших значениях L в
элементе объема dak содержится
d°k(±y	A5.3)
различных векторов k.
Вопрос о нормировке ряда A5.1) можно решить с помощью
подходящего выбора коэффициентов сь. Запишем интеграл от
квадрата модуля волновой функции по объему куба периодич-
периодичности:
(L»)	* *'
Интеграл в правой части этого равенства обращается в нуль,
если k'' фк, и равен L3, если k=k, поэтому
§ |г|>|8Л*: = 51|сй|2.	A5.4)
а»)	*
Пусть теперь PL есть вероятность обнаружить частицу внутри
куба периодичности L3, тогда \cu\2Pl будет вероятностью обна-
обнаружить частицу в кубе периодичности с импульсом %k, a |cft|2—
вероятностью обнаружить у частицы импульс Kk при условии,
что она находится внутри куба периодичности L3.
Переходя к пределу бесконечно больших L, можно заменить
ряд Фурье A5.1) интегралом Фурье по ft-пространству. Согласно
A5.2) и A5.3), это можно сделать с помощью правила:
l3k.	A5.5)

15. Пространство импульсов	39
Тогда равенство A5.1) даст
J	r~^d3k.	A5.6)
Данный интеграл Фурье представляет ограниченную волновую
функцию с не зависящими от L значениями в том и только в
том случае, если величина
A5.7)
имеет конечный предел при L—юо. Тогда волновую функцию
можно нормировать следующим образом:
(*'-*>'• d3x, A5.9)
где последний интеграл берется по всему пространству,
J e«(*'-fe)T ^ = Bя)'б (Л'—Л).	A5.10)
Поэтому для интеграла A5.9) получаем
, t)\*d3k,	A5.11)
что, кстати говоря, есть просто преобразование суммы A5.4) в
интеграл с помощью правила A5.5) и с учетом соотношения
A5.7). Полученный результат означает, что вероятность обна-
обнаружить у частицы импульс в пределах элемента d?k безотноси-
безотносительно к ее местоположению в конфигурационном пространстве
равна
d	k\fk, t)\\	A5.12)
Замечание. При изменении порядка интегрирования необходимо соблюдать
известную осторожность, если / (к) не является непрерывной функцией к.
Пусть, например,
тогда в соответствии с равенством A5.8) имеем
г|)(г, 0 = е'<*0''"Шо°.	A5.14)
Интеграл A5.11) и интегралы A5.9) с измененным порядком интегрирования
содержали бы в этом случае квадрат б-функции и были бы совершенно бес-
бессмысленными. Если же выполнить интегрирование по конфигурационному про-
пространству в конце, то равенство A5.9) дает
что находится в согласии с выражением для волновой функции A5.14).

II. Одночастичные задачи
без учета спина
А. Одномерные задачи
Одномерные задачи, будучи в известном смысле чрезмерной
идеализацией, тем не менее могут быть использованы для выяс-
выяснения основных особенностей квантовой механики. Эти задачи
возникают при рассмотрении трехмерного волнового уравнения
в котором потенциал зависит от одной-единственной^- декартовой
координаты х. С помощью факторизации
y:=eUk,y+k,i)<f(Xt fj	(A 2)
получаем
*
Последнее уравнение можно еще более упростить, положив
ф(*. о = *-""••'«(*. *), A©e = -^(ftj + ftj). (A.3)
В результате мы приходим к одномерному волновому уравнению
-?& + •'*<>'—тж-	<А-4>
Экспоненциальные множители в формулах (А.2) и (А.З) описы-
описывают распространяющиеся перпендикулярно оси х плоские волны,
которые не влияют на поведение волновой функции в направле-
направлении оси х.
Задача 16. Фундаментальные решения
в случае свободного движения
Решить одномерное волновое уравнение в случае V — 0. Обсу-
Обсудить физический смысл полученных решений.
Решение. Волновое уравнение
_.*!*$._ _Ai*	П6П»
2от дх* ~ i dt	I10-1;
11 Здесь и далее будем обозначать через \|> одномерную волновую функцию,
удовлетворяющую уравнению (А.4), а через и — ее пространственную часть.

16. Фундаментальные решения в случае свободного движения	41
допускает разделение переменных:
y(x,t) = u(x)g(t),	A6.2)
так как при подстановке выражения A6.2) в уравнение A6.1)
получаем
Ц
где через %ы обозначена постоянная разделения. Разбивая A6.3)
на два отдельных уравнения, находим
g=—i(og, т.е.. g(t) = e-t№t,	A6.4)
и
«• + ^« = 0.	A6.5)
Ъ
Если ш—действительная величина, то волновая функция будет
периодической и |т)з|2 не будет зависеть от времени (стационар-
(стационарное состояние). Если со — положительная величина, то
&2	A6.6)
также положительная величина, поэтому решение A6.5) будет,
кроме того, периодической функцией пространственной пере-
переменной х.
Комплексная форма A6.4) зависимости волновой функции от времени
составляет примечательную особенность квантовой механики: действительные
функции sin a>t и cos at не являются решениями дифференциального урав-
уравнения A6.4). Это столь разительное отличие от классической физики обуслов-
обусловлено тем, что уравнение Шредингера является уравнением первого порядка по
времени.
Физический смысл параметра со можно выяснить, рассматри-
рассматривая оператор в левой части уравнения A6.1) в качестве опера-
оператора Гамильтона, который в данном случае состоит из одного
оператора кинетической энергии. Отсюда следует, что величина
? = Д(о представляет собой кинетическую энергию частицы и,
таким образом, должна быть положительна, а наше решение
есть собственная функция гамильтониана.
Так как кг — положительная постоянная, общее решение
уравнения A6.5) или уравнения
= 0	A6.7)
имеет вид
u(x) = Aeikx + Be-'kx,	A6.8а)
поэтому одномерная волновая функция
хр(х, /) = Ле'(**-""»+ 5е-"*Л+ш'>	A6.86)

42	//. Задачи без учета спина. А. Одномерные задачи
состоит из двух волн, распространяющихся в противоположных
направлениях. У обеих волн фазовая скорость равна Оф = со/&.
Физический смысл пространственной части волновой функции
A6.8а) станет ясен, если записать в явном виде выражения для
плотности
р = 1|>*1|>	A6.9)
и для потока
Согласно A6.86), мы имеем
р = | А |2 +1В |2 + (АВ*еШх + А*Ве~21кх),
Две волны с амплитудами А и В соответствуют, как видно,
двум противоположно направленным потокам, интенсивность
которых определяется относительными нормировочнмми постоян-
постоянными волн и пропорциональна к. Выражение для плотности ука-
указывает на наличие интерференции двух (когерентных) волн, обу-
обусловливающей пространственную периодичность.
Когда нет особых причин (например, граничных условий)
добиваться когерентности, разумно рассматривать каждую волну
отдельно, полагая либо 5 = 0, что дает s > 0, либо Л = 0, что
дает s < 0. В результате получается прямолинейное движение
частицы либо в том, либо в другом направлении. Считая, что
величина k может быть обоих знаков, можно резюмировать наши
результаты следующим образом:
? = ?co, k* = ^,	A6.11)
Ъ
р = |СТ, s = —|C|a.
Исключая со, находим
E = ^,	A6.12)
поэтому импульс частицы и ее классическая скорость соответ-
соответственно равны
p = %k	A6.13)
и
»=?.	06.14)
Последняя совпадает отнюдь не с фазовой
со Е I

17. Волновой пакет в случае свободного движения	43
а с групповой скоростью волны
	 dco 	 dE
°гр = "Ж ~~ ~dp = У"
Замечание. Основное дифференциальное уравнение A6.1) можно рассмат-
рассматривать как уравнение диффузии с мнимым коэффициентом диффузии D:
дх2 dt '	2т
Так как разделение переменных играет важную роль в квантовой теории, а не
в теории диффузии, то решения, типичные для задач диффузии (с действи-
действительным коэффициентом D),
1 7^	Vim (х-Ы
не находят применения в квантовом случае.
Обращение времени в уравнении A6.1) ведет к замене г|) на г|э*.
Задача 17. Волновой пакет в случае свободного движения
Построить волновой пакет и исследовать его временную эво-
эволюцию.
Решение. Мы начнем с частного решения волнового уравне-
уравнения, записав его в ранее найденном виде A6.11):
i|>(?; х, t) = C(k)ei0!X-atK	A7.1)
а С (k) — произвольная постоянная амплитуда. Здесь k—все еще
свободный параметр, так что общее решение волнового уравнения
записывается в виде любого сходящегося интеграла по k от вы-
выражения A7.1):
ц(х, t)= 5 !>(*; х, t)dk.	A7.3)
— 00
Равенство A7.3) описывает одномерный волновой пакет наиболее
общего вида. Чтобы интеграл сходился, амплитуда С (k) должна
стремиться к нулю при |?|-»-оо, по крайней мере как l/k. Вся-
Всякая выбранная подходящим образом амплитуда С (k) приводит к
решению определенного вида.
Теперь построим волновой пакет таким образом, чтобы в на-
начальный момент времени ^ = 0 вероятность обнаружить описы-
описываемую им частицу заметно отличалась от нуля лишь внутри малой
окрестности точки х = 0 и чтобы частица двигалась с импульсом

44	//. Задачи без учета спина. А. Одномерные задачи
po = fiko. Этого можно добиться, положив
Ч> (х, 0) = А ехр [- ^ + ikox] .	A7.4)
Действительно, в этом случае плотность
р(х, 0) = |Ч>(*. 0)|а-|Л
отвечает частице, локализованной в области | x|^a, a поток A6.10)
равен
s(x> У^Ш2^ Л1'ехР(—?) = Pm*»'
поэтому величина и0 = fikjtn есть скорость частицы, a po=mvo=fiko—
импульс пакета. Так как волновая функция описывает одну час-
частицу, то имеет место условие нормировки
т. е.
|Л|2=-1=.	A7.5)
аул
Выражение A7.4) можно разложить по плоским волнам, ис-
используя соотношения A7.3) и A7.1):
со
г|>(х, 0)= J C(k)eikxdk.	A7.6)
— оо
Но этот интеграл есть интеграл Фурье, обращая который, полу-
получаем
Вычисляя последний интеграл с помощью хорошо известной фор-
формулы
со
-**dz = Vn,	A7.7)
— ОО
окончательно находим
С (А) = -^|= ехр [—!(*-*/] .	A7.8)
Этот результат легко понять, привлекая на помощь соотношение
неопределенности Гейзенберга. В начальном состоянии неопреде-
неопределенность координаты частицы, согласно выражению A7.4), имеет
порядок Ах « а. С другой стороны, как показывает выражение
A7.8), основной вклад в волновую функцию дает та часть спектра

17. Волновой пакет в случае свободного движения
45
волновых чисел k (или импульсов p = %k), которая лежит в по-
полосе шириной Akttl/a (или Apz&fi/a) вблизи k = k0. Следова-
Следовательно, независимо от выбора величины а имеет место соотношение
Ах- Ар « %,
A7.9)
но это и есть соотношение неопределенности Гейзенберга.
Определив амплитуду С (k) по начальному состоянию при / =- О,
мы можем теперь перейти к вычислению общего интеграла A7.3)
для любого момента времени:
Здесь в экспоненте стоит квадратичная форма k, так что этот
интеграл снова можно привести к интегралу ошибок A7.7).
Результат имеет вид
-5т)
та2 J
ma2
A7.10)
В этом довольно сложном выражении нетрудно разобраться,
снова рассмотрев плотность р и поток s, но теперь уже для лю-
любого момента времени t. Плотность в этом случае равна
/ Ш \211/2
ехр
.A7.11)
Как функция координаты х она все еще имеет форму колоколо-
образной кривой, однако максимум ее теперь сдвинут из точки
х = 0 в точку x = (rlkjm)t. Следовательно, максимум „цуга волн",
описываемого выражением A7.10), перемещается со скоростью
vo — 1ikalm (групповая скорость равна скорости частицы). В то
же самое время знаменатель в экспоненте A7.11) показывает,
что ширина волнового пакета увеличилась от значения а при
t = 0 до значения
а'=а
при t = t. Этот эффект легко объяснить, исходя из вида спект-
спектральной функции A7.8). Так как спектр волновых чисел имеет
ширину Ak ж I/a, то скорости отдельных волн разбросаны в об-
области шириной Av = (h/m) Ak = fi/tna, поэтому пакет расплывется
на величину Ах— tAv= (%/ma) t, что и было найдено выше.

46	П. Задачи без учета спина. А. Одномерные задачи
Выражение для потока получается из A7.10) с помощью со-
соотношения
! | х
1 +*
Непосредственное вычисление после сравнения с формулой A7.11)
дает
s(x, t) = 9(x,t)v0	ТТГЬ--	A7Л2)
Отсюда видно, что для произвольных времен мы отнюдь не имеем
s = pv0, как это было при ^ = 0, что опять-таки является след-
следствием конечной ширины спектра скоростей. Для максимума
пакета xo = vot, и равенство A7.12) приводит к элементарному
соотношению s = pu0. С другой стороны, для х^х0 мы имеем
s^pv0, и это вполне разумно, так как к моменту времени t до
точки х < х0 (х > х0) доходят лишь те части волнового пакета,
скорость которых меньше (больше) у0.
В заключение следует упомянуть, что условие нормировки
^ pdx— 1 выполняется для всех времен, это является выражением
закона сохранения вещества.
Задача 18. Стоячие волны
Частица заключена между двумя непроницаемыми стенками,
расположенными в точках х — — а и х=-\-а. (Стенки служат
идеализацией сильного отталкивания, испытываемого частицей
при приближении к указанным границам.) Найти собственные
состояния и обсудить их свойства.
Решение. Для стационарных состояний мы имеем
ф (х, t) = и (х) е~ Т .	A8.1)
Пространственная часть волновой функции и(х) удовлетворяет
уравнению Шредингера
u" + **« = 0,	A8.2)
где
2^	A8.3)
и в самом общем случае имеет вид
u{x) = Aeikx-\-Be-'kx.	A8.4)

18. Стоячие волны	47
Наличие непроницаемых стенок налагает граничные условия
ы(а) = 0, и(—а) = 0,	A8.5)
что в сочетании с условием нормировки,
а
\\и(х)\Ых=\,	A8.6)
— а
если отвлечься от фазового множителя, выбор которого никогда
не регламентируется в квантовой механике, позволяет полностью
определить собственные функции.
Подставляя выражение A8.4) в соотношения A8.5), получаем
для определения А к В систему двух линейных однородных
уравнений:
Aik Bl 0
Эта система допускает нетривиальное решение только в том слу-
случае, если ее определитель равен нулю:
eikae-ik
g — ihagtka
= 0, или sin2/so = 0.	A8.7)
Условию A8.7) удовлетворяют лишь собственные значения 1гп,
определяемые формулой
ftn = |.n, n = ±l, ±2, ±3, ...	A8.8)
Значение k — О, также удовлетворяющее условию A8.7), должно
быть исключено как противоречащее условию нормировки A8.6).
Из соотношений A8.3) и A8.8) для собственных значений энер-
энергии получаем
На основании A8.8) имеем
я
etkna ^е Т
поэтому
Если п—нечетное целое число, то В = А, а нормированные вол-
волновые функции равны
и*(х) = а 2cosknx = a 2cos^^, n=±l, ±3, ... A8.10а)
Е'-сли же п—четное целое число, то В = —А, и мы имеем
и~(х)—а ^sin&r — а 2~ gin nnx n — -t-2 -4-4	HRlOfii

48
//. Задачи без учета спина. А. Одномерные задачи
Так как функции ип, если отвлечься от несущественного изме-
изменения знака в формуле A8.106), не зависят от знака п, то от-
отрицательные значения п можно не принимать во внимание, поэ-
поэтому, например, волновые функции четырех наинизших состояний
будут равны
п=1, Е, = ?г^, uX = a~2cosnr
?i 8/ла2*
п = 2, E2 = 4Elt
л = 4, ?4=16?,,
ur = t
la '
L nx_
2 sin a ,
A8.11)
= a"^cos^.
la
Следует отметить, что собственные функции попеременно то чет-
четные (п нечетное), то нечетные (п четное) по отношению к инвер-
Фиг. 1.
Первые четыре собственные функции в одномерном потенциальном
ящике с бесконечными стенками.
сии с центром в начале координат. Об этом свойстве волновых
функций говорят как о четности состояния: в случае симмет-
симметричной функции мы говорим, что четность положительна, в про-
противном же случае—отрицательна. В принятых обозначениях (и*,
и^) четность состояния отмечается верхними индексами „+" и „-".
Первые четыре собственные функции изображены на фиг. 1.
Так как пространственные части собственных функций
действительны, то результирующий ток вероятности не может
существовать ни в одном состоянии. Это является следствием
того, что в формуле A8.4) (вспомните рассуждения, приведенные
в задаче 16) |/4| = |ZJ|. Волны с амплитудами А и В в выраже-
выражении A8.4) дают противоположные вклады в токи и импульсы.

19. Полупроницаемая перегородка
49
Следовательно, собственные функции гамильтониана, принадле-
принадлежащие дискретным собственным значениям энергии, не являются
собственными функциями оператора импульса
_ % д
р~тш-
Действительно, дифференцирование функций A8.10а) и A8.106)
ведет не к воспроизведению, а к замене синусоидальных решений
косинусоидальными. Среднее же значение импульса можно вы-
вычислить по формуле
, а
<п | р | п> = — J ип (х) A lln (x) dx.
—а
Для всех состояний этот интеграл исчезает, так как подынтег-
подынтегральное выражение является нечетной функцией х. Таким обра-
образом, <л | /71 п> = 0 в согласии с обращением в нуль плотности тока
вероятности.
Замечание. В математическом отношении это по существу та же самая
задача, что и классическая задача о колебаниях струны. Единственное разли-
различие заключается в том, что здесь квадратичному закону A8.9) следуют соб-
собственные значения энергии, там же ему подчиняются собственные частоты.
Классическая энергия колебаний не имеет, однако, никакого аналога в кван-
квантовом случае, поскольку она зависит от амплитуды колебаний — последняя же
может быть произвольной, в то время как амплитуда волновой функции фик-
фиксирована условием нормировки A8.6), т. е. тем обстоятельством, что число
частиц равно единице.
Задача 19. Полупроницаемая перегородка
Дополнительно к условиям предыдущей задачи в точке х = 0
вводится бесконечно узкая и бесконечно высокая полупроницае-
полупроницаемая перегородка. Выяснить влияние пе-
перегородки на стационарные состояния.
Решение. Полупроницаемую перего-
перегородку (фиг. 2), разделяющую всю область
на две равные части, можно получить как
предельный случай барьера конечной ши-
ширины 2е (между точками х= — е и х— +е)
и конечной высоты Vo. Для краткости _
введем обозначения
2т?_,2 2/П/у_р\_, t\q \\
0
+а
Фиг. 2. Потенциальный
ящик с полупроницаемой
перегородкой.
Кроме двух граничных условий ы(±а) = 0, благодаря наличию
барьера мы имеем еще четыре граничных условия, так как функ-
функции и (х) и и'(х) должны быть непрерывны в точках х=±ъ.
Удовлетворяя первым двум условиям и беря решение в дейсг-

2
в-сЛ
50	//. Задачи без учета спина. А. Одномерные задачи
вительной форме, имеем
(A1sink(xJra), —а^л;^—е,
Ве~кх -\-Секх, —S5^;cs^8,	A9.2)
A9sink(x — а), е^Сх^а.
Требование непрерывности при х=±е теперь дает
и(—s) = Ах sin k (a—s) = Bexe-\-Ce~Ke,	A9.3а)
и' ( — e) = kAl cosk(a— e) = и( — Веяе + Се-Яе), A9.36)
u( + e) = Assmk (e —а) = 5е-ие + Сеие,	A9.Зв)
и' (-f e) = fei42cos^ (e — а) = х (— fie-^-f СеКЕ). A9.3г)
После исключения А1 и Аг из равенств A9.3а), A9.36) и A9.Зв),
A9.3г) соответственно остаются два соотношения
и + и,	1	-Ве2хе+С
kctgk(a — e) = x	^
k4\gk (a — е) = х
Из тождественности их левых частей следует равенство правых
частей. Последние же равны в том и только в том случае, если
В = ±С. При В = + С из равенств A9.3а) и A9.Зв) следует, что
А± = —Л2, и мы получаем решения с положительной четностью,
если же В = — С, то Аг= А2, и мы получаем решения с отрица-
отрицательной четностью. Следовательно, как и в предыдущей задаче,
стационарные состояния разделяются на два класса, характери-
характеризующиеся различными четностями.
Теперь перейдем к пределу е—> 0, и—>¦ оо так, чтобы хе—»¦ 0,
но величина
х2е = Й	A9.5)
оставалась конечной. Величину Q будем называть коэффициентом
непроницаемости перегородки, так как с ростом Q она стано-
становится все более непроницаемой. При положительной четности
(В = С) соотношение A9.4) после разложения его правой части
в ряд дает
kctgka = — Q.	A9.6а)
При отрицательной четности (В = — С) аналогичным путем полу-
получаем
kctgka—-> — оо.	A9.66)
Второй случай проще. Собственные функции обращаются на
перегородке в нуль, так что решение имеет вид
A sin k~ (x + a), —а^л:<0,
' k-l	0	A9.7а)
я = /ш, п=1, 2, 3 ...,
"	'	а

19. Полупроницаемая перегородка
51
Что же касается уравнения A9.6а), то оно позволяет определить
собственные значения k+ лишь численно. Исключение представ-
представляют только два предельных случая:
1)	полностью непроницаемая перегородка (Q—> оо), когда для
собственных значений получается тот же результат, что и в слу-
случае уравнения A9.66), т. е. k* = nn;
2)	полностью проницаемая перегородка (Q = 0), когда k%=
Таким образом, при конечном коэффициенте непроницаемости
собственное значение k+ заключено между k~ и k~_lt т. е. уровни
с положительной и отрицательной четностями так же, как и
в предыдущей задаче, чередуются. Собственные функции можно
записать в виде
J — Asmk
Asmk+(x—a),
л= 1, 2, 3,
A9.76)
Их значения при х = 0 конечны, а на графиках имеются изломы.
В прилагаемой таблице даны численные значения произведе-
произведения k%a, найденные с помощью уравнения A9.6а) для низших
состояний при некоторых значениях безразмерного параметра па:
Qa
0
1/4
1/2
1
2
4
10
00
л=1
1,571
1,715
1,835
2,023
2,282
2.568
2,866
3,142
л = 2
4,712
4,765
4,816
4,915
5,091
5,361
5,763
6,283
п = Ъ
7,854
7,886
7,917
7,979
8,097
8,305
8,711
9,425
10,996
11,018
11,040
11,085
11,173
11,335
11,704
12,566
п = 5
14,137
14,155
14,171
14,208
14,276
14,408
14,734
15,708
Полученные таким образом уровни изображены на фиг. 3, где
сплошные линии относятся к состояниям с положительной чет-
четностью, а пунктирные—к состояниям с отрицательной. Крайним
слева на фиг. 3 показан случай Q = 0, когда перегородка пол-
полностью прозрачна, что соответствует ситуации, обрисованной
в задаче 18. Чем непрозрачней становится перегородка, т. е. по
мере приближения к правому краю фигуры, тем выше подни-

•g
к
15
К
13
1Z
П
10
и
4~~
-4+-
з'-
т-
-2"-
+-
-Г"
'Г-
0 1
Прозрачная
перегородка
10
Sla
Непрозрачная
перегородка
Фиг. 3. Расположение уровней при различных
значениях коэффициента непроницаемости перего-
перегородки.
Сплошные ланчи — состояния с положительной четностью,
пунктирные линии — состояния с отрицательной четно-
четностью.
Фиг. 4. Волновые функ-
функции двух первых стацио-
стационарных состояний при
различных-гзначениях ко-
коэффициента непроница-
непроницаемости перегородки.
Вверху — состояние 1 +, вни-
внизу— состояние 1~.
Яа=О
Яа=1
Яа=2
?2а=оо
-а
+а

	20. Полупроницаемая перегородка	53
маются уровни с положительной четностью; уровни же с отри-
отрицательной четностью остаются на прежнем месте. Это находит
отражение и в поведении четных собственных функций. В качестве
примера одна такая функция для п=1 показана на фиг. 4
(волновые функции не нормированы). В случае непроницаемой
перегородки (Q—*• оо) она при х = 0 обращается в нуль, и обе
части ящика становятся независимыми друг от друга. За исклю-
исключением знака в левой части ящика эта функция совпадает с пер-
первой нечетной собственной функцией, показанной в нижней части
фиг. 4; таким образом, в пределе Q—>¦ оо энергетические уровни
становятся вырожденными (крайняя правая полоса на фиг. 3).
Задача 20. Полупроницаемая перегородка в виде
б-образного потенциального барьера
Потенциальную стенку предыдущей задачи с равным успехом
можно описать с помощью б-функции Дирака, полагая
V(x) = ^Q8(x).	B0.1)
Докажите это и обсудите обусловленные наличием такой стенки
граничные условия.
Решение. Нам нужно решить уравнение Шредингера
u"+[k2 — 2Q8(x)]u = 0.	B0.2)
Прежде всего мы видим, что и дифференциальное уравнение B0.2),
и граничные условия «(±а) = 0 инвариантны относительно ин-
инверсии х-—>— х. Следовательно, решениями этой задачи, которая
определяется дифференциальным уравнением и граничными усло-
условиями, могут быть только собственные функции оператора чет-
четности (он заменяет х на —х). В этом можно убедиться следую-
следующим образом. Всякую функцию и (х) можно разбить на две части:
четную /(*) = /(—х) и нечетную g{x) = — g(— х), поэтому
u(~x) = Af(x)-Bg(x).
Если и (х) есть решение нашей задачи, то таковым будет и и (— х),
а так как вырождение отсутствует, решение с точностью до муль-
мультипликативной постоянной, скажем а, должно быть однозначным.
Следовательно,
и (—х) = аи (х),
или
Так как fug линейно независимы, последнее возможно тогда
и только тогда, когда А = аА и В = — аВ, т. е. когда а =1,

54	//. Задачи без учета спина. А. Одномерные задачи
6 = 0, так что и (х)— четная функция, или же когда а = — 1,
.4 = 0, так что и (х) — нечетная функция.
Рассмотрим теперь окрестность вблизи потенциальной стенки.
Интегрирование уравнения B0.2) по указанной окрестности
[функция и (х) предполагается непрерывной] дает
ы'( + 0) —ы'(__0) = 2Q«@).	B0.3)
Другими словами, логарифмическая производная
Кх) = ^-Щ	B0.4)
х ' и (х)	v '
терпит на стенке разрыв со скачком 2Q:
) — L(—0) = 2Q.	B0.5)
Таким образом, довольно трудоемкую предельную процедуру,
использованную нами в задаче 19, можно заменить в известной
мере искусственным, но очень простым граничным условием на
потенциальной стенке. Следует отметить, что мы получили это
граничное условие, рассматривая поведение дифференциального
уравнения лишь в непосредственной окрестности потенциальной
стенки; поэтому оно должно удовлетворяться и в том случае,
когда дополнительно имеется какой-либо несингулярный потен-
потенциал V(x), а также любые граничные условия, наложенные
в каком-либо ином месте.
Обратимся теперь к вопросу о собственных функциях. Что
касается нечетных решений, то функции и~ (х) обращаются в нуль
на потенциальной стенке: ы~@) = 0. Но тогда в силу равенства
B0.3) производная не будет иметь никакого скачка и будет не-
непрерывной. Таким образом, оказывается, что наличие перегородки
не влияет на нечетные решения, каков бы ни был коэффицент
непроницаемости. Это полностью согласуется с результатом, по-
полученным в задаче 19 [см. равенства A9.7а)].
С другой стороны, четные решения по необходимости должны
иметь вид, предписываемый равенствами A9.76):
Отсюда
так что в силу условия B0.5)
g = — Q
в согласии с уравнением A9.6а). Таким образом, дальнейшие
рассуждения дословно повторяют соответствующие рассуждения
задачи 19.

21. Рассеяние на Ь-образном потенциальном барьере	55
Задача 21. Рассеяние на б-образном потенциальном барьере
Слева на потенциальный барьер
V(x)^Q8(x)	B1.1)
падает поток частиц с энергией Е. Показать, что наличие барьера
приводит к появлению разбегающейся в обе стороны от него
„рассеянной" волны.
Решение. Всюду, кроме бесконечно малой окрестности точки
х = 0, общее решение уравнения Шредингера можно записать
в виде
u{x) = Aeikx + Be-ikx, k* = ~, k > О,	B1.2;
л2
где А и В — константы, имеющие различные значения для об-
областей х < 0 и х > 0; подбирая их, можно добиться, чтобы ре-
решение B1.2) удовлетворяло граничному условию. Наше решение
можно записать несколько иначе, если выбрать нормировку таким
образом, чтобы амплитуда падающей волны равнялась единице,
ikx + Be-ikx, x<0,
Здесь В и F — соответственно амплитуды рассеяния назад и вперед.
Согласно равенству B0.3), позедение функции и (х) в точке
х = 0 определяется условиями
и(+0) = и(—0) и и'( + 0)~ ы'( — 0) = 2Qu@). B1.4)
Эти соотношения дают B = F и
ik(l+F) — ik{l — B) = 2Q(l+B),
поэтому окончательно
B = F = ^.	B1.5)
В решении B1.3) можно различить три волны: падающую
волну единичной интенсивности, отраженную с интенсивностью
| В [2 и прошедшую с интенсивностью \l~\-F\2. Из соотношения
B1.5) следует
Это приводит к закону сохранения (уравнение непрерывности)
1 = |B|2 + |1+F|2,	B1.7)
согласно которому сумма интенсивностей прошедшей и отражен-
отраженной волн равна интенсивности падающей волны.
Если потенциальный барьер почти непроницаем (Q —* оо),
то в силу B1.5) fi« —1 и l-f-.FwO, поэтому мы имеем почти

56	//. Задачи без цчгта спина. А. Одномерные задачи
полное отражение. Если же потенциальный барьер почти про-
прозрачен (Q—>-0), то
Q
и интенсивность рассеянной волны становится обратно пропорцио-
пропорциональной энергии частицы. Разумеется, это верно лишь в пре-
предельном случае высоких энергий и не имеет места при малых
энергиях частицы (k^.Q). Здесь мы имеем дело с частным слу-
случаем первого борновского приближения, которое справедливо,
как известно, при высоких энергиях. Следует, однако, отметить,
что для справедливости последнего вовсе не требуется (как
иногда утверждают), чтобы кинетическая энергия была всюду
велика по сравнению с потенциальной энергией V(x). Действи-
Действительно, в приведенном примере потенциальная энергия прил: = 0
становится даже бесконечно большой.
Равенство амплитуд рассеяния вперед и назад для любых
значений энергии является специфической чертой потенциала B1.1).
Задача 22. Рассеяние на симметричном потенциальном барьере
Поток частиц с энергией Е падает на потенциальный барьер
V(x), ограниченный областью —а^.х^.а. Предполагается, что
потенциал представляет собой четную функцию х:
V(x) = V(—x).	B2.1)
Требуется выразить амплитуды рассеяния вперед и назад через
логарифмические производные волновой функции в точках х= ±а.
Решение. Из условия симметрии B2.1) вытекает важное следст-
следствие: при любом значении энергии Е уравнение Шредингера имеет
как четное решение
и+(х) = и+(—х), и'+(х) = — и'+(—х),	B2.2а)
так и нечетное решение
и _(*) = — «-(— х), и'.(х) = и'_(—х).	B2.26)
Эти решения, разумеется, линейно независимы, поэтому общее
решение можно записать в виде их произвольной линейной ком-
комбинации. В интервале —а^.х^а частные решения ы+ и и_
в крайнем случае можно определить с помощью численных мето-
методов, положив в точке х = О
и+@) = 1, ы'+@) = 0
и
ы_@) = 0, и'_@)=-1.
Конечно, при этом нормировка базисных решений оказывается
довольно произвольной. Таким образом, мы можем вычислить

22. Рассеяние на симметричном потенциальном барьере	57
их логарифмические производные в точке х — а, которые для
удобства запишем в безразмерном и не зависящем от их относи-
относительной нормировки виде
au'+(a)/u+(a) = L + , au_(a)/u.(a) = L_.	B2.3)
Логарифмические производные аи± ( — а)/и±( — а) в точке х = — а
в силу соотношений B2.2) будут равны — L+ и —L_.
Решение, отвечающее падающей слева волне с единичной
амплитудой, имеет вид
{е"гх + Ве-'кх,	— оо<х<—а,
C1u+(x)+Ciu^(x), —а< х<а,	B2.4)
(l+F)eikx,	а<л:<оо.
Требование непрерывности и(х) и и' (х) в точках х=±а дает
четыре условия:
е-"га + Ве1ка=--С1и+ {а) — Сги_ (а),	B2.5а)
ik (e-ika—Beika) = — Ctu'+ (а) +С2ы1 (о),	B2.56)
(l+F)e<*" = C1u+(a)+C2u_(a),	B2.5в)
ik(l+F)eika^C1u'+(a)+Ciui(a).	B2.5г)
Складывая равенства B2.5а) и B2.5в) и вычитая из равенства
B2.56) равенство B2.5г), получаем справа соответственно 2СХ«+ (а)
и 2Схи+(а). Взяв теперь их отношение, находим
L + = ika —.	+i+ +T .	B2. 6a)
+	e-ika + {\+F + B)eika	^ Ua>
Аналогичная процедура, но с переменой знаков дает
B2.66)
Разрешая уравнения B2.6а) и B2.66) относительно \-\-F±B
и полагая для простоты
ka = ?,	B2.7)
окончательно получаем следующие выражения для амплитуд:
На основании уравнения непрерывности, следует ожидать,
что сумма интенсивностей отраженной и прошедшей волн будет
равна интенсивности падающей волны. Действительно, из соот-
соотношений B2.8а) и B2.86) следуют формулы

58	//. Задачи без учета спина. А. Одномерные задачи
так что ожидаемое равенство
|В|2 + | 1 + F |2 = 1,	B2.10)
очевидно, выполняется.
Таким образом, проблема нахождения амплитуд рассеяния
вперед и назад свелась к отысканию логарифмических произ-
производных B2.3) четной и нечетной волновых функций в точке
х~а. Разумеется, эту последнюю задачу нельзя решить, пока
потенциал B2.1) не задан в явном виде.
В противоположность результату задачи 21 равенство B — F
теперь уже не имеет места. Если
q\L+-L_\>\L+L_+q*\,
то преобладает рассеяние вперед, в противном случае — рассея-
рассеяние назад.
Задача 23. Отражение от прямоугольного барьера
Общую формулу, полученную в задаче 22, применить к по-
потенциальному барьеру вида
^V(x) = k\, И<а	B3.1)
и V — 0 вне этого интервала. Вычислить коэффициент прохож-
прохождения.
Решение. Внутри барьера уравнение Шредингера запишем
в виде:
и" + {k2—kl)u = 0.	B3.2)
Оно имеет решения двух типов: для кинетической энергии ниже
порога (k < k0) и для кинетической энергии выше порога (k > k0).
Мы начнем с первого случая. Положим
kl—k* = %2,	B3.3)
тогда
и"—и2и = 0.
Поэтому для четного и нечетного решений имеем соответственно
u+(x)=chnx, u+@) = l, ы;@) = 0	B3.4а)
и
и. (х) = -sh ш, ы_@)=-0, ы1@)=1.	B3.46)
Следовательно,
L+ = au\ (a)/u+ (a) = xothxo,	B3.5а)
L_ = аи'_ (а)/и_ (а) = па cth на.	B3.56)

23. Отражение от прямоугольного барьера	59
Для коэффициента прохождения с помощью формулы	B2.96)
после элементарных преобразований получаем
Л	•	B3.6)
14-
Коэффициент отражения находится с помощью B2.10):
Я = |В|2 = 1— Т.	B3.7)
В классической механике падающий слева поток целиком
отразился бы от барьера и мы имели бы |б|2 = 1 и 11-f F |2 = 0.
Согласно же формуле B3.6), это может быть только при усло-
условии ха—coo, т. е. только в том случае, когда над энергети-
энергетическим уровнем частицы возвышается огромная „потенциальная
гора". Коэффициент прохождения становится при этом очень
малым, хотя и конечным („туннельный эффект"), и приближенно
его можно записать в виде
Порядок величины коэффициента прохождения в основном опре-
определяется экспоненциальным множителем.
В дальнейшем для показателя экспоненты нами будет получено общее
выражение (см. задачу 116) в виде интеграла
при произвольном потенциале V (х).
Когда кинетическая энергия частицы превышает высоту по-
потенциального барьера, величина к, определенная соотношением
B3.3) становится чисто мнимой. Вводя для удобства обозначение
К» =*»_?* = _х»,	B3.9)
мы можем теперь вместо B3.6) написать
Т=		•	B3Л0)
В классической механике при рассматриваемых энергиях должно
было бы быть Т = 1 и R = 0, коэффициент же прохождения,
определяемый формулой B3.10), достигает максимального значе-
значения Т=1 только при 2Ка — пп (п—\, 2, 3, ...). Между этими
максимумами в точках 2/Са = (п -f 72) л находятся минимумы,
которые лежат тем ближе к значению Т = 1, чем меньше мно-
множитель при синусе в формуле B3.10), другими словами, чем

60
//. Задачи без учета спина. А. Одномерные задачи
больше энергия частицы по отношению к высоте потенциального
барьера.
Зависимость коэффициента прохождения Т от отношения
энергии к высоте барьера (скажем. U) показана на фиг. 5, где
я=0,5
Фиг. 5. Зависимость коэффициента прохож-
прохождения 7* от отношения энергии к высоте барь-
барьера (при Е > U).
изображен график функции Т (E/U) для
случая 2kaa = 3n. На фиг. 6 иллюстри-
иллюстрируется поведение волновой функции:
на ней изображена зависимость плот-
плотности вероятности | и |2 от координаты х.
По правую сторону от барьера |и|2 =
= | 1 -f F |а, т. е. плотность вероятности
постоянна, слева же от барьера имеет
место интерференция между отражен-
отраженной и падающей волнами. На фиг. 6
показан случай k2 = х2 = 1/а^о для барь-
барьеров различной ширины. Чем шире
барьер, тем меньше интенсивность
прошедшей волны и тем ярче выраже-
выражено явление интерференции.
а=1
Л/1
Фиг. 6. Зависимость плот-
плотности вероятности | «21 от
координаты л: для потока час-
частиц, падающих слева на пря-
прямоугольный барьер в случае
Е < U.
Парой вертикальных линий от-
отмечена ширина барьера а. Ос-
Осцилляции слева от барьера обу-
обусловлены интерференцией между
отраженной и падающей волна-
волнами.
Задача 24. Инверсия отражения
Пусть слева на препятствие в виде потенциального барьера
V (х) > 0, расположенного в области 0 < х < а, падает волна.
Показать, что независимо от формы потенциала коэффициент
отражения будет иметь то же самое значение и в том случае,
когда волна падает на барьер справа.
Решение. Пусть и (х) и v(x)—два независимых действитель-
действительных решения уравнения Шредингера для области 0 < х < а
с вронскианом
uv' — vii=\.	B4.1)

24. Инверсия отражения	61
В случае волны, падающей слева, волновая функция имеет вид1'
(е'кх + Re~ikx, х < О,
Аи (х) + Bv (x), 0<х<а,	B4.2)
Се'к <-х-"\	х>а,
и требование непрерывности i|) и i|/ в точках х = 0 и х = а дает
1 -\- R — Аи @) -\- Bv @),
Au(a)+Bv{a) = C,
Аи' (а) + Bv' (a) = ikC.
С помощью соотношения B4.1) из последней пары уравнений
находим
A=C[v'(a)-ikv(a)],
B = —C[u'(a) — iku(a)].	K '
Подставив полученные для Л и В выражения в первую пару
уравнений B4.3), имеем
\ + R = (pOa — iq)C, \—R = (pa0—ir)C,	B4.5)
где в целях сокращения записи положено
pOa==u(O)v'(a)-v(O)u'(a),
aq = k[u@)v(a)-v@)u{a)],	B4.6)
r=j[u'@)v'(a)-v'@)u'(a)].
С помощью соотношений B4.5) окончательно получаем
D \Роа Рай) * \Я ^)	/ол v\
так что коэффициент отражения будет равен
| г> 12	 (Роа — РаоJ + (Я — ГJ
Рассмотрим теперь второй случай, когда первоначальная волна
падает справа. Для этого волновую функцию B4.2) достаточно
заменить выражением
Се-'кх,	х<0,
= •{ Au(x) + Bv(x),	0<x<a,	B4.9)
и Через ф мы в этой задаче обозначаем пространственную часть волновой
функции, так как символ и уже использован с иной целью.

62	//. Задачи без учета спина. А. Одномерные задачи
Условия непрерывности теперь гласят:
a),	B4.10)
Au@)+Bv@) = C,
Аи' @) + Bv' @) = — ikC.
Они имеют ту же структуру, что и уравнения B4.3), из кото-
которых их можно получить, заменив k на —k и поменяв аргу-
аргументы а и 0 местами. Это преобразование применительно к со-
соотношениям B4.6) дает
Роа-+Рао, РаО—>-рОа, <7 ~* <7. Г—* Г.	B4.11)
Таким образом, окончательные формулы будут отличаться от
формул B4.7) и B4.8) лишь тем, что рОа и ра0 поменяются мес-
местами. Так как выражение B4.8) симметрично по отношению к р„а
и ра0, то коэффициент отражения
|Я|* = |Я|"	B4.12)-
будет иметь одно и то же значение для волны, падающей слева,
и для волны, падающей справа. Это, однако, не имеет места для
амплитуды R. Действительно, равенство B4.7), будучи записано
в виде отношения R = a/?> двух комплексных чисел аир, со-
согласно соотношениям B4.11), преобразуется к виду /? = — а*р.
Задача 25. Прямоугольная потенциальная яма
Найти связанные состояния и соответствующие им собствен-
собственные значения в случае прямоугольной потенциальной ямы
Г25П
о, |х|>а.	(ZbA)
Решение. Результаты двух предыдущих задач позволяют без
труда разобраться в поведении состояний с положительной энер-
энергией, поэтому достаточно рассмотреть случай отрицательных
энергий, соответствующих связанным состояниям.
Потенциал инвариантен по отношению к инверсии V(х) = V {—х),
так что решения обязаны быть либо четными, либо нечетными
(см. задачу 20). Положив
?	и Ш *' *3'	B52)

25. Прямоугольная потенциальная яма	63
можно записать эти решения в следующем виде:
четные
( А . cos kx,	0 <! л: <! а,
и (х) — <
+ К ' \ Л+cos to* «-*>, х>а,
И + \	Л^ — w _^ V /»	y^tO .Oaf
—j- = -j- [ka -f- sin ka cos ka] -\— cos2 ka;
нечетные
A _ sin kx,	0 ^ x ^C a,
ЛС1П bap^- (^ — ^)	v ""*>. /y
«_ (— x) — — u_ (x),	B5.36)
1 i	.	i
—— = -r [ka — sin ka cos ka] -\— sin2 ka.
д_ к	х
Выше амплитуды внутри и вне потенциальной ямы были выбраны
таким образом, чтобы функция и (х) оставалась непрерывной
в точке х = а. Нормировочная постоянная была определена из
условия
09
dx=\.
\ и
— 00
Требование непрерывности и' в точке х~а дает еще условие:
четные
— k sin ka = — х cos ka,
или
igka = ~\	B5.4a)
B5.46)
& cos to = — x sin fea,
или
С помощью соотношений B5.4) и B5.2) можно упростить выра-
выражения для нормировочных постоянных, получая в обоих случаях
одно и то же равенство:
+ 1	B5.5)
л2
Чтобы из уравнений B5.4) можно было найти собственные
значения, заменим в правых частях этих уравнений величину х
в соответствии с выражением B5.2) и введем обозначение
C = kaa.	B5.6)

64
//. Задачи без yygmA спина. А. Одномерные задачи
В результате получим
четные
tg ka = ¦
ka
B5.7а)
нечетные
ka
.	B5.76)
При данном потенциале величина С является постоянной, зави-
зависящей лишь от размеров ямы (Са~?/а2), и уравнения B5.7а) и
Фиг. 7. Графическое решение уравнений B5.7а) и B5.76).
На фигуре показаны точки пересечения кривых, изображающих правые части уравнений
при различных значениях параметра С, с тангенсоидой tg ka. Кривые с положительными
ординатами относятся к четным состояниям, кривые с отрицательными ординатами —
к нечетным.
B5.76) дают возможность определить все значения ka, a
самым и все значения энергии
ka
тем
E=—l
B5.8)
реализующиеся в яме данных размеров.
На фиг. 7 tg ka, а также правые части уравнений B5.7а) и
B5.76) показаны как функции переменной ka. Собственные зна-
значения находятся как абсциссы точек пересечения двух послед-
последних кривых с тангенсоидой. Упомянутые кривые, разумеется,
зависят от параметра С, определяемого размерами ямы. Начав,
например, со значения С=1, мы получаем одну точку пересе-
пересечения, обозначенную буквой а, в четном случае и вообще
не получаем ни одного пересечения в нечетном случае. Следова-
Следовательно, в яме такого размера имеется не более одного связан-
связанного состояния с положительной четностью. Эта яма с соответ-
соответствующим уровнем показана на фиг. 8,а. Для ямы больших

25. Прямоугольная потенциальная яма
65
размеров, С =1,5, кривые на фиг. 7 пересекаются в точке Р;
по-прежнему имеется только одно состояние с положительной
четностью (фиг. 8,6), причем ?р < Еа, поскольку (ka)§ > (ka)a.
Если еще увеличить размер ямы, взяв, например, С = 2, то пере-
пересечение в точке у Даст еще более низкое состояние с положи-
положительной четностью (?v<?p), но, кроме того, к нему добавится
сг=г,г5

СгЧ6


е
Фиг. 8. Энергетические уровни (а—е) в потенциальных ямах при различном
значении характеристического параметра С.
Сплошные линии — состояния с положительной четностью, пунктирные линии—со-
линии—состояния с отрицательной четностью.
состояние с отрицательной четностью, соответствующее пересе-
пересечению в точке а' (фиг. 8, в). С дальнейшим увеличением разме-
размеров ямы ее „вместимость" возрастает (фиг. 8, г—е): число свя-
связанных состояний растет линейно с ростом С, образуя чередую-
чередующиеся серии состояний с положительной и отрицательной чет-
четностью. Что касается собственных функций, то они следуют
общему правилу: чем больше у них нулей, тем выше их поло-
положение на шкале энергий. Волновые функции четырех низших
состояний показаны для случая С = 5 на фиг. 9.
В классической механике частица могла бы колебаться между
стенками (точки х = ±а), ограничивающими яму, при любом
значении энергии. Вне ямы ее кинетическая энергия была бы
отрицательна, поэтому область вне ямы классически недостижима.
В квантовой механике мы не имеем такого жесткого ограниче-
ограничения. Вероятность Pt обнаружить частицу внутри ямы оказы-
№ Ю50

66
//. Задачи без учета спина. А. Одномерные задачи
вается меньше единицы:
+а
B5.9)
Таким образом, имеется конечная вероятность того, что частица
находится снаружи. Для всякого конечного интервала вне ямы
Фиг. 9. Энергетические уровни и собственные функции для случая С = 5.
Сплошные линии — состояния с положительной четностью, пунктирные линии — состоя-
состояния с отрицательной четностью.
вероятность убывает экспоненциально, как е-ач<|Л:|-а\ по мере
увеличения расстояния |jt|—а между частицей и ямой.
Задача 26. Прямоугольная потенциальная яма между двумя
бесконечными стенками
Найти решения уравнения Шредингера для потенциала,
изображенного на фиг. 10. Особо рассмотреть состояния с поло-
положительной энергией в предельном случае /—<-оо.
Решение. Начнем с беглого рассмотрения „связанных" состоя-
состояний, для которых ?<0. Используя прежние обозначения &2, k\
и к2, определенные посредством B5.2), и условие нормировки
\
можем записать волновые функции следующим образом:

26. Потенциальная яма между двумя бесконечными стенками	67
четные
0<лг<а,
(
. cos kash x (/— х)
Л ;
sh2x(/ —a)J '
B6.1a)
_ sin kx,
Здесь, как и ранее в задаче 25,
рывности и(х) при х = а, но
требование непрерывности про-
производной и'(х) в этой точке дает
нам дополнительное условие:
четные
/—a), B6.2a)
a), B6.26)
B6.16)
мы уже позаботились о непре-
непреКг
нечетные
-х
-и-
r.J
которое и позволяет вычислить собственные значения. Мы не будем,
однако, углубляться в дальнейшие детали и лишь заметим, что при
обе гиперболические функции быстро стремятся к единице. При
этом уравнения B6.2а) и B6.26) переходят в уравнения для
собственных значений B5.4а) и B5.46) предыдущей задачи, а нор-
нормировочные соотношения B6.1а) и B6.16) для 1/Л± — в соответ-
соответствующие соотношения B5.3а) и B5.36). В выражениях же B6.1а)
и B6.16) для самих волновых функций,когда \х\ </, нок(/—*)^>1,
можно положить
shx (/-<),„_,»
shx(/-a) e
снова возвращаясь, таким образом, к волновым функциям B5.3а)
и B5.36).
Гораздо более интересен вопрос о состояниях с положитель-
положительной энергией. При конечных значениях / имеются дискретные
собственные значения, образующие по мере роста / все более

68	//. Задачи без учета спина. А. Одномерные задачи
плотную систему уровней, которая в предельном случае /—>¦ оо
переходит в континуум. Введя вместо Е > 0 новую переменную
/С2 = -к2 = ^-^(	B6.3)
мы можем записать волновые функции в виде:
четные
( А + cos kx,	О < х < а,
B6.4а)
нечетные
(A_s\nkx,
1 1 г,	. ,	, -,
— = T[ka-smkacoska]
B6.46)
Согласно этим выражениям, функция и(х) уже непрерывна, тре-
требование же непрерывности производной и' (х) снова дает условие:
четные
tgb=^ctg/C(/-a),	B6.5а)
нечетные
|a),	B6.56)
которое позволяет вычислить собственные значения. Используя
это условие, мы можем заменить ctg/C(/ — а) во вторых скобках
в нормировочных выражениях для 1/Л±. В результате получим
—- = -т- [ka + sin ka cos&a] +
— — sintecos&a B6.6a)
—Г = ¦?¦ [^й—sin ka cos &a] +
B6.66)
Если /—»-оо, то второй член в этих выражениях неограниченно

	26. Потенциальная яма между двумя бесконечными стенками	69
возрастает, поэтому
—j-«/ ( cos2 ka + -gz sin2 ka ),
A+ V	а	у	B6?)
Амплитуды вне ямы можно, однако, определить непосредственно
из B6.4а) и B6.46)
sin»/С (<-а) _^ ;	sinaAT(i—а) _^
так что при л: > а обе волновые функции принимают вид
u±=y=rsinK(l—x).	B6.8)
Здесь величина / все еще входит в фазу волновой функции, но
ее можно исключить, воспользовавшись снова уравнениями B6.5а)
и B6.56), определяющими собственные значения:
четные
/* +tgfeatg Ka\
Kl = arctg -	_	 ,	B6.9а)
нечетные
( ^\
Ю = arctg 	j,	 .	B6.96)
U + ^-tgkatgKa
Наиболее примечательной особенностью этой системы волновых
функций являются их энергетические уровни, плотность которых
можно определить из уравнений B6.5а) и B6.56) для случая очень
больших, но все еще конечных значений /. Правые части этих
уравнений пробегают всю действительную ось от —оо до оо,
когда переменная Ю пробегает интервал шириной п. В каждом
таком интервале существует ровно одно решение как у одного,
так и у другого уравнения; поэтому мы получаем чередующиеся
четные и нечетные уровни, расположенные в среднем на расстоя-
расстоянии АК = п/B1) (в шкале переменной К) друг от друга. Среднее
же расстояние между уровнями в энергетической шкале, согласно
B6.3), равно
?/?	B6Л0)
Таким образом, среднее расстояние между последовательными
уровнями растет лишь как Е1'1 и обратно пропорционально длине

70
//¦ Задачи без учета спина. А. Одномерные задачи
нормировочного интервала. Следовательно, в пределе / —>¦ оо ди-
дискретный энергетический спектр переходит в непрерывный.
Поведение амплитуды при переходе к непрерывному спектру
для случая &оа^С = 2 показано на фиг. 11. Безразмерная ве-
величина А21 представляет собой меру квадрата амплитуды внутри
ямы, когда нормировка на всем протяжении вне ямы остается
одной и той же, а величина I велика. График этой величины
в зависимости от (КаJ, т. е. в зависимости от энергии в безраз-
безразмерных единицах, построен с помощью формул B6.7). Ясно, что
Четные Нечетные
0,3
0,8
%0,7
0,6
-/Л
1
/
/
—-*
10 гО SO 40 50 60 70
Фиг. 11. Виртуальные состояния в непрерывном спектре.
имеется бесконечное число последовательных значений энергии,
для которых величина Л2/ принимает максимальное значение,
равное единице. Между максимумами лежат минимумы амплитуды,
выраженные тем слабее, чем выше энергия (обратите внимание, что
нижняя половина оси ординат на фиг. 11 не показана). При
энергиях, соответствующих максимумам амплитуды, рассматри-
рассматриваемые состояния, хотя их энергия положительна, все еще сохра-
сохраняют некоторые черты связанных состояний, так как в этих
состояниях достигается максимально возможная концентрация
волновой функции в области, занятой ямой. По этой причине
о ник часто говорят как о виртуальных состояниях в противо-
противоположность „истинным" связанным состояниям с отрицательной
энергией.
Задача 27. Виртуальные уровни
Потенциальная „полость" между точками х = 0 и х=о огра-
ограничена справа, как это показано на фиг. 12, полупроницаемой
стенкой (см. задачу 20) так, что между волновыми функциями
внутри и вне полости существует лишь слабая связь. Показать,
что при большом коэффициенте непроницаемости существуют узкие
полосы энергии, для которых упомянутая связь становится до-
довольно сильной. Рассмотреть числовой пример Qa/n = 50.

27. Виртуальные уровни
71
Решение. В данном случае спектр энергии непрерывен и вол-
волновые функции, нормированные так, чтобы их амплитуда равня-
равнялась единице вне полости, имеют вид
j A sin kx,
оо.
B7.1)
Граничные условия на стенке с конечным коэффициентом непро-
непроницаемости Q, согласно задаче 20, выгля-
выглядят следующим образом:
| = ы(а—0),
¦и' {а—0) + 2Яи(а).
Для функций B7.1) это дает
sin (ka + б) =¦ Л sin &а,
= &Л cos &а + 2QA sin i
B7.2)
О а
Фиг. 12. Потенциальная
полость, ограниченная по-
полупроницаемой стенкой.
Эти два соотношения определяют фазовый угол б:
и амплитуду А волновой функции внутри полости:
~м— 1 + 4 -г sin ka cos te + 4 гг sin2 fta,
или
B7.3)
B7.4)
B7.4a)
В случае непроницаемой стенки (Я —* оо) амплитуда А обращается
в нуль: колебания, имеющиеся снаружи, не могут проникнуть
внутрь полости — она оказывается совершенно не связанной
с внешним пространством. Однако при больших, но конечных
значениях Я допустимо появление малых амплитуд A~k/Q.
Если же значения тригонометрических функций в формуле B7.4)
близки к нулю, то не исключено появление даже весьма больших
амплитуд.
Пусть произведение ka велико по сравнению с я(/?а^>2я),
тогда полному периоду изменения тригонометрических функций
будет соответствовать такой интервал изменения переменной k,
в котором отношение Q/k будет оставаться почти постоянным.
В таком случае максимальные и минимальные значения величины
Л2 с разумной степенью точности можно найти, дифференцируя
выражение B7.4а) по переменной 2ka при условии Q//fe== const:

72	//. Задачи без учета спина- А. Одномерные задачи
Таким образом, имеем
tg2ta = — -j~.	B7.5)
Обозначая решения уравнения B7.5) через kn и полагая
|f = е„,	B7.6)
получаем
2kna = nn—arctgen,	B7.7)
где п—целое число, и, следовательно,
/	1 \ и -1. 1	&П
= (-l)	.
У 1 + е2„
Подставляя эти выражения в равенство B7.4а), для экстремаль-
экстремальных значений величины 1/Ла находим при четных п = 2, 4, 6, ...
а при нечетных п=\, 3, 5, ...
-±- = 1 + -7J==f + 4 A + тт=ЦЛ •	B7.86)
Так как е„<^1, то последние выражения можно разложить по
степеням е„:
1Г = Те« = & при л = 2, 4, 6, ...	B7.9а)
и
1	4	1	4Q2
7Г = — + 2-те^«-г при п = 1, 3, 5, ... B7.96)
Выше отброшены все члены, имеющие порядок е*.
Таким образом, при четных значениях п, т. е. при значениях
произведения ka, близких целым кратным л, мы имеем макси-
максимальные амплитуды:
2О
4,.M«c=ftf>l,	B7.10)
а при нечетных п, т. е. для значений ka, близких полуцелым
кратным л,— минимальные амплитуды:
Л„,ии„ = ^<1.	B7.11)
Следовательно, заметная связь внешнего пространства и полости
имеет место- лишь при тех значениях энергии, которые близки

77. Виртуальные уровни
73
к энергиям, обеспечивающим выполнение соотношения B7.10),—
только в этом случае наружная волна проникает заметным образом
сквозь потенциальный барьер. С классической точки зрения это
означает существование резонансных частот, при которых воздей-
воздействие извне способно возбудить
собственные колебания полости. Ю
Согласно соотношению B7.7),
резонансы имеют место, если
произведение kna лишь незначи- 8
тельно отличается от пп, где п —
целое число, т. е. для тех зна- . 7
чений k, при которых волновая \ в
функция внутри полости, опре- ^
деляемая формулой B7.1), весь- 5
ма близка к собственной функ-
функции в случае непроницаемой
стенки (Я —>- оо)
ип (х) = A sin '¦
ип(а) =
1,5 г,о
Фиг. 13. Резонансный уровень.
Зависимость амплитуды волновой функции
от энергии.
Следовательно, резонансные
уровни располагаются вблизи
собственных значений энергии
полости при Q—>оо. По этой
причине их называют виртуаль-
виртуальными уровнями.
На фиг. 13 показано поведе-
поведение амплитуды А при изменении
произведения 2ka от 18я до 22л, а численное значение величины
Яа взято равным 50я= 157,08. В этом случае ?/2Я « 0, 1, и не-
нетрудно видеть, что амплитуда А, как правило, имеет такой же
порядок. Исключение представляет очень узкая область, распо-
расположенная немного левее точки 2&а=*20я, где ее поведение носит
типично резонансный характер. Разлагая величину \/А3 в сте-
степенной ряд вблизи резонансной энергии, определяемой соотно-
соотношением
2koa =* 2пп— arctg -^,
приближенно получаем
B7
Таким образом, ширина резонанса по порядку величины равна
Ы~тъ-	B7.13)
Нам осталось обсудить поведение фазового угла, определяемого
соотношением B7.3). Несложные тригонометрические преобразо-

74	//. Задачи без учета спина. А. Одномерные задачи
вания дают
B7.14)
Если отношение Q/k велико, то мы, как правило, можем прене-
пренебречь единицей в знаменателе, так что выражение B7.14) стано-
становится не зависящим от Q:
, е	1 — cos 2 ka	it.
tg б «	г—н-г— = — tgka.
s	sin 2 ka	&
Это снова соответствует случаю непроницаемой стенки с волновой
функцией
и (х) = sin k (x—a)
при х > а. Такое приближение неприменимо лишь для тех зна-
значений k, которые близки к корням уравнения
sin2?a = — ¦?-.	B7.15)
Имеется два типа решений уравнения B7.15): когда 2ka немного
больше Bп + 1)я и когда 2ka немного меньше 2пп. В первом
случае числитель 1—cos2?a близок к 2 и почти постоянен.
Но тогда tg б обращается в бесконечность, т. е. б становится
полуцелым кратным я, для определенности, скажем, я/2. В этой
области фазовая кривая имеет постоянный наклон и в ее пове-
поведении не наблюдается сколько-нибудь существенных особенностей.
С другой стороны, если 2ka лежит вблизи 2пп, то числитель
раЕвн нулю, причем этот нуль, хотя и лежит вблизи, но не
Совпадает с нулем знаменателя, положение которого определяется
уравнением B7.15), поэтому tg б внутри очень узкого интервала
изменений переменной 2ka пробегает значения от бесконечности
до нуля, а фазовый угол б — от л/2 до я. Выше мы видели, что
в областях, близких к точкам 2ka=2nn, имеются резонансы,
а скачкообразное изменение фазы при прохождении через резо-
резонанс является характерной особенностью колебательных систем.
На фиг. 14 показано изменение фазового угла в том же ин-
интервале значений 2ka, который приведен на фиг. 13. Если бы
величина Q была бесконечно большой, то поведение фазового
угла описывалось бы пунктирной кривой. При построении этой
кривой мы для удобства в точке 2&а = 20я произвольно добавили
скачок фазы, равный я, что влечет за собой скачкообразное
изменение знака волновой функции, который сам по себе, как
известно, не имеет физического смысла. Для выбранного нами
конечного значения Q поведение фазового угла показано на
фиг. 14 сплошной кривой. Согласно этой кривой, для последо-
последовательных значений энергии мы получаем набор волновых функ-
функций, которые по фазе не слишком отличаются от волновых

28. Периодический потенциал
75
функций, соответствующих непроницаемой стенке, но которые
тем не менее непрерывным образом переходят друг в друга при
прохождении через резонансное значение энергии, так что в этом
случае скачок фазы приобретает реальное значение.
Зя
4
-
V
NT
V
/9х	ZOji	Zlifi
Фиг. 14. Резонансный уровень.
Зависимость фазового угла от энергии.
Задача 28. Периодический потенциал
Получить общие соотношения для волновых функций и энер-
энергетического спектра в случае периодического потенциала.
Решение. Если V(х) — периодическая функция с периодом а,
то уравнение Шредингера инвариантно по отношению ко всем
трансляциям, кратным а:
V(x + a) = V(x), х-^х + па, п = 0, ±1, ±2	 B8.1)
Обозначим через ых (х) и и2 (х) два линейно независимых решения
уравнения Шредингера, тогда функции «х (х-\-а) и и2 (х-{-а) также
должны быть решениями этого уравнения. Так как любое реше-
решение можно представить в виде линейной комбинации их (х) и и2 (х),
то это должно быть справедливо и в отношении решений их(х-\-а)
и и2 (х-{-а):
1	11 1	12 г	B8.2)
Теперь можно доказать (теорема Флоке), что среди этих решений
имеются два, скажем ty1 и ф2, таких, что
г|з (х + а) = Лг|) (х),	B8.3)
где множитель Я—постоянная. В этом случае, очевидно,
q(x + na)=k"q(x), п = 0, ±1, ±2, .... B8.3а)

76	//. Задачи без учета спина. А. Одномерные задачи
Искомое доказательство выглядит следующим образом:
(x),	B8.4)
и, согласно B8.2),
гр (х+а) = (АСи + ВСг1) и, (х) + (ЛС„ + ДС„) и, (х).
Последнее же выражение равно Ягр (х), если
Система B8.5) двух однородных линейных уравнений относи-
относительно А и В имеет нетривиальное решение тогда и только тогда,
когда обращается в нуль детерминант:
\ =0.	B8.6)
Это—квадратное относительно Я уравнение, двум корням кото-
которого, \ и Я2, соответствуют две функции, г^,^ и г|за.
Из формулы B8.3) можно усмотреть, что определитель Врон-
Вронского
удовлетворяет соотношению
По теореме Грина определитель Вронского D не зависит от х,
отсюда следует, что
3^=1.	B8.7)
О параметрах Ях и К2 можно получить более подробные све-
сведения, рассмотрев равенство B8.3а). Пусть |Я| > 1, тогда ампли-
амплитуда волновой функции гр будет неограниченно возрастать при
х—> оо и неограниченно убывать при х—>—оо. Противополож-
Противоположный случай имеет место, если |Я|< 1. Такие решения не нор-
нормируемы даже в том смысле, который мы вкладываем в это
понятие в случае плоских волн, поэтому физически значимые
решения существуют лишь при |Я|=1, т. е. когда
X1 = eiKa и Я2 = е-'№,	B8.8)
а К—действительная величина. Так как егп1п= 1, то можно огра-
ограничиться теми значениями К, которые лежат в интервале
-?<*<?,	B8.9)
что даст нам полный набор всех допустимых волновых функций.
Таким образом, для всех ограниченных решений г|з(л;) имеем
B8.10)

28. Периодический потенциал	77
Последнее возможно лишь в том случае, если
$(х) = е'к*ик(х),	B8.11)
а ик(х) — периодическая функция, т. е.
B8.12)
Этот результат составляет содержание теоремы Блоха.
Обратимся теперь к вопросу об энергетическом спектре.
В интервале О^лг^а построим решение ij) из двух каких-либо
решений и1 и у, так же, как это сделано в B8.4). Для соседнего
интервала периодичности а^.х^.2а в соответствии с формулой
B8.10) получаем
$(х) = е'Ка [Аи^х—ф + Ви^х—а)],	B8.13)
причем значения аргумента х—а попадают в предыдущий ин-
интервал. На границе этих интервалов, в точке х~а, должны
совпадать как сами выражения B8.4) и B8.13), так и их про-
производные:
Аи(а) + ВиМ = е1Ка[АиЛ®)+ВиЩ
Эта однородная относительно А и В система уравнений разре-
разрешима в том и только в том случае, если обращается в нуль
детерминант:
ut (а) — eiKaux @) у 2 (а) — е'Каиг @)
и[{а) — е'^и'^О) u'2(a)~eiKau'2(Q) =0#
Раскрывая детерминант, окончательно приходим к соотношению
сое Ка - [Ul @)"'(а)+Ul (а) "*@)] ~[ @) Ul (a) +  (а) и1 @)] B8 15)
2(UM ««)
Здесь в знаменателе стоит вронскиан, взятый для любого значе-
значения аргумента (так как вронскиан есть константа, то нет необ-
необходимости указывать его конкретное значение).
Уравнение B8.15) представляет собой условие существования
собственных значений. Оно разрешимо только в том случае, если
абсолютная величина правой части не превышает единицы, тогда
с помощью этого уравнения можно вычислить величину К.
Имеются целые интервалы значений энергии, удовлетворяющие
указанному условию, и чередующиеся с ними интервалы значений
энергии, для которых это условие не выполняется. Таким обра-
образом, энергетический спектр состоит не из отдельных уровней,
а представляет собой чередующиеся последовательности разрешен-
разрешенных и запрещенных энергетических зон. Границы энергетических
зон определяются согласно B8.15) из соотношения cos/Ca = ±l-
Замечание. Так как функции их и иг можно заменить любой другой па-
парой линейно независимых решений vx и v2, то уравнение B8.15) с таким же

78	//. Задачи без учета спина. А. Одномерные задачи
успехом можно записать через функции v. Оно, однако, должно приводить
к тем же самым энергетическим зонам. В этом нетрудно убедиться, подставив
выражения
в уравнение B8.15). Несложные выкладки показывают, что при использовании
функций v получается в точности то же самое выражение, что и при исполь-
использовании функций и, если детерминант Цс/^Ц не обращается в нуль.
Задача 29. Дираковская потенциальная гребенка
Дан периодический потенциал, образованный последователь-
последовательностью б-функций Дирака (интервал между соседними особыми
точками постоянен и равен а):
?	B9.1)
Определить зоны разрешенных значений энергии.
Решение. Начнем с фундаментальных решений
u1(x) = e!kx и иг{х) = е-Шх.	B9.2)
Если
и (х) = Aeikx + Be~ikx	B9.3)
— решение в интервале О^х^а, ограниченное в смысле за-
задачи 28, то в соседнем интервале а ^ х ^ 2а будем иметь
u(x)=eiKa [Ле'*и-а) + ?е-'А(д;-а)].	B9.4)
Далее при х—а должны выполняться граничные условия
поэтому
е!ка (А + В) = Aeika + Ве~1ка	B9.6a)
и
ikeiKa {A — B) = ik {Aeika—Be-ika) + 2Q (Aeika + Be~ika). B9.66)
Уравнения B9.6а) и B9.66) представляют собой однородную
систему линейных уравнений относительно А и В—ее детерми-
детерминант должен обращаться в нуль. Тривиальные преобразования
дают
cosKa = coska-\--r-s'mka.	B9.7)
Следовательно, зоны разрешенных значений энергии определя-
определяются неравенством
cos ka + -p- sin ka <1,	B9.8)

29. Дираковская потенциальная гребенка
79
или
У l+(Qa/ka)* '
а собственные значения энергии равны
B9.9)
Щ\	B9.10)
На фиг. 15—18 приведены результаты расчетов для случая
Qa = 4. Функции переменной ka, стоящие в правой и левой частях
неравенства B9.9), показаны на фиг. 15.
Точки пересечения соответствующих кри-
кривых изображены кружками, а интервалы, в
которых выполняется неравенство B9.9),
отмечены на оси ka жирными линиями.
Верхним границам зон соответствуют точки,
30-
0,1
о 1
IS
Фиг. 15. Графическое определение зонной Фиг. 16. Зонная структу-
структуры.	ра в случае дираковской по-
потенциальной гребенки.
кратные л; согласно уравнению B9.7), в этих точках cos /<a=cos ka.
Положение зон на энергетической шкале, найденное с помощью
фиг. 15, показано на фиг. 16, где разрешенные энергетические
зоны заштрихованы. По мере роста энергии разрешенные зоны
расширяются, так что энергетический спектр приближается
к непрерывному. Тем не менее он никогда полностью не совпа-
совпадает с ним: даже при самых высоких энергиях всегда имеются
запрещенные зоны, примыкающие сверху к точкам ka~rm.
На фиг. 17 и 18 показана зависимость энергии (в безразмерных
единицах) от переменной Ка для первых трех зон. На фиг. 17
переменная Ка монотонно возрастает от зоны к зоне, а на фиг. 18
ее изменение ограничено интервалом —л^/Са^я. Пунктирная
кривая на фиг. 17 представляет собой параболу K = k, прохо-
проходящую через точки, соответствующие верхним границам разре-
разрешенных зон.

80
//. Задачи без учета спина. А. Одномерные задачи
Все приведенные фигуры относятся к случаю Qa = 4, поэтому
по ним нельзя судить о влиянии проницаемости стенки на энер-
энергетический спектр. Для меньших значений О,а правая часть
неравенства B9.9) будет быстрее приближаться к единице, и
соответствующая кривая на фиг.
15 будет пересекать косинусо-	g
иду в точках, более близких
к максимумам последней. Это,	8
Зл
-л
О	*П
¦ Ля —»-	Ля —*-
Фиг. 17. Зависимость энергии от пе-	Фиг. 18. Зависимость энергии от пе-
переменной Ка для трех первых зон	ременной Ка.
(одномерные ЗОНЫ Бриллюэна).	Приведенное представление.
Пунктирная кривая —парабола, отвечаю-
отвечающая энергии свободной частицы.
разумеется, означает, что запрещенные зоны станут уже. Так как
положения верхних границ разрешенных зон (точки ka = nn) не
зависят от па, то по мере уменьшения этой величины будут
смещаться вниз на фиг. 16 лишь одни нижние границы этих
зон. При Qa = 0 запрещенные зоны исчезают, но при этом исче-
исчезает и наш потенциал, и мы приходим к случаю свободного дви-
движения, которому соответствует непрерывный спектр. С другой
стороны, если па—>-оо, то разрешенные зоны вырождаются
в дискретные уровни ka — nn, В этом случае стенки полностью
изолируют потенциальные ямы друг от друга и рассматриваемый
спектр сводится к спектру задачи 18, только теперь расстояние
между стенками равно а, в задаче же 18 оно равнялось 2а.
Литература
Kronig R. de L., Penney W., Proa Roy. Soc, 130, 499 A931).

30. Гармонический осциллятор	81
Задача 30. Гармонический осциллятор
Найти собственные значения и собственные функции в случае
осцилляторного потенциала
У(л:) = утаЛс2.	C0.1)
Решение. Введя обозначения
k* = *2* и Х = ^,	C0.2)
уравнение Шредингера можно записать в виде
jg+(tf_XV)u=0.	C0.3)
Решения этого дифференциального уравнения асимптотически
при \x\^>kjX ведут себя как exp (±Vab:s). Если выделить эту
экспоненту из функции и (х), положив
u(x) = e-*'**v(x),	C0.4)
то функция v(x), удовлетворяющая уравнению
v"—2Xxv' + (k2—Л) о = 0,	C0.5)
будет либо полиномом, либо пропорциональна е***. Решая урав-
уравнение C0.5) с помощью разложения в ряд
v(x)=^a,xf,	C0.6)
/=о
получаем рекуррентное соотношение
—k2	/ол-7v
+i)ar	<30J>
При /—ссхэ имеет место асимптотическое соотношение а;-+2 =
= BK/j)alt соответствующее степенному разложению функции еКх*.
Таким образом, решение C0.4) нельзя нормировать, если ряд
C0.6) не обрывается на конечном члене, что происходит при
условии ап+3 = 0, т. е. когда
В этом случае, согласно C0.2), имеем
у), л = 0, 1, 2, ...	C0.8)
Собственные функции ип (х) можно определить с помощью соот-
соотношения C0.7) и нормировать их в соответствии с условием
S «„•(*)**=!•	C0-9)

82
//. Задачи без учета спина. А. Одномерные задачи
Несколько первых собственных функций приводятся ниже:
с—-тгкх* \е
C0.10)
«4 = С, { 1 -
у Л,1** J е- '
а соответствующие нормировочные постоянные равны
'П~\И) с»' С°~1' Ci-V2k> С*~-[7Т>
Iх/
C0.11)
Три первые собственные функции показаны на фиг. 19.
Легко видеть, что собственные функции обладают определен-
определенной четностью. В самом деле, в силу симметрии потенциала,
V(—x) = V(x), функция ц„(— х)
является решением дифференци-
дифференциального уравнения наряду с функ-
функцией ип (х) и принадлежит тому же
самому собственному значению
- !* C0.8). Так как вырождение от-
~Е'~г ш сутствует, то оба решения могут
различаться лишь постоянным
множителем /, причем в силу ус-
-Ea=Lbco ловия нормировки |/|2=1. При
г повторном изменении знака х мы
возвращаемся к исходному реше-
решению, поэтому /2=1 или / = ±1,
следовательно, всякая собствен-
фу	*JT	„
ции гармонического осциллятора. четной, лиоо нечетной.
Этот факт можно подтвердить
непосредственно, если в уравнение C0.5) ввести вместо х новую
переменную
У=--Ьх\	C0.12)
тогда v(y) будет удовлетворять дифференциальному уравнению
для вырожденной гипергеометрической функции:

30. Гармонический осциллятор	83
Если положить
4?Jb	C013>
то общее решение этого уравнения будет иметь вид
. C0.14)
Так как вырожденный гипергеометрический ряд tFx есть целая
функция, то первое слагаемое в решении C0.14) четное, а второе
нечетное по отношению к переменной х. При у—>-оо оба слагае-
слагаемых расходятся как еУу"-1^ и решение и нельзя нормировать»
если ряды не исчезают и не обрываются. Гипергеометрический
ряд обрывается только тогда, когда его первый аргумент равен
целому отрицательному числу, поэтому у нас имеется две воз-
возможности. Если
a=—n, или ?2n = 7ko( 2n + y J,	C0.15а)
то обрывается первый ряд и для собственной функции получаем
-л, у; КхЛе-1/'^'.-	(ЗО.16а)
у = — п, или E,n+1 = im(^2n + ~y C0.156)
Если же
то обрывается второй ряд и собственная функция будет равна
«•»«(*) = вх Л (—я, у ; >^2) е-1'**.	C0.166)
Эти результаты полностью согласуются с формулой для собствен-
собственных значений C0.8) и собственными функциями C0.10).
Многочлены, определяемые равенствами C0.16а) и C0.166),.
называются полиномами Эрмита. С вырожденной гипергеометри-
гипергеометрической функцией они связаны соотношениями:
C0 17)
2п+1\ъ)—\—I)
Кроме того, имеет место формула
^™ (Е) = (—1)" ^' ^я— •	C0.18)
Таким образом, в общем случае нормированные собственные функ-
функции [см. C0.9)] имеют вид

84	//. Задачи без учета спина. А. Одномерные задачи
Для вычисления нормировки в формуле C0.19) можно вос-
воспользоваться следующим приемом. Запишем собственную функ-
функцию в виде
тогда в силу условия C0.9) должно быть
С
— 00
Заменим теперь один из полиномов #„(?) его выражением C0.18).
Беря получающийся интеграл
п раз по частям, окончательно находим
Поскольку #„(!)—многочлен л-й степени относительно ?, то
после n-кратного дифференцирования останется вклад лишь от
высшей степени |:
в полном согласии с формулой C0.19).
Задача 31. Осциллятор в абстрактном гильбертовом
пространстве (осциллятор в представлении Фока)
Используя операторы
Ь = -7===г{р—штх), tf=-7J===-(p-\-i(umx), C1.1)
У 2mta	У 2тПю
найти собственные значения энергии гармонического осциллятора
и построить соответствующие им собственные векторы, не конк-
конкретизируя абстрактное гильбертово пространство состояний.
Решение. Подставляя оператор b и эрмитово сопряженный
ему оператор Ь+ в гамильтониан
П ~2тР Т 2 Х '	F1-2>

31. Осциллятор в абстрактном гильбертовом пространстве	85
получаем
Н = ^1шф&+ЬЩ.	C1.3)
Легко видеть далее, что из канонического перестановочного соот-
соотношения рх—xp = %/i следует
Ш—Ь*Ь=1.	C1.4)
Равенства C1.3) и C1.4) служат математической основой для
построения гильбертова пространства состояний.
Предположим, что существует по крайней мере один кет-век-
тор | tyO, принадлежащий собственному значению X оператора b+b:
fct&|^> = M^>;	C1.5)
этот вектор будем предполагать нормированным:
<%|%>= 1.	C1.6)
Если теперь умножить равенство C1.5) на бра-вектор <%|, то
левую часть получающегося равенства
можно преобразовать, воспользовавшись определением эрмитово
сопряженного оператора
В результате найдем
*| «	*»	C1-7)
Таким образом, величина X, будучи квадратом нормы вектора
| Ьг|зх>, должна быть действительной и положительной:
Х>0,	C1.8)
причем Х = 0 только тогда, когда &|%> = 0. Все это справедливо
для любого собственного значения, так как в нашем распоря-
распоряжении пока еще нет способа отличить одно собственное значение
от другого.
Собственное значение, отличное от К, можно найти, умножив
равенство C1.5) слева на & и перегруппировав затем сомножи-
сомножители с учетом закона ассоциативности и перестановочного соот-
соотношения C1.4):
Таким образом,
или
Поэтому кет-вектор | Ьрх> является собственным вектором опера-
оператора №Ь и принадлежит собственному значению К— 1. Этот век-
вектор пока еще не нормирован, но, как показывает равенство C1.7),

86	//. Задачи без учета спина. А. Одномерные задачи
нормированный собственный вектор должен иметь вид
\Ъ>	Ь\Ъ>	C1.9)
Такую процедуру можно повторить, и мы получаем убываю-
убывающую последовательность собственных значений, причем
\rX(X-[)(X-2)...(X
C1.10)
Для всех п > X эти собственные значения отрицательны, что про-
противоречит неравенству C1.8). Противоречие не возникает только
в том случае, если собственные значения целочисленные, так
как при этом последовательность C1.10) обрывается на векторе
|г|зо> ввиду того, что, согласно C1.9), Ь|г|зо> = О.
Возрастающую последовательность собственных значений мож-
можно построить путем повторного умножения на оператор &+. Так
как
ftt фЩ = Ы (Ш— 1) = фЩ fct_&t,
то из равенства C1.5) следует
Здесь снова вектор |Ы%> еще не нормирован:
Следовательно,
(ЗМ2>
Подытожим теперь наши результаты. Собственными значе-
значениями оператора Ъ^Ь являются целые числа м = 0, 1, 2, ... .
Оператор bbf, как следует из соотношения C1.4), имеет ту же
систему собственных векторов, но его собственные значения равны
п-)-1. Следовательно, для гамильтониана C1.3) справедливо соот-
соотношение
#|^„> = у&й>Bл+1)|^„>, п = 0, 1, 2 ... . C1.13)
Отсюда для энергии осциллятора получаются хорошо известные
значения, найденные нами с помощью координатного представ-
представления в задаче 30.
Векторы состояний |г|з„> не являются собственными векторами
операторов b и &+, однако матрицы этих операторов можно легко
построить, взяв векторы |г|зп> в качестве координатных векторов
гильбертова пространства.

32. Использование лестничных операторов	87
С помощью формул C1.9) и C1.11) соответственно находим
<г|3„_1|&|^п> = К«	C1.14)
C1.15)
Все другие матричные элементы исчезают благодаря ортогональ-
ортогональности векторов | г|з„>. В этом нетрудно убедиться непосредствен-
непосредственной проверкой:
<Ч>„ | ЬЩпУ = п <г|>м | г|>„> =
<ЬЩт [ Ч>„> = т <фя | г|>„>
и, следовательно,
(n-m)<^M|^> = 0,
поэтому либо п = т, либо <^т\^„> = 0- Матрицы C1.14) и C1.15)
можно записать следующим образом:
0 0 0 0..
0 0 0..
Ь = [ 0 V2 0 0 ..
о о Кз о ..
0
0
0
Vi
0
0
0
V2
0
0 ...
0 ...
Va ...
C1.16)
Литература
Becker R., Leibfried G., Zs. Phys., 125, 347 A949).
Задача 32. Использование лестничных операторов для
нахождения собственных функций осциллятора
Найти собственные функции осциллятора, переведя операторы
b и 6+ предыдущей задачи на язык координатного представления.
Решение. Введенные с помощью соотношений C1.1) операторы
b и Ь+ являются линейной комбинацией операторов р их. В коор-
координатном представлении х—классическая переменная, а
— дифференциальный оператор. Здесь удобно выбрать в качестве
единицы длины величину
/=1/ —	C2.2)
у та	v '
и во всех соотношениях пользоваться безразмерной переменной
6 = j	C2-3)

88	//. Задачи без учета спина. А. Одномерные задачи
вместо переменной х. При этом имеем
(i) C24)
Наинизшее состояние, согласно результатам предыдущей задачи,
определяется соотношением &г|з0 = 0 или
d ,
o(S) = "O.	C2.5)
Это есть дифференциальное уравнение с общим решением
где постоянную интегрирования следует выбрать, руководствуясь
соображениями нормировки так, чтобы
Таким образом, получаем
г|3оA) = я-1/</-'/ге-1Л1'.	C2.6)
Полный набор собственных функций теперь можно построить,
применяя последовательно оператор ft+:
|0	C2J>
т. е. путем повторного дифференцирования формулы C2.6). Если
мы напишем
Ъ„ = СаНа®е-ЧА\	C2.8)
то тогда в соответствии с C2.7) функции Я„(|) будут многочле-
многочленами п-я степени от ?, причем для них должно выполняться
рекуррентное соотношение
Ся+1Нп+1 = - у^гц Сп(Н'п-21Нп).	C2.9)
Если мы выберем нормировочные постоянные таким образом,
чтобы
с-«=ужщщс-	C2ло)
то тогда формула C2.9) просто превратится в рекуррентное соот-
соотношение для полиномов Эрмита:
где

33. Гармонический осциллятор в матричном представлении	89
Сравнение с формулой C0.19) показывает, что полученный там
нормировочный множитель, если отвлечься от i, удовлетворяет
соотношению C2.10), поэтому
И Х=1*-
Множитель i, разумеется, произволен, так как условие норми-
нормировки оставляет фазовый множитель всякой собственной функции
неопределенным.
Задача 33. Гармонический осциллятор в матричном
представлении
Получить матрицы ртп и хтп для импульса р и координаты х
гармонического осциллятора, определяемого гамильтонианом
Я = Ш^ + ^Г*2'	C31>
в представлении, где оператор Я диагоналей. Чему равны соот-
соответствующие собственные значения?
Решение. Отправной точкой для нас послужит диагональность
гамильтониана
Нтп = ^ L P*kPk« + ^f ? Х-пЛп = ? А„,	C3.2)
k	k
где Еп—собственные значения. Кроме того, у нас имеются (см.
задачу 8) соотношения
?L = -±-(Hp-pH), ™.= ^±-(Hx-xH), C3.3)
которые в матричных обозначениях с учетом равенств дН/дх =
и дН/др = р/М можно записать следующим образом:
1	, i
IV\ ftin ' +
k
С помощью формулы C3.2) они легко приводятся к виду
Мш*хтп=-\(ЕЯ-Еа)ртп,
L _ I	C3.4)
iy[Pmn ~Г + \Е-т ^п)хтп-
Эта система однородных уравнений относительно хтп и ртп
будет совместной, если исчезают оба матричных элемента или

90	//. Задачи без учета спина. А. Одномерные задачи
если ее определитель равен нулю; в последнем случае
C3.5)
Упорядочив собственные значения в соответствии с неравенствами
...<?,< ?2 < ?„ < ....
мы получаем, что разность двух последовательных собственных
значений равна гш и что
?„ = йсо (я 4-е), /г = 0, 1, 2, ...,	C3.6)
где е — постоянная, общая для всех собственных значений. Но
тогда единственными, не равными нулю матричными элементами
будут элементы рп,п±\ и хп,п±\, которые в силу C3.4) должны
удовлетворять соотношению
/)„,„±1 = ТШша;„,„±1.	C3.7)
Теперь попытаемся получить более подробную информацию
о нашем гамильтониане. Начнем с матриц р2 и х2. Согласно
соотношению C3.7), имеем
(Р2)в* —Рп, n+lpn+l, k-\-pn. n-\Pn-l, k,
где только при k = n, n 4-2, п — 2 левая часть не обращается
в нуль. Аналогичное соотношение имеет место и для матричных
элементов х2. Подставляя их в формулу C3.2), для недиагональ-
недиагональных элементов гамильтониана получаем
Я1	, Ма>2
В, П+2	2М У"' П + 1УП + 1, В + 2 "Г 2 Л". В + Л + 1, Л + 2
*°* ХП, B + 1-^B+l, В + 2	gyVf	~~2	*"
То же самое справедливо и для матричных элементов Нп< „_2,
что полностью согласуется с фактом диагональности оператора Н,
послужившим основой вывода уравнений C3.4). Что касается
диагональных матричных элементов, то они имеют вид
п — 5hM W», п + iPn + l, в \ Рп, n — lPn-1, n) Г
Согласно соотношению C3.7), слагаемые в правой части равны
между собой, поэтому
Еп = М<и2 (х„,п+1хп+1, „ + х„, „_ А_ь „).	C3.8)
Равенства C3.8) и C3.6) устанавливают соотношение мел&ду мат-
матричными элементами оператора х. Учет эрмитовости оператора х
дает еще одно соотношение
хп± 1. п =хп, п±ь	C3.9)

33. Гармонический осциллятор в матричном представлении	91
Таким образом, получаем
Ьй (п + 6) = УИсо2 (| хп, я+112 +1 *„-!, „ |*)-	C3.10)
Вводя обозначение
хК-ь„12 =/(«),	(зз-п)
последнее уравнение можно записать в виде
Решением этого функционального уравнения является функция
C3.12)
в чем нетрудно убедиться, представив / (п) в виде ряда по степе-
степеням п. Из соотношения C3.11) далее следует
Теперь у нас есть все необходимое, чтобы определить постоян-
постоянную е. Правая часть равенства C3.10) не может быть отрица-
отрицательной, следовательно, не отрицательно и собственное значение,
стоящее в левой части этого равенства. Предположим, что я = 0
есть наименьшее значение п, тогда матричный элемент
должен обратиться в нуль. Не будь этого, равенство C3.10)
можно было бы использовать в качестве рекуррентного соотно-
соотношения для вычисления матричных элементов я„_ь „ вплоть до
п — — оо, что противоречило бы неравенству п + е>0. Прирав-
Приравняв нулю матричный элемент C3.14), находим искомую постоян-
постоянную е
е-]-,	C3.15)
а тем самым и собственные значения (83.6),
«+т).	C3.16)
так же, как и матричные элементы х, которые, согласно C3.9)
и C3.13), равны

92	//. Задачи без учета спина. А. Одномерные задачи
Задача 34. Волновые функции осциллятора в пространстве
импульсов
Определить волновые функции осциллятора в пространстве
импульсов.
Решение. Очевидно, что у потенциала
V(x)=??*	C4.1)
не существует фурье-образа, поэтому нельзя воспользоваться
интегральным уравнением A4.6). Вместо этого нам придется вер-
вернуться к исходным определениям:
00
ы(х) = Bл)-'/« \eikxf{k)dk,	C4.2)
—	00
00
f(k) = Bn)-'/' \e-ikxu(x)dx.	C4.3)
—	00
Подставив выражение C4.2) в уравнение Шредингера
d2u , 2т
после дифференцирования
— 00
и двукратного интегрирования по частям
00
х*и = — Bя) - v. J eikxf" (k) dk
— 00
получаем
со
Bл)-'/. je/**[_feV(ft) + ^/(*) + (^)V(*)]dft = O. C4.5)
— 00
Вводя обозначения
Х-=. „-^.	C4.6)
которые уже использовались нами при рассмотрении осциллятора
в задаче 30, убеждаемся, что уравнения C4.4) (координатное
пространство) и C4.5) (импульсное пространство) по существу
идентичны.

35. Ангармонический осциллятор
93
Координатное пространство
•?= У~Хх
d?u
±± + Bll-x^)u = 0
dx2
Импульсное пространство
г+(?-?),-.
_ ъ
и к
j?L-|-B^-*»)/ = 0
dk2
Следовательно, с точностью до нормировки функция / зависит
от k точно так же, как функция и зависит от х. Так как из
условия
00
\\u(x)\*dx=\,
— 00
как было показано в конце задачи 14, следует
то отсюда
где f так же зависит от Ъ, как и от х, а эта последняя функция
была найдена в задаче 30.
Задача 35. Ангармонический осциллятор
Оценить энергетические уровни ангармонического осциллятора
Т 7 / \	'	9
^, 1 =
ты '
C5.1)
в первом и втором порядке теории возмущений.
Решение. В первом порядке теории возмущений сдвиг уров-
уровней гармонического осциллятора с энергией
C5.2)
= -?¦	C5.3)
и нормированными собственными функциями

94	//. Задачи без учета спина. А. Одномерные задачи
определяется диагональными матричными элементами энергии
возмущения:
ЛA>?п=?„-?° = $(е1?« + еД«)[и° (*)]¦<**.	C5.4)
— 00
Так как [и?]2 — четная функция х, то член е^3 не дает вклада
в первую поправку ДA)?п. Таким образом, первая поправка равна
ДA>?„ = е2
„
— 00
и ее можно вычислить тем же приемом, что и нормировочный
интеграл: заменить один из полиномов Эрмита Нп (?) в подынтег-
подынтегральном выражении, согласно формуле
Hn(t) = (-l)»et'-^e-t\	C5.5)
и произвести n-кратное интегрирование по частям. В" результате
получим
2	Г р-Ъ? JP_ (t«H
Многочлен (п+4)-й степени, который требуется продифференци-
продифференцировать п раз, начинается с членов
C5.6)
поэтому
d" ,Е4 „ ._„„ I (п+4)! ?4 1 / п \ (я + 2) 1 „ , 3 /п\ .)
¦^-U л«;-^ \ 4! ё 2 V 2 У 2! e+TV4y Г
Учитывая значения хорошо известных интегралов
C5.7)
окончательно приходим к выражению
ДA>?„ = |-еаBп2 + 2/г + 1).	C5.8)
Результат первого порядка теории возмущений можно качест-
качественно пояснить следующим образом. Малая добавка к потенциалу
е^3 вызывает небольшую асимметрию параболы V(x), но еще не
меняет для низко лежащих уровней ее ширины. Следовательно,
движение осциллирующей массы происходит в области таких же
размеров, что и в случае гармонического осциллятора, поэтому
нет причин, которые вызывали бы изменение энергии. Добавоч-

35. Ангармонический осциллятор	95
ный же член e2g4 при е2 > 0 (е2 < 0) симметричным образом под-
поднимает (опускает) обе ветви параболы, тем самым уменьшая
(увеличивая) ширину параболы и размеры области движения
даже для самых малых энергий, поэтому все энергетические
уровни смещаются вверх (вниз) в согласии со знаком правой
части формулы C5.8).
Во втором порядке теории возмущений к энергиям C5.2) и
C5.8) мы должны добавить поправку
+f >\2 .	C5.9)
Для осциллятора отличны от нуля только следующие недиаго-
недиагональные матричные элементы [они вычисляются тем же методом,
который использовался при вычислении поправки C5.8)]:
C5.10)
C5.11)
(n-2) (n —3).
С учетом значений этих матричных элементов общая формула
C5.9) дает
C5.12)
Если теперь ввести обозначения
15/ 24_ . 11N
4 V	оО /
C5.13)

96
//. Задачи без учета спина. А. Одномерные задачи
то выражение для энергии с точностью до членов второго порядка
включительно принимает вид
()>} C5.14)
Значения коэффициентов для четырех низших уровней приведены
в таблице:
n
0
1
2
3
11
~8~
71
T
191
8
371
8
B«)
3
4
15
4
39
4
75
4
21
8
165
8
615
8
1575
8
Следовательно, положение последних теперь нетрудно рассчитать.
Для возмущения ех|3 оно показано на фиг. 20 в зависимости от
безразмерного параметра ejfm. Так как в данном случае эффект
первого порядка отсутствует, то кривые, характеризующие поло-
положение уровней, представляют собой параболы с вершинами на
прямой ех.= 0. Отрицательный знак возмущения обусловлен тем,
что описывающая потенциал парабола уширяется в области более
высоких значений е^ где пренебречь этим эффектом уже нельзя.
Роль эффекта уширения все более возрастает по мере продвиже-
продвижения в область высоких энергий, где даже второй порядок теории
возмущений становится все менее надежным. В точке ? = —Aco/^eJ
у потенциальной энергии имеется максимум VMaKC = флоK/E4ef),
поэтому для энергий Е > VwaKC дискретные уровни перестают су-
существовать: эффект, который нашим приближением не учиты-
учитывается1'.
Приведенные кривые в целом показывают, что чем выше
энергия уровня, тем меньше значения параметра tjlUa, характе-
характеризующего возмущение, для которых используемое приближение
дает надежные результаты. Это же подтверждает и фиг. 21, где
1) Строго говоря, при наличии возмущения s^3 энергетический спектр
является непрерывным, так что дискретных уровней в этом случае вообще не
существует. См., например, Давыдов А. С., Квантовая механика, Физматгиз,
М., 1963, стр. 195 и далее.— Прим. ред.

36. Приближенные волновые функции
97
пунктирные и сплошные линии относятся соответственно к по-
поправкам первого и второго порядков. Разумеется, на результаты
второго приближения совершенно нельзя полагаться там, где
Возмущение е, f*
/ Возмущение е?*
Фиг. 20. Энергетические уровни ангар-
ангармонического осциллятора с асимметричным
возмущением.
Вклады отвозмущения возникают только во вто-
втором приближении. Линия V /пи грубо ха-
рактеризуетобласть применимости использован-
использованного приближения.
Фиг. 21. Энергетические уровни
ангармонического осциллятора с
симметричным возмущением.
Пунктирные линии соответствуют од-
одному первому приближению, сплошные
линии построены с учетом второго
приближения.
соответствующие поправки, достигнув максимума, начинают
убывать.
Задача 36. Приближенные волновые функции
Частица свободно движется по оси х между двумя абсолютно
жесткими стенками, расположенными в точках л:=±а. Аппрок-
Аппроксимировать волновые функции основного и первого возбужденного
состояний простейшими нормированными полиномами, имеющими
те же нули, что и точные волновые функции, и сравнить точные
значения энергии с приближенными.
Решение. Пусть иа и и1—точные волновые функции, а Ео и
Е1—соответствующие им точные энергетические уровни двух
4 М> 1050

98	//. Задачи без учета спина. А. Одномерные задачи
рассматриваемых состояний. Тогда (см. задачу 18)
пх с %г п
Е
ип = —==- cos—, Еп =	—
К а 2а	2та2 4
И
пх с %г п2	/ос 1Ч
cos—, Еп =	—	C6.1)
2	22 4
C6.2)
„1= Sin 2?, ?1==JL.«.
К а	а	2та2
Простейшие полиномы с теми же нулями имеют вид
Все четыре волновые функции C6.1) — C6.4) нормированы со-
согласно условию
Максимум функции ы0 при х = 0 равен 1 (в единицах а"'7»),
у функции и0 максимум расположен в той же точке и равен
A5/16)'/« = 0,970, что лишь на 3% меньше. У функции щ экстре-
экстремумы находятся в точках х—±1/2а и равны ±1, в то время
как экстремумы функции их равны ± C5/36)v' = ±0,986 и рас-
располагаются в точках х= ± A/К 3) а = ±0,577а, так что согла-
согласие по величине здесь еще лучше, но имеется сдвиг в поло-
положении.
Энергия во всех рассматриваемых случаях определяется вы-
выражением
~ fa' С fdu\* ,
Е = -к— \ т- dx.
2от J \dx)
— а
Для приближенных значений энергий уровней элементарное ин-
интегрирование дает
Ъ fa 5	р ft* 21
Выбрав в качестве единицы величину Ь?1Bта*), можно сравнить
численные значения энергий C6.1), C6.2) и C6.5):
?0 = 2,4674, ?, = 2,5000,
Ех = 9,8696, ^=10,5000.
В обоих случаях приближенные значения энергий превышают
точные. Значения ?0 и Ёо весьма близки друг к другу, согла-

37. Потенциальная ступенька	99
сие между Ег и Ёг несколько хуже, но и здесь ошибка не пре-
превышает 6%.
Задача 37. Потенциальная ступенька
Определить коэффициент отражения в поле потенциальной
ступеньки:
Решение. Рассматриваемый потенциал монотонно возрастает
от значения V = 0 при х =—оо до значения V = V0 при х=-\-<х>,
при этом наиболее существенное возрастание потенциала проис-
происходит на отрезке —2а < х < 2а:
V(—2a) = 0,l\9Va и
Волновая функция, описывающая приходящую слева волну,
должна иметь асимптотический вид
u = e'fcx +Re~'kx	при х—>•—с»,
Се~Кх, если Е < Vo при х—» + <х>, C7.2)
Ceik'x, если Е > Vo при х —+ оо.
Величина |^|2 и есть искомый коэффициент отражения. Чтобы
решить уравнение Шредингера
-0	,37.3,
с потенциалом C7.1), введем вместо х новую переменную
Используя далее обозначения
х« = *«а.~^Я, ^ = ^V0	C7.5)
и учитывая, что
d	1 ,, > d
Тх=—а-У^-У)Ту'
l + thi = 2(l-y),
получаем
УA-У)^2 + A-2г/)^+[^г=7)-7]« = О. C7.6)
Это дифференциальное уравнение имеет три особые точки у = 0,
1, оо, и, следовательно, его решение выражается через гипер-
гипергеометрическую функцию. С помощью подстановки
C7.7)

100	//¦ Задачи без учета спина. А. Одномерные задачи
где
V2 = >.2 —к2, (Xs = — И2,	C7.8)
уравнение C7.6) после несложных преобразований приводится
к гипергеометрическому уравнению Гаусса в стандартной форме:
У A-У)Г + [Bv + l)-B|i + 2v + 2) у] f-
-(H+v)(|x + v + l)/ = 0.	C7.9)
Сейчас мы покажем, что частное решение этого уравнения
f(y) = CtFl(ii + v, ц + v + l, 2v + l; У)	C7.10)
при надлежащем выборе постоянной С как раз удовлетворяет
граничным условиям C7.2).
Начнем с предела х—> + оо, когда j«r''a—> (), и, следова-
следовательно, решение C7.10) стремится к f(O) = C, так что
u(y)—>-Cyv^Ce-vx.	C7.11)
Теперь необходимо различать две возможности.
а)	X > х, v—действительное число и больше Нуля. В этом
случае выражение C7.11) экспоненциально убывает, как и должно
быть при Е < Уо. Таким образом, получаем
и—*Се-к* и Л:* = ^ = 4^-(УО — Е).	C7.12а)
а2 п,2
б)	X < и, v = —ik'a—чисто мнимое число. Тогда
и-+Се!к'х и kri = -=P-(E — V0).	C7.126)
л2
С другой стороны, при х—>—оо, когда у—>• 1 и 1—г/да
« e*/a —> 0, можно применить хорошо известные правила преоб-
преобразования гипергеометрической функции от аргумента у в гипер-
гипергеометрическую функцию от аргумента 1—у:
.Mli + v, |i + v+l, 2v+l; y) =
С учетом равенства 1—y = ex/a это дает
U^cl ,ГBу+1)Г(-2ц)	,а + ГBу+1)ГBр)	/а)
После подстановки
[J, = ix, 7 = (й	C7.13)
видим, что наше решение по форме будет совпадать с C7.2),
если положить
Г(-2ц)

37. Потенциальная ступенька	101
Г(+2ц)Г(у-ц)Г(у-ц+1)
Теперь снова необходимо различать две возможности:
E>V0 и E<V0.
а) Е < Vo, ц. = tx — чисто мнимое число, v—действительное
число и больше нуля. Числитель и знаменатель дроби C7.15)
представляют собой комплексно сопряженные величины, поэтому
т. е. имеет место полное отражение.
б) Е > Vo, ц — ix и v = —ia—величины чисто мнимые. Теперь
только множители T(±2\i), являющиеся комплексно сопряжен-
сопряженными величинами, не дают вклада в коэффициент отражения
| R |2. Так как далее
то
|ГA-*(х + о))
Теперь можно воспользоваться элементарной формулой
Для коэффициента отражения окончательно получаем
I	~h—?—Т—^ '	'	'
ИЛИ
I di»_ [shn(k-k')a-\*	,o7 ,7Ч
где ft и ft' —волновые числа соответственно слева и справа от
потенциальной ступеньки.
Замечание 1. В предельном случае очень малых а, т. е. в случае кусочно
постоянного потенциала со скачком в точке д: = 0, последнее выражение при-
принимает вид
C7.18)
Конечно, в этом случае нет необходимости пользоваться гипергеометрическими
функциями, так как теперь граничные условия C7.2) выполняются не асимп-
асимптотически, а на протяжении всей полупрямой:
kx	при жо,
u = Ceik'x	при оО
(мы рассматриваем лишь физически интересный случай „б"). Требование непре-
непрерывности и и и' при х = 0 дает
ik(l—R) = ik'C,

102
//. Задачи без учета спина. А. Одномерные задачи
следовательно,
k—k'
~'k+k'
Заметим, что эти выражения удовлетворяют соотношению
fe A—Л2) = *'С2,
C7.20)
C7.21)
которое вытекает из непрерывности плотности тока вероятности в точке, где
потенциал имеет разрыв.
Замечание 2. Новая переменная у, равенство C7.4), вводится для того,
чтобы сделать коэффициенты дифференциального уравнения рациональными
функциями и тем самым вернуться к классу хорошо изученных дифферен-
дифференциальных уравнений. Этой же цели можно добиться путем другой замены
переменных:
у = {\-\-е-х'а)-1.	C7.4а)
Замена переменных C7.4) была выбрана с таким расчетом, чтобы частное реше-
решение C7.10) удовлетворяло граничным условиям нашей весьма специальной
задачи, что при замене переменных C7.4а) было бы невозможно. Тем не менее
весьма поучительно провести все расчеты, пользуясь заменой переменных
C7.4а).
Задача 38. Потенциальная яма Пешля — Теллера
Решить уравнение Шредингера с потенциалом
V(x)--
v W- 2
—]
40 г
sin2 ax cos2 ах
где к > 1
П v %*а*
читься
Фиг. 22. Три различные потен-
потенциальные ямы Пешля — Теллера,
соответствующие Х = 2 и %sX.
Потенциальная яма симметрична толь-
только при к—%..
и К > 1. Ограни-
Огранирассмотрением интервала
на границах кото-
которого потенциал V (х) обращается
в бесконечность.
Решение. Потенциал C8.1) по-
показан на фиг. 22 для случая А, = 2
и нескольких значений к > 1. Если
к = Я, то яма оказывается симмет-
симметричной по отношению к прямой
ах = я/4, если же и > к, то яма
перекашивается таким образом,
что ее минимум сдвигается в сто-
сторону больших значений х. При
1 < у. < А, минимум ямы сдвигается
в противоположную сторону, а
имеющаяся в точке х = 0 сингуляр-
сингулярность становится менее четко выра-
выра1В
р
женной и наконец совершенно исчезает, когда и = 1. В этом случае
потенциальные ямы, имеющиеся в интервалах — п/2а^.х^.О и
0^х^я/2а, объединяются в одну потенциальную яму большего
размера. Рассмотрение последней можно свести, однако, к случаю

38. Потенциальная яма Пешля — Теллера	103
¦ к, если воспользоваться тождеством
1 Г	1	,	1
cos2 ах 4 I . . / ах я \ ~ „( ах
и, кроме того, заменить а на 1/2а и Уо на 1/iV0.
Разумеется, потенциал C8.1) является периодическим, но
практически это несущественно для решений уравнения Шредин-
гера, так как между соседними ямами имеются непроницаемые
барьеры, обусловленные сингулярностями потенциала V(x).
Таким образом, можно ограничиться рассмотрением одной-един-
ственной потенциальной ямы, скажем в интервале 0^х^я/2а,
и решать в этом интервале уравнение Шредингера с граничными
условиями
ы = 0 при х = 0 и * = -^-.	C8.2)
Путем замены независимой переменной
у = sin2 ах	C8.3)
уравнение Шредингера приводится к виду
/1 \ » i / ! \ i i 1 Г*2 х(х—1) Я (Я—1) Л /оо .,
где
Это дифференциальное уравнение имеет три регулярные особые
точки, у = 0, 1, оо, поэтому подстановкой
u = 0*(l-y)v/@)	C8.5)
и надлежащим выбором значений (д. и v оно приводится к гипер-
гипергеометрическому уравнению. В самом деле, положив
получаем
|[^	] = 0.	C8.7)
Общее решение этого уравнения имеет вид
/ = Сх 2/?1 (а, Ь, с; г/) + C.^1-%F1 (а + 1 -с, Ь+ 1 -с, 2-е; у), C8.8)

104	//. Задачи без учета спина. А. Одномерные задачи
где
k
C8.9)
В выражении C8.8) мы еще должны определить постоянные
интегрирования Сх и Сг так, чтобы выполнялись граничные
условия C8.2), которые, если пользоваться переменной у, гласят
ц@) = 0, иA) = 0.	C8.2а)
В точке у = 0 оба гипер геометрических ряда обращаются в еди-
единицу, поэтому
Так как х> 1, то у второго слагаемого имеется сингулярность,
отсюда следует, что Са = 0. Чтобы рассмотреть случай у=\,
воспользуемся преобразованием
Так как с—а—b = 1/i—К, то второе слагаемое в этом выраже-
выражении дает вклад в решение и в окрестности точки у—\\
и ...
1 и)
у)	Г (а) Г F)
При показателе
этот вклад сингулярен, и граничному условию можно удовле-
удовлетворить только в том случае, когда во втором слагаемом обра-
обращается в нуль множитель, содержащий Г-функции, другими
словами, лишь тогда, когда либо а, либо b—целое отрицатель-
отрицательное число. Если
а = —п, тг = О, 1, 2, ... ,	C8.10)
то в силу равенства C8.9)
и, следовательно, b—положительное число. Если же Ь = — п, то
а=к-{-к-\-п. Так как при замене параметра а параметром b
волновая функция не меняется, то оба условия приводят к тому
же самому решению. Заменяя в равенстве C8.10) параметр а
его выражением C8.9), получаем следующую формулу для собст-

38. Потенциальная яма Пешля—Теллера
105
венных значений:
или ?„ =
(х + X, + 2/t)\ C8.11)
Соответствующие им собственные функции имеют вид
un (x) = Cj sin*
ах x
-g-; sin2
C8.12)
где постоянную Сх следует выбрать сообразно условию норми-
нормировки. На фиг. 23 показана зависимость энергетических уровней
от параметра асимметрии х при К = 2.
Сопоставляя приведенные результаты с
кривыми потенциальной энергии, изо-
изображенными на фиг. 22, мы видим, что,
чем уже потенциальная яма, тем выше,
как и следовало ожидать, располага-
располагаются энергетические уровни. Если
2/г^>х+^, то собственные значения
C8.11) приближенно описываются фор-
формулой ?2 = 4а2/г2 (/t=l, 2, ...), соот-
соответствующей случаю прямоугольной по-
потенциальной ямы. Этот результат также
вполне разумен, поскольку по мере роста
энергии искривление дна потенциаль-
потенциальной ямы должно играть все меньшую
и меньшую роль.
100
90
80
70
» 60
? 50
40
30
го
to
Замечание. Вблизи минимума кривую потен-
потенциальной энергии приближенно можно заменить
параболой, т. е. потенциалом осциллятора. Ог-
Ограничиваясь случаем х = Х, когда потенциал
имеет минимум в точке оис=я/4, и вводя переменную
Фиг. 23. Зависимость энер-
энергетических уровней от пара-
параметра асимметрии к для по-
потенциалов Пешля — Теллера
Х 2
имеем
= W0\ (Х- 1) Гу
Положим далее множитель при гг равным
тогда
Если теперь пренебречь отклонением нашего потенциала от потенциала гар-
гармонического осциллятора, то допустимые значения энергии будут равны
или
'- = 2

106
II. Задачи без учета спина. А. Одномерные задачи
Это приближение, разумеется, оправдано только в том случае, если в клас-
классических точках поворота г< величина 1/а гораздо больше | г |, другими сло-
словами, если
Этот результат является точным в пределе а—>-0, А,—>-оо при постоянном
Литература
P6schl G., Teller E., Zs. Phys., 83, 143 A933).
Rosen N., Morse P. M., Phys. Rev., 42, 210 A932).
Lotmar W., Zs. Phys., 93, 528 A935).
Задача 39. Модифицированная потенциальная яма Пешля —
Теллера
Решить одномерное уравнение Шредингера с потенциалом
(фиг. 24)
У(х\ =	 даМ^ — *)	/on i\
v '	2т ch2 ах '	\ ¦ г
где Я> 1. Для положительных энергий определить коэффициент
отражения и коэффициент прохождения,
2 для отрицательных — энергетические
уровни связанных состояний.
Решение. Перейдем в уравнении
Шредингера
= 0, C9.2)
где &2 = 2тЕ/%г, к новой переменной
у = ch2 ax.	C9.3)
Это даст
Ф и г. 24. Потенциальная яма	,.	„
в случае модифицированного У ' * У> и
потенциала Пешля — Телле-
Теллера.
д — у) if —
После подстановки
u = y№v(y)	C9.4)
последнее уравнение приводится к гипергеометрическому уравнению
Вводя обозначения

39. Модифицированная потенциальная яма Пешля — Теллвра	107
можно записать общее решение уравнения C9.5) в виде1'
1-у) +В {\-у)ЧгХ
1, |; 1-у),	C9.7)
так что при х — 0 или г/=1 волновая функция будет стремиться
к выражению
и@)=шА + ВA—уУ*.	C9.8)
В качестве фундаментальной системы решений выберем два дей-
действительных стандартных решения ие и и0 соответственно, четное
и нечетное по отношению к изменению знака переменной х:
и,(—х) = и.(х), ио(—х) = -ио(х).	C9.9)
При 5 = 0 и А = 1 получаем стандартное четное решение
C9.10а)
а при Л = 0 и B = i—стандартное нечетное решение
). C9.106)
Свойства этих решений мы подробно обсудим ниже.
Для ответа на вопросы задачи нам прежде всего необходимо
выяснить асимптотическое поведение решений C9.10а) и C9.106)
при больших отрицательных значениях аргумента:
Хорошо известные формулы дают
Г (ft-а)
Г (а) Г [1—Ь
ll C9.
J
11а)
х) Нас интересует решение в области 0<;|лг| < оо или 1 ^ у < со. Гипер-
Гипергеометрическое уравнение
i/(l— y)v" + [c — (a + b + \)y]v'— abv = 0
после перехода к новой независимой переменной г=1—у принимает вид
с'— (а + Ь+\)г) v'—abv = 0,
где с' = а + 6 + 1—с. Для новой независимой переменной г решение C9.7)
принимает стандартную форму. Нужной нам областью изменения г является
полупрямая — оо < й(>

108
//. Задачи без учета спина. А. Одномерные задачи
и
«0 (х) ¦
± 2~<л
х|
Г (ft —а)	О2Д4-1 с-г2д-и> а|
Г{а~&)	г26*^-"*-1-1)»!*!!, C9.116)
где
х <
а и
знаки + и — относятся соответственно к случаям х > 0 и
0. Если энергия положительна, то в силу равенства C9.6)
Ь—комплексно сопряженные величины, поэтому
ие(х)-*Т
I — In 2
Г (— (ft/a) e a
-i—- In 2
Г ((ft/a) e a
Г<Т + '-2а)Г
__
2a
elk\x\
±Г 4
( — In 2
-Г— In 2
Г ((ft/a) e a
gift I * l
Вводя обозначения
-I— In 2
Г (ift/a) e a
+'
Г ((ft/a) e a
~2 !"' 25
-< — In 2
C9.12a)
. C9.126)
C9.13a)
C9.136)
можно записать последние выражения в более компактном виде
ue-*Cecos(k\x\+(pey,
(p0) при х>0 и х<0. ( ' ;

39. Модифицированная потенциальная яма Пешля — Теллера	109
Фигурирующие здесь амплитуды можно было бы вычислить с по-
помощью соотношений C9.12а) и C9.126), однако их конкретные
значения для дальнейшего несущественны.
Образуем теперь линейную комбинацию рассмотренных выше
фундаментальных решений:
так что для случаев х > 0 и х < 0 соответственно будем иметь
и = у Се (е'фее'** +е """«е-'**) + \ Со (e'V** + <г№-'**)
и
и - 4 Се (в'ф«в- '** + «""••в'**) — у Со (е!<°°е-1кх
Нас интересует решение с асимптотикой
telkx + Re-tkx при х<0,
и = \Т#»	пРи,>0.
Следовательно, в нашем случае должно быть
Из второго и четвертого уравнений можно определить произве-
произведения АСе и ВС0, а затем из первого и третьего —амплитуды
Т и Я;
7=1 («"">« -в8".), /? = j (в2*. +•"*•). C9.16)
Зная амплитуды для коэффициентов прохождения и отражения,
получаем соответственно выражения
|T|» = sina(q>,-cp0)	C9.17)
и
|#|* = cos2(<p, — Фо).	C9.18)
Эти выражения удовлетворяют соотношению
и зависят только от разности фазовых углов собственных функ-
функций, но не зависят от их нормировки.

110	//. Задачи без учета спина. А. Одномерные задачи
Чтобы вычислить коэффициенты C9.17) и C9.18), вернемся к
соотношениям C9.13), из которых следует
C9.19)
где
Из общей формулы
Г(г)ГA — г)=^—
4 ' v ' sin яг
вытекает
argT(z) — argTd— z*)= —argsinnz.,	C9.20)
Полагая далее
l
. о — Z.2)
имеем
to+ 4—4=1— zT и
Теперь с помощью формулы C9.20) можно объединить соответ-
соответствующие пары аргументов, фигурирующие в выражении C9.19),
что в итоге даст
Фе—фо= — argsinn f-^ + t^Wargsinnfy
= arctg (ig -тр th я^J + arctg (ctg -^- th j
Последнее выражение после элементарных преобразований при-
принимает вид
Если параметр К, характеризующий глубину ямы, является целым
числом, то знаменатель дроби обращается в нуль, так что
ц»е—фо = я/2, и в силу соотношений {39.17) и C9.18) имеем
|7|а=1, |/?|2 = 0. В этом случае волна, соответствующая пада-
падающей частице, независимо от ее энергии проходит через область,
занятую ямой, совершенно не отражаясь (заметим, что при Х= 1
этот результат самоочевиден). В предельном случае ? = 0« (т.е.
л&/а = 0) в выражении C9.21) обращается в нуль числитель,
поэтому для нецелых значений Я разность сре — фо = 0, и мы имеем
дело с полным отражением: | Г |2 = 0, J R |2 = 1.

39. Модифицированная потенциальная яма Пешля — Теллера
111
Коэффициенты | Т |2
можно записать в виде
при произвольных значениях
\R
1+P2
C9.22)
где

sh яА/ое
На фиг. 25 показана зависимость коэффициента отражения от
глубины потенциальной ямы для двух энергий, соответствующих
значениям &/2а = 0,1 и &/2а = 0,2.
Эта же картина повторяется и в лю- ""
бом другом интервале п < А. < п 4-1,
где п — целое число.	»
Связанные состояния. При от- J_
рицательных энергиях существуют 2* 4
дискретные собственные значения.
В этом случае можно положить k = ix,
так что энергия будет равна
C9.23)
/
1.5
X-
а параметры C9.6)
,oq 24\
Фиг. 25. Зависимость коэф-
фициента отражения от глубины
потенциальной ямы для двух
значений энергии.
будут действительными величинами. Снова можно воспользо-
воспользоваться асимптотическими формулами C9.11а) и C9.116), однако
теперь в этих формулах первое и второе слагаемые ведут себя
соответственно как е*1 и е~*1*1. При х > 0 существование
нормируемых решений возможно лишь в том случае, когда фигу-
фигурирующий в первом слагаемом множитель обращается в нуль.
Теперь все аргументы Г-функций действительны, а их полюсы
расположены в точках, соответствующих целым отрицательным
числам —я(п = 0, 1, 2, ...), поэтому собственные значения
находятся из соотношений: в случае четных состояний
1-Я,
или
а в случае нечетных состоянии
1	к , К

112
//. Задачи без учета спина. А. Одномерные задачи
ИЛИ
— =Л,—2 — 2/t.
а
Отсюда после очевидных изменений в обозначениях для уравне-
уравнений энергии получаем
_/ г з 4 5	_	й.2„2
4 ""¦'	/t<A,— 1. C9.25)
.	\ \ \ *я=г ^РИ четных п эта формула
\ т~	\\ \	дает уровни четных состоя-
состояний, а при нечетных п — уров-
уровни нечетных состояний. На
фиг. 26 показана зависимость
энергии связанных состояний
от размера потенциальной
ямы. Следует отметить, что
при целом А, всеРда имеется
один связанный уровень(п =
=Я—1) с нулевой энергией.
Задача 40. Свободное падение
вблизи земной поверхности
Частица движется водно-
родном гравитационном поле
над поверхностью земли, которая предполагается абсолютно упругой
(например, стальной шарик, танцующий на стеклянной горизон-
горизонтальной пластине). Проанализировать эту классическую задачу
с точки зрения квантовой теории.
Решение. В квантовой теории скачкам стального шарика соот-
соответствует стационарное состояние. Для отыскания этого состо-
состояния необходимо решить уравнение Шредингера
Фиг. 26. Зависимость энергии связан-
связанных состояний от размера модифициро-
модифицированных потенциальных ям Пешля — Тел-
лера.
Пунктирная линия характеризует глубину
потенциальной ямы.
-Е)и =
D0.1)
в области x>Q. Выше через х обозначена высота над поверх-
поверхностью земли, а гравитационный потенциал взят, как обычно,
в виде V (х)^ mgx. Предположение об абсолютно упругом харак-
характере отражения при х — 0 приводит к граничному условию
и@) = 0.	D0.2а)
Кроме того, сюда следует добавить естественное условие
ы(оо) —0.	D0.26)

40. Свободное падение вблизи земной поверхности
113
Если ввести обозначения
2тЕ
I*
и безразмерную переменную
D0.3)
D0.4)
где / — характерная длина, то уравнение D0.1) и граничные
условия D0.2а) и D0.26) примут соответственно вид
D0.5)
D0.6)
/Л,
/
Фиг. 27. Первые десять энергети-
энергетических уровней в гравитационном
поле над поверхностью земли.
Фиг. 28. Функция Эйри.
Классически разрешенная область движения заключена между
классическими точками поворота ?=—Я и | = 0 (фиг. 27), т.е.
ей соответствуют исключительно отрицательные значения пере-
переменной |.
Решения дифференциального уравнения D0.5) выражаются
через функции Бесселя порядка 1/3. Решение же, удовлетворя-
удовлетворяющее граничному условию ы(оо) = 0, представляет собой функцию
Эйри (см. фиг. 28)х>
u(g) = C-Aig.	D0.7)
Для положительных значений \, т. е. правее точки поворота
? = 0(л: = Л/) на фиг. 27, эту функцию можно выразить через
модифицированную функцию Ханкеля:
Т„ ( 2
3
Aii=4
&>о.
D0.8)
1( В настоящее время имеются хорошие таблицы функции Эйри и ее нулей.
См., например, Abramowitz M., Stegun I. E., Handbook of Mathematical
Functions, New York, Dover Publ., 1965 Приводимая ниже таблица нулей
взята из указанного источника. (См. также Яковлев Г. Д., Таблицы функций
Эйри, изд-во „Наука", М., 1969.— Прим. ред.)

114
//. Задачи без учета спина. А. Одномерные задачи
Ее асимптотика получается из общей формулы
*vB)—¦ ]/?е-г, г — оо,
в силу которой
«(&)¦
ПРИ
D0.9)
В классической области, т. е. для отрицательных значений ?,
функция Эйри выражается линейной комбинацией функций
Бесселя:
или
D0.10)
В силу второго граничного условия D0.6) решение-должно обра-
обращаться в нуль при |= —К. Так как величина X при подходящем
выборе единиц представляет собой энергию, то отсюда для опре-
определения допустимых значений энергии получаем
Ai(—Я) = 0	D0.11а)
или
(	)	{	) 0-	D0.116)
Первые десять нулей функции Эйри приведены в нижеследующей
таблице.
А1(-Я.в) = 0
n
1
2
3
4
5
6
7
8
9
10
п
2,338
4,088
5,521
6,787
7,944
9,023
10,040
11,009
11,936
12,829
Соответствующие этим нулям уровни энергии показаны на фиг. 27.
Для определения более высоких уровней, когда А,^>1, можно

40. Свободное падение вблизи земной поверхности	115
воспользоваться асимптотическими формулами
2	( л
из которых следует, что при больших отрицательных значениях |
^v. cos (|-| 61'/.—J-).	D0.12)
Отсюда в дополнение к приведенной таблице при тг^>1 полу-
получается соотношение
Последнее после очевидных преобразований принимает вид
\^-Ы—^Г'при п>1.	D0.14)
Замечание 1. Асимптотические формулы D0.9) и D0.12) полностью согла-
согласуются с формулами, которые получаются с помощью метода ВКБ (см. за-
задачу 115, где рассмотрен вопрос об аналитическом продолжении волновой
функции за классическую точку поворота без использования функции Эйри).
Замечание 2. Характерную длину /, фигурирующую в данной задаче,
можно вычислить для любого значения массы т. Для электрона мы находим
/ = 0,088 см, для частиц с большей массой получаются меньшие значения
(/ ~ т~ /•). Фундаментальная энергетическая постоянная данной задачи,
согласно равенству D0.14), имеет вид
В~ 2ml* '
что в случае электрона составляет 1,03хЮ~26 эрг1'. Порядки приведенных
величин дают наглядное представление о крайней малости квантовых эффектов
в случае макроскопических тел. Для таких тел длина волны, отвечающая
функции D0.12), будет чрезвычайно мала и, следовательно, лишь усредненное
по многим периодам выражение и2 будет иметь непосредственный физический
смысл:
2л
Обозначая через h = Xl высоту в классической области, мы, таким образом,
имеем
Vh—x '
что в точности соответствует предсказаниям классической теории. В самом
деле, и2 dx есть вероятность обнаружить частицу (танцующую в стационарном
состоянии!) в интервале dx. Так как эта же вероятность пропорциональна
" Приведенные значения прежде всего следует сравнить со значениями
соответствующих величин в задачах атомной физики. Так, радиус первой
боровской орбиты равен 5,29хЮ~в см, а энергия ионизации атома водорода
составляет 2,18xlO-u эрг. Это сравнение показывает, что в задачах атомной
физики влияние силы тяжести можно не учитывать.— Прим. ред.

[16
//. Задачи без учета спина. А. Одномерные задачи
времени dt, в течение которого частица находится в указанном интервале, то
~u?dx~dt,
и для скорости частицы получаем v = dxjdt ~ yOi—х, что, очевидно, согла-
согласуется с классическим выражением
и= V2g(h—х).
Любопытно отметить значительные математические трудности, возникающие
при решении рассматриваемой задачи, которая в классической механике
является одной из самых простейших.
Замечание 3. В данной задаче нулевая энергия, Е1 = еХ1, по порядку ве-
величины равна е. Этот результат легко получается с помощью соотношения
неопределенности, Др-Дх = й.. Действительно, Др « \ 2тЕ, а размеры клас-
классической области равны &x = E/mg. Таким образом, имеем
mg
что для энергии дает величину ожидаемого порядка:
з
у
-1 fc mg* = e.
Задача 41. Ускоряющее электрическое поле
Пусть металлическая пластина испускает в положительном
направлении оси х поток электронов с начальной энергией Е,
которые потом ускоряются электрическим
полем g, приложенным в том же направ-
направлении. Сопоставить классическую форму-
формулу для скорости электронов на расстоянии
х от поверхности излучающей пластины,
~2mv"
+ egx,
D1.1)
с результатами квантовомеханического ана-
анализа данной аадачи.
Фиг. 29. Ускорение элек-
электронов однородным элек-
электрическим полем.
Решение. Так как V (х) ~ — е?х, то
необходимо решить уравнение Шредингера
— ¦^-^г—еёхи^Еи	D1.2)
2т dx*	v * • /
в области х > 0 (фиг. 29), причем нужные нам решения этого
уравнения должны представлять собой волны, распространя-
распространяющиеся в положительном направлении оси х. Как и в преды-
предыдущей задаче, введем характерную длину / и безразмерный энер-
энергетический параметр Я, определенные соотношениями
= ~,	D1.3)

41. Ускоряющее электрическое пом	117
а также безразмерную переменную
6 = у + Ь.	D1-4)
В результате получаем дифференциальное уравнение
¦|г + 6и = 0.	D1.5)
которое требуется решить в области \ > К.
Решение, соответствующее расходящимся волнам, имеет вид
D1.6)
Как следует из формулы
„A) -,/~Т~ \.( Ъп\Л
III/	I/	„ tAU I (• I С	| q J I 9
'3	г jIZ	I \	1Z j J
оно имеет асимптотику ^
ы(Е) —Ce~"IFg-1/4e"8 .	D1.7)
Чтобы сопоставить выражение D1.1) с нашими результатами,
сравним теперь плотность потока частиц
«•?-«^	D1-8)
\ dx	dx J
с плотностью частиц
p = u*u;	D1.9)
отношение этих плотностей даст нам скорость частицы v. Из фор-
формулы D1.7) иолучаем
так что соотношение D1.8) теперь дает
А
или
р ml m
11 Заметьте, что асимптотика D1.7) совпадает с асимптотикой, получаемой
методом ВКБ. Здесь, как и в предыдущей задаче, мы не пользуемся функцией
Эйри, поскольку в данном случае никаких трудностей с аналитическим про-
продолжением не возникает. Более того, нужное нам решение представляет собой
линейную комбинацию функций Эйри первого и второго рода:
Сл
и = С \Гш 6 [Ai (-!)-/Bi(-|)].

118 //. Задачи без учета спина. Б. Задачи с двумя или тремя степ, свободы
что с помощью равенств D1.3) можно записать в виде
в полном согласии с формулой D1.1).
В наших рассуждениях мы пользовались асимптотикой вол-
волновой функции, т. е. считали, что Е^>1 или х^>1. Характерную
длину / можно вычислить по формуле D1.3). В случае электрона
и для вполне разумного значения напряженности поля <?=300 В/см
(или 1 эл. стат. ед.) получаем / = 3,69 X 10~6 см. Таким образом,
условие х^>1, как правило, выполняется очень хорошо.
Б. Задачи с двумя или тремя степенями свободы
без сферической симметрии
Задача 42. Круговой осциллятор
Исследовать движение точечной частицы в двумерном потен-
потенциальном поле
o>*(x*+y*)	D2.1)
Решить задачу в прямоугольных декартовых и полярных коор-
координатах с
г* = х2 + у2.	D2.2)
Полученные результаты сравнить.
Решение
а. В прямоугольных декартовых координатах уравнение Шре-
дингера допускает разделение переменных:
причем каждый из сомножителей удовлетворяет уравнению для
одномерного осциллятора (см. задачу 30):
/" + {Щ - №) f = о, g"+№- »?) g=o,
где
Таким образом, для собственных значений имеем
или
f	+ l), п1г nt = 0,l, 2, ....	D2.3)

42. Круговой осциллятор	119
а соответствующие волновые функции имеют вид
«л,/!, (х, y) = fni{x)fnt{tj),
где посредством fn обозначены одномерные осцилляторные функ-
функции, определяемые выражением C0.10) с нормировочными посто-
постоянными C0.11). Энергетические уровни в данном случае вырож-
вырождены, потому что сумму
лх+ «, = «,	D2.4)
входящую в выражение для энергии, можно составить из двух
целых чисел п -f-1 различными способами, и, следовательно,
общее решение имеет вид линейной комбинации
п
ип{х, у)= 23 4.Л, (*)/»-„, (у),	<42-5)
где
2 14., 1В=1-	D2.6)
б. В полярных координатах потенциал зависит только от г
и здесь также допустимо разде^ние переменных:
и (г, ф) = v (г)ешч>, /И = 0, ±1, ±2, 		D2.7)
Это приводит к дифференциальному уравнению
первая скобка в левой части которого получилась из лапласиана.
После подстановки
для функции F (г) получается дифференциальное уравнение
F" + B] Mrl + l-2lA F — [2А,(| Ж | + \) — k*\ F = 0,
которое с помощью замены независимой переменной г на
t =--- А,га
преобразуется в уравнение Куммера
Решением этого уравнения, регулярным при t = 0, является вы-
вырожденный гипергеометрический ряд
F(t) = lFl(a, \M\+l; (),

120 //. Задачи без учета спина. Б. Задачи с двумя или тремя степ, свободы
где
a = l(|Af|+l)-?.	D2.8)
При больших значениях t этот ряд расходится как е1, что де-
делает нормировку решения невозможной. Только в том случае,
если
а = — пг, где пг = 0, 1, 2, ...,	D2.9)
вырожденный гипергеометрический ряд обрывается, превращаясь
в полином, и волновую функцию можно нормировать. В таком
случае имеем
- — г»
и„г м(г, <р) = С„г,мг\м1е * Л (—«г. |Af| + l; W*»
D2.10)
.	D2.11)
Так же, как и в случае равенства D2.4), можно положить
и снова подсчитать кратность вырождения, для которой полу-
получается то же самое значение, что и выше.
в. Сравнение результатов. Каждое решение D2.10), с одной
стороны, есть собственная функция оператора проекции момента
на ось, перпендикулярную плоскости движения,
г~ i 5ф '
принадлежащая собственному значению %М:
Lzunr, М=-Ыи„г, „.	D2.12)
С другой стороны, за исключением основного состояния, отдель-
отдельные сомножители в волновой функции, полученные разделением
переменных в прямоугольных декартовых координатах, не явля-
являются собственными функциями оператора момента. Однако можно
найти такие значения постоянных Ani в формуле D2.5), чтобы
получающаяся линейная комбинация вырожденных функций сво-
сводилась к выражению вида D2.10). Ниже приведено несколько
примеров, относящихся к первым трем низшим состояниям;
в правильности соответствующих формул можно убедиться не-
непосредственной проверкой.
я = 0 (основное состояние, невырожденное); «г = 0, /И = 0,
л = 0, E = fuo,
«o.o (г. Ф)= ]/ \е~^Г' = ии{х)и0(у).

	43. Эффект Штарка для двумерного ротатора	ПМ
п = 1 (дважды вырожденные состояния); пг = 0, УИ = ±1,
/г=1, E = 2fuo,
к -->•	1
«o.±i(r, ф) = е а e±lv
п = 2 (трижды вырожденные состояния); пг=1, М = 0 и
и, = 0, /И = ±2, ? = 3&со,
"ьо(л Ф)=
и..±.(г, ф)= )/^ ^'е±"ф =
= i-[ы0 (х) и, (у) — и, (л) ы0 (г/) ± i |/Т и, (х) и, (у)].
Замечание. Полученные здесь результаты следует сравнить с результатами
задач 65 и 66, где рассмотрен трехмерный изотропный осциллятор.
Задача 43. Эффект Штарка для двумерного ротатора
В плоскости вращается жесткий ротатор с моментом инерции
9 и электрическим дипольным моментом р. Исследовать влияние
однородного электрического поля ?, направленного по оси х,
на уровни энергии ротатора.
Решение. Невозмущенный ротатор описывается уравнением
Шредингера
26 Лр2	С*а-Ч
Собственные функции и собственные значения соответственно
имеют вид
\-em<f, m = 0, ±1, ±2, ...	D3.2)
*. = ^Г.	D3.3)
Возмущающий потенциал
D3.4)
достигает минимума (—р?) при ф = 0 и максимума (-\-рё) при
<р = л. В первом порядке сдвиг невозмущенных уровней D3.3)
определяется формулой
2л

122 //. Задачи без учета спина. Б. Задачи с двумя или тремя степ, свободы
Так как интеграл в последнем выражении обращается в нуль, то
А1?и = 0.	D3.5)
Эффект Штарка второго порядка, пропорциональный ?2, вычис-
вычисляется по формуле
Л.*.= Е '^'У1'.	D3.6)
Фигурирующие в этой сумме недиагональные матричные элементы
V равны
2л
= — ^ Се
о
.m-l).	D3.7)
Таким образом, сумма D3.6) состоит всего-навсего из двух сла-
слагаемых с т' = т ± 1:
или
Собственные функции в этом приближении определяются по
общей формуле
?	<?Щр>	D3.9)
где сумма опять-таки содержит только два слагаемых:
-1)ф]} • D3-Ю)
В том же приближении для относительной вероятности различ-
различных ориентации диполя получаем
i|T	D3.11)
В случае, когда т — 0, имеем
т. е. вероятность обнаружить диполь, ориентированный по полю
(ф = 0), максимальна, а против поля (ф = л) минимальна. Этот
результат, как очевидно, соответствует статической ориентации
диполя в классической теории. Если же т^=0, то у дополни-
дополнительного слагаемого в формуле D3.11) изменится знак и пове-
поведение диполя будет иметь противоположный характер. Этот ре-
результат также можно уяснить с помощью классических модель-
модельных представлений: при своем вращении диполь проходит поло-

	44. Ион молекулы водорода	123
жение ф = 0, где потенциал минимален, с большей скоростью,
чем противоположное положение. Следовательно, если сделать
большую серию статистически независимых моментальных сним-
снимков, то на них диполь чаще будет обнаружен вблизи положения
Ф = я, чем вблизи положения ф = 0.
Замечание 1. Состояния | т > и |—ту вырождены, однако нет никакой
необходимости использовать вместо самих волновых функций | ту и |—т> их
линейную комбинацию
|m||-m>. ?=!- 2-
Это объясняется тем, что матричный элемент энергии возмущения <—т \ V \ ту
равен нулю, и, следовательно, возмущение не смешивает указанные пары вы-
вырожденных состояний.
Замечание 2. Если задать магнитное поле Э?, направленное перпендику-
перпендикулярно плоскости движения ротатора, то в гамильтониане появится дополни-
дополнительный член, обусловленный энергией взаимодействия
1/маг = — еМ-И,
где JH — магнитный момент ротатора, связанный с его моментом количества
движения соотношением
а М и е — масса и заряд ротатора соответственно. Таким образом,
и уравнение Шредингера D3.1) теперь заменится уравнением
Решениями последнего по-прежнему являются функции D3.2), однако принад-
принадлежат они другим собственным значениям:
Эти собственные значения уже более ие вырождены по отношению к знаку т
(эффект Зеемана на плоскости).
Задача 44. Ион молекулы водорода
Получить приближенное значение энергии диссоциации для
реакции Н%—>Н-\-Н+, взяв электронные волновые функции
в виде линейной комбинации функций
\ay = ^Le~yra и \b> = ^Le~yrb,	D4.1)
У п	у п
где га и гь (фиг. 30) — расстояния между электроном и протонами,
расположенными на фиксированном расстоянии R друг от друга.
Параметр у считать вариационным параметром Ритца. Определить

124 //. Задачи без учета спина. Б. Задачи с двумя или тремя степ, свободы
равновесное расстояние Ro между протонами и в дальнейшем
учесть нулевую энергию их колебаний.
Решение. Сначала будем считать, что положения двух про-
протонов фиксированы и расстояние между ними равно R (прибли-
(приближение Борна — Оппенгеймера). В этом слу-
случае уравнение Шредингера для электрона в
атомных единицах принимает вид
= Е.и. D4.2)
где Ее—энергия электрона. При этом энер-
энергия молекулы для фиксипованного положе-
положения ядер будет равна
± + Ее.	D4.3)
Мы будем пользоваться вариационным методом, согласно кото-
которому последнее выражение должно иметь минимально возможное
значение:
ЕМ0Л=<и\Н\и> + -^- = Минимум	D4.4)
при условии
<и|и>=1.	D4.5)
Рассмотрим линейную комбинацию
и = а\ау + р\Ь>,	D4.6)
где функция |а> так же зависит от переменной га, как функция
|Ь> от переменной гь. С учетом нормировки наших функций
имеем
<а|а>=1, <&|&>= 1, <a\b> = <b\ay = S, D4.7)
где через 5 обозначили так называемый интеграл перекрытия.
Теперь выражения D4.4) и D4.5) можно записать в более раз-
развернутом виде
?мол = (а2 + р2) <а\Н |а> + 2офф \ Н | а> + -^- = Минимум D4.8)
а8 + р2 + 2ар5=1.	D4.9)
Из соображений симметрии непосредственно очевидно, что
имеется два решения — симметричное
D410)
и антисимметричное
„_ а	'	F <а\Н\а>-<Ь\Н\а>

44. Ион молекулы водорода	125
Симметричное решение принадлежит более низкому энергетиче-
энергетическому уровню и, таким образом, соответствует основному со-
состоянию молекулы, поэтому в дальнейшем мы ограничимся рас-
рассмотрением соотношений D4.10).
Для нормированных функций | а> и | by, определенных соот-
соотношениями D4.1), непосредственное вычисление дает
поэтому
D4.12)
<fc| Я|a> = -^(Vv <'<•+'*>( — -iY2 + ml	L)dx. D4.13)
Я J	\ *	ra	rb 1
Вводя обозначения
и учитывая, что в силу определения D4.7)
S = -?- f е-? "<¦+'¦<•> dx,	D4.15)
после несложных преобразований получаем
Y2 + A)_ <g	D4.16)
и
<b\H\ay^-\fS + (y-2)S,	D4.17)
поэтому
Нам осталось вычислить интегралы %, $ и S. Так называемый
кулоновский интеграл # характеризует кулоновское притяжение
между протоном Ь и „облаком" отрицательного заряда, которое
окружает протон а и описывается волновой функцией \ау. Этот
интеграл можно вычислить, воспользовавшись разложением
(см. фиг. 30):
J_
л=0
л-0
Из этого разложения только член с п = 0 дает вклад в интег-
интеграл '€, вычисление которого теперь тривиально:
S[l 0+?/?)r2v«]	D4.19)

126 //. Задачи без учета спина. Б. Задачи с двумя или тремя степ, свободы
Интеграл ? называется обменным интегралом. Он характеризует
обменную энергию, являющуюся следствием симметризации соб-
собственных функций (замена электрона, находящегося вблизи а,
электроном, находящимся вблизи Ь). Обменная энергия не имеет
классического аналога. Обменный интеграл ? можно вычислить,
перейдя к вытянутым эллипсоидальным координатам с фокусами
в точках, где находятся протоны. Для этого надо положить
а в качестве третьей координаты наряду с \ и ц использовать
угол поворота ф вокруг оси молекулы. В этих координатах
элемент объема равен
а область интегрирования определяется неравенствами 1 ^С| < оо,
— 1^т]^+1. 0^ф^2л. Такой же способ можно применить
и для вычисления интеграла перекрытия 5. Соответствующие
результаты имеют вид
<§ = уA -\-yR) e~vR	D4.20)
и
S= ( 1 4-vR 4-—v2R2 1 e~yR	/44 21)
\	J
Если теперь в соответствии с формулой D4.18) записать энер-
энергию молекулы ?мол, то она будет зависеть от двух параметров у
и R. Для дальнейшего вместо у и /? в качестве параметров
Ритца, минимизирующих энергию, удобнее использовать вели-
величины у и
p=yR.	D4.22)
Подставив в формулу D4.18) вместо 5 выражение D4.21),
а вместо % и <§ соответственно выражения
!р]	D4.23)
D4.24)
(все три выражения зависят только от параметра р), получим
Последнее выражение можно представить в виде
и из соотношения

44. Ион молекулы водорода
127
определить оптимальное значение параметра у. В результате
имеем
.. _ 8 (Р)
2/(р)
и, следовательно,
f __
Теперь мы должны определить минимум этого выражения, рас-
рассматривая его как функцию переменной р.
Численные расчеты не представляют труда, хотя и требуют
известного времени. Основные результаты таких расчетов приво-
приводятся в нижеследующей таблице.
V« = P
1,0
1,5
2,0
2,3
2,5
2,8
3,0
3,5
V
0,832
1,113
1,216
1,235
1,240
1,228
1,216
1,180
~ мол
0,300
0,500
0,573
0,5848
0,5865
0,5827
0,578
0,560
R
1,200
1,345
1,645
1,86
2,02
2,28
2,47
2,96
Минимум можно определить с еще большей степенью точ-
точности, чем это следует непосредственно из таблицы, если аппро-
аппроксимировать энергию параболой, проходящей через три точки
р = 2,3, 2,5 и 2,8. Путем интерполяции находим
?иол = 0,0380 (# —2.08J—0,5866.
D4.26)
Таким образом, равновесное расстояние, соответствующее мини-
минимуму энергии, равно
«„ = 2,08 ат. ед. = 1,10 А,
а глубина потенциальной ямы составляет
Vo = — 0,5866 ат. ед.
Чтобы найти энергию диссоциации D, мы должны учесть нуле-
нулевую энергию колебаний молекулы, 1/г%и>, соответствующую ос-
цилляторному ядерному потенциалу D4.26), и вычесть из энер-
энергии связи молекулы энергию связи атома водорода, которая
равна V» ат. ед. Таким образом
D = - ~— (Vo
у?со) = 0,0866—1 fm = 2,36эВ—i-

128 //. Задачи без учета спина. Б. Задачи с двумя или тремя степ, свободы
Грубую оценку нулевой энергии колебаний можно получить,
ограничившись гармоническим приближением D4.26). Для этого,
очевидно, следует положить 1/2Mco2 = 0,0380 (см. задачу 30), где
М — приведенная масса колеблющихся протонов. Отсюда полу-
получаем i^to = 0,00913 ат. ед., так что нулевая энергия колебаний
равна
у ?<о = 0,00457 ат. ед. =0,124 эВ.
Отсюда для энергии диссоциации окончательно находим D — 2,24 эВ.
Это приближенное значение следует сравнить с эксперименталь-
экспериментальным значением D3KCn = 2,65 эВ. Такое согласие можно считать
хорошим, особенно если учесть, что в нашей теории приближае-
приближаемой величиной является не энергия диссоциации D, а глубина
потенциальной ямы Vo; экспериментальное же "значение Vo равно
—0,6017, и, следовательно, теоретическое значение—0,5866 со-
содержит ошибку, составляющую всего-навсего 2,6%.
Задача 45. Наклонное падение плоской волны
На прямоугольную потенциальную ступеньку
0, х < 0,
V~'x Vo, x>0
наклонно падает плоская волна. Найти законы отражения и
преломления, а также вычислить интенсивности пучков отра-
отраженных и прошедших частиц. Особо рассмотреть случай полного
отражения.
Решение. Всюду в дальнейшем будем пользоваться сокра-
сокращенными обозначениями
ft2	ft2
Предположим сначала, что Vo < Е, т. е. что величина К дейст-
действительная (сюда автоматически включается случай отрицатель-
отрицательных Vo). В полупространстве х < 0 решение уравнения Шредин-
гера при стандартной нормировке имеет вид
u=eikr+Reik'r, x<0,	D5.2а)
где k (kx, ky, kz) — волновой вектор падающей волны, a R и
k' (k'x, k'y, k'2) — соответственно амплитуда и волновой вектор отра-
отраженной волны. В полупространстве х > 0 имеется только про-
прошедшая волна:
х>0,	D5.26)

45. Наклонное падение плоской волны
129
с амплитудой Т и волновым вектором К(КХ, Ку, Кг)- Упомянутые
волновые векторы удовлетворяют соотношениям
b* = k'* = V, /Г = /С2.	D5.3)
На поверхности х = 0 функции и, определяемые формулами
D5.2а) и D5.26) и зависящие от переменных у и г, должны
совпадать; то же самое относится и к их производным ди/дх.
Отсюда следует, что должны быть рав-	<Q .Q
ны как их фазы	>чЛг
v	y	D5.4)
так и их амплитуды
1+7? = Т, kx + Rkx=TKx. D5.5)
Прежде всего исследуем уравнения Фиг. 31. К определению
D5.4). Последующие рассуждения можно волновых векторов и углов
существенно упростить, если выбрать ось при наклонном п™и-
г таким образом, чтобы &г = 0, т. е. направить эту ось перпенди-
перпендикулярно плоскости падения. Тогда, согласно уравнениям D5.4),
k'z и Кг также будут равны нулю, и, следовательно, оба вектора,
k' и К, будут лежать в плоскости ху. На фиг. 31 показано вза-
взаимное расположение волновых векторов и определены исполь-
используемые ниже углы а, а', |J. С учетом этих определений уравне-
уравнения D5.4) принимают вид
k sin a — k sin а' =/С sin p.
Из них сразу же следует закон отражения, а = а', и закон пре-
преломления Снеллиуса,
sin а К	,.r a \
т,	D5.6а)
sin
позволяющий тем же путем, что и в оптике, определить показа-
показатель преломления:
Теперь из уравнений D5.5) найдем амплитуды R и Т:
Kx — kx	 К cos Р — k cos a 	 sin (a — P)
„

k'x—Kx
kx — kx •
~k cos a~^cosP
— k cos a — k cos a
sin
2 cos a sin
D5.7)
k'x—Kx ~ ?cosa— /Ccosp sin(a+P)
Найденные амплитуды позволяют вычислить интенсивности пуч-
пучков, которые мы определим как плотности потоков соответ-
соответствующих частиц:
D5.8)
S № 1060

130 //. Задачи без учета спина. Б. Задачи с двумя или тремя степ, свободы
В полупространстве х < 0 в силу формулы D5.2а) имеем
и, следовательно,
s = A [k + R*k' + R(k + k') cos {k — k') r],
или более подробно
!	D5.9)
sy = -^ 6 sin a [ 1 + /?2 + 2R cos Bfcc cos a)].
По другую сторону потенциальной ступеньки (х > 0) формула
D5.26) дает
или более подробно
sx = — /Сcos р-Г2; s = — AT sin р-Г2.	D5.10)
Из непрерывности плотности потока частиц следует, что ком-
компонента sx должна иметь одно и то же значение по обе стороны
плоскости * = 0, где потенциал претерпевает разрыв:
Используя формулы D5.6а) и D5.7), нетрудно показать, что при-
приведенное выше соотношение действительно является тождеством.
Что же касается компоненты sy, то на нее не налагается никаких
ограничений подобного рода, если, конечно, не считать, что она
не должна зависеть от координаты у. Интересно, однако, отме-
отметить, что благодаря интерференции между падающей и отражен-
отраженной волнами sy зависит от координаты х. Эта периодическая за-
зависимость от расстояния до потенциальной ступеньки нигде не
приводит к изменению знака, так как выражение, стоящее в квад-
квадратных скобках в формуле D5.9), осциллирует между значениями
A — RJ и A+#)\ но оба они положительны.
Если произвести усреднение по области протяженностью
в несколько длин волн, интерференционный член в результате
усреднения пропадет и выражения для падающего, отраженного
и прошедшего потоков примут соответственно вид
S0 = Aft; вг = АяЪ'; 8Х = ^ГК.	D5.11)
Абсолютные величины этих векторов называют интенсивностями,
а об отношениях sr/s0 = R* и Sf/Sg — nT2 говорят, заимствуя тер-
терминологию из оптики, как о коэффициентах отражения и про-
прохождения соответственно.

46. Симметричный волчок	131
Полное отражение имеет место, когда Vo > Е, т. е. когда ве-
величина К в формуле D5.1) является чисто мнимой:
Уравнения D5.4) остаются в силе и в данном случае, поэтому
К.у = k sin а и Кг = О, так что
Следовательно, величина К\ отрицательная, а Кх = 1у-х—чисто
мнимое число. Уравнения D5.5) в рассматриваемом случае при-
принимают вид
l+R = T, kx + Rk'x = Tixx.	D5.5а)
Закон отражения остается прежним, а о законе преломления
говорить, конечно, не имеет смысла. Что касается амплитуд, то
вместо выражений D5.7) теперь имеем выражения
р _ Ых — k cos a	j, _ —2fe cos a	,.~ j >
—kcosa — ixx' ~ — k co's a — ixx '	^ ' '
Отсюда следует, что j R |2 = 1 и, таким образом, интенсивность
отраженной волны равна интенсивности падающей волны, что
присуще в случае полного отражения волнам любой природы.
Замечание. Решение этой задачи во многом аналогично решению соответ-
соответствующей оптической задачи. Однако из-за векторной природы световых волн
теория отражения и преломления света значительно сложнее простого случая
скалярной волны, с которым мы имели дело в нашей задаче. Заметим, что
наша формула D5.7) соответствует формуле Френеля для компоненты электри-
электрического вектора, перпендикулярной плоскости падения.
Задача 46. Симметричный волчок
Вращение весьма большого класса молекул можно трактовать
как вращение твердого тела, если не принимать во внимание
колебания ядер и не учитывать движение электронов. Пусть мо-
молекула имеет форму симметричного волчка с моментом инерции С
относительно оси молекулы и моментом инерции А относительно
любой из перпендикулярных осей, проходящих через ее центр
масс. Исходя из классической функции Гамильтона, получить
уравнение Шредингера для свободных вращений и определить
собственные значения энергии.
Решение. Если положение оси волчка задается двумя сфери-
сферическими углами ¦& и ф, а поворот волчка вокруг этой оси углом я|з,
то классическое выражение для кинетической энергии имеет вид11:
4	.	D6.1)
11 Вывод этого выражения можно найти в учебниках по классической
механике. См., например, Fliigge S., Lehrbuch der theoretischen Physik, Bd. II,
S. 50, 75. (См. Ландау Л. Д. и Лифшиц Е. М., Механика, Физматгиз, 1958,
§ 32 и 35.— Прим. ред.)

132 //. Задачи без учета спина Б. Задачи с двумя или тремя степ, свободы
В этой задаче три эйлеровых угла ft, ф, г|э являются обобщен-
обобщенными координатами, а кинетическая энергия Ткл представляет
собой квадратичную форму в переменных ft, ф и ij>, поэтому для
написания соответствующего квантовомеханического оператора
мы можем воспользоваться методом, развитым в задаче 13. Опре-
Определенный там метрический тензор в нашем случае имеет следующие
ковариантные компоненты:
= Л sin2 ft + С cos2 ft, gv^ = Ccosb, D6.2)
= 0, g^y = С cos ft,	gw = С,
а соответствующий ему определитель равен
g=A*C sin2 ft.	D6.3)
Контравариантные компоненты метрического тензора вычисляются
с помощью формулы gik = Giklg и имеют вид
в**	^ 0	fif** 0
= О
A sin2 О' 8	A sin2 О
C0S °
Л sin* О'
Оператор кинетической энергии теперь можно получить путем
непосредственного расчета по формуле A3.11). Это дает
Т- %\ ' д ^inft д
Так как в отсутствие внешних сил оператор Гамильтона совпа-
совпадает с оператором кинетической энергии Т, то уравнение Шре-
дингера для свободно вращающегося волчка записывается в виде
Ти = Еи.	D6.6)
Уравнение D6.6) с оператором Т, определенным равенством
D6.5), можно решить методом разделения переменных:
D6.7)
Чтобы волновая функция и была однозначной, квантовые числа
М и К должны быть целыми, так как областью изменения и угла ф
и угла г|э является интервал длиной 2л. Эти квантовые, числа
имеют простой физический смысл: %М — проекция момента коли-
количества движения волчка на неподвижную в пространстве ось г
(полярная ось сферической системы координат), а Кк, — проекция
момента количества движения волчка на его ось симметрии.

46. Симметричный волчок	133
После подстановки выражения D6.7) в уравнение D6.6) мы
для функции / {&) получаем дифференциальное уравнение вида
&	. „ d \
2А [ШЪШ\5т d$)~^
Дифференциальное уравнение D6.8) можно записать несколько
по-иному, если ввести обозначение
^()	D6.9)
и новую переменную
i	s<l.	D6.10)
s = i-(l+cosfl) = cos~,
Имеем
D6.11)
Вместо квантовых чисел М и К удобно ввести положительные
числа р и q:
±	q = ±\M-K\,	D6.12)
удовлетворяющие соотношениям
Теперь уравнение D6.11) с помощью подстановки
f(s) = SP(l— s)*F(s)	D6.13)
легко приводится к гипергеометрическому уравнению
)-b]F = 0. D6.14)
Регулярное в точке s = 0 {& = п) решение этого уравнения имеет вид
F^fiip + q+l + J, P + Q-J, 2/^+1; s), D6.15)
где
Х = /(/ + 1),	D6.16)
так что теперь выражение для,энергии Е с учетом формулы D6.9)
приобретает вид
|	!A±)	D6.17)
Второе решение уравнения D6.14) имеет сингулярность в точке
s = 0 (F ~ s~2p,. f ~ s~p), и его можно не рассматривать.

134 //. Задачи без учета спина. Б. Задачи с двумя или тремя степ, свободы
Необходимо подчеркнуть, что величина J не обязана быть
целым числом (пока что это всего лишь новое сокращенное обоз-
обозначение) и формула D6.17) еще не определяет искомые собствен-
собственные значения. Однако в нашем распоряжении есть еще второе
граничное условие. В точке s= 1 (¦§ = 0) гипергеометрический ряд
D6.15) имеет сингулярность типа F ~ A—s)~2? и, следовательно,
наше решение / ведет себя как A—s)~q\ исключением является
случай, когда гипергеометрический ряд D6.15) обрывается, что
происходит всякий раз, когда либо первый, либо второй аргумент
функции D6.15) равен целому отрицательному числу. Поскольку
первый аргумент в силу своего определения положителен, в на-
нашем случае должно быть
p + q — J^ — n, n=\, 2, 3, ...,	D6.18)
при этом функция F становится полиномом п-й степени и волно-
волновая функция оказывается конечной для любых физических зна-
значений угла. Как следует из формулы D6.12), сумма p + q есть
положительное целое число, равное либо \К\, либо \М\ в зави-
зависимости от того, какая из этих величин больше, поэтому вели-
величина J, равная сумме n-{-p-\-q, также есть целое положительное
число, всегда превосходящее или в крайнем случае равное боль-
большему из чисел \К\ и \М\. Этот результат выглядит вполне ра-
разумным, если понимать под J (хотя мы этого еще не показали)
полный момент количества движения волчка, поскольку всякий
вектор всегда не меньше любой из своих компонент. Только те-
теперь, после того как выяснен вопрос о допустимых значениях
величины J, мы можем сказать, что формула D6.17) является
решением поставленной задачи.
В том, что величина J действительно является квантовым
числом полного момента количества движения, проще всего убе-
убедиться, сопоставив классическое выражение
g квантовой формулой D6.17).
Замечание 1. Собственные функции в стандартных обозначениях имеют вид
где
dJUK = NJUKsP(\— s)q iF^(p-\-q-\-J-\-\, p-\-q — J, 2p+lj s). D6.20)
Они нормированы таким образом, что
л	2л 2л
11 \ Лр \ I @)мк \г dty— 1	D6.21)
о о

47. Бесконечно малые вращения	135
j sin ft |d^K|add=l.	D6.22)
о
Определенная с помощью последних соотношений нормировочная постоянная
NJMK выражается формулой
j	/27+T f(J+p + q)\(J + p-q)\
NMK= 2Bp)l V {j-p+q)i(J-p-q)r .	<4623)
С математической точки зрения эти функции примечательны тем, что матрица
<2) с элементами eDJ^j^ реализует B7 + 1)-мерное представление группы 3-мер-
3-мерных вращений. В этой связи см. также задачу 55.
Замечание 2. Применительно к твердому телу метод построения оператора Т
[формула D6.5)] нельзя ни в коей мере считать обоснованным: в задаче 13
разбирался исключительно вопрос об обобщенных координатах для системы
точечных масс. Более того, в квантовой механике вообще не может быть абсо-
абсолютно твердого тела, так как последнее понятие предполагает наличие таких
ограничивающих внутренние движения связей, которые приводят к бесконечной
нулевой энергии. Только путем корректного отделения этих внутренних дви-
движений от вращения системы в целом можно решить указанную проблему. Эта
программа была выполнена в работе Флюгге и Вейгани [Flugge S., Weiguny A.,
Zs. Phys., 171, 171 A963)], где было произведено упомянутое отделение внут-
внутренних движений и выполнен предельный переход к бесконечно малым коле-
колебаниям составляющих систему частиц около их равновесных положений1'.
Что же касается самого выражения D6.5) и квантовой теории симметрич-
симметричного волчка, то они, разумеется, были получены значительно раньше; первой
относящейся сюда работой мы обязаны Рейхе [Reiche F., Zs. Phys., 39, 444 A926)].
В. Момент количества движения
Задача 47. Бесконечно малые вращения
Показать, что результат преобразования скалярной функции
/ (г) при бесконечно малом вращении системы координат простым
образом выражается через операторы момента количества движения.
Решение. Пусть поворот системы координат описывается фор-
формулами
r' = Rr, R=l+A,	D7.1a)
где R и А—трехрядные матрицы, причем
О ег -
= | — е, 0 в,).	.	D7.16)
гу -гх О
11 Впервые эта проблема рассматривалась в работе Уилкера [Welker H.,
Zs. Phys., 101, 95 A936)].

136	//. Задачи без учета спина. В. Момент количества движения
Фигурирующие здесь бесконечно малые величины е^ представляют
собой углы поворота относительно трех осей х, у, г. Заметим, что
обратное преобразование можно получить, либо изменяя знак всех
трех величин е^, либо переходя к транспонированной матрице А.
Следовательно,
Л = — А.	D7.1в)
В результате преобразования D7.1а) — D7.1в) функция /(г)
перейдет в функцию /' (г') от новых координат. Эту функцию
можно выразить через старые координаты г, воспользовавшись
разложением в ряд Тейлора:
/'(r') = /'(r) + Fr-v)/'(r).	D7.2)
где бг = г' — г~Аг\ в D7.2) все члены, содержащие более вы-
высокие производные, отброшены. Как следует из формулы D7.16),
ггу —гуг\
Аг=[—вжх +гхг\,	D7.3)
)
поэтому равенство D7.2) можно записать в виде
Г ('') = /'
Собирая здесь члены с одинаковыми е, и вводя операторы мо-
момента количества движения
Lx = — (y^—2л~) и т- Д- (циклические перестановки), D7.4)
получаем
?г),	D7.5)
где через е обозначен вектор с компонентами ех, еу, г2. Так как
последний член в выражении D7.5) есть величина бесконечно малая,
то здесь мы можем пренебречь различием между /' (г) и /' (г'),
поэтому выражению D7.5) можно придать иную форму:
/'(r)=[l + j(«•?)] ПО-	D7.6)
До сих пор мы не пользовались тем, что функция f (г) является
скаляром, т. е. инвариантна по отношению к вращениям:
/'(/") = /(/•)•	D7.7)
Последнее равенство позволяет все величины, входящие в соотно-
соотношение D7.6), выразить через старые координаты г, так что окон-

	48. Момент количества движения в сферических координатах	137
чательно оно принимает вид
+ j (е-L)]/(r).	D7.8)
Задача 48. Момент количества движения
в сферических координатах
Воспользовавшись результатами предыдущей задачи, выразить
компоненты оператора момента количества движения через сфе-
сферические координаты.
Решение. В равенстве D7.5) мы вместо /' будем писать ip,
так что оно запишется в виде
?]>(r).	D8.1)
Прежде всего произведем поворот вокруг оси г. Этому повороту
соответствует преобразование r' — r, ft' = ft, ф'=ср — ег. Отсюда
с помощью разложения в ряд Тейлора получаем
С другой стороны, в соответствии с формулой D8.1) имеем
i|J(r')=[l--?(eA)]i>('>).
Сравнение этих выражений дает
Рассмотрим теперь поворот системы координат на угол &х вокруг
оси х. В этом случае по-прежнему будет г' = г, но оба сфери-
сферических угла О и ф изменятся:
ft'= ft-f-6ft, ф' = ф + бф.
В прямоугольных координатах рассматриваемый поворот, соглас-
согласно D7.1а) и D7.16), описывается формулами
* = *', y'=y + exz, г' = г—гху.
Так как, с одной стороны,
z = r cos ft, у = г sin •& sin ф
и
г'=r cos ¦&' = г (cos ft — 60 sin ft),
а, с другой стороны,
г' — г—ъху~г (cos ft—ex sin ft этф),
то из сравнения этих выражений вытекает
6ft = exsincp.	D8.3)

138	//. Задачи без учета спина. В. Момент количества движения
Аналогичным образом, сравнивая выражения
у' = г sin ft' sin ф' = г (sin ft sin ф + 6ft cos ft sin ф 4- бф sin ft cos ф)
и
у' = у + e,xz = г (sin ft sin ф + e,x cos ft),
получаем
6ft cos ft sin ф + бф sin ft cos ф = sx cos ft,
что с учетом формулы D8.3) для 6ft дает
бф = 6.,. cos ф ctg ft.	D8.4)
Используя формулы D8.3) и D8.4), запишем разложение в ряд
Тейлора в виде
Из соотношения D8.1) следует
сравнение этих двух выражений дает
|	^)	D8.5)
Рассмотрим, наконец, поворот системы координат на угол гу
вокруг оси у. Снова обозначим приращения углов ft и ф через
6ft и бф, которые теперь имеют иные значения, определяющиеся
соотношениями
х' = r sin ft' соэф' = r (sin ft cos ф 4- 6ft cos ft cos ф—бфзтдзтф) =
= x—ZyZ = r (sin ¦&cos(f — e^cosft) D8.6a)
и
г' = r cos ft' = r (cos ft — 6ft sin ft) =
= г -f ъух = r (cos ft 4- ъу sin ft cos ф). D8.66)
Из формулы D8.66) получаем
6ft = — вуСОЭф,	D8.7)
а из формулы D8.6а) следует
бф = ъу sin ф ctg ft.	D8.8)
Таким образом,
1|э (г') =i|j (г) + гу (—cos ф щ + sin ф ctg ft А) у (Г))
но последнее выражение должно согласовываться с соотношением

49. Момент количества движения и оператор Лапласа	139
вытекающим из формулы D8.1), поэтому
flA).	D8.9)
Вместо самих компонент D8.5) и D8.9) обычно удобнее поль-
пользоваться их комбинациями:
L(±	±) D8.10a)
D8.106)
Выражениями D8.2), D8.5) и D8.9) полностью исчерпывается
решение поставленной задачи.
Задача 49. Момент количества движения и оператор Лапласа
Записать оператор L2 в сферических координатах. Полученное
выражение сравнить с оператором Лапласа и с оператором кине-
кинетической энергии.
Решение. Используя операторы L+ и L~, определенные фор-
формулами D8.10а) и D8.106), можно написать
^	D9.1)
Произведение L+L~ равно
Учитывая перестановочное соотношение
позволяющее исключить экспоненту, и принимая во внимание,
что
приходим к выражению
Аналогичным образом можно найти и оператор L~L+; от только
что найденного соответствующее выражение отличается знаком
последнего члена. Таким образом, формула D9.1) теперь дает
или

140	//. Задачи без учета спина. В. Момент количества движения
В этой последней записи выражение, стоящее в квадратных
скобках, совпадает с выражением для угловой части оператора
Лапласа, поэтому можно написать
v. *+2а !_?..	D9.4)
дг2 ' г or %гтг	v '
Как известно из классической механики, кинетическую энер-
энергию частицы можно представить в виде
Так как ей соответствует квантовомеханический оператор
(—%2l2m) V2, то равенство D9.4) приводит к соотношению
„__*,._?__»(? + 1|).	D9.5,
которое показывает, что оператор р? с точностью до множителя
совпадает с радиальной частью оператора Лапласа. Оператор же,
соответствующий классическому радиальному импульсу рг, теперь
получается из выражения D9.5) путем факторизации:
В самом деле, последнее выражение, будучи применено дважды,
дает правую часть равенства D9.5). Можно показать, что опе-
оператор рГ эрмитов (см. задачу 59) и что он и координата г удо-
удовлетворяют каноническим перестановочным соотношениям.
Задача 50. Преобразования в гильбертовом пространстве
Показать, что любой квантовомеханический оператор F при
бесконечно малом повороте преобразуется в соответствии с фор-
формулой
F' = UFU*,	E0.1)
где унитарный оператор U имеет вид
U = 1 — j(b-L).	E0.2)
Пользуясь этим преобразованием, найти коммутаторы Lf с xk,
Pk> Lk и L\
Решение. На основании соотношения D7.8) мы знаем, что
всякие скалярные волновые функции я|з и ср преобразуются при
поворотах по закону г|/ = ?/г|) и ф' = ^/ф, где оператор U опре-
определяется равенством E0.2). Всякая измеримая величина (т. е.
всякий матричный элемент, получаемый из оператора F) должна
быть инвариантна по отношению к выбору системы координат,

	50. Преобразования в гильбертовом пространстве	141
поэтому
<i|>'|F|q>'> = <i|j|F|<p>.	E0.3)
Заменяя здесь \|/ и ср', получаем
<г|/ | F' | ф'> = <Uq | F' | (/ф> = <ф | i/+ Ft/ | q». E0.4)
Сравнивая последнее выражение с правой частью равенства E0.3),
находим искомый закон преобразования E0.1).
Подставляя в равенство E0.1) выражение E0.2) и учитывая,
что рассматриваемое преобразование является бесконечно малым,
получаем
F' = F — b-[L, F],	E0.5)
где [а, Ь] означает, как обычно, квантовую скобку Пуассона:
[a, b] = j{ab-ba).
Если теперь в качестве оператора F взять прямоугольные коор-
координаты х, у, z, то, с одной стороны, должны выполняться соот-
соотношения
x' = x—e-[L, х],
y'=y—B-[L, у],	E0.6)
z' = z—e-[L, г],
а с другой стороны, как мы знаем, в соответствии с формулой
D7.3) должно быть
х' = х + егу—гуг,
,	E0.7)
Сравнивая соотношения	E0.6) и E0.7), находим
[Lx, x] = 0, [Ly, x] = z, [Lz, x] = —y,
[Lx, у] = -г,	[Lv, y] = 0, [Lz, y] = x,	E0.8)
[Lx, z] = y, [Ly, z] = — x, [Lz, z] = 0.
Компоненты всякого вектора преобразуются по формулам, име-
имеющим такую же структуру, как и формулы E0.7), отсюда
с необходимостью следует, что и перестановочные соотношения
с компонентами оператора момента количества движения должны
иметь тот же самый вид, например,
[Lx, px] = 0, [Lv, px] = pz, [Lz, px]=—py и т.д. E0.9)
Поскольку момент количества движения сам является вектором,
то вышеприведенные соображения относятся и к его собственным
компонентам, поэтому
[Lx, LJ = O, [Ly, LX] = LZ, [Lz, Lx] = -Ly и т. д. E0.10)

142	//. Задачи без учета спина. В. Момент количества движения
Скалярный же оператор при вращениях не изменяется, и, следо-
следовательно, в силу соотношения E0.5) он коммутирует с компо-
компонентами оператора момента количества движения. В частности,
(L2)' = L2, поэтому
[L, L2] = 0	E0.11)
и аналогично
[L, r2] = 0, [L, р2] = 0 и т. д.	E0.12)
Задача 51. Коммутаторы в координатном представлении
Непосредственным вычислением в координатном представлении
проверить, что для системы из N частиц имеют место переста-
перестановочные соотношения
[Lx, Y] = -Z, [Lx, Lv] = -Lt,	E1.1)
где L—оператор момента количества движения системы в целом,
а X, Y, Z—координаты ее центра масс.
Решение. Согласно определению,
/*/' /=1. 2, .... tf, E1.2)
где т.-—масса /-й частицы, а М—суммарная масса всей системы
и, следовательно,
iLx> У] = мЦ Цrnk[Llx, yk],
! k
[Lx> Ly\ = 2j 2j \.LfXt '-ftyj-
/ *
Фигурирующие здесь операторы L/x действуют только на коор-
координаты /-й частицы и коммутируют со всеми операторами, дейст-
действующими на координаты других частиц, поэтому приведенные
выше двойные суммы сводятся к одинарным:
[Lx,Y] = ^mk[Lkx, yk],	E1.3)
k
^, Lky].	E1.4)
Вклад каждого слагаемого можно оценить, непосредственно вы-
вычисляя соответствующие производные:

52. Частица со спином 1	143
Подстановка полученных результатов в формулы E1.3) и E1.4)
дает
[Lx, У] = -1Е'ПА = -2 и [Lx, Lv] = — 2^ = — Lz,
чем и доказывается справедливость соотношений E1.1).
Задача 52. Частица со спином 1
Рассмотрев бесконечно малые вращения системы координат,
показать, что векторное поле ¦ф пригодно для описания частицы
со спином 1.
Решение. Если бесконечно малое вращение, как и в задаче 47,
описывать формулой
r' = (l + A)r,	E2.1)
то векторное поле будет преобразовываться точно так же, как
радиус-вектор г, поэтому
.	E2.2)
Из решения же задачи 47 нам известно, что разложение в ряд
Тейлора каждой компоненты г|э,: (г') в окрестности г должно при-
приводить к соотношениям
>Нг).	E2.3)
Мы получим решение нашей задачи, проведя сравнение этих двух
выражений.
С этой целью воспользуемся для матрицы А выражением
D7.16), которое запишем в виде разложения:
/о о о\ /о о — Л /01 о\
А = вх\0 0 1 +е„ 0 0 0+eJ-lOo), E2.4I»
\0 — 10/	\1 0 0/ \ 0 0 0/
или более компактно:
' "	E2.5)
11 Три матрицы E2.4) суть генераторы группы вращений SOC) в трех-
трехмерном представлении.

144
//. Задачи без учета спина. В. Момент количества движения
так что равенство E2.2) теперь примет вид
E2.7)
Комбинируя равенства E2.3) и E2.7), можно исключить ip' (rr).
Это дает
или
где
/ft = Lft+Sft.	E2.9)
Отсюда следует, что три матрицы Sk суть компоненты спина,
J—полный момент количества движения, a L—его орбитальная
часть. Пользуясь определениями E2.6), нетрудно показать, что
операторы 5А подчиняются перестановочным соотношениям для
компонент оператора момента количества движения:
[Sj, Sk] = —St (j, k, 1-х, у, г и их циклические перестановки).
Каждая из матриц E2.6) имеет собственные значения +1,0,-1,
так как они отличаются от двухрядной матрицы Паули ау, имею-
имеющей собственные значения +1 и —1, лишь одной дополнитель-
дополнительной строчкой и одним дополнительным столбцом нулей (если
отвлечься от знака матрицы Sy), что приводит к собственному зна-
значению 0 в дополнение к собственным значениям матрицы ау. Таким
образом, проекция спина на любое направление имеет соб-
собственные значения +jfc, 0, —ft. Наконец, квадрат спина равен
/0 0 0\ /10 0\ /1 0 0^
0 1 0 + 0 0 0 +( 0 10
ДО 0 1/ \0 0 1/ \0 0 0/_
или Sa = 2&2. В соответствии с общей формулой S2 = ]
получаем для спина векторного поля значение s= 1.
Задача 53. Перестановочные соотношения компонент тензора
Рассмотрев бесконечно малые вращения системы координат,
получить перестановочные соотношения компонент симметричного
тензора с компонентами оператора момента количества движения.
Решение. Как было показано в задаче 50, всякий квантово-
механический оператор при бесконечно малых вращениях пре-

	53. Перестановочные соотношения компонент тензора	145
образуется по закону
F' = F—е- [L, F].	E3.1)
Если преобразование координат задается формулой г' = Rr, та
тензор определяется трансформационными свойствами своих ком-
компонент:
Та = 2 2 Я*д Rkv T^ = (RTR)ik.	E3.2>
Так как при бесконечно малых вращениях R — l-\-A и А — — А,
то отсюда
Т' = A + А)ТA—А) = Т + (АТ — ТА);	E3.3)
сравнив с соотношением E3.1), находим
е-[?, Т] = ТА — AT.	E3.4>
Формула E3.4) является основой для решения нашей задачи.
Ниже мы ограничимся вращением вокруг оси х, когда
'О О
О
v0 — 1 О/
В этом случае
/О - Т13 Tlt\	/ О О
= *х[0 -Т„Т„), АТ = гх[ Т31 Т3
\п	т т /	\	т 	т 	т
\и 	 'S3 J 32/	\	 ' 21 	 1 22	•• 23
поэтому для симметричного тензора разность
(О 	 т з Т \
-Т13 -27\3 Т„-Тп)	E3.5)
т т 	т it I
\ 1 12 1 22	1 33	*¦* 23 /
также оказывается симметричной. Левая часть этого равенства,
согласно E3.4), должна равняться гх [Llt T], следовательно,
|у т'1=0	Г/ Т 1 =	Т	Г/ Т 1 — Т
L'-'l» 1 llj 	 U»	1Ь1> ' 12J 		•* 13»	L^l» •* lSj 	 J 12»	/ГО CV
г г 'тч т	ОТ4	Г / Т1 1 	 7	Т1	Г А Т4 1 ОТ4	^'-'t-' •"/
L^l ¦* 22j	^ 23»	L 1' 23 J	22 ~ 33» 11» ¦• Зз] == -^ ¦* 23"
Перестановочные соотношения с компонентами /,2 и L3 можно
найти, рассмотрев вращения вокруг осей у и z или, что еще
проще, с помощью циклических перестановок символов в форму-
формулах E3.6):
L^2> ^22J=^'	[^2> ^2з] = 	 7\г»	1^2» ^12j==^23» /КС>7\
\i т I	от	и т 1 — Т 	Т Г/ Т 1 — IT @0-'/
1^2» ' 33j	* is»	С'-'г» * 13J J зз J ii» L^a» J nj А/ is
И
L^3» ^ 11J	^ 12» L 8» ^ 12J	11 ^ 22» L 3» * 22J == ^ 12'

146	//. Задачи без учета спина. В. Момент количества движения
Следует отметить, что все три компоненты Lk коммутируют
со следом тензора:
[L, SpT]=0.	E3.9)
Последнее обстоятельство становится понятным, если записать
симметричный тензор в виде
где Sp9 = 0. Следовательно, след тензора Sp T представляет
собой скаляр (тензорный инвариант), но, как было показано
в конце задачи 50, скаляр всегда коммутирует с компонентами Lk.
Задача 54. Тензор квадрупольного момента. Сферические
гармоники
Тензор квадрупольного момента Q, определяемый соотноше-
соотношением
Qik = Qki = 3xiXk-r*8ik,	E4.1)
является симметричным тензором со следом, равным нулю, и,
следовательно, он имеет пять линейно независимых компонент.
Эти компоненты (с точностью до множителя г2) можно предста-
представить в виде линейной комбинации пяти сферических гармоник
второго порядка. Воспользовавшись найденными в задаче 53
перестановочными соотношениями, вычислить перестановочные
соотношения сферических гармоник с компонентами оператора
момента количества движения.
Решение. Сферические гармоники F2>m с
можно выразить через декартовы координаты1'
г272, о = С (Зг2-/-2), r*Y2, ±, = ±
r*Y2, + 2
= с 1 Кб (х ± iyf, с = Y-m'	E4-2)
§\
Y
i,
Эти хорошо известные формулы позволяют выразить сферические
гармоники через компоненты тензора квадрупольного момента:
2, о = CQ33, r*Y2, ±, = ± С Y\ (Qi. ± 'Q«),
E4'3)
11 Выбор знака в выражениях для сферических гармоник произволен,
однако различие в знаках у Y2 j и Y2 _j упрощает окончательные резуль-

54. Тензор квадрупольного момента	14?
Чтобы вычислить интересующие нас коммутаторы, воспользуемся
теперь равенствами E3.6) — E3.8).
Так как ось г является полярной осью сферических гармо-
гармоник, то мы начнем с равенств E3.8), которые с учетом того, что
L3 есть соответствующая проекция момента количества движе-
движения, дают
r2[Lz, Y2,o]=C[L3, 0зз]=0,
4{L3, Qu]±i[L,, Q»
\(- Q*3 ± tQ») = ± ir*Y2. ±i,
[Lz, Y2, ±2] =C ]/| {i- [L3, Qu] - у [^. QJ± / [L,, Qlt]
| {-QM- QM±f (Qu-Q22)} =
2, ±2.
Эти три результата можно объединить в одно соотношение
[Lz, Y2im]=imY2,m,	E4.4)
которое становится почти очевидным, если принять во внимание,
что в координатном представлении Lz = (fl/i) (д/ду) и Y2y m~eimf.
Действительно,
[L,, emf\ = — e'm(P — eimf 4~ = imeimf.
1 z' J дц>	dtp
Теперь мы воспользуемся равенствами E3.6) и E3.7), чтобы
вычислить перестановочные соотношения с операторами
L+ = Lx-\-iLy и L~ = LX—iLy.
Мы имеем
[L\ Q11]=2iQ18,	[L-, Qu]=-2jQ13,
E4.5)
= -2Q23,	[L-, Q22]=-2Q23,
Непосредственное применение формул E4.3), а затем формул
E4.5) и снова формул E4.3) приводит нас к перестановочным
соотношениям между сферическими гармониками и оператором
момента количества движения. Ниже дано несколько типичных

148	//. Задачи без учета спина. В. Момент количества движения
примеров:
= - 2iC Y\ {y (Qn - Q22) + JQ12} = - 2ir*Y2,2.
2) r*[L-, Y2,i]=Cyr^{[L-, Ql3]+i[L-, Q23]} =
Так как
то выражение в круглых скобках равно —3Q33> поэтому
r*[L~, Y2,i]=-iVGr*Y2.o
И наконец, коммутаторы, содержащие сферические гармоники
с максимальным значением т, обращаются в нуль:
3) r*[L\ 72>2]=
Полученные результаты можно объединить в две простые фор-
формулы:
[L+, Y2. m]= — iV§ —m(m+l)Y2,m+l	E4.6)
и
[L-, Y2, т] = -1Уб-(т-1)ш72,т.,	E4.7)
Равенства E4.4), E4.6) и E4.7) дают нам полный набор искомых
коммутаторов.
Задача 55. Преобразование сферических гармоник
Пусть конечный поворот системы координат характеризуется
тремя углами Эйлера а, Р, у. Выяснить трансформационные
свойства волновых функций, являющихся сферическими гармо-
гармониками.
Решение. Начнем с общепринятого определения углов Эйлера.
Исходная система координат х, у, г сначала поворачивается на
угол а вокруг оси г, причем 0^а^2я. В результате полу-
получается система координат хх, уг, гх, которую теперь следует
повернуть на угол Р(О^р^л) вокруг оси ух. Получающуюся
таким образом промежуточную систему координат х2, уг, гг

55. Преобразование сферических гармоник
149
в заключение поворачивают на угол у (О ^ у ^ 2я) вокруг оси
z2, и она переходит в систему координат х', у', г'.
Путем последовательного применения формул D8.1) нетрудно
убедиться, что всякая волновая функция ty (г) при повороте
вокруг оси А на конечный угол гА преобразуется по закону
z=z,
, где Ще^е^Ч E5.1)
Таким образом, закон преобразования волновой функции при
трех следующих друг за другом эйлеровых поворотах имеет вид
q(r') = D(a, р, y)q(r),	E5.2)
где
D(a, р, y) = e~TVVe~irfV<f TaL* # E5.3)
Теперь мы попытаемся выразить три поворота вокруг осей
г, у13 2а, фигурирующие в формуле E5.3), через повороты вокруг
осей исходной системы координат.
Чтобы произвести поворот на угол р
вокруг оси у1г обратимся к фиг. 32, а,
на которой оси г и z1 совпадают
между собой и перпендикулярны
плоскости чертежа, а оси у и у^ об-
образуют угол а. Мы заменим поворот
на угол р вокруг оси yt сначала об-
ратным поворотом системы координат
xlt уг, zx на угол —а вокруг оси z,
затем произведем поворот на угол р
вокруг оси у вместо оси уг и наконец повернем систему коорди-
координат снова вокруг оси г на угол -\-а. Таким образом, имеем
Др\ = е-?аЧе-7РЧе?а\	E5.4)
Аналогичным образом мы разложим поворот на угол у вокруг
оси z2 (фиг. 32,6). Для этого сначала повернем ось z2 назад на
угол —Р вокруг оси уг, затем повернем ось у1 на угол у вокруг
оси z и наконец восстановим исходное положение оси гг с по-
помощью поворота на угол р вокруг оси у{.
e-TT4 = e-t^,.e-T^.eT4	E5.5)
Комбинируя равенства E5.3) — E5.5), в результате находим
D(a, p, 7) = Г^Ч Л*\еТРЧе-ТРЧе-Та^
Фиг. 32. Повороты осей ко-
ординатных систем.

150	//. Задачи без учета спина. В. Момент количества движения
ИЛИ
D(a, p, v) = e"K z-e~ft y¦ е~У г.	E5.6)
Формула E5.6) является весьма общей и по существу чисто
геометрической формулой; ниже мы ее применим в частном слу-
случае сферических гармоник. Функция YLtM является собственной
функцией оператора L2, принадлежащей собственному значе-
значению %М. Оператор Ly, как нетрудно усмотреть из результатов
задачи 56, может изменять только индекс М, но не индекс L,
поэтому в новой системе координат ft', ф' мы в соответствии
с формулой E5.2) будем иметь
= 2 DLMtM.YLtM.(u, Ф).	E5.7)
M' = ~L
Перейдем к вычислению коэффициентов разложения:
DLM, м- = § Yl, м- (ft, ф) YL> м (ft', <
(a, р,
или короче
Dai. м- =
E5.8)
где D (а, р, 7) — оператор, определенный формулой E5.6). Далее
мы можем написать 1)
е~тУ '|
<LM"\e
-+-*l.
и, следовательно,
где
E5.9)
%
— довольно сложная функция переменной р. Таким образом,
закон преобразования сферических гармоник имеет вид
-(О,
E5.10)
х) Знак в формуле с бра-вектором может показаться сомнительным. Тем
не менее мы имеем
1М"
л'1,
поскольку Y*L м" ~
' l, м
и, кроме того.
_ и<*м»
„-taM
'(ш-
L, М"
'i,M- = -^"Yl<M,,.

56. Построение собственных векторов оператора Lz	151
Задача 56. Построение собственных векторов оператора Lz
в абстрактном гильбертовом пространстве
Пусть атомная система находится в состоянии, которое ха-
характеризуется определенным орбитальным квантовым числом /.
Требуется построить собственные векторы оператора Lz, восполь-
воспользовавшись для этого методом задачи 31.
Решение. Мы выберем такую гильбертову систему координат,
в которой оператор L2 диагоналей, т. е. для всех рассматривае-
рассматриваемых векторов (в единицах А)
L* = ±(L+L-+L-L+) + Ll = t(l+ 1).	E6.1)
Пусть далее |^т>—собственный вектор оператора Lz, принадле-
принадлежащий (еще не определенному) собственному значению т. Подей-
Подействуем на этот вектор оператором
L+ = Lx + iLy,	E6.2)
который удовлетворяет (см. задачу 51) перестановочному соот-
соотношению
L+Lz — LzL+ = — L+.	E6.3)
Тогда, учитывая равенство
Lz\qm> = m\ 4>m>,	E6.4)
получаем
L+Lz | !>«> = (Lz-1) | L+tym> = m | L^my,
или
Lz\L+ym-> = (m + \)\L+ypm>.	E6.5)
Отсюда следует, что вектор |L+^m> является собственным векто-
вектором оператора Lz, принадлежащим собственному значению т-\-\.
Этот вектор пока еще не нормирован, так как скалярное про-
произведение
<L+i|>m |L+i|>m> = <L~L^m | !>.>, где L~ = (L+)t,
не равно единице. Из равенства E6.1) и перестановочного соот-
соотношения
L+L-—L~L+ = 2LZ	E6.6)
находим
L-L+ = L* — L\—Lt,	E6.7)
поэтому
Таким образом, нормированный собственный вектор, принадле-
принадлежащий собственному значению /п + 1, имеет вид
'^1^	E68)

152	//. Задачи без учета спина. В. Момент количества движения
Эту процедуру можно повторять вплоть до значения т = Л Сле-
Следующий шаг по необходимости приводит к соотношению L+| 1|>г> = О,
в результате чего последовательность собственных векторов обры-
обрывается, а вектора |1)зг+1> просто не существует.
Кроме возрастающей последовательности, можно построить
убывающую последовательность путем повторного применения
эрмитово сопряженного оператора
L~ = Lx-iLy,	E6.9)
который удовлетворяет перестановочному соотношению
L-LZ~LZL- = L-.	E6.10)
Действуя оператором L~ на обе части равенства E6.4), получаем
Lt\L-ym> = (m-\)\L-*m>.	E6.11)
Собственный вектор здесь снова не нормирован, так как
<L-1>« | L-qm> = <L+L~ym | Ч>.> = <(La-LI +Ьг) уя \ут> =
Отсюда следует
С помощью этой формулы можно получать собственные векторы,
принадлежащие даже отрицательным собственным значениям т
вплоть до значений т = — /. Следующий шаг должен был бы
привести к соотношению
1||> 0
так что вектора | л^_г_х> не существует.
Замечание 1. Из теории Шредингера нам известно, что сферические функции
1*»> = ^.«(#. ф)	E6.13)
с точностью до произвольных фазовых множителей представляют собой реали-
реализацию рассмотренных выше нормированных гильбертовых векторов. Следова-
Следовательно, формулы E6.8) и E6.12), опять-таки с точностью до фазового множи-
множителя, который обычно выбирают равным (—\)т, идентичны рекуррентным
соотношениям для сферических функций:
Замечание 2. В приведенном решении молчаливо предполагалось, что
/—целое число. Так как при каждом действии операторов L+ и L~ число т
изменяется на ±1, а максимальное и минимальное значения т соответственно
равны -\-1 и — /, то разность этих граничных значений, равная 21, должна
быть целым числом. Но это возможно как при целых значениях I Й т, так и
при полуцелых. Таким образом, перестановочные соотношения для компонент
момента количества движения в принципе допускают квантование с помощью
полуцелых чисел. Такое квантование не возникает при рассмотрении момента

	57. Ортогональность сферических гармоник	153
количества движения материальной точки, но это отнюдь не ограничивает воз-
возможностей теории. Указанные полуцелые значения появляются в том случае,
когда наряду с «орбитальным» моментом в рассмотрение включается спиновый
момент частицы.
Задача 57. Ортогональность сферических гармоник
Показать, что выведенные в предыдущей задаче собственные
векторы оператора Lz при фиксированном значении числа / обра-
образуют ортогональную систему, и определить по отношению к ней
матричные элементы операторов L+ и L~.
Решение. Как было показано, векторы |ifm> удовлетворяют
соотношениям
,	E7.1а)
.	E7.16)
Образуем два равных скалярных произведения:
<L+ojw | Ь+Цт> = O|w | L-L+oj3m>	E7.2a)
<L+^m'|L+tm> = <L-L+i|w|a|3m>.	E7.26)
Применяя к правым частям этих равенств соотношение E7.1а),
соответственно получаем выражения
[/(/ + 1)—m(m + l)]o|vl1'»>
[I (I + \)—т' (т' + 1)] <o|w 11>т>.
Разность этих выражений равна нулю:
[от (т + 1)—от' (т' + 1)] <iv №m> - 0.	E7.3)
Второй сомножитель в левой части должен равняться нулю за
исключением тех случаев, когда равен нулю первый сомножи-
сомножитель. Таким образом, искомая ортогональность доказана для
всех случаев, кроме т = т либо т' = —т — 1. Чтобы исключить
последнюю возможность, воспользуемся соотношением E7.1б}„
В полной аналогии с предыдущими выкладками имеем
— m (/n— 1)] <ipm. | фт> =
Снова рассматривая разность
[m(m— 1)—m'(m' — 1)] <o|v|4>m>,	E7.4)
видим, что на этот раз первый сомножитель обращается в нуль
при т' — т и т' = —„от+1, но не при от'= — т—1. Следова-
Следовательно, оба соотношения E7.3) и E7.4), рассматриваемые сов-

154 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
местно, приводят к искомому условию ортогональности:
<*|W | ЧртУ = $т'т	E7.5)
(выше мы воспользовались нормировкой, введенной в предыду-
предыдущей задаче).
С помощью соотношений E6.8) и E6.12) теперь нетрудно
получить матричные элементы операторов L+ и L". Придержи-
Придерживаясь соглашения о знаке E6.14), имеем
+1	т	.	'	E7.6)
все прочие матричные элементы исчезают в силу соотноше-
соотношения E7.5).
Г. Сферически симметричные потенциалы
а. Связанные состояния
Чтобы решить уравнение Шредингера в случае сферически
симметричного потенциала, зависящего только от г (центральные
силы), целесообразно с помощью формул
х = г sin Фсоэф,
y = r sin йзтф,	(а.1)
2 = Г COS'S"
ввести сферические координаты (фиг. 33). Ось
г называется полярной осью, Ф—угол меж-
между полярной осью и радиус-вектором г
__ (О^Ф^я), а угол ф характеризует поворот
у вокруг полярной оси @^ф^2я). В этих
координатах оператор Лапласа имеет вид
Фиг. 33. Сфериче-
Сферические координаты.
г д% , 2 д . 1
где Л — оператор, зависящий только от углов:
_ 1 д I . „ д \	1 as
~ЖЪ д® [sm w дь) + ШЧд$
В рассматриваемом случае уравнение Шредингера
допускает разделение переменных
(а.2)
(а.З)
(а.4)
(а.б)

а. Связанные состояния	155
Функция Хг (г) удовлетворяет радиальному волновому уравнению
fa IdH, 1A+1) \ , Лт, >	г-	, С\
-2^(^	4Нх«) + ^(/-)Х| = ?х«.	(а.6)
а функции y,t m удовлетворяют дифференциальному уравнению
для сферических гармоник
Величина /(/ + 1) играет здесь роль постоянной разделения пере-
переменных г и Ь, ф. Несингулярные решения существуют лишь
в том случае, если /—целое число: / = 0, 1,2, ... . Для каждого
целого / существует 2/+1 несингулярных однозначных решений,
отвечающих различным значениямm(m = — I, —/+ 1, ..., /— 1, /).
В нижеследующих задачах мы всегда будем пользоваться
нормировкой сферических гармоник в соответствии с условием
Частное решение при т = 0 будем записывать в виде
Оно зависит только от угла $ и называется зональной сфериче-
сферической гармоникой. Функция Рг нормирована таким образом, что
Р1A)=1, и представляет собой полином степени / относитель-
относительно cosft; ее называют полиномом Лежандра.
В сферических координатах компоненты оператора момента
количества движения частицы имеют вид
(a.10)
z i дц>
Оператор квадрата момента количества движения
(а.11)
выражается в сферических координатах следующим образом:
1 а. /
Л_|_ *^*!L1	(a.12)
Если воспользоваться сокращенным обозначением (а.З), послед-
последнюю формулу можно записать короче:
D = — h%d.	(а. 13)

156 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Как следует из уравнения (а.7), функции YUm являются соб-
собственными функциями оператора квадрата момента количества
движения L\ принадлежащими собственным значениям fl2l(l-\- 1).
Так как зависимость функций Ylt m от угла ф имеет вид eimf,
то из равенства (а. 10) следует, что Yly m есть собственная функ-
функция оператора Lz, принадлежащая собственному значению %т,
где |т|=^/. Эти два свойства волновых функций частицы в поле
с центральной симметрией являются применительно к квантовой
механике своеобразным отражением классического закона сохра-
сохранения момента количества движения.
Равенства (а.2) и (а.10), разумеется, можно получить с помощью преобра-
преобразования координат (а.1). Однако этот прямой путь оказывается довольно гро-
громоздким. Более изящный метод, использующий связь между оператором
момента количества движения и бесконечно малыми поворотами системы коор-
координат, был изложен в задачах 47—49.
Математические детали, касающиеся сферических гармоник, приведены
в приложении, том 2, стр. 296.
Задача 58. Средние значения компонент момента
количества движения
Что можно сказать о компонентах момента количества дви-
движения Lx, Ly, Lz в следующих двух случаях?
а)	Волновая функция частицы, движущейся в центральном
поле, зависит от углов как Yu m.
б)	При данном значении / функции Yu m и Yu -m зависят от
угла Ф одинаковым образом. Оба решения вырождены, поэтому
их линейные комбинации, пропорциональные cos mcp и sin ту,
по-прежнему являются решениями уравнения Шредингера в слу-
случае центральных сил.
Решение
а. Сферическая гармоника Y^ m есть собственная функ-
функция операторов L2 и Lz, принадлежащая соответственно соб-
собственным значениям %г1A-\-\) и %т. Следовательно, компонента
Lz имеет вполне определенное значение в рассматриваемом состо-
состоянии. Две другие компоненты Lx и Lv по необходимости не имеют
определенных значений, так как компоненты момента количества
движения описываются некоммутирующими операторами (см. за-
задачи 50 и 51). Эту ситуацию можно пояснить с помощью сле-
следующей классической картины. Для каждого отдельного движения
все три компоненты L имеют фиксированные значения:
Lx = Lsin ¦frcoscp,
LZ = L cosft.
В нашем распоряжении, однако, имеется лишь неполная инфор-
информация, позволяющая точно определить Lz, но не содержащая

58. Средние значения компонент момента количества движения 157
никаких сведений относительно «фазового» угла ф. Тогда в каж-
каждом отдельном случае мы можем определить лишь фазовое сред-
среднее, например,
2я
г, - i 1
Так как величина Lz не зависит от угла, ф, то она имеет вполне
определенное значение; что же касается средних значений Lx и
Ly, то они обращаются в нуль. Различие между классической и
квантовой механикой состоит в том, что в первом случае в прин-
принципе можно было бы получить полную информацию и тем самым
сделать фазовое усреднение ненужным, во втором же случае
получить полную информацию из-за некоммутативности операто-
операторов вообще невозможно, так что приходится довольствоваться
средними значениями.
Вместо классического среднего по фазе квантовая механика
позволяет нам вычислить математическое ожидание, т. е. среднее
по состоянию:
<Lx>=<$YlmLxYl,mdU и т.д.
Математическое ожидание описывает средний результат, получен-
полученный на основании большого числа независимых измерений, про-
произведенных над системами, которые находились в одном и том
же состоянии. Если все эти измерения приводят к одному и тому
же результату (именно такова ситуация в нашем случае с ком-
компонентой Lz), то мы имеем дело с вполне определенным значением,
и математическое ожидание переходит в собственное значение.
Если же различные измерения приводят к разным результатам,
то на основании квантовой теории мы можем получить только
соответствующее среднее значение1}.
Вместо того чтобы вычислять средние значения компонент
момента, целесообразнее иметь дело с их комбинациями L+ и L~.
Действие операторов (а. 10) на функцию YUm дает [см. приложе-
приложение, а также соотношения E6.14)]
+т + 1) (l-m) Yu я+1,
7
Следовательно, в выражениях <L+> и <L"> появляются лишь
интегралы вида
Х) Квантовая теория дает возможность не только предсказать средний ре-
результат большого числа независимых измерений, но и указать вероятность
появления каждого отдельного результата.— Прим. ред.

158 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
обращающиеся в нуль в силу ортогональности сферических гар-
гармоник. Таким образом, математические ожидания Lx и Ly так же,
как и фазовые средние в классической картине, равны нулю.
б. Две действительные волновые функции, рассматриваемые
в этом случае, имеют вид
и+ =4-(*",,„ +К,. -J ~ cosmq),
1	E8.2)
U. = 2Г (Yl, m — Yl, -m)	i
Обе функции являются собственными функциями оператора L2,
но не являются собственными функциями ни одного из операто-
операторов Lx, Ly, Lz l), так как
±l\,	E8.3)
Yt, m±, -
Lzu_ — — hmiu+.	E8.4)
Следовательно, во всех трех случаях нас должны интересовать
лишь средние значения. Для Lx и Ly (или L+ и L") мы по су-
существу должны повторить выкладки, которые были сделаны
в случае „а"; для математических ожиданий, как и ранее, в силу
ортогональности сферических гармоник получаются нулевые зна-
значения. Что касается Lz, то равенства E8.4) и здесь приводят
к нулевым средним значениям, поскольку
<Lzy =§u± Lzu±dQ = ± hmi § н±«т dQ = О,
а функции и+ и ц_ также ортогональны. Это нетрудно усмотреть,
заметив, что
2я
Между математическими ожиданиями <_LX> и ФУУ, с одной
стороны, и математическим ожиданием <L2> — с другой, однако,
имеется существенное различие. В классической картине волно-
волновым функциям и+ и и_ все еще соответствуют состояния, для
которых фазовый угол ф так же, как и в случае „а", может при-
принимать все возможные значения. Угол же й может принимать
всего два различных значения: й] = '9' и Ф2 = я—¦&, поэтому
х> Исключение представляет случай т = 0.— Прим ред.

59. Радиальная компонента оператора импульса	159
/^ = ±Lcosu и LZ = L costf — L cosft = 0.
В квантовой механике математическое ожидание Lz проистекает
из смеси взятых с равными весами состояний с Lz=-\-fim и
Lz =— %т. В этом можно убедиться с помощью равенств E8.3)
и E8.4): при действии операторов Lx и Ly вместо функций и+ и
ц_ получаются совершенно иные функции, в то время как при
действии оператора Lz функции и+ и и_ просто меняются места-
местами, поэтому из их линейной комбинации мы снова можем обра-
образовать собственные функции оператора Lz- Действительно,
Lzu1 = hmu1 для «1 = и++ш_
и
Lzu2 = — %тиг для u2 = u+ — ш_.
Замечание. Действительные комбинации типа E8.2) играют роль в кван-
квантовой химии, где предпочтительнее рассматривать не момент количества дви-
движения, а избранные направления, определяемые местоположением соседних
атомов в молекуле.
Задача 59. Радиальная компонента оператора импульса
Получить оператор, канонически сопряженный координате г.
Каков явный вид этого оператора в координатном представлении?
Решение. В классической механике импульс рг, сопряженный
радиусу г, определяется как проекция вектора р на направление
радиус-вектора г:
Рг = -г(рг).	E9.1)
В квантовой механике это определение из-за некоммутативности
компонент р и г становится двусмысленным: классическому
выражению E9.1) априори могла бы соответствовать любая ли-
линейная комбинация вида
pr=^f + (l-X)-^/>.	E9.2)
Оператор рг должен быть эрмитов, т.е. рг — р\. Это дает
Х=1—X или Я=Уг и, следовательно,
Чтобы показать, что это симметричное выражение действительно
является оператором, канонически сопряженным с радиусом г,
мы должны проверить справедливость перестановочного соотно-
соотношения
Prr — rpr = —	E9.4)

160 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
при условии, что оно выполняется для прямоугольных декарто-
декартовых компонент. Для доказательства справедливости соотноше-
соотношения E9.4) воспользуемся равенством
которое сразу же следует из формулы скалярного произведения
в прямоугольной декартовой системе координат. Мы имеем
—rpr = ^ [(pr)+y(rp)r—
Здесь
r2(pr) = >
¦z2)(pxx + puy + pzz),
и так как
и мы получаем
Тем самым справедливость соотношения E9.4) установлена.
Чтобы найти явный вид оператора рг в координатном пред-
представлении, запишем равенство E9.3) в декартовых координатах
1 I х , ._ и , г , х , и .2 \
и учтем, что
х i дх
и т. д.
Следовательно,
х . х \ % X д ( х ,\ . х д-$Л
г | r rx j t t [дх \ г Y J ' г дх \
Добавляя сюда аналогичные результаты, относящиеся к у и г,
и замечая, что
окончательно получаем (см. также задачу 49)
А /" а , 1 \
гг j \дг ' /¦;

60. Решения, близкие к собственным функциям	161
Эрмитовость этого оператора легко показать, непосредственно
проверив справедливость соотношения
<ы | prv> = <рги | v>
для любой пары комплексных функций и и v, для которых эти
интегралы имеют смысл. Мы находим
4
Эти два интеграла будут равны в том случае, если
А С [ а dv , ,1 , ди* , .1
ИЛИ
f л2
~r u*v ] dr = 0.
Внутренний интеграл можно преобразовать к виду
о
так что он действительно обращается в нуль, если функции и* и
v конечны в точке г = 0 и исчезают на бесконечности. Следует,
однако, заметить, что нормировочные интегралы <ы | и> и <d|u>
существуют и в том случае, когда функции и и v имеют в начале
координат особенность вида 1/л. Таким образом, одного условия
нормировки не всегда бывает достаточно для исключения не
имеющих физического смысла решений, например в случае сфе-
сферически симметричной ямы при 1 = 0.
Задача 60. Решения, близкие к собственным функциям
Дана потенциальная яма радиусом а с характеристическим
безразмерным параметром
где VQ — глубина ямы. Построить графики волновых функций
для / = 0 и ka = 2,20; 2,28; 2,36 (k — волновое число внутри
ямы). Эти значения произведения ka выбраны таким образом,
что они лежат довольно близко к наинизшему собственному
значению.
Решение. Обозначим посредством
EШJ = 1Г2—(ka)*	F0 1)
6 № 1050

162 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
энергетический, параметр вне ямы, тогда волновая функция
внутри и вне ямы будет соответственно иметь вид
1
ka'
и
cos ka , г .
щ^-^smikax)
sin ka
ka
F0.2а)
:—1)], F0.26)
где
Х~ а
F0.3)
— безразмерная радиальная координата с радиусом ямы в каче^
стве единицы длины. Нормировка волновой функции выбрана
г, го
-0,4
г,г&
г,го
Фиг 34. Волновые функции для энергетических уровней, близких к собст-
собственному значению гамильтониана.
таким образом, чтобы выполнялись начальные усдрвия « = 0
и du/dx=: 1 при х = 0, а коэффициенты функции ие(х) определены
из условия непрерывности и и и' на границе ямы в точке х= 1.
Для получения собственных значений необходимо потребо-
потребовать, чтобы коэффициенты при гиперболических функциях в фор-
формуле F0.26) удовлетворяли соотношению
cos ka	sin ka
ka
которое с учетом равенства F0.1) можно записать в виде
tg ka _	1
F0.4)
(ср. задачу 25). Для случая №2 = 9 решение равно
ka = 2,2789.	F0.5)
Волновые функции F0.2а) и F0.26) изображены на фиг. 34,
здесь же схематически показаны потенциальная яма и соответ-

61. Квадрупольныи момент	163
ствующие энергетические уровни. Если выбранное значение энер-
энергии Fа = 2,20) меньше собственного значения, то длина волны
внутри ямы оказывается слишком большой, и уменьшение ампли-
амплитуды волновой функции на границе ямы недостаточно для того,
чтобы заставить ее асимптотически стремиться к нулю—на боль-
больших расстояниях волновая функция вновь возрастает. С другой
стороны, если выбранное значение энергии (?а = 2,36) слишком
велико, а следовательно, длина волны внутри ямы слишком
мала, то уменьшение амплитуды волновой функции на границе
ямы оказывается чрезмерным и она обращается в нуль уже на
конечном расстоянии, но в дальнейшем, будучи отрицательной,
вновь возрастает по абсолютной величине. Промежуточное зна-
значение энергии (?а = 2,28) настолько близко расположено к соб-
собственному значению F0.5), что волновая функция вне ямы почти
точно стремится к нулю. Так как тем не менее эта энергия все-
таки немного больше энергии основного уровня, то амплитуда
волновой функции на большом расстоянии от ямы становится
отрицательной и растет по абсолютной величине — это возраста-
возрастание отсутствует лишь для того значения произведения ka, кото-
которое определяется формулой F0.5).
Задача 61. Квадрупольныи момент
Для частицы в сферически симметричном поле вычислить
квадрупольныи момент в случае состояния с определенными зна-
значениями квадрата момента и его проекции на ось г.
Решение. Волновая функция, описывающая интересующее нас
состояние, имеет вид
и = 7-Х|(/-)У|..(«, Ф).	F1.1)
а тензор квадрупольного момента, согласно определению за-
задачи 54, равен
Q/* = 3*,x*-/-«6rt.	F1.2)
Мы должны вычислить квантовомеханические средние
\$\	F1.3)
о
Недиагональные компоненты тензора Qik зависят от угла <р соот-
соответственно как cos ф sin ф, соэф и БШф, в то время как |У1>т|2
от угла ф не зависит, поэтому соответствующие интегралы обра-
обращаются в нуль. Для диагональных компонент
1),
— 1),
б*

164 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
интегрирование по <р дает множитель V», и так как
-1
-| sins ¦ft—1 = —-1C cos2 ft— I),
то интегралы <QXX> и <Qyy> можно свести к интегралу <Q«>:
<Q**> = «?,„>=-у <Q«>-	F1.4)
Вводя сокращенное обозначение
г*\Х1(г)\*йг,	F1.5)
б
мы, таким образом, имеем
<Q«> = <г*> § C cos2 ft— 1) | Yu m \*d?t.	F1.6)
Интеграл в F1.6) легко вычислить, если воспользоваться соот-
соотношением
cos ft Yu m (ft, Ф) = аи mYl+u m + at.u mYt_u „	F1.7)
где
Учитывая ортогональность сферических функций, получаем
<Q«> = <'"'>(ai.m + a?-i.m)
и элементарное вычисление теперь дает
Мы видим, что квадрупольный момент отсутствует только
у S-состояний (ш = / = 0), что является следствием сферической
симметрии11. Для Я-состояний мы, например, имеем
Состояние с т = 0, соответствующее распределению вытянутой
формы, характеризуется положительным значением <QiZ>. У со-
состояний с т = ± 1 компонента <QZZ> в 2 раза меньше по вели-
величине и отрицательна, что, очевидно, соответствует распределению
сплюснутой формы. Это представляется вполне разумным, так
как суперпозиция всех трех состояний приводит к сферически
симметричной конфигурации (конфигурация замкнутой оболочки).
На самом деле эффект замкнутой оболочки имеет место для
любых значений /. Суммируя по всем состояниям, относящимся
11 Квадрупольный момент исчезает также при /=3, т = 2, однако это
является единственным исключением из правила по крайней мере вплоть до
значений /= 16.

	62. Частица внутри непроницаемой сферы	165
к данной оболочке, получаем
(Mm2/+a)
m= —/	m=—l
но сумма, стоящая в правой части этого равенства, равна нулю,
так как
i
Задача 62. Частица внутри непроницаемой сферы
Определить уровни энергии частицы, находящейся в сфери-
сферически симметричном потенциальном ящике с бесконечными стен-
стенками и радиусом R.
Решение. Уравнение Шредингера допускает разделение пере-
переменных, и его решение можно записать в виде
и (г, О, Ф)-|Х1(/-)У|..(*.Ф).	F2.1)
Радиальная волновая функция удовлетворяет уравнению
F2.2)
в интервале 0<1г<1/? и равна нулю всюду вне его. Это урав-
уравнение после введения новой переменной z — kr и замены
Xi = zf/np B)
можно привести к виду
Но это есть уравнение Бесселя, решениями которого являются
функции J / 1 \ (z). Таким образам, общее решение уравне-
уравнения F2.2) можно записать в виде
X,(r)= l/?"[ci/'+I/,(*'") + C1/-H+./i)(ifer)].	F2.3)
Обычно вводят в рассмотрение так называемые сферические
функции Бесселя:
F2.4)

166 //¦ Задачи без учета спина. Г. Сферически симметричные потенциалы
с асимптотикой
¦ sin (г_?), rt,(z)^_cos(z-§) F2.5)
при больших положительных значениях г. Вблизи начала коор-
координат, когда \г\<^.1-\-11г, эти функции аппроксимируются пер-
первыми членами соответствующих степенных рядов:
/,«-^-zl+1, n,« —^z.	F2.6)
" -B/+1I	2«Л	;
Второе слагаемое в решении F2.3) при г—>0 дает вклад
в зсг~/--' и в и~г~1~х. Следовательно, чтобы обеспечить суще-
существование нормировочного интеграла
J|xil1d/-=l,	F2.7)
о
необходимо положить в формуле F2.3) С2 = 0. Эти соображения,
однако, не применимы к случаю 1 — 0, когда сингулярность функ-
функции и слишком слабо выражена и не может привести к расхо-
расходимости интеграла в точке г — 0. Но и в этом случае мы должны
исключить сингулярное решение, так как оно приводит к расхо-
расходимости в точке г = 0 интеграла для среднего значения энергии1':
t	F2-8)
(см. также задачу 65). Таким образом, в качестве нормируемого
решения мы должны взять
%i{r) = Ci,(kr).	F2.9)
Из этого набора решений собственные функции отбираются
путем наложения условия
/,(*/?) = О,	F2.10а)
или
/,+./,(?#) = 0.	F2.106)
Для каждого фиксированного значения величины / + 7» функ-
функция Бесселя обладает бесконечным числом нулей, поэтому мы
получаем бесконечное число значений knr, i и бесконечное число
энергетических уровней
Е"г.1 = -шк*"г.1	F2.11)
для каждого значения величины 1{пг=\, 2, 3 ...—радиальное
квантовое число, определяющее число нулей).
11 Для / = 0 и малых г это решение принимает вид и~ 1/г, а интеграл
для кинетической энергии записывается как Е ~ Ыг,/.г*.

62. Частица внутри непроницаемой сферы
167
Для низших значений / сферические функции Бесселя имеют
вид
sin г
= -j	cos г,
c°s г
F2:12)
а для более высоких значений / явный вид этих функций легко
находится с помощью рекуррентного соотношения
h (z) = 7-/*-х (z) — ii-i (z)-	F2.13)
200
180
160
140
I no
^100
80
60
40
го
nr-l nr=Z nr=3 nr~4 Все термы
Фиг. 35. Энергетические уровни частицы внутри непроницаемой сферы.
Их нули можно определить, решая несложные трансцендентные
уравнения:
/0(z) = 0, если sin z=0 или г — ппп
/j(z) = O, если tg z = z,	F2.14)
/2(z) = 0, если tgz = -3—^2" и т- Д-
Все они стремятся либо к пп в случае четных /, либо
к (« + 1/г)л в случае нечетных /. На фиг. 35 показаны нижние
энергетические уровни (в единицах A2/2mR2), а значения пара-
" 9
- 8
- 7
-
6
. 5
- 4
3
г
1
0
	5_
4
3
- г
- 1
——
i
3
- 2
1
0
1 1


168 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
метра
не превышающие 15, приведены в таблице
F2.15)
0
1
2
3
4
б
6
7
8
9
1
3,142
4,493
5,764
6,988
8,183
9,356
10,513
11,657
12,791
13,916
2
6,283
7,725
9,095
10,417
11,705
12,967
14,207
3
9,425
10,904
12,323
13,698
4
12,566
14,066
Замечание. Эта задача тесно связана с более простой одномерной пробле-
проблемой, рассмотренной нами в задаче 18. Решения при / = 0 точно соответствуют
антисимметричным волновым функциям для одномерного случая.
Задача 63. Сферически симметричная прямоугольная яма
конечной глубины
Для значений / = 0, 1, 2 определить энергетические уровни
связанных состояний в сферически симметричной прямоуголь-
прямоугольной яме
V(r)
J
-Л, r<R,
0, r>R,
F3.1)
Довести расчеты до численных результатов в том случае, когда
характеристический параметр 2mV0R*/fi2 — 100.
Решение. Пусть
2т\Е\ _
fa
p
_
	 /С ,
F3.2)
тогда радиальное уравнение Шредингера для связанных состоя-
состояний внутри и вне ямы соответственно будет иметь вид
= 0	F3.3а)
, = 0.	F3.36)

	63. Сферически симметричная прямоугольная яма конечной глубины 169
Уравнение F3.3а) с очевидным граничным условием ^z @) = 0
имеет своим решением сферическую функцию Бесселя
X, (/¦)=-Л/, (ftr). r<R.	F3.4a)
ени
, яв
мого аргумента:
X, (/¦)=-Л/, (ftr). r<R.	F3.4a)
Решением уравнения F3.36), убывающим при больших значе-
значениях г как е~хг, является сферическая функция Ханкеля мни-
мнимого аргумента:
r>R.	F3.46)
Фигурирующие здесь постоянные А и В следует определить,
руководствуясь соображениями непрерывности и нормировки.
Если записать условие непрерывности логарифмической произ-
производной на границе ямы (/- = #), то указанные постоянные
взаимно сократятся:
h №)
Здесь штрих означает производную по соответствующим аргу-
аргументам. Так как уравнение F3.5) связывает между собой х и k,
то оно тем самым фиксирует нам, согласно формулам F3.2),
собственные значения энергии для каждой данной ямы.
Для низших значений / функции, фигурирующие в уравне-
уравнении F3.5), имеют следующий вид:
^ (z) _. g}n 2i	/j(D B) =	lelz^
F3.6)
При ббльших значениях I можно воспользоваться рекуррентными
формулами
Если ввести сокращенные обозначения
ип	 „ Ъ D -г- v		% uD	 v \/ \ ?2	/со с»
К[\ —Л, К0Д =Л0, -г-— S, й«—Ло у 1 	ё >	^ОО.О)
где xl — указанный в условии характеристический параметр, то
уравнение F3.5) после элементарных, но довольно длинных вы-
выкладок можно привести к виду
*ё (хо%) — ft (ХЛ)	F3.9)

170 П. Задачи без учета спина. Г. Сферически симметричные потенциалы
и
F3.10а)
(*». S) = *oS
+
ч^-Z*[i-~
4141-
F3.106)
F3. Юв)
Значения переменной|, а тем самым и переменной х, удовлетворяю-
удовлетворяющие этим уравнениям, лроще всего находятся графическим методом.
Фиг. 36. Графическое определение собственных значений в случае сферически
симметричной прямоугольной ямы конечной глубины
На фиг. 36 дана функция tg*0? для физической области изме-
изменения переменной, 0<;?^1, в случае *0=10. Ее точки пере-
пересечения с функциями ft(l) находятся сначала непосредственно
по фигуре, а затем их положение уточняется вплоть до четвер-
четвертого знака при помощи табулирования рассматриваемых функ-
функций в окрестностях точек пересечения. Окончательные резуль-
результаты для случая хо=10 приведены в нижеследующей таблице.
Сюда же для сравнения помещены и соответствующие результаты,
относящиеся к сферически симметричному ящику с бесконечными
стенками, полученные нами в предыдущей задаче.

64. Потенциал Вуда—Саксона
171
Яма конечной глубины, значения
параметра х для
/ = 0
2,853
5,679
8,422
/ = 1
4,070
6,958
9,625
1 = 2
5,226
8,124
Ящик с бесконечными стенками,
значения параметра х для
/ = 0
3,142
6,283
9,425
4,493
7,725 .
10,904
1 = 2
5,764
9,095
Следует отметить, что в яме конечной глубины положение всех
уровней несколько смещено вниз, поэтому нужно ожидать, что
в рассматриваемом примере возможно появление связанных со-
состояний, по крайней мере, вплоть до значений / = 5, как это
видно из таблицы, приведенной в предыдущей задаче, где зна-
значения параметра х даны для больших значений /.
Замечание. Эта задача тесно связана с более простой одномерной пробле-
проблемой, рассмотренной нами в задаче 25. Наши решения при / = 0 точно соот-
соответствуют антисимметричным решениям для одномерного случая.
Задача 64. Потенциал Вуда — Саксона
Сферически симметричная потенциальная яма описывается
потенциалом
1,5 r/R
r-R
F4.1)
'. R. Требуется определить энер- ~°'г
гию связанных состояний с/ = 0.
-0,4
Замечание. Этот потенциал использовал-
использовался для описания взаимодействия нейтрона ^^g
с тяжелым ядром. Параметр R интерпрети- '
руется как радиус ядра, другой параметр а
характеризует толщину поверхностного слоя, _^^
внутри которого потенциал падает от значе-
значения V = 0 снаружи ядра до значения V — —Vo
внутри ядра (фиг. 37). При а = 0 получается -1,0
простая потенциальная яма со скачком по-
потенциала на поверхности ядра.
0,5
1.0
Решение. После введения обозна-
обозначений
Фиг. 37. Потенциал Вуда —
Саксона для случая a/R =0,2
и сферически симмегричная пря-
прямоугольная яма, соответствую-
соответствующая случаю a/R = 0
2тЕ
2mVn
F4.2)
уравнение Шредингера
йги , 2 du
2m

172 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
путем замены независимой переменной
У =	т=2	F4-3)
1 -\- e "
приводится к виду
К этому уравнению необходимо присоединить граничные условия
_R_ '	F4.4)
Х=0 при ух 1—е а w 1 (г = 0).
Полагая далее
%(y) = yv(l—y)^f(y)>	F4.5)
получаем
У Г 1— У УA—У) ]'	К '
Если параметры v иц выбраны таким образом, что
v = p, fAa=p3—у2,	F4.7)
то множитель при / в уравнении F4.6) не будет зависеть от у
и оно перейдет в гипергеометрическое уравнение
F4.8)
Соответствующее (ненормированное) решение имеет вид
X = yv(l-y)V1(|A + v, ц + v + l, 2v + l; у). F4.9)
Другое независимое решение можно получить, заменяя v на —v,
однако оно не удовлетворяет первому из граничных условий
F4.4). В случае больших значений г (у—«-О) равенство F4.9)
дает
х~ев«/«ехр(- |/2-^1
Таким образом, наше решение обладает правильным асимптоти-
асимптотическим поведением.
Другому граничному условию при (или вблизи) у=\ удов-
удовлетворить не так просто. Чтобы выяснить поведение решения

64. Потенциал Вуда—Саксона173
F4.9) вблизи точки у=\. мы воспользуемся соотношением
ГBу+1)Г(-2>г)
r(v_ft+[)r(v_f
1, 2ц + 1; 1— У)
U+V + 1 оу I 1- и)- ГBу+1)Г(-2>г)
в силу которого
ГBу+1)Г(-2|Д) A ...	ГBу+1)ГBц)
*~ Г(у-ц+1)Г(у-ц) U W + Г(у + ц+1)Г(у + ц) I1 »' •
F4.10)
Чтобы проанализировать это выражение, прежде всего заметим,
что у > Р, и поэтому величина |и, согласно равенству F4.7),
является чисто мнимой:
[i = i?i, Х = Уу2 — р*.	F4.11)
Таким образом, можно написать
х [A-1/)'*+ гBа)Г(р + 1-а)Г(р-^) п_ x-
х [U W +Г(-2й)Г(Р+1+й)Г(Р + й) { У}
Вблизи точки /- = 0 экспонента в правой части равенства F4.3)
очень мала, поэтому здесь мы можем приближенно положить
1—у«е-«/«.	F4.13)
Пусть далее по определению,
ip = argr(P + a)t i|) = argrBu).	F4.14)
Если теперь опустить множитель, стоящий перед квадратными
скобками в выражении F4.12), что мы вполне можем сделать,
так как наша функция не нормирована, и затем подставить туда
вместо 1—у выражение F4.13), то граничное условие нам даст
,-
е а +ехр \2п|) — 4йр — 2i arctg p ) е а =0.
Отсюда для собственных значений получается уравнение
exp U (^—2ф — arctg j)j cos (^ + i|5—2ф — arctg j) = 0,
или
М. + ^,_2ф —arctgj = Bn—D-5-, n = 0, ±1, ±2,...
F4.15)
Это уравнение действительно устанавливает связь между р и К,
а следовательно, и между Е ш Vo при данных значениях пара-
параметров R и а.

174 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Формула F4.15) все еще мало пригодна для практического
использования. Однако с помощью разложения1)
Г (х + iy) =
где С = 0,5772 . . .—постоянная Эйлера, мы можем получить для
аргументов <р и г|> Г-функций удобные для практических целей
явные выражения:
Подставляя эти выражения в уравнение F4.15), получаем
:j = im. F4.16)
Для дальнейшего анализа удобно ввести новые параметры:
[2т „, щи!'/. х_ JL_ Г?^| ? ll'7'
F4.17)
Эти параметры не зависят от толщины поверхностного слоя
а и поэтому сохраняют смысл в предельном случае простой
потенциальной ямы, когда а—>-0. Используя введенные пара-
параметры, уравнение F4.16) можно переписать в следующем виде:
F4.18)
При а—>¦ 0 сумма, стоящая в квадратных скобках, обращается
в нуль, и мы возвращаемся к уравнению для уровней энергии
в простой потенциальной яме:
11 Это разложение можно легко вывести из станаартных формул, которые
собраны в обычных математических справочниках, например у Янке —Эмде —
Лёша или Магнуса—Обергеттингера.

65. Изотропный осциллятор	175
Производя в F4.18) разложение в ряд по степеням малого пара-
параметра
<* = ¦%,	F4.19)
окончательно находим
~ f=tg \х-2а
% F) (>--^*у +
где в целях сокращения мы положили kR — x и v.R = y.
Задача 65. Изотропный осциллятор
Путем разделения переменных в сферических координатах
решить уравнение Шредингера для осцилляторного потенциала
V(r) =уш<в1г1.	F5.1)
Решение. Обычная процедура разделения переменных
и (г, §, Ф) = |х*('')У|.-(*, Ф),	F5.2)
приводит к радиальному уравнению
^^O.	F5.3)
При / = 0 оно оказывается идентичным уравнению одномерного
осциллятора (см. задачу 30). Когда же 1ф0, центробежные силы
отбрасывают частицу от центра, что ведет к существенно иным
решениям.
Вводя обозначения
^	%	^	F54)
можно записать уравнение F5.3) в стандартном виде
х, = 0.	F5.5)
Анализ поведения решения при г = 0 и г—>-оо, которое опреде-
определяется соответственно центробежным и осцилляторным членами,
наводит на мысль искать решение в виде
b = rl+le-Tr'v{r)	F5.6)
и по аналогии с одномерным случаем ввести вместо г новую

176 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
переменную
t = Xr2.	F5.7)
В результате получаем уравнение Куммера
общее решение которого имеет вид
] [ ' . 1 ,2 1 ,-BZ +1) /СС О\
I ~-\—— , ЛГ I '	(DO.о)
Наличие второго слагаемого в этом выражении несовместимо
при г = 0 с условием нормировки1', поэтому С2 = 0. Это сущест-
существенно отличается от задачи об одномерном осцилляторе, где
нет никаких граничных условий в начале координат.
Вырожденная гипергеометрическая функция при больших
положительных значениях ее аргумента ведет себя-как
^(а, с; г)-+Ц±е*га-с,
что с учетом равенств F5.6) и F5.8) приводит к экспоненциально
возрастающему решению
Этого возрастания можно избежать лишь тогда, когда а = —пг
(пг = 0, 1, 2, ...), т. е. в том случае, когда ги пер геометрический
ряд вырождается в полином степени пг. Таким образом, имеем
-пг.	F5.9а)
так что с учетом выражений F5.4) уровни энергии будут равны
^, nr = 0, 1,2	 F5.96)
Число пг можно назвать радиальным квантовым числом. Система
энергетических уровней начинается с нулевой энергии 3/Jm (это
соответствует наличию трех степеней свободы в нашей задаче) и
так же, как в случае одномерного осциллятора, все уровни рас-
располагаются эквидистантно:
?B = ftco(n4-!),	F5.10)
где
п = 2пг + 1.	F5.11)
1( При / = 0 второе слагаемое также нормируемо, однако его присутствие
приводит к расходимости интеграла, соответствующего среднему значению
кинетической энергии (см. также задачу 62).

	66. Вырожденные состояния изотропного осциллятора	177
Собрав вместе результаты, содержащиеся в формулах F5.6),
F5.8) и F5.9а), приведем окончательное выражение для собст-
собственных функций
и (г, ft, <p)=C/VTVi(—«r, ' + i; Kr*)Y'.m(®> Ф). <65'I2>
где постоянную С следует определять с помощью условия нор-
нормировки.
За исключением основного состояния, для которого м = 0,
все энергетические уровни вырождены, так как, согласно фор-
формуле F5.11), четные «можно получить 1/2п-\-\ различными спо-
способами, а нечетные п можно получить Va(" + 1) способами. Кроме
того, следует учесть, что для каждого значения / имеется 2/-f 1
различных значений т, заключенных между —/ и -f/, что приво-
приводит к дополнительному увеличению кратности вырождения.
Замечание. Полученные здесь результаты целесообразно сравнить с резуль-
результатами задачи 42, где был рассмотрен изотропный осциллятор на плоскости.
Задача 66. Вырожденные состояния изотропного осциллятора
Показать, что собственную функцию изотропного осцилля-
осциллятора с квантовыми числами 1 = 2, /л = 0, пг= 1 можно сконструи-
сконструировать как линейную комбинацию вырожденных функций, полу-
полученных разделением переменных в прямоугольных декартовых
координатах.
Решение. В прямоугольных декартовых координатах уравне-
уравнение Шредингера для изотропного осциллятора можно записать
в виде
[0	]O,	F6.1)
где
К] -\- К% ~\- «з ^ К ,
a k% и К обозначают те же величины, что и в предыдущей
задаче. С помощью разделения переменных
и(х, у, z) = f(x)g(y)h(z)	F6.2)
для каждой из независимых переменных х, у и z мы получаем
простые осцилляторные уравнения, первое из которых, например,
имеет вид
¦j? + (*i-bV)/ = 0.	F6.3)
Соответствующие собственные значения равны Aco^j + Va). a nt—

178 //• Задачи без учета спина. Г. Сферически симметричные потенциалы
целое неотрицательное число. Как было показано в задаче 30,
(ненормированная) собственная функция уравнения F6.3) при
четных п1 = 2п равна
; kx*y	F6.4a)
F6.46)
а при нечетных nl = 2n-\-\ равна
То же самое имеет место и для функций g (у) и h (г) (соответст-
(соответствующие квантовые числа мы будем обозначать посредством п2 и
п3), поэтому полная энергия должна быть равна
F6.5)
С другой стороны, при разделении переменных в сферических
координатах, как мы видели,
(|)	F6.6)
следовательно, в состоянии с квантовыми числами 1 = 2, т = 0,
пг~\ мы имеем 2^-f/ = 4, а соответствующая собственная функ-
функция, согласно формуле F5.12), равна
u = r'ie~r\F1 ( — 1, -j; Xr2) Я2 (cosd).	F6.7)
Теперь наша задача состоит в том, чтобы записать выраже-
выражение F6.7) в прямоугольных декартовых координатах и результат
выразить в виде линейной комбинации функций /(x)-g{y)-h(z),
для которых
«!+•«, + «, = 4.	F6.8)
Мы имеем
-Y^-jy' + z'). F6.9)
В каждом произведении fgh присутствует один и тот же экспо-
экспоненциальный множитель, который в дальнейшем, при сравнении
функций, мы опустим. Так как «1^4, то в формулах F6.4а) и
F6.46) первый параметр п вырожденной гипергеометрической
функции не может превосходить 2. Эти же соображения, разу-
разумеется, относятся и к гипергеометрическим функциям, через
которые выражаются функции g(y) и h(z). Поэтому нам при-

66. Вырожденные состояния изотропного осциллятора
179
дется иметь дело лишь со следующими полиномами:
1,1;
2
F6.10)
l, ¦§-; Ь
Как показано в нижеследующей таблице, число 4 [см. фор-
формулу F6.8)] можно разбить на сумму трех целочисленных ела-
nt n, пг
0 0 4
0 1 3
0 2 2
0 3 1
0 4 0
1 0 3
1 1 2
1 2 1
1 3 0
2 0 2
2 1 1
2 2 0
3 0 1
3 1 0
4 0 0
Собственные функции прн разделении переменных в пря-
прямоугольных декартовых координатах
(экспонента опущена)
4
{1_2^)A-2^)
yz^l-lly^
1-4^ + 4 XV
XZ I1 ~~ *Ау \
/ Q \
A — 2Л.х2) A — 2Л.г2)
4,A-4**)
3
Умножается
на коэффи-
коэффициент
—6/28Л
0
-1/28Л
0
3/28А,
0
0
0
0
—1/28А,
0
2/28А,
0
0
3/28Х

180 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
гаемых пятнадцатью различными способами. Так как интересую-
интересующий нас полином F6.9) содержит только четные степени пере-
переменных х, у и г, то 9 функций, полученных разделением пере-
переменных в прямоугольных декартовых координатах, в которых
фигурируют нечетные степени х, у и z (это те функции, где
хотя бы одно из трех чисел п1г n2, ns нечетное), в искомую
линейную комбинацию вклада не дадут. В последнем столбце
таблицы мы приводим коэффициенты, на которые необходимо
умножить соответствующие функции для того, чтобы их сумма
оказалась равной полиному F6.9). Так как в нашем распоря-
распоряжении имеется всего 6 слагаемых, а полином F6.9) содержит
10 членов, то у нас остается еще 4 соотношения, которые
можно использовать для контроля правильности вычислений.
Замечание. Сопоставьте этот анализ с результатами задачи 42, где разби-
разбирался вопрос о вырожденных состояниях изотропного осциллятора на плос-
плоскости.
Задача 67. Проблема Кеплера
Решить уравнение Шредингера для связанных состояний элект-
электрона в поле бесконечно тяжелого точечного ядра с зарядом Ze.
(При Z=\ мы имеем дело с теорией атома водорода.)
Решение. Введя обозначения
"=^- -W-ZE»/Zff	№7Л)
и используя обычный способ разделения переменных
и = 7-Х»И^.«(*, Ф),	F7.2)
мы приходим к радиальному уравнению Шредингера вида
-0.	F7.3)
Это уравнение имеет регулярную особую точку при г = 0 и
существенно особую точку при г = оо. Вблизи точки г = 0 оно
решается путем разложения в ряд, что приводит к решениям,
которые пропорциональны либо rl+1, либо г~1. При г—»• оо его
решения ведут себя как е±чг. Только те решения, которые при
малых значениях г ведут себя как rl+l, а при больших значе-
значениях г как e~vr, можно нормировать в соответствии с условием1'
(r)dr=*l.	F7.4)
" Решение с поведением типа г~1 при / = 0 также может быт*> нормиро-
нормировано, однако в этом случае теряет смысл интеграл, описывающий среднее зна-
значение кинетической энергии, поэтому указанное решение тоже необходимо отбро-
отбросить (см. задачу 62).

67. Проблема Кеплера	181
Таким образом, мы должны положить
Xi = rl+le-vf(r).	F7.5)
Если теперь вместо г ввести безразмерную переменную
z = 2vr,	F7.6)
то придем к дифференциальному уравнению
z/* + B/ + 2 —z)/' — (/+1-х)/= О,	F7.7)
которое представляет собой уравнение Куммера. Нам необходимо
рассмотреть только одно решение этого уравнения, а именно
/»=Л('+1 — х, 2/+ 2; г),	F7.8)
так как только оно регулярно в начале координат, а о гранич-
граничном условии мы уже позаботились, введя посредством форму-
формулы F7.5) новую неизвестную функцию. При больших значе-
значениях z вырожденная гипергеометрическая функция F7.8) ведет
себя как ez, что находится в противоречии с условием норми-
нормировки. Противоречие не возникает лишь в том случае, когда
она вырождается в полином, т. е. когда
/+ 1__х = _ пп пг = 0, 1,2		F7.9)
Так как величина х в силу F7.1) связана с энергией, то урав-
уравнение F7.9) определяет искомые собственные значения. Если
ввести главное квантовое число
n=nr + l+l,	F7.10)
то мы получим х = м или
?»=-?pif-	F7Л1)
Энергетические уровни вырождены, так как каждому из них при
п > 1 принадлежит несколько собственных функций:
ип. i,m = Crle-1>r1F1(l + l — n, 21 + 2; 2уг) У,, т (¦&, ср), F7.12)
различающихся значениями орбитального квантового числа
/ = 0, 1, ..., п—1 и магнитного квантового числа /л = 0,
±1, •••, ±/- Таким образом, для каждого значения п всего
имеется
]?B/+1) = гса	F7.13)
собственных функций. Только основное состояние с квантовыми
числами п—1, 1 — 0, т = 0 оказывается невырожденным.
Радиальные части волновых функций, нормированные в соот-

182 //. Задачи без t/нета спина. Г. Сферически симметричные потенциалы
ветствии с условием F7.4) для значений п = 1, 2 и 3, приведены
в таблице на стр. 183. Следует иметь в виду, что в ней мы
пользуемся атомными единицами (m=l, e—l, h=\), поэтому
Z
—
V
F7.14)
Графики некоторых функций |х/.пг|а приведены на фиг. 38.
Кроме того, мы даем сводку явных выражений сферических
о, г
О,!
1 г з 4 5
Фиг. 38. Функции
/О
15
го
Z5
п I, описывающие радиальную плотность вероят-
вероятности в случае атома водорода.
функций, нормированных согласно условию
Замечание. Относительно взаимного движения ядра и электрона около их
общего центра масс см. задачу 150. Вопросы тонкой структуры и реляти-
релятивистские эффекты разобраны в задачах 202 и 203. Теория строения атомов
с двумя и более электронами, основанная на водородоподобных волновых
функциях, рассматривается в задаче 154 и ряде следующих за ней задач.

Таблица водородоподобных функций
а) Радиальные части волновых функций для л=1, 2, 3, 4
n
1
2
3
4
i
0
0
1
0
1
2
0
1
2
3
"r
0
1
0
2
1
0
3
2
1
0
Символ
Is
2s
3s
3p
3d
4s
4p
"
4/
* 7я/, -Zr/2 (л • 7 \
1
/24
2 7*/,rc-Zr/3 (, 2 2 Л
3/3 V 3 27 У
27 У Т Г в V " ГУ
4 77/,гз,-2г/3
81/30
1 77/.гзс-2г/4 Л 1 z \
64/5 V 12 У
1 „V» 4 -Zr/4
768/35
б) Угловые части волновых функций для / = 0, 1, 2, 3
0
1
2
0
0
±1
0
±1
¦',.-«>¦ я»
1
/4л"
/4cosd
1/ —~~ I ^i^ wo \S	^Г 1
К 8яSI" °S

184 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
I
3
m
0
±>
±2
±3
4- l/ — Ecos3d — 3cos
4 г я
±4-1/ — sin 0E cos2 fl-
or Я
— J/ ^ sin cos
8 г я
Продолжение таблицы
в)
-i,.±*
'ф
Задача 68. Потенциал Хюльтена
Решить уравнение Шредингера и определить уровни энергии
в случае так называемого потенциала Хюльтена
V(r) = -V»TJbe^T«	F8Л>
при / = 0.
Решение. .Мы будем пользоваться безразмерной переменной
x = -j	F8.2а)
и введем обозначения
a=-^fl>0' P2 = -#«2>0-	F8-26)
причем будем считать, что а > 0 и р > 0. Радиальное дифферен-
дифференциальное уравнение для функции % (г) = rty (r) теперь можно за-
записать в виде
-Л-\-\—а2 + Р2т—	Их — О-	F8.3)
Замена переменной
е-х = у	F8.4)
позволяет сделать коэффициенты уравнения рациональными функ-
функциями:
= 0.	F8.5)
Мы должны решить это уравнение при граничных	условиях:
Х = 0 при у = 0, г-ч-оо,	F8.6а)
Х = 0 при у=\, г = 0.	F8.66)
Решение находится с помощью подстановки
^ = t/«(l—y)w(y),	F8.7)

68. Потенциал Хюльтена	185
в результате которой уравнение F8.5) приводится к гипергеомет-
гипергеометрическому уравнению
1/A— y)w" + [{2а+\) — Bа+ 3)|/] а/ — Bа+1 — р')ви = О. F8.8)
Общее решение этого уравнения имеет вид
, a+1 — у, 2a+U y) + By-f*x
,—a+1—у, —2a+l; у),	F8.9)
где
Первое граничное условие F8.6а) при а>0 дает В — О. Вто-
Второе граничное условие F8.66) требует более тщательного ана-
анализа в окрестности точки у — 1. Это нетрудно сделать, восполь-
воспользовавшись тождеством
а+1-7, 2а' + 1; */) =
-У)' Г (аГ+2Г++7)'гГ(«'+16-7) 8Л(^-Т+ е,а +7 + в, в; 1 -ц,
г
где е = 2(а'— а). Так как далее
2/г1 (а, Ь, е; 1 —у) =14— A —у) +. ..,
то первый член в точке г/=1 в пределе е -»• 0 становится равным
ГBа+1) ,. Г(е-1)
Поскольку
Г(е—1)	п„+1
первый член будет конечным, если и только если
а—у = — п, л = 0, 1, 2, 3 ....
В знаменателе второго члена имеется множитель
Г(а+1— у) — оо,
поэтому этот член обращается в нуль, за исключением случая
а—y = 0> когда он равен
и, следовательно, расходится при у-*\. Таким образом, мы при-
приходим к выводу, что при п = 0 граничное условие F8.66) не вы-
выполняется и поэтому собственные значения определяются из
условия
a — y= — n, /1=1,2,3...,	F8.10)

186 //. Задачи бгз t/чета спина. Г. Сферически симметричные потенциалы
а принадлежащие им (ненормированные) собственные функции
имеют вид
x = e-a*(l_e-')tFlBa+l+n, 1-я, 2о + 1; е~х). F8.U)
Отметим, что в этом случае гипергеометрический ряд вырождаете^
в полином относительно переменной е~х.
Из условия F8.10) получаем
2п
F8.12)
Кулоновский -?Ш-агу Потенциал
потенциал
3 2 1
Фиг. 39. Кулоновский потенциал и потенциал Хюльтена с одинаковыми син-
гулярностями.
Обратите внимание на сдвиг энергетических уровней
Так как а > 0, то по необходимости должно выполняться нера-
неравенство
Р2>л2.	F8.13)
Оио означает, что для существования дискретных уровней энер-
энергии размеры потенциальной ямы должны превышать некий мини-
минимум, определяемый равенством Р2=1. Точнее говоря, неравен-
неравенство F8.13) определяет число связанных состояний, реализующихся
в потенциальной яме данных размеров. Используя равенства

69. Молекулярный потенциал Кратцера
187
F8.26), соотношение F8.12) можно записать в виде
F8.14)
Потенциал Хюльтёна при малых значениях г ведет себя напо-
наподобие кулоновского потенциала
а при больших значениях г он убывает экспоненциально, поэтому
в хюлтеновскую потенциальную яму „вмещается" меньше связан-
связанных состояний, чем в кулоновскую. На фиг. 39 представлены
для сравнения оба потенциала при числовом значении р2 = 30:
кулоновский потенциал изображен слева, а потенциал Хюльтёна—
справа. Здесь же показаны энергетические уровни: кулоновские
уровни всегда располагаются ниже хюлтеновских, число которых
остается конечным (в нашем примере их всего пять).
Задача 69. Молекулярный потенциал Кратцера
Для анализа вращательно-колебательного спектра двухатом-
двухатомной молекулы Кратцер предложил использовать потенциал вида
КИ_-И,(А-^) F9.1) щ
с минимумом V (а) =— D (фиг. 40).
Решить уравнение Шредингера,
считая, что один из атомов зна-
значительно тяжелее другого (при-
(примером может служить молекула
HJ). В этом предположении тя-
тяжелый атом можно считать непод-
неподвижным и связать с ним начало
системы координат (в противном
случае нам пришлось бы решать в
эквивалентную одночастичную за-
задачу—см. подробности В задаче Ф и г- 40- Молекулярный потен-
у
150).
циал Кратцера.
Решение. Движение легкого атома массы т описывается урав-
уравнением Шредингера
|[	(fl^)]	F9.2)
F9.3)
допускающим разделение переменных

188 П. Задачи без учета спина. Г. Сферически симметричные потенциалы
Используя безразмерные величины
г Q,	2/тш2 г, о 2та2
Х Р	? Y
F9-4)
где у > 0, а р в случае связанных состояний действительно и
также больше нуля, мы получаем для радиальной части волно-
волновой функции %( дифференциальное уравнение вида
г==0.	F9.5)
Оно имеет существенно особую точку при х — оо, вблизи которой
нормируемые решения, соответствующие связанным состояниям,
ведут себя как е~&х, и другую особую точку при % = 0, где
X, ~ хх, а показатель К является корнем характеристического
уравнения
-1) = Y2
Из двух корней этого квадратного уравнения на^ нужен лишь
положительный корень:
Так как Я>1, то волновая функция обращается в нуль при
г = 0, что объясняется наличием сильного отталкивания между
атомами (см. фиг. 40). Приведенные соображения наводят на
мысль положить
F9.7)
Подстановка выражения F9.7) в уравнение F9.5) приводит к
уравнению Куммера общего вида для вырожденной гипергеомет-
гипергеометрической функции:
f.	F9.8)
Стандартная форма уравнения Куммера получается после замены
х на г = 2$х. Таким образом, имеем
-^, 2Я; 2Рх).	F9.9)
Теперь мы по отдельности разберем случаи отрицательных и по-
положительных энергий.
а. Отрицательные энергии. Для связанных состояний р > 0 и
решение (нормировка произвольная) принимает вид
" -	Х	F9.10)
Для больших значений х вырожденная гипергеометрическая функ-
функция пропорциональна е2$х, поэтому функция %t неограниченно
возрастает при %-»оо, если функция 1Fl не вырождается в поли-

69. Молекулярный потенциал Кратцера	189
ном. Когда же такое вырождение имеет место, функция %{ стре-
стремится к нулю при х -» оо и решение действительно становится
нормируемым. Следовательно,
*.—? = —о, о = 0, 1, 2		F9.11)
Соотношение F9.11) определяет собственные значения р и при-
приводит к следующей формуле для энергетических уровней:
р	*!?.
эту формулу с учетом соотношения F9.6) можно записать в виде
Остановимся на анализе этой формулы несколько подробнее.
Так как для большинства молекул 7^>1, то выражение F9.12)
можно разложить в ряд по степеням 1/у. Это даст
F9.13)
Выражение F9.1) для потенциала V (г) также можно разложить
вблизи минимума в точке г = а:
I/(,-) = ?> <Lz?)!_ d.	F9.14)
Отсюда для классической частоты малых гармонических колеба-
колебаний получается выражение
со= j/^.	F9.15)
Заменяя в формуле F9.13) величины D и у на частоту со и мо-
момент инерции
в=та\	F9.16)
получаем
2в
Первый член в этом выражении является постоянной и непосред-
непосредственно не сказывается на положении спектральных линий, хотя
его значение и можно вычислить на основании спектроскопичес-
спектроскопических данных. Второй член описывает колебательные уровни, ха-
характеризующиеся колебательным квантовым числом у. Третий член

190 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
соответствует вращательным уровням с постоянным моментом
инерции [так как (/ -)-1/2J = / (/ + 1) -f-1/4, то это слагаемое содер-
содержит еще один постоянный член]. Четвертый член ведет к неко-
некоторому понижению колебательных уровней, обусловленному
ангармоничностью потенциала. Наконец, пятый член характери-
характеризует связь между вращениями и колебаниями, что опять-таки
обусловлено ангармоничностью потенциала. Разумеется, наше
разложение оказывается тем хуже, чем больше квантовые
числа, особенно колебательное квантовое число v, и поэтому им
нельзя пользоваться в случае энергий, близких к энергии дис-
диссоциации (у-->оо). Однако для таких энергий вся модель вообще
теряет смысл из-за нефизического характера поведения потенциала
при очень больших и очень малых г.
В заключение приведем формулу для энергии диссоциации
молекулы, получающуюся из выражения F9.17) при у = 0, / = 0:
?дясс = |вШ«-1Л(о+^ + т^ + ... . F9.18)
б. Положительные энергии. В этом случае Р — чисто мнимая
величина. Если ввести волновое число k, то, как показывает
определение, мы можем написать р = — ika и, следовательно,
Рх= — ikr. Вместо решения F9.10) теперь имеем
-fg, 2к -2ikr).	F9.19)
(Здесь нормировка по-прежнему произвольна). Как и раньше,
в точке г = 0 волновая функция обращается в нуль. Ее асимп-
асимптотика определяется с помощью известной формулы
которая выполняется на всей комплексной плоскости г с разре-
разрезом вдоль положительной мнимой полуоси. Применение этой
формулы к выражению F9.19) после довольно длинных преоб-
преобразований дает
, cos (kr +Jiln2&--^-ii,),	F9.20)
где фазовый угол т], определяется соотношением
e '*=—)	з-f,	F9.21)
г x—i 4-
a Cj—(не представляющая интереса) нормировочная постоянная.
С точностью до логарифмического члена радиальные части
волновых функций F9.20) оказываются периодическими, когда

70. Потенциал Морса
191
расстояние между атомами велико. Логарифмическое искажение
периодичности обусловлено тем, что рассматриваемый потенциал
асимптотически подобен кулоновскому потенциалу (см. задачу 111).
Интерпретируя потенциал Кратцера как потенциал взаимодейст-
взаимодействия пары ионов, каждый из которых имеет электрический заряд е,
мы находим, что 2?>а = е2 и y2/ka = e2/Av (где v—скорость), и, таким
образом, действительно можем отождествить логарифмический
член формулы F9.20) с логарифмическим членом в кулоновском
поле.
Замечание. Потенциал Кратцера сыграл большую роль на ранней стадии
развития квантовой механики, так как он позволял получать точные решения
даже в том случае, когда / > 0. Однако этот потенциал гораздо менее физичен,
чем потенциал Морса, который тем не менее все еще достаточно прост, чтобы
с его помощью можно было построить теорию рассматриваемого круга явле-
явлений. Потенциалу Морса будут посвящены две следующие задачи. Полученные
там результаты, по крайней мере для связанных состояний, можно будет
сравнить с результатами, найденными нами в случае потенциала Кратцера.
Литература
Kratzer A., Zs. Phys., 3, 289 A920) (классическая трактовка задачи).
Fues E., Ann. Phys., 80, 367 A929) (квантовая трактовка задачи).
Задача 70. Потенциал Морса
Колебания двухатомной молекулы прекрасно описывает потен-
потенциал Морса
V(r) = D(e-™*—2e-ax), х = ^—^-.	G0.1)
Решить уравнение Шредингера для связанных состояний при / = 0.
Для количественного анализа воспользоваться приведенными ниже
экспериментальными данными для трех типичных молекул
Молекула
на
НС1
h
	Г .см
60,8296
10,5930
0,0374
D, см->
38292
37244
12550
а
1,440
2,380
4,954
Здесь М—приведенная масса атомов, а энергия дана, как это
принято в спектроскопии, в см [Е (эВ) = Е (см) х 1,2398 х 10].
Решение. Начнем с небольшого обсуждения свойств потен-
потенциала, который впервые Евел Морс (фиг. 41). На больших
расстояниях он соответствует силам притяжения, в точке х = 0

192 П. Задачи без учета спина. Г. Сферически симметричные потенциалы
(г = л0) у него имеется минимум, равный—D, и, наконец, при
дальнейшем сближении атомов он приводит к сильному оттал-
отталкиванию. В окрестности точки л; = 0 потенциал G0.1) можно
разложить в ряд
V(г) = ?>(—1 -\-а*х%...) = — D + y Мо)а(г—/¦0J + ..., G0.2)
где
2?><х»
т-г/щ
Фиг. 41. Потенциал Морса для молекулы НС1.
Пунктирная кривая — аппроксимирующая парабола.
Таким образом, для низких колебательных уровней энергети-
энергетический спектр, как можно ожидать, будет не слишком отличаться
от спектра гармонического осциллятора
G0.3)
jj, v=0, I, 2, ...
с колебательным квантовым числом v. По мере роста энергии
почти эквидистантные уровни становятся более плотными, что
обусловлено ангармоничностью потенциала, не учтенной нами
при написании формулы G0.2).
Введем теперь обозначения
G0.4)
где по определению р>0 и v>0i и перейдем от переменной г
к переменной х, тогда радиальное уравнение Шредингера для
случая / = 0 запишется в виде
+ (— Ра + 2v2e-aj(—y2e~ ««*) Хо = 0.
G0.5}
Чтобы сделать коэффициенты этого дифференциального уравнения
рациональными функциями, надо перейти к новой независимой
переменной, которая простым образом выражается через функ-

70. Потенциал Морса			193
цию е~ах. Если в качестве такой переменной взять выражение
0 = ?*-<", ? = -^,	G0.6)
то уравнение G0.5) будет выглядеть особенно просто:
У% + УХо + ( -11- +1У —f У) X» = 0.
Точки (/ = 0 и г/=оо являются особыми точками этого уравне-
уравнения: в окрестности точки (/ = 0 решение Хо должно быть пропор-
пропорционально ух, где К = ± Р/а, а на бесконечности должно быть
П. Таким образом, если положить
и ввести параметры
c = 2-?+l и fl = |c_J-f	G0.7)
то функция F (у) будет удовлетворять дифференциальному урав-
уравнению Куммера для вырожденной гипергеометрической функции
в стандартной форме, поэтому полное решение уравнения G0.5)
можно записать в виде
/'y{AllF1(a, с; y) + AtlFl(a-c + l, 2-е; y)
G0.8)
Чтобы удовлетворить граничному условию %в = 0 при г—>-оо или
у = 0, необходимо положить Л2 = 0, так как степень
в которую возводится у, оказывается отрицательной. Значение
постоянной А1 фиксируется условием нормировки.
Второе граничное условие %о = 0 при г = 0 (х = —1) или
y = y, = Ua	G0.9)
приводит к соотношению
А (а, с; г/0) = 0;	G0.10)
из него должны определяться собственные значения. Это соот-
соотношение является весьма сложным трансцендентным уравнением,
о точном решении которого трудно сказать что-либо определен-
определенное. Однако для всех реальных молекул значения параметров а
и 7 таковы, что мы можем воспользоваться очень простым, но
тем не менее весьма хорошим приближением.
В нижеследующей таблице представлены числовые значения
ряда величин для трех типичных молекул, полученные на осно-
основании данных, приведенных в условии задачи.
7 № 1050

194 //. Задачи без t/чета спина. Г
Сферически симметричные потенциалы
НС1
V
25,09
59,30
579,51
а
1,440
2,380
4,954
Е
34,9
49,8
234
Уа
147
539
33200
0./Е
4,22
10,80
142
а
5,6
270
31240
Мы видим, что во всех случаях г/0 ^> 1. Чтобы можно было вос-
воспользоваться асимптотическим выражением для гипергеометри-
гипергеометрической функции G0.10), величина \уа\ должна быть достаточно
велика по сравнению со значениями параметров |а\ и \с\. Согласно
формуле G0.7), оба параметра зависят от величины р, т. е. от
собственных значений, которые нами пока еще не определены.
Однако мы знаем, что во всяком случае должно выполняться
неравенство
— D<E<0, или 0<р<7,	G0.11)
так как энергия связанного состояния должна быть отрицательной
и не может быть ниже минимума потенциальной энергии. Это
ограничивает область изменения параметров а и с интервалами
1<с<1 + ? и \{\ — 1)<а<\.	G0.12)
Из таблицы видно, что ? всегда остается значительно меньше у0
(это верно даже в наиболее неблагоприятном случае молекулы
водорода). Таким образом, для реальных значений у0 у нас есть
все основания воспользоваться асимптотическим разложением:
xFx(a, с; г/0) » е-'™ Г ^а) г/0~а Л-Щ^еу<~с = 0- G0.13)
Полагая в уравнении G0.13)
и ип = ?еа,
можем записать его в виде
или
Г(а) = — einaT(a
Кроме того, мы имеем
-«-in с).
1
-«-ш о j. = о,
G0.14)
и так как, согласно табличным данным, даже для водорода ве-
величина ? настолько велика, что а + ?> 17,95, то мы можем
применить к функции ГA/аA+С)) формулу Стирлинга. Это дает

70. Потенциал Морса	 195
оценку	__
\Y{a)\>VTne°,
причем показатель G, определяемый выражением
G0.15)
мы можем вычислить, не имея никаких дополнительных сведений
о собственных значениях; соответствующий цифровой материал
приводится в последнем столбце нашей таблицы. Даже в наибо-
наиболее неблагоприятном случае молекулы водорода мы имеем
| Г (а) | > 675. Следовательно, во всех случаях величина | Г (а) |
очень большая, поэтому можно считать, что аргумент Г функции а
практически совпадает с одним из целых отрицательных чисел
(напомним, что а < 1/2). Таким образом, получаем
а = —и, у = 0, 1, 2, 3, ... .	G0.16)
Следует иметь в виду, что ряд чисел v не является неограни-
неограниченным, так как условие
означает
о<1(?-1).	G0.17)
С помощью формул G0.16), G0.7) и G0.4) теперь получаем
2 У	V 2
и, следовательно, энергия выражается через колебательное кван-
квантовое число в виде
^{{i)i^y\ G0Л8)
Первые два члена в этой формуле полностью согласуются с фор-
формулой G0.3) для гармонического осциллятора, поскольку
1Мг%
последний же член представляет собой поправку на ангармонич-
ангармоничность колебаний. Если полученную формулу записать в виде
G0-19)
то на основании неравенства G0.17) можно заключить, что ан-
ангармонический член всегда меньше гармонического.
Литература
Morse Р. М., Phys. Rev., 34, 57 A929); см. также замечание в конце
следующей задачи.

196 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Задача 71. Ротационные поправки к формуле Морса
Вращательная энергия молекулы обычно значительно меньше
ее колебательной энергии, поэтому в предыдущей задаче она
вообще не учитывалась. Вращательную энергию можно включить
в рассмотрение, либо прибегая к теории возмущений, либо за-
заменив истинный центробежный потенциал некоторым прибли-
приближенным выражением, позволяющим без существенных новых
математических осложнений ввести величины р и у из преды-
предыдущей задачи. Требуется проанализировать второй из указанных
выше способов.
Решение. Если 1=?0, то к потенциалу в радиальном уравне-
уравнении Шредингера необходимо добавить центробежный член
, Pi (l + l)	j n
V	2Mr* '	A '
Используя обозначения, принятые в предыдущей задаче, его
можно записать в виде
^Ь()8	G1-2)
Таким образом, этот член, если отбросить случай неоправданно
больших /, крайне мал по сравнению с величиной D, так как
значения г не слишком отличаются от г0. Даже в мало благо-
благоприятном случае молекулы водорода, когда у лишь слегка пре-
превосходит 25, наше заключение остается в силе по крайней мере
для тех /, которые существенно меньше 25. Следовательно, мы
можем рассматривать центробежный потенциал в качестве малой
поправки практически во всех случаях.
Расстояние г между атомами, конечно, не является постоян-
постоянным, однако даже для довольно высоких колебательных уровней,
как показывает детальное исследование собственных функций
G0.8), оно не слишком отличается от равновесного расстояния г0.
(Кстати, для классических точек поворота имеет место неравенство
х2 = Bу+ 1)/Y°sa<^ 1.) Таким образом, если разложить потенциал
G1.1) вблизи точки /"=/¦„ в ряд по степеням величины х—(г—ro)lro,
-4^ + ...), G1.3)
то в этом разложении нам достаточно будет учесть несколько
первых членов. Теперь заменим потенциал V (г) выражением
у2	0	1	2
где мы положили
Зо	л	с.	10
г ¦ - i	j_	г	г"=-	I	^715^

	71. Ротационные поправки к формуле Морса	197
Так как выражение G1.4) разлагается в ряд в соответствии с
формулой
то оно отличается от выражения G1.3) лишь членами порядка
х3 и выше. Используя потенциал V' вместо истинного центро-
центробежного потенциала V, мы можем записать радиальное уравнение
Шредингера при /^0 в виде
dx*
где
G1.7)
Это дифференциальное уравнение по форме почти совпадает с
уравнением G0.5), только вместо постоянных р и у в нем стоят
соответственно постоянные pt и ylt y3, поэтому для его решения
можно воспользоваться той же процедурой, что и раньше. Введем
новую переменную
у = ^е-ах, U = ~.	G1-8)
а также параметры
с\Л+1, «=-И-Ж	G1.9)
и найдем решение
которое приводит к уравнению для определения собственных
значений
1F1(a, с; г/0) = 0, где г/0 = ?2еа.	G1.11)
Так как параметры а и с отличаются от параметров а а с только
малыми поправками, то все качественные соображения относи-
относительно приближенного решения этого трансцендентного уравнения
остаются в силе и в данном случае. Следовательно,
a = — v, у = 0, 1, 2, 3, ...	G1.12)
и в силу равенств G1.9)
— Р? = — \~—a(v + i)Y-	G1.13)
Отсюда видно, что в формуле для уровней энергии	мы должны

198 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
величину у заменить величиной
а величину р*2—выражением, стоящим в правой части равенства
G1.13). С учетом формулы G1.7) это дает
Выражая здесь постоянные С{ через а в соответствии с опреде-
определениями G1.5), мы окончательно получаем следующую формулу
для уровней энергии:
В первой строке здесь стоят в точности те же члены, что и по-
полученные нами в предыдущей задаче: глубина потенциальной ямы
(—D), гармонический член и антигармоническая поправка. Во
второй строке стоят три новых члена: вращательная энергия,
соответствующая фиксированному расстоянию между атомами г0,
член, обусловленный связью колебаний с вращениями, и, наконец,
нелинейная поправка к вращательным уровням. Два последних
члена дают отрицательный вклад, так как большим квантовым
числам соответствуют такие состояния, в которых среднее рас-
расстояние между атомами несколько превосходит равновесное рас-
расстояние /¦„.
Замечание. Одно из возможных обобщений потенциала Морса примени-
применительно к колебаниям двухатомных молекул рассмотрено в работе Флюгге
[Flugge S., Walger P., Weiguny A., Journ. Molec. Spectrosc, 23, 243 A967)].
Задача 72. Потенциал Юкавы
Дан потенциал Юкавы
УМ —У.-^Г".	G2.1)
соответствующий наличию притяжения между двумя частицами
(например, между двумя нуклонами). В рамках вариационной
процедуры Ритца найти для случая / = 0 оптимальное решение,
используя пробную волновую функцию
и = ±х(П,	G2.2)

72. Потенциал Юкавы	199
где
х
а а —вариационный параметр Ритца. При каком минимальном
размере потенциальной ямы возможно существование связанных
состояний? (В системе центра масс проблема сводится к одно-
частичному уравнению Шредингера с приведенной массой т*,
см. задачу 150.)
Решение. Прежде всего найдем постоянную С с помощью ус-
условия нормировки
о
Отсюда имеем
С = 2а8/..	G2.3)
Среднее значение энергии Е представляет собой сумму двух
интегралов:
hYdr
°.	G2.4)
Г е~г/а
0
Элементарное интегрирование дает
Для дальнейшего удобно ввести безразмерные переменные
р = 2аа, K = 2-^fV0.	G2.6)
Первая из них представляет собой отношение среднего радиуса
потенциальной ямы к среднему радиусу той области, где волно-
волновая функция заметно отличается от нуля, вторая же характери-
характеризует эффективный размер потенциальной ямы. Теперь мы можем
преобразовать равенство G2.5) к виду
<72-7)
Используя в качестве вариационного параметра вместо величи-
величины а величину р, получим оптимальное решение из условия
dE/dp = 0, которое сразу же дает
Если теперь выражение G2.8) подставить в формулу G2.7), то

200 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
оптимальное значение энергии будет равно
Е= ур*(р— 1) ^	^2.9)
Так как величина р по определению положительная, то связан-
связанные состояния могут существовать только в том случае, когда
р > 1 или, как это следует из формулы G2.8), когда К > 2.
В рассматриваемом приближении этим неравенством и опреде-
определяется минимальный размер потенциальной ямы, в которой воз-
возможно существование связанных состояний. Ниже мы приводим
цифровые данные, полученные по формулам G2.8) и G2.9).
р
,00
,05
,ю
,15
,20
,30
,40
К
2,000
2,025
2,050
2,08
2,11
2,18
2,24
-E/V,
0
0,0017
0,0036
0,0058
0,0081
0,0135
0,0198
р
1,50
1,60
1,70
1,80
1,90
2,00
2,50
К
2,32
2,39
2,!б
2,54
2,62
2,70
3,12
-E/V,
0,0270
0,0349
0,0438
0,0532
0,0633
0,0740
0,1364
Замечание. Использованное приближение является довольно хорошим.
Если пробную функцию G2.1) заменить менее удачной функцией
то вариационная процедура даст
К 2(Р+1N
F--V рЪ (р~3)
°8(р+1M-
Очевидно, в этом случае связанные состояния могут существовать только при
условии р > 3, т. е. для значений
Задача 73. Изотопический сдвиг границы рентгеновского
излучения
В тяжелых атомах средний радиус орбиты /(-электрона при-
примерно в 100 раз превышает радиус ядра R. Следовательно, бла-
благодаря конечному размеру ядра энергетический уровень /(-элект-
рона должен претерпеть небольшое смещение. Рассчитать указан-
указанное смещение, считая электрический заряд равномерно распреде-
распределенным по объему ядра. Кроме того, определить изотопическое
смещение границы рентгеновского Л>излучения таллия (Z = 81)

73. Изотопический сдвиг границы рентгеновского излучения	201
для двух изотопов с атомными весами А = 203 и А = 205, поль-
пользуясь для радиуса ядра формулой
R = r0A1'; го= 1,2.10-» см. "	G3.1)
Эффектом экранировки /(-электрона пренебречь.
Решение. Энергия взаимодействия электрона с ядром имеет
вид
\7j; 7Л	G32)
Начнем с невозмущенной задачи о движении электрона в поле
точечного ядра (? = 0). В этом случае
V9 = — — (всюду),	G3.3)
Здесь и0 (г) и Ео — соответственно волновая функция и энергия
основного состояния кеплеровской проблемы (см. задачу 67).
Энергия возмущения равна разности
@, r>R,
* Ъ R\	G3.4)
Отсюда для сдвига энергетического уровня получаем
G3.5)
В области интегрирования показатель 2уг всегда меньше 2-у# «
»0,02, поэтому в подынтегральном выражении G3.5) мы можем
положить
e-2v« 1.
Используя далее величину r/R в качестве переменной интегри-
интегрирования, после элементарных вычислений получаем
где ао = Д2/(/ие2) означает боровский радиус.
В случае Z = 81 формула G3.3) дает
?„ = — Z2- 13,60 эВ = — 88,3 кэВ.	G3.7)
Полный сдвиг уровня АЕ для изотопа с атомным весом А = 203,

202 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
согласно формулам G3.1) и G3.6), оказывается равным
АЕ = | Еа |• 0,935 х Ю-4 = 8,25 эВ.	G3.8)
Изотопический сдвиг, т. е. разность между значениями АЕ в
случае А = 203 и в случае А + АЛ = 205 получается отсюда диф-
дифференцированием:
с dAE dR . , 2 ДЛ „
S = -lR-dAAA = -3^AE-
Для рассматриваемого примера это приводит к значению
5==0>00656А? = 6,14х10-'|?0|.	G3.9)
В то время как абсолютное значение энергии /(-оболочки,
согласно формуле G3.8), сдвигается вверх на вполне заметную
величину АЕ/Е ~ 10~4, разностный эффект для соседних изото-
изотопов S/E (который можно было бы обнаружить по расщеплению
/(-линии рентгеновского излучения, будь он достаточно велик)
составляет, согласно G3.9), менее одной миллионной.
Замечание. Эффект экранировки, конечно, значительно больше рассмот-
рассмотренных сдвигов, однако он совершенно одинаков для обоих изотопов. Экспе-
Эксперимент для границы /С-линии таллия дает значение 6310 ридберг, или 85,9 кэВ,
вместо нашего неэкранированного значения G3.7). Что касается изотопиче-
изотопического расщепления, то оно почти не зависит от этой поправки.
Задача 74. Основное состояние мезоатома
Вычислить энергию связи [i-мезона в ls-состоянии в поле того
же ядра (Z = 81), которое рассматривалось в предыдущей задаче.
а)	Почему в этом случае нельзя использовать применявшуюся
там теорию возмущений?
б)	Применить вместо теории возмущений вариационный метод
Ритца, взяв в качестве пробной функции выражение вида
u = C{l+ar)e-ar,	G4.1)
в котором считать величину а вариационным параметром.
Решение
а. Масса [i-мезона ц в 207 раз больше массы электрона т, и
вместо атомных единиц длины и энергии
а, = — = 5,29x10-" см, ?, = ^ = 27,236,
те2	п2
мы теперь имеем мюонные единицы
ai = ^L = 2,56x10"" см, ?1 = ^-?1 = 5,63 кэВ. G4.2)
В невозмущенном состоянии (точечное ядро) средние радиусы
электронной ajZ и (i-мезонной ajZ орбит в соответствующих

74. Основное состояние мезоатома	203
единицах в обоих случаях равны l/Z= 1,236 X 10~а. С другой сто-
стороны, радиус ядра /? = 7,05х 10~м см в атомных единицах равен
l,33xlO~4, а в мюонных 2,75х 10~2. Таким образом, радиус
электронной орбиты примерно в 100 раз превышает радиус ядра,
а радиус (л-мезонной орбиты равен примерно половине ядерного
радиуса. Следовательно, (л-мезон находится главным образом вну-
внутри, а электрон — вне ядра, поэтому (л-мезонная волновая функ-
функция определяется осцилляторным потенциалом внутри ядра, а
электронная волновая функция — кулоновским потенциалом вне
ядра.
Эти геометрические различия отражаются и на значениях
энергии. Отношение АЕ/\Е0\, равное для электрона [согласно
формуле G3.8)] 4/5 Z2(R/aj* = 0,935 х 10~4, в случае [i-мезона бу-
будет равно 4/6Z2 {Rja^f = 3,98, следовательно, в этом последнем слу-
случае „возмущающая" энергия не является малой по сравнению
с энергией невозмущенного состояния, более того, она значительно
превосходит ее.
б. Внутри ядра имеется осцилляторный потенциал
у (/•) =-^1 (ra	3R2),	G4.3)
для которого волновая функция основного состояния (см. за-
задачу 65) имеет вид
ДЮ fi
°Л3/>е~*ь ,	G4.4а)
где
^	G4.46)
in а а \
G4.4b)
а соответствующая энергия равна
с- 3 i	3Ze%
Приближенно решение G4.4а) должно быть верным при малых
значениях г, для которых его можно разложить в ряд
G4-5)
С другой стороны, при больших значениях г истинный потен-
потенциал стремится к нулю, а не к бесконечности, что имеет место
в случае потенциала G4.3), поэтому поведение истинной волно-
волновой функции будет определяться множителем
е-*\ где х2 = М^-	G4.6)
л2
и она будет убывать значительно медленнее, чем функция G4.4а).

204 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Разложение пробной функции G4.1) имеет теперь вид
сравнение этого выражения с разложением G4.5) позволяет ожи-
ожидать для а2 значение, близкое к (хсо/Й. Кроме того, пробная функ-
функция в отличие от G4.6) асимптотически ведет себя как е~аг, что
гораздо больше похоже на поведение истинной функции, чем
поведение функции G4.4а), но хорошего результата от пробной
функции можно, разумеется, ожидать только в том случае,
если а « х.
В мюонных единицах, как следует из формул G4.46) и G4.4в),
<в= 1,98х 103 и Ео — —1,46х 108 и, следовательно, в соответствии
с G4.6) х=54. Если для того, чтобы отождествить функции
G4.4а) и G4.1) при малых значениях г, мы положим а2 = |д,<в/Д,
то в принятых единицах а = [Лв будет равно 44,5, что не так
уж сильно отличается от х = 54. Таким образом, у нас есть все
основания ожидать, что пробная функция G4.1) обеспечивает хо-
хорошее описание реальной ситуации.
Заметим здесь же, что использованная далее вариационная процедура приво-
приводит к следующим значениям: а « 64 и х « 60.
Перейдем теперь непосредственно к приближенному вычисле-
вычислению энергии основного состояния, при этом мы всюду будем
пользоваться мюонными единицами ([х=1, Й=1, е = 1). Норми-
Нормируя функцию G4.1), получаем
С* = ^-	G4.7)
Вычисление среднего значения кинетической энергии дает
V2«dT = ^a2.	G4.8)
-потен = 4зх С /"V ~ ^_з) dr — 4л J rV у dr,
Что же касается вычисления среднего значения потенциальной
энергии
R
i	R
то оно оказывается несколько более затруднительным. Однако,
если перейти к безразмерным величинам
2ar = x, 2aR = K	G4.9)
и воспользоваться известной из анализа формулой
х"е-* dx ^п\ е-

75. Модель дейтрона с центральным взаимодействием	205
то это вычисление по существу становится элементарным. Окон-
Окончательный результат можно представить в форме
^	G4.10)
где
f(l) = (j}-28}-e-bB-? + ^ + 8O + Ul + l*y G4.11)
Условие Ритца,
дЕ-0
дк~~и>
приводит к уравнению для определения X
^ ?	G4.12)
где
Ф (Я,) = 216 + 216Я.+ 108Я2 + 33?i3 + 6Я4 + у V.
Для значения ZR = 2,23 из уравнения G4.12) мы получаем, что
X да 3,5. Этому соответствует минимизированное значение энергии
Е =—1808 мюонных единиц или Е — —10,18 МэВ.
Замечание. Более детально эта задача, а также некоторые имеющиеся здесь
тонкие эффекты рассмотрены Флюгге и Цикендратом [Fliigge S., Zickendraht W.,
Zs. Phys., 143, I A955)]. (Полезные сведения по данному кругу вопросов можно
найти в обзорной статье Д. Д. Иваненко и Г. Е. Пустовалова [УФН, 61, 27
A957)]. — Прим. ред.)
Задача 75. Модель дейтрона с центральным взаимодействием
Идеализируя реальную ситуацию, будем предполагать, что
взаимодействие между нейтроном и протоном описывается сфери-
сферически симметричным потенциалом
V(r) = — Ae-"a.	G5.1)
Решить уравнение Шредингера для эквивалентной одночастичной
задачи (см. задачу 150) в случае связанных состояний с 1 = 0
(дейтрон). Экспериментально установлено, что существует только
одно связанное состояние с энергией
? = —2,23 МэВ.
Найти связь между параметрами А я а, при которой для энер-
энергии Е получается указанное значение, считая, что значения а
близки к 2 ферми A ферми = 10~13 см). Для установления иско-
искомой связи использовать три метода:
а) точное решение уравнения Шредингера;

206 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
б)	приближенную волновую функцию вида
обладающую правильным асимптотическим поведением при над-
надлежащем выборе у;
в)	метод Ритца с однопараметрическим семейством экспонент
в качестве пробных функций.
а. Точное решение. Полагая при / = 0
и = у%(г),	G5.2)
мы имеем следующее уравнение Шредингера для эквивалентной
одночастичной задачи:
?l + ^(E+Ae- r/a)% = 0,	G5.3)
dr* %г
где m* = 1/s m — приведенная масса нуклонов (мы считаем, что
массы нуклонов равны). Переходя к новой независимой переменной
у = е-«*°,	G5.4)
получаем
где
^	^а2>0.	G5.6)
Уравнение G5.5) есть уравнение Бесселя с общим решением
% = С^д(су) + С^.д(су).	G5.7)
Согласно равенству G5.4), точке у — О соответствует точка г = оо,
где функция х должна обращаться в нуль. Следовательно, С2 = 0
и волновая функция будет равна
и = ^J9 (<%-"*').	G5.8)
С другой стороны, точке у = 1 соответствует точка г = 0, где
волновая функция и обязана быть конечной, поэтому для функ-
функции Бесселя должно выполняться равенство
У,(с) = О.	G5.9)
При заданных числовых значениях величин т* и Е мы на осно-
основании формул G5.6) имеем
<7 = О,458а, А =2,23-^,	G5.10)
где значения а берутся в единицах ферми, а значения А в МэВ.
Пусть нам задано значение величины а, тогда величину q мы

75. Модель дейтрона с центральным взаимодействием
207
можем найти по формуле G5.10). Затем из уравнения G5.9) на-
находим величину с и, наконец, снова с помощью формулы G5.10)
определяем соответствующее значение глубины потенциальной
ямы А. Следует подчеркнуть, что нужно брать наименьший ко-
корень уравнения G5.9), так как именно в этом случае получается
наименьшее значение А, что соответствует потенциальной яме
с одним-единственным связанным состоянием. Результаты числен-
численных расчетов значений величин А я а приводятся в нижеследую-
нижеследующей таблице11.
q
0,2
0,4
0,6
0,8
0,9
1,0
1.1
1,2
1,4
а
0,436
0,873
1,310
1,747
1,963
2,180
2,40
2,62
3,05
с
2,707
2,999
3,283
3,560
3,696
3,832
3,966
4,099
4,363
А
409
125
67
44
37
32
28
26
21
,0
,5
,5
,7
,1
,1
,7
б. Приближенное решение. Волновая функция
г
3L
G5.11)
в точке г=0 имеет конечное значение,
и убывает экспоненциально на больших расстояниях г, причем
коэффициент спадания имеет правильное значение:
Нормировочная постоянная С получается из условия
со
4л J r*u2(r)dr = l,
о
которое дает
С= /ЦТ.
G5.12)
11 Решения уравнения G5.9) можно взять из таблиц Янке и Эмде.
(Имеется перевод: Янке Е., Эмде Ф., Лёш Ф., Специальные функции, изд-во
„Наука", М., 1968. — Прим. перев.)

208 П. Задачи без учета спина. Г. Сферически симметричные потенциалы
Теперь с помощью этой волновой функции мы определим сред-
среднее значение энергии, для которого имеет место формула
Если в подынтегральное выражение G5.13) подставить точную
волновую функцию G5.8), то в результате мы получили бы точ-
точное собственное значение Е. Используя же приближенную функ-
функцию и G5.11), мы получаем приближенное собственное значе-
значение Е, которое, согласно вариационному принципу Шредингера
(см. задачу 2), должно несколько превышать точное собственное
значение Е.
Интеграл G5.13) с функцией G5.11) вычисляется элементарно,
и окончательный результат имеет вид
Ё?*А (Ь+М G5Л4)
Если теперь подставить сюда значения а = 2,18 ферми и Л =
= 32,7 МэВ, найденные нами ранее, то для Ё получится значе-
значение Е = —2,18 МэВ. Если же, с другой стороны, потребовать,
чтобы формула G5.14) давала правильное значение энергии,
Е = —2,23 МэВ, при q = 1 и а = 2,18, то для этого придется
глубину ямы А взять равной Л =33,5 МэВ. Таким образом, при
правильном значении глубины потенциальной ямы у нас полу-
получается значение энергии, завышенное примерно на 2,5%, для
получения же правильного значения энергии требуется потен-
потенциальная яма несколько большей глубины А.
в. Метод Ритца. В качестве пробных функций возьмем нор-
нормированные функции вида
и определим значение параметра а из условия минимальности
выражения G5.13) для среднего значения энергии Е. Подставив
выражение G5.15) в формулу G5.13), после элементарных вычис-
вычислений получаем
E=8m^a*~ (l+aK A	G5.16a)
и
дЁ %г	ЗА _ „
a	'	G5.166)

75. Модель дейтрона с центральным взаимодействием
209
ИЛИ
12т*аМ
А2
G5.17)
Для значений а = 2,18 ферми и А =32,7 МэВ правая часть равен-
равенства G5.17) будет равна 22,3, откуда следует, что а = 1,34. Учи-
Учитывая, что п2/(8т*а*) =2,21 МэВ, мы в соответствии с форму-
формулой G5.16а) получаем для энергии значение
? = 3,97 МэВ —6,15 МэВ=— 2,18 МэВ.
Мы видим, что приближенное значение снова больше точного.
На фиг. 42 представлены графики всех трех волновых функ-
функций и (точная), и, и с учетом правильной нормировки (правиль-
0,3
о, г
0,1
\
\
V
г/а —*
Фиг. 42. Точная и две приближенные волновые функции для модели дейтрона
с центральным взаимодействием.
ную нормировку для функции и можно найти лишь численным
методом). О5е приближенные функции при малых г принимают
слишком большие значения, что, однако, не играет особой роли,
так как благодаря множителю гг в элементе объема практически
не сказывается ни на нормировке, ни на величине интеграла
G5.13). Кроме того, это отклонение компенсируется тем, что при
больших г обе функции принимают заниженные значения. В асим-
асимптотическом поведении всех трех кривых не наблюдается сколько-

210 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
нибудь существенного различия:
¦ ua*l> -^0,308 — , ua"'' —-0,346 e-^,
где х = г/2а.
Задача 76. Импульсное представление для волновых функций
в поле центральных сил
В обычном пространстве волновая функция разбивается на
радиальную и угловую части, причем последняя представляет
собой сферическую гармонику. Показать, что в импульсном про-
пространстве волновая функция допускает точно такую же фактори-
факторизацию.
Решение. Будем предполагать, что в формулах, осуществляю-
осуществляющих связь между координатным и импульсным представлениями,
G6.1)
=77^77 U-^u(r)d^x,	G6.2)
функция и имеет вид произведения:
G6.3)
Чтобы найти фурье-образ этой функции, разложим экспоненту,
фигурирующую в формуле G6.2), по сферическим гармоникам,
которые, очевидно, будут функциями угла у, образованного век-
вектором г и вектором k (см. задачу 81). Это разложение имеет вид
BЯ, + 1) i-^K, о (cosy). G6.4)
С помощью теоремы сложения сферических гармоник функцию
Yx, о (cosy) можно выразить через сферические углы Ф, ф век-
вектора г и сферические углы в, Ф вектора k
(«,ф). G6.5)
Подставляя теперь формулу G6.5) в правую часть формулы G6.4),
а затем полученный результат и выражение G6.3) в интеграл G6.2),
получаем

76. Импульсное представление для волновых функций	211
Интегрирование по направлениям вектора г можно выполнить
с помощью формулы
$ К;, д (#, ср) У г, m (#, Ф) dQr = 6a8mM.
В результате от двойной суммы у нас останется только один
член с индексами ! и /пи мы получаем
	 «
kf (*) = у \ i~l J /, (kr) ъ (г) ¦ Yu m (в, Ф) dr.
о
Таким образом, волновая функция f (k) в пространстве импуль-
импульсов может быть представлена в виде произведения
4|..(в."Ф),	G6.6)
где
		оо
si № = У ff'' 1 /«^ X' ^ dr-	G6-7>
о
Мы видим, что радиальные части волновых функций g: (k)
и i~l%i(r) связаны между собой преобразованием Ханкеля. Пре-
Преобразование, обратное преобразованию G6.7), записывается в виде
I i (*) ^-	G6-8)
о
Если в координатном пространстве волновая функция и нор-
нормирована так, что допускается ее обычная вероятностная интер-
интерпретация, т. е.
00
jlXiWl*dr=l,	G6.9)
о
то подстановка выражения G6.8) в формулу G6.9) даст
со	оо	со
-1Jdr^dk JU (kr) gl (k) U (k'r)gt (k') dk'=\.
0 0	0
Выполняя здесь сначала интегрирование по г и учитывая, что
§k-k'),	G6.10)
о
получаем
со
§	G6.11)

212 И. Задачи без учета спина. Г. Сферически симметричные потенциалы
Таким образом, в пространстве импульсов правомерна та же
самая вероятностная интерпретация: в рассматриваемом кванто-
квантовом состоянии абсолютное значение импульса частицы будет
обнаружено в интервале между k и k + dk с вероятностью
\gt(k)\*dk.
Задача 77. Уравнение Шредингера в импульсном представлении
в поле центральных сил
В задаче 14 было получено интегральное уравнение, которому
в общем случае должны удовлетворять волновые функции импульс-
импульсного представления. Показать, что в поле центральных сил реше-
решения этого уравнения можно представить в виде произведения
f{k) = ^gl(k)YUm{<d,Q».	G7.1)
В частном случае атома водорода получить инте-рральное урав-
уравнение для функции gt (k).
Решение. Интегральное уравнение A4.6), записанное в атом-
атомных единицах, имеет вид
d3k',	G7.2)
где
w \iv) —z p з \ б v \i) a x.	y/1 toj
В том случае, когда потенциал V (г) зависит только от модуля г
радиус-вектора г, оно сводится к интегральному уравнению для
функции gt{k). Действительно, в этом случае в формуле G7.3)
можно произвести интегрирование по телесному углу, так что
в результате получится ядро, зависящее только от модуля век-
вектора к:
Но тогда ядро интегрального уравнения G7.2) будет функцией
переменной
(k — k'Y=k2 + k'2—2kk'cosy,	G7.5)
где у—угол, образованный векторами к и k', и ядро W можно
будет разложить в ряд по полиномам Лежандра. Это разложе-
разложение имеет вид
00
Z),	G7.6)

77. Уравнение Шредингера в импульсном представлении	213
причем коэффициенты разложения ап зависят только от абсо-
абсолютных значений k и k'. Именно это обстоятельство позволяет
представить волновую функцию в виде произведения G7.1).
Подставляя в интегральное уравнение G7.2) вместо функ-
функции f (k) ее выражение G7.1), получаем
), Ф) =
" \(cosy)Ylim(Q\(\>')dQ'.
п О
Интеграл по углам можно вычислить с помощью теоремы сло-
сложения:
п
д=-п
В результате от суммы остается только член с индексами п — /
и р. = m, и мы получаем
По угловым переменным последнее равенство является тождест-
тождеством, что подтверждает корректность представления G7.1). Что
же касается функции gt (k), то для нее мы имеем интеграль-
интегральное уравнение
оо
¦ kz— Е) gt(k) = —-^j § k'at{k, k')gl(k')dk'. G7.7)
о
В частном случае атома водорода
V(r)=—y,	G7.8)
и интеграл G7.4) с помощью предельного перехода
со
lim С e~iXs\nxdx= I
Е~* о
можно вычислить до конца, в результате получаем
W (&) =	L_ .	G7.9)
Отсюда, согласно формуле G7.5),
V« —« ; — —2л2|А— А'р= ~4n2fefe'B — cosy)

214 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
<77-10>
Полагая cosy=^, замечаем, что в рассматриваемом случае равен-
равенство G7.6) представляет собой хорошо известное разложение
СО
—— — У\ Brt+ 1) Q {z) Р @>	G7.11)
коэффициентами которого служат так называемые функции
Лежандра второго рода
j^	G7.12)
-1
Следовательно, в нашем случае
{^f\	G7.13)
и интегральное уравнение окончательно принимает вид
l(k')dk'. G7.14)
о
Замечание. Интегральное уравнение G7.14) было решено В. Фоком [см. Zs.
Phys., 98, 145 A935)]. При таком подходе волновые функции в импульсном
представлении находятся без помощи собственных функций в координатном
представлении. Однако в случае кулоновского поля второй способ оказывается
более простым, и мы рассмотрим его в следующей задаче.
Задача 78. Водородные волновые функции
в импульсном пространстве
Найти импульсное представление волновых функций, принад-
принадлежащих низшим уровням (Is, 2s, 2p) атома водорода.
Решение. В задаче 76 мы уже показали, что в поле централь-
центральных сил волновой функции в координатном представлении
и{г)=±гЧл(г)Уит(Ъ, Ф)	G8.1)
в импульсном представлении соответствует функция
/(*)=у?»(*)^.»(в,Ф),	G8 2)
поэтому нам остается определить лишь „радиальную" функцию
gj (k), связанную с функцией ii (r) преобразованием Ханкеля:
(*'')Xi@^.	G8.3)

79. Штарк-эффект у пространственного ротатора	215
Для трех заданных состояний, используя атомные единицы,
можно написать
Is: Xio(r) = 2r<T',
2s- y (r> =
2p:
= j/|-2 Jrsin
0
=-J= f (r—1- r2) sin fere-r/2 dr;
Вычисление этих интегралов элементарно, хотя и несколько
громоздко. Результаты вычислений дают
G8-4б)
G8.4в)
Непосредственной проверкой можно убедиться, что во всех слу-
случаях выполняется условие нормировки
]k=l,	G8.5)
о
как это и должно быть согласно общей теории [см. формулу
G6.11)].
Задача 79. Штарк-эффект у пространственного ротатора
Во втором порядке теории возмущений рассчитать штарк-
эффект у пространственного ротатора с электрическим дипольным
моментом р.
Решение. Невозмущенному уравнению Шредингера удовлет-
удовлетворяют сферические гармоники:
|	?(y,,.,	G9.1)

216 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
причем для собственных значений имеет место формула
?г = ^&^-	G9.2)
Энергия возмущения при наличии произвольно направленного
электрического поля ? равна
V = — р (<§х sin •& cos ф + ?у sin ft sin <p + ?г cos ft). G9.3)
Чтобы определить матричные элементы энергии возмущения V,
</', m'\V\l, m> = /y;,im,V(O, <?)YLmdQ,	G9.4)
воспользуемся соотношениями1(
smfte'vYt, m = att mYl+u m+1 — a,_lt -m^Yt.u m+1>
sin«8-"'r,te = —alf _„, Y^.^^ + a^^Y^,^,, G9.5)
cos «У,, e = blt mYl+lt m + b,_i. »У«-1. «..
где
_ /~(/ + m+l)(/ + m + 2) , _ At + m+lHl-m+l)
ai,m— у B1+1) B1 + 3) ' Um V B1+\)B1 + Ъ)
G9.6)
Если теперь учесть свойство ортонормированности сферических
гармоник, то окажется, что для каждой данной пары квантовых
чисел I и т отличными от нуля будут следующие шесть матрич-
матричных элементов:
m + l\V\l, m> = — j(?
m + \\V\l, m> = + y(tf
m—1 |V|/, OT> = + y(tf
m-\\V\l, m> = —2tf
, m\V\l, m> = —gzpbltm,
</—1, т|У|/, т> = — €жрЬ,_ия.
Среди них нет ни одного диагонального матричного элемента
A = 1'). Это означает, что поправка первого порядка теории воз-
возмущений равна нулю:
А1?г = </, m\V\l, m> = 0,	G9.8)
т. е. в рассматриваемом случае линейный эффект Штарка отсут-
отсутствует. Это же утверждение сохраняет силу и для матричных
11 См., например, Bethe H. A., Salpeter E. Е. в книге: Encyclopedia of
Physics, vol. 35, Springer, Berlin — Gottingen — Heidelberg, 1957, p. 432. (Имеет-
(Имеется перевод: Бете Г., Солпитер Э., Квантовая механика атомов с одним и
двумя электронами, Физматгиз, 1960, стр. 542.—Прим. перев.)

80. Интерференция падающей и рассеянной волн	217
элементов вида </, т'|У|/, ту, поэтому возмущение не приводит
к смешиванию вырожденных состояний, принадлежащих одному
и тому же значению / и разным значениям т. Следовательно,
мы можем воспользоваться более простыми формулами теории
возмущений без вырождения.
Таким образом, для расчета квадратичного эффекта Штарка
мы будем иметь
I'm-
В этой сумме, согласно G9.7), содержатся шесть слагаемых,
а их знаменатели находятся с помощью формулы G9.2), поэтому
26 /1 ,?2 о2, Г aim+aj -m
u+lJ/ G9-10)
Подставляя в последнее выражение значения коэффициентов
ai, m и blt m из G9.6), мы окончательно получаем
Найденная формула не применима к случаю / = 0. Это не-
нетрудно понять, если принять во внимание, что в состоянии Уо< 0
нет никакого выделенного направления, поэтому возмущение
должно быть просто пропорционально <?2. Вычисления, анало-
аналогичные выполненным выше, показывают, что в этом случае из
шести матричных элементов G9.7) отличны от нуля только три
матричных элемента <1, m'|V|0, 0> с m' = -fl, О, —1. Окон-
Окончательный результат имеет вид
Аг-^о, о= —ъЦТ$'	G9.12)
Литература
Meyenn K-, Zs. Phys., 231, 154 A970). В работе рассмотрен случай силь-
сильных полей, а также установлены границы применимости второго порядка тео-
теории возмущений.
б. Упругое рассеяние
Задача 80. Интерференция падающей и рассеянной волн
В задачах рассеяния на волновую функцию необходимо на-
наложить асимптотическое граничное условие (так называемое

218 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
условие излучения Зоммерфельда)
e^, kr-^oo.	(80.1)
Показать, что на больших расстояниях от рассеивателя оно
приводит к суперпозиции падающего и рассеянного потоков без
заметной интерференции между ними, и установить соотношение
между амплитудой рассеяния и сечением рассеяния.
Решение. К волновой функции, имеющей вид (80.1), можно
применить формулу для плотности тока
N(u*VuuW*),	(80.2)
в которой нормировочная постоянная N характеризует интен-
интенсивность потока частиц. В сферических координатах оператор
градиента имеет компоненты:
д	1 д	1 д	,ar. n ..
Vr = 57' V» = 71' ?ч> = Г5ПП*дф-	(80>3а)
Так как функция и не зависит от угла <р, то, очевидно, sv = 0.
Для двух других компонент вектора s с помощью формулы (80.2)
после несложных вычислений получаются выражения
J,
—^ N sin®+^.N{(f'-ikr sin
-(/*' + ikr sin <>/•)e-^^j> + ^ N (f'p-
здесь штрих означает производную по ¦&. Полученные формулы
должны выполняться лишь асимптотически (kr—> оо), поэтому
мы можем пренебречь последним членом, который пропорциона-
пропорционален г~3, по сравнению с плотностью потока рассеянной волны,
пропорциональной г~2. Что касается интерференционных членов,
стоящих в фигурных скобках, то мы оставим только те из них,
которые содержат в качестве множителя величину kr. Таким
образом, для дальнейшего анализа у «ас остаются значительно
более простые выражения
JV { sin * -
В этих формулах первые слагаемые не зависят от г. Они
представляют собой г- и ¦О-компоненты направленного вдоль

80. Интерференция падающей и рассеянной волн	2И)
оси z вектора плотности тока s0 = fikN/m, порожденного плоской
волной. Так как hk/m = v есть скорость частицы, то величину'iV
следует понимать как плотность падающих частиц. Второе сла-
слагаемое в выражении для sr представляет собой радиальный
поток, который мы можем отождествить с плотностью потока
рассеянных частиц. При любого рода наблюдениях для получе-
получения конечной интенсивности мы должны по необходимости ис-
использовать какой-то детектор, который виден из рассеивателя
под малым, но обязательно конечным телесным углом 8Q. Если
детектор находится на расстоянии г от рассеивателя, то в каж-
каждую секунду через его поверхность, равную r25Q, пройдет и будет
зарегистрировано
65= {(Ц-N ^-\ridu==^rN f l/№	(80-4)
рассеянных частиц. Разделив этот поток на плотность потока
{hkjm) N падающих частиц, получим величину
6ст= $|/(#)|2dQ»|/(#)p6Q,	(80.5)
во
не зависящую от первичной интенсивности и являющуюся, таким
образом, характеристикой рассеивающих свойств взаимодействия,
вызывающего рассеяние. Это отношение имеет размерность пло-
площади и носит название дифференциального сечения рассеяния
в телесный угол 6Q. Отсюда для полного сечения рассеяния
получаем
o=(f\f(®)\*dU.	(80.6)
Нам осталось разобрать вопрос об интерференционных членах
в формулах (80.36), которые, будучи пропорциональными \/г,
на первый взгляд играют даже более важную роль, чем члены,
отвечающие плотности потока рассеянных частиц. Во всех этих
членах имеются сомножители, меняющиеся медленно, и сомно-
сомножители, меняющиеся быстро при изменении телесного угла.
При интегрировании любого из них по малому, но конечному
телесному углу 6Q медленно меняющиеся сомножители (такие,
как sin ft) можно считать постоянными, так что остается лишь
рассмотреть интегралы вида
^coskir — z)du или [sink(r — z)dQ.	(80.7)
Если kr очень велико, то даже при интегрировании по сравни-
сравнительно небольшому телесному углу 5Q изменения аргумента
k(r — z)=kr{\— cos ft)
вызовут большое число осцилляции периодических функций,
стоящих под знаком интеграла в (80.7). Следовательно, эти

220 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
интегралы практически будут равны нулю (во всяком случае,
их вклад не будет пропорционален 5Q), и поэтому в пределе
очень больших kr мы вправе опустить интерференционные члены
и рассматривать потоки от падающей и рассеянной волн как
независимые.
В этой связи стоит, пожалуй, отметить, что
и 2пг
Ьг —
й X •
где к — длина волны де Бройля, которая обычно имеет порядок атомных (или
даже ядерных размеров, т. е., скажем, 10~8 см. Величина же г — это макро-
макроскопическое расстояние между частями экспериментальной установки, равное
по крайней мере 10 см. Таким образом, величина kr равна 6-10е и, действи-
действительно, очень велика.
Задача 81. Разложение плоской волны по парциальным волнам
Разложить плоскую волну по парциальным волнам, соответ-
соответствующим состояниям с определенным моментом- количества
движения.
Решение. Плоская волна
u = e''fa = e'*'cos*	(81.1)
является решением уравнения Шредингера для свободного дви-
движения:
V2u + ft3« = 0, &2 = ^.	(81.2)
л2
Общее решение этого уравнения, полученное путем разделения
переменных в сферических координатах, имеет вид
« ;
» = 57Z ? {Ai. mi i (kr) + В ,ш mn,(kr)\Pf (cos О)е*»ф, (81.3)
ЫО m=-l
где
(81.4)
Каждый член суммы (81.3) представляет собой вклад состояния,
характеризующегося вполне определенным моментом количества
движения, т. е. квантовыми числами / и т.
Представляя плоскую волну (81.1) в виде разложения (81.3),
сразу же можно добиться двух упрощений.
1. Вклад в сумму дают только слагаемые с т — 0, так как
выражение (81.1) не зависит от угла <р. Физически это связано
с тем, что пучок частиц параллелен оси z, и поэтому проекция
момента количества движения на ось z равна нулю.

81. Разложение плоской волны по парциальным волнам	221
2. Функции n(, будучи сингулярными в начале координат,
не могут давать вклада в искомое разложение.
Следовательно, разложение плоской волны по состояниям
с определенным моментом должно иметь вид
со
eikr cos О = j_ ? A{h {kr) ?l (cos Щ^	(81.5)
1 = 0
и наша задача сводится к определению коэффициентов At. С по-
помощью условия ортонормированности
(81.6)
где t = cos ¦&, эта задача решается аналогично задаче об опреде-
определении коэффициентов Фурье. Таким образом, имеем
(81.7)
Чтобы определить коэффициент Л, из этого уравнения, следо-
следовало бы вычислить интеграл, стоящий слева, и результат инте-
интегрирования сравнить со сферической функцией Бесселя, стоящей
справа. Эта процедура, будучи вполне элементарной, довольно
громоздка. К счастью, использовать ее нет необходимости, так
как нам достаточно сравнить выражения, стоящие в обеих частях
равенства (81.7) при больших значениях произведения kr. В этом
....
]t(kr)
sml kr —-g 1
(81.8)
а наш интеграл последовательным интегрированием по частям
можно представить в виде разложения по отрицательным степе-
степеням величины kr:
Асимптотически важен лишь первый член этого разложения.
Учитывая, что
мы, таким образом, получаем
\ eikrtPt (t) dt
Frsm[>
(81.9)

222 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Подстановка выражений (81.8) и (81.9) в равенство (81.7) те-
теперь дает
At = Bl+l)il,	(81.10)
так что окончательно разложение (81.5) принимает вид
Fr	).	(81.11)
Если воспользоваться нормированным выражением для сфе-
сферических гармоник
то разложению (81.11) можно придать несколько иную форму:
li0^).	(81.13)
1 = 0
Обоими разложениями (81.11) и (81.13) можно пользоваться
с равным успехом.
Замечание 1. Из равенства (81.7) и соотношения (81.10) вытекает интег-
интегральное представление для сферических функций Бесселя
1
J ^Pt(t)dt.	(81.14)
Метод, использованный нами при решении этой специальной задачи, часто
применяется для нахождения подобных интегральных представлений.
Замечание 2. Для т=0 проекция момента количества движения на ось г
равна нулю, Lz = 0, две другие проекции. Lx и Lv, не имеют определенного
значения. Это находит отражение и в классической картине, когда пучок па-
падающих частиц расслаивают на тонкие цилиндрические слои радиуса р. Для
каждого такого слоя, имеющего ось г в качестве оси симметрии, величина L
имеет определенное значение (L = mvp), но при этом все еще допустимы все-
всевозможные способы разбиения вектора L на компоненты Lx и Ly. Бесхитрост-
Бесхитростное квантование, L я nl, приводит к соотношению
mv 2л '
где %—длина волны де Бройля, а р является грубой мерой расстояния, на
котором частица с квантовым числом / пролетает мимо начала координат.
Такое выделение из полной суммы одного отдельного члена разложения,
разумеется, некорректно: наблюдаемые величины по необходимости выражаются
через билинейные комбинации и и и* (или их производные), что ведет к воз-
возникновению интерференционных членов. Только в пределе больших квантовых
чисел / можно дать классическую интерпретацию отдельной парциальной
волне. Дело в том, что высокие сферические гармоники быстро осциллируют,
поэтому усреднение даже по небольшому интервалу углов приводит к выпаде-
выпадению интерференционных членов.

82. Разложение амплитуды рассеяния по парциальным волнам	223
Замечание 3. Пусть плоская волна	распространяется не в направлении
оси г, а в направлении вектора к со	сферическими углами в и Ф. Если
посредством д' обозначить угол между	векторами ft и г, то в соответствии
с формулой (81.13) будем иметь
Применяя к этому выражению теорему сложения сферических гармоник
У 4я
т=-1
получаем разложение более общего вида
4
k-r=-^rj^ X ''//(**¦) W. m (в. Ф)П,и(д, ф).	(81.16)
Задача 82. Разложение амплитуды рассеяния
по парциальным волнам
Пусть внутри сферы радиуса R имеется потенциал V (г)
и пусть вне этой сферы потенциал равен нулю. В этом потен-
потенциальном поле рассеивается пучок частиц, описываемый плоской
волной. Воспользовавшись разложением в ряд по парциальным
волнам, вычислить амплитуду рассеяния и выразить ее затем
через значения логарифмических производных парциальных волн
на сфере r = R.
Решение. В области г < R волновую функцию можно запи-
записать в виде
« = ^?»'1BЛ-1)Х*(*. OP,(cosО),	(82.1)
1 = 0
где
[^f]	(82.2)
Граничные условия определяют функции %г с точностью до
постоянной амплитуды, но логарифмические производные,
t	(82.3)
от этой постоянной амплитуды не зависят. Ниже предполагается,
что величины Lt известны.
Вне сферы г = R можно написать
\	ТаМ" <*r>] Л (cos*).. (82.4)
1 = 0

224 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Если бы все аг==0, это выражение совпадало бы с разложением
плоской волны из задачи 81; члены, пропорциональные сфери-
сферическим функциям Ханкеля первого рода, соответствуют наличию
дополнительных расходящихся сферических волн. Действительно,
/г<1> (kr) = /, (At) + int (kr) — i~u+1) eikr.	(82.5a)
Вспомнив далее асимптотическое поведение функций /,
(82.56)
находим, что на больших расстояниях разложение (82.4) для и
ведет себя как
"-*-2^г?B/+1)[A+а,)е'*г-(-1)'е-'*г]Я,(соз*). (82.6)
1 = 0
Основываясь на законе сохранения числа частиц при упру-
упругом рассеянии, можно заключить, что квадраты модулей ампли-
амплитуд сходящихся и расходящихся волн должны совпадать, а именно
|1+а,|*=1.	(82.7)
Другими словами, должно выполняться равенство
al = eii('i—\,	(82.8)
с учетом которого разложение (82.6) можно записать в более
компактной форме
GO
и — ^?B/+l)f'Asin(*r —^ + 6/)p,(cos#), (82.9)
/=о
где величины бг, как очевидно, представляют собой асимптоти-
асимптотический сдвиг фаз решения уравнения (82.2) по отношению к ре-
решению (82.56) уравнения Шредингера для свободного движения.
Амплитуда рассеяния /(¦&) связана с рассеянной волной us
соотношением
us~u~eikz—*f(^)~,	(82.10)
поэтому
fw=4kXBl+l)atp^cos^- (82Л1а>
С учетом равенства (82.8) эту формулу можно записать несколько
иначе:
ш

83. Рассеяние при низких энергиях	225
Теперь нам осталось выразить коэффициенты at через лога-
логарифмические производные Lt, определенные посредством фор-
формулы (82.3). Последняя задача решается с помощью условий
непрерывности функций %t и d^Jdr на поверхности сферы r=R.
Мы имеем
Xl(k, R)=jl(kR) + \ath\»(kR),
Здесь штрих означает производную не по г, а по kr. Деля вто-
второе из приведенных соотношений на первое, имеем
L, = x	=	, x=kR,	(82.12a)
2
и отсюда находим
at = — 2 Lil(x)~xll.j!? ¦	(82.126)
•L/ft/ (x)—xhl (x)
Разумеется, полученное выражение опять удовлетворяет закону
сохранения числа частиц (82.7). В этом нетрудно убедиться,
введя сферические функции Ханкеля второго рода и исключив
функции jt(x) с помощью соотношения
/, (х) = -i [hj" (x) + hf (x)\,	(82.13)
если учесть, что при действительных значениях аргумента функ-
функции hf (x) комплексно сопряжены с функциями Щи (х). Действи-
Действительно, в соотношении
1+СТг=,_П[пкл>~м\). "	(82.14)
числитель дроби комплексно сопряжен с ее знаменателем, поэтому
j ] ~[-ос/1 = 1 в полном согласии с равенством (82.7).
Задача 83. Рассеяние при низких энергиях
Разложение амплитуды рассеяния по сферическим гармоникам
сходится тем лучше, чем меньше параметр x = kR. Убедиться
в справедливости этого утверждения прямым вычислением коэф-
коэффициентов аг при л:<^1 и получить разложение коэффициентов
а0 и а1 по степеням х, считая, что коэффициент а2 мал и им
можно пренебречь.
8 № 1050

226 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Решение. Мы начнем с формулы (82.126) предыдущей задачи:
а 2 У*"*!*? •	(83-1)
1	Llh\1)(x)-xhY) (х)	V
Воспользуемся определениями
К1' (х) = // (х) + in, (х), А{» (х) = /, (х) - щ (х) (83.2а)
и заменим сферические функции Ханкеля функциями /, и п„
для которых степенные разложения имеют вид
где
Если л:<^1, то достаточно учесть только первый член каждого
ряда. В этом случае имеем
h<^\ni\ и Лр'даш,,
следовательно,
Btx-1,
поэтому из формулы (83.1) с учетом соотношений (83.2в) вытекает
(83.3)
В этой формуле сохранен лишь основной член, а все более вы-
высокие степени х отброшены.
Как мы знаем, для амплитуды рассеяния имеет место разло-
разложение
1 = 0
При х<^1 этот ряд очень хорошо сходится, так как в силу
формулы (83.3)
B/+3)аг+1 _ 1	Lt+l
Если характер сходимости ряда (83.4) позволяет пренебречь
членом с 1 — 2, то, согласно равенству (83.3), это эквивалентно
тому, что в амплитуде рассеяния мы пренебрегаем членами с хь
и более высокими степенями х. В этом случае с помощью рядов
(83.26) удается получить разложение коэффициентов, а0 и ах
с точностью до х4 включительно. Однако тот же самый результат
можно получить значительно проще, рассмотрев непосредственно
функции

84. Рассеяние на сферически симметричном барьере	227
Л«» (х) = — ieix, h? (x) = — [\+-)elx	(83.5a)
и
/гJ) (*) = h\1}* (x) для действительных х.	(83.56)
Если вместо равенства (83.1) воспользоваться эквивалентным ему
равенством (82.14) предыдущей задачи,
Lthf (x)~xhT' (х)
= -'	(836)
то для интересующих нас коэффициентов получатся следующие
точные выражения:
\±^	(83.7а)
-e~2tx
Разлагая эти выражения в ряд и ограничиваясь требуемой сте-
степенью точности, находим
В разложении коэффициента ах член, пропорциональный xi,
отсутствует. В том случае, когда член с /=1 начинает только-
только сказываться, мы должны для получения достаточной сте-
степени точности удерживать в разложении (83.8а) три или даже
четыре члена, в связи с этим часто оказывается проще вместо
формулы (83.8а) пользоваться точным соотношением (83.7а).
Задача 84. Рассеяние на сферически симметричном
прямоугольном потенциальном барьере
Дан потенциал V = Vo > 0 при г < R и V = Q при r>R. Для
случая / = 0 найти зависимость фазы рассеяния So и парциаль-
парциального сечения 0О от энергии падающих частиц.
Решение. Вводя обозначения
К1=^. *а = ^- Х = 1/7СГ=*\	(84.1)
можно записать радиальную волновую функцию %о(г) при 1 = 0
следующим образом:

228 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
если энергия Е меньше порогового значения Vo, то
sh кг,	г < R,
<84
если же энергия Е выше порогового значения Vo, то
A' sinxV, г < R,
sin (*г +в.), r>tf;	<84'2б>
в последнем случае величина и оказывается чисто мнимой:
ч = /ч'. У волновой функции вне сферы нормировка во всех
случаях одинакова, поэтому амплитуды А а А' характеризуют
степень возбуждения области, заключенной внутри сферы. Заме-
Заметим, что приведенные выше выражения уже написаны с учетом
граничного условия.
Непрерывность функций %0 и %о в точке r = R предполагает
непрерывность логарифмической производной, значение которой
при r — R, т. е.
можно получить двумя способами, беря для волновой функции
выражения, соответственно справедливые либо в области г < R,
либо в области г > R. Таким образом, имеем
L03s*/?ctg(*/? + 60) = x/?cthx#, E<VQ, (84.4a)
и
L0^kRctg{kR + 6a) = x'Rctgx'R, E>V0. (84.46)
Только в случае Е > VQ решение во внутренней области оказы-
оказывается периодическим и выражение для амплитуды А' представ-
представляет интерес:
Л'2 =	Lj	:	.	(84.5)
sin2 х'#+-^2- cos2 x'R
Прежде всего обсудим полученные формулы для предельно низ-
низких энергий. Когда k—»-0, величину ч следует заменить вели-
величиной Ко- Кроме того, чтобы величина Lo была конечной, аргу-
аргумент котангенса в правой части равенства (84.4а) должен стре-
стремиться к нулю как k. Таким образом, в этом предельном случае
равенство (84.4а) принимает вид
Lo = щ+s; = -Ко# cth K0R,
и, следовательно,
(^~ l).	(84.6)
Если высота потенциального барьера Vu очень велика (т. е.
/ео—юо, жесткая сфера), то при всех энергиях мы можем пре-

84. Рассеяние на сферически симметричном барьере
229
небречь величиной k2 по сравнению с К1, поэтому соотношение
к = К0 и равенство (84.6) будут иметь место для всех энергий.
Это означает, что величина фазы б0 растет линейно с ростом
параметра kR, как показано на фиг. 43 (прямая линия /). Кри-
Кривая 2 на этой же фигуре рассчитана по формулам (84.4а) и
(84.46) для численного значения параметра K0R — 4. Мы видим,
что даже на начальном участке, т. е. вблизи kR = 0, наклон
фазовой кривой для потенциального барьера конечной высоты
О
-0,5
-1
1,5
•г
-г,5
~3 12 3 4-K0R5 6 7 8 в 10
I.
V
V
\\
\
\
V
\
\
ч
-
1
J
f
/
Фиг. 43. Зависимость фазы 60 от kR.
Прямая линия / соответствует случаю жесткой сферы (ЛГ0Я = ю); кривая 2 построена для
случая Ко^? = 4. Пунктирная линия построена на основании первого борновского при-
приближения. Резонансы (максимумы амплитуды) отмечены кружками, минимумы ампли-
амплитуды — крестиками.
заметно отличается от наклона фазовой кривой в случае рассея-
рассеяния на жесткой сфере. Это является характерной особенностью
квантовой механики, согласно которой частицы могут проникать
внутрь потенциальной сферы даже тогда, когда их энергия не
превышает порогового значения, причем глубина проникновения
зависит от высоты потенциального барьера. В классической
механике, где такое проникновение попросту невозможно, высота
потенциального барьера не может сказаться на рассеянии частиц,
энергия которых меньше пороговой.
Если энергия Е (или параметр kR), увеличиваясь, начинает
превышать высоту потенциального барьера, то фазовая кривая 2
сначала достигает минимума, а затем начинает приближаться
к нулю, имея при этом отчетливо выраженный ступенчатый ха-
характер. В предельном случае очень больших энергий (kR—>оо),
разумеется, снова бо = 0, так как при E^>V0 потенциальный
барьер не является для частиц существенным препятствием. При-
Причину ступенчатого характера фазовой кривой можно понять,
вычислив по формуле (84.5) амплитуду А' волновой функции во

230 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
внутренней области. Для случая /C0i? = 4 результаты этих рас-
расчетов показаны на фиг. 44, а. Мы видим, что имеются такие
значения kR, т. е. такие длины волн стационарного пучка ча-
частиц, на которых происходит возбуждение колебаний внутренней
части потенциальной сферы и возникают максимумы ампли-
амплитуды А'. Следовательно, существуют такие полосы частот, при
1,0
sA
kR-
8
6
D
-г
-4
-6
-а
-ю
-1Z
\
8 V
Фиг. 44. а —амплитуда А' волновой функции внутри области, занятой барье-
барьером (/Со/? = 4), в зависимости от энергии.
Кривая имеет резонансный характер.
б—логарифмическая производная волновой функции Lo.
Сингулярности соответствуют резонансным значениям энергии.
которых колебания внутренней области попадают в резонанс
с колебаниями, воздействующими на нее извне. Между каждой
парой резонансов имеются минимумы амплитуды А', где А'~\;
это происходит всякий раз, когда cosx'i? = 0 или WR — (n + Va) Я-
Каждому такому минимуму амплитуды соответствует нуль
логарифмической производной Lo (она показана на фиг. 44, б),
поэтому при г = R волновая функция имеет горизонтальную ка-
касательную и одну и ту же амплитуду внутри и вне рассеиваю-
рассеивающей сферы. Между этими значениями энергии вблизи точек
n'R = nn, т. е. вблизи сингулярностей величины Lo, распола-
располагаются резонансные энергии. В самих же этих точках.волновая
функция при r~R обращается в нуль, но ее касательная при
переходе через точку r = R не меняет своего наклона, благодаря
чему амплитуда во внутренней области с ее более высокими зна-

84. Рассеяние на сферически симметричном барьере
231
чениями длин волн достигает наибольшего возможного зна-
значения.
Далее, мы знаем общую закономерность всех резонансных
явлений —при прохождении через резонанс фаза (в идеальном
случае) скачком изменяется на я. Этой закономерностью и объяс-
объясняется резкий рост фазы между точками, соответствующими
минимумам амплитуды (на кривой 2 фиг. 43 они отмечены крести-
крестиками, а резонансы — кружками).
Зная фазовую кривую, нетрудно рассчитать зависимость пар-
парциального сечения рассеяния
о0 — -р-sinzo0	(84.7)
от параметра kR. Результаты этих расчетов представлены на
фиг. 45. В низкоэнергетическом пределе, когда kR—*0, фаза
0,05
0,05
0,04
0,03
о,ог
0,0!
12
0,6
0,5
0,4
о,г
0,1
>J
\
\
\
1
1
\
\
\
/
-1
6
ля-
ляФиг. 45. Зависимость сечения s-расмяния а0 от kR (в двух различных
масштабах).
Вкладом высших значений момента I можно пренебречь только при kR <^ 1. Резонансный
максимум вблизи kR = 5 в эксперименте будет выражен по этой причине менее отчетливо.
60, согласно равенству (84.6), становится малой величиной, так
что в формуле (84.7) sin60 можно заменить его аргументом:
;).	(84.8)
Величина a0, определенная равенством (84.8), называется длиной
рассеяния потенциала. Для нашего числового примера а0 = 0,75/?.
(О роли длины рассеяния см. задачу 88.) По мере роста энер-
энергии на виде кривой сечения рассеяния начинают сказываться
резонансы, но в нашем примере только первый из них, располо-
расположенный вблизи kR = 5,l, приводит к отчетливо выраженному
эффекту. Высшие резонансы почти не заметны на кривой сече-
сечения рассеяния. Экспериментальная ситуация в этом отношении
еще менее благоприятна, так как здесь приходится иметь дело
со все возрастающими вкладами в сечение о от волн с 1фО.
Таким образом, кривая сечения рассеяния содержит не очень
много информации.

232 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Замечание. Каким образом фаза рассеяния б0 стремится к нулю при
очень больших энергиях, можно выяснить, воспользовавшись первым борнов-
ским приближением (см. задачу 105). При 1 = 0 имеем
00
откуда для частного вида потенциала, рассматривавшегося выше, получаем
R
кг С	к2
60=	-?- \ sin* krdr = — ¦— BkR — sin2W?).	(84.9)
ft J	4ft
0
Рассчитанная по этой формуле фаза рассеяния показана на фиг. 43 пунктир-
пунктирной линией. Для представленной там энергетической области значения фазы
рассеяния еще довольно велики, поэтому от борновского приближения не сле-
следует ожидать результатов, удовлетворительных в количественном отношении.
Замечательно уже то, что даже для этих энергий борновская формула, если
отвлечься от смещения резонансов, правильно передает ход фазовой кривой,
включая ее ступенеобразный характер; последнее, конечно, объясняется нали-
наличием члена с синусом в формуле (84.9).	*
Задача 85. Аномальное рассеяние
Изменим потенциал предыдущей задачи таким образом, чтобы
центр сферы был окружен потенциальной ямой:
г1<г<«1',	(85.1)
Вычислить изменение фазы 80, определенной в предыдущей за-
задаче, и проанализировать случай /С0# = 4 (прежнее значение),
К1г1=\,Ь и r1 = 1^2R.
Решение. Рассматриваемый потенциал схематически изобра-
изображен на фиг. 46. Введем обозначения
v? = Kl—k\ /С2 = /С! + ^2,	(85.2)
смысл которых для энергий, не превышающих порогового зна-
значения (k2 < Kl, x—действительная величина), разъяснен на той
же фигуре. В этих обозначениях радиальная волновая функция
Хо (г) записывается в виде
! В sin Кг,	0<г<Г!,
A(shxr + ychKr), гх </-</?,	(85.3)
Для энергий, превышающих пороговое значение, величина к
будет чисто мнимой, ч = /к' (ч'—действительная величина),

85. Аномальное рассеяние
233
однако формулы (85.2) и (85.3) после указанной формальной
замены можно использовать и в этом случае. Рассматриваемая
задача отличается от предыдущей наличием дополнительного
граничного условия при г —г,. Следовательно, при г, —О она
точно переходит в задачу, рассмотренную ранее: формально
в этом можно убедиться, положив в формуле (85.3) у = 0.
«a
h
хг<
„г
ко
Фиг. 46. Рассеивающий потенциал задачи 85.
Теперь в нашем распоряжении имеется два условия непре-
непрерывности логарифмической производной функции (85.3); одно
в точке г = г„ другое в точке r = R. Эти условия гласят:
Lo (г,) = Кг, ctg Кг, = кг,
(kR + b0).
Из соотношения (85.4а) мы находим величину у,
-тг tg Krx — th кг,
А
1— -ьг ig Kr, th кг,
А
а затем из условия (85.46) — величину 60,
1+Ythx/?/ •
(85.4а)
(85.46)
(85.5)
(85.6)
Выражение (85.5) показывает, что при г, = 0, действительно,
у = 0, на что мы уже обращали внимание выше. С точки зрения
числовых расчетов выражение (85.5) для у удобнее сразу же
подставить в формулу (85.6). Такая подстановка после элемен-
элементарных преобразований дает
(85.7)
Зависимость фазы рассеяния б0, вычисленной по формуле
(85.7) для значений параметров /C1/'1=l,5, K0(R—О^З,

234 // Задачи без учета спина. Г. Сферически симметричные потенциалы
K0R = 4, от kR показана на фиг. 47. Там же для сравнения
изображены результаты, полученные в предыдущей задаче (кри-
(кривая б0), и результаты для случая рассеяния на жесткой сфере
радиуса R (прямая линия). Между кривыми б0 и б0 мы не ви-
видим существенного различия при энергиях, меньших kR&2.
0,4
о, г
о
-а г
-0,4
-0,6
-0,8
-I
-г
-з
-
\
1
1
1
\\
Жесткая \
сфера \
1
Л
к
/
J
1
Фиг. 47. Зависимость фазы 60 от й/? для случая 1 = 0 при аномальном рас-
рассеянии, которое вызвано потенциальной ямой внутри рассеивающей сферы.
Для сравнения приведена фаза рассеяния 60 в отсутствие потенциальной ямы, опреде-
определенная в предыдущей задаче. Прямая линия получена для рассеяния на жесткой сфере.
Из этого можно сделать вывод, что волна не проникает глубоко
внутрь рассеивающей сферы и поэтому потенциальная яма, окру-
окружающая ее центр, не оказывает заметного влияния на характер
рассеяния. Однако положение дел в корне меняется в интервале
энергий 3 < kR < 6, где поведение фазовых кривых носит су-
существенно различный характер. Резкий подъем кривой б0 в окрест-
окрестности точки kR — З указывает на наличие резонанса при этой
энергии.
Следующие рассуждения позволяют понять причину аномаль-
аномального поведения фазовой кривой б0. Предположим, что значе-
значение R бесконечно велико. В этом случае мы имели бы дело
просто с потенциальной ямой глубиной
б которой были бы принадлежащие связанным состояниям энер-

86. Рассеяние на резонансных уровнях	235
гетические уровни, определяемые уравнением
В рассматриваемом числовом примере этому уравнению удовлет-
удовлетворяет значение Кг1 = 2,125, которому, если вернуться к перво-
первоначальной величине R, будет соответствовать значение kR = 3,\4,
т. е. как раз точка фазовой кривой на фиг. 47, указывающая
на наличие резонансного уровня.
Задача 86. Рассеяние на резонансных уровнях
Сферическая полость радиуса R окружена тонкой потенциаль-
потенциальной стенкой, непроницаемость которой характеризуется безраз-
безразмерным коэффициентом Q, так что потенциал имеет вид
V(r)=~|-6(r-/?).	(86.1)
Исследовать рассеяние парциальной волны с / = 0.
Замечание. Эта задача тесно связана с одномерным случаем, рассмотрен-
рассмотренным нами в задаче 27. Однако определение коэффициента непроницаемости
здесь отличается от определения, данного в задаче 20 и использованного
в задаче 27, наличием множителя 2R в знаменателе формулы (86.1). Дело в том,
что в одномерном случае в нашем распоряжении не было характерного пара-
параметра, имеющего размерность длины, который был бы подобен радиусу сфери-
сферической полости настоящей задачи. Заметьте, кстати, что одномерная б-функция
имеет размерность обратной длины.
Решение. Уравнение Шредингера для радиальной волновой
функции %0(г) в случае потенциала (86.1) имеет вид
. = 0.	(86.2)
Сама функция %0 должна быть непрерывной в точке, где у по-
потенциала имеется сингулярность, ее же производная Хо в этой
точке претерпевает разрыв, что можно установить, проинтегри-
проинтегрировав уравнение (86.2) вблизи поверхности потенциальной
стенки. Это интегрирование дает
R-e
так что для логарифмической производной
(86-3)
в результате получаются граничные условия
Lv(R + e)-L0(R-e) = Q.	(86.4)

236 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
С помощью соотношения (86.4) теперь можно связать выраже-
выражения для волновой функции внутри сферической полости:
Хо (г) = Л sin Лг,	/-</?,	(86.5а)
и вне ее
X0(r) = sin(?r + 60), r>R.	(86.56)
В результате имеем
Q.	(86.6)
Последнее уравнение можно переписать в виде, более удобном
для определения фазы:
t	гяе x = kR.	(86.7)
Амплитуда А, фигурирующая в выражении (86.5а), легко нахо-
находится с помощью условия непрерывности функции Хо (&¦
Исключая отсюда с помощью уравнения (86.7) фазу б0, получаем
Как нетрудно убедиться, для непроницаемой потенциальной
стенки (Q—* оо) из уравнения (86.7) следует результат, соответ-
соответствующий предельному случаю рассеяния на жесткой сфере:
tg(jc + 60) = 0, или бо = — х.	(86.9)
В этом случае амплитуда А, согласно формуле (86.8), обра-
обращается в нуль.
При конечных, но достаточно больших значениях Q, вблизи
нулей знаменателя дроби, стоящей справа в уравнении (86.7),
имеются такие узкие полосы значений энергии, для которых
в характере рассеяния наблюдаются существенные отличия от
рассеяния на жесткой сфере. Это те же самые узкие энергети-
энергетические полосы, для которых, как показывает формула (86.8),
амплитуда А внутри полости становится большой. Таким обра-
образом, налицо типичное явление резонанса, когда для узких
энергетических полос имеется сильная связь между колебаниями
внутри и вне полости, а для всех прочих энергий такая связь
почти полностью отсутствует. Чем более проницаема потенциаль-
потенциальная стенка, тем менее отчетливо выражено явление резонанса.
Если Q^-l, то резонансы имеют место вблизи точек х = гт.
Но это соответствует как раз тем энергиям, для которых
Хо(Я) = О, другими словами, это собственные уровни полости

86. Рассеяние на резонансных уровнях
237
в том случае, когда она окружена непроницаемой потенциаль-
потенциальной стенкой. Таким образом, резонансные уровни, отвечающие
максимальной связи, совпадают или весьма близки к собствен-
собственным энергетическим уровням полости.
Ниже обсуждаются результаты числовых расчетов для слу-
случаев Q = 4 и Й=10. Для меньшего значения, Q = 4, зависимость
фазы рассеяния от х показана на фиг. 48. При малых энергиях
наша кривая не очень отличается от прямой, соответствующей
рассеянию на жесткой сфере, однако тангенс угла наклона на-
начального участка нашей кривой равен —Q/(l-j-Q) = —0,8 вместо
—1 в случае жесткой сферы. Первые два нуля знаменателя
дроби в (86.7) расположены соответственно при ^ = 2,57 и
\
\
\\
/
1
J
\
I/
У
1
1
4
0 г г з 4 s_
\ '0,5
-1,0
-1,5
Фиг. 48. Зависимость фазы рассеяния б0 от kR для сферической полости
с Q = 4.
При больших значениях ?2 резонансы выражены отчетливее (см. фиг. 49, а).
л:2 = 5,35 (на фигуре их положение отмечено вертикальными
пунктирными линиями). Эти резонансные энергии лежат заметно
левее точек х = пл, в которых фаза рассеяния вновь обращается
в нуль. При больших значениях Q резонансные энергии распо-
располагаются ближе к точкам х = пп, так, например, для значения
Q= 10 первый резонанс сдвигается в точку ^ = 2,86, а второй —
в точку х2 = 5,76 (см. фиг. 49, б). Подъем фазовой кривой ста-
становится при этом круче, и резонанс выражен более отчетливо.
В пределе Q—^oo мы имеем в точках хп = пк скачки фазы
Дбо = я. Разумеется, это не противоречит линейному закону
(86.9) для случая жесткой сферы, так как к фазе б0 всегда
можно добавить целое кратное я.
Проанализируем явление резонанса в случае Q=10 более
подробно. На фиг. 49, б изображена амплитуда А, рассчитанная
по формуле (86.8). Мы видим, что у амплитудной кривой имеется
два отчетливо выраженных резонансных максимума, лежащих
в тех же точках х, которые отмечены на фазовой диаграмме
(фиг. 49, б) вертикальными пунктирными линиями. Из фиг. 49, а
видно, что сечение рассеяния, по крайней мере для первого из

238 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
0,8
I 0,6
а %о,4
о, г
\
\
1
0,04
0,03
0,0 г
i,
г
1
———
\
/
,	-
1

л
/
/
\
	-
о
-0,5
-1,0
-г,о
-Z,5
01Z345678
АЯ-^
_0 12 3 4 5 6 7 8
\
\
Жес/г
сере/:
\
каяу
ш \
|\
!
\
\ 1
1
\
\
|
Л
\
Я=10
Фиг. 49. а —сечение рассеяния при / = 0 (на фигуре использованы два раз-
различных масштаба).
Несмотря на пренебрежение высшими моментами количества движения, на кривой сечения
рассеяния даже для отчетливо выраженного резонанса при */? = 2,86 имеется всего лишь
довольно незначительный пик.
б — резонансы на амплитудной кривой.
в — та же фаза рассеяния о0, что и на фиг. 48, но для случая Q= 10
этих значений х, имеет небольшой, но не очень отчетливо выра-
выраженный резонансный пик. По обе стороны от каждого резонанса
имеются две точки, для которых /1=1 и, следовательно,
^=±1.	(86.10)
Верхнему знаку отвечают точки х=пп, где 60 = 0 и ао = О.
Последний результат совсем нетрудно понять, если заметить, что
в этом случае волновые функции внутри и вне полости тожде-
тождественно совпадают и поэтому не возникает никакой рассеянной

87. Вклад состояний с высшими значениями момента количества движения 239
волны вообще. Нижнему знаку в формуле (86.10) отвечают
точки, расположенные вблизи минимумов фазы рассеяния. Из
соотношения
dx ~u
легче получить, что фаза рассеяния стационарна в точках
tgx =	2_
х	Q—1 "
Для случая Q = 10 мы находим х = 2,616 и х= 5,406, в то время
как формула (86.10) при выборе нижнего знака дает
tg*_ 2
х ~ Q '
что при том же значении Q приводит к значениям х — 2,654 и
х = 5,454, располагающимся очень близко к точкам минимумов
фазовой кривой.
Кривая сечения рассеяния содержит довольно скудную ин-
информацию (см. фиг. 49,а). Первый резонанс приводит лишь
к небольшому пику. На кривой не заметно никаких следов вто-
второго резонанса, если не считать двух нулей, расположенных
много правее и много левее от него. Наличие этих нулей гово-
говорит лишь о том, что где-то между ними имеется резонанс неиз-
неизвестной высоты и ширины. Еще меньше сведений мы можем
получить из экспериментальной кривой сечения рассеяния, так-
как возрастающий с ростом х вклад состояний с высшими зна-
значениями момента может замаскировать наличие нулей на кривой
сечения а0.
Задача 87. Вклад состояний с высшими значениями момента
количества движения
Для потенциала, рассмотренного в предыдущей задаче, вы-
вычислить фазы рассеяния и парциальные сечения рассеяния вплоть
до значений / = 2.
Решение. При любом значении / радиальную волновую функ-
функцию можно записать в виде
для r<R, (87.1а)
Xi(r)-= it (kr)cos8i — nt(kr) sin8t для г > R. (87.16)
Так как при kr^>l сферические цилиндрические функции имеют
асимптотику
¦h (kr) — sin ( kr-~^j , n, (kr) —-cos ( kr — Y
то выражение (87.16) приводит к следующей асимптотической

240 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
формуле для функции %г:
Хг—-sinlfcr —
(87.2)
Следовательно, бг есть фаза рассеяния 1-й парциальной волны,
а соответствующее парциальное сечение
Для определения фазы рассеяния бг мы снова воспользуемся
граничными условиями в точке r*=R, где функция Хг должна
!(R	быть непрерывна, а ее логарифми-
0 1 г з 4 s ческая производная, ry_\ (r)/%t (r),
имеет скачок, равный по величине
Q. Таким образом, имеем
Aih (х) = It (х) cos6\ — nl (x) sin бг,
(87.4)
-0,5
,5
~г,о
1,0
0,8
К,,
\
Лч
\
\
\
Чг
\
\
А
V
\
>
f n{x) —
__ и(х) \ _ g
ii(x) f
(87.5)
\
k
Л
/
\
4N
I
Здесь x = kR, а штрих означает
производную по аргументу kr.
Уравнение (87.5) позволяет по-
получить для фазы рассеяния б( вы-
выражение вида
tg6, =	/?W r , (87.6)
которое можно подставить в со-
соотношение (87.4) с тем, чтобы
найти явное выражение для ам-
амплитуды Av
При I = 0 сферические цилин-
цилиндрические функции сводятся со-
соответственно к /0 (х) = sin х и
по (х) — — cos л:, а формулы (87.4)
и (87.6) точно переходят в фор-
формулы предыдущей задачи.
На фиг. 50, а показаны фа-
фазовые кривые, соответствующие
значениям / = 0, 1,2. Расчеты проводились для случая Q = 10,
а значения х брались в интервале О^лг^б. Все фазовые кривые
зависят от х аналогичным образом, и основное различие между
ними состоит в том, что при малых х по мере роста / они все
медленнее удаляются от прямой 6 = 0. При низких энергиях
t.0,4
о,г
12 3 4 5
АН ——
Фиг. 50. Фаза рассеяния (а) и
сечение рассеяния (б) в случае сфе-
сферической полости с учетом вклада
высших моментов.
Пик при /г/? = 2,86 еще можно заметить.

	88. Приближение, не зависящее от формы потенциала	241
вклад дают только центральные столкновения с / = 0. Начиная
со значений х= 1 и выше становится существенным вклад волны
с /= 1, а со значений л: = 2— и волны с 1 = 2. На кривых пар-
парциальных сечений для / = 0 и /=1 заметны небольшие резо-
резонансные пики (фиг. 50,6), однако на плавно меняющейся сум-
суммарной кривой а = ац + ст1-т-а2 они проявляются лишь в виде
небольших возвышений. (Резкий спад этой кривой справа от точки
х — А обманчив: на самом деле здесь уже велик вклад от неуч-
неучтенной нами волны с / = 3.)
Задача 88. Приближение, не зависящее от формы потенциала
Показать, что при низких энергиях имеет место разложение
в ряд по степеням k2, начало которого имеет вид
где длина рассеяния а и эффективный радиус г0—единственные
параметры, зависящие от потенциала.
Из существования подобного разложения следует, что в области энергий,
достаточно низких, чтобы можно было ограничиться двумя первыми членами
(т. е. там, где еще не наблюдаются эффекты, связанные с / = 1), любая экспе-
экспериментальная кривая а (Е) содержит информацию, достаточную лишь для
определения двух констант. Это означает, что таким путем нельзя определить
фэгму потенциала. Последнее обстоятельство особенно важно в ядерной физике
низких энергий, где оно является одной из причин нашего незнания коли-
количественных законов для ядерных сил.
Решение. В этой низкоэнергетической области мы будем иметь
дело только со случаем / = 0. Обозначим посредством %»(/") ра-
радиальную волновую функцию состояния с энергией ftafca/2m,
а посредством %0(г) — волновую функцию состояния с нулевой
энергией. Эти две функции подчиняются дифференциальным
уравнениям
Xl-U(r)K = 0	(88.1а)
» + [*1-t/(r)]x* = O1	(88.16)
где
а также граничным условиям
Ь@)=0, х*@)=0.	(88.2)
Поведение этих функций в области г > Ro, где потенциал счи-
считается равным нулю, определяется формулами
%0 = C(r-a), x* = sin(*r + 60).	(88.3)
причем постоянная а может быть любого знака.

242 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Умножая уравнение (88.1а) на %k, а уравнение (88.16) на х0
и вычитая одно из другого, получаем
Проинтегрируем это уравнение от 0 до г и воспользуемся усло-
условиями (88.2):
Г
X* (г) Хо (г) — Хо И Ъ (г) = k2 J
ИЛИ
Хо
Хо Ik	Хо (г) tk (r) '
Если в качестве верхнего предела интегрирования взять какое-
либо значение радиуса R > Ro, то в левой части последнего
равенства мы сможем воспользоваться выражениями (88.3) и
в результате получим
R
[ Хо И tk (r) dr
Теперь мы можем заменить здесь котангенс суммы по формуле
В результате уравнение (88.4) превратится в линейное уравне-
уравнение относительно ctg60, и его решение будет иметь вид
где
R
Хо (г) Xk
До сих пор мы не делали никаких приближений.
Разложим теперь наши выражения в ряды по степеням
Для этого сначала заменим тангенс его разложением:
О
а затем заменим величину Q, определяемую формулой (88.6),
более простым выражением:
8-7)

88. Приближение, не зависящее от формы потенциала	243
где
R
S Xo2 (r) dr
(88-8>
В результате этих преобразований в числителе и знаменателе
дроби (88.5) получаются выражения, верные с точностью до
членов k2 включительно, так что после соответствующей пере-
перегруппировки мы приходим к формуле искомого вида:
*ctg60 = —i- + -iro*»f	(88.9)
где эффективный радиус определяется соотношением
=?)'.	(88Л0)
Нам осталось разобраться в двух вопросах.
1.	Величина R, удовлетворяющая неравенству /?>/?„, в ос-
остальном совершенно произвольна, поэтому необходимо убедиться,
что эффективный радиус (88.10) от нее не зависит.
2.	Если величина г0 действительно имеет смысл эффективного
радиуса, то следует проверить, всегда ли эта постоянная должна
быть положительной.
В первый вопрос легко внести ясность, рассмотрев изменение
выражения (88.10) при переходе от R к R + dR. Мы имеем
Из определения (88.8) следует
или
~dR~~l~R-a'	(M.IZ)
поэтому, подставляя (88.12) в уравнение (88.11), сразу же получаем
каково бы ни было значение R, лишь бы оно превосходило Rn.
Следовательно, постоянная г0 не зависит от выбора R.
Чтобы ответить на второй вопрос, предположим, что /?>|а|,
тогда первый член в правой части (88.10) будет положительным,
второй же член в силу неравенства X > 0—отрицательным.
Таким образом, эффективный радиус будет положительной вели-
величиной, если первый член рассматриваемого выражения больше

244 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
второго, т. е.
Это неравенство эквивалентно условию
R	R
в чем нетрудно убедиться с помощью определения (88.8). В случае
а<0 (фиг. 51, о) справедливость нашего неравенства следует
а и а<0
а
Фиг. 51. Волновая функция %0 (г) состояния с нулевой энергией и ее асимп-
асимптотическое поведение при различных знаках длины рассеяния а.
а) а < 0; б) а > 0.
из того, что график функции %0 всюду располагается под пря-
прямой С (г—а). Оно справедливо и в случае а>0 (фиг. 51,6),
если только точка г = а расположена не слишком далеко от нуля
функции Хо (г)-
Замечание. С помощью равенства
R
[С [г — a)]2dr = -^C2 {(к—аK-|-а3[
0
формулу для эффективного радиуса (88.10) можно привести к виду
R
1
Обычно в литературе используют такую нормировку, при которой асимптоти-
асимптотически }(о —*¦ 1—г/а и, следовательно, С = —1/а. Кроме того, в рассмотрение
вводят разность этой асимптотики и функции %0
что позволяет записать формулу для эффективного радиуса в виде
00
4-/-«= Сф(/-) |~2 A-— ^-<р(/-)] dr.

59. Рассеяние на сферически симметричной прямоугольной яме 245
В качестве верхнего предела интегрирования здесь взята бесконечность, но
функция ф (г), конечно, равна нулю правее точки r = R0.
Задача 89. Низкоэнергетическое рассеяние на сферически
симметричной прямоугольной яме
Исследовать низкоэнергетическое разложение
*ctg 80 = -1 + 1г0*«
(89.1)
в случае сферически симметричной прямоугольной потенциаль-
потенциальной ямы радиуса R и глубины
Vt = %*Kl/2m (фиг. 52):
а)	получить формулу (89.1) Е
непосредственно из граничных ус- 0
ловий при г= R;
б)	использовать общую форму-
формулу для г0, полученную в преды-
предыдущей задаче, применительно к
потенциалу рассматриваемого ча-
частного вида.	~vo
1
1
4
•
кг
Фиг. 52. Потенциальная яма с
обозначениями, используемыми в
тексте.
Общий множитель 2m/ti> не указан.
Решение. Для заданного по-
потенциала имеем, если г < R,
Xft = Ak sin Кг, Хо = Л sin Кйг,
(89.2)
и, если r>R,
Xft = sin(?r + 60), Xo = C(r—a).	(89.3)
Логарифмическая производная Lo волновой функции состояния
с нулевой энергией в точке r = R будет равна
- К R ctg /С R —	—		(89 4)
а. Запишем логарифмическую производную функции х*
в точке r = R:
Lk = KRctgKR = kRctg(kR + 50).	(89.5)
Так как
(89.6)
eg (rk -t- o0; - j +ctg 6o tg kR,
то, решая это уравнение относительно ctg60, получаем
kR~LktgkR '
Разложение в ряд по степеням k проще всего сделать в два
этапа. Сначала, воспользовавшись тем, что kR<^.\, разложим

246 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
tgkR. В результате находим
[^^Ы (89-7)
Следует заметить, что равенства (89.6) и (89.7) выполняются
для любого потенциала, лишь бы он обращался в нуль при
r~^R. Специальным видом нашего потенциала мы воспользуемся
на втором этапе при разложении логарифмической производной Lk
в ряд. Введем обозначения:
X0 = K0R, X = KR, x = kR.	(89.8)
Тогда первое равенство (89.5) примет вид
Lk = XcigX,
где
Л = У Лота =Л0~Г о у | • • •	(."У -У/
и, следовательно,
Отсюда получаем
х* Л
La(\-L0)j\'
2X1 Ч
поэтому первое слагаемое в формуле (89.7) можно разбить на
два члена: один из них дает вклад в длину рассеяния,
—l-=R(lL^L(j),	(89.10)
а другой, пропорциональный k2,— в эффективный радиус. Во
втором слагаемом в формуле (89.7) в нашем приближении мы
можем заменить Lk на Lo и в результате получим
^	2Хй 1— Lo\ 4A —Lo)/
Выразим в последней формуле логарифмическую производную Lo
через безразмерную величину
а = -^-.	(89.11)
Учитывая теперь, что
1	in	1	1	1	а
1 — (X	1 — L>q	ОС	1 — /*0	СС
и приводя подобные члены, получаем
'	"' ' f|-ib	(89.13)

90. Рассеяние и связанные состояния	247
Теперь нам осталось с помощью равенства (89.4) записать окон-
окончательное выражение для длины рассеяния. Оно имеет вид
(89.14)
Формулы (89.13) и (89.14) совместно с равенством (89.1) дают
полное решение нашей задачи.
б. Общий метод предыдущей задачи не дает никакого иного
пути определения длины рассеяния, кроме пути, основанного
на использовании равенства (89.4), что приводит непосредственно
к формуле (89.14). Однако для вычисления эффективного радиуса
уже нет необходимости вводить %* или Lk, если мы с самого
начала пользуемся общим выражением (88.10), которое в обо-
обозначениях (89.11) принимает вид
lro=fl|('-^2+K3-9fib^},	(89.15)
где
R
\ Хо (г) dr
xUR)
Постоянная 9С получается элементарным интегрированием, если
учесть, что функция %0 (г) в нашем случае определяется равен-
равенством (89.2). Мы имеем
2A0sinz
и так как
)
то выражение для ЭС можно преобразовать к виду
(89Л6)
Подставляя выражение (89.16) в (89.15), легко получаем для
эффективного радиуса формулу (89.13).
Задача 90. Низкоэнергетическое рассеяние и связанные состояния
Исследовать поведение функции ctg б0 в окрестности точки
& = 0 на комплексной плоскости k. Рассмотреть вопрос о суще-
существовании связанного состояния (k2 < 0) в той области значений k,
где еще можно пользоваться разложением для ctg60.
Решение. Если для малых значений k существует разложение
вида
Q = -±- + ±rok>+...,	(90.1)

248 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
то ctg б0 будет аналитической функцией комплексной переменной k
с полюсом в точке k = 0. Связанным состояниям отвечают зна-
значения переменной k, лежащие на положительной мнимой полуоси.
Положим
k = ix,	(90.2)
где и—действительная и положительная величина. Подставляя
выражение для k в формулу (90.1), получаем
т. е. ctg60 на мнимой оси становится чисто мнимой величиной.
Мы знаем, что фаза рассеяния б0 играет важную физическую
роль по той причине, что асимптотика радиальной волновой
функции s-состояния имеет вид
Основываясь на аналитичности функции у<0, мы можем для отри-
отрицательных энергий с учетом соотношения (90.3) написать
Функция с таким поведением будет волновой функцией связан-
связанного состояния только в том случае, если при к > 0 будет вы-
выполняться равенство
е-'б°=0,	(90.4)
так как только при таком условии функция %0 будет нормируема.
Условие (90.4) можно записать по-иному:
cos60 — i sin бо = 0,
или
ctg60=/	(90.5)
Подставляя равенство (90.5) в формулу (90.3), получаем
это соотношение связывает характеристическую величину и с па-
параметрами рассеяния а и г0. Этой связью можно воспользоваться
двояким образом.
1. Определение энергии связи из данных по рассеянию. Пред-
Предположим, что в соотношении (90.6) второе слагаемое в правой
части играет роль малой поправки. В этом случае соотношение
(90.6), рассматриваемое в качестве уравнения относительно х,
имеет решение

	91. Дейтронный потенциал с жесткой сердцевиной и без нее	249
поэтому энергия связанного состояния будет равна
¦ц-?).	(90.8)
"	2т"
Так как здесь фигурирует только и2, то необходимо подчеркнуть,
что, согласно равенству (90.7), связанное состояние в рамках
нашего приближения может существовать только при положи-
положительных длинах рассеяния.
2. Определение сечения рассеяния по энергии связи. Данная
задача не допускает столь полного решения, так как при этом
требуется найти значение двух параметров, а в нашем распоря-
распоряжении имеется лишь один (энергия связи). Запишем выражение
для сечения рассеяния
а„ = ^ sin2 60 = ~ • t+ct ,а	(90.9)
и в том же приближении, в котором получено равенство (90.7),
разрешим уравнение (90.6) относительно а:
_ 1 1
Далее из формулы (90.1) следует
и поэтому
Таким образом, мы приходим к знаменитой формуле Бете—Пай-
ерлса из ядерной физики:
^A +^о)-	(90.10)
Она справедлива при малых энергиях и условии иго<^1.
Литература
Bethe H. A., Peierls R., Ргос. Roy. Soc, A148, 146 A935).
Задача 91. Дейтронный потенциал с жесткой сердцевиной
и без нее
Используя условие существования связанного состояния
ctg80 = i, так подобрать глубину сферически симметричной пря-
прямоугольной потенциальной ямы радиуса R (фиг. 53), чтобы
у дейтрона было одно связанное состояние с энергией ED=
= — 2,23МэВ. Радиус ямы взять равным R= 1,2 ферми A ферми —
= 10~18см). Чему будет равна глубина потенциальной ямы, если
вблизи центра имеется жесткая сердцевина радиуса а = 0,2 ферми?

250 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Решение. При положительных энергиях волновая функция,
s-состояния, удовлетворяющая граничному условию Хо(а) = О.
имеет вид
- — а), а<г</?,
, R<r;
требование непрерывности логарифмической производной в точке
V(r)	V{r)
•г
где
а
0), (91.1)
(91.2)
нее.
Вырезая жесткую сердцевину, мы должны
сделать яму глубже, если намерены сохра-
сохранить энергию связи неизменной.
Для связанного состояния с
отрицательной энергией сле-
следует положить
k = iK, x = i\, l = xR, (91.3)
тогда энергия будет равна
(91-4)
где т* —приведенная масса пары нуклонов (т* = т/2, см. за-
задачу 150). Вместо энергии ED можно ввести характеристическую
длину
1= .г	- = 4,312 ферми,	(91.5а)
и отсюда
1 = ^ = 0,2783.	(91.56)
В задаче 90 мы показали, что для существования связанного
состояния должно выполняться условие
е-'Л =0, или ctg60 = i,
то тогда, как очевидно, должно выполняться и условие
е-м*+б<,) = о, или ctg (х + 60) = I,
поэтому равенство (91.1) дает
XctgpX = —?.	(91.6)
Так как в правой части этого равенства стоит знак минус, то
аргумент котангенса должен иметь значение в интервале между

91. Дейтронный потенциал с жесткой сердцевиной и без нее	251
я/2 и я1'. Если же принять во внимание, что величина ? мала,
то можно заключить, что оно довольно близко к я/2. Таким
образом, можно написать
pX = -J + e, ctgpX = -tge.	(91.7)
Нам нужно определить глубину потенциальной ямы, т. е.
значение параметра Xjj в предположении, что величина | задана
равенством (91.56). С этой целью мы сначала вычислим величину е:
подставим X из (91.7) в равенство (91.6) и произведем там раз-
разложение по степеням е и |. В результате получим
Подставив теперь полученное выражение в соотношение
будем иметь
X2 —
0 ~~
— 4 —
0
4- — 4-1^1	-
Обсудим полученный результат. Если жесткая сердцевина
отсутствует, то C=1 и Хо должно быть чуть больше я/2. Будь
Х0 = я/2, энергия связи была бы равна нулю (| = 0), но так как
связь несколько сильнее (| > 0), то и яма несколько глубже.
При наличии жесткой сердцевины это предельное значение па-
параметра Хо сдвигается и становится равным Х0 = я/2|3 > я/2:
в этом случае, чтобы сохранить энергию связи неизменной, по-
потенциальная яма должна быть глубже, чем в отсутствие жесткой
сердцевины.
Для значения ?=0,278 мы в соответствии с формулой (91.9)
получаем
где Vo — глубина потенциальной ямы. Если жесткой сердцевины
нет (C=1), то отсюда Х*о = 3,070 и УО = 88,4 МэВ. При наличии
жесткой сердцевины радиуса а = 0,2 ферми (Р = 0,8333) мы имеем
Х1 = 4,267 и Уо= 122,9МэВ. На фиг. 53 оба потенциала изо-
изображены в соответствии с этими числовыми результатами.
х) Это утверждение справедливо, если в потенциальной яме, как в случае
дейтрона, имеется только одно связанное состояние. Для ямы с двумя связан-
связанными состояниями уравнение (91.6) имело бы два корня и низшему энергети-
энергетическому уровню соответствовал бы интервал л < р"Х < 3/2 л.

252 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Задача 92. Низкоэнергетическое рассеяние при наличии жесткой
сердцевины и без нее
Для двух рассмотренных в предыдущей задаче дейтронных
потенциалов рассчитать длину рассеяния и низкоэнергетический
предел сечения рассеяния нейтронов на протонах.
Решение. Длина рассеяния а связана с предельным значением
логарифмической производной при k—>О в точке r = R соотно-
соотношением (89.10), так что мы имеем
С другой стороны, согласно равенству (91.1), для рассматрива-
рассматриваемых потенциалов должно быть
Lo = XoctgpXo.	(92.2)
Низкоэнергетический предел сечения рассеяния при-&—>-0 равен
а @) = 4яаа.	(92.3)
Так как значения параметров Хо и |3, полученные в предыдущей
задаче, согласуются с правильным значением энергии связи дей-
дейтрона, то для вычисления величин а и а @) мы можем просто
воспользоваться формулами (92.1)—(92.3). Результаты числовых
расчетов таковы:
1.	Потенциальная яма без жесткой сердцевины (Р=1,
XJ = 3,070):
Lo = — 0,3214, о = 4,934 ферми, а = 3,059 барн.
2.	Потенциальная яма с жесткой сердцевиной (|3 = 0,8333,
XI = 4,267):
Lo = —0,3135, а =5,028 ферми, ст = 3,177 барн.
Эти результаты представляют определенный интерес, так как они
показывают, что при заданных значениях радиуса потенциальной
ямы и энергии связи дейтрона наличие жесткой сердцевины очень
незначительно, всего на 3,8%, изменяет низкоэнергетическое
сечение нейтрон-протонного рассеяния. Таким образом, экспери-
эксперименты при низких энергиях практически не позволяют решить
вопрос о существовании жесткой сердцевины в нуклон-нуклон-
ных взаимодействиях.
Следует отметить, что благодаря спиновой зависимости ядерных сил и
большого вклада в рассеяние ^-состояния экспериментальное сечение рассея-
рассеяния фактически составляет примерно 21 барн. Полученные же из нашей мо-
модели числовые результаты хорошо согласуются с данными по рассеянию
в ^-состоянии.

93. Рассеяние на модифицированном потенциале	253
Задача 93. Низкоэнергетическое рассеяние на модифицированном
потенциале Пешля —Теллера
Используя сферически симметричный потенциал
являющийся результатом обобщения потенциала задачи 39 на
трехмерный случай, получить сечение рассеяния в пределе малых
энергий (/ = 0).
Решение. Найденные в задаче 39 одномерные решения при
/ = 0 можно использовать и в трехмерном случае, следует лишь
учесть, что дополнительному граничному условию %о@)=0
удовлетворяют только нечетные решения, поэтому ниже нам
понадобятся лишь соотношения C9.126), C9.136) и второе из
равенств C9.14). С учетом упомянутых формул имеем
ХоОО —sin(fcr + 80),	(93.2)
Дальнейшая, по существу чисто математическая, задача состоит
в том, чтобы придать выражению (93.3) вид, удобный для число-
числового расчета.
Введя обозначения
перепишем (93.3) в более компактной форме:
Из хорошо известных тождеств
Г Bг) = -—г е2г 1п 2 Г (г) Г (z + ^-
и
ГB)ГA—2) = -г^-
v ' ч ' sin яг
вытекают следующие соотношения для фаз:
arg Г (г) + arg Г A — г) = — argsin лг.

254 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Исключая из них arg Г (г), получаем
—arglY г + -2-) + argr(l— 2) =—argrB2) + 21n2- Imz—argsin nz.
Если теперь заменить здесь величину z ее выражением (93.4),
то формула (93.5) приобретет вид
б0—у = {arg Г Biq)—2q In 2} + { — arg Г (X + 2iq)+2q In 2-
— argsin jt (— -f iq J }•,
или
б0 = | + arg Г Bj<7) - arg Г (*. + 2iq) -
— arctgf eighth nq\ (93.6)
Для аргументов, фигурирующих в последнем выражении Г-функ-
ций, имеют место следующие представления:
поэтому их разность запишется в виде
Отсюда окончательно получаем
б0 = arctg -^ — arctg ( ctg ~ th nq ) +
и=1
(93.7)
Нетрудно убедиться, что фаза рассеяния стремится к нулю
при стремлении к нулю энергии рассеиваемой частицы (q—>-0).
Действительно,

93. Рассеяние на модифицированном потенциале	255
Что же касается сечения рассеяния
^)\	(93.9)
то оно стремится тогда к конечному пределу. Исключениями
являются случаи, когда к равно целому четному числу, т. е.
когда ctgirV2 обращается в бесконечность. В этих случаях
сечение а стремится к бесконечности, что можно объяснить нали-
наличием резонансного уровня в потенциальной яме, которому при
рассматриваемых значениях к соответствует энергия, в точности
равная нулю.
Расчет величин б0 и о по формулам (93.7) и (93.9) представ-
представляет чисто техническую задачу, и мы не будем вдаваться в соот-
соответствующие детали. Заметим лишь, что для целых к (четных
или нечетных) бесконечный ряд в формуле (93.7) вырождается
в конечную сумму, а второй член в этой формуле равен либо
нулю (нечетные к), либо я/2 (четные к), т.е., если к = 2т,
2т-1
и=1
а если к = 2т -f-1,
2m
В том случае, когда Я не является целым числом, бесконечную сумму
в формуле (93.7) можно разложить в ряд по степеням 2q. Вводя обозначение
X — iV = |x, где N ¦—наибольшее целое число, не превосходящее Я@ < ц, < 1),
можно написать
arctg -г—г—= У arctg —?—
N	^
Х + п
n=o	n=N
±
= у ( i)v v Bqfv+l,
v= 0
где
с _ у ( '	!_1_ у ' ГЛ , jM-Bv+"_il
v~Bt^U«+|iJv+1 «2V+1/ hn2v+i^ п'	J
Каждый член этого биномиального разложения можно выразить через ?-функ-
цию от аргументов 2v-j-2, 2v + 3 и т. д. Предлагаемый метод приводит к пред-
представлению фазы б0 в виде быстро сходящегося ряда.

256 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
10
л
Некоторые результаты числовых расчетов показаны на фиг. 54,
где изображена зависимость сечения рассеяния от энергии пада-
падающих частиц (обе величины взяты в подходящих единицах).
Гипербола 1/B<7J соответствует предельному значению сечения
а = 4я/?2; оно всегда превосхо-
превосходит значение парциального се-
сечения рассеяния с / = 0. В слу-
случае Я = 2 мы имеем резонанс
при нулевом значении энергии,
для двух других кривых, со-
соответствующих	значениям
к = 2,5 и к = 3, предельное сече-
сечение рассеяния конечно. В случае
К = 2,5 вблизц точки B<7J=0,6
имеется виртуальный уровень
F0 = jt/2), поэтому кривая се-
сечения рассеяния^ в этой области
энергий проходит очень близко
от предельной гиперболы. Для
значения ^ = 4 (эта кривая не
показана на фигуре) сечение
спадает до нуля (бо = я) в точ-
точке BqY = l, но затем по мере
0,Z 0,4 0,6 0,8
Фиг. 54. Сечения рассеяния на трех
различных модифицированных потен-
потенциалах Пешля — Теллера.
Гипербола определяет предел 4л/кг, кото-
который никогда не может быть превзойден
сеченнем о0.
роста энергии снова возрастает.
Задача 94. Радиальное интегральное уравнение
Заменить радиальное уравнение Шредингера
(94.1)
где
2тЕ
U{r) =
2mV (г)
интегральным уравнением. Каким образом превратить это урав-
уравнение в интегральное уравнение с симметричным ядром? Как
записать интегральное выражение для асимптотического значения
фазы волновой функции %fi Как связано решение этого уравне-
уравнения, найденное методом последовательных приближений, с после-
последовательными борновскими приближениями?
Решение. Уравнение (94.1) формально можно записать в виде
неоднородного дифференциального уравнения
_Dii = F{r),	(94.2)
где
г» '	(94.3)

94. Радиальное интегральное уравнение	257
а выражение F (г) можно рассматривать в качестве неоднород-
неоднородности. Однородное уравнение
имеет фундаментальную систему решений
/,(*,-) —sin (*/--?), nt(kr)-+-cos(kr-l-%y (94.4)
Общее решение неоднородного уравнения (94.2) представляет собой
суперпозицию общего решения однородного уравнения и частного
решения неоднородного уравнения, причем последнее опреде-
определяется функцией Грина G (г, г'). Таким образом, имеем
li (r) = A}t (kr) + Bnt (kr) + S G (r, r') F (r') dr'. (94.5)
о
Функция Грина G (г, г') определяется как решение уравнений
DG{r, r')=b{r — r') и D'G(r, r') = b{r — r'),
и ее можно взять, например, в виде
i(kr'), r<r',
G(r, /¦') = <! i	(94.6)
I -frhikr^n^kr), r > r'.
Так как нас интересует только волновая функция %1 (г), ре-
регулярная в точке г = 0, то в равенстве (94.5) мы должны поло-
положить В = 0; кроме того, мы можем выбрать такую нормировку,
при которой Л=1. В результате искомое интегральное уравне-
уравнение приобретает вид
со
')# (ОХ» (О <*''•	(94.7)
Теперь можно перейти к ответам на вопросы, поставленные
в условии задачи.
а. Симметричное ядро. Неоднородное интегральное уравнение
(94.7) имеет несимметричное ядро G(r, r')U(r'). Однако с по-
помощью подстановки
iiibr), (94.8)
К (г, r') = VU(r)U(r')G(r, r')
оно преобразуется в уравнение
со
y(r)=f(r) + ^K{r, r')y{r')dr'	(94.9)
о
9	№ 1050

258 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
с симметричным ядром
К (г, г') = К(г', г).	(94.10)
В преимуществах такого преобразования позволяет убедиться
задача 95.
б. Асимптотическое значение фазы. Если нас интересует реше-
решение хЛг) интегрального уравнения (94.7) при больших значениях
г, то мы можем во всей области интегрирования пользоваться
тем выражением функции Грина из (94.6), которое написано для
/">/¦'. Эта возможность обусловлена наличием под знаком интег-
интеграла множителя U(r'), благодаря которому основной вклад
в интеграл происходит от области 0 ^r' < R, где R — величина
порядка атомных размеров. С учетом изложенных соображений
получаем
(94.11)
Последнее выражение можно записать по-иному:
^.,	(94.12)
где асимптотическое значение фазы 8t определяется интегралом
tg^t= —j^U (r) it(kr)Xl(r)dr.	(94.13)
о
в. Последовательные приближения. Эти приближения	к реше-
решению нашего интегрального уравнения имеют вид последователь-
последовательности Неймана:
х}"> = /,(*л),	(94.14а)
{r, r')U{r')jt(kr')dr',	(94.146)
l\n) = It ikr) + S G (r, r') U (г') хГ" (rr) dr'. (94.14в)
о
Можно показать, что рекуррентная формула (94.14в) с точностью
до нормировочных постоянных совпадает с формулой гс-ro бор-
новского приближения (см. задачу 105):
^Уг, | {/(г'К-аг')**'. (94.15)
Чтобы убедиться в эквивалентности соотношений (94.14з) и
(94.15), разложим функции, фигурирующие в (94.15), по парци-

94. Радиальное интегральное уравнение	259
альным волнам. Мы имеем (см. задачи 81 и 82)
"» И = Т7 X К4яB/+1)г'хГ (г) Г,, о (О) (94.16)
/ = о
Bl+l)il]l(kr)Ytt0{&),	(94.17)
(= о
кроме того,
eik\r-r'\	, " .
\r-r'\ =7F 1* К4яB/ + 1)Гг(г, r')Y,,0(y), (94.18a)
где
{^YHkr'), r<r',
Г, (г, /•')=<{ ,	(94.186)
а у—угол между векторами гиг'.
Выделим теперь из рекуррентного соотношения (94.15) 1-ю
парциальную волну. Для этого умножим обе части (94.15) на
Ylt о (¦&) и проинтегрируем по всем направлениям вектора г. Учи-
Учитывая, что
§ У и о (О) Г,.
в результате получаем
(^«„-.(П-^ГЛг, г')
В последнем интеграле вместо функции un_t (r') мы можем взять
ее разложение, аналогичное разложению (94.16). Это даст
Х> @ = /г (*r)- S U (г') Гг (г, г') х!"-1' (г') dr'.	(94.19)
о
Полученное рекуррентное соотношение уже очень похоже на со-
соотношение (94.14в). Чтобы убедиться в их идентичности, заме-
заменим сферическую функцию Ханкеля в выражении для Гг в соот-
соответствии с ее определением
В результате имеем
г') = 4
9*
, {г, г') = 4 /, (kr) }t (kr')-G (r, r'),	(94.20)

260 II Задачи без учета спина. Г. Сферически симметричные потенциалы
где через G обозначена функция Грина, определенная равенством
(94.6). Первый член выражения (94.20) приводит к интегралу,
который пропорционален /, (kr), и его можно объединить с пер-
первым членом в правой части (94.19), поэтому
Й"' (г) = Ajt {kr) + J U (rr) G {г, г') х(Г1( (П dr', (94.21)
о
причем постоянная А определяется равенством
со
А = 1 -± J U (г') h (Аг')зс/(п-" (г') dr'.	(94.22)
о
Если отвлечься от этой постоянной, которая ведет лишь к не-
некоторому изменению нормировки, то последнее соотношение дей-
действительно идентично рекуррентной формуле (94.14в).
Замечание. Если сравнивать точное интегральное уравнение (94.7) для
функции %i(r) с точным интегральным уравнением
, Г eik\r-r'\
U(r) = elkz_	I	 U(r')u(r')d4',	(94.15a)
^л J \f—г \
то для этого достаточно в (94.21) опустить верхние индексы я —1, п и т. д.
Полагая теперь
мы видим, что интегральное уравнение, аналогичное уравнению (94.21), преоб-
преобразуется в уравнение (94.7), а формула (94.22) заменяется формулой
A = \-~A§U(r')jl(kr')Xl(r')dr'.	(94.22а)
о
Эту формулу можно упростить, воспользовавшись соотношением (94.13):
A = l+lAtg6[,
или
A=em'cos6i.
Разложение (94.16), если учесть асимптотическую формулу (94.12), теперь дает
СО
"(г) — TF 21 ^4n
( + ) ilel sin (kr —
что находится в полном согласии с найденной ранее формулой (82.9).
Задача 95. Вариационный принцип Швингера
Исходя из выведенного в предыдущей задаче интегрального
уравнения с симметричным ядром, установить вариационный
принцип для определения фазы рассеяния.

	95. Вариационный принцип Швингера	261
Решение. Оставляя неоднородность в правой части, запишем
интегральное уравнение (94.9) в виде
00
у (г) -J К (г, r')y{r')dr' = f{r).	(95.1)
о
Умножим обе части этого уравнения на у (г) и проинтегрируем
по г. Это даст
К = К,	(95.2)
где
во	/	со	\
h=\dry(r)\y{r)-\K{r, r')y(r')dr'\	(95.3)
о • v о	;
и
СО
l% = \y{r)f{r)dr.	(95.4)
Эти два интеграла равны между собой при условии, что-функ-
что-функция у (г) удовлетворяет уравнению (95.1). Из предыдущей задачи
нам известно, что
CD
Л = $ U (r) U ikr) Ъ (г)dr = -ktg б,.	(95.5)
о
Возьмем теперь вместо истинного решения у (г) близкую к нему
функцию у{г) + Ьу(г). При этом несколько изменятся и значения
наших интегралов:
6/t = 2 S dr Ьу {г) [у (г)-IК (г, г')у (rf) dr'	(95.6)
о	V о	;
(95.7)
Следует заметить, что равенство (95.6) написано в предположении,
что ядро интегрального уравнения симметрично. Дело в том, что
при варьировании у (г') первоначально возникает вариация 8у(г'),
и, чтобы вернуться к вариации бг/(г), мы должны в правой части
равенства (95.6) произвести замену переменных интегрирования,
в результате которой ядро К (г, г') перейдет в ядро К (г1, г).
Так как выше у (г) означает истинное решение интегрального
уравнения (95.1), то в правой части равенства (95.6) выражение,
стоящее в фигурных скобках, можно заменить функцией /(/¦),
поэтому мы получаем
6^ = 26/,.	(95.8)
9* №. 1050

262 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Последнее равенство с помощью соотношения (95.2) можно запи-
записать по-иному:
1	~Т~ — и>
ПЛИ
6 DНО-	(95-9)
Это и есть искомый вариационный принцип. Согласно этому
принципу, требуется, чтобы величина S^IJIl, или, подробнее,
величина
а	(	со	^
J dr U (r) %l (г) \ %l (r) ~ J %1 (/¦') U (/"') G (r, r') dr'}
^°
(95.10)
U (r) ti (r) It (kr) dr
6
была экстремальна и, следовательно, чтобы
65^ = 0.	(95.11)
Смысл величины St нетрудно установить, если принять во вни-
внимание равенство (95.5) и учесть, что /1 = /2. Мы имеем
S* = -|ctg6,.	(95.12)
Таким образом, экстремальное значение величины S[ непосредст-
непосредственно связано с правильным значением фазы рассеяния 6г.
Следует отметить, что сформулированный вариационный прин-
принцип не зависит от нормировки волновой функции. В этом легко
убедиться, заменив в (95.10) волновую функцию хг функцией C%t.
В результате этой замены числитель и знаменатель дроби (95.10)
умножаются на С2, поэтому сама величина St остается неизменной.
Замечание. В области очень малых энергий (k —»¦ 0), когда взаимодействие
имеет характер притяжения, в рассеянии участвует только s-волна (Z = 0).
Как было показано в задаче 88, в этом случае мы можем ввести длину рассеяния
"о = — -j tg 60.
Равенство (95.12) показывает, что
поэтому сформулированный вариационный принцип с успехом можно исполь-
использовать для определения длины рассеяния.
Литература
Schwinger J., Phys. Rev., 72, 742А A947).
Blatt J. M., Jackson J. D., Phys. Rev., 76, 18 A949).

96. Последовательные приближения для фазы рассеяния	263
Задача 96. Последовательные приближения для фазы рассеяния
Радиальное уравнение Шредингера для s-волны формально
можно рассматривать как неоднородное дифференциальное урав-
уравнение, считая неоднородностью член, содержащий потенциальную
энергию. „Решение" этого уравнения представляет собой интег-
интегральное уравнение для функции Хо, и его можно решать методом
последовательных приближений. Используя указанную процедуру,
найти интегральное выражение для второго приближения к функ-
функции tg60.
Решение. Радиальное уравнение Шредингера при 1 = 0 запи-
запишем в виде
%' + к*% = и%, V = 2fj(r).	(96.1)
Здесь и далее мы опускаем индекс 0 у функций %о, б0 и т. д.
Рассматривая в этом уравнении правую часть как неоднородность,
мы можем выразить его решение через функцию Грина Q (г, г'),
которая является решением уравнений
5J + *2G = 6(r-r') = gS + ?2G.	(96.2)
Таким образом, имеем
$(r, r') U (r') % (rr)dr'. (96.3)
Функцию Грина в (96.3) можно выбирать различными способами,
для дальнейшего ее удобно взять в виде
G(r,r') = (-TsIn*(r-r>' '<'.	(96.4)
I	0,	г' > г,
так как при этом мы сможем удовлетворить граничному условию
Х@) = 0, просто положив В = 0. Выбирая далее в качестве усло-
условия нормировки, которая не является существенной для опреде-
определения фаз, условие Л=1, мы приходим к интегральному урав-
уравнению Вольтерра
г
X (г) = sin kr—j j sin k (r' — r) U (rr) x (/¦') dr'. (96.5)
о
Расписав sink(r' — r), мы можем представить наше решение %{г)
в виде
X (г) = С (г) sin kr + S(r) cos kr,	(96.6a)

264 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
где
С(г) = 1 +1
г
С(г) = 1 +1 jcosfer' U (r')x(r')dr't
(96.66)
о
Обе амплитудные функции С (г) и 5 (г) при г —* оо стремятся
к конечным пределам при условии, что потенциал ведет себя как
/—', где <? > 1, в этом предельном случае из (96.6а) следует:
%(r) ~ sin (kr + 8).
Таким образом, фазу рассеяния б мы можем определить из соот-
соотношения
tge-|g|.	(96.7)
Выражения (96.66) совместно с соотношением (96.7) дают строгое
решение задачи.
Интересующие нас последовательные (борновские) приближения
строятся в предположении, что потенциал U (г) является величиной
первого порядка малости. Для удобства выкладок будем временно
писать W вместо U и разложим функцию % в ряд по степеням
„параметра порядка" %:
X = Xo + bXi + *fX. + -...	(96.8)
где индексы, очевидно, означают порядковые номера приближе-
приближений. Уравнение (96.5) во втором приближении записывается
следующим образом:
Отсюда, приравнивая члены одинакового порядка малости, по-
получаем
X0(r) = sin&r,	(96.9а)
г
%1 (г) = — i- f sin k (r' —r) U (г') sin kr' dr', (96.96)
о
X, (') = ^ j dr' sin * (r' -r)U (r') x
T*
X Uin k (r" — r') U (/-") sin kr" dr".	(96.9b)

96. Последовательные приближения для фазы рассеяния	265
Здесь Хо представляет собой вклад от невозмущенной плоской
волны. В первом порядке имеем х —Хо + Хи и> расписывая снова
s\nk(r' — r) так, как это было сделано при получении соотноше-
соотношений (96.6), находим
г
C(r)=l+-j^U (г') cos kr' sin kr' dr',
'	(96.10)
S(r) = —g-V U (r') sin2 kr'dr'.
Таким образом, в первом порядке амплитуду S (г) можно отож-
отождествить с выражением (96.7), так что для фазы рассеяния мы
имеем формулу
tg6 = — ±^U (r') sin2 kr'dr',	(96.11)
которая, действительно, совпадает с формулой первого борнов-
ского приближения (см. задачу 106). Во втором порядке к при-
приведенным выражениям мы должны добавить функцию х2- Это даст
г
С (г) = 1 +1- J dr' U {r') cos kr' x
о
X | sin kr' — j j U (г") sin k (r" - r') sin kr" dr" I,
;	n	^ (96.12)
^r'U (r') sinЛг'X
о
т'
X \ sinkr'—г \ U (г") sin k (г"—г') sin kr" dr" \.
X К slnkr'—г-
I
Мы видим, что наше приближение представляет собой разложе-
разложение по отрицательным степеням k в соответствии с тем, что бор-
новский метод применим в области высоких энергий. Наряду
с возрастающими отрицательными степенями величины k в высших
приближениях появляются и все более высокие степени потен-
потенциала U.
Если теперь подставить выражения (96.12) в формулу (96.7)
для tg6, то величину 1/С(оо) мы можем разложить аналогичным
образом. Так как S(oo) пропорционально l/k, то амплитуду С(оо)
можно взять в первом приближении, если нас интересует ре-
результат, верный лишь с точностью до членов \/k2 включительно.

266 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Таким образом, имеем
( °°
tg6 = \—\\u (г) sin2 krdr +
4- 4f [ dr U (r) sin kr^U (r') sin k (/•' — r) sin kr' dr' I x
0	0	^
/oo	\	oo
IIP	llP
X < 1 — jlf (r') cos kr' sin &r' dr' > = — -г- \ i/ (r) sin2 /sr dr +
00	00
+ тг \ dr U (r) sin2 kr \U (r') sin ?r' cos ^r'dr' +
о	J/
oo	Г
+ i Г dr i/ (r) sin Jfer С ?/ (r') sin/г (r' — r) sin kr' dr'.
о	о
После очевидной перегруппировки членов, имеющих порядок \/ka,
окончательному результату можно придать одну из следующих
форм:
00	/	00	\
tg б = — ijdr i/ (r) sin2fcr j 1—-i J i/ (/¦') sin 2 fcr' dr' 1 , (96.12a)
- или
tg б = — -j \ dr U (r) sin kr | sin kr—|-cos /гг С U (r') sin2 /sr' dr' I.
(96.126)
Это есть приближение второго порядка для фазы рассеяния.
Замечание. Данный метод можно применять к парциальным волнам с / > 0.
Единственное отличие состоит в том, что тригонометрические функции sin kr и
cos kr придется заменить на сферические функции Бесселя ji(kr) и — ;
Задача 97. Уравнение Калоджеро
Для отношения
!$	(97Л)
где S{r) и С (г) — амплитудные функции, введенные в предыдущей
задаче, вывести нелинейное дифференциальное уравнение первого
порядка. Найти приближенное решение этого уравнения, соот-
соответствующее второму борновскому приближению.

97. Уравнение Калоджеро	267
Решение. Мы показали, что в выражении
у> (г) = С {г) sin kr + S (r) cos kr	(97.2)
амплитудные функции и их производные определяются соотно-
соотношениями
г
С (г) = 1 + \ J U (r') cos kr'% (/¦') dr',
(97.3)
S (r) = — \ j f/ (r') sin kr' % {r') dr',
0
S'(r) =-± U (r) sinkrX(r).
Дифференцируя равенство (97.1), получаем
, _CS'—SC
где
CS' — SC = — ^ x {С sin kr+S cos kr} = — ~ xa (r).
Следовательно,
^p = — -jU^ is[nkr + * (r)cos krY-	(97-4)
Это и есть искомое дифференциальное уравнение для t (r), извест-
известное как уравнение Калоджеро.
Последовательные борновские приближения нетрудно полу-
получить, заменив опять U на W и разложив затем функцию t (r)
в ряд по степеням Я,. Мы имеем
/ = Я,/х + А,2г2 + Л.3/8+... .	(97.5)
Приравнивая теперь в уравнении (97.4) члены одинакового по-
порядка малости, находим
t\ = — -j- sin2 kr,	(97.6a)
/; = —-j-/xsin2*r,	(97.66)
/g = — -у {/„ sin 2fer + ^ cos2 Ar}	. (97.6b)
и т. д. Каждое последующее уравнение этой цепочки допускает
решение в квадратурах.

268 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Уравнение (97.6а) соответствует первому борцовскому приб-
приближению, и его решение имеет вид
г
t, (г) = - If U (г') sin2 kr' dr',	(97.7)
так что для фазы рассеяния в этом приближении получается
формула
00
tg б = tx (оо) = — i С U (г) sin2 kr dr.	(97.8)
Во втором борновском приближении t — tx^t%, поэтому с учетом
уравнений (97.6а) и (97.66) имеем
t(r) = — i- f dr' U(r') sin kr' sin kr'—|cos kr' f U (r*)sin2 kr" dr" [,
0	'	0	)
(97.9)
и, следовательно,
tg б = — -i f dr i/ (r) sin &r I sin fer —~ coskr f i/ (/¦') sin2 йг' dr' 1
4	{	i	)
(97.10)
в полном согласии с формулой (96.126) предыдущей задачи.
Задача 98. Линеаризация уравнения Калоджеро
Найти приближенное решение дифференциального уравнения
Калоджеро (97.4) в предположении, что |/()|^1
Решение. В правой части уравнения Калоджеро
§ = - j- U (r) {sinkr +1 (r) cos kr\\	(98.1)
или
~r = — ¦%¦ {sin2 kr +1 sin 2kr + /2cos2 kr),
последний член при малых / (г) можно отбросить. Таким обра-
образом, приближенное решение t должно удовлетворять линейному
уравнению вида
¦§¦=* — -^-{sin2^r+?sin2fer}.	(98.2)
Сравнивая уравнение (98.2) с уравнением для второго борнов-
ского приближения
2Г (<i + f0 = - Т isin2 kr + h sin

	99. Длина рассеяния потенциала	269
которое легко получается из (97.6), мы находим, что второе бор-
новское приближение несколько хуже, чем приближение (98.2).
В правой части уравнения (98.2) вместо функции tx фигурирует
сама функция Г, что эквивалентно включению в уравнение пер-
первого члена из третьего борновского приближения (97.6в). Таким
образом, линеаризация сразу же приводит к решению, которое
в качественном отношении занимает промежуточное положение
между вторым и третьим борновскими приближениями.
Решение уравнения (98.2), удовлетворяющее граничному ус-
условию
?@)=0,	(98.3)
находится стандартным методом и имеет вид
г
?(') = — х j dr'u (r')sin2 kr> х
ехр ( —-±- J U (г") sin 2kr" dr\ . (98.4)
Разлагая здесь экспоненту по степеням l/k, мы можем вернуться
ко второму борновскому приближению. Следует подчеркнуть,
что приближение (98.4) значительно лучше борновского, так как
даже при очень малых значениях k [или же при очень больших
значениях U(r), как в случае сингулярных потенциалов], когда
формулы борновских приближений теряют смысл, мы все еще
имеем вполне определенное решение по крайней мере для потен-
потенциалов, соответствующих силам отталкивания.
Задача 99. Длина рассеяния потенциала, имеющего вид
степенной функции
Определить длину рассеяния потенциала, описываемого фор-
формулой
g	^(Uy\	(99.1)
а)	путем точного интегрирования уравнения Шредингера при
б)	путем решения линеаризованного уравнения Калоджеро.
Решение
а. Радиальное уравнение Шредингера для случая / = 0 и ? = 0
имеет вид
•Хл—8*х-а%а = 0, х = -~.	(99.2)

270 //, Задачи без учета спина. Г. Сферически симметричные потенциалы
Решением этого уравнения, удовлетворяющим граничному усло-
условию 5С0 @) = 0, является функция
& = С К*/Cjl (!¦*-*), ^~,	(99.3)
где Kv (z) означает модифицированную функцию Ханкеля
*v(z)=2in^r['-v(z)-/vB)] = fe2 ^(iz), (99.4)
асимптотика которой при \z\—>-оо имеет вид
:е-*.	(99.5)
Когда значения переменной х очень малы, аргумент функции К
в (99.3) становится большим и мы можем воспользоваться фор-
формулой (99.5). В результате имеем
в „-*.
Функция Хо> очевидно, удовлетворяет граничному условию
Хо(О) = О-
С другой стороны, если значения х велики и значения г
малы, то мы можем воспользоваться степенными разложениями
функций /±v (z), что с учетом равенства (99.4) дает
4A—v)
*
2
Чтобы получить асимптотическую формулу для функции %0 при
больших значениях г, мы оставим у каждого слагаемого в фи-
фигурных скобках только главный член разложения. В результате
имеем
Г 1+^-
Последнее выражение представляет собой линейную функцию
переменной х, и его можно записать в виде
(99.7)

99. Длина рассеяния потенциала	271
где а по определению есть длина рассеяния (см. задачу 88).
Сравнивая выражения (99.6) и (99.7), получаем
-r
e
(i—L
б. С помощью линеаризации уравнения Калоджеро мы нашли
[см. соотношение (98.4)]
tg6e=—?fdr(^)" sin» Лгх
0 о
Xexpj —¦??(¦?)" sin 2Jfer'dr'|; (99.9)
кроме того, для случая асимптотического поведения %0 при
k—>-0 имеем
Х„ ~ sin (&г + 50) = s'n ^r cos ^o +
+ cosfersinS0—>sin боA +/гг ctg 60).
Сравнивая это выражение с равенством (99.7), мы приходим
к формуле, определяющей длину рассеяния через фазу рассеяния:
а = ~ lim-Ц^-.	(99.10)
*о к
Подставляя сюда выражение (99.9) и используя в качестве без-
безразмерных переменных интегрирования величины г/го~х и
Г'/Го — У> получаем следующее приближенное выражение для
длины рассеяния:
<Ю	/	GO	v
a = g\ J dx х*-п exp ( -2g2 J /-" dy).
0	\	x	1
Показатель экспоненты легко вычисляется и равен —2gixi~n[{n—2),
а оставшийся интеграл с помощью подстановки
п-2х	%
сводится к интегралу Эйлера, так что окончательно имеем
(99Л1)
Это приближенное выражение можно сравнить с точной фор-
формулой (99.8). В обоих случаях длина рассеяния одинаковым
образом зависит от безразмерной константы взаимодействия g2,

272 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
а отношение приближенного и точного выражений
t
1%
(99.12)
представляет собой функцию Я, т. е. зависит только от показа-
показателя л = 2(Я+1) в выражении для потенциала. О качестве при-
приближения (99.11) можно судить по приведенной таблице:
п
3
4
5
6
8
10
12
00
а 1а
1
0,886
0,810
0,762
0,702
0,665
0,642
0,500
Мы видим, что при п = 3 отклонение отсутствует, затем ошибка
возрастает и становится равной 50% в случае жесткой сферы
(Я=оо).
Задача 100. Второе приближение к уравнению Калоджеро
Связать процедуру линеаризации уравнения Калоджеро с ме-
методом последовательных приближений и на этой основе вычис-
вычислить во втором приближении длину рассеяния потенциала, рас-
рассмотренного в предыдущей задаче.
Решение. Если точное уравнение
~г = — х {sin2 kr +1 sin 2 kr +1% cos2 kr)	A00.1)
заменить цепочкой уравнений
^г= — -^-{sin2^r + /nsin2^/- + /2_1cos2fer}, *0 = 0,	A00.2)
то в первом приближении мы снова получим линейное уравнение
A00.3)
решенное нами в задаче 98. Каждое последующее приближение
получается из предыдущего путем решения линейного уравнения
в квадратурах, только в разных случаях приходится иметь дело

	100. Второе приближение к уравнению Калоджеро	273
с различными неоднородностями:
г
К (г) = — -j J dr' U (rr) [sina kr'+Pn_l {r') cos* kr'\ x
о
X ехр I — -j j U (О sin 2kr"dr"\. A00.4)
Таким образом, чтобы найти второе приближение, нам доста-
достаточно в подынтегральное выражение для линеаризованного ре-
решения ввести дополнительный множитель
[1+'? (О ctga ?/"'].	A00.5)
Что же касается длины рассеяния, то здесь можно добиться еще
больших упрощений. Введем „интерполированную" длину рассея-
рассеяния а (г), определив ее соотношением
а(г) = — Пт'-Р-.	A00.6)
* -*о R
В первом приближении имеем
ах (г) =\dr'U {r')r'\xp I — 2 J U (r") r"dr"\. A00.7)
0	v	г"	I
Отсюда для длины рассеяния во втором приближении [а2 = аг (оо)]
получаем
\-2^U(r')r'dr'\ .	A00.8)
Соотношения A00.7) и A00.8) теперь можно использовать для
вычисления длины рассеяния потенциала
A00-9)
рассмотренного в предыдущей задаче. Вводя обозначения
A00.10)
'о
получаем
а, (О = g\ J dyy*-n ехр {-2g2 J z1-ndz\ =
0	V	у	I
X
= ё*г„ [у-гХ&хр1^-(х-^— y~tX)\ dy.

274 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Последнее выражение после замены
s = ¦?*-•»¦ и t = ^-y—K	A00.11)
принимает вид
4(?)теф"^в-<Л.	A00.12)
Подставляя его теперь в формулу A00.8), получаем
1 <ю	1	/	if0!	^
\ CISS С К 1 —I т~ S € I \ X С dt I \ . (lUU.lo)
о	V	Lo	-i )
Если в фигурных скобках оставить только первый член, то это,
разумеется, даст нам формулу первого приближения (99.11). Что
касается поправки
а = ^^-1, a^a^l+a),	A00.14)
то для нее из A00.13) легко получается выражение вида
а = -
A00.15)
Этот интеграл сходится, и его в общем случае можно вычислить
численным интегрированием.
Имеются два случая, а именно л = 4 и л—* оо, когда оценка
интеграла особенно проста.
Если п = 4 или Я,= 1, имеем
2
a = —^ Г
4 \Tn J
или
Численное интегрирование по методу Симпсона и использование
в области | > 2,4 вместо функции ошибок ее асимптотического
выражения приводят к значению a = 0,0770. Как мы видели (см.
стр. 272), в первом приближении
flj = 0,886a,
когда п = 4, поэтому во втором приближении получаем
а, = 0,886-1,077a = 0,954a.
Таким образом, ошибка, составляющая в первом приближении
11,4%, теперь будет равна 4,6%.

101. Длина рассеяния для сферически симметричной ямы	275
В случае п -»¦ оо, или 1/А, = 0, сходимость метода несколько
хуже. Выражение A00.15) в этом случае дает
и так как
а^ 0,500а,
то
«2 = 0,625а.
Задача 101. Длина рассеяния для сферически симметричной пря-
прямоугольной потенциальной ямы
В случае сферически симметричной прямоугольной потенци-
потенциальной ямы
сравнить точное выражение для длины рассеяния с приближен-
приближенным выражением, полученным на основании линеаризованного
уравнения Калоджеро. Обсудить также случай сил отталкива-
отталкивания, который получается при перемене знака в формуле A01.1)
Решение. Введем обозначения
kR = x, K0R = X0, KR = X = VXl + x\	A01.2)
В этих обозначениях, согласно задаче 89, мы имеем следующее
точное выражение:
Для потенциала A01.1) логарифмическая производная [см. равен-
равенство (89.5)] равна
L = XctgX.	A01.4)
Что же касается длины рассеяния, определяемой выражением
fc-s-0 K
то для нее в рассматриваемом случае [см. также (89.14)] имеет
место формула
а = _д Ига *!»•	^(leXo—i) .	A01.6)
0 х	\ Ло	/
С другой стороны, линеаризованное уравнение Калоджеро,
как мы знаем из задачи 98, приводит к соотношению
00	Г
tg60 = —~ \ drU (r) sin*krexpl — -J- Jt/ (r') sin 2kr
L
0
'dr' ,
J

276 //¦ Задачи без учета спина. Г. Сферически симметричные потенциалы
что с учетом определения A01.5) дает
1
A01.7)
Отсюда в случае потенциала A01.1) получаем
определения A01.5) дает
а= Jdrrst/(r)exp — 2 J r'U (r')dr' .
0	L	г	J
а = -К1S
exp [KI (Яа-
или
A01.8)
где мы ввели обозначение
Если воспользоваться тождеством
dt = \ j в"*1 dt —i-
о
то интеграл в правой части равенства A01.8) можно привести к
функции ошибок. Окончательный результат имеет вид
A01.9)
Длины рассеяния, рассчитанные по точной формуле A01.6) и по
приближенной формуле A01.9), для сравнения приведены в ни-
нижеследующей таблице для нескольких значений Хо:
1
1
1
1
,0
,2
,4
,6
a/R
—0,557
—1,142
—3,14
+20,4
Притяжение
~a/R
—0,515
—0,912
-1,632
—3,02
Отталкивание
a/R
0,238
0,305
0,368
0,424
~a/R
0,231
0,289
0,337
0,375
Ниже точки Л0 = 0,7 различие становится совершенно незначи-
незначительным. С другой стороны, при Л0 = л/2 точная формула »в слу-
случае сил притяжения приводит к расходимости и, кроме того,
длина рассеяния меняет знак. Эту особенность длины рассеяния
наше приближение передать не в состоянии. Таким образом,

102. Длина рассеяния потенциала Юкавы	277
линейной аппроксимацией можно пользоваться без опасений только
в том случае, когда уровни связанных состояний располагаются
заметно ниже нуля.
В случае сил отталкивания, когда потенциал имеет вид
мы аналогичным образом для длины рассеяния находим точную
формулу
^thX^	A01.11)
2
и приближенную формулу
( -х2 Хо	\
a = —^R -^-Je'VH-l .	A01.12)
В случае сил отталкивания резонансные эффекты отсутствуют,
поэтому наше приближение, как показывают последние два столбца
таблицы, оказывается более удовлетворительным.
Задача 102. Длина рассеяния потенциала Юкавы
Определить длину рассеяния в случае сил притяжения, опи-
описываемых потенциалом Юкавы:
V{r) = -Vorfe-«r., Vo = ^.	A02.1)
Рассмотреть три метода:
а)	метод линеаризованного уравнения Калоджеро;
б)	метод численного интегрирования уравнения Шредингера
при g=l;
в)	Метод Борна.
Решение. И линеаризованное уравнение Калоджеро, и бор-
новское приближение — это методы, типичные для области высо-
высоких энергий, поэтому не следует ожидать, что они дадут надеж-
надежные результаты для длины рассеяния, т. е. в области низких
энергий. В задаче 98 было показано, что линеаризованное урав-
уравнение Калоджеро лучше второго и тем более лучше первого бор-
новского приближений. Таким образом, данная задача может
служить иллюстрацией того, что эти приближения с точки зрения
их качества располагаются именно в таком порядке, как указано
выше. В этой связи весьма удивительно, что полученные ниже
результаты в общих чертах все же передают основные особен-
особенности рассеяния даже при нулевой энергии.

278 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
а. Воспользовавшись, выражением (98.4) для функции ? (г) и
определением длины рассеяния
a~ — lim-
и введя обозначения
j j / \ 2/7z t, , ,	g e~x	т
ft2	r0 x	ro
мы получим следующую приближенную формулу:
a = — gr0
Подставив в эту формулу
найдем
2g
а = — -g- r0 J еУ (In 2g—In у) dy.
Вводя интегральную экспоненту
A02.2)
A02.3)
A02.4)
= 2ge~x,
2g
и интегрируя по частям, окончательно получаем
A02.5)
где С = 0,5772... — постоянная Эйлера. Числовые результаты для
некоторых значений константы взаимодействия g приведены в
нижеследующей таблице:
g
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
-а/г„
0,1052
0,2220
0,3518
0,4967
0,6589
0,8413
1,0468
1,2790
t
0,9
1,0
1,1
1,2
1,3
1,4
1,5
-а/г.
1,5425
1,8420
2,1835
2,5740
3,0217
3,5362
4,1290

102. Длина рассеяния потенциала Юкавы
279
б. Длину рассеяния можно определить, зная решение ради-
радиального уравнения Шредингера при нулевой энергии
которое определяется начальными условиями
Х.@) = 0, Ь(О)=1.
A02.6)
(Ю2.7)
При очень больших значениях х член, содержащий потенциаль-
потенциальную энергию, практически равен нулю, поэтому асимптотическое
решение представляет собой линейную функцию:
Хо
A02.8)
где постоянная а связана с длиной рассеяния а соотношением
A02.9)
а
а — — .
Разрешая асимптотическое равенство A02.8) относительно
лучаем
по-
поA02.10)
Ниже в таблице приведены интересующие нас величины, полу-
полученные численным интегрированием уравнения A02.6) при на-
начальных условиях A02.7) для случая g= 1.
X
0
1
2
3
4
5
5,5
6
X
0
0,638
1,040
1,312
1,559
1,798
1,916
2,033
х'
1
0,457
0,298
0,255
0,241
0,237
0,236
0,235
— а
0
0,348
1,484
2,15
2,47
2,60
2,63
2,65
Из таблицы видно, что величина а, рассчитанная по формуле
A02.10), при х = 0 равна нулю, а затем с ростом х медленно воз-
возрастает, стремясь к некоему постоянному пределу, который и
определяет длину рассеяния. В нашем примере имеем
а = —2,65г0.	A02.11а)
Это значение следует сравнить с приближенным значением A02.5),

280 //¦ Задачи без учета спина. Г. Сферически симметричные потенциалы
которое при g= l равно
а = —1,842г„.	A02.116)
в. Формулу первого борновского приближения можно полу-
получить из формулы A02.4), если оставить там только член, линей-
линейный по g. Таким образом, имеем
а1 = — gr0 $ xe~x dx = — gr0,
о
что в случае g= 1 дает
«! = — /-„.	A02.Ив)
Если же в разложении подынтегрального выражения в A02.4) мы
учтем еще и член, квадратичный по g, то в результате у нас по-
получится формула второго борновского приближения:
Отсюда для случая g=\ находим
а, = —1,500г0.	A02. Иг)
В заключение заметим, что чем сильнее взаимодействие, тем,
разумеется, больше отклоняются от точного все три рассмотрен-
рассмотренные нами приближенные значения. Классификация этих прибли-
приближений в качественном отношении вполне соответствует той, кото-
которая предсказывалась нами в самом начале задачи.
Литература к задачам 96—102
Calogero F., Nuovo Cimento, 27, 261, A963).
Klar Й., Kruger H., Zs. Rhys., 191, 409 A966).
Kruger H., Zs. Rhys., 204, 114; 205, 338A967).
Задача 103. Улучшение сходимости рядов сферических гармоник
Используя рекуррентные соотношения, связывающие соседние
полиномы Лежандра, получить вместо ряда
более быстро сходящийся ряд для функции A—x)f(x).
Решение. Чтобы получить интересующий нас ряд, мы можем
воспользоваться рекуррентным соотношением
Pl{x).	A03.2)

103. Улучшение сходимости рядов сферических гармоник	281
Это дает
A— X)f (*)==Х/г \Pi~2r+TPl+l~2r+lPl
1=0
Выделяя здесь первое слагаемое и переобозначая индекс сумми-
суммирования, находим
со
A-*)/(*)=/„-4-/i+EfaM*). A03'3)
1=1
где
fi^fi 21 — 1 '**** 2Г+3^'+1#	A03.4)
Теперь, чтобы получить представление о достигнутом улучше-
улучшении сходимости, положим для больших I
Тогда выражение
при /^>1 можно разложить следующим образом:
Члены, содержащие /° и Z, взаимно сокращаются, так что основ-
основной член разложения становится равным
J - _f
It	li 2/
и мы, действительно, имеем значительное улучшение сходимости.
Замечание. Приведенные формулы еще больше упрощаются, если положить
как это чаще всего и бывает в приложениях. В этом случае получается
формула
Литература
Yennie D. R., Ravenhall D. 0., Wilson R. N., Phys. Rev., 95, 600 A964).
10 № 1050

282 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Задача 104. Интеграл по прицельному расстоянию
Когда kR^>\, где R — эффективный размер области взаимо-
взаимодействия, основной вклад в амплитуду рассеяния дают состояния
с Z^>1. Заменив сумму по I интегралом по прицельному рас-
расстоянию Ь и взяв для фазы рассеяния б (Ь) выражение, получен-
полученное методом ВКБ, определите сечение рассеяния.
Решение. В общую формулу амплитуды рассеяния
/ @) = ~ V B1 + 1) (е«\ - 1) Pt (cos Щ	A04.1)
введем прицельное расстояние
Ь^—^-	A04.2)
и используем его в качестве переменной интегрирования:
b [e2™ <») — 1] Pt (cos Щ db.	A04.3)
о
Замена нижнего предела интегрирования l/Bk)^.R нулем
в данном случае вполне допустима. Несколько труднее предста-
представить полином Лежандра Pt в виде функции прицельного рас-
расстояния Ь. По определению полиномы Лежандра связаны с гипер-
гипергеометрической функцией соотношением
Ц+1, -1,1; sin»?J,	A04.4а)
или подробнее
P<(cos0)=l-^sin4 +	sin4+... •
A04.46)
Отсюда нетрудно получить асимптотическое выражение для зна-
значений /^>1. Введем обозначение
Ь = * + у.	(Ю4.5)
тогда, очевидно,

104. Интеграл по прицельному расстоянию	283
и, следовательно, коэффициенты ряда A04.46) отличаются от Я,2"
лишь членами порядка к~2. Если пренебречь этими поправками
в случае больших /, то равенство A04.46) можно записать в виде
но последний ряд, как известно, представляет функцию Бесселя,
поэтому окончательно получаем
lim Рг (cos #) = ./„ (B/ + l)sin^).	A04.6)
Подставляя выражение A04.6) в формулу A04.3) и учитывая
соотношение A04.2), находим
00
/ (О) = — ik f Ь [е2'6 <">— 1] Jo Bkb sin i)d6. A04.7)
Так к.ак энергия рассеиваемой частицы велика, то мы можем
для вычисления фазы рассеяния б (Ь) применить приближение
ВКБ, воспользовавшись методом квазипотенциала, развитым
в задаче 124. Согласно равенству A24.7), имеем
где функцию Q (t) в области высоких энергий, а точнее, при
условии
|
для всех значений г, можно заменить потенциалом V{r). Если
теперь от переменной / вернуться к переменной г, то у нас
получится следующее простое соотношение:
Ш=.	A04.8)
Стоит заметить, что это соотношение линейно по потенциалу V (г),
поэтому, когда потенциал состоит из отдельных простых слагае-
слагаемых, как, например, межмолекулярный потенциал Леннарда —
Джонса, содержащий две отрицательные степени г и т. п., их
вклады в фазу рассеяния просто суммируются.
В заключение запишем формулу для полного сечения рас-
рассеяния, применив к соотношению A04.7) оптическую теорему
ю*

284 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Это даст
СО
о = 4п \ b [I—cos 28 (b)]db.	A04.9)
о
Замечание. Аппроксимация A04.6) очень удобна в задачах рассеяния в тех
случаях, когда энергия велика. Она значительно лучше известного асимпто-
асимптотического выражения
Р, (cos*) — 1/_J_cos|(/ + JrU--j-|.	A04.6а)
^(cos &)~J0 (г/sin^)
Фиг. 55. Полином Лежандра Plo (cos ¦&) (сплошная линия) и аппроксимирую-
аппроксимирующая его функция Бесселя A04.6) (пунктирная линия).
которое имеет особенности в точках д = 0 и Ф = я. Вблизи О = 0 (рассеяние
вперед, представляющее наибольший интерес) равенство A04.6) является почти
точным. По мере роста угла •& точность приближения ухудшается, и в точке
¦&=я мы получаем /0B/-|-1) вместо нужного значения (—1)'. На фиг. 55
для сравнения изображены полином Р10 и аппроксимирующая его функция
A04.6). Так как с ростом энергии (kR^>\) рассеяние назад становится все
менее существенным, то эта ошибка нашей аппроксимации не играет сколько-
нибудь заметной роли.
Литература
Moli'ere G., Zs. Naturforsh., 2a, 133 A947).
Blankenbecler R., Goldberger M. L., Phys. Rev., 126, 766 A962).
Flugge S., Kruger H., Zs. Phys., 216, 213 A968).
Задача 105. Борновское рассеяние. Последовательные приближения.
Решить задачу о потенциальном рассеянии, рассматривая
рассеивающий потенциал в качестве малого возмущения. Разо-
Разобрать более подробно случай центральных сил.

105. Борновское рассеяние	285
Решение. Запишем уравнение Шредингера в виде
V*u + kiu = gW (г)и,	A05.1)
где
Щ	r) = 2^V(r).	A05.2)
Функция Грина, соответствующая оператору, стоящему в левой
части уравнения A05.1), имеет вид
G(r, г') = -^?Рг	(Ю5.3)
Рассматривая формально правую часть уравнения A05.1) в каче-
качестве неоднородности, мы можем применить к нему стандартный
метод решения неоднородных дифференциальных уравнений. Таким
образом, имеем
и (г) = и0 (г) +g J G (г, r') W (г') и (г') dV', A05.4)
где ио(г) — решение однородного уравнения. Равенство A05.4)
представляет собой интегральное уравнение для функции и (г).
Нетрудно убедиться, что интегральный член в A05.4) асимп-
асимптотически, при больших г, описывает расходящуюся сферическую
волну. Действительно, с ростом г' потенциал достаточно быстро
убывает, что практически делает область интегрирования конеч-
конечной, поэтому в выражении для функции Грина A05.3) мы можем
считать, что г^>г' и, следовательно,
G(r, r')__«_e-«r'co.e'f	(Ю5.5)
где в' означает угол между векторами г и г'. В задачах рас-
рассеяния в качестве решения однородного уравнения и0 (г) следует
брать плоскую волну, описывающую пучок падающих частиц.
Пользуясь стандартной нормировкой, запишем ее в виде
«„(г)-^»'; |*,| = Л.	A05.6)
Решение уравнения A05.4) можно получить методом после-
последовательных приближений:
"„ (г) = "о (г) +g J G (r, r') W (г') «„_! (г') dV. A05.7)
Другими словами, его можно записать в виде ряда Неймана:
и (г) = u0 (r) +g S d*r'G {r, r') W (г1) К (г') +
Последний представляет собой ряд по степеням „константы взаи-
модействия" g. Для нахождения n-го приближения необходимо
вычислять Зп-кратный интеграл, что делает расчет всех членов,
кроме первого, весьма громоздким.

286 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Формула первого борновского приближения заметно упро-
упрощается в том случае, когда потенциал W (г) зависит только от
модуля вектора г. В этом случае асимптотическое поведение
функции и^г), согласно формулам A05.7), A05.6) и A05.5), будет
описываться равенством
их (г) = в».-' — ^ je~ikr'cos в' W (rr) eik°-r'd3r'. A05.8)
Введем вектор klt совпадающий по направлению с вектором г
и такой, что \k^\ — k. Тогда
kr' cos6' = {kx-r')
и интеграл A05.8) принимает вид
¦<*.-*»)-'-'W(r')dQ'. A05 9
Фиг. 56. Волновые
векторы и угол рас- Вектор
сеяния-	K^K-ka	A05.10)
представляет собой импульс (в единицах 1ь), переданный частице,
рассеянной в направлении вектора г. Обозначив посредством #
угол рассеяния, т. е. угол между векторами k0 и г, мы можем
написать (фиг. 56)
/C = 2Asiny.	A05.11)
Выполняя в выражении A05.9) интегрирование по углам, получаем
tSHL^,	(Ю5.12)
так что формула первого приближения A05.8) окончательно при-
приобретает вид
e^,	A05.13)
где
f (#) = _g^r'W (r')Щ^-dr'.	A05.14)
о
Амплитуда рассеяния f (Щ простым образом связана с диф-
дифференциальным сечением рассеяния:
-g- = |/(#)|2.	A05.15)
Формулой A05.14) для амплитуды рассеяния, разумеется,
нельзя пользоваться, если интеграл расходится на верхнем или
на нижнем пределе. Следовательно, в окрестности точки г' — О

106. Рассеяние на потенциале Юкавы	287
потенциал должен расходиться не сильнее, чем г'~8+Е(е>0).
С другой стороны, при больших г' он должен убывать быстрее
кулоновского потенциала, т. е. по крайней мере как г'-1~е.
Задача 106. Рассеяние на потенциале Юкавы
В первом борновском приближении найти амплитуду рассея-
рассеяния в случае сил притяжения, описываемых потенциалом Юкавы:
^о—у.-^. «Нг-	о06-1)
Оценить качество приближения, используя разложение по пар-
парциальным волнам.
Решение. В первом борновском приближении имеем
Кг	A06.2)
# = 2?sin —
Применительно к потенциалу A06.1) элементарное интегрирова-
интегрирование дает
, ,	(Ю6.3)
где постоянная
Vj4	A064)
характеризует „размер" потенциальной ямы.
С другой стороны, разлагая амплитуду рассеяния по пар-
парциальным волнам, имеем
^) = ш11B/+1Не2'б<-1)/Мсозд)-	(Ю6.5)
г=о
Чтобы оценить качество первого борновского приближения A06.3)
с помощью фаз рассеяния б2, мы должны либо разложить выра-
выражение A06.3) по сферическим гармоникам, либо произвести это
разложение непосредственно в формуле A06.2) и лишь затем
перейти к частному случаю потенциала Юкавы. Разумеется, оба
пути ведут к одному и тому же конечному результату.
1. Разложение амплитуды рассеяния A06.3) по парциальным
волнам имеет вид

288 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
где
X0 = kr0.	A06.6)
Пользуясь ортогональностью сферических гармоник, получаем
е'— 1 _ Р С Pt (t)dt
2i ~ ~4^J ta — t '
-1	A06.7)
Фигурирующие здесь интегралы
--Qt(t0)	A06.8)
-i
определяют функции Лежандра второго рода (t0 > 1). Две пер-
первые из них имеют вид
1 t 1 1
Qo^o)=Tln7^-'
<M'.)=T<oin-?±!-i.
Заменяя здесь переменную t0 переменной х0, окончательно полу-
получаем
&i ~ -fy~ {e2i&i—1) = Ptfi (x0),	A06.9)
причем
2. Чтобы разложить амплитуду рассеяния A06.2), восполь-
воспользуемся тождеством
-i!^ = llB/+l)/7(?r)/>,(cos#).	A06.10)
Сравнивая теперь выражения A06.2) и A06.5), получаем соотно-
соотношение
со
6, да 4- (е2^-1) = —|J- A j /-2V (r) /J (kr) dr. A06.11)
Если подставить сюда вместо V (г) выражение для потенциала
Юкавы A06.1) и ввести обозначения
и	all
*г=, и а = т = ^ = -,

106. Рассеяние на потенциале Юкавы
289
то это соотношение примет вид
С помощью известной формулы
я/2
}\{z) = ~ \ /,B2sin
о
A06.12)
интеграл A06.11) можно преобразовать таким образом, чтобы
функция Бесселя входила в подынтегральное выражение линей-
линейно. Учитывая далее, что'
Jz'+1/,(bz),
A06.13)
0,4
0,1
0,1 0,2 0,5
5 10 20 50 100
hr0
Фиг. 57. Первое приближение для фаз рассеяния на потенциале Юкавы
бг = — Рщ (kr0).
Р — параметр, характеризующий размер ямы. По оси абсцисс отложен энергетический
параметр в логарифмическом масштабе.
я/2
Г
окончательно получаем
fi ~J 1еШ	 п — р Г sin2
2«	2д;0 J (si
О
С помощью замены переменной интегрирования
A06.14)
последний интеграл приводится к более простому виду
у ) 	^m	"*	(Ш6.15)
и его можно вычислить для каждого значения /. В результате,
разумеется, снова получается найденная выше формула (Ю6.9).
Чтобы можно было судить о качестве сделанного приближе-
приближения, на фиг. 57 изображены графики функций ф0 (х0) и q^ (*0)

290 //¦ Задачи без учета спина. Г. Сферически симметричные потенциалы
(по оси абсцисс отложена переменная х0 в логарифмическом мас-
масштабе). При хо = О обе функции обращаются в нуль и при малых
энергиях они ведут себя соответственно как
4>о(хо)=хо {1—2x1+...),	A06.16)
<Pi W=y^oA— 4xS+...)•
Далее обе они проходят через максимум и при больших энер-
энергиях снова стремятся к нулю. Борновское приближение оказы-
оказывается хорошим в том случае, если для интересующего нас зна-
значения энергии выполняются неравенства
РФо<^1 и Аго>1.
Может случиться, что произведение Рф0 не очень мало по срав-
сравнению с единицей, но все еще имеет место неравенство /'ф!^ 1,
в таком случае можно написать
где индексом В отмечены амплитуда и фаза рассеяния в бор-
борновском приближении, определяемые равенствами A06.3) и A06.9).
Точный расчет здесь требуется только для определения фазы
60(/=0), остальная же часть амплитуды / (#), т. е. fB{$), нахо-
находится по формуле A06.3).
Замечание. В первом борновском приближении и амплитуда рассеяния A06.3)
и выражение A06.9) для функции б;
ZX
оказываются действительными. Это возможно лишь в том случае, когда истин-
истинная фаза рассеяния удовлетворяет условию |6/|<^1, поскольку разложение
интересующего нас выражения в ряд по степеням б; имеет вид
Вообще говоря, достаточным является даже условие 6?<^1, так как в пол-
полное сеченне рассеяния
1=0
входит только
Задача 107. Рассеяние на экспоненциальном потенциале
В первом борновском приближении определить амплитуду
рассеяния на потенциале вида
V(r)=—Voe-'»:	A07.1)
В этом же приближении найти фазы рассеяния б0 и бх, обуслов-
обусловленные вкладом состояний с /==0 и /=1. С помощью метода,

107. Рассеяние на экспоненциальном потенциале	291
развитого в задаче 96, вычислить фазу рассеяния 6„ во втором
борновском приближении и результат расчета сравнить с полу-
полученным ранее.
Решение. В первом борновском приближении амплитуда рас-
рассеяния имеет следующий вид:
A07.2)
^-.
Вводя безразмерные- величины
jh2 ' ° °
и используя в качестве переменной интегрирования величину
х = г/г0, амплитуде рассеяния можно придать следующую форму:
PC	ft
< =-^-\xe~xs'm qxdx, q—2xnsm-^-.	A07.4)
о
Последний интеграл вычисляется элементарно, и окончательный
результат имеет вид
Р Iq
= 1ГA+</2J'
или
Р / гуч	2гТл
'*"' (а-6 cos ftJ'	A07_5)
п— 1 4-9у2 h — 2 г2
Для амплитуды такого вида нетрудно рассчитать и полное
сечение рассеяния:
d (cos ft)
а — b cos ftL '
-1
Этот интеграл также вычисляется элементарно, и в результате
получаем
32яр2/.а 1+24	A07.6)
3 D(l+4SL
Наше приближение, разумеется, не улавливает ни резонансных
эффектов, ни зависимости от знака величины Р (случай притя-
притяжения и случай отталкивания). Так как формула A07.6) отно-
относится к области высоких энергий, то xl^>\ и ее можно еще
более упростить:
4	LiPl
4

2Э2 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Мы видим, что с ростом энергии Е сечение убывает как 1/Е.
Перейдем теперь к вычислению фаз рассеяния бг в первом бор-
новском приближении. Как мы знаем, имеет место разложение
A07.7)
и, следовательно,
J
Подставляя сюда вместо / (Щ выражение A07.5), мы после не-
несложных вычислений, в частности, получаем
'	J^	A07.9)
' (еио, -1) = р J '
21	I *o
- ' In
44
, A07.10)
Левые части этих равенств можно записать в виде
е*6/ sin 6f,
причем последнее выражение можно заменить на бг, если фаза
рассеяния мала. Зависимость фаз рассеяния б0 и 6^ измеренных
в единицах Р, от величины х0 показана на фиг. 58. На фигуре
о,/ о,г о,5 I г 5 ю го so wo
Ф и г. 58. Борцовские фазы рассеяния б0 и ftx на экспоненциальном потенциале.
Р — параметр, характеризующий размер ямы. По оси абсцисс отложен энергетический
параметр в логарифмическом масштабе.
отчетливо видно, что для небольших значений величины х0 выпол-
выполняется условие 6,^6,,, которое означает, что р-рассеянием можно
пренебречь по сравнению с s-рассеянием. Интересно, что эта
типичная для области малых энергий особенность рассеяния
правильно отражается борновским приближением, специально
приспособленным к области высоких энергий. Если д;0^>1, то
обе фазы рассеяния б0 и 6t оказываются величинами одного по-
порядка и преобладающим становится рассеяние вперед.
Чтобы иметь представление о границах применимости первого
борновского приближения, мы с помощью формулы (96.12а) вычис-

107. Рассеяние на экспоненциальном потенциале	293
лим фазу рассеяния б0 во втором борновском приближении.
Согласно (96.12а), имеем
Со	CD
tg60=—j jdrt/(r) sin» ftr{ 1— y \u(r')sln2kr'dr'\, A07.11)
о	о
где
Для потенциала A07.1) с учетом равенств A07.3) отсюда полу-
получается
^ бо = Т- [ dx е~Х sin2 (V) { 1 + -f f е~у sin 2х*У йУ \ •
0	x
выше мы воспользовались безразмерными величинами х = г/г0
и у = г'/г0 в качестве переменных интегрирования. Внутренний
интеграл легко вычисляется:
sin 2x0y dy= ~^ | sin 2xox + 2x0 cos 2.v
Чтобы найти оставшийся интеграл, тригонометрические функции
удобно заменить экспонентами. Дальнейшие выкладки совершенно
тривиальны, хотя и несколько громоздки. Окончательный резуль-
результат имеет вид
ЫУ} (Ш7Л2)
Первый член здесь идентичен выражению A07.9), и если второй
член в фигурных скобках мал по сравнению с единицей, то можно
рассчитывать на хорошую сходимость борновского метода. Таким
образом, границы его применимости определяются условием
8A+4H+44)
График функции g(xa) изображен на фиг. 59, причем в левой
и правой половинах фигуры для удобства использованы различ-
различные масштабы.
Числовой пример. Пусть параметр Р, характеризующий размер потенциаль-
потенциальной ямы, равен 3, и пусть ошибка в амплитуде не привышает 2 % (для интен-
интенсивности это составляет 4 %). Тогда условие применимости первого борновского
приближения принимает вид
*0)| < 0,02 или | g(*0)| < 0,0067.

294 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Граничное значение достигается в точке хо = 4, чем и определяется наимень-
наименьшее значение энергии, для которой мы еще можем пользоваться первым бор-
новским приближением. С помощью фиг. 58 нетрудно установить, что для этого
значения энергии фаза рассеяния б0 оказывается примерно равной 21°.
0,6
0,5
0,4
0,2
о, г
0,0
\
\
\
1
\
0,1 0,2
-о.ог
Фиг. 59. График функции g (x0).
Чтобы первое борновское приближение было хорошим, функция | Pg | должна быть мала.
Задача 108. Борновское приближение для рассеяния
на сферически симметричном распределении заряда
В первом борновском приближении вычислить дифференциаль-
дифференциальное сечение рассеяния электронов на ядрах, считая, что плот-
плотность электрического заряда ядра р (г) сферически симметрична.
Полученные результаты применить к случаю, когда заряд распре-
распределен по объему ядра с постоянной плотностью.
Решение. Если рассеиваемой частицей является электрон с
зарядом — е, то уравнение Пуассона классической электроста-
электростатики, связывающее потенциал V (г) и плотность р(г), можно
записать в виде
rV^±-§i(rV) = 4neP(r).	A08.1)
Плотность заряда ядра положительна и нормирована в соответ-
соответствии с условием
4я JJ /-2р (г) dr = Ze.
A08.2)
В первом борновском приближении амплитуда рассеяния
определяется формулой
A08.3)

	 108. Борновское приближение	295
Необходимо отметить, что вне ядра
и поэтому интеграл при бесконечном верхнем пределе, строго
говоря, не имеет смысла. Указанная трудность легко устраняется,
если в подынтегральное выражение ввести обрезающий множи-
множитель е~аг, а затем в окончательном результате положить а = 0;
это впервые было показано Вентцелем11. Физическим основанием
этой несколько сомнительной математической процедуры может
служить экранирующее действие атомных электронов.
Рассмотрим тождество, полученное двукратным интегрирова-
интегрированием по частям:
СО	СС
f (rV)<***dr = ^ U' (rV—L{rV)')] *-± J (rV)V*' dr.
о	о
Благодаря математическому трюку Вентцеля подстановка на
верхнем пределе обращается в нуль. В окрестности точки г = 0
функция V (г) должна иметь вид
V = V0-Vir*+...,
поэтому rV—*0 и (rV)'—*Vn. Следовательно, вклад от подста-
подстановки будет равен —VJK*- Но точно такой же вклад даст под-
подстановка и в интеграл, комплексно сопряженный с только что
рассмотренным, поэтому в разности этих интегралов, которая
равна интегралу, фигурирующему в формуле A08.3), вклада от
подстановки содержаться не будет. Что касается интегрального
члена, то в нем производную (rV)" можно заменить правой частью
уравнения A08.1). Это даст
^\	A08.4)
Здесь уже никаких трудностей с расходимостью не возникает.
Если бы ядро можно было рассматривать как точечное, то
вклад в интеграл происходил бы от малой окрестности точки
г = 0 и мы могли бы воспользоваться непосредственно форму-
формулой A08.2), поэтому амплитуда рассеяния / (•&) в этом случае
была бы равна
'°^ = ~*^~=~1	л~-	A08.5)
Учитывая, что
fik — mo и -к-ти2 = ?,
Wentzel G., Zs. Phys., 40, 590 A927).

296 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
последнее выражение можно записать в виде
4? sin2 -у
Отсюда для дифференциального сечения рассеяния получается
известная формула Резерфорда
dQ	— < sin%
Выражению A08.4) можно придать иную форму:
/(#) = /„ (#)/=¦ (/С),	A08.7)
где формфактор
оо
f(/C) = ^. f r"p (r) -5^Д^сЕг.	A08.8)
о
Он характеризует отклонение сечения рассеяния от резерфор-
резерфордовского:
^- = Я(/с).	A08.9)
В качестве простейшего примера рассмотрим случай, когда
заряд ядра распределен с постоянной плотностью внутри сферы
радиусом R. Для такого распределения условие нормировки
A08.2) и формфактор соответственно имеют вид
{sinKR—KRcosKR}, A08.10)
о
или
3/г BkR sin 4-)
^^	A08.11)
При изменении угла в интервале О^Ф^я аргумент сфериче-
сферической функции Бесселя меняется от 0 до 2kR. Если учесть, что
для применимости борновского приближения должно выполняться
неравенство kR ;=> 1, то указанный интервал оказывается довольно
большим и функция Бесселя должна в нем иметь несколько
нулей. Таким образом, вместо монотонно убывающего с ростом
угла резерфордовского сечения рассеяния мы теперь будем иметь
последовательность дифракционных максимумов, так же как это
бывает в аналогичных задачах классической оптики. Число мак-

108. Борноеское приближение	297
симумов при условии, что все они разрешимы, позволяет полу-
получить грубое представление о размере ядра.
Замечание. Если считать, что потенциальная энергия нейтрона в поле,
созданном другим нуклоном, приближенно описывается потенциалом Юкавы
V(r) = — ?-e-*r,	A08.12)
то для описания взаимодействия нейтрона с ядром, плотность частиц в кото-
котором равна р, можно написать дифференциальное уравнение, аналогичное
уравнению Пуассона:
-^ (rV) — х2 (rV) = 4ng2p (r) r.	A08.13)
Условие нормировки теперь имеет вид
4я [ r2p(r)dr = A,	A08.14)
о
где А'—атомный вес ядра. В математическом трюке Вентцеля в данном,случае
нет необходимости, и без него интегрирование по частям дает
С (rV) sin K.rdr = —-^{ (rV)" sinKrdr.
о	о
Если воспользоваться уравнением A08.13), то последнюю формулу можно
записать в виде
СО	00
Г (rV) sin Kr dr = — -^ С {4я#2р/-+х2 (rV)} sin Kr dr
О	о
и, следовательно,
i" (rV) sin Krdr = — lnf 2 [ rp (/¦) sin Kr dr.
j	л -)-х j
о	о
В случае точечного ядра имеем
а для протяженного ядра должно быть
/ (О) = /0 (О) F(K),	A08.16)
где формфактор
00
!Р (г) S'" fГ dr	A08.17)
по существу определяется тем же выражением, что и раньше.

298 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Задача 109. Высокоэнергетическое рассеяние на жесткой сфере
Показать, что сечение рассеяния на жесткой сфере радиусом
R для очень больших энергий приближается к значению 2nR2.
Решение. Борновское приближение, обычно применяемое в об-
области высоких энергий, становится несостоятельным в случае
сингулярных потенциалов, так как фигурирующий в нем инте-
интеграл расходится. По этой причине мы вынуждены использовать
метод разложения по парциальным волнам, несмотря на
то, что сходимость этого метода с ростом энергии ухудшается.
Для любого значения I радиальная волновая функция вне
жесткой сферы имеет вид
%i (г) = /, (kr) cos &t-nt (kr) sin бг — sin (&¦_? + 6j) A09.1)
и должна удовлетворять граничному условию
Xt(R) = O.	A09.2)
Таким образом, имеем
tg 6, =-?$-, x = kR,	A09.3)
и, следовательно, сечение рассеяния будет равно
1. „09.4,
Если энергия столь велика, что х^>1, то бесконечную сумму
A09.4) можно разбить на две части. Члены суммы, для которых
/<х, описывают частицы, сталкивающиеся со сферой (hl<.nwR),
и соответствующие функции /, и nt можно заменить их асимпто-
асимптотическими выражениями:
- /,(*) = Sin [X	2") ,
( 'м	A09-5)
= —cos ^j
Членам же с / > х в классической картине соответствуют части-
частицы, пролетающие мимо сферы, не сталкиваясь с ней (Ш > tnvR).
В этом случае функции /, и nt можно заменить первыми членами
их разложения в степенной ряд. Так как при такой замене
\1~х1+х и nt~x-1,
то отношение, фигурирующее в формуле A09.4), оказывается
очень малой величиной и всеми этими слагаемыми можно пре-
пренебречь. Таким образом, в рассматриваемом приближении можно
написать
I*]
°«$-?Bi + l) sin» (*--?).	(Ю9.6)

109. Высокоэнергетическое рассеяние на жесткой сфере	299
Конечно, все эти рассуждения теряют силу применительно к тем
членам, для которых / ж х и где неправомерна ни одна из упо-
употребленных нами аппроксимаций функций \1 и nt. Однако чем
больше величина х и чем больше членов содержит сумма A09.6),
тем меньшую роль играет эта небольшая группа членов и тем,
следовательно, меньше ошибка нашего приближения в целом.
Преобразуем правую часть равенства A09.6) с помощью
тождества
sin2 (х	?-) = sin2 x -\- sin'2 -?-cos 2x.
В результате имеем
Ы	Г*]
;=о	/=1, з, 5...
Обе суммы вычисляются элементарно и соответственно равны
2B/+1) = (х+1J
1 = 0
и
1=1, 3, 5...
Поэтому получаем
^	У A09.7)
Так как наше приближение справедливо лишь при условии
х^>1, то в этой формуле достаточно удержать только основной
член. Таким образом, окончательно наша формула принимает
вид
что и доказывает утверждение, сформулированное в условии
задачи.
Замечание редактора перевода. Может показаться странным, что эффектив-
эффективное сечение рассеяния равно удвоенному геометрическому поперечному сече-
сечению. Однако этот эффект хорошо известен в классической волновой оптике и
объясняется тем, что рассеянная волна состоит из двух частей одинаковой
интенсивности: одна из них соответствует волне, отраженной от препятствия,
другая обеспечивает образование тени. Для каждой из них поперечное сечение
равно nR2. Подробное обсуждение этого вопроса можно найти, например, в
монографии: Морс Ф., Фешбах Г., Методы теоретической физики, т. 2, ИЛ,
I960, стр. 354 и далее.

300 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Задача 110. Формула Резерфорда
Решить задачу о рассеянии точечного заряда в кулоновском
поле другого точечного заряда, воспользовавшись параболиче-
параболическими координатами.
Решение. Запишем уравнение Шредингера
—^\и = 0,	A10.1)
воспользовавшись стандартными обозначениями:
Л = ™, * = -?gL, 2kK = %.etet,	A10.2)
где е1 и ег — величины точечных зарядов, т—масса рассеиваемых
частиц, a v — их скорость на бесконечности. Задача обладает
очевидной симметрией относительно поворотов вокруг оси z,
поэтому решение зависит лишь от координат, характеризующих
положение частицы в меридиональной плоскости, таких, скажем,
как г и Ь, или же если пользоваться параболическими коор-
координатами, то от
В целесообразности применения этих координат нетрудно убе-
убедиться, вспомнив, как выглядит формула Резерфорда. Если
отвлечься от фазового множителя, то асимптотика решения, при-
приводящего к формуле Резерфорда, должна иметь вид
+
S
Отсюда следует, что имеется надежда с помощью разделения
переменных
u = eikzv{\)	A10.4)
свести задачу к нахождению функции, зависящей только от одной
переменной |.
Подставляя выражение A10.4) в уравнение Шредингера
A10.1), получаем
причем на функцию v пока еще не наложено никаких специаль-
специальных ограничений. Пользуясь определениями A10.3) и опуская

ПО. Формула Резерфорда	301
производные по переменным т] и ф, можно написать
dv?|^	L
Г
	?|_^		Lis
~dz"~ |+TJd|' Г~ 2 ^ + T1)'
так что наше дифференциальное уравнение приводится к виду
ф	|0.	A10.5)
Это — известное уравнение Куммера, решениями которого явля-
являются вырожденные гипергеометрические функции. Решение, регу-
регулярное в точке | = 0, имеет вид
v = C1Fl(—ix, 1; 1Щ.	A10.6)
Отсюда для волновой функции и, отвечающей задаче рассеяния,
получаем
u = Ceik*1Fl(— tx, 1; ikl),	A10.7)
причем постоянную С еще следует выбрать надлежащим обра-
образом. Чтобы убедиться в этом, мы должны найти асимптотику
волновой функции A10.7) при больших абсолютных значениях
чисто мнимого аргумента <ik\ (k\ > 0). Здесь имеется одна неболь-
небольшая математическая трудность, связанная с тем, что в данном
случае мы не можем воспользоваться известным асимптотическим
выражением
р (л п- 2\ 	j.p-ina Г(С) , 2-a_L ?l?j_pz?a-c	П 10 81
iri V"> с> *¦) *е р (с	а\с ' т (а)	'	lyj-o)
|г|>|а|, |г|>|с|, с^ — п, п = 0, 1,2....
Дело в том, что приведенная асимптотическая формула для
вырожденной гипергеометрической функции справедлива на ком-
комплексной плоскости z с разрезом вдоль положительной мнимой
полуоси. Однако эту трудность легко обойти, если заметить, что
к комплексно сопряженной функции и* формулу A10.8) можно
применять без всяких опасений. Таким образом, имеем
Учитывая далее, что
In \ — Ы	як
)
и что
находим
як
у	хГA+(к)е	k\ }¦
A10.9)

302 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Произведем в этой формуле комплексное сопряжение и подста-
подставим получающийся результат в правую часть равенства A10.7),
положив там
як
C = e~~T(l+ix).	A10.10)
Если, кроме того, принять во внимание, что г-\-\ = r, то окон-
окончательное выражение для асимптотики волновой функции A10.7)
будет иметь вид
Г	(	»\1
i \ kz + x In ( 2kr sin* "г" )
( Лг-xln ( 2kr sin2 y)
e-	,	A10.11)
хе2Й1°
где
rio = argr(l + /x).	A10.12)
Мы видим, что рассматриваемое решение действительно имеет
стандартную нормировку и отвечает задаче рассеяния. Единст-
Единственное его отличие от волновых функций, встречавшихся нам
в других подобных задачах,— это характерное для кулоновского
поля логарифмическое искажение фазы. Зная выражение для
амплитуды расходящейся сферической волны, мы можем сразу
же написать формулу Резерфорда для дифференциального сече-
сечения рассеяния:
1П }|	A10ЛЗ)
Замечание 1. При г = 0 из формулы A10.7) следует, что и=С, поэтому
с учетом равенства A10.10) имеем
Пользуясь известными свойствами Г-функции, последнее выражение можно
записать в виде
Для положительных значений к оно всегда меньше единицы, если же 2яи^> 1,
то это выражение становится экспоненциально малой величиной. Вспоминая, что
пи
мы, таким образом, видим, что в случае одноименных зарядов вероятность
проникновения сквозь потенциальный барьер характеризуется множителем
(фактор Гамова), который очень быстро убывает по мере уменьшения энергии
рассеиваемой частицы.
Замечание 2. Мы вывели асимптотическую формулу A10.11) в предположе-
предположении, что k^^c, где c*g> 1, а не в предположении, что kr ^> 1. Следовательно,

111. Разложение кулоновской функции по парциальным волнам 303
она выполняется не для точек, расположенных вне сферы r = c/k, а для точек,
лежащих вне параболоида
2?/-sin24=c, или г — 2 = 4" •	A10.15)
Таким образом, эта формула может оказаться неверной даже для очень боль-
больших значений г, если только значения угла д достаточно малы. Однако прак-
практически это ограничение не является существенным. В большинстве случаев
длина волны не превышает атомных размеров, так что, скажем, 1/?=10~7 см,
счетчик же, детектирующий рассеяние частицы, находится от мишени по край-
крайней мере на расстоянии /¦=10 см. Таким образом, kr=\Os. Пусть далее
ск Ю3, тогда формула A10.15) приводит к значению д=Ю~6, но для таких
малых углов вряд ли можно надеяться отделить рассеянный пучок от падаю-
падающего.
Задача 111. Разложение кулоновской функции
по парциальным волнам
Разложить по парциальным волнам волновую функцию, полу-
полученную в предыдущей задаче.
Решение. Так как кулоновский потенциал зависит только
от г, то кулоновскую волновую функцию с таким же успехом
можно найти, пользуясь разделением переменных в сферических
координатах. В этом случае она должна иметь вид
cosft),	A11.1)
1 = 0
причем радиальные функции %t обязаны удовлетворять уравне-
уравнению
[*-^-^]х, = О	A11.2)
и граничному условию
Xi @) = 0.	A11.3)
С помощью подстановки
Xl = Bkr)l+1eikrF{p), p = —2ikr	(Ш.4)
уравнение A11.2) приводится к уравнению Куммера
pFt + Bl + 2 — p)F'~(l + \+in)F = 0,	A11.5)
регулярное решение которого имеет вид
ix, 2/+2; —2ikr).	A11.6)
Нормировочную постоянную а, мы выберем позднее. Асимпто-
Асимптотику решения A11.6) можно найти непосредственно с помощью
формулы A10.8) предыдущей задачи. Полагая
Ti/=argr(/ + l-H'x),	A11.7)

304 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
получаем
Подставляя это выражение в формулу A11.4) и выбирая постоян-
постоянную аь в виде
находим, что функция
Xl(r) = a[Bkr)l+1el^1F1(l + l+in, 21 + 2; -2ikr) A11.9)
имеет асимптотику вида
^)	A11.10)
Теперь наша задача состоит в том, чтобы выразить опреде-
определенную в предыдущей задаче функцию и в виде ряда A11.1)
с функциями %г> заданными формулами A11.8) — A11.10). Функ-
Функция и, записанная в сферических координатах, выглядит сле-
следующим образом:
як
u{r, ^)^=e~TT(l+ix)eikrco^ 1F1[— w, 1; ikr{\ — cosG)].
A11.11)
Обращая ряд A11.1), находим
s#). A11.12)
Если теперь подставить сюда выражение A11.11) и ввести
новую переменную
x = — lkl = — ikr (l—cosb),	A11.13)
то нетрудно получить соотношения
^Jt	A11.14)
J	(^^Fj	A11.15)
-2ikr
При этом мы учли, что с помощью тождества
ex1F1(a> с; —x) = 1F1(c—a, с; х)

///. Разложение кулоновской функции по парциальным волнам 305
выражение
як	_
и = е~т Г A + tx) eikrex ^ (— ix, 1; — х)
приводится к виду
и = е~ Г A + Ы) eikr 1F1 (I + m, 1; х).
Таким образом, наша задача теперь сводится к вычислению
интегралов Jh в частности, при условии kr^>\. Это можно сде-
сделать с помощью повторного интегрирования по частям, если
принять во внимание тождество
rFAa, 1; x) = ±[1Fl(a, 1; x)~lFl(a-l, 1; *)]. A11.16)"
В результате n-кратного интегрирования по частям Pt в подын-
подынтегральном выражении заменится производной
(через Р{р мы обозначаем n-ю производную Рг по его аргу-
аргументу). Но Pt представляет собой полином степени /, поэтому
процедура интегрирования по частям оборвется на 1-й шаге.
Детали этого расчета даны в приложении, помещенном в конце
задачи, а результат при kr^>\ имеет вид
X
P-2ikr 1
A11.17)
Если п = 0, то оба члена в фигурных скобках имеют одинако-
одинаковый порядок величины, в противном случае вклад дает лишь
второй член. С помощью приведенного в приложении равен-
равенства A11.22) после небольших преобразований получаем
r + lH In 2kr
l) Указанное тождество следует из общей формулы
~ [^ [а, с; х) -!/=¦, (а-1, с; *)] = ^, (а, с; х)+^ ^ (а, с + 1; *),
если в ней положить с=1; эту формулу легко вывести с помощью соотноше-
соотношений, приведенных в приложении (см. т. 2, стр. 304).

306 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
Можно показать, что коэффициент в квадратных скобках равен
е
и, следовательно,
( 2 e~ilir
A11.18)
Подставляя это выражение в равенство A11.14) и используя
асимптотику A11.10) для функции %lt получаем
Ct = iB/ + l)iV\	A11.19)
поэтому окончательно искомое разложение при больших kr при-
принимает вид
X sin Г^г—и In 2kr + 4i—y) Pi (cos ft).	A11.20)
Заметим, что в известном смысле волновая функция A11.11)
и ее разложение по парциальным волнам аналогичны плоской
волне и ее разложению по парциальным волнам. Если исклю-
исключить влияние кулоновского поля, положив я = 0, то, согласно
равенству A11.7), мы будем иметь г|г = 0, и, следовательно, функ-
функция 11У определяемая выражением A11.9), перейдет в сфери-
сферическую функцию Бесселя, а волновая функция и и разложение
A11.20) соответственно перейдут в плоскую волну и ее разло-
разложение по парциальным волнам.
Приложение. Ниже вместо XF^ (a, 1; х) мы будем просто писать Fa. Одно-
Однократное интегрирование по частям дает
= Pi (Fa + 1-Fa)+yr J Pi (Fa + l-Fa) dx.
Повторяя эту процедуру / раз, получаем
I
X
На верхнем пределе, когда х = 0, все Fv = 1 и выражение в фигурных скоб-
скобках обращается в нуль. Таким образом, у нас остается только вклад от ниж-

112. Аномальное рассеяние	307
него предела, где x = —2ikr и аргументы полиномов Лежандра равны —1,
поэтому имеем
v=-l
При fe/- ^> 1 имеет место асимптотическая формула
r
"v +
Первый член в ней пропорционален (kr)v, а второй — (kr)~v~x. В сумме
A11.21) значение v ограничено интервалом —l<v<n, поэтому ее асимпто-
асимптотическое выражение будет определяться первым членом слагаемого с v = n и
вторым членом слагаемого с v = — 1, так что в результате мы получим фор-
формулу A11.17), приведенную выше.
Значения производных полиномов Лежандра легко получить, воспользо-
воспользовавшись соотношением
i
, -/, 1; 0= У, (-'
I — т)\ m\i
где
Дифференцируя обе части этого равенства л раз по t и полагая затем / =
(cos 0=1), находим
df -"" " (l-n)\nl*
и, следовательно,
(n,	dnpl(\)	l + n (l+
' у ' (dcosd)" l ; 2"(/ —
n)! n\
Задача 112. Аномальное рассеяние
Пусть наряду с кулоновским полем предыдущей ?адачи имеется
короткодействующий потенциал (например, ядерные силы или
конечное распределение электрического заряда) и пусть kR<^.\,
где R — радиус действия этих дополнительных сил. Выразить
амплитуду рассеяния через дополнительный сдвиг фаз рассеяния.
Решение. Если kR<^.\, то благодаря наличию дополнитель-
дополнительных короткодействующих сил изменится лишь одна фаза s-pac-
сеяния. Вместо асимптотической формулы A11.10) предыдущей
задачи мы теперь имеем формулу
Хо — A sin (kr—x In 2kr + % + бо).	(*12- 0

308 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
где б0—дополнительный сдвиг фазы рассеяния. Это выражение
мы должны сравнить с первоначальной формулой для точечного
заряда:
Хо—> sm(kr—я1п2/гг + гH).	A12.2)
Их разность
% 	% 	> — le{ (kr-it\n2kr+r\0)
1I
должна содержать только одну расходящуюся сферическую волну,
следовательно, должно быть
Ae~i&° = l	A12.3)
и
±l)eMfcr-Kln2ftr + no).	A12.4)
Таким образом, необходимо дополнить правую засть равен-
равенства A11.20) новым членом
Заменяя далее разложение A11.20) выражением A10.11), полу-
получаем для рассеянной волны формулу вида
(л
v	-Ы In sin8 —
	^е	*-»(*»».-1)
},(П2.5)
-	J
поэтому амплитуда рассеяния теперь равна
-<Х In Sin2-г-	1
+т(еш°-Я (П2.6)
Следует отметить два обстоятельства: во-первых, дополнительный
член не зашисит от угла рассеяния и сильнее всего скажется
при больших углах, где собственно резерфордовский член мал;
во-вторых, в сечении рассеяния |/(Ф)|2 теперь будет присутство-
присутствовать интерференционный член резерфордовского и аномального
рассеяния.
Задача 113. Преобразование Зоммерфельда — Ватсона
Пусть амплитуда рассеяния
/W=SB/+l)/,/>,(cos*)	A13.1)
записана в виде контурного интеграла в плоскости комплексной
Переменной / в предположении, что каждый член суммы A13.1)

	11$, Преобразование Зоммерфельда—Ватсона	309
есть вычет подынтегрального выражения в точке с целочислен-
целочисленным значением /. Считая, что /2 ==/(/)—мероморфная функция
переменной I, представить этот интеграл в виде суммы полюсных
членов и интеграла, взятого по прямой, параллельной мнимой
оси и проходящей через точку / = — х/2-
Решение. Целесообразно переменную / заменить комплексной
переменной
K = l + j.	A13.2)
Тогда формулу (П3.1) можно заменить равенством
где контур интегрирования С показан на фиг. 60. Действительно,
функция
1
cos nX	sin nl
-з/г-i/z
ImA
t/г з/г 5/г 7/г 9/г С
-Re Л
имеет простые полюсы во всех
целочисленных точках / = 0, ±1,
±2, ... (т. е. в точках А,=
= ± 72> ± V". ± 6/2, ¦ • •)' и ее ВЫ- Фиг. 60. Контур интегрирования
четы в них равны (—1)' + 1. Если ос- в комплексной^ плоскости перемен-
перементальные сомножители подынтег-
подынтегрального выражения A13.3) регулярны на положительной действи-
действительной полуоси, то интеграл по контуру С можно заменить
суммой интегралов, каждый из которых берется в направлении
часовой стрелки (множитель —2ш) по малой окружности с цен-
центром в одном из упомянутых полюсов. Таким образом, имеем
( |)	A13.4)
С учетом четности полиномов Лежандра:
(— \I Pt{— cosd)=P?(cos#), /—целое число, A13.5)
выражение A13.4) в точности переходит в формулу A13.1).
Деформируем теперь контур интегрирования в комплексной
плоскости К таким образом, чтобы он проходил по мнимой оси и
замыкался бесконечной полуокружностью, лежащей в правой по-
полуплоскости. Последняя не будет давать вклад в интеграл, если
подынтегральная функция убывает на ней по крайней мере как
|^|-i-ej чт0 и предполагается всюду в дальнейшем. В резуль-
результате у нас остается вклад от интеграла по мнимой оси и вклад
от всех полюсов, которые расположены в правой полуплоскости
и которые наш контур пересекал в процессе деформации. Пусть

310 //. Задачи без учета спина. Г. Сферически симметричные потенциалы
эти полюсы располагаются в точках X = ап и пусть вычеты функ-
функции /(/) равны в них р„, тогда вклад полюсных членов в ам-
амплитуду рассеяния будет иметь вид
га Р~, 1/ (—cos Ф)
/р(О)=2урп^-^^	:.	(пз.6)
IFX ' ?^rn	cos яа„	v	'
п
Что касается интегрального члена, то с помощью замены пере-
переменной
К = iy,
где у—действительная величина, его можно записать следующим
образом:
Мы видим, что амплитуда рассеяния / (¦&) действительно разби-
разбивается на две существенно различные части:
Замечание. Полюсы амплитуды рассеяния /(/) в плоскости комплексной
переменной / называют полюсами Редже, а линии, по которым они перемеща-
перемещаются в этой плоскости при изменении энергии,—траекториями Редже. Важ-
Важность полюсов Редже обусловлена тем, что они дают в наше распоряжение
альтернативную возможность описать взаимодействие между сталкивающимися
частицами, которое обычно описывается с помощью потенциала. Если положе-
положение полюсов ап и вычеты в них амплитуды рассеяния |3„ известны, то рассея-
рассеяние можно описать с помощью этих параметров. Этот метод, по-видимому, должен
быть особенно удобен в физике элементарных частиц, так как эксперименталь-
экспериментальные данные свидетельствуют о наличии резко выраженных резонансных состоя-
состояний (промежуточные частицы или резононы). Конечно, там приходится иметь
дело с очень высокими энергиями, и вся теория должна быть сформулирована
релятивистским образом. Что касается нерелятивистской теории, то ее можно
использовать в ядерной физике для описания компаунд-ядра.
Задача 114. Полюс Редже
Пусть при данном значении энергии полюс функции f (/) рас-
располагается вблизи физического значения /, например вблизи l = L,
где L—целое число. Какая физическая ситуация описывается
этим полюсом, если значение энергии подвергается небольшому
изменению?
Решение. Мы будем рассматривать вклад в амплитуду рас-
рассеяния от одного-единственного члена суммы A13.6), который,
опуская индекс п, можно записать в виде
В этой формуле
±	A14.2)

114. Полюс Редже	311
а оба действительных числа, ? и г], предполагаются малыми
(|||<^1, |т]|<^1). Таким образом, имеем
соэла = (— l^sinn^ + rn).	A14.3)
Функцию Лежандра с комплексным индексом v = a —1/2 можно
выразить через обычные полиномы Лежандра:
^	Р'<),	A14.4)
(v — п) (v
поэтому в рассматриваемом нами случае должно быть
/>«_.,,(-cos д) ==(-1)?зтя
и, следовательно,
Bn+l)Pn(cos'
До сих пор мы не делали никаких приближений, и вклад по-
полюсного члена учитывался точно. Теперь мы воспользуемся ма-
малостью величин | и т), из-за которой первый сомножитель в зна-
знаменателе дроби A14.6) становится при n — L очень малой вели-
величиной. По этой причине указанный член оказывается значительно
больше других членов и в резонансном приближении последние
можно не учитывать. Таким образом, имеем
.	A14.7)
Перейдем теперь к изучению зависимости этого выражения от
энергии Е рассеиваемой частицы. Положению полюса в точке
к = а, разумеется, соответствует некоторое определенное действи-
действительное значение энергии Е, но момент количества движения при
этом не является целочисленным и, следовательно, не соответст-
соответствует никакому реальному физическому состоянию. Если теперь
предположить, что состояние, отвечающее физическому целочи-
целочисленному значению момента количества движения L, располагается
вблизи рассматриваемого полюса, то энергия такого состояния
будет комплексной величиной — ее действительная часть Еа будет
близка к Е, а мнимая часть мала. Таким образом, можно напи-
написать
EL = E0--LiT.	A14.8)

312 //. Задачи без учета спина. Г, Сферически симметричные потенциалы
Согласно соотношению A14.2), это означает, что величины | и
г], рассматриваемые как функции энергии, должны быть связаны
равенством
Пусть теперь Е—действительная энергия реального физического
состояния и пусть она не слишком отличается от EL, тогда можно
написать
Ед-	(П4.10)
Подставляя последнее выражение в формулу A14.7), получаем
Такому виду амплитуды рассеяния отвечает типичное резонанс-
резонансное сечение рассеяния Брейта—Вигнера:
г	)
(Е-?„)»+.!. Г»
Здесь Ео имеет смысл резонансной энергии, а Г означает ширину
резонансной линии, связанную со средним временем жизни про-
промежуточного резонансного состояния соотношением % = %1Т.
Предположим теперь, что значению энергии Е = Е0 на траек-
траектории Редже соответствует точка, для которой ? и ц равны со-
соответственно |„ и гH, тогда для значения A,=L + V2 мы имеем
что с учетом соотношений A14.9) и A14.8) дает
^Ц-	<114ЛЗ>
Оказывается, что производная (da/dE)B_E практически является
действительной величиной (см. ниже), и поэтому |о = 0, а
-	<114Л4>
причем величина гH может служить мерой ширины резонансной
линии.
Замечание. В случае потенциального рассеяния доказать, что производная
da/dE вблизи от резонанса является действительной величиной, можно до-
довольно легко: см. De Alfaro V., Regge Т., Potential Scattering, Amsterdam, 1965,
p. 104. (Имеется перевод: де Альфаро В., Редже Т., Потенциальное рас*сеяние,
изд-во „Мир", 1966, стр. 138.— Прим. ред.) Если # —эффективный размер
области рассеяния, а о—скорость рассеиваемых частиц, то, кроме того, можно
показать, что da/dE w RftfLv).

115. Разложение эйконала	313
Д. Приближение Вентцеля — Крамерса —
Бриллюэна (ВКБ)
Задача 115. Разложение эйконала
Решить уравнение Шредингера, воспользовавшись известным
из оптики методом решения волнового уравнения
V2« + ?2n2 (г) « = 0	A15.1)
с помощью процедуры последовательных приближений. С этой
целью ввести эйконал S(r), положив
u = e^S(r),	A15.2)
где k = 2n/k—длина волны в вакууме, и разложить его в ряд по
степеням к. Показатель преломления п (г) считать медленно ме-
меняющейся функцией координат.
Решение. Пусть к означает волну де Бройля во всех точках,
где V (г) = 0, тогда
г, +
Л —	 ,	и — у &IIIJ-, — (Itv.	( 1 Ю .О I
р
Введем далее показатель преломления
-V~P-	(H5.4)
Условие медленного изменения показателя преломления п озна-
означает, что он меняется заметным образом на расстоянии /, кото-
которое значительно больше к, иначе говоря,
7<Т-	A15-5>
Подставляя выражение A15.2) в уравнение A15.1), приходим
к уравнению Риккати:
Если бы п было постоянным, то эйконал S был бы линейной
функцией координат и v2S = 0. В случае медленно меняющегося п
можно ожидать, что по крайней мере на расстояниях порядка л
влияние нелинейности на экспоненту A15.2) будет мало. Так как
для любого направления х имеет место разложение
S (х + к) = S(x) + kS' (x) + ±VS" (x) + ...,
то вклад нелинейного члена 1/2k2S" будет мал при условии, что
X
11 iVs 1050
2л '	 " ' или

314	//. Задачи без учета спина. Д. Приближение ВКБ
В этом случае первый член уравнения Риккати A15.6) мал
по сравнению с двумя другими членами, поэтому в первом при-
приближении оно заменяется уравнением эйконала:
(V<SJ = n2.	A15.7)
Разложим теперь эйконал в ряд по степеням безразмерного
параметра К/2м1. Мы имеем
причем
Подставляя это разложение в уравнение A15.6), получаем сле-
следующую систему равенств:
VS2 -f 2VSO • VS3 = 0
и т. д.
Эти равенства содержат только производные искомых функций,
поэтому мы можем ввести безразмерные векторы
yn = \Sn.	A15.11)
Выражения вида
будут тогда представлять собой безразмерные дивергенции век-
векторов уп, а равенства A15.10) приобретут вид
A15Л2)
и т. д.
С их помощью можно последовательно определить все ректоры
уп, через которые, согласно A15.11), величины Sn выражаются
в квадратурах. В заключение заметим, что вопрос о граничных
условиях пока остается открытым.

116. Применение метода ВКБ к радиальному уравнению	315
Задача 116. Применение метода ВКБ к радиальному уравнению
Развитый в предыдущей задаче метод применить для нахож-
нахождения радиальной волновой функции в случае сферически сим-
симметричного потенциала.
Решение. Если эйконал зависит только от одной переменной
г, то волновое уравнение
Xi + Q2(/-)b = 0,	A16.1)
где
A* '
с помощью подстановки
Х, = Д-5(Г), л = ^,	A16.3)
приводится к уравнению Риккати
Разложение
f(fJ3+...	A16.5)
по степеням безразмерного параметра
^1,	(П6.6)
где /? — эффективный радиус области взаимодействия, позволяет
получить следующую систему равенств:
С' С' 		1 Г> О"
(П6.7)
]
2
S'SJ,=—д- [??SJ> -j~ 2515^] и т. д.
После введения безразмерных функций
yn(r) = S'(r)	A16.8)
и*

316	//. Задачи без учета спина. Д. Приближение ВКБ
эти равенства принимают вид
У = ±
,. _
У*-
С их помощью мы можем последовательно выразить функции
у„ (г) через функцию уд (г) и ее производные:
h— о .. > У2— , \ .2 Т~3"
^ УО	4 Ч УО	2 У0 ,	,jjg g.
^ = "f №-6^+65)ИТ-Д-
8 \ {/о	г/о	{/о '
Если
— действительная величина, то действительными будут и все
функции уп(г), а так как мы разлагаем функцию S по степеням
чисто мнимого параметра e/i, то последовательные приближения
Sn будут попеременно то действительными, то мнимыми и будут
давать вклад то в фазу, то в амплитуду радиальной волновой
функции х^г):
¦¦¦}%¦
Если мы изменим знак величины у0, то нечетные функции ytn+1
не изменят своего знака, а следовательно, не изменятся и ампли-
амплитудные поправки, четные же функции у2п изменят свой знак,
так что в результате у нас получится комплексно сопряженное
решение. Таким образом, развитый метод позволяет найти фун-
фундаментальную систему решений.
Задача 117. Граничное ВКБ-условие Лангера
Рассмотрим потенциал, соответствующий силам отталкивания.
В классической точке поворота r = rt решение ВКБ имеет осо-
особенность, что не позволяет сформулировать граничное условие.
Эту трудность можно обойти следующим образом. Заменим диф-
дифференциальное уравнение, имеющее в качестве своих точных
решений функции ВКБ, другим дифференциальным уравнением,
которое, во-первых, согласуется с уравнением Шредингера вблизи

117. Граничное В К Б -условие Лангера	317
классической точки поворота и, во-вторых, согласуется с диф-
дифференциальным уравнением ВКБ во всей остальной области. Эту
программу проще осуществить, используя в качестве независимой
переменной вместо г величину
x=) Q (r)dr.	(П7.1)
Решение. Так как в классической точке поворота выражение
обращается в нуль, то функции ВКБ,
u=Q-'/. exp{±t \ Q(r)dr \,	A17.3)
j
имеют сингулярную амплитуду при r = rt. Нас интересует реше-
решение, конечное в точке r — rt\ это позволит нам продолжить осцил-
осциллирующее решение из области г > rt в область г < г,, где оно
должно экспоненциально убывать.
Замену переменной A17.1) нетрудно сделать, заметив, что
±=п±
йг ч их'
После указанной замены радиальное уравнение Шредингера при-
принимает вид
x+-|i+x=°.	{U7A)
где точкой обозначено дифференцирование по переменной х.
С другой стороны, функции ВКБ,
u = Q-v.g±<«,	A17.5)
образуют фундаментальную систему решений дифференциального
уравнения
где штрих означает дифференцирование по переменной г. Пере-
Переходя к переменной х, можно записать это уравнение в виде
Вблизи точки поворота r — rt функция Q2 становится линейной
функцией разности г — rt, поэтому интеграл A17.1) будет пропор-
пропорционален (г — rtyt'. Таким образом, имеем

318	//. Задачи без учета спина. Д. Приближение ВКБ
и, следовательно,
Q~*v.,	A17.8)
поэтому в непосредственной близости от точки поворота должны
выполняться равенства
А=± н А=	L
Q Зх	Q	9x2 '
и мы можем при гтагх заменить дифференциальные уравнения
A17.4) и A17.7) соответственно уравнениями
^	(П7.4а)
iC&)=°-	<117-7а>
После подстановки
% = х'',<?(х), и = **/./(*)	A17.9)
эти уравнения принимают вид
ф+1ф + A—э^)ф = 0	A17.46)
и
/ + т/ + A-1^)^°-	A17-7б>
Оба уравнения являются уравнениями Бесселя и имеют соот-
соответственно решения
Ф (х) = /±./, (х) и f{x) = J±4,{x).
Так как при малых значениях х функция Бесселя Jv(x) про-
пропорциональна xv, то фундаментальные решения / ведут себя как
хй и хг/*, т. е. оба конечны в точке х = 0. Что же касается реше-
решений и, то они ведут себя как х~ *'• и д;*/«, т. е. одно из них
имеет особенность, а другое равно нулю при * = 0. Это та самая
особенность решения ВКБ в классической точке поворота, которая
не позволяет сформулировать граничное условие. Ее можно
устранить, заменив в уравнении A17.76) член V4*2 на 1/»х*-
Другими словами, мы должны к коэффициенту при неизвестной
функции в уравнениях A17.76), A17.7а) и A17.7) добавить
слагаемое ^1зехг. В результате уравнение ВКБ A17.7) изменится
лишь в непосредственной близости от точки х=0, а во всей
остальной области практически останется неизменным. Пусть
функция v(x) удовлетворяет этому новому дифференциальному
уравнению, заменяющему собой уравнение ВКБ A17.7):

	117. Граничное ВКБ-условие Лангера	319
Записав решение этого уравнения в форме, аналогичной выра-
выражению A17.3) или A17.5):
v(x) = Q-l>-F(x),	A17.11)
мы приходим к уравнению
] = 0'	<117Л2)
общее решение которого имеет вид
v(x)= yr-~{ClJi/s(x)+C2J^/3(x)}.	A17.13)
Благодаря соотношению A17.8) это решение не имеет особенно-
особенностей в точке х = 0, а от решения ВКБ оно отличается лишь
заменой функций е±1х функциями У xJ±i/,(x), которые асимпто-
асимптотически при х^>1/3 ведут себя как
(JJ)	A17.14)
Теперь мы можем перейти к формулировке граничного условия.
Зная общее решение A17.13) для области г > rt, где Q>0 и
х > 0, мы должны найти его продолжение в область г < гь где
Q = l\Q\, x = e~\, ?>0.	A17.15)
Для малых значений комплексной переменной х имеют место
равенства
поэтому для чисто мнимых л:, определяемых соотношением A17.15),
должно быть
Для действительных положительных значений аргумента | так
называемые модифицированные функции Бесселя /v(?), опреде-
определяемые равенствами
/'/. (х) = Ич. (I), /- •/. (х) = - if- ч. (?).
принимают действительные значения. Этим же свойством обла-
обладает и модифицированная функция Ханкеля,
ivn

320	//. Задачи без учета спина. Д. Приближение ВКБ
асимптотика которой при больших положительных | имеет вид
e-1-	A17.16)
Пользуясь этими математическими сведениями, мы можем за-
записать общее решение A17.13) для значений аргумента х A17.15)
следующим образом:
В области потенциального барьера интересующее нас решение
должно убывать по мере роста | наподобие функции A17.16),
поэтому мы должны положить
C1 = Ct=C.	A17.17)
Таким образом, получаем
Эта формула позволяет зафиксировать относительную фазу ре-
решений ВКБ в области х > 0. Действительно, если теперь вер-
вернуться к равенствам A17.14) и A17.13), то в силу соотношения
A17.17) получим
или
"(х)-*СУ ^sm[x + i).	A17.18)
Этот результат асимптотически согласуется с решением ВКБ
A17.3), если там определенным образом зафиксировать относи-
относительную фазу.
Замечание. Вопрос о решении вблизи классической точки поворота можно
несколько упростить, воспользовавшись функциями Эйри (см. задачу 40).
Литература к задачам 113—115
Wentzel G., Zs. Phys., 38, 518 A926).
Kramers H. A., Zs. Phys., 39, 828 A926).
Brillouin L., Cont. Rend. Acad. Sci., Paris, 183, 24 A926).
Longer R. E., Phys. Rev., 51, 669 A937).

118. Гармонический осциллятор в приближении ВКБ	321
Задача 118. Гармонический осциллятор в приближении ВКБ
Найти энергетическиеу ровни гармонического осциллятора, при-
применив к волновым функциям ВКБ граничные условия Лангера.
Решение. В случае осцилляторного потенциала
V(r)=-g-m©V	A18.1)
значению энергии
E = ±mv\	A18.2)
где v—классическая скорость частицы при х — 0, соответствуют
классические точки поворота
х=±ха, х9 = ^.	A18.3)
Отсюда следует, что
(П8.4)
Волновая функция, найденная методом ВКБ и удовлетворяющая
граничному условию Лангера в точке поворота х =— х0, должна
иметь вид
( х	\
?(x) = Q-'/.COs { J Q (x) dx—-Jj.	A18.5)
Подставляя сюда вместо функции Q (х) ее выражение A18.4) и
учитывая, что
2A
получаем
Теперь мы должны потребовать, чтобы это решение удовлетво-
удовлетворяло граничному условию Лангера в другой точке поворота
х — х0. Таким образом, оно должно быть либа четной, либо нечет-
нечетной функцией переменной х.
Вводя обозначения
(х) = f [
M
у (х) = f [arcsin -f + J
M F ° *> V	**	A18.7)
E n n	ч	'
где функция у (х), очевидно, нечетная [у(—х) = — у(х)], получаем
и (х) = Q~ Чг cos {у (х) + ф} ~ Q~ '^{"соэг/соэф — sin у sin <p}.

322
//. Задачи Ьгз учета спина. Д. Приближение В К Б
Таким образом, если
Ф = 2л^, u2n(*) = Q-v'(-l
то решение и будет четной функцией; если же
A18.8а)
)|, «2n+1(*) = Q-v'(-l)n+1sint/, A18.86)
то и будет нечетной функцией. Оба ограничения на фазу ер
можно объединить в одной формуле, полагая
Отсюда, согласно соотношению A18.7), получаем
±\
A18.9)
Отрицательные значения п можно исключить из рассмотрения,
так как они не удовлетворяют условию
выполнение которого необходимо для применимости приближения
ВКБ.
Чтобы составить представление о качестве приближения ВКБ
для волновых функций, интересно сравнить расположение нулей
функций ВКБ ип и точных решений ип, найденных в задаче 30.
Соответствующие данные приведены в нижеследующей таблице:
Л
0
1
2
3
4
Значения х/х0
и
п
0
± 0,320
0
±0,466
±0,1754
± 0,553
для нулей функций
и
п
0
±0,316
0
± 0,462
±0,1750
± 0,550
Задача 119. Уровни ВКБ в однородном поле
Пользуясь методом ВКБ, получить энергетические уровни
стационарных состояний в гравитационном поле
V (z) = mgz

119. Уровни ВКБ в однородном поле	323
над отражающей поверхностью (z = 0). Результаты сравнить
с точным решением, найденным в задаче 40.
Решение. Здесь имеются две классические точки поворота
*i = 0 и z^=Elmg. Условие Лангера для левой точки поворота1(
г1 = 0 дает
M(z) = Q-v.Cos(f Q(z)dz— ?l,	A19.1)
4
где
Q(y\ 	 h 1/ 1 	 *Ш. 7	i\ 1Q 9\
и после элементарного интегрирования получаем
С другой стороны, условие Лангера должно выполняться и в точ-
точке z = z2. Если ввести переменную г/ = — z, то она снова будет
левой точкой поворота, поэтому
. — 2
u(z)=±Q-1/'Cos\ Г Q(~y)dy—~
= ±Q-1/«cosj-JQ(z)dz-i[,
или
и (г) = ± Q"'/. cos К Q (z) dz 4-J|.	A19.4aJ'
Так как равенство A19.1) в общем случае можно записать в виде
п (г) = Q" '/. cos (Jq (Z)d* --J-j ,	A19.46)
то аргументы косинусов в формулах A19.4а) и A19.46) могут
отличаться лишь на целое, кратное л:
г	г
х> В точке ^ = 0 имеется непроницаемая стенка, поэтому вместо условия
Лангера следовало бы положить г|з(О) = О. В этом случае формула A19.5) при-
принимает вид
!) я.
— Прим. ред.
2) Наличие двух знаков в этой формуле связано с тем, что при выводе
формулы Лангера вопрос о знаке остается открытым, поскольку последняя
не зависит от нормировки.

324	//. Задачи бея учета спина. Д. Приближение ВКБ
ИЛИ
A19.5)
г,
Такова общая формула, определяющая уровни энергии в при-
приближении ВКБ. Применительно к частице в нашем гравитацион-
гравитационном поле получаем
!(!)	(П9.6)
Выразив здесь величину k через энергию и положив z2 = E/mg,
окончательно найдем
?.	(Н9.7)
Эта формула согласуется с асимптотикой D0.14) точного решения.
Замечание. Формулу A19.5) нетрудно применить к гармоническому осцил-
осциллятору, рассмотренному в задаче 118. В этом случае
1
что сразу же приводит к формуле для уровней
Задача 120. Проблема Кеплера в приближении ВКБ
Определить энергетические уровни частицы в кулоновском
поле притяжения
применив метод ВКБ к радиальному волновому уравнению.
Решение. Условие квантования
I
, лг = 0, 1, 2, .... A20.1)
где
Q3 =^[?—^афф (г)],	A20.2)
a /"j < г2—две классические точки поворота, можно применять
как при положительных, так и при отрицательных значениях
энергии Е. Под Уэфф подразумевается потенциальная энергия,
в которую включен центробежный член, где произведена замена

120. Проблема Кеплера в приближении ВКБ	325
величины 1A-\-\) на (/ + У2J (см. задачу 121I). В нашем случае
С помощью обозначений
k*=MH, fl = -*!-, * = / + !	A20.4)
ft2	me2	2
выражение A20.3) можно записать в виде
где точки поворота лх и г2 определяются формулами
A20.6)
В этих обозначениях условие квантования приобретает вид
.	A20.7)
Вычисление интеграла A20.7) можно разбить на три этапа. Сначала с по-
помощью замены переменной интегрирования
квадратичная форма под знаком радикала приводится к диагональному виду.
Затем с помощью второй подстановки
у—
подынтегральное выражение приводится к рациональному виду
где
И наконец, последний интеграл берется вычетами. Для этого путь интегриро-
интегрирования следует замкнуть полуокружностью бесконечно большого радиуса, рас-
расположенной в верхней полуплоскости комплексной переменной у, и учесть,
что полюсы подынтегрального выражения находятся в точках y = ip и y — i,
причем последний является полюсом второго порядка. Окончательно получаем
-	{120-8)
11 По поводу строгого обоснования замены величины / (/+1) на (/-f-l/2J CM-
Соколов А. А., Терние И. М., Квантовая механика и атомная физика, изд-во
„Просвещение", 1970, стр. 200. — Прим. ред.

326	//. Задачи без учета спина. Д. Приближение ВКБ
Полагая Xka = t, этот результат.можно записать в виде
2t	\ г i_ j/~i _^2 J ~ r "¦"~2 '
После упрощений это дает
Х^- = пг+±.	A20.9)
Отсюда
t=-
г' 2
ИЛИ
1
ka = -
и, следовательно, в силу равенства A20.4)
A20.10)
Так как Л, = Z -f- a/2, то этот результат совпадает с известной точ-
точной формулой для собственных значений, причем
n = nr + l+l	A20.11)
есть главное квантовое число.
Замечание. Для получения этого результата весьма существенна сделанная
нами замена в центробежном члене величины I (/+ 1) на (Z + VaJ- Это означает,
что центробежный член даже для s-состояний не обращается в нуль. Если бы
мы опустили указанный член и пользовались выражением
то в результате у нас получились бы полуцелые квантовые числа п. В этом
нетрудно убедиться, учтя, что при Х = 0 точки поворота, согласно A20.6),
расположены в л1 = 0 и r2 = 2/(k2a) и что условие квантования A20.8) в дан-
данном случае приводит к равенству
Задача 121. Фазы ВКБ для свободного движения
Показать, что с помощью замены в выражении для радиаль-
радиальной волновой функции величины /(Z-|-l) на A-\-1/2)г получается
волновая функция, обладающая правильным асимптотическим
поведением в случае свободного движения.

122. Вычисление фаз ВКБ	327
Решение. При свободном движении V = 0, и в силу равен-
равенства A17.18) можно написать (нормировка произвольная)
где X2 = Ц1-{-1) и rt = \/k — классическая точка поворота. При
больших значениях г амплитудный множитель этой функции
стремится к единице, и его можно опустить при обсуждении во-
вопроса об ее асимптотическом поведении. Интеграл легко вычис-
вычисляется, и мы получаем
J
Разлагая последнее выражение по степеням rt/r<^l, находим
Таким образом, функция ВКБ при больших значениях г при-
принимает вид
х
С другой стороны, для точного решения при той же нормировке
имеет место формула
(%)	A21.3)
Выражения A21.2) и A21.3) становятся тождественными при боль-
больших г, если положить
\—Y = l или Х = 1 + ±-,	A21.4)
что и означает замену в центробежном члене величины 1A+1)
на (/ + 1/*J-
Задача 122. Вычисление фаз ВКБ
Показать, что асимптотическое значение фазы радиальной вол-
волновой функции ВКБ, определяемой условием Лангера (см. за-
задачу 117), где предварительно сделана замена величины /(/+1)
на I2,
DJ	A22.1)
можно найти с помощью формулы
6, = й Um
j	I

328	//. Задачи без учета спина. Д. Приближение
т. е. как предел разности интегралов ВКБ при наличии рассеи-
рассеивающего потенциала и без него, причем в каждом случае ниж-
нижним пределом интегрирования служит своя собственная точка
поворота.
Решение. Лангеровское выражение для фазы бг следует из
формулы A17.18), которая асимптотически при больших значе-
значениях г дает
( г
поэтому
1г(
Vt	)
Тождественность выражений A22.2) и A22.3) легщэ показать,
если учесть (см. задачу 121), что интеграл
г
J У l
J	[^-l + arcsin—-y
\lk
при больших значениях г стремится к выражению
k [x/k 2}~Г k 2~Г~ fe\ + 2) 2 ¦
Подставляя это выражение вместо второго интеграла в фор-
формулу A22.2), мы убеждаемся, что она приводит к A22.3).
Задача 123. Расчет кулоновских фаз методом ВКБ
Определить в приближении ВКБ асимптотику парциальных
волн в кулоновском поле. Полученные выражения сравнить
с точными решениями.
Решение. Пользуясь обозначениями
2m? = A,2) W=Xf 1+±=K	A23.1)
%2	hv	2
асимптотическое выражение для точного решения (см. задачу 111)
можно записать в виде
2
где
sin ( kr — -?—Kln2kr+4lj,	A23.2)
+ /x).	A23.3)

123. Расчет кулоновских фаз методом ВКБ	329
С другой стороны, метод ВКБ приводит к результату
Хг-зт^г-^ + б,).	A23.4)
где
(г 		г		 \
i — пт | \ 1/ /г2	-р^ dr— \ у /г2 — -^dr} . A23.а)
Таким образом, мы должны показать, что формула A23.5) яв-
является аппроксимацией точного выражения
8l = — H\n2kr + t\l,	A23.6>
в котором величина ¦ц1 определяется равенством A23.3).
Переходя к новой переменной x — kr и полагая
— X 	ZXa	Л ,
можно написать
6,= lim
где
Учитывая теперь значение неопределенного интеграла
мы после подстановки пределов получаем
Г . ш-{-№	. Я ] |
arcsin —,	—arcsin— \
[	xYy?+№	x\i
Предел нетрудно вычислить, разложив это выражение по степе-
степеням 1/х. Окончательный результат имеет вид
х
ё, = —х + х lnl/x2 + ^2 + ^ arcsin -	—х In 2л;.
*	Ух2+Р
Таким образом, с учетом соотношения A23.6) мы можем сказать,
что в приближении ВКБ
,		,	A23.7)
Теперь нам осталось сравнить приближенное выражение ВКБ
A23.7) с точным выражением A23.3),

330
//. Задачи без учета спина. Д. Приближение ВКБ
В приведенной ниже таблице мы даем несколько числовых
значений величины т|, для случая х=2.
0
1
2
3
4
Значение rj.
точное
0,130
1,237
2,022
2,610
3,074
в приближении ВКБ
0,110
1,222
2,012
2,610
3,076
Вычисление значений г\1 в приближении ВКБ производится
непосредственно по формуле A23.7), что же касается вычисления
величин т]г, определяемых формулой A23.3), то оно выполняется
с помощью соотношений
A23.8а)
1
1
360х3 " ' "
A23.86)
Заметим, что ряд A23.86) быстро сходится при и > 2.
Из таблицы видно, что результаты находятся в хорошем
.согласии между собой. В случае / = 0, когда г-=к/н—ги<^1,
выражение A23.7) можно разложить в ряд
¦Ю -4Т^Ш" Ч 8x^192x3 ••• '
поэтому разность между этим выражением и точным выражением
A23.86) будет примерно равна
- — %» —24^-
С другой стороны, если
следует
, то из равенства A23.7)
\ВКБ х	х
в то время как соответствующее точное выражение в силу A23.8а)
можно записать в виде
х	v	х	х3
/^ 	,у. Чточн —. Jz	 |
Л 2,К	4А	оА
Разность двух приведенных выражений убывает как ()
Это значит, что при продолжении нашей таблицы (/ > 4) 'мы
не получим сколько-нибудь заметных различий между точными
и приближенными значениями фаз.

124. Квазипотенциал	331
Задача 124. Квазипотенциал
Вместо переменной г часто полезно ввести новую переменную
A24.1)
~
(преобразование Сабатьера). Показать, что выражение для фазы
ВКБ можно представить в виде простого интеграла по перемен-
переменной t, в котором квазипотенциал
Q(t)=2E\n^p-	A24.2)
по существу заменяет потенциал V (г).
Решение. Если ввести величину
Ь = —~	A24.3)
(прицельное расстояние), то, согласно формуле A22.2), выраже-
выражение для фазы ВКБ можно записать в виде
(г
		г		 \
_iL—b~dr-\ l/l—b~dr,
b	}
A24.4)
где rt — наибольший корень выражения, стоящего под радикалом
в первом интеграле. Некоторое неудобство этой формулы состоит
в том, что предел при г —>• оо имеет лишь разность интегралов,
сами же интегралы расходятся, а нижние пределы различны.
Эту трудность можно устранить, воспользовавшись преобра-
преобразованием A24.1), в результате которого первый из интегралов
A24.4) приводится к виду
t
i/"i v b% a. fdlnr(O./.2 ,2 ,,	л24^
I/ i •—— ——	— (^if 	 i 	-у-	у t	и ttt-.	I lul.u'l
rt	'	b
Разумеется, это возможно лишь в том случае, если преобразо-
преобразованию t=t(r) соответствует единственное обратное преобразо-
преобразование r = r(t), т. е. если t представляет собой монотонную функ-
функцию г. Подставляя выражение A24.5) в формулу A24.4) и
обозначая во втором интеграле переменную г через t, получаем
J{^^f}	A24.6)
ь
ь
Последний интеграл еще более упрощается с помощью интегри-
интегрирования по частям. С учетом тождества
d\nr(t) 1 d , r(t)
dt	t ~ dt t

332	//. Задачи без учета спина. Е. Магнитное поле
окончательный результат принимает вид
6,	'ftf-gm "L_,	A24.7)
2 J ? Yt*o*
где функция Q (t) определяется равенством A24.2).
Если \V(r)\<^E, то функция Q (t) лишь немного отличается
от потенциала V (г). В этом нетрудно убедиться, переписав
равенство A24.2) в виде
Q (/)=—? In (l —-^г)-	A24.8)
Отсюда в первом приближении следует, что Q(t) = V (r). Заметим,
кстати, что нули функции Q (t) в точности совпадают с нулями
функции V (г).
Замечание. В работе Сабатьера [Sabalier Р. С, Nuovo Cimento, 37,
1180 A965)] введено преобразование A24.1). Метод квазипотенциала был раз-
развит в работе Вольмера и Крюгера [Vollmer G., Krilger #., Plj-ys. Lett., 28A,
№ 2 A968)]. Дополнительные подробности можно найти в статье Вольмера
\Vollmer G., Zs. Phys., 226, 423 A969)].
Е. Магнитное поле
Задача 125. Введение магнитного поля
Получить выражение для гамильтониана заряженной частицы
при наличии магнитного поля и показать, что присутствие в
уравнении Шредингера векторного потенциала не противоречит
калибровочной инвариантности.
Решение. В классической механике показывается11, что при
наличии магнитного поля, описываемого вектор-потенциалом А,
импульс р любой частицы с зарядо.,1 е заменяется величиной
Р=р~А,	A25.1)
поэтому нерелятивистская функция Гамильтона имеет вид
') + V(r),	A25.2)
1} Это делается следующим образом. С помощью функции Гамилыона
A25.2) находятся канонические уравнения движения, из которых затем исклю-
исключается импульс, что в результате приводит к уравнению движения
В правой части этого уравнения стоит правильное выражение для силы
Лоренца действующей на частицу с зарядом е.

125. Введение магнитного поля	333
где Ф—скалярный потенциал электромагнитного поля, а V(г) —
потенциал, обязанный силам неэлектромагнитного происхождения
(например, ядерным силам). Соответствующий этому классиче-
классическому выражению гамильтониан получается заменой вектора р
оператором (fl/i) у. В результате мы получаем обобщенное урав-
уравнение Шредингера
где
Так как
V-.<4i|} = i|)div A + А -уф,
то последнее выражение можно упростить:
В классической теории Максвелла, кр_оме того, показывается,
что векторный потенциал А и скалярный потенциал Ф можно
подвергнуть одновременному калибровочному преобразованию
где х—произвольная функция координат и времени, при этом
напряженности полей
Я=то1А, & = —grad<I>—±-A	A25.6)
останутся неизменными. Если физические явления определяются
напряженностями полей, а не их потенциалами, то эта калиб-
калибровочная инвариантность должна иметь место и в квантовой
теории.
Если мы теперь просто подставим выражения A25.5) в гамиль-
гамильтониан A25.4), то это, разумеется, приведет к появлению целого
ряда дополнительных членов, что нарушит калибровочную инва-
инвариантность уравнения Щредингера. Имеется единственная воз-
возможность избавиться от этих членов: для этого нужно, чтобы
сама волновая функция участвовала в калибровочном преобра-
преобразовании. Так как произведение i|>*i)j имеет непосредственный
физический смысл, то оно, так же как и напряженности полей,
не должно меняться при калибровочном преобразовании. Таким
образом, это преобразование должно иметь вид
ц—+ц' = е1ац,	A25.7а)
где а —некоторая функция rat. При этом, очевидно, должно

334	//. Задачи без учета спина. Е. Магнитное поле
быть
у Y = е'а {у2ф -f 2iyi|)• ya + *фу2(* — (V«L}.
Подставляя эти выражения в гамильтониан A25.4) и заменяя
там потенциалы А и Ф потенциалами Л' и Ф' в соответствии
с равенствами A25.5), получаем
^' = — ^ {V2i|3 + 2tya
Последнему выражению после перегруппировки членов можно
придать вид
Дополнительные члены, фигурирующие в этом выражении, дей-
действительно взаимно сокращаются, если положить
a = -rX,	A25.76)
так что в результате мы приходим к равенству
Так как наше преобразование одновременно изменяет и левую
часть уравнения Шредингера A25.3)
__ е-'аф' = _._ (ф + »аф) = — т ф—f хФ.
то последние члены в обеих частях уравнения A25.3) взаимно
уничтожаются и оно будет выполняться для штрихованных вели-
величин так же, как и для нештрихованных. Этим и доказывается
калибровочная инвариантность теории, если волновая функция i)>
преобразуется согласно соотношениям A25.7а) и A25.76).
Задача 126. Плотность тока в присутствии магнитного поля
Вывести формулу для плотности тока в случае уравнения
Шредингера с векторным потенциалом. Доказать, что плотность
тока калибровочно инвариантна.

126. Плотность тока в присутствии магнитного поля	335
Решение. В задаче 1 был получен закон сохранения вероят-
вероятности. При выводе этого закона мы исходили из уравнения Щре-
дингера и уравнения, комплексно сопряженного с уравнением
Шредингера, и строили с их помощью уравнение непрерывности.
В этой задаче мы поступим аналогичным образом и начнем
с уравнений
A26.1а)
= ТдГ-	A26.16)
Умножая уравнения A26.1а) и A26.16) соответственно на г|з* и i)>
и вычитая их одно из другого, получаем
fc 2	2 ^
?ft	1 - »	h д
тс	т\тт/ тт	j	i dt
Так как далее
и
А ¦ у (г|з*г|з) + i|A|) div Л = div (Лт^),
то левую часть этого уравнения можно представить в виде ди-
дивергенции некоторого вектора. Таким образом, сохраняя прежнее
определение плотности вероятности
p = i|A|>,	A26.2)
мы приходим к уравнению непрерывности
!f	A26.3)
в котором плотность тока вероятности s имеет вид
A26.4)
Последняя формула является обобщением формулы A.6), выве-
выведенной ранее для случая А =0.
Выполняя калибровочное преобразование, рассмотренное
в предыдущей задаче,
А' = А + \%, ф'=е'«ф, a = fx,	A26.5)

336	//. Задачи без учета спина. Е. Магнитное поле
находим
-2» ^ (Л^)' = - 2t i-
= — 2t f-
Отсюда следует, что плотность тока вероятности A26.4) калибро-
вочно инвариантна. Очевидно, что определяемая равенством A26.2)
плотность вероятности р также калибровочно инвариантна, сле-
следовательно, этим же свойством обладает и сам закон сохранения.
Задача 127. Нормальный эффект Зеемана
На электрон, помещенный в центральное поле, дополнительно
воздействует однородное магнитное поле %. Определить стацио-
стационарные состояния электрона. Спин электрона не учитывать.
Решение. В пренебрежении релятивистскими эффектами диф-
дифференциальное уравнение для стационарных состояний электрона
с зарядом —е имеет вид
-^42u-~ri(A-\)u + Vu = Eu,	A27.1)
причем выше мы воспользовались калибровкой div A = 0 и опу-
опустили член, пропорциональный А2. В случае однородного поля Ж,
направленного вдоль оси г, мы можем удовлетворить условию
калибровки, положив
^	у ^	А2 = 0,	A27.2)
при этом
1
и уравнение A27.1) можно записать в виде
Заметим, что член, содержащий магнитное поле, можно перепи-
переписать несколько по-иному:
6 H-L,	A27.5)
2тс
где L — оператор момента количества движения, z-компонента

127. Нормальный эффект Зеемана	337
которого равна
г п, д
2 = Т дер '
Согласно максвелловской теории электромагнетизма, движущаяся
частица с зарядом —е и моментом количества движения L по-
порождает магнитное поле, обусловленное дипольным магнитным
моментом
,	A27.6)
поэтому величину A27.5) можно записать в виде —М-Ж. По-
Последнее выражение представляет собой, на самом деле, хорошо
известную потенциальную энергию диполя М в магнитном поле Ж.
Решение дифференциального уравнения A27.4) можно искать
в виде
" = fi{r)Y,ill(b, ф),	A27.7)
тогда член, содержащий магнитное поле, даст а уравнение вклад
и вместо A27.4) теперь можно написать
Это уравнение по форме совпадает с дифференциальным уравне-
уравнением для случая 5Jf = O. Отсюда следует, что под действием
магнитного поля энергетические уровни расщепляются:
^	A27.9)
Здесь через ?°, / обозначены собственные значения для случая
Ж~0. Учитывая, что %\i. = Lz, и принимая во внимание равен-
равенство A27.6), последнее соотношение можно преобразовать к виду
Ea,i,v = E°a 1—M-X,	A27.10)
что и следовало ожидать исходя из классических соображений.
Характерный магнитный момент eh/Bmc) называют магнето-
магнетоном Бора, а квантовое число ц—магнитным квантовым числом.
В рассматриваемом случае система собственных состояний та же
самая, что и при 5? = 0, но магнитное поле уничтожает простран-
пространственное вырождение энергетических уровней.
Замечание. Формулу A27.9), определяющую уровни энергии, можно полу-
получить, рассматривая оператор магнитной энергии A27.5)
A27.11)

338	//. Задачи без учета спина. Е. Магнитное поле
в качестве возмущения. В первом порядке теории возмущений сдвиг уровней
определяется диагональным матричным элементом оператора WMaT, вычислен-
вычисленным по невозмущенным собственным функциям:
2^	A27.12)
Совпадение приближенного результата с точной формулой A27.9) объясняется
тем, что волновые функции нулевого приближения в интеграле A27.12) сов-
совпадают с точными решениями уравнения A27.4). В связи с вопросом о прави-
правилах отбора см. задачу 216.
Задача 128. Парамагнитная и диамагнитная восприимчивости
без учета спина
Вычислить парамагнитную и диамагнитную восприимчивости
на один связанный электрон, находящийся в центральном поле.
Спин электрона не учитывать.
Решение. Пусть на рассматриваемый атомный электрон, дви-
движение которого описывается гамильтонианом Но, дополнительно
действует магнитное поле Ж || z. Выбирая калибровку, при кото-
которой дивергенция вектор-потенциала обращается в нуль, получаем
?^	A28.1)
Чтобы удовлетворить условию калибровки, положим
I	I
Л 	 	 <%f и	Л 	 О^-и Л 	П	/1 ОЙ 0\
**х —	о"^^У»	у — "о" Jl'X'y f*z — »	yl^O.Zf
тогда
0 ' тс 2 \vдх ду J ' 2тс2 4 v
ИЛИ
— И | е<^ Г | е '^> r2 cin2ft	Л 98 Ч\
0 ' 2тс z ' 8тс2	v	'
Магнитная энергия в состоянии | п> (посредством п обозна-
обозначена вся совокупность квантовых чисел, характеризующих одно-
электронное состояние) с точностью до членов второго порядка
равна
(Г28.4)
Пусть далее все атомы вещества находятся в основном состоя-
состоянии (такое предположение действительно разумно, так как энер-

128. Парамагнитная и диамагнитная восприимчивости	339
гия возбуждения, как правило, составляет несколько электрон-
вольт, что значительно больше тепловой энергии). Допустим, что
в этом основном состоянии рассматриваемый электрон обладает
орбитальным моментом Ш и, следовательно, может иметь раз-
различные значения проекции момента flml на направление магнит-
магнитного поля. В этом случае первый член формулы A28.4) даст
в магнитную энергию (отнесенную к одному электрону) вклад
вида
В состоянии теплового равновесия число электронов с проек-
проекцией момента %mt пропорционально, согласно Больцману,
ехр {— Ell)/kT\, поэтому средняя магнитная энергия, приходя-
приходящаяся на один электрон, будет равна
где
2тс kT
Безразмерная величина а для всех разумных значений напря-
напряженности поля Ж значительно меньше единицы, и фигурирую-
фигурирующие выше экспоненты можно разложить в ряд. Таким образом,
имеем
2 ^ "ч •
Все эти суммы симметричны относительно т1 — О, поэтому суммы,
содержащие нечетные степени ть обращаются в нуль, и мы можем
написать
¦ = —а
причем здесь мы опустили члены порядка а2 и выше. Отсюда
для плотности магнитной энергии получаем
где N — число электронов с моментом / в 1 см3. Следует заме-
заметить, что плотность энергии пропорциональна квадрату напря-

340	//. Задачи без учета спина. Е. Магнитное поле
женности поля, хотя исходная энергия ?A) зависела от поля
линейно.
Второй член формулы A28.4)
-^|r<n|r!sin2ft|n>	A28.8)
оказывается (см. ниже) значительно меньше, чем ?ш, поэтому
он не играет большой роли в тех случаях, когда первый член
отличен от нуля. Эти же соображения относятся и к третьему
члену формулы A28.4). Таким образом, для всех / > 0 магнит-
магнитные свойства вещества определяются первым членом, в случае
же / = 0 эти свойства определяются энергией ?B). Так как
2
то мы можем написать
где |0> означает волновую функцию, соответствующую основному
s-состоянию, а <0|г2|0>—среднее значение г2 в этом состоянии.
В данном случае необходимость в температурном усреднении от-
отпадает. Первый и третий члены формулы A28.4) в случае s-состоя-
ния обращаются в нуль, так как Lz|0> = 0, поэтому теперь их
можно не рассматривать.
Согласно электродинамике Максвелла, изменение поля Ж на
ЬЖ приводит к изменению плотности магнитной энергии:
ЬЕ = —ЛЪЖ,	A28.10)
где <М—так называемая намагниченность, т. е. магнитный диполь-
ный момент 1 см3 вещества, индуцированный полем Ж. Предпо-
Предполагается, что она пропорциональна полю Ж:
а€ = 1Ж.	A28.11)
Коэффициент пропорциональности % называется магнитной вос-
восприимчивостью. Комбинируя соотношения A28.10) и A28.11),
получаем
6Е
и, следовательно, плотность магнитной энергии будет равна
Е=—~гЖ\	A28.12)
Если %—положительная величина, то мы говорим о парамагне-
парамагнетизме, если % — отрицательная величина, то — о диамагнетизме.
Макроскопическое выражение A28.12) для плотности ма*гнит-
ной энергии мы должны отождествить либо с выражением A28.7),
если /=й=0, либо с умноженным на jV выражением A28.9), если

128. Парамагнитная и диамагнитная восприимчивости	341
= 0. В первом случае мы имеем дело с парамагнетизмом, причем
Хпара з V 2mcy kT '
во втором же случае
^>,	A28.14)
и, следовательно, мы имеем дело с диамагнетизмом.
Как и следовало ожидать, формула A28.13) совпадает с клас-
классической формулой Ланжевена, полученной усреднением по ориен-
тациям постоянного дипольного момента
* = -?el-	<128-15>
Диамагнитная восприимчивость значительно меньше парамагнит-
парамагнитной восприимчивости, поэтому ее можно не учитывать при рас-
рассмотрении парамагнитных веществ. В этом можно убедиться,
оценив отношение
^W/-	<12816>
Фактически это есть отношение вращательной и тепловой энер-
энергий электрона. Первая из них составляет несколько электрон-
вольт, вторая по порядку величины равна 0,03 эВ при комнат-
комнатной температуре1'.
11 Величина <л2> по порядку совпадает с квадратом боровского радиуса
(felme2J. Полагая для оценки в числителе отношения A28.16) 1 = \ъ находим,
что он равен mei/1i2 = 27,2 эВ.