Автор: Подстригач Я.С.
Теги: механика деформируемых тел упругость деформация физика теплопроводность твердое тело
Год: 1977
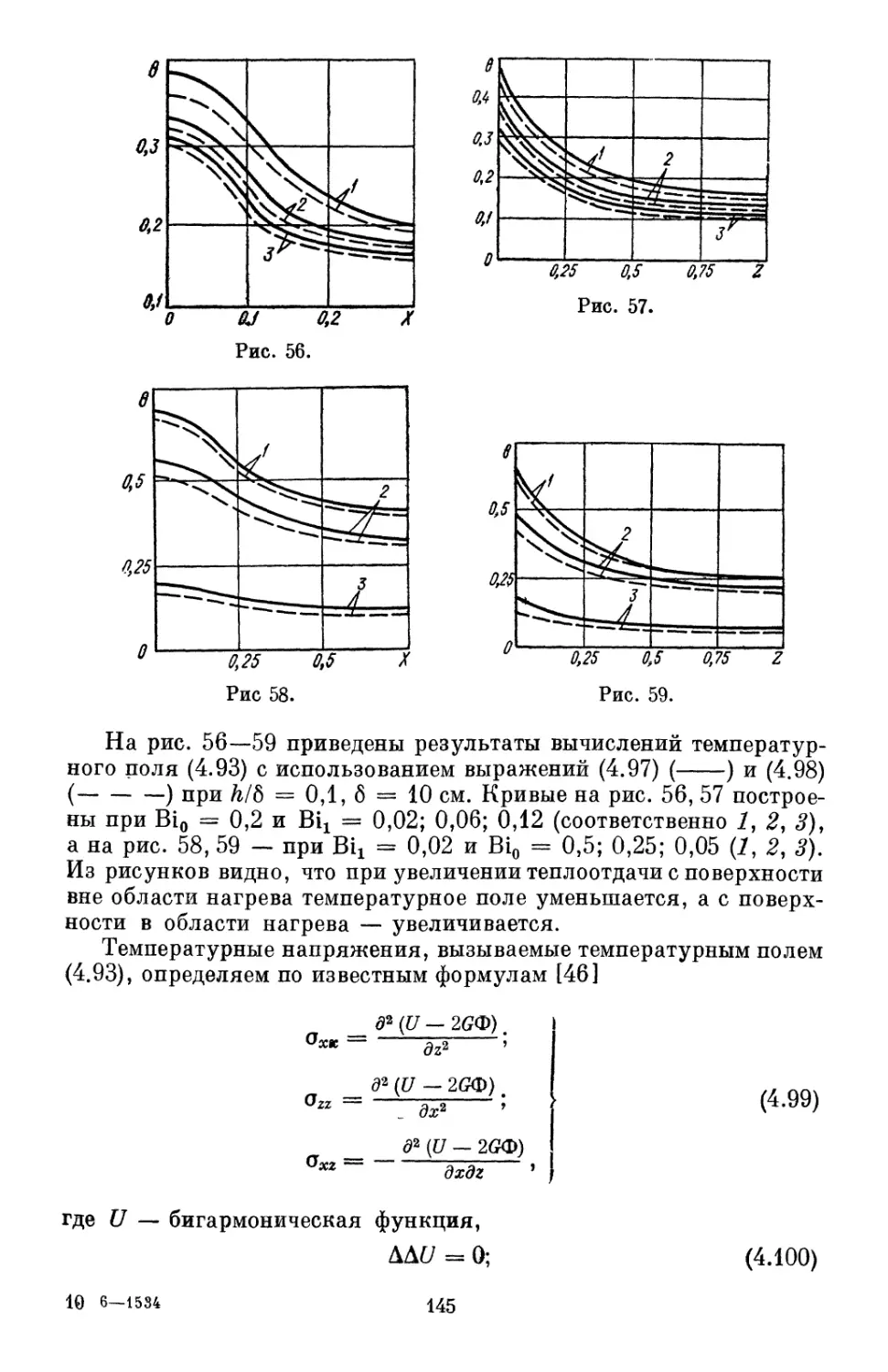
Текст
АКАДЕМИЯ НАУК УКРАИНСКОЙ ССР
ЛЬВОВСКИЙ ФИЛИАЛ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
ИНСТИТУТА МАТЕМАТИКИ
ТЕРМОУПРУГОСТЬ ТЕЛ
ПРИ ПЕРЕМЕННЫХ
КОЭФФИЦИЕНТАХ
ТЕПЛООТДАЧИ
КИЕВ
«НАУКОВА ДУМКА»
1977
531
Т35
УДК 539.3
В монографии изложены основы теории
теплопроводности и термоупругости анизотропных v
изотропных тонкостенных элементов конструкций и
некоторых массивных тел с зависящими от температуры,
времени и координаты коэффициентами теплоотдачи.
Развиты аналитические методы расчета
температурных полей и напряжений в пластинках, оболочках,
стержнях — важнейших составных частях
современных машин, сооружений, электровакуумных
приборов и других конструкций.
Рассчитана на научных работников,
занимающихся механикой деформируемого твердого тела.
Может быть также полезной аспирантам и
студентам старших курсов вузов, специализирующимся
в этой области знаний.
АВТОРЫ
Я. С. П О Д С Т Р И Г А Ч,
Ю. М. К О Л Я Н О,
В. И. ГРОМОВЫ К,
В. Л. Л О 3 Б Е Н Ь
Рецензенты
Т. Л. Мартынович,
О. Н. Романив
Редакция физико-математической
литературы
т 20304-039 _
М221@4)-77 *W "
ХУ) Издательство «Наукова думка», 1977
ОГЛАВЛЕНИЕ
Предисловие 5
Принятые обозначения 7
Глава 1
Уравнения теплопроводности и термоупругости тел
при переменных коэффициентах
теплоотдачи
Аппроксимация зависимостей коэффициентов теплоотдачи
от температуры, времени и координаты , . 9
Уравнения теплопроводности пластинок при зависящих от
температуры коэффициентах теплоотдачи , . . 13
Уравнения тэплопроводн )стя пластинок, оболочек и т.рж-
ней при нестационарном теплообмене 21
Уравнения теплопроводности тонкостенных элементов
конструкций при зависящих от координаты коэффициентах
теплоотдачи 31
Температурные поля при узкозональном нагрев4 тел . . 33
Уравнения и соотношения термоупругости пластинок с
прямолинейной и цилиндрической анизотропией 35
Уравнения и соотношения термо упругости изотропных
пластинок и оболочек 44
Глава 2
Термоупругость тел
при зависящих от температуры
коэффициентах теплоотдачи
Исследование температурных полей и напряжений в пластин- 4Ф
ках при сварке ... . ,
Исследование температурных полей и напряжений в
твердых телах при закалке 64
3
Глава 3
Термоупругость тонких пластинок
при нестационарном теплообмене
Температурные поля и напряжения в анизотропных
пластинках , . . 80
Температурные поля и напряжения в изотропных
пластинках 105
Г л а в а 4
Термоупругость тел
при зависящих от координаты
коэффициентах теплоотдачи
Исследование температурных полей и напряжений в
пластинках и оболочках при кусочно-постоянных коэффициентах
теплоотдачи , 126
Исследование температурных полей и напряжений в твердых
телах при узкозональном нагреве ....,.,., 137
Литература * 155
ПРЕДИСЛОВИЕ
Задачи теплопроводности и термоупругости тел с теплообменом, как
правило, решаются в предположении, что коэффициент теплоотдачи является
постоянной величиной. Однако развитие многих областей современной
техники тесно связано с изучением температурных полей и напряжений в
элементах конструкций, коэффициенты теплоотдачи которых зависят от
температуры, времени или координаты. Для изучения термопрочности
элементов конструкций в условиях аэродинамического нагрева, тепловых и
механических процессов жидкостной закалки стекла, сварки элементов конструкций
и других технологических процессов необходимо знание температурных полей
и напряжений в телах с зависящими от температуры или времени
коэффициентами теплоотдачи. При локальном нагреве тонкостенных элементов
конструкций, нагреве тел по областям малых размеров коэффициент
теплоотдачи является функцией координаты, которую с удовлетворительной степенью
точности можно аппроксимировать ступенчатой функцией. Важное
практическое значение имеет исследование тепловых режимов конструкционных
элементов в условиях, когда изменяются в зависимости от времени коэффициент
теплоотдачи и температура внешней среды. Задачи такого рода возникают
при исследовании охлаждения тел воздушным потоком с переменной
скоростью обтекания, изменения температуры 'в цилиндрах двигателей, при
изучении явления турбулентности, контактного измерения температуры
реактивной струи, выходящей из сопла с нарастающими скоростью и
температурой. Знание температурного поля в этих условиях позволяет оценить
скорость нагрева и рассчитать напряжения. Определению одномерных
температурных полей в массивных телах при заданных законах изменения
коэффициентов теплоотдачи в зависимости от времени или температуры
поверхности посвящены работы Ю. В. Видина [9—11], В. Н. Гревцевой и
В. И. Киршбаума [15, 16), Ф. Зелига [72], М. А. Каганова и Ю. Л. Розенштока
[24], В. Н. Козлова [27], Ю. С. Постолъника [S3], Ю. Л. Розенштока [54, 55],
В. В. Саломатова и Э. И. Гончарова [57—59], В. В. Саломатова, В. В.
Иванова и Э. И. Гончарова [60], В. С.Саркисяна [61], М. М.Сидляра [62—64],
В. М. Юдина [67, 68] и др. Конвективный теплообмен между телами и
методика определения коэффициента теплоотдачи рассмотрены в исследованиях
Я. М. Чанга и А. Д. Андерсона [69], П. Р. Хилла [70], Я. А. Шетца и
Р- Айхорна [73]. Методика решения в аналитически замкнутом виде задач
5
теплопроводности пластинок и стержней при произвольном изменении в
зависимости от времени коэффициента теплоотдачи с боковых поверхностей
предложена в работах В. В. Иванова [22], Ю. М. Коляно B9J, Я. С Под-
стригача и Ю. М. Коляно \47].
В данной монографии впервые изложены результаты исследований
температурных полей и напряжений в изотропных и анизотропных тонкостенных
-элементах конструкций при произвольной зависимости коэффициента
теплоотдачи от времени, температуры и координаты В первой главе основное
внимание уделено развитию теории теплопроводности и термоупругости
тонкостенных элементов конструкций при переменных коэффициентах
теплоотдачи Рассмотрены наиболее характерные зависимости этих коэффициентов
от температуры, времени, координаты и способы их аппроксимации.
Выведены уравнения теплопроводности пластинок, оболочек и стержней и, исходя
из гипотезы Кирхгофа — Лява, уравнения и соотношения квазистатической
задачи термоупругости анизотропных и изотропных пластинок и
изотропных оболочек* Вторая глава посвящена исследованию
термонапряженного состояния элементов конструкций в условиях электрошлаковой сварки и
жидкостной закалки стекла.
На основании полученных в первой главе уравнений и соотношений в
третьей главе определяются и исследуются нестационарные температурные поля
и напряжения, возникающие в нагреваемых внешними потоками тепла,
внешней средой или внутренними источниками тепла анизотропных, ортотроп-
ных и изотропных пластинках при нестационарном теплообмене
(коэффициент теплоотдачи с боковых поверхностей является функцией времени).
Рассматриваются частные случаи: экспоненциальное изменение в зависимости
от времени коэффициента теплоотдачи, аэродинамический нагрев, тепловое
воздействие как заданная функция координаты (периодическая, разрывная
и др.) и единичная функция времени.
При локальном нагреве твердых тел коэффициент теплоотдачи с
поверхности области нагрева отличается от коэффициента теплоотдачи с
поверхности вне этой области. В последней, четвертой главе предлагается
способ определения температурных полей и напряжений в тонкостенных
элементах конструкций, области поверхности которых подвергаются
локальному нагреву внешней средой, а также конструкций, нагреваемых внутренними
источниками тепла. Определяется термонапряженное состояние массивных
тел и тонкостенных элементов конструкций, нагреваемых по узким зонам.
Рассматривается класс задач, в которых коэффициент теплоотдачи можно
выразить через дельта-функцию Дирака.
В подготовке рукописи к изданию принимали участие В. 3. Дидык,
С» Т. Стасюк и О. 3. Худа, за что авторы приносят им благодарность.
Авторы
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
а — %t/Cv — коэффициент температуропроводности
Bi = azb/Xt — критерий Био
С = 2сг,д — приведенная объемная теплоемкость
с — удельная теплоемкость
cv = ср — объемная теплоемкость
#__n(D — функция параболического цилиндра (функция Вебера)
Е — модуль упругости
Ei (—р — интегральная показательная функция
ег^ (£) — интеграл вероятности
'**> 'уу* ег» еху = «Ух» V в *гУ' **г = егх ~ КОМПОНвНТЫ
тензора деформаций в декартовых координатах
ет *ФФ. ezz> erq> = V' егг = ezr, ещ = ещ - компоненты
тензора деформаций в цилиндрических координатах
Fo — ат/б2 — критерий Фурье
G — модуль сдвига
^v Ю ~ модифицированная функция Бесселя первого рода
порядка v
^v ©' ^v © — функция Бесселя первого и второго рода
порядка v
Kv (£) — функция Бесселя от мнимого аргумента порядка v
(функция Макдональда)
Mi = BiFo — критерий Михеева
щ, п2 — компоненты вектора внешней нормали п к
цилиндрической поверхности S пластинки
Ре = Vbl2a — критерий Пекле
q — мощность источников тепла
г, ф, z — цилиндрические координаты
тъ = 26Д3з — удельное термосопротивление
|1. С>о,
£(£) = { V2» С = 0> — симметричная единичная функция
10, £<0,
+ ( I о : < о ® I о t < о, ~" асимметРичные еди-
ничные функции
7
7\ 71* — интегральные характеристики температуры пластинок
и оболочек
t — температура точек тела
tc — температура сред, омывающих поверхности z = ± 6
пластинки и у= f б оболочки
** — температура среды, омывающей поверхность S пластинки
U — функция напряжений Эйри
и, у, м; — компоненты вектора перемещений в декартовой или
цилиндрической системе координат
V — скорость движения источника тепла
wt — плотность источников тепла
х, у, z — прямоугольные декартовы координаты
а> Р> У — триортогональная система координат оболочки
aU> ah "— температурные коэффициенты линейного расширения
и сдвига анизотропного тела
ап — коэффициент теплоотдачи, зависящий от координаты
aR — коэффициент теплоотдачи с поверхности г — R стержня
кругового сечения
as — коэффициент теплоотдачи с цилиндрической поверхности
S пластинки
at — температурный коэффициент линейного расширения
изотропного тела
ах, а , аг — коэффициенты теплоотдачи с поверхностей стержня
прямоугольного поперечного сечения
а*, а* — коэффициенты теплоотдачи с боковых поверхностей
z = db б пластинки и у = ±6 оболочки, зависящие от температуры
или времени
у (v, Q — неполная гамма-функция
А — оператор Лапласа
б — полутолщина пластинки или оболочки
8 (С) ~~ дельта-функция Дирака
б// — символ Кронеккера
к, \х — постоянные Ламе
Aij = 2Kt-d — приведенный коэффициент теплопроводности
^h (*> 7=1? 2, 3) — коэффициенты теплопроводности
анизотропного тела
Xt — коэффициент теплопроводности изотропного тела
v — коэффициент Пуассона
р — плотность
°хх> ауу агг> °ху = Gyx' °yz = °zy °zx = °хг ~ Компоненты
тензора напряжений в декартовых координатах
т — время
¥ — термоупругий потенциал перемещений
Гла ва 1
УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
И ТЕРМОУПРУГОСТИ ТЕЛ
ПРИ ПЕРЕМЕННЫХ КОЭФФИЦИЕНТАХ
ТЕПЛООТДАЧИ
Аппроксимация зависимостей
коэффициентов теплоотдачи от температуры,
времени и координаты
Зависимости коэффициента теплоотдачи от температуры при
закалке стеклянных пластинок в жидких средах рассмотрены в
работе [5]. Такие зависимости с достаточной точностью могут быть
аппроксимированы дельта-образной последовательностью:
az(T) = a0 + -^-
(Т — Т J 1—1
( "' +в» , A.1'
где Т — средняя по толщине температура пластинки; а0 —
значение коэффициента теплоотдачи при малых температурах; аг =
= ат — а0; 8 — безразмерный параметр; Тт — температура,
соответствующая максимальному значению коэффициента
теплоотдачи ат; Та — коэффициент с размерностью температуры. На рис. 1
показана зависимость коэффициента теплоотдачи полиэтилсилок-
сановой жидкости от температуры (——), аппроксимированная
дельта-образной последовательностью A.1) при Та = 280° С
( ) и Та = 300° С (-•-), е - 0,318, Тт = 640° С.
При резком локальном возрастании коэффициента
теплоотдачи в окрестности некоторого значения температуры и
последующем резком его уменьшении для сравнительного анализа влияния
зависимости az (T) на температурное поле и напряжения в
пластинке вместо A.1) можно использовать представление
а2(Л=«о + М(^-^т), A.2)
где а2 ■— коэффициент с размерностью а0Т [кал/(см2 • с)]; 6 (Т —
— Тт) — дельта-функция Дирака. Учитывая, что
вместо A.2) получаем
6 (т — т )
az (т) = а0 + а2 | f/ (т } [ , A.4)
где тт — время, по истечении которого достигается температура
1 гп*
9
Рассмотрим другой способ аппроксимации зависимостей
коэффициента теплоотдачи от температуры. Если кривые, приведенные
в работе [5], аппроксимировать ломаной, изменяющейся
скачкообразно, т. е. представить в виде алгебраической суммы единичных
функций Хевисайда а*£ (Т — Т{), то вследствие замены
S+ (Т — Тп) = 5+ (тп — т) (при охлаждении пластин), A.5)
S+ (Т — Тп) = £_!_ (т — тп) (при нагревании пластин) A.6)
коэффициент теплоотдачи, зависящий от температуры, становится
функцией времениа2 (т), где т7 — время, за которое пластинка
охлаждается (нагревается) до температуры Т{. Для решения
задачи можно использовать линейное уравнение теплопроводности
с переменным коэффициентом теплоотдачи. При закалке
стеклянной пластинки в полиэтилсилоксановой жидкости зависимость
коэффициента теплоотдачи от температуры имеет вид (рис, 2)
az (Т) = а0 + (<х8 - оо) S (Т - Г8), A.7)
где а3 = 6а0; а0 = 5 • 1(ГГ кал/(см2. с - °С); Тъ = 440° С.
Используя замену A.5), вместо соотношения A.7) получаем
аг (т) = а0 + (а3 — а0) S (т3 — т), A.8)
где т = 2,5 с — время, по истечении которого достигается
температура Т3.
Если коэффициент теплоотдачи, являющийся функцией
температуры, представить в виде (рис. 3)
а2 (Т) = а0 + 2а0 [S (T -T2)-S(T- Тг)] + Aa0S (T - Г3), A.9)
$00 800' 700 600 500 400 Т
Рис 1.
10
0,05
0,02
0,01
С005\
О
^
^
00 81
1
А
1
10 7i
'
1
1
1
ч!
i4"
70 S00 500 400 Т
ом\
0,02\
0,0/
0,005
О ;
500 400 Т
Рис. 2.
Рис. 3.
то, используя замену A.5), находим следующую зависимость
коэффициента теплоотдачи от времени охлаждения:
а2 (т) = а0 + 2а0 [S (т2 - т) - S (т: - т)] + 4а05 (т8 - т). A.10)
На рис. 4 ломаной линией показано изменение коэффициента
теплоотдачи в зависимости от времени, соответствующее аппроксимации
A.10).
Наконец, если
а7 (Т) = (<х8 - a0)S(T - Т3) + а, 4- а2б(Г - Тт), A.11)
то, используя соотношения A.3) и A.5), вместо A.11) получаем
ncz (т) = (а3 — а0) 5 (т3 — т) + а0 + а2
I Г (tJ I
A.12)
Полагая в A.12) а2 = 0, приходим к выражению A.8), а при а3 =
= а0 — к соотношению A.4)
Процесс аппроксимации коэффициента теплоотдачи ломаной
совершенствуется при увеличении количества скачков,
позволяющем более точно отображать экспериментальную кривую
Например, построена ломаная, соответствующая коэффициенту
теплоотдачи, изменение в зависимости от времени которого записывается
в виде
a2(T) = a0[l + 2 S(Ti-T)-
i=1
A.13)
т. е. было восемь скачков. При этом
количестве скачков зависимость
коэффициента теплоотдачи от времени,
построенная согласно A.13), практически
совпадает с экспериментальной кривой,
полученной в работе [5]
Заметим, что результат
аппроксимации экспериментальной зависимости
коэффициента теплоотдачи от температуры
74
до \
г LY
Ч 1
\ 1
|\
1
1
2 4
Рис. 4.
11
<%| I I ] 1 1 I ломаной линией (рис. 5) при вы»
Р"%] числении температурного поля
ом щ—4г практически совпадает с резуль-
А Г\ I—I татом, полученным при аппро-
ощ —-J-X —ЛН—|—1 ксимации в виде дельта-образ-
V/ >1 | ной последовательности A.1).
5,о\^\ " ir^L^ ^Ри электРошлаков°й свар-
0qq\ * |^d ке пластинок в стык из малоуг-
о\ I 1 1 I 1 | леродистых и низколегирован-
900 800 700 600 500 400 т ных сталей зависимость
коэффициента теплоотдачи от
температуры имеет вид [12]
а2 = 24- КГ^еГ1'61, A.14)
где 8 — степень черноты поверхности тела (для проката черных
металлов 8 = 0,9). Температура по оси сварного шва может быть
выражена через параметры режима сварки [12]. Следовательно,
зависящий от температуры коэффициент теплоотдачи после
некоторых преобразований становится функцией времени, т. е. возможна
аппроксимация вида
700 600
Рис. 5.
/(т) = 0,1бГЬоТ + 0,15бГЬ1Х + 0,75е~
где Ь0 = 1200^; Ъг = 44F; Ъ2 = 1,16^;
A.15)
F =
V2
2а
27,2-Ю-'ае Ujg^1,61
2cJ>V
V = 0,1 см/с; а = 0,08 см2/с; cv = 4,8 дж/(см3 • °С) — объемная
теплоемкость; q = 2,75 дж/с; 26 = 0,4 см.
Пусть цилиндрическая оболочка, пластинка толщины 26,
стержень кругового поперечного сечения радиуса R подвергаются
локальному нагреву внешней средой температуры вс по области
| £ | < h каждой боковой поверхности или равномерно
распределенными по толщине оболочки (пластинки), сечению стержня
внутренними источниками тепла мощности q, действующими в
области | £ | < А. Зависимость коэффициента теплоотдачи с боковых
поверхностей тонкостенного элемента от координаты с
удовлетворительной точностью можно аппроксимировать ступенчатой
функцией:
ab(Q = *l+(a0-a1)[S-& + h)-S+&-h)], A.16)
где а0 — коэффициент теплоотдачи с участка |£|<1А боковой
поверхности; ах — коэффициент теплоотдачи с остальной части
боковой поверхности тонкостенного элемента.
Если длина области локального нагрева соизмерима с толщиной
тонкостенного элемента, с диаметром 2R сечения стержня, то,
осуществляя в выражении A.16) предельный переход при h -> 0
12
и сохраняя при этом постоянной величину Л0 = 2ha0, получаем
оь(£) = а1-МоA-ЯаЖ9> A-17)
где
#а = а1/а0.
A.18)
Уравнения теплопроводности пластинок
при зависящих от температуры
коэффициентах теплоотдачи
Рассмотрим однородную анизотропную пластинку толщины
26, имеющую в каждой точке плоскость тепловой симметрии, к
которой нормальна ось z (рис. 6). Пластинка нагревается
произвольно распределенными по ее объему источниками тепла плотности
Wt (х, yy z, t) и внешней средой, теплообмен с которой происходит
по закону Ньютона.
Пусть коэффициенты теплоотдачи с боковых поверхностей
пластинки z = + б являются функциями температуры
соответствующих поверхностей пластинки t , остальные теплофизические
характеристики от температуры не зависят. В этом случае t (#, у, z, т)
определяется из уравнения теплопроводности [44, 51 ]
дН
+ рЧ =
hs
A.19)
где выражение для оператора, соответствующего случаю
пластинки с прямолинейной анизотропией, имеет вид
д2 , от д* , , д2 id
Р2 = *и
дх2
■ + 2k
12
дхду
+ ^2:
ду*
дх
A.20)
а для оператора, соответствующего случаю пластинки с
цилиндрической анизотропией,—
P' = *u4-iHri-) + 2^
<92
дгду
<9ф2
1
д
дт
; A.21)
кгз = ^г;Азз (i, } = I; 2); а33 = %^lcv — коэффициент
температуропроводности в направлении оси z при граничных условиях на
поверхностях пластинки
4з|-±а^±) (*-**) = 0,1
z = ± б; I
на цилиндрической поверхности S
Lst+as(t-tsc) = Q A.23)
и начальном условии
t = t0 при т = 0,
A.24)
Рис. 6.
13
где Ls — операторы, соответствующие случаям пластинок с
прямолинейной,
Ls = /н (ti, 4г + Х'„ -£-) + », Х'и -£- + Х122 -£- , A.25)
и цилиндрической,
Ls=nA Х'п -г- +
?ц9
± /Л+
<9г
I I Л1 д I
д22
дф
A.26)
анизотропией; аг (£~), а^ — коэффициенты теплоотдачи с
поверхностей z = + б и S\ t*, tc — температуры сред, омывающих
поверхности z — ± б и 5; ^ — компоненты вектора внешней
нормали /г к поверхности 5.
Применяя операторный метод, аналогично тому, как это
сделано в работе [51], общее решение уравнения A.19) записываем в
виде
, , , , sin pz ( dt \ . w()
t = cos pzt z=0 H — -r- Л r1— i
A.27)
где w0 = p f sin p (£ — z)u?t d£. Вводя интегральные характеристики
о
температуры
1
26
tdz, Г* =
262
f z£dz,
A.28)
-б
интегрируя выражение A.27) в соответствии с A.28) и учитывая
соотношение -т~- = — р2 (w0 + и>*)» находим
т sin рб , . <?
г* =
sin рб
р26
Рб
cos рб
dt_
dz ]z~
+ ,t
ЧзР*
где
<? = --w{w + -^
dz
2б2р2
i<~"^o~"-6
dz
<9z
"•" « dz
26
A.29)
A.30)
W
= Г Ш/С?2, PF* = — f zwtdz — соответственно отнесенная к
единице площади срединной плоскости пластинки плотность
источников тепла и плотность «моментов» источников тепла, характе-
14
ризующая неравномерность распределения источников по
толщине; Wq , ( J° )" — значения функции wQ и ее производной по
z при z = + б.
Из соотношений A.29) следует
(l^^^fS Д; /*) = 4 ■ * РЧ1 Г**> A-31)
|Z sin рб ' \ dz )Z=Q 3 sm рб — рб cos рб ' v ;
где R = T — Q/Хззр2; #* = Г* — QV^kp2- Подставляя выражения
A.31) в A.27), выражаем температуру через ее интегральные
характеристики:
t =
р cos pzR +
р2б2
sin рб
3 sin рб — рб cos рб
sin pzR* +
43Р2
A.32)
Для определения интегральных характеристик температуры Т и
Г* подставляем выражение A.32) в граничные условия A.22).
Учитывая соотношения A.30), получаем следующую систему
дифференциальных уравнений бесконечно высокого порядка [48]:
р2б2
рб ctg рб
26XVr - «+рб ctg pbR -af ^ffL 6 Л* = - («+4+
+ a_*l) -W + ■
Ц3Р2
[a^^rf+arnwir];
28X33p2T* -
2Ло
33
+ a+^
Р2б2
у 1 — рб ctg рб
J?* —
I A.33)
— 3a_ p8 ctg />6i?
'l +
■3(а+*1 + а_ф-И^* + -
Р2б
X
X
a+ (*+)
азз
■6) i/;^ — A 4 ^ б wo \;
^33
a+ = at (t+) ± аГ (О; £± = » и' как слеДУет из
выражения A.32), при z = ±8
t* = рб ctg p8R ± —
Р2б2
p6ctgp6 ^Зр2
A.34)
Условия теплообмена на цилиндрической поверхности S A.23)
и начальное условие A.24) после интегрирования по z в
соответствии с A.28) принимают вид
LsT + ab(T-Tsc) = 0;
LST* + as (T* - Г?) = 0;
Т = Т0; Т = То при т = О
15
A.35)
A.36)
где
г°= ж J*od2; r°= "W" I ^°d2; A-37)
-6 -б
П = ^( № 7Т = -ggr J **&- A-38)
—б —б
Если на поверхности S задается тепловой поток qs, в
граничных условиях A.35) произведения asTsc и asTsc следует заменить
выражениями
1 * 3 ?
^s ^ 6" J ^srfz; ^s* = 6^" J ^*&' A*39)
-б* -6
а а5 положить равным нулю. Если на поверхности S задается
граничное значение температуры, в условиях A.35) следует
перейти к пределу при as -> со.
Система уравнений A.33) вместе с выражением A.32) вполне
эквивалентна уравнению A.19) и граничным условиям A.22),
поэтому ее решение является точным решением задачи
теплопроводности анизотропной пластинки произвольной постоянной
толщины 26.
Найдем теперь приближенную систему уравнений
теплопроводности тонких анизотропных пластинок. Полагая \рпТ\ < + оо;
\рпТ*\ < + °о, переходим в системе A.33) и выражении A.34)
к пределу при б -*- 0 (сохраняем при этом постоянными Ai;, С, г2,
W, W *). В результате получаем следующую систему уравнений
[50]:
LT - (ос+Г + а_Г*) = - (W + оцД + <*-*-); I AЛ0)
LT* - 3 (а0Г* + а_Г) = - (W* + За+£ + За_ф, I
где выражения для оператора, соответствующего случаям
пластинки с прямолинейной и цилиндрической анизотропией, имеют
вид
д2 д% д2
Ли -^г- + 2Л12 -ЩГ + Ла2 ~^>
дг \ дг J l r дгдц)
<У22 <?2
г2 дф2
-с4-; 1
A.41)
ос0 = 4/гг -f a+; t* = Т + Г*. Когда Г и Г* найдены,
температура в любой точке пластинки может быть определена из
соотношения A.32). Переходя в выражении A.32) к пределу при б -МЗ
и сохраняя постоянным отношение z/б, получаем соотношение
t = T + zT*/6, A.42)
по которому температура при известных Т и Г* определяется
приближенно. Таким образом, уравнения A.40) и A.42) являются
16
приближенными нелинейными уравнениями теплопроводности
тонких анизотропных пластинок при переменных коэффициентах
теплоотдачи с боковых поверхностей.
Приведем точную систему уравнений теплопроводности
пластинок с зависящими от температуры поверхности коэффициентами
теплоотдачи, необходимую для определения граничных значений
температуры пластинки £*. Используя представление A.34), после
некоторых преобразований находим
tgP5 / t++t
рд
wt + wo \ , Q
2^3Р2
4зР2 '
Г* ==
3A— pftctgpb) I &—i
Р2б2
,&.
2^3Р2
+
} A.43)
ЧзР*
или
tgp6
t+ + f
W+ + WQ)
3 A — рб ctg рб) f *+ — *~
p262
wt~wo
| A-44)
Подставляя соотношения A.43) и A.44) в уравнения A.32) и A.33),
получаем нелинейную систему уравнений для определения
граничных значений температуры пластинки
XUp tg РЬ (t+ + Г) - -%р- (w+ + щ) -
v+ <t+\ U+
[аТ (Г) (Г - tT) + а.7 (П (*- - £")]
B6<? + W);
lisp ctg P8(t+- Г) + ± I-L- - ctg рб\ (w+ - ш0-) +
\ A-45)
»+/*-Ь/*+
+ [«7 (Г) (Г - *+) - «Г (П (*- - Q] = 4- Bб(?* + ^*)
и уравнение для определения температуры, выраженной через ее
граничные значения,
+
cos pz 1 t^~ + t~
~~ cos рд \ 2
sin pz ( f^ — Г~
sin pb \ 2
wt + wo
*ЧзР2
2^3P2 /
)-
4зР2
A.46)
Если задача теплопроводности симметрична относительно
срединной плоскости z = О пластинки, т. е. tt = t^~ = £с;
а+ (*+) = аГ (П = az (Г); W* = 0; Г* = 0, A.47)
2 6—1534 17
то вместо системы A.40) получаем следующее нелинейное
уравнение теплопроводности для определения нестационарного
обобщенного плоского температурного поля в анизотропной пластинке [29]:
LT - 2az (Т)(Т - tc) = - W. A.48)
В этом случае справедливы первые из краевых условий A.35)?
A.36).
Аналитическое решение нелинейного уравнения
теплопроводности A.48) сопряжено с известными трудностями. Если же
теплопроводность в направлениях срединной плоскости значительно
меньше теплопроводности в направлении оси з, а коэффициент
теплоотдачи изменяется в зависимости от температуры
скачкообразно, уравнение A.48) можно линеаризовать с помощью
соотношений
S+ (Т — Тп) = S+ (тп — т) (при охлаждении); A.49)
5+ (Т — Тп) = S+ (т — тп) (при нагревании), A.50)
где Тп — заданная температура. После подстановки
Т = 9 ехр
X
_-i-J «,(£)(*£
A.51)
о
получаем выражение для температуры в пластинке
X Х0 \
Т = -±-[ Baztc + W) ехр I -f- (' azd^ dx0 +
cv J ^ cv j J
+ Гсехр/--А-|аг^), A.52)
где т — время, по истечении которого пластинка охладилась или
нагрелась до Тп. Это время в каждой точке пластинки
определяется из соотношения A.52) при Т = Тп.
Найдем теперь уравнения теплопроводности анизотропных
пластинок, соответствующие квадратичному, кубичному и четвертой
степени законам распределения температуры по толщине
пластинки. Если источников тепла нет, системы A.33), A.45) принимают
соответственно вид
г U T* i
28&рТ - а+Р8 ctg рбГ £- «_£° „д Т* =
jfi
р8 ctg p8
= — (<М+ + «-*-): ' A.53)
= — 3 (a+tt + а_ф; '
18
A.54)
Я-ззр tg рб (t+ + Г) - |o+ (i+) (t+ - t+) +
+ аГ (П (f - £")l = У;
Ьзз/xstg рб (i+ - Г) + [at (t+) (t+ - tt) -
-<хГ<П(*~-*Л]=0,
i
а выражения для температуры A.32), A.46) —
1 p282
t = pb csc pS . cos pz • Г + _ sinp6lp6cQSp6 sin р.Г*; A.55)
t =
cos pz г+ + t'
cos p5
+
sin pz f^ — f
sinp5
A.56)
Разлагая операторы, входящие в систему A.53), в ряд по степеням
р8 и ограничиваясь членами не выше второй степени, вместо A.53)
получаем
26%ззР2Т - а+ (l - ^pj T - а_Г* = - (а+4 + а_*1);
28ХззР2Т* - 3 /-А- + а+) Г* - За_ (l - -S Г =
= — 3(оц-£_ + а_ф-
A.57)
J
Соответствующий этой системе закон изменения температуры по
толщине находим по соотношению A.55):
р2б2
A + "^)Г + —2 2
7Ъа.
A.58)
Удерживая в разложениях операторов в ряд по степеням рб,
входящих в систему A.53) и выражение A.55), слагаемые не выше
третьей и четвертой степеней относительно рб, получаем
следующие системы уравнений и соответствующие им законы изменения
температуры по толщине:
28^-а+A з Г -Г " 15
= - (а+4 + а_*1);
26^Р2Г* - 3 (± + а+) A - Sg) Г* - За_ (l - £*!) Т - } A'5в)
= — 3 («+£. + а_ф;
-('+JS=-)'+(n-^)-?—^'-■SF-td*»
2*
19
26XlsP2T-a+(l--^-
p464
525
+ a+
p464
— a_A —
p262
15
28%i3p2T* - 3
_ p464
15
T* = - (a+4 + a_£);
р2б2 p464
^ = A + 4^ +
- i +
P262
60
45
7p4S4
'360
p2T
_ _ T*
15 525 '
Г = -3(а+£с_ + а_ф;
} A.61)
T + (l +
66
p262
10
б
z* +
р4Г
24
A.62)
Запишем теперь системы уравнений, которым удовлетворяют
граничные значения температуры, а также уравнения для
определения интегральных характеристик температуры, выраженных
через граничные значения, при квадратичном, кубичном и
четвертой степени распределениях температуры по толщине пластинки.
Эти системы уравнений и соотношения можно получить либо так,
как были получены системы уравнений и выражения A.57) —
A.62), либо подстановкой найденных из соотношений A.58),
A.60), A.62) выражений интегральных характеристик температуры
в соответствующие системы уравнений A.57), A.59), A.61). При
квадратичном и кубичном законах распределения температуры по
толщине пластинки системы уравнений, которым удовлетворяют
граничные значения температуры, совпадают:
Х|зр26 (t+ - Г) - [а+ (t+) (t+ ~ t$) + а~ (О (Г - t~)\ = 0; )
4з (х
РЧ
4-+
Л /t+\ (t+
3 ,(Г-Г) + [а1"(И(*'1
*+•
Ч)-
■оГ(Г")(Г~-*с)] = 0.
A.63)
Однако интегральные характеристики, выраженные через
граничные значения температуры, отличаются. Так, при
квадратичном законе
Г = A
а при кубичном
р262
Т= 1 +
3
р2б2
t+ + r
t+ + t~
Т7* —
р- - г
1 +
р252
15
&-t~
A.64)
A.65)
Система уравнений и соотношения интегральных характеристик и
траничных значений температуры при четвертой степени распре-
20
деления температуры по толщине имеют вид
?4(р26 +
р4бз
(t+ + r)-{a+(t+)(t+-tt) +
+ оГ(П(*~"-£")] = 0;
^зз I
Р26
р46з
*( 8 3 45
-оГ(Г-) (*""-£")] = 0;
-к
(Г-П + [а"*"(П(*'
*+
*с+)~
A.66)
r = (i + ^!_+4r^W+ + -
J1*
1 +
3
Р2б2
15
+
120
р4§4
225
/+_/-
A.67)
В случае изотропных пластинок в уравнениях A.53), A.54), A.57),
A.59), A.61), A.63) и A.66) нужно положить >4; = Mv
Запишем уравнения, к которым сводятся системы A.57),
A.59) и A.61), соответствующие квадратичному, кубичному и
четвертой степени законам изменения температуры по толщине
симметрично охлаждаемой (нагреваемой) изотропной пластинки, при
постоянном коэффициенте теплоотдачи с ее боковых поверхностей:
Р2б2
p*6sr-Bi 1-
р2й2Г_В1 !__
р2б2
р4б4
15
= - Bi U\
Т = - Bi *c,
A.68)
A.69)
где Bi = azb/Xt. Системы A.57), A.59) сведены к уравнению A.68),.
A.61) — к уравнению A.69).
Уравнения теплопроводности
пластинок, оболочек и стержней
при нестационарном теплообмене
Если коэффициенты теплоотдачи с боковых поверхностей
пластинок зависят от времени, то температура t (x, у, 2, т) в
произвольной точке пластинки в момент времени т определяется из уравнения
теплопроводности
№ р«*=—£- A.70)
dz2
Aq
33
и краевых условий A.22)—A.24). При этом в граничном условии
A.22) необходимо положить a* (t) = af (т). Общее решение
уравнения A.70) имеет вид
* = С - Щ) |,=о ch p z + -L- (t - w0) |2=о ^ + w0, A.71),
21
где
wn
щг1т{0е~*~^;
n2
*" дх*
+ 2кп ■
дхду
I д22 я,/2
Щ
д
~дтГ
Интегрируя A.71) в соответствии с A.28), находим
Т =
Т7* =
где
sh рб
Рб
|2=0 ■
^0 |г=0] +
Ло
'33^
р2б
ch рб
sh рб
dz /z=0
dz Jz=0
+
4зР2
^ = Ж J(l-e-pechpS)«;<(adC =
-б
= ж(и/_ J *-р9сЬр&МСк);
^* = -Jr jk-e-p6shpC(e + y-)]
« I \ /J
и>*@# =
W*
-С
s 3
6 + -i-]shp£u;(S)d£
Из соотношений A.72) получаем
* 12=° = ■ sh рб
i? + w012=0;
р8б2
3 (рб ch рб — sh рб)
Д* +
5г
A.72)
A.73)
A.74)
=0 ° V^u ^" ^и — 0il ^и^ \ "* /г=0
Подставляя A.74) в A.71), выражаем температуру через ее
интегральные характеристики:
Р5 „и Л„ю . Р262
£ =
ch pzi? +
shpzR* + u>0.(lJ5)
sh рб ^ 3 (рб rh рб — sh рб)
Для определения интегральных характеристик температуры
Т и Т * подставляем A.75) в граничные условия A.22). Учитывая
соотношения A.73), после сложения и вычитания полученных
уравнений для определения Т и Т * находим следующую систему двух
дифференциальных уравнений бесконечно высокого порядка:
« п2Л2
26ХззР2Т + а+рб cth рб Я
-ь:
33
ди)п \ +
\ dz
dz
3 1 — рб cth рб
Я* = 2б(?
+ а2 (wq — tc )];
22
26?4p2r* + 3a_p6cthp6i?
+ a+
РЧ2
1 — рб cth рб
/?* = | A.76)
= 2б<?*-за
V33
II *
+
^0
<9z
-+/„,+
-f aj {wj — #") —
■+\
— az (wo — tc)
Условия теплообмена на цилиндрической поверхности S A.23) и
начальное условие A.24) после интегрирования по z в
соответствии с A.28) записываются в виде A.35) и A.36). Если на
цилиндрической поверхности S задается теплопоток qSi то условия A.35)
принимают вид [49]
LsT + Qs = 0; LsT* + Q; = 0. A.77)
Поступая аналогично тому, как это сделано в предыдущем
параграфе, из системы A.76) получаем приближенную систему A.40),
в которой вместо a* (t±) следует подставить а* (т). Если af (т) =
= о&Г (т) = olz (т), то вместо системы A.40) получаем
LT - 2az(x)(T ~ t%) = -W;
12
L71* - 6a, (т) (Г* - tL) - -^ Г* = - И^*.
A.78)
Если задача теплопроводности симметрична относительно
срединной плоскости z = 0 пластинки, т. е.
t+ - Г
v+<
tc; аТ (т) = аГ (т) - az (т); 1У* =0; Г* - 0, A.79)
из системы уравнений A.40) следует уравнение теплопроводности
для определения нестационарного обобщенного плоского
температурного поля в анизотропной пластинке:
LT - 2а2(т) (Т - tc) = - W. A.80)
Краевые условия в этом случае принимают вид
LJ — as(T — Tbc)=z0; Т = Т0 при т - 0.
Разлагая операторы, входящие в систему A.76), в ряд по степеням
рб и ограничиваясь членами не выше третьей степени, если нет
источников тепла, получаем
\33p*T + a+(l + -^
2б2
3
Л3зР2^ + 3(-^+а+)A +
рЧ'
p42
15
15
г* +
} A.81)
+ 3а_ 1 +
Т= -3(а+^1 + а_ф.
23
Соответствующий этой системе кубичный закон распределения
температуры по толщине находим из соотношения A.75) в виде
< = (i_J^r + (i ^
ю
j- Т* + -££- Т + -^-Т*, A.82)
где
1
рЦ2 \ t++t~
71* = ' 1
Раб2
15
t+-r
A.83)
При квадратичном законе распределения температуры по
толщине, если at (т) = а7 (т) = аг (т),
LT - 2а* (г) (Т - t\) = 0;
LT* - 6аг (т) (Т* - f_)
12
7** = о,
A.84)
где а * (т) = ЗА,з3аг(т)/(За,зз + баг (т)). Если <+ = <"= гс, Т* =
= 0, то вместо A.84) получаем
LT - 2аг' (т) (Т - tc) = 0. A.85)
После подстановки [49]
Г = 9/(т); Г = е/!К(т); Г* = 9*/*(т) A.86)
краевые задачи теплопроводности A.78), A.84), A.35), A.36)
принимают соответственно вид
LQ=-Qca; L9*=-ec*№; A.87)
L9 = -ec; LB* -9S; A.88)
L,e + a,(9 + eS = 0; Ls + as(9* - 9?) = 0; A.89)
9 = r0; 0*= при т = 0, A.90)
где
/(т) = ехр
/* (т) = exp
c о
f 6
= exn /
/* (x) = exp
■j-r+ fa,(»#
9^/ (т) = 2az (t) t% + JP; 9c/* (x) = 2a* (т) 4;
ecV* (t) = 6a2 (т) fL + W*; 6C/* (т) = 6аг (т) f 1;
A.91)
PS/(T) = fc
OS/* (г)
6cV* (T) = П
24
Если коэффициенты теплоотдачи с боковых поверхностей
пластинок постоянные, в уравнениях A.40), A.76), A.78), A.80), A.81),
A.84), A.85) следует положить
а?(т) = ос*; а2(т)
а*. A.92)
Если материал пластинок ортотропен, в уравнениях A.40),
A.76), A.78), A.80), A.81), A.84), A.85) следует положить
Х12 = Х21 = 0; Хп = Хх; Я22 = ку. A.93)
При изотропном материале пластинок в этих уравнениях
необходимо принять
^12 = ^21 = 0; Xn = X22 = h. A.94)
В частности, уравнение теплопроводности для определения
нестационарного обобщенного плоского температурного поля в
изотропных пластинках с постоянными коэффициентами
теплоотдачи имеет вид
2az(T-tc)=cv-^--W. A.95)
ЛД71
Рассмотрим теперь однородную изотропную оболочку толщины
26, нагреваемую произвольно распределенными по ее объему
источниками тепла плотности wt (а, р, у, т) и внешней средой,
теплообмен с которой через поверхности оболочки происходит по
закону Ньютона. Пусть коэффициенты теплоотдачи на поверхностях
оболочки у = ± б являются функциями температуры
соответствующих поверхностей, остальные теплофизические
характеристики от температуры не зависят. В этом случае температура t (a, C,
Y, т) в произвольной точке оболочки в момент времени т
определяется из уравнения теплопроводности [49]
м +
дЧ
Iff
1 ду
dt
д%
при граничных условиях на ее поверхностях
и
dt
± а* (£*)(** - *±) = 0
и начальном условии
*(а, р, у, т) = *0(а, Р, у) при т = 0,
A.96)
A.97)
A.98)
где А =
АВ
д
да
А да
^ д$ [ В
А, В — коэффи-
кх + к2
циенты первой квадратичной формы; к = ' ""* средняя
кривизна срединной поверхности оболочки; а* (£*) —
коэффициенты теплоотдачи с поверхностей у = ± б; £*, **
—-температуры соответственно сред, омывающих эти поверхности, и боковых
поверхностей. Если оболочка незамкнутая, то могут быть
записаны краевые условия, аналогичные условиям A.97).
25
Введем замену
t = Be-***.
Тогда уравнение A.96) преобразуется к виду
ду'
X,
A.99)
A.100)
1 д
Здесь п* = п2 — к2: р2 = Д —; а = wtekv. Учитывая замену
A.99), с помощью операторного метода из уравнения A.100)
находим
t = e~hv
sin pjY
Pi
sin pxy I dt
COSPlY + к -^L- ) ty=0 + ~^- (-£-) +
Qo
A.101)
Где g0 = px I sin px (£ — -y) qdt,. Вводя интегральные характеристики
температуры
и учитывая соотношение
-6
д2Яо __
Г ytdy
A.102)
ду2
— р] (?о + ?)> интегрируем
A.101) в соответствии с A.102):
Г = М^=0 + ЛЧ^-
0*
^ /т=о ^ '
Г* = МП^0+#*НН n +
<9£
<?Y /v=o ^
A.103)
Здесь
А:2
М - -4g- Bй sh /гб cos Pl6 + — ch *8 sin PiS
/V = 2x~ (~~ & cn ^ sin Pi$ + P sn ^6 cos p26);
M* = ( ~ 2 — 2/c5 ch /сб cos px6 H —^ sh /c8 cos pxS +
A:2 — p? 3pl—k2 \
_| _ g sn £g sjn pt§ _| _— k ch /со sin pjO I;
Pi
PiP*
q / p? — к2
/V* = —ttvt ^6 sh /c8 sin Pl8 + —Ц ch кб sin px5
Pi (рбJ \ ri p2
— px6 ch /1:6 cos px6 -] p~ sn ^ cos Pi$J»
}A.104)
26
o-M+nv+i
-fed
dQo
ду
-г-
{A — Щ e~ktq+ — A+Щ e^q-
2 (рбJ
_6|е-ы/_«9Ь_У-
*-)++-(-*-)-]--i-fr)"
И"
TF
= f wtdy; W* = -г- f ywidy — сооть етственно отнесенная к еди-
-б ~б
нице площади срединной поверхности оболочка плотность
источников тепла и плотность «моментов» источников тепла,
характеризующая неравномерность распределения источников по
толщине; д*,
— значения функции д0 и ее производной по
7 при у = +б. Из соотношения A.103) следует
tv=a = -£- (RN* - tf*W); (|L) =Q = -I- (MR* - M*R), A.105)
где
А, = MN* - M*N =
3
PiP463
-^— sin 2рхб -f
+ 2k2b ch2/c6 sin 2ргб + -Ц- (ch 2&6 - cos 2p,6)
Я = Г
V?
д* ___ у7*
<2*
Vi
Подставляя A.105) в A.101), выражаем температуру через ее
интегральные характеристики:
t = -i- е-*У | (cos plT + к sinpPiy \ (RN* - R*N) +
+
sinpjY
Pi
(МЯ* — M*R) +
9o
hP]
A.106)
Для определения Г и Г* используем условия на поверхностях
У = ±8. Подставляя A.106) в A.97), после несложных
преобразований получаем следующую систему дифференциальных
уравнений бесконечно высокого порядка:
J4_ |2 ( hM*-p*N* ch кЬ gin ftfi + ж* sh kf> cQs pigJ д +
+ 2 / p2iV ~ kM ch Л6 sin Лв - M sh A6 cos Л6j Л* +
27
dq0 \+
pfe6
5Y / \ dy
N*k — M*
■fc(#-?5->l} +
+ -д^-11 «1 sin pj6 + A7*a^_ cos PxSj i? +
M—/ciV
+
+ ■
Pi
a*_ sin Pl8 — iVa* cos Pl6) Л* +
+
a+ (*+) g~fe V + аГ (Г") е*У
| — (a+*+ + a_*L) = 0;
_^_ j _ 2 / kM*-p*N* gh feg gin ^fi + M# ch ftg cog pigj д
2 ( p2N ~ Ш sh A;6 sin Pl6 - M ch k& cos Р1б) Д* +
A.107)
Pi
1
"a7
dy
+
-*6|-^о_Г + ^б[ U4«
d%
dy
— k{q+ + q~
+
N*k — M*
Pi
- a* sin Pl6 + N*a*_ cos Pl6 i R +
_|_ j 1 a* sjn p^ _ TVoc^ COS /7XS ] /?* +
+ -V (a+ (i+) e-k6qt - оГ (П екЩ -
Afp1 J
- (a+£. + a_4) = 0-
Здесь a± = e~fe6a+ (t+) ± Л~~ (Г~); ^ = (t£ ± £Г)/2; при 7 =
= ± б, как следует из формулы A.106),
' 'cos Pl6 ± к sin Pl6 ) (ЯЛГ* - i?*iV)
Ai
Pi
±-
sinPl6 (МД* - M*/?) +
ад-
Pi
Vi
A.108)
Система уравнений A.107) вместе с выражением A.106) вполне
жвивалентна уравнению A.96) и граничным условиям A.97).
Поступая так же, как при выводе системы уравнений A.40),
приближенную систему уравнений для тонких изотропных оболочек
записываем в виде
Ар2Т - а+ (Т - ф - а_ (Г* - tt) + 4/сХ/Г* = — W; }
1? A.Ю9)
Лр*Г* — Зоц. (Г* - ф - 3a_ (T - ф ~ — ^* = - ^*5
где rY = 26/?w
28
Рассмотрим сплошной изотропный цилиндр, через поверхности
г = Л, z = =Ь б которого происходит теплообмен с внешней средой
температуры tc, t? соответственно.
Уравнение теплопроводности для определения температурного
поля цилиндра имеет вид
ч.
граничные условия
^^+ад(т)(*-*с) = 0 при r^R- A.111)
h^-± а± (* — *с) = 0 при z = ± б, A.112)
начальное условие —
*|т=0 = *о- (L113)
Здесь р2 = —у^ ^—— ; aR (т), ех± — коэффициенты
теплоотдачи с поверхностей соответственно г = R, z = ±6. Решение
уравнения A.110) имеет вид
* = 4/0 (рг) + BY0 (pr) + -£- [ [J0 (pr) Y0 (p® -
' о
~ /о (р£) П (И1 £">* (Б, *. х) d£ A.114)
Учитывая условие симметрии — = 0, получаем
г
t = /0 (pr) f |г=0 + -^- j [/0 (pr) Y0 (pQ -
О
-Y0{pr)JM] t,wt(l z, T)d£. A.115)
Введем в рассмотрение интегральную характеристику
температуры
r = -|rj№*,T)dC. A-116)
о
Решение A.115) теперь нетрудно записать в виде
1="§Й§- (' - tS-)+-к- j ^ « г. <* -
-Y0(pr)J0(pt)]twtfc,z,i)dZ,-
R ' Y, (PR)
■ir-roU>r)^\JM-j^—Yo{PQ
о L
29
&*,(£, 2,т)С A.117)
2 г * ,„ х 7. W
где W* = -^- J £и;*(£, 2, r)d£ = -^ . Подставляя A.117) в A.111),
о
получаем уравнение
ан(т)
^-^{^Tr^+vJ^h^-
ло>в-=г
">/ (£. г> т) 1 ,«. „, 1 I47*
рД/i (рД)
4-2^0 =-^-. A.118)
Интегрируя граничные условия A.112) и начальное условие A.113)
в соответствии с A.116), находим
А*-|£- ± ос,* (Г - Ге*) = 0, при z = ± б; A.119)
24x^0 = ^о, A.120)
где Гс* = -|r J fctfdfc П = -|г { УД-
2 ?.^„ т 2 н
Введем в рассмотрение приведенную теплопроводность Л =
= XfF, теплоемкость С = cvF, сопротивление теплообмену на
поверхности г = R AR(%) = Bяан(т)/?)-~\ где ,Р = nR2 —
площадь поперечного сечения цилиндра. Разлагая в A.118) операторы
в ряды, переходим к пределу при R -> 0, сохраняя при этом
постоянными Л, С, AR, W. В результате получаем уравнение
теплопроводности для стержней при нестационарном теплообмене
После подстановки [22]
Г = 6/(т), A.122)
, краевая задача теплопроводности
где/(т) = ехр[--И~^
о
A.121), A.119), A.120) преобразуется к виду
Х,-?-±а±(8-в±) = 0 при z = ±& A.124)
в|т=о = Г0, A.125)
где 9CW = I An1 (t) *t + W] Г1 Wi 6? = ^Г1 (t).
30
Уравнения теплопроводности
тонкостенных элементов конструкций
при зависящих от координаты
коэффициентах теплоотдачи
Рассмотрим оболочку, отнесенную к триортогональной
системе координатных линий (а, р, у), являющихся соответственно
линиями главных кривизн срединной поверхности и внешней
нормали к ней. Уравнение теплопроводности для определения
нестационарного температурного поля t в оболочке толщины 26
имеет вид
где 2k = кх + /с2; кг, к2 — кривизны координатных линий;
р2 _ Д _ J_
1 д А 1
д% ' ЛЯ
da ^ Л doc j + ap \ В д$
А, В — коэффициенты Ламе срединной поверхности оболочки.
Пусть через поверхности у = ± б оболочки теплообмен с
внешней средой происходит в соответствии с законом Ньютона, т. е.
h -^ ± а* (а, Р) (t - *±) = 0 при у = ± б, A.127)
где а^ (а, р) — коэффициенты теплоотдачи с поверхностей у -
= ±б; tc (а, р, т) — температуры сред, омывающих эти
поверхности. На торцевой поверхности S оболочки заданы условия
теплообмена первого — третьего рода, начальное условие принимаем
в виде
*|t=o = *0- A-128)
Если температура по толщине оболочки изменяется по линейному
закону
t = T + yT*,6, A.129)
то, интегрируя уравнение A.126) в соответствии с интегральными
характеристиками температуры
Т = -1- J tdy; T* = JL. j ytdy, A.130)
—6 -Ь
приходим к следующей системе уравнений теплопроводности
тонких оболочек:
дг - п\{т ~ ф - х!(Г* - £.) + -f- т* = 4- —5г;
ДГ* - 3 [kz+(T* - *L) + х!(Г - ф + бП = -^- -^ ,
A.131:
31
где
+ 2Kf6 ' * 2
w*= ~i~ f w*v.
26;
-б
Интегрируя A.128) в соответствии с A.130), получаем
Т = Т0; Г* = Го при т = 0. A.132)
Аналогично следует проинтегрировать заданное на торцевой
поверхности S оболочки условие теплообмена.
Для тонких пластинок в уравнениях A.131) полагаем
д2 д2
к = 0; у = z; А = -^- + -р- , а± (ж, г/),
ИЛИ 1 в / 0 \ 1 0*
А = -— (г^т) + — -v". а» ('"' <р>-
В симметричной относительно срединной поверхности
оболочки (пластинки) задаче теплопроводности система уравнений A.131)
сводится к уравнению вида
&T-x*(T-t0) = -£---%-, A.133)
где х2 = an/Xt&; an — переменный коэффициент теплоотдачи с
боковых поверхностей оболочки (пластинки); tc — температура
среды, омывающей эти поверхности.
Для вывода уравнения теплопроводности стержней кругового
поперечного сечения рассмотрим цилиндр радиуса R, через
поверхность г = R которого происходит теплообмен с внешней
средой температуры tc по закону Ньютона, т. е.
h-^r+an(z)(t--tc)==0 при r = R. A.134)
На торцевой поверхности z = ± / цилиндра заданы условия
теплообмена первого —- третьего рода. Начальное условие имеет
вид A.128). Вводя в рассмотрение интегральную характеристику
температуры
T = ^L\rtdr A.135)
О
и интегрируя аналогично предыдущему уравнение
теплопроводности цилиндра
f-!-('-£-)+-£-4---5- <1ЛЗв)
32
в соответствии с A.135), приходим к уравнению теплопроводности
стержней кругового поперечного сечения
dz2
2ап (г)
■>i*{z){T-tc) =
W
A.137)
где к2(z) = ^R— ; ап(г) — коэффициент теплоотдачи с поверх-
2 R
ности г = R; W = -™- 1 rwtdr. Аналогично следует проинтегриро-
6
вать заданное на торцевых поверхностях z = ± / цилиндра
условие теплообмена и начальное условие.
Температурные поля
при узкозональном нагреве тел
Пусть твердое тело в виде изотропного параллелепипеда | х | <
< а, \у\ < Ь, | z\ < б подвергается нагреву внешней средой
температуры 80 по области | х | < h, \ у | < dy причем h и d очень малы
по сравнению с размерами а, 6, б. Остальные поверхности
параллелепипеда нагреваются внешней средой температуры 9С < 80.
Через поверхности рассматриваемого твердого тела происходит
теплообмен с внешней средой в соответствии с законом Ньютона,
т. е.
^ Dг Г + а^ + IK - «с)t+ - «оУ N = 0, |
dz
h
dt
dz
dt
dz
= —- a~t
__ dt
~ dz
z=-6'
++
z=-f6
dt
r^fl^+e;
■w
&c
1 V I V=
|x==±a
x=±a'
л 5i
dy
\y=±b
= +*P\y~±V
A.138)
A.139)
где t = 9 — 9C; J0 = 90 — 8C; 9 — температура тела; a0, ac —
коэффициенты теплоотдачи соответственно с области | х | <; /г,
|г/|< <i и остальной части поверхности z = + б; а7, а*, а^ —
коэффициенты теплоотдачи с поверхностей z = — б, ж = ± а,
0=± Ь; ^(*> у) = [S-(x + h)-S„(x~h)} [S„(y + d)-S^(y - d)].
Решение краевой задачи теплопроводности A.19), A.138),
A.139), A.24) рассматриваемого твердого тела из-за разрывного
коэффициента в граничном условии A.138) сопряжено с
известными математическими трудностями. Поскольку h и d очень малы
по сравнению с а, 6, б, температурное поле t+ (х, у) = t (x, у} б)
в области \х\ <; /г, \у\ ^ d можно заменить его интегральной
3 6—1534
33
характеристикой
h d
0= JL. j* Г *+<fcwfy. A.140)
—Л — d
При нагреве конечного цилиндра г < р, | z| <с б по области г <
<С R, z = -f- б малого радиуса Л внешней средой температуры В0 и
остальных его поверхностей средой температуры 9С в условии
A.138) N (г) = S+ (R — г), г+ (г) заменяется интегральной
характеристикой
«= -gr С Лг, A.141)
о
а условия A.139) — условием Xt -у- + <М= 0 при г = /?, где
аг — коэффициент теплоотдачи с поверхности г = р; г —
полярный радиус.
Таким образом, в обоих случаях краевая задача
теплопроводности становится линейной. Дальнейшее упрощение ее решения
возможно в случаях, когда толщина 26 параллелепипеда или
цилиндра мала по сравнению с их другими размерами. Предполагая,
что температура по толщине рассматриваемой пластинки
изменяется по линейному закону A.42) и внутренних источников гепла
нет, для определения интегральных характеристик Г и Г*
температурного поля получаем следующую систему уравнений
теплопроводности:
ДГ _ у*т - х2Г* = -QN; \
A.142)
ДГ* - Щт - Зк2,Т* = - 3QN, \
д2 д2
где Д = -д~г + ~JT > N = N (ж> У) ~~ Для прямоугольной пластинки
d2 1 d
Д = -—- -| — , N — N (г) — для круглой пластинки; к2 =
= д ; х^ = с л г ; к^ = ^ + б-2; Л = 2Ь,6; <? =
^с — ^о сСп
= ф _j—_2_ ^. $ дЛЯ прямоугольной пластинки имеет
вид A.140), для круглой — A.141). Граничные условия на торцевых
поверхностях пластинок следует усреднить в соответствии сГи Г*.
Система уравнений A.142) сводится к разрешающим уравнениям
Дфг ~ Р!фг = ~ QiN, A.143)
где ф| = Т + щГ»; р? = х2 + Зи,х2; & = A + Зщ) <?;
ц1|2 = * t2*2 + Зб ± 1Bх2 + Зб~2J + 12уЦ]1'»}; i = 1; 2.
6хл
34
Уравнения и соотношения термоупругости пластинок
с прямолинейной и цилиндрической
анизотропией
Температурные напряжения, обусловленные Г и Г*, если
справедлива гипотеза о неизменяемости нормального элемента и
Ozz = 0» определяются по формулам [51]
&хх = &11е11 i £>12^22 "Г" Н 16^12 — г 11^ »
(Jyy = П12еи + £>22^22 "Г ^26^12 Р22^ »
#ху = ^16^11 "Г" ^26^22 Т" ^66^12 — Pl2* ' '
а;х = 2Euxu + В12х22 + 2/?ихи - риГ*/б);
Kv = Z (S12X11 + #22*22 + 2S26*12 ~ ft^*/6);
A.144)
axy = 2 Ewxn + #26*22 + 2Be6x12 — р12Г*/б),
A.145)
где ^ii = -^-i Чч
d2W _
^2~ » X12 — ~
~%" ' 6l2 = "fly" +
&c' *" -
5%
Xo
dy2
d2w
дхду
дх2 ' 2 ~~
деформации срединной плоскости и
—l/
изменения кривизны; #^ = с\-} — йз^з^зз (i> / = 1; 2; 6); Cij —
постоянные, выражающиеся через упругие постоянные а^ [51, 66];
Рп = aii5ii + a^ia + «'А»'
|322 = а^512 + <42#22 + а\2В^ I A.146)
Pl2 — ац^16 4" а22 26 ~Г °Ч2 66*
Компоненты перемещений точек срединной плоскости пластинки
а, у, w удовлетворяют уравнениям
В
о2и „ а2 а „
д2у
11 ^,2
+ (*i, + ^ье)
ду2
д2и
16 й*2
+ А
26'
ду2
25
16
д2ц
дхду
+
_в .«L-b — -о-
Я
а2и
16 дх>
+ (Ви + Вм)
B<>R -7ГИ Ь Ве
26 ду2
д2и
дх
d2v
дх2
д2и d2v
+ В22 -д-а" + 2526 +
%2
дхду
дхду
дТ
дх
Pi2 -тгг — Р22 -£- = °;
д" -&- + «>.. w +2 V» + ^ w +
^ ^26 я,,я,,з + /*
+ Й
22-
дхду*
д2Т*
~ду2~~"==
22
^ I ft* i!Zl__i_ft*
13" + Р« "ЙГ" + Р12
дядг/
+
о,
A.147)
3*
35
где fij = 2б2ръ/3 (t, / = 1; 2); D{j = 2б35ъ/3 (i, / - 1; 2; 6) -
жесткости анизотропной пластинки Фи, #22» ^66* ^ie> ^26 — жесткости
соответственно изгиба вокруг осей г/, х, кручения и побочные).
При заданных граничных условиях для напряжений
температурные напряжения A.144) можно выразить через функцию
напряжений F:
d*F d2F d2F .. ,/0ч
где функция F удовлетворяет уравнению
d*F 9 d*F /9 d*F 9 d*F
а™ 1х^~ ~ М** дхЧу + (^12 + а™> дхЧу* ~" Zttl6 дхду* +
+ a"-J^- = - aii -S3T + а12 -щг -**-*зг* I1-149)
В случае изотропных пластинок вместо A.149) используем
уравнение
AAF = -atEAT, A.150)
где F = U — 2G¥, С/ — бигармоническая функция, т. е.
ДД£/ = 0, A.151)
а 4х — частное решение уравнения
AT = cxt(l +v)T. A.152)
Если коэффициент теплоотдачи с боковых поверхностей пластинки
зависит от времени, то перемещения и, vy напряжения вхх, оуу,
оху, функцию напряжений F, а также U и W при обобщенном
плоском термонапряженном состоянии можно представить в виде
A.153)
<*а = o$V (т); и = и0/ М; *> = *V М;
F = F0f(T); U=U0f(T); W = ¥0/(т),
а прогиб м? и напряжения изгиба а^- — в виде
и> = "V* (т); 0$*/* (т) - <4 i, 1 = х, у. A.154)
Здесь / (т) и /* (т) имеют вид A.91). Учитывая представление
интегральных характеристик температуры A.86), после подстановки
соотношений A.153), A.154), A.86) в формулы A.148), A.149),
A.145) и в последнее из уравнений A.147) соответственно получаем
@)„_^о_. a@)_J!^L_. a<0)e_J!£o_. A155)
_ d*Fn 0_ <э^0 , о /. , «ее \ w0
^о о. ^0 , о //, 4- fl6e
22 ^ ^6 ^3<fy "Г " ^12 Т 2 J дх*ду*
9 _^о , J!Zo __ t дЩ ,
~" ^16 &t%* "Г аП ~д^ ~ ai1 ЦуГ "Г
36
, t дЩ
дхду
•a;
22 дх2
oS* = z (дцх8> + 2?Mxgf + 2Вих® - P„
<C* = г (£12xff + ЯИХ$ + 2Bux№ - 622
JO)*
JO)
@)
z BukW + Вы-*№ + 2Вихй' - B:
,@)
e*
A.156)
A.1 7)
^^-+^^ + 2(^ + 2^)^ + 4-^ +
711 ~~Ш~
+ #22 -^r- + Pit ~^2- + P12 -^^7 + P22 '
0y*
дхду
ду*
О, A.158/
где %f> = Xi,-/*_1 (x), i, / = 1; 2.
В случае ортотропных пластинок функция ^0 удовлетворяет
уравнению
d*Fn
Еу а*
+ft
d4F0 1 d*F0
Exj дхЧу* "*" ^ ду*
• ат
— aw
t дЩ
х ду2 у дх* '
а формулы A.157) и A.158) принимают вид
A.159)
A.160)
С = 2&$*;
Ог
d*wn
дх*
где Вп =
+ 2Д3^ + ^ = -б^-р^, A.161)
3 дх2ду2
Е
\ — v v
Х V0C V7/
ду* Vi дх2 г* ду2
*. 5i2 = 51Л = #22^; Pi = #ц (a£ + ayvy); 522 =
263
= d^vvv ; p2 = S22D + ^); Д = 5г^- (* = 1; 2); £>3 -
263
262
= ^ivy + A<; DB = G -Sj- ; ft* - ft-|- (* = 1; 2); JDlf ZJ, A,-
жесткости изгиба и кручения для главных направлений, или
главные жесткости.
Если пластинка изотропна, функция FQ удовлетворяет
уравнению
ДД^0= — а,ЯД6, A.162)
где F0 = UQ — 2G¥0, причем U0 — бигармоническая функция, т. е.
ДД[/0 = 0, A.163)
37
я ¥0 -- частное решение уравнения
Д¥0 = а'A +v)9.
Выражения A.160), A.161) имеют вид
2Gz
иосх
т<°)* —
1
2Gz
Jyy
[xf?
,((>)
■vx$
@)
«/(l+v)*];
= T^V lVK« + *22 -«*(! + v) j-];
X0)* = 2M?;
ах4
+
а4ш„
A.164)
A.165)
дх2ду2
= — a/
1 + v
( &r2
<92e*
%2
A.166)
Уравнения равновесия в перемещениях A.147) в случае
обобщенного плоского напряженного состояния ортотропных
пластинок принимают вид
~2и , г <92y 0 (9Г
GA«+(*u-G)-^+VS'-Pu-sr;
бгДу + (Я
22 '
■G)-S- + V
<fy2
дхду
д2и
дхду
= Р2
дГ
fy ;
A.167)
где b0 = J512 + G; ри = £u (a* + a^vy); |322 = 522 (а{, + a*vx),
соотношения обобщенного закона Гука —
ди
dv
ax* = Вп — + £12 — риГ;
<9w
dy
jyy — х^12 -^- + В22 -щ- — р^Г; }
дх
ди
^ дх J
A.168)
Общее решение взаимосвязанных уравнений A.167) можно
записать в виде
, д2Ч
А
г д2Ф R д2Ф
i> = В,
дх2
д2Х¥
ду2
+ G
-ь0
дхду '
#2ф
A.169)
11 дх2 ' " ду2 ^ дхду '
где функции Ф и W удовлетворяют соответственно уравнениям
L =
+ 2р
а4
&г4
Х~; ^
+ д
<?4
; 2р = еу\-тг —-тг-
ду* ' ^ ~" *"у \ G
-Q- (a* + ayVy); со2 = -^- (ау + axvx)
38
A.170)
Подставляя A.169) в соотношения A.168), получаем формулы для
определения температурных напряжений:
cv = G lBn
дхъ
%3
>УУ
G (Bt9 -^г- + В22 -^ж- ) + 50
'12
G
Д
&с3
и дхз
+ В*
ду3
Вл
дхду2
дхъду
d3W
дхду2
д3Ф
■РиГ;
~ B**G ~bxW ~~ р22Г; I
^ дх2ду)у
A.171)
где #0 — ВиВ22 — #1260. Так как через поверхности z = + б
пластинки происходит нестационарный теплообмен с внешней
средой, то, используя представления типа A.153) и A.86), т. е.
oy = ai?/(Fo); 0 = 00/(Fo). «F = ¥0/(Fo);
7, = 9/(Fo); a = u0/(Fo); у = i;0/(Fo),
A.172)
где
/ (Fo) = exp
Fo
Bi (o di
ar @ &
выражения для определения uQl vQl Ф0, *F0 и aff записываем
соответственно в форме
дх2
»o = G°$-+Bu
22 ^у2
W0
дх2
дхдц
ь д2ф°
0 дхду
A.173)
A.174)
дх3
■ДпС-^-Рпв;
а?у3
дхду2
дх2ду
<№=GIB.
12 9гЗ
i~ D22 ду3 I "I" О0 -&25(/
1A.175)
-bvg4£?-№;
°ху — G
я,
а«т0 <?3Ф0
дхду*
дх2дц
По соотношениям A.173) —A.175) можно определять
температурные напряжения при нестационарном теплообмене в случае
закрепленных пластинок [19].
39
Рассмотрим пластинку, отнесенную к цилиндрической системе
координат г, ф, z. В каждой точке пластинки, как и в пластинке с
прямолинейной анизотропией, есть плоскость тепловой и упругой
симметрии; ось z совмещается с осью анизотропии. Поперечные
сечения пластинки после деформации не искривляются и остаются
нормальными к срединной плоскости, azz = 0 по всей толщине
пластинки. Температурные напряжения, обусловленные Г и Г*
определяются по формулам
+
<Vp = 512-f +B22-L(u + -JL) +526[-i-(~-^) +
!A.176)
дг
+
ГФ — 6 дг
ди
+ ^26 —
(«+■£■) +
■вй1
ди
дер
-v) +
дг
d2w
В
11
дг2
+вп[
дю
~dF
1 d2w
X
~7~ "^Г + Ри
■^фф ■
— 2
<9
^12 ^2 + #22 ~аГ + — -^F
<9г^
+ 2В1в^~Х
+
+ P8e-V-
'Гф
5
д2ш
+в2
и б
dw
A.177)
16 5г2 Гв( 0Г
1 Й0 >
+
1 Л
дф2
Н-+
+^4-D-£' + с
т*
12 —
где коэффициенты Z?^ и Si; выражаются соответственно через aik
и а^- [51], а перемещения точек срединной плоскости а, у, ы;
определяются из уравнений
Я_1а ^ , „ / д2и 2_ &их В^_ ,j_ дЪ_ \
ВпДи + -
дгдер
+ в,
16^ 5г2
1 <52^
дер2 ~~*~
г дгдф j
д2и 1
дф2
дг;
di;
дгдер г с
дт , Bi* ar . ри-
, 7Л _ А ^ , Pi. ^ ,
Т;
40
В12
+ -
+
+
г дгдц! гг \ йф2 6'ф
■Мир-+т--£)+ ',A'178>
326
а2у 4- — -^- 4- — 4- —
Л. R /JL_^_ 4.
1 д2ц
г дгдф
^ о» дТ
+ <9г2 + г дг г2 ) ~~ Р12 ( <9г + г Т) +
дф '
В11 ~jjpr + 2 (В12 + 256б) ТЗ"
з4и>
+-М.
+
Всъ,
+ 2566 + 522)
1 d2u;
11 5г3 I г2
1 д2ш
■(?
Зг2дф2
1 d*w d2w
dzw
Зф4
дг2
дгдцр
+
Д,
+
+
дф2
1 ^
dw . 4 R / д4ш
' ~дГ + Т~ 16 (~^30ф +
дгдф
+ 4"*:
.3 ^26
дф3$Г
1 d3w
дгдц ~ г дц ) ~ 6 11 u
^22 д2Г* | 2Р12
г2 дф2 "•" г2
дГ*
6>ф
0Г2
2'ц
,, дТ*
дг
A.179)
При решении осесимметричной задачи формулы A.176), A.177)
записываются в виде
A.180)
Qrr ' Zi-jj.
С^ФФ == ^й
grr = — z/?^
^фф = — Z&*
Е
г
УГф УфГ
\( д
(± +
(^4~
^HL.\u—atT
*
-+-£-) u-ajw]
% \ dw , * Т*
*
'
. кЛ dw . t А2Г*1
; at = а,. + vr<1
t .
р^-ф?
a
* ]
5 __
Is
A.181)
где Е*
Перемещения точек срединной плоскости определяются из
уравнений
Дц — к2 -
дг*
2 д3ш
+ г 5гз
* дГ . о Т
а yat —
дг ■ г
/с \2 / d2w
I к \2 / а2ш 1 ^ш \
* о
а, а; яг*
1_ д т1* L
6 б 5г
A.182)
A.183)
41
где at = at — /na¥; Д = —^ + — -^-. В случае изотропной
пластинки Er = /?ф = /?; ar = аф == af; v<pr = vr(p = v и, следовательно,
соотношения A.180) — A.183) принимают вид
OVnfD
2G
1 —v
261
Orr = ~
J<p<p ■ I ^
2S
1- v
0фф " T^=T
^r + 4)M_ai(l + v)r
v4-+-r)M-a^1 + v)JT
а . v \ dw , /A , ч T*
а . l
V1F + —
3u?
+ a*
(l+v)V]i
Ли-—= a,(l +V)^T;
d*w 2
dr4 + г
дъш
HP~~
1
" —
/ d2w
~d?
1
r
dw
~дГ
/4.x11 д / дТ* \
A.184)
A.185)
A.186)
A.187)
Если коэффициент теплоотдачи с боковых поверхностей пластинки
зависит от времени а2 (т), то, используя представления
напряжений и перемещений A.153), прогиба w и напряжений изгиба A.154),
а также интегральных характеристик температуры Т и Г* A.86),
приходим к следующим выражениям:
^ = Вп-^+В12±(и0 + Щ+В1в{±(^-,0)+^
+
dva
дг
— Ргг^;
^-Влл-^-+В, — '•< J--^
'26
г \Ы'+ 8»
-$-)+ч-м-
0Цр
ч> +
+ _*Sl
dr
<т<Г = - ж
A.188)
5
11 5г2
+ »-TD-5-) + fc.-f.
42
<->фф — 6
в,.2ь-+вп№ + ±-А)± +
12 дг2
д / 1 dw.
22 I дг
е*
, ОД ^ / 1 ^0 \ , О в«
"Г ^^26 -^г ^— ^ф j "г Р22 -g-
Ощ z\ #16 —^г- + #26 Г
, о» д / 1 dw0
^2 4- — ^о \ 1 I
дг ~^ г дф2 I г '
1 ^0 \ I D 6*
~Г Pl2~F~
A.189)
причем компоненты перемещений точек срединной плоскости
удовлетворяют уравнениям вида A.178), A.179), в которых и, и, w, T
и Т* записываются соответственно и0, v0, w0, 0 и 6*.
Соотношения A.177) — A.179) имеют вид
- ^* j \-^г + -у~) Щ — а* 8
,(»)*
т@)*
— £^2
^г+чч-^+а;
ar
+ ■
дг
/С2 \ 010,
е*
Т
t е*
о е
дг*
А 7 9 ^П * СО . 0 О
Л "о — к2 -^- = а t -^ + а, —;
^ г ) у дг2 г дг J
о_ I JL ^Х / к \2 ( д*Щ * ^о
ar3
= - -/■ де*
о
Щ дд*
6 ~~дГ" *
A.190)
A.191)
A.192)
A.193)
Обобщенное плоское термонапряженное состояние анизотропной
пластинки определяется по системе A.190) и уравнению A.192).
В случае изотропной пластинки соотношения A.190) — A.193)
имеют вид
(Т@)-
Urr —
ст@) -
1 — V
2G
+ -fK-a,(l+v)9
ст@)* = _
a@)* —
w= i_v |(v"^ + ~)"o — «t(l +vN
(-J" + т) ■*- + ««(*+^7°*.
1 — V
2G
1 — v
A.194)
A.195)
43
+
Ди0 —
2 d3w(
1°_ =
r2
o«(l+v)
dr?
-(
d8
i
dr2
1
— oc*(l +v)-^-A6*.
_dw±
dr
A.196)
A.197)
Уравнения и соотношения термоупругости
изотропных пластинок и оболочек
Температурные напряжения и t перемещения в изотропных
пластинках в случае обобщенного плоского термонапряженного
состояния определяются по формулам [45]
&хх —
2G д
1 —v ду
2G д
д2
ду2
дх2
U — 2G
d2W
ду2
ЛУУ '
Jxy
1 — V ду
2G д
д2
ду2
+ B + v).
дх2
дщ
u-2G-d-'< \ (Lis)
dW_
дх
1 — v дх \ дх2
1 + у d2U
1 — v дхду
V =
U + 2G
2
+
<92¥
дхду
d2U
1
дх2
+
д2и
ду2
A.199)
где U — бигармоническая функция, удовлетворяющая уравнению
A.151); W — термоупругий потенциал перемещений, являющийся
частным решением уравнения A.152). Учитывая A.86) и используя
подстановки A.153), соотношения A.198) и A.199) преобразуем
к виду
а@)
2G
1 — v ду
@) _ 2G д
д2
ду2
д2
иху — |
2G
д_
v дх
ду2
д2
дх2
дх2
+ B + V)
д2
и0-
д2
дх2
2G д2Ур-°~
U о
ду2 '
- 2G ^^-
дх2
\ A.200)
— v
ду'
1 + v d2U0
U0 + 2G -д*?°-
дхду
дх
1 — v дхду
Vn =
+
d2Un
дх2
^ ду2
A.201)
где U0 удовлетворяет уравнению A.163); ¥0 — частное решение
уравнения A.164).
Рассмотрим тонкую изотропную оболочку толщины 26,
отнесенную к криволинейной системе координат a, P, у, в которой
базисной является ее срединная поверхность [49], а Rx и R2 —
главные радиусы кривизны срединной поверхности недеформиро-
44
ванной оболочки. Предполагаем, что нормальный элемент оболочки
не изменяется и компоненты тензора деформации еау, е$у, еуу
мало влияют на величину компонентов еа$, еаа, е$$, а нормальные
напряжения ауу пренебрежимо малы по сравнению с другими
компонентами тензора напряжений, т. е.
cav
0; е$у = 0; еуу = 0;
Jvv
0.
A.202)
Интегрируем геометрические соотношения для оболочек по у в
границах от нуля до у. В результате получаем выражения для
компонент перемещения срединной поверхности оболочки:
и (а, р, у) = и (а, р) — flyy;
у (а, р, y) = z> (a, P) — %у;
w (а, р, у) = а? (а, р),
A.203)
где
u = u (а, р, 0); i; == у (а, р, 0), w = w (a, p, 0);
5^ , а 1 дш , т 1
к2 —
Физические соотношения при этих предположениях имеют вид
Е
1 —v2
Е
1
+ V^aa)
1 — V
t;
atE ,
E
A.204)
a<*P = 2A + v) eap.
Компоненты деформации срединной поверхности оболочки
выражаются через компоненты ее перемещении:
^ _ 1 дА
л да +
1 gy
в ар +
лв ар
1 дв
■ v + kxw;
АВ да
и + &2И>;
&12
5
X, =
д
1 а
А да
-LJL
в ар
^ А да [ В
1 а^
А да
dw
кги
АВ
— к2и
1 а#
ля аа
дА I i dw 7 \ I
аи; 7 \
— 1 / d2w LJ?£_^1 1 дВ dw \
*12 ~Ш \"аоар а ар аа """ в да ар J "+"
+ Л* ~в "ар" (Т) + *» ~Т 1ST ("Г/ •
45
Компоненты деформации в произвольной точке оболочки
выражаются через компоненты деформации ее срединной плоскости:
еаа ^= Ч + кгу\ *эз = ea + x2v; еа$ = е12 + 2к12у. A.206)
Рассматривая соотношения A.205) как дифференциальные
уравнения относительно перемещений при заданных компонентах
деформации, видим, что три компоненты перемещения
определяются с помощью шести дифференциальных уравнений.
Следовательно, между шестью компонентами деформации существуют
дополнительные дифференциальные соотношения, которые обеспечивают
совместность этой системы дифференциальных уравнений.
Уравнения совместности записываются в виде
дВ дАкЛ9 дА . )
"ян" Н12 +
дВк2
да
дАкг
да
дВе9
дАуп,
да
дА
i дВ i
х« —
да
дВкь
да
+ ^2 ( Я?Г~ + "Ж" 82 +
ар
дЛ&12
дВ
да
дВгл,
дЬ
^2Х1 + ^1Х2 4Б
1 а^е^ J_
Х12 +
+ иг» Ягу. 812 ~ U»
+
ар
ал
+ "ар"в2
2
1 дВг-
д
да
дА
ар 8*2
1
+
аа ' /с,
дВ&,
да
1
+ аа £l +
ар 5
1 дВ \
да 8l2
а^
a,j
+
-0.
2 аа ' 2
Уравнения статики элемента оболочки имеют вид
A.207)
)
dBNx
да
дВ N dAS12
да
+ I±S 4- к I dBMl
да
dAN,
дВ М2 + 2 дАН»
д$
+ 2"НИ
{ да
12, АВ {q1 + ^mj);
04
0BS,
«р
ар
^i + J^i2- + ^^+^
-Ж^1 + 2
аа
дВН12 . у кг
да ' к2
дВ
да
дАМ2
ар
дВ
да
H12)=-AB(q2+k2m2);
(M^i + &2iV2) -
1
АВ
дА „ \ а 1 /
да
дАМ,
]_>_двм1_
А \ да
дА
дВ
дАНь
да
Mt + °-2£L +
м, + 4^ +
аа
"*" да П™
?п + ~АВ
дВт^ дАт2
да
00
A.208)
46
где
N,
A + к2у) Oaady; N2 = [ A + kty)a^dy;
—ь
5lo = N„ — KM™ = 501 = Nn — А^М12;
л,2хгл 21
J2\ — iy 21
6
M1== \ A+^7OG^7; M2 = 1 A+^7O0^7;
Я„ = 4 (Mla + Ma) = Я21 = -1 (M21 + M]2); ?1 =r o+ - a-;
mx = 8 (ajv + dav); <?2 = a3v — <W> m2 = 8 (ojy + a£~v);
gn = a^, — a7v; N12 = \ A + &2v) o^dy;
M2i = f (i + *iv) y<w*y; ^2i =1A+ *iy) <Wy;
6 б
\ A + A2v) \e<x$dy\ Q2 = \ A + Aw) a^cfy;
M
~6
(?!=](! +/c27)oavd7.
Здесь g1? g2, gn, mlt m2 — компоненты поверхностной нагрузки;
NVN12,N2, Qi, Q2,ML, M12, M2 — компоненты векторов усилий и
моментов. Компоненты деформации срединной поверхности
оболочки выражаются через усилия и моменты:
-^-(N.-vN^ + atT; я, = -^- (М, - vM2) + *
е, =
+ -£-Т*,
2Е8
№г
vNJ + atT; х2 = -^ (М3 - vMx) + | A_209)
-г б
D12
1 + V
Е8
3 1+V тт
2 £63 12*
Подставляя A.209) в A.207), получаем формулы для определения
компонент деформации eaai e$$, еа$ в произвольной точке тонкой
оболочки, выраженных через компоненты векторов усилий и
моментов. Если подставить эти выражения еаа, е$$у ^а$ в A.204),
то получим формулы для определения компонент напряжений
47
ааа, #33' ^аз в произвольной точке тонкой оболочки:
^ = ^(^ + 3M2^-) + ^-v(f + Xr*_^)
1
26
S12 + 3#x
-)
A.210)
Отметим также, что соотношения A.209) при известной
температуре t вместе с уравнениями равновесия A.208),
неразрывности деформации A.207) и соотношениями компонент перемещения
срединной поверхности оболочки и компонент ее деформации
A.205) составляют полную систему уравнений теории тонких
оболочек, из которых при заданных граничных условиях могут бытв
определены величины N±, S12, N2 и Мъ H12l М2.
Если на границе срединной поверхности оболочки задаются
обобщенные перемещения, напряженно-деформированное
состояние определяется с помощью системы дифференциальных
уравнений для непосредственного определения перемещений срединной
поверхности оболочки. Для получения такой системы уравнений
выполняются следующие операции: решается система A.209)
относительно усилий и моментов, в полученную систему вносятся
выражения A.205) и после подстановки выражений для усилий и
моментов в уравнения статики A.208) составляется искомая
система дифференциальных уравнений
Lnu + L12u + L
13'
w
atEb
-Qi + 2 i—7
L21u + L22u + L23w
q, + 2T
atE6
дТ кхЬ
да + з
дТ
+
3
kJ>
дТ*
да
дТ*
ар
}A.211)
а*Е6 ( R \
L31u + L32v + L33w = qn + 2 T4-v (-J- ДГ* - 2kT),
где Lij (ij = 1, 2, 3) — в общем случае дифференциальные
операторы с переменными коэффициентами не выше четвертой степени;
к = у (к± + к2).
Глава 2
ТЕРМОУПРУГОСТЬ ТЕЛ
ПРИ ЗАВИСЯЩИХ ОТ ТЕМПЕРАТУРЫ
КОЭФФИЦИЕНТАХ ТЕПЛООТДАЧИ
Исследование температурных полей и напряжений
в пластинках при сварке
Рассмотрим тонкую полубесконечную изотропную пластинку,
нагреваемую линейным источником тепла постоянной мощности
д/26, движущимся с постоянной скоростью V в положительном
направлении оси х, перпендикулярно кромке пластинки (рис. 7).
Через боковые поверхности пластинки происходит теплообмен с
внешней средой нулевой температуры по закону Ньютона, причем
коэффициент теплоотдачи является функцией времени az (т).
Температурное поле в пластинке, согласно A.48), описывается
уравнением теплопроводности
AT
K2^T==±JL^ q
где к2 (т) = az (т)А6. Граничные и начальное условия имеют вид
ОТ
:0- iL
х—0, х-*<х>
1 У 1->оо
■L |х-*<х>, | у |-юо
После подстановки
У = 9/(т); /(т) = ехр
уравнение B.1) и условия B.2) принимают вид
V%, у);
8(x~Vxiy), B.1)
е условия имеют вид
0; Т (я,р,0) = 0.B.2)
-aJx»(Qd£
aq 1 59 q _i л
е
X-voo, 1 у [-юо
2Ы J
и' 5*
58
5а:
0;
_ае_
B.3)
B.4)
B.5)
= 0; 0(я, z/,0) = 0.
С помощью интегральных преобразований Фурье и Лапласа
получаем решение краевой задачи теплопроводности B.4), B.5):
х [х+У (T-QP [х-У (T-Q]2 у2
п Ь
4 6—1534
49
где Q = д/8лАД Подставляя выра-
^^-^г жение B.6) в соотношение B.3),
получаем общее решение задачи
теплопроводности B.1), B.2)
рассматриваемой пластинки.
Напряжения, вызываемые найденным
температурным полем,
определяем по формулам A.155);
d2Fa
-г(°>
d2F0 .
о@)-
о@)-
дх2
d2F0
дхду
B.7)
где функция F0 = £/0 —26?Y0 удовлетворяет уравнению A.162),
a U0 и W0 определяются соответственно из уравнений A.163),
A.164). Поскольку рассматривается незагруженная пластинка,
компоненты температурных напряжений удовлетворяют таким
условиям:
х = О, #->оо, |г/|->оо. B.8)
О хх — Qx.ii — vJ
-»эсу
при
Применяя преобразование Лапласа к соотношениям B.7) и
уравнениям A.163), A.164), соответственно находим
гг@) — — r\2F •
'(О)
Jyy
d*F0
dx*
2 ;
dx*
dx2
-rf)W0
a^y = Щ ■
0;
dx
-Ч2] U0
a,(l+vN
Решение уравнения B.10) ищем в виде
U0 = (Ас + В) е~' л '* + (С* + D) е1 * 1х.
B.9)
B.10)
B.11)
B.12)
Определяем постоянные интегрирования А, В, С, D w находим
частное решение уравнения B.11). Подставляя найденную для
этого случая F0 в формулы B.7), записываем выражение компонент
тензора напряжений в изображениях:
-@) <> f / yi . г. ч — I T1 IX 1т-,,г1 !
Оу0) = {[ h | B - |tj | x) Cs - rfDs\ e~'ч |x + Г,7, - LLS);
1т*(-г)
B.13)
50
где
"(О)
g<°> - g« ■ г
°г atEQ0 > <"
Dt
hl--£-(-£- + ?.)(?,-hi|)
a ( ь
Y5[Ys + -f)(-^T-^
v? = is + -f; rs
F , s \2
£s =
1
X exp
(i-Tf)(i-Tia)
X
г v
*-[f*'(f)-^++Hf
<?o
— Q
2V6k
tyin
M
а\/ определяем по формуле
1
-j-OO 0-{-ioQ
3/h
] \ afe'^^d^ds.
Bя) . „ооа.гоо
Подставляя теперь эти выражения в первое из соотношений A.153),
получаем формулы для расчета температурных напряжений. В
связи с трудностями математического характера, возникающими при
переходе к оригиналам, расчет целесообразно проводить
численными методами [71].
Исследуем тонкую полубесконечную пластинку, нагреваемую
линейным источником тепла постоянной мощности д/26,
движущимся с постоянной скоростью V в положительном направлении
оси у на расстоянии х = d от края пластинки (рис. 8). Через
поверхности пластинки z = dz б происходит теплообмен с
внешней средой нулевой температуры, причем коэффициент
теплоотдачи с ее поверхностей является функ- л_у о
цией времени. Поверхность х = 0
пластинки теплоизолирована.
Уравнение теплопроводности, согласно
A.48), имеет вид [41]
ДГ-х2(т)Г = —
дТ
~дтГ
2Ь6
X
X 6(s-d, у — Vx), B.14)
граничные и начальное условия —
B.2). Используя подстановку
r = 0/(r), B.15)
Рис. 8.
4*
51
преобразуем уравнение B.14) и условия B.2) к виду
Ае = 4- -W~-il Г1 ЮН*-* у-Угу, B.16)
^ |х=0, ос-v оо ^
= 0;
I ^ Ко° \ B.17)
в(ж,у,0) = 0.
Записываем полученное с помощью преобразований Фурье и
Лапласа решение краевой задачи B.16), B.17):
в^С^Г^-Ш* 4aS +e kal }e kal -%-. B.18)
о ' ь
Подставляя выражение B.18) в B.15), получаем общее решение
задачи теплопроводности рассматриваемой пластинки. Напряжения,
вызываемые температурным полем, определяем по формулам A.155),
причем функция напряжения^ =U0 — 2GWQ удовлетворяет
уравнению A.162), а U0 и ¥0 — соответственно A.163), A.164).
Поскольку пластинка предполагается незагруженной, компоненты
температурных напряжений удовлетворяют следующим условиям:
в{х1 = Оху = 0 при # = 0, #->оо, |г/|-^оо. B.19)
С помощью интегральных преобразований Фурье и Лапласа
вместо A.155), A.163), A.164) получаем
(^-^0 = 0; B.21)
^-v?j% = at(l + v)Q. B.22)
Записываем решение уравнения B.21)
U0 = {Ах + В)е~Ы1х + (Сх + D)e^ lx B.23)
и частное решение уравнения B.22)
S
■ \ -Л I (*+<*) ^— l "Л I \ *-d j
|T|| |T||
где Г1 - f Г1 (т) e~x (S-^V) d% = Г'(8 - *t)V); 7? = *12 + — • Onpe-
0 a
деляя постоянные интегрирования А, В, С, D с учетом граничных
условий B.19), после некоторых преобразований и перехода от
52
трансформант к оригиналам находим
+ {х [(х + d)l+ — {x — d)Z_] +r+ — r_} erfc (■
-^[р--2х(г+ + г-)]е kal +4
У ml
- 2x(x + d)l+ - r+ + г \ d£;
} erfc I——r-
1
+ — (o>+ + co_) —
rr(°>
= 2ajr
^4)ж+НМе*"Ыс(тйг))-
+-^rf(i+4)^HMeYarerfc(iwj)+
+ {x [(x + d)l+-(x-d) U - r+ + r_} erfc (-£=-
\ 2 у at,
d?
-±=-lp+-2x(r++r_)]e~ 4aS +ijl-(, + <IFx
]} -|^p- ^ "^~+4- {i - (^ - ^ x
X
|*+|» + lal
X ' ' - "> r ta\
l г |2
-ur- + -k}}jhrr kal -2<*+^++
,£> = 2a j /-1 (t - 0 <(x lm {[b - ^ P2 + ^A + -^
X
xP1]/U-erfcG^f)} + (,1+yD{^±i
I 2 i I9
i +
^ h+|2j + Ю2 I 4e£ + |s_|»)
■ (vi + m* /i i«+i'-4(* + <i>1 i«_i'-4(«-d)-
2 U l*+l' 1г-1в
X
53
X
' 2Vat I 2Vn(ar)h I
+ (jfi+VQ
2x
4 (x + df - | 2+ |
Д + d , x— d \
TZ ij "Г -Г-. FT" I X
*+'
.*_l*
Xfl+_|^e *<
где
of =
гтСО)
\
<&
27V
1 1
(i = x, y); |3fe = —- + -^ ; z0 = ж + (yx + FQ i;
*+
z± = x ± d + i (уг + VI); l± =
4 (x ± d)« - 3 | z . |2
l*±l6
r+ =
2 (^ + ^J — I *± I2
2 ! г |4
P±
4a£
Г*(*+<*) + (У1 + П)я , *(*-<Q + (!/i + ^J , ,
-— 1 ^_^ -+-
l*± I2
@+ = ^
4a£
~ 2
1 +
1 J x -\- d x — d
2 H r: f2*
*+i
z+ I2 — (ж ± d)* 2{x ± cZJ
2a:
К
т@) -
o@)
2iV
/V - а,Я().
Подставляя выражения B.25) в первое из соотношений A.153),
получаем общее решение квазистатической задачи термоупругости
рассматриваемой пластинки.
Предположим, далее, что зависимость Bi (Fo) представляется
в виде
Bi (Fo) = Bix (Fo) 5_ (F0l - Fo) + Bi2 (Fo) S+ (Fo — Fo,), B.26)
где изменение Bix в зависимости от Fo иллюстрируется известной
кривой [1], которая удовлетворительно аппроксимируется
выражением
Bi (Fo) = Bi0FoV
Ъ—Шо
B.27)
Bi0 = 6723,4; Ъ = 1,3; к = 10,2. Функция / (т), если Bi2 (Fo)
представляется в виде B.27), принимает вид
/ (Fo) = exp j - £_ (¥ог - Fo) |37 (Ь + 1, к Fo) -
Fo \
-S+(Fo-F0l)\° Bl2(t)dt ,
i J
54
B.28)
где р = Bi0/kb+\ Подста вл яя соотношение B.28) в формулы
B.25), получаем выражения компонент температурных
напряжений, которые на крае пластинки при d = О имеют вид
о?
0; т^=0;
&„' = 2 ехр - 5_ (Foj — Fo) Pv (Ь + 1, A Fo) - 5+ (Fo -
Fo
Fo
- FoJ J Bi2 (t) Л f exp 5_ (F0l - Fo + 0 Py [6 + 1,
Fo-? |
^ (Fo - £)] + 5+ (Fo - Foj - £) j Bi2 (t) dt\ {
•2Г +
+
exp
iI±l^|-2(y + 2PeCr2}^
B.29)
/
У + 2РеО
где Y = г//б; Ре = Vb/2a — критерий Пекле. При Fo <; Fox
Fo
oy = 2 f exp {- $[y(b + 1, Fo) - у F + 1, A (Fo - £))]} f [ -,1
b
+
+
(У+2Ре£)«
exp
(Y + 2 Pe gJ
4C
(Y + 2 Pe ps
U 2s
d£. B.30)
На рис. 9 показаны графики изменения ау, построенные по
формуле B.30), в зависимости от безразмерного времени Fo при
фиксированных значениях критерия Пекле (безразмерной
скорости): Ре = 0; 1; 10 (кривые соответственно 7, 2, 3), Из графиков
следует, что с увеличением скорости движения источника тепла
температурные напряжения в пластинке по абсолютной величине
уменьшаются. Максимального значения ау достигает при
неподвижном источнике тепла, Ре = 0. На рис. 10 для сравнения приведены
графики изменения напряжений, вызванных подвижным
источником тепла в полубесконечной пластинке при переменном и неко-
6,0
п
rio1
I J^
Л
0,06 0,12 FO
Рис. 9.
•e9-ff
6,0
3,0
0
/YJ
\
0,0$ 0J2 Fo
Рис. 10.
55
тором постоянном среднем значениях коэффициента теплоотдачи.
При постоянном коэффициенте теплоотдачи (кривые 1, 2)
напряжение в конструкции возрастает до определенной постоянной
величины. Переменному коэффициенту (кривые 3, 4) соответствует
напряжение, в начальной стадии резко возрастающее с
последующим таким же резким уменьшением до уровня, который начиная с
Fo ^ 0,12 уменьшается незначительно, но существенно ниже
напряжения при постоянном коэффициенте. Пик напряжения
заметно выше его максимального значения при постоянном
коэффициенте теплоотдачи. С возрастанием скорости различие между
уровнями напряжений при постоянном и переменном
коэффициентах теплоотдачи несколько уменьшается: от приблизительно 2,1
безразмерных единиц при Ре = 0,01 (кривые 1, 3) до 1,2 при Ре =
= 10 (кривые 2,4).
Следовательно, характер изменения напряжений существенно
зависит от функционального представления коэффициента
теплоотдачи. Напряжение в пластинке при постоянном коэффициенте
теплоотдачи возрастает до тех пор, пока мощность источника тепла
не исчерпается теплопроводностью материала и теплообменом с
окружающей средой. При переменном коэффициенте теплоотдачи
возникает пик напряжений, объясняющийся тем, что в начальный
момент времени величина коэффициента теплоотдачи не постоянна
(средняя), возрастает, но она все-таки меньше его среднего
значения. Именно в этот момент и появляется пик напряжений,
поскольку прогрев материала, а следовательно, и вызванный им рост
напряжений происходит интенсивнее, чем увеличение
коэффициента теплоотдачи. Затем теплопроводность материала и
значительно возросшая теплоотдача исчерпывают мощность
источника тепла и вызывают понижение уровня напряжений (Fo > 0,12).
Используя известную в практике сварочного производства [12]
зависимость коэффициента теплоотдачи от температуры
(аппроксимированную в виде A.15)), получаем следующие выражения
компонент температурных напряжений на крае пластинки:
а„ = 2
Ve.expf-^Fo)
г=1
3
2>iexp[-MFo-S)]
г=1
2£ ^(У+2Ре£J
X
X ехр
(У+ 2 Ре О2
С
(Y + 2PeQ*
<К\ ох = хху = 0, B.31)
где ах = 0,1; а2 = 0,15; а3 = 0,75; Ьг = 34,091; Ь2 =■ 1,25; Ь3 =
= 0,033. Характер напряжений, вычисленных по формуле B.31)
при Ре = 0,01; 10 (кривые соответственно 1,2), показан на рис.11.
Как видно, напряжения изменяются по такому же закону, как и на
рис. 9, отличие состоит лишь в их величине. Вычисление проводи-
56
us
uo
Q,$\
лось при следующих значениях
теплофизических и механических
характеристик: at = 12 • 10~6 1/°С;
26 - 0,4 см; Е = 2,1 . 106 кГ/см2;
^ = 0,376 дж/(см • с • °С). Мощность
источника тепла q в первом и втором
случаях соответственно равна 275 и
4,182 . 103 дж/с. Нетрудно
убедиться, что размерные значения ау
в первом и втором случаях одного
порядка.
Решение задачи B.14), B.2) при
постоянном коэффициенте
теплоотдачи х2 = const, независимо от
приведенного выше, получено в работе [42].Выражения для
температурного поля B.18) и вызываемых им напряжений B.25) в этом случае
соответственно имеют вид
>2
0,1 0,2
Рис. 11.
0,3 Fo
Т = Q [дг0 (р+, со+) + Зъ0(р_, ©_)] в
-Vi<0i.
ох = — 2а
—ак*1
V
Re(M^~
+ ■
Z0X
х
X
+ч-
ч-
4а?:
1 +
2а?:
'+
г+г
xf + r-» 4а£ «*ЬЗ=г +
+ \х
(x + d)
4(x+d)*-3\z+\
|z+l6
(x-d)
2yar
i{x — df ■
X
■3|*_[»
z_l6
+
+ ^
2 (x + dJ-} z+ |2 2 (x — dJ — | г_ Р
41
erf с I -
d
Vnal
4a?
x(x+d) + (Vl + Vtf
z+l
+
l г у<ь
x{x-d) + (yl + VQZ
— X
2 (ж + dJ — | z+ p 2 (x — dJ
П^ 1 т
."i+4-{
2 (ж + dJ ■
l*+'8 .
2{x— dJ
1 +
|z+|2-(*-
41
df
+
1*4-1
•+'
+ e
4a£
1 +
2a£
|2 — (x — dJ
2z (x + d)
2a£
4 (X _j_ dJ — 3 | z.
'+'
4 s
2 (x + dJ - | z+ |2 2 (ж - dJ — | z_ |2 ч
2|z,
21 z
dfc
57
ov = 2a \ e~^
-a.Y.% /
0(Кт+т)-И1 + ^
X
zst_
Aat
l + -^-)x + z0
2a
i + T""*
X e ^ erfc[—y=)) + Iх
(x + d)
(x-d)
4(x— dJ — 3 | z_ |2 1 j
2 (я — dJ __ | z__ |2
erfc
4 (x + d) — 3 | z+1
2(x + d)*-\z+ |
h+4l
=■ X
2 У"а£ / V паъ
X
4<
sfo + cQ + fa + yp» , * (г - <9 + fri + ^J
2(o: + dJ— |Z+|2 2 (a:— dJ
iz+I4
K
+
+
i [ x -\- d x — d
d2
+
4a£
+ 4-
1-(^ + ^J(ттЧ +
-+i
+ ■
2al
»+l
1 - (ж — dJ
+
|z_l2
+
2a£
l*_l
, , , ~ 4(s + dJ — 31 z. I2
I г
•+l
3 2(» + «i)'-|i+|' 2(g-d)»-|«_|»\
тжу = 2a \ e
-a^^Im
V
—+ —
%
1
2«£ I ^ + zl_ I +
+ 4aC l1+ 2a£ Д s+ + z_ jj
Ч-2-
+ 0/1 + П)
+
x -\- d
z+l
4a:
1 + 1
•+■
e 4a£ erfc (
_±f±_!L
e 4a£ +
Zq \ 1
+
ж — d
ю2
4a!:
+
__I*-T
I z_ |2
I z_ |2 — 4 (x — dJ
ГСП5
, (У1 + УР « If I z+ I3 ~ 4 (* + rfJ _
^ 2 \| |,+ |«
erfc ITjT^f) ~ 2у-дю3/2 Inn*"+
58
+
2x
4 {X + df - | z+ |«
2a:
4a£
\
В этих выражениях приняты следующие обозначения:
с
5in (р, <о) = в\ оO1-1 ехр 1~ (ш + -JJ-)
Ло (и = 0, ± 1, ± 2, .. .);
Р± = ю^а ]/(ж ± йJ -4- г/?; о>± = VaFx/f/' (х ± aJ + yf,
z±=x±d + i(y1 + VQ; z0 = x + 1(уг + VQ\
щ = У/2а; v* = 1 + (х/согJ; у± = у - Ут.
При нагревании пластинки неподвижным источником тепла,
У — 0, выражение безразмерного напряжения ау на ее крае
значительно упрощается:
р пЯ0(р+,а>) + 4-
гч+
^х(р+, со) —2
1-е
,—BiFo
п+
II
где р± = ]/Bi (У2 ± D2); У = у/в; © = 2BiFo/p+; D = d/б.
Изменение напряжения оу|х==0, у=о с течением времени, вычисленное
по этой несложной формуле, показано на рис. 12 при D = 2
(кривые 7, 2), D = 5 (кривые 5, 4) и Bi = О (кривые 1, 5), Bi = 1
(кривые 2, 4). Наибольшего значения в случае Bi = 1 это
напряжение достигает при стационарном тепловом режиме. Если учесть
коэффициент теплоотдачи, то напряжения уменьшаются. С
удалением источника тепла от края пластинки х = 0 напряжение
уменьшается. Переходя к пределу (к -> 0, х -> 0, d-+ 0) в
выражениях для ах, оу, тху при постоянном коэффициенте теплоотдачи
с боковых поверхностей пластинки,
получаем
2F
Оу\х^0 = е~Ш1\
+ '
4i?
, 2 /F
61 >
+ /?)
sign I +
-lb
где £ = ^7/2**; F = У2т/4а. При
квазистационарном тепловом
режиме, F-^oo, величина этого
напряжения совпадает с величиной
напряжения, полученной в работе [12]
применительно к сварке. Изменение
напряжения ву \x=zq рдоль подвижной
0J
0,6
0А
0,2.
\л
\г
Ь
V /
)tL
3 у
/
А
**~^'
\
н
2 4
Рис. 12.
Fo
59
-2
-f 0
-//!
-2 /
-3
2
/>^^
3>^
S*3
Рис. 13.
безразмерной координаты! приF = 0,25; 1;
сю (соответственно кривые 1,2,3)
показано на рис» 13. Видно, что с течением
времени это напряжение увеличивается.
Максимального значения, например при F = 1,
оно достигает при | = 0,3. При
автоматической сварке металлическим электродом
под флюсом и при ручной сварке
тонкостенных элементов конструкций из
малоуглеродистой стали [56] а = 8 • 10~~6 м2/с,
скорость перемещения дуги V
соответственно равна 3 • 10~3 и 10~3 м/с. При этом
максимального значения напряжение ау \х==о достигает через 3,56 и
32 с после начала действия источника тепла в точках
соответственно у = 0,0123 и у = 0,0358 м.
Рассмотрим полубесконечную пластинку, край которой (х = 0)
закреплен и теплоизолирован, нагревается источником тепла
мощности д/26, движущимся с постоянной скоростью V в
положительном направлении оси у на расстоянии d от ее края. Через
поверхности пластинки происходит теплообмен с внешней средой
нулевой температуры, причем коэффициент теплоотдачи является
функцией времени аг (т).
Возникающее нестационарное температурное поле в пластинке
определяем из уравнения теплопроводности
д2Г
дх2
+
д2т
- х2 (т) Т - —
4 ' а
дТ
дх
2Xfi
б (я _ d, у - Ут), B.32)
где х2 (т) = а2 (т) АД Краевые условия имеют вид
дТ
У |-*оо
1 У 1-*о
= 0;
дТ
дх
я=0
= 0, Г (ж, г/, 0) = 0. B.33)
Используя подстановку A.153), уравнение B.32) и краевые
условия B.33) преобразуем к виду
1 дВ
,-1
m=lTl>r-f M-ij-Hx-d, y-Vx);
B.34)
Х-юо
| У I-►«>
0;
<99
I I/ !-><»
= o- JL
u' дх
x—Q
= 0; 6 (ж, i/, 0) = 0. B.35)
После преобразований Фурье и Лапласа решение краевой задачи
B.34), B.35) получаем в виде
A L
о
-Ьехр
(У-Гт0)«+(* + <*)'
4а (т — т0)
+
(y~VToJ + (x-d)*
4а (т — т0)
d%n
B.36)
60
где Q (%) = -rfy- / 1 (т); / (т) = exp
2^6
a U2(D^
о
. Таким
образом, общее решение задачи теплопроводности рассматриваемой
пластинки имеет вид
Г = 0/(т). B.37)
Для определения вызываемых температурным полем B.37)
температурных напряжений, воспользуемся формулами A.200).
Граничные условия:
и0 = 0; v0 = 0 при х = 0, lim of = 0. B.38)
Применяя к уравнениям A.200), A.163), A.164) и условиям B.38)
преобразования Фурье и Лапласа, находим
"@)
иХХ
:@)
T^r^(-v^--^-)t/0 + 2rlW0;
°УУ ~*
2G
"(О).
Jxy ■
1 — V
2G d
Щ
_y,* + B + v)-
d2
77 _ 9П d^°
1 — v dx \ dx2
d2
vr\2\U0-2ir\G
dW0
dx
d2
(-e--^Y0 = (l+v)«A
и0 = 0, v 0 = 0 при я = 0, lim olf = 0.
x-*-oo, I y [-*-oo
Решение уравнения B.40) с учетом B.42) имеет вид
U0 = (A+Bx)exp(— х\г\\),
частное решение уравнения B.41) —
_ (l+v)«t ТЛ exy[-\x-d\y) exy[-\x-d\\r\\]
п~~ а'-л ~п \ у |ti|
2 (у2 _ ^2)
ехр [— (х + d) у] ехр [—(х + d) \ г\ \]
У ^ 1ч1
B.39)
B.40)
B.41)
B.42)
B.43)
- +
B.44)
где
-f-oo -f-°°
N:
= -±=- J J <? (т) 8 (y - Ft) e^-'dydv, Y = j/rf + JL
K~2S _M 0
Решая краевую задачу B.39), B.42), определяем Оу'. Переходя к
оригиналам и подставляя результат в первое равенство A.153),
61
находим выражения температурных напряжении
а/ (т) f ,-1 tr ~ /г
а
4C-
^■^-'(х-а^кв^ку-^р^ + га + ^х
х *pLj + ii±^- р_х^ +
1
« г— . ^ f(v-DP+ + 2(l+v)x
Xxf+\ Lt+ [(v -1) f+ + 2A + v)жpL] if- 4A + v) X2+3 +
+ C - v) (CD+Z+2 + co_zI2 + pL) - 4z+2} + Im (ii+^-i x
X p_LF +
at
1 [(v-l)P+ + 2(l+v)«pL]LT +
/2a£
+ [(v - 1) РГ, + 2 A + v) «pi] LT+ C ~ v).^ " F£)
X
x(^± +
■ dl;
ov=aJL+^nu\ri{x_0
2C-v) .1
Re(8p2_ + _£-P_L3+ +
+ •
YZaZ,
$+Lt + P+Lt-2z+2 +Im
/2a£
M>2~ +
+ P+£f)
C - v) (ю+ + а>_)
4 A + v) ai
dt, — ax;
^ = -4^.fr1(^-D<Re{7|f[P+-(i+v)x
X *pL] LT - ^Ц^ P-LT + 2 [p2, - A + v) *pl] LT -
~ C~У} (^ + ^)} + Im{2(v-l)^2-
- 2e [PL - A + v) *pL] + A + !)ж p_£j-
/2aJ
■IP+-
r +
- A + v) *pl] /^ - 2 [p'+ - A + v)*pi] LJ- - 4A +v) xz?+
+ C - v) ((o+2+2 + co_2I2 + pi))\ d£,
!B
где
(J/ =
27V
(/ = s, y); 6 = erfc
2Val
JUy
Yin [
D.
Uexp^J^) +
'"'y^ir^r 4<*
62
+ 0-v
V'lal
• Уг+Vt
exp l — ix *
4a:
exp
*'-(У1+П)а-2<Р
2± = (^±d) + i(ft + Р£); co± = exp —
8аГ
(* ± df + (У1 + FQ«
К
£7
/2я
Mw)exp
te-ft + ^-
-Z)_v
z0
/^.
/ • У1 + Ч
exp I - ю y\ar
exp
*2 - (yx -f VQ2 - 2d?
(v = 1, 2, 3);
o„
z0 = x + i{y1 + VQ; %xy - -5L.
У1 = »-П; N = atEQQ; Q0
IN '
я
2nXtb
Переходя в формулах B.45) к пределу при х -> 0, получаем для
края пластинки такие выражения температурных напряжений в
подвижных координатах:
Fo >
а* =
X
/(Fo)
3 —v
r'CFo-Q exp
о
D2 + (Y + 2Pe p2
4£
X
/}2 __ (у -)- 2Ре СJ
(У + 2Ре£J
[Я2 + (У + 2Ре О»]» 2С [Я2 + (У + 2Ре £J]
_ Д2-(У + 2Рер2 )
Fo
% = vo* - Ш- I /-1 (Fo - 0 exp
Fo
/(Fo) Г Г1^о-0(Г + 2РвО
■ v .)
xv 3 —v .! [Я2 + (У + 2Pe £JP
Д2+(У + 2Ре£J
5.
B.46)
exp I i
Ш ([Z>2 + (F + 2Pe 02!Л
l;
(У + 2Ре£J
4C
jpfil] + [/?• _ (у + 2РеО»1ЛЧ
(У — 2Pe gJ
2 '
2
где tFx (a; 7; z) — вырожденная гипергеометрическая функция;
Y = ^/6; Z) = <2/S. Учитывая зависимость A.14) и переходя в
A.15) к безразмерным величинам, находим
/(Fo) = 0,l<TBoFo + G,15e~BlFo + G,75<rB2Fo, B.47)
63
is
ho
д,5
Y^-'-
р—
й
/*
/2
/
0>1 0,2
Рис. 14.
Fo
где В0 = 34,091; Ях - 1,25; В2 =
= 0,033. Графики изменения в
зависимости от времени безразмерных
температурных напряжений ах (кривые 2, 2)
и ау (кривые 3, 4) на крае пластинки,
вычисленных по формулам B.46) при
Ре = 0,01 (кривые 2, 4) и Ре = 10
(кривые 2, 5), представлены на рис. 14.
С уменьшением скорости движения
источников тепла напряжения
возрастают. Напряжения ох значительно
меньше напряжений ау.
Исследование температурных полей
и напряжений
в твердых телах при закалке
Рассмотрим тонкую пластинку, обладающую тепловой и
упругой цилиндрической анизотропией и имеющую в каждой точке
плоскость тепловой и упругой симметрии, к которой нормальна ось
z. Через боковые поверхности пластинки происходит теплообмен
с внешней средой постоянной температуры tQ по закону Ньютона,
причем коэффициент теплоотдачи зависит от температуры az (T).
В начальный момент времени температура пластинки
предполагается постоянной
1 |т=о ~ ±п
B.48)
пластинки в срединной
теплопроводностью в на-
Если теплопроводность анизотропной
плоскости очень мала по сравнению с
правлении оси z и источников тепла в пластинке нет, уравнение
теплопроводности A.80) для определения обобщенного плоского
температурного поля в ней имеет вид [38]
-az(T)(T-t0) = cv-^-. B.49)
Любую зависимость коэффициента теплоотдачи от температуры
с удовлетворительной степенью точности можно
аппроксимировать кусочно-непрерывной функцией температуры.
Экспериментальные данные зависимости коэффициента теплоотдачи от
температуры при жидкостной закалке стеклянных пластинок
приведены в работе [5]. Такую зависимость приближенно можно
аппроксимировать ступенчатой функцией [39]:
а* (Т) =а0+ К - а0) [S+ (Г - Тх) - S+ (T - Г0)], B.50)
где аг > а0; ах = const; а0 = const; Т0 > Т±; Тх = const; T0 =
= const. Учитывая зависимость 5+ (Т — Г*) = S+ (п — т),
получаем
а* (т) = а0 + (ах - а0) [S+ (т - т0) - S+ {% - %г)]. B.51)
64
Решение уравнения B.49), в котором коэффициент
теплоотдачи имеет вид соотношения B.51), при начальном условии B.48)
записывается в виде
9 = ехр {— Mi — В [(Mi — Mi0) £+ (Mi — Mi0) -
- (Mi - р Mi0) S+ (Mi - j3Mi0)]}, B.52)
где 0 =» (Г - t0)/(Tn - g; В = ах/а0 - 1; p = MVM^; Mi0 =
= a0x/cv8; Mix = а0тг/cv8.
Определим теперь температурные напряжения в свободной
от внешней нагрузки кольцевой пластинке при условии, что
внутренняя (г = d) и внешняя (г = D) концентрические поверхности
теплоизолированы. Вместо и0 и ви* подставляем и, а и. Так как
радиальные перемещения удовлетворяют уравнению A.192), по
формулам A.190) находим безразмерные температурные
напряжения в кольцевой пластинке [7, 8]:
аг = {or [E*N (/+ (m) - I)] - *0} (Tn - g
a; = {аф [E+N {kf~ (m) - l)] - t0] (Tn - g
-l
B.53)
где
ЛГ =
E„
A + vrq>) + at; k2 = -/- =
a*t = ar + vrq)oc(p; a{ = a£vr<p + &2<4;
m =
D
f
г,А+1
n2fe
ft+1
1—771'
fe-1
„2ft
DГ.
Температурные напряжения в круговой, бесконечной с
круговым отверстием и бесконечной пластинках находим, полагая
соответственно в формулах B.53) d = 0 и D = оо, d = 0, D = оо.
На рис. 15, 16 приведены графики изменения безразмерных
температурных напряжений аф в зависимости от параметров р и В.
Кривые 1—3 на рис. 15 построены соответственно при В = 0,5,
0,5\
НйЕ
/ 2 Mi
Рис. 16.
5 6—1534
65
*
20
/S
w
!\\Ч/
jW4
0,5
UO
Рис. 17.
f,s
Fo<
Mi0 = 0,5 и р = 1,5; 2; 4; кривая
4 - при 5 = 2, Mi0 = 1, P =
= 1,5; кривые 2—^ на рис. 16 —-
соответственно при 5=0; 0,5; 1; 2.
Неустановившиеся температурные
напряжения значительно
уменьшаются при увеличении
параметра В (относительной «высоты»
ступеньки) с момента, когда
коэффициент теплоотдачи начинает
U возрастать. Изменение ширины сту-
[J пеньки р при фиксированном В не
оказывает существенного влияния
на распределение безразмерных
температурных напряжений. На
рис. 17, 18 приведены графики
изменения температурных напряжений аф) аг в зависимости
от безразмерного параметра Fo при Bi = 1; 2; 3
(соответственно кривые 7, 2, 3). Напряжения сгф, аг отличаются лишь
количественно. Рассмотрим подробнее, например, график сгф.
Как видно, увеличение коэффициента теплоотдачи (критерия Био)
вызывает более быстрое падение напряжений. Точки сопряжения
кривых соответствуют моменту «включения» скачка ах — а0.
Скорость остывания пластинки связана с величиной критерия Био,
т. е., чем выше коэффициент теплоотдачи, тем скорее пластинка
остывает, это приводит к тому, что «включение» происходит в
разные моменты времени.
Рассмотрим бесконечную стеклянную пластинку с начальной
температурой tH, которая подвергается закалке (охлаждению)
в воздухе температуры tc [40]. Возникающее при этом
температурное поле A.32) можно записать в виде
t
Рб
jg- cos pzT,
B.54)
1
где р* = — -д—. Интегральную характеристику температуры
Т находим из уравнений теплопроводности A.48), A.69), A.68),
соответствующих линейному, квадратичному и четвертой степени
законам изменения температуры по толщине пластинки:
-BL-Fo
T = tc + (tH-tc)e-
(i = 0, 1, 2,
B.55)
где
Bi2 =
T^V; «.-i/HH£ +
+ 45-
11
2
— /—2 и 1
■> I Bio +
66
Подставляя выражение B.55) в ^
формулу B.54), находим
X cosec \/Шг cos 1/ВГг Z, B.56)
20
где В = t — tQ; 6Н= tn — tc; Z = -|- .
Согласно теории закалки стекла f0^ 05 ^ f-5 ^-с
[23], напряжения в каждом слое ' Рис' |g
пластинки определяются разностью
средней остаточной деформации еь и остаточной деформации еь в
каждом слое, т. е.
4v</
1Г
м
(
II
ill)
-—j)l
—-fln
Е
1 — v
(еь — еь),
где
1 . /—г
eb (Z) = а(9, f (sin J/Щ - sin УЩ £) &;J±\ -^j- ;
•> cos21/ Вь t l — ь
B.57)
B.58)
У о — £ — i a
(^ — температура стеклования). Средняя остаточная деформация:
eb{Z) = T^-T\eb{l)<K.
Z
B.59)
Подставляя выражение B.58) в уравнение B.59) и вычитая его
после интегрирования [14], получаем
еъ — еъ = — atQg 1 —
sin |/Bi£- — sin]/"Bii Z
g{ " увц A — Z) cos |/Bi{Z
После подстановки формулы B.60) в равенство B.57)
Е
B.60)
— afig
sinl/BL — sin]/~Bi.Z ,
1 J... г ,. \r=L- I • B.61)
g i — v \" у вц (i — z) cos ут{ z
В средней плоскости пластинки
СГо.г
aft
*. fi_ sin]i3 , = -»*
1 — V \
|/"В1,
1— V
Ф (KBiO,
B.62)
где ф (f/BiJ — функция закалки, равная степени закалки,
отнесенной к постоянной к = atEQgB • 107A — v); В — оптическая
постоянная упругости.
На рис. 19 приведены функции закалки, вычисленные согласно
теориям, изложенным в работах [3] (кривая 2) и [23] (кривая 3).
67
0,3
о,г\
о,<
8rWA
<
° / ол
ь/У^
J °о 1
В/
При этом использовано
приближенное выражение
температурного поля для слоя. Проследим, как
изменяется функция закалки в
зависимости от уточненного решения
задачи теплопроводности. Если
интегральная характеристика Т
определяется из уравнения
теплопроводности, соответствующего
линейному закону изменения
температуры по толщине слоя,
функция закалки описывается кривой
7, что вполне удовлетворительно
согласуется с
экспериментальными данными О [3], Д, Ф [4]. При
определении Т из уравнений,
соответствующих квадратичному и
четвертого порядка законам
изменения температуры по толщине
слоя, кривые функции закалки
в рассматриваемом промежутке изменения критерия Био
практически совпадают (кривая 4). Величины предельной степени
закалки, вычисленные по формулам, соответствующим линейному,
квадратичному, четвертого и шестого порядков законам изменения
температуры по толщине слоя, имеют соответственно значения:
1; 0,43; 0,375; 0,366. Отметим, что в работах [3, 23] приведены
величины предельной степени закалки 0,69 и 0,363. Таким образом,
результаты приближенной [23] и уточненной теорий хорошо
согласуются.
Пусть тонкая полубесконечная пластинка (рис. 20)
погружается с конечной скоростью V в полиэтилсилоксановую жидкость,
которая служит охлаждающей средой. Для определения
нестационарного температурного поля, усредненного по толщине
пластинки, используем уравнение теплопроводности A.48),
которое, принимая во внимание изотропию
материала и отсутствие источников
тепла, записываем в виде [37]
Рис. 19.
Л
-2\a{T)S„{Vx-x) +
+ abS+(x-Vx)](T-T0)
- cv -|f + 2аъ (Т0 - Тв) S+ (х - Ft),
B.63)
где 5_ (Ft - х) = 1 — S+ (x - Ft);
а (Т) — коэффициент теплоотдачи с
поверхности пластинки в жидкость; а& —
68
постоянный коэффициент теплоотдачи пластинки в воздухе с
температурой Тв; Т0 — температура жидкости. Если предположить,
что теплоотдача с части поверхности пластинки, находящейся в
воздухе, очень мала, то уравнение B.63) принимает вид
Л -^ - 2а (Т) S„ (Ft - z) (T - TQ) = cv-^-. B.64)
дх*
При интенсивном теплообмене со средой и быстром погружении в
охлаждающую среду тонких пластинок составляющая потока в
срединной плоскости их мала по сравнению с составляющей потока
через поверхность и ею можно пренебречь, уравнение B.64)
имеет вид
- 2а (Т) S_ (Ft -х){Т- Г9) = с, -^-. B.65)
Интегрируя B.65) с учетом A.1), находим зависимость времени
охлаждения данной точки пластинки от температуры:
% = D(T)-D(Tn), B.66)
где
D (Т) = In (Т - Tf [(Г - Tmf + C2ГА/2 + АВ arctg (T ~ Tm) (Г1;
Я = (Гт - TQ) Г1; А = c^ajl {nal [(Tm - T0f + P2]};
c0 = cvb;
Tn — начальная температура пластинки. Если коэффициент
теплоотдачи изменяется по закону A.12), уравнение B.65)
записывается в виде
ОТ
С° д% "+"
(а3 — а0) S (т3 — т) + а0 + а.
6 ft — тт)
'2 |Г(тЛ
X
X (Г - Г0) = 0. B.67)
Интегрируя уравнение B.67) от нуля до т и учитывая, что Т |т=о =
= Ти, находим
Г* = (Г** - 1) ехр -со
(а3 — а0) (т3 + (т — т3) б' (т3 — т)) +
+ а°т+Т5%Г5(т~т4 + 1>
B.68)
где Т# = 777V Полагая в соотношении B.68) а2 = 0, получаем
выражение
Г* = (Г.н - 1) ехр {- аз~а° [т3 + (х - тя) S (х, - т)] -
-31-1 + 1, B.69);
69
соответствующее представлению коэффициента теплоотдачи в виде
скачкообразной функции температуры A.7). Записываем выражение
для Т%, используя представление зависимости коэффициента
теплоотдачи от температуры в виде дельта-функции A.4). Полагая
в соотношении B.68) а3 == а0, находим
(Т.н - 1) ехр
—i
а°т+Тг7Ьг5(т~Тт)
+ 1. B.70)
Дифференцируя B.70) по т и переходя к пределу слева при т -> т„
получаем
Т (тт) | = -
а0
(Г*н-1)ехр --^т,
Если в B.70) т = тт, то
7\т = (ГЙЯ - 1) ехр
«0^
+ 1.
B.71)
B.72)
Соотношения B.71), B.72) позволяют записать выражение для
безразмерной температуры в виде
(Т*н — 1)ехр
а0т
+
*о(Т«т-1)Т(
■$ (т — тт)
+ 1. B.73)
Если используется свойство дельта-функции (Т — Г0) б (Г — Г™) =
= (Тт— Т0) Ь (Т — Тт) и ее представление A.3), уравнение
теплопроводности для определения температурного поля в
погруженной в жидкость части пластинки B.67) записывается
несколько иначе:
дТ
+ а0(Т-Т0)
ос,
2 \T'(iJ\
(Tm-T0). B.74)
Принимая во внимание B.71), B.72), с помощью преобразования
Лапласа находим такое решение этого уравнения:
Т* = 1+е
-Mi
1-
оЛ
Т — 1
(Г.н - 1), B.75)
где Mi = ос0т/с0; с0 = сД Если а (Т) равно некоторому среднему
значению ас, из B.73) и B.75) при а0 = ас, а2 = 0 получаем
1-(Т.в-1)е
-м-
B.76)
где Mic = аст/с0.
Если коэффициент теплоотдачи имеет вид зависимости A.10),
то, согласно уравнению B.65),
дТ
X (Т - Г0) = 0. B.77)
Интегрируя это выражение, находим
Т+ = 1 + (Г« — 1) ехр [-Mi - 4Mi3
70
2Mi2 - 2Mix +
+ 4 (Mi — Mi8) S (Mi, - Mi) 4- 2 (Mi, - Mi) 5 (Mi - Mia) -
- 2 (Mi - Mit) 5 (Мц - Mi)], B.78)
где
Mi^-^- (* = 1,2,3); т^-^ШГ,; т, = --^ In Г,+
+ -¥"• -.—й-ЬГ. + ^-т,); Г|в^1
(* = 1; 2; 3).
Если принять Гн = 720, Тг = 680, Г2 - 600, Г3 = 480° С, то
тг = 0,33115, т2 - 0,85976, т3 = 2,2379 с.
При построении графиков изменения температурных полей в
зависимости от времени коэффициенты теплоотдачи с боковых
поверхностей пластинки аппроксимировались различными
способами. Численные значения теплофизических характеристик стекла
приняты следующие: Xt = 24 • 10~ кал/(см • с • °С); а = 48 X
X Ю~д см2/с; р = 2,5 г/см3; cv — 0,2 кал/(г • °С); толщина
пластинки — 4,8 мм, начальная температура выбиралась в промежутке
650—760° С и считалась постоянной для всей пластинки стекла.
На рис. 21 изображены графики изменения температурного поля
в пояубесконечной пластинке, построенные по соотношению B.66)
при Тя = 760, 720, 680 °С (кривые соответственно 2, 2, 3), а также
график изменения температурного поля Т = Г*Г0,
вычисленный по формуле B.76), при среднем значении коэффициента
теплоотдачи 0,02 кал/(см2 • с • °С) и при Тн = 720° С (кривая 4).
График изменения в зависимости от времени температуры Т =
= Т*Т0, построенный по формуле B.75), при Тн = 720° С
показан на рис. 22 (кривая 2). Для сравнения приведены также кривые,
полученные по соотношениям B.66) (кривая 3) и B.76) (кривая 4).
Q 5 10 15 20 т
Рис. 21.
71
Видно, что кривая 3, которая может соответствовать реальному
температурному полю, отличается от кривой 1 на интервале 0 <1
< i < тт = 2,5 с. Этот интервал играет решающую роль при
вычислении временных и остаточных температурных напряжений.
Используем такое выражение для температуры:
ап% а0т
T* = [l+e~~(TtH-l)]S+(%m-x)+l[l + e '• |>.н - 1 +
а0тт
1 -ос0Г0 Г,н_1
Из него следует
71 — 1 2
5_(т-тт). B.79)
ОС0Т^
Г,т=1 + е «. (Г.„-1),
откуда
в С° = [(У.н - l)/(^m - I)]2-
Соотношение B.79) принимает вид
B.80)
B.81)
Т* = \1+е со (T>R-l)]S+(im-i) + \l+(T*H-l)e
X
X
1 - -jgr Gm - D^ (T - TW) ] j S_ (T - Tm).
B.82)
Кривая 2, построенная по этой формуле, на интервале ГО; 2,5]
значительно меньше отличается от кривой 3. При т >> тт кривые
7, 2, построенные соответственно по формулам B.75) и B.82),
идентичны. В этом легко убедиться, положив в соотношении B.82)
i > тт. При этом получаем аналитическое выражение,
совпадающее с B.75).
600
440
280
120
1
10 15
Рис. 22.
72
20
г
m\
440
280
/20
\
V^
5^
^JA
^^T^
3
4?==
T
600
440
280
/20
^/
0
'—-.
_ 1
J
Ю 15
Рис. 23.
20
0
/0 /5
Рис. 24.
20
На рис. 23 представлен график изменения температуры
(кривая i), построенный по формуле B.78). Для сравнения приведены
данные (кривые 2—4), вычисленные по зависимости B.66) при
а0 = 0,005; 0,006; 0,007 кал/(см2 . с • °С) соответственно и по
формуле B.76) (кривая 5). Отклонение кривых 2—4 от кривой 1
при т > гт обусловлено тем, что аппроксимация A.1)
удовлетворительна приблизительно до Т = 400° С (см. рис. 1). На рис. 24
приведены кривые изменения температурного поля, вычисленные по
формулам B.69), B.75) и B.66) (кривые 2, 2, 3; кривая 4
соответствует кривой 5 на рис. 23).
Представленные на рис. 21—24 графики изменения
температурного поля позволяют сделать следующий вывод: учет зависимости
коэффициента теплоотдачи от температуры играет значительную
роль при исследовании распределения температурного поля во
всем диапазоне изменения температур и, следовательно, при
определении временных температурных напряжений.
Рассмотрим процесс затвердевания стекла. В качестве
основной модели этого процесса примем [3] скачкообразное изменение
вязкости стекла в точке стеклования Tg от нуля до
бесконечности. В этом случае задача об определении временных
температурных напряжений сводится к задаче термоупругости свободной от
внешней нагрузки бесконечной полосы-пластинки, ширина
которой Ft* изменяется с течением времени (т* = т — т#, xg —
время, начиная с которого затвердевает край полубесконечной
пластинки х = 0, т. е. интервал, по истечении которого достигается
температура стеклования Tg). Формула для определения
временных температурных напряжений в полосе-пластинке, по ширине
которой температурное поле распределено несимметрично, имеет
вид [6]
i
4 Л. 3 х \ Г m ,*ч .«. 6
Jyv
= -г.
+4(*-4^И
T*®ai
г2
■(«-**)
X
X
J>*(DC
B.83)
73
где ащуу = оуу!щЕТ0. При т = т§, когда край пластинки
охлаждается до температуры стеклования Tg, согласно B.75), B.72),
в затвердевшей части пластинки
2 (м\ -{-Mi )
2\ = i+e-Mi[r;-l-Le m *S+(Mi*-MC)l, B.84)
где
Mi* = Mi - Mi.; Mi„ = -^-; Mim =
olm
L =
а0Г0 7\H-1
Подставляя выражение B.84) в формулу B.83) и учитывая, что
т — тё — xlV, находим a^ на нижнем (х* = 0) и верхнем (я* =
= Z) краях затвердевшей части пластинки:
>уу \х*=о "- \
4
/п,_гЛ^1 - . ~-Ш-
D + Le
— В + е
Ш
то- A + Mim) -
мС
5+(Mi* - Mim) >5+ (Miw - Mi*) -f \D - LAe 8 m] x
* . / 2Mi +Mi
<4 U-, = </>* + /> m e
X 5+(Mi*-Mim);
2 -4
B.85)
£* +
1-
ML
X
Mi* \ Mi
X S+ (Mi - Mim)\ S+ (Mim - Mi*) + \D* - LA*e-2u,™+ms\ x
X S+ (Mi* - Mim), B.86)
где
D = e-meA{Tl-l); В = (l - -^
6 \ —Mi*
Mi
Л-5 +
Mi*
B*= 1 +
Mi*
6 \ —Mi
Mi
2 / 3
л* =
Mi* Mi*
l) - B*.
40 U
Рис. 25.
74
о s to ts и;
Рис. 26.
Полагая в формулах B.85), B.86) а2 == О, а0 = ас, а (Г) = ас,
находим температурные напряжения на нижнем и верхнем краях
затвердевшей пластинки при некотором среднем постоянном
коэффициенте теплоотдачи.
На рис. 25, 26 представлены кривые изменения безразмерных
временных температурных напряжений соответственно на нижнем
и верхнем краях затвердевшей части пластинки, вычисленные с
учетом зависимости коэффициента теплоотдачи от температуры
( ), а также в случае постоянного его значения, равного
0,02 кал/(см2 . с • °С) ( ) при Tg = 580 ~ 630° С, at =
= 95 • 1(Г7 1/°С, Е = 6800 кГ/мм2, v = 0,22. Кривые 1—4 на
рис. 25 вычислены при zg = 1,5; 2; 2,5; 3,5, а кривые 1— 3 на
рис. 26 — при Tg = 1,5; 2,5; 3,5 соответственно. Как видно из
рисунков, на нижнем крае (х* = 0) возникают временные
температурные напряжения растяжения, на верхнем — сжатия. При
учете зависимости коэффициента теплоотдачи от температуры
временные температурные напряжения существенно изменяются.
Более длительному промежутку времени, на протяжении которого
материал достигает температуры стеклования (больше ig),
соответствуют меньшие по абсолютной величине напряжения и
наоборот (как при постоянном коэффициенте теплоотдачи, так и при
изменении его в зависимости от температуры). Заметим, что
временные температурные напряжения, соответствующие
зависящему от температуры коэффициенту теплоотдачи, при тё <; тш
существенно превышают напряжения, соответствующие
постоянному (среднему) коэффициенту теплоотдачи. Если xg > тт,
напряжения, соответствующие переменному коэффициенту
теплоотдачи, приблизительно равны по величине напряжениям,
вычисленным при постоянном коэффициенте (последние даже несколько
выше). Изменение времени стеклования ig по сравнению с
интервалом тт, которому соответствует максимальное значение
коэффициента теплоотдачи, оказывает решающее влияние на величину
0уу при переменном коэффициенте теплоотдачи. Временные
температурные напряжения при %g < %ш в несколько раз выше а*уу при
75
Выражение для температурного поля B.79) при т = %g
принимает вид
Г* = [1 + *-6(Mr+MVG\H - 1)J S+ (Mim - Mi*) + {1 +
x5^(Mi*-MC). B.87)
Подставляя соотношение B.87) в формулу B.83) и учитывая, что
х* == т — тё = #*/У, находим напряжения на нижнем и верхнем
краях затвердевшей части пластинки:
6Mi*
ОуУ \X*=Q = — 1 е S (тт — т*) +
^-6Mi* __ 2
3Mi*
S(t*-t4I X
х(г;-1),-6^ + -1^
Ar,-Mig/,-Mi- + ^_,-Mi*\ +
+ 1^ + 1)Г6(Ш^)
M:
* I /ф* л\ —6 (Mi*+MiJff) с iJ ^*\ AT„— (Mi*+Mi„) w
2
X 5 (x* - tm)
Mi*
-Mi
m i о —Mi*4
iVe-™«(e m + 2e~m!) +
+ ^-(T«-\)e-mHi-e Ш1т)\ + М,
B.88)
где
TV = TH - 1
<^2 W»
Гт-1 2(Mi +MiJ
m' g'
a0T0 T* _ i
M = -4r (TV \e Wm (Mi; + 1) - e-Mil e-Mi* +
«2
Mi
+ -i-(r;-i)e-6Mi.
4-(*"+4-)- -]
При а (Г) = ac = const в выражениях B.88) следует положить
a2 — 0, a0 = ac. Если т = xg, выражение температурного поля
B.69) в затвердевшей части пластинки записывается в виде
Т* = 1 + /Vexp {- Mi* - 5 (Mi* - Mis) S(Mi3 - Mi*)}, B.89)
где iV = (Г,н ~ 1) exp (- 5М1з - 6Mig); Mis = ^-. Определим
вызванные этим полем температурные напряжения при ж* = 0 и
х* = I:
0*yV\x*=o=-N(C-2A-B); ayy|x*^ = - N (С + А + В), B.90)
где
С = exp I- Mi* + 5 (Mi*3 - Mi*) S (Mf3 - Mi*)];
76
А = —
3Mi*
Eе
-Mi, 5Mi, „,.
3 + e 3 + 6e-M' );
B " eS* [36 A + Mi*} e_Mi' ~ 5 FМз + 7) e_M'3 ~ '""'I'
При x > т5 выражение B.78) принимает вид
T* = iV exp [ — Mi* - 4 (Mi* - Mia) 5 (Mis - Mi*) +
+ 2 (Mi* - Mil) 5 (MiJ - Mi*) - 2 (Mi* - Mil) 5 (Mil - Mi*)] + 1,
B.91)
где N = (Г* — 1) exp [— 5Mig — 4Mis — 2 (Mi2 — Mil)].
Напряжения, обусловленные полем B.91) на концах затвердевшей
пластинки, записываются в виде
оУу\х*=о = N BА - В + С); <4 !*■«< = # (- Л + В + С), B.92)
где
Mi*
—Mi о
-5Mi
2+4Mi3
ibB8e 6+2e " й + le
- 2e~7Mii+2Mi2+4Mi3) _ -m\
■2Mi*+2Mi2-fiMi3
В
Mi*
24
25 -39
-ф- Mi*) exp (- 7MiI + 2Mi*2 + 4MiS) +
+ J^ exp (- 2Mi; + Ml + 4Mi*3) + (A. Mi*2 + ^-)
X
34
—Mi,
x exp (- 5Mi2 + 4MQ +1-g- + -f- Mi5) * ~3 U (Mi* +1) <гш J;
С = - exp [Mi* -f 4 (Mi* - MiJ) 5 (Mis - Mi*) +
+ 2 (MiJ - Mi*) S (Mia - Mi*) - 2 (Mi* - Mil) 5 (Mil - Mi*)].
Временные температурные напряжения, вычисленные по формулам
B.88), B.90), B.92), практически не отличаются. Расчеты
представлены на рис. 27. Напряжения на нижнем (положительные) и
верхнем (отрицательные) краях
пластинки вычислены с учетом
зависимости коэффициента
теплоотдачи от температуры ;(кривые 1) 2,б\
и при некотором среднем его
значении, равном 0,02 кал/(см2 . с • °С)
(кривые 2). Результаты полу- q \
чены при Tg — 600° С.
Совпадение временных температурных
напряжений, обусловленных -2,5[
температурными полями B.87), ° 2>5 5
B.89), B.91), свидетельствует об Рис. 27.
jTV
й
Ны
3
/
--" ■"'" "
—•—.
—■ .J
7,5 МГ
77
удовлетворительной аппроксимации зависимости коэффициента те»
плоотдачи от температуры в виде обобщенных функций A 2), A.9).
Напряжения растяжения (на нижнем крае пластинки) в несколько
раз превышают временные температурные напряжения сжатия.
Рассмотрим упругое полупространство при tu = const,
охлаждающееся средой также постоянной температуры tc = const.
Через поверхность полупространства (х = 0) происходит
теплообмен со средой по закону Ньютона, причем коэффициент
теплоотдачи, являющийся функцией температуры, резко изменяется в
некоторой температурной точке tm. Аппроксимируя его с помощью
дельта-функции Дурака, получаем
ап (tn) =a0 + am6 (tu — tm). B.93)
Учитывая, что температура поверхности полупространства tn
является функцией одной переменной tn (x, т) |т=0, и используя
известное свойство дельта-функции [13, 43], записываем
коэффициент теплоотдачи в виде
ап (т) = а0 + атб (х — тт)/| tn (тт) |, B.94)
где а0 = const; am = const; am ^> а0; tu (x) содержит только
простые нули (в данном случае — единственный нуль в точке
т = тш); tm — температура, которая достигается за промежуток
времени тт. В этом случае закон Ньютона с учетом формального
соотношения [43 ] / (х) о (х — а) = — [/ (а + 0) -f- / (а — 0) ] X
X б (х — а) описывается формулой
h -g- = а0 (t - tc) + ат (tm - t0) |(T/ ~ TJ- при* = 0. B.95)
С помощью уравнения теплопроводности вида
дН 1 dt
B.96)
дх2 а дх
и преобразования Лапласа [20, 21, 65] находим
* = (*о - *н) ierfc (—$=■) -ех?\-%*-(х + -£- ах) \ erfc f—х— +
а0УИ \| «m/a(*m-g Г 1 expf — ** )
+ h /I Xf|t'(Tm)| \Vn(x-Xm) У{ 4a(t-xm)j
У~аап
■ л ° ехр
х + -^- а (т — хт) \
h \ ' Я,
erfc ( —- +
2/a(T-xJ
+ а0|/а(ГТт) )\S+(*- тт) + tH. B.97)
'Н
78
Определяем tn (x) = tn (rm):
tn (lm) — (cc *н)"
У а
X erfc
—= ji- exp
V^aTm)
a%m\ x
B.98)
Подставляя выражение B.98) в B.97), получаем следующее
выражение нестационарного температурного поля:
t (х, т) = (*с — *н) J erfc / —у=А — ехР X" Г ~*~ ~ТГ ат)
Xerfcf-^- +^-У^)\+^Л
X
-^- exp I —~ атт 1 erfc
(-г-*
с н
-1
Уяч
-хАуФ^ех*(-^^)-^Гаехр[^(х+
+ -=-£- а (т — т^)
erfc
2/а(т-тт) ^
|2- "|/"а (х — тте)
+ *н
B.99)
где erfc (£) = 1 — erf (£). При постоянном коэффициенте тепло*
отдачи и ат = О, а0 = ап = const в B.99)
t (х, т) = (*с — *н) jerfc ( * ) — exp Г -~- (х +
+ ^г™
erfc
I7s+ttH) + '- <2Л00)
Квазистатические температурные напряжения в
полупространстве определяются по формуле
= °zz = fZT '(*»*)•
B.101)
Глава 3
ТЕРМОУПРУГОСТЬ ТОНКИХ ПЛАСТИНОК
ПРИ НЕСТАЦИОНАРНОМ ТЕПЛООБМЕНЕ
Температурные поля и напряжения
в анизотропных пластинках
Рассмотрим ортотропную неограниченную полосу-пластинку
(рис. 28) [32], через поверхности которой z = ± S происходит
теплообмен с внешней средой по закону Ньютона, причем
коэффициент теплоотдачи и температура внешней среды являются
произвольными функциями времени. На поверхности х = О задается
тепловой поток как произвольная функция координаты и времени
q (г/, Fo). Поверхность х = I пластинки предполагается
теплоизолированной, температура в начальный момент времени —
равной нулю. Для определения нестационарного температурного
поля в пластинке используем уравнение теплопроводности A.80)
в|безразмерном виде
Д,Г - Bi (Fo) [Т - Тс (Fo)] = -JL- C.1)
д¥о
и краевые условия
«t дТ
ОТ
х=0
-6G (У, Fo); -гг
дх
х=1
0; Г (ро^о = 0, C.2)
где Дг =
д*
+
оператор Лапласа; ух = у/Уку. С помощью
замены типа A.86), т. е.
r = e/(Fo), C.3)
уравнение C.1) и краевые условия C.2) преобразуем к виду
= — <?о (у» F°);
\х=0
дх
дх
\х—1
0; 0|fo=o = O, C.5)
где
Fo
/(Fo) = exp -J Bi(£)d£
<?o =
6q
^/(FO) '
0c(Fo) = Bi(Fo)rc(Fo)/-1(Fo).
Пользуясь интегральными преобразованиями Фурье и
Лапласа, решение уравнения C.4) при условиях C.5) записываем
80
в виде
6 =
-foo a-f-ioo
• QQ ch у (x — /)
ни
B;
^гРМ'
— оо СГ—гоо
у sh 7^
Fo
X
ш\п\ни\\\
х e-^+^ds + Г ecds, C.6)
Рис. 28.
где
-{-оо оо
<?0 = -L- j % j <?0 (у, Fo) е'вд- Forf Fo; у = jAyif + *.
" —оо О
Подставляя C.6) в C.4), находим общее решение нестационарной
задачи теплопроводности рассматриваемой пластинки в виде
Т = -Щ* Г dT1 f g.cbyfr-*) (TO+e ^
Bn)v«i ' '. ?9hY*
—оо (J—гоо
Fo
+ /(Fo)(ee(£)d£. C.7)
О
Возникающие в полосе-пластинке температурные напряжения
определяем по формулам A.148), записывая их в безразмерном виде
__ д2Ф _ д2Ф _ д2Ф
О'хх —
^2 » ^УУ- дх2
где Ф — общее решение уравнения
■>ху
ЬФ = -ок^--а: д2Т
L =
дх*
+ 2р
д*
дх2ду2
2 дх*
+ q-
ду*
1 ду* '
дхду '
2^12 4" Я6<
C.8)
C.9)
2а«
at ... at
/7 — U • ГУ* WX • ГУ* ~"У
я22 а22 * а22
Если пластинка свободна от внешней нагрузки, компоненты
напряжений C.8) должны удовлетворять условиям
ахх = аху = О при х = О, х = 1. (ЗЛО)
Согласно A.153)
*« = o<S/(Fo); <% = *$/(**<>); a*y = og/ (Fo), C.11)
где
^2Фо
0@):
1/У
д2Ф(
о
0<О):
ху
ху1
*ф0
&с2 ' «у да%
Учитывая C.3), решение уравнения C.9) ищем в виде
a> = ay(Fo),
6 6—1534 81
C.12)
где функция Ф0 удовлетворяет уравнению
^.--<ч^-«1-т^ C-13)
Fo
e0 = e-Jec(C)^. C.14)
О
Применяя к соотношениям C.11), C.13) и условиям C.10)
преобразования Фурье и Лапласа, соответственно находим
5S = - г)*фо; 5Й = #-; 25 = щ -#-; C.15)
грл1 "#- + дЛ = - Ъ -S" + airfB, C.16)
ds* ^ч d*2 ' ^ ' ° z d;r2
a^ = Оху = 0 при х = 0, х = Z, C.17)
где а#\ Ф0 — трансформанты Фурье и Лапласа функций ay, Ф0*>
Используя преобразованное по Фурье и Лапласу уравнение
теплопроводности C.4), частное решение Ф@Г) уравнения C.16)
записываем в виде
Ф&г) = Qe0, C.19)
а*т]2 — c^y2 —*
где Q = ^ __ 2^2р + ^4 . Общее решение Ф0 однородного
уравнения C.16) в зависимости от корней характеристического
уравнения
fi* — 2р|ха + g = 0, C.20)
как известно [2], имеет следующий вид:
а) если корни уравнения C.20) вещественные и неравные
(± jii, ± н.2, Mi > 0, \х2 > 0),
Фо = A ch цгх + В sh цхх + С ch ц2х + D sh ц2х; C.21)
б) если корни вещественные и попарно-равные (± jx0, |ш0 >> 0),
ф^ = (А + Вх) ch гHх + (С + Dx) sh V; C.22)
в) если корни комплексные (u. rb п; — М ± ^, М> > 0, г > 0),
Фо = (A cos цгх + 5 sin т]гх) ch ц^х +
+ (С cos цтх + Z) sin цгх) sh %#, C.23)
где r\t = |jti jr| |; ц^ = £ \ц |; i = 0, 1, 2. Определив постоянные 4Г
В, С, D в соответствии с C.15), C.17) и трансформантами Фурье и
Лапласа температурного поля C.18), можно найти выражения
трансформант температурных напряжений.
82
[ C-24)
Случай «а»:
Ж = - Л^о I AT1 (Л, ch щх + D2 sh цгх + Ds ch ц2х +
+ D4 sh т]2я) + ch у (х — /)];
a^ = ОД 0 {AT1 hi (Dj ch %x + D2 sh т^) + r| (Z?8 ch V +
+ £>4 sh г|2я)] + Y2 ch у (x — I)};
o(®> = iv\QR0 {A-1 [% (Z?! sh %х + D2 ch tjjz) +
+ ?]2 (Z?a sh rj2a; + Z>4 ch T|2x)] + у sh у (я — I)},
где
Л° = vshV ' D° = 2и1М* (Ch %/ °h %Z ~ ^ —
Dx = [i2 ch yZ [|i2 sh r^Z sh rJZ + [xx A — ch цх1 ch t]2Z)] +
+ -щ- sh yZ (\ix ch T]XZ sh r|2Z — \i2 ch y]2Z sh %Z) + ^^ (ch y]^ — ch rJZ);
Z>2 = ji2 ch yZ (fxu sh т|^ ch iq2Z — j^2 sh yJZ ch %Z) + —^- sh yZ [ji2 x
X (ch ti-jlZ ch r\2l — 1) — \хг sh r\2l sh r^Z] -f- |ы2 (fx2 sh %Z — ^ sh r^Z);
ZK = jj,x ch yl [ji2 A — ch %Z ch r|2Z) + Hi sh r|2Z sh %Z] +
+ --r-r sh yZ (|i2 sh r^Z ch r]2Z — Hi sh ri2Z ch %Z) — fx^ (ch %Z — ch r\2l);
У
D± = jbtx ch yZ (ji2 sh r\2l ch T)XZ — Hi sh t]1Z ch tj2Z)
ИI
shy/ffx^l
■|i2shri2Z).
— ch цг1 ch T]2Z) -f [x2 sh %Z sh T]2Z] -f jix (|хх sh r]1Z
Случай «б»:
с4°х} = Л2^ {ch У1 [ch г]0ж + 2Z?io (I — x) ch T]0«r —
— ch t]0 BZ — x) -f r]0 BZ — x) sh y]0£ — #% sh t]0 BZ — x)] +
4- 7 sh yl [2y]0Z (я — Z) sh ц0х + # ch % BZ — ж) — x ch %#] —
— 2 [(sh %Z + t]0Z ch tHZ) sh %# — r\0x sh T]0Z ch rHx —
— г\Цх ch Y]0 (Z — #)]} — rj2Q0 ch 7 (Z — a:);
a^ = —- QQS }r|o ch yl [21 (I — x) rjo ch r\Qx — ch r\Qx —
— BZ -f- x) % sh yi0x + ch % B1 — x) — a:ri0 sh r|0 BZ — ^)] +
+ y sh ylr\0 [2lr^(x — I) sh r\Qx — 2 sh r\0x + rj0 DZ —- ^) ch ц0х —
— 2 sh % BZ — x) + xr\0 ch rj0 B1 — x)] + 2т|§ [sh щ1 sh tj0 я? +
+ | tj ((x — Z) sh т|0/ ch r]0«r — /% sh rj0 (Z — ^) +
+ ^Zr]2 ch гH (Z — x)]} + £20Y2 ch у (x - Z);
6* 83
C.25)
Q{xy = — ir\Q0S {r\2 ch yl [2x\0l (I — x) sh rj0 x — x ch туе +
+ x ch r\Q B1 — x)] + у sh 7/ [% B/ — ж) sh r\0x +
+ 2Zr]g (# _ i) ch т]0^ — ch r\0x -f ch T]0 B1 — x) —
— xk}0 sh T]0 BZ — .z)] + 2тт| [(x — Z) sh r\Ql sh r]0;r —
— х1ц0 sh т]0 (Z — x)\) -j- ^0t]y sh y (x — Z),
где
(а|Л2 - а|т2) R0
Q0 =
G2 ~ Л0J
$fto) = [2(Ti§P-shVl
-1
Для случая «в» в выражениях C.24) необходимо положить
\i± = \х + п, |ы2 = fx — п. Для получения общего решения
задачи термоупругости полосы-пластинки, соответствующего
произвольному изменению в зависимости от времени коэффициента
теплоотдачи и произвольной зависимости от координаты у и времени
теплового потока, заданного на крае, следует в C.6), C.24) и
C.25) перейти от изображений к оригиналам и полученные
выражения для В, 0$ подставить соответственно в C.3) и C.11).
Пусть граничное значение теплового потока есть
периодическая функция координаты и асимметричная единичная функция
времени, т. е.
q = q0 cos ®yS+ (Fo), q0 = const. C.26)
Подставляя равенство C.26) в C.18), C.24), C.25) и переходя к
оригиналам, находим
Q = 6q0 cos щ г ,-i ^ ^©«fyCFo-ug, /
^ о' ^
где Ф (и, и) — тэта-функция.
Случай «а»:
I — х
1
@)* _
— CD'
А
— (D\ ch щх + ^2 sh co^ + />з ch щх +
+ #1 sh аJ£) + ЛГ
g*;
С C.27)
47 = -гг И (Я1 ch со^ + ^2* sh со^) + ш1 (ZM ch щх + i C.28)
^0 -
+ Z)Ishco2a:) + iV;]g*;
0^* = [сог (DJ sh щх -f- #2 ch са^) -f co2 (£>з sh cd2# -f
+ DUh<o2z) + N'x](q*)'y,
84
где
ai!" =
d; = d<
0|Tli=©it
Z)j = jli2 [ja2 sh cDj/ sh oJl -f px A —- ch C0j/ ch o>2Z)] N |x==0 —
— со-1 (\xx eh coj/ sh co2Z — ju2 ch co2Z sh coxZ) i¥x jx==o +
/?2 = |i2 (ux sh o)^ ch oo2Z — ji2 sh co2Z ch cox/) N \x==q —
— (o-1 [[Li2 (ch (x)xl ch o)aZ — 1) — \хг sh cd2Z sh сог/] Nx |x=0 +
+ ji2 (|i2 sh GJZ — [Ax sh щ1) N |x^;
Dl = (x1 [pi2 A — ch щ1 ch co2Z) + щ sh co2Z sh coxZj N |x=o —
— со-1 (|i2 sh (ог1 ch co^ — fij sh co2/ ch щ1) Nx \x==q —
— fijji^ (ch coxZ — ch a2Z) iV Jx==r5
^4 — j^i (Щ°h ^l sh °M — I1! sh o)xZ ch co2Z) N |ж=о +
+ со-1 [ jix A — ch щ1 ch co2Z) + \i2 sh ^V sh ЩЦ N'x \x==o +
+ Iх! (l^i sh &>iZ — \x2 sh co2Z) iV |x==;;
> (s_v Fo ~ D - ф {s2, ro — g ^ а * = X
g0
Po
N--
(si ~ h)
7@ ^ g "
Ф («i, Fo) =
Случай «б»:
Si,2 = (o2(p± Yp2 -
Po
exp l(Si ~0J/c )Fo] \ #
6
i = l, 2.
e);
/ — a:
11
Si4;
T@)*
= co2<5(co0) {coo [ch co0,r + 2to0 (Z — #) chщх ■
— ch co0 B1 — ж) + oH BZ — ж) sh со0£ — хщ sh co0 BZ —
— x)] M |xs=0 — [2co0Z (x — Z) sh (xHx + # ch щ B1 — x) —
— ^crch щх] Mx \x=q — 2 [(sh w0l -\- щ1 ch co0Z) sh щх —
— щх sh (o0Z ch co0«r — щ1х ch co0 (/ — x)\ M \x=i) g* ~ wWg*;
aiS' = — $ (шо) {©о [2^ (Z — x) coo ch co0a: — ch щх —
— B1 -j- a;) co0 sh щх + ch ш0 B/ — ж) -~ a? co0 sh co0 B1 —
— x)} M |x==o + [2 sh щх + 2Zcog (Z — ж) sh o>0x — щ DZ —
— ж) ch щх + 2 sh co0 B/ — x) — дхо0 ch 0O B/ ~ x)} M'x |x==o +
+ 2co§ [sh co0/ sh co0^ + щ (x — Z) sh co0Z ch oH/ — 1щ sh c»H (Z —
-x) + xl<& ch co0 (Z - s)] M |x==^} g* + M"xq*;
85
И3
с4°у* = S (co0) {coo !2co0Z (I — a;) sh щх — х eh co0^ -f ж с1! со0 B/ —
— х)\ М |х==0 — |со0 B1 — х) sh со0£ + 2/соо (ж — 1) ch оз0х — ch co0x +-
+ ch (o0 BZ — ж) — ш0 sh co0 BZ — ^r)J Мх |Хв0 + 2соо [(# —
— Z) sh co0Z sh со0 ж — х1щ sh со0 (Z — а;)] М \x=t] (q*)y — М'х (q*)'v,
где
[— а* + (а*1©2 — об2(Оо) (Fo — £ ■
о
М =
Ш
I
о
Подставляем теперь C.20) в C.6), а затем в C.3) и получаем
решение задачи теплопроводности полосы-пластинки, граничное
значение теплового потока которой имеет вид C.26), а температура
среды, омывающей ее боковые поверхности, и коэффициент
теплоотдачи с этих поверхностей — произвольные функции времени.
Температурные напряжения, обусловленные этим температурным
полем, находим, подставляя формулы C.28), C.29) в соотношения
C.11).
Общее решение задачи теплопроводности и термоупругости
полубесконечной пластинки можно получить с помощью предельного
перехода в формулах C.27), C.29) при / ->- оо. Если значение
теплового потока, действующего на крае х = 0 полубесконечной
пластинки, задается в виде C.26), то вместо C.27)—C.29)
получаем
Fo
0 = 8д0 cos ыу С ехр [- feyoJ (Fo - Q]
о
Случай «а»:
0@)* = оJ ( Г— (е-®.* — е-»!*) N'x L=o —
- ((X2e-».* - ще-**) N |ж=0 1- N\ q*;
C.30)
o«»* =
w i ц, — fig
[щщ {\Kie-^x - fi2e-»^) N\x=0 +
+ (ffl^e-"»»* - a>j|V-««*) #я |a=0] + iVK 5*;
<C = - {[(соЛе-<^ - щ^е-»»*) # |x=0 +
} C-31)
где
Ро
N:
(p(sb Fo-£)-q>(sa, Fo-g)
d£,
<p (sit Fo) =
T^i
(*i-*t)/@
Случай «б»:
<tS* = со2 {[A + a»0) ^ l*-o + *Л*х |x=01 *_и°* - М\ g*;
oS* = {- % [©o K* - 1) M jx=0 + B - хщ) М'х |ж=о] e~a«* +
+ M"x) <?*:
o£}* = - {\<*lxM |x=0 - (co0* - 1) M'x |ж=0| e-*°x + M'x) (q*)y, )
C.32)
где
M
Fo г
= f (ajco2 - a*0H2) (Fo - J - -Ar~) erf (co0 УШ=® _ a» +
+ AH^
^G)*(Fo-£)
«Dg-^ffl^CPO-O ^
/(E)
Подставляя выражение C.30) в уравнение C.7), при I ->• оо
получаем решение задачи теплопроводности полубесконечной
пластинки. Температурные напряжения, обусловленные этим
температурным полем, находим, подставляя значения C.31), C.32) в
соотношения C.11).
Исследуем влияние ортотропии и коэффициента теплоотдачи
на температурные напряжения в полубесконечной пластинке,
изготовленной из стеклотекстолита КАСТ-В [2]. Корни
характеристического уравнения C.20) для такой пластинки вещественные и
неравные: (% = 1, fx2 = 0,83. Предположим, что коэффициент
теплоотдачи изменяется в зависимости от времени по
экспоненциальному закону [16], т. е.
Bi (Fo) = Bi0 e~KFo; Bi0 = const, К = const.
C.33)
Используя формулы C.11), где а{ц имеют вид C.31), и учитывая
значения C.33), при х = 0, у = 0 находим
г
о L
-*ifi
УК
И-1 г*2
8|*2-1
exp
87
2^_е-МA_ехС)!
dt. C.34)
где оу = Оуу \х=о1У=0а)Х1/д0ахЕу8; г = ау1а!х\ В^ = Bi0co 2; F = со2 Fo.
В случае изотропной пластинки из C.34) следует
оу = J 12 erfc "Кё -
о *-
*-Е
V4
ехр
_£**-« (l_eXE)
d£, C.35)
где ау = Оуу \x==o>y=Q(£>Xt/q0atE8. При if = 0 (постоянном
коэффициенте теплоотдачи [28]) из C.34), C.35) соответственно находим
1 — ей? F(m,?-b -ft,,) л /.-
а„ = - - о _ — * * * у erfc (|ч К^) +
+
(И-i — И*) ОЧ — ^о:
1 — в|4
(И-i — М-г) (^| — 5о ~
■V
/(^B-verfc(^2^) +
+
[1 - 8 B?Q+ у] {erf (YiPn + ку)F) [|x^2 + £w + у -)/ 5tt+^ (^+щ)}
0*1-я*-У 0*1-**
У)/"^о) + ^
Ог, =
2
5,.
2/^co + l
C.36)
erf (У(В@+ \)F) - <TB@jFerfc (j/^)
По формулам C.34)-
C.37)
-C.37) при Вш = 1; 5 рассчитаны
напряжения av, результаты представлены на рис. 29 (кривые 1,2 —
соответственно К = 1; 0). Как видно, при учете ортотропии
материала пластинки и зависимости коэффициента теплоотдачи от
времени температурные
напряжения увеличиваются. Если
коэффициент теплоотдачи
постоянный, то температурные
напряжения достигают
максимального значения при малых
значениях критерия F в изотропной
( ) и ортотропной ( )
пластинках, а если он
изменяется в зависимости от времени,
то — только в изотропной
пластинке, в ортотропной
напряжения достигают максимума при
стационарном тепловом режиме.
Найдем общее решение
квазистатической задачи
термоупругости полубесконечной
ортотропной пластинки. Тепловой
поток, которым она нагревается
по краю х = О, является
функцией координаты и времени.
0,8 1,2
Рис. 29.
Предположим, что температура среды, омывающей боковые по-
верхнооти пластинки, и начальная температура равны нулю, а
коэффициент теплоотдачи с поверхностей z = ± б зависит от
времени.
Для определения обобщенного плоского температурного поля
в пластинке из A.78) и A.77) с учетом A.194) получаем
следующие уравнение теплопроводности и краевые условия:
Я2° +*„-S—^ C.38)
дх2
ду2
д¥о
%*-дх~
х=0
-gB/,Fo)r1(FoN;
C.39)
e|Fo=0=0. C.40)
Применяя к уравнению C.38) и соотношениям A.195)—A.197)
интегральные преобразования Фурье по координате у и Лапласа
по безразмерному времени Fo при условии C.40), соответственно
находим
0 = Qe-v*;
Ъ -В ^
дх2
ц2в^0 + щЬ0-
дх
дх
C.41)
C.42)
й4ф„
О 2 д2ф0 . 2 ?Ъ б6
дх4
s- — 2тJр
дх2
дх
дх2
+ ц2д^о = — щ®&
:@)
= G[Bn^--i^Bn
Уо)-г\2В0
дх
+
+ *\BnG%-
Рпё;
5<°> = G (я„ -£§*- + *rf ад,) - й#, ^J- +
+ r\2B22G^--^2Q;
дх
C.43)
C.44)
;<о)
*ху
где
Oacv = ^
to»
<?¥„
&г
з (ч, *) б
to2 /J' j
C.45)
/ (О ^Y ''WIT'
F(tj, s) = —Lr- f е{^£?г/ l" ^(г/, Fo)e-^°dFo.
У2я J„ n'
89
Общее решение уравнения C.43) имеет вид
ф0 = Ае-ъх* + Be-w _ Q^ye-v*, C.46)
а частным решением уравнения C.44) является функция
% = -щ^0е~у\ C.47)
Q
где <?0
; т|;. = (i;-1 г) | (/ = 1; 2); ± и., — вещественные
1>4 — 2pr[2v2 + qrf
и неравные корни уравнения
и.4 - 2pfi2 + ? = 0. C.48)
Рассмотрим два случая закрепления пластинки по краю х = 0.
1. Пусть пластинка закреплена по краю х = 0 и свободна от
напряжений на бесконечности, т. е.
й0 = Ъ0 = 0 при х=. 0; о^ Uco = ° & 1 = *; »)• C-49)
Определяем постоянные интегрирования А и В, входящие в C.46),
и находим такие выражения трансформант напряжений и
перемещений:
гу^цЛФл
I4I
+ y40))
£-т),* _ ^^2
Ь1(Л*Ск»8 + «^0))'
<C = 5MGJV {%иГ [Yu.A (tMU) - v» 6Ц) - | т] | Ь, (т]2Ссой + { C5())
+ 72@<°))] e-ч.* - t|,|if [YjiA (tJcoO - fCcoJ - | л | b, (t)*G©2 + '
+ yM0)I е_Г1гЗС} + Y2^e-^;
a@) = _ jT)GiV522 {uf [7fx260 (T,2cof - fGMl) - | n 16, (тJ&о, +
+ v2©<°>)] в-ч.* - u.<<» [Wl&0 (rfcof) - 72GcoJ — | Л I *x (*12£«>2 +
+ у2©'0))] е-^*} — irjTfie-vx;
u0 = N {bx [y\xj>0 (rf©|0) - Y2GWl) - | Tj | 6, (rf Gco2 + ^
+ 7H0))l е~^х ~ b* fYI*A (*lM0) - -fGuJ -\1\\Ъг (r,2GoJ +
+ Y2o>«»)] е-1!'*} + <?oY(n2®(i0) - Y2G4) е-чх;
y0= iti^bJuj
+ Y2<40))
-j^- bofi2 (Ti2©f) - уЮщ) - b2 (r]2Gco2 + I C.51)
e~^x — jut2
щ- *№i ОтЧ°> - Y2G«x) - К (r]2G(o2 +
+ Y2»^) I е-1!»*} + jt)(?0 (tJGco2 + Y2(o(t») «-*«,
90
где
'V = <Л !(Ц, - Щ) (■%> + G|xlMj) bj-1: Q = <?0£2 (a,V - alf)
cof = Я 2
<> = «f
E,
a{+o|iv1--J-);
b,- = 5„ - G^; A,- = G (v2 + |^) - E2; fif) = 1 + tyv " / = 1; 2
2. Пусть пластинка свободна от внешней нагрузки, т. е.
aS = о^у = 0 при ж = 0; а}?} I*-*, - 0. C.52)
Выражения трансформант напряжений и перемещений
записываются в виде
1@)
Т]2Й
1
f^i — И-2 \ \ I Л I
V
ji2U-^x
1 hi
(ij e~^x
1
— e-v* ;
Hi P2
— (Y — 4i) h^-^l - y2e~yx
1
} C.53)
a^ = ivfcl j-
Ha — H*
f(Y ~ %) М""Л1Х - (V ~ %) IV'11*]-
u0 = QM [Ьг (h J nf + w*4) e~^x ~ &2 (I % I Hi0) +
+ YMi) ^*1 + <?oY (Л2Ц0) - Y2G%) ^"vx;
^0 = 1фМ\ j ^ (i4°> + j^p e2u.2) *-%* -
+ ^o№J +
} C.54)
~ ^2 (^
'Р)+-|^вЛ/*-ПвЯ
+ 7аЦ°)) e-v*,
где М = A — vxv2) [fxl(x2 (^ - н.2) (^^Vi - G£8vi + GE^]; e,- =
Для получения общего решения квазистатической задачи
термоупругости закрепленной или свободной ортотропной пластинки
следует перейти в C.41), C.50), C.51), C.53) и C.54) от
изображений к оригиналам и подставить полученные значения в A.194).
С помощью предельного перехода при \i± ->- ji2 = jx в выражениях
C,50), C.51), C.53) и C.54) находим решение задачи для случая
равных корней уравнения C.48). Если корни уравнения C.48)
91
комплексные, то в решении следует положить fJi = fi + r/, ji2 =
= {ш — ri (jlx >> 0). Полагая в данном решении Bi (Fo) — const,
получаем общее решение задачи для случая пластинки с
постоянным коэффициентом теплоотдачи [35].
Пусть на край х = О ортотропной пластинки действует
тепловой поток
q (у, Fo) = qQ6 (у) б (Fo); q0 =-» const, C.55)
т. е. следует найти фундаментальное решение задачи. Подставляя
C.55) в C.41), C.50)—C.54) и переходя к оригиналам, с учетом
A.194), получаем фундаментальное решение задачи
соответственно для случаев закрепленной и свободной пластинок. При
этом
go/(FoN
ехр
1
4Fo/c
(у2 + кух2
у
C.56)
Выражения напряжений и перемещений, возникающих в свободной
от внешней нагрузки пластинке, при действии теплового потока
C.55) имеют вид
охх = К
1
Ml — 1*2
•*11 *12 1Ы
/2] + /22--^ЯП + ЯГ2 + I
Mi
+ #il - -£. Я21
Gm, — К
Jyy
1
М<2
± (яй - #й) - -J- (я£ + #г2)
1*1 G11 — hi) + 1*2 GИ - 712) —
Hi
- М1ц2 ЯП - Jii #Г2 - -^ Яг! + Нгг
+
Ml
т±
И2
щ\+\ ец|+1
+
(#22 — #22)
е (И>1 - и!)
I4FO
ехр
1
4Fo^-(V2 + ^2)
а,, = if {-^4^- Il*i (рй - i>a - Я22 + Я.л) +
} C-57)
1
Vf^^-^^j + ^fi-^-
~~ ih НЦ + bi^4 (уй"~^ + 6#A ^" T12)
2
Щ+'
92
v = КМЬ0 {ц1И2 \г2 (Р\{ - P'2l) + е, (Р;2 - PSj)] - } C-58)
™2 + «^1 /г+ s r_^ т2 + ш*и| ,
L Mepf + l)
(£Й + LIT) -
где
£ =
И* (ем-2 + 1)
6g0^2^i
(£22 + £22)
л/ 2 9 /(Fo);
/г? = Fi%j
\k§x—iy\ 1 р.х + iy
/2 Fo x.
я5 = |/А^фад2 —
n=0 V
ft
2n+l
+ 1)!! ^+3/2
*oV>-
]/ Fo x,
± [i.x — iy
-2n—3
/2 Fo k.
+
, ± Д>е + iy
+ f±Z)_2n_3'
У г Fo &y
Pj = — iFwu
Ш
±lijx—iy \ ( ± p.x + iy
|/ Fo xz
2n-f-l
/2 Fo x,
Мчя — iy
ь,— У± *.*т2BЛ'т^>. [^Мтшк)~
- l|$#-2n~3
Hf + II/
V2Fokv
Hb-Y^Ffill^ —
^n+1
n=0
+ \|)+ZL_2n-2
Bm+1)!!^+1
jx^ + ty
*5J^
•2n—2
Ц-Х — iy
/2 Fo ky
+
Yl Fo Ay
± цл — iy
v5 - 2^,фгЦ^, +^,(^L)j:
PJ--2^/Fox,фу
j^z — iy
/2 Fo xz
©1 = -fr — w8; ^1 = j- A + ev2);
ft
r* 1/ 2 .„ ^ ft | l3:n / ±^ — W \
93
-f±Z)„2n-2
IQJ
\ У 2 Fo к
®l=mi--G-
Щ = -щ-(ь + vj;
ц.х
Ft
E\X2r
1
4 Fox
щ = ку-у% Фц-ехр^ j8FqX; j; ^ = exp^±T^-j;
/
Z, /=1; 2; <p0i = q>0- L 0
4>S =
*«li*i-o-
Рассмотрим неограниченную ортотропную полосу-пластинку,
через поверхности Z = ± 1 которой происходит теплообмен с
внешней средой по закону Ньютона, причем коэффициент теплоотдачи^
температура внешней среды являются некоторыми функциями
времени, удовлетворяющими условиям для преобразования Лапласа.
Торцевые поверхности х = Zi, х = 12 пластинки
теплоизолированы (рис. 30).
Предположим, что пластинка нагревается системой мгновенных
равноотстоящих источников тепла, расположенных вдоль оси у
(начальная температура равна нулю). Возникающее при этом
нестационарное обобщенное плоское температурное поле определяем с
помощью дифференциального уравнения теплопроводности и
краевых условий [18]:
ДХГ - Bi (Fo) [T - Ts (Fo)]
дТ -<?06H6(Fo) *
dFo
2c
дТ
дх
+2 2 cos v™y '•>
m=l /
-0; r|F0=
о
0,
1 +
C.59)
C.60)
где <?0
w*
2\t& '
X—li, X——1%
с — полурасстояние между двумя соседними
источниками тепла; vm = ; Zx, Z2 — составляющие ширины
полосы-пластинки. После подстановки C.3) уравнение
теплопроводности C.59) и краевые условия C.60) принимают вид
А18=tw - ^б {х) б (Fo) 4~ A+2 5 c°s v-H -е* (р°)' (з-61)
2с
ее
дх
x=lti x=—l2
Рис. 30.
0; 6|Fo=o = 0,
C.62)
где 9S (Fo) = Bi (Fo) Ts (Fo)/(Fo).
Используя интегральные преобра-
94
зования Фурье и Лапласа, решение уравнения C.61) при
условиях C.62) для симметричной (k = /2 = I) и несимметричной
AХ = I, 12 = 0) задач находим в виде
где
в£
6с = Во |Bi=o + 6Г; 8Н = во |Bi=o + 9r> C.63)
°° —kvvmFo \
+ 2 * cosvmy;
™— А !
-тП, . / ж Fn х / 1 ~ -feo.vi Fo
е~*Ш<?о А / * Fcm / 1
0 2/с 3\ 2/ ' I
Fo
вг = I Qs (£) dt;, 0o = 2Эо — известные [51 ] решения для симмет-
6
ричной и несимметричной задач при постоянном значении
коэффициента теплоотдачи и температуре среды, равной нулю;
#3 (и, v) — тэта-функция. Подставляя C.63) в C.60), получаем
решение симметричной и несимметричной задач теплопроводности
ортотропной полосы.
Температурные напряжения, возникающие в полосе-пластинке,
определяем по формулам C.11) — C.13). Если пластинка свободна
от внешней нагрузки, компоненты напряжений должны
удовлетворять условиям
вхх = Оуу = 0 при х= lv х = — Za. C.64)
Применяя к формулам C.63) и уравнению C.13) преобразования
Фурье и Лапласа, получаем уравнение для определения
изображения функции напряжений с учетом преобразованного
уравнения теплопроводности C.61). Общее решение такого уравнения
совпадает с приведенным в работе [51 ] при Bi = 0. Определив
необходимые постоянные в соответствии с C.8), C.64) и описанным
общим решением, получим выражения трансформант в$.
Положив в этих выражениях h = Z2 = I и h = I, 1% = 0 и перейдя от
изображений к оригиналам, после подстановки их в C.11)
получим указанные решения симметричной и несимметричной задач.
При предельном переходе, когда с ->• оо, получаем формулы для
определения температурных напряжений в ортотропной полосе,
нагреваемой действующим в начале координат линейным
источником тепла
В случае нагрева полосы-пластинки равномерно
распределенным источником тепла интенсивности w\ = б (х) S+ (Fo) решения
симметричной задачи теплопроводности и термоупругости при
переменном значении коэффициента теплоотдачи с поверхностей
Z = ± 1 имеют вид
Fo Fo—t,
r = /(Fo){-l-J exp[ J Bi ©<$]<>,(-£-, -§r)rf£ + e'}; <3-65>
95
Fo
x. „ Fo—£
°^ = --£-/<Fo)Jexp[ J Bi©*
0 L 0
a&*
X
X
Г
-fr^1
С
C.66)
где @* = д/2Хьх; e = aylax. Переходя в C.66) к пределу при I ->-
-> оо, получаем решение задачи термоупругости бесконечной орто-
тропной пластинки, нагреваемой плоским источником тепла вдоль
оси у, в виде
iFo Fo—t
При Bi
о u о
const формула C.67) принимает вид
8
C.67)
Jy
4J/Bi
_ е\х\ vm erfc
е-\х\ /Bi erfc / _i£JL
\ 2yrFo
"[/"Mi) -
2/Fo
+ ]Ali
C.68)
Пусть пластинка толщины 26 = 4 • 10 м изготовлена из
стеклотекстолита КАСТ-В [2] со следующими характеристиками:
ап = 0,518 • 10~10 м2/н; а*х = 3 . 10~5 1/° С; а\ = 4 . Ю 1/° С;
а22 = 0,749 • КГ10 м2/н; ах = 0,196 . 10~8 м2/с; %1 = 0,209 X
X 10~2 вт/(м • ° С); ^ - 0,335 • 10 вт/(м . ° С). В условиях
аэродинамического нагрева изменение коэффициента
теплоотдачи в зависимости от времени можно представить в виде известной
кривой, изображенной на рис. 31 (—) [1]. Эта кривая
удовлетворительно аппроксимируется ( ) функцией (в безразмерных
величинах)
Bi (Fo) = d ¥obe~k Fo, 0 < Fo < 0,353. C.69)
Подставляя C.69) в формулу C.67),
получаем
/Fo ,
ay = --JL_ J exp{-60[v(b + l;
*/
/2
в\
4\
в
W'1
//
11
//
//
//
//
//
//
//
II
И
f
' t
7"
>
<
t 6
«^ I
1
I
1
Т/Г*
kFo) — y(b + l; A(Fo
е2)I-
к
С
C.70)
Рис. 31.
где Ъ0 = d/kb+\ Ъ = 1,3; d =
= 0,67234-104; к = 10,2. На рис. 32,
33 показано изменение напряжения
оу, рассчитанное по формуле
C.70) соответственно при х = 0
и в зависимости от безразмер-
86
-/?,
У
008
0,06
ОМ
0,02
0
_
//
^2
0,1 0,2 0,3 Fo
Рис. 32.
ной координаты х при Fo = 0,04
(кривые 1\ кривые 2 — изменение
напряжений в изотропной
пластинке при ап = а22 = 0,749 X
X 1(Г10 м2/н;
-0,08
-0,0$\
-ом
-0,02
^\
N
W
_^2
#Ztf 0,i DJ5
Рис. 33.
«*
а*
а«
3 • 10~5 1/°С; Л£ = ^ = 0,209 х
X 10~2 вт/(м • °С)). Видно, что при учете ортотропии материала
в случаях как изменяющегося в зависимости от времени, так и
постоянного коэффициента теплоотдачи температурные
напряжения увеличиваются [47], во всей области они сжимающие и при
Fo = 0,353 достигают значения —0,102.
Рассмотрим тонкую полубесконечную анизотропную пластинку,
которая имеет либо ось симметрии, либо плоскость зеркальной
симметрии, к которой нормальна ось Z. На крае х = 0
пластинки задан тепловой поток как произвольная функция координаты и
времени q (г/, т). Через боковые поверхности Z = ± 1
пластинки происходит теплообмен с внешней средой нулевой температуры
по закону Ньютона. Начальная температура принимается равной
нулю. Пусть в пластинке нет источников тепла. В этом случае,
как следует из A.80) при L A.41), W = 0 и tc = 0, нестационарное
температурное поле в пластинке определяется с помощью
уравнения теплопроводности [17, 31]
г 7 д*Т U- /Т7^\ Т дТ
д2Т 9, дЧ
ду*
C.71)
дх* ' ху дхду
и краевых условий A.77), т. е.
q{y\¥o) б = 0 при х = 0, Т l^oo - 0; C.72)
дТ . , дТ
дх
и
Г|Ро=о = 0, C.73)
где кху = кУкгц. После первой подстановки A.86) уравнение
C.71) и краевые условия C.72), C.73) принимают вид
Л2° . 97, ^8 ■ и дЩ m . П7£\
_сЮ_ , ,. дд
дх
0 |fo=o = 0»
dFo
-S-+**v-^- + ^ <»• F°) = 0 при х = 0, 6 \х^ = 0; C.75)
C.76)
7 6—1534
97
где
Fo
6(y,Fo) = ^''^f ; /(Fo) = exp|-f Bi(Qdd. C.77)
k^J (ГО) | J j
Применяя к C.74) и к первому условию C.75) преобразования
Фурье по координате у и Лапласа по Fo, получаем
2b^r-(kyrf + s)Q^0; C.78)
dx2 dx
_|_ _ Ье + 9 = 0 при х = 0, C.79)
где
4 +00 °°
9 = —^==- ( eiT"tfff \ Qe-sFodFo; C.80)
-f"°° (T-f-ioo
0 = —L— Мл \" ee-iw+sFo^. C.81)
—oo G—гоо
Выражение трансформанты функции температуры находим из
C.78) при условии C.79) в форме
0 = Q<r*(v-b), C.82)
где Q = Qy~l\ у = |/"s + т]2 (Ау — &2y); 6 = jr^. Подставляя
C.82) в формулу обращения C.81), а затем выражение функции
0 в A.86), получаем общее решение задачи теплопроводности
рассматриваемой пластинки
-f-oo G-J-гоо
т =
/(Fo)
^7 J di\ j Q exp [— x (у — b) — щу + s Fo] d*. C.83)
Bя)
—oo G—гоо
Для определения возникающих при этом квазистатических
температурных напряжений используем формулы A.155) и уравнение
A.156). Применяя к ним преобразования Фурье и Лапласа,
получаем
5^ = -Л; af = #-; ЗЭ-fti-g-; C.84)
{-&- + 2Р°^ -£r ~ 2K -£ 2Я0Щ3 -&• + <?П4) Фо =
= ~ к 4г + <Л 4- - Л3) в, C.85)
У dx2 ' «У • &
где
1*
F0a22X,11 a12 a22
98
%
2gl2 + Дб|
Zttoo
J4^, <»-£&-; *= const.
Если корни характеристического уравнения
u4 - 2Poit3 + 2№2 - 2qolx + q = 0, C.86)
соответствующего однородному уравнению C.85), не равны,
трансформанты функций а\} (i = х, у), т^у свободной от внешней
нагрузки пластинки имеют вид
1
Й^-чМ
е—гц,х
Ц1 — Ц2
+ i(y — b)] +e-*(v-b)|.
[Ъ + ЧУ-Ь)]-
~гт12х
Л1 — Л2
t% +
%-л2
Ai\2 — i(y — b)] —
+ г G — 6)] — i (y — b) е-х(У~ьА;
%*"
-IY\2X
ni — Л2
hi +
} C-87)
5f = л
[т|, + * (V — b)l +
gg-iih*
Л2 — *)l
m-^2
[% +
+ /G-6)]+(Y-6J^(v~b)J,
где
A.
-Qn
1\* + *Щ*ху(У-Ь)-а?у(у~Ъ)*
(Y - Ъ)* - 2p0i*l (V - bK - ^2 (Y - bf + 2g0JT]3 (Y - b) + grj*
Ц,-^; <?<> =
hi
4C6
<?; rji = ли-
Переходя в C.87) от трансформант к оригиналам и подставляя по*-
лученные выражения в первое из соотношений A.153), где / (Fo)
имеет вид C.77), получаем общее решение квазистатической
задачи термоупругости анизотропной полуограниченной пластинки при
нестационарном теплообмене.
Рассмотрим пример, когда тепловой поток является разрывной
функцией координаты и асимметричной единичной функцией
времени [31], т. е.
q (у, Fo) = qcS+ (Fo) ^ IS (U-) - S (*/+)],
C.88*
n=0
7*
99
где у± — у — пс — Bп ± 1) d;
| JtJHJl N = 0, ± 1, ± 2,...; с - рас-
"* ' '"*"" стояние между участками
действия теплового потока,
отнесенное к полутолщине
пластинки б (рис. 34); 2d — длина
участков, на которых действует
тепловой поток, отнесенная к
толщине пластинки 26.
Пусть коэффициент
теплоотдачи изменяется в зависимости
от времени по
экспоненциальному закону C.33). Подставляем выражения C.88) и C.33) в C.83).
После необходимых вычислений интегралов находим
jexp
J 71=0
2кХ1п \' ку -
У-~ихух
xy 0
Bi0 -KFo{i
R e {i
y+-hxyx
o,
x2 +
кУ ~ kxy
<№ C.89)
где Г (a, x) — неполная гамма-функция. Если п = 0, т. е. если
тепловой поток действует лишь на участке (— d, d), из C.89) по-
лучаем Ро
Т = с С ехр
2яХ\Уку-к2ху „
y+d-hxvx
__^_e-KFoA_
-4»] I.
О, -^|J+ , £,2 ||«. C.90)
У " ^хуХ
Если коэффициент теплоотдачи постоянный, то из C.89) и C.90)
соответственно получаем
а б N у-~Ъхух
Т = t Jc 2 ^ J Яо(Р. *) <*& C-91)
y+d—fexyx
Г = ^с 2 J #о(Р.<»)<« C-92)
2яХи У ку — кху y_d_hxyX
(функция 9С0 (р, со) = J ехр | --|- (ю + 4-)|— протабулиро-
вана в работе [51]; р = 1/ BL ^—я М2); ш ^
= 2Fo
Bi„
fcV ~ kxy
6» + *» (*„-**,)
]
)•
100
Если материал ортотропен, в решениях C.89) — C.92)
необходимо аринять кху = 0, k\i = Хх, Лгг = ку. При N — 0 выражения
C.90) и ( .92) имеют вид
Т = -
rlexp
2п%1 Vk
У+d
_ J|l e-KPo A _ екщ
X
X
Iг "■ *("+-«
V-d
т =
«
?сб
V+d
2<v\ „_,
3C0(Pi. «i)^,
C.93)
C.94)
2/-d
= /Bi«(t
гдеР1=^/ Biol^-.+a*); eot = 2Foy Bi0 gl+» ,
При a: = i/ = 0 —
Fo
Tn =
vr
jexp
Big
-KFo
A - eK&)
X
*j[-*(--dM
_ Fo
r0 = 2l/nj e-BUerfr
*id£;
2/£(l-e)
C.95)
C.96)
где T0 = 2я^цГ/д0б; e = fc^/fc,,; Z) = dlVky.
Для теплоизолированной (Bi0 = 0) по поверхностям Z = ± 1
ортотропной пластинки из C.94) находим
Г* = ]/Fo
erf
r + d
2 /Fo kv
— erf
£ — d
V 2VFokv
+
+ _i±i_l_Ei
2 Vnky
2ynky
У + d
2}/Fo ky
J y-d
{ 2VFoky
C.97)
Здесь Г* = ynhxT/qcb. Совершая в C.90) предельный переход прж
Fo -> оо, кху = 0, Bi (Fo) = Bi0, получаем решение стационарной
задачи теплопроводности ортотропной пластинки в виде
C/-Н) Ymjuy
Г*
f *0<0«.
где К0 (£) — функция Макдональда нулевого порядка.
101
C.98)
Определим теперь температурные напряжения, вызываемые
температурным полем C.90). Подставляя C.88) при п = 0 в
выражения C.87), переходя от изображений к оригиналам п
подставляя результаты в соотношения A.153), при Bi (Fo) C.33)
находим
ах = - f г) sin r\d ( ю (Fo - Q 2 » К ~ Д» +
-+ -L еЬжф-) + Dn (Si - s2 + 4- еЬЖ(Р+I «*nC~1,14d»i;
«*- j -^-jco(Fo-92 {-rh^ + 1^- +
+ -4- еЬж ф_ (p2 - rfkxy) - 2ЬрФ+ +
4£
/я;
)]
+
+ Dn | - tif^ + r]|S2 + 4" в6* (ф+ (Р2 - Л) +
+ 4ZL^_e П « _2%p_
-j-oo
Txy = \ sin rid ^ со (Fo — 0 ^ \-jT ЛЛ ~ Ла^г —
—00 6 n=l
2 \' ' ' ГяС
Здесь введены следующие обозначения:
Oj = —т— G = я, У);
a^S
irt
<o (Fo — Q = exp
Bi0
e~K Fo ^ _ ^
Сп = ФЫ№иа
,—1
^
*2 =
-гтьае
"Hi —"Па
1(Ч2 + Чкху)ет{фУ1) + ф];
-%4\%X
tp± «= exp (— #P) erf с
% —%
X
\ C.99)
fOl!+ i« erf (p ]/£)+$];
2n - pKS; ± exp (*fj) erfc (-^_ + p VI)
102
Dn = X (sn) f^s (sn)]
-i
s1 =
S2 =
-IT^X
Ъ — Л2
% — ^2
Л2 + Л**!/ + I
rji + ti**i/ + i
-К-^у-КуЖ
Vnt
+ Perf(PVl)
— +perf(p1/o
/sc
sn — корни полинома я4 + Pt& + 2P2s2 + 4P3s + P&
* = У*п+*(ку-к& xxy = "Yf11 :
Ф E) - fe</ + /-lS» + b2s + bs; Ц (s) = (s - sx) (^ - s2) E -
X {5) = d0 s2 + dxs + d2; fe0 = — o$
Ьг = if (aa — 2ax — aya3);
b2 = n4 B^3 + я2а3 — 4ax (^ — A^,));
6g = Za^ (/c^ — /cXy) A — ky -f- /c^cy);
do= *n (ai — 2c4); rfi = ^л3 Bй2 — 2o4 (*y — ft2?/) +
+ axa3 + 2ayK3); d2 = 2агг)Б (fcy — k% — #8);
*з) (s ~ S*Y>
#1 — С^ху ttxyOby'i
1 ~T &>xykxy — ft?/°C</ "T A&ykxy'i
a3 — Z (% — kxy — a2);
Л = Л2 (*, - ftx,Po - P + Po2)' *• = ~ 4№#3 + № +
+ Зг]4 {fo - 4) [fty - /4 - 2 (*, - *i)]}; P* = - 4r]7 (£, -
- A&) JT^ + л6 {(*» - ft*y) [(ft„ - klyf + K\ - ЪКг + К, +
+ (ky-kly)K21]-.K1K2 + K3};
P4=- 8х\*КгКъ (ky - klyf + rf{(/% - k2xy)[(ky - Л&)8 + 4 (*„ -
- ft2,J (#2 - к2) + 2 (^ - 4) (#4 + 24) + 4 (Я, - /?2й:4)] + #!};
^ = 2й*у + p0; K2 = 3 kxy (kxy + pQ) + p;
Ks = kxy Bk2xy 4- 3ual/p0 + 2p) + g0;
Я = kxy (kxy + 2/c3cyp0 — 2kxyp — 2q0) + q.
При попарно-равных корнях уравнения C.86) формулы для
определения напряжений получаем из C.92 с помощью
предельного перехода, принимая jx2 -> \iv Если корни уравнения C.86)
комплексные, то в решении C.92) необходимо принять \it = u. +
+ п, fx2 = [i — ri. Если коэффициент теплоотдачи не зависит от
времени, в решении C.92) необходимо перейти к пределу при К ->
->0.
103
to
6,6
6,2
5,8
5,4
5,0
4^2
V
zOO
3
<
?
4
/
L&
i
UyS
w
0,2
0,8
На рис. 35 приведены
результаты вычислений но формулам C.95)
(Fo = 1, К = 1, Bi0 = 1) и C.96)
(Fo = 1, Bi0 = 1) при переменном
(К = 1, кривые 2, 2, 3) и
постоянном (кривые 4, 5, #)
коэффициентах теплоотдачи в анизотропной
пластинке (D = оо — кривые 5, 4;
£) = 2 — кривые 2,6; D = 4 —
кривые 2, 5). Видно, что при
учете коэффициента теплоотдачи
температура в пластинке повышается.
Если тепловой поток действует по
всему краю пластинки, т. е. D =
= оо, то в обоих случаях
температура постоянная, но разная.
При постоянном коэффициенте теплоотдачи с увеличением s
температура повышается и приближается к постоянной, а при
изменяющемся в зависимости от времени коэффициенте
понижается и также стремится к постоянному значению.
На рис. 36, 37 представлены вычисления изменения
температурного поля в пластинке из стеклотекстолита КАСТ-В при заданном
потоке тепла C.88) в зависимости от координаты у {Х1Х — 0,209 х
X 10~~2 вт/(м -° С); ^ = 0,335 . 10 вт/(м.° С); в случае
изотропной ( ) пластинки Я£ = %1у = 0,209 . 10~2вт/(м.°С)) —
по формулам C.97) и C.98). Температурное поле в
теплоизолированной пластинке увеличивается с течением времени, при этом
возрастает относительное влияние степени ортотропии (см. рис. 36);
0,4 0,6
Рис. 35.
2 4 6 у
Рис. 37.
104
стационарное температурное поле при увеличении коэффициента
теплоотдачи с боковых поверхностей пластинки уменьшается,
при этом уменьшается и относительное влияние степени ортотро-
пии на распределение температурного поля (см. рис. 37, Bi = ОД;
0,5; 1,0 — кривые соответственно 1, 2, 3).
Температурные поля и напряжения
в изотропных пластинках
Рассмотрим свободную от внешней нагрузки бесконечную
пластинку толщины 26 с круговым отверстием (рис. 38), на
цилиндрической поверхности г — R которой задан тепловой поток q (Fo).
Через боковые поверхности пластинки Z =±1 происходит
теплообмен с внешней средой температуры tc (Fo), причем коэффициент
теплоотдачи является произвольной функцией времени Bi (Fo).
Начальная температура равна нулю, на бесконечности пластинка
предполагается теплоизолированной.
Возникающее нестационарное температурное поле в пластинке
согласно A.80) определяем с помощью уравнения
теплопроводности [34]
дЧ 1
дТ
дг
- Bi (Fo) (T - tc) =
дТ
C.100)
при краевых условиях
дТ
h-
дг
г=я
= 8g(Fo);
дТ
дг
= 0; Г|Ро = о = 0, C.101)
где Л — отнесенный к полутолщине б пластинки радиус кругового
отверстия.
Посредством замены типа A.86) уравнение C.100) и краевые
условия C.101) приводим к виду
дг
д2В 1 дд __
дг2 + г дг ~ '
= &7(Fo); -§-
r=R or
did
д¥о
= 0
Г-*оо
бс!
C.102)
0; 6 |Fo = о = 0, C.103)
где 0C = Bi (Fo) tc (Fo) Г1 (Fo);
Fo
/ (Fo) = exp [ — { Bi (£) (%). При-
6
меняя к уравнению C.102) и
граничным условиям C.103)
преобразование Лапласа по Fo,
получаем
r = 6/(Fo), C.104)
Рис. 38.
105
где
О = J" \QR (Fo-О ЩЬ& + 0C (С) j rf£; QB = -&- Г* (Fo): j
<?v(r, Fo) =
2
J C.105)
nr
00 /v (Er) Yt (Ш — Fv (gr) /1 (Ш
\ (i - ^Fo) ;|2 ;2'1. JzLi ль
0 . *[/fF^) + Y\№\
Квазистатические температурные напряжения, вызываемые
температурным полем C.104), определяем по формулам
o,, = ag)/(Fo) (/ = г,ф),
где crS* определяется из соотношений A.185), т. е.
аф)-
a@) -
иФФ
2G
1 — V |
W 1
1 — V
ir+-rK-Ml + v)9
(v^- + -f)«0-af(l+v)9
(и0 удовлетворяет уравнению A.186)). Учитывая, что
а„ \r=R = 0; lira o,j = 0,
из C.107), где 8 имеет вид C.105), находим
Fo
a%> = -atE\ QR (Fo-Q
dQi (r, Q
dfc
Fo
a$ = atE f <?R (Fo - Q -iL [<?г (r, Q - <?0 (r, 0] d£.
C.106)
C.107)
C.108)
C.109)
Подставляя C.109) в C.106), получаем общее решение
квазистатической задачи термоупругости рассматриваемой пластинки.
Пусть тепловой поток на крае г = R пластинки изменяется в
начальный момент времени на некоторую величину q0l оставаясь в
дальнейшем постоянным, а коэффициент теплоотдачи в случае
аэродинамического нагрева есть функция времени C.69), т. е.
Bi(Fo)=^Fo66f-ftFo. C.110)
Подставляя C.110) в C.109) и затем в C.106), приходим к
следующим выражениям температурных напряжений в пластинке:
Fo
arr =
ЩЕд0Ь п dQx (r, £)
У dQl^] exp{-60[Y(fr + l; k¥o)
■ vF + i; *(Fo-c))]}d&
Fo
ff- = V° \ 4r [<?i (r, 0 - Qo (r, t)} exP {- b0 iy(b + j
1C.111)
J<№
'4
dt
0
+ 1; fcFo)-v(b + l; Л (Fo-£))]}<£>
106
где b0 = dk ь 1. На крае г = R пластинки
Огг = 0;
Од, =
УЧф|г^
afEq06
Fo
| iV0(C)№p{-be[vF + l; l C.112)
ftFo)-v(& + l; &(Fo-£))]}£, !
где #ft (£) = —5- \ —о s ~ • Если коэффициент теплоот-
дачи изменяется в зависимости от времени по экспоненциальному
закону C.33), т. е.
Bi (Fo) = B\Qe-KFo, C.113)
где Bi0, К — постоянные, то
afEan$ ( г ц\п 1
а" = ~ ~Чг {<?! <r' F°) <яр - -^- A - е~* Fo) | -
Fo
- Bio J Qx С, С) ехр [Bi0 Я A - eKl) e~K Fo -
(Fo-£)£]#};
0<РФ —
*7
^(r.Fo)-^, Fo)]exp
Bip
К
C.114)
X
x A _ e-KFo)] + Bi0 J \Qt (r, у _ <?0 (r, g; exp [Bi0 Я X
A _ ещ e-K fo _ (Fo _ g #j ^j .
X
на крае пластинки
arr = 0; аф = ttb* - ~ <?Г (Fo) exp
i+i
atEq0RQ
F
о
Д
_-2L(l -«-**)
A _ *3S) e-P* _ (F - £) p J dC (З.И5)
где
Я0 = В10Д2; Bi0 = ^-; $ = KR*, F = /T2Fo; X
00 —tap
V°W" ^2 J Ail) + Y\(i) I9
\ C.110)
107
-0,2
-0,1
n
>
0,1 0,2
Рис. 39.
аз fo
-го
~hS
-!,0
(функция Qt протабулирована
[25]). Переходя в C.115) к
пределу при Р -^ 0, получаем-
выражение сгф при постоянном
коэффициенте теплоотдачи с боковых
поверхностей пластинки:
-0,5
и'"
7
>2
-——4
2,5
5 7,5
Рис. 40.
аф = — Qfe~
B0F
~B^Qtg)e-B&dl. C.117)
На рис. 39, 40 приведены вычисления безразмерных
кольцевых температурных напряжений сгф, выполненные по формуле
C.112) при значениях постоянных, принятых в C.70), а также по
формулам C.115) при р = 1 и C.117) при В0 = 0,1; 0,5 (
изменение температурных напряжений в зависимости от времени
при переменном, —- при постоянном коэффициентах
теплоотдачи). Если коэффициент теплоотдачи изменяется по закону
аэродинамического нагрева (см. рис. 31), то напряжения аф достигают
максимального значения при Fo — 0,353 (см. рис. 39). Если в
случае Bi (Fo) = const напряжения сгф (см. рис. 40) при В0 = 0,1
(кривые 1) и В0 = 0,5 (кривые 2) отличаются существенно,
достигая в условиях стационарного теплового режима конечного
значения, то в случае изменения коэффициента теплоотдачи в виде
C.113) при В0 = 0,1 и В0 = 0,5 они отличаются незначительно,
достигая в этих же условиях бесконечно большого значения.
Рассмотрим неограниченную полосу-пластинку,
теплоизолированную по поверхностями = 4h I (I = 1г -f- h)- Через
поверхности Z = =Ь 1 пластинки происходит теплообмен с внешней средой
нулевой температуры по закону Ньютона, причем коэффициент
теплоотдачи является некоторой
функцией времени. Пусть в начальный
момент времени в точках (Z2, — 2с),
j (— hi — 2с) (рис. 41) начинают
действовать сосредоточенные источники
тепла постоянной мощности q [33].
При Fo = Fox подключается следую-
Рис. 41. щая пара источников тепла такой
*эт
2с
j
108
же мощности, действующая в точках A2, 0), ( — 12, 0). Наконец,
третья пара источников тепла действует с момента Fo = Fo2.
Решение нестационарной задачи теплопроводности и
соответствующей квазистатической задачи термоупругости
рассматриваемой пластинки необходимо для изучения процессов сварки в
микроэлектронике. Нестационарное температурное поле в
пластинке определяется с помощью уравнения теплопроводности A.80),
выражений A.93), A.94):
AT - Bi (Fo) T = -Ц- -Q[b(x-lj + 6{z + l2)] [8Q/ +
+ 2c) S+ (Fo) + 8 (y) S+ (Fo - ¥ог) + б (у - 2c) S+ (Fo - Fo2)], C.118)
при краевых условиях
дТ
дх
= 0; Т =™=0, г/-^±оо; C.119)
x=±i °У
Гк=о = 0, C.120)
где ly с — отнесенные к полутолщине 8 полуширина пластинки
и полурасстояние между соседними источниками тепла; Q = д/2ХД
Используя замену C.3) и применяя к полученному уравнению
для определения функции 9 интегральные преобразования Фурье
по у и Лапласа по Fo, находим
О F.°
Q = TftTT\ r1(Fo-0[<tf(Fo--o +
о
I! +
/ V-2c ,2
+ S+g-Fo2)e U/рЗЧ ij-^L^-, C.121)
где Оз" (I) = % (J—fj-1-1- , -^-1 • Подставляя выражение C.121)
в формулу C.3), получаем решение задачи теплопроводности
рассматриваемой пластинки.
Квазистатические температурные напряжения в
полосе-пластинке, обусловленные температурным полем C.121), определяем
по формулам A.148). В случае свободной от внешней нагрузки
полосы-пластинки компоненты температурных напряжений A.148)
должны удовлетворять граничным условиям
Согла
где
охх = аху = 0 при х = ± 1;
Охх = ОуУ — аху = 0 при у = ± со.
сно A.153)
охх = а№/ (Fo); ovy = o%f (Fo); oxy = a^f (Fo),
** ~ dua ' uw— to2 ' зд— to% '
C.122)
C.123)
C.124)
C.125)
109
F0 удовлетворяет уравнению A.162). Применяя к выражениям
C.125), A.163), A.164) и представленным согласно A.153)
условиям C.122) преобразования Фурье и Лапласа, получаем
а@)
v?Fv
(-
f d*
dx2
а@)-
Uxx —
-@) _ d°~F0 t -@)
°УУ — ^д.2 ' °xy —
^Г-Л")'^-05
-TfyY0 = *(l+v)e;
Oxy = 0 при x = ± I.
Щ
dFa .
dx '
C.126)
C.127)
C.128)
C.129)
Решение уравнения C.127) ищем в виде
U0 = (A + Вх) сМх | ц | + (С + Dx) sh х \ х\ |. C.130)
Частным решением уравнения C.128) является функция
0|<? A + ^)
У 2ns
где
9 - -А- (*H*-'«lN + бН^-ЫМ) j f C.131)
e = -^L[ch7(Z-k-/2|) + chv(Z-|a; + /2|)]; iV = (YshY0~1;
<?0 = — (e~2iTlc + £~s FOj + ^2iTic~s Fo*); у = ]ЛJ + s;
_ +00 OO
0 = ■-—==- I i ee*w-eFodydFo.
" — 00 б
Определяем постоянные интегрирования и по формулам C.126)
находим выражения трансформант функций о$. Переходя
затем от изображений к оригиналам и используя аппроксимацию
Снеддона
loSlHT « 4%-^ + {± - 3.1Й,) г«Ч , C.132)
находим
°S = - НйГ- f 23 a~ ^Г1 (Fo - X) ЛС; C.133)
о i=1
Fo
4
a® = -^- J 2 <C' W Г1 (Fo - X) dl; C.134)
6 ^=1
a EO Fo
<C = - °S + ~br- .1 t7* <c> + (x - F°J 7з @) +
6
+ (X - Fo2) /8 (— с)] Г1 (Fo - X) ЯС — atEQ. C.135)
110
В mix выражениях введены следующие обозначения:
ctS1 = Ux (с) + (Х - Fox) 1, @) + (X - Fo2) /x (- с);
а!Г = -L Re ( #э -^-, ^=±) HIT {с) - (F0l - 0 If> @) -
-(Fo.-0/f (-c)|fl5;
4? = г [Шх (с) + (X - Fox) Afj. @) + (X - Fo2) Mt (- c)];
aS'1 = 4 ^2 Re J [d^ (X - Q + ^ (X - Q] [£г$0) (c) -
■ (*4 - Q г|)@) @) - (Fo2 - С) Ф<0) (- e)]
X
dl
(X_gK/2 •
of* = XI, (c) + (X - Fox) /f @) + (X - Fo2) /2 (- c);
o$* - 4- Im J #3 (i^iL_ , J^L j ,yf (C) _ (F0l - 0 4°> @) -
-(Fo2-a/B0)(-c)]C
og8 = 2 {[XMf (c) + (X - F0l) M2+ @) + (X - Fo2) M2+ (- c)] sign (z +
+ Z2) + [Ш2~ (с) + (X - F0l) M2~ @) + (X - Fo2) Щ (- e)] X
x sign (г — Z2)};
a@L _
X (sin я/
Imf 2 (-l)'+1/exp
r2y2
Я7
■(x-0
X
J _ I x — У , . . l—\x + L\
'—. У- + Sin nj ' , al
- (F0l - 0 a|f>@) - (Fo2 - 0 r|f > (- c)] -^;
I^zUl (qf>- - Ф№+ + qf>- - Ф№+) + 4" (<PB2)- ~ Ф22)+ +
+ qf- - ф^+) - ЗД/ (ф<3>- - qf'+ + ф<3>- - <$>+)] - 4" D^ x
X f l (Ф<33> + + Ф^ - - Ф<3> + + ф(93>-) + 4 (<Pf)+ + Ф?0" + 4f)+ +
+ф^ )++<pf -+фй)++^?-)+4* («f)++Фр^+qf)++ф?^ -
+ 4[Мф12)+ + ф12)- + ф^+ +
- Ф?)+ - Фр- - <pg>+ _ фB)-)
ш
+ «Pi!") + "Г (ф21>+ + ^1>_ + ф81)+ + ф81,_ ~ Ф61>+ ~ ф61,_ - ф12+ ~
Фи") -3'1Z
/ (фC)+ +фC)- + фC)+ + ф^з,-) + -i-(q^)+ + cpf- +
1
+ qf>+ + qf >- + ф|? )+ + qf»~ + ф^+ + ф$-) + -f (ф?)+ + ф22) - +
+ ф£2)+ + ф£2>- - qf+ - ф^- - ф$+ - ф$-) ]};
[зг щ»+ + ^<Г + ^v+ + *$>-) +
/f =
/
(X - О2
+ V2 (X - О (^(|)+ + Ч$- - г|$+ - г|>$-) - 3* (г|$- - Ч$+ +
+ ^46)+-^Г)] +
4/2(Х-£K/»
Z (ф(|)+ + л^С|>- + г|$+ + ^-) +
+ V^^T-W®* + <№~ ~ ^(n)+ ~ Ч®~) - * Ш~ + 4f7)+ ~
.^3)+_^3,-)
3,11
4flC-0»
[3/ (г|^+ + ^)- + ^7)+ + ^-) +
/ - — —
* 9. 1
+ V2 (X - О ОД*>+ + a|f5>- - г|$+ - ^~) -
- Ъх (!$- - Ц$+ + г|$+ - ^D)-)];
4/ (cof+ + cof- + cof+ + of»-) + -i- (©B)+ + cof- +
+ С0<2>+ + Of >-) - 3,1/ (cof+ + Cof ~ + шC)+ + ^C)-) |
- JL [ 4/ (cof)- - cof >+ + of)- - cof + + of)- - cof+ + со®- -
- <°11)+) + 4" И1)_ ~ <в^1>+ + С0в2)_ - Ч2 >+ + <°Р~ - <42)+ +
+ cog)- - cof+) - 3,1/ (cof- + cof- + cof- + cof- - cof + -
- cof+ - cof+ - <of+)
++
4/ (cof- -j- cof- + cof- + cof- -
. @C)+ _ 0,C)+ _ ^C)+ _ @C)+) + J_ (&)p- + юB)- + (oB)- _|_ ЮС|_ _
- cof + - cof + - cof + - cof+) + 3,1/ (cof- + cof- + cof- +
+ Cof" - Cof + - Cof + - (Of + - C0f2)+I + 4/ (cof- _|_ @C)- _
- cof+ - cof+) + i- (cof- - cof + + cog)- - cof+) _
- 3,1/ (cof- + cof0>- - cof + - cog) ty
112
3/
- УГ ~ *fiPfl - 4K2(X1_Dv, ЖР" + ТЯГ - ^+ - ^+
- x (Щ>- + tl>f+ - г|$- - t|f7>+)J - 9,3 —i-j-j^)- + o|f7>-
/s = 4/ (q>f+ + qf»- + qf>+ + qf>-) + -i" (<$)+ + Ф^~ +
+ <Й1)+ + qf-) ~ 3,« (qf>+ + qf> ~ + qf>+ + qf");
/f = Re ft$- - t|f3>+ + ^|)- - ipgH-);
<#>±
/>ft±*
qrf3)± =
(pft±zK-3(pft±*N2
qf>± =
«*
(pft±*J-&2 ,
(р„±*L+ь* ;
ft
,<1>± =
«K
X2)± =
[(Pft±*J + b2l3
2 (рь ± г) 6
(Рь±х)* + Ь* ' Ш" [(Pft ± *J + *>2]3
(рА±*J + Ьа '
Ъ(рк±хуъ-Ъ*
№± =, exp
(Pk±* + ib)*
/>-»[■
ph±x + ib
MJ =
(*-*2>8-
i|><0> = exp
8(X-0
n = 2; 3; 4; ft = l; 2;
-6* (a. + y»_6«
(* + у* + ы
V2(X-0
...; 17;
M± _ I ж ± /2 | &
2 ~ (*±У4 + ь* •
fc2
L /2(X-0 J' "^
8(X-0
p^l + W, p2 = l,8l + k; p3 = 2l + lx; pi = 2,8l + l1;
p^Zl + li, Pe = 3,8l + lv p7 = 2i + /2; p8 = 2,8/ + /a;
p9 = 3Z + гз; pw = 3,8J + Z2; рц = 4/ + /а; pl2 = 4,81 + l2;
Р13 = h Pu — — к Р\ь = 1|8^; Pu = 3Z; p17 = 3,8£.
Подставляя выражения C.133) — C.135) в формулы C.124),
получаем решение данной задачи термоупругости при нестационарном
теплообмене.
В случае постоянного коэффициента теплоотдачи решение задач
теплопроводности и термоупругости записывается в виде
Fo
т - w\ '<*(Fo - ® + «*(Fo -?)!,ехр [-ti^v) +
+ 5+(g-Fol)exp(-1T^-ir) +
8 6—1S34
113
_Bi(F0-£)
dfc C.136)
*—wsrg0^ (ЗЛ37)
ffy = -o* + 2/1вп [Я/,(с) + HJt@) + Я2/3(-c) +
Fo
+ V2e-m ] #8 (A±A-, J*£U (Я<°>4°> (с) + ЯМ> @) +
2Z
7@O@),
+ Н$>1Г(-с)
dL
где
/2яа.;.
°> ~ atEQ ' v*"
(Fo-5)'/. ' Г°;
T = _L у a(i)
1/2яож
C.138)
C.139)
1>XV
ху ,
XX
„-Mi
aB) = _ i_^
__ f2nT
afEQ ' х°~~ Q
a(i> = tf/x (с) + HJX @) + #2 Ix (- с);
Re
Fo
•J М-
2/2 + h Fo-g
гг
о
7@) 7@)
)(Я@)/Г(С)
+
@O@),
+ тГ@) + яГ/И-с))<£
a<?> = г (ЯЛ/х (с) + НХМХ @) + Я2МХ (- с));
тD).
Fo.
|«-Ы Fo-g \
2/
+
Fo-g
*,(■
| x + i2 |
2l , p-)][FflV(c) + 5f>4^>@) +
oW = Я/2 (с) + ЯЛ @) + Я2/2(- с);
21, + ^ Fo-C
-Mi F°
es---v-imJ^(
г\
^d^/i
f@ +
+ M,,/f@) + 4°,/f,(-cM;
og? = 2 [(ЯМ2+ (с) + HtMt @) + Я2М2Ь (- с)) sign (ж + ^ +
+ (M2-(c) + ЯхМГ@) + Н2М^(- c))sign (ж - д];
114
0D)
ху
-р— Im I 2 ("~ !) 7* (sin Я7
/ — | Д? — /а |
+
+ sin щ ±zi£±liL J (#«y<» (с) + Н[°>№ @) +
+ MV)(-0)-l^T-;
Я = 1 - ехр (— Mi); Нг = 1 - ехр (- Mi + Mix);
#2 = 1 — ехр (— Mi + Mi2);
Я@) = 1 - ехр (Bi£); #(i0) = ехр (MiJ - ехр (Bi£);
#f = exp(Mi2)-exp(Bi£);
в обозначениях для/^0)(/ = 1; 2; 3), г|4п) вместо X следует
записать Fo.
Полагаем в выражениях C.121), C.133) — C.135) (с учетом
формул C.3) и C.124)), а также в C.136), C.139) с = О, 1Х = О,
12 = 1у х2 = %1 = 0. Делим результат на три, интегрируем его по
у в пределах от — оо до -f- oo и находим температурные поля и
вызываемые ими температурные напряжения для случая, когда
полоса-пластинка нагревается по краям плоскими источниками
тепла, соответственно при переменном и постоянном
коэффициентах теплоотдачи:
Ро
TsajP$Q_\ ^(Po-^/^.D^ C.140)
о v '
Fo
/(Fo) (' ,_i
Jr1(Fo-0[l-d,(-|->-L)]dC;
Fo
°v = -T
Fo
1-е1
Mi
Bi
-ЬНг'-^И4
C.141)
C.142)
C.143)
где oy = Oyy/octEQ. При ж = ± / формулы C.141) и C.143)
записываются в виде
C.144)
J, = -2/2
*J лДО + ВП2
=1 l
1 — exp
r_(n%a + Bi?)_*LJj. C.145)
115
-2,5\
"Щ
-0,5\
>^х
££~
<
л
у
А
л
^^ 1
|\
РП
\Л
2\
Ы
\у \
г
Если коэффициент теплоотдачи
изменяется в зависимости от
времени по экспоненциальному закону
C.33), то формула C.144)
принимает вид
av =
X
еХр[-^'~КР°]
+
Fo оо
О j=l
Bi0
яар
с +
AS
1
Рис.
U5
42.
Fo
К
g-X(Fo-S)
d£. C.146)
На рис. 42 представлены
результаты вычислений изменения
температурных напряжений в зависимости от времени при переменном
( ) и постоянном ( ) коэффициентах теплоотдачи при
ширине полосы-пластинки I = 10 по формулам C.146) (Bi0 = 0,5;
К = 1) и C.145) (Bi = 0; 0,5; 1 — кривые соответственно 7, 2, 3).
Видно, что при постоянном коэффициенте теплоотдачи напряжения
увеличиваются с уменьшением критерия Био, достигая в условиях
стационарного теплового режима конкретного значения, при
переменном коэффициенте — увеличиваются в зависимости от времени
и достигают в равных условиях бесконечно большого значения.
Определим нестационарное температурное поле и вызываемые
им температурные напряжения в тонкой изотропной пластинке,
нагреваемой по торцу г = R постоянным тепловым потоком q =
= const. Теплообмен с внешней средой через поверхности
пластинки z = ± б происходит по закону Ньютона, коэффициенты
теплоотдачи с боковых поверхностей являются функциями времени,
&t (т) = «Г (т) = а2(т). Усредненное по толщине температурное
поле находим с помощью дифференциального уравнения
д2Т , 1 дТ ^. ,™ . tm m ч дТ
дг2
+ ■
дТ
дг
-Bi(Fo)(r-rc) =
<9Fo
C.147)
при начальном условии
Г (г, Fo) |Fo=o = 0
и граничном —
дТ
дг
г=Н
= ?•
C.148)
C.149)
Используя замену A.86) и применяя к уравнению C.147)
преобразование Лапласа по Fo, получаем
*в , 1 «» , й ей
C.150)
116
где 9С = Тс j Bi (Fo)/^(Fo) е~~ *FodFo. Решение уравнения C.150)
о
ищем в виде
Q = AI0(rVS) + -S-.
C.151)
Определив постоянную интегрирования из преобразованного с
помощью замены A.86) и преобразования Лапласа граничного
условия C.149), записываем решение C.151):
6 =
<?<*)
— I0(rVs)+-i-,
C.152)
%tV sh(Rfs)
00
где Q (s) = \ qf1 (Fo) e~ sFod Fo; Ix (R jA) — модифицированная
о
функция Бесселя первого рода первого порядка.
Трансформированные по Лапласу соотношения
квазистатической задачи термоупругости в полярных координатах в осесим-
метричном случае имеют вид
"(О)
"(О)
Уфф
=
=
1
1
2G [
— V I
2G
— V
дг
4- + -тк-««A + *)в
дг
+ 7-k -«t(l+v)9
C.153)
где щ (преобразованное по Лапласу радиальное перемещение)
удовлетворяет уравнению
Решение уравнения C.154) ищем в виде
Щ = Схг + " Н ; \ r0odr,
о
где %== Q (s) I0 (r Y s)/%t Yslx {R Ys). Постоянные
интегрирования определяем из условия симметричности нагрева и
незагруженности пластинки:
щ |г=о = 0, aS} \t=r = 0.
C.154)
C.155)
C.156)
Подставляя найденные постоянные в соотношения C.155),
получаем
*-4<*+^+4
r+(i^iMtai. C.1^7)
117
Изображения температурных напряжений записываем в виде
_l_ h (r yi)
-<0) __ J7_0i±
1
V
* г/1(Д/*)
Я / S rV sh{R У 8)
C.158)
- h(rVfL 1. C.159)
Л (R У*) \ к '
Переходя в формулах C.158), C.159) к оригиналам и учитывая
первое из соотношений A.153), находим безразмерные
температурные напряжения в круговой пластинке:
Fo оо I г
'i (ft, д-
ог = ехр
-j°BHII]
X
X ехр
О п=1 R
VnJo W
[-(^) (Po-0 + jBi(Fo)dPo
огф = ехр
Fo
о
Fo оо
<*£;
Л ("»т) —й-/в ("» Т,
1
^" -^Г Мо (Ип)
} C.160)
X ехр
о n=i
X
-&)Vo-0+\Bi(Fo)dFo
С
где 0^ = au%tR/2atEq (i = г, ф); fx^ — корни функции Бесселя
Jx (\\). Следовательно, существует бесчисленное множество корней
ДЛЯ S, Sn = — (Lln/i?2.
На рис. 43, 44 представлены результаты вычислений сгф, ov
в зависимости от Fo по формуле C.160) при переменном
коэффициенте теплоотдачи, аппроксимированном выражением C.69), и
фиксированных значениях r/R = 0,25; 0,5; 0,75 (кривые соответ-
Щ
№
\[\
й*
р
ч^
**—
ом
0,01
ОМ OJZ Fo
Рис. 43.
№
0,00 0,12 Fo
Рис. 44.
118
ственно 2, 2, 3). Кольцевые напряжения значительно превышают
радиальные.
Рассмотрим прямоугольную пластинку длины /, ширины b и
толщины 26, отнесенную к декартовым координатам х, у, z. Пусть
в некоторой точке (х0, у0) пластинки действует источник тепла
мощности g05+ (Fo) (g0 = const). Теплообмен поверхностей
пластины Z = ± 1 с внешней средой происходит по закону Ньютона,
причем коэффициент теплоотдачи является произвольной
функцией безразмерного времени Fo. Температура в начальный момент
времени и по краям пластинки в любой момент времени Fo > О
предполагается равной нулю. Остальные тепловые и механические
свойства материала принимаются постоянными. Так как задача
симметрична относительно срединной плоскости пластинки, то,
полагая в уравнении A.80) tc = 0, Х{2 = Я21 = 0, %\^ = Х22 = h,
получаем уравнение теплопроводности
AT - Bi (Fo) T = -^-Q0b(x-x0,y- y0) S+ (Fo) C.161)
и краевые условия
T @, у, Fo) = T (I, у, Fo) = Т (х, 0, Fo) = Т (х, Ь, Fo) = 0
при Fo>0; C.162
Г = 0 при Fo = 0, C.163)
где Q0 = q0/h- Используя замену A.86), уравнение C.161) и
краевые условия C.162), C.163) приводим к виду
де = -ш - Q»ri (Fo) б {х - х»у - ^ s+(Fo); (ЗЛ64)
6 @, у, Fo) = 6 (I, у, Fo) = 9 (я, 0, Fo) = 9 (х, 6, Fo) = 0
при Fo>0; C.165)
9=0 при Fo = 0. C.166)
Применяя к уравнению C.164) и граничным условиям C.165) при
начальном условии C.166) двойное преобразование Фурье по
координатам х, у и преобразование Лапласа по времени Fo и
учитывая A.86), температурное поле, возникающее в пластинке,
записываем в виде
т^_ 4Q0/(Fo) j, | ^^>?/£«fr x
1Ъ 71=1 7^1 0
X Г1 (£) sin amx0 sin $ny0 sin amx sin pn*/d£, C.167)
где am = nmlly pn = nnlb. Переходя к пределу при 6-> оо,
а затем при I ->- оо, получаем решения задачи теплопроводности
пол у ограниченной полосы-пластинки и клина, ограниченного
119
.2 _,_.*,„*? ,„2
яг 6 «-« о
линиями х = 0, у = О, соответственно в виде
* m х
X jf (С) sin (Xm^sin am:r sin t]z/0 sin r|i/dT|c^; C.168)
ooooFo
T = 4<?0/ (Fo) Г i- ^ ^-(IM-ti^Fo-t) ,-i /£ч х
0 0 0
X sin Y]z/0 sin ri# sin £;r0 sin \хд,х\д£><]%. C.169)
Квазистатические температурные напряжения, вызываемые
температурным полем C.167), определяем по формулам A.153), где
6ij — символ Кронеккера; ^¥0 и U0 удовлетворяют уравнениям
B.164), B.163). В случае свободной от внешней нагрузки
прямоугольной пластинки компоненты тензора напряжений должны
удовлетворять следующим условиям:
охх=оХу = 0 при х = 0, I; C.170)
Оуу = оух = 0 при у = 0,Ь. C.171)
Принимаем W0 = 0 при х = 0, / и у = 0, Ь. Решением
уравнения A.164) является функция
n=l m=\ am г" Рп 0
X Z" (С) sin am^0 sin $ny0 sin am.r sin pn#^ C.172)
a бигармонического уравнения A.163) —
oo
^o = 2 Pn2 (-4n sh f3nz + 5npn# ch $nx) sin pni/ +
n=l
oo
+ 2 <x~2 (Cm sh amy + Dmamy ch amy) sin aw:z, C.173)
m=l
где An, Bn, Cm, Dm — постоянные, определяемые из граничных
условий. Подставляя C.172), C.173) в выражения для напряжений
A.153), а затем в граничные условия C.171), получаем
бесконечную систему уравнений для определения постоянных АП1 ..., Dm
в виде
оо оо \
2 [(Ап + Вп) ch <ря + ВпЦ)п sh <pn] cos pnz/ + 2 (— 1)т X
X [{Cm + Dm) ch amy + Dmamy sh amy] = j
120
_ 4Qba*E V V (~~ i)m+la™P* -<°M>Fo v
- гь Zi Zj< a2 4-B2
FO о о
/гу —Uft ^7"
X \ * /"*(£) sin Отаг0 sin Pny0 cos p„yd£;
0
oo oo
2 (- l)n [(Л„ + 5n) ch M + #»Pn*sh pnz] + 2 KG» +
n=l m=l
+ A„) ch \|)w + Dmtym sh tyw] cos c^z =
C.174)
4Q0aiE
lb
££
\*+i.
Fo
(~ ^ЧЛ -<+^n)Fo Г }<+K*
< + fn
X
n=im=l ^m i Hn 0
X Г (£) sin amx0 sin pnz/0 cos amxd£;
An sh фп + Bn(pn ch cpn == 0; Cm sh -фте + Z)m\|)m ch г|э„
0,
где фп = fU; \|>m = aw6.
Таким образом, рассматривая только к элементов, из системы
C.174) получаем 2к уравнений для определения Ап и Ст.
Постоянные Вп и Dm находим из последних двух соотношений C.174):
Вп =
Ath9n; Dm = -^thtym. C.175)
Теперь с достаточной точностью можем определить функцию Эри
£/0, а по A.153) полностью найти распределение температурных
напряжений в рассматриваемой пластинке. Переходя в
полученных решениях для прямоугольной пластинки к пределу при Ь-> оо,
затем при I -> оо, получаем решения квазистатической задачи
термоупругости соответственно полуограниченной
полосы-пластинки и клина. При постоянном коэффициенте теплообмена в
выражениях C.172), C.174) необходимо положить Bi (Fo) = Bi =
= const, если пластинка теплоизолирована по поверхностям
Z = ± 1, то следует перейти к пределу при Bi ->- 0.
Рассмотрим сначала бесконечную упругую пластинку,
нагреваемую неподвижным линейным источником тепла, мощность
которого изменяется только в начальный момент времени (на
некоторую величину). Коэффициенты теплоотдачи с боковых
поверхностей пластинки z = ± б являются функцией времени <xz (т).
Начальная температура пластинки равна нулю.
Нестационарное температурное поле в пластинке определяем
по первому выражению A.86). Функция 0 удовлетворяет
уравнению
дл 1 06 , * б (Г)
C.176)
121
где
-^L = 6(x,y); ?oW=4+(T)rl(T);
/(т) = е ° ; х2(т) = ■ 2
А,<6
После преобразований Ханкеля и Лапласа
е-<?(,« *е*-о_< C.177)
О *
где г = |/~;г2 + ^2; (? = q/2An. Следовательно,
Г_<?1.-1"да,-в£'_Аг. C.178)
О *
Температурные напряжения, обусловленные температурным
полем C.178), определяем по формулам
oxx = -2G^-; a„--2G-g-; охг/ = 20^, C.179)
где W — частное решение уравнения A.152). Используя
представления A.153), получаем выражения
@) __ оа дЩ0 % @) 9Г д2У0 . @) _ 9а <?2У0 q 1ЯП
ж уравнение A.164). Применяем, далее, к C.180), A.164) и C.177)
преобразования Фурье и Лапласа В результате
Jyy
dx2
or ^o . "(О) or,„ ^0 .
-Т12¥0 = а4A+т)ё;
_ ,-|*lY
9 = ^^Г-.
C.181)
C.182)
C.183)
где N = __ \ qQ (т) е nd%\ y= 1/ г]2 + — . Частным решением
у 2л J fa
уравнения C.182) является функция
'.-S4-T—^ Cл84)
122
где ЛГ = at A + v) N12. После подстановки C.184) в C.180)
\
'(О)
^-а'М\ц\(е
2G
•\х\\ч\\
И1 е- \x\y\.
<*УУ = -Г aMiVi (*"
■1*11*11
У
.\х\
е mv)sign;r; I C.185)
2G -w-
_^_aM(h|^|x|1,ll-Y^lX|V).
Переходя в C.185) к оригиналам и подставляя результат в
A.153), получаем такие выражения квазистатических
температурных напряжений в пластинке:
40
2a(x—Q
Ь ~ г» J /
4a (T-£)
#;
W
(?)
r2 — -
-1]-
C.186)
2«(t-D
<»"t> Л- =-
dS =
a i /
E _ 2джу Г /(т)
/(t) « 4a(x-"
@
t-C
d&
^ОД
'4 J /@
1 +
e *»(t-C) _14,
4a(T-Qj
где of = afi/2atEQ (i — x, y)\ %% = c^yl2atEQ. Если коэффициент
теплоотдачи является постоянной величиной, выражения
напряжений C.186) принимают вид
„е 1
хл — у'
4г2 | гаи
~У2Ж0(р, а>)\;
гЗ£1(Р,со) + ^-(е-2'
1)
4г2
/■^(р, ©)+-£-(*-*■«-!)
Тосу —
— #22£0(р, <o)j;
г[г5€х (р, со) + \ (е-""» - 1)] + ^ ^о <Р, со) | ,
C.187)
где ?■
\п (р, со) = С (o^-% 2 Iе0 "/ йщ
кг; со =
2ха
123
-0,2
-0,1
О
ш
0,15
0,05
О
-0,05
ч
|\
^
^^
J-J
■
0,5
1,5
Fo
0,5
Рис. 45.
/
Рис. 46.
1,5
Fo
Рассмотрим пластинку, нагреваемую линейным мгновенным
источником тепла мощности q0. Температура внешней среды и
коэффициент теплоотдачи с боковых поверхностей являются
произвольными функциями времени. В этом случае
Г-
i
9 (х, у, т) + a J х2 @ tc (О Г1 @ dd / (т), (ЗЛ88)
где 0 == QQe 4ат /т; <?0 = ^0/4Ля. Температурные напряжения,
обусловленные температурным полем C.188), определяем по формулам
C.179) и уравнению A.152):
„2
ог= (е
4Fo
-1)
/(Fo)
S+(Fo);
Осп =
е ^Шб+^о),
2Fo
C.189)
где о{ = Ou62/atEQQa; г*= г/б. Если коэффициент теплоотдачи
изменяется в зависимости от времени по закону
C.190)
C.191)
а2 (т) = а0 — (ах — а0) S+ (хг - т),
то функция / (Fo) в C.189) имеет вид
/ (Fo) = ехр [- FoBi0 - Fox (Bix - Bi0) -
- (Bix - Bi0) (Fo - FoJ S+ (Fox - Fo)].
По формулам C.189), C.191) вычислены температурные
напряжения при г* = 2, ¥ог = 1, Bi0 = 0,5, Bix - 1 (рис. 45, 46,
кривые 1). Для сравнения показаны изменения напряжений,
вычисленные при постоянном коэффициенте теплоотдачи (Bi0 = Bix =
= 0,5, кривые 2). Из графиков следует, что зависимость
коэффициента теплоотдачи от температуры влияет на распределение
температурных напряжений в пластинке, в данном случае они
уменьшаются.
124
Для определения температурных напряжений в вязкоупругой
пластинке воспользуемся принципом соответствия, который для
среды Максвелла и Кельвина выражается в следующем:
X
в\. = <j§ - хм \ <rXM(T~D ag (z, i/, Q dZ; C.192)
6
т
<т?. = о% A + Р) - рхк { е-ин(т~у erg- (*, у, С) С C.193)
О
где км = Е/Зц; г\ — коэффициент вязкости; (J = 2 A + v)/(l —
— 2v); кк = 3/A — 2v) т*; т * — время запаздывания.
Подставив вместо ofj выражения C.186), получим общее решение задачи
термовязкоупру гости бесконечной пластинки, соответствующее
произвольному изменению коэффициента теплоотдачи в
зависимости от времени.
Глава 4
ТЕРМОУПРУГОСТЬ ТЕЛ
ПРИ ЗАВИСЯЩИХ ОТ КООРДИНАТЫ
КОЭФФИЦИЕНТАХ ТЕПЛООТДАЧИ
Исследование температурных полей и напряжений
в пластинках и оболочках
при кусочно-постоянных коэффициентах теплоотдачи
Пусть полубесконечная пластинка, край которой х = О
закреплен, нагревается полосовым источником тепла ширины 26 и
мощности q, действующим на расстоянии d от ее края. Через
поверхности z = ± б пластинки происходит теплообмен с внешней
средой нулевой температуры по закону Ньютона.
Стационарное температурное поле в пластинке определяем из
уравнения теплопроводности A.133), которое в данном случае
имеет вид [36]
•7271 а„ (х) п
»w .T^-^-[S_{x-d)-S+{x-c*)}, D.1)
= 0. D.2)
Х=0
dx2 Xt6 aj
где ап (х) = a -\- (a0 — a) [£_ (x — d) — S+ (x — с*)], с * =
= d + 2b; a0 — коэффициент теплоотдачи с областей d < х <
<; с * поверхностей z = ± б; a — коэффициент теплоотдачи с
остальных областей этих поверхностей. Краевые условия:
Для решения краевой задачи D.1), D.2) рассмотрим однородное
уравнение . .
Последовательно умножая его на асимметричные единичные
функции S+ (х — с*), £_ (я — d), вводя замены
ц+ = T0S+ (х - с*); гг_ = roSL (яг - d) D.4)
и учитывая равенства
S± (х — х$ S± (х — Xj) = S± (х — хтах ij); D.5)
/ (х) б'± (х) = / @) б; (х) - f @) б± (Ж), D.6)
получаем систему двух уравнений с постоянными коэффициентами
относительно неизвестных функций:
-^±- - х*и+ = Т0 Bс* - я) б; (х - с*);
d%_ 2
dx2
xoa_ = Г0 Bd - x) б_ (х — d) — Ри+,
D.7)
126
где х2 = a/kt8; %l = а0Д,*6; Р = (Oq — а)ДД Общее решение
первого уравнения D.7) имеет вид
и+ - Аег** + Be™ + ±JL[T0 Bс* - £) sh х (g - *)]6вС, х
X S+ (х - с*). D.8)
Из D.4) следует, что и± === 0 при х <Z d, поэтому в решении
D.8) А = В = 0. Таким образом,
ц+ = -1- -А. [То Bс* - Q sh х (g - ar)]6ec*5+ (о: - с*). D,9)
Подставляя решение D.9) во второе уравнение D.7), получаем
и- = ~ ^ -~ [Т0 Bd -1) sh х0 (I - *) W_ (z-d) +
+ |-i- [Г,Bс* - Й sh х (g - *)]|=с. -
i- \Т0 Bс* -1) sh х0 (| - *)]|=с») S+ (х - е*)\ . D.10)
На основании D.4), D.9), D.10) уравнение D.3) сводится к
частично вырожденному уравнению вида
*Т9
- Х2Тп =
х0
■щ- {[Т0 Bd - I) sh х0 (£ - *)]6=dS_ (x-d)~
- [Г0 Bс* - I) sh х0(| - x)]l=c,S+ (x - с*)}.
D.11;
Общее решение этого уравнения, являющееся общим решением
уравнения D.3), ищем в виде
Г0 = Го1 + Г02, D.12)
где Го1 = CiChux + C2shxx; частное решение определяется
методом вариации постоянных:
Тог - —■ {[Т0Bd -1) R]l=dS-.(x-d)
-[TuBc*-i)R]^c,S+(x-c*)};
D.13)
R =
sh x0 (| — a) sh x (| — s)
Xq X
)
Из системы
Г0 (d) = Г01 (d) + Т02 (d); T0 (с*) = Го, (с*) + Гог (с*);
dT0 (с*) ^01 (с*)
dr„(rf) __ «gpiW df02(d)
Ac da: ' dx
dx
dx
+
+
^02 (c*)
dx
D.14)
127
определяем TQ(d), Г0(с*), —j~' —*J£ и подставляем в D.12).
Получаем следующее общее решение однородного уравнения D.3):
Г0= chxz +
-\ sh xd sh х0 (х — d)
х0
— ch kx + ch xd ch x0 (л; — d) +
S„(x - d) + (KXL + K2N) S+(x - c*)lCx +
-[- jsh кх +
— sh x# + sh xd ch x0 (x — d) H ch xd sh x0 (.z -
• d)l S_(x - d) + (#3L + Z4A0 S+ (a: - c*)l C„ D.15)
где
/^ = ch xd ch x0 (c* — d) -\ sh xd sh x0 (c* — d);
#2 = x0 ch xd sh x0 (c* — d) + x sh xd ch x0 (c* — d);
K3 = sh xd ch x0 (c* — d) -\ ch xd sh x0 (c* — d);
K^ = x0 sh xd sh x0 (c* — d) -f- x ch xd ch x0 (c* — d);
r i / *ч г, / *ч at sh и (# — с*) sh x0 (# — c*)
L = ch x (# — c*) — ch x0 (ж — с*); /V = * - ^ ' .
Зная общее решение однородного уравнения D.3), частное
решение неоднородного уравнения D.1) находим методом вариации
постоянных в виде
[1 — ch х0 (х — d)\ £_ (х — d) + ch x0 (x — d) -f
XtKQ
+ A — ch х0 (с* — d)) ch х (# — с*) ~ sh х0 (с* — d) sh x (x —
х
-с*) -ljS+(« —с*)' D.16)
и общее решение имеет вид
Т = Т0 + Тч. D.17)
Удовлетворяя граничным условиям D.2), получаем общее решение
задачи теплопроводности рассматриваемой пластинки:
в =-j^-Z^ch 1/ВГХ + I/- Z0 chl/BiX-
- У-щ-^sh VW0(X -D)- /ach УЩХ -D)-m\s_(X -
-D) + h4 и, -1) ch КвГ (х - щ + j/-|i- i, [sh УЩ(Х - /)) -
128
-L
+ I, [ch VW0 (X - D) - Y^- h] ~ '5 [1 + (U - 1) X
X ch |/Bi (X - C)\ +1, [ch VBi(X -C)-sh УЩХ - С)] +
+ mj5+(Z-C)\. D.18)
Здесь
6 = ?w77g62; l = h + l3(Y^h+V^1^)'
Bi0 = a08/Kt; l0 = Z4 + j/1^- /3 - 1; Bi = об/*,*
Х = ж/6; /1 = sh]/BTO; Z2 = chKBlZ); D = d/8;
TO = /1[chKBT0(X-C) -"[/"-|i-sh/Bi;(X-C)];
Z4 = ch2l/BT0B;
5 = 6/6; Z3 = sh2l/BT05; h = h{h+hY,
C = D + 2B;
Если а0 = а, то решение D.18) принимает вид
6 = -±r- {(e-mD - e~^c)oh КВГХ +
+ [1 - ch J/Ш (X - D)} S„(X - £) +
-f [chYWi(X~C)— l]S+(X-~C)}. D.19)
Температурные напряжения и перемещения определяем по
известным формулам [45]
охх = 0; Оуу = — 2(тФ"; аху = . __ ^
•%'";
и = Ф'; v =
X",
1 — V
где функции Ф и 1 удовлетворяют уравнениям
ф" = A+^а*Г; X(IV) = 0,
Граничные условия принимаем в виде
и @)^0; у@) = 0; а^\х^ = 0.
Решая краевую задачу D.20) — D.22)т получаем
ох = 0; оу = — 6; %ху = 0,
где 0У = GyyXtlatEqb2.
9 6—1534 129
D.20)
D.21)
D.22)
D,23)
-щ
-од
•Щ
Л
1
)\
-А
к
V
20 40 60 X
Рис. 47.
-J2
-Я
46
-8
п
\
20 40 60 tO
Рис. 48.
По формулам D.23), D.18) произведены расчеты распределер я
температурных напряжений при переменном коэффициенте
теплоотдачи с поверхностей пластинки (рис. 47, 7, Bi = 0,01, Вз0 =
В = 5, D = 20) и постоянном коэффициенте (рис. 47, 2, В10
= Bi = 1; рис. 48, В10 — Bi = 0,01). Изменение коэффициента
теплоотдачи влияет на распределение температурных напряжений в
пластинке, нагреваемой полосовым источником тепла, причем эта
влияние во втором случае (Bi0 = Bi = 0,01) значительно больше,
чем в первом (Bi0 = Bi = 1).
На рис. 4J показано изменение температурных напряжений е
полубесконечной пластинке, нагреваемой полосовым источником
тепла ширины 45 (В = 2), действующим на расстоянии 103 (D =
= 10), при Bi0 = 1 и разных значениях коэффициента
теплоотдачи с поверхности вне области нагрева (Bi = 0,04; 0,25; 0,5; 1,0 —
кривые соответственно 1, 2, 3, 4). Как видно, с ростом
коэффициента теплоотдачи напряжения уменьшаются.
Рассмотрим случай нагрева бесконечной пластинки полосовым
источником тепла. Производя в D.23), D.18) замену хх = х — d —
— Ь, при d ->■ оо решение задачи получаем в виде
Су = - (BiotfJ-1 /я2 + (Ях - Я, - Я3) S- (Хг + В) +
+ {h ih - 1) ет~ + h [к +Уж) е~т~ ~ 2l* *4 + <*« ~ № т-] +
где
+ Н3- Bi, Z3J S+ (Х1 - В)\ ■ ох = хху = 0,
Я, = 21, + В1Ж /„; Я2 = (z4 + ]/"-gjL /3 _ lj em+; Xl = f;
Я3 = 2 (Я0 + |/-|- f0) Ch /Щ, Zi; m± = /Ш (Xx ± B);
F0 = sh 1/Bi0 fi; Я0 = ch /Bi0 5; Bix =
Bi + Bi0
/BiBio
130
4 8 12 fS 20 24 a
Рис. 49.
При а0 = a
Oy = - -gj- [sh |/Bi Bevm ** + A - ch m+) S_ (Xx + B) +
+ (ch m_ - 1) 5+ (X2 - 5)]; a* = тх2/ = 0.
Изменение напряжений, возникающих в нагреваемой
полосовым источником тепла при ширине 105 (В = 5) бесконечной
пластинке, показано на рис. 50 (Bi = 0,01; Bi0 = 1 — кривая 2;
Bi = Bi0 = 1 — кривая 2). На рис. 51 показано изменение
напряжения при Bi = Bi0 = 0,01. Из графиков видно, что если
теплоотдача с поверхностей области нагрева равна теплоотдаче с
поверхностей за ее пределами, то максимальные значения
температурных напряжений практически не отличаются. Если
теплоотдача с поверхностей пластинки за пределами области нагрева
равна теплоотдаче с поверхностей области нагрева (см. рис. 51), то
максимальные значения температурных напряжений
увеличиваются по сравнению с реальными (см. кривую 1 на рис. 50) почти в
40 раз.
Рассмотрим тонкую прямоугольную пластинку толщины 26,
ширины d и длины 2Z, изготовленную из разнородных
прямоугольных пластинок ширины dx и d2. Ее поверхности х = 0, х = d
поддерживаются при постоянных температурах t0 и td, а
поверхности у = ± I теплоизолированы. Через поверхности z = ± 6
происходит теплообмен с внешней средой нулевой температуры.
Физико-механические характеристики такой пластинки можно
представить в виде
п-1
р(х)=*р1+ 2 (Pi+i — Pi) S~ (x — х{). D.24)
г=1
9*
131
-0,8
-0,6\
-0,4
-0,2
О
h
г
\/
20
Рис. 50.
40 //
'32
-24
46
-8
л
20 40 //
Рис. 51.
Подставляя D.24) в уравнение теплопроводности неоднородной
пластинки, получаем
d2T -х?[1 + Ь5_(*-<у]Г = A-Ль)^| в_(*-£у, D.25)
dx*
dx
x=dt
где б_ (х — с?х) =
dS__ (х — dx)
dx
Я(/>6
; av a2 — коэффициенты
теплоотдачи с поверхностей z = ± 6 первой и второй сопрягаемых
пластинок; Х(/\ Xf] — коэффициенты теплопроводности; Ь =
= Х2/К1 — 1. Умножаем D.25) на 5L (о: — d). Вводя замену
W (х) = b*\S- (ж - dx) Г0, D.26)
получаем
rf2¥
dx2
-х|ЧГ = (х1-Х?)[-
<*г0
d#
Решение этого уравнения имеет вид
6_(*-^) +
D.27)
¥ =
2 2
^2—х1 5
Х2
^- [Т0 Bd, -1) sh х2 (| - s)fc_dl.S_ (х - dt). D.28)
Теперь соответствующее уравнению D.25) однородное уравнение
приводим к частично вырожденному дифференциальному
уравнению вида
"о JtT —
1 Щ* о —
dx2
н1—к2
e ~V^ ~W~ [Г°B^ ~ B sh *2 (|~~ *)] ^-*5-{х ~ dl)' D>29)
132
Общее решение этого уравнения имеет вид
Т0 = 6 (х) + — -£- {[Сch *! Bdx - 9 + Dsh v,x Bd, - |)] sh x2 E -
-*)}|*«с^-(*-<*1), D.30)
где 8 (х) = (Cchx^ + ^shx^) S+(dx — #). Частное решение
уравнения D.25), найденное методом вариации постоянных С и D,
записывается так:
dT
rr = (ftx-l)shx1(d1-x)^.
c£r
x=d,
5_ (ж — dx),
D.31)
dT
где &x = ^ VaZA Из D.30), D.31) определяем -—^- I и под-
ставляем в D.31). Получаем общее решение уравнения D.25) в виде
Т = 9 (х) + 6* (я), D.32)
где
9* (х) = [ЛГ sh х2 (а: — dx) + М ch х2 (л: — dt)] £_ (# — dx);
iV =
Кх
Иа*л
(С sh %xdx + D ch x^); M = С ch x,*^ + D sh x^.
Удовлетворяем граничным условиям на поверхностях х = О,
х = I, находим постоянные интегрирования
£ =
ch х^ ch x2d2 +
xx
хг\
sh x1/1shx2^2
ch Kxdx sh x2d2 + sh x^ ch x2<22
x2A^
C = t0.
D.33)
Обусловленные температурным полем D.32), D.33)
температурные напряжения в незакрепленной пластинке определяем по
следующей формуле:
d
и
+ -т(-Ц--1)$*к(х)Т(х)<1х
D.34)
где к (х) = at (x) Е (х)\ щ (х) — температурный коэффициент
линейного расширения. Согласно D.24)
к (х) = а\Х)Ег + {а?Ег - а\1)Ег) 5_ (х - dx) =
= К + (къ - кг) S^ (x - dt). D.35)
Подставляя D.32), D.33) и D.35) в D.34), получаем искомые
температурные напряжения в кусочно-однородной пластинке
оуу = - Агв (х) - к2в* («) + -L / B - -^-) (-£- [С sh Xld +
133
+ D (Сь x,d - 1)] + J£- [N (ch >v4 - 1) + M sh x2rf2] +
+ T(-7--*)|-£|C('-**4 + i:Tr,t) +
Ч-Л^сЬк^-^)]
I ^2
+ M I d sh x2d<
'2U2
N id ch x0d0 - d - ili^L ] +
\
1 — ch x2d2
Kg
D.36)
Если ширина dx и толщина 25 одного порядка малости, то решение
D.36) справедливо для случая пластинки с краем, подкрепленным
тонким стержнем прямоугольного поперечного сечения. Решение
задачи для слоя с покрытием следует из D.36) при а( — О, к\ —
= a^Ei/il - vi).
Рассмотрим закрепленную и теплоизолированную по краю
а = О круговую цилиндрическую оболочку, которая нагревается
по кольцевой области ширины 2Ь внешней средой температуры
t0 или внутренними источниками тепла мощности qXJ действующими
на расстоянии d от ее края. Через поверхности у = ± б оболочки
происходит теплообмен с внешней средой нулевой температуры по
закону Ньютона.
Подставляя в решении D.18) а вместо х, Q вместо q, получаем
такое выражение установившегося температурного поля в
рассматриваемой оболочке:
Т = —~— ( l4 ch ха + \h — h cn ха & sn хо (а ~ d) ™"
^t^O з
Кп
f %
• Z ch х0 (а — d) — A; ch х0 (а — с*) sh x0 (а — с*)
X
х
X 5_(а — d)+ /0(L — l)chx(a — 26) + — к [sh х0(а— d) — к0] +
1 %0
+ *
ch к0 (а — d) -2- &0
/1[l + (Z0-l)chx(a-C*)] +
ch x0 (a — ^
с*) —
+ /2 [°п х (а — с*) — sh х (а — с*)] + /с
- -£- sh х0 (а - с*)] j S+ (а - с*)\ , D.37)
где Q = qx при нагреве внутренними источниками тепла; Q =
= £0а0/6 при нагреве внешней средой; 1Ъ = ( & И—- l)k0 + /х;
/4 = /0 -| 2- /с0 —-1; Z = ch xd; /с = sh xd; a0, a2 — соответственно
коэффициенты теплоотдачи с поверхностей d <I a <i с*, у = ±6
и 0 < a < d, a > с*, -у = ± S; Z0 = ch 2х06; 1г = (к + I) 10; 12 =
= (кк0 + -^- *, к0; к0 = sh 2x0&.
134
При aQ = а
Q
ltY?
{(e-*'] — e~^) ch %d + [1 — ch x (a — d)\ 5_ (a — d) +
+ [ch x (a - c*) — 1] 5+ (a — с*) |. D.38)
Если в D.37) и D.38) положить d = О, то выражения
температурного поля в оболочке, нагреваемой по кольцевой области от края
a = 0, соответственно при переменном и постоянном
коэффициентах теплоотдачи имеют вид
т Q
—9— т — ch x0a
т — ch х0ос •
S+(a-2b)|, m = ^k0 + l0; D.39)
Г = -
^x2
A _ е~ъФ ch Xa - [1 — ch x(a - 2b)] S+ (a - 26)}. D.40)
Производя в D.37) и D.38) замену a* = a — d — b и переходя к
пределу при d -> оо, находим установившееся температурное поле
в бесконечной оболочке соответственно при переменном и
постоянном коэффициентах теплоотдачи:
Т = Q9 //г2ек(а*+Ь) + iK - V(a*+b) - К ch >W**1 ^- (а* + 6) +
+ {/0A0 - 1) **(«*-*> + ko(kQ + ^ e-^-b) __ 2/о [4 + {iQ _ 4) х
X ch х (a* - 6)] + Д3 ch х0а* - рй0| S+ (а* - Ь)\ , D.41)
где Ь,г = 210 + рк0; /г2 =/0 +-^-/с0 — 1; А3 = 2 fchx06+-^- х
X shx06;; р = (х2 + хо) (ххо)";
Г = -Y^V {sh xbe*«* + [1 — ch x (a* + b)] S__ (a* + 6) +
+ [ch x (a* - 6) - 1] S+ (a* - 6)}. D.42)
Сделав в D.41) и D.42) замену a = a* + b и перейдя затем к
пределу при b-+ оо, найдем температурное поле в бесконечной
оболочке, нагреваемой по области а >< 0, соответственно при <х0 Ф
Ф аг и а0 = ах:
0 f к° -*" ' 1л 1 (х«/а + х^-а) р_(а)'; D.43)
Г =
9 f *о
4*0 I X + %о
•em+jl
х + хп
г = _2—Г-
V2 [
A — ch ха) 5__ (а)
D.44)
135
Температурные напряжения в оболочке определяем по
формулам A.210), которые в данном случае имеют вид
®аа —
Тб-^1 + 3-^Мх); орр-^^ + З-Х-Л^). D.45)
Выражая усилия и моменты из соотношений A.209) через
деформации срединной поверхности оболочки и учитывая A.205), находим
#i
2Е8
М1=-
2Е&
^. + vii_A + v)a(r
! d2w
N2=j
3 A — v2) da2 '
I Л> -.
da ' R
v^+4-d+v)^
; м.2 = vMv
D.46)
где компоненты перемещений w, и определяются согласно A.211)
из уравнений
*» + п* (w - atRT) + -^ГА10= 0;
do}
b2R2
D.47)
и= [\(l + v)atT-v^-
da+AW-Jf +^40,
D.48)
где лг4 = 3 A — v2)/62/?2, R — радиус срединной поверхности
цилиндрической оболочки. С помощью преобразования Фурье
находим частное решение уравнения D.47)
-f оо п | a—I \ _
п\а-\\
nRa*
wv = —l T(l)e ^2
2/2 _^
п (а — I) . .
cos —v *'—h sin •
У 2
v,2 ^10
Общее решение этого уравнения ищем в виде
па
in па . ~ . па \ ~77Ч" .
w = 1С1 cos -—=г + С3 sm —— )е у 2 +
у-2
V-2
D.49)
х in • па . п т
-f 62 sm + C4 cos —7:
/
+ wr.
D.50)
D.51)
V ' ^ 2
Удовлетворяя граничным условиям
lim {Nv 7V2, Mx) = 0,
получаем общее решение уравнения D.47) для случая бесконечной
цилиндрической оболочки:
-f-oo nja*—11
л (a* - |)
nRa*
w =
2/2
Г©*
V~2
cos
1Г2
-f- sin
w I a» — 11
V~2
D.52)
136
Подставляя D.52), D.48) в D.46) и полученный результат — в-
D.45), находим температурные напряжения в рассматриваемой
бесконечной оболочке:
Oaa^-^rw"(a*); ом = Е^+хоаа~агЕТ(а*). D.53)
Исследование температурных полей и напряжений
в твердых телах при узкозональном нагреве
Рассмотрим бесконечные цилиндрическую оболочку, пластинку
толщины 26, стержень кругового поперечного сечения радиуса
Д, которые подвергаются термоудару внешней средой температуры
6С в области | £ | < h каждой боковой поверхности или
равномерно распределенными по толщине оболочки (пластинки), сечению
стержня внутренними источниками тепла мощности д,
действующими в области |^| < h. Согласно A.133), A.137) температурное
поле в них определяем из уравнения теплопроводности [52]
-|^ - к\Т = -L + [(х§_ Х2)Г _ QS+(x)] [5_ (i + h) -
-S+&- ft)], D.54)
где к^ = > д ; xi = , * ; а0 — коэффициент теплоотдачи с бо-
ковой поверхности элемента на участке | £ | < h\ аг — коэффициент
теплоотдачи с остальной части поверхности; Э = -— при нагреве
?
элемента внутренними источниками тепла, 9 = щВс при
нагреве элемента внешней средой; для пластинки и оболочки C^ = б,
для стержня C* = Л/2; для пластинки £ = х, для оболочки
£ = а и для стержня £ = z\ S± (ц) — асимметричные единичные
функции; Т |т==0 = 0.
Пусть длина области локального нагрева соизмерима с
толщиной 25 оболочки (пластинки) или с диаметром 2R сечения
стержня. Переходим в уравнении D.54) к пределу при h ->• 0, сохраняя:
при этом постоянными приведенные величины Q = 2А9, А0 =
= 2haQ. В результате получаем
^г - п\Т = -f- + [2mT 1^0 - QS+ (г)] б (Q, D.55)
где m = А0 A — Ка)/А; б (£) — дельта-функция Дирака; Л =
= 2^6; Ка = ах/а0. После применения преобразования Лапласа
уравнение D.55) принимает вид
™--№=BтТ- 4) б (С); v. = ]/"x! + -f • D.56)-
Так как решение уравнения D.56) имеет вид
г-(^-а^И °J:,ICI> • («')
137
то f |,=0
Q/2s (ys + m). Следовательно,
<?exp(-YJU)
T =
2s (ys
D.58)
Переходя в D.58) от изображения к оригиналу, получаем искомое
выражение температурного поля в рассматриваемых тонкостенных
элементах конструкций:
Q*
+
T(Z, Fo)
exp (| Z 1 УШ)
b ~ }ABi
exp (— | Z | j/Bi)
erf с
b+ |ABi
enc
2|/ Fo
+ i Mi
2]/Fo
26
4=--} Mi) +
b2-Bi
• exp F | Z | +
62Fo
Mi)erfcf |ZL + fcJ/"Fo)
• 2/Fo '
D.59)
= £/p*;
где Bi - a^JXu Fo - ят/|Г; b= m^; Q* = Qfc Z =
6* = б для пластинки (оболочки); C^ = R/2 для стержня.
Обусловленные температурным полем D.59) квазистатические
температурные напряжения, например, в локально нагреваемой
источниками тепла свободной от внешней нагрузки бесконечной
пластинке определяем по известной формуле [6]
УУ
Т (X, Fo)
-у - a]EQ* ~ Q* ' D'6°)
где at — температурный коэффициент линейного расширения;
Е — модуль упругости; X = х/8.
На рис. 52 представлены графики изменения безразмерных
температурных напряжений ау в зависимости от безразмерного
времени Fo в сечениях X = 0; 1 пластинки при h = б, переменном
{Bi = a^/Xt = 0,25; Bi0 = a0b/Xt = 0,89) и постоянном (Bi =
Bin
ностеи
поверх-
о - 0,89;
-0,9\
-0,6
-0,3
= 0,25) коэффициентах теплоотдачи с боковых
Кривая 1 соответствует X = 1, Bi = 0,25, Bi
кривая 2 — X = 0, Bi = 0,25,
Bi0 = 0,89; кривая 3 — X = 1,
Bi = Bi0 = 0,25; кривая 4 -— X =
- 0, Bi - Bi0 = 0,25. Из
графиков следует, что неравномерность
теплоотдачи с боковых
поверхностей тонкостенных элементов
конструкций при локальном
нагреве значительно влияет на
распределение температурных
напряжений.
Пусть в области R — h < г <;
< R -f hj | z | <; 6 бесконечной
изотропной пластинки толщины 26
действуют источники тепла плот-
/
ь
Ё
/"
^=-
--—
\
5
/
-
6
Рис. 52.
Fo
138
ностж Wi = qN (r), где
Л' (г) = S_ (r ~ R + h) - S+ (r - Я - А). D.61)
Через поверхности z = ± б плаетинки происходит теплообмен с
внешней средой нулевой температуры, причем коэффициент
теплоотдачи есть функция координаты г,
а (г) = аг + (а0 - а,) N (г), D.62)
где а0 — коэффициент теплоотдачи с части Л — А <. г </?-(- /г
боковых поверхностей z = + б; аг — коэффициент теплоотдачи
с остальных частей поверхности z = ± б.
Установившееся температурное поле в пластинке определяем
из уравнения теплопроводности
-£ + -!-т-т5?-'~тг-"<1 <«з)
при граничных условиях
IT
= 0; TVoo-0. 0.64)
Вводим приведенную теплоотдачу А0 = 2a0h и приведенную
мощность источников тепла Q ~ gF*, где F* = 4й/гб; d = 2л/?.
Если ширина 2/г и толщина 26 пластинки одного порядка,
переходим в D.63) к пределу при h ->- 0, сохраняя при этом
постоянными А0 и Q и используя равенство
lim iV(r)/2/z - б (г - /?). D.65)
В результате получаем
«+4-f-«--f*ri~.-4-)-J£jJ!- («б»
dr2 ' r Jr \ >r===jK d J Л
где х2 = ал/М; М = 2Л0 A - /fa); #a = OLjaQ; A = 2А,Д
Решение уравнения D.66) ищем в виде
Т = СЯ0 (кг) + Dl0 (хг) + JL [ -§- - МГ |r=RJ [/0 (xr) А'0 (хЯ) -
-70(хД)*о(хг)]5(г-Д). D.67)
При условиях D.64) из D.67) получаем
с=:0. D== QKq (хД) .
2n[A-1MRIQ(KR)K0(%R) — l] '
T\r=R = DI0(>tR). D.68)
Подставляя выражения D.68) в D.67), находим искомое
температурное поле в рассматриваемой пластинке
Т = Q ^J° (кг) Z° (х/?)'- 7° (кД) Ж°(xr)J S(r-~R)~K0 (хД) /р (хг)} D б9)
2я [1 - A^MRlo (хД) Z0 <хД)]
139
Переходя в D.69) к безразмерным величинам, записываем
е =
[/„ (jo) К0 (Дд) - /„ (Дд) К0 (g0)] 5 (г0 -Р)-Ка (Дд) /0 (Ь)
1-2Р#(В;0-ЕИ)/0(Дд)ЛГ0(Дк)
, D.70)
где 5В = J/Bi P; Bi0 = а0бД4; Bix = с^бДй ?0 = /Ш г0; г0 = г/б;
P = R/fr, H = h/8.
Температурные напряжения, возникающие в пластинке,
определяем по формулам
Огт —
2G
СТфф — '
1 — V
2G
du
1
dr +v-f -at(i+v)T.
где и — радиальное смещение точки пластинки,
d2u 1 du и ,A..dT
D.71)
D.72)
Решение уравнения D.72) ищем в виде
Dr о,A+v)
u = Crr H 1
У £Г (о d£.
Постоянные интегрирования Сг и Dr находим с помощью условий
Огг |г->оо = 0; и |г==0 = 0.
Переходя в формулах D.71) к безразмерным величинам, получаем
аг =
h°rr
2atEqd2
го о
•о
j£9@d& аф=-аг-0 (/•„). D.73)
После подстановки в D.73) выражения D.70) и интегрирования —
(Wi (lo) - Ph{BR)\ К0 (Б,) + го^ (У - J>*x (Дв)} 5 (г„ - Р) - j
- гаКй (Дд) /, A„)
0\.= — ■
От — — 0"г
У"В1 r§ [1 _ 2РЯ (Bi0 - ВЩ /0 (Дд) Я0 (ДдI
•в(г0).
Принимая в формулах D.74), D.70) г = R, находим
1 h (br)
Or =
Offi =
BR h (BR)
1 А (Дд)
e(P);
-1
9(P);
#o (Дй) /о (Br)
2РЯ (Bio - Bid h (BR) Ka (BR) - 1
140
D.74)
D.75)
D.76)
в
o,s
0,2
0,f
0
-o,f
&
20
<&,
40
6%,
60
80 б\
По формулам D.75), D.76) при Р = 10,
Я = 1, Bti = 0,01 произведены расчеты
температурного поля и напряжений в
зависимости от параметра г = ~-. Резуль-
тг
таты расчета представлены на рис. 53.
Видно, что при увеличении теплоотдачи
с поверхности нагрева температура и
напряжения уменьшаются.
Рассмотрим однородную изотропную
полосу-пластинку ширины 21 и толщины 26.
В области R — h^x*CR + h, |z | < б
действуют равномерно распределенные
источники тепла плотности w% = qN (x), где
N{x) = S„{x — R + h) — S+ (x — R — h).
D.77)
Поверхности x = ± l пластинки предполагаются
теплоизолированными, а через поверхности z = ± б происходит теплообмен
с внешней средой по закону Ньютона. Коэффициент теплоотдачи с
поверхностей z = ± б пластинки можно представить аналогично
D.62) в виде
а (х) = аг+ (а0 — ах) N (х), ' D.78)
где а0 — коэффициент теплоотдачи с части R — h^.x^R-\-h
боковых поверхностей z = ± б; ах — коэффициент теплоотдачи
с остальных частей поверхностей z = ± б.
Установившееся температурное поле в пластинке определяем
из уравнения теплопроводное^
Рис. 53.
d2T
dx2
при граничных условиях
а (х)
Т = -
■N(x)
dT
dx
= о.
х=±/
D.79)
D.80)
Аналогично тому, как это сделано выше, получаем следующее
уравнение для определения температурного поля в пластинке:
d*T
dx2
где Q = qF; F = 4fe5. Общее решение уравнения D.81) ищем в виде
Q-MTI
- к*Т = (МТ |х==й - <?) д(Х~Щ , D.81)
нения D.81
?=*Le-\x-R\x.t D.82)
Т = С ch ш + D sh кх
2Лх
Отсюда определяем Т \X=R и с помощью условий D.80) находим
постоянные интегрирования С и D и получаем искомое выражение
141
температурного поля в пластинке
_0_
м
[sh 2nle- u-н i к _|_ сь у _|_ д) хек (ос-о _f_
+ ch (Z — R) не-***+*>]
1 +
2хЛ
"Ж"
у,
sh 2и/ + ch 2kR + e-*Al
. D.83)
Температурные напряжения в свободной от внешней нагрузки
пластинке определяем по известной формуле
i i
оуу = atE[-T + -±- \ Tdx + ^l xTdx). D.84)
Подставляя в нее D.83), получаем
Xt°yy
2atEqb2
shB
chB
зх
QB [~~~ ' LB
+ chB(BReB-B-l)]\--Q,
e~B [sh BR(B ch В - sh B) +
D.85)
где
В = : Bix L; X = x/fr, L = Z/6; Вд = j/B^ P;
Я.21
0 = W = -4r <sh 2^~ '/Bi X~BR' + *-B l<* (^ + **> */Ш1 *
2g62
Q = (Bi0— Bix)
+ ch (B — BR) e~Y^i *\
Bsh2£
Принимая в D.85) P = 0, X = 0, находим
СУ» =
D.86)
-0,2\
Nc
4
_Z_
Я [1 + g~2i? + A - В-1) sh 2Б]
2 [/Bli sh 2£ + 2Я (Bi0 — By ch2£]
По формуле D.86) вычислены
температурные напряжения в
зависимости от параметра 8 = Bi0/Bix
при Я - 0,01; 0,2; 0,4; 0,8
(кривые соответственно 1, 2, 3,4) и
L = 10, В^ = 0,01. Результаты
20 40 80 80
Рис. 54.
*9\
-1,2
-0,8
-0,4
0
0,
2
0
Г
4 0
>ис. 5*
6
0,
8
Н
142
расчетов представлены на рис. 54. Из графиков следует, что
при увеличении теплоотдачи с поверхности области нагрева
напряжения уменьшаются, а при увеличении ширины источника —
возрастают. На рис. 55 показана зависимость температурных
напряжений, возникающих в пластинке при постоянном
коэффициенте теплоотдачи (Bi0 = Bit = 0,01), от величины Я. При
принятых выше значениях L, BilT X ау = — 0,79Я [30].
Пусть массивное тело нагревается внешней средой температуры
t0 по зоне | х\ <; hповерхности S. Через эту поверхность
происходит теплообмен с внешней средой по закону Ньютона, т. е.
h -r~ + о,* + [(а0 - аг) t - аоу N (х) - 0, D.87)
где п —- внешняя нормаль к поверхности S\ %t — коэффициент
теплопроводности; а0 — коэффициент теплоотдачи с части | х j <;
<; h поверхности S; ах — коэффициент теплоотдачи с остальной
части этой поверхности; N (х) = £_ (x -f- h) — S+ (х — h).
Температура внешней среды вне области нагрева равна нулю.
Решение двумерной задачи теплопроводности тел, на граничной
поверхности которых выполняется условие D.87), сопряжено со
значительными трудностями. Однако, если локальная область
нагрева узка, граничное значение температурного поля в зоне j x \ <;
<^ h можно аппроксимировать его интегральной характеристикой
* = -w I Ых- <4-88>
—Л
Рассмотрим простейший пример. Пусть полупространство
z > 0 нагревается внешней средой по зоне ( х | < h. Тогда
установившееся температурное поле в кем определяется из уравнения
теплопроводности
to = 0 D.89)
и граничное условие при z = 0 имеет вид
где А = -r-j- + —рг • Применяя к D.89), D.90) интегральное
преобразование Фурье по переменной х, получаем
dH _t27.
■£ - Hj\^ = [(Я0 _ tfj О - HQtQ] X
х/А_£Ер_т D.91)
где Я0 = aQ/Xt; Нг = aJX^ Поскольку температура
полупространства на бесконечности равна нулю, решение уравнения D.91|
с учетом условия D,91) записывается в виде
t ~ l/— \(~^- - lU 4- Л Я°8Ь^ в—IS К D.92)
143
Переходя в D.92) к оригиналу, находим
в(Х, Z) = -|2- j (-Щ- - lj T + 1]ф0 (X, Z). D.93)
Здесь
Ф. (X, Z) = +, ""ЧД-'Д d4, D.94)
—оо
Z = z/б; 9 = £/£0; е = fc/б; ц = £б; Г = ФД0; б — характерный
размер. При Z > О
Ф0 (X, Z) = -A- /arctg -£±i- - arctg -^^ +
+ exp (Z Bij) |-1 cos Bix (X + е) [Ei (С+) - Ei (C$] +
+ \ sin Bix (X + e) [Ei {C%) + Ei (<?+)] - -i- cos Bi, (X - e) X
X [Ei (CZ) - Ei (C±)] - sin Bix (X - e) [Ei (CI) + Ei (C±)] \\ , D.95)
где C$ = -Bi1[Z±i(X + E)];Ct= - Bix[Z ± i(X - e)]. При Z =
Ф0(Х, 0) = -±- {-f sign (X + 8) - -2L sign (X - 8) +
+ cos Bix (X + 8) si [Bix (X + e)] — sin Bix (X + e) ci [Bix (X + e)] —
- cos Bix(X — e) si [Bix(X — e)] + sin Bix (X — e) ci [Bix(X - 8)] j. D.96)
Подставляя D.93) в D.88), приходим к уравнению, из которого
определяем Т:
Т = Bi0 F (BiQ (/ q74
яВ11 + (В10-В11)^(В11)' V*'*''
где F (BiJ «= -^L — с + cos 2 Bixci B Bix) + sin 2 Bixsi B Bix) —
—- In BBix); с — постоянная Эйлера. После подстановки D.97)
в D.93) получаем выражение температурного поля в
рассматриваемом полупространстве.
Если значение температурного поля на граничной поверхности
в зоне | х | < h заменить значением t @, 0), то выражение его в
полупространстве примет вид D.93), в котором Т следует заменить
на 6 @, 0). Из D.93) получаем
А/О 0\ Bip Y (В1г) nQ4
6 <°' °> = nBix + CBio-BWYfBiO ' D'98)
где W (Bix) = л + 2 cosBi^i (Bix) — 2 sin Bixci (Bix).
144
0,4
oj
0,2
o,t
\к
^
zS
2
g£-'t=r=
.: Jsl
Tl
0,25 0,5 0,75
Рис. 57.
0,5
Ш
re'
H^
1^
J
— —.——.
0,25 0,5 0,75 Z
Рис. 59.
На рис. 56—59 приведены результаты вычислений
температурного поля D.93) с использованием выражений D.97) ( ) и D.98)
( ) ПрИ д/s = 0,1, 6 = 10 см. Кривые на рис. 56, 57
построены при Bi0 = 0,2 и Bix = 0,02; 0,06; 0,12 (соответственно 7, 2, 3),
а на рис. 58, 59 — при Bix = 0,02 и Bi0 = 0,5; 0,25; 0,05 B, 2, 3).
Из рисунков видно, что при увеличении теплоотдачи с поверхности
вне области нагрева температурное поле уменьшается, а с
поверхности в области нагрева — увеличивается.
Температурные напряжения, вызываемые температурным полем
D.93), определяем по известным формулам [46]
Охж =
д* (U — 26Ф),
д2 (U — 2£Ф) ф
_ дх2 '
ОЧ;2 =
д2 {U — 2£Ф)
дхдг '
D.99)
где U — бигармоническая функция,
ДД£/ = 0;
D.100)
10 6—1534
145
Ф — термоупругий потенциал, являющийся частным решением
уравнения
Если полупространство свободно от внешней нагрузки,
компоненты температурных напряжений D.99) должны удовлетворять
следующим граничным условиям:
Огг = Ozx = 0 при Z = 0, Z -> ОО. DЛ 02)
Применяя к формулам D.99) — D.102) интегральное
преобразование Фурье по я, с учетом изображения температурного поля D.92),
соответственно получаем
d2 {U— 2&Ф) . \
^=-Г(^-2СФ);
dz2
I2) Е/ = 0;
х
Я0 sin gfe
III*
КШ + Я,)
Общее решение уравнения D.104) имеет вид
й=(А + Bz)e~zn* +(C + Dz)ezUi .
Частное решение уравнения D.105) записываем в виде
D.103)
D.104)
X
D.105)
D.106)
+ t0
Y2n 1 — v
Н0 sin %h
D.107)
\U\l\ + Bi)\l\
Определив постоянные интегрирования А, Ву С, D из
трансформированных условий D.102) и подставив их значения в D.106),
получаем
#0 sin %h
■ zr^U,
Ш'КШ + #1)
Из D.107) и D.108), как и следовало ожидать, следует
D.108)
oZz = 0;
oxz =* 0;
146
0.
Аналогично можно определить температурное поле и
напряжения и в других массивных телах, нагреваемых по узким зонам,
например в цилиндре, слое, пространстве с цилиндрической
полостью.
Пусть бесконечная изотропная пластинка нагревается в
области г < R, z = -f- б температурой 0О, остальные ее
поверхности нагреваются температурой 8С. В этом случае в уравнениях
A.143) N (г) = S+(R — г). Используя преобразование Хан-
келя, находим такое решение уравнений A.143):
QiR
1
Pi
S+(R-r) +
-^-/0(M*i(Pi#)
+ ^I1®iR)KQ($ir)S^(r~R).
Согласно A.42), A.44)
^1 — fA2
Подставляя D.109) в D.110), а затем полученное выражение для
(^ — в A.141), получаем уравнение, из которого # находим в
виде
D.109)
D.110)
# =
(«о — eg ^ + (н - |4Я) л '
D.111)
где
* = 2 [Qi, - 1) Р2 A + Зщ) - (jx2 - 1) Рг A + 3^)];
P. __L
./^фадд)
Обусловленные Г и Г* температурные напряжения определяем
по формулам
<у„ = -^4-(я*-П афф = 2С^(^-¥), D.112)
dr
где f и w — соответственно термоупругий потенциал радиальное
го перемещения и прогиб,
AW = at(l+v)T; AAw = —ot*A + v) -~^-. D.113)
Частные решения уравнений D.113) имеют соответственно вид
¥ = а,Д
1 + У
^1— Й2
1ш^ЛИ-|*19Л(г)];
ш = а< "Г 117—^7"[<?Л (г)~ ^л (r)] '
D.114)
ю*
147
где %i (г) - \ /хг(Ду •/° ^ t%. Подставляя D.114) в D.112), полу-
чаем такие выражения температурных напряжений в пластинке:
агг =
И-1 — ^2 г
(l*i--f)^0»W"" I
■(м.-т)^ф1(г)];
■>фф
D.115)
где
Ф|(г) = РГ^-др -Oi(r, Л) - [-£^*L -0,(г, i?) +
+ 0*(Д,г)]5.(г^Д));
При г = О выражения D.115) принимают вид
Grr = Ot
фф
atER
(Д.! — Ц3
-(ib-f)
(h~i
QM@)\
D.116)
* 1 Г 1 1
где Фг(О) «« 0PQ -5 i?^ {Cii?) , в безразмерных величинах —
ar = (Z-n1)M2-(Z-lx2)M1;
o-m =
D.117)
где
о\=
_ 9а
atEt0
A = Г, ф);
Mi = {т ~ т h (Вф) Кх {Bik) ~~ [т {* -
Р2
-^/,E^)^E^) +
+ -2-/1'(fiiu)Jf1(firf))LS_(p-u)
Bi0 (I + Зщ)
^(В^-ву + гв?^-^) '
л
148
^ = 1/^ + 3^; Fi = B\F;
Pi =
Bic
Ф? = A+3^)
I- -I^Bik) КХ{ВЩВТ2;
«с6 t (fa-^)92-(^2-Z)(pi
Bi0 (p-i — ц2)
|il — Ц2
-{l-BikI0(Bip)K1(Bik)-
F. (Bi0 - Bic) + 2Bf (p.! - Ц,)
- [1 - /0 EiP) ЯГ, (Bik) - Ix (Bik) K0 (Вф)] 5_ (p - k)};
^ = -^=r [У+ + 3 ± KG+ + 3J + 3 (V-J]; v± = Bic±Bi7;
На рис. 60, 61 представлены результаты расчетов безразмерных
радиальных и кольцевых температурных напряжений,
выполненных по формулам D.117) при к = 0,5, Bi0 = 1, Bi7 = 0, Bic =
— 0,01 (кривые 1), 0,25 B), 1 C) на верхней ( ), срединной
( ) и нижней ( ) поверхностях пластинки, на рис. 62,
63 — результаты, полученные при к = 1.
Рис. 60.
149
Если бесконечная изотропная пластинка нагревается в области
г <* R каждой боковой поверхности z = ± б температурой 0О,
а остальные ее поверхности — температурой 0С, то для определения
температурного поля Т в ней вместо системы A.142) используется
одно уравнение
АГ - х2Г = - QN, D.118)
где
Ко
= -§-; ^ = (^2-^)# + ^0;
D.119)
0--£-Ji№ Л^ = ^+(Л —г).
о
Применяя преобразование Ханкеля, находим
+ 1г (хД) #0 (хг) ^ ] S_ (г - Л)} . D.120)
Подставляя D.120) в выражение D.119), получаем
2nh0M (R)
0 = ^LJJ D.121)
1 Г 1 1
где М (R) = -^2~ h (пЩ %i (х^) • Следовательно,
<? - *о*о{* + (^ ~ 1) [1 - 2/х (кД) #х (хДИр1. D.122)
150
Обусловленные температурным полем D.120), D.122)
температурные напряжения находим по формулам D.112), где z = 0,
a W определяется из первого уравнения D.113), в таком виде:
Or = - 8 {4- - -£ h (КвГсР) К, (Утск) +
+ ± U (УЩр) Kt (УШ) - h (КВД К, A/ЁГср) -
От = — О Т —
D.123)
где
е = -Ж; {* + ft ~ 4)[1 ~ 2/l {VBick) *» ^Bloft)]} S
-f- = e < 1 - к КвГо/о (КвГсР) # i (V^cfc) +
+ {ft I/ вй [/0 (/вир) kx (i/Brcft) + /x (j/вд к0 (КвГср)] -
-l}S_(p-ft)>.
На рис. 64, 65 представлены расчеты безразмерных радиальных
и кольцевых температурных напряжений, выполненные по
формулам D.123) при k = 0,5 ( ); к = 1 ( ), Bi0 = 1;
Bic = 0,01 (кривые 1); Bic = 0,25 B); Bic = 1 E).
На основании результатов расчетов, приведенных на рис. 60—
65, можно сделать вывод, что при увеличении коэффициента
теплоотдачи с поверхности вне области нагрева максимальные
значения температурных напряжений уменьшаются. Изменение
теплоотдачи существенно влияет на распределение температурных
напряжений.
Рассмотрим бесконечную круговую цилиндрическую оболочку
толщины 26. По узкой кольцевой области | а | < h оболочка
нагревается равномерно распределенными источниками тепла мощности^.
Коэффициент теплоотдачи ап является функцией координаты а
и согласно A.17) изменяется по закону
ап (а) = аг + А0 A - Ка) б (а), D.124)
где AQ = 2а0А, а0 — коэффициент теплоотдачи с. области |а| < h
поверхностей 7 = ± б оболочки; ах — коэффициент теплоотдачи
с остальной части этих поверхностей.
Установившееся температурное поле в оболочке согласно A.133)
определяем из уравнения теплопроводности
д?Т <*п(а) rp 2hq&(a)
da2
Kfi
Г=-
D.125)
151
6V
ц2о
'0,24
-o,z
-0,16
■0,/2
-0,08
-од
0
ОМ
\
Л
\
\\
kV
\\
V
j^
\^c-
>2
J^f
***■""
"~"l
/ 2 3
Рис. 65.
4 p
решение которого имеет вид
Т (а)
Л
2к
■*-*i*if D.126)
^-2-^A-Яа)Г|а=
где Q = Ah8q; Л = 2А*6* к2 = о^/ЯД Из D.126) находим Т |а=0, и
Г = 5ег-*|0И. D.127)
Здесь В =
2Лх
4,A-*а)
Ли + А0 A - К)
- 1
Поскольку задача осе-
симметрична и напряженно-деформированное состояние оболочки
не зависит от р, система дифференциальных уравнений в частных
производных A.211) относительно компонентов вектора
перемещений сводится к одному дифференциальному уравнению для
определения прогиба
{-Щ- + п*)w = n*atRT - W" Ao D-128)
и одному равенству для определения перемещения в направлении а
и = J [A + v) atT - vw/R] da + Aloa/R + 440, D.129)
152
где n4 = 3 A — v2)/i?262; R — радиус срединной поверхности
оболочки. Решение уравнения D.128) ищем в виде
w
i па \ (п па . п я. па \ .
= ехр т^Н i W cos —=- + С-sin —г=- +
па . ~ . па
Уг 4 /2
+ exp^)^3cos^|-+C4sin^|-)+u;<r>, D.130)
где выражение
ы/г) =
3v
g2#2 ~Ю
Ло +
2n*atBx,R { cos£a
» (£4 + n4) (g« + н2) ^ DЛ31)
является частным решением уравнения D.128), найденным с
помощью преобразования Фурье по а. Постоянные интегрирования
Ci> С2, Сз> Q» ^ю» ^40 определяются из следующих условий:
lim {Nv Nt, Мг) = 0. D.132)
Усилия и моменты NX1 N2, Mv M2, согласно A.209) и A.205),
записываются в виде
,т 2ЕЬ Г du . vw /Л . ч „,]
Ni = Т=^-[-Щ- +-R -<4 + v) а'Г|;
2#6 Г <fo , W /л i \ m'
Ж
Ml 3(i-v2;
da2
M„
D.133),
Удовлетворяя граничным условиям D.132), общее решение
уравнения D.128) получаем в виде
w =
2n*atBnR
cos£a
(£4 + )(?2 + *2)
dg.
D.134)
Формулы для определения температурных напряжений в
рассматриваемой оболочке, согласно A.210), имеют вид
°™=4r(N* + 3M*lh); ^ = ^(^2 + ЗМ2-Х-). D.135)
Подставляя D.134), D.129) в D.133), а затем полученный
результат в D.135), находим такие выражения температурных
напряжений в оболочке:
2BEyn*atKR i*
A - v2) я J (g4 + /г4) (|2 + к2)
I2 cos |a
4;
0РЭ = Я^-а^ +
vaa
153
Переходя теперь к безразмерным величинам, при у = 8 получаем
оо
aa = fl(l-v!!)-1(' л V
2 cos a*'
46«) (? + ^ Bix)
dfc
ap = vaa + A + v) Q
„P- VWtR, i a»
«,
Г cosa*g j DЛ36)
8&4 /Bix
где
50л^(Т«
Qi <?£a^4
Q =
V*h
/Bh + AiBioa-y '
£ = £Я; a* = a/#;
4&4=3(l-v2)/??; 7?! = /?/б.
Вычисленные значения напряжений aa и op по формулам D.136)
в точке а* = 0 при Bi0 = Bi2 = 0,01 и Bi0 = 0,1, В^ = 0,01
соответственно равны 0,31; 0,16; 3,3; 1,7, т. е. при увеличении
коэффициента теплоотдачи с области нагрева по сравнению с
коэффициентом вне этой области продольные и кольцевые напряжения
уменьшаются.
ЛИТЕРАТУРА
1. Алексашенко В. А. Температурное поле в стекле фотолюка при
постоянных и переменных коэффициенте теплоотдачи и температуре внешней
среды.— Труды ЦАГИ, 1966, 1003, 14—40.
2. Амбарцумян С. А., Дургарьян С. М. Некоторые нестационарные
температурные задачи для ортотропной пластинки.— Изв. АН СССР. ОТН.
Механика и машиностроение, 1962, 3, 120—127.
3. Бартенев Г. М. Механические свойства и тепловая обработка стекла.
Госстройиздат, М., I960, 167 с.
4. Бартенев Г. М., Колбасникова А. И. К сравнению теории закалки с
экспериментом.— ЖТФ, 1958, 28, 6, 37—39.
5. Богуславский И. А. Управляемое упрочнение стекла жидкостной
закалкой.— ДАН СССР, 1967, 173, 6, 1298-1301.
6. Боли Б., Уэйнер Дж. Теория температурных напряжений. «Мир», М.,
1964. 517 с.
7. Болотин В. В., Болотина К. С. Термоупругая задача для кругового
цилиндра из армированного слоистого материала.— Механика полимеров,
1967, 1, 136-141.
8. Болотина Я*. С. Механические и теплофизические характеристики
слоистого материала.— Изв. вузов. Машиностроение, 1966, 12, 23—28.
9. Видин Ю. В. Нагревание цилиндрического тела с внутренним
тепловыделением при переменном коэффициенте теплообмена.— ИФЖ, 1966, 11, 2,
166—170.
10. Видин Ю. В. О температурном поле неограниченной пластины при
переменном коэффициенте теплообмена.— Изв. вузов. Авиационная техника,
1967, 7, 65-69.
11. Видин Ю. В. Температурное поле составного тела при переменном
коэффициенте теплоотдачи.— Изв. вузов. Энергетика, 1969, 2, 107—110.
12. Винокуров В. А. Сварочные деформации и напряжения.
«Машиностроение», М., 1968. 233 с.
13. Гельфанд И. М., Шилов Г. Е. Обобщенные функции и действия над ними.
Физматгиз, М., 1959. 470 с.
14. Градштейн И. С, Рыжик И. М. Таблицы интегралов, сумм, рядов и
произведений. «Наука», М., 1971. 1108 с.
15. Гревцева В. Н., Киршбаум В. И. Температура полуограниченного
стержня с коэффициентом теплообмена, экспоненциально зависящим от
времени.— В кн.: Механика. Изд. Куйбышевск. политехи, ин-та, Куйбышев,
1969, 72—76.
16. Гревцева В. Н., Киршбаум J5. И. Теплопроводность твердых тел с
теплообменом, линейно зависящим от времени.— В кн.: Сборник трудов по
физико-математическим наукам. Изд. Куйбышевск. политехи ин-та,
Куйбышев, 1970, 17—21.
155
17. Громовик В. I. Нестацюнаряе температурив поле в ашзотроптй пластин-
щ з щ1 линою.— У кн.: Тези допов1дей П'ято'! науково! конференцы мо-
лодих математишв Украши. Вид. 1н-ту математики АН УРСР, К., 1970,
218.
18. Громовик В. И. Температурные напряжения в нагреваемых ортотропных
пластинках с переменным коэффициентом теплоотдачи.— ПМ, 1973, 9,
9, 94-98.
19. Громовых, В. И. К определению температурных напряжений в
ортотропных пластинках с защемленным ортотропным подкрепляющим
элементом.— В кн.: Тезисы докладов XIII Научного совещания по тепловым
напряжениям в элементах конструкций. «Наукова думка», К., 1974, 23—
24.
20. Диткин В. А., Прудников А. П. Справочник по операционному
исчислению. «Высшая школа», М., 1965. 466 с.
21. Дёч Г. Руководство к практическому применению преобразования
Лапласа. Физматгиз, М., 1960. 207 с.
22. Иванов В. В. Температурный режим твердого тела при переменных
условиях теплообмена на его поверхности.— Изв. вузов. Авиационная
техника, 1967, 1, 133—134.
23. Инденбом В. Л. К теории закалки стекла.— ЖТФ, 1954, 24, 5, 925—
928.
24. Каганов М. А., Розеншток Ю. Л. О температуре тел в среде с
пульсирующей теплоотдачей и температурой.— ПМТФ, 1962, 3, 90—92.
25. Карслоу Т., Егер Д. Теплопроводность твердых тел. «Наука», М., 1964.
487 с.
26. Коваленко А. Д. Основы термоупругости. «Наукова думка», К., 1970. 307 с.
27. Козлов В. Н. Решение задачи теплопроводности при переменном
коэффициенте теплообмена.— ИФШ, 1970, 18, 1, 133—138.
28. Коляно Ю. М. Температурные напряжения в ортотропной
полосе-пластинке с теплоотдачей. — ПМ, 1967, 3, 6, 39—47.
29. Коляно Ю. М. Определение температурных полей в тонких
анизотропных пластинках с переменным коэффициентом теплоотдачи.— ДАН БССР,
1970, 14, 11, 1000-1002.
30. Коляно Ю. М., Громовик В. И. Влияние переменной теплоотдачи на
напряжения в пластинках, обусловленные источниками тепла. — ПМ, 1976, 12,
12, 101—106.
31. Коляно Ю. М., Громовик В. И. Нестационарное температурное поле в
анизотропной пластинке при заданном тепловом потоке на краю.— ИФЖ,
1972, 22, 6, 1125-1126.
32. Коляно Ю. М.} Громовик В. И. Температурные напряжения в
ортотропных пластинках с переменным коэффициентом теплоотдачи.— ПМ, 1972,
8, 1, 56—61.
33. Коляно Ю. М., Громовик В. И. Неустановившиеся температурные поля
и напряжения в полосе-пластинке, обусловленные сосредоточенными
источниками тепла.— ФХОМ, 1974, 6, 25—30.
34. Коляно Ю. М., Громовик В. И. Напряжения в пластинке с отверстием при
нестационарном коэффициенте теплоотдачи.— Проблемы прочности, 1974,
12, 18—20.
35. Коляно Ю. М., Громовик Б. И. Квазистатические температурные
напряжения и перемещения в ортотропных пластинках.— В кн.: Динамика и
прочность машин, 24. Изд-во Харьковск. ун-та, Харьков, 1976,
93—99.
36. Коляно Ю. М., Дидык В. 3., Кордуба Б. М. Учет переменной
теплоотдачи при нагреве пластинки полосовым источником тепла. Деп. в ВИНИТИ,
№ 102-76.
87. Коляно Ю. М., Лозбенъ В. Л. К определению нестационарных
температурных полей и напряжений при закалке стеклянных пласгинок.— В кн.:
Тезисы докладов Первой республиканской конференции молодых ученых
по механике твердого деформируемого тела. Изд. Ин-та механики
АН УССР, К., 1969, 53-54.
156
38. Коляно Ю. М., Лозбень В. Л. Температурные напряжения в кольцевой
анизотропной пластинке с зависящим от температуры коэффициентом
теплоотдачи.— Механика полимеров, 1971, 5, 949—950.
39. Коляно Ю. М., Лозбень В. Л. Визначення температурних напружень у
деяких ашзотропних пластинках з залежним в!д температури коефь
щентом тепловвддачь— У кн.: Тези доповщей Перпнн конференцп моло-
дих вчених Захщних областей УРСР. Вид. Льв1вськ. обкому ЛКСМУ
Львгв, 1972, 271—273.
40. Коляно Ю. М,, Лозбень В. Л. Воздухоструйная закалка стеклянной
пластинки.— ФХММ, 1973, 2, 112—114.
41. Коляно Ю. М., Лозбень В, Л. Нагрев движущимся источником тепла
полубесконечной пластинки с переменным коэффициентом
теплоотдачи.— ПМ, 1974, 10, 3, 42—47.
42. Коляно Ю. М., Лозбень В. Л., Стасюк С. Т. Неустановившиеся
температурные напряжения в полубесконечной пластинке, нагреваемой
движущимся линейным источником тепла.— Изв. вузов. Машиностроение, 1974,
р4, 10—14.
43. Корн Г., Корн Т. Справочник по математике для научных работников и
инженеров. «Наука», М., 1968. 720 с.
44. Лыков А. В. Теория теплопроводности. «Высшая школа», М., 1967. 599 с.
45. Новацкий В. Вопросы термоупругости. Изд-во АН СССР, М., 1962. 364 с.
46. Паркус Г. Неустановившиеся температурные напряжения. Физматгиз,
М., 1963. 252 с.
47. Шдстригач Я. С, Коляно Ю. М. Температурив поле в тонких пластинках
при зм!яному коеф1щбнт! тепловщдач! з бокових поверхонь.— ДАН
УРСР. Сер. А, 1971, 1, 75-78.
48. Шдстригач Я. С, Коляно Ю. М., Лозбень В. Л. Р1вняння теплопров!д-
HocTi для ашзотропних пластинок i3 залежними вщ температури поверх-
m коефщ1ентами тепловцшачь — ДАН УРСР. Сер. А, 1972, 6, 551 —
555.
49. Шдстригач Я. С, Ярема С. Я. Температурш напруження в оболонках.
Вид-во АН УРСРТ К., 1961. 212 с.
50. Подстригач Я. С, Коляно Ю. М. О нагреве источниками тепла тонких
пластинок с теплообменом.— ИФЖ, 1964, 7, 2, 79—86.
51. Подстригач Я. С, Коляно Ю. М. Неустановившиеся температурные поля
и напряжения в тонких пластинках. «Наукова думка», К., 1972.
308 с.
52. Подстригач Я. С, Коляно Ю. М. Учет теплоотдачи при локальном
нагреве тонкостенных элементов конструкций. —ДАН СССР, 1975, 225, 4,
778—781.
53. Постольник Ю. С. Конвективный нагрев при линейной зависимости
коэффициента теплообмена от времени.— Изв. вузов. Черная металлургия,
1970, 6, 143—148.
54. Розеншток Ю. Л. Температурное поле неограниченной пластины в
условиях зависимости температуры внешней среды и коэффициента
теплообмена от температуры.— ИФЖ, 1963, 6, 3, 45—50.
55. Розеншток Ю. Л. Решение задачи теплопроводности при коэффициенте
теплоотдачи, зависящем от времени.— ГТМТФ, 1963, 1, 136—137.
56. Рыкалин Н. Я. Тепловые основы сварки. Ч. 1. Изд-во АН СССР, М.—
Л., 1947. 272 с.
57. С ало матов В. В., Гончаров Э. И. Температурный режим
тепловыделяющих элементов при переменных значениях коэффициента теплообмена и
температуры внешней среды.— Изв. АН СССР. Энергетика и транспорт,
1967, 4, 99—103.
58. Саломатов В. В., Гончаров Э. И. Температурное поле неограниченной
пластины при переменных значениях коэффициента теплообмена и
температуры внешней среды.— ИФЖ, 1968, 14, 4, 743—745.
59. Саломатов В. В., Гончаров Э. И. К расчету теплопроводности при
нестационарном коэффициенте теплообмена.— Изв. АН СССР. Энергетика
и транспорт, 1968, 6, 154—159.
157
60. Саломатов В. В., Иванов В. В., Гончаров 3. И. Исследования переноса
тепла в твердых телах при переменном коэффициенте теплообмена.— Изв.
АН СССР. Энергетика и транспорт, 1968, 4, 144—147.
61. Саркисян В. С. Температурные напряжения в анизотропных (неорто-
тропных) пластинках.— В кн.: Тепловые напряжения в элементах
конструкций, 5. «Наукова думка», К., 1965, 127—137.
62. СЬдляр М. М. Визначення нестационарного температурного поля вдво-
шаровш пластинщ у випадку змшного в qaci коефицента тепловщдачь —
ПМ, 1963, 9, 3, 309-314.
63. Сидляр М. М. Об интегрировании уравнения теплопроводности в случае
изменения во времени коэффициента теплоотдачи.— В кн.: Тепловые
напряжения в элементах конструкций, 3. «Наукова думка», К., 1963,
38-44.
64. Сидляр М. М. Нестационарное температурное поле бесконечного
цилиндра при переменном коэффициенте теплоотдачи.— ПМ, 1965, 7, 1, 11—13.
65. Снеддон И. Преобразование Фурье. ИЛ, М., 1955. 667 с.
66. Уздалев А. И. Некоторые задачи термоупругости анизотропного тела.
Изд-во Саратовск. ун-та, 1967. 168 с.
67. Юдин В. М. Решение задачи теплопроводности для полуограниченного
тела при переменном коэффициенте теплообмена.— ИФЖ, 1964, 7, 12,
90-94.
68. Юдин В М. Метод решения задачи теплопроводности при переменном
коэффициенте теплоотдачи — В кн.: Тепловые напряжения в элементах
конструкций, 5. «Наукова думка», К., 1965, 68—75.
69. Chung P. M., Anderson A. D. Unsteady Laminar Free Convection. — Trans.
ASME. Heat Transfer, 1961, S.C, 83, 4, 78—89.
70. Hill P. R. A Method of Computing the Transient Temperature of Thick
Walls from Arbitrary Variation of Adiabatic Wall Temperature and Heat
Transfer Coefficient.— NACA. Report 1372, 1958, 21.
71. Papoulis А. Л. New Method of Inversion of the Laplace Transfor.— Quart.
Appl. Math., 1957, 14, 4, 405-414.
72. Selig F. Ebene Warmeleitprobleme mit variablem Ubergangs koeffizi-
ent.— Z. angew. Math, und Mech., 1957, 37, 7-8, 73—77.
73. Schetz J. A., Eichorn R. Nonstationary Free Convection along Infinite
Vertical Plate.— Trans. ASME. Heat Transfer, 1962, 84, 4, 42—44.
Ярослав Степанович Подстригай
Юрий Михайлович Коляно
Василий Иванович Громовык
Виталий Леонидович Лозбень
ТЕРМОУПРУГОСТЬ ТЕЛ
ПРИ ПЕРЕМЕННЫХ КОЭФФИЦИЕНТАХ
ТЕПЛООТДАЧИ
Печатается по постановлению ученого совета
Львовского филиала математической физики
Института математики АН УССР
Редактор Е. Л. Орлик
Оформление художника Д. Д. Грибова
Художественный редактор Я. П. Антонюк
Технический редактор Б. М. Кричевская
Корректор И. В. Точаненко
Сдано в набор П.VI 1976 г. Подписано в печать, 8.XII.1976 г. БФ 08115.
Зак № 6—1534. Тираж 1750 экз. Формат 60y90l/ie. Бумага типогр № 1
Усл. печ. л. 10. Учетно-изд. л. 9,26. Цена 1 руб. 17 коп.
Издательство «Наукова думка», 252601, Киев—601, ГСП. ул. Репина, 3
Изготовлено Нестерове кой городской типографией Львовского облполиграфиздата
(г. Нестеров, ул. Горького, 8) с матриц Головного предприятия республиканского
производственного объединения «Полиграфкнига» Госкомиздата УССР (г. Киев.
Довженко, 3), зак. 522.
В 1977 г. В ИЗДАТЕЛЬСТВЕ «НАУКОВА ДУМКА»
ВЫЙДЕТ В СВЕТ КНИГА:
Термоуцругость электропроводных тел.
Язык русский. 20 л. Цена 2 руб. 41 коп.
Книга посвящена дальнейшему развитию расчетных схем и
эффективных аналитических методов решения комплексной задачи об определении
электромагнитных, температурных полей и напряженно-деформируемого
состояния электропроводных тел, в частности пластин и оболочек, при
индукционном нагреве; исследованию и оптимизации термоупругого
состояния применительно к задачам индукционной термообработки элементов
металлических конструкций.
Предназначена для научных работников, занимающихся
исследованиями в области механики деформируемого твердого тела и математической
физики, а также для специалистов, интересующихся вопросами
упрочняющей термообработки металлических конструкций.
Наиболее продолжительное время заказы на эту книгу принимает мага-
sun издательства «Наукова думка» B52001, Киев-1, ул. Кирова, 4), который
после выхода книги из печати вышлет ее иногородним заказчикам
наложенным платежом.