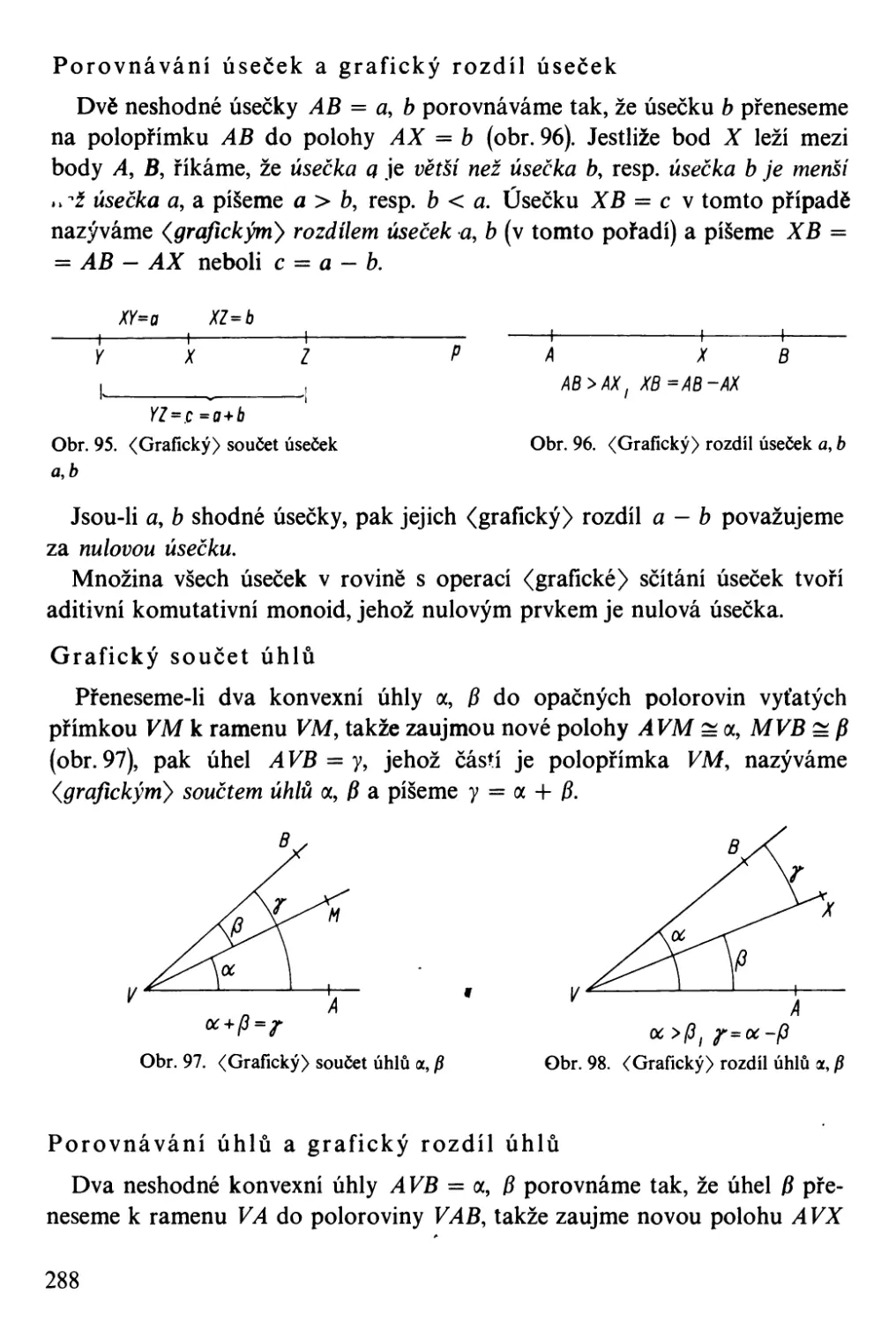
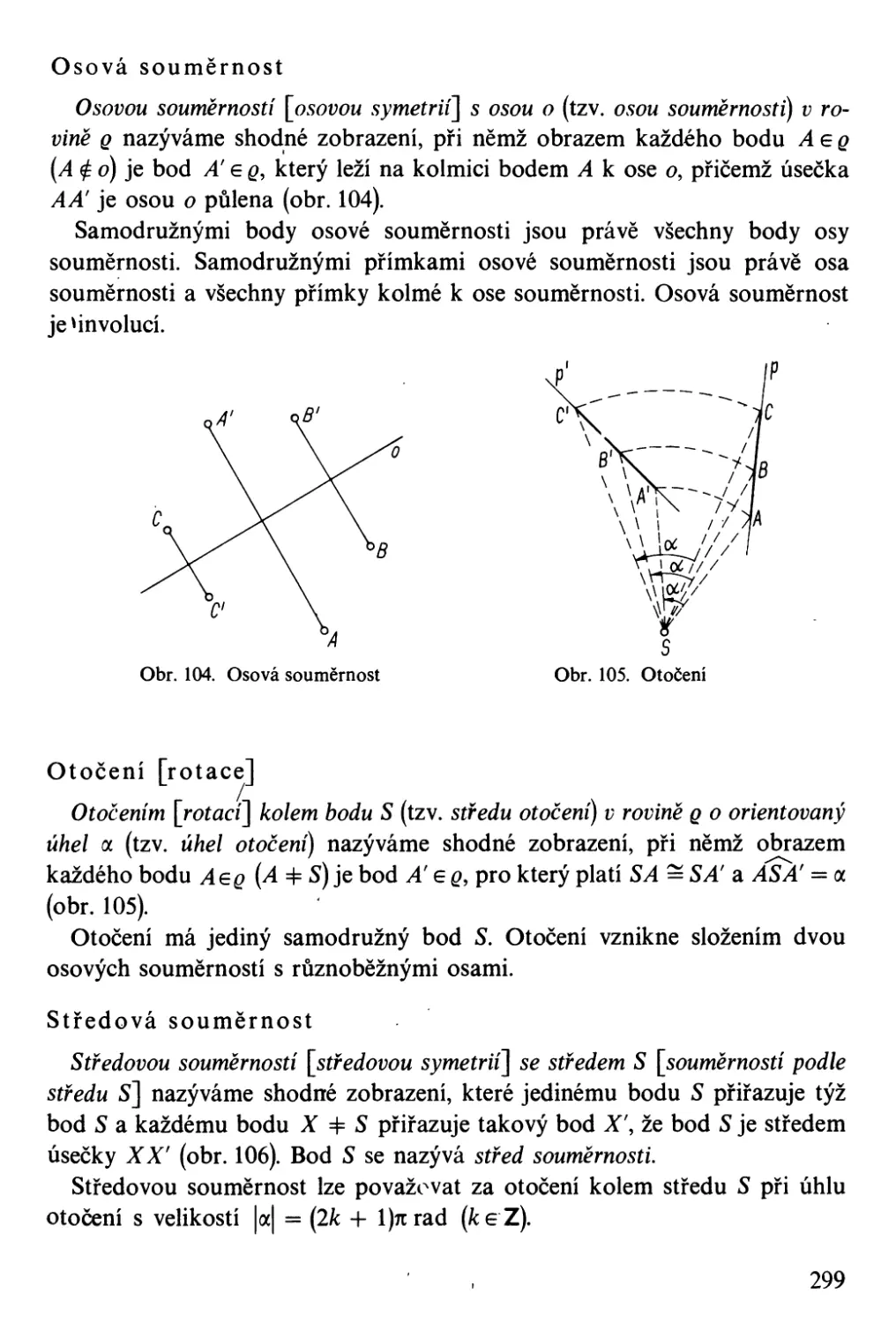
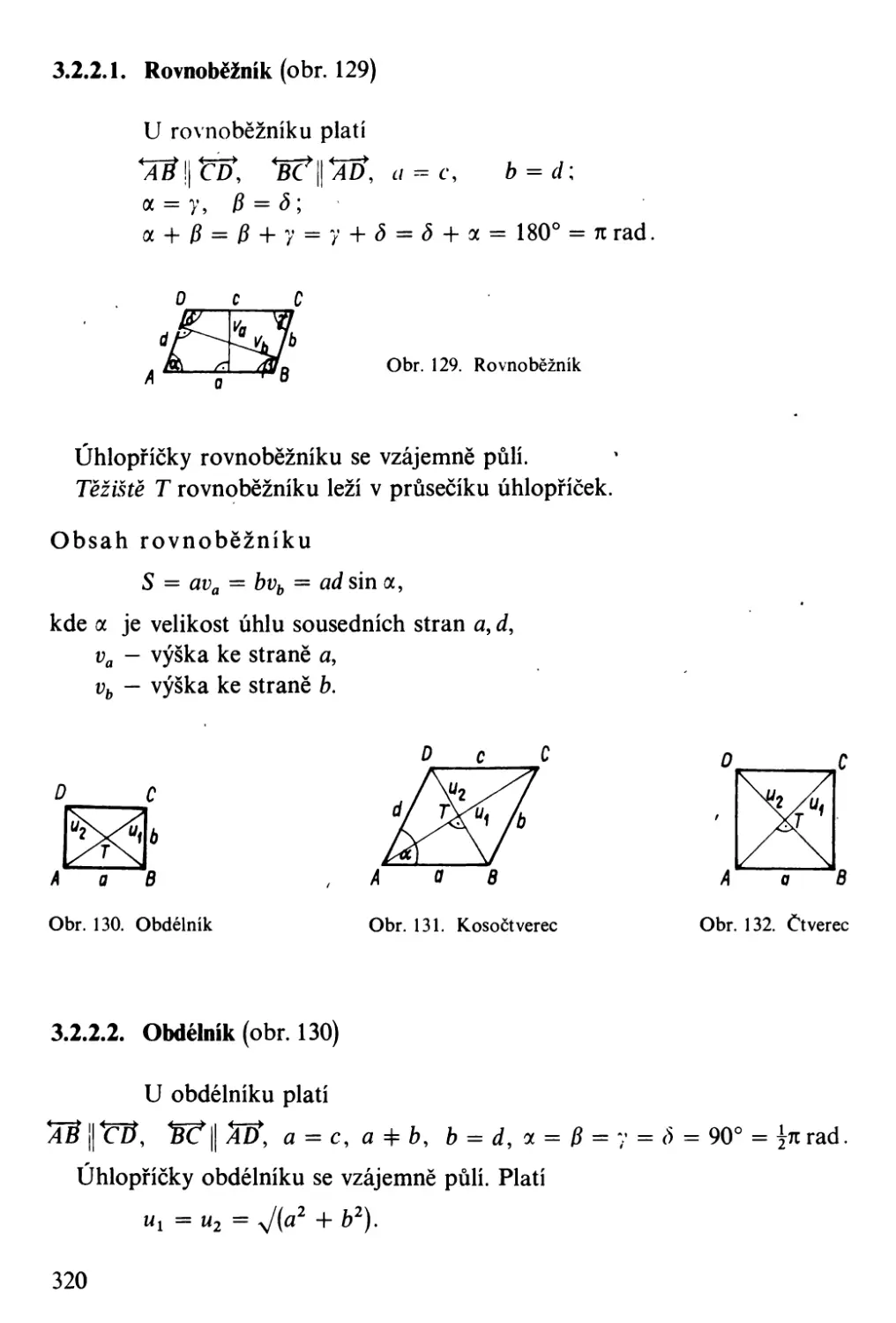
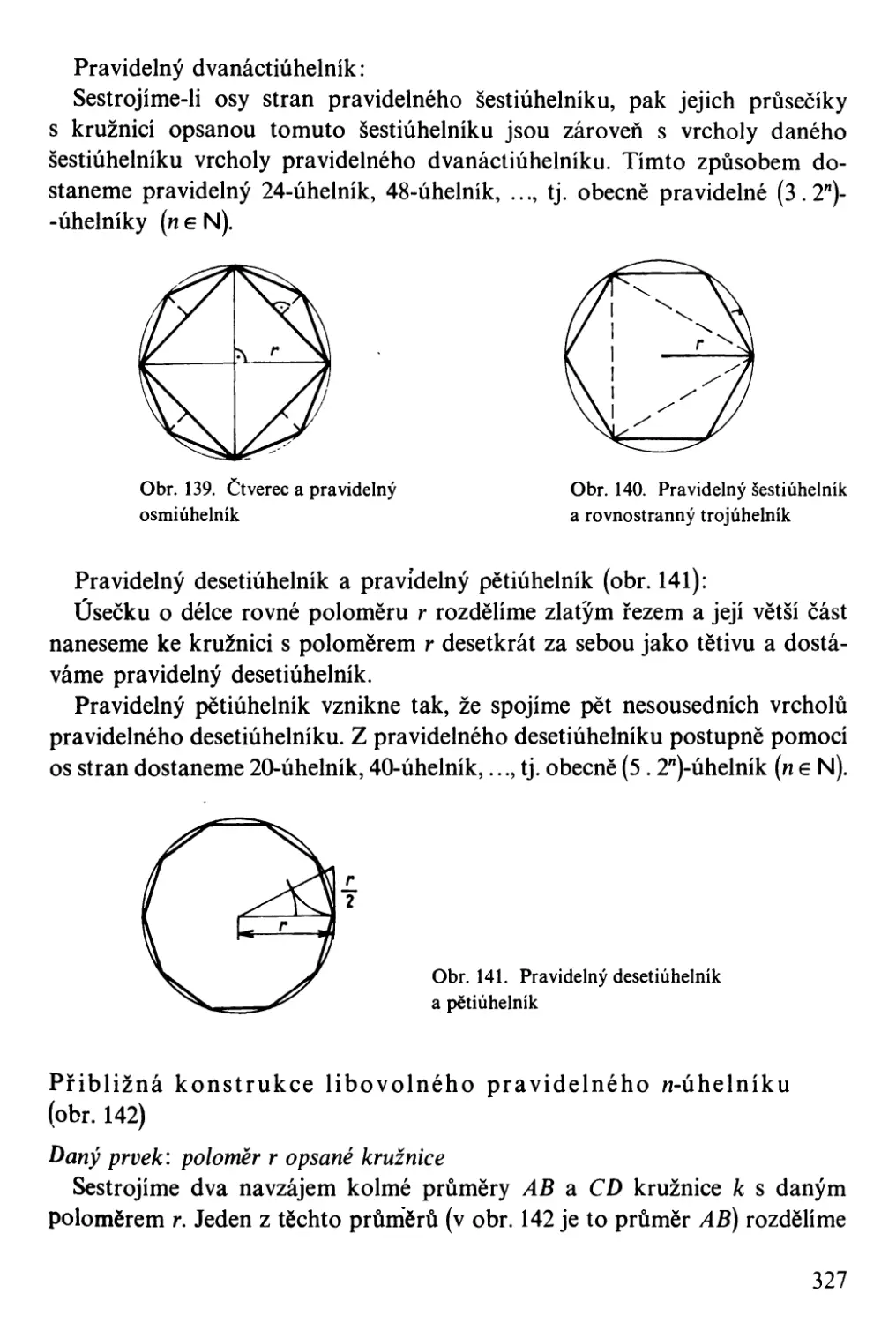
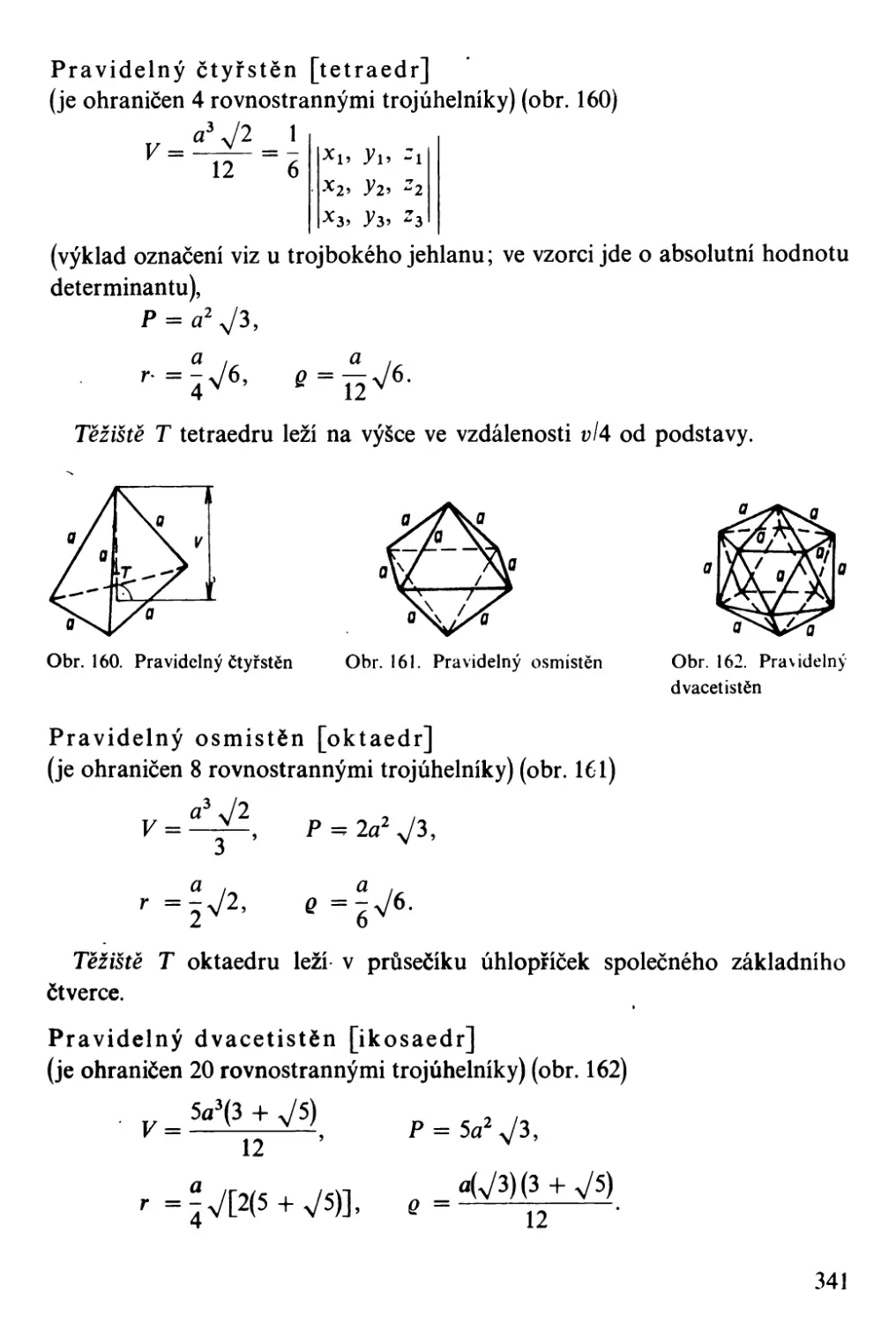
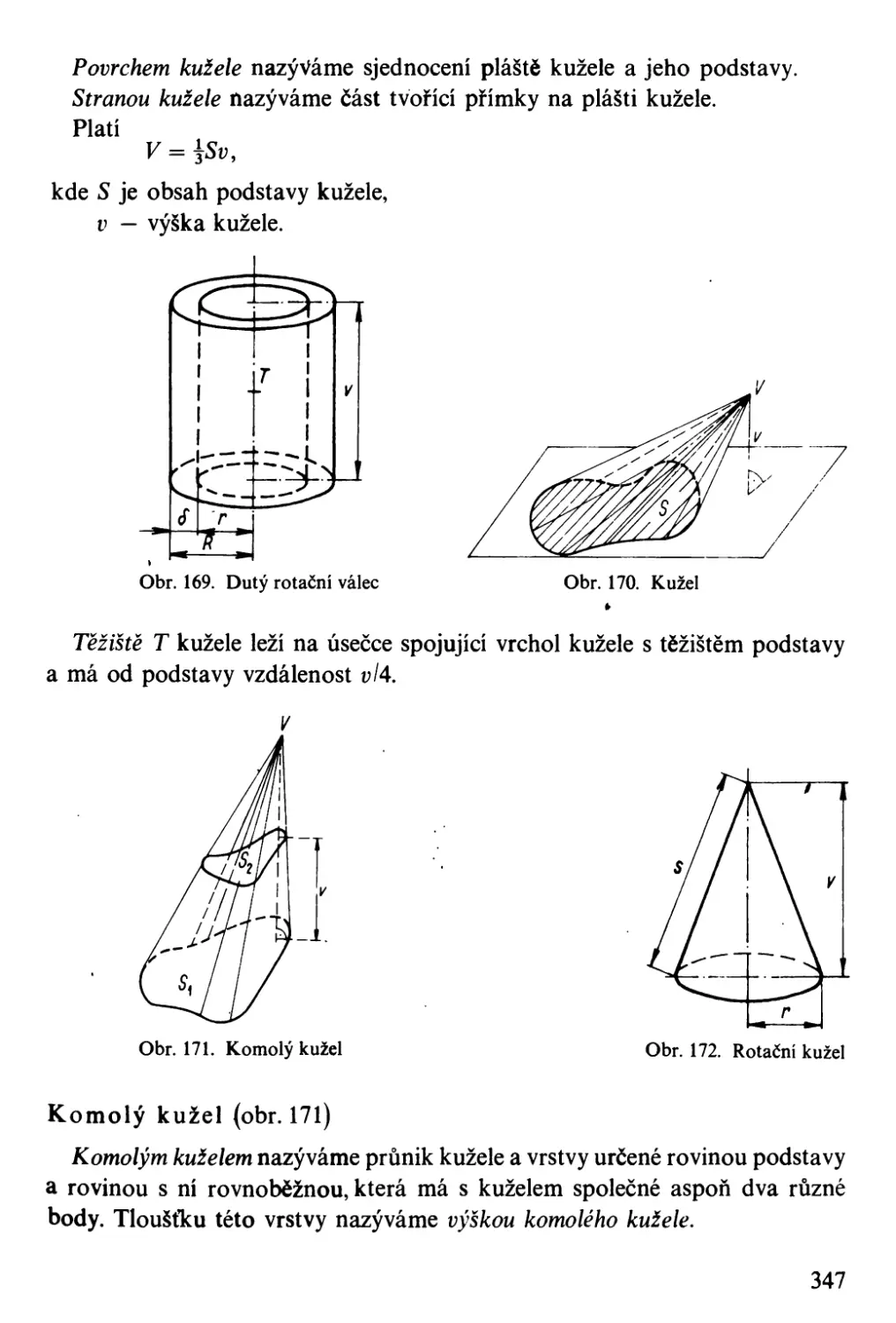
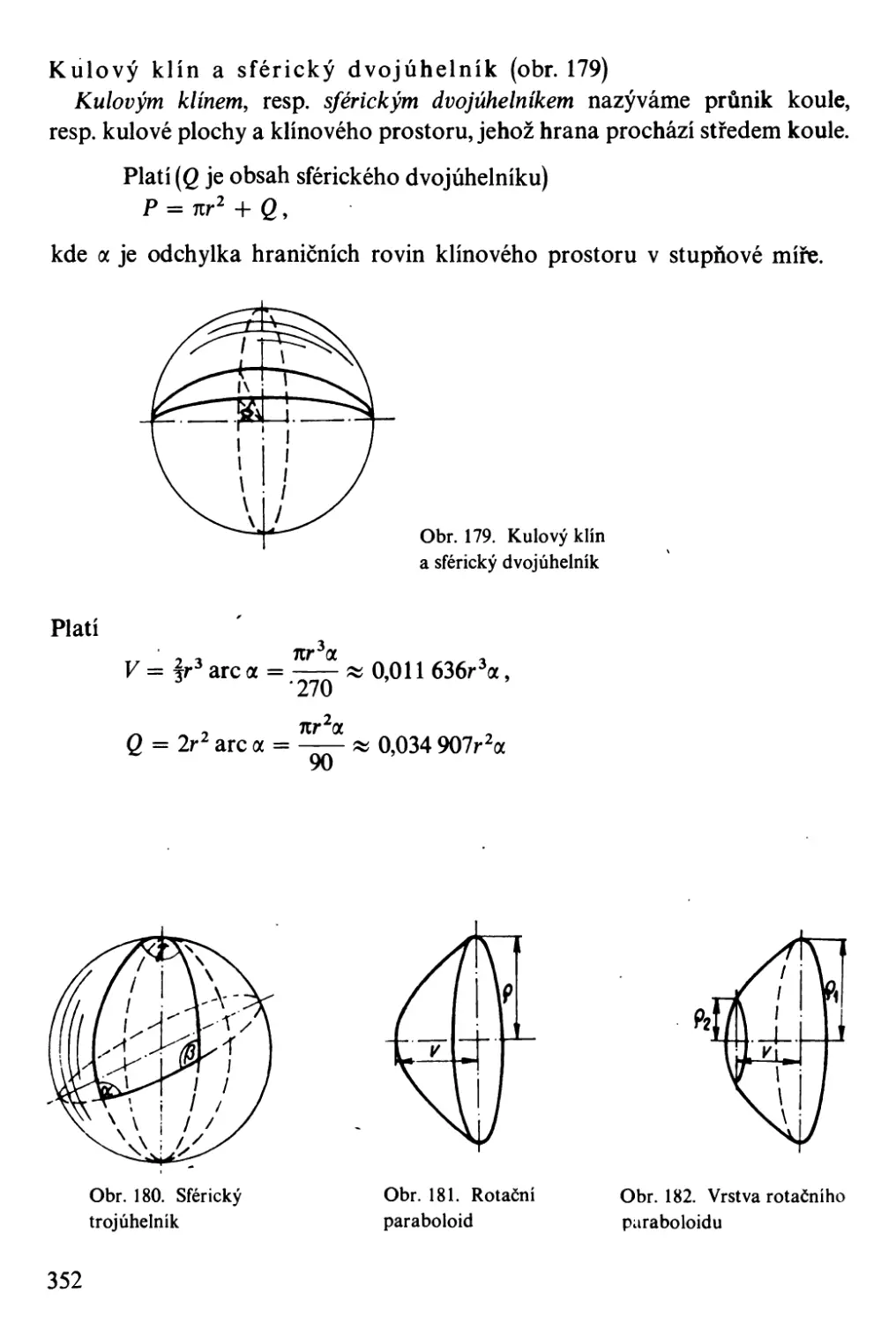
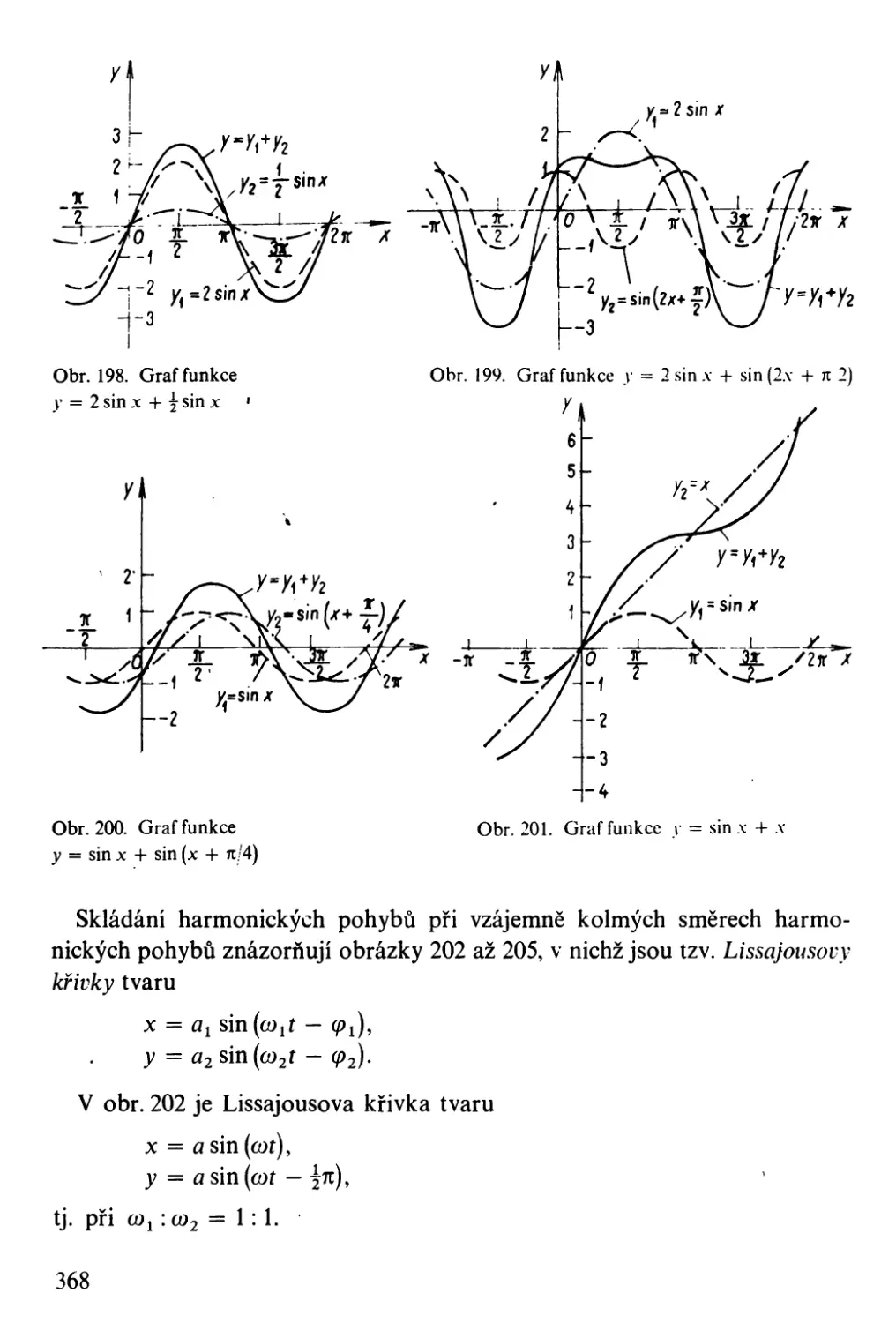
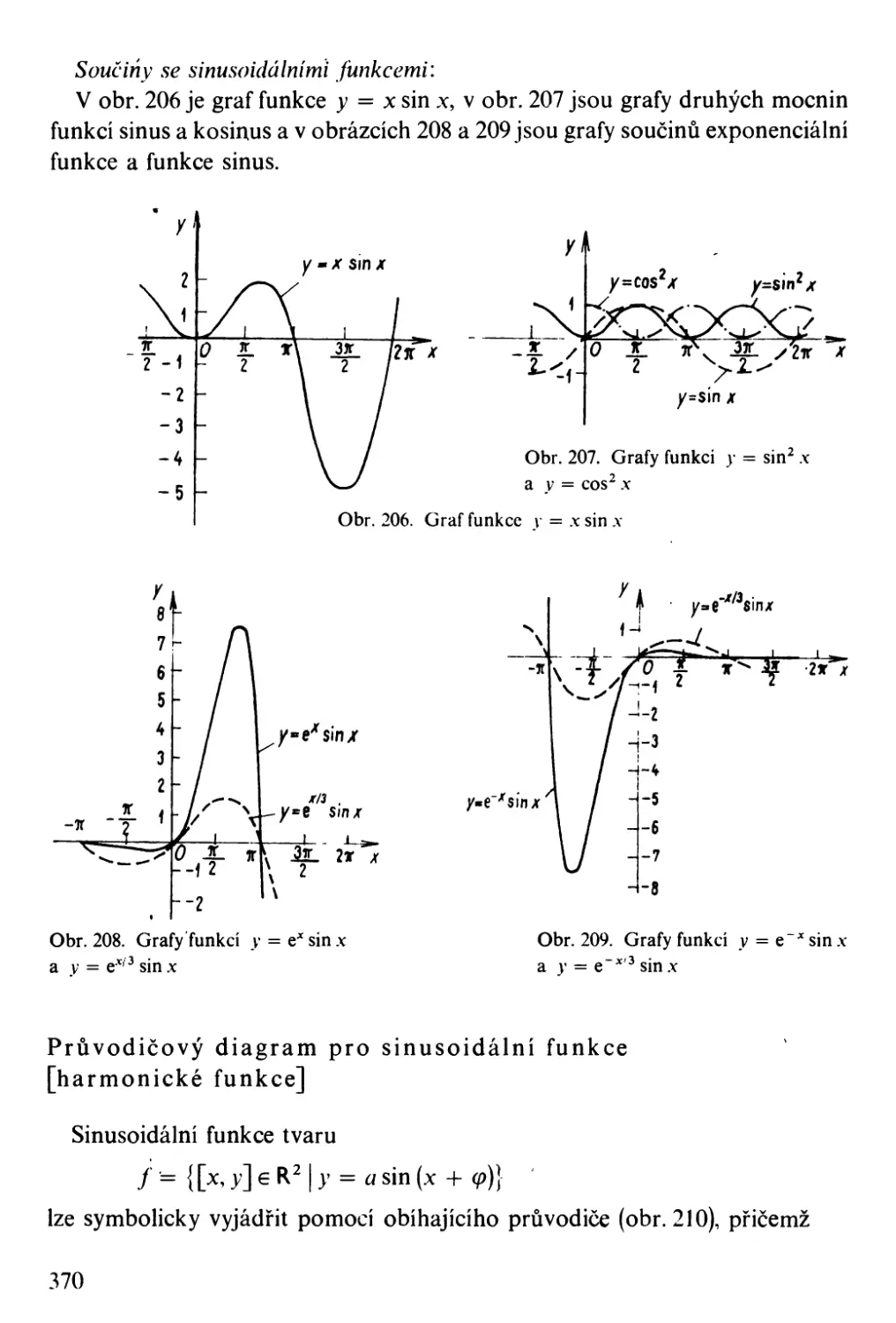
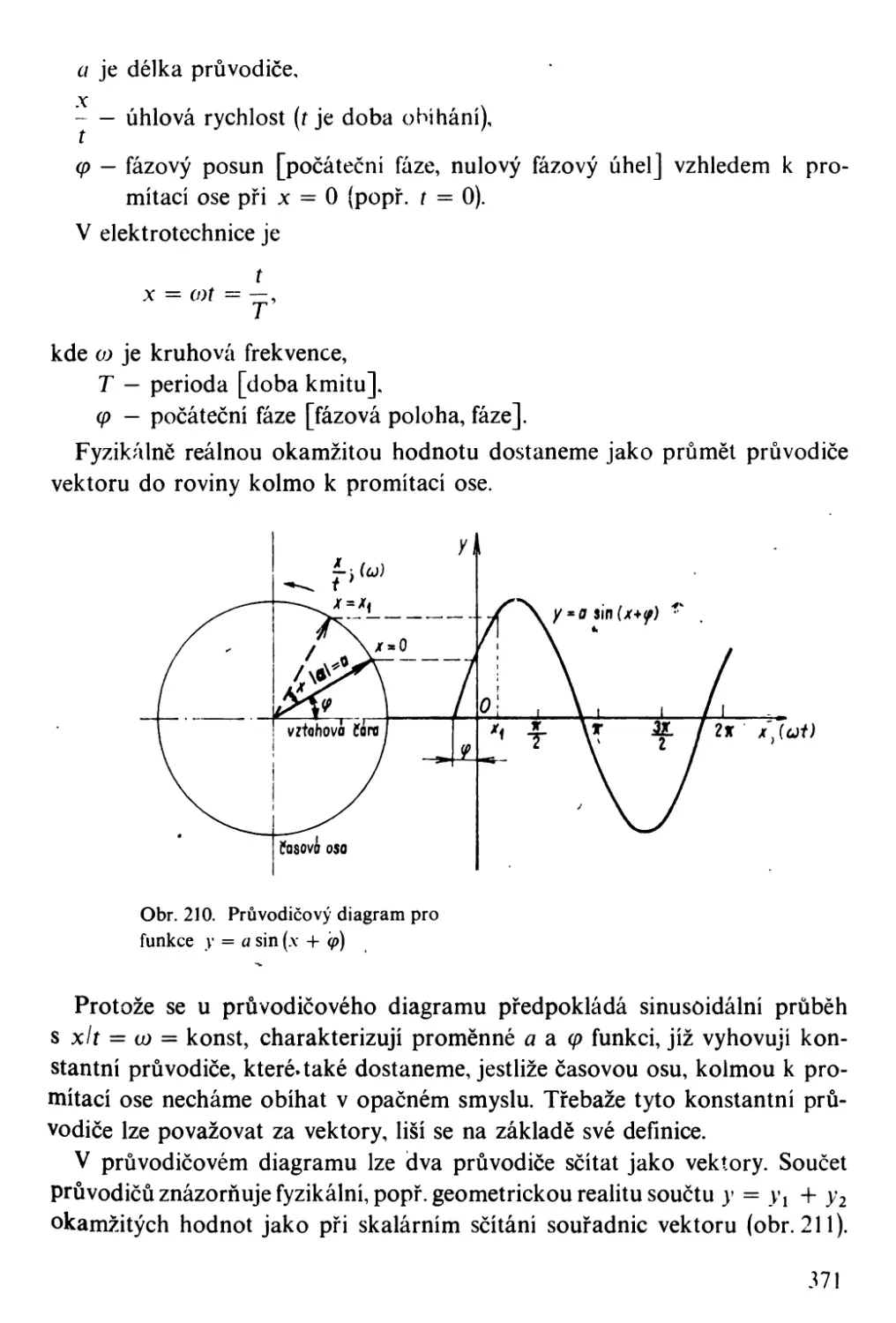
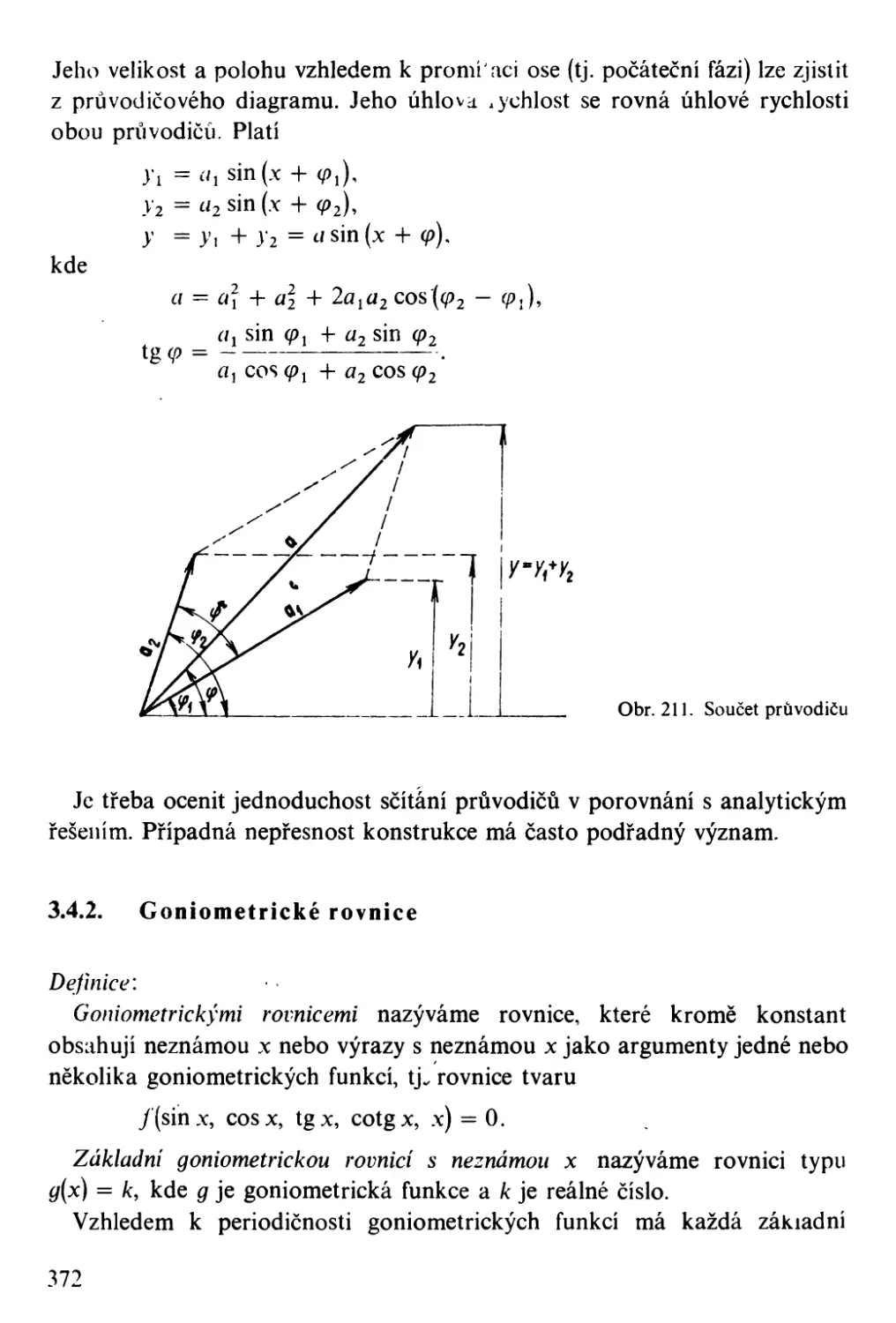
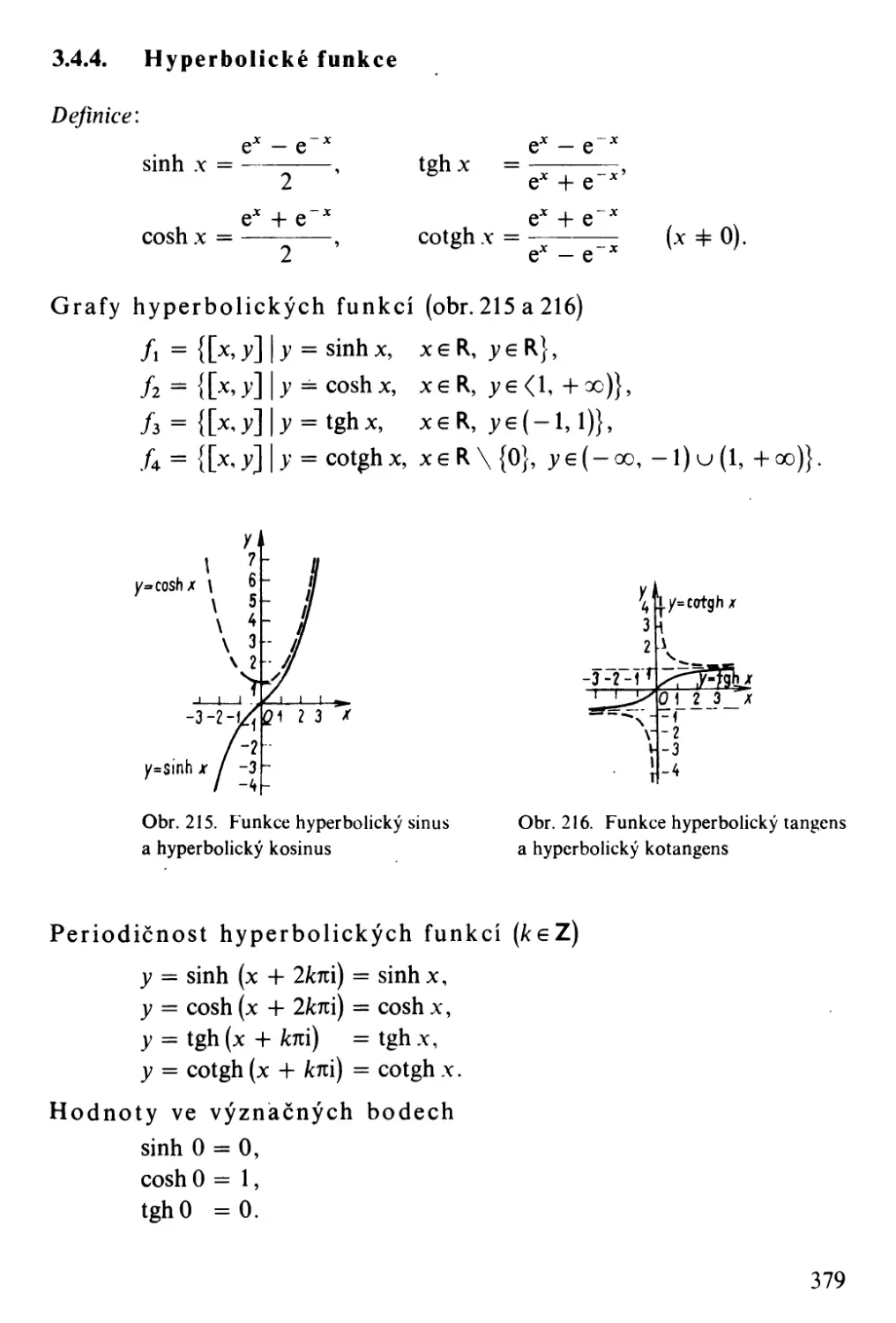
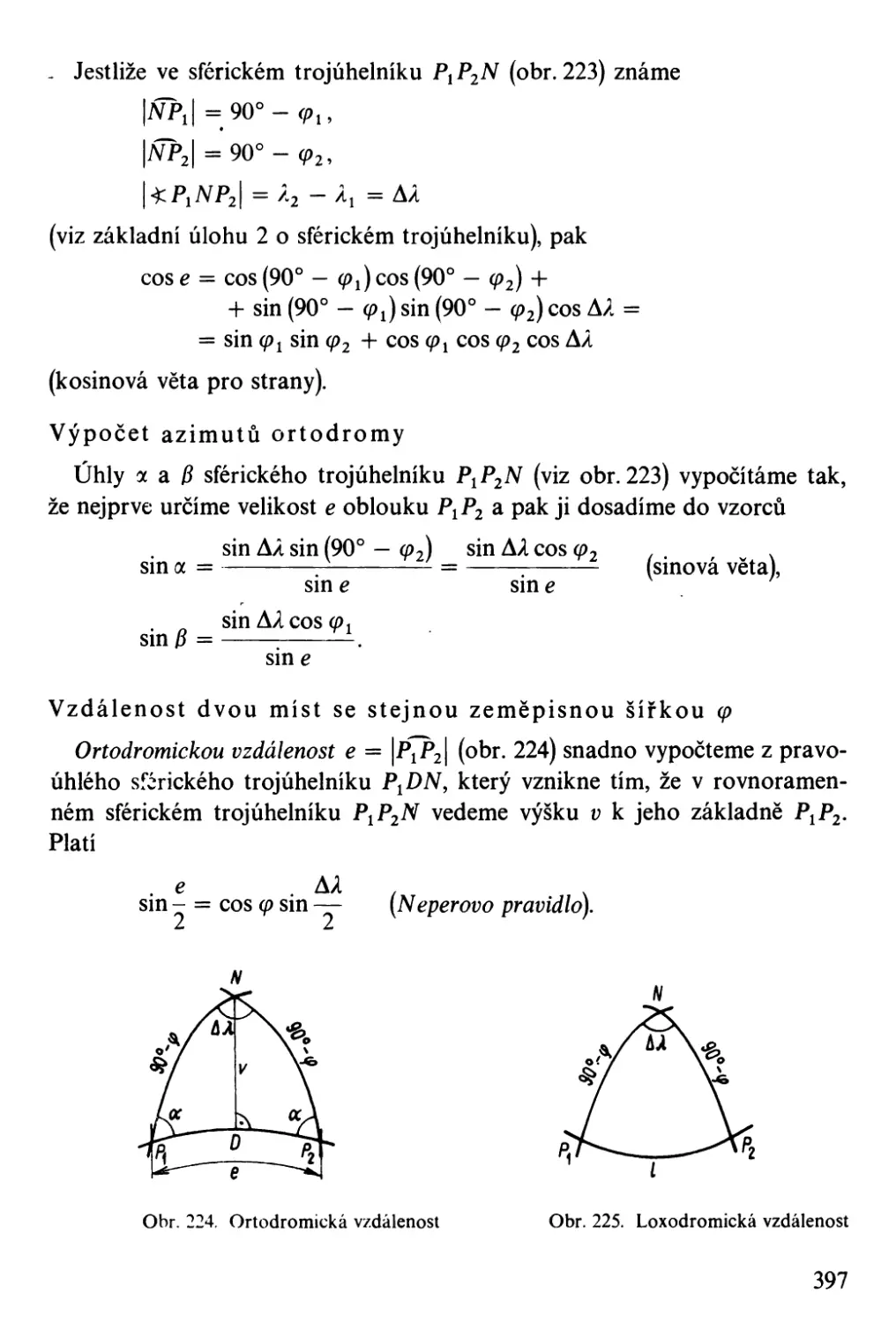
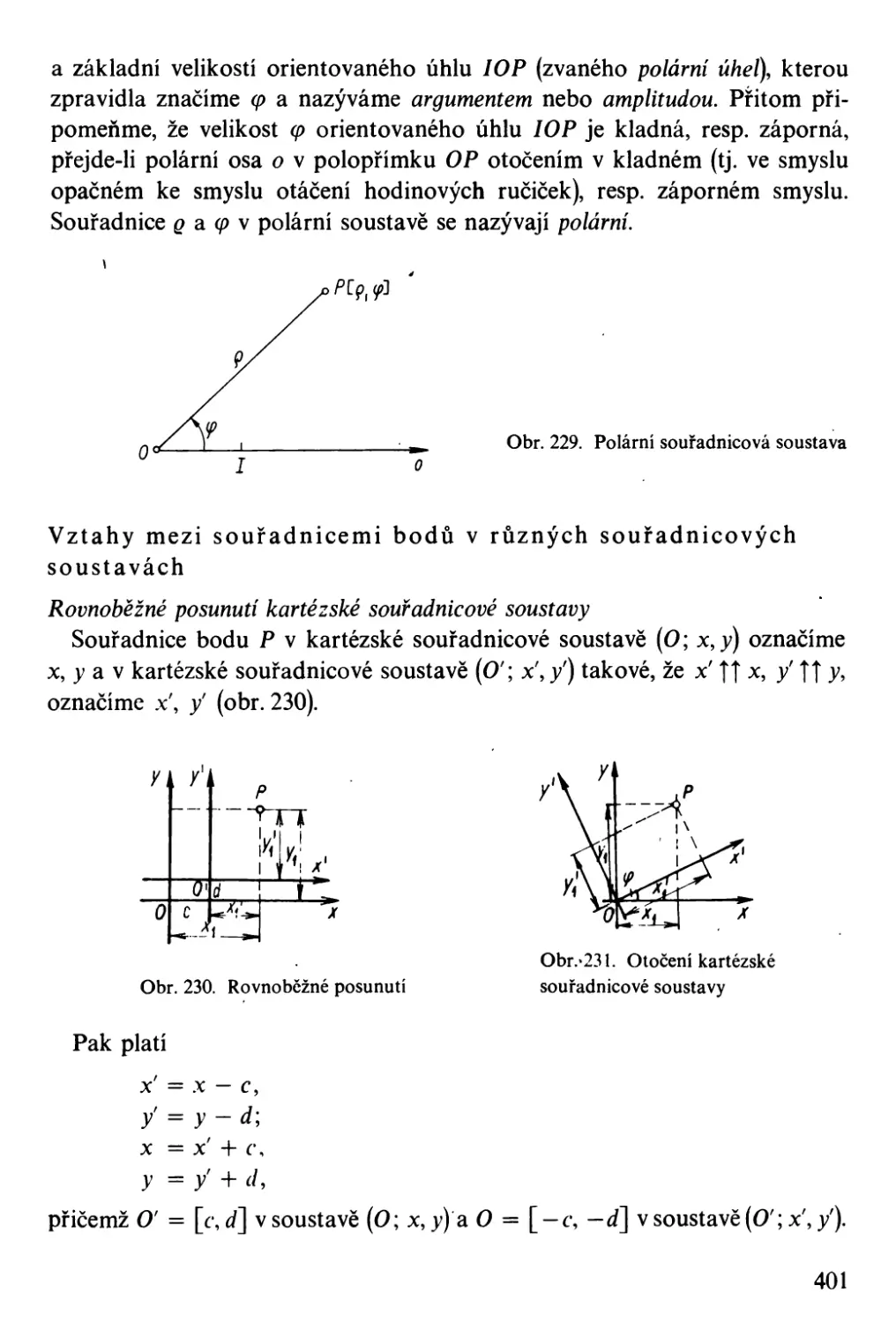
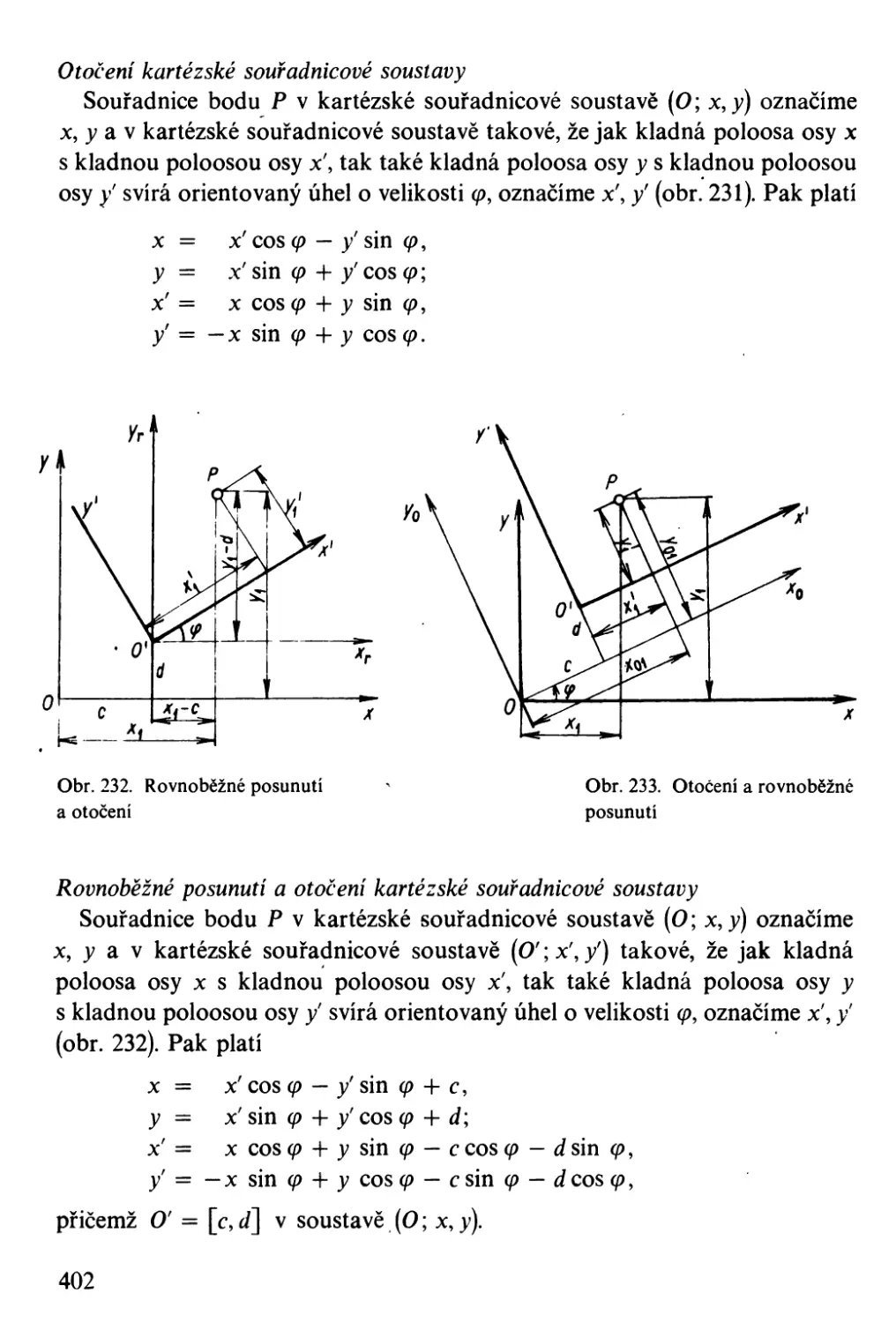
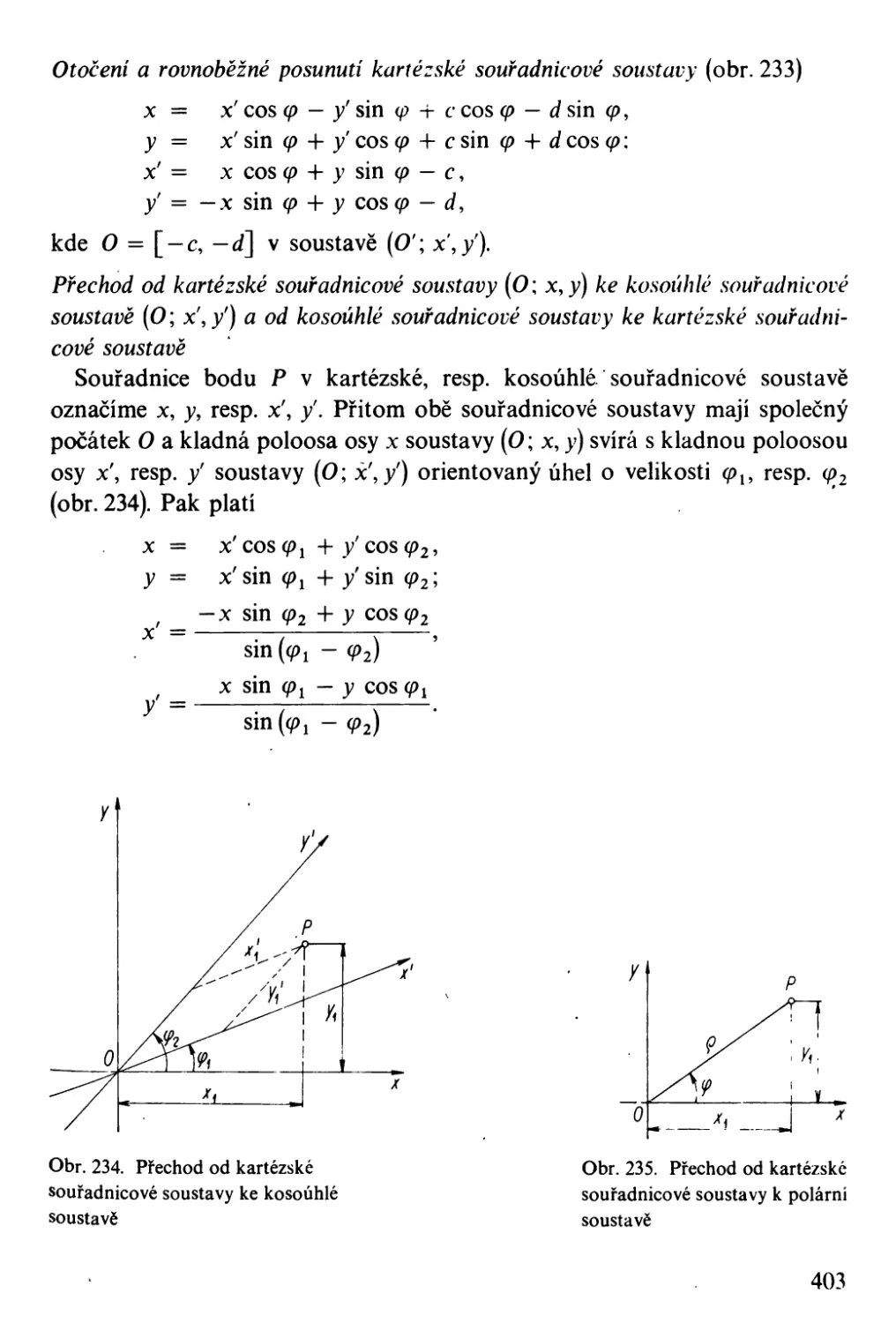
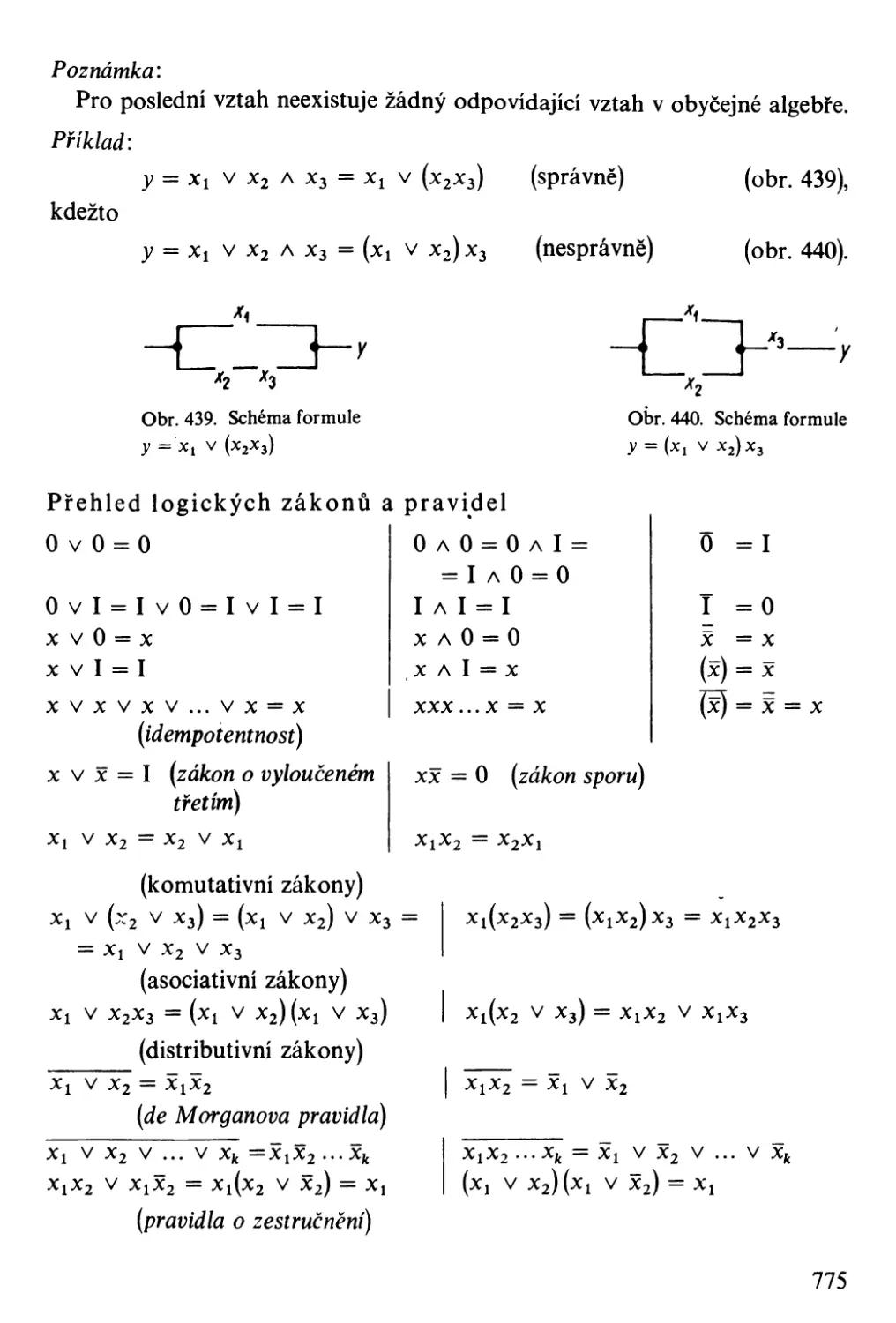
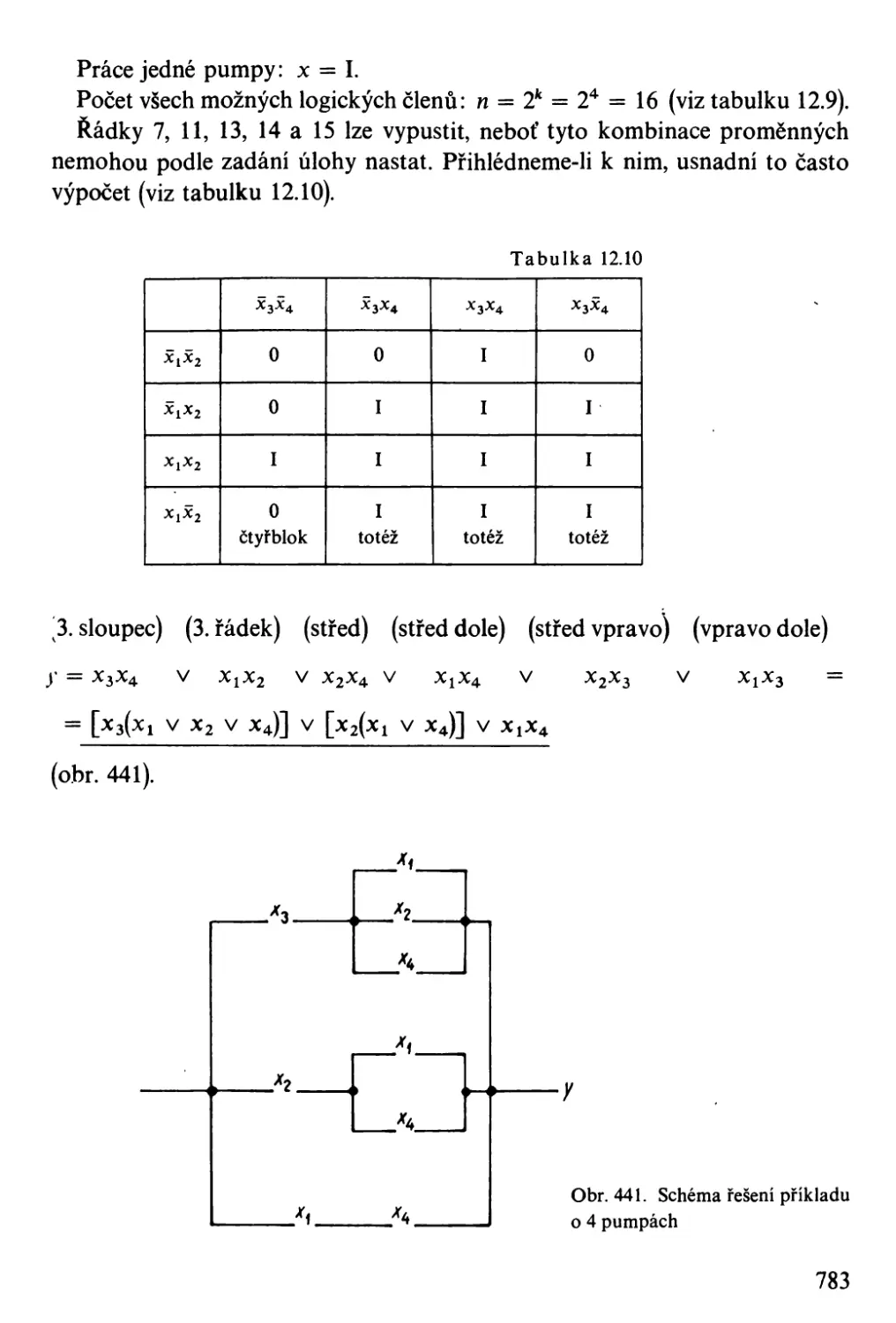
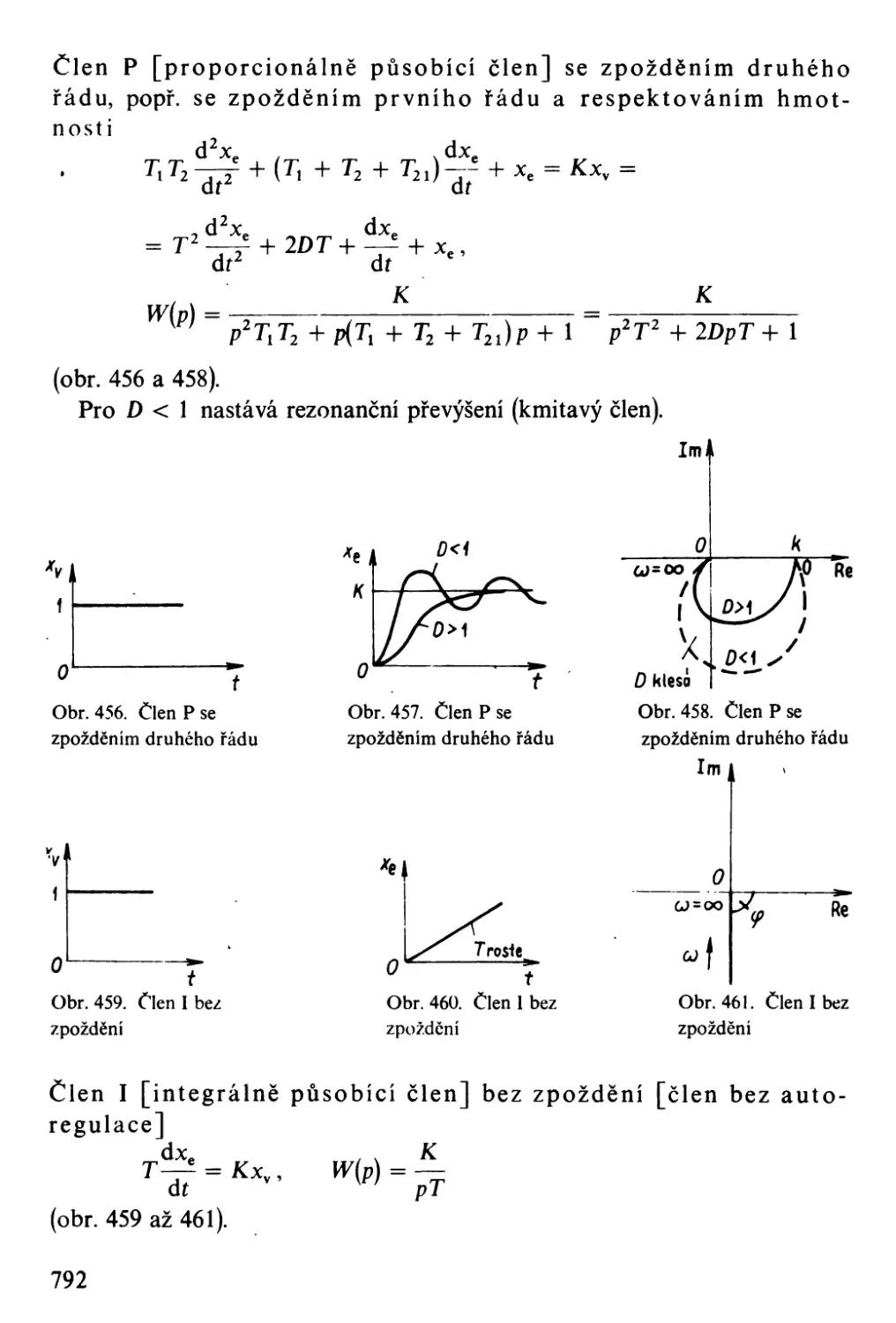
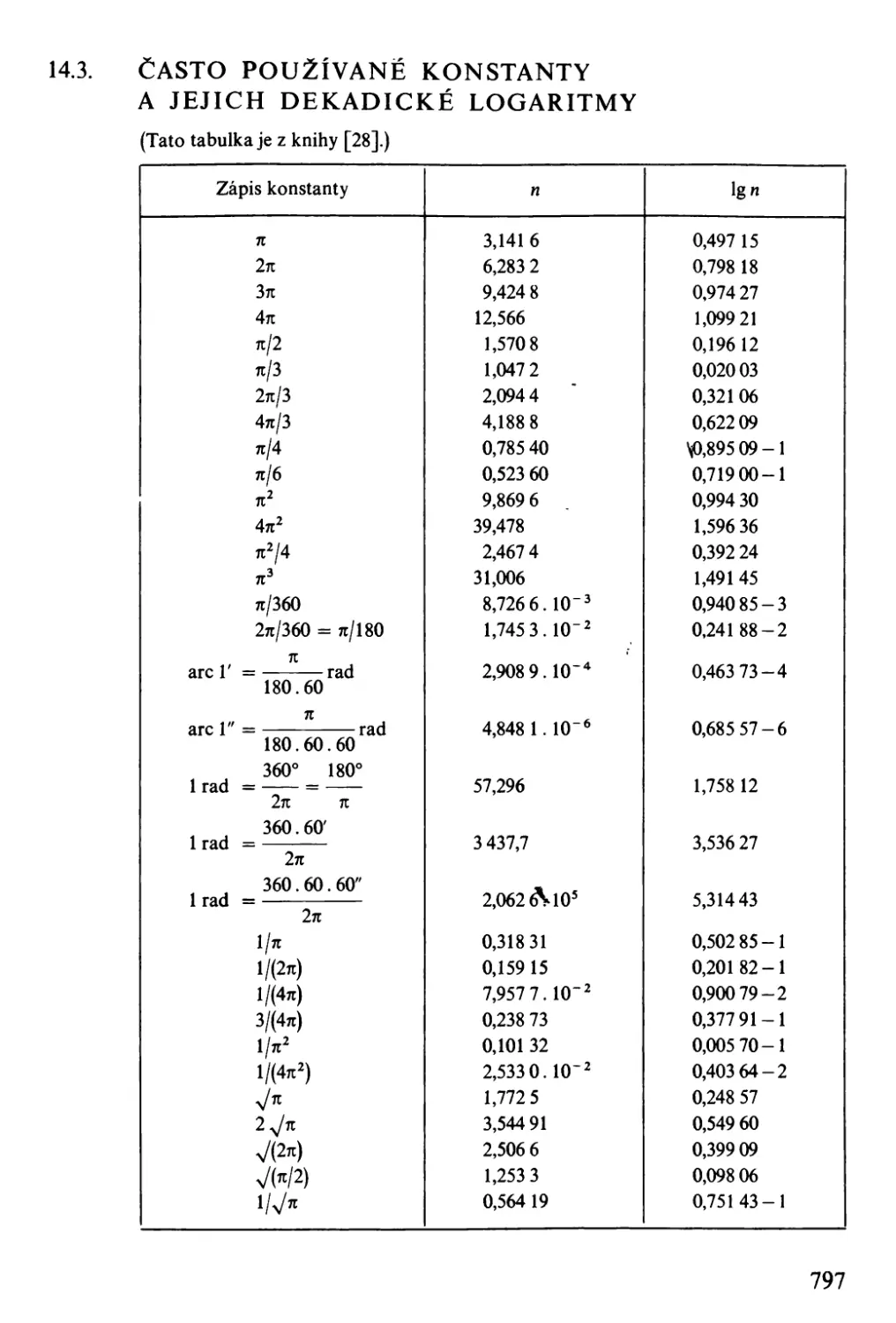
Автор: Bartsch H-J.
Теги: matematika počítání vzorce matematické vzorce česky logika množiny algebra a aritmetika
Год: 1983
Текст
MATEMATICKÉ VZORCE
SNTL
,
MATEMATICKE
v z o RC E Dr. Ing. Hans-Jochen Bartsch
Př ložil, upravil a doplnil
. Ing. Zdeněk Tichý
Praha 1983
SNTL -
Nakladatelství
technické
literatury
Příručka zahrnuje nejdůležitější definice, věty a metody ze základních oborů užité matematiky.
Zvláštní pozornost je věnována výběru matematických vzorců a ilustrativním řešeným příkladům.
Kromě základů matelp tické logiky a teorie množin ob ahuje aritmetiku a elementární algebru,
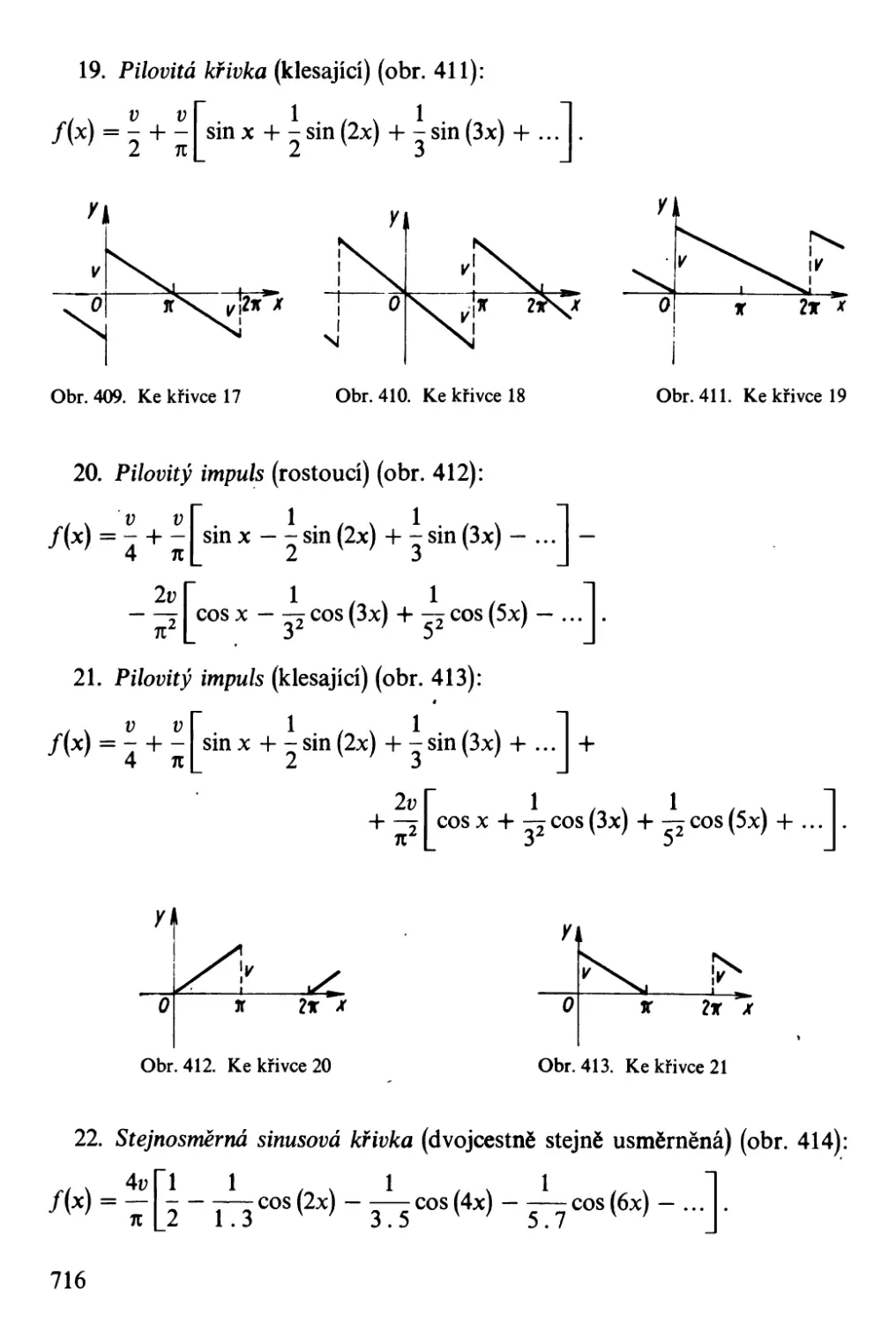
. rovnice a nerovnice, základní funkce, procentový a úrokový počet, vektorový a l11aticový pqčet,
elelnentární geometrii, rovinnou a sférickou trigonometrii, analytickou geometrii v rovině a pro-
storu. diferenciální a integrální počet, diferenciální geometrii, obyčejné a parciální diferenciální
rovnice, posloupno ti a řady, Fourierův integrál a Laplaceovu transformaci, počet pravděpodob-
nosti a Qlatematickou statistiku, lineární optimalizaci, spínačovou aTgebru a vzorce z regulační
techniky.
Příručku doplňují matematické tabulky, přehled znaků a symbolů, přehled literatury a věcný
rejstřík.
Je určena studujícím střednícl} škol 'všech zaměření, posluchačům vysokých škol technických,
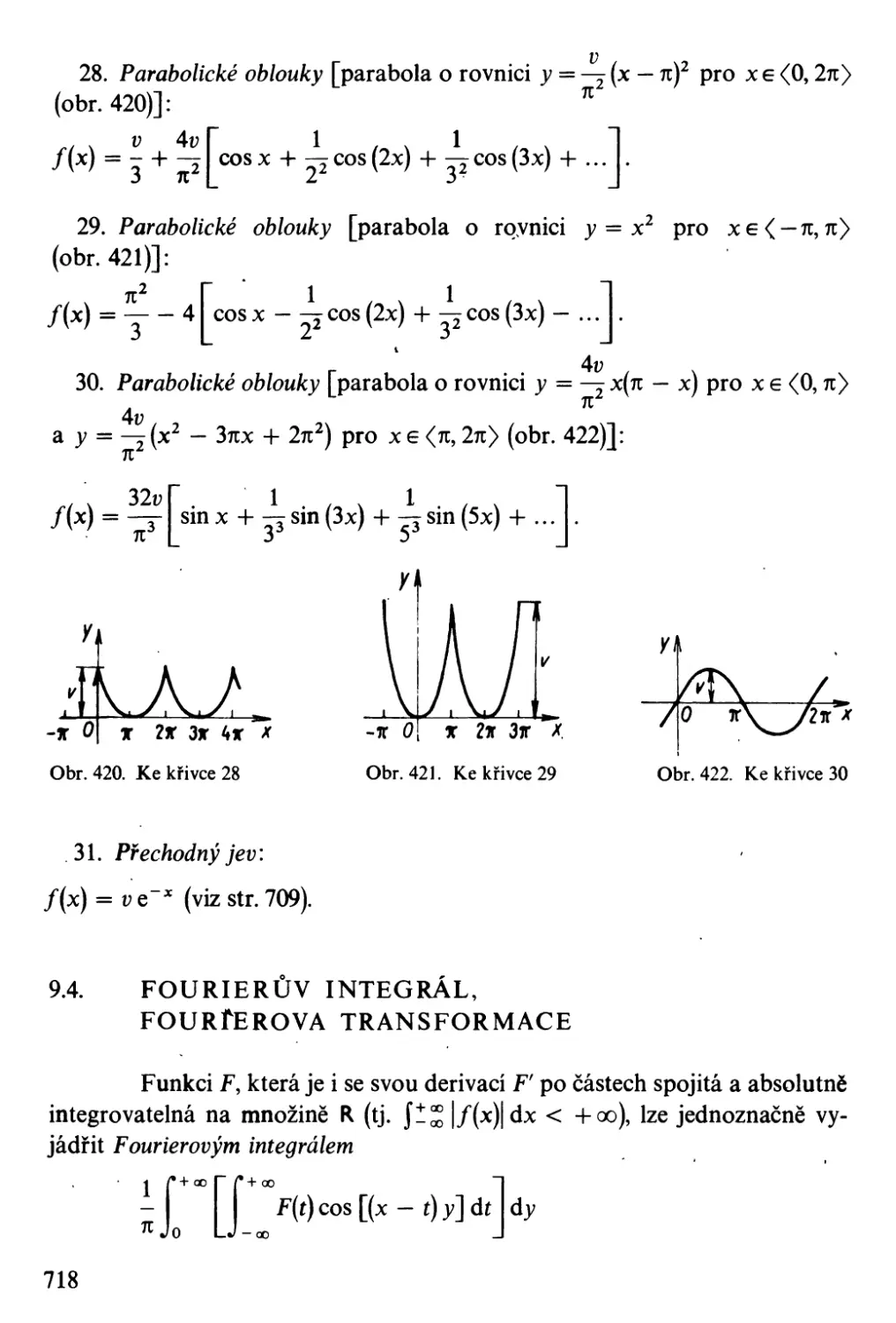
ale hlavně těm čtenářům, kteří při své pracovní nebo studijní činnosti potřebují rychlou a přesnou
informaci ze základních oblastí aplikované matematiky.
Redakce teoretické literatury
Hlavní redaktorka RNDr. Blanka Kutinová, CSc.
Odpovědný redaktor Vladimír Doležal, promovaný matematik
@ Dr. Ing. Hans-Jochen Bartsch: Taschenbuch mathematischer Formeln. 17. Auflage. Leipzig,
VEB Fachbuchverlag 1979
Tr nslation @ Ing. Zdeněk Tichý, 1983
OBSAH
PŘEDMLUVA K ČESKÉMU VYDÁNÍ. . . . . . . . . . . . . .
PŘEDMLUVA K 17. NĚMECKÉMU VY-DÁNÍ. .... . . . .
O. PŘEHLED ZNAK Ů A SYMBOL Ů, ČíSELNÉ T ABULK Y, MATEMATICKÁ
LOGIKA A M'NOŽINY . . . .
0.1.
0.1.1.
0.1.2.
0.1.3.
0.1.4.
0.1.5.
0.1.6.
0.1. 7.
0.1.8.
0.1.9.
0.1.10.
0.1.1 L
0.1.12.
0.1.13.
0.1.14.
0.1.15.
0.1.16.
0.2.
0.2.1.
0.2.2.
0.2.3.
0.2.4.
0.2.5.
0.3. i
0.3.1.
0.3.2.
0.4.
0.4.1.
0.4.2.
0.4.3.
0.4.4.
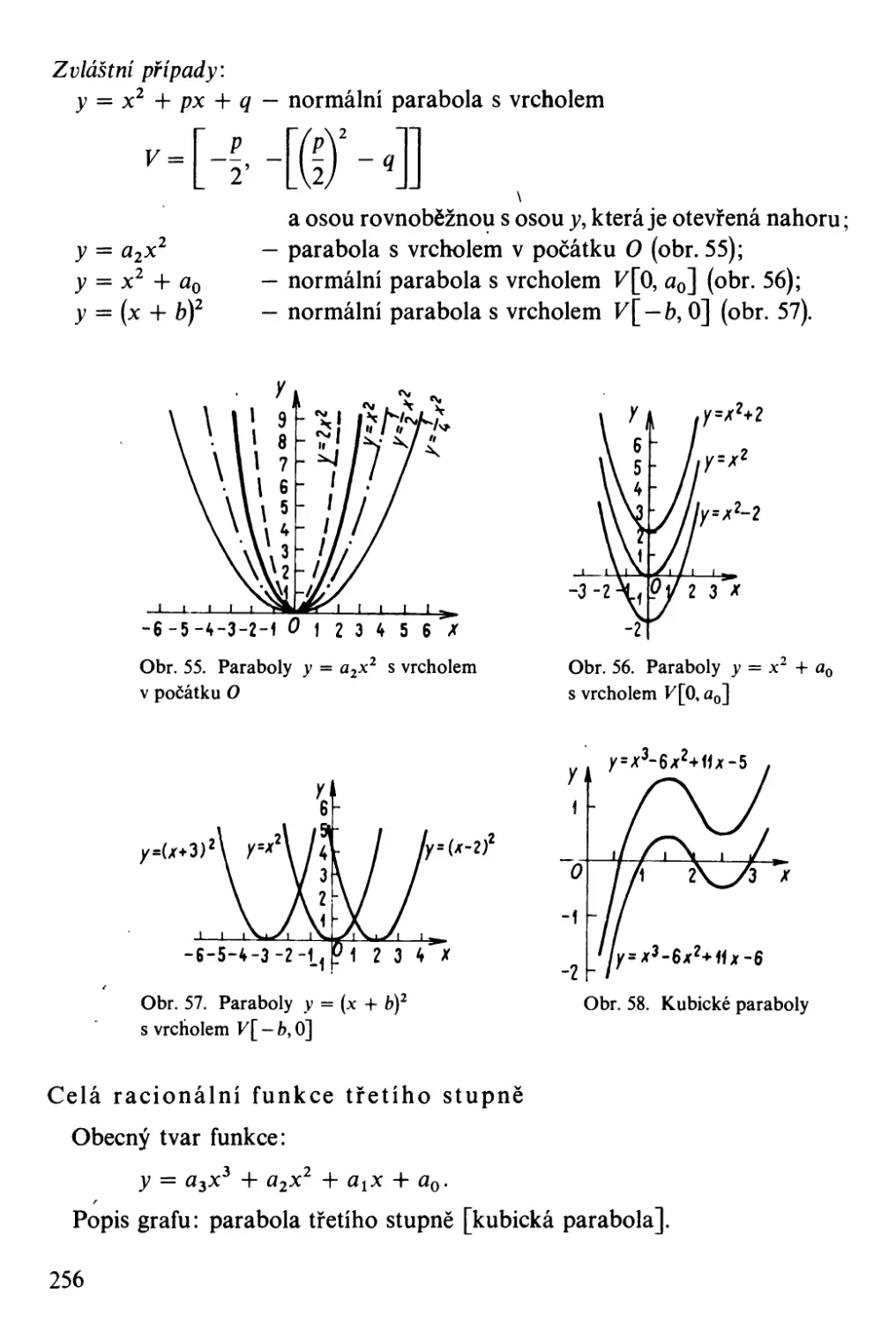
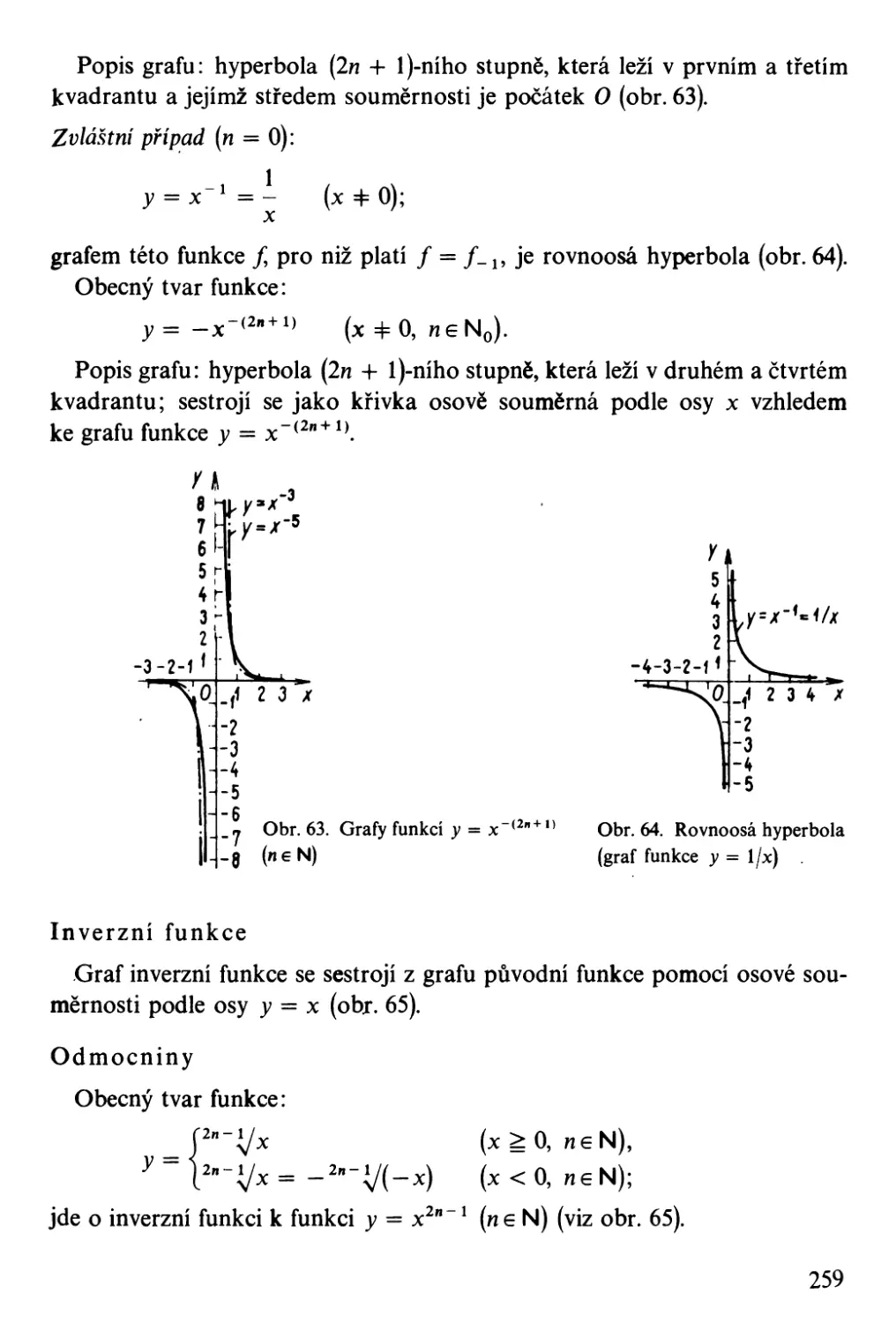
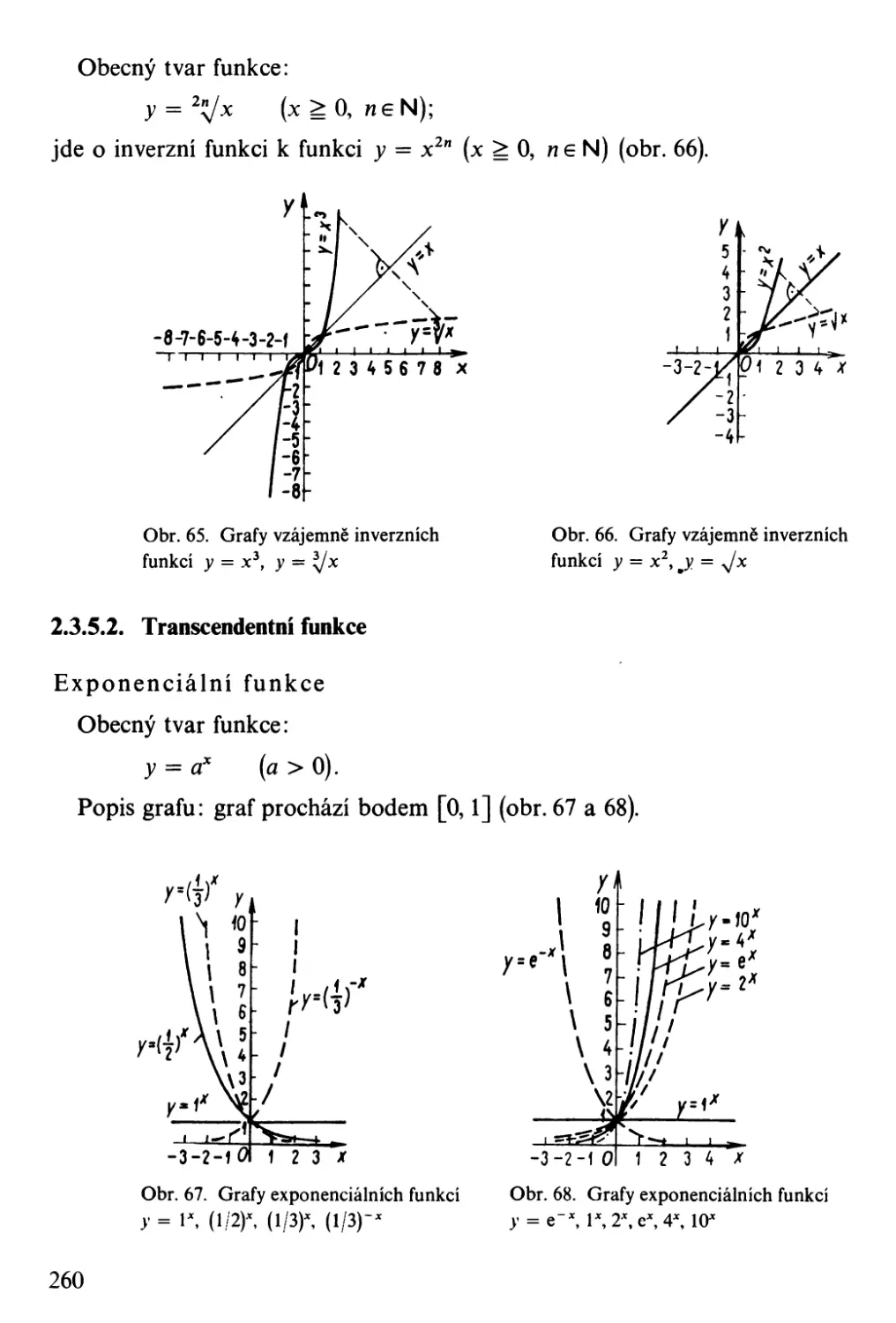
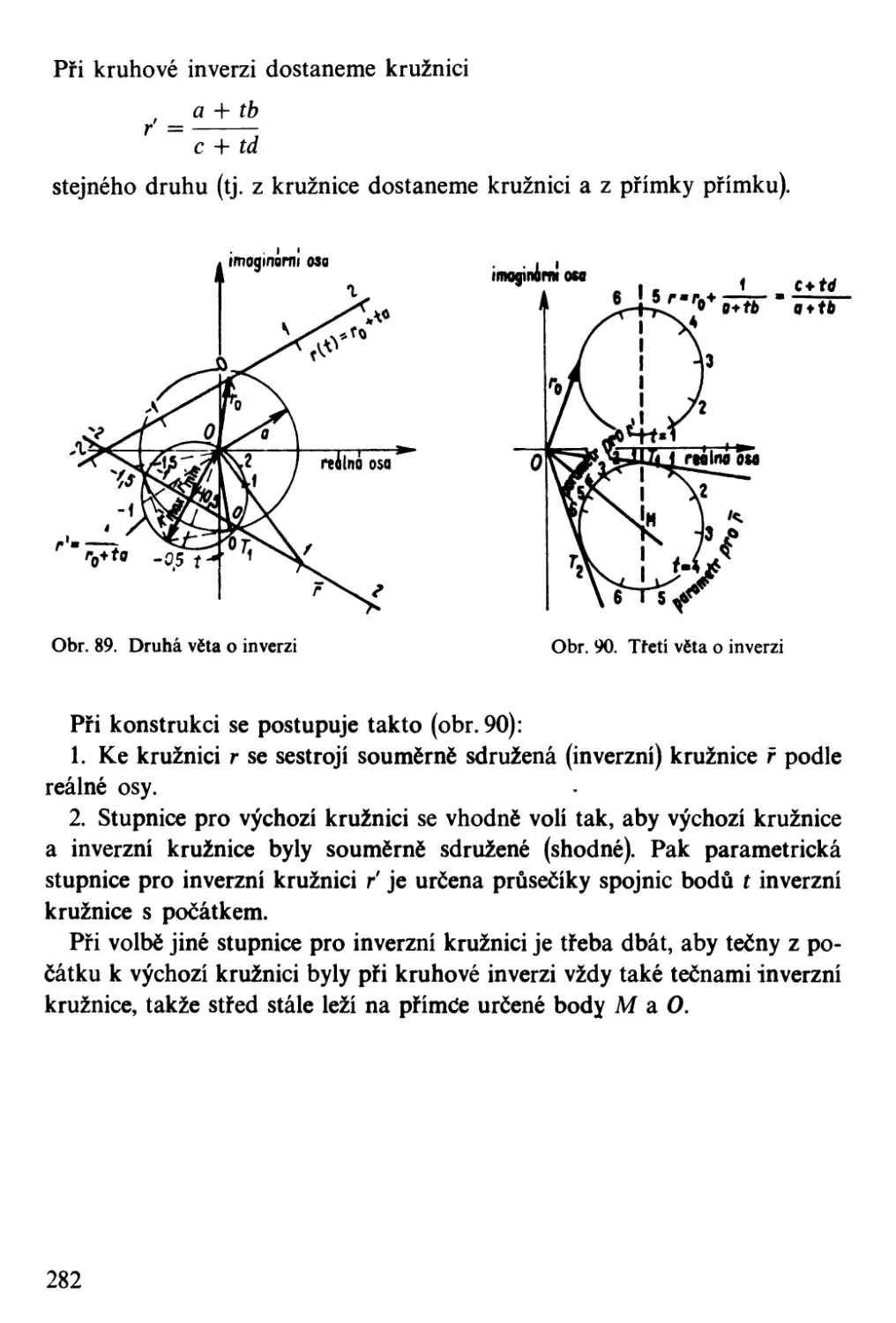
Přehled znaků a symbolů . .
Matematická logika. . . .
Množiny, zobrazení, funkce. .
Standardní <,značení některých množin. . .
Číselné konstanty. . . . . . . .
Elementární aritmetika a algebra . . .
Komplexní čísla . . . . . . . . . .
Vektorová algebra a vektorová analýza
Matice a determinanty .
Geometrie. . . . .
Matematická analýza .
Elementární funkce . . . . .
Speciální funkce . .
Diferenciální geometrie
Laplaceova transformace. .
Počet pravděpodobnosti, matematická statistika a teorie chyb. .
Regulační technika .
Číselné tabulky. .
Tabulky hodnot n 2 , n 3 , Jn, !1tn 2 , 1tn a 19 n pro n od do 100 ,'. .
Goniometrické funkce. .
Mocniny o základu 2 . . .
Desítkové zápisy pro a. 8" . . . .
Osmičkové zápisy pro a. 10" . . . . .
Matematicka logika .
Výrokový počet. . .
Predikátový počet. .
Množiny, zobrazení a funkce
Množiny. . . . . . .
.
Množinové operace . . . .
,Věty o množinách. . . . .
Kartézský s&učin dvou množin
I
14
16
19
19
19
20
24
26
27
28
28
30
31
34
38
40
41
42
42
44
45
45
. 47
56
57
58
59
59
65
68
68
71
73
76
5
0.4.5.
0.4.6-
0.4.7.
Ó.4.8.
0.4.9.
1.
1.1.
1.1.1.
L 1.2.
1.1.3.
1.1.4.
1.2.
1.2.1.
1.2.2.
1.2.3.
1.2.4.
1.2.5.
1.2.6.
1.3.
1.3.1.
1.3.2.
1.3.3.
1.3.4.
1.3.5;
1.3.6.
1.4.
1.4.1.
1.4.2.
1.4.3.
1.5.
1.6.
1.6.1.
1.6.2.
1.6.3.
1.6.4.
1.7.
1. 7.1.
1. 7.2.
1. 7.3.
1. 7.4.
6
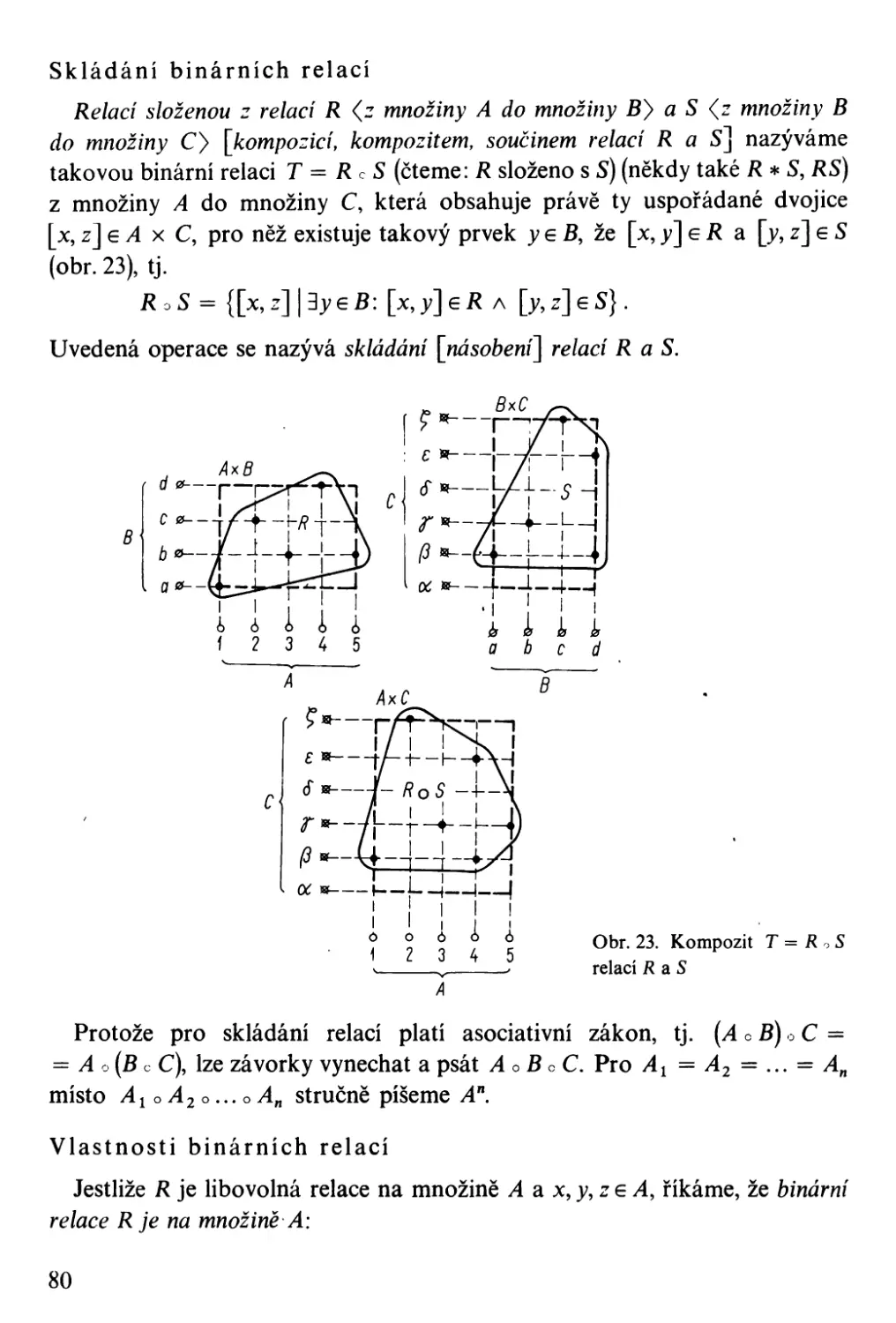
Binární relace . . . . . . . . . . . . . . . . . . '.' .
Zobrazení, operace, funkce. . . ',' . . . . . . .' . . . . . . .
Konečné, nekonečné a spo tné množiny, mohutnost množiny. .
Algebraické struktury . . . . . . . .
Několik topologických pojmů . . . . . . .. . . .
ARITMETIKA A ELEMENTÁRNÍ ALGEBRA.
77
83
89
91
98
103
103
103
104
105
106
106
106
110
111
114
121
128
129
129
131
132
134
138
139
143
143
144
146
Číselné množiny . . . . . . .
Nlnožina všech přirozených čísel
Množina všech celých čísel. . . . . . . . .
. Množina všech racionálních čísel
Množina všech reálných čísel. .
/
Operace na množinách Z, Q a R
Základní operace na množinách Z, Q aR.
Absolutní hodnota reálného čísla .
Mocnina a odmocnina. . . . . . . . . .
. Číselné sousta vy . . . . . . . . . . . . . . . . .
Dělení se zbytkem a beze zbytku v množině Z. Dělitelnost v množině Z '. .
. .
UspořÚdání na množině R .
'"
Komplexní čísla . . . .
I
Množina všech komplexních čísel . .'
Ryze imaginární čísla . . . '. .
Komplexní čísla v kartézském tvaru .
Komplexní čísla v goniometdckém tvaru .
Komplexní čísla v exponenciálním tvaru .
Grafické metody . . . . . . . . . . .
Přibližná čísla a jejich chyby .
Přibližná čísla . . . . . .
Zaokrouh lená čísla . . . . . . . . .
Pravidla pro přibližné výpočty
Úměry . . . .
Logaritmování
. . . . . 149.
151
151
,153
153
155
156
156
160
. 163
164
,
Základní pojmy.
Vlastnosti logaritmů. . -. . . . . . .
Určování desítkových, logaritmů z logaritmických tabulek. . . '. .
Přirozené logaritmy komplexních čísel . . J'
Kombinatorika. . . . . . . . . . .
Binomické koeficienty, binomická věta. . . . .
Permutace. . . . . .
Variace . .'. .
Kombinace .
1.8.
1.8.1.
1.8.2.
1.8.3.
1.8.4.
1.9.
1.9.1.
1.9.2.
1.9.3.
1.9.4.
1.10.
1.10.1.
1.10.2.
1.10.3.
1.10.4.
1.11.
1.11.1.
1.11.2.
1.11.3.
2.
2.1.
2.1.1.
2.1.2.
2.1.2.1.
2.1.2.2.
2.1.2.3. .
2.1.2.4.
2.1.3.
2.1.3.1.
2.1.3.2.
2.1.4.
2.1.4.1.
2.1.4.2.
2.1.4.3.
2.1.4.4.
2.1.5.
2.1.5.1.
2.1.5.1
2.1.5..J.
2.1.5.4.
2.1.5.5.
2.2.
Posloupnosti reálných čísel.
Základní pojmy. . . . . . .
Aritmetické posloupnosti. . .
Geometrické posloupnosti-:
Vyvolená čísla . . . . . . .
Procentový počet, úrokový počet .
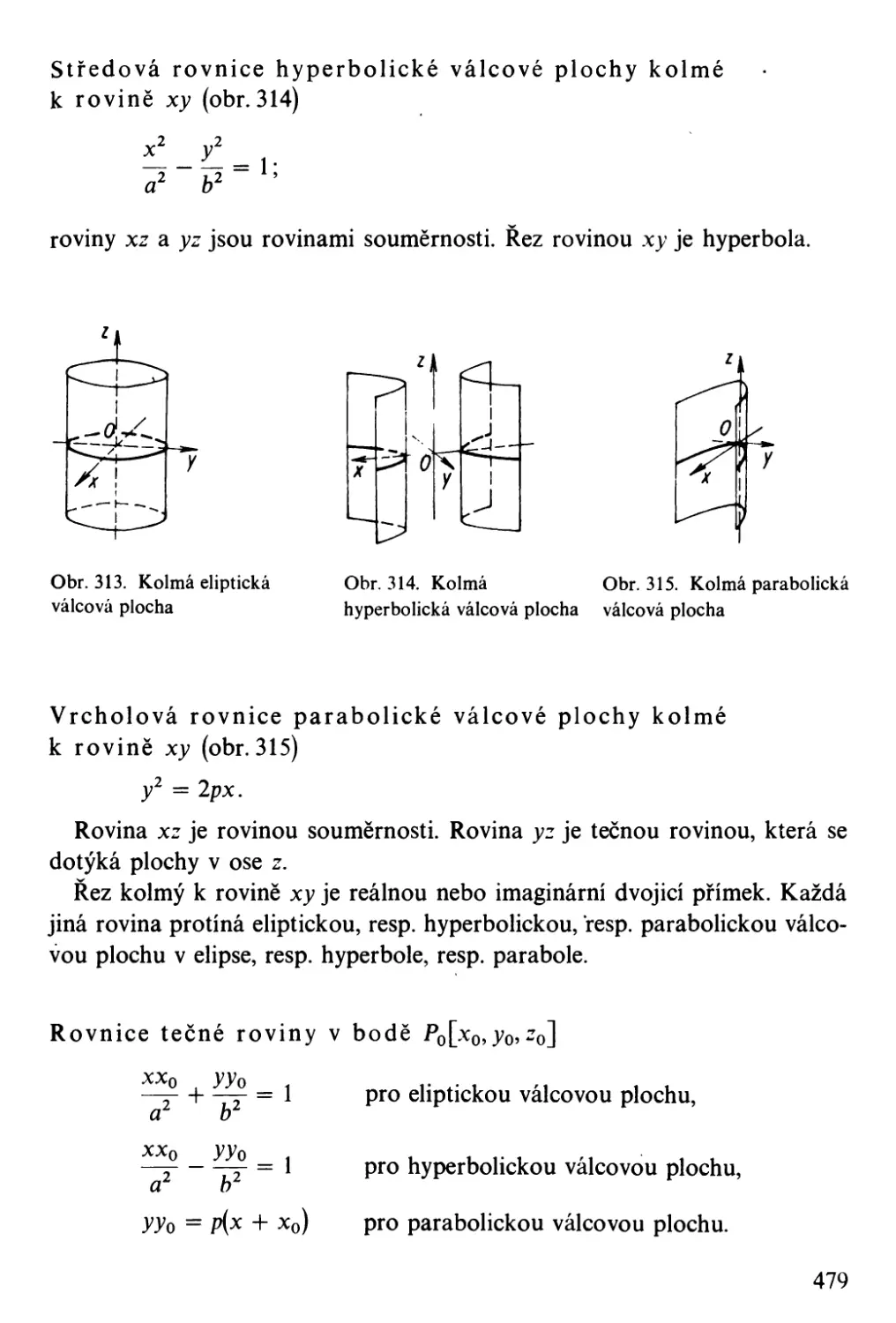
Procentový počet, promiJový počet
Úrokový počet . . . .
Složený úrokový počet.
Důchodový počet.
Matice . . . . .
Základní pojmy. . .
Operace s maticemi . . . . .
Některé typy matic
Použití maticového počtu
Determinanty . . . . . . .
Základní pojmy. . . . .
Vlastnosti determinantu čtvercové matice. .
Ř.ešenÍ soustavy lineárních rovnic pomocí determinantů
ROVNICE, FUNKCE, VEKTOROVÝ POČET.
Rovnice . . . . . . . . . . . . . .
Základní pojmy. . . . . . . . . . .
Algebraické rovnice s jednou neznámou
Lineární rovnice s jednou neznámou. .
K vadratická rovnice s jednou neznámou
Kubická rovnice s jednou neznámou. . .
Algebraická rovnice n-tého stupně s jednou neznámou . .
Transcendentní rovnice . . . .
Exponenciální rovnice. . . . . . . . . . . .
LogaritJ11ické rovnice . . . . . . . . . . . . . .
Přibližné metody k určení kořenů rovnice '.
Metoda,tětiv [regula falsi, lineární interpolace]
Metoda tečen [Newtonova metoda] . . . . . .
Iterační metoda. . . . . . .
Grafické řešení rovnic . . . . . .
Soustavy rovnic. . . . . . . . . . .
Soust;;lVY lineárních rovnic se dvěma neznámými. . .
Soustavy lineárních rovnic se třemi neznámými . . .
Soustava n lineárních rovnic s n neznámými. . . . . . .
Soustava dvou kvadratických rovnic se dvěma ne námými
Grafické řešení soustav rovnic se dvěma neznámými
Nerovnice . . . . . . . . . . . . . . . . . . .
. . "
165
165
167
170
171
172
172
174
175
177
180
180
184
193
196
198
198
202
207
209
209
209
211
212
212
214
217
220
220
221
222
222
223
225
225
227
227
230
233
235
237
239
7
2.2.1.
2.2.2.
2.3.
2.3.1.
2.3.2.
2.3.3.
2.3.4.
2.3.5.
2.3.5.1.
2.3.5.2.
2.4.
2.4.1.
2.4.2.
2.5.
3.
3.1.
3.1.1.
3.1.2.
3.1.3.
3.1.3.1.
3.1.3.2.
3.1.3.3.
3.1.3.4.
3.1.3.5.
.
3.1.3.6.
3.1.3.7.
3.1.4.
3.1.5..
3.2.
3.2.1.
3.2.1.1.
3.2.1.2.
3.2.1.3.
3.2.2.
3.2.2.1.
3.2.2.2.
3.4.2.3.
3:2.2.4.
3.2.2.5.
3.2.2.6.
3.2.2.7.
3.2.2.8.
3.2.3.
8
Základní pojmy.
Řešení nerovnice .
Reálné funkce . . .
. .'
239
239
241
241
250
252
253
254
254
260
261
261
273
279
. . ,
Základní pojmy.
Přibližné vyjádření funkcí pomocí interpolačních vzorců
Funkce několika proměnných.' . . . .
Implicitní funkce . . . . . . . . . . . .
Kartézské grafy funkcí .
Algebraické funkce . . .
Transcendentní funkce. .
Vektorový počet . . .
Základní pojmy. . . .
Použití vektorového počtu v geometrii. .
Kruhová inverze . . . . . . . . . .
ELEMENTÁRNÍ GEOMETRIE. .
Základní pojmy. . . . . . . . . . .
Přímka, rovina, prostor a j jich části .
Rovinný a prostorový úhel "
Míry v geometrii.. . . . . . .
Míra jako zobrazení. . . . .
Součet úseček a součet úhlů
Délka [velikost] úsečky
Velikost úhlu.. . . .
Obsah obrazce .
Objem telesa. .
Pojem veličiny . . . . ..' . . .
Geometrická zobrazení v rovině.
. Použití shodnosti a p<?dobno'sti .
Planimeti-ie . . .' . . .
. \.
. ',283
283
283
286
287
287
287
289
290
296
296
296
298
301
307
307
317
318
319
319
320
320
321
321
322
J22
323
323
323
Trojúhelník . . . . .
Pravoúhlý trojúhelník .
Rovnoramenný trojúhelník.
Rovnostranný trojúhelník
Čtyřúhelní y .
Rovnoběžník .
Obdélník .
Kosočtverec .
Čtverec . . .
Licho běžník
Tětivový čtyřúhelník . . .
Tečnový čtyřúhelník. .
Deltoid . . . . . .
Mnohoúhelníky [n-úhelníky]. .
. .' .
3.2.3".1.
3.2.4.
3.2.5.
3.2.6.
3.2.7.
3.2.7.1.
3.2.7.2.
3.2.7.3.
3.3.
3.3.1.
, 3.3.2.
3.3.3.
3.4.
3.4.1.
3.4.2.
3.4.3.
3.4.4.
3.4.5.
3.5.
3.5.1.
3.5.2.
3.5.3.
3.5.4.
4.
4.1.
4.1.1.
4.1.2.
4.1.3 -
4.1.4.
4.1.5.
4.1.6.
4:t.7.
4.1.8.
4.2.
4.2.1.
4.2.2.
4.2.3.
4.24.
4.2.5.
4.2.5.1.
4.2.5.2.
4.2.5.3.
Pravidelné n-úhelníky. .
Kružnice a kruh
Kruh'ová úseč . . . . . . .
Mezikruží . . . . . .
Elipsa, hyperbola a parabola .
Elipsa. . . . . . . .
Hyperbola .
Parabola . . . . . . . . .
324
. . . . 328
. . . . . 330
. . . . . 331
332
332
" r 333
334
. . .. . . .
Stereometrie .
Obecné věty . . . . .
Mnohostěny
Oblá tělesa a jejich části
334
335
335
344
357
357
372
376
379
384
386
386
388
389
394
399
399
399
404
406
413
. . 418
427
438
449
Goniometrické, cyklometrické, hyperbolické a hyperbolometrické funkce .
Goniometrické funkce. . . . .. !.
Goniometrické rovnice . . . . . .. ........
Cyklometrické funkce . '.
Hyperbolické funkce '.' .
Hyperbolometrické funkce .
. . . . . .
Sférická trigonometrie . I. . .
Základní pojmy. . . . . . .
Pravoúhlý sférický trojúhelník
Kosoúhlý sférický trojúhelník.
Matematický zeměpis . . . . . .
ANALYTICKÁ GEOMETRIE
,
Analytická geometrie v rovině
. Různé souřadnicové soustavy.
Body a úsečky
Přímka . .
Kružnice
Parabola
Eli psa. . . . . . . .
Hyperbola. . . . . . . . .
Obecná algebraická rovnice druhého stupně v x a y
Analytická geometrie v prostoru
Různé souřadnicové soustavy .
. Body a úsečky v prostoru . .
Rovina v prostoru. . .
Přímka v prostóru. . .
Plochy druhého stupně
Kulová plocha
Elipsoid. . .
Hyperboloid .
455
455
459,
461
466
471
471
472
473
9
4.2.5.4.
4.2.5.5.
4.2.5.6.
4.2.6.
5.
5.1.
5.1.1.
5.1.2.
5.2.
5.3.
5.4.
5.5.
5.6.
5.7.
5.8.
5.9.
5.10.
5.11.
5.11.1.
5. tl.2.
5.11.3.
5.11.4.
6.
6.1.
6.1.1.
6.1.2. .
6.1.2.1.
6.1.2.2.
6.1.2.3.
6.1.2.4.
6.1.2.5.
6.1.2.6.
6.1.2.7.
6.1.2.8.
6.1.2.9.
6_2.
6.2.1.
6.3.
10
Paraboloid. . .
Kuželová plocha .
Válcová plocha. . . . . . .
Obecná algebraická rovnice druhého stupně v proměnných x, y a z. . . . . .
DIFERENCIÁLNÍ POČET .
Limity. :. . . . . .
Limity posloupností.
Limity funkcí. . . .
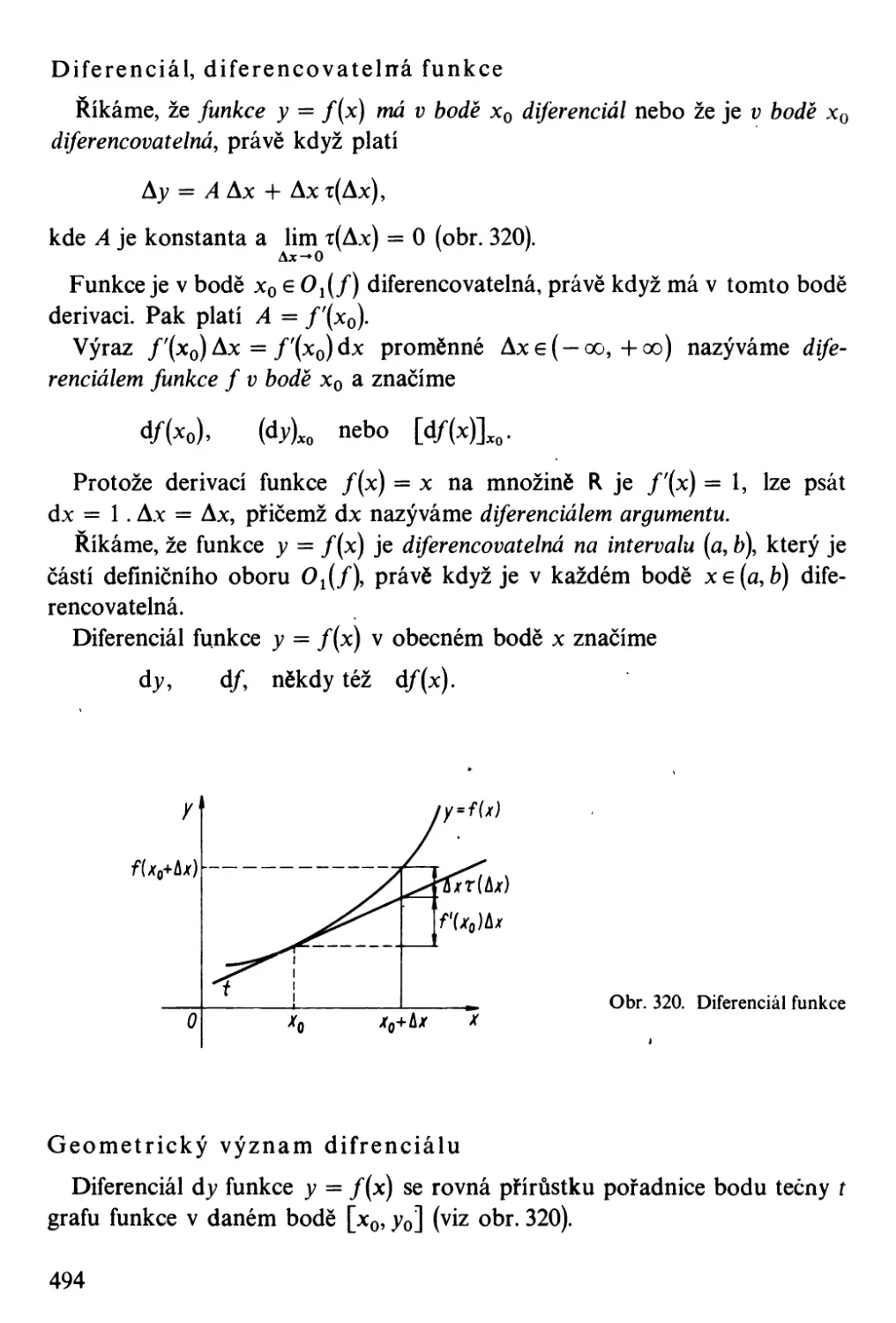
Diferenční podíl, derivace, diferenciál
Pravidla pro derivování funkcí . . . .
Derivace funkcí několika proměnných, totální diferenciál . .
Derivace elementárních funkcí . . . . . .
Derivování vektorové funkce v E3 .
Grafické derivování .
Extrémy funkcí .
Inflexní body. . .
Věty o střední hodnotě v diferenciálním počtu.
Neurčité výrazy. : . . . .
Limita typu 0/0 nebo 00100 . ....
Limita typu O. 00 . .. .....
Limita typu 00 - 00 . . .'. .
L . . t t o 0 0 o l aJ
lml y ypu , 00 , ...
DIFERENCIÁLNÍ GEOMETRIE
Rovinné křivky. . . . . . . . .
Základní prvky rovinných křivek .
Některé důležité rovinné křivky. .
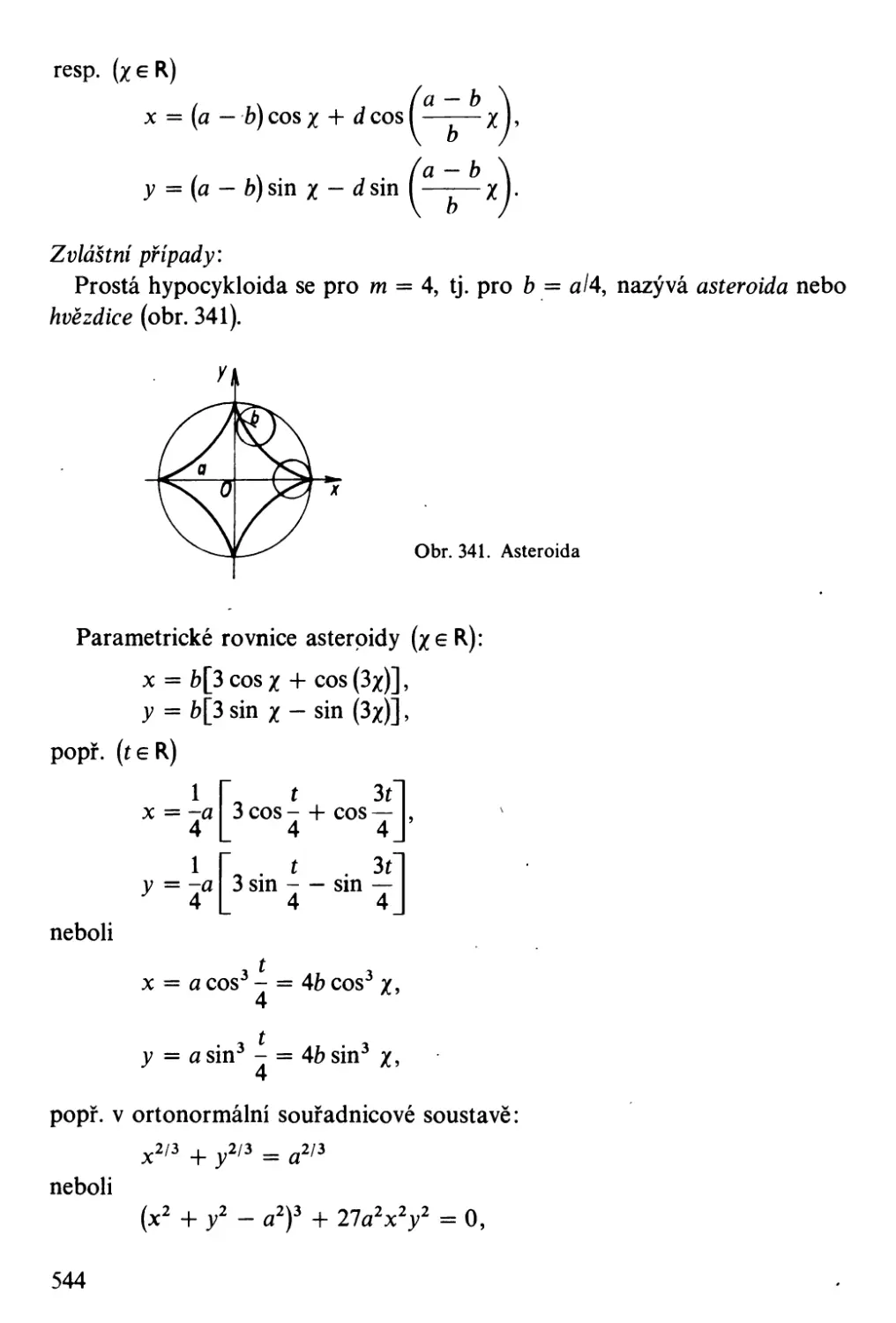
Semikubická parabola [Neilova parabola] .
, Cyklické křivky [trochoidy]
Cassiniovy křivky. .
Spirály . .
Řetězovka .
Traktrix. .
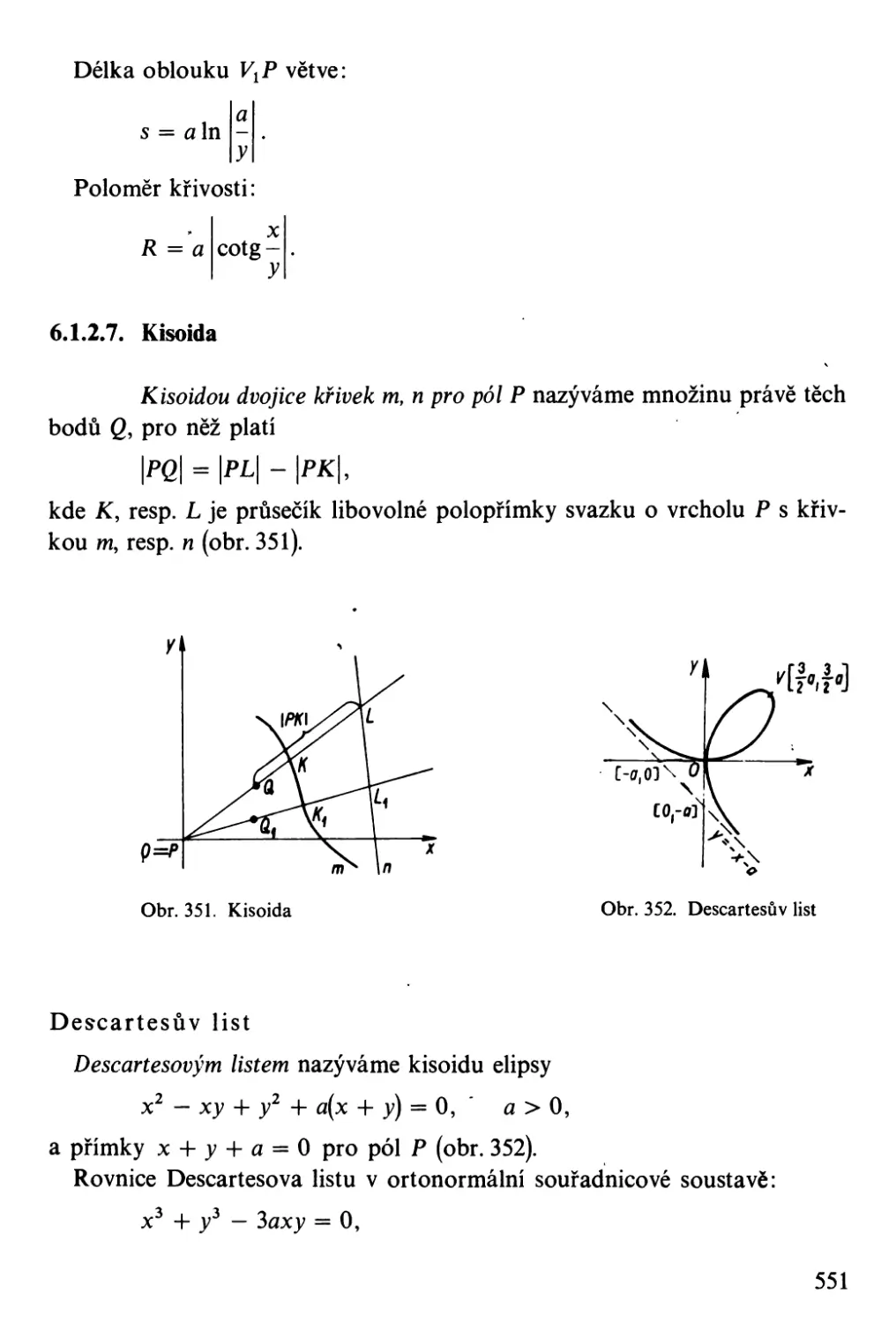
Kisoida . .
Strofoida .
Konchoida. .
I
Prostorové křivky: . . . .
Základní prvky prostorových křivek .
Plochy . . . . . . . . . . . . . .
475
477
478
480
482
482
482
486
491
496
499
505
508
511
511
518
519
520
520
521
522
522
524
524
525
537
537
537
545
547
549
550
551
553
,554
556
557
567
7. '
7.1.
7.2.
7.3.
7.4.
7.4.1.
7.4.2.
7.4.3.
7.4.4.
7.4.5.
7.4.6.
7. .7.
7.4.8.
7.5.
7'.5.1.
7.5.2.
7.5.3.
7.5.4.
7.5. .
7.5.6.
7.5.7.
7.5.8.
7.6.
7.6.1.
7.6.2.
7.6.3.
7.7.
7.7.1.
7.7.2.
8.
8.1.
8.2.
8.2.1.
8.2.2.
8.2.3.
8.2.4.
8.2.5.
8.2.6.
8.2.7.
8.2.8.
INTEGRÁLNÍ POČET FUNKCÍ JEDNÉ PROMĚNNÉ
571
571
571
573
585
585
587
589
594
597
598
599
600
601
601
602
604
607
607
609
616
619
631
631-
633
634
635
635
642
648
648
649
649
652
654
658
659
660
662
663
Definice neurčitého integrálu . .
Z kladní integrály . . . . .
Základní integrační pravidla
Některé důležité integrály .
Integrály racionálních funkcí
Integrály iracionálních fljl1kcí. .
I tegrály goniometrických funkcí . . . . . .
Integrály hyperbolických funkcí. .
Integrály exponenciálních funkcí
Integrály logaritmických funkcí .
Integrály cyklometrických funkcí
Integrály hypebolometrických funkcí. . . . .
,
Určitý integrál . . . . . . . . . . .
Základní pojmy. . . . . . . . " .
Věty o střední hodnotě integrálního počtu
Přibližné metody pro výpočet určitých integrálů. .
Grafická integrace . . . . . . . . . . . .
Nevlastn integrály,. . . . . . . . . .
Přehled některých určitých integrálů. .
Vyjádření některýc.t1 integrálů řadami . . . . .
Použití určitých integrálů
. c.. . .
. I. . . .
Křivkový integrál. . . . . . . . .
Křivkový integrál po oblouku rovinné křivky. .
Křivkový integrál po pro orové křivce.
Křivkový integrál vektoru . . . .
Množné [n-rozměrné] integrály .
Dvojné [dvojro,změrné] integrály .
Trojné [trojrozměrné] integrály'.
DIFERENCIÁLNÍ ROVNICE.
Obyčejné diferenciální rovnice .
Obyčejné diferenciální rovnice prvního řádu
Geometrický význam . . . . . . . . . . . . .
Diferenciální rovnice se separovanými proměnnými
Lineární di(ere.nciální rovnice prvního řádu. . .
Homogenní diferenciální rovnice prvního řádti
Exaktní diferenciální rovnice prvního řádu .
Integrující faktor [Eulerův multiplikátor]. .
Bernoulliova <diferenciální) rovnice. .
Riccatiova < diferenciáln,í) rovnice .
.
11
8.2.9.
8.3.
8.3.1.
8.3.2.
8.3.3.
8.3.4.
8.3.5.
8.3.6.
8.3.7.
8.4.
8.4.1.
8.4.2.
K5.
8.6.
8.6.1.
8.6.2.
8.6.3.
9.
9.1.
9.1.1.
9.1.2.
9.1.3.
9.1.4.
9.1.5.
9.2.
9.3.
9.4.
9.5.
Clairau tova <diferenciální> rovnice . . . .'.
Obyčejné diferenciální rovQice druhého řádu . . . . . .
Zvláštní případy . . . . . . . . . . . . . . . . . .
Homogenní lineární diferenciální rovnice druhého řádu s konstantními koe-
ficienty . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Homogenní lineární diferenciální rovnice druhého řádu s proměnnými koeficienty
Eulerova diferenciální rovnice druhého řádu bez pravé strany [homogenní
Eulerova diferenciální rovnice] . . . . . . . . . .'. . . . . . . . . . .
Nehomogenní lineární diferenciální rovnice druhého řádu. . . . . . . . . .
Nehomogenní lineární diferenciální rovnice druhého řádu s konstantními koe-
ficien ty . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . '.
Eulerova diferenciální rovnice druhého řádu s pravou stranou [úplná Eulerova
diferenciální rovnice] . . . . . . . . .
Obyčejné diferenciální rovnice třetího řádu . /. ....
Homogenní lineární diferenciální ra.vnice třetího řádu s konstantními koeficienty
\ Nehomogenní lineární diferenciální rovnice třetího řádu s konstantními koe-
fi . ..
lClenty . . . '. . . . . . . . . . . . . . . . . . . .
Integrování diferenciálních rovnic pomocí mocninných řad .
Parciální 'diferenciální rovnice: . . . ...
Základní pojmy. . " . . . . . . . . . . . . . .
Jednoduché parciální diferenciální rovnice . . . .
Lineární parciální diferenciální rovnice prvního řádu ve dvou proměnných
NEKONEČNÉ ŘADY, FQURIEROVY ŘADY, FQURIERŮV INTEGRÁL,
LAPLACEOV A TRANSFORMACE . . . . . . . .
Řady . . . . . . . . . . .
Zákla ní pojmy. . . . .
Kritéria konv rgence řad. . . . . . . . . .
Některé nekonečné konvergentní Číselné řady.
, Mocninné řady. . . . . . . . . '. . . .
\Přibližné vzorce' pro počítání s malými čísly. . .
Základní pojmy k Fourierovým řadám.
Výpočet Fourierovy řady; příklady . . .
Fourierův integrál, Fourierova transformace
Laplaceova transformace. . . . . . . . . .
664
665
666
672
673
675
677
680
682
684
684
685
686
688
688
689
690
692
692
692
692
695
697
705
706
709
718
720
9.6. Použití Laplaceovy transformace k řešení diferenciálních rovnic 725
9.7. Tabulka korespondencí některých racionálních Laplaceových integrálů. 730
10. POČET PRA VDĚPODOBNOSTI, MATEMATICKÁ STATISTIKA, TEORIE
CHYB A VYROVNÁ V ACÍ POČET . . .. .... 732
10.1. Počet pravděpodobnosti '. . . . . . . .'. . . . . . . . . . . . . . . . 732
12
10.2.
10.2.1.
10.2.2.
10.2.3.
10.2.4.
10.2.,5.
10.2.6.
10.3.
10.4.
11.
11.1.
11.2.
11.3.
11.4.
Matematická statistika.
Sumační znak . . . .
Multiplikační znak .
Střední hodnoty . .
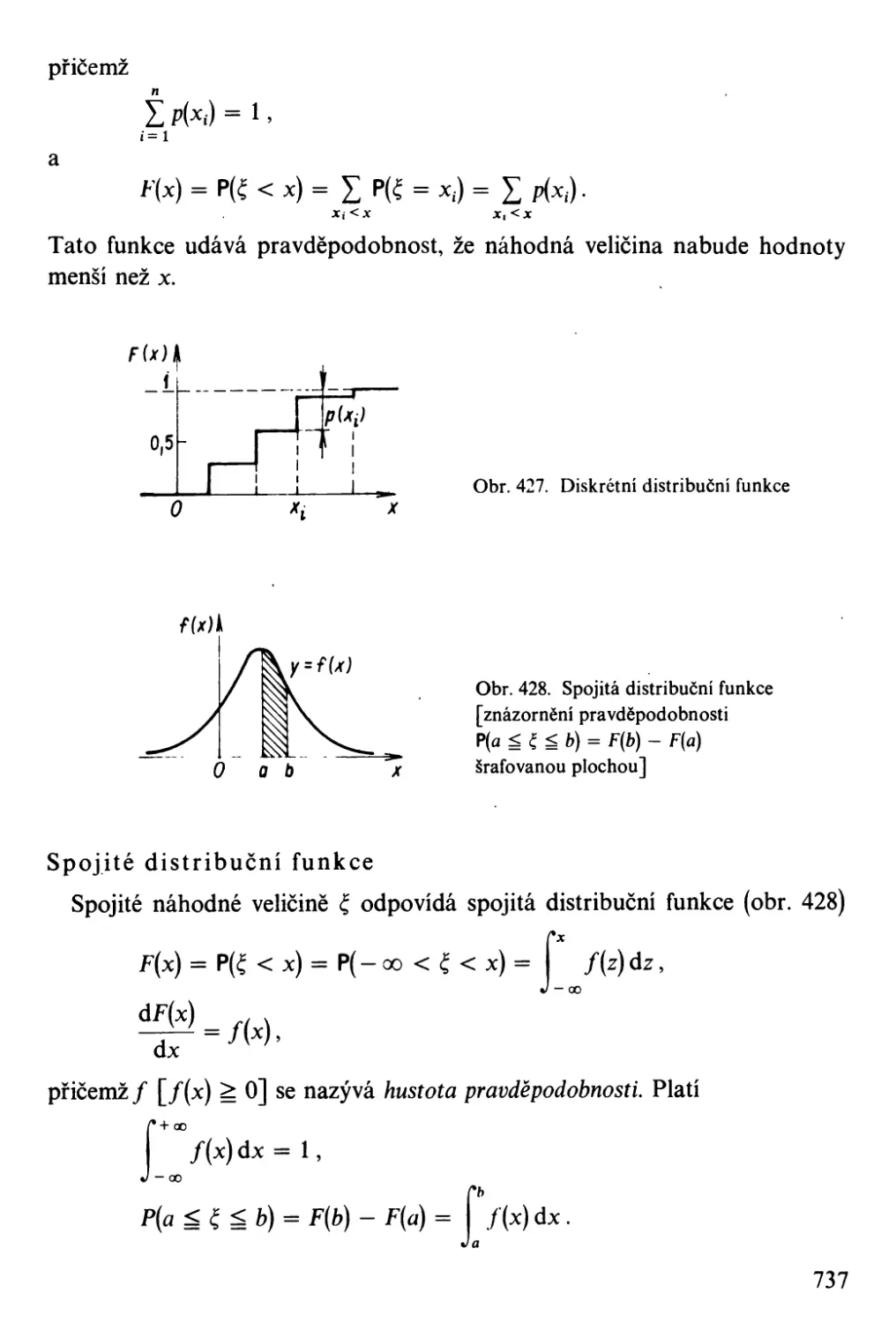
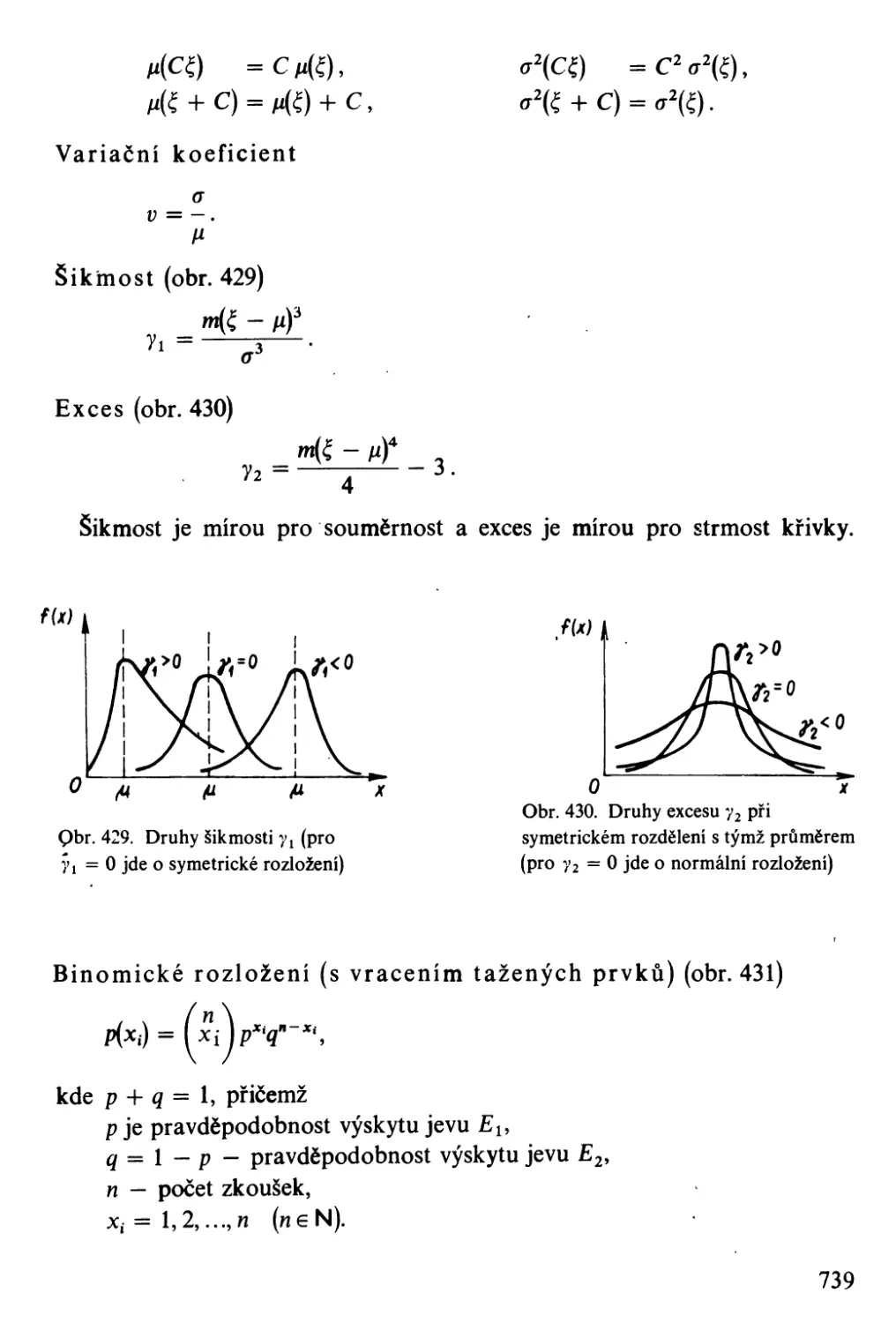
Míry rozptýlení. .
Metoda nejmenších čtverců.
Lineární regrese, lineární korelace. .
"
743
. . .. 743
744
745
. . . . 747
j
. " 749
751
752
753
760
Teorie chyb '. . .
Vyrovnávací počet
LINEÁRNÍ OPTIMALIZACE [LINEÁRNÍ PROGRAMOVÁNÍ]
Základní pojmy. . . .
760
762
764
770
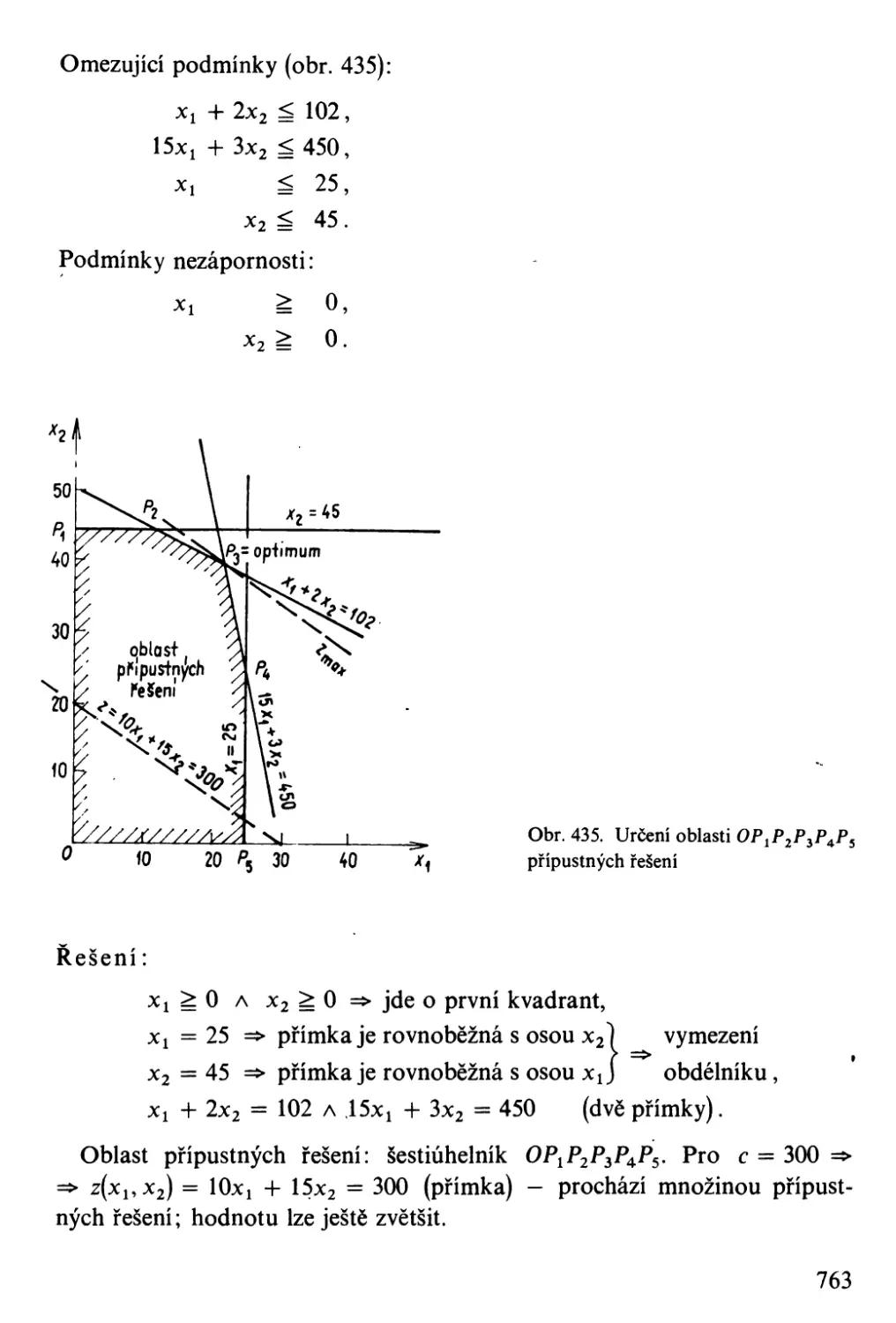
Grafická metoda řešení
Simple ová metoda . . . . .
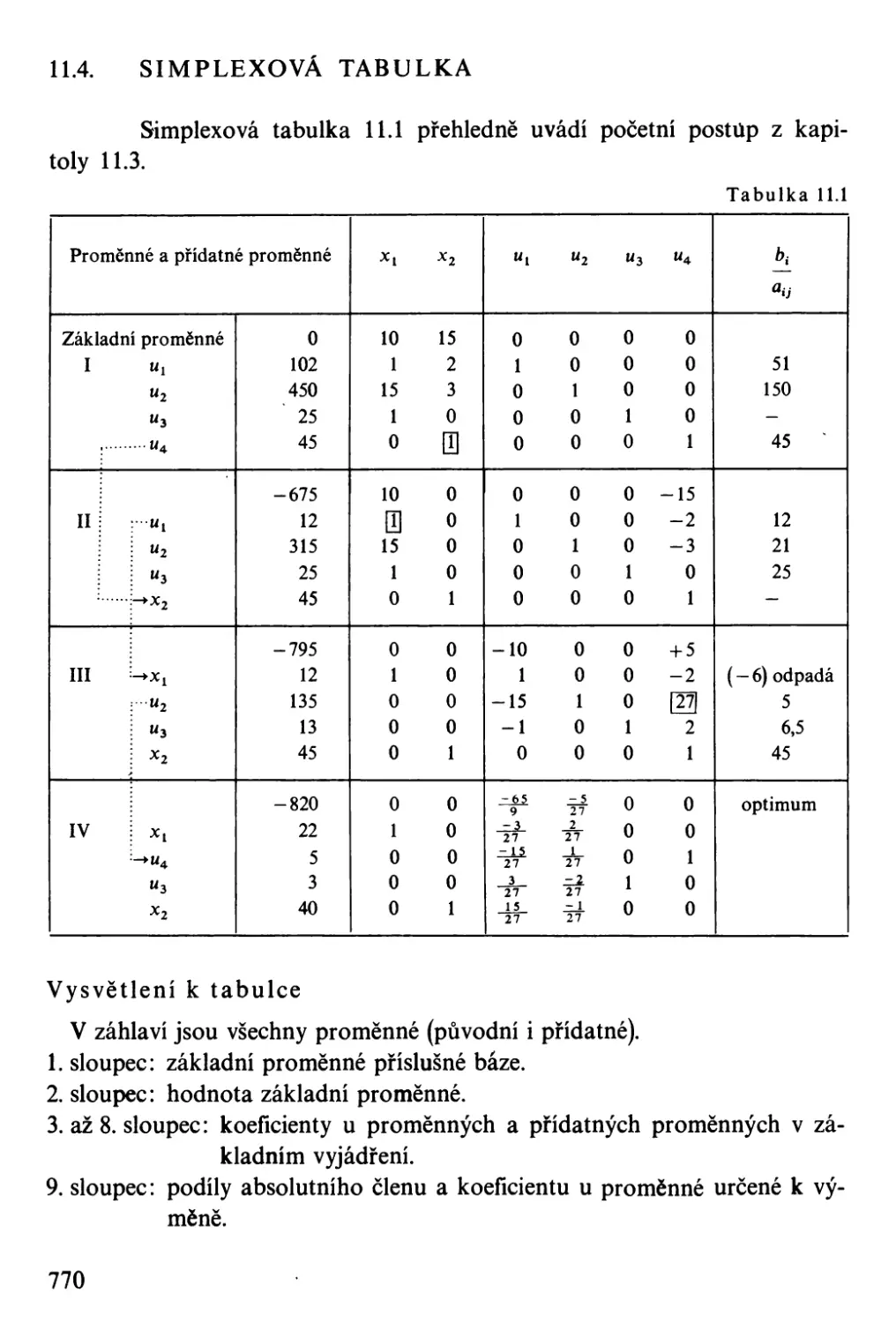
Simplexová tabulka.
12. LOGICKÁ ALGEBRA [SPÍNAČOVÁ ALGEBRA] . 772
12.1. Základní pojmy. . . . . . . . . . . . . 772
12.2. Základní logické zákony a pravidla 774
12.3. Další bo<?lovské funkce se dvěma proměnnými [lexikografické uspořádání] .. 776
12.4. Normální t ary. . . . . 779
12.5.
13.
\ 13.1.
13.2.
13.3.
13.4.
13.5.
14.
14.1.
14.2.
14.3.
15.
15.1.
15.2.
-15.2.1.
15.2.2.
15.2.3.
Karnaughovy mapy .
781
784
784
785
787
790
791
795
795
796
797
799
.799
801
801
802
.802
VZORCE Z.REGULAČNÍ TECHNIKY.
Základní pojmy. . . . . . .
Testovací [zkušební] funkce .
Symbolická vyjádření . . . . . . .
Řazení řídicích [regulačních] členů
. .
....
. ,. . . .
Charakteristické hodnoty některých přenosových členů. . .
DO D A TK Y . '. . : . . . . . .'. .
Řecká abeceda . . . . . . . . . . . . . .
Německá abeceda [gotické písmo] . . . . .
Často používané konstanty a jej i,ch. dekadické logaritmy
LITERATURA. . . . . . . . .
Literatura z německého originálu .
Literatura připojená při českém překladu. .
Matematická IObika a množiny . . . .
Algebra (rovnice, matice, determinanty)
Analytická geometrie : . . . . . . .
. . . ,. . . . .
13
15.2.4.
15.2.5.
15.2.6.
15.2.7.
15.2.8.
15.2.9.
15.2.10.
15.2.11.
15.2.12.
15.2.13.
14
Matematická analýza . . . . . . . .
Nekonečné řady . . . . . . ". . . .
Diferenciální geometrie křivek a ploch .
Obyčejné a parciální diferenciální rovnice. .
Funkce komplexní proměnné . . . . .
Laplaceova transformac.e. . . . . . . . .
Numerické a grafické metody. . . . . . .
Počet pra vděpodo bnosti a matematická statistika
Příručky, sbírky příkladů a přehledy vzorců.
Tabulky konstant a funkcí . . . . .
VĚcNÝ REJSTŘÍK.. . . . . . .
. . . . . . . . . . . 803
. . . . . . . . . . . . 804
. . . . . -'"'804
. . . . . . . . . 804
805
. . " 805
805
806
. . . . . . . . .. 806
807
,
. . . . .
,
808
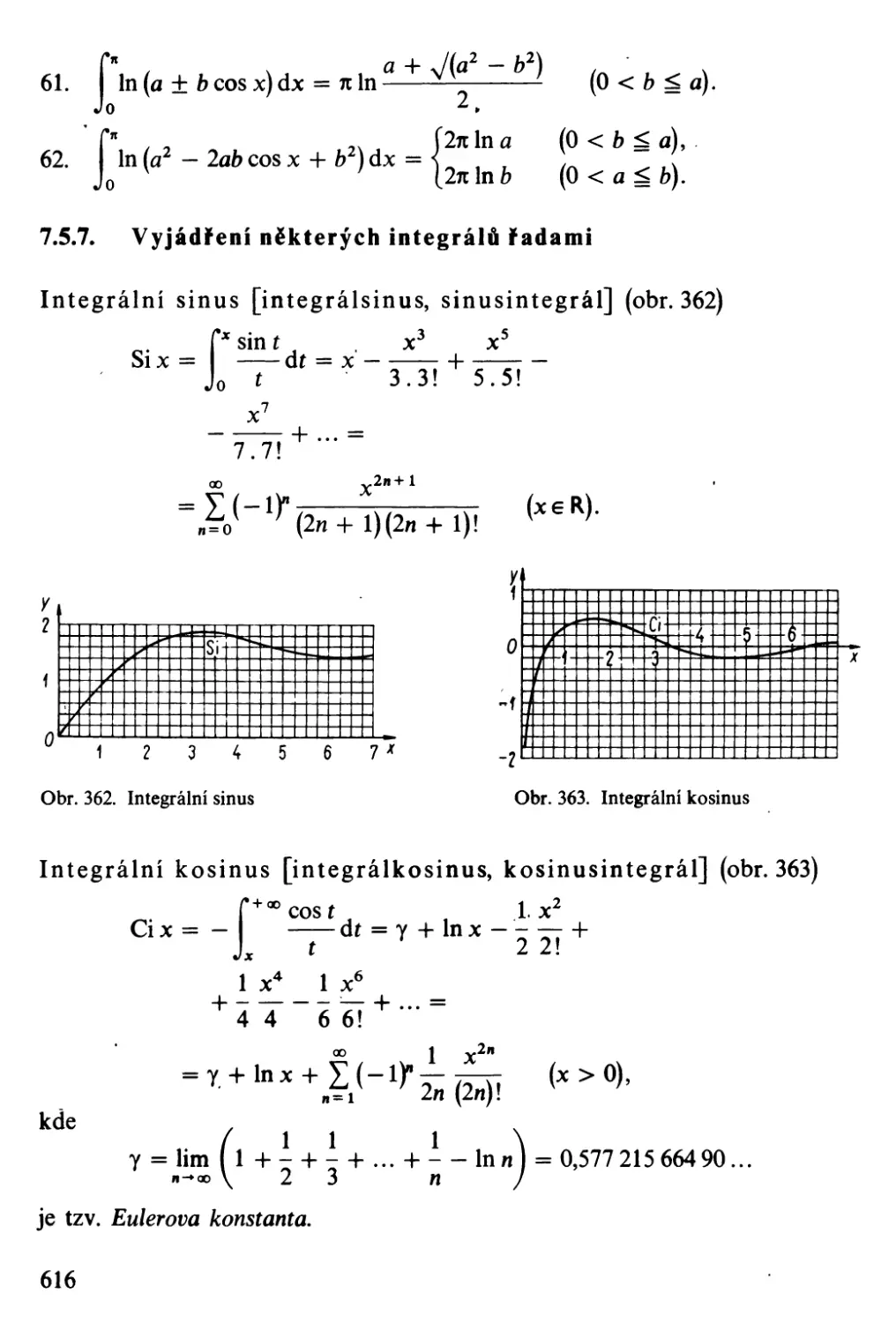
PŘEDMLUVA K ČESKÉMU VYDÁNÍ
Příručka "M atematické vzorce" se v původním německém znění i v pře-
kladech všestranně osvědčila, o čemž svědčí dosavadních sedmnáct vydání
v Německé demokratické republice, čtyři vydání v Německé spolkové republice
a Švýcarsku, překlad do angličtiny a tři předchozí vydání v češtině podle pů'vodního
zpracování (v druhém německém vydání), která měla u širokého okruhu českých
čtenářů velmi dobrý ohlas a stala se vyhledávanou pomůckou v technické praxi
i na středních a vysokých školách.
Posláním této obsažné příručky je dát studujícím na středních a vysokých
školách s převážně technickým zaměřením, stejně jako technickým pracovníkům
a inženýrům na pracovišti pohotově a spolehlivě bezprostředně použitelné mate-
matické poznatky a vzorce s udáním podmínek jejich platnosti pro řešení prak-
tických problémů. Přitom .vzhledem k charakteru této sbírky matematických
vzorců lze považovat za samozřejmé, že do ní nebyly zařazeny ryze teoretické
poznatky ani důkazy uváděných pouček a algoritmů; lze z ní však vycházet při
studiu speciální teoretické literatury. .
Názorný výklad pojmů a četné řešené příklady usnadňují pochopení látky,
která byla do příručky pojata s přihlédnutím k různým potřebám techniků
. v , o
a lnzenyru.
Při zavádění názvů v definicích jsou v českém překladu pro lepši srozumitelnost
dávány alternativní termíny do lomených závorek a fakultativní roz íření termínů
do úhlových závorek. Odvolávky na pořadová čísla bibliografických citací z pře-
hledu literatury na konci knihy jsou uváděny v lomených závorkách.
Nynější české vydání je zcela novým překladem podle úplně přepracovaných,
doplněných a modernizovaných posledních německých vydání. Přitom v osobní
spolupráci mezi autorem a překladatelem bylo se souhlasem autora nové české
znění přizpůsobeno domácím zvyklostem nejen v "terminologii, dikci a značení,
ale také v pojetí a způsobu výkladu příslušných matematických oborů na střed-
ních a vysokých školách v ČSSR.
Stávající české vydání je tedy založeno na moderně pojatých matematických
pojmech ve snaze zajistit maximálně možnou přesnost formulaci definic, matema-
tických vět a početních metod.
15
Můj vřelý dík patří překladllteli Ing. Zdeň/"u Tichému za uvědomělé zprqco-
vání mé knihy při překladu i za jeho doplňky a úpravy, kterými české znění při-
způ obil způsobu podání v češtině.
Dr. Ing. Hans-Jochen Bartsch
Karl-Marx-Stadt, 1980
16
PŘEDMLUVA K 17. NĚMECKÉMU VYDÁNÍ
V dnešní době, kdy věda a technika učinily o ro.vské pokroky, jsou
na celý výchovný systém, zejména však na výchovu vědeckotechnických kádrů
kladeny značně zvý ené požadavky. Platí to ovšem hlavně pro matematiku.
Jen spolehlivé á moderně pojaté matematické znalosti umožňují inženýrům,
technikům, konstruktérům a mistrům neustále držet krok s technickým
rozvojem -a s matematickou přesností plnit požadavky na ně kladené. Před-
pokladem k tomu je především' pečlivá .základní matematická výchova r.a
školách všech stupňů a v příslušných institucích. Této přípravě má pomáhat
i tato sbírka vzorců, která vychází v podstatě z všeobecných poznatků získa-
ných v základní desetileté škole a je určena hlavně studujícím na odborných
školách a posluchačům vysokých škol. Avšak také žákům odborných střed-
ních škol a gymnázií, stejně jako pracujícím, kteří si s rozsáhlou pomocí vlády
zvyšují při povolání svou kvalifikaci při samostatném, dálkovém nebo večerním
studiu, může tato příručka být účinným pomocníkem při racionalizaci duševní
práce.
Samozřejmě nebylo možno do této knihy pojmout všechny,speciální obory
matematiky. Výběr látky této sbírky vzorců, která kromě základních početních
operací a metod, planimetrie a stereometrie, analytické geometrie v rovině
a prostoru, lineární algebry a vektorového počtu, diferenciálního a integrál-
ního počtu, diferenciální geometrie a diferenciálních rovnic obsahuje také
Fourierovy řady a základy,' počtu pravděpod<:>bnosti, lineární optimalizace,
matematické logiky a Laplaceovy transformace, je však tak široký, že vyhovuje
potřebám velkého okruhu zájemců o literaturu tohoto druhu.
Již dvanácté německé vydání bylo vylepšeno, pokud jde o uspořádání
.,a umístění některých výkladových celků v rámci této příručky. Zároveň bylo
zpracování ještě více přizpůsobeno modernímu výkladu matematiky na zá-
kladě matematické logiky a teorie množin. Aby čtenář snadno našel, co x>ka-
mžitě potřebuje, byla zvláštní pozornost věnována věcnému rejstříku a pře-
hlednému členění látky.
17
Četné řešené příklady mají čtenářům usnadnit pochopení abstraktních
matematických vzorců. Poznámky v textu mají čtenáře vést k tomu, aby
ke studiu matematiky nepřistupoval jen formálně, ale aby si ji osvojil vlastním
myšlením. Mají zároveň přispívat k tvůrčímu použití matematiky v praxi.
Autor a nakladatelství
18
o. PŘEHLED .ZNAKŮ A SYMBOLŮ,
ČíSELNÉ TABULKY, MATEMATICKÁ 'LOqlKA
A, MNOŽINY
..... o o
0.1. PREHLED.ZNAKU A SYMBOLU
t.
0.1.1. atematická logika
x, y, z, .. .
.qJ, t/J, x, ...
- -" ,
cp, -, cp, cp, non cp, <p
cp 1\ t/J, cp. t/J, cpt/J, cp n t/J, cp & t/J
cp v t/J, cp + t/J, cp u t/J, cp vel t/J
cp t/J, cp t/J,"- cp ::::> t/J
cp t/J, cp t/J.
cplt/J
cp <= t/J, cp +- t/J, cp c t/J
cp++t/J
,
cp+-+t/J
výrokové proměnné, též výroky
výrokové formule, též výroky .
není pravda, že cp; negace výrokové
I
formule (popř. výroku) cp
cp a <zároveň) t/J, qJ i t/J; konjunkce
[logický součin] výrokových formulí .-
(popř.' výroků) cp, t/J
cp nebo t/J; 4isjunkce [logický součet]
výrokových formulí (popř . výroků) cp, t/J
jestliže cp, <pak) t/J; <příma) implikace
výrokových formulí (popř . výroků) cp, t/J
(v tomto pořadí)
cp, právě když t/J; cp tehdy a jen tehdy,'
když t/J;,ekvivalence výrokových
formulí (popř . výroků) cp, t/J
negace konjunkée [operace NAND,
Shefferova operace, funkce ani]
výrokových formulí (popř. výroků) cp, t/J
nepřÍIná [zpětná] implikace výrokových
formulí (popř . výroků) cp, t/J
(v tomto pořadí)
negace implikace [inhibice, přímá
inhibice, nonimplikace] výrokových
formulí (popř. výroků) cp, t/I
(v tomto pořadí)
negace nepřímé implikace . [nepřímá
inhibice, zpětná inhibice] výrokových
formulí (popř . výroků) cp, t/J
(v tomto pořadí)
I . I
19
3
.
negace ekvivalence [antivalence, alterna-
tiva, operace "bud", nebo"" operace
vylučovací nebo, .nonek vivalence,
logický součet modulo 2] výrokových
formulí (popř. výroků) qJ, .p
pravdivostní ohodnocení výroku qJ
qJ je logicky ekvivalentní s t/J
obor pravdivosti predikátové formule
[výrokové formy]
pro všechna, pro libovolné; obecný
[velký] kvantifikátor, obecný [velký]
kvantor, generalizátor
existuje; existenční [malý] k vanti-
fikátor, existenční [malý] kvantor,
partikular,izátor
pro nekonečně mnoho
pro nejvýše konečně mnoho
existuje právě jeden
existuje nekonečně mnoho
existuje nejvýše konečně mnoho
({J >=< .p, ({J (f) t/J., ({J t/J
p( ({J )
({J = t/J
p
v
3
00
v
<:x:
V
3 !
"X.
3
.... .k
0.1.2. Množiny.. zobraze-ní, funkce
A=t=B
(je) prvkem <množiny), patří do
<množiny); incidence [příslt]šnost]
prvk u k množině .
není prvkem <množiny>, nepatří do
<množiny)
XI E A 1\ X 2 E A !\ ... A X n E A
množina A se rovná množině B;
rovnost množin A, B ·
Innožina A se nerovná množině B:
nerovnost množin A, B
množina A = X I' X 2' ..., xn} =
- f-" l (1. (l b h .
- l X I J U lX 2 j U ... u l X n j o sa uJe
prÚ vě jen prvky x 1'1 X 2 , ..., X n
E
ft
.\' 1 .. Xl" .. '" :(11 E A
A=B
1 ' x '. \ . 1
" = l' I"" 2" .. .. . n'
o
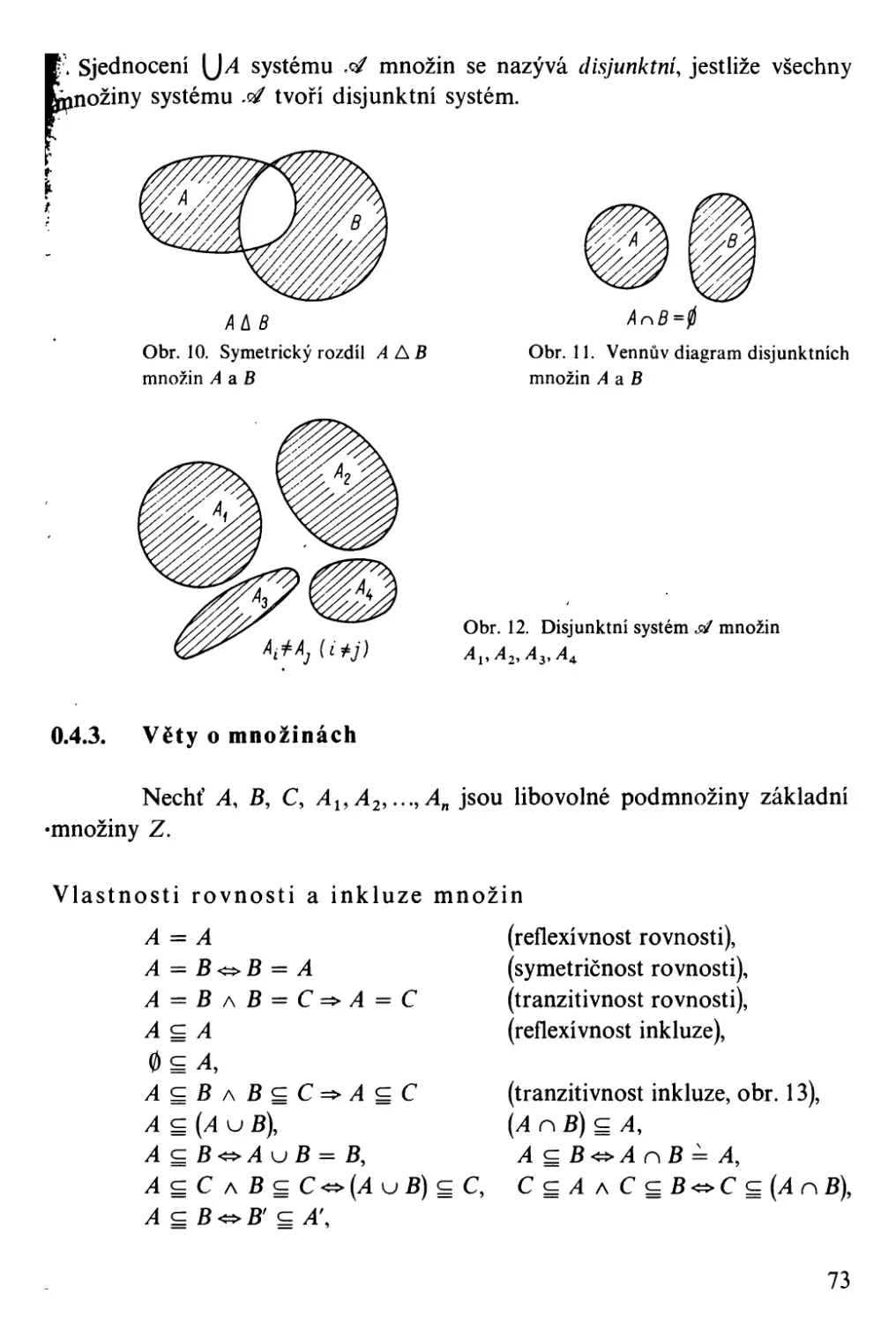
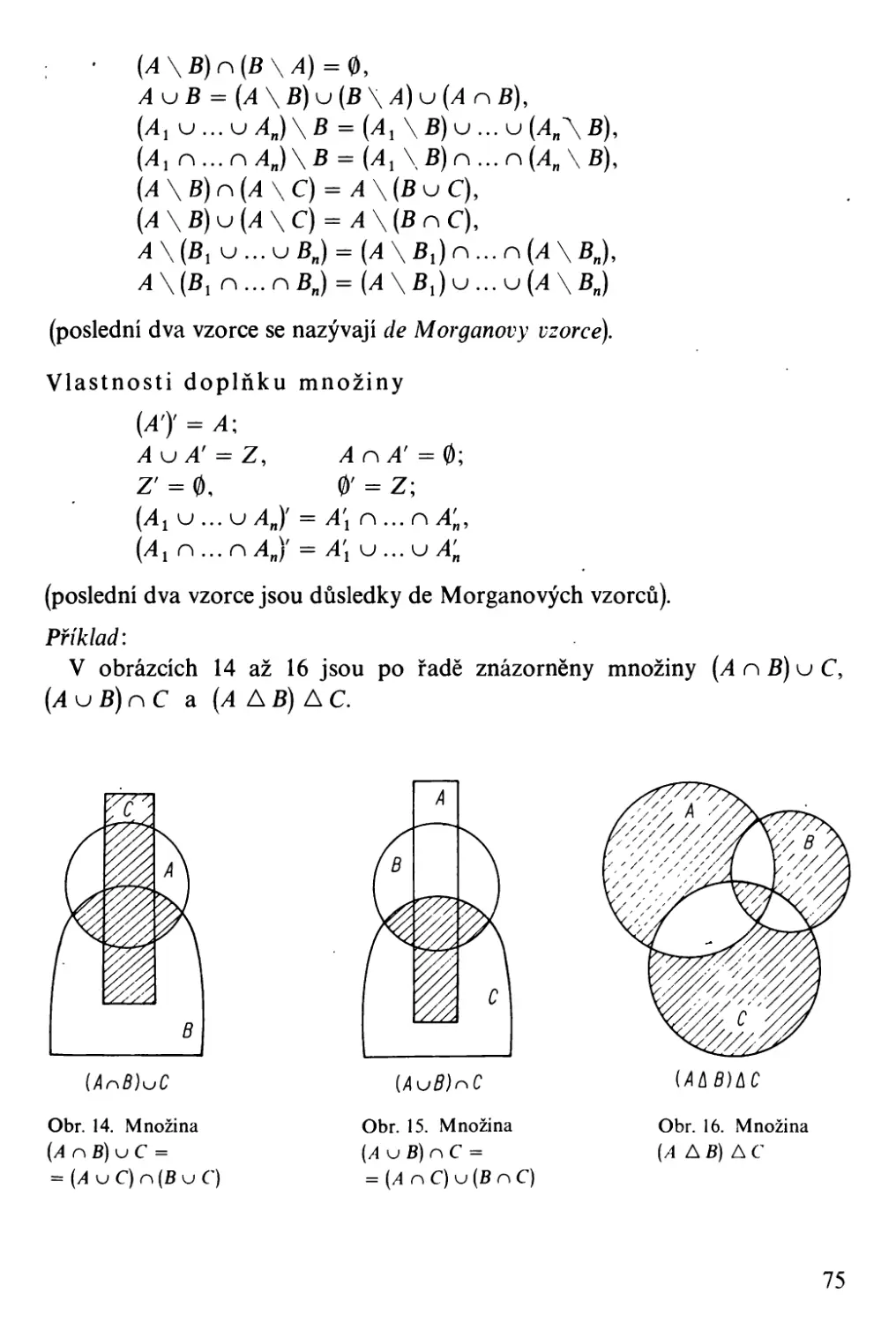
0, { }
d = {A i' A 2 , ..", An}
prázdná množina
systém .sti množin obsahuje právě jen
množiny A i' A 2 , . o o., An
množina právě těch prvků oboru U
proměnné x, které mají vlastnost V
{x E U I V(x)},
{x E U: V(x)},
{XEU; V(x)}
Vx E M [V(x)],
tlx EM: V(x),
VXEM; V(x)
3x E M [V(x)],
3XEM:V(x),
3x EM; V(x)
A c B, A c B
pro každý prvek x množiny M platí
vlastnost V(x)
existuje aspoň jeden prvek množiny M, ,
pro který platí vlastnost V(x)
AcB
množina A je částí [podmnožinou]
množiny B; neostrá inkluze množin
A, B (v tomto pořadí)
množina A je vlastní částí [vlastní pod-
množinou] množiny B; ostrá inkluze
množin A, (v tomto pořadí)
množina A je nadmnožinou množiny B
množina A je vlastní nadmnožinou
množiny B
sjednocení [součet] množin (tříd) A, B
průnik množin (tříd) A, B .
rozdíl množin (tříd) A, B (v tomto pořadí)
symetrický rozdíl množin (tříd) A, B
doplněk množiny A v <základní>
. množině Z
A => B, A => B
A=>B
A u B, A + B
A n B, AB
A \ B, A - B
A B, A B
A , Ai, CzA, Ai
n n
Ai .u A 2 U ... U An' U Ai' UA i
i = 1 i
sjednocení množin AI' A 2 , o.., An
Us
Sel/'
sjednocení systému Y množin S
n n
Ai n A 2 n ... n An' n Ai' nA i průnik množin Ai' A 2 , 00" An
i = 1 1
nS
Sefl
[a,b]
a l' a 2' . . ., a n ]
4 x B
průnik systému !f/ množin S
uspořádaná dvojice objektů a, b
uspořádaná n-tice objektů a 1 , a 2 , .. o, a n
kartézský součin množin A, B
(v tomto pořadí)
21
A 2 , A x A
druhá kartézská mocnina
[kartézský čtverec] množiny A
n ,.
A. X A 2 X ... X An, XA i , XA i kartézskýsoučinmnožin A.,A 2 ,...,A n
i = . 1
.
'n-tá kartézská mocnina množiny A
<binární) relace R mezi množinami A, B
(v tomto pořadí)
J <binární) relace v množině M
x je v <binární) relaci R s <prvkem) y,
prvku x je přiřazen prvek y v relaci R;
přiřazení prvku y prvku x v relaci R
prvku x je přiřazen prvek y
<prvek) x není v <binární) relaci R
s <prvkem) y .
první [definiční, vstupní, levý] obor
[ vzor] relace R
druhý [výstupní, pravý] obor [obraz]
relace R
in verzní relace k relaci R
R složeno s S; relace složená z relací
R a S, kompozice [kQmpozit, součin]
relací R a S
identická relace [relace identity]
na množině M .
ryze [striktně] předchází, (je) menší než;
znak ostrého uspořádání
, ryze [striktně] následuje za, (j ) větší
než; znak ostrého uspořád4ní
předchází, (je) nejvýše roven, není
větší než; znak <neostrého) uspořádání
následuje, je nejméně roven, není menší
než; znak <neostrého) uspořádání
prvek y je obrazem prvku x v zobrazení f,
hodnota zobrazení (funkce) f v bodě x,
též funkce f jedné < nezá visle) pro-
měnné [argumentu] x (y je závisle
proměnná)
A n
[R;A,B], R:A B
[R; M], R: M M
R R
xRy, XH y, x-+ Y
XH y, x-+ y,
x R y
01(R), D(R), dom.R
02(R), R(R), rng R, H(R)
R_bR- 1
R o S, R * S, RS
id M , L1 M', BM
-<
>-
, f f
f: x H y, X H y, X -+ y, y = fx,
y = f(x),f(x)
22'
sup A, sup A
M
zobrazení i množiny A do množiny B
zobrazení i množiny A na množinu B
vzájemně jednoznačné zobrazení
[bijekce] f množin A, B
obraz množiny A v zobrazení i
vzor množiny B v zobrazení i
inverzní zobrazení (funkce) k zobrazení
(funkci) i
jediný vzor prvku y v zobrazení i
parciální zobrazení (funkce) indukované
na množinu M zobrazením (funkcí) f,
parcializace [zúžení, restrikce]
zobrazení (funkce) i na množinu M
složené zobrazení (funkce) h s vnější
složkou g a vn třní složkou i
hodnota složeného zobrazení (funkce) h
s vnější složkou g a vnitřní složkou i
v bodě x, též zobrazení (funkce) h
složené ze zobrazení (funkcí) g a i
. .,
při argum"entu x (y je závisle proměnná)
hodnota zobrazení (funkce) i v bodě
[x l' xz, ..., x n ],. též zobrazení (funkce) i
<nezávisle> proměnných [argumentů]
Xl' X 2 , ..., X n (y je závisle proměnná) .
árnost operace w
množina A je ekvivalentní [ekvipolentní]
s množinou B
mohutnost" [kardinální číslo] množiny A
mohutnost ..[kardinální číslo] ,konečné
množiny A
alef nula; mohutnost množiny No
alef; mohutnost kontinua
mohutnost systému JH všech podmnožin
množiny M
supremum množiny A v množIně M
i:A B
i: A . B
i: A B
i(A)
i-I (B), i-I (B)
i-I' i-I
.
i- 1 (y), i- 1 (y)
ilM
h = g(i), h = g o i
y = g(i(x)) = h(x)
y = i(X.l' x 2 , ..., x n ),
i (x 1 , X 2' . . ., X n )
a(w)
A B
card A, m(A)
IAI
o
2 m (M)
inf A, inf A
M
infimum množiny A v množině M
23
maxA
max {X1, Xl' ..., Xn}
min A
min {x l' X 2' · . ., Xn}
(M, Q)
AO AO
M'
Ext M A, Ext A
Fr M A, Fr A
A M , A
maximální prvek úplně uspořádané
množiny A
maximální prvek číselné množiny
{ Xl' X 2, . . ., xn}
minimální pryek úplně uspořádané
množi y A
minimální prvek číselné množiny
.{x 1, X2, ..., xn}
metrický prostor s nosičem M
a metrikou Q
vnitřek množiny A v metrickém
prostoru (M, Q)
vnějšek množiny A v metrickém
prostoru (M, Q)
hranice množiny A v metrickém
- prostoru (M, Q)
uzávěr množiny A v metrickém
prostoru (M, Q)
0.1.3. ' Stand rdní 9značení některých množin
N
No
z
Q
R Rt
,
z-
Z-
o
Q+
Q;
..
Q-
Qů\
24
-
{I, 2, 3, ...}; množina všech kladných
celých čísel '
N u {O}; množina všech nezáporných
celých čísel (viz článek 1.1.1)
množina všech celých čísel
množina všech racionálních čísel
množina všech reálných čísel, reálná
[číselná] osa .
množina všech záporných celých čísel
množina všech nekladných celých čísel
množina všech kladných racionální h čísel
množina všech nezáporných
racionálních čísel
množina všech záporných
racionálních čísel
množina vŠ,e<:h nekladných
racionálních čísel
R+
R+
o
-00
+00
00
množina všech kladných reálných čísel
množina všech nezáporných
r álných čísel
množina všech záporných reálných čísel
množina všec1l. ne ladných reálných čísel
množina všech uspořádaných n-tic
reálných čísel
minus nekonečno
plus nekonečno
<bod) nekonečno; nevlastní prvek,
. .
nekonečně vzdálený bod
Ru{+oo}
R u { - 00, + 00 }; rozšířená reálná
[číselná] osa
Ru{oo}
množina všech konečných komplexníc
.čísel, otevřená <Gaussova) rovina
<komplexních čísel)
C \ {O}
množina všech uspořádaných n-tic
, konečných komplexních čísel
C u { 00 }; uzavřená [rozšířená] Gaussova
rovIna
{O, 1, 2, """, n}; n-tý úsek množiny No
{1, 2, " ""' n}; n-tý úsek množiny N
{x E R I a < x < b}; otevřený interval
od a do b [s krajními body a, b ]
{x E R I a < x < b}; uzavřený interval
od a do b [s krajními body a, b ]
{x E R I a < x < b};. zleva uzavřený
a zprava otevřený interval od a do b
rpolouzavřený interval od a do b ]
{x E R I a < < b}; zleva otevřený
a zprava uzavřený interval od a do b
[polootevřený interval od a do b]
{xERla < x}
{xERla<x}
{xERlx < a}
R-
R-
o
Rn
R*
R*, Ef, < oo, +(0)
*R *E
, 1
C, C , G
p
C n
* -
C , S, G
U On
U n
(a, b)
<a,b)
\ a, b)
(a, b )
< a, + 00 )
(a, + 00 )
(- , a)
, . 25
En
{xERlx<a}
množina R všech reálných čísel
(a - tJ, a + tJ); tJ-okolí [tJ-ové okolí]
bodu a <v prostoru El>
U(a, tJ) \ {a}; neúplné tJ-okolí
[tJ-ové okolí] bodu a <v prostoru E 1 >
< otevřená> koule v metrickém prostoru
(M, Q) (se středem a a poloměrem tJ),
tJ-okolí bodu a v metrickém prostoru
(M, Q) .
K(a, tJ) \ {a}; neúplné tJ-okolí bodu a
v metrickém prostoru (M, Q)
n-rozměrný <bodový> euklidovský
prostor
n-rozměrný afinní prostor
n-rozměrný projektivní prostor
pro tor spojitých funkcí na množině M;
pro M = (a, b), resp. M = <a, b>
se používá symbolu C(a, b), resp.
C<a, b>
prostor spojitých funkcí na množině M
se spojitými derivacemi až do řádu n
včetně, resp. všech řádů
( - 00, a)
(-00, +00)
l!(a, tJ), U (a), U(a)
U(a, tJ), U (a), U(a)
K(a, tJ), K (a), K(a)'
K(a, tJ), K (a), K(a)
An
Pn
C(M)
c<n)(M), resp. C<OO)(M)
0.1.4. Číselné konstanty
e 2,718 281 828459 O...; Eulerovo číslo
1t 3,141 592 654 . . .; LudQlfovo číslo
y 0,57721566490...; Eulerova konstanta
M 19 e . 0,434 294 48; součinitel pro převod
přirozeného logaritmu na dekadický
logaritmus
m ln 10 ...:.. 2,302 585 09; součinitel. pro
převod dekadického logaritmu
na přirozený logaritmus
26
Elementární aritmetika a algebra
(je)' rovno
není rovnE>, je různé od
(je> identicky rovno
. není identicky rovno
(je> přibližně rovno
(je> po zaokrouhlení rovno
(je> menší než
(je> mnohem [řádově] menší než
< je > větší než
<je> mnohem [řádově] větší než
(je> menší nebo rovno, (je> nejvýše
rovno, není větší než
(je> větší nebo rovno, (je> nejméně
rovno, není menší než
plus; kladné znaménko
minus; záporné znaménko
krát, násobeno; při násobení čísel
vyjádřených písmeny lze tyto znaky
vyne hat
,
lomeno, děleno; šikmá, popř. vodorovná
zlomková čára
(je> úměrno
odpovídá
okrouhlé, lomené, složené a úhlové
závorky
n faktoriál, faktoriál čísla n
1 . 3 . . .. . (2n + 1)
. 2 . 4 . .. . . (2n)
0.1.5.
=F
$
f"Oto.I
f"Oto.I
<
>
<
>
+ ,
., x
I, -, :
f"Oto.I
(), [], { }, < > .
n!
(2n + I)!!
( 2n ) ! !
( ). Ck(n), C
C ( n)
(n)
00
.
n nad k; kombinační číslo, binomický
koeficient; počet k-prvkových
kombinací [počet kombina í k-té třídy]
z n prvků
počet k-prvkových kombinací
[počet kombinací k-té třídy J z n prvků
s opakováním
počet k-prvkových variací [počet variací
k-té třídy] z n prvků .
127
V (n)
počet k-prvkových variací [počet variací
k-té třídy] z n prvků s opakováním
suma [součet] čísel Xl' Xl' ..., X n
n n
Xl + Xl + ... + X m L Xi' LXi
i = 1. 1
n n
X I X 2 ... X n ' n Xi' n Xi
i= 1 I
součin čísel Xl' X 2 , ..., X n
0.1.6. Komplexní čísla
1
z=a+bi
imaginární jednotka (v elektrotechnice j)
komplexní číslo z s reálnou částí a
a imaginární částí b
reálná část komplexního čísla z
imaginární část komplexního čísla z
.
absolutní hodnota [modul, velikost,
délka] komplexního čísla z
komplexně sdružené číslo
ke komplexnímu číslu z
argument [amplituda] komplexního
čí sla z
Rez
Imz
Izl
-;; "7'*
"-,
argz
0.1.7. Vektorová algebra a vektorová analýza
a ii b
vektory a, b, c (v. obrázcích se někdy
'..... -+ .....
značí a, b, c, ... v této knize se však
v obrázcích značí stejně jako v textu
tučným písmem)
nulový vektor
n-rozměrný nulový vektor
vá aný vektor [umístění vektoru,
orientovaná úsečka] s počátečním
bodem A a koncovým bodem B
rovnost vektorů a, b
vektor a je kolineární [rovnoběžný] .
s vektorem b
vektor a je 'souhlasně kolineární
[souhlasně rovnoběžný] s vektorem b
a, b, c, ...
o
On
AB , [A, B], a(A), B - A
a=b
a II b
28
aj! b
vektor a je nesouhlasně kolineární
[nesouhlasně rovnoběžný]
s vektorem b
jednotkový vektor souhlasně kblineární
[souhlasně rovnoběžný]
s vek.torem a
n-rozměrný reálný (popř. komplexní)
vektorový prostor
základ,ní vektory [orty] souřadnicové
soustavy (O; i,j, k), resp. (O; e 1 , e2' e 3 )
průměty polohového vektoru a
do souřadnico ých os x, y, z
[složky vektoru a]
souřadnice polohového vektoru a
vzhledem k základním jednotkovým
vektorům i, j, k [projekce polohového
ektoru a do souřadnicových os x, y, z]
velikost úhlu nenulových vektorů a, b
a s = [a cos (a?)] 5°; projekce vektoru a
do vektoru [směru] 5
Os = a cos (a ); průmět vektoru a
do vektoru [směru] 5
n-rozměrný vektor se souřadnicemi
aO
i, j, k, resp. e 1 , e 2 , e 3
a x , ay, Oz
a x ' a y , a z
(a, b)
a s
a s
(a 1 ,a 2 ,...,a n )
[ obc ]
a 1 ,a 2 ,...,a n
velikost [modul, délka] vektoru a = AB
součet vektorů a, b .
rozdíl vektorů a, b (v tomto pořadí)
součin vektoru a a skaláru c [c-násobek
vektoru a]; násobení vektoru a
skalárem c
opačný vektor k vektoru a
a skalárně b; skalární součin vektorů a, b
skalární kvadrát vektoru a
.'
a vektorově b; vektorový součin
vektorů a, b _
smíšený součin vektorů a, b, c
(v tomto pořadí)
vektorová funkce [vektorové pole]
v skalární <reálné> proměnné t
a, lal, I AB I
o+b
o-b
ca
-a a
,
ab, a. b, (a, b)
0 2
a x b, [a, b]
v(t)
29
0.1.8. Matice a determinanty
Poznámka:
Je-li znám typ, popř. řád matice, pak' se v příslušném symbolu neuvádí.
A, S, C, . . . matice
matice A typu (m, n) s prvky a ik
(i = 1, 2, . . ., m; k = 1, 2, . . ., n)
( a 1 l' a 1 z, ..., a 1 n \
: ' ::.:. .) .
[ .a. I . 1 : . 1.2.' ..:.: .a.l . J '
a m1 , a mZ '...' a mn
. .a. I . 1 :. I. 2.' .. :.: .a.l .I I I ..
," I
l'a m1 , amz,...,amnfl
(aik ' (aik)(m,n),
[aik] ' II aik II , .
(aik)' [aik]' II aik II
A(m,n)
n
S(A)
a i
aJ
.
A=S
A+S
ClA
AS = C
\.
mcttice A typu (m, n) .
<čtvercová) matice A řádu n
stopa matice A
i-tý řádkový vektor matice A .
k-tý sloupcový [transponovaný] vektor
matice A
nulová matice typu (m, n), resp. řádu n
ř dkový nulový vektor
sloupcový [transponovaný] nulový vektor
diagonální matice řádu n
násobná [skalární] matice řádu n
jednotková matice řádu n
transponovaná matice k matici A
nulita [defekt, degenerace] matice A
hodnost matice A
m,atice A je ekvivalentní s maticí S
[matice A, S mají stejnou hodnost]
rovnost matic A, S
součet matic A, S
součin matice A a skaláru.Cl
součin mafic A a S
O(m,n), resp. Om O
o
OT
Dn, D.
Sn' S
En, (eik)n, E
A T
')7, nul A
h( A), h
A",S
30
A*
A n
adjA
A, det A, IAI
I a 11' a 1 2' ..., a 1 n :
!..... ........ .,
lanI' a n2 , ..., lI nn :
det (aik)n, laik ln
M ik
t
Aik
V(a 1 , {l2' ..., (ln)
0.1.9. Geometrie
-
,-
.'$
JI
.':: t
"
':ti
.\it
i
'"
'-I
přímka A, AR: AB
. -
. polopřímka AB, AB, AB, AB
>4B, +- AB7 <--iAB
usečka AB, AB
IABIE' d(AB)E' g(A, B)E
. orientovaná úsečka AB, .4B
",IIABIIE
oblouk AB, ÁB
komplexně sdružená matice k matici A
n-tá mocnina matice A
adjungovaná matice k čtvercové matici A
determinant čtvercové matice A
determinant l1-tého řádu s prvky a ik
(i, k = 1, 2, .. ., n)
subdeterminant [minorJ příslušný prvku
a ik determinantu A
Aik = (-l)i+k M ik ; <algebraický>
doplněk prvku aik determinantu A
Vandermondův determinant
(je> totožné, (je> identické, splývá
není totožné, není identické, nesplývá
(je> rovnoběžné
není rovnoběžné
(je> souhlasně rovnoběžné
(je> nesouhlasně rovnoběžné
(je> kolmá na [k J
(je> shodné
(je> podobné
přímka určenÚ body A, B (A =t= B)
polopřímka s počátkem A a v"nitřním
bodem B
'opačná polQpřímka k polopřímce AB
úsečka s krajními body A, B
délka [velikost] úsečky AB [vzdálenost
bodů A, B] při délkové jednotce E
orientovaná úsečka s počátečním bodem
A a koncovým bodem B, vázaný
vektor umístěný do bodu A
orientovaná délka [velikost]
orientované úsečky AB při délkové
jednotce E
oblouk s krajními body A, B
31
,-....
oblouk ACB, ACB
IÁBI
rovina ABC, ABC
rovIna pq
rovina pA
----+
poloprostor A, A
. ---+
polorovlna ABC, ABC,
ABC, I-+ABC \-
ABC, +- ABC, ABC
polorovii1a pA, pA, pA, I-+pÁ
.
pA , pA, +-tpA
Q(A, M)
IApl
úhel A VB, A VB
I A VBIE' v( !Í VB)E
<3 A VB
I AVBIE' v( 'AVB)E
,
.
orientovaný úhel ABJ< VB
,
.....-...
IA VB E' v(A VB)E
pq
Q(]
PQ
o
"
32
oblouk s ktajními body A, B a vnitřním
f ,
bodem C
délka [velikost] oblouku AB
rovina určená třemi různrmi body
A, B, C, které neleží v téže pří mce
rovina určená přímkami p, q (p 4= q)
. ,
rovina určená přímkou p a bodem A
(A p)
poloprostor určený rovinou a bodem
A (A )
poloroviná s hraniční přímkou AB
a s vnitřním bodem C
opačná polorovina k polo.rovině ABC
polorovina s hraniční přímkou p
a vnitřním bodem A
opačná polorovina k polorovině pA
vzdálenost bodu A od množiny
(útvaru) M
vzdálenost bodu A od přímky'p
konvexní (neorientovaný> úhel
s vrcholem Va rameny VA, VB
velikost konvexního (neorientovaného>
úhlu A VB při úhlové jednotce E
nekonvexní úhel ke konve nímu úhlu A VB
velikost nekonvexního
(ne,orientovaného> úhlu A VB
p,ři úhlové jednotce E
orientovaný úhel s vrcholem
počátečním ramenem V A a koncovým
ramenem VB
(orientovaná> velikost' orientovaného
úhlu A VB při úhlové jednotce E
od hylka přímek p, q
odchylka rovin Q, (]
odchylka .přímky p a roviny Q
t .... } \ ·
- s upen " hl ,. d k ....,
. t u ove Je not y v stupnove
m t l a míře (při šedesátinném dělení)
v erlna
.
rad
A[x]
A[ x, y]
A[e, cp ]
A [ x, y, z ]
radián
(úhlóvá jednotka v obloukové míře)
arkus úhlu ; oblouková míra úhlu
grad úhlové jednotk
centigrad, setina gradu při setinném
centicentigrad, dělení
desetitisícina gradu
lomená čára s počát ním bodem P,
koncovým bodem K a vrcholy
AI' A 2 , o. o, A" (v tomto pořadí)
uzavřená lomená čára s vrcholy
At,A2,o.o,A"
trojúhelník s vrcholy A, B, C
čtyřúhelník s vrcholy A, B, C, D
(v tomto pořadí)
kružnice k se středem S a poloměrem r
poloprostor s hraniční rovinou' ABC
a vnitřním bodem D
poloprostor s hraniční rovinou e
a vnitřním bodem D
čtyřstěn s vrcholy A, B, C, D
kvádr s protějšími stěnami ABCD,
A' B'C' D' (AA' II BB' II cc' II DD')
kulová plocha x se středem S
a poloměrem r
dělicí poměr bodu C na přímce
vzhledem k základním bodům A, B
na téže přímce
dvojpoměr bodů A, B, C, D
(v tomto pořadí)
bod A na přímce se souřadnicí x
(někdy také A = [x])
bod A v rovině s kartézskými
souřadnicemi x, y
bod A v rovině s polárními
souřadnicemi e, cp
bod A v prostoru s kartézskými
souřadnicemi x, y, z
arc
.
c '
,
cC "
,
lomená čára PAtA2 .00 A"K
A t A 2 o o o A"A 1
trojúhelník ABC, ABC
čtyřúhelník ABCD
k = (S, r), k(S, r)
poloprostor ABC D
poloprostor eD
čtyřstěn ABC D
kvádr ABCDA'B'C'D'
x = (S, r), x(S, r)
AABCl (ABC), A
ABCD' (ABCD),
33
A[e, cp, z]
A[e, cp, .9]
(O; x), O(x)
(O; x, y), O(x, y)
(O; , y, z), o(x, y, z)
( O; e, lp), o(e, lp)
(O'; e, lp, z o(e, lp, z)
(O; (!, cp, .9), o((!, lp, -9)
0.1.10. Matematická analýza
{a,,}:= h {a,,}, (a,,), (al, a2, ...)
&l"
!!"a
"
n-+oo
n-+-oo
x-+a
x' -+ a +
x -+ a-
iim a" = a
" CIJ
lim a" = + 00, resp. lim a " = - 00
" CIJ " CIJ
lim sup a", lim a"
" CIJ " CIJ
34
bod A v prostoru s cylindrickými
souřadnicemi e, cp, z
bod A v prostoru se sférickými
souřadnicemi e, cp, .9
souřadnicová soustava na přímce
s počátkem O a souřadnicí x
kartézská souřadnicová soustava v rovině
s počátkem O a souřadnicemi x, y
kartézská souřadnicová soustava
v prostoru s počátkem O
a souřadnicemi x, y, z
polární souřadnicová soustava v rovině
s.pólem O, průvodičem e
a argumentem li'
cylindrická souřadnicová soustava
s počátkem O, průvodičem (!,
argumentem li' a souřadnicí z
sférická souřadnicová soustava
s počátkem O a souřadnicemi (!, cp, -9
(nekonečná) posloupnost čísel al' a 2 , ...
!!a" = a" + 1 - a"
!!" a =!!" - 1 a - !!n - I a
" ,,+1 "
n (n E N) se blíží k plus nekonečnu
[ n roste bez omezení v kla ných
celých číslech]
n (n E Z) se blíží k minus nekonečnu
x se blíží k a [x konverguje k a]
x se blíží k a zprava
x se blíží k a zleva
(vlastní) limita posloupnosti {a,,}
pro n -+ 00 se rovná číslu a
posloupnost {a,,} pro n -+ 00 má nevlastní
limitu + 00, resp. - 00
limes superior posloupnosti a"
lim inf a,., lim a,.
11-+ 00
f(x), resp. Pl f(x)
limes inferior posloupnosti a,.
maximum (reálné) funkce f (reálné) ,
proměnné x na intervalu (a, b),
resp. na množině A
minimum (reálné) funkce f (reálné)
proměnné x na intervalu (a, b),
resp. na množině A
supremum (reálné) funkce f (reálné)
proměnné x na intervalu (a, b),
resp. na množině A
infimum (reálné) funkce f (reálné)
proměnné x na intervalu (a, b),
resp. na množině A
limita (reálné) funkce f (reálné)
proměnné x v bodě a
limita (reálné) funkce f (reálné)
prominné x v bodě a zprava
limita (reálné) funkce f (reálné)
proměnné x v bodě a zleva
limita (reálné) funkce f (reálné)
proměnné x v nevlastním bodě + 00,
resp. - 00
přírůstek [diference] argumentu x
"v bodě Xo
přírůstek [diference] funkce f
[přírůstek závisle proměnné y]
v bodě Xo
(první) derivace (reálné) funkce f
(reálné) proměnné x
(y je závisle proměnná)
(první) derivace (reálné) funkce f
(reálné) proměnné x v bodě x,
též (první) derivace (reálné) funkce f
(reálné) proměnné x
(y je závisle proměnná)
d d . . , I ' ,
-;. l1erenCla nI operator
dx
,t f(x), resp'IllT f(x)
sup f(x), resp. sup f(x)
(a,b) xeA
a'J, f(x), resp. ! J f(x)
\
!ig) f(x)
xlllJ1+f(x), f(a +), f(a + O)
xli.T-f(x f(a-), f(a - O)
lim f ( x ) , resp. lim f ( x )
x -+ +-00 x -+ - 00
Ax
L\y, L\f(x)
, df d , dy
f , dx ' dx f, Df, y. dx
d f ( x )
f'(x dx ' Df(x). y'(x). y
D
35
, dy df
f (xo), dx (x o ), dx (xo),
Df(xo), y o' y'(xo)
j, f.
f(t o ), f.(t o )
(první) derivace (reálné) funkce f
(reálné) proměnné x v bodě Xo
(y je závisle proměnná)
(první) derivace (reálné) funkce f
v bodě Xo zprava
(první) derivace (reálné) funkce f
v bodě Xo zleva
(první) derivace (reálné) funkce
y = f( t) podle par metru t
(první) derivace (reálné) funkce
y = f(t) podle parametru t v bodě to
f (xo)' f'(x o +)
f (xo)' f'(x o - )
" df' d 2 f "dy' d 2 y
f , dx ' dx 2 ' Y , dx ' dx 2
druhá derivace (reálné) funkce f
(reálné) proměnné x
(y je závisle proměnná)
druhá derivace <reálné) funkce y = f(t)
podle parametru t
n-tá derivace <reálné) funkce f
(reálné) proměnné x
(y je závisle proměnná)
f, fu
d lf <"-l) d"£
f <,,) J
, dx ' dx'"
d y <"-l) d " y
(,,)
y, dx ' dx"
dx
dj;dy
,df(x), dy:c
lim f( x ) ,
.-G'
_ lim .f(x I' X2, ..., x,,)
:CI QI,.oot:Cn-Un
diferenciál argumentu x
diferenciál (reálné) funkce y = f(x)
diferenciál (reálné) funkce f v bodě x,
též diferenciál (reálné) funkce f
(reálné) proměnné x
(y je závisle proměnná)
hodnota (reálné) funkce f n (reálných)
pro ěnných v bodě x = (Xl' x 2 , ..., x..
též (reálná) funkce f n (reálných)
proměnných
limita (reálné) funkce f n (reálných)
proměnných pro Je -+ G, tj. pro
Xl -+ a l , x 2 -+ a2, ..., X.. -+ a.., přičemž
G = (a l , a 2 , ..., a..)
f(x), f(x I' X2, ..., x,,)
36
of f' f
-;--, JXk' JXk
uX"
parciální derivace (prvního řádu)
(reálné) funkce y = f(x) podle
proměnné x"
!-(a f Ja)
uX"
parciální derivace (reálné) funkce
y = f(x) podle proměnné x" v bodě
a = (a l' a 2, ..., a..)
e 2 f'
2 ' f; .\ k' fXkXk
uX"
parciální derivace druhého řádu (reálné)
funkce y = f(x) dvakrát podle
proměnné x"
02f 1''' I'
a ' J XiXj' J XiXj
X. uX'
I J
F
ff(X) dx
ff(X) dx
parciální derivace druhého řádu (reálné)
funkce y = f(x) nejprve podle
proměnné Xi a pak podle proměnné x j
[smíšená parciální derivace druhého
řádu]
totální [úplný] diferenciál (reálné)
funkce y = f(x)
totální [úplný] diferenciál n-tého řádu
(reálné) funkce y = f(x)
totální [úplný] diferenciál (reálné)
funkce y = f(x) v bodě a
totální [úplný] diferenciál n-tého řádu
(reálné) funkce y = f(x) v bodě a
primitivní funkce k (reálné) funkci f
neurčitý integrál (z) (reálné) funkce
y = f(x)
df (.
d"f
df(a)
d"f(a)
I x' resp. ly, resp. I z
určitý integrál (z) (reálné) funkce
y = f(x) od a do b
[na intervalu (a, b)]
[F(x)]: = F(b) - F(a)
statický moment vzhledem k ose x, resp. y
statický moment vzhledem k rovině xy,
resp. xz, resp. yz
moment setrvačnosti vzhledem k ose x,
resp. y, resp. z
[F(x)]:, F(x)l:
Sx, resp. Sy
SXY' resp. Sxz, resp. SyZ
37
Ip
D XY' resp. D xz' resp. D yz
f:(p dx + Q dy)c
f:(PdX + Qdy + R dz)c
f
f:(F dr)c
fI/(x, y) dS, fI/(x, y) dx dy
ffI/(x, y, z) d v,
ffI/(x, y, z) dx dy dz
ex:> co
L a", La", La"
,,=1 1
R"
moment setrvačnosti vzhledem k počátku
deviač í moment vzhledem k osám x a y,
resp. x a z, resp. y a z
křivkový integrál (reálných) funkcí
z = P(x, y) a z = Q(x, y) po oblouku
rovinné křivky C od A do B
křivkový integrál (reálných) funkcí
u = P( x, y, z), u = Q( x, y, z) a
u = R(x, y, z) po oblouku prostorové
křivky C od A do B ·
znak křivkového integrálu po uzavfené
křivce
křivkový integrál vektoru F po křivce C
ve vektorovém tvaru r = r(t) od A do B
dvojný [dvojrozměrný] integrál (
(reálné) funkce z = f(x, y) přes
rovinnou uzavřenou oblast a 2
trojný [trojrozměrný] integrál (z)
(reálné) funkce u = f(x, y, z) přes
prostorovou uzavřenou oblast a 3
nekonečná řada se členy ai (i = 1, 2, ...)
zbytek nekonečné řady po n-tém členu
0.1.11. Elementární funkce (x E R, ZE C)
sgnx
[x], E(x)
r
41
X',z"
38
signum [znaménko] reálného čísla x
celá,část (reálného) čísla x
obecná mocnina (reálného) -čísla x
s exponentem s (x > O, SE R)
obecná mocnina (komplexního) čísla z
s exponentem s (z E P, SEC)
n-tá mocnina (n E N)
'!Jx, X l / n
.
n-tá odmocnina (z) (reálného) čísla x
(x > O, neN); ;jx = Jx
n-tá odmocnina (z) (komplexního)
čísla z (z e P, n e N)
(obecná) exponenciální funkce
proměnné x se základem a (a > O)
(obecná) exponenciální funkce
proměnné z se základem a (a * O)
přirozená exponenciální funkce
(tj. se základem e)
(obecná) logaritmická funkce
proměnné x se základem a
(x > O, a > O, a * 1), logaritmus
(reálného) čísla x (x> O) se základem a
(a > O, a * 1)
logaritmická funkce proměnné x
se základem 10 (x > O),
desítkový [dekadický, Briggsův]
logaritmus (reálného) čí la x (x > O)
přirozená logaritmická funkce proměnné x
(x > O), přirozený logaritmus (reálného)
čísla x (x > O) (tj. se základem e)
'!Jz, Zl/"
té, eXPa x
tf, eXPa z
eX, exp x, e Z , exp z
log" x
19 x, log x
ln x
ln z
(přirozená) logaritmická funkce
. proměnné z (z e P), přirozený logaritmus
(komplexního) čísla z (z * O)
. .
sIn us x, sIn us =
kosinus x, kosinus z
tangens x [x * (k + t) 1t, k e Z],
tangens z
kotangens x (x * k1t, k e Z kotangens z
sekans x [x * (k + t) 1t, k e Z]
kosekans x (x * k1t, k e Z)
arkussinus x (x e < -1, 1»), arkussinus z
arkuskosinus x (x e ( -1, 1)
arkuskosinus z
arkustangens x, arkustangens z
arkuskotangens x, arkuskotangens z
. .
sIn x, sIn z
cos x, cos z
tg x, tg z
cotg x, cotg z
sec x
cosec x
arcsin x, arcsin z
arccos x, arccos z
arctg x, arctg z
arccotg x, arccotg z
39
sinh x, sinh z
hyperbolický sinus x, hyperbolický
sInus z
hyperbolický kosinus x, hyperbolický
kosinus z
hyperbolický tangens x, hyperbolický
tangens z
hyperbolický kotangens x (x =t= O),
hyperbolický kotangens z
argument hyperbolického sinu x,
argument hyperbolického sinu z
argument hyperbolického kosinu x
[x E (1, + 00 )], argument
hyperbolického kosinu z
argument hyperbolického tangens x
[x E ( 1, 1)], argument hyperbolického
tangens z
argument hyperbolického kotangens x
[x E ( - 00, -1) u (1, + 00 )], argument
hyper olického kotangens z
cosh x, cosh z
tgh x, tgh z
cotgh x, cotgh z
argsinh x, argsinh z
argcosh x, argcosh z
argtgh x, argtgh z
argcotgh x, argcotgh z
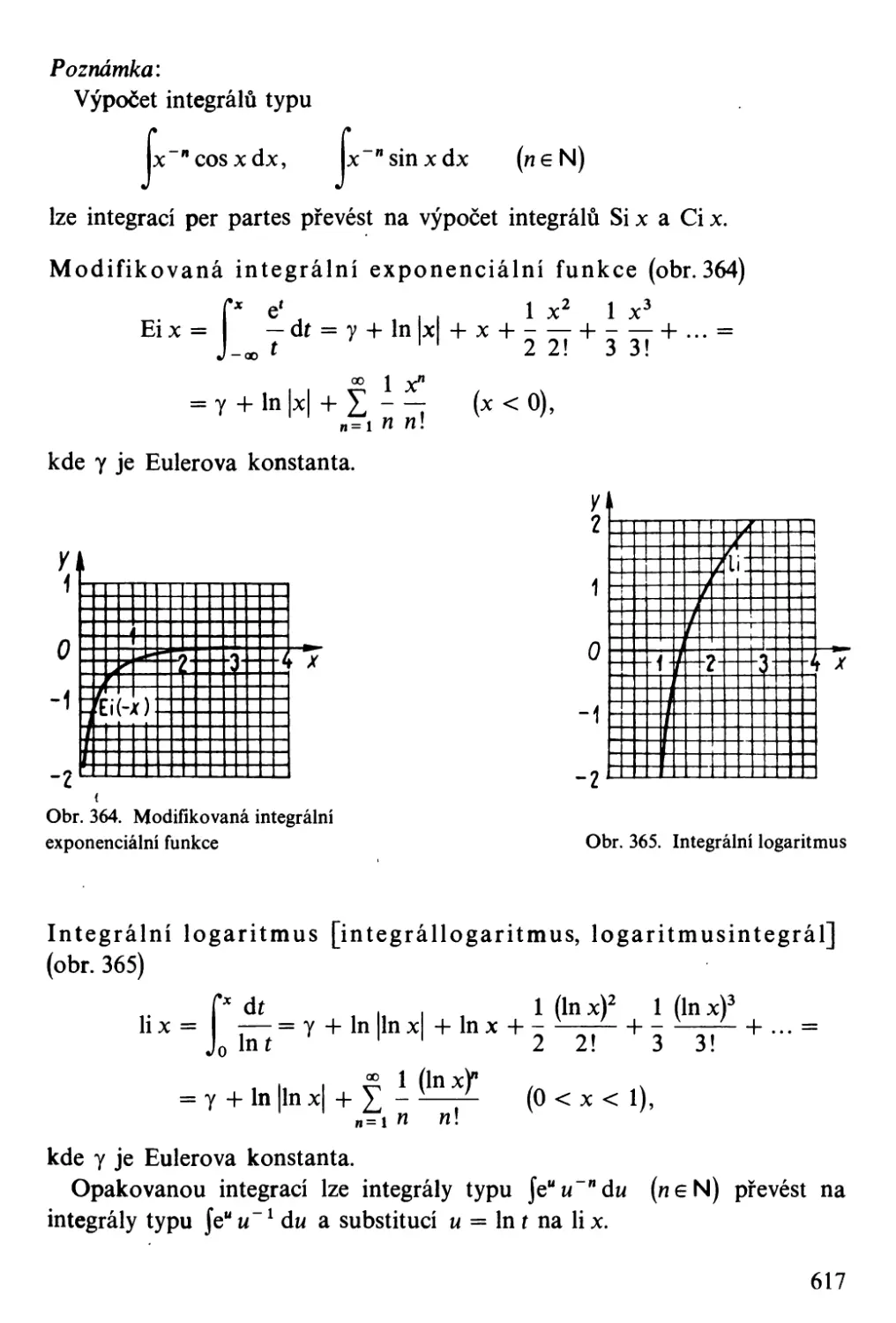
0.1.12. Speciální funkce
r(x)
B(p, q)
J p( x)
Yp(x)
Np(x)
Ep(x)
H l)(X), H 2)(X)
Eix
funkce gama
funkce beta
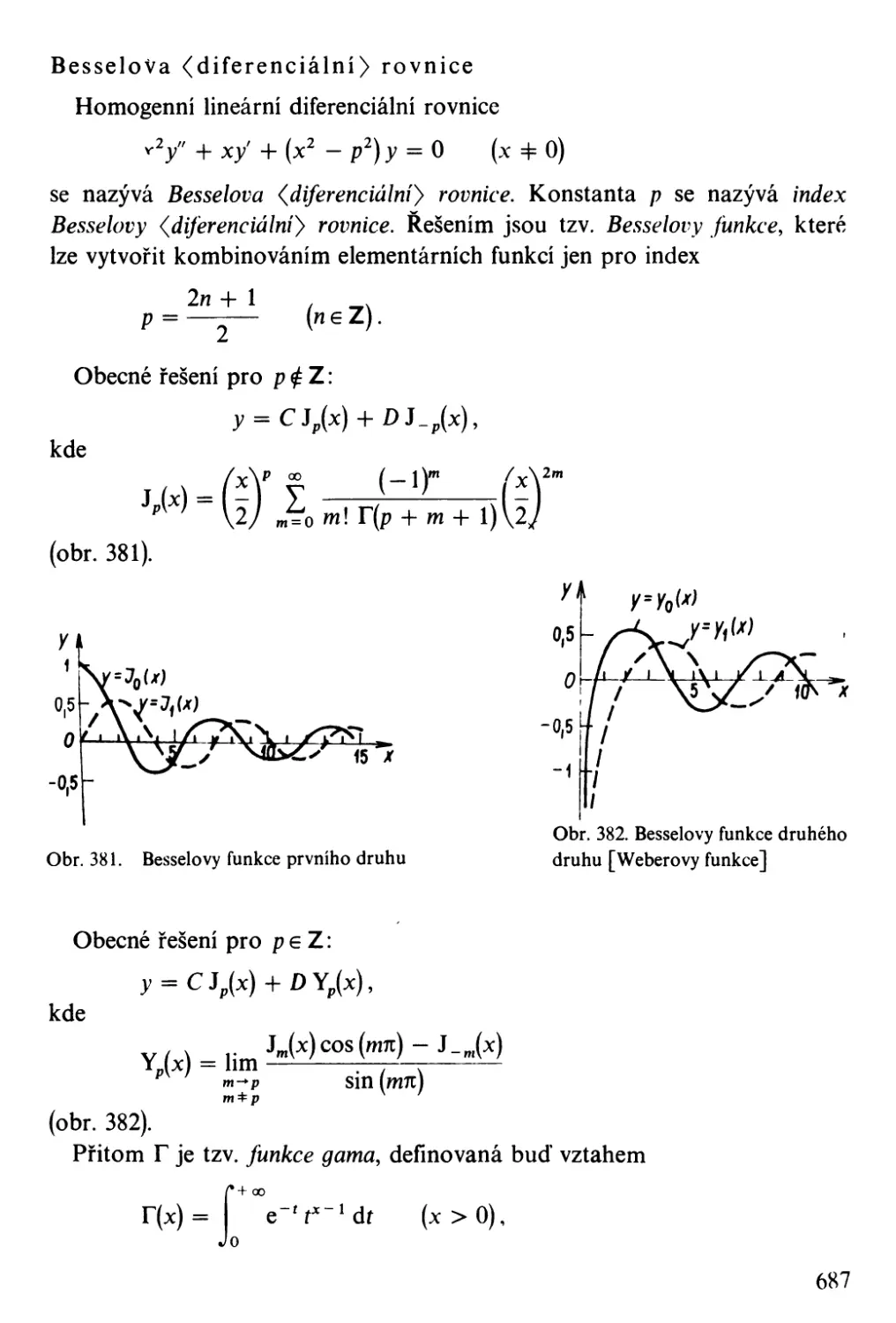
Besselovy funkce [cylindrické funkce]
prvního druhu
Besselovy funkce [cylindrické funkce]
druhého druhu
Neumannovy funkce
,Weberovy funkce
Besselovy funkce [cylindrické funkce]
třetího druhu [Hankelovy funkce
prvního a druhého druhu]
integrální sinus [integrálsinus,
sinusintegrál]
integrální kosinus [integrálkosinus,
kosinusintegrál]
modifikovaná integrální exponenciální
funkce
Si x
Ci x
40
1ix
integrální logaritmus
[integrállogaritmus,logaritmusintegrál]
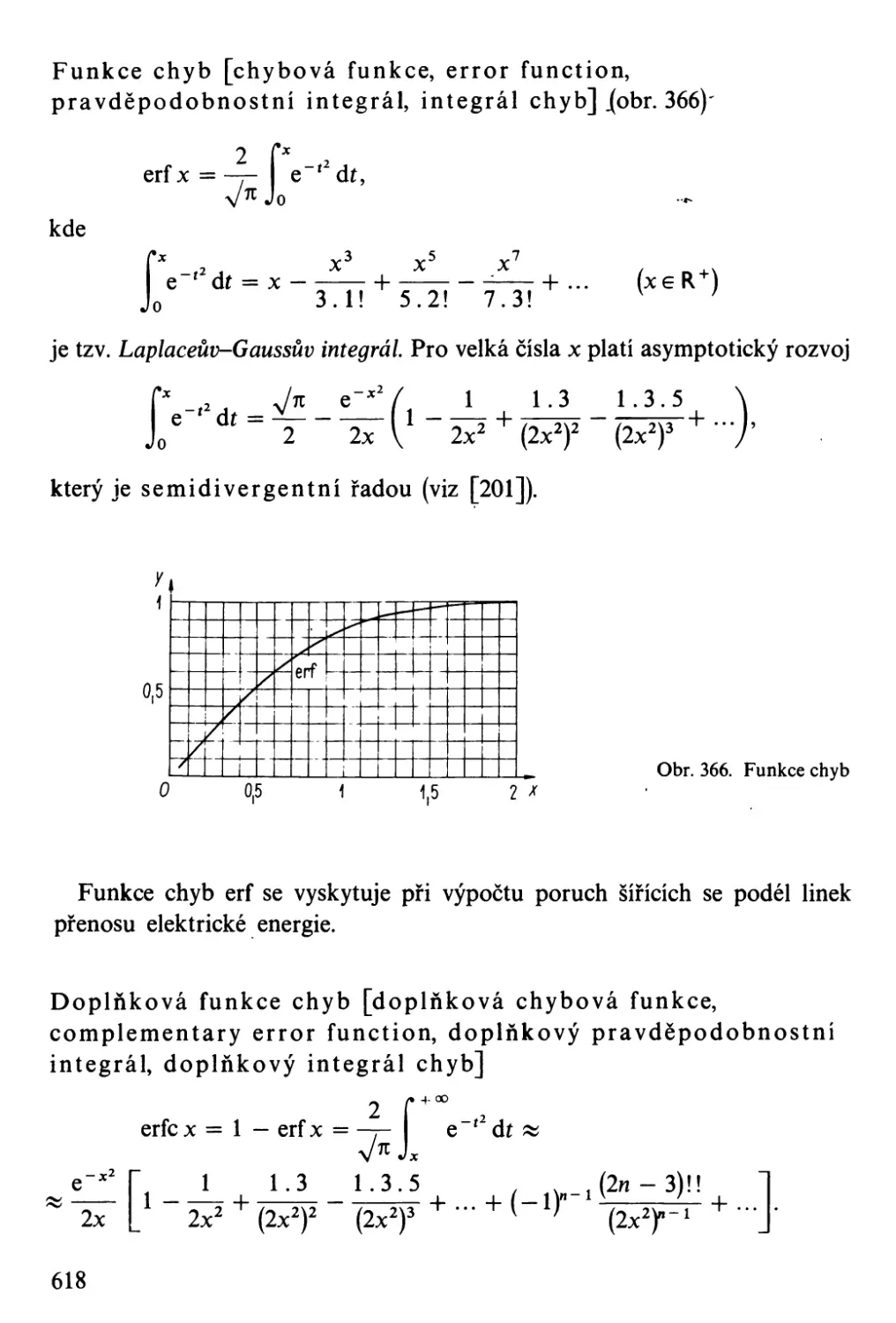
funkce chyb [chybová funkce
error function]
doplněk funkce chyb [error function
complement]
Gaussův pravděpodobnostní integrál
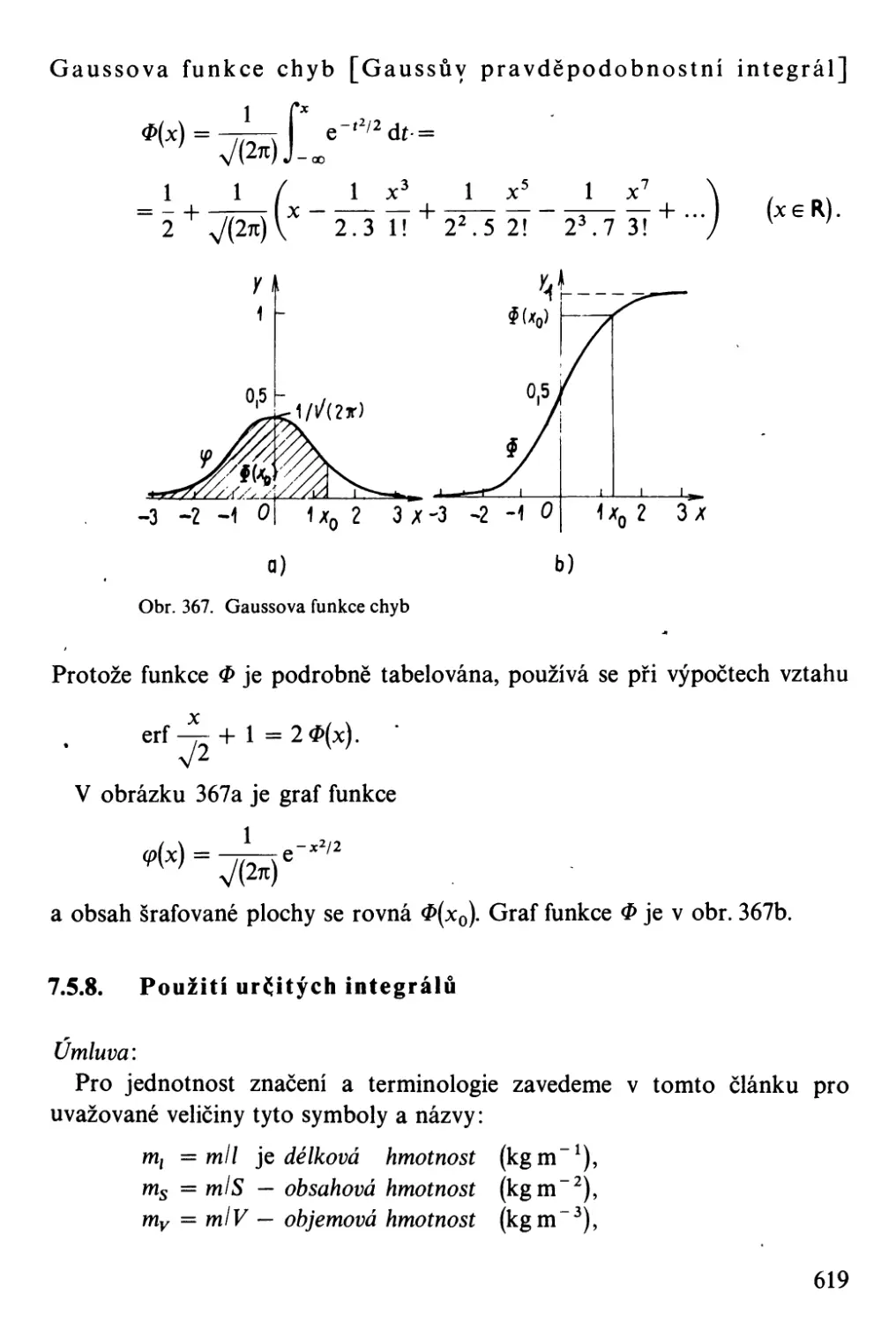
[Gaussova funkce chyb]
neúplný eliptický integrál prvního druhu
neúplný eliptický integrál druhého druhu
úplný eliptický integrál prvního druhu
úplný eliptický integrál druhého druhu ,
erf x
erfc x
cP( x) .
F(k, qJ)
E(k, qJ)
K, F(k,1t/2)
E, E(k,1t/2)
0.1.13. Diferenciální geometrie
,
r = r( t)
T
r(t) = (x(t), y(t), z(t)); vektor skalárního
argumentu t
délka úseku tečny [tangenta] rovinné
křivky
délka úseku normály [normála] rovinné
křivky
subtangenta rovinné křivky
subnormála rovinné křivky
délka úseku polární tečny rovinné křivky
délka úseku polární normály rovinné
křivky
polární subtangenta rovinné křivky
polární subnormála rovinné křivky
poloměr <první) křivosti rovinné křivky
<první) křivost [flexe] rovinné křivky
poloměr druhé křivosti [poloměr torze]
druhá křivost [torze, kroucenost]
Kroneckerův symbol
[Kroneckerovo delta]
N
ST
SN
t
n
St
Sn
R,R l
X, Xl
R 2
X 2
b ik
41
0.1.14. Laplaceova transformace
F(P) = 2{f(t)} = Yj:
j'(t) F(p), f(t) F(p)
!e _ 1 {F(p)} = !e - 1 F(p) = f(t),
F(p) f(t), F(p) .r(t)
fl (t) * fz(t)
funkce F je Laplaceovým obrazem
funkce f; Laplaceova transformace
funkce f proměnné t
inverzní Laplaceova transformace
funkce F proměnné p
konvoluce funkcí ft, fz
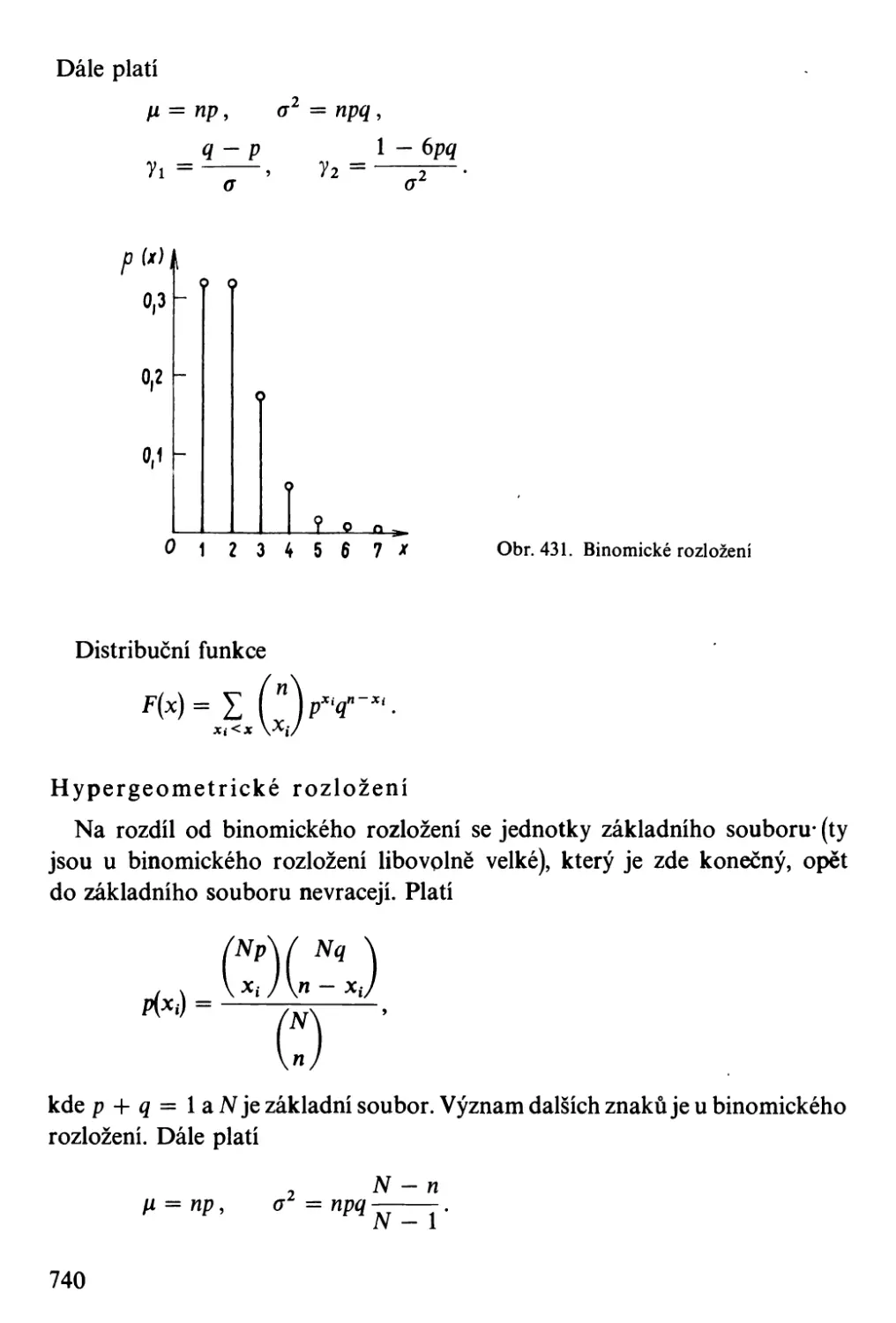
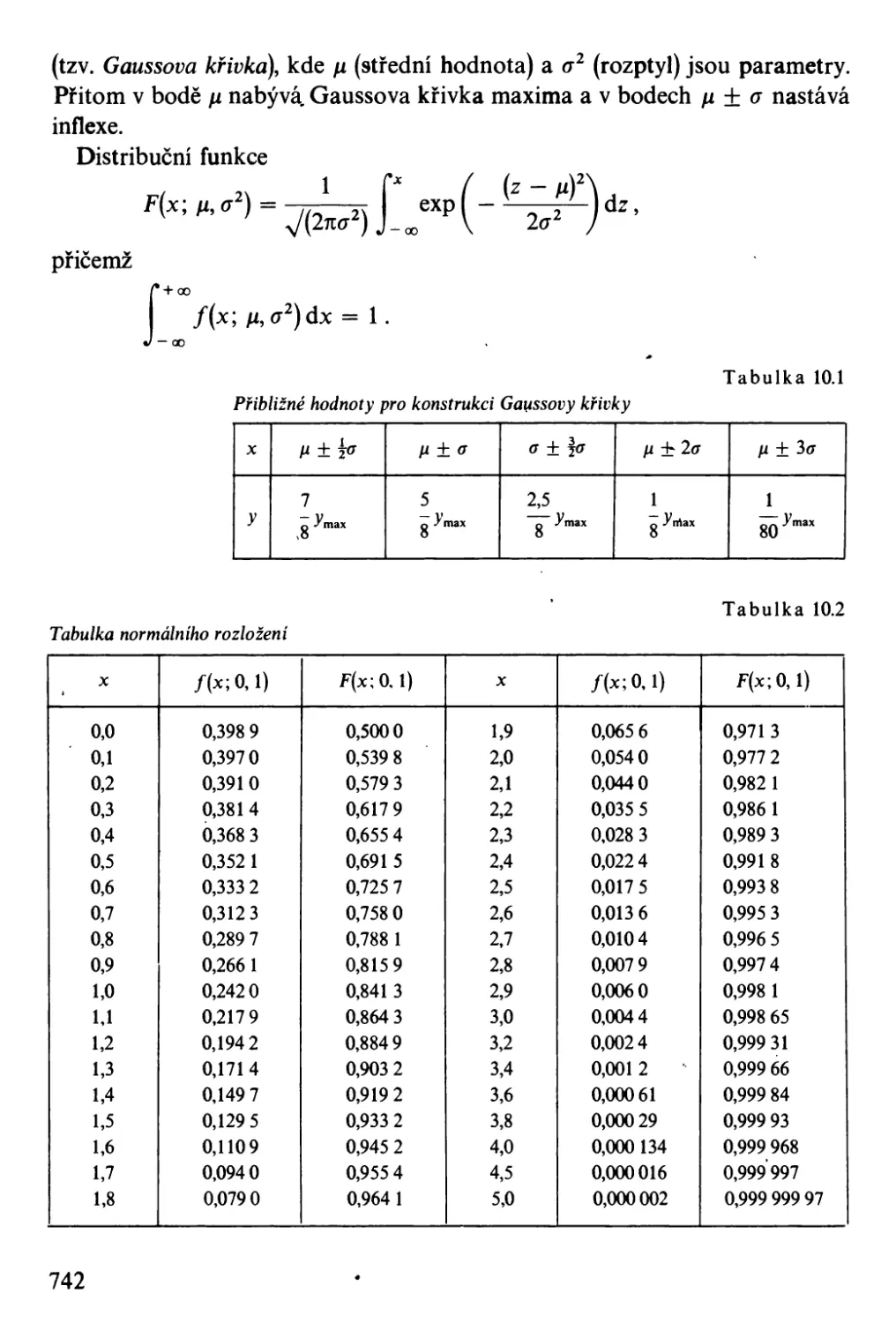
0.1.15. Počet pravděpodobnosti, matematická statistika
a teorie chyb
El,Ez,...
0, V
U
E
P(E)
P( E z/ E 1 )
P n( ml' m z , . . ., m n )
.
'Pn(m)
, X
F(x), P( < x)
p(x)
f(x)
m( - xr
m( - cr
m( )
42
náhodné jevy
nemožný náhodný jev
jistý náhodný jev
opačný náhodný jev k náhodnému jevu E
pravděpodobnost náhodného jevu E
podmíněná pravděpodobnost náhodného
jevu Ez za podmínky, že nastal
náhodný Jev E 1
pravděpodobnost, že při n pokusech
náhodný jev E i nastal mi-krát
k
(i = 1, 2, ..., k); j mj = n);
multinomické rozložení
binomické rozložení
náhodné veličiny
'distribuční funkce náhodné veličiny
hustota pravděpodobnosti diskrétní
náhodné veličiny
hustota pravděpodobnosti spojité
náhodné veličiny
moment k-tého řádu pro diskrétní
náhodnou veličinu
moment k-tého řádu pro spojitou
náhodnou veličinu '
počáteční moment pro spojitou náhodnou
veličinu
'.
m( - Jlf
centrální moment pro spojitou náhodnou
veličinu
střední hodnota [očekávaná hodnota]
náhodné veličiny
rozptyl náhodné veličiny
směrodatná odchylka, střední kvadratická
odchylka
variační koeficient
šikmost
špičatost [exces]
obecné normální rozložení s parametry
Jl:u 2
<Gaussova> hustota pravděpodobnosti
rozložení N(Jl, ( 2 )
<Gaussova> distribuční funkce rozložení
N(Jl, ( 2 )
normované normální rozložení
s parametry Jl = O, u 2 = 1
<Gaussova> hustota pravděpodobnosti
rozložení N(O, 1)
<Gaussova> distribuční funkce rozložení
N(O, 1)
výběrový průměr
výběrový rozptyl
výběrová směrodatná odchylka
empirický rozptyl
empirická směrodatná odchylka
< empirický> aritmetický průměr
< empirický> vážený aritmetický průměr
< empirický> geometrický průměr
< empirický> vážený geometrický průměr
průměrné tempo
<empirický> kvadratický průměr
< empirický> vážený kvadratický průměr
< empirický > armonický prů ěr
<empirický> vážený harmonický průměr
<empirický> medján
Jl, E
(J2, D
(J
V
Yl
Y2
N(Jl, ( 2 )
f(x; Jl, ( 2 )
( X - Jl. )
F(x; f1, (1:), f/> (1
N(O, 1)
-
f(x; O, 1), qJ(x) "
F(x; O, 1), (/)(x)
X
S2
S
S2
S
X
x'
x G
-,
.x G
W
x K
-,
x K
x H
-,
x H
X
43
A
X
R
d
v-
x
Sxy, cov (X, y)
r xy
[a]
[ab]
X
X.
I
Gi
X
tJ
x
V.
I
m
m-
x
0.1.16. Regulační technika
Xv( t)
Xe(t)
K(t)
a( t)
h(t)
G(iw)
tJ( t)
j'( iw )
g(t)
G(p)
44
< empirický> .mod us
< empirické> rozpětí
< empirická> střední odchylka
výběrový variační koeficient
výběrová kovariance dvojice náhodných
veličin x, y
<empirický> korelační koeficient dvojice
náhodných veličin x, y
n
L a i ; Gaussův sumační symbol
i = 1
alb l + a 2 b 2 + ... + anb n
skutečná hodnota měřené veličiny
naměřená hodnota měřené veličiny
<nevyhnutelná> skutečná chyba měřené
veličiny
absolutní chyba měřené veličiny
relativní chyba měřené veličiny
zdánlivá <střední> hodnota měřené
veličiny
zdánlivá [domnělá] chyba [oprava
střední chyba jednotlivé hodnoty
[míra rozptýlení]
střední chyba aritmetického průměru
vstupní veličina
výstupní veličina
přenosová funkce
jednotková skoková funkce
přechodová funkce
komplexní frekvenční přenos,
frekvenční charakter'istika
impulsová funkce, Diraco:va funkce delta
spektrum impulsu delta
impulsová přechodová funkce
přenosová: funkce
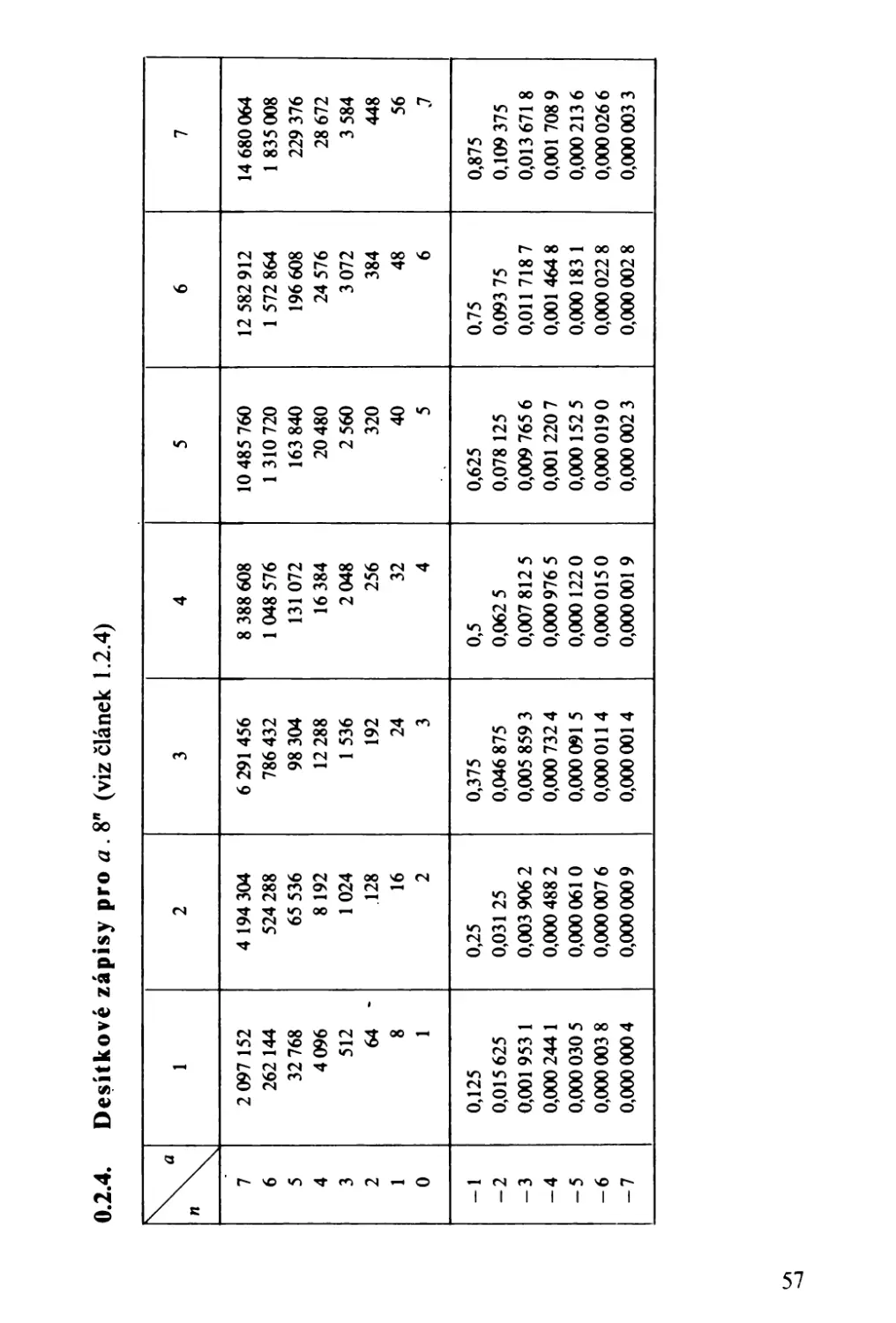
0.2.
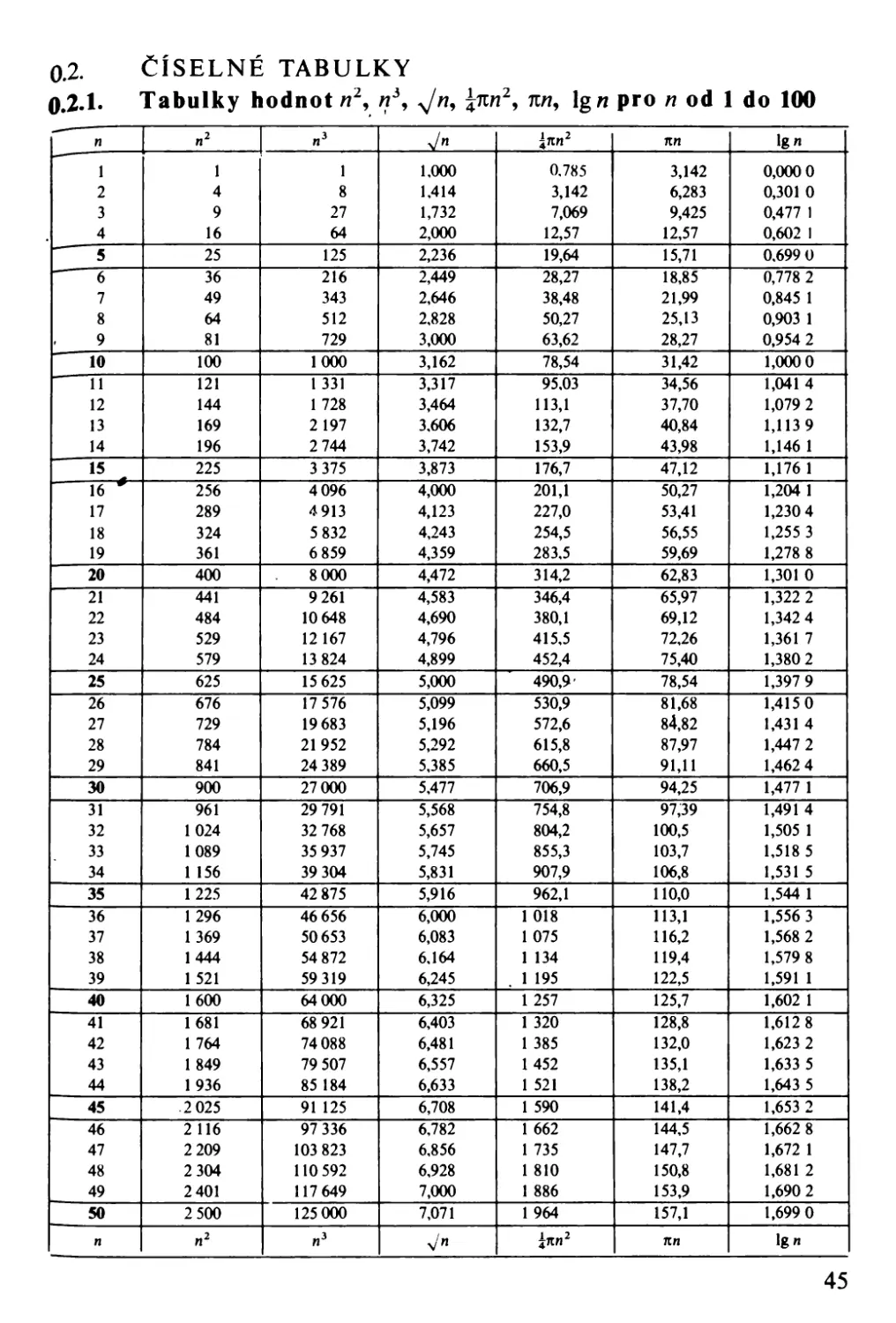
0.2.1.
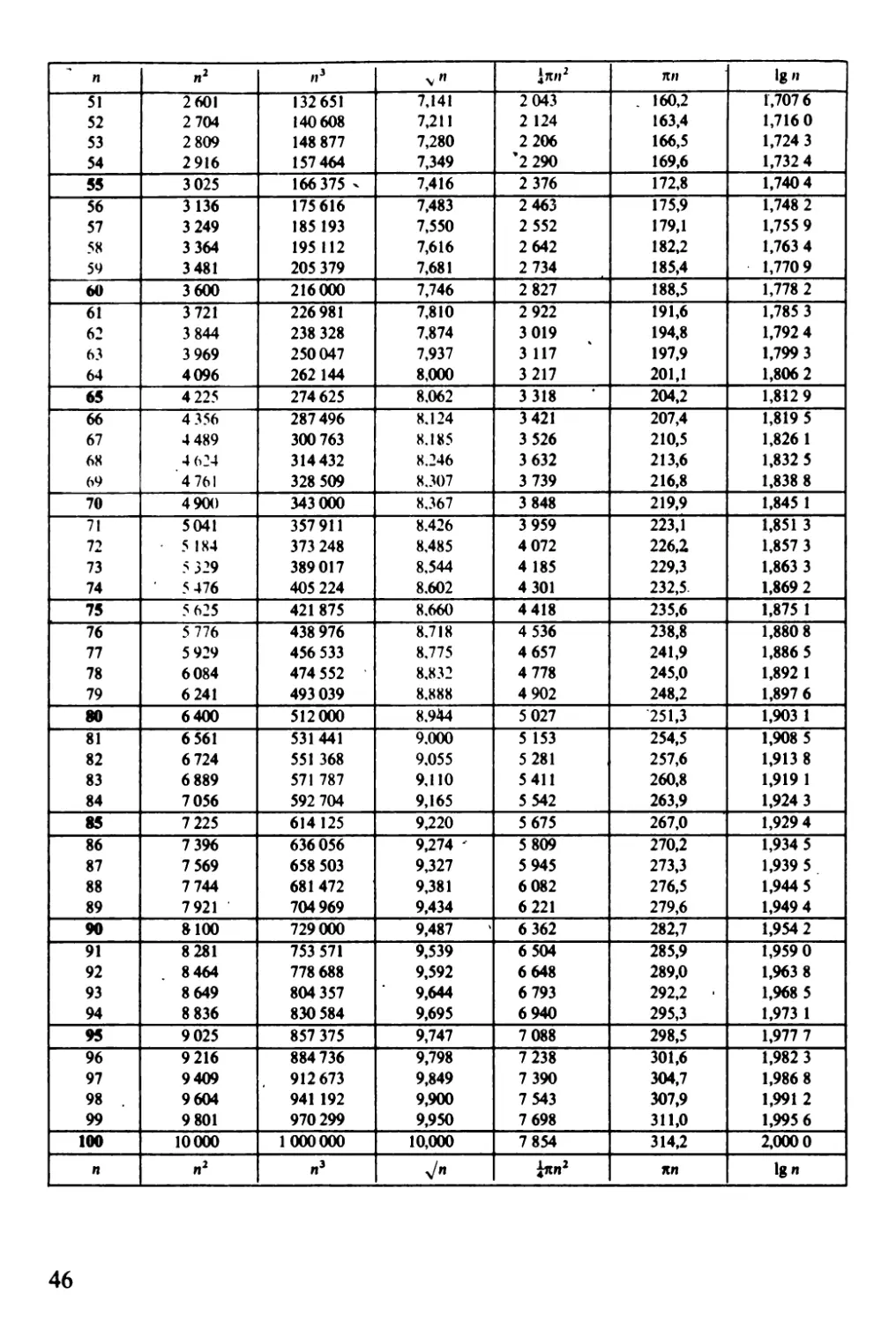
ČíSELNÉ TABULKY
2 .3 / 1 2
Tabulky hodnot n " '! , vn, ;{1tn , 1tn, 19 n pro n od 1 do 100
- n 2 n 3 Jn i1tn 2 19 n
n 1tn
-
1 1 1 1.000 O.7 5 3,142 0,000 o
2 4 8 1.414 3,142 6,283 0,301 o
3 9 27 1,732 7 J)69 9,425 0,4 77 1
4 16 64 2,000 12,57 12,57 0,602 1
- 5 25 125 2,236 19,64 15,71 0.699 o
6 36 216 2,449 28,27 18,85 0,778 2
7 49 343 2,646 38,48 21,99 0,845 1
8 64 512 2.828 50,27 25,13 0,903 1
, 9 81 729 3,000 63,62 28,27 0,954 2
10 100 1000 3,162 78,54 31,42 1,000 o
11 121 1 331 3,317 95.03 34,56 1,041 4
12 144 1 728 3,464 113,1 37,70 1,079 2
13 169 2 197 3.606 132,7 40,84 1,113 9
14 196 2744 3,742 153,9 43,98 1 , 146 1
15 225 3375 3,873 176,7 47,12 1,176 1
-
16 - 256 4096 4,000 201,1 50,27 1,204 1
17 289 4- 913 4,123 227,0 53,41 1,230 4
18 324 5832 4,243 254,5 56,55 1,255 3
19 361 6859 4,359 283.5 59,69 1,278 8
20 400 8000 4,472 314,2 62,83 1,301 o
21 441 9261 4,583 346,4 65,97 1,322 2
22 484 10648 4,690 380,1 69,12 1,342 4
23 529 12 167 4,796 415.5 72,26 1,361 7
24 579 13 824 4,899 452,4 75,40 1,3802
25 625 15 625 5,000 490,9 . 78,54 1,397 9
26 676 17 576 5,099 530,9 81,68 1,415 o
27 729 19 683 5,196 572,6 84,82 1,431 4
28 784 21 952 5,292 615,8 87,97 1,447 2
29 841 24 389 5.385 660,5 91,11 1,462 4
30 900 27 000 5.477 706,9 94,25 1,477 1
31 961 29791 5,568 754,8 97;39 1,491 4
32 1024 32 768 5,657 804,2 100,5 1,505 1
33 1089 35937 5,745 855,3 103,7 1,518 5
34 1 156 39 304 5,831 907,9 106,8 1,531 5
35 1225 42875 5,916 962,1 110,0 1,544 1
36 1 296 46 656 6,000 1 018 113,1 1,556 3
37 1 369 50 653 6,083 1 075 116,2 1,568 2
38 1444 54872 6.164 1 134 119,4 1,579 8
39 1 521 59 319 6,245 1 195 122,5 1,591 1
40 1600 64 000 6,325 1 257 125,7 1,602 1
41 1 681 68921 6,403 1 320 128,8 1,612 8
42 1 764 74088 6,481 1 385 132,0 1,623 2
43 1 849 79 507 6,557 1 452 135,1 1,633 5
44 1 936 85 184 6,633 1 521 138,2 1,643 5
45 .2025 91 125 6,708 1 590 141,4 1,653 2
46 2 116 97 336 6.782 1 662 144.5 1,662 8
47 2209 103 823 6.856 1 735 147,7 1,672 1
48 2304 110592 6.928 1 810 150,8 1,681 2
49 2401 117 649 7,000 1 886 153,9 1,690 2
50 2500 125 000 7,071 1 964 157,1 1 ,699 O
n n 2 n 3 ,jn 1 1tn2 1tn 19 n
45
n 2 '1 3 i7t1l 2 19 II
n "n 7t1l
51 2601 132 651 7.141 2043 _ 160.2 r,707 6
52 2704 140 608 7.211 2 124 163,4 1,716 O
53 2809 148877 7,280 2206 166,5 1,724 3
54 2916 157 464 7,349 "2290 169,6 1,7324
55 3025 166 375 " 7,416 2376 172,8 1,740 4
56 3 136 175616 7,483 2463 175,9 1,748 2
57 3249 185 193 7,550 2552 179,1 1,755 9
5 3364 195 112 7,616 2642 182,2 1,763 4
5Y 3481 205 379 7,681 2734 185,4 1,770 9
60 3600 216000 7,746 2827 188,5 1,778 2
61 3721 226 981 7.810 2922 191,6 1,785 3
6:! 3844 238 328 7.874 3019 194,8 1,7924
.
63 3969 250 047 7,937 3 117 197,9 1,799 3
64 4096 262 144 8.000 3217 201 , 1 1,806 2
65 4225 274625 8.062 3318 204,2 1,8129
66 4356 287496 K.124 3421 207,4 1,819 5
67 489 300 763 K.I t(5 3526 210,5 1,826 I
68 6 -t 314 432 K.246 3632 213,6 1,832 5
6Y 4761 328 509 8.307 3739 216,8 1,838 8
70 4900 343 000 8.367 3848 219,9 1,845 1
71 5041 357911 M.426 3959 223,1 1,851 3
72 5 18 373 248 8.485 4072 226,2. 1,857 3
73 :' 329 389 017 8.544 4 185 229,3 1,863 3
74 5 -t 76 405 224 8.602 4301 232,5. 1,869 2
75 5625 421 875 8.660 4418 235,6 1,875 1
76 5776 438 976 8.718 4536 238,8 1 ,880 8
77 5 9:!9 456533 8.775 4657 241,9 1 ,886 5
78 6084 474 552 8.83:! 4778 245,0 1,892 I
79 6241 493 039 8.888 4902 248,2 1,897 6
80 6400 512000 8.944 5027 '251,3 1,903 1
81 6561 531 441 9.000 5 153 254,5 1,908 5
82 6724 551 368 9.055 5281 257,6 1,913 8
83 6889 571 787 9.110 5411 260,8 1,919 1
84 7056 592 704 9,165 5542 263,9 1,924 3
SS 7225 614 125 9,220 5675 267,0 1,9294
86 7396 636 056 9,274 .. 5809 270,2 1,934 5
87 7569 658 503 9,327 5945 273,3 1,939 5 .
88 7744 681 472 9,381 6082 276,5 1,944 5
89 7921 ' 704 969 9,434 6221 279,6 1,9494
90 8100 729 000 9,487 , 6362 282,7 1,954 2
91 8281 753 571 9,539 6504 285,9 1,959 O
92 8464 778 688 9,592 6648 289,0 1,963 8
93 8649 804 357 9,644 6793 292,2 1,968 5
94 8836 830 584 9,695 6940 295,3 1,973 I
9S 9025 857 375 9,747 7088 298,5 1,977 7
96 9216 884736 9,798 7238 301,6 1,982 3
97 9409 912673 9,849 7390 304,7 1,986 8
98 9604 941 192 9,900 7543 307,9 1,991 2
99 9801 970 299 9,950 7698 311,0 1,995 6
100 10000 1 000 000 10,000 7854 314,2 2,000 O
n n 2 n 3 .Jn inn 2 Kn 19 n
46
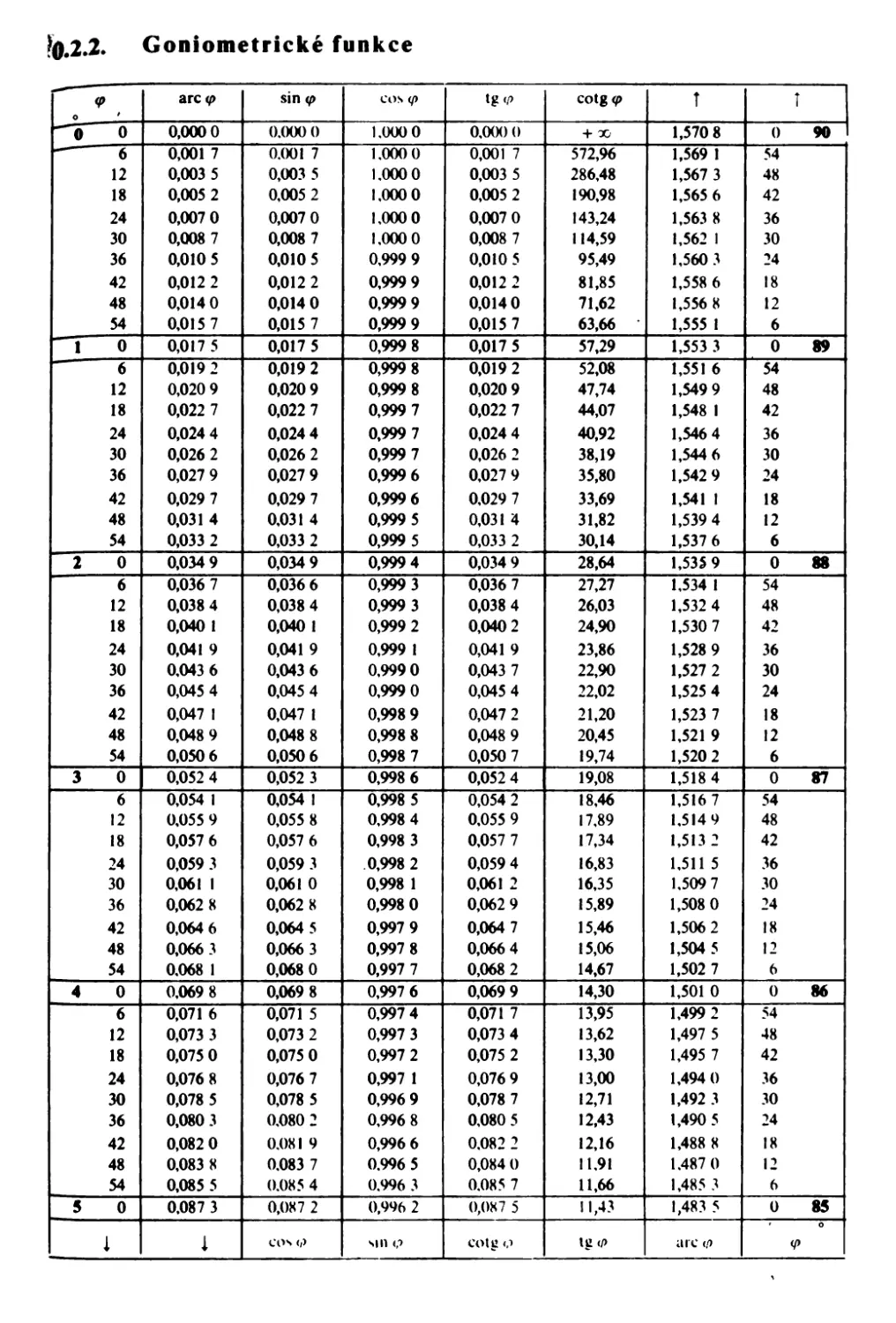
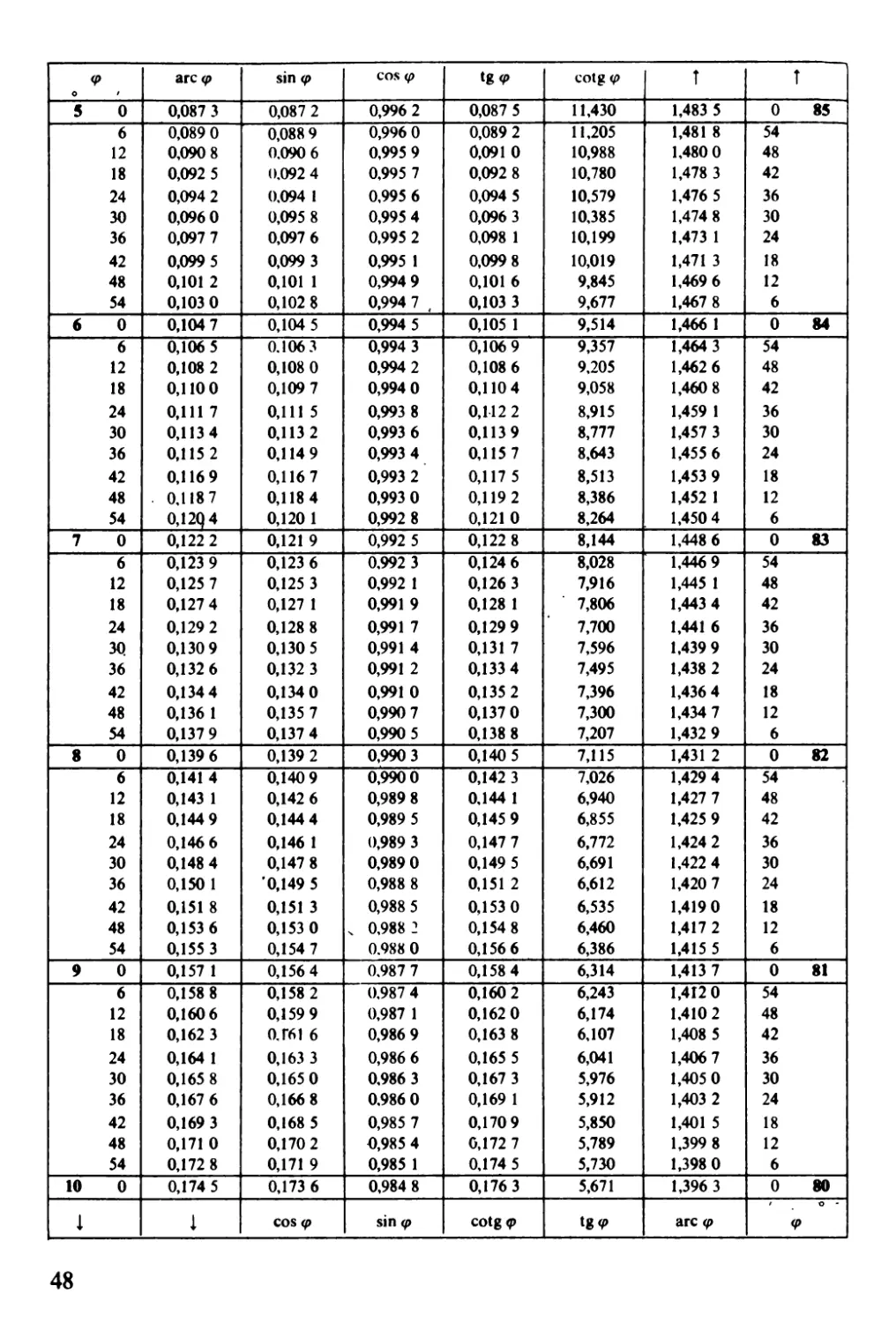
O.2.2.
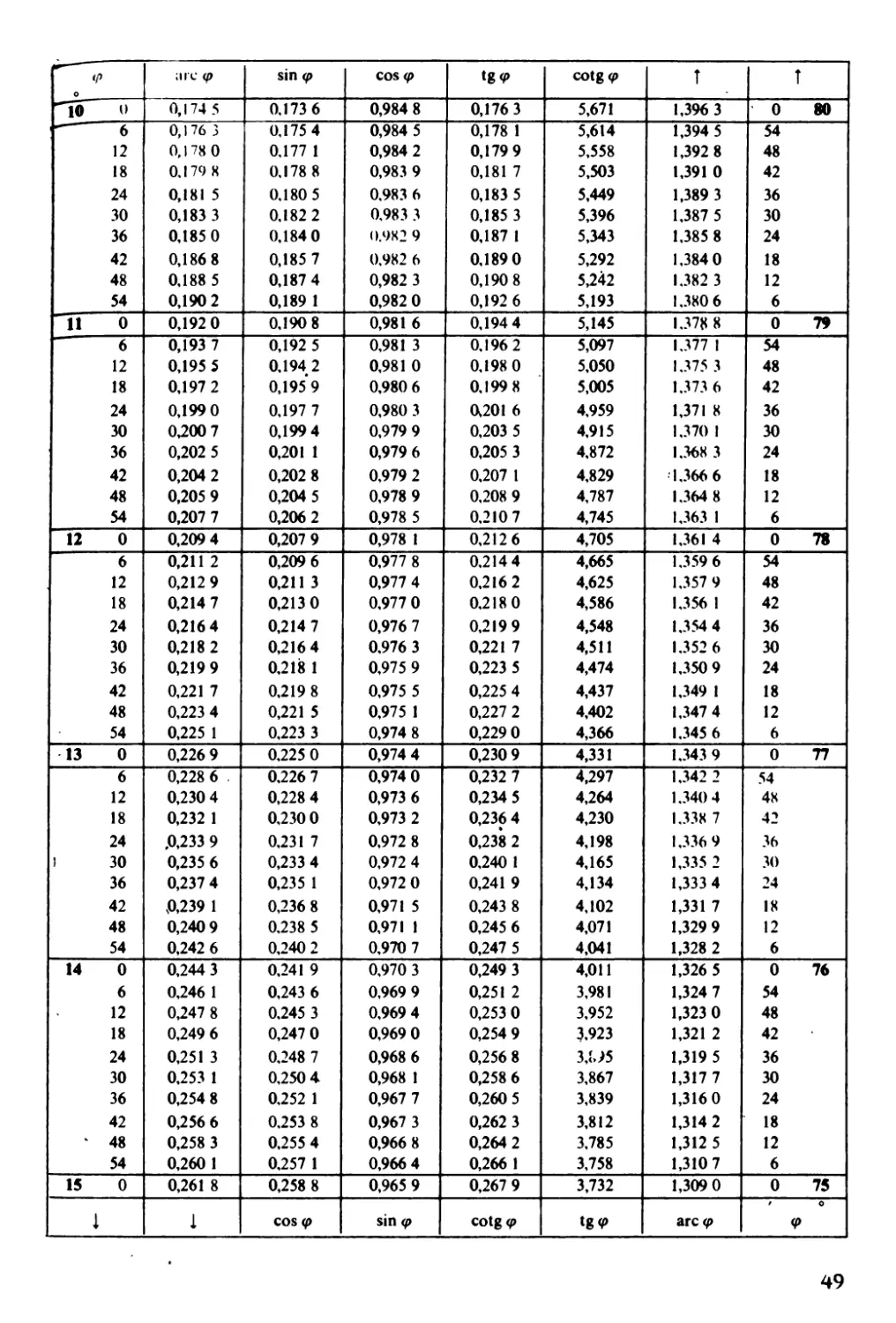
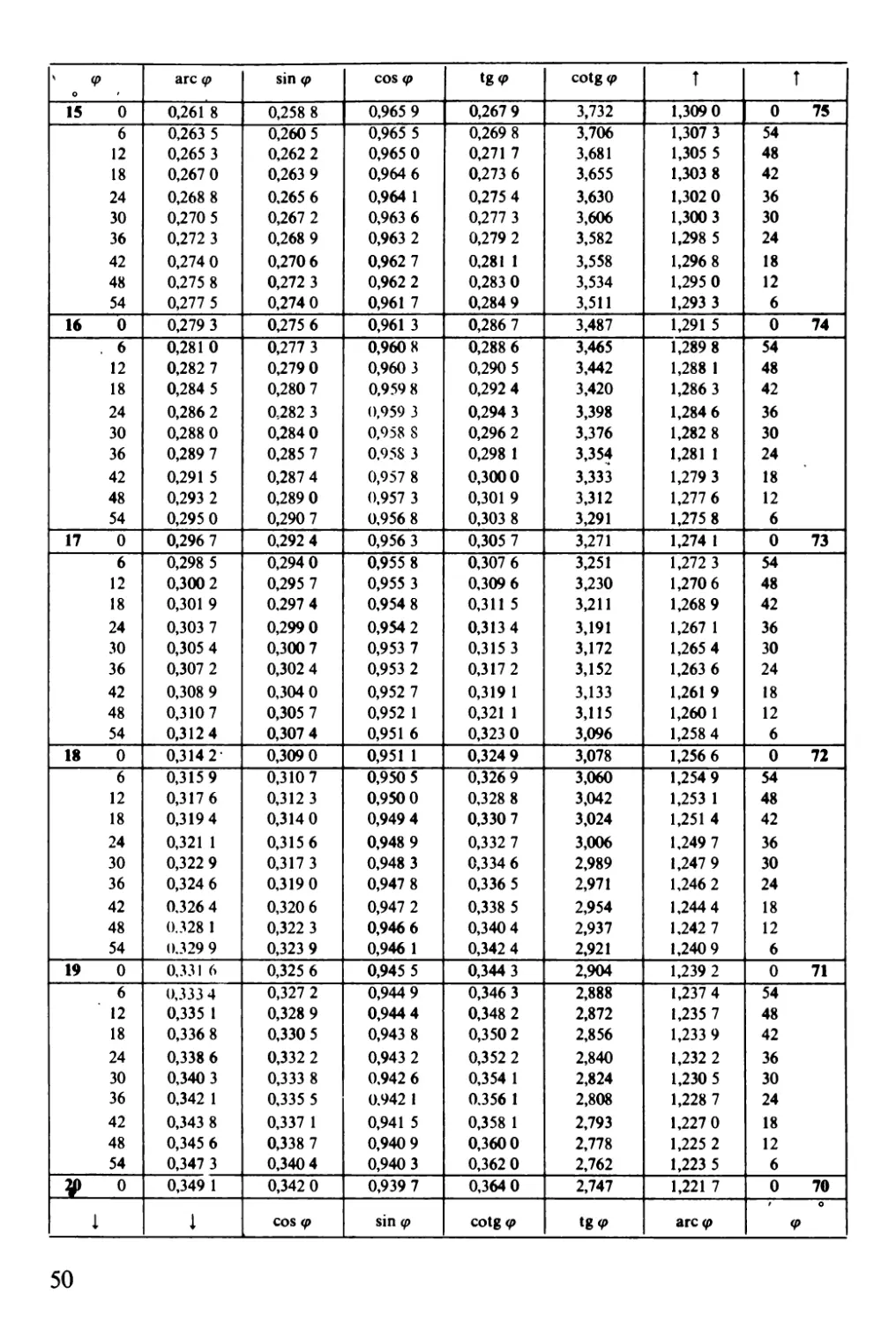
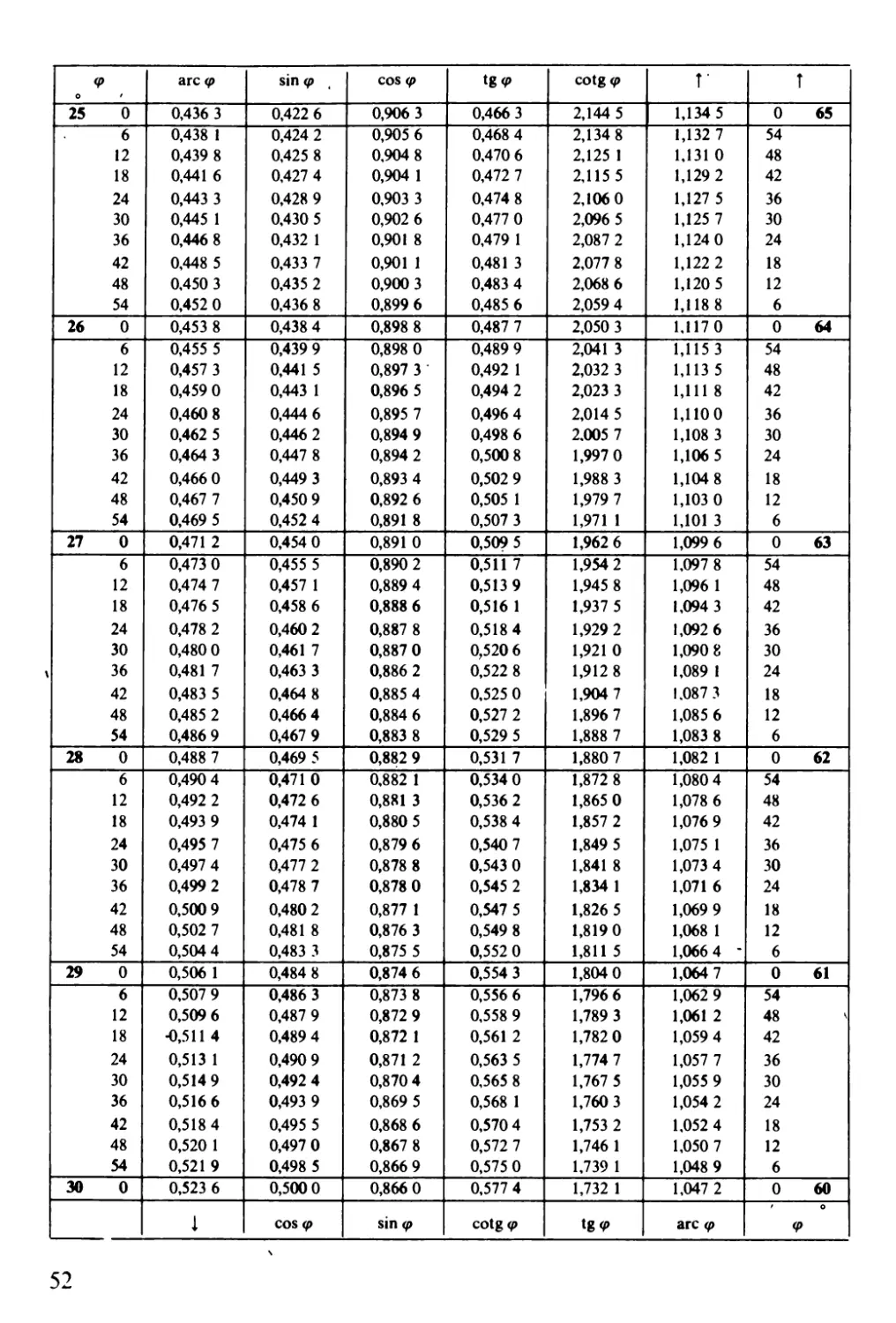
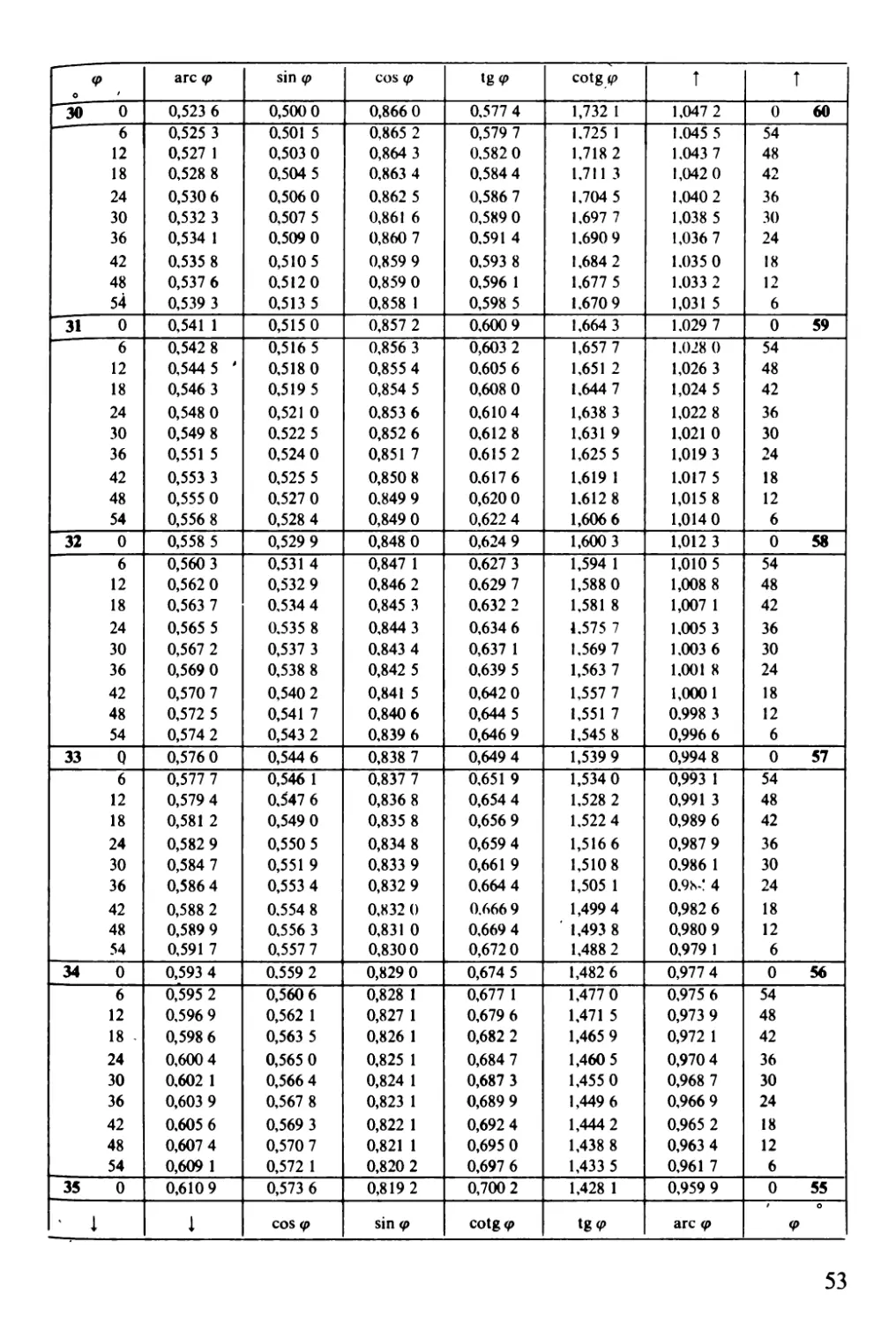
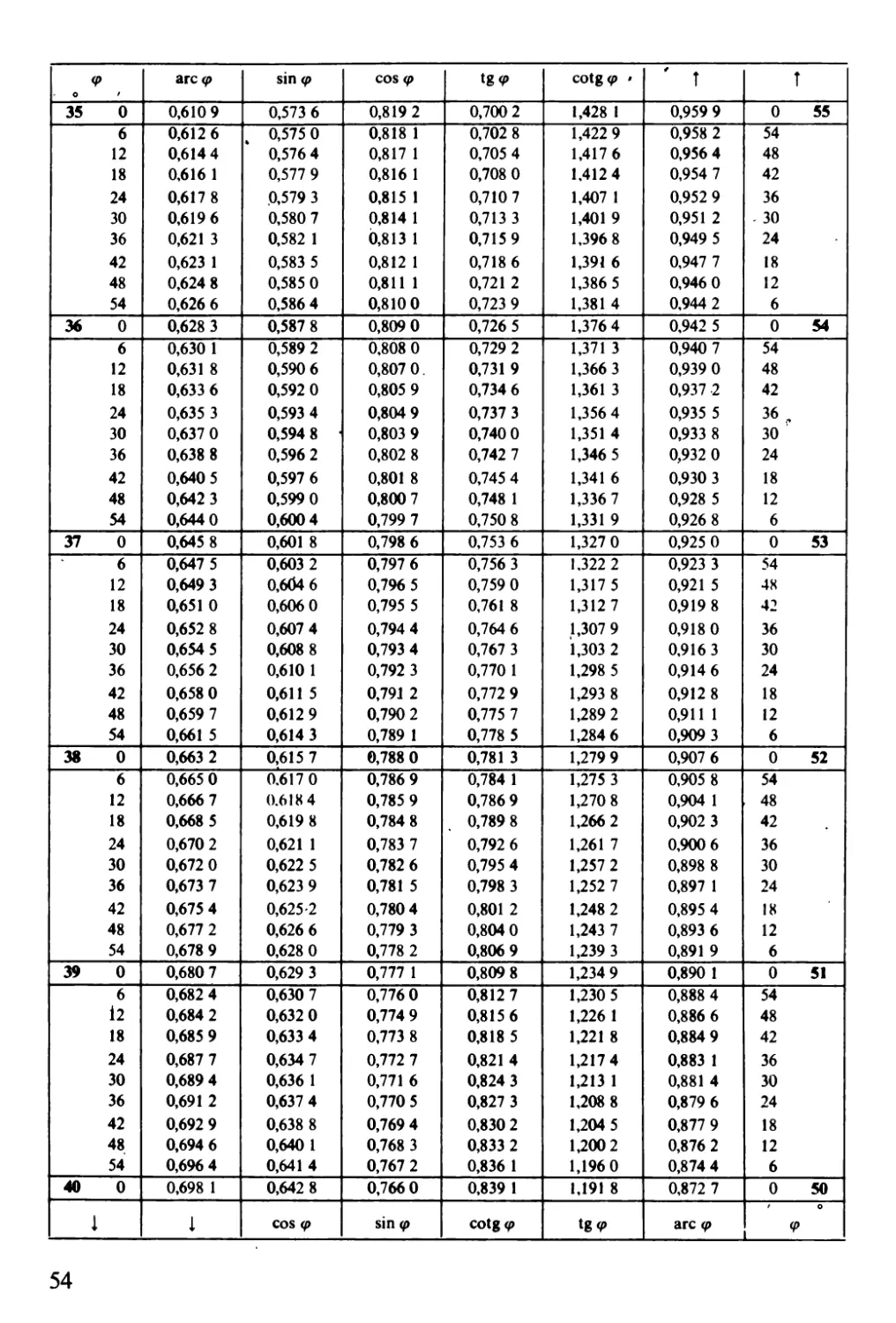
Goniometrické funkce
- - si n qJ f
qJ are qJ \,;',) <f' tg (t> cotg li' i
o ,
-. ° 0,000 O (). noo n 1.000 O O.O()O () +XJ 1,570 8 () 90
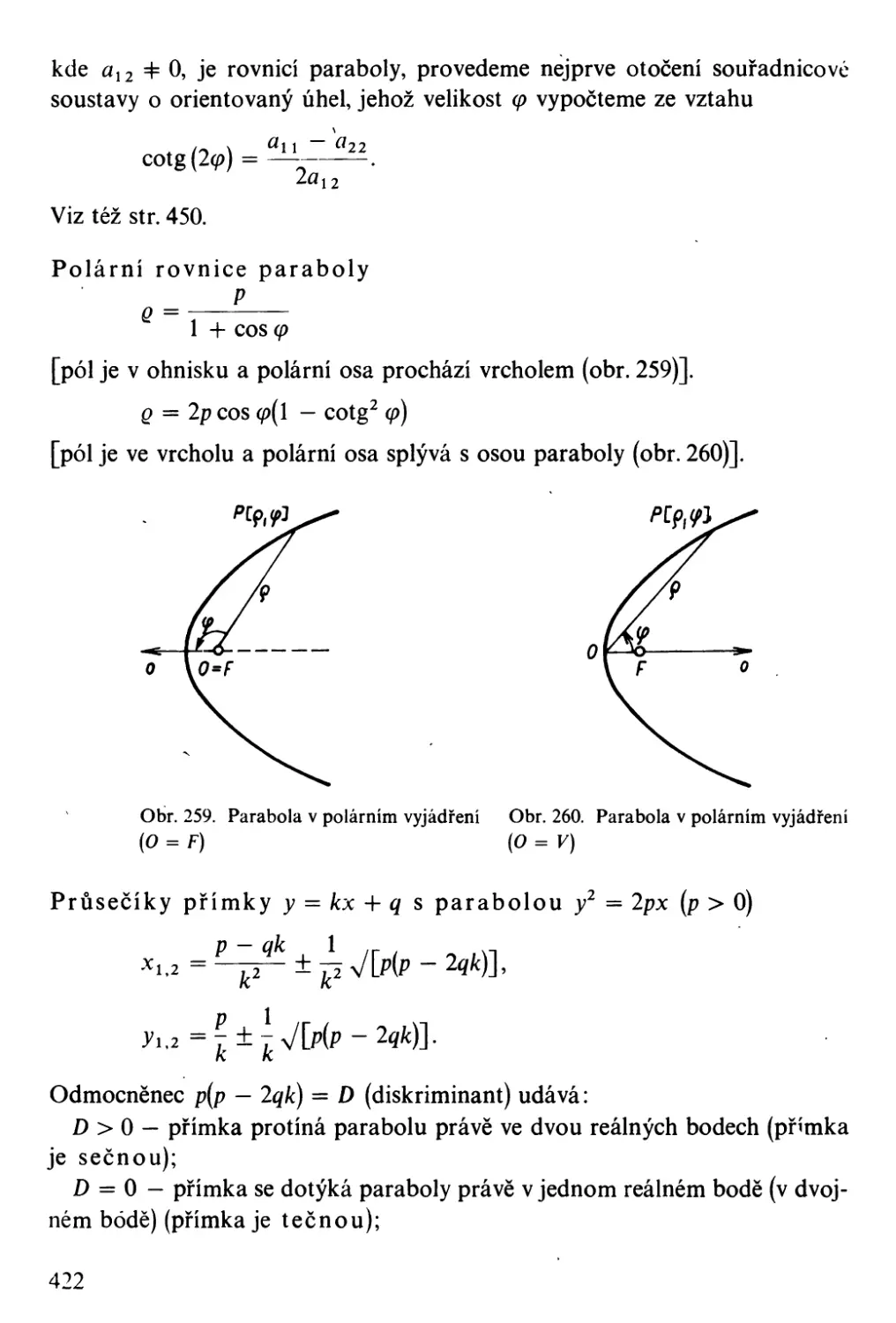
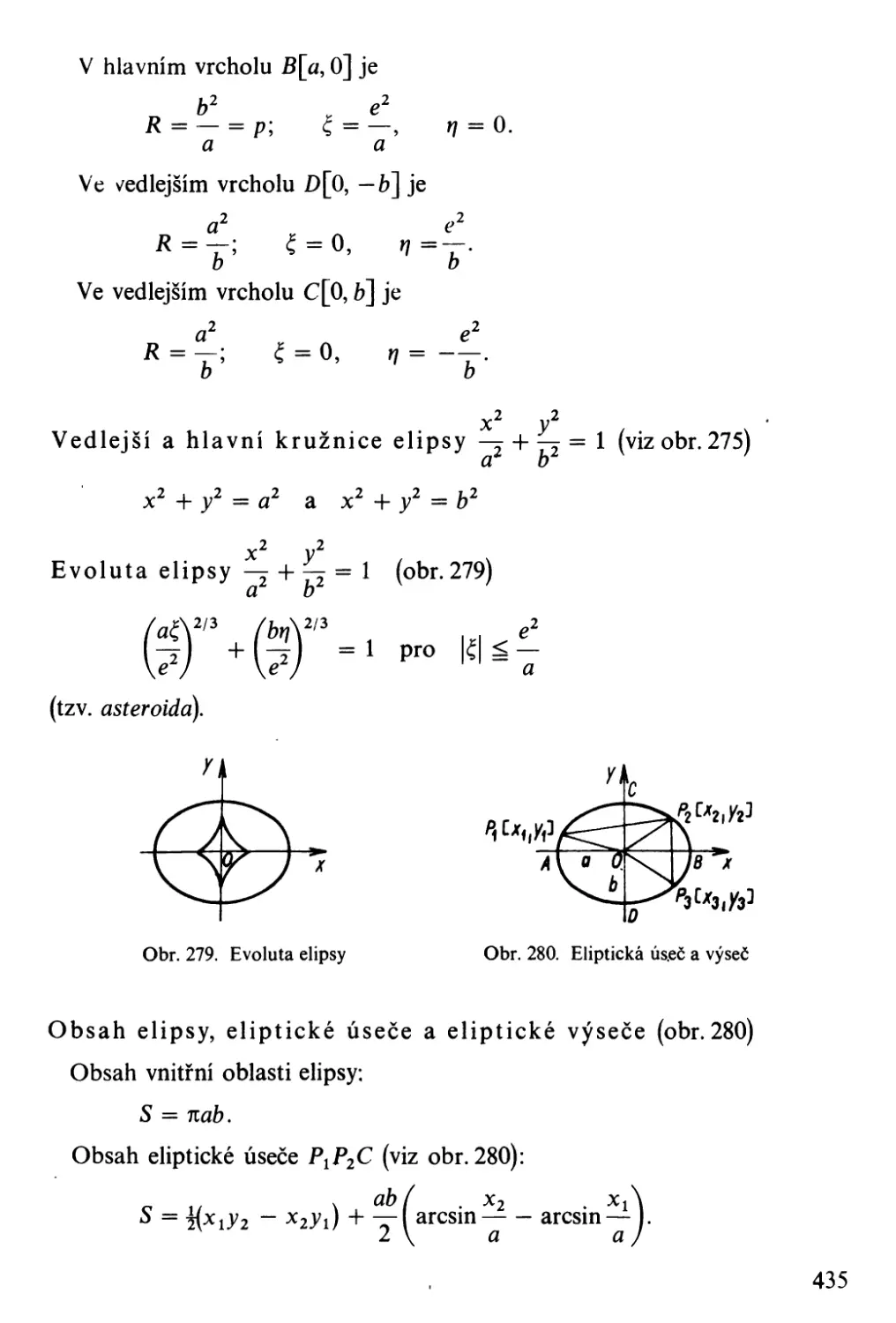
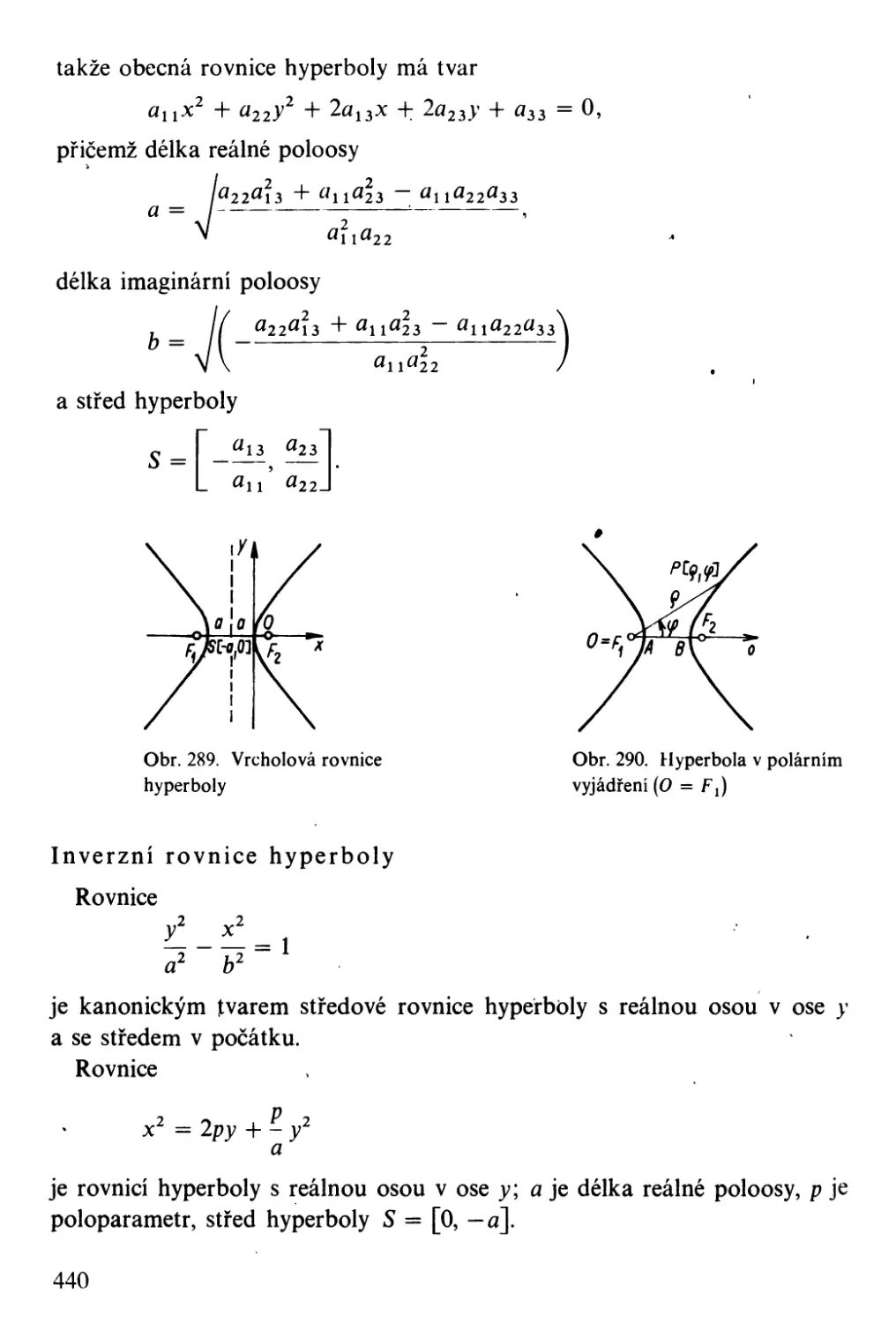
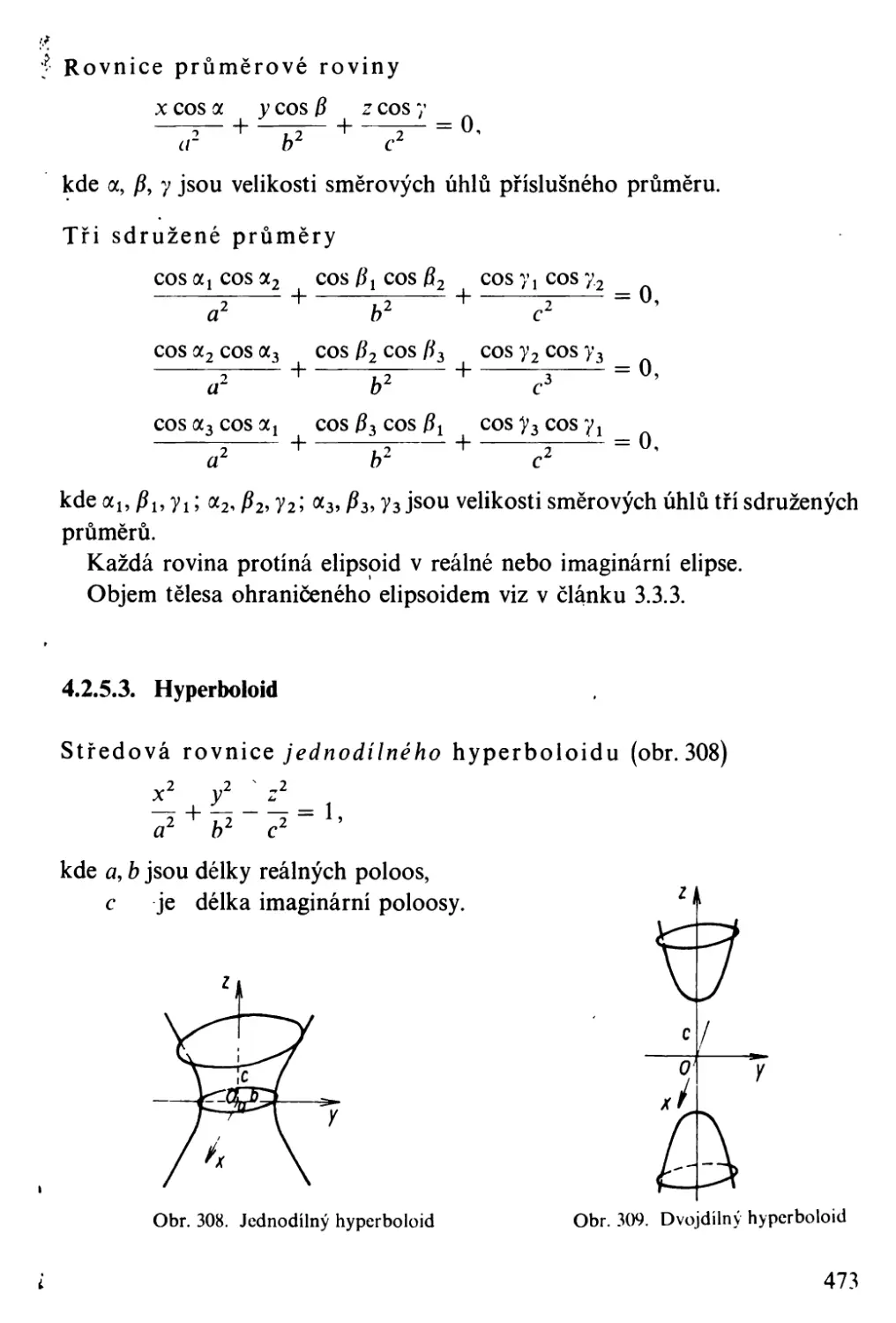
- 6 0,001 7 o.no I 7 1.000 O 0,001 7 572,% 1,569 I 54
12 0,003 5 0,003 5 1.000 ° 0,003 5 286.48 1,567 3 4
18 0,005 2 0,005 2 1.000 ° 0,005 2 190,98 1,565 6 42
24 0,007 ° 0,007 O 1.000 ° 0,007 O 143,24 I ,563 36
30 0,008 7 0,008 7 1.000 O 0,008 7 114,59 1,562 1 30
36 0,0 I ° 5 0,0 I ° 5 0.999 9 0,010 5 95,49 1.560 3 4
42 0,012 2 0,012 2 0,999 9 0,012 2 81,85 1,558 6 18
48 0,014 O 0,014 ° 0,999 9 0,014 ° 71,62 I ,556 12
54 0,015 7 0,015 7 0,999 9 0,015 7 63,66 1,555 I 6
1 ° 0,0 I 7 5 0,017 5 0,999 8 0,017 5 57,29 1,553 3 ° 19
-- 6 0,019 2 0,019 2 0,999 8 0,019 2 52,08 1,551 6 54
12 0,020 9 0,020 9 0,999 8 0,020 9 47,74 1,549 9 48
18 0,022 7 0,022 7 0,999 7 0,022 7 44,07 1,548 I 42
24 0,024 4 0,024 4 0,999 7 0,024 4 40,92 1,5464 36
30 0,026 2 0,026 2 0,999 7 0,026 2 38,19 1,544 6 30
36 0,027 9 0,027 9 0,999 6 0,027 9 35,80 1,542 9 24
42 0,029 7 0,029 7 0,999 6 0.029 7 33,69 1,541 I 18
48 0,031 4 0.031 4 0,999 5 0,031 31,82 1,539 4 12
54 0,033 2 0,033 2 0,999 5 0,033 2 30,14 1,537 6 6
1 ° 0,034 9 0,034 9 0,999 4 0,034 9 28,64 1,53S 9 ° 88
6 0,036 7 0,036 6 0,999 3 0,036 7 27,27 1.534 I 54
12 0,038 4 0,038 4 0,999 3 0,038 4 26,03 1,532 4 48
18 0,040 I 0,040 I 0,999 2 0,040 2 24,90 1,530 7 42
24 0,041 9 0,041 9 0,999 I 0,041 9 23,86 1,528 9 36
30 0.043 6 0,043 6 0,999 ° 0,043 7 22,90 1,527 2 30
36 0,045 4 0,045 4 0,999 ° 0,045 4 22,02 1,525 4 24
42 0,047 I 0,047 I 0,998 9 0,047 2 21,20 1,523 7 18
48 0,048 9 0,048 8 0,998 8 0,048 9 20,45 1,521 9 12
54 0,050 6 0,050 6 0,998 7 0,050 7 19,74 1,5202 6
3 ° 0,052 4 0,052 3 0,998 6 0,0524 19,08 1,518 4 O 87
6 0,054 I 0,054 I 0,998 5 0,054 2 18,46 1,516 7 54
12 0.055 9 0,055 0.998 4 0,055 9 17.89 1.514 ') 48
18 0,057 6 0,057 6 0,998 3 0,057 7 17,34 I ,513 42
24 0,059 3 0,059 3 .0,998 2 0,059 4 16,83 1.511 5 36
30 0,061 I 0,061 O 0,998 I 0,061 2 16,35 1.509 7 30
36 0,062 {( 0,062 0,998 ° 0,062 9 15,89 1,508 O 24
42 0,064 6 0,064 5 0,997 9 0,064 7 15,46 1,506 2 I
48 0,066 3 0,066 3 0,997 8 0,066 4 15,06 1,504 5 12
54 0.068 I 0,068 O 0,997 7 0,068 2 14,67 1,502 7 6
4 ° 0,069 8 0,069 8 0,997 6 0,0699 14,30 1,501 O O 86
6 0,071 6 0,071 5 0,997 4 0,071 7 13,95 1,499 2 54
12 0,073 3 0,073 2 0,997 3 0,073 4 13,62 1,497 5 8
18 0,075 ° 0,075 ° 0,997 2 0,075 2 13,30 1,495 7 42
24 0,076 8 0,076 7 0,997 1 0,0769 13,00 1,494 O 36
30 0,078 5 0,078 5 0,996 9 0,078 7 12,71 1,492 3 30
36 0,080 3 0.080 2 0.996 8 0.0805 12,43 t ,490 5 24
42 0,082 ° O.O I 9 0,9966 0.082 2 12, 16 1,488 8 18
48 0,083 8 0.083 7 0.996 5 0,0 4 () 11.91 1.487 O 12
54 0,085 5 ().O 5 4 0.996 3 0.085 7 11,66 1,485 3 6
5 ° 0.087 3 0,OX7 2 0,996 2 O,OX 7 5 IIA3 I ,4 B 5 O SS
o
! ! \,;',), (/) '111 (,'> cotg f,) tg (I> a rc (f) <f'
li' are li' sin li' cos ({J tg li' cotg ({J f f
o ,
5 ° 0,087 3 0,087 2 0,996 2 0,087 5 11,430 1,483 S ° 85
6 0,089 ° 0,088 9 0,996 ° 0,089 2 11 ,205 1,481 8 54
12 0,090 8 0.090 6 0,995 9 0,091 ° 10,988 1,480 ° 48
18 0,092 5 ().092 4 0,995 7 0,092 8 10,780 1,478 3 42
24 0,094 2 0.094 1 0.995 6 0,094 5 10,579 1.476 5 36
30 0,096 ° 0,095 8 0,9954 0,096 3 10,385 1,474 8 30
36 0,097 7 0,097 6 0,995 2 0.098 I 10,1 99 1,473 1 24
42 0,099 5 0,099 3 0,995 1 0,099 8 10,019 1,471 3 18
48 0, I ° 1 2 0,101 I 0,994 9 0, I ° 1 6 9,845 1.469 6 12
54 0, I 03 ° 0,102 8 0,994 7 I 0,103 3 9,677 1,467 8 6
6 ° 0,104 7 0,104 5 0,994 5 0, I 05 I 9,514 1,466 1 ° 84
6 0, I 06 5 O. I 06 ) 0,994 3 0, I 06 9 9,357 1,464 3 54
12 0,108 2 0,108 ° 0,994 2 0,108 6 9.205 1,462 6 48
18 0,110 ° 0,109 7 0,994 ° 0, II ° 4 9,058 1,460 8 42
24 0, III 7 0,111 5 0,993 8 0,1,12 2 8,915 1,459 1 36
30 0,113 4 0,113 2 0,993 6 0,113 9 8,777 1,457 3 30
36 0,115 2 0,114 9 0,993 4 0,115 7 8,643 1,455 6 24
42 0,116 9 0,116 7 0,993 2 0, II 7 5 8,513 1,453 9 18
48 0.118 7 0,118 4 0,993 ° 0,119 2 8,386 1,452 1 12
54 0, 12Q 4 0,120 1 0,992 8 0,121 ° 8,264 1,450 4 6
7 ° 0,122 2 0,121 9 0,992 5 0,122 8 8,144 1,448 6 ° 8J
6 0,123 9 0,123 6 0.992 3 0,124 6 8,028 1.446 9 54
12 0,125 7 0,125 3 0.992 1 0,126 3 7,916 1,445 1 48
18 0,1274 0,127 1 0,991 9 0,128 1 7,806 1,443 4 42
24 0,129 2 0,128 8 0,991 7 0,129 9 7,700 1,441 6 36
3Q 0,130 9 0,130 5 0,991 4 0,131 7 7,596 1,439 9 30
36 0,132 6 0,132 3 0,991 2 0,133 4 7,495 1,438 2 24
42 0,134 4 0,134 ° 0,991 ° 0,135 2 7,396 1,436 4 18
48 0,136 1 0,135 7 0,990 7 0,137 ° 7,300 1,434 7 12
54 0,137 9 0,137 4 0,990 5 0,138 8 7,207 1,432 9 6
8 ° 0, 139 6 0,139 2 0,990 3 0,140 5 7,115 1,431 2 ° 82
6 0,141 4 0,140 9 0,990 ° 0,142 3 7.026 1,429 4 54
12 0,143 I 0,142 6 0,989 8 0.144 1 6.940 1,427 7 48
18 0,144 9 0,144 4 0,989 5 0,145 9 6,855 1,425 9 42
24 0,146 6 0,146 1 0,989 3 0,147 7 6,772 1,424 2 36
30 0,148 4 0,147 8 0,989 ° 0,149 5 6,691 1.422 4 30
36 0, ISO 1 .0,149 5 0,988 8 0, 151 2 6,612 1,420 7 24
42 0,151 8 0,151 3 0,988 5 0,153 ° 6,535 1,419 ° 18
48 0,153 6 0,153 ° " 0.988 0,154 8 6,460 1,417 2 12
54 0,155 3 0,154 7 0.98M ° 0,156 6 6,386 1,415 5 6
9 ° 0,157 1 O, 156 4 0.987 7 0,158 4 6,314 1,413 7 ° 81
6 0,158 8 0,158 2 0.987 4 0,160 2 6,243 1,412 ° 54
12 0,160 6 0,159 9 0,987 1 0,162 ° 6,174 1.4102 48
18 0,162 3 O. ff; 1 6 0,9869 0,163 8 6.107 1,408 5 42
24 0,164 1 0,163 3 0,986 6 0,165 5 6,041 1,406 7 36
30 0, 165 8 0,165 ° 0,986 3 0,167 3 5,976 1,405 ° 30
36 0,167 6 0,166 8 0.986 ° 0,169 1 5,912 1,403 2 24
42 0,169 3 0, 168 5 0,985 7 0,170 9 5,8SO 1,401 5 18
48 0,1 71 ° 0,170 2 ,985 4 0,172 7 5,789 1,399 8 12
54 0,172 8 0,1 71 9 0,985 1 0,174 5 5,730 1,398 ° 6
10 ° 0,174 5 0,173 6 0,984 8 0, I 76 3 5,671 1,396 3 ° 80
, o -
! ! cos li' sin li' cotg tp tg li' arc li' li'
48
--- sin li' tg li' f f
tf" an: cp cos li' cotg li'
o
-10 U O, I 7 5 0.1 73 6 0,984 8 0,176 3 5,671 1,396 3 O 80
- 6 O, I 76 3 0.175 4 0,984 5 0,1 78 1 5,614 1,394 5 54
12 O, 17M O 0.177 1 0,984 2 O, 1 79 9 5.558 1,392 8 48
18 0.179 0.178 8 0,983 9 0,181 7 5,503 1.391 O 42
24 0, 18 I 5 0.180 5 0.983 () 0.183 5 5.449 1,389 3 36
30 0,183 3 0.182 2 0.983 3 0,185 3 5,396 1.387 5 30
36 0.185 O 0.184 O O.9K 9 0.187 I 5,343 1.385 8 24
42 0,186 8 0,185 7 O. 9 2 6 0,189 O 5,292 1.384 O 18
48 0,188 5 0,187 4 0,982 3 0,190 8 5,242 1.3 2 3 12
54 0,190 2 0,189 1 0,982 O 0,192 6 5.193 1.3 0 6 6
11 O 0,192 O 0,190 8 0,981 6 0,194 4 5,145 1.3 7 O 79
6 0,193 7 0,192 5 0,981 3 0.196 2 5,fJ)7 1.377 1 54
12 0,195 S 0,194. 2 0.981 O O,19 O 5.050 1.:'75 3 48
18 0.197 2 0,1959 0,980 6 0.199 8 5,005 1,373 6 42
24 0,199 O 0.197 7 0.980 3 0.20 I 6 4,959 1.3 71 36
30 0,200 7 0,199 4 0.9799 0.203 5 4.915 1.370 1 30
36 0,202 5 0.20 I 1 0,979 6 0.205 3 4,872 1.36M 3 24
42 0,204 2 0,202 8 0.979 2 0,207 1 4,829 : 1.366 6 18
48 0,205 9 0,204 5 0,978 9 O,20 9 4,787 1.364 8 12
54 0,207 7 0,206 2 0,978 5 0.210 7 4,745 1,363 I 6
1% O 0.2fJ) 4 0,207 9 0,978 I 0,212 6 4,705 1.3614 O 78
6 0,211 2 0,2fJ) 6 0.977 8 0,214 4 4,665 1.359 6 54
12 0,212 9 0.211 3 0,977 4 0.216 2 4,625 1.357 9 48
18 0,214 7 0.213 O 0,977 O 0,2 18 O 4,586 1,356 I 42
24 0,216 4 0,214 7 0,976 7 0.219 9 4,548 1,354 4 36
30 0,218 2 0,216 4 0,976 3 0.221 7 4,511 1.352 6 30
36 0,219 9 0,218 1 0,975 9 0.223 5 4,474 1,350 9 24
42 0.221 7 0.219 8 0.975 5 0,225 4 4,437 1,349 I 18
48 0.223 4 0,221 5 0,975 1 0,227 2 4.402 1.347 4 12
54 0,225 1 0,223 3 0,974 8 0,229 O 4,366 1,345 6 6
-13 O 0,226 9 0,225 O 0,974 4 0,230 9 4,331 1,343 9 O 77
6 0,228 6 . 0,226 7 0.974 O 0,232 7 4,297 1.342 2 54
12 0,230 4 0,228 4 0,973 6 0,234 5 4,264 1.340 .. 4X
18 0,232 1 0.230 O 0.973 2 0,23 4 4,230 1.33M 7 4
24 ,0,233 9 0,231 7 0.972 8 0,238 2 4.198 1,336 9 .16
I 30 0,235 6 0,233 4 0.972 4 0,240 I 4.165 1.335 2 3()
36 0,237 4 0,235 1 0,972 O 0.241 9 4,134 1,333 4 24
42 ,0,239 1 0.236 8 0.971 5 0.243 8 4.102 1,331 7 I
48 0,240 9 0.238 5 0,971 1 0.245 6 4.071 1,3299 12
54 0.242 6 0,240 2 0,970 7 0,247 5 4,041 1,328 2 6
14 O 0.244 3 0.241 9 0,970 3 0,249 3 4,011 1,326 5 O 76
6 0,246 1 0,243 6 0.969 9 0,251 2 3.981 1,324 7 54
12 0,247 8 0.245 3 0,969 4 0,253 O 3,952 1,323 O 48
18 0.249 6 0,247 O 0.969 O 0,254 9 , 923 1,321 2 42
24 0.251 3 0,248 7 0,968 6 0,256 8 3.f»)5 1 ,319 5 36
30 0.253 1 0,250 4 0,968 1 0,258 6 3.867 1,317 7 30
36 0.2548 0.252 1 0,967 7 0,260 5 3.839 1,316 O 24
42 0,2566 0.253 8 0,967 3 0,262 3 3.812 1,314 2 18
. 48 0,258 3 0.255 4 0,966 8 0,264 2 3.785 1,312 5 12
54 0.260 1 0,257 1 0,966 4 0,266 1 3.758 1,310 7 6
15 O 0,261 8 0,258 8 0,965 9 0,267 9 3,732 1,3fJ) O O 7S
, o
! 1 cos li' sin li' cotg li' tg li' arc li' li'
49
, qJ arc qJ sin qJ cos qJ tg qJ cotg qJ f f
o ,
15 O 0,261 8 0,258 8 0,965 9 0,267 9 3,732 1,309 O O 75
6 0,263 5 0,260 5 0,965 5 0,269 8 3,706 1,307 3 54
12 0,265 3 0,262 2 0,965 O 0,271 7 3,681 1,305 5 48
18 0,267 O 0,263 9 0,964 6 0,273 6 3,655 1,303 8 42
24 0,268 8 0.265 6 0,964 1 0,275 4 3,630 1,302 O 36
30 0,270 5 0,267 2 0,963 6 0,277 3 3,606 1,300 3 30
36 0,272 3 0,268 9 0,963 2 0,279 2 3,582 1,298 5 24
42 0,274 O 0,270 6 0,962 7 0,281 1 3,558 1,296 8 18
48 0,275 8 0,272 3 0,962 2 0,283 O 3,534 1,295 O 12
54 0,277 5 0,274 O 0,961 7 0,284 9 3,511 1,293 3 6
16 O 0,279 3 0,275 6 0,961 3 0,286 7 3,487 1,291 5 O 74
6 0,281 O 0,277 3 0,960 H 0,288 6 3,465 1,289 8 54
12 0,282 7 0,279 O 0,960 3 0,290 5 3,442 1,288 1 48
18 0,284 5 0,280 7 0,959 8 0,292 4 3,420 1,286 3 42
24 0,286 2 0,282 3 0.<)59 3 0,294 3 3,398 1,284 6 36
30 0,288 O 0,284 O 0.958 8 0,296 2 3,376 1,282 8 30
36 0,289 7 0,285 7 O. <) 58 3 0,298 1 3,35 1,281 1 24
42 0,291 5 0,287 4 0,957 8 0,300 O 3,333 1,279 3 18
48 0,293 2 0,289 O 0,957 3 0,301 9 3,312 1,277 6 12
54 0,295 O 0,290 7 0.956 8 0,303 8 3,291 1,275 8 6
17 O 0,296 7 0,292 4 0,956 3 0,305 7 3,271 1,274 I O 73
6 0,298 5 0,294 O 0,955 8 0,307 6 3,251 1,272 3 54
12 0,300 2 0,295 7 0,955 3 0.309 6 3,230 1,270 6 48
18 0,301 9 0.297 4 0,954 8 0,311 5 3,211 1,268 9 42
24 0,303 7 0,299 O 0,954 2 0,313 4 3,191 1,267 1 36
30 0,305 4 0,300 7 0,953 7 0,315 3 3,172 1,265 4 30
36 0,307 2 0,302 4 0,953 2 0,317 2 3,152 1,263 6 24
42 0,308 9 0,304 O 0,952 7 0,319 1 3,133 1 ,261 9 18
48 0,310 7 0,305 7 0,952 1 0,321 1 3,115 1,260 1 12
54 0,312 4 0,307 4 0,951 6 0,323 O 3,096 1,258 4 6
18 O 0,3142' 0,309 O 0,951 1 0,3249 3,078 1,256 6 O 72
6 0,315 9 0,310 7 0,950 5 0,3269 3,060 1,254 9 54
12 0,317 6 0,312 3 0,950 O 0,328 8 3,042 1,253 1 48
18 0,319 4 0,314 O 0,949 4 0,330 7 3,024 1,251 4 42
24 0,321 1 0,315 6 0,948 9 0,332 7 3,006 1.249 7 36
30 0,322 9 0,317 3 0,948 3 0,334 6 2,989 I ,247 9 30
36 0,324 6 0,319 O 0,947 8 0,336 5 2,971 1.246 2 24
42 0.326 4 0,320 6 0,947 2 0,338 5 2,954 1,244 4 18
48 0.328 I 0,322 3 0,946 6 0,340 4 2,937 1.242 7 12
54 0.329 9 0,323 9 0,946 1 0,342 4 2,921 1,240 9 6
19 O 0.331 6 0,325 6 0,945 5 0,344 3 2,904 1,239 2 O 71
6 0,333 4 0,327 2 0,944 9 0,346 3 2,888 1,237 4 54
12 0,335 1 0,328 9 0,944 4 0,348 2 2,872 1,235 7 48
18 0,336 8 0,330 5 0,943 8 0,350 2 2,856 1,233 9 42
24 0,338 6 0,332 2 0,943 2 0,352 2 2,840 1,232 2 36
30 0,340 3 0,333 8 0.942 6 0,354 1 2,824 1,230 5 30
36 0,342 1 0,335 5 0.942 I 0.356 1 2,808 1,228 7 24
42 0,343 8 0,337 1 0,941 5 0,358 1 2,793 1,227 O 18
48 0,345 6 0,338 7 0,940 9 0,360 O 2,778 1,225 2 12
54 0,347 3 0,340 4 0,940 3 0,362 O 2,762 1,223 5 6
J» O 0,349 1 0,342 O 0,939 7 0,364 O 2,747 1,221 7 O 70
, o
! ! cos qJ SIO qJ cotg qJ tg qJ arc qJ qJ
50
- sin li' f
li' arc li' cos li' tg li' cotg li' f
o ,
-. ° 0,349 1 0,342 O 0,939 7 0,364 O 2,747 5 1,221 7 O 70
- 6 0,350 8 0,343 7 0,939 I 0,365 9 2,7326 1,220 O 54
12 0,352 6 0,345 3 0,938 5 0,367 9 2.71 7 9 1,218 2 48
18 0,354 3 0,346 9 0.937 9 0,369 9 2,703 4 1,216 5 42
24 0,356 ° 0,348 6 0.937 3 0,371 9 2.688 9 1,214 7 36
30 0,357 8 0,350 2 0.936 7 0,373 9 2.674 6 1,213 ° 30
36 0,359 5 0,351 8 0,936 I 0,375 9 1.660 5 1,211 3 24
42 0,361 3 0,353 5 0.935 4 0,377 9 2.646 4 1 ,209 5 18
48 0,363 ° 0,355 1 . 0.934 8 0,3799 2.632 5 1,207 8 12
54 0,364 8 0,356 7 0.934 2 0,381 9 1,618 7 1,206 ° 6
Zl O 0,366 5 0,3584 0.933 6 0,383 9 2,605 I 1,204 3 O 69
6 0,368 3 0,360 ° 0.933 O 0,385 9 2.5916 1,202 5 54
12 0,370 O 0,361 6 0.932 3 0,387 9 2,578 2 1,200 8 48
18 0,371 8 0,363 3 0.931 7 0,389 9 2.564 9 1,199 O 42
24 0,373 5 0,364 9 0.931 1 0.391 9 2,551 7 1,197 3 36
30 0,375 2 0,366 5 0,930 4 0.3939 2.538 6 1,1956 30
36 0,377 ° 0,368 I 0,929 8 0.395 9 1.525 7 1,193 8 24
42 0,378 7 0,369 7 0,929 1 0.397 {) 2,512 9 1,192 1 18
48 0,380 5 0,371 4 0,928 5 OAOO O 2,50() 2 1,190 3 12
54 0,382 2 0.373 O 0,927 8 0.402 O 2.487 6 1,188 6 6
ZZ ° 0,384 ° 0.374 6 0,927 2 OA04 O 2.475 I 1, I 86 8 O 61
6 0,385 7 0.376 2 0,926 5 0.406 I 2.462 7 1,185 I 54
12 0,387 5 0.377 8 0,925 9 OAm I' 2,450 4 1,183 3 48
18 0,389 2 0,379 5 0.925 2 OA 1 U I 2,438 3 1.181 6 42
I
24 0,391 O 0,381 I 0.924 5 UA 12 2 2,426 2 1.1 79 8 36
30 0,392 7 0,382 7 0.923 9 0.414 2 2,414 2 1.1 78 I 30
36 0,394 4 0,384 3 0.923 2 OAl Ó 3 2,402 3 1.176 4 24
42 0,396 2 0,385 9 0.912 5 OA 18 3 2,390 6 I, 174 6 18
48 0,397 9 0,387 5 0.921 9 0.420 4 2,378 9 1, 1 72 9 12
54 0,399 7 0,389 1 0:921 2 0.422 4 2,367 3 1,171 I 6
Z3 ° 0,401 4 0,390 7 0.920 5 OA24 5 2,355 9 1, 169 4 ° 67
6 0,403 2 0,392 3 0,9 19 M OA26 5 2,344 5 1,1676 54
12 0,404 9 0,393 9 0.919 1 OA2X 6 2,333 2 1,1659 48
18 0,406 7 0,395 5 0.91 g 4 OA30 7 2.322 O 1,164 I 42
24 0,4084 0.397 I 0.91 7 8 0.432. 7 2.310 9 1,1624 36
30 0,4102 0.398 7 0.917 I 0.434 8 2.299 8 1,160 6 30
36 0,411 9 0.400 3 0.916 4 0.4 36 9 2.288 9 1,158 9 24
42 0,413 6 0.401 9 0.9 I 5 7 0.439 O 2.278 I 1,157 2 18
48 0,415 4 0.403 5 0.915 O 0.441 I 2.267 3 1,155 4 12
54 0,417 1 0,405 1 0.914 3 0.443 1 2.256 6 1,153 7 6
Z4 ° 0,418 9 0.406 7 0.9 I 3 5 0.445 2 2.246 O 1,151 9 O 66
6 0,420 6 0.408 3 0.91 2 8 0,447 3 2.235 5 1,150 2 54
12 0,422 4 0.409 9 0,912 1 0.449 4 2,225 I 1.148 4 48
18 0,424 1 0.4115 0,911 4 0.451 5 2,214 8 1,146 7 42
24 0,425 9 0.413 I 0.9107 0,453 6 2,204 5 1,144 9 36
30 0,427 6 0.414 7 0,910 ° 0,455 7 2.194 3 i,143 2 30
36 0,429 4 0.416 3 0.909 2 0,457 8 2, 184 2 1,141 4 24
42 0,431 1 0,417 9 0.908 5 0,459 9 2, 174 2 1,139 7' 18
48 0,432 8 0,419 5 0,907 8 0,462 1 2,164 2 1,138 ° 12
54 0,434 6 0,421 ° 0,907 O 0,464 2 2,154 3 1,136 2 6
25 ° 0,436 3 0,422 6 0,906 3 0.466 3 2,144 5 1,134 5 O 6S
, o
! ! cos li' sin li' cotg li' tg li' are <p li'
51
li' arc li' sin li' . cos li' tg li' cotg li' f' f
o ,
25 O 0,436 3 0,4226 0,906 3 0,466 3 2, 144 5 1,134 5 O 65
6 0,438 I 0,424 2 0,905 6 0,468 4 2, 134 8 1,132 7 54
12 0,439 8 0,425 8 0.904 8 0,4 70 6 2,125 I 1,131 O 48
18 0,441 6 0,427 4 0,904 1 0,472 7 2, 115 5 1 , 129 2 42
24 0,443 3 0,428 9 0,903 3 0,474 8 2, 106 O 1,127 5 36
30 0,445 1 0,430 5 0,9026 0,4 77 O 2,096 5 1,125 7 30
36 0,446 8 0,432 1 0,90 I 8 0,479 1 2,087 2 1 , 124 O 24
42 0,448 5 0,433 7 0,901 1 0,4813 2,077 8 1, 122 2 18
48 0,450 3 0,435 2 0,900 3 0,483 4 2,068 6 1, 120 5 12
54 0,452 O 0,436 8 0,8996 0,485 6 2,059 4 1,1188 6
26 O 0,453 8 0,438 4 0,898 8 0,487 7 2,050 3 1.1170 O 64
6 0,455 5 0,439 9 0,898 O 0,489 9 2,041 3 1,1153 54
12 0,457 3 0,441 5 0,897 3 ' 0,492 1 2,032 3 1,113 5 48
18 0,459 O 0,443 1 0,896 5 0,494 2 2,023 3 1,111 8 42
24 0,460 8 0,444 6 0,895 7 0,496 4 2,014 5 1,110 O 36
30 0,462 5 0,446 2 0,894 9 0,498 6 2.005 7 1 ,108 3 30
36 0,464 3 0,447 8 0,894 2 0,500 8 1,997 O 1,106 5 24
42 0,466 O 0,449 3 0,893 4 0,502 9 1,988 3 1,104 8 18
48 0,467 7 0,4509 0,892 6 0,505 1 1,979 7 1,103 O 12
54 0,469 5 0,452 4 0,891 8 0,507 3 1,971 1 1,101 3 6
27 O 0,471 2 0,454 O 0,891 O 0,509 5 1,962 6 1,099 6 O 63
6 0,473 O 0,455 5 0,890 2 0,511 7 1,954 2 1,097 8 54
12 0,4 74 7 0,457 1 0,889 4 0,513 9 1,945 8 1 ,096 1 48
18 0,4 76 5 0,458 6 0,888 6 0,516 1 1,937 5 1,094 3 42
24 0,478 2 0,460 2 0,887 8 0,518 4 1,929 2 I ,092 6 36
30 0,480 O 0,461 7 0,887 O 0,5206 1,921 O 1,090 8 30
36 0,481 7 0,463 3 0,886 2 0,522 8 1 ,912 8 1,089 I 24
42 0,483 5 0,464 8 0,885 4 0,525 O 1,904 7 1.087 3 18
48 0,485 2 0,466 4 0,884 6 0,527 2 1,896 7 1 ,085 6 12
54 0,486 9 0,4679 0,883 8 0,529 5 1,888 7 1,083 8 6
28 O 0,488 7 0,469 5 0,8 2 9 0,531 7 1,880 7 1,082 1 O 62
6 0,490 4 0,471 O 0,882 1 0,534 O 1,872 8 1,080 4 54
12 0,492 2 0,472 6 0,881 3 0,536 2 1,865 O 1,078 6 48
18 0,493 9 0,474 1 0,880 5 0,538 4 1,857 2 1,076 9 42
24 0,495 7 0,475 6 0,879 6 0,540 7 1,849 5 1,075 1 36
30 0,497 4 0,477 2 0,878 8 0,543 O 1,841 8 1,073 4 30
36 0,499 2 0,4 78 7 0,878 O 0,545 2 1,834 1 1,071 6 24
42 0,500 9 0,480 2 0,877 1 0,54 7 5 1,826 5 1,069 9 18
48 0,502 7 0,481 8 0,876 3 0,549 8 1,819 O 1,068 1 12
54 0,504 4 0,483 3 0,875 5 0,552 O 1,811 5 1,0664 - 6
29 O 0,506 1 0,484 8 0,874 6 0,554 3 1,804 O 1,064 7 O 61
6 0,507 9 0,486 3 0,873 8 0,556 6 1,796 6 1,062 9 54
12 0,509 6 0,487 9 0,872 9 0,558 9 1,789 3 1,061 2 48
18 .0,511 4 0,4894 0,872 1 0,561 2 1,782 O 1,059 4 42
24 0,513 1 0,490 9 0,871 2 0,563 5 1,774 7 1,057 7 36
30 0,5149 0,492 4 0,870 4 0,565 8 1,767 5 1,055 9 30
36 0,516 6 0,493 9 0,869 5 0,568 1 1,760 3 1,054 2 24
42 0,518 4 0,495 5 0,868 6 0,570 4 1,753 2 1.052 4 18
48 0,520 1 0,497 O 0,867 8 0,572 7 1,746 1 1,050 7 12
54 0,521 9 0,498 5 0,866 9 0,575 O 1,739 1 1,048 9 6
30 O 0,523 6 0,500 O 0,866 O 0,577 4 1,732 1 1,047 2 O 60
, o
! cos li' sin li' cotg li' tg li' arc li' li'
52
li' arc li' Sin li' COS li' tg li' cotg,fP i i
o ,
30 O 0,523 6 0,500 O 0,866 O 0,577 4 1,732 1 1,047 2 O 60
6 0,525 3 0,501 5 0,865 2 0,579 7 1. 725 1 1.045 5 54
12 0,527 1 0,503 O 0,864 3 0,582 O 1,7182 1.043 7 48
18 0,528 8 0,504 5 0,863 4 0,584 4 1.7113 1,042 O 42
24 0,530 6 0,506 O 0.862 5 0,586 7 1. 704 5 1.040 2 36
30 0,532 3 0,507 5 0,861 6 0,589 O 1.697 7 1,038 5 30
36 0,534 1 0,509 O 0,860 7 0.591 4 1,690 9 1,036 7 24
42 0,535 8 0,510 5 0,859 9 0,593 8 1,684 2 1.035 O 18
48 0,537 6 0,512 O 0,859 O 0.596 1 1.677 5 1.033 2 12
54 0,539 3 0,513 5 0,858 I 0,598 5 1.6709 1,031 5 6
31 O 0,541 1 0,515 O 0,857 2 0,600 9 I ,664 3 1.029 7 O 59
6 0,542 8 0,516 5 0.856 3 0,603 2 1,657 7 1.028 O 54
12 0,544 5 , 0,518 O 0,855 4 0.605 6 1,651 2 1,026 3 48
18 0,546 3 0,519 5 0,854 5 0,608 O 1.644 7 1,024 5 42
24 0,548 O 0,521 O 0,853 6 0,610 4 1,638 3 1,022 8 36
30 0,549 8 0,522 5 0,852 6 0,612 8 1,631 9 1,021 O 30
36 0,551 5 0,524 O 0,851 7 0.615 2 1,625 5 1,019 3 24
42 0,553 3 0,525 5 0,850 8 0.617 6 1.619 1 1.017 5 18
48 0,555 O 0,527 O 0.849 9 0,620 O 1.612 8 1,015 8 12
54 0,556 8 0,528 4 0,849 O 0,622 4 1,606 6 1,014 O 6
32 O 0,558 5 0,529 9 0,848 O 0,624 9 1,600 3 1,012 3 O 58
6 0,560 3 0,531 4 0,847 1 0,627 3 1,594 1 1,010 5 54
12 0,562 O 0,532 9 0,846 2 0.629 7 1,588 O 1,008 8 48
18 0,563 7 0.534 4 0,845 3 0,632 2 1.581 8 1,007 1 42
24 0,565 5 0,535 8 0,844 3 0,634 6 1.575 7 1,005 3 36
30 0,567 2 0,537 3 0,843 4 0,637 1 I. 569 7 1.003 6 30
36 0,569 O 0,538 8 0,842 5 0,639 5 1,563 7 1,001 H 24
42 0,570 7 0,540 2 0,841 5 0,642 O 1,557 7 1,000 1 18
48 0,572 5 0,541 7 0,840 6 0,644 5 1,551 7 0.998 3 12
54 0,574 2 0,543 2 0.839 6 0,646 9 1,545 8 0,996 6 6
33 Q 0,576 O 0,544 6 0,838 7 0,649 4 1,539 9 0,994 8 O 57
6 0,577 7 0,546 1 0,837 7 0.651 9 1,534 O 0,993 1 54
12 0,579 4 0.547 6 0,836 8 0,654 4 1,528 2 0,991 3 48
18 0,581 2 0,549 O 0,835 8 0,656 9 1.522 4 0,989 6 42
24 0,582 9 0,550 5 0,834 8 0,659 4 1,516 6 0,987 9 36
30 0,584 7 0,551 9 0,833 9 0,661 9 1,510 8 0.986 1 30
36 0,586 4 0,553 4 0,832 9 0,664 4 1,505 1 0.9 . 4 24
42 0,588 2 0,554 8 0,M32 O 0.666 9 1,499 4 0,982 6 18
48 0,589 9 0,556 3 0.831 O 0,669 4 1,493 8 0,980 9 12
54 0,591 7 0,557 7 0.830 O 0,672 O 1,4882 0.979 1 6
34 O 0,593 4 0.559 2 0,829 O 0,674 5 1,482 6 0,977 4 O 56
6 0,595 2 0,560 6 0,828 1 0,677 1 1,477 O 0,975 6 54
12 0.596 9 0,562 1 0,827 1 0,679 6 1,471 5 0,973 9 48
18 . 0,598 6 0,563 5 0,826 1 0,682 2 1,465 9 0,972 1 42
24 0,600 4 0,565 O 0,825 1 0,684 7 1,460 5 0,970 4 36
30 0,602 1 0,566 4 0,824 1 0,687 3 1,455 O 0,968 7 30
36 0,603 9 0,567 8 0,823 1 0,689 9 1,449 6 0.9669 24
42 0.605 6 0,569 3 0,822 1 0,692 4 1,444 2 0,965 2 18
48 0,607 4 0,570 7 0,821 1 0,695 O 1,438 8 0.963 4 12
54 0,609 1 0,572 1 0,820 2 0,697 6 1,433 5 0,961 7 6
35 O 0,6109 0,573 6 0,819 2 0,700 2 1,428 1 0,959 9 O 55
, o
! ! cos li' sin li' cotg li' tg li' are li' li'
53
sin li' , f f
li' arc li' cos li' tg li' cotg li' ,
o ,
35 O 0,6109 0,573 6 0,819 2 0,700 2 1,428 1 0,959 9 O 55
6 0,612 6 0,575 O 0,818 1 0,702 8 1,4229 0,958 2 54
.
12 0,6144 0,576 4 0,81 7 1 0,705 4 1,4176 0,956 4 48
18 0,616 1 0,577 9 0,816 1 0,708 O 1.4124 0,954 7 42
24 0,61 7 8 9,579 3 0,815 1 0,710 7 1,407 1 0,952 9 36
30 0,619 6 0,580 7 0,814 1 0,713 3 1 ,401 9 0,951 2 - 30
36 0,621 3 0,582 1 0,813 1 0,715 9 1,396 8 0,949 5 24
42 0,623 1 0,583 5 0,812 1 0,718 6 1,391 6 0,947 7 18
48 0,624 8 0,585 O 0,811 1 0,721 2 1,386 5 0,946 O 12
54 0,626 6 0,586 4 0,810 O 0,723 9 1,381 4 0,944 2 6
36 O 0,628 3 0,587 8 0,809 O 0,726 5 1,376 4 0,942 5 O 54
6 0,630 1 0,589 2 0,808 O 0,729 2 1 ,371 3 0,940 7 54
12 0,631 8 0,590 6 0,807 O , 0,731 9 1,366 3 0,939 O 48
18 0,633 6 0,592 O 0,805 9 0,734 6 1,361 3 0,937 -2 42
24 0,635 3 0,593 4 0,804 9 0,737 3 1,356 4 0,935 5 36 ."
30 0,637 O 0,594 8 0,803 9 0,740 O 1,351 4 0,933 8 30
36 0,638 8 0,5962 0,802 8 0,742 7 1,346 5 0,932 O 24
42 0,640 5 0,597 6 0,801 8 0,745 4 1,341 6 0,930 3 18
48 0,642 3 0,599 O 0,800 7 0,748 1 1 ,336 7 0,928 5 12
54 0,644 O 0,600 4 0,799 7 0,750 8 1,331 9 0,926 8 6
37 O 0,645 8 0,60 1 8 0,798 6 0,753 6 1,327 O 0,925 O O 53
6 0,647 5 0,603 2 0,797 6 0,756 3 1,322 2 0,923 3 54
12 0,649 3 0,604 6 0,796 5 0,759 O 1 ,31 7 5 0,921 5 4
18 0,651 O 0,606 O 0,795 5 0,761 8 1 ,312 7 0,919 8 42
24 0,652 8 0,607 4 0,794 4 0,764 6 ,1,307 9 0,918 O 36
30 0,654 5 0,608 8 0,793 4 0,767 3 1,303 2 0,9163 30
36 0,656 2 0,610 1 0,792 3 0,770 1 1,298 5 0,9146 24
42 0,658 O 0,611 5 0,791 2 0,772 9 1,293 8 0,912 8 18
48 0,659 7 0,6129 0,790 2 0,775 7 1,289 2 0,911 1 12
54 0,661 5 0,614 3 0,789 1 0,778 5 1 ,284 6 0,909 3 6
38 O 0,663 2 0,615 7 6,788 O 0,781 3 1,2799 0,907 6 O 52
6 0,665 O 0.617 O 0,786 9 0,784 1 1,275 3 0,905 8 54
12 0,666 7 O.tJl 4 0,785 9 0,786 9 1,270 8 0,904 1 48
18 0,668 5 0,619 8 0,784 8 0,789 8 1,266 2 0,902 3 42
24 0,6702 0,621 1 0,783 7 0,792 6 1,261 7 0,900 6 36
30 0,672 O 0,622 5 0,782 6 0,795 4 1,257 2 0,898 8 30
36 0,673 7 0,623 9 0,781 5 0,798 3 1,252 7 0,897 1 24
42 0,675 4 0,625 - 2 0,780 4 0,801 2 1,248 2 0,895 4 I
48 0,677 2 0,626 6 0,779 3 0,804 O 1,243 7 0,893 6 12
54 0,678 9 0,628 O 0,778 2 0,806 9 1,239 3 0,891 9 6
39 O 0,680 7 0,629 3 0,777 1 0,809 8 1,234 9 0,890 1 O 51
6 0,682 4 0,630 7 0,776 O 0,812 7 1,230 5 0,888 4 54
12 0,6842 0,632 O 0,774 9 0,815 6 1,226 1 0,886 6 48
18 0,685 9 0,633 4 0,773 8 0,818 5 1,221 8 0,884 9 42
24 0,687 7 0,634 7 0,772 7 0,821 4 1,217 4 0,883 1 36
30 0,689 4 0,636 1 0,771 6 0,824 3 1 ,213 1 0,881 4 30
36 0,691 2 0,637 4 0,770 5 0,827 3 1,208 8 0,879 6 24
42 0,692 9 0,638 8 0,7694 0,830 2 1,204 5 0,877 9 18
48 0,6946 0,640 1 0,768 3 0,833 2 1,200 2 0,876 2 12
54 0,696 4 0,641 4 0,767 2 0,836 1 1,196 O 0,8744 6
40 O 0,698 1 0,642 8 0,766 O 0,839 1 1,191 8 0,872 7 O 50
, o
! ! cos li' 510 li' cotg li' tg li' are li' li'
54
..
-
li' are li' sin li' cos li' tg li' cotg li' f f
o ,
-40 O 0.698 I 0,642 8 0,766 O 0,839 I 1,191 8 0,872 7 O 50
6 0,699 9 0,644 I 0,764 9 0,842 1 1,187 5 0,870 9 54
12 0,70 I 6 0,645 5 0,763 8 0,845 I 1,183 3 0,869 2 48
18 0,703 4 0,646 8 0,762 7 O.X4X I 1, 1 79 2 0,867 4 42
24 0.705 1 0,648 I 0,761 5 O,M51 I 1,1750. 0,865 7 36
30 n,706 9 0,649 4 0,760 4 0,854 I 1 , 1 70 8 0,863 9 30
36 0.708 6 0.650 8 0,759 3 0,857 I 1, 166 7 0,862 2 24
42 0.710 3 0,652 1 0,758 I 0,860 1 1, 162 6 0,860 4 18
f 48 0,712 I 0,653 4 0,757 O 0,863 2 1,158 5 0,858 7 12
54 0,713 8 0.654 7 0,755 9 0,866 2 1, 154 4 0,857 O 6
- 41 O 0,715 6 0,656 1 0.754 7 0,869 3 1, 150 4 0,855 2 O 49
6 0,71 7 3 0,657 4 0,753 6 0,872 4 1,146 3 0,853 5 54
12 0,719 1 0,658 7 0,752 4 0,875 4 1,142 3 0,851 7 48
18 0,720 8 0,660 O 0,751 3 0,878 5 1,138 3 0,850 O 42
24 0,722 6 0,661 3 0,750 1 0,881 6 1,134 3 0,848 2 36
30 0..724 3 0,662 6 0,749 O 0.884 7 1, 130 3 0,846 5 30
36 0,726 1 0,663 9 0,747 8 0,887 8 1,126 3 0,844 7 24
42 0,727 8 0,665 2 0,746 6 0,891 O 1,122 4 0,843 O 18
48 0,729 5 0,666 5 0,745 5 0,894 1 1,1184 0,841 2 12
54 0,731 3 0,66 7 8 0,744 3 0,897 2 1,114 5 0,839 5 6
42 O 0,733 O 0,669 1 0,743 1 0,900 4 1,1106 0,837 8 O 48
6 0,734 8 0,6704 0,742 ° 0,903 6 1,106 7 0,836 O 54
12 0,736 5 0,671 7 0,740 8 0,906 7 1.102 8 0,834 3 48
18 0,i38 3 0.673 O 0,739 6 0,909 9 1,099 O 0.832 5 42
24 0,740 O 0,674 3 0,738 5 0.9 J 3 1 1,095 1 0,830 8 36
30 0.741 8 0,675 6 0,737 3 0,916 3 1,091 3 0,829 O 30
36 0,743 5 0,676 9 0,736 I 0,919 5 1.087 5 0,827 3 24
42 0,745 3 0,678 2 0,734 9 0.922 8 1,083 7 0,825 5 18
48 0,747 O 0,679 4 0,733 7 0,926 O 1,079 9 0,823 8 12
54 0,748 7 0,680 7 0,732 5 0,929 3 1,076 1 0,822 1 6
43 O "0,750 5 0,682 O 0,731 4 0,932 5 1,0724 0,820 3 O 47
6 0.752 2 0,683 3 0.730 2 0,935 8 1,068 6 0,818 6 54
12 0,754 O 0,684 5 0,729 O 0,939 1 1,064 9 0,816 8 48
18 0,755 7 0,685 8 0,727 8 0,942 4 1,061 2 0,815 I 42
24 0,757 5 0,687 1 0,726 6 0,945 7 1,057 5 0,813 3 36
30 0,759 2 0,688 4 0,725 4 0,949 O 1,053 8 0,811 6 30
36 0,761 O 0,689 6 0,724 2 0,952 3 1,050 1 0,809 8 24
42 0,762 7 0,690 9 0,723 O 0,955 6 1,0464 0,808 1 18
48 0,764 5 0,692 1 0,721 8 0,959 O 1,042 8 0,806 3 12
54 0,766 2 0,693 4 0,720 6 0,962 3 1,039 2 0,804 6 6
44 O 0,7679 0,694 7 0,719 3 0,965 7 1,035 5 0,802 9 O 46
6 0,769 7 0,695 9 0,718 I 0,969 1 1,031 9 0,801 1 54
12 0,771 4 0,697 2 0,716 9 0,972 5 1,028 3 0,799 4 48
18 0,773 2 0,698 4 0,715 7 0,975 9 1,024 7 0,797 6 42
24 0,7749 0.699 7 0,714 5 0,97rJ 3 1,021 2 0,795 9 36
30 0,776 7 0,700 9 0:713 3 0,982 7 1,017 6 0.794 1 30
36 0,7.78 4 0,702 2 0,712 O 0,986 1 1,014 I 0,792 4 24
42 0,7802 0,703 4 0,710 8 0,989 6 1,010 5 0,790 6 18
48 0,781 9 0,704 6 0,709 6 0,993 O 1,007 O 0,788 9 12
54 0.783 7 0,705 9 0,708 3 0,996 5 1,003 5 0,787 1 6
45 O 0,785 4 0,707 1 0,707 1 1,000 O 1,000 O 0,785 4 O 45
, o
! ! co li' sin li' cotg li' tg li' are li' li'
55
0.2.3. Mocniny o základu 2
n 2" 2 -ft
o 1 I
1 2 0,5
2 4 0,25
3 8 0,125 .
4 16 0,062 5
5 32 0,031 25
6 64 0,015 625
7 128 0,0078125
8 256 0,003 906 25
9 512 0,001 953 125
10 1024 0,000 976 563
11 2048 0,000 488 281
12 4096 0,000 244 141 ,
13 8 192 0,000 122 070
14 16 384 0,000 061 035
15 32 768 0,000 030 518
16 65 536 0,000 015259
17 131 072 0,000 007 629
18 262 144 0,000 003 815
19 524 288 0,000 00 1 907
20 1 048 576 0,000 000 954
56
r-
\O
V'I
,-..
N
---
aJ
C
..
...
)C)
N
.-
>
'-"
I:
00
f"")
"
...
c:a.
fIj
N
.-
c:a.
.."
NI!
..
"
.=.c
..
..-
fIj.
Q
-
OO \ON OO\Or--.
8 V'I
OV'lO'\OOf"")
00 f"") N N
\OOON
-
-
N oo\ON oo\O
-\OOr-r-OO
0'\ 00\C)V'I Of"")
NN\O f"")
00 r- 0'\ N
V'lV'I-
N -
-
OOO V'I
V'lf"")
V'lOf"")ON
OO-\ON
f"")-
0-
-
OO\ON OO\ON
8 f"")
OOOO-\ON
-
00 -
\ON OO\ON f"")
V'lf"")OOOf"")O'\N
f"")NV'I-
-\oOON-
O'\-
\O
OO\ON OO\ON
OOOf"")O'\NN-
f"")NV'I-O-
V'l00-
0'\ N \O
- V'I
N OO\ON OO-
\O
r-NN
f"")
N
.
N
=
/.,......0.,., '" N - O
00 0'\ \O \O f"")
V'I - 00 f"") \O f"")
gN 8
88
óóóóóóo
r-OO-oooo
8
V'lf"")=-
d ÓÓÓ
\Or-V'lOf"")
V'lV'IONO'\N
o8
8
óóooooo
V'lV'IOOO'\
N\ONV'I-
V'loo o8
V'l8
óóooooo
f"") V'I
V'lO'\N---
o8
8
óóóoooo
NNO\OO'\
88
óoooooo
--V'loo
f"")
\OO'\N08
-
-o ..
óóooooo
-Nf"") V'I\Or-
I I I I I I I
57
N
.
aJ
=
..
...
>O
N
.-
>-
I:
o
"
..
A.
rI2
.-
A.
,"
NI!
,
"
)(J
.-
E
fIj
o
v)
N
=
/:
0'\
00
r---
\O
V')
M
-
N
V')
(""-I
N
V
OO š N -
N V') !"""'I
\O -
V') r--- - -
V')N
N
00
N -
-
-NVr----
- -
ON
\O
M
8 ;! r---
r--- - V') V') N .....
r---r---OV')-
N--
V') V') N
N N
\O V') -
ON \0-
r--- N -
\O N
N
O \O
r---
.....
8000 MV')
V') ::Or---\O
V')O--
, -
-
N
><88 0
N-
r---
N -
r--- -
.....
OO
N V')
\O
8 :};
r--- \O
-NV')
-r---
-
-
-
M r-
o
V')
r-
OO N
N - N
r-
8 000 N-
NV')"d"-
.....N r----
- -
N
\CV') N-O
--
V') V') N
r---N
or---
8
ód
-
\O
-
r---
Ó
000
..........
- -
-
...o V') \O
r-O
óóó
V
N
\O
V
-
\O
V')
Ó
r--- r---
\O N
r--- V')
\O
8
óeS
0\0\0
.....0\0
V') \O
V')o
\O
- V')
\O
88
óóó
"d"V')V')
r-"d"V')
r- ..... V')
r--- \O
r--- \O
r---v
r--- ..... N
88
óóó
O-t
;
V') o Jh
\O
,.,... =>
V N
8
óó
-
\O
"d"
-
Ó
- N
ON
\O r--- N
"d"N
- r--- -
.....O
MOO
óóó
ONN
ON
\Or-N
N
-0-
M-O
\O N -
:!:88
oóó
.....-
- -
M-
. 8
88
óóó
- N
I I I
příklad:
K desítkovému zápisu 579 čísla najdeme jeho dvojkový a osmičkový zápis
pomocí tabulek 0.2.3 a 0.2.5.
579 = 512 + 64 + 2 + 1 = 2 9 + 2 6 + 2 1 + 2° = (1001000011)2;
579 = 5.10 2 + 7 .10 1 + 9.10° = (764)8 + (106)8 + (11)8 =
= (1103)8'
0.3. MATEMATICKÁ LOGIKA
V této kapitole uvedeme základní pojmy a pravidla matematické
logiky, zatímco v částech 12 a 13 se poznatky matematické logiky budeme
zabývat z hlediska technických aplikací.
0.3.1. Výrokový počet
Výrokovým počtem [výrokovým kalkulem] rozumíme tu část mate-
matické logiky, která vyšetřuje vztahy mezi výroky jen se zřetelem .k jejich
pravdivosti nebo nepravdivosti, aniž se zabývá vnitřní strukturou atomárních
výroků nebo zákonitostmi, podle nichž se tyto výroky tvoří.
Abeceda, druhy slov, metaznaky
Abecedou v nějaké oblasti matematiky nazýváme seznam všech znaků,
kterých se v této oblasti používá. Skupina konečně mnoha znaků psaných
zleva doprava se nazývá slovo v dané abecedě. Přitom každý znak abecedy
se považuje za slovo. Abecedu a souhrn všech slov v této abecedě nazýváme
jazykem příslušné oblasti matematiky. Slova označujeme znaky (tzv. metaznaky)
z nové abecedy (tzv. metaabecedy). Skutečnost, že slovo označené metaznakem
qJ je totožné se slovem označeným metaznakem t/J, zapisujeme ve tvaru cp t/J.
. Slovem složeným ze slov qJ a t/J (v tomto pořadí) v nějaké abecedě nazýváme
slovo v téže abecedě, které dostaneme tak, že slova qJ a t/J napíšeme zleva
doprava bezprostředně za sebou ve tvaru qJt/J.
Prázdným slovem nazýváme slovo, k jehož zapsání nepoužijeme žádného
znaku.
Slovo qJ nazýváme podslovem slova t/J [říkáme také, že slovo qJ se vyskytuje
ve slově t/J], právě když existují taková slova X, y, že platí
t/J '" x. qJr' .
59
Přitom jedno ze slov X' I' může být prázdné nebo obě tato slova mohou být
prázdná.
Výroky, funktory, složené výroky
Každé sdělení, u něhož má smysl se ptát, zda je nebo není pravdivé (tzv.
princip vyloučení třetího), a pro něž může nastat právě jedna z těchto možností
(tzv. princip sporu), se nazývá výrok.
Znaky (nebo jejich slovní vyjádření), pomocí nichž se tvoří nové výroky,
se nazývají (výrokotvorné> funktory [logické spojky].
Nejdůležitějšími jsou tyto funktory (alternativní znaky a slovní vyjádření
pro tyto funktory viz v článku 0.1.1 a v části 12):
Funktor negace se značí znakem - (pruh) nebo vyja řuje slovy "není pravda,
že" .
Funktor konjunkce se značí znakem /\ nebo vyjadřuje slovy "a (zároveň>".
Funktor disjunkce se značí znakem v nebo vyjadřuje slovem "nebo".
Funktor implikace se značí znakem nebo vyjadřuje slovy "jestliže...,
(pak>".
Funktor (logické> ekvivalence se značí znakem <=> nebo vyjadřuje slovy
"právě když" ["tehdy a jen tehdy, když"].
,Znaky a slovní vyjádření pro ostatní funktory viz v článku 0.1.1, popř.
v části 12. '
Atomárním výrokem výrokového počtu nazýváme výrok bez funktorů.
Výrok, který není atomární, se nazývá složený.
Proměnná, obor proměnné
Každému objektu studovanému v matematice jednoznačně přiřazujeme
název [jméno], popř. znak (zpravidla písmeno), který nazýváme konstantou.
Název, popř. znak, kterého používáme místo určitých konstant, se nazývá
názvová [jmenná] proměnná nebo stručně proměnná. Stručně říkáme, že dosa-
zujeme za proměnnou příslu. né objekty, místo správného vyjádření, že dosa-
zujeme za proměnnou názvy, popř. znaky příslušných objektů. Názvovou
proměnnou, za kterou je možno dosazovat právě jen čísla, resp. právě jen
výroky, resp. právě jen množiny, lze nazývat číselnou, resp. výrokovou, resp.
množinovou proměnnou.
Konstanty, které lze za proměnnou x dosazovat, se nazývají hodnoty pro-
měnné x. Množina právě těch konstant, které lze za proměnnou x dosazovat,
se nazývá (definiční> obor proměnné x.
60
Abeceda výrokového počtu
Abecedu výrokoveno počtu [výrokovou abecedu] tvoří tyto znaky:
- znaky výrokových proměnných (např. písmena malé latinské abecedy);
- znaky funktorů -, /\, v, =>, <=>;
- znaky (, ) pro levou a pravou závorku;
- znak "" pro totožnost výroků.
Výrokové formule
Výrokové formule, popisující strukturu výroků, jsou definovány takto:
a) Každá výroková proměnná je výrokovou formulí.
b) Jsou-li slova qJ, t/J výrok9vými proměnnými, pak každé ze slov (qJ),
(qJ) /\ (t/J), (qJ) v (t/J), (qJ) => (t/J), (qJ) <=> (t/J) je výrokovou formulí.
c) Žádné slovo, které nelze vytvořit postupným použitím zásad a) a b),
není výrokovou formulí.
Vynechá vání zá vorek ve výrokovém počtu
Zápisy výrokových formulí lze zjednodušit vynecháním závorek podle
těchto zásad:
r ex) Jestliže v zápisu výrokové formule je podslovo (x), kde x je výroková
proměnná, pak závorky vynecháme.
) Znaku - (prúh) se dá přednost před ostatními funktory a závorky, které
tuto přednost stanoví, se vynechají.
y) Znakům /\, V se dá přednost před znaky => a <=> a závorky, které tuto
přednost stanoví, se vynechají.
Počet levých závorek se vždy musí rovnat počtu pravých závorek.
Při větším počtu dvojic závorek lze dvojice okrouhlých závorek vhodně
nahrazovat dvojicemi lomených, popř. složených závorek.
Příklad 1:
Místo (x) /\ (y) lze psát x /\ y.
Příklad 2:
Místo (x) => ((x) v (y)) lze psát x => x v y, ale místo (x) v ((y) => (z)) a
((x) => (y)) v (z) lze psát jen x v (y => z) a (x => y) v z, kde závorky již nelze
vynechat.
Příklad 3:
Slovo x => ((u /\ v) V (v /\ z)), které lze psát ve tvaru
x => [(u /\ v) V (v /\ z)]
.11
61
neboli podle zásady y)
x => (u 1\ v) V (v 1\ z),
je výrokovou formulí, neboť podle bodu a) je x výrokovou formulí, takže
qJ '" x. Slova u 1\ v a v 1\ z jsou podle bodů a), b) výrokovými formulemi,
stejně jako slovo t/J '" (u 1\ v) V (v 1\ z). Dané slovo qJ => t/J je tedy podle
bodu b) výrokovou formulí.
Úmluva:
Protože po dosazení výroků za všechny výrokové proměnné do dané vý-
rokové formule cp dostaneme výrok, lze výrokovou formuli qJ považovat za
zápis tohoto výroku. Proto místo o výrokové formuli qJ, která popisuje
strukturu daného výroku, se někdy stručně mluví o výroku qJ. Z téhož důvodu
se výrokové formule tp, cp 1\ t/J, cp v ,t/J, qJ => t/J, qJ <=> t/J, které se správně po-
stupně nazývají negace výrokové formule qJ, konjunkce, disjunkce, implikace
a ekvivalence [oboustranná implikace] výrokových formulí qJ a t/J, obvykle
postupně nazývají negace výroku qJ, konjunkce, disjunkce, implikace a ekvi-
valence [oboustranná implikace] vý oků qJ a t/J.
Pravdivostní ohodnocení výrokových formulí
Rozšíříme-li výrokovou abecedu o znak I (někdy se používá znaku 1) pro
pravdivost a znak O pro nepravdivost výroku, lze použít označení
. p(cp) = I pro pravdivý výrok qJ,
p( cp) = O pro nepravdivý výrok qJ.
Znaky I, O se nazývají pravdivostní hodnoty.
Pravdivostním ohodnocením výrokové formule nazýváme tzv. pravcjivostní
tabulku (podmínky pravdivosti pro danou výrokovou formuli), která uvádí,
jakých pravdivostních hodnot nabude výroková formule při všech možných
pravdivostních hodnotách výrokových proměnných. Tabulky 0.1 a 0.2 jsou
pravdivostními ohodnoceními výrokových formulí tp, qJ 1\ t/J, qJ V t/J, qJ => t/J
a cp t/J.
Tabulka 0.1
p(q» P( )
O I
I O
62
Ta bulka 0.2
p(q» p( t/J ) p( q> /\ t/J) p(q> v t/J) p(q> t/J) p(q> t/J)
O O O O I I
O I O I I O
I O O I O O
I I I I I I
Předpoklad a zá věr implikace
V implikaci qJ => t/J se výrok qJ nazývá předpoklad [premisa, přední člen,
antecendent, postačující podmínka nebo stručně podmínka J a výrok t/J závěr
[tvrzení, zadní člln, konsekvent, nutná podmínka J. Říkáme tedy, že v implikaci
qJ => t/J výrok qJ je postačující podmínkou pro výrok t/J, zatímco výrok
(závěr) t/J je nutnou podmínkou pro výrok (předpoklad) qJ.
Ekvivalentní výrokové formule
Výrokové formule qJ a t/J nazýváme logicky ekvivalentními a píšeme qJ = t/J,
právě když mají stejnou tabulku pravdivostních hodnot neboli mají stejné
pravdivostní ohodnocení.
T a u t o log i e, k on t rad i k c e
Výroková formule qJ, resp. t/J, jejíž pravdivostní hodnota je p(qJ) = 1, resp.
p(t/J) = O pro jakoukoli volbu pravdivostních hodnot výrokových proměn-
ných, které se v této výrokové formuli vyskytují, se nazývá tautologie, resp.
kontradikce výrokového počtu. '
N :
Ověřme, že výroková formule ip => (qJ => t/J) je tautologií.
Tabulka 0.3
p(q» p( t/J ) p( ) p(q> t/J) p( (q> t/J))
O O I I, I
O I I I I
I O O O I
I I O I I
Z pátého sloupce pravdivostní tabulky 0.3, v níž jsme nejprve určili pravdi-
vostní hodnoty atomárních výrokových formulí, je zřejmé, že daná výroková
formule je tautologií (pátý sloupec obsahuje totiž ve všech řádcích jen znak I).
63
Některé zákony a vztahy výrokového počtu
Zákony idempotence:
CP/\CP = qJ,
cp v cp , = cp .
Vztah mezi ekvivalencí a implikacemi:
cp t/J = (cp => t/J) /\ (t/J => cp).
Zákon o vyloučeném třetím [tercium non datur]:
p(cp v íP) = I .
f.
Zákon sporu:
p( cp /\ íP) = O.
Zákon identity:
p(cP => cp) = I .
Zákon simplifikace:
p(cp => (t/J => cp)) = I ·
Zákon tral'spozice:
cp=> t/J = tp=>ip.
Pravidlo odloučení [modus ponens]:
p(cp) =. I /\ p(cp => t/J) = I => p(t/J) = I.
De M organo vy zákony:
CP/\ t/J= ipvtp,
cpv t/J= ip/\tp.
V článku 12.2 je obsáhlý přehled logických zákonů a vztahů pro konjunkci
a disjunkci, který doplňuje tyto logicky ekvivalentní výrokové formule:
cp t/J . t/J cp,
cp => 'P = íP v t/J,
p(cp=> cp V t/J) = I,
p(cP /\ t/J => cp) = I ·
Příklad:
Dokažme zákon transpozice cp => '" == tp => íP.
64
Tabulka 0.4
p(qJ) p( '" ) p( qJ => "') p(t/i) p( ip) p( tli => )
O O I I I I
O I I O I I
I O O I O O
I I I O O I
Porovnáním třetího a šestého sloupce v tabulce 0.4 lze zjistit, že výrokové
formule qJ => t/J a t/J => ip jsou logicky ekvivalentní.
0.3.2. Predikátový počet
Predikátovým počtem [predikátovým kalkulemJ rozumíme tu část
matematické logiky, která se zabývá popisem a studiem vnitřní (sémantické)
struktury atomárních výroků pomocí slov ve vhodné abecedě. .
Abeceda predikátového počtu
Abecedu predikátového počtu [predikátovou abecedu] tvoří tyto znaky:
a) znaky proměnných pro objekty, které jsou předměty úvah;
b) znaky -, /\, v,. =>, <=> pro logické spojky (funktory),
c) znak V pro obecný [velký] kvantifikátor [obecný [velký} kvantor, gene-
ralizátor], který čteme: "pro všechna" nebo "pro libovolné";
d) znak 3 pro existenční [malý] kvantifikátor [existenční [malý] kvantor,
partikularizátor], který čteme; "existuje";
e) znaky (, ) pro levou a pravou závorku;
f) specifické znaky pro obor, který chceme predikátorovým počtem po-
pisovat, a znak pro totožnost predikátových formulí.
Někdy se do predikátové abecedy zařazují ještě např. tyto kvantifikátory:
00
V čteme "pro nekonečně mnoho",
<00
V čteme "pro nejvýše konečně mnoho",
3! čteme "existuje právě jeden",
00
3 čteme "existuje nekonečně mnoho",
<00
3 čteme "existuje nejvýše konečně mnoho".
65
Primitivní predikátová formule
Atomárním výrokem predikátového počtu nazýváme výrok bez logických
spojek a kvantifikátorů.
Primitivní predikátovou formulí [primitivním predikátem] nazýváme slovo
v predikátové abecedě, které se stane zápisem atomárního výroku po dosazení
konkrétních objektů daného oboru za všechny jeho proměnné.
Druhy proměnných
Proměnná x se nazývá vázaná ve slově qJ, právě když slovo \:Ix nebo 3x
(předpokládáme, že predikátová abeceda obsahuje jen kvantifikátory \:I a 3)
je pod slovem slova qJ. Proměnná, která není ve slově qJ vázaná, se nazývá
volná ve slově qJ (volnou proměnnou je tedy také každá proměnná, která se
ve slově qJ nevyskytuje). Vyskytuje-li se ve slově qJ volná proměnná, nazýváme
ji podstatně volnou proměnnou ve slově qJ.
Slučitelná slova .
Dvě slova qJ a t/J se nazývají 'slučitelná, právě když žádná vázaná proměnná
ve slově qJ není podstatně volnou proměnnou ve slově 1/1, a obráceně.
Predikátová formule
Predikátová formule [v.vroková forma, predikát] nebo stručně formule
(predikátového počtu) se definuje takto:
a) Každá primitivní predikátová formule je predikátovou formulí.
b) Je-li slovo qJ predikátovou formulí, pak také slovo ( ) je predikátovou
formulí.
c) Jestliže slova qJ, t/J jsou slučitelná a jsou predikátovými formulemi, pak
také slova (qJ) 1\ (t/J), (qJ) v (t/J), (qJ) => (t/J), (qJ) (t/J) jsou predikátovými
formulemi [na tyto formule včetně formule (qJ) přenášíme odpovídající názvy
z výrokového počtu J.
d) Jestliže slovo qJ je predikátovou formulí, jejíž proměnná x není vázanou
proměnnou, pak také slova (\:I x) qJ, (3x) qJ jsou predikátovými formulemi.
e) Žádné slovo, které nelze vytvořit postupným použitím bodů a) až d),
není predikátovou formulí.
Podstatně volnou 'proměnnou lze v predikátové formuli nahradit indivi-
duálním objektem, ale vázanou proměnnou jím nahradit nelze.
66
Vynechávání závorek v predikátovém počtu
Úmluvy z výrokového počtu v článku 0.3.1 o vynechávání závorek lze
zachovat také u predikátových formulí. Kromě toho budeme kvantifikátorům
V, 3 dávat přednost před znaky pro logické spojky, takže závorky určující
toto pořadí lze vynechat.
Uzavřené a otevřené predikátové formule
.
Predikátová formule, která neobsahuje podstatně volné proměnné, se na-
zývá uzavřená. Predikátová formule s podstatně volnými proměnnými se
se nazývá otevřená.
Definiční obor a obor pravdivosti predikátové formule
Predikátovou formuli, která obsahuje právě jen proměnné Xl' X 2 , ..., X n ,
označíme V(x l' X2, ..., x n ). Množina právě těch uspořádaných n-tic
(al' a 2 , ..., (ln) [a i (i = 1, 2, ..., n) je konstanta z oboru proměnné Xi]' že po
dosazení všech členů každé z těchto n-tic za všechny' proměnné predikátové
formule V(x I' x 2 , .. ., X n ) se tato formule změní ve výrok, resp. v pravdivý
výrok, se na ývá <definiční> obor D, resp. obor pravdivosti P predikátové formule
V(x l , X 2 , ..., x n ).
Tautologie a kontradikce predikátového počtu
Tautologií, resp. kontradikcí <predikátového počtu> nazýváme predikátovou
formuli, která se stane zápisem pravdivého, resp. nepravdivého výroku,
jestliže do ní za všechny podstatně volné proměnné dosadíme libovolné
konkrétní objekty bez ohledu na obor studovaný predikátovým počtem.
Při zjišťování existence tautologie a kontradikce predikátového počtu
je nutno používat deduktivních metod, neboť obecná metoda není k dispozici.
Vlastnosti kvantifikátorů
Označíme-li V(x) predikátovou formuli s právě jednou podstatně volnou
p.roměnnou x, říkáme, že objekt, pro který po dosazení jeho znaku do pre-
dikátové formule V(x) dostaneme pravdivý výrok, má <charakteristickou>
vlastnost JI: Slovo-
Vx [V(x)]
čteme "každé x má vlastnost V", popř . "všechna x mají vlastnost V' , přičemž
predikátová formule J/(x) se nazývá dosah obecného kvantifikátoru. Obdobně
,slovo
3x [V(x)]
67
čteme "existuje (aspoň jedno) x, které má vlastnost V", popř. "pro některá x
platí V''', přičemž predikátová formule V(x) se nazývá dosah existenčního
kvant(fikátoru.
Pořadí kvantifikátorů V, 3 u predikátových formulí se dvěma proměnnými
nelze obecně zaměňovat.
Oe Morganovy zákony pro predikátový počet
[negace uzavřených predikátových formulí]
Není-li pravda, že objekt x s vlastností V existuje, pak žádný objekt x n má
vlastnost JI: a obráceně, tj.
3x [V(x)] <=> Vx [V(x)] .
Není-li pravda, že každý objekt x má vlastnost JI: pak existuje objekt x,
který nemá vlastnost JI: a obráceně, tj.
Vx [V(x)] <=> 3x [V(x)] .
Není-li pravda, že ke každému objektu y existuje objekt x s vlastností JI:
pak existuje takový objekt }, Le žádný objekt x nemá vlastnost JI: a obráceně, tj.
.
(3x Vy) [V(x, y)] <=> Vx 3y [V(x, y)] .
Příklad:
Výrok "neexistuje n ejvětší reálné číslo y" lze vyjádřit ve tvaru (x E R)
3y Vx (x < y) <=> Vy 3x (x > y) .
0.4. MNOŽINY, ZOBRAZENÍ A FUNKCE
0.4.1. Množiny
Soubor právě těch objektů, které mají určitou vlastnost JI: se nazývá
množina definovaná vlastností JI: Přitomje třeba poznamenat, že nejde o přesnou
definici pojmu množiny, ale jen o intuitivní vymezení pojmu množiny (korektní
definici množiny v implicitním tvaru axiomatického systému viz např. v [45]).
Množinu lze tedy považovat za určenou [danou, definovanou ],jestliže o každém
objektu lze jednoznačně rozhodnout, zda danou vlastnost má nebo nemá,
tj. zda do uvažované množiny patří nebo nepatří.
Množiny se v této příručce zpravidla označují velkými písmeny latinské
abecedy.
68
Objekty patřící do množiny A se nazývají prvky množiny A a v této příručce
se zpravidla označují malými písmeny latinské abecedy.
Množina jejíž prvky jsou množiny, se nazývá systém lnnožin. Systémy
množin označujeme zpravidla velkými skriptovými písmeny (např. '"w, ;?d, .lf).
Rčení ,,(prvek> a patří do (množiny> A", resp. ,,(prvek> a nepatří do
(množiny> A" zapisujeme
a E A, resp. a A .
Přitom místo Xl E A, Xl E A, ..., x n E A, resp. Xl A, Xl A, ..., x n A lze
stručně psát
Xl' x 2 , ..., X n E A, resp. Xl' Xl' ..., X n A.
Vztah E se nazývá incidence [přísluL nost] prvku k množině.
Je-li možno vyjmenovat všechny prvky množiny M (tzv. výčet prvků), pak
se při jejím zápisu znaky všech jejích prvků umístí mezi složenými závorkami
(popř. se vypíšou jen některé její prvky, je-li zřejmé, jak lze vypsat všechny
ostatní prvky); např. množina A, kterou tvoří právě prvky 3, 7 a 11, se zápíše
ve tvaru
A = {3, 7, II} ,
.
přičemž nezáleží na pořadí prvků (znak = zde vyjadřuje, že jde o různé zápisy
téže množiny).
Množina, která obsahuje právě ty prvky oboru U proměnné X, které mají
vlastnost V(x), tj. tvoří obor pravdivosti predikátové formule V(x) (viz článek
0.3.2), se zapisuje
{x E U I V(x)}, {x E U: V(x)}, nebo {x E U; V(x)}
(čteme: množina právě těch prvků X množiny U, které mají vlastnost V)
nebo stručně
{X I V(X'I}, {X: V(x)} nebo {x; V(x)},
není-li třeba připomínat obor U proměnné x.
K názornější interpretaci množin se používá tzv. Vennových diagramů,
kde množina M se znázorňuje jako množina právě těch bodů, které leží
ve vnitřní oblasti rovinné jednoduché uzavřené Jordanovy křivky (obr. 1)
(definice Jordanovy křivky je např. v [199]).
Množina A se nazývá část lpodmnožina] množiny B (popř. množina B
se nazývá nadmnožina množiny A), přičemž píšeme
A c B nebo B ::::> A ,
69
právě když každý prvek množiny A je zároveň prvkem množiny B (obr. 2), tj.
\Ix (x E A X E B) <=> A c B .
Vztah c se nazývá (neostrá> inkluze.
Jestliže pro množiny A, B neplatí A c B, píšeme 4 $ B nebo B A
(obr. 3).
Obr. 1. Vennův diagram množiny M
A 8
A B
Obr. 2. Podmnožina A množiny B
Obr. 3. Vennův diagram množin A, B
(A $ B $ A)
Existuje právě jedna množina, která neobsahuje žádný prvek. Označuje se 0
a nazývá prázdná množina. Přitom pro každou množinu A platí '0 c A.
Říkáme, že množina A se' rovná množině B [množiny A, B jsou identické,
sobě rovné, splývají] a píšeme A = B, právě když A c BaB c A, tj.
A c B/\B c A<=>A=B
/.
(antisymetričnost inkluze).
Jestliže pro množiny A, B neplatí A = B, píšeme A * B a říkáme, že
množina A je různá od množiny B [množina A se nerovná množině B].
Množina A se nazývá vlastní část [vlastní podmnožina] množin y B, přičemž
píšeme
A c B nebo B::::> A ,
právě když A c B a zároveň A =t= B, tj.
A c B/\A=t=B<=>AcB.
Relace c se nazývá ostrá inkluze.
70
Tvoří-li množinu n prvků, pak počet všech jejích podmnožin se rovná 2 n .
Systém všech podmnožin množiny M se značí 9(M) (někdy také 2 M nebo
exp M) a nazývá se potenční množina množiny M.
0.4.2. Množinové operace
Sjednocením množin A a B nazýváme množinu A n B (čteme: A sjed-
noceno s B) právě těch prvků, které patří aspoň do jedné z množin A a B
(obr. 4).
Sjednocením neprázdného systému .sl množin A nazýváme množinu
U A (stručně UA)
Aed
právě těch prvků, které patří aspoň do jedné z množin patřících do systému .rd
(obr. 5). Sjednocení konečného systému množin AI' A 2 , ..., An' resp. neko-
nečného systému množin AI' A 2 , ... značíme
n
AI U A 2 U ... U An = U Ai'
i = I
00
resp. A I U A 2 U ... = U Ai .
i = I
G
5
OA.
i =1 L
AuB
Obr. 4. Sjednocení A u B množin A a B
.
Obr. 5. Sjednocení UA systému
.r;i = {Al'A 2 ,A 3 ,A 4 ,A s }
Průnikem množin A a B nazýváme množinu A n B (čteme: A průnik B)
právě těch prvků, které patří do množiny A a zároveň do množiny B (obr. 6).
Průnikem neprázdného systému ..9/ množin A nazýváme množinu
n A (stručně nA)
Aed
právě těch prvků, které patří zároveň do všech množin patřících do systému .sl
(obr. 7). Průnik konečného systému množin AI' A 2 , ..., An' resp. nekonečného
systému množin AI' A 2 , ... značíme
n
AI nA 2 n...nA n = nAi'
i = 1
00
resp. AI n A 2 n ... = n Ai .
i = 1
71
Rozdílem množin A a B (v tomto pořadí) nazýváme množinu A \ B (někdy
také A - B) právě těch prvků, které patří' do množiny A, ale nepatří do
mnoŽiny B, tj. rozdíl A \ B obsahuje právě ty prvky množiny A, které nepatří
do množiny B (obr. 8).
B
Af\ B
4
nA,
L
i =1
Obr. 6. Průnik A n B množin A a B
Obr. 7. Průnik n A systému
,Qj = fA., A 2 . A 3 , A 4 }
z
A"B
Obr. 8. Rozdíl A '" B množin A a B
Obr. 9. Doplněk A množiny A
v množině Z
Dopliíkem [konlplementem] n1nožiny A V množině Z :::::> A nazýváme množinu
A = Z \ A (někdy ji také značíme Ai, CzA nebo A ) (obr. 9). Množina Z
se nazývá základní nlnožina nebo univerZtl1n. Je-li zřejmé, ke které základní
množině se doplněk vztahuje, lze jej stručně označit A' nebo A "'.
Symetrick)Jm rozdílem [symetrickou diferel1ci] rnlložin A a B nazýváme
množinu (obr. 10)
A B = (A \ B) u (B \ A)
(někdy ji také značíme A B).
Množiny A, B se nazývají disjunktni, resp. konjunktni, právě když A n B = (/)
(obr..ll), resp. A n B =t= (/) (viz obr. 6).
Systém .sI množin se nazývá disjunktní, právě když každé dvě různé mno-
žiny systému .cd jsou disjunktní (obr. 12); říkáme také, že n1110žiny systénui .cI
tvoří disjunktní systénl [jsou po dvou disjunktní].
"
72
:, Sjednocení UA systému ." množin se nazývá disjunktní, jestliže všechny
nožiny systému .'7/ tvoří disjunktní systém.
f'
f.
AtJ8
Obr. 10. Symetrický rozdíl A B
množin A a B
G
0.4.3. Věty O množinách
o
Ar. B =
Obr. 11. Vennův diagram disjunktních
množin A a B
Obr. 12. Disjunktní systém $I množin
AI' A 2 , A 3 , A4
Nechť A, B, C, AI' A 2 , ..., An jsou libovolné podmnožiny základní
.množiny Z.
Vlastnosti rovnosti a inkluze množin
A=A
A=B<::>B=A
A=B/\B=C=>A=C
A c A
(/) c A,
A c B/\B c C=>A c C
A c (A u B),
A c B <=> A u B = B,
A c C /\ B c C <=> (A u B) c C,
A c B <=> B' c A',
(retlexívnost rovnosti),
(symetričnost rovnosti),
(tranzitivnost rovnosti),
(retlexívnost inkluze),
(tranzitivnost inkluze, obr. 13),
(A n B) c A,
A c B <=> A n B ' A,
C c A /\ C c B <=> C c (A n B),
73
A n B = (/) <=> A c B',
A u B = Z <=> A' c B,
A n B = (/) <=> B c A',
A u B = Z <=> B' c A.
C
8
A
Obr. 13. Tranzitivnost inkluzí A B,
B C
Vlastnosti sjednocení.. a průniku množin
AuB=BuA,
AnB=BnA
(komutativnost sjednocení a průniku),
(A u B) u C = A u (B u C) = A u B u C ,
(A n B) n C = A n (B n C) = A n B n C
(asociativnost sjednocení a průniku),
(AI u... u An) n B = (AI n B) u ... u (An n B)
(distributivnost sjednocení vzhledem k průniku),
(AI n ... n An) u B = (AI U R) n ... n (An u B)
(distributivnost průniku vzhledem k sjednocení),
AuA=A,
AnA=A
(idempotentnost sjednocení a průniku),
AuZ=Z, AnZ=A,
Au0 =A, An0 =0,
A n (A u B) = A .
Vlastnosti rozdílu množin
0\A=0, A\0=A, A\A=0;
A \ B c A,
A \ B = A \ (A n B),
(A \ B) n B = 0,
(A \ B) n (A n B) = 0,
74
(A \ B) n (B \ A) = 0,
A u B = (A \ B) u (B \ A) u (A n B),
(AI u...uAn)\B = (AI \B)u...u(An\B),
(A In... n An) \ B = (A I \, B) n ... n (An \ B),
(A \ B) n (A \ C) = A \ (B u C),
(A \ B) u (A \ C) = A \ (B n C),
A \ (B I u... U Bn) = (A \ B I ) n... n (A \ Bn),
A \ (B ln. .. n Bn) = (A \ B I ) U ... U (A \ Bn)
(poslední dva vzorce se nazývají de Morganovy vzorce).
Vlastnosti doplňku množiny
(A')' = A
A U A' = Z, A n A' = 0;
z' = 0, (/)' = Z;
(AI U ... U An)' = A ' I n... n A ,
(AI n... n AnY = A / I U ... U A
(poslední dva vzorce jsou důsledky de Morganových vzorců).
Příklad:
V obrázcích 14 až 16 jsou po řadě znázorněny množiny (A n B) U C,
(A U B) n C a (A 6. B) 6. C.
B
{AnB)uC
(AvB)nC
Obr. 14. Množina
(A n B) u C =
= (A u C) n (B u C)
Obr. 15. Množina
(A u B) n C =
= (A n C) u (B n C)
Obr. 16. Množina
(A B) C
75
0.4.4. Kartézský součin dvou množin
U spořádanou dvojicí objektů a a b (v tomto pořadí) nazýváme systém
[a, b J = {{a}, {a, b} }
,množin, kde a, resp. b se nazývá první, resp. druh v člen uspořádané dvojice [a, b J.
Přitom
[a,bJ * [b,a] a * b
neboli
[a,b] = [b,a] a = b.
Obdobně se zavádí pojem uspořádané n-tice [a l , a 2 , ..., (ln].
Neuspořádanou dvojici objektů a, b nazýváme množinu
{ a, b} = {a} u {b} .
Obdobně se zavádí pojem neuspořádané n-tice {a l ,a 2 ,...,a n }.
I
I I
o 6
Q1 Oz aJ
'----v--J
A
y
3
2
AxB
o
--
2 3 4 x
Obr. 17. Kartézský součin množin A a B
Obr. 18. Kartézský součin intervalů
< 1, 4> x < 2, 3)
Kartézským součinem A x B neprázdné rnnožiny A a neprázdné množiny B
(v tomto pOř'1\dí) nazývám množinu právě těch uspořádaných dvojic [a, b ],
kde a E A a b E B (obr. 17 a 18). Jestliže aspoň jedna z množin A, B je prázdná,
klademe A x B = 0.
Kartézský součin množin
A = {a l , a 2 , ..., a m },
B = {bl' b 2 , ..., b n } ,
se tedy rovná
A x B = {[al' bl]' ..., [a l , b n ], [a2' bl]' [a 2 , b 2 ], .J..
. .., [ a 2, b n]' ..., [ a m , b I ], [ a m , b 2]' .. ., [a m , b n]} ,
což lze zapsat ve tvaru tabulky 0.5.
76
Tabulka 0.5
hl b 2 .. . h"
lil [£II' b l ] [a l ,h 2 ] .. . [(II' h,,]
a 2 [a 2 ,b l ] [a 2 ,b 2 ] [a 2 . b,J
.. .
.. .
.. .
a m [am,h l ] [a m .h 2 ] .. . [ lim' h,,]
Speciálně při A = B se kartézský součin A .x A nazývá druhá karté:skÚ
mocnina Innožžny A a značí 'se stručně" A z.
Obdobně A 1 X Az x ... x Am kde AI, Az, ..., An jsou neprázdné množiny,
značí množinu. právě těch uspořádaných n-tic [a 1 a2 ..., an] kde ai E Ai pro
i = 1, 2, . .., n. Speciálně A 1 X A 2 X ... x An pro AI = A 2 = ... = An = A
se nazývá n-tá kartézská lnocl1ina 111l1ožiny A a značí se stručně A n .
Množiny, jejichž prvky jsou právě jen čísla (reálná, popř. komplexní),
se nazývají číselné množiny (viz tabulku 0.6 na str. 90).
0.4.5. Binární rel ace
D e f i nic e b i n á r n í r.e I a c e
Každou podmnožinu R kartézského součinu A x B nazýváme <binární>
relací z množiny Á do množiny B [(binární> relací lnezi rnnožina111i A a B
(v tomto pořadí)] a zapisujeme jako uspořádanou trojici [R; A, B] (obr. 19).
Známe-li množiny A, B nebo uvažujeme-li o vlastnostech binárních relací
bez ohledu na tyto množiny, pak místo [R; A, B] lze stručně psát jen R
a mluvit o (binární> relaci R. Je však třeba si uvědomit, že i při R 1 = Rz je
[R 1 ; A,B] = [Rz; C,D], právě když A = C a B = D.
Jestliže [x, y ] E R, říkáme, že (prvek> x je v (binární> relaci R s (prvkeln> y,
a píšeme
R
xRy nebo x - y ,
77
přičemž tyto zápisy představují tzv. přiřazení prvku y v <binární) relaci R
prvku x. Proto také říkáme, že prvek y je v <binární) relaci R přiřazen prvku x.
Jestliže [x, y] R píšeme x R y a říkáme že <prrek) x není v <binární)
relaci R s <prvkeln) y.
02 (R) =B i u 8 2
Ax8
8i ------
1
I
Bi
j
- - _. .- - -
.
,----- -- ----- -_ .
8 2 I
L__ ---------.-------. I
I
I
!
R=PuQ
Ai
A 2
Obr. 19. Binární relace
I ; 01 (RJ=AtuA z R c A x B
T
A
První,n [dejiničnínI. vstupnín1, lev.vn1] oborem nebo vzorem 0 1 (R) [někdy též
D(R), dom R] relace [R; A, B] nazýváme množinu právě těch prvků x E A,
z nichž ke každému existuje aspoň jeden takový prvek Y E B, že xRy, tj.
°l(R) = (xEAI3YEB:xRy}
(viz obr. 19).
Druhým [vJ J stupníI11, praV)ltl1] obore111 nebo obrazenI 02(R) [někdy "také
R(R}, rngR] relace [R;A,B] nazýváme množinu právě 'těch prvků YEB,
z nichž ke každému existuje aspoň jeden takový prvek x E A, že xRy, tj.
02(R) = {y E B 13x E A: xRy} .
I
Relace v množině a na množině
Speciálně každou podmnožinu R množiny A x A = A 2 nazýváme <binární)
relací v množině A a značíme [R; AJ (obr. 20); přitom množinu A nazýváme
nosnou lnnožinou [nosičem] <binární) relace R. Protože
A x B C (A u B) x (A u B) ,
lze místo relace [R: A, B] uvažovat relaci [R; MJ, kde nosná množina
M = A u B.
78
Každou podmnožinu R množiny A x A = A 2 , kde A = Ol(R), nazýváme
<binárnľ) relací[R; AJ na množině A (obr. 21). Každá relace [R; AJ na množině
A je zřejmě také relací [R; AJ v množině A, ale ne každá relace [R; AJ v mno-
žině A je relací na množině A. V binární relaci [R; AJ na množině A je tedy
každý z prvků množiny A prvním členem aspoň jedn z uspořádaných dvojic
z binární relace [R; A].
A2
A2
A
I
L RJ_ _
A
02 (R)
J____ '____ _____
I
I
I
I
I
I
I
""'--"-- - --
I
I
1--
I
01 (R)
A
A =01 (R)
Obr. 21. Binární relace na množině A
Obr. 20. Binární relace v množině A
ln verzní relace
Inverzní relací k relaci R [inverzľ relace R] z množiny A do množiny B na-
zýváme takovou binární relaci R _ 1 (někdy se také značí R - 1) z množiny B
do množiny A, která obsahuje právě ty uspořádané dvojice [y, x] E B x A,
že [x, y] E R (obr. 22), tj.
R-l = {[y, x] I [x, y] E R} .
8
b .--
A
I I
'* Jr
a b
8
I
-I
L_J
I I
I I
. j
c d
Obr. 22. Inverzní re'lace R - 1
k relaci R
I
\. a -
b
1
79
Skládání binárních relací
Relaci složenou z relaci R (= množiny A do množiny B) a S (z množiny B
do množiny C) [kompozici, kompozitem, součinem relaci R a S] nazýváme
takovou binární relaci T = R c S (čteme: R složeno s S) (někdy také R * S, RS)
z množiny A do množiny C, která obsahuje právě ty uspořádané dvojice
lx, z ] E A x C, pro něž existuje takový prvek y E B, že [x, y ] E R a [y, z ] E S
(obr. 23), tj.
R 8 S = {[ x, z] I 3 y E B: [x, y ] E R /\ [y , z] ES} .
Uvedená operace se nazývá skládáni [násobení] relaci RaS.
8
'-
B
c
Obr. 23. Kompozit T = R r) S
relací R a S
Protože pro skládání relací platí asociativní zákon, tj. (A c B) <) C =
= A o (B c C), lze závorky vynechat a psát A oB c C. Pro AI = A 2 = ... = An
místo A I o A 2 o . .. o An stručně píšeme A n.
Vlastnosti binárních relací
Jestliže R je libovolná relace na množině A a x, y, z E A, říkáme, že binární
relace Rje na množině'A:
80
- identická [identitou' totožnost," rovností], a označujeme ji id A , právě když
pro \Ix E A z přiřazení x id A Y plyne x = y E A;
- reflexívní, právě když pro \Ix E A platí xRx, tj. právě když idA c R
(obr. 24);
- are.flexívní, právě když pro Vx E A platí x R x (z každého přiřazení xRy
plyne x * y), tj. právě když id A n R = 0;
- sYlnetrická, právě když z každého přiřazení xRy plyne yRx, tj. právě
když R = R _ 1 (viz obr. 24);
- aSY111etrická, právě když z každého přiřazení xRy plyne y R x, tj. právě
když RnR_ 1 =(/);
- flntisymetrická, právě když z každých dvou přiřazení xRy, yRx plyne
x = y, tj. právě když R n R-I C id A ;
- tranzitivní, právě když z každých dvou přiřazení xRy, yRz plyne xRz,
tj. právě když R ,) R C R (obr. 25);
00-
A
A 2
5 0--- 1 --,-- --.,..-
I I I I
4o--- L --- --+---t--+
I I i I I
I
3 0--- -l---+--t--
R I I
2 0-- +--t--I-- -l
I I I I I
1 0-- -- -,.__-L__.J
I I I
! I I
Ó 6 b
3 4 5
A 2
d -
co--
A
b 0--
,
ó
o
I
g
I
I
<:>
1
I
6
2
A
id A R
A
[ 4, 3 ] I [3, 5] E R [4 1 5] E R
Obr. 24. Reflexívní a symetrická relace
Obr. 25. Tranzitivní relace
atranzitivní, právě když z každých n (n > 2) přiřazení Xl Rx 2 , X2 Rx 3, ...
_ 00
..., xnRx n + I plyne xl R x n + l' tj. právě když ( U Rk) n R = (/);
k=2
- úplná, právě když obsahuje všechna přiřazení xRy, yRx, tj. právě když
R n R _ 1 :::::> A 2 \ id A ;
- univerzální, právě když obsahuje všechna přiřazení xRx, ,xRy, yRx,
tj. právě když R n R-l = A2;
81
00
cyklická, právě když U Rk c R_ 1 ;
k=l
00
acyklická, právě když (U ,Rk) n R - 1 = (/).
, k=l
Druhy binárních relací
Binární relaci nazýváme:
- tolerancí [relací tolérance], právě když je reflexívní a symetrická;
- ekvivalenci [relací ekvivalence], právě když je reflexívní, symetrická
a tranzitivní;
- kvaziuspořádáním, právě když je reflexívní a tranzitivní;
- <neostrým) uspořádáním [relací <neostrého) uspořádání] (znak ),
právě když je reflexívní, antisymetrická a tranzitivní;
- ostrým uspořádáním [relací ostrého uspořádání] (znak -<), právě když je
areflexívní a tranzitivní;
- úplným <neostr.vm) uspořádáním, resp. úplným ostrým uspořádáním
[lineárním <neostr.vm) uspořádáním, resp. lineárním ostrým uspořádáním],
právě když relace R je <neostrým) uspořádáním, resp. ostrým uspořádáním
a pro každou dvojici různých prvků x, y E A platí bud' xRy, nebo yRx.
Uspořádaná a úplně uspořádaná množina
Množina A, v níž je dáno uspořádání , resp. ostré uspořádání -< se nazývá
uspořádaná, resp. ostř uspořádaná a značí se [ ; A], resp. [ -<; A].
Uspořádanou množinu, v níž uspořádání je úplným uspořádáním, nazý-
váme úplně [lineárně] uspořádanou množinou nebo řetězcem.
Porovnatelné prvky
Prvky x, y E [ ; A] se nazývají porovnatelné, resp. neporovnatelné, právě
když platí aspoň jedno z přiřazení x y, y x, resp. neplatí žádné z nich.
Prvek a se nazývá maximalní, resp. minimální prvek uspořádané množiny
[ ; A], právě když pro všechny prvky x E A z přiřazení a x, resp. x a
plyne a = x. Prvek a se nazývá největší, resp. nejmenší prvek uspořádané
množiny [ ; A], právě když pro všechny prvky x E A je x a, resp. a x.
Maximální, resp. minimální prvek úplně uspořádané množiny A značíme
max A, resp. min A.
Dobře uspořádaná množina
Dobře uspořádanou n1nOZlnou nazýváme úplně uspořádanou množinu,
právě když každá její neprázdná podmnožina obsahuje nejmenší prvek.
82
Horní a dolní zá vora úplně uspořádané množiny
H orní, resp. dolní, závorou [horní, resp. dolní mezí] <úplně uspořádané)
množiny [ : A] v <úplně uspořádané> lnnožině [ ; MJ (A c M) nazýváme
každý takový prvek kE M, že x k, resp. k x pro všechny prvky x E A.
Supremum a infimum úplně uspořádané množiny
Supremem, resp. infirnem <Úplně uspořádané> 1111ložiny [ ; A] r <Úplně
uspořádané> 111nožině [ ; M] [A c M) nazýváme nejmenší horní závoru,
resp. největšÍ dolní závoru množiny A v množině M. Supremum, resp. infimum
množiny A v množině M zhačÍme
sup A, resp. inf A (stručně sup A, resp. inf A).
M M.
Speciálně v množině R zavádíme:
Prvek T E R nazýváme supremeln neprázdné množiny A G R, splňuje-li
tyto podmínky:
1. Pro každý prvek x E A platí x < T.
2. Jes liže T' < T, pak existuje takový prvek Xo E A, že Xo > T'.
Prvek t E R nazýváme infinleln neprázdné l11nožiny A c R, splňuje-Ii tyto
podmínky:
1. Pro každý prvek x E A platí x > t. ,
2. Jestliže ť > t, pak existuje takový prvek Xo.E A, že Xo < ť.
.
0.4.6. Zobrazení, operace, funkce
Zobrazení
Zobrazení,n j' z množiny A do n1110žiny B (A =F (/), B =F 0) nazýváme binární
relaci [J; A, B], o níž platí, že každému prvku x E A je přiřazen nejvýše jeden
takový prvek Y E B, že [x, y] E j' (obr. 26). Zobrazení má tedy tu vlastnost,
o
2
Ó
7
Obr. 26. Zobrazení.ľ z množiny A
do množiny B
A
8J
že jestliže [x 1')'1], [X2' Y2] E ,ľ a XI = x 2 , pak Yl = Y2' Místo [x, y] E f často
píšeme y == ,ľ(x) [někdy též )' = .lx, .ť: x y nebo x y, popř. jen x y,
víme-li, o jaké zobrazení jde J. Prvek y = .ľ(x) E B nazýváme hodnotou ::ob-
rll:el1í ,ť ľ hodě x nebo ohrll:eln prrku x r :obrazení f; 'kdežto prvek x E A
nazýváme r:orel11 piTku)' == .ľ(x) r =()bra el1í .l Množinu všech vzorů prvku
.r E B nazýváme LÍp111J 111 rZOrel11 prrku y v :obrazellí j: Má-li prvek y právě
jeden vzor, pak tento vzor označujeme j'-- 1 (y).
Množinu ()lCľ) [někdy také j'-l(B), DC/,) nebo domj] právě těch prvků
x E A, z nichž ke každému existuje právě jeden takový prvek Y E B, že [x, y] E f,
nazýválTIC <d tilli{llíI11> oburern nebo <ÚpbZ.Vlll> vzorenl zobrazeni f z nUložiny
1 do 1111zo=illY B.
Množinu 0lCľ) [někdy také'.ľ(A), RCl), H(j') nebo rng!] právě těch prvků
.r E B, z nichž ke každélTIU exist uje aspoň jeden takový prvek x E A, že [x, y] E f,
nazýváme ohorťlll hodnot nebo obrll:eln =obra ení ,ľ = n1nožiny A do množiny B.
Jestliže lvI c 01(!), pak množina {f(a) I a EM} = f(M) se nazývá obraz
Innožiny 1\1. v zobrazení f
Jestliže N c 02(j'), pak množina {aE0 1 (!)lf(a)EN} =f-l(N) se nazývá
<úpln.\ > vzor množiny N z; zobrazení f
Druhv zobrazení
01
Zobrazení .ľ z množiny A do množiny B se nazývá:
- :oh"(l ení.ť I1zlložiny A do nll10žžny B, právě když vzorem zobrazení! je
množina A (obr. 27), tj.
"
f'-- 1 ( B) = A 1\ .ľ ( A) c B
(toto zobrazení se někdy značí .ť: A B);
Ax8
AxB
B j }O:(f
l
B
Oz (f)
,-- ----
I
A
I I I
I
I 01 (f) I I
t.- ..... I- I
, I
'---- -- y
A
: 01 (f) I
1---- -------.I
I
- - - --- --...,--- ---'
()br, 27. Zobrazení.ľ množiny A
do n1nožiny B
Obr. 28. Zobrazení f z množiny A
na množinu B
84
"
zobrazení j' z lnnožiny A na lnnožinu B [suljektivní zobrazeni, surjekce,
nakrytí z 111nož;ny A na n1110žinu B], právě když obrazem zobrazení f je mno-
žina B (obr. 28), tj.
j l(B) c A /\ ť(A) = B
- zobrazení f n1110žiny A na množinu B Lsurjektivní zobrazení, surjekce,
nakrytí n1110žiny A na množinu B], právě když vzorem, resp. obrazem zobrazení
f je množina A, resp. B (obr. 29), tj.
j l(B) = A /\ f(A) = B
(toto zobrazení se někdy značí f: A B);
- prosté [injektivní] zobrazeňi [injekce, vloženi] f z množiny A do množiny B,
právě když pro každé dva různé prvky Xl' X 2 Ef-I(B) platí f(x l ) * f(x 2 )
....
(obr. 30), tj. právě když
f-I(B) c A 1\ f(A) c B 1\ (v[ Xl' YI] ,
[X 2 , Y2] E f: Xl * X 2 => YI * Y2);
AxB
AxB
r __h
r----- --
8 02 (f)
J__h
I
I
I
I
---l------
!
I
-------1
I
I
I
I
(
I
B1I0 2 (f)
01 (f)
1-- - -- - -
I
, I
,
I 01 (f)
r--
---
- ---/
'----
.....
A
A
Obr. 29. Zobrazení f množiny A
na množinu B
Obr. 30. Prosté [injektivní] zobrazení f
z množiny A do množiny B
1
B !
AxB
I
I
I
I
Ir
.
"
0 1 (f)
....
I
I
I
I
'I
Obr. 31. Vzájemně jednoznačné
[bijektivní] zobrazení množin A a B
--
A
85
- r::ájel1111ě jedlloznačné [iedl1ojedno načl1é, bUektivní] zobrazení [bijekce]
,ľ 1111l0=;11 A a B (v tomto pořadí), právě kdyžje prostým zobrazením množiny A
na množinu B (obr. 31), tj. je injektivním [prosté] a surjektivním zobrazením
množiny A na množinu B (toto zobrazení se někdy značÍ ,ľ: A +-+ B);
- identické ::ohra::ellí .ľ Innožiny A l1a I'l'lnož;nu A, právě když každému
prvku x E A je přiřazen právě prvek x;
- :: )brazení j' r I1zllož;ně A, právě když A = B;
- :ohra::ení .ľ Ila 111l1ož;ně A, právě když je zobrazením množiny A do
množiny B = A.
Parciální zobrazení
Jestliže ,ľ je zobrazení množiny A do množiny B a platí M c A, pak zob-
razení j'l M, jehož definičním oborem je množina M a které každému prvku
x E M přiřazuje právě prvek tť I M) (x) = j'(x), nazýváme parciálním zobra-
Zeníl11 .ľ I M <;lldllkoraIlJ 111 na l11nožinu M zobrazením I> nebo parcializací
[zÚžením, restrikcí] :: množiny A na množinu M zobrazení I.
Zúžení a prodloužení zobrazení
Jsou-li 1 a 9 dvě zobrazení, pak zobrazení 1 nazýváme parcializací
[zÚže ím] zobrazeni g z 01(g) na 0 1 (1) a zobrazení 9 nazýváme prodloužením
obra::eni .ľ :: 0IC() na 01(g), právě když 01(j') c 01(g) a 9 I 0 1 (1) = f.
Inverzní zobrazení
Jestliže .ť je bijektivní zobrazení množin A a B, pak ke ka dému prvku
Y E B existuje právě jeden takový prvek x E A, že j'(x) = y. Tím je definováno
inverzní ::obrazení ..f- 1 k zobrazení f.
Složené zobrazení
Jestliže j' je zobrazení množiny A do množiny B a g je zobrazení množiny
I(A) do množiny C, pak zobrazení h, které každému prvku x E A přiřazuje
právě prvek h(x) = g(j'(x)) E C, se nazyvá složené zobrazení h s vnější složkou 9
a vnitřní složkou .ť; píšeme h = g(j') nebo h = g C ,f (v některé literatuře je
zaměněno pořadí a píše se 1 g).
Operace
Zobrazení (JJ Il-té kartézské mocniny A" do množiny A nazýváme n-arnl
operací l1a nznožině A (11 E N); l1ulární (O-ární) (11 = O) operací na množině A
rozumíme volbu určitého (tzv. vy::načeného) prvku z množiny A. Číslo n = a(w)
86
se nazývá árnost operace w, přičemž pro n = O, 1, 2, 3, . .. se příslušná operace
postupně nazývá nulární, unární, binární, ternární,... operace na množině A.
příklad:
Jestliže A = {1, O} je množina všech pravdivostních ohodnocení výro-
kových proměnných, kde 1, resp. O značí pravdivost, resp. nepravdivost, pak
negace N je unární operací na množině A, kdežto konjunkce K, disjunkce D,
implikace I a ekvivalence E jsou binárními operacemi na množině A.
Označíme-li
a = [1, 1], b = [1, O], c = [O, 1], d = [O, O],
platí
N = {[I, O], [O, l]},
K = {[a, l], [b, O], [c, O], [d, O]},
D = {[q,I], [b,1], [c,I], [d,O]},
1= {[a,l], [b,O], [c,l], [d,I]},
E = {[a, l], [b, O], [c, O], [d, l]}.
Mnohoznačné zobraze.ní
Někdy se zavádí pojem mnohoznačného zobrazení rJ.. z množiny A do množiny B
(tj. některému prvku x E A jspu přiřazeny aspoň dva prvky množiny B)
tak, že se místo množiny B uvažuje systém 2 B a prvku x E dom a je přiřazena
právě jedna množina Bx E 2 B . Dříve definované zobrazení se pak pro o lišení
nazývá jednoznačné.
Funkce
Funkcí nazýváme zobrazení f z libovolné množiny A do nějaké číselné
množiny B. Funkce f z množiny A do číselné množiny B je tedy binární relací
[f; A, B], o níž platí, že každému určitému prvku x E A je přiřazeno nej výše
je dno takové číslo Y E B, že [x, Y ] E h tj. jestliže [Xl' Yl]' [X 2 , Y2] E J a Xl =
= X 2 ' pak Yl = Y2' Místo [X,Y]EJ často píšeme Y =J(x) (někdy též
Y = fx, f: X Y nebo X Y, popř. jen x Y, víme-li, o jakou funkci jde).
Číslo Y z uspořádané dvojice [x, y] E f nazýváme (funkční> hodnotou funkce
f v prvku x E A.
Množinu 0l(J) [někdy také f-l(B), D(f) nebo domf] právě těch prvků
x E A, z nichž ke každému existuje p r á věj e dno takové číslo Y E B, že
[x, y] E h nazýváme (definičním> oborem funkce f. Množinu 02(J) [někdy
také f(A), R(j'J nebo rngf] právě těch prvků Y E B, z nichž ke každému
existuje aspoň jeden takový prvek xEA, že [X,Y]Ej; nazýváme ohoreln
87
<.funkčních) hodnot [funkčním oborem, množinou všech funk ních hodnot]
funkce f
Rovnost funkcí
Jestliže funkce j' a 9 mají stejný definiční obor ° 1 (f) = ° 1 (g) = A =t= 0
a pro každý prvek x E A platí rovnost .f(x) = g(x), říkáme, že funkce 1 a y
JSOll si rovny na množině A.
Součet, součin a podíl funkcí
Mají-li funkce f' a 9 stejný definiční obor 01(f) = 02(g) = A =t= (/), pak
funkci h, resp. k nazýváme součtem, resp. součinem fÚnkcí j' a 9 na množině A,
jestliže pro každý prvek x E A platí h(x) = f(x) + g(x), resp. k(x) = j'(x) g(x).
Jestliže pro každý prvek x E A platí g(x) =t= O a l(x) = f(x)1 g(x), pak funkci I
,nazýváme podílem funkci 1 a 9 na ml10žině A.,
Prostá funkce
Funkce f se nazývá prostá, právě když pro každé dva různé prvky Xl' x 2 E
E 0 1 (f) platl f(x 1 ) =t= l(x 2 ).
Druhy funkcí
Funkci f nazýváme:
- reálnou funkcí (jedné) reálné proměnné, právě když
, ° 1 (f) c R,
02(f) c R;
- reálnou funkcí n reálných proměnných, právě když
01(f) C Rn,
02(f) c R;
- reálnou funkci (jedné> komplexní proměnné, právě když
01(f) c C*,
02(f) c R;
- reálnou funkci n komplexních proměnnýc.h, právě když
0l(f) C (c*)n,
02(f) c R;
- komplexní funkcí (jedné) reálné proměnné, právě když
° 1 (f) c R,
02(f) c c*;
- komplexní funkci n reálných proměnných, právě když
01(1) C Rn,
02(1) c C*;
88
komplexní ,funkcí (jedné> kOlnplexní proměnné právě když
0 1 (f') c C # ,
02(f') C c#;
komplexni funkci n komplexních proměnných, právě když
01(f) C (C#r,
02(.f) C C# .
.
Posloupnosti
(Nekonečnou> posloupností nazýváme Zohľd7ťní množiny N všech klad-
ných celých čísel do libovolné množiny M. K onei'I1()U posloupností nazýváme
zobrazení úseku U n = {1, 2, ..., n} do libovolné množiny M. Je-li M = R,
mluvíme o posloupnosti reálných či sel. Je-li M systém funkcí, mluvíme o po-
sloupnosti funkcí.
0.4.7. Konečné, nekonečné a spočetné množiny,
mohutnost množiny
Říkáme, že lnnožiny A a B jsou ekriv.alentni [ekvipolentni] nebo že
množina .4 je ekvivalentní [ekvipolentni] s množinou B, a píšeme A '" B, právě
když existuje bijektivní zobrazení množin A a B.
Množina \4 se nazývá konečná, právě když není ekvivalentní se žádnou
svou vlastní podmnožinou, tj. právě když každé injektivní zobrazení
f: M M je surjektivní. Množina se nazývá nekonečná, právě když není
konečná, tj. právě když je ekvivalentní s nějakou svou vlastní podmnožinou.
Množina se nazývá spočetná, právě když je ekvivalentní s podmnožinou
množiny No všech přirozených čísel. (Někdy se za spočetné množiny
považují právě jen množiny ekvivalentní s množinou No. Pak konečné množiny
a spočetné množiny se souhrnně nazývají nejvý. e spočetné n1nožiny )
Říkáme, že množiny A a B n1ají stejnou mohutnost nebo že množiny A a B
mají stejné kardinálni číslo, právě když jsou ekvivalentní. Mohutnost množiny A
se značí card A [nebo též nt(A), popř. IAI jde-li o konečnou množinu].
Pro konečné množiny pojem mohutnosti splývá se známým pojmem
počtu prvků množiny. Mohutnost množiny No všech přirozených čísel
se značí o (čteme: alef nula). Říkáme, že nlnožžna má mohutnost kontinua,
právě když je ekvivalentní s množinou R všech reálných čísel; tato mohutnost
se značí .
Existuje-li bijektivní zobrazení mezi množinami A a M, přičemž M c B
(tj. M je vlastní částí množiny B), ale neexistuje-li bijektivní zobrazení mezi
89
množinami A a B, pak říkáme, že množina A má menší mohutnost než množina B,
nebo že množina B má větší mohutnost než množina A.
Systém . (M) všech podmnožin množiny M má větší mohutnost než mno-
žina M. Označíme-li 2 m (M) mohutnost m(.A) systému .A všech podmnožin
množiny M, platí m(M) < 2 m (M). Platí 2 No = , tj. mohutnost systému
všech podmnožin množiny No všech přirozených čísel se rovná mohutnosti
kontinua.
Číselné množiny
Tabulka 0.6
Popis množiny Označení Proveditelné operace a vlastnosti
Množina všech nezáporn.vch No = {O, 1, 2, ...} sčítání, násobení
cel)ích čísel [111110žina všech
přirozenJJch čísel]
Množina " ech kladn.vch N = {I, 2, 3, ...}
cel.ťch čísel
Množina všech celých Z = {..., - 2, - 1, O, 1, 2, . .. }, sčítání, odčítání, násobení;
čísel N e No e Z tvoří k o m u ta t i vn í o k r u h
Al nožina všech racionálních Q = {pjq I pE Z /\ q E N}, sčítání, odčítání, násobení,
čísel ZcQ dělení; tvoří komutativní
těleso (tzv. těleso racionálních
čísel)
Množina všech reálných R, sčítání, odčítání, násobení,
čísel QeR dělení (věta o supremu a jnfimu);
tvoří kom u ta t i vní' těleso
(tzv. těleso reálných čísel); ob-
sahuJe těleso racionálních čísel
a všechny nekonečné desítkové
rozvoje (reálná čísla, která
nejsou racionální, se nazývají
iracionální čísla, přičemž
jejich desítkové rozvoje nejsou
. periodické)
Množina v. ech (konečných) C = {a + bi I a, bER /\ i 2 = stejné operace jako u množiny R
komplexních čísel = -1\ (každá algebraická rovnice
J'
ReC má v množině C aspoň jeden
kořen); tvoří komutativní
těleso (tzv. těleso komplexních
čísel)
90
0.4.8. Algebraické struk tury
Rovnost na množině
Každý neprázdný disjunktní systém .0/ množin, jehož sjednocením je mno-
žina M =F (/), nazýváme rozkladem < v třúiy> na nlnožině M [r()zkladen1 mno-
žiny M, rozkladem pokrývajícím množinu M, j'a,ktorol'ou lnl1()žinou na 11111()-
žině M]. Řekneme, že dva prvky a, b E M jsou si rovny a píšeme a = b, právě
když prvek a patří do téže třídy rozkladu na množÍně M jako prvek b.
Řekneme, že dva prvky a, b E M jsou od sebe různé, a píšeme a =F b, právě
když prvky a a b patří do různých tříd rozkladu na množině M. Tím jsou
definovány rovnost a nerovnost na množině M. Na rovnost na množině M
(a, b, c E M) klademe tyto základní požadavky (tzv. axiólny rovnosti na mno-
žině M):
Ro: Pro každé dva prvky a, b platí právě jedno ze d vou přiřazení a = b,
a =F b.
Rl (axióm rejlexívnosti): Pro každý prvek a platí a = a.
R 2 (axióm symetričnosti): Jestliže a = b, pak b = a..
R3 (axiónl tran itivnosti): Jestliže a = bab = c, pak a = c.
Z axiómu R3 plyne, že místo a = b, b = c lze stručně psát a = b = c.
Příklad 1:
Množinu N všech kladných celých čísel lze vyjádřit jako disjunktní systém
jednoprvkových množin, takže každé kladné celé číslo pokládáme za různé
od všech ostatních kladných celých čísel.
Příklad 2:
Množinu M všech uspořádaných dvojic kladných celých čísel lze vyjádřit
jako takový disjunktní systém, že uspořádané dvojice [a, b], [f, d] E AI patří
do téže třídy (tj. [a, b] = [c, d]), právě když součiny ad a bc jsou týmž kladným
celým číslem.
Algebraické struktury
Binární operaci [stručně operací] nebo rnltrl11111 =Úkollenz konlpo=ice D
na množině M nazýváme zobrazení D: M 2 lvi, přičemž prvek li D h
(a, b, a D b E M) nazýváme k0l11PO=icí prvků li, b r=hledťl11 k hinÚrní operaci D
na množině M. .
Podle základních požadavků (tzv. axiómů) kladených na binární operace
(vyšetřované v algebře) na dané množině dostáváme objekty s různými algeb-
raickými vlastnostmi neboli dostáváme tzv. algebraické struktury. Binární
operace na určité množině, které splňují ,axiómy příslušné algebraické slruk-
tury, nazýváme operacemi této struktury.
.
91
Komutativní grupa
Komutativní grupou [Abelovou grupou] [M: O] s grupovou operací O na-
zýváme algebraickou strukturu definovanou na množině M jedinou binární
operací O na množině M, která splňuje tyto axiómy:
G o (uzavřenost operace O): Ke každé uspořádané dvojici [a, b J prvků
a, b E M je přiřazen právě jeden prvek množiny M, který označujeme a O b
a nazýváme kompozicí prvků a, b E M vzhledem k vnitřnímu zákonu kompozice
O na množině M.
G 1 (asociativní zákon pro operaci O):
a O (b O c) = (a O b) O c
."
pro všechny prvky a, b, C E M.
G 2 (komutativní zákon pro operaci O):
aOb=bOa
pro všechny prvky a, b E M.
G 3 (existence neutrálního prvku vzhledem k operaci O): Existuje takový
prvek e E M (tzv. neutrální prvek vzhleden1 k vnitřnímu zákonit kompozice O
na množině M), že pro každý prvek a E M platí
aOe=eOa=a.
G 4 (existence sYlnetrického prvku vzhledem k operaci O): Ke každému
prvku a E M existuje takový. prvek a' E M (tzv. symetrick.v prvek k prvku a
množiny M vzhledem k vnitřnímu zákonu kompozice O na množině M, majícímu
neutrální prvek e EM), že platí
a O a' = a' O a = e.
Pro konkrétní binární operace ,se místo znaku O používá speciálntch znaků.
U konkrétní algebraické struktury se kromě toho používá jednak speciálního
názvu pro každou binární operaci této struktury, jednak speciálního názvu
pro kompozici prvků vzhledem k příslušné binární operaci.
Nejčastěji se používá aditivního a multiplikativního označení
a příslušné terminologie.
Aditivní komutativní grupa
Použije-li se pro binární operaci komutativní grupy aditivního označení
(názvem operace je pak sčítání a znakem operace je +), dostaneme aditivní
92
, kO»1utat;vní grupu [M + J. Příslušné axiómy pak místo (lO až G 4 značíme
. Ao až A4'
Prvek a + b nazýváme součtel11 prrklí (tzv. sčítallcIi) li. h E A1 <r:h/edeI11
k sčítání + na nlnož;ně lvI).
Neutrální prvek vzhledem k sčítání + nazýváme Illl/{)r.\ 111 prrke111 nebo
nulou (vzhledem k sčítání + na Innožině M) a značíme O.
Symetrický prvek k prvku a vzhledem k sčítání + nazýváme opačným prvkenl
k prvku a a značíme - a.
Příklad:
Množina Z všech celých čísel s obvyklým sčítáním tvoří aditivní komuta-
tivní grupu, přičemž nulovým prvkem je číslo O E Z a opačným prvkem
k číslu a E Z je číslo -a E Z.
Multiplikativní komutativní grupa
Použije-li se pro binární operaci komutativní grupy multiplikativního
označení (názvem operace je pak násobení a znakem operace je .), dostaneme
multiplikativní komutativní grupu [M: . J. přislušné axiómy pak místo G o až G 4
značíme Mo až M4'
Prvek a. b (stručně ab) nazýváme soUČinel11 prvk{i (tzv. čill;tehi) a, b E M
(vzhledeln k násobení. na 111l1ožině Ai).
Neutrální prvek vzhledem k násobení . nazýváme jedllotkovJ 111 prrkel11
nebo jednotkou (vzhledem k násobení. na množině M) a značíme 1.
Symetrický prvek k prvku a vzhledem k násobení . nazýváme ;lleer=llínl
prvkem nebo převrácenÝ111 prvke111 k prrku a a značíme a-I.
Příklad:
Množina Q všech racionálních čísel různých od nuly s obvyklým násobením
tvoří lTIultiplikativní komutativní grupu přičemž jednotkovým prvkem
je čísl 1 a inverzním prvkem k číslu a E Q je číslo a- 1 E Q.
Obecnější algebraické struktury než komutativní grupa jsou algebraické
struktury grupoid, kvazigrupa, lupa pologrupa a monoid.
Grupoid
Grupoidenl [M; O] nazýváme algebraickou strukturu definovanou na
množině M (na tzv. nosiči ?Jrupoidu) jedinou binární operací O na množině M
(tzv. operace grtlpoidu), přičemž na operaci grupoidu se nekladou žádné po-
žadavky. Je-li operací grupoidu sčítání, resp. násobenL nazýváme jej lIditil'llíI11,
resp. multiplikativnín1 grupo;dern.
93
K vazigrupa
Kvazigrupoll nazýváme takový grupoid [M; OJ, že pro každé dva prvky
a, b E M má každá z rovnic a O x = b, y D a = b právě jedno řešení v mno-
žině M.
Lupa
Lupou nazýváme kvazigrupu, jejíž operace má neutrální prvek.
Pologrupa
Pologrupou [senli{jrupou, asociativním grupoidem] nazýváme grupoid, jehož
operace je asociativní, tj. platí axiómy G o a G l'
Monoid
Monoidem nazýváme pologrupu, jejíž operace má neutrální prvek, tj. platí
axiómy G o , G 1 a G 3 .
Je-li operace dosud uvedených struktur komutativní, připojí se k jejich
názvům přívlastek "komutativní".
Poznámka:
Monoid [M; O], v němž ke každému prvku množiny M existuje inverzní
prvek vzhledem k operaci monoidu, tj. platí axiómy G o , G b G 3 a G 4 , na-
zýváme grupou.
Distributivní zákony
Říkáme, že binární operace O je distributivní zprava vzhledem k binární
operaci O, platí-li axióm:
Dl (pravý distributivní zákon): .
aO (b Oe) = (a O b) O (a O c).
Říkáme, že binární operace O je distributivní zleva vzhledem k binární
operaci O, platí-li axióm:
D 2 (levý distributivní zákon):
(a O b)O c = (a O c) O (bO c).
Jestliže axiómy Dl a D 2 platí zároveň, říkáme, že binární operace O je
distributivní vzhledem k binární operaci O.
Okruh
Okruheln [M; +, .] nazyvame algebraickou strukturu definovanou na
množině M takovými dvěma binárními operacemi + (sčítání) a . (násobení),
94
že [M; + ] je komutativní grupa s grupovou operací + (tzv. aditivní grupa
okruhu [M; +, . ]), [M; .] je grupoid (tzv. multiplikativní grupoid okruhu
[M; +, .]) a operace . je distributivní vzhledem k operaci +.
-. Pro operace + a . okruhu tedy platí axiómy Ao až A 4 , Mo a Dl a O 2 ,
Aso ci a ti vní ok ruh, k om u ta t i vn í ok ruh, ok ru h s j ed n ot k o u
Jestliže násobení na okruhu [M; +, .] je asociativní, resp. je komutativní,
resp. má jednotkový prvek e E M, pak okruh [M; +, .] nazýváme asocia-
tivním okruhem, resp. komutativním okruhem, resp. okruhem s jednotkou.
Prvek a E M se nazývá levý, resp. pravý dělitel nuly v okruhu. [M; +, .],
právě když a =t= O a existuje takový prvek b E M, b =t= O, že platí a. b = O,
resp. b. a = O. Platí-li a. b = O a zároveň b. a = O, pak prvek a E M na-
zýváme dělitelem nuly v okruhu [M; +, .].
Prvek a E M okruhu [M; +, .] s jednotkou se nazývá levý, resp. prav)
invertovatelný prvek okruhu [M; +, .], právě když k němu existuje inverzní
prvek a-I, pro který platí a-I. a = 1, resp. a. a-I = 1. Platí-li a-I. a = 1
a zároveň a. a- 1 = 1, pak prvek a E M nazýváme invertovatelným prvkem
okruhu [M; +, .].
Singulárním prvkem okruhu nazýváme prvek, který není invertovatelný.
Regulárním prvkem okruhu nazýváme invertovatelný prvek asociativního
okruhu.
Asociativní o.kruh nemá dělitele nuly, právě když v tomto okruhu lze krátit
nenulovým prvkem, tj. právě, když z každé rovnosti a. x = b . x, x. a = x . b
při x * O plyne a = b (takový okruh se nazývá asociativní okruh bez dělitelů
nuly).
Přík Zad 1:
Množina všech sudých čísel s obvyklými operacemi sčítání a násobení
tvoří asociativní a komutativní okruh bez jednotky a bez dělitelů nuly.
Příklad 2:
Množina Z všech celých čísel s obvyklými operacemi sčítání a násobení
tvoří asociativní a komutativní okruh s jednotkou bez dělitelů nuly. Neutrálním
prvkem vzhledem k sčítání, resp. násobení je číslo O, resp. 1.
Obor integrity
Oborem integrity nazýváme asoC'iativní a komutativní okruh bez dělitelů
.
nuly, tj. pro operace oboru integrit platí axiómy Ao až A 4 , Mo až M 2 , Dl a O 2 ,
Platí-li také axióm M 3 , mluvím_e o oboru integrity s jednotkou.
95
Příklad:
Množina všech reálných čísel tvaru a + b J2 (a, bEZ) s obvyklými ope-
racemi sčítání a násobení je oborem integrity s jednotkou.
Těleso
Tělesem nebo asociativnfm okruhem s dělením [division ring] nazýváme
asociativní okruh s jednotkou, jehož každý nenulový prvek je invertovatelný,
tj. pro operace tělesa platí axiómy Ao až A 4 , Mo, Ml' M 3 , M 4 , Dl a D 2 .
Nenulové prvky tělesa tvoří vzhledem k násobení grupu (tzv. multiplikativní
grupu tělesa). Je-li tato grupa komutativní (tj. platí-li ještě axióm M 2 ), pak
příslušné těleso nazýváme komutativním tělesem nebo polem.
Příklady:
S obvyklými operacemi sčítání a násobení tvoří komutativní tělesa např.
tyto množiny: množina Q všech racionálních čísel (tzv. těleso racionálních
čísel), množina R všech reálných čísel (tzv. těleso reálných čísel) množina C
všech komplexních čísel (tzv. těleso komplexních čísel).
Poznámka:
V matematické literatuře se někdy asociativní okruh nazývá stručně
okruhem. U oboru integrity se někdy nepožaduje komutativnost násobení
a někdy se požaduje existence neutrálního prvku vzhledem k násobení.
Vnější zákon kompozice
VnějL í operaci [operátorovou operací, vnějším zákonem kompozice] L na
množině M s množinou operátorů A [vnější operací z množiny A na množinu M]
nazýváme zobrazení L: A x M M, přičemž prvek a L a (a E A, a EM)
nazýváme kompozicí operátoru a a prvku a vzhledem k vnější operaci L z mno-
žiny A na množinu M.
Modul
Modulem LM, O, L] nad asociativním okruhem [A, +, .1 (stručně modulem M
nad okruhem A) nazýváme algebraickou strukturu definovanou na množině M,
přičemž [M, O] je komutativní (zpravidla aditivní) grupa a L je vnější operace
na množině M s asociativním okruhem [A, +, .] jako množinou operátorů.
Vnější operace L je distributivní vzhledem k sčítání + na množině A a vzhle-
dem k binární operaci O na množině M a je asociativní vzhledem k násobení.
na množině A, tj. pro každé dva prvky Cť, B E A a pro každé dva prvky a, b E M
..
96
'; pta tí
( + B) a = (ex L a) O (B L a),
ex L (a O b) = ( a) O ( b),
C( L(/J a) = (ex. D) a.
Lineární prostor
Lineárním prostorem [vektorovým prostorem] L nad tělesem T ,nazýváme
modul L nad tělesem T, takže pr9 každý prvek a E L platí
e a = a,
kde e je jednotkový prvek těl sa T. Prvky lineárního prostoru nazýváme body
nebo vektory. Těleso T nazýváme tělesem skalám a jeho prvky skaláry. Je-li
nosičem tělesa T množina R, resp. C, mluvíme o reálném, resp. komplexním
lineárním prostoru.
Příklad:
Množina všech volných vektorů v rovině je lineárním prostorem nad tě-
lesem reálných číse1.
"
Us ořádaná grupa.
Uspořádanou grupou [M; O, ] nazýváme grupu [M; O] s grupovou
operací O, právě když množina M je uspořádaná a pro každé dva porovna-
telné prvky a, b E M, a b, a libovolný prvek C E M platí
aOc bOc
a zároveň
cO'a cOb.
,Prvek a E M se nazývá kladný, resp. nezáporný, právě když a e, a =F e,
resp. a e, kde e je neutrální prvek grupy [M; OJ. Prvek a E M se nazývá
záporný, resp. nezáporný, právě když a e, a * e, resp. a e.
Uspořádaná grupa [M; O, ] se nazývá úplně uspořádaná [lineárně uspo-
řádaná], právě když je úplným uspořádáním.
V úplně uspořádané grupě [M; O, ] tedy platí tyto tzv. axiómy uspo-
řádání:
U o (axióm trichotomie): Pro každé dva prvky a, b E M platí právě jedno
ze tří přiřazení
a -< b, a = b, b -< a.
97
U 1 (axiÓm tranzitivnosti): Jestliže pro nějaké prvky a, b, c E M platí a b,
b c, pak a c.
U 2 (axióm monotonie): Jestliže pro nějaké prvky a, b E M platí a b,
pak a D c b O c a cO a c O b pro každý prvek c EM.
Uspořádaný okruh
Uspořádaným okruhem [M; +, ., ] nazýváme okruh [M; +, .], právě
když množina M je uspořádaná, pro každé dva porovnatelné prvky a, b E M,
a b, a pro všechny prvky C E M platí
a+c b+c,
a pro prvky a, b E M, a O, b O, platí
ab O 1\ ba O .
Uspořádaný okruh [M; +, ., ] se nazývá úplně uspořádaný [lineárně
uspořádaný], právě když grupa [M; + ] je úplně uspořádaná.
V úplně uspořádaném okruhu [M; +. " ] tedy platí axiómy uspořádání
U o , Ul' U 2 (v tomto případě axióm U 2 nazýváme axiómem monotonie pro
sčítání) a kromě toho tento axióm:
U 3 (axióm monotonie pro násobení): Pro prvky a, b E M, a O, b O, platí
ab O 1\ ba O .
0.4.9. Několik topologických pojmů
Metrický prostor
Metrickým prostorem (M, g) nazýváme neprázdnou množinu M, na níž je
definováno zobrazení g: M 2 R, které splňuje tyto axiómy:
a) g(x, y) > O pro Vx, yE M.
b) g(x, y) = O <=> x = y (axióm totožnosti).
c) g(x, y) = g(y, x) pro V x, y E M (axióm symetričnosti).
d) g(x, y) < g(x, z) + g(z, y) pro Vx, y, zEM (trojúhelníková nerovnost).
Přitom prvky množiny M se nazývají body, zobrazení g se nazývá metrika
a číslo g(x, y) se nazývá vzdálenost bodů x, y.
Nemůže-li dojít k nedorozumění, lze metrický prostor značit stejným
písmenem jako samu množinu M.
98
Euklidovský prostor
Euklidovskou metrikou na množině Rn všech uspořádaných n-tic reálných
čísel nazýváme metriku g(x, y), při níž vzdálenost
g(x, y) = J[(XI - Yl)2 + ... + (xn - Yn)2J
kde x = (Xt,...,xn) a y = (Yl""'Y")'
. Množina Rn s euklidovskou metrikou se nazývá n-rozměrný euklidovský
prostor a označuje se En'
Otevře ná koule,. okolí bod u
(Otevřenou) koulí v metrickém prostoru (M, ()) (se středem a a poloměrem
b, [) > O) [[)-okolím bodu a] nazýváme množinu všech bodů x E M, jejichž
vzdálenosti (}(x, a) od bodu a jsou menší než tJ; značíme ji K(a, tJ), K<5(a) nebo
stručně K (a).
Neúplným b-okolím bodu a nazýváme množinu K(a, b) \ {a) kterou značíme
K(a, b), K,,(a) nebo stručně K(a).
Okolí bod u a E EI
Jestliže a je libovolné reálné číslo a [) > O, pak:
a) levým, resp. pravým b-okolím bodu a nazýváme interval tvaru (a - b, a),
resp. (a, a + tJ); značíme je U _(a, b), resp. U + (a, tJ), popř. stručně U _(a),
resp. U +(a);
. b) tJ-okolím bodu a nazýváme interval tvaru (a - tJ, a + tJ); značíme je
U(a, tJ), U <5(a) nebo stručně U(a); ,
c) levým, resp. pravým neúplným b-okolím, resp. neúplným b-okolím bodu a
nazýváme množinu U_(a, [)) \ {a}, resp. U+(a,b)\{a}, resp. U(a,b)\{a}
a značíme po řadě a _(a, tJ), a +(a, b) a a(a, b).
Spojité zobrazení
Spojitým zobrazením metrického prostoru (X, (}1) do metrického prostoru
(1': (2) v bodě a nazýváme takové zobrazení f, že k libovolnému bodu okolí
K(f(a), e) existuje takové okolí K(a, tJ), že f(x) E K(f(a), e)' pro všechny body
x E K(a, tJ).
Spojitým zobrazením metrického prostoru (X, (lI) do metrického prostoru
(1': (}2) nazýváme zobrazení, které je spojité v každém bodě metrického pro-
storu (X, (} I)'
Otevřená a uzavřená množina
Vnějším bodem množiny A c (M, (}) v prostoru (M, (}) nazýváme bod prostoru
(M, g), právě když nějaké jeho okolí je disjunktní s množinou A.
99
Vnitřním bodem množiny A c (M, g) v prostoru (M, g) nazýváme bod pro-
storu (M, g), právě když nějaké jeho okolí je částí množiny A.
Hraničním bodem množiny A c (M, Q) v prostoru (M, Q) nazýváme bod
prostoru (M, g), právě když každé jeho okolí obsahuje aspoň jeden bod patřící
do množiny A a aspoň jeden bod nepatřící do množiny A.
Izolovaným bodem množiny A c (M, Q) nazýváme bod a E A, právě když
existuje takové okolí bodu a v prostoru (M, Q), že z tohoto okolí patří do
množiny A jen bod a.
Vnitřkem A (stručně A O), resp. vnějškem Ext M A (stručně Ext A), resp.
hranicí Fr M A (stručně Fr A) množiny A c (M, e) v prostoru (M, Q) nazýváme
množinu všech vnitřních, resp. všech vnějších, resp. všech hraničních bodů
množiny A.
Otevřenou množinou v prostoru (M, Q) nazýváme množinu A c (M, g),
právě když existuje její neprázdná hranice a všechny body množiny A jsou
vnitřními body.
Uzavřenou množinou v prostoru (M, Q) nazýváme množinu A c (M, Q),
právě když je sjednocením svého vnitřku a své neprázdné hranice.
Obojetnou množinou v prostoru (M, e) nazýváme množinu A c (M, e),
právě když její hranice je prázdnou množinou.
Příklady:
V prostoru E I je interval (a, b> uzavřenou množinou, interval (a, b) otevře-
nou množinou, interval (- 00, a) otevřenou množinou, interval (a, + oo)
uzavřenou množinou a interval ( - 00, + oo) obojetnou množinou.
Souvislá množina
Souvislou množinou v prostoru (M, Q) nazýváme množinu A c (M, g),
právě když pro každé dvě disjunktní neprázdné podmnožiny A., A 2 množiny A,
pro něž platí AI u A 2 = A, existuje aspoň jeden bod v množině A, který je
společným hraničním bodem množin AI' A 2 , tj. platí
A = AI U A 2 /\ AI * 0 =F A 2 /\ AI n A 2 = 0 =>
=> A n Fr M AI n Fr M A 2 =F 0.
Sjednocení dvou souvislých množin AI' A 2 , které mají aspoň jeden bod
společný, je souvislou množinou. Protože lomená čára ie souvislou množinou,
je každá množina, jejíž každé dva body lze spojit lomenou čárou, souvislou
množinou.
100
oblast
Oblastí nazýváme souvislou otevřenou množinu.
- U zavřenou oblastí [kontinuem] nazýváme sjednocení oblasti a její ne-
.prázdné hranice.
Oblast D 2 c E 2 se nazývá ohraničená [omezená], právě když existuje
takový uzavřený kruh K 2 s konečným poloměrem, že D 2 c K 2 .
Ohraničená oblast D 2 c E 2 se nazývá jednoduše souvislá, právě když její
doplněk E 2 \ D 2 je souvislou množinou.
Příklady:
Vnitřek kruhu a vnějšek kruhu jsou jednoduše souvislými oblastmi. Vnitřek
kruhu bez libovolného bodu tohoto vnitřku a vnitřek mezikruží nejsou
jednoduše souvislými oblastmi.
Oblast D3 c E3 se nazývá ohrat:ličená [omezená], p ávě když existuje
taková uzavřená koule K3 s konečným poloměrem, že Q3 c K .
Ohraničená oblast D3 c E3 se nazývá jednoduše souvislá, právě když
existuje taková uzavřená koule K 3 a ,takové zobrazení f, které je spojité
a prosté a jehož inverzní zobrazení je také spojité; že platí f(K 3 ) = D3.
Příklady:
Vnitřek koule je jednoduše souvislou oblastí. Vnitřek koule z libovolného
bodu tohoto vnitřku a vnitřní oblast anuloidu nejsou jednoduše souvislými
oblastmi.
Vnitřní a vnější oblast kružnice, popř. kulové plochy
Vnitřní oblastí kružnice Kl v prostoru E 2 nazýváme oblast D 2 c E 2 , která
obsahuje střed kružnice K 1 a jejíž hranicí je kružnice K 1. Vnější oblastí kruž-
nice K 1 v prostoru E 2 nazýváme množinu E 2 \ (D2 U K 1 ). Sjednocení vnější
a vnitřní oblasti kružnice je vnějškem kružnice v prostoru E 2 . Vnitřek kružnice
v E 2 je prázdnou množinou.
Vnitřní oblastí kulové plochy K 2 v prostoru E3 nazýváme o last D3 c E 3 ,
která obsahuje střed kulové plochy K 2 a jejíž hranicí je kulová plocha K 2 .
Vnější oblastí kulové plochy K 2 v prostoru E3 nazýváme množinu
E3 \ (D3 U K 2 ).
Podobně se definuje vnitřní a vnější oblast např. elipsy, n-úhelníku
a elipsoidu.
Poznámka:
Vnitřní oblast kružnice v prostoru E 2 je vnitřkem příslušného kruhu.
Vnější oblast kružnice je vnějškem příslušného kruhu, ale není vnějškem
101
kružnice. Vnější bod kružnice je bodem vnějšku kružnice, tj. bodem
vnitřní nebo vnější oblasti kružnice, kdežto vnitřní bod kružnice neexistuje.
Mluvíme-li o bodu uvnitř, resp. vně kružnice, pak tím zpravidla myslíme,
že jde o bod vnitřní, resp. vnější oblasti kružnice.
Hromadný bod, deri vace a uzá věr množiny
Hromadným bodem množiny A c (M, g) v prostoru (M, e) nazýváme bod
a E (M, e), právě když v každém okolí bodu a leží aspoň jeden bod množiny A,
který je různý od bodu a.
Množinu všech hromadných bodů množiny A c (M, e) nazýváme derivací
množiny A vzhledem k prostoru (M, e).
Sjednocení množiny A c (M, e) a derivace n'1nožiny A vzhledem k prostoru
(M, e) nazýváme uzávěrem množiny A v prostoru (M, e) a označujeme AM
nebo stručně A.
102
1. ARITMETIKA A ELEMENTÁRNí ALGEBRA
1.1. ČíSELNÉ MNOŽINY
1.1.1. Množina vAech přirozených čísel
Přirozeným [l1e:Úporným celým] číslem nazýváme kardinální číslo
konečné množiny.
Množina
No = {O, 1,2,3, ...}
všech přirozených čísel s obvyklou operací + (sčítání) a s obvyklým uspo-
řádáním < je komutativní dobře uspořádaná pologrupa s neutrál-
ním prvkem O (tj. platí axiómy U o až U 3' AI až A 3 ), v níž lze krátit, tj. pro
každé tři prvky a, b, cENo z předpokladu a + c = b + C plyne a = b.
Množina No s obvyklou operací . (násobení) a s obvyklým uspořádáním <
je komu ta ti vní do bře us pořádaná polo gru pa s neu trá I ní m prvkem 1
(tj. platí axiómy U o až U 3' Ml až M 3 ), v níž lze krá ti t nen ulovým prvkem,
tj. pro každé tři prvky a, b, cENo (c 9= O) z předpokladu ac = bc plyne
a = b. Pro každé tři prvky a, b, cENo platí (a + b) c = ac + bc.
Peanovy axiómy
1. Jestliže x E No, pak x + 1 E No.
2. O E No.
3. Jestliže x E No, pak x + 1 9= O.
4. Jestliže x, y E No a x + 1 = y + 1, pak x = y.
5. Jestliže M C No, O EMa z předpokladu x E M plyne x + 1 E M, pak
M = No (tzv. princip matematické indukce).
Důkaz matematickou indukcí
Důkaz matematickou indukcí se skládá z těchto dvou kroků:
1. Ověříme, že výrok platí pro n = p (p E No).
2. Předpokládáme platnost výroku pro n = k > p a dokážeme platnost
výroku Jt;. pro n = k + 1 (tzv. indukční krok).
Pak výrok JI;. platí pro všechna přirozená čísla n > p.
103
Příklad:
Dokažme matematickou indukcÍ platnost vzorce
1 + 3 + 5 + ... + (2n - 1) = n 2 .
Vzorec je zřejmě správný pro n = 1, neboť 1 = 1 2 .
Z předpokladu, že daný vzorec platí pro n = k, dokážeme platnost vzorce
pro n = k + 1:
[1 + 3 + 5 + ... + (2k - 1)] + (2k + 1) = k 2 + (2k + 1) = (k + 1)2.
Daný vzorec tedy platí pro všechna přirozená čísla n > 1.
Úsek množiny No
Podmnožinu {O, 1, 2, 3, ..., n} množiny No všech přirozených čísel na-
zýváme n-tým úsekem množiny No a označujeme U 011 (např. U 04 = {O, 1,2,3, 4}).
1.1.2. Množina vAech celých čísel
Množina
z {..., - 2, - 1, O, 1, 2, ...}
/
všech celých čísel s obvyklými operacemi sčítání a násobení a s obvyklým
uspořádáním tvoří uspořádaný obor integrity s jednotkovým prv-
kem 1 a nulovým prvkem O. Opačným prvkem k číslu k je číslo -k.
Rozdílem celých čísel a, b (v tomto pořadí) nazýváme celé číslo d, pro něž
platí a = b + d, a píšeme a - b = d. Číslo a, resp. b se nazývá menšenec,
resp. menšitel.
Pro a, bEZ platí
..
.
a>b a-bEN.
Konstrukce množiny Z
Celá čísla lze sestrojit jako třídy ekvivalence na množině všech uspořádaných
dvojic přirozených čísel, splňují-li tyto požadavky (ml' m2, ni' n2 E No):
[m l ,m 2 ] = [nl,n 2 ] ml + n 2 = m 2 + ni'
[m l ,m 2 ] < [n l ,n 2 ] ml + n 2 < m2 + nI'
[ml,m2] > [n l ,n 2 ] ml + n2 > m 2 + ni'
[ml' m 2 ] + [n I' n2] = [ml + ni' m 2 + n 2 ],
[ml' m 2 ] [ni' n 2 ] = [min I + m2 n 2, m l n 2 + m2 n 1 ].
104
Kladným celým číslem k nazýváme třídu obsahující dvojici tvaru [k + 1, '1]
a ztotožňujeme je s přirozeným číslem k * O. Množinu všech kladných
celých čísel značíme N.
Záporným celým číslem - k nazýváme třídu obsahující dvojici tvaru
[l,k+l]. .
Celým číslem nula nazýváme třídu obsahující dvojici tvaru [1, 1] a ztotož-
ňujeme je s přirozeným číslem o.
Množina Z je tedy rozšířením množiny No o všechna záporná celá čísla
a na rozdíl od množiny No je uzavřená vzhledem k operaci odčítánÍ.
Úsek množiny N
Podmnožinu {I, 2, 3, ..., n} množiny N všech kladných celých čísel nazý-
váme n-tým úsekem množiny N a označujeme U" (např. U 4 = {I, 2,3, 4}).
1.1.3. Množina vAech racionálních čísel
Množina Q všech racionálních čísel s obvyklými operacemi sčítání
a násobení a s obvyklým uspořádáním tvoří uspořádané komutativní
těleso s jednotkovým prvkem 1 a nulovým prvkem O:
Podílem racionálních čísel p, q (q * O) nazýváme racionální číslo r, pro něž
platí P = qr, a píšeme p: q nebo ve tvaru zlomku !!., popř. plq. Číslo. p, resp. q
q
se nazývá dělenec, resp. dělitel (u zlomku čitatel, resp. jmenovatel).
Konstrukce množiny Q
Racionální čísla lze" sestrojit jako třídy ekvivalence na množině všech
uspořádaných dvojic celýcfi čísel, splňují-li tyto požadavky (Pt, P2, qt, q2 E Z,
P2 9= O, q2 9= O):
[Pl,P2] = [ql,q2] Plq2 = P2qt,
[Pl, P2] < [ql, q2] <=> (Plq2 < P2ql pro P2q2 > O) V
V (Pl q2 > P2qt pro P2q2 < O),
[Pt, P2] > [Ql, q2] (Ptq2 > P2Ql pro P2Q2 > O) V
V (Pt Q2 < P2Ql pro P2Q2 < O).
[p t, P2] + [Q l' Q 2] = [p 1 Q 2 + P 2 Q l' P2 q 2] ,
[p t, P 2] [Q l' Q 2] = [p 1 Q t, P 2 Q 2] .
Třídu obsahující dvojici tvaru [p, 1] ztotožňujeme s celým číslem p.
105
Třídu obsahující dvojici tvaru [1, p] ztotožňujeme s inverzním číslem
k číslu p a zapisujeme lip nebo P- I. Třídu obsahující dvojici tvaru [Pl' P2]
pak zapisujeme PIl P2'
Množina Q je tedy rozšířením množiny Z o všechna necelá racionální čísla
P 1 1p2, kde Pl, P2 (P2 * O) jsou nesoudělná celá čísla, a na rozdíl od množiny Z
je uzavřená vzhledem k operaci dělení.
1.1.4. Množina vAech reálných čísel
Množina R všech reálných čísel s obvyklými operacemi sčítání
a násobení a s obvyklým uspořádáním tvoří uspořádané komutativní
těleso s jednotkovým prvkem 1 a nulovým prvkem O.
Konstrukce množiny R
Množinu R lze sestrojit několika způsoby. Hlavní z nich jsou konstrukce
reálných čísel pomocí Dedekindových řezů a konstrukce reálných čísel pomocí
cauchyovských posloupností (viz např. [73], [101 ]).
.
Množina R je rozšířením množiny Q o všechna tzv. iracionální čísla a na
rozdíl od množiny Q existuje ke každému kladnému reálnému číslu a a ke
každému celému číslu n právě jedno takové kladné číslo b, že b n = a. Každá
neprázdná shora, resp. zdola ohraničená množina reálných čísel má supremum,
resp. infimum. Každá cauchyovská posloupnost reálných čísel má v množině
R limitu.
1.2. OPERACE NA MNOŽINÁCH Z, Q A R
1.2.1. Základní operace na množinách Z, Q a R
Sčí tání a odčí tán í na množinách Z, Q a R
a + (b + c) = (a + b) + c = a + b + c
a + b = b + a,
a + O = O + a = a,
(+a) + (+b) = +(a + b) = a + b,
(-a)+ (-b) = -(a + b),
(+a) + (-b) = +(a - b) = -(b - a),
(-a) + (+b) = -(a - b) = +(b - a),
(+a) - (+b) = (+a) + ( -b) = a - b,
(-a) - (-b) = (-a) + (+b) = b - a,
106
(+a) - (-b) = (+a) + (+b) = a + b,
(-a) - (+b) = (-a) + (-b) = -(a + b).
Odstraňování závorek obsahujících slučování výrazů
Závorky, před nimiž je znak sčítání (plus), lze vynechat.
Závorky, před nimiž je znak odčítání (minus), lze vynechat, jestliže' se zá-
roveň uvnitř závorek změní všechny znaky sčítání a odčítání v opačné (včetně
prvního členu, i když je znak plus vynechán).
Příklady:
a + (b + c - d) = a + b + c - d,
a - (b + c - d) = a - b - c + d.
Zavedení závorek u slučovaných výrazů
Slučované výrazy lze uzavřít do závorek, jestliže před závorky dáme znak
sčítání (plus). Jestliže však před nově zavedenými závorkami dáme znak
odčítání (minus), pak v závorkách musíme změnit všechny znaky sčítání
a odčítání v opačné (včetně prvního členu, i když je znak plus vynechán).
Příklady:
a + b - c + d = a + (b - c + d),
a ....:. b - c + d = a - (b + c - d).
N áso bení na množinách Z, Q a R
a(bc) = (ab) c = abc,
ab = ba,
-il . 1 = 1 . a = a,
a . O = O . a = O,
ab = O a = O v b = O.
( + a) . ( + b) = + ab , ( - a) . ( + b) = - ab ,
( + a) . ( - b) = - ab , ( - a) . ( - Ď) = + ab .
Distributivní zákon pro násobení na množinách Z, Q a R
vzhledem k sčítání
(a + b) c = c(a + b) = ac + bc.
Součet několika čísel násobíme číslem tak, že tímto číslem násobíme
všechny sčítance a pak je sečteme.
Jestliže všechny sčítance obsahují téhož činitele, pak tohoto činitele lze
vytknout před závorky.
107
N áso bení mnohočlen u mnoho členem (viz články 2.1.1 a 2.3.1)
(a + b - c) (d - e + f) = ad + bd - cd - ae - be + ce + af + bf - cf
(každý člen v prvních dvou závorkách se násobí každým členem z dalších
dvou závorek).
Příklady:
(a + b - c) m = am + bm - cm,
am + bm - cm = m( a + b - c),
(a + b) (c + d) = ac + bc + ad + bd,
(a + b) (c - d) = ac + bc - ad - bd,
(a - b) (c + d) = ac - bc + ad - bd,
(a - b) (c - d) = ac - bc - ad + bd.
Dělení na množinách Q a R (počí tání se zlomk y)
Ve zlomku
a
-=c
b
se číslo a, resp. b (b * O) nazývá čitatel, resp. jmenovatel. Ve všech zlomcích
uvažujeme vždy jmenovatele různého od nuly.
Rovnost zlomků
a c
- = - <=> ad = bc.
b d
Rozšiřování zlomků
a ac
-
b
bc
(zlomek alb byl rozšířen číslem c 9= O).
Jestliže některé sčítance neobsahují téhož činitele in 9= O, lze je před vy-
týkáním před závorky činitelem m rozšířit.
Příklad :
( )
cm c
am + bm - c = am + bm - m = m a + b - m .
108
Krácení zlomků
a a: c
b b: c
(zlomek alb byl krácen číslem c * O).
Při rozšiřování a krácení zlomku nenulovým číslem se hodnota zlomku
nezmění.
Početní operace se zlomky
a l b 2 al + a2
b+b= b
a l a2
a. - a 2
b b
b
a. a2 a. b 2 + a 2 b.
-+-=
bld b 2 d b l b 2 d
a l a2
a.b 2 - a 2 b l
b l b 2 d
. b1d b 2 d
a ac
-c=-
b . b '
a a 1 a
-:C=-.-=-,
b bc bc
a ca
c-=-
. b b'
al a2 a l a2
----,
b l b 2 b l b 2
b c ac
a:-=a.-=-,
c b b
a. a2 a l b 2 a l b 2
b. : b 2 = b; a2 = b l a2
Součet několika čísel dělíme číslem tak, že tímto číslem dělíme všechny
sčítance a pak výsledné podíly sečteme.
Přík lad :
a b c a+b-c
(a + b - c)/m = - + - - - = .
m m m m
'.
Složený zlomek (bcd 9= O)
a
-
b a c ad
- - - - -
c b d bc
-
d
Delší zlomková čára mezi tzv. jednoduchj mi zlomky alb a cld se nazývá hlavní
zlomková čára, kdežto ostatní zlomkové čáry jednoduchých zlomků se nazý-
vají vedlejší zlomkové čáry. Čísla a, d, resp. b, c nazýváme vnějšími, resp. vnitřními
členy složeného zlomku.
109
Složený zlomek převedeme na jednoduchý, tak, že součin jeho vnějších
členů lomíme součinem jeho vnitřních členů.
Je-li v čitateli a jmenovateli složeného zlomku součet jednoduchých zlomků,
pak složený zlomek převedeme na jednoduchý tak, že jej rozšíříme nejm nším
společným násobkem jmenovatelů všech jednoduchých. zlomků.
Příklad:
1 2 G-D84
- --
2 3 42 - 56 14
- - - --
I 5 G + ) 84 21 + 60 81
-+-
4 7
1.2.2. Absolutní hodnota reálného čísla
Absolutní hodnota reálného čísla a se značí lal a definuje jako nezáporný
prvek množiny {a, - a}, tj. lal = max {a, - a}. Platí tedy
a > O => lal = a,
a < O => lal = -a.
Platí
a < laj,
lal = O a = O,
lal > O <=> a =t= O,
labl = lallbl,
a lal
b = lb! (b + O),
lal-Ibl < Ilal-lbll < la + bl < lal + Ibl
(trojúhelníková nerovnost),
lal - I-al,
la 1 + a 2 + ... + ani < I a 11 + la 21 + ... + I a..l.
Signum [znaménko] reálného čísla
{ I (a > O),
sgn a = O (a = O),
-1 (a < O),
lal
sgn a = -
a
(a * O).
110
:1.2.3. Mocnina a odmocnina
Mocnina
-tá mocnina aa. (a, E R) reálného čísla a, kde číslo a, resp. se nazývá
základ mocniny [mocněnec], resp. exponent [mocnitel], je definována v zá-
vislosti na o boru proměnné (1.
Mocnina s kladným celým exponen tem (a E R, nE N)
li' == aa . . . a.
.....
....
n-krát
Platí (a, bER; m, nE N):
O" = O, ln = 1,
( - 1 )2... = 1 , ( - 1 )2m + 1 = - 1 ,
amb m = (aby",
amď = a m + n
,
(amr = a mn .
Mocnina s celočíselným exponentem (a E R \ {O}, nE Z)
1
a- n = - aO = 1.
n '
a
Platí (a, bER \ {O}, k, I E Z):
1 k = 1, ( - 1 )2k = 1,
ďb k = (abf,
ďa' = ď+',
cf = cf-I
, ,
a
(ď)' = ď .
( - 1 )2k + 1 = - 1 ,
..
Odmocnina (a, bER;, nE N):
Nezáporné číslo b, pro něž platí b ra = a, se nazývá n-tá odmocnina (z)
čísla a a značí se "J a (místo V a píšeme J a). Číslo a se nazývá základ odmocniny
[ odmocněnec] a číslo n se nazývá odmocnitel.
1 11
Pro odmocniny platí (a, b E Rt, m, nE N, k E Z): Existuje právě jedno
číslo b, pro něž platí b n = a. Dále
O=O, 1=1, Va=a,
(ab) = ( a) b,
J a a
n b = b (b *' O).
( af = cf = d',n (a =t= O),
':j a = m a,
( a)':ja = m am+n,
Ja + Jb = J[a + b + 2J(ab)],
Ja - Jb = J[a + b - 2J(ab)] (a > b),
J(a + Jb) = J a + J 2 - b) + J a - J 2 - b)
(a 2 > b).
Usměrňování zlomků [racionalizování jmenovatele]
U směrnit zlomek znamená odstranit odmocninu nebo odmocniny ze jmeno-
vatele vhodným rozšířením zlomku.
Příklady:
1 Ja
-
Ja a
1 a + Jb
-
a + Jb a 2 - b
1 _ Ja + Jb
Ja ' + Jb - a - b
(a > O),
(a 2 =t= b, -b > O),
(a =t= b, a > O, b > O)"
Odmocnina ze záporného čísla (a E Rt, m E No, n = 2m + 1)
(-a) = - a.
Pro m-tou odmocninu z m-té mocniny platí (a E R;, m E N):
am = a,
(-ar = - an = -a (n = 2m + 1),
(-ar = a (n = 2m).
Každá m-tá (m E N) odmocnina z m-té mocniny racionálního čísla je opět
racionálním číslem. Každá m-tá odmocnina z nezáporného reálného čísla,
které není m-tou mocninou racionálního čísla, je iracionálním číslem.
112
Příklady:
[J(3a)] [J(5b)] [J(ISab)] = J(3d. Sh. 15ab) = J(15 2 a 2 b 2 ) = 15ab
(a, bER;),
V(27x 3 ) = (V27) VX3 = 3x (x E R)
3 / x 4n J x4n
-::!_-- = 3 - = X4n-n = VX 3n = X n
VXn X n
J 49 p2q4 J(49p2q4) 7pq2
25nz 2 n 6 = J(25m 2 n 6 ) = 5m1l 3
X = X = l1JX (x E RJ),
642 = (V64)2 = 4 2 = 16,
a2 = 1?ja 4 = 1 a6 = ... (a E R),
(-5)5 = -5, (-5)6 = 5.
(xER \ {O}),
(n1, 11 E R \ {O}, p, q E R),
Mocnina s racionálním exponentem (aER+, mEZ, nEN)
a m / n = "J a m .
Mocnina s reálným exponentem [obecná mocnina]
(lIER+ 'XER)
a 7 = lim a 2n ,
n-CI)
kde {Cl. n } je taková libovolná posloupnost racionálních čísel n' že lim IXn = .
Pro (X > O se definuje ()« = o. n-ex'
Pro mocniny s reálným exponentem platí tytéž vzorce jako pro mocniny
s celočíselným exponentem.
Příklady:
44C 4 d 4 = (4cd)4 (c, dER),
(O,Sax)3 = 0,125a 3 x 3 (a, x E R),
0,14 4 = ( 0'14 ) 4 = ( ) 4 == 1
0,21 4 0,21 3 g 1 '
( ?YX ) 2 = (5xý)2 = 25x 2 yL
(x, Y E R, z E R \ {O}) ,
2z (2Z)2 4Z2
(-tr')2n ! = _(a 3 )2n-1 = _(/3(2n-1) = _a ón - 3
(llEN. oER).
t t 3
Dělení mnohočlenu mnohočlenem (viz články 2.1.1 a 2.3.1)
1. krok: Členy v obou mnohočlenech uspořádáme podle sestupných
mocnin téhož základu.
2. krok: První člen dělence dělíme prvním členem dělitele a dostaneme
první člen podílu.
3. krok: Dělitele násobíme prvním členem podílu, který dostaneme při
2. k fO k u, a odečteme tento součin od dělence. Zbytek dělíme týmž způsobem.
Pokračujeme tak dlouho, až je zbytek bud' nula, nebo mnohočlen nižšího
stupně než dělitel.
Přiklad:
(a 2 - 2ac - b 2 + c 2 ): (a - c + b) = a - c - b
-(a 2 - ac + ab)
ac - b 2 + c 2 - ab
-( - ac + c 2 - bc)
- b 2 - ab + bc
-( - b 2 - ab + bc)
O
1.2.4. Císelné soustavy
Množina určitých znaků s pravidly, která slouží k zobrazení čísel,
se nazývá čiselná soustava.
K zápisu reálných čísel používáme pozičních soustav, u nichž význam znaku
závisí na jeho poloze v zápisu a z nichž nejrozšířenější jsou polyadické číselné
soustavy.
Polyadické číselné s ustavy
V z-adické číselné soustavě lze každé přirozené číslo p vyjádřit ve tvaru tzv.
z-adického rozvoje
n
P - " a i - a n + a n-l + + a 2 + a 1 + a O
- i'" - n'" n - 1':" . . . 2'" I"'" O... ,
i=O
kde ZE N \ {I}, aj E U O ,z-1 a pak zapsat pomoéí tzv. z-adického zápisu
[z-adického číselného obrazu J
(CXnCl n - 1 ... CX 2 CX 1 cxo)z,
Zde = se nazývá základ [bá.:e J z-adické číselné soustavy a cx i jsou znaky repre-
zentující čísla ai' Znaky Cli (popř. někdy také čísla a;) se nazývají čis ice [cifry J.
1 14
Index i číslice i' resp. pozice, která tomuto indexu v číselném obrazu přísluší,
se nazývá řád číslice (Xi, resp. řád číselného obrazu. Číslice s indexem i se nazývá
číslice řádu i nebo číslice i-tého řádu. Nenulová číslice, která je v číselném obrazu
přirozeného čísla p první zleva, se nazývá číslice největšího řádu čísla p. Řád
číslice největšího řádu přirozeného čísla p se nazývá řád přirozeného čísla p.
Přirozené číslo řádu n - 1 se nazývá n-ciferné.
Číslo Zi se nazývá jednotka řádu i nebo jednotka i-tého řádu. Jednotka nultého
řádu se nazývá základní jednotka nebo stručně jednotka.
Polyadická soustava se základem dvě se nazývá dvojková [binární, dyadická],
se základem tři trojková [ternární], se základem osm osmičková' [oktalová],
se základem deset desítková [dekadická], se základem šestnáct šestnáctková
[hexadecimální] atd.
Nekonečný z-adický zlomek
Každé nezáporné reálné číslo a lze vyjádřit ve tvaru
a=k+d
[k E No, d E < O, 1)],
kde číslo k se nazývá celá část čísla a a číslo
d= f a;
I
i= 1
(ZE N \ {I}, ai E UO,Z-l)
(viz část 9) se nazývá nekonečný z-adický zlomek nebo zlomková část čísla a
a zapisuje se ve tvaru z-adického zápisu
(O - 1 - 2 ... (X - n ...)z
(n E N),
kde O je znak reprezentující nulu a (Xi jsou znaky (tzv. číslice) reprezentující
čísla ai' Jestliže i = O pro všechny indexy i < - n a (X-n * O, říkáme u desít-
kového zápisu, že číslo a má n desetinných míst. Číslo a = k + d pak zapisu-
jeme ve tvaru z-adického zápisu
(% - 1 - 2 ... (X - n . . . )z,
kde x je z-adický zápis čísla k. Je-li reálné číslo a záporné, zapisujeme je
ve tvaru
a = (-% CI.-l(X-2'" (X-n ...)z.
S výjimkou čísel tvaru mf zn (m E Z \ {O}, nE N), která lze zapsat ve tvaru
dvou různých z-adických zápisů, je z-adický zápis každého z ostatních reálných
čísel jednoznačný.
115
Poznámka:
Nemůže-li dojít k nedorozumění, lze u z-adického zápisu reálného čísla
vynechat závorky i základ z, což se zpravidla dělá u desítkové, popř. dvojkové
číselné soustavy.
Číslice polyadických číselných soustav
Pro zápis reálných čísel se běžně používá desítkové číselné soustavy, kde
číslicemi jsou znaky O, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Za číslice dvojkové číselné soustavy se zpravidla volí znaky O, 1 (někdy také
znaky O, I).
U ostatních z-adických číselných soustav se základem z < 10 se většinou
používá číslic desítkově číselné soustavy. Při z > 10 se číslice desítkové
číselné soustavy zpravidla doplňují velkými písmeny latinské abecedy.
Příklad 1:
Desítkový číselný obraz
O
1
2
3
4
5
6
7
8
9
Dvojkový číselný obraz
0=0
1 = I
10 = 10
11 = II
100 = 100
101 = 101
110 = 110
111 = III
1000=1000
1 001 = I 001
30
11 110 = II 110
Příklad 2:
(30).0 = (lE)16, neboť (E)16 = (14)10.
Příklad 3:
Dva různé desítkové číselné obrazy
0,002 000 . . . ,
0,001 999 ... ,
vyjadřují totéž číslo 2/10 3 .
116
Základní operace
v různých polyadických číselných soustavách
Provádějí se obdobně jako v desítkové číselné soustavě tak, že kdykoli při
sčítání (resp. násobení) v některém řádu dostaneme součet (resp. součin) větší
nebo roven základu příslušné číselné soustavy, je třeba provést přenos do
nejblíže většího řádu.
Příklady:
(423 )6
+ (1 341)6
+ (521 )6
(3 125)6
(42 714)8
-(17043)8
(23 651)8
Násobení a dělení usnadní tabulka násobení pro příslušnou číselnou sou-
stavu, sestavená ze součinů všech čísel menších než základ dané soustavy.
Příklad 1:
Před výpočtem součinu (325)6. (245)6 sestavíme tabulku násobení pro
šestkovou soustavu.
1 1
2 2 4
3 3 10 13
4 4 12 20 24
5 5 14 23 32 41
1 2 3 4 5
Příklad 2:
(352)6
. (245)6
(3124)6
(2332)6
( 1144)6
(145244 )6
(120101)3 : (102)3 = (1101)3
(102)3
(111 )3
(102)3
(201 )3
(102)3
(22)3
t 17
Převádění p-adické ho zápisu čí sla na z-adický
Při převádění p-adického zápisu přirozeného čísla na z-adický zápis dělíme
p-adický zápis základem z a dostaneme jako zbytek číslici o (tj. číslici řádu O)
.:-adického zápisu. Potom částečný podíl dělíme opět základem z a dostaneme
číslici CX I (tj. číslici řádu 1) z-adického zápisu. Takto postupně určujeme
všechny hledané číslice z-adického zápisu čísla daného v p-adickém zápisu,
dokud nedostaneme nulový částečný podíl.
Příklady:
(3287)10 :7 (100)10 :2
4 469 :7 O 50 :2
O 67 :7 O 25 :2
4 9 :7 1 12 :2
2 1 :7 O 6 :2
1 O O 3 :2
1 1 :2
1 O
(212)3 :2
1 102 :2
1 12 :2
1 2 :2
O 1 :2
1 O
Dostali jsme tyto výsledky:
(3 287)10 = (12404)7 ,
(100)10 = (1100 100)2'
(212)3 = (10 111)2'
Při převádění p-adického zápisu reálného čísla na z-adický zápis převe-
deme zvlášť jeho celou část a zvlášť jeho zlomkovou část. Přitom z-adický
zápis zlomkové části určíme tak, že zlomkovou část v p-adickém zápisu vy-
násobíme základem z a dostaneme CX_ 1 (tj. číslici řádu -1) jako celou část
118
součinu. Po vynásobení zlomkové části tohoto součinu opět základem =
dostaneme a_ 2 jako celou část takto získaného součinu. Tak postupujeme dále,
dokud zlomková část součinu není nulová.
Příklad:
(25,3125)10 = (11 001,010 1)2'
neboť
(25)10 :2 (0,3125)10 .2
1 12 :2 O 0,625 .2
O 6 :2 1 0,25 .2
O 3 :2 O 0,5 .2
1 1 :2 1 O
1 O
Nepolyadick.é číselné soustavy
Poziční číselné soustavy, které nejsou polyadické, se nazývají nepolyadické.
Z nepolyadických soustav uvedeme římskou číselnou soustavu.
Římská číselná soustava
Římská číselná soustava je založena na použití zvláštních znaků jednak
pro jednotky řádů O, 1,2 a 3 desítkové číselné soustavy: I = 1, X = 10, C =
= 100 a M = 1 000, jednak pro poloviny jednotek řádů 1, 2 a 3 desítkové
číselné soustavy: V = 5, L = 50, D = 500. Římskými číslicemi lze zapsat
jen kladná celá čísla podle těchto pravidel:
a) Římské číslice zapisujeme zprava doleva podle nerostoucích řádů
s výjimkou pravidla d).
b) Číslice I, X a C lze zapsat nejvýše třikrát bezprostředně za sebou, kdežto
číslice V, LaD nejvýše jednou.
c) Jsou-li větší číslice před menšími nebo jsou-li stejné číslice vedle sebe,
pak tyto číslice sčítáme (např. CCLXII = 100 + 100 + 50 + 10 + 1 + 1 =
= 262).
d) Je-li právě jedna z číslic I, X a C před větší číslicí, pak se menší číslice
odečte od číslice větší [např. CMXLIV = (1 000 - 100) + (50 - 10) +
+ (5 - 1) = 944, XMIV = (1 000 - 10) + (5 - 1) = 994]. Tímto pravidlem
se nahrazuje čtyřnásobné opakování některé z číslic I, X a C.
119
Periodická a neperiodická čísla
.:-adický zápis
(( sgn a) (Xm(Xm - 1 ... (Xo, (X - 1 (X - 2 ... (X - k(X - k-I (X - k - 2 ... (X - k - r)z
,(k, m E No, r E N) reálného čísla a se nazývá periodický, právě když existují
taková čísla k" r E N, že a _ n _ r = _ n pro všechna kladná celá čísla n > k.
Polyadický zápis reálného čísla, který není periodický, se nazývá
neperiod;ck.v.
Reálné číslo, které má (resp. nemá) periodický polyadický zápis, se nazývá
periodické (resp. neperiodické).
Právě všechna racionální, resp. právě všechna iracionální čísla jsou perio-
dická, resp. neperiodická.
Příklad:
-
Racionální čísla 0,750000... = 0,750, 0,592 a 0,64096 jsou periodická,
kdežto iracionální čísla J2 = 1,41421 ... a J1t = 1,77245... jsou ne-
periodická.
Ryze periodická a neryze periodická čísla
Periodický polyadický zápis se při k = O, resp. k > O nazývá ryze, resp.
neryze periodický. Reálné číslo, které má ryze, resp. neryze periodický poly-
adický zápis, se nazývá ryze, resp. neryze periodické.
Předperioda a perioda periodického čísla
Číslo u, resp. v, které má z-adický zápis
(CX- 1 CX- 2 ... cx-k)z při k > O, resp. (CX-.k-l(X-k-2 ... cx-k-r)z
a bylo vytvořeno z číslic periodického z-adického zápisu reálného čísla a,
se nazývá předperioda, resp. perioda periodického čísla a.
Převádění periodických čísel na obyčejný zlomek
Ryze periodické číslo a (O < a < 1) v desítkovém zápisu lze zapsat jako
obyčejný zlomek, jehož čitatelem je perioda a jm.enovatelem je kladné celé
číslo s desítkovým zápisem, který obsahuje právě tolik devítek, kolik číslic
má perioda (tj. r deví tek).
Přík Lad :
--- 592 592:37 16
0,592 = 999 = 999 : 37 - 27
120
Neryze periodické číslo a (O < a < 1) v desítkovém zápisu lze zapsat jako
obyčejný zlomek. Jeho čitatelem je rozdíl, kde menšencem je kladné celé číslo
s desítkovým zápisem vytvořeným právě z číslic před periody a periody ve stej-
ném pořadí jako v číselném zápisu a menšitelem je před perioda. Jmenovatelem
je číslo s desítkovým zápisem, který obsahuje nejprve právě tolik devítek,
kolik číslic má perioda, a za nimi právě tolik nul, kolik číslic má před perioda.
Příklad:
_ 64096 - 640
0,640 96 =
99 000
63 456 : 24
99 000 : 24
2644
-
4125
1.2.5. Dělení se zbytkem a beze zbytku v množině Z.
Dělitelnost v množině Z
Dělení se zbytkem v množině Z
Dělením se zbytkem v množině Z všech celých čísel nazýváme zobra-
zení, které každé uspořádané dvojici [a, b] (b * O) celých č(sel přiřazuje
uspořádanou dvojici [q, r] celých čísel, přičemž platí
a = bq + r, O < r < Ibl.
Číslo q se nazývá částečný [neúplný] podíl čísel a, b (v tomto pořadí) a číslo r
nejmenší nezáporný zbytek čísla a při děleni čislem b [nejmenší nezáporný zbytek
čísla a podle modulu b [modulo b ]], stručně zbytek při dělení.
Dělení beze zbytku v množině Z
Ve speciálním případě pro r = O mluvíme o dělení beze zbytku.
Dělitelnost v množině Z
Říkáme, že číslo bEZ je dělitelem čísla a E Z [číslo b dělí číslo a, číslo a
je dělitelné číslem b, číslo a je násobkem [q-násobkem] čísla b], a označujeme
b I a, právě když existuje takové číslo q E Z, že a = bq. Číslo q se nazývá
podíl čisla a při dělení číslem b. Neplatí-li b I a, říkáme, že čislo b není dělitelem
čísla a [číslo b nedělí číslo a] a píšeme b % a.
Zobrazení I v množině Z nazýváme dělitelností v množině Z.
Pro dělitelnost I na množině Z platí (a, b, c, m, nE Z):
a I b /\ b I c => a I c . (tranzitivnost dělitelnosti),
c I a /\ c lb=> c I am + bn ,
alb => albc,
a lb=> lal < Ibl (b * O) .
121
Každé celé číslo je dělitelem nuly, ale nula není dělitelem žádného celého
čísla různého od nuly.
Každé číslo a E Z je dělitelné tzv. nevlastními [samozřejmými] děliteli
1, - 1 a, - a. Existují-li další dělitele čísla a E Z, nazývají se vlastní [nesamo-
zřejmí] dělitelé.
Kongruence na množině Z
Jestliže rozdíl a - b (a, bEZ) je dělitelný číslem m E N, říkáme, že číslo a
je kongruentní s číslem b podle modulu m'[ stručně kongruentní s b modulo m]
a píšeme a = b mod m.
Každá množina těch celých čísel, která při dělení číslem m E N dávají týž
nejmenší nezáporný zbytek, se nazývá zbytková třída podle modulu m [modulo m]
nebo zbytková třída mod m.
Kritéria dělitelnosti celým číslem
Určit dělitele celého čísla zapsaného v desítkové číselné soustavě nebo
zjišťovat zbytky při tomto dělení, umožňují bez dělení pravidla, zvaná kritéria
[znaky] dělitelnosti celým číslem, která se zakládají na této větě: Jestliže celé
číslo b lze napsat jako součet dvou sčítanců, z nichž jeden je násobek kladného
celého čísla a, pak druhý sčítanec patří do téže zbytkové třídy podle modulu a
jako číslo b.
Celé číslo má týž zbytek při dělení číslem:
2 (resp. 5, resp. 10) jako při dělení jeho číslice řádu O číslem 2
(resp. 5, resp. 10);
3 (resp. 9) jako při dělení součtu jeho číslic číslem 3 (resp. 9);
4 jako při dělení součtu jeho číslice řádu O a dvojnásobku číslice
řádu 1;
4 (resp. 20, resp. 25, resp. 50, resp. 100) jako při dělení jeho posledního dvoj-
číslí číslem 4 (resp. 20, resp. 25, resp. 50, resp. 100);
7 (resp. 13) jako při dělení rozdílu posledního trojčíslí a čísla psaného ostat-
ními číslicemi číslem 7 (resp. 13); je-li menšenec menší než menšitel,
pak menšence zvětšíme nebo menšitele zmenšíme o vhodný ná-
sobek čísla 7 (resp. 13).
8 (resp. 40, re p. 125, resp. 200, resp. 250, resp. 500-, resp. 1000) jako při dělení
posledního trojčíslí číslem 8 (resp. 40, resp. 125, resp. 200, resp.
250, resp. 500, resp. 1(00);
11 jako při dělení rozdílu součtu číslic sudých řádů a součtu číslic
lichých řádů číslem 11; je-li menšenec menší než menšitel, z t-
šíme jej o vhodný násobek čísla 11;
122
11 jako při dělení součtu dvojčíslí počínajíc od číslice řádu O;
27 (resp. 37) jako při dělení součtů posledního trojčíslí a čísla psaného ostat-
ními číslicemi číslem 27 (resp. 37).
Příklad 1:
Číslo 4 193 dává při dělení číslem 3, resp. 9 zbytek 2, resp. 8, neboť 4 + 1 +
+ 9 + 3 = 17 = 5 . 3 + 2 = 9 + 8.
Příklad 2:
Číslo 4210 573 dává při dělení číslem 11 zbytek 4, neboť 3 + 5 + 1 + 4 -
-(7 + O + 2) = 13 - 9 = 4, popř. podle druhého kritéria 73 + 05 + 21 +
+ 4 = 103 a dále 03 + 1 = 4.
Příklad 3:
Číslo 941 326 dává při dělení číslem 7, resp. 13 zbytek 1, resp. 9, neboť
(700 + 326) - 941 = 326 - (941 - 7(0) = 85 = 7 . 12 + 1, resp. (650 + 326) -
- 941 = 326 - (941 - 650) = 35 = 13.2 + 9.
P r v očí s I a, s I o žen á čís I a
Každé celé číslo p (lpi 9= 1, p 9= O), které má jen nevlastní dělitele, se nazývá
prvočíslo (někdy se za prvočísla považují jen všechna kladná celá čísla n > 1,
vyhovující uvedeným podmínkám).
Každé celé číslo různé od nuly, které má aspoň jednoho vlastního dělitele,
se nazývá složené.
Čísla 1, -1 nejsou ani složenými čísly, ani prvočísly.
Celá čísla 2k, resp. 2k + 1 (k E Z) se nazývají sudá, resp. lichá.
Je-li složené číslo a dělitelné prvočíslem p, pak prvočíslo p nazýváme prvo-
činitelem čísla a.
Věty o prvočíslech
Každé složené číslo m má aspoň jednoho kladného prvočinitele p, pro něhož
platí p < Jimi. Z toho plyne, že každé celé číslo m > 1 je prvočíslem, právě
když všechna dělení prvočísly p (p2 < m) jsou dělením s nenulovým zbytkem.
Každé liché prvočíslo p (p > 3, p < - 3) lze psát ve tvaru 6k - 1 nebo
6k + 1 (k E Z). Každé číslo tvaru 6k - 1 nebo 6k + 1 (k E Z) nemusí však
být prvočíslem.
Malá Fermatova věta: Jestliže p > 1 je prvočíslem, pak každé číslo tvaru
a P .- a (a E Z) je násobkem prvočísla p.
Wilsonova věta: ,Jestliže p > 1 (p E N), pak číslo (p - I)! + 1 je dělitelné
číslem p, právě když číslo p je prvočíslem.
123
Příklad 1:
Číslo 137 je prvočíslem, neboť žádné z dělení prvočísly 2, 3, 5, 7 a 11 (pomocí
kritérií dělitelno ti) není beze zbytku. Prvočíslem 13 již není třeba dělit, neboť
13 > J137.
Příklad 2:
Prvočísla 53 a 37 lze psát po řadě ve tvaru 6. 9 - 1 a 6. 6 + 1. A však
35 = 6.6 - 1, 25 = 6.4 + 1.
Příklad 3:
Podle malé Fermatovy věty pro prvočíslo p = 3 a číslo a = 5 E Z Je
aP - a = 53 - 5 = 120 40-násobkem prvočísla 3.
Příklad 4: .
Číslo (p - I)! + 1 = (5 - I)! + 1 = 25 je podle Wilsonovy věty dělitelné
prvočíslem p = 5. .
Příklad 5:
Všechna prvočísla od 2 do n najdeme pomocí metody zvané Eratostenovo
síto takto: Napíšeme za sebou celá čísla 2 až n. Prvočíslo 2 ponecháme a škrt-
neme všechny jeho větší násobky. První neškrtnuté číslo je prvočíslo (3).
Číslo 3 ponecháme a škrtneme všechny jeho větší násobky, pokud nebyly
již škrtnuty. První neškrtnuté číslo je opět prvočíslo (5). Tak postupujeme dále,
až škrtneme všechny větší násobky čísel menších než Jn. Všechna neškrtnutá
čísla jsou hledaná prvočísla.
Rozklad složeného čísla v prvočinitele
Každé složené číslo a lze jednoznačně až na pořadí a znaménka činitelů
vyjádřit jako součin konečně mnoha prvočísel. Napíšeme-li složené číslo a
pomocí prvočísel Pl, P2, ..., Pn (která nemusí být od sebe různá) ve tvaru
a = PIP2 ... Pn ,
říkáme, že Jsme provedli rozklad složeného čísla a v prvočinitele [rozklad slo-
ženého čísla a v součin prvočísel, prvočíselný rozklad složeného čísla aJ.
Vyjádříme-li složené číslo a ve tvaru
a = P e 1 p e 2 P em
1 2'" m
(Pl' P2, ..., Pm jsou vzájemně různá prvočísla a el, e 2 , ..., e m E N), říkáme,
že jsme provedli kanonický rozklad složeného čísla a v prvočinitele.
124
Příklad:
Rozklad 2 2 .3 2 .5.7. 17 čísla 21 420 v prvočinitele najdeme takto:
21 420 I 2
10710 I 2
5 355 I 3
1 785 I 3
595 I 5
119 I 7
17 I 17
1 I
tj. zjistíme nejmenší prvočíslo, kterým je dané číslo dělitelné, a zapíšeme je
do pravého sloupce. Se získaným podílem, který zapíšeme do levého sloupce
pod dělence, postup opakujeme, dokud nedostaneme podíl rovný číslu 1.
Každé složené číslo a je dělitelné libovolným součinem s (Isl < a) svých
prvočini tel ů.
Společný dělitel celých čísel
Celé číslo d * O, které je dělitelem každého z daných čísel a l' a 2 , ..., a n E Z
(n > 1), se nazývá společný dělitel celých čísel al, a 2 , ..., an0
Protože čísla 1, - 1 jsou společnými děliteli každých dvou celých čísel,
nazývají se nevlastní [samozřejmí] společní dělitelé. Ostatní společní dělitelé
se nazývají vlastní.
Celá čísla al, a2, ..., a n (n > 1) se nazývají nesoudělná, právě když nemají
jiné společné dělitele než nevlastní společné dělitele. Celá čísla a 1 , a2, ..., a n
(n > 1) se nazývají po dvou nesoudělná, právě když jsou nesoudělná každá
dvě čísla ai, aj (i * j). Celá čísla, která mají aspoň jednoho vlastního společ-
ného dělitele, se nazývají soudělná,
Příklad:
Čísla 25, 12 a 24 jsou nesoudělná, ale nejsou po dvou nesoudělná, neboť
čísla 12 a 24 jsou soudělná.
Největší společný dělitel celých čísel
Společného dělitele celých čísel al, a2, ..., a n , který je násobkem každého
jiného jejich společného dělitc1e (tj. je největším ze, společných dělitelů), na-
zýváme největším společn.vm dělitelem celých čísel al, a2, ..., a n a značíme
D(a 1 , a2' ..., a n ) nebo stručně D. Jestliže ai = O pro i = 1, 2, ..., n, pak
D(a 1 , a 2 , ..., a n ) = O. Jestliže aspoň jedno číslo ai je různé od O, pak vždy
125
existují dva největší společní dělitelé Dl' D 2 , pro něž platí D 1 (a 1 , a2, .0., a n ) =
= -D 2 (al'u 2 "",u n ).
Společný násobek celých čísel
Celé číslo k, které je násobkem každého z daných čísel al, a 2 , ..., U n E Z
(n > 1), se nazývá společný násobek cel.vch čísel a l' a 2 , ..., an0
Nejmenší společný násobek celých čísel
Společný násobek celých čísel al, a2, ..., a n , který je dělitelem každého
jiného jejich společného násobku, nazýváme nejmenším společným násobkem
celých čísel ap a 2 , ..., a n a značíme n(a 1 , a 2 , . o., u n ) nebo stručně n. ·
Jestliže aspoň jedno číslo a; = O, pak n(al' a 2 , ..., a n ) = O. Jestliže a; * O
pro i = 1, 2, o o o, n, pak existují dva nejmenší společné násobky ni' n 2 , pro něž
platí n 1 (a 1 , a 2 , ..., a n ) = -n 2 (al, a2, .0., a n ).
Výpočet D(a 1 ,a2,o.o,a,,) a n(a1,a 2 ,...,a n )
Největšího společného dělitele n kladných celých čísel a 1 , a 2 , .0., a n
určíme pomocí jejich kanonických rozkladů v prvočinitele
a . = P ei1 p ei2 P eim
I 1 2 o.. m
(i = 1, 2, o o ., n) ,
kde P1, P2, o o., p". jsou vzájemně různá kladná prvočísla, mezi než patří všechna
prvočísla, která dělí aspoň jedno číslo ai, a exponenty eij E No jsou jedno-
značně určeny čísly a; a Pj (i = 1, 2, ..., n; j = 1, 2, .. '.' m). Největší společný
dělitel čísel a 1 , a 2 , ..., a n je číslo
D( a l' a 2' . o ., a,,) = p{ 1 p{ 2 .. o p' m ,
kde
jj = min {e 1j , e2j: ..., e"j}
(j = 1, 2, . .., m) o
Největšího společného dělitele několika kladných celých čísel vypočteme
tedy tak, že každé z daných čísel rozlQžíme v součin prvočinitelů a z těchto
prvočinitelů vybereme všechny, jež se zároveň vyskytují ve všech rozkla-
dech (tj. každého prvočinitele vezmeme s nejmeušín1 mocnitelem, jaký se
vyskytuje v rozkladech všech daných čísel). Součin takto vybraných prvo-
činitelů je hledaným největším společným dělitelem.
Nejmenší společný násobek n kladných celých čísel al, a2, ..., U n
je číslo
n(a 1 , a 2 , .. o, a,,) = MI 2 ... p9",m,
kde
9 j = max. { e 1 j' e 2j' o o o, e nj }
(j = 1, 2, ..., m) .
126
Nejmenší společný násobek, několika kladných celých čísel vypočteme tak,
že každé z daných čísel rozložíme v součin prvočinitelů a z těchto prvočinitelů
vybereme všechny, jež se vyskytují aspoň v jednom rozkladu (tj. každého
prvočinitele vezmeme s nej větší m mocnitelem, jaký se vyskytuje v rozkladu
aspoň jednoho z daných čísel). Součin takto vybraných prvočinitelů je
hledaným nejmenším společným násobkem.
Příklad:
Protože 24 = 2 3 .3.5°, 60 = 2 z .3.5 a 72 = 2 3 . 3 z . 5°, dostaneme
D(24, 60, 72) = 2 2 .3.5° = 12,
n(24, 60, 72) = 2 3 .3 2 .5 = 360.
Platí
D(a 1 , a2, ..., a n ) = D(a i1 , a i2 , ,.., ai,),
n(a1' a2, ..., a n ) = n(akl' a k2 , ..., ak")'
kde
{ i l' i z, .. ., in} = {k 1 , k 2' . . ., k n } = {1, 2, ..., n} ,
tj. největší společný dělitel a nejmenší společný násobek nezávisí na pořadí
čísel a1' a z , ..., an0
Platí D(a l , a2, ..., a n ) = D(Dl' D 2 ), kde Dl = D(a l , (1z, ..., a k ), D 2 =
= D(a k +1,a k +2,...,a n ) (k > 1), přičemž pro k = 1 klademe Dl = a 1 a pro
k = n - 1 klademe D 2 = an0
Obdobně n(a 1 , a 2 , ..:, a n ) = n(n l' n z ), kde nI = n(a p a z , ..., a k ), n z =
= n(ak+ l' a k +2, ..., a n ) (k > 1), přičemž pro k = 1 klademe nI = al a pro
k = n - 1 klademe n 2 = an0
Označíme-li P = a 1 a2 .. ° a n (a i E N) a AI = pla 1 , Az = plaz, ..., An = Pla n ,
platí
n(a1' a z , "0' a n ) D(A l' A 2 , ..., An) = P
neboli speciálně
, a 1 a2
n( a l' a 2) = ( ) ·
Dal' a 2
Euklidův algoritmus pro celá čísla
Při výpočtu největšího společného dělitele D(a,_ b) (a, bEZ \ {O},-a > b)
podle Euklidova algoritmu postupujeme takto: Číslo a dělíme číslem b. Při
zbytku r1 * O dělíme číslo b číslem r 1 a určíme zbytek r2' Při r z * O dělíme
číslo r l číslem r 2 0 Dojdeme-li po n krocích ke zbytku r n = O, je D(a, b) = r n - 1 .
127
Příklad:
Postup výpočtu D(648,252) zapíšeme do schématu
2 1 1 3
648 252 144 108 36
144 108 36 O
tak, že v prostředním řádku napíšeme nejprve větší číslo 648 (co do absolutní
hodnoty) a pak menší dané číslo 252. Jejich neúplný podíl 2 napíšeme
do prvního řádku nad dělitele 252 a do třetího řádku napíšeme zbytek 144,
který zároveň vypíšeme do středního řádku za číslo 252. Takto postupujeme
až k dělení beze zbytku. Poslední nenulový zbytek 36 = D(648,252).
1.2.6. U spořádání na množině R
· Říkáme, že číslo a je menší (resp. větší) než číslo b, jestliže číslo b - a
je kladné (resp. záporné) a píšeme a < b (resp. a.> b). Zápis a < b (resp. a > b)
znamená, že a < b nebo a = b (resp. a > b nebo a = b). Relace [<; R],
[ > ; R], [ < ; R] a [ > ; R] se nazývají nerovnosti na množině R.
Z axiómů uspořádání U o až U 3 plynou tyto axiómy pro nerovnosti na
.množině R:
Pro každá dvě čísla a, bER platí právě jedno z přiřazení
a = b,
a < b,
a > b.
Pro každá tři čísla a, b, cER platí:
a < b /\ b < (' => a < c,
a < b => a + c < b + c,
a < b /\ O < c => ac < bc.
Z axiómů pro nerovnosti plynou tato pravidla (a, b, c, dER, k, u, VE R +):
a < b /\ C < d => a + c < b + d,
a < b /\ C < d => a + c < b + d,
a < b /\ C < O <=> ac > bc,
O < a < b <=> O < lib < lla,
a <,b < O <=> lib < 11 a < O,
u < V /\ a > O => ua < va,
128
u < V 1\ a < O => ua > Va,
Li > 1 1\ a < b => II < U b ,
Zl < 1 f\ a < b => ua > u b ,
b - k < a < b + k la - bl < k.
Intervaly
,
Množinu všech reálných čísel x, pro něž platí
a < x < b
a < x < b,
a < x < b,
a < x < b,
a < x
a < x
x < b,
x < b,
označujeme po řadě
<a,b),
< a, b),
(a, b),
(a, b),
<a, + ťx)),
(a, + (0),
(-x,b),
(-oo,b)
a nazýváme intervalem v prostoru EI' Interval <a, b), resp. (a, b) se nazývá
uzavřen.v, resp. otevřen.v. Intervaly <a, b) a (a, b) se nazývají polootevřelJé
[polouzavřené]. Interval <a, a) = {a} je jednobodovou množinou. Interval
( - oc, + 00) značí množinu R všech reálných čísel. Interval <a, b), <a, b),
(a, b), (a, b) se nazývají ohraničené, kdežto intervaly (- 00, b), (- 00, b),
(a, + Cf:)), <a, + 00), (- 00, + (0) se nazývají neohraničené.
Symbol < - JJ, + 00) = R u { + OC, - JJ} = R # = Ef, kde + 00, - 00 jsou
nevlastní body reálné osy, značí tzv. roz. ířenou reálnou [číselnou] osu.
1.3. KOMPLEXNÍ ČíSLA
1.3.1. Množina všech komplexních čísel
Množina C všech uspořádaných dv jic [a, b ] reálJJ.ých čísel s rovností
a operacemi sčítání a násobení, které jsou definovány vztahy
Cal' b l ] = [a2' b 2 ] <=> a l = a2 /\ b l = b 2 ,
Cal' b l ] + [a2' b 2 ] = [a I + a 2 b l + b 2 ],
Cal' b l ] [a 2 , b 2 ] = [a l a 2 - b t b 2 , a l b 2 + a2 b l]'
tvoří komutativní těleso s nulovým prvkem [0,0] a jednotkovým
prvkem [1, O]. Prvky tohoto tělesa se nazývají komplexní čísla. Pro uvedené
129
operace sčítání a násobení na množině C tedy platí axiómy Ao až A 4 , Mo až
M 4 , Dl a D 2 , takže pro Zl' Z2, Z3 E C platí
Zl + (Z2 + Z3) = (z 1 + Z2) + Z3'
(asociativní zákony),
Zl(Z2 Z 3) = (Z l Z2)Z3
+ - +z
l 2 - 2 .'
Z.Z2 = Z2 Z .
(komutativní zákony),
(Zl + Z2)Z3 = Z l Z3 + Z2 Z 3,
'Z3(Zl + Z2) = Z3 Z 1 + Z3 Z 2
(distributivní zákony).
Opačným prvkem k prvku z = [a, b] je prvek ž = [ -a, -b] a převráceným
[inverzním] prvkem k prvku z = [a, b] 9= [O, O] je prvek
1 1 [ a b ]
z = zž z = a 2 + b 2 ' - a 2 + b 2 .
Komplexní .číslo [0,1] se nazývá (ryze) imaginární jednotka a značí se i,
popř. v elektrotechnice j. Pro číslo i platí i 2 = [ -1, O].
Množina všech komplexních čísel tvaru [a, O] tvoří podtěleso komutativního
tělesa C a je izomorfní s tělesem R reálných čísel, takže lze klást [a, O] = a;
speciálně [O, O] = O. Těleso C vznikne připojením prvku i k tělesu R.
Pro komplexní číslo z = [a, b] se zavádějí tyto pojmy:
a = Re z, resp. b = lm z se nazývá reálná, resp. imaginární část komplex-
ního čísla z.
ž = [a, -b] se nazývá číslo komplexně sdružené k číslu z -[čísla z, ž se na-
zývají (vzájemně) komplexně sdružená].
. Izl = J(a 2 + £,2) se nazývá absolutní hodnota [modul] komplexního čísla z.
Reálné číslo a 2 + b 2 se nazývá norma komplexního čísla z.
Komplexní číslo z, kde lm z 9= O, se nazývá imaginární číslo. Imaginární
číslo z, kde Re z = O, se nazývá ryze imaginární číslo.
Z definic sčítání a násobení na množině C plynou tyto další operace:
Rozdíl komplexních čísel
Zl - Z2 = [a, b] - [c, d] = [a - c, b - d].
Podíl komplexních čísel
Zl = [a, b] = Zl Ž 2 = [ ac + bd bc - ad J
Z2 [c, d] I Z 21 2 c 2 + d 2 ' c 2 + d 2
(Z2 9= O).
130
, Pro každá dvě komplexně sdružená čísla z = [a, b], z = [a, - b] platí:
(z) = Z,
z + z = 2a,
(Zl + Z2) = Zl + Z2'
(Z l Z2) = Z I Z2'
(-z) = -z,
ZZ = a 2 + b 2 ,
(Zl - Z2) = Zl - Z2'
(Zn) = (z)",
(;:) = ::
(Z2 =t= O).
Pro absolutní hodnoty libovolných komplexních čísel z, Zl' Z2 platí:
Izl = J(a 2 + b 2 ) > O,
Izl = O <=> z = O,
Izl = 1- zl = Izl = J(zz),
I Z lz21 = I Z lllz21,
Zl Iz 11 )
- = - I I (Z2 =t= O ,
Z2 6.2
Iz 11 - I Z 21 < Iz 1 + Z21 < Iz 11 + I Z 21 (trojúhelníková nerovnost),
Re Z < Izl, lm Z < Izl.
1.3.2. Ryze imaginární čísla
Imaginární jednotka
'2 1
1=-.
Mocniny imaginární jednotky
i 4n _ 1 ,
. 4n + 1 .
1 = 1,
i 4n + 2 = - 1
,
. 4.. + 3 .
1 = -1
pro "V n E Z .
Řešení rovnice x 2 = -a (a E R +)
Oborem pravdivosti rovnice x 2 = - a = ( - 1) a je množina
p = {i J a, - i J a} .
Součet ryze imaginárních čísel je buď ryze imaginárním číslem, nebo
nulou.
131
Příklad y:
4i - 7i + 9i = 6i,
4i - 7i + 3i = O.
Součin ryze imaginárních čísel je bud' reálným číslem, nebo ryze ima-
ginárním číslem.
Příklady:
5i.7i = 35i 2 == -35,
5i . 7i . 8i = 280i 3 = - 280i .
Podíl ryze imaginárních čísel je vždy reálným číslem.
Příklad:
14i 14
15i 15
Znázornění ryze imaginárních čísel
Ryze imaginární číslo bi se v kartézské souřadnicové soustavě znázorňuje
jako bod [O, b] osy y, která se proto nazývá imaginární osa (obr. 32). Osu x
pak nazýváme reálnou osou.
5i
4i
2. kvadrant 3 i. 1. kvadrant
2i
l
Obr. 32. Znázornění ryze imaginárních
čísel na imaginární ose
-6-5-4-3 -2 -ji.
-2i
3.kvadrant -3 4 4.Kvodront
- 1.
1.3.3. Komplexní čísla v kartézském tvaru
Protože platí
z = [a,b] = [a, O] + [0,1] [b,O],
lze komplexní čísla z ps t v tzv. kartézském [algebraickéln, binomickém] tvaru
z = a + ib = a + bi
(a, bER),
132
kde a = Re z, resp. b = lm z je reálná, resp. imaginární část komplexního
čísla z, a počítat s nimi .jako s dvojčleny.
Vzorce pro počítání s komplexními čísly lze přepsat v kartézském tvaru
takto:
Komplexně sdružená čísla
z = a + ib, z = a - ib.
Rovnost komplexních čísel
a + ib = c + id <=> a = c /\ b = d;
speciálně
a + ib = O <=> a = O /\ b = O.
Sčítání komplexních čísel
(a + ib) + (c + id) = (a + c) + i(b + d),
(a + ib) + (a - ib) = 2a.
Odčítání komplexních čísel
(a + ib) - (c + id) = (a - c) + i(b - d),
(a + ib) - (a - ib) = 2ib.
,
Násobení komplexních čísel
(a + ib) (c + id) = (ac - bd) + i(ad + bc),
(a + ib) (a - ib) = a 2 + b 2 .
Dělení komplexních čísel (usměrňování jmenovatele)
a + ib (a + ib)(c - id) ac + ibc - iad - i 2 bd
- -
c + id (c + id) (c - id) c 2 - i 2 d 2
(ac + bd) + i( bc - ad) ac + bd . bc - ad
= +1
c 2 + d 2 c 2 + d 2 c 2 + d 2 .
Násobíme-li dělence a dělitele číslem komplexně sdruženým k děliteli,
dostaneme vždy podíl ve tvaru zlomku, jehož jmenovatel je reálným číslem.
Příklad:
1 + 2i
3 - i
(1+2i)(3+i)
-
(3 - i) (3 + i)
1 + 7i 1 7
10 =lO+ i to '
133
Umocňování komplexních čísel
(a + ib)2 = a 2 + 2abi + b 2 i 2 = a 2 + 2abi - b 2 ,
(a + ib)3 = a 3 + 3a 2 bi + 3ab 2 i 2 + b 3 i 3 =
= a 3 + 3a 2 bi - 3ab 2 - b 3 i,
(a + ib)4 = a 4 + 4a 3 bi + 6a 2 b 2 i 2 + 4ab 3 i 3 + b 4 i 4 =
= a 4 + 4a 3 bi - 6a 2 b 2 - 4ab 3 i + b 4 .
Komplexní hodnoty odmocniny z komplexního čísla
Kořeny rovnice X2 = a + ib = z jsou komplexními hodnotami Xl' x 2
odmocniny z komplexního čísla z:
Xl,2 = + (J a + ..j( 2 + b 2 ) + ib J 2[a + J( 2 + b 2 )] ).
Znázornění komplexních čísel
Protože každému komplexnímu číslu z přísluší právě jedna uspořádaná
dvojice [a, b], lze je znázornit jako bod [a, b] v kartézské souřadnicové sou-
stavě. Jde tedy o bijektivní zobrazení množiny C = R 2 = R x R na množinu
všech bodů tzv. Gaussovy rODiny [roviny komplexních čísel] (obr. 33).
l2-- 5 + 3í 4i
t- - - - i -
I 2i
I i
-6-5-4 -3 - -jL
1-2i
-3i
2 . cl4i
Z3=- -41. -5L
Zf= 3+2 i
--
I
1 2 3 4 5 6
---
Z4= 5-2i.
Obr. 33. Znázornění komplexních čísel
v Gaussově rovině
V obrázku 33 jsou v Gaussově rovině znázorněna čísla Zl = 3 + 2i, Z2 =
= -5 + 3i, Z3 = -2 - 4i a Z4 = 5 - 2i.
1.3.4. Komplexní čísla v goniometrickém tvaru
Každé komplexní číslo z lze znázornit jako bod v rovině s polární
souřadnicovou sousta vou a vyjádřit pomocí polárních souřadnic qJ a (l
(obr. 34):
z = a + ib = Izl (cos qJ + i sin qJ) = Q( cos qJ + i sin qJ) =
= Q[ cos (qJ + 2k1t) + i sin (qJ + 2k1t)] pro \fk E Z.
134
Proměnná (l E Rri je absolutní hodnota komplexního čísla z; proměnnou
cp = arg z nazýváme argumentem [amplitudou] komplexního čísla z. Platí
a = (l cos cp, b = (! sin cp,
a a
cos cp = ..j(a 2 + b 2 ) = '
b
tg cp = -
a
. b b ( )
SIn cp = ..j(a 2 + b 2 ) = Izl z =F O ·
(čísla a a b určují polohu bodu v Gaussově rovině, a tedy také úhel o velikosti cp).
. ."
.maglnClm' osa
z = Q+ bi
O .. . I
I a reau.a osa
Obr. 34. Modul Q a argument cp
komplexního čísla z '
Argument cp je komplexním číslem z (z * O) určen jednoznačně, požadu-
jeme-li, aby platily nerovnosti -1t < cp < 1t; argument z tohoto intervalu
se nazývá hlavní hodnota argumentu komplexního čísla z a značí se Arg z.
Příklad:
Vyjádřeme číslo z = 3 - 4i v goniometrickém tvaru:
(l = J[3 2 + (_4)2] = 5;
-4 4
tg ({J = 3 = -3' ({J = - 53°8' = -0,93 rad,
3 - 4i = 5[ cos ( - 53°8') + i sin ( - 53°8')] .
[Druhá hodnota 126°52' argumentu cp z intervalu (0°, 360°) nepřichází v úvahu,
neboť při a > O a b < O je obraz daného čísla z ve čtvrtém kvadrantu.]
Násobení komplexních čísel v goniometrickém tvaru
Zl = (lI (cos ({JI + i sin ({JI)' Z2 = (l2(COS ({J2 + i sin ({J2)'
Z l Z2 = r1r 2 [cos (({JI + ({J2) + i sin (({JI + ({J2)]'
135
Dělení komplexních čísel v goniometrickém tvaru
Zl = (JI (cos (/JI + i sin (/JI)' Z2 = (J2(COS lp2 + i sin qJ2),
z 1 (J 1 [ ( ) . . ( )]
-, = - cos qJI - qJ2 + I sIn lpI - lp2 .
Z2 (J2
'-
Umocňování komplexních čísel v goniometrickém tvaru
z = (!(cos qJ + i sin qJ),
:! = gk[ cos (kqJ) + i sin (klp)] pro \fk E Z
(tzv. M oivrova věta), speciálně
(cos li' + i sin qJf = cos (klp) + i sin (klp).
Odmocnina z komplexního čísla v goniometrickém tvaru
Pro každé komplexní číslo z a pro libovolné přirozené číslo n > 2 nazýváme
n-tou odmocninou (z) komplexního čísla z takové komplexní číslo x, pro něž
platí = z. Značíme je V z. Je-li komplexní číslo z vyjádřeno v goniometric-
kém tvaru z = e(cos lp + i sin lp), pak n-tými odmocninami z čísla z jsou
prá vě čísla
" ( lp + 2k1t .. li' + 2k1t )
X k + 1 = (VZ)k+ 1 = (V(!) cos + I sIn ,
. n n
kde k = O, 1, 2, . .., n - 1.
Komplexní n-té odmocniny' z jedné
\ ,
Ze vzorce pro n-tou odmocninu komplexního čísla dostaneme pro (! = 1
a qJ = O právě njednoduchých kořenů x ,...,x rovnice ,X' = 1 (nEN):
2k1t 2k1t
, . .
x k + 1 = cos - + I sIn -
n n
pro Y k E {O, 1, 2, . . ., n - I}.
Rovnice
x" = - 1
má právě n jednoduchých kořenů x , ..., x :
1t + 2k1t 1t + 2k1t
" . .
x k + 1 = cos + I sIn
n n
pro \f k E {O, 1, 2, . . ., n - I}.
136
Příklad y:
"
x 1 =
1 ,
x 1 =
1 J3.
-+-1
22'
X3 = 1
1 J3.
=> X 2 = -2 + 2 1 ,
1 J3.
x = -- - -1'
3 2 2'
x 3 = - 1 =>
X2 = - 1 ,
.X 3 =
1 J3.
- - -1.
2 2'
X4 = 1 =>
X4 = - 1 =>
J2 . J2 .
x 1 = 2+2 1 ,
J2 J2 .
x = --+-1
2 22'
J2 J2 .
x3=-2-2 1 ,
J2 . J2 .
x 4 = - - -1.
2 2
Xl = 1,
X 2 = I,
X 3 = - 1 ,
X 4 = -I;
Řešení binomických rovnic
Binomická rovnice
xn-z=O
(n E N, ZE C)
má pro z = e( cos cp + i sin cp) právě n jednoduchých kořenů Xl'.." XII:
n ( CP + 2k1t .. cp + 2k1t )
Xk+ 1 = (Vi l! ) cos n + I SIn n
pro Y k E {O, 1, . .., n - I}.
Speciálně pro a E R v množině C platí
+ a = O,
{ ( a) Xk+ I pro a > O a (Xk+ 1)" = -1,
X -
k+l - [V(-a)]x +1 pro a < O a (X +lr = 1
pro \f k E {O, 1, 2, ..., n - I}, přičemž x + l' resp. X; + 1 je komplexní n-tá od-
mocnina z čísla 1, resp. - 1.
137
1.3.5. K o m p I e x n í čís I a v e x po n e n c i á I ním t v a r u
Z Eulerových vzorců (viz str. 366)
sin cp = i (ei(q> + 2kx) - ei(q> + 2kn)),
cos cp = (ei(q> + 2kn) + ei(q> + 2kn J )
2
plyne
ei(<p + 2k1t) = cos (qJ + 2k1t) + i sin (qJ + 2k1t),
takže
z = Izl ei(<p+ 2k1t) = Izl [cos (4-> + 2k1t) + i sin (qJ + 2k1t)] =
= a + ib pro Vk E Z.
Vyjádřeme číslo z = - 2 + 3i v exponenciálním tvaru:
(1 = J[( _2)2 + 3 2 ] = J13,
3
tg qJ = _ 2 = -1,5, qJ = 123°41' = 2,16 rad
(obraz čísla z je v druhém kvadrantu);
z = -2 + 3i = (JI3)e 2 ,16i.
Stručný zápis v technických aplikacích:
- 2 + 3i = (JI3) e 2 ,16i = (JI3) 1123°4 !
přičemž symboll!t (kde qJ je ve stupňové míře) čteme: verzor qJ.
Příklad 2:
Vyjádřeme 17 eO,65i v algebraickém tvaru a + ib;
0,65 rad = 37°22',
17 eO,65i = 17(cos 37°22' + i sin 37°22') =
= 17(0,795 + 0,607i) = 13,5 + 10,3i.
Násobení komplexních čísel v exponenciálním tvaru
- n e i<Pl }
'" 1 - 1 , . ( + )
. Z Z = n o e l <PI <P2
1<P2 1 2 11O;,1
Z2 = (12 e ,
pro V Zl' Z 2 E C .
138
Dělení komplexních čísel v exponenciálním tvaru
'7 - n e iqJ I } '7 I)
1 - 1 . ' _ _ e i (qJl -qJ2) \,../ C \,../ P
pro v ZlE 1\ v Z 2 E .
'7 - O e lqJ2 .., n
""'2 - 1;;2 , 2 2
Umocňování komplexních čísel v exponenciálním tvaru
= = {! e iqJ ,
Z' = on e inqJ
....
pro \In E N, \lz E C.
I
n..tá odmocnina z komplexního čísla v exponenciálním tvaru
z = {! e iqJ , (?J Z)k + 1 = X k + 1 = (?J (!) e[(<p + 2k1t)ín]i
(k = O, 1, 2, . . ., n - 1).
Zvláštní hodnoty činitele ei<p
e(2k + 1 )1ti =
I, }
-1
pro \I k E Z,
e 2k1ti
e(1t/2)i e(21t,' 3)i 1 J3.
- 1, - -- +-1
2 2'
e(31t í 2)i -1, e(41t/3)i 1 J3.
- - -- - - 1
2 2'
e 2k1ti - 1 e<P + 2k1ti = e<P (k E Z).
Periodou exponenci*lní funkce je tedy 2ITi.
Vztahy mezi exponenciálními a goniometrickými funkcemi viz na str. 366.
1.3.6. Grafické metody
,G r a f i c k é s I u č o v á n í k o m p I e x n í c h čís e 1
Protože komplexní čísla lze považovat za dvojrozměrné vektory v Gaussově
rovině, vede grafické sluč vání komplexních čísel na slučování vektorů.
Při grafickém výpočtu součtu Zl + Z2 komplexních čísel se k vektoru
Zl = OA pomocí rovnoběžného posunutí připojí vektor Z2 = OB podle
obrázku 35. 'Součtem komplexních čísel Zb Z2 je pak komplexní číslo
z = Zl + Z2 = OC.
Při konstrukci rozdílu
'7-'7 _'7 -.... +( _.., )
-- - l 2 - l --2
se postupuje tak, že se k vektoru Zl = OA místo vektoru Z2 = OB pomocí
rovnoběžného posunutí připojí opačný vektor AC = - Z2 (obr. 36).
139
Grafické násobení komplexních čísel
Grafické násobení komplexních čísel neodpovídá žádnému z možných
vektorových násobení.
Ze vzorce
'7 '7 - O O e i(<Pl + <P2) - '7 - n ei<p
1 2 - 1 2 - - -
pro součin komplexních čísel Zl' Z2 dostaneme porovnáním argument ({J =
= qJl + ({J2 a modul (1 = (11(12, přičemž poslední rovnost lze vyjádřit jako
úměru (1: (] 2 = (] 1 : 1.
. ., I
Imagmarnl oso
o
, ,I J
t Imoglnorm oso
I
c
. . I I
J m09tnornl osa
A
f
I I I
rea na osa
1.\
-- --",- T-
reolna osa
I
rea(na osa
o
o
Obr. 35. Grafické sčítání
kom plexních čísel
Obr. 36. Grafické odčítání
kom plexních čísel
Obr. 37. Grafické násobení
komplexních čísel
Konstrukce (obr. 37):
1. krok: Sestrojíme vek ory O A a OB , odpovídající po řadě komplexním
", 1 0
CIS um Zl a Z2'
2. krok: K vektoru OB naneseme podle rovnosti ({J = ({J 1 + ({J2 v kladném
smyslu úhel velikosti ({JI'
3. krok: Od bodu O naneseme na reálnou osu úsečku délky 1 a dostaneme
bod C.
4. krok: Vedeme spojnici bodu C s bodem A.
5. krok: K úsečce OB naneseme úhel OCA velikosti rJ.. tak, že bod B je
vrcholem sestrojeného úhlu.
Průsečík D ramen úhlů sestrojených podle kroků 2 a 5 určuje vektor
součinu Zl Z2'
Odůvodnění: LOCA '" LORD (trojúhelníky se shodují ve dvou úhlech),
takže platí uvedená úměra (]: (]2 = l! 1 : 1.
140
Grafické dělení komplexních čísel
Ze vzorce
Z I Q 1 . ( .
- = - e l (fJI - (fJ2) = Z = (l el(fJ
Z2 (l2
pro podíl komplexních čísel Zl' Z2 dostaneme porovnáním argument ({J =
:::: ({JI - ({JI a modul (l = (l11(l2' přičemž poslední rovnost lze vyjádřit jako
úměru Q: (lI = 1 : Q2'
Konstrukce (obr. 38):
, 1. krok: Sestrojíme vektory O A a OB , odpovídající po řadě komplexním
číslům Z 1 a Z2'
2. krok: K vektoru OA naneseme podle rovnosti ({J = ({JI - ({J2 v záporném
smyslu úhel velikosti ({J2 neboli naneseme orientovaný úhel velikosti - ({J2'
3. krok: Od bodu O naneseme na reálnou osu úsečku délky 1 a dostaneme
bod C.
4. krok: Vedeme spojnici bodu B s bodem C.
5. krok: K úsečce O A naneseme úhel O BC velikosti rJ.. tak, že bod A je
vrcholem sestrojeného úhlu.
Průsečík D ramen úhlů sestrojených podle kroků 2 a 5 určuje vektor po-
dílu Z 11 z 2'
Odůvodnění: LOCB '" LODA (trojúhelníky se shodují ve dvou úhlech),
takže platí uvedená úměra (l: Q I = 1 : (]2.
. . I I
t Imog,"orm so
,
8
Obr. 38. Grafické dělení komplexních
čísel
o
f C
I I
realno osa
Grafické umocňování komplexních čísel
Postup grafického výpočtu n-té mocniny zn (n E N) komplexního čísla z
je založen na n-násobném provedení grafického násobení (obr. 39).
141
'Jiný způsob grafického výpočtu mocniny zn vychází z výpočtu argumentu
nlfJ modulu (ln (obr. 40). Obrázky 39 a 40 uvádějí konstrukce mocniny z"
pro n = 4.
I I
rea lna osa
. . I I
l,ma 9 1"am, osa
I
I
I
, I I
reo no osa
Obr. 39. Grafické umocňování
komplexních čísel
Obr. 40. Grafické umocňování
komplexních čísel
Grafické znázornění hodnot u-té odmocniny
komplexního čísla ---
n-tá odmocnina 'Zl z komplexního čísla z je dána všemi řešeními rovnice
x n = z = g(cos lfJ + i sin lfJ)
v proměnné x.
Postup grafického výpočtu odmocniny 'Zl z vychází z výpočtu argumentu
lfJ/n a modulu 'ZI(l.
Obrázek 41 uvádí konstrukci hodnot Xl' X2' X 3 a X 4 odmocniny 'Zl z pro
n = 4, jejichž obrazy leží na ramenech úhlů, posunutých vždy o 21t/n rad =
= 21t/4 rad = 90°.
, ,I'
Imagmcrm osa
J(.
'4
Obr. 41. Grafické odmocňování
komplexních čísel
X 3
Grafické znázornění hodnot n-té odmocniny čísel 1 a -1
V obrázcích 42 až 45 jsou po řadě znázorněny všechny hodnoty odmocnin
tJl, (-1), tJl, (-1). Body Xi znázorňující n-té odmocniny čísel 1 a -1
142
rozdělují jednotkovou kružnici (tj. kružnici o poloměru 1) na n (n = 3, 4)
stejných částí.
. I I
imag1narOl osa
-f
x 2
Obr. 42. Grafické znázornění tf I
Obr. 43. Grafické znázornění tf( - I)
X3
-1
. I I
imaglnorm osa
Obr. 44. Grafické znázornění I
Obr. 45. Grafické znázor!1ění ( - 1)
1.4. PŘIBLIŽNÁ ČíSLA A JEJICH CHYBY
1.4.1. Přibližná čísla
o mnoha údajích, které konkrétně zjišťujeme v technické praxi nebo
ve výzkumu, nelze vždy tvrdit, že jsou úplně přesné.
.
Označíme li d, resp. h číslo, o němž určitě víme, že je menší, resp. větší než
přesná hodnota X vyšetřované veličiny, pak rozdíl h - d (h > d) nazýváme
nepřesností. Číslo h, resp. d se nazývá horní, resp. dolní odhad přesné hodnoty X.
Za odhad přesné hodnoty X mohou sloužit všechna čísla x z intervalu (d, h),
která nazveme přibližným číslem [neúplným číslem]. Přitom h, resp. d nazveme
horní, resp. dolní mezí přibližného čísla. Číslo x, které vyhovuje nerovnostem
d < x < h, se nazývá přípustná hodnota [přibližná hodnota, aproximace, odhad]
přibližného čísla.
Podrobnější informace o přibližných číslech dávají tyto charakteristiky:
143
a) Středni hodnota přibližného čisla se rovná
d+h
a=
2
nahrazujeme jí přesnou hodnotu X, kterou neznáme.
b) Prostá [absolutní] chyba [stručně chyba] přibližného čísla se rovná
h-d
!Iv = = h - a (d < h).
2
Přibližné číslo tedy definujeme jako množinu všech reálných čísel x, která
vyhovují nerovnici
lx - al < !Iv
a která se zapisují ve tvaru x = a + !Iv.
c) Poměrná [relativní] chyba přibližného čísla se rovná
!Iv
e =-.
,a
1.4.2. Zaokrouhlená čísla
Úmluva:
Budeme uvažovat, že reálná čísla jsou vyjádřena v desítkovém zápisu.
Jestliže přibližné číslo x má střední hodnotu
a k = ao . 10"
a prostou chybu
!lv k = ! . 10",
nazýváme je čislem zaokrouhleným na jednotky řádu k [stručně zaokrouhlenýnl
číslem] a místo
(ao E Z) .
x = ao . 10" + ! . 10"
stručně píšeme
x ...:. k ao . 10",
kde znak "':' k čteme ,,(je> po zaokrouhlení na jednotky řádu k rovno". Říkáme
také, že přibližné číslo x jsme zaokrouHlili na jednotky řádu k. Číslo a k ve tvaru
I
144
ao . t O" nazýváme hodn.otou přibližného čísla x při zaokrouhlení na jednotky
řádu k [stručně zaokrouhlenou hodnotou J. Všechny číslic čísla ao E Z nazý-
váme platnými číslicemi. Zaokrouhlit (přibližné, popř. přesné> číslo na n plat-
ných číslic znamená, že číslo ao má n platných číslic, přičemž prvních n - 1
platných číslic čísla a o nazýváme správnJ J n1i číslicemi.
Zobrazení [ ...:... k; R J množiny R všech reálných čísel s poslední číslicí řádu
menšího než k na množinu všech reálných čísel zaokrouhlených na jednotky
řádu k, tj. na množinu všech uzavřených okolí U(a o . 10", t. 10"), nazýváme
zaokrouhlením na jednotky řádu k. Přitom víme-li, že jde o zaokrouhlení
na jednotky řádu k (a nemůže-li dojít k nedorozumení), píšeme místo. ...:.. k
jen ' . To umožňuje zjednodu. en.v tvar zaokrouhlené hodnoty, jímž lze nahradit
tvar a o . 10" (ao E Z) zaokrouhlené hodnoty tak, že číslo a o . 10" vyjádříme
v pouhém jeho desítkovém zápisu jen s tou výjimkou, že při k > O posledních k
nul desítkového zápisu bude mít menší velikost.
Příklad:
Zaokrouhlené hodnoty 428. 10 0 (k = O), 78 651 . 10- 3 (k = - 3), 110. 10 3
(k = 3 > O) lze po řadě psát v zjednodušeném tvaru 428; 78,651; 110000.
Pravidlo pro zaokr0uhlení
Viz ČSN 01 \010 Zaokrouhlování čísel a jejich zápis, 1975.
Máme-li dané (přibližné, popř. přesné) číslo a s poslední číslicí řádu r < k
nahradit číslem b s poslední číslicí řádu k při prosté chybě 1. 10 k (tzv.
zaokrouhlovací chybě), používáme k tomu tohoto pravidla pro zaoki-vuhlení
na jednotky řádu k neboli stručně zaokrouhlovacího pravidla (píšeme pak
a . b):
a) Všechny číslice řádů enších než k vypustíme [s výjimkou při lal
(O, 10);' a E Z, kdy místo vypuštěných číslic píšeme m lé nuly] a zbývající
číslice ponecháme s případnými změnami podle bodů c) až e).
b) Je-li číslice řádu k-I menší než 5, pak číslice řádů větších než k-I
ponecháme beze změny, a dostaneme tak číslo p (např. při -k = .-1 je 8,739 ...:..
. 8,7).
c) Je-li číslice řádu k-I větší než 5, přičteme k číslu p, získanému podle
bodu b), jednotku řádu k (např. při k = - 2 je 0,176 . 0,18).
d) Pravidlo sudé číslice: jestliže číslice řádu k-I je 5 a všechny číslice
daného čísla a řádů menších než k-I jsou nuly (popř. číslice 5 řádu k-I
je poslední číslicí daného čísla a), pak je-li číslice řádu k sudá, ponecháme ji
beze změny, aje-li I ichá, přičteme k číslu p, získanému podle bodu b),jednotku
řádu k (např. při k = 3 je 14 500 ...:... 14000 a při k = - 2 je 0,035 . 0,04).
145
e) Jestliže číslice řádu k-I je 5 a číslice kteréhokoli řádu menšího než
k-I je u daného čísla a různá od nuly, pak k číslu p, získanému podle bodu b),
přičteme jednotku řádu k (např. při k = O je 37,500 02 -.:.. 38).
P I a t n Ý m i čís I i ce m i 'hodnoty přibližného čísla při zaokrouhlení na jed-
notky řádu k jsou všechny její číslice bez nul vlevo od první nenulové číslice
a bez případných (malých) nul řádů menších než k.
Příklad:
Zaokrouhlené hodnoty
0,003 08; 308; 30,8; 30 800
mají všechny právě po třech platných číslicíC,h 3, O, 8. Zaokrouhlené hodnoty
0,430 O; 4300; 430000
mají všechny právě po čtyřech platných číslicích 4, 3, O, O.
Zaokrouhlení nahoru a dolů
Jestliže při a -.:.. b je a < b, resp. a > b, říkáme, že jsme číslo a zaokrouhlili
nahoru (a někdy pak pod poslední platnou číslicí čísla b děláme pruh), resp.
dolů (a někdy pak nad poslední platnou číslicí čísla b děláme tečku).
Příklad:
247,36 -.:.. 247, (zaokrouhlení nahoru),
247,45 . 247,4 (zaokrouhlení dolů).
Znak přibližné rovnosti
Víme-li že číslo a se od čísla b liší jen o zaokrouhlovací chybu, píšeme
a . b, kdežto jinak pro přibližnou rovnost používáme znaku .
Příklad:
247,36 -.:.. 247,4, ale 247,36 240.
1.4.3. Pravidla pro p.řiblifné výpočty
V praxi je při výpočtech s přibližnými čísly třeba se omezit na takový
počet platných číslic u daných údajů, mezivýsledků a výsledků, který zaručí
výsledek s minimální chybou. Přitom se používá těchto pravidel pro přibližné
výpočty:
1. Při sč í tán í a od čít á ní přibližných čísel vypustíme podle zaokrouhlo-
146
vacího pravidla číslice těch míst, na nichž aspoň v jednom z přibližných čísel
není platná číslice.
Při sčítání a odčítání přibližných čísel s desetinnými místy ponecháme
ve výsledku tolik platných desetinných mist, kolik jich íná přibližné číslo
s nejmenším počtem platných desetinných míst.
Prostá chyba součtu několika přibližných čísel je rovna součtu prostých
chyb všech sčítanců. Pro Xl = al + l a x 2 = a 2 + rl 2 platí tedy
Xl + X 2 = (a I + a 2 ) + (Cl. 1 + cx 2 ).
Poměrná chyba součtu kladných přibližných čísel leží mezi největší a nej-
menší po ěrnou chy ou sčítanců.
Při sčítání kladného přibližného čísla s kladným přesným číslem je po-
měrná chyba součtu menší než poměrná chyba přibližného čísla.
Prostá chyba rozdílu dvou přibližných čísel je rovna součtu prostých chyb
menšence a menšitele. Pro Xl = al + cx I a X 2 = a 2 + 2 tedy platí
Xl - X 2 = (a I - a 2 ) + (CtI + 2)'
Prostá chyba algebraického součtu několika přibližných čísel je rovna
součtu prostých chyb sčítanců.
Poměrná chyba rozdílu dvou přibližn)!ch čísel navzájem blízkých může
být velká, i když jsou poměrné chyby těchto čísel malé.
2. Při nás o b e n í a děl e n í přibližných čísel ponecháme ve výsledku tolik
platných číslic, kolik jich má dané přibližné číslo s nejmenším počtem platných
číslic. Výjimkou (kdy ponecháváme o jednu platnou číslici více) je případ,
kdy součin začíná číslicí 1 a při1;>ližné číslo s nejmenším počtem platných
číslic začíná nějakou jinou platnou číslicí.
Pro prostou chybu součinu dvou přibližných čísel Xl = a l + ctI a X2 =
= a 2 + CX 2 platí
X I X2 -= la2 + (a l cx 2 + a2 cx I)'
Poměrná chyba součinu několika kladných přibližných čísel o malých po-
měrných chybách je přibližně rovna součtu poměrných chyb všech činitelů.
Při násobení přibližného čísla přesným číslem roste prostá chyba úměrně
s přesným číslem a poměrná chyba zůstane beze změny.
Pro prostou chybu podílu dvou přibližných čísel Xl = a l + CtI a X2 =
= a2 + cx 2 platí
Xl a l a l cx 2 + a 2 cx l
-=-+
- 2
X2 a 2 a 2
147
Poměrná chyba podílu dvou kladných přibližných čísel malých poměrných
chybách je přibližně rovna součtu poměrných chyb dělence a dělitele.
Při dělení přibližného čísla přesným číslem X se zmenší prostá chyba
podílu X -krát, kdežto poměrná chyba zůstane beze změny.
3. Při umocňování dvěma nebo třemi ponecháme ve výsledku tolik
platných číslic, kolik jich má umocňované přibližné číslo. Přitom poslední
číslice druhé, a zejména třetí mocniny je méně spolehlivá než poslední číslice
umocňova ého přibližného čísla.
4. Při odmocňování dvěma nebo třemi ponecháme ve výsledku tolik
platných číslic, kolik jich má odmocňované přibližné číslo. Přitom poslední
číslice druhé, a zejména tře.tí odmocniny je spolehlivější než poslední číslice
odmocňovaného přibližného čísla.
5. Při vyčíslování dílčích výsledků bereme o jednu číslici více, než
se doporučuje v předchozích pravidlech. Přitom v mezivýpočtech "zásobní
číslice" nepovažujeme za platné.
Není-li ve výpočtu sčítání nebo odčítání, lze v konečném výsledku ponechat
tolik platných číslic, kolik jich má číslo s nejmenším počtem platných číslic.
Přitom lze všechny. mezivýpočty provádět s počtem platných míst o jeťlnotku
větším. V konečném výsledku zásobní číslice po zaokrouhlení zmizí. Zásobní
číslice je vhodné při výpočtech psát menším písmenem nebo podtrhnout.
6. Mají-li při.sčítání nebo odčítání některá čísla větší počet desetin-
n Ý c h mís t, resp. při násobení, dělení, umocňování nebo odmocňování vět š í
počet platných číslic než ostatní, pak je před výpočtem zaokrouhlíme
na nejmenší počet desetinných míst, resp. platných číslic, který se v daných
číslech vyskytuje, zvětšený o jednu číslici.
7. Vyhledání čísla v tabulkách se považuje za samostatný výkon. Jde-li
o mezi výsledek, bereme je s jednou zásobní číslicí.
8. Lze-li čísla brát s libovolnou přesností, pak k tomu, abychom dostali
konečný výsledek s k platnými číslicemi, musíme přibliž1!á čísla za-
okrouhlit na takový počet platných číslic, aby předběžný výsledek měl
k + 1 platn¥ch číslic.
9. Při výpočtech pomocí logaritmů volíme takové tabulky, které mají
o jedno desetinné místo více než logaritmované přibližné číslo s nejmenším
počtem platných číslic. V konečném výsledku se poslední platná číslice po za-
okrouhlení vypustí.
148
Při použití pravidel pro výpočty s přibližnými čísly je nutno pamatovat.
že nezaručují správnost poslední číslice výsledku. Chyba této poslední číslice
řádu r může v některých případech činit i několik jednotek řádu r.
1.5. ÚMĚR Y
Názvy a označení
Rovnost dvou poměrů
a
a : b = c: d neboli
c
(abcd =F O)
b
-
d
se nazývá Úměra, přičemž se pro členy a, b, c, d úměry zavádějí tyto názvy:
a, d jsou
b, c
vnější členy,
vnitřní členy,
přední členy,
zadní členy,
a, c
b, d
Rozšiřování a krácení členů úměry (rE R \ {O}):
{ ar: br = c : d,
a:b = c:d =>
ar: b = cr: d;
a b
-:-=c :d,
r r
a:b = c:d =>
a c
-:b =-:d.
r r
Platí
a : b = c : d <=> ad = bc,
tj. součin vnějších členů se rovná součinu vnitřních členů.
Vzájemná výměna členů úměry
Z úměry a: b = c : d plyne:
a:c = b:d,
d:b=c:a,
d:c = b:a.
149
Sč í táTi í a od čít á n í v ú mě r á c h
Z úměry a: b = c: d pro všechna čísla p, q, r, s E R, 'pro něž jmenovatelé
zlomků nejsou rovni nule, plyne
pa + qb pc + qd
- ,
ra + sb rc + sd
pa + qe pb + qd
- rb + sd'
ra + se
.. .
odkud při speciální volbě čísel p, q, r a s dostaneme (pokud úměry mají smysl)
(a + b) : a = (c + d): c,
(a + b) : b = (e + d): d ,
(a - b): a = (c - d): c,
(a - b): b = (e - d): d,
(a + b): (a - b) = (e + d): (c - d):
Součinitel úměrnosti
a : b = c : d => a = pc /\ b = pd,
kde p se nazývá součinitel úměrnosti.
Spojitá úměra
a:b = b:c
(vnitřní členy jsou si rovny).
Třetí úměrná
b 2
x=-
a
(x se nazývá třetí úměrná k číslům a a b).
a:b = b:x;
Čtvrtá úměrná
a:b = e:x;
bc ..
x=-
a
(x se nazývá čtvrtá 1íměrná k číslům a, b, c). Geometrický význam viz na str. 302.
Střední úměrná
a:x = x:b;
x = J(ab) (ab > O)
150
(x se nazývá středni úměrná [geometrický průměr] z čísel a a b). Geometrický
význam viz na str. 303.
Spojitá harmonická úměra
(a - x):(x - b) = a:b;.
2ab
x=
a+b
(x se nazývá harmonický průměr z čísel a a b) neboli v jiném tvaru
1 1 ( 1 1 )
-=- -+- .
x 2 a b
Postupná měra
a:b:c:d:... = al :b l :c I :d l :...<=>
<=> a 1 = pa /\ b I = pb /\ c I = l!c /\ d I = pd /\ ....
Každou postupnou úměru lze rozepsat v jednotlivé úměry:
a : b = a l : b l ,
a : c = al : CI'
a:d=al:d l ,
b:c = b l :c l ,
b:d=bl:d l ,
c : d = CI: dl' atd.
1.6. LOGARITMOVÁNÍ
1.6.1. Základní pojmy
Pojem logaritmu a označení
Logaritmem kladného reálného čísla x při základu a E R + \ {1} nazýváme
takové reálné číslo
y = loga x,
že a Y = x. Číslo a se nazývá základ [báze], x numerus [logaritmované číslo]
a y logaritmus.
Logaritmování
Logaritmováníje při daném základu inverzní operací k umocňování, přičemž
k dané hodnotě x mocniny a Y se základem a hledáme exponent y. Platí
a 10ga x = x, loga (a Y ) = y, loga' (a - Y) = - Y .
151
Desítkové logaritmy
Logaritmus při základu 10 značíme
y = log1o X = 19 x (x > O)
a nazýváme desítkovým [dekadickým, Briggsovým] logaritmem, tj.
19 x = Y <=> x = 1 ()Y.
Přirozené logaritmy
Logaritmus při základu
e = lim. ( 1 + ! ) n = lim (1 + h)llh = 2,7182818284590...
" oo n h-O
značíme
10g e x = ln x (x > O)
a nazýváme přirozeným [N apierovým] logaritmem, tj.
ln x = y <=> x e Y .
Vztah mezi soustavami logaritmů
1
10g b a '= 1 b logc a = 10g b c 10& a,
ogc
kde převodní součinitel
1
1 b = 10g b C
ogc
se nazývá modul přechodu od soustavy logaritmů o základu b k soustavě logaritmů
o základu c.
Vztahy mezi desítkovými a přirozenými logaritmy
ln tI
19 a = = 19 e ln a,
ln 10
kde
1
- = 19 e = M = 0,434 294 48 .. .
ln 10
se nazývá modul soustavy dekadických logaritmů;,
ln a = ln 10 19 a,
152
kde
1
ln 10 = - = m = 2 , 302 585 0 9
M ...
se nazývá modul soustavy přirozených logaritmů.
1.6.2. V I a s t n o s t i log a r i t m ů
Pro \I a, cER + /\ \lb E R + \ {I} /\ \Ir E R /'.. \In E N platí:
10g b (ac) = log b a + 10g b c,
a
10g b - = 10g b a - 10g b c ,
c
10 gb ar
= r 10g b a,
1
= - 10gb a ,
n
= 1
,
= O.
10gb 'V a
10g b b
10g b 1
1.6.3. Určování desítkových logaritmů z logaritmických tabulek
Protože každé kladné číslo N lze vyjádřit ve tvaru N = 1 on No,
kde No E (I, 10) a n je celé číslo, můžeme jeho desítkový logaritmus vyjádřit
jako součet log N = n + log No, kde celé číslo n, které je řádem první nenulové
číslice čísla N, se nazývá charakteristika a log No E (O, 1) se nazývá mantisa.
Charakteristika nepravého desetinného zlomku (tj. čísla většího než 1)
s n místy před desetinnou čárkou se rovná n - 1.
Charakteristika pravého desetinného zlomku je záporná a rovná se počtu
nul před první nenulovou číslicí, počítajíc v to i nulu před desetinnou čárkou.
Je-li N > 1, resp. N < 1, píšeme log N ve tvaru n,a 1 a2 ... a s (n > 1),
resp. O,a 1 a 2 ... a s - Inl (n < O), kde n je charakteristika čísla log N.
Příklad:
Charakteristiky čísel 3 745; 75; 4; 0,007 3 jsou po řadě 3, 1, O, - 3.
Mantisy logaritmů najdeme v logaritmických tabulkách.
Má-li logaritmované číslo (numerus) o jednu platnou číslici více, než uvádějí
tabulky, pak k nalezené hodnotě v tabulkách pomocí lineární interpolace
připojíme přírůstek
d _ Dp
-10'
153
kde D je tabulková diference (tabulkový rozdíl mezi bezprostředně následující
hodnotou v tabulkách a nalezenou hodnotou) a p je další číslice, která se má
vzít v úvahu.
Příklad 1:
19 37 489 4,573 91,
neboť podle pětimístných tabulek je
19 37 480 . 4,573 80,
19 37490 4,57392.
Tabulková diference D = 12; další číslice je p = 9, takže přírůstek je
d= Dp = 12.9 = 108 · 11.
10 10 '
Dostaneme
19 37 489 4,573 80
+ 11
4,573 91.
Příklad 2:
Podobně vypočteme
19 0,123 67 0,09227 - 1,
1a
přičemž
D = 35
,
p = 7,
35.7
d = ...:.. 25.
10
Přírůstek mantisy lze také přímo najít v tabulkách poměrných částí, které
jsou ve všech logaritmických tabulkách.
Hledání logaritmovaného čísla (numeru) k danému logaritmu
Charakteristika logaritmu udává přímo polohu desetinné čárky ve výsledku
(v numeru). Je-li příslušná mantisa právě uvedena v tabulkách, můžeme
všechny číslice numeru přímo číst. Jinak najdeme v tabulkách nejblíže nižší
hodnotu a z přírůstku d mantisy a tabulkové diference D vypočteme další
číslici p numeru:
10d
p=-.
D
Také při hledání numeru je výhodné používat tabulek poměrných částí.
154
Příklad 1:
19 x = 3,598 14,
x 3 964,1 ,
d = 1
,
D = 11
,
10 . 1
p = . 1. .
11
Příklad 2:
19 x = 0,99637 - 3,
x 0,009 916 8,
d = 3
,
D = 4
,
10.3
p = ...:.. 8.
4
1.6.4. Přirozené logaritmy komplexních čísel
Přirozeným logaritmem [stručně logaritmem] komplexního čísla
z = e(cos qJ + i sin qJ) pro '1z E P
je komplexní číslo
ln z = ln [g(cos qJ + i sin qJ)] = ln Q + i(qJ + 2k1t) pro Yk E Z.
Hlavní hodnotou Ln z přirozeného logaritmu komplexního čísla
= g(cos li' + i sin qJ) nazýváme kompl xní číslo
Ln z = ln Q + iqJ, li' E ( - 1t, 1t>.
-
41 -:
Příklad:
Vypočtěme ln (3 - 7i).
r = J(9 + 49) = J58,
-7 '
t g ff) = - = - 2 j
3 ' ,
li' 293 °12' ...:.. 5,12 rad;
ln (3 - 7i) = ln .J58 + i(5,12 + 2k1t) =
= 2,03022 + i(5,12 + 2k1t);
k = O: ln (3 - 7i) 2,030 22 + 5,12i,
k = 1: ln (3 - 7i) 2,03022 + i(5,12 + 21t) 2,03022 + 11,4i,
k = 2: ln (3 - 7i) 2,03022 + i(5,12 + 41t) 2,03022 + 17,68i,
atd.
155
Zvláštní případy
Ryze imaginární číslo bi (b > O):
ln (bi) = ln (b e i (x/2+ 2b)) = ln b + i G + 2k1t) pro Vk E Z.
Ryze imaginární číslo - bi (b > O):
ln ( - bi) .= ln (b e i (3x/2+ 2b)) = ln b + i G 1t + 2k1t) pro Vk E Z .
Kladné reálné číslo a:
ln a = ln (a ei(O + 2k1t)) = ln a + 2k1ti
Záporné reálné číslo -a (a > O):
ln ( - a) = ln (a ei(1t + 2k1t)) = ln a + i(1t + 2k1t)
Pro Vk E Z tedy je
ln 1 = 2k1ti,
ln (-1) = i(1t + 2k1t),
ln i = i(-!1t + 2k1t),
ln ( - i) = i(!1t + 2k1t).
pro Vk E Z.
pro Yk E Z .
1.7.. KOMBINATORIKA
1.7.1. Binomické koeficienty', binomická věta
Faktoriál čísla n
Faktoriálem čísla n [n-faktoriálem] nazýváme funkci F na množině všech
..
nezáporných celých čísel, definovanou takto:
F(O) = 1 ,
F(n + 1) = (n + l)F(n) (ne No).
Místo F(n) píšeme n!. Platí O! = 1. Pro n > 1 je
n! = 1.2.....(n.. l)n.
Binomický koeficient
ro libovolné komplexní číslo (X a celé číslo k se tzv. binomický koeficient
156
[binomické číslo] C) (čteme: IX nad k) definuje takto:
ťX( ex - 1) (ťX - 2) oe. (ťX - k + 1)
k!
1
O
(:)=
(k > O),
(k = O),
(k < O).
Pro binomické koeficienty platí vztahy (ťX, B E C, k, n E Z)
(:) + C : 1) = (: : ).
f ( ex + k ) = ( ex + n + 1 ) ,
k=O k n
f ( ex ) ( B ) = ( ex + B )
k=O k n - k n.
Kombinační čísla
Pro nezáporná celá čísla k, n se tzv. kombinační číslo ( ) definuje takto:
( n ) ! n( n - 1) (n - 2)... (n - k + 1) = n !
k = C: = k! k !(n - k)!
O
(n > k),
(O < n < k).
Platí
( ) = (:) = 1.
Příklady:
( 10 ) = 10. 9 . 8 · 7 = 5 040 = 210,
4 1 . 2 . 3 . 4 24
( -5 ) ( - 5) ( - 6) ( - 7)
- - 35
3 - 1.2.3 --,
( -1 ) = (-!)(-1 )=
2 1.2 8'
( 3 ) 3 . 2 . 1 . O . ( - 1)
- _ O
5 - 1.2.3.4.5 - .
157
Pascalův trojúhelník k určení kombinačních čísel
.. 11=0 1
n' = 1 1 1
11 = 2 1 2
n = 3 1 3 3 1
n=4 1 4 6 4 1
11 = 5 1 5 10 10 5 1
První a poslední číslo v každém řádku schématu je vždy rovno 1. Každé
číslo uvnitř chématu se rovná součtu dvou nejbližších čísel z předchozího
řádku. Kombinační číslo (n) je v tomto schématu v (n + 1)-ním řádku na
(k + 1 )-ním místě. k
Příklad:
G) = 6 je v 5. řádku na 3. místě.
Vztahy mezi kombinačními čísly (k, nE No)
( n ) ( n ) /1 ! (symetričnost),
k - n - k - k !(n - k)!
C) + C : 1) = C : }
C : 1) - c) : : ,
G) + (k : 1) + (k : 2) + ... + c) = C : }
( ) + (k : 1) + (k ; 2) + ... + (k : /1) = (k + : + I)
C;) = C n .) = n,
( ) + (;) + G) + ... + (:) =kto C) = 2 n ,
( ) - (;) + (;) -... + (-1)"(:) =Jo(-q(:) = O,
15S
( ) + (;) + (:) + ... = 2n l,
(;) + (;) + G) + ... = 2 n - l ,
( y + (;y + (;y + ... + Cy = C:).
Binomická věta pro kladné celočíselné exponenty n
(a + br = ( ) a n + (;) an-Ib + (;) a n - 2 b 2 + G) a n - 3 b 3 +
+ . ... + ( n ) abn - 1 + ( n ) bn = f ( n ) an - k bk ,
n - 1 n k=O k
(a - br = ( }ď - (;)an-Ib + (;)a n - 2 b 2 - (;)ď- 3 b 3 +
+...+(-l)n-IC n l)abn-I+(-lr(:)bn=
= t (-l)k ( n ) an-kbk.
k=O k
.
Obecná binomická věta pro reálné exponenty rJ..
(a + b)a = ( )aa + G)aa-Ib + G)aa- 2 b 2 + (;)aa- 3 b 3 + ....
(viz též str. 702). Podmínka konvergence: Ibl < lal.
Binomická věta pro některé exponenty
(a + b)2 = a 2 + 2ab -+- b 2 , odkud (a + b)2 = (a - b)2 + 4ab,
(a + b)3 = a 3 + 3a 2 b + 3ab 2 + b 3 ,
(a + b)4 = a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4 ,
(a + b)5 = a 5 + 5a 4 b + 10a 3 b 2 + 10a 2 b 3 + 5ab 4 + b 5 .
.,
(a 1 + a2 + ... + amr = ai + a + ... + a; +
+ 2(al a 2 + al a 3 + ... + al a m + a 2 a3 + a 2 a4 + ... + a2 a m +
+ ... + a m - 1 a m ) .
159
Součty a rozdíly mocnin
a 1 - b 2 = (a + b) (a - b),
a 2 + b 2 = (a - b)2 + 2ab = (a + ib) (a - ih),
a 3 + b 3 = (a + b) (a 2 + ab + b 2 ), .
a 4 + b 4 = (a 2 + b 2 + ab J2) (a 2 + b 2 - ab J2), J
a 4 - b 4 = (a 2 + b 2 ) (a 2 - b 2 ) = (a 2 + h 2 ) (li + h) (li - h).
a n - b n = (a - b)(a n - I + a n - 2 b + a n - 3 b 2 + ... + ab n - 2 + b n - 1 )
(n E N),
a n + b n = (a + b) (a n - I - a n - 2 h + a n - 3 b 2 _ ... _ a b n - 2 + b n - I )
(n = 2n1 + 1, m E N),
Příklady (m, n E N):
(a 6 - b 6 )/(a 3 - b 3 ) = a 3 + b 3 ,
(a 6 - b 6 )/(a 3 + b 3 ) = a 3 - b 3 ,
(a 4 - b 2 )/(a 2 + b) = a 2 - b,
(a 2m _ b 2n )/(a m _ b n ) = a m + b n ,
(a 2n _ b 2n )/(a 2 _ b 2 ) = a 2n - 2 + a 2n - 4 b 2 + a 2n - 6 b 4 +
+ ... + a 2 b21J - 4 + b2n - 2,
(a 3m + b 3m )/(a m + bm) = a 2m + amb'" + b 2m ,
(a n - 1) I (a - 1) = a n - 1 + a n - 2 + a n - 3 + ... + a + 1,
(a 2n + 1 + 1 )/(a + 1) = a 2n - a 2n - I + a 2n - 2 - + ... - a + 1.
1.7.2. Permutace
Permutace bez opakování
Permutací [pořadím] z n-prvkové množiny M (bez opakování> nebo n-člennou
permutací [n-členným pořadfm] (bez opakování> nazýváme každou uspořá-
danou n-tici navzájem různých prvků vytvořenou z prvků množiny M.
Počet všech permutací z n prvků bez opakování:
p( n) = 1 . 2 . 3 . ... . n = n! .
Permutace s opakováním
n-člennou permutaci z p-prvkové množiny M = {a 1 , a2, ..., ap} s opakováním
prvku a 1 právě k1-krát, prvku a2 právě k 2 -krát, ..., prvku ap právě kp-krát nazý-
váme každou takovou uspořádanou n-tici vytvořenou ze všech p (p < n)
prvků množiny M, že se v této uspořádané n:.tici prvek a l vyskytuje právě
kl-krát, prvek a 2 právě k 2 -krát, ..., prvek ap právě kp-krát (k l + k 2 + ...
... + kp = n).
160
Počet všech n-členných permutací z p-prvkové množiny {a t, a2, ..., ap}
s opakováním prvku a t právě kt-krát, prvku a 2 právě k 2 -krát,..., prvku ap
právě kp-krát:
P I. k2. .... d n ) = C J , k2 " ., kJ = k J ! k2 !". k/
kde symbol
C J, k 2 , ", k J
se nazývá polynomický koeficient.
Speciálně pro p = 2 počet všech n-členných permutací ze dvou prvků al, a2
I
s opakováním p vku a 1 k-krát a prvku a 2 (n - k)-krát je
P .n-k(n) =,C, nn_ k) = k!(nn k)! .
Číslo ( " n ) je rovno číslu ( n ) .
k,n-k k
Příklad 1:
Kolik různých pětimístných kladných celých čísel lze vytvořit z číslic 2, 3 a 5,
jestliže se v každém čísle každá z číslic 3 a 5 vyskytuje právě dvakrát?
( ) 5! 1.2.3.4.5
P 5 = = = 30
1,2.2 1!2!2! 1.1.2.1.2 .
Příklad 2:
, Kolik různých šestimístných kladných celých čísel lze vytvořit z číslic 1 a 4,
jestliže se v každém čísle číslice 1, resp. 4 vyskytuje právě dvakrát, resp. právě
čtyřikrát?
( ) _ ( 6 ) _ 6 ! _ 1 . 2 . 3. . 4 . 5 . t> _ 5 . 6 _
P 2 4 6 - - - - - - - 15.
, 2 2!4! 1.2.1.2.3.4 2
Transpozice
Permutaci, v níž vzájemně zaměníme dva členy a všechny ostatní členy
ponecháme beze změny pořadí, nazýváme transpozicí původní permutace.
Každou permutaci lze převést v jinou permutaci postupnými transpozicemi.
Základní permutaci nazýváme pevně zvolenou permutaci, s níž se porovnávají
jiné permutace.
161
Permutace množiny
Permutací množiny M nazýváme každé prosté zobrazení množiny M
na množinu M.
Speciálně permutaci P množiny (úseku) U n = {I, 2, ..., n} zapisujeme
ve tvaru schématu
( 1, 2, . . ., n )
P=
k 1, k 2' . · ., k n '
kde k i = P(i) je číslo z množiny U n , které je při permutaci P obrazem čísla
i EM. Mezi čísly k 1 , k 2 , ..., kra se vzhledem k definici permutace každé číslo
z čisell, 2, ..., n vyskytuje právě jednou. Základní [hlavní, identickou] permutací
množiny U n nazýváme permutaci
P = ( 1, 2, . .., n ) .
1, 2, .. ., n
Inverzní permutací k permutaci
( 1, 2, . .., n )
p = k 1 , k 2 , ..., k n
nazýváme permutaci
_ ( k 1 , k2' . .., k n )
P- 1 - .
1, 2, ..., n
Inverze u permutace
Říkáme, že permutace
( 1, 2, ..., n )
p = k 1 ,k 2 ,...,k n
množiny U n = {I, 2, ..., } má inverzi, právě když existují takové .indexy i, j
(i < j), že k i > k j (i, jE U n ). Označíme-li v(p) počet všech inverzí v permutaci P,
pak permutaci P nazýváme sudou, resp. lichou, právě když v(p) je sudé, re p.
liché číslo. Znaménko [signum] permutace P je číslo
z(p) = ( -1 )V(P.).
Obdobně se definuje inverze u permutace
P = ( i h i 2, ..., in )
k 1, k 2, ..., kra
162
libovolné n-prvkové množiny M = {i l' i 2 , ..., in} tak, že permutace P má
inverzi, právě když pro ;m < in je km > k n (im, in E !\tf), přičemž <, resp. >
je znakem předcházení, resp. následování.
příklad:
Permutace
,
".-
p = ( 4,5,6.7,8 )
8, 4, 6, 5, 7
má právě pět inverzí
8 a 4, 8 a 6, 8 a 5, 8 a 7, 6 a 5,
takže jde o lichou permutaci.
Počet všech možných sudých permutací množiny o mohutnosti n se rovná
počtu všech jejich možných lichých permutací, tj. n! 12.
1.7.3. Variace
Variace bez opakování
Variací k-té třídy z u-prvkové množiny <bez opakování) nebo variací k-té
třídy z n prl,ků <bez'opakování) nazýváme každou uspořádanou k-tici na-
vzájem různých prvků, vytvořenou z n-prvkové množiny, tj. každý prvek
z daných n prvků se v jedné variaci může vyskytnout právě jednou.
Počet všech variací k-té třídy z n-prvkové množiny bez opakování:
v,,(n) = n( n - 1)( n - 2)... (n - k + 1) = ( n!) = ( " ) k! .
n-k! k '
Variace n-té třídy z n prvků bez opakování je tedy permutací z n prvků, takže
platí
(n) = P( n) = 11! .
Mohutnost systému všech prostých zobrazení množiny B o mohutnosti k
do množiny A o mohutnosti 11 se rovná (n).
Příklad:
Považujme za zdařilý takový vrh, při němž třikrát za sebou hodíme kostkou
a pokaždé padne jiný počet bodů. Kolik takových různých zdařilých vrhů
existuje, přihlížíme-li k pořadí bodů ve vrhu?
V 3 ( 6) = 6 . 5 . 4 = 120.
163
Variace s opakováním
. Variací k-té třídy z n-prvkové množiny M s opakováním nazýváme každou
uspořádanou k-tici vytvořenou z prvků množiny M tak, že v této uspořádané
k-tici se každý prvek z prvků množiny M může vyskytovat až k-krát.
Počet všech variací k-té třídy z n prvků s opakováním:
.
V (n) = n k .
Mohutnost množiny všech zobrazení množiny B o mohutnosti k do množiny
A o mohutnosti n se rovná V;(n).
Příklad:
Kolik možností je při vyplňování sázenky Sazky o 12 utkáních?
n = 3 (vítězství, prohra, nerozhodně),
k = 12,
V{2(3) = 3 12 = 531441.
1.7.4. Kombinace
Kombinace bez opakování
Kombinací k-té třídy z n-prvkové množiny <bez opakováni) nebo kombinaci
k-té třídy z n prvků. <bez opakování) nazýváme každou k-prvkovou podmnožinu
n-prvkové množiny, tj. u kombinace bez opakování nepřihlížíme k uspo-
řádání prvků a každý prvek z daných n prvků s v jedné kombinaci může
vyskytnout nejvýše jednou.
P č t všech kombinací k-té třídy z n prvků bez opakování:
( ) _ ( n ) _ n( n - 1)... (n - k + 1) _ n ! _
C k n - - --
k 1 .2. ... . k k! (n - k)!
(n)
P(k)
(n > k).
Má-li systém &'(A) všech podmnožin množiny A mohutnost 2", pak systém
&'(A) obsahuje právě Ck(n) k-prvkových podmnožin množiny A.
Příklad :
Kolik možností by bylo při tahu Sportky, kdyby se počet sportů rozšířil
na 90 a počet tažených čísel se zm nšil na pět?
n=90 k= 5
, ,
( 90 ) ,
C s (90) = 5 = 43 949268. \
164
Kombinace s opakováním
Kombinací k-té třídy z n-prvkové množiny M s opakováním nazýváme každou
skupinu o k prvcích vytvořenou z prvků množiny M tak, že v této skupině
se každý prvek může vyskytovat až k-krát.
Počet všech kombinací k-té třídy z n prvků s opakováním:
' ( ) _ ( n + k - 1 ) _ (n + k - 1)!
Ckn - - .
k k!(n-l)!
příklad:
Kolik kombinací třetí třídy s opakováním lze vytvořit z pěti číslic 2, 3, 4, 5, 6?
, ( ) _ ( 5 + 3 - 1 ) _ ( 7 ) _ 7 o 6 . 5 _
C 3 5 - - - - 35.
3 3 1.2.3
108. POSLOUPNOSTI REÁLNÝCH ČíSEL
1.8.1. Základní pojmy
(Nekonečnou) posloupností reálných čísel [(nekonečnou) posloup-
ností, číselnou (nekonečnou) posloupností] nazýváme každé zobrazení mno-
žiny N všech kladných celých čísel do množiny R všech reálných čísel.
Konečnou posloupnosti reálných čísel [konečnou posloupností] nazýváme
každé zobrazení množiny (úseku) U n = {1, 2, ..., n} do množiny R všech
reálných čísel (na neprázdnou podmnožinu množiny R)o
(Nekonečná) posloupnost, resp. konečná posloupnost reálných čísel je tedy
reálná funkce jedné reálné proměnné, jejímž definičním oborem je množina N,
resp. nějaký úsek U" množiny No
Označení:
n je index (vzor),
a 1 - počáteční člen,
a n - n-tý člen posloupnosti (obecný člen posloupnosti, obraz),
{a n } = l' popřo {a n } f, popř. (a 1 , a2, o. o), popř. a 1 , a2, ... - posloupnost,
{ } k '" { } k '" ( ) v k "':
a n n= l' popr. a n l' popr. a1, a2, .0., a k , popro a1, a2, .0., a k - onecna
posloupnost.
Posloupnost je dána:
- slovním vyjádřením: například každému kladnému celému číslu' n je při-
řazena jeho druhá mocnina;
analyticky (vzorcem pro n-tý člen): například a n = n 2 pro Vn E N:
165
- tabelárně (výčtem všech členů): například {n 2 }:>= 1 = (1,4,9,16, ...),
- rekurentně '(tj. je dáno několik prvních členů posloupnosti a je dán před-
pis, jak se vypočte n-tý člen na základě znalosti předchozích členů): například
a 1 = 1, a2 = 4, a n - 2a n - 1 + a n -2 = 2, takže a3 = 2 + 2.4 - 1 = 9.
Diferenční posloupností prvního řádu k posloupnosti {a n } nazýváme po-
sloupnost { 1 a n } = { an} = {b n }, kde b n = a n + 1 - a n = an pro \In E N.
Přík lad :
Diferenční posloupností prvního řádu k posloupnosti
H} = 1 = ( 1 , t, t, . ..)
je posloupnost
{ ( )} = (-t, -k, - /2 ' ...).
- nn l :1
Diferenční posloupností k-tého řádu posloupnosti {a n } nazýváme diferenční
posloupnost { kan} diferenční posloupnosti (k - 1 )-ního řádu { k - 1 a n }
k posloupnosti {a n }. '
Podilovou posloupností k posloupnosti {a n }, kde a n 9= O pro \In E N, je po-
sloupnost {b n }, kde b n = a n + l/a n pro \In E N. \
Posloupností částečných součtů posloupnosti {a n } nazýváme posloupnost
{ sn} = 1 ,
n
Sn = L a k .
k=l
Příklad:
Posloupností částečných součtů posloupnosti
,
{ 2n }:= 1 = (2, 4, 6, ...)
je posloupnost
{ n( n + 1)}:= 1 = (2, 6, 12, .. .) .
Posloupností s kladnými, resp. nezápornými členy nazýváme takovou po-
sloupnost '{a n }, že a n > O pro \In E N, resp. a,. > O pro \In E N.
Alternující posloupností nazýváme takovou posloupnost {a n }, že a n =
= ( - 1 r b n , popř. a,. = ( - 1 r + 1 b n , kde b n > O.
Rostoucí
Klesající
Neklesající
Nerostoucí
.
posloupností nazýváme takovou posloupnost
{a n , žé pro \In E N platí
a n < a n + 1 ,
a n > a n + 1 ,
a n < a n + 1 ,
a,. > a n + 1 .
166
Rostoucí, klesající, neklesající a nerostoucí posloupnosti se souhrnně na-
nazývají monotónní posloupnosti. Rostoucí a klesající posloupnosti se souhrnně
nazývají ryze monotónní posloupnosti.
Konstantní posloupnosti nazýváme takovou posloupnost {a n }, že a n = konst
pro \In E N.
Posloupnost {a n } se nazývá shora, resp. zdola ohraničená [shor.a, resp. zdola
omezená], právě když existuje takové číslo K, resp. k, že pro všechny indexy n
platí a n < K, resp. a,. > k.
Posloupnost a,. se nazývá ohraničená [omezená], právě když je shora i zdola
ohraničená, tj. právě když existuje takové reálné číslo K > O, že lani < K
pro \In E N.
Vybranou posloupností z posloupnosti [pod posloupností posloupnosti]
{a,.}:= 1 nazýváme posloupnost {b n }:= l' k níž existuje taková rostoucí po-
sloupnost {k,.}:= 1 kladných celých čísel, že b,. = a kn .
Příklad :
Posloupnost {n2} =1 je vybranou posloupností k posloupnosti {n}:'=l.
1.8.2. Aritmetické posloupnosti
Posloupnost {a n } se nazývá (nekonečná) aritmetická posloupnost [aritme-
tická posloupnost prvního řádu], právě když platí a,. - a n - 1 = d = konst
pro \In E N neboli právě když její diferenční posloupnost prvního řádu je
konstantní. Číslo d = konst se nazývá diference aritmetické posloupnosti, {a n }.
Aritmetickou posloupností nultého [O-tého] řádu nazýváme konstantní
posloupnost.
Příklad:
Posloupnost 1,4, 7, 10, ... je aritmetickou posloupností s diferencí d = 3.
Pro aritmetickou posloupnost platí
a,. = al + (n - 1)d pro \lnEN,
a n = ak + (n - k)d pro \lnEN \lkEN;
a n = !-(a n - k + a n + k ) pro \In E N \lk E U n - 1 .
Pro součet Sn prvních n členů aritmetické posloupnosti platí
a 1 + a n n [
Sn = a 1 + a 2 + ... + a,. = n = - 2a 1 + (n - 1) d] .
2 2
167
Příklady:
Součet prvních n kladných celých čísel:
sn = t k = n(n + 1) .
k=l 2
Součet prvních n kladných sudých čísel:
n
Sn = L 2k = n(n + 1).
k=l
Součet prvních n kladných lichých čísel:
n
Sn = L (2k - 1) = n 2 .
k=l
Posloupnost {a,,} se názývá aritmetická posloupnost k-tého řádu, právě když
její diferenční posloupnost k-tého řádu {Dka,,} je k'onstantní.' .
Posloupnost {a n } se nazývá aritmetická posloupnost k-tého řádu, právě když
její diferenční posloupnost k-tého řádu { kan} je konstantní.
Příklad:
{a n } = {2, 3, 8, 18, .36, 67, 118, ...},
{L\a,,} - {I, 5, 10, 18, 31, 51, ...} (diferenční posloupnost 1. řádu),
{L\ 2 a n } = {4, 5, 8, 13,' 20, ...} (diferenční' posloupnost 2. řádu),
{ 3an} = {I, 3, 5, 7, o..} (diferenční posloupnost 3. řádu),
{ 4 a n } _ {2, 2, 2, ...} (konstantní diferenčn! posloupnost 4. řádu).
Posloupnost {a n } je aritmetickou posloupností 4. řádu ·
Rekurentní vzorce pro aritmetické posloupnosti
vyšších řádů
Aritmetická posloupnost druhého řádu:
Jsou-li dány členy a 1 ,.a2 a diference d, resp. člen a l a čísla dl' d 2 , platí
a n - 2a n - 1 + a n - 2 = d
pro \:In E N .
resp.
a n = al + (n - 1) dl + (n - 1)2 d 2
pro \:In E N..
Aritmetická posloupnost třetího řádu:
Jsou-li dány členy a 1 , 2' a3 a diference d, resp. člen a 1 a čísla dl' d 2 , d 3 , platí
a" - 3a n - 1 + 3a n - 2 - a n - 3 = d pro \:In E N \ U 3 '
168
resp.
a n = a 1 + (n - 1) d 1 + (n - 1)2 d 2 + (n - 1)3 d 3 pro
Aritlnetická posloupnost m-tého řádu:
Jsoll;-li dány členy a 1 , a 2 , ..., a m a diference d resp. člen al a čísla dl' d 2 , ..., dm'
platí
a n - (;) a n - 1 + ( ) a n - 2 - .., + ( - l)m a n - m = d pro Vn E N \ U m ,
resp.
a n = a I + (n - 1) li I 7 (n - 1)2 d 2 + ... + (11 - 1 r dm
pro \:In E N.
Interpolace aritmetické posloupnosti prvního řádu
Jestliže mezi každé dva sousední členy aritmetické posloupnosti s diferencí d.
vložíme m členů tak, aby nově vzniklá posloupnost byli také aritmetická,
říkáme, že me provedli lineární interpolaci aritmetické posloupnosti prvního
řádu. Nová aritmetická posloupnost má diferenci ·
d
dl = ' .
nI + 1
Příklady: .
Součet druhých mocnin prvních n kladných celých čísel:
Sn = t k 2 =. n(n + 1)(2n + 1) .
k=l 6
Součet třetích mocnin prvních n kladných celých čísel:
n 3 ( n(n + 1 ) ) 2 ( n ) 2
sn='Lk= = 'Lk.
k=l. 2 k=l
Součet čtvrtých ffi0cnin prvních n kladných celých čísel:
Sn = t k 4 = n(n + 1)(2n + 1)(3n 2 + 3n - 1) .
k=1 30
Další vzorce:
p + (p + 1) + (p + 2) + .'0 + (q --.: 1) + q = (q + p)(q + 1 - p) =
2
q2 + q _ p2 + P
2
pro \:Iq E N /\ \:Ip E U q ,
169
2 2 2 ( ) 2 _ n( 2n + 1) (2n - 1) _ n( 4n 2 - 1
1 + 3 + 5 +. .. + 2n - 1 - 3 - 3 '
1 3 + 3 3 + 53 + ... + (2n - 1)3 = n 2 (2n 2 - 1).
1.8.3. Geometrické posloupnosti
/
Posloupnost {a n } se nazývá (nekonečná) geometrická posloupnost,
právě když platí
a,. + 1 = anq
pro ' \:In E N ,
kde číslo q = konst =F O se nazývá kvocient geometrické posloupnosti {a,.}.
Je tedy
{a,.} = (a 1 , a 1 q, a1q2, ...).
Pro q > 1 je geometrická posloupnost při a 1 > O, resp. a 1 < O rostoucí,
resp. klesající.
Pro O < q < 1 je geometrická posloupnost při al > O, resp. a 1 < O
klesající, resp. rostoucí.
Pro q < O je geometrická posloupnost alternující (se střídavými znaménky).
Pro q = 1 dostaneme konstantní posloupnost, tj. posloupnost s konstant-
ními členy.
Pro geometrickou posloupnost platí
a,.=alq'-l pro VneN,
a,. + 1 = anq,
la,.1 = J (a,. - tJl,. + k)
nS- r
a s = a r '1 ·
pro "Vn e .\1 \ {I} /\ "V k e U,. - 1 ,
Součet prvních n členů geometrické posloupnosti {a,.}
a 1 (q" - 1) anq - a 1
s = -
n q-1 q-1
s,. = a 1 n (q = 1).
(q =F 1),
Součet nekonečné geometrické řady
-1 al
s = i.J a. cf =
,.=1 1 - q
pro Iql < 1.
170
Interpolace geometrické posloupnosti
Jestliže mezi každé dva členy geometrické posloupnosti s kvocientem q
vložíme m členů tak, aby nově vzniklá posloupnost byla také geometrická,
říkáme, že jsme provedli interpolaci geometrické posloupnosti. Nová geo-
metrická posloupnost má kvocient
ql = m+ !jq.
1.8.4. V y vol e n á čís I a
(
I
Normalizovaná [normální] vyvolená čísla jsou všechny členy některé
z geometrických posloupností (tzv. základních [teoretick) ch] posloupností
vyvolených čísel)
{(I()"/ 40 r- 1 }:= 1 = R k
(r = 2 m pro m = 1,2,3,4; k = 40Ir), vyjádřené v desítkovém zápisu na tři
platné číslice. Jsou-li tyto členy vyjádřeny na pět pl?tných číslic,
mluvíme (nevhodně) o přesných vyvolených číslech. Prvním členem každé
základních posloupností R k je číslo 1.
K vocientem základní posloupnosti vyvolených čísel je číslo qJ = 10 1 ík,
přičemž k = 40lr je součást označení příslušné základní posloupnosti R k
vyvolených čísel a k-I je počet členů mezi dvěma mocninami 10", 10"+ 1
(n E No). Součin a podíl dvou vyvolených čísel, stejně jako n-tá ,mocnina vy-
voleného čísla (n E N \ {I}) je zřejmě opět vyvoleným číslem.
Odro=enou [vyhranou] posloupnost vyvolených čísel dostaneme z některé
ze základn h posloupností vyvolených čísel tak, že za první člen odvozené
posloupnosti vohme některý člen a n základní posloupnosti a za kvocient
odvozené posloupnosti volíme p-tou mocninu (p E N \ {I } kvocientu
základní posloupnosti, takže ze základní poslvupnosti bereme vždy každý
p-tý člen od zvoleného členu. f)dvozenou posloupnost vyvolených čísel pak
označujeme R kjp (..., a n , .. .).
Základní i odvozené posloupnosti vyvolených čísel mají velký význam při
normalizování hodnot technických veličin (rozměrů strojních součástí,
rychlostí, frekvencí otáčenÍ. tlaků, \:, :'.onů, napětí aj.). Pojednává o nich
ČSN 01 0201 Vyvolená čísla 19f Písmeno R v označení posloupností
vyvolených čísel pochází od jejich navrhovatele Ch. Renarda.
171
Příklad 1 :
Kvocientem posloupnosti R 20 je číslo qJ = 10 J / 20 ...:... 1,122. Z teoretických
vyvolených čísel
10, 10.10 1 / 20 , 10. (10 1 / 2 °)2, 10. (101120)3, ...
odvozené posloupnosti R 20 (..., 10, ...) dostaneme příslušná normalizovaná
vyvolená čísla
10; 11,2; 12,6; 14,1; 15,8; 17,6;....
Příklad 2:
Odvozená posloupnost R 40i6 (...; 300; ...) představuje normalizovaná
vyvolená čísla 300, 425, 600, 850,..., neboť qJ = 1 0 6 / 40 J2. Posloupnost
R 40/6 (...; 300; ...) se tedy přibližně shoduje s posloupností rozměrů světových
formátů.
1.9. PROCENTOVÝ POČET, úROKOVÝ POČET
1.9.1. Procentový počet, promilový počet
Procentov)- d promilový poměr
Čísla (nebo veličiny téhož druhu při téže měřicí jednotce) a, b (v tomto pořadí)
lze porovnávat bud' r_ozdílem a - b (popř. absolutní hodnotou la -' bl
rozdílu), nebo podílem [poměrem] alb neboli a: b (čteme: a ku b). Při
vhodné volbě jednoho z čísel c, d lze rozdíl a - b vyjádřit pomocí rozdílové
[aritmetické] úměry
a-b=c-d
a podíl alb pomocí (podílové> úměry
a:b = c:d.
V praxi se často v p:lpadě podílové úměry klade d = 100, resp. d = 1 000,
takže
a:b = p: 100, resp. a:b = m: 1000,
což zapisujeme ve tvaru
a : b = p %, resp. a : b = m o 100'
Výraz p % (čteme: p procent), resp. 111 o/no (čterrle: m promile) tedy značí q =
= pil00, resp. r = mil 000 a nazývá se rrocentový poměr [procentový podíl],
resp. promilový poměr [promilový podíl] čísel a, b (v tomto pořadí). Číslo p,
172
resp. m se nazývá procentová míra [počet procent], resp. promilová míra [počet
promilí].
Pozná Inka :
Určit zlomek alh z čísla [= celku] c neboli změnit číslo c r poměru alb (poměr
je jiný název pro zlomek) znamená určit číslo ac/ho
Procentový počet (ze základu) (procentový počet fe sta]
Obrácenými úlohami k úloze určit, jakým zlomkem p/l00 (tj. kolik procent
neboli setin) z čísla Ku je číslo C, jsou úloha určit číslo C jako zlomek plloo
(tj. p procent neboli p %) z čísla Ku a úloha určit číslo Ko k danému číslu C,
které je daným zlomkem piloo z čísla Ko.
Platí
C : p = Ko : 100,
odkud
Kop
C = 100 = Koq,
T lODC C
K - -
o - -- - -,
p q
lOOC
p = Ko = lOOq,
přičemž zavádíme tyto názvy:
Ko - (procentový> základ,
p - procentová míra (ze sta> [počet procent (ze sta>],
C - procentová část.
Procentový počet ze zvětšeného základu
[procentový počet na sto]
Jestliže součet Ko + C nazveme zvětšeným základem a označíme K(+), platí
C : p = K( +) : ( 1 00 + p),
odkud
K(+)p
C-
- - ,
100 + P
100K(+ )
K -
o - 100 + p'
lOOC
p = K( +) - C'
Procentový počet ze zmenšeného základu
'[p r o cen t o v Ý poč e t ves tu]
Jestliže rozdíl Ko - C nazveme zmen. enJJm základen1 a označíme K(-), platí
C : p = K( - ) : (100 - p),
odkud
K(- )
C' = P
100 - p'
1OOK(-)
K ----
o - 100 _ p'
looC
p = K( --) + c'
173
Procentová míra <na sto> poměru procentové části
a zvětšeného základu
< +) _ looC '
p - K(+.-
looC
-
Ko + C
toop
-----
-
100 + p'
kde p je procentová míra ze sta.
Procentová míra <ve stu> poměru procentové části
a zmenšeného základu
(_) _ l00C
p - K( -) -
looC
K - C
o
loop
,
100 - p
kde p je procentová míra ze sta.
Příklad 1:
Přičteme-li k výrobní ceně 15procentní přirážku, dostaneme velkoobchodní
cenu. Přirážka tedy činí p % = 15 %. z výrobní ceny a
(+)0 = loop 0/ = 100.15 0 /-=-13°/
P % 1()() + /0 1()() + 15 /0 - /0
P .
z velkoobchodní ceny.
Příklad 2:
Ztráta na materiálu při určité výrobě činí p % = 23 z hmotnosti surovin.
Z hlediska hotových výrobků ztrátě p % = 23 % z hmotnosti surovin odpovídá
ztrá ta .
lOOp 100.23
P < -) 0/ = 0/ = 0/ . 29 9 o
/ o 100 _ P /0 100 _ 23 / o , o
z hotových výrobků.
1.9.2. Úrokový počet,
o značeni:
Ko - základní částka Distina],
p - úroková míra,
t r - počet roků,
t m - počet měsíců,
t d - počet dnů,
u -:... úrok.
174
Výpočet úroku:
Kopt r Kopt m
u = 100 ' popř. u = 100.12 ' popř.
Výpočet základní částky:
lOOu
Ko = -, popř.
pt r
Výpočet úrokové míry:
Kopt d
U = -----.
100.360
100. 12u
Ko = --
ptm
100. 360u
popř. KO = -----.
pt d
lOOu
p=-,
Kot r
Výpočet doby:
lOOu
t r = -,
Kop
100. 12u
popř. p =
Kot m '
, 100. 360u
popř. p =
KOt d
popř. t m =
100. 12u
Kop
popř.
100. 360u
t d =
Kop
Úrokové číslo a úrokový dělitel
Při výpočtu úroku podle počtu dnů platí
N
u =-
D'
kde
KOt d
N=-
100
je tzv. úrokové číslo a
360
D=-
p
je tzv. úrokový dělitel.
1.9.3. Složený úrokový počet
Označení:
K o je počáteční [základní] jistina, diskontovaná částka [hotovost],
Kn - konečná [výsledná] jistina na konci n-tého úrokovacího období,
n - počet úrokovacích období,
p - úroková míra,
i = p = pllOO - úrokový poměr,
175
r = 1 + i - úrokový faktor,
r" = (1 + ir - úročitel,
(X - splátka [pravidelná splátka, anuita],
1
v = - diskontní faktor,
1 + i
tf' = ( 1 ) " - odúročitel.
1 + i
Konečná jistina na konci n-:tého roku při ročním připisování úroků:
K" = Kor".
Při připisování úroků pololetně je relativní úro ková míra pj2, takže
. p
r=I+-
200'
při připisování úroku čtvrtletně je relativní úro ková míra pj4, takže
r=I+-.L
400'
atd. Ve vzorci K" = Kor" značí n po řadě počet pololetí, čtvrtletí atd.
Výpočet. počáteční j istin y :
K"
Ko = -.
r"
Výpočet počáteční jistiny [hotovosti] se nazývá diskontováni.
Výpočet úrokové míry: Z úrokového faktoru
r = J Kn
Ko
dostaneme
p = l00(r - 1).
Výpočet počtu úrokovacích období:
19 Kn - 19 Ko
n=
19 r
Konečná jistina po n úrokovacích obdobích při pravidelných platbách:
K = ťX(ť' - 1)
" r - 1
176
pro platby na konci roku (při polhůtní [dekurzívní] platbě ),
ťXr(r n - 1)
K =
n r - 1
pro phitby na začátku roku (při předlhůtní [anticipativní] platbě ex).
1.9.4. Důchodový počet
Konečná jistina po n úrokovacích obdobích a při předlhůtním
vkladu '1:
ťXr(r n - 1) i
Kn = = r.t.S n ,
r - 1
kde
. r(r" - 1) ( . ) (1 + ir - 1
Sl= =1+z
n 1 .
r- z
je tzv. předlhůtní střadatel.
Konečná jistina po n úrokovacích obdobích a při polhůtním vkladu ťX:
r" - 1)
K = = Sil
" 1 '"
r-
kde
. r n - 1
S il -
n -
r - 1
(1 + i)n - 1
i
je tzv. polhůtní střadatel.
Počáteční jistina při n úrokovacích obdobích a při předlhůtním důchodu :
ťX( r" - 1) i
Ko = -1 ( ) = an'
ť' r - 1
kde
r n - 1 1 - v"
a i = = (1 + i)
n r n - 1 (r - 1) i
je tzv. před lhůtní zásobitel.
Počáteční jistina při n úrokovacích obdobích a při polhůtním důchodu :
r" - 1) il
K o = ( ) = ťXa n ,
r n r - 1
\
kde
rn(r - 1) , i
je tzv. polhůtni zásobitel.
a il _
n
r" - 1 1 - v"
177
Výpočet důchodu nebo splátky [anuity] a z konečné, resp. počáteční jistiny
při polhůtním umořování:
Kn(r - 1)
a =
ť' - 1 '
resp.
Kor"(r - 1) 1
a = = Ko '
J.n - 1 a I
n
kde
1 r"( r - 1) l
aŽ!
n
r n - 1
1 - tf
je tzv. umořovatel.
Výpočet důchodu nebo splátky [anuity] a z konečné, resp. po áteční jistiny
při předlhůtním umořování:
Kn(r - 1)
a=
r(r" - 1) ,
resp.
Kor"-l(r - 1)
rJ..-
- r n -1 .
Výpočet počtu n úrok ovacích období z konečné, resp. počáteční jistiny:
19 [Kn(r - 1) + a] - 19 a
n=
19 r
19 [Kn(r - 1) + rJ..r] - 19 (ťXr)
n=
19 r
při polhůtní platbě a,
při předlhůtní platbě ,
resp.
19 rJ.. - 19 (ťX + Ko - Kor)
n = při polhůtní platbě a,
19 r
19 ťX + 19 r - 19 (Ko + ar - Kor)
n = při předlhůtní platbě rJ...
19 r
Počáteční jistina trvalého důchodu [renty]:
a
Ko=
r r- 1
(polhůtní důchod),
rJ..r
Ko=
r - 1
(předlhůtní důchod).
178
očáteční jistina při periodick)'ch platbách C( měnových jednotek:
C((,.n - 1)
Ko = ---
,."(1'-1)
(,'I - 1)
K - -----
o - r" - 1 (r - 1)
pTI) platby na konci roku
pro platby na začátku roku.
Konečná jistina při počáteční jistině Ko a při pravideln}'ch vkiadech. resp
výběrech a měnových jednotek-:
, y :ť( r" - 1)
Kn = Kor" + ---- 1 - při vkladech na konci roku,
r-
ar("" - 1)
Kn = Ko,'l + při vkladech na začátku roku.
r - 1
resp. (zbytek dluhu po zaplacení n anuit (1)
T e«"" - '1)
Kn = Ko"" - 1 při výběrech na konci roků,
r-
o ar(,.1I ,- 1)
Kn = Ko"" - při výběrech na začátku roku.
f r - 1
.
Umořování dluhu [půjčky, výpůjčky]
Umořovací splátka [anuita], má-li být Iuh umořen právě ti splátkami:
K orn( r - 1) , 1
a = n 1 = Ko b'
r - a n
kde Ko je dlužná [umořovací] částka.
Umořovací sazba (procentová míra, při které se bude dlužná ( :'tstka
umořovat):
p
li n = JI 1 '
, -
kde p je procentová míra zúročenÍ.
Počet n období (doba úmoru), za něž se dlužná částka umoří:
19 (1 + plUn)
n -
- 19 r - .
Spojité [organické] zúročenÍ základní jistiny Ko za n roků:
Kn = Koe pn 100.
179
Obdobně pro spojitý pokles platí
K n = K o e - pni I O O .
Organický růst vyjadřuje funkce
w = Ko ear,
kde je intenzita růstu,
Ko - počáteční hodnota.
Pro C( < O popisuje růstový zákon tlumené procesy (radioaktivní rozpad,
ochlazování, vybíjení kondenzátoru).
1.10. MATICE
1.10.1. Základní pojmy
D e fi nic e a o z nač e ní:
Maticí typu (In, 11) [maticí typu m x n] nazýváme schéma
A = lilI' a 1 2' ..., a 1" ,
£121' a 22 , ..., a 2 "
li ml, a m 2 , ..., a m II
které označujeme (aik) nebo stručněji (a ik ) (m, nE N), utvořené z mn objektů a ik ,
které nazýváme prvky matice (čteme: a jedna jedna, a jedna dvě atd.). Prvky
a i l' (li2, ..., ain' resp. a li' a 2i , ..., ami tvoří i-tý. řádek, resp. i-tý sloupec matice
(typu (m,I1). První index udává tedy vždy pořadové číslo řádku a druhý
index pořadové číslo sloupce. Řádky a sloupce označujeme společným názvem
řady. Prvky matice bývají zpravidla reálná, popř, komplexní čísla, ale mohou
také záviset na nějakém parametru.
Pro matici A typu (m, n) se také používá těchto označení:
a l1 , a 12 , ..., a 1n '
a21, a 2 2, ..., a 2n
41b a12, ..., atn '
a2t, a22, ..., a 2n
a m 1, a m2 , ..., a mn
a m l' Qm2, ..., a mn
(aik)(m.np [aik] ' II aik II , [a ik ], II aik II (m, n E N).
Matice A s m řádky a n sloupci se při m =f: n nazývá obdélníková matice typu
(m, n) a někdy se značí A(m.n>, kdežto při m = n se matice A nazývá čtvercová
matice n-tého řádu [matice řádu n. n-rozměrná matice] a někdy se značí An',
180
Všechny prvky aii (tj. prvky a t I' a 22 ,.. ..(lmnJ} :'1\. hlarní prvky), rt;sp. prvky
aml, a m - 1,2' ..., atm čtvercové matice A = (a ik ) typu (nt, m) tvoří tzv. hlavní
diagonálu (al l , a22, ..., a mm ), resp. vedlej. i diagonálu (a mt , aru -1.2' ..., (ltm) Ina-
tice A. Součet hlavních prvků matice A typu (In, ln) <;e nazývá stopa
m
S(A) = I a rr
r=1
matice A. ,
Matici tvořenou jedním řádkem [tj. matici typu (1, n)J resp. jedn"jln sloup-
cem [tj. matici typu (m, 1)] nazýváme řádkovou Inuticí nebo <11-rOZ"lěrll) /n>
vektorem, resp. sloupcovou maticí nebo (m-rozlněrným> transpol1ovan.Í'nz
vektorem.
Řádkovým vektorem matice A typu (111, n) nazýváme každý vektor
a i = (a i1 , a i2 , ..., a in ), i E { 1, 2, ..., m)- .
Sloupcovým vektorem matice A typu (111, n) nazýváme každ)t vektor
ar - a 1 k k E {1, 2, . .., 11 } .
a2k
a mk
Matici A typu (m, n) s řádkovými, popř. sloupcovýn1i vektory zapisujeme
takto:
,
A=
a 11' a I 2' ..., a I Fa
a21' a 22 , ..., a 2n
°1
°2
. Q f ,, 1 0 1 )
= \, J .:,,;. 2' , . ., n .
a m1 , a m2 , ..., a mn ,Om,
Každou matici, jejíž všechny prvky jsou rovny nule a která rná ln řádků
'a n sloupců, nazýváme nulovou matici typu (nI.. n) a označujeme O(m,n) nebo
stručně O. Obdobně každý n-rozměrný vekto , re3p. n-rozměrný transponovaný
vektor, jehož všechny prvky (tzv. souř-adnice) jsou rovny nule, nazýváme
n-rozměrným nulovým vektorem, resp. n-rozměrným transpol1ovaným nulovým
vektorem a označujeme 0m resp. O , popř. jen stručně o, resp. o T.
Příklady:
o = O, O, ..., O
O, O, ..., O
o = (O, O, ..., O),
T
o = O .
O
O, O, ..., O / O
,
Čtvercová nulová matice n-tého řádu se značí On nebo stručně O.
181
DŽl1gonálni matžci řádu Il I1Hzýváme čtvercovou matici Dn = (d ik ) (stručně D)
řádu 11, právě když všechny její hlavní prvky jsou čísla různá od nuly a ostatní
prvky jsou rovny nule, tj. d ik = O pro \Ii, k E U n : ; =t= k. Platí tedy
Dn = D = dlI' O, O, ..., O = (ť5 ik d ik ),
O, d 22' O, ..., O
o, O, O, . .., d nn
kde
{ O (i * k),
ť5 ik = 1
(i = k)
je tzv. Kroneckerův symbol [Kroneckerovo delta J.
IV ásobnou l kalárl1i] maticí Sn = (a ik ) (stručně 5) řádu n nazýváme diago-
nální matici, právě když se všechny její hlavní prvky rovnají témuž číslu k
(a 11 = a22 = ... == a,," = k), tj.
.
SPI = 5 = k, O, O, ..., O .
O, k, O. ..., O
O, O, k, ..., O
\0. . o. O, ..., k
J ednotkovou n1aticí E. n =-- (l ik) ( tručně E) řádu n nazýváme násobnou matici,
prÚvě když všechny její hlavní prvky jsou rovny číslu 1, tj.
E" = E = 1, O, O, ..., O = (eik)'
O, 1, O, ..., O
O, O, 1, ..., O
O, O, O, ..., 1
Horní [prarou], .resp. dolní [levou] tr júhelníkovou maticí (a ik ) nazýváme
čtvercovou matici, právě když pod (resp. nad) všemi hlavními prvky a ii jsou
samé nuly, takže ažk = O pro Vi, k E U n takové, že i > k (resp. ; < k).
pf.rkllldy:
1atice
A = ( 11,2,7 ) , resp. B = ( '3, O, O )
O, 3, 4 7, 4, O
O, O, 2 .9, 1, 6
je horní, resp. dolní trojúhelníkovou maticí.
182
Hodností h = h(A) nlatice A typu (m, n) nazýváme maximální počet lineárně
nezávislých řádkových vektorů, který je roven maximálnímu počtu lineárně
nezávislých sloupcových vektorů matice A.
Hodnost matice A se rovná číslu h, právě když existuje nenulový subdeter-
minant matice A h-tého řádu a všechny subdeterminanty řádů větších než h
jsou rovny nule nebo neexistují.
Má-li čtvercová matice A n-tého řádu hodnost h = n (tj. det A * O), resp.
hodnost h < n (tj. det A = O), nazývá se regulární, resp. singulární.
Nulitou [defektem, degenerací] ", = nul A matice A typu (m, n) nazýváme
rozdíl ", = n - h počtu n sloupců matice A a hodnosti h matice A.
Pro každou obdélníkovou matici typu (m, n) o hodnosti h platí:
h < min {m, n} .
Jestliže h = n = min {m, n}, resp. h = m = min {m, n}, pak sloupcové
resp. řádkové vektory matice typu (m, n) jsou lineárně nezávislé. .
Hodnost matice A se nezmění (tj. z matice A vytvoříme novou matici 8
o téže hodnosti), jestliže s řádky, popř. sloupci (tj. s řadami) provedeme některou
z těchto elementárních úprav:
1. Napíšeme řady matice A v jiném pořadí.
2. Násobíme některou řadu matice A číslem k * O.
3. Přidáme k matici A řadu, terá je lineární kombinací ostatních řad této
matice.
4. Vynecháme v mati i A řadu, která je lineární kombinací ostatních řad
této matice.
5. Přičteme k některé řadě matice A lineární kombinaci ostatrllch řad
této matice.
o rndtici B, která má stejný počet řádků, popř. sloupců jako matice A,
ríK!inlt . 't.e je ekvivalentní s maticí A, jestliže matice 8 vznikla z matice A ně-
kterou z elementárních úprav, tj. jestliže matice A, 8 mají stejnou hodnost.
Píšeme pak A '" 8.
Příklad:
A=
( --1, 4, 1, 3 ) .
2, - 2, - 2, O
O, 2 O, 2
183
Přičteme-li k prvnímu sloupci třetí sloupec, dostaneme
( O. 4, 1, 3 ' ) '
O, - 2, - 2, O
O, 2, O, 2 /
Všechny s1Jbdeterminanty třetího řádu jsou rovny nule, neboť tři z nich mají
v prvním sloupci jen nuly a čtvrtý subdeterminant má po odečtení druhého
sloupce od prvního sloupce dva sloupce stejné:
4, 1, 3
-2 -2 O
, ,
2, O, 2
3, 1, 3 = O.
O, - 2, O
2, O, 2
Protože jeden ze subdeterminantů druhého řádu, např.
-1, 4,
\2, - 2
je různý od nuly, má vyšetřovaná matice hodnost h = 2.
K určení hodnosti matice lze použít 9aussovy eliminační etody
(viz např. [194]).
1.10.2. Operace s maticemi
Rovnost matic
A = 8, právě když a ik = b ik pro \:Ii E U m /\ \:Ik EU",
tj. právě když matice A a 8 jsou téhož typu a každý prvek aik matice A se rovná
stej 01ehlému prvku b ik matice 8.
Součet dvou matic
A + 8 = (aik + b ik ) = (Cik) = C pro Yi E U /\ Yk E U n ,
tj. právě když matice A, 8, C jsou téhož typu a každý prvek Cik se rovná součtu
"
stejnolehlých prvků aik, b ik matic A, 8. '
Komutativní zákon pro sčítání matic: A + 8 = 8 + A.
r\ _ ociativní zákon pro sčítání matic: (A + 8) + C = A + (8 + C).
N.áso bení matice reá I ný m, popř. kom plex ní m čí s lem
(skalárem)
exA = ((Xa i1 J = A(X.
\
184
Distributivní zákon pro součin součtu skalárů a matice:
((l + B) A = (lA + BA.
Distributivní zákon pro součin skaláru a součtu matic:
(X(A + 8) = (lA + (X8.
Asociativní zákon pro součin skalárů a matice:
(X(BA) = ((lB) A = Cl.BA.
N áso bení ř ádk ového a sl ou pcovéh( ''- k t o r u (sk alá rn í so uč i n)
ab T ,= (a l , a2, ..., a n ) b l
b 2
n
= L aibi'
i = I
b n
Násobení matic
Součinem matice A = (aik) typu (m, n) a matice B = (b ik ) typu (n, p) (v tomto
pořadí) nazýváme matici C typu (m, p), kterou označujeme A8 nebo A. 8
(tečku používáme jen výjimečně) a pro jejíž prvky platí:
n
C' k = a.b k T = a..b' k
1 1 i..J I))
j=1
pro 'tieU m 1\ 'tkeU p ,
..
takže
C = A8 = (aibl) = ( t aijb jk ) = (Cik).
)=1 I
Prvek Cik matice C = A8 tedy dostan me jako skalární součin řádkového
vektoru a i (i-tého řádku) a sloupcového vektoru br (k-tého sloupce). Při
C = A8 říkáne, že matici A násobíme matici 8 zprava, popř. že matici 8 náso-
bime maticí' A zleva. .
Podmínka pro součiI?- A8 matic A a 8: Počet .sloupců matice A
se rovná počtu řádků matice 8.
Příklad:
alb l =
a. (b l , b 2 , ..., b n ) =.
a2
a l b 1 , a l b 2 , ..., alb n ,
a2 b l' a2 b 2 , ..., a2 b n
a m
a m b 1 , a m b 2 , ..., amb n
185
Formální schéma pro násobení matic
n p p
m0. n 0=m l C=AS/
nebo ve tvaru součinu zlomků
m n m
,
n p p
tj. při násobení matice A ty; ":; n) maticí 8 typu (II, p) zprava dostaneme
matici C typu (m, p).
Přík lad :
A8 = ( 1, 3, 2 ) ( 1, O ) =
2, 4, 1 2, 3
4, 1
= ( 1 . 1 + 3 . 2 + 2 . 4, 1._0 + 3 . 3 + 2 . 1 ) = ( 15, 11 ) .
2 . 1 + 4 . 2 + 1 . 4, 2. O + 4 . 3 + 1 . 1 14, 13
Falkovo multiplikační schéma
p
r: 8
n
A A8
m
m
p
Prvek Cik matice C = A8 je v průsečíku i-tého řádku matice A a k-tého
sloupce matice 8 a je jejich skalárním součinem.
Příklad:
2
2
1, O
3 2, 3
3 4, 1
1, 3, 2 15, 11
2, 4, 1 14, 13
2
2
186
Zkoušku správnosti výpočtu podle Falkova schématu lze provést pomocí
tzv. řádkové zkoušky:
8 b
A A8 = C c
,
Součty řádků mé}tice B připojínle jilko sloupcový vektor b a součty řádkú
matice C připojíme jako sloupcový vektor c. Pak platí Ab = c.
Příklad:
1, O 1
2, 3 5
4, 1 ' 5
1, 3, 2 15, 11 26
2, 4, 1 14, 13 27
+- 1.1 +5.3+5.2
Obdobně lze provést tzv. sloupcovou zkou. ku, při níž sečtením sloupců
matice A dostaneme vektor o, kdežto sečtením sloupců matice A8 dostaneme
vektor d, přičemž oB ' d:
Příklad:
8
A AB = C
o d
1, O
2, 3
4, 1
1, 3, 2 15, 1 1
2, 4, 1 14, 13
3, 7, 3 29, 24
i 1.3+2.7+4.3
f.
Obě zkoušky lze kom inovat.
187
Komutativní zákon pro součin matic obecně neplatí:
AB =t= BA,
tj. při násobení matice B maticí A zleva dostaneme obecně jiný výsledek než
při jejím násobení maticí A zprava.
Jestliže při čtvercových maticí:.'h platí AB = BA, pak se matice A, B na-
zývají zaměnitelné [komutujícíJ.
Násobení jednotkovou maticí E, popř. nulovou matici O
Pro čtvercové matice A, E a O téhož řádu platí
AE = EA = A,
AO = OA = O.
Matice E a O mají v maticovém počtu týž význam jako 1 a O při násobení
na množině R.
PO 1!Ún1ka :
Rovnost A8 = O nemusí nutně znamenat, že A = O nebo 8 = o. Jestliže
AB ,:= O, přičemž A =t= O a zároveň 8 =t= O, pak matice A,' 8 jsou singulární.
Ma1 ice A, B se v tomto případě nazývají dělitelé nuly.
Násobení diagonální maticí D (d ii = di)
Násobení diagonální maticí D n-tého řádu zprava:
AD = (aikd k ) = all dl' a 2 d 2' ..., atndn .
a 21 d t , a22 d 2 ,' ..., a2n d n
a ml dl, a m 2 d 2' ..., amnd n
Násobení diagonální maticí D m-tého řádu z I e va:
DA = (aikd i ) = alld l , a l2 d l , ..., alnd l .
a 21 d 2 , a 22 d 2 , ..., a2n d 2
a 1 dm' a m 2 d m, ..., amnd m
Násobení tří matic
Asociativní zákon pro součin matic:
(AB) C = A(BC) = A8C.
Předpoklady: Matice A je typu (m,I1), matice 8 typu (n, p) a matice C
typ" (p, q).
JRX
Pravý distributivní zákon vzhledem k součtu matic:
(A + B) C = AC + SC.
Levý distributivní zákon vzhledem k součtu matic:
A( B + C) = AS + AC.
Mocniny matic
Pro čtvercovou matici A pro n činitelů definujeme:
A" = AA .. . A
\
(n E N),
(n E N),
A-" = A-1A- 1 ...A- 1
n činitelů
AO
přitom platí
= E'
,
AmA" = Am+n
(n,mEZ).
Záměnná matice B
Záměnnou maticí nazýváme čtvercovou matici B, která v každém řádku
a v každém sloupci má jen jeden prvek 1, ale jinak obsahuje samé nuly. Při
násobení matice A maticí 8 zleva způsobuje prvek t v r-tém řádku a s-tém
sloupci matice B, že r-tý řádek matice BA a s-t). řádek matice A jsou stejné.
Příklad:
8A = O, 1, O, O 1, 3, O, 2 -- 4. 7, 3
O, r-, 2, 4, 7, 3 ,-- - - - -. - ,. -- - --,
r O, L 1..J O ' 3 \),\ -+ 1 +-r
L:L____ _ __
1, O, O, O r--------, 1, 3, O, ")
L1_Q,__4i_!l +-s
O, O, O, 1 5, 2, 1, 1 5, 2, 1, 1
i
s
Při násobení matice A maticí S zprava způsobuje prvek 1 v r-tém řádku
a s-tém sloupci matice B, že s-tý sloupec matice AB a r-tý sloupec matice A
jsou stejné.
Příklad:
AB = ( 11, 2, 4, O' )
2, 4, 6, 1
1, 3, O, 3
O, O, O, 1
1, O, O, O
O, 1, O, O
O, O, 1, O
= ( 2, 4, O, 1 \ ) .
4, 6, 1, 2
3, O, 3, 1
189
Dosadíme-Ii za prvek 1 v záměnné matici číslo Pik' znásobíme tím ještě
zaměněný řádek, popř. sloupec číslem Pik'
Determinant součinu čtvercových matic
det (AB) = det A det 8.
Inverzní matice
Jc tliže k matici A typu (m, n) existuje taková matice 8 typu (n, m), resp. C
typu (n, m), že platí A8 = E, resp. CA = E, kde E je jednótková matice m-tého,
resp. n-tého řádu, pak matici 8, resp. C nazýváme inverzní matici zprava,
resp. : leva k matici A.
Jestliže matice A je čtvercovou maticí řádu n, pak inverzní matice zprava
k matici A se rovná inverzní matici zleva k matici A. Tuto matici nazýváme
inverzni matici k matici A a označujeme A-I. Platí
AA - 1 = A-I A = E
,
kde E je jednotková matice řádu n. Matice A a A - 1 jsou tedy zaměnitelné.
.I
K čtvercové matici A řádu n existuje jediná inverzní matice A-I řádu n,
právě když matice A je regulární, tj. právě když hodnost h(A) = n. Jestliže
= (aik) = a1 1 , a12, ..., a 1n 1\ h(A) = n,
a2 b a22, ..., a2n
a n l' G 2" ..., a nn
pak
8 = {hiJ A -- I -
I A 1 I' A 2 1 ..., An 1
A
A 11 , A 22 , ..., A n2
1 1
= -adj A = -(Aki)'
A A
.
A 1 n' A 2n' ..., Ann
kde Aki (k, i = 1, 2, ..., n) je algebraický doplněk prvku aki matice A (viz str. 199),
A = det A *= {) je determinant regulární matice A a adj A je tzv. adjungovaná
matice (transponovaná matice algebraických doplňků) k matici A, kterou
dostaneme tak, že v transponované matici A T k původní matici A = (a ik )
každý prvek a ki nahradíme příslušným algebraickým doplňkem.
Prvky b řk = AkJ A (všimněte si indexů) inverzní matice 8 = A-I k matici A
se nazývají redukované algebraické doplňky.
Inverzní matice A - I k regulární matici A je regulární maticí.
K singulární čtvercové matici řádu n (tj. h < n) inverzní matice neexistuje.
190
K matici A typu (m, n) a hodnosti h existuje inverzní matice zprava nebo
zleva, právě když h = min {m, n}, přičemž
- pro m < n existuje nekonečně mnoho inverzních matic zprava a ne-
existuje žádná inverzní matice zleva;
- pro m > n existuje nekonečně mnoho inverzních matic zleva a ne-
existuje žádná inverzní matice zprava;
- pro m = n existuje právě jedna inverzní matice k matici A.
Ke každé inverzní matici C zprava, resp. zleva k matici A typu (m, 11) (m 9= n)
existuje taková matice 8 typu (n, m), že čtvercová matice A8, resp. BA je re-
gulární a C = 8(A8)- 1, resp. C = (8A)- 1 8. Této vlastnosti se používá
ke konstrukci inverzní matice zprava, resp. zleva.
Pro regulární matice A, 8 platí
(A- 1 )-1 = A,
det (A --1) = (det A)-I,
1
( cxA ) - 1 = - A-I (ex * O),
ex
(A8) - 1 = 8 - 1 A-I,
(AE) - I = £ - 1 A-I.
K výpočtu inverzní matice se používá tzv. Gaussovy metody inverze matic
[Gaussovy metody konst;ukce inverzní matice] (viz např. [194]), která je za-
ložena na tom, že inverzní matici A-I k regulární čtvercové matici A lze určit
pomocí jen řádkových (popř. sloupcových) elementárních úprav matice A,
přičemž nejprve dostaneme jednotkovou matici a pak stejnými elementárními
úpravami v témže pořadí přejde tato jednotková matice v inverzní matici A-I.
Předností Gaussovy metody je malý počet algebraických operací při větším
řád.u matice A vzhledem k počtu těchto operací při výpočtu inverzní matice
pomocí algebraických doplňků prvků matice. A.
Příklad :
A = (1, O, 3)' A = det A = 1, O, 3 = 13.
,
2, - 3, 1 2, - 3, 1
1, 2, 2 1, 2, 2
A l1 = ( _ 1 )2 -3 1 = -8,
,
2, 2
A 12 = ( _ 1 )3 2, 1 = -3
,
1, 2
. 191
A 1 3 = (- 1)4 2, -3 - 7 ,
1 2
A 2t = (_ 1)3 O, 3 - 6,
\
2, 2 \.
A 22 =(-1)4 1, 3 = -1
,
1, 2
A 23 = (-1)5 1, O = -2,
1, 2
A 3 t = (- 1)4 O, 3 - 9,
-3 1
, '
A 32 = (-1)5 1, 3 - 5 ,
2, 1
A33 = (-1)6 1, O - -3.
- ,
2, -3
A- 1 = /3 (-8, 6, )'
-3 -1
, ,
7, -2 -3
,
Limi ta ma tice A(t)
Je-li A(t) matice, jejíž prvky jsou funkce aik(t), pak matici, jejíž každý prvek
je limitou prvku aik(t) pro t to, nazýváme limitou matice A(t) v bodě to, tj.
lim A(t) = (lim aik(t)).
t-+to t-+to
Derivace matice A{t)
Derivací matice A(t) = (aik(t)) podle proměnné t, kde a ik jsou diferencovatelné
funkce, nazýváme matici
dA(t) = ( daik(t) ) .
dt dt
Jsou-li A(t), 8(t) matice téhož typu a , f3 skaláry, platí
d dA d8
-( A + B8) = rx- + B-.
dt dt dt
192
I Jestliže A(t) je matice typu (m, n) a 8(t) matice typu (n, p), pak pro derivaci
matice A8 platí
d dA d8
- A8 = - S + A -.
dt dt dt
Integrál matice
Integrálem matice A(t) = (aik(t)), kde a ik jsou integrovatelné funkce, nazý-
váme matici
fA(t)dt = (faik(t)dt).
1.10.3. Některé typy matic
Transponovaná matice A T
Transponovanou maticí A T = (a ) typu (m, n) k matici A . (a ik ) typu (n, m)
nazýváme matici, kterou z matice A dostaneme vzájemnou záměnou
(transpozicí) řádků za sloupce. Lze také říci, že matice A T vznikne překlopením
matice A kolem její hlavní diagonály. Z řádkového vektoru se tedy při trans-
pozici stane sloupcový vektor, tj.
A = (a ik ) 1\ A T = (a ) => al = a ki .
Platí
(AT)T = A,
(A + S)T = A T + ST,
(cxA)T = cxA T ((1 je skalár).
(AS)T = ST AT;
. pro regulární mat ci A platí
(AT)-1 = (A -1)T (kontragredientní matice k matici A),
A - 1 = (A - 1)T pro A = A T ,
det A T = det A.
Souměrná [symetrická] matice
Čtvercová matice A = (a ik ) řádu n, pro kterou platí A = A T , tj. aik = al =
= a ki pro \:Ii, kE U n , se nazývá souměrná [symetrická].
193
Příklad:
A = ( 1,
5,
7,
5, 7 ) = A T .
2 -6
,
-6 8
,
Skoro polosouměrná matice
Čtvercová matice A = (a ik ) řádu 11, pro jejíž všechny prvky platí:
aik = -a ki pro i * k 1\ 3 iE U n (a ii * O),
se nazývá skoro polosouměrná matice.
Polosouměrná matice
Čtvercová matice A = (a ik ) řádu n, pro kterou platí
aik = - aki pro i * k /\ 3i E U n (aii * O) ,
se nazývá polosouměrná [antisymetrická, polosymetrická, alternující]. Všechny
hlavní prvky polosouměrné matice musí být zřejmě rovny nule.
Příklad:
Matice
(- : _ : -i) , resp. (- : _ : -i)
je skoro polosouměrnou, resp. polosouměrnou maticí.
Komplexně sdružená matice A*
Konlplexně sdruženou [komplexně konjugovanou] maticí A* = (a ) typu
(n1, n) ke komplexní matici A = (aik) typu (m, n) nazýváme matici, která vznikne
z matice A, zaměníme-li v matici A každý prvek a ik komplexně sdruženým
číslem Qik' tj.
A = (aik /\ A*) = (ai'k)
* -
aik = aik
pro \:Ii E U n /\ \:Ik E U n .
Příklad:
A = (1 + 3i, 2 - 5i ) ,
5, 7 + 2i,
A* = (1 - 3i, 2 + 5 ' ) .
,5, 7 - 21
194
Platí
(A*)* = A,.
(A + B)* = A* + 8*,
(cxA)* = A* (Cť je komplexní číslo),
(A8)* = B*A*,
(A *) - 1 = (A - 1 )* (det A * O) ,
A* = (A - 1)* (det A * O, A = A*),
(A*)T = (AT)*.
Hermitovsky transponovaná matice
Hermitov$ky transponovanou maticí typu (m, n) ke komplexní matici A na-
zýváme matici (AT)* typu (n, m).
Hermitovsky souměrná matice.
Komplexní čtvercová matice A = (aik) řádu n, pro kterou platí
A = (AT)*, takže aik = Qki pro \Ii, kE U n ,
se nazývá hermitovsky souměrná [hermitovská, hermitovsky symetrická] matice.
Všechny hlavní prvky hermitovsky souměrné matice musí zřejmě být reálná
čísla, kdežto prvky souměrně ležící podle hlavní diagonály jsou komplexně
'sdružená čísla.
Příklad:
A = (A T )* = 12, I - 2i, 3 + 5i ) .
I I + 2 , 3, . 2 - i
3 - 51, 2 + 1, 5
Hermitovsky polosouměrná matice
Komplexní čtver'cová matice A = (aik) řádu n, pro kterou platí
A = _(AT)*, takže a ik = - Qki pro \Ii, kE U n ,
se nazývá hermitovsky polosouměrná [antihermitovská, polohermitovská, hermi-
tovsky polosymetrická]. Všechny hlavní prvky hermitovsky polosouměrné
matice musí zřejmě být rovny nule.
Příklad:
A = -(A T )* = ( O, 1 - 2i, 3 + 5i ) .
- 1 - 2i, O, 2 - i
- 3 + 5i, - 2 - i, O /
195
Reálná hermitovská, resp. hermitovsky polosouměrná matice je tedy sou-
měrnou, resp. polosouměrnou maticí.
1.10.4. Použití maticového počtu
Soustavou m lineárních algebraických rovnic s n neznámými nazýváme
soustavu rovnic
a 11 Xl + a 1 2 X 2 + ... + a 1 n X n = b 1 ,
a21 x 1 + a22 x 2 + ... + a2n X n = b 2 ,
a m1 X 1 + a m 2 X 2 + ... + amnX n = bm
nebo stručně
n
L aikx k = b i
k=l
pro \:Ii E U m ,
kde a ik , b i jsou daná komplexní čísla. Soustava lineárních algebraických rovnic
se nazývá homogenní, resp. nehomogenní, právě když b i = O pro \:Ii E U m ,
resp. b i * O pro aspoň jeden index i E U m . Matici
A = (aik) = a l 1, a 12 , ..., a 1n
a21, a 22 , ..., a2n
typu (m, n),
a m 1, a m 2, ..., a mn
utvořenou z koeficientů u neznámých na levých stranách všech rovnic soustavy,
nazýváme maticí soustavy a matici
(aik i b i ) = a1 1 , a22, . . ., a1n' 1 b 1 typu (m, n + I),
1
a21, a 22 , . . ., a2n' 1 b 2
1
. . . . . . . . . . . . . . . .1' . .
a m1 , m2' a mn , I bm
. . ., 1
vzniklou připojením absolutních členů k matici soustavy, nazýváme rozšířenou
maticí soustavy. Označíme-li
x = (Xl ,
l 2
X n
resp. b = b 1 ..
-b 2
bm
196
tzy. vektor neznámwvch, resp. vektor pravých stran, můžeme soustavu lineárních
algebraických rovnic vyjádřit jedinou maticovou rovnicí
Ax = b .
Hodnosti soustavy lineárních algebraických rovnic je hodnost matice soustavy.
Řešením soustavy lineárních algebraických rovnic nazýváme takovou n-tici
kOJI1plexních čísel, že po jejich dosazení za neznámé dostaneme ze všech rovnic
rovnosti [identity J. Soustavu lineárních algebraických rovnic nazýváme
řešitelnou, právě když existuje aspoň jedno její řešenÍ. Řešitelná soustava
lineárních rovnic ,se nazývá určená, resp. neurčená, právě když existuje právě
jedno její řešení, resp. má aspoň dvě řešenÍ. Dvě soustavy lineárních algebraic-
kých rovnic o témže počtu neznámých se nazývají ekvivalentní, právě když
mají touž množinu všech řešení neboli týž obor pravdivosti.
Podmínky řešitelnosti soustavy lineárních rovnic
Nehomogenní soustava m lineárních algebraických rovnic o n neznámých
je řešitelná, právě když matice soustavy a rozšířená matice soustavy mají
stejnou hodnost h.
Při h = n existuje prá vě jedno řešení soustavy.
Při h < n existuje nekonečně mnoho řešení soustavy.
Příklad:
r
3x + 2y + 5z = 10,
6x + 4 y + 10z = 30,
12x + 8y + 20z = 40.
Matice soustavy
( 3, 2, 5 )
6, 4, 10
12, R, 20
má hodnost h = 1 (viz str. 183). Rozšířená matice soustavy
( 3, 2, 5, 10 \ )
6, 4, 10, 30
, 12, 8, 20, 40
má hodnost h > 1, neboť např.
5, 10 * O.
10, 30
Vyšetřovaná soustava nemá žádné řešení (rovnice si vzájemně odporují).
197
Homogenní soustava m lineárních algebraických rovnic o n neznámých
je vždy řešitelná a má netriviální řeštní (triviální řešení představuje nulový
vektor), právě když hodnost matice soustavy je menší než n. /
/
/
1.11. DETERMINANTY
1.11.1. Záléladní pojmy
Definice" a označení
Determinantem matice A n-tého řádu [stručně, determinantem n-tého řádu,
n-řádovým determinantem] nazýváme číslo.
LZ(P) atkJ a2k2 ... a,.k n ,
p
kde
P _ ( 1, 2, . .., n )
- k l , k 2 , ..., k,.
je permutace množiny U,. = {I, ,..., n}, z(p) je ,znaménko příslušné permu-
tace a kde sčítáme přes všech n! součinů, přičemž n! je pdČet všech permutací
množiny U,. (viz článek.J.7.2). / .
Determinant matice A n-tého řádu označujeme
-
Li = det A = det (a ik ) = IAI = A = laikl,. =
= det all' a l 2, ..., a tn - at t , a t 2, ..., a t ,.
a 2t , a 22 , ..., a 2 ,. a 2t , a22, -..., a2,.
/'
a,.t , a n 2' .. ., a,.,.
a,.t, a,. 2' . .., a,.,.
Ačkoli determinant A n-tého řádu je číslo přiřazené příslušné čtvercov matici,
zavádějí se často tyto názvy v souvislosti se schematickým zápisem deter-
minantu:
Čísla aik (v počtu n 2 ) se nazývají prvky determinantu A (čteme: a jedna jedna,
a jedna dvě, atd.). .
Prvky ai1, ai2, ..., ai,., resp. a1i, a 2i , ..., ani tvoří tzv. i-tý řádek, resp. i tý
sloupec determinantu A.
První, resp. druhý index prvku \aik udává tedy pořadové číslo řádku, resp.
sloupce determinantu A.
Sloupcům a řádkům říkáme souhrnně řady determil,antu A.
198
Všechny prvky a ii , i = 1, 2, ..., n (tj. all, a22, ..., a nn ), resp. všechny prvky
ai,n - i + l' i = 1, 2, ..., n (tj. al n , a2,n - 1, a3,n - 2' ..., a n .) tvoří tzv. hlavní, resp.
vedlejší diagonálu [úhlopříčku] determinantu A.
Sčítance z(p) a 1k1 a2k2 ... ank n se nazývají členy determinantu A. Člen
al1 a22 ... a nn (tj. součin prvků hlavní diagonály) se nazývá hlavní člen deter-
minantu A.
Subdeterminantem [minorem] k-tého řádu matice A typu (m, n) nazýváme
determinant takové matice, která vznikne z matice A po vypuštění tolika
řádků a sloupců, aby z ní zbyla čtvercová matice k-tého řádu.
Příklad:
A = 1, 2, 2, 3, 4 .
2, 3, 6, 5, 2
4, O, 1, 3, 1
1, 1, 2, 4, 2
Subdeterminantem 4. řádu matice A je
1, 2, 2, 3 nebo 1, 2, 3, 4 atd.
2, 3, 6, 5 2, 3, 5, 2
4, O, 1, 3 4, O, 3, 1
1, 1, 2, 4 1, 1, 4, 2
Subdeterminantem 3. řádu matice A je
1, 2, 2 nebo 2, 6, 5 nebo
2, 3, 6 4, 1, 3
4, O, 1 1, 2, 4
2, 3, 4 atd.
O, 3, 1
1, 4, 2
Subdeterminantem 2. řádu matice A je
1, 2 nebo 3, 5 nebo 2, 6 atd.
2, 3 O, 3 1, 2
Subdeterminantem [minorem] M ik [přesněji subdeterminantem řádu n - 1,
minorem řádu n - 1, prvním minorem] příslušným prvku aUt matice A řádu n
nazýváme determinant matice, kterou dostaneme z matice A, vynecháme-li
v ní i-tý řádek a k-tý sloupec.
(Algebraickým) doplňkem Aik prvku aik matice A řádu n nazýváme součin
subdeterminantu M ik a čísla ( - l)i + k, tj.
( ) i + k
Aik = -1 M ik .
199
Rozvoj determinantu podle jedné řady
Determinant A matice A řádu n se rovná součtu součinů, které dostanem"e,
vynásobíme-li každý prvek některé řady jeho algebraickým doplňkem.
Tomuto postupu při výpočtu determinantu A říkáme rozvoj determinantu A
podle prvků jedné řady.
Rozvoj determinantu A podle prvků i-té ho řádku:
n
A = L aikA ik
k=l
pro \:Ii E U n .
Rozvoj determinantu A podle prvků k-tého sloupce:
n
A = I aikAik
i = 1
pro \:Ik E U n .
Příklad 1 :
a 1 l' alt' a 1 3 ' = a 1 1 A 1 1 + a 1 2 A 1 2 + a 1 3 A 1 3 =
a21' a 22 , a 23
a31, a32, a33
= a 11 a 22 , a 2 3 - a 1 2 a2b a 2 3 + a13 a2b a22 .
a32, a33 a31, a33 a31, a32
Příklad 2:
3, 7, 4, 6 = 3A 11 + 7A 12 + 4A 13 + 6A 14 =
10, 5, 9, 6
1, 2, 7, 8
5, 4, 2, 9
. L
= 3 5, 9, 6 - 7 10, 9, 6 + 4 10, 5, 6 - 6 10, 5, 9
2, 7, 8 1, 7, 8 1, 2, 8 1, 2, 7
4, 2, 9 5, 2, 9 5, 4, 9 5, 4, 2
(rozvoj determinantu podle prvků prvního řádku).
Výpočet determinantu druhého řádu
.1= alb a 12 =al1a22-a12a21"
X
a 2 '1' a22
- +
Determinant .1 se rovná rozdílu součil1u prvků hlavní diagonály a součinu
prvků vedlejší diagonály.
200
Příklad:
2, 4 = 2 .7 - 4.6 = -10.
6, 7
Sarrusovo pravidlo pro výpočet determinantů třetího řádu
Postup při výpočtu determinantu třetího řádu
- all a 22 a33 - a l1 a 23 a 32 +
+ a 1 2 a 23 a 31 - a l2 a21 a 33 +
+ a l3 a2l a 32 - al3 a 22 a 31
je možno si zapamatovat tak, že k matici A daného determinantu připíšeme
první dva sloupce, resp. první dva řádky (tj. první dvě řady) matice A jako
čtvrtý a pátý sloupec, resp. čtvrtý a pátý řádek podle schématu
A = det (aik) = a 1 1, a12, a l 3
a21, a22' a23
a 31 , a 3 2, a 33
a ll , (112' (lIJ- (lIl' 1112 \,
YX/
(/21/ ' -a2x2 (/22
a1 1 - (/1 2 ' 1 1. a' l - li,."
-' -' - -, . -
// + +
resp.
(131'
/
all, lI 12 - £1 1 J'
""" /
lilI' (121' 1I 2J
:/
132- cl J3
+
(ltt-
/
al
=+
+
.a od tří součinů prvků na jednoduchých přímých čarách odečteme tři součiny
prvků na dvojitých přímých čarách (znaménka ve schématech naznačují,
že součiny prvků na dvojitých čarách je nutno ještě vynásobit číslem - 1).
Při dostatečné praxi není třeba vypisovat celou rozšířenou matici a k vý-
201
počtu determinantu podle Sarrusova pravidla postačí toto schéma
determinantu:
'l
.--:
'l
'l
'l
'l
'l
{/II al :/{/13
.'" J',
lI21, (122' /' a 2 3 I :j
/ ijY( ' i " +
{/3 t "',,{/32' a3 '+
.a+
£
t..:
/
1.11.2. Vlastnosti determinantu čtvercové matice
1. Determinant matice A se rovná determinantu transponované
matice A T , tj. determinant A se nezmění, zaměníme-li v matici A řádky za
sloupce při zachování jejich pořadí neboli překlopíme-li matici A kolem
hlavní diagonály.
Příklad:
2, 7, 13
4, 6, 9
16, 3, 8
2, 4, 16
7, 6, 3
13, 9, 8
2. Jestliže v matici A vzájemně zaměnírr.e dvě rovnoběžné řady, změní
determinant A znaménko.
Přfklud:
2, 7, 13 - 4, 6, 9 I.
4, 6, 9 2, 7, 13
I 16, 3, 8 16, 3, 8
3. Společného nenulového činitele k všech prvků jedné řady matice A lze
vytknout před determinant A/k.
Příklad:
2, 7, 13 = 2 1 , 7, 13 .
4, 6, 9 2, 6, 9
16, 3, 8 8, 3, 8
Obráceně platí: Jestliže všechny prvky jedné libovolné řady matice A
násobíme libovolným číslem k, dostaneme matici, jejíž determinant se rovná kA.
102
Příklad:
5 2, 7, 13 -
4, 6, 9
16, 3, 8
2, 35, 13
4, 30, 9
16, 15, 8
4. Determinant A matice A se rovná nule, právě když
- všechny prvky aspoň jedné řady jsou rovny nule;
- jedna řada matice A je lineární kombinací řad s ní rovnoběžných.
Příklad 1:
2, 7, 13 = O.
4, 6, 9
8, 12, 18
Příklad 2:
2, 7, 13 = O,
4, 6, 9
16, 32, 53
neboť třetí řádek je součtem dvojnásobku prvního řádku a trojnásobku
druhého řádku.
5. Jestliže prvky jedné řady čtvercové matice A násobíme příslušnými
algebraickými doplňky prvků jiné řady matice A s ní r?vnoběžné, pak součet
všech těchto součinů se rovná nule.
Příklad:
K dané matici
A = ( 2, 7, 13 )
4, 6, 9
, 16, 3" 8
.
vypočteme algebrajcké doplňky prvků prvního sloupc :
A 11 = 6, 9 = 21, A 21 = - 7, 13 = - 17 , A 31 = 7, 13 = - 15 .
3, 8 . 3, 8 6, 9
Podle věty 5 platí
a 12 A 11 +a22 A 21 +a 32 A 31 =7.21 +6.(-17)+3.(-15)=0.
6. Determinant matice A se rovná determinantu matice B, která vznikne
tak, že k libovolné řadě matice A přičteme lineární kombinaci ostatních řad
s ní rovnoběžných. Z toho speciálně plyne, že determinant matice A se rovná
203
determinantu matice C, která vznikne tak, že ke každému prvku libovolné
řady matice A přičteme k-násobek příslušného prvku jiné řady s ní rovnoběžné.
Přík Lad :
2, 7, 13 -
4, 6, 9
16, 3, 8
2, 7, 13
4, 6, 9
16 + 5 . 4, 3 + 5 . 6, 8 + 5. 9
7. Determinant matice A se rovná determinantu atice 8, která vznikne
z matice A tak, že se k ní od jejího rohu připojí jeden sloupec 3: jeden řádek,
přičemž jejich společným prvkem je číslo 1, všechny ostatní prvky jedné
přidané řady jsou rovny nule a ostatní prvky druhé přidané řady jsou libo-
volné konstanty. S takto vzniklým determinantem lze tento postup opakovat,
aniž se změní jeho hodnota.
Příklad 1:
a 11' ..., a 1 m - a 11' ..., a 1 m' O, ..., O
a m 1, ..., a mm a m1 , ..., a mm , O, ..., O
O, . .., O, 1,. .., O }
. . . . . . . . . . . . . . . . . . n - m řádků
O, . .., O, O,. .., 1
\r...
T
Příklad 2:
2, 7, 13 -
4, 6, 9
16, 3, 8
n - m sloupců
1, O, O, O
18, 2, 7, 13
4, 4, 6, 9
-6, 16, 3, 8
8. Součtové pravidlo pro determinanty: Součet determinantů čtvercových
matic AI a A 2 téhož řádu, které se liší jen v prvcích libovolné i-té řady, se rovná
determinantu matice A, jejíž prvky i-té řady jsou součty příslušných prvků
i-tých řad matic AI a A 2 a ostatní prvky se nezmění.
Obráceně platí: Jestliže každý z prvků i-té řady čtvercové matice A lze vy-
jádřit jako součet dvou sčítanců, pak determinant matice A se rovná součtu
determinantů matic AI a A 2 , které se od matice A liší jen tím, že v i-té řadě
matice AI jsou první sčítance a v i-té řadě matice A 2 jsou druhé sčítance i-té
řady matice A.
204
Příklad :
2, 7, 13 + 2, 7, 13 - 2, 7, 13
4, 6, 9 5, - 2, 9 9, 4, 18
16, 3, 8 16, 3, 8 16, 3, 8
9. Pravidlo pro součin determinantů: Součin determinantů matic A = (aik)
a 8 = (biJe) n-tého řádu se rovná determinantu matice C = (Cik) n-tého řádu,
jejíž prvky vypočteme kterýmkoli z těchto čtyř způsobů:
a) Cik = ai1 b kl + ai2 b k2 + ... + ai,.b k ,.;
b) Cik = ai1 b lk + ai2 b 2k + ... + ainb"k;
c) C ik alibkl + a2i b k2 + ... + Q,.ibk,.;
d) C ik = aliblk + a2ib2k + ... + a,.ib"k'
Příklad :
Jestliže
A = all' a 1 2, al3 ,
a21, a22, a23
a31, a32, a33
B = bIl' b 12 , b l3 ,
b 21 , b 22 , b 23
b 31 , b 32 , b 33 I
pak podle d) je
C = AB = allb ll + a21b21 + a31 b 3b a ll b 12 + a21 b 22 + a31b32, allb 3 + a21 b 23 + a31b33 .
a 1 2 b ll + a22 b 21 + a32 b 3b a12 b 12 + a22 b 22 + a32 b 32, a12 b 13 + a22 b 23 + a32 b 33
a13 b ll + a23 b 21 + a33 b 31; a13 b 12 + a23 b 22 + a33 b 32, a13 b 13 + a23 b 23 + a33 b 33
Vandermondův determinant
= V( a I' a 2' . . ., a n ) = 1, a l , 2 3 dl-I
a l , a l , . . ., -
1, a 2 , 2 3 -l
a 2 , a 2 , . . .,
1, a3, 2 3 aj-I
a3, a3, . . .,
1 2 3 .....n-l
, a n , a n , a,., ..., u,.
= (a 2 - a 1) (a 3 - a I) . .. (a,. - a 1) .
. (a3 - a 2) (a 4 - a 2) . .. (a n - a 2) .
. (a 4 - a 3) (a 5 - a 3) . . . (a n - a3)'
· (a,. - a,. - 1) =
n-l [ n ]
=}J Jll(a s - ar) ,
kde a 1 , a2, ..., a,. E C.
205
Jsou-li mezi komplexními čísly a 1 , a2, ..., a n aspoň dvě stejná, pak = O.
Příklad:
Při výpočtu determinantu
A = 1, 7, 5, 4
-4, 4, 12, 8
2, 6, 9, - 2
3, 1, 7, 3
postupujeme podle uvedených vět o determinantech takto:
1. krok: Vytkneme společného čibitele 4 prvků druhého řádku.
2. krok: Druhý řádek přičteme k prvnímu řádku.
3. krok: Druhý sloupec odečteme od třetího sloupce.
4. krok: Determinant rozvineme podle prvků prvního řadku.
5. krok: U prvního determinantu odečteme třetí sloupec od druhého
sloupce a u druhého determinantu přičteme první sloupec k druhému sloupci.
6. krok: U prvního determinantu vytkneme společného činitele 3 prvků
třetího řádku a u druhého determinantu přičteme dvojnásobek prvního
sloupce k třetímu sloúpci.
7. krok: Oba determinanty rozvineme podle prvků prvního řádku.
Postupně tedy dostaneme (pořadová čísla kroků uvádíme nad rovnítkem)
1, 7, 5, 4 1 4 1, 7, 5, 4 2
-4, 4, 12, 8 -1, 1, 3, 2
2, 6, 9, - 2 2, 6, 9, - 2
3, 1, 7, 3 3, 1, 7, 3
2 4 O, 8, 8, 6 3 4 . O, 8, O, 6 4
-1, 1, 3, 2 -1, 1, 2, 2
2, 6, 9, - 2 2, 6, 3, - 2
3, 1, - 7, 3 3, 1, 6, 3
4 4( - 8) - 1, 2, 2 + 4( - 6) - 1, 1, 2 5
2, 3, - 2 2, 6, 3
3, 6, 3 3, 1, 6
5 ' 6
= - 32 -1., O, 2 - 24 -1, O, 2 -
2, 5, - 2 2, 8, 3
3, 3, 3 3, 4, 6
6 7
- 32 . 3 - 1, O, 2 - 24 - 1, O, O
2, 5, - 2 2, 8, 7
1, 1, 1 3, 4, 12
206
7 _ 96( - 1) 5, - 2 - 96 . 2 2, 5 - 24( - 1) 8, 7 -
1, 1 1 , 1 4, 12
= 96(5 + 2) - 192(2 - 5) + 24(96 - 28) = 2880.
1.11.3. Řešení soustavy lineárních rovnic pomocí determinantů
Determinantem matice D soustavy n lineárních rovnic s n neznámými
allx l + at2 X 2 + ... + alnX n = b l ,
a2l x I + a22 x 2 + ... + a2n x n = h 2 ,
ant X t + a n 2 x 2 + ... + annX n = b n
nazýváme determinant
D = alt' a12, ..., al n ..
a21, a22, ..., a 2n
ani' a n2 , ..., a nn
Cramerovo pravidlo
Jestliže D * O, pak soustava n lineárních rovnic má právě jedno řešení
[x I' x 2 , ..., x n ], kde
D.
Xi = ; pro '<lŽE U n ,
přičemž- Di je determinant matice Di' která vznikne z matice D soustavy tak,
že v ní i-tý sloupec nahradíme sloupcem pravých stran soustavy lineárních
rovnIC.
Cramerovo pravidlo se k praktickému řešení soustavy n lineárních rovnic
o n neznámých s nenulovým determinantem příliš nehodí, neboť vyžaduje
výpočet n + 1 determinantů n-tého řádu. Je proto vhodnější používat Gaus-
sovy eliminační metody.
Přík lad :
Pomocí Cramerova pravidla vypočteme
x- y+2z= 7,
2x - 3y + 5z = 17,
3x - 2y - z = 12.
207
D = 11 -1 2 - O, -1, 21=
, ,
2, -3 5 -1 -3 5
, , ,
3, -2 -1 t, -2 -1
, ,
=1 -1 2 + 1 -L 2 = 5 + 1 = 6,
,
-2 -1 -3 5
, ,
Dx = 7, -1,
17, - 3,
I 12, - 2,
= 7 - 3, - 1
-2 -5
,
Dy = 1, 7, 2
2, 1 7, 5
3, 12, - 1
2 - 7, - t, O
5 17, -3, -1
- 1, I I t 2, - 2, - 5
+117, -1 =7(15-2)+1(-85+12)=18,
12, - 5
= -12, Dz = 11, -1, 7 = 6.
2, - 3, 17
3, - 2, 12
Daná soustava má právě jedno řešení
r x = = 3 Y = -12 = -2
L 6' 6 '
tj. obor proavdivosti P = {[3, - 2, 1 ]}.
Jestliže D = O a Di = O pro \:Ii E U n , pak soustava n lineárních rovnic o 11
neznámých má nek()nečně mnoho řešení, neboť má nejvýše n - 1 nezávislých
rovnIC.
Jestliže D = O a aspoň pro jeden index i platí Di * O, pak rovnice'si od-
porují a obor pravdivosti P = 0.
6
---- 1
- - -
6
208
2. ROVNICE, FUNKCE, VEKTOROV Ý POČET
2.1. ROVNICE
2.1.1. Základní pojmy
Termy
(A ritn1etickýl11 > nebo (a IgebraickÝl11 > termem [(aritmetickýl11> nebo
(algebraickýn1> výrazen1] nazýváme takové slovo vytvořené z čísel, podstatně
volných číselných proměnných a matematických operačních znaků, které má
nějaký smysl a které nabude určité číselné hodnoty, jestliže za proměnné
dosadíme libovolná čísla z oborů těchto proměnných (viz články 0.3.1 a 0.3.2).
Příklad 1 :
Lineární term:
T(XI' X2, ..., x n ) = a o + QI X l + ... + anX n
(n E N),
kde a o , a 1 , ..., a n jsou konstanty a Xl' X 2 , ..., X n jsou číselné proměnné.
Příklad 2:
C elJ racionální ternl [nlno!zočlel1, polynom]:
T(x,y) = ax3 + bx 2 + cxy + dy2 + ex + fy + g,
kde a, b, ..., g jsou konstanty a x, y jsou číselné proměnné.
Příklad 3:
Racionální term:
n n-l
( ) anx + a n - 1 X + ... + a 1 x + ao
Tx =
bmx'" + b m _ I x m - 1 + ... + b 1 x + b o
kde a o , a I' . .., a m bo, b l' .. ., bm jsou konstanty a x je číselná proměnná.
(m, n E N),
Příklad 4:
Lineární konlbinace termů:
111 1 TI + n1 2 T 2 (n1 1 , m 2 E R).
Ohvren1 pr0I11ěl111J ch tertl1u T(x, y, ...) nazýváme množinu M = X x y x ....
kde X, Y:... jsou o bory všech proměnných x, y, . .. .
209
Rovnice
Predikátová formule TI = Tz, kde TI' T2 jsou termy, se nazývá rovnice.
Soustava predikátových formulí TI = Tz, T3 = T 4 ,..., T:a - I = ,..., T 2n - I =
= TZn' kde TI' Tz, ..., TZn jsou termy, se nazývá soustava n rovnic.
(Definičním> oborem rovnice TI(x, y,...) = T 2 (x, y, .. .), resp. soustavy rovnic
TI(x,y",,) = Tz(x,y,...),..., TZn-I(X,y,,,,) = Tzn(x,y,...) nazýváme kartézský
součin O = X x Y x ... oborů proměnných x, y, ... dané rovnice, resp.
daných n rovnic. Přitom X = X I n X 2 n ..., Y = Y I n Y 2 n ..., kde X, Y I , ...
jsou obory všech proměnných x, y, ... termu TI' X z, Yz,... jsou obory všech
proměnných x, y, . .. termu Tz atd.
Rovnice bez číselných proměnných představuje bud' pravdivý výrok
(pravdivou rovnost), nebo nepravdivý výrok; např. 7 = 3 + 4 je pravdivý
výrok, ale 7 = 3 + 5 je nepravdivý výrok.
Rovnice s aspoň jednou číselnou proměnnou představuje predikátovou
formuli, která se změní bud' v pravdivý výrok (pravdivou rovnost), nebo v ne-
pravdivý výrok, jestliže za všechny číselné proměnné dosadíme hodnoty
odpovídající definičnímu oboru dané rovnice.
Řešeníln [pravdivostním prvken1] rovnice TI (x, y, ...) = Tz(x, y, ...) s n čísel-
nými proměnnými nazýváme každou takovou uspořádanou n-tici [xo, Yo, .. .],
kde Xo EX, Yo E 1': . ., že po dosazení jejích členů Xo, Yo, ... do rovnice
TI (x, y, ...) = Tz(x, J7, ...) dostaneme pravdivý výrok. Řešení rovnice o jedné
neznámé se někdy nazývá kořen rovnice. '
Oborem pravdivosti P rovnice nazýváme množinu všech řešení neboli mno-
žinu všech pravdivostních prvků rovnice. Obor pravdivosti P rovnice je tedy
podmnožinou oboru O rovnice.
Z působ zápisu oboru pravdivosti:
P = {[x,y,...] I TI(x,y,...) = T 2 (x,y,...)},
je-li definiční obor rovnice zřejmý;
P = {[ x, y, ...J I x E X 1\ Y E Y 1\ ... 1\ TI (x, y, ...) =
= T 2 (x, y'," .)} ,
je-li třeba uvést definiční obor rovnice.
Identita
I dentitou nazýváme rovnici
TI (x, y, ...) = Tz(x, y, .. .),
210
kde obor pravdivosti P se rovná definičnímu oboru O rovnice. Například
. I
rovnIce
TI (x) = T2(X)
s jednou proměnnou x je při P = O identitou, a lze ji proto zapsat ve tvaru
P = {xix EX 1\ Tl(X) = T 2 (x)} = X.
Příklad:
Rovnice
sin (2x) = 2 sin x cos x
je identitou vzhledem k tělesu R neboli
P = {XIXER 1\ sin (2x) = 2sinxcosx} = R.
Definice neřešitelnosti rovnIce
P = 0.
Příklad:
3 X = - 4
,
O ' R
,
P = 0,
r
tj.
P = {x I x E R 1\ 3 x = - 4} = 0.
Ekvivalentnost rovnic
"
, Rovnice TI = T 2 , jejíž obor pravdivosti obsahuje obor pravdivosti rovnice
T3 = T4 s týmž definičním o orem, se nazývá důsledková rovnice vzhledem
k rovnici T3 = T4'
Dvě rovnice s definičními obory 0 1 a O 2 se nazývají <vzájemně) ekvi-
valentní vzhledem k definičnímu oboru O = 0 1 n O 2 , právě když mají týž obor
pravdivosti při definičním oboru O.
Úpravou rovnice nazýváme postup, kterým dané rovnici přiřadíme jinou
rovnici. Úprava, při níž rovnici s oborem pravdivosti P 1 přiřadíme rovnici
s oborem pravdivosti P 2 , přičemž P 1 c P 2 , resp. P 1 = P 2 , se nazývá důsled-
ková, resp. ekvivalentní.
2.1.2. Algebraické rovnice s jednou neznámou
Rovnici tvaru
n n-l O
anx + a n - 1 X + ... + a 1 x + ao =
(n E N, až E C; i = O, 1, ..., 11; a n * O)
211
nazýváme algebraickou rovnicí n-tého stupně s jednou neznámou. Čísla
£li;, a l' . .., a n se nazývají koeficienty rovnice; výrazy a o , a 1 x, a2 x2 , aix se po
řad.ě nazývají absolutní člen, lineární člen, kvadratický člen, člen i-tého stupně.
Komplexní číslo, které je kořenem aspoň jedné algebraické rovnice s racio-
nálními koeficienty se nazývá algebraické. Komplexní číslo (X se nazývá
transcendentní, právě když neexistuje žádná algebraická rovnice s racionál-
ními koeficienty, která má kořen rJ...
2.1.2.1. Lineární rovnice s jednou neznámou
Lineární rovnicí s jednou neznámou nazýváme algebraickou rovnici prvního
stupně, tj. rovnici tvaru
ax + b = O (a, b E C, a * O).
Obor pravdivosti této rovnice je
p = { - }.
2.1.2.2. Kvadratická rovnice s jednou neznámou
Kvadratickou rovnicí s jednou neznámou nazýváme algebraickou
rovnici druhého stupně, tj. rovnici tvaru
ax 2 + bx + c = O (a, b, c E C, a 9= O).
Číslo D = b 2 - 4ac se nazývá diskriminant kvadratické rovnice.
Kvadratická rovnice s reálnými koeficienty
ax 2 + bx + c = O
má obor pravdivosti
p = { - b + -J D - b - J D }
, 2a ' 2a
p = {- ;J
p == { - b + i -JIDI , - b - i JIDI }
2a 2a
(a, b, cER, a * O)
(D > O),
(D = O),
(D < O).
Pro D > O má tedy kvadratická rovnice právě dva navzaJem různé
reálné kořeny, pro D = O má právě jeden .reálný dvojnásobný kořen
a pro D < O má právě dva komplexně sdružené kořeny.
212
Zvláštní případy
a) Ryze kvadratická rovnice:
x 2 + c = O (c E R);
obor pravdivosti
P={iJc, -iJc} (c>O),
P = {O} (c = O),
P = {J( -c), -J( -c)} (c < O).
b) Kvadratická rovnice bez absolutního členu:
ax 2 + bx = O (a, bER, a * O);
obor pravdivosti
p = {O, - }. J
c) Normovaný tvar kvadratické rovnice [normovaná kvadratická rovnice]:
x 2 + px + q = O (p, q E R);
diskriminant
Dl = p2 - 4q.
Obor pravdivosti
p = { - + J[ ( y - q J. - - J[ ( y - q J}
p = { - }
p = {- + iJ[q - ( YJ. - - iJ[q - ( YJ}
(Dl > O),
(Dl =0),
(Dl < O).
Každou kvadratickou rovnici ax 2 + bx + c = O lze převést dělením
koeficientem a na normovaný tvar
2 b c
x + - x + - = O.
a a
Každou kvadratickou rovnici v normovaném tvaru x 2 + px + q = O lze
substitucí x = y - pl2 převést na ryze kvadratickou rovnici
l - ( Y + q = O.
213
Rozklad v součin kořenových činitelů
Kvadratickou rovnici ax2 + bx + c = O (a 9= O), resp. X2 + px + q = O
s kořeny Xl' X2 lze vyjádřit v ekvivalentních tvarech
a(x - Xl) (X - x 2 ) = O, resp. (X - Xl) (X - x 2 ) = O,
kde činitelé X - X I' X - X2 se nazývají kořenoví činitelé.
Pro kořeny Xl' X2 kvadratické rovnice ax2 + bx + c = O (a * O) platí tzv.
Vietovy vzorce: b
Xl + X 2 = --,
a
C
X I X 2 = -.
a
Kvadratická rovnice s komplexními koeficienty
ax2 + bx + c = O
obor pravdivosti
p = { b + J D - b - J D }
2a ' 2a '
kde J D je pevně zvolená odmocnina z komplexního čísla D (viz články 1.3.3
až 1.3.5).
(a, b, c E C, C * O);
2.1.2.3. Kubická rovnice s jednou neznámou
Kubickou rovnicí s jednou neznámou nazýváme algebraickou rovnici
třetího stupně, tj. rovnici tvaru
ax3 + bX2 + ex + d = O (a, b, c, d E C, a * O).
Každou kubickou rovnici l.lX3 + bX2 + cx + d = O lze dělením číslem a
převést na tzv. normovaný tvar
x 3 + Ax2 + Bx' + c = O.
Každou kubickou rovnici v normovaném tvaru X3 + Ax2 + Bx + C = O lze
substitucí x = y - AI3 převést na tzv. redukovaný tvar
y3 + PY'+ q = O.
Redukovaný tvar kubické rovnice
[kubická rovnice bez kvadratického členu]
x 3 + px + q = O (p, q E C);
214
diskriminant
D = ( y + ( r.
Obor pravdivosti
{ u+v u-v
P = li + v - + --- i /3
, 2 2 'V'
ll+V u-v }
- - i /3
2 2 'V '
kde
u = J( + JD ). v = J( - - JD ).
přičemž třetí odmocniny volíme tak, aby 3uv = - p a JD je pevně zvolená
druhá odmocnina z komplexního čísla D (Cardanovy vzorce).
V případě k ubické rovnice s reálnými koeficienty z těchto vzorců
dostáváme:
pro p = q = O jeden reálný trojnásobný kořen rovný nule;
pro D = O, pq =t= O dva reálné kořeny - 2 J q , J ll, z nichž druhý je
d ., b ' 2 2
vOJnaso ny;
pro D > O jeden kořen reálný a dva komplexně sdružené.
Pro D < O má kubická rovnice s reálnými koeficienty tři reálné kořeny.
Tyto kořeny v reálném tvaru nelze pomocí Cardanových vzorců najít (casus
irreducibilis). Lze je však vypočítat goniometrickým řešením:
Xl = 2 ( JI I )cos , X2 = -2 ( JI I )cos ( - ),
X3 = -2( JI I )cos ( + ; ),
kde qJ lze vypočítat z rovnice
q
2
cos cp = J(!ilf .
Přiklad 1:
Rovnici
x 3 - 3x 2 + 4x - 4 = O,
215
-3
lze substitucí x = y - 3 = y + 1 převést na tvar
takže
Pak
(y + 1)3 - 3(y + 1)2 + 4(y + 1) - 4 = O,
y3 + Y - 2 = O,
p = 1,
q = -2,
( 1 ) 3 28
D = 1 + 3 = 27 > O.
u = J{ - 22 + J[( 22 Y + GY]} = J(l + J ) 1,264,
v = J( l - J 28 ) . -O 264'
. 27"
y 1 = 1,264 - 0,264 = 1, Xl = 2;
1 1,528. / 1 /
Y 2 = -"2 + 2 1 'V' 3 , X 2 = I + 0,7 64i 'V' 3 ;
Y = - _ 1,528 1 . / 3 1 /
3 2 2 'V" X 3 = I - 0,764 i 'V' 3 ;
P = {2; ! + 0,764i J3; t - 0,764i J3}.
....-.
Příklad 2:
Rovnice
X3 - 21x - 20 = O
má diskriminant
(již redukovaný tvar)
D = (-10)2 + (_7)3 = 100 - 343 < O.
Použijeme goniometrického způsobu řešení:
10
cos qJ = / '
v 343
Xl = 2(J7) cos 19°6',
X 2 = -2(J7) cos (-40°54'),
X3 = -2(J7) cos 79°6',
qJ = 57°19';
Xl = 5 ;
X 2 = -4 ;
X 3 = -1.
Zvláštní případy
a) Binomická rovnice
216
y3 + q = O
(q E R);
obor pravdivosti
p = {- q, -Wq)( - + J3). -Wq)( - - J3)}.
b) Binomická rovnice
y3 + q = O (q E C);
viz článek 1.3.4.
c) Rovnice
y3 + py = y(y2 + p) = O
obor pravdivosti
P = {O, J( -p), -J( -p)}
P = {O, i J p, - i J p }
d) Rovnice
y3 + py = y(y2 + p) = O
obor pravdivosti
(p E R);
(p < O),
(p > O).
(p E C);
P = {O, J( -p), -J( -p)},
kde J( - p) je pevně zvolená druhá odmocnina z komplexního čísla p.
"
2.1.2.4. Algebraická rovnice n-tého stupně s jednou neznámou
Základní věta algebry
Každá algebraická rovnice n-tého stupně (n > 1) s jednou neznámou má
v tělese komplexních čísel aspoň jeden kořen. Obor pravdivosti P každé alge-
braické rovnice s oborem O c C není tedy nikdy prázdnou množinou.
Rozklad mnohočlenu v součin kořenových činitelů
Mnohočlen n-tého stupně Pn(X) = x" + a,r_lXn-1 + ... + a o s nulovým
bodem [kořenem] Cťl tj. Pn(CX I ) = O, lze rozložit v součin (x - CX I ) Pn-- I (x).
Říkáme, že x - CX I je k-násobný kořellovJ čin;tel jestliže p(x) = (x - l)k .
. Pn-k(X), kde P n -- k je polynom (n - k)-tého stupně nad tělesem komplexních
čísel a J-k(CXI) =f: O. Číslo k se nazývá násobnost kořene l a Cť 1 se nazývá
k-násobnJ kořen rovnice Pn(x) = O nebo P01Yl10111l1 P,r' Místo názvu j ed 11 o-
n á s o b n Ý k oře n používáme názvu jedlloduch.\ koi'ell.
217
Každý mnohočlen Pn(x) = x n + a n _ 1 x n - I + ... + a o lze jednoznačně roz-
ložit v součin kořenových činitelů
Pn(x) = (x - r1 l r l (x - CX 2 )k 2 ... (x - cxrr r (k l + k 2 + ... + k r = n),
kde CX I , G(2, ..., a n jsou všechny navzájem různé kořeny mnohočlenu Pne Jestliže
CXi je k-násobný kořen, pak komplexně sdružený kořen i je také k-násobný.
Známe-li jeden kořen Xl' lze stupeň rovnice snížit tím, že rovnici dělíme
příslušným koř novým činitelem x - x l'
Vietovy vztahy
Pro všechny kořeny Xl' X 2 , ..., X n (k-násobný kořen CXi se tedy uvádí k-krát)
algebraické rovnice n-tého stupně
n + ...JI - 1 O
x a n - 1 Á + ... + ao =
platí tzv. Vietovy vztahy:
n
LX i =Xl +X 2 +X3+",+ x n= -a n -l'
i = I
n
L XiX j = XI X 2 + X I X 3 +... + X2 X 3 + X 2 X 4 + ... + X n -l X n = a n - 2 ,
i,j= 1
i<j
n
L XiXjXk = X I X 2 X 3 + XI X 2 X 4 + ... + X2 X 3 X 4 + X 2 X3 X S + ...
i, j. k = I + X X X
i < j < k . . . n - 2 n - 1 n = - a n - 3 ,
XI X 2 X 3'" X n = (-1)" ao.
Máme-li 'algebraickou rovnici n-tého stupně v normo\'aném tvaru s celo-
číselnými koeficienty, lze pomocí Vietových vztahů zjistit, zda tato rovnice
má celočíselné kořeny. Jako celočíselné kořeny přicházejí totiž v úvahu jen
dělitelé absolutního členu.
Příklad:
X4 - X3 - 7X2 + x + 6 = O.
Platí
X I X2X3X4 = 6 (absolutní člen).
Dělitelé absolutního členu jsou + 1, + 2, + 3 a + 6. Zkusmo najdeme:
x 1 =1, x 2 =-1, x 3 =-2, x 4 =3.
Při resení algebraických rovnic lze také použít Hornerova schématu
(viz str. 247).
218
Reciproká rovnIce n-tého stupně
Reciprokou rovnicí nazýváme každou rovnici tvaru
n n-l O
aox + a I x + ... + a n = ,
de bud" a i = a n _ i (i = O, 1, ..., n) (tzv. kladně rec;proká rovnice), nebo ai =
= -a n - i (i = 0,1, ..., n) (tzv. záporně reciproká rovnice).
Každá kladně re iproká rovnice lichého stupně a každá záporně reciproká
rovnice sudého stupně má kořen -1. Každá záporně reciproká rovnice
má kořen 1.
Z každé r ciproké rovnice lze po odstranění možného kořenového činitele
x - 1, popř. x + 1 získat kladně reciprokou rovnici sudého stupně m = 2k
tvaru
b O X2k + b I X2k - I + ... + bkx k + ... + b o = O (b o =F O, k E N) ,
z níž po dělení mocninou Xk (nula totiž nemůže být kořenem) dostaneme
( k 1 ) ( k-I 1 ) ' ( 1 )
. b o x + Xk + b I X + X'k - 1 +... + b k - I X + x + b k = O.
Po substituci y = x + 1/ x dostaneme rovnici k-tého stupně v proměnné y,
z jejíchž kořenů Yi (i = 1, 2, ..., k) dostaneme po řešení k kvadratických rovnic
x 2 - Y i X + 1 = O (i = 1, 2, . . ., k)
všechny kořeny dané reciproké rovnice.
Příklad:
x 6 + x 5 - 5x 4 + 5x 2 - x-I = O
(záporně reciproká rovnice sudého stupně).
Po dělení součinem kořenových činitelů (x + 1) (x - 1) máme
x 4 + x 3 - 4x 2 + x + 1 = O
(kladně reciproká rovnice sudého stupně),
(X2 + :2 ) + (x + ) - 4 = O.
Protože ·
x2 + = ( X + ) 2 _ 2,
x 2 X
po substituci Y = x + l/x dostaneme
y2 + Y - 6 = O , Y 1 = 2,
Y2 = - 3,
219
takže
x 2 - 2x + 1 = O,
x 2 + 3x + 1 = O,
Xl = 1, x 2 = t;
-3 + J5
2
X 4 =
-3 - J5
2
X3 =
2.1.3. Transcendentní rovnice
Transcendentni rovnici nazýváme rovnici f(x) = O, kde f je trans-
cende tní funkce (viz článek 2.3.1).
V tomto článku uvedeme jen exponenciální a logaritmické rovnice. O gonio-
metrických rovnicích se pojednává až v článku 3.4.2.
2.1.3.1. Exponenciální rovnice
Exponenciálni rovnicí nazýváme rovnici, kde proměnná x se vyskytuje
v exponentu. Obecně lze exponenciální rovnice řešit jen graficky nebo při-
bližnými numerickými metodami. Jen v některých jednoduchých zvláštních
případech lze tyto rovnice převést na algebraické rovnice.
Základní exponenciální rovnici
a X = b
(a > O, a * 1, b > O)
lze řešit:
a) bez logaritmování, jestliže lze členy rovnice vyjádřit jako mocniny
téhož základu:
c px = c q <=> x = ,
p
neboť exponenciální funkce je prostá.
b) logaritmováním,: ..
19 b
x = loga b, popř. x 19 a = 19 b x = -.
19 a
..
Přiklad 1:
ax+2 = Ja x - s .
Řešení:
a(x + 2)/3 = a(x - S)í2 ,
x+2 x-5
3 2
2x + 4 = 3x - 15, x = 19.
220
Přík lad 2:
2 x + 1 + 3x- 3 = 3 x - 1 _ 2x- 2.
Řešení:
2 x . 2 + 3 x . 3 - 3 = 3 x . 3 - 1 - 2 x . 2 - 2,
216 . 2 X + 27 . 2 x = 36 . 3 X - 4 . 3 x ,
243 . 2 X = 32 . 3 x ,
GY = ;:3 = : = GY, x = 5 .
Příklad 3:
4 3x . 5 2x - 3 = 6x.
Řešení:
3xlg4 + (2x - 3)lg5 = xlg6,
x(31g4 + 2lg5 -lg6) = 31g5,
3lg 5
x= .
3 19 4 + 2 19 5 - 19 6
2.1.3.2. Logaritmické rovnice
Logaritmickou rovnici nazýváme rovnici, kde proměnná x se vyskytuje
v logaritmickém výrazu (termu). Obecně lze logaritmické rovnice řešit jen
graficky nebo přibližnými numerickými metodami. Jen v některých jedno-
duchých zvláštních případech lze tyto rovnice převést vhodnou substitucí
na algebraické rovnice.
Základní logaritmická rovnice: loga x = b (a > O, a * 1).
Platí-li b = loga c, pak
loga x = loga c <=> x = c ,
jinak je
x = a b .
Vyskytuje-li se proměnná x nebo mnohočlen P jen jako argument logaritmu,
lze logaritmickou rovnici převést na algebraickou v těchto případech:
a) Rovnice obsahuje logaritmy téhož argumentu. Takové rovnice se řeší
tak, že logaritmus tohoto argumentu považujeme za novou neznámou y,
najdeme kořeny nové rovnice a umocněním základu logaritmu těmito kořeny
dostaneme kořeny dané rovnice.
221
b) Logaritmická rovnice tvaru
CI loga P I (x) + C2 loga P 2 (x) + ... + C n loga Pn(x) = O,
kde P 1 , P 2 , . . ., Pn jsou mnohočleny v proměnné x, se na algebraickou rovnici
převedou odlogaritmováním. V tomto případě je třeba se vždy přesvědčit,
zda pro nalezené kořeny má původní rovnice smysl a zda jí tyto kořeny
vyhovují.
Příklad 1 :
3 ln (2x -,7) + 8 = J[ln (2x - 7) + 20].
/
Ř e sen Í: Zavedeme substituci y = ln (2x - 7) a dostaneme kvadratickou
rovnicI
3y + 8 = J(y + 20),
9y2 + 47y + 44 = O
se dvěma kořeny YI = -11/9 a Y2 = -4. Ze substituce Y = ln (2x - 7)
pak plyne e Y 2x - 7, tj. e- II / 9 = 2x - 7, e- 4 = 2x - 7, odkud lze vy-
e- II / 9 +7 e- 4 +7
počítat kořen y x I = a X 2 = dané rovnice z nichž kořen
22'
x 2 dané rovnici nevyhovuje (- 4 * J 16).
Příklad 2:
Ig(x2 + 1) = 21g(3 - x).
Řešení:
19 (X2 + 1) = 19 (3 - X)2,
X2 + 1 = (3 - X)2,
X2 + 1 = 9 - 6x + X2,
4
X--
, - 3'
2,,1.4. Přibližné metody k určení kořenů rovnice
2.1.4.1. Metoda tětiv [regula falsi, lineární interpolace]
Jestliže rovnice f(x) = O má mezi hodnotami Xl a x 2 právě jeden
kořen [tj. jestliže platí f(x I) f(X2) < O a funkce f je spojitá a ryze monotónní
na intervalu <Xl' X2)] a nemá v tomto intervalu inf1exi, pak první aproximací
kořene vzhledem k bodům Xl a X2 je
(X2 - xl)f(x l )
X3 = Xl - f(x 2 ) - f(x l ) .
222
Další lepší aproximaci kořene získáme obdobně v tom z intervalů <x 1, X 3 >,
<X 3 , xz>' kde platí uvedené předpoklady.
Geometrický význam metody tětiv (obr. 46)
Křivka se nahradí tětivou vedenou body P 1 a Pz (z toho plyne název metoda
tětiv). Přitom aproximace x 3 kořene je první souřadnicí průsečíku osy x
s přímkou P 1 Pz.
Příklad:
Najděme jeden z prvků oboru pravdivosti
P = {x E R I X3 - x + 7 = O}.
Řešení: Příslušná funkční rovnice je
f(x) = x 3 - x + 7.
y
o
I
_l
Xz x
f (.x 2 )
f(x 1 )
Obr. 46. Určení kořene metodou tětiv
Po ověření platnosti předpokladů metody tětiv najdeme v tabulce funkčních
hodnot tyto hodnoty:
Xl = - 2,5,
X2 = - 2,
f(x l ) = -6,125,
f(x 2 ) = 1 ;
( - 2 + 2,5) . 6,125
x 3 = - 2,5 + ...:. - 2,07,
1 + 6,125
f(x 3) 0,200 .
Použijeme-li znovu metody tětiv na intervalu <Xl' X3 >, dostaneme další
(lepší) aproximaci kořene.
2.1.4.2. Metoda tečen [Newtonova metoda]
Jestliže v rovnici ,f(x) = O je f funkcí, která má na intervalu <a, b>
spojitou druhou derivaci, j'(a) j'(b) < O, derivace ,f' a j'" jsou na intervalu
223
<a, b) různé od nuly a Xl E (a, b) je takový bod, že f(x 1 ) f"(x l ) > O, pak
první aproximací kořene rovnice f(x) = O je bod
f(XI)
X2 = Xl - f'(x l )'
Po výpočtu aproximace x 2 kořene lze metody tečen znovu použít pro nalezení
lepší aproximace kořene. Přitom při každém dalším kroku se počet správných
číslic aproximace kořene prakticky zdvojnásobí.
Geometrický význam metody tečen (obr. 47)
Křivka se nahradí tečnou v bodě P I = [Xt,f(xt)] (z toho plyne název
metoda tečen).
y
I
O I
b x
P(x f )
Obr. 47. Určení kořene metodou tečen
Příklad:
Najděme jeden z prvků oboru pravdivosti
P = {x E R I X3 + 2x - 1 = O}.
Řeš e ní: Příslušná funkční rovnice je
f(x) = x 3 + 2x - 1,
odkud
f'(x) = 3x 2 + 2,
f"(x) = 6x. .
Předpoklady metody tečen jsou splněny na intervalu (O, 1). Zvolme Xl = 0,5.
Pak
.{(X I ) = 0,125,
f' (x I) = 2,75,
f"(XI) = 3,
takže
0,125 .
X2 = 0,5 - 0,5 - 0,045 = 0,455,
2,75
f(x 2 ) 0,004.
224
2.1.4.3. Itera ní metoda
Danou rovnici f(x) = O vyjádříme ve tvaru x = qJ(x). Známe-li při-
bližnou hodnotu Xl kořene Xo rovnice a je-li pro tuto hodnotu Xl splněna
podmínka IIp'(xl)1 < m < 1, pak
X 2 = qJ( X I )
je lepší aproximací. Při dalším použití této metody dostaneme ještě lepší
aproximaci kořene. Při lp'(X) < O leží dvě po sobě jdoucí aproximace po
různých stranách kořene, a lze tedy odhadnout dosaženou přesnost.
Při IqJ'(x)1 > 1 je třeba použít inverzní funkci k funkci qJ.
Příklad:
Najděme jeden z prvků oboru pravdivosti
p = {x E R I X3 + 2x - 6 = O}.
Řešení: Přibližná hodnota Xl = 1,45 pro kořen dává f(x l ) = -0,051 375.
Danou rovnici vyjádříme ve tvaru
6 - X3
X = 2 = q>(x),
3X2
q>'(x) = - 2' 1q>'(x 1 )1 = 1q>'(1,45)1 = 3,153 75 > 1 ·
Proto je třeba danou rovnici řešit pomocí inverzní funkce k funkci qJ:
6 - x J
y=
x 3 = 6 - 2y,
X = V(6 - 2y) = t/1(y),
-2
It/I'(1,45)1 = 3 V3;1 2 < 1.
2
-2
t/I'(y) = 3 V(6 - 2y)2 '
Z 'toho plyne
Xl = 1,45 ,
X 2 = V(6 - 2 . 1,45) 1,458 1 ,
x 3 = V(6 - 2.1,458 1) 1,4556 ,
atd.
/
,
2.1.4.4. Grafické fdení rovnic
Rovnice f(x) = O v normovaném tvaru se vyjádří jako funkční vztah
tím, že se její levá strana položí rovna y. Z grafu funkce y = f(x) dostaneme
reálné kořeny rovnice f(x) = O jako první souřadnice průsečíků tohoto grafu
s osou X (y = O).
225
Někdy je vhodné rovnici f(x) = O, která se má řešit, napsat ve tvaru
qJ(x) = tjJ(x) a sestrojit grafy funkcí Y = qJ(x) a y = tjJ(x). První souřadnice
průsečíků grafů obou funkcí jsou pak reálnými kořeny rovnice f(x) = O.
Příklad 1:
Určeme obor pravdivosti
P = {x E R I x 2 - X - 6 = O}.
Řeš e ní: Průsečíky grafu funkce
y = x 2 - X - 6
s osou x jsou (obr. 48)
Xl = -2, x 2 = 3, takže P = {-2, 3}.
x
Obr. 48. Grafické řešení rovnice
x 2 - x - 6 = O
Obr. 49. Grafické řešení rovnice
x 3 - 1,5x - 0,5 = O
Příklad 2:
Určeme obor pravdivosti
P = {x E R I X3 - 1,5x - 0,5 = O}.
Řeš e ní: Danou rovnici napíšeme ve tvaru
x 3 = 1,5x + 0,5.
První souřadnice, průsečíků grafů funkcí
oY = (p(x) = x 3 ,
Y = tjJ(x) = 1,5x + 0,5
jsou kořeny dané rovnice (obr. 49)
Xl = -1, X2 ...:.. -0,4, X3 ...:.. 1,35,
takže
P = { -1; -0,4; 1,35}.
226
1.1.5. Soustavy rovnic
K jednoznačnému určení mnozlny všech řešení soustavy rovnic
s n neznámými je třeba n vzájemně nezávislých a vzájemně si neodporujících
rovnic. Způsob řešení záleží v tom, že se n rovnic s n neznámýoli postupně
redukuje na jednu rovnici s jednou neznámou. Pomocí hodnoty jedné neznámé
vypočtené z této rovnice lze postupně najít hodnoty ostatních neznámých.
Máme-li soustavu r vzájemně nezávislých rovnic s n neznámými (r < n),
pak n - r proměnných zvolíme za volné parametry (nezávisle proměnné).
Za tyto proměnné lze dosadit libovolné hodnoty z oboru soustavy rovnic.
Obor pravdivosti P soustavy rovnic' se rovná průniku oborů pravdivosti
P t , P 2 , ..., Pr jednotlivých rovnic:
P=P 1 nP 2 n...nP r .
2.1.5.1. Soustavy lineárních rovnic se dvěma neznámými
Jedna lineární rovnice se dvěma neznámými a1x + a2Y = b
Obor pravdivosti P rovnice a.x + a2Y = b je množina všech uspořádaných
dvojic [x, y] E R x R, pro něž z predikátové formule a 1 x + a2Y = b dosta-
neme pravdivý výrok.
Způsob zápisu:
P = {[x,y] I [X,Y]E R x R 1\ a1x + a2Y = b; a 1 , a2, bE R},
popř. při zřejmém oboru rovnice stručněji
P = {[x,y] I a1x + a2Y = b}.
Považujeme-li x za nezávisle proměnnou a Y za závisle proměnnou, pak obor
pravdivosti je
{ \ b - a1x }
p = [x, y ] I x E R /\ Y = - a2 '
který představuje zobrazení f': x Y, jehož grafem je přímka.
"
Soustava dvou lineárních rovnic se dvěma neznámými
allx+a12y=bl'
a21 x + a22Y = b 2 .
Obor pravdivosti P této soustavy dvou rovnic se dvěma neznámými je
množina všech uspořádaných dvojic (x, y] E R x R, pro něž z uvedených
predikátových formulí dostaneme pravdivé výroky.
227
Způsob zápisu:
P = {[x, y] I [x, y] E R x R A U 1 lX + a12Y = hl A a2l x + a22Y = h 2 },
popř. při zřejmém oboru rovnice stručněji
P = {[x,y] I allx + a l 2Y = hl /\ a2l x + a22Y = h 2 }.
Dosazovací [substituční, vylučovací] metoda
Řešíme jednu z rovnic v kterékoli z neznámých a získaný term (výraz) pro
tuto neznámou dosadíme do druhé rovnice. Tím eliminujeme jednu ne-
známou.
Pokud po dosazení termu pro jednu neznámou do druhé rovnice dostaneme
rovnost O = O, resp. nepravdivý výrok, má soustava nekonečně mnoho řešení,
resp. nemá žádné řešenÍ.
Příklad:
Určeme obor pravdivosti
P = {[x, y] 13x + 7y - 7 = O A 5x + 3y + 36 = O}.
Řešení:
3x + 7y - 7 = O ,
5x + 3 y + 36 = O .
7 - 3x
y = (řešení první rovnice vy),
7
7 - 3x
5x + 3, 7 + 36 = O (po dosazení do druhé rovnice),
35x + 21 - 9x + 252 = O,
x = -10,5 , y = 7 + 1,5 = 5,5,
takže P = {[ -10,5; 5,5]}.
Porovná vací [kom par ač ní] metoda
Obě rovnice řešíme v téže proměnné a naleze'né termy (výrazy) položíme
sobě rovné. Tím se jedna neznámá eliminuje. (Případ rovnosti O = O, popř.
nepravdivého výroku viz u dosazovací metody.)
228
příklad:
Určeme obor pravdivosti
p = {[x, y] 13x + 7y - 7 ---- O 1\ 5x + 3y + 36 = O}.
." .... ,
Resenl:
3x + 7y - 7 = O,
5x + 3y + 36 = O;
- 3x + 7 - 5x - 36
-
7 3
-9x + 21 = -35x - 252,
7y = -3x + 7,
3y = - 5x - 36;
x = -10,5,
y = 5,5,
takže
- 3x + 7
y=
7
- 5x - 36
y=
3
p = {[ -10,5; 5,5]}.
Sčítací [a di ční, slučovací] metoda
Obě strany každé z rovnic znásobíme takovým vhodným číslem, aby u jedné
z neznámých byl v obou rovnicích týž koeficient. Odečtením obou rovnic
se příslušná neznámá eliminuje. (Případ rovnosti O = O, popř. nepravdivého
výroku viz u dosazovací metody.)
Příklad:
Určeme obor pravdivosti
p = {[ x, y] I 3x + 7 y - 7 = O 1\ 5x + 3 y + 36 = O}.
Řešení:
3x + 7y - 7 = O, .3
5x + .3y + 36 = O; .7
9x + 21y - 21 = O, .(-1)
35x + 21y + 252 = O;
26x + 273 = O,
x = -10,5,
y = 5,5,
takže P =, {[ -10,5; 5,5]}.
Další způsob řešení soustavy dvou rovnIC o dvou neznámých pomocí
determinantů viz v článku' 1.11.3.
229
2.1.5.2. Soustavy lineárních, rovnic se třemi neznámými
Soustava dvou lineárních rovnic se třemi neznámými
a 11 x + a 1 2Y + a 1 3 Z = b 1 ,
a21 x + a22Y + a23 z = b 2 .
Homogenní soustava (b l = b 2 = O)
all x + a 1 2Y + a13z = O,
a21 x + a22Y + a23 z = O.
Předpokládáme, že determinant
A = A3 = all, a12 =F O.
a21' a 22
Soustavu upravíme na tvar
a 11 x + a 12 y = -a13 z ,
a21 x + a22Y = -a23 z .
Označme
A = -a 13 z, a12 - -z a 13 , a 12 =z a 12 , a 13 = ZAl'
x
-a23 z , a 22 a23, a 22 a 22 , a 23
A = a l l, -a13 z - -z all , a 13 - - .,. A
, 41 2.
a2h -a23 z a21, a23
Podle Cramerova pravidla (viz článek 1.11.3) platí
Ax ZAl
x=-=
A A
A,
y=-=
A A
Alt,
kde
tE R,
- zA 2
- -A 2 t,
z = A 3 t.
Obecné řešení je
[x,y,z] = [Alt, -A 2 t,A 3 t],
t E R.
Pro pevně zvolené číslo t = to dostaneme uspořádanou trojici
[ AI to, - A 2 t o ; A 3 t O ] ,
kterou nazýváme partikulárním řešením.
230
Příklad:
3x + 7y - . 7z = O,
5x + 3y + 36z = O.
JI = 7, -7 = 273. A 2 = 3, -7 = 143,
3, 36 5, 36
[x, y, z] = [273t, -143t, - 26t], 't E R.
Soustavu dvou lineárních rovnic o třech neznámých lze také řešit tak,
že jednu neznámou převedeme jako parametr (nezávisle proměnnou) na pravou
stranu a takto vzniklou soustavu pak řešíme jako soustavu dvou lineárních
rovnic o dvou neznámých.
A3 = 3, 7 = -26;
5, 3
N ehomog.enní soustava
Nejsou-li všechny determinanty Ai rovny nule, pak obor pravdivosti ne-
homogenní soustavy tvoří součet obecného řešení homogenní soustavy
a jednoho řešení nehomogenní soustavy.
Soustava tří lineárních rovnic se třemi neznámými
Postup řešení je obdobný jako u soustavy dvou rovnic se dvěma neznámými.
Dosazovací [substituční, vylučovací] metoda
Příklad 1:
3x + 3y + z = 17, (I)
3x+ y+3z=15, (II)
x + 3 y + 3z = 13. (III)
teše-ní: Z rovnice (I) dostaneme
z = 17 - 3x - 3y.
Po dosazení do rovnic (II) a (III) máme
3x + y + 3(17 - 3x - 3y) = 15,
x + 3y + 3(17 - 3x - 3y) = 13;
-6x - 8y = -36,
- 8x - 6y = - 38 ;
x - 22
-" 7 ,
\.' _ U
.f - 7,
.. -
- 7'
231
takže
p = {[ 22 .!2 8 J} .
7' 7' 7
Porovná vací [kom par ač ní] metoda
Příklad 2:
3x + 3y + z = 17,
3x + y + 3z = 15,
x + 3y + 3z = 13.
Řešení:
z=
z.= 17-3x-3y,
15 - 3x - Y
3
13 - x - 3y'.
-
- 3 '
\
,
15 - 3x - Y
17-3x-3y= 3
15 - 3x - y 13 - x - 3y
3 3
Výsledek viz u příkladu 1.
Sčítací [a di ční, sl učovací] metoda
Příklad 3:
3x + 3 y + z = 17, . 3 (I)
3x + y + 3z = 15, .(-1) (II)
x + 3 y + 3z = 13. . ( - 1) (III)
Řešení: Po uvedeném vynásobení' rovnic sečteme nejprve rovnice (I) a (II)
a pak rovnice (I) a (III):
6x + 8y = 36,
8x + 6y = 38 .
Výsledek viz u příkladu 1.
232
2.1.5.3. Soustava n lineárních rovnic s n neznámými
Gaussova eliminační metoda
Soustavu n lineárních rovnic s n neznámými:
allxl + a12 x 2 + ... + a1n X n = hl'
a21 x 1 + a22 x 2 + ... + a2n x n = b 2 ,
(1)
ani Xl + a n 2 x 2 + ... + annx n = b n ,
kde a 11 =F O a determinant soustavy L1 =F O, lze řešit pomocí tzv. Gaussovy
eliminační metody:
První rovnici soustavy (1) vynásobíme zlomkem -a21/all a sečteme
s druhou rovnicí. Potom vynásobíme první rovnici soustavy (1) zlomkem
- a31/al1 a sečteme s třetí rovnicí, atd., až se všechny členy obsahující ne-
známou Xl u všech rovnic kromě první rovnice eliminují a původní soustava
rovnic (1) přejde v soustavu, kde k první rovnici soustavy (1) je připojena
soustava n - 1 rovnic s n - 1 neznámými:
I I + ' b '
a22 x 2 + a23 x 3 + ... a2n X n = 2'
, I I b '
a32 x 2 + a33 x 3 + ... + a3n X n = 3'
..............................
(2)
, I I h '
a n 2 X 2 + a n 3 X 3 + ... + annX n = n'
Postupujeme-li u soustavy (2) obdobně, dostaneme soustavu n - 2 rovnic
o n - 2 neznámých, atd. Konečně ze soustavy (1) dostaneme tuto soustavu
s trojúhelníkovou maticí, která je ekvivalentní se soustavou (1):
a 11 X 1 + a 12 X 2 + a 1 3 X 3 + ... + a I nXn = b 1 ,
, + I' + + I b '
a22 x 2 a23 x 3 ... a 2n X n = 2'
" + + " b "
a33 x 3 ... a3n X n = 3 ,
, (3)
a(n,- l)X = b(n - 1)
nn n n ,
z níž lze postupně vypočítat hodnoty všech neznámých, počínajíc výpočtem
hodnoty neznámé x n z poslední rovnice.
Příklad:
X + 2y - 0,7z =
3x + 0,2y - z =
0,9x + 7y - 2z =
21, .(-3)
24,
27.
,
. ( -0,9)
233
x + 2y - 0,7z = 21,
- 5,8y + 1,lz = -39,
5,2y - 1,37z = 8,1;
x + 2y - 0,7z = 21,
5,8y + 1,lz = -39,
11,13 779,1
-
-
29 29
5,2
5,8
z = 70
,
y = 20,
x = 30,
takže ,P = {[30, 20, 70]}.
Tabulka 2.1
Výpočetní schéma
ai1 ai2 ai3 . . . a i.. b,
I
(11 (12 (13 . . . (1,. (1 (1 + L(1t = LSi
E. ř. a l1 a12 a 13 . . . a 111 b l Sl
e21 a2t a22 a23 . . . a2.. b 2 S2
e2t a a ... ................... .....
e 3t a31 a32 a33 . . . a 3 .. b 3 S3
e nt alt! a.. 2 a n3 . . . a"" bIt S..
E. ř. O . . .
Symboly v uvedeném výpočetním schématu mají tento význam:
aik jsou koeficienty u neznámých,
b i - absolutní členy,
"
(1k = Laik (k E {I, 2, ..., n}) - sloupcové součty,
i = I
"
Si = Laik (i E { 1, 2, ..", n}) - řádkové součty,
1=1
"
(1 = L b i je součet absolutních členů,
i= I
a i1 Š . '" , Č . . I
ei1 = -- - roz lrovaCl Inlte,
all
E.ř. - eliminovaný řádek.
234
Příklad :
x + 2y - 0,7z = 21,
3x + O,2y - z = 24,
O,9x + 7y - 2z = 27.
Výpočetní schéma
a i1 a i2 a i3 b.
I
4,9 9,2 -3,7 72 82,4
E. ř. 1 2 -0,7 21 23,3
-3 3 0,2 -1 24 26,2
(-3).a1k -3 -6 2,1 -63 -69,9
-0,9 0,9 7 -2 27 32,9
(0,9) . a 1k -0,9 -1,8 0,63 -18,9 - 20,97
E. ř. O -5,8 1,1 -39 - 43,7
5,2 O 5,2 -1,37 8,1 11,93
-
5,8
5,2 ., -5,2 0,986 -35 - 39,214
-. tln
5,8 \
O - 0,384 - 26,9 - 27,284
Cramerovo pra vidlo (viz článek 1.11.3)
2.1.5.4. Soustava dvou kvadratických rovnic se dvěma neznámými
Tabulka 2.2
L
Soustavu rovnic tvaru
alx2 + b 1 xy + c 1 y 2 + d 1 x + e.y + f. = O,
a 2 x 2 + b 2 xy + C2y2 + d 2 x + e 2 y + f2 = O
lze řešit dosazovací metodou, přičernž však tento postup je početně velmi
nepohodlný, neboť vede na rovnici čtvrtého stupně.
Zvláštní případy
a) Soustava jet;fné kvadratické a jedné lineární rovnice
Takovou soustavu lze řešit dosazovací metodou.
235
Příklad :
X 2 + y2 = 25, I
x - y = 4.
Řešení: Po dosazení y = x - 4 do první rovnice dostaneme kvadratickou
ro vnlCI
x 2 + (x - 4)2 = 25.
b) Soustava dvou ryze kvadratických rovnic (bez členu s xy)
Takovou soustavu lze řešit sčítací metodou.
Příklad :
9x 2 -2y2= 18, .3
5x 2 + 3y2 = 47; .2
37x 2 = 148,
x 2 - 4,
'x I = 2, X 2 = 2, X 3 = -2,
Yt = 3,
Y2 = -3,
Y3 = 3,
x 4 = -2 ,
Y4 = -3,
takže
P = {[2, 3], [2, -3], [ -2,3], [ -2, -3]}.
c) Soustava rovnic, v nichž se z kvadratických členů vyskytuje jen xy
Takovou soustavu lze řešit sčítací a dosazovací metodou.
Příklad:
5x+y+3=2xy, I (I)
xy = 2x - y + 9; . (II)
-2xy + 5x + y + 3 = O,
xy - 2x + y - 9 = O; . 2
x + 3y - 15 = O,
x = 15 - 3y.
Po dosazení x = 15 - 3y do rovnice (II) dostaneme kvadratickou rovnici
v proměnné y:
y(15 - 3y) = 2(15 - 3y) - y + 9,
takže P = {[6, 3], [2, ¥]}.
236
d) Soustava dvou homogenních kvadratických rovnic
K vadratická funkce dvou proměnných x a y se nazývá homogenní, jestliže
její analytické vyjádření obsahuje jen členy druhého stupně, tj. má-li tvar
f(x, y) = ax 2 + bxy + cy2.
Substituce y = xz vede na kvadratickou rovnici v proměnné z.
Příklad:
x 2 - xy + y2 = 39,
2X2 - 3xy + 2 y 2 = 43;
y = xz
x 2 - x 2 z + X 2 Z 2 = 39,
2X2 - 3x 2 z + 2X 2 Z 2 = 43;
./
x 2 (1 - z + Z2) = 39,
x 2 2 - 3z + 2Z2 = 43;
2 - 3z + 2Z2
7
Zl =-,
5
1 - z + Z2 39
43
5
Z2 = 7 .
(kvadratická rovnice v proměnné z),
Po dosazení Zl' resp. Z2 dostaneme kvadratické rovnice v proměnné Xl'
resp. X2'
2.1:5.5. Grafické fdení soustav rovnic se dvěma neznámými
Soustavy rovnic prvního stupně
Každou rovnici prvního stupně v proměnných X a y lze považovat za ana-
lytické vyjádření funkce (neboli za funkční rovnici), jejímž grafem je přímka.
Souřadnice průsečíku S přímek udávají pak reálné řešení soustavy rovnic.
Příklad:
X + 3y = 3,
X - 3y = 9.
Řešení (obr. 50):
y = -j-x + 1,
y = lx - 3.
Xs = x = 6,
ys = y = -1, takže P = {[6, -tJ}.
237
Pozllil1nka:
Jsou-li přímky různými rovnoběžkami, resp. vzájemně splývají, pak rovnice
soustavy si odporují, resp. nejsou vzájemn nezávislé.
Soustavy rovnic druhého stupně
Každou rovnici druhého stupně v proměnných x a y lze považovat za ana-
lytické vyjádření funkce (funkční rovnici), jejímž grafem je kuželosečka
(parabola, elipsa, hyperbola). '
Je-li druhá rovnice soustavy lineární, představuje přímku, jejíž průsečíky
s kuželosečkou určují řešení soustavy rovnic.
Jsou-li obě rovnice kvadratické, pak grafy příslušných funkcí jsou kuželo-
sečkami. Souřadnice průsečíků (průsečík může být jeden nebo průsečíky
mohou být dva až čtyři) udávají pak reálná řešení soustavy rovnic.
x
Obr. 50. Grafické řešení soustavy rovnic
prvního stupně
Obr. 51. Grafické řešení soustavy rovnic
druhého stupně
I
(I)
(II)
Řešení (obr. 51): Rovnice (I) představuje kružnici s poloměrem r = 5
a středem v počátku, kdežto rovnice (II) představuje parabolu s vrcholem [O, 3].
Souřadnice průsečíků jsou
Xl . 2 7 , Y 1 . - 4,2 ,
Příklad:
x 2 + y: = 25,
x 2 + y = 3.
/'
X 2 ...:. - 2,7 ,
Y2 . -4,2,
takže .
P = {[2,7; -4,2], [-2,7; -4,2]}.
238
2.2. NEROVNICE
2.2.1. Základní pojmy
Predikátové formule tvaru TI N T 2 , kde N značí kterýkoli ze znaků
>, > , <, < , *, vysvětlených v článku 0.1.5, se nazývají nerovnice.
Definiční obor, řešení a obor pravdivosti nerovnice se definují stejně jako
u rovnIc.
Definičním oborem nerovnice TI (x, y, ...) N T 2 (x, y, ...) nazýváme kartélský
součin O = X x Y x ... oborů promčnných termů TI a T 2 .
Řešenínl [pravdivostním prvkem] nerovnic TI (x, y, ...) N T 2 (x, y, ...) s n čí-
selnými proměnnými nazýváme takovou uspořádanou n-tici [xo, Yo, .. .] E
E X' X Y X ..., že po dosazení jejích členů do dané nerovnice dostaneme
pravdivý výrok. Oborem pravdivosti P nerovnice nazýváme množinu všech
jejích řešení.
Nerovnice bez čís lných proměnných představuje buď pravdivý výrok
(pravdivou nerovnost), nebo nepravdivý výrok; např. 7 < 5 je nepravdivý
výrok.
Nerovnice s aspoň jednou číselnou proměnnou představuje predikátovou
formuli, která se změní bud' v pravdivý výrok (pravdivou nerovnost), nebo
v nepravdivý výrok, jestliže za všechny číselné proměnné dosadíme všechny
členy některé uspořádané n-tice z definičního oboru dané nerovnice.
2.2.2. Řešení nerovnice
Nerovnice tvaru
(x - a 1) (x - a 2) . . . (x - a n ) NO,
popř. tvaru
(x - a I) (x - a 2) . .. (x - a m )
(x - a m + 1 )(x - a m +2)'.'(X _ a,,) N O,
(1)
(2)
kde každá dvě z čísel a 1, a 2, . ., a n jsou různá a N zastupuje některý ze znaků
> < '" "" t kt
=, =, >, <, -r, reslme a o :
Nulové body a l' a2, ..., a n lineárních dvojčlenů uspořádáme podle velikosti
a přesvědčíme se, zda je nerovnice splněna v libovolném intervalu (ai, aj + 1),
kde a i a a i + 1 jsou dva sousední nulové body. Další intervaly, kde je nerovnice
splněna, pak se určí tak, že interv.aly, kde je nerovnice splněna, se střídají
s intervaly, kde nerovnice splněna není.
239
Nerovnici (1) nulové body at, a2, ..., a,. splňují, právě když znak N za-
stupuje znaky > , < . Nerovnici (2) nulové body al, a2, ..., a". splňují, právě
když znak N zastupuje znaky > , < , ale nulové body a". + t, a", + 2' ..., a,. tuto
nerovnici nesplňují. O tom, zda určitý interval vyhovuje nebo nevyhovuje
dané nerovnici, lze rozhodnout dosazením libovolného čísla x = k z vnitřku
tohoto intervalu do dané rovnice. Přitom říkáme, že provádíme pokus pro
x = k. Postup výpočtu ukážeme na příkladu.
Příklad:
(x-l)(x+2)(x-3) .
(x + 4)(x - 5)(x + 6) > O.
Nulové body: -6, -4, -2,1,3,5; přitom body -2,1,3 nerovnici vy-
hovují, ale body - 6, - 4, 5 nerovnici nevyhovují.
Dosadíme-li x = O, dostaneme
(-1).2.(-3) > O
4 . ( - 5) . 6 = ,
což je nepravdivý výrok. Řešením jsou tedy intervaly
( - 00, - 6), (-4, - 2), < 1, 3), (5, + (0).
Nerovnice tvaru
ax 2 + bx + c N O
(a =t= O) ,
kde N zastupuje některý ze znaků > , < , >, <, =t=, řešíme takto:
I Má-li levá strana různé reálné kořeny, píšeme
ax 2 + bx + c = a(x - Xl) (X - x 2 )
a nerovnlCl
a(x - xl)(x - X2) N O
řešíme jako v předchozím případě.
Má-li levá strana uvedené nerovnice dvojnásobný kořen, píšeme
ax 2 + bx + c = a(x - Xt)2.
Nerovnice a(x - Xt)2 > O je splněna pro všechna čísla X E R v případě,
že a > O, a pro x = Xt v případě, že a < O.
Nerovnice a(x - X I )2 > O j( splněna pro všechna čísla XE R \ {Xl} v pří-
padě, že a > O, a není splněria pro žádné číslo X E R v případě, že a < O.
Nerovnice a(x - Xt)2 < O je splněna pro všechna čísla X E R v případě,
že a < O, a pro x = Xl v případě, že a > O.
240
Nerovnice a(x - X l )2 < o je splněna pro všechna čísla XE R \ {Xl} v pří-
padě, že a < O, a není splněna pro žádné číslo X e R v případě, že a > O.
Má-li levá strana komplexně sdružené kořeny, pak rovnice ax 2 + bx + c N O
je bud' splněna pro všechna čísla X e R, nebo není splněna pro žádné číslo
X e R. O tom, který z obo'u případů nastává, se rozhodne dosazením x = O.
2.3. REÁLNÉ FUNKCE
2.3.1. Základní pojmy
Pojem reálné funkce
Reálnou funkcí f (jedné) reálné proměnné x [stručně (reálnou) funkci f
proměnné x nebo jen funkcí] nazýváme každé zobrazení v množině R všech
reálných čísel (viz článek 0.4.6), tj. množinu f právě těch uspořádaných 'dvojic
[ x, y ] e R 2 , které lze vytvořit podle nějakého (funkčního) předpisu tak,
že každému číslu xe,R je přiřazeno nejvýše jedno číslo yeR. Přitom
proměnná x se nazývá nezávisle proměnná [argument] a proměnná y se na-
zývá závisle proměnná.
Pro určité číslo x e R se číslo y e R, pro něž platí [x, y ] e f, nazývá (funkční)
hodnota funkce f v čísle x a označuje se f(x). Téhož symbolu f(x) výjimečně
používáme nro funkci f, chceme-li zdůraznit, že nezávisle proměnnou funkce f
značíme x. '4
Množina D = ° 1 (/) c R, která má tu vlastnost, že ke každému číslu x E D
je přiřazeno prá vě jedno takové číslo y, že [x, y] e f, se nazývá (definiční)
obor funkce f, kdežto množina G = O 2 (/), která má tu vlastnost, že ke každému
číslu ye G existuje takové číslo x e D, že [x, y ] e f, se nazývá funkční obor
[obor funkčních hodnot] funkce f.
"-
Reálnou funkci f proměnné x na množině D = 0 1 (/) (viz článek 0.4.6)
značíme
f: D G,
kde G :::> O 2 (/). Je-li D = 0 1 (/) a U = O 2 (/), píšeme
f: D G .
Reálnou funkci /: D G lze uvádět v množinovém zápisu:
f= {[x,y]eR2Iy=f(x), xeD, yeG}
nebo stručně
f= {[x,y]ly=f(x), xeD}.
241
Zápis y = f(x) značí, že jsme pro nějakou funkci zvolili znak f, pro nezá-
visle proměnnou znak x a pro závisle proměnnou znak y.
Funkční předpis je zpravidla dán v analytickém tvaru, tj. nějakým vzorcem
pro výpočet hodnot závisle proměnné (např. y = x 2 , Y = sin x apod.). Je-li
funkční předpis tvaru y = f(x), říkáme, že funkce f je dána v explicitním tvaru
[explicitně], a mluvíme o explicitní funkci. Je-li funkční předpis tvaru
F(x, y) = O, říkáme, že funkce f je dána v implicitním tvaru [implicitně], a mlu-
víme o implicitní funkci (viz článek 2.3.4). Funkce bývá také dána kartézským
grafem, orientovaným grafem, tabulkou funkčních hodnot, graficky nebo
jiným způsobem (např. jako součet funkční řady).
Rovnost, součet, součin a podíl reálných funkcí
Nechť fa g jsou dvě reálné funkce proměnné x s definičními obory Dl a D 2
a platí D c Dl n D 2 (D * 0). Pak říkáme, že funkce f, g jsou si rovny na mno-
žině D,jestliže pro každé číslo x E D platí f(x) = g(x). Dále říkáme, že funkce h,
resp. k je součtem, resp. součinem funkcí f a g na množině D, jestliže pro každé
číslo x E D platí h(x) = f(x) + g(x), resp. k(x) = f(x) g(x). Funkce I se na-
zývá podíl funkcí fa g na množině D,jestliže pro každé číslo x E D platí g(x) * O
a I(x) = f(x)/g(x).
Kartézský graf funkce
(Kartézský.> grafem funkce y = f(x), jejímž definičním oborem je mno-
žina D, nazýváme množinu právě těch bodů v rovině xy s kartézskou sou-
řadnicovou soustavou (O; x, y), které mají tvar [x, f(x)] (obr. 52).
Ydt
----------
G! __ _ f: D-6
I
I
i
o
a '-- -----
D
' b
Obr. 52. Kartézský graf funkce y = J(x)
na intervalu (a, b>
x
Algebraické funkce
Reálná funkce jedné proměnné se nazývá algebraická, jestliže ji lze vyjádřit
vzorcem vytvořeným z konstant a z nezávisle proměnné pomocí konečného
242
počtu základních početních operací, za nez považujeme sčítání, odčítán Í,
násobení, dělení a umocňování při racionálním exponentu. Funkce, která
není algebraická, se nazývá transcendentní.
Rozdělení
algebraických funkcí
Reálná algebraická funkce
I I
iracionální funkce
1 , . I , 1 ' f k
ce e raclona nI un ce
. ' l " f k
raClona nI un ce
I
1 ' . 1 ' 1 ' f k
omene raclona nI ut) ce
Celá racionální funkce n-tého stupně (polynom [mnoho člen]
n-tého stupně): '
P ' () n + n-l + + +
x = anx a n - 1 X . . . a 1 x ao
(n E N; ak E R; k = O, 1, ..., n; a n * O).
Lomená racionální funkce
R(x) = P(x) = anx n + an_1x n - 1 + ... +"a1x + ao
Q(x) bmx m + bm_1x m - 1 + ... + b1x + b o
(m, n E N; ak, h, E R; k = O, 1, .. ., n; I = O, 1, ..., m; a n * O, bm * O).
Jestliže n < m, jde o ryze lomenou racionální funkci.
Jestliže n > m, jde o neryze lomenou racionální funkci.
Jestliže n = m = 1, jde o lineární lomenou racionalní funkci.
Sudé a liché funkce
Funkce y = f(x) se nazývá sudá, resp. lichá, právě když definiční obor D
funkce f je souměrný podle počátku souřadnicové soustavy (tj. s každým
bodeffi/ x E D patří do oboru D také bod - x) a pro každé čislo x E D platí
f( -x) = f(x), resp. f( -x) = -f(x).
Graf sudé funkce je souměrný podle osy y, kdt'lto graf liché funkce je sou-
iněrný podle počátku O.
Ohraničené [omezené] funkce
Existuje-li taková konstanta K, že pro všechna čísla x E DI C D, kde D je
definiční obor funkce j; platí j'(x) < K, resp. j'(x) > K, resp. Ij'(x)1 < K, pak
se funkce f nazývá shora ohraničená [shora omezená], resp. zdola ohraničená
[zdola omezená], resp. ohraničená [omezená] na množině DI'
243
Monotónní a ryze monotónní funkce v bodě
Jestliže funkce y = J(x) je definována na okolí U(xo) nějakého bodu
Xo E R a platí:
a) J(x) < f(xo) pro \Ix E a -(xo) a f(xo) < f(x) pro \Ix E a +(xo), říkáme,
že funkce f je rostoucí v bodě xo;
b) f(x) > f(xo) pro \Ix E a -(xo) a J(xo) > j'(x) pro \Ix E O +(xo) říkáme,
že funkce f je klesající v bodě Xo;
c) f(x) < f(xo) pro \Ix E a -(xo) a f(xo) < f(x) pro \Ix E a +(xo). říkáme,
že funkce f je neklesající v bodě xo;
d) f(x) > f(xo) pro \Ix E a -(xo) a f(xo) > f(x) pro \Ix E a +(xo) říkáme,
že funkce f je nerostoucí v bodě xo.
Monotónní a ryze monotónní funkce na množině
Jestliže funkce y = f(x) je definována na množině D, Dl c D a pro každá
dvě čísla Xl' X2 E Dl (Xl < x 2 ) platí nerovnost:
a) f(x l ) < f(x 2 ), říkáme, že funkce f je rostoucí na množině Dl;
b) f(XI) > f(X2)' říkáme, že funkce f je klesající na množině Dl;
c) f(x l ) < f(X2), říkáme, že funkce f je neklesající na množině Dl;
d) f(x 1) > f(x 2 ), říkáme, že funkce f je nerostoucí na množině Dl'
Neklesající funkce a nerostoucí funkce nazýváme souhrnně monotónními
funkcemi, kdežto rostoucí funkce a klesající funkce nazýváme souhrnně ryze
monotónními funkcemi.
Jestliže funkce f je rostoucí, resp. klesající, resp. neklesající, resp. nerostoucí
v každém bodě x intervalu I, pak je rostoucí, resp. klesající, resp. neklesající,
resp. nerostoucí na intervalu I.
Konvexní a konká vní funkce v bodě
Jestliže funkce y = f(x) je definována na okolí U(x ) nějakého bodu
Xo E R, v němž existuje vlastní derivace f'(x o ) (viz kapitolu 5.2), a platí:
a) f(x) < f(x o ) + (x - xo) f'(xo) \lxE U(xo), říkáme, v funkce f
pro ze
je v bodě Xo ryze konkávní;
b) f(x) > f(x o ) + (x - xo) f'(xo) pro \Ix E U(xo), říkáme, v funkce f
ze
je v bodě Xo ryze konvexní;
c) f(x) < f(xo) + (x - xo) f'(x o ) pro \Ix E U(xo), říkáme, v funkce f
ze
je v bodě Xo konkávní;
d) f(x) > f(xo) + (x - xo) f'(xo) pro \Ix E U(x o ), říkáme, v funkce j'
ze
je v bodě Xo konvexní.
244
Konvexní a konkávní funkce na intervalu
Jestliže funkce y = f'(x) je definována na intervalu J a pro každé tři body
PI[xl,f(x l )], P 2 [ x 2 ,f(x 2 )], P 3 [X3,f(X3)] (Xl' X2, X3 E J, Xl < X2 < X3) platí,
že '
a) bod P 2 leží pod přímkou určenou body P I a P 3 , říkáme, že funkce f je
ryze konvexní na intervalu J;
b) bod P 2 leží nad přímkou určenou body P I a P 3 , říkáme, že junkce j
je ryze konkávní na intervalu I:
c) bod P 2 leží bud" pod přímkou určenou body P 1 a P 3 , nebo na ní, říkáme,
že .funkce f je konvexní na intervalu J;
d) bod P2 leží bud' nad přímkou určenou body P I a P 3 , nebo na ní, říkáme,
že funkce f je konkávní na intervalu J.
Homogenní fun ce jedné proměnné
Funkce y = f(x) se nazývá hOlnogenní funkce k-tého stupně na množině D,
právě když pro každé číslo z určitého okolí čísla t = 1 patří do množiny D
s každým číslem X také číslo tx a platí
f(tx) = ť< f(x),
kde k se nazývá stupel1 homogenní funkce .f
Periodická funkce
Funkci y = f(x) nazýváme periodickou funkcí s periodou p. existuje-li
takové nejmenší číslo p > O, že platí:
a) Je-li funkce f definován v bodě xo, je definována také v bodech X k =
= Xo + kp pro všechna celá čísla k.
b) Pro všechna čísla X z definičního oboru funkce f platí f(x) = f(x + kp).
Složená funkce
Jestliže funkce u = qJ(x) je definována na oboru Dl a funkce y = f(u)
na oboru D 2 a jestliže množina D je takovou podmnožinou množiny Dl'
že pro každé číslo X-E D patří příslušné číslo qJ(x) = u do množiny D 2 , pak
funkce y = f(qJ(x)) [která se také značí y = Cľ o qJ) (x)], definovaná na oboru D,
se nazývá složená funkce s ,vnitřní složkou u = qJ(x) a vněj. í složkou y = f(u).
Prostá funkce
Funkce y = f(x) s definičním oborem D se nazývá prostá, jestliže pro každá
dvě čísla X I ,X 2 ED (Xl * x 2 ) platí .ľ(x l ) =t=j'(x 2 ).
245
Inverzní funkce
Jestliže .funkce y = f(x) je prostá na oboru D a jejím funkčním oborem
je množina G, lze na množině G definovat funkci, která každému číslu y E G
přiřazuje právě to číslo x E D, pro které je f(x) = y, a která se nazývá inverzní
funkce k funkci f a značí se f-l [někdy také f- 1 nebo 1]. Funkce I a 1-1
se nazývají vzájemně inverzn.í a platí pro ně rovnosti
l-l(l(x)) = x
1(1-1 (y)) = Y
pro \:Ix E D,
pro \:I Y E G .
Funkce x = I-I(Y)' inverzní k funkci y = I(x), má za argument pro-
měnnou y, kdežto její závisle proměnnou je x. Protože však argument obvykle
označujeme písmenem x a závisle proměnnou písmenem y, budeme funkci 1-1
často psát ve tvar y = l-l(X).
Definičním oborem funkce 1- l' inverzní k funkci f, je funkční obor funkce f,
a funkčním oborem funkce 1-1 je definiční obor funkce f. Grafy funkcí I a 1-1
jsou souměrné podle přímky y = x.
Jestliže funkce I je dána v analytickém tvaru y = I(x), pak analyticky
tvar inverzní funkce dostaneme tak, že v analytickém tvaru funkce I všude
místo x píšeme y a místo y píšeme x a v takto získaném vyjádření osamostat-
níme proměnnou y.
Příklad:
Funkce
x
y=1+x
je prostá, neboť pro každou dvojici čísel X b X 2 E R \ { -1} (Xl * X2) platí
Xl + XIX2 :f: X2 + X 1 X2,
x 1 (1 + x 2 ) =t= x 2 (1 + Xl)'
Xl X 2
:f: .
1+x 1 1+x 2 .
Proto k ní existuje inverzní funkce. Jestliže ve vzorci y = x/(l + x) vzájemně
zaměníme proměnné X a y, pak
y
x=
,
1 + Y
246
odkud dostaneme inverzní funkci
x
y=
1 - x
k dané funkci.
Hornerovo schéma
Pomocí Hornerova schématu lze rychle 'určit funkční hodnotu p(x 1 ) celé
racionální funkce
y = P(x) = a"X' + a n _ 1 x n - 1 + ... + ao
Hornerovo schéma se sestavuje takto:
pro x = x I .
a n a n -1 a n -2 a n -3 . . .
O 2 3 2
anx I a n x 1 + a n -1 X 1 a n x 1 + a n - 1 x 1 + a n - 2 X 1
a n x 1 + a,,_ 1 2 3 2
Qn anx 1 + a" - 1 Xl + a n - 2 anx 1 + a n -1 X 1 + a n - 2 X l + a n - 3
ao
n n-1 JI-2
a"x 1 + a n - 1 Xl + a n - 2 Á 1 + . . . + a 1 x 1
n n - 1 n - 2 f( )
anx 1 + a n - 1 Xl + a n - 2 Xl + . . . + a 1 Xl + a o = Xl
První řádek obsahuje koeficienty polynomu. Je třeba pamatovat, že je-li
některý z koeficientů a k roven nule, je nutno na příslušném místě v prvním
řádku Hornerova schématu napsat nulu.
1. krok: Koeficient a" vynásobíme číslem Xl a k součinu přičteme a n - l'
2. krok: Součet opět vynásobíme číslem x 1 a k součinu přičteme a n - 2'
3. krok: Součet opět vynásobíme číslem x 1 a k součinu přičteme a n - 3' atd.
Takto postupujeme až k poslednímu součtu, který je hledanou funkční
hodnotou v bodě Xl.
Příklad:
Má se vypočítat hodnota funkce
f(x) = X4 + 2X3 - 5x + 7 vbodě Xl = 2,3.
Pomocí Hornerova schématu dostaneme
120
O 2,3 9,89
1 4,3 9,89
Je tedy f(2,3) 47,82.
-5
22,747
17,747
7 (řádek koeficientů)
40,818 1
47,818 1 = f( 2,3 )
247
Nulové body a póly
Nulovým bodem Xo funkce f nazýváme takovou hodnotu nezávisle pro-
měnné x, pro kterou f(xo) = O. Pólem Xo funkce f nazýváme takovou hodnotu
nezá visle proměnné x, pro kterou
lim .r(x) = + 00 nebo lim f(x) = + 00.
X-Xo+ X-Xo-
Spojitost funkce
Říkáme, že funkce f = {[x,f(x)] I x E D, f(x) E G}, jejíž definiční obor D
obsahuje okolí U(c) bodu c, je spojitá v bodě c, právě když ke každému číslu
B > O existuje takové číslo 1J = 1J(B) > O, že pro každé číslo x E U(c,1J) je
If(x) - f(c)1 < B.
Řík me, že funkce f= {[x,f(x)]lxED, f(X)EG}, jejíž definiční obor D
obsahuje levé okolí U _(c), resp. pravé okolí U +(c) bodu c, je spojitá zleva,
resp. spojitá zprava v bodě c, právě když ke každému číslu B > O existuje takové
číslo 1J = 1J(B) > O, že pro každé číslo XE U_(c,1J), resp. XE U+(c,1J) je
If(x) - f(c)1 < B.
uÍ1kce f je spojitá v bodě c, právě když má tyto tři vlastnosti:
a) Funkce f je definována v bodě x = c [hodnota f(c) je tedy konečná],
tj. [c, f(c)] E f
b) Existuje limita limf(x) = C (viz definici limity funkce v článku 5.1.2).
x-c '
c) Platí f(c) = C.
Funkce j' je s poj i t á z I e v a, resp. s poj i t á z p r a v a v bod ě c, právě
když má tyto tři vlastnosti:
a) Funkce f je definována v bodě x = c, tj. [c, f(c)] E f
b) Existuje lim f(x) = C l' resp. lim f(x) = C 2 .
x c- x c+
c) Platí f(c) = C., resp. f{c) = C 2 .
Jsou-li funkce fa g spojité v bodě c, pak funkce af + bg (a, bER) a fg jsou
také spojité v bodě c. Je-li y(c) * O, pak také funkce flg je spojitá v bodě c.
Body nespojitosti funkce
Bod, v němž funkce .r není spojitá, se nazývá bod nespojitosti funkce f
Jestliže v bodě c obě jednostranné limity funkce y = f(x) existují, jsou
konečné a jsou rovny číslu C, tj. lim f(x) = lim j(x) = C, ale funkce f buď
x c + x-c-
není v bodě c definována, nebo f(c) * C, pak říkáme, že funkce f má v bodě c
odstr,anitelnou nespojitost.
248
Bod nespojitosti c, v němž existují vzájemně různé vlastní limity funkce
y = f(x) zpra.a a zleva, tj. lim f(x) 9= lim .f(x), se nazývá bod nespojitosti
x-e+ x-c-
prvního druhu funkce f. Číslo lim f(x) - lim f(x) se nazývá skok funkce f
b d v x-c+ x-e-
voe c.
Bod nespojitosti c, v němž buď neexistuje limita funkce f, nebo aspoň jedna
z jednostranných limit funkce f není konečná, se nazývá bod nespojitosti
druhého druhu funkce f.
Příklad 1:
Funkce y = 1/x je v bodě x = O nespojit . Bod x = O je pólem.
Příklad 2:
Funkce
3
y = 1 - e l / x
je v bodě x = O nespojitá. Bod x = O je bodem nespojitosti prvního druhu.
Příklad 3:
Funkce
x 3 - 1
y = 2 1
x -
je v bodech x = + 1 nespojitá. V bodě x = 1 má tato funkce odstranitelnou
nespojitost, neboť
x 3 - 1 3
lim 2 -
x-I x-I. 2
Bod x = -1 je pólem.
Spojité funkce na intervalu
Funkce f se nazývá spojitá na otevřeném intervalu (a, b), právě když je spojitá
v každém bodě intervalu (a, b).
Funkce f se nazývá spojitá na uzavřeném intervalu (a, b), právě když je
spojitá v každém vnitřním bodě tohoto intervalu, v bodě a je spojitá zprava
a v bodě b je spojitá zleva.
Funkce po částech spojité
Funkce, která je spojitá na intervalu (a, b) s výjimkou konečně mnoha
bodů, v nichž má odstranitelnou nespojitost nebo které jsou body nespojitosti
prvního druhu, se nazývá funkce po částech spojitá na interralu (a b).
249
Stejnoměrně spojité funkce
Funkce Y = f(x) se nazývá stejnoměrně spojitá na intervalu (a, b), právě
když ke každému číslu 8 > O existuje takové číslo {) = £5(8) > O (tj. číslo £5
závisí jen na čísle 8), že pr{) každá dvě čísla x a x + h z intervalu (a, b), jejichž
vzdálenost Ihl < {), platí nerovnost
If(x + h) - f(x)1 < 8.
Jsou-li funkce f a g stejnoměrně spojité na intervalu (a, b), pak funkce
cf + dg (c, dER) a fg jsou také stejnoměrně spojité na intervalu (a, b).
Jestliže v každém bodě intervalu (a, b) je g(x) =t= O, pak také funkce flg je
stejnoměrně spojitá na intervalu (a, b).
2.3.2. Přibližné vyjádření funkcí pomocí interpolačních vzorců
Lagrangeův vzorec
( ) (x - X 2) (x - x 3 ) (x - x 4 )... (x - x n )
y = f x = YI +
(Xl - X 2 ) (Xl - X 3 ) (Xl - X 4 )... (Xl - X n )
(X - Xl) (X - X 3 ) (X - X 4 )... (x - X n )
+ Y2 (X2 - X 1 )(X2 - X 3 )(X2 - X 4 )... (X2 - X n ) + o..
(X - Xl) (X - X 2) (x - X 3) . . . (X - X n - I)
... + Yn (Xn - Xl)(X n - X2)(X n - X3) ... (Xn - X n - 1 )'
,
přičemž hodnoty Y l' Y2, ..., Y.. funkce v bodech X I' X2, X3, ..., X n jsou známé
nebo jsou předem dány.
Příklad:
Jaké přibližné vyjádření polynomem minimálního stupně má funkce daná
tabulkou:
1 4 6 9 ?
Y 2 5 3 6.
(x - 4) (x - 6) (x - 9) (x - 1)(x - 6) (x - 9)
Y = 2. (1 _ 4)(1 - 6)(1 - 9) + 5. (4 - 1)(4 - 6)(4 - 9) +
(x - 1)(x - 4) (x - 9) (x - 1)(x - 4) (x - 6)
+ 3. (6 _ 1)(6 - 4)(6 - 9) + 6. (9 - 1)(9 - 4)(9 - 6) ;
Y = - io(x 3 - 19x 2 + 114x - 216) +
+ -t(x 3 - 16x 2 + 69x - 54)-
- -Mx 3 - 14x 2 + 49x - 36) +
+ io(x 3 - l1x2 + 34x - 24),
Y = lO X3 - ix 2 + 3l x - 3.
250
Newtonův vzorec [Newtonův interpolační polynom]
Y = YI + AI(X - Xl) + A 2 (x - xI)(x - X2) +
+ A3(X - Xl) (x - X2) (X - X3) + ...
... + An(x - Xl) (X - X2) (x - X3) ... (X - X n ).
Přitom
A - Y2 - YI (Y3 - YI) -:- A I (X3 - Xl)
1 - , A 2 = ( ) ( \,
X2 - Xl X3 - Xl X3 - X2)
(Y4 - YI) - A I (X 4 - Xl) - A 2 (X 4 - Xl) (X 4 - X 2 )
A3 =
(X 4 - Xl) (X 4 - X2) (X 4 - X3)
atd. Tento vzorec se podstatně zjednoduší, jsou-li hodnoty X ekvidistantní,
tj. je-li X k - X k - 1 = h.
Položíme-li
Y2 - Yl = YI'
Y3 - Y2 = Y2'
Y4 - Y3 ' Y3' ...;
Y2 - L\YI = 2Yl'
Y3 - Y2 = 2Y2'
Y4 - Y3 = 2Y3' ...;
2Y2 - 2YI = 3YI'
2Y3 - 2Y2 = 3Y2'
2Y4 - 2Y3 = 3Y3' ...;
.........................
n-2Y2 - n-2YI = n-IYI'
n-2Y3 - n-2Y2 = n-IYt,
n-2 n-2 An-l
Y4- Y3=L1 Y3'.'"
dostaneme
Yl(X'- Xl) 2YI(X - XI)(X - X 2 )
Y=YI + l!h + 2!h 2 +
D3YI(X - Xl) (x - X 2 ) (X - X3)
+ 3! h 3 + ...
D n - 1 YI(X - Xl) (X - X2) (X - X3) ... (X - X n - l )
... +
(n - I)! h n - I '
popř. s novou proměnnou t: x = Xl + th:
Y = YI + G)AYt + G)A 2 YI + G)A 3 Yt + ... + G)AnYt.
251
Příklad:
Jaké přibližné vyjádření má funkce daná tabulkou
2 345 6 ?
yl3 5427'
1. krok: Určíme diference:
YI = 5 - 3 = 2
Y2 = 4 - 5 = - 1
Y3 = 2 - 4 = -2
Y4 = 7 - 2 = 5
3Yl = -1 + 3 = 2
3y? =, 7 + 1 = 8
2Yl = -1 - 2 = -3
2Y2 = -2 + 1 = -1
2Y3 = 5 + 2 = 7
4YI = 8 - 2 = 6
2. k r o k: Po dosazení do před posledního vzorce dostaneme
2(x - 2) -3(x - 2) (x - 3)
y=3+ 1!.1 + 2!.12 +
2(x - 2) (x - 3) (x - 4)
+ 3!.13 +
6(x - 2) (x - 3)(x - 4) (x - 5)
+ 4! .1 4 =
= 3 + 2x - 4 - X2 - 5x + 6) +
+ i(x 3 - 9x 2 + 26x - 24) +
+ !(x 4 - 14x 3 + 71x 2 - 154x + 120),
y = ix 4 - Il x 3 + 54 3 X 2 -!lfx + 12.
2.3.3. Funkce několika proměnných
Každé zobrazení množiny D 2 uspořádaných dvojic [x, y] E R 2
do množiny R nazýváme (reálnou) funkcí dvou (reálných) proměnných x, y.
Způsob zápisu:
z = f(x, y)
nebo v množinovém zápisu:
f = {[[x, y], z] I z = f(x, y), [x, y ] E D 2 } .
Zobrazení množiny Dn uspořádaných n-tic [x l' X2' .. ., X n ] E R n do množiny R
nazýváme (reálnou) funkcí n (reálných) proměnných Xl' X2' ..., X n .
252
Zpúsob zápisu:
y = f(x t , x 2 , ..., x n )
nebo v množinovém zápisu:
f = {[[Xl' X2, ..., x n ], y] ly = f(x l , X2, ..., X n ), [Xl' X2, ..., Xn] e Qn} =
= {[X,y]ly =f(X), [X]eQn}'
Homogenní funkce n proměnných
Funkce y = f(x l' X2, ..., X n ) se nazývá homogenní funkce k-tého stupně
na množině Qn, právě když pro každé číslo z určitého okolí čísla t = 1 patří
do množiny Qn s každou n-ticí [Xl,X 2 ,.,.,x n ] také n-tice [tXt,tx2,...,txn]
a platí
f(tx l , tX2, ..., tx n ) = ť< f(x l , X2, ..., x n ),
kde k se nazývá stupeň homogenní funkce f.
Spojitost funkcí několika proměnných
Říkáme, že reálná funkce f n reálných proměnných, jejíž definiční obor Qn
obsahuje okolí K(c) bodu c = [C.,C2'...'C n ], je spojitá v bodě c, právě když
ke každému číslu B > O existuje takové číslo tJ > O, že pro všechna čísla
x e K(c, tJ) je
If(x l , X2, ..., x n ) - f(c l , C2, ..., cn)1 < B.
Funkce y = f(x l , X2, ..., x n ) je spojitá v bodě [CI' C2, ..., c n ], právě 'když
má tyto tři vlastnosti:
a) Funkce f je definována v bodě [Xl' X 2 , ..., Xn] = [C t, C2, ..., C,,].
b) Existuje vlastní limita C funkce fv bodě [CI' C2, ..., C,,] (viz článek 5.1.2).
c) Platí f(c l , C2, ..., c n ) = C.
2.3.4. Implicitní funkce
Je-li dána rovnice
"
F(x, y) = O,
kde F je funkce dvou proměnných na množině D 2 , pak říkáme, že funkce
y = f(x) je na množině D řešením této rovnice, jestliže pro každé číslo x E D
je [x, f(x)] E Q2 a
F(x, f(x)) = O.
253
Funkci f, která je řešením rovnice F(x, y) = O, nazýváme funkcí danou v impli-
citním tvaru [funkcí danou implicitně, implicitní funkcí].
Příklad:
Na intervalu < - a, a> jsou řešeními rovnice x 2 + y2 - a 2 = O tyto funkce:
YI = J(a 2 - x 2 ),
Y2 = -J(a 2 - x 2 ).
Věta o implicitních funkcích: Má-li funkce F(x, y) na okolí bodu [c, d] spojité
parciální derivace prvního řádu (viz kapitolu 5.4), přičemž
cF
-;- (c, d) * O,
(lY
pak na určitém okolí bodu c existuje jediná funkce y = f(x), která je řešením
rovnice F(x, y) = O a vyhovuje pO,dmínce d = f(c). Funkce f je na tOltlto
okolí bodu c spojitá.
Obdobně definujeme řešení y = f(x I' X2, ..., x n ) rovnice
F( Xl' X 2' . . ., x n , y) = O.
Má-li funkce F(x I' X 2, ..., X m y) na okolí bodu [c I' C 2, ..., Cm d] spojité
parciální derivace prvního řádu, přičemž platí
cF
cy (Cl' C2, ..., C n , d) =F O,
pak na určitém okolí bod u [C I' C 2, ..., c n ] existuje jediná funkce y =
= f(x l' X2' ..., x n ), která je řešením rovnice F(x I' X2, ..., X n ) = O a vyhovuje
podmínce d = .{(c I , C2, ..., c n ). Funkce f je na okolí bodu [CI' C2, ..., c n ]
spojitá.
2.3.5. Kartézské grafy funkcí
2.3.5.1. Algebraické funkce
Celá racionální funkce prvního stupně [lineární funkce]
Obecný tvar funkce: y = aIx + a o .
Popis grafu: přímka.
Koeficienty mají tento význam:
aI = tg C( - směrnice přímky, která je grafem lineární funkce
(viz článek 4.1. 3) ;
254
a 1 > o
a. < O
ao
a o = O
al = O
- směrnice grafu rostoucí lineární funkce:
- směrnice grafu klesající lineární funkce;
- úsek (vyťatý přímkou) na ose y;
- přímka prochází počátkem O;
- přímka je rovnoběžná s osou x.
Y=.!..X'fo3
3
f
__Y='3 X + 2
f
Y=3 x + f
x
f
y-= 3' x
y=t X - 1
1
y= 3" x - J
Obr. 53. Grafy lineárních funkcí při
a 1 = konst
Obr. 54. Grafy lineárních funkcí při
a o = konst
Příklady:
V obrázcích 53 a 54 jsou grafy lineárních funkcí.
Celá racionální funkce druhého stupně [kvadratická funkce]
Obecný tvar funkce:
y = a 2 x 2 + a 1 x + a o .
Popis grafu: parabola druhého stupně [kvadratická parabola], jejíž osa
je rovnoběžná s osou y.
Koeficient a2 má tento význam:
a 2 > O - parabola je otevřená nahoru;
a 2 < O - parabola je otevřená dolů.
Vrchol paraboly
[ -a 1 al ]
v= -, - +ao .
2a2 4a2
255
ZvláL tní případy:
y = x 2 + px + q - normální parabola s vrcholem
v= [ - , -[( y - qJJ
_ 2
Y - a2 x
2
y = x + ao
y = (x + b)2
\
a osou rovnoběžno,:! s osou y, která je otevřená nahoru;
- parabola s vrcholem v počátku O (obr. 55);
- normální parabola s vrcholem V[O, ao] (obr. 56);
- normální parabola s vrcholem V[ -b, O] (obr. 57).
---LJ.
-6-5-4-3-2-f O t 2 J 456 X
Obr. 55. Paraboly y = a 2 x 2 s vrcholem
v počátku O
Obr. 56. Paraboly y = x 2 + a o
s vrcholem V[O, a o ]
o
y = x 3 - 6 x 2 + ff x - 6
y
f
-t
-2
Obr. 57. Paraboly y = (x + b)2
s vrcholem V[ - b, O]
Obr. 58. Kubické paraboly
Celá racionální funkce třetího stupně
Obecný tvar funkce:
y = a 3 x 3 + a 2 x 2 + al x + a o .
,
Popis grafu: parabola třetího stupně [kubická parabola J.
256
Koeficienty a3' a o mají tento význam:
a3 > O - parabola probíhá z dolní poloroviny roviny xy do její horní
poloroviny (obr. 58);
a3 < O - parabola probíhá opačně než při a 3 > O;
a o - úsek (vyťatý křivkou) na ose y.
Zvláštní případ:
y = x 3 - normální kubická parabola (obr. 59).
Sudé mocninové [potenční] funkce
Obecný tvar funkce:
y = x 2n (nE N).
Popis grafu: normální parabola (2n)-tého stupně s vrcholem V[O, O], která
je otevřená nahoru (obr. 60).
Obecný tvar funkce:
y = _x 2n (nE N).
Popis grafu: normální parabola (2n)-tého stupně, která je otevřená dolů.
y= x 3
'::;.
2 3 ,f
Obr. 59. Normální kubická parabola
(graf funkce y = x 3 )
Liché mocninové [potenční] funkc'e
Obecný tvar funkce:
y = x2n+l (n E N).
Popis grafu: normální parabola (2n + 1)-ního stupně, která leží v prvním
a třetím kvadrantu a jejímž středem souměrnosti je počátek O (obr. 61).
257
Obecný tvar fUllkce:
Y=_X 2n + 1 (neN).
Popis grafu: normální parabola (2n + 1 )-ního stupně, která leží v druhém
a čtvrtém kvadrantu a jejímž středem souměrnosti je počátek O; sestrojí se
jako křivka osově souměrná podle osy x vzhledem ke grafu funkce y = x 2n + 1 .
/'
Sudé mocninové [po ten ční] funkce se záporným exponentem
Obecný tvar funkce:
y = x - 2n (x * O, n E N).
Popis grafu: hyperbola (2n)-tého stupně, která leží v prvním a druhém
kvadrantu (obr. 62).
y
8
7
G
5
ft
3
2
-3-2-f f
23ft x
Obr. 61. Grafy funkcí y = X2.. + 1
(n E N)
Obr. 62. Grafy funkcí y = x - 2..
(n E N)
Obecný tvar funkce:
y = _x- 2n (x * O, nE N).
Popis grafu: hyperbola (2n )-tého stupně, ktera leží v třetím a čtvrtém kva-
drantu; sestrojí se jako křivka osově souměrná podle osy x vzhledem ke grafu
funkce y = x- 2n :
Liché mocninové [p'otenční] funkce se záporným exponentem
Obecný tvar funkce:
y = X-(2n+ 1)
(x * O, ne No).
258
Popis grafu: hyperbola (2n + 1 )-ního stupně, která leží v prvním a třetím
kvadrantu a jejímž středem souměrnosti je počátek O (obr. 63).
Zvlá. tní případ (n = O):
- 1 1 ( )
y=x =- X9=O;
x
grafem této funkce f, pro niž platí i = i-I' je rovnoosá hyperbola (obr. 64).
Obecný tvar funkce:
y = _X-(2n+ 1) (x =F O, nE No).
Popis grafu: hyperbola (2n + l)-ního stupně, která leží v druhém a čtvrtém
kvadrantu; sestrojí se jako křivka osově souměrná podle osy x vzhledem
ke grafu funkce y = X-(2n+ 1).
y
8 y:ax- 3
7 . Y = x- 5
6 - r
5 r .
I
4r-
3 :.-
2 I.
-3-2-1 f . .
,O 1
-1
. -2
. -3
-4
-5
-6
-7 Obr. 63. Grafy funkcí y = x-(2n+ I)
-8 (neN)
y
5
4
3
2
-4-3-2 -1 f
O -11
-2
-3
-4
-5
Obr. 64. Rovnoosá hyperbola
(graf funkce y = 1/ x)
Inverzní funkce
,Graf inverzní funkce se sestrojí z grafu původní funkce pomocí osové sou-
měrnosti podle osy y = x (obr. 65).
Odmocniny
Obecný tvar funkce:
{ 2n-!J x
y = 2n - !J x = - 2n - !J ( - x)
jde o inverzní funkci k funkci y = x 2n - 1
(x > O, nE N),
(x < O, nE N);
(n E N) (viz obr. 65).
259
Obecný tvar funkce:
y = 2r;j X (x > O, nE N);
jde o inverzní funkci k funkci y = x 2n (x > O, nE N) (obr. 66).
Obr. 65. Grafy vzájemně inverzních
funkcí y = x 3 , Y = x
Obr. 66. Grafy vzájemně inverzních
funkcí y = x 2 ,.y = Jx
2.3.5.2. Transcendentní funkce
Exponenciální funkce
Obecný tvar funkce:
y=a x (a >0).
Popis grafu: graf prochází bodem [O, 1] (o br. 67 a 68).
I
I
,
I f -I
r Y={3}
I
I
I
/
\
\
y = e- x \
\
-3 -2 - f O 1 2 3 4 x
Obr. 67. Grafy exponenciálních funkcí
y = 1 x, (1 j 2 Y , (1/3)X, (1/3) - x
Obr. 68. Grafy exponenciálních funkcí
y = e - X, 1 X, 2X, eX, 4 X, HP
260
Logaritmické funkce
Obecný tvar funkce:
y=logax (x>O, a>O, a* 1).
Popis grafu": graf prochází bodem [1, O] (obr. 69).
y
3 .
2
f
-1
-2
-3
-4
Obr. 69. Grafy logaritmických funkcí
v = lo g x
, a
Logaritmická funkce je inverzní funkcí k odpovídající exponenciální funkci.
O goniometrických funkcích, cyklometrických funkcích, hyperbolických
funkcích a hyperbolometrických funkcích viz v příslušných článcích. O plo-
chách druhého stupně viz v kapitole 4.2.
2.4. VEKTOROVÝ POČET
2.4.1. Základní pojmy
Definice aritmetického vektoru jako uspořádané n-tice neboli
řádkové matice, uvedená v článku 1.10.1, připouští po připojení pojmu
velikosti geometrickou interpretaci, která má důležité uplatnění v technic-
kých a přírodních vědách.
Protože u mnoha geometrických a fyzikálních veličin (např. u síly, rychlosti,
zrychlení, intenzity elektrického pole a posunutí bodu v geometrii) jsou pod-
statné velikost, směr a orientace, vytváří se jejich model (tzv. geometrický
vektor) pomocí pojmu orientované úsečky neboli pomocí uspořádané dvojice
bodů v trojrozměrném euklidovském prostoru. Na rozdíl od těchto veličin
existují ještě veličiny (např. hmotnost, teplota, doba, hustota, odpor vodiče,
délka úsečky, obsah plochy a objem tělesa), které mají jen velikost a nemají
směr ani orientaci a které nazýváme skalárními veličinami nebo stručně skaláry.
Protože však v matematice abstrahujeme od měřicích jednotek, rozumí se
slovem skalár libovolné reálné číslo.
261
o mluva:
V této kapitole se při vyšetřování vektorů omezíme na trojrozměrný eukli-
dovský prostor E3.
Vázaným vektorem nazýváme orientovanou úsečku AB nebo uspořádanou
dvojici [A, B] bodů, přičemž bod A, resp. B nazýváme poČátečním, resp.
koncovým bodem vektoru, který označujeme AB (obr. 70).
Nositelkou vázaného vektoru AB nazýváme přímku AB.
Polohovým vektorem [rádiusvektorem, průvodičem] rB bodu B vzhledem
k bodu O nazýváme vázaný vektor, který má počáteční bod v počátku O
souřadnicové soustavy a koncový bod v daném bodě .B.
II-A8
B
A
Obr. 70. Vázaný vektor (J = AB
Umístěním soustavy vázaných vektorů ve společném bodě P nazýváme taková
jejich rovnoběžná posunutí (translace), že počátečn! body všech vázaných
vektorů soustavy se ztotožní s bodem P. Vázané vektory, které dostaneme
pomocí takového umístění soustavy vázaných vektorů do bodu P, se nazývají
umístěné [centrované, centrální] vektory; říkáme pak, že jsme dané vázané
vektory umístili [centrovali] do bodu P.
Dva vázané vektory se nazývají sobě rovné [vzájemně ekvivalentní], právě
když se po umístění v společném bodě ztotožňují.
< Volným> vektorem [geometrickým vektorem] nazýváme množinu všech
vzájemně ekvivalentních vázaných vektorů.
Vektory se zpravidla označují polotučnými písmeny malé latinské, popř.
otické abecedy (např. a, b, c, ..., Q, b, c, ...) nebo stejně jako orientované
úsečky, neboť volný vektor jakožto množina všech vzájemně ekvivalentních
vázaných vektorů je v důsledku tranzitivnosti rovnosti určen kterýmkoli
z těchto vázaných vektorů.
V rukopisech lze vektory označovat bud' podtrženými malými latinskými
písmeny, nebo týmiž písmeny se šipkou.
Je-li vektor a určen vázaným vektorem AB , pak vektor AB nazýváme
umístěním vektoru a do bodu A a píšeme a = AB .
Velikostí [délkou, absolutní hodnotou, modulem, normou] vektoru a = AB
nazýváme délku úsečky AB a značíme ji
lal = a,
I AB I = IABI.
Nulovým vektorem nazýváme vektor, jehož prvkem je orientovaná úsečka
262
nulové délky, tj. orientovaná úsečka, jejíž počáteční bod splývá s koncovym
bodem. Nulový vektor se značí o. Platí 101 = O.
Jednotkovým vektorem nazýváme každý vektor o velikosti rovné číslu 1.
Jednotkové vektory označujeme 0°, bO, ... (0° čteme: o na nultou).
Jednotkové vektory se společným počátečním bodem O (tj. umístěné do
počátku O souřadnicové soustavy), jejichž směry a orientace jsou dány sou-
řadnicovými osami kartézské souřadnicové soustavy (O; x, y, z) se nazývají
základní vektory a označují se i, j, k (obr. 71).
zt
1
1
. O - -----..
1 f j y
xl
Obr. 71. Základní vektory i, J, I<
V dalším textu budeme vždy uvažovat jen pravotočivou souřadnicovou
soustat'u, která je charakterizována tím, že otočení kladné části osy x do kladné
části osy y se současným posunutím ve směru osy z dává pravotočivý
šroubový pohyb.
Vektory o, b se nazývají kolineární [rovnoběžné], právě když po umístění
v společném bodě mají společnou nositelku. Kolineární vektory o, b se na-
zývají souhlasně kolineárni [souhlasně rovnoběžné], právě když po umístění
do bodu A leží v téže polopřímce s počátečním bodem A (píšeme o ii b).
Kolineární vektory o, b se nazývají nesouhlasně kolineární [nesouhlasně
rovnoběžné], právě když po umístění do bodu A leží ve vzájemně opačných
polopřímkách s počátečním bodem A (píšeme o i! b).
Vektory o, b, c se nazývají komplanární, právě když po umístění v společném
bodě leží v právě jedné rovině.
Kolineární vázané vektory AB , CD s různými nositelkami jsou s o u h I a s n ě
kolineární, právě když jejich koncové body leží v téže polorovině s hraniční
přímkou AC. Mají-li ektory AB , CD společnou nositelku, jsou souhlasně
kolineární, právě když jedna z polopřímek AB, CD je částí druhé.
Vyjádření vektoru pomocí jeho souřadnic
Jestliže AB je umístění vektoru o a počáteční, resp. koncový bod vektoru
AB má souřadnice xl' YI, Zl' resp. X2' Y2, Z2' pak souřadnicemi vektoru o
vzhledem k základním vektorům ;,j, k nazýváme čísla
..
a x = X2 - Xl'
a y = Y2 - YI,
a z = Z 2 - Z I .
Píšeme o = (a x , aJ" a z ).
263
Vyjádření polohového vektoru bodu B[XB' YB, ZB] pomocí souřadnic:
rB = (XB' YB, ZB)'
Vyjádření základních vektorů pomocí souřadnic:
; = (1, O, O),
j = (O, 1, O),
k = (O, O, 1).
Vyjádření velikosti vektoru a = (a x , a y , a z ) pomocí souřadnic:
lal = J(a; + a; + a:) =
= .J[(XB - X A )2 + (YB - YA)2 + (ZB - ZA)2].
Příklad:
Vektor a = (5,2, -6) má velikost
lal = .J[5 2 + 2 2 + (-6)2] = .J65 8,062.
Sčítání a odčítání vektorů
Jestliže o, b jsou dva vektory, vektor AB je umístěním vektoru a do bodu A
a vektor BC je umístěním vektoru b do bodu B, pak součtem a + b vektorů
a, b nazýváme vektor, jehož umístěním do bodu A je vektor AC (obr. 72).
.o
a '" b
CIt "-
-----
d-a-b
K
e
Saa+b+C+6+.
Obr. 72. Sčítání a odčítání vektorů
Obr. 73. Vektorový mnohoúhelník
Vektory a, b se nazývají vzájemně opačné, právě když platí o + b = o.
Říkáme také, že b je antivektor vektoru a, a obráceně..
Odčítání vektoru se převede na přičtení opačného vektoru (viz obr. 72):
d = a - b = a + (-b).
Sčítání několika vektorů vede .při tomto způsobu určení součtu vektorů
k vektorovému mnohoúhelníku, který je uzavřen součtem vektorů
(obr. 73).
Komutativní zákon pro sčítání vektorů:
a+b=b+o.
Asociativní zákon pro sčítání vektorů:
a + (b + c) = (o + b) + c.
264
Pro velikosti vektorů G, b platí
la + bl < lal + Ibl,
la - bl > Ilal -Ibll.
Jestliže a = (a x , a y , a z ) a b = (b x , by, b z ), pak platí
a + b = (a x + b x , a y + by, a= + b z ).
Jestliže a ii b, pak la + bl = lal + Ibl.
Jestliže a i ! b, pak la + bl = Ilal - Ibll.
Násobení vektoru skalárem
Jestliže cER (c * O) a a je nenulový vektor, pak c-násobkem vektoru a
nazýváme vektor b, který má velikost Ibl = Icllal, a platí a ii b při c > O
a a i ! b při c < O. Jestliže vektor a = o nebo skalár c = O, pak c-násobkem
vektoru a nazýváme nulový vektor.
Komutativní zákon pro násobení vektoru skalárem:
ca = ac.
Asociativní zákon pro násobení vektoru skalárem:
CI (C2 a ) = (CI C 2 ) a.
Distributivní zákon pro násobení vektoru skalárem vzhledem k sčítání vektorů:
c(a + b) = ca + cb.
Distributivní zákon pro násobení vektoru skalárem vzhledem k sčítání skalárů:
(CI + c2)a = cla + C2 a ..
Platí
o 1
a = ];fa.
Jestliže a = (a x , a y , a z ) a cER, pak platí
ca = (ca x , ca y , ca z ).
Vektor a = (a x , a y , a z ) lze vyjádřit ve tvaru
a = axi + aj + azk.
Příklad:
a = -5i + t2j + 7k, b = 3i - 6j - 7k;
s = a + b = (- 5 + 3) i + (12 - 6)j + (7 - 7) k = - 2i + 6j.
265
Množina všech vektorů se zavedenou rovností a definovanými operacemi
sčítání a násobení skalárem tvoří vektorový prostor (viz článek 0.4.8).
Rozkladem vektoru o do směrů b, e nazýváme součet klb + k 2 e = o (obr. 74).
.ff 6 b
- Obr. 74. Rozklad vektoru (J do směrů b, c
Lineární závislost a lineární nezávislost vektorů
Lineární kombinací vektorů 0 1 , O 2 , ..., On (n E N) nazýváme vektor
o = ClO l + C2 0 2 + ... + cno n '
kde Ci (i = 1,..., n) jsou reálná čísla, zvaná koeficienty lineární kombinace.
Při c. = c 2 = ... = c n = O mluvíme o triviální lineární kombinaci. O netriviální
lineární kombinaci mluvíme, právě když aspoň jeden z koeficientů Ci (i = 1,..., 11)
je různý od nuly.
Vektory 0i (i = 1,..., n) se nazývají lineárně závislé, právě když aspoň jedna
jejich netriviální lineární kombinace je nulovým vektorem, tj. existují taková
reálná čísla Ci (i = 1,..., n), z nichž aspoň jedno je různé od nuly, že
CIO. + C2 0 2 + ... + cno n = o.
Vektory Oi (i = 1,..., n; n < 3) se nazývají lineárně nezávislé, právě když
každá jejich netriviální lineární kombinace je nenulovým vektorem. Vektory Oi
(i = 1,..., n) jsou tedy lineárně nezávislé, právě když nejsou lineárně závislé.
Každé dva kolineární vektory o, b jsou lineárně závislé, tj. platí
3t E R (o + tb).
Každé tři komplanární ve tory o, b, e jsou lineárně závislé, tj. platí
3s, t E R (e = so + tb).
Vektory o, b, e jsou lineárně zá vislé, právě když
L1= a x , b x , C x = O.
a y , by, c y
a z , b z , C z
Pro L1 9= O jsou vektory o, b, e lineárně nezávislé. Vektory Oi
(i = 1, 2, ..., n; n > 3) jsou vždy lineárně závislé (viz úmluvu na str. 262).
266
Říkáme, že soustava vektorů a 1 , a 2 , ..., a n má hodnost h (1 < h < 3), právě
když m zi vektory a 1 , a 2 , ...,a n existuje h lineárně nezávislých vek orů., ale
pro každých h + 1 vektorů z vektorů a l' a 2' .. ., On platí, že jsou již lineárně
závislými vektory.
Skalární součin [vnitřní součin] vektorů
".-...,
Velikostí (a, b) úhlu dvou nenulových nekolineárních vektorů a jj OA,
b jf OB nazýváme velikost konvexního úhlu sevřeného polopřímkami
OA a OB. Jsou-li vektory a, b souhlasně, resp. nesouhlasně kolineární, pak
klademe (a, b) = O, resp. (o, b) = 1t.
Skalárním součinem ab (používáme také symbolu a. b) dvou nenulových
vektorů a a tJ nazýváme skalár
ab = lallbl cos (a, b),
kde lal, resp. Ibl je velikost vektoru a, resp. b.
Jestliže aspoň jeden z vektorů je n u lov ý, definujeme ob = O.
Komutativní zákon pro skalární násobení vektorů:
ab = ba.
Pro a ji b platí af) = lallbl.
Pro a i! b platí ab = -Iallbl.
Pro a .1 b platÍ' ab = O.
Platí aa = a 2 = lal 2 ,
II = 1, JJ = 1, kk = 1,
IJ = JI = O, ik = ki = O, jk = kj = O.
Distributivní zákon pro skalární násobení vektorů vzhledem k sčítání vektorů:
a(b + c) = (b + e)a = ab + ae.
Asociativní zákon pro násobení skalárního součinu skalárem:
c(ab) = (ca) b = a(cb).
Pro skalární násobení vektorů asociativní zákon neplatí, tj. obecně (ab) e 9=
=F a(be).
Jestliže a = (a x ' a y , a z ) a b = (b x ' by, b z ), pak platí
ab = axb x + ayb y + azb z ,
aa = a 2 = a 2 + a 2 + a 2
x y z,
( ".-..., ) . ab axb x + ayb y + azb z
cos a, b = lallbl = J[(a; + a; + a;) (b; + b; + b;)]'
267
K ritérium kolmosti vektorů o, &:
axb x + ayb y + azb z = O.
K osinová věta:
(o + &)2 = a 2 + 2ab + &2,
la + &1 = J(02 + 2ab + b 2 ),
(a + b)2 - (a - b)2 = 4ob.
Příklad:
a = 16; + 4j - 7k, b = 3i - 9j - 4k;
ab = 16.3 + 4.(-9) + (-7)(-4) = 40;
lal = J(16 2 + 4 2 + 7 2 ) = J321 17,9,
Ibl = J(3 2 + 9 2 + 4 2 ) = JI06 10,3,
40
cos (a, b) . 0,217 O; (a, b) 77°29'.
. 1 7,9 . 10,3
Průmětem vektoru a do vektoru s [složkou vektoru a ve směru s] nazýváme
vektor as, jehož velikost je
I 1 = lasl
a. Isl
a který je souhlasně kolineární s vektorem s pro as > O a nesouhlasně koli-
neární s vektorem s pro as < O.
Skalár
as
a. = lal cos (a, s) =
se nazývá projekce vektoru a do vektoru [směru] s.
y
x
Obr. 75. Vektorové složky vektoru (J
Platí
lasl = lasl.
Průmět vektoru a do vektoru i, resp. j, resp. k nazýváme složkou a x , resp. ay,
resp. Oz vektoru a (obr. 75); platí
a x = axi,
o}' = aJ,
a z = azk.
268
Projekcí vektoru a do vektoru i, resp. j, resp. k je souřadnice a x , resp. a y ,
resp. a= vektoru a; platí
a x = ai, a y = aj, a z = ak.
Směrové kosiny
Směrovými úhly vektoru a *= o s velikostmi cx, {3, y nazýváme úhly s velikostmi
............... ............... ...............
ex = (a, i), {3 = (a, j), y = (a, k), sevřené vektorem a a vektory i, j, k.
Pro kosiny velikostí směrových úhlů neboli pro tzv. směrové kosiny platí
ai a x
cos (J( = la i = j;!'
aj a y
cos 8 = lGT = j;!'
ok a_
cos Y = r;r = I I"
Platí
cos 2 a + cos 2 B + cos 2 y = 1.
Platí
o = a[; cos (cO) + j cos (ti)) + k cos (cG)].
Příklad:
Směrové kosiny vektoru a = (5,2, - 6) (viz příklad na str. 264) jsou
cos (cO) 5 _ 0,6202,
8,062
cos (ti}) 2 - 0,248 1,
8,062
............... -6
cos (o, k) . -0,7442,
8,062
(cO)
51 °40' .
,
(ti})
75°38' ;
...............
(o, k) 138°6'.
Vektorový součin [vnější součin vektorů]
Způsob zápisu: a x b (čteme: a křížek b, popř. o vektorově b) nebo [o, b].
Definice:
Vektorovým součinem nenulových neko/ineárních Dektorů umístěných v témže
bodě nazýváme vektor
c = a x b,
který má tyto vlastnosti (obr. 76):
269
1. Velikost Icl = lallbl sin (cí)J), tj. rovná se obsahu rovnoběžníku sestro-
jeného z vektorů G, b.
2. Vektor c je kolmý k vektorům G, b.
3. Vektory G, b, c tvoří pravotočivou [kladně orientovanou] soustavu
[tj. pozorujeme-li rovnoběžník sestrojený z vektorů a, b z koncového bodu
vektoru c, pak přechod (při menším úhlu otočení) od vektoru a k vektoru b
se děje proti smyslu otáčení hodinových ručiček].
Jsou-li vektory a, b kolineární nebo je-li aspoň jeden z nich' nulový, klademe
a x b = o.
c
Obr. 76. Vektorový součin c = (J x b
a
Komutativní zákon pro vektorové násobení neplatí, ale platí
a x b = -(b x a) = (-b) x a = b x (-a).
Asociativní zákon pro násobení vektoru skalárem vzhledem k vektorovému
náso bení :
k(a x b) = (ka) x b = a x (kb).
Distributivní zákon pro vektorové násobení vzhledem k sčítání vektorů:
(a + b) c = a x c + b x c,
G x (b + c) = a x b + a xc.
Pro a ii b a a i! b platí a x b = o.
Pro a .1 b platí la x bl = lallbl.
Pro základní vektory platí
; x ; = o,
; x j = k,
j x ; = -k,
j x J - o,
j x k = I,
k x j = -I,
k x k = o,
k x; = j,
1 x k = -j.
270
Vyjádření vektorového součinu pomocí složek:
o x b = (ayb z - bya z ) 1 + (azb x - bzax)j + (axb y - bxa y ) k,
o x b = I, J, k .
a x , a y , a z
b x , by, b=
Příklad:
o = 161 + 4j - 7k, b = 3; - 9j - 4k;
o x b = I, J, k = -79; + 43j - 156k.
16, 4,-7
3 -9 -4
, ,
Součiny se třemi a více vektory
Pro skalární součin ani pro vektorový součin neexistují zákony pro vázání
tří a více vektorů. V jedné početní operaci lze vždy jen dva vektory vázat
skalárně nebo vektorově.
Protože skalární součin je skalárem, je v dalších pravidlech vždy napřed
nutno určit vektorový součin.
Smíšený součin tří vektorů
[obc] = (o x b)c = a x , a y , a z
b x , b)" b z
cx, c y , C z
přičemž L1 > O, jestliže vektory o, b, c jsou nekomplanární a tvoří pravo-
točivou soustavu.
Smíšený součin [obc] = L1 = O, právě když aspoň jeden z vektorů o, b, c
je nulový nebo tyto vektory jsou komplanární (tj. leží v právě jedné rovině).
Distributivní zákon pro smíšené násobení vektorů vzhledem k sčítání
vektorů:
[(o + b) cd] = [acd] + [bcd].
=L1
,
Asociativní zákon pro smíšené násobení vzhledem k násobení vektoru
skalárem :
[(mo)bc] = m[obc].
Platí tyto vztahy:
[obc] = (o x b) c = o(b x c) = (b x c) o = b(c x o) =
= c(o x b) = (c x o) b,
[obc] = -o(c x b) = -(o x c)b = -b(o x c) =
= -(b x o)c = -c(b x o) = -(c x b)o.
271
Geometrický význam:
Absolutní hodnota smíšeného součinu tří vektorů se rovná objemu
rovnoběžnostěnu, jehož tři hrany vycházející z téhož vrcholu jsou určeny
danými vektory, tj. = IAI. Příslušný čtyřstěn má o jem = il L1 l.
Příklad:
Má se určit objem rovnoběžnostěnu určeného vektory
o = 3i + 6j - 2k,
b = 5i - J + 7k,
e = 6i - 3j + 8k.
Objem
= [obe] = 3, 6, - 2 = 69.
5, -1, 7
6, - 3, 8
(tj. asociativní zákon neplatí),
(vyjádření bez vektorového
násobení) .
Skalární součin dvou vektorových součinů (Lagrangeova identita)
(o x b) (e x d) = oe, be = (oe) (bd) - (od) (be),
od, bd
Dvojný vektorový součin
o x (b x e) 9= (o x b) x e
(o x b) x e = (oe)b - (be) o
(ci X b)2 = 00, ob = 02b 2 - (Ob)2.
ob, bb
Vektorový součin dvou vektorových součinů
(o x b) x (e x d) = e[obd] - d[obe] = b[oed] - o[bed].
Vektorový součin s dvojným vektorovým součinem
[(o x b) xc] x1d = (oe) (b x. d) - (be) (o x d) =
= [abd]e - (cd) (a x b).
Součin dvou smíšených součinů tří vektorů
[obc][ def] = od, oe, of I;
bd, be, bf I
cd, ee, cf
272
[obe]2 = r(o,b,e) = 0 2 , ob, oe > O
bo, b 2 , bc
co, cb, c 2
je tzv. Gramův determinant [gramián], který se rovná nule, právě když vektory
o, b, c jsou lineárně závislé.
2.4.2. Použití vektorového počtu v geometrii
Vzdálenost dvou bodů P 1 a P 2 (obr. 77)
d = I p 1 P 2 1 = Idl = Ir2 - r 1 1.
Dělení úsečky s krajními body A[rA]' B[rBJ v poměru A. (obr. 78)
r A - A.r B
r - .
D- 1+A.'
dělicí bod D[r D ] je pro ).. > O vnitřním bodem, pro A < O vnějším bodem
a pro A = 1 středem S[rs]'úsečky AB, tj.
r A + rB
rs =
2
\
Rovnice přímky určené bodem Po[ro] a směrovým vektorem s
(obr. 79)
r = ro + ts
pro \j t E R.
z
y
y
d
8
y
o
Obr. 77. Vzdálenost
dvou bodů
Obr. 78. Dělení úsečky
v daném poměru
x
Obr. 79. Přímka daná bodem
a směrovým vektorem
Příklad:
Po[3, -4,6], s = 2i + 4j - 5k;
r = 3i - 4j + 6k + t(2i + 4j - 5k).
273
Rovnice přímky jdoucí dvěma body Pt[r l ] a P 2 [r 2 ] (obr. 80)
r = r I + t( r 2 - r I) pro \j t E R.
Příklad:
P I [ -1,5,7], P 2 [3, -4,2];
r = (- 1) ; + 5j + 7k + t[3; - 4J + 2k - ( - 1) ; - 5J - 7k] =
= -; + 5j + 7k + t(4; - 9j - 5k).
z
Obr. 80. Přímka daná dvěma body
Odchylka dvou přímek
/'- lobl
(a, b) = arccos lalIbl ,
Nejkratší vzdálenost dvou přímek v prostoru
[vzdálenost dvou mimoběžek]
V (oxb)(r 1 -r 2 ) [obr]
d --- --
- - --
S oxb oxb
L1
,
oxb
kde V = [obr] = Sd je objem rovnoběžnostěnu určeného směrovými vektory
o = (a x , a y , a z ), b = (b x , by, b z )
mimoběžek a r = r 1 - r 2 , přičemž
r 1 = Xl' + y.j + zlk, resp. r 2 = X2; + yJ + Z2 k
je polohový vektor libovolného bodu na první, resp. druhé přímce; S = 10 x bl
je obsah rovnoběžníku určeného vektory o, b a
L1 = a x , a y , a z
b x , by, b z .
Xl - X2' Yl - Y2, Zl - Z2
Jestliže L1 = O, pak se přímky protínají.
274
Příklad:
'1 = 3; - j + 2k + t(2i + 4j + 3k),
'2 = -; + 5J + 10k + t( -41 + 4J + 6k);
L1 = 2, 4, 3 = O,
- 4, 4, 6
4 -6 -8
, ,
takže přímky se protínají.
Pro poslední řádek determinantu byly VZf1ty za základ polohové vektory
bodů přímek, které dostaneme při t = O a t = O.
Průsečík přímek dostaneme tak, že položíme sobě rovny pravé strany rovnic
daných přímek a porovnáme koeficienty u základních vektorů:
3; - j + 2k + t(21 + 4J + 3k) =
= -; + 5j + 10k + 't( -4; + 4j + 6k),
3 + 2t = - 1 - 4t,
- 1 + 4t = 5 + 4't,
2+3t= lO+6!.
.
z
l
y
)
r- ro+ t .
s
d
..-
Obr. 81. Vzdálenost bodu od přímky
Obr. 82. Rovnoběžné posunutí
souřadnicové soustavy
Z libovolných dvou rovnic této soustavy vypočtěme
t -1.
- 3'
7
t = -6"
Tyto dvě hodnoty musí také vyhovovat třetí z rovnic, neboť v opačném pří-
padě se přímky neprotínají.
Polohový vektor průsečíku P je
rp = 31 - J + 2k + M2; + 4j + 3k) = II I + ti + 3k.
Vzdálenost bodu P.[r 1 ] od přímky r = ro + ts (obr. 81)
(rl- r O)s
d = ro - r. + 2 s ·
s
275
Rovnoběžné posunutí souřadnicové soustavy (obr. 82)
,
r 1 = r I - ro.
Rovnice roviny procházející třemi body, které neleží
na téže přímce (obr. 83)
[(r - l) (r - r 2 ) (r - r 3 )] = O.
Tento smíšený součin lze vyjádřit ve tvaru determinantu:
x - Xl' Y - YI, Z - Zl = O.
x - X2' Y - Y2, Z - Z2
X - X3, Y - Y3, Z - Z3
Z toho po ovroubení dostaneme determinant
I x, Y, ,., 1 =0
"',
Xl' YI, ,., 1
"'1'
X 2 , Y2' ,., 1
"'2'
X3, Y3, ,., 1
"'3'
S řešením
Ax + By + Cz + tJ = O,
kde A, B, C, D jsou algebraické doplňky prvků prvního řádku posledního
determinantu.
lj
I
y
x
Obr. 83. Rovina daná třemi body
Obr. 84. Rovina (} daná parametricky
třemi body
Úsekový tvar rovnice roviny (p, q a r jsou po řadě úseky roviny na osách
X, Y a z):
X, y, ,., 1 =0
"',
p, O, O, 1
O, q, O, 1
O, O, r, 1
1
276
neboli
x y z
-+-+-=1.
p q r
Parametrické vyjádření roviny (! (obr. 84):
r = r 1 + s( r 2 - r 1) + t( r 2 - r 3) ,
kde s, t jsou parametry,
r 1 , r 2 , r 3 - polohové vektory tří různých bodů roviny, které neleží
v téže přímce.
Zřejmě platí (obr. 85)
r = r ° + SG + tb,
kde s, t jsou parametry,
r o je polohový vektor daného bodu roviny,
G, b jsou nekolineární směrové vektory.
l
J -- 9
SI
Obr. 85. Rovina (l daná parametricky
bodem a dvěma směrovými vektory
x
y
Rovnice roviny určené bodem a normálovým vektorem
Rovnice roviny procházející bodem Po [r o ] kolmo k normálovému vektoru n
,
ma tvar
n(r - r o ) = O,
odkud
nr = nr °
neboli
nr + D = O.
Normálový tvar rovnice roviny
nOr - d = O,
kde nO = n/lnl je jednotkový normálový vektor.
" .
277
Vzdálenost počátku O souřadnicové soustavy od rovIny
nr + D = O
d=
D
Inl'
Vzdálenost ,bodu Po [roJ od rovIny nOr - d = O
1£51 = Inoro - dl,
přičemž je-li £5d > O, leží bod Po na téže straně od dané roviny jako počátek O,
a je-li £5d < O, leží bod Po na opačné' straně od roviny než počátek O.
Platí
1£51 = I n O(rl - ro)l,
kde r 1 je polohový vektor libovolného bodu ,roviny' n(r, - r o ) = O,
I I axo + byo + CZo + d ( )
(j = ,J( 2 2 2) , kde n = a, h, c ·
a +b +c
Odchylka cp přímky r = ro + ts a rovIny nr = nro
. Insl
cp = arcsm Inllsl ·
Odchylka cp dvou rovin
I n l n 21
cos cp = I n llln21 '
kde nI' n 2 jsou normálove vektory daných rovin.
o bsah Sn rovin néh o n-úheln ík u
Sn = tl r l X r 2 + r 2 X r3 + ... + r n X r 1 1,
kde r l' r 2, . .., r n jsou polohové vektory vrcholů n-úhelníku.
Pro r i = (Xi' Yi) (i = 1, 2, ..., n) platí
S _.1
n - 2
Xb X2 + X2, X3 +... + X n , Xl .
Yl, Y2
Y2, Y3
Yn' Yl
Obsah S3 rovinného trojúhelníku
. .
S3 = tl r l X r 2 + r 2 X r 3 + r 3 x r 1 1,
kde r l' r 2 a r 3 jsou polohové vektory vrcholů trojúhelníku.
278
Pro r i = (Xi' Yi) (i = 1, 2, 3) platí
S 3 = - XI' Yl' t
Xl' Y2, 1
X3, Y3' 1
(ve vzorci jde o absolutní hodnotu determinantu).
Objem V 4 čtyřstěnu s vrcholem v počátku
V 4 =tl(r 1 x r 2 )r 3 1,
kde r l , r 2 , r 3 jsou polohové vektory vrcholů čtyřstěnu mimo počátek. .
...
Objem V 4 čtyř stěnu v libovolné poloze
V 4 = il [( r 1 - r 4) (r 2 - r 4) (r 3 - r 4)] I '
V 4 =t XI' YI, Zl' 1 'I
X2' Y2' =2' 1
X3, Y3' 23' 1
I X4' Y4, Z4' 1
(ve vzorci jde o absolutní hodnotu determinantu), kde ri = (Xi' Yi' Zi)
(i = 1, 2, 3,4) jsou polohové vektory vrcholů čtyřstěnu. Všechny čtyři vrcholy
leží v téže rovině, právě když uvedený determinant se rovná nule.
Rozklad vektoru a v součet složek kolineárních s vektory
b,c,d
b[acd] + c[bad] + d[bca]
a=
[bcd] .
2.5. KRUHOVÁ INVERZE
Kruhovou inverzí (obr. 86) nazýváme zobrazení na množině C.tf:,
definované přiřazením
I I . 1.
a = a e''I' 1-+ b = e -1'1' .
Použití: metoda frekvenčních charakteristik, přepočet odporu na vodivost
[konduktanci] apod.
279
Bod b k bodu a se při kruhové inverzi podle uvedené rovnice sestrojí gra-
fickým způsobem pomocí jednotkové základní kružnice inverze (obr. 87):
, 1. Sestrojí se komplexně sdružený bod a = lal e - i<P.
2. Sestrojí se tečny z koncového bodu průvodiče bodu či ke kružnici.
3. Spojnice dotykových bodů tečen protne průvodič bodu a v bodě B,
který je koncovým bodem průvodiče bodu b.
.,
o
. ,I I
,Imaglnorn, OSG
I .,,'-
I \'
.,,
I
,
, I J
6 - reolna osa
4) , 'i
imogin&m osa
-1
Obr. 86. Body komplexně sdružené při
kruhové inverzi
-t O
Obr. 87. Jednotková základní kružnice
ln verze
Odůvodnění:
-
1 -Ibl'
S ohledem na měřicí jednotku při kruhové inverzi platí:
r = 1 ..... a měřicích jednotek veličiny a <:>
<:> lfa měřicí jednotky veličiny b.
OBD ODA,
Například
poloměr r = 1 .:. 5 Q <=> t S
při přepočtu odporu na vodivost.
Inverze čar
/
První věta o inverzi: Z přímky procházející počátkem dostaneme při kruhové
inverzi opět přímku jdoucí počátkem.
. Je dána přímka
r(t) = ta
(t E R #, a E C) .
Při kruhové inverzi dostaneme přímku
1 1
,
-=-=r.
r ta
280
Při konstrukci se postupuje takto (obr. 88):
1. K bodu a se sestrojí komplexně sdružený bod Q.
2. Nanese se stupnice s parametrem t pro
1
,
r -
ta
, . I I
.maglnarnl osa
Obr. 88. První věta o inverzi
Druhá věta o inverzi: Z přímky neprocházející počátkem dostaneme při
kruhové inverzi kružnici procházející počátkem.
Je dána přímka
1 t) = r o + ta (t E R #, a E C) ·
Při kruhové inverzi dostaneme kružnici
1 1
,
-=r=
r ro + ta
Při konstrukci se postupuje takto (obr. 89):
1. K přímce r se sestrojí souměrně sdružená přímka r podle reálné osy.
2. Sestrojí se normála n k přímce r, čímž dostaneme r min jako průsečík
přímek ran.
3. Při kruhové inverzi s jednotkovou základní kružnicí dostaneme bod r:nax.
Dotykové body TI a T 2 jsou průsečíky přímky r s jednotkovou kružnicí
a zároveň také body kružnice, kterou dostaneme při kruhové inverzi.
Třeti věta o kruhové inverzi: Z kružnice neprocházející počátkem dostaneme
při kruhové inverzi opět kružnici neprocházející počátkem.
Je dána kružnice
1
r(t) = ro +
a + rb
c + td
a + tb
281
Při kruhové inverzi dostaneme kružnici
a + tb
r' =
c + td
stejného druhu (tj. z kružnice dostaneme kružnici a z přímky přímku).
;rnaginla 011
Jr\O
, , fO
f\\
Obr. 89. Druhá věta o inverzi
Obr. 90. Ttetí věta o inverzi
Při konstrukci se postupuje takto (obr. 90):
1. Ke kružnici r se sestrojí souměrně sdružená (inverzní) kružnice ř podle
reálné osy.
2. Stupnice pro výchozí kružnici se vhodně volí tak, aby výchozí kružnice
a inverzní kružnice byly souměrně sdružené (shodné). Pak parametrická
stupnice pro inverzní kružnici r' je určena průsečíky spojnic bodů t inverzní
kružnice s počátkem.
Při volbě jiné stupnice pro inverzní kružnici je třeba dbát, aby tečny z po-
čátku k výchozí kružnici byly při kruhové inverzi vždy také tečnami inverzní
kružnice, takže střed stále leží na přímée určené body M a O.
282
3. ELEMENTÁRNÍ GEOMETRIE
3.1. ZÁKLADNÍ POJMY
3.1.1. Přímka, rovina, prostor a jejich části
Základními útvary geometrie jsou bod, přímka, rovIna a (troj-
rozměrný) prostor.
Množinu bodů na přímce, v rovině nebo v prostoru nazýváme (geo-
metrickým) útvarem.
Uzavřenou oblast v rovině, resp. v prostoru nazýváme obrazcem, resp.
tělesem.
Rovina a poloprostor
Roviny se značí malý i řeckými písmeny (1, a, 1t, .... Jsou-li A, B, C tři
různé body roviny, které neleží v téže přímce, pak se tato rovina značí
"rovina ABC".
Roviny (!, G V trojrozměrném prostoru, které mají společnou právě jen
přímku, se nazývají různoběžné (píše se (1-H" a). Roviny (1, a v trojrozměrném
prostoru, které nemají žádný společný bod, se nazývají (různé) rovnoběžné
(píše se (! II G). Roviny (!, G V trojrozměrném prostoru, které jsou si rovny,
se nazývají splývající rovnoběžné roviny.
Rovina (X dělí prostor ve dV3; vzájemně opačné poloprostory se společnou
hraniční rovinou (x. Je-li X vnitřním bodem jednoho z těchto poloprostorů,
tj. jestliže X ti (x, pak se tento poloprostor značí buď "poloprostor a.X", nebo
stručně a.X
Přímka, polorovina a polopřímka
Přímky se značí malými latinskými písmeny a, b, p, q, .... Jsou-li A, B dva
různé body přímky, pak se tato přímka značí buď "přímka AB", nebo stručně
AB: popř. +-+AB.
Přímka p = B dělí rovinu ve dvě vzájemně opačné poloroviny se společnou
hraniční přímkou p (obr. 91). Je-li bod X vnitřním bodem jedné z těchto polo-
rovin, tj. jestliže X ti p, pak tato polorovina se zna čí bu ď "polorovina pX",
popř. "polorovina ABX", nebo stručně pX, popř. AB X: popř. --.ABX.
283
Přímky p, q v rovině, které mají právě jeden společný bod, se nazývají
různoběžné přímky nebo různoběžky (píše se p -H" q). Přímky p, q v rovině, které
nemají žádný společný bod, se nazývají rovnoběžné přímky nebo (různé)
rovnoběžky (píše se p II q). Přímky p, q v rovině, které jsou si rovny, se nazývají
splývající [totožné] rovnoběžky. Přímku různoběžnou s rovnoběžkami p, q
nazýváme příčkou rovnoběžek p, q.
..
----
XA
A
I
X
XA
..
Obr. 92. Vzájemně opačné polopřímky
A
8
p
Obr. 91. Polorovina pX
Přímky p, q v trojrozměrném prostoru, které neleží v téže rovině, se nazývají
mimoběžky. Každá přímka protínající dvě mimoběžky se nazývá příčka
mimoběžek. Přímka kolmá k oběma mimoběžkám se nazývá osa mimoběžek.
Bod X dělí přímku ve dvě vzájemně opačné polopřímky se společným po-
čátkem X. Je-li bod A vnitřním bodem jedné z těchto polopřímek, tj. jestliže
.14 * X (obr. 92), pak tato polopřímka se značí bud' "polopřímka XA", nebo
stručně XA, popř. XA. Opačná polopřímka k polopřímce XA se stručně
značí XA, popř. +-XA.
Pás a vrstva
Pásem určeným přímkami p, q nazýváme průnik dvou polorovin pB a qA,
jejichž hraniční přímky p, q jsou rovnoběžné a A E p, B E q.
Vrstvou určenou rovinami cx, B nazýváme průnik dvou poloprostorů cxB a BA,
jejichž hraniční roviny cx, (3 jsou rovnoběžné a A E ex, B E B.
Vzdálenost přímek p, q, resp. rovin (1, f3 se nazývá šířka pásu, resp. tloušťka
vrstvy.
Úsečka
Úsečkou AB nazýváme průnik dvou polopřímek AB a BA (obr. 93), který se
značí bud' "úsečka AB", nebo stručně AB. Bod se považuje za nulovou úsečku.
A A8 8
I I .
. -
--- AB
BA
284
Obr. 93. Úsečka A B
Bod ležící mezi body
Ze tří různých bodů přímky leží vždy právě jeden bod mezi ostatními
dvěma. body. Bod B leží me=i body A a C, právě když bod B je vnitřním bodem
úsečky AC. Říkáme také, že bod B odděluje body A, C.
Lomená čára
Jsou-li AI' A 2 , ..., An vzájemně různé body, pak množinu úseček A I A 2 ,
A 2 A 3 , ..., An-l An (resp. A I A 2 , A 2 A 3 , ..., An- lAn' An A 1) nazýváme lomenou
čárou (resp. uzavřenou lomenou čárou) a označujeme AIA2 ... A (resp. A 1 A 2 ...
... AnAI)' Body AI' A 2 , ..., An nazýváme vrcholy lomené čáry AIA2 ... An
a úsečky AžAž + I (i = 1, 2, ..., n - 1) nazýváme stranami lomené čáry
AIA2 ... An.
Klínový prostor
Klínovým prostorem [někdy také klínem] nazýváme průnik dvou polo-
prostorů, jejichž hraniční roviny jsou různoběžné. Hranou klínového prostoru
nazýváme společnou hraniční přímku dvou polorovin, jejichž sjednocením
je hranice klínového prostoru.
Hranolový a jehlanový prostor
n-bokým hranolovrvm pro torem nazýváme množinu všech bodů všech
vzájemně rovnoběžných (tvořících) přímek procházejících všemi body
(řídicího) n-úhelníku, přičemž tyto přímky nejsou rovnoběžné s rovinou
tohoto n-úhelníku. Hranici n-bokého hranolového prostoru nazýváme
n-bokou hranolovou plochou. Hranou hranolového prostoru nazýváme jeho
tvořící přímku procházející vrcholem jeho řídicího mnohoúhelníku.
n-bokÝ"1 jehlanovým prostorem nazýváme množinu všech bodů všech
(tvořících) přímek procházejících bodem V (tzv. vrcholem) a všemi body
(řídicího) n-úhelníku, přičemž bod V neleží v rovině n-úhelníku. Hranici
n-bokého jehlanového prostoru nazýváme ll-bokou jehlanovou plochou.
Hranou jehlanového prostoru nazýváme jeho tvořící přímku procházející
vrcholem řídicího mnohoúhelníku.
Válcový a kuželový prostor
Válcovým prostorem nazýváme množinu všech bodů všech vzájemně rovno-
běžných (tvořících) přímek procházejících všemi body (řídicí) jednoduché
uzavřené křivky a její vnitřní oblasti, přičemž tyto přímky nejsou rovnoběžné
285
s rovinou tohoto geometrického útvaru. Hranici válcového prostoru nazýváme
válcovou plochou.
Kuželovým prostorem nazýváme množinu všech bodů všech <tvořících)
přímek procházejících bodem V (tzv. vrcholem) a všemi body <řídicí) jedno-
duché uzavřené křivky a její vnitřní oblasti, přičemž bod V neleží v rovině
tohoto geometrického útvaru. Hranici kuželového prostoru nazýváme
kuželovou plochou.
Rovinný řez
<Rovinným) řezem geometrického útvaru U rovinou (l nazýváme průnik
roviny (l a útvaru U.
Konvexní geometrický útvar
Geometrický útvar, jehož každé dva body lze spojit úsečkou, která je částí
tohoto útvaru, se nazývá konvexní.
3.1.2. Rovinný a prostorový úhel
<Rovinným) úhlem n ýváme množinu všech bodů všech polopřímek
VX se společným počátkem kde bod X patří do daného oblouku AB
kružnice se středem v bodě V (obr. 94). Takto definovaný úhel se značí "úhel
v
Obr. 94. Úhel A VB
A VB"'. Bod V se nazývá vrchol úhlu A VB a polopřímky V A a VB se nazývají
ramena úhlu A VB. Množina právě těch bodů úhlu A VB, které nepatří do polo-
přímek V A a VB, se nazývá vnitřek úhlu A VB. Množina právě těch bodů
roviny, které nepatří do úhlu A VB, se nazývá vnějšek úhlu A VB. Je-li oblouk
AB podmnožinou nějaké polokružnice, pak úhel A VB se nazývá konvexní
a značí se stručně A VB. Je-li nějaká polokružnice vlastní podmnožinou
oblouku AB, pak úhel A VB se nazývá nekonvexní a značí se stručně (3:: A VB.
Je-li oblouk AB celou k užnicí, resp. polokružnicí, resp. nulovým obloukem,
pak úhel A VB se nazývá plný, resp. přímý, resp. nulový.
286
Osa úhlu
Osou úhlu nazýváme množinu právě těch bodů úhlu, které mají od obou
ramen úhlu stejnou vzdálenost.
Orientovaný úhel
Orientovaným úhlem A VB (stručně AVB) nazýváme uspořádanou dvojici
polopřímek V A, VB se společným počátkem JI': přičemž polopřímka V A,
resp. VB se nazývá počáteční, resp. koncové rameno a bod V se nazývá vrchol
orientovaného úhlu A VB. Při V A * VB je tedy AVB 9= BVA.
Prostorový úhel
Prostorovým úhlem nazýváme množinu všech bodů všech polopřímek VX
se společným počátkem kde bod X patří do daného kulového vrchlíku
se středem v bodě JI: Bod V se nazývá vrchol prostorového úhlu.
3.1.3. Míry v geometrii
3.1.3.1. Míra jako zobrazení
Mírou (v geometrii) nazýváme takové zobrazení J.l systému ff po-
rovnatelných geometrických útvarů (tj. geometrických útvarů téhož druhu)
do množiny Rt, které má tyto vlastnosti (X, 1': E E ff):
a) X Y => J.l(X) = J.l( Y).
b) Nemají-li geometrické útvary X a Y žádný vnitřní bod společný, pak
J.l(X u Y) = J.l(X) + J.l( Y).
c) Pro nějaký předem zvolený geometrický útvar E E ff platí J.l(E) = 1.
Geometrický útvar E nazýváme měřicí jednotkou míry J.l a hodnotu J.l(X)
nazýváme (číselnou) velikostí geometrického útvaru X při měřicí jednotce E.
Shodnost geometrických útvarů viz v článku 3.1.4.
3.1.3.2. Součet úseček a součet úhlů
Grafický součet úseček
Naneseme-li úsečky a, b na přímku p tak, aby pro body X, Z přímky p
platily vztahy XY = a, XZ = b a bod X ležel mezi body Z (obr. 95), pak
úsečku YZ = c nazýváme (grafickým) součtem úseček a, b a píŠeme YZ =
= Xy + X Z neboli c = a + b.
287
Porovnávání úseček a grafický rozdíl úseček
Dvě neshodné úsečky AB = a, b porovnáváme tak, že úsečku b přeneseme
na polopřímku AB do polohy AX = b (obr. 96). Jestliže bod X leží mezi
body A, B, říkáme, že úsečka a je větší než úsečka b, resp. úsečka b je menší
u"ž úsečka a, a píšeme a > b, resp. b < a. Úsečku XB = c v tomto případě
nazýváme (grafickým) rozdílem úseček .a, b (v tomto pořadí) a píšeme XB =
= AB - AX neboli c = a - b.
I
Y
I .
XY=a Xl= b
I
X
I
Z
I
p
I I I
A X B
A B > AX I XB = A B - AX
Y Z = ,c = a + b
Obr. 95. (Grafický) součet úseček
a,b
Obr. 96. (Grafický) rozdíl úseček a, b
Jsou-li a, b shodné úsečky, pak jejich (grafický) rozdíl a - b považujeme
za nulovou úsečku.
Množina všech úseček v rovině s operací (grafické) sčítání úseček tvoří
aditivní komutativní monoid, jehož nulovým prvkem je nulová úsečka.
Grafický součet úhlů
Přeneseme-li dva konvexní úhly , B do opačných polorovin vyťatých
přímkou VM k ramenu VM, takže zaujmou nové polohy A VM , MVB P
(obr. 97), pak úhel A VB = y, jehož částí je polopřímka VM, nazýváme
(grafickým) součtem úhlů , B a píšeme y = + B.
,
v
A
v
rx+(3=T
Obr. 97. (Grafický) součet úhlů , P
A
> (J I r = rx -{3
Obr. 98. (Grafický) rozdíl úhlů , P
Porovnávání úhlů a grafický rozdíl úhlů
Dva neshodné konvexní úhly A VB = , B porovnáme tak, že úhel B pře-
neseme k ramenu V A do poloroviny V AB, takže zaujme novou polohu A VX
288
(obr. 98). Jestliže bod X je vnitřním bodem úhlu A VB, říkáme, že úhel rxje vět. i
než úhel {3, resp. úhel {3 j"e men. í než úhel (X a píšeme (X > {3, resp. f3 < . Úhel
X VB = " v tomto případě nazýváme <gra.fickJ 'n) ro=dílern úhlů CI., IJ (v tomto
pořadí) a píšeme }' = CI. - (je
Jsou-li Cť, tJ shodné úhly, pak jejich <grafický) rozdíl 'Y. - IJ považujeme
za nulový úhel.
Jsou-li .dva úhly totožné, říkáme také, že jsou si rovny.
Množina všech úhlů v rovině s operací <grafické) sčítání úhlů tvoří
aditivní komutativní monoid, jehož nulovým prvkem je nulový úhel.
3.1.3.3. Délka r velikost] úsečky
Hodnotu míry Jl(X): .Cf R;, kde.Cf je systém všech Úseček a X E /f,
nazýváme délkou [relikostí] Úsečky "t. Nenulovou úsečku E, pro niž platí
Jl(E) = 1, nazýváme délkovoujednotkoll [jednotkou délky,jednotkovou úsečkou].
Délkou Úsečky při délkové jednotce E je tedy hodnota zobrazení Jl, které
každé úsečce přiřazuje nezáporné číslo a má tyto vlastnosti:
a) Shodné úsečky mají stejnou délku.
b) Délka <grafického) součtu dvou úseček se rovná součtu jejich délek.
c) Zvolená nenulová úsečka má délku 1.
Délku úsečky X = AB při délkové jednotce E značíme
IXIE' g(A, B)E nebo d(AB)E'
popř. bez uvádění délkové jednotky, nemůže-li dojít k nedorozumění.
Čast..o se nerozlišuje úsečka a její délka a pro oba pojmy se používá téhož
označení a někdy i téhož názvu. V této příručce jde např. o názvy poloměr,
,
průměr, výška a obvod.
Vzdálenost
Vzdáleností dvou bodů A, B [vzdáleností bodu A od bodu B], kterou značíme
IABI, Q(A, B) nebo d(A, B), nazýváme délku úsečky AB.
Vzdáleností bodu A od přímky a, kterou značíme IAal, Q(A, a) nebo v(A, a),
nazýváme vzdálenost bodu A od paty kolmice vedené z bodu A k přímce a.
Vzdáleností bodli A od roviny Cť, kterou značíme IArxl, Q(A, rx) nebo v(A, rx),
nazýváme vzdálenost bodu A od paty kolmice vedené z bodu A k rovině rx.
Vzdáleností dvou rovlloběžll.f:ch přímek a, b, kterou značíme labl, Q(a, b)
nebo v(a, b), nazýváme vzdálenost libovolného bodu jedné přímky od druhé
přímky.
2S9
Vzdáleností dvou rovnoběžných rovin (1, B, kterou značíme lexBI, g(ex, B) nebo
v(cx, B), nazýváme vzdálenost libovolného bodu jedné rov1ny od druhé roviny.
Vzdálenosti dvou mimoběžek a, b, kterou značíme labl, g(a, b) nebo v(a, b),
nazýváme vzdálenost dvou rovnoběžných rovin procházejících těmito mimo-
běžkami.
V=dáleností přimky a od roviny ex s ni rovnoběžné, kterou značíme lacxl, g(a, ex)
nebo v(a, ex), nazýváme vzdálenost libovolného bodu přímky a od roviny ex.
3.1.3.4. Velikost úhlu
Veliko'st <neorientovaného> úhlu
Hodnotu míry ,u(X): !/ Rt, kde ff je systém všech <neorientovaných>
úhlů a X E!/, nazýváme velikostí úhlu X. Nenulový úhel E, pro který platí
,u(E) = 1, nazýváme úhlovou jednotkou.
Velikosti <neorientovaného> úhlu při úhlové jednotce E je tedy hodnota
zobrazení ,u, které každému neorientovanému úhlu přiřazuje nezáporné
číslo a má tyto vlastnosti:
a) Shodné úhly mají stejnou velikost.
b) Velikost úhlu A VB E // se rovná součtu velikostí úhlů A VX a XV A,
kde X je vnitřní bod úhlu A VB.
c) Zvolený nenulový úhel má velikost 1.
Velikost <neorientovaného> úhlu X při úhlové jednotce E značíme IXIE
nebo V(X)E' popř. stručně IXI nebo v(X), nemůže-li dojít k nedorozumění,
který úhel jsme zvolili za jednotkový.
Často se nerozlišuje úhel a jeho velikost a pro oba pojmy se používá téhož
označení.
Úhlové míry
V praxi se velikost úhlu pova uje za veličinu, takže se k velikosti úhlu při-
pojuje značka úhlové jednotky. Pouze u údajů v obloukové míře se značka
rad zpravidla vynechává. Úhly se zpravidla měří v stupňové, setinné nebo
obloukové míře.
Hodnota IXlrad obloukové [radiánové] míry úhlu A VB = X se rovná délce
kružnicového oblouku AB, který je průnikem úhlu A VB a kružnice se středem
ve vrcholu V úhlu A VB a s poloměrem rovným číslu 1. Úhlová jednotka
obloukové míry se nazývá radián a označuje se rad, takže arc rad = 1
(obr. 99).
290
Úhlovou jednotkou stupňové [devadesátinné] míry je (úhlový) [(devade-
sátinný)] stupeň (značka tJ), pro který platí
1t
1 ° = 180 rad.
Úhlový stupeň se dělí na 60 (úhlových) minut (10 = 60') a úhlová minuta
se dělí na 60 (úhlových) vteřin (1' = 60").
o br. 99. Radián
v
Úhlovou jednotkou setinné míry je grad [setinný stupeň] (značka g), pro
který platí
1t
1 g = - rad.
200
Grad se dělí na 100 setinných minut [centigradů] (lg = lOOc = 100') a setinná
minuta se dělí na 100 setinných vteřin [centicentigradů] (l C = 100 cC = 100").
Dílec je úhlovou jednotk u, pro kterou platí
1t 3°
1 dílec = rad = - .
3 000 50
Dělostřelecký dílec je úhlovou jednotkou, pro kterou platí
1t 9°
1 dělostřelecký dílec = rad = -
3 200 160 .
M atematii.:ký dílec (značka dc) je úhlovou jednotkou, pro který platí
1
1 dc = rad.
1000
291
Převodní vztahy pro velikosti úhlů
Jestliže stupňovou, resp. obloukovou míru úhlu označíme cp, resp. arc cp,
platí
1t
arc cp = - cp ,
180
180
cp = -arcqJ.
1t
Dále platí (1 R = ; rad)
4 R = 360° = 4()()K = 2n rad.
,
1 rad 0,636619 8 R 57,295 78° 57°17'45" 63,661 98 1 ;
30° = lx rad, 45 0 = in rad, 60° = tx rad,
90° = in rad, 180° = n rad, 270° = Pc rad,
1 0 = 0,017 453 29 rad,
l' ...:.. 0,000 29 rad;
1t
19 = 0,01 R = 0,9° = rad ...:.. 0,01570796 rad,
200
3° .
1 dílec = - = 3,6',
50
50 -
1 ° = - dílce = 16,6 dílce;
3 .
1
1 dc 1 571 R, 1 dc 3'26,3", 1 o 17,45 dc.
Při 1 ldc < 250 dc s přesností na dvě platné číslice platí
II 1 ldc
tg ex dc .
1000
10 1
1 0 - -.
- ,
9
Dílcové pravidlo
Je-li oko pozorovatele ve výšce dolního konce předmětu, pak při Inl dC <
< 250 dc s přesností na dvě platné číslice platí formální vzorec
v
B ""'-
"'" ,
d
kde v (m) je výška pozorovaného předmětu,
d (km) - vodorovná vzdálenost pozorovatele,
B (dc) - velikost zorného úhlu.
292
U rčujeme-li výšku v, resp. vzdálenost d, pak výsledek zvětšíme, resp. zmen-
šíme o jeho 5 %.
Příklad:
Je-li tyč o délce 4 m vidět pod zorným úhlem velikosti 20 dc, dostaneme podle
dílcového pravidla vztah 20 4/d, odkúd vzdálenost od pozorovatele
d ( - ) km = 190m.
20 100
Klasifikace úhlů podle jejich velikostí
nulový úhel ( = 0°),
ostrý úhel (0° < !Iv < 90°),
pravý úhel (!Iv = 90°),
tupý úhel (90° < (X < 180°),
kosý úhel (0° < < 90° a 90° < < 180°),
přímý úhel (!Iv = 180°),
konvexní [vypuklý] úhel . (0° < !Iv < 180°),
nekonvexní úhel (180° < !Iv < 360°),
plný úhel (!Iv = 360°).
Přehled názvů konvexních úhlů
I
ostrý úhel
I
kosý úhel
I
konvexní úhel
I
I
přímý úhel
I
pravý úhel
I
nulový úhel
I
tupý úhel
Styčné, vedlejš-í a vrcholové úhly
Styčnými úhly nazýváme dva úhly, jejichž součet velikostí je menší než
velikost plného úhlu a jejichž dvě ramena splývají a zbývající dvě ramena
leží ve vzájemně opačných polorovinách s hraniční 'přímkou obsahující
společné rameno (obr. lOOa).
Vedlejšími úhly nazýváme styčné úhly, jejichž nesplývající ramena jsou
vzájemně opačné polopřímky. Dva shodné vedlejší úhly se nazývají pravé
(obr. lOOb).
Vrcholovými úhly nazýváme úhly, jejichž vrcholy splývají a ramena jsou
vzájemně opačné polopřímky. Vrcholové úhly jsou shodné (obr. l00c).
293
Úhly sevřené dvěma rovnoběžkami a jejich příčkou (obr. 101)
Souhlasné úhly jsou si rovny:
íJ.. = íJ.. 1 ,
8 = 8 1 ,
Y = Yl'
tJ = tJ 1 .
Střídavé úhly jsou si rovny:
íJ..=Yl,
8 = tJ 1 ,
Y = íJ.. 1 ,
tJ = 8 1 .
Přilehlé úhly mají součet velikostí roven 180 tJ :
íJ.. + tJ 1 = 180°, Y + 8 1 = 180°,
f3 + Yl = 180°, tJ + (Xl = ,180°.
a)
b)
c)
Obr. 100. a) Styčné úhly; b) vedlejší úhly; c) vrcholové úhly
Obr. 101. Souhlasné,
střídavé a přilehlé úhly
Doplň ové a výplňkové úhly
Dva úhly, jejichž grafickým součtem je pravý, resp. přímý úhel, se nazývají
doplňkové, resp. výplňkové.
Rozdíl mezi vedlejšími a výplňkovými úhly je v tom, že u vedlejších úhlů
záleží na jejich vzájemném umístění, kdežto u výplňkových úhlů jde jen
o vztah platný pro jejich velikosti. Všechny vedlejší úhly jsou tedy výplňkové,
ale výplňkové úhly nemusí být vedlejšími úhly.
Velikost orientovaného úhlu
Základní velikost 'orientovaného úhlu A VB je velikost neorientovaného úhlu,
jehož všemi body proběhne počáteční rameno V A při otočení do polohy
koncového ramena VB v kladném smyslu (obr. 102).
Velikostí orientovaného úhlu je v stupň'ové míře íJ.. + k . 360° a v obloukové
míře a + 2k1t rad, přičemž íJ.. je základní velikost orientovaného úhlu a k E Z.
294
../'-.. "........."
V elikost orientovaného úhlu (1, resp. A VB se značí lexl, resp. IA T/BI. V praxi
se orientovaný úhel i jeho velikost označuje zpravidla týmž znakem, např.
ex, B, .. ..
Příklad:
Orientovaný úhel o velikosti - 3 030° má základní velikost 210°, neboť
- 3 030° = 210° - 9 .360°.
Velikost prostorového úhlu
Velikost úJ prostorového úhlu, který vyjadřuje rozbíhavost kužele, se de-
finuje jako poměr obsahu S kulového vrcqIíku, který daný prostorový úhel
vymezuje na kulové ploše se středem ve vrcholu prostorového úhlu, a druhé
mocniny poloměru r této kulové plochy, tj. úJ = S/r 2 (obr. 103).
Obr. 102. Velikost orientovaného úhlu
Obr. 103. Velikost prostorového úhlu
Měřicí jednotkou pro určování velikosti prostorového úhlu je prostorový
úhel s vrcholem ve středu kulové plochy, který na této ploše vytíná vrchlík
o obsahu rovném obsahu čtverce se stranou rovnou poloměru kulové plochy.
Tato jednotka se nazývá steradián a označuje se sr. Pro plný prostorový úhel,
který se nazývá spat a označuje se sp, platí
1 sp. = 41t sr .
Odchylka dvou přímek
Odchylkou dvou přímek nazýváme velikost nulového, ostrého nebo pravého
úhlu, který má libovolně zvolený vrchol V a ramena na přímkách, které pro-
cházejí bodem V a jsou rovnoběžné s danými přímkami.
Odchylkou dvou rovin nazýváme odchylku průsečnic těchto rovin s třetí
rovinou, která je k oběma daným rovinám kolmá. Rovnoběžné roviny mají
odchylku rovnou nule.
Odchylkou přímky a roviny nazýváme odchylku dané přímky a průsečnice
dané roviny s rovinou, která obsahuje danou přímku a je kolmá k dané rovině.
295
3.1.3.5. Obsah obrazce
Hodnotu míry ,u(X): //J R +, ,kde //) je systém všech obrazců a
X E ff/, nazýváme <plošn Í'm> obsahem obrazce X. Za obrazec E, pro který
platí J1(E) = 1, volíme čtverec se stranou délky 1 a nazýváme jej plošnou
jednotkou [jednotkou obsahu, obsahovou jednotkou].
Obsahem obra::ce při obsahové jednotce E je tedy hodnota zobrazení J1,
které každému obrazci přiřazuje kladné číslo a má tyto vlastnosti:
a) Shodné obrazce mají stejný obsah.
b) Nemají-li dva obrazce žádný vnitřní bod spblečný, pak obsah jejich
sjednocení se rovná součtu jejich obsahů.
c) Zvolený obrazec E má obsah 1.
3.1.3.6. Objem tělesa
Hodnotu míry J1(X): .g; R +, kde // je systém všech těles a X E //J,
nazýváme objemem tělesa X. Za těleso E, pro které platí J1(E) = 1, volíme
krychli s hranou délky 1 a nazýváme ji objemovou jednotkou [jednotkou
objemu ].
Objemem tělesa při objemové jednotce E je tedy hodnota zobrazení J1, které
každému tělesu přiřazuje kladné číslo a má tyto vlastnosti:
a) Shodná tělesa mají stejný objem.
b) Nemají-li dvě tělesa žádný vnitřní bod společný, pak objem jejich
sjednoceni 'se rovná součtu jejich objemů.
c) Zvolené těleso E má objem 1.
3.1.3.7. Pojem veličiny
Délkovou, úhlovou, plošnou a objemovou jednotku souhrnně na-
zýváme měřicími jednotkami.
Protože se ve fyzice a v technických vědách používá různých měřicích
jednotek, považuje se tam hodnota m = J1(X) míry pro nějaký objekt X
za veličinu neboli za formální součin číselné hodnoty {m} a zvolené měřicí
jednotky [m] a zapisuje se ve tvaru
{m} Em], {m}. Em] nebo {mhm]'
296
Příklad:
Délka d = IXI = 5 úsečky X se při délkové jednotce centimetr zapíše jako
veličina ve tvaru
d = {d} Cd] = 5cm,
kde {d} = 5 je číselná hodnota a [d] = cm zvolená délková jednotka.
Měnitel
Jestliže nějaká veličina a má číselnou hodnotu {a }j, resp. {a}j' při mčřicÍ
jednotce j, resp. j', platí
, {a}j' = k{a}j'
kde k je konstanta (tzv. měnitel), terá udává velikost měřicí jednotky j při
měřicí jednotce j'. V tomto případě říkáme, že měřicí jednotkaj je k-násobkelll
měřicí jednotky j'.
Tabulka 3.1
Předpony a znaky SI pro t('orbu
násobných a dílčích jednotek
Násobitel Předpona Znak
10 18 exa E
10 15 peta P
10 12 tera T
10 9 glg G
10 6 mega M
10 3 kilo k
10 2 hekto h
10 deka da
10- 1 deci d
10- 2 centi c
10- 3 mili m
10- 6 mikro Ji
10- 9 nano n
10- 12 piko p
10- 15 femto f
10- 18 atto a
fO
Příklad:
Pro {a}m = 500 platí
{aJkm = k{a}m = 1 5 : = 0,5,
neboť 1 m = 10- 3 km (tj. k = 10- 3). Je tedy a = 500 m = 0,5 km.
297
V praxi se za délkové jednotky volí násobky a díly základní jednotky SI,
zvané metr (značka m), jejichž názvy a symboly se tvoří pomocí tabulky 3.1.
Příklad:
1 m = 10- 3 fm = 10 dm = 10 2 cm = 10 3 mm = 10 6 J.1m,
kde číselné hodnoty jsou měniteli.
3.1.4. Geometrická zobrazení v rovině
Při geometrickém zobrazení v rovině je každému Q.odu (tzv. vzoru) A
útvaru U přiřazen právě jeden bod (tzv. obraz) A' útvaru U' (U' je tzv. obraz
útvaru U; U je tzv. vzor útvaru U'). Při A = A' se bod A nazývá samodružný.
Při U = U' se útvar U nazývá samodružný [invariantní].
Říkáme, že dva různé body A, B roviny tvoří při daném zobrazení involutorni
dvojici, právě když bod B je obrazem bodu A a zároveň bod A je obrazem
bodu B. Zobrazení v rovině, které není identitou a při němž každý bod roviny,
k.terý není samodružný, patří involutorní dvojici, nazýváme involutorním
zobrazením [involuci].
Shodnost útvarů
Jestliže se dva útvary U l' U 2 dají přemístit tak, že se navzájem kryjí (tj. libo-
volný bod útvaru U 1 splývá s bodem útvaru U 2 a zároveň libovolný bod
útvaru U 2 splývá s bodem útvaru Ul)' nazýváme je shodn vmi a píšeme U 1 U 2'
Shodnost úseček a, b, resp. úhlů (x, f3 však někdy nevhodně zapisujeme stručněji
a = b, resp. (X = p.
Shodné zobrazení v rovině
Shodnýln zobrazenim [shodnosti, izometrií].. v rovině nazýváme zobrazení,
při němž každé úsečce je přiřazena shodná úsečka. Přímá, resp. nepřímá
shodnost převádí každý orientovaný úhel v souhlasně, resp. nesouhlasně
orientovaný úhel. Přímou, resp. nepřímou shodnost lze realizovat přemístěním
průsvitky s obkresleným útvarem, která se ponechá lícem nahoru, resp. se
obrátí na rube
Jsou-li dva geometrické útvary U a U' shodné, pak lze najít takové shodné
zobrazení, že útvar U převede v útvar U'.
Identita
I delltitou v rovině (] nazýváme shodné zobrazení, při němž obrazem každého
bodu A E g je týž bod A.
29X
Osová souměrnost
Osovou souměrností [osovou symetrií] s osou o (tzv. osou souměrnosti) v ro-
vině (l nazýváme shodné zobrazení, při němž obrazem každého bodu A E (l
(A o) je bod A' E (1, který leží na kolmici bodem A k ose o, přičemž úsečka
AA ' je osou o půlena (obr. 104).
Samodružnými body osové souměrnosti jsou právě všechny body osy
souměrnosti. Samodružnými přímkami osové souměrnosti jsou právě osa
souměrnosti a všechny přímky kolmé k ose souměrnosti. Osová souměrnost
je 'involucí.
p' p
---
-- -
, - -..... C
C \
\ - - /
B' - -.. i-
\ / 8
\ \ A I - -.. - I /
\ \ I .... / '1
\ I A
\ \ \ I I
\ \ IIV 11/
, /I/
//
\ '. "J 17 /
\\ /
f/
S
Obr. 105. Otočení
Obr. 104. Osová souměrnost
Otočení [rotace]
!
Otočením [rotací] kolem bodu S (tzv. středu otočení) v rovině (l o orientovaný
úhel rJ.. (tzv. úhel otočení) nazýváme shodné zobrazení, při němž obrazem
každého bodu A E (! (A * S) je bod A' E (1, pro který platí SA SA ' a ASA ' = rJ..
(obr. 105).
Otočení má jediný samodružný bod S. Otočení vznikne složením dvou
osových souměrností s různoběžnými osami.
Středová souměrnost
Středovou souměrností [středovou symetrií] se středem S [souměrností podle
středu S] nazýváme shodné zobrazení, které jedinému bodu S přiřazuje týž
bod S a každému bodu X * S přiřazuje takový bod X', že bod S je středem
úsečky X X' (obr. 106). Bod S se nazývá střed souměrnosti.
Středovou souměrnost lze považ(\vat za otočení kolem středu S při úhlu
otočení s velikostí 1rJ..1 = (2k + 1)1t rad (k E" Z).
299
Středová souměrnost má jediný samodružný bod S. Samodružnými přím-
kami středové souměrnosti jsou právě všechny přímky procházející středem
souměrnosti. Středová souměrnost je involucí.
A'
A
I
I '
AI I
El I
I
I
I
h
/
/
I
I
I
C
A
Obr. 106. Středová souměrnost
Obr. 107. Posunutí
Souměrně sdružené a souměrné útvary
Daný útvar a jeho obraz v souměrnosti podle osy, resp. podle středu se na-
zývají souměrne sdružené útvary podle osy, resp. podle středu. Jestliže pro daný
útvar existuje taková osová, resp. středová souměrnost, 'v níž daný útvar
je samodružný, říkáme, že daný útvar je souměrný podle osy, resp. podle středu,
popř. říkáme, že je osově, resp. středově souměrný.
Posunutí
Posunutím o vektor v v rovině (1 nazýváme shodné zobrazení, při němž
obrazem každého bodu A E (1 je takový bod A' E (1, že vektor AA ' = v (obr. 101).
Podobné zobrazení v rovině
"-
Podobným zobrazením [podobností] v rovině nazýváme zobrazení, při němž
každé úsečce AB je přiřazena úsečka A' B ' s délkou kIABI, kde kER + je tzv.
poměr podobnosti.
Každá podobnost při k = 1 je shodností.
Dva útvary U a U' nazýváme podobnými a píšeme U U', je-li možno
najít podobné zobrazení, které převádí. útvar U v útvar U'.
1
Stejnolehlost [homotetie]
Stejnolehlostí [homotetií] se středert S a koeficientem stejnolehlosti x
(x E R \ {O, I}) v rovině (l nazýváme podobné zobrazení, při němž obrazem
300
každého bodu A E (l (A *= S) je takový bod A' E (l, že vektor SA ' = x . SA
(obr. 108).
Každá stejnolehlost je podobností s poměrem podobnosti k = Ixl. Stejno-
lehlost s koeficientem x = - 1 je středovou souměrností.
Ú tvar a jeho obraz ve stejnolehlosti se nazývají stejnolehlé útvary [útvary
sdružené ve stejnolehlosti].
s
SA '-::=,£SA
Obr. 108. Stejnolehlost
3.1.5. Poulití shodnosti a podobnosti
Věty o svazku přímek
První věta o svazku přímek: Jsou-li přímky svazku přímek proťaty rovno-
běžkami (obr. 109), pak délky vzniklých úseček na jedné přímce svazku jsou
v témže poměru jako délky odpovídajících úseček na každé jiné přímce svazku.
Druhá věta o svazku přímek: Jsou-li přímky svazku přímek proťaty rovno-
běžkami (viz obr. 109), pak délky stejnolehlých úseček na rovnoběžkách jsou
v témže poměru jako délky odpovídajících úseček na kterékoli přímce svazku.
\
\
s
c X
Obr, 110. Čtvrtá geometrická
úměrná
Obr. 109. Svazek přímek a rovnoběžky
Úměry plynoucí z vět o 'svazku přímek
První věta o svazku přímek:
ISA!I: ISA 2 1: ISA 3 1 = ISBII: ISB 2 1: ISB 3 1 = ISCII: ISC 2 1: Isc 3 1
301
nebo
ISAII: I A IA21: IA2A31 = ISBII: I B IB21: IB2B31 = I'SCII: IC l c 2 1: IC 2 C 3 1
atd.
Druhá věta o svazku přímek:
IAIBII: IA2B21: I A 3 B 31 = ISAII: ISA 2 1: ISA 3 1
nebo .
IBICII: IB 2 C 2 1: IB 3 C 3 1 = Iscll: ISC 2 1: Isc 3 1
atd. Z toho plyne
IAIBII:IBICII = IA 2 B 2 1:IB 2 C 2 1 = IA 3 B 3 1:IB 3 C 3 1.
Čtvrtá (geometrická) úměrná (obr. 110)
Čtvrtou (geometrickou) úměrnou nazýváme úseč u s délkou x, pro kterou
pta tí '
a:b = c:x,
kde a, b, c jsou délky daných úseček.
Rozdělení úsečky v daném poměru
Úsečka se má rozdělit v poměru m: n (obr. 111 a 112).
Získaný dělicí bod se přesněji nazývá vnitřní dělicí bod.
A O B
A
A Dl 8 De
Obr. 111. Dělení úsečky
v poměru m: n
. ,
Obr. 112. Jiná konstrukce
dělicího bodu D
Obr. 113. Použití první věty
o svazku přímek
,
Dělicí poměr uspořádané trojice bodů přímky
Dělicím poměrem bodu C na přímce vzhledem k základním bodům A, B (B * C)
se nazývá číslo
IACI
A.(ABC) = B IBCI '
kdé e = -1, resp. e = 1, jestliže bod C leží, resp. neleží mezi body A, B.
302
Dvojpoměr uspořádané čtveřice bod ů přímky
Dvojponrerem čtyř bodů A, B, C, D (v tomto pořadí) na přímce se nazývá číslo
A ( ABC )
l5(ABCD) =
A(ABD)
[}y(ABD) =*= O].
Harmonická čtveřice bodů
Harlnonickou čtveřicí bodů přímky nazýváme body A, B, Di De (v tomto
pořadí), jejichž dvojpoměr A(ABDiDe) = -1, přičemž Di' resp. De se nazývá
vnitřní, resp. vnější dělicí bod, kdežto body A, B se nazývají základní
(obr. 113 a 114). Říkáme, že body Db De jsou harmonicky sdružené vzhledem
k bodům A, B.
V každém trojúhelníku protíná osa vnitřního úhlu a osa příslušného
vnějšího úhlu přímku obsahující protější stranu po řadě ve vnitřním 'a vnějším
dělicím bodě z harmonické čtveřice bodů, jejímiž základními body jsou
vrcholy protější strany trojúhelníku. Přitom např. platí (obr. 115)
lADil: IBDil = IADel : IBDel = Ibl : lal '
kde a, b jsou zbývající strany trojúhelníku.
Obr. 114. Použití druhé věty
o svazku přímek
A
Di 8
De
Obr. 115, Apolloniova kružnice
Kružnice sestrojená nad úsečkou DiD e jako průměrem je množinou vrcholů
všech trojúhelníků, jejichž jedna strana (AB v obr. 115) je pevná a poměr
délek zbývajících dvou stran je předem dán (tzv. Apolloniova kružnice).
Střední, (geometrická> úměrná [geometrický průměr]
Označení:
a - délka přepony,
a 1 , a2 - délky úseků přepony.
Podle Eu.klidovy věty o odvěsně (obr. 116) platí
x 2 = aa 1 neboli a:x = x:a 1 ,
kde lit je délka úseku přepony přilehlého k odvěsně s délkou x.
303
Podle Euklidovy věty o vÝL ce (obr. t 17) platí
x 2 = a l a 2 neboli a l : x = x: a 2 ,
kde x je délka výšky k přeponě.
O další konstrukci viz u věty o tečně a sečně (viz obr. 121).
8t
A 2
S 02
Obr. 116. Euklidova věta
o odvěsně
Obr. 117. Euklidova věta
o výšce
Obr. 118. Věta o tětivách
Mocnost bodu ke kružnici
Věta o tětivách (obr. 118): Jestliže se bodem K vnitřní oblasti kružnice
vedou její sečny, protínající kružnici v bodech AI' A 2 , popř. B I , B 2 , pak součjn
délek a l = IAIKI a a2 = IA2KI se rovná součinu délek hl = IBIKI a b 2 =
= IB2KI, tj.
al a2 = hl b 2 neboli a l : b l = h 2 : a 2 .
Věta o sečnách (obr. 119): Jestliže se bodem M vnější oblasti kružnice .vedou
její sečny/protínající kružnici v bodech AI' A 2 , popř. B I , B 2 , pak součin délek
a l ' IMA 2 1 a a2 = 1M AI I se rovná součinu délek b l = IMB 2 1 a hl = IMBII,
tj.
a l a 2 = b l b 2 neboli al :b l = b 2 :a 2 .
8
B
H
/II
Obr. 119. Věta o sečnách
Obr. 120. Věta o tečnč a sečně
T
Obr. 121. Střední
geometrická úměrná x
Věta o tečně li sečně (obr. 120): Jestliže se bodem M vnější oblasti kružnice
vede její sečna protínající kružnici v bodech A, B a tečna dotýkající se kružnice
304
v bodě pak součin délek {lI = IMBI a (12 = IMAI se rovná druhé mocnině
délky x = IA T!, tj.
a l a2 = x 2 neboli a l .: x = x: a2'
Délka x = IA TI je tedy střední geometrickou umernou délek a l = 1M BI
a a 2 = 11\1 AI (v obr. 121 je další konstrukce střední geometrické úměrné).
Zlatý řez
Říkáme, že úsečka je ro:dělena Zla(vnl řezem, je-li rozdělena J,odem na dvě
části tak, že délka x větší ze vzniklých úseček je střední geometrickou úměrnou
k délce a celé úsečky a délce a - x menší úsečky vzniklé rozdělením, tj.
x 2 = a( (l - x) ne boli a : x = x : (a - x),
odkud
J5 - 1 '
x = a O,618a.
2
K onstrukce zlatého. ře=u (obr. 122):
V bodě B úsečky AB o délce a sestrojíme kolmou úsečk BC o délce ta,
spojíme bod A s bodem C, sestrojíme kružnici se středem C a poloměrem
o délce ta, která protne úsečku AC v bodě D, a naneseme úsečku AD na úsečku
AB od bodu A. Bod E, který dostaneme, rozdělí úsečku AB zlatým řezem.
p o u žit í: Strana pravidelného deseti úhelní k u má stejnou délku jako větší
úsečka vzniklá rozdělením poloměru kružnice opsané desetiúhelníku zlatým
fuze \
A
Obr. 122, Zlatý řez
Věty o podobnosti mnohoúhelníků
Definice:
Trojúhelníky se nazývají podobné, shodují-li se v poměrech délek odpoví-
dajících si stran.
Dva trojúhelníky jsou podo bné, shodují-li se
a) ve dvou úhlech (věta uu);
b) v poměrech délek dvou stran a v úhlu jimi sevřeném (věta sus):
c) v poměrech délek dvou stran a v úhlu proti větší z nich (věta Ssu).
O:'
Podobné trojúhelníky lze odpovídajícími výškami nebo osami úhlů nebo
těžnicemi rozložit v podobné trojúhelníky. V podobných trojúhelnících jsou
délky odpovídajících si výšek, os úhlů (osa úhlu je zde úsečkou) a těžnic
v témže poměru jako délky odpovídajících si stran.
Obvody podobných trojúhelníků jsou ve stejném poměru jako délky
odpovídajících si úseček (stran, výšek, těžnic atd.), tj.
01 : 02 = a1 : a2 = hl : b 2 = CI : C 2 = k,
kde k se nazývá koeficient podobnosti nebo poměr podobnosti (při k > 1 poměr
=vět. ení a při O < k < 1 poměr zmenL eni).
Obsahy podobných trojúhelníků jsou v témže poměru jako druhé mocniny
délek odpovídajících si úseček (stran, výšek, těžnic atd.), tj.
S . S - a 2 . a 2 b 2 . b 2 C 2 . C 2 k 2
l' 2- l' 2= l' 2= l' 2= ,
kde k je koeficient podobnosti.
Mnohoúhelníky jsou pod o b n é, jsou-li délky odpovídajících si stran v témže
poměru nebo shodují-li se všechny odpovídající si úhly.
Obvody podobných mnohoúhelníků jsou v témže poměru jako délky
odpovídajících si úseček (stran, výšek, úhlopříček atd.), tj.
01 : 02 = a 1 : a 2 = b 1 : h 2 = ... = k.
Obsahy podobných mnohoúhelníků jsou v témže poměru jako druhé
mocniny délek odpovídajících si úseček (stran, výšek, úhlopříček atd.), tj.
S . S - a 2 . a 2 - h 2 . h 2 - - k 2
l' 2 - l' 2 - 1. 2 - ... - .
Poměr zvětšení, popř. poměr zmenšení obsahů podobných mnohoúhelníků
se tedy rovná druhé mocnině koeficientu podobnosti.
Stejnolehlost mnohoúhelníků
Podobné mnohoúhelníky jsou stejnolehlé, jestliže odpovídající si strany
jsou rovnoběžné a odpovídající si body leží na přímkách svazku přímek
(obr. 123). Střed S svazku přímek se nazývá střed stejnolehlosti.
o k
S C c'
SA J -. SA (ae>O)
Obr. 123. Stejnolehlost mnohoúhelníků
306
Věta o shodnosti mnohoúhelníků
Mnohoúhelníky jsou shodné, jsou-li jak všechny odpovídající si strany,
tak všechny odpovídající si úhly shodné.
Věty o shodnosti trojúhelníků
Trojúhelníky jsou s hod n é, shodují-li se
a) v jedné straně a v obou úhlech k ní přilehlých (věta usu);
b) ve dvou stranách a v úhlu jimi určeném (věta sus);
c) ve dvou stranách a v úhlu proti větší z nich (věta Ssu);
d) ve všech třech stranách (věta ss s).
3.2. PLANIMETRIE
3.2.1. Trojúhelník
Trojúhelníkem nazýváme n-úhelník pro n = 3.
Af
._-
.
8 2 Obr. 124. Prvky trojúhelníku
Označení (obr. 124):
A, B, C - vrcholy trojúhelníku ABC,
(1, B,)' - velikosti vnitřních úhlů [(x, B, Y E (O, 1t)],
a. 1 , B l' Y 1 - velikosti vnějších úhlů,
a - délka protější strany k vrcholu A,
b - délka protější strany k vrcholu B,
307
c - délka protější strany k vrcholu C,
S - obsah trojúhelníku,
s = !(a + b + c) - poloviční obvod trojúhelníku,
Va' Vb,'V c - délky výšek [stručně výšky] po řadě k stranám a, b, c,
ta' lb' t c - délky těžnic po řadě k stranám a, b, c,
0a, op, 0'1 - délky os po řadě vnitřních úhlů ex, 8, y,
oal,opl,o'1l - délky os po řadě vnějších úhlů (Xl,8 l ,Yt,
r - délka poloměru [stručně poloměr] opsané kružnice,
(! - délka poloměru [stručně poloměr] vepsané kružnice,
(la' (lb' (lc - délky poloměrů [stručně poloměry] připsaných kružnic
po řadě k stranám a, b, c.
Vztahy pro velikosti úhlů trojúhelníku
(X + 8 + y = 180 0 = 1t rad,
(Xl + 8 1 + Yl = 360 0 = 21trad;
(Xl = f3 + )' = 180 0 - (X, Pt = (X + )' = 180 0 - P, }'t = (X + P = 180 0 - )';
. I. 8 . 4 (X tJ Y
sIn ex + sIn + sIn y = cos - cos - cos -,
, 2 2 2
8 1 4 . (x. 8. Y
cos ex + cos + cos)' = + sIn - sIn - sIn -;
. 2 2 2
sin (2ex) + sin (28) + sin (2y) = 4 sin (X sin 8 sin y,
cos (2(X) + cos (28) + cos (2y) = -(4 cos (X cos 8 cos y + 1);
tg (X + tg 8 + tg Y = tg (X tg 8 tg Y (neplatí pro pravoúhlý trojúhelník);
sin 2 (X + sin 2 8 + sin 2 )' = 2(1 + cos (X cos 8 cos }');
cos 2 (X + cos 2 8 + cos 2 Y = 1 - 2 cos (X cos 8 cos y;
cotg (X cotg 8 + cotg (X cotg y + cotg 8 cotg Y = 1;
ex 8 y (X 8 y
cotg 2 + co g 2 + cotg 2 = cotg 2 cotg 2 cotg 2 ;
(sin (X + sin 8 + sin }') (sin (X + sin 8 - sin y) .
. (sin (X - sin 8 + sin y) ( - sin (X + sin 8 + sin }') = 4 sin 2 (X sin 2 8 sin 2 y. -
,
Sinová věta
a : b : c = sin ex : sin 8 : sin y .
Kosinová věta .
a 2 = b 2 + c 2 - 2bc cos (X ,
b 2 = a 2 + c 2 - 2ac cos 8,
c 2 = a 2 + b 2 - 2ab cos y .
308
Mollweidovy vzorce
(X-O (X-tJ
a+b cos sin
2 a-b 2
- -- -
c y c y
sin - cos-
2 2
O-y O-y
cos sin
b+c 2 b-c 2
-
a (X a (X
sln- cos-
2 2
(X-y (X-y
cos sIn
a+c 2 a-c 2
- -
b O b O
sln- cos-
2 2
Tangentová věta
(X-O (X-O
a-b tg 2 tg 2
- -
a+b (X+O y
tg 2 cotg -
2
tg O-y tg O-y
b-c 2 2
- -
b+c O+y (X
tg-- cotg -
2 2
tg (X-y tg (X-y
2 2
a-c
- -
a+c (X+y O
tg 2 cotg -
2
Vztahy pro velikosti vnitřních úhlů
a délky stran trojúhelníku [s = t(a + b + c)]
sin = J (s - b)(s - c) , sin 8 = J (s - a) (s - c) ,
2 bc 2 ac _
309
sin = J (s - a) (s - b) .
2 ab'
rJ.. J s(s - af
cos - =
2 bc'
cos = j s(s - c) .
2 ab'
tg = j (s - b) (s - c)
2 s( s - a) ,
tg = j (s - a) (s - b)
2 s( s - c) .
cos B = j s(s - b) ,
2 ac
tg B = j (s - a)(s - c) ,
2 s(s - b)
Proti shodným stranám trojúhelníku Ježí shodné vnitřní úhly. Proti větší
straně trojúhelníku leží větší vnitřní úhel. Proti tupému nebo pravému vnitř-
nímu úhlu trojúhelníku leží jeho největší strana.
Vztahy pro délky stran trojúhelníku
a + b > c, la - bl < c,
b + c > a, lb - ci < a,
a + c > b, la - ci < b.
Těžnice
Úsečka spojující vrchol trojúhelníku se středem protější strany se nazývá
těžnice.
Průsečík těžnic se nazývá těžiště T.
Vzdálenost těžiště od středu příslušné strany se rovná třetině délky těžnice.
Vzdálenost těžiště od strany trojúhelníku se tedy rovná třetině délky pří-
slušné výšky. I
Dělicí poměr těžiště vzhledem k vrcholu a středu protější strany trojúhelníku
se rovná
;. = 2.
Platí
ta = t .J[2(b 2 + c 2 ) - a 2 ] = t .J(b 2 + c 2 + 2bc cos (1),
t b = t .J[2(a 2 + c 2 ) - b 2 ] = t J(a 2 + c 2 + 2ac cos B),
t c = t J[2(a 2 + b 2 ) - ("2] = t J(a 2 + b 2 + 2ab COS y).
310
Osy vnitřních a vnějších úhlů trojúhelníku
Každá z os vnitřních úhlů trojúhelníku rozděluje protější stranu v poměru
délek přilehlých stran, tj. dělicí poměr každého z uvedených průsečíků vzhle-
dem ke krajním bodům příslušné strany se v absolutní hodnotě rovná poměru
délek přilehlých stran.
Každá z os vnějších úhlů trojúhelJ1íku protíná prodloužení protější strany
v bodě, jehož dělicí poměr vzhledem ke krajním bodům příslušné strany se
rovná poměru délek přilehlých stran.
Plat tedy
IAMil : IBMil = b: a,
IBKil : ICKil = c: b,
ICLil : IALil = a: c,
lAMel: IBMel = b: a,
IBKel : ICKel = c: b,
ICLel : IALel = a: c,
kde K i , Li' Mi jsou po řadě průsečíky os vnitřních úhlů trojúhelníku se stra-
nami BC, C A, AB a Ke, Le, Me jsou po řadě průsečíky os vnějších úhlů troj-
úhelníku s prodlouženími stran RC, C A, AR (obr. 125). Úsečky AK i , BL i
a C Mi nazýváme osami vnitřních úhlů trojúhelníku (definovan.vmi jako úsečky),
úsečky AKe' BLe a CM e nazýváme osami vnějších úhlů trojúhelníku (defino-
vanými jako úsečky).
Ke
...... -_..- --
\
\
\
-
\
\
\
\
/
...........
.........
--
Me
Obr. 125. Osy vnitřních a vnějších
úhlu trojúhelníku
Pro délky os vnitřních úhlů trojúhelníku platí
a
2bc cos --
I 2
0a = IAKil = J{bc[(b + C)2 - a 2 ]} = --,
b+c b+c
311
B
2ac cos -
1 2
op = IBLil = J{ac[(a + C)2 - b 2 ]} =
a+c a+c
'"
I
2ab cos-
o.. = ICMil = 1 y'{ab[(a + bY _ c 2 ]} = 2
I a+b a+b
Výšky trojúhelníku
Úsečka spojující vrchol trojúhelníku s patou kolmice k protilehlé straně
(popř. k prodloužení protileh é strany) se nazývá liÝL ka trojÚhelníku. Délku
výšky obvykle nazýváme také vÝL kou.
Průsečík' výšek trojúhelníku se nazývá ortocentrul11.
Platí
111
Va : Vb : lie = - : - : - ;
a b c
li a = b sin i' = c sin B,
. .
Vb = a sin }' = c sin rJ..,
Ve = a sin B = b sin rJ...
Kružnice opsaná trojúhelníku
Středem kružnice opsané trojúhelníku je průsečík os stran.
Pla tí
li
b
c
2 . ,
sin y
r=-
2 sin rJ..
2 sin tJ
rJ.. B t'
s = 41" cos - cos - cos - ,
222
a + b -+ c
s=
2
he lIC ab abc
r = ---- = - = - = -
2ra 2rb 2v e 4S'
K .... . ,. , h I ' k ( a + b + C )
ruznlce vepsana troJu e nI u s = 2 .
Středem kružnice vepsané trojúhelníku je průsečík os vnitřních úhlů.
312
!Platí (! = s = J (s - a)(s - b)(s - c) ,
s s
tj
!! = (s - a)tg2: = (s - b)t g 2 = (s - c)tg ,
B " .
o = s t g - t g - t g -
... 2 2 2'
(.} ,
4 . . IJ . I
o = r sin - sin - sin - .
2 2 2
Vzdálenost d středu kružnice opsané trojúhelníku od středu kružnice
vepsané trojúhelníku se rovná
d = J(r 2 - 2rQ).
Kružnice připsané trojúhelníku
Středem kružnice připsané trojúhelníku vzhledem ke straně a, resp. b, resp. c
je průsečík os úhlů BAC, B 1 BC a CI CB, resp. ABC, A 1 AC a C 2C A, resp. AC B,
A 2 AB a B 2 1JA (viz obr. 124).
Platí
s
S.
Qb = ,
s-b
s
Qa =
s-a
Qc =
s-c
1 111
-=-+---,
Q a Vb V c Va
1 111
-=-+---,
Qb Va Ve Vb
1 111
- + .
--- ---,
Qc Va Vb Ve
1 1 1 1 1 1 1 1
-=-+-+-, -=-+-+-;
Q Va Vb Ve Q Qa Qb (Je
Qa + Qb + Qe = 4r +' Q ,
B }'
a cos - cos -
rJ.. 2 2
Qa = s tg 2 = rJ..
cos-
2
rJ.. Y
b cos - cos -
2 2
B
cos-
2
B '
Qb = s tg - =
2
'Yv B
c cos - cos -
y 2 2
Q = s tg - =
2 )'
cos-
2
313
Obsah ,trojúhelníku (. = a + + c )
abe
S = = J((l(UM1J,
av bv ev
S= = =
2 2 2'
S = J[s(s - a) (s - h) (s - e)] (Heronův vzorec),
S = (1S = (1a(s - a) := b(S - b) = (1c(s - c),
S = tab sin y = tbc sin ex tac sin B ,
a 2 sin B sin y b 2 sin ex sin y c 2 sin ex sin B
S- - -
- 2 sin ex - 2 sin B - 2 sin y ,
S = 2r 2 sin Cť sin B sin y ,
ex B y'
S = S2 t g - t g - t g -
2 2 2'
C( B )'
S = (12 cotg - cotg - cotg - .
222
Jsou-li A[X 1 ,Y1,ZI]' B[X 2 'Y2,Z2] a C[X3'Y3,Z3] vrcholy trojúhelníku
dané v kartézské souřadnicové soustavě, platí
S* = t[x I (Y2 - Y3) + X2(Y3 - YI) + X3(Y1 - Y2)],
S* = t[(x I - x 2 ) (Y1 + Y2) + (X2 - X3) (Y2 + Y3) +
+ (X3 - Xl) (Y3 + YI)] =
1 1 I
= '2 XI' YI, = '2 X 2 - XI' Y2 - Y1 .
. X 2 , Y2, 1 X3 - Xl' Y3 - Y1
X3, Y3, 1
Jsou-li A[(ll' qJ1]' B[U2, qJ2] a C[Q3' qJ3] vrcholy trojúhelníku dané v po-
lární souřadnicové soustavě, platí
S* = ![(11(12 sin (lpI - qJ2) + (12(13 sin (qJ2 - qJ3) + (13(11 sin (qJ3 - qJ1)J .
.
Vyjde-li S* > O, pak obsah trojúhelníku je S = S* a smysl obíhání vrcholů
trojúhelníku je kladný. Vyjde-li S* < O, pak obsah trojúhelníku je S = -S*
a smysl obíhání vrcholů trojúhelníku je záporný (kladným smy lem obíhání
se rozumí opačný smysl ke smyslu otáčení hodinových ručiček). Vyjde-li
S* = O, leží body A, B, C v přímce.
314
Zobecněná Pythagorova věta
a 2 = b 2 + c 2 + 2bp pro rJ.. 90 0 ,
b 2 = c 2 + a 2 + 2cq pro {J 90 0 ,
('2 = a 2 + b 2 + 2ar pro y 90 0 ,
kde p je délka průmětu strany (' do strany b,
q - délka průmětu strany a do strany c,
r - délka průmětu strany b do strany a.
Věty o určenosti trojúhelníku
Trojúhelník je jednoznačně určen, jsou-li dány tyto jeho určovací prvky:
a) délka strany a velikosti dvou k ní přilehlých úhlů, jejichž součet velikostí
je menší než 180 0 (věta usu);
b) délky dvou stran a velikost úhlu jimi sevřeného (věta sus);
c) dvě různé délky stran a velikost ú.hlu protilehlého k delší straně (věta Ssu);
d) délky tří stran, pro něž platí
la - bl < c < a + b
(věta sss).
Základní úloha 1 (k větě usu):
Jsou dány délka strany a velikosti dvou k ní přilehlých úhlů, jejichž součet
je menší než 180 0 (např. a, B, y).
Řešení:
rJ.. = 180 0 - (13 + y),
a sin B
b = . (sinová věta),
sin rJ..
a sIn y
c =
sIn rJ..
(sinová věta).
Základní úloha 2 (k větě sus):
Jsou dány délky dvou stran a velikost úhlu jimi sevřeného (např: a, c, p).
Způso b řešení 1:
rJ..-y
tg
2
a-c IJ
- cotg --
a + c 2
(tangentová věta),
odk ud se určí 1( Q: - ,').
315
Sečtením, resp. odečtením hodnot výrazů
Q: - ". Q: + Y 13
I a = 90 0 _ _
2 2 2
dostaneme , resp. y. Konečně
a sin B
b = .
sin ex
(sinová věta).
Způsob řešení 2:
b = J(a 2 + c 2 - 2ac cos B)
. a sin B
sIn a =
(kosinová věta),
(sinová věta),
b
y = 180 0 - (ex + B).
Základní úloha 3 (k větě Ssu):
Jsou dány dvě různé délky stran a velikost úhlu protilehlého k větší straně
(např. a, b, ex, a >. b).
Řešení:
b sin C(
sin B =
a
(sinová věta),
y = 180 0 - ( + B),
a sIn y
c = .
sin ex
( sinová věta).
Základní úloha 4 (k větě sss):
Jsou dány délky a, b, c tří stran, pro něž platí la - bl < c < a + b.
Způsob řešení 1:
tg = J (s - b)(s - c)
2 s( s - a)
(věta o velikosti vnitřního úhlu),
. B b sin ex
sIn =
a
(sinová věta),
}' = 180 0 - (ex + B).
316
Způsob řešení 2:
b 2 + c 2 - a 2
cos rJ.. =
(kosinová věta),
2bc
. B . b sin rJ..
sIn =
a
(sinová věta),
y = 180° - (rJ.. + B).
3.2.1.1. Pravoúhlý trojúhelník
Označení (obr. 126):
a, b - délky odvěsen,
y = 90° = 11t rad - velikost úhlu proti přeponě,
C - délka přepony,
V c - výška k přeponě,
C a , resp. c b - délka průmětu strany a, resp. b do přepony C
(tzv. úseky přepony).
c
o c
B
Obr. 126. Pravoúhlý trojúhelník
A
Pythagorova věta
a 2 + b 2 = c 2
(y = 90°).
Pythagorejská čísla
Členy každé uspořádané trojice [a, b, c] celých čísel (v uvedeném pořadí),
která je řešením rovnice a 2 + b 2 = c 2 , nazýváme pythagorejskými čísly.
Jsou-li čísla p, q E Z, pak čísla
a = 2pq, b = p2 - q2, C = p2 + q2
jsou pythagorejskými čísly. Jsou-li čísla a, b, c (v tomto pořadí) pythagorej-
skými čísly, pak čísla Aa, Ab, AC (A E Z) (v tomto pořadí) jsou také pythagorej-
skými čísly. Proto jestliže všechny členy kterékoli uspořádané trojice [a, b, c]
z tabulky 3.2 vynásobíme číslem A E Z, dostaneme další uspořádanou trojici
pythagorejských čísel.
317
Tabulka 3.2
p q a b c
2 1 4 3 5
3 1 6 8 10
4 1 8 15 17
5 1 10 24 26
3 2 12 5 13
4 2 16 12 20
5 2 20 21 29
4 3 24 7 25
5 3 30 16 34
5 4 40 9 41
Jsou-li délky stran trojúhelníku pythagorejskými čísly, pak tento troj-
úhelník je pravoúhlý.
Euklidova věta o odvěsně
2
a = CCa'
b 2 -
- CC b .
Euklidova věta o výšce
2
Ve = CaCb.
Obsah pravoúhlého trojúhelníku
- ev" ab
S = 2 = 2'
Těžiště pravoúhlého trojúhelníku
Vzdálenost těžiště T od přepony C se rovná tv e .
Vzdálenost těžiště T od odvěsny a se rovná tb.
Vzdálenost těžiště T od odvěsny b se rovná ta.
3.2.1.2. Rovnoramenný trojúhelník
a = b - délka ramen,
c - délka základny,
= {3, y - velikosti vnitřních úhlů.
318
3.2.1.3. Rovnostranný trojúhelník (obr. 127)
a = b = c - délka stran,
C( = 8 = y = 60 0 = )1t rad - velikost vnitřních úhlů;
aJ3
V=-
2 '
a 2 J3
S = .
4
Vzdálenost těžiště T rovnostranného trojúhelníku od kterékoli jeho strany
, a
se rovna - J3.
6
D
B
c
A
Obr. 127. Rovnostranný trojúhelník
A
Obr. 128. Čtyřúhelník
3.2.2. Ctyřúhelníky
Čtyřúhelnikem nazýváme ll-úhelník pro n = 4.
'Označeni (obr. 128):
a, b, c, d - délky stran,
, 8, y, tJ - velikosti vnitřních úhlů,
(Xl' 8 1 , Y1, tJ 1 - velikosti vnějších úhlů,
Ut' u 2 - délky úhlopříček,
({J - odchylka úhlopříček.
Součty velikostí úhlů čtyřúhelníku
+ 8 + Y + tJ = 360 0 = 2n rad,
1 + 8 1 + f1 + tJ 1 = 360 0 = 2n rad.
Obsah čtyřúhelníku
S = 1U1U2 sin ({J.
.
319
3.2.2.1. Rovnoběžník (obr. 129)
U rovnoběžníku platí
AB!i CV., (BC II AD , li == c, b = ti:
= }', B = tJ ;
rJ.. + B = B + t' = }' + tJ = tJ + C( = 180 o = 7t rad.
o c C
m
A Q' B
Obr. 129. Rovnoběžník
Úhlopříčky rovnoběžníku se vzájemně půlí.
Těži. tě T rovn<?běžníku leží v průsečíku úhlopříček.
Obsah rovnoběžníku
s = aV a = bV b = ad sin rJ..,
kde rJ.. je velikost úhlu sousedních stran a, d,
Va - výška ke straně a,
Vb - výška ke straně b.
o
c
c
o
a
D C
b
A Q 8
a
B
A
A
Obr. 130. Obdélník
Obr. 131. Kosočtverec
Obr. 132. Čtverec
3.2.2.2. Obdélník (obr. 130)
U obdélníku platí
ABIIW, BCII Ád, a=c, a:i=b, b=d,':l=B=:.'=()=90 o =!7trad.
Úhlopříčky obdélníku se vzájemně půlí. Platí
Ul = U2 = J(a 2 + b 2 ).
320
Obsah obdélníku
S = ab.
Těži.ště T obdélníku leží v průsečíku úhlopříček.
3.2.2.3. KosOCtverec (o br. 131)
U kosočtverce platí
AB II CD, BC) II AD,
(X = y 9= 90 o = 11t rad,
(X + B = 180 0 = 1t rad.
a=b=c=d
,
B = tJ * 90° = t1t rad,
Úhlopříčky kosočtverce jsou vzájemně kolmé, vzájemně se půlí a půlí
vnitřní úhly kosočtverce.
Obsah kosočtverce
Ul U 2 2'
S = - = a sIn rJ...
2
Těžiště T kosočtverce leží v průsečíku úhlopříček.
3.2.2.4. Ctverec (obr. 132)
U čtverce platí
AR II CD, II AD, a = b = c = d,
rJ.. = B = y = tJ = 90 0 = i1t rad.
Úhlopříčky čtverce se vzájemně půlí a jsou k sobě kolmé. Platí
Ul = U2 = a J2.
Obsah čtverce
S = a 2 = tui .
'- Těžiště T čtverce leží v průsečíku úhlopříček.
Pravoúhelník je spol čný název pro obdélník a čtverec.
321
3.2.2.5. Lichoběžník (obr. 133)
U lichoběžníku platí AR II E15, AD -H" BC.
Obsah lichoběžníku
a+c
S= v=mv
2 '
kde v je vzdálenost rovnoběžných stran lichoběžníku,
m = (a + c)/2 - délka střední příčky lichoběžníku.
O
D
A
8
DU
Obr. 133. Lichoběžník
Obr. 134. Tětivový čtyřúhelník
Těžiště T lichoběžníku leží na spojnici středů U, V základen ve vzdálenosti
.
v a + 2c
3 a + c
od delší základny a.
3.2.2.6. Tětivový čtyřúhelník (obr. 134)
Čtyřúhelník, jemuž lze opsat kružnici, se nazývá tětivový.
U tětivového čtyřúhelníku platí
rJ.. + y = B + tJ = 180 0 = 1t rad;
S = J[(s - a) (s - b)(s - c)(s - d)],
kde s = t(a + b + c + d);
ac + bd = U t U 2 (Ptolemaiův vzorec);
Ul = j (ac + bd) (bc + ad) , U 2 = j (ac + bd) (ab + cd) ;
ab + cd bc + ad
r _ 1 j (ab + cd) (ac + bd) (bc + ad)
- 4 (s - a) (s - b) (s - c) (s - d) ,
kde r je poloměr opsané kružnice.
322
I
3.2.2.7. Tečnový čtyřúhelník (obr. 135)
Čtyřúhelník, jemuž lze vepsat kružnici, se nazývá tečnový.
U tečnového čtyřúhelníku platí
a + c = b + d;
S = (lS,
kde (l je poloměr vepsané kružnice
s = !(a + b + c + d).
D
A
c
A
a
8
Obr. 135. Tečnový čtyřúhelník
Obr. 136. Dcltoid
B
3.2.2.8. Deltoid (obr. 136)
U deltoidu platí
a=b
,
c=d
,
AC 1- B15;
s _ U 1 U 2
- 2 .
Čtverec, obdélník a rovnoramenný lichoběžník jsou speciálními případy
tě t i v o v é h o čtyřúhelníku. Čtverec, kosočtverec a deltoid jsou speciálními
případy tečnového čtyřúhelníku.
3.2.3. Mnohoúhelníky [n-úhelníky]
n-úhelníkem (n E {n E Nin > 3} ) [obecně mnohoúhelníkem] nazý-
váme uzavřenou rovinnou oblast, jejíž hranicí je jednoduchá uzavřená lomená
.čára s n vrcholy, přičemž zpravidla předpokládáme, že žádné dvě sousední
strany lomené čáry neleží na téže přímce.
323
Součet velikostí úhlů n-úhelníku
Součet velikostí v nit ř n í c h úhlů n-úhelníku se rovná
(2n - 4) . 90 0 = (2n - 4) . in rad.
Součet velikostí vnějších (popř. středových) úhlů n-úhelníku se rovná
360 0 = 2n rad.
Počet úhlopříček n-úhelníku
n(n - 3)
Vn = .
2
Obsah n-úhelníku
n-úhelník se rozloží bud' v trojúhelníky (obr. 137) pomocí 'úhlopříček vy-
cházejících z jednoho vrcholu, nebo v pravoúhlé trojúhelníky a lichoběžníky
pomocí kolmic vedených z vrcholů k vhodné úhlopříčce (obr. 138). Pak platí
k
S = L Si'
i= 1
kde Si je obsah trojúhelníku, popř. lichoběžníku.
Obr. 137. Rozklad n-úhelníku
v trojúhelníky
Obr. 138. Rozklad n-úhelníku v
v trojúhelníky a lichoběžníky
3.2.3.1. Pravidelné n-úhelníky
Všechny strany, stejně jako všechny úhly pravidelného n-úhelníku
jsou shodné.
O značení:
a n - délka strany pravidelného n-úhelníku,
r n - poloměr kružnice opsané n-úhelníku,
{ln - poloměr kružnice vepsané n-úhelníku,
n - velikost vnitřního úhlu pravidelného n-úhelníku,
a - velikost vnějšího (popř. středového) úhlu pravidelného n-úhelníku,
Sn '- obsah pravidelného n-úhelníku.
324
Těžiště Tpravidelného n-úhelníku leží ve středu kružnice opsané n-Úhelníku.
Velikosti úhlů pravidelného n-úhelníku:
"
360°
,
ťX n = -.
n
2n - 4
(ln = . 90°,
n
Vztah mezi a m r n a Qn:
. - 1. / (4 2 2 )
Qn - 2 V r n - a n .
Výpočet délky a2n strany pravidelného 2n-úhelníku pomocí délky a,. strany
pravidelného n-úhelníku:
a2,. = J[2r; - r,. J(4r; - a;)] = J(2r; - 2r,.(),.).
Obsah pravidelného n-úhelníku:
nanl!n na,. J(4r; - a;) nr;. ,
S = = = - sIn ťX .
n 2 4 2 n
Jednoduché pravidelné mnohoúhelníky
Daný prvek: poloměr r n opsané kružnice
Rovnostranný trojúhelník:
a 3 =r 3 J3,
Čt verec :
1
Q 3 = "2 r 3 ,
S3 = ir J3.
a 4 = r4 J2, Q4 = t r 4 J2,
Pravidelný pětiúhelník:
as = trs J(lO - 2 J5),
. .
Ss = ir J(lO + 2 J5).
Pravidelný šestiúhelník:
a6 = r6, Q6 = t r 6 J3,
Pravidelný osmiúhelník:
as = r8 J(2 - J2), Qs = trs J(2 + J2), SS = 2ri J2.
Přibližná hodnota pro délku a9 strany pravidelného devítiúhelníku (r = 1):
2 J5 + 1
a9 8 .
S4 = 2r;.
,
l!s = !rs(J5 + 1),
S6 = 1r J3.
325
Pra videlný desetiúhelník:
al0 = t r lo(J5 - 1), QI0 = *r 1 0 J(10 + 2 J5),
. S10 = irio J(10 - 2 J5).
Daný prvek: délka a n strany n-úhelníku
Rovnostranný trojúhelník:
r3 = t a 3 J3, , (13 = !-a 3 J3, S3 = *a J3.
Čtverec:
r 4 = ta J2,
1
Q4 = Ia 4 ,
S4 = a .
Pravidelný pětiúhelník:
rs = lo as J(50 + 10 J5), Qs = lo a s J(25 + 10.J5),
Ss . !a .J(25 + 10 J5).
Pravidelný šestiúhelník:
r6 = a6, Q6 = t a 6 J3, S6 = !a J3.
Pravidelný osmiúhelník:
r8 = t a 8 J(4 + 2 J2), Q8 = t a 8(.J2 + 1),
S8 = 2a (J2 + 1).
Pravidelný desetiúhelník:
r 10 = talo(J5 + 1), QI0 = ta 1 0 J(5 + 2.J5),
S10 = iaio J(5 + 2 J5).
Konstrukce některých pravidelných mnohoúhelníků
I
Daný prvek: poloměr r opsané kružnice
Čtverec a pravidelný osmiúhelník (obr. 139):
Sestrojíme dva vzájemně kolmé průměry kružnice s daným poloměrem r.
Krajní body těchto průměrů jsou vrcholy čtverce.
Sestrojíme-li osy stran čtverce, pak jejich průsečíky s kružnicí opsanou
čtverci jsou zároveň s vrcholy daného čtverce vrcholy pravidelného osmi-
úhelníku. Tímto způsobem dostáváme pravidelné 2 n -úhelníky (n E N \ {I}).
Pravidelný šestiúhelník a rovnostranný trojúhelník (obr. 140):
Úsečku délky r naneseme šestkrát za s bou jako tětivu kružnice s daným
poloměrem r a dostaneme pravidelný šestiúhelník.
Rovnostranný trojúhelník vznikne tak, že spojíme tři nesousední vrcholy
pravidelného šestiúhelníku.
326
Pravidelný dvanáctiúhelník:
Sestrojíme-li osy stran pravidelného šestiúhelníku, pak jejich průsečíky
s kružnicí opsanou tomuto šestiúhelníku jsou zároveň s vrcholy daného
šestiúhelníku vrcholy pravidelného dvanáctiúhelníku. Tímto způsobem do-
staneme pravidelný 24-úhelník, 48-úhelník, ..., tj. obecně pravidelné (3 .2 n )_
- úhelníky (n E N).
Obr. 139. Čtverec a pravidelný
osmi úhelník
Obr. 140. Pravidelný šestiúhelník
a rovnostranný trojúhelník
Pravidelný desetiúhelník a pravÍdelný pětiúhelník (obr. 141):
Úsečku o délce rovné poloměru r rozdělíme zlatym řezem a její větší část
naneseme ke kružnici s poloměrem r desetkrát za sebou jako tětivu a dostá-
váme pravidelný desetiúhelník.
Pravidelný pětiúhelník vznikne tak, že spojíme pět nesousedních vrcholů
pravidelného desetiúhelníku. Z pravidelného desetiúhelníku postupně pomocí
os stran dostaneme 20-úhelník, 40-úhelník, ..., tj. obecně (5 . 2 n )-úhelník (n E N).
r
2
Obr. 141. Pravidelný desetiúhelník
a pětiúhelník
Přibližná konstrukce libovolného pravidelného n-úhelníku
(obr. 142)
Daný prvek: poloměr r opsané kružnice
Sestrojíme dva navzájem kolmé průměry AB a CD kružnice k s daným
poloměrem r. Jeden z těchto průměrů (v obr. 142 je to průměr AB) rozdělíme
327
pak na n stejných dílů (v obrázku 142 je n = 11) a kolem jednoho z krajnlch
bodů tohoto průměru (v obrázku Je to bod A) opíšeme kružnici I s polo-
měrem 2r, která obě prodloužení dl 'ůhého p.4ůměru protne v bodech E a F.
[
A
Obr 142. Přibližná konstrukce
pravidelného n úhelníku
Z bodů E a F vedeme polopřímky dělicími body prvního průměru AB, přičemž
postupně vždy vynecháme jeden dělIcí bod, a v jejich průsečících s opsanou
kružnicí k dostaneme vrcholy n-úhelníku.
3.2.4. Kružnice a kruh
..
Kružnicí k se středem S.lc a poloměrem r nazýváme množinu právě těch
bodů, které mají stejnou vzdálenost r od pevného bodu Sk' zvaného střed
kružnice k.
Poloměrem kružnice podle souvislosti nazýváme jednak každou úsečku,
jejímž jedním krajním bodem je střed kružnice a druhým krajním bodem
je libovolný bod této kružnice, jednak délku této úsečky. Podle potřeby lze
však mluvit o délce poloměru. Obdobně průměrem kružnice nazýváme jednak
každou tětivu kružnice, která obsahuje střed této kružnice, jednak délku
této tětivy. Podle potřeby lze též mluvit o délce průměru.
Kruhem k se středem Sk a poloměrem r nazýváme množinu právě těch bodů,
které mají od pevného bodu Sk (zvaného střed kruhu k) vzdiÍlenost nejvýše
rovnou číslu r.
Obloukem kružnice nazýváme souvislou část kružnice ohraničenou dvěma
jejími body.
Kruhovou výsečí nazýváme průnik kruhu a úhlu s vrcholem ve středu kruhu.
328
O=l1uČ'ellí:
r - po)oměr,
d - pr-: 1 měr.
Velikost o bvo dového úhl u (obr. 143) se rovná polovině velikosti
středově-ho úhlu příslušného k témuž oblouku kružnice.
Thaletova věta
Obvodový úhel nad průměrem je pravý, tj. jeho velikost je 90° = in rad
(obr. 144). .
Velikost úsekového úhlu (obr. 145) se rovná polovině velikosti stře-
dového úhlu příslušného k témuž oblouku kružnice, takže se rovná velikosti
obvodového úhlu příslušného k témuž oblouku kružnice.
(Mocnost bodu ke kružnici viz na str. 304 a 305.) ,
Obr. 143. ,Obvodový
a středový úhel
Obr. 144. Obvodový úhel
nad prů měrem
Obr. 145. Úsekový úhel
Délka kružnice [obvod kruhu]
o = 2nr = nd.
Délka oblouku kružnice (obr. 146)
nrrl ndrx
[ = - = - = r arc rx 0,017 453rrx,
180 360
..
kde rx je velikost příslušného středového úhlu v stupňové míře;
I J(t 2 + 13 V2),
kde t je délka příslušné tětivy,
v - výška příslušné kruhové úseče.
Těžiště T kružnicového oblouku délky [leží na ose příslušného středového
úhlu ve vzdálenosti rt II od střed u kružnice, na níž oblouk leží, přičemž t
je délka tětivy příslušné k danému oblouku kružnice.
329
Obsah kruhu
1td 2
S = 1tr 2 = -.
4
Těžiště T kruhu leží ve středu kruhu.
I
l
Obr. 146. Kruhová výseč
Obsah kruhové výseče (viz obr. 146)
1tr2 1 2 Ir
S = - ="2r arc rJ.. = -,
360 2
kde I je délka příslušného oblouku kružnice,
rJ.. - velikost příslušného středového úhlu v stupňové míře.
Těžiště T kruhové výseče leží na ose souměrnosti dané kruhové. výseče
ve vzdálenosti trtll od středu Sk příslušné kružnice k, přičemž I je délka pro'
oblouku a t délka tětivy příslušného oblouku kružnice.
3.2.5. Kruhová úseč
Kruhovou úsečí nazýváme průnik kruhu a poloroviny, jejíž hraniční
přímka má od středu kruhu vzdálenost menší než jeho poloměr.
Označení (obr. 147):
t - délka tětivy AB,
v - výška kruhové úseče,
I - d.élka příslušného oblouku kružnice,
rJ.. - velikost příslušného středového úhlu v stupňové míře.
Platí
t = 2 J(2vr - v 2 ) = 2r sin-,
2
v = r - tJ(4r 2 - t 2 ) = tttg-
4
pro konvexní středový úhel.
330
I
l
"
Obr. 147. Kruhová úseč
Obsah kruhové úseče
Obsah kruhové úseče se rovná rozdílu obsahu kruhové výseče a obsahu
trojúhelníku ASkB, tj.
S = t[lr ,- t(r - v)] = tr 2 C - sin (x).
Těžiště T kruhové úseče leží na ose souměrnosti dané kruhové výseče
ve vzdálenosti
rJ..
4r sin 3 -
2
12S ( o1trJ.. )
3 - - sin rJ..
180
od středu Sk příslušné kružnice.
t 3
1
3.2.6. Mezikrufí
Mezikružím nazýváme množinu právě těch bodů, které mají o
pevného bodu Sk' zvaného střed mezikruží, vzdálenost aspoň r a nejvýše R.
Označení (obr. 148):
R, resp. r - vnější, resp. vnitřní poloměr mezikruží (R > r),
D, resp. d - vnější, resp. -vnitřní průměr mezikruží (D > d),
rs = !(R + r) - poloměr střední kružnice mezikruží,
b = R - r - šířka mezikruží.
Obsah mezikruží
S = 1t(R 2 - r 2 ) = !1t(D2 - ( 2 ) = 21tr s l5 (r < R).
Těžiště mezikruží leží ve středu Sk příslušných kružnic k 1 a k 2 .
331
Výsečí mezikruží nazýváme průnik mezikruží a úhlu s vrcholem ve středu
mezikruží.
d
O
Obr. 148. Mezikruží
,I
Obr. 149. Výseč mezikruží
Obsah výseče mezikruží (obr. 149)
1t
S = 360 (R 2 - r 2 ) = r/) are ()( ,
kde je velikost příslušného středového úhlu v stupňové míře.
Těžiště T výseče mezikruží leží na ose souměrnosti dané výseče mezikruží
ve vzdálenosti
.
Sln-
4 R 3 - r 3 2
3 R 2 - r 2 1t
180
od středu Sk příslušných kružnic k 1 a k 2 , přičemž (X je velikost příslušného
středového úhlu v stupňové míře.
3.2.7. Elipsa, hyperbola a parabola
3.2.7.1. Elipsa
Definici elipsy viz v článku 4.1.6.
Délka elipsy
o 1t[1,5(a + b) - J(ab)],
64 - 31 4
o 1t( a + b) 2 '
64 - 161
a-b
kde 1 = .
a+b
332
Obsah (uzavřené) vnitřní oblasti elipsy
s = 1tab,
kde a, resp. b je délka hlavní, resp. vedlejší poloosy elipsy.
Těžiště T (uzavřené) vnitřní oblasti elipsy leží ve středu Se elipsy e.
Obsah výseče OMN (uzavřené) vnitřní oblasti elipsy
[o bsah eli ptic ké výseče] (obr. t 50)
Při konvexním úhlu MON a MN .1 AR platí
a v
S = - S' = ab arccos -,
b a
kde S' je obsah příslušné kruhové výseče OM ' N',
v - výška trojúhelníku OMN ke straně MN.
A
B x
x
c
Obr. 150. Eliptická výseč
Obr. 151. Hyperbolická úseč
3.2.7.2. Hyperbola
Definici hyperboly viz v článku 4.1.7.
Obsah hyperbolické úseče (obr. 151)
I
( a+v h )
S = (a + v) h - ab ln a + b '
kde a, resp. b je délka hlavní, resp. vedlejší poloosy hyperboly,
\
2h - délka tětivy M N,
v - výška úseče.
333
3.2.7.3. Parabola
Definici paraboly viz v článku 4.1.5.
Délka oblouku BVE paraboly (obr. 152)
/
c 2 { 4h 1 }
1 = !-J[c 2 + (4h)2] + -ln - + -J[(c 2 + (4h)2] ,
8h c c
1 C[l + GY - 3 s 2 Cr J
pro malé číslo hlc. Význam znaků je zřejmý z obr. 152.
I
I
I
O =v
x
c
2
Obr. 152. Parabolická úseč
Obsah parabolické úseče
S = 1.tv sin rJ..
, 3 ,
takže se rovná dvěma třetinám obsahu rovnoběžníku ABCD.
Těžiště T parabolické úseče BVE leží na ose paraboly ve vzdálenosti 3hj5
od vrcholu V paraboly.
3.3. STEREOMETRIE
Označeni:
V - objem,
P - obsáh povrchu,
Q - obsah pláště,
S - obsah (dolní) pod stavy,
Sl - obsah horní podstavy,
v r - výška,
Ut - délka tělesové úhlopříčky.
334
3.3.1. Obecné věty
Cavalieriův princip
Tělesa se stejně velkými podstavami a výškami mají tyž objem, jestliže
jejich řezy rovnoběžné s podstavou a vedené ve stejné vzdálenosti od podstavy
mají stejný obsah.
Simpsonovo pravidlo
Jestliže těleso má právě dvě rovnoběžné podstavy a každý s nimi rovno-
běžný řez, vedený ve výšce x, má takový obsah, že je hodnotou celé racionální
funkce nejvýše třetího stupně v proměnné x, pak platí
V = iv(S + Sl + 4S s )'
kde Ss je obsah středního řezu.
Guldinova pravidla
Objem V rotačního tělesa, které vznikne při rotaci rovinného (tvořícího>
obrazce U kolem osy, která leží v téže rovině jako obrazec U a neprotíná
obrazec U, se rovná součinu obsahu S obrazce U a délky kružnice opsané
těžištěm obrazce U, tj.
V = 21tYTS = 21tS x ,
kde S je obsab tvořícího obrazce,
YT - vzdálenost těžiště T od osy x otáčení,
Sx - statický moment vzhledem k ose x.
Obsah Q pláště rotačního tělesa, které vznikne při rotaci rovinné rektifikace
schopné (tvořící> křivky k kolem osy o, která leží v téže rovině jako křivka k
a neprotíná křivku k, se rovná součinu délky křivky k a délky kružnice opsané
těžištěm křivky k, tj.
Q = 21tYT 1 ,
kde 1 je délka tvořící křivky,
YT - vzdálenost těžiště T od osy otáčenÍ.
3.3.2. Mnohostěny
n-stěn (n E {n E Nin > 4} ) [obecně mnohostěn, polyedr] je těleso,
jehož hranice je takovým sjednocením n hraničních mnohoúhelníků, že strana
každého z nich je zároveň stranou jiného mnohoúhelníku, přičemž žádné dva
335
mnohoúhelníky neleží v téže rovině. Každý z mnohoúnelníků, jejichž sjed-
nocením je hranice n-stěnu, se nazývá stěna n-stěnu. Strany stěn se nazývají
hran y n-st ěnu.
Eulerova věta o mnohostěnech
Jestliže mnohostěn je konvexní, platí
e + .f - h = 2,
kde e je počet vrcholů,
f - počet stěn,
h - počet hran.
Kolmý a kosý hrano I (obr. 153)
n-bokým hranolem [stručně hranolem] nazýváme (n + 2)-stěn, který je prů-
nikem n-bokého hranolového prostoru a vrstvy určené rovinami, které nejsou
rovnoběžné s hranami tohoto hranolového prostoru. Tloušťku této vrstvy
nazýváme výškou hranolu.
"
Obr. 153. Kosý hranol
Mnohoúhelníky, které jsou průniky hraničních rovin vrstvy a hranolového
prostoru, se nazývají podstavy [podstavné stěny] hranolu. Všechny stěny
.
hranolu, které nejsou jeho podstavami, se nazývají boční stěny.
Pláštěm hranolu nazýváme sjednocení všech jeho bočních stěn. Povrchem
hranolu nazýváme sjednocení všech jeho stěn.
Strany pod stavy hranolu se nazývají podstavné hrany, ostatní hrany se na-
zývají boční hrany.
Kolmým hrano/em nazýváme hranol, jehož boční hrany jsou kolmé na rovinu
podstavy. Hranol, který není kolmý, se nazývá kosý.
N ormálovým řezem hranolu nazýváme neprázdný řez hranolu rovInou
kolmou k jeho bočním hranám a protínající všechny boční hrany.
336
Platí
v = Sv = Na,
P=Q+2S,
kde N je obsah normálového řezu hrano lem,
a - délka boční hrany.
Těži. tě T hranolu leží ve středu úsečky spojující tě iště dolní a horní
podsta vy.
Rovnoběžnostěnem nazýváme čtyřboký hranol, jehož podstavou je
rovnoběžník.
K vádr (obr. 154)
Kvádrem nazýváme kolmý hranol, jehož podstavou je pravoúhelník.
Platí
v = abc,
P = 2(ab + ac + bc),
Ut = J(a 2 + b 2 + c 2 ).
Těžiště T kvádru leží v průsečíku tělesových úhlopříček.
"" c
I u-y""
L ____
/""
L,/ b
. a
a
Obr. 154. Kvádr s rozměry a, b, C
Obr. 155. Krychle s hranou délky a
Krychle (obr. 155)
Krychlí [hexaedrem] nazýváme kolmý hranol, jehož všechny stěny jsou
čtverce.
Platí
v = a 3
,
P = 6a 2 ,
u t =aJ3.
Těžiště T krychle leží v průsečíku tělesových úhlopříček.
337
Trojboký kolmý hranoI
seříznutý rovinou nerovnoběžnou s rovInou podstavy (obr. 156)
V=S. a+b+c .
3
Trojboký kosý hranol
seříznutý rovinou nerovnoběžnou s .rovlnou podstavy (obr. 157)
a+b+c
V=N. ,
3
kde N je obsah normálového řezu hranolem.
Při seříznutí trojbokého kolmého hranolu rovinou nerovnoběžnou s ro-
vinou podstavy se obsah N normálového řezu hranolem rovná obsahu S
dolní podstavy.
a b c
Obr. 156. Trojboký kolmý hranol
seříznutý rovinou nerovnobčžnou
s rovinou podsta vy
Obr. 157. Trojboký kosý hranol
seříznutý rovinou nerovnoběžn u
s rovinou podstavy
n-boký kolmý hrano I
seříznutý rovinou nerovnoběžnou s rovInou podstavy
V = Nt,
kde t je vzdálenost těžišť dolní a horní podstavy,
N - obsah rovinného řezu kolmého ke spojnici těžišť horní a dolní
podstavy.
Jehlan (kolmý a kosý) (obr. 158)
n-bokým jehlanem [stručně jehlanem] nazýváme (n + 1 )-stěn, který je prů-
nikem n-bokého jehlanového prostoru a vrstvy, jejíž jedna hraniční rovina
338
má s jehlanovým prostorem společJJÝ jen vrchol jehlanového prostoru (tzv.
hlavní vrchol jehlanu). l'loušťku této vrstvy nazýváme výškou jehlanu.
Mnohoúhelník, který je řezem jehlanu tou hraniční rovinou vrstvy, která
neprochází vrcholem jehlanového prostoru, nazýváme podstavou jehlanu.
Všechny stěny jehlanu, které nejsou jeho podstavou, se nazývají boční stěny.
Obr. 158. Jehlan
Pláštěm jehlanu nazýváme sjednocení všech jeho bočních stěn. Povrchem
jehlanu nazýváme sjednocení všech jeho stěn.,
Kolmým jehlanem nazýváme takový jehlan, že řídicí n-úhelník má střed
souměrnosti a přímka určená tímto středem a vrcholem jehlanového prostoru
je kolmá na rovinu podstavy. Jehlan, který není kolmý, se nazývá kosrÍ'.
Platí
v = tSv,
P = S + Q.
Těžiště T jehlanu leží na úsečce spojující hlavní vrchol s těžištěm podstavy
a od podstavy má vzdálenost v/4.
Trojboký jehlan [čtyřstěn]
Jestliže [xi, YI, Zl]' [X2, Y2' Z2] a [X3, Y3, Z3] jsou vrcholy pod stavy troj-
bokého jehlanu a hlavní vrchol leží v počátku souřadnicové soustavy, platí
V =! Xl' Yl, Zl
X2, Y2, Z2
X3, Y3' Z3
(ve vzorci jde o absolutní hodnotu determinantu).
Komolý jehlan (obr. 159)
. Komolým jehlanem nazýváme průnik jehlanu a vrstvy určené rovinou pod-
stavy a rovinou s ní rovnoběžnou, která má s jehlanem společné aspoň dva
body. Tloušťku této vrstvy nazýváme výškou komolého jehlanu.
339
Platí
v = tv[S + J(SSl) + Sl]'
P = S + Sl + Q,
kde S, resp. S 1 je obsah do ní. resp. horní podstavy.
Obr, 159. Komolý jehlan
Těžiště T komolého jehlanu leží na úsečce spojující těžiště dolní a horní
pod stavy a má od dolní (tj. větší) pod stavy vzdálenost
/
v S + 2.J(SSl) + 3S 1
4 S + (SSl) + Sl ·
Přibližný vzorec pro objem komolého jehlanu
S + Sl
V v.
2
Vzorec dává dobré přibližné hodnoty, jestliže se obsahy S a Sl podstav málo
liší. I
Pět pravidelných mnohostěnů
o značení:
a - délka hrany,
r - poloměr opsané kulové plochy,
(l - poloměr vepsané kulové plochy.
Pravidelným n-stěnem [obecně pravidelným mnohostěnem] nazýváme kon-
vexní n-stěn, jehož všechny stěny jsou shodné pravidelné mnohoúhelníky.
V každém jeho vrcholu se sbíhá stejný počet hran, přičemž všechny vrcholy
leží na téže kulové ploše. Existuje prá vě pět pravidelných mnohostěnů.
340
Pravidelný čtyř stěn [tetraedr]
(je ohraničen 4 rovnostrannými trojúhelníky) (obr. 160)
a 3 J2 t
V = = - Xl' YI, =1
12 6
, X2' Y2, Z2
X3, Y3, Z3
(výklad označení viz u trojbokého jehlanu; ve vzorci jde o absolutní hodnotu
determinan tu),
P=a 2 J3,
a
r. = 4: ..)6,
a
U = -J6.
12
Těžiště T tetraedru leží na výšce ve vzdálenosti v/4 od podstavy.
Q
Obr. 160. Pravidelný čtyřstěn
Obr. 161. Pravidelný osmístěn
Obr, 162, Pra \ ideln}'
dvacetistěn
Pravidelný osmistěn [oktaedr]
(je ohraničen 8 rovnostrannými trojúhelníky) (obr. 1(1)
a 3 J2
V=
3 '
a
r = - /2
2 V '
P ::; 2a 2 J3,
a
(! = - J6
6 ·
Těžiště T oktaedru leží. v průsečíku úhlopříček společného základního
čtverce.
Pravidelný dvaceti stěn [ikosaedr]
(je ohraničen 20 rovnostrannými trojúhelníky) (obr. 162)
5a 3 (3 + J5)
v=
12 '
a
r = - J[2(5 + J5)],
4
P = 5a 2 J3,
(l -
a(J3) (3 + J5)
12
341
Krychle [hexaedr] (je ohraničena 6 čtverci)
V = a 3 , P = 6a 2 ,
a
r = - /3
2 V '
a
n -
- 2'
Těži. tě T krychle leží v průsečíku tělesových úhlopříček.
Pravidelný dvanáctistěn [dodekaedr]
(je ohraničen 12 pravidelnými pětiúhelníky (obr. 163)
V = .a 3 (15 : 7 J5) , P = 3a 2 J[5(5 + 2 J5)] ,
a(J3)(1 + J3) aJ[10(25 + 11 J5)]
4 (l = 20 .
r -
o
Obr. 163. Pravidelný dvanácti stěn
Prismatoid
Prismatoidem nazýváme každé těleso, které má přímé hrany a je ohraničeno
rovinnými mnohoúhelníky, přičemž všechny jeho vrcholy a obě podstavy leží
ve dvou rovnoběžných rovinách. Boční stěny mohou být trojúhelníky nebo
lichoběžníky. (Objem prismatoidu lze vypočítat pomocí Simpsonova pravidla
ze str. 335.)
Prismatoid, jehož podstavy mají týž počet hran a boční stěny jsou jen
lichoběžníky, se nazývá obelisk. Obelisk, jehož podstavami jsou podobné
mnohoúhelníky, je komolým jehlanem. Obelisk, jehož podstavami jsou
obdélníky, se nazývá hranolec. Zvlášt ím případem prismatoidu je klín,
což je těleso, jehož dolní podstava je mnohoúhelníkem, horní podstava se re-
dukuje na úsečku rovnoběžnou s rovinou dolní podstavy a boční stěny jsou
trojúhelníky, lichoběžníky nebo rovnoběžníky.
342
Hranolec (obr. 164)
Podstavami uvažovaného hranolce jsou nepodobné obdélníky s rozměry
a, b a a I' b I' ležící v rovnoběžných rovinách majících vzdálenost v, přičemž
protější boční stěny mají stejné odchylky od pod stavy, ale neprotínají se
v právě jednom bodě.
Platí
v = i-v[(2a + a l ) b + (2al + a) b l ] =
= i-v[ ab + (a + a I) (b + b I) + a I b I)] .
Vzdálenost těžiště T hranolce od dolní (tj. větší) podstavy s rozměry a, b
se rovná
v ab + ab l + alb + 3a 1 b.
2 2ab + ab l + alb + 2a l b.
v
v
a
a
Obr. 164. Hranolec
Obr. 165. Klín
Klín s obdélníkovou podstavou (obr. 165)
Dolní podstavou uvažovaného klínu je obdélník s rozměry a, b, kdežto
horní podstava je redukována na úsečku délky al rovnoběžnou s rovinou
dolní podst vy ležící ve vzdálenosti v. Jednu dvojici protějších bočních stěn
tvoří shodné rovnoramenné trojúhelníky a druhou dvojici bočních stěn tvoří
shodné rovnoramenné lichoběžníky.
Platí
v = ibv(2a + a l ).
Těžiště T klínu leží na úsečce spojující střed horní hrany a střed podstavy
s rozměry a, b a má od této pod stavy vzdálenost
v a + a l
2 2a + al
343
3.3.3. Oblá tělesa a jejich části
o značení:
r - poloměr,
li - průměr.
Kosý a kolmý válec
Válcem (resp. pláštěm válce) nazýváme průnik válcového prostoru (resp.
hranice válcového prostoru) a vrstvy, jejíž hraniční roviny nejsou rovnoběžné
s tvořícími přímkami válcového prostoru. Tloušťku této vrstvy nazýváme
vý. kou válce.
Řezy válcového prostoru hraničními rovinami vrstvy ,se nazývají podstavy
vá lce.
Povrchem válce nazýváme sjednocení pláště vá1ce a obou jeho podstav.
Stranou válce nazýváme část tvořící' přímky na plášti válce.
Kolmým válceln nazýváme válec, jehož strany jsou kolmé na roviny jeho
podstav. Válec, který není kolmý, se nazývá kosý.
N ormálovýln řezem válce nazýváme neprázdný řez válce rovinou kolmou
k jeho stranám a protínající všechny strany válce.
Platí
V = Sv,
Q = os,
kde S je obsah pod stavy válce,
v - výška válce,
o - obvod normálového řezu válce rovinou,
s - délka strany válce.
Rotační válec [kolmý kruhový válec] (obr. 166)
Kruhovým válcem nazýváme válec, jehož podstavami jsou kruhy. Kolmý
kruhový válec nazýváme rota ním válcem.
v
Obr. 166. Rotační válec
344
Platí
1td 2
V = 1tr 2 v = - v
4 '
Q = 21trv = 1tt/v,
P = 21tr(r + v) = 1td(td + v),
kde v je výška rotačního válce.
Těži. tě T rotačního válce leží na ose válce ve vzdálenosti vl2 od pod stavy,
tj. leží ve středu úsečky spojující těžiště obol! pod stav válce.
Rotačn i válec seříznutý rovinou nerovnoběžnou s rOVInou
podstavy a neprotínající podstavu (obr. 167)
1tr 2 1td 2
V = -(Sl + S2) = -(Sl + S2)'
2 8
1td
Q = 1tr( S I + S2) = - (Sl + S2)'
2
P = r{sl + S2 + r + J[r2 + CI S2Y J},
kde s 1 resp. S2 je největší, resp. nejmenší z délek stran válce.
$2
--
.......,
fP ')
/
",
Sf
Obr. 167. Rotační válec seříznutý
rovinou nerovno běžnou s podsta vou
Obr. 16X. Úsek rotačního válce
Těži. tě T šikmo seříznutého rotačního válce leží na ose válce a má od dolní
podstavy vzdálenost
S + s 1 r 2 t g 2 a
1 2 + _ ,
4 4 Sl + S2
.
kde a je odchylka roviny horní pod stavy od roviny dolní pod stavy.
345
Rotační válec seříznutý rovinou nerovnoběžnou s rovinou
pods ta vy a protí naj ící dolní podsta vu [úsek rotačního válce,
v á I c o v Ý k I í n, v á I c o v é k op y to] (obr. 168)
V = [ a(3r 2 - a 2 ) + 3r 2 (b - r) qJ ] ,
3b 2
Q = 2;V [(b - r) + a 1
kde qJ je velikost středového úhlu v obloukové míře, příslušného průsečnici
s podstavou,
2a - délka přímé hrany válcového klínu,
v - největší/, z délek stran pláště válcového klínu,
b - vzdálenost průsečíku nejdelší strany pláště válcového klínu s pod-
stavou od přímky obsahující přímou hranu válcového klínu.
Pro cp = 1t je a = b = r a platí
V = tr 2 v,
Q = 2rv = dv.
Dutý rotační válec [rotační válcová trubice] (obr. 169)
V = 1tV(R2 - r 2 ) = i1tv(D2 - d 2 ) = 1tav(2R - b) =
/ = 1tav(2 + b) = 21tr s bv,
Q = 21tv(R + r),
P = 21t(R + r) (v + R - r),
kde R, resp. r je vnější, Jresp. vnitřní poloměr,
D, resp. d - vnější, resp. vnitřní průměr,
b = R - r - tloušťka trubice,
rs = -MR + r) - střední poloměr.
Těžiště T rotační válcové trubice leží na ose trubice a má od podstávy
vzdálenost v12.
K užel (obr. 170)
Kuželem (resp. pláštěm kužele) nazýváme průnik kuželového prostoru
(resp. hranice kuželového prostoru) a vrstvy, jejíž jedna hraniční rovina má
s kuželovým prostorem společný jen vrchol kuželového prostoru. Tloušťku
této vrstvy nazýváme výškou kužele.
Řez kužele tou hraniční rovinou vrstvy, která neprochází vrcholem kuželo-
vého prostoru, nazýváme podstavou kužele.
346
Povrchem kužele nazýváme sjednocení pláště kužele a jeho podstavy.
Stranou kužele nazýváme část tv'ořící přímky na plášti kužele.
Platí
v = tSv,
kde S je obsah podstavy kužele,
v - výška kužele.
f
v
v
V
1---- --7
/"-.../ '
i . "\, /
",/ /
/
/
/
/
Obr. 169. Dutý rotační válec
Obr. 170. Kužel
.
Těžiště T kužele leží na úsečce spojující vrchol kužele s těžištěm podstavy
a má od podstavy vzdálenost v/4.
v
-1
_I
v
r
Obr. 171. Komolý kužel
Obr. 172. Rotační kužel
Komolý kužel (obr.I7!)
Komolým kuželem nazýváme průnik kužele a vrstvy určené rovinou podstavy
a rovinou s ní rovnoběžnou, která má s kuželem společné aspoň dva různé
body. Tloušťku této vrstvy nazýváme výškou komolého kužele.
347
Platí
..
v = 1V[Sl + S2 + J(SlS2)]'
kde Sl' resp. S2 je obsah dolní, resp. horní podstavy,
v - výška komolého kužele.
Rotační kužel [kolmý kruhový kužel] (obr. 172)
Kruhov.vm,kuželem nazýváme kužel, jehož podstávou ie kruh.
Rotačním kuželem [kolmým kruhovým kuželem] naz'ýváme kruhový kužel,
jehož vrchol leží na kolmici jdou í středem podstavy na rovinu podstavy.
Kruhový kužel, který není rotační, se nazývá kosý.
Platí
v = t1tr 2 v = /2 1td2V, 0,261 8d 2 v,
Q = 1trs = 11tds,
p = 1tr(r + s),
kde s = J(r 2 + v 2 ) je délka strany rotačního kužele,
v - výška rotačního kužele.
Těžiště T rotačního kužele leží a ose kužele a má od podstavy vzdálenost v/4.
Komolý rotační kužel (obr. 173)
V = t1tv(R 2 + Rr + r 2 ) = /2 1tv(D2 + Dd + d 2 ),
Q = 1ts(R.+ r) = 11ts(D + d),
P = 1t[R 2 + r 2 + s(R + r)] = !n[D 2 + d 2 + 2s(D + d)],
kde r, resp. R je poloměr menší" resp. větší podstavy,
d, resp. D - průměr menší, resp. větší podstavy,
v - výška komolého rotačního kužele a
s = J[v 2 + (R - r)2] = 1J[4v 2 + (D - d)2]
je délka strany rotačního komolého kužele.
r
R
Obr. 173. Komolý rotační kužel
348
Těži. tě Tkomolého rotačního kužele leží na ose tohoto kužele a má od dolní
(tj. větší) pod stavy vzdálenost
v R 2 + 2Rr + 3r 2
4 R 2 + Rr + r 2 .
Přibližné vzorce pro objem komolého kužele
V t1tv(R 2 + r 2 ) = t 1tV (D 2 + d 2 )
(vzorec dává dobré přibližné hodnoty, jestliže se hodnoty R a r málo liší),
V v(R + r)2 = /6 1tv(D + d)2,
V "'" 1t 2 - 1. 1tvd 2
"'" vr s - 4 s ,
kd R + r. I d ' h '"
e rs = Je po omer stre nI o rezu,
2
d D + d o", t '" d ' h
s = 2 - prumer s re nI o rezu.
Obr. 174. Koule
Obr. 175. Kulová úseč
Koule (obr. 174)
Koulí (resp. povrchem koule [kulotou plochou,- sférou]) se středem S a polo-
měrem r nazýváme množinu právě těch bodů, jejichž vzdálenost od bodu S
se rovná nejvýše číslu r (resp. právě číslu r).
Platí
1 J P3
V = k r 3 = - - 4188 8r 3
.1"" 6 1t ' ,
P = 41tr 2 = 1td 2 = V(361tV 2 ) 12,566r 2 ,
1 J p /3 V
r = 2: 1t = 4 '
J p _/3 V
d = 1t = 2 41t .
Těžiště T koule leží ve středu koule.
V = !M 3 0,5236d 3 ,
349
Kulová úseč a kulový vrchlík (obr. !'5)
Kulovou úseči nazýváme průnik koule a poloprostoru, jehož hraniční
rovina protíná kouli v kruhu; tento kruh nazýváme podstavou úseče.
Kulovým vrchlíkem nazýváme průnik kulové plochy a poloprostoru, jehož
hraniční rovina protíná kulovou plochu v kružnici.
Platí
v = -btv(3g. 2 + v 2 ) = tTtv 2 (3r - v) = -btv 2 (3d - 2v),
Q = 27trv = 1tdv = 1t(Q2 + v 2 ) (obsah kulového vrchlíku),
P = 1t(2rv + (2) = 1t(v 2 + 2 ( 2) = 1tv(4r - v),
kde Q = J[ v(2r - v] je poloměr podstavy kulové úseče,
v - výška kulové ús če.
Těžiště T kulové úseče leží na ose souměrnosti kulové úseče a má od středu
koule vzdálenost
3 (2, - V)2
4 3r - v '
v
Obr. 176. Kulová výseč
Obr. 177. Kulová vrstva
Kulová výseč (obr. 176)
Kulovou výsečí nazýváme průnik koule a prostorového úhlu s vrcholem
ve středu koule.
Platí
21tr 2 v
V = ' 2,0944r 2 v,
3
P = 1tr(2v + Q),
kde v je výška příslušné kulové úseče,
Q - poloměr pod stavy příslušné kulové úseče.
Těžiště T kulové výseče leží na ose souměrnosti kulové výseče a má od
středu koule vzdálenost
i(2r - v).
1td 2V
V = - 0,523 6d 2 v,
6
350
Kulová vrstva a kulový pás (obr. 177)
Kulovou vrstvou (resp. kulovým pásem) nazýváme průnik koule (resp. kulové
plochy) se středem S a poloměrem r a vrstvy určené dvěma rovnoběžnými
rovinami, jejichž vzdálenosti od středu S jsou al a a2 (O < a 1 < a2 < r).
Platí
v = -btv(3Qf + 3Q + v 2 ),
Q = 21trv = 1tdv (obsah kulového pásu),
P = 1t(2rv + Qi + Q ) = 1t(dv + (li + Q ),
kde Ql' Q2 jsou poloměry kruhových podstav,
v - výška kulové vrstvy, popř. kulového pásu (v = a2 + a 1)'
Platí
( 2 2 2 ) 2
2 _ 2 + e. - e2 - v
r - Ql
2v
(Q2 < Ql)'
Jestliže Ql = r, pak
V = 1tv(r 2 - tv 2 ).
P2
v
" /'
b) ""'---.........
P4
a)
Obr. 178. Prstenec
Prs tenec (obr. 178)
Prstencem nazýváme (množinový) rozdíl kulové vrstvy a vepsaného
rotačního komolého kužele (popř. rotačního válce).
Jestliže Vľ je objem rotačního komolého kužele (popř. rotačního válce)
vepsaného do kulové vrstvy a s délka strany vepsaného rotačního komolého
kužele (popř. rotačního válce), pak pro objem V p prstence platí
= V - ,V 1 = -btvs 2 ,
kde V je objem kulové vrstvy.
351
K úlový kl ín a sférický d voj úhelník (obr. 179)
Kulovým klínem, resp. sférickým dvojúhelníkem nazýváme průnik koule,
resp. kulové plochy a klínového prostoru, jehož hrana prochází středem koule.
Platí (Q je obsah sférického dvojúhelníku)
P = nr 2 + Q,
kde je odchylka hraničních rovin klínového prostoru v stupňové míře.
Obr. 179. Kulový klín
a sférický dvojúhelník
Platí
, xr3
V = *r 3 arc = - 0 , 011 636r3 ,
oJ . 270
xr2
Q = 2r 2 arc = - 0,034 907r2
90
, P2
Obr. 180. Sférický
trojúhelník
Obr. 181. Rotační
paraboloid
Obr. 182. Vrstva rotačního
paraboloidu
352
Sférický trojúhelník (obr. 180)
1tr 2 [-;
s-
- 180 '
kde G = C( + B + " - 180 0 je sfé!"ický exces [nadbytek] sférického troj-
úhelníku, přičemž Ct, tJ, " jsou velikosti úhlů sférického trojúhelníku (v stup-
ňové míře).
Rotační paraboloid (obr. 181)
Rotačnín1 parabolo;denl v tomto článku nazýváme těleso ohraničené plochou
vzniklou při rotaci části paraboly s jejím vrcholem kolem její, osy a kruhem,
jehož rovina je kolmá k ose rotace paraboly á protíná osu paraboly.
Platí
v . !1tg 2 z: 1,570 796Q 2 v,
21t
Q = 3q [Jk)2 + q2)3 - q3],
kde Q je poloměr kruhové podstavy,
r - výška,
q = (l2/( 2r).
Těži. tě T rotačního paraboloidu leží na jeho ose a ,má od vrcholu para-
boloidu vzdálenost 2r /3.
Vrstva rotačního paraboloidu [komolý rotační paraboloid]
(obr. 182)
V = !1tv(Qf + Q ),
kde (lI' Q2 jsou poloměry kruhových podstav v rovnoběžných rovinách,
z: - výška vrstvy rotačního paraboloidu.
z
Obr. 183. Trojosý elipsoid
Trojosý elipsoid (obr. 183)
Trojos.vm elipsoidem v tomto článku nazýváme těleso ohraničené plochou
definovanou v odstavci 4.2.5.2.
353
Platí
v = 11tahc,
2 21t b [ 2 ( ( 2 - 2 ) ( )]
P = 21tc + ,J(a 2 _ c 2 ) c F k, Ip) + a - c E k, Ip ,
kde a, b, c (a > b > c) jsou délky poloos elipsoidu,
F(k, Ip) = r'l' ,J( d . 2 ) (eliptický integrál prvního druhu),
Jo 1 - k sIn t/J
E(k, Ip) = 1'1' ,J(l - e sin t/J) dt/J (eliptický integrál druhého druhu),
b
qJ = arccos - ,
a
k _ _ a J b 2 - c 2
(modul integrálů F a E).
b a 2 - c 2
Rotační protáhlý elipsoid
\
Rotačním protáhlým elipsoidem v tomto článku nazýváme těleso ohraničené
plochou vytvořenou při rotaci elipsy s poloosami délek a, b (a > b) kolem
hlavní osy (obr. 184).
z
-
y
--
y
Obr. 184. Rotační protáhlý elipsoid
Obr. 185. Rotační zploštělý elipsoid
Platí
v = 17tab2,
( , arcsln B )
p , 27t b- + ab B '
P 2(J2) 7tb J(a 2 + b 2 ),
kd J(a2 - b 2 ). o I , , ..., d I .
e B = Je cIse na vystre no st e IPSY.
a
354
Rotační zploštělý elipsoid
Rotačním zplo. tělÝI11 elipsoiden1 [L réroidem] v tomto článku nazýváme
těleso ohraničené plochou vytvořenou při rotaci elipsy s poloosami délek
a, b (a > b) kolem vedlejší osy (obr. t 85).
Platí
v = 11ta2h
( , b 2 t + D )
P = 21t a-, + ln ---
_t 1 - 8
kde
I; -
J(a 2 - b 2 )
a
je číselná výstřednost elipsy.
Rotační jednodílný hyperboloid
Rotačním jednodibl.}Jm hyperbolo;dem v tomto článku nazyvame těleso
ohraničené plochou vytvořenou při rotaci hyperboly s poloosami' délek a, b
(a > b) kolem vedlejší osy a dvěma shodnými kruhy, jejichž roviny jsou kolmé
k ose rotace hyperboly (obr. 186).
Obr. 186. Jednodílný rotační
hypcrboloid
Obr. ] X7. Dvojdílný rotační
hypcrboloid
Pla tí
v = {-1tv(2a 2 + Q2),
kde.v je výška,
a - délka hlavní poloosy tvořící hyperboly,
(l - poloměr shodných kruhových podst v v rovnoběžných rovinách.
355
Rotační dvojdílný hyperboloid
Rotačním dvojdíln Í'm hyperboloidem v tomto článku nazýváme těleso
ohranÍčené plochou vytvořenou při rotaci hyperboly s poloosami délek a, b
(a > b) kolem hlavní osy a dvěma shodnými kruhy, jejichž roviny jsou kolmé
k ose rotace hyperboly (obr. 187).
Platí ( b2V2 )
Jl = l. 1tV 3n 2 - --
3 2'
a
kde a, resp. b je délka hlavní, resp. vedlejší poloosy tvořící hyperboly,
v - výška "skořepiJ?Y"\
(l - poloměr shodných kruhových podstav v rovnoběžných rovinách.
Anuloid [torus, kruho ý prstenec] (obr. 188)
Anu/oid vznikne při rotaci kružnice s poloměrem r kolem osy ležící v rovině
této kružnice ve vzdálenosti R (R > r) od střed u kružnice.
Pro těleso ohraničené anuloidem platí
V = 21t 2 ,.2R 19,739r 2 R,
P = 41t 2 rR 39,478rR.
R
v
Obr. 18K Anuloid
Obr, 189. Sud
S ud (obr. 189)
Sud s tvořící křivkou tvaru oblouku kružnice:
V = t1tv(2R 2 + r 2 ) = /2 1tv (2D 2 + d 2 ) 0,261 8v(2D2 + d 2 ).
Sud s tvořící křivkou tvaru oblouku paraboly:
V = fsnv(8R2 + 4Rr + 3r 2 ) = i o 1t v(8D2 + 4Dd + 3d:l)
, 0,05236v(8D 2 + 4Dd + 3d 2 ).
Přitom R, resp. D je poloměr, resp. průměr středního řezu sudu, kdežto r,
resp. d je poloměr, resp. průměr podsta vy.
ro jiné tvary tvořící křivky sudu dávají uvedené vzorce přibližné hodnoty.
356
\
3.4. G O N 10M E T R I C K É, C Y K LOM E T R I C K É,
HYPERBOLICKÉ A HYPERBOLOMETRICKÉ
FUNKCE
3.4.1. Goniometrické funkce
Definice goniometrických funkcí
Goniometrické funkce je společný název pro funkce sinus (symbol sin),
kosinus (symbol cos), tangens (symbol tg), kotangens (symbol cotg), sekans
(symbol sec) a kosekans (symbol cosec).
c
A
c
8
OhL 190. .Pravoúhlý trojúhelník
V pravoúhlém trojúhelníku s přeponou AR o délce c a s odvěsnami RC
a AC o délkách a a b pro ostrý úhel CAB o velikosti rJ.. platí (obr. 190):
. a délka protilehlé odvěsny
sIn rJ.. = - =
c délka přepony
b délka přilehlé odvěsny
cos rJ.. = - =
c délka přepony
sIn rJ.. a délka protilehlé odv sny
tg rJ.. = - - -
cos rJ.. b délka přilehlé odvěsny ,
cos rJ.. b délka přilehlé odvěsny
. cotg rJ.. = . - -
sIn rJ.. a délka protilehlé odvěsny'
... 1 c délka přepony
sec rJ.. = - - -
cos a b délka přilehlé odvěsny'
1 c délka přepony
cosec rJ.. = . -
sIn rJ.. a délka protilehlé odvěsny
V praxi se goniometrických funkcí sekans a kosekans používá jen zřídka.
357
Rozšíření definic goniometrických funkcí
Definiční obor goniometrických funkcí sin a cos lze rozšířit na celou mno-:
žinu R všech reálných čísel. Funkční hodnoty funkcí sin a cos jsou pak defi-
novány pomocí kartézských souřadnic průsečíku M = [x, y] koncového
ramena orientovaného úhlu AOM (jehož vrchol leží v počátku O a počáteční
rameno splývá s kladnou částí osy x) s jednotkovou kružnicí se středenl
ve vrcholu O a poloměrem r = 1 (obr. 191):
sin = y, cos rJ.. = x,
kde (X je velikost orientovaného úhlu AOM a x, y jsou souřadnice průsečíku M.
-1
IK[u, v]
T(r,'s]
I
I
I
I
u = cotg lt
.
x
tečna hodnot
funkce Katangens
te na hodnot
funkce tangens
Obr. 191. Znázornění hodnot
goniometrických funkcí pomocí
jednotkové kružnice
/
Pomocí funkcí sin a cos definujeme ostatní funkce takto:
sin rJ.. Y 't (X E {rJ.. E R I (X * (2k + 1). tn; k E Z} ,
tg rJ.. = - - pro
cos rJ.. x
cos rJ.. X 't rJ.. E {rJ.. E R I rJ.. * kn; k E Z} ,
cotg rJ.. = - pro
sin rJ.. y
popř. také málo používanou funkci sekans:
1
1
pro 't(X E {rJ.. E R I rJ.. * (2k + 1). in; k E,Z}
sec rJ.. =
cos (X
x
a málo používanou funkci kosekans:
1 1
cosec rJ.. = - = -
sin eX y
-pro 't rJ.. E {(X E R I rJ.. * kn; k E Z} .
3Sg
Pomocí souřadnic průsečíků T = (r, s] a K = (u t:] přímky obsahující
koncové rameno orientovaného úhlu AOM s velikostí r.x a tečen v bodech A, B
jednotkové kružnice k lze funkce tg a cotg také vyjádřit takto:
tg C( = s
cotg C( = u
pro 'tex E { E R I + (2k + 1). i1t k E Z}
pro 'tex E f E R I + k1t; k E Z} .
Znaménka hodnot goniometrických funkcí v jednotlivých kvadrantech
uvádí tabulka 3.3.
, Tabulka 3.3
Znaménka hodnot goniometrick.Í'ch funkcí
rjednot firJlch kradrantech
Kvadrant SIn cos tg cotg
I + + + +
II + - - -
III - - + +
IV - + - -
Goniometrické funkce lze také definovat pomocí množiny všech komplex-
ních jednotek
J = cos ex + i sin ex = [x, y]
tak, že
sIn = y,
cos ex = x)
kde ex je amplituda komplexní jednotky J:z,
x, resp. y - reálná, resp. imaginární část komplexní jednotky JJ.'
V matematické analýze se velikost orientovaného úhlu zpravidla uvádí
v obloukové míře a vynechává se značka rad, kdežto v geometrických a trigono-
metrických úlohách se z tradičních důvodů používá stupňové míry.
Goniometické funkce jsou proto zpravidla tabelovány pro stupňovou míru,
k čemuž je nutno při výpočtech přihlížet.
359
Vztahy mezi goniometrickými funkcemi doplňkových úhlů
sin ex = cos (90° - ex),
cos ex = sin (90° - ex),
tg (X = cotg (90° - Cť),
cotg ex = tg (90° - ex).
Pomocí tabulky 3.4 lze každou goniometrickou funkci libovolného argt:-
mentu (p převést na funkci argumentu C( E (0°, 90°>.
,
Tabulka 3.4
Přerod goniometrickJ\'h funkcí do prrního krlldrantu
Funkce
s argumentem -':J. 90 0 ::t ':J. 180 0 ::t :x 270 0 ::t :x 360 0 - :x
cp
sin cp -sin ':J. cos :x =+= sin :x -cos ':J. -SIn ':J.
cos cp cos :x =+= sin :x - cos :x ::t sin :x cos :x
tg cp - tg :x =+=cotge< ::t tg :x =+= cotg :x -tg ':J.
cotg cp - cotg C( =+=tg ':J. :t cotg ':J. =+= tg :x - cotg :x
Periodičnost goniometric ých funkcí
sin ex = sin (ex + k . 360°),
cos ex = cos (ex + k . 360°),
tg (X = tg (ex + k . 180°),
cotg ex = cotg (Cť + k . 180°)
pro \f k E Z .
Grafy goniometrických funkcí (obr. 192 a 193)
fl = {[x, y] ly = sin x, x E R, , Y E ( -1, I>} (sinusoida),
f2 = {[x, y] I y = cos x, X E R, y E ( - 1, t > } (kosinusoida),
f3 = {[ x"y] ly = tg , X E R \ {(2k + 1).!1t I k E Z}, Y E R} (tangentoida),
14 = {[x, y] ly = cotg x, x E R \ {k1t I k E Z}, Y E R} (kotangentoida).
Příklady:
sin ( - 500°) = - sin 500° = - sin 140° = - sin 40° = - cos 50°;
cos 1 ()()()O = cos 280° = cos 80° = sin 1 U :
tg 1 500° = tg 60° = cotg 30°;
cotg ( - 2 000°) = - cotg 2 ()()()O = - cotg 20° = - tg 70°.
360
.
I
I
Obr. 193. Funkce tangens a kotangens i
I
I
3
2
Obr. 192. Funkce sinus a kosinus
\ r
\ i
"l
\ I
ti
Poznámka:
Dolní, resp. horní znaménko čísla v tabulce 3.5 platí pro hodnoty arg -
mentu ex, uvedené v prvním, resp. druhém řádku. Symbol + x (resp. + x)
I
znamená, že limita zleva příslušné funkce se v tabelovaném bodě rovná + x
(resp. - 'X)) a limita zprava se rovná - x (resp. + x).
Tah u I k a 3,5
Hodnut\' tjo17io11lerriclq:( h IUIlh.<" '/wo l',:::l1l1l'Ill; Úh'-r
I
FlIl1k( () J() 45' 60° 90 0
s argu mel1 tenl 'J. IXO' 150-' 135 0 120 0 270 0
O 1 !J2 1 / :tI
sin 'J. i 2V 3
cos :tI +1 '3 +1 " +1 O
-2\; -2V- -2
tg O :t 1,.)3 :tI :t v '3 :tx.
cotg +x :t ,,' 3 :tI +J '3 O
-3\/
Úl11111va:
Všechny dále' uvedené vzorce platí jen pro přípustné hodnoty argumentů.
Vztahy mezi goniometrickými funkcemi stejného argumentu
sin 2 + cos 2 ex = 1, tg ex cotg ex = 1,
sIn ex
tg ex = --,
cos
cos ex
co t g ex = . ,
SIn a
1 +
2 1
tg a = 2 '
cos ex
1
1 + cotg 2 = . .
sln 2 ex
..
361
Vyjádření goniometrické funkce pomocí ostatních goniometrických funkcí
stejného argumentu uvádí tabulka 3.6.
Ta bu I ka 3.6
Vyjádření gon;ometrkké.funkce pomocí j;né.f;u1kce stejného argumentu
.
Hledaná
funkce sIn cos tg cotg a
-
Isin I (1 - OS2 =<) Itg e<1 1
- --- ---- - -- ---- ----
J(1 + tg 2 ti) v/( 1 '+ cotg 2 =<)
Icos I J(1 - sin 2 ) 1 Icotg I
- -- --- - - - ---
(1 + tg 2 ) J( 1 + cotg 2 !X)
Itg =<1 Isin al .J( 1 - cos 2 e<) 1
-- - --- -- --- ------- -- - ---
)(1 - sin 2 Ct) Icos !XI Icotg C(I
Icotg I ,,(1 - sin 2 lX) Icos I 1
----- -- -- --- - --- -
Isin I /( 1 - cos 2 ) Itg I
Goniometrické funkce součtu a rozdílu argumentů
sin (IJ. + 8) = sin cos B + cos et sin 8,
cos (IJ. + B) = cos IJ. cos B + sin CI. sin B,
tg IJ. :t tg B
t + tgIJ.tgB'
( ) cotg et cotg B + 1
cotg IJ. j: B = ,
cotg 8 + cotg IJ.
sin ( + 8) sin (IJ. - 8) = cos 2 8 - cos 2 IJ.,
cos (IJ. + B) cos ( - 8) = cos 2 B - sin 2 IJ..
tg (et + B)
Goniometrické funkce dvojnásobku a poloviny argumentu
sin (2IJ.) = 2 sin IJ. cos IJ., . et _ _ J I - cos et
sin -
cos (2IJ.) = cos 2 IJ. - sin 2 Q: = 2 2'
= 1 - 2 sin 2 Q: = CI. _ _ J I + cos et
cos-
= 2 cos 2 'X - 1, 2 2'
__ 2 t _ Q: _ _ J I - cos ,
tg (2et) - tg--
I - tg 2 2 1 + cos :ť
l
362
tg (2ex) 2 ex 1 - cos ex
- , tg- -
cotg fY. - tg Cť 2 SIn ex
cotg Z Cť - 1 sin ex
cotg (2Cť) = - 1 + cos a ,
2 cotg ex
cotg - tg ex ex = J os ex
- cotg -
2 2 1. - cos ex '
(J. Cť
sin = 2 sin -- cos - , a 1 + cos Cť
.2 2 cotg -
ze( . 2 ex 2 sin ex
cos ex = cos - - sIn - - sin e(
2 2
--
I - cos ex ,
zex
= 1 - 2 sin - = . _ JI - cos (2a)
2 Isin al
- ----
ze( 2 '
= 2 cos - - 1
2 ' Icos I JI + cos (2a)
= --- - ,
Cť 2'
2 tg- JI - cos (2:x)
2 Itg al
tg ex , = - -,
zex 1 + cos \2:l)
1 - tg -
2 sin (2Cť)
2 tg a - -
1 + cos (2a)
1 - cos (2(1)
cotg.- - tg-
2 2 sin (2a)
2 ex Icotg al = Jl- os _( 2a)
cotg - ,- 1
2
cotg 'Y... - 1 - cos (2cx)
li..
2 cotg - _ si (2 _
2 cotg 'Y...
- 1 -- cos (2ex) -
C( Cť
cotg - tg- 1 + cos (2ex)
2 2
- - - sin (2C()
.,
Goniometrické funkce dalších nÚsobků argumentu
sin (3ex) = 3 sin a - 4 sin 3 a,
sin (4ex) = 8 sin fY. cos 3 C( - 4 sin a C0 -/.
sin (5Cť) = 16 sin ex cos4. - 12 sin 'Y OS2 'Y... + sin c(,
363
sin (nťX) = n sin ťX cos" - 1 ťX - (;) sin 3 ' ťX cos" - 3 ťX + ( ) sin 5 ťX cos" - 5 ťX -
cos (3ex) = 4 cos 3 ex - 3 cos ex,
cos (4ex) = 8 cos 4 ex - 8 cos 2 ex + 1,
cos (5ex) = 16 cos 5 ex - 20 cos 3 ex + 5 os ,
cos (nťX) = cos" ťX - (;) sin ťX cos" - 2 ťX + ( ) sin 4 ťX cos" -4 ťX - o o.,
, ) _ 3 tg Ct - tg 3 ex
tg (3ex - 2 '
1 - 3 tg ex
4 tg ex - 4 tg 3 ex
ex)= ,
. 1 - 6 tg 2 ex + tg 4 ex
n tg ťX - G) tg 3 ťX + (;) tg 5 ťX - o o .
tg (nex) = ,
1 - (;) tg 2 ťX + ( ) tg 4 ťX - ( ) tg 6 ťX + 00.
( ) _ cotg 3 ex - 3 cotg ex
cotg 3ex - 2 '
3 cotg ex - 1
( ) cotg4 ex - 6 cotg 2 ex + 1
cotg 4ex = .
4 cotg 3 a - 4 cotg ex
c tg" - (;) cotg"-2,ťX + ( ) cotg"-4 ťX - o..
cotg (nex) = .
n cotg"-l ťX - (;) cotg"- 3 ťX + G) cotg"- 5 ťX - ...
Součty a rozdíly goniometrických funkcí
. ex+O ex-O
sin ex + sin O = 2 sIn cos ,
2 2
ex+O. ex-O
sin ex - sin O = 2 cos -- sIn
22'
cx+O ex-tJ
cos ex + cos B = 2 cos -'- cos --
2 "2'
. ex+IJ. a-O
cos ex - cos a = - 2 sIn -- sIn
p 2 2'
364
tg C( + tg 8 =
s in (:>: i: (3)
cos cos B '
sin (8 + Cť)
----- ---
sin sin tJ '
cotg rJ.. + cotg 8 =
...
cos (,): + fJ)
tg C( + cotg fl = + - --:--
cos sIn tJ
cos + sin = (\/2) sin (45 0 + ) = (J2) cos (45 0 - )
cos rJ.. - sIn = (J2) cos (450 + Cť) = (J2) sin (450 - rJ..).
Součiny goniometrických funkcí
sin rJ.. sin B = t[ cos (Ct - tJ) - cos (rJ.. + fJ)]
cos rJ.. cos B = i[ cos (rJ.. - B) + cos (rJ.. + tJ)],
sin C( cos 8 = t[ sin (a + B) + sin (a - B)],
cos Cť sin B = t[ sin (rJ.. + B).- sin ( - B)],
tg rJ.. + tg B
tg Cť tg tJ =
cotg + cotg B'
tg rJ.. - tg B
cotg tj. - cotg B'
cotg (X + cotg B
cotg rJ.. cotg B =
tg rJ.. + tg B '
cotg rJ.. - cotg B
tg Cť - tg B '
tg rJ.. + cotg B
tg a cotg B =
cotg rJ.. + tg B
tg (X - cotg B
cotg rJ.. - tg tJ '
cotg Cť + tg tJ
cotg rJ.. tg tJ =
tg rJ.. + cotg B '
cotg rJ.. - tg {j
tg Cť -. cotg B '
sin:>: sin B sin ' = i[ sin (:1 + B - y) + sin (tJ + Y - rJ..) +
+ sin (:' + rJ.. - B) - sin (rJ.. + B -t- }')],
365
cos a cos Bcos}' = ![cos(ex + B - y) + cos(fj + ' - ) +
+'cos (,' + - B) + cos (ex + fj -t' y)],
sin sin Bcos ' = k[ -cos( + 8 - :J) + cos(/J +,' - ) +
+ cos (,' + - tJ) - cos (CI. + B + }')] ,
sin ex cos IJ cos I' = ![ sin (CI. + tJ - ,') - sin (/j + ' - ) +
+ sin("/ + C( - 13).- sin (a + tJ + I)]'
. Mocniny goniometrických funkcí
sin 2 ex = t[l - cos (2ex)],
cos 2 C( = t[ 1 + cos (2Cť)],
sin 3 ex = 1[3 sin a - sin (3ex)] ,
cos 3 ex = ![3 cos ex + cos (3ex)],
sin 4 Cť = k[ cos (4Cť) - 4 cos (2cx) + 3],
cos 4 (1 = k[ cos (4ex) + 4 cos (2ex) + 3]_
sin 5 ex = /6 [10 sin a - 5 sin (3a) + sin (5a)],
cos 5 ex = /6 [ 1 O cos ex + 5 cos (3ex) + cos (5(1)] ,
sin 6 Cť = 3 1 2-[ 10 - 15 cos (2ex) + 6 cos (4ex) - cos (6ex)] ,
cos 6 a = 3 1 2 [10 + 15 cos (2(1) + 6 cos (4ex) + cos (6.:ť)].
Exponenciální funkce imaginárního argumentu (Eulerovy vzorce)
e ilp = cos qJ + i sin qJ,
e - i<p = cos qJ - i sin qJ.
Z toho plyne
ei<p - e - i<p
2i
cos
e ilp + e - i<p
qJ = --2--
sin 0/ =
i( ei<P - e - i<P)
tg qJ = - i<p - iep ,
e + e
i( e ilp + e - i<P)
cotg cp == ---;----- 0- , - .
el<P - e - lep
Goniometrické funkce
imaginárního a komplexního argumentu viz na str. 383.
':;bb
Přibližné vzorce pro malé hodnoty argumentů
sin x x tg x,
sin (Ct + 8) sin a + sin 8
tg (C( + B) tg + tg tJ,
sin (na) n sin
tg (n ) . n tg ex.
Grafické znázornění sinusoidálních [si nových] funkcí
Změna amplitudy a:
Na obr. 194 je graf funkce y = a sin x pro amplitudu a = 3 (tj. Y = 3 sin x),
který se;orovnává s grafem funkce y = sin x.
4
Změna kruhové frekvence (o:
Na obr. 195 jsou grafy funkcí y = sin ((J)x) pro (1) = 2 a (t) =:t [tj. y =
=d sin (2x), y = sin (ix)], které se porovnávají s grafem funkce y = sin x.
:t
2
x
Obr. 194. Graf funkce .r = 3 sin x
rt
I . X
y=s," T
_ r '; -.:. "- , ; X
Z /-1 r - 2 "
y=sin (2x) ycsin x
()hr. 195. (jrafy funkcí y = sin (wx) ((I) = i, 2)
Skládání s;nusoidálních .fÚnkcí je naznačeno na obr. 196 až 201
- 2 1'2 = COS x
I
Obr. 196. Graf funk c .r = sin x + cos x
=2 sin X
V
\ ,-."
\. .
x
()hr. 197. Graf funkce.r == 2 sin x + in (2x)
J67
Obr. 198. Graf funkce
y = 2 sin x + t sin x
Obr. 200. Graf funkce
y = sin x .+ sin (x + 1t/4)
y
2
= 2 sin x
/ 1
.
\
Ohr. 199. Graf funkce .r = 1 sin x + sin (2x + 1t 2)
Y
6
5
I
X -1r
4
3
2 /. Y" Y'+Y2
1 y,=sinx
,
_L _--L-_ _._ __L_
- t A O t 1t", 1[. ;I'''Z'!r ,(
....... -:;' j, -1 ....J__
./
/
-2
-3
-4
Obr, 201. Graf funkce .r = sin x + x
Skládání harmonických pohybů při vzájemně kolmých směrech harmo-
nických pohybů znázorňují obrázky 202 až 205, v nichž jsou tzv. Lissajollsovy
křivky tvaru
x = a 1 sin (ro l t - qJl),
Y = a2 sin (ro 2 t - qJ2).
V obr. 202 je Lissajousova křivka tvaru
x = a sin (rot),
y = a sin (rot - in),
tj. při ro 1 : ro 2 = 1 : 1. '
368
V obr. 203 je Lissajousova křivka tvaru
x = asin(o)t),
Y = li sin (wt - j1t),
tj . při. (I) 1 : (I) 2 = 1 : 1.
r,
-
x
()br. 202. Lissajousova křivka
x = II sin (wt),
.r = li sin ((1)1 - 1ti2),
(') 1 : w 2 = 1 : 1
V obr. 204 je Lissajousova křivka tvaru
x = a sin ((vt),
y = a sin (2(vt - *1t)
..tj. při w 1 : (})2 = 1 : 2.
V obr. 205 je Lissajousova křivka tvaru.
x = a sin (2o)t),
Y = li sin (3wt), ,
tj. při 0)1 : (1)2 = 2 : 3.
y
x
Obr. 204. Lissajousova křivka
x = ti sin ((}Jr).
Y = li sin (2(1)1 - 1t:'4).
W 1 : (')2 = 1 : 2
y
I
x
Obr. 203. Lissajousova křivka
x = li sin (wt), "
Y = II sin (rot - nf3),
(1)1 :w 2 = 1: 1
x
Obr. 205. Lissajousova křivk"
x = a sin (2Wl),
y = a sin (3wt),
(1)1 :(1)2 = 2:3
369
Součiny se sinusoidálníml .funkcemi:
V obr. 206 je graf funkce y = x sin x, v obr. 207 jsou grafy druhých mocnin
funkcí sinus a kosinus a v obrázcích 208 a 209 jsou grafy součinů exponenciální
funkce a funkce sinus.
.
y
71"
- '2-1
-2
-3
-4
-5
y - x Sin X
x
Obr. 207. Grafy funkcí r = sin 2 x
a y = cos 2 X
Obr. 206. Graf funkce .r = x sin x
y.e- X sin x
Y t . y e-.t/38inx
f.-. I
\ ...... - "'"'
- -11' ..: -i - O ..... T .....
, /. .......-f
_/ '
I
--2
I
'1- 3
I
-f-It
I
-5
-6
-7
"
t
7:-
6
5
4
3
2
f
-8
-2
Obr. 208. Grafy'funkcí y = eX sin x
a y = e,'C{3 sin x
Obr. 209. Grafy funkcí y = e -x sin x
a y = e - x' 3 sin x
Průvodičový diagram pro sinusoidální funkce
[harmonické funkce]
Sinusoidální funkce tvaru
j' '- {[x, Y ] E R 2 I y = a sin (x + qJ)}
lze symbolicky vyjádřit pomocí obíhajícího průvodiče (obr. 210), přičemž
370
li je délka průvodiče,
x )
- - úhlová rychlost (t je doba ohi hání
t
lfJ - fázový posun [počáteční fáze, nulový fázový úhel J vzhledem k pro-
mítací ose při x = O (popř. t = O).
V elektrotcchnice je
t
x = (1Jt = -
T'
kde (1) je kruhová frekvence,
T - perioda [doba kmitu J-
lfJ - počáteční fáze [fázová poloha, fáze J.
Fyzikil1ně reálnou okamžitou hodnotu dostaneme jako průmět průvodiče
vektoru do roviny kolmo k promítací ose.
. "..
yzQ Sin (X+,) .'
..
-
x-) ( (.)t )
Obr. 210. Průvodičov}' diagram pro
funkce y = a sin (x + ip) .
Protože se u průvodičového diagramu předpokládá sinusoidální průběh
s xlt = w = konst, charakterizují proměnné a a lfJ funkci, jíž vyhovují kon-
stantní průvodiče, které. také dostaneme, jestliže časovou osu, kolmou k pro-
mítací ose necháme obíhat v opačném smyslu. Třebaže tyto konstantní prů-
vodiče lze považovat za vektory liší se na základě své definice.
V průvodičovém diagramu lze dva průvodiče sčítat jako vektory. Součet
průvodičů znázorňuje fyzikální, popř. geometrickou realitu součtu)' = Yl + Y2
okamžitých hodnot jako při skalárním sčítání souřadnic vektoru (obr. 211).
371
Jeho velikost a polohu vzhledem k pron1Í Jací ose (tj. počáteční fázi) lze zjistit
z průvodičového diagramu. Jeho úhlo\ld .l ychlost se rovná úhlové rychlosti
obou prťlvodičů, Platí
Y 1 = li 1 sin (x + <P 1 )
Y2 = li2 sin (x + (fJ2),
Y = Y1 + )'2 = LI sin (x + (fJ),
kde
a = ai + a + 2a 1 a 2 COS{4?2 - (Pl),
{lI sIn (fJl + a 2 sin (fJ2
tg qJ = -
a] co (fJl + a 2 cos (fJ2
Obr. 211. Součet pruvodiču
Je třeba ocenit jednoduchost sčít ní průvodičů v porovnání s analytickým
řešením. Případná nepřesnost konstrukce má často podřadný význam.
3.4.2. Goniometrické rovnice
Dej; nice:
Gon;ometr;ckýlni rovnicemi nazýváme rovnice, které kromě konstant
obsahují neznámou x nebo výrazy s neznámou x jako argumenty jedné nebo
I
několika goniometrických funkcí, tj., rovnice tvaru
j'(sin x, cos x, tg x, cotg x, x) = O.
Základní goniometrickou rovnici s neznámou x nazýváme rovnIcI typu
g(x) = k, kde g je goniometrická funkce a k je reálné číslo.
Vzhledem k periodičnosti goniometrických funkcí má každá základní
372
goniometrická rovnice bud' prázdný nebo nekonečný- obor pravdivosti.
Zpravidla hledáme jen řešení z intervalu <0°, 360°) neboli <0 rad, 2n rad >,
tj. hledáme tzv. základní hodnoty.
Početní způsob řešení
Pomocí goniometrických vzorců převedeme goniometrické funkce s pří-
padnými různými argumenty na funkce s týmž argumentem. Potom případné
různé goniometrické funkce vyjádříme jedinou goniometrickou funkcí.
Získané řešení je třeba vždy ověřit dosazením do výchozí rovnice, neboť
úpravy rovnic nemusely být ekvivalentní.
Příklad 1:
Určeme množinu {x E <0°, 360°> I sin (2x) = sin x}.
Podle vzorce pro sin (2x) je
2 sin x cos x = sin x,
2 sin x cos x - sin x = O.
Z poslední rovnice lze vytknout sin x:
(sin x) (2 cos x-I) = O;
sin x = O dává základní hodnoty
Xl = 0°, X2 = 180 d , X 3 = 360°;
I
2 cos x-I = O, odkud cos x = t dává základní hodnoty
X 4 = 60°, Xs = 300°.
Zkouška ukazuje, že všechna nalezená řešení splňují danou rovnici, ta že
obor pravdivosti
p = {0°, 60°, 180°, 300°, 360°} .
Příklad 2 (kvadratický typ):
Určeme množinu {x E <0°, 360°> 117 sin 2 x - 3 cos 2 X = 2}.
17 sin 2 x - 3( 1 - sin 2 x) = 2,
20 sin 2 x = 5,
(sin X)1,2 = + !;
(sin X)l = t dává základní hodnoty
Xl = 30°,
x 2 = 150°;
(sin X)2 = -! dává základní hodnoty
X3 = 210°, X4 = 330°.
373
Všechna uvedená řešení splňují danou rovnici, takže obor pravdivosti
P = {30°, 150°,210°, 330°}.
Příklad 3:
Určeme množinu {x E (0°, 360°) 12 sin x + cos x = 2}.
Postup řešení 1:
cos x = 2 - 2 sin x;
po umocnění dvěma je
cos 2 x = 4 - 8 sin x + 4 sin 2 x,
t - sin 2 x = 4 - 8sinx + 4sin 2 x,
(sin X)I,2 = ! + J( - ) = + t;
(sin X)l = 1 dává základní hodnotu
Xl = 90°;
(sin X)2 =! dává základní hodnoty
X2 = 36°52', X3 = 143°8'.
Zkouškou se zjistí, že z nalezených řešení pouze řešení X3 nesplňuje danou
rovnici, takže obor pr:n'dlvosti
P = {90°, 36°52' f'
Postup řešení 2:
Metoda pomocného úhlu
Pro danou rovnici typu a sin x + b cos x = c použijeme substituce tg z =
= b! a.
2 sin x + cos x = 2 => sin x + i cos x = 1.
Po substituci tg z = t => z = 26°34' dostaneme
sin x + tg.:cosx = 1,
sin = .,
sin x + - cos x = t,
cos z
sin x cos.: + sin z cos x = cos =,
sin (x + z) = cos z = cos 26 °34' . 0,894 4,
(x + =)1 = 63°26' dává Xl = 36°52',
(x + Z)2 = 116°34' dává X 2 = 90°.
374
PříkLad 4:
Určeme množinu {x E <0°, 360°> I sin (2x) = tg x}.
sin x
2 sin x cos x = ---,
cos x
2 . 2 . O
sin x COS x - sin x = ,
(2 cos 2 x-I) sin x = O;
sin x = O dává základní hodnoty
x I = 0°, X 2 = 180°, x 3 = 360°;
2 cos 2 x-I = O,
cos 2 x=!;
(cos X)1.2 = :t!.J2 dává základní hodnoty
X4 = 45°, Xs = 135°, X 6 = 225°, x 7 = 315°.
Všechna nalezená řešení splňují danou rovnici, takže obor pravdivosti
p = {OO 45°, 135° 1800 225°, 3 J 5°, 360°}.
Grafický způsob řešení
Upravíme danou rovnici na tvar qJ(x) = tjJ(x) a pro \Ix E <0°, 360°> sestro-
jíme grafy funkcí y = qJ(x) a y = t/J(x). Řešeními (základními hodnotami) jsou
první souřadnice průsečíků těchto grafů.
y
.
. _J
Obr. 212. 'Grafické řešení rovnice
2 sin x + cos x = 2
Příklad 5:
Obor pravdivosti P = {36°52', 90°} příslušný k množině
{x E <0°, 360°> 12 sin x + cos x = 2}
je zřejmý z grafického řešení na obr. 212 a z početního řešení příkladu 3.
375
3.4.3. Cyklometrické funkce
Cyklometrickými funkcemi nazýváme inverzní funkce ke gonio-
metrickým funkcím. Protože goniometrické funkce jsou ryze monotónní jen
na určitých intervalech, existují inverzní funkce jen na těchto intervalech.
Funkce arkussinus
fl = {[ x, y] I y = arcsin x, x E < - 1, 1), y E < - l1t, !7t) }
je inverzní funkcí k funkci sin na intervalu < -11t, 11t), funkce arkuskosinus
j = {[x, y] I y = arccos x, x E < - 1, 1), y E <O, 1t) }
je inverzní funkcí k funkci cos na intervalu <O, 1t), funkce arkustangens
f3 = {[ x, y] ly = arctg x, x E R, y E ( -1 1t , l 1t )}
je inverzní funkcí k funkci tg na intervalu (-17t, i1t) a funkce arkuskotangens
, f4" = {[x, y] ly = arccotg x, x E R, ,y E (O, 1t)}
je inverzní funkcí k funkci cotg na intervalu (O,1t).
y
r- 1['
\
y.arccos x',
I
.. x
2
. ------ y .
y = a rccotg x ......" I '
I \
r
,y
"-
.......
.............-..
-
x
r
- --
2
Obr. 213. Funkce arkussinus
a arkuskosinus
Obr. 214. Funkce arkustangens
a arkuskotangens
Grafy cyklometrických funkcí lze pomocí osové souměrnosti s osou y = x
sestrojit z grafů goniometrických funkcí na intervalech, kde jsou ryze mono-
tónní a které obsahují počátek O (obr. 213 a 214).
376
Vyjádření cyklometrické funkce pomocí jiné cyklometrické
funkce stejného argumentu
1
arcSln x = i1t - arccos x
x
= arctg J(l _ x 2 )
arccos x = i1t - arcsin x
x
-= arccotg - J( _ 2 )
. 1. x
(Ixl < 1),
,
(lxl < 1),
(Ixl < 1),
(Ix; < 1),
arctg
,
1 . X
X = 11t - arccotg x = arcsm J(l +- x 2 ) '
. I X
arccotg x = 11t - arctg x = arccos ( ----;;- ) '
.J 1 + x-
1
arccotg x = arctg-
x
(x > O),
1
= arctg - + 1t
x
(x < O).
Cyklometrické funkce ,vzájemně opačných argumentů
arcsin (- x) = - arcsin x (Ixl < 1),
arccos (- x) = 1t - arccos x (Ixl < 1),
arctg (-x) = -arctg x,
arccotg ( - x) = 1t - arccotg x .
Součty a rozdíly cyklometrických funkcí
arcsin x I + arcsin X2 = arcsin [x I .J'( 1 - x ) + X2 ..J( 1 - ,xi)]
,
(X I X 2 < 0 nebo xi+x < l),
- 1t - arcsin [Xl J(1 - x ) + X2 J(1 - xi)] (XI> O, X2 > O, xi + x > 1)
= -1t - arcsin [Xl J(1 - X ) + X 2 J(l - xi)] (XI < O x 2 <ů, xi + x > 1),
arcsin XI - arcsin x 2 = .
= arcsin [XI J(1 -;- x ) - x 2 J(t - xi)] (X I X 2 > O nebo xi + x < 1),
- 1t - arcsin [Xl J(1 - X ) - X2 J(l - xi)] (Xl> O, X2 < O, X: + X > 1),
== -7t - arcsin [Xl J(l - X ) - X2 J(1 - X )] (Xl < O, X2 > O, xT + x > 1),
377
arccos x 1 + arccos x 2 =
,= arccos {X I X 2 - [J(1 - xi)] Jíl - x }
= 21t - arccos {X I X 2 - [J(1 - xi)] J(I - x }
(Xl + X 2 > O) ,
(Xl + X 2 < O),
arccos X I - arccos X 2 =
= -arccos {X I X2 + [J(1 - xi)] J(1 - x )}
- arccos {X I X2 + [J(1 - xi)] J(1 - x )}
(Xl > X2),
(Xl < X2),
arctg Xl + arctg X 2 =
,X 1 + X2
= arctg - --
I - X I X 2
Xl + X2
- 1t + arctg
I - X I X 2
Xl + X2
= -1t + arctg
1 - XIX2
(.\1'\2 < 1)
(Xl> O, XIX2 > 1),
(Xl < O, XIX > 1),
arctg Xl - arctg X 2 =
Xl - X 2
= arctg
1 + XIX2
(X I X 2 > -1),
Xl - X2
1t + arctg
1 + X I X2
Xl - X 2
= -1t + arctg
1 + X I X2
(Xl> O, XIX2 < -1),
(Xl < O, X I X2 < -1),
X I X 2 - 1
arccotg Xl + arccotg X2 = arccotg
Xl. + X 2
X I X2 - 1
arccotg x I + arccotg X 2 = arccotg + 1t
X2 + Xl
(Xl> -X 2 ),
(Xl < -X 2 ).
Vztahy mezi cyklometrickými funkcemi a logaritmickou funkcí
arCSln X = -i ln [ix + J(1 - X2)],
arccos X = -iln[x + J(X2 -1)],
1 1 + ix
arct g X = - ln
2i 1 - ix'
1 ix + 1
arccotg X = --ln "
2i ix - 1
378
3.4.4. Hyperbolické funkce
Definice:
sinh x =
eX - e - X
tgh x
2
eX + e - X
cosh x = ,
2
eX - e- X
eX + e - x'
eX + e- X
cotgh x = --
eX - e- X
(x * O).
Grafy hyperbolických funkcí (obr. 215 a 216)
fl = {[x, y] I y = sinh x, x E R, y E R} ,
f2 = {[x,y] ly coshx, xER, YE(l, + )},
j = {[x, y] I y = tgh x, x E R, y E ( - 1, I)},
.f 4 = {[x, yJ ly = cot h x, x E R \ {O}, Y E ( - 00, -1) u (1, + oo)}.
\
y=cosh,( \
\
\
y=sinh x
Obr. 215. Funkce hyperbolický sinus
a hyperbolický kosinus
Periodičnost hyperbolických funkcí
y = sinh (x + 2k1ti) = sinh x,
y = cosh (x + 2k1ti) = cosh x,
y = tgh (x + k1ti) = tgh x,
y = cotgh (x + k1ti) = cotgh x.
Hodnoty ve význačných bodech
sinhO=O,
cosh O = 1,
tghO = O.
Obr. 216. Funkce hyperbolický tangcns
a hypcrbolický kotangens
(k E Z)
379
Pro x = O není funkce cotgh definována v bodě x = O se její limita zprava,
resp. zleva rovná + 'X), resp. - tYJ.
Hyperbolické funkce vzájemně opačných argumentů
sinh (-x) -
cosh (-x) =
tgh (-x) -
cotgh (-x) =
- sinh x,
cosh x ,
- tg x,
-cotg x.
Vztahy mezi hyperbolickými funkcemi stejného argumentu
sinh x + cosh x eX ,
sinh x - cosh x - -e- X '
,
cosh 2 x - sinh 2 x = 1 ;
sinh x
tgh x = ,
cosh x
1
cotgh x = .
tgh x'
2 1
1 - tgh x = -
cosh 2 x'
cosh x
cotgh x = . ;
slnh x
1
cotgh 2 x-I = . 2
slnh x
Tabulka 3.7
Vyjádření hyperbolické jil1lkce pomocí jiné hyperbolické funkce stejného argumentu
Daná funkce
Hledaná sinh cosh tgh cotgh
funkce
(cosh2 x-I) Itgh xl 1
Isinh xl - --- ----
..J( 1 - tgh 2 x) J(cotgh 2 x-I)
1 Icotgh xl
cosh x J(sinh 2 x + 1) -
J(1 - tgh 2 x) J(cotgh 2 x-I)
Itgh xl Isinh xl J(cosh 2 x-I) 1
- --- -
J(sinh 2 x + 1) cosh x ---
Icotgh xl
J(sinh2 x + 1) cosh x 1
Icotgh xl --- --- -- -
Isinh xl v'(cosh 2 x-I) Itgh xl
380
Hyperbolické funkce součtu a rozdílu dvou argumentů
sinh (x + y) = sinh x cosh y + cosh x sinh y,
cosh (x + y) = cosh x cosh y + sinh x sinh y,
tgh x ::t tgh Y
1 + tghxtghy'
( ) 1 + cotgh x cotgh y
cotgh x + y = - .
- cotgh x + cotgh y
tg (x + y)
Hyperbolické funkce dvojnásobku argumentu
sinh (2x) = 2 sinh x cosh x,
cosh (2x) = sinh 2 x + cosh 2 x,
2 tgh x
tgh (2x) . - 1 + tgh 2 x '
( ) _ 1 + cotgh 2 x
cotgh 2x - h '
2 cotg x
Hyperbolické funkce dalších násobků argumentu
sinh (3x) = sinh x (4 cosh 2 .'; - t),
sinh (4x) = sinh x cosh x «: cosh 2 \: -- .,
'sinh (5x) = sinh x(1 - 12cosh 2 x -+ 1('l0sh x
cosh (3x) = cosh x (14 cosh 2 x -- 3),
cosh (4x) = 1 - 8 cosh 2 x + 8 cosh x.
cosh (5x) = cosh x (5 - 20 cosh 2 x + 16 cosh 4 x).
sinh (nx) = G) cosh n - 1 x sinh x + (;) coshn- 3 x sinh 3 x +
( n )
n-5 . 5
+ 5 cosh x slnh x + ...,
cosh (nx) = cosh n x + G) coshn- 2 x sinh 2 x +
( n )
n-4 . 4
+ cosh x slnh x + ....
4 ..
381
Hyperbolické funkce polovič ího argumentu
. x J COSh x-I Isinh xl
slnh - -
2 -, -2- - = J[2(cosh x + 1)]'
cosh = J COSh x + 1 = Isinh xl
2 2 J[2(cosh x-I)]'
sinh x cosh x-I
x
tgh-
2
x
tgh-
2
cosh x + 1
J COSh x-I
cosh x + l'
sinh x
sinh x
x
cotgh - - --- ----- -
2 cosh x-I
x _ _ J COSh x + 1 .
cotgh -
2 cosh x-I
cosh x + 1
sinh x
Mocniny hyperbolických funkcí
sinh 2 x = t[ cosh (2x) - 1],
cosh 2 X = t[ cosh (2x) + 1].
sinh 3 x = i[ - 3 sinh x + sinh (3x)],
cosh 3 X =: lr3 cosh x + cosh (3x)],
sinh 4 x == !: t:\ - 4 cosh (2x) + cosh (4x)],
c0sh 4 x l3 + 4 cosh (2x) + cosh (4x)],
sinh 5 x = 1 [10sinhx - 5si11b(3x) + sinh(5x)],
cosh 5 x = /b [lOcoshx + 5cosh(3x) + cosh(5x)],
sinh 6 x = l2 [ -10 + 15cosh(2x) - 6cosh(4x) + cosh(6x)],
cosh 6 x = 3 1 2 [10 + 15 cosh (2x) + 6cosh(4x) + cosh(6x)].
Součty a rozdíly hyperbolických funkcí
x+y x + y
sinh x + sinh y = 2 sinh - cosh ,
2 2
cosh x + cosh y
x+y x-y
= 2 cosh cosh ,
2 2
cosh x - cosh y
. x+y. x-v
= 2 slnh slnh . ,
2 2
382
sinh (x :t y)
cosh x cosh y'
sinh (x + y)
cotgh x + cotgh y = . . ,
slnh x slnh y
sinh (y - x)
cotgh x - cotgh r = --- - .
r sinh x sinh y
tgh x + tgh y
M oi vrovy vzorce
(sinh x + cosh xt = sinh (I1X) + cosh (llx),
(cosh x - sinh xt = cosh (nx) - sinh (nx).
Součiny hyperbolick)'ch funkcí
sinh x sinh y = J[ cosh (x + y) - cosh (x - y)],
cosh x cosh y = t[ cosh (x + y) + cosh (x - y)],
sinh x cosh y = t[ sinh (x + y) + sinh (x - y)],
tgh x + tgh Y
cotgh x + cotgh y
tgh x tgh y
Vztahy mezi hyperbolickými funkcemi a exponenciální funkcí
sinh x + cosh x = eX,
x
1 + tgh 2
sinh x - cosh x = -e- x ,
eX =
x
1 - tgh 2
(další vzorce viz, v definicích hyperbolických fun cí na začátku článku 3.4.4).
Goniometrické a hype!bolické funkce imaginárního
a komplexního argumentu
cosh (ix) - cos x, cosh x - cos (ix),
sinh (ix) I sIn x, sinh x = - i sin (ix),
tgh(ix) itgx, tghx = -i tg (ix),
cotgh (ix) = - i cotg x, cotgh x .- i cotg (ix),
sin (x + iy) = sin x cosh y + i cos x sinh y,
cos (x + ir) = cos x cosh y + i sin x sinh y,
383
tg (x + iy)
sin (2x) :t i sinh (2y)
cos (2x) + cosh (2y)
sin (2x) + i sinh (2yr
2(sin 2 x + sinh 2 y)
sin (2x) :t i sinh (2y)
----
2(cos 2 x + sinh 2 y) ,
sin (2x) + i sinh (2y)
cos (2x) - CQsh (2y) ,
cotg (x + iy) -
sinh (x + iy) = sinh x cos y + i cosh x sin y,
cosh (x + iy) = cosh x cos y + i sinh x sin y,
sinh(2x):t i sin (2y)
cosh (2x) + cos (2y) ,
( . ) sinh (2x) + i sin (2y)
cotgh x + lY = .
. cosh (2x) - cos (2y)
tgh (x + iy)
3.4.5. Hyperbolometrické funkce
Hyper.bolometrick.vmi funkcemi (reálné proměnné> argsinh (argunlent
hyperbolického sinu), argcosh (argument hyperbolického kosinu), argtgh
(argument hyperbolického tangens) a argcotgh (argument hyperbolického
kotangens) nazýváme inverzní funkce po řadě k hyperbolickým funkcím
sinh, cosh, tgh a cotgh.
i y.. argtgh x .
13
:2
-ft-J-2-f i
, : -f li 2 3 4 x
'1 -21
-3 1
-Ir I
Obr. 217. Funkcc argumcnt
hyperbolického sinu a argument
hypcrbolického kosinu
Obr. 218. Funkce argument
hyperbolického tangens a argumc
hyperbolického kotangens
Grafy hy per bolomet ric k ých funk cí (obr. 217 a 218)
.ft = { [x, y] ly = argsinh x, x E R, Y E R},
.f = {[x, y] I r = argcosh x, x E (1, + x), y E (O, + x.)},
.f3 = {[x, y] I y = argtgh x, x E ( - 1, 1), Y E R } ,
.f = {[x, y] I y = argcotgh , x E ( - x, - 1 ) u (1, + x), Y E P \ (O 1 .
384
Vyjádření hyperbolometrické funkce
pomocí jiné hyperbolometrické funkce
argsinh x - argcosh J(x 2 + 1) (x > O),
,
= - argcosh J(x 2 + 1) (x. < O),
argtgh x
- J(x 2 + 1)'
J(x 2 + 1) (x * O);
- argcotgh
x
argcosh x - argsinh J(x 2 - 1) (x > 1),
argtgh J(x 2 - 1) (x > 1),
-
x
x (x > 1);
- argcotg J(x 2 - 1)
argtgh x argsinh x '( - 1 < x < 1),
- J(1 - x 2 )
1 (O < x < 1),
- argcosh J(1 - x 2 )
1 (-1 < x < O),
= - argcosh J(1 - x 2 )
1 (-1 < x < 1, x 9= O);
- argcotgh -
x
1 (x > 1),
argcotgh x = argsinh J(x 2 - 1)
t (x < -1),
= - argsinh J(x 2 --1)
x' (x > 1),
- argcosh J(x 2 - 1)
1 (Ixl > 1).
- argtgh -
x
385
Součty a rozdíly hyperbolometrických funkcí
argsinh x + argsinh y = argsinh [x J(1 + y2) + Y J(1 + X2)],
largcoshx + .argcoshyl = argcosh {xy + J[(X2 - 1)(y2 - I)]}
(x > 1, y > I),
argtgh x + argtgh y ·
x+y
= argtgh -
1 + xy
(Ixl < 1, Iyl < I).
Hyperbolometrické funkce imaginárního argumentu
argsinh (ix) - i arcsin x,
argcosh (i x) = 1 arccos x,
argtgh (ix) - i arctg x,
argcotgh (i x) = -i arccotg x.
Vztahy mezi hyperbolometrickými funkcemi
a přirozeným logaritmem
argsinh x = ln [x + J(x 2 + 1)],
argcosh x = ln [x + J{x 2 - 1)] (x . > I),
argtghx = !ln 1 + x (Ixl < 1),
'I - x
, 1 X + 1 (I I )
argcotgh x = "2 ln x > 1 .
x-I
3.5. SFÉRICKÁ TRIGONOMETRIE
3.5.1. Základní pojmy
Hlavní kružnicí kulové plochy [sféry] nazýváme průnik kulové plochy
a roviny procházející středem kulové plochy.
Vedlej. í kružnicí kulové plochy [sféry] nazýváme neprázdný průnik kulové
plochy a roviny neprocházející středem kulové plochy.
Sférickou vzdáleností bodů A, B kulové plochy, které neleží na témže prů-
m u, nazýváme délku menšího oblouku z oblouků hlavní kru nice pro-
cházející body A, B. Sférická vzdálenost protějších bodů kul,?vé plochy se rovná
polovině délky hlavní kružnice.
Sjerickým dvojúhelníkem nazýváme část kulové plochy ohraničenou oblouky
dvou různých hlavních kružnic.
386
Sférickým trojúhelníkem nazýváme část kulové plochy ohraničenou tako-
vými oblouky (stranami sférického trojúhelníku) tří různých hlavních kružnic,
které spojují tři body A, B, C kulové plochy (body A, B, C neleží na téže hlavní
kružnici) a které se kromě bodů A, B, C neprotínají. Jestliže se délky všech
stran sférického trojúhelníku rovnají sférickým vzdálenostem, pak tento
sférický trojúhelník nazýváme Eulerovým trojúhelníkem (obr. 219).
,
Obr. 219. Eulerův trojúhelník ABC
Úmluva:
V dalším textu budeme uvažovat jen Eulerovy trojúhelníky při polo-
měru r = 1 kulové plochy.
Stranami sférického trojúhelníku jsou oblouky hlavních kr'užnic, takže při
r = 1 jsou přímo určeny velikostmi úhlů BSC, ASC a ASB polopřímek SA,
SB a SC (S je střed kulové plochy) v obloukové míře. Mluvíme proto o veli-
kostech stran sférického trojúhelníku.
Polopřímky, jejichž počátkem je střed S kulové plochy a vnitřními body
jsou vrcholy A, B, C sférického trojúhelníku, tvoří tzv. základní trojhran SABC.
Velikosti (1, B, y úhlů sférického trojúhelníku ABC se rovnají odchylkám
stěn základního trojhranu SABC.
Označení vrcholů a velikostí stran a úhlů sférického trojúhelníku odpovídá
označení u rovinného trojúhelníku. Prvky a, b, c, ex, B, y se nazývají =ákladní
prvky sférického trojúhelnlku.
Polární trojhran SA' B' C' má hrany kolmé k stěnám základního trojhranu
SABC a určuje na kulové ploše Eulerův polární trojúhelník A'B'C'. .
Podmínky pro velikosti stran a úhlů sférického trojúhelníku
O < a + b + c < 21t,
1t < ex + tJ + Y < 31t.
Platí a > b, resp. a = b, resp. a < b, právě když ex > B, resp. ex = tj,
resp. ex < B.
387
Platí a + b > 1t, resp. a + b = 1t, resp. a + b < 1t, právě když rJ.. + B > 1t,
resp. rJ.. + B = 1t, resp. rJ.. + B < 1t.
Obdobné vztahy platí také pro ostatní strany a úhly.
Číslo
e=rJ..+B+y-1t
se nazývá sférický exces [sférický nadbytek J.
Číslo
d = 21t - (a + b + c)
se nazývá sférický defekt.
Velikosti stran a úhlů polárního trojúhelníku
Velikosti stran polárního trojúhelníku A' B' C' jsou
a' = 1t - rJ..,
b' = 1t - B,
c' = 1t - Y
a velikosti jeho úhlů jsou
rJ..' = 1t - a
,
B' = 1t - b,
/=1t-c.
Nahradíme-li tedy v kterémkoli vzorci velikosti stran velikostmi výplňků
úhlů a velikosti úhlů velikostmi výplňků stran, dostaneme nový vzorec
(např. výplněk úhlu o velikosti rJ.. má velikost a' = 1t - rJ.. a výplněk strany
o velikosti a má velikost rJ..' = 1t - a).
.
3.5.2. Pravoúhlý sférický trojúhelník
Použív se téhož označení jako u rovinného pravoúhlého troj-
úhelníku [tj. při y = t1t znaky a, b znamenají velikosti odvěsen a znak c
velikost přepony (obr. 220)].
c
c
(l
A
B
'Jr'
--b
2
11"
--o
2
Obr. 220. Pravoúhlý sférický trojúhelník
Obr. 221. Schéma k Neprerovu pravidlu
388
Neperovo pravidlo pro pravoúhlý sférický trojúhelník
Jestliže velikost c přepony, velikosti Q:, f3 úhlů a velikosti !7t - a, tn - b
doplňků stran po řadě o velikostech a, b napíšeme k vrcholům pětiúhelníku
v pořadí zřejmém z obr. 221, pak kosinus libovolného prvku se rovná součinu
sinů dvou protilehlých prvků nebo součinu kotangent dvou sousedních prvků.
Podle Neperova pravidla lze základní prvky pravoúhlého sférického troj-
úhelníku vypočítat. ze dvou daných prvků pomocí vzorců
. ..
sIn a = sin sIn c ,
sin a = tg b cotg B ,
sin b = sin c 4 sin B,
sin b = tg a cotg Cl,
cos c = cos a cos b,
cos c = cotg rJ.. cotg B,
cos rJ.. = cos a sin B,
cos rJ.. = cotg c tg b,
cos B = sin rJ.. cos b,
cos B = cotg c tg a.
Sférický exces B v pravoúhlém sférickém trojúhelníku
Bab
tg - = tg - tg - .
222
3.5.3. Kosoúhlý sférický trojúhelník (obr. 222)
Používáme téhož označení jako u rovinného kosoúhlého troj-
úhelníku (viz obr. 124).
c
"
A
R
Obr. 222. Kosoúhlý sférický trojúhelník
Sinová věta
sin a : sin b : sin c = sin Q: : sin B : sin }' .
389
Kosinová věta pro strany
cos a = cos b cos c +. sin b sin c cos rJ.. ,
cos b = cos c cos a + sin c sin a cos 8 ,
cos c = cos a cos b + sin a sin b cos " .
Kosinová věta pro úhly
cos rJ.. = -cos IJ cos y + sin 8 sin y cos a,
cos 8 = - cos y cos rJ.. + sin y sin rJ.. cos b,
cos y = -cos rJ.. cos 8 + sin sin 8 cos c.
Věta o polovičních stranách, sférického trojúhelníku
Pro a = i(rJ.. + 8 + y) platí
sin = J( - cos cos O" - IX) ) ,
2 sin 8 sin y
a _ _ J cos(a - 8) cos (a - y)
cos-
2 sin 8 sin y ,
a J( cos a cos (a - rJ..) )
tg "2 = - cos (O" - 8) cos (O" - y) ,
a J( cos (a - 8) os (a - y) )
cotg - = - .
2 cos a os (a - rJ..)
Cyklickou záměnou dostaneme vzorce pro bl2 a c/2.
Věta o polovičních úhlech sférického trojúhelníku
Pro s = t(a + b + c) platí
. a _ _ J Sin(s - b)sin(s - c)
sin -
2 . sin b sin c '
a _ _ J Sin s sin (s - a)
cos-
2 sin b sin c '
t = J sin (s - b) sin (s - c)
g 2 .. ( ) '
sin s sin s - a
rJ.. J sin s sin (s - a)
cot g - = , .
2 sin (s - b)sin(s - c)
Cyklickou záměnou dostaneme vzorce pro 812 a y12.
390
Gaussovy vzorce
a+O a-b a+O a+b
sin COS COS COS
2 2 2 2
- -
}' c '" C
I
cos- cos- sln- cos-
2 2 2 2
a-O a-b rx-B a+b
sin sin cos sin
2 2 2 2
- -
y C "11 C
I
cos- sln- sin - sln-
2 2 2 2
Cyklickou záměnou dostaneme dalších osm vzorců.
Neperovy analogie
a+b a' - O +O a-b
tg cos tg cos
2 2 2 2
- a + O' - ,
c )' a+b
tg- cos cotg - cos
2 2 2 2
a-b a-O a-O a-b
tg sin tg sin --
2 2 2 2
- fl + O' -
c y a+b
tg- sin cotg - sin
2 2 2 2
,
I
'Cyklickou záměnou dostaneme dalšÍ vzorce.
oloměr r kružnice opsané a poloměr (l kružnice
vepsané sférickému troj ú'hel ník u
, Pro a = 1(a + O + y) a s = t(a + b + c) platí
,
t. J( cos (a - (1) cos (a - O) cos (a - f') )
ť cotg r = - ,
cos a
' tgQ = J Sin(s - a)sin( - b)sin(s - c) ,
. sin s
a
cotg r = cotg - cos (a - a), I
(cyklickou záměnou dostaneme
dalšÍ vzorce).
tgQ - tg 2 sin(s -a)
L
I
L
391
L'H uilierů v vzorec
Pro s = t(a + b + c) a sférický exces B platí
B J( S S - a s - b s - C )
tg - = tg - tg tg tg ,
4 2 2 2 2
s-b s-c
tg tg
2 2
( rJ.. e )
tg 2 - 2 .=
s s - a
tg - tg
2 2
Sférický defekt
Pro (] = -!( rJ.. + B + y), (] 1 = (] - rJ.., (] 2 = (] - B a (] 3 = (] - y a pro
sférický defekt d platí
.
tg = J[ -t g ( : - u)t g ( : - l )tg (: - 2 )tg( : - 3 )J.
I
Legendrova věta
Sférický trojúhelník o malých stra1?-ách lze nahradit rovinným trojúhelníkem
jehož velikosti úhlů jsou o třetinu .sférického excesu menší než velikosti úhlů
sférického trojúhelníku.
Obsah sférického trojúhelníku a sférického dvojúhelníku
viz v článku 3.3.3
Řešení kosoúhlých sférických trojúhelníků
Základní úloha 1:
Jsou dány velikosti tří stran.
Způsob řešení 1:
Vypočteme velikost jednoho úhlu pod e kosinové věty pro strany (např. eť):
cos a - cos b cos c
cos rJ.. =
sin b sin c
. B sin b sin rJ..
sin = .
sin a
(sinová věta),
. .
. sin c sin rJ..
sin y =
sin a
(sinová věta).
392
Způsob řešení 2:
Všechny velikosti úhlů vypočteme podle kosinové věty pro strany.
Způsob řešení 3:
Všechny velikosti ,úhlů vypočteme podle věty o polovičních úhlech, popř.
velikost jednoho úhlu vypočteme podle věty o polovičních úhlech a velikosti
ostatních úhlů vypočteme podle sinové věty jako v způsobu řešení 1.
Základní úloha 2:
I
Jsou dány velikosti dvou stran a velikost úhlu jimi sevřeného (např. b, c, ex).
Způ'so b řešení 1:
cos a = cos b cos c + sin b sin c cos ex (kosinová věta pro strany),
sin b sin ex'
sin B = . ( sinová věta),
sIn a
. .
. sIn c sIn ex
sIn y =
sIn a
(sinová věta).
Způsob řešení 2:
O+y
tg
2
b - c ex
cos cotg -
2 2
b+c
cos
2
. (Neperova analogie),
O-y
tg
2
b - c (X .
sin cotg -
2 2
-
. b + c
sIn
2
(Neperova analogie).
z !(O +.Y) a t(O - y} dostaneme oba úhly O a y. Dále vypočteme
b+c B+y
tg cos
2 2 ·
O-y
cos
2
a
tg- =
2
(Neperova analogie).
Základní úloha 3:
\
Jsou dány velikosti dvou stran a velikost úhlu proti větší z nich (např. b, c, O;
b > c).
393
Řešení:
sIn y -
a
tg- -
2
(X
cotg - =
2
sin c sin B
sin b
b+c B+y
tg cos
2 2
B-y
cos
2
B+y b+c
tg 2 cos 2
, b - c
cos
2
(sinová věta),
(Neperova analogie),
(Neperova analogie)
nebo úhel rJ.. vypočteme podle sinové věty.
Základní úloha 4:
Je dána velikost strany a velikosti obou k ní přilehlých úhlů (např. a, B, y).
Způsob řešení 1:
cos rJ.. = - cos ,B cos y + sin B sin y cos a (kosinová věta pro úhly),
sin B sin a
sin b = . (sinová věta),
sIn rJ..
. .
. sIn Y sIn a
sIn c =
sIn rJ..
B-y a
cos 2 tg "2
-
B+y
cos
2
. B-y a
sIn 2 tg "2 .
-
. B + Y
sIn
2
Z t(b + c) a t(b - c) dostaneme velikosti obou stran b a c. Dále vypočteme
. sin a sin B '
sIn rJ.. = (sinová věta).
sin b
Způsob řešení 2:
b+c
tg
2
b-c
tg
2
394
(sinová věta).
(Neperova analogie),
(Neperova analogie).-
Základní úloha 5:
Jsou dány tyto prvky: velikost strany, velikost přilehlého úhlu a velikost
protilehlého úhlu (např. b, B, y).
Řešení:
a
tg-
2
sin '" sin b
. I
sIn c =
sin {J
b+c fJ+y
tg cos --
2 2
B - y .
cos
2
(sinová věta),
(Neperova analogie),
. sin a sin B
sIn rJ.. =
sin b
( sinová věta).
Základní úloha 6:
J sou dány velikosti tří úhlů.
Způso b řešení 1:
cos rJ.. + cos B cos }'
cos a =
sin B sin y
sin {J sin a
sin b = .
sIn rJ..
(kosinová věta pro úhl)),
(sinová věta),
. .
sin '" sIn a
. I
sIn c =
sIn rJ..
(sinová věta).
Způsob řešení 2:
\" l kost jedné strany vypočteme podle věty o polovičních stranách; dále
postupujelne ja k \) v způsobu řešení 1.
3.5.4. Matematický zeměpis
Důležité délky a délkové měřicí jednotky
Střední poloměr Země podle Hayforda z r. 1910 je r H = 6371,229 km.
Přibližný poloměr referenční koule je r = 6 371,1 km.
Délka hlavní poloosy zemskéhc' c ;nsoidu podle Krasovského z r. 1940
je a = 6 378,245 km.
Délka zemského rovníku se . ,lle 'Krasovského z r. 1940 rovná
,
40 075 695 km.
395
Délka oblouku hlavní kružnice (zemského rovníku) zemské sféry odpoví-
dajícího jednomu stupni, resp. jedné minutě zeměpisné délky se přibližně
rovná 111,3 km, resp. 1,852 km = 1 n mile (nautical mile neboli námořní míle).
1 zeměpisná míle = 4 n mile = 7,408 km.
1 námořní čárka kompasové růžice se rovná 11*°.
Souřadnicová soustava Země
První osou A je rovník a druhou osou qJ je nultý poledník (greenwichský
poledník, čti: grynyčský).
Zeměpisné souřadnice
Zeměpisná délka A. se udává bud' jako délka oblouku zemského rovníku
mezi nultým a místním poledníkem, nebo jako odchylka roviny nultého
poledníku a roviny místního poledníku, přičemž od 0° do 180° jde o kladnou
odchylku (ve smyslu otáčení Země) neboli o východní zeměpisnou délku a od 0°
do -180° jde o zápornou odchylku (proti smyslu otáčení Země) neboli
o západní zeměpisnou délku.
Zeměpisná ířka qJ je odchylka přímky, která prochází uvažovaným místem
a středem zemské sféry, a roviny zemského rovníku, přičemž od 0° do 90°
jde o kladnou odchylku (od rovníku k severnímu pólu) neboli o severní
zeměpisnou šířku a od 0° do -90° o zápornou odchylku (od rovníku k již-
nímu pólu) neboli o jižní zeměpisnou šířku.
N
Obr. 223. Délka ortodromy
Nejmenší vzdálenost dvou bodů na sféře
Velikost oblouku hlavní kružnic.e spojujícího body P 1 [A. 1 , lpI] a P[ A.2, qJ2]
(tj., délka tzv. ortodromy), která je jejich nejmenší vzdáleností (tzv. ortodromická
vzdálenost e), se vypočte takto:
396
- Jestliže ve sférickém trojúhelníku Pt P 2 N (obr. 223) známe
I &PIl . 90 o - (P 1 ,
1&P 2 1 = 90 0 - ({J2,
I PINP21 = ; 2 - AI = A
(viz základní úlohu 2 o sférickém trojúhelníku), pak
cos e = cos (900 - ({JI) cos (90 0 - ({J2) +
+ sin (900 - ({J I) sin (90 0 - ((J2) cos ) =
= sin ({JI sin ({J2 + cos ({JI cos ({J2 cos A
(kosinová věta pro strany).
Výpočet azimutů ortodromy
Úhly a B sférického trojúhelníku P 1 P 2 N (viz obr. 223) vypočítáme tak,
že nejprve určíme velikost e oblouku P 1 P 2 a pak ji dosadíme do vzorců
. sin A. sin (90 0 - ({J2) sin A. cos ({J2
sin rJ.. = - . = . ( sinová věta),
sin e sin e
r
. B sin A cos ({JI
sin = . .
sin e
Vzdálenost dvou míst se stejnou zeměpisnou šířkou ({J
Ortodromickou vzdálenost e = Ip'J'21 (obr. 224) snadno vypočteme z pravo-
úhlého sf rického trojúhelníku P 1 DN, který vznikne tím, že v rovnoramen-
ném sférickém trojúhelníku P 1 P 2 N vedeme výšku v k jeho základně P 1 P 2 -
Platí
. e . A.
sin - = cos ({J sin -
2 2
(N eperovo pravidlo).
N
N
L
Ohr, 224. Ortodromická vzdálenost
Obr. 225. Loxodromická vzdálenost
397
Loxodromickou vzdálenost (velikost oblouku na rovnoběžkové kružnici) I
(obr. 225) vypočteme podle vzorce
I = A cos qJ (0),
nebo
1[r A. cos qJ
1 = 180 0 (km),
kde
r 6370km.
Poznámka:
Loxodroma je křivka na kulové ploše, která všechny poledníky [meridiány]
protíná pod stejným úhlem. Je-li tento úhel různý od 90°, pak se loxodroma
spirálovitě blíží k pólu. Každá rovnoběžková kružnice je loxodromou, která
poledníky protíná pod pravým úhlem.
398
4. ANALYTICKÁ GEOMETRIE
4.1. ANALYTICKÁ GEOMETRIE V ROVINĚ
4.1.1. Různé souřadnicové sousta vy
Při zavádění souřadnicových soustav jde o zavedení prostého
zobrazení všech bodů roviny na množinu R 2 = R x R.
Kosoúhlá so uř adn icová so us ta v a (O; x, y)
V rovině zvolíme různoběžky x, y (I xyl * in) s průsečíkem O, který na-
zveme počátkem souřadnicové soustavy (obr. 226). Přímku x, resp. y nazveme
první, resp. druhou osou kosoúhlé souřadnicové soustavy. Dále zvolíme body I E X,
JE y, I * O * J. Počátek O dělí každou z os na dvě polopřímky. Polopřímku
01, resp. OJ nazveme první, resp. druhou kladnou p%osou kosoúhlé souřad-
nicol,é soustavy. Polopřímku opačnou k polopřímce OI resp. OJ nazveme
první, resp. druhou zápornou p%osou kosoúhlé souřadnicové soustavy. Úsečku
DI, resp. OJ považujeme za jednotkovou úsečku na ose x, resp. y.
----7'P[x 11.]
/ 0,,0
/
/
/
/
/
/
I [xo, OJ x
oc E(O, )v( , )
Obr. 226. Kosoúhlá souřadnicová
sousta va
Polohu libovolného bodu P roviny určíme takto: Bodem P vedeme rovno-
běžky s osami x a y a jejich průsečíky s osami x a y označíme po řadě P 1 a P 2 .
První souřadnicí [souřadnicí x] bodu P nazýváme číslo Xo = (sgn e) IOP 1 1,
přičemž sgn e = 1, resp. sgn e = -1, právě když bod P 1 leží v první kladné,
resp. první záporné poloose. Druhou souřadnicí [souřadnicí y, pořadnicí]
bodu P nazýváme číslo Yo = (sgn e) IOP21, kde sgn e = 1, resp. sgn e = -1,
399
právě když bod P2 leží v druhé kladné, resp. druhé záporné poloose. Počátek O
má .souřadnice Xo = O a Yo = O. Souřadnice x a y v kosoúhlé souřadnicové
soustavě se nazývají kosoúhlé. Bod P se souřadnicemi Xo a Yo označujeme
p[xo, Yo] nebo P = [xo, Yo] (obsahují-li souřadnice desetinnou čárku, pak
v uvedených symbolech místo čárky píšeme středník). Někdy je vhodné sou-
řadnice bodu P označovat Xp a yp.
Poznámka:
Nemůže-li dojít k nedorozumění, lze souřadnice bodu P značit stejnými
písmeny jako souřadnicové osy x a y, tj. používat označení p[x, y] nebo
P = [x, y ].
Pravoúhlá [ortogonální] souřadnicová soustava (O; x, y)
Osy x a y volíme k sobě kolmé (obr. 227). Souřadnice x a y v pravoúhlé
souřadnicové soustavě se nazývají pravoúhlé [ortogonální].
/ . y
Ya -- --I P[x o , Yo] Yo ----]' P[xo,yoJ
J I I
I I
I I
I J I
I
I I
O I Xo x O I ,fo x
Obr. 227. Pravoúhlá [ortogonální]
souřadnicová soustava
Obr. 228. Kartézská [ortonormální]
souřadnicová sousta va
Kartézská [ortonormální] souřadnicová soustava (O; x,y)
, Osy x a y volíme k sobě k o lm é a jednotkové úsečky na osách x a y volíme
shodné, tj. volíme 01 OJ (obr. 228). Souřadnice x a y v kartézské sou-
řadnicové soustavě se nazývají kartézské [ortonormálni].
Polární souřadnicová soustava (O; (l, qJ)
V rovině zvolíme polopřímku 01, přičemž bod O nazveme pólem a polo-
přímku o = OJ polární osou (obr. 229). Polohu libovolného bodu P určíme
vzdáleností bodu P od pólu O (neboli velikostí vektoru OP , který nazýváme
průvodičem nebo rádiusvektorem bodu p), kterou zpravidla značíme (l (popř. r)
400
a základní velikostí orientovaného úhlu lOP (zvaného polární úhel), kterou
zpravidla značíme qJ a nazýváme argumentem nebo amplitudou. Přitom při-
pomeňme, že velikost qJ orientovaného úhlu 10P je kladná, resp. záporná,
přejde-li polární osa o v polopřímku OP otočením v kladném (tj. ve smyslu
opačném ke smyslu otáčení hodinových ručiček), resp. záporném smyslu.
Souřadnice (l a qJ v polární soustavě se nazývají polární.
ti
P[9,lp]
o
Obr. 229. Polární souřadnicová soustava
I
o
Vztahy mezi souřadnicemi bodů v různých souřadnicových
soustavách
Rovnoběžné posunutí kartézské souřadnicové soustavy
Souřadnice bodu P v kartézské souřadnicové soustavě (O; x, y) označíme
x, y a v kartézské souřadnicové soustavě (O'; x', y') takové, že x' ii x, y' ii y,
označíme x', y' (obr. 230).
y
yl
p
'- O
I, I
I '
I f i .xl
y'
o
x
Obr. 230. Rovnobčžné posunutí
Obr.'231. Otočení kartézské
souřadnicové soustavy
Pak platí
,
x = x - c,
y'=y-d;
,
x = x + c
y=y'+d,
přičemž O' = [c, d] v soustavě (O; x, y)"a O = [ -c, -d] v soustavě (O'; x', y').
401
Otočení kartézské souřadnicové soustavy
Souřadnice bodu_ P v kartézské souřadnicové soustavě (O; x, y) označíme
x, y a v kartézské souřadnicové soustavě takové, že jak kladná poloosa osy x
s kladnou poloosou osy x', tak také kladná poloosa osy y s kladnou poloosou
osy y' svírá orientovaný úhel o velikosti qJ, označíme x', y' (obr: 231). Pak platí
x = x' cos qJ - y' sin qJ,
y = x' sin qJ + y' cos qJ;
x' = x cos qJ + Y sin qJ,
I .
Y = - x sIn qJ + y cos qJ.
Yr
y
Yo
x
...-
X r
o c x -c
i
._-
,(
Obr. 232. Rovnoběžné posunutí
a otočení
Obr. 233. Otočení a rovnoběžné
posunutí
Rovnoběžné posunuti a otočeni kartézské souřadnicové soustavy
Souřadnice bodu P v kartézské souřadnicové soustavě (O; x, y) označíme
x, y a v kartézské souřa nicové soustavě (0 ' ; x', y') takové, že jak kladná
poloosa osy x s kladnou poloosou osy x', tak také kladná poloosa osy y
s kladnou poloosou osy y' svírá orientovaný úhel o velikosti qJ, označíme x', y'
(obr. 232). Pak platí '
x = x' cos qJ - y' sin qJ + c,
Y = x' sin qJ + y' cos qJ + d;
x' = x cos qJ + Y sin qJ - C cos qJ - d sin qJ,
y' = - x sin qJ + y cos qJ - C sin qJ - d cos qJ,
přičemž 0 ' = [c, d] v soustavě, (O; x, y).
402
Otočení a rovnoběžné posunutí kartézské souřadnicové soustavy (obr. 233)
x = x' cos ({J - y' sin <tJ + c cos ({J - d sin ({J,
y = x' sin ({J + y' cos qJ + c sin ({J + d cos qJ:
x' = x cos ({J + Y sin qJ - C,
y' = - x sin ({J + y cos ({J - d,
kde O = [ -c, -d] v soustavě (O'; x', y').
Přechód od kartézské souřadnicové soustavy (O: x, y) ke kosoÚhlé souřadnicové
soustavě (O; x', y') a od kosoúhlé souřadnicové soustavy ke kartézské souřadni-
cové soustavě .
Souřadnice bodu P v kartézské, resp. kosoúhlé.' souřadnicové soustavě
označíme x, y, resp. x', y'. Přitom obě souřadnicové soustavy mají společný
počátek O a kladná poloosa osy x soustavy (O; x, y) svírá s kladnou poloosou
osy x', resp. y' soustavy (O; x', y') orientovaný úhel o velikosti ({JI' resp. ({J2
(obr. 234). Pak platí '
y -
I I
X cos ({J I + Y cos ({J 2 ,
I . I .
X sIn ({JI + y sIn ({J2;
-x sin ({J2 + Y cos ({J2
sin (({JI - ({J2)
x sIn ({JI - Y cos ({JI
sin (({JI - ({J2)
x =
X'-
y' =
y
y
p
I 'f..
O __ X 1 ----J X
,
I Y1'
Obr. 234. Přechod od kartézské
souřadnicové sousta vy ke kosoúhlé
sousta vě
Obr. 235. Přechod od kartézské
souřadnicové sousta vy k polární
sousta vě
403
Poznú,nka:
Při qJ2 = CPI + 1tí2 dostáváme vzorCl: p,-O otqčení kartézské souřadnicové
soustavy o orientovaný úsel velikosti ({JI' Vzorců lze také použít pro přechod
od jedné kartézské souřadnicové soustavy k jiné opačně orientované kartézské
souřadnicové soustavě (např. ({JI = 1t, qJ2 = 1t/2, popř. ({JI = O, qJ2 = 31t/2).
Přechod od kartézské souřadnicové soustavy (O; x, y) k polární souřadnicové
soustavě (O; {l, ({J) a od polární souřadnicové soustavy ke kartézské souřadnicové
sou tavě
Souřadnice bodu P v kartézské, resp. polární souřadnicové soustavě
označíme x, y, resp. (1, qJ. Přitom soustava (O; (!, qJ) je orient,ována stejně jako
soustava (O; x, y), tj. polární osaje totožná s kladnou poloosou osy x (obr. 235).
Pak platí
x = e cos qJ, } y
. => - = tg qJ;
Y = (1 sIn qJ . x
(1 = J(x 2 ,+ y2),
Y
qJ = arctg- (x > O, y > O),
x
qJ = tx (x = O, y > O),
y
qJ = 1t + arctg-
x
(x < O, 'ty E R),
qJ = 1 1t
(x = O, y < O),
y
qJ = 21t + arctg-
x
(x, > O, y < O).
4.1.2. Body a úsečky
Vzdálenost d dvou bodů PI[X I , YI] a P 2 [X2' Y2] (obr. 236)
d = J[(X2 - XI)2 + (Y2 - YI)2].
y t 1(X2. Y2 J
1/
I
0 1 P, (X, I ¥,]
y
(X2 , Y2 J
>
x
[Pf I J
r921"J
Pf
P2
O --
o
x
Obr. 236. Vzdálenost dvou bodů' Obr. 237. Vzdálenost dvou bodů
v kartézských souřadnicích v polárních souřadnicích Obr. 238. Směrnice úsečky
404
Vzdálenost d dvou bodů PI[gl, qJt] a P2[Q2,l{J2] (obr. 237)
d = J[gf + g - 2g l Q2 cos (qJ2 - qJI)]'
Souřadnice bod u D[XD' YD] s dělicím poměrem )\, vzhledem
k bodům P 1 [XI,YI] a P 2 [X 2 ,Y2] (D:FP 2 ) ,.
Xl - A.X 2 YI - A.Y2
X D = 1 -)..' YD = 1 _ )"
(definice dělicího poměru je na str. 302).
Střed Po [xo, Yo] úsečky P I P 2 (A = -1)
YI + Y2
Yo =
2
Xl + X2
Xo =
2
Těžiště T[xr,Yr] trojúhelníku s vrcholy PI[XI,YI], P 2 [X2,Y2]
a P 3 [ X 3 , Y3]
Xl + X 2 + X 3
X r =
3
YI + Y2 + Y3
Yr =
3
Jsou-li P 1 , P 2 a P 3 hmotnými body po řadě s hmotnostmi ml' m2 a m3' pak
pro těžiště T soustavy bodů P I , P 2 , P 3 platí
mlx l + m2 x 2 + m3 x 3
Xr =
ml + m 2 + m3
mlYI + m2Y2 + m3Y3
Yr =
ml + m2 ,t nt3
obecně pro souřadnice těžiště T n hmotných bodů s hmotnostmi po řadě
ml' m2, . . ., m n platí
n
L mkxk
k=l
Xr = n
L m k
k=l
n
L mkYk
k=l
Yr = n
L m k
k=l
Směrnice úsečky s krajními body PI[XI, Yi] a P 2 [X2, Y2) (Xl 9= X 2 )
Y2 - YI
tg qJ = k = ,
X2 - Xl
kde qJ je orientovaný úhel sevřený kladně orientovanou osou X a přímkou P I P 2
(měřený v kladném smyslu); výraz tg qJ se nazývá směrnice [stoupání] úsečky
(obr. 238).
405
Obsah trojúhelníku s vrcholy P1[XI,Yt], P 2 [X 2 'Y2] a P3[X 3 'Y3]
S = t1X t (Y2 - Y3) + X2(Y3 - YI) + X3(Yt - Y2)1 =
I 1 I
.= '2 X I' Y 1 , = I l x 2 - X I' Y 2 - Y 1 I
X 2 , Y2' 1 X 3 - Xl' Y3 - YI
X3' Y3, 1
(ve vzorcích jde o absolutní hodnoty determinantů).
Ousah trojúhelníku s vrcholy P1[QI' qJt], P 2 [g2, qJ2] a P 3 [Q3, qJ3]
S = -!IQIQ2 sin (qJI - qJ2) + g2Q3 sin (qJ2 - qJ3) + Q3Ql sin (qJ3 - qJt)l.
Obsah konvexního n-úhelníku s vrcholy
PI[X 1 , YI]' P 2 [X 2 , Y2]' ..., Pn[Xn, Yn]
S.= tI X I(Y2 - Yn) + X2(Y3 - YI) + X3(Y4 - Y2) + ... + Xn(YI - Yn-I)I '
= tl(X I - X 2 ) (YI + Y2) + (;X 2 - X 3 ) (Y2 + Y3) + ... + (Xn - Xl) (Yn + YI)I =
== t IX t, x 2 1 + I X2, X 3 1 +... + I Xn' X l I
YI' Y2 Y2' Y3 Yn, YI
n
= 11 L Xk(Yk+1 - Yk-t)!
k=l
(v posledním výrazu klad me Yo = Yn a Yn+ t = YI)'
4.1.3. Přímka
Směrnicový tvar rovnice [směrnicová rovnice] přímky, která
není rovnoběžná s osou Y (obr. 239)
y = kx + q,
kde k = tg qJ je t,zv. směrnice přímky, přičemž qJ je orientovaný úhel, jehož
vrchol je v počátku souřadnicové soustavy, první rameno tvoří první
kladná poloosa a druhé rameno je rovnoběžné s danou přímkou
libovolně orientovanou;
q - tzv. úsek (vyťati přínlkou) na ose y tj. druhá souřadnice průsečíku
přímky s osou y. '
Pro k > O, resp. k < O je příl11ka grafem rostoucí, resp. klesající funkce
Y = kx + q. Pro k = O je přímk rovnoběžná s osou .x a pro q = O prochází
počátkem.
406
Úsekový tvar rovnice [úseková rovnice] přímky, která není
rovnoběžná s žádnou souřadnicovou osou ani neprochází
počátkem (obr. 240)
x y
-+-=1,
p q
p * O,
q * O,
.
kde p je tzv. úsek (vyťatý přímkou> na ose x, tj. první souřadnice průsečíku
přímky s oso.u x,
q - tzv. úsek (vyťatý přímkou> na ose y, tj. druhá souřadnice průsečíku
přímky s osou y.
y
y
x
x
Obr. 239. Směrnicový tvar
rovnice přímky
Obr. 240. Úsekov)' tvar
rovnice přímky
Obr. 241. Normálový tvar
rovnice přímky
Normálový tvar rovnIce [normálová rovnice] přímky (obr. 241)
x cos t/J + Y sin t/J - n = O, n > O,
kde n je vzdillenost počátku O od přímky,
t/J - velikost orientovaného úhlu, jehož prvn rameno je první kladná
poloosa a druhé rameno je polopřímka s počátečním bodem O
vedená kolmo k přímce.
Obecný tvar rovnice [obecná rovnice] přímky
ax + by + c = O,
kde a, b, c jsou konstanty, přičemž konstanty a a b nejsou zároveň rovny nule.
Převedení obecného tlJaru rovnice přímky v směrnicový tvar:
a c
Y = -b x - b (b * O),
k=
a
b'
c
q=
b
407
Převedení obecného tvaru rovnice přímky v úsekový tvar:
x y
- + - = 1 (a, b, c * O),
c c
a b
c
c
p=
,
a
q=
b
Převedení obecného tvaru rovnice přímky v normálový tvar:
a b c
/; ,J(a 2 + h 2 ) x + /; ,J(a 2 + h 2 ) Y + /; ,J(a 2 + h 2 ) = O,
kde B = 1, resp. B = -1, jestliže sgn c = -1, resp. sgn c = 1.
Zvláštní případy polohy přímky:
Rovnice přímky procházející počátkem:
y = kx; ax + by = O.
Rovnice rovnoběžky s osou x:
y = q;
by + c = O.
Rovnice rovnoběžky s osou y:
x = p; ax + c = O.
Rovnice osy x:
y = o.
Rovnice osy y:
x = O.
y
y
P2 CX 2,Y,]
e'f ,y,]
o
o
'X
o
x
otk
Obr. 242. Přímka daná bodem
a směrnicí
Obr. 243. Přímka daná
dvěma body
()br, 244. Polární tvar
rovnice přímky
Rovnice přímky dané bodem p[x 1 , YI] a směrnicí k = tg qJ
(obr. 242)
y - YI = k(x - x l ).-
408
Rovnice přímky dané dvěma bodyPI[XI,YI] a P 2 [X2,Y2] (X2 =* Xl)
(obr. 243)
,
Y - YI X2 - YI
x - Xl X2 - Xl
neboli
Y2 - YI ( )
Y - YI = X - Xl
X 2 - Xl
neboli ve tvaru determinantu
x, Y, 1 = O.
Xl' YI' 1
X 2 , Y2, 1
Jestliže Xl = X 2 , pak rovnice přímky je X = Xl. Podmínka, aby tři body
P 1 [X 1 , YI]' P 2 [ x 2 ' Y2] a P 3 [ x 3 ' Y3] ležely na téže přímce, á tvar
Xl' YI, 1 = O.
X2, Y2, 1
X3, Y3' 1
Polární tvar rovnice [polární rovnice] přímky jdoucí bodem
p[Q, qJ] (obr. 244)
n
Q=
cos (t/J - qJ)'
kde n je vzdálenost přímky od pólu O;
t/J - orientovaný Í1hel, jehož vrchol je v pólu O, první rameno tvoří
polární osa a druhé rameno tvoří polopřímka s počátečním bodem O
vedená kolmo k přímce.
V zdá lenos t d bod U P I [Xl' YI] od pří mk y s rovn icí
v normálovém tvaru
. laXI + bYl + ci
d = lx I cosrjJ + YI smrjJ - ni = -/ ( 2 2) .
. V a + b
409
Průsečík p[xp,Yp] dvou přímek
Rovnice daných přímek považujeme za soustavu rovnic, jejíž řešení (prvek
oboru pravdivosti) dává souřadnice průsečíku přímek. Například průsečík P
přímek daných rovnicemi (k l *= k 2 )
y = klx + ql ,
Y = k 2 x + q2
v směrnicovém tvaru má souřarlnice
ql - q2 lJl k 2 - q2 k l
X p = k 2 - k l ' Yp = k 2 - k l
Podobně v případě rovnic
alx + bly + CI = O,
a2 x + b 2 y + C2 = O
dostaneme
b l , CI
b l C2 - b 2 C l b 2 , C2
xp = - ,
a l b 2 - a 2 b l al, b l
a2, b 2
CI a2 - C2 a l
YP =
a l b 2 - a 2 b l
CI' al.
C2, a 2 ( al, b l =FO}
-
a l , b l a2, b 2
a 2 , b 2
přímky dané . .
rovnIcemI
Podmínka, aby se tři
alx + bly + CI = O,
a2 x + b 2 y + C2 = O,
a3 x + b 3 y + C3 = O
protínaly v prá vě jednom bodě:
a l' b l , CI = O.
a2, h 2 , C2
a3' b 3 , C3 I'
Odchylka qJ dvou přímek Pl, P2 (obr. 245) daných rovnicemi
Y = klx + ql'
Y = k 2 x + q2
410
se určí podle vzorce
k 2 - k l I
tgq> = 1 + k 1 k 2 1
popř. rovnicemi
. alx + blx + c. = O,
a 2 x + b 2 x + c 2 = O
se určí podle vzorce
a.b 2 - a2 b .
tg <p = --
a.a2 + b l b 2
(<p je velikost ostrého úhlu).
yA
I
x
(k.k2 =t= -1),
(a.a 2 +'b.b 2 =t= O)
Obr. 245. Odchylka dvou přímek
Podmínka rovnoběžnosti dvou přím,ek daných r.ovnicemi
y=k.x+q.,
y = k 2 x + {j2
Je
k l = k 2 ,
popř. rovnicemi
alx + b.y + CI = O,
a 2 x + b 2 y + ('2 = O
Je
a., b l = (I.h 2 - a2bl = O neboli a.: a2 = b l : b 2 .
a2' b 2
Podmínka kolmosti dvou přímek daných rovnicemi
y = k.x + q.,
Y = k 2 x + q2
Je
k 1 k 2 + 1 = O neboli kt-
1
k 2 '
411
popř. rovnicemi
aIx + bly + CI = O,
a2 x + b 2 y + C2 = O
Je
aIa 2 + b l b 2 = O.
Rovnice svazku přímek
Jestliže R. = O, R 2 = O, kde
RI = aIx + bly + CI'
R 2 = a2 x + b 2 y + C2
jsou rovnice dvou různoběžek, pak rovnice svazku přímek se středem v prů-
sečíku těchto různoběžek má tvar
JLRt + AR 2 = O,
kde JL, A. jsou vhodná reálná čísla, která nejsou zároveň rovna nule.
Osy o. a 02 různoběžek PI a P2 (obr. 246)
Jsou-li různoběžky dány rovnicemi v obecném tvaru
at X + bly + CI = O,
a 2 x + b 2 y + C2 = O,
pak rovnice os různoběžek jsou
at X + bly + Ct + a2 x + b 2 y + C2 = O.
J(ai + bi) - J(a + b )
y
Obr. 246. Osy různoběžek
o
x
Jsou-li různoběžky dány rovnicemi v normálovém tvaru
x cos t/J I + Y sin t/J. - nI = O,
x cos t/J 2 + Y sin t/J 2 - n 2 = O,
pak rovnice os různoběžek jsou
x(cos t/J I + cos t/J2) + y(sin t/J I + sin t/J2) - (nI + n 2 ) = O.
412
4.1.4. Kružnice
Definice kružnice.. poloměru kružnice a.průměru kružnice viz v člán-
ku 3.2.4.
Rovnice kružnice se středem S v počátku 0[0, O] (obr. 247)
x 2 + y2 = r2,
kde r je poloměr kružnice.
y
y
x
x
x
....
Obr. 247. Kružnice
Obr. 248. Kružnice
v obecné poloze
Obr. 249, Vrcholová
rovnice kružt\Íl'e
Obecná rovnice kružnice se středem S[m, n] a poloměrem r
v kartézských souřadnicích (obr. 248)
(x - m)2 + (y - n)2 = r 2 .
Vrcholová rovnice kružnice (obr. 249)
y2 = 2rx - x 2 .
Obecná algebraická rovnIce druhého stupně
vyjadřující kru nici
Obec á rovnice druhého stupně v x a y
.allx2 + 2a 1 2 x y + a22y2 + 2a 1 3 x + 2a 23 y + a 33 = O
vyjadřuje kružnici, právě když
alt =a22 =FO,
al2 = O,
2 2 O
a13 + a23 - all a 33 > ,
takže obecná rovnice kružnice má tvar
2 2-
a 11 x +a 11 y +2a13x+2a23y+a33 =0.
413
Střed kružnice
s = [ - , - a 23 J .
a ll a ll
Poloměr kružnice
1 / ( 2 'z )
r = - '\/ a l 3 + a23 - all a33 .
a 11
Rovnice kružnice procházející třemi body
Pl[X t 'YI]' P 2 [X 2 ,Y2] a P 3 [X 3 'Y3]
X2 + y2, x, y, 1 = O.
2 2 1
Xl + YI, XI' Yl ,
2 2 1
X 2 + Y2, X 2 , Y2'
2 2 1
x 3 + Y3' X3, Y3'
Parametrické rovnice kružnice se středem S[m, n] a poloměrem r
(obf;-250)
x = ln + r cos t ,
Y = n + r sin t,
kde t E (O, 2n) je proměnný parametr.
y
---
x
o
m
:.
o
Obr. 251. Kružnice v polárním vyjádření
Obr. 250. Kružnice v parametrickém
vyjádření
Rovnice kružnice v polárních souřadnicích se středem S[Qo, qJo]
a poloměrem r (obr. :51)
g2 - 2QQo cos (qJ - qJo) + Q = r 2 ,
kde (l, qJ jsou souřadnice obecného bodu P na kružnici.
414
Zvláštní případy: ,
Pól O leží na kružnici a střed kružnice leží na polární ose (obr. 252):
(1 = 2r cos qJ.
o
p
o
o
Obr. 252. Pól leží na kružnici a polární
osa prochází středem kružnice
Obr. 253. Pól leží na kružnici a polární
osa neprochází středcm kružnice
Pól O leží na kružnici a polární osa svírá s průměrem procházejícím pólem O
úhel qJo (obr. 253):
(1 = 2r cos (qJ - qJo)'
Pól O neleží na kružnici a střed S[Qo, O] leží na polární ose (obr. 254):
{!2 - 2(1(10 cos qJ + l! = r 2 .
Pól O leží na kružnici a úseky na osách x, y kartézské souřadnicové soustavy
jsou po řadě p, q (obr. 255):
(1 = p cos qJ + q sin qJ .
o
p (p, ,)
o
o
Obr. 254. Pól neleží na kružnici
a polární osa prochází středem kružnice
Obr. 255. Pól leží na kružnici a p a q
jsou úseky na souř.adnicových osách
Průsečíky přímky y = kx + q a kružnice x 2 + y2 = r 2
Yl.2 =
qk 1 j [ 2 ( 2 ) 2 ]
- 1 + k 2 + 1 + k 2 V r 1 + k - q ,
1 : k 2 + 1 : k 2 J[r2(1 + k 2 ) - q2].
Xl.2 =
415
Odmocněnec r 2 (1 + k 2 ) - q2 = D (diskriminant) udává:
D > O - přímka protíná kružnici právě ve dvou reálných bodech (přímka
je sečnou);
D = O - přímka se dotýká kružnice právě v jednom reálném bodě (v dvoj-
ném bodě) (přímka je tečnou);
D < O - přímka kružnici neprotíná v žádném reálném bodě (přímka je
vnější přímkou kružnice).
y
x
Obr. 256. Tečna a normála kružnice
Tečna a normá!a kružnice X2 + y2 = r 2 v bodě Pl [Xl' YI] (obr. 256)
Rovnice tečny:
XXI +YYI =r 2 ;
směrnice
XI
kt = --o
YI
Rovnice normály:
yx. - XYI = O;
směrnice
k = YI
n .
Xl
Délka úseku tečny
rYl
t = -.
Xl
Délka úseku normály
n = r.
Délka subtangenty
yi
St =
Xl
416
Délka subnormály
Sn = X I .
Polára bodu po[xo,Yo] vzhledem ke kružnici x 2 + y2 = r 2
XXo + YYo = r 2 .
Polárou bodu Po vzhledenl ke kružnici nazyvame množinu všech bodů
harmonicky sdružených s bodem Po vzhledem k průsečíkům přímek jdoucích
bodem Po s danou kružnicí.- Bod Po se nazývá pól poláry vzhledem ke kružnici.
K přímce ax + by + c = O jako poláře vzhledem ke kružnici x 2 + y2 = r 2
přísluší pól Po se souřadnicemi
ar 2
Xo = --,
c
br 2
Y -
o - --o
C
Mocnost m bodu Po[xo,Yo] ke kružnici x 2 + y2 = r 2
2 2 2
m = Xo + Yo - r .
Tečna a normála kružnice (x - m)2 + (y n)2 = r 2 v bodě
P I [x I' Y I]
Rovnice tečny:
(x - m)(x 1 - m) + (y - n)(Yl - n) = r 2 ;
směrnice
k =
t
X I - 111
YI - n
Rovnice normály:
(y - y 1) (x I - m) = (x - X I) (y I - n);
směrnice
YI - n
k n = .
Xl - m
Polára bodu po[xo,Yo] vzhledem ke kružnici (x-m)2+(y-n)2=r 2
(x - m)(xo - ln) + (y - n)(yo - n) = r 2 .
Mocnost m bodu po[xo,Yo] ke kružnici (x - m)2 + (y - n)2 = r 2
m = (xo - m)2 + (Yo - 1,1)2 - r 2 .
417
Chordála dvou kružnic
Chordálou dvou kružnic nazýváme množinu právě těch bodů, které mají
k oběma kružnicím stejnou mocnost.
Jestliže R 1 = O, R 2 = O, kde
Rt = (x - m1)Z + (y - n})Z ,- ri,
Rz = (x - mz)Z + (y - nz)Z - r
jsou rovnice daných kružnic, pak rovnice chordály těchto kružnic má tvar
R} - Rz = O.
Ch rdála je kolmá ke spojnici středů daných dvou kružnic.
Svazek kružnic
Jestliže R} = O, Rz = O, kde
Rt = (x - m1)Z + (y - nl)Z - rf,
Rz = (x - mz)Z + (y - n z )2 - r
jsou rovnice dvou daných kružnic, pak rovnice svazku kružnic pro A 9= -1
má tvar
Rl + ARz = O.
4.1.5. Parabola
Definice:
Parabolou nazýváme množinu právě těch bodů roviny, které mají stejné
vzdálenosti od pevného bodu F této roviny (tzv. ohniska) a od pevné přímky d
této roviny (tzv. řídicí přímky), přičemž přímka d neprochází bodem F.
d Y
L
Obr. 257. Parabola
418
Označení a názvy (obr. 257):
F - ohnisko paraboly,
d - řídicí [určující] přímka [direktrix],
o = ff - osa paraboly,
V - vrchol paraboly,
IDFI = lpi - poloparametr paraboly (někdy se tato vzdálenost nazývá
parametr),
21DFI - parametr paraboly,
PF - ohniskový průvodič,
P L - řídicí průvodič.
Kanonický [normální] tvar rovnice paraboly s osou vose x
a s vrcholem v počátku souřadnicové soustavy
y2 = 2px,
přičemž pro p > O, resp. p < O je parabola otevřená doprava, resp. doleva.
Řídicí přímka má rovnici
p
x =--
2
a ohnisko
F = [ , OJ.
y
n
v
Obr. 258. Parabola v normální poloze
Kanonický tvar rovnice paraboly v normální poloze
(osa je rovnoběžná s osou x a vrchol V = Cm, n]) (obr. 258)
(y - n)2 = 2p(x - m),
přičemž pro p > O, resp. p < O je parabola otevřená do p r a v a, resp. d o I e v a.
419
Řídicí přímka má rovnici
p
x=m--
2
a ohnisko
F = [ m + , n J.
Obecná algebraická rovnice druhého stupně
a 11 x 2 + 2al2xy + a 22 y 2 + 2a l 3 x + 2a23Y + a33 = O
vyjadřuje parabolu v normální poloze (osa paraboly je rovnoběžná s osou x),
právě když
all = a l 2 = O,
al3a22 =F O,
takže obecná rovnice paraboly má tvar
a 2 2y 2 + 2al3x + 2a 2 3Y + a 33 = O.
Řídicí přímka má rovnici
a 3 + ai3 - a22 a 23
x=
2a22al3
ohnisko
2 2 J
F = a23 - al3 - a2 2 a 33 _ a 23 ,
2a22al3 a 2 2
vrchol
[ a 3 - a22 a 33
v=
,
2a22al3
_ 923 J
a22
a parametr
1 2 pl =
2a 1 3
a 22
Kanonický tvar rovnice paraboly s osou vose Y a vrcholem
v počátku souřadnicové soustavy
x 2 = 2py,
přičemž pro p > O, resp. p < O je parabola otevřená nahoru, resp. dolů.
420
Řídicí přímka má rovnici
Y=
P
2
a ohnisko
F = [O, J.
Kanonický tvar rovnice paraboly v normální poloze
(osa paraboly je rovnoběžná s osou y a vrchol V = [m, n])
(x - m)2 = 2p(y - n),
přičemž pro p > O, resp. p < O je parabola otevřená nahoru, resp. dolů.
Obecná algebraická rovnice druhého stupně
a 1 1 x2 + 2a 1 2 X Y + a22y2 + 2a 1 3 X + 2a23Y + a 33 = O
vyjadřuje parabolu v normální poloze (osa paraboly je rovnoběžná s osou y),
právě když
a 12 = a 22 = O,
a11 a 2 3 =F O,
takže obecná rovnice parabolv má tvar
a 1 Íx 2 + 2a13x + 2a23Y + a 3 3 = O.
Řídicí přímka má rovnici
ai3 + a 3 - a 11 a 3 3
Y=
2a11 a23
ohnisko
F = [ _ a 13 , ai3 - a 3 - a l1 a 33 ] ,
a 11 2a 1 1 a 23
vrchol
[ a13 ai3 - a 11 a 33 ]
, V = - al1 ' 2alla23
a parametr
1 2 pl =
2a23
a 11
Máme-li rozhodnout, zda obecná algebraická rovnice druhého stupně
a 11 x 2 + 2a 12 xy + a22y 2 + 2a 13 x + 2a23Y + a 3 3 = O,
421
kde a l2 *= O, je rovnicí paraboly, provedeme nejprve otočení souřadnicové
soustavy o orientovaný úhel, jehož velikost qJ vypočteme ze vztahu
\
al l - a22
cotg (2qJ) = ---.
2al2
Viz též str. 450.
Polární rovnice paraboly
, p
{!=
1 + cos qJ
[pól je v ohnisku a polární osa prochází vrcholem (obr. 259)].
Q = 2p cos qJ(l - cotg 2 qJ)
[pól je ve vrcholu a polární osa splývá s osou paraboly (obr. 260)].
o
o
Obr. 259. Parabola v polárním vyjádření
(O = F)
Obr. 260. Parabola v polárním vyjádření
(O = V)
Průsečíky přímky y = kx + q s parabolou y2 = 2px (p > O)
p - qk 1
X1,2 = k 2 + k 2 J[p(p - 2qk)],
p 1
Yl.2 = k + k J[p(p - 2qk)].
Odmocněnec p(p - 2qk) = D (diskriminant) udává:
D > O - přímka protíná parabolu právě ve dvou reálných bodech (přimka
je sečnou);
D = O - přímka se dotýká paraboly právě v jednom reálném bodě (v dvoj-
ném bádě) (přímka je tečnou);
422
D < o - přímka parabolu neprotíná v žádném reálném bodě (přímka
je vn ěj šíp ří m k o u paraboly).
Tečna a normála paraboly y2 = 2px v bodě PI[X I , YI] (obr. 261)
x
prDm"rov p :m a
x
Obr. 261. Úsek tečny a úsek normály
paraboly
Obr. 26 . Průměrová přímka paraboly
Rovnice tečny:
YYI = p(x + Xl);
směrnice
p
kt = -.
YI
Rovnice normály:
p(y - Y I) + jJ I (X - X I) = O;
v f
smernlce
k = _ YI
n .
p
Délka úseku tečny
t = J(yf + 4xf).
Délka úseku normály
n = J(yi + p2).
Délka subtangenty
St = 2x 1 .
Délka subnormály
sn = p.
423
Polára bodu Po [xo, Yo] vzhledem k parabole y2 = 2px
YYo = p(x + xo) .
Polárou bodu Po vzhledem k parabole nazýváme množinu všech bodů
harmonicky sdružených s bodem Po vzhledem k pr,ůsečíkům přímek jdoucích l
bodem Po s danou parabolou. Bod Po se nazývá pól poláry vzhledem k parabole.
Průměrová přímka y2 = 2px (obr. 262)
p
y = k'
kde k je směrnice přiřazených rovnoběžných tětiv, které jsou průměrem půleny.
Tečna v průsečíku průměru s parabolou je rovnoběžná s přiřazenou osnovou
tětiv. .
Tečna a normála paraboly (y n)2 = 2p(x - m) v bodě PI[X I , YI]
Rovnice tečny:
(y - n) (YI - n) = p(x + Xl - 2m);
směrnice
P
kt =
YI - n
Rovnice normály:
P(y - YI) + (YI - n) (x - Xl) = O;
směrnice
k = _ YI - n
n .
p
Polára bodu po[x o , Yo] vzhledem k p.arabole (y - n)2 = 2p(x - m)
(y - n) (Yo - n) = p(x + Xo - 2m).
..
O.bsah S parabolické úseče
Jestliže tětiva P I P 2 (P I = [Xl' YI], P 2 = [x 2 , Y2]) není kolmá k ose paraboly
y2 = 2px (obr. 263), je
S = (YI - Y2)3 _ (XI - X2) (YI - Y2Y
12p 6(YI + Y2)
424
Je-Ii tětiva p. P 2 kolmá k ose paraboly (obr. 264), je
S = 1XtYl'
Délka tětivy jdoucí ohniskem kolmo k ose paraboly má délku 2p.
Poloměr křivosti R a střed křivosti Sk[ ' 11] paraboly y2 = 2px
v bodě p t [X t 'Yl] a ve vrcholu V
. Pro Pt * V platí
J(yf + p2)3
R=
p2
n 3
-
p2'
kde n je délka úseku normály (viz str. 423);
= 3Xl + p,
11=
yi
2 .
,p
Pro vrchol V[O, O] platí
R = lpi, = p,
11. = O.
y
y
I
o
x
Obr. 263. Parabolická. úseč Obr. 264. Parabolická úseč Obr. 265. Evoluta paraboly (Neilova
s tětivou libovolného směru s tětivou koln10u k ose x neboli semikubická parabola)
.
Evoluta paraboly y2 = 2px (obr. 265)
2 8( - p)3
n P ro > P
fl = 27p
(tzv. N eilova [semikubická] parabola).
425
Délka oblouku OP I paraboly y2 = 2px
1 ó1 \1 = {J[ 2;1 (1 + 2;1 )] + ln [ J2;1 + J( 1 + 2;1 ) J} =
= J(p2 + yD + E ln Yl + J(p2 + yD =
2p 2 p
= Yl J(p2 + yD + E argsinh Yl .
2p 2 P
Přibližná hodnota pro malý poměr XI/YI:
lóPII YI [ 1 + ( XI ) 2 ( XI ) 4 J .
3 YI 5 YI
Délka d ohniskového průvodiče k bodu PI[XI,YI]
p
d = Xl + -.
2
Konstrukce paraboly
J sou dány ohnisko a řídicí přímka (obr. 266) .
Bodem F (ohniskem) vedeme kolmici FD (osu paraboly) k řídicí přímce d
a v libovolných bodech AI' A 2' A 3 , ... osy paraboly sestrojíme k ní kolmice.
Potom opíšeme kolem bodu F kružnice s poloměry DAl' DA 2 , DA 3 , ..., které
protnou příslušné kolmice v bodech paraboly.
Střed úsečky FD je vrchol pataboly.
d ".. d
/'
/ Af
/
A 2
O'
"-
..........
,
,
Obr. 266. Konstrukce paraboly (jsou
dány F a d)
Obr. 267. Konstrukce paraboly (jsou
dán y F a d)
Jsou dány ohnisko a řídicí přímka (o&r. 267)
Libovolný bod A I řídicí přímky d spojíme s ohniskem F a sestrojíme osu
úsečky AlF, která kolmici v bodě A 1 k řídicí přímce protíná v bodě P I paraboly.
426
Opakujeme-li týž postup s dalšími body A 2 , A 3 ,... řídicí přímky, dostaneme
další body paraboly.
Jsou dány ohnisko a vrcholová tečna (obr. 268)
Spojíme různé body vrcholové tečny s ohniskem F a sestrojíme k takto
získaným spojnicím v jednotlivých bodech vrcholové tečny kolmice, které
parabolu obalují.
,/
a
-a y
>
o
-
o
Q p
>
V
o=v
x
Obr. 268. Konstrukce paraboly (jsou
dány F a vrcholová' tečna)
Obr. 269. Konstrukce paraboly (jsou
dány souřadnicové osy, vrchol V = O
a bod paraboly)
J sou dány souřadnicové osy, vrchol paraboly v počátku a bod P paraboly (obr. 269)
Z bodu P vecjeme kolmici PQ k ose y a rozdělíme úsečky PQ a VQ na stejný
počet stejných dílů. Dělicí body na úsečce PQ spojíme s vrcholem V a dělicími
body na úsečce VQ vedeme rovnoběžky s osou x. Průsečíky odpovídajících
rovnoběžek se spojnicemi vycházejícími z vrcholu V jsou hledané body
paraboly.
t>
Body paraboly ležící pod osou x jsou souměrně sdruženy s nalezenými body
paraboly podle osy paraboly.
4.1.6. Elipsa
Definice: /
Elipsou nazýváme množinu právě těch bodů P v roviné, které mají od dvou
pevných bodů Ft, F 2 (tzv. ohnisek) konstantní součet vzdáleností !PF 1 ! +
+ !PF 2 ! = 2a, přičemž je 2a > IFtF21 = 2e > O.
427
Z podmínky IpP'11 + IPF 2 1 = 2a plyne vláknová [nitková] konstrukce
elipsy.
Označení a názvy (obr. 270):
Ft, F 2 - ohniska,
".
A, B - hlavní vrcholy,
C, D - vedlejší vrcholy,
S - střed elipsy,
Ip Ftl + Ip F21 = 2a - konstantní součet,
PF 1 , PF 2 - průvodiče,
IABI = 2a - délka hlavní osy,
a - délka hlavní poloosy,
ICDI = 2b - délka vedlejší osy,
b - délka vedlejší poloosy (b < a),
IFIF21 = 2e,
e = J(a 2 - b 2 ) - délková [lineární] výstřednost [délková excentricita],
e
- = B - číselná [numerická] výstřednost [číselná excentricita],
a
2b 2
2p = - - parametr (délka tětivy kolmé k hlavní ose a procházející
a ohniskem).
A
b
D
Obr. 270. Elipsa
m X
Obr. 27). Elipsfi v normální poloLe
Kanonický tvar středové rovnice elipsy s hla vní osou vose x
(viz obr. 270)
x2 y2
- + - = 1 neboli b 2 x 2 + a 2 y2 - a 2 b 2 = O.
a 2 b 2
Kanonický tvar rovnice elipsy v normální poloze (hlavní os.a
elipsy je rovnoběžná s osou x a střed S = [m, n]) (obr. 271)
( X - m ) 2 (y - n)2 _
2 + 2 -1.
a b
428
Vrcholová rovnIce elipsy '(obr. 272)
p
y2 = 2px - - x 2 .
a
y
P[p, ff]
x
B o
Obr. 272. Vrcholová rovnice elipsy
Obr. 273. Elipsa v polárním vyjádření
(O = F 2)
Obecná rovnIce druhého stupně vyjadřující elipsu v normální
poloze
Obecná rovnice druhého stupně v x a y
a ll x 2 + 2a l2 xy + a22y2 + 2al3x + 2a 2 3Y + a33 = O
vyjadřuje elipsu v normální poloze (hlavní osa elipsy je rovnoběžná
s osou x), právě když
sgn a ll = sgn a22 = sgn (a 22 ai 3 + a ll a 3 - a ll a 22 a33)'
a l2 = O, lalll < la 22 1, .l
takže obecná rovnice elipsy má tvar
a ll x 2 + a22y2 + 2a l3 x + 2a 2 3Y + a33 = O,
přičemž délka hlavní poloosy
J ' 2 2
_ a22 a l3 + al l a 2 3 - all a 22 a33
a - 2 '
a ll a 22
délka vedlejší poloosy
J 2 2
b = a22 a 13 + a ll a 23 2 - all a 22 a 33
a ll a 22
a střed elipsy
S= [ _ a I 3 , _ a23 J .
al l a 22
29
Inverzní rovnIce elipsy
Rovnice
y2 x2
-+-=1
a 2 b 2
je kanonickým tvarem středové rovnice elipsy s hlavní osou vose y; a, resp. b
je délka hlavní, resp. vedlejší poloosy; střed elipsy je v počátku.
Rovnice
P
x 2 = 2py _ _ y2
a
. .
je vrcholovou rovnicí elipsy s hlavní osou vose y; a je délka hlavní poloosy.
Polární rovnice elipsy
,
Jestliže ohnisko F 2 je pQlem O a polární osou o je polopřímka F 2 B (obr. 273),
Je
p
(} = (8 < 1).
1 + 8 cos qJ
Jestliže střed elipsy je pólem O a polární osou o je polopřímka OB (obr. 27'4),
Je
b 2
{!2 =
1 - 8 2 cos 2 qJ
(8 < 1).
\.
vedlejll kru!n;ce hlavni kru!nice
Obr. 274. Elipsa v polárním vyjádření
(O = S)
Obr. 275. Elipsa v parametrickém
vyjádření
Parametrické rovnice elipsy (obr. 275)
x = a cos t ' }
pro \jt E (O, 2n);
y = b sin t
t je excentrická anomálie.
430
x 2 v 2
Průsečíky přímky y = kx + q s elipsou a 2 + [,2 = 1
a 2 kq ab / ( 2 2 2 2 )
X 1 . 2 = b 2 + a 2 k 2 + b 2 + a 2 k 2 vak + b - q ,
b 2 q ,abk / ( 2 2 2 2 )
Y1.2 = b 2 + a 2 k 2 + b 2 + a 2 k 2 vak + b - q .
Odmocněnec a 2 k 2 + b 2 - q2 = D (diskriminant) udává:
D > O - přímka protíná elipsu právě ve dvou reálných bodech (přímka
je sečnou); ,
D = O - přímka se dotýká elipsy právě v jednom bodě (v dvojném bodě)
(přímka je tečnou);
D < O - přímka elipsu neprotíná v žádném reálném bodě (přímka je
vněj ší přímko u elipsy).
X2 y2
Délky průvodičů PF 1 a PF 2 elipsy 2" + 1: = 1 s bodem p[x,y]
a b
'IPF 1 ! = a + BX,
IPF 2 ! = a - BX,
přičemž
!PF 1 1 + IPF 2 1 = 2a.
X2 y2
Tečna a normála elipsy - + - = 1 v bodě P 1 [X , 1, Yl] (obr. 276)
a 2 b 2
Rovnice tečny:
XXI YYl
7 + b2 = 1;
směrnice
b 2 xl
kt = - .
a Yl
y
Obr. 276. Úsek tečny a úsek normály
elipsy
431
Rovnice normály:
a 2 YI
Y - YI = - b 2 (x - Xl)
Xl
směrnice
a 2 YI
k n = .
b Xl
Délka Úseku tečny
t = J[Yi + (: - xIYJ.
Délka úseku normály
b J(a 4 - e 2 xf)
n = 2 .
a
Délka subta,ngenty
a 2
St = - - Xl .
Xl
Délka subnormály
b2XI
s =
. n 2.
a
(X - m)2 (y - n)2
Tečna a normála elipsy 2 + 2 = 1 v bodě PI[XI' YI]
a b
Rovnice tečny:
(x - m) (Xl -lm) (y - n) (Yi - n) .
a 2 + b 2 = 1,
směrnice
b 2 (XI - m)
kt = - 2 ( ) .
a YI - n
Rovnice normály:
a 2 (YI - n) .
Y - YI = b 2 (xI _ m) (x - Xl)'
směrnice
k = a 2 (YI - n)
n 2 ( ) .
b Xl - m
432
. X2 )'2
Polára bodu po[xo,Yo] vzhledem k elIpse -- + -- = 1
a 2 b 2
.
xXo yYo
+-Z=1.
a b
Polárou bodu Po vzhledem k elipse nazýváme množinu všech bodů harmo-
nicky sdružených s bodem Po vzhledem k průsečíkům přímek jdoucích bo-
dem Po s danou elipsou. Bod Po se nazývá.pól poláry vzhledem k elipse.
(x - m)2 (y - n)2
Polára bodu po[xo,Yo] vzhledem k elipse 2' + 2 = 1
a b
(x - m) (xo - m) (y - n) (Yo - n)
2 + 2 = 1.
a b
Průměrová přímka elipsy (obr. 277)
Průměrem M N elipsy nazýváme úsečku, která obsahuje střed S elipsy a jejíž
krajní body M, N leží na elipse. Polovina průměru elipsy se nazývá poloměr
elipsy. Průměrovou přímkou M N elipsy (někdy se také stručně nazývá prů"iěr
elipsy) nazýváme přímku, která obsahuje průměr MN elipsy.
Rovnice průměrové přímky elipsy:
b 2
y = - a 2 k x,
kde k je směrnice příslušných rovnoběžných tětiv, které jsou průměrovou
přímkou půleny.
pra rovo y
p lmka
H
y
x
x
Obr. 277. Průměrová přímka elipsy
Obr, 278, Sdružené průměry elipsy
Průměrová přímka osnovy rovnoběžných tětiv elipsy prochází dotykovými
body tečen rovnoběžných s těmito tětivami. Průměrová přímka tětivy elipsy,
v jejíchž krajních bodech jsou vedeny tečny, prochází průsečíkem těchto tečen.
433
Sdruženými průnlěry elipsy (obr. 278) nazýváme takové dva prů'měry elipsy,
že tečny elipsy v krajních bodech jednoho průměru jsou rovnoběžné s prů-
měrovou přímkou druhého průměru, tj. takové dva průměry elipsy, z nichž
každý půlí tětivy I elipsy rovnoběžné s druhým průměrem. Poloviny al, b l
dvou sdružených průměrů elipsy se nazývají sdružené poloměry elipsy. Sdruže-
n.vm; průměrovými přímkami u, v elipsy nazýváme takové dvě průměrové
přímky, které obsahují sdružené 'průměry.
Přímky
y = k 1 x a y = k 2 x
jsou sdruženými průměrovými přímkami elipsy, právě když
b 2
k l k 2 = -2'
" a
Pro dva sdružené průměry elipsy o délkách 2a 1 a 2b 1 platí
af + bf = a 2 + b 2 ,
a 1 b 1 sin (qJI - qJ2) = ab,
což slovy lze vyjádřit takto: Obsah trojúhelníku vytvořeného ze dvou sdruže-
ných poloměrů elipsy a ze spojnice jejich krajních bodů na elipse je konstantní.
Rovnice elipsy dané dvěma sdruženými poloměry o délkách a1 a ,JI má tvar
x2 y2
2: + 2 = 1.
a l b l
x2 y2
Poloměr křivosti R a střed křivosti Sk[ ' ] elipsy a 2 + b 2 = 1
'"
V bodě P1 [Xl' Y1] je
R = l ( a 4 y 2 + b4x2 ) 3 = J(a 4 - e 2 xf)3, = n 3
4 b 4 '\/ I 1 4 b 2 '
a a p
kde n je délka úseku normály (viz str. 432);
e 2 xi e 2 yi B 2 a 2 yi
= 7' 17 = -y = b 4 .
V hlavním vrcholu A[ -a, O] je
b 2 e 2
R = - = p; = 11 = O.
a a
434
V hlavním vrcholu B[ a, O] je
b 2 e 2
R = - = p; = -,
a a
11 = o.
Ve vedlejším vrcholu D[O, -b] je
a 2 e 2
R=b; =O, 11=/;.
Ve vedlejším vrcholu C[O, b] je
a 2
R =-.
b '
= O,
e 2
11=
b
V d 1 ....., h 1 ' k ..... 1 . X2 y2 1 ( . b 275)
e eJ SI a a VDI rUZDlce e Ipsy a 2 + b 2 = VIZ o r.
x 2 + y2 = a 2 a X2 + y2 = b 2
x2 y2
Evoluta elipsy 1: + 1: = 1 (obr. 279)
a b
(: r /3 + e r /3 = 1 pro I I <
(tzv. asteroida).
x
CXf,¥f J
A
8 x
Obr. 279. Evoluta elipsy
Obr. 280. Eliptická ús.eč a výseč
o b S a h e 1 i psy, e 1 i pti c k é ú seč e a e 1 i pti c k é v Ý seč e ( o br. 280)
Obsah vnitřní oblasti elipsy:
S = 1tab.
Obsah eliptické úseče PIP2C (viz obr. 280):
) ab ( . x 2 . Xl )
S = !(X 1 Y2 - X2Yl + - arcsln - - arcsID - .
2 a a
435
Obsah eliptické úseče P2P3B (viz obr. 280)
X2
S ab arccos - - X2Y2'
a
Obsah eliptické výseče P20P3B (viz obr. 280)
X2
S = ab arccos-.
a
Obsah eliptické výseče P l OP 2 C (viz obr. 280)
ab ( . x 2 . Xl )
S = - arcSID - - arcsln - .
2 a a
Délka elipsy
[ ( 1 ) 2 2 ( 1 · 3 ) 2 84 ( 1 .3 . 5 ) 2 86 ]
d = 21ta 1 - 2 B - 2. 4 "3 - 2. 4 . 6 5 - ... ·
Přibližné vzorce:
d 1t[t(a + b) - J(ab)],
d t1t[a + b + J[2(a 2 + b 2 )].
Konstrukce elipsy
Jsou dána ohniska a délka 2a hlavni osy (obr. 281)
Kolem ohnisek Fl a F 2 opíšeme kružnice s poloměry p < 2a a 2a - p
a dostaneme průsečíky, které jsou čtyřmi souměrně sdruženými body elipsy.
p
2Q
+- ---
./ "
/ \
I \
I o o 1
\ Ff F 2 /
\ /
' -- --*'
20
Obr. 281. Konstrukce elipsy (jsou dány
délka hlavní osy a ohniska)
Obr. 282. Konstrukce elipsy (jsou dány
délka hlavní osy a ohniska)
\
Jsou dána ohniska a délka 2a hlavní osy (obr. 282)
Kolem ohniska Ft opíšeme kružnici s poloměrem 2a (tzv. řidici kružnici),
spojíme libovolný bod P 2 řídicí kružnice s druhým ohniskem F 2 a sestrojíme
436
osu takto vzniklé spojnice P2f'2' Průsečík £2 této osy s úsečkou P 2 F I je bode nI
elipsy. Stejně lze postupovat u řídicí kružnice opsané kolem ohniska F 2 .
Jsou dány délky a a b p%os
1. způsob konstrukce (obr. 283)
Kolem bodu O opíšeme vedlejší kružnici s poloměrem b a hlavní kružnici
s poloměrem a. Potom sestrojíme k ose x libovolnou kolmici p, která protne
hlavní kružnici v bodech AI a A 2 . Spojnice OA I a OA 2 protínají vedlejší
kružnici v bodech Bl a B 2 . Rovnoběžky s osou x, vedené body B 1 a R 2 , protínají
kolmici p ve dvou bodech £1 a £2 elipsy.
y rt
£4 C
--
T
}} A - . - t- - - - --
x
[1
£3
8
x
£2
Obr. 283. Konstrukce elipsy (jsou dány
délky poloos)
Obr. 284. Konstrukce elipsy (jsou dány
délky poloos)
y
y
-
x
x
Obr. 285. Proužková konstrukce elipsy
(\QRI = a - b)
Obr. 286. Proužková konstrukce elipsy
(IQR\ = a + b)
2. způso b k ons trukce (obr. 284)
Vrcholy A, B, C, D vedeme rovnoběžky s osami souřadnic, které se vzájemně
protnou v bodech E 1 , E 2 , E 3 , E4' Potom rozdělíme úsečky OC a E 3 C na stejný
počet stejných dílů. Vedeme spojnice dělicích bodů úsečky oe a bodu A
a spojnice dělicích bodů úsečky E 3 C a bodu B. Průsečíky odpovídajících si
43'7
spojnic jsou hledané body elipsy. Sestrojíme body souměrně sdružené podle
osy x, popř. y a dostaneme ostatní body elipsy.
3. způsob konstrukce (proužková konstrukce) (obr. 285)
Na proužek papíru s přímou hranou naneseme na sebe od bodu P obě
poloosy o délkách IPQI = a a IPRI = b (IQRI = a - b). Posunujeme-li nyní
proužek papíru tak, aby se bod Q pohyboval po ose y a bod R po ose x, opisuje
bod P elipsu (jde o princip elipsografu).
4. způsob konstrukce (obr. 286)
Na proužek papíru s přímou hranou naneseme za sebou obě poloosy
o délkách IPQI = a a IPRI = b (IQRI = a + b). Posunujeme-li nyní proužek
papíru tak, aby se bod Q pohyboval po ose y a bod R po ose x, opisuje bod P
elipsu.
4.1.7. Hyperbola
Definice:
Hyperbolou nazýváme množinu právě těch bodů P v rovině, které mají
od dvou pevných bodů F l , F 2 (zvaných ohniska) konstantní rozdíl IPFll -
- IPF 2 1 = 2a vzdáleností, přičemž je O < 2a < 2e = IFlF21.
Obr. 287, Hyperbola
Obr. 288. Hyperbola v normální poloze
Označení a názvy (obr. 287):
F l , F 2 - ohniska,
A, B - hlavní vrcholy,
C, D - vedlejší vrcholy (imaginární),
S - střed hyperboly,
IPF 1 1-lpF 2 1 = 2a (konstantní rozdíl),
438
Pl: 1 , PF 2 - průvodiče,
ISAI = ISBI ' a - délka reálné poloosy AS, popř. SB,
IABI = 2a - délka reálné osy AB,
Isel = ISDI = b - délka imaginární poloosy SC, popř. SD,
ICDI = 2b - délka imaginární osy CD,
1 F t F 2 1 = 2e,
e = J(a 2 + b 2 ) .- délková [lineární] výstřednost [délková excentricita],
e
- = [; - číselná [numerická] v.vstřednost [číselná excentricita], 8 > 1,
a
2b 2
2p = - ;- parametr (délka tětivy kolmé k hlavní ose a procházející
a ohniskem).
Kanonický tvar středové rovnice hyperboly s reálnou osou
vose x (viz 9br. 287)
x2 y2
--- - - = 1 neboli b 2 x 2 - a 2 y2 - a 2 b 2 = O.
a 2 b 2
Kanonický tvar rovnice hyperboly v normální poloze
(tj. reálná osa AR hyperbolý je rovnoběžná s osou x a střed S = [m, n])
(obr. 288)
(x - m)2 (y - 11)2
a 2 b 2 = 1.
Vrcholová rovnice hyperboly (obr. 289)
P
y2 = 2px + - x 2
a
se středem S = [-a, O].
Obecná algebraická rovnice druhého stupně
vyjadřující hyperbolu v normální potoze
Obecná rovnice druhého stupně v x a y
a tt x2 + 2a l2 xy + a22y2 + 2al3x + 2a23Y + a 33 = O
vyjadřuje hyperbolu v normální poloze (tj. reálná osa hyperboly je rovno-
běžná s osou x), právě když
sgn al l =F sgn a22 = sgn (a22 a I3 + alla 3 - a ll a22 Q 33)' a l2 = O.
439
takže obecná rovnice hyperboly má tvar
allx2 + a22y2 + 2a l 3 X + 2a 23 y + a33 = O,
přičemž délka reálné poloosy
..
a = J 22ai3 + a1 a 3 -: a 11 a 22 a 33 ,
a 1 1 a 2 2
délka imaginární poloosy
b = J( - a22ai3 + a11a 32 - a 11 a 22 a 33 )
a ll a 22
a střed hyperboly
S = [ - a 13 , a 23 J .
a ll a2 2
Obr. 289, Vrcholová rovnice
hyperboly
..
.
Obr. 290. Hyperbola v polárním
vyjádření (O = F 1)
Inverzní rovnice hyperboly
Rovnice
y2 x2
---=1
a 2 b 2
je kanonickým tvarem středové rovnice hype'rboly s reálnou osou vose y
a se středem v počátku.
Rovnice
P
x 2 = 2py + _ y2
a
je rovnicí hyperboly s eálnou osou vose y; a je délka reálné poloosy, p je
poloparametr, střed hyperboly S = [O, -a].
440
Polární rovnice hyperboly
Jestliže ohnisko F. je pólem O a polární osou o je polopřímka F. A (obr. 290),
Je
p
(1 = (D > 1), ,
1 + e cos qJ
přičemž těm hodnotám argumentu qJ, pro které vyjde (1 > O, resp. Q < O,
přiřazujeme bod [g, qJ], resp. [ - (1, qJ + 7t].
Jestliže střed hyperboly je pólem O a polární osou () je polopřímka SB,
(tj. první kladná poloosa (obr. 291), je '
b 2
0 2 = (D > 1).
.. f,2 cos 2 qJ - 1
Obr. 291. Hyperbola v polárním
vyjádření (O = S)
Parametrické rovnice hyperboly
a
x=-,
cos t
x = + a cosh t,
y = + b tg t:
y = b sinh t.
Rovnice rovnoosé hyperboly
x 2 _ y2 = a2
(b = a).
x2 y2
Délky průvodičů PF. a PF 2 hyperboly -, - - = t s bodem
P[x,y] a- b 2
IPF.! = f,X + a,
!PF 2 1 = ex - a,
přičemž
!PF.I -IPF 2 1 = 2a. .
441
x2 y2
Průsečíky přímky y = kx + q s hyperbolou - - - = 1
a 2 b 2
a 2 kq ab / ( 2 2 2 2 ) "
X1.2 = b 2 _ a 1 k 2 + b 2 _ a 2 k 2 '\/ b + q - a k ,
b 2 q abk
)'1,2 = b 2 _ a 2 k 2 + b 2 _ a 2 k 2 J(b 2 + q2 - a 2 k 2 ),
Odmocněnec b 2 + q2 - a 2 k 2 = D (diskriminant) udává:
D > O - přímka protíná hyperbolu právě ve dvou reálných bodech (přímka
je sečnou);
D = O - přímka se dotýká hyperboly právě v jednom bodě (v dvojném
bodě) (přímka je tečnou); ,
D < O - přímka hyperbolu neprotíná v žádném reálném bodě (přímka je
vnější přímkou hyperboly).
Zvlá. tní případy:
1. b 2 - a 2 k 2 = O, k =t= O, q * O.
Přímka protíná hyperbolu právě v jednom bodě [xo, Yo] a je rovnoběžná
s jednou ze dvou asymptot:
q2 + b 2 q2 _ b2
Xo = - 2kq' Yo = 2q
2. b 2 - a 2 k 2 = O, k * O, q = O.
,
b 2 - a 2 k 2 * O.
Přímka je asymptotou a její rovnice má tvar jedné z rovnic pro asymptoty:
b
y = + - x.
a
x2 y2
Tečn a normála hyperboly 2 - b 2 = 1 v bodě PI[X I , )'1]
(obr. 292) a
Rovnice tečny:
xx I YY 1 _ 1 .
7-/;2- ,
směrnice
b 2 x I
kt = .
a YI
442
Rovnice normály:
a 2 YI
Y - YI = -- b 2 (x - Xl);
Xl
směrnice
k =
n
a 2 YI
--
b2XI'
x
Obr. 292. Úsek tečny a úsek normály
hyperboly
Délka úseku tečny
t = J[Yi + (Xl - :: rJ.
Délka úseku no.rmály
b
n = 1: J(e 2 xi - a 4 ).
a
Délka subtangenty
a 2
St = Xl - - .
Xl
Délka subnormály
b2Xt
s =
n
., .
a-
(X - m)2
Tečna a normála hyperboly
a 2
PI[XI, YI]
(y - nV = 1 v bodě
b 2
Rovnice tečny:
(x - m)(xI - m) (y - n)(YI - n)
2 - 2 = 1 ;
a b
.
443
směrnice
b 2 (x 1 - ln)
k: = 2 ( ) .
a YI - 11
Rovnice nor má ly:
a 2 (YI - n)
Y - YI = - b 2 (XI _ m) (x - Xl);
směrnice
k =
n
a 2 (YI - 11)
b 2 (xI - mf
Asymptoty
Asymptotou hyperboly nazýváme takovou přímku p, že vzdálenost bodu M
hyperboly od přímky p konverguje k n le, jestliže p.rvní souř dnice bodu M
konverguje k + 'ryj, popř. I' -'oc. Asymptoty procházejí středem hyperboly
a mají rovnice
b
y :-: + -x.
a
Část T 2 každé tečny mezi asymptotami je půle 'na svým dotykovým
odem , . (obr. 29 ), takže p atí
ITIEI = IT2EI
Věta o trojúhelníku s konstantním obsahem (viz obr. 293)
Obsah trojúhelníku TI OT 2 je konstantní (8 = ab).
Obr. 293. Asymptoty hyperbofy
Věta o rovnoběžniku s konstantním obsahem
Jsou-li EF a EG rovnoběžky s asymptotami (viz obr. 293),je obsah vzniklého
rovnoběžníku oGEF konstantní (S = ubI2).
444
Asymptotická rovnice hyperboly
Zvolím -li asymptoty za souřadnicové osy, dostaneme pro hyperbolu
(při a *= b) kosoúhlou souřadnicovou soustavu, v níž má rovnice hyperboly
tvar
e 2
, ,
xy =-.
4
Asymptoty rovnoosé hyperboly (tj. při a = b)jsou k sobě kolmé, takže v tomto
případě je souřadnicová soustava pravoúhlá. Rovnice rovnoosé hyperboly
má pak tvar
a 2
, ,
xy =-.
2
Každá rovnice tvaru
Ax + B
y = Cx + D
(AD - BC *= O, C *= O)
vyjadřuje hyperbolu, jejíž asymptoty jsou rovnoběžné se souřadnicovými
osamI.
x2 y2
Polára bodu po[xo, Yo] vzhledem k hyperbole 1: - 1: = 1
a b
xXo _ YYo = 1
a 2 b 2 .
Polárou bodu Po vzhledem k hyperbole nazýváme množinu všech bodů
harmonicky sdružených s bodem Po vzhledem k průsečíkům přímek jdoucích
bodem Po s danou hyperbolou. Bod po[xo, Yo] se nazývá pól poláry vzhledem
k hyperbole.
Průměrová přímka hyperboly
Průměrem MN hyperboly nazýváme úsečku, která obsahuje střed hyperboly
a jejíž krajní body M, N leží na hyperbole (obr. 294). Přímka MN se nazývá
průměrová přímka hyperboly [někdy stručně průměr hyperboly J.
Rovnice průměrové přímky:
b 2
y = x,
a k
kde k je směrnice příslušných rovnoběžných tětiv, které jsou průměrovou
přímkou půleny.
Sdruženými průměry hyperboly nazýváme takové dva průměry hyperboly,
že tečny hyperboly v krajních bodech jednoho průměru jsou rovnoběžnp
445
s průměrovou přímkou druhého průměru, tj. takové dva průměry hyperboly,
z rtichž každý půlí tětivy hyperboly rovnoběžné s druhým průměrem. Poloviny
dvou sdružených průměrů hyperboly se nazývají sdružené poloměry hyperboly.
Sdruženými průměrovými přímkami hyperboly nazýváme takové dvě průměrové
přímky, které obsahují sdružené průměry.
Obr. 294. Průměrová přímka hyperboly
Přímky
y = klx a y = k 2 x
jsou sdruženými průměrovými přímkami, právě když
b 2
k l k 2 = 2'
a
....
Pro dva sdružené průměry o délkách 2a l a 2b l platí
af - bf = a 2 - b 2 .
Rovnice hyperboly dané dvěma sdruženými poloměry o délkách a l a b l
,
ma tvar
x2 y2
---=1
af bf .
x2 y2
Poloměr křivosti R a střed křivosti Sk[ ' 11] hyperboly --- = 1
a 2 b 2
V bodě PI[XI'YI]
_ 1 / ( 4 2 4 2 ) 3 _ J(e 2 xf - a 4 )3
R - a 4 b 4 V b Xl + a YI - a 4 b -
n 3
2'
P
kde n je délka úseku normály (viz str. 44 );
/'
e 2 YI -B 2 a 2 YI
11=
-Y - b 4
e 2 x3
= -T,
a
446
Ve vrcholu A[ - a, O] je
b 2
R = - = p;
a
=
e 2
tf = O.
a
Ve vrcholu B[ a, O] je
b 2
R = - = p;
a
e 2
t =-
- ,
a
11 = O.
Hlavní kružnice hyperboly:
X2 + y2 = a 2 .
X2 y2
Evoluta hyperboly 2: - 2" = 1 (obr. 295)
a b
(: Y/3 _ e; Y/3 = 1
e 2
pro I I > -.
a
y
y
--
x
Obr. 295. Evoluta hyperboly
Obr. 296. Hyperbolická úseč
a hyperbolIcká výseč
Obsah hyperbolické úseče P I BP 2 (obr. 296)
( Xl VI ) Xl .
S = X I Y I - ab ln - + =-- = x I Y I - argcosh - .
a b a
Obsah hyperbolické výseče OP 2 BP I
( Xl YI ) Xl
S = ab ln - + - = argcosh - .
a b a
447
Konstrukce hyperboly
Jsou dána ohniska a délka 2a hlavni osy (obr. 297)
Kolem ohnisek Ft a F 2 opíšeme kružnice s libovolným poloměrem p a s po-
loměrem 2a + p. Dostaneme jako průsečíky čtyři souměrně sdružené body
hyperboly. Při jiném poloměru p dostaneme další body hyperboly.
Jsou dány délky a a b poloos (obr. 298)
Kolem středu O opíšeme kružnice s poloměry a a b. K těmto "řídicím
kružnicím ' vedeme tečny s a t kolmé k ose x. Libovolná přímka p, vedená
středem S = O, protne tyto tečny v bodech A a B. Potom opíšeme kolem
bodu O kružnicový oblouk s poloměrem OB a sestrojíme v jeho průsečíku
s osou x kolmici k ose x. Průsečík této kolmice a rovnoběžky s osou x vedené
bodem A je bod P hyperboly.
20
x
p
Obr. 297. Konstrukce hyperboly (jsou
dány délka hlavní osy a ohniska)
Obr. 298, Konstrukce hyperboly (jsou
dány délky poloos)
J sou dány souřadnicové osy jako asymptoty a bod' P rovnoosé hyperboly (obr. 299)
Z bodu P vedeme ko mice PQ'a PR k souřadnicovým osám, prodloužíme
PR za bod P a spojíme libovolné body na prodloužení s počátkem O. Průsečíky
těchto spojnic s přímkou PQ vedeme rovnoběžky s osou x. Potom vedeme
dělicími body na prodloužení úsečky PR rovnoběžky s osou y. Jejich průsečíky
s odpovídajícími rovnobižkami s osou x jsou body P hyperboly.
Obdobnou konstrukcí ve třetím kvadrantu dostaneme druhou větev
hyperboly.
Jsou dány asymptoty a bod Pt hyperboly (obr. 3(0)
Vedeme libovolnou přímku bodem P 1 , která protne asymptoty v bodech
Qt a Q2, a naneseme-li na ni úsečku Q2 P 2 QtPt. Bod P 2 je dalším bodem
1-typerboly. Vedeme-li bodem Pt další přímky, dostaneme další bo y hyperboly.
_/
448
R
Q
)(
o
Obr. 299. Konstrukce hyperboly
(souřadnicové osy jsou asymptotami,
P je bod rovnoosé hyperboly)
Obr. 300. Konstrukce hyperboly (jsou
dány asymptoty a bod hyperboly)
4.1.8. Obecná algebraická rovnice druhého stupně v x a y
Rovnicí
F(x, y) = allx 2 + 2al2XY + a 22 y 2 + 2al3x + 2a 23 y + a33 = O,
kde koeficienty a ik jsou reálná čísla, lze vyjádřit každou kuželosečku (tj. kruž-
nici, elipsu, hyperbolu, parabolu, dvojici přímek a bod).
I n v a r i a nt y křivky druhého stupně:
A= alt' a t2 , al3 , tJ= alt' al2 ,
a 2t a22, a23 a 2t , a22
a 31 , a 32 , a33
přičemž L1 se nazývá diskriminant kuželosečky a tJ diskriminant kvadratick) ch
členů.
Poznámka:
V determinantech L1 a t5 platí aik = aki'
lnvarianty jsou veličiny, které se při transformaci souřadnic nezměnÍ.
Každá obecná rovnice druhého stupně vyjadřuje vlastní kuželosečku
jestliže číslo L1 * O, kdežto degenerovanou kuželosečk u jestliže číslo L1 = O.
Při tJ * O jsou obecnou algebraickou rovnicí druhého stupně určeny
elipsa nebo hyperbola, kdežto při tJ = O je jí určena parabola.
449
Pří pad 1: b =F O
".
Rovnoběžné posunutí kartézské souřadnicové soustavy
Transformační rovnice:
x = x' + u,
Y = y' + v,
kde x, y jsou původní souřadnice,
x', y' jsou nové souřadnice,
[u, v] je nový počátek --vzhledem k původní souřadnicové soustavě:
,I
{)
a l2 a l 3 - a 11 a23
v=
a l2 a 23 - a 2 2 a l3
u=
£5
Určovací rovnice pro u a v jsou
cF(u, v)" 8F(u, v)
= O a = O'
,
cu . cV
[u, v] je střed kuželosečky.
Transformovaná rovnice má tvar
,2 + 2 ' , + '2 + O
allx a l 2 x y a22Y a 44 = ,
kde
L1
(144 = al3 u + a23 v + a33 = -.
tJ
Otočení kartézské souřadni ové soustavy (O; x, y) o úhel
( ) 2a I 2
tg 2ex =
a ll -a 22
(ex < 90°).
Transformační rovnice:
x' = cos ex - 11 sin ex,
y' = sin ex + 11 cos ex,
kde , 11 jsou nové souřadnice.
Transformovaná rovnice m,á tvar
bll 2 + b 22 11 2 + a 44 = O,
(1)
kde
bIl = !{ all + a22 + .J[(all - a22)2 + 4af 2]}'
b 22 = t{ all + a 22 + .J[(a ll - a22)2 + 4af 2]}'
přičemž horní, resp. dolní znaménko se vezme při kladném, resp. záporném
koeficientu a 1 2'
450
/
Invariant
bIl + b 22 0 = a ll + a22
označíme S.
Rovnice (1) vyjadřuje pro tJ > O a L1 * O elipsu, a to reálnou elipsu při
bil> O, b 22 > O, a44 < O a imaginární elipsu při bil> O, b 22 > O, a 44 > O.
Je-li () > O, ale L1 = O, degeneruje elipsa v imaginární dvojici přímek s reál-
ným průsečíkem v konečnu. Jestliže L1 = O, pak také a44 = O.
Rovnice (1) vyjadřuje pro tJ < O a L1 * O hyperbolu, která při L1 = O dege-
neruje v reálnou dvojici protínajících se přímek.
Případ 2: tJ = O
Otočení k,artézské souřadnicové soustavy o úhel
) 2a I 2
tg (2(1 =
all - a22
(ex < 90°).
Transformační rovnice:
x = X' cos ex - y' sin ,
y = x' sin ex + y' cos ex,
kde x, y jsou původní souřadnice,
x', y' - nové souřadnice.
Transformovaná rovnice má tvar
b 11 X '2 + 2b 13 X ' + 2b 23y ' + a 3 3 = O,
kde
bIl = a ll + a 22 ,
b _ a13 .Ja ll + a23 .Ja22
13 -
J(a ll +a22) ,
h _ a23 Jal l - a 1 3 Ja22
23 - .
, J(al l + a22)
Rovnobě=llé posunuti kartézské souřadnicové soustavy (O; x', y,)
Transformační rovnice:
X' = _ biJ ,
bIl
I b ll a 33 - bi3
y = 11 - .
2b l b 23
451
Transformovaná rovnice má tvar
2 = _ 2b 2 3 17. (2 )
bil
Rovnice (2) vyjadřuje pro L1 * O parabolu. Jestliže L1 = O, degeneruje
křivka v dvojici přímek, a to
ve dvě různé reálné rovnoběžky, jestliže
ai3 - a ll a 33 > O;
ve dvojici splývajících rovnoběžek (tj. v dvojnou přímku), jestliže
ai3 - a ll a33 = O.
ve dvě imaginární rovnoběžky, jestliže
ai3 - a ll a3 3 < O.
Tabulka 4.1
Shrnutí
"
ť5=t=0 ť5=0
kuželosečky se středem kuželosečky bez středu
(středové kuž osečky) (nestředové kuželosečky)
ť5>0 ť5<0
"
L1.S<O
reálná
L1 =t= O eli psa
vlastní hyperbola parabola
kuželosečky L1.S>O
imaginární
elipsa
dvojice nerovnoběžných
L1=0 (protínajících se) dvojice rovnoběžek
přímek
nevlastní
(degenerované) imaginární 2
a 13 - a ll Q 33
kuželosečky přímky reálné >0 =0 <O
s reálným přímky 2 různé 2 splývajíCÍ 2 imaginární
průsečíkem reálné
v konečnu rovnoběžky rovnoběžky rovnoběžk)
452
Příklad 1:
5x 2 + 4xy + 2 y 2 - 18x - 12y + 15 = O;
all = 5, a 12 = 2,
Li = 5, 2, - 9
2, 2, - 6
-9 -6 15
, ,
a22 = 2, a l 3 = -9, a 23 = -6,
* O; tJ = 5, 2 = 10 - 4 > O.
2, 2
a33 = 15;
Rovnice určuje e I i psu.
Výpočet souřadnic u a v:
cF(u, v)
= 10u + 4v - 18 = O,
ex
c F( u v)
. , = 4u + 4v - 12 = O,
cv
u = 1, v = 2.
Střed elipsy v původní souřadnicové soustavě je S = [1, 2].
Výpočet a44:
a 4 4 = al3u + a23v + a 33 = (-9).1 + (-6).2 ir 15 = -6.
Transformovaná rovnice po rovnoběžném posunutí:
5X,2 + 4x'y' + 2y,2 - 6 = O.
Výpočet úhlu otočení ex:
( ) 2a I 2
tg 2ex =
a ll - a22
Po dosazení do rovnice
bIl = t{ a ll + a22 + J[(all - a22)2 + 4ai ;]}
(vzali jsme horní znaménko, neboť koeficient al2 je kladný), dostaneme
bIl =t{5 + 2 + J[(5 - 2)2 + 4.22]} = 6.
4
3'
ex = 26°34';
= _e
Podobně po dosazení je
b 22 = t{ a ll + a 22 - J[(all - a 22 )2 + 4ai 2]} = t(7 - 5) = 1.
Transformovaná rovnice po otočení:
6 2 + 11]2 - 6 = O,
2 1]2
-+-=1
1 6
453
což je rovnice elipsy s poloosami o délkách a = J 6 a b = 1 a s středem
v počátku soustavy (8; , 17). Hlavní osa leží vose 17 (obr. 301).
Otázka: Při jaké hodnotě absolutního členu a33 rovnice dojde k dege-
neraci elipsy?
"E-
,x'
x Obr. 301. Rovnoběžné posunutí
a otočení elipsy
Podmínka zní: L1 = O neboli a44 = o. Z rovnice
a44 = a 1 3 u + a23 v + a33 = O
po dosazení dostaneme
-9-12 a33 =0;
a33 = 21.
Rovnice 5x 2 + 4xy + 2 y 2 - 18x - 12y + 21 = O vyjadřuje tedy elipsu,
která degeneruje ve svůj střed.
Příklad 2:
I
. 9x 2 - 24xy + 16 y 2 + 220x - 40y - 100 = O;
a 11 9, a 12 - 12, a22 = 16, a 13 = 110, a23 = - 20,
a 33 = -100;
L1 = 9, - 12, 110 9= O,
- 12, 16, - 20
11 O, 20, - 100
tJ = 9, 12 = 144 - 144 = O.
- 12, 16
Rovnice určuje parabolu.
Otočení souřadnicové soustavy:
2a 1 2
tg (2cx) =
a 11 -a 22
-24
-7
24
.
7 '
ex = 36°52'.
,
454
bIl =a 11 +a 22 =25,
al3 .J a 11 + a23 .J a22 110.J9 + ( - 20) .J16
b l3 = = = 50
.J(a 11 + a 22 ) .J25 '
a 23 .J a I 1 - a 1 3 .J a 2 2 - 20 .J 9 - 110.J 16
b 23 = = = -100.
.J(a 11 + a 2 2) .J25
Transformovaná rovnice po otočení:
25x,2 + 100x' - 200y' - 100 = O,
X,2 + 4x' - 8y' - 4 = O.
Transformovaná rovnice po rovnoběžném posunutí:
,
-200
2 = - 25 17 ,
což je rovnice paraboly s vrcholem v počátku soustavy (O'; , 17) (obr. 302)
a s parametrem 2p = 8. Osa paraboly splývá s osou 11.
2 = 811,
"
r " r - x'
rz\ \ 11'
\ ",
\ //' /r
\ \\ O ",/ ./
-\-- -
\ /
/'(
>-
x
\
\
Obr. 302. Otočení a rovnoběžné
posunutí paraboly
/"
",
4.2. ANALYTICKÁ GEOMETRIE V PROSTORU
4.2.1. Různé souřadnicové soustavy
Kartézská [ortonormální] souřadnicová soustava (O; x, y, z)
Kartézská [ortonormální] souřadnicová soustava v prostoru se zavádí
obdobně jako kartézská souřadnicová soustava v rovině, přičemž za třetí osu
souřadnicové soustavy (O; x, y, z) se volí přímka OJ 3 = z, kolmá na rovinu
01 1 1 2 (obr. 303). Polopřímku OJ 3 , resp. polopřímku k ní opačnou nazveme
třetí kladnou, resp. třetí zápornou poloosou soustavy (O; x, y, z).
455
Pravotočivá kartézská souřadnicová soustava
PravotJčivá soustava je charakterizována pravotočivým šroubovým po-
hybem, přičemž se první kladná poloosa otáčí do polohy druhé kladné polo-
osy a zároveň se posunuje vzhůru ve směru třetí kladné poloosy (viz obr. 303).
Souřadnice bodu P v prostoru značÍmé x, y, z.
Způsob zápisu bodu: p[x, y, z] nebo P = [x, y, z J.
Čáry v prostoru, v jejichž rovnicích se mění jen jedna souřadnice, jsou
rovnoběžkami se souřadnicovými osami. Plochy, v jejichž rovnicích je jedna
souřadnice konstantní (tj. roviny x = konst, y ' konst a z = konst) jsou
rovinami rovnoběžnými se souřadnicovými osami.
U kartézské souřadnicové soustavy v prostoru jde o vzájemně jednoznačné
[bijektivní] zobrazení množiny všech bodů prostoru na množinu všech
uspořádaných trojic [x, y, z], kde x, y, z E R.
l
z
p
I .
I
'- :z
, J
o 9' I
'-..J f}
p
J 3 J 2 : l
..,0
V}.L I / X Y
, _ _ _ _ __ _ -l/
1 y
Obr. 303. Kartézská souřadnicová
soustava
Obr. 304. Válcová [cylindrická]
souřadnicová soustava
Cylindrická [válcová, semipolární] souřadnicová soustava
(O; (l, cp, z) (obr. 304)
Souřadnice bodu P značíme (1, cp, z.
Způsob zápisu bodu: p[Q, cp, z] nebo P -. [Q, cp, z].
. Cylindrická souřadnicová soustava (O; (1, cp, z) se zavádí takto: V prostoru
zvolíme rovinu a v ní zavedeme polární souřadnicovou soustavu (O; (1, cp).
Za kladnou poloosu souřadnicové osy z zvolíme polopřímku OJ, kolmou
k zvolené rovině. Souřadnice (1, cp jsou tedy polárními souřadnicemi průmětu
bodu P na rovinu xy a souřadnice z je třetí kartézskou souřadnicí bodu P.
Plochy (l = konst jsou rotační válcové plochy se společnou osou z.
Plochy cp = konst jsou poloroviny, jejichž hraniční přímky splývají
s přímkou OJ.
Plochy z = konst jsou roviny kolmé k ose z.
456
Vztahy mezi cylindrickými a kartézskými souřadnicemi
Souřadnice bodu v kartézské souřadnicové soustayě (O; x, y, z), resp.
v cylindrické souřadnicové soustavě (O; (l, qJ, z) značíme x, y, z, resp. (], qJ, z.
Přitom polární osa je totožná s první kladnou poloosou soustavy (O; x, y, z)
a kladná poloosa osy z soustavy (O; (l, qJ, ) splývá s třetí kladnou poloosou
soustavy (O; x, y, z).
Platí'
(1 = J(x 2 + y2),
. Y
sin qJ = -,
(1
Y
tg qJ = -
x
x
cos qJ = -
(1
pro \/qJ E (O, 2n),
pro \/qJ E (O, 2n) \ {-!1t, ín}.
x = (1 cos qJ,
y = (l sin qJ,
- -
.., - ..,.
Sférická [kulová, polární] souřadnicová soustava (O; (2, qJ, 8)
(obr. 305)
Souřadnice bodu P značíme (1, qJ, 8.
Způsob zápisu bodu: p[(1, qJ, 8] nebo P = [(1, qJ, 8].
O 2
p
°1
'J P1
Obr. 305. Kulová [sférická]
souřadnicová soustava
S,ľérická souřadnicorlÍ soustava (O; (1, qJ, 8) se zavádí takto: V prostoru
zvolíme rovinu a v ní polopřímku OA. Dále zvolíme polopřímku OB, kolmou
k zvolené rovině. Souřadnice (1 bodu P je vzdálenost 10PI bodu P od počátku
(pólu) O. Souřadnice qJ je velikost orientovaného úhlu, který svírá polopřímka
O A a polopřímka O Ph kde P 1 je průmět bodu P do zvolené roviny (O < qJ < 2n).
Souřadnice 8 je velikost orientovaného úhlu, který svírá polopřímka OP
s polopřímkou OB (Q < 8 < n).
Plochy (1 = konst jsou soustředné kulové plochy se středem v pólu O.
Plochy qJ = konst jsou poloroviny, jejichž hraniční přímky splývají
s přímkou OB.
457
Plochy 8 = konst jsou rotační kuželové plochy s vrcholem v pólu O a s osou
splývající s přímkou OB.
Vztahy mezi sférickými a kartézskými souřadnicemi
Souřadnice bodu v kartézské souřadnicové soustavě (O; x', y, z), resp. ve
sférické souřadnicové soustavě (O; (l, q>, 8) značíme x, y, z, resp. (l, lp, 8. Přitom
polopřímka OA splývá s kladnou částí osy x soustavy (O; x, y, z) a polopřímka
O B splývá s kladnou částí osy z sousta vy (O; x, y, z).
(l = J(X2 + y2 + Z2),
. Y x
SIn CP. = J(x2 + l), cos cp . J(x2 + y2)
z J(x 2 + y2)
cos 8 = -, tg 8 =
(l z
Y
tg lp = -
z
pro 't lp E (O, 2n),
pro 't8 E (O, n),
pro 'tlp E (O, 2n) \ (!1t, !n} ,
x = (l sin 8 cos lp ,
Y = (l sin 8 sin lp ,
z = Q cos 8 .
z'
y'
Obr. 306. Rovnoběžné posunutí
Transformace kartézské souřadnicové soustavy
1. Rovnoběžné posunuti (obr. 306):
I
X = X + m,
y = y' + n,
- ' + P .
- ,
x' = x - m
. ,
y' = y - n,
I
z = Z - p,
kde x, y, z jsou původní souřadnice,
x', y', z' nové souřadnice,
m, n, p - souřadnice nového počátku v původní soustavě.
458
2. Otočeni:
x = x' cos rJ.. 1 + y' cos (X2 + z' cos rJ.. 3 ,
Y = x' cos 8 1 + y' cos 8 2 + Z' cos 8 3 ,
Z = x' cos Y 1 + y' cos Y 2 + Z' cos Y 3 ;
Z' = X cos rJ.. l + Y cos 8 1 + z cos Y 1 ,
y' = X cos rJ.. 2 + Y cos 8 2 + z cos Y2,
z' = x cos (X3 + Y cos 8 3 + z cos Y3,
kde rJ..l, Pl, Yl jsou velikosti úhlů, které svírá první kladná poloosa soustavy
(O; x', y', Zl) s kladnými poloosami soustavy (O; x, y, z).
rJ.. 2, f3 2' Y 2 velikosti úhlů, které svírá druhá kladná poloosa sousta vy
(O; x', y', z,) s kladnými poloosami soustavy (O; x, y, z).
(X3, P3, Y3 velikosti úhlů, které, svírá třetí kladná poloosa sou tavy
(O; x', y', z') s kladnými poloosami soustavy (O; x, y, z).
Vztahy mezi směrovými kosiny nových os:
,
cos 2 rJ.. l + cos 2 8 1 + cos 2 Yl = 1,
2 2 2 - 1
cos rJ.. l + cos (X2 + cos rJ..3 - ,
cos rJ.. l cos rJ..2 + cos 8 1 cos 8 2 + cos Yl cos Y2 = O,
cos rJ.. l cos 8 1 + cos (X2 cos 8 2 + cos rJ.. 3 cos 8 3 = o.
Další vzorce se dostanou cyklickou záměnou.
Platí
"
L1 = cos rJ.. I , cos 8 1 , cos YI = 1.
cos 2' cos 8 2 , cos Y2
cos (X3, cos 8 3 , cos Y3
4.2.2. Body a úsečky v prostoru
Vzdálenost tJ dvou bodů PI[X l , Yl, Zl] a P 2 [X 2 , Y2, Z2]
IP 1 P 2 1 = .J[(Xl - X2)2 + (Yl - Y2)2 + (Zl - Z2)2] = tJ.
Průmět [projekce] ,úsečky délky. tJ = IP l P 2 1 do souřadnicových os
tJ x = tJ cos (X , by = tJ cos P , tJ z = tJ cos Y
459
(Q:, f3, y jsou velikosti směrových úhlů vektoru P I P 2 ).
£52 = t5; + £5; + t5; ,
t5 = t5 x cos a + t5 y cos B + t5 z cos }' ,
cos 2 rJ.. + cos 2 B + cos 2 y = 1,
kde cos rJ.., cos {3, cos y jsou směrové kosiny vektoru P I P 2 .
Souřadnice bodu D s dělicím poměrem A. vzhledem k bodům
P I a P 2
Xl - A. X 2
XD = 1 - A. '
YI - A.Y2
YD = 1 - A. '
Z 1 - A.Z 2
ZD = ,
1 - A.
přičemž A. > O, resp. A < O, jestliže bod D je vnějším, resp. vnitřním dělicím
bodem úsečky P 1 P 2 .
Střed po[xo, Yo, zo] úsečky P I P 2
Xl + X 2
Xo =
2 ,
YI + Y2
Yo =
2
Zl + Z2
-
"'O -
2
Těžiště T[xT' YT, ZT] trojúhelníku s vrcholy PI[XI, YI]' P 2 [X2, Y2]
a P 3 [X3' Y3]
Xl + X2 + X3
X T =
3
YI + Y2 + Y3
YT = 3'
Zl + Z2 + Z3
ZT =
3
Pro hmotné body s hmotnostmi ml' m2 a m3 ve vrcholech trojúhelníku
P I P 2 P 3 platí
mlx l + m2 x 2 + m 3 x 3
XT =
ml + m 2 + m3
mlYI + m2Y2 + m3Y3
YT =
ml + m2 + m3
ZT =
mIzl + m2 z 2 + m3 z 3
ml + m2 + m 3
a obecně pro n hmotných bodů platí
n
L mk x k
k=l
X T =
n
L m k
k=l
460
"
L mkY"
k=l
YT = n
L m k
k=l
n
L mkzk
k=l
ZT = n
L m k
k=l
Obsah trojúhelníku P I P 2 P 3 v prostoru
S = J(Si + S + S ),
kde
Sl = t Yl, 1 S2 = t Xl' 1
"'1' "'1,
Y2, Z2, 1 X2, 1
"'2'
Y3, Z3, 1 X3, 1
"'3,
83 =! Xb Yb 1
X2, Y2, 1
X3, Y3, 1
Objem čtyřstěnu P1P2P3P4 (Pl je hlavní vrchol)
V-1. Xb Yl, 1 1 Xl - X2, Yl - Y2, Zl - Z2
-6 "'1' . 6
X2, Y2, Z2, 1 Xl - X3, Yl - Y3, - Z3
"'1
X3, Y3, Z3, 1 Xl - X4, Yl - Y4, - Z4
"'1
X4, Y4' 1
"'4'
(ve vzorcích jde o absolutní hodnoty determinantů).
Jestliže všechny čtyři body leží v jedné a téže rovině, pak determinant
6 V = O.
Úhel dvou rádiusvektorů OP 1 = r 1 a OP 2 = r2 o velikosti qJ
cos qJ = cos CX 1 cos CX 2 + cos 8 1 cos 8 2 + cos Yl cos 'V2 =
X 1 X 2 + YIY2 + Z1 Z 2 '
r 1 r 2
kde 1' Pp }'1' resp. 2' {32' }'2 jsou velikosti směrových úhlů rádiusvektoru
- -
OP 1 , resp. OP 2 .
Vektory r 1 , r 2 jsou vzájemně kolmé, právě když cos qJ = O.
4.2.3. Rovina v prostoru
Obecný tvar rovnice roviny (]
(] = ax + by + cz + d = O, stručně R = O.
(koeficienty a, b, c nejsou zároveň rovny nule).
Úseky na souřadnicových osách
d
,
a
q=
d
b'
d
p=
r=
c
461
Vzdálenost počátku O od roviny
Vzdálenost počátku O od roviny ax + by + cz + d = O se rovná číslu 1£51,
kde
d '
£5=
J(a 2 + b 2 + c 2 ).
Směrové kosiny roviny ax + by + cz + d = O
a
cos íJ.. = ,
B J(a 2 + b 2 + c 2 ).
b
cos B = ,
B J(a 2 + b 2 + c 2 )
c
cos y = . ,
B J(a 2 + b 2 + c 2 )
kde B = 1, resp. G = -1 podle toho, zda sgn d = -1, resp. sgn d = 1.
Veličiny íJ.., {3, Y jsou velikosti směrových úhlů kolmice k počátku O k dané
rovině, tj. velikosti úhlů, které kolmice k svírá s kladnými poloosami sou-
řadnicových os.
Rovnice souřadnicových rovin:
z = O je rovnice roviny xy,
y = O je rovnice roviny xz,
x = O je ovnice roviny yz.
Zvláštní případy:
d = O - rovina prochází počátkem:
ax + by + cz = O;
a = O . - rovina je rovnoběžná s osou x:
by + cz + d = O;
b = O - rovina je rovnoběžná s osou y:
ax + cz + d = O;
c = O - rovina je rovnoběžná s osou z:
ax + by + d = O;
a = b = O - rovina je rovnoběžná s rovinou xy:
cz + d = O;
462
a = c = O - rovina je rovnoběžná s rovinou xz:
by + d = O;
b = c = O - rovina je rovnoběžná s rovinou yz:
ax + d = O;
a = d = O - rovina prochází osou x:
by + cz = O;
b = d = O - rovina prochází osou y:
ax + cz = O;
c = d = O - rovina prochází osou z:
ax + by = O.
Úsekový tvar rovnice roviny
x y z
-+-+-=1,
p q r
kdep, q, r jsou tzv. úseky (vyťaté rovinou) na souřadnicových osách (viz str. 461).
N ormálový tvar rovnice roviny
x cos rJ.. + y cos B + z cos y - n = O,
kde n je vzdálenost počátku O od roviny, tj. délka kolmice z počátku O k rovině.
Veličiny cos rJ.., cos {3, cos y jsou směrové kosiny roviny (viz str. 462).
Transformace obecného tvaru rovnice roviny v normálový tvar:
ax + by + cz + d = O
B J(a 2 + b 2 + c 2 ) ,
kde B = 1, resp. B = -1 padle toho, zda sgn d = -1, resp. sgn d = 1.
Vzdálenost bodu Po[xo,yo,zo] od roviny (] ax + by + cz + d = O
Vzdálenost bodu Po od roviny (] je číslo 1£51, kde
£5 = axo + byo + cZo + d
J(a 2 + b 2 + c 2 ) ,
přičemž při £5 < O leží bod Po na téže straně od roviny (] jako -počátek O,
kdežto při £5 > O leží bod Po na opačné straně od roviny (] než počátek O.
Platí
£5 = Xo cos rJ.. + Yo cos B + Zo cos y - n.
463
Rovnice svazku rOVIn
Jsou-li
alx + bly + ClZ + dl = O,
a2 x + b 2 y + C2 Z + d 2 = O
rovnice dvou daných rovin, přičemž označíme
Rl = al,x + bly + ClZ + dl' R 2 = a2 x + b 2 y + C2 Z + d 2 ,
pak svazek rovin procházejících průsečnicí dvou daných rovin Rl = O,
R 2 = O má rovnici
JlRl + AR 2 = O,
kde čísla Jl, A E R nejsou zároveň rovna nule.
Roviny půlící úhly dvou různoběžných rOVIn
Jsou-li aix + biy + CiZ + di = O (i = 1, 2) rovnice' dvou daných rovin
v obecném tvaru, pak rovnice rovin půlících úhly dvou různoběžných rovin
mají tvar
at X + blc + ClX + dl a2 x + b 2 y + c 2 z + d 2
J( 2 2 2) + J( 2 2 2) = O,
8 1 a l + b l + CI - 82 a2 + b 2 + C2
kde 8 1 = -sgn dl a 8 2 = -sgn d 2 .
P r ů seč í k P [ x p, Y p, z p] tří r o v i n
Jsou-li aix + biy + Ci + di = O (i = 1, 2, 3)
tvaru, pak jejich průsečík má souřadnice
L1x L1y
x p = L1' Yp = L1' zp =
rovnice tří rOVIn v obecném
L1z
L1'
kde
L1 - al, b l , CI
a2, b 2 , C2
a3, b 3 , C3
L1x = dl, b l , CI ,
d 2 , b 2 , C2
d 3 , b 3 , C3
. L1y = al, dl' CI ,
a2, d 2 , C2
a3, d 3 , c 3
464
Az = al, hl' dl
a2, h 2 , d 2
a3, b 3 , d 3
Podmínka: A =t= O.
Podmínka, že čtyři rovIny procházejí právě jedním bodem
a l , b l , CI' dl
a 2 , b 2 , c 2 , d 2
a 3 , b 3 , c 3 , d 3
a4, b 4 , c 4 , d 4
kde aj, b i , Ci' di jsou koeficienty rovnic aix + bix + CiX + di = O (i = 1, 2, 3, 4)
čtyř rovin v obecném tvaru.
=0
,
Odchylka qJ dvou rovin
Jsou-li aix + bix + CiX + di = O (i = 1, 2) rovnIce dvou daných rOVIn
v obecném tvaru, platí
a l a2 + b l b 2 + C l C2
cos cp = J[(ai + bi + d) (a + b + d)]
Dvě roviny jsou rovnoběžné, právě když
al:bl:c l =a2: b 2: c 2 ,
tj. právě když a2 = Aa l , b 2 = Ab., C2 = ACl pro vhodné číslo A.
Dvě roviny jsou vzájemně kolmé, právě když
a l a2 + b l b 2 + ClC2 = O.
(0° < qJ < 90°).
Obsahy SXy, SYZ' Sxz průmět ů rovin ného o brazce o o bsah u S
do rovin xy, yz, xz
SXy = Scosy, SYZ = Scos , Sxz = ScosB,
kde cx, {3, y jsou velikosti směrových úhlů kolmice k z počátku O k rovině,
v níž leží daný rovinný obrazec o obsahu S, tj. velikosti úhlů, které kolmice k
svírá s kladnými poloosami souřadnicových os.
Platí
S2 = S;y + S;z + S;z,
S = SXy cos y + SYZ cos cx + Sxz cos B.
465
4.2.4. Přímka v prostoru
Obecný tvar rovnice přímky
,
{ a 1 x + b 1 Y + C 1 z + dl = O,
a2 x + b 2 y + C2Z + d 2 = O,
Přímka je průsečnicí dvou rovin.
stručně
stručně
Rl = O,
Rz = O.
Rovnice přímky ve dvou promítacích rovinách
{ y = mx + q (rovnice roviny kolmé k rovině
z = nx + r (rovnice roviny kolmé k rovině
Transformace obecného tvaru v právě uvedený tvar:
al=-m, b l =l, cl=O, dl=-q,
a 2 =-n, b 2 =0, c2=1, d 2 =-r.
Zvláštní případy:
Přímka je rovnoběžná s rovinou xy:
Přímka je rovnoběžná s rovinou xz:
Přímka je rovnoběžná s rovinou yz:
Přímka je rovnoběžná s osou x:
Přímka je rovnoběžná s osou y:
Přímka je rovnoběžná s osou z:
Přímka prochází počátkem O:
Rovnice souřadnicových os:
{ y = O
Osa x:
z = O;
osa y: {; ;
osa z: {; :
466
{ y = mx + q,
z = r.
{ Z _ nx + r,
y -. q.
{ Z = oy + r,
x = p.
{ y = q,
z = r.
{ X = p,
z = r.
{ X = p,
y = q.
{ y = mx,
z = nx.
xy),
xz).
Odchylky ťx, 8, y přímky { : ' a souřadnicových os
1 hl' CI a 1 CI' a 1
COS (X = - COS IJ = -
N b 2 , C2 N C 2 , a 2
1 a l , b l ,
cos y = - a2, h 2
N
N 2 = hl' CI 2+ CI' a l 2 + al, b 1 2
h 2 , C2 C 2 , a2 a2, h 2
Od h lk a v, k { y = mx + q, v d . , h
c y y CX, IJ, Y P r 1 m y a S O u ran 1 c O v y c O s
z=nx+r
1 m
cos IX = ,J ( 2 2)' cos 8 = ,J ( 2 2 r
1.+m +n l+m +n
n
COS Y = / ( 2 2 ) ;
v 1 + m + n
cos 2 cx + COS 2 {3 + COS 2 Y . 1.
Rovnice přímky určené bodem P1[X b Yl,Zl] a směrovými
O d c h y I k a m i cx, {3, }'
x - Xl · Y - Yt
-
COS cx COS {3
-
1
COS Y
Parametrické rovnice přímky určené bodem P 1 [X 1 , Y1, Zl]
a směrovými kosiny
X = Xl + t COS cx ,
Y = Y 1 + t COS {3,
z = Z 1 + t COS Y
(t je parametr).
Obecné parametrické rovnice přímky procházející bodem
P1[XbY1,Zl]
x = Xl + at,
Y = Y1 + bt,
z = Zl + ct,
kde veličiny a, b, C nemusí již splňovat podmínky pro směrové kosiny, ale
stejně jako veličiny X l' Y l' Z I mohou být libovolnými' čísly.
467
Rovnice přímky procházející dvěma body P.[Xl,y.,Zl]
a P 2 [ X2, Y2' Z2]
x - Xl
Y - Yl
z - Zl
X2- X l Y2-Yl Z2- Z .
Zvláštní případy:
1. Přímka prochází bodem Pl[X.,Yl'Z.] a počátkem o:
X
Y
41
Xl Yl Zl
2. Přímka prochází bodem p. [Xl' Yl, Zl] a je kolmá k rovině R = O:
x - Xl Y - Yl
-
a b
-
41 411
c
X - Xl
Průsečík p[xp, YP, zp] přímky
s rovinou R = O cos ('J.,
Y - Y.
-
cos B.
z - Zl
cos y
x p = Xl - t cos ex,
YP = Yl - t cos B,
z p = Z. - t cos y,
kde
aX l + bYl + eZ l + d
t=
a cos ex + b cos B + c cos Y
Přímka
x = Xl + t cos cx, Y = Y. + t cos B , z = Z 1 + t cos y
je rovnoběžná s rovinou ax + by + ez + d = O, právě když
a cos ex + b cos B + e cos y = O.
, { y - mx + q
Průsečík P přímky - , s rOVInou ax + by + ez + d = O
z=nx +r
qb + re + d .
a + mb + ne'
souřadnice YP a Zp dostaneme dosazením do výchozích rovnic.
Daná přímka je rovnoběžná s rovinou ax + by + cz + d = O, právě když
a + mb + ne = O.
Xp =
46R
Podmínka pro průsečík d vou přímek
Dané přímky
{ a 1 x + b 1 Y + CI z + dl'
a2 x + b 2 y + C2 Z + d 2 ,
{ a 3 x + b 3 y + C3 Z + d 3 ,
a4 x + b 4 y + c 4 z + d 4
se protínají právě v jednom bodě, právě když
a1, b 1 , c., dl = O.
a 2 , b 2 , C2, d 2
a3, b 3 , C3, d 3
a 4 , b 4 , c 4 , d 4
Průsečík p[x p , YP, zp] dvou přímek
{ y = m 1 x + q1, a { y = m2 x + q2,
z = n 1 x + r 1 z = n 2 x + r2,
q2 - q1 r2 - r 1
xp = ,
ml - m2 nI - n2
m1q2 - m 2 q1
YP =
ml - m 2
n 1 r 2 - n 2 r 1
11 1 - n 2
-
p -
Podmínky, aby se dvě přímky proťaly:
q1 -- q2 ml - m 2
r 1 - r2 nI - n 2
x - x Y - Y z - Zl
Odchylka qJ přímky 1 = 1 _ a rovIny R = O
cos rJ.. cos B cos y
a cos rJ.. + b cos B + c cos y
J(a 2 + b 2 + c 2 )
sin cp =
(0° < qJ < 90°).
Přímka je rovno běžná s rovinou, právě když
a cos rJ.. + b cos B + C cos Y = O.
469
Přímka je k o lm á k rovině, právě když
a b c
- -
cos cx cos 8 cos y
x - Xl Y - Y1 - X - X2
6.. 6..1
Odchylka cp přímek - - a -
cos cx 1 cos 8 1 cos Y 1 cos CX 2
Y - Y2 Z - Z2
- -
cos 8 2 cos Y2
cos qJ = cos CX 1 cos CX 2 + cos 8 1 cos 8 2 + cos Y1 cos Y2'
Podmínky rovnoběžnosti přímek:
cos cx 1 = cos cx 2 , cos 8 1 = Cos 8 2 , COS}'l = cos 'Y2'
Podmínka k o I m o s t i přímek:
cos cx 1 COŠ cx 2 '+ cos 8 1 cos 8 2 + cos Y1 cos Y2 = o.
Od h Ik ...., k { y=m1X+Q1' { y=m2X+Q2'
c y a qJ prlme a
z = n 1 x + '1 z = n2 x + '2
1 + m1 m 2 + n 1 n2
COSqJ = J[(l + m + nD(l + m + nm
Podmínky rovnoběžnosti přímek: mľ = m2, nI = n 2 .
Podmínka kolmosti přímek: 1 + m 1 m 2 + n 1 n 2 = O.
Vzdálenost dvou mimoběžek v prostoru
Dané přímky
x - Xl Y - Yl Z - Zl
- -
cos cx 1 cos 8 1 cos }' 1
X - X2 Y - Y2 -
6.. 6..2
- -
cos cx 2 cos 8 2 cos Y 2
mají vzdálenost
Xl - X2, Y1 - Y2, -
6..1 6..2
cos cx 1 , cos 8 1 , cos Y 1
I
£5= cos (X2, cos 8 2 , cos Y 2
( COS 8 1 , COS Y 1 2 + cos }' l' cos cx 1 2 + cos ClI' COS 8 1 2) .
cos 8 2 , cos Y 2 cos }'2, cos cx 2 cos cx 2 , cos 8 2
470
4.2.5. Plochy druhého stupně
4.2.5.1. Kulová plocha
o becná fO vn ice k u lové ploch y se středem S[ m, n, p] a
poloměrem r
,(x - m)2 + (y - n)2 + (z - p)2 - r 2 = O.
Středová rovnice kulové plochy
x 2 + y2 + Z2 - r 2 = O
(střed kulové plochy je v počátku O).
Kvadratická rovnice vyjadřující kulovou plochu
A(x 2 + y2 + Z2) + Bx + Cy + Dz + E = O (A * O),
přičemž střed kulové plochy
S = [ - 2 ' - 2 ' - ;: ]
a poloměr
1
r = 2A J(B2 + C 2 + D 2 - 4AE),
kde B 2 + C 2 + D 2 > 4AE.
XRovnice tečné roviny v bodě Po [xo, Yo, zo] ke kulové ploše
(x - m)2 + (y - n)2 + (z - p)2 - r 2 = O
(x - nI) (xo - m) + (y - n) (Yo - n) + (z - p) (zo - p) - r 2 = O.
Neleží-li bod Po na kulové ploše, vyjadřuje tato rovnice polární rovinu bodu Po
vzhledem ke kulové ploše.
Mocnost J1 bodu po[xo, Yo, zo] ke kulové ploše
(x - m)2 + (y - n)2 + (z - p)2 - r 2 = O
J1 = (xo - m)2 + (Yo - n)2 + (zo - p)2 - r 2 .
I
Rovnice potenční roviny dvou kulových ploch
(x - m 1 )2 + (y - n 1 )2 + (z - Pl)2 - ri = O,
(x - ln 2 )2 + (y - n 2 )2 + (z - P2)2 - r = O:
K 1 -K 2 =O,
471
kde
K I = (x - ml)2 + (y - nl)2 + (z - pt)2 - ri,
K 2 = (x - m2)2 + (y - n 2 )2 + (z - P2)2 - r .
PotenčnÍ rovina je kolmá k spojnici středů daných dvou kulových ploch.
Potenční křivka vzhledem ke třem daným kulovým plochám
K I = O, K 2 = O a K 3 = O:
KI - K 2 _ O, }
KI - K3 - O.
4.2.5.2. Elipsoid
Středová rovnice (trojosého> elipsoidu (střed elipsoidu je
v počátku O) (obr. 307):
x 2 y2 Z2
-+-+-=1
a 2 b 2 c 2
kde a, b, c jsou délky poloos hlavních řezů.
Mají-li dvě osy elipsoidu stejnou délku, jde o rotační elipsoid.
Mají-li všechny tři osy elipsoidu stejnou délku, .jde o k u lov o'u p I o c h u.
l
--
y
Obr. 307. Trojosý elipsoid
Rovnice tečné roviny bodu Po[xo, Yo, Zo] k elipsoidu
x 2 y2 Z2
2+2+2=1:
a b c
XXo YY6 ZZo
-+-+-=1.
a 2 b 2 c 2
Neleží-li bod Po na elipsoidu, vyjadřuje tato rovnice polární rovinu bodu Po
vzhledem k elipsoidu.
472
:.
.?, Rovnice průměrové rovIny
x cos a y cos 8 z cos j'
') + b 2 + 2 = O
ll- C
de cx, {3, y jsou velikosti směrových úhlů příslušného průměru.
Tři sdružené průměry
cos cx I cos 2 cos tJ I cos B 2 cos }'I cos /.2
2 + 2 + ') = O,
a b c
cos a 2 cos CX 3 cos tJ 2 cos {-J 3 cos }'2 cos }'3
') + b 2 + 3 = O,
a- C
cos cx 3 cos I cos 8 3 cos 8 1 cos Y3 cos (1
a2 + b 2 + c 2 = O
kde CXb {31, Y1; CX2 {32, Y2; CX3, {33, Y3jSOU velikosti směrových úhlů tří sdružených
o .., o
prumeru.
Každá rovina protíná elipsoid v reálné nebo imaginární elipse.
I
Objem tělesa ohraničeného elipsoidem viz v člÍl;nku 3.3.3.
4.2.5.3. Hyperboloid
St ř e d o v á r o v nic e j e d 11 o d i ln é ho h y per b o I o i d u (o br. 308)
x 2 y2' Z2
-+---=1
a 2 b 2 c 2 '
kde a, b jsou délky reálných poloos,
c -je délka imaginární poloosy.
y
y
z
Obr. 308. Jcdnodílný hyperboloid
Obr, 309. Dvojdíln}' hypcrboloid
473
Středová ro vn ice dvojd í lné ho hyperboloi d u (obr. 309)
x 2 y2 Z2
-+---= -1
u 2 b 2 c 2
kde c je délka reálné poloosy,
u, b jsou dél y imaginárních poloos.
\
Rovnice asymptotické kuželové plochy pro oba hyperboloidy
x2 y2 :2
-+---=0
a 2 b 2 c 2
Při a = b je hyperboloid rotační (osou otáčení je osa z).
Veličiny a, b, c jsou délky poloos hlavních řezů.
Rovnice průměrové roviny pro oba hyperboloidy
x cos rJ.. Y cos B z cos y
2 + b 2 - 2 = O,
a c
kde rJ.., {3, Y jsou velikosti směrových úhlů příslušného průměru.
Rovnice tečné roviny bod u Po [xo, Yo, =0] k hyperboloid u
x 2 y2 Z2
- + - - - + G = O:
a 2 b 2 c 2
xXo yYo ZZo
+ ---z - 2 + e = O,
a b c
kde G = 1, resp. G = -1 platí pro dvojdílný, resp. jednodílný hyperboloid.
Neleží-li bod Po na hyperboloidu, vyjadřuje uvedená rovnice polární rovin
bodu Po vzhledem k hyperboloidu.
Rovnice povrchových přímek jednodílného hyperboloidu
x z ( Y )
-+-=x 1 +-,
a a b
: - = : (l-ť)
První osnova:
pro 't x E R \ { O} ;
474
druhá osnova:
x z ( Y )
a + =A I-I;'
x _ = ( 1 + )
a c).. b
pro 't J.. E R \ {O}.
Každá povrchová přímka první osnovy protíná každou' povrchovou přímku
druhé osnovy.
Rovina protíná hyperboloid v hyperbole, resp. parabole podle toho, zda je
rovnoběžná právě s dvěma obalovými přímkami, resp. právě sjednou obalovou
přímkou asymptotické kuželové plochy. Není-li rovina rovnoběžná se žádnou
obalovou přímkou asymptotické kuželové plochy, protíná hyperboloid
v elipse. .
Objem rotačního jednodílného hyperboloidu
Rotační jednodílný hyperboloid uvažovaný jako těleso definované v člán-
ku 3.3.3, které vznikne ,při rotaci hyperboly x21 a 2 - y21 b 2 = 1, jestliže osou
otáčení je osa y a otáčí se jedna z větví hyperboly pro - YI < Y < YI' má
objem
v = 21ta 2 Yl(yi + 3b 2 )
3b 2 .
Objem rotačního dvojdílného hyperboloidu
Rotační dvojdílný hyperboloid uvažovaný jako těleso definované v článku
3.3.3, které vznikne při rotaci hyperboly x 2 /a 2 - y2/b 2 = 1, jestliže osou
otáčení je osa x a otáčejí se obě větve hyperboly pro a < x < X I a - x I <
< X < -a, má objem
21tb 2 (XI - a)2 (Xl + 2a)
V = 2 .
3a
4.2.5.4. Paraboloid
Střed ová rovn ice e 1 i pt ie ké ho par a b o 10 id u (obr. 310)
X2 y2
1: + 2" - 2z = O.
a b
475
S tře d o v á r o vn 1 c e h y per b O I i c k é h o par a b o I o i d u (obr. 311)
x2 y2
2 - 1: -.2z = O.
a b
Osa paraboloidu splývá s osou z.
Vrchol paraboloidu je v počátku O.
Při a = b jde o r'otační paraboloid s osou z jako osou otáčenÍ.
Rovina xy je tečnou rovinou k oběma paraboloidům v počátku O.
Každá rovina rovnoběžná s osou z protíná eliptický paraboloid v parabole;
každá jiná rovina jej protíná v reálné nebo imaginární elipse.
Každá rovina rovnoběžná s osou z protíná hyperbolický paraboloid
v parabole; každá jiná rovina jej protíná v hyperbole.
Roviny xz a yz jsou rovinami souměrnosti pro oba paraboloidy.
y
.
y
Obr. 310. Eliptický paraboloid
x
Obr. 311. Hyperbolický paraboloid
Rovnice tečné roviny bodu po[xo,yo,zo] k paraboloidu
x2 y2
a 2 + b 2 - 2z = O:
xXo yYo ( )
7 + b 2 - z + Zo = O.
Neleží-li bod Po na paraboloidu, vyjadřuje uvedená rovnice polární rovinu
bodu Po vzhledem k paraboloidu.
Rovnice povrchových přímek hyperbolického paraboloidu
x y
-+-=x
a b '
x y 1
---=-.2z,
a b x
První osnova:
-
476
tj. přímky rovnoběžné s rovinou
x y
- + - = O.
a b '
druhá osnova:
xy"
---=A
a b '
x Y 1
-+-=-.2z,
a b A
tj. přímky rovnoběžné s rovinou
x Y
- - - = O.
a b
"
U vedené rovnice platí pro \j x \j A. E R \ {O}.
Objem V a obsah Q pláště úseče rotačního paraboloidu
uvažovaného jako těleso (viz článek 3.3.3)
OtáčÍ-li se. parabola kolem osy x a PI[XI, YI] je bod hrany podstavy, je
V I 2
= 2'X I YI,
1ty 1 [ 3
Q = _ 6 2 (yi + 4xi) /2 - Yi]
Xl '
(YI je poloměr pod stavy a Xl výška paraboloidu).
4.2.5.5. Kuželová plocha (obr. 312)
Vrcholová rovnice kuželové plochy
X2 y2 Z2
-+---=0
a 2 b 2 c 2 '
,
..
1
Obr. 312. Kuželová plocha
477
kde a, b jsou délky poloos elipsy, která je řídicí křivkou kuželové plochy a jejíž
rovina je kolmá k ose z;
c je vzdálenost roviny elipsy od roviny xy.
V rchol kuželové plochy je v počátku O.
x 2 y2 Z2
Tečná rovina ke kuželové ploše s rovnicí - + - - - = O
a 2 b 2 c'2
v bodě Po [xo, Ýo, zo]:
. .
xXo YYo ZZo
-+ --=O
a 2 b 2 c 2 .
Rotační kuželová plocha
Při a = b je řídicí křivka kružnicí; rotační kuželová plocha má pak rovnici
x 2 + y2 Z2
a 2 - c 2 = O;
její tečná rovina má rovnici
XXo + YYo zZo
2 - 2 = O.
a a
..
Rovnice povrchových přímek kuželové plochy
x z 1 Y
- + - = - -,
a c A b
x z - Y
- - - - -).-
a c - .. b
přímky osnovy procházejí vrcholem kuželové plochy.
pro 't ;.. E R \ {O};'
4.2.5.6. V álcová plocha
.
Středová rovnice eliptické válcové plochy kolmé k rovině xy
(obr. 313)
x2 y2
- + - = 1;
a 2 b 2
roviny xz a yz jsou rovinami souměrnosti.
Rovnice je identická s rovnicí průsečné elipsy v rovině xy.
478
Středová rovnice hyperbolické válcové plochy kolmé
k rovině xy (obr. 314)
x2 y2
- 1 .
a 2 - b 2 - ,
roviny xz a yz jsou rovinami souměrnosti. Řez rovinou xy je hyperbola.
I
Obr. 313. Kolmá eliptická
válcová plocha
Obr, 314. Kolmá
hyperbolická válcová plocha
Obr. 315. Kolmá parabolická
válcová plocha
Vrcholová rovnice parabolické válcové plochy kolmé
k rovině xy (obr. 315)
y2 = 2px.
Rovina xz je rovinou souměrnosti. Rovina y.: je tečnou rovinou, která se
dotýká plochy vose z.
Řez kolmý k rovině xy je reálnou nebo imaginární dvojicí přímek. Každá
jiná rovina protíná eliptickou, resp. hyperbolickou, .resp. parabolickou válco-
vou plochu v elipse, resp. hyperbole, resp. parabole.
Rovnice tečné rovIny v bodě Po [xo, Yo, zo]
xXo + yYo = 1
a 2 b 2
pro eliptickou válcovou plochu,
xXo yYo - 1
7 - b 2 -
yYo = p(x + xo)
pro hyperbolickou válcovou plochu,
pro parabolickou válcovou plochu.
479
4.2.6. Obecná algebraická rovnice
druhého stupně v proměnných x, y a z
j'(x,y,z) = a l1 x 2 + 2a12xy + a22y2 + 2a13xz +
+ 2a23YZ + a 33 z 2 + 2a14X +
+ 2a24Y + 2a 34 z * a44 = O.
Ortogonální invarianty plochy druhého stupně
Diskriminant
.
A= all, a12, a13, d 14 ,
a2l, a22, a23, a24
a3b a32' a 3 3, a34
a 41 , a42' a 43 , a44
subdeterminant A44 diskriminantu
A44 = a 11' a 12 , a13 ,
a 2l , a22, a23
a3l' a32, a33
kvadratický invariant
1 2 = a l 1, a 12 + a22, a 2 3 + a33, a31 ,
a 1 2, a22 a23, a33 a3l, a l 1
lineární invariant
11 = a l1 + a 22 + a33'
Poznámka:
V determinantech platí a ik = a ki .
Obecná funkční rovnice druhého stupně vyjadřuje plochu druhého stupně
(kvadriku). Kvadrika má jediný střed v konečnu, právě když A44 9= O
(tzv. středová kvadrika). Tětivy procházející středem se nazývají průměry.
Množina všech středů rovnoběžných tětiv je průměrová rovina. Průměr pří-
slušný k tětivám je sdružen s průmě ovou rovinou.
Plocha druhého stupně degeneruje ve dvojici rovin, právě když
alb a12, a 1 4 + a11, a13, a14 + a 22 , a23' a24 = O.
I a 21 , a22' a 2 4 aj l' a 3 3, a 3 4 a32' a33, a34
a 41 , a 4 2' a44 a 41 , a43' a44 a42, a43, a44
4RO
Pro reálné, nedegenerující plochy druhého stupně platí podmínky uvedené
v tabulkách 4.2 a 4.3. '
Tabulka 4.2
Případ 1 : A44 * O (středové kvadriky)
11 A44 > O, 1 2 > O 1 1 A44 a 1 2
nejsou zároveň větší než O
A < O elipsoid dvojdílný hyperboloid
A> O imaginární elipsoid jednodílný hyperboloid
A = O imaginární kuželová plocha kuželová plocha
Tabulka 4.3
Případ 2: A44 = O (nestředol,é kl'adriky)
A < O, 1 2 > O A > O 1 2 < O
A * O eliptický paraboloid hyperbolický paraboloid
1 2 > O 1 2 < O 1 2 = O
A=O eliptická hyperbolická parabolická
válcová plocha válcová plocha válcová plocha
481
5. DIFERENCIÁLNÍ POČET
Úmluva:
V celé části 5 se uvažuje jen o posloupnostech reálných čísel a o reálných
funkcích reálné proměnné. Pouhým slovem číslo, popř. bod budeme zde
rozumět reálné číslo.
5.1. LIMITY
5.1.1. Limity posloupností
Definice limity posloupnosti
Říkáme, že posloupnost {ak} má (vlastní, konečnou) limitu a nebo že kon-
verguje k číslu a [je konvergentní], a píšeme lim ak = a, jestliže ke každému
k cx>
číslu B > O existuje takové kladné číslo. nt' že pro všechny indexy n > ne
(tj. pro skoro všechny indexy k) platí (obr. 316)
lan - al < B.
y
Q+e
Q
Q-£
o 1 2 3 4 5
Obr. 316. K definici limity
nE n n+f n+2 n+J . ., x posloupnosti
Platí
lim ak = a lim (ak - a) = O,
k cx> k cx>
přičemž posloupnost, jejíž limitou je číslo nula, nazýváme nulovou posloup-
ností.
482
Nemá-li posloupnost vlastní limitu, pak se nazývá divergentní, popř. říkáme,
že diverguje.
Říkáme, že posloupnost {a k } má nevlastní limitu + 00, resp. - 00 [diverguje
k + 00, resp. - 00], a píšeme
lim a k =. + 00, resp. lim'a k = - 00,
k-oo k-oo
právě když ke každému číslu K existuje takové číslo n K > O, že pro všechny
indexy n > nK je a n > K, resp. a n < K.
Posloupnost, která má nevlastní limitu + 00, popř. - 00, se nazývá určitě.
divergentní.
Hromadný bod posloupnosti
Říkáme, že posloupnost {a k } má hromadný bod a, jestliže ke každému číslu
e > O existuje nekonečně mnoho takových indexů n, že platí (viz též článek
0.4.9)
lan - al < e.
Existuje-li limita posloupnosti, pak tato limita je jediným hromadným
bodem této posloupnosti.
Věty o limitách posloupností
Jestliže členy posloupnosti {a n } jsou pro skoro všechny indexy n rovny
témuž číslu a, pak lim a n = a.
n-oo
Každá konvergentní posloupnost je ohraničená.
Jestliže posloupnost. {a n } má limitu a, pak každá z ní vybraná posloupnost
{ a kn } má také limitu a.
Jestliže posloupnosti {a n }1I {b n } mají vlastní limity lim a n = l:l, lim b n = b,
pak n- 00 n- 00
a) lim lani = lal;
n-oo
b) lim (a n + b n ) = a + b;
n-oo
c) lim (a n - b,.) = a - b;
n-oo
d) lim (anb n ) = ab, lim ca n = c lim a n ;
n-oo n-oo n-oo
) 1 . an a ( )
e lm - = - b * O ;
"-00 b b
, n
f) jestliže pro skoro všechny indexy je a n < b n , platí a < b.
Jestliže lim lani = O, pak lim a n = O.
n-oo n-oo
483
Věta o limitě sevřené posloupnosti: Jestliže pro skoro všechny členy po-
sloupnosti {c n } platí a n < C n < b n a lim a n = lim b n = a, pak existuje
n-oo n-oo
lim C n = a..
n-oo
Jestliže lim a n = + 00, lim b n = - 00, lim C n = C > - 00 a lim d n =
n-oo n-oo n-oo n-oo
= d < + 00, přičemž může být také c = + 00 nebo d = - 00, platí
lim (a n + c n ) = + 00, lim (b n + d n ) = - 00.
n-oo n-oo
Jestliže lim a n = + 00, lim b n = - 00, lim C n = C > O a lim d n = d < O,
n-oo n-oo n-oo n-oo
přičemž může být také C = + 00 nebo d = - 00, pak
lim (anc n ) = lim (b,.dn) = + 00 ,
n-oo n-oo
lim (and n ) = lim (bnc n ) = - 00 .
n-oo n-CIJ
Jestliže neklesající posloupnost {a n } je (resp. není) shora ohraničená, pak
má vlastní limitu (resp. nevlastní limitu lim a n = + 00 ).
n-oo
Jestliže nerostoucí posloupnost {a n } je (resp. není) zdola ohraničená, pak
má vlastní limitu (resp. nevlastní limitu lim a n = - 00 ).
n-oo
Některé limity posloupností
lim a: = (lim an)cx (a n > O, E R);
n-oo n-oo
n-oo
. b lim b n ( )
hm a n = a n -+ oo a > O ;
lim 10gb a n = 10gb lim a n
n-CIJ n-oo
(a n > O, bER + \ {I});
I . an .
1m - b = O, jestlIže
n-oo n
lim a n = O
n-oo
a lim b n * O;
n-oo
1 . an
1m - = O, jestliže
n-oo b
n
lim b n = + 00
n-oo
a
{a n } je ohraničená
posloupnost;
I , an
1m - = + 00 , jestliže
n-oo b
n
je ohraničená posloupnost;
anb n > O, lim lani = + 00
n-oo
a
{b n }
484
lim a n = - 00, jestliže anb n < O, lim lani = + 00 a {b n }
n oo b n oo
n
je ohraničená posloupnost;
. . . v . a n + 1
hm Van = a, Jesthze hm - = a (a n > O);
n 00 n 00 a n
. a 1 + a 2 + ... + a n
hm = a, jestliže
n oo n
lim a = a'
n ,
n oo
lim ( 1 + ! ) n = e = 2,718281 828459 O ... (základ přirozených
n oo n
logaritmů [Eulerovo číslo]);
lim ( 1 + ) n = ea. (oc E R);
n oo n
lim, ex n = O (Iexl < 1);
n oo
lim Vp = 1 (p > O);
n oo
(x < 111, ex E R);
(Ial < 1),
(a = 1),
(a > 1);
(O < a < 1),
(a = 1),
(a > 1);
lim ( V ex + V B ) n = J(ocB)
n oo 2
lim Vn = 1;
n oo
lim V(n!) = + 00,
n oo
o n1
hm - = O o
,
n 00 nn
(J,n
lim - = O;
n 00 n!
lim (nax n ) = O
n oo
1 { I
1 . 1
1m = 2'
n oo 1 + ci' O
n { O
. a 1
hm = "2
n 00 1 + a n 1
1 k + 2 k + .. o + n k
lim k + 1
n 00 n
lim J = O,
n 00 n!
. V(n!) 1
hm = _o
,
n oo n e
(ex > O, B > O);
1
-
k + 1
(k E N);
485
lim ( 1 k + 2 k + ... + n k _ n ) = !
n - co n k k + 1 2
(k E N);
. 1 - 2 + 3 - ... - 2n
! J(n 2 + 1) = -1;
lim ( 1 + 2 + oe. + n _ !!. ) = _ ;
n-co n + 2 2 2
I . 1 . 2 + 2. 3 + 3 . 4 + ... + n( n + 1) 1 .
lm --
n-oo n 3 - 3 '
lim 1 2 + 3 2 + 52 + ... + (2n - 1 V = .
n- 00 n 3 3 '
1 [( 1 ) 2 ( 2 ) 2 ( n - 1 ) 2 J 1
! (X + + (X + n +. · . + (X + n = (X2 + (X + 3;
lim ( 1 + + + ... + - ln n ) = lim ( f - ln n ) '=
n-oo 2 3 n n-oo k= 1 n
= 'Y = C = 0,577 215 66490... (Eulerova konstanta);
nf
lim. _ . J = J(21t) (Stirlingův vzorec);
n - 00 nn e n n
lim [( 2.4.6..... (2n) ) 2 J = 1t (Wallisův vzorec).
n - 00 1 . 3 . 5 . ... . (2n - 1) 2n 2
5.1.2. Limity funkcí
Limita funkce
Říkáme, že funkce y = f(x) má v bodě x = a, v němž nemusí být definována,
(vlastní, konečnou) limitu A, a píšeme lim j'(x) = A, právě když ke každému
x-a
číslu B > O existuje takové číslo tJ > O, že pro všechny body x, pro něž je
O < lx - al < tJ, platí If(x) - AI < B, tj. že pro 'Ix E O(a, tJ) je f(x) E
E (A - B, A + B ) (obr. 317). '
Limitu lim f(x) nelze zaměňovat s funkční hodnotou f(a).
x-a
486
Limita funkce zleva a zprava
Říkáme, že funkce y = f(x) má v bodě a (vlastní) limitu zprava A, resp.
zleva A [píšeme lim J(x) = A, resp. lim f(x) = AJ, právě když ke každému
x a+ x a-
číslu B > O existuje takové číslo b > O, že pro všechny body x z intervalu
(a, a + c5), resp. (a - tJ, a) platí If(x) - AI < B.
y
A+
A
A -t
o
0-6' Q a+cf x
"
u(o,o)
Obr. 317. K definici limity funkce
Nevlastní limita funkce
Říkáme, že funkce y = f(x) má v bodě a nevlastní limitu + 00, resp. - 00
[píšeme limf(x) = + 00, resp. limf(x) = - 00], právě když ke každému
x a x a
číslu K existuje takové číslo [) > O, že pro všechny body x, pro něž je O <
< lx - al < tJ, platí f(x) > K, resp. f(x) < K.
Obdobně se definují nevlastní limity funkce zprava a zleva v bodě a:
lim f(x) = + 00 ('tK 3[) > O Vx E (a, a + c5) => f(x) > K),
x a+
lim f(x) = - 00 (V K 3b > O Vx E (a, a + tJ) => f(x) < K),
x a+
lim J(x) = + 00 (V K 3[) > O Vx E (a - tJ, a) => f(x) > K),
x a-
xl _f(x.t = - 00 (V K 3b > O Vx E (a - b, a) => f(x) < K).
Limita funkce v nevlastním bodě
Říkáme, že funkce y = f(x) má v nevlastním bodě '+ 00, resp. - 00 (vlastní)
limitu A [píšeme lim f(x) = A, resp. lim f(x) = A], právě když ke každému
x + 00 x - 00
číslu B > O existuje takový bod c, že pro všechny body x > c, resp. x < c
platí If(x) - AI < B.
487
Nevlastní limita funkce v nevlastním bodě
Říkáme, že funkce y = f(x) má v nevlastním bodě + 00, resp. - 00 nevlastní
limitu + 00 [píšeme lim f(x) = + 00, lim f(x) = + 00], právě když ke
x + 00 x - 00
každému číslu K existuje takový bod c, že pro všechny body x > c, resp.
x < c platí f(x) > K.
Říkáme, že ,funkce y = j'(x) má v nevlastním bodě + 00, resp. - 00 nevlastní
Limitu - 00, právě když ke každému číslu K existuje takový bod c, že pro
všechny body x > c, resp. x < c platí f(x) < K.
Věty o limitách funkcí
Funkce má v bodě nejvýše jednu limitu, nejvýše jednu limitu zprava a nej-
výše jednu limitu zleva.
Platí
lim f(x) = lim f(x) = A lim f(x) = A.
x a+ x a- x a
Funkce f je spojitá v bodě a, právě když lim f(x) = f(a). Funkce f je spo-
x a
jitá v bodě a zprava, resp. zleva, právě když lim f(x) = f(a), resp. lim f(x). =
x a+ x a-
= f(a).
Limita konstantní funkce f(x) = c se v každém bodě a E 01(f) rovná c.
Platí lim x = a pro každý bod a E 0 1 (f(x) = x).
x a
Jestliže funkce f, 9 mají vlastní limity lim f(x) = A, lim g(x) = B, pak
, x a x a
a) lim If(x)1 = IAI;
x a
b) lim [f(x) + g(x)J = A + B;
x a
c) lim [f(x) - g(x)] = A - B;
x a
d) lim [f(x)g(x)J = AB, lim [cf(x)] = c limf(x);
x a x a x a
e) lim j(x) = A (B =to O).
x a g(x) B
Jestliže lim If(x)1 = O, pak lim ,f(x) = O.
x a x a
Věta o limitě sevřené funkce: Jestliže lim f(x) =- lim h(x) = A a na ne-
x a x a
úplném okolí D(a, (5) platí f(x) < g(x) < h(x), pak existuje limita lim g(x) = A.
x a
488
Jestliže lim J(x) -- + 00, lim g(x) = - 00, lim h(x) = C > - 00, lim k(x) =
x-a x-a x-a x-a
= D < + 00, přičemž může být také C = + 00, D = - 00, platí
lim [f(x) + h(x)J = + 00, lim [g(x) + k(x)J = - 00.
x-a x-a
Jestliže lim .f(x) = + 00, lim g(x) = - 00, lim h(x) = C > O, lim k(x) =
x-a x-a x-a x-a
= D < O, přičemž může být také C = + oc, D = - 00, pak
lim [f(x) h(x)] = lim [g(x) k(x)] = + 00,
x-a x-a
lim [f(x) k(x)] = lim [g(x) h(x)] = - 00.
x-a x-a
Platí
lim [f(x)]" = [lim f(x)]n
x-a x-a
limVf(x) = Vlimf(x)
x-a x-a
[f(x) > O, nEN],
[f(x) > O].
Jestliže platí lim qJ(x) = b, lim f(y) = A a, existuje takové číslo {) > O,
x-a y-b
že qJ(x) =4= b platí pro všechny body x E O(a, (5), pak je Ilmf(qJ(x)) = A.
.X-Q
Při vý očtech limit se často používá těchto tvrzení: -
lim f(x) = A lim f ( ! ) .= A,
x - ,.f, 00 y - o + y
lim j'(x) = A . lim f ( ! ) = A.
x--oo y-O- y
....,
Některé limity funkcí
lim ( 1 + ) X . lim (1 + xfx = e:
x-f:oo x x-Of:
lim ( 1 + a ) X = e", lim ( 1 + a ) X = e";
x-+oo X x--oo X
X< - a k ' ,
lim = ka k - 1 (k E N, (X > O);
x-a X - a
lim f(x)
lim f(X) = ax-.a ((X > O);
.\' -+ (I
lim [logp f(x)] = logp [lim f(x)] [f(x) > O, B > O, B =4= 1];
x- x-a
lim a X = O (O < (X < 1),
x- + 00
489
lim rJ..x = + 00
x- - 00
lim rJ..X = + 00
x- + 00
lim rJ..X = O
X- - 00
sin x
lim- = 1,
x-o x
. sin (rJ..x)
hm = rJ..
x-o X
. tg x
hm - = 1,
x-o x
(O < rJ.. < 1),
(rJ.. > 1),
(rJ.. > 1);
sin x
lim -.= O;
x- + 00 X
(x E R);
lim tg ((Xx) = (X
x-o X
(x E R);
I . 1 1t
1m arctg x = lim arctg - = -;
x- + 00 x- o + X 2
I . I . 1
1m arctg x = 1m arctg - =
x--oo x-o- X
eX - 1
lim
x-o ,x
= 1.
,
rJ..X - 1
lim =lnrJ..
x-o x
1t
2'
(rJ.. > O);
x
lim = O, ((1 E R, f3 > O);
x:-+ + 00 e
In a x
lim - = O (rJ..-E R, f3 > O);
x- + 00 x fJ '
lim [x fJ ( -In x)a] = O (rJ.. E R, B > O);
x-o+
pro aj, bjE R (i = O, 1, ..., m; j = O, 1, ..., n; a m 9= O, b n 9= O) platí
m m-l
I . amx + am-1x
1m
x- + 00 bnx n + b n - lX n - 1
490
O (m < n),
+ ... + ao
+ ... + b o
a m
,b n
+00
(m > n, amb n > O) ,
(m > n, amb n < O);
(m = n),
-00
o (m < n),
m m-l a m
1 . amX + a m - 1 X + ... + a o
lm b n b n - 1 b - b n
x - - 00 nX + n - 1 X + ... + o
+00
-x
(m = n),
(m > n, (_l)m-n amb n > O),
(m > n, (_l)m-n amb n < O);
sIn x
lim 3 = 1
_\-0 X cos X
(Maskelynovo pravidlo).
Limita funkce n proměnných
Říkáme, že funkce y = f(x l' x 2 , .. ., x n ) má v bodě [C l' C 2' ..., C n ] (vlastní,
konečnou> limitu, a píšeme
lim f(X 1 ,X2,.."X n ) = A,
[XI. X2. .... Xn] - [CI. C2. .... c n ]
právě když ke každému číslu G > O existuje takové neúplné okolí
K([ C}, C2, ..., c n ], (5), pro jehož všechny body [x}, x 2 , ..., x n ] platí
If(X 1 ,X 2 ,...,x n ) - AI < G.
5.2. DIFERENČNÍ PODÍL, DERIVACE, DIFERENCIÁL
Diferenční podíl
Je-li funkce y = f(x) definována na nějakém okolí U(xo, (5), pak rozdíl
L\x = x - Xo nazýváme přírůstkem [diferencí] argumentu x v bodě Xo a rozdíl
y = f(x) - f(x o ) nazýváme přírůstkem [diferencí] funkce f [přírůstkem
(závisle> proměnné y] v bodě xo.
Poměr přírůstků
L\y f(x) - f(xo) f(xo + x) - f(xo)
- = = = tg (]
L\x x - Xo x '
který se nazývá diferenční podíl ji111kce j' v bodě Xo, udává směrnici sečny PoP
(obr. 318). Trojúhelník PoAP se naLývá sečnový trojÚhelník.
491
Derivace funkce v bodě
Existuje-li vlastní, resp. nevlastní limita
lim L\y = lim f(x) - f(xo) = lim f(xo + L\x) -: f(xo) = tg. o
x-o x X-Xo X - Xo x '
Xo, Xo + x E 0 1 (f), Yo = f(x o ) E 02(f),
říkáme, že funkce j' má v bodě Xo vlastní, resp. nevlastní derivaci. Tuto limitu
značíme
dy df ' I I
f'(X O )' - d (xo), - d (xo), Df(xo), Yxo nebo y (xo)
x x
a nazýváme vlastní, resp. nevlastní derivací funkce f v bodě xo.
Neexistuje-li uvedená limita (vlastní ani nevlastní), říkáme, že funkce f
nemá v bodě Xo derivaci.
Místo o vlastní derivaci mluvíme také o konečné derivaci nebo zpravidla
jen o derivaci.
Derivace funkce v bodě Xo udává směrnici tg 'to tečny křivky dané rovnicí
y = f(x) v bodě Po (obr. 319). Trojúhelník PoBC se nazývá tečnový trojúhelník.
y
y
---;.
x
o
x
o
Obr. 318. Diferenční podíl
Obr. 319. Derivace funkce
ti
Příklad:
Je-li x doba a y dráha, pak derivace funkce y = f(x) v bodě a udává oka-
mžitou rychlost v okamžiku a.
Existuje-li vlastní limita
f ' ( ) - 1 . f(x) - f(xo)
+ Xo - lm ,
X-Xo+ X - Xo
resp.
j'(x) - f(xo}
f (xo) = lim
X-Xo- x - Xo
\
\
492
v bodě xO' nazýváme ji (vlastní, konečnou) derivací funkce y = f(x) v bodě Xo
zprava, resp. zleva.
Platí
,
j (xo) = f (xo) = a <=> f'(x o ) = a.
Obdobně se definuje nevlastní derivace funkce v bodě zprava, popř. zleva.
Má-li funkce y = f(x) v každém bodě intervalu (a, b) vlastní derivaci,
resp. derivaci zprava, resp. derivaci zleva, řikáme, že funkce f má (vlastní)
derivaci, resp. (vlastní) derivaci zprava, resp. (vlastní) derivaci zleva na inter-
valu (a, b). Jestliže funkce y = f(x) má vlastní derivaci na intervalu (a, b)
a zároveň má v bodě a vlastní derivaci zprava a v bodě b vlastní derivaci zleva,
říkáme, že funkce f má (vlastní) derivaci na intervalu (a, b).
Funkce na intervalu (a, b), jejíž funkční hodnota v každém bodě x E (a, b)
je f'(x), se nazývá derivace funkce f na intervalu (a, b) a značí se
f',
df
dx '
y',
dy ,
- nebo Yx'
dx
někdy též
f'(x),
dl (x) , ( )
y' x ,
dx
dy
- (x) nebo Df(x).
dx
Funkce na intervalu (a, b), která je derivací funkce f na intervalu (a, b) a jejíž
funkční hodnota v bodě a, resp. b je vlastní derivací funkce f zprava, resp.
zleva, se nazývá derivace funkce f na intervalu (a, b ).
Jestliže funkce y = f(x) má v bodě Xo vlastní derivaci, resp. vlastní derivaci
zprava, resp. vlastní derivaci zleva, pak funkce f je v bodě Xo spojitá, resp.
spojitá zprava, resp. spojitá zleva. Obrácená implikace však neplatí. Například
spojitá funkce f(x) = Ixl nemá v bodě o derivaci, neboť f (O) = 1 a f (O) =
= -1. Stejně tak neplatí uvedená věta pro nevlastní derivaci, neboť např.
funkce
{ 1 (x > O),
f(x) = O (x = O),
- 1 (x < O)
má derivaci f'(O) = f (O) = f (O) = + 00, ale je v bodě Xo = O nespojitá.
Funkce, která má na intervalu (a, b) spojitou derivaci, stejně jako křivka,
která je jejím grafem, se nazývá hladká [spojitě diferencovatelná] na intervalu
(a, b ).
493
Diferenciál, diferencovatelná funkce
Říkáme, že funkce y = f(x) má v bodě Xo diferenciál nebo že je bodě Xo
diferencovatelná, právě když platí
y = A x + x 't( x),
kde A je konstanta a lim 't( x) = O (obr. 320).
L\x - o
Funkce je v bodě Xo E 0 1 (f) diferencovatelná, právě když má v tomto bodě
derivaci. Pak platí A = f'(xo).
Výraz f'(x o ) x = f'(x o ) dx proměnné x E ( - 00, + (0) nazýváme dife-
renciálem funkce f v bodě xo a značíme
df(xo),
(dy)xo nebo [df(x)]xo.
Protože derivací funkce f(x) = x na množině R je f'(x) = 1, lze psát
dx = 1 . x = x, přičemž dx nazýváme diferenciálem argumentu.
Říkáme, že funkce y = f(x) je diferencovatelná na intervalu (a, b), který je
částí definičního oboru 0 1 (f), právě když je v každém bodě x E (a, b) dife-
rencovatelná.
Diferenciál funkce y = f(x) v obecném bodě x značíme
dy, df, někdy též df(x).
y
Obr. 320. Diferenciál funkce
f(xo+tJx) ----------
o
Xo
lO+tJX X
Geometrický význam difrenciálu
Diferenciál dy funkce y = f(x) se rovná přírůstku pořadnice bodu tečny t
grafu funkce v daném bodě [xo, Yo] (viz obr. 320).
494
Oerivace vyšších řádů
Existuje-li vlastní, resp. nevlastní limita
f ,, ( ) - I . f'(xo + L\x) - f'(xo)
Xo - 1m A '
x o LlX
říkáme, že funkce f má v bodě Xo vlastní, resp. nevlastní druhou derivaci [derivaci
druhého řádu], a hodnotu f"(xo) nazýváme vlastní, resp. nevlastní druhou
derivací [derivací druhého řádu] funkce f v bodě xo. Obdobně se definují de-
rivace vyšších řádů v bodě Xo, které po řadě označujeme f"'(x o ), f(4)(X O )'
f(5)(x o ) atd. .
Jestliže funkce J' má v každém bodě definičního oboru (a, b) funkce f
vlastní derivaci, pak derivaci funkce f' na intervalu' (a, b) nazýváme druhou
derivací [derivací druhého řádu] funkce f na intervalu (a, b). Obdobně zavá-
díme derivace vyšších řádů funkce f proměnné x, přičemž používáme těchto
označení:
Druhá derivace [derivace druhého řádu]:
f ff , d2f " d 2 y "
dx 2 ' Y , dx 2 ' Yx'
někdy též
[f'(x )]',
f"(x) ,
02f(x) ,
d 2 1 (x) nebo df'(x)
dx 2 dx
1řetí derivace [derivace třetího řádu]:
d 3 f d 3 y
I"', dx 3 ' y"', dx 3 '
",
Yx'
někdy též
[f"(x )]',
f"'(x),
03f(x),
d 3 f
dx 3 (x),
df"(x)
dx
n-tá derivace [derivace n-tého řádu]:
dnf dny
Y (n) ,
dX-'
f(n) ,
dx n '
Y (II)
x ,
někdy též
[J n - l)(x )]/,
"
f(n)(x) ,
onf(x),
dnf(x)
dx"
dj'(n - 1 )(x)
nebo
dx
495
Difrenciály vyšších řád ů
Říkáme, že funkce y = f(x) má v bodě Xo n-tý diferenciál [diferenciál n-tého
řádu], právě když všechny derivace funkce f až do řádu n - 2 mají diferenciál
na okolí bodu Xo a derivace (n - 1 )-ního řádu funkce f má v bodě Xo diferenciál.
n-tý diferenciál funkce f v bodě Xo značíme dnj'(xo)' V obecném bodě x po-
užíváme těchto označení:
Druhý diferenciál [diferenciál druhého řádu]:
d 2 y, d(dy), d(df), někdy též d 2 f(x).
Platí d ť(x) = f"(x) dx 2 .
1řetí diferenciál [diferenciál třetího řádu]:
d 3 y, d(d 2 y), někdy též d 3 f(x).
, Platí d 3f(x) = f"'(x) dx 3 .
n-tý diferenciál [diferenciál n-tého řádu]:
dny, d(d n - l y), někdy též dnf(x).
Platí d'j(x) = f(n)(x) dx n .
\
5.3. PRAVIDLA PRO DERIVOVÁNÍ FUNKCÍ
Derivování funkcí daných explicitně
Úmluva:
u, v, Ul' U2, ..., u n , W jsou diferencovatelné funkce proměnné x.
..
1. y = k = konst => y' = O.
2 + + + " + ' + + "'
. Y = U I U2 . . . U n => Y = U I U2 . . . U n
(pravidlo pro derivování součt.u funkcí).
3 " + '
. y = uv => y = u v uv
(pravidlo pro derivování součinu dvou funkcí),
, , + ' + '
y = uvw => y = u vw uv w uvw ,
" + ' + + ,.
Y = UIU2." Ú n => Y = UIU2 ... U n U I U2'" U n ... UIU2 ... Un-IU n ,
popř.
y' = U t U2 ... U n ( u; +, u + ... + U ) (Ul * O, U 2 * O, ..., U n * O).
U 1 U 2 U n ·
4. y = ku => y' = ku' (k je konstanta).
496
u u' v - uv'
5. y = - (v * O) => y' = 2
V V
(pravidlo pro derivování podílu dvou funkcí).
6. Derivace složené funkce: Má-li funkce u = g(x) (vnitřní složka složené
funkce) vlastní derivaci v bodě Xo a funkce y = f(u) (vnější složka složené
funkce) vlastní derivaci v bodě Uo = g(xo), pak složená funkce y = f(g(x))
má v bodě Xo vlastní derivaci
y o = f'(u o ) g'(xo) = j"(g(xo)) g'(xo)
Má-li funkce u = g(x) vlastní derivaci na intervalu (a, b) a funkce y = f(u)
vlastní derivaci na intervalu (ex, B) a pro všechna čísla x E (a, b) platí g(x) E (ex, B),
pak složená funkce y = j'(g(x)) má na intervalu (a, b) derivaci
[f(g(x))J' = f'(g( )) g'(x)
neboli
dy
dx
dy du
--
du dx
7. Obdobně jako v bodě 6 se postupuje při výpočtu derivace složené funkce
s několika vnitřními slo kami, např.
[f(g(h(x)))J' = f'(g(h(x))) g'(h(x)) h'(x)
(tzv. řetě ()vé pravidlo).
8. Jestliže x = g(y) je inverzní funkcí k funkci y = f(x) a existuje-li v bodě c
derivace f'(c) 9= O, pak v bodě d = f(c) existuje g'(d) a platí
1
g'(d) = f'(c)
neboli
( :; \ -
1
( d Y ) .
dx c
Příklady:
V příkladech jsou odvolávky na pravidla z této kapitoly a na vzorce z ka-
pitoly 5.5.
1. y = - 9 ; y' = O (pravidlo 1).
2. y = x 5 + x 2 - x 7 ; y' = 5x 4 + 2x - 7x 6 (pravidla 2, 4 a vzorec 3).
497
3. y = (x 3 + a) (x 2 + 3b) (a, b jsou konstanty);
x 3 + a = u; u' = 3x 2 ;
x 2 + 3b = v; v' = 2x;
y' = 3x 2 (X 2 + 3b) + (x 3 + a) . 2x (pravidla 1, 2, 3 a vzorec 3),
y' = 5x 4 + 9bx 2 + 2ax .
4. y = lOx 6 ; y' = 10.6x s (pravidlo4avzorec3),
y' = 60x 5 .
x 3 + 2x
5. y = 4x2 _ 7 ;
x 3 + 2x = u; u' = 3x 2 + 2;
4x 2 - 7 = v; v' = 8x;
I (3x 2 + 2) (4x 2 - 7) - (x 3 + 2x).8x
y = (4x 2 _ 7Y (pravidlo 5),
4x 4 - 29x 2 - 14
I
Y = (4x 2 - 7)2
6. y = (1 - cos 4 X)2 = u 2 = f(u), kde u = 1 - cos 4 x;
f'(U) = 2u = 2(1 - cos 4 x),
U = 1 - cos 4 X = 1 - v 4 = g( v), kde v = cos x,
g'(V) = -4v 3 = -4cos 3 x,
V = cos x = h(x); h'(x) = - sin x (vzorec 8); .
dy = f'(u) g'(v) h'(x) = 2(1 cos 4 x) (-4 cos 3 x) (-sin x) (pravidlo 7);
dx
dy
- = 8(1 - cos 4 x) sin x cos 3 x.
dx
7. y = arctgx; inverzní funkce je x = tgy = g(y);
1
g'(y) = 2 = 1 + tg 2 Y (pravidlo 8 a vzorec 9);
cos y
111
L = f'(x) = g'(y) = 1 + tg 2 Y - 1 + x 2 ·
Logaritmické derivování i
Někdy je vhodné k určení derivace funkce y = f(x) najít přirozený loga-
ritmus této funkce a potom tento logaritmus derivovat podle x (tzv. logarit-
nJ;cké derivování).
498
Zvlášť vhodný je tento postup u funkcí tvaru y = u(x)l'{X) [u(x) > O]:
ln y = v(x) ln u(x),
1 u'(x)
- y' '= v'(x) ln u(x) + v(x) - ( ) '
y ux
[ u'(x ) ]
y' = y v/(x) ln u(x) + v(x) u(x) ,
y' = u(x)V(x{ v'(x) ln u(x) + v(x) ( j J.
Příklad 1:
(xx)' = xX(lnx + 1) (x > O).
Příklad 2:
y = (arctg xY [x E (O, 1t/2)];
ln y = x ln (arctg x),
1 x 1
- y' = ln (arctg x) + 2 '
Y arctg x 1 + x
. y' = (arctg xt [ ln (arctg x) + ( ;; ] .
1 + x arctg x
5.4. DERIVACE FUNKCÍ NĚKOLIKA PROMĚNNÝCH,
TOTÁLNÍ DIFERENCIÁL
P.arciální derivace
/
Existuje-li vlastní limita
I . f(xo + x, Yo) - f(xo, Yo)
lm ,
x o x
resp.
1 . f(xo, Yo + y) - f(xo, Yo) ,
lm , ,
}'-o x ,
říkáme, že funkce z = f(x, y) má v bodě [xo, Yo] parciální derivaci podle x,
resp. podle y. V obecném bodě [x, y] používáme těchto označení:
lx, Zx'
499
někdy též
[I'
?x (x, y),
oz ·
ex (x, y), .I:(x, y) nebo J,,(x, y),
resp.
h., z)'
někdy též
cf
-;- (x, y),
cy
cz
oy (x, y), J;(x, y) nebo /y(x, y).
Obdobně se definují parciální derivace yyšších řádů.
Parciální derivace druhého řádu
!xx, 02Z o ( :)
"'xx, C 2 ' OX ,
IX
02Z ° ez)
oy
hy, z J'}' , "" 2 ' oy ,
oy
Ixy, 02Z C ( :)
... xy , OX oy' ay ,
,.
!,x,
41)'X ,
02Z
oy Ox'
o ( ;)
lX
Parciální derivace zx)" Zyx se nazývají smíšené.
Za předpokladu, že obě smíšené derivace jsou spojité v bodě [x, y], platí
tzv. Schwarzova věta:
02Z 02Z
ex oy - oy ex .
Obdobně se definují parciální derivace funkce n proměnných.
500
Totální diferenciál
Říkáme, že funkce z = j'(x, y) má v bodě [xo, Yo] totální [úplný] diferenciál
nebo že je v tomto bodě diferencovatelná, právě když na okolí bodu [xo, Yo]
platí
z = A dx + B y + (l !( x, y),
kde A, B jsou konstanty, (l = J[( X)2 + ( y)2] a lim 't( x, y) = O.
L\x - o
y-O
Je-li funkce f v bodě [xo, Yo] diferencovatelná, pak má parciální derivace
prvního řádu a platí
af
A = ox (xo, Yo),
cf
B = oy (xo, Yo).
Výraz
af af
o) xo, Yo) Ax + oy (xo, Yo) Ay =
af af
= -;-(xo,yo)dx + (xo,fo,yo)dy
li x (, Y
nazýváme totálním diferenciálem funkce f v bodě [xo, yo].
Říkáme, že funkce z = f(x, y) má v bodě [xo, Yo] totální diferenciál n-tého
řádu [n-tý diferenciál], právě když všechny parciální derivace až do řádu
n - 2 mají totální diferenciál na okolí bodu [xo, Yo] a všechny parciální
derivace (n - l)-ního řádu mají v bodě [xo, Yo] totální diferenciál. Pro n = 2
Je
2 a 2 z 2 a 2 z a 2 z 2
d z = ox 2 dx + 2 ox oy dx dy + oi dy ·
Obdobně definujeme totální diferenciál pro funkci y = f(xl' X2, ..., x n )
n proměnných. Je-li f diferencovatelná funkce, pak platí
cy ty ; y
dy = -dx} + dx2 +... + dxn'
ex} CX2 CX n
501
Příklad:
'.
z = Y 2 eX.
, ,
e
= y2 eX
?x '
ez
- = 2 y eX
ey ,
a 2 i)2 Z C 2 Z
: = y2 eX, ;") 2 = 2e x , c = 2 y eX;
(.IX' vy X o Y
dz = y2 eX dx + 2 y eX d y = y eX(y dx + 2 d y),
d 2 z = y2 eX dx 2 + 2. 2y eX dx dy + 2e X 'd y 2 =
= e X (y2 dx 2 + 4y dx dy + 2 dy2).
Derivování funkcí daných implicitně
Jestliže funkce y = f(x) je dána implicitně rovnicí f(x, y) = O, parciální
derivace fx, h existují a h :F' O, pak první derivaci funkce f vypočteme podle
vzorce
dy _ ' _ r.f _ fx
dx - Y - - a - - Ir ·
""
cy
Pokud existují parciální derivace druhého řádu fxx' hy, fxy, je druhá derivace
e 2 f ( ť f ) 2 _ 2 02f cf of + 02f ( Of ) 2
d 2 y " cx 2 ay ex ey ex ay oy2 ex
dx 2 = y - (% y
fxxh2 - 2fx y fxh + hyfx2
h 3
Příklad:
f(x,y) = x 3 - x 2 y + y5 = O;
f . 2 cf 4 2
-;- = 3x - 2xy = fx, -;- = 5y - x = h,
vX (jY
a c 3
= 6x - 2y.= fxx' = 20y = hy,
lX cy
e 2 f '
"" = -2x = fx)' = f}'x;
(,X cy
502
3x 2 - 2xy
5 y 4 - X 2 '
dy
dx
d 2 y
dx 2
(6x - 2x) (5y4 - y2)2 - 2( - 2x) (3x 2 - 2xy) (5y4 - X 2 ) + 22y3(3x 2 - 2Xy)2
(5y4 _ X 2 )3
Derivování funkcí daných parametricky
Jestliže funkce f je dána parametricky rovnicemi
x = qJ(t), y = tjJ(t) pro \lt E M
a dqJldt = ljJ(t) + O, dt/lldt = .jJ(t) existují, pak
dy
dy _ _ .jJ(t)
dx - dx - ljJ(t).
dt
. Pokud existují Ip, .ji, resp. ip, i/i, platí
d 2 y dx d 2 x dy
-----
d 2 y d , dt 2 dt dt 2 dt .ji(t) ljJ(t) - ip(t) .jJ(t)
dx 2 = dx (y) = (:: Y - [ifÍ(tW
neboli
d 2 y
dx 2 =
resp.
d 3 y
dx 3 =
Příklad:
x = ln t,
dx
--
dt
dy
dt
d ( d Y )
dx dt
,
dt dx
ljJ2i/i - ljJ.jJ-q; - 3ljJip.ji. + 3ip2.jJ
· s
li'
1
1
y = ;
1 - t
d 2 x 1
-
dt 2
dt
dx = t,
2
(1 - t)3'
,
t
2'
t
1
(1 - t)2'
d 2 y
dt 2
503
první derivace
dy
dx
1 1
(1 - t)2 . t
t
.
(1 t)2'
druhá derivace '
2 1 1 1
-+-
(1 - t)3 t t 2 (1 - t)2
C y
d 2 y
dx 2 -
2t 2 '+ t ,. t 2
(1 - 1)3
t 2 + t
(1 - t)3
neboli
d 2 Y { d [ t J} 1 + t t 2 + t
dx 2 = dt (1 - t)2 t = (1 - t)3 t = (1 - t)3.
Derivování funkcí daných polárními souřadnicemi
Diferenční podíl funkce (l = f( qJ), dané polárními souřadnicemi (l, qJ, je
Ae (l .
- = - = (l cotg (] ,
qJ tg (]
kde (] je odchylka sečny pp! a přímky OP! (obr. 321).
pater", osa
o
Obr. 3Z1. Derivace funkce dané
polárními souřadnicemi
o
Derivace
d(l . Ae (l
- = hm - '= - = (l cotg l' ,
dqJ <p-o qJ tg l'
kde l' je odchylka tečny v bodě P a přímky OP.
504
Pro polární souřadnice
x = (l cos qJ,
Y = (l sIn qJ
z rovnIc
dx = dg cos qJ - (l sin qJ dqJ,
dy = dg sin qJ + g cos qJ dqJ
dostáváme
dy dg .
- sIn qJ + g cos qJ
I dqJ dy dqJ
y =-=-=
dx dx dg .
- - cos qJ - g sIn qJ
dqJ ,dqJ
5.5. DERIVACE ELEMENTÁRNÍCH FUNKCÍ
,
Pokud nejsou uvedeny omezující podmínky, je u následujících
vzorců oborem proměnné x a všech konstant množina R všech reálných čísel:
1. y = konst (tzv. aditivní konstanta) => y' = O.
2. y = x n => y' = nx n - 1 (n E N). Speciálně
y = x => y' = 1.
3. y = x- n => y' = -nx- n - 1 (x * O, nE N). Speciálně
1 1
y = - => y' = -- (x 9= O ) .
X x 2
4. y = x a => y' = ax a - 1 (x > O, a E R). Speciálně
1
y = n / x =:> y' = "J -1 (x > O, nE N).
'\/ n n x n
Pro některá reálná čísla a lze obor proměnné x rozšířit; např.
(x 1 / 3 )' = t x - 2/3 (x E R \ {O}),
ale
1
y = Jx => y' =
2Jx
5. y = a X => y' = a X ln a
y = eX => y' = eX.
(x > O).
(a > O), Speciálně
505
1
6. y = loga x y' = (x > O, a > O, a 9= 1). Speciálně
x ln a
1
y = ln x => y' = - (x > O);
x
1 0,434 3
y = 19 x => y' = -lg e
x x
(x > O). Dále
1
y = ln [x + J(x 2 + a 2 )] y' = J(x 2 + a 2 ) ;
y = ln [x + J(x 2 - a 2 )] y' = J(x 21 _ a 2 )
[x > lal, x + J(x 2 - a 2 ) > O];
(x > lal, a 9= O);
1 x - a
y = - ln => y' =
2a x + a x 2 - a 2
1 a + x 1
y = -ln => y' = (x > lal, a 9= O).
2a a - x a 2 - x 2
7. y = sin. x => y' = cos x. Dále
y = ln Isin xl => y' = cotg x (x 9= k1t; k E Z).
8. y = cos x => y' = -sin x. Dále ..
y = ln Icos xl y' = - tg x [x + (2k '+ 1) ; ; k E Z J.
9. y=tgx y'= \ =1+tg 2 x [ X+(2k+l) 1t ;kEZ J . Dále
cos x 2
I X 1
y = ln tg - => y' = -:-- = cosec x (x =t= k1t; k E Z).
2 sIn x
1
10. y = cotg x => y' = - . 2 = -(1 + cotg 2 x) (x 9= k1t; k E Z). Dále
sin x
y = ln tg ( 1t + X ) y' = 1 = sec x [ X + (2k + 1) 1t ; k E Z J .
4 2 cos x 2
11. y = sec x y' = SlOt = tgxsecx [ X + (2k + 1) 1t ; kEZ J .
cos x 2 . .
cos x
12. y = cosec x => y' = - . 2 = -cotg x cosec x (x 9= k1t; k E Z).
sin x
1
14. y = arccos x
1
y' = J(1 _ x 2 ) (Ixl < 1).
1
y' = - J( 1 _ x 2 ) (Ixl < 1).
13. y = arcsln x
506
1
15. y = arctg x => y' = 1 + x2 o
1
16. y = arccotg x I
=> Y = - 2'
l+x
17. y = sinh x => ,y' = cosh x.
18. y = cosh x => y' = sinh x. I
1
19. y = tgh x I
=>y= cosh 2 X
1 (x * O).
20. y = cotgh x I
=>y=-
sinh 2 X
1
21. y = argsinh x I
=:> Y = J(l + x 2 )"
1 (x > 1).
22. y = argcosh x I
=> Y = J(x 2 - 1)
1 (Ix I < 1).
23. y = argtgh I
=>y=
1 - x 2
1 (Ix I > 1).
24. y = argcotgh x => y' = 2
, I-x
25. y = lnf(x) I f'(X) [j(x) > O]
=> y = f(x)
(tzv. logaritmická derivace)o
Derivace vyšších řádů některých funkcí
V následujících vzorcích je n E N.
26. y = x a => y(n) = a( a-I) (a - 2)... (a - n + 1) x a - n (x > O, a E R);
y = x r . => y(n) = O (r E Z, n > r);
y = x n => y(n) = n!;
1 \ 1
y = - => y(n) = (-I)na(a + 1 )( a + 2)...(a + n - 1)- +
x a xa n
(x > O, a E R);
1
y = mj X => y(n) = ( - 1 t - 1 -- - (m - 1) (2m - 1)...
'\/ n° rt .
1
... [(n - 1) m - 1] vtx mn - I (x > O, m E N). Dále
y = anx n + an_1x n - 1 + (ln_2 Xn - 2 + o.. + a1x + ao => y(n) = ann!.
507
27. y = a X => y(n) = aX(ln ar (a > O). Speciálně
y = eX => y(n) = eX;
y = d'x => y(n) = (k ln ar a kx (a > O, kER);
y = e ax => y(n) = (ln e ax (a E R).
(n - 1)'
28. y = loga x => y(n) = ( - 1 r + 1 -- (x > O, a > O, a * 1).
x n ln a
Speciálně
(n - I)!
y = ln x => y(n) = (_I)n-l (x > O).
x n
29. y = sin x y(n) = sin (x + n;).
30. y = cos x ln) = cos (x + n; ).
31. y = sin (ax) y<n) = ď sin (ax + n;) (a E R).
32. y = cos (ax) y(n) = ď cos (ax + n 2 1t) (a E R).
33 -' h (n) _ { sinh x (n je sudé číslo),
. y - sIn x => y - h ( . I . h ' .." I )
cos x n Je IC e CIS o .
_ h (n) _ { COSh x (n je sudé číslo),
34. y - cos x => y - . h ( . I . h ' .." 1 )
sIn x n Je IC e CIS o .
35. y = uv y(n) = u(n)v + ( ) u(n-l) v' + (;) u<n-2) v" + .:.
... + ( n ) u'v(n-l) + uv(n) = f ( n ) u(k)v(n-k)
n - 1 k=O k
(n, kE N, u(O) = U, v(O) = v; u, v jsou funkce reálné proměnné x)
(tzv. Leibnizův vzorec). (Leibnizův vzorec lze odvodit podle binomické
věty, viz str. 159.)
.
5.6. DERIVOVÁNÍ VEK TOROVÉ FUNKCE V E3
Vektorová funkce
v = v(t) nazýváme vektorovou funkcí [vektorovým polem] skalární (tj. reálné)
proměnné t, právě když každé hodnotě proměnné t z definičního oboru
vektorové funkce v je přiřazena právě jedna hodnota vektorové proměnné
v E M, kde M je množina všech vektorů z prostoru E3'
508
Vektorová funkce má v složkovém vyjádření tvar
v = v x + Vy + v z = v x ; + vJ + vzk,
kde V x = vx(t), Vy = vy(t), V z = vz(t) jsou skalární (tj. reálné) funkce skalární
proměnné t, které určují závislosti souřadnic x, y, z vektoru na proměnné t
(obr. 322).
lt
I /
. I /
\ I I
-___ _____.1/
VA'
----- -- - ---
// I
/
V /
y
o
Obr. 322. Složkové vyjádření vektorové
funkce
Obr. 323. Derivace vektorové funkce
Limita vektorové funkce
Říkáme, že vektorová funkce v(t) má v bodě to limitu vo, právě když ke každému
reálnému číslu B > O existuje takové číslo bť" že pro všechna čísla t, pro něž
platí O < It - to I < bť" je Iv(t) - vol < B, a píšeme
lim v( t) = V o .
t-to
Z toho pro V o = (ml' m2, m3) plynou limity
lim vx(t) = ml , lim vy(t) = m 2 , lim vz(t) = m3 .
t-to t-to t-to
Říká e, že vektorová funkce v(t)je spojitá v bodě to, právě když lim v(t) = v(t o ).
t-to
...
Derivace vektorové funkce
Existuje-li limita
dv . . v(t + t) - v(t) dv x . dv y . dv z
- = v = hm = -, + - J + - k =
dt I1t-O t dt dt dt
= v x ; + vJ + vzk,
říkáme, že vektorová funkce v(t) má v bodě t derivaci podle skalární proměnné t,
a limitu v nazýváme derivací funkce v podle skalární proměnné t (obr. 323).
509
Diferenciál- vektorové funkce
Říkáme, že vektorová funkce v(t) má v bodě t diferenciál nebo že vektorová
funkce v(t) je diferencovatelná v bodě t, právě když platí
dv = v t + £(dt) L\t,
kde
lim £(L\/) = O
L\t -+ o
tj. přírůstek vektoru dV' lze nahradit tzv. diferenciálem dv(t) = v At = v dt
vektorové funkce v( t) v bodě t.
Derivace a diferenciály vyššíctt řádů vektorových funkcí se zavádějí obdobně
jako pro skalární funkce.
.
Geometrický a kinematický význam ve torové funkce
Derivace v(t o ) udává směr, tečny v bodě M(t o ) k trajektorii (hodografu)
příslušné k da é vektorové funkci v(t).
Považujeme-li t za časovou proměnnou, pak derivace v(t o ) udává rychlost
bodu M(t), pohybujícího se po trajektorii příslušné k vektorové funkci v(t),
v okamžiku t = to.
Pravidla pro deri\'ování vektorových funkcí
dv
1. - = O pro v( t) = V o (konstantní vektor).
dt
d(v 1 + v 2) dv 1 dv 2
2. dt = dt + dt"
d(gv) dg dv
3. dt = dt v + 9 dt '
. kde 9 = g( t) je skalární funkce skalární proměnné t.
d(V 1 V 2 ) dVl .' dV 2 dV t dV 2
4. = -- v + v - = v - + - v .
dt dt 2 1 dt 2 dt dt 1
d(v 1 v 2 v 3 ) - [ dV 1 J [ dV2 . J [ dV3 J
5. dt - d"t V2V3 + VI d"t V3 + "I V 2 d"t .
d(v 1 x v 2 ) dV 1 dV 2 dV 1 dV 2
6. dt = d"t x V 2 + y 1 X dt = dt x V 2 - dt x VI'
510
d(v I X V2 X V 3 ) _ dV I ( . )
7. dt - dt X V 2 X V 3 + VI
( dV 2 )
X dl X V 3 +
( d V3 )
+ VI X V 2 X dl .
d dv dqJ
8. dt v( (j)(t)) = d(j) Cit'
kde qJ = qJ( t) je skalární funkce skalární proměnné t.
5.7. GRAFICKÉ DERIVOVÁNÍ
Grafickým derivováním nazýváme bodovou konstrukci grafu funkce
y' = f'(x) na základě grafu funkce y = f(x).
Je-li dán graf funkce y = f(x), sestrojíme graf její derivace takto (obr. 324):
V dostatečně mnoha bodech AI' A 2 , A 3 , ... daného grafu (tyto body volíme
blíže sebe tam, kde se graf více mění) sestrojíme tečny a vedeme k nim bodem
p = [ -1, O] na ose x rovnoběžky, které protnou osu y po řadě v bodech
B I , B 2 , B 3 , .... Body Bt, B 2 , B 3 , ... vedeme rovnoběžky s osou x, které protnou
kolmice z bodů Ai, A 2 , A 3 , ... na osu x v bodech CI' C 2 , C 3 , .... Body CI' C 2 ,
C 3 , ... Jsou body hledaného grafu derivace f'.
V
I
Obr. 324. Grafické derivování
v
..
5.8. EXTRÉMY FUNKCÍ
Extrémy funkcí daných explicitně
Jestliže funkce y = f(x) má v bodě Xo kladnou, resp. zápornou derivaci,
pak je v bodě Xo rostoucí, resp. klesající.
Jestliže funkce y = J (x) má v každém vnitřním bodě intervalu I kladnou,
resp. zápornou, resp. nezápornou, resp. nekladnou derivaci, pakje na intervalu I
rostoucí, resp. klesající, resp. neklesající, resp. nerostoucí.
511
Říkáme, že funkce y = f(x) na definičním oboru D má v bodě Xo E D
absolutní maximum, f(x) < f(xo)
absolutní minimum, f(x) > f(xo)
právě když pro \Ix E D platí
ostré absolutní maximum, f(x) < f(xo) .
ostré absolutní minimum, J (x) > f(xo)
Říkáme, že funkce y = f(x) na definičním oboru D má v bodě Xo E D absolutní
extrém (resp. ostrý absolutní extrém), právě když má v bodě Xo absolutní
maximum nebo absolutní minimum (resp. ostré absolutní maximum nebo
ostré absolutní minimum). ' "
Říkáme, že Junkce y = f(x) na definičním oboru D má v bodě Xo E D [O(xo)
je neúplné okolí bodu xo]
lokální maximum, J (x) < f(x o )
lokální minimum, právě když pro \Ix E a(xo) c D platí f(x) > f(xo)
ostré lokální maximum, J (x) < f(xo) .
ostré lokální minimum, f(x) > f(x o )
Říkáme, že Junkce y = f(x) na definičním oboru D má v bodě Xo E D lokální
extrém (resp. ostrý lokální extrém), právě když má v bodě Xo lokální maximum
nebo lokální minimum (resp. ostré lokální maximum nebo ostré lokální
minimum).
Body x k ' v nichž f'(x) = O, se nazývají stacionární body funkce J nebo nulové
body derivace J".
Má-li funkce y = f(x) v bodě Xo lokální extrém a existuje-li f'(x o ), platí
J '(xo) = O (nutná podmínka pro lokální extrém).
Jestliže Xo je stacionárním bodem funkce y = J (x) a existuje f"(xo), pak
funkce f má v bodě Xo
- ostré lok lní maximum, jestliže f"(xo) < O;
- ostré lokální minimum, jestliže J "(xo) > O.
Jestliže f"(xo) = O, pak platí:
Má-li funkce y = f(x) na okolí U(xo) spojitou derivaci řádu m > 3, přičemž
Je
f'(x o ) = f"(xo) = ... = f(m - l)(XO) = O,
f(m)(x o ) =t= O,
pak
je-li m liché číslo, f(m)(xo) > O, je funkce f v bodě Xo ros to ucí;
je-li m liché číslo, f<m)(xo) < O, je funkce f v bodě Xo klesaj ící;
je-li m sudé číslo, f(m)(xo) > O, má funkce f v bodě Xo ostré lokální minim um;
je-li m sudé číslo, f(m)(x o ) < O, má funkce f v bodě Xo ostré lokální maxim urn.
512
Absolutní extrémy funkce na množině
Říkáme, že funkce y = f'(x) nabývá v bodě Xo E A c D(J ) (absolutního>
maxima, resp. (absolutního> minima na množině A, jestliže pro všechny body
x E A platí J (x) < J (xo)' resp. f(x) > J (xo)' Absolutní maximum a absolutní
minimum funkce f na množině A souhrnně nazýváme (absolutními) extrémy
funkce J na množině A. (Absolutní) maximum, resp. (absol tní) minimum
funkce y = J (x) na množině A značíme
max J (x), resp. min J (x) [stručně max J (x), resp. min J (x)].
XEA xEA A A
Supremum a infimum funkce na množině
Supremem, resp. infimem ohraničené reálné funkce f na množině A C D(f)
nazýváme supremum, resp. infimum množiny f(A) (viz článek 0.4.5). Supre-
mum, resp. infimum funkce y = f(x) na množině A značíme
sup f(x), resp. inf f(x) [stručně sup f(x), resp. inf f(x)] .
XEA xEA A A
Poznámka:
Má-li reálná funkce na množině A absolutní aximum M, resp. absolutní
minimum m, pak číslo M, resp. m je supremem, resp. infimem funkce f na
množině A.
Úmluva:
V dalším vý.kladu budeme ostré lokální maximum, resp. ostré lokální
minimum stručně nazývat maximem, resp. minimem (souhrnně budeme mluvit
o extrému).
Příklad:
Máme najít extrémy funkce y = x 3 - 15x 2 + 48x - 3.
y' = 3x 2 - 30x + 48,
y" = 6x - 30;
y' = O => 3x 2 - 30x + 48 = O => Xl = 8 /\ X 2 = 2;
f'''(x l ) = 6 . 8 - 30 = 18 => v bodě Xl nastává minimum,
J "(X2) = 6.2 - 30 = -18 => v bodě X2 nastává maximum.
Příslušné extrémy: YI = - 67, Y2 = 41.
Extrémní body:
El[8, -67] (minimum),
E 2 [2, 41] (maximum).
513
Zjednodušený výpočet extrémů u racionálních lomených funkcí
Jestliže f(x) = g(x)/h(x), pak první derivace f'(X) = p(x)/q(x) je rovněž
racionální lomenou funkcí, takže podmínka pro existenci extrému zní:
p(x) = g'(X) h(x) - g(x) h'(X) = O,
q( x) * O .
o druhu extrému se rozhodne podle znaménka druhé derivace, která pro
nulové body funkce p nabývá jednoduchého tvaru
J " ( ) = p'(X)
X q( x) ·
Příklad:
Máme najít extrémy funkce
2 - 3x + x 2
Y =
2 + 3x + X2.
I ( - 3 + 2x) (2 + 3x + x 2 ) - (2 - 3x + x 2 ) (3 + 2x) 6x 2 - 12 p(x)
y - -
- (2 + 3x + X 2 )2 - (2 + 3x + X 2 )2 - q(x)'
V nulových bodech funkce p platí
I 12x
y' = (2 + 3x + x 2 f ;
y' = O => 6x 2 - 12 = O => Xl,2 = + J2;
12J2
1"("/2) - ( 2)2 > O =:> v bodě ../2 nastává minimum,
2 + 3x + x
f " ( / 2) -12 J2 O b d " / 2 " .
-v = (2 3 2 ) 2 < voe -" nastava maXImum.
+ x+x
Příslušné extrémy:
4 - 3 J2
YI = 4 + 3../2'
4 + 3 J2
Y2 = 4 - 3../2'
Extrémní body:
[ 4 - 3 J2 ]
£1 ../2, 4 + 3 J2
[ 4 + 3 J2 ]
£2 -J2, 4 - 3../2
(minimum),
(maximum).
514
Extrémy funkcí daných implicitně
Funkce y = <p(x), daná implicitně ve tvaru f(x, y) = O, má extrém v bodě xo,
platí-li tyto podmínky:
f(x o , Yo) = O,
fx=O, j ,*O.
Maximum nastává, jestliže v příslušném bodě je fxxlh' > O.
Minimum nastává, jestliže v příslušném bodě je fxxlfy < O.
Příklad:
Máme najít extrémy funkce f(x, y) = x 3 - 3a 2 x + y3 = O (a > O).
J = 3x 2 - 3a 2 , h = 3y2, fxx = 6x;
f(x, y) = O 1\ fx = O 1\ h * O => x 3 - 3a 2 x + y3 = O 1\
1\ 3x 2 - 3a 2 = O 1\ 3y2 * O;
oborem pravdivosti je P = {[a, a 2], [ -a, -a 2]}.
Pro [a, a tf2] platí:
6a
fxx = 6a =:> fx)/Y = 2 > O =:> v bodě a nastává maximum.
3a 4
Pro [-a, -a tf2] platí:
I' I' I I' - 6a O b d " ". .
Jxx = -6a => Jxx Jy = 2 3/ < => voe -a nastava mInImum.
3a v4
Extrémy funkcí daných parametricky
Funkce y = f(x), daná parametricky rovnicemi x = <p(t), y = tjJ(t), má
ex t r é m pro t = to, jestliže platí tyto podmínky:
.jJ(t o ) = O,
(to) * O.
Maximum nastává, jestliže je .ji(t o ) < O.
Minimum nastává, jestliže je .ji(t o ) > O.
515
Příklad:
Máme najít extrémy funkce. (a, b > O)
x = a cos t = qJ( t) ,
y = b sin t = tjJ(t).
q,( t) = - a sin t, .jJ( t) = b cos t,
.jJ(t) = O => b cos t = O s kořeny
t 1) + O, q,(t 2 ) + O;
.. ) 1t
tJI(t 1 = -b sin - = -b < O => V tI nastává maximum,
2
.ji(t 2 ) = b > O => V t 2 nastává minimum.
Příslušné extrémy:
.ji ( t) = - b sin t;
1t 31t
t - t __o
1 - 2 ' 2 - 2'
1t
Xl = acos- = O,
2
31t
X2 = acos- = O,
2
1t
Y 1 = b sin - = b;
2
31t
Y2 = bsin- = -b.
2
Extrémní body:
E 1 [O, b ]
E 2 [0, -b]
(maximum),
(minimum).
. ;
Ex trémy funkce z = f(x, y) (maximální a minimální body plochy)
Absolutní a ostré absolutní extrémy, stejně jako lokální a ostré lokální
extrémy se u funkcí několika proměnných zavádějí obdobně jako u funkce
jedné proměnné.
Funkce z = f(x, y) má v bodě [xo, Yo] ostrý lokální extrém, jestliže
v tomto bodě platí tyto podmínky:
fx O,' J = O, !xx!" - (f:c,)2 > O.
Maximum nastává pro f:cx < O.
Minimum . nastává pro fx:c > O.
Jestliže fxx!'y - (!x,)2 < O, pak říkáme, že funkce z = f(x, y) má v bodě
[xo, Yo] minimax, a bod [xo, Yo, zo] nazýváme sedlovým bodem.
Pro !x:c!,y - (fx,)2 = O nelze rozhodnout, zda le v bodě [xo, Yo] maximum
nebo minimum nebo zda v něm vůbec nastává extrém.
516
Vázané extrémy (metoda Lagrangeových multiplikátorů)
Funkce z = f(x, y) má v bodě [xo, Yo] extrém vázaný vedlejší pod-
mínkou <p(x, y) = O, jestliže v tomto bodě platí tyto podmínky:
<p(x, y) = O,
c
ex [J(x, y) + A <p(x, y)] = o,
(}
-;- [f(x, y) + A <p(x, y)] = O, kde)w E R.
liY
Druh extrému se určí takto: Jestliže druhý diferenciál
Li = d 2 (f + A<p) =
= 02(f + A<p) ( a<p ) 2 _ 2 fP(J + A<p) alp o<p + 02(J + A<p) ( e<p ) 2
ex 2 ay ex ay ax ay ay2.. ax
je v příslušném bodě záporný, resp. kladný, pak'funkce z = f(x, y) má v tomto
bodě maximum, resp. minimum.
Uvedenou metodu lze analogicky použít pro n nezávisle proměnných s m
vedlejšími podmínkami (n + m rovnic).
Příklad:
Máme určit extrémy funkce z = f(x, y) = x 2 + xy + y2 s vedlejší
podmínkou
<p(x, y) = xy - 9 = O.
Řešíme soustavu rovnic
<p(x, y) = O => xy - 9 = O,
e
ox [J(x, y) + A. <p(x, y)] = O 2x + y + AY = O ,
e
oy [J(x, y) + A <p(x, y)] = O x + 2y + AX = O,
X 1 ,2 = + 3,
Yl,2 = + 3,
A = -3.
Extrémní body jsou P 1 [3, 3, 27] ,a P 2 [ - 3, - 3, 27].
517
Druh extrému určíme takto:
a 2 (f + AqJ)
ex 2 = 2,
aqJ
ax = y,
( aqJ ) 2 = 2
ay x ,
aqJ
=x,
oy
e 2 (j' + ) qJ)
=1+A.
ex oy ,
e2(J + AqJ)
2 = 2.
ay .
Je tedy
A = 2X2 - 2(1 + ) ) xy + 2 y 2.
Pro bod P 1 platí:
Li = 2.9 - 2(1 - 3).3 . 3 + 2.9 = 72 > O => v bodě [3,3]
nastává minimum.
Pro bod P2 platí:
A =2.9 - 2(1 - 3).9 + 2.9 = 72 > O => v bodě [-3, -3]
nastává minimum.
5.9. INFLEXNÍ BODY
Jestliže funkce y = J (x) má v bodě Xo. kladnou, resp. zápornou
druhou derivaci, pak je v bodě Xo ryze kon vexní, resp. ryze konká vnL
Jestliže funkce y = J (x) má v každém vnitřním bodě intervalu I kladnou,
resp. zápornou, resp. nezápornou, resp. nekladnou druhou derivaci, pak
na intervalu I je ryze konvexní, resp. ryze konkávní, resp. konvexní,
resp. konká vnL
Říkáme, že funkce y = f(x) na množině D má v bodě Xo E D, v němž existuje
vlastní derivace f'(xo), injlexi, právě když
a) pro \Ix E O -(xo) platí f(x) < f(xo) + (x - xo) f'(xo) a pro \:Ix E O +(xo)
platí f(x) > f(xo) + (x - Xo f'(xo);
b) pro \Ix E O _( ) platí f(x) > f(xo) + (x - xo)f'(x o ) a pro \Ix E O +(xo)
platí f(x) < f(xo) + (x - xo)f'(x o ).
Jestliže funkce y= j(x) má v bodě Xo inf1exi a existuje f"(xo), platí f"(xo) =0
(nutná podmínka pro injlexi v bodě xo).
Jestliže f"(x o ) = O a existuje f"'(xo), pak funkce f má v bodě Xo in flexi,
jestliže f"'(x o ) * O.
Nechť f"'(x o ) = O. Má-li funkce y = f(x) na okolí U(xo) spojitou derivaci
řádu m > 4, přičemž je
f'(x o ) = f"(xo) = ... = f<m - 1 )(xo) = O,
f<m)(xo) =t= O,
518
pak platí:
a) Je-li m liché číslo, pak funkce f má v bodě Xo in flexi [pro rostoucí
hodnoty proměnné x při f(m)(xo) > O přechází graf funkce f v bodě Xo z po-
lohy pod tečnou do polohy nad tečnou, kdežto při f(m)(x o ) < O přechází
graf funkce f z polohy nad tečnou do polohy pod tečnou].
b) Jestliže m je sudé číslo a f(m)(x o ) > O, pak funkce f je v bodě Xo ryze
konvexní.
c) Jestliže m je sudé číslo a f(m)(xo) < O, pak funkce f je v bodě Xo
ryze konkávní.
5.10 VĚTY O STŘEDNÍ HODNOTĚ
V DIFERENCIÁLNÍM POČTU
Rollova věta
Jestliže funkce' y = f(x) je spojitá na uzavřeném intervalu (a, b), má
v každém bodě otevřeného intervalu (a, b) vlastní nebo nevlastní první derivaci
a platí f(a) = f(b) (obr. 325), pak existuje aspoň jeden takový bod E (a, b),
že platí
f'( ) = o.
-
:f(o): 'f(b)
I
o a f b x
Obr. 325. Význam Rollovy věty
y (b)
O a b X
Obr. 326. Význam Lagrangeovy věty
Geometrický význam Rollovy věty: Za uvedených předpokladů existuje
aspoň jeden takový bod [ , f( )] grafu funkce y = f(x), definované na inter-
valu (a,b), mezi body [a,f(a)] a [b,f(b)], že tečna grafu v bodě [ ,f( )]
je rovnoběžná s osou x.
Lagrangeova věta [první věta o přírůstku funkce]
Jestliže funkce y = f(x) je spojitá na uzavřeném intervalu (a, b) a má
v každém bodě otevřeného intervalu (a, b) vlastní nebo nevlastní první deri-
vaci, pak existuje aspoň jeden takový bod E (a, b), že platí
f(b) - f(a) = f'( )
b-a
519
(obr. 326). Jiný zápis:
j(x + h) - f(x) = f'(x + 9h)
h
pro -9 E (0,1).
Geometrický význam Lagrangeovy věty: Za uvedených předpokladů existuje
aspoň jeden takový bod [ ,f( )] grafu funkce y = f(x), definované na inter-
valu (a,b), mezi body [a,j'(a)] a [b,f(b)J, že tečna grafu v bodě [ ,f( )]
je rovnoběžná se spojnicí bodů [a, f(a)], [b, f(b)]. '
Cauchyova věta
[druhá [zobecněná] věta o přírůstku funkce]
Jestliže funkce y = f(x) J a y = g(x) jsou na uzavřeném intervalu (a, b)
spojité a mají v každém bodě otevřeného intervalu (a, b) vlastní první derivace,
přičemž' pro všechna čísla x E (a, b) je g'(x) * O, pak existuje 3:spoň jeden
takový bod E (a, b), že pla!í
f(b) - f(a) f'( )
g(b) - g(a) g'( r
Pro g(x) = x dostáváme Lagrangeovu větu.
5.11., NEURČITÉ VÝRAZY
5.11.1. Limita typu O/O nebo 00/00
Říkáme, že podíl f(x)/g(x) je pro x a limitou [neurčitým výrazem]
typ 0/0, resp. 00 100, jestliže platí
limf(x) = lim g(x) = O,
x a x a
resp.
limf(x) = + 00,
x a
lim g(x) = + 00
x a
(místo x a lze uvažovat x a+, x a-, x +00, x -(0).
K určení lim [f(x)/g(x)] v těchto případech často používáme I'Hospitalova
x a
pravidla:
Jestliže bud' lim f(x) = lim g(x) = O, nebo lim Ig(x)1 = + 00 .(0 funkci f
x a x a x a
není třeba nic předpokládat) a existuje vlastní nebo nevlastní limita
520
lim [f'(x)lg'(x)J, pak existuje lim [f(x)lg(x)J a platí
x-a x-a'
lim f(x) = lim f'(x) .
x-a g(x) x-a g'(x)
Jestliže lim [f'(x)/g'(x)J je opět limita typu 0/0 nebo
ľHospitalova pravidla znovu.
Příklad:
( ) _ sin (2x) - 2 sin x . O
qJ x - 2 ' lim q>(x) je typu -.
2e X - x - 2x - 2 x-o O
2 cos (2x) - 2cosx
lim qJ(x) = lim
x-o x-o 2e X - 2x - 2
00 100, použijeme
. -4sin (2x) + 2 sin x
=hm =
x-o 2e X - 2
-8 cos (2x) + 2 cos x
= 'lim = -3.
x-o 2e x
5.11.2. Limita typu O . 00
Jestliže limita funkce q>(x) = f(x)/g(x) je pro x = a typu O. 00, platí
lim cp(x) = lim f(x) nebo lim g(x) ,
x-a x-a 1 x-a 1
- -
g(x) f(x)
čímž dostaneme limitu typu 0/0 nebo 00 100.
Příklad:
qJ(x) = (1 - sin x) tg x;
lim qJ(x) je typu O. 00 .
x-ft/2 +
1 - sin x
lim . = lim
x-ft/2 + 1 x-ft/2 +
- cos x
1 1
- lim
x-ft/2 +
tg x
cos 3 X
c os 2 x
sin 2 x
tg 2 X cos 2 X
= lim (cos x sin 2 x) = O.
x-ft/2 +
521
5.11.3. Limita typu 00 - 00
Jestliže limita funkce qJ(x) = f(x) - g(x) je pro x a typu 00 - 00,
platí
I 1
---
lim [J(x) - g(x)] " = lim g(x) J(x)
x-'a x-.a I I
--
J(x) g(x)
čímž dostaneme limitu typu 0/0.
Příklad:
I I
qJ(x) = - -;
x-I ln x
lim qJ(x) je typu 00 - 00.
x-.l
1
--1
1 . ln x - (x - I) x
1m = lim
x-.l (x - 1) ln x x-.l I
I + ln x - -
x
I-x -1
= lim = lim
x -. 1 X + x ln x - I x -. 1 I + I + ln x
1
- --.
2
5.11.4. Limity typů 0°, 00°, 1 00
Jestliže limita funkce qJ(x) = f(xr(X) je pro x a typu 0° nebo 00°
nebo 1 00 , platí
lim f (x )9(X) = lim e 9 (x) ln (f(x)) ,
x-'a x-.a
čímž exponent převedeme na limitu typu O. 00.
Příklad:
qJ(x) = (sin x)tgx;
lim qJ(x) je typu 1 00 .
x-.7t/2 +
lim e tg x ln (sin x)
x-7t/2 +
má tvar e 00 . ° .
522
Pro exponent platí
lim ln (sin x) = lim
X-7t/2 + 1 X-7t/2 +
1
---:-- cos x
sIn x
1 1
tg X tg 2 X cos 2 X
= lim (-cotg x tg 2 x cos 2 x) = lim (-sin x cos X ) = O
X-7t/2 + X-7tí2 + .
Je tedy
lim (sin x)tgx = e O = 1.
x-7t/2 +
Poznámka:
Někdy vede rozvoj podle rostoucích mocnin proměnné x (rozvoj v řadu)
rychleji k výsledku.
Příklad:
( ) 1 - cos qJ ( ) I
qJ x = . lim qJ x je typu O O .
sin 2 qJ' x-o
x 2 x 4 ( 1 x 2 )
1 - cos x = 2! - 4! + ... = X 2 2! - 4! + ... ,
sin 2 x = (;, - ; + ...y = x 2 G! - ; + ...y;
1 x 2
1 - cos x V - 4f + ... 1
lim 2 = lim ( . 2 . )2 -
x-o sin x x-o 1 x 2
1!-3!+."
/
523
6. DIFERENCIÁLNÍ GEOMETRIE
V diferenciální geometrii se studují křivky a plochy metodami
diferenciálního počtu.
6.1. ROVINNÉ KŘIVKY
Křivkou definovanou parametricky v dvojrozměrném euklidovském
prostoru E 2 nazýváme množinu právě těch bodů, jejichž kartézské souřadnice
x, y jsou dány rovnicemi
x = qJ(t),
y = t/J( t) ,
kde qJ, t/J jsou reálné funkce reálné proměnné t, definované na nějakém inter-
valu J, k eré mají spojité derivace podle t aspoň prvního řádu a pro něž vztahy
<iJ(t) = O,
.jJ(t) = O
oba zároveň platí jen v izolovaných bodech intervalu J.
Bod [qJ(t o ), t/J(t o )] křivky se nazývá regulární, jestliže aspoň jedna z derivací
<iJ(t o ), .jJ(t o ) je různá od nuly a bodu [qJ(t o ), t/J(t o )] odpovídá právě jedna hod-
nota parametru t. Ostatní body kři .ky se nazývají singulární.
Přísluší-li několika hodnotám parametru t jediný bod, pak takový bod
se nazývá několikanásobný.
Rovnice x = qJ(t), y = t/J(t) nazýváme parametrickými rovnicemi křivky.
Křivkou dejinovanou implicitně v dvojrozměrném euklidovském prostoru E 2
nazýváme množinu právě těch bodů, jejichž kartézské souřadnice x, y jsou
dány rovnicí
F(x, y) = O,
kde F je reálná funkce dvou reálných proměnných na množině Q2 c E 2 ,
která má spojité první parciální derivace a pro niž vztahy
F(xo, Yo) = O,
cF
(xo, Yo) = O,
(,X
cF
(xo, Yo) = O
(."y
všechny tři zároveň platí jen v izolovaných bodech oboru Q2'
524
Bod [xo, Yo] křivky se nazývá regulární, jestliže spoň jedna z parciálních
d . , cF ( ) oF ( ) . o , d I
erlvaCl Xo, yo , Xo, Yo Je ruzna o nu y.
ex vy
Je-Ji křivka definována implicitně, pak ji lze v dostatečně malém okolí
každého jejího bodu vyjádřit parametricky, a obráceně, je-li definována
parametricky, pak ji lze na okolí každého jejího bodu vyjádřit implicitně.
Graf spojitě diferencovatelné funkce y = f(x) (x E (a, b » je křivka defino-
vaná parametrickými rovnicemi x = t, Y = f(t) (t E (a, b». Graf diferenco-
vatelné funkce y = f(x), (x E (a, b » je křivka definovaná implicitně rovnicí
F(x, y) = y - f(x) = o.
Vektorový zápis rovinné křivky:
r(t) = qJ(t); + tjJ(t)j.
Vyjádření rovinné křivky v polárních souřadnicích:
Q = f(qJ) nebo F(Q, qJ) = O.
.
6.1.1. Základní prvky rovinných křivek
Diferenciál [element] oblouku křivky:
ds = J(<iJ2 + .jJ2) dt
pro křivku danou parametricky;
ds = J(l + y'2) dx
pro křivku y = f(x);
ds = J[e 2 + G rJd
pro křivku Q = f(qJ).
Délka oblouku křivky dané parametricky s krajními body P(t 1 ) a p(t 2 )
je dána vzorcem
f2J{[q,(t)J2 + [q,(t)]2} dto
Délka oblouku křivky dané rovnicí y = f(x) s krajními body [xl,f(x 1 )]
a [x 2 , j'(X2)] je dána vzorcem
f,2J{1 + [f'(x)]2} dx.
525
Délka oblouku křivky dané rovnicí (l = f( qJ) s krajními body [(lI' cp 1]
a [(l2, qJ2] je dána vzorcem
f: 2 J[Q2 + ( : rJd .
Oblouk jako parametr
Jestliže x = qJ(t), y = t/J(t) jsou parametrické rovnice křivky k a t(-r) je
funkce definovaná na intervalu J', která má na intervalu ,J' spojitou derivaci
dtld-r * O, pak také x = qJ(t(-r)) a y = t/J(t(-r)) jsou parametrické rovnice
křivky k. . .
Říkáme, že v parametrických rovnicích x = qJ(s), y = ,,(s) křivky k je para-
metrem oblouk, jestliže délka křivky k s krajními body p(s 1) a P(S2) se rovná
číslu S2 - Sl' Jsou-li x = qJ(t), y = t/J(t) parametrické rovnice křivky k, pak
x = qJ(t(s)), y = t/J(t(s)), kde f(s) je inverzní funkce k funkci
s(t) = 1: J{[q,(L)Y + [tfr(L)]2} dL,
jsou parametrické rovnice téže křivky k, kde parametrem je oblouk.
Př(klad:
Jestliže x = r cos t, y = r sin t (t E R) jsou parametrické rovnice kružnice
s poloměrem r, pak platí
s(t) = l J [( - r sin tY + (r cos tY] dL = rt,
S
t( s) = -
r
a
s
x=rcos-,
r
. S
Y = r sIn -
r
(S E R)
jsou parametrické rovnice téže kružnice, kde parametrem je oblouk.
Tečný a normálový vektor
Tečným, resp. normálovým vektorem v regulárním bodě p[ xo, Yo] křivky dané
parametrickými rovnicemi x = (t), Y = "'(t) [xo = (to)' Yo = "'(to), q,o =
= ( : ) _ ' tfro = ( d dt/J ) _ ] nazýváme vektor
t t - to t t - to
to = ( o' tfro),
526
resp.
.
no = (.jJo, -<Po)'
Je-li parametr t = s obloukem, je Itol = Inol = 1.
Tečným, resp. normálovým vektorem v regulárním bodě p[xo, yo] křivky
dané implicitně rovnicí F(x, y) = O [ F = F (xo, Yo), F = F (xo, Yo) ] na-
zýváme vektor ox y
to = ( - F y O , F ),
resp.
no = (F , F y O ).
Tečným, resp. normálovým vektorem v regulárním bodě p[ xo, yo] křivky
y = i(x) [ y = ( di ) ] nazýváme vektor
dx x = xo
to = (1, y ),
resp.
no = (y , - 1 ) .
x
o
Obr. 327. Tečna a normála křivky
Obr. 328. Úhel tečny a průvodiče
Pro úhel velikosti (1, který svírá tečný vektor s první kladnou poloosou platí
. dy dx dy
sIn (X = -, cos (X = -, tg (X = - (obr. 327).
ds ds dx
Pro úhel B, který svírá tečný vektor s kladně orientovaným průvodičem,
platí
dqJ
sin B = g -,
ds
dg
cos B = ds '
g
tg B = -
dg
dqJ
(obr. 328).
527
Tečna a normála
Přímka obsahující. tečný vektor se nazývá tečna.
Rovnice tečny v regulárním bodě po[ xo, Yo] křivky dané parametrickými
o v ( n e ) mi X ] : (j)(t),. y = t/I(t) [xo = (j)(t o ), yo = t/I(t o ), o = ( : }=to' tÍ10 =
dt t = to
(X - xo) tfro - (y - Yo) <Po = O.
Rovnice tečny v regulárním bodě Po[xo, Yo] křivky dané implicitně rovnicí
( ' ) [ Oe F ( ) o a F ( )] .
F x, Y = o Fx = ox xo, yo, Fy = oy xo, Yo ·
(X - xo)F + (y - yo)F = o.
Rovnice tečny v regulárním bodě po[ xo, Yo] křivky y = f(x)
[ y = ( d f ) ]
dx X=Xo
(y - Yo) - y (X - xo) = o.
Takto zavedená tečna je limitní polohou sečny, jestliže její dva průsečíky
s křivkou splynou v jediný bod. Regulární bod P nazýváme dotykovým bodem
tečn y ke křivce.
Přímka obsahující normálový vektor se nazývá normála.
Rovnice normály v regulárním bodě po[ xo, Yo] křivky dané parametrickými
ro v ( n ; ) mi X ] : qJ(t), y = t/I(t) [xo = (j)(to o = t/I(t o ), 4Jo = ( : }=to' tÍ10 =
dt t = to
(X - xo) <Po + (y - Yo) tfro = O.
Rovnice normály v regulárním bodě pol xo, Yo] křivky dané implicitně
., ( ) [ Oe F ( ) o a F ( )]
rovmCl F x, y = o Fx = ox xo, Yo, Fy = oy xo, Yo :
(X - xo)F '- (y - yo)F2 = O.
Rovnice normály v regulárním bodě Po [xo, Yo] křivky y = f(x)
[ y = ( d f ) . ] .
ex X=Xo .
1
(X - xo) + Yo (Y - Yo) = o ·
Tečna a normála jsou přímky navzájem kolmé.
528
Úseky tečny a normály
Pro křivku y = J(x) (obr. 329a) a dotykový bod P[ x, y] platí:
Délka úseku tečny (tzv. tangenta), tj. vzdálenost dotykového bodu od prů-
sečíku tečny s osou x, se rovná
t = J( 1 + y'2) .
y'
Délka úseku normály (tzv. normála), tj. vzdálenost dotykového bodu od prů-
sečíku normály s osou x, se rovná
n = ly" '(1 + y'2 )1.
Subtangenta, tj. délka průmětu úseku tečny do osy x, se rovná
y
St = - .
y'
Subnormála, tj. délka průmětu úseku normály do osy x, se rovná
sn = Iyy'l.
x
.
O
a)
Obr. 329. Úsek tcčny a úsek normály
kři vk y
Pro křivku (l = f( qJ) (obr. 329b) a dotykový bod P[Q, qJ] platí:
Délka úseku polární tečny, tj. vzda enost dotykového bodu od průsečíku
tečny s přímkou vedenou pólem kolmo k průvodiči dotykového bodu, se rovná
t = d: J[Q2 + ( :: YJ ·
dqJ
529
Délk,a úseku polární l1ornuí/y, tj. vzdálenost dotykového bodu od průsečíku
normály s přímkou vedenou pólem kolmo k průvodiči dotykového bodu,
se rovná
n = J[ e 2 + G rJ .
Polární subtangenta, tj. délka průmětu polární tečny do přímky vedené
pólem kolmo k průvodiči dotykového bodu, se rovná
g2
St = dg .
dlp..
Polární subnormála, tj. délka průmětu polární normály do přímky vedené
pólem kolmo k průvodiči dotykového bodu,"se rovná
.'
dg
Sn = - .
dqJ
Styk dvou křivek
Jestliže křivka k, resp. k' je dána parametrickými rovnicemi
x = qJl(S),
y = t/Jl(S),
resp.
x = qJ2(S), Y = t/J2(S),
kde parametrem je oblouk S, pak říkáme, že rovinné křivky k, k' mají ve společ-
ném bodě S = O styk [dotyk] nejméně q-tého řádu [styk [dotyk] nejméně
(q + l)-bodový], právě když
qJl(O) = qJ2(O), t/Jl(O) = t/J2(O),
(d l ).=0 = (d 2 ).=0' (d l ).=0 = (d 2 ).=0'
...............................................
(d l ).=O = (d 2 ).=0.
( d qqJ 1 ) ( dqqJ2 )
ds q s = o = ds q s = o '
Říkáme, že rovinné křivky y = J(x) a y = g(x) mají v bodě po[ xo, Yo] styk
[dotyk] nejméně q-tého řádu [styk [dotyk] nejméně (q + 1 )-bodový], právě
když
Yo = J(xo) = g(xo) ,
J'(xo) = g'(xo), ..., J(q)(xo) = g(q)(xo) .
530
Mají-Ii dvě křivky k I a k 2 styk nejméně q-tého řádu, ale nemají-Ii již styk
(q + 1 )-ního řádu, říkáme, že mají styk právě q-tého řádu.
o s k u I ač ní k r u žni c e, po lom ě r k ř i vos t i, k ř i vos t, st ř e d k ř i vos t i
Oskulační kružnicí [kružnicí křivosti] křivky v jejím bodě nazýváme kružnici,
která má v tomto bodě s křivkou styk nejméně druhého řádu. Její poloměr R,
resp. střed Sk nazýváme poloměrem, resp. středem (první) křivosti křivky.
Střed křivosti Sk [ ,.11] ležÍ" na normále v dotykovém bodě křivky.
Převrácené číslo k poloměru 1"řivosti R se nazývá (první) křivost [flexe]
x křivky: x = 1/ R.
Poloměr křivosti , křivost x a souřadnice středu křivosti Sk[ ' 11] vypoč-
teme podle těchto vzorcú: '
Pro křivku y = ,j'(x) v jejím bodě p[x, y] pro y" =F O je
(1 + y')3/2
R=
II
Y
"
y
x=
(1 + y'2)3/2 '
1 + y' 2
11=y+ II '
Y
;; = x _ y'( 1 + y '
':> ",
y
Pro křivku F(x, y) = O v jejím bodě p[x, y] při tečně různoběžné s osou y je
1
R = Iml J(F; + F;), x = I I J( 2 2)'
m Fx + Fy
= x - mFx, 11 = Y - mF,v,
kde
F; + F}
m= 2 2 '
FxxF}. - 2FxyFxFy + FyyFx
Pro křivku x = qJ(t), y = t/J(t) v jejím bodě P(t) je
liJ, .jJ
ip, tli
x = (cp2 + tjJ2)3/2'
(liJ2 + .jJ2)3/2
R=
liJ, tj!
ip, tli
.jJ(liJ2 + .jJ2)
=x- .. ,
qJ, t/J
ip, tli
liJ ( liJ 2 + .jJ2)
11 = Y + .. .i, .
qJ, Y'
ip, tli
531
Pro křivku g = f(cp) v jejím bodě P[(), cp] je
( d Q ) 2 d2Q
Q2 + 2 - - g-
dqJ dqJ2
[Q2 + ( :: rr!2
R=
[Q2 + (:: YJ/2
x=
( dg ) 2 d2e'
Q2 + 2 _ - e -
\ dep dep2
[Q2 + (*YJ [Q cos + *sin ]
= Q cos - 2 2 ( dl! ) 2 d2Q
Q + - - Q-
.. dqJ dqJ2
. [Q2 + (*rJ [Q sin - *cos- ]
17=Qsm - 2 2 ( dl! ) 2 d2Q
Q + - -Q-
dqJ dep2
..
Pro R, popř. x dále platí
1 L\s ds
R = - = lim - = -,
X t-O 1' d1'
kde L\1' je odchylka tečny v daném bodě P a tečny v sousedním bodě P 1 (obr. 330)
a s je délka oblouku mezi body P a P 1 . Úhel 1' se nazývá kontingenční úhel.
Vrcholem rovinné křivky nazýváme bod, v němž má tato křivka (lokálně)
extrémní hodnotu poloměru křivosti. Rozeznáváme hlavní a vedlejší vrcholy.
x
Obr. 330. Kontingenční úhel
Konvexnost a konkávnost křivky
Křivku nazýváme konvexní v bodě P, jestliže pro křivost x křivky v tomto
bodě platí x < O. Křivku nazýváme konkávní v bodě P, jestliže pro křivost x
křivky v tomto bodě platí x > O.
532
Inflexní body
lnjlexním bodem křivky k nazýváme takový její bod, v němž bud' konvexnost
křivky se změní v konkávnost, nebo konkávnost se změní v konvexnost.
Nutnou podmínkou pro inf1exní body u křivky x = qJ(t), y = tjJ(t) je
liJ, tjJ = O,
ip, .ji
u křivky g = f( qJ) je
2 ( dg ) 02 d2g
g +2 - -g-=O
dqJ dqJ2
a u křivky F(x, y) je
Fxx, Fxy, Fx = O.
Fyx, Fyy, Fy
Fx, Fy, O
Singulární body
Singulárním bodem křivky F(x, y) = O nazýváme bod, jehož souřadnice
vyhovují zároveň rovnicím
F(x, y) = O, Fx = O, Fy = O.
Dvojnásobným bodem křivky F(x, y) = O nazýváme její singulární bod,
pro který aspoň jedna z parciálních derivací druhého řádu je různá od nuly.
Dvojnásobný bod se nazývá:
- uzlový bod [uzel], jestliže F;y > FxxFyy;
- hrot [bod vratu], jestliže F;y = FxxFyy;
- izolovaný [osamocený] bod, jestliže F;y < FxxF}'}. .
V každém uzlovém bodě má křivka právě dvě reálné různé tečny.
V každém hrotu má křivka jedinou společnou tečnu.
V izolovaných bodech neexistují reálné tečny.
Příklad 1:
Vyšetřeme singulární body křivky F(x, y) = x 3 + y3 - 3axy = O.
Fx = 3x 2 - 3ay,
Fy = 3y2 - 3ax,
Fxy = -3a, Fxx = 6x, Fyy = 6y;
533
F(x, y) = o 1\ Fx = o 1\ Fy = O => obor pravdivosti P =' {[O, OJ} =>
=> křivka má jedi!1Ý singulární bod U = [O, O];
F;y = 9a 2 1\ Fxx = O 1\ Fyy = O => F;y > FxxFyy =>
=> bod U = to, O] je uzlovým bodem.
Viz Descartesův list na str. 551.
Příklad 2:
Vyšetřeme singulární body křivky F(x, y) = x 3 - y2(a - x) = O.
Fx = 3x 2 y2,
Fy = 2xy - 2ay,
Fxy = 2y, Fxx = 6x, Fyy = 2x - 2a;
F(x, y) = O 1\ Fx = O 1\ Fy = O => obor pravdivosti
P = {[O, O]} => křivka má jediný singulární bod H = [O, O];
F;}. = O 1\ Fxx = O /\ Fyy = - 2a => F;y = FxxFyy =>
=> bod H = [O, O] je hrotem.
Viz kisoidu na str. 551.
y
3
2 -
1 -
.
x
Obr. 331. Graf funkce z příkladu 3
Příklad 3:
Vyšetřeme singulární body křivky F(x, y) = y2 - x 3 + 7x 2 - 16x + 12 = O.
Fx = -3X2 + 14x - 16,
Fy = 2y,
Fxy = O, Fxx = -6x + 14, Fyy = 2;
F(x, y) = O 1\ Fx.= O 1\ Fy = O => obor pravdivosti
P = {[2, O]} => křivka má jediný singul rní .bod 1 = [2, O];
F;y = O 1\ Fxx = 2 1\ Fyy = 2 => F;y < FxxF}.y =>
=> bod 1 = [2, O] je izolovaným bodem (obr. 331).
534
Asymptoty rovinných ,křivek
Asymptotou rovinné křivky nazýváme takovou přímku, že vzdálenost d
bodu P na křivce od této př mky konverguje k -nule, jestliže aspoň jedna sou-
řadnice bodu P roste nade všechny meze, tj.
lim d = O.
p- :t 00
U křivek y = f(x) rozeznáváme vertikální [nesměrnicové] asymptoty
o rovnici x = Xo (tj. asymptoty rovnoběžné s osou y) a směrnicové asymptoty
o rovnici y = kx + q.
Křivka y = f(x) má vertikální asymptotu o rovnici x = xo, právě když
platí
lim f(xo) = + 00, popř. lim f(x) = + 00, popř. lim f(x) = + 00 .
X-%o %-%0+ X-Xo-
Křivka y = f(x) má směrnicovou asymptotu o rovnici y = kx + q,
existují-li vlastní limity
k = lim f(x) ,
x-j:oo X
q = lim (f(x) - kx].
%- :t 00
Směr asymptoty křivky (l = f(cp) v polárních souřadnicích je určen úhlem
CPo, jestliže
lim (l = + 00 .
li' - (/10
Pro vzdálenost p pólu od asymptoty platí
p = lim [e sin (CPo - cp)].
li' - (/10
Obalová křivka [obálka]
Říkáme, že rovnicí F(x, y, p) = O je určena jednoparametrická soustava
rovinných křivek, jestliže každému parametru p z určitého intervalu přísluší
určitá rovinná křivka o rovnici F(x, y, p) = O.
Křivka, jejíž rovnici G(x, y) = O dostaneme vyloučením parametru p
z rovnIC
F(x, y, p) = O,
oF(x, y, p)
op = O,
se nazývá diskriminantní křivka jednoparametrické soustavy křivek o rovnici
535
F(x, y, p) = O. Oiskriminantní křivku nebo její část nazyvame obalovoll
křivkou [obá'?kou] jednoparametrické soustavy křivek, jestliže se v každém
svém bodě dotýká někteté křivky zjednoparametrické soustavy křivek a každá
křivka této soustavy se dotýká diskriminantní křivky.
Tečna v každém bodě obálky je zároveň tečnou některé z křivek jedno-
parametrické soustavy křivek.
Evoluta
Evolutou křivky nazýváme množinu všech jejích středů křivosti.
Rovnici evoluty dostaneme vyloučením x a y z rovnice křivky a z rovnic
pro souřadnice , 11 středu křivosti, přičemž , 11 pak představují souřadnice
běžného bodu evoluty.
Tečny evoluty jsou zároveň normálami dané křivky.
Rozdíl dvou poloměrů křivosti se rovná délce oblouku mezi příslušnými
středy křivosti. (Rovnice evoluty pro parabolu, elipsu a hyperbolu viz na
str. 425, 435 a 447.)
Traj ek torie
Trajektorií nějaké soustavy křivek nazýváme křivku, která protíná všechny
křivky této soustavy podle nějakého zákona.
1 zogonální, resp. ortogonální trajektorie soustavy křivek protíná všechny
křivky této soustavy pod týmž úhlem, resp. pod pravým úhlem.
Evolventa
Při kotálení tečny evoluty po evolutě opisuje každý bod tečny křivku rovno-
běžnou [ekvidistantní] s původní křivkou (vzdálenost mezi dvěma evolventami
měřená na společné normále je totiž konstantní). Prvky této soustavy rovno-
běžných křivek, k nimž také patří původní křivka, se nazývají evolventy dané
křivky.
Evolventa křivky k je křivka, jejíž evolutou je křivka k.
Evolventa křivky k kolmo protíná soustavu tečen křivky k, tj. evolventa
křivky k je ortogonální trajektorií tečen křivky k.
Každá normála evolventy je tečnou její evol ty s dotykovým bodem
ve středu křivosti evolventy.
Poměr poloměrů křivosti evoluty a evolventy se rovná poměru příslušných
eleme'1tů oblouků.
536
Evolventa kružnice
Při valení tečny po dané kružnici (obr. 332) opIsuJe každý bod tečny
evolventu kružnice, danou rovnicemi
x = a( cos t + t sin t),
Y = a(sin t - tcos t),
kde a je poloměr an kružnice,
t - velikost úhlu odvalení.
p [x, y 1
x
Obr. 332. Evolventa kružnice
Rovnice evolventy kružnice v polárních souřadnicích:
= J( : - 1) - arctgJ( : ; - 1)
(valení se začíná v bodě A).
6.1.2. Některé důležité rovinné křivky
6.1.2.1. Semikubická parabola [Neilova parabola]
y = ax2/
(x E R, a * O)
(obr. 333).
6.1.2.2. Cyklické křivky [trochoidy]
Jestliže se kružnice k 1 (tzv. hybná kružnice [hybná poloida]) kotálí
po kružnici k 2 (zvané nehybná kružnice [nehybná poloida]) ve vnější nebo
vnitřní oblasti kružnice k 2 , pak body hybné kružnice k 1 nebo body s ní pevně
spojené vytvářejí tzv. cyklické křivky neboli trochoidy.
Prostá cykloida
Bod kružnice, která se beze skluzu kotálí po přímce, opIsuJe prostou
[obecnou, obyčejnou] cykloidu (obr. 334).
537
Rovnice prosté cykloidy (t E R):
= a( t - sin t),
Y = a( 1 - cos t),
kde a je poloměr kružnice,
t - velikost úhlu odvalení.
Obr. 333. Semikubická parabola
[Neilova parabola] y3 = 2X2
Obr. 334. Prostá cykloida
Explicitní vyjádření první, resp. druhé poloviny prvního oblouku prosté
cykloidy:
.
a-y
x = a arccos - .J[y(2a - y)]
a
(y E (O, 2a»),
resp.
( a-y )
x = a 21t - arccos a + J[y(2a - y)]
Délka oblouku OP o:
8 0 = 8asin 2 : = 4a(1 - cos )
Délka větve: s = 8a.
Obsah plochy ohraničené jednou větví prosté cykloidy a osou x:
S = 3na 2 .
(y E (O, 2a»).
(t E (O, 2n»).
Primitivní perioda: 2na.
Evolutou cykloidy je shodná cykloida posunutá o na ve směru osy x sou-
hlasně s její orientací a o 2a ve směru osy y nesouhlasně s její orientací.
538
Zkrácená cykloida
Zkrácená cykloida vznikne, jestliže tvořící bod pevně spojený s kotálející se
(hybnou> kružnicí leží ve v nit ř n í oblasti této kružnice ve vzdálenosti d
(d < a) od středu kružnice o poloměru a (obr. 335).
Parametrické rovnice zkrácené cykloidy (t E R):
x = at - d sin t,
Y = a - d cos t.
y
.
Obr. 335. Zkrácená cykloida
Obr. 336. Prodloužená cykloida
Prodloužená cykloida
I
Prodloužená cykloida vznikne, jestliže tvořící bod pevně spojený s kotálející
se (hybnou> kružnicí leží ve vně j š í oblasti této kružnice ve vzdálenosti d
(d > a) od středu kružnice o poloměru a (obr. 336).
Parametrické rovnice prodloužené cykloidy (t E R):
x = at - d sin t,
Y = a - d cos t.
x Obr. 337. Prostá epicykloida
Prostá epicykloida
Bod kružnice, která se beze skluzu kotálí po nehybné kružnici v její vnější
oblasti, opisuje prostou [obecnou, obyčejnou] epicykloidu (óbr.337).
539
Parametrické rovnice prosté epicykloidy (t E R):
x = (a + b)COS( t) - b cos ( a : b t).
y = (a + b) sin ( t) - b sin ( a : b t).
popř. (X E R)
( a + b )
x = (a + b) cos X - b cos b X,
y = (a + b) sin X - b sin ( a : b X).
kde a je poloměr nehybné kružnice,
b - poloměr hybné kružnice,
t - velikost úhlu odvalení,
X - velikost úhlu otočenÍ.
Je-li poměr alb = m celým číslem, pak prostá epicykloida je uzavřenou
křivkou s m větvemi, které vzniknou při jednom oběhu hybné kružnice kolem
nehybné kružnice.
Je-li poměr alb = plq = m racionálním číslem v základním tvaru plq,
pak prostá epicykloida je 'uzavřenou křivkou s p větvemi, které vzniknou
při q obězích hybné kružnice kolem nehybné kružnice.
Je-li poměr alb = m iracionálním číslem, pak prostá epicykloida není
uzavřenou křivkou a obsahuje nekonečně mnoho větví.
Délka oblouku větve:
-
8(a + b) . 2 ax
So = sIn -
m 4b
(XE\O, 2:n )).
Délka větve:
8(a + b)
S= .
m
Délka prosté epicykloidy pro mEZ:
1 = 8( a + b).
Obsah plochy ohraničené jednou větví prosté epicykloidy a příslušným
obloukem nehybné kružnice:
S = nb 2 (3a + 2b) .
a
540
Zkrácená a prodloužená epicykloida [epitrochoidy]
Zkrácená, resp. prodloužená epicykloida vznikne, jestliže tvořící bod pevně
spojený s hybnou kružnicí (kotálející se po nehybné kružnici o poloměru a
v její vnější oblasti) leží ve vnitřní, resp. vnější oblasti této kružnice ve vzdá-
lenosti d < b, resp. d > b od středu hybné kru2nice o poloměru b (v obr. 338
je k 1 , resp. k 2 zkrácená, resp. prodloužená epicykh)ida). .
Parametrické rovnice zkrácené, resp. prodlouženl epicykloidy (t E R):
,x = (a + b) cos ( t) - d cos ( a : b t).
y = (a + b) sin ( t) - d sin ( a : b t).
resp. (X E R)
x = (a + b)cosX - dCO ( a: b x).
y = (a + b) sin X - d sin ( a : b X).
Z vláš tní případ:
Prostá epicyklo.ida se pro a = b, tj. pro m = 1, nazývá kardioida nebo
sr'lcovka (obr. 339).
Yt
x
Obr. 338. Prodloužená a zkrácená
epicykloida
Obr. 339. Kardioida
"
Parametrické rovnice kardioidy (t E R):
x = a[2 cos t - cos (2t)],
Y = a[2 sin t - sin (2t)],
541
popř. V ortonormální souřadnicové soustavě:
(x 2 + y2 _ (12)2 = 4a 2 [(x _ (1)2 + y2],'
přičemž počátek je ve středu nehybné kružnice a osou x je prodloužení úsečky
spojující počátek s hrotem, popř. v polární- souřadnicové soustavě:
(l = 2a(1 - cos qJ)
(qJ E R),
přičcnlŽ pól leží na nehybné kružnici a polární osou je prodloužení úsečky
spojující pól a střed nehybné kružnice.
ProstÚ hypocykloida
Bod kružnice, která se beze skluzu kotálí po nehybné kružnici v její vnitřní
oblasti, opisuje prostou [obecnou, obyčejnou] hypocykloidu (obr. 340).
(
\
\
"
"
-.....
Obr. 340. Prostá hypocykloida
Parametrické rovnice prosté hypocykloidy (t E R):
x = (a - b) cos ( t) + b cos ( a : b t),
y = (a - b)sin ( t) - bsin ( a: b t),
popř. (X E R)
( a - b )
x=(a-b)cosX+bcos b X.,
. , ( a - b )
y = (a - b) sin X - b sin b X,
kde a je poloměr nehybné kružnice,
b - poloměr hybné kružnice,
t - velikost úhlu odvalení,
X - velikost úhlu otočenÍ.
542
Je-li poměr alb = m celým číslem (v obr. 340 je m = 3), pak prostá hypo-
cykloida je uzavřenou křivkou s m větvemi, které vzniknou při jednom oběhu
hybné kružnice kolem nehybné kružnice.
Je-li poměr alb = plq = m racionálním číslem v základním tvaru plq,
pak prostá hypocykloida je uzavřenou křivkou s p větvemi, které vzniknou
při q obězích hybné kružnice kolem nehybné kružnice. ..
Je-li poměr alb = m iracionálním číslem, pak prostá hypocykloida není
uzavřenou křivkou a obsahuje nekonečně mnoho větví.
Délka oblouku větve od bodu t = O do bodu t:
8( a - b) . 2 ax
So = sIn -
m 4b
(XE\O. 2:n )).
Délka větve:
8(a - b)
S= .
m
Délka prosté hypocykloidy pro mEZ:
I = 8( a - b).
Obsah plochy ohraničené jednou větví prosté hypocykloidy a příslušným
obloukem nehybné kružnice:
,.
1tb 2 (3a - 2b)
s= .
a
Zkrácená a prodloužená hypocykloida [hypotrochoidy]
Zkrácená, resp. prodloužená hypocykloida vznikne, jestliže tvořící bod
pe.vně spojený s hybnou kružnicí (kotálející se po nehybné kružnici o polo-
měru a v její vnitřní oblasti) leží ve v nit ř n í, resp. vně j š í oblasti této kružnice
ve vzdálenosti d < b, resp. d > b od středu hybné kružnice o poloměru b.
Parametrické rovnice zkrácené, resp. prodloužené hypocykloidy (t E R):
. ( b ) ( a - b )
x = (a - b) C08 t + d cos a t.
Y = (a - b)COS (: t) - dCOS( a: b t).
543
resp. (X E R)
( a - b )
x = (a -b)cosX + dcos b X,
( a - b )
y = (a - b) sin X - d sin b X.
Zvláštní případy:
Prostá hypocykloida se pro m = 4, tj. pro b.= a/4, nazývá asteroida nebo
hvězdice (obr. 341).
x
Obr. 341. Asteroida
Parametrické rovnice asterpidy (X E R):
x = b[3 cos X + cos (3X)],
y = b[3 sin X - sin (3x)],
popř. (t E R)
1 [ t 3t J
x = -a 3 cos - + cos - ,
4 4 4
1 [ . t . 3 t J
y = 4: a 3 sIn 4: - sIn 4
neboli
t
x = a cos 3 - = 4b cos 3 v
4 "'-,
Y = a sin 3 = 4b sin 3 v
4 ",-,
popř. v ortonormální souřadnicové soustavě:
x2/3 + y2/3 = a2/3
neboli
(x 2 + y2 _ a 2 )3 + 27a 2 x 2 y2 = O,
544
přičemž počátek je ve středu pevné kružnice a osou x je prodloužení úsečky
spojující počátek s hrotem.
Prostá hypocykloida přéchází pro m = 2, tj. pro b = a/2, v úsečku,
neboť degeneruje v průměr nehybné kružnice (toho se využívá k přeměně
otáčivého pohybu v pohyb sem a. tam, což má technické použití při řezání
ozubení). .
Zkrácená a prodloužená hypocykloida přechází pro m = 2, tj. pro d =*
* b = a/2, v elipsu s rovnicemi (tE R)
x = ( + d ) cos ,
'2 2
v = ( - d ) sin
.22
,
(toho se využívá k přeměně otáčivého pohybu v eliptický pohyb).
6.1.2.3. Cassiniovy křivky
Cassiniovou křivkou nazýváme množinu všech, takových bodů,
že součin jejich vzdáleností od dvou různých pevných bodů (tzv. ohnisek)
F 1 a F 2 je konstantní.
Rovnice Cassiniovy křivky v ortonormální souřadnicové soustavě:
(x 2 + y2)2 _ 2e 2 (x 2 _ y2) = a 4 _ e4,
popř. v polární souřadnicové soustavě:
(12 = e 2 cos (2qJ) + J[ e 4 cos 2 (2qJ) + a 4 - e 4 J,
kde e = IFIF21/2.
Pro a 2 > 2e 2 má Cassiniova křivka tvar podobný elipse (obr. 342).
Pro e 2 < a 2 < 2e 2 má Cassiniova křivka dva průhyby (obr. 343).
Pro a 2 = e 2 dostaneme Bernoulliovu lemniskátu (viz dále).
y
y
x }
e e
O
X Ia
a 2 > 2 e 2
0 2 < 2e 2
a 2 > e 21
Obr. 343. Cassiniova křivka
(e 2 < (12 < 2e 2 )
Obr. 342. Cassiniova křivka (a 2 2e 2 )
545
Pro a 2 < e 2 se křivka skládá ze dvou samostatných vejčitých částí, z nichž
každá obklópuje jedno ohnisko (obr. 344).
Bernoulliova lemniskáta
Berno.tlliova lemniskáta Je zvláštním případem Cassiniovy křivky pro
a 2 = e 2 (obr. 345).
y
t e
Ff
o
F. x 1°
2
Q2< e2
x Io
a 2 = e 2
Obr. 344. Cassiniova křivka (a 2 < e 2 )
Obr. 345. Bernoulliova
lemniskáta (a 2 = e 2 )
Rovnice Bernoulliovy lemniskáty v ortonormální souřadnicové soustavě:
(x 2 + y2)2 = 2a2(x2 _ y2),
popř. v polární souřadnicové soustavě:
(1 = a J[2 cos (2qJ)]
(qJ fi < -tn, tn) u < , in»),
popř. v parametrickém vyjádření (t E R):
1 + t 2
x = at(J2) 4 '
1 + t
1 - t 2
Y = at(J2) 4 .
1 + t
Poloměr křivosti:
R _ 2a 2 _ a ../(1 + t 4 )
- 3(1 - 31tl
pro t * O, popř. (l 9= o.
Obsah jedné smyčky:
S = a 2 .
546
6.1.2.4. Spirály
Logaritmická spirála
Logaritmickou spirálou nazýváme křivku (obr. 346), která protíná všechny
polopřímky vycházející z počátku pod konstantním úhlem velikosti rJ... Je tedy
izogonální trajektorií svazku přímek procházejících pólem O, který je asympto-
tickým bodem této trajektorie. Proto se používá v technické praxi (u rotujících
nožů, ozubených kol apod.) a v námořnictví v souvislosti s loxodromou,
která je nejvhodnější křivkou pro plavbu lodí a jejímž průmětem na stereo-
grafickou síť je právě logaritmická spirála.
,c; CPfl 'fJ
Obr. 346. Logaritmická spirála
o
Rovnice logaritmické spirály v polární souřadnicové soustavě:
(1 = a ek({J (qJ E R, a > O, k > O),
kde
cotg rJ.. = k.
Délka oblouku P 1 P2 :
s = - k 1Il !2 -l!11 J(l + k 2 ) = b -l!II .
cos rJ..
Délka oblouku OP 2 :
! l!2 J(l + k 2 ).
k
Obsah výseče pro tento mezní případ:
(12
s=-
4k
Poloměr křivosti:
R = g J(l + k 2 ).
547
Archimédova spirála
Archimédovou spirálou nazýváme křivku vytvořenou bodem, který se po
polopřímce od jejího počátečního bodu v pólu O pohybuje konstantní rych-
lostí, zatímco se polopřímka sama otáčí kolem pólu při konstantní úhlové
rychlosti (obr. 347).
P2
o
i<oW: - Spd F-
O .
Obr. 348. Hyperbolická spirála
,,>0
Obr. 347. Archimédova spirála
Rovnice Archimédovy spirály v polární souřadnicové soustavě:
(! = acp (cp > O, a > O).
Délka oblouku OP o :
a .
So = - [cp .J(cp2 + 1) + arcslnh cp] =
2
a
= - {qJ .J (cp2 + 1) + ln [cp + .J (cp2 + 1)]};
2
pro velká čísla cp:
acp2
S o -.
. 2
Obsah výseče P 1 0P2:
a 2 ( 3 3 )
S = 6 CP2 - CP. ·
Poloměr křivosti:
(a2 + (!2)3/2
R=
2a2 + (!2
a( cp2 + 1 )3/2
cp2 + 2
Hyperbólická spirála
Hyperbolickou spirálou nazýváme křivku, pro kterou je součin průvodiče
a argumentu (tj. součin polárních souřadnic) konstantní (obr. 348).
548
Rovnice hyperbolické spirály v polární souřadnicové soustavě:
a
{!=-
qJ
(qJ > O, a > O).
Asymptota: y = a.
Obsah výseče P 1 OP2:
S = a; ( 1 - J .
Poloměr křivosti:
R = ; ( J(l ; q12) Y = Q ( :: + 1 Y/ 2 .
6.1..2.5. letězovka
Každé homogenní dokonale ohebné hmotné vlákno, které je zavěšeno
ve dvou bodech, má v rovnovážné poloze tvar řetězovky (obr. 349).
Rovnice řetězovky:
a x
y = _(e x / a + e- x / a ) = acosh-.
2 a
x
y =-a coshi
yt I
IPCt, Y J r.( ,2
I ¥=t 2a +Q
: VrO,a]
a .
01 x
Obr. 349. Řetězovka
Vrcholem řetězovky je bod V[O, a].
Obecná řetězovka a parabola y = a + x 2 f(2a) mají ve vrcholu V[O, a]
styk třetího řádu.
Obsah plochy ohraničené řetězovkou a úsečkami na ose x a rovnoběžkách
.
x = O a x = x:
x e x / a - e -x/a
S = a 2 sinh - = a 2
a 2
549
Délka oblouku VP:
x ex/a - e -x/a
S = a sinh - = a
a 2
Poloměr křivosti:
y2 2
R = -- = a cosh -.
a a
6.1.2.6. Traktrix
Hmotný bod na konci neroztažitelného přímého vlákna konstantní
délky a opisuje křivku zvanou traktrix, jestliže se druhý krajní bod vlákna
pohybuje po přímce y = O a vlákno se zároveň beze skluzu otáčí (obr. 350).
Tangenta každého bodu této křivky, tj. úsek tečny mezi bodem dotyku a jejím
průsečíkem s osou x, má konstantní délku a.
y
[O,Q]
P(x,Y)
a
x
Obr. 350. Traktrix
Traktrix je evolventou řetězovky, tj. při kotálení tečny po řetězovce vytváří
vrchol řetězovky traktrix.
Parametrické rovnice traktrix [t E ( -1t, O) U (O, 1t)]:
x = a (ln tg + cos t).
y = a sin t,
(parametr t je velikost úhlu, který tečna svírá s osou x), popř. v ortonormální
souřadnicové soustavě:
a
x = arccosh - + J(a 2 _ y2) =
Y
= a ln a:t ,J(a 2 - l) + ,J(a2 _ y2),
Y
Iyl < a.
Asymptota traktrix: y = o. ,
Body Vt[O,a] a V 2 [0, -a] jsou body vratu [hroty].
550
Délka oblouku V1P větve:
a
s = a ln - .
y
Poloměr křivosti:
:o X
R = a cotg - .
Y
6.1.2.7. Kisoida
Kisoidou dvojice křivek m, n pro pól P nazýváme množinu právě těch
bodů Q, pro něž platí
IPQI = Ip LI -IPKI,
kde K, resp. L je průsečík libovolné polopřímky svazku o vrcholu P s křiv-
kou m, resp. n (obr. 351).
y
,
v[/a,fa]
p =P
( -OJ O] '-. -X
"
[o,-aJ l "
,; ,
,
+,'-.
(;)-
Obr. 351. Kisoida
Obr. 352. Descartesův list
Descartesův list
Descartesovým listem nazýváme kisoidu elipsy
x 2 - xy + y2 + a(x + y) = O, - a > O,
a přímky x + y + a = O pro pól P (obr. 352). ,
Rovnice Descartesova listu v ortonormální souřadnicové soustavě:
x 3 + y3 - 3axy = O,
551
popř. v polární souřadnicové soustavě:
3a sin qJ cos qJ
(l = 3 (qJ E (O, tn) u (in, n) u (in, n»
sin 3 qJ + cos qJ
neboli
3a sin (2ep)
(l = 2 sin 3 qJ + cos 3 qJ'
popř. v parametrickém vyjádření (t E R \ { -I}):
3at
x=
1 + t 3 '
3at 2
y = 1 + t 3 '
Asymptota Descarteso a listu: y = - X :- a.
Vrchol Descartesova listu: V = [!a, !a].
Obsah S smyčky Descartesova listu se rovná obsahu plochy ohraničené
Descartesovým listem a jeho asymptotou:
S = ía 2 .
"
Dioklova kisoida -
Dioklovou kisoidou nazýváme kisoidu kružnice
(x - r + y2 - ( r = O
a přímky x = a (a > O) pro pól p[O, O], tj. množinu právě těch bodů, jejichž
vzdálenosti d od pólu P se rovnají délkám úseček, jejichž krajní body dosta-
neme jako průsečíky polopřímek svazku o vrcholu P s kružnicí k (se středem
S[a/2, O] a průměrem a) a její tečnou x = a (obr. 353).
Ix=a
I
I
x
Obr. 353. Dioklova kisoida
552
Rovnice Dioklovy kisoidy v ortonormální souřadnicové soustavě:
y2(a - x) = x 3
neboli
x 3
y2 =
a-x
[x E (O, a)],
popř. v polární souřadnicové soustavě:
a Sil}2 qJ .
(l = = a sIn qJ tg qJ [qJ E (O, tn) u (!n, 2n> ],
cos qJ
popř. v parametrickém vyjádření (t E R):
at 2
x=
1 + t 2 '
at 3
y = 1 + t 2 .
Asymptota Dioklovy kisoidy: x = a.
Obsah plochy ohraničené Dioklovou kisoidou a její asymptotou:
S = !na 2 .
6.1.2.8. Strofoida
Přímou strofoidou [stručně s trofoidou ] nazýváme množinu všech
průsečíků každé ze svazku kružnic, které mají společnou teČrlU vose x s bodem
dotyku T[O, O], s jejím průměrem ležícím na polopřímce svazku o vrcholu
V[ - a, OJ, a > O (obr. 354).
Obr. 354. Strofoida
Rovnice strofoidy v ortonormální souřadnicové soustavě:
(a - x) y2 = (a + x) x 2
[XE(-a,a)]
553
neboli
2 2 a + x
y = x ,
a-x
popř. v polární souřadnicové seustavě
-a cos (2qJ)
(l = [qJ E <in, tn) u (in, in> u (!n, n>],
cos qJ
popř. v parametrickém vyjádření (t E R):
· -a(l - t 2 )
x=
1 + t 2
- at(l - t 2 )
Y = 1 + t 2
Vrchol strofoidy: V = [ -a, O].
Asymptota strofoidy: x = a.
Obsah smyčky strofoidy:
na 2
Sl = 2a 2 - -.
2
Obsah plochy ohraničené strofoidou a její asymptotou:
na 2
S2 = 2a 2 +-.
2
6.1.2.9. Konchoida
Přímou konchoidou [stručně konchoidou] řídicí křivky k pro pól P
nazýváme množinu právě těch bodů, které dostaneme tak, že na každou
přímku p svazku přímek o vrcholu P naneseme od průsečíku přímky p a křivky k
na obě strany úsečky konstantní délky b (obr. 355). Získané krajní body těchto
úseček mimo křivku k jsou body přímé konchoidy.
Nikomédova konchoida
f:Jikomédovou konchoidou nazýváme přímou konchoidu, jejíž řídicí křivkou
je přímka x = a > O (obr. 356).
Rovnice Nikomédovy konchoidy v ortonormální souřadnicové soustavě:
(x - a)2 (x 2 + y2) = b 2 x 2 ,
554
popř. V polární souřadnicové soustavě:
a
(l = + b (Q > O).
cos qJ
Vrcholy Nikomédovy konchoidy jsou VI [a + b, O] a VI [a - b, O].
y
p=o
o=p
Obr. 355. Přímá konchoida
Obr. 356. Nikomédova konchoida
Asymptota Nikomédovy konchoidy: x = a.
Pól p[O, O] Nikomédovy konchoidy je
- pro b < a izolovaným bodem (viz obr. 356),
pro b > a dvojnásobným bodem (jedna větev má v pólu uzel),
- pro b = a hrotem.
Pascalova závitnice
Pasca/ovou závitnicí L konchoidou kružnice] nazýváme přímou konchoidu
kružnice (2x - a)2 + 4y2 = a 2 pro pól P na řídicí kružnici a parametr b > O.
Rovnice Pascalovy závitnice v ortonormální souřadnicové soustavě:
(x 2 + y2 _ ax)2 _ b 2 (x 2 + y2) = O,
popř. ,v polární souřadnicové soustavě:
Q = a cos qJ + b (Q > O),
popř. v parametrickém vyjádření (t E R):
x = a cos t b cos 2t),
y =\ a sin t - b sin (2t).
Pro b = a je Pascalova závitnice totožná s kardioidou o rovnici
Q = a( cos qJ + 1),
přičemž rovnici Q = a(cos qJ - 1) sph\uje jen bod [O, O] (hrot).
555
Pól (počátek O) Pascalovy závitnice je
- pro b < a uzlem,
- pro b > a izolovaným bodem,
- pro b = a hrotem (kardioida).
6.2. PROSTOROVÉ KŘIVK Y
Křivkou definovanou parametricky v troJrozměrném euklidovském
prostoru E3 nazýváme množinu právě těch bodů, jejichž kartézské souřadnice
x, y, z jsou dány rovnicemi
x = qJ(t), y = t/J(t), z = X(t),
kde qJ, t/J, X jsou reálné funkce reálné proměnné t, které jsou definovány
na nějakém intervalu J a mají spojité derivace podle t aspoň prvního řádu,
přičemž vztahy
ljJ(t) . O, .jJ(t) = O, i(t) = O
platí všechny zároveň jen v izolovaných bodech intervalu J. Bod P = [qJ(t o ),
t/J(t o ), X(t o )] křivky se nazývá regulární, jestliže aspoň jedna z derivací ljJ(t o ),
.jJ(t o ), i(t o ) je různá od nuly a bodu P přísluší právě jedna hodnota parametru t.
Ostatní bod) křivky se nazývají singulární. Jestliže několika hodnotám para-
metru t přísluší právě jeden bod, pak takový bod se nazývá fJ, kolikanásobný.
Rovnice x = qJ(t), y = tfJ(t), z = X(t) nazýváme parametrickými rovnicemi
křivky.
Křivkou definovanou implicitně v trojrozměrném euklidovském prostoru E3
nazýváme množinu právě těch bodů, jejichž kartézské sOQřadnice x, y, z jsou
dány rovnicemi
F(x, y, z) = O,
I#-
G(x, y, z) = O,
kde F, G jsou reálné funkce tří reálných proměnných na množině Q3 c E 3 ,
které mají spojité první parciální derivace, přičemž existuje aspoň jeden bód
[xo, Yo, zo], pro který platí:
a) F(xo, Yo, zo) = O,
b) matice
oF
ox (xo, Yo, zo),
oG
-;- (xo, Yo, zo),
vX
G(xo, Yo, zo) = O;
oF
0Y (xo, Yo, zo),
oG
oy (xo, Yo, zo),
oF
Oz (xo, Yo, zo)
oG
oz (xo, Yo, zo)
má hodnost 2.
556
Vektorový zápis prostorové křivky:
r = r(t) = cp(t); + t/J(t) j + X(t) k.
Je-li křivka definována implicitně, pak ji lze na dostatečně malém okolí
každého jejího bodu vyjádřit parametricky, a obráceně, je-li křivka definována
.
parametricky, pak ji lze na okolí každého jejího bodu vyjádřit implicitně.
6.2.1. Základní prvky prostorových křivek
Diferenciál [element] oblouku prostorové křivky pro křivku danou
parametricky:
ds = J(liJ2 + .jJ2 + X 2 ) dt .
Délka oblouku prostorové křivky dané parametricky s krajními body
P(t 1 ) a P(t 2 ) je dána vzorcem
1: 2 J {[ <i>(t)] 2 + [tfr(t)Y + [i(t)y} dt ·
Oblouk jako parametr
Jestliže x == cp(t), y = t/J(t), z = x(t) jsou parametrické rovnice křivky k
a t(-r) je funkce definovaná na intervalu J', která má na tomto intervalu spojitou
derivaci dtldt * O, pak také x = cp(t(-r)), y = t/J(t(-r)), z = X(t(-r)) jsou para-
metrické rovnice křivky k.
Říkáple, že v parametrických rovnicích x = qJ(s), y = t/J(s), z = X(s) křivky k
je parametrem oblouk, jestliže délka oblouku křivky k s krajními body P(Sl)
a P(S2) se rovná číslu S2 - Sl' Jsou-li x = cp(t), y = t/J(t), z = X(t) parametrické
rovnice křivky k, pak x = cp(t(s)), y = t/J(t(s)), z = X(t(s)), kde t(s) je inverzní
fU'nkce k funkci
s(t) = 1: J {[ <i>(-r)Y + [tfr(-r)Y + [i(-r)Y} d. ,
,
jsou parametrické rovnice téže křivky, kde parametrem je oblouk.
557
Příklad:
Jsou dány parametrické rovnice x = r cos t, y = r sin t, z = t šroubovice.
Pak platí
s(t) = LJ(r 2 + 1) dL = t J(r 2 + 1),
s
t(s) = J(r2 + 1)'
takže
s . s s
x = rcos J(r 2 + 1)' Y = rsm J(r2 + 1)' z = J(r 2 + 1)
jsou parametrickými rovnicemi šroubovice, kde parametrem je oblouk.
Tečný vektor
Tečným vektorem v regulárním bodě p[xo, yo, zo] křivky dané parametricky
rovnicemi x = q>(t.), y , I/I(t), z = X(t) [xo = q>(t o ), Yo = I/I(t o ), Zo = X(t o ),
· ( dli' ) · ( d"' ) : ( d X ) ]
qJo = - , 1/10 = - , Xo = - nazýváme vektor
dt t = to dt t = to" dt t = to
to = (CPo,tfro,Xo).
Je-li parametrem t = s oblouk, je Itol = 1.
Tečným vektorem v regulárním bodě p[xo, Yo, zo] křivky dané implicitně
rovnicemi F(x, y, z) = O, G(x, y, z) = 'O [ F = : (xo, Yo, zo) atd. ] nazýváme
vektor .
to = ( FyO, Fzo, Fzo, F , F , Fi ) 0
G , G G , G G , G
Tečným vektorem v regulárním bodě p[ xo, Yo, zo] křivky dané vektorovou
rovnicí r = r(t) nazýváme vektor
;'0 = ( dr )
, dt t = to .
Tečna
Přímka obsahující tečný vektor se nazývá tečna. .
Rovnice tečhy v regulárním bodě p[xo, Yo, 2 0 ] křivky dané parametricky
558
rovnicemi x = q>(t), y = "'(t), z = x(t) [xo = q>(t o ), 'Yo = "'(to),
liJo = ( dli' ) tfro = ( dt/J ) Xo = ( d X ) ] .
dt t=to' dt t=to' dt t=to .
X - Xo y - Yo Z - Zo
- -
tbo
Zo = X(t o ),
liJ o
.
1..0
Rovnice tečny v regulárním bodě p[ xo, Yo, zo] křivky dané implicitně
rovnicemi F(x, y, z) = O, G(x, y, z) = O [F . : (xo, Yo, zo), ...]
X - Xo y - Yo Z - Zo
Fi, Fzo - Fzo , F - F , Fyo .
G , G G , G G , G
Rovnice tečny v regulárním bodě p[ xo, Yo, zo] křivky dané vektorovou
rovnicí r = r(t) [ ro = r(t o ), ;'0 = ( dr ) ] :
dt t=to
r = ro + ).;0.
Tečna takto zavedená je lineární polohou sečny, jestliže její dva průse-
číky s křivkou splynou v jediný bod. Regulární bod P nazýváme do ykovým
bodem tečny ke křivce. Každá rovina procházející tečnou křivky v bodě P
se nazývá tečná rovina.
Vektor hlavní normály a binormály
Vektorem hlavní normály v regulárním bodě p[ xo, Yo, zo] křivky dané para-
metricky rovnicemi x = qJ(s), y = t/J(s), z = X(s), kde parametrem s je oblouk
[xo = qJ(so), Yo = t/J(so), Zo = X(so)], nazýváme vektor
( ( d 2qJ ) ( d2"' ) ( d2x ) )
no = --'2 ' --'2 ' .
ds s=so ds S=So ds s=so
Vektorem hlavní normály v regulárním bodě p[ xo, Yo, zo] křivky dané vekto-
rovou rovnicí r = r(s) nazýváme vektor
( d 2 r )
"
ro= -
ds 2 s=so.
559
Vektorem binormály v regulárním bodě p[ xo, Yo, zo] křivky dané parametricky
rovnicemi x = qJ(S}, Y = t/J(s), z = x(s), kde parametrem s je oblouk
[xo = qJ(so), Yo = t/J(so), Zo = X(so)], nazýváme vektor
b o = dt/J dX dX dqJ dqJ dt/J
- - - - - -
ds , ds , ds , ds , ds , ds
d 2 t/J d 2 X d2X d 2 qJ d 2 qJ d 2 t/J
-- -- --
ds 2 ' ds 2 ds 2 ' ds 2 ds 2 ' ds 2
Vektorem binormály v regulárním bodě p[xo, Yo, zo] křivky dané vektorovou
rovnicí r = r(s) nazýváme vektor
r x r = ( dr ) ( d2 ) .
ds S=So ds S=So
Platí
b o to no
-=-x-
Ibol Itol Inol'
to no b o
-=-x-
Itol Inol Ibol.
no b o to
-=-x-
I n o1 Ibol Itol'
Hlavní normála a binormála
Přímka obsahující vektor hlavní normály se nazývá hlavní normála.
Rovnice hlavní normály v regulárním bodě p[xo, Yo, zo] křivky dané para-
metricky rovnicemi x = qJ(s}, y = t/J(s}, z = x(s} [xo = qJ(so}, Yo = t/J(so),
Zo = X(so}]:
x - Xo
( d 2qJ )
ds 2 s=so
y - Yo
-
( ::: ).=.0
z - Zo
-
( d 2X ) .
ds 2 s=s()
Rovnice hlavní normály v regulárním bodě p[xo, Yo, zo] křivky dané vek-
torovou rov,nicí r = r(s) [ ro = r(so), ro = ( d2 ) J :
ds s = So
r = r o + A.r .
Přímka obsahující vektor binormály se nazývá binormála.
560
Rovnice binormály v regulárním bodě p[xo, Yo, zo] křivky dané para-
metricky rovnicemi x = <p(s), y = t/J(s), z = X(s) [xo = <p(so), Yo = t/J(so),
:o = X(so)]:
x - Xo y - Yo Z - Zo
- -
dt/J dX dX d<p d<p dt/J
- - - - - -
ds , ds ds , ds ds , ds
d 2 t/J d 2 X d 2 X d 2 <p d 2 <p d 2 t/J
-- -- --
ds 2 ' ds 2 ds 2 ' ds 2 ds 2 ' ds 2
Rovnice binormály v regulárním bodě p[xo, Yo, zo] křivky dané vektorovou
rovnicí r = r(s) [ ro = r(so), r = ( dr ) r = ( d 2 : ) J :
ds s=So ds s=so
r = r o + A.( ro x ro).
Směrové úhly tečny, hlavní normály a binormály
Pro velikosti (1, p, y směrových úhlů tečny platí
cos rJ.. = ( d dX ) , cos B = ( :Y ) , cos y = (d dZ ) .
s s = so S s = so S s = so
Pro velikosti 1, m, n směrových úhlů hlavní normály platí
( d 2 x ) ( d2y )
cos I = R 1 --:-2 ' cos m = R 1 d 2 '
ds S=So s S=So
kde
( d 2 Z )
cos n = R 1 d 2 '
S s = So
. J[( d 2 X ) 2 ( d2y ) 2 ( d2Z ) 2 ]
Rl = + +
ds S=So ds s=so ds s=so
je poloměr první křivosti.
Pro velikosti A., J1, v směrových úhlů binormály platí
[ ( dY ) ( d2Z ) ( dz ) ( d2y ) ]
cos A. - R - - - - -
- 1 ds S=So ds 2 S=So ds s= o ds 2 S=So '
[( dZ ) ( d2X ) ( dX ) ( d2Z ) ]
cos Jl - R - - - - -
. - 1 ds s=so ds 2 s=So ds S=So .ds 2 S=So '
[( dX ) ( d2y ) ( dY ) ( d2X ) ]
cos v - R - - - - -
- 1 ds S=So ds 2 S=so ds S=So ds 2 S=so '
561
kde
J[( d 2 X ) 2 ( d2y ) 2 ( d2z ) 2 ]
Rt = + +
ds S=So ds S=So ds S=So
je poloměr první křivosti.
Normálová, oskulační a rektifikační rovIna
Normálovou rovinou v bodě Po prostorové křivky k nazýváme rovinu kolmou
k tečně křivky v bodě Po a procházející bodem Po. Normálová rovina je
určena bodem Po, vektorem hlavní normály a .vektorem binormály (obr. 357).
Každá přímka procházející bodem Po a ležící v normálové rovině se nazývá
normála prostorové křivky v bodě Po.
Rovnice normálové roviny v regulárním bodě Po [ xo, Yo, zo] ke křivce dané
parametricky rovnicemi x = Ip(t), y = "'(t), z = X(t) [xo = Ip(t o ), yo = "'(to),
Zo = X(t o ), CPo = ( : ) _ ' .jJo = ( :"' ) , Xo = ( :: ) J :
t - to t t = to ,t = to
(X - xo) CPo + (y - Yo).jJo + (Z - zo) Xo = O.
Rovnice normálové roviny v regulárním bodě Pol xo, Yo, zo] ke křivce dané
implicitně rovnicemi F(x,y,z) = O, G(x,y, z) = O [F = (XO,YO,zo),...}
X - xo, Y - Yo, Z - Zo = O.
F , F , Fzo
G , G , G
Rovnice normálové roviny v regulárním bodě Po L xo, Yo, zo] ke křivce dané
vektorovou rovnicí r = r(t) [ ro = r(so), 'o = ( dr ) J :
dt t = to
(r - ro);'o = O
Oskulační rovinou v bodě Po prostorové křivky k nazýváme rovinu kolmou
k binormále křivky v bodě Po a procházející bodem Po. Oskulační rovina
je určena bodem Po, tečným vektorem a vektorem hlavní normály (viz obr. 3.57).
Takto zavedená oskulační rovina je limitní polohou rovin procházejících
tečnou v bodě Po a bodem P 1 křivky pro P 1 Po.
Rovnice oskulační roviny v regulárním bodě Po[xo, Yo, zo] ke křivce dané
parametricky rovnicemi x = qJ(s), y = tjJ(s), z = X(s), kde parametrem s
562
je oblouk [Xo = qJ(So), Yo = .p(Std, Zo = x(so)]:
X - Xo, y - Yo, Z - Z J i = o.
dqJ d'" dx
--- --
ds' ds' ds
d 2 qJ d 2 ", d2x
ds 2 ' ds 2 ' ds 2
Rovnice oskulační roviny v regulárním bodě Po [xo, Yo, zo] ke křivce dalié
vektorovou rovni í r = r(s) [ ro = r(5 0 ), r = (d d ) _ ' r = ( d d2 ) _ J :
s s u so 5 s - so
(r - r o) (r x r ) = O.
Obr. 357. Prostorová křivka
Rektifikační rovinou v bodě Po prostorové křivky k nazýváme rovinu kolmou
k hlavn.í normále křivky v bodě Po a procházející bodem Po (viz obr. 357).
Rektifikační rovina je určena bodem Po, tečným vektorem a vektorem
binormály.
Rovnice rektifikačnÍ roviny v regulárním bodě Po[ xo, Yo, Zo] ke křivce dané
parametricky rovnicemi x = qJ(S), Y = ",(s), z = x(s), kde parametrem s
je oblouk [xo = qJ(so), Yo = ",(so), Zo = X(so)J:
( d 2qJ ) ( d2"' ) ( d2X )
(X - xo) + (Y - Yo) +(Z - Zo) = O.
ds S=So ds S=So ds S=So
. Rovnice rektifikačnÍ roviny v regulárním bodě Po [x o, Yo, Zo] ke křivce dané
vektorovou rovnicí r = r(s) [ro = r(so), r "= (:: ).=.ol
(r - r o) r = O.
563
Styk dvou prostorových křivek
Jestliže křivka k, resp. k' je dána parametricky rovnicemi
x = lfJI(S), Y = t/JI(S), Z = Xl(S),
resp.
x = lfJ2(S), Y = t/J2(S), Z = X2(S),
kde parametrem je oblouk s, pak říkáme, že prostorové křivky k, k' mají ve
společném bodě s = O styk [dotyk] nejméně q-tého řádu [styk [dotyk] nejméně
(q + l bodový], právě když
lfJl(O) = lfJ2(O), t/Jl(O) = t/J2(O), Xl(O) = X2(O),
(::1 ).=0 = ( ::2 )s=o' (:: 1 ).=0 = ( ::2 ).=0' ( ::1 ).= = ( ::2 ).=0'
............................................................".....
( d 4qJ I ) ( d4lfJ2 ) ( d4t/Jl ) ( d4t/J2 ) ( d4XI ) ( d4X2 )
ds q s = o = ds4 s = o' dl' s = o = dl' s = o' dl' s = o = ds 4 s = o'
Osk ulační kružnice, poloměr kři vosti, kři vos t,
s tfed kři vos ťi
Oskulační kružnicí [kružnicí křivosti] prostorové křivky v jejím bodě na-
zýváme kružnici, která má v tomto bodě s křivkou styk nejméně druhého řádu.
Její poloměr R I , resp. střed Sk nazýváme poloměrem, resp. středem (první)
křivosti prostorové křivky. Střed křivosti Sk[ C;, ", (] leží na normále v doty-
kovém bodě křivky.
Převrácené číslo k poloměru křivosti R 1 se nazývá (první) křivost [flexe]
Xl prostorové křivky: Xl = l1R 1 .
Pro křivku danou parametricky rovnicemi x = q>(s), y = t/J(s), z = X(s)
v jejím bodě p(so} platí [xo = q>(so), Yo = t/J(so), Zo = X(so)]:
J[( d 2lfJ ) 2 ( d2t/J ) 2 ( d2X ) 2 ]
Xl = + + '
ds S=So ds S=So ds S=So
( d 2lfJ )
= Xo + R I - d 2 '
s s=so
( d2 t/J )
" = Yo + Rl d2 '
s s = so
( d 2X )
( = Zo + Rl ·
ds s = so
564
Pro křivku danou vektorovou rovnicí r = r(s) v jejím bodě ro = r(so) platí
r=rO+RlnO.
Pro R I' popř. x I dále platí
1 . s ds
Rl = - = hm - = -
Xl t-+O t dt'
kde t je odchylka tečny v daném bodě P a tečny v sousedním bodě P 1 a s
je délka oblouku s krajními body P a P I . Úhel t se nazývá kontingenční úhel.
Druhá křivost [torze]
Označíme-li As délku oblouku prostorové křivky s krajními body P 1 a P 2
a B velikost tzv. úhlu torze, který svírají binormály v bodech P 1 a P 2 , platí
B dB 1
lim - = - = - = x 2
As-+O /!s ds R 2 '
kde číslo X 2 se nazývá druhá křivost [torze, kroucenost] a číslo R 2 se nazývá
poloměr druhé křivosti [poloměr torze].
řivka je ve svém bodě pravotočivá, resp. levotočivá (smysl kroucení proti
smyslu, resp. ve smyslu otáčení hodinových ručiček), jestliže druhá křivost
je v tomto bodě kladná, resp. záporná.
Křivkaje rovinná, právě když ve všech jejích búdech platí X 2 = O. Prostorové
křivky, pro něž platí, že první a druhá křivost jsou nenulové, se někdy v apli-
kacích nazývají křivky dvojí křivosti.
Druhá křivost v bodě p[ xo, Yo, zo], kde x = lp(so), Yo = ",(so), Zo = X(so):
( :: ). =so' ( :: ) &=so' ( : )&=so
(::: )&= so' ( ::t) & = so' ( : )&=&O
( )&=so' ( )&=so' ( )&=so
X 2 = ( d 2lp ) 2 ( d2"' ) 2 ( d2X ) 2.
ds 2 &=so + ds 2 &=50 + ds 2 &=&0
Příklad: {
v
K dané obyčejné šroubovici [x, y, z] E R 31 x = r cos t, y = r sin t, z = - t;
} 2n
v, t E R , kde lvi je výška závitu, určeme prvnj a druhou křivost.
565
Parametrické rovnice dané šroubovice, kde parametrem s je oblouk, mají
tvar
21ts
q>(s) = r cos J( 2 2 2)'
41t r + v
vs
x.(s) = J(41t2r2 + v 2 )"
I /I ( ) . 21ts
'I' S = r sIn / ( 2 2 2 ) '
V 41t r + v
Vypočteme
dqJ 21tr. 21ts
- = - sIn ,
ds J(41t 2 r 2 + v 1 ) J(41t 2 r 2 + v 2 )
dt/J
ds
21tr 21ts
J(41t 2 r 2 + v 2 ) cos J(41t 2 r 2 + v 2 )'
dX v
---
ds J{41t 2 r 2 + v 2 )'
d 2 qJ 41t l r 21ts
-- = - COS -
ds 2 41t 2 r 2 + 1)2 J(41t 2 r 2 + 1)2)'
d 2 t/J 4Jr; (. 21ts'
- = ------- SIn ,
ds 2 41t 2 r 2 + v 2 J(41t 2 r 2 + v 2 )
..
d2X
ds 2 = o.
Pak první křivost
41t 2 r
:< 1 == - .
41t 2 ,.2 + v 2 .
Dále vypočteme
d 3 qJ
ds 3
81t 3 r . 21ts
[J(41t 2 r 2 + t;2)]3 SIn J(41t 2 r 2 + v2)'
d 3 t/J 87[ 3 r 21ts
---- = - cos
ds 3 [J(41t 2 r 2 + V 2 )]3 J(41t 2 r 2 + v 2 )'
d3X
=o.
ds
566
Pak druhá křivost
x 2 = ( 41t 2 r 2 + V2 ) 2.
41t 2 r
2nr 2ns
- -- --- sin
(4n2r2 + (12) J(4n 2 r 2 + v 2 )
2nr
J(4n 2 r 2 + v 2 )
2ns ('
cos - -- -----
J(4n 2 r 2 + v 2 )' J(4n2r2 + ( 2 )
4n 2 r 2ns 4n 2 r 2ns
- [J(4n 2 r 2 + ('2)]2 cos J(4n2r2 + (2)' - r ( 4n2r2 + V 2 )]2 sin J(4n 2 r 2 + v2)'
o
8 n 3 r 2ns 8n 3 r 2ns
[J(4n2r2 + (2)]3 sin J(4n 2 r 2 + v 2 )' - [J(4n 2 r 2 + V 2 )]3 cos J(4n 2 r 2 + ( 2 )'
( 41t 2 r 2 + V 2 ) 2 V 321t 5 r 2 _ 21tv
- 41t 2 r J(41t 2 r 2 + v 2 ) {J(41t 2 r 2 + V 2 )]5 41t 2 r 2 + v 2 .
o
6.3. PLOCHY
Plochou definovanou parametricky v trojrozměrném euklidovském
prostoru E3 nazýváme množinu právě těch bodu, jejichž kartézské souřadnice
x, y, z jsou dány rovnicemi '
x = (u, v),
y = 17(u, v),
z = ((u, v),
kde , 17, 'jsou reálné funkce dvou reálných parametrů, definované na množině
Q2' které mají spojité parciální derivace aspoň prvního řádu, přičemž matice
a a" o,
- -
ou' ou' ou
(1)
a 017 o,
- --
ov' ov' ev
má hodnost 2 na určitém dvojrozměrném intervalu JI >< J 2'
Body, v nichž matice má hodnost 2, nazýváme regulárními body plochy.
Ostatní body nazýváme singulárními body. Rovnice x = (u, v), y = 17(u, v),
z = '(u, v) nazýváme parametrickými rovnicemi plochy.
Plochou definovanou implicit!1ě v trojrozměrném .euklidovském prostoru E3
nazýváme množinu právě těch bodů, jejichž kartézské souřadnice jsou dány
rovnicí
F(x, y, z) = O,
kde F je reálná funkce tří reálných proměnných na množině Q3 c E 3 , která
má spojité parciální derivace na množině Q3 a v žádném bodě množiny
Q c Q3 zároveň neplatí
567
cF cF cF
- - _ O
t 1 x - cy- - cz - .
(2)
Body, ve kterých neplatí rovnosti (2), nazý:váme regulárními body. Ostatní
body nazýváme singulárními body.
(J raf spojitě diferencovatelné funkce z = f(x, y) je plochou definovanou
para 111Ct ricky rovnicemi
x = u,
y = v,
z = f (u, v)
a plochou definovanou implicitní rovnicí
:: - f(x,y) = O.
Souřadnice na ploše
Hodnoty parametrů u, v se nazývají křivočaré souřadnice bodu p[ x, y, z]
plochy.
Pro konstantní parametr u a proměnný parametr v, resp: pro konstantní
parametr v a proměnný parametr u dostáváme v-čáry, resp. u-čáry.
Křivky na ploše
Rovnice
u = qJ(t),
v = tjJ(t)
(t E J)
(3)
definují parametricky křivku na ploše
x = (u, v), y = ,,(u, v), z = '(u, v) (u, VE D 2 ),
jestliže funkce (3) splňují na intervalu J tyto podmínky:
a) Jsou spojité a mají spojité aspoň první derivace, které nejsou obě zároveň
rovny nule.
b) Body [qJ(t), tjJ(t)] leží pro všechny hodnoty parametru t E J v množině D 2 .
c) Prvky matice (1) nejsou. pro všechny body [qJ(t), tjJ(t)] všechny zároveň
rovny nule.
Rovnice (3) nazýváme parametrickými rovnicemi křivky na ploše.
Tečná rovina a normála plochy
Tečnou rovinou plochy v jejím regulární 111 bodě Po nazýváme rovinu, kterou
tvoří tečny ke všem křivkám ležícím na ploše a procházejícím dotykovým
bodem Po.
Normálou plochy v jejím bodě Po nazýváme přímku, která prochází bodem
Po kolmo k tečné rovině této plochy v bodě Po.
568
Rovnice tečné roviny v regulárním bodě P[ xo, Yo, Zo] k ploše dané para-
metricky rovnicemi:
x = (u, v), Y = 17(u, v), z = '(u, v)
[xo = (uo' vo), Yo = 17(u o , vo), Zo = '(uo, v o )]:
X-xo, Y-Yo, Z-Zo =0.
G ) u =uo. v= vo' G: ) U=uo. ,.= vo' ( ) .=uo. v = vo
( ) u=uo,v=vo' G ) u=uo,v=vo' (:D U= o. v=Vo
Rovnice tečné roviny v regulárním bodě p[ xo, Yo, Zo] k ploše dané implicitní
rovnicí F(x, y, z) = o:
( CF ) ( CF )
(X - xo) ex x=Xo,y=yo,z=zo + (y - yo) ey x=xo.y=Yo.z=zo +
.
+(Z-zo) ( e ť ) =0.
e z x = Xo. Y = Yo. z = Zo
Rovnice tečné roviny v regulárním bodě p[ xo, Yo, Zo] k ploše dané rovnicí
z = f( x, y): .
Z - Zo = (X - xo) ( ez ) + (y _ yo) ( 8z ) .
e x x = XQ. Y = YO C Y x = Xo Y = Yo
Rovnice normály v regulárním bodě p[ xo, Yo, zo] k ploše dané parametricky
rovnicemi x = (u, v), y = 17(u, v), z = '(u, v) [xo = (uo' vo), Yo = 17(u o , Do),
Zo = '(uo, v o )]:
x - Xo
y - Yo
-
( ) u=uo. ,.= vo' ( ) u=Oo. ,,= Vo
( : ) u=uo. ,. = "0' ( ) u=uo. v= Vo
G: )u=uo. v=vo' G ) u=Uo. v=vo
( : ) u = Uo. v = "0 ' ( ) u = Uo. v = Vo
Z - Zo
-
( c ) ( 017 ) .
cu u=UQ,v=...,o' cu u=uo.(,'=vo
( )u=uo. "='.0' G: ) u=uo. V=Vo
569
Rovnice normály v regulárním bodě P[ xo, Yo, zo] k
rovnicí F(x, y, z) = O:
X - Xo
G: ) X=Xo.y= Yo,Z=Zo
570
y - Yo
( :: ) x=Xo.Y=Yo,Z=Zo
ploše dané implicitně
z - Zo
( : ) X=Xo. y= yo. Z=Zo .
7. INTEGRÁLNÍ POČET FUNKCÍ JEDNÉ
PROMĚNNÉ
7.1. DEFINICE NEURČITÉHO INTEGRÁLU
I
Primitivní funkce
Funkce F se nazývá primitivní funkce k funkci f na intervalu (a, b)
(připouští se a = - 00, b = + (0), jestliže pro 'v'x E (a, b) platí F'(x) = .f(x).
Neurčitý integrál
..
Zápis Jf(x)dx představuje množinu všech primitivních funkci
k funkci f a nazývá se neurčitý integrál (z) funkce f.
Jf(x) dx = F(x) + C, přičemž F'(x) = f(x) a C je libovolná konstanta.
Funkce f se nazývá integrand nebo integrovaná funkce, x integrační pro-.
měnná, C integrační konstanta a J integrační znak:
Protože integrační konstanta C může nabývat libovolného reálného čísla,
přísluší danému integrandu nekonečně mnoho primitivntch funkcí. KažJé
určité hodnotě integrační konstanty C přísluší právě jedno parciální ře. ení.
Geometricky to znamená, že existuje nekonečně mnoho integrálních křivek,
které vzniknou jedna z druhé rovnoběžným posunutím ve směru dru hé
souřadnicové osy.
Funkce f se nazývá integrovatelná, existuje-li k ní primitivní funkce F.
Každá spojitá funkce je integrovatelná.
7.2. ZÁKLADNÍ INTEGRÁLY
Pokud u vzorců nejsou v závorkách připojeny další omezující pod-
mínky, platí vzorce pro 'v'x E R a pro všechny reálné hodnoty uvedených
konstant. Přitom např. místo omezení platnosti vzorce na 'v'x E (- 00, 1) u
u (1, + (0) se stručně uvádí x =t= 1. V omezujících' podmínkách je všude
vynechán obecný kvantifikátor.
f xn+l
1. dx = + C
n + 1
(x > 0 1 nE R \ { - t}).
571
2. f dx = ln Ixl + C
x = ln (kx)
3. fe x dx = eX + C.
r a X
4. rř dx = ln a + C = a X log" e + C
5. fin xdx = -cos x + c.
6. fcos x dx = sin x + c.
f dx - ( '(2k + 1)1t kE z).
7. 2 - tg x + C x =F ,
cos x 2
8. f .d: = -cotg x + C (x + n1t, nE Z).
sIn x
9. f J(l dx x 2 ) = arcsin x + C = -arccos x + CI
(x =F O),
(kx > O).
(a > O, a * 1).
10. f 1 :x2 = arctg x + C = -arccotg x + CI'
11. finh x dx = co h x + c.
12. fCOShXdX = sinh x + C.
13. f d h x2 = tgh x + c.
cos x
14. f . d = -cotghx + C
slnh x
(x =F O).
(Ixl < 1).
15. f J(x x+ 1) = argsinh x + C = ln [x + J(x 2 + 1)] + C.
16. f J(x x_ 1 ) ln lx + J(x 2 - 1)1 + c,
= argcosh x + C
(Ixl > 1),
(x > 1).
572
f dX 11+x
17. 2 = -ln + C
I-x 2 I-x
= argtgh x + C
= argcotgh x + c
Ze vzorce 17 plyne
f dx 1 x-I
x 2 -1 = 2 In x + 1 + C
= -argtgh x + c
= -argcotg x + c
(Ixl + 1),
(I x I < 1),
(Ixl > 1).
(I x I + 1),
(I x I < 1),
(Ixl > 1).
7.3. ZÁKLADNÍ INTEGRAČNÍ PRAVIDLA
I ntegrace součtu nebo rozdílu funkcí (I, g a h jsou integrovatelné
funkce) :
f[J(x) + g(x) - h(x)] dx = ff(X)dX + fg(X)dX - fh(X)dX.
I ntegrace funkce s multiplikační konstantou (f je integrovatelná funkce):
Je f(x) dx = c ff(X) dx.
Substituční metoda
a) Neurčitý integrál Jf(qJ(t)) qJ'(t) dt vypočteme tak, že najdeme libovolnou
primitivní funkci F(x) k funkci f(x) a do výsledku za proměnnou x dosadíme
x = qJ(t):
ff(CP(t)) cp'(t) dt = F(cp(t)) + C .
Přitom předpokládáme, že funkce qJ má spojitou derivaci qJ' na intervalu ((1, 8),
funkce f je spojitá na intervalu (a, b) a qJ(t) E (a, b) pro všechna čísla t E (Li, 8).
b) Neurčitý integrál Jf(x)dx vypočteme tak, že najdeme libovolnou
primitivní funkci G(t) k funkci f(qJ(t)) qJ'(t) a do výsledku za proměnnou t
dosadíme t = t/J(x), kde t/J je inverzní funkce k funkci qJ na intervalu (rx, 8):
ff(x) dx = G(t/I(x)) + c.
573
Přitom kromě' předpokladů uvedených v bodě a) ještě předpokládáme
existenci inverzní funkce t/J. Protože zpravidla z dané funkce t = t/J(x) odvo-
zujeme vztah x = <p(t), je třeba také ověřit existenci a spojitost funkce <p
na intervalu ( , B).
Často se vyskytující substituce
1 (a * O);'
= t, dx = - dt
a
= t, dx = a dt (a =t= O);
ax + b
x
a
a
= t,
x
a X
=' t
,
eX = t,
ln x = t,
a + bx 2 = t,
a 2 + x 2 = t,
J(a 2 + x 2 ) = t,
J(a 2 - x 2 ) = t,
J(x 2 - °a 2 ) = t,
J(a + bx) = t,
J x = t,
, V(a + bx) = t,
574
a
dx = --i dt (a * O, x =t= O);
t
dt
dx = (a =t= 1, a > O);
t ln a
1
dx = -dt;
t
dx = e t dt (x > O);
dt
dx =. -J(b ) (x > O nebo x < O, b + O);
2 t -- ab
dt
dx = 2 "'/(t _ a 2 ) (x > O nebo x < O);
t dt
dx = ,J(t 2 _ a 2 ) ;
t dt
dx . - ,J(a 2 _ ( 2 ) (Ixl < lal);
, t dt
dx = ,J(t 2 + a 2 ) (Ixl > a);
2t dt
dx = - (a + bx > O, b * O);
b
di = 2t dt (x > O);
nť-l dt
dx = b. (a + b > O, b + O).
Substituce pro speciální integrály
1: fJ(X, .J(a 2 x 2 )) dx (Ixl < lal).
Substituce
x = a sin t,
dx = a cos t dt
dává
fJ(a sin t, a cos t) a cos t dt.
Po integraci dosadíme
. x
t = arCSln-,
a
. x
sIn t = -,
a
J(a 2 - x 2 )
cos t = ,
a
x
tg t = J(a 2 _ x 2 )'
l ( a 2 X2 )
cotg t = V .
x
Příklad:
ln tegrál
f.J(a - x 2 ) dx
vypočteme pomocí substituce x = a sin t, dx = a cos t dt. Dostaneme
f[ .J(a 2 - a 2 sin 2 t)] a cos t dt = a fcos 2 t dt =
2 ( 1 . 1 )
= a "2 cos t sIn t + It ,
kde jsme použili vzorce 14 z článku 7.4.3. Po zpětném dosazení máme
f a2 J(a 2 - x 2 ) x a 2 x
J(a - x 2 )dx = - - + -arcsin- =
2 a a 2 a
x (!2 x
= - J(a 2 - x 2 ) + arcsin-.
2 2 a
2. fJ(x, .J(a 2 - x 2 )) dx (Ixl < laj).
575
Substituce
x = a tgh t,
adt
dx =
cosh 2 t
dává
f ( a ) a dt
a t gh t, .
f cosh t cosh 2 t
Po integraci dosadíme
x
t = argtgh-,
a
x ,.
sinh t = J(a 2 _ X2) '
a
cosh t = J(a2 _ x 2 )'
3. ff (x, J(a 2 + x 2 )) dx .
Substituc
x = a tg t,
a dt
dx =
cos 2 t
dává
f ( a ) a dt
f a tg t, .
cos 2 t cos 2 t
Po integraci dosadíme
x
t = arctg-,
a
. x
S10 t = J(a2 + x 2 )'
a
cos t = J(a 2 + x 2 )'
4. ff(X, J(a 2 + x 2 )) dx.
Substituce
x = a sinh t ,
x
tgh t = -,
a
a
cotgh t = -.
x
x
tg t = -,
a
a
Gotg t = -.
x
dx = a cosh t dt
576
dává
f!(a sinh t, a cosh t) a cosh t dt.
Po integraci dosadíme
x
t = argsinh -,
a
. h x
sin t = -,
a
J(a 2 + x 2 )
cosh t = ,
a
x
tgh t =
J(a 2 + x 2 )'
l(a 2 + x 2 )
cotgh t = V .
x
5. f!(x, J(x 2 - a 2 )) dx (Ixl ;;> laj).
Substituce
a
x=-
,
cos t
dx = a sin t dt
cos 2 t
dává
Jf( a ) a sin t dt
-, atgt .
cos t cos 2 t
Přitom platí
. J(x 2 - a 2 )
sin t = ,
x
tg
J(x 2 - a 2 )
t =
,
a
a
cos t = -,
x
a
cotg t = J(x 2 _ a 2 ).
6. f!(x, J(x 2 - a 2 )) dx (Ixl > lal).
Substituce
x = a cosh t ,
dx = a sinh t dt
dává
f!(a cosh t, a sinh t) a sinh t dt.
577
Přitom platí
l ( x 2 - a 2 )
sinh t = '\/ ,
a
tgh
J(x 2 - a 2 )
t= ,
x
x
cosh t = -,
a
x
cotgh t = J(x 2 _ a 2 )'
7. fR(sin x, cos x, tg x, cotg x) dx (R je racionální funkce).
Substituce
x
t g - = t
2 '
2
dx = 2 dt
1 + t
dává
f ( 2t 1 - t 2 2t 1 - t 2 ) 2 dt
J 1 + t 2 ' 1 + t 2 ' 1 - t 2 ' 2t 1 + t 2 '
8. fR(sinh x, cosh x, tgh x, cotgh x) dx (R je racionální funkce).
Substituce
x
tgh - = t,
2
dx = 2 dt
1 - t 2
dává
f R ( 2t 1 + t 2 2t 1 + t 2 ) 2 dt
1 - t 2 ' 1 - t 2 ' 1 + t 2 ' 2t 1 - t 2 .
9. fJ(e X ) dx.
Substituce
eX = t,
dx = dt
t
dává
fJ(t) dt.
10. fJ(x, V(ax + b)) dx (x > - ).
578
Substituce
ax + b = t,
kt k - l dt
dx =
a
dává
fI(t) dt.
11. J f ( X' ( ax + b ) l/P, ( ax + b ) ll q , ... ) dx (p, q,... E Z).
ex + d ex + d
Substituce
ax + b
=t"
ex + d
dává
fI(t) dt
(n je nejmenší společný násobek jmenovatelů p, q, ...; ad - bc * O).
12. fI(x, J(ax 2 + bx + c)) dx .
Používáme těchto substitucí, které integrály tohoto typu převedou na
integrály racionálních funkcí:
Případ 1: a > O.
Substituce:
J(ax 2 + bx + e) = x Ja + t,
t 2 - C - t 2 J a + bt - c J a
x = , dx = 2 dt .
b - 2tJa (b - 2tJa)2
Případ 2: e>O, x*O.
Substituce
J(ax 2 + bx + c) = xt + Je,
2t Je - b 2a Je - 2bt + 2t 2 Je
x = 2 ' dx = ( 2Y dt .
a-t a-t
Případ 3: Odmocněnec má reálné kořeny Xl a x 2 .
Substituce ·
J(ax 2 + bx + e) = t(x - Xl),
t2XI - aX 2 2at(x 2 - Xl)
x = 2 ' dx = (2 )2 dt .
t - a t - a
579
I.n tegrace per partes
Na otevřeném intervalu J platí
fuv' dx = uv - fvu' dx,
kde u = u(x), v = v(x) jsou funkce proměnné x, které mají na intervalu J
spojité derivace.
Jiný způsob psaní:
fUdV = uv - fVdU.
Příklad:
Má se vypočítat integrál
fx 3 1n x dx.
Pomocí substitucí
u = ln x,
1
du = - dx,
x
dv = x 3 dx,
x 4
V =-
4
dostaneme
f X4 1 f X4 x 4 1 f .
x 3 ln x dx = -ln x - - - dx = - ln x - - x 3 dx =
4 4 x 4 4
x 4 1 x 4 x 4 ( 1 )
= -ln x - - - + C = - ln x - - + C.
444 4 4 .
Integrace rozkladem v částečné [parciální] zlomky
Při rozkladu zlomku flg, kde f, 9 jsou mnohočleny a f je stupně nižšího
než g, v částečné [parciální] zlomky rozlišujeme tyto čtyři případy:
..
Případ 1
Rovnice g(x) = O má jen jednoduché. reálné kořeny Xl' x 2 , .... Pak
lze fl 9 rozložit v částečné [parciální] zlomky takto:
f ) A B C
( ) + + + ... ,
9 x x - Xl X - X2 X - X3
580
kde
A = f(x l ) B = f(X2) f(X3)
g'(X 1 )' g'(X 2 )' c = g'(X3)' ....
Je tedy
f f(X) f dx f dx f dx
, - ( ) dx = A + B -- - + c + ....
9 x x - Xl X - X2 X - X3
Čitatele A, B, C, ... částečných zlomků lze také (a často ještě rychleji) najít
metodou neurčitých součinitelů [koeficientů], které se určí porovnáním
koeficientů u týchž mocnin proměnné X v čitatelích zlomků.
Příklad:
Má se vypočítat integrál
f 15x2 - 70x - 95
X3 _ 6X2 - 13x + 42 dx ·
Protože
x 3 - 6x 2 - 13x + 42 = O => Xl = 2/\ X2 = -3 /\ x 3 = 7 ,
Je
15x 2 - 70x - 95 A B C
= + + =
x 3 - 6x 2 - 13x + 42 X - 2 X + 3 X - 7
A(x + 3) (x - 7) + B(x - 2) (x - 7) + C(x - 2) (x + 3)
(x - 2) (x + 3) (x - 7)
(A '+ B + C) x 2 - (4A + 9B - C) x - (21A - 14B + 6C)
(x - 2) (x + 3) (x - 7)
Porovnáním koeficientů u týchž mocnin proměnné x v čitateli prvního a po-
sledního zlomku dostaneme soustavu rovnic
A + B + C = 15, }
4A + 9B - C = 70,
21A - 14B + 6C = 95
popř. pomocí první z uvedených metod je
f(XI) -175
A = ( ) = atd.
g' Xl - 25
=> A = 7 /\ B = 5 /\ C = 3,
581
Z toho plyne
f 15x2 - 70x - 95 r dx r dx r dx
x 3 _ 6x 2 - 13x + 42 dx = 7 J - 2 + 5 J + 3 + 3 J - 7 =
= 7 ln lx - 21 + 5 ln lx + 31 + 3 ln lx - 71 + C.
Případ 2
Rovnice g(x) = O má jen reálné kořeny, z nichž některé jsou však několika-
násobné, napřo kořen Xl je -násobný, kořen x 2 O-násobný atd. Pak lze flg
rozložit v částečné zlomky takto:
f(x)
g(x)
AI A 2 A3 Aa
= ( ) a + ( ) a-l + ( \a-2 + 0.0 + +
x - Xl X - Xl X - XII X - Xl
BI
+
(X - X 2 Y
CI
+
. (X - X 3 )y
B 2
+ (x - X2y-t
C 2
+
" ( ) y - I
X - X3
B3
+
(X - X 2)P - 2
C 3
+
(X ""7 X 3 )Y-2
+ ... +
+ 000 +
Bp
+
X - X2
C y
+ ....
X - X3
Součinitele AI' A 2 , 000' Aa, B I , B 2 , 000' Bp, CI' C 2 , ..o, C y , 00' vypočteme po-
rovnáním koeficientů u týchž mocnin proměnné X v čitatelích zlomkůo
Příklad:
Má se vypočítat integrál
F x 3 +. 10x 2 - X
(2 Y dx.
X - 1
Protože
/""
(X2 - 1)2 = O => Xl = X 2 = 1 /\ X3 = x 4 = -1,
Je
3x 3 + 10x 2 - X
(X2 - 1)2
AI A 2 BI B 2
- ( ) 2 + + + -
X - 1 x-I (x + 1)2 x + 1
= AI(X + 1)2 + A 2 (x + 1)2 (X - 1) + BI(X - 1)2 -+= B 2 (x - 1)2 (X + 1)
(x - 1)2 (x + 1)2
582
(A2 + B2)X3 + (AI + A 2 + BI - B2)X 2 + (2A. - A 2 - 2B. - B 2 )x
= +
(X - 1)2 (X + 1)2
A. - A 2 + BI + B 2
.+
(x - 1)2 (X + 1)2 .
Porovnáním koeficientů dostaneme sOllstavu rovnic
A 2 +B 2 = 3,
A. + A 2 + BI - B 2 = 10,
=> A I =3I\A 2 =4I\B I =2I\B 2 =-1.
2A I - A 2 - 2B I - B 2 = - 1 ,
AI - A 2 + BI + B 2 = O
Z toho plyne
f 3X 3 + lOx 2 - x dx =
(X2 - 1)2
= 3 f1 x \)2 + 4 t 1 + 2 f1 x :xW - t 1 =
3 2
= - + 4 ln lx - 11 - - ln lx + 11 + C.
x-I x+1
Případ 3
Rovnice g(x) = O má kromě reálných kořenů také jednoduché komplexní
kořeny (vždy dva a dva komplexně sdružené). Uvedených metod rozkladu
v částečné zlomky lze použít také zde, přičemž se ovšem zároveň vyskytují
komplexní čitatelé. Počítání s komplexními výrazy se lze vyhnout, jestliže
částečné zlomky, které vzniknou dosazením komplexně sdružených kořenů,
uvedeme na společného jmenovatele. Jsou-li např. Xl a X 2 dva komplexně
sdružené koře.:ty, použijeme vyjádření
A
B
Px + Q
-
(x - Xl) (x - x 2 )'
X - Xl
+
x - X2
kde součinitele opět určíme porovnáním koeficientů u týchž mocnin proměnné
i) x v čitatelích zlomků.'
Integrál výrazu
Px + Q
(x - Xl) (x - X2)
Px + Q
-
X2 + px + q'
kde
p2
q -->O
4 '
583
lze vypočítat podle vzorce
f Px + Q . P
2 dx = -ln (x 2 + px + q) +
x + px + q 2
Pp p
Q-- x+-
+ n arctg n '
Příklad:
Má se vypočítat integrál
r 7x 2 - 10x + 37
J 3 - 3x 2 + 9x + 13 dx.
Protože
x 3 - 3x 2 + 9x + 13 = O => Xl = -1 /\ X2 = 2 + 3i /\ X3 = 2 - 3i,
Je
7x 2 - 10x + 37 A Px + Q
- + -
x 3 - 3x 2 + 9x + 13 - x + 1 x 2 - 4x + 13 -
A(X2 - x + 13) + (Px + Q)(x + 1)
x 3 - 3x 2 + 9x + 13
(A + p) x 2 - (4A - Q - p) x + (13A + Q)
x 3 - 3x 2 + 9x + 13
Porovnáním koeficientů dostaneme soustavu rovnic
A +P= 7 ' 1
4A - Q - P = 10, => A = 3 /\ P = 4/\ Q = -2.
13A + Q = 37 I
Z toho plyne,
f 7X2 - 10x + 37 f dx f 4x - 2
dx = 3 + dx =
x 3 - 3x 2 + 9x + 13 X + 1 x 2 - 4x + 13
x-2
=31nlx+ll+21n(x 2 -4x+13}+2arctg 3 +c.
Případ 4
Rovnice g(x) = O má kromě reálných kořenů také několikanásobné kom-
plexní kořeny. V tomto případě je opět nejlépe zlomky, které vzniknou do-
sazením komplexně sdružených kořenů, uvést na společného jmenovatele.
584
AI A 2 A3
- (X - Xl)3 + (X - Xd 2 + X - Xl +
PtX + Ql P 2 X + Q2
+ (X2 + pX + q)2 + X2 + pX + q'
kde kořen Xl je trojnásobným reálným kořenerf1 a komplexně sdružené kořeny
jsou dvojnásobnými kořeny. Integrál
r Plx + Ql d
J(x2 + px + q)2 x
viz vzorce 20 a 21 z článku 7.4.1.
Například
f(x)
g(x)
7.4. ' NĚKTERÉ DŮLEŽITÉ INTEGRÁLY
Poznámka:
U neurčitých integrálů jsou pro přehlednost vynechány integrační konstanty.
Obory pravdivosti jsou uváděny jen tam, kde jsou méně zřejmé.
'.4.1. Integrály racionálních funkcí
Nechť nE N. Ve výrazu ax + b je a * O, b * O. Ve výrazech ax 2 + bx + c
a 4ac - b 2 * O je a * O. Ve výrazu x 2 + á 2 je a > O.
} (ax + br+ l
1. (ax + br dx = ( )
a n + 1
2. r dx = ln lax + bl.
J x + b a
f (ax + b)n+2 b(ax + br+ 1
3. x(ax + br dx = 2( ) 2( ) -
an+2 an+l
a(n+l)x-b +1
= a2(n + l)(n + 2) (ax + br .
l x dx x b
4. = - - - ln lax + bl.
ax + b a a 2
X dx b 1
5. = + - ln lax + bl.
(ax + b)2 a 2 (ax + b) a 2
585
r x dx a(l - n) x - b
6. J{ ax + br a 2 (n - l)(n - 2)(ax + br- t
f 1 [ (ax + br+ 3 2b(ax + br+ 2 b 2 (ax + b r + 1 J
7. x 2 (ax + br dx = 3 - + .
á n+3 n+2 n+l
8. r x 2 dx = -; [ (ax + bY _ 2b(ax + b) + b 2 1n lax + bi J .
J x+b a 2
9. r ( X2 dx Y = -; ( ax + b 2b ln lax + bl _ b 2 ) .
J(ax + b a ax + b
10. r x 2 dx = ( In lax + bl + 2b _ b 2 )
J(ax + b)3 a 3 ax + b 2(ax + b)2 .
r x 2 dx 1 ( 1
11. J( ax + b)" = a 3 - (n - 3)(ax + b)"-3 +
2b b 2 )
+ ( )( r 2 - ( )( r t (n =to 1, 2, 3).
n - 2 ax + b - n - 1 ax + b -
f dx 1 ax + b
12. x(ax + b) = -b ln x ·
f dx 1 a ax + b
13. x 2 (ax + b) = - bx + b 2 ln x ·
f dx ( 1 1 2 aX+b )
14. x2(ax + b)2 = -a b 2 (ax + b) + ab 2 x - b 3 1n x ·
f dx 1 x
15. 2 2 = - arctg-.
x +a a a
f dx 1 x 1 a - x
16. = -- argtgh - = -ln ( I x I < a ) .
x 2 - a 2 a a 2a a + x
f dx 1 x 1 x-a
17. 2 2 = -- argcotgh - = -ln (Ixl > a).
x - a a. a 2a x + a
(n =t= 1, 2).
18. f X2 +d x + c
2 2ax + b
= J(4ac - b 2 ) arctg J(4ac _ b 2 )
(4ac - b 2 > O),
586
2 h 2ax + b
argtg
J(b 2 - 4ac) J(b 2 - 4ac)
1 2ax + b - J(b 2 - 4ac)
ln
J(b 2 4ac) 2ax + b + J(b 2 - 4ac)
19. r 2 x dx = ln lax 2 + bx + ci - r 2 dx .
J x. + bx + c 2a 2a J x + bx + c
(4ac - b 2 < O),
(4ac - b 2 < O).
r dx 2ax + b
20. J(ax2 + bx + cr = (n - 1 )(4ac - b 2 )(ax 2 + bx + cr- 1 +
(2n - 3)2a r dx (n 9= 1).
+ (n - 1 )(4ac - b 2 ) J(ax 2 + bx + cr- 1
r x dx bx + 2c
21. J(ax2 + bc + cr = - (n - 1)(4ac - b 2 )(ax 2 + bx + cr- 1 -
b( 2n - 3) r _ dx
(n - 1)(4ac - b 2 )J ( ax 2 + bx + cr- 1 (n 9= 1).
r dx 1 x 2 . b r dx
22. Jx(ax2 +. bx + c) = 2c ln ax 2 + bx + c - 2cJ X2 + bx + c
(c * O).
7.4.2. Integrály iracionálních funkcí
Ve výrazech a 2 + x 2 a x 2 - a 2 je a > O. Ve výrazech ax 2 + bx + c
a 4ac - b 2 * O je a * O.
1. ax + b)' dx = ( 1) (ax + b)'+ 1 (a 9= O, b 9= O, r E R \ { -I}) .
J' r + -1 a
f r - a(r+l)x-b r+l
2. x(ax + b) dx - 2( )( ) (ax + b)
a r+l r+2
I , (a * O, r E R \ { - 1, - 2}) .
3. fJ(a 2 - x 2 ) dx = [x J(a 2 - x 2 ) + a 2 arcsin : ] (Ixl < a).
4. fx J(a 2 - x 2 ) dx = t J(a 2 - X 2 )3 = --i(a 2 - x 2 )J(a 2 - x 2 )
. (Ixl < a).
5. f J(a 2 - x 2 ) dx = J(a 2 _ x2) _ a ln a + J(a 2 - x 2 ) (Ixl < a).
x x
587
6. f:j(a2d x 2 ) = arcsm :
r x dx / ( 2 2 )
7. J:j(a 2 _ x 2 ) = -" a - x
8. ',Jt: dx 2) = _ x ,J(a 2 _ x 2 ) + a 2 arcsin x
J: a - x 2 2 a
9. f,J(x 2 + a 2 ) dx = [x ,J(x 2 + a 2 ) + a 2 argsinh : J.
10. fx ,J(x 2 + a 2 ) dx = t ,J(x 2 + a 2 )3 = -l(x 2 + a 2 ) ,J(x 2 + a 2 ).
f J(x 2 + a 2 ) dx / ( 2 2 ) a + J(x 2 + a 2 )
11. = V x + a - a ln .
x x
f dx . x x + J(x 2 + a 2 )
12. ,J( 2 2) = argsmh - = ln ·
x +a a a
(Ixl < a).
(Ixl < a).
-.
(Ix I < a).
r x dx / ( 2 2 )
13. J :j(X2 + a 2 ) = "x + a ·
f X2 dx x a 2 x
14. ,J( 2 2) = - ,J(x 2 + a 2 ) - - argsinh - =
x +a 2 2 a
= x ,J(x 2 + a 2 ) _ a 2 ln x + ,J(x 2 + a 2 ) .
2 2 a'
f dx _ _! . a _ _ a + J(x 2 + a 2 )
15. ,J( 2 2) - argsmh - ln ·
x x +a a x a x
r dx J(x 2 + a 2 )
16. JX 2 ,J(X 2 + a 2 ) = - a 2 x ·
17. f,J(x 2 - a 2 ) dx = [x ,J(x 2 - a 2 ) + a 2 argcosh : ] =
= t[ X J(x 2 - a 2 ) + a 2 ln (Ixl + J(x 2 - a 2 )] (lxl > a),
kde znaménko minus, resp. plus. platí pro x > q, resp. x < O.
18. fx ,J(x 2 - a 2 ) dx = t ,J(x 2 - a 2 )3 = -l(x 2 - a 2 ) ,J(x 2 - a 2 ) (Ixl > a).
588
f I ( X2 - a 2 ) dx a
19. " x = .J(x 2 - a 2 ) - a arccos
f: dx _ x _ [ Ix l + (X2 - a 2 ) ]
20. .j( 2 2) - argcosh - ln
x -a a a
r x dx / ( 2 2 )
21. JJ(x 2 _ a 2 ) = "x - a
f: X2 dx x a x
22. J( 2 2) = - .J(x 2 - a 2 ) + - argcosh - -
x -a 2 2 a
= {x J(x 2 - a 2 ) + a 2 ln [ Ixl + J 2 - a 2 ) ]}
23. rJ( 2 dx ) = InI2.J[a(ax 2 + bx + e)] + 2ax + bl (a > O).
J: ax + bx + c V a
1 2ax + b
= jargsinh .J( 2) (a > O, 4ae - b 2 > O).
va 4ae - b
1
= .Ja ln 1 2 ax + bl
1 . 2ax + b
= - / ( ) arcsln / ( 2 )
V -a V b - 4ac
(a < O, 4ae - b 2 < O).
r x dx (ax2 + bx + c) b r dx
24. JJ(ax 2 + bx + e) = a - 2a J (ax2 + bx + e)"
(Ixl > a).
(Ixl > a).
(Ix I > a).
(Ixl > a).
(a > O, 4ae - b 2 = O).
7.4.3. Integrály goniometrických funkcí
Všude se předpokládá, že c * o; m, n E N, r E R.
Integrály obsahujícÍ sinus:
1. fsin (ex) dx = - : cos (ex).
} sinn-l (ex) cos (ex) n - 1 }
2. sin n (ex) dx = - + sin n - 2 (ex) dx
ne n
f . ( ) sin (ex) x cos (ex)
3. x sIn ex dx = 2 - .
C C
(n > 1).
589
I n I
4. x n sin (ex) dx = - cos (ex) + X'-1 cos (ex) dx.
5. (sin (ex) dx = ex _ (ex)3 + (ex)5 _....
J- x 3 . 3 ! 5 . 5 !
Ý Sin (ex) 1 sin (ex) e f cos (ex) d
6. dx = - + . X
x n n - 1 x n - 1 n - 1 x n - 1
J; dx 1 ex
7. =-ln tg-.
sin (ex) e 2
r dx 1 cos (ex) n - 2 r dx
8. J inn (ex) = - c(n - 1) sin n - 1 (ex) + n - 1 J inn-2 (ex)
9. I dx 1 ( ex 1t )
1 + sin (ex) = e tg 2: + 4 ·
10. I1 :s :(ex) = > g( - : )+ :2 ln cos (e; - : ).
1-1. I x x = x cotg ( 1t _0 ex ) + ln sin ( 1t _ ex ) .
1 - sIn (ex) e 4 2 e 2 4 2,
I Si (ex) dx 1 ( 1t _ ex )
12. . = + x + - tg - + - .
1 + sIn (ex) - e 4 2
Integrály obsahující kosinus:
13. fcos (ex) dx = sin (ex).
} ( ) cosn -1 (ex) sin (ex) n - 1 } - 2 ( ) d
14. cos n ex dx = + cos n ex x
ne n
I ( ) cos (ex) x sin (ex)
15. x cos ex dx = 2 + .
e e
I xn sin (ex) n I
16. X' cos (ex) dx = e - x n - 1 sin (ex) dx.
17. (cos (ex) dx = ln !ex I _ (exy + (ex)4 _ ....
J- x 2.2! 4.4!
(cos (ex) dx = _ cos (ex) _ e (sin (ex) dx
18. J x n (n - 1)x n - 1 n - 1 J X'-1
590
,n > 1).
(n > 1).
(n > 2).
(n > 1).
19. i dx 1 (ex n)
= -ln tg - + -
cos (ex) e 2 4.
20. i dx 1 sin (ex) n - 2 i dx (n > 1).
cos" (ex) = e(n - 1) COS"-l (ex) + n - 1 COS"-2 (ex)
dx 1 ex
21. = - tg -
1 + cos (ex) e 2.
dx 1 ex
22. 1 - cos (ex) = - e cot g T .
f x dx x ex 2 ex
23. = - tg - + - ln cos - .
1 + cos (ex) c 2 e 2 2
24. f x dx . x ex 2 . ex
= --cotg- + -ln sln- .
1 - cos (ex) e 2 e 2 2
25. f ces (ex) dx = x _ tg ex .
1 + cos (ex) c 2
26. fcos(ex)dx = -x _ cotg ex .
1 - cos (ex) c 2
Integrály obsahující sinus a kosinus:
i dx 1 ( ex n)
27. = -ln tg - + - .
cos (ex) + sin (ex) e J2 2 - 8
Ii dx 1 ( n)
28. [cos (ex) + sin (ex)Y = 2e tg ex + 4 .
29. i cos (ex) dx x 1 . (viz 58).
() . ( ) = - + -ln Ism (ex) + cos (ex)1
cos ex + sIn ex 2 2e
30. i cos (ex)dx x 1 . (viz 59).
() . ( ) = - - -ln I m (ex) - cos (ex)1
cos ex - sIn ex 2 2e
31. i sin (ex) dx x 1 . (viz 60).
() . ( ) = - - -ln Ism (ex) + cos (ex)1
cos ex + sIn ex 2 2e
I
32. f sin (ex)dx x 1 . (Viz 61).
. = -- - -ln Isin (ex) - cos (ex)1
cos (ex) - sIn (ex) 2 2e
591
f cos (ex) dx 1 2 ex 1 I e
33. Js in (cx)[ 1 + cos (cx)] = - 4e tg 2 + 2e n tg-l
r cos (ex) dx 1 2 ex 1 ex
34. J Sin(cx)[1 _ cos (ex)] = - 4e cotg 2 - 2c ln t g 2 .
35. f sin (ex) dx = cotg 2 ( cx + 1t ) + ln tg ( ex + 1t )
J os (cx) [1 + sin (ex)] 4c 2 4 2c 2 4.
36. f sin (ex) di 1 2 ( ex 1t ) 1 ( ex 1t )
J os ( x) [1 - sin (cx)] = 4e tg. 2 + 4 - 2c ln tg 2 + 4 ·
} . 1
37. sin (cx) cos (cx) dx = - sin 2 (cx). .
2c
} . ( ) . ( ) sin ((CI - C 2) x) sin (( CI + C 2) x) (I 1 1 I)
38. S10 CIX S10 C2X dx = ( ) - ( ) CI =F C2 .
2CI- C 2 2CI+C2
J ' sin ((CI - C2) x) sin ((CI + C2) x) .
39. COS(CIX)COS(C2X)dx= 2( ) + 2( ) (Icll =F le 2 1).
CI - C2 CI + C2 '
40. f sin (CIX) cos (C2 X ) dx = - cos (CI+ C2i x) - cos (el - C2i x) (!ctI =F hl).
J 2 CI + C2 2 CI - C2
41. f sin ' (cx) cos (ex) dx = (1 ) sin'+ 1 (ex) (r =F -1).
J C r + 1
} 1 I
42. sin (cx) cos' (cx) dx = - ( I ) cos'+ 1 (ex). (r =F -1).
C r + 1
43. fSin" (e ) cos m (cx) dx =
sin n -1 (ex) cos m + I (CX) n - 1 }
= - ( )' + sin"-2 (ex) cos m (ex) dx =
en+m n+m
sinn+ I (cx) cos m - I (cx) m - 1 } .
= ( ) + sin" (ex) cos m - 2 (CX) dx (m, n > 1).
cn+m n+m
j . dx 1
44. . () () = -ln Itg (ex)l.
sIn cx cos ex C
f dx 1 f dx
45. Jsin (cx) cos" (ex) = c(n - 1) cos"- 1 (ex) + Jsin (cx) cos"- 2 (ex) (n > 1).
592
r dx 1. r dx
46. j sinn (ex) cos (ex) = - e(n - 1) sin n - I (ex) + js in n - 2 (ex) cos (ex)
(n > 1).
Y Sin 2 (ex) dx 1 1 ( 1t ex )
47. = -- sin (ex) + -ln tg - + - .
cos ( ex) e e 4 2
in2 (ex) dx sin (ex) 1 C dx
48. J cos n (ex) = e(n - 1) cos n - 1 (ex) - n - 1 j osn-2 (ex)
(sin n (ex) dx = _ sin n - I (ex) + fsin n - 2 (ex) dx
49. J cos (ex) e(n - 1) J cos (ex)
Y inn (ex) dx =
50. )
cosm(ex
sinn+ 1 (ex) n - m + 2 fsin n (ex) dx
= e(m - l)cos m - 1 (ex) - m - 1 J osm-2(ex)
sin n - 1 (ex) n - 1 Csin n - 2 (ex) dx
= - e(n - m) cos m - I (ex) + n - mJ cos m (ex)
sin n - 1 (ex) n :- 1 fsin n - 1 (ex) dx
= e(m - l)cos m - 1 (ex) - m - 1 J- cosm- 2 (ex)
51. fcos ((x) t x = ( COS (ex) + ln tg ex ) .
J- sIn ex e 2
Ccos 2 (ex) dx 1 . ( cos (ex) C dx )
52. J sin n (ex) = - n - 1 e sin n - I (ex) + js in n - 2 (ex)
Ccos n (ex) dx = cos n - 1 (ex) fcosn- 2 (ex) dx
53. J sin (ex) e(n - 1) + J sin (ex)
J cos n (ex) dx =
54. ( )
sin m ex
cos n + 1 (ex) n - m + 2 Ccos n (ex) dx
= - e(m - 1) sin m - 1 (ex) - m - 1 J-sin m - 2 (ex)
cos n - 1 (ex) n - 1 Ccos n - 2 (ex) dx
= e(n - m) sin m - I (ex) + n - mJ sin m (ex)
cos n - 1 (ex) n - 1 Ccos n - 2 (ex) dx
= - e(m - 1) sin m - 1 (ex) - m - 1 J- sin m - 2 (ex)
(n > 1).
(n > 1).
(m > 1),
(m * n, n > 1),
(m 1).
(n > 1).
(n > 1).
(m > 1),
(m =t= n, n > 1),
(m > 1).
593
Integrály obsahující tangens a katangens:
55. fg (ex) dx = - ln Icos (ex)l.
56. fgn(ex)dx = e(n 1) tgn-t (ex) - f g n-2 (ex)dx
Y gr (ex) dx 1 + 1
57. 2 ( ) = ( ) t gr ( ex )
cos ex e r + 1
58. r (d; = x + ln Isin (ex) + Cos (ex)l.
Ji g ex + 1 2 2e
59. r (d; = _ x + ln Isin (ex) - cos (ex)l.
Ji g ex - 1 2 2e
r tg (ex) dx r dx x 1 .
60. li g (ex) + 1 = 1 1 + 'cotg (ex) = 2 - 2e ln Ism (ex) + cos (ex)l.
J; t g (ex) dx f dx x 1
61. () = ( ) = - + -ln Isin (ex) - cos (ex)l.
tg ex - 1 1 - cotg ex 2 2e
62. fcot g (ex) dx = ln Isin (ex)l.
63. fcotg" (ex) dx = - r(n 1) cotg"-t (ex) - fcotg"-2 (ex) dx
Y cot gr (ex) dx' 1 + 1 ( )
64. = - cotg r ex
sin 2 (ex) c(r + 1)
f dx rtg (ex)dx
65. 1 1 + cotg (ex) li g (ex) + 1 .
r dx ftg(ex)dx
66. 1 1 - cotg (ex) - li g (ex) - 1 ·
7.4.4. J'ntegrály hyperbolických funkcí
1. fsinh (ex) dx = cosh (ex).
594
(n > 1).
(r * -1).
(n > 1).
(r * -1).
2. fCOSh (ex) dx = sinh (ex).
-3. r sinh 2 (ex) dx = sinh (2ex) _ x .
J 4e 2
4. rcos h 2 (ex) dx = sinh (2ex) + x .
J' 4e - 2
5. finh n (ex) dx =
1 n-l }
= - sinh n - 1 (ex) cosh (ex) - sinh n - 2 (ex) dx
en n
6. fCOSh n (ex) dx =
1 n-l }
= -sinh(ex)coshn- 1 (ex) + coshn- 2 (ex)dx
en ..
(n > 1).
(n > 1).
J; dx 1 ex 1 cosh (ex) - 1
7. = -ln tgh - = - ln =
sinh (ex) e 2 c sinh (ex)
1 sinh (ex) 1 cosh (ex) - 1
= - ln = - ln
e cosh (ex) + 1 2e cosh (ex) + 1
i dx 2
8. h ( ) = -arctge cx .
cos ex e
9. Lin::(ex)-
1 cosh (ex) n - 2 r dx
= - e(n - 1) sinh n - 1 (ex) - n - 1 J inhn- 2 (ex)
10. f os::(ex) =
1 sinh (ex) n - 2 r dx
= e(n - 1) coshn- 1 (ex) + n - 1 J osh n-2 (ex)
Ý COSh n (ex)
11. dx =
sinh m (ex)
(n > 1).
(n > 1).
595
1 cosh n - 1 (ex) n - 1 Y coshn- 2 (ex)
= + -- dx
e(n - m) sinh m - 1 (ex) n - m sinh m (ex)
1 coshn+ 1 (ex) n - m + 2 J; coshn (ex)
= - + dx
c(m - 1) sinh m - 1 (ex) m - 1 sinhm-2(ex)
1 cosh n - 1 (ex) n - 1 coshn - 2 (ex)
- + dx (m > 1, n > 1).
- - e(m - 1) sinh m - 1 (ex) m - 1 sinh m - 2 (ex)
t inhm (ex)
12. ( ) dx =
cosh n ex
1 sinh m - 1 (ex) m - 1 Ý Sinh m - 2 (ex)
= - dx (m 9= n, m > 1),
e(m - n) cosh n - 1 (ex) m - n cosh n (ex)
1 sinh m + 1 (ex) m - n + 2 1 sinhm (ex)
= - dx
e(n - 1) cosh n - 1 (ex) n - 1 coshn- 2 (ex)
1 sinh m - 1 (ex) m - t t inhm - 2 (ex)
+ dx (n > 1, m > 1).
e(n - 1) cosh n -1 (ex) n - 1 cosh n - 2 (ex)
13. I x sinh (ex) dx = x cosh (ex) - sinh (ex).
e e
14. I x cosh (ex) dx = x sinh (ex) - cosh (ex).
e c
15. fgh (ex) dx = : ln Icos (ex)l.
16. fcotgh (ex) dx = ln Isinh (ex)l.
17. fghn(ex)dx= e(n l) tghn-l(ex)+ fghn-2(ex)dx
18. fcotghn (ex) dx =
= - (1 ) cotghn-1 (ex) + rcotghn-2 (ex) dx
e n - 1 J'
19. finh (bx) sinh (ex) dx =
1
= b 2 _ e 2 [b sinh (ex) cos (bx) - e cosh (ex) sinh (bx)]
(rn 9= n, n > 1),
(m > 1),
(n > 1),
(n.> 1).
(n > 1).
(b 2 * e 2 ).
596
20. fCOSh (bx) cosh (ex) dx =
1
=. 2 2 [b sinh (bx) cosh (ex) - c sinh (ex) cosh (bx)] (b 2 =t= c 2 ).
b - e
21. fCOSh (bx) sinh (ex) dx =
1
= 2 2 [b sinh (bx) sinh (ex) - e cosh (bx) cosh (ex)] (h 2 =t= c 2 ).
b -e
22. fsinh (ax + b) sin (ex + d) dx =
a c
= 2 2 cosh (ax + b) sin (ex + d) - 2 2 sinh (ax + b) cos (ex + d).
a +e a +e
23. finh (ax + b) cos (ex + d) dx =
= 2 a 2 cosh (ax + b) cos (ex + d) + 2 c 2 sinh (ax + b) sin (ex + d).
a +e a +e
24. fCOSh (ax + b) sin (ex + d) dx =
= 2 a 2 sinh (ax + b) sin (ex + d) - 2 e 2 cosh (ax + b) cos (ex + d).
a +e a +e
25. fcosh.(ax + b) cos (ex + d) dx =
= 2 a 2 sinh(ax+b)cos(cx+d)+ 2 e 2 cos h (ax+b)sin(cx+d).
a +e a +e
7.4.5. Integrály exponenciálních funkcí (e =1= O; n E N)
1. fe cx dx = e CX .
f eCX
2. xecxdx = "?(cx - 1).
3. f x 2 eCX dx = eCX ( x 2 _ 2x + 2. ) .
e e 2 e 3
597
4. fxnecxdx = X'ecx - fxn-l ecxdx.
Y ecx dx ex (CX)2
5. = ln Ixl + - + - + ... .
x 1.1! 2.2!
Y ecx dx 1 ( eCx Y ecx dX )
6. = -- 1 + e 1
x n n - 1 x n - x n -
7. fe cx ln x dx = (e cx ln x - f CXxdX )
} eC x _
8. e CX sin (bx) dx = 2 2 [e sin (bx) - b cos (bx)].
e + b
9. le cx cos (bx) dx = 2 e CX 2 [c cos (bx) + b sin (bx)].
J e + b
io. }cx sin n x dx =
e CX sin n - 1 x n(n - I) }
= 2 2 (c sin x - n cos x) + 2 2 e Cx sin n - 2 x dx.
e + n e + n
11. fe cx cos n x dx =
e CX cosn- 1 X n(n - I) }
= (e cos x + nsinx) + ecxcosn- 2 xdx.
e 2 + n 2 e 2 + n 2
7.4.6. Integrály logaritmických funkcí (x > O; nE N, r E R)
1. ftn x dx = x ln x - x.
2. JIn xY dx = x(In X)2 - 2x ln x + 2x.
3. JIn x)" dx = x(In x)" - n JIn X)"-l dx.
dX (ln X)2 (ln X)3
4. -- = ln Iln xl + ln x + + + ... .
ln x 2 . 2! - 3. 3 !
598
(n > 1).
(x > O).
..
r dx x 1 r dx
5. J(ln x)" = - (n - 1)(ln X)"-1 + n - 1 J(ln X)"-1
6. I x: ln x dx = x r + 1 ( ln x - ( 1 ) 2 )
r+1 r+1
I xr+l(lnxr n I
7. X:(ln xr dx = - xr(ln xr- 1 dx
r+l r+1
J ln xy dx = (ln xy+ 1
8.
x r + 1
r x r dx x: + 1 r + 1 r x r dx
9. J(ln x)" = - (n - 1 )(ln x)" -1 + n - 1 J(ln X)"-1
10. I dx = ln Iln xl.
J ln x
I x dx = Ý e-Y d y,
11. kde y = -(r + l)lnx
ln x y
12. fsin (ln x) dx . [sin (ln x) - cos (ln x)J.
13. fcos (ln x) dx = [sin (ln x) + cos (ln x)J.
( 1 ( fecx dX )
14. r cx ln x dx = c e CX ln x - J x ·
7.4.7. Integrály cyklometrických funkcí (c =1= O; n E N)
1. larcsin x dx = x arcsin x + J(c 2 _ x 2 ).
Ji: C c
2. I x rcsin x dx = ( x 2 _ c 2 ) arcsin x + x J(c 2 _ x 2 ).
C 2 4 c 4
I X x 3 X x 2 + 2c 2
3. x 2 arcsin - dx = - arcsin - + J(c 2 x 2 ).
C 3 c 9
4. larccos x dx = x arccos x - J(c 2 _ x 2 ).
Ji: C C
(n > 1).
(r =t= - 1) .
(r * -1).
(r =t= -1).
(n > .1).
(r * -1).
599
5. I x arccos x dx = ( x 2 _ c 2 ) arccos x _ X J(e 2 _ x 2 ).
e 2 4 e 4
I X x 2 X x 2 + 2e 2
6. x 2 arccos-dx = -arccos- - J(e 2 - x 2 ).
e 3 e 9
7. farctg x dx = x arctg x - ln (c 2 + x 2 ).
Je e e 2
f X e 2 + x 2 X ex
8. x arctg - dx = arctg - - -.
e 2 e 2
9. f x 2 arctg x dx = x 3 arctg x _ cx 2 + c 3 ln (c 2 + x 2 ).
c 3 e 6 6
' f X xn+l X e I xn+ 1 dx
10. x n arctg - dx = -- arctg - - -- .
c n + 1 e n + 1 c 2 + x 2
11. farccotg x dx = x arccotg x + ln (c 2 + x 2 ).
Je e e 2
f x e 2 + x 2 X ex
12. x arccotg - dx = arccotg - + -.
c 2 e 2
f x x 3 X ex 2 e 3
13. x 2 arccotg - dx = - arccotg - + - - -ln (e 2 + x 2 ).
e 3 e 6 6
f x x n + 1 X l x n + 1 dx
14. x n arccotg -- dx = -- arccotg - + 2 2 '
e n+l e n+lc+x
7.4.8. Integrá"ly hyperbolometrických funkcí (c # O)
1. fargsinh x dx = x argsinh x - ,J(x 2 + c 2 ).
Je e e
. 2. fargcosh x dx = x argcosh - ,J(x 2 - c 2 ).
J' c e
} x xc'
3. argtgh - dx = x argtgh - + -ln le 2 - x 2 1.
e c 2 .
4. fargcotgh dx = x argcotgh x + ln Ix 2 - c 2 1.
J' c c 2
600
7.5. URČITÝ INTEGRÁL
7.5.1. Z ákladní pojmy
N ewt on ova defi nice urči tého integrál u
K danému integrandu přísluší nekonečně mnoho primitivních funkcí.
Jsou-li F a G libovolné dvě primitivní funkce příslušné integrandu f, platí
.
F(b) - F(a) = G(b) - G(a)
pro libovolná čísla a a b z definičního oboru integrandu.
(N e\1,'tonovým) určitým integrálem spojité filnkce f promě.nné x v mezich
od a do b nazýváme přírůstek
ff(X) dx = F(b) - F(a),
který také zapisujeme ve tvaru
[F(x)I nebo F(X):,
kde F je primitivní funkce k funkci f na intervalu (a, b), přičemž F'(a + ) = f(a),
F'(b -) = f(b); interval (a, b) nazýváme integračnim oborem a číslo a, resp. b
dolní, resp. horni (integrační) mezí.
Výpočet určitého integrálu se takto převádí na určení primitivní funkce,
do níž se za proměnnou dosadí postupně horní a dolní mez integrálu a výsledné
hodnoty (v uvedeném pořadí) se odečtou.
Riemannova součtová definice určitého integrálu
Je-li dáno n + 1 čísel Xo, Xl' ..., X n tak, že
- 00 < a = Xo < Xl < ... < X n = b < + CIJ ,
říkáme, že je dáno děleni. Dn intervalu (a, b). Jestliže {Dn} je taková posloup-
nost dělení, že !
Y(Dn) = m {Xi - Xi-I} O
I
pro 11 . 00
a existuje limita integrálních součtů:
n
lim a(Dn) = lim L f( ;) (Xi - Xi - 1)
n-oo n-oo i= 1
(X i - I < i < Xi) nezávisle na volbě posloupnosti {Dn} a bodů i' pak se tato
601
limita nazývá Riemannův nebo Cauchyův-Riemannův určitý integrál [stručně
určitý integrál nebo jen integrál] funkce f na intervalu (a, b> a značí se stejně
jako Newtonův integrál symbolem S: f(x) dx.
Dále definujeme
ff(x) dx = O,
ff(x)dX = - ff(X)dX
(a > b).
Existuje-li Newtonův určitý integrál S: f(x) dx, resp. Riemannův určitý
integrál S: f(x) dx, říkáme, že funkce f je integrovatelná v N ewtonově, resp.
,.
v Riemannově smyslu. Je-li funkce integrovatelná v Newtonově nebo Rieman-
nově smysl , říkáme stručně, že je integrovatelná.'
Každá po částech spojitá funkce (a tedy také každá spojitá funkce) na inter-
valu (a, b> je na tomto intervalu integrovatelná v Newtonově i Riemannově
smyslu a platí, že určitý integrál S: f(x) dx v Newtonově smyslu se rovná
určitému integrálu S: f(x) dx 'V Riemannově smyslu.
Základní vlastnosti určitého integrálu
Pro integrovatelné funkce f a g platí
ff(x) dx = ff(x) dx + ff(X) dx (c E (a, b»,
f[J(x) + g(x)]dx = ff(x)dX + fg(X)dX,
fCf(X)dX = C ff(X)dX.
Přík lad :
f(2X' + 3x 2 )dx = [X2 + X3]: = (9 + 27) - (1 + 1) = 34.
ft'
7.5.2. V ěty o střední hodnotě integrálního počtu
První věta o střední hodnotě integrálního počtu
.
Jestliže funkce f a g proměnné x jsou spojité na intervalu (a, b), funkce g
je nezáporná, popř. nekladná na intervalu (a, b), pak existuje takové číslo
602
E <a, b), že platí
ff(x) g(x) dx =f( ) fg(X)dX
neboli
ff(X) g(x) dx = f(a + 9(b - a)) f g(x) dx
(O < 9 < 1).
Speciálně pro g(x) = 1 je
ff(X)dX = (b - a)f( )
neboli
ff(X) dx = (b - a) f(a + 9(b - a))
(O < 8 < 1).
Střední hodnotou funkce y = f(x) v mezích" od a do b nazýváme číslo
1 l b
f( ) = b _ a /(x)dx.
"
Kvadratickou střední hodnotou funkce y = f(x) v mezích od a do b nazývárr!e
číslo ·
k = J{ b a f[J(x W }dx.
Druhá věta o střední hodnotě integrálního počtu
Jestliže funkce'f a g proměnné x jsou spojité na intervalu <a, b), funkce g
je na to to intervalu nezáporná a nerostoucí, pak existuje takové číslo
E <a, b), že platí
ff(X) g(x) dx = g(a) ff(X) dx.
Je-li funkce g na intervalu <a, b) nezáporná a neklesající,. platí
ff(x)g(X)dX = g(b) ff(x)dX.
603
Určitý integrál jako funkce integrační meze
U rčitý integrál spojité funkce f s proměnnou horní, resp. dolní integrační
mezí je spojitá funkce této integrační meze:
ff(X) dx = F(x) - F(a), .
resp.
ff(X)dX = F(b) - F(x).
Derivace určitého integrálu podle proměnné meze
.Jestliže funkce f proměnné x je spojitá, platí
d: [ff(t)dt] = f(x),
dd x [ff(t)dt] = - d: [ff(t)dt] = -f(x).
.
7.5.3. Přibližné metody pro výpočet určitých integrálů
Obdélníková metoda (obr. 358)
. f bf(X) dx b - a (Yo + YI + Y2 + ... + Yn-I)' Yo = f(a),
a n
f bf(X) dx b - a (YI + Y2 + .... + Yn), Yn = f(b),
a n
kde n je počet stejně dlouhých částečných intervalů, na které je rozdělen
interval (a, b).
Při pevném čísle n a ryze monotónní funkci Y = f(x) na intervalu (a, b)
je při použití obdélníkové metody absolutní hodnota chyby
b-a
AI = IYn - Yol.
n
Lichoběžníková metoda (obr. 359)
f b b-a
f(x)dx (Yo + 2Yl + 2Y2 + ... + 2Yn-l + Yn)'
2n '
a Yo = f(a),
kdt,; n je počet stejně dlouhých částečných intervalů.
Yn = f(b),
604
Při použití lichoběžníkové metody je absolutní hodnota chyby
(b - a)3
A 2 = 2 M 2'
12n
jestliže, pro x E (a, b> platí Ij'''(x)1 < M 2'
:t. J
n=8 b x
Obr. 358. Obdélníková metoda
y
(o Y, Y2 ((b)
O Q n=5 b x
Obr. 359. Lichoběžníková metoda
Tečnová metoda (obr. 360)
l b 2(b - a)
f(x)dx (YI + Y3 + Ys + ... + Yn-I)
a n
(n je kladné sudé číslo).
Při použití tečnové metody je absolutní hodnota chyby
(b - a)3
A3 = 2 M 2 ,
24n
jestliže pro x E (a, b> platí
If"(x)1 < M 2.
y
Yf
Y s
Obr. 360. Tečnová metoda
o a
b .x
n=6
Simpsonova metoda [parabolická metoda]
l b b "
f(x) dx - a (Yo + 4Yl + 2Y2 + 4Y3 + 2Y4 + ... + 2Yn-2 + 4Yn-t + Yn)'
a 3n
kde n = 2k (k E N) je počet stejně dlouhých částečných intervalů.
605
Při použití Simpsonovy metody je absolutní hodnota chyby
L1 _ (b - a)5 M4
4 - 2 880 k 4 '
jestliže pro x E (a, b) platj Ij'(4)(x)1 < M 4'
Při klad:
f 1t/2
cosxdx = [sinx] ;/2 = 2.
- Ttl 2
Pomocí Simpsonovy metody při n = 2 dostaneme
f Tt/2 n 2n
cosxdx -(O + 4.1 + O) = - . 2,094.
- Tt/2 6 3
Newtonová-Cotesova metoda
Jestliže funkce Y = f(x) je spojitá reálná funkce na intervalu (a, b), platí
i b b-a
f(x) dx (ConYo + C1nYl + C 2n Y2 + ... + CnnYn),
a n
kde
_ (- 1 r - k i n t( 1. - 1) (t - 2)... (t - n)
C kn - ( ) , dt
k! n-k! o. t-k
(n E No; k = O, 1, 2, ..., n).
Odhady zbytků viz např. v [199].
Integrace pomocí rozvoje v řadu
Je-li možno funkci, jejíž integrál máme najít, rozvinout v stejnoměrně
konvergentní mocninnou řadu f(x) = ao + a1x + a 2 x 2 + ... s poloměrem
konvergence r, platí
ff(X)dX = ao fdX + a 1 fXdX + a2 fx 2 dX + ...,
pokud
lal < r,
Ibl < r
(r je poloměr konvergence).
606
7.5.4. Grafická integrace
Při konstrukci grafu primitivní funkce F(t) = J f(x) dx, příslušné
dané křivce y = f(x) na intervalu (a, b >, nahradíme křivku y = f(x) stup-
ňovou funkcí se "stupni" rovnoběžnými s osou x (obr. 361). Body Ai zvolíme
tak, aby vždy oba šrafované křivkové trojúhelníčky nad křivkou a pod ní,
umístěné mezi dvěma sousedními "stupni", měly přibližně stejný obsah.
Konečně na osu y naneseme pořadnice "stupňů" a body B I , B 2 , ..., které
takto dostaneme, spojíme s pólem P = [ -1, O]. K těmto spojnicím vedeme
rovnoběžky, počínajíc v bodě Co, který je pravoúhlým průmětem bodu Ao
do osy x, tak, aby CoC\ II PEl' C l c 2 11 PE 2 , C 2 c 3 11 PE 3 ,.... Lomená čára,
kterou takto dostaneme, je tečnovou lomenou čarou k hledané integrální
křivce, která se integrální křivky dotýká v bodech Co, Dl' D 2 , D 3 , ... . Integrální
křivku samu nakreslíme podle křivítka.
PC-I,O]
8 7
Obr. 361. Grafická integrace
7.5.5. Nevlastní integrály
Definice
Jestliže funkce f je integrovatelná na každé konečném intervalu (a, b>
a existuje vlastní limita
lim f 'f(X) dx,
t- + 00
a
resp.
I cx) ff(X) dx,
. 607
pak tuto limitu nazýváme konvergentním nevlastním integrálem s nekonečnými
mezemi [nevlastním integrálem vlivem intervalu] a píšeme
i+ "'f(x) dx,
resp.
f '" f(x) dx.
Jestliže uvedené limity neexistují, říkáme, že nevlastní integrál diverguje
[je divergentní].
Konvergují-li integrály
f",f(X)dX,
1+ '" f(x} dx,
říkáme, že integrál
L+: f(x)dx
konverguje [je konvergentní], a píšeme
L+: f(x)dx = f",f(X)dX + i+"'f(X)d X .
Neexistuje-li aspoň jeden z integrálů J 00 f(x) dx a S: 00 f(x) dx, říkáme, že
integrál S : f(x) dx diverguje [je divergentní].
Jestliže funkce f je integrovat lná na každém konečném intervalu (a, b>
a neohraničená na okolí bodu b, resp. na každém konečném intervalu (c, b>
a neohraničená na okolí bodu a (přičemž v obou případech je a < c < b)
a existuje vlastní limita
c ff(X)dX,
resp.
c ff(X) dx,
pak tuto limitu nazýváme konvergentním nevlastním integrálem vlivem funkce.
Jestliže uvedené limity neexistují, říkáme, že nevlastní integrály divergují
[jsou divergentní].
608
Příklad 1:
f l dx i 1 dx [ Xl -" ] 1 [ 1 ti -" ]
- = lim - = lim = lim - .
o x" t O t x" t O 1 - n t t O 1 - n 1 - n
Protože
t 1 -"
lim
t O 1 - n
existuje pro 1 - n > O neboli n < 1 a m hodnotu O, je
f l dx = 1
oxn l-n
(n < 1).
Přík lad 2:
1
--1
i + 00 dx i b dx [ X l - n J b bn - 1
- = lim - = lim - lim
1 X' b + 00 1 x" b + 00 1 - n 1 b + 00 1 - n
Tato limita existuje pro n - 1 > O => n > 1. Je tedy
i + oo dx _ _ 1
(n > 1).
1 x: n-l
Přík lad 3:
Nevlastní integrál
f l dx
o x
diverguje, neboť
lim f l dx = lim [ln x ],1 = lim ( -ln t) = + 00 .
t O t X t O t O.
7.5.6. Přehled některých určitých integrálů
V tomto článku všude m, nE N, , b, c, p, rE R, y = 0,577215664 90...
(Eulerova konstanta),
f +oo
r(x)= o e-'ř- 1 dt
(x > O),
609
přičemž
r(x + 1) = xr(x) (x > O),
r(t) = J1t, r(l) = 1, r(n + 1) = n!,
1t
r(x)r(l-x)= . () (O<x<l),
sin 1tX
je funkce gama,
B ( ) = r(p) r(q)
p, q r(p'+ q)
je funkce beta,
(p > O, q > O)
( 1t ) i ft/2 dqJ
K=Fk-=
, 2 o (1 - k 2 sin qJ)1/2'
resp.
E = E( k, ;) = f: 1 2(1 - k 2 sin 2 (j))1/2 d(j)
je úplný eliptický integrál prvního, resp. druhého druhu (O < k < 1).
Přehled některých určitých [vlastních] integrálů
1. i lt sin (px) dx = 1 - os (p1t) (p 9= O);
o p
speciálně
i ft 1 + ( - 1 r + 1
sin (nx) dx = .
o n
i ft sin (p1t)
2. cos (px) dx =
o P
(p * O);
speciálně
f:cos(nx)dx = O.
i 1t / 2 dx _ 1t
3. o a 2 cos 2 x + b 2 sin 2 x 2ab
f C + 2ft { O
4. 1 sin (mx) sin (nx) dx = 1t
(a > O, b > O).
(m =t= n),
(m = n).
610
5. f+2"COS (mx) cos (nx) dx = {
6. f+2"sin (mx) cos (nx)dx = O.
7. ("sin (mx) sin (nx) dx = ("cos (mx) cos (nx) dx = { ( (m 9= n ) ),
Jo. Jo 2 1t m - n .
71 I O (m - n je sudé číslo),
8. (sin (mx) cos (nx) dx = 2m
Jo m 2 _ n 2 (m - n je liché číslo).
1 71 / 2 . 2 d l Tt/2 2 d l. 3 · 5 · .. . . (2n - 1) 1t
9. sIn n X X = cos n X X = - .
o o. 2 . 4 . 6 . ... . (2n) 2 '
speciálně
("/2 sin 2 x dx = ("/2 cos2 X dx = 1t .
Jo Jo 4
1 71 / 2 . 2 + 1 d 1 71/2 2 + 1 2 . 4 . 6 · ... . (2n)
10. sIn n X X = cos n X dx = .
o o 1 . 3 . 5 . ... . (2n + 1)
(m 9= n),
(m = n).
1 71 / 2 . 2 2 d l. 3 . 5 . ... . (2m - 1). 1 . 3 . 5 . ... . (2n - 1) 1t
11. sIn m X cos n X X = - .
o 2 . 4 . 6 . ... . (2m + 2n) 2
1 71 / 2 1 m' n'
12. sin 2m + 1 X COS 2n + 1 X dx = - ( ..)
O - 2 m+n+l!
13. J: / 4 tg X dx. = ! ln 2.
l ft/ 2 dx
14. = 1
o 1 + cos x .
1 1 ln (1 + x) 1
15. 2 dx = 81t ln 2.
o x + 1
16. J: / 4 1n (1 + tg x) dx = in ln 2.
17. ( 1 dx
Jo 1 + 2x cos a + x 2
a
(O < a < t1t).
2 sin a
611
i 2b 1tb2
18. J(2bx - x 2 ) dx = -.
o 2
J I a2 - 1
19. a X dx = (a > O, a * 1).
- 1 a ln a
10 1t cos (sx) 1tb s
20 dx =
. 1 - 2b cos x + b 2 1 - b 2
(s E No, Ibl < 1).
1 1t/ 2 sin xiI + k
21. / ( dx = - ln
o V 1 - k 2 sin 2 x) 2k 1 - k
1 1t/2 cos x 1
22. / ( 1 k 2' 2 ) dx = - arcsin k
o V - sIn x k
[1t/2 sin 2 x 1
23. Jo J(1 _ k 2 sin 2 x) dx = k 2 (K - E)
(Ikl < 1).
(Ikl < 1).
(O < k < 1)
1 1t/2 'cOS2 X 1
24. ( 2 2) dx = _ 2 [ E - ( 1 - k 2 ) K ]
o 1 - k sin x k
(O < k < 1).
Přehled některých nevlastních integrálů
(1 dx (Jn)r( )
25. Jo J(1 - x a ) - arC a)
speciálně
r 1 dx 1t
Jo J(1 - x 2 ) = 2 .
1 + 00 dx
26. ( )
o l+xx a
(a * O);
1t
(O < a < 1);
sin (a1t)
speciálně
f + 00 dx
Jo (1 + x) Jx = n.
27. f J[(x - )(b _ x)] = n.
612
i a . dx ft
28. o .J(a 2 - x 2 ) = 2
i + 00 dx ft
29. o a 2 + x 2 = 2a
(a > O).
(a > O).
i a X2 3fta 2
30. o .J(ax _ x 2 ) dx = 8
31. i +ooxre-oxdx = r(r + 1)
ar+ 1
o
speciálně
(a > O).
(a > O, r > - 1);
i + oo n!
xne-axdx =-
o (/'+1
i + oo
o xNe-Xdx=n!.
(a > O),
"
32. io +ooxre-OX2dx = r(r: 1 /2 )
2a(r + 1)
(a > O, r > - 1);
speciálně
i + 00 2k - 2 1 . 3 . 5 . ... . (2k - 1) J n
x eaxdx=
o 2 k + 1 a(2k + 1 )/2
(a > O, k E No),
i + 00 k'
X2k+ 1 e- ax2 dx = .
o 2a k + 1
(a > O, k E No),
i + oo 11t
-a 2 x2 d V
e x=-
o 2a
i + oo
o e- x2 dx = t J'Tt,
i + oo ln
2 -a 2 x2 d V
x e x =-
4a 3
o
(a > O) (Laplaceův-Gaussův integrál).
(a > O).
f +oo Jn
33. e - a 2 x2 + bx dx = _ e b2/ (4a 2 )
-00 a
(a > O).
613
3iJ. 1 + 00 X dx = 1t 2 .
o eX - 1 6
1 + 00 x
35. o eX + 1 dx = 12 .
1t 2
36. L+ooe-xlnxdx = flnllnxldx = -y.
37. i 1 ln x dx = 1t 2 .
ox-l 6
38. i 1 ln x d x = _ 1t 2 .
o x + 1 12
i 1 ln x _ 1t 2
2 dx - .
o x-I 8
i 1 ln ( 1 + x) _ 1t
40. 2 dx - - ln 2.
o x+l 8
41. f (ln : Y dx = r(a + 1)
i + 00 sin (ax) { 1t/2
42. dx = /
o x -1t2
i b cos (ax)
43. dx = + 00
o x
i + oo cos (ax) - cos (bx) b
44. dx = ln-
o x a
j 1t/2 (Ial < 1),
45. i+ oo sin x cos (ax) dx = 1t14 (Ial = 1),
o x O (Ial > 1).
46. L+oo s : dx = L+oo ců.jxx dx = J; (Fresnelovy integrály).
i + oo i +oo J 1t
47. o sin (x 2 ) dx = o cos (x 2 ) dx = 2 (Fresnelovy integrály).
i + oo x sin (bx) 1t
48. dx = (sgn b) - e -Iabl.
o a 2 + x 2 2
39.
(-ľ<a< +(0).
(a > O),
(a < O);
(b > O; integrál je divergentní);
(a > O, b > O).
614
i + co sin 2 (ax) _ 1t
49. o x 2 :- 2 lal.
50. i "/\n (sin x) dx = i "/2 1n (cos x) dx = - 1t ln 2.
o o 2
i 1t 1t2 ln 2
51. x ln (sin x) dx = - .
o 2
52. i "/\in x ln (sin x) dx = ln 2 - 1.
o \
53. f/\n (tg x) dx = O.
i + co b
54. e -ax sin ( bx ) dx =
o a 2 + b 2
55. i + e-ax cos ( bx ) dx = a
o a 2 + b 2
i + 00 e- ax sin (bx) b
56. dx = arctg-
o x a
i 1t / 2 1 r(p) r(r)
57. sin 2 p-l x COS 2r - 1 X dx = - ( ) = ! B(p, r)
o 2rp+r
(a > O).
(a > O).
(a > O).
(p > O, r > O);
speciálně
(viz též 9 až 12).
58. i 1xa (1 _ x)bdx = 2 i lx2a+l(1 _ x 2 fdx = r(a + l)r(b + 1) =
o o r(a + b + 2)
= B(a + 1, b + 1).
59. i + 00 x a - 1 dx = 1t
o 1 + b x . a1t
b sin -
b
(p > O)
(O < a < b).
i + co dx a
60. 2 -
o 1 + 2x cos a + x sin a
(O < a < l1t) .
615
1 11 a + J(a 2 b 2 )
61. In (a + b cos x) dx = 1t ln 2
o
fn { 21t ln a
62. Jo ln (a 2 - 2ab cos x + b 2 ) dx = 21t ln b
(o < b < a).
(O < b < a), .
(O < a < b).
7.5.7. Vyjádření některých integrálů řadami
Integrální sinus [integrálsinus, sinusintegrál] (obr. 362)
l x sin t x 3 x 5
Si x = - dt = x' - + -
o t '3.3! 5.5!
x 7
- + -
7.7! ...-
00 x2n+l
= n o (-Ir (2n + 1)(2n + I)!
(x E R).
y
2
I I
I I
_... I- Ci :
.....""" 4 -- . -- t ---
J ..... -
-1 .....-, -- " ....... ...... X
4
Si .....
,.... --
I I
I
" I
o
-1
o
2 3 4 5 6 7 X
-z
Obr. 362. Integrální sinus
Obr. 363. Integrální kosinus
kde
Integrální kosinus (integrál kos inu s, kos in us integrál] (obr. 363)
i + 00 cos t 1. x 2
Ci x = - - dt = 'Y + ln x - '- - +
x t 2 2!
1 x 4 1 x 6
+ - - - - =-- + ... =
4 4 6 6!
00 1 x2n
= 'Y + ln x + L (-Ir - -
. n = 1 2n (2n)!
( 1 1 1 )
'Y = lim 1 + - + - + ... + - -lnn = 0,57721566490...
n oo 2 3 n
(x > O),
je tzv. Eulerova konstanta.
616
Poznámka:
Výpočet integrálů typu
fX-II cos x dx, fX-II sin x dx (n E N)
lze integrací per partes převést na výpočet integrálů Si x a Ci x.
Modifikovaná integrální exponenciální funkce (obr. 364)
I x et 1 x 2 1 x 3
Ei x = - dt = }' + ln Ixl + x + - - + - - + ... =
-00 t 2 2! 3 3!
00 1 x:
= y + ln lx I + L - -, (x < O),
n=l n n.
kde 'Y je Eulerova konstanta.
y
1
,.. ,. x
::: tj(-x )
J
.
1
r
I ti
I I
I
, ,
- 1 f- 2- . -
..... - - "") fo- - "4 X
I
I
y
2
o
-1
o
-1
-z
-2
{
Obr. 364. Modifikovaná integrální
exponenciální funkce
Obr. 365. Integrální logaritmus
ln tegrální 10 gari tm us [in tegrá Ilo gari tm us, 10 gari trn us in tegrá I]
(obr. 365)
I x dt 1 (ln X)2 1 (In X)3
li x = - = y + ln Iln xl + ln x + - + - + ... =
o ln t 2 2 ! 3 3 !
00 1 (In x)"
= y + ln Iln xl + L - , (O < x < 1),
n=l n n.
kde y je Eulerova konstanta.
Opakovanou integrací lze integrály typu Jeli u- n du (n E N) převést na
integrály typu Jeli U-I du a substitucí u = ln t na li x.
617
Funkce chyb [chybová funkce, error function,
pravděpodobnostní integrál, integrál chyb] lobr. 366)-
2 l x
erf x = J'Tt o e- t2 dt,
.....
kde
l x X3 x 5 X 7
- t 2 d .
e t = x - + - + ...
o 3.1! 5.2! 7.3!
(x E R +)
je tzv. Laplaceův-Gaussův integrál. Pro velká čísla x platí asymptotický rozvoj
l x - t 2 J 1t e - x 2 ( 1 1 . 3 1 . 3 . 5 )
e dt = - - - 1 - + ( 2 ) 2 - ( 2)3 +... ,
o 2 2x 2x 2x 2x
který je semidivergentní řadou (viz (201]).
r.
1
. :......... v -+-t-f- I
-f-- :7'
...
I erf I I
- P - - I I
I
/1 - - -rl-
I /
v. I T i
/, - .- - I I
/ i I I
Obr. 366. Funkce chyb
°1 5
o
°1 5
1,5
2 x
Funkce chyb erf se vyskytuje při výpočtu poruch šířících se podél linek
přenosu elektrické, energie.
Doplňková funkce chyb [doplňková chybová funkce,
co mp leme nt ary error function, doplňkový pravděpodobnostní
in t e g r á I, do plň k o v Ý in t e g r á I c h y b ]
2 f +oo
erfc x = 1 - erf x = J'Tt x e - t 2 dt
e - x 2 [ 1 1 . 3 1 . 3 . 5 ( ) n - 1 (2n - 3)!! ]
h 1 - 2X2 + (2x2)l - (2X 2 )3 + ... + -1 (2X2)"-t +... .
618
Gaussova funkce chyb [Gaussůy pravděpodobnostní integrál]
1 f x
CP(x) = e- t2 / 2 dt.=
J(21t) -00
1 1 ( 1 x 3 1 x 5 1 x 7 )
= 2: + J(21t) x - 2.3 T! + 2 2 .5 2! - 2 3 .7 3! + ...
(x E R).
-3
a)
b)
Obr. 367. Gaussova funkce chyb
Protože funkce cp je podrobně tabelována, používá se při výpočtech vztahu
x
erf Ji + 1 = 2 (x).
V obrázku 367a je graf funkce
Ip(x) = 1 e - x 2 f2
J(21t)
a obsah šrafované plochy se rovná CP(xo). Graf funkce cp je v obr. 367b.
7.5.8. Použití ur itých integrálů
Úmluva:
Pro jednotnost značení a terminologie zavedeme v tomto článku pro
uvažované veličiny tyto symboly a názvy:
m, = mil je délková hmotnost (kg m - 1),
ms = miS - obsahová hmotnost (kgm- 2 ),
mv = mlV - objemová hmotnost (kgm- 3 ),
619
kde m je hmotnost (kg),
I - délka (m),
S - (plošný) obsah (m 2 ),
V - objem (m 3 ).
Poznamenejme, že veličina m, se také někdy nazývá lineární hmotnost
a veličina ms má v technické praxi zpravidla název plošná hmotnost. Poměr
hmotnosti m a objemu V se ve fyzice a v technické praxi nazývá měrná hmotnost
nebo hustota a označuje se (!. Název objemová hmotnost a symbol (lv se v tech-
nické praxi používají pro střední hustotu nespojitě rozložené látky.
Použití určitých integrálů v geometrii
Výpočet obsahu části roviny
1. Obsah S části roviny ohraničené grafy funkcí y = f(x) a y = g(x),
spojitých na intervalu (Xl' x 2 ), přičemž v každém bodě X E (Xl' X 2 ) platí
O < g(x) < f(x), resp. f(x) < g(x) < O, a příslušnými úsečkami na přímkách
x = Xl a X = X 2 (obr. 368):
S = f:2[J(X) - g(x)J dx,
S = - f:2[J(X) - g(x)J dx.
Speciálně pro g(x) = O platí'
S = rXj(x) dx, resp. S = - r X2 f (x) dx
JXl JXJ
(obr. 369).
resp.
y
y
o
x 2 X
X f
o
/f
Xz
/
Obr. 368. Obsah části roviny
Obr. 369. Obsah části roviny
620
Obsah S plochy ohraničené křivkou y = f(x) a příslušnými úsečkami
na přímkách x = Xl' X = x 2 a na ose x tedy je "
s = f: 2If (x)1 dx ,
neboť v elementární geometrii se obsah plochy definuje jako kladné číslo.
Příklad:
Jaký obsah má část roviny ohraničená grafem funkce
y = fo(x 3 - 2X2 - 15x)
a příslušnými úsečkami na přímkách x = -4 a x = 4 a na ose x (obr. 370)?
Obr. 370. Graf funkce
y = -M X3 - 2X2 - 15x)
Nulové body:
Xl = -3,
X 2 = O,
X3 = 5,
přičemž pouze body Xl' X2 leží uvnitř integračního oboru < -4,4).
S = f:4 If (x)1 dx = t-:f(x) dx + f /(x) dx + 1 4f (x) dx -
= f -3(X3 - 2X2 - 15x)dx + f O (X3 - 2X2 - 15x)dx +
10 -4 10 - 3
+ r 4 (x 3 _ 2X2 - 15x) dx =
10 Jo
= [ X4 _ 2x 3 _ 15X 2 J -3 + [ X4 _ 2x 3 _ 15X 2 J O +
10 4 3 2 -4 10 4 3 2-3
+ [ x 4 _ 2x 3 _ 15X 2 J 4 =
10 4 3. 2 o
_ 1 ( 117 40 ) 1 11 7 1 296
- 10 -4 + 3 + 10 4 + - 10 3 -
= 1 4 6 plošných jednotek.
621
2. Obsah části roviny ohraničené grafem funkce dané parametricky
rovnicemi x = qJ(t), y = t/J(t) [funkce qJ, t/J jsou spojitě diferencovatelné,
liJ(t) * O, t/J(t) = O (t E (tI' t 2 »)] a příslušnými úsečkami na ose x a na přím-
kách x = qJ(t 1 ) a x = qJ(t 2 ):
I t 2
S = t/J(t) liJ(t) dt .
tJ
Obsah části roviny ohraničené grafem funkce dané parametricky rovnicemi
x = qJ(t), y = t/J(t) [funkce qJ, t/J mají spojitou derivaci, qJ(t) > O, .jJ(t) * O,
t (tI' t 2 )] a příslušnými úsečkami na ose y a na přímkách y = t/J(t 1 ) a y =
= tfJ(t 2 ):
I t 2
S = qJ(t) .jJ(t) dt.
tJ
. 3. Obsah části roviny ohraničené grafem spojité a nezáporné funkce, dané
v polárních souřadnicích rovnicí (1 = f(qJ) a průvodiči (lI = f(qJl) a (12 =
= f(qJ2) bodů grafu dané funkce, přičemž O < qJl < qJ < qJ2 < 21t (obr. 371):
1 1 ({J2
S = - (12 dqJ
2 ({JJ
(Leibnizův vzorec pro rovinnou výseč).
Obr. 371. Obsah rovinné výseče
o
4. Obsah části roviny ohraničené grafem funkce dané parametricky
rovnicemi x = qJ(t), y = t/J(t) [funkce qJ, t/J mají spojitou derivaci, liJ(t) * O]
a průvodiči OP l a OP 2 bodů P l , P 2 grafu:
1 I t 2 ·
S = - (qJt/J - liJt/J) dt
2 tt
(Leibnizův vzorec pro rovinnou výseč).
Délka oblouku křivky [rektifikace křivky]
1
Jestliže množina M délek všech možných lomených čar vepsaných oblouku
křivky c je ohraničená, pak délkou oblouku křivky nazýváme supremum
množiny M a říkáme, že křivka c je schopná rektifikace [rektifikovatelná].
622
1. Délka s části rovinné křivky, ohraničené body P I a P 2 (předpokládá se
spojitost prvních derivací daných funkcí na integračním oboru):
s = I2 J[1 - (: Y]dX
pro křivku Y = f(x) a body P I [Xl' f(XI)]' P 2 [X2, f(X2)];
s = f2 J[1 + (:; Y]dY
pro křivku x = g(y) a body P 1 [g(Yl), YI], P 2 [g(Y2), Y2];
f t 2
s = J(liJ2 + .jJ2) dt
tJ
pro křivku x = qJ(t), Y = t/J(t) a body P I [qJ(t l ), t/J(t l )], P 2 [ qJ(t 2 ), t/J(t 2 )];
s = f:'2J[e 2 + ( : YJd = f2 J[1 + e 2 ( :; Y]d e
pro křivku (l = f(qJ) a body PI[(lb qJI], P 2 [e2, qJ2]'
2. Délka s části pro s t o r o v é křivky, ohraničené body P 1 a P 2 (předpokládá
se spojitost prvních derivací daných funkcí na integračním oboru):
s = f l2 J(q,2 + .j,2 + X 2 ) dt
tJ
pro křivku x = qJ(t), Y = t/J(t), z = X(t) a body P I [qJ(t l ), t/J(t l ), X(t l )],
P 2 [ qJ( t 2)' tfJ( t 2)' X( t 2) ].
Obsah pláště rotačního tělesa [komplanace]
Obsah Q pláště rotačního tělesa (předpokládá se spojitost prvních derivací
daných funkcí na integračním oboru):
Qx = 2 I2y J[ 1 + ( : Y ] dx
při rotaci křivky Y = f(x) [f(x) > O, X E (Xl' X2)] kolem osy X;
Qy = 2 f:'x J[ 1 + (:;Y ] dy
při rotaci křivky x = g(y) [g(y) > O, Y E (YI, Y2)] kolem osy Y;
f t 2
Qx = 21t t/J J(liJ2 + .jJ2) dt
tJ
..
623
při rotaci křivky dané parametricky rovnicemi x = q>(t), y = tjJ(t) [q,(t) =F O,
tfJ(t) > O, tE(t 1 ,t 2 )] kolem osy x,
Qy = 21t 1 /2 q> J(cp2 + .j,2) dt
h
při rotaci křivky aané parametricky rovnicemi x = qJ(t), y = tfJ(t) [qJ(t) > O,
.jJ(t) 9= O, t E (tI' t 2 )] kolem osy y;
Qx = 2 f: 2e sin q> J[ e 2 + ( ::Y J dq>,
resp.
Qy = 2 f: 2e cos q> J[e 2 + ( :: YJdq>
při rotaci křivky dané v polárních souřadnicích rovnicí (! = f( qJ) (O < li' 1 <
< li' < qJ2 < 1t, resp. -1t/2 qJl < li' < qJ2 < 1t/2) kolem osy x, resp. y.
Objem rotačních těles [kubatura]
1. Objem V rotačního tělesa (předpokládá se spojitost prvních derivací
daných funkcí na integračním oboru):
= f:2[J(X)Y dx
při rotaci křivky y = f(x) [f(x) > O, X E (Xl' x 2 )] kolem osy X;
= 1t 1 Y2 [g(y)] 2 dy
YI
při rotaci křivky X = g(y) [g(y) > O, Y.E (Yl' Y2)] kolem osy y;
V x = 1t i '2 t/J2q> dt
tI .
při rotaci křivky dané parametricky rovnicemi X = qJ(t), y = tjJ(t) [tjJ(t) = O,
ljJ(t) 9= O, t E (tI' t 2 )] kolem osy x;
= 1t i '2 q>2t/J dt
tJ
při rotaci křivky dané parametricky rovnicemi X = qJ(t), y = tjJ(t) [qJ(t) > O,
.jJ(t) 9= O, t E (tI' t 2 >] kolem osy y;
f «J2 ( dg )
= 7t (12 sin 2 qJ - cos qJ - (1 sin qJ dli',
«JI dqJ
624
resp.
f (/J2 ( dg )
V, = 1t Q2 cos 2 q> dq> sin q> + r cos q> dq>
(/JI
při rotaci kř'ivky dané v polárních souřadnicích rovnicí g = f( cp) (O < ({J. <
< cp < ({J2 < 1t/2, resp. -1[/2 < CP. < cP < CP2 < 1t/2) kolem osy x, resp. y.
2. Objem rotačního tělesa, jehož podstavy jsou v rovinách x = x., x = X 2
a jehož obsah řezu rovinou kolmou k ose rotace je S(x):
1 S2
w= Fds,
SI
Použití integrálního počtu v technické' mechanice
Práce
f. S 2
W = F ds,
SJ
kde F je velikost síly působící po úsečce s krajními body Sl a S2.
Statické momenty
Úmluva:
Předpokládá se spojitost prvních derivací daných funkcí na příslušných
integračních oborech.
1. tatický moment Sx' resp. Sy oblouku homogenní rovinné křivky
v souřadnicové rovině xy vzhledem k ose x, resp. y (délková hmotnost m, =
= 1 kg m - · ) :
1 X 2
Sx = y J(l + ,y'2) dx,
XJ
1 X2
Sy = x J(1 + y'2) dx
XI
pro křivku y = f(x) (x E (Xl' x 2 »;
I t 2
Sx ' t/1 J(q, + .jJ) dt,
tJ
I t 2
Sy = ({J J(q, + .jJ) dt
tJ
625
pro křivku danou parametricky rovnicemi x = qJ(t), y = t/J(t) (t E (ti' t 2 »)
Sx = f: 2e J(e 2 + :: ) sin d ,
Sy = f:' 2e J[e 2 + ( : rJCOS d
pro křivku danou v polárních souřadnicích rovnicí (l = f(qJ) (li' E «({JI, qJ2».
2. Statický moment SXY' resp. Sxz, resp. SyZ oblouku homogenní prostorové
křivky vzhledem k rovině xy, resp. xz, resp. yz (délková hmotnost
m, = 1 kg m - I):
I t 2
Sxy = X J(liJ2 + .jJ2 + X 2 ) dt,
tJ
I t 2
Sxz = '" J(liJ2 + .jJ2 + X2) dt,
tJ
I t 2
SyZ = ({J J(liJ2 + .jJ2 ,+ X2) dt
tJ
pro křivku danou parametricky rovnicemi x = qJ(t), y = t/J(t), z = X(t)
(t E (t I' t 2 > ).
3. Statický moment Sx, resp. Sy homogenního rovinného obrazce ohra-
ničeného grafem funkce y = f(x) [f(x) > O] a příslušnými úsečkami na ose x
a na přímkách x = Xl a x = X 2 vzhledem k ose x, resp. y (obsahová hmotnost
ms = 1 kgm- 2 ):
1 1 X2
Sx = - y2 dx,
2 XJ
1 X2
Sy = xydx.
XJ
4. Statický moment Sx, resp. Sy homogenního rovinného obrazce ohra-
ničeného grafy funkcí y = f(x), . y = g(x) [O < g(x) < f(x), X E (Xl' X2)]
a příslušnými úsečkami na přímkách X = Xl a X = X2 vzhledem k ose x,
resp. y (obsahová hmotnost ms = 1 kg m - 2):
1 1 X2
Sx = - {[f(X)]2 - [g(X)]2} dx,
2 XJ
Sy = {2 X [J(X) - g(x)] dx.
626
5. Statický moment SyZ homogenní rotační plochy vytvořené při rotaci
grafu funkce y = f(x) [f(x) > O, X E (Xl' x 2 )] kolem osy x vzhledem k ro-
vině yz (o bsahová hmotnost ms = 1 kg m - 2) :
SYZ = 21t f: 2 X f (x)J{1 + [J'(x)] }dx
(SXY = Sxz = O).
6. Statický moment SyZ homogenního rotačního tělesa, jehož plášť se vy-
tvoří při rotaci grafu funkce y = f(x) [f(x) > O] kolem osy X a které má
podstavy v rovinách X = Xl a x = X2, vzhledem ,k rovině yz (objemová
hmotnost mv = 1 kgm- 3 ):
I X2
SyZ = 1t xy2 dx
XI
(SXY = Sxz = O).
Těžiště
1. Souřadnice těžiště T oblouku homogenní rovinné křivky y = f( )
(x E (Xl' x 2 »):
f:2xJ(1 + y'2)dx Sy
XT =
f:2J(1 + y'2)dx
f:2y J(l + y'2) dx Sx
YT = [X2J(1 + y'2)dx --;
JXI
s
kde s je délka uvažovaného oblouku (délková hmotnost m, = 1 kg m - I)
a Sx, Sy jsou příslušné statické momenty.
2. Souřadnice těžiště T oblouku homogenní prostorové křivky x = q>(t),
y = t/J( t), z = X( t) (t E (t l' t 2 ) ) :
I t 2
X J( liJ 2 + .jJ? + X 2 ) dt
ti S yz
x T = I t 2 . = ----;-
J(liJ2 + .jJ2 + X2) dt
ti
627
l t2 rjJ .J(<řJ 2 + tb 2 + X 2 ) dt
tJ S xz
YT = l t2 J(<řJ2 + tb 2 + X2) dt =---;-'
tJ
l t2 ({J J(<řJ 2 + tb 2 + X2) dt
tJ S xy
- --
T - t2 - ,
I J(<iJ2 + .jJ2 + x 2 ) dt S
tJ
kde s je délka uvažovaného oblouku (délková hmotnost m, = 1 kg m - I)
a SXY' Sxz, SyZ jsou příslušné statické momenty.
3. Souřadnice těžiště T homogenního rovinného obrazce ohraničeného
grafem funkce Y = f(x) [f(x) = O] a příslušnými úsečkami na ose x a na
přímkách x = Xl a x = X 2 :
r X2 xy dx
J XJ _ Sy
XT = I X2 S '
ydx
XJ
r X2 y2 dx
J XJ Sx
YT = 2 r X2 Y dx - S'
JXJ
kde S je obsah uvažovaného rovinnéhq obrazce (obsahová hmotnost ms =
= 1 kg m - 2) a Sx, Sy jsou příslušné statické momenty.
4. Souřadnice těžiště T homogenního rovinného obrazce ohraničeného
grafy funkcí y = f(x) a y = g(x) [O < g(x) < f(x), X E (Xl' x 2 )] a příslušnými
úsečkami na přímkách x = Xl a x = X 2 :
f2 X [J(x) - g(x)] dx Sy
XT = f: 2 [J(x) _ g(x)J dx - s'
r X2 {[J(x)Y - [g(x)Y} dx
J Xl Sx
YT = r X2 [J(x) _ g(x)] dx = s'
JXl
kde S má význam jako v odstavci 3 a Sx, Sy jsou příslušné statické momenty.
628
5. Souřadnice těžiště T homogenního rotačního tělesa, jehož plášť se vytvoří
při rotaci grafu funkce y = f(x) [f(x) > O, X E (Xl' X2>] kolem osy x:
i X2
xy2 dx
Xl
x T = i X2
y2 dx
Xl
SYZ
V'
YI' = O, ZT = O,
kde V je objem uvažovaného tělesa (objemová hmotnost mv = 1 kg m - 3)
a SyZ je statický moment.
Jde-li o křivky v parametrickém, popř. polárním vyjádření, pak se souřad-
nice těžiště uvažovaného geometrického útvaru vypočtou jako podíly pří-
slušných statických momentů a délky příslušného oblouku, popř. obsahu
příslušného rovinného obrazce, popř. obsahu pláště příslušného tělesa, popř.
objemu příslušného tělesa.
Momenty setrvačnosti (nauka o pevnosti)
1. Moment setrvačnosti IX' resp. lY' resp. lz oblouku homogenní rovinné
křivky vzhlede k ose x, resp. k ose y, resp. k počátku (délková hmotnost
m, = 1 kg m - I):
lx = i X2y2 J(l + y'2)dx,
XI
ly = i X2X2 J(l + y'2) dx,
Xl
lz = f: 2 (X 2 + y2) J(l + y'2) dx
pro křivku y = f(x) (x E (Xl' x 2 »;
I t 2
1 x = t/J2 J( <iJ2 + .jJ2) dt ,
t 1
I t 2
I}. = qJ2 J(<iJ2 + .jJ2) dt ,
ti
I t 2
lz = (qJ2 + t/J2) J(<iJ2 + .jJ2) dt
ti
629
pro křivku danou parametricky rovnicemi x = qJ(t), y = t/J(t) (t E (tI' t 2 »;
lx = f "J2(/ sin2 q> ,J((/ + Q'2) dq>,
lpI
ly = f "'2 Q2 cos 2 q> ,J(Q2 + Q'2) dq> ,
lpI
I z = f "'2 Q2 ,J(Q2 + Q'2) dq>
lpI
I
pro křivku danou v polárních souřadnicích rovnicí (l = f( qJ) (qJ E (qJ I' qJ 2> ).
2. Moment setrvačnosti I x' resp. ly, resp. I z oblouku homogenní prostorové
křivky vzhledem k ose x, resp. y, resp. z (délková hmotnost m, = 1 kg m - I):
,
I x = J I2(1/I2 + X 2 ) ,J( 2 + tÍ1 2 + X 2 ) dt ,
tI
ly = J t2(q>2 + X2) ,J( 2 + tÍ1 2 + X2) dt,
tI
lz = f2(q>2 + 1/12) ,J( 2 + tÍ1 2 + X2) dt
pro křivku danou parametricky rovnicemi x = qJ(t), y = t/J(t), z = x(t)
(t E (t I' t 2> ).
3. Moment setrvačnosti I x' resp. ly, resp. I z homogenního rovinného obrazce
ohraničeného grafem funkce y = f(x) [f(x) > O] a příslušnými úsečkami
na ose' x a na přímkách x = Xl a X = X2 vzhledem k ose x, resp. k ose y, resp.
k počátku (obsahová hmotnost ms = 1 kgm- 2 ):
l l x 2
I x = - y3 dx ,
3 XI
ly = rX2x2y dx,
JXI
rX2 ( y3 )
lz = lx. 3 + x 2 y dx.
4. Moment setrvačnosti I x' resp. ly, resp. I z homogenního rovinného obrazce
ohraničeného grafy funkcí y = f(x) a y = g(x) [O < g(x) < f(x), XE (x b X2>]
630
a příslušnými úsečkami na přímkách x = Xl a x = X 2 vzhledem k ose x,
resp. k ose y, resp. k počátku (obsahová hmotnost ms = 1 kg m - 2):
l l X2
Ix = - {[j>(X)]3 - [g(X)]3} dx,
3 Xl
I X2
ly = x 2 [j'(x) - g(x)Jdx,
Xl
1= = lx + ly .
5. Moment setrvačnosti I x homogenní rotační plochy vytvořené při rotaci
grafu funkce y = f(x) [f(x) > O, X E (Xl' x 2 > J kolem osy x vzhledem k ose X
(obsahová hmotnost ms = 1 kgm- 2 ):
Ix = 21t 1 2 [J(xW J{l + [f'(X)J2} dx.
6. Moment setrvačnosti lx homogenního rotačního tělesa, jehož plášť se
vytvoří při rotaci grafu funkce y = f(x) [f(x) > O] kolem osy x a které
má 'lodstavy v rovinách X = Xl a X = x 2 , vzhledem k ose x (objemová hmot-
nost mv = lkgm- 3 ):
1t l x 2
lx = - [f(X)J4 dx .
2 Xl
7.6. KŘIVKOVÝ INTEGRÁL
7.6.1. Křivkový integrál po oblouku rovinné křivky
Jsou-li P(x, y), Q(x, y) spojité funkce na rovinné oblasti D 2 , v níž
leží křivka C, daná parametricky rovnicemi x = f(t), y = g(t), t E (tA' t B »,
pak integrály
J B [P(x, y) dx Je = l IB P(J(t), g(t)) f'(t) dt ,
A tA
J B [Q(x, y) dy Je = l IB Q(J(t), g(t)) g'(t) dt
A tA
se nazývají křivkové integrály po oblouku rovinné křivky C v mezích od A do B.
Hodnota křivkového integrálu nezávisí na volbě souřadnicové soustavy ani
631
na volbě parametrického vyjádření. Závisí však na integrační cestě (tj. na
oblouku křivky C). Je-li C k(ivka C s opačnou orientací, pak platí
f)P(x,y)dxJe = - f)P(X,y)dX J e ,
f)Q(x, y) dy Je = - f: [Q(x, y) dy Je ·
Jestliže C je orientovaná křivka s počáte.čním bodem A a koncovým bodem B
a hodnota integrálu
f:[P(x,y)d y + Q(x,y)dyJe
závisí jen na volbě bodů A, B, a nikoli na křivce spojující body A a B, říkáme,
že integrál nezávisí na integrační cestě.
Jsou-li P, Q, op/oy, oQ/ox spojité funkce na jednoduše souvislé rovinné
oblasti Q2' pak nutná a postačující podmínka, aby integrál
f: [P(x, y) dx + Q(x, y) dy Je
nezávisel v oblasti Q2 na integrační cestě, je, aby na oblasti Q2 byla splněna
podmínka
ap oQ
oy ox .
Jsou-li P, Q spojité funkce na oblasti Q2' pak nutná a postačující podmínka,
aby integrál
f:[ p(x, y) dx + Q(x, y) dy Je
nezávisel v oblasti Q2 na integrační cestě, je, aby na oblasti Q2 existovala taková
funkce qJ(x, y), že
P(x, y) dx + Q(x, y) dy
je jejím totálním diferenciálem (tzv. Schwarzova podmínka).
Je-li C kladně orientovaná uzavřená křivka vzhledem k oblasti Q2 (tj. tak
orientovaná křivka,. že probíháme-li křivku souhlasně s její orientací, leží
4-
o bla-st vlevo), pak místo J píšeme .
632
Obsah rovinného obrazce
S = t t (x dy - y dX)e ,
kde C je hraniční křivka dané oblasti.
Příklad 1:
Vypočtěme křivkový integrál
f)(x y + l)dx + xdyJe
po oblouku paraboly y = 2X2 ohraničeném body A[O, O] a B[2, 8 J.
Při explicitním tvaru křivky lze za parametr zvolit jednu z neznámých.
Zvolme tedy za parametr neznámou x, takže y = 2x 2 , dy = 4x dx. Dostaneme
1 2 (x.2x 2 + 4x 4 + x. 4x) dx = 44-fs.
Příklad 2:
Vypočtěme křivkový iQtegrál z příkladu 1 po úsečce na přímce y , 4x,
ohraničené body A[O, O] a B[2, 8].
Dostaneme dy = 4 dx, takže
f)(x y + l)dx + xdyJe = f(X.4X + 16x 2 + x.4)dx = 91t.
7.6.2. Křivkový integrál po prostorové křivce
Jsou-li P, Q, R, spojité funkce v prostorové oblasti Q3, v níž leží
křivka C, daná parametricky rovnicemi x = f(t), y = g(t), z = h(t) (te«(-t, tB»)'
pak integrály
J B f. tB
[P(x, y, z) dX]e = P(f(t), g(t), h(t)) f'(x) dt ,
A tA
J B f. tB
.( [Q(x, y, z) dy Je = c< Q(J(t), g(t), h(t)) g'(t) dt ,
. J B [R(x, y, z) dz Je = f. IB R(J(t" g(t), h(t)) h'(t) dt
A tA
se nazývají křivkové integrály po oblouku prostorové křivky C v mezích od A do B.
633
Mají-li funkce P, Q, R spojité parciální derivace prvního řádu na jednoduše
souvislé prostorové oblasti (23' pak nutná a postačující podmínka, aby integrál
f) P(x, y, z) dx + Q(x, y, z) dy + R(x, y, z) dz Je
nezávisel v oblasti Q3 na integrační cestě, je, aby byly zároveň splněny tyto
p'odmínky (tzv. Schwarzovy podmínky integrovatelnosti):
oP
oy
oQ
-
ox '
ap oR
oz - cx '
oQ aR
oz - oy '
7.6.3. Křivkový integrál vek toru
Vektorová funkce
F = P( x, y); + Q( x, y) i ,
popř. vektorová funkce
F = P(x, y, z); + Q(x, y, z) i + R(x, y, z) k
určuje vektorové pole. .
Je-li rovnice křivky C dána ve vektorovém tvaru r = r(t) (t E (tA' t B », pak
křivkový integrál
f:(F dr)e ,
.
kde dr = ; dx + j d y, resp. dr = ; dx + J d y + k dz, se nazývá křivkový in-
tegrál vektoru F po křivce C v mezích od A do B.
Příklad:
Je dáno silové poie
1
F = - yl + xi + k .
z + 1
Jakou práci W = F dr je třeba vynaložit, ab se hmotný bod v silovém poli
dostal podél šroubovice
r = (a cos t); + (a sin t)i + ctk
z bodu p. [a, O, O] do bodu P 2 [ a, O, 21tc] (c E N)?
634
Z rovnice šroubovice plyne
x = a cos t , Y = sin t , z = ct ,
dx = - a sin t dt , d y = a cos t dt ,
z = c dt .
Je tedy
dr = [(...:. a sin t) I + (a cos t) j + ck] dt .
Vypočteme integrační meze:
y sin t
- = - = tg t ,
x cos t
Y
t = arctg - + k1t
x
(k E Z) .
Pro bod P 1 platí
O
tI = arctg O + k1t (k E Z) /\ tI = - => tI = O .
c
Pro bod P2 platí
21tc
t 2 = arctg O + k1t (k E Z) /\ t 2 = - => t 2 = 21t .
C
Křivkový integrál má tedy tvar
W = (2" [ ( -a sin t); + (a cos t) J + 1 Ic ] .
J o ct + 1
. [( - a sin t) I + (a cos t) j + ck] d t =
= C 27t ( a 2 sin2 t + a 2 cos 2 t '+ c ) dt =
Jo - ct + 1 .
= 21ta 2 + ln (21tc + 1).
7.7. MNOŽNÉ [n-\ROZMĚRNÉ] INTEGRÁLY
7.7.1. Dvojné [dvojrozměrné] integrály
,
Nechť z = f(x, y) je funkce dvou proměnných na uzavřené rovinné
oblasti (dále budeme mluvit jen o oblasti) Q2 = (a, b) x (c, d). Jestliže
intervaly (a, b) a (c, d) rozdělíme na podintervaly Xi' Yj (i = 1, 2, ..., m;
j = 1, 2, ..., n) a vytvoříme integrální součet
Gij = Lf(x i , Yj) Xi Yj ,
i,j
635
kde f(Xi' Yj) je funkční hodnota z v libovolném bodě Pij [ Xi' Yj]' Xi E Xi'
Yj E Yj' pak existuje-li limita integrálních součtů:
lim (] ij
... oo. n oo
nezávisle na volbě podintervalů Xi' Yj (i = 1, 2, ..., m; j = 1, 2, ..., n) a bodů
Pij[X i , Yj]' označujeme ji
fI2 f(x, y) dS
a nazýváme dvojným l dvojrozměrným] integrálem funkce f přes oblast D 2 .
Je-li Q2 libovolná ohraničená rovinná oblast, sestrojíme uzavřený obdélník
M :::> Q2 a definujeme funkci g(x, y) = f(x, y) pro [x, y] E D 2 a g(x, y) = O
pro [x, y] E M\D 2 . Dvojný integrál přes oblast D 2 definujeme vztahem
_ fI/(x, y) dS = ffMg(x, y) dS .
Funkce f(x, y), pro niž existuje dvojný integrál
fI; f(x, y) dS ,
se nazývá integrovatelná. Každá spojitá funkce f na oblasti Q2 je na této oblasti
integrovatelná.
Geometricky dvojný integrál z nezáporné funkce f vyjadřuje objem
tělesa ohraničeného rovinnou oblastí D 2 v souřadnicové rovině xy, přísluš-
nými úsečkami na rovnoběžkách s osou z, procházejícími body hranice
oblasti Q2' a částí plochy z = f(x, y), příslušnou oblasti Q2 (obr. 372).
l 1 = f(x,y)
y
Obr. 372. Význam dvojného integrálu
Jestliže plocha z = f(x, y) protíná souřadnicovou rovinu xy v oblasti Q2'
pak je nutno při určování objemu rozdělit oblast D 2 na takové podoblasti,
aby na nich bylo bud' f(x, y) > O, nebo f(x, y) < O. Hledaný objem je pak
součtem absolutních hodnot příslušných dílčích dvojných integrálů.
636
Pro z = f(x, y) = 1 dává hodnota dvojného integrálu
S = fL2dS
obsah oblasti D 2 .
Výpočet dvojného integrálu (převedení dvojného integrálu
na dvojnásobný integrál)
Jestliže f je integrovatelná funkce na oblasti D 2 , jejíž hranice je tvořena grafy
funkcí y = gl (x), Y = g2(X) [gl (x) < g2(X), X E (a, b)] a příslušnými úseč-
kami na přímkách x = a, x = b (obr. 373), pak platí.
JI i b [i 92(X) , ]
f(x, y) dS = f(x, y) dy dy.
02 a 91(X)
Podobně, má-li oblast D 2 hranici tvořenou grafy funkcí x = h1(y), X = h 2 (y)
[hl(Y) < h 2 (y), Y E (c, d)] a příslušnými úsečkami na přímkách y = c, y = d
(obr. 374), pak platí
JI f(x, y) dS = i d [i "2(),) f(x, y) dX ] dy ·
02 C hl(Y)
l
l
o A
Q ;;: Y
b - y=g2(X)
X 8
Obr. 373. výpočet dvojného integrálu
s mezemi Yi = gi(X) (i = 1,2)
o C d
Č ' y
I '/
C O
,r =h,(y)
Obr. 374. Výpočet dvojného integrálu
s mezemi Xi = hJy) (i = 1,2)
Má-li oblast D 2 hranici tvořenou grafy funkcí (l = gl(qJ), (l = g2(lfJ)
[O < gl(qJ) < g2(qJ), qJ E (qJl' qJ2)] (obr. 375), lze výpočet dvojného integrálu
fL/(x, y) dS
převést na výpočet dvojnásobného integrálu
i <P2 [i 92 (C'p) ]
f({l cos qJ, (l sin qJ) (l d{l dqJ.
<Pl 9d<p)
637
Příklad:
Vypočtěme objem koule x 2 + y2 +, Z2 < r 2 .
Stačí určit objem osminy koule v prvním oktantu pro x > 0, y > O a z > O,
neboť koule je souměrné těleso (obr. 376). Platí
V = JI f(x,y)dS, .
8 02
kde
z = f(x, y) = J(r 2 - x 2 _ y2).
V ypočteme in tegrační meze:
.
Proměnná x probíhá od O do J(r 2 - y2), což plyne z rovnice koule pro
z = O, tj. z rovnice kruhu x 2 + y2 < r 2 . v souřadnicové rovině xy.
9=g2((')
f I
R 2
I
I.
l: Pz
O
o
Obr. 375. Výpočet dvojného integrálu
s polárními mezemi (li = gJq» (i = 1,2)
Obr. 376. Výpočet objemu osminy
koule
Proměnná y probíhá od O do r.
Je tedy
V i r [i J<r2-Y2) ]
"8 = o o J(r 2 - x 2 y2) dx dy.
Zavedeme substituci
x = J(r 2 - y2) sin qJ ,
dx = J(r 2 - y2) cos li' dli'
a dostaneme nové integrační meze:
Pro x = O je qJ = O a pro x. = J(r Ž - y2) je qJ = 1[/2. Po substituci máme
V i r {i ft/ 2 }
"8 = o o J[r2 - (r 2 - y2) sin 2 cp - l] J(r 2 - y2) COS cp dcp dy =
= fJf:12 J[(r 2 - y2)(1 - sin 2 cp)] J(r 2 - y2) cos cp dCP} dy =
638
= fIJ:/ 2 (r 2 - y2) cos 2 lp dlp ] dy =
= JJ(r 2 -l { + !sin(2lp)]f 2dY =
= i '(r 2 - y2) 1t dy = 1t [ r 2y _ l ] r _ 7t
o 4 4 3 o 6
Objem koule tedy je
V = 17tr3.
Použití dvojných integrálů
O významu integračních mezí viz na str. 637.
1. Obsah 8 rovinného obrazce (uzavřené rovinné oblasti) Q2 v souřadni-
cové rovině xy:
Obecně platí:
s = JI2 dS ,
v kartézských souřadnicích
f b (f 92(%» ) f d (f, h2(Y) )
8 = dy dx = dx dy
a 91(%) c ht<y)
a v polárních souřadnicích
f «J2 (f 92(f/J) )
8 = g dg dqJ.
«JI 91(f/J)
2. Obsah 8 0 části plochy o rovnici z = f(x, y), jejíž průmět do souřadni-
cové roviny xy má obsah 8:
Obecně platí (y je odchylka tečné roviny k plošnému elementu a souřadni-
cové roviny xy)
fI d8
8 0 =
02 cos Y ,
v kartézských souřadnicích
f X2 [f. 9 (X) ]
8 0 = J(fx2 + h 2 + l)dy dx
XI 91(X)
639
a v polárních souřadnicích
i lp2 [f. '2(lp) ]
So = .J(flp2 + (12f(/ + (12) de dli'.
lpi 'l(lp)
3. Statický moment rovinné oblasti Q2 vzhledem k ose x, popř. y:
Sx = fl/ dS ,
Sy = fL2XdS,
v kartézských souřadnicích
1 X2 (f. 92 (X) )
Sx = y dy dx,
XI 91(X)
1 X2 (f. '2(X) )
S, = x dy dx
XI 'I(X)
a v polárních souřadnicích
f. lp2 (f. '2(lp) )
Sx = e 2 de sin li' dli' ,
lpi Ih(lp)
f. lp2 (f. '2(lp) )
S, = e 2 de cos li' dli' .
lpi 111 (lp)
4. Moment setrvačnosti rovinné oblasti D 2 vzhledem k ose x, popř. y:
Obecně platí
Ix = fL2 ldS ,
ly = fL2X2 dS,
v kartézských souřadnicích
1 X2 (f. 'I2(X) )
= y 2 dy dx,
XI 9t(X)
1 X2 (f. 92 (X) )
4= x 2 dy dx
XI 91(X)
640
.
a v polárních souřadnicích
i (fJ2 (i 92 «(fJ) )
lx= g3dg sin 2 epdep,
lpi 9 1((fJ)
i (fJ2 (i 92 «(fJ) )
ly = g3 dg cos 2 qJ dqJ .
lpi gl«(fJ)
5. Moment setrvačnosti rovinné oblasti Q2 vzhledem k počátku:
Obecně platí
Ip = fL2r2 dQ2 ,
v kartézských [ortonormálních J souřadnicích
i X2 [f. g2 (X) ]
Ip = (x 2 + y2)dy dx
XI gl(X)
a v' polárních souřadnicích
i (fJ2 (f. g2 «(fJ) )
1 p = . (! 3 dg dep.
lpi gJ((fJ)
6. Moment setryačnosti ,lq rovinného obrazce Q2 vzhledem k ose q, pro-
cházející těžištěm 0[0, OJ obrazce Q2 a svírající s osou x úhel velikosti Cť,
se rovná
lq = lx cos 2 - 2Dxy sin ex cos + ly sin 2 ,
kde lx, resp. ly je moment setrvačnosti rovinného obrazce Q2 vzhledem k ose x,
resp. y a Dxy je deviační moment.
7. Steinerova věta pro rovinný obrazec: Moment setrvačnosti rovinného
obrazce Q2 s obsahem S (obsahová hmotnost ms = 1 kg m- 2 ) vzhledem
k ose p se rovná
Ip = lq + d 2 S,
kde lq je moment setrvačnosti rovinného obrazce Q2 vzhledem k ose q,
rovnoběžné s osou p a procházející těžištěm 0[0, OJ obrazce Q2;
d - vzdálenost os p a q.
8. Deviační [odstředivýJ moment rovinného obrazce Q2 vzhledem k osám
x a y:
Dxy = fL2 XYdS .
641
9. Objem V tělesa ohraničeného plochou z = f(x, y) > O, rovinným ob-
razcem Q2 v souřadnicové rovině xy a příslušnými úsečkami na rovnoběžkách
v hraničních bodech obrazce Q2 s osou z:
Obecně platí
V = J i z dS ,
. U3
v kartézských [ortonormálních] souřadnicích
i X2 (f. g2 (X) )
V = zdy dz
XI gl(X)
a v polárních souřadnicích
f. <P2 (f. 92(fP) )
V = ZQ dQ dqJ.
lpi gl(<p)
7.7.2. Trojné [trojrozměrné] integrály
Trojný [trojrozměrný] integrál se definuje obdobně jako dvojný in-
tegrál s tím rozdílem, že v něm vystupují funkce tří proměnných 'U = f(x, y, z)
(x, y, z jsou souřadnice kartézské [ortonormální] souřadnicové soustavy),
popř. u = f(g, qJ, z) (Q, cp, z jsou souřadnice válcové [cylindrické, semipolární]
souřadnicové soustavy), popř. u = f(Q, qJ, 8) (Q, qJ, 8 jsou souřadnice kulové
[sférické, polární] souřadnicové soustavy) a regulární uzavřená prostorová
oblast Q3'
Funkce f, pro niž exisl 1 Jje trojný integrál, se nazývá integrovatelná. Každá
spojitá funkce f na oblasti Q3 je na této oblasti integrovatelná.
Výpočet trojného integrálu (převedení trojného integrálu
na trojnásobný integrál)
V kartézských souřadnicích platí
III f. b {f. g2(X) [i h2(X,Y) ] }
f(x, y, z) d V = f(x, y, z) dz dy dx
a3 a 91(X) hl(x,y)
za předpokladu, že trojrozměrná oblast Q3 je množinou právě těch bodů
[x, y, z] E E 3 , že x E (a, b), pro každý pevně zvolený bod x E (a, b) platí
gl(X) < Y < g2(X) (gl a g2 jsou spojité funkce) a pro aždou pevně zvolenou
642
"přípustnou" uspořádanou dvojici lx, y] platí hl (x, y) < z < h 2 (x, y) (hl a h 2
jsou spojité funkce dvou proměnných) (obr. 377).
Obr. 377. Výpočet trojného integrálu
Ve válcových souřadnicích platí
III I(e, cp, z) d V = r<P 2 {f g2 (f/J) [ "2(l/,q>f(e, cp, z) e dz J de } dli'
a3 J<Pl g1ťf/J) Jia 1 (Q,<p)
za předpokladu, že trojrozměrná oblast Q3 je množinou právě těch bodů
[Q, qJ, z] E E 3 , že qJ E < qJl, qJ2 >, pro každou pevně zvolenou hodnotu qJ E < qJl, qJ2 >
platí gl(qJ) < Q < g2(qJ) (gl a g2 jsou spojité funkce) a pro každou pevně
zvolenou "přípustnou" uspořádanou dvojici [Q, qJ ] platí hl (g, qJ) 2:: Z = h 2 (Q, qJ)
(hl a h 2 jsou spojité funkce dvou proměnných).
V kulových souřadnicích platí
III f <p2 {f g2(<P) [l h2u .<P) J }
f(Q, qJ, 8) d V = f(Q, qJ, 8) Q2 dQ sin 8 d8 dqJ
fJ3 <p 1 9 t(<p) h t(8-.<p)
za předpokladu, že trojrozměrná oblast Q3 je množinou právě těch bodů
[Q, qJ, 8) E E 3, že qJ E < qJI, qJ2 >, pro každou pevně zvolenou hodnotu qJ E < qJI, qJ2 >
platí gl(qJ) < 8 < g2(qJ) (gl a g2 jsou spojité funkce) a pro každou pevně
zvolenou "přípustnou" uspořádanou dvojici [8, qJ] platí h l (8, qJ) < Q < h 2 (8, qJ)
(hl a h 2 jsou spojité funkce dvou proměnných).
.'Pří klad:
Na tělese 11 3 , znázorněném v obr. 377, ukážeme, jaký geometrický význam
mají v tomto případě integrační meze trojnásobného integrálu.
Integrační mez hl (x, y), resp. h 2 (x, y) trojnásobného integrálu představuje
dolní hraniční plochu z = hl (x, y), resp. horní hraniční plochu z = h 2 (x, y)
trojrozměrné uzavřené oblasti Q3, přičemž tyto plochy mají společnou hra-
'niční křivku k. Průmětem těchto ploch do roviny xy je uzavřená oblast Q2'
jejíž hraniční křivka k' je průmětem křivky k. -
643
Integrační mez gl (x), resp. g2(X) představuje dolní část y = gl (x), resp.
horní část y = g2(X) křivky k'.
Integrační meze a, b jsou krajní body úsečky, která je průmětem každé
z. křivek y = gl (x) a Y = g2(X) do osy x.
Použití trojného a trojnásobného integrálu
O významu integračních mezí viz na str. 637.
1. Objem tělesa V:
Obecně platí
v = ffI3dV,
v kartézských souřadnicích
i X2 [f. g2(X) (l h2(X,Y) ) ]
V = dz d y dx,
XI gt(x) hl(x,y)
ve válcových souřadnicích
1 ({J2 [f. g2 «{J) (i h2 (q,({J) ) ]
V = g dz dg dqJ
({J I g I «{J) hl (q, ((J)
a v kulových souřadnicích
1 ({J2 [f. g2«{J) (i h2UJ.,({J» ) ]
V = g2 dg sin 8 d8 dqJ.
({JI gl«{J) hIUJ.,({J)
2. Statický moment SXY' resp. Sxz' resp. SYZ homogenního tělesa vzhledem
k rovině xy, resp. xz, resp. yz (objemová hmotnost mv = 1 kg m - 3):
Obecně platí
SXY = ffI3 Z dV,
Sxz = ffI/dV,
SYZ = ffI3 XdV
644
a v kartézských souřadnicích
_ l X2 [f 92 (X) (i h2 (X,Y) .., ) ]
Sx}' - dz dy dx,
Xl gdx) ht<x.}')
_ l X2 [f 92 (X) (f h2 (X.y) ) ]
Sx= - y dz dy dx,
Xl 9t(x) ht<x,y)
l X2 [f g2 (X) (i h2 (X.}') ) ]
S y= = x dz d y dx.
Xl gdx) hdx.y)
3. Těžiště T homogenního tělesa s objemem V:
Obecně platí
ffL,XdV ffL/dV ffL,ZdV
X1' = V ' YT = . V ' Z1' = V
a v kartézských souřadnicích
1 i X2 [f g2(X) (f h2(X.y) ) ]
X T = - x dz dy dx,
V Xl gl(X) hdx,y)
- 1 i X2 [f. g2(X.) (i h2(X,Y) ) ]
YT - V y dz d y dx,
Xl 91(X) hl(x,y)
1 i X2 [f. 92(X) (i h2(X,y) ) ]
ZT = - z dz dy dx.
V Xl 91(X) hl(X.Y)
4. Moment setrvačnosti lx, resp. ly, resp. 1 z homogenního tělesa Q3 vzhle-
dem k ose x, resp. y, resp. z (objemová hmotnost mv = 1 kg m- 3 ):
Obecně platí
Ix = ffL,(l + z2)dV,
ly = ffL,(x 2 + z2)dV,
Iz = ffL,(x 2 + l)dV
645
a v kartézských souřadnicích
I X2 {f. g2 (X) [i h2 (X.y) ] }
lx = (y2 + Z2) dz dy dx,
Xl gt<x) ht(x,y)
i X2 {f g2(X) [f, h2(X,y) ] }
1 y =. (X2 + Z2) dz dy dx,
. Xl gl(X) ht(x,y)
I X2 {f. g2 (X) [ f h2(X,y) ] }
Iz = (x 2 + y2)dz dy dx.
Xl gt(x) Jht(x,y)
5. Moment setrvačnosti homogenního tělesa Q3 vzhledem k ose otáčení
(objemová hmotnost my = 1 kgm- 3 ):
1 = ffI3 r2dV ,
kde r je vzdálenost bodu [x, y, z] od osy otáčenÍ.
6. Moment setrvačnosti Iq tělesa Q3 vzhledem k ose q, procházející těžištěm
0[0, O, O] tělesa Q3 a svírající se souřadnicovými osami úhly s velikostmi
, B, y, se rovná
Iq = Ix cos 2 + ly cos 2 B + Iz cos 2 Y -
- 2Dxy cos cos B - .2D xz cos cos y - 2Dyz cos B cos}' ,
kde lx, resp. ly, resp. 1 z je moment setrva nosti tělesa Q3 vzhledem k ose x,
resp. y, resp. z a Dxy, resp. Dxz, resp. Dyz je deviační moment tělesa Q3 vzhle-
dem k osám x a y, resp. x a z, resp. y a z.
7. Steinerova věta pro těleso: Moment setrvačnosti Ip tělesa Q3 s objemem V
(objemová hmotnost my = 1 kg m - 3) vzhledem k ose p se rovná
Ip=Iq+d 2 V,
kde Iq je moment setrvačnosti tělesa Q3 vzhledem k ose q, rovnoběžné s osou p
a procházející těžištěm 0[0, O, O] tělesa Q3;
d - vzdálenost os p a q.
8. Deviační [odstředivý] moment Dxy, resp. Dxz, resp. Dyz homogenního
tělesa Q3 vzhledem k osám x a y, resp. x a z, resp. y a z (objemová hmotnost
my = 1 kg m- 3 ):
Dxy = ffI3 XYdV ,
646
Dxz = ffL,xz dV,
Dyz = ffL/z dV.
Příklad:
Vypočtěme objem tělesa
Q3 = {[x, y, z] E R 31 (x - 2)2 + y2 < 4 1\ Y > O 1\ O < Z < 2x2y} .
..
.
Vypočteme integrační meze:
Proměnná z probíhá od O do 2x 2 y.
Proměnná y probíhá od O do J(4x - x 2 ), neboť
(x - 2)2 + y2 < 4 ,
x 2 - 4x + 4 + y2 < 4,
O < Y < J(4x - x 2 ).
Proměnná x probíhá od O do 4, což plyne z analytického vyjádření kruhu.
Je tedy
V = LlLJ(4X - x2) (fX 2 Y dz ) d y J dz =
i 4 (i J (4X-X 2 ) )
= 2x2ydy dx =
o o
= L4[X2i] (4X-X2)dX = L4(4X 3 - x 4 )dx =
[ X5 J 4
= x 4 - 5 0=51,2
(objemové jednotky).
647
8. DIFERENCIÁLNÍ ROVNICE
.
8.1. OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE
Základní pojmy
Obyčejnou diferenciální rovnicí n-tého řádu v implicitním tvaru nazýváme
rovnici tvaru
F( , (n » - O
x, y, y , .. ., y - ,
kde 'nEN a F: Qn+2 R, Qn+2 C Rn+2. Přitom levá strana rovnice závisí
v každém případě na proměnné y(n>.
Obyčejnou diferenciální rovnicí n-tého řádu v explicitním tvaru [obyčejnou
diferenciální rovnicí rozřešenou vzhledem k derivaci největšího řádu] nazýváme
rovnici tvaru
(n> _ f( , (n - 1 »
y - x, y, y , ..., y ,
(1)
(2)
kde n E N aJ: Qn + 1 R, Qn + 1 C Rn + I .
Jsou-li splněny předpoklady plynoucí z věty o implicitních funkcích, lze
rovnici (1) převést na rovnici (2).
Řešením [integrálem, partikulárním řešením, partikulárním integrálem] rov-
nice (1), resp. (2) na intervalu J c R nazýváme každou funkci cp: J R,
která má na intervalu J derivace až do n-tého řádu včetně a která po dosazení
do rovnice (1), resp. (2) tuto rovnici splňuje. Řešení nemusí být dáno v expli-
citním tvaru y = qJ(x), ale může být dáno i implicitně rovnicí h(x, y) = O.
Řešení rovnice (1), resp. (2) na intervalu J, které závisí na n podstatných
konstantách (tj. takových konstantách, že žádnou z nich nelze vyjádřit pomocí
zbývajících konstant), se nazývá obecné řešení [obecný integrál] rovnice (1),
resp. (2). Obecné řešení nemusí být dáno v explicitním tvaru y = cp(x, CI' ..., C n ),
ale může být dáno i implicitně rovnicí h(x, y, CI' .. ., C n ) = O. Volbou určitých
hodnot za parametry CI'...' C n ve vyjádření obecného řešení dostaneme ře-
šení partikulární. Jestliže [a, b o , b l , ..., b n - l ] E J x Rn a y = cp(x) je takové
řešení diferenciální rovnice (1), resp. (2) na intervalu J, že platí
cp(a) = b o , cp'(a) = b l , ..., qJ(n - I >(a) = b n - 1 ,
pak říkáme, že řešení y = cp(x) je dáno počátečními podmínkami (3).
(3)
648
Počáteční úlohou [Cauchyovou úlohou] pro obyčejnou diferenciálnf rovnici
n-tého řádu nazýváme úlohu najít řešení rovnice (1), resp. (2), dané počáteční
podmínkou (3). Taková počáteční úleha nemusí mít žádné řešení, může mít
právě jedno řešení nebo několik řešenÍ.
Věta o existenci řešení: Jestliže v diferenciální rovnici (2) je f: Dn + 1 R
spojitou funkcí na okolí bodu [a, bo, b l' . . ., b n - 1] E Qn + l' pak existuje řešení
této rovnice na intervalu J, které splňuje počáteční podmínku (3).
Věta o jednoznačnosti řeL ení:. Jestliže v diferenciální rovnici (2) jsou
funkce f: Dn+l R, of/ay, af/oy', ..., of/ c y(n-l) spojité na okolí bodu
[a, bo, b l , ..., b n - l ] E D,,+ l' pak existuje právě jedno řešení této rovnice na
intervalu J, které splňuje počáteční podmínku (3).
Singulárním řešením diferenciální rovnice (1), resp. (2) nazýváme takové řešení,
v jehož každém bodě je porušena jednoznačnost.
Příklad 1:
Rovnice x + yy' = O je obyčejnou diferenciální rovnicí prvního řádu
v implicitním tvaru (n = 1, Q3 = R 3). Rovnicí x 2 + y2 = C 2 je dáno její
obecné řešení v implicitním tvaru.
Příklad 2:
Rovnice y' = - x/ y je obyčejnou diferenciální rovnicí prvního řádu roz-
řešenou yzhledem k derivaci (n = 1, D 2 = R x (R\{O}). Rovnicí y =
= + J( C 2 - x 2 ) je dáno její obecné řešení v explicitním tvaru.
8.2. OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE
PRVNÍHO ŘÁDU
8.2.1. Geometrický význam
Jestliže Q3 c R 3 a F: Q3 R, resp. Q2 c R 2 a f': D 2 R,
pak rovnicí
F(x, y, y,) = O, (4)
resp. rovnicí
y' = j'(x, y)
(5)
je bodům [x, y] definiční oblasti funkce F, resp: j' přiřazen směrový element y'
(obr. 378). Říkáme, že na Q2 je definováno směrové pole. Grafickým znázQr-
něním obecného řešení rovnice (4), resp. (5) je jednoparametrická soustava
křivek; každé partikulární řešení odpovídá určité křivce (tzv. integrální křivce)
649
této. soustavy. Přitom platí, že směrnice tečny integrální'křivky v bodě [x, y]
je dána rovnicí (4), resp. (5).
Singulárním řešením je obalová křivka (existuje-li) jednoparametrické sou-
stavy integrálních křivek.
[KO , Yo, y'( ' 0 »
Yo ----
I
I
I
I
I
I
Y
OL-
Xo
---
x
Obr. 378. Směrový element ze svazku
křivek
Čáry spojující všechny body se stejným směrem se nazývají izoklíny (y' =
= onst). Z jejich znalosti lze přibližně určit integrální křivky.
Příklad 1:
y' = tx
([ x, y ] E < - 2, 2> x R +) .
Rovnice izoklín: y' = !x = c => x = 2c (rovnoběžky s osou y) (obr. 379).
"
+ t
1
r
y
0,5
C=-f
-- - - 0,75
-'- --- - -- -0,5
--.. -0,25
-2 -15-1-05 O 05 1 152 x
, , , ,
'", , .............. "'-... - L
0,5 1 1,5
,
Z x
Obr. 379. Izoklíny rovnice y' = tx
Příklad 2:
Obr. 380. Izoklíny rovnice y' = - y
([ x, y ] E R 2) .
I
Y =-y
.
Rovnice izoklín: y' = - y = C => y = -C (rovnoběžky s osou x) (obr. 380).
Je-li dána jednoparametrická soustava křivek F(x, y, C) = O, resp. y =
= f(x, C), pak eliminací konstanty C z rovnic
cF cF
F(x, y, C) = O a -;- + y' = O ,
ux cy
650
popř. z rovnic
y = f(x, C) a y' = f (x, C)
lze při splnění předpokladů plynoucích z věty o implicitních funkcích najít
diferenciální rovnici této sousta vy.
Křivka, která každou křivku soustavy protíná v právě jednom bodě, se
nazývá trajektorie této soustavy. Trajektorie, která každou křivku soustavy
protíná pod shodným, resp. pod pravým úhlem se nazývá izogonální, resp.
ortogoOO lní trajektorie. Diferenciální rovnici izogonální trajektorie protínající
křivky soustavy pod úhlem velikosti qJ * n/2 dostaI?-eme eliminací .kon-
stanty C z rovnic (opět při splnění předpokladů z věty o implicitních funkcích)
F(x, y, c) = O ,
[ 1. + ( aF / OF ) tg qJ ] y' = tg cp _ OF / fJF ,
ox ay ex oy
resp. z rovnIC
y = f(x, c) ,
[1 - f'(x, C) tg qJ] y' = f'(X, C) + tg qJ .
Diferenciální rovnici ortogonální trajektorie dostaneme eliminací konstan-
ty C z rovnic
F(x, y, C) = O,
oF aF
---y'=O
oy ax "
resp. z rovnIC
y = f(x, C) ,
1 + f:(x, C) y' = O .
Příklad 1:
Je dána soustava křivek
4x 2 + 5y + C = O .
Konstantu C eliminujeme derivováním_ takže diferenciální rovnice dané sou-
stavy je
8x + 5 y' = O .
651
Diferenciální rovnice sousta vy ortogonálních trajektorií je
5 - 8xy' = O .
Diferenciální rovnice soustavy izogonálních trajektorií, kde úhel protínání
má velikost qJ = 30°, je
( 1 + 8x ,J3 ) y' = ,J3 _ 8x
5 3 3 5
neboli
(15 + 8xJ3)y' = -24x + 5J3.
Příklad 2:
Je dána soustava křivek
y = Cx 2 .
Diferenciální rovnici soustavy vypočteme z rovnic
y = Cx 2 ,
y' = 2Cx ;
dostaneme (pro x * O)
y' = 2 . Y .
x
Diferenciální rovnici soustavy ortogonálních trajektorií vypočteme z rovnic
y = Cx 2 a 1 + 2C xy ' = O .
Pro x * O dostaneme
2 . Y y' = - 1 .
x
8.2.2. Diferenciální rovnice se separovanými proměnnými
Jestliže funkce qJ, resp. t/J [t/J(y) 9= O] je spojitá na otevřeném inter-
valu JI' resp. J 2' p k rovnice
I qJ(X)
t/J(y) y' = (j)(x) neboli y = t/J(y)
652
se nazývá d ťerel1ciální rovnice se separovanými proměnnými. Na množině
JI X J 2 je její obecné řešení tvaru
ft/J(y) dy = fQJ(X) dx .
Každým bodem množiny J 1 X J 2 prochází aspoň jedna integrální křivka.
Jestliže funkce t/J' je na intervalu J 2 spojitá, pak každým bodem množiny
JI X J 2 prochází právě jedna integrální křivka. Na hranici množiny JI X J 2
je třeba rovnici vyšetřit zvlášť.
Příklad 1 :
xe X
yy' = xe x + y neboli y' = _Y
ye
je rovnice se separovanými proměnnými: qJ(X) = x eX, JI = R, t/J(y) = y e - Y,
J 2 = R -, popř. J 2 = R +. Na množině JI X j 2 je její obecné řešení tvaru
fye- Y dy = fx eX dx
neboli (integrací per partes)
-ye- Y + fe-YdY = xe X - fexdx
neboli
-e- Y (y + 1) = eX (x - 1) + C ,
CE R.
Každým bodem množiny JI X J 2 prochází právě jedna integrální křivka.
Příklad 2:
2x2 - 3x - 14
y'(2x - 7) + y(2X2 - 3x - 14) = O neboli y' = - Y
2x -7
je rovni e se separovanými proměnnými:
2X2 - 3x - 14
qJ(x) = - = -(x + 2),
2x - 7
JI = (- 00, t), resp. JI = (t, + 00); t/J(y) = lly, J 2 = R -, resp. J 2 = R +.
Na množině JI X J 2 je její obecné řešení tvaru
ft dY = - Jx + 2)dx
653
neboli
x 2
ln Iyl = - - - 2x + CI
2
(C1ER)
neboli
lyl = e,xp ( - 2 _ 2x + CI) = C 2 exp ( _ 2 - 2x ) ,
neboli
C.2 = e C1 (C 2 > O)
y=c 3 ex p ( _ 2 -2X), C 3 =C 2 (y>O), C 3 =-'C 2 °(y<O).
,
Protože funkce
y=O (XEJ 1 )
Je také řešením dané rovnice, je funkce y = C exp ( - 2 - 2X) (C E R)
jejím obecnýin řešením.
Každým bodem množiny JI X R prochází právě jedna ip.tegrální křivka.
8.2.3. Lineární diferenciální rovnice prvního řádu
Jestliže funkce a [a(x) 9= O], b, c jsou spojité funkce na intervalu J,
pak rovnice
a(x) y' + b(x) y + c(x) = O
se nazývá lineární diferenciální rovnice prvního řádu. Diferenciální rovnice
y' + p(x)y + q(x) = O,
kde p, q jsou spojité funkce na intervalu J, se nazývá lineární diferenciální
rovnice prvního řádu v normovaném tvaru.
Homogenní line"ární diferenciální rovnice prvního řádu
Homogenní lineární diferenciální rovnicí prvního řádu nazýváme rovnICI
y' + p(x)y = O. Je to rovnice se separovanými proměnnými: qJ(x) = -p(x),
J. = J, tfJ(x) = lly, J 2 = R -, popř. R +. Na množině J x R -, popř. J x R +
je jeií obecné řešení tvaru
ft dY = - fP(X)dX
654
neboli
Iyl = CI e-P(X), kde P'(x) = p(x) (CI> O).
Protože y = O dané rovnici také vyhovuje, je na množině J x R funkce
y = C e-P(X), pI(X) = p(x) (C E R), jejím obecným řešením. Každým bodem
množiny J x R prochází právě jedna integrální křivka, která je definovaná
pro všechna čísla x E J. \
Nehomogení lineární diferenciální rovnice prvního řádu
Nehomogenní lineární diferenciální rovnicí prvního řádu nazýváme rovnici
y' + p(x) y + q(x) = O.
1. způsob řešení (řešení pomocí substituce):
Zvolíme libovolné nenulové řešení u rovnice u' = p(x) u (x E J). Pak
u'(x)
y' + u(x) y + q(x) = O
neboli
u(x) y' + u'(x) y + u(x) q(x) = O
neboli
(uy)' + uq = O .
Na množině J x R je tedy funkce
y = - u( ) fu(x) q(x) dx
obecným řešením dané rovnice. Každým bodem množiny J x R prochází
právě jedna integrální křivka, definovaná pro všechna čísla x E J.
Příklad:
y' sin x + y = cos x
[J = (0,1t)]
neboli
1
y' + y = cotg x .
sIn x
x
Partikulárním řešením rovnice U' = u/sin x Je např. funkce u = tg-.
2
Položíme-li u'fu = l/sin x, dostaneme
I
U
y' + - Y = cotg x
u
655
neboli
x 1
uy' + u'y = tg-cotg x = 1 -
2 x
2 cos 2 -
2
neboli
(uy)' = 1 -
x
. 2 cos 2 -
2
1
Odtud
y = cotg ; J ( 1 - 1 2 x ) dx = cotg (x - tg + c ) =
2 cos -
, 2
x
= (x + C)cotg- - 1
2
(C E R) .
Každým bodem množiny (0,1t) X R prochází právě jedna integrální křivka,
definovaná pro všechna čísla x E (O, 1t).
2. způsob řešení (metoda variace konstant): .
Nejprve najdeme obecné řešení y = C e-P(X), p'(x) = p(x) (C E R) příslušné
homogenní lineární diferenciální rovnice
y' + p(x) Y = O .
Konstantu C nahradíme, neznámou funkcí z a výraz
, y = z(x) e-P(X)
dosadíme do nehomogenní rovnice: .
z' e-P(X) - z p(x) e-P(x) + z p(x) e-P(x) + q(x) = O
neboli
z' = - q(x) eP(X) .
Odtud vypočteme pomocnou funkci:
z = - fq(x) eP(x) dx ;
pak
y = -e-P(X) fq(x) eP(X) dx.
656
Příklad:
y' sin x + y = cos x
neboli
[J = (0,1t)]
1
y' + y = cotg x .
sin x
Obecné řešení rovnice
1
y' + y = O
sin x
[x E (O, 1t)]
Je
x
y = C cotg - .
2
Položíme
x
y = z(x) cotg-
2
a po dosazení máme
x . 1. x
z' cotg - sin x - z sin x + z cotg - = cos x
2 x 2
2 sin 2 -
2
neboli
x 1
z' = cotg x tg - = 1 -
2 x
2 cos 2 -
2
neboli
z = ]( 1 - 1 x ) dX = x - tg +.e
2 cos 2 -
2
(C E R).
Odtud
.
IX
Y = (x + C) cotg - - 1
2
(C E R) .
Každým bodem množiny (0,1t) X R prochází právě jedna integrální křivka,
definovaná pro všechna čísla x E (O, 1t).
3. způsob řešeni (řešení při známém partikulárním řešení yp):
Najdeme obecné řešení Yh příslušné homogenní lineární diferenciální rov-
nice. Obecné řešení nehomogenní lineární diferenciální rovnice pak je y =
657
= Y p + Yh' Známe-li dvě partikulární řešení Y p l, Yp2 nehomogenní rovnice,
pak obecné řešení nehomogenní lineární diferenciální rovnice je
Y = Y p l + C(Y p 2 - Y p l).
8.2.4. Homogenní diferenciální rovnice prvního řádu
Jestliže f(x, y) je homogenní funkce nultého stupně, tj. platí-li
f(tx, ty) = f(x, y) pro všechna čísla t z nějakého okolí bodu t = 1, pak dife-
renciální rovnici
y' = f(x, y)
nazýváme homogenní diferenciální rovnicí nultého stupně. Jestliže funkce z je
na intervalu J řešením diferenciální rovnice z' = [f(1, z) - z ]Ix se separova-
nými proměnnými, pak funkce y(x) = x z(x) je řešením dané homogenní
rovnice na témže intervalu J. Při vyšetřování musíme vyloučit body x = O.
Příklad:
y'=3-2. y
x
.
.
(x E R -, popř. R +, Y E R) .
Fun ce f(x, y) = 3 - 2ylx je na intervalu R -, popř. R + homogenní rovnicí
nultého stupně. Dostaneme f(1, z) - z = 3 - 2z - z = 3 - 3z. Řešíme lineární
rovniCI
1 - z
z' = 3
,
x
což je rovnice se separovanými proměnnými, kde qJ(x) = 31x, JI = R --,
popř. R +, tjJ(z) = 1/(1 - z), J 2 = (- 00, 1), popř. (1, + (0). Na množině JI x J 2
je její obecné řešení tvaru
f dz = 3 f dX
1 - z x
neboli
neboli
-ln 11 - zl = 3 ln Ixl + CI
-ln Ix 3 (1 - z)1 = CI
(C 1 E R)
neboli
Ix 3 (1 - z)1 = e C1 = C 2
(C 2 > O) .
65X
Protože funkce z = 1 je také řešením rovnice z' = 3(1 - z)/x, je na množině
JI X R jejím obecným řešením funkce
C
z=l--
x 3
(C E R) .
Každým bodem. množiny JI X R prochází právě jedna integrální křivka,
definovaná pro všechna čísla x E JI'
Dosadíme-li za z do vztahu y = xz, dostaneme na množině JI X R obecné
řešení rovnice y' = 3 - 2yjx ve tvaru
c
y=x--
x 2
(C E R) .
Každým bodep1 množiny JI X R prochází právě jedna integrální křivka,
definovaná pro všechna čísla x E JI'
8.2.5. Exaktní diferenciální rovnice prvního řádu
,
Exaktní diferenciální rovnici prvního řádu nazýváme rovnici
(x,y)dx + (x,y)dy = O,
kde levá strana rovnice je v oblasti Q2 totálním diferenciálem nějaké funkce
F(x, y) (tzv. kmenové funkce). Na oblasti Q2 je pak F(x, y) = C obecným
řešením dané rovnice.
Nutnou a postačující podmínkou, aby na oblasti Q2 byla rovnice tvaru
(x,y)dx + (x,y)dy = O
exaktní rovnicí, je
a et/!
-
GY ex
Funkci F(x, y) pak najdeme ze vzorce
f f[ ' f C (x,y) ] '
F(x, y) = JP(x, y) dx+ t/J(x, y) - oy dx dy = C ,
popř.
F(X. y) = ft/J(x, y) dy + f[ cp(x, y) - f ct/J y) dy ] dx = C .
Přitom všechny integrační konstanty jsou zahrnuty do konstanty C. V bodech
[xo, YoJ E Q2' kde (xo' Yo) * O je zaručena existence řešení y jako argumentu
(6)
659
funkce x. Jestliže t/J(xo, Yo) = O, ale qJ(x o - Yo) :f: O, můžeme najít x jakožto
funkci argumentu y. Body [xo, Yo], kde 4- ( -(o .\'0) = t/J(x o , Yo) = O, se nazývají
singulární body rovnice.
Příklad:
(3x 2 + 8ax + 2b y 2 + 3y) dx + (4bxy + 3x + 5) dy = O .
Protože
a(3x 2 + 8ax + 2b y 2 + 3y)
- = 4b y -t- 3,
. oy
a(4bxy + 3x - 5)
= 4by + 3 ,
()x
je levá strana rovnice na celé rovině totálním diferenciálem nějaké funkce
F'( x, y). Použijeme vzorce (6) k určení obecného řešení:
F(x, y) =
= J3X2 + 8ax + 2by2 + 3y) dx +
+ f[4bX Y + 3x + 5 - J4b Y + ;)dx ]d Y =
= x 3 + 4ax 2 + 2bxy 2 + 3xy + f[4bX y + 3x + 5 - (4bxy + 3X)]d Y =
= x 3 + 4ax 2 + 2b xy 2 + 3xy + 5y = C .
Singulární body najdeme řešením soustavy rovnic
3x 2 + 8ax + 2b y 2 + 3y = O,
4bxy + 3x + 5 = O .
8.2.6. Integrující faktor [Eulerův multiplikátor]
Výraz J1.(x, y) nazýváme integrujícím [integračním] faktorem [Eulero-
vým multiplikátorem] diferenciální rovnice (která není exaktní)
(x,y)dx + t/J(x,y)dy = O,
jestliže levá strana této rovnice po vynásobení integrujícím faktorem J1.(x, y)
bude na oblasti D 2 totálním diferenciálem nějaké (kmenové) funkce F(x, y),
tj. jestliže bude
a[J1.(x, y) (x, y)] o[J1.(x, y) t/J(x, y)]
ay ex
660
Ve speciálních případech lze řešení zpravidla Jcdnodušit tím, že integrující
faktor ,u(x, y) hledáme jako funkci bud' jen argumentu x, nebo jen argumentu y,
popř. jako funkci argumentu x 2 + y2, xfy apod..
Speciální integrující faktory
Integrující faktor závisí jen na argumentu x:
,u = exp [ - f ( et/J - alp ) d X ] .
t/J ex oy
Integrující faktor závisí jen na argumentu y:
,u = exp [f ( ot/J - alp ) d Y ] .
lp ex oy
Integrující faktor závisí jen na součinu xy:
,u = exp [f 1 ' ( ot/J - OqJ ) dZ ] ,
XqJ - yt/J ex oy
Integrující faktor závisí jen na podílu xfy:
[f X2 ( Ot/J CqJ ) ]
,u = exp - - - dz ,
XqJ + yt/J ox oy
Integrující faktor závisí jen na souétu X2 + y2:
Jl = exp [ f2(Y49 x ) G - ; ) dz l
Příklad (srov. příklad v článku 8.2.4):
(3x - 2y) dx - x dy = O.
Protože
o(3x - 2y)
oy = - 2 ,
e( - x)
= -1
ox '
z = xy .
y
z::.: -.
X
z = x 2 + y2 .
není rovnice exaktní.
Předpoklad: Integrující faktor závisí jen na argumentu x:
Jl = exp [ - f- 1) - 1 + 2) dx ] = exp (f ) = e 1n Ixl = ;.
661
Násobíme-li výchozí rovnici integrujícím faktorem ,u(x, y) = x, dostaneme
diferenciální rovnici
(3x 2 - 2xy)dx - x 2 dy = O,
jejíž levá strana již je totálním diferenciálem kmenové' funkce.
Řešení:
x 3 - x 2 Y = C
(C E R) .
Singulární body najdeme řešením soustavy rovnic
3x 2 - 2xy = O,
-x 2 =.0,
tj. x = O.
8.2.7. Bernoulliova <diferenciální> rovnice
Jestliže qJ, t/J (t/J * O) jsou spojité funkce na intervalu J, pak rovnici
y' + qJ(x) Y = t/J(x) yY
(f' E R \ {O, I})
nazýváme Bernoulliovou (diferenciálnl) rovnicí. Rovnici vyšetřujeme na mno-
žině H = R x R + . Jestliže y > O, pak také funkce y = O je řešením Bernoulliovy
rovnice. Jestliže y je liché číslo, pak řešením Bernoulliovy rovnice je také
funkce - y. Jestliže y je sudé číslo, pak řešeni Bernoulliovy rovnice, na mno-
žině H* = R x R - najdeme jako řešení rovnice
y' + qJ(X) Y = - t/J(x) yl .
Každým bodem množiny J x H prochází právě jedna integrální křivka.
Jestliže na intervalu JI c J je z > O řešením lineární rovnice
Z' + (1 - y) qJ( x) z = (1 - y) t/J(x) ,
pak y = Zl/(l - i') je řešením Bernoulliovy rovnice
y' + qJ(x) Y = t/J(x) Y"
na témže intervalu J.
pjcíklad:
y' + y - x 2 y3 = O
X
(J = R -, popř. R +, Y E R) .
662
Řešíme lineární rovnici "'"
I 2 2
Z - - z = - 2x .
x
Obecným řešením této rovnice na, intervalu J je funkce
z = X2( C - 2x).
Podmínce z > O vyhovují řešení z = X2(C - 2x), kde C > O na intervalu
(O, Cj2), a řešení z = x 2 (C - 2x), kde C < O na intervalu (- 00, Cj2).
Na množině J x H je obecné řešení dané Bernoulliovy rovnice tvaru
x 2 y2(C - 2x) = 1 .
Jestliže C > O, pak funkce Y je obecným řešením rovnice na intervalu (O, Cj2),
a jestliže C < O, je funkce y obecným řešením na intervalu ( - 00, Cj2).
Na množině J x H* je obecné řešení dané rovnice také. tvaru
x 2 y2(C - 2x) = 1 .
Funkce y = O je řešením dané rovnice na intervalu J.
8.2.8. Riccatiova < difer.enciální > rovnice
Jestliže qJ, t/J, w [qJ(x) * O, w * O] jsou spojité funkce na intervalu J,
pak rovnici
y' = qJ(x) y2 + t/J(x) y + w(x)
nazýváme Riccatiovou <diferenciální> rovnicí. Každým bodem množiny J x R
prochází právě jedno řešení této rovnice. Tato řešení však nelze obecně najít
pomocí kvadratur (tj. její řešení nelze převést jen na výpočet integrálů). Jestliže
však známe partikulární řešení YI, pak lze najít obecné řešenÍ. .
Jestliže je na intervalu JI c J funkce z * O řešením rovnice
Z' = - [t/J(x) + 2qJ(x) YI] Z - qJ(x),
pak na tomto intervalu je funkce
1
Y = YI + -
z
řešením dané Riccatiovy rovnice.
663
Příklad:
Rovnice
, 2 1 1 ( + )
Y = Y - - Y -- - J = R -, popř. R , Y E R
X x 2
má partikulární integrál y = lfx. Řešme lineární rovnici
z' = ( - 2 ) z-I = _ z _I. -
x x x
Její obecné řešení je
x C
z= --+-
2 x
(XEJ, CeR).
Pro C < O je z(x) * O na celém intervalu J. Pro C > O je z(x) = O v bodě
x = .J(2C), popř. x = - .J(2C Obecné řešení Riccatiovy rovnice je pak
1 2x
y = - +.' 2C 2 .
x -x
.
Jestliže C < O, je jeho definičním oborem celý interval J, a jestliže C > O,
jsou definičními obory dva intervaly (- 00, -.J(2C)) a (-.J(2C), O), popř.
dva intervaly (O, .J(2C)) a (.J(2C), + (0).
8.2.9. Clairautova <diferenciální) rovnice
Jestliže cp je spojitá diferencovatelná funkce na intervalu J, která není
lineární [tj. qJ(t) není tvaru at + b], pak rovnici
y = xy' + qJ(Y')
nazýváme Clairautovou (diferenciální) rovnicí na množině R - x R x J, popř.
R + x RO x J. Jejím obecným řešením je funkce
y = kx + qJ(k)
(k E J, x * O) .
Singulárním řešením je funkce y, splňující vztah
x + qJ'(Y') = O.
Příklad:
y = xy' - 2y'2 + y'
(J = R, x * O) .
Pak qJ(t) = -2t 2 + t, qJ'(t) = -4t + 1. Řešením je soustava přímek
y = kx - 2k 2 + k
664
a křivka splňující vztah
x + 1 - 4y' = O
neboli
x + 1
y' =
4
Po dosazení nalezené derivace y' do původní rovnice dostane e singulární
integrál
x + 1 ( X + 1 ) 2 x + 1 x 2 + 2x + 1
y=x -2 + = .
4 4 4 8
.
8.3. OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE
DRUHÉHO ŘÁDU
Diferenciální rovnice druhého řádu určují pro každý bod
[x, y] E Q2 E R 2 směr a křivost elementu oblouku. Určení diferenciální rov-
nice dvouparametrické soustavy křivek F(x, y, CI' C 2) = O se provádí ob-
dobně jako u jednoparametrické soustavy (viz článek 8.2.1.).
Příklad:
Určeme diferenciální rovnici všech parabol s vrcholem na ose y.
Rovnici paraboly
(y - d)2 = 2px
dvakrát derivujeme:
2(y - d) y' = 2p,
(y - d) y" + y' 2 = O .
Z prvních dvou rovnic dostaneme
(y - d)2 = 2(y - d) y' X ,
(y - d) = 2 y' X
a dosadíme do třetí
2xy'y" + y'2 = O,
2x y" + y' = O .
665
8.3.1. Zvl áštní případy
Diferenciální rovnice bez x a y' (qJ je spojitá funkce na inter-
valu J)
y" = qJ(Y).
Je-li k nulový bod funkce qJ, pak y = k je řešením dané rovnice. Vynásobme
rovnici výrazem 2y'. Pak
neboli
2y' y" = 2 qJ(Y) y'
(y'2)' = 2 qJ(Y) y' .
Integrací dostaneme
y,2 = 2 fcp(y) y' dx = 2 fcp(y) dy ·
Řešení vyhovující rovnicím
, = J[2 fCP(Y)dyJ a y' = - J[2 fCP(Y)dyJ
bude vyhovovat dané rovnici. Podmínkami y(xo) = Yo, y'(xo) = y ,
[xo, Yo, y ] E R x J x .R je dáno aspoň jedno řešenÍ. Má-li qJ spojitou derivaci,
pak uvedenými podmínkami je dáno právě jedno řešenÍ.
Příklad: '
1
"
y=--
y3
(y * O) .
Zřejmě počátečními podmínkami y(xo) = Yo 9= O, y'(xo) = y je určeno
právě jedno řešenÍ. Je-li Yo > O, je y(x) >. O; je-li Yo < O, je y(x) < O. Je-li y
řešením dané rovnice, je také - y řešením dané rovnice. Stačí tedy rovnici
vyšetřovat na množině R x R + x R. Rovnici násobíme výrazem 2y'. Dosta-
neme
2y'y" = -2 L
y3
neboli
(y'2)' = ( ;2 )'
666
neboli
1
y,2 = - + c
y2
Nyní musíme rozlišit tři případy:
1. C = O (pak ly 1 = llyo),
2. C > O (pak ly 1 > llyo),
3. C < O (pak ly 1 < Ilyo).
V 'prvním případě řešíme rovnici
(C E R) .
,2 1
y -
- y2
neboli
1 1
y' = - , popř. y' = - - (y > O).
y Y
Obecné řešení rovnice y' = 11 y je tvaru
y = J[2(x + D)]
(D E R, x > - D) .
Obecné řešení rovnice y' = -lly je tvaru
y = J[ -2(x + D)] (DER, x < -D).
V druhém případě řešíme rovnici
1
y'2 = - + C
y2
(C > O, y > O)
neboli
y' = J(;2 + C ), popř. y' = - J (;2 + C ).
Tyto rovnice upravíme na tvar
neboli
, ,
yy 1 v yy = - 1
J(l + Cl) = , popr. J(l + Cy2) ,
Kyy' Kyy'
= 1 popř. = -1
J(K2 + y2)' J(K2 + y2)
(K2 . > O ) .
K yy' .
Obecné řešení rovnice J( 2 2) = 1 Je tvaru
K + Y
J (X + D)2 - K 4 J[ l J
Y = K 2 = C(X + DY - c
(x + D > > O) ;
667
K y y' .
obecné řešení rovnice .J(K2 + y2) = -1 Je tvaru
- J (X + D)2 - K 4 J[ 1 J
y - K 2 = C(x + DY - c
Ve třetím případě řešíme rovnIci
y,2 = ;2 + c ( c < O, .J cl > y > O)
ne boli
y' = J ( ;2 + c ) , popř. y' = - J (;2 + c ) ·
Tyto rovnice upravíme na tvar
yy' yy'
.J(1 + Icl y2) = 1, popr. .J(1 + Icl y2) = -1
neboli
Kyy'
.J(K2 _ y2) = 1, popř.
Kyy' =-1
.J(K2 _ y2) "
(x + D < - < O ) .
( K 2 = I I > O ) .
Kyy' .
Obecné řešení rovnice .J(K2 _ y2) = 1 Je tvaru
y=J K4_ 2+Dt =J[C(X+Dy- J (- >X+D>O);
obecné řešení rovnice
Kyy'
= -1
.J(K2 _ y2)
je tvaru
_ J K4-{X+D)2 - J[ ( ) 2 1 J
Y - - Cx+D--
K 2 C
(O>X+D> ) .
Diferenciální rovnice 'bez x a y [li' je spojitá funkce na intervalu J,
qJ( x) =t= O]
y" = qJ(Y').
668
Substitucí y' = p, y" = p' převedeme danou rovnici na rovnici prvního řádu
p' = lp(p) se separovanými proměnnými. V množině R x J má obecné řešení
tvar
f cp p) dp = x .
Předpokládejme, že tuto rovnici lze rozřešit vzhledem k p:
p = f(x, C) ;
y = ff(X, C) dx ·
Každým bodem [xo, Yo, y ] E R x R x J prochází aspoň jedno řešenÍ. Je-li lp'
spojitá funkce, pak každým bodem [xo, Yo, y ] E R x R x J prochází právě
jedno řešení.
pak
Příklad:
y" = 2y,2
(J = R).
Počáteční podmínkou y(xo) = Yo, y'(xo) = y je určeno právě jedno řešenÍ.
Zřejmě y = k je řešenÍ. Ostatní řešení splňují bud' y' > O, nebo y' < O.
Substitucí y' = p převedeIrae danou rovnici na rovnici
p' = 2 p 2 .
Separací proměn ých dostaneme na množině R x R -i- " 'ecné řešení tvaru
, 1 '
- - = 2(x - C)
p
'1
neboli
1
p =-
2(x - C)
( CER, x < c) ;
na množině R x R - obecné řešení tvaru
1
- - = 2(x - C)
p
neboli
1
p = -
2(x - C)
(C E R, x > C).
669
Po integrování máme
y = - f 1 dx = -t ln lx - ci + D -.-
2(x - C)
D
= ln ( CER, D > O, x < C),
Jlx - Ci
popř.
D
y = ln J(x - C)
( CER, D > O, x > C).
Diferenciální rovnice bez Y (qJ je spojitá funkce na množině Q2 c R2):
y" = qJ(x, y') .
Substitucí y' = p dostaneme rovnici
p' = qJ(x, p) .
...
Jestliže p = p(x, C) je obecné řešení této rovnice, pak
. y = fp(x, C) dx. .
Každým bodem [xo, y , Yo] E Q2 x R prochází aspoň jedno řešenÍ. Spojitost
funkce oqJjoy' zaručuje jednoznačnost řešenÍ. .
Příklad:
xy' I y' - 1 = O
(x *'0)
neboli
, 1
"y O
y +---= .
x x
Funkce
v-I
qJ(u, v) = -
u
je spojitě diferencovatelná pro u * O. Substitucí y' = p převedeme danou rov-
nici na lineární rovnici prvního řádu tvaru
, p 1
p +---=0.
x x
Obecným řešením homogenní róvnice
p' + p = O
x
670
je funkce
c
p-
x
Metodou variace konstant dostaneme obecné řešení nehomogenní rovnice
c
p=-+l.
x
Obecné řešení původní rovnice je
y = f( + 1) dx = C ln Ixl + x + D
(x :i= O) .
Diferenciální rovnice bez x (qJ je spojitá funkce na množině Q2 c R2):
y" = qJ(Y, y,) .
Každým bodem [Xo, Yo, Y ] E R X Q2 prochází aspoň jedno řešenÍ. Spojitost
funkcí Clp/ay, cqJ/cy' zaručuje jednoznačnost. Nejprve najdeme obecné řešení
p = p(y, C) rovnice
dp 1
- d = qJ(Y, p)-.
y p
Obecné řešení dané rovnice najdeme ze vztahu
y' = p(y, C) .
Příklad:
" '2 1 ( )
y=y- y:i=O.
y
Každým bodem [xo, Yo, y ] E R 3 (Yo 9= O) bude procházet právě jedno ře-
šenÍ. Nejprve řešíme rovnici
dp 2 IIp
-=p ---
dy y p y
Obecné řešení této rovnice na množině (R\{O}) x R je tvaru
f = f ;
neboli
p = Cy
(y :i= O, CER).
671
Obecné řešení dané rovnice dostaneme ze vztahu
, y' = Cy
neboli
y = D e Cx
(x E R, D * O) .
8.3.2. Homogenní lineární diferenciální rovnice
druhého řádu s konstantními koeficienty
ay" + by' + cy = O
(a, b, ,c E R, a * O) .
Každým bodem [xo, Yo, Yó] E R 3 procházÍ právě jedno řešenÍ. Najdeme řešení
r - _ + J b 2 - 4ac
1,2 - 2a - 4a 2
charakteristické rovnice
ar 2 + br + c = O .
Případ 1:
r 1 * r2
(rb r2 E R):
Pak řešení diferenciální rovnice je
/
y = C 1 e r 1 x + c 2 e r2X
( CI' C 2 E R, x E R) .
Případ 2:
rl = r 2 = r
(r E R):
Pak řešení diferenciální rovnice je
y = e rx (C 1 x + C 2 )
(CI' C 2 E R, x E R).
,
Případ 3:
r 1 ,2 ,- !Iv + iB ( , BER):
Pak řešení diferenciální rovnice je
y = e ax [CI cos (Bx) + C 2 sin (Bx)] = C e ax sin (Bx + qJ)
(c l' C 2 E R, x E R, popř. C, qJ E R, x E R).
Příklad 1:
2y" - 8y' + 6y :::: O .
672
Charakteristická rovnice je
2r 2 - 8r + 6 = O,
r 2 - 4r + 3 = O ; r 1 = 3 , r 2 = 1
Obecné řešení
y = CI e 3x + C 2 eX .
(pří pad 1).
Příklad 2:
3 y" + 18 y' + 27 Y = O .
Charak teristická rovnice je
3r 2 + 18r + 27 = O ;
r1.2 = -3
(pří pad 2).
Obecné řešení
Y = e- 3x (C I x + C 2 ).
Příklad 3:
y" + 2y' + 5y = O .
Charakteristická rovnice je
r 2 + 2r + 5 = O ;
Obecné řešení
"
r 1,2 = - 1 + 2i
(pří pad 3).
y = e - X [CI cos (2x) + C 2 sin (2x)] .
8.3.3. Homogenní lineární diferenciální rovnice
druhého řádu s proměnnými koeficienty
y" qJ(x) + y' t/J(x) + Y w(x) = O,
kde qJ [qJ(x) * O], t/J a w jsou spojité funkce na nějakém intervalu J. Každým
bodem [xo, Yo, y ] E J x R x R prochází právě jedno řešenÍ.
K řešení dané rovnice je třeba najít partikulární integrál YI' Pak můžeme
na intervalu, kde Y * O, zavést substituci
Y = YIZ,
Daná rovnice přejde v rovnici
YI z" qJ(x) + [2y; qJ(x) + YI t/J(x)] z' = O.
673
Zavedením další substituce z' = u vznikne diferenciální rovnice prvního řádu
(snížení řád u ) :
y; u' qJ(x) + [2y'l qJ(x) + YI t/J(x)] u = O .
Příklad:
x 2 (ln Ixl - 1) y" - xy' + y = O
[J = ( - 00, -e), popř. (-e, O), popř. (O, e), popř. (e, + (0)] .
Každým bodem J x R x R prochází právě jedno řešenÍ.
Partikulární integrál: Yl = x.
Substituce:
Y = Y 1 Z = xz ,
, , +
Y = xz z ,
y" = xz" + 2z' .
Po dosazení dostaneme
x 3 (ln lx I - 1) z" + x2(21n Ixl - 3) z' = o.
Po substituci z' = u, z" = u' dostaneme diferenciální rovnici prvního řádu
(snížení řád u ) :
xu'(ln Ixl - 1) = u(3 - 21n Ixl) .
Po separaci proměnných je na množině JI X J 2, kde JI je ( - 00, -e), popř.
( -e, O), popř. (O, e), popř. (e, + (0) a J 2 je R -, popř. R +, obecné řešení
f dU f 3 - 2 ln Ixl
-; = x(ln Ixl - 1) dx .
V integrálu na pravé straně rovnice zavedeme substituci
ln Ixl = v .
Dostaneme
f 3 - 2 ln Ixl dx = 3 f dv - 2 f v dv =
x(ln Ixl - 1) v-I v-I
= 3ln Ip - 11 - 2 f( 1 + v 1 ) dv =
= 3 ln Iv - 11 - 2v - 2 ln Iv - 11 + ln le 11 =
I I ln Ixl - 1 )
= ln C 1 2 ( C I * O .
x
674
Pak obecné řešení je
ln Ixl - 1
u = CI
x 2
( CI> O, Ixl > e),
popř.
ln Ixl - 1
u = CI
x 2
( CI < O, O < Ixl < e).
Odtud
_ f ln Ixl - 1
z - CI 2 dx .
x
Integrováním dostaneme
. . CI
- Z = C 2 --lnlxl,
x
odkud pro x E J plyne
y = C 2 x - f 1 ln Ixl.
8.3.4. Eůlerova diferenciální rovnice d uhého řádu
bez pravé strany [homogenní Eulerova diferenciální
rovnice]
ax 2 y" + bxy' + cy ='0,
kde a (a * O), b, c jsou konstanty a x E R -, popř. x E R +. Každým bodem
[xo, Yo, y ] E R 3 (xo f= O) prochází právě jedno řešenÍ.
Najdeme řešení charakteristické rovnice:
ar(r - 1) + br + c = O,
ar 2 + (b - a) r + c = O ;
_ a - b '. J( a - b 2 _ c )
'1.2 - + 2 .
2a 4a a
Případ 1: r 1 9= r2 (r 1 , r 2 E R):
Pak řešení diferenciální rovnice je
y = C 1 X r1 + C 2 X r2
( CI' C 2 E R, x 9= O) .
Případ 2: '1 = '2 = r (r E R):
- 675
Pak řešení diferenciální rovnice je
y=xr(CIlnlxl+ C 2 ) (C b C 2 ER,x:FO).
Případ 3: r1.2 = Q: + Bi (ex, BER):
Pak řešení diferenciální rovnice je
y = x 2 [ C I cos (8 ln Ixl) + C 2 sin (B ln Ixl)
Přiklad 1:
x 2 y" + 5xy' - 12y = O .
Charakteristická rovnice:
( CI' C 2 E R, x :F O) .
r(r - 1) + 5r - 12 = O,
r 2 + 4r - 12 = O ; r 1 = 2 , r 2 = - 6
Řešení diferenciální rovnice je
2 C -6 C 2 C 2
y = C 1 x + 2 X = IX + .
X
(pří pad 1).
Příklad 2:
4x 2 y" - 16xy' + 25y = O.
Charakteristická rovnice:
-4r(r - 1) - 16r + 25 =.'Ó,
4r 2 - 20r + 25 = O ; r I = r 2 = !
Řešení diférenciální rovnice je
(pří pad 2).
-
y = x S / 2 (C 1 In Ixl + C 2 ) = (y'X S ) (CI ln Ixl + C 2 ) =
= x 2 (Jx) (CI ln Ixl + C 2 ).
Příklad 3:
x 2 y" - 7xy' + 20y = O.
Charakteristická rovnice:
r(r - 1) - 7r + 20 = O,
r 2 - 8r + 20 = O; r1,2' = 4 + 2i
Řešení diferenciální rovnice je
(případ 3).
y = x 4 [ C 1 cos (2 ln Ixl) + C 2 sin (2 ln Ixl)
676
8.3.5. Nehomogenní lineární di fefenciální rovnice druhého řádu
y" <Pt (x) + y' <P2(X) + y <P3(X) = <P4(X),
kde lpi (i = 1, 2, 3, 4) jsou spojité funkce na nějakém intervalu J, <P I (x) * O
a funkce <P4 není identicky rovna nule. Po dělení funkcí <PI dostáváme normo-
vaný tvar uvedené rovnice
y" + y' <p(x) + y t/J(x) = w(x)
(w * O) .
Každým bodem [xo, Yo, y ] E J x R x R prochází právě jedno řešenÍ.
Postup řešení: Jsou-li YI a Y2 taková dvě partikulární řešení homogenní
rovnIce
y" + y' <p(x) + y tjJ(x) = O,
že
YI, Y2 * O
I I
YI, Y2
V každém bodě x E J, pak óbecné řešení této rovnice je tvaru
Y = CIYI + C 2 Y2.
Obecne řešení nehomogenní rovnice najdeme metodou variace konstant:
Y = CI (x) YI + C 2 (x) Y2 ;
pak
y' = C (X)Yi + CI(x)y; + C (X)Y2 + C2(X)Y .
Položíme
Pak
C (x) YI + C (x) Y2 = O.
y" = C; (x) Y'I + C I (x) Y + ,C (x) Y; + C 2 (x) Y
a po dosazení do rovnic máme
C;(x)y; + Ct(X)y'{ + C;(x)y; + C2(X)Y +
+ C I (x) Y'l <p(x) + C 2(X) y <p(x) + C I (x) YI t/J(x) + C 2(X) Y2 t/J(x) =
= C; (x) Y'I + C;(x) Y = w(x) .
Získali jsme tedy pro funkce C t a C 2 soustavu dvou rovnIC
C'I (x) YI + C (x) Y2 = O,
C'I (x) y't + C (x) Y; = w(x).
677
Protože determinant soustavy je pro každé číslo x E J různý od nuly, lze z této
soustavy vypočítat funkce C a C a integrací najít funkce Cla C 2'
Obecné řešení nehomogenní rovnice pak je
Y = C IYI + C 2 Y2 + C I (x) YI (x) + C 2 (x) Y2(X).
. Příklad:
x 2 y" - 2xy' + (X2 + 2) Y = x 4
(x + O) .
Dělíme-li danou rovnici mocninou x 2 , dostaneme normovaný tvar nehomo-
genní diferenciální rovnice druhého řádu:
2 x 2 + 2
y" _ _ly' + Y = x 2
X x 2
Nejprve řešíme homogenní diferenciální rovnici
2 x 2 + 2
y" - - y' + Y = O .
X x 2
Tato rovnice má partikulární integrál YI = x sin x. Postupujeme podle člán-
ku 8.3.3.
Položím -li Y = YIZ = zx sin x [x E (2n, (2k + 1) n), popř. x E ((2k + 1) n,
(2k + 2) n); k E Z] dostaneme rovnici
z"x sin x + (2 sin x + xcosx + 2sinx)z' =
= z" sin x + z' cos x = O.
Položíme-li z' = u, dostaneme rovnici u' sin x + u cos x = O. Její obecné ře-
šení je
c
u = ---:--
sIn x
(x + 2kn; k E Z, CER).
Pak
f; dX
z = C ---:-- = C cotg x + D
sin x
Odtud hledaný obecný integrál homogenní diferenciální rovnice tedy je
(x + 2kn; k E Z, C, DER) .
Y = (Ccotgx+D)xsinx = x(Dsinx+Ccosx)
(C, DER).
Tato funkce je spojitá ve všech bodech x, kde daná rovnice má smysl.
678
Obecný integrál nehomogenní diferenciální rovnice najdeme nyní pomocí
metody variace konstant. Dosadíme-li za CaD po řadě funkce C(x) a D(x),
máme
y = x[C(x) cos x + D(x)sinxJ.
Dosadíme-li tuto funkci do nehomogenní diferenciální rovnice a klademe-li
C'(x) cos x + D'(x) sin x = O,
pak
y' = C(x) cos x + D(x) sin x + x[ -C(x) sin x + D(x)cosx],
y" = [ - C(x) sin x + D(x) cos x] .2 +
+ x[ - C'(x) sin x + D'(x) cos x - C(x) cos x - D(x.) sin x] ,
a tedy
2[ -C(x) sin x + D(x) cos x] +
+x[ -C'(x) sin x + D'(x) cos x - C(x) cos x - D(x) sin x] -
- 2 [c(x) cos x + D(x) sin x] - 2[ -C(x) sin x + D(x) cos x] +
x .
x 2 + 2
+ [C(x) cos x + D(x) sin x] =
x
= x[ -C'(x) sin x + D'(x) cos x] = x 2 .
Dohromady s dodatečnou podmínkou platí tedy soustava rovnic
- C'(x) sin x + D'(x) cos x = x ,
C'(x) cos x + D'(x) sin x = O .
Její determinant soustavy je
- sin x, cos x = - 1 .
cos x sin x
Soustava má tedy řešení
C'(x) = x, cos x = - x sIn x ,
O, sin x
D'(x) = -sin x x = xcosx,
cos x, O
679
odkud
C(x) = fxsin x = xcosx - sin x,
D(x) = - Ix cos x = x sin x + cos x..
Obecný integrál nehomogenní diferenciální rovnice na množině (R\,[O}) x
x R x R je
. y = x[ C cos x + D sin x J +
+ x [ - sin x cos x + x cos 2 x + x sin 2 x + cos x sin:: J =
= Cx cos x + Dx sin x + x 2 .
8.3.6. Nehomogenní lineární diferenciální rovnice druhého řádu
- ,
s konstantními koeficienty
ay" + by' + cy = s(x) (x E J) ,
kde a (a * O), b, c jsou konstanty a s je spojitá funkce na intervalu J.
Nejprve řešíme homogenní diferenciální rovnici pro s(x) = O, jak je uvedeno
v článku 8.3.2. Potom hledáme partikulární řešení nehomogenní diferenciální
rovnice (tj. s pravou stranou) metodou variace konstant. V jednotlivých pří-
padech lze najít partikulární integrál rovnice s pravou stranou rychleji:
Nechť p + qi není kořenem charakteristické rovnice. Nechť funkce s má tvar
s(x) = ePx[p(x) cos (qx) + Q(x) sin (qx)J '
kde P a Q jsou po řadě mnohočleny m-tého a n-tého stupně. Pak partikulární
in tegrál rovnice
ay" + by' + cy = s(x)
má tvar
yp(x) = e PX [R(x) cos (qx) + S(x) sin (qx)J '
kde R, S jsou mnohočleny stupně max {m, n}.
Je-li p + qi jednoduchým kořenem charakteristické rovnice, pak partiku-
lární integrál má tvar
yp(x) x e PX [R(x) cos (qx) + S(x) sin (qx)J '
kde R, S jsou opět mnohočleny stupně max {m, n}.
680
Je-Ii p dvojnásobným kořenem charakteristické rovnice a funkce s je tvaru
s(x) = p(x) e Px ,
kde P je mnohočlen m-tého stupně, pak partikulární integrál rovnIce
ar" + by' + cy = s(x) má tvar
Y p = x 2 R(x) e PX ,
kde R je mnohočlen m-tého stupně. Je-li funkce s součtem funkcí Si tvaru
e PX [P(x) cos (qx) + Q(x) sin (qx)] , pak partikulární řešení rovnice
ay" + by' + cy = s(x)
je součtem partikulárních řešení rovnic
ay" + by' + cy = Si(X).
Řešení nehomogenní diferenciální rovnice se pak rovná součtu obecného
řešení příslušné homogenní diferenciální rovnice a partikulárního řešení ne-
homogenní rovn'ice.
Příklad 1:
y" - 2y' - 8y = 3 sin x .
Řešení příslušné homogenní diferenciální rovnice:
y" - 2 y' - 8 y = O .
Charakteristická rovnice:
r 2 - 2r - 8 = O .
,
r 1 =4, r2= -2.
Řešení homogenní diferenciální rovnice tedy je
YI = C 1 e 4x + C 2 e - 2x .
Protože s(x) = 3 sin x, hledáme partikulární integrál ve tvaru
y - A sin x + B cos x ,
y' - A cos x - B sin x,
y" = - A sin x - B cos x .
Po dosazení do výchozí rovnice máme
- A sin x - B cos x - 2A cos x + 2B sin x - 8A sin x - 8B cos x =
= 3 sin x .
681
Porovnáním koeficientů dostaneme
-9A + 2B = 3,
- 9 B - 2A = O ,
odkud
A=
27
85 '
6
B =-.
85
Obecné řešení dané diferenciální rovnice tedy je
4x C 2 27. 6
y = C e + - - - sin x + - cos x .
I e 2x 85 85
Příklad 2 (případ rezonance):
y" + y' - 2 y = !ex .
Charakteristická rovnice příslušné homogenní diferenciální rovnice:
r 2 + r - 2 = O ; r I = 1, r 2 = - 2 .
Obecné řešení homogenní diferenciální rovnice je
y = C I eX + C 2 e - 2x .
Protože s(x) = t eX, hledáme řešení ve tvaru
y = Ax eX ,
y' = A eX + Ax eX ,
y" = 2A eX + Ax eX .
Po dosazení do výchozí rovnice máme
2A eX + Ax eX + A eX + Ax eX - 2Ax eX = 3A eX = t eX .
Odtud A = i, a obecné řešení dané rovnice tedy je
y = CI eX + C 2 e- 2x + t,e x .
8.3.7. Eulerova diferenciální rovnice druhého řádu
s pravou stranou [úplná Eulerova diferenciální rovniceJ
ax 2 y" + bxy' + cy = qJ(x),
kde a (a * O), b, c jsou konstanty a qJ(x) je spojitá funkce na intervalu J
(O J).
682
Nejprve řešíme homogenní Eulerovu diferenciální rovnici
ax 2 y" + bxy' + cy = O,
jak je uvedeno v článku 8.3.4. Potom hledáme partikulární řešení nehomogenní
rovnice metodou variace konstant. V jednotlivých případech lze najít parti-
kulární integrál rovnice s pravou stranou rychleji tímto postupem:
a) Pravá strana rovnice je polynom n-tého stupně. Hledáme řešení ve tvaru
y = Axn + Bxn-t + Cx n - 2 + ... + K .
b) Pravá strana rovnice je funkce obsahující výraz e nx . Hledáme řešení ve
tvaru
y=Ae nx ,
kde e nx je výraz vyskytující se na pravé straně.
c) Pravá strana je funkce sin (mx) nebo cos (mx) nebo lineární kombinace
obou těchto funkcí. Řešení hledáme ve tvaru
y = A sin (mx) + Bcos(mx).
d) Pravá strana je funkce sinh (mx) nebo cosh (mx) nebo lineární kom-
binace obou těchto funkcí. Řešení hledáme ve tvaru
y = A sinh (mx) + B siQh (mx).
e) Pravá strana je algebraickým součtem předchozích jednotlivě uvedený h
funkcí. Řešení je pak rovněž algebraickým součtem příslušných tvarů řešenÍ.
Řešení diferenciální rovnice s pravou stranou je pak součtem obecného řešení
rovnice bez pravé strany a nalezeného partikulárního řešení rovnicé s pravou
stranou.
Příklad:
x 2 y" - 2xy' - 10y = 2X2 - 3x + 10.
Řešení příslušné homogenní diferenciální rovnice:
x 2 y" - 2xy' -_ 10y = O.
Charakteristická rovnice:
r(r - 1) - 2r - 10 = O,
r 2 - 3r - 10 = O; r I = 5, r 2 == -2.
Homogenní diferenciální rovnice má tedy obecný integrál
y = CIX S + C 2 X- 2 .
Partikulární integrál se určí takto:
683
Vzhledem k tvaru pravé strany hledáme řešení ve tvaru
y = AX2 + Bx + C ,
y' = 2Ax + B ,
y" = 2A .
Po dosazení do výchozí rovnice je
x 2 . 2A - 2x(2Ax + B) - lo(Ax2 + Bx + C) = 2X2 - 3x + 10
Porovnáním koeficientů dostaneme
x 2 (2A - 4A - 10A) = 2x 2 ,
x( -2B - 10B) -3x,
- 10C O .
Je tedy
A= -t, B=1, C= -1.
Partikulární integrál je
1 . 2 1
Yl = -(jx + 4X - 1 .
Diferenciální rovnice s pravou stranou má tedy obecné řeš ní
C 5 C 2 1 2 1 1
y = 1 X + 1: - 6"X + 4 X - .
x
8.4. OBYČEJNÉ DIFERENCIÁLNÍ ROVNICE
TŘETÍHO ŘÁDU
8.4.1. Homogenní lineární diferenciální rovnice třetího řádu
s konstantními koeficienty
y'" + a y" + by' + c Y = O,
kde a, b, c jsou konstanty.
Najdeme řešení charakteristické rovni e
r 3 + ar 2 + br + c O .
Případ .1: r 1 * r2 * r3, r3 * rl
Pak řešení diferenciální rovnice je
(r 1 , r2, r 3 E R):
y = C 1 e r 1 x + c 2 e r2X + C 3 e r 3X .
684
Případ 2: r 1 = r2 = r, r3 9= r (r,r3 E R):
Pak řešení diferenciální rovnice je
Y = (C 1 x + C 2 )e rX + C 3 e r3X .
Případ' 3: r 1 = r 2 = r 3 = r (r E R):
Pak řešení diferenciální rovnice je
Y = (C 1 X 2 + C 2 x + C 3 )e rx .
Případ 4: rl E R, r 2 ,3 = (X + iB ( , tJ E R):
Pak řešení diferenciální rovnice je
Y = CI e rtX + [C 2 cos (Bx) + C 3 sin ( x)] cczx.
Tuto metodu lze snadno zobecnit pro homogenní diferenciální rovnIce
n-tého řádu s konstantními koeficienty.
Má-li homogenní lineární diferenciální rovnice n-tého řádu n nezávislých
řešení Yl, Y2, ..., Yn (tj. determinant
Y l' ..., Y n
, ,
Y l' . .., Y n
Y (n - 1) ,,(n - 1 )
1 , ..., J n
je různý od nuly), pak obecné řešení má tvar
Y = C 1 Yl + C 2 Y2 + ... + CnYn'
8.4.2. Nehomogenní lineární diferenciální rovnice
třetího řádu s konstantními koeficienty
y'" + ay" + by' + cy = qJ(x),
kde a, b, c jsou konstanty a qJ(x) je spojitá funkce na intervalu J.
Tato diferenciální rovnice se obdobně jako nehomogenní diferenciální rov-
nice druhého řádu (viz str. 677) vyšetřuje tak, že se nejprve řeší příslušná homo-
genní diferenciální rovnice a pak se bud" pomocí vhodné substi-tuce, nebo
metodou variace konstant hledá partikulární integrál. Součet obecného řešení
homogenní rovnice a partikulárního řešení nehomogenní rovnice dává ()hecné
řešení dané diferenciální rovnice.
Této metody lze také obdobně použít při řešení diferenciálních rovnic
vyššího řád u.
685
8.5. INTEGROVÁNÍ DIFERENCIÁLNÍCH ROVNIC
POMOCÍ MOCNINNÝCH ŘAD
Je-li f(x, y) analytická funkce na. oboru Xo - a < x < Xo + a,
Yo - b ' < y < Yo + b, pak na určitém okolí bodu Xo existuje analytické řešení
ex:>
y(x) = Yo + L aix i
i = 1
rovnIce
y' = f(x, y),
y(xo) = Yo . /
Koeficienty rozvoje řešení y určíme porovnáním koeficien ů u stejných mocnin.
Každý částečný součet řady pro y(x) lze považovat za přibližné řešehÍ úlohy.
Poloměr konvergence mocninné řady určíme známými metodami teorie moc-
ninných řad.
Příklad :
y' = y2 + x3 ,
Položíme
Y.o = y(O) = -1 .
00
y = - 1 + L aix i ;
i= 1
pak
00
y' = L iai xi - 1 .
i= 1
Po dosazení do výchozÍ rovnice máme
ex:>' ( ex:> ) 2
.L ia i x i - 1 = -1 +.L aixi + x 3 .
1=1 1=1
Porovnáním koeficientů máme
a. = 1 ,
2a2 = - 2a 1'
3a3 = af - 2a2 ,
4a4 = 1 - 2a3 + 2a1a2,
Přibližné řešení:
a1 = 1 ,
a2 = - 1 ,
a3 = 1(1 + 2) = 1 ,
a4 = f(1 - 2 - 2) = -i, atd.
y - 1 + x - x 2 + x 3 - ix 4 .
686
BesseloVa (diferenciální> rovnice
Homogenní lineární diferenciální rovnice
y2 y " + xy' + (X2 - p2)y = O
(x * O)
se nazývá Besselova (diferenciální> rovnice. Konstanta p se nazývá index
Besselovy (diferenciální> rovnice. Řešením jsou tzv. Besselovy.funkce, které
lze vytvořit kombinováním elementárních funkcí jen pro index
2n + 1
p=
2
(n E Z) .
Obecné řešení pro pf/Z:
y = C Jp(x) + DJ_p(x),
kde
( X ) P 00 ( - 1 )m I X ) 2m
Jp(x) = 2 m o m! r(p + m + 1) \ 2
(obr. 381).
y
1
Obr. 381. Besselovy funkce prvního druhu
Obr. 382. Besselovy funkce druhého
druhu [W eberovy funkce]
Obecné řešení pro p E Z:
y = CJp(X) + DYp(x),
kde
( ) . Jm(X) cos (m1t) - J -m(X)
Y X = hm
p m-p sin (m1t)
m*p
(obr. 382).
Přitom r je tzv. funkce gama, definovaná bud' vztahem
f+ 00
r(x) = Jo e- t ř- 1 dt
(x > O),
6R7
nebo vztahem
p! pX-l
r(x) = lim
p - 00 x( x + 1) (x + 2)... (x + P - 1)
(p E N, X E R) .
Funkce gama splňuje tyto vztahy:
r(x + 1) = x r(x) ,
1t
r(x) r(l - x) = . ( )'
sin 1tX
r(x) r(x + t) = 2 1 r(2x) ;
pro x E N platí
r(x) = (x - I)!.
Funkce J p a Y p jsou pro pEN tabelovány (viz např. [206]).
Mezi Besselovými funkcemi s různými indexy platí vztahy
2p
J p - 1 (x) + J p + I(X) = - Jp(x),
x
dJp(x) p
d = --JAx) + Jp-l(X).
x x
8.6. PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE
8.6.1. Základní pojmy
Parciální diferenciální rovnicí n-tého řádu v m proměnných Xl' X2, ..., X m
nazýváme rovnici tvaru
F ( Xl' ..., x m , Y, oY , ..., OY , 0 2 [ , ..., on! ) = O,
Xl X m Xl X m
(1)
kde mEN a F: Qmn+m+l R (Qmn+m+l C Rmn+m+l). Přitom levá strana
rovnice závisí v každém případě aspoň na jedné n-té derivaci hledané funkce.
ŘeL ením [integrálem, integrální plochou, integrální varietou] rovnice (1) na
určité oblasti Dm c R m nazýváme každou funkci qJ: Dm => R, která má všech-
ny požadované parciální derivace na oblasti Qm a která po dosazení do rov-
nice (1) tuto rovnici splňuje. Řešení nemusí být dáno v explicitním tvaru
688
y = qJ(X 1 , ..., xm) ale může být dáno i implicitně rovnicí u(x 1 , x 2 , ..., x m , y) = o.
U parciálních diferenciálních rovnic nelze mluvit o obecném řešenÍ. U ně-
kterých jednoduchých rovnic lze uvést obecný integrál, který závisí na jedné
nebo několika libovolných funkcích.
8.6.2. Jednoduché parci ální di ferenc i ální rovnice
V následujícím přehledu symboly ,v, Wl' W2 značí libovolné funkce,
které mají dostatečný počet derivacÍ.
Rovnice
Řešení
z = O
x
Zy = O
Zxx = O
- - O
":'yy -
Z x}' = O
..,. - Z - O
"'x y -
z = w(y)
z = w(x)
z = x Wl(y) + W2(y)
z = y w 1 (x) + w 2 (x)
z = w 1 (x) + W2(Y)
z = w(x + y)
z = JJf(x, y) dx dy + w 1 (x) + W2(y)
z = Wl(X + y) + w 2 (x - y)
z = w(x - y)
z = w 1 (x + ty) + w 2 (x - ty)
(t 2 * O je reálná konstanta)
z = w(ay - bx)
z = Wl(X + iy) + w 2 (x - iy)
z = w(g(x, y))
(g je daná 'funkce proměnných x, y)
z = w(xy)
z = w(x 2 + y2)
ZX\' = f(x, y)
zxx - z},y = O
Zx + Zy = O
z)'}' O
z ---=
xx t 2
az x + bz y = O
Zxx + Zyy = O
zxg}. - z'ygx = O
xZx - YZy = O
yzx - XZy = O
689
8.6.3. Lineární parciální diferenciální rovnice prvního řádu
ve dvou proměnných
Lineární parciální diferenciální rovnicí prvního řádu ve dvou proměn-
ných nazýváme rovnici
cz, (''I Z
P(x, y, z) + Q(x, y, z) = R(x, y, z) ,
ex cy
kde P, Q, R jsou spojité funkce proměnných x, y, z na nějaké oblasti Q3'
Najdeme-li řešení soustavy obyčejných diferenciálních rovnic
dy
dx
Q
P'
ve tvaru
(2)
dz
dx
R
P
(3)
u(x, y, z) = CI'
v(x,y,z) = C 2 ,
pak obecné řešení rovnice (2) je tvaru
w( u, v) = O,
kde w je libovolná diferencovatelná funkce dvou proměnných. K tomu, aby-
chom mohli funkci w jednoznačně určit, je třeba znát tzv. okrajovou podmínku.
Poznámka:
Místo soustavy (3) můžeme řešit soustavu
dx P
- -
dy R'
popř. soustavu
dx P
- R'
dz
dz R
-
dy Q'
dy Q
-
dz R
o řešení takové soustavy viz např. [147]. V následujícím příkladu ukážeme
jednoduchý případ.
Příklad:
t z tz
2xy + 4y2 = x 2 y.
('X (')'
69(,
Pak soustavě
dy 2y
- -
dx x
dz x
- - -
dx 2
vyhovují řešení
y = C I x 2 ,
x 2
Z = - + C 2 ,
4
neboli
Y
2 = CI ,
X
(4)
x 2
z--=C 2 .
4
Obecné řešení dané rovnice je
( Y x 2 )
w- z-- =0
x 2 ' 4 '
kde w je libovolná diferencovatelná funkce dvou proměnných.
Požadujeme-li, aby hledané řešení splňovalo podmínku z(x,4) = X2, pak
z rovnic (4) dostaneme
4
CI = 2'
x
5 2/
C 2 =4 x2 - : =x 2 ,
Odtud CIC 2 = 4, a tedy
y ( X2 ) '
x 2 Z - 4 = 4
neboli
4x 2 x 2 2 ( 4 1 )
z=-+-=x -+- .
Y 4 y 4
691
9. NEKONEČNÉ ŘADY, FOURIEROVY ŘADY,
FOURIERŮV INTEGRÁL,
LAPLACEOVA TRANSFORMACE
9.1. ŘADY
9.1.1. Základní pojmy
Definice:
Je-li {Uk} číselná posloupnost, pak nekonečnou číselnou řadou (stručně čí-
selnou řadou nebo řadou) nazýváme výraz
00
a 1 + a 2 + ... + a k + ... = L ak ,
n=1
(X)
který často -stručněji značíme Lak nebo Lak' Sčítanec a k se nazývá k-tý člen
n 1
řady. Výraz sn = I a k = al + (z2 + ... + a n se nazývá n-tý částečný součet
r:r: i=l
řady Lak' Posloupnost
n=l
{Sk} = (Sl,S2,S3"") = (a., al +a2, al +a 2 +a3, ...)
00
se n"zývá posloupnost částečných součtů řady Lak.
n=l
Příklad"V:
{a k } = (1, t,!, t, ...),
{Sk} = (1, 1 + 1, 1 + t + !,
= (1, lt, 1 , 1 , ...),
1 + t + i + t, ...) =
00
" 1 1 1 1
i..J ak = + 2 + 4 + 8" + ... ·
k=l
"
9.1.2. Kri téria konvergence řad
Konvergentní a divergentní řady
00
Říkáme, že řada L a k je konvergentní [konverguje], jestliže existuje limita
k=l n.
lim Sn posloupnosti částečných součtů Sn = L a k a má konečnou hodnotu s,
n-oo k= 1
která se nazývá součet (konvergentní) řady.
692
Řada {a k } se nazývá určitě divergentní, resp. neurčitě divergentní, jestliže
posloupnost {sn} jejích částečných součtů má nevlastní limitu, resp. neexistuje
její vlastní ani nevlastní limita.
00
Říkáme, že řada L a k je absolutně konvergentní [konverguje absolutně],
k=l
00
jestliže řada L lakl konverguje.
k=l
00
Říkáme, že řada L ak je neabsolutně [relativně] konvergentní [konverguje
k-=l
00 00
neabsolutně [relativně]], jestliže řada L ak konverguje, ale řada L lakl
diverguje. k = 1 k = 1
Říkáme, že řada je nepodmíněně, resp. podmíněně konvergentní [konverguje
nepodmíněně, resp. podmíněně], jestliže součet řady nezávisí, resp. závisí na
přerovnání členů řady.
Absolutně, resp. neabsolutně konvergentní řada je nepodmíněně, resp. pod-
míněně konvergentní.
Vynecháme-li v dané řadě L a k prvních n členů a 1 , a 2 , ..., a n , dostaneme
řadu k= 1
.JI
00
a n + 1 + a n + 2 + ... = L a n + k ,
k=l
00
kterou nazýváme zbytkem řady L ak po n-tém členu. Je-Ii 'laná řada konver-
k=l
gentní a má-li součet s, pak zbytek této řady po n-tém členu je také konver-
g ntní řada a její součet Rn se rovná rozdílu součtu s a částečného součtu sn:
Rn = S - sn .
Pro konvergentní řady platí
lim Rn = O .
n-oo
00
Základní kritérium konvergence řady L a k
k=l
lim (Sk+P - Sk) = O pro \Ip E N .
k-oo
Toto kritérium je nutné a postačující.
Nutnou,. ale nikoli postačující podmínkou konvergence řady
lim a k = O .
k-oo
00
L a k Je
k=l
693
Řady s kladnými členy
00
Řada L a k se nazývá řada s nezápornými členy, resp. řada s kladnými členy,
k=l
jestliže pro všechny indexy k platí a k > O, resp. a k > O.
00
Řada L a k s nezápornými nebo kladnými členy se nazývá majorantni
k=l 00
[ majoranta], resp. minorantni [minoranta] k řadě L b k , jestliže pro skoro
k=l
všechny indexy k platí a k > b k , resp. ak < b k .
Postačující, ale nikoli nutnou podmínku konvergence, popř. divergence
obsahují tato kritéria:
00
Podilové [d'Alembertovo] kritérium: Jestliže L a k je řada s kladnými
k=l
členy, platí O < q < 1 a pro skoro všechny indexy k platí
a k + 1
- < q,
a k
a k + 1
resp. - > 1 ,
a k
pak řada je konvergen tní, resp. divergentní.
00
Limitní podílové' [limitni d' Alembertovo] kritérium: Jestliže L ak je řada
k=l
s kladnými členy, existuje lim (ak + ljak) = q, pak při q <' 1, resp. q > 1 je
n-+ 00
I
řada konvergentní, resp. divergentní. Jestliže 4 = 1, pak o konvergenci řady
nelze podle tohoto kritéria rozhodnout.
. 00
Odmocninové [Cauchyovo] kritérium: Jestliže L ak je řada s kladnými
k=l
členy, platí O < q < 1 a pro skoro všechny indexy k je
k / < esp k / >/ 1
'\/ a k = q, r . V a k = ,
pak řada je konvergentní, resp. divergentní.
00
Limitní odmocninové [limitní Cauchyovo] kritérium: Jestliže L a k je řada
k=l
s 'kladnými členy, existuje lim Vak = q, pak při q < 1, resp. q > 1 řada
k-+oo
konverguje, resp. diverguje. Jestliže q = 1, pak o konvergenci řady nelze podle
tohoto kritéria rozhodnout.
00
Porovnávaci kritérium: Řada L ak s kladnými členy konverguje, jestliže
· k=l 00
k ní existuje konvergentní majoranta. Jestliže řada L a k diverguje, pak je
k=l
divergentní každá její majoranta. '
694
Alternující řady
a)
Řada I ( - 1 r + 1 a k , kde Uk > O, se nazývá alternující.
k=l
Alternující řada konverguje, jestliže příslušná řada absolutních hodnot
konverguje.
00
Leibnizol'o kritériu'11 pro alternující řady: Jestliže I ( - l)k + 1 ak, kde
k=l
a k > O, je alternující řada, posloupnost {a k } je nerostoucí a lim a k = O, pak
řada je konvergentní. k-oo
Operace s řadami
Konvergentní řady lze člen po členu sčítat nebo odčítat, tj. jestliže
00 00
I a k = A, I b k = B, pak platí
k=l k=l
00
I (a k + b k ) = A + B ,
k=l
00
I (a k - b k ) = A - B .
k=l
00 a) .
Jestliže řady I a k = A, I b k = B jsou absolutně konvergentní, pak kon-
k=l k=l
00
verguje absolutně také řada I Ck' kde
k=l
C k = akbl + a k - 1 b 2 + o.. + a 1 b k ,
a platí
00
I C k = AB .
k=l
00
Řada L C k se nazývá cauchyovský součin daných řad.
k=l
9.1.3. Některé nekonečné konvergentní číselné řady
111
1. + 1! + 2! + 3! + ... = e
111
1 - 2 + "3 - 4 + o.. = ln 2
111
1+-+-+-+...=2
248
(a k = (k 1)) ;
( a = ( -lf- 1 ) o
k k '
(nk = 2 k 1 ) ;
695
1 1 1 1t 2
1 + 2 2 + 32 + 42 + ... = 6
1 1 1 1t 2
1 - - + -- - - + ... = -
2 2 3 2 4 2 12
1 1 1 1t 2
--, + -2 + 2 + ... = -
1- 3 5 8
1 1 ]
+ 3 + 3. 4' ... = 1
1 1 1 1
1.3 + 3.5 + s.-i + ... = 2
1 1 1 1
-- + + + ... = -
1.2.3 2.3.4 3.4.5 4
(a k = k 12 ) ;
( _ ( _ l)k - t ) .
a k - 2 '
k
(a k = (2k 1 )2 ) ;
(a k = k(k 1) ) ;
(a k = (2k _ 1)1(2k + 1) ) ;
(a k = k(k + 1 (k + 2) ) .
Další nekonečné řady pro číslo 1t dostaneme z rozvojů eyklometrických
funkcí v řady (viz str. 704):
1t 111
- = arct g 1 = 1 - - + - - - +
4 3 5 7 ...
1t 1 1 ( 1 1 )
4 = arctg 2 + arctg 3 = 2 + 3 -
- ( ;3 + 3 13 ) + (;5 + 315 ) - ...
1t 1 1
- = 4 arctg- - arctg- =
4 5 239
= 4 G - 3 \3 + 5 \5 - ...) -
( 1 1 '. 1 )
- 239 - 3 . 239 3 + 5. 239 5 - ... ,
1t 1 1 1
4 = arctg 2 + arct g "5 + arctg 8 '
1t 1 1 1
- = 8 arctg - - arctg - - 4 arctg - .
4 10 239 515
696
(Leibnizova řada),
(Eulerova řada),
9.1.4. Mocninné řady
Posloupností .funkcí [.funkční posloupností] na množině J nazýváme
zobrazení množiny N všech kladných celých čísel do množiny LJ všech ko-
nečných reálných, popř. komplexních funkcí definovaných na množině J.
Posloupnost funkcí zapisujeme
: .f = l' Lhcj, (f , .f , ...) nebo .f , .f ,....
Pro určité číslo Xo E J dostaneme z posloupnosti {.f } čís e I n o u p o s 10 u p-
no st {fi(xo)}. Je-li posloupnost {fi(xo)} konvergentní, říkáme, že funkční
posloupnost {.f } konverguje r bodě Xo. Jestliže pro každé číslo x E M c J
existuje vlastní limita lim .f (x) = .ť(x), říkáme, že jÚnkční posloupnost {f }
k - r.(\
,k{)llrergl ie na nl11o=žně 1\1 k .funkci ,{
Jestliže {.f } je funkční posloupnost na množině J, pak výraz
oc
.f + f + ... = I .f = Lf
k=l
nazýváme řadou funkcí [funkční řadou J. Funkci fk nazýváme k-tým členem
n
řady a funkci Sn = I f n-(Í'ln částečn.vm součtem řady. Posloupnost {sn)
k=l 00
nazýváme posloupností částečných součtů .funkční řady I f .
k=1
00 00
Pro určité číslo Xo E J dostaneme z řady L f číselnou řad u I Á(xo).
k=1 k=1
00 00
Je-li řada I fi(xo) konvergentní, říkáme, že funkční řada L f konverguje
k=l k=l
00
v bodě xo, který pak nazýváme bodem .konvergence. řady L "'. Jestliže pro
k=1
00 00
každé číslo x E M c J je řada L Á konvergentní, říkáme, že řada I f
k=l k=l
konverguje na množině M; množinu M všech bodů konvergence dané funkční
řady nazýváme oborenl konvergence této řady. Každému bodu x z oboru kon-
00
vergence dané funkční řady I h je pomocí této řady př řazeno číslo s(x) =
k = 1
<:J..J 00
= L f (x), takže na oboru konvergence je funkční řadou I.f definována
k=l k=l
OC'
funkce s, která se nazývá součet .filnkční řady L.f
k-=l
697
Říkáme, že funkční posloupnost {f } konverguje stejnoměrně [je stejnoměrně
konvergentní] k funkci j' na intervalu M, právě když k libovolnému číslu
B > O existuje takové číslo ko, že pro všechny indexy k > ko a pro všechny
body x E M platí If (x) - f(x)1 < B.
00
Říkáme, že funkční řada I h stejnoměrně konverguje [je stejnoměrně
k=l
konvergentní] k funkci s na intervalu M, právě když posloupnost {sn} jejích
částečných součtů stejnoměrně konverguje k funkci s na intervalu M.
Mocninnou [potenční] řadou v jedné reálné proměnné se středem v bodě Xo
nazýváme funkční řadu tvaru
00 00
I Á = ao + a 1 (x - XO) + a 2 (x - XO)2 + ... = I ak(x - XO)k,
k=O k=O
kde ao, a 1 , a 2 , ... jsou reálné konstanty. Pro Xo = O dostaneme mocninnou
řadu se středem v bodě O tvaru
00
k 2
i.J akx = ao + a 1 x + a2 x +....
k=O
Abelova věta o konvergenci mocninné řady
00
Konverguje-li mocninná řada I akx" v bodě Xl * O, konverguje absolutně
k=O 00
v každém bodě x, pro nějž platí Ixl < x.". Diverguje-li mocninná řada I akx k
k=O
v bodě Xl' diverguje v každém bodě x; pro nějž platí Ixl > x l'
Věta o konvergenčním intervalu
00
Ke každé mocninné řadě I akJ! existuje takové číslo (tzv. poloměr kon-
k=O
vergence) r > O (připouštíme i r = + 00), že pro všechna čísla x, pro něž
Ixl < r (tzv. interval konllergence [konvergenční interval]), je mocninná řada
absolutně konvergentní a pro všechna čísla x, pro něž Ixl > r, je divergentní.
V bodech x, pro něž Ixl :=: r, nelze obecně rozhodnout, zda mocninná řada je
konvergentní nebo divergentní. Je-li r = O, pak mocninná řada je konver-
gentní jen v bodě x = O. Jestliže r = + 00, pak mocninná řada je konvergentní
na množině R.
Cauchyova-Hadamardova věta
Pro poloměr konvergence r mocninné řady platí
1 1
r---
,- Jl - rrm Vlakl '
k-oo
698
popř.
1
r ---
- -
J.l
1
lim
k-oo
U k + 1
a k
přičemž pro J.l = O klademe r = + 00 a pro J.l = + oc klademe r = O. Symbol
rrm Vlakl = lim sup Vlakl
k-oo
značí tzv. limes superior [horní limitu] posloupnosti {Vlak I}, což je největší
hromadný bod posloupnosti
lall, Jla 2 1, tll a 31, ..., Vlakl, ... .
Podobně symbol
t==- a k + 1
11m -
k - 00 a k
značí limes superior posloupnosti
a2 a3 a n +l
, ..., , ... .
a 1 a 2 a n
Existuje-Ii limita
.- ak + 1 r== k / 1 I
J1 = lm -, resp. J.l = 11m V ak ,
k-oo k-oo
pak pro poloměr konvergence r platí
1
r =-,
J1
přičemž při J1 = O, resp. J1 = + 00 je r = -+- x, resp. r = O.
>t.
Vlastnosti mocninné řady
Mocninná ř a konv rgentní na intervalu J = (-r, r), kde r je její kon-
vergenční poloměr, má tyto vlastnosti:
1. Konverguje stejnoměrně na každém uzavřeném intervalu I c J.
2. Součet s mocninné řady je spojitou funkcí na intervalu J.
3. Na každém intervalu 1 c J je diferencovatelná a integrovatelná člen
po členu, přičemž řady takto vzniklé mají stejný konvergenční poloměr jako
původní řady.
69Q
Příklad:
f x dz
arctg x = 2 .
') 1 + z
Mocninná řada
1 - Z2 + Z4 - Z6 + ...
konverguje pro každé číslo z, pro něž platí Izl < 1, stejnoměrně k součtu
1 (1 + Z2). Integrací řady člen po členu dostaneme
x 3 x 5
arctg x = x - 3 + 5 - ... (Ixl < 1).
Tato řada konverguje kromě toho ještě pro x = + 1 podle Leibnizova kri-
téria konvergence pro alternující řady (viz str. 695).
Rozvoj funkce v mocninnou řadu
Taylorův vzorec: Jestliže reálná funkce j' reálné proměnné x na inter\lalu
(a, x> pro " > a, resp. na intervalu (x, a> pro x < a má spojité derivace až
do n-tého řádu včetně a na intervalu (a, x), resp. na intervalu (x, a) má spojitou
derivaci (n + 1 )-ního řádu, pak vzorec
j"(a) f"(a)
j'(x) = f(a) + -(x - a) + (x - a)2 + ...
I! 2!
f(n>(a) n.'
... + (x - a) + Rn + 1 ,
n!
kde, zbyte Rn + I lze uvést na některý z těchto tvarů:
"
(x at+ 1
R = f (n + 1 > ( a + 8- ( x - a )) , ( O < 8- < I )
n+l (n+l)!
(Lagrangeův tvar),
(x a)n + 1
Rn+ 1 = , (1 - 1])n f(n+ l>(a + 1](x - a))
n.
(O < 1] < I)
(Cauchyův tvar), popř. na integrální tvar
l x ( X t ) n
R = f (n + l> ( t ) dt
n+1 "
II n.
se nazývá TaJ lorůr l'zorec.
700
Poznámka:
Píšeme-li x = a + h, dostaneme tento tvar Taylorova vzorce:
f( a + h ) = f( a ) + f' ( a) h + f'J ) h 2 + ... + p n'(a) h n + R
. 1 , 2 ' ,n. 1 -
.. 11 .
kde
f(n + 1 ) ( a + 1 9h )
R - . h n + 1
n + 1 - (n + I)!
f (n + l> ( a + h )
R = 11 ( 1 _ ) n hn + 1
n+l , 11
n.
(O < 19 < 1)
(O < ti < 1),
l a+h ( a + h t\ll
Rn+ 1 = f(n+ l>(t) I dt.
a n!
Taylorova řada: Jestliže funkce .f na intervalu <a, x) pro x > (I, resp. na
intervalu <x, a) pro x < a má derivace všech řádů, pak mocninná řada
f'( ). f"( )
f(a)+ (x-a)+ (l (x_a)2+...
1 ! 2 !
v bodě x konverguje a její součet se rovná .ť(x) právě když
lim R n + l(X) = O,
n-oo
kde R n + l(X) je některý z uvedených zbytků.
M aclaurinův vzorec: Jestliže v Taylorově vzorci položíme a = O, pak vzorec
f' ( O) j''' ( O ) j'(n> ( o )
f( x ) = f( O ) + - x + x 2 + ... + -- x n + R
I! 2! n! n+l,
kde zbytek
xn+ 1
R = .r(n + 1 > ( 8x )
n+l (n+l)!J
(Lagrangeův tvar), popř.
xn+ 1
Rn + 1 = ----,- (t - t1)n j'(n + 1)(11X)
n.
(O < 8 < 1)
(O < 11 < 1)
(C auchyůz; tvar), se nazývá M aclaurinův vzorec.
701
M aclaurinova řada: Jestliže funkce f má na intervalu (O, x), resp. ( - x, O)
spojité derivace všech řádů, pak mocninná řada
. j(O) + 1'(0) x + 1"(0) x 2 + ...
1 ! 2!
v bodě x konverguje a její součet se rovná f(x), právě když
lim Rn+ l(X) = O,
n-CX)
kde Rn+ l(X) je některý z uvedených zbytků.
Přehled rozvojů v řady, zejména mocninné
Binomická řada
(1 + xY = 1 + G)x + (;)X2 + (;)x 3 + ... . (rE R),
kde
( r ) = r( r - 1)... (r - k + 1)
k k! '
je konvergentní pro všechna čísla Ixl < 1. Pro Ixl = 1 je třeba konvergenci
řady vyšetřovat zvlášť. Pro Ixl > 1 řada diverguje. Pro r = n E N je (:)
binomickým koeficientem, který se pro n > r rovná nule, a vzorec tedy pře-
chází ve vzorec binomické věty (viz str. 159).
Výraz
(a + xY' = a" (1 + : )"
lze rozvinout pomocí uvedené řady, jestliže proměnnou x nahradíme zlomkem
x/a. Konverguje pro Ix/al < 1.
Příklady:
(1 + X)1/2
1 1 1.1 2 1.1.3 3 1.1.3.5 4 II )
= +-x--x + x x +... (x < 1,
- 2 2.4 - 2.4.6 2.4.6.8-
, 1 1.2 2 1.2.5 3 1.2.5.8 4 II
= 1 + - x - - x + x - x +. . . (x < 1),
- 3 3 . 6 - 3 . 6 . 9 3 . 6 . 9 . 12 -
1 1 . 3 2 1 . 3 . 7 3 1 . 3 . 7 . 11 4 (I I )
=1 + - 4 x--x + x - x +... x < l,
4 . 8 4 . 8 . 12 4 . 8 . 12 . 16 - -
(1 + X)1/3
(1 + X)1/4
702
(1 + X)-l = 1 + x + X 2 + X 3 + X 4 + ...
( ) _ 1'2 - 1 1 . 3 2 _ t .3. 5 3 1 .3, 5 . 7 4-
l+x I =I+-x+-x + X +-- X +...
- 2 2.4 2.4.6 2.4.6.8
( ) _ 1/3 - 1 1 . 4 2 _ 1 . 4 . 7 J 1 . 4 . 7 . 10 4 _ ,
1 + x = 1 + - x + - x + --- X + x +..
- 3 3.6 3.6.9 3.6.9.12
qxl < 1),
(Ixl < 1),
(Ixl < 1),
( ) _ 1/4 _ -! ! 2 - 1. 5 . 9 3 5 . 9 . 13 4 _ ( I _ I ) .
1 + x-I + x + x + x + x +... x < 1 ,
- 4 4.8 4.8.12 4.8.12.16
(Ixl < 1).
(1 + X)-2 = 1 + 2x + 3x 2 + 4x 3 + 5x 4 + ...
Řady pro exponenciálnf funkci:
X x 2 00 Xk
eX = 1 + - +, - + ... = I -
I! 2! k=ok!
x ln a x 2 ln 2 a x 3 ln 3 a
a X = eX ln a = 1 + + + + ...
I! 2! 3!
(Ixl < + ex:: ),
(Ixl < + OC, a > O).
Řady pro logaritmickou funkci:
x-I (x - 1)2 (x - 1)3
ln x = - + -
123
x-I (x - 1)2 (x - 1)3
ln x = + 2 + 3 +. . .
x 2x 3x
( X - 1 (x - 1)3 (x - 1) 5 )
ln x = 2 + - + - - +
x + 1 3(x +#1)3 5(x + 1)5 ...
x 2 x 3 x 4
10(1 + x) = x - 2 + 3 - 4 + ...
10(1 _ x) = _ (x + + 3 + :4 + ...)
1 + x ( X3 x 5 x 7 )
ln -- = 2 argtgh x = 2 x + - + - + - + ...
I-x 3 5 7
x + 1 ( I 1 1 )
ln = 2 argcotgh x = 2 - + + -S + ...
x-I. x 3x 5x
(O < x < 2),
(x > t),
(x > O),
( - 1 < x < 1),
( - 1 < x < 1),
(I x I < 1),
(Ixl > 1).
703
Řady pro goniometrické .funkce:
SIn x
x 3 x 5 x 7
-x--+----+
- 3! 5! 7! ...
(Ixl < + 00 ),
COSX
x 2 x 4 x 6
= 1 - 2! + 4! - 6! + ...
1 3 2 5 17 7
=x+-x +-x +-x +...
3 15 315
(Ix I < + oc ),
tg x
(Ixl < 1t/2),
1 1 \13 25 ( II )
cotg x = - - - x - - x - - x O < x < 1t .
x 3 45 945
Řady pro cyklometrické funkce:
1 x 3 1 . 3 x 5 , 1. 3 . 5 x 7
arcsm x = x + "2 3 + 2 . 4 5 + 2 . 4 . 6 7 + ... (Ixl < 1),
7t 1 x 3 1 . 3 x 5 1 . 3 . 5 x 7
areeos x = - - x - - - - - - - - - \ (Ixl < 1),
2 2 3 2.4 5 2.4.6 7
x 3 x 5 x 7
are tg x = x - 3 + 5 - 7 + ...
(I x I < 1),
1t x 3 x 5 x 7
areeot g x = - - x + - - - + - -
2 3 5 7 ...
(Ixl < 1).
Řady pro hyperbolické funkce:
x 3 x 5 x 7
sinh x = x + - + - + - + ...
3! 5! 7!
(Ixl < + oc),
x 2 x 4 x 6
eosh x = 1 + - + - + - +
2! 4! 6! ...
1 3 2 5 17 7
=x--x +-x --x +...
3 12 315
(Ixl < + 00 ),
tghx
(Ix I < 1t/2),
1 X x 3 2x 5
eotghx ="- + - - - +:-- - ...
x 3 45 945
Řady pro hyperbolometrické funkce:
1 x 3 1 . 3 x 5 1 . 3 . 5 x 7
argsinh x = x - - - + - - - - + ...
2 3 2.4 5 2.4.6 7
(O < Ixl < 1t).
(Ixl < 1),
704
[ ( ) 1 1.3 1.3.5 J
argcosh x = + ln 2x - 2 - 5 - 6 - ...
- 2 . 2x 2 . 4 . 4x 2 . 4 . 6 . 6x
,
x 3 x 5 x 7
argtgh x = x + - + - + - + ...
357
1 1 1 1
argcotgh x = - + + ---s + ---;:; + ...
x 3x 5x 7x
(x > 1),
(Ixl < 1),
(Ixl > 1).
9.1.5. 'Přibližné vzorce pro počítání s malými čísly
Pro malá čísla e (v absolutní hodnotě) dostaneme z mocninných řad
přibližné vzorce, kterých se v praxi často použív .
Platí
(1 + er 1 + ne
(a + er a n (1 + )
Speciálně
(1 + e)2 1 + 28,
(1 + e)3 1 + 3e,
. 8
J(l + e) 1 + 2'
1
1 + 8,
1 + 8
1 e
J(l + e) 1 + 2'
P
V(l + e}P 1 + - e,
q
1 -- 1 - p
V(1 + e)p + q I: ,
e E 1 + C,
ln (1 + [;) 8 ,
(CE R, lel 1);
(8 a).
(a + eY a 2 (1 + e ),
(a + e)3 a3(1 + e ):
J(a + e) (Ja) (1 + ;a )'
1 ! ( 1 + ) ,
a + e a a
1 1 ( e )
J(a + e) J a 1 + 2a '
ar. 1 + e ln a ,
705
1 + e
ln 2e
1 - e
ln [e + J(r,2 + 1)] e,
sIn e e,
tg e e,
£2
COS e 1 - -
2'
1
cotg e - ,
e
arcsln e e,
sinh e e ,
arctg e e,
tgh e e ,
1
cotgh e - ,
e
argtgh e e .
e 2
cosh e 1 + -,
2
argsinh e e ,
Obecně platí
f(e) f(O) + f'(O) e.
9.2. ZÁKLADNÍ POJMY K FOURIEROVÝM ŘADÁM
Nechť f je periodická funkce S periodou To [tj. f(x) = f(x + kTo)
pro \Ix E R a \lk E Z] a nechť fa f' jsou po částech spojité funkce na intervalu
(O, To).
Trigonometrickou Fourierovou řadou [Fourierovým rozvojem] funkce f na-
zýváme řadu
a 00
; + k l [a k cos (kwox) + h k sin (kwox)] ,
kde
2 1 1 '0
a k = - f(x) cos (kwox) dx,
To o
2 1 1 '0
b k = - ,f(x) sin (kwox) dx'
To o
jsou tzv. F ourierovy koeficienty [F ourierovy konstanty] funkce j' vzhledem k tri-
gonometrickému systému
1, cos (wox), sin (wox), cos (2w o x), sin (2wox), ... ,
a o /2 je střední hodnota funkce f (váha) a
2n
W o = - = 2nfo .
To
706
Speciálně pro periodu To = 21t dostaneme řadu
00
ao + L [a k cos (kx) + b k sin (kx)] ,
2 k= 1
kde
\
a k = i 2 " f(x) cos (kx) dx ,
1t o
b k = i 2 " f(x) sin (kx) dx .
1t o
V každém bodě xo, v němž je funkce f spojitá, konverguje Fourierova řada
funkce f k hodnotě f(xo), a v každém bodě xo, v němž není funkce f spojitá,
k hodnotě
t[ lim f(x) + lim f(x)].
X-Xo+ x-xo-
Spektrální tvar Fourierovy řady je
00
ao + L Dk sin (kwox + lI'k),
2 k= 1 '
kde
Dk = J(a; + b;),
a k
({Jk = arctg-
b k
(obr. 383).
Ok
Obr. 38 K spektrálnímu vyjádření
Fourierovy řady
Komplexní tvar Fourierovy řady je
00 00
L c k eikcoox = Co + L (C k eikCOo + C -k e - ikCOQX) ,
k=-oo k=l
/
kde
1 i TO .
C k = - . f(x) e -Ikcoox dx
o o '
(k E Z) .
707
Speciálně pro periodu To = 21t platí
00 00
L Ck e ikx = Co + L (Ck e ikx + C- k e- ikx ),
k=-oo k=l
kde
C k = 1 2" j(x) e- ikx dx (k E Z).
21t o
Platí vztahy
ak=ck+c-k
b k = i(c k - c- k ) (k E N) .
Případy souměrnosti pro Fourierovy řady
Případ 1 (obr. 384):
Sudá funkce
f(x) = f( -x)
má graf souměrný podle osy y. Platí b k = O (k E N) a Fourierova řada sudé
funkce tedy neobsahuje členy s funkcí sinus.
Případ 2 (obr. 385):
Lichá funkce
/(x) = -f( -x)
má graf středově souměrný vzhledem k počátku. Platí a k = O (k E No), a Fou-
rierova řada liché funkce tedy obsahuje jen členy s funkcí sinus.
y
x
x
Obr. 384. Sudá funkce
Obr. 385. Lichá funkce
Případ 3 (obr. 386):
Funkce, jejíž graf se skládá z částí (polovIn příslušných poloviční periodě)
téhož tvaru, které zaujímají touž polohu vzhledem k ose x:
f(x) = f(X + :0 ).
708
Platí
a2k + 1 = O ,
b 2k + 1 = O,
a Fourierova řada této funkce tedy obsahuje jen takové členy s funkcemi sinus
a kosinus, jejichž koeficienty a k , b k mají sudé indexy.
Připad 4 (obr. 387): I
Funkce, jejíž graf se skládá z částí (polovIn příslušných poloviční periodě)
téhož tvaru, které však zaujímají různou polohu vzhledem k ose x:
f(x) = -f(X + :0 ).
Platí
a 2k = O,
b 2k = O,
a Fourierova řada této funkce tedy obsahuje jen takové členy s funkcemi
sinus a kosinus, jejichž koeficienty a k , b k mají liché indexy.
o
y
x
y
x
Obr. 386. Pol6vlny ve stejné poloze
k ose x
Obr. 387. Poloviny v různé poloze
k ose x
9.3. VÝPOČE'T FOURIEROVY ŘADY; PŘÍKLADY
Rozvoj funkce
f(x) = ve- X [x E (O, 21t)] ,
To = 21t ,
popisující harmonický vyrovnávací proces (přechodný jev), máme rozvinout
ve Fourierovu řadu:
1. způsob řešeni (výpočet Fourierových koeficientů v trigonometrickém
tvaru):
1 i 21t V i 21t
ak = - ve-Xcos(kx)dx = - e-Xcos(kx)dx
1t o 1t o
(k E N)
709
(obr. 388). Integrováním per partes vypočteme
1 271 e - x 271 1 1 271
e- X cos (kx) dx = - sin (kx) + - e- X sin (kx) dx =
o k o k o
[ -x -x ] 271 1 1 271
= sin(kx) - cos(kx) - 2" e- X cos (kx)dx,
k k o k o .
a po úpravě dostaneme
( 1 ) C27t [ -x -x ] 271
1 + k 2 J6 e -x cos (kx) dx = e k sin (kx) - e k2 .cos (kx) o
1 271 k2 [ e -x e -x ] 271
e-Xcos(kx)dx = 2 -sin (k x) - cos(kx) .
o . 1+k k k o
Yf
v
2...
Obr. 388. Přechodný jev
o
I
Odtud
v(l - e- 27t )
a =
k n( 1 + k 2 ) .
Podobným způsobem dostan me
vk( 1 - e - 271)
b -
k - n( 1 + k 2 ) .
Z toho plyne
v( 1 - e - 271) v( 1 - e - 271) v( 1 - e - 271)
ao = , a 1 = , a 2 = . ,..
n 2n 5n
v( 1 - e - 271) 2v( 1 - e - 271)
b o = o , b 1 = b 2 =
2n' 5n'
710
Hledaná Fourierova řada má tedy tvar
v( 1 - e - 271) [ 1 00 1 00 k ]
f(x) = - + L -2 cos (kx) + L 2 sin (kx) =
n 2 k= 1 1 + k k= 1 1 + k
v( 1 - e - 271) [ 1 1 1 1 2 ]
= - + - cos x + - cos (2x) + ... + - sin x + - sin (2x) + ... .
n 2 2 5 2 5
2. způsob řešení (výpočet Fourierových koeficientů v komplexním tvaru):
1 1 271 . V 1 271 ,
C k =- ve-xe-1kxdx=- e-(1+lk)xdx
2n o 2n o
(k E Z). I
Intěgrováním ihned dostaneme
- v e - (1 + ki) x 271 - V . v( 1 - e - 271)
C k = 21t(1 + ki) o = 21t(1 + ki) (e-2" - "k - 1) = 21t(1 + ki) .
1
Z C k vypočteme koeficienty a k a b k :
v( 1 - e - 271) ( 1 1 )
ak = Ck + C - k = + =
2n 1 + ki 1 - ki
v(1 - e- 27t ) 1 - ki + 1 + k i v(1 - e- 27t )
- -
2n 1 + k 2 n( 1 + k 2 ) ,
b - ( c _ C ) i _ vi( 1 - e - 2,,) ( 1 _ 1 ) _
k - k - k - 2n 1 + ki 1 - ki -
vi( 1 - e - 271) 1 - ki - 1 - ki vk( 1 - e - 2k)
= 'I = .
2n 1 + k 2 n(l + k 2 )
21f Re ť k
f y E
-4 -3 -2 -f O
-.-l_-L
2 3 4 k
Zn-Zmc k
4
I -vit
v r 1+k 2 = f (Id (kEl)
I
----1- LlJo t -1I1111-r-
- 4 - 3 - 2 - f ot *' *- 'I. *3 *4 k
- O.5v I
Obr. 390. Čárové spektrum funkce l' e- X
(imaginární část)
v
1 : Jc2 = f ( k ) ( /( € Z)
Obr. ,389. Čárové spektrum funkce ve -.
(reálná část)
711
Při obou způsobech výpočtu dostaneme ovšem tytéž výrazy pro Fourie-
rovy koeficienty. Zřejmě při výpočtu těchto koeficientů v komplexním tvaru
dostáváme podstatně j dnodušší integrály, takže druhý způsob výpočtu je
početně méně namáhavý, a to zejména tehdy, jestliže f je exponenciální funkcí.
Čárové spektrum funkce f dostaneme ve tvaru
v( 1 - e - 2n) v( 1 - e - 2n) (1 - ki)
2nc = = =
k 1 + ki 1 + k 2
v( 1 - e - 2n) . vk( 1 - e -- 2n) V . vk
= -1 -1
1 + k 2 1 + k 2 1 + k 2 1 + k 2 '
neboť e- 2n 1 (obr. 389 a 390).
.
Speciální Fourierovy řady
1. Pravoúhelníková křivka (obr. 391):
4v
f(x) = -;- [sin x + t sin (3x) + t sin (5x) + ...] .
2. Pravoúhelníková křivka (obr. 392):
4v
f(x) = - [cos x - }cos (3x) + tcos (Sx) - ...].
n
I v
-o i-
v
I
I I
1'1 Zl'
I
>-
x
ib
r-
I v I I
- I I I I
1r O .. I I J :-
-_I -I r K 21' x
2 !
y
r--
r ! J, !
- -1 '
I Vz
- t- -- 1 - j -
O I 'Jr l' 2,r, x
y
Obr. 391. Ke křivce 1
Obr. 392. Ke křivce 2
Obr. 393. Ke křivce 3 pro
V 2 =F O
3. Pravoúhelníková křivka (posunutá ve směru osy y) (obr. 393):
( ) VI + v 2 2( VI + v 2)
f x = 2 + 1t [sin x + tsin(3x) + tsin(5x) + ...].
Pro V2 = O dostaneme pravoúhelníkový impuls (obr. 394).
712
4. Pravoúhelníková křivka [posunutá ,ve směru osy y (obr. 395)]:
( VI + v 2 2( VI - V 2) [
fx)= 2 + 1t cosx-tcos(3x)+!cos(5x)-...].
Pro V2 = O dostaneme pravoúhelníkový impuls (obr. 396).
y
I V I I
I f I
--ar- t
y
in y 1 ;-
I 1J'f: I
- L 4- - -1 __ -1 I I
_1L O j .!.. 7r 1.", 21'
2 2 2
Obr. 396. Ke křivce 4 pro
V 2 = O
r-
I
I
I =-
21' X
r--
I I I
I ! . I
---I fU I
I .ť 1 I L
_ Jr.. O .!. Jr I,.. 2Jr X
222
Obr. 395. Ke křivce 4 pro,
u 2 =F O
Obr. 394. Ke křivce 3 pro
l'2 = O
5. Pravoúhelníkový impuls (obr. 397):
2v' ( qJ sin qJ sin (2íp) sin (3qJ) )
f(x)=- -+ cos x + cos (2x) + 3 cos(3x)+....
n 2 1 2
6. Pravoúhelníkový impuls (obr. 398):
4v ( COS qJ cos (3qJ) cos (5qJ) )
f(x) = - sinx + sin (3x) + sin (5x) + ... .
n 1 1 5
;L,
j;Qv
01 1('
y
I I I
21r X
f'I
___ v '
O 11' V I I 271' X
I I
L.J
Obr. 398. Ke křivce 6
Obr. 399. Ke křivce 7
Obr. 397. Ke křivce 5
7. ,Lichoběžníková křivka (rovnoramenný lichoběžník) (obr. 399):
4v [ 1 1 1 ]
j'(x) = - 1: sin qJ sin x + 2 sin (3qJ) sin (3x) + 1: sin (5qJ) sin (5x) + ... .
nqJ 1 3 5
713
8. Lichoběžníkový impuls (rovnoramenný lichoběžník (obr. 4(0):
( ) _ 4v [ sin ex - sin qJ . sin (3cx) - sin (3qJ) . ( )
f x - ( ) 2 sm x + 2 sm 3x +
1tCX-qJ 1 3
sin (5ex) - sin (5qJ) . ( ) ]
+ 2 sIn 5x +... .
5
y
I
y
- + -
01 -
, 2
I
Obr. 400. Ke křivce 8
I
I
I
Obr.401. Ke křivce 9
Obr. 402. Ke křivce 10
9. Trojúhelníková křivka (rovnoramenný trojúhelník) (obr. 401):
8v [ 1 1 1 ]
f(x) = 2 1: sin x - 1: sin (3x) + 1: sin (5x) - ... .
x 1 3 5
10. Trojúhelníková křivka (rovnoramenný trojúhelník) (obr. 402):
8v [ 1 1 1 ]
f(x) = 2 2COS X + 1: cos (3x) + 1: cos (5x) + ... .
1t 1 3 5
o
ft'
31' X
21' x
l vfZL
r 21' x
y
Obr. 403. Ke křivce 11
Obr. 404. Ke křivce 12
Obr. 405. Ke křivce 13
11. Trojúhelníková křivka (roynoramenný trojúhelník) (obr. 403):
".
v. 4v [ 1 1 1 ]
f(x) = _ 2 + 2" 1: cos x + 1: cos (3x) + zcos(5x) + ... .
1t 1 3 5
12. Trojúhelníková křivka (rovnoramenný trojúhelník) (obr. 404):
v 4v [ 1 1 1 ]
f(x) = _ 2 - 2 zCosx + 1: cos (3x) + zcos(5x) + ... .
x 1 3 5
714
13. Trojúhelníkový impuls (rovnoramenný trojúhelník) (obr. 405):
- VqJ 2v [ 1 - cos qJ '1 - cos (2qJ)
f(x) = - + - , cos x + - cos ( 2x ) +
2 'TtqJ 1 2 2 2
1 - cos (3qJ) ]
+ 3 2 cos (3x) + ... .
14. Pilovitá křivka (rostoucí) (obr. 406):
j(x) = 2v [ sin x - sin (2x) + sin (3x) - . .. ] .
'Tt 2 3
15. Pilovitá křivka (rostoucí) (obr. 407):
j(x) = - 2v [ sin x + sin (2x) + sin (3x) + ... ]
'Tt 2 3
16. Pilovitá křivka (rostoucí) (obr. 408):
v V [ 1 1 ]
j(x).= 2 - 1t sin x + 2 sin (2x) + "3 sin (3x) + ... ·
. Yf J I
I
IV
I I
- --
0" IZI' X O 21' X
V
Obr. 406. Ke křivce 14
Obr. 407. Ke křivce 15
Obr. 408. Ke křivce 16
17. Pilovitá křivka (kJesající) (obr. 409):
2v [ 1 1 ]
f(x)=- sinx+-sin(2x)+-sin(3x)+... .
'Tt 2 3
18. Pilovitá křivka (klesající) (obr. 410):
2v [ 1 1 ]
f(x) = - -sin x + - sin (2x) - - sin (3x) + ... .
'Tt 2 3
715
19. Pilovitá křivka (klesající) (obr. 411):
f(x) = + v [ sin x + ! sin (2x) + ! sin (3x) + ... ] .
2 1t 2 3
Yf
y
, v :v
'oi I' 21' x
I
j
rA
v
Obr. 409. Ke křivce 17
Obr. 410. Ke křivce 18
Obr.411. Ke křivce 19
20. Pilovitý impu s (rostoucí) (obr. 412):
, [ 1 1 ]
f(x) = v + sin x - -sin (2x) + -sin (3x) - ... -
4 1t 2 3
2v [ 1 1 ]
-"2 cos x - 1: cos (3x) + 1: cos (5x) - ... ·
1t 3 5
.
21. Pilovitý impuls (klesající) (obr. 413):
.
v V [ 1 1 ]
f(x)=-+- sinx+-sin{2x)+-sin(3x)+... +
4 1t 2 3
2v [ 1 1 ]
+"2 cos x + 1: cos (3x) + 1: cos (5x) + ... .
1t 3 5
Yi
I
y
21' X
o
,.,
21' X
o
I'
Obr. 412. Ke křivce 20
Obr. 413. Ke křivce 21
22. Stejnosměrná sinusová křivka (dvojcestně stejně usměrněná) (obr. 414),:
4v [ 1 1 1 1 ]
f(x) = - - - -cos (2x) - -cos (4x) - -cos (6x) - ... .
1t 2 1.3 3.5 5.7
716
23. Stejnosměrná kosinová křivka (dvojcestně stejně usměrněná) (obr. 415):
4v [ 1 1 1 1 ]
f(x) = - -; + -cos (2x) - -cos (4x) + -cos (6x) -... .
1t 2 1.3 3.5 5.7
24. Sinusový impuls (jednocestně stejně usměrněný) (obr. 416):
v v 2v [ 1 1 1 ]
f(x) = - + -sin x - - -cos (2x) + -cos (4x) + -cos (6x) + ... .
1t 2 1t 1.3 3.5 5.7
y
y
y
J'
2r x
o
I"
21' x
Obr. 414. Ke křivce 22
Obr. 415. Ke křivce 23
Obr. 416. Ke křivce 24
25. Kosinusový impuls (jednocestně stejně usměrněný) (obr. 417):
v v 2v [ 1 1 1 ]
f(x) = - + -cosx + - -cos (2x) - -cos (4x) + -cos (6x) - ... .
1t 2 7t 1.3 3.5 5.7
26. Stejnosměrný trojfázový (střídavý) proud (obr. 418):
3v J3 [ 1 1 1 1 ]
f(x) = - - -cos (3x) - -cos (6x) - cos (9x) - ... .
1t 2 2 . 4 5 . 7 8 . 10
y
y
-11' 11' 21' 311' 4,... x
Obr. 417. Ke křivce 25
Obr. 418. Ke křivce 26
br. 419. Ke křivce 27
v
27. Parabolické oblouky [parabola o rovnici y = - x 2 pro x E ( -1t, 1t)
1t 2
(obr. 419)]:
j(x) = - : [cos x - ;2 cos (2x) + 3 12 cos (3x) - ..J.
717
v
28. Parabolické oblouky [parabola o rovnici y = 2" (x - 1t)2 pro x E (O, 21t)
(obr. 420)]: 1t
v 4v [ 1 1 ]
f(X)=-+2 cosx+ 2 cos(2x)+2cos(3x)+... .
3 x 2 3,
29. Parabolické oblouky [parabola o rQynici y = x 2 pro x E < -1t, 1t)
(obr. 421)]:
J(x) = 1t 2 - 4 [ co x - cos (2x) + cos (3x) - · .. ] .
323
L
4v
30. Parabolické oblouky [parabola o rovnici y = 1: x(1t - x) pro x E (O, 1t)
4v 1t
a y = 1: (x 2 - 31tx + 21t 2 ) pro x E (1t, 21t) (obr. 422)]:
1t
32v [ '1 1 ]
f(x) = 3"" sin x + 3 sin (3x) + 3 sin (5x) + ... .
. 1t 3 5
YI
I
T 2r 31' 41' x
Obr. 420. Ke křivce 28
Obr. 421. Ke křivce 29
Obr. 422. Ke křivce 30
.31. Přechodný jev:
f(x) = ve- X (viz str. 709).
9.4.
o ,
FOURIERUV INTEGRAL,
FOURtEROVA TRANSFORMACE
Funkci F, která je i se svou derivací F' po částech spojitá a absolutně
integrovatelná na množině R (tj. J : If(x)1 dx < + (0), lze jednoznačně vy-
jádřit Fourierovým integrálem
. : L+OO[f:: F(t) cos [(x - t)Y]dtJd Y
718
nebo v komplexním tvaru
1 f + 00 [f + 00 . ]
- F(t)el(X-t)Ydt dy.
2n - 00 - 00
V každém bodě xo, v němž je funkce F spojitá, se Fourierův integrál funkce F
rovná hodnotě F(x o ), kdežto v každém bodě xo, v němž není funkce F spojitá,
se Fourierův integrál funkce F rovná hodnotě ![ lim F(x) + lim F(x)].
X-Xo+ X-Xo-
Fourierovým obrazem funkce (tak zvaného vzoru nebo předmětu) F(t)
(J:: IF( t)1 dt < + (0) nazýváme funkci
j(y) = r+: F(t)e-iY1dt.
Zobrazení, které funkci (vzoru) F přiřazuje její Fourierův obraz se nazývá
F ourierova transformace.
Inverzní vzorec pro Fourierovu transformaci
1 f + 00
F(t) = - f(y) e iyt dy .
2n - 00
Příklad (srov. str. 709):
F(t) = { e-'
[t E <O, + 00 )] ,
[tE(-oo,O)].
Fourierův obraz funkce F je
f +oo 1 +00 1 +00
.f(Y) = F(t)e- iyt dt = v e- t e- iyt dt = v e-(1+iy)t dt.
-00 o o
Integrováním dostaneme
-1 . +00 v
f(y) = v . e-(l +Iy)t = . -
1 + lY o 1 + lY
v . vy
-I
1 + y2 1 + y2"
Fourierův integrál je
1 f +oo [f +oo . ]
F(x) = 21t _ CX) _ CX) F(t) e'(X-I)y dt dy =
1 f + 00 . V v f + 00 1 - iy .
= - e 1xy dy = - 2 e 1XY dy .
2n - 00 1 + iy 2n - 00 1 + Y
Grafické znázornění funkce j' dává spojité spektrum (obr. 423 a 424).
719
v
f+y2 = (Y)
lm f(y)
.:!L
1+y2 = ((y)
O,5v
_ _.l__...L _
-4 -3 -2 -1 O
-- -
f 23ft Y
y
Obr. 423. Spojité spektrum funkce
ve -, (reálná část)
Obr. 424. Spojité spektrum funkce
l' e - r (imaginární část)
9.5. LAPLACEOVA TRANSFORMACE
Přiřazení
f+OO
F(p) = Jo f(t) e - pt dt = ff' {J(t)} = ff' f
(p E C, P = x + iy, x > (] > - 00 )
se nazývá Laplaceova transformace, přičemž funkce F se nazývá obraz funkce f
v Laplaceově transformaci [Laplaceův obraz funkce fJ a funkce f proměnné
t E (O, + 00) se nazývá vzor [originál, předmět J Laplaceova obrazu F. Integrál
J 6" 00 f(t) e - p(t) dt se nazývá Laplaceův integrál funkce f
Kritéria pro existenci Laplaceovy transformace F na o boru t > O
1. 1+ OOlf(t)1 dt <'- + oc (funkce f je po částech spojitá);
2. 1 T2If (t)1 dt = }. o f:' 2If (t)1 dt;
3. T 2 > TI; pro aspoň jedno číslo Po E C je
1 1 '2
lim e C Pot f(t) dt = O.
T2-+oo TI' .
Funkce, které splňují podmínky 1 až 3 se nazývají L-:funkce [funkce třídy L J.
.4. Jestliže Laplaceův integrál 2{f(t)} konverguje pro číslo, Po, pak také
konverguje pro všechna čísla p z poloroviny Re p > Re Po = Xo. Jestliže
Xo = (X je taková konstanta, že pro všechna čísla p z poloroviny Re p > ,
resp. Re p < (X Laplaceův integrál konverguje, resp. diverguje, pak se kon-
720
stan ta nazývá úsečka konvergence Lap/aceova integrá /u [úsečka konvergence
I předmětu j] (obr. 425). Jestliže < + 00, pak funkci.ľ nazýváme laplaceovsky
\ transj'ornl0vatelnou.
iy t
. polorovina konversence
-+.p. x+ yi
o xi Re Po x
Obr. 425. Polorovina konvergence
La placeova integrálu
Funkce, jejichž Laplaceovy integrály konvergují absolutně, tj.
L+ ool.f(t) e - Pf! dt < + 00
pro Re p = x > a,
se nazývají La-funkce. La-funkce jsou zároveň L-funkcemi.
Laplaceova transformace:
{f(t)} = Ie j(t) = F(p).
Inverzní [zpětná] Laplaceova transformace:
2-1{F(p)} = 2_ 1 F(p) =f(t).
Je-li j' laplaceovsky transformovatelná funkce, pak
y _ 1 { 2 { F(p) }} = F(p),
- 1 (P{f(t)}} = r(t).
Základní věty o Laplaceově transformaci
Věta o lineárnosti Laplaceovy transjormace:
{a f (t) + b .f 2 (t)} = a F 1 (p) + b F 2 (p) ,
popř.
2 {JI Ci j;(t)} = it 1 Ci F;(p),
kde a, b, Ci jsou komplexní konstanty a .t;(t) jsou laplaceovsky transformova-
telné funkce.
Jsou-li a 1 , C(2, ..., n úsečky konvergence po řadě předmětů fl (t), j (t), . :., .f (d,
n
pak úsečka konvergence předmětu L Ci j;(t) se rovná
i = 1
max { 1' a 2 , ..., C(n} .
721
Inverzní transformace:
2_ 1 {a F 1 (p) + b F 2 (p)} = a -1 {F 1 (p)} + b 2_ 1 {F 2 (p)} .
Věta o obrazu funkce násobené exponenciální funkcí [vět!l o posunu obrazu,
věta o tlumení]:
2 { e - at f( t)} = F(p + a),
kde a E C a f je laplaceovsky transformovatelná funkce. Je-li úsečka kon-
vergence předmětu f, pak úsečka konvergence předmětu e -at f se rovná
rJ.. - Re a.
Inverzní transformace:
2_ 1 {F(p + a)} = e- at f(t).
. Věta o změně měřítka [věta o podobnosti]:
Y{J(at)} = F( )
nebo
Y{ fG t)} = F(py),
kde a, y > ° jsou reálné konstanty a f je laplaceovsky transformovateln,
fynkce. Je-li (X úsečka konvergence předmětu f(t), pak úsečka konvergenct
předmětu f(at) se rovná aa a úsečka konvergence' přédmětu ! f ( ! t ) se
1 y Y
rovná - (X.
Y
Inverzní transformace:
Y-l{F( )} = af(at),
Y -l{F(yp)} = fG) (y > O).
Věta o translaci předmětu:
2 {fl (t)} = e - pto F(p),
kde
fl (t) = { (t - to)
[t E (O, to)] ,
[t E (to, + (0)],
722
nebo
Y {f(t - to)} = e - pto F(p) [t E (to, + (0)] ,
!e{J(t + a)} = e ap [F(P) - J: f(t) e- pt dt].
kde to, a > O jsou reálné konstanty a f je laplaceovsky transformovatelná
funkce.
Inverzní transformace:
2_ {e- Pto F(p)} = { O '
1 f(t - to)
[t E (O, to)] ,
(t > to).
Věta o obrazu derivace:
2{f(n)(t)} = pn P(p) _'.pn-l f(O+) _,pn-2 1(0+) - pn-3 J(O+) - ...
. .. - f(n - 1)(0 + ) ,
kde f(n) je laplaceovsky transformovatelná funkce, f(k)(O+) = lim f(k)(t),
t-+O +
k O, 1, .. ., n - 1. Je tedy
!e{ d t) } = pF(p) - f(O+),
.p eX t) } = p2 F(p) - p f(O+) - j(O+),
atd.
ln verznÍ transformace:
df(t)
.P_dpF(p) - f(O+)} = dl'
d 2 j'(t)
!e_ t {p2 p(p) - pf(O+) - j(O+)} = dt '
atd.
Věta o derivaci obrazu: .
dnF(p) = !e{J(t)} = (-1)" !e{ť' f(t)},
dpn dpn
kde f je laplaceovsky integrovatelná funkce. Je tedy
F'(p) = -2{t f(t)},
F"(p) = 2{t 2 f(t)},
atd.
723
Inverzní transformace:
g;_I{ d ) } = (-I)"t" f(t).
V'ětll o obrazu integrálu:
g;{l f (')d'} = F(P)'
kde .ť je laplaceovsky transformovatelná funkce.
Inverzní transformace:
. 2- I HF(P)} = If(,) dL.
Věta o integrálu obrazu:
i+ 00 F((1) clu = 2{ f t) } ((1 E C) ,
kde I je laplaceovsky transformovatelná funkce.
Konvoluce
fl(t) * j (t) = 1 fl (,) f2(t - ,) d, ·
Komutativní zákon pro konvoluci:
11 (t) * 12(t) = 12(t) * 11 (t) .
Asociativní zákon pro konvoluci:
[11 (t) * 12(t)] * 13(t) = 11 (t) * [12(t) * 13(t)] .
.
Věta o obrazu konvoluce:
F 1 (p) F 2 (p) = 2{ll(t)} 2{12(t)} = Y{ll(t) * 12(t)} =
= 2{f>I(,)f2(t -")d'},
kde j , j .jsou funkce, jejichž Laplaceovy integrály konvergují absolutně pro
Re P > rJ...
ln verzní transformace:
2_ 1 {F 1 (p)F 2 (p)} = .!e-l{F 1 (p)} * 2-1{F2(P)}.
724
Věty O limitách
lim' f(t) = lim p F(p),
1-0+ p-+oo
lim j'(t) = lim p F(p) ,
1-+00 p-o+
kde f je laplaceovsky transformovatelná funkce.
9.6. POUŽITÍ LAPLACEOVY TRANSFORMACE
K ŘEŠENÍ DIFERENCIÁLNÍCH ROVNIC
Schematický početní postup:
diferenciální
rovnIce
počá teční
+ podmínky
Laplaceova
transformace
(početní
pra vidla,
1 tabulky)
-----+
řešení y
I prostor vzoru
lineární algebraická rovnice -----+
in verzní
transformace
(početní
pravidla,
tabulky)
řešení !£ {y} I prostor obrazu
Provedeme-li Laplaceovu transformaci na diferenciální rovnici s přihlédnu-
tím k počátečním podmínkám, převedeme ji na algebraickou rovnici. Tuto
algebraickou rovnici rozřešíme a k řešení najdeme inverzní transformací ře-
šení původní diferenciální rovnice. Podmínkou je, že pravá strana rovnice
musí mít Laplaceův obraz.
Příklad 1:
Řešme diferenciální rovnici
y + 5y + 4y = t
s počátečními podmínkami y(O) = O, y(O) = O.
Podle věty o obrazu derivace dostaneme
p22{y} - p y(O) - y(O) + 5p P{y} - 5 y(O) + 4 {y} = Y{t} .
Přihlédneme-li k počátečním podmínkám, dostaneme
p22'{y} + ,5p .P{y} + 4 Y{y} = Y{t} .
725
Podle korespondence 3 z tabulky v kapitole 9.7 dostaneme
1 1 1 1 1
.P{y} = p2 p2 + 5p + 4 - p2 P + 1 p + 4 .
Rozklad v součet částečných zlomků dává
111. A BC D
- . =-+-+ + ,
p2 P + 1 p + 4 p2 P P + 1 p + 4
1 A(p + 1)(p + 4) + BP(p + 1)(p + 4)
= +
p2(p + 1)(p + 4) p2(p + 1)(p + 4)
Cp2(p + 4) + Dp2(p + 1)
+ p2(p+1)(p+4) .
Porovnáním koeficientů dostaneme
1
A =-
4'
Z toho plyne
{ II I } 1 { I } 5 { I }
y = .P - 1 p2 P + 1 p + 4 = 4 .P - 1 . p2 - 16 .P - 1 P +
. 1 { I } l' { I }
+3.P-l p+1 - 4S .P-l p+'4 .
5
B=--
, 16 '
1
C =-
3 '
1
D = --.
48
a podle korespondencí 3, 1 a 5 z tabulky v kapitole 9.7 plyne
t 5 1 _ t 1 - 4t
y=---.+-e --e
4 16 3 48
Příklad 2:
Řešme diferenciální rovnici
y - 4 y = 2 sinh t
s počátečními podmínkami y(0) = O, y(O) = O.
Podle věty o obrazu derivace dostaneme
p22{y} - P y(0) - y(O) - 42{y} = 2 Y{sinh t}.
Přihlédneme-li k počáte ním podmínkám, dostaneme
p22{y} - 42{y} = 2 2{sinh t} ,
2
.P{y} = 2 4 .P{sinh t} ·
p -
726
1. způsob řešení:
Podle korespondence 9 z tabulky v kapitole 9.7 platí
2 .
2 = 2{Slnh (2t)} ,
p - 4
odkud
y {y} = .!.f { sinh (2t)} Y {sinh t} .
Podle věty o obrazu konvoluce je
2{y} = 2{sinh (2t) * sinh t},
Y = -1 { {sinh (2t) * sinh t}} = sinh (2t) * sinh t =
= lsinh (t - .) sinh (2.) d. .
Dvojím integrováním per partes postupně dostáváme
y = [ ! sinh (t - .) cos (2.) J ' +
2 t=O
1 f t
+"2 o cosh (t - .) cosh (2.) d. =
= - ! sinh t + [ !.! cosh (t - .) sinh (2.) J ' +
2 2 2 t=O
1 f t
+ - sinh (2-r) sinh (t - -r) d-r =
4 o
111
= - 2 sinh t + 4 sinh (2t) + 4 y ,
2 1
y = - 3 sinh t + 3 sinh (2t).
2. způsob řešeni:
Podle korespondence 9 z tabulky v kapitole 9.7 platí
. 1
2{slnh t} = 2 '
P - 1
odkud
2 1
!e{y} = p2 _ 4 p2 _ 1 .
727
Rozklad v součet částečných zlomků dává
2 A B
- +
(p2 _ 4) (p2 _ 1) - p2 - 4 p2 - 1 .
[Rozklad v činitele (p - 2) (p + 2) (p - 1) (p + 1) není účelný, neboť aj(p2 - a 2 )
je obraz Laplaceovy transformace.]
Porovnáním koeficientů dostaneme
A _1-
- 3'
B - -
- 3 .
Z toho plyne
Y=.fe- 1 { 2 2 2 1 } ,
p-4p-l
y = t Y - 1 t2 4 } - f Y - 1 t2 I }'
y = t sinh (2t) - t sinh t
(jako dříve) podle korespondence 9 z tabulky v kapitole 9.7.
Příklad 3:
Řešme diferenciální rovnici y = b rovnoměrně zrychleného pohybu při
y(O) = Yo, y(O) = VOe
Podle věty o ,obrazu derivace je
p22{y} - P y(O) - y(O) = {b}.
Přihlédneme-li k počátečním podmínkám, dostaneme I
p2 Y {y} - pYo - Vo 0;= ,
p
{ } b Yo vo
2 Y =-+-+-.
p3 P p2
Použijeme-li věty o obrazu konvoluce na rovnici
b b 1
- = - - = 2 { bt } { 1 }
p3 p2 P
(dostali jsme ji podle korespondencí 1 a 3 z tabulky v kapitole 9.7), pak máme
. y = Y_dY{bt} Y{1}} + Y- 1 { ; } + Y-l t } =
728
= .P_1{Y{bt* I}} + Yo + vot = f>rdL + Yo + rot,
b
y = - t 2 + vot + Yo .'
2
Z tohoto příkladu je vidět, že metoda řešení diferenciálních rovnic pomocí
Laplaceovy transformace je výhodná.jen u některých typů rovnic.
-o
-+-
CI:
gz
a..
Yo
Obr. 426. Harmonické kmitání
Pří klad 4:
Řešme diferenciální rovnici harmonického kmitání (obr. 426)
d 2 y
m dt 2 = -mg + k(a - y)
s počátečními podmínkami y(O) = O, y(O) = Vo (k je konstanta pružiny).
Pro -mg = ka je
my = -ky,
k
y+-y=O,
m
k
p22{y} - py(O) - y(O) + -2{y} = O.
m
.
Přihlédneme-li k počátečním podmínkám, dostaneme
k
p2 {y} - V o + - 2 {y} = O,
m
(p2 + : ) .P{y} = v o ,
Y{y} = V o
k
p2 +_
m
729
Zpětná transformace:
y = Vo 2 - 1
1 k = Vo ( J: ) !I! - l J k
p2 + _ p2 + _
m m
y = Vo ( J: ) sin (t J )
podle korespondence 17 z tabulky v kapitole 9.7.
9.7. TABULKA KORESPONDENCÍ NĚKTERÝCH
,. ,. ,. ,. o
RACIONALNICH LAPLACEOVYCH INTEGRALU
V zor f Obraz F(p) = .P {f(t)}
h
1. h -
p
a(t) (pružinová konstanta) 1
2. - (p > O)
P
1
3. t -
p2
,n 1
4. - (n E Z)
n! p" + 1
e :t al 1
5. - (Re p > Re a)
p+a
a' 1
6. p - ln lal
7. (a + e-Ir I (n) r A
k=O k p + k
8. - a e - al p
-
'P+a
sinh (at) a
9. p2 _ a2
10, cosh (at) p
p2 _ a2
1 1
11. - (e al - 1) --
a p(p - a)
730
Vzor f
Obraz F(p) = .!R{f(t)}
b-a
1
(p =+= a)2
1
(p - a) (p - b)
p
(p - a) (p - b)
12. t e:tll t
e ht - elit
13.
b-a
14.
h e ht - a elit
15. e- ht sin (at)
a
16. e-btcos(at)
(p + b)2 + a 2
p+b
(p + b)2 + a 2
17. sin (at)
a
p2 + a2
(a =4= O)
18. cos (at)
p
(a O)
p2 + a2
ť'- 1
w p.
2 2 cos cp + 2 2 sin fP
p +w p +ro
(p - a Y
p(p2 + a2)
p2 + 2a2
p(p2 + 4a2)
p2 _ 2a2
p(p2 _ 4a2)
1
(a O)
19. sin (rot + cp)
20. 1 - 2.sin (at)
21. cos 2 (at)
(a O)
22. cosh 2 (at)
(a O)
23.
(n - I)!
p"
(n > O)
Rozsáhlé tabulky vzorů a příslušných obrazů jsou ve speciální literatuře (např. v [155],
[157] a [159]).
731
10. POČET PRAVDĚPODOBNOSTI,
MATEMATICKÁ STATISTIKA,
TEORIE CHYB A VYROVNÁVACÍ POČET
10.1. POČET PRAVDĚPODOBNOSTI
Jevy
Náhodné jevy mohou nastat za určitých podmínek, ale jejich výskyt není
jistý.
Deterministické jevy nastanou za určitých podmín k s naprostou jistotou
(jistý jev).
Zákonitosti počtu pravděpodobnosti mají hromadný charakter, tj. platí jen
pro dostatečně velký počet pokusů.
O jednou možné jevy jde tehdy, jestliže za určitých podmínek jeden z těchto
. o . .
Jevu s JIstotou nastane.
O neslučitelné [po dvou disjunktní] jevy jde tehdy, jestliže jeden jev ostatní
s jistotou vylučuje..
E 1 je částečný jev jevu E 2 , právě když jev E 1 vždy následuje po jevu E 2 :
\
E 1 C E 2 , popř. E 2 => £1 (čteme: E 1 je částečný jev jevu E 2 ).
Ekvivalentní jevy se buď zároveň vyskytují, nebo nevyskytují:
E 1 = E 2 => E 1 C E 2 /\ E 2 C E 1 .
Logická disjunkce jevů E 1 a E 2 je jev E 3 , při němž aspoň jeden z jevů E 1
nebo E 2 nastane:
E3 = E 1 U E 2 (čteme: E3 se rovná E 1 sjednoceno s E 2 ).
Logická konjunkce jevů E 1 a E 2 je jev E 3 , při němž jevy E 1 a E 2 zároveň
nastanou:
E3 = E 1 n £2 (čteme: E3 se rovná E 1 průnik s E 2 ).
Logický rozdíl jevů E 1 a E 2 je jev E 3 , při němž jev E 1 nastane, ale jev E 2
nenastane:
E3 = E 1 \E2 .
Nemožné jevy 9 nenastanou nikdy, jisté jevy nastanou vždy.
O opačné jevy E 1 a £1 jde tehdy, jestliže výskyt jednoho z nich podmiňuje
nevýskyt druhého.
732
Definice
Každému jevu E, tj. každému možnému výsledku pokusu, je přiřazeno číslo
P = P(E), zvané pravděpodobnost jevu E, pro něž platí
O < P(E) < 1 .
PrQ jistý jev je
P(E) = 1 .
Pro nemožný jev je
P(E) = O.
Elementární definice pravděpodobnosti
m
P(E) = -
n
(m, n E N) ,
tj. při pokusu je pro jev E z n možných výskytů m výskytů příznivých.
Příklad:
Pravděpodobnost, že při vrhání kostkou padne číslo 6, je P = 1/6.
Statistická definice pra vděpodo bnosti
P(E) = lim p ,
n- 00 n
tj. při n-násobném provedení pokusu se jev E vyskytuje p-krát.
Pravděpodobnost P(E), že jev E nenastane (tj. nastane jev E), je
P(E) = 1 -.P(E).
Částečný jev E 1 c E 2
P(El) < P(E 2 ).
Součtová věta počtu pravděpodobnosti
[pravděpodobnost "bud', nebo"]
"
Pravděpodobnost, že jeden z neslučitelných jevů E l' E 2 , ..., Ek nastane, je
P(El u E 2 U ... u E k ) = P(El) + P(E 2 ) + ... + P(Ek)'
Příklad:
Pravděpodobnost, že při vrhu kostkou padne číslo 3 nebo 6, je
P Il _ 1
=6+6-3.
733
Speciálně platí
P(El u E 2 ) = P(E l ) + P(E 2 ) - P(El n E 2 ),
kde jevy £1' E 2 se vzájemně n musí vylučovat.
Podmíněná pravděpodobnost
Pravděpodobnost jevu E 2 za předpokladu, že jev £1 již nastal, se nazývá
podmíněná pravděpodobnost P(E2/EI) jevu E 2 a platí
( / ) P( E 1 n E 2)
P £2 £1 - () ·
P El
Jsou-li jevy El a E 2 vzájemně nezávislé, .pak čísla P(E 1 ) a P(E 2 ) nazýváme
nepodmíněné pravděpodobnosti.
Věta o násobení pravděpodobností
[pravděpodobnost "a zároveň"]
Pravděpodobnost, že zároveň nastanou vzájemně nezávislé jevy E l , E 2 ,..., E k ,
Je .
P(El n E 2 n ... n E k ) = P(E l ) P(E 2 ) ... P(Ek)'
Pro vzájemně závislé jevy El a E 2 s podmíněnými pravděpodobnostmi
P(E 1/ E 2 ) a P(E 2 / E 1) platí
P( E 1 h E 2) = P( E 1) P( E 2/ E 1) = P( E 2) P( E 1/ E 2) ·
Příklad:
Vytáhneme-li z karetní hry o 32 kartách jednu kartu, pak pravděpodobnost,
že je to král, je P(El) = 4/32 = 1/8. Je-li vytažená karta král a vytáhneme-li
nyní další kartu, pak pravděpodobnost, že je to opět král, je P(E2/El) = 3/31.
Vytáhneme-li z uvedené karetní hry dvě karty, pak pravděpodobnost, že
vytáhneme dva krále, je
1 3
P = P(El) P(E 2 !E l ) = -. - 0,012.
8 31
I
Pro nezávislé jevy E l , E 2 platí
P(E2/El) = P(E 2 ), popř. P(El/E2) = P(El).
\
Pro k nezávislých jevů E l , E 2 , ..., Ek pravděpodobnost, že zároveň nastanou,
. .. I ,
Je
P = P(El) P(E 2 ) ... P(Ek)'
734
pravděpodobnost, že žádný z nich nenastane, je
P = [1 - P( E I )] [1 - P( E 2)] ... [1 - P( E k )] ,
a pravděpodobnost, že aspoň jeden z nich nastane, je
P = 1 - [1 - P(EI)] [1 - P(E 2 )] ... [1 - P(E k )] .
Vzorec pro celkovou pravděpodobnost
Pravděpodobnost, že jev E nastane zároveň s právě jedním z k neslučitel-
ných jevů E I' E 2 , ..., E k , je
, P(E) = P(E 1 ) P(EjE I ) + P(E 2 ) P(EjE 2 ) + ... + P(Ek) P(EjEk) =
k
= L P(Ei) P(Ej E i ) .
i= 1
Bayesův vzorec [vzorec pro pravděpodobnost hypotéz]
Nechť E je jev, který nastane právě s jedním z k neslučitelných jevů
E l' E 2 , ..., Ek' Pravděpodobnost jevu E i za předpokladu, že jev E již nastal, je
( j ) _ P(E i ) P(EjE i )
P E i E - k .
L P(Ej) (P(EjEj)
j= 1
Výsledky nezávislých pokusů
Dva pokusy se nazývají vzájemně nezávislé, jestliže výsledek jednoho z nich
nemá vliv na výsledek druhého pokusu. Provedeme-li n nezávislých pokusů,
přičemž při každém pokusu nastane právě jeden z k neslučitelných jevů
E l' E 2 , ..., Ek s pravděpodobnostmi po řadě P 1 = P(E 1)' P 2 = P(E 2)' ...
..., P k = P(Ek)' a označíme-li Pn(m}, m2, ..., mk) pravděpodobnost, že při
n pokusech jev E1" nastane ml-krát, ..jev E. 2 m2-krát, .., jev. Ek mk-krát
(ml + m 2 + ... + m k = n), pak platí
n!
P n (m 1 , m 2 , ..., m k ) = p';lp 2 ... Pkmk.
ml! m 2 ! ... m k !
Speciálně pro k = 2 dostaneme tzv. Bernoulliovo schéma:
Jestliže
P I = P , P 2 = 1 - P = Q , ml = m, m 2 = n - m,
pak
n'
Pn(m) = . pmQn-m.
m!(n - m)!
735
V I a s t n o s t i k oe f i c i e n t ů P n( m)
n
I Pn(m).= 1 ,
m=O
kde Pn(m) je koeficieQt u x m v rozvoji polynomu (Q + px)n podle mocnin
proměnné x (binomický zákon rozložení pravděpodobnosti). Přitom
Pn(m) < Pn(m + 1)
Pn(m) > Pn(m + 1)
Pn(m) = Pn(m + 1)
pro m < nP - Q ,
pro m > nP - Q ,
pro m = nP - Q .
Maximum koeficien u P(m) je při J1 = momo = nP - Q, přičemž
_ { mo, } .. { celým číslem,
mo = . "" I , "', I k ' b h . je-II mo I , "', I
nejmenSl ce e CIS o, tere o sa Uje mo, nece ym CIS em.
Náhodné veličiny
Náhodné veličiny [náhodné proměnné] jsou proměnné, jejichž hodnoty při
konstantních podmínkách závisí na náhodě, přičemž každá z těchto hodnot
vystupuje s určitou pravděpodobností. Náhodné veličiny mohou být diskrétní
(x k ), popř. spojité. Odpovídá jim diskrétní, popř. spojitá distribuční funkce
F(x) = P( < x).
Vlastnosti distribuční funkce F
Distribuční funkce F je monotónní neklesající funkce, tj. z Xl < X2 plyne
F(x 1) < F(x 2 ).
Funkce F má nejvýše spočetně mnoho bodů nespojitosti a je spojitá zleva.
Platí
F( - (0) = O,
F( + 00) = 1 .
Diskrétní distribuční funkce [stupf1ové funkce] "-
Náhodná veličina, která může nabývat jen konečně mnoha hodnot X j
'(i = 1, 2, ..., n), určuje diskrétní distribuční funkci. Hodnotami proměnné
jsou body nespojitosti a příslušnými pravděpodobnostmi jsou hodnoty dis-
tribuční funkce v bodech nespojitosti.
Rozložení pravděpodobnosti v případě, že náhodná veličina nabývá hod-
noty Xi (obr. 427), je
.. p(xJ = P( = Xi)
(i E N) ,
736
přičemž
n
L p( Xi) = 1 ,
i = 1
a
f'(x) = P( < X) = L P( = Xi) = L P(X i ).
Xi <x
x.<x
Tato funkce udává pravděpodobnost, že náhodná veličina nabude hodnoty
menší než x.
F (X)
f
0,5
P (xi)
I
I
I
Obr. 427. Diskrétní distribuční funkce
o
X'
t
x
f(x)!
I
o a b
>
x
Obr. 428. Spojitá distribuční funkce
[znázornění pravděpodobnosti
P(a b) = F(b) - F(a)
šrafovanou plochou]
SpoJité distribuční funkce
Spojité náhodné veličině odpovídá spojitá distribuční funkce (obr. 428)
F(x) = P( < x) = P( - 00 < < x) = foof(Z)dZ,
d: X) = f(x) ,
přičemž f [f(x) > O] se nazývá hustota pravděpodobnosti. Platí
f:: f(x)dx = 1,
P(a < < b) = F(b) - F(a) = ff(x) dx .
737
Momenty
n
m( - xf = L x P(x i )
i = 1
pro diskrétní náhodnou veličinu (tzv. moment k-tého řádu),
m( - cf = L+:(x - cf f(x) dx
pro spojitou náhodnou veličinu .
.
Pro c = O se momenty m( ) nazývají počáteční. Pro c = J1 se momenty
m( - J1f nazývají centrální.
Očeká vaná hodnota
Očekávaná hodnota J1 je počáteční moment prvního řádu, popř. vážený
aritmetický průměr:
n
J1 = E = L Xi P(x i )
i = 1
pro diskrétní náhodnou proměnnou ,
f +oo
Ji = E = -00 x f(x)dx
pro spojitou náhodnou proměnnóu .
Rozptyl [variace]
Rozptyl (]2 je centrální moment druhého řádu, přičemž (] se nazývá směro-
datná odchylka [střední kvadratická odchylka]:
n
(]2 = C2 = E( - E )2 = L (Xi - J1)2 P(x i )
i = 1
pro diskrétní náhodnou veličinu ,
a 2 = D2 = E( - E Y = L+:(x - JiY f(x)dx
pro spojitou náhodnou veličinu .
Poč e t n í p r a v i d I a (C je konstanta; , 11 jsou různé náhodné veličiny)
J1( c) = c ,
J1( + 11) = J1( ) + J1( 11 ) ,
J1( 11 ) = J1( ) J1( 11) ,
(]2(C) = O,
(]2( + 11) = (]2( ) + (]2(11),
738
,u( c ) = c ,u( ) ,
Ji( + C) = ,u( ) + c ,
a 2 ( C ) = C 2 a2( ) ,
a2( + c) = a2( ).
Variační koeficient
a
v =-.
Ji
Šikmost (obr. 429)
m( - Jl)3
Yl = 3
(1
Exces (obr. 430)
Y2 = m( - 11)4 - 3 .
4
Šikmost je mírou pro' souměrnost a exces je mírou pro strmost křivky.
f(x)
,,(x)
o ,ti
Po
x
o x
Obr. 430. Druhy excesu 12 při
symetrickém rozdělení s týmž průměrem
(pro y 2 = O jde o normální rozložení)
1 2 >0
12=0
12<0
9br. 4 9. Druhy šikmosti )'1 (pro
l' 1 = O jde o symetrické rozložení)
Binomické rozložení (s vracením tažených prvků) (obr. 431)
P(Xi) = (:i) pX'qn-x"
kde p + q = 1, přičemž
p je pravděpodobnost výskytu jevu E l'
q = 1 - p - pravděpodobnost výskytu jevu £2'
n - počet zkoušek,
Xi = 1, 2, ..., n (n E N).
739
Dále platí
J.l = np,
(12 = npq ,
1 - 6pq
Y2 = (12
q-p
}'l =
(1
P (x)
0,3
0,2
0,1
01234567X
Obr. 431. Binomické rozložení
Distribuční funkce
F(x) = L ( n ) pXiqn-Xi.
Xi <x Xi
Hypergeometrické rozložení
Na rozdíl od binomického rozložení se jednotky základního souboru. (ty
jsou u binomického rozložení libovolně velké), který je zde konečný, opět
do základního souboru nevracejí. Platí
p( . ) = (::)C qx)
XI ( )'
kde p + q = 1 a N je základní soubor. Význam dalších znaků je u binomického
rozloženÍ. Dále platí
Jl = np,
N - n
(12 = npq .
N -1
740
Distribuční funkce
F(x) = L (: ) C qx) .
Xi <X. ( )
Poissono o rozložení (obr. 432)
"X
I.. A.
f(x) = - e - .
x!
Platí
J1 = )'"
1
11= JJl. '
Distribuční funkce
(]2 = A
,
1
Y2 = - .
J.l
l x )..%
F(x)= -e-A.dz.
o z!
f(x) ,
0,28
°1 24
0.20
0,16
0,12 r
I
0,08 1
0,04
O 2 4 6 8 10 12 x
Obr. 432. Poissonovo rozložení
Poissonova rozložení lze prakticky použít jen při malých hodnotách pravdě-
podobnosti p (p < 1/2). Při velkých hodnotách pravděpodobnosti p se počítá
s q = 1 - p.
Normální rozložení [Gaussovo-Laplaceovo rozložení]
Hustota pravděpodobnosti
2 1 ( (x - J1)2 )
j(x; Jl., (1 ) = J(21t(12) exp - 2(12
(x E R)
741
(tzv. Gaussova křivka), kde J.l (střední hodnota) a (12 (rozptyl) jsou parametry.
Přitom v bodě J.l nabývá.. Gaussova křivka maxima a v bodech J.l + (1 nastává
inflexe.
Distribuční funkce
1 I x ( (z - J.l)2 )
F(x; Jl., (12) = J( 2) exp - 2 dz ,
21t(1 - 00 2(1
přičemž
f +oo
_ CX) j(x; Jl., (12) dx = 1 ·
Tabulka 10.1
Přibližné hodnoty pro konstrukci Ga ssovy křivky
x Jl + 10' Jl + O' O' + 30' Jl ::f:- 2 O' Jl :t 30'
- 2 -2
7 5 2,5 1 1
y ,8 y max 8" Ymax 8' Ymax '8 Y n\ax 80 Y max
Tab u I k a 10.2
Tabulka normálního rozložení
x f (x; O, 1) F( x O. 1) x f(x; O, 1) F(x; 0,1)
I
0,0 0,398 9 0,500 O 1,9 0,065 6 0,971 3
0,1 0,397 O 0,539 8 2,0 0,054 O 0,9772
0,2 0,391 O 0,579 3 2,1 0,044 O 0,982 1
0,3 0,381 4 0,617 9 2,2 0,035 5 0,986 1
0,4 0,368 3 0,655 4 2,3 0,028 3 0,989 3
0,5 0,352 1 0,691 5 2,4 0,022 4 0,991 8
0,6 0,333 2 0,725 7 2,5 0,017 5 0,993 8
0,7 0,312 3 0,758 O 2,6 0,013 6 0,995 3
0,8 0,2897 0,788 1 2,7 0,0104 0,996 5
0,9 0,266 1 0,815 9 2,8 0,0079 0,997 4
1,0 0,242 O 0,841 3 2,9 0,006 O 0,998 1
1,1 0,2179 0,864 3 3,0 0,004 4 0,998 65
1,2 0,194 2 0,884 9 3,2 0,002 4 0,999 31
1,3 0,171 4 0,903 2 3,4 0,001 2 " 0,999 66
1,4 0,149 7 0,919 2 3,6 0,000 61 0,999 84
1,5 0,129 5 0,933 2 3,8 0,000 29 0,999 93
1,6 0,110 9 0,945 2 4,0 0,000 134 0,999 968
1,7 0,094 O 0,955 4 4,5 0,000 016 0,999 997
1,8 0,079 O 0,964 1 5,0 0,000 002 0,999 999 97
742
.
Normované normální rozložení (o- = 1, J1.= O) (obr. 433)
,
Hustota pravděpodobnosti
1 2
cp(x) = f(x; O, 1) = J(21t) e -x I
Distribuční funkce
1 f x
4>(x) = F(x; 0,1) = J(21t) -00 e- t2/2 dto
Každé normální rozložení f(x, J1, 0'2) lze transformací (tzv. normalizací)
Xnenorm - J1
X norm =
a
uvést na normovaný tvar.
f(x j O,1J
-3cr -26 -O' O 6' 2(J' 36' x Obr. 433. Normované normální
rozložení ((J = 1, Jl = O)
10.2. MATEMATICKÁ STATISTIKA
10.2.1. Sumační znak
n
L ai = a m + a m + 1 + ... + a n
i=m
(m, nE N, m < .n).
Gaussův sumační symbol:
n
L a i = [a] = a 1 + a2 + ... + a n .
i = 1
743
Platí
n n n
, ( a. + b, ) , = , a. + ' b.
I-I I- I'
i=1 i=1 i=1
n n
L cai = c L a i
i=1 i=1
(c je konstanta),
m n n
L a i + L a i = L ai ,
i=1 i=m+l i=1
m n n m
L ai + L a i = L a i + L a i
i=1 i=k i=1 i=k
m n n k-I
L a i + L ai = L a i - L a i
i= 1 i=k i= 1 i-=m+ 1
(k < m < n)
(m < k < n),
n
Lc=(n-m+l)c
(c je konstanta, m < n),
i=m
d n n' d
dx i l J;(x) = i l dx J;(x),
n n+c-m
L a i = L ak-c+m
i=m k=c
(transformace- indexů),
m n n m
L Laik = L Laik
i=1 k=1 k=1 i=1
(dvojný součet je součet řádků a sloupců).
10.2.2. Multiplikační znak
n
O ai = ama m + 1 ... a n
i=m
(m, nE N, m < n),
takže
Platí
n
n! = O x.
x=1
n n n
n a.b. = n a. O b,
I I I I
i=1 i=l i=1
(platí také pro dělení),
n n
O ca. = lfI n a.
I I ,
i=1 i=1
m n n
n a i O a i = n a i
i=1 i=m+l i=1
(m < n),
744
m n n m
n a i n ai = n až n až
i=1 i=k i=1 ž=k
m n n I k-I
,n až .n ai = .n a i . n a i
1=1 I=k 1=1 l=m+l
(k < m < n),
(m < k < n),
n
ne = ť--m+l
ž=m
(e je konstanta, m < n).
10.2.3. Střední hodnoty
Aritmetický průměr
_ Xl+X2+...+ X n
x=
n
LXi
i= 1
n
n
[Je to vážený, aritmetický průměr pro h i = h (i = 1, 2, ..., n).]
Vážený aritmetick.v průměr:
_I x1h 1 + x2h + ... + xnhn
X =
hl + h 2 + ... + h n
n
x.h.
i..J I I
i = 1
n
x.h.
i..J I I
i = 1
n
L h i
i = 1
N
kde h i je četnost (váha) i-tého pozorování (viz str. 755),
N -, počet všech pozorování,
Xi - hodnota i-tého pozorování.
Není-li možno zjistit jednotlivé hodnoty pozorování, ale jen jejich dílčí
soubory (třídy), pak místo jednotlivých hodnot Xi bereme pro i-tou třídu
třídní třední hodnotu mi znaku a třídní četnost h i .
Vlastnost aritmetického průměru jako těžiš tě :
n
L (Xi - x) h i = O,
i = 1
1 n
- L (Xi - C) h ž = x - c,
N i= 1
f h i
i..J Xi -
1 n ;=1 e _
- ex.h, = ex ale = x
N i..J II' I
i= 1 t
i= 1 e
(c * O) .
745
Minimálnost součtu čtverců odchylek od aritmetického průměru x [kvadra-
tická minimálnost aritmetického průměru]:
n n
L (Xi - x)2 h i < L (Xi - a)2 h i
i=1 i=l
pro X 9= a .
Pro aritmetický průměr n tříd (dílčích souborů, podsouborů) platí
_ XINl+X2N2+,,,+xnNn
X=
NI + N 2 + ... + Nn
kde Ni je četnost i-té třídy.
Geometrický průměr
X G = V(X1 X 2 ... X n ) = JlJ Xi
1 n
19 XG = - L 19 Xi
ni=1
(Xi >0),
(Xi > O).
Vážený geometrický průměr
X = J Ii X ; . kde N = f h i .
i=1 i=l
Průměrné tempo [průměrný koeficient] růstu
W ' (n- J:: ).100%.
K vadratický průměr
J 2' 2
_ Xl + X 2 + ... + X n
X K =
n
1 J n
= / L xf .
'\In i=l
Vážený kvadratický průměr
XK = J( it Xth ),
n
kde N = L h i .
i= 1
Harmonický průměr
n
n
Xli =
1 1 1
- + - + ... + -
Xl X 2 X n
n 1
L-
i = 1 Xi
746
Vážený harmonický průměr
N
-,
X H = n '1
L -h i
i = 1 Xi
kde
n
N=Lh i .
i = 1
Cauchyova věta:
Pro Xi * x k (i, k = 1, 2, ..., n) platí
X max > XK > X > x G > Xli > x min .
Med ián [pros třed ní hod not a zn ak u, s třední hodnota poloh y] x
Po uspořádání pozorovaných hodnot ai v rostoucí pasloupnost je mediánem
prostřední hodnota, jejíž index při lichém rozsahu n výběru je
n + 1
=> x = X(n+ 1)/2 ;
2
při sudém rozsahu n výběru mají prostřední hodnoty indexy
n n
- a -+1
2 2
a mediánem je aritmetick.ý průměr obou prostředních hodnot:
_ X n /2 + x n / 2 + 1
x=
2
Minimálnost součtu 'odchylek od mediánu x [lineární minimálnost me-
diánu] :
n n
L tX i - :xl h i < L IX i - al h i
i=l i=l
pro x * a .
Modus
Modus x je nejčetnější hodnotou znaku v daném souboru, tj. modus je
.
pozorovanou hodnotou s třídní četností h imax .
10.2.4. Míry rozptýlení
Mírou rozptýlení [mírou variace] nazýváme číslo charakterizující
stupeň proměnlivosti pozorovaných hodnot v daném souboru.
Rozpětí, výběrové rozpětí
4
R = X max - x.:nin .
747
Střední odchylka
1 n
d = - L IX i - TI h i ,
N i=1
n
kde N = L h i a T je vhodná hodnota (x nebo x). Pro soubor vytvořený z ně-
i= 1
kolika tříd (podsouborů) místo jednotlivých hodnot Xi znaku bereme pro
i-tou tř-ídu třídní hodnotu mi znaku.
Směrodatná odchylka
s = J[ N 1 itt(X i - xY hiJ,
Pro h i = 1 je
n
kde N = L h i .
i= 1
s = J[ .f (Xi - xy ] = J[ ( .f xt - x.f Xi )] .
n 11=1 n 11=1 1=1
Pro soubor vytvořený z několika tříd místo Xi bereme opět mi.
Variační koeficient [koeficient variace]
Vx = . 100 % .
X
Problém odlehlých hodnot
.
..
Odlehlými hodnotami ve výběru nazýváme takové hodnoty pozorované ve
výběru, jichž je malý počet a které jsou tak vzdáleny od ostatních hodnot, že
buď pocházejí zjiného základního souboru, nebo výběrový postup byl chybný.
,
k
7
6
5
4
3
2
1
O
fO 20 50 100 200 500 1000 n Obr. 434. Diagram pro součinitele k
748
Předpokládejme, že ve výběru o n + 1 měřených hodnotách je jedna (označ-
me ji X n + 1) nápadně velká, základní soubor má normální rozložení a x, resp. s
je aritmetický průměr, resp. výběrová směrodatná odchylka bez odlehlé hod-
noty. Odlehlá hodnota se vypustí, je-li
X n + 1 > X + ks,
přičemž hodnotu součinitele k lze určit z diagramu na obr. 434. V praxi postačí
pro rozsah N výběru z intervalu < 10, 1 (00) vzít k = 4.
Při elkých výběrových hodnotách Xi je vhodné zavést předběžný odhad
aritmetického průměru D a položit Zi = Xi - D. Pak dostaneme
1 n
· X = D + - L Zi = D + z,
ni=i
s = J[ 1 1 f (Xi - X)2 J = J[ 1 f (Zi - zy J .
n - i=l n - 1 i=l
10.2.5. Metoda nejmenších čtverců
Základem je časová řada [dynamická řada], v níž empirické hodnoty
jsou přiřazeny nějakému časovému okamžiku. Zjistitelný vývojový směr se
nazývá základní směr [vývojový směr, trend]. Metoda nejmenších čtverců dává
aproximační funkci, při níž součet čtverců odchylek funkčních hodnot Yi
od statistických údajů Si je nejmenší.
Gaussova podmínka minimálnosti:
.
n
S = L (Si - Yi)2 min.
i= 1
Pomocí substituce
Yi = f(x i ) = ao + al x i + a2 x f + ... + amx
dostaneme
n
S = L(Si - ao - a1xi - a2x{ - ... - am )2 min.
i= 1
Koeficienty ak se vypočtou pomocí parciální derivace normálních rovnIC
a anulováním.
V praxi zpravidla stačí omezit se na lineární a kvadratickou (progresívní,
popř. degresívní) závislost (viz též vyrovnávací počet na str. 756 a 757).
..
749
Lineární závislost:
n n
L Si = aon + a 1 L Xi'
i=l i=l
n n n
L SiXi = ao L Xi + al L X? .
i=l i=l i=l
K vadratická závislost (při týchž sčítacích nlezích):
LSi = aon + al LXi + a2 LX? ,
LSiXi = a o LXi + al LX? + a Lxf ,
LSi X ? = ao LX? + al Lxf + a2 Lxi.
Výpočet koeficientů a k se zjednoduší, volíme-li časové úseky Xi tak, že
n
L xt k - 1 = O
i= 1
(k = 1, 2, . .., m) .
Při týchž sčítacích mezích dostaneme:
Lineární závislost:
LSi = aon,
LSiXi = a 1 LX? .
Kvadratická závislost:
LSi = aon + a2 LXi,
LSixi = a 1 LX? ,
LSi x ? = ao LX? + a2 Lxi .
Uvedená podmínka bude splněna, jestliže polovina hodnot Xi je kladná,
popř. záporná (prostřední člen má časovou hodnotu nula).
Stupeň absolutní kompatibility [stupeň absolutní slučitelnosti]:
Vak = J L(S; Yi)2 .
Stupeň relativní kompatibility [stupeň relativní slučitelnosti]:
. Vak
Vrk = - L .100 %.
s.
1
n
750
10.2.6. Lineární regrese, lineární korelace
Úkolem je vyšetřit závislost řad měření se dvěma znaky (korelační
vztah mezi hodnotami Xi a Yi)' Regresní rovnice je analytickým vyjádřením
vztahu mezi proměnnými. Získaná přímka optimálně prokládá soustavu bodů
(regre ní přímka [vztahová přímka]).
Substituce:
ji = ao + a. X ,
kde a 1 je regresní koeficient.
Lineární regresní rovnice (při stejných sčítacích mezích jako dříve):
_ _ _ + LXiYi - Y LXi ( . _ )
Y-Y 2 _ x-x,
i.JXi - X i.JXi
přičemž
s = J[ n 2 itl (Yi - Yi)lJ.
Stupeň závislosti (přesnost lineárního vztahu) vyjadřuje korelační koeficient
[koeficient korelace]
L(Xi - x) (Yi - y)
r X }' = JII(Xi - x)2 L(Yi - y)2] ,
r xy E < - 1, 1 > .
Pomocí kovariance
1
Sxy = cov (x, y) =
n - 1
(L - LXi LYi )
x. y .
I I
n
dostaneme
Sxy
r xy = - ,
SxSy
Sx
r xy = a 1 - .
Sy
Míra variability
S}'
al =r xv -
, Sx
B xy = r y .
751
tO.3. TEORIE CHYB
Označeni a názvy:
X - skutečná hodnota,
Xi - naměřená hodnota,
Li = X - Xi - (nevyhnutelná> skutečná chyba,
L\x (Xi - dx < X < Xi + dx) - absolutní chyba,
- L\x - oprava,
L\x L\x
tJ = . - - - relativní chyba,
X x'
l
l00tJ / - procentuální relativní chyba.
Počáteční chyba
Chybu výpočtu, která vznikne vlivem nepřesnosti vstupních údajů, nazý-
váme počáteční chybou.
Jsou-li dXbdx2,...,dxn chyby po řadě veličin X I ,X2,.."X n , pak veličina
y = f(x I' X 2 , .. ., x n ) má počáteční chybu
A f cf(x l , x 2 , ..., x n ) - d
L1 Y "" i.J dx v - y.
\' = I C Xv
Největší absolutní počáteční chyba
n cf
L\Ymax < L L\x\.
V = I C Xv
Pro y =f(x) je
dYmax = f'(x) dx .
Největší relativní počáteční chyba
Cf
dYmax f. ex\.
tJ max = < i.J L\x\.
Y \'=1 f
Zvláštní případy:
a) Y = Xl + X 2 + ... + X n :
dy < L\x 1 + dX2 + ... + dx n ,
L\x l dX 2 dX n
tJ < + + ... +
Xl
X2
X n
752
b) .V = Xl - X2:
dy < dXI + dX 2 ,
dX I + dX2 )
£5 < (X I * X 2 .
- XI - X 2
c) Y = ex 1 X 2 ... X n :
L\y < lel [ldx l x 2 ... xnl + IX I dX 2 X 3 ... Xnl +... + Ix l x 2 ... X n - l L\xnll,
£5 < I ci [ L\x 1 + L\x 2 +... + L\x n ] .
Xl X2
) Xl
d y = - (X2 * O):
X 2
L\y < I X 21 L\x I lx I I L\ X 2 ,
X2
dXI dX2 ( )
U < - + Xl * O .
Xl X2
e) y = X n (X > O):
dy < dxlnxn 1i.
dx
tJ < n-.
X
f) y = C loga X (X > O):
C dx
L\y < ln a
X
1 dx
£5 <
ln a X loga X
10.4. VYROVNÁVACÍ POČET
Pozorování o stejné přesnosti
Označení a názvy:
X - skutečná hodnota,
Xi - naměřená hodnota, .
[x] = X I + X2 + ... + X n - Gaussův sumační symbol.
753
Zdánlivá hodnota [střední hodnota]:
_ [x]
X=-.
n
Zdánlivá chyba:
Vi = X - Xi => [v] = O
Skutečná chyba:
(zkouška) .
Gi = X - Xi .
Střední chyba jednotlivé hodnoty [míra rozptýleni]:
m = + J [ ] + J [vv] ,
n n - 1
přič'emž symbol [ab] = a l b l + a2b2 + ... + anb n .
Středni chyba aritmetického průměru x:
mx- = = + J [ ] + J ([ vv] r
'\In n nn-l
Výsledek souboru měření pak je x + mx.
Podmínka pro vyrovnání:
[ vv] min .
Gaussův zákon o přenášení chyb pro střední chyby
Při několika souborech měření s výsledky Xi + m Xi (i = 1, 2, ..., n) má
funkce y = f(x l, X2, ..., x n ) střední chybu
my = + JLtl (: . rm vJ.
Přiklad:
Určeme tloušťku stěny dutého válce s vnějším průměrem D a vnitřním prů-
měrem d.
Tloušťka stěny
t = !(D - d),
odkud
ct 1 ct 1
- - --
cD 2' cd 2
754
K určení průměrů bylo provedeno pět měření podle tabulky 10.3.
Ta bulka 10.3
D v' VjVj d v' ViV i
I I
9,98 - 0,01 0,000 1 9,51 +0,01 0,000 1
9,97 - 0,02 0,000 4 9,47 - 0,03 0,000 9
10,01 + 0,02 0,000 4 9,50 + 0,00 0,000 O
9,98 - 0,01 0,000 1 9,49 -0,01 0,000 1
10,02 + 0,03 0.000 9 9,52 +0,02 0,000 4
49,96 +0,01 0,00 1 9 47,49 - 0,01 0,00 1 5
Vypočteme
mj) 0,01 ,
47,49
d - . 9,50,
5
J O,OOl 5
m = -.;.. 0,02,
- 4
1nj 0,01 .
49,96
jj - . 9,99,
5
m = J O, l 9 ..:.. 0,02,
Pro tloušťku stěny pak podle Gaussova zákona o přenášení chyb dostaneme
- 11- :T\ 0,49
t = 2\D - d J = 2 = 0,245 ,
m, = J(im + imi-) = J(0,25 .0,000 1 + 0,25 .0,000 1) =
0,01
= ../2 ..:.. 0,007 07 ..:.. 0,007 ·
Pozorování o nestejné přesnosti
Při sdružování výsledků z několika dílčích souborů o různých přesnostech
je třeba tyto výsledky opatřit příslušnými vahami h i . Nejjednodušší je vzít
vážený ritmetický průměr:
_ [hx ] hl Xl + h 2 X] + ... + hnxn
x - -
- [h ] - hl + h 2 + ... + h n '
hl: h 2 = m : mi ,
kde h i je váha i-tého souboru,
Xi - střední hodnota i-tého souboru,
mi - střední chyba i-té ho souboru.
755
Zdánlivá chyba střední hodnoty Xi:
Vi = X -, Xi , [hv] = O.
Střední chyba váhové jednotky:
mo = + J [hVV] .
n - 1
Střední chyba váženého aritmetického průměru:
mo J [hvv]
m x = J[h] = + [h](n - 1)"
Měření o různých přesnostech se na stejnou přesnost normují tak, že se
naměřená hodnota Xi vynásobí číslem Jhi'
Podmínka pro vyrovnání:
[hvv] min .
Zprostředkující pozorování
a) Lineární závislost
Bylo naměřeno n dvojic [Xi' Yi] (i = 1, 2, ..., n) hodnot o stejné přesnosti
(n > 2), které mají splňovat lineární rovnici y = ao + al X tzv. vyrovnávací
přímky.
. Substituce: ao + al Xi - Yi = Vi' [vv] min.
Koeficiel)ty ao, a 1 se určí z tzv. normálních rovnic:
na o + a.[x] = [y],
ao[x] + al[xx] = [yx].
Střední chyba jednotlivé hodnoty:
m= + J [vv] .
- n-2
Mají-li (r + 1 )-tice [Yi, Xli' X 2i ' ..., x ri ] (i . 1, 2, ..., n; n > r + 1) být řeše-
ními nějaké lineární rovnice, pak koeficienty ai lineární rovnice y = a o +
+ a 1 x 1 + a2x2 + ... + arX r je třeba určit z těchto normálních rovnic:
nao + a1[xl] + a2[x2] + ... + ar[xr] = [y],
aO[xi] + a 1 [x t x i ] + a2[x2 x i] + ... + ar[xrx i ] = [YXi]
(i = 1, 2, ..., r) .
/
756
Příklad:
Bylo naměřeno n = 5 dvojic čísel:
[4,3], [7; 4,5], [8,5], [9; 6,1], [10; 6,41.
Máme určit příslušnou vyrovnávací přímku.
Vypočteme
[x] = 4 + 7 + 8 + 9 + 10 = 38 ,
[y ] = 3 + 4,5 + 5 + 6,1 + 6,4 = 25 ,
[xx] = 16 + 49 + 64 + 81 + 100 = 310,
[yx] = 12 + 31,5 + 40 + 54,9 + 64 = 202,4.
Normální rovnice mají tvar
5a o + 38a 1 = 25,
38ao + 310a 1 = 202, ,
odkud -
25 . 310 - 38 .202,4
a = ...:.. O 555
o 5.310 -- 38.38 "
5 . 202,4 - 25 . 38
al = 5. 310 _ 38. 38 ...:.. 0,585 . /'
Vyrovnávací přímka má tedy rovnici
y = 0,555 + 0,585x .
Při nestejné' přesnosti jednotlivých hodnot tj. má-li (r + 1 )-tice
[Yi' Xli' X2i, ..., Xri] váhu h i , určí se koeficienty aj z těchto normálních rovnic:
ao[h] + a. [hx t ] + ... + ar[hxr] = [hy] ,
ao[hx i ] + a 1 [hXl Xi] + ... + ar[hxrx i ] = [hyx i ]
(i = 1, 2, ..., r) .
b ) Nelineární závislost
Naměřené dvojice [Xi' Yi] (i = 1, 2, ..., n) hodnot mají splňovat celou ra-
cionální funkci
Y = ao + a 1 X + ... + arx r (r + 1 < n).
Úloha se řeší pomocí normálních rovnic z odstavce a) s tím že místo Xi
-píšeme Xi.
757
Přjklad:
Je-li vyrovnávací křivkou parabola, dostaneme tyto normální rovnice:
nao + al[x] + a2[x 2 ] = [y],
ao[x] + al[xx] + a2[x 2 x] = [yx],
a o [x 2 ] + a 1 [xx 2 ] + a 2 [x 2 x 2 ] = [yx 2 ].
Závislá pozorování
V jednom souboru měření byly zjištěny hodnoty x;, x;, ..., x; o stejné přes-
nosti. Tyto hodnoty mají přesně splňovat t lineárních podmínkových rovnic
[aix] = ai1 x l + a i2 x 2 + ... + airX r = Ci
(i = 1, 2, ..., t) .
Opravy Vn (n = 1, 2, ..., r) pro naměřené hodnoty se vypočtou z korelát k j
(j = 1, 2, ..., t):
t
Vn = L aink i
i= I
(n = 1, 2, . . ., r) .
Koreláty se počítají z normálních rovnic:
[aial] k l + [a i a2] k 2 + ... + [aiat] kt = W i
Wi = Ci - [aix'] .
(i = 1, 2, ..., t) ,
Jestliže hodnoty x;, x , ..., x; byly zjištěny při různých přesnostech,. tj.
byla-li hodnota X n určena s váhou hm pak pro Vn a k i máme tyto určovací
rovnIce:
Opravy:
aink i
v=i..J-
n i = I h n
(n =. 1, 2, . . ., r) .
Normální rovnice pro koreláty:
[ a i a 1 ] [ aia2 ] aia t ]
h k l + h k 2 + ... + h kt = Wi,
(i = 1, 2, ..., t) ,
W i = Ci - [aix'].
Příklad:
Hodnoty X'I = -1,2 a x; = 1,9 mají přesně splňovat rovnice
3x I + 4x 2 = 5,
-7x 1 + 2x 2=11.
758
Pak platí
WI = 5 - 3X'1 - 4x; = 5 + 3,6 - 7,6 = 1 ,
W2 = 11 + 7X'1 - 2x; = 11 - 8,4 - 3,8 = -1,2,
[a 1 al] = a ll a1l + a l 2 Q l2 = 3.3 + 4.4 = 25,
[a 1 a 2 ] = a 11 a 21 + a 12 a 22 = 3 . ( -7) + 4.2 = -13,
[a 2 al] = a 21 al1 + a 22 a l 2 = ( -7).3 + 4.2 = -13,
[a 2 a2] = a21 a 21 + a22 a 22 = ( -7). ( -7) + 2 . 2 = 53 .
Normální rovnice mají tvar
25k I - 13k 2 = 1 ,
-13k 1 + 53k 2 = -1,2,
odkud dostaneme
...........-
k l . 0,032,
k 2 ...:.. -0,015.
Nyní lze vypočítat opravy. Platí
VI = allk l + a 2l k 2 = 3 .0,032 + (-7). (-0,015) . 0,2,
V2 = a12 k l + a 22 k 2 = 4.0,032 + 2. (-0,015) ...:.. 0,1 .
Přičteme-li tyto opravy k výsledkům X'l' x; měření, dostaneme konečné
hodnoty Xl = -1 a X 2 = 2, které přesně splňují podmínkové rovnice.
759
11. LINEÁRNÍ OPTIMALIZAC
[LINEÁRNÍ PROGRAMOVÁNÍ]
.
11.1. ZÁKLADNÍ POJMY
Optimalizaci rozumíme metody, s jejichž pomocí lze optimalizovat
určitý záměr při racionálním využití daných možností. Zadání úlohy vede
k maximalizační nebo minim'alizační úloze, která zpravidla obsahuje mnoho
proměnných.
Lineárni programováni je matematická metoda pro. určení optimálního ře-
šení matematického modelu vytvořeného z lineárních rovnic nebo nerovnic,
přičemž optimalizovaná účelová funkce je také lineární. Matematický model
je matematickou formulací zadání úlohy.
Řešeni optimalizačního problému představuje splnění optimalizačního kri-
téria pro danou úlohu.
Lineární programování má hlavní použití při řešení ekonomických nebo
technicko-ekonomických problémů, z nichž jen poměrně jednoduché problémy
(jen s několika proměnnými)je efektivní řešit ručními,výpočty. Složité problémy
vyžadují zpracování na počítačích s dosti značnými požadavky na kapacitu
paměti počítače.
Metoda určení extrémní hodnoty pomocí diferenciálního počtu selhává"
neboť při derivování proměnné z lineá ních rovnic zmizí. \
Kanonickým tvarem lineární optimalizace nazýváme maximalizační úlohu,
při níž omezující podmínky mají jen nezáporné absolutní členy.
Algoritmus řešeni použitého matematického modelu je souhrnem všech po-
kynů pro výpočet. Z mnoha metod pojednáme jen o grafické metodě a o sim-
plexovém algoritmu [simplexové metodě].
Sestavení matematického modelu
Učelová funkce:
z(x l' . . ., X n ) = CI X 1 + C 2 X 2 + C 3 X 3 + ... + CnX n =
n
= L CkX k optimum ;
k=l
760
v maticovém vyjádření má tvar
ex optimum ,
kde
e = (CI' C2, C 3 ,..., C n )
je řádkový vektor a
x = XI
X2
/'
X n
sloupcový vektor.
Vlastní omezení (při maximalizační, resp. minimalizační úloze platí znak < ,
resp. » :
a 11 Xl + a 1 2 X 2 + ... + a 1 nXn b I ,
,
a 21 x 1 + a22 x 2 + ... + a 2n X n b 2 ,
a m1 X 1 + a m 2 X 2 + ... + amnX n ;: bm'
popř.
n
I aikx k ;: b i
k=l
(i = 1, 2, . .., m)
neboli v maticovém tvaru
Ax ;: b ,
kde
A=
a 11 , a12,
a21, a22, ...,
. . .,
a 1n
a2n
a m 1, a m 2, ..", a mn
je matice koeficientů a
b = b 1
h 2
hm
je sloupcový vektor absolutních členů.
Podmínky nezápornosti:
Xk > O (k = 1, 2, .. ., n) .
761
Omezující podmínky a podmínky nezápornosti určují definiční obor úče-
lové funkce.
Podmínku Ax < b, popř. Ax > b lze pomocí ekvivalence o > b
<=> -o < -b vždy splnit.
Množinu všech přípustných řešení tvoří všechny vektory x, pro které platí
omezující podmínky a podmínky nezápornosti.
Řešení Xo, pro které účelová funkce je optimem, se nazývá optimální řešení.
11.2. GRAFICKÁ METODA ŘEŠENÍ
Této metody lze použít pro řešení úloh se dvěma proměnnými.
V kartézské souřadnicové soustavě s osami Xl a x 2 nejprve určíme množinu
všech uspořádaných dvojic [Xl' X 2 ], na níž jsou splněny omezující podmínky
a podmínky nezápornosti tím, že se rovnice
allxl + a l2 x 2 = hl '
a21 x l + a 2 2 x 2 = h 2 ,
atd.
přímek vyjádří graficky. Jsou-li omezující podmínky dány nerovnicemi, roz-
děluje každá z těchto přímek rovinu na "přípustnou" polorovinu, jejíž body
příslušnou podmínku splňují, a na polorovinu, jejíž body příslušnou pod-
mínku nesplňují. Přípustná řešení leží v lnnožině, která je průnikem "pří-
pustných" polorovin.
Optimální řešení se najde pomocí grafického znázornění účelové funkce
z(x I , X2) = CIXI + C 2 X 2 = C (c je libovolná konstanta) a rovnoběžného po-
sunutí této funkce:
c C max => optimum = maximum.
Optimální řešení je bud' právě jedno, jestliže přímka prochází jedním vrcho-
lem přípustné oblasti (tzv. vrcholové řešení), nebo existuje nekonečně mnoho
optimálních řešení, jestliže graficky znázorněná účelová funkce probíhá rovno-
běžně s nějakou z uvedených přímek z omezujících podmínek.
Při minimalizaci je třeba přímku posunout ve směru C C min .
Příklad:
Máme určit optimální řešení úlohy s účelovou funkcí
z(x I , X2) = 10xI + 15x 2 max-:
762
Omezující podmínky (obr. 435):
Xl + 2x 2 < 102,
t5x I + 3X2 < 450,
Xl < 25,
X2 < 45.
odmínky nezápornosti:
Xl > O,
X 2 > O .
X 2 t
30
Xz = 45
P3= optimum
l
", l 10i"
"
.t
40
'"
20
fa
fa
20 P5 30
I
40
::>-
Xi
Obr. 435. Určení oblasti OPtP2P3P4PS
přípustných řešení
Řešení:
Xl > O /\ X2 > O => jde o první kvadrant,
Xl = 25 => přímka je rovnoběžná s osou X2 } vymezení
X2 = 45 => přímka je rovnoběžná s osou Xl => obdélníku,
Xl + 2X2 = 102 /\ J5x I + 3X2 = 450 (dvě přímky) .
Oblast přípustných řešení: šestiúhelník OPIP2P3P4Pso Pro c = 300 =>
=> z(x I , x 2 ) = tO XI + I X2 = 300 (přímka) - prochází množinou přípust-
ných řešení; hodnotu lze ještě zvětšit.
763
Rovnoběžné posunutí přímky z tak, že prochází b0genf P 3 => optimum =
= maxImum:
P 3 = [22,40].
. Hodnota účelové funkce optimálního řešení:
zmax = 10.22 + 15.40 = 820.
11.3. SIMPLEXOVÁ METODA
Simplexovou metodou nazýváme iterační metodu postupného zlepšo-
vání řešení, které lze použít pro dvě i více proměnných. Lze ji zjednodušit pro
řešení opravního problému (minimalizace celkových přepravních nákladů).
Základním řešením nazýváme každé řešení splňující omezující podmínky,
které má ,nejvýše tolik nenulových proměnných (tzv. základních proměnných),
kolik existuje vzájemně nezávislých omezujících podmínek, přičemž sloupcové
vektory matice A, které přísluší nenulovým proměnným, jsou lineárně nezá-
vislé. Množina všech základních proměnných se nazývá báze. Proměnné,
které nepatří do báze, se nazývají nezáklad.ní [nebazické] proměnné.
Podmínky nezápornosti se při této metodě automaticky respektují a ne-
rozhodují při volbě počtu základních proměnných.
Každé základní řešení odpovídá jednomu vrcholu přípustné oblasti při
grafické metodě (viz kapitolu 11.2).
Postup řešení
1. Převedení úlohy na kanonický tvar ,
Omezující podmínky dané nerovnicemi Ax < b se zavedením tzv. přídat-
ných [fiktivních, doplňkových] proměnných změní v rovnice
.
a 11 X I + a 1 2 X 2 + ... + a I nXn + u I
a2l x l + a22 x 2 + ... + a2"X n + U2
= b l ,
= b 2 ,
.............................................
aml Xl + a m 2 x 2 + ... + amnx n
+ U m = bm ·
Přídatné proměnné podávají v základních řešeních informaci o ještě nevyuži-
tých rezervách.
Účelová funkce nabývá tvaru
Z(XI, X2, ..., X"' Ul' U2, ..., U m ) =
= CIXI + C2 X 2 + ... + C"X" + Ou l + 0u 2 + ... + Ou m -+ max.
764
Účelové funkce z mIn se násobením číslem - 1 převedou na účelové
funkce z max.
Omezující podmínky dané rovnicemi Ax = b se převedou , a kanonický
tvar zavedením umělých proměnných, přičemž se účelová funkce (v případě
maximalizace) změní takto:
z = C 1 X 1 + C 2 X 2 + ... + CnX n - N(u 1 + U2 + U3 + ...),
kde N C 1 'C2'....
Omezující podmínky dané jako nerovnice Ax > b se zavedením přídatných
proměnných změní v rovnice:
a 11 XI + a 1 2 X 2 + ... + a 1 nXn - Ul = b 1 ,
atd.
Máme-li dostat kanonický tvar, musí přídatné proměnné být kladné, což
dosáhneme tím, že každý řádek odečteme od řádku s největším absolutním
členem b i . Rozdíly a řádek s největším absolutním členem b i , doplněný o umě-
. ,
lou proměnnou, tvoří soustavu rovnic v kanonickém tvaru.
2. Nalezení výchozího základního řešení
Položme všechny proměnné x k = O, všechny U, * O => všechny U, patří do
báze prvního základního řešenÍ.
Základní vyjádření prvního základního řešení:
Ul = b 1 - a 11 Xl - a 1 2 X 2 - ... - a 1 n..Xn ,
U2 = b 2 - a 21 x l - a22 x 2 - ... - a2n X n'
U m = bm - a m l X l - a m2 X 2 - ... - amnXn'
První základní řešení lze vyjádřit takto:
Zl = C 1 X l + C 2 X 2 + ....
Základní řešení:
.
[ X h X 2, ..., X,., U h U 2, . . ., U m ] = [O, O, . . ., O, b h b 2, .. ., bm] .
3. Ověření, zda základní řešení je optimální (test optima)
Kritérium:
U optimalizačních úloh lze výsledek tak dlouho zlepšovat, dokud se v zá-
kladním vyjádření účelové funkce vyskytují koeficienty Ci > O (pro případ
maximalizace).
765
4. Vybrání některé dosavadní nezákladní proměnné k výměně za základní
.
proměnnou
Zavedeme takovou nezákladní proměnnou z účelové funkce Zl' která má
největší koeficient Ci' neboť tato proměnná způsobuje největší zvětšení hodnoty.
5. Vybrání jedné z dosavadních základních proměnných, která má být vyměněna
Vytvoříme všechny podíly bdaij pro aij > O, přičemž Xj je nová základní
proměnná, kterou je nutno zavést. Nejmenší z těchto podílů určuje tu základní
proměnnou určenou k výměně, která patří k stejné rovnici (Ul).
6. Výměna proměnných
Transformací odpovídající rovnice ze základního vyjádření prvního zá-
kladního řešení dostaneme jednu rovnici pro novou základní proměnnou:
b, a' l
) 1
X j = - - - Xl - ... - U, ,
aij aij
jejíž pravá strana se dosadí do ostatních rovnic pro x j.
7. Druhé základní ře el1í
( b. a"l )
u I = b I - a I 1 X I - a I 2 X 2 - ... - a I j -1.... - Xl - ... - U, -. .. - a I nXn ,
a.. a' I
I) 1
U 2 = b 2 - a: 1 XI - ... ,
Uj-l =...,
Uj+l =...,
b. a" 1
) 1
X j =---XI-.'.-U , .
aij aij
Vlevo je nová báze, v níž vzhledem k první bázi jsou členy X, a u, vyměněny.
Metoda potom pokračuje dále, jak je popsáno v bodě 2, a to tak dlouho,
doku všechny koeficienty základního vyjádření účelové funkce p-tého zá-
kladního řešení nejsou rovny nule. Pak je dosaženo optima.
Příklad:
Úlohu, kterou Jsme v kapitole 11.2 řešili graficky, budeme nyní řešit sim-
plexovou metodou:
z(X., X2) = 10x I + 15x2 max.
766
Omezující podmínky:
Xl + 2x 2 < 102,
15x l + 3X2 < 450,
Xl < 25,
X2 < 45.
Podmínky nezápornosti:
Xl > O,
X2 > O .
..
Poznámka:
Simplexová metoda je již při dvou proměnných značně náročnější než gra-
fická metoda. ·
1. Kanonický tvar úlohy:
,
Xl + 2X2 + Ul
15XI + 3X2
X2
= 102,
+ U 2 = 450,
+ U3 - 25,
+ U4 = 45;
Xl
Z(X I , X2) = 10XI + 15x 2 .
2. Výchozí základní řešení:
Základní vyjádření:
Ul = 102 - Xl - 2X2 ,
U2 = 450 - 15xI - 3X2,
U3 = 25 - Xl ,
U4 = 45
Základní řešení:
[0,0,102,450,25,45]
(tomuto řešení odpovídá bod Po grafického řešení).
Základní vyjádření účelové funkce:
Zl = 10XI + 15x 2 .
Hodnota účelové funkce:
- X2'
Z I = 10. O + 15. O + O. 102 + O . 450 + O. 25 + O. 45 = O .
767
3. Test optima:
Řešení není optimální, neboť v základním vyjádření je CI> O, C 2 > O.
4: Nová základní ptoměnná je X 2 , neboť má v základním vyjádření největší
koeficient.
s: Dosat'adní základní proměnná určená k výměně
b l 102
- = - = 51 ,
al2 2
b 2 450
- = - = 150,
a22 3
b 4 45
- = - = 45
a42 1
(nejmenší hodnota); je tedy třeba vyloučit proměnnou u 4 .
6. V.vnlěna proměnné
. X2 = 45 - u 4 .
7. Druhé základní ře. ení
Ul = 102 - Xl - 2(45 - U4) = 12 - Xl + 2U4 ,
u 2 = 450 - 15x I - 3(45 - U 4 ) = 315 - 15x I + 3U4,
U3 = 25 - Xl - 25 - Xl ,
X2:=' 4 - li4 = 45 - u 4 .
Základní řešení: [0,45,12,315,25, O] => bod P I .
Základní vyjádření: z; = 10XI + 15(45 - u 4 ) = tOXI 15u4 + 675.
Hodnota účelové funkce: Z2 = 10. O + 15.45 = 675.
8. Řešení není optimální, neboť koeficient u proměnné Xl je kladný, takže
je třeba vyměnit Xl'
b'l 12
= - = 12 (nejmenší hodnota) => vypustit Ul,
alt 1
b 315 ,
- = - = 21
a; I 15
9.
b 25
- = - = 25 .
a l 1
10. Třetí základní ře. ení
Xl = 12 - Ul + 2U4 - 12 - Ul + 2U4,
X2 = 45 - u 4 - 45 - U4 ,
U2 = 315 - 15(12 - Ul + 2U4) + 3U4 = 135 + 15uI - 27u4'
U3 = 25 - (12 - Ul + 2U4) = 13 + Ul - 2u 4 .
768
Základní řešení: [12, 45, O, 135, 13, O] => bod P2.
Základní vyjádření:
Z = 10(12 - Ul + 2U4) + 15(45 - U4) = -10u1 + 5U4 + 795 .
Hodnota účelové funkce: Z3 = 10.12 + 15.45 = 795.
11. Řešení není optimální, neboť koeficient u proměnné U4 je kladný, taki
je třeba vyměnit U4.
( b = _ 12 _ _ _ 6 )
12. , 2 ' odpadá kvůli a 6 < O ,
al6 -
b 45
- = - = 45
a " 1
26
.
b" 135
3 5 .
-'= - = => V yp ustIt U 2 ,
a;6 27
b 13
-=-=65.
" 2 '
a 4 6
13. Ctvrté základní řešení
Xl = 12 - Ul + 2(5 + MU 1 - l7 U 2) = 22 + lU I - -l7u2 ,
X2 = 45 -
(5 + U 1 - -&u2) = 40 - i-ul + l7 U 2 ,
U3 = 13 + Ul - 2(5 + UI - l7 U 2) = 3 - 1 + £7 U 2 ,
U4 ;::
5 + U I - l7 U 2 = 5 + iu1 - -hu 2 .
Základní řešení: [22,40, O, O, 3, 5] => bod P 3 .
Základní vyjádření:
z = 10(22 + 1 - 22 7 U2 ) + 15(40 - iU I + l7 U 2) =
= 820 - ¥Ul - f, U 2 .
Hodnota účelové funkce:
= 10.22 + 15.40 = 820 .
769
11.4. SIMPLEXOVÁ TABULKA
Simplexová tabulka 11.1 přehledně uvádí početní postůp z kapi-
toly 11.3.
Ta bu lka 11.1
Proměnné a přídatné proměnné Xl X 2 Ul U 2 U3 U 4 b,
I
-
a..
IJ
Základní proměnné O 10 15 O O O O
I Ul 102 1 2 1 O O O 51
u 2 450 15 3 O 1 O O 150
U 3 25 1 O O O 1 O -
:........' U 4 45 O [!] O O O 1 45
-675 10 O O O O -15
II :... U I 12 [!] O 1 O O -2 12
U2 315 15 O O 1 O -3 21
U 3 25 1 O O O 1 O 25
.. ..,. X2 45 O 1 O O O 1 -
-795 O O -10 O O +5
III : Xl 12 1 O 1 O O -2 (- 6) odpadá
:"'U 2 135 O O -15 1 O [TIJ 5
U3 13 O O -1 O 1 2 6,5
X 2 45 O 1 O O O 1 45
.-
-820 O O -65 -5 O O optimum
27
IV Xl 22 1 O --=.l.... 2 O O
27 27
: U4 5 O O .::.li 1 O 1
27 27
U 3 3 O O 3 .=1. 1 O
27 27
X 2 40 O 1 15 -1 O O
27 27
Vysvětlení k tabulce
V záhlaví jsou všechny proměnné (původní i přídatné).
1. sloupec: základní proměnné příslušné báze.
2. sloupec: hodnota základní proměnné.
3. až 8. sloupec: koeficienty u proměnných a přídatných proměnných v zá-
kladním vyjádření.
9. sloupec: podíly absolutního členu a koeficientu u proměnné určené k vý-
měně.
770
První základní řešení
1. řádek: účelová funkce; je určen největší koeficient 15; je třeba vyměnit x'}.
2. až 5. řádek: kanonický tvar.
Nejmenší podíl 45 určuje výměnu proměnné l!4.
Hlavní prvek (koeficient u proměnné X2 v rovnici pro u 4 ) [!] je označen
rámečkem (zarámečkován).
Druhé základní řešení
5: řádek: dělíme 5. řádek části I hlavním prvkem 1.
1. řádek: odečteme 15-násobek 5. řádku od 1. řádku v části I, aby ve sloupci
proměnné x 2 určené k výměně byl koeficient O.
,
2. řádek: odečteme 2-násobek 5. řádku od druhéhó řádku v části I.
3. řádek: odečteme 3-násobek 5. řádku od 3. řádku v č ti I.
4. řádek: odečteme nulový násobek 5. řádku od 4. řádku v části I, tj. 4. řádek
zůstává beze změny.
Nejmenší podíl 12 určuje výměnu proměnné Ul za proměnnou Xl' u níž je
největší koeficient v účelové funkci.
Hlavní prvek je [!].
1řetí základní řešení
2. řádek: dělíme 2. řádek v části II hlavním prvkem 1.
1. řádek: odečteme 10-násobek 2. řádku od 1. řádku v části II a dostaneme
základní vyjádření třetího základního řešenÍ.
3. řádek: odečteme 15-násobek 2. řádku od 3. řádku v části II.
Uvedeným způsobem pokračujeme tak dlouho, až 1. řádek (základní vy-
jádření) již neobsahuje žádné koeficienty větší než nula.
Zvláštní pi'ípady
Vyskytují-li se v řádku účelové funkce z pro nezákladní proměnné částečně
nuly nebo samé nuly, pak je další výměna možná, čímž dostaneme jiné opti-
mální řešení se stejnou hodnotou účelové funkce.
Úloha je degenerovaná, jestliže nějaká základní proměnná nabude nulové
hodnoty.
771
12. LOGICKÁ ALGEBRA [SPÍNAČOVÁ ALGEBRA]
12.1. ZÁKLADNÍ POJMY
Vhodným aparátem pro popis vztahů mezi výroky je jako logický
počet vytvořená Boolova algebra, pomocí níž lze matematicky odůvodnit
pravdivost nebo nepravdivost složených výroků. Její převedení na spínačovou
algebru se zakládá na tom, že v číslicové technice bezpaměťových členů jsou
možné jen stavy ,,zapnuto" (znak I) a "vypnuto" (znak O), tj.
x = I, právě když x * O,
x = O, právě když x * I.
Proměnná x je dvouhodnotová a nazývá se boolovská proměnná.
k-místným logickým členem [k-místnou boolovskou funkcí] F je každé uspo-
řádané k-tic [Xl' X 2 , ..., Xk] výroků (hodnot argumentů) jednoznačně přiřazen
výrok F(XI' X2, ..., x k ) (hodnota funkce).
Boolovské funkce jsou dvouhodnotové, neboť oborem hodnot je množina
obsahující jen dva prvky, které označíme O a I. Každou z nich lze přehledně
vyjádřit pomocí tzv. pravdivostní tabulky, která se v řídicí technice nazývá
tabulka stavů.
Označení (pro logicky ekvivalentní výrokové formule se v této části používá
rovnítka): ..
Pravdivostní ohodnocení výroků: pravda - nepravda, ano - ne, zapnu-
to - vypnuto, platí - neplatí.
Znaky pro pravdivostní ohodnocení: I-O, 1-0, P-N.
V stupní proměnné: xv'
Počet vstupních proměnných: k.
Hodnota boolovské funkce: y, popř. F(x 1 , X2, ..., x k ).
Stálé spojení: I.
Stálé přerušení: O.
Dosazení znaků I a O za vstupní proměnné: f" (n viz dále).
Při k proměnných existuje nejvýše 2 k kombinací.
Boolovská funkce: F , kde k je počet vstupních proměnných a n stavový
index řádku v pravdivostní tabulce (viz tabulku 12.3).
772 .
Počet n všech boolovských funkcí při k vstupních proměnných je
n = 2 2k ;
např. pro k = 2 dostaneme 16 možností (viz tabulku 12.3).
Elementární logické operace
Struktura elementárních logických operací je ú p 1 n á, neboť z jejích operací
lze vyjádřit všechny dvouhodnotové funkce.
Disj u I}kc [logické sčí tání, logické nebo, někdy al tern a ti va]
(viz tabulku 12.1)
Způsob zápisu: y = Xl V X2 (čteme: Xl nebo x 2 ) (další používané znaky:
+, u, vel).
Obvodová technika: paralelní řazení členů (obr. 436).
.
I
:;; A'2 y
st", nl ----1.--
x1
Obr. 436. Schéma disjunkce y = x I V X 2 (paralelní řazení členů)
X1 :J-r
+
Konjunkce [logické násobení, logické a] (viz tabulku 12.1)
Způsob zápisu: Y = Xl /\ X 2 [čteme: Xl a (zároveň) X 2 , popř. Xl i x 2 ]
(ji.né používané znaky: ., (1, &, popř. bez znaku).
Ta bulka 12.1
Pravdivostní tabulky
pro disjunkci a konjunkci
Xl X2 Xl V X 2 Xt X 2
O O O O
O I I O
I O I O
I I I I
Poznámka:
Bez uvedení znaku tedy vždy uvažujeme, že jde o konjunkci. V dalším
textu. budeme znak konjunkce zpravidla vynechávat.
773
Obvodová technika: sériové řazení členů (obr. 437).
Negace [logický zápor, inverze] (viz tabulku 12.2)
Způsob zápisu: y = x (čteme: není pravda, že x; x neplatí) (jiné používané
znaky: l, -, " non).
Obvodová technika: klidový [normální] kontakt (obr. 438).
A' " Xv
I C>--Y =9 -x t -x 2 -Y
stru n
Obr. 437. Schéma konjunkce y = Xl x 2
(sériové řazení členů) ,
I
x-
o o
y
j
Obr. 438. Schéma negace y = x
Ta b u I k a 12.2
Pravdivostní
tabulka pro negaci
x X
O I
I O
12.2. ZÁKLADNÍ LOGICKÉ ZÁKONY A PRAVIDLA
Úmluva:
Při určování pravdivostní hodnoty složen'ých výroků se při odstranění
závorek dává přednost konjunkci před disjunkcí.
Komutativní zákony:
Xl V X2 = X2 V Xl ,
X I X2 = X2 X I .
Asociativní zákony:
Xl v (X2 V X3) = (Xl V X2) V X3 = Xl V X 2 V X3 ,
XI(X2 X 3) = (X I X 2 )X3 = X I X2 X 3.
Distributivní zákony:
X I (X 2 v X3) = X I X2 v X I X3,
Xl V X2X3 = (Xl v X2) (Xl v X3).
774
Poznámka:
Pro poslední vztah neexistuje žádný odpovídající vztah v obyčejné algebře.
Příklad:
kdežto
Y = Xl V X2 /\ X3 = Xl V (X 2 X3)
(obr. 439),
(správně)
(nesprávně)
Y = Xl V X2 /\ X3 = (Xl V x 2 ) x 3
Přehled logických zákonů a pravidel
.
OvO=O 0/\0=0/\1=
=1/\0=0
1/\1=1
x/\O=O
x/\I=x
-cXf y
x2 x3
Obr. 439. Schéma formule
y = 'Xl V (X 2 X 3 )
Ovl=IvO=lvl=1
xvO=x
xvl=1
(obr. 440).
-e Xf =t- X3 ---': y
X 2
obr. 440. Schéma formule
Y=(X I VX 2 )X 3
o = 1
I = O
-
X = X
(x) = X
=x=x
X V X V X V ... V X = X xxx . . . X = X
(idempotentnost)
X V X = I (zákon o vyloučeném xx = O (zákon sporu)
třetím)
Xl V X2 = X 2 V Xl
(komutativní zákony)
Xl V (:-:2 V X3) = (Xl V X2) V X3 =
= Xl V X 2 V X3
( asociativní zákony)
Xl V X2X3 = (Xl V X 2 ) (Xl V x 3 )
(distributivní zákony)
Xl V X2 = XIX2
(de Morga nova pravidla)
X I V X2 V ... V Xk = X I X2 ... Xk
X I X 2 V XIX 2 = XI(X 2 V X2) = Xl
(pravidla o zestručnění)
X I X 2 = X 2 X I
XI(X2 X 3) = (X I X 2 )X3 = X I X2 X 3
X 1 (X 2 V X3) = XIX2 V X I X3
XIX2 = Xl V X2
XIX 2 ... X k = Xl V x 2 V ... V X k
(Xl V X2) (Xl V X 2 ) = Xl
775
Xl V X1X2 = xI(I V X2) = Xl
XI(XI V X2) = Xl
(zákonyabsorpce)
Xl V XIX2 = Xl V X2
X I X2 V XIX3 = X I (X2 V X3)
XI(XI V X2) = XIX2
(Xl V X2)(X I V X3) = Xl V X2 X 3
(odstranění závorek)
(Xl V X2) (Xl V X3) = X I X3 V XIX2
X I X2 V X I X3 V X2X3 = X I X3 V X2X3 (Xl V X2) (Xl V X3) (X2 V X3) =
= X 2 X3 V XIX3
F(XI' X2, ..., X k ) = Xl /\ F(1, X2, ..., X k ) V Xl /\ F(O, X2' ..., x k )
(rozklad funkce F podle proměnné Xl).
/
Pro Xfi (a i E {O, 1}) a XO = X, X'l = X (tj. pro i = O je proměnná Xi
negována, kdežto pro aj = 1 není proměnná Xi negována) lze rozklad podle
proměnných Xl' X2, ..., Xh obecně vyjádřit takto:
F(XI' X2, ..., X h , ..., x k ) =
V (11 (12 (1h F( )
- Xl X2 ... Xh a 1, a 2' ..., a h, X h + l' ..., X k .
[(11 , (12, ..', (1 h]
12.3. DALŠí BOOLOVSKÉ FUNKCE
SE DV MA PROMĚNNÝMI
(LEXIKOGRAFICKÉ USPOŘÁDÁNÍ)
Z šestnácti možností (operací) uvedených v tabulce 12.3 je šest
triviálních (O, 3, 5, 10, 12, 15).
Pro technickou praxi jsou důležité zejména tyto logické operace:
Negace disjunkce [negace logického sčítání, funkce [operace,
člen] NOR, Peirceova operace, funkce ani] (viz tabulku 12.4)
Y = Xl V X2 = Xl /\ X2 .
Negace konjunkce [negace logického náso bení, funkce [operace,
členJ 'NAND, Shef ferova operace] (viz tabulku 12.4)
Y = Xl I X2 = Xl /\ X 2 = Xl V x 2 .
776
Tabulka 12.3
Xl I I O O
X2 101 O F 2 Název
"
n
O O O O O F 2 =0 konstanta [přerušení]
o
1 O O O I Ff --- NOR [Peirceova operace]
= Xl V X 2 = X I X2
.-
2 O O I O F 2 = Xl +-fo X2 = XIXl nepřímá inhi bice
2
3 O O I I F = Xl negace
4 O I O O F 2 = Xl ++ X2 = X I X2 přímá inhibice
4
.
5 O I O I F; = X2 negace
6 O I I O F = X l )=:::( X 2 =Xt$X2= antivalence
= X t X2 v X I X2
7 O I I I F =x l lx2= X l X2 = NA ND
= Xl v x 2 [Shefferova operace]
8 I O O O F 2 = x t x 2 = Xl " X2 konjunkce
8
9 100 I F = XI <:> x 2 = ek vi valence
= X I X 2 v XIX2
10 I O I O F 2 - identita
10 - X2
11 101 I F 2 - X2 = Xl V X 2 implikace
11 - Xl
12 I I O O Ff2 = Xl identita
13 I I O I F 2 - V X2 negace nepřímé inhibice
13 - Xl
14 I I I O F 2 V X2 disjunkce
14 = Xl
15 I I I I Ff 5 = I konstanta [skrat]
Tabulka 12.4
Pravdivostní tabulky
pro negaci disjunkce
a negaci konjunkce
---
Xl X2 Xl V X 2 X 1 X 2
O O I I
O I O I
I O O I
I . I O O
777
Poznámka:
I Pomocí funkcí NOR a NAND lze rovněž vyjádřit všechny boolovské
funkce (tyto funkce tedy tvoří ú p I n o u logickou soustavu).
Implikace [přímá implikace] (viz tabulku 12.5)
Y = Xl => X 2 = Xl V X 2
(jiné používané naky: , )}.
Nepřímá implikace (viz tabulku 12.5)
Y = Xl X2 = X 2 => Xl
(jiné používané znaky: +-, C).
Ta bulka 12.5
Pravdivostní tabulky pro přímou
a nepřímou implikaci a pro přímou
a nepřímou inhibici
Xl X2 X I => X2 Xl <= X 2 Xl ++ X 2 x I ++ X2
O O I I I O O
O I I O O I
I O O I I O
I I I I O O
Inhi bice [pří má inhi bice, nonimplikace, negace implikace] (viz
tabulku 12.5)
Y = Xl ++ X2 = Xl => X2 .
Tabulka 12.6
Pravdivostní
tabulky pro ekvivalenci
a antivalenci
Xl X 2 Xl <=> X2 Xl >==< X2
O O I O
O I O I
I O O I
I I I O
778
Nepřímá inhibice (viz tabulku 12.5)
Y = Xl ++ X2 = Xl X2 .
Ekvi valence (viz tabulku 12.6)
Y = Xl <=> X2 = (Xl /\ X2) V (Xl /\ X2)
(jiné používané znaky: , = ).
N on e k v i val e n c e [a n t i val e n c e, a I t e r n a t i va, o per a c e v y I U č o va c í
nebo, negace ekvivalence, logické sčítání modul o 2] (viz tabulku 12.6)
Y = Xl X2 = (Xl /\ X2) V (Xl /\ X2)
(jiné používané znaky: , +++, =t=).
12.4. NORMÁLNÍ TVARY
Úplný konjunktivní normální tvar (zkratkou ÚKNT) [elem.en-
tární konjunkce]
k
K = I\xv
v= 1
(čteme: součet všech konjunkcí pro v = 1 až v = k). Počet všech možných
úplných konjunktivních normálních tvarů je 2 k .
Výraz K se nazývá úplný konjunktivní normální tvar (zkratkou ÚKNT),
obsahuje-li konjuktivní vazbu všech k vstupních proměnných (negovaných
nebo nenegovaných), přičemž počet ohodnocení je dán k-to mocninou čísla 2.
Příklad:
6
K 8 = I\x = XIX2X3X4XSX6
v=l
s ohodnocením 100110 dává n = 38.
Ú pl ný d isj unk ti vní n ormál ní tvar (zkratkou ÚDNT) [elemen tá rní
disjunkce]
k
D k = V x
n v
v= 1
(čteme: součet všech disjunkcí pro v = 1 až v = k). Počet všech možných
úplných disjunktivních normálních tvarů je 2 k .
779
Výraz D: se nazývá úplný disjunktivní normální tvar (zkratkou ÚDNT),
obsahuje-li disjunktivní vazbu všech k vstupních proměnných (negovaných
nebo nenegovaných), přičemž počet,phodnocení je dán k-tou mocninou čísla 2.
Příklad:
4
Di 1 = V Xv = Xl V X2 V X3 V x 4
v=l
s ohodnocením 1011 dává n = 11.
Disjunktivní normální tvar, konjunktivní normální tvar
Každé disjunktivní spojení konjunkcí (základních výrazů) se nazývá dis-
junktivní normální tvar, např. y = XIX3X4 V X3X4 V X2' Obdobně definujeme
konjunktivní normální tvar, např. y = (Xl V X 2 ) (Xl v X 3 V X 4 ) (Xl v 'x 4 ).
Výrokové termy, které nelze rozložit v složené termy, se nazývají elementární
výrokové termy dané výrokové funkce.
Kanonický disjunktivní normální tvar představuje sériově paralelní obvod.
Kanonický konjunktivní normální tvar představuje paralelní sériový obvod.
Každé disjunktivní spojení úplných konjunktivních normálních tvarů na-
zýváme kanonickým disjunktivním normálním tvarem:
I = VK
n
(je přednostně používán). Obdobně definujeme kanonický konjunktivní nor-
'mální tvar
I = I\D .
.
n
Počet všech možných kanonických disjunktivních normálních tvarů je
n = 2 2k ,
kde k je počet vstupních proměnných.
Příklad:
Tři vstupní proměnné Xl' X 2 , X3 jsou s výchozí proměnnou y podle technické
úlohy spojeny dále uvedeným způsobem. Vypočtěme logickou funkci v mini-
málním tvaru.
Tabulka 12.7 uvádí 2 k mCi>žností odezvy (k je počet vstupních proměnných).
Pro y = I platí kanonický disjunktivní normální tvar:
y = VKn
(n = O, 1, 2, 3, 4, 5) ,
n
y = Ko V KI V K 2 V K3 V K4 V Ks =
780
= XIX2 X 3 V XIX2X3 V XIX2X3 V XIX2X3 V XIX2X3 V XIX2X3 =
= Xt X 2(X3 v X3) v X I X2(X 3 V X3) V XIX2(X3 V X3) =
= XtX2 v XIX2 V X I X2 = X I (X2 V X2) V X I X2 = Xl V X t X2 =
= Xl V X 2 ·
Protože jen ve dvou řádcích tabulky 12.7 je y = O, je lépe zvolit pro kano-
nický konjunktivní normální tvar ohodnocení O a výsledek pak negovat:
Ji = K6 V K7 =
= X t X2 X 3 v XIX2X3 = X I X 2 (X3 v X3) = X I X 2 ,
odkud
y = X I X 2 = Xl V X 2 ,
což je týž výsledek jako dříve.
Ta bulka 12.7
n Xl X2 X 3 Kn
O O O O I
1 O O I I
2 O I O I
3 O I I I
4 I O O I
5 I O I I
6 I I O O
7 I I I O
12.5. KARNAUGHOVY MAPY
Každé pole Karnaughovy mapy (tabulka 12.8) představuje konjunkci
vstupních proměnných, uvedených na jejím levém a horním okraji. Kar-
naughovy mapy se v rovině sestavují až do pěti vstupních proměnných (to
odpovídá 32 polím). Při větším počtu proměnných nejsou Karnaugl}ovy mapy
operati vnL
Od sloupce k sloupci a od řádku k řádku se pokaždé mění jen jedna pro-
měnná (tzv. Grayův kód). To platí také pro okraje Karnaughovy mapy, např.
mezi prvním a čtvrtým sloupcem, popř. řádkem se vždy mění jen jedna pro-
měnná.
781
Příklad: 4 _ ( . )
K 13 = X1X2X3X4 .... 1101 VIZ tabulku 12.8 ·
Do průsečíků řádků a sloupců zaneseme k příslušným elementárním k n-
junkcím Kn výchozích. proměnných žádanou výchozí hodnotu I nebo O. Pole
jsou spojena spojkou "nebo".
Tab u I k a 12.8
X3 X 4 X3 X 4 X3 X 4 X3 X 4
X I X 2 ססoo 0001 0011 0010
Ko KI K3 K 2
X I X 2 0100 0101 0111 0110
K4 Ks K7 K6
X I X 2 1100 1101 1111 1110
K l2 K l3 K IS K l4
X I X2 '1000 1001 1011 1010
Ks K9 Kll K 10
Pravdivostní ohodnocení dostaneme tak, že vytvoříme pokud možno velké
dvojbloky, čtyřbloky nebo csmibloky s Kn = I (popř. Kn = O), které se mohou
také rozšířit přes okraje. Ohodnotíme-li bloky, přičemž zmizí všechny ty
vstupní proměnné, jejichž hodnota se uvnitř bloků mění, pak dostaneme pri-
mitivní součásti (implikanty) logické funkce.
Příklad:
Ze čtyř pump mají současně pracovat nejvýše dvě. Máme zabránit tomu,
aby více než dvě pumpy byly současně zapojeny (činnost blokovacího [za-
bezpečovacího] zařízení Kn = I).
Ta bu lka 12.9
n Xl X2 X 3 X 4 ' Kn n Xl X 2 X 3 X 4 Kn
,
O O O O O O 8 I O O O O
1 O O O I O 9 I O O I I
2 O O I O O 10 I O I O I
3 O O I I I 11 I O I I I
4 O I O O O 12 I I O O I
5 O I O I I 13 I I O I I
6 O I I O I 14 I I I O I
7 O I I I I 15 I I I I I
782
Práce jedné pumpy: x = I.
Počet všech možných logických členů: n = 2 k = 2 4 = 16 (viz tabulku 12.9).
Řádky 7, 11, 13, 14 a 15 lze vypustit, neboť tyto kombinace proměnných
nemohou podle zadání úlohy nastat. Přihlédneme-li k nim, usnadní to často
výpočet (viz tabulku 12.10).
Tabu I k a 12.1 O
X 3 X 4 X3 X 4 X 3 X 4 X 3 X 4
Xt X 2 O O I O
X t X 2 O I I I .
X 1 X2 I I I I
X 1 X 2 O I I I
čtyřblok totéž totéž totéž
3. sloupec) (3. řádek) (střed) (střed dole) (střed vpravo) (vpravo dole)
J' = X3 X 4 V X I X2 V X2X4 V X I X4 V
X 2 X 3
v
X I X3
= [X3(Xt V X2 v X4)] V [X2(Xl v x 4 )] V XIX 4
(obr. 441).
y
X 3 x 2
X2 --[ Xf
X4
X f
X 4
Obr. 441. Schéma řešení příkladu
o 4 pumpách
783
13. VZORCE Z REGULAČNÍ TECHNIKY
13.1. ZÁKLADNÍ POJMY
Vzhledem k zvláštnímu způsobu vyjádření je následujícím vzorcům
věnována samostatná část.
Lineárnost
Přenosový člen pro signály (regulovaná soustava, zesilovač, měřicí za-
řízení) se nazývá lineární (obr. 442), jestliže
xe(t) = K(t) Xy(t),
kde x y ( t) je vstupní veličina,
xe(t) - výstupní veličina,
K(t) - přenosová funkce.
Přitom platí
n xe(t) = n K(t) Xy(t) ,
x e I ( t) = K 1 ( t) Xy I ( t) ' } ( ) ( ) )
( ) = K ( ) ( ) xel + x e2 = KIt XYI t + K2(t) X y2 (t
x e 2 t 2 t Xy 2 t ,
(zákon o superpozici).
Xv (t) I J ,
- linearn. pl'enosova f'unkct
xe(f)
U R
-
Obr. 443. Závislost napětí u na proudu i
při konstantním odporu R
Obr. 442. Lineární přenosová funkce
o
1
Působení žádaných vlivů xyi(t) a poruchových veličin Zi(t) se sčítají nezávisle
na sobě. Funkce K(t) = K (K je konstanta) vyjadřuje statickou lineárnost,
přičemž grafické znázornění vztahu mezi vstupními a výstupními veličinami
se nazývá statická charakteristika (obr. 443).
784
Chování lineárních členů popisuje nehomogenní lineární diferenciální rov-
nice (omezíme se na technicky důležité diferenciální rovnice s konstantními
koeficienty), popř. rovnice dopravního zpoždění:
d n x dn - 1 X dx
e e e
a n dl" + a n - 1 dl" - 1 +... + a 1 dt + Xe =
dxv dmxv dz
=boxv+b 1 - d +...+bm- d +Coz+Cl- d -....
t t m t
V praxi je m < n, tj. Xe plyne z Xv podle daných podmínek.
Členy s autoregulací Xe jsou různé od O, kdežto členy bez autore-
gulace Xe jsou rovny O. Řešení diferenciální rovnice (viz str. 680 a 685) se
skládá ze stacionárního řešení (partikulární řešení úplné Eul rovy diferen-
ciální rovnice) :
xe s ( t)
a z astatického řešení (obecné řešení homogenní diferenciální rovnice)
xep(t) ,
takže
Xe(t) = Xe (t) - Xe (t).
s p
V charakteristické rovnici (viz str. 673), odvozené z diferenciální
rovnice, se v regulační technice obvykle píše p místo r, přičemž p vyjadřuje
chování astatického členu takto:
Při p < O jde o "klesající" křivku,
při p > O jde o křivku "neohraničeně rostoucí",
při p = tJ + iw jde při tJ < O o oscilující křivku s klesající amplitudou a při
(j > O o oscilující křivku s rostoucí amplitudou.
13.2. TESTOVACÍ [ZK UŠEBNÍ] FUNKCE
Při určování charakteristických hodnot členu (velikost a průběh)
se berou za základ standardizované vstupní signály a počáteční podmínky,
s jejichž pomocí lze určit všechny údaje pro popis chování při libovolném
vstupním signálu.
Jednotková skoková funkce (obr. 444)
(t < O),
(t O) .
u(t) = {
785
Přechodová charakteristika [odezva na skokovou funkci]
(obr. 445)
Xy(t) = x Yo a(t) xe(t).
Xv
Ke
Xvo
o
t
o
t
Obr. 444. lednotková skoková funkce
Obr. 445. Odezva na skokovou funkci
XV o 6'(t)
-
, I I
l. near", sous,ova
Xe=Xvo h(t)
ó(t)
g(t)
( . " to
:... .near", sous va
Obr. 446. Přechodová funkce
Obr. 447. Impulsová funkce a její odezva
Přechodová funkce (obr. 446)
h(t) = xe(t) ,
xYo
kde xe(t) je skoková odezva,
h(t) = G(p) ,
P
kde G(p) je přenosová funkce,
p - diferenciální operátor,
2 i + 00 p(w)
h(t) = - - sin (wt) dw ,
1t o w
přičemž G(iw) = P(w) + i Q(w) je frekvenční přenos.
Impulsová funkce [Diracova funkce delta]
O (t < O),
. 1 1
l5(t) = hm - [a(t) - a(t - t)] = A t (O < t < t),
t-O t L1
O (t > t) ,
i + 00 i t d t '
l5(-r)d-r = lim - = 1.
o t-O o dt
786
Poznámka:
V klasickém matematickém významu není Diracova funkce delta funkcí
(viz teorii distribucí).
Spektrum impulsu delta (obr. 447)
j(iw) = t+: £5(t)e- iwt dw = 1
(viz str. 707),
2 {l5( t)} = 1 ,
2{l5(t - to)} = e- pto (to> O),
t+: j(t) £5(t - to) dt = j(t o ).
Impulsová přechodová funkce [odezva na impulsovou funkci]
[xe(t) = ] g(t) = 1! h(t) - h? - At) = d t) (t > O),
xe(t) = xv(t) * g(t) = ft xlr) g(t - .) d. =
d f t Jo
= - xvCr) h(t - -r) d-r .
dt o
Duhamelův vzorec
2{g(t)} = G(p),
kde G(p) je přenosová funkce.
13.3. SYMBOLICKÁ VYJÁDŘENÍ
Z možných časových funkcí pojednáme pro zjednodušení jen o ně-
kterých z nich:
Xv(t) = xvo e pt ,
kde p = l5 + iw je diferenciální operátor (Heavisideův operátor). .Je tedy
dx d 2 x 2
dt = px , dt 2 = P x, . . . ,
fx dt = : x , ffx 2 (dtY = :2 x ,
787
Převedení diferenciální rovnIce do podoblasti Laplaceovy transformace
člen po členu dává při
2{xe(t)} = Xe(P), {Xv(t)} = Xv(p)
a při nulových počátečních podmínkách vztah
(anpn + a n _ . p" -. + ... + 1) X e(P) =
= (bmpm + bm_.pm-. + ... + 1) Xv(p).
Obrazová přenosová funkce
G(p) = X e(P) = .<l' {xe(t)}
X v(p) 2 {xv(t)} .
Póly přenosové funkce jsou kořeny charakteristické rovnice diferenciální
rovnice. Pro stabilní soustavy leží všechny v levé polorovině Gaussovy roviny.
Pomocí symbolické metody lze často diferenciální rovnici dané soustavy
vhodně odvodit tak, že místo dxldt = px, ... položíme x dt = xl p, ....
Příklad:
Je dán elektrický obvod podle obrázku 448. Určeme přenosovou funkci
a diferenciální rovnici daného schématu.
Pro
u = rž dt = i
. c C J' pC
dostaneme
,
Xe(P) = G(p) =
X v(p)
( R +- )
pC l 2 pC 2
1 1
R 2 + - + -
pC. pC 2
( R + )
pC l 2 pC 2
R.+
1 1
R 2 + - + -
pC l pC 2
1
1
pC 2
1
R +-
2 pC 2
P 2 t(!2 + P't 2l + pt I + pt 2 + 1 '
kde ti = CIR I , 't 2 = C 2 R 2 , t 21 = C 2 R I .
788
Diferenciální rovnice zní:
d2Xe ( ) dxe
C 1 C 2 R 1 R 2 - d 2 + C 2 R 1 + C1R 1 + C 2 R 2 - d + Xe = Xv'
t t '
Rt
R 2
o
T C1
T C 2 : e
Obr.44K Schéma elektrického obvodu
Xv
K témuž výsledku dojdeme podle KirchhofTových zákonů:
Xv = i 1 ( R 1 + P J - P 1 '
O = i 1 ( -1 \ + i 2 ( R2 + + C I ) .
pC; pC 2 P 1
Frekvenční přenos [frekvenční [kmitočtová] charakteristika]
Při sinusovém vstupním signálu Xv = xvo cos (rot) po doplnění imaginární
části dostaneme
Xv = xvo[ cos (rot) + i sin (rot)] = xvo eiCJ>t ,
X = X e iCJ>t + ({J
e eo .
Reálné, popř. imaginární části jsou si rovny.
Komplexní frekvenční přenos
[frekvenční [kmitočtová ] charakteristika]
G(iw) = xeo eiq> = P(w) + i Q(w),
x VQ
přičemž
P(ro) = p( -ro),
Q(ro) = -Q( -ro).
Lze jej snadno vypočítat z přenosové funkce pro p = iro.
789
kde
Obecně platí
Xy = X Yo cos (wt) = Re xvo eiCJ>t ,
Xe = Re G(iw) Xv = Re xYOIG(iw)1 ei(CJ>t + <p) =
= xvoIG(iw)1 cos (wt + qJ),
lm G(iw)
qJ = arctg G( ' )
Re lW
je fázový posuv výchozí proměnné xe vzhledem k vstupní proměnné Xy. Výraz
IG(iw)1 znam ná poměr amplitud veličin Xe a Xy (v stacionárním stavu). Kon-
cové body průvodičů (tzv. fázory) hodnot funkce G(iw) pro w E (O, + (0)
jako parametr tvoří fázovou křivku frekvenční charakteristiky v komplexní
rovině.
Z frekvenční charakteristiky se odvodí Bodův diagram:
19 G(iw) = 19 IG(iw)1 ei<p = IgIG(icb)1 + iM 10qJ .
Přitom se vyjadřuje:
- amplitudová charakteristika 19 IG(iw)1 = f(lg w),
- fázová charakteristika qJ = f(lg w).
Poznámka:
Poměr amplitud se často udává při měřicí jednotce decibel (dB) ve tvaru
IG(iw 1 )1
20 19 IG( iw 2)I '
13.4. ŘAZENÍ ŘÍDICÍCH [REGULAČNÍCH] ČLENŮ
Sériové řazení členů:
Gers(P) = G 1 (p) G 2 (p)... Gn(p).
Paralelní řazení členů (obr. 449):
Gers(P) = G 1 (p) + G 2 (p).
Xv
Xy + + f
Gf(p)
X ef
- Xe
xe2
b2(P)
Obr. 449. Paralelní zapojení
790
Antiparalelní řazení členů:
G 1 (p)
Gers(p) = 1 + G 1 (p) G 2 (p) .
13.5. CHARAKTERISTICKÉ HODNOTY NĚKTERÝCH
PŘENOSOVÝCH ČLENŮ
Člen P [proporcionálně působ ící člen] bez zpožděn í [člen s au to-
regulací]
Xe = Kxy,
(obr. 450 až 452).
W(p) = K
1m
Xv
Xe
K
w = O. .00
O K Re
t
o
=--
t
o
Obr. 450. Člen P bez
zpoždění
Obr. 451. Člen P bez
zpoždění
Obr. 452. Člen P bez
zpoždění
Re t
Xv
,xe
K
tp K
i c.J=O lm
-,\,- /C4}
f t:)
1.r' T
Obr. 455. Člen P se
zpožděním prvního řádu
1
O
o
t
Obr. 453. Člen P I e
zpožděním prvního řádu
t
Obr. 454. Člen P se
zpožděním prvního řádu
Člen P [proporcionálně působící člen] se zpožděním prvního
řádu
dXe
T - + Xe = Kxy,
dt
(obr. 453 až 455).
K
W(p) = pT + 1
791
Člen P [proporcionálně působící člen] se zpožděním druhého
řádu, popř. se zpožděním prvního řádu a respektováním hmot-
nosti
d2xe ( ) dXe
TI T 2 dt 2 + 11 + T 2 + T 2I dr + Xe = Kx y =
2 d2xe dXe
= T - d 2 + 2DT + - + Xe ,
t dt
. K K
W(p) = 2 -
P TIT2 + P(Tt + T 2 + T 21 )P + 1 p 2 T 2 + 2DpT+ 1
(obr. 456 a 458).
Pro D < 1 nastává rezonanční převýšení (kmitavý člen).
Im+
Ke D<f O k
Xv w=oo ! \ Re
K I I
r D>1
X I
D<f / /
O O I -. --
t O ktesa
Obr. 456. Člen P se Obr. 457. Člen P se Obr. 458. Člen P se
zpožděním druhého řádu zpožděním druhého řádu zpožděním druhého řádu
lm
I;"
'v
Xe
o ste
t
Obr. 460. Člen I bez
zpoždční
o
(.J = 00
ffJ
Re
o
VJt
t
Obr. 459. Člen I beL
zpoždění
Obr. 461. Člen I bez
zpoždění
Člen I [integrálně působící člen] bez zpoždění [člen bez auto-
regulace]
dXe ( ) K
T - = Kxy, W p =-
dt pT
(obr. 459 až 461).
792
Člen I [integrálně působící člen] se požděním prvního řádu
d2xc qXe ( K
TI T 2 d t 2 + TI _ dl = Kxv, W p) = 2
P TI T 2 + pTI
(obr. 462 až 464).
Xv f
c=>
t
lm I
I
,
i
Xe :0
Re
o
t
Obr. 462, Člen I se
zpožděním prvního řádu
Obr. 463. Člen I 'se
zpožděním prvního řádu
Obr. 464. Člen I se
zpožděním prvního řádu
lm
A'v
.Ke
too
wt
o
t
o
.
t
w=o
0,
ip
.
Re
Obr. 465. Člen D
realizovatelný jen s členem P
Obr. 466. Člen D
realizovatelný jen s členem P
., Obr. 467. Člen D
realizovatelný jen s členem P
lm
Xv
Xe
o
Re
o - ---.-
t
Obr. 468. Člen D se
zpožděním prvního řádu
t
Obr. 469. Člen D se
zpožděním prvního řádu
Obr. 470. Člen D se
zpožděním prvního řádu
793
Člen D [derivačně působící člen] realizovatelný jen s členem P
dx y ( )
xe = KT dt ' W p = pT
(obr. 465 až 467).
Člen D [derivačně působící
[poddajná zpětná vazba]
dXe dxy
T - + X e = KT-
dt dt '
(obr. 468 až 470).
člen] se zpožděním prvního řádu
KpT
W(p) = pT + 1
Člen s dopravním zpožděním
dnx dn-1x
on dť'e + 0n-1 dť'-/ + ... + Xe = K.xv(t - "Id)
(člen s autoregulací a dopravním zpožděním),
W(p) = e- pTd pro xe = Kxv(t - )
(obr. 471 až 473).
1m
- -- --
t
Xv
Xe
f
o
o
Obr. 471. Člen s dopravním
zpožděním
Obr. 472. Člen s dopravním
zpožděním
Obr. 473. Člen s dopravním
zpožděním
,
794
14. DODATKY
14.1. ŘECKÁ ABECEDA
Pí"smena řecké abecedy Odpovídající písmena
latinské abecedy
stojatá velká ležatá velká stojatá malá ležatá malá název
,
A A alfa a
B B P tJ beta b
r r 'Y y gama I g
A Li o delta d
E E E e epsílon e
Z Z , dzéta dz
,
H H 11 " éta é
e 8 3,9 9,0 théta th
I I 1 l ióta 1
.
K K x x kappa k
A A A A. lambda I
M M J.1 JI. mí m
N N v v ný n
- - c; xí (ksí) x
... ,..
- -
O O o o omikron o
n n 1t 1t pí p
P P Q ť! ró r
1: I a G sigma s
T T t f tau t
y Y u v ypsilon y
ci> fP cp cp ti f
X X X X chí ch
'I' 'JI '" IjI psí ps
n D <O OJ ómega ó
Poloha písmen malé abecedy v řádku:
(J.tJy e' ,.,:JlXA.JI. ve; 01tť!GfVCP xljI OJ
795
14.2. . NĚMECKÁ ABECEDA [GOTICKÉ PÍSMO]
Písmena Písmena
velká malá velká malá
Q 91 n
b tJ o
(t c p
1) b .Q q
(f e 9t r
f 6 s
ffi 9 :t t
U u
3 i u
3 I m ID
5\ f I
( 1)
9Jl m 3 3
,-'
796
14.3. ČASTO POUŽÍVANĚ KONSTANTY
A JEJICH DEKADICKÉ LOGARITMY
(Tato tabulka je z knihy [28].)
Zápis konstanty n 19 n
1t 3,141 6 0,497 15
21t 6,283 2 0,798 18
31t 9,4248 0,97427
41t 12,566 1,09921
1t/2 1,570 8 0,196 12
1t/3 1,0472 0,020 03
21t/3 -
2,094 4 0,321 06
41t/3 4,1888 0,622 09
1t/4 0,785 40 \(),895 09 - 1
1t/6 0,523 60 0,71900-1
1t 2 9,869 6 0,99430
41t 2 39,478 1,596 36
1t 2 /4 2,4674 0,39224
1t 3 31,006 1,491 45
1t/36O 8,7266. 10- 3 0,940 85 - 3
21t/36O = 1t/180 1,7453. 10- 2 0,241 88 - 2
1t i
are l' = rad 2,9089. 10- 4 0,46373-4
180 . 60
1t 4,848 1.10- 6
are I" = rad 0,68557 - 6
180 . 60 . 60
360 0 180 0
lrad =-=- 57,296 1,758 12
21t 1t
360.60'
1 rad = 3437,7 3,536 27
21t
360 . 60 . 60" 2,062 lOs
1 rad = 5,31443
21t
1/1t 0,31831 0,50285 -1
1/(21t) 0,159 15 0,201 82-1
1/(41t) 7,9577. 10- 2 0,900 79 - 2
3/(41t) 0,238 73 0,37791-1
1/1t 2 0,101 32 0,005 70 - 1
1/(41t 2 ) 2,533 O. 10- 2 0,403 64 - 2
J1t 1,7725 0,248 57
2 J1t 3,544 91 0,549 60
J(21t) 2,506 6 0,399 09
J(1t/2) 1,253 3 0,098 06
I/J1t 0,564 19 0,75143-1
797
Zápis konstanty n 19 n
C = 2/Jrr 1,128 4 0,052 46
&1/C = Jrr/2 0,886 23 0,947 54-1
CI = J(40/rr) 3,568 2 0,552 46
J(2/rr) 0,797 88 0,901 94-1
rr J2 4,442 9 0,647 66
n J3 . 5,441 4 0,735 71
rr/ J2 2,221 4 0,34663
n/J3 1,813 8 0,258 59
n 1,464 6 0,16572
e 2,718 3 0,434 29
e 2 7,389 1 0,868 59
M = 19 e 0,434 29 0,63778 -1
m = 1/ M = ln 10 2,3026 0,362 22
l/e 0,367 88 0,565 71 -1
l/e 2 0,135 34 0,131 41 - 1
e1l: 23,141 1,364 38
Je 1,648 7 0,217 15
g 9,806 65 0,991 52
g2 96,170 1,983 04
l/g 0,101 97 0,008 48 - 1
1/(2g) 5,0986. 10- 2 0,70745 - 2
l/g2 1,0398. 10- 2 0,01696-2
Jg 3, 131 6 0,495 76
J(2g) 4,428 7 0,64628
rrJg 9,838 1 0,992 91
v
I/Jg 0,31933 0,504 24 - 1
rr/Jg 1,003 2 0,00 1 39
2n/ J g 2,006 4 0,302 42
J2 1,4142 0,150 51
J3 1,732 1 9,238 56
, I/J2 0,707 11 0,849 49 - 1
I/J3 0,577 35 0,76144- 1 I.
798
15. LITERATURA
15.1. LITERATURA Z NĚMECKÉHO ORIGINÁLU
1. ALgebra und Geometrie fUr 1 ngen;eure. 8. Aufl. Zi.irich - FrankfurtjMain - Thun, Verlag
Harri Deutsch.
2. AnaLysis fUr blfJenieure. 11. Aufl. Zi.irich - FrankfurtjMain - Thun, Verlag Harri Deutsch.
3. Ausgewahlte KapiteL der Mathematik fur Ingenieure und Ďkonomen. 8. Aufl. Ziirich -- Frank-
furtjMain- Thun, Verlag Harri Deutsch 1974.
4. Bar, D.: Einfi.ihrung in die Schaltalgebra. 2. Aufl..Berlin, VEB Verlag Technik 1966.
5. Baule, B.: Die Mathematik des Naturforschers und Ingenieurs. Band I - VIII. Leipzig,
S. Hirzel Verlag:
Band I: Differential- und Integralrechnung. 16. Aufl. 1970;
Band II: Ausgleichs- und N aherungsrechnung. 8. Aufl. 1966;
Band III: Analytische Geometrie. 8. Aufl. 1968;
Band IV: Gewohnliche Differentialgleichungen. 9. Aufl. 1970;
Band V: Variationsrechnung. 7. Aufl. 1968;
Band VI: Partielle Differentialgleichungell. 8. Aufl. 1970;
Band VII: D tJerentialgeometrie. 6. Aufl. 1965:
Band VIII: Aufgabensammlung. 2. Aufl. 1966.
6. Brauning: Gewohnliche Differentialgleichungen. 4. Aufl. Zi.irich - FrankfurtjMain - Thun,
Verlag Harri Deutsch 1975.
7. Brónstein, I. N. - Semendjajew, K. A.: Taschenbuch der Mathematik. 15. Aufl. Ziirich - Frank-
furtjMain-Thun, Verlag Harri Deutsch 1975 (překlad z ruštiny).
Bronštejn, I. N. - Semenďajer, K. A.: Príručka matematiky pre inženierov a pre študujúcich.
3. vyd. Bratislava, SVTL 1964 (překlad z ruštiny).
8. Dietrich, G. - Stahl, H.: Grundzi.ige der Matrizenrechnung. 9. Aufl. Thun - Frankfurt/Main,
Verlag Harri Deutsch 1975.
9. Doetsch, G.: Anleitung zum praktischen Gebrauch der Laplace- Transformation. 3. Aufl.
Mi.inchen, R. Oldenbourg Verlag 1967.
10. Dreszer: \1athematik-Handbuch rur Technik und Naturwissenschaft. Thun - Frank-
furtjMain, Verlag Harri Deutsch 1975.
11. Fucke, R. - K;rch, K. - Nickel, H.: Darstellende Geometrie. 8. Aufl. Ziirich - Frankfurt/
Main - Thun, Verlag Harri Deutsch 1975.
12. Gnedenko, B. W. - Chintschin, A. J.: Elementare Einfi.ihrung in die Wahrscheinlichkeits-
rechnung. 9. Aufl. Berlin, VEB Deutscher Verlag der Wissenschaften 1973 (překlad z ruštiny).
Gněděnko, B. V. - Chinčin, A. J.: Elementární úvod do teorie pravděpodobnosti. Praha,
SNTL 1954 (překlad z ruštiny).
13. GoLdner, K.: Mathematische Grundlagen fi.ir Regelungstechniker. 2. Aufl. Zi.irich - Frank-
furtj Main - Thun, Verlag Harri Deutsch 1969.
799
14. Gorke, L.: Mengen - Relationen - Fuqktionen. 4. Aufl. Ziirich - Frankfurt/Main - Thun,
Verlag Harri Deutsch 1974.
15. Greuel, O.: Mathematische Erganzungen und Aufgaben fi.ir Elektrotechniker. 6. Aufl. Mi.in-
chen, Carl Hanser Verlag 1972.
16. H ess, A.: Analytische Geometrie. 11. Autl Berlin, Springer- Verlag 1965.
17. He)'man1l: Trigonometrie der Ebene. Leipzig, VEB Fachbuchverlag 1959.
18. H oltmann, F.: Mathematik. Band I und II. Leipzig, VEB Fachbuchverlag 1969.
19. Hůtte: Des Ingcnieurs Taschenbuch. Band I. Berlin, Verlag Wilhelm Ernst und Sohn 1955.
20. I SllllCSOtJ, E. - Keller, B.: Analyse numerischer Verfahren. Zi.irich - Frankfurt!Main - Thun,
Verlag Harri Deutsch 1973.
21. Joos, &, - Richter, E. W.: Hohere Mathematik fi.ir den Praktiker. 11. Aufl. Leipzig, Verlag
Ambrosius Barth 1969.
22. Kleine Enzyklopadie Mathematik. Neuautl Zi.irich - FrankfurtjMain - Thun: Verlag Harri
Dcutsch 1972,
23. Krekó - Bélll: Lehrbuch der linearen Optimierung. Berlin, Deutscher Verlag der Wissenschaf-
ten 1964.
24. Lehr- und Uhungsbuch M athematik. Zi.irich - Frankfurt/Main - Thun, Verlag Harri Deutsch:
Band I. Aritmetik, Algebra und elementare Funktionslehre. 13. Aufl.;
Band II. Plan;metrie, Stereometrie und Trigonometrie der Ebene. 14. Autl;
Band III. A1lalytische Géometrie, Vektorrechnung und lnfinitesimalrechnung. 13. Aufl.
25. Moderner Vorkurs der Elementarmat ematik. 2. Aufl. Zi.irich - Frankfurt/Main - Thun, Verlag
Harri Deutsch 1973.
26. Lehrhr;efe .fUr das F ernstudium, Technische Hochschule Dresden. Hohere Mathematik.
Berlin, VEB Verlag Technik.
27. Ma;baum, G.: Wahrscheinlichkeitsrechnung. Zi.irich - FrankfurtjMain - Thun, Verlag Harri
Deutsch 1972.
28. lI, Mangoldt, H. - Knopp, K.: Einfi.ihrung in die hohere Mathematik. Leipzig - Stuttgart,
S. Hirzel Verlag:
Band I: Zahlen, Funktionen, Grenzwerte, Analyt;sche Geometrie, Algebra, Mengenlehre.
14. Autl 1971
Band II: Different;alr chnung. U nendliche Reihen, Elemente der Differentialgeometrie und
F unktionent heorie. 13. Autl 1968:
Band III: lntegralrechnung und ihre Anwendungen, Funktionentheorie, Differentialgleichungen.
13. Autl1967
Band IV: Mengenlehre, Lebesguesches Mass und lntegral. Topologische Raume, Vektorraume,
Funktionalanalysis, lntegralgleichungen 1973.
29. Metz, J. - Merbeth, G.: Schaltalgebra. Zi.irich - Frankfurt/Main - Thun, Verlag Harri Deutsch
1970.
30. Muller, F.: Fi.infstellige Logarithmčn und andere mathematische Tafeln. Fi.ir sexagesimal-
geteilten Altgrad, 15. Aufl. Zi.irich - Frankfurt/Main - Thun, Verlag Harri Del!tsch 1970.
Muller, F.: Pětimístné logaritmy a jiné matematické tabulky. Praha, SNTL 1956 (překlad
z němčiny).
31. Naas, J. - Schmid, H. L.: Mathematisches Worterbuch. Nachdruck der 3. Aufl. Berlin, Aka-
demie-Verlag; Leipzig-Stuttgart, B. G. Teubner Verlagsgesellschaft 1972.
32. Rint, C.: Handbuch fi.ir Hochfrequenz- und Elektro-Techniker. Berlin, Verlag fi.ir Radio-
-Foto-Kino-Technik GmbH.
800
.ll Ri('hter. K ,-.I: Methoden der Optimierung. Band I: Lilleare Optimierung. 4. Autl Leiplig.
V FB Fachbll:hverlag 1971.
J4. Ringle,.. F, O Mathcmatische Formelsammlung. 8. Autl Berlin, Walter de Gruyter und Co.
196 t
35, Rump./; K, II. Pulrers, M.: Transistor-Elektronik. 5. Aufl. Berlin, VEB Verlag Technik 1973.
3ft, Se !z efľers, G., Lehrbuch der Mathematik, 15. Autl Berlin, Walter de Gruyter und ('o. 1962,
37, Speiser. A. p, Digitale Rechenanlagc. Neudruck der 2. Aufl. Berlin -Gottingen - Heidelberg,
Springer- Ver lg 1967,
3X, Storm, R,: Wahrschcinlichkeitsrechnung, mathcmatische Statistik und statistische QualiHits-
kontrolle. 5. \ufl. Leipzig. VEB Fa hbuchverlag 1974.
39, Thompson, S p,: Hoherc Mathematik - und doch versHindlich! Eine leichtversHindliche
Einftihrung ir die Differential- und Integralrechnung. 10. Aufl, Ztirich - FrankfurtjMain-
Thun, Verlag Harri Deutsch 1972.
40. Weyh. U,: Eltmente der Schaltungsalgebra. 7. Aufl. Mtinchen, R. Oldenbourg 1972.
41. H-'i , llers F, A Elcmentarmathematik, 13. Aufl. Dresden, Verlag Steinkopff 1968.
42, Zu,.,niihl, R.: rraktische Mathematik fi.ir Ingenieure und Physiker. 5. Aufl. Berlin, Springer-
- Verlag 1965.
15.2. LITERATURA PŘIPOJENÁ
PŘI ČESKÉM PŘEKLADU
15.2.1. Matematická logika a množiny
43. Alexandrof, P. S.: Úvod do obecné teorie množin a funkcí. Praha, NČSA V 1954 (překlad
z ruštiny).
44. Bel'L'ář. J, - Bicl1 n , L. - Ježek, J. - Kepka, T. - Němec, P.: Seznamujeme se s množinami. Praha,
SNTL 1981.'
45. Blažek, J. - Ku,sorá, B.: Množiny a přirozená čísla. Praha, SPN 1977.
46. Gr=egorc=rk, A,: Populární logika. Praha, SPNL 1957 (překlad z polštiny).
47, llorsk V, Z.: Matematika pro vysoké školy technické. Sešit I: Množiny a matematické struktury.
Praha: SNTL 1 79. ·
48. Ilru, a, K.: Základy moderní matematiky. Díly I, II. 3. vyd. Praha, SPN 1975.
49, llrll. a, K. - Dlot1hý, Z. - Rohlíček, J.: Úvod do studia matematiky. Praha, SPN 1963.
50. Kemeny, J. G. ./ Snell, J. L. - Thompson, G. L.: Úvod do finitní matematiky. Praha, SNTL
1971 (překlad 1 angličtiny).
51. Kolmogoror, A, N. - F omin, S. V.: Základy teorie funkcí a funkcionální analýzy. Praha,
SNTL 1975 (pNklad z ruštiny).
52, Kosmák, L.: MI,ožinová algebra. Bratislava, Alfa 1978.
53. (,llil')\ J.: O ml>dernizaci školské matematiky. 2., rozšířené vydání. Praha, SPN 1973.
54, . reider, J. A.: Binární relace. Praha, SNTL 1978 (překlad z ruštiny).
55. l'arski, A.: ÚV{,d do logiky a metodologie deduktivních věd. 2. vyd. Praha, Academia 1969
(překlad 3, angl,ckého vydání).
56. Vilenkin, N, J.: Vyprávění o množinách. Praha. SPN 1973 (překlad z ruštiny).
801
15.2.2. Algebra (rovnice, matice, determinanty)
57. Bican, L.: Lineární algebra. Praha, SNTL 1979,
58. Borůvka, O.: Základy teorie matic. Praha, Academia 1971.
59. Bydžovsk.Í', B.: Úvod do theorie determinantů a matic a jich užití, Praha, J CM F 1947,
60. Čech, E.: Čísla a početní výkony. Praha, SNTL 1954.
61. Čulík, K. - DoLežaL, V. - F;edler, JI:: Kombinatorická analýza v praxi. Praha, SNTL 1967,
62. Dant:ig, G. B.: Lineárne programovanie a jeho rozvoj. Bratisla\a, SVTL 1963 (překlad z an-
gličtiny).
63. Fiedler, M.: Speciální matice a jejich použití v numerické matematice. Praha, SNTL 1981.
64. Frazer, R. A. - Duncan, W. J. - Col/,"', A. R,: Základy maticového počtu, jeho aplikace v dy-
namice a v diferenciálních rovnicích. Praha, SNTL 1958 (překlad z angličtiny).
65. (jantmacher, F. R,: Teorija matric. Mosk\'a. Gostc hnoizdat 1953.
66. Garaj, J.: Základy vektorového počtu. 3. vyd. Bratislava, SVTL 1969.
67. GeLfand, J. M.: Lineární algebra. Praha, NČSA V 1953 (překlad I. ruštiny).
68. Horský, Z.: Matematika pro vysoké školy technické. Sešit II: Vektororé prostory. Praha.
SNTL 1980.
69. Chudý, J.: Determinanty a matice. 2. vyd. Praha, SNTL 1974.
70. llkot'ič, D.: Vektorový počet. 2. vyd. Praha, Přírodovědecké nakladatelství 1950.
71. Jarník, J. - Sísler, M.: Jak řešit rovnice a jejich soustavy. 2. vyd. Praha, SNTL 1969.
72. Kolek, L.: Základy algebry pro techniky. Praha, SNTL 1969.
73. Kořínek, V.: Základy algebry. 2. vyd. Praha, NČSA V 1956.
74. Kuroš, A.: Kapitoly z obecné algebry. 2. vyd. Academia, Praha 1977 (překlad z ruštiny).
75. Mac Lane, S. - BirkhojJ, G.: Algebra. Bratislava, Alfa 1973 (překlad z angličtiny),
76. Pachová, Zs. - Frey, T.: Vektorová a tenzorová analýza. Praha, SNTL 1964 (překlad z ma-
ďarštin y).
177. Schmidtmayer, J.: Maticový počet a jeho použití v technice. 2. vyd. Praha, SNTL 1974.
78.. Schwarz, S.: O rovnicích. 2. vyd. Praha, JČMF 1947.
79. Schwarz, S.: Základy náuky o riešení rovníc. Praha, NČSA V 1958,
80. Ter-Manuelianc, A.: Metody operační analýzy I. Praha, SNTL 1967.
81. Vyšín, J.: Základy vektorové algebry. Praha, SPN 1966.
15.2.3. Analytická geometrie
82. Bydžovský, B.: Úvod do analytické geometrie. 3. vyd. Praha, NČSA V 1956.
83. Cech, E.: Základy analytické geometrie. Díly I (1951) a II (1952). Praha, Přírodovědecké
vyda vatelství.
84. Klapka, J.: Analytická geometrie. Praha, SNTL 1960.
85. Kraemer, E.: Analytická geometrie lineárních útvarů. Praha, NČSA V 1954.
86. M astn)J, E.: Úvod do analytické geometrie lineárních útvarů a kuželoseček. Praha, NČSA V
1953.
87. PeschL, E.: Analytická geometrie a lineární algebra. Praha, SNTL 1971.
88. PrivaLor, I. I.: Analitičeskaja geometrija. 22. izd. Moskva, Gostechizdat 1957.
89. Sindelář, K.: Analytická geometrie pro začátečníky. Praha. S NTL 1956.
90. Vančura, Z.: Analytická metoda v geometrii. Díly I (1957), II (1958). Praha. SNTL.
802
15.2.4. Matematická analý za
91. Cech, E.: Elementární funkce. Praha, JČM F 1947.
92, Dani/ov, V. L. a kol.: Přehled matematické analýzy I. Praha, SNTL 1968 (překlad z ruštiny).
93. Fichtengolc, G. M.: Kurs differenciaľnogo i integraľnogo isčislenija. Časti I, II. III. Moskva-
Leningrad, Gostechizdat 1951.
94. Gillman. L. - M cDo\\'ell, R. JI.: Matematická analýza. Praha, SNTL 1980.
95. Grebenča, .'W. K. - Noroselor, S. L.: Učebnice matematické analysy. Díly I. II. Praha, NČSA V
1955,
96, Hadíček, K.: Diferenciální počet pro začátečníky. 2. vyd. Praha, SNTL 1962,
97. Harlíček. K.: Integrální počet pro začátečníky. 2. vyd. Praha, SNTL 1963.
98, Horský, Z.: M.atematika pro vysoké školy technické. Sešit II: Diferenciální počet. Praha,
SNTL 1981.
99. Horský, Z.: Učebnice matematiky pro posluchače VŠE I. 5. upravené vydání.' Praha - Bra-
tisla va, SNTLi Alfa 1981.
100. Hrllša, K.: Deset kapitol z diferenciálního a integrálního počtu. 3. vyd. Praha, NČSA V 1959.
101. Jarník, v.: Diferenciální počet I. 6. vyd. Praha, Academia 1974.
102. J arník, V.: Diferenciální počet II. 3. vyd. Praha, Academia 1976.
103. J arník, V.: Integrální počet I. 5. vyd. Praha, Academia 1974.
104, Jarník, V.: Integrální počet II. 2. vyd. Praha, Academia 1976.
105. Kluvánek, 1. - Mi. ík, L. - Svec, M.: Matematika pre štúdium technických vied. Díly I (2. vyd.,
1964), II (1961 ). Bratislava, S VTL.
I
106, Knichal, V. - Ba. ta, A. - Pišl, M. - Rektorys, K.: Matematika I. Praha - Bratislava, SNTL-
SVTL 1965.
107. Knichal, V. - Bašta, A. - Pišl. M. - Rektorys, K.: Matematika II. Praha - Bratislava, SNTL-
S VTL 1966.
108. Ljusternik, L. A. a kolektir: Přehled matematické analýzy II. Praha, SNTL 1969 (překlad
z ruštiny).
109. R vchnorsk}\ R.: Úvod do vyšší matematiky. Třetí, rozšířené vydání. Praha, SZN 1968.
110. Smi,.,1Or, JI: I.: Učebnice vyšší matematiky. Díly I (1954), II (1956). Praha, NČSA V (překlad
z ruštiny).
111. Ši/ar, G. E. - Gllrevič. B, L.: Integrál, míra a derivace. Díl I. Praha, SNTL 1968 (překlad
z ruštiny). '
112. Si/ov, G. E. - Fan Dyk Tin: Integrál, míra a derivace. Díl II. Praha, SNTL 1971 (překlad
z ruštiny).
113. Sindelář, K.: Diferenciální počet funkcí více proměnných. Praha, SNTL 1972.
114, Skrá. ek. ;r, - Tichý, Z.: Základy aplikované matematiky I. Matematická logika, množiny,
základy algebry, analytická geometrie, diferenciální počet, numerické a grafické metody.
Praha, SNTL 1983.
115. Skrá. ek, J. - TicJl,Ý, Z.: Základy aplikované matematiky II. Integrální počet, nekonečné
řady, diferenciální geometrie, obyčejné a parciální diferenciální rovnice, funkce komplexní
proměnné, Laplaceova transformace, diferenční rovnice. Praha, SNTL (v tisku).
116. Škrá. ek, J. - TichJ\ Z.: Základy aplikované matematiky III. Počet pravděpodobnosti, ma-
tematická statistika, stochastické procesy: teorie informace. variační počet, integrální rovnice,
lineární a nelineÚrní programování. úvod do dějin matematiky, Praha, SNTL (v tisku).
117. J '!lIsor. .4, K,: Učehnice vyšší matematiky. DítI. čÚst I (t 957), část 2 (1958); díl II. část I (1958),
čÚ t 2 (llJ59), Praha, SNTL (upraven)' překlad z ruštin) ,.
803
15.2.5. Nekonečné řady
118. Hardy, G. H. - Rogos;nsk;, W. W.: Fourierovy řady. Praha - Bratislava, SNTL - Alfa 1l)71.
119. Kufner, A. - Kadlec, J.: Fourierovy řady. Praha, Academia 1969.
120. Romanorskij, p, l.: Fourierovy řady, Teorie pole. Analytické funkce. Praha, SNTL 1964
(překlad z ruštiny).
121. Salát, T.: Nekonečné řady. Praha, Academia 1974.
122. Vyšín, J.: O nekonečných řadách. Praha, JČMF 1948.
123. Zygmund, A.: Trigonometrical Series. Warszawa - Lwów, Kultura narodowa 1936; 2. ed.,
V olumes I, II. New Y ork, Cambridge University Press 1959.
15.2.6. Diferenciální geometrie křivek a ploch
124. Budinský, B. - Kepr, B.: Základy diferenciální geometrie s technickými aplikacemi. Praha,
SNTL 1970.
125. Dvořák, J. - Svec, A.: Technické křivky. Praha, SNTL 1962.
126. Finikov, S. P.: DifTerencial'naja geometria. Moskva, Izdateľstvo Moskovskogo universiteta
1961
127. Kohout, V.: Diferenciální geometrie. Praha, SNTL 1971.
15.2.7. O byčejné a parciální diferenciální rovnice
128. Borůt'ka, O.: Lineare DifTerentialtransformationen 2. Or nung. Berlin, VEB Deutscher Verlag
der Wissenschaften 1967.
129. Collatz, L.: Numerische Behandlung von Differentialgleichungen. 2. Auflage. Berlin - Got-
tingen - Heidelberg, Springer- Verlag 1955.
130. Fučík, S. - Kufner, A.: Nelineární diferenciální rovnice. Praha, SNTL 1978.
131. J arník, V.: Diferenciální rovnice v komplexním oboru. Praha, Academia 1975.
132. Kamke, E.: DifTerentialgleichungen. Bande I, II; 5. Auflage. Leipzig, Akademische Verlags-
gesellschaft 1962, 1964.
133. Kamke, E.: DifTerentialgleichungen. Losungsmethoden und Losungen. Bande I, II; 4. und
6. Auflage. Leipzig, Akademische Verlagsgesellschaft 1959.
134. Kneschke, A.: DifTerentialgleichungen und Randwertproblemc. Bande I, II, III; 2. Auflage.
Berlin, VEB Verlag Technik 1960.
135. Kurzweil, J.: Obyčejné diferenciální rovnice. Úvod do teorie obyčejných diferenciálních rovnic
v reálném oboru. Praha, SNTL 1978.
136. Legras, J.: Praktické metody pro řešení parciálních diferenciálních rovnic. Praha, SNTL
1960 (překlad z francouzštiny). ,
137. A1ichlin, S. G. - Smolickij, Ch. L.: Približné metoQY riešenia difTerenciálnych a integrálnych
rovníc. Bratislava - Praha, SNTL - Alfa 1973.
138. Míka, S. - Kufner, A.: Matematika pro vysoké školy technické. Sešit XIX: Okrajol'é úlohy pro
obyčejné diferenciální rornice. Praha, SNTL 1981.
139. Nagy, J.: Elementární metody řešení obyčejných diferenciálních rovnic. Praha, SNTL 1978.
140. Nagy, J.: Matematika pro vysoké školy technické. Sešit IX: Elementární metody řešení
obyčeJn.\ích d(terenciálních rornic. Praha, SNTL 1978.
804
141. N £lgy, J.: MatematiKa pro vysoké školy technické. Sešit XV: Soustavy obyčejn,rch df(erellc;ÚI-
nÍl-+t rornic, Praha, SNTL 1980.
142. Nagy, J.: Matematika pro vysoké školy technické. Sešit XVI: Stabilita ;'e. el1í obyčejn,vch
diferenciálních rovnic. Praha. SNTL 1980,
143: Panov D. J.: Příručka k numerickému řešení parciálních diferenciálních rovnic. Praha,
SNTL 1958.
144. Petrovskij, I. G.: Parciální diferenciální rovnice. Praha, Přírodovědecké vydavatelství 1952
(překlad z ruštiny).
145. Rychnorsk.Í', R.: Obyčejné diferenciální rovnice a jejich řešenÍ. 2. vyd. Praha, SNTL 1972.
146. Rychnovský, R. - Výborná, J.: Parciální diferenciální rovnice a j jich některá řešení. Praha,
SNTL 1963.
147. Stěpanov, V. V.: Kurs diferenciálních rovnic. 2. vyd. Praha, Přírodovědecké vydavatelství
1952.
15.2.8. Funkce komplexní proměnné
148. Černý, I.: Základy analysy v komplexním oboru. Praha, Academia 1967.
149. Fuks, B. A. - Sabat, B. V.: Funkce komplexní proměnné. 2. vyd. Praha, NČSA V 1961.
150. Jevgrafov, M. A.: Funkce komplexní proměnné. Praha, SNTL 1981 (překlad z ruštiny).
151. Jevgrafov, M. A. - Bežanot:, K. A. - Fedorjuk, M. V. - Sabunin, M. I.: Sbírka úloh z teorie
funkcí komplexní proměnné. Praha, SNTL 1976 (překlad z ruštiny).
152. Privalov, I. I.: Analytická funkce. Praha, NČSA V 1955 (překlad z ruštiny).
153. Sulista, M.: Matematika pro vysoké školy technické. Sešit XIII: Základy anal.Í'zy r komplex-
ním oboru. Praha, SNTL 1981.
15.2.9. Laplaceova transformace
154. Čížek, V.: Diskrétní Fourierova transformace a její použití. Praha, SNTL 1981.
155. Ditkin, V. A. - Kuzněcot', P. I.: Příručka operátorového počtu. Praha, NČSA V 1954 (překlad
z ruštiny).
156. Kontorovič, M. I.: Operátorový počet a přechodné jevy v elektrických sítích. Praha, SNTL
1953 (překlad z ruštiny).
157. Pírko, Z. - Veit, J.: Laplaceova transformace. Praha, SNTL 1970.
158. Salamon, M.: Matematika pro regulaci a automatisaci. Praha, SNTL 1957.
159. Veit, J.: M tematika pro vysoké školy technické. Sešit XIV: Integrální transformace. Praha,
SNTL 1979.
160. Vích, R.: Transformace a některá jejich použití. Praha, SNTL 1980.
15.2.10. Numerické a grafické metody
161. Col/atz, L.: Funkcionální analýza a numerická matematika. Praha, SNTL 1970.
162. Děmidovič, B. P. - Maron, J. A.: Základy numerické matematiky. Praha, SNTL 1966 (překlad
z ruštiny).
163. Faddějev, D. K. - Fůddějel'orá. V. N,: Numcrické metody lineární algebry. Praha, SNTL
1964 (překlad z ruštiny).
805
164. Gass:-S. I.: Lineárne programovanie. Metoda a aplikácie. Bratislava, SVTL 1965 (překlad
z angličtiny).
165. Habr, J.: Lineární programování. 2. vyd. Praha, SNTL 1960.
166. H ruša, K.: Počítání s neúplnými čísly. Praha, JČMF 1949.
167. Nekl'inda, M, - Srubař, J. - Vi/d, J.: Úvod do numerické matematiky. Praha. SNTL 1976.
168. Ralston, A.: Základy numerické matematiky. Praha, Academia 1973 (překlad z angličtiny).
169. Slavíček, O. a kol.: Základní numerické metody. Praha, 1964.
170. V/ach. M.: Základní numerické metody. Praha, SNTL 1971.
15.2.11. Počet pra vděpodobnosti a matematická statistika
171. Anděl, J.: Matematická statistika. Praha - Bratislava, SNTL - Alfa 1978.
172. Cramer, H.: Mathematical Methods oe. Statistics. Princeton, Princeton University Press 1946.
Kramer, G.: Matematičeskije metody statistiki. Moskva, lIL 1948.
173. Dupač, V. - Hájek, J.: Pravděpodobnost ve vědě a technice. Praha, NČSA V 1962.
174. F abián, V.: Základní statistické metody. Praha, NČSA V 1963.
175. Feller, W.: An Introduction to Probability Theory and its Applications. Vol. 1 (1957),2 (1966).
New Y ork, Wiley.
Feller, v.: Vvedenije v teoriju verojatnostej ij jo primenenija. Tomy 1 (2. izd., 1964),2 (1967).
Moskva, Mir.
176. Hald, A.: Statistical Theory with Engineering Applications. New Y ork - London, Wiley
1952.
Chatd, A.: Matematičeskaja statistika s techničeskimi priloženijami. Moskva, lIL 1955.
177. Jakovler, K. P.: Matematické zpracování výsledků měření. Praha, SNTL 1958 (překlad
z ruštiny).
178. Janko, J.: Jak vytváří statistika obrazy světa a života. Díly I (1947), 11(1948).2. vyd. Praha,
JČMF.
179. Kladivo, B.: Mčřičské chyby a jejich vyrovnání (podle methody nejmenších čtverců). Praha,
Přírodovědecké nakladatelství 1950.
180. Likeš, J. - Laga, J.: Základní statistické tabulky. Praha, SNTL 1978.
181. Likeš, J. - Machek, J.: Matematika pro vysoké školy technické. Sešit VIII: Základy počtu
prarděpodobnosti. Praha. SNTL 1982.
,
182. Reisenaur, R.: Metody matematické statistiky a jejich aplikace v technice. 2. vyd. Praha,
SNTL 1970.
183. Rényi, A.: Teorie pravděpodobnosti. Praha, Academia 1972.
184. Tutubalin, V. N.: Teorie pravděpodobnosti. Praha, SNTL 1978.
185. Vau der Waerden, B.: Mathematische Statistik. Bertin, Springer 1957.
Van der Vardell, B. L.: Matematičeskaja statistika. Moskva, lIL 1960.
15. .12. Příručky, sbírky příkladů a přehledy vzorců
186. Angot, A.: Užitá matematika pro elektrotechnické inženýry. 2. vyd. Praha, SNTL 1972.
187. Dubbel, H.: Inženýrská příručka pro stavbu strojů. Praha, SNTL 1961 (překlad z němčiny).
188. Eliaš, J, - Horl'áth, J. - Kajan. J.: Zbicrka úloh z vyššej matematiky. Časti I (3. vyd" 1971),
2 (3. vyd., 1972), 3 (2. vyd., 1971). Bratislava, Alfa.
806
189. Eliaš, J. - Hort'ách, J. - Kajan, J, - Sulka, J.: Zbierka úloh z vyššej matematiky. Časť 4;
2. vyd. Bratislava. Alfa 1970.
190. Frank, L. a kol.: Technický průvodce. Matematika. Sv. 1. Praha, SNTL 1973.
191. Hlat'áček, A. - DoLanský, P.: Sbírka řešených příkladů z vyšší matematiky pro přípravu
pracujících ke studiu na vysokých školách. Druhé, změněné vydání. Díly I, II. Praha, SPN
1971.
192. Hořejšorá, M.: Řešené příklady z matematiky pro VŠE. Praha, SNTL 1980.
t 93. Hruša, K. - Kracmer, E. - Sedláček, J. - Vyšín, J. - Ze linka, R.: Přehled elementární matema-
tiky. 4., znovu revidované vydání. Praha, SNTL 1965.
194. Jirásek, F. - KriegeLstein, E. - Tichý, Z.: Sbírka řešených příkladů z matematiky. Logika
a množiny, lineární a vektorová algebra, analytická geometrie, posloupnosti a řady, diferen-
ciální počet funkcí jedné proměnné. Druhé, nezměněné vydání. Praha, SNTL 1981.
195. KohLmann, ť.: Matematika ve sdělovací technice. 2., zcela přep_racované a doplněné vydání.
Praha, SNTL 1960.
196. Koníček, O. - Tichý, Z. - Veselka, J.: Strojnická příručka. Díly I (1956), II (1957). Praha
SNTL (upravený překlad z ruštiny).
197. Medek, V. - Mištk, L. - Salát, T.: Prehl'ad stredoškolskej matematiky. Bratislava, SVTL
1963.
198. M inorskij, V. P.: Sbírka úloh z vyšší matematiky. 2. vyd. Praha, SNTL 1964 (překlad z ruštiny).
199. Oborové encyklopedie SNIL. Aplikovaná matematika I, II. raha, SNTL 1977, 1978. '
200. Panov, D. J.: Logaritmické pravítko v praxi. Praha, SZN 1971.
201. Rektorys, K. a spoLupracovníci: Přehled užité matematiky. Čtvrfé, nezměněné vydání. Praha,
SNTL 1981.
202. Schleicher, F.: Příručka pro stavební inženýry. Díl I. Praha, SNTL 1960 (překlad z němčiny).
203. Salát, T. ti koL.: Malá encyklopedie matematiky. Bratislava, Obzor 1967.
204. Vygodskij, M. J.: Príručka elementárnej matematiky. 2. vyd. Bratislava, SVTL 1963 (překlad
z ruštiny).
15.2.13. Tabulky konstant a funkcí
205. Grad. tejn, I. S. - Ryžik.I. M.: Tablicy integralov, summ, rjadov i proizvedenij. Izd. 4. Moskva,
Fizmatgiz 1962.
206. J ahnke, E. - Emde, F.: Tablicy funkcij s formulami i krivymi. 3. izd. Moskva, Fizmatgiz 1959
(překlad anglického vydání: New Y ork, Dover Publication 1945).
207. MikuLčák, J. - Krkavec, J. s kol.: Matematické, fyzikální, chemické tabulky pro SVVŠ.
Praha, SPN 1966.
208. Smoljanskij, M. I.: Tabulky neurčitých integralov. Bratislava, SVTL 1965 (překlad z ruštiny).
>.
807
VĚCNÝ REJSTŘÍK
A
axiómy G I až G 4 92
- metrického prostoru 9X
- rovnosti 91
- Peanovy 103
- Ro až Rj 91
- U o až U 2 97.9X
- uspořádání 97
azimut ortodromy 397
A beceda predikátová 65
- výroková 61
algoritmus Euklidův 127
- řešení matematického modelu
760
alternativa 773, 779
amplituda konlplexního čísla 135
analogie Neperovy 391
nomálie excentrická 430
antecedent implikace 63
antivalence 777. 779
antivektor vektoru 264
anuloid 356
argument funkce 241
- hyperbolického kosinu 384
- - kotangens 384
- - sinu 384
- - tangens 384
- komplexního čísla 135
arkuskosinus 376
arkuskotangens 376
arkussil)us 376
arkustangens 376
asteroida 435, 544
asymptota křivky 535
- -, nesměrnicová 535
- -. směrnicová 535
- -, vertikální 535
axióm 91
- monotonic 98
- - pro násobení 98
- symetričnosti 98
- totožnosti 98
- tranzitivnosti 98
- trichotomie 97
B
Báze (množina základních proměnných)
764
bijekce 86
binormála křivky 560
bod derivace, nulový 512
- funkce. nulový 248
- -, stacionární 512
- inflexnÍ 518
- invariantní 298
-" křivky, dvojnásobný 533
- -, inflexní 533
- -, izolovaný 533
- -, několikanásobný 524, 556
- -, o amocený 533
- -, regulární 524, 525, 556
- -, singulární 524, 533, 556
- -, uzlový 533
- lineárního prostoru 97
- metrického prostoru 98
- mezi body 285
- mnohočlenu, nulový 217
- množiny, hraniční 100
- -, hromadný 102
- -, izolovaný 100
- -, vnější 99
- -.vnitřní 100
808
bod nespojitosti 248
-- - druhého druhu 249
- - prvního druhu 249
- plochy, regulární 567
- -. ingulÚrní 567
- posloupnosti. hromadný 483
- s dčlicím poměrem 460
- satnodružný 298
- cdlový 516
i ngulární (diferenciální rovni e)
660
- vratu 533
c
čísla pythagorejská 317
- soudětná 125
- vyvolená 171
- -, normalizovaná 171
- '-. přesná 171
číslice 114 - 116
- i-tého řádu 115
- největšího řádu 115
- platná 145
- správná 115
číslo binomické 157
- celé. kladné 105
- --, nezáporné 103
- -, záporné 105
- Eulcrovo 485
- imaglnarní 130
- kardinální 89
- kombinační 157, 158
- komplexně sdružené 130
- komplexní 129
- -. algebraické 212
- -. transcendentní 212
- - v exponenciálním tvaru
138
- - v goniometrickém tvaru
134
- - v kartézském tvaru 132
- neperiodické 120
- neryze periodické 120
- neúplné 143
- opačné 104
- periodické 120
- přibližné 143
- přirozené 103
- ryze imaginární 130
- - periodické 120
- složené 123
- úrokové 175
- zaokrouhlené 144
čtverec 321, 325. 326
čtveřice bodů, harmonická 303
čt vrtá úměrná 150, 302
čtyřstěn pravidelný 341
čtyřúhelník 319
- tcčnový 323
tčtivov}'. 322
Casus irreducibilis 215
centiccntigrad 291
centigrad 291
centrování soustavy vázaných vektorů
262
romplcmentary error function 618
ykloida obecná 537, 538
- obyčejná 537, 538
- prodloužená 539
- prostá 537. 538
- zkrÚcená 539
c
Čára lomená 285
- -.uzavřená 285
část čísla. celá 115
- -, zlomková 115
- komplexního čísla, imaginární
130
- - -. reálná 130
c
- množiny 69
- -. vlastní 70
člen algebraické rovnice. absolutní
212
- -- -. i-tého stupně 212
determinantu. hla Vl1í 199
-- s autorcgulací 784
činitel kořenový 214. 217
čísla ncsoudťlná 125
-- po dvou ncsoudčlná 125
gQ9
D
derivace množiny 102
- složené funkce 497
- smíšené 500
- určitého integrálu 604
- vektorové funkce 509
- vyšších řádů 495
derivování grafické 511
- logaritmické 498, 499
deseti úhelník pravidelný
325-327
determinant Gramův 273
- matice n-tého řádu 198
- - sousta vy 207
devítiúhelník pravidelný 325
diagonála determinantu, hlavní
199
- -, vedlejší 199
- matice, hlavní 181
- -, vedlejší 181
diagram průvodičový 370, 371
diference argumentu 491
- aritmctické posloupnosti 167
- funkce 491
- množin, symetrická 72
diferenciál argumentu 494
- funkce 494
- -, n-tý 496
- -, totální 501
- -, úplný 50 I
- oblouku prostorové křivky 557
- - rovinné křivky 525
- vektorové funkce 510
diferenciály vyšších řádů 496
dílec 291
- dělostřelecký 291
- matematický 291
direktrix 419
disj unkce 62, 773
- jevů, logická 732
diskontování 176
diskriminant kubické rovnice 215
- kuželosečky 449
- kvadratické rovnice 212, 213
- kvadratických členů kuželoscčky
449
dodekaedr 342
Defekt matice 183
- sférický 388, 392
definice pravděpodobnosti,
elementární 733
- -, statistická 733
degenerace matice 183
dělení mnohočlenu mnohočlenem
113,114
- se zbytkem 121
- úsečky v poměru 273
dělitel 105, 121
- nesamozřejmý 122
- nevlastní 122
- nuly 95, 188
- samozřejmý 122
- společný 125
- -, nevlastní 125
- -, samozřejmý 125
- úrokový 175
- vlastní 122
dělitelnost v množině všech celých
čísel 121
délka úsečky 289
- elipsy 436
- oblouku křivky 622, 623
- vektoru 262
- zelněpisná 396
deltoid 323
derivace elementárních funkcí 505
- funkce dané parametricky 503
- - - polárními souřadnicemi
504
- -,konečná 492
- -, logaritmická 507
- - na intervalu 493
- -, nevlastní 492
- -, n-tá 495
- -, parciální 499, 500
- - v bodě 492
- -, vlastní 492
- - zleva, nevlastní 493
- - zprava, nevlastní 493
- implicitní funkce 502
- matice 192
810
doplněk množiny v množině 72
- prvku matice, algebraický 199
- - -, redukovaný algebraický 190
dvacetistěn pravidelný 341
dvanáctistěn pravid lný 342
dvanáctiúhelník pravidelný 327
dvojice bodů, involutorní 298
- neuspořádaná 76
- uspořádaná 76
dvojpomčr čtyř bodů 303
dvojúhelník sférický 352. 386
důkaz matematickou indukcí' 103
extrém funkce. absolutní 512, 513
- -, lokální 512
- -, ostrý lokální 512
- -,vázaný 517
extrémy funkce 511-518
- - dané parametricky 515
- implicitní funkce 515
F'
E
Faktor diskontní 176
- integrujíCÍ 660. 661
- úrokový 176
faktoriál čísla 11 156
flexe křivky 531. 564
forma výroková 66
formule predikátová 66
- -, atomární 66
- -, otevřená 67
- -,uzavřená 67
- výroková 61
- výrokové, ekvivalentní 63
- -, - (vzorce) 775, 776
funkce 87, 241
- algebraická 242. 243
- Besselovy 687
- beta 610
- boolovská. k-místná 772
- cyklometrické 376
- delta, Diracova 786
- diferencovatclná 494. 50 I
- distribuční 736, 737, 743
- dvou proměnných. reálná 252
- explicitní 242
- exponenciální 260
- -, modifikovaná integrální 617
- gama 610.687,688
- goniometrické 357
- harmonické 370, 371
- hladká 493
- homogenní 245. 253
- hyperbolické 379
- hyperbolometrické 384
- chyb 618
- -. doplňková 618
- implicitní 242. 254
Ek vi valence 62, 82, 777, 779
elcment oblouku křivky 525
- - prostorové křivky 557
elipsa 332. 333, 427-438
elipsoid protáhlý, rotační 354
- trojosý 353, 354, 472
- zploštělý, rotační 355
epicykloida obecná 539-541
- obyčejná 539-541
- prodloužená 541
- prostá 539-541
- zkrácená 541
epitrochoidy 541
error function 618
evoluta cykloidy :"38
- elipsy 435
- hyperboly 447
- křivky 536
- paraboly 425
evolventa kružnice 537
- křivky 536
excentricita elipsy, čí-selná
428
- -, délková 428
- hyperboly, číselná 439
- -, délková 439
exces 739
- sférický 388, 389
existence neutrálního prvku 92
- symetrického prvku 92
exponent III
811
funkce impulsová 786
- integrovatelná 574, 602, 636
- inverzní 246, 259
- klesající 244, 512
- kmenová 659
- komplexní 88, 89
- konkávní 244.245,518
- konvexní 244.245, 518
- kvadratická 255, 256
- -, homogenní 237
- laplaceovsky transformovatelná
721
- lichá 243
- lineární 254. 255
- logaritmická 261
- mocninová 257-259
- monotónní 244
- n reálných proměnných, reálná 252
- NAND 776, 777
- neklesajíCÍ 244
- nerostoucí 244
- NOR 776, 777
- ohraničená 243
- - shora 243
- - zdola 243
- periodická 245
- po částech spojitá na intervalu
249
- potenční 257-259
- primitivní 571
- prostá 88, 245
- přechodová 786
- přenosová 784
- racionální 243
- -, celá 243, 254-257
- -, lineární lomená 243
- -, lomená 243
- -,neryze lornená 243
- -,ryzelornená 243
- reálná 88
- reálné prot.něnné, reálná 241
- - -,vektorová 508
- rostoucí 244, 512
- ryze monotónní 244
- - konkávní 244.245, 518
- - konvexní 244,245,518
funkce s odstranitdnou nespojitostí
248
- sinusoidální (grafické znázornění)
367
- skalární proměnné. vektorová
508, 509
- skoková, jednotková 785
- složená 245
- spojitá v bodě 248. 253. 488
- - na intervalu 249
- - zleva 248, 488
- - zprava 248,488
- spojitě diferencovatelná 493
- stupňová 736
- sudá 243
- testovací 785-787
- transcendentní 243, 260, 261
- třídy L 720
- účelová 760, 764, 765
funktor disjunkce 60
- ekvivalence 60
- implikace 60
- konjunkce 60
- negace 60
- výrokotvorný 60
G
Generalizátor 65
grad 291
graf funkce, kartézský 242, 254-261
gramián 273
gru pa 94
- Abelova 92
- komutativní 92
- -, aditivní 92
- -, multiplikativní 93
- lineárně uspořádaná 97
- okruhu. aditivní 95
- tčlesa. 111uhiplikativní 96
- úplně uspořádaná 97
- uspořádaná 97
grupoid 93
- asociativní 94
- multiplikativní 93
- okruhu, multiplikativní 95
812
H
hustota pra vděpodo bnosti 737
- - normálního rozložení 741,
743
- - normovaného normálního
rozložení 743
hvčzdice 544
hyperbola 258 259, 333.
438-449
- rovnoosá 259,441
hyperboloid dvojdílný 474
- -,rotační 356.475
- jednodíln)' 473
- -,rotační 355.475
hypocykloid-a obecná 542
- obyčejná 542
- prodloužená 543
- prostá 542
- zkrácená 543
hypotrochoidy 543
Hexaedr 337, 342
hmotnost délková 620
- lineární 620
- měrná 620
- objemová 620
- obsahová 620
- plošná 620
hodnost matice 183
- soustavy vektorů 267
hodnota argumentu komplexního čísla.
hlavní 135
- číselná 296
- funkce 87, 241
- -. kvadratická střední 603
- -. střední 603
- očekávaná 738
- komplexního čísla, absolutní
131
- polohy, střední 747
- proměnné 60
- přibližná 143
- přibližného čísla. střední
144
- přípustná 143
- přirozeného logaritmu komplexního
čísla. hlavní 155
- reálného čísla, absolutní 110
- střední 745, 754
- vektoru. absolutní 262
- zaokrouhlená 145
- zdánlivá 754
- znaku, prostřední 747
- zobrazení 84
hodnoty výběru odlehlé 748
- základní u goniometrické rovnice
373
homotetie 300
hranice množiny 100
hranol 336
- kolmý 336
- kosý 336
- n-boký 336
hranolec 342, 343
hrot křivky 533
CH
Charakteristika logaritmu 153
chordála dvou kružnic 418
chyba absolutní 144, 752
- aritmetického průměru, střední
754
- jednotlivé hodnoty, střední
754, 756
- počáteční 752
- poměrná 144
- prostá 144
- relativní 144. 752
- skutečná 752, 753
- střední hodnoty, zdánlivá 756
- váhové jednotky, střední 756
- váženého aritmetického průměru,
střední 756
- zdánlivá 754
I
Identita 81,210
- Lagrangeova 272
- v rovině 298
ikosaedr 341
813
implikace 62, 777. 778
- oboustranná 62
- nepřímá 777, 77X
- přímá 77X
incidence prvku k množinč 69
index Besselovy rovnice 6X7
- členu posloupnosti 165
infimum funkcc 513
- množiny 83
inflexe funkcc 51 X
inhibice 778
- nepřímá 777, 779
- přímá 777, 778
injekce 85
inkluze neostrá 70
- ostrá 70
integrace rozkladem v částečné zlomky
580
- per partes 550
integrál diferenciální rovnice,
partikulární 648
- dvojnásobný 637
- dvojný 636
- dvojrozměrný 636
- eliptický druhého druhu 354
- - - -,úplný 610
- - prvního druhu 354
- - - -,úplný 610
- Fourierův 718
- chyb 618
- křivkový 631-634
- Laplaceův 720
- Laplaceův-Gaussúv 618
- matice 193
- neurčitý 571
- nevlastní vlivem funkce 608
- - - intervalu 608
- nezávislý na integrační cestě 632
- parciální diferenciální rovnice
688
- pravdivostní 618
- trojnásobný 642, 643
- trojný 642
- trojrozměrný 642, 643
- určitý, Cauchyův-Riemannův
601,602
integrál určitý, Ncwtonův 601
- -, Ricmannúv 60 I, 602
- vektoru, křivkový 634
integrály Fresnelovy 614
- základní 571-573
integrand 574
interpolace lineární 222,
223
interval neohraničený 129
- ohraničený 129
- otevřený 129
- polootevřený 129
- poJouzavřený 129
- za vřený 129
invariant kvadratický 480
- lineární 480
invarianty plochy druhého st-upně,
ortogonální 480
inverze kruhová 279-282
- křivek 280
- relace 79
- v permutaci 162
- ve výrokovém počtu 774
involuce 298
izometrie 298
J
Jazyk 59
jednotka 93, 115
- délková 289
- imaginární 130
- ;-tého řádu 115
- měřicí 296
- míry, měřicí 287
- objemová 296
- obsahu 296
- plošná 296
- úhlová 290
- základní 115
jehlan kolmý 339
- komolý 339. 340, 342
- kosý 339
- n-boký 338
- trojboký 339
814
jev částečný 732, ?33
- d tcrministický 732
- jistý 732, 733
- náhodný 732
- nemožný 732. 733
- přechodový 718
jevy ekvivalentní 732
- jednou možné 732
- neslučitelné 732
- po dvou disjunktní 732
- vzájemně opačné 732
jmenovatel 105, 108
K
Kalkul predikátový 65
kardioida 541
kisoida Oioklova 552
kisoidy 551-553
klín 285,342
- kulový 352
- s obdélníkovou podsta vou 343
- válcový 346
kód Grayův 781
koeficient binomický '156
- korelační 751
- polynomický 161
- růstu, průměrný 746
- stejnolehlosti 300
- variační 739, 748
koeficienty algebraické rovnice
212
- Bernoulliova schématu 735, 736
- F ourierovy 706
- lineární kombinace 266
- normálních rovnic 756
kolmost dvou přímek 411
- - vektorů 268
kombinace 164
- lineární netriviální 266
- -, tri viální 266
- s opakováním 165
- termů, lineární 209
- vektorů, lineární 266
komplanace 623, 624
konlplement množiny v množině 72
\,
kompozice 80
- prvků vzhledem k binární operaci
91
kompozit 80
kongruence 122
konchoida kružnice 555
- Nikomédova 554
- přímá 554
konchoidy 554, 555
konjunkce 62, 773
- jevů, logická 732
konsekvent implikace 63
konstanta 60
- aditivní 505
- Eulerova 609, 616, 617
- integrační 574
konstanty Fourierovy 706
konstrukce elipsy 436-438
- -, nitková 428
- -, vláknová 428
- hyperboly 448
- paraboly 426, 427
kontinuum 101
kontradikce predikátového počtu
67
-'" výrokového počtu 63
konvoluce 724
kopyto válcové 346
koreláty 758
kořen mnohočlenu 217
- -,k-násobný 217
- rovnice 210
kosekans 357, 358
kosinus 357, 358
- integrální 616
kosinusoida 360
kosiny vektoru, směrové 269
kDsočtverec 320
kotangens 357, 358
kotangentoida 360
koule 349
- otevřená 99
kůvariance 751
kritéria dělitelnosti 122, 123
kritérium konvergence alternující řady,
Leibnizovo 695
815
kritérium konvergence řady,
d'Alembertovo 694
- - -,Cauchyovo 694
- - -, limitní d'Alembertovo
694
- - -,- Cauchyovo 694
- - -, - odmocni nové 694
- - -, - podílové 694
- - -, odmocninové 694
- - -,podílové 694
- - -, porovnávací 694
kroucenost křivky 565
kruh 328-330
kružnice 328, 329
- Apolloniova 303
- elipsy, hlavní 435
- -, vedlejší 435
- hybná 537
- křivosti křivky 531. 564
- kulové plochy, hlavní (vedlejší) 3S6
- nehybná 537
..:.. opsaná trojúhelníku 312
- oskulační 531, 564
- připsaná trojúhelníku 313
- vepsaná trojúhelníku 312
krychle 337, 342
křivka daná implicitně 524, 556
- - parametricky 524, 556
- diskriminantní 535
- dvojí křivosti 565
- ekvivalentní 586
- Gaussova 742
- integrální 649
- konkávní 532
- konvexní 532
- obalová 535, 536
- potenční 472
- prostorová 556, 568
- rektifikovatelná 622
- schopná rektifikace 622
křivky Cassiniovy 545, 546
- cyklické 537-545
- Lissajousovy 368, 369
křivost křivky. první 531, 564
- -,druhá '565
kubatura 624,625
kužel 346
- komolý 347
- kosý 348
- kruhový 348
- -. kolmý 348
- rotační 348
- -. komolý 34H. 349
kvádr 337
kvadrika 480
- středová 480
kvantifikátor existenční 65
- malý 65
- obecný 65
- velký 65
kvantor existenční 65
- malý 65
- obecný 65
- velký 65
kvazigrupa 94
kvaziuspořádání 82
kvocient geometrické posloupnosti
170
L
"
Lemniskáta Bernoulliova 547
L-funkce 720
lichoběžník 322
limes superior posloupnosti 691
limita funkce 486-491
- -.konečná 486
- - n proměnných 491
- -, nevlastní 487
- - v nevlastním bodě 486, 487
- -. vlastní 486
- - zleva 487
- - zprava 487
- lnatice 192
- posloupnosti, horní 699
- -,konečná 482
- -. nevlastní 483
- -, vlastní 4R2
- typu O; O 520
- - x x 520
- - O.:k 521
- - _ - -:1_ 522
816
limita typu 0° 522
- - y o 522
- - I (c, 522
- vektorové funkce 509
'Iineárnost statistická 784
list Descartesův 551
logaritmování 151
logaritmus 151
- desítkový 152
- integrální 616
- komplexního čísla, přirozený
155
- přirozený 152
loxodroma 398
lupa 94
M
Mantisa logaritmu
mapa Karnaughova
maximum absolutní
- -. ostré 512
- lokální 512
- -, ostré 512, 513
matice adjungovaná 190
- alternující 194
- antihermitovská 195
- antisymetrická 194
- čtvercová 180
- diagonální 182
- ek vivalentní 183
- hermitovská 195
- hermitovsky polosouměrná
- - souměrná 195
- - transponovaná 195
- inver7ní 190
- jednotková 182
- komplexně sdružená 194
- komutující I R8
- násobná 182
- nulová 181
- o bdélníková I gO
- polohermitovská 195
- polosouměrná 194
- řádková 181
- řádu Il 181
153
781
512, 513
195
matice skoro polosouměrná 194
- sloupcová 181
- souměrná 193
- soustavy 196
- --, rozšířená 196
- symetrická 193
- transponovaná 193
- trojúhelníková 182
- typu (m, n) ) 80
- zaměnitelné 188
- zamenná 189
medián 747
měnitel 297
menšenec 104
menšitel 104
metaa beceda 59
metajazyk 59
metoda adiční 229. 232
- dosazovací 228, 231
- eliminační. Gaussova 233
- integrování per partes 580
- - rozkladem v částečné zlomky
580
- -, substituční 573
- iterační 225
- komparační 228, 232
- konstrukce inverzní matice,
Gaussova 191
- Lagrangeových mu 1tiplikátorů
517
- lichoběžníková pro výpočet určitých
integrálů 604
- Newtonova 223, 224
- Newtonova-Cotesova pro výpočet
určitých integrálů 606
- obdélníková pro výpočet určitých
integrálú 604
- parabolická pro výpočet určitých
integrálů 604
- pomocného úhlu 374
- porovnávací 228, 232
- sčítaCÍ 229, 232
- simplcxová 764, 766
- Silnpsonova pro výpočet určitých
integrálu 605
- slučovad 229. 232
Xl?
metoda substituční 228, 231
- tečen 223, 224
- tečnová pro výpočet určitých
integrálů 605
- těti v 222, 223
- variace konstant 656
- vylučovací 228, 231
metody k určení kořenu rovnic,
přibližné 222-226
metrika euklidovská 99
mezikruží 331
míle námořní 396
- zeměpisná 396
mimoběžky 284
minimax 516
minimum absolutní 512, 513
- . -, ostré 512
- lokální 512
- -, ostré 512.513
mi nor matice 199
míra devadesátinná 291
- oblouková 290
- procentová 173
- radiánová 290
- rozptýlení 747, 754
- setinná 291
- stupňová 291
- v geometrii 287
- variability 751
- variace 747
mnohočlen 209
- n-tého stupně 217
mnohostěn 335
- pravidelný 340
mnohoúhelník 323, 324
- pravidelný 324-328
- řídicí 285
- vektorový 264
množina číselná 77
- - (rozdělení) 90
- definovaná vlastností 68
- dobře uspořádaná 82
- faktorová 91
- konečná 89
- lineárně uspořádaná 82
- mohutnosti kontinua 89
množina nejvýše spočetná 89
- nekonečná 89
- nosná 78
- obojetná 100
- ostře uspořádaná 82
- otevřená 100
- potenční 71
- prázdná 70
- souvislá 100
- spočetná 89
- úplně uspořádaná 82
- uspořádaná 82
- uzavřená 100
- všech celých čísel 104
- - kladných celých čísel 105
- - komplexních čísel 129
- - přirozených čísel 103
- - racionálních čísel 105
- - reálných čísel 106
- základní 72
množiny disjunktní 72
- ekvipolentní 89
- ekvivalentní 89
- identické 70
- konjunktní 72
- po dvou disjunktní 72
- sobě rovné 70
- splývající 70
- stejné mohutnosti 89
mocněnec III
mocnina matice 189
- komplexního čísla. n-tá 136,
139
- množiny, n-tá kartézská 77
- obecná 113
- s celočíselným exponentem 111
- s kladným celým exponentem
III
- s racionálním exponentem 113
- s reálným exponentem 113
mocnitel III
'mocnost bodu ke kružnici 304,
417
- - ke kulové ploše 471
model matematický 760
modul nad okruhem 96
g18
modul soustavy dekadických logaritmů
152
- - přirozených logaritmů 153
- vektoru 262
modus 747
- ponens 64
mohutnost kontinua 89
moment deviační 641, 646
- k-tého řádu 738
- - -, centrální 738
- - -. počáteční 738
- odstředivý 641, 646
momenty setrvačnosti 629-631,
640.641,645,646
- statické 625-627, 640, 644.
645
monoid 94
multiplikátor Eulerův 660, 661
N
nezávisle proměnná 241
nonekvivalence 779
nonimplikace 77X
nonna vektoru 262
nOfmála elipsy 431
- hyperboly 442-444
- křivky 528, 529, 562
- -. hlavní 560
- paraboly 423
- plochy 568
nosič relace 7X
nositelka vázaného vektoru 262
II-stěn 335
- pravidelný 340
ll-úhelník 323, 324
- konvexní 406
- pravidelný 324-328
nula 93, 105
nulita matice 183
numcrus 151
Nadbytek sférický 388
nadmnožina množiny 69
náhodná proměnná 736
nakrytí množiny na množinu 85
nasobek čísla 121
- společný 126
- -, nejmenší 126
- vektoru 265
násobení relací 80
násobnost kořene mnohočlenu 217
nautical mile 396
negace 774
- uzavřených výrokových formulí
68
- výrokové formule 62
nepřesnost 143
nerovnice 239
- s jednou proměnnou 239, 240'
nerovnost 91, 128
- množin 70
- trojúhelníková 98. 110, 131
nespojitost funkce 248
- - druhého druhu 249
- -. odstranitelná 248
- - prvního druhu 249
o
Obálka 535, 536
obdélník 320, 321
o belisk 342
objem čtyřstčnu 279, 461
- dvojdílného hyperboloidu 475
- jednodílného hyperboloidu 475
rotačního tělesa 624, 625
- ro\noh('ino'\tčnu 272, 274
- tělesa 296
oblast 101
- jednoduše souvislá 101
- kružnice, vnější 101
- -, vnitřní 101
- ohraničená 101
- uzavřená 101
oblouk jako parametr 526, 557
- paraboly 334
obor funkce, definiční 87, 241
- funkční 87, 241
- integrační 601
- integrity 95
- - s jednotkou 95
- konvergence řady funkcí 697
g\9
ohor nerovnice. definiční 239
- pravdivosti nerovnice 239
- - predikátové formule 67
- - rovnice 210
- predikátové formule. definiční
67
- proměnné. definiční 60
- proměnných tcrnl li 209
- relace. definiční 7X
- -, druh}' 7X
- -, první 7'8t
- rovnice, definiční 210
- soustavy rovnic. definiční
210
- zobrazení, definiční 84
obraz číselný, =-adický 114
- funkce v Laplaceově transformaci
720
- - ve Fourierovč transformaci
719
- relace 78
- zobrazení 84
obrazec 2'8t3
obsah eliptické úseče 435, 436
- - výseče 436
- hyperbolické úsečc 44 7
- - výseče 447
- Il-úhelníku 278, 406
- obrazce 296,620-622,639
- parabolické úseče 424
- pláště rotačního tělesa 623,
624
- pravidelného n-úhelníku 325
- trojúhelníku 279, 314, 406,
461
- vnitřní oblasti elipsy 333,
435
odchylka dvou přímek 274, 295, 410,
411
- kvadratická, střední 738
- smčrodatná 738, 748
- střední 748
odmocnina III. 134, 259, 260
odúročitel 176
ohodnocení výrokové formule,
pravdivostní 62
okolí bodu (různé druhy okolí)
99
okruh 94
- asociativní 95
- bez dělitelů nuly, asociativní
95
- komutativní 95
- lineárně uspořádaný 98
- s dělením. asociativní 96
- s jednotkou 95
- úplně uspořádaný 98
- uspořádaný 9R
oktaedr 341
operace binární 87, 91
- n-ární 86
- Peirceova 776. 777
- Shefferova 776. 777
operátor Heavisideův 787
originál Laplaceova obrazu
720
ortodroma 396
osa mimoběžek 284
- reálná. rozšířená 129
- úhlu 287
osmistěn pravidelný 341
osmiúhelník pravidelný 325, 326
otočení 299
- kartézské soustavy 402, 403. 450,
451
p
Parabola 255-258,418-427
- Neilova 425, 537
- semikubická 425, 537
paraboloid eliptický 475
- hyperbolický 476
- rotační 353,476
- -, komolý 353
parametr paraboly 419
parcializace zobrazení 86
partikularizátor 65
pás 284
'- kulový 351
perioda funkce 245
- periodického čísla 120
820
permutace 160
- množiny 162
- -. hlavní 162
- -, identická 162
- -, inverzní 162
- -, základní 162
- s opakováním 160
- základní 161
pětiúhelník pravidelný 325-327
plocha hranolová 285
- integrální 688
- jehlanová 285
- kulová 386,471
- kuželová 286,474,477
- -,rotační 478
- válcová 286
- -, hyperbolická 479
- -, parabolická 479
počet predikátový 65
- procentový na sto 173
- - ve stu 173
- - ze sta 173
- - ze zmenšeného základu 173
- - ze zvětšeného základu 173
podíl částečný 121
- diferenční 491
- neúplný 121
podmínka implikace, nutná 63
- -, postačující 63
- minimálnosti, Gaussova 749
okrajová 690
- Schwarzova pro nezávislost integrálu
na integrační cestě 632
podmínky integrovatelnosti,
Schwarzovy 634
- počáteční 648
podmnožina množiny 69
- -, vlastní 70
podobnost 300
pod posloupnost posloupnosti 167
pod slovo slova 59
pól poláry 417, 424, 433, 445
polára bodu 417, 424, 433, 445
pole 96
- směrové 649
- vektorové 508
pologrupa 94
poloida hybná 537
- nehybná 537
poloměr druhé křivosti 565
- první křivosti 531, 564
- torze 565
poloměry elipsy, sdružené 434
- hYl?erboly, sdružené 446
poloparametr paraboly 419
polyedr 335
polynom 209
- interpolační. Newtonův 151
- n-tého stupně 243
poměr 172
- bodu, dělicí 302
- procentový 172
- promilový 172
pořadnice 399
posloupnost alternující 166
- aritmetická 167
- - k-tého řádu 168
- částečných součtů posloupnosti
166
- diferenční k-tého řádu 166
- divergentní 483
- funkcí 89
- -, konvergentní 697
- geometrická 170
- klesající 166
- konečná 89, 165
- konstantní 167
- konvergentní 482
- monotónní 167
- neklesající 166
- nekonečná 89, 165
- nerostoucí 166
- nulová 482
- ohraničená 167
- - shora 167
- - zdola 167
- pod ílová 166
- reálných čísel. konečná 89,
165
- - -,nekonečná 89,165
- rostoucí 166
- ryze monotónní 167
821
posloupnost určitě divergentní
483
- vybraná z posloupnosti 167
- vyvolených čísel, odvozená 171
- - -. základní 171
posunutí kartézské soustavy, rovnoběžné
276.401-403,450.451
pravdčpodobnostjevu 733
- nepodmínčná 734
- podmíněná 734
pravidla de Morganova pro výrokový
počet 775
- Guldinova 335
- pro derivování funkcí 496, 497
- - - vektorových funkcí 510. 511
- pro integrování 573
- pro přibližné výpočty 147-149
pravidlo Cramerovo 207
- d ílcové 292
- l'Hospitalovo 520
- Maskelynovo 491
- Neperovo 389,397
- odloučení 64
- pro zaokrouhlení 145
- řetězové 497
- Sarrusovo pro výpočet determinantu
201
- Simpsonovo 335
pravoúhelník 321
predikát 66
- primitivní 66
premisa implikace 63
princip Cavalierův 335
- matematické indukce 103
- sporu 60
- vyloučení třetího 60
prismatoid 342
prodloužení zobrazení 86
projekce vektoru do vektoru 268
proměnná 60
- číselná 60
- integrační 574
- jmenná 60
- náhodná 736
- názvová 60
- podstatně volná ve slově 66
822
proměnná vázaná ve slovč 66
- volná ve slově 66
- výroková 60
prostor euklidovský. II-rozměrný
99
- hranolový 2X5
- jehlanový 285
- klínový 285
- kuželový 286
- lineární 96
- -, komplexní 97
- -, reálný 97
- metrický 98
- válcový 285
- vektorový 96,266
prstenec 351
- kruhový 356
průměr aritmetický 745
- -,vážený 738.745
- elipsy 433
- geometrický 303. 746
- -,vážený 746
- harmonický 147. 746
- -.vážený 747
- hyperboly 445
- kvadratický 746
- -,vážený 746
- středové kvadriky 480
průměry elipsy. sdružené 434
- hyperboly, sdružené 445.
446
průmět vektoru do vektoru 268
průnik množin 71
- systému množin 71
průvodič 400.419,428,439
prvek invertovatelný 95
- inverzní 93
- jednotkový 93
- kladný 97
- maximální 82
- minimální 82
- množiny 69
- nejmenší 82
- největší 82
- neutrální 92
- nulový 93
prvek okruhu, regulární 95
- -, singulární 95
- opačný 93
- převrácený 93
- symetrický 92
- záporný 97
prvky neporovnatelné 82
- porovnatelné 82
- sférického trojúhelníku. základní
387
prvočinitel 123
prvočíslo 123
předmčt Fourierova obrazu 719
před perioda periodického čísla
120
před poklad implikace 63
převod na jinou číselnou soustavu
118
příčka mimoběžek 284
přímka elipsy, průměrová 433
- hyperboly, průměrová 445
- paraboly, průměrová 424
- regresní 751
- vyrovnávací 756, 757
- vztahová 751
přírůstek argumentu 491
- funkce 491
přiřazení 78
R
relace inverzní 79
- mezi množinami, binární
77
- na množině, binární 79
- neostrého uspořádání 82
- ostrého uspořádání 82
- reflexívní 81
- složená 80
- symetrická 81
- tolerance 82
- tranzitivní 81
- univerzální 81
- úplná 81
- v množině. binární 78
- z množiny do množiny, binární
77
restrikce zobrazení 86
rotace 299
rovina Gaussova 134
- komplexních čísel 134
- normálová 562
- oskulacní 562
- potenční 472
- průměrová 474,48{)
- rektifikační 562
-'tečná 471,474,476,478.479.
568
rovnice 210
- algebraická n-tého stupně 211, 212,
220
- binomická 137
- diferenciální, Bernoulliova 662
- -, Besselova 687
- - bez pravé strany, Eulerova
675
- -, Clairautova 664
- -.exaktní 659
- -, homogenní Eulerova 675
- -, - lineární 654, 672, 673. 684.
685
- -, lineární 654
- -, - parciální 690
- -, nehomogenní lineární 655, 677,
680,684
- - n-tého řádu. obyčejná 648
- - - -. parciální 688
Racionalizování jmenovatele 112
radián 290
rádiusvektor 262,400
regula falsi 222, 223
rektifikace křivky 622
relace 77
- acyklická 82
- antisymetrická 81
- areflexívní 81
- asymetrická 81
- atranzitivní 81
- binární 77
- cyklická 82
- ekvivalence 82
- identická 81
823
rovnice diferenciální. Riccatiova
663
- - s pravou stranou. Eulerova 682.
683
- -. úplná Eulerova 682. 6X3
- druhého stupně. obecná algebraická
420.449
- d usledková 211
- ekvivalentní 211
- elipsy 428. 429, 430
- exponenciální 220
- goniometri ká 372
- -. základní 372
- homogenní 237
- hyperboly 439.440,441
- jednodílného hyperboloidu 473
- kladQě reciproká 219
,
- kružnice 41 3--415
- křivky, parametrické 524
- kubická 214-217
- kulové plochy 471
- kuželové plochy 477
- kvadratická 212-214
- lineární 212, 227
/
- logaritmi ká 220
- normální 756 759
- normály kružnice 416, 417
- osr znobčžek 412
- paraboly 419, 42
- přímky 273, 2-74,406-409
467.468.476
- rc iproká 219
- regresní. lineární 751
- roviny 276, 277, 463
- svazku přímek 412
- tečny kružnice 416. 417
- transcendentní 220
- /Úporně reciproká 219
ro nobčžky 284.452
rovnobč7ník 320
ro noběžnost dvou přímek 411,
412
rovnobčlno těn 337
ro\ nost 81, 91
Inati I X4
n1noiin 70
rozdíl jevů, logický 732
- Innožin 72
- -, symetrick}' 72
- úhlu. grafický 289
- úseček. grafický 2XX
rozklad mnohočlenu v součin kořenových
činitelú 217
- nlnožiny 91
- sloleného čísla v prvočinitele
124
- vektoru 266, 279
rozložení binomické 739
- Gaussovo-Laplaceo\'o 741
- hypcrgeometrické 740
- normální 741
- -,norrnované 743
- Poissonovo 741
rozpětí 747
- výběrové 747
rozptyl 738
rozšiřování zlomků 108
rozvoj determinantu podle prvků řady
200
- F ouricrův 706
- =-adický 114
ruznoběžky 284
A
Řád číslicc 115
- přirozeného čísla 115
řada absolutně divergentní 693
- binomická 702
- časová 749
-- číselná 692
- dynamická 749
- Fouricrova 707-712
- -, trigonometrická 706
- funkcí 697
- - stejnoměrně konvcrgentní 698
- konvergentní 692
- Maclaurinova 702
- matice I HO
- mocninná 698. 699
- neabsolutně konvergentní 693
-- nepodmíněně konvcrgentní 693
X24
řada neurčitě divergentní 6 3
- podmíněně konvergentní 693
- potenční 698. 699
- relativně konvergentní 693
- Taylorova 70 I
- určitě divergentní 693
řádek matice 180
řad y Fourierovy. speciální
712- 718
řešení diferenciální rovnice, obecné
648
- - -. partikulární 648
- - -. singulární 649
- nerovnice 239, 240
- optimalizačního problému
760
- - -. vrcholové 762
- optimální 762, 765
- parciální diferenciální rovnice
6XX
- rovnice 210
- -.grafické 225.226
- sousta \' nn.nic. partikulární 230
- základni při simplexové metodě
764. 767
řetězec 82
řetězovka 549
řez hranolu, normálový 336
- rovinný 286
- válce. normálový 344
- zlatý 305
s
Sekans 357, 358
semigrupa 94
sféra 349, 386
sféroid 355
shodnost 298
- nepřímá 298
- přímá 298
schéma Bernoulliovo 735
- Hornerovo 247
- multiplikační, Falkovo 186
signum permutace 162
_ rcÚln ho čísla 110
,
sInus 357. 358
- integrální 616
sinusoida 360
sjednocení množin 71
- systému množin 7 t
skalár 97. 261, 267
kládání relací 80
kok funkce 249
Ioupcc tllaticc I XO
slova slučitelná 66
slovo prázdné 59
- složené 59
- ve slově 59
složka vektoru ve směru 268
směrnice přímky 406
- úsečky 405
smysl obíhání. kladný 314
součet řady 692
- - funkcí 697
- -. ll-tý částečný 697
- úhlů. grafick)' 288,
- úseček, grafický 287
součin matic 185
- množin, kartézský 76
- relací 80
- vektorový 269,270
- -, dvojný 272
- -, smíšený 271, 272
- vektorů, skalární 267
- -, vnější 269, 270
- -, vnitřní 267
souměrnost osová 299
- středová 299, 300
souřadnice kartézské 400
- kosoúhlé 400
- kři vočaré 568
- ortogonální 400
- ortonormální 400
polÚrní 40 I
- pravoúhlé 400
- vektoru 19 1. 263
- zeměpisné 396
soustava číselná. nepolyadická
119
- -. římská 119
- -. polyadická 114
825
soustava číselná, -adická 114
- kladně orientovaná 270
- kvadratických rovnic 235
- lineárních algebraických rovnic
196,227-231. 233. 237. 23X
- - - -.neurčená 197
- - - -. řešitelná 197
- - - -. určená 197
-- pravotočivá 270, 456
- rovnic 210. 227
- souřadnicová. cylindrická
456
- -.kartézská 400,455
- -, kosoúhlá 399, 400
- -, kulová 457
- -, ortogonální 400
- -,ortonormální 400, 455
- -, polární 400, 457
- -, pravotočivá 263
- -, pravoúhlá 400
- -. semipolární 456
- -, sférická 457
- -, válcová 456
- Země, souřadnicová 396
soustavy lineárních algebraických
rovnic. ekvivalentní 197
spat 295
spirála Archimédova 548
- hyperbolická 548
srdcovka 541
stejnolehlost 300
steradián 295
stopa matice 181
stoupání úsečky 405
strofoida přímá 553
struktura algebraická 91
střadatel polhůtní 177
- předlhutní 177
střed křivosti 531. 564
střední úměrná 150. 303
stupeň absolutní slučitelnosti
750
- relativní slučitelnosti 750
- úhlový 291
styk dvou křivek 530. 564
subdeterminant matice 199
subnormála elipsy 432
- hyperboly 443
- kružnice 417
- křivky 529
- -. polární 530
- paraboly 423
subtangenta elipsy 432
- hyperboly 443
- kružnice 416
- křivky 529
- -, polární 530
- paraboly 423
sud 356
supremum funkce 513
- množiny 83
surjekce 85
svazek kružnic 418
- přímek 301, 464
symbol Kroneckerův 282
- sumační, Gaussů\' 743, 753
systém množin 69
- množin, disjunktní 72
š
Šestiúhelník pravidelný 325, 326
šikmost 739
šířka zeměpisná 396
T
Tabulka korespondencí Laplaceových
integrálů 730, 731
- neurčitých integrálů 585-600
- normálního rozložení 742
- pravdivostní 62, 772
- určitých integrálů 609-616
tangens 357, 358
tangenta křivky 529
tangentoida 36Ů
tautologie predikátového počtu 67
- výrokového počtu 63
tečna elipsy 431, 432
- hyperboly 442, 443
- křivky 528, 558
- paraboly 423.424.427
826
tčlc o 96. 2X)
- komplexních čísel 90. 96
- komutativní 96
- racionálních čísel 90. 96
- reálných čísel 90. 96
- skaláru 97
tempo rustu, průměrné 746
terciunl non datur 64
ternl algebraický 209
- aritmetický 209
- lineární 209
- racionální 209
- --, celý 209
- výrokový, základní 780
test optima 765, 768
tetraedr 341
tčžiště jako aritmetický průmčr
745
- oblouku křivky 627, 628
- obrazce 628
- tělesa 629, 645
- trojúhelníku 310, 405, 460
tolerance 82
torus 356
torze křivky 565
totožnost 81
trajektorie izogonální 536,
651
- ortogonální 536, 651
traktrix 550
transformace Fourierova 719
- kartézské soustavy 458
- Laplaceova 720
transpozice permutace 161
trend 749
trochoidy 537-545
trojhran základní 387
trojúhelník 307-317
- Eulerův 387
- Pascalův 158
- polární, Eulerův 387
- pravoúhlý 317, 318
- rovnoramenný 318
- rovnostranný 319. 325,
326
- sečnový 491
trojúhelník sférický 353, 387
- -. kosoúhlý 389
- -, - (řešení) 392-394
- -, pravoúhlý 388
- tečnový 492
trubice válcová, rotační 346
třetí úmčrná 150
třída zbytková 122
tvar normální, úplný disjunktivní
779;780
- -. - konjunktivní 779
tvrzení implikace 63
u
Úhel dvou rádiusvektorů 461
- kontingenční 532
- konvexní 286, 293
- nekonvexní 286,293
- nulový 286, 293
- obvodový 329
- orientovaný 287
- ostrý 293
- plný 286, 293
- polární 401
- pravý 293
- prostorový 287
- přímý 286, 293
- rovinný 286
- tupý 293
- úsekový 329
- vypuklý 293
úhly doplňkové 294
- přilehlé 294
- souhlasné 294
- střídavé 294
- styčné 293
- vedlejší 293. 294
- vektoru, směrové 269
- vrcholové 293
- výplňkové 294
úloha Cauchyova 648
- počáteční 648
úměra 149, 150
- aritmetická 172
-' harmonická. spojitá 151
827
úměra podílová 172
- postupná 151
- rozdílová 172
- spojitá 150
umístění sousta vy vázaných vektorů
262
- vektoru do bodu 262
umořova tel I 77
11niverzum 72
úprava rovnice 211
- -, důsledková 211
- -, ekvivalentní 211
úpravy determinantu 202-205
- matice, elementární 183
úročitel 176
úrok 175
úseč eliptická 435, 436
- hyperbolická 333, 447
- kruhová 330, 331
- kulová 350
- parabolická 334
úsečka 284
- jednotková 289
- nulová 288
úsek množiny všech přirozených čísel
104
- - - kladných celých čísel 105
- na druhé ose 406, 407
- na první ose 407
- normály elipsy 432
- - hyperboly 443
- - kružnice 416
- - křivky 529
- - paraboly 423
- polární normály 530
- - tečny 529
- rotačního válce 346
- tečny hyperboly 443
- - kružnice 416
- - křivky 529
- - paraboly 423
úseky přímky na o"Úch 46 I. 46
USlllčrI'1ování zlomku 112
uspořádání lexikografické 776, 777
- lineární. neostré 82
- -. ostré 82
uspořádání na množinč všech reálných
čísel 128
- neostré 82
- ostré 82
- úplné, neostré 82
- -, ostré 82
útvar geometrický 283
- invariantní 298
- samodružný 298
útvary shodné 298
uzávěr množiny 102
uzel křivky 533
v
Válec 344
- kolmý 344
- kosý 344
- kruhový 344
- -, kolmý 344
- rotační 344
- -, dutý 346
variace 163, 738
- s opakováním 164
varieta integrální 688
vektor 97
- aritmetický 261
- binormály 560
- centrální 262
- centrovaný 262
- geometrický 261. 262
- hlavní normály 559
- jednotkový 263
- neznámých 197
- normálový 526, 527
- n-rozměrný 181
- nulový 181,262
- polohový 262
- pravých stran 197
- řádkový 181
- sloupcový 181
- tečný 526, 527. 558
- transponovaný 181
- umístěný 262
- vázaný 262
- volný 262
828
vektory ekvivalentní 262
- komplanární 263
- lineárně nezávislé 266
- - závislé 266
- nesouhlasně rovnoběžné 263
- rovnobčžné 263
- souhlasnč rovnoběžné 263
- vzájemnč opačné 264
- základní 263
veličina 296
- náhodná 736
velikost geometrického útvaru 2R7
-- orientovaného úhlu 294. 295
- prostorového úhlu 295
- st any sférického trojúhelníku 387,
388
- úhlu 290
- úsečky 289
- vektoru 262
věta algebry, základ ní 21 7
- binomická 159
- Cauchyova o průměrech 747
- - o přírůstku funkce 520
- Cauchyova-Hadamardova 698
- F ermatova, malá 123
- kosinová 308
- - pro strany 390
- - pro úhly 390
- - pro vektory 268
- Lagrangeova 519
- Legendrova 392
- Moivrova 136
- o implicitních funkcích 254
- o konvergenci mocninné řady, Abelova
698
- o konvergenčním intervalu 698
- o limitě sevřené funkce 488
- - - - posloupnosti 484
- o mnohostěnech, Eulerova 336
- o násobení pravděpodobností 734
- o odvěsnč, Euklidova 303, 318
- o přírůstku funkce, druhá 520
- - - -, první 519
- - - -.zobecněná 520
- o sečnách 304
- o shodnosti mnohoúhelníků 307
věta o tečnč a sečně 304
- o tětivách 304
- o výšce. Euklidova 304, 318
- Pythagorova 317
- -,zobecněná 315
- Rollova 519
- Schwarzova 500
- sinová 308
- - pro sférický trojúhelník 389
- součtová počtu pravdčpodobno li
733
- Steinerova pro rovinný obrazec 64.1
- - pro těleso 646
- tangentová 309
- Thaletova 329
- Wilsonova 123
věty o inverzi 280, 281
- o Laplaceově transfonnaci, základní
721-725
- o limitách funkcí 488
- - - on'\loupnosti 483
- o množinách 73-75
- o podobnosti mnohoúhelníků 305
- o prvočíslech 123
- o sférickém trojúhelníku 390
- o shodnosti trojúhelníků 307
- o střední hodnotě diferenciálního
počtu 519
- - - - integrálního počtu 602,
603
- o svazku přímek 30 I
- o určenosti trojúhelníku 315
vložení 85
vnějšek množiny 100
- úhlu 286
vnitřek množiny 100
- úhlu 286
vrchlík kulový 350
vrstva 284
- kulová 351
- rotačního paraboloidu 353
výraz algebraický 209
- aritmetický 209
- neurčitý 520
výrok 60
- atomární 60, 66
829
výseč eliptická 333, 436
- hyperbolická 447
- kruhová 328, 330
- kulová 350
- mezikruží 332
- vnitřní oblasti elipsy 333
výstřednost elipsy, číselná 428
- -, délková 42X
- hyperboly, číselná 439
- -, délková 439
vzdálenost bodu od přímky 275, 289
- - od roviny 278, 289, 463, 473
- dvou bodů 98, 273, 289, 404, 405,
459
- - - kulové plochy, sférická 386,
396
- - mimoběžek 274, 290, 470
- - rovnoběžek 289
- - rovnoběžných rovin 290
- loxodromická 398
- ortodromická 396, 397
- roviny od počátku 278, 462
vzor Fourierova obrazu 719
- Laplaceova obrazu 720
- prvku v zobrazení, úplný 84
- relace 78
- zobrazení, úplný 84
vzorce Cardanovy 215
- de Morganovy pro množiny 75
- Eulerovy 366
- Gaussovy 391
- interpolační 250-252
- Moivrovy 383
- Mollweidovy 309
- pro cyklometrické funkce 377,
378
- pro goniometrické funkce
360-367
- pro hyperbolické funkce 379-384
- pro hyperbolometrické funkce 385,
386
- pro limity funkcí 489-491
- - - posloupností 4X4
- pro logaritmování 153
- pro logické, operace 775, 776
- pro množinové vztahy 72-75
vzorce pro počítání s malými čísly
705, 706
- pro rozvoje v řady 702-705
- pro strany trojúhelníku 309, 310
- pro úhly trojúhelníku 308, 309
.- Vietovy 214,218
vzorec Bayesúv 735
- Duhamelúv 787
- Heronův 314
- Lagrangeův 50
- Leibnizův 508
- - pro rovinnou výseč 622
- ľH uilierův 392
- Newtonuv 251
- pro celkovou pravděpodobnost 735
- pro pravděpodobnost hypotéz 735
- Ptolemaiův 322
- Taylorův 700, 701
z
Základ číselné soustavy 114
- logaritmu 151
- mocniny III
- odmocniny III
zákon asociativní 92
- distributivní, levý 94
- -,pravý 94
- identity 64
- kompozice, vnější 96
- -, vnitřní 91
- komutativní 92
- o přenášení chyb, Gaussův 754,
755
- o superpozici 784
- o vyloučeném třetím 64, 775
- rozložení pravděpodobnosti,
binomický 736
- simplifikace 64
- sporu 64, 775
- transpozice 64
zákony absorpce 776
- de Morganovy pro predikátový počet
68
- - - pro výrokový počet 64
- distributivní 94
830
zákony idempotence 64
- množinového počtu 72-75
- pro násobení vektoru skalárem
265
- pro sčítání na množině vektorů 264,
265
- pro skalární násobení na množině
vektoru 267
- pro smíšené násobení na množině
vektorů 271
- pro vektorové násobení 270
zaokrouhlení nahoru a dolů
146
zaokrouhlování na jednotky k-tého
řádu 145
zápis =-adický 114
- -, neperiodický 120
- -, neryze periodický 120
- -, periodický 120
- -. ryze periodický 120
zásobitel polhůtní 177
- předlhůtní 177
závěr implikace 63
závisle proměnná 241
závislost kvadratická 750
- lineární 750, 756
- nelineární 757
závitnice Pascalova 555
závora množiny, dolní 83
- -, horní 83
zbytek
1aclaurinova vzorce
(Cauchyůvtva
701
- - - (Lagrangeův tvar) 701
- při dělení 121
- řady 693
zbytek Taylorova vzorce
('auchyuv tvar) 700.701
- - - (integrální tvar) 700, 701
- - - (Lagrangeův tvar) 700, 70 I
zlomek složený 109
- =-adický. nekonečný 115
zlomky IlI8. 109
- částečné 5HO
- parciální 580
znak multij,likační 744
- sumační 743
znaky dělitelnosti 122, 123 ..
znaménko permutace 162
zobrazení bijektivní 86
- identické 86
- injektivní 85
- inverzní 86
- involutorní 598
- jednojednoznačné 86
- jednoznačné 87
- metrického prostoru, spojité 99
- mnohoznačné 87
- množiny do množiny 84
- na množině 86
- parciální 86
- podobné 300
- prosté 85
- shodné 298
- složené 86
- surjektivní 85
- v množině 86
I
- vzájemně jednoznačné 86
- z množiny do množiny 83
- - - na množinu 85
zúžení zobrazení 86
.
MATEMATICKÉ VZORCE
Dr. Ing. Hans-Jochen Bartsch
Podle německého originálu Taschenbuch mathematischer Formdn, 17. Auf1age.
vydaného nakladatclstvím VEB Fachbuchverlag, Leipzig. roku 1979
přeložil, upravil a doplnil Ing. Zdeněk Tich}'
, '
DT 51 (083)
Vydalo SNTL - Nakladatelství technické literatury, n. p..
Spálená 5L 11302 Praha 1, v roc
ItJ83 jako svou 9299. publikaci
Redakce teoretické literatury
Odpovědný redaktor Vladimír DoležaI. promovaný matematik
Vazbu a přebal navrhl Jiří Ledr
Grafická úprava a technická rcdakce Jana Doubětová
Vytiskla Polygrafia, n. p., Praha 2, Svobodova I
832 stran, 473 obrázků, 32 tabulek
Typové číslo LI1-EI-IV-5If 11839. Vydání první
Náklad 30200 výtisků. 56.00 AA, 59,44 V A
03/2
Cena brožovaného výtisku 51, - Kčs
Cena v.ázaného výtisku 55, - Kčs
505,21. 85.6
Publikace je určena žákům středních škol, posluchačúm v}sokých škol technických a těm,
kteří ve své praxi nebo při studiu používají základních oboru matematiky.
04-019-83 b.
04-020-83 v.
K čs 51.-
Kčs 55,-